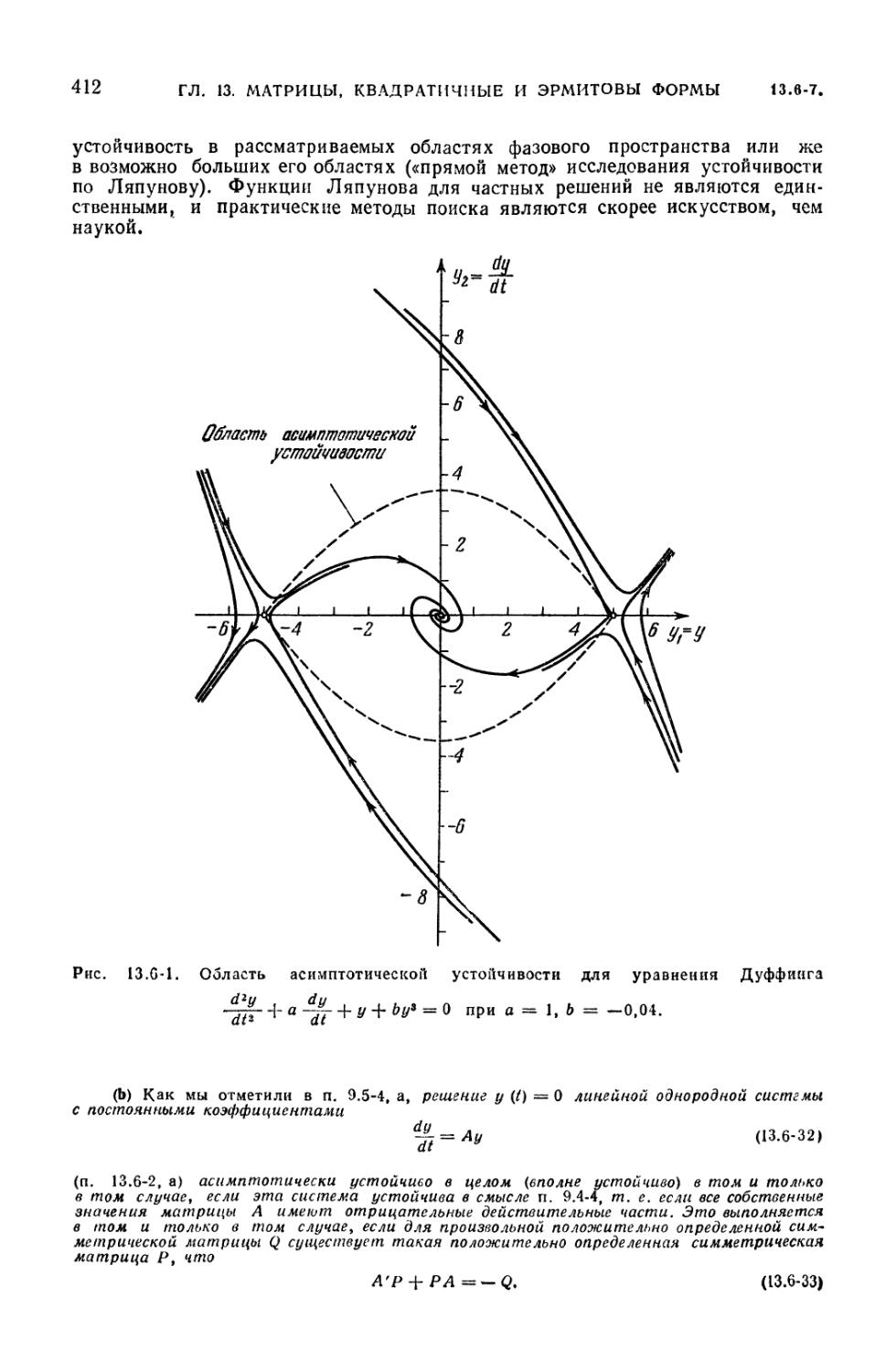
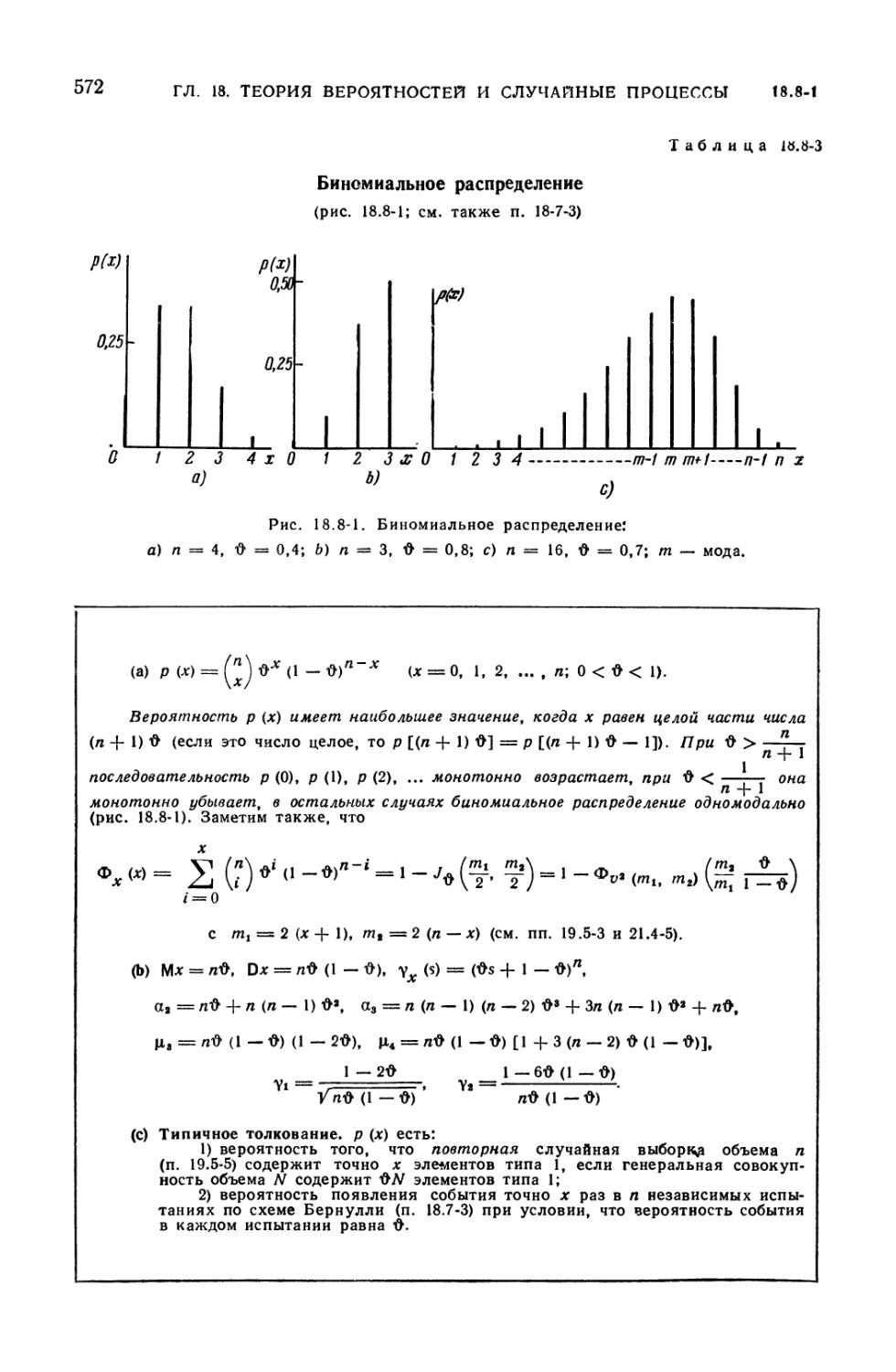
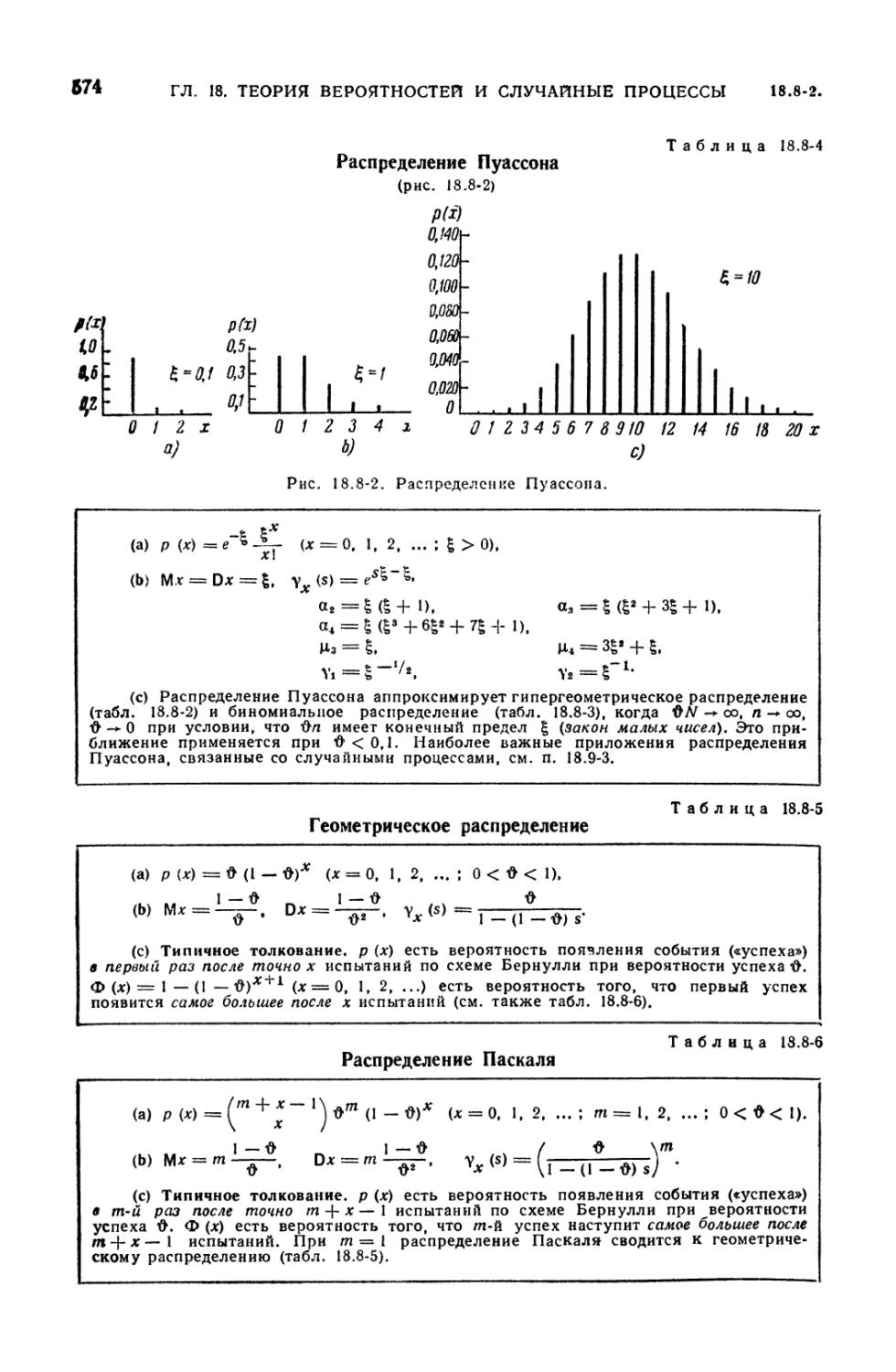
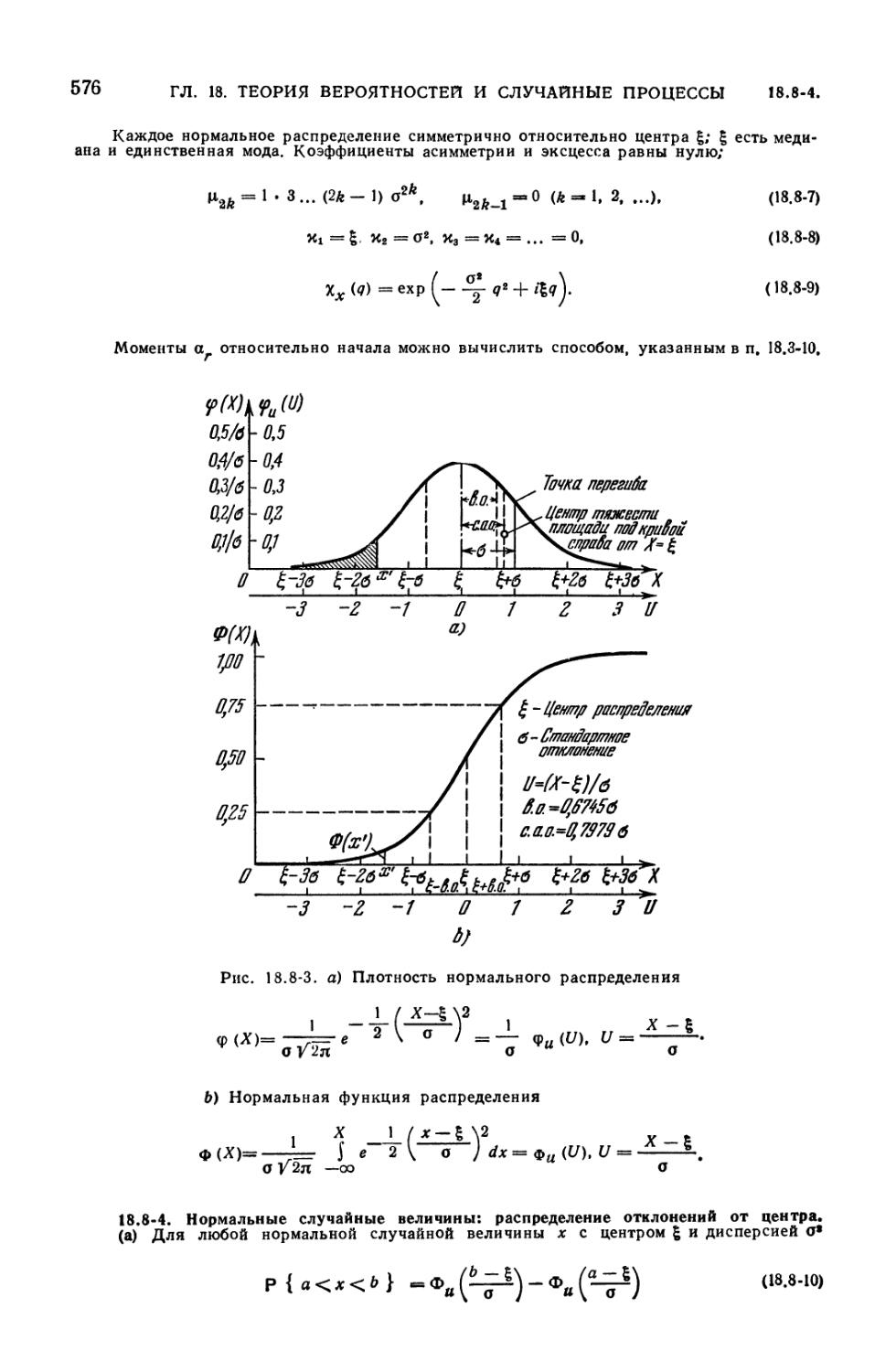
Text
Г. КОРН и Т. КОРН
СПРАВОЧНИК
ПО МАТЕМАТИКЕ
ДЛЯ НАУЧНЫХ РАБОТНИКОВ
И ИНЖЕНЕРОВ
ОПРЕДЕЛЕНИЯ, ТЕОРЕМЫ, ФОРМУЛЫ
Перевод со второго американского переработанного издания
И. Г. АРАМАНОВИЧА, А. М. БЕРЕЗМАНА,
И. А. ВАЙНШТЕЙНА, Л, 3. РУМЫНСКОГО, Л. Я. ЦЛАФА
Под общей редакцией И, Г, АРАМАНОВИЧА
§
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1973
51
K67
УДК 510
Справочник по математике (для научных работников и инженеров). Г. Корн,
Т. Корн.
«Справочник» содержит сведения по следующим разделам: высшая алгебра,
аналитическая и дифференциальная геометрия, математический анализ (включая
интегралы Лебега и Стилтьеса), векторный и тензорный анализ, криволинейные
координаты, функции комплексного переменного, операционное исчисление,
дифференциальные уравнения обыкновенные и с частными производными, вариационное исчисление»
абстрактная алгебра, матрицы, линейные векторные пространства, операторы и теория
представлений, интегральные уравнения, краевые задачи, теория вероятностей и
математическая статистика, численные методы анализа, специальные функции.
В настоящем издании заново написаны главы 11, 20 и значительная часть глав
13 и 18. Книга пополнилась значительным количеством новых разделов.
MATHEMATICAL
HANDBOOK
FOR SCIENTISTS AND ENGINEERS
DEFINITIONS, THEOREMS AND FORMULAS
FOR REFERENCE AND REVIEW
SECOND, ENLARGEND
AND REVISED EDITION
GRANINO A. KORN, PH. D.,
THERESA M. KORN, M. S.
McGraw-Hill Book Company
New York San Francisco Toronto London Sydney, 1968
0223-1741
K 042(02)-73 /&'/d
ОГЛАВЛЕНИЕ
Перечень таблиц 20
Предисловие переводчиков 23
Из предисловия авторов ко второму американскому изданию • 25
ГЛАВА 1
ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ
И ТРИГОНОМЕТРИЯ (ПЛОСКАЯ И СФЕРИЧЕСКАЯ)
1.1. Введение. Система действительных чисел 27
1.1-1. Вводные замечания (27). 1.1-2. Действительные числа (27). 1.1-3.
Отношение равенства (28). 1.1-4. Отношение тождества (28). 1.1-5.
Неравенства (28). 1.1-6. Абсолютные величины (28).
1.2. Степени, корни, логарифмы и факториалы. Обозначения сумм и
произведений 28
1.2-1. Степени и корни (28). 1.2-2. Формулы для уничтожения
иррациональности в знаменателе дроби (29). 1.2-3. Логарифмы (29). 1.2-4. Факториалы
(30). 1.2-5. Обозначения сумм и произведений (30). 1.2-6. Арифметическая
прогрессия (30). 1.2-7. Геометрическая прогрессия (30). 1.2-8. Некоторые
числовые суммы (31).
1.3. Комплексные числа 31
1.3-1. Вводные замечания (31). 1.3-2. Изображение комплексных чисел
точками или радиусами-векторами. Тригонометрическая форма
комплексного числа (32). 1.3-3. Представление суммы, произведения и частного.
Степени и корни (32).
1.4. Различные формулы 33
1.4-1. Бином Ньютона и родственные формулы (33). 1.4-2. Пропорции (34).
1.4-3. Многочлены. Симметрические функции (34).
1.5. Определители 35
1.5-1. Определение (35). 1.5-2. Миноры и алгебраические дополнения.
Разложение определителя по строке или по столбцу (35). 1.5-3. Примеры. (35).
1.5-4. Дополнительные миноры. Разложение Лапласа (36). 1.5-5.
Различные теоремы (36). 1.5-6. Умножение определителей (37). 1.5-7. Изменение
порядка определителей (37).
1.6. Алгебраические уравнения: общие теоремы 37
1.6-1. Вводные замечания (37). 1.6-2. Решение уравнения. Корни (37).
1.6-3. Алгебраические уравнения (37). 1.6-4. Соотношения между корнями
и коэффициентами (38). 1.6-5. Дискриминант алгебраического уравнения
(38). 1.6-6. Действительные алгебраические уравнения и их корни (39).
1.7. Разложение многочленов на множители и деление многочленов.
Элементарные дроби 41
1.7-1. Разложение многочленов на множители (41). 1.7-2. Деление
многочленов. Остаток (41). 1.7-3. Общие делители и общие корни двух
многочленов (41). 1.7-4. Разложение на элементарные дроби (42).
1.8. Линейные, квадратные, кубичные уравнения и уравнения четвертой степени 43
1.8-1. Решение линейных уравнений (43). 1.8-2. Решение квадратных
уравнений (43). 1.8-3. Кубичные уравнения: решение Кардано (43).
1.8-4. Кубичные уравнения: тригонометрическое решение (44). 1.8-5.
Уравнения четвертой степени: решение Декарта — Эйлера (44). 1.8-6.
Уравнения четвертой степени: решение Феррари (44).
1.9. Системы уравнений 45
1.9-1. Системы уравнений (45). 1.9-2. Системы линейных уравнений:
правило Крамера (45). 1.9-3. Линейная независимость (45). 1.9-4. Системы
4
ОГЛАВЛЕНИЕ
линейных уравнений: общая теория (46). 1.9-5. Системы линейных
уравнений: п однородных уравнений с п неизвестными (46).
1-10. Формулы, описывающие плоские фигуры и тела 47
1.10-1. Трапеция (47). 1.10-2. Правильные многоугольники (48). 1.10-3.
Круг (48). 1.10-4. Призмы, пирамиды, цилиндры и конусы (48). 1.10-5.
Тела вращения (48). 1.10-6. Правильные многогранники (49).
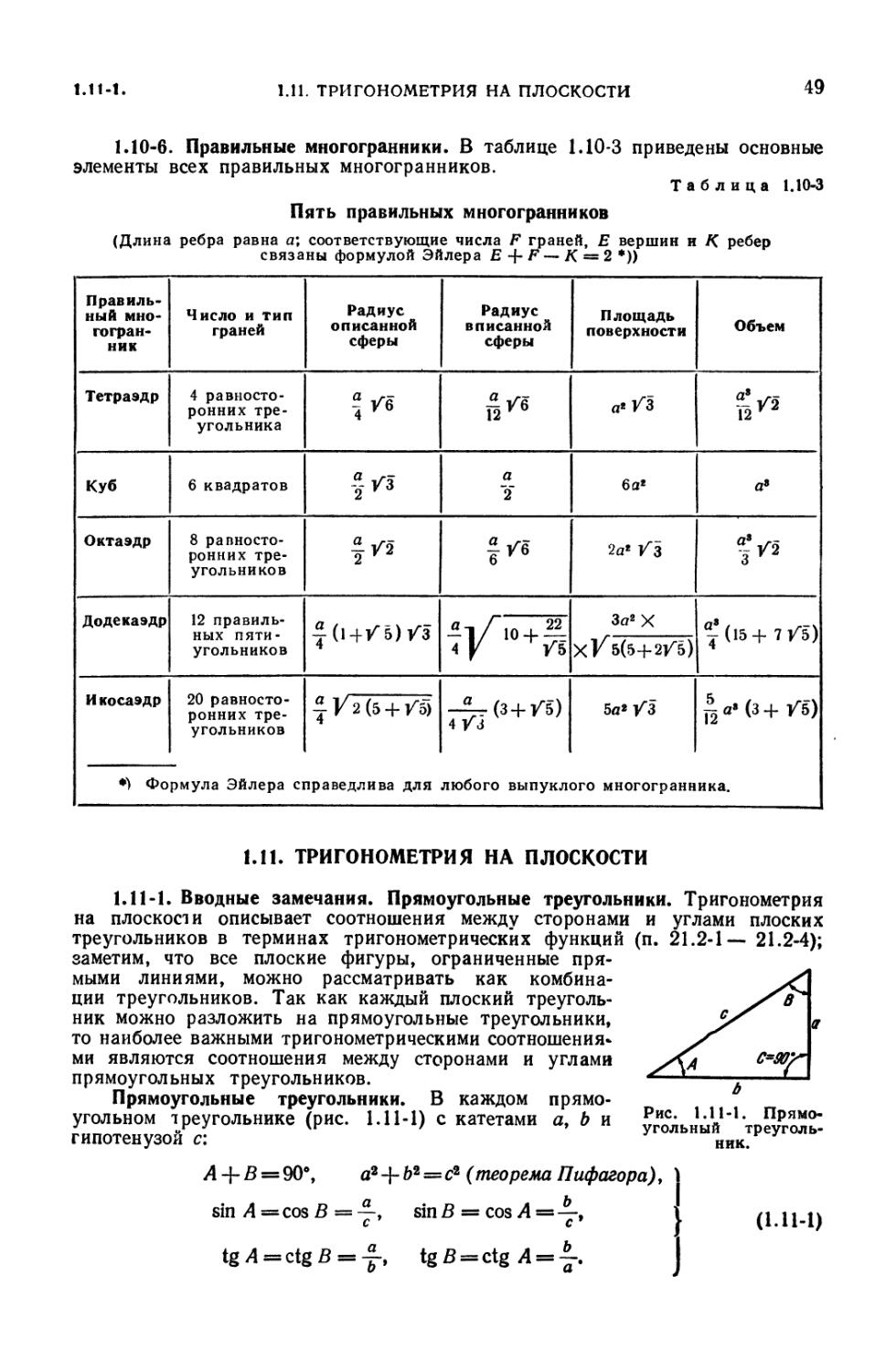
1.11. Тригонометрия на плоскости 49
1.11-1. Вводные замечания. Прямоугольные треугольники (49). 1.11-2.
Свойства плоских треугольников (50). 1.11-3. Формулы для решения
треугольников (50).
1-12. Сферическая тригонометрия 51
1.12-1. Введение. Сферические треугольники (51). 1.12-2. Свойства
сферических треугольников (52). 1.12-3. Прямоугольный сферический
треугольник (53). 1.12-4. Формулы для решения сферических треугольников (53).
ГЛАВА 2
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.1. Введение и основные понятия 56
2.1-1. Вводные замечания (56). 2.1-2. Декартова система координат (56).
2.1-3. Правая декартова прямоугольная система координат (57). 2.1-4.
Основные формулы в декартовых прямоугольных координатах (57). 2-1-5.
Преобразование декартовых координат при параллельном переносе осей (58).
2.1-6. Преобразование декартовых прямоугольных координат при повороте
осей (58). 2.1-7. Одновременный перенос и поворот координатных осей (58).
2.1-8. Полярные координаты (59). 2.1-9. Способы задания кривых (60).
2.2. Прямая линия 60
2.2-1. Уравнение прямой линии (60). 2.2-2. Другие способы задания
прямой (61).
2.3. Взаимное расположение точек и прямых 62
2.3-1. Точки и прямые (62). 2.3-2. Две или несколько прямых (62). 2.3-3.
Тангенциальные координаты (63).
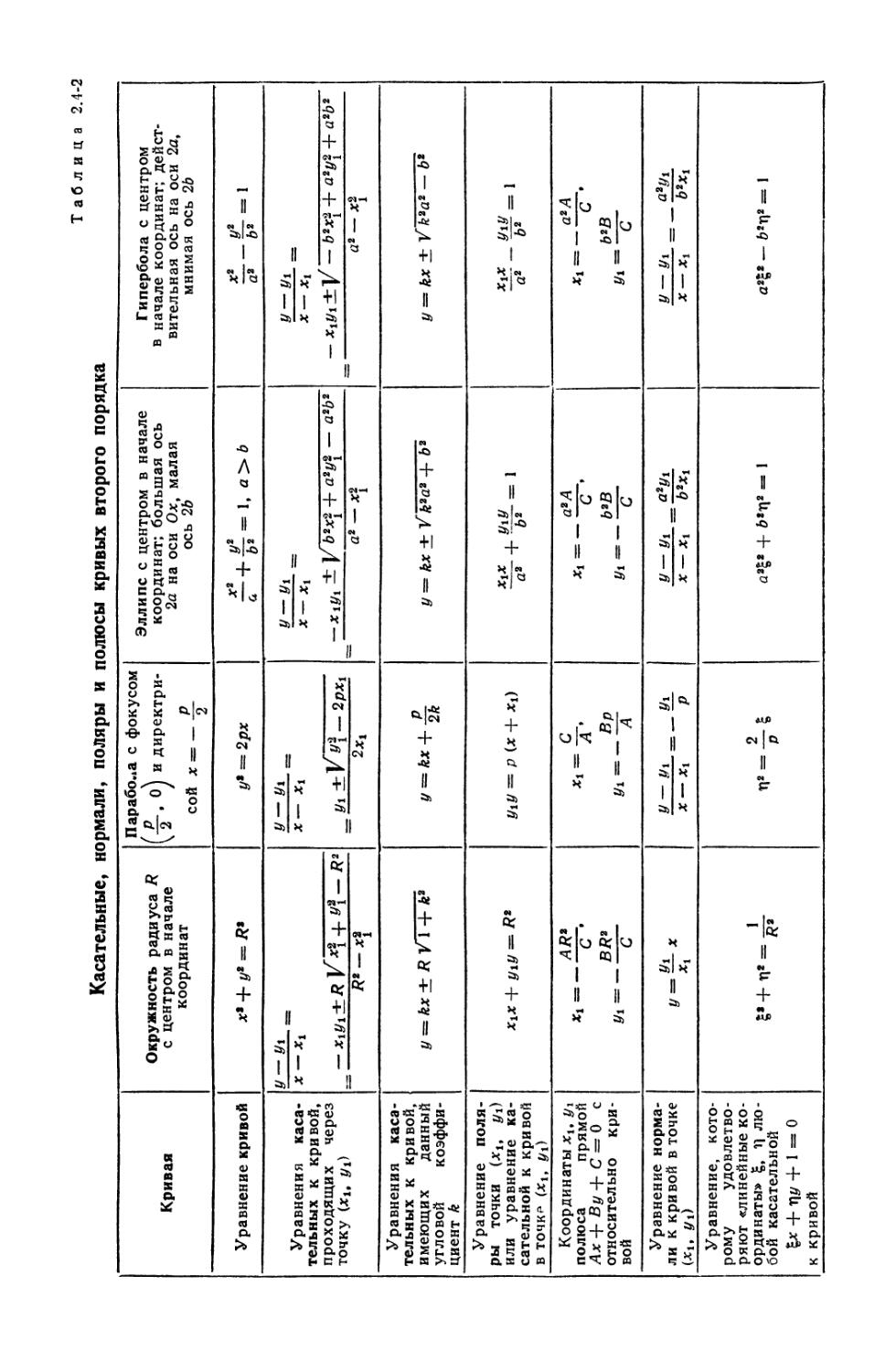
2.4. Кривые второго порядка (конические сечения) 64
2.4-1. Общее уравнение второй степени (64). 2.4-2. Инварианты (64).
2.4-3. Классификация кривых второго порядка (64). 2.4-4. Условие
подобия невырожденных кривых второго порядка (64). 2.4-5.
Характеристическая квадратичная форма и характеристическое уравнение (64). 2.4-6.
Центры и диаметры кривых второго порядка (64). 2.4-7. Главные оси (66).
2.4-8. Приведение уравнения кривой второго порядка к стандартному
(каноническому) виду (66). 2.4-9. Геометрическое определение
невырожденной кривой второго порядка (67). 2.4-10. Касательные и нормали к кривым
второго порядка. Полюсы и поляры (67). 2.4-11. Другие способы задания
кривых второго порядка (69).
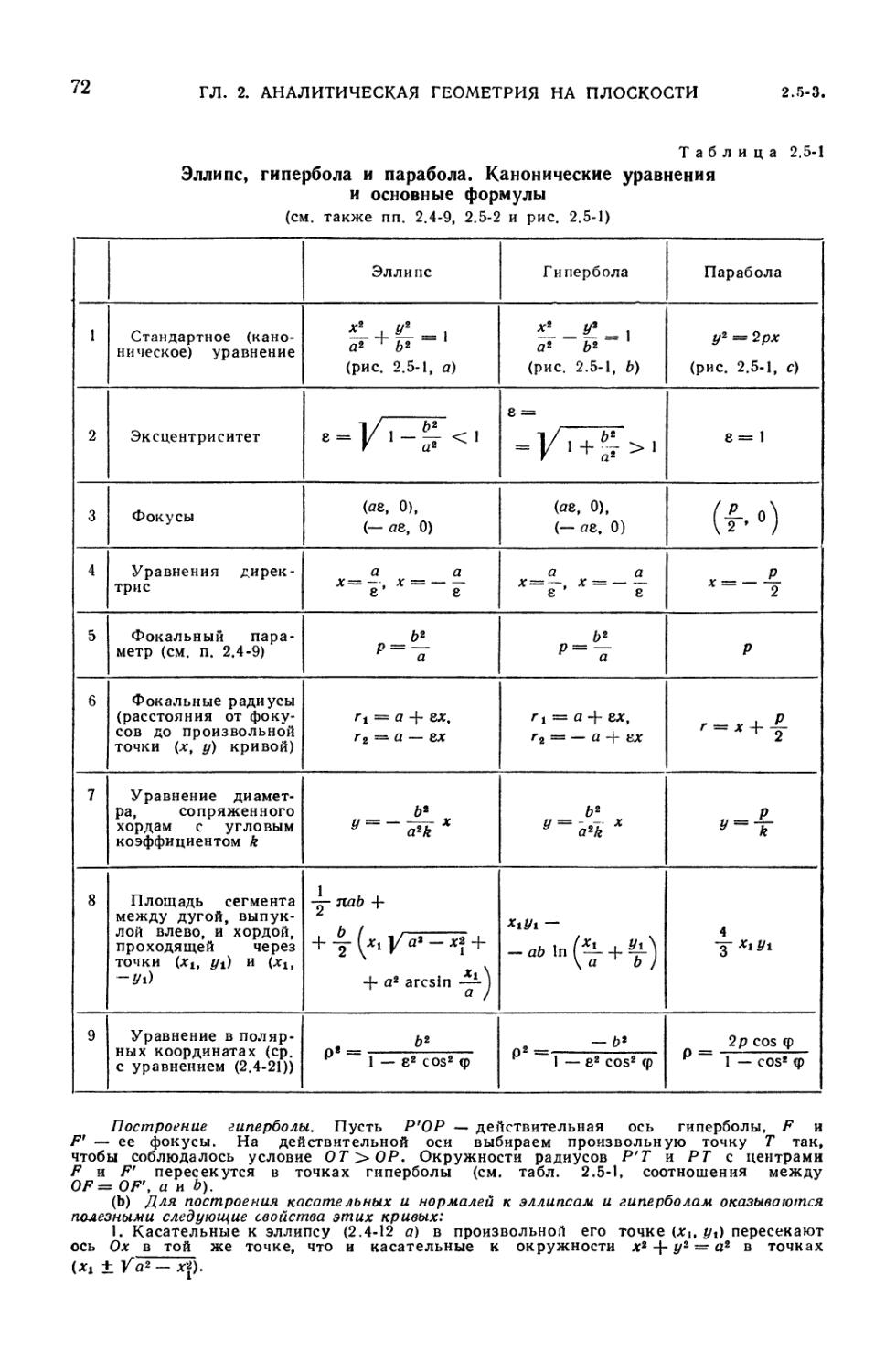
2.5. Свойства окружностей, эллипсов, гипербол и парабол 70
2.5-1. Окружность: формулы и теоремы (70). 2.5-2. Эллипс и гипербола:
формулы и теоремы (70). 2.5-3. Построение эллипсов и гипербол, их
касательных и нормалей (71). 2.5-4. Построение параболы, ее касательных
и нормалей (73).
2.6. Уравнения некоторых плоских кривых 73
2.6-1. Примеры алгебраических кривых (73). 2.6-2. Примеры
трансцендентных кривых (74).
Г Л А В А 3
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
3.1. Введение и основные понятия 76
3.1-1. Вводные замечания (76). 3.1-2. Декартова система координат (76).
3.1-3. Правая система осей (76). 3.1-4. Правая декартова прямоугольная
система координат (76). 3.1-5. Радиус-вектор (77). 3.1-6. Цилиндрическая
и сферическая системы координат (77). 3.1-7. Основные формулы в
декартовых прямоугольных координатах и в векторной форме (77). 3.1-8.
Направляющие косинусы (78). 3.1-9. Проекции (79). 3.1-10. Вектор площади
(79). 3.1-11. Вычисление объемов (79). 3.1-12. Преобразование декартовых
прямоугольных координат при параллельном переносе и повороте осей
ОГЛАВЛЕНИЕ О
(79). 3.1-13. Аналитическое задание кривых (81). 3.1-14. Способы задания
поверхностей (81). 3.1-15. Специальные типы поверхностей (82). 3.1-16.
Поверхности и кривые (82).
3.2. Плоскость 83
3.2-1. Уравнение плоскости (83). 3.2-2. Параметрическое задание
плоскости (84).
3.3. Прямая линия 84
3.3-1. Уравнения прямой (84). 3.3-2. Параметрические уравнения прямой
(85).
3.4. Взаимное расположение точек, плоскостей и прямых 85
3.4-1. Углы (85). 3.4-2. Расстояния (80). 3.4-3. Специальные случаи
взаимного расположения точек, прямых и плоскостей (87). 3.4-4.
Тангенциальные координаты плоскости и принцип двойственности (88). 3.4-5.
Некоторые дополнительные соотношения (88).
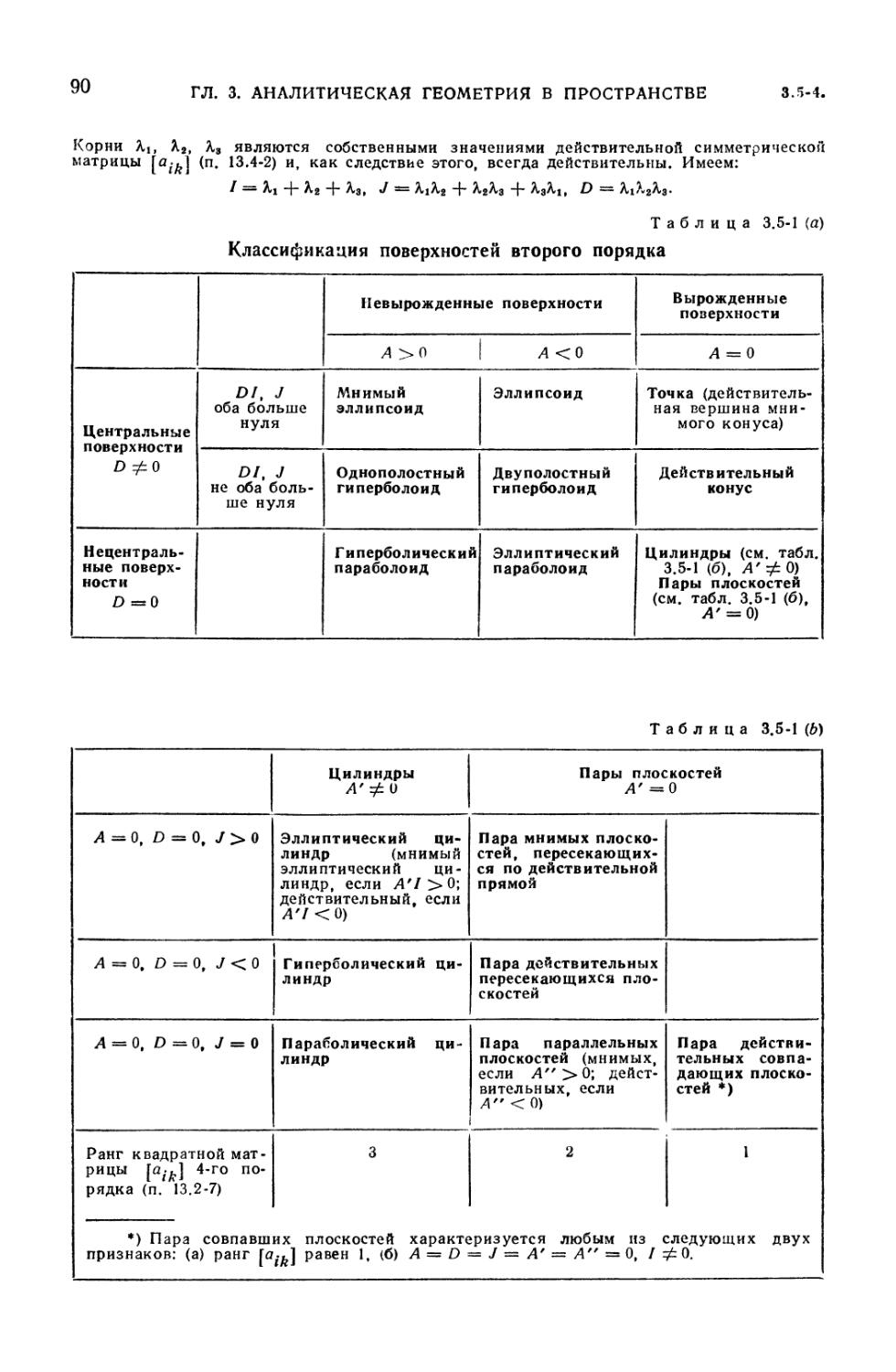
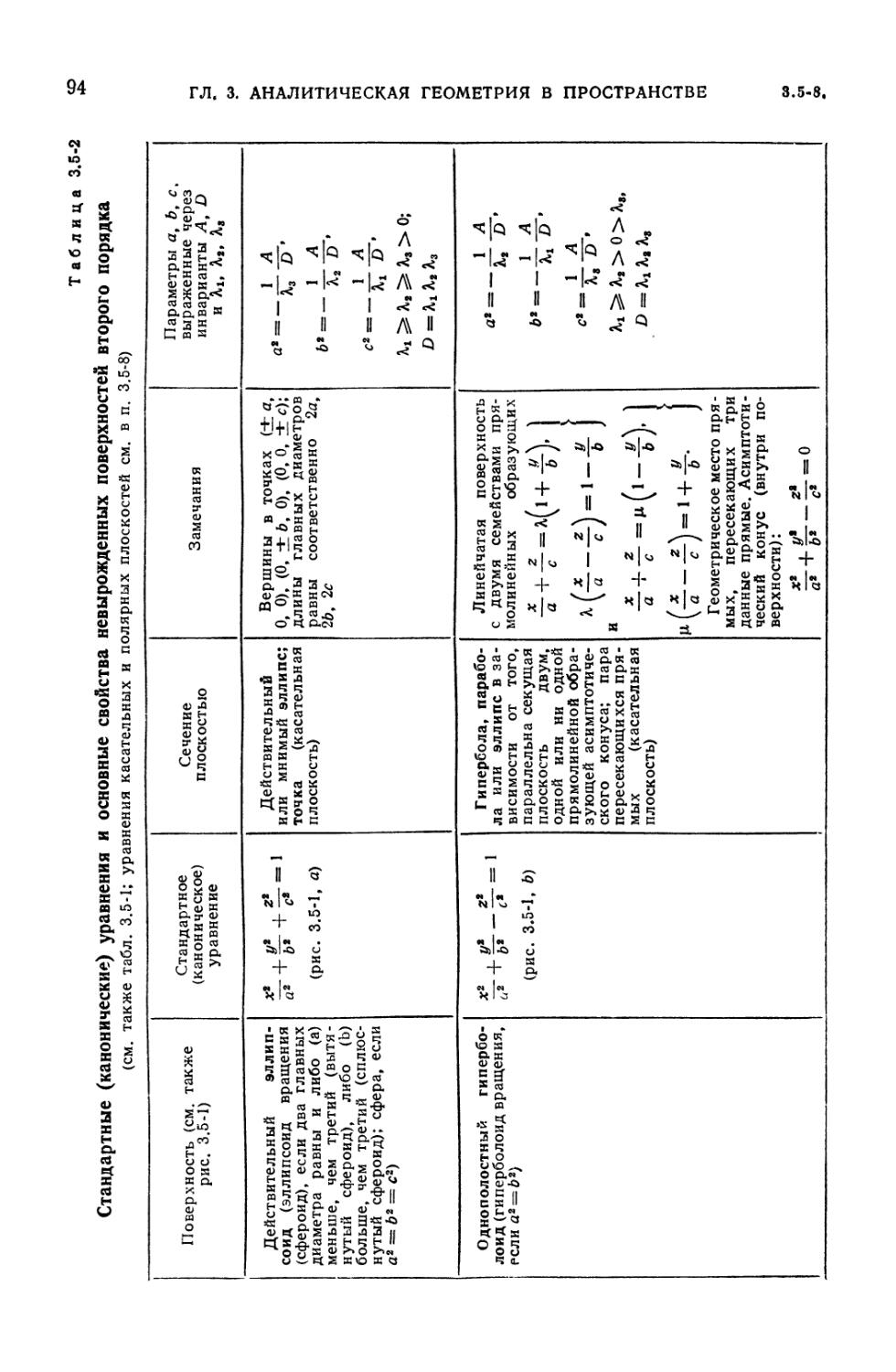
3.5. Поверхности второго порядка 89
3.5-1. Общее уравнение второй степени (89). 3.5-2. Инварианты (89).
3.5-3. Классификация поверхностей второго порядка (89). 3.5-4.
Характеристическая квадратичная форма и характеристическое уравнение (89).
3.5-5. Диаметральные плоскости, диаметры и центры поверхностей второго
порядка (91). 3.5-6. Главные плоскости и главные оси (91). 3.5-7.
Приведение уравнения поверхности второго порядка к стандартному
(каноническому) виду (92). 3.5-8. Касательные плоскости и нормали поверхности
второго порядка. Полюсы и поляры (93). 3.5-9. Некоторые дополнительные
формулы и теоремы (96). 3.5-10.. Параметрическое задание поверхностей
второго порядка (97).
Г Л А В А 4
ФУНКЦИИ И ПРЕДЕЛЫ. ДИФФЕРЕНЦИАЛЬНОЕ
И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
4.1. Введение 93
4.2. Функции 93
4.2-1. Функции и переменные (93). 4.2-2. Функции со специальными
свойствами (99).
4.3. Точечные множества, интервалы и области 99
4.3-1. Вводные замечания (99). 4.3-2. Свойства множеств (100). 4.3-3.
Границы (100). 4.3-4. Интервалы (101). 4.3-5. Определение окрестностей (101).
4.3-6. Открытые и замкнутые множества и области (101).
4.4. Пределы, непрерывные функции и смежные вопросы 102
4.4-1. Пределы функций и последовательностей (102). 4.4-2. Операции над
пределами (103). 4.4-3. Асимптотические соотношения между двумя
функциями (103). 4.4-4. Равномерная сходимость (104). 4.4-5. Пределы по
совокупности переменных и повторные пределы (104). 4.4-6. Непрерывные функции
(104). 4.4-7. Односторонние пределы. Односторонняя непрерывность (105).
4.4-8. Монотонные функции и функции ограниченной вариации (106).
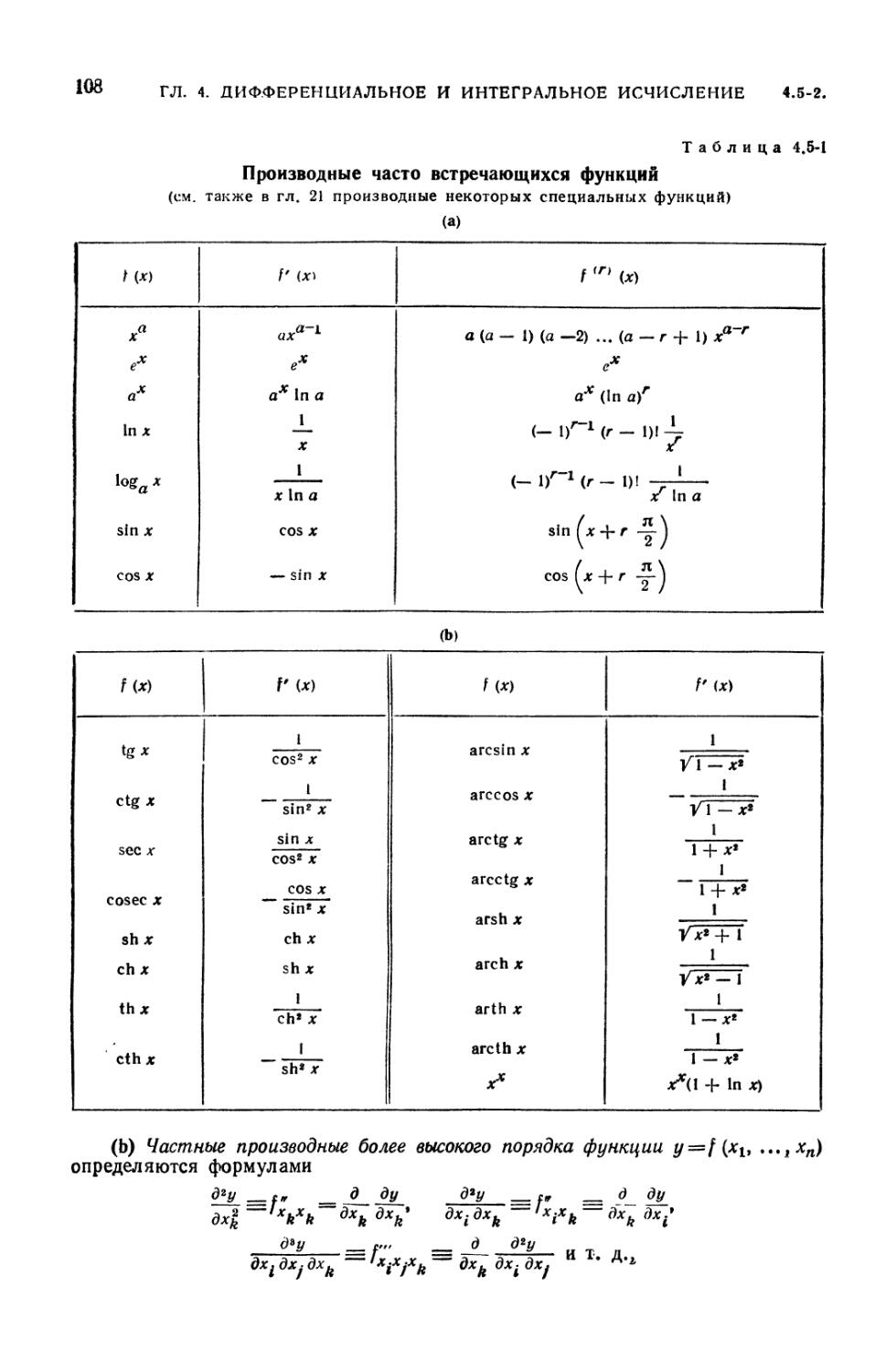
4.5. Дифференциальное исчисление 107
4.5-1. Производные и дифференцирование (107). 4.5-2. Частные производные
(107). 4.5-3. Дифференциалы (109). 4.5-4. Правила дифференцирования
(ПО). 4.5-5. Однородные функции (112). 4.5-6. Якобианы и
функциональная зависимость (112). 4.5-7. Неявные функции (112).
4.6. Интегралы и интегрирование ИЗ
4.6-1. Определенные интегралы (интеграл Римана) (113). 4.6-2. Несобственные
интегралы (115). 4.6-3. Среднее значение (117). 4.6-4. Неопределенные
интегралы (117). 4.6-5. Основная теорема интегрального исчисления (117).
4.6-6. Методы интегрирования (117). 4.6-7. Эллиптические интегралы (119).
4.6-8. Кратные интегралы (119). 4.6-9. Длина дуги спрямляемой кривой
(120). 4.6-10. Криволинейные интегралы (120). 4.6-11. Площади и объемы
(121). 4.6-12. Интегралы по поверхности и по объему (122). 4.6-13. Замена
переменных в интегралах по объему и по поверхности (123). 4.6-14. Мера
Лебега. Измеримые функции (123). 4.6-15. Интеграл Лебега (124). 4.6-16.
Теоремы о сходимости (теоремы о непрерывности) (126). 4.6-17. Интеграл
Стилтьеса (126). 4.6-18. Свертки (128). 4.6-19. Неравенства Минковского
и Гельдера (1.23).
6
ОГЛАВЛЕНИЕ
4.7. Теоремы о среднем значении. Раскрытие неопределенностей. Теоремы Вейер-
штрасса о приближении 129
4.7-1. Теоремы о среднем значении (129). 4.7-2. Раскрытие
неопределенностей (130). 4.7-3. Теоремы Вейерштрасса о приближении (131).
4.8. Бесконечные ряды, бесконечные произведения и непрерывные дроби .... 131
4.8-1. Бесконечные ряды. Сходимость (131). 4.8-2. Ряды функций.
Равномерная сходимость (132). 4.8-3. Операции над сходящимися рядами (132).
4.8-4. Операции над бесконечными рядами функций (133). 4.8-5. Улучшение
сходимости и суммирование рядов. Суммы некоторых рядов (134). 4.8-6.
Расходящиеся бесконечные ряды (136). 4.8-7. Бесконечные произведения
(137). 4.8-8. Непрерывные (цепные) дроби (138).
4.9. Признаки сходимости и равномерной сходимости бесконечных рядов и
несобственных интегралов 139
4.9-1. Признаки сходимости бесконечных рядов (139). 4.9-2. Признаки
равномерной сходимости бесконечных рядов (140). 4.9-3. Признаки
сходимости несобственных интегралов (140). 4.9-4. Признаки равномерной
сходимости несобственных интегралов (142).
4.10. Разложение функций в бесконечный ряд и представление их интегралом.
Степенные ряды и ряд Тейлора 142
4.10-1. Разложение функций в бесконечный ряд и представление их
интегралом (142). 4.10-2. Степенные ряды (143). 4.10-3. Теоремы Абеля и Таубера
(145). 4.10-4. Ряд Тейлора (145). 4.10-5. Кратный ряд Тейлора (146).
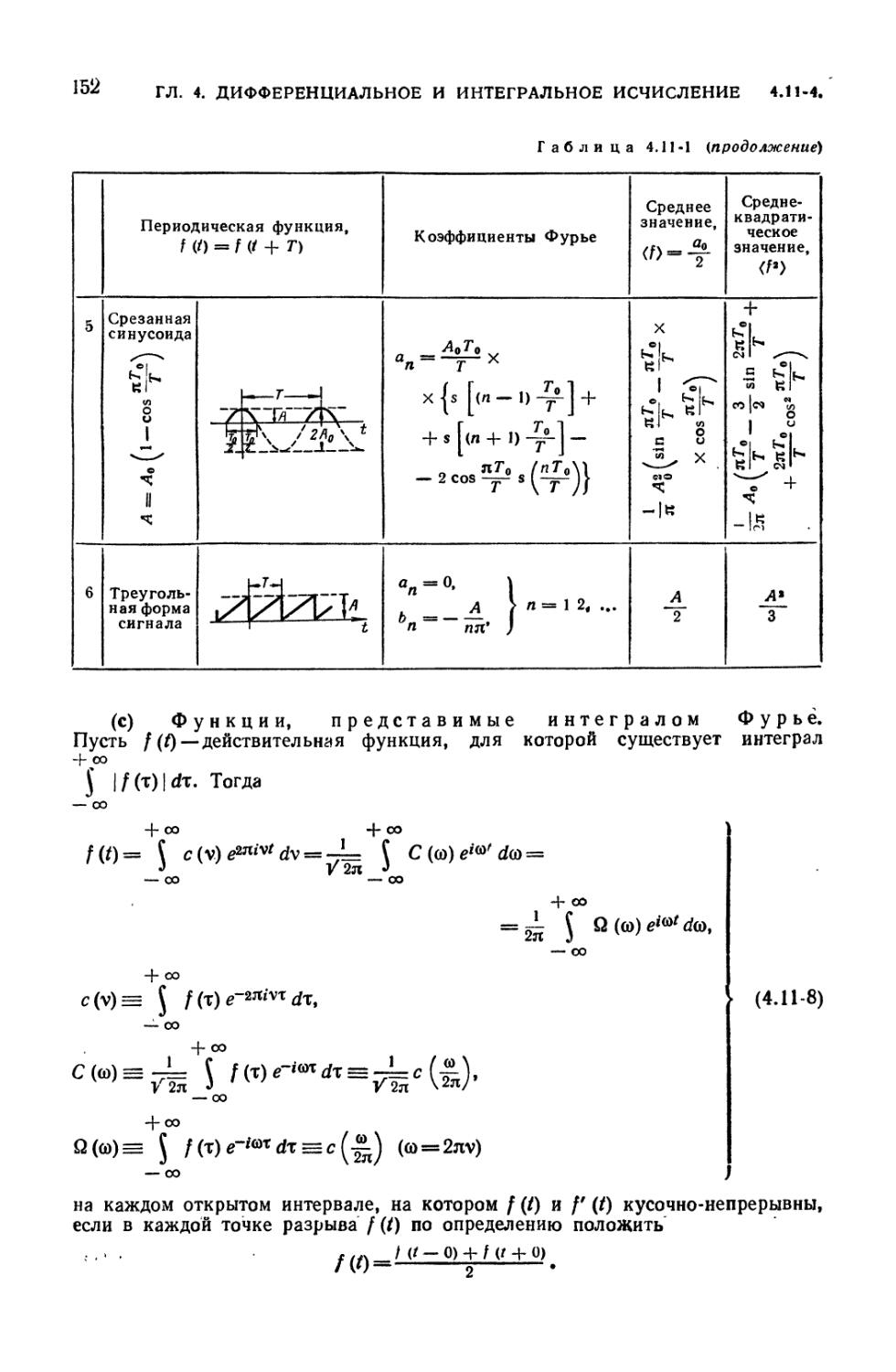
4.11. Ряды Фурье и интегралы Фурье 146
4.11-1. Вводные замечания (146). 4.11-2. Ряды Фурье (146). 4.11-3. Интеграл
Фурье и преобразование Фурье (148). 4.11-4. Функции, разложимые в ряд
Фурье и представимые интегралом Фурье. Гармонический анализ (149).
4.11-5. Некоторые свойства коэффициентов Фурье и преобразования Фурье
(156). 4.11-6. Интегралы Дирихле и Фейера (157). 4.11-7. Суммирование
средними арифметическими (160). 4.11-8. Кратные ряды и интегралы Фурье
(160).
Г Л А В А 5
ВЕКТОРНЫЙ АНАЛИЗ
5.1. Векторы в евклидовом пространстве 162
5.2. Векторная алгебра 162
5.2-1. Сложение векторов и умножение вектора на (действительный) скаляр
(162). 5.2-2. Разложение векторов по базисным векторам (163). 5.2-3.
Декартовы прямоугольные координаты вектора (163). 5.2-4. Векторы и
физические размерности (163). 5.2-5. Модуль (норма, абсолютная величина, длина)
вектора (164). 5.2-6. Скалярное (внутреннее) произведение двух векторов
(164). 5.2-7. Векторное произведение двух векторов (164). 5.2-8. Смешанное
(векторно-скалярное) произведение (165). 5.2-9. Другие произведения,
содержащие более двух векторов (166). 5.2-10. Разложение вектора а по
направлению единичного вектора и и ему перпендикулярному (166). 5.2-11.
Решение уравнений (166).
5.3. Векторные функции скалярного аргумента 166
5.3-1. Векторные функции и их пределы (166). 5.3-2. Дифференцирование
(166). 5.3-3. Интегрирование и обыкновенные дифференциальные уравнения
(167).
5.4. Скалярные и векторные поля 163
5.4-1. Вводные замечания (168). 5.4-2. Скалярные поля (168). 5.4-3.
Векторные поля (168). 5.4-4. Векторный элемент линии и длина дуги (168). 5.4-5.
Криволинейные (линейные) интегралы (169). 5.4-6. Поверхностные
интегралы (169). 5.4-7. Объемные интегралы (170).
5.5. Дифференциальные операторы 170
5.5-1. Градиент, дивергенция и ротор; инвариантные определения (170).
5.5-2. Оператор V (171). 5.5-3. Полный дифференциал, полная производная и
производная по направлению (172). 5.5-4. Производные высших порядков
по направлению. Ряд Тейлора (173). 5.5-5. Оператор Лапласа (173). 5.5-6.
Операции второго порядка (173). 5.5-7. Операции над простейшими
функциями от г (174). 5.5-8. Функции от двух и более радиусов-векторов (174).
5.6. Интегральные теоремы 175
5.6-1. Теорема о дивергенции и связанные с ней теоремы (175). 5.6-2. Теорема
о роторе и связанные с ней теоремы (176). 5.6-3. Поля с разрывами на
поверхностях (176).
ОГЛАВЛЕНИЕ
7
6.7. Отыскание векторного поля по его ротору и дивергенции 175
5.7-1. Безвихревое векторное поле (176). 5.7-2. Соленоидальные
(трубчатые) векторные поля (177). 5.7-3. Отыскание векторного поля по его ротору
и дивергенции (177).
Г Л А В А 6
СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
6.1. Вводные замечания 179
6.2. Системы криволинейных координат 179
6.2-1. Криволинейные координаты (179). 6.2-2. Координатные поверхности
и координатные линии (179>. 6.2-3. Элементы длины дуги и объема (179).
6.3. Криволинейные координаты вектора 180
6.3-1. Координаты вектора и локальный (местный) базис (180). 6.3-2.
Физические координаты вектора (182). 6 3-3. Контравариаитные и ковариант-
ные координаты вектора (182). 6.3-4. Запись векторных соотношений в
криволинейных координатах (183).
6.4. Системы ортогональных координат. Векторные соотношения в
ортогональных координатах • • 183
6.4-1. Ортогональные координаты (183). 6.4-2. Векторные соотношения
(184). 6.4-3. Криволинейный интеграл, поверхностный интеграл и
объемный интеграл (185).
6.5. Формулы для специальных систем ортогональных координат 185
Г Л А В А 7
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
7.1. Вводные замечания . . . ^ 197
7.2. Функции комплексного переменного. Области в комплексной плоскости 19/
7.2-1. Функции комплексного переменного (197). 7.2-2. г-плоскость и
^-плоскость. Окрестности. Бесконечно удаленные точки (197). 7.2-3. Кривые и
контуры (200). 7.2-4. Границы и области (200). 7.2-5. Комплексные
контурные интегралы (200).
7.3. Аналитические (регулярные, голоморфные) функции 201
7.3-1. Производная функция (201). 7.3-2. Уравнения Коши — Римана (201).
7.3-3. Аналитические функции (202). 7.3-4. Свойства аналитических
функций (202). 7.3-5. Теорема о максимуме модуля (203).
7.4. Многозначные функции 203
7.4-1. Ветви (203). 7.4-2. Точки разветвления и разрезы (203), 7.4-3. Рима-
новы поверхности (204).
7.5. Интегральные теоремы и разложения в ряды 205
7.5-1. Интегральные теоремы (205). 7.5-2. Разложение в ряд Тейлора (206).
7.5-3. Разложение в ряд Лорана (206).
7.6. Нули и изолированные особые точки 207
7.6-1. Нули (207). 7.6-2. Особые точки (207). 7.6-3. Нули и особенности в
бесконечности (209). 7.6-4. Теоремы Вейерштрасса и Пикара (209), 7.6-5.
Целые функции (209). 7.6-6. Разложение целой функции в произведение
(210) 7.6-7. Мероморфные функции (210). 7.6-8. Разложение мероморфных
функций на простейшие дроби (211). 7 6-9. Нули и полюсы мероморфных
функций (211).
7.7. Вычеты и контурные интегралы 211
7.7-1. Вычеты (211). 7.7-2. Теорема о вычетах (212). 7.7-3. Вычисление
определенных интегралов (212). 7.7-4. Применение вычетов к суммированию
рядов (213).
7.8. Аналитическое продолжение 214
7.8-1. Аналитическое продолжение и моногенные аналитические функции
(214). 7.8-2. Методы аналитического продолжения (214).
7.9. Конформное отображение 215
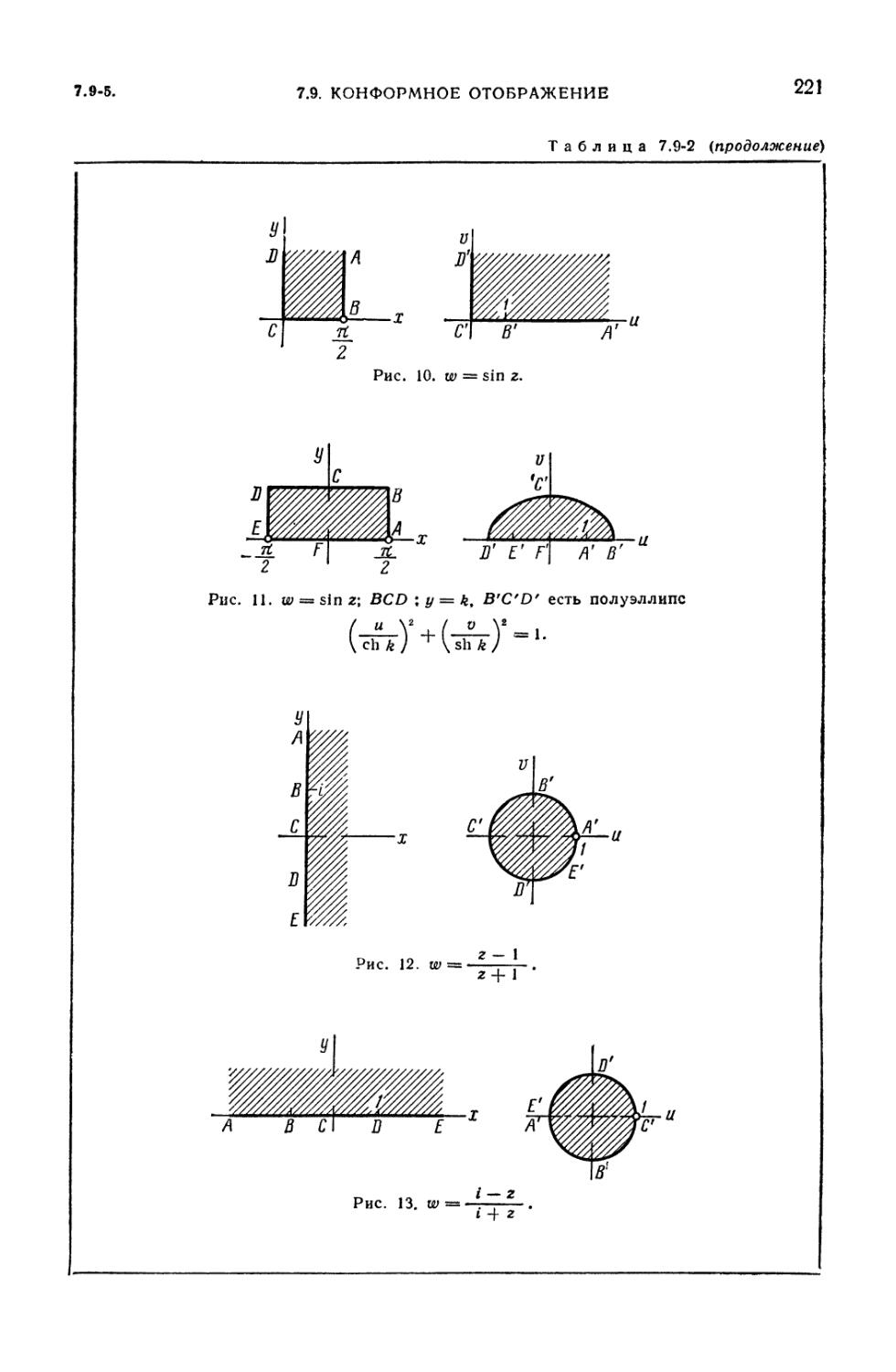
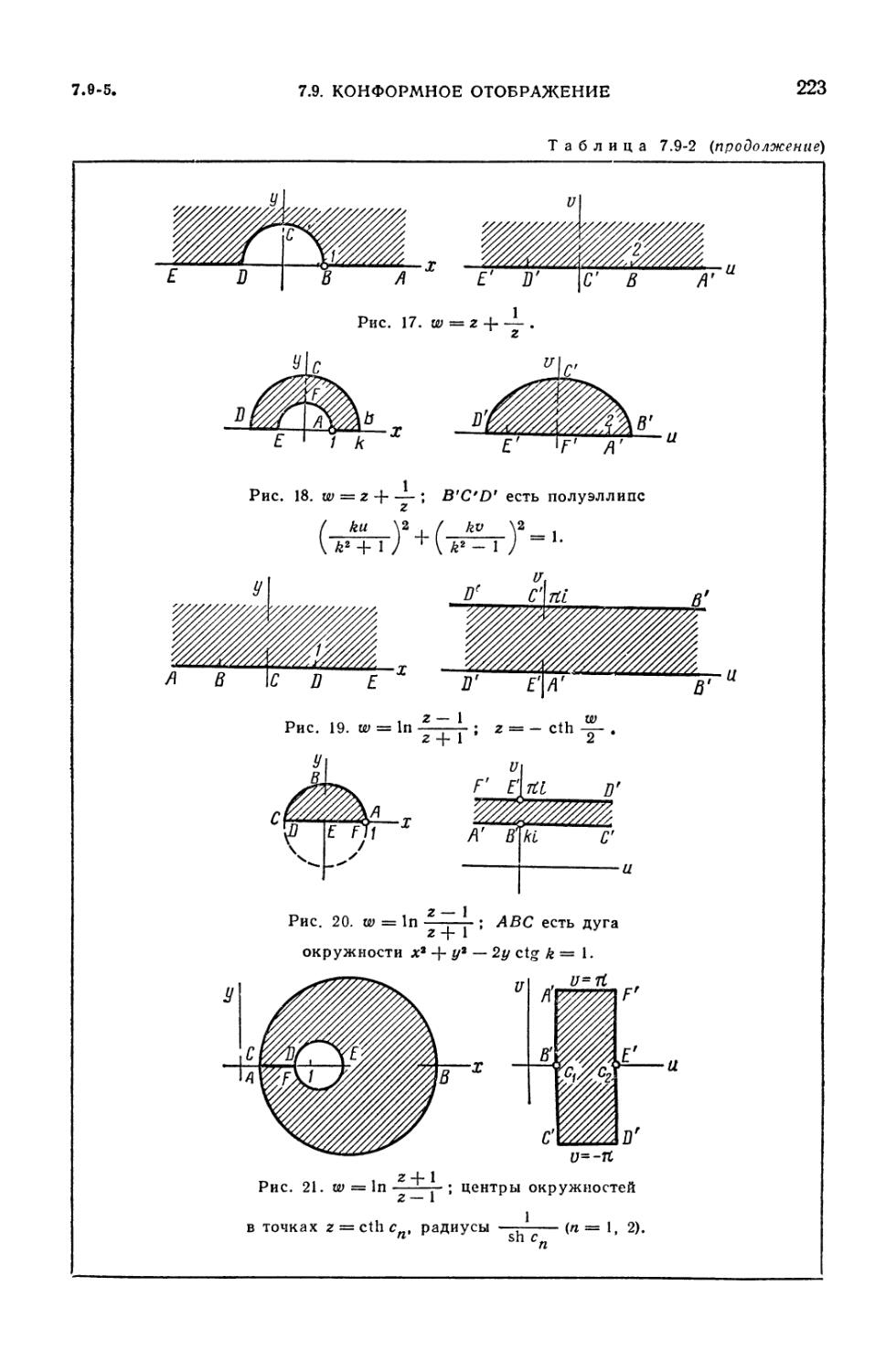
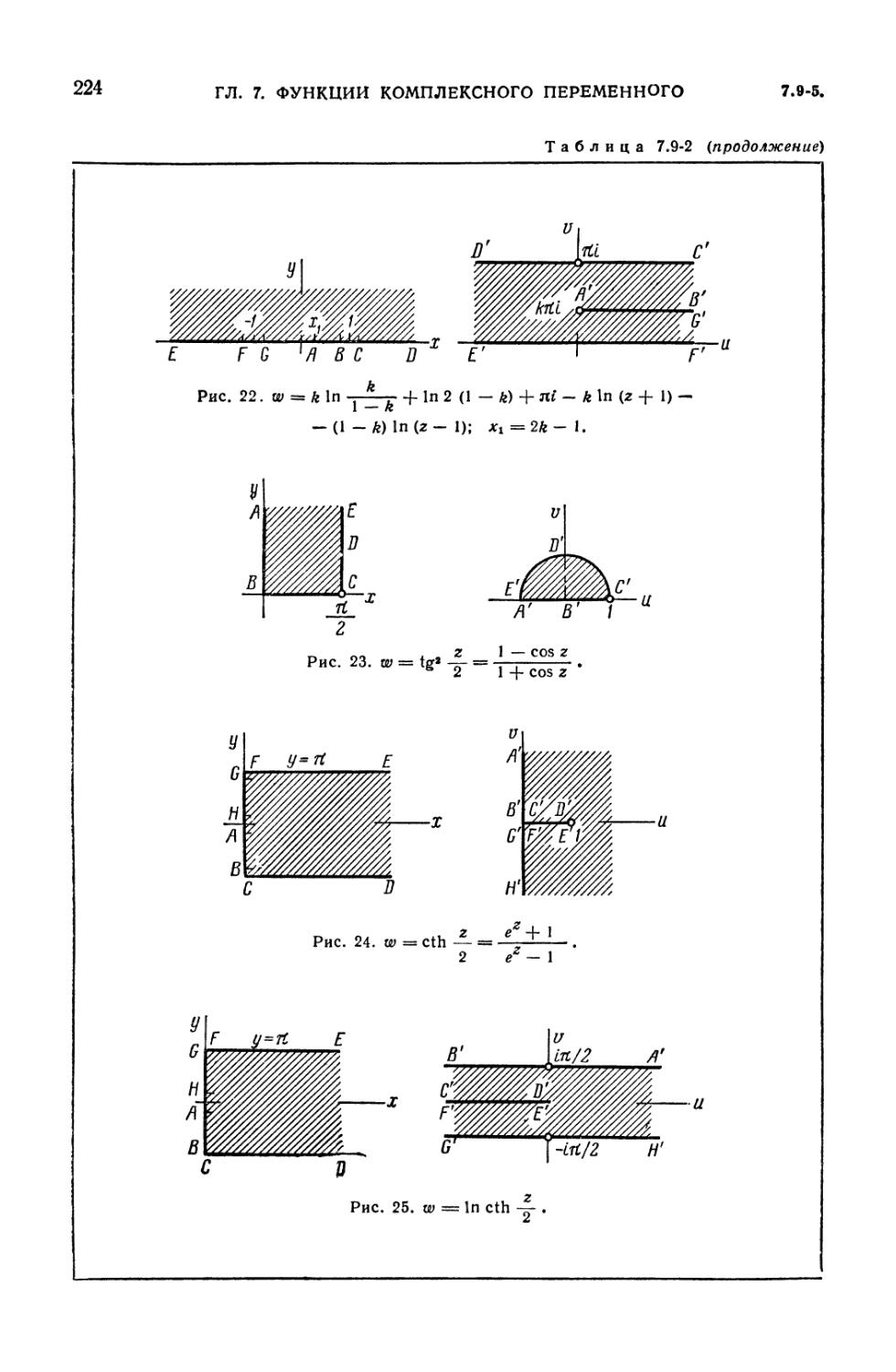
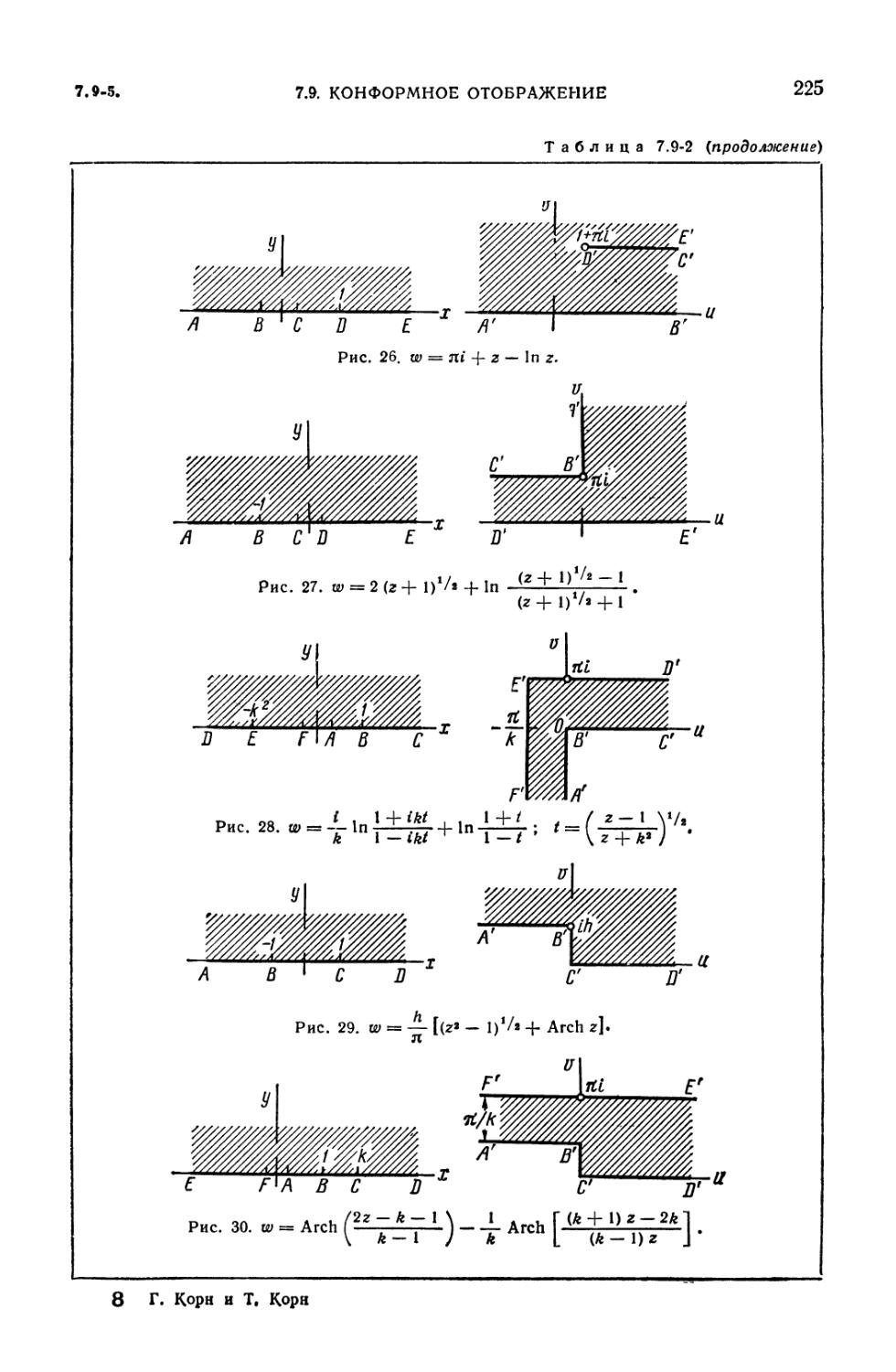
7.9-1. Конформное отображение (215), 7.9-2. Дробно-линейное
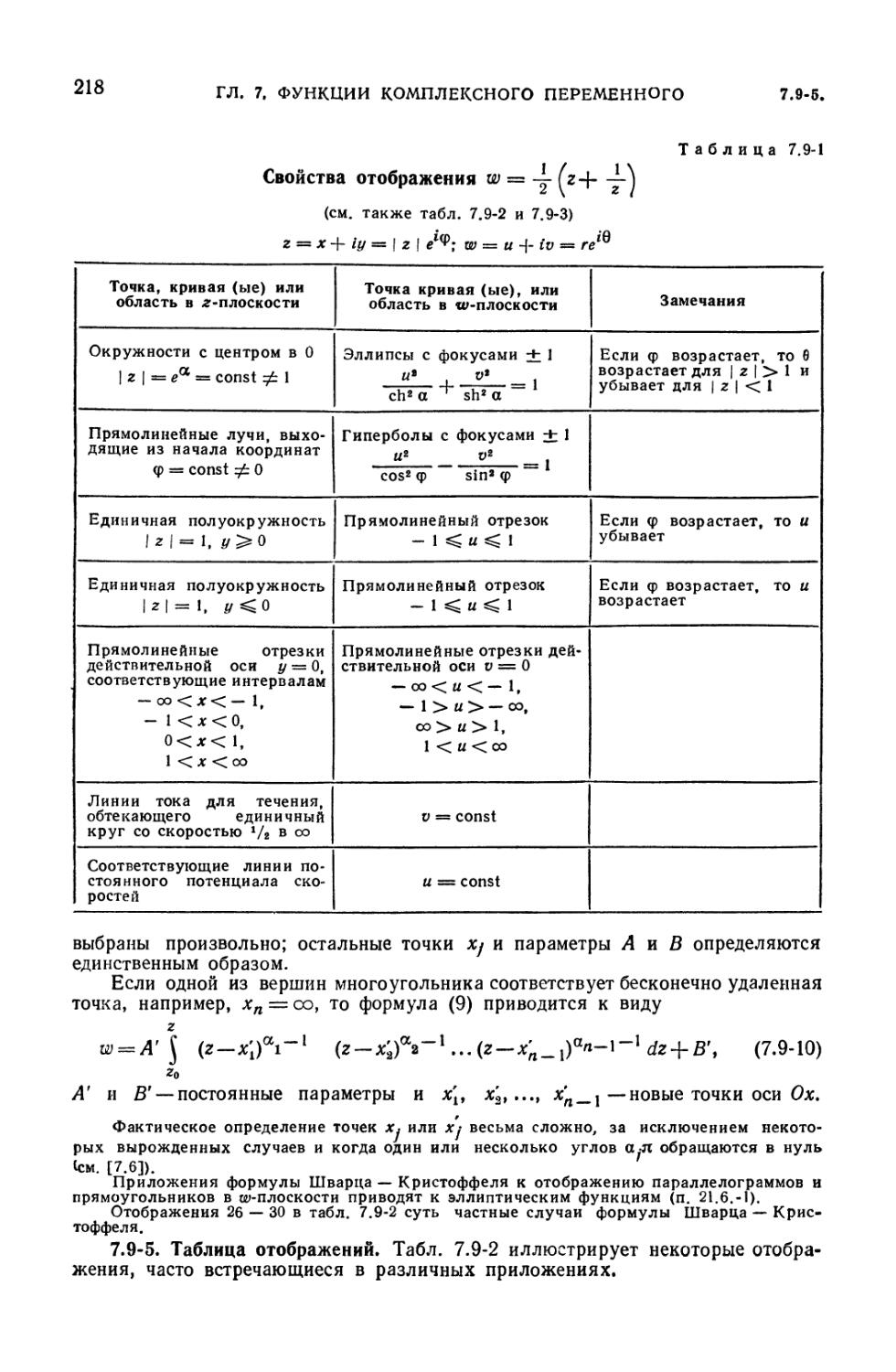
отображение (преобразование) (216), 7.9-3. Отображение w = -^- (г -\ ) (217).
ь
ОГЛАВЛЕНИЕ
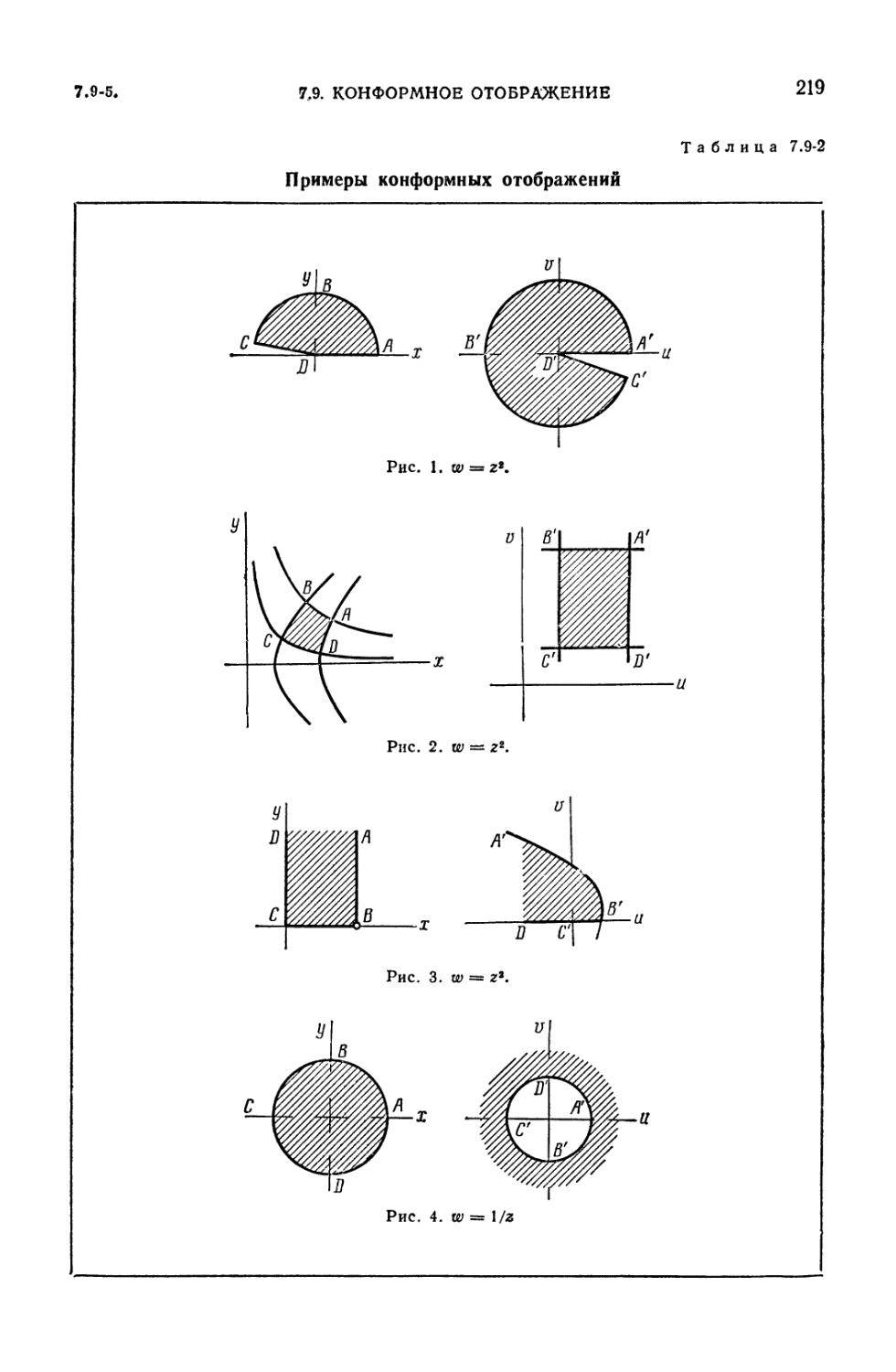
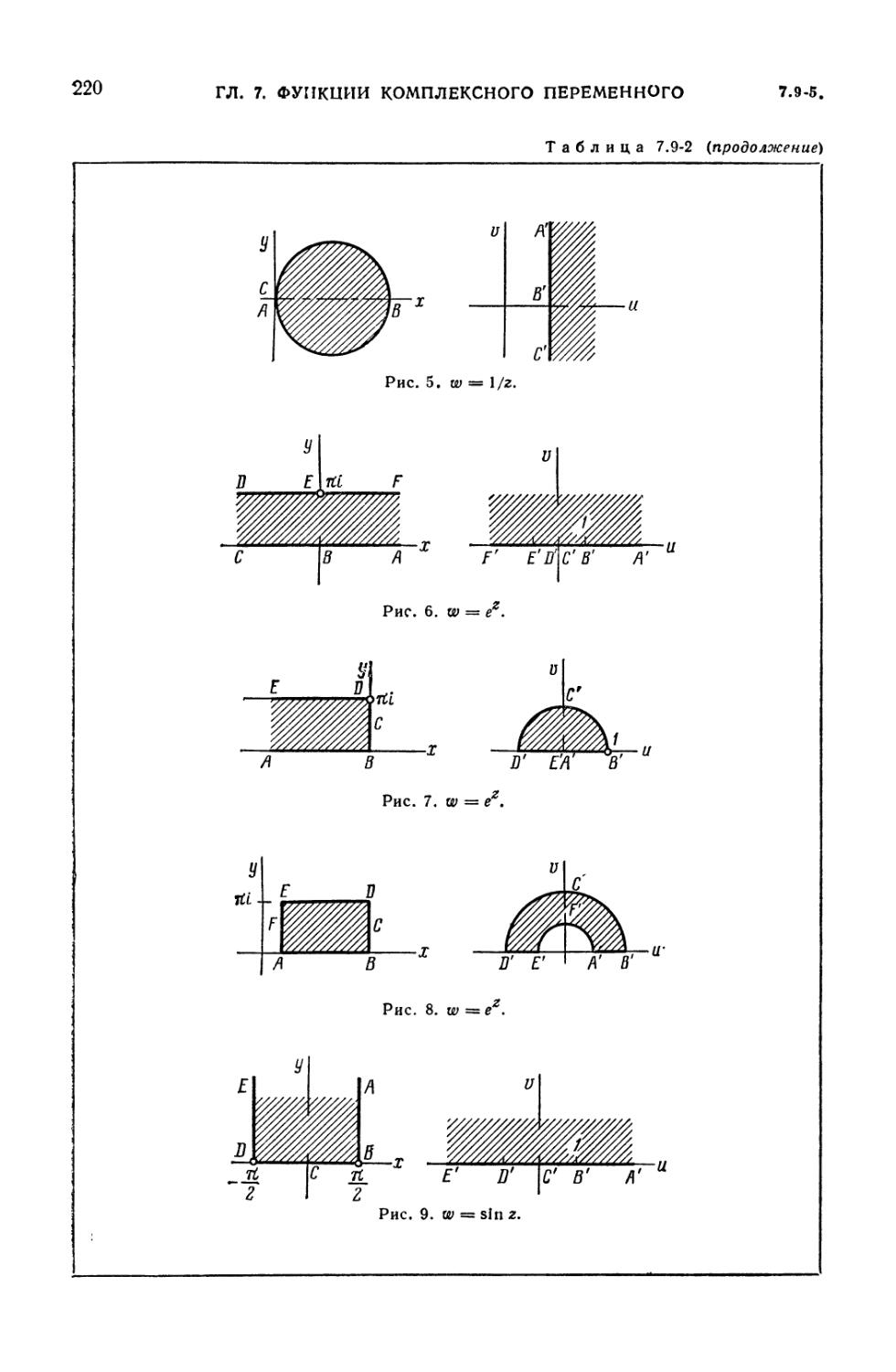
7.9-4. Интеграл Шварца — Кристоффеля (217). 7.9-5. Таблица отображений
(218). 7.9-6. Функции, отображающие специальные области на единичный
круг (227).
Г Л А В А 8
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ДРУГИЕ ИНТЕГРАЛЬНЫЕ
ПРЕОБРАЗОВАНИЯ
8.1. Вводные замечания 228
8.2. Преобразование Лапласа 228
8.2-1. Определение (228). 8.2-2. Абсолютная сходимость (228). 8.2-3. Область
определения (229). 8.2-4. Достаточные условия существования
преобразования Лапласа (229). 8.2-5. Обратное преобразование Лапласа (229). 8.2-6.
Теорема обращения (229). 8.2-7. Существование обратного преобразования
Лапласа (230). 8.2-8. Единственность преобразования Лапласа и его
обращения (230).
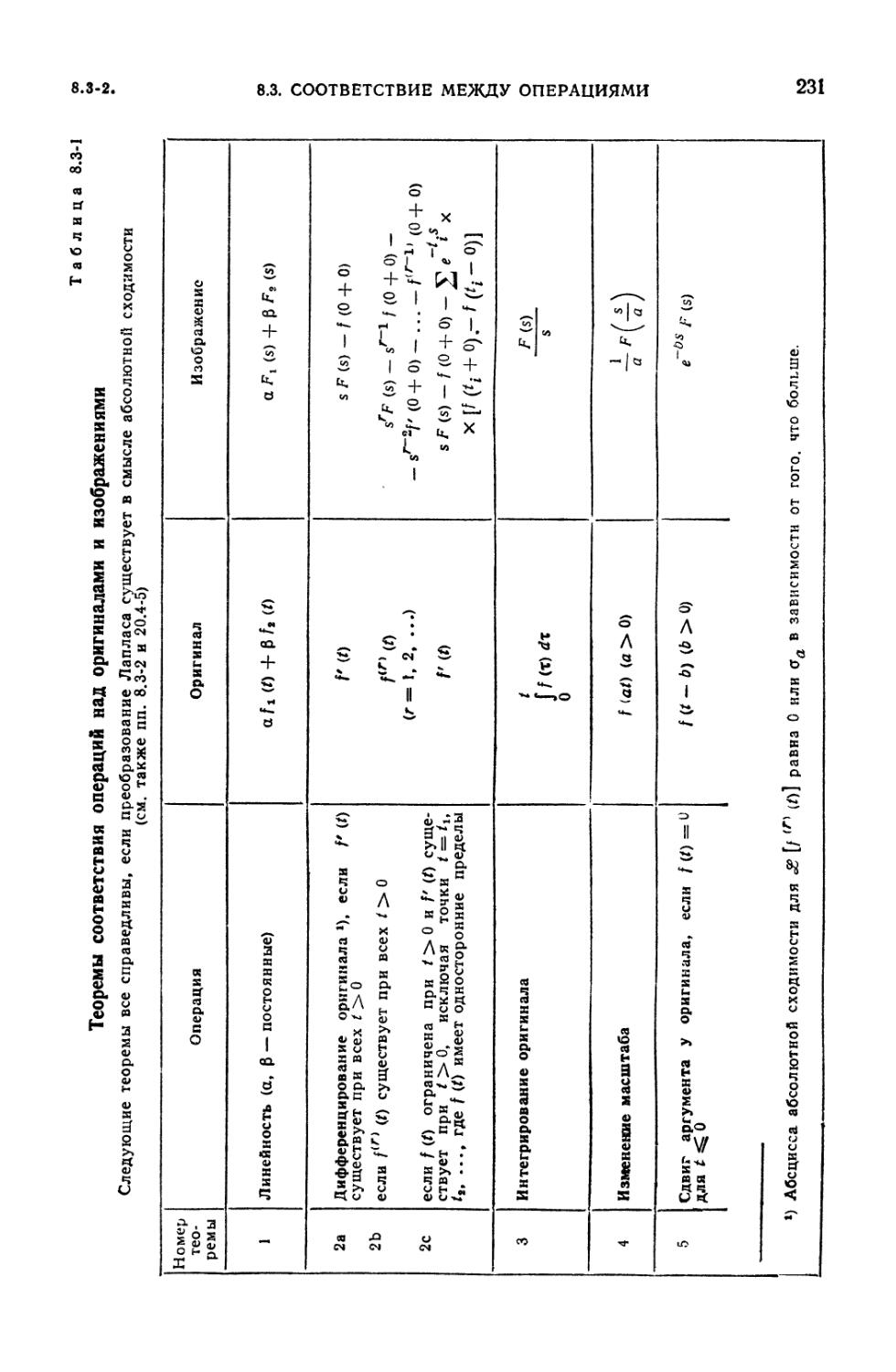
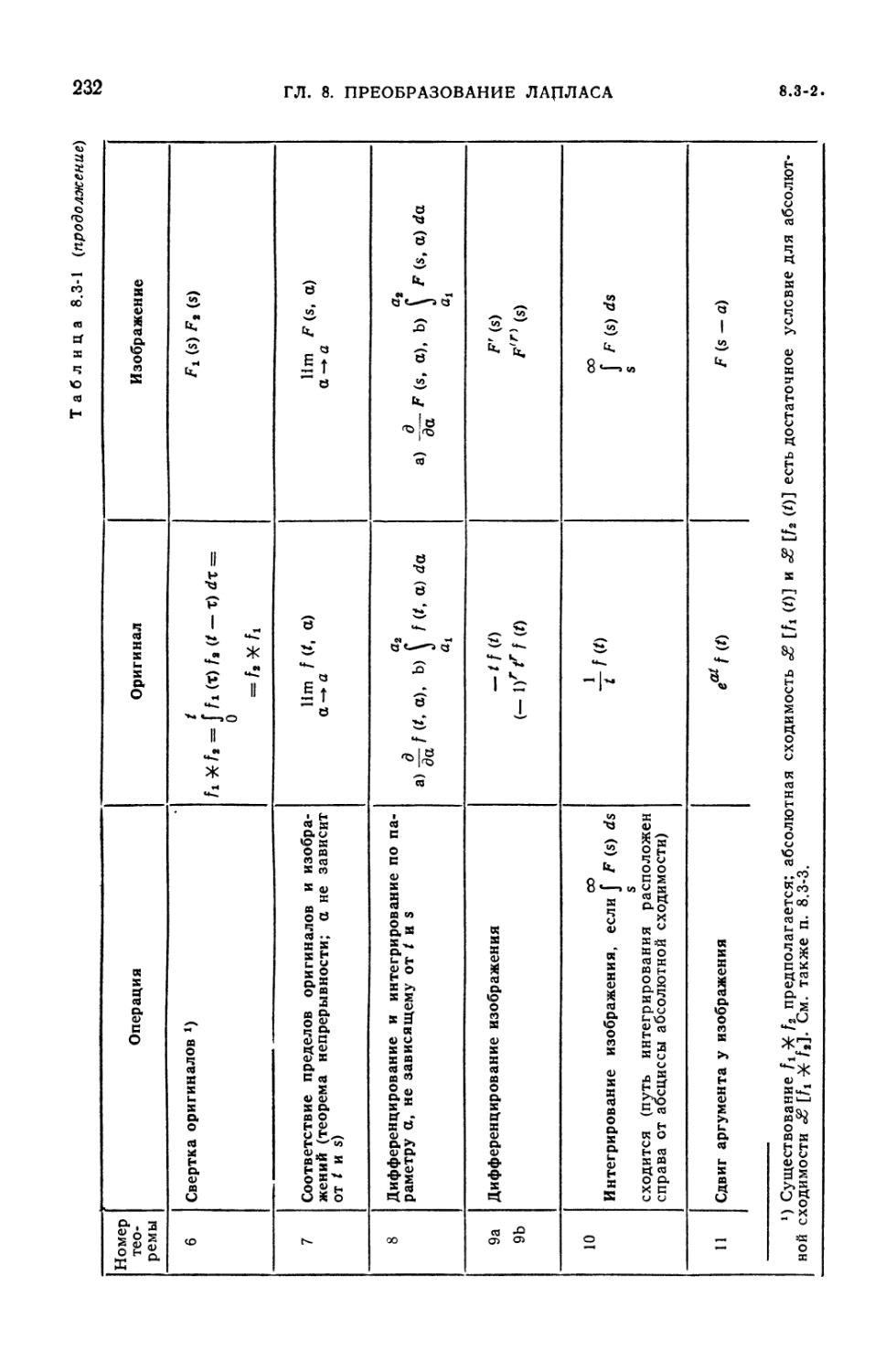
8.3. Соответствие между операциями над оригиналами и изображениями . . 230
8.3-1. Таблица соответствия операций (230). 8.3-2. Преобразования Лапласа
периодических функций и произведений оригиналов на синус или косинус
(230). 8.3-3. Преобразование произведения (теорема о свертке) (233). 8.3-4.
Предельные теоремы (233).
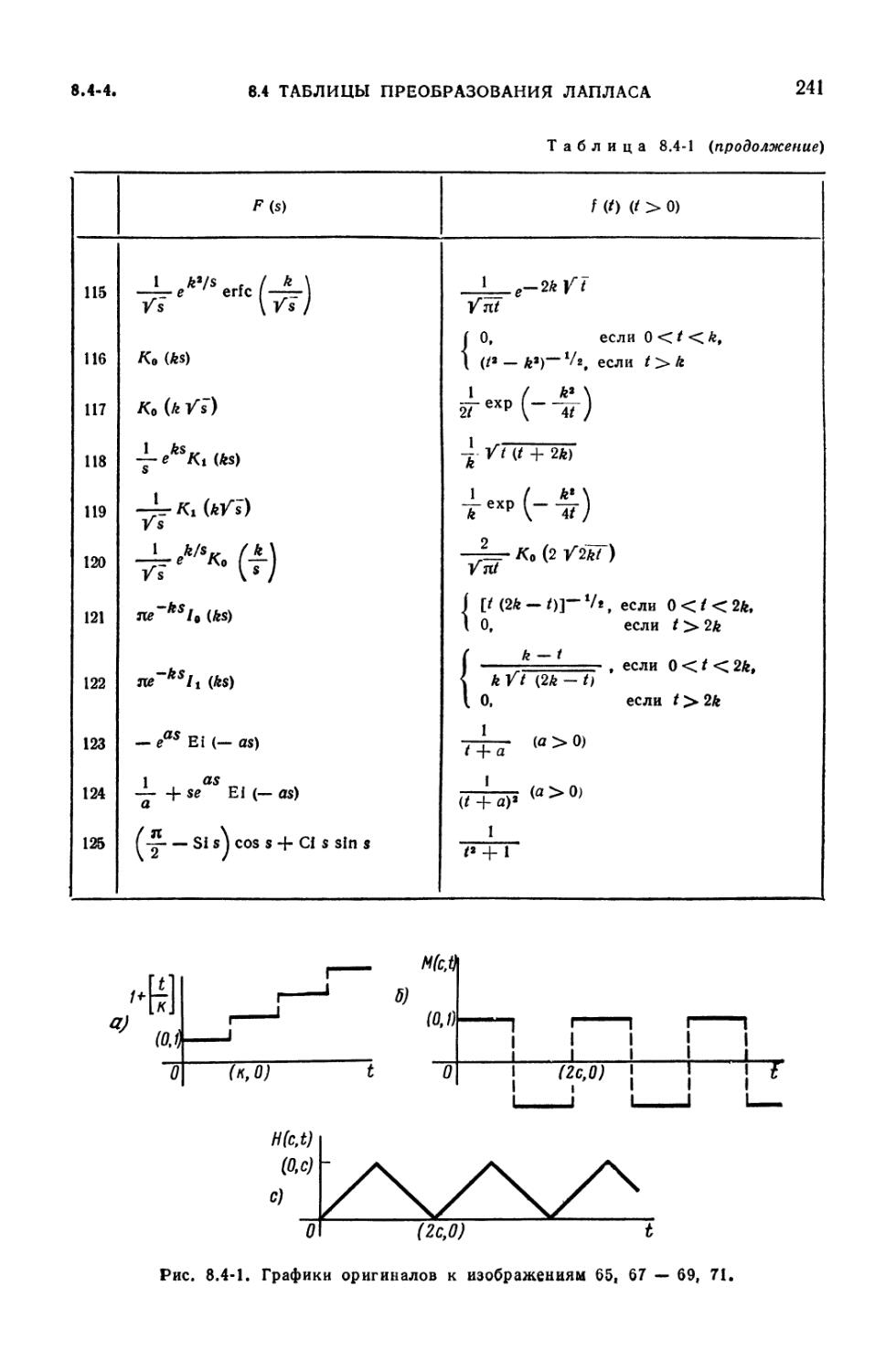
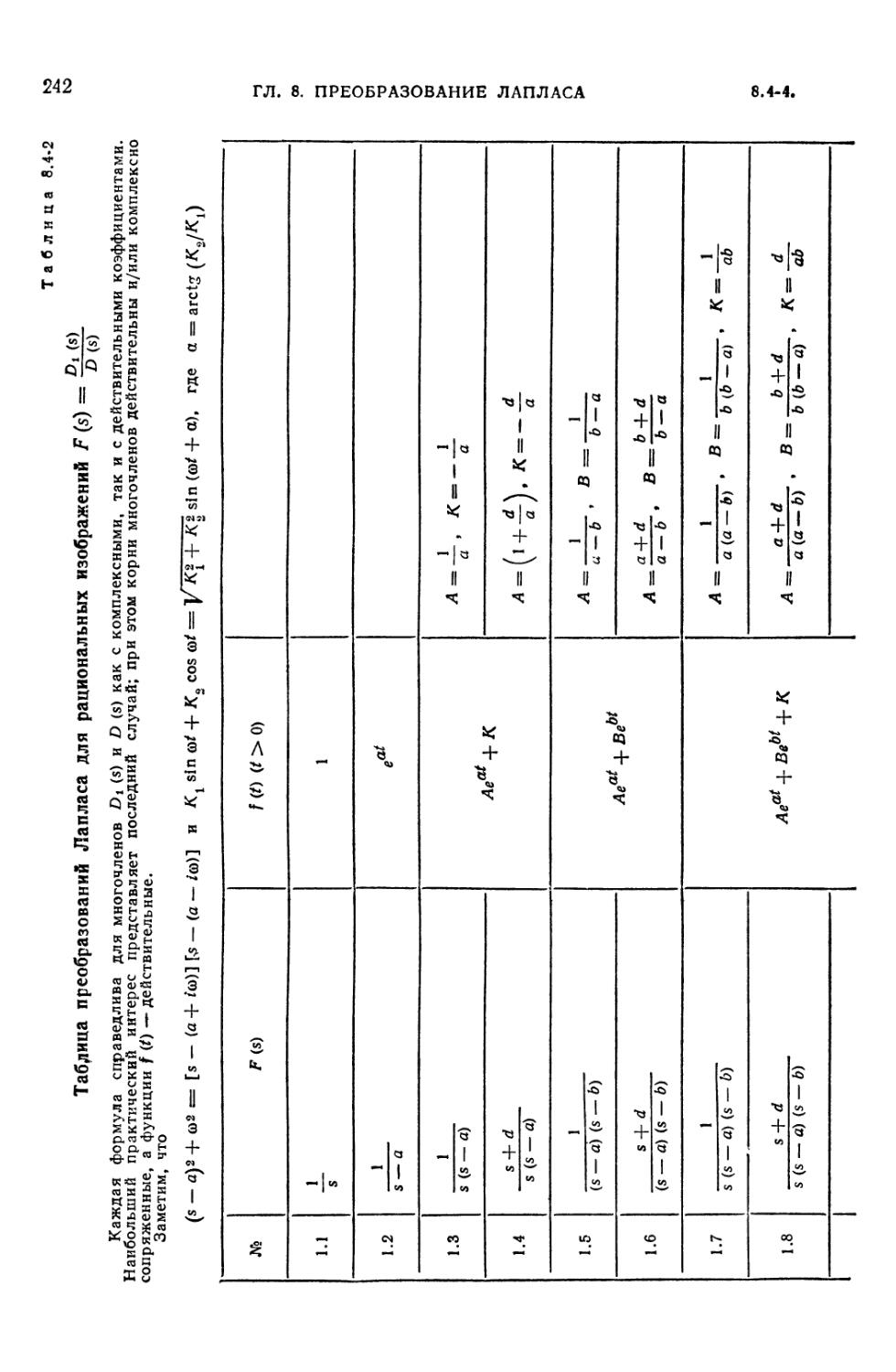
8.4. Таблицы преобразования Лапласа и вычисление обратных преобразований
Лапласа 234
8.4-Г. Таблицы преобразования Лапласа (234). 8.4-2. Вычисление обратных
преобразований Лапласа (234). 8.4-3 Применение контурного
интегрирования (234). 8.4-4. Обратное преобразование Лапласа для рациональных
алгебраических функций: разложение Хевисайда (234). 8.4-5. Обратное
преобразование Лапласа для рациональных алгебраических функций:
разложение на простейшие дроби (252). 8.4-6. Разложения в ряды (252).
8.4-7. Разложения по степеням / (253). 8.4-8. Разложения по многочленам
Лагерра (253). 8.4-9. Разложения в асимптотические ряды (254).
8.5. Формальное преобразование Лапласа импульсных функций 255
8.6. Некоторые другие функциональные преобразования 256
8.6-1. Вводные замечания (256). 8.6-2. Двустороннее преобразование
Лапласа (256). 8.6-3 Преобразование Лапласа в форме интеграла Стилтьеса
(256). 8.6-4. Преобразования Ганкеля и Фурье — Бесселя (258).
8.7. Конечные интегральные преобразования, производящие функции и г-пре-
образование v 260
8.7-1. Ряды как функциональные преобразования. Конечные
преобразования Фурье и Ганкеля (260). 8.7-2. Производящие функции (260). 8.7-3.
г-преобразование. Определение и формула обращения (263).
Г Л А В А 9
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
9.1. Введение 265
9.1-1. Вводные замечания (265). 9.1-2. Обыкновенные дифференциальные
уравнения (265). 9.1-3. Системы дифференциальных уравнений (266). 9.1-4.
Существование решений (266). 9.1-5. Общие указания (266).
9.2. Уравнения первого порядка 26S
9.2-1. Существование и единственность решений (266). 9.2-2.
Геометрическое толкование. Особые интегралы (267). 9.2-3. Преобразование
переменных (268). 9.2-4. Решение специальных типов уравнений первого
порядка (268). 9.2-5. Общие методы интегрирования (270).
9.3. Линейные дифференциальные уравнения 271
9.3-1. Линейные дифференциальные уравнения. Принцип наложения (271).
9.3-2. Линейная независимость и фундаментальные системы решений (271).
9.3-3. Решение методом вариации постоянных. Функции Грина (272). 9.3-4.
Приведение двухточечных краевых задач к задачам Коши (275). 9.3-5.
Линейные дифференциальные уравнения в комплексной области.
Тейлоровские разложения решения и влияние особенностей (275). 9.3-6. Решение
однородных уравнений путем разложения в ряд в окрестности правильной
особой точки (276). 9.3-7. Методы интегральных преобразований (277).
9.3-8. Линейные уравнения второго порядка (278). 9.3-9.
Гипергеометрическое дифференциальное уравнение Гаусса и Р-уравнение Римана (279).
ОГЛАВЛЕНИЕ
9
9.3-10. Вырожденные гипергеометрические функции (282). 9.3-11.
Обобщенные гипергеометрические ряды (283).
9.4. Линейные дифференциальные уравнения с постоянными коэффициентами 283
9.4-1. Однородные линейные уравнения с постоянными коэффициентами
(283). 9.4-2. Неоднородные уравнения (285). 9.4-3. Свертки и функции Грина
(286). 9.4-4. Устойчивость (287). 9.4-5. Операторный метод решения (288).
9.4-6. Периодические внешние нагрузки и решения (289). 9.4-7.
Передаточные функции и частотные характеристики (290). 9.4-8. Нормальные
координаты и собственные колебания (291).
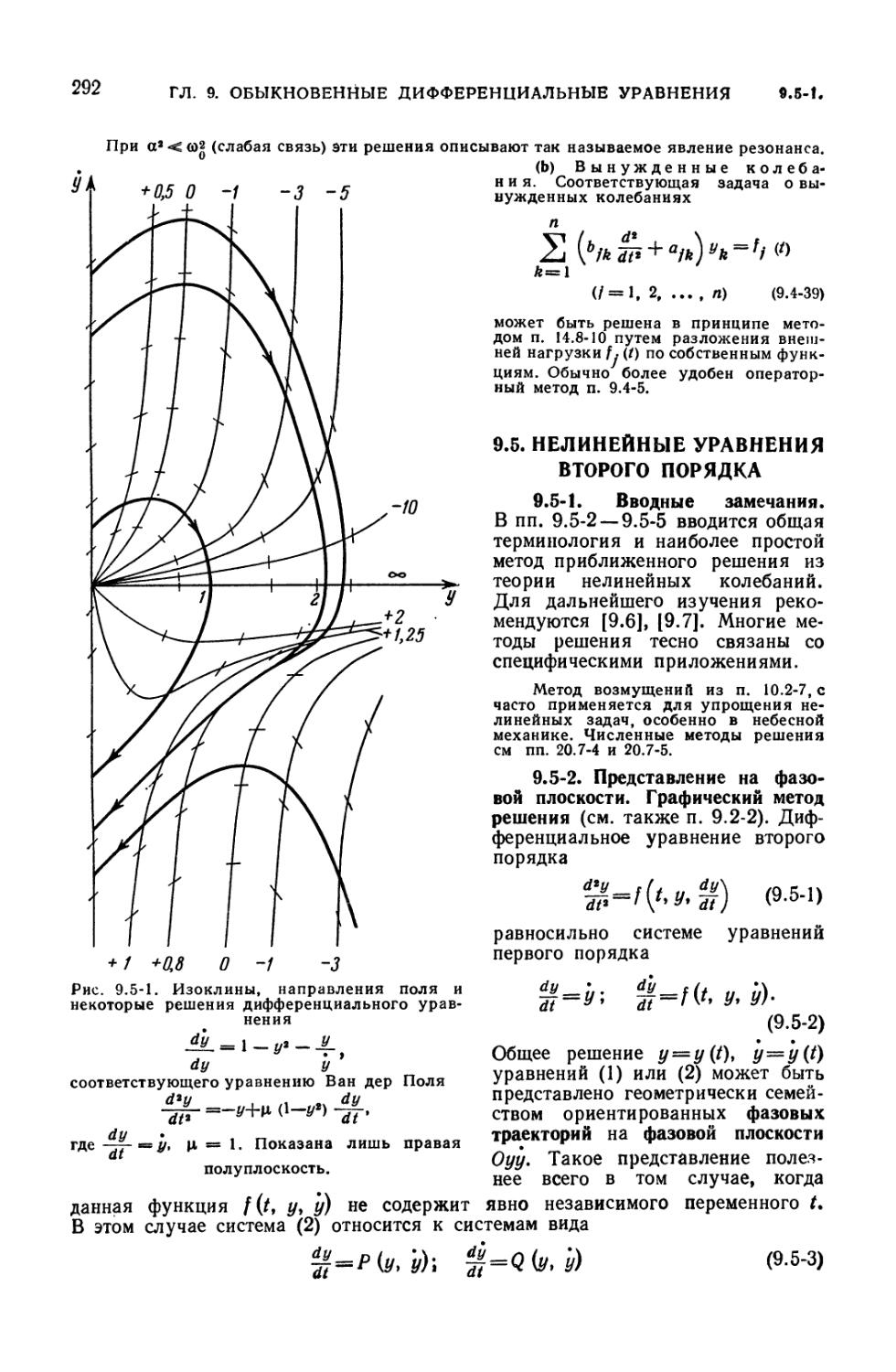
9.5. Нелинейные уравнения второго порядка 292
9.5-1. Вводные замечания (292). 9.5-2. Представление на фазовой плоскости.
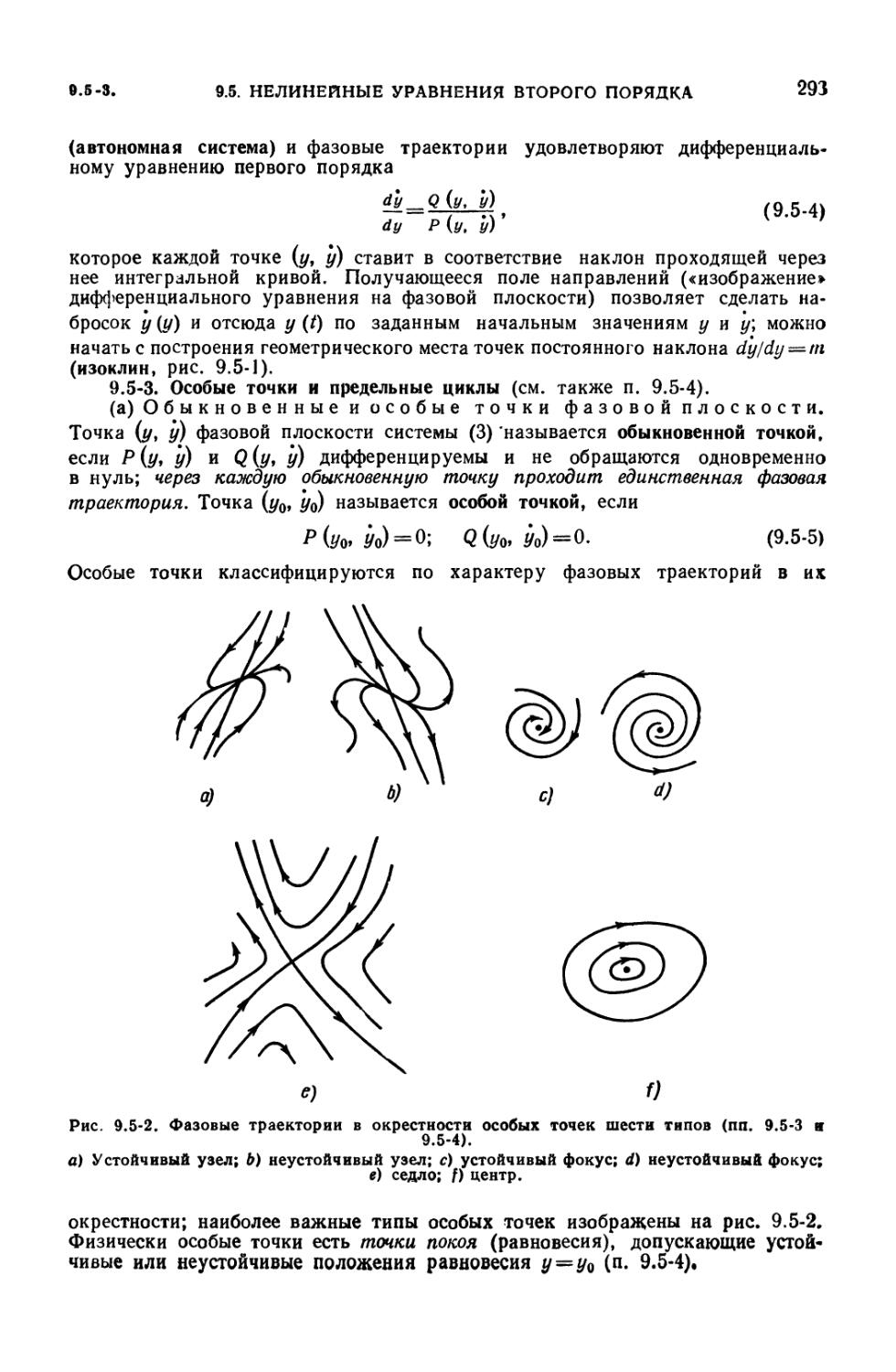
Графический метод решения (292). 9.5-3. Особые точки и предельные циклы
(293). 9.5-4. Устойчивость решений по Ляпунову (294). 9.5-5. Приближенный
метод Крылова и Боголюбова (296). 9.5-6. Интеграл живых сил (297).
9.6. Дифференциальные уравнения Пфаффа 298
9.6-1. Дифференциальные уравнения Пфаффа (298). 9.6-2. Вполне
интегрируемый случай (298).
ГЛАВА 10
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
10.1. Введение и обзор 299
10.1-1. Вводные замечания (299). 10.1-2. Дифференциальные уравнения
с частными производными (299). 10.1-3. Решение дифференциальных
уравнений с частными производными; разделение переменных (300).
10.2. Дифференциальные уравнения с частными производными первого порядка 301
10.2-1. Уравнения с двумя независимыми переменными. Геометрическая
интерпретация (301). 10.2-2. Задача с начальными условиями (задача Коши)
(302). 10.2-3. Полные интегралы. Общие, частные, особые интегралы;
решения характеристических уравнений (303). 10.2-4. Уравнения с п
независимыми переменными (304). 10.2-5. Преобразования соприкосновения (306).
10.2-6. Канонические уравнения и канонические преобразования (307).
10.2-7. Уравнение Гамильтона — Якоби. Решение канонических уравнений
(310).
10.3. Гиперболические, параболические и эллиптические дифференциальные
уравнения с частными производными. Характеристики 312
10.3-1. Квазилинейные уравнения с частными производными второго порядка
с двумя независимыми переменными. Характеристики (312). 10.3-2. Решение
гиперболических уравнений методом характеристик (313). 10.3-3.
Преобразование гиперболических, параболических и эллиптических уравнений к
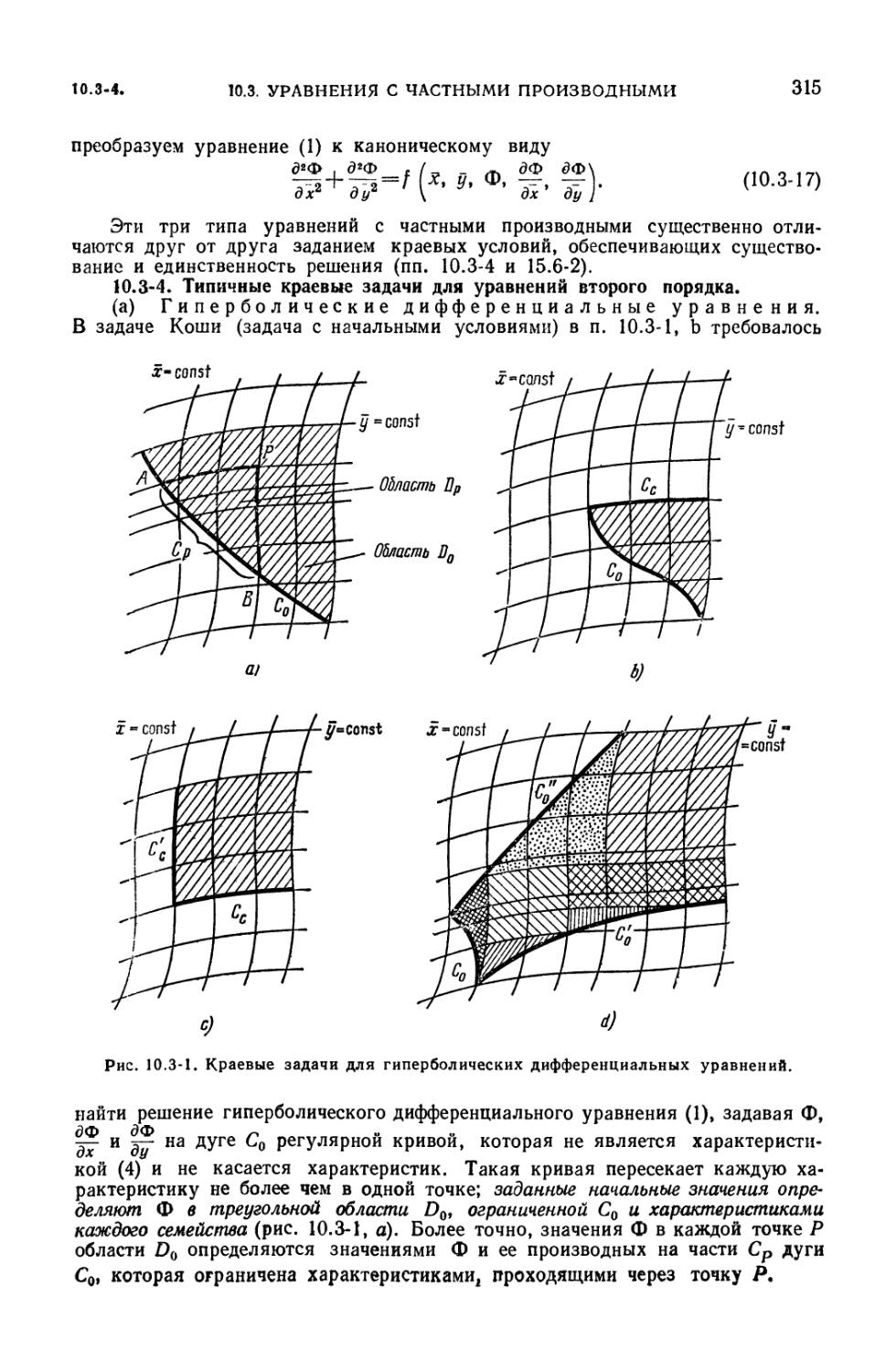
каноническому виду (314). 10.3-4. Типичные краевые задачи для уравнений
второго порядка (315). 10.3-5. Одномерное волновое уравнение (316). 10.3-6.
Метод Римана — Вольтерра для линейных гиперболических уравнений
(317). 10.3-7. Уравнения с тремя и более независимыми переменными (318).
10.4. Линейные уравнения математической физики. Частные решения 319
10.4-1. Физические основы и обзор (319). 10.4-2. Линейные краевые задачи
(321). 10.4-3. Частные решения уравнения Лапласа: трехмерный случай
(322). 10.4-4. Частные решения для трехмерного уравнения Гельмгольца
(324). 10.4-5. Частные решения двумерных задач (325). 10.4-6. Уравнение
Шредингера (326). 10.4-7. Частные решения для уравнения
теплопроводности и диффузии (326). 10.4-8. Частные решения для волнового уравнения.
Синусоидальные волны (326). 10.4-9. Решение краевой задачи разложением
в ортогональные ряды. Примеры (328).
10.5. Метод интегральных преобразований 329
10.5-1. Общая теория (329). 10.5-2. Преобразование Лапласа по временнбй
переменной (330). 10.5-3. Решение краевых задач методом интегральных
преобразований. Примеры (331). 10.5-4. Формулы Дюамеля (332).
ГЛАВА 11
МАКСИМУМЫ И МИНИМУМЫ
11.1. Вводные замечания 333
11.2. Экстремумы функций одного действительного переменного 333
11.2-1. Локальные максимумы и минимумы (333). 11.2-2. Условия
существования внутренних максимумов и минимумов (333).
10
ОГЛАВЛЕНИЕ
11.3. Экстремумы функций двух и большего числа действительных переменных 334
11.3-1. Локальные максимумы и минимумы (334). 11.3-2. Формула Тейлора
для приращения функции (334). 11.3-3. Условия существования внутренних
максимумов и минимумов (334). 11.3-4. Условные экстремумы. Метод
множителей Лагранжа (335). 11.3-5. Численные методы (336).
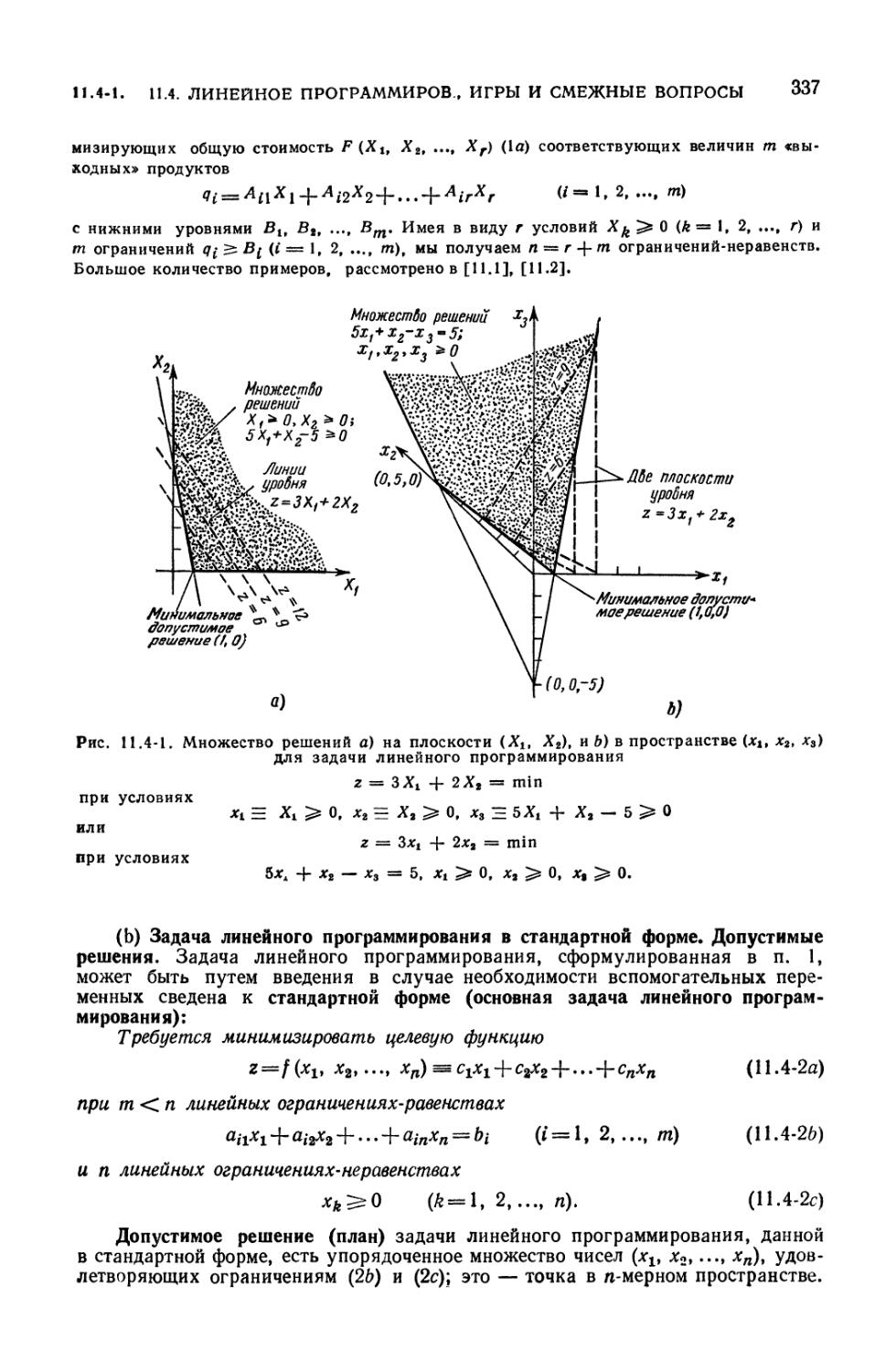
11.4. Линейное программирование, игры и смежные вопросы 33S
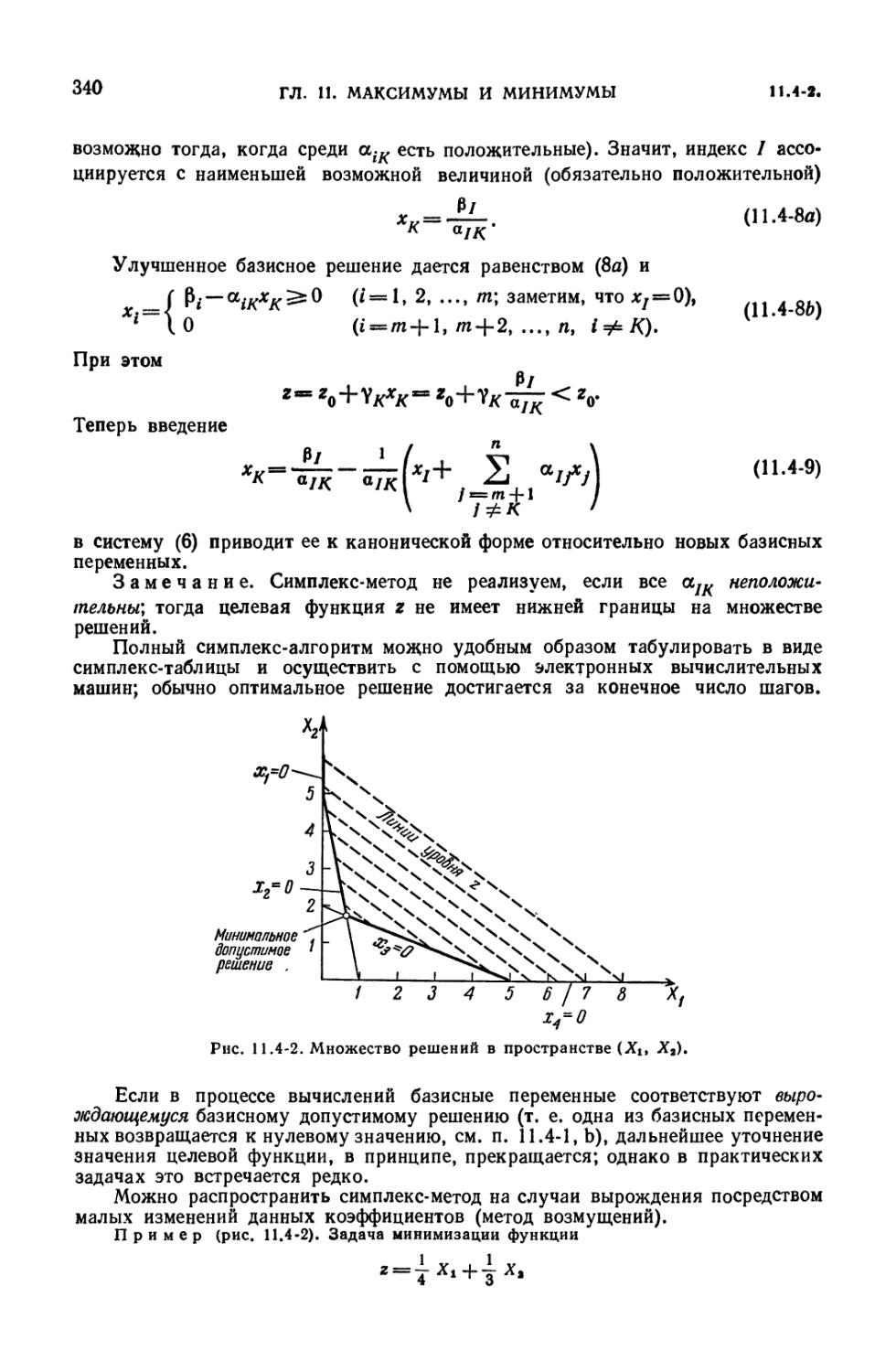
11.4-1. Задача линейного программирования (336). 11.4-2. Симплекс-метод
(339). 11.4-3. Нелинейное программирование. Теорема Куна — Такера (342).
11.4-4. Введение в конечные игры двух партнеров с нулевой суммой (342).
11.5. Вариационное исчисление. Максимумы и минимумы определенных
интегралов 344
11.5-1. Вариации (344). 11.5-2. Максимумы и минимумы определенных
интегралов (345). 11.5-3. Решение вариационных задач (346).
11.6. Экстремали как решения дифференциальных уравнений: классическая
теория 346
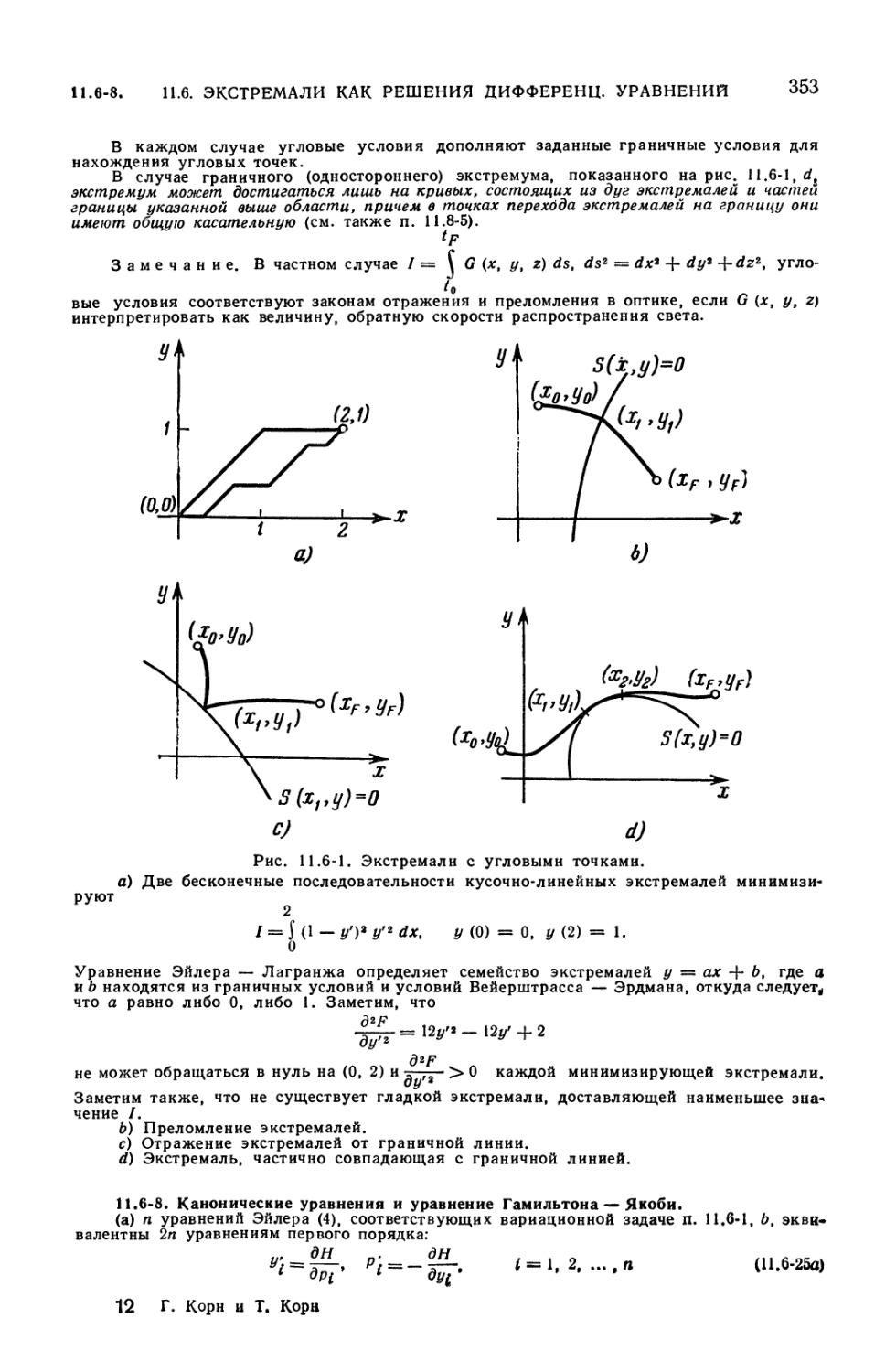
11.6-1. Необходимые условия максимумов и минимумов (346). 11.6-2.
Условные экстремумы. Метод множителей Лагранжа (348). 11.6-3. Изопериметри-
ческие задачи (349). 11.6-4. Решение вариационных задач в случае, когда
подынтегральная функция содержит производные высших порядков (350).
11.6-5. Вариационные задачи с неизвестными граничными значениями и
неизвестными пределами интегрирования (350). 11.6-6. Задачи Больца
и Майера (351). 11.6-7. Ломаные экстремали. Отражение, преломление и
односторонние экстремумы (352). 11.6-8. Канонические уравнения и
уравнение Гамильтона — Якоби (353). 11.6-9. Вариационные задачи в случае
нескольких независимых пер змеиных: максимумы и минимумы кратных
интегралов (354). 11.6-10. Достаточные условия для максимума и
минимума в простейшей задаче (355).
11.7. Решение вариационных задач прямыми методами 353
11.7-1. Прямые методы (356). 11.7-2. Метод Релея — Ритца (357). 11.7-3.
Приближение у (х) полигональными функциями (357).
11.8. Задачи управления и принцип максимума 357
11.8-1. Постановка задачи (357). 11.8-2. Принцип максимума Понтрягина
(360). 11.8-3. Примеры (362). 11.8-4. Матричные обозначения в задачах
управления (364). 11.8-5. Ограничения-неравенства для переменных состояния.
Угловые условия (365). 11.8-6. Метод динамического программирования (366).
11.9. Шаговые задачи управления и динамическое программирование 3G6
11.9-1. Постановка задачи (366). 11.9-2. Принцип оптимальности Беллмана
(367).
ГЛАВА 12
ОПРЕДЕЛЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ: СОВРЕМЕННАЯ
(АБСТРАКТНАЯ) АЛГЕБРА И АБСТРАКТНЫЕ ПРОСТРАНСТВА
12.1. Введение 363
12.1-1. Математические модели (368). 12.1-2. Обзор (369). 12.1-3. «Равенство»
и отношения эквивалентности (369). 12.1-4. Преобразования, функции,
операции (369). 12.1-5. Инвариантность (370). 12.1-6. Представление одной
модели другой: гомоморфизмы и изоморфизмы (370).
12.2. Алгебра моделей с одной определяющей операцией: группы 371
12.2-1. Определение и основные свойства группы (371). 12.2-2. Подгруппы
(371). 12.2-3. Циклические группы. Порядок элемента группы (372). 12.2-4.
Произведения подмножеств. Смежные классы (372). 12.2-5. Сопряженные
элементы и подгруппы. Нормальные делители. Фактор-группы (372). 12.2-6.
Нормальный ряд. Композиционный ряд (372). 12.2-7. Центр.
Нормализаторы (373). 12.2-8. Группы преобразований или операторов (373). 12.2-9.
Гомоморфизмы и изоморфизмы групп. Представление групп (373). 12.2-10.
Аддитивные группы. Классы вычетов и сравнимость (374).
12.3. Алгебра моделей с двумя определяющими операциями: кольца, поля и
области целостности 374
12.3-1. Определения и основные теоремы (374). 12.3-2. Подкольца и под-
поля. Идеалы (375). 12.3-3. Расширения (375).
12.4. Модели, включающие в себя более одного класса математических
объектов: линейные векторные пространства и линейные алгебры 375
12.4-1. Линейные векторные пространства (375). 12.4-2. Линейные алгебры
ОГЛАВЛЕНИЕ
11
12.5. Модели, допускающие определение предельных процессов: топологические
пространства 377
12.5-1. Топологические пространства (377). 12.5-2. Метрические пространства
(378). 12.5-3. Топология, окрестности и сходимость в метрическом
пространстве (378). 12.5-4. Метрические пространства со специальными свойствами.
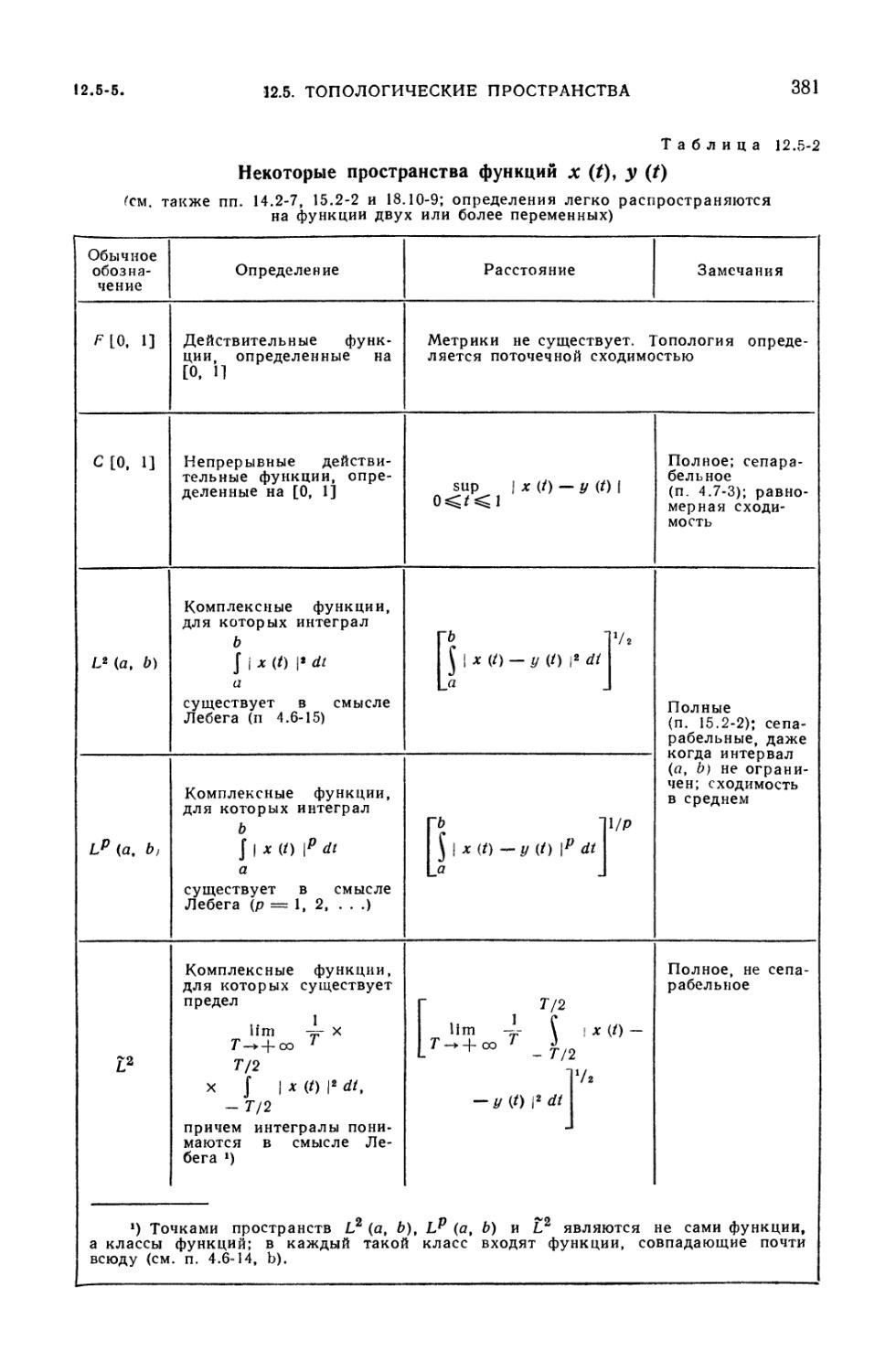
Теория точечных множеств (379). 12.5-5. Примеры: пространства числовых
последовательностей и функций (380). 12.5-6. Теорема Банаха о сжатых
отображениях и последовательные приближения (382).
12.6. Порядок 382
12.6-1. Частично упорядоченные множества (382). 12.6-2. Линейно
упорядоченные множества (382). 12.6-3. Упорядоченные поля (383).
12.7. Комбинации моделей: прямое произведение, топологическое произведение
и прямая сумма 383
12.7-Ь Декартово произведение (383). 12.7-2. Прямое произведение групп
(383). 12.7-3. Прямое произведение действительных векторных пространств
(383). 12.7-4. Топологическое произведение (384). 12.7-5. Прямая сумма (384).
12.8. Булевы алгебры 384
12.8-1. Булевы алгебры (384). 12.8-2. Булевы функции. Приведение к
каноническому виду (385). 12.8-3. Отношение включения (386). 12.8-4. Алгебра
классов (386К 12.8-5. Изоморфизм булевых алгебр. Диаграммы Венна (386).
12.8-6. Алгебры событий и символическая логика (387). 12.8-7.
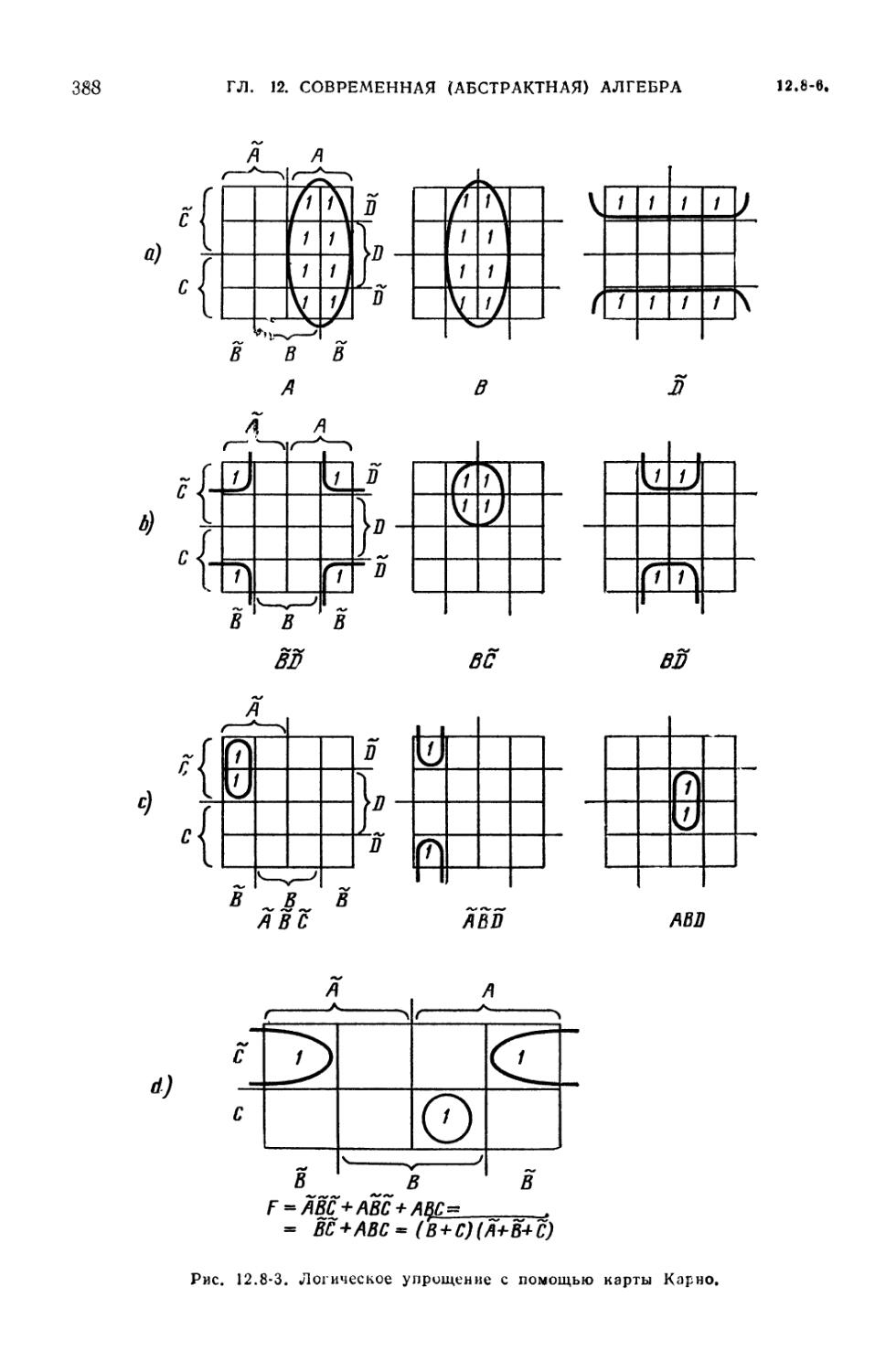
Представление булевых функций истинностными таблицами. Карты Карно (389).
12.8-8. Полная аддитивность. Алгебры меры (389).
ГЛАВА 13
МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ
13.1. Вводные замечания • . 390
13.2. Алгебра матриц и матричное исчисление 390
13.2-1. Прямоугольные матрицы (390). 13.2-2. Основные операции (392).
13.2-3. Нулевая и единичная матрицы; обратные матрицы (393). 13.2-4.
Целочисленные степени квадратных матриц (393). 13.2-5. Матрицы как
строительные блоки математических моделей (393). 13.2-6. Умножение на
матрицы специального вида. Матрицы перестановки (394). 13.2-7. Ранг, след
и определитель матрицы (394). 13.2-8. Разбиение матриц (394). 13.2-9.
Клеточные матрицы. Прямые суммы (395). 13.2-10. Прямое (внешнее)
произведение матриц (395). 13.2-11. Сходимость и дифференцирование (395). 13.2-12.
Функции матриц (395).
13.3. Матрицы со специальными свойствами симметрии 396
13.3-1. Транспонированная и эрмитово сопряженная матрица (396). 13.3-2.
Матрицы со специальными свойствами симметрии (396). 13.3-3. Правила
комбинирования (396). 13.3-4. Теоремы о разложении. Нормальные матрицы
(397).
13.4. Эквивалентные матрицы, собственные значения, приведение к
диагональному виду и смежные вопросы 398
13.4-1. Эквивалентные и подобные матрицы (398). 13.4-2. Собственные
значения и спектры квадратных матриц (398). 13.4-3. Приведение квадратной
матрицы к треугольному виду. Алгебраическая кратность собственного
значения (399). 13.4-4. Приведение матриц к диагональному виду (399).
13.4-5. Собственные значения и характеристическое уравнение матрицы
(400). 13.4-6. Собственные значения клеточных матриц (прямых) сумм
(401). 13.4-7. Теорема Кэли — Гамильтона и смежные вопросы (401).
13.5. Квадратичные и эрмитовы формы 401
13.5-1. Билинейные формы (401). 13.5-2. Квадратичные формы (401). 13.5-3.
Эрмитовы формы (402). 13.5-4. Преобразование квадратичных и эрмитовых
форм. Приведение к сумме квадратов (402). 13.5-5. Одновременное
приведение двух квадратичных или эрмитовых форм к сумме квадратов (404).
13.5-6. Признаки положительной определенности, неотрицательности
и т. д. (404).
13.6. Матричные обозначения для систем дифференциальных уравнений
(динамических систем). Возмущения и теория устойчивости Ляпунова 405
13.6-1. Системы обыкновенных дифференциальных уравнений. Матричные
обозначения (405). 13.6-2. Линейные дифференциальные уравнения с
постоянными коэффициентами (406). 13.6-3. Линейные системы с переменными
коэффициентами (407). 13.6-4. Методы возмущений и уравнения в вариациях
(408). 13.6-5. Устойчивость решений: определения (409). 13.6-6. Функции
Ляпунова и устойчивость (410). 13.6-7. Приложения и примеры (411).
12
ОГЛАВЛЕНИЕ
ГЛАВА 14
ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И ЛИНЕЙНЫЕ
ПРЕОБРАЗОВАНИЯ (ЛИНЕЙНЫЕ ОПЕРАТОРЫ). ПРЕДСТАВЛЕНИЕ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МАТРИЦАМИ
14.1. Введение. Системы отсчета и преобразования координат 414
14.1-1. Вводные замечания (414). 14.1-2. Числовое описание математических
моделей: системы отсчета (414). 14.1-3. Преобразования координат (414).
14.1-4. Инвариантность (415). 14.1-5. Системы мер (415).
14.2. Линейные векторные пространства 415
14.2-1. Определяющие свойства (415). 14.2-2. Линейные многообразия и
подпространства в U (416). 14.2-3. Линейно независимые и линейно
зависимые векторы (416). 14.2-4. Размерность линейного многообразия или
векторного пространства. Базисы и системы координат (системы отсчета) (416).
14.2-5. Нормированные векторные пространства (417). 14.2-6. Унитарные
векторные пространства (417). 14.2-7. Норма, метрика и сходимость в
унитарных векторных пространствах. Гильбертовы пространства (418). 14.2-8.
Теорема о проекции (419).
14.3. Линейные преобразования (линейные операторы) 419
14.3-1. Линейные преобразования векторных пространств. Линейные
операторы (419). 14.3-2. Множество значений, ядро и ранг линейного
преобразования (оператора) (419). 14.3-3. Сложение и умножение на скаляры.
Нулевое преобразование (420). 14.3-4. Произведение двух линейных
преобразований (операторов). Тождественное преобразование (420). 14.3-5.
Невырожденные линейные преобразования (операторы). Обратные
преобразования (операторы) (420). 14.3-6. Целые степени операторов (420).
14.4. Линейные операторы в нормированном или гильбертовом пространстве.
Эрмитовы и унитарные операторы 421
14.4-1. Ограниченные линейные преобразования (421). 14.4-2.
Ограниченные линейные операторы в нормированном векторном пространстве (421).
14.4-3. Сопряженный оператор (421). 14.4-4. Эрмитовы операторы (422).
14.4-5. Унитарные операторы (422). 14.4-6. Симметрические, кососиммет-
рические и ортогональные операторы в действительных унитарных
векторных пространствах (422). 14.4-7. Правила комбинирования (423). 14.4-8.
Теоремы о разложении. Нормальные операторы (423). 14.4-9. Сопряженные
векторные пространства. Более общее определение сопряженных
операторов (424). 14.4-10. Бесконечно малые линейные преобразования (424).
14.5. Матричное представление векторов и линейных преобразований
(операторов) 425
14.5-1. Преобразование базисных векторов и координат векторов:
«активная» точка зрения (425). 14.5-2. Матричное представление векторов и
линейных преобразований (операторов) (426). 14.5-3. Матричные обозначения для
систем линейных уравнений (426). 14.5-4. Диадическое представление
линейных операторов (427).
14.6. Замена системы координат 427
14.6-1. Преобразование базисных векторов и координат векторов:
«пассивная» точка зрения (427). 14.6-2. Представление линейного оператора в
различных базисах (428). 14.6-3. Последовательное применение операторов
(428).
14.7. Представление скалярного произведения. Ортонормированные базисы , . . 429
14.7-1. Представление скалярного произведения (429). 14.7-2. Замена
системы координат (430). 14.7-3. Ортогональные векторы и
ортонормированные системы векторов (430). 14.7-4. Ортонормированные базисы (полные
ортонормированные системы) (430). 14.7-5. Матрицы соответствующие
сопряженным операторам (431). 14.7-6. Взаимные базисы (432). 14.7-7.
Сравнение обозначений (433).
14.8. Собственные векторы и собственные значения линейных операторов . . . 433
14.8-1. Вводные замечания (433). 14.8-2. Инвариантные многообразия.
Разложимые линейные преобразования (линейные операторы) и матрицы
(433). 14.8-3. Собственные векторы, собственные значения и спектр (434).
14.8-4. Собственные векторы и собственные значения нормальных и
эрмитовых операторов (435). 14.8-5. Определение собственных значений и
собственных векторов: конечномерный случай (436). 14.8-6. Приведение и
диагоналнзация матриц. Преобразование к главным осям (437). 14.8-7.
«Обобщенная» задача о собственных значениях (439). 14.8-8. Задачи о
собственных значениях как задачи о стационарных значениях (439). 14.8-9.
Границы для собственных значений линейных операторов (441). 14.8-10.
Неоднородные линейные векторные уравнения (442).
ОГЛАВЛЕНИЕ
13
14.9. Представления групп и смежные вопросы 443
14.9-1. Представления групп (443). 14.9-2. Приведение представлений (443).
14.9-3. Неприводимые представления группы (444). 14.9-4. Характер
представления (445). 14.9-5. Соотношения ортогональности (445). 14.9-6. Прямые
произведения представлений (446). 14.9-7. Представления колец, полей и
линейных алгебр (446).
14.10. Математическое описание вращений 446
14.10-1. Вращения в трехмерном евклидовом векторном пространстве (446).
14.10-2. Угол поворота. Ось вращения (447). 14.10-3. Параметры Эйлера и
вектор Гиббса (448). 14.10-4. Представление векторов и вращений спиновыми
матрицами и кватернионами. Параметры Кэли — Клейна (448). 14.10-5.
Вращения вокруг осей координат (449). 14.10-6. Углы Эйлера (450). 14.10-7.
Бесконечно малые вращения, непрерывное вращение и угловая скорость
(452). 14.10-8. Группа трехмерных вращений и ее представления (454).
ГЛАВА 15
ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ, КРАЕВЫЕ ЗАДАЧИ
И ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
15.1. Введение. Функциональный анализ 456
15.1-1. Вводные замечания (456). 15.1-2. Обозначения (456).
15.2. Функции как векторы. Разложения по ортогональным функциям 457
15.2-1. Квадратично интегрируемые функции как векторы. Скалярное
произведение и нормирование (457). 15.2-2. Метрика и сходимость в L2.
Сходимость в среднем (458). 15.2-3. Ортогональные функции и ортонормированные
последовательности функций (459). 15.2-4. Полные ортонормированные
последовательности функций. Ортонормированные базисы (459). 15.2-5.
Ортогонализация и нормирование последовательности функций (460).
15.2-6. Аппроксимации и разложения в ряды по ортогональным функциям
(460). 15.2-7. Линейные операции над функциями (460).
15.3. Линейные интегральные преобразования и линейные интегральные
уравнения 461
15.3-1. Линейные интегральные преобразования (461). 15.3-2. Линейные
интегральные уравнения. Обзор (462). 15.3-3. Однородное интегральное
уравнение Фредгольма второго рода. Собственные функции и собственные
значения (463). 15.3-4. Теоремы разложения (463). 15.3-5. Итерированные
ядра (464). 15.3-6. Эрмитовы интегральные формы. Задача о собственных
значениях как вариационная задача (465). 15.3-7. Неоднородное уравнение
Фредгольма второго рода (465). 15.3-8. Решение линейного интегрального
уравнения (16) (467). 15.3-9. Решение линейного интегрального уравнения
Фредгольма первого рода (468). 15.3-10. Интегральные уравнения Воль-
терра (469).
15.4. Линейные краевые задачи и задачи о собственных значениях для
дифференциальных уравнений 470
15.4-1. Линейные краевые задачи. Постановка задачи и обозначения (470).
15.4-2. Дополнительное дифференциальное уравнение и краевые условия
для линейной краевой задачи. Теоремы о суперпозиции (470). 15.4-3.
Эрмитово сопряженные и сопряженные краевые задачи. Эрмитовы операторы
(471). 15.4-4. Теорема Фредгольма об альтернативе (473). 15.4-5. Задачи о
собственных значениях для линейных дифференциальных уравнений (473).
15.4-6. Собственные значения и собственные функции эрмитовой задачи
о собственных значениях. Полные ортонормированные множества
собственных функций (474). 15.4-7. Эрмитова задача о собственных значениях
как вариационная задача (475). 15.4-8. Одномерная задача Штурма —
Лиувилля о собственных значениях (476). 15.4-9. Задача Штурма — Лиу-
вилля для уравнений с частными производными второго порядка (477).
15.4-10. Теоремы сравнения (477). 15.4-11. Решение дискретных задач
о собственных значениях методами возмущений (478). 15.4-12. Решение
краевых задач посредством разложений в ряды по собственным функциям
(479).
15.5. Функции Грина. Связь краевых задач и задач о собственных значениях
с интегральными уравнениями ...» 480
15.5-1. Функции Грина для краевой задачи с однородными краевыми
условиями (480). 15.5-2. Связь краевых задач и задач о собственных значениях
с интегральными уравнениями. Резольвента Грина (481). 15.5-3.
Приложение метода функций Грина к задаче с начальными условиями:
обобщенное уравнение диффузии (482). 15.5-4. Метод функций Грина для
неоднородных краевых условий (483).
14
ОГЛАВЛЕНИЕ
15.6. Теория потенциала 484
15.6-1. Введение. Дифференциальные уравнения Лапласа и Пуассона
(484). 15.6-2. Трехмерная теория потенциала. Классические краевые условия
задачи (484). 15.6-3. Теорема Кельвина об инверсии (485). 15.6-4. Свойства
гармонических функций (485). 15.6-5. Решения уравнений Лапласа и
Пуассона как потенциалы (486). 15.6-6. Решение трехмерных краевых задач
посредством функций Грина (488). 15.6-7. Двумерная теория потенциала.
Логарифмический потенциал (490). 15.6-8. Двумерная теория потенциала;
сопряженные гармонические функции (490). 15.6-9. Решение двумерных
краевых задач. Функции Грина и конформные отображения (492). 15.6-10.
Распространение теории на более общие дифференциальные уравнения.
Запаздывающие и опережающие потенциалы (493).
ГЛАВА 16
ПРЕДСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. ТЕНЗОРНАЯ
АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ
16.1. Введение 494
16.1-1. Вводные замечания (494). 16.1-2. Системы координат и допустимые
преобразования (494). 16.1-3. Компоненты объектов. Индексные
обозначения (494). 16.1-4. Системы отсчета и индуцированные преобразования.
Геометрические объекты (495).
16.2. Абсолютные (истинные) тензоры и относительные тензоры (псевдотензоры) 496
16.2-1. Определение абсолютных и относительных тензоров, основанное на
законе преобразования их компонент (496). 16.2-2. Инфинитезимальное
перемещение. Градиент скалярного поля (498).
16.3. Тензорная алгебра: определение основных операций 499
16.3-1. Равенство тензоров (499). 16.3-2. Нуль-тензор (499). 16.3-3.
Сложение тензоров (499). 16.3-4. Умножение тензора на абсолютный скаляр (499).
16.3-5. Свертывание смешанного тензора (499). 16.3-6. Произведение
(внешнее) двух тензоров (500). 16.3-7. Внутреннее произведение (500). 16.3-8.
Признак тензора (500).
16.4. Тензорная алгебра. Инвариантность тензорных уравнений ......... 501
16.4-1. Инвариантность тензорных уравнений (501).
16.5. Симметричные и антисимметричные тензоры 502
16.5-1. Симметричные и антисимметричные объекты (502). 16.5-2. Символы
Кронекера (502). 16.5-3. е-объекты (символы Леви-Чивита) (503). 16.5-4.
Альтернированное произведение двух векторов (503).
16.6. Локальная система базисных векторов (локальный базис) 504
16.6-1. Выражение векторов и тензоров через векторы локального базиса
(504). 16.6-2. Преобразование локального базиса при преобразовании
координат (504).
16.7. Тензоры в римановых пространствах. Ассоциированные тензоры 505
16.7-1. Риманово пространство и фундаментальные тензоры (505). 16.7-2.
Ассоциированные тензоры. Поднятие и опускание индексов (506). 16.7-3.
Эквивалентность ассоциированных тензоров (506). 16.7-4. Операции над
тензорами в римановых пространствах (507).
16.8. Скалярное произведение векторов и связанные с ним понятия 507
16.8-1. Скалярное (внутреннее) произведение двух векторов в римановом
пространстве (507). 16.8-2. Скалярные произведения локальных базисных
векторов. Ортогональная система координат (507). 16.8-3. Физические
компоненты тензора (508). 16.8-4. Векторное произведение и смешанное
произведение (508).
16.9. Тензоры ранга 2 в римановом пространстве 509
16.9-1. Диадные произведения (509). 16.9-2. Умножение тензоров ранга 2
и векторов и связанная с ним система обозначений (510). 16.9-3. Собственные
векторы и собственные значения (510).
16.10. Абсолютное дифференциальное исчисление. Ковариантное
дифференцирование 510
16.10-1. Абсолютные дифференциалы (510). 16.10-2. Абсолютный
дифференциал относительного тензора (512). 16.10-3. Символы Кристоффеля (512).
16.10-4. Ковариантное дифференцирование (513). 16.10-5. Правила ковари-
антного дифференцирования (514). 16.10-6, Ковариантные производные
высших порядков (514). 16.10-7. Дифференциальные операторы и
дифференциальные инварианты (515). 16.10-8. Абсолютные (внутренние) производ-
ОГЛАВЛЕНИЕ
15
кые и производные по направлению (515). 16.10-9. Тензоры, постоянные
вдоль кривой. Уравнения параллелизма (517). 16.10-10. Интегрирование
тензорных величин. Элемент объема (517). 16.10-11. Дифференциальные
инварианты тензоров ранга 2; интегральные теоремы (517).
ГЛАВА 17
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.1. Кривые на евклидовой плоскости 518
17.1.1. Касательная к плоской кривой (518). 17.1-2. Нормаль к плоской
кривой (518). 17.1-3. Особые точки (519). 17.1-4. Кривизна плоской кривой
(519). 17.1-5. Порядок касания плоских кривых (520). 17.1-6. Асимптоты
(520). 17.1-7. Огибающая семейства плоских кривых (520). 17.1-8.
Изогональные траектории (520).
17.2. Кривые в трехмерном евклидовом пространстве 521
17.2-1. Вводные замечания (521). 17.2-2. Подвижной трехгранник (521).
17.2-3. Формулы Фроне — Серре. Кривизна и кручение пространственной
кривой (522). 17.2-4. Уравнения касательной, нормали и бинормали;
уравнения соприкасающейся, нормальной и спрямляющей плоскостей (523).
17.2-5. Дополнительные замечания (523). 17.2-6. Порядок касания (524).
17.3. Поверхности в трехмерном евклидовом пространстве 524
17.3-1. Вводные замечания (524). 17.3-2. Касательная плоскость и нормаль
к поверхности (524). 17.3-3. Первая основная квадратичная форма
поверхности. Дифференциал длины дуги и элемент площади (525). 17.3-4.
Геодезическая и нормальная кривизна кривой на поверхности. Теорема Менье (526).
17.3-5. Вторая основная квадратичная форма. Главные кривизны, гауссова
кривизна и средняя кривизна (527). 17.3-6. Некоторые направления и кривые
на поверхности. Минимальные поверхности (528). 17.3-7. Поверхности
как римановы пространства. Трехиндексные символы Кристоффеля и
параметры Бельтрами (529). 17.3-8. Уравнения с частными производными,
связывающие коэффициенты основных квадратичных форм. Theorema Egregium
Гаусса (530). 17.3-9. Определение поверхности коэффициентами ее основных
квадратичных форм (530). 17.3-10. Отображения (530). 17.3-11.
Огибающие (531). 17.3-12. Геодезические линии поверхности (531). 17.3-13.
Геодезические нормальные координаты. Геометрия на поверхности (532).
17.3-14. Теорема Гаусса — Бонне (533)
17.4. Пространства с кривизной 533
17.4-1. Вводные замечания (533). 17.4-2. Кривые, длины и направления
в римановом пространстве (533). 17.4-3. Геодезические линии в римано-
вом пространстве (534). 17.4-4. Римановы пространства с неопределенной
метрикой. Изотропные направления и геодезические нулевой длины (535).
17.4-5. Тензор кривизны риманова пространства (535). 17.4-6.
Геометрическое истолкование тензора кривизны. Плоские пространства и евклидовы
пространства (536). 17.4-7.Специальные координатные системы (537).
ГЛАВА 18
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
18 1. Введение 539
18.1-1. Вводные замечания (539).
18.2. Определение и представление вероятностных моделей 539
18.2-1. Алгебра событий, связанных с данным испытанием (539). 18.2-2.
Определение вероятности. Условные вероятности (540). 18.2-3. Независимость
случайных событий (540). 18.2-4. Сложные испытания. Независимые
испытания и повторные независимые испытания (540). 18.2-5» Правила сочетаний
(541). 18.2-6. Теоремы Байеса (542). 18.2-7. Представление событий как
множеств в пространстве выборок (542). 18.2-8. Случайные величины (542).
18.2-9. Описание вероятностных моделей на языке случайных величин и их
функций распределения (542).
18.3. Одномерные распределения вероятностей 543
18.3-1. Дискретные одномерные распределения вероятностей (543). 18.3-2.
Непрерывные одномерные распределения вероятностей (543). 18.3-3.
Математическое ожидание и дисперсия. Числовые характеристики одномерного
распределения вероятностей (544). 18.3-4. Нормирование (546). 18.3-5.
Неравенство Чебышева и связанные с ним формулы (546). 18.3-6. Единое
описание распределений вероятностей с помощью интеграла Стилтьеса (546).
18.3-7. Моменты одномерного распределения вероятностей (547). 18.3-8. Ха-
16
ОГЛАВЛЕНИЕ
рактеристические и производящие функции (548). 18.3-9. Семиинварианты
(549). 18.3-10. Вычисление моментов и семиинвариантов через % (<7). М (s)
и у (s). Соотношения между моментами и семиинвариантами (549).
18.4. Многомерные распределения вероятностей 550
18.4-1. Многомерные случайные величины (550). 18.4-2. Двумерные
распределения вероятностей. Распределения координат случайной величины
(550). 18.4-3. Дискретные и непрерывные двумерные распределения
вероятностей (550). 18.4-4. Математическое ожидание, моменты, ковариация
и коэффициент корреляции (551). 18.4-5. Условные распределения
вероятностей, связанные с двумя случайными величинами (552). 18.4-6.
Регрессии (553). 18.4-7. м-мерные распределения вероятностей (553). 18.4-8.
Математические ожидания и моменты (555). 18.4-9. Регрессия. Коэффициенты
корреляции (556). 18.4-10. Характеристические функции (557). 18.4-11.
Независимость случайных величин (557). 18.4-12. Энтропия распределения
вероятностей (558).
18.5. Функции от случайных величин. Замена переменных 559
18.5-1. Вводные замечания (559). 18.5-2. Функции (или преобразования)
одномерной случайной величины (559). 18.5-3. Линейные преобразования
одномерной случайной величины (560). 18.5-4. Функции (или
преобразования) многомерных случайных величин (561). 18.5-5. Линейные
преобразования (562). 18.5-6. Математическое ожидание и дисперсия суммы случайных
величин (562). 18.5-7. Суммы независимых случайных величин (563). 18.5-8.
Распределение суммы случайного количества случайных величин (564).
18.6. Сходимость по вероятности и предельные теоремы 564
18.6-1. Последовательность распределений вероятностей. Сходимость по
вероятности (564). 18.6-2. Пределы функций распределения,
характеристических и производящих функций. Теоремы непрерывности (564). 18.6-3.
Сходимость в среднем (565). 18.6-4. Асимптотически нормальные распределения
вероятностей (565). 18.6-5. Предельные теоремы (565).
18.7. Специальные методы решения вероятностных задач 566
18.7-1. Вводные замечания (566). 13.7-2. Задачи с дискретным
распределением вероятностей: подсчет событии и комбинаторный анализ (567). 18.7-3.
Применение производящих функций. Теорема Пойа (569). 18.7-4. Задачи
с дискретным распределением вероятностей: успехи и неудачи в
составляющих испытаниях (571).
18.8. Специальные распределения вероятностей 571
18.8-1. Дискретные одномерные распределения вероятностей (571). 18.8-2.
Дискретные многомерные распределения вероятностей (573). 18.8-3.
Непрерывные распределения вероятностей: нормальное распределение (Гаусса)
(575). 18.8-4. Нормальные случайные величины: распределение отклонений
от центра (576). 18.8-5. Различные непрерывные одномерные распределения
вероятностей (582). 18.8-6. Двумерные нормальные распределения (582).
18.8-7. Круговое нормальное распределение (583). 18.8-8. /г-мерные
нормальные распределения (583). 18.8-9. Теоремы сложения для
специальных распределений (583).
18.9. Теория случайных процессов 584
18.9-1. Случайные процессы (584). 18.9-2. Описание случайных процессов
(584). 18.9-3. Средние по множеству наблюдений. Корреляционные
функции (585). 18.9-4. Интегрирование и дифференцирование случайных
функций (586). 18.9-5. Процессы, определяемые случайными параметрами (588).
18.9-6. Разложение по ортонормированной системе (588).
18.10. Стационарные случайные процессы. Корреляционные функции и
спектральные плотности 589
18.10-1. Стационарные случайные процессы (589). 18.10-2. Корреляционные
функции по множеству наблюдений (589). 18.10-3. Спектральная плотность
по множеству наблюдений (590). 18.10-4. Корреляционные функции и спектры
действительных процессов (590). 18.10-5. Спектральное разложение средней
«мощности» действительных процессов (590). 18.10-6. Другие виды
спектральной плотности по множеству наблюдений (591). 18.10-7. Средние по
времени и эргодические процессы (591). 18.10-8. Корреляционные
функции и спектральные плотности по времени (592). 18.10-9. Функции с
периодическими компонентами (593). 18.10-10. Обобщенные преобразования Фурье
и спектральные функции (595).
18.11. Типы случайных процессов. Примеры 696
18.11-1. Процессы с постоянными и периодическими реализациями (596).
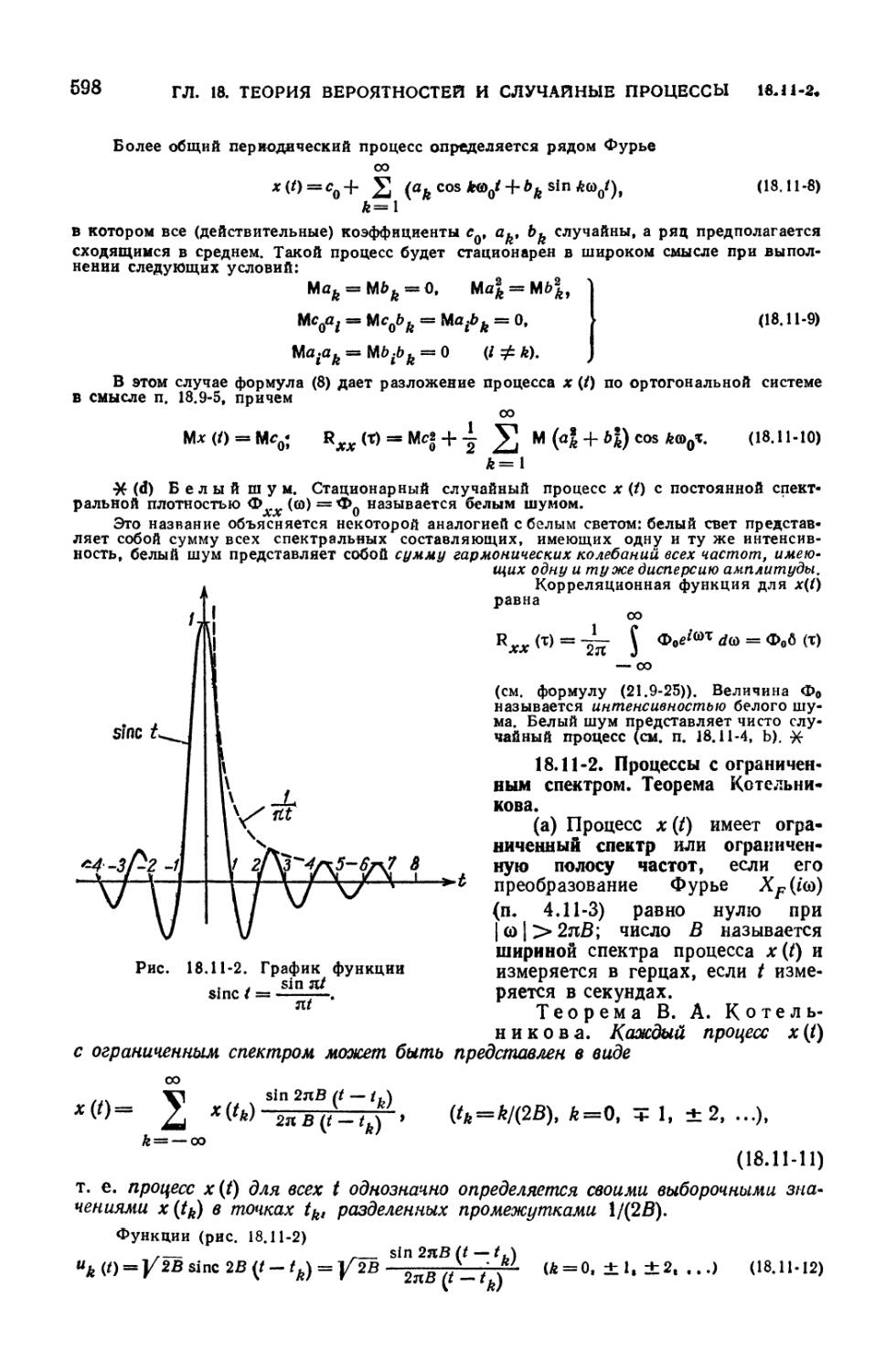
18.11-2. Процессы с ограниченным спектром. Теорема Котельникова (598).
18.11-3. Гауссовские случайные процессы (599). 18.11-4. Марковские
процессы и процесс Пуассона (599). 18.11-5. Некоторые случайные процессы.
ОГЛАВЛЕНИЕ
17
порождаемые процессом Пуассона (601). 18.11-6. Случайные процессы,
порождаемые периодической выборкой (602).
18.12. Действия над случайными процессами 603
18.12-1. Корреляционные функции и спектры сумм (603). 18.12-2.
Соотношения между входным и выходным сигналами для линейных систем (604).
18.12-3. Стационарный случай (604). 18.12-4. Соотношения для
корреляционных функций и спектров по времени (605). 18.12-5. Нелинейные операции
(605). 18.12-6. Нелинейные операции над гауссовскими процессами (606).
ГЛАВА 19
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.1. Введение в статистические методы . . .* 607
19.1-1. Статистики (607). 19.1-2. Классическая вероятностная модель:
статистики случайной выборки. Понятие о генеральной совокупности (607).
19.1-3. Связь вероятностной модели с опытом: оценка и проверка (608).
19.2. Статистическое описание. Определение и вычисление статистик случайной
выборки 609
19.2-1. Относительные частоты (609). 19.2-2. Распределение выборки.
Группированные данные (609). 19.2-3. Выборочные средние (610). 19.2-4.
Выборочные дисперсии и моменты (611). 19.2-5. Упрощенное вычисление
выборочных средних и дисперсий. Поправка на группировку (612). 19.2-6.
Размах выборки (613).
19.3. Типовые распределения вероятностей 613
19.3-1. Вводные замечания (613). 19.3-2. Класс распределений Кэптейна
(613). 19.3-3. Ряды Грама — Шарлье и Эджворта (614). 19.3-4. Усеченные
нормальные распределения и распределение Парето (614). 19.3-5. Типы
распределений Пирсона (615).
19.4. Оценки параметров 615
19.4-1. Свойства оценок (615). 19.4-2. Некоторые свойства статистик,
применяемых в качестве оценок (616). 19.4-3. Нахождение оценок. Метод
моментов (617). 19.4-4. Метод наибольшего правдоподобия (617). 19.4-5.
Другие методы нахождения оценок (618).
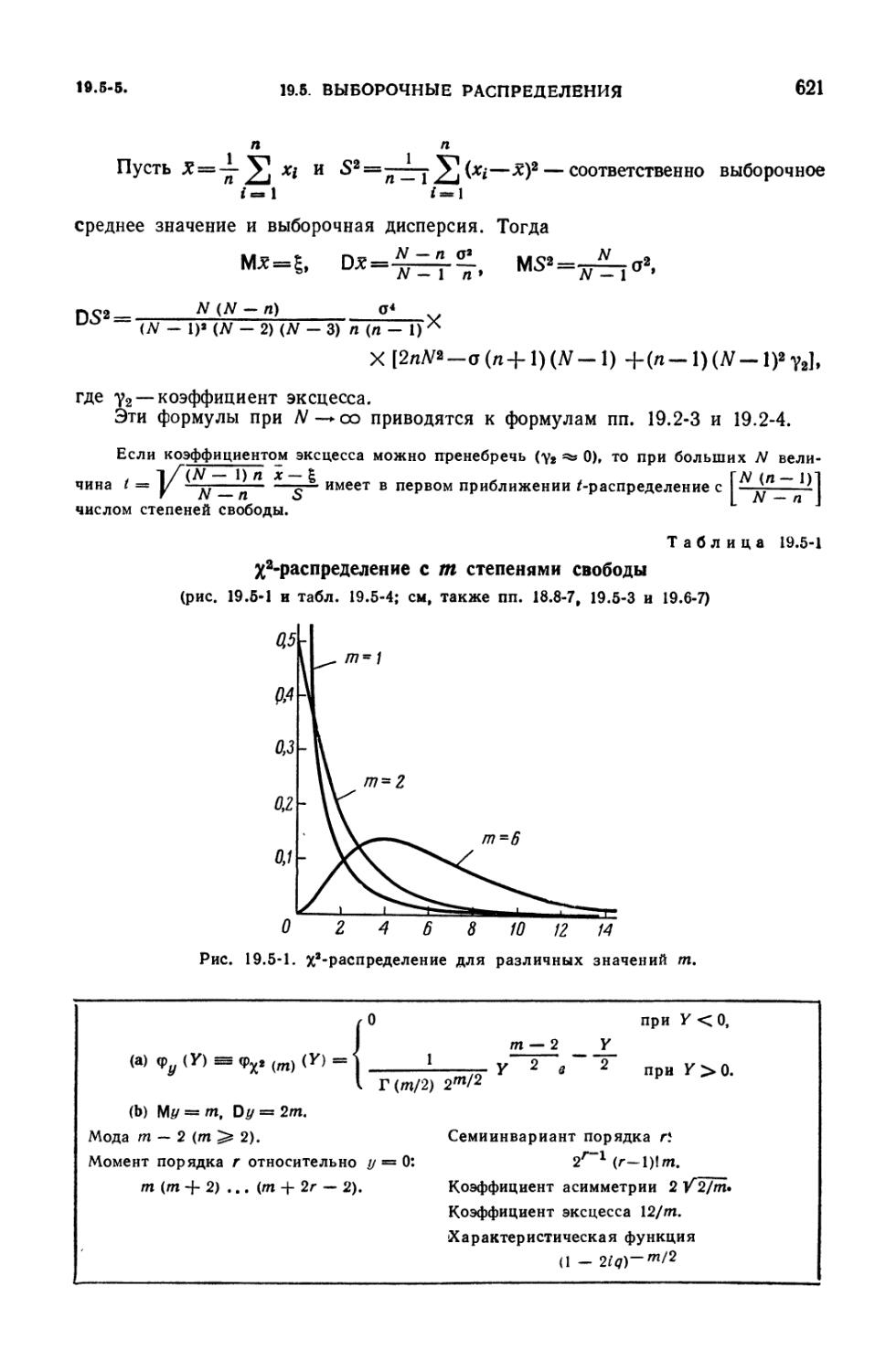
19.5. Выборочные распределения 618
19.5-1. Вводные замечания (618). 19.5-2. Асимптотически нормальные
выборочные распределения (618). 19.5-3. Выборки из нормальной совокупности.
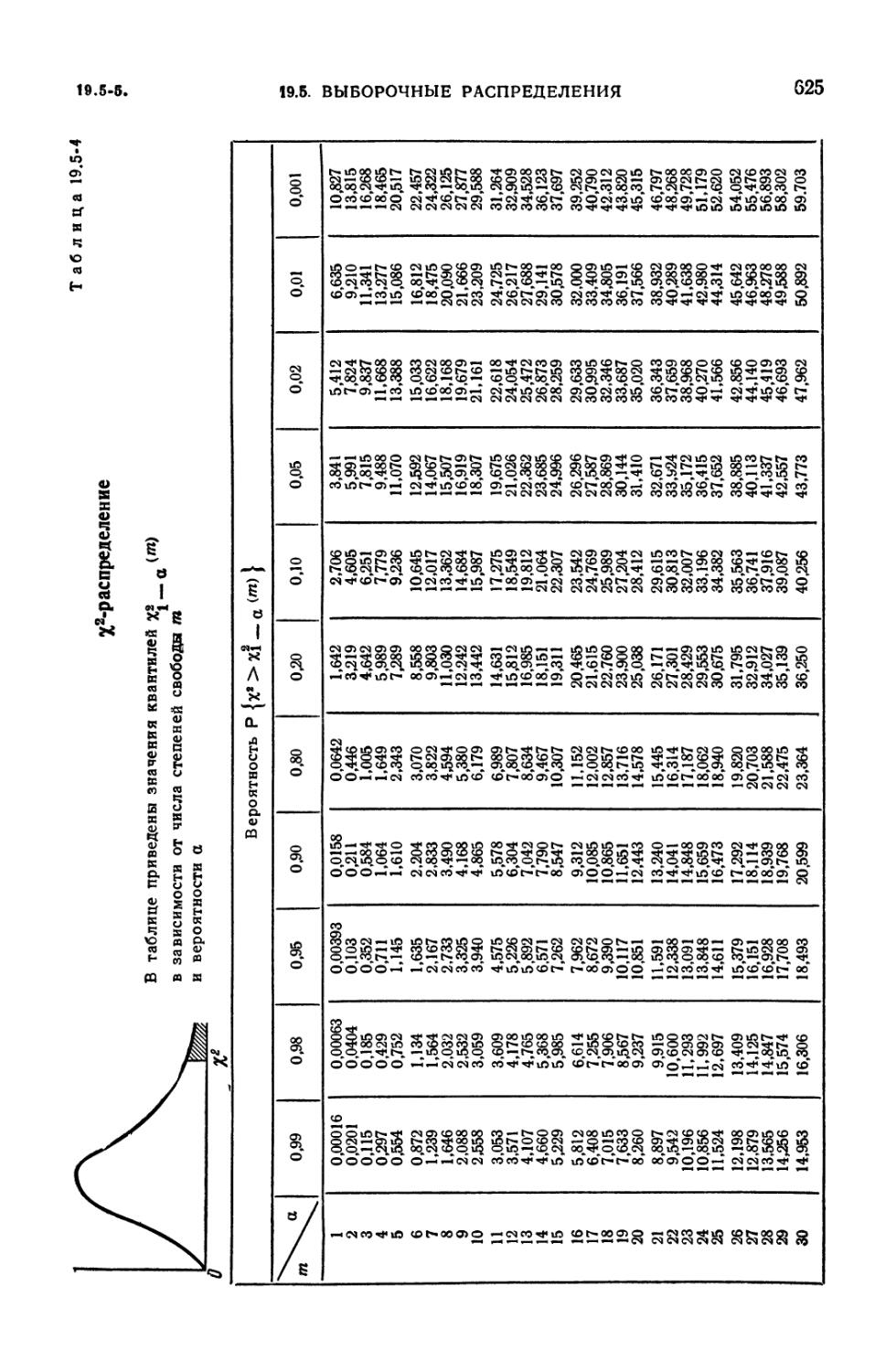
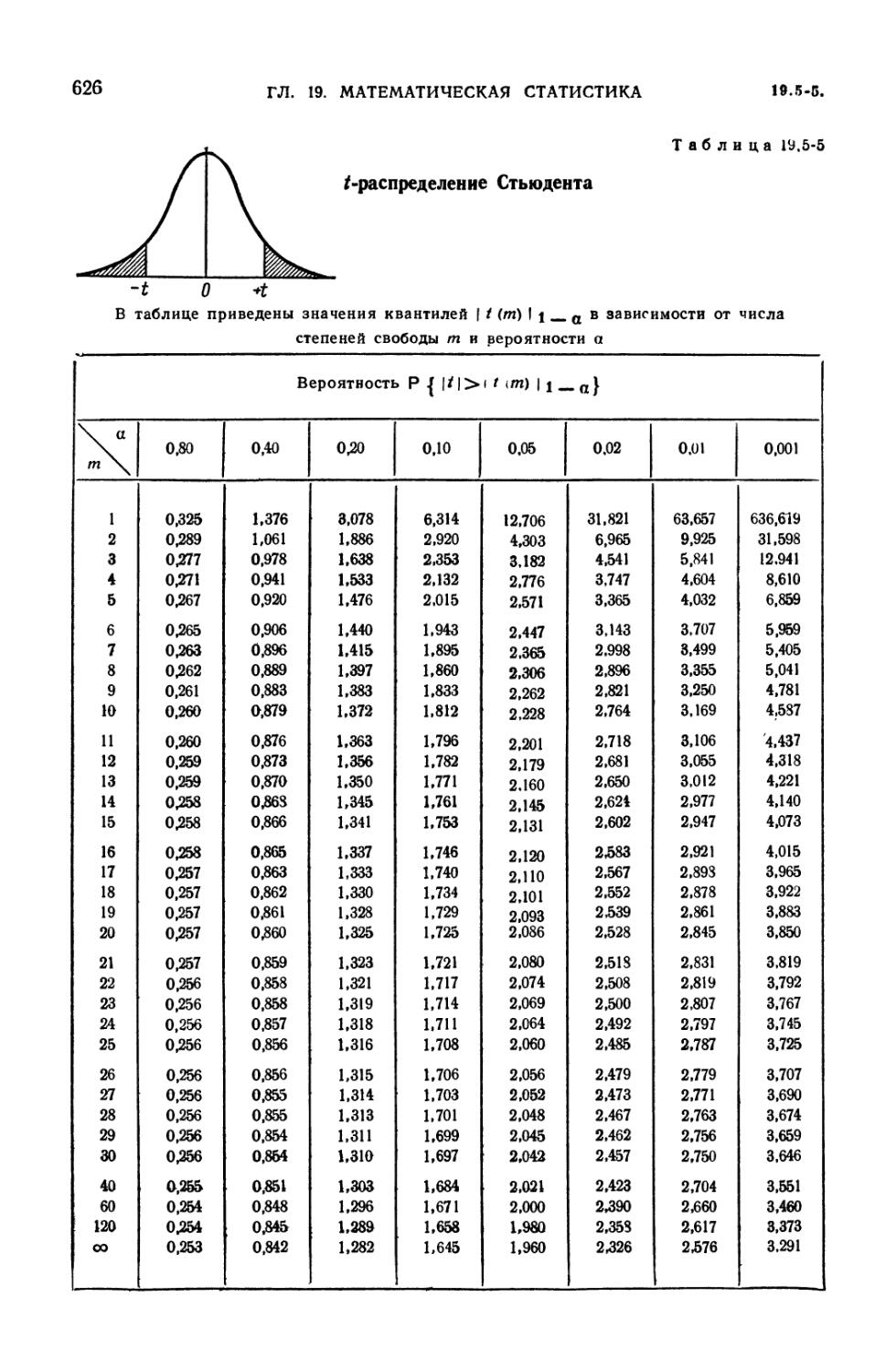
Распределения %2, t и v2 (619). 19.5-4. Распределение размаха выборки (619).
19.5-5. Выборочный метод для конечной совокупности (620).
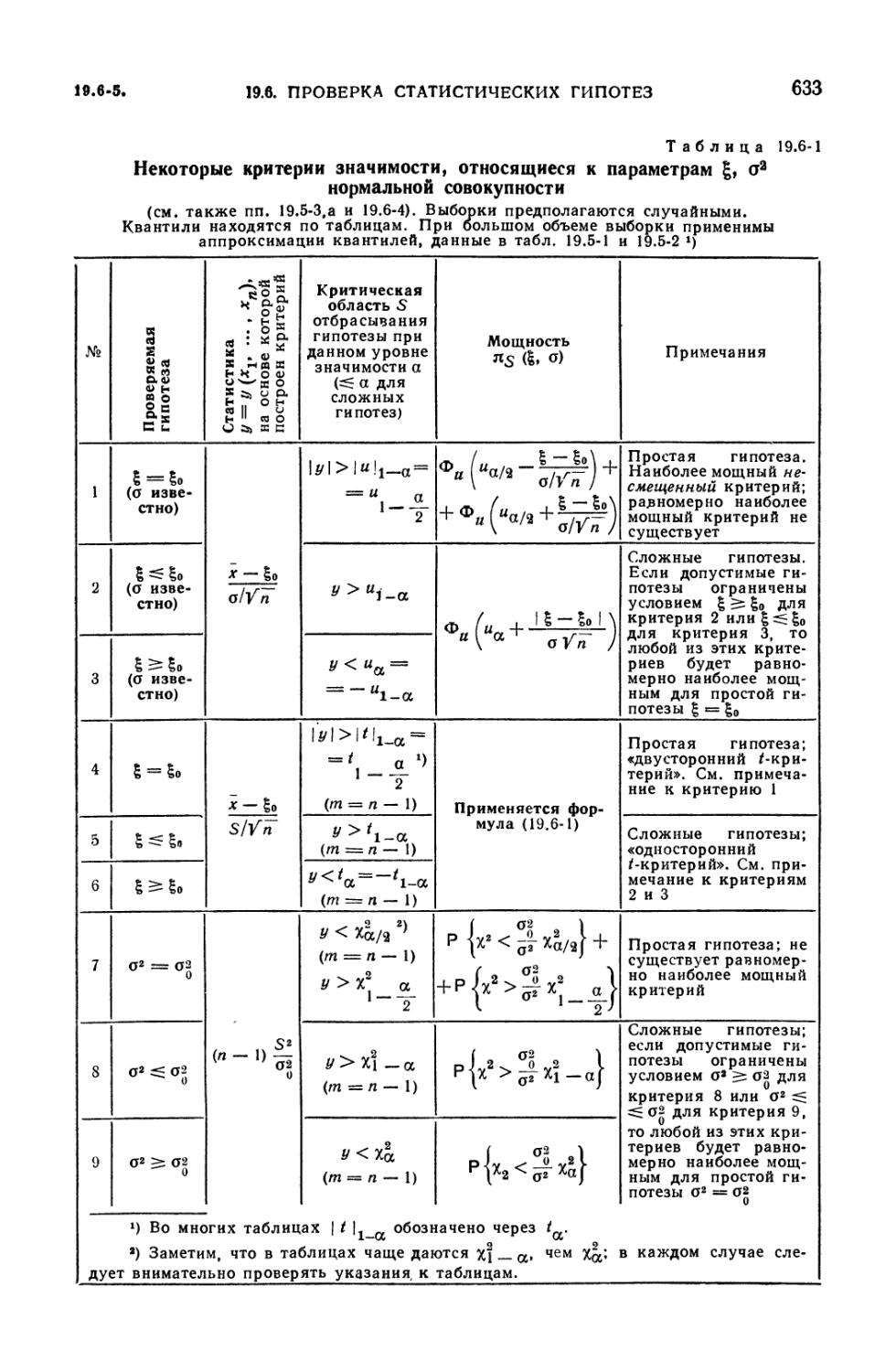
19.6. Проверка статистических гипотез 630
19.6-1. Статистические гипотезы (630). 19.6-2. Критерии с фиксированной
выборкой; определения (630). 19.6-3. Уровень значимости. Правило
Неймана — Пирсона отбора критериев для простых гипотез (630). 19.6-4.
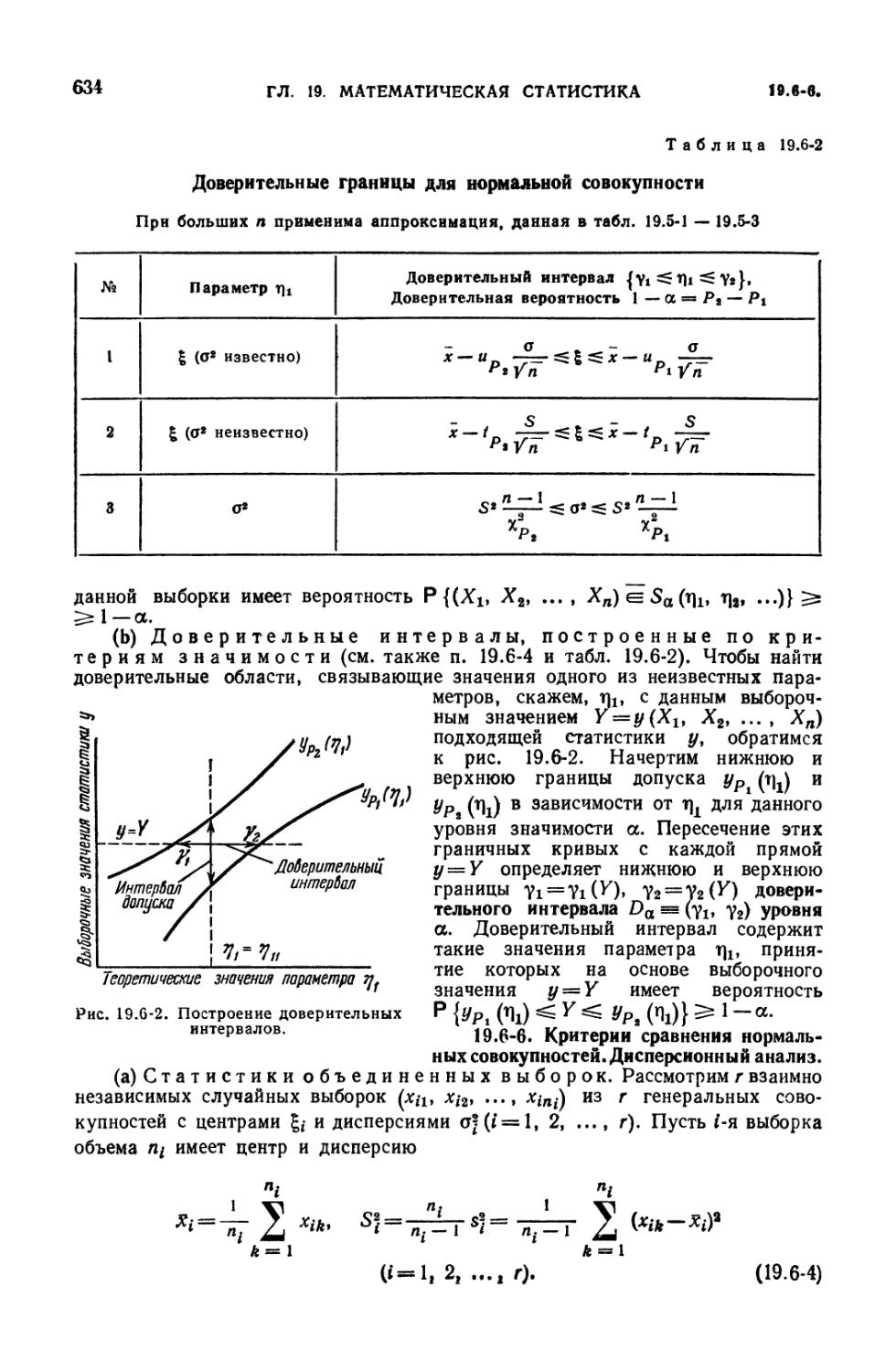
Критерии значимости (632). 19.6-5. Доверительная область (632). 19.6-6.
Критерии сравнения нормальных совокупностей. Дисперсионный анализ (634).
19.6-7. Критерий согласия у} (637). 19.6-8. Непараметрическое сравнение
двух совокупностей: критерий знаков (638). 19.6-9. Обобщения (638).
19.7. Некоторые статистики, выборочные распределения и критерии для
многомерных распределений 638
19.7-1. Вводные замечания (638). 19.7-2. Статистики, получаемые на основе
многомерных выборок (638). 19.7-3. Оценки параметров (639). 19.7-4.
Выборочные распределения в случае нормальной совокупности (640). 19.7-5.
Выборочная средняя квадратическая сопряженность признаков. Критерий
независимости двух случайных величин, основанный на таблице
сопряженности признаков (642). 19.7-6. Порядковая корреляция по Спирмену.
Непараметрический критерий независимости (642).
19.8. Статистики и измерения случайного процесса 643
19.8-1. Средние по конечному промежутку времени (643). 19.8-2.
Усредняющие фильтры (644). 19.8-3. Примеры (645). 19.8-4. Выборочные средние
(646).
19.9. Проверка и оценка в задачах со случайными параметрами . . 647
19.9-1. Постановка задачи (647). 19.9-2. Оценка и проверка с помощью
формул Байеса (648). 19.9-3. Случай двух состояний, проверка гипотез (648).
19.9-4. Оценки по методу наименьших квадратов (650).
18
ОГЛАВЛЕНИЕ
Г Л А В А 20
ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ
20.1. Введение 652
20.1-1. Вводные замечания (652). 20.1-2. Ошибки (652).
20.2. Численное решение уравнений 652
20.2-1. Вводные замечания (652). 20.2-2. Итерационные методы (653). 20.2-3.
Вычисление значений многочлена (655). 20.2-4. Численное решение
алгебраических уравнений. Итерационные методы (655). 20.2-5. Специальные методы
решения алгебраических уравнений (656). 20.2-6. Системы уравнений н
экстремальные задачи (659). 20.2-7. Градиентные методы (660). 20.2-8.
Метод Ньютона и теорема Канторовича (661).
20.3. Системы линейных уравнений и обращение матриц. Собственные
значения и собственные векторы матриц 662
20.3-1. Методы исключения (662). 20.3-2. Итерационные методы (663). 20.3-3.
Обращение матриц (665). 20.3-4. Решение системы линейных уравнений и
обращение матриц при помощи разбиения на клетки (666). 20.3-5.
Собственные значения и собственные векторы матриц (667).
20.4. Конечные разности и разностные уравнения 668
20.4-1. Конечные разности и центральные средние (668). 20.4-2.
Операторные обозначения (669). 20.4-3. Разностные уравнения (670). 20.4-4.
Линейные обыкновенные разностные уравнения (671). 20.4-5. Линейные
обыкновенные разностные уравнения с постоянными коэффициентами (672). 20.4-6.
Методы преобразований для линейных разностных уравнений с
постоянными коэффициентами (672). 20.4-7. Системы обыкновенных разностных
уравнений. Матричная запись (674). 20.4-8. Устойчивость (675).
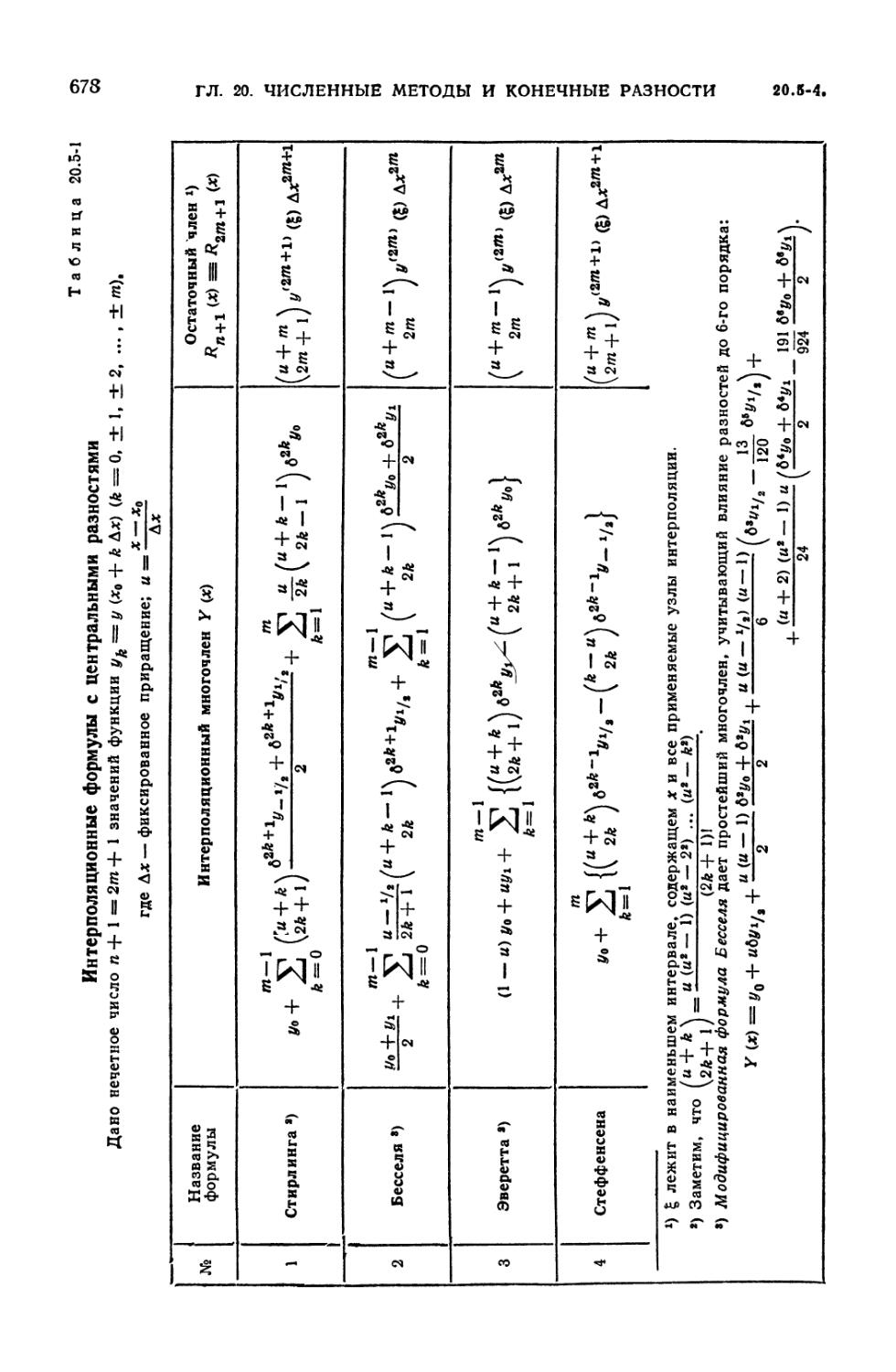
20.5. Интерполяция функций 675
20.5-1. Вводные замечания (675). 20.5-2. Общие формулы параболической
интерполяции (значения аргумента могут быть и неравноотстоящими)
(675). 20.5-3. Интерполяционные формулы для равноотстоящих значений
аргумента. Ромбовидные диаграммы (677). 20.5-4. Обратная интерполяция
(677). 20.5-5. Интерполяция с оптимальным выбором узлов (682). 20.5-6.
Интерполяция функций нескольких переменных (682). 20.5-7. Обратные
разности и интерполяция рациональными дробями (683).
20.6. Аппроксимация функций ортогональными многочленами, отрезками ряда
Фурье и другими методами 683
20.6-1. Вводные замечания (683). 20.6-2. Приближения функций
многочленами по методу наименьших квадратов на интервале (683). 20.6-3.
Приближения функций многочленами по методу наименьших квадратов на
дискретном множестве точек (684). 20.6-4. Равномерные приближения (686).
20.6-5. Экономизация степенных рядов (686). 20.6-6. Численный
гармонический анализ и тригонометрическая интерполяция (687). 20.6-7. Разные
приближения (693).
20.7. Численное дифференцирование и интегрирование 695
20.7-1. Численное дифференцирование (695). 20.7-2. Численное
интегрирование для равноотстоящих узлов (696). 20.7-3. Квадратурные формулы
Гаусса и Чебышева (698). 20.7-4. Построение и сравнение квадратурных
формул (700). 20.7-6. Вычисление кратных интегралов (700).
20.8. Численное интегрирование обыкновенных дифференциальных уравнений 701
20.8-1. Вводные замечания (701). 20.8-2. Одношаговые методы решения
задачи Коши. Методы Эйлера и Рунге — Кутта (701). 20.8-3.
Многошаговые методы решения задачи Коши (703). 20.8-4. Улучшенные многошаговые
методы (704). 20.8-5. Сравнение различных методов решения. Контроль
величины шага и устойчивость (704). 20.8-6. Обыкновенные
дифференциальные уравнения высших порядков и системы дифференциальных уравнений
(706). 20.8-7. Специальные формулы для уравнений второго порядка (707).
20.8-8. Анализ частотных характеристик (708).
20.9. Численное интегрирование уравнений с частными производными, краевые
задачи; интегральные уравнения 709
20.9-1. Вводные замечания (709). 20.9-2. Двухточечная краевая задача для
обыкновенных дифференциальных уравнений (709). 20.9-3. Обобщенный
метод Ньютона (квазилинеаризация) (710). 20.9-4. Разностные методы
численного решения уравнений с частными производными для случая двух
независимых переменных (710). 20.9-5. Двумерные разностные операторы
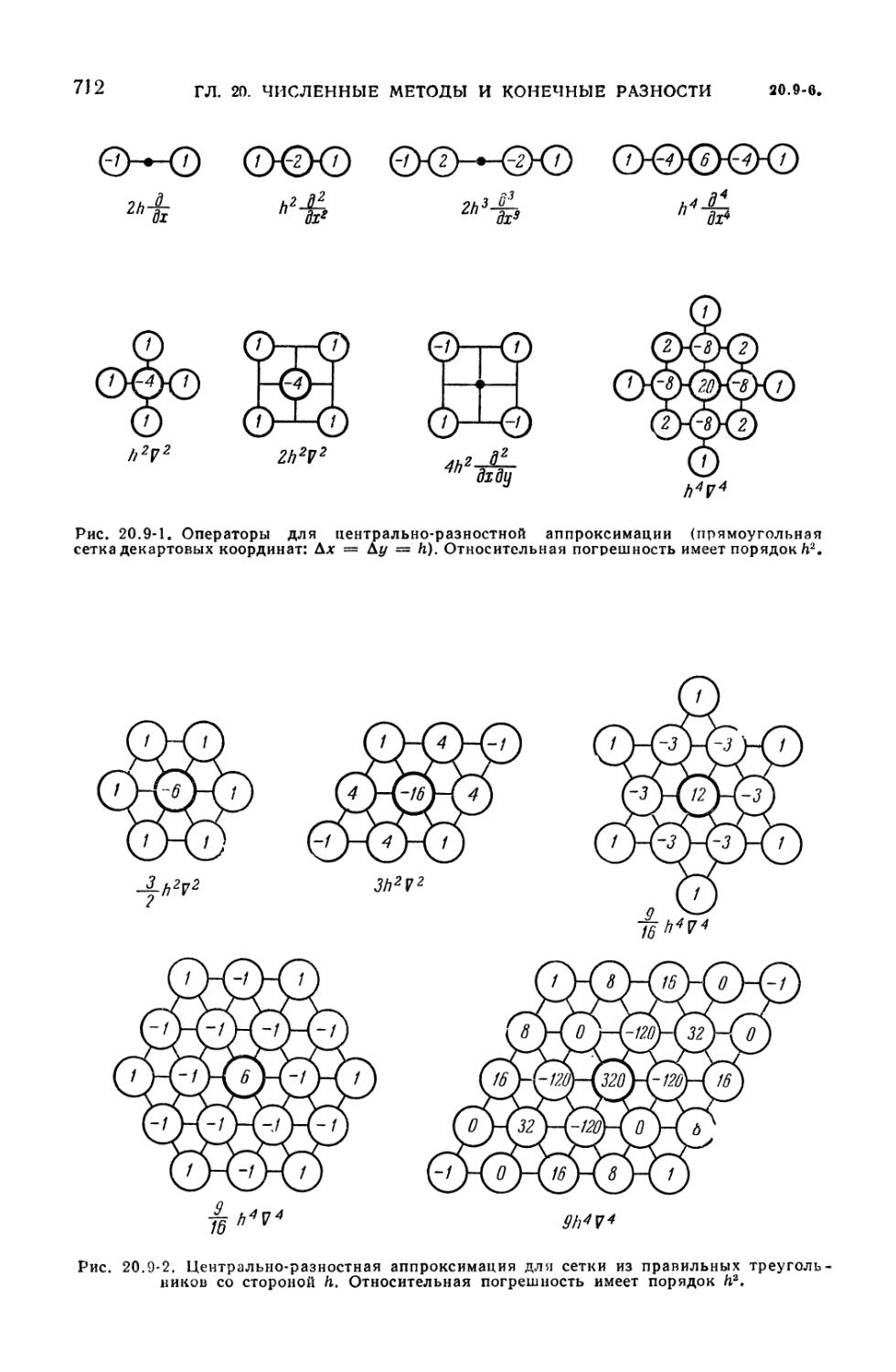
(711). 20.9-6. Представление краевых условий (711). 20.9-7. Задачи,
содержащие более двух независимых переменных (714). 20.9-8. Пригодность
разностных схем. Условия устойчивости (714). 20.9-9. Методы аппроксими-
ОГЛАВЛЕНИЕ
19
рующих функций для численного решения краевых задач (715). 20.9-10.
Численное решение интегральных уравнений (716).
20.10. Методы Монте-Карло 717
20.10-1. Методы Монте-Карло (717). 20.10-2. Два метода уменьшения
дисперсии оценки (718). 20.10-3. Использование предварительной информации.
Метод значимой выборки (719). 20.10-4. Некоторые методы генерирования
случайных чисел. Проверка случайности (719).
Г Л А В А 21
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.1. Введение 720
21.1-1. Вводные замечания (720).
21.2. Элементарные трансцендентные функции 720
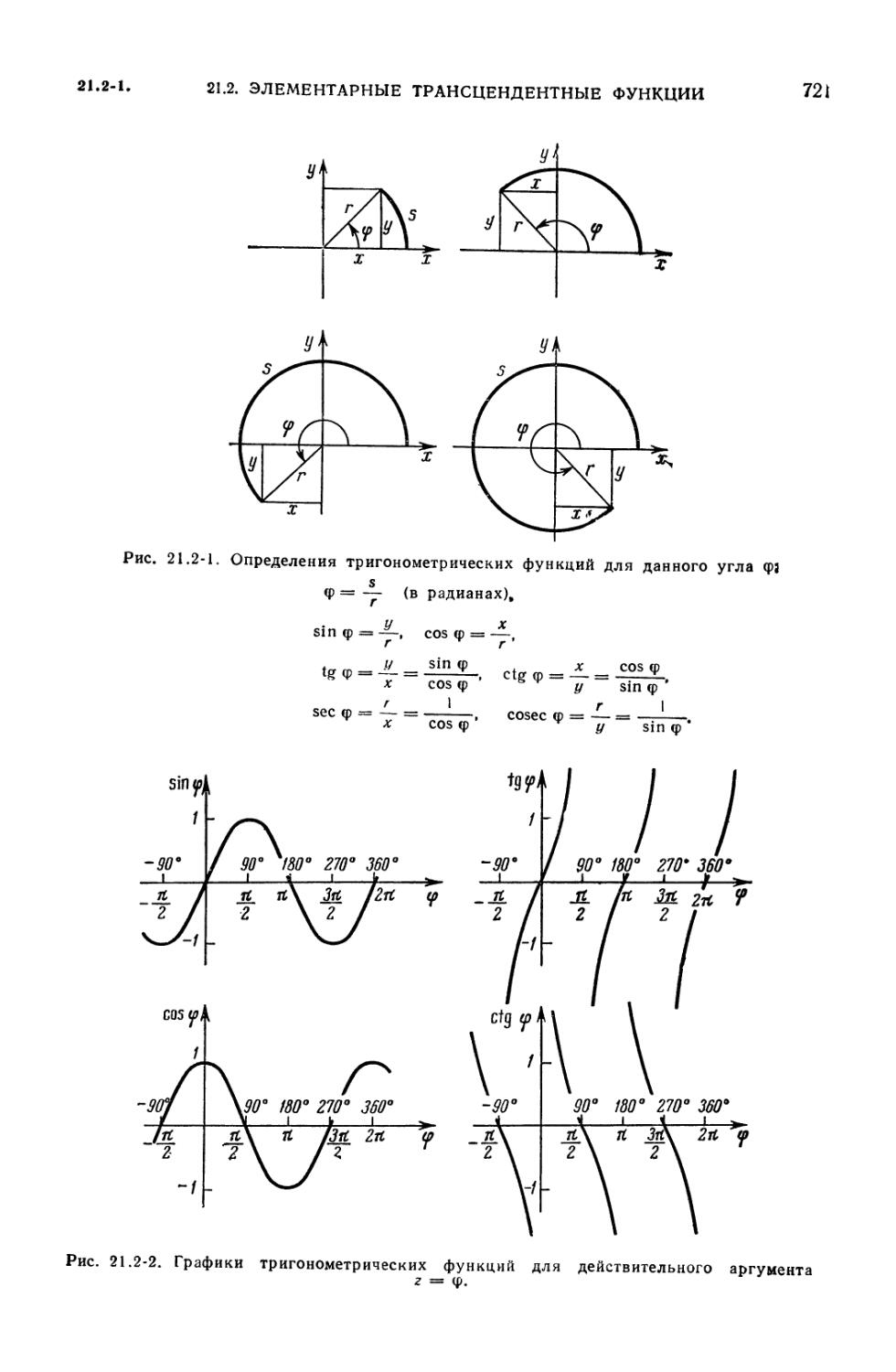
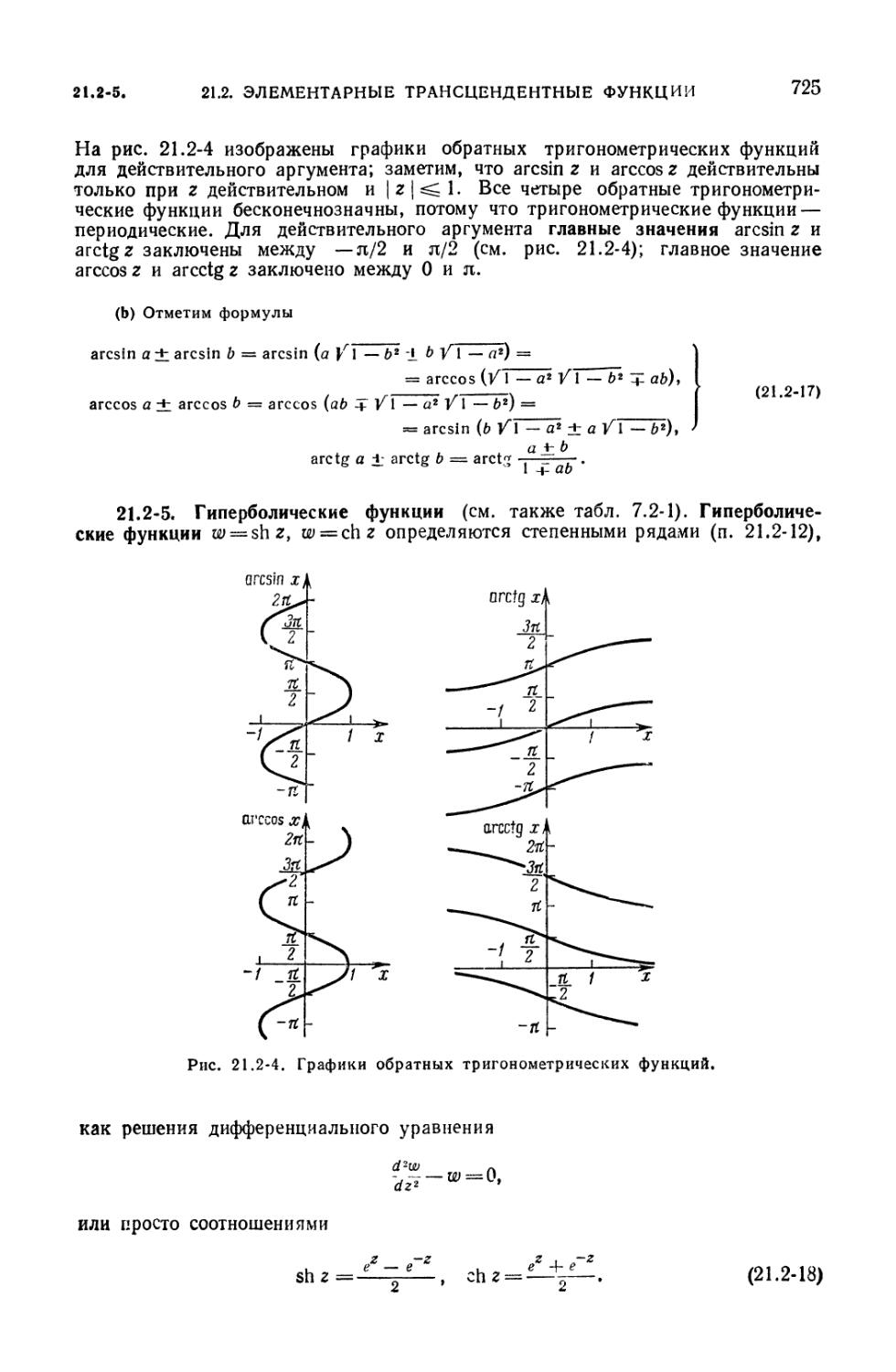
21.2-1. Тригонометрические функции (720). 21.2-2. Соотношения между
тригонометрическими функциями (722). 21.2-3. Теоремы сложения и формулы
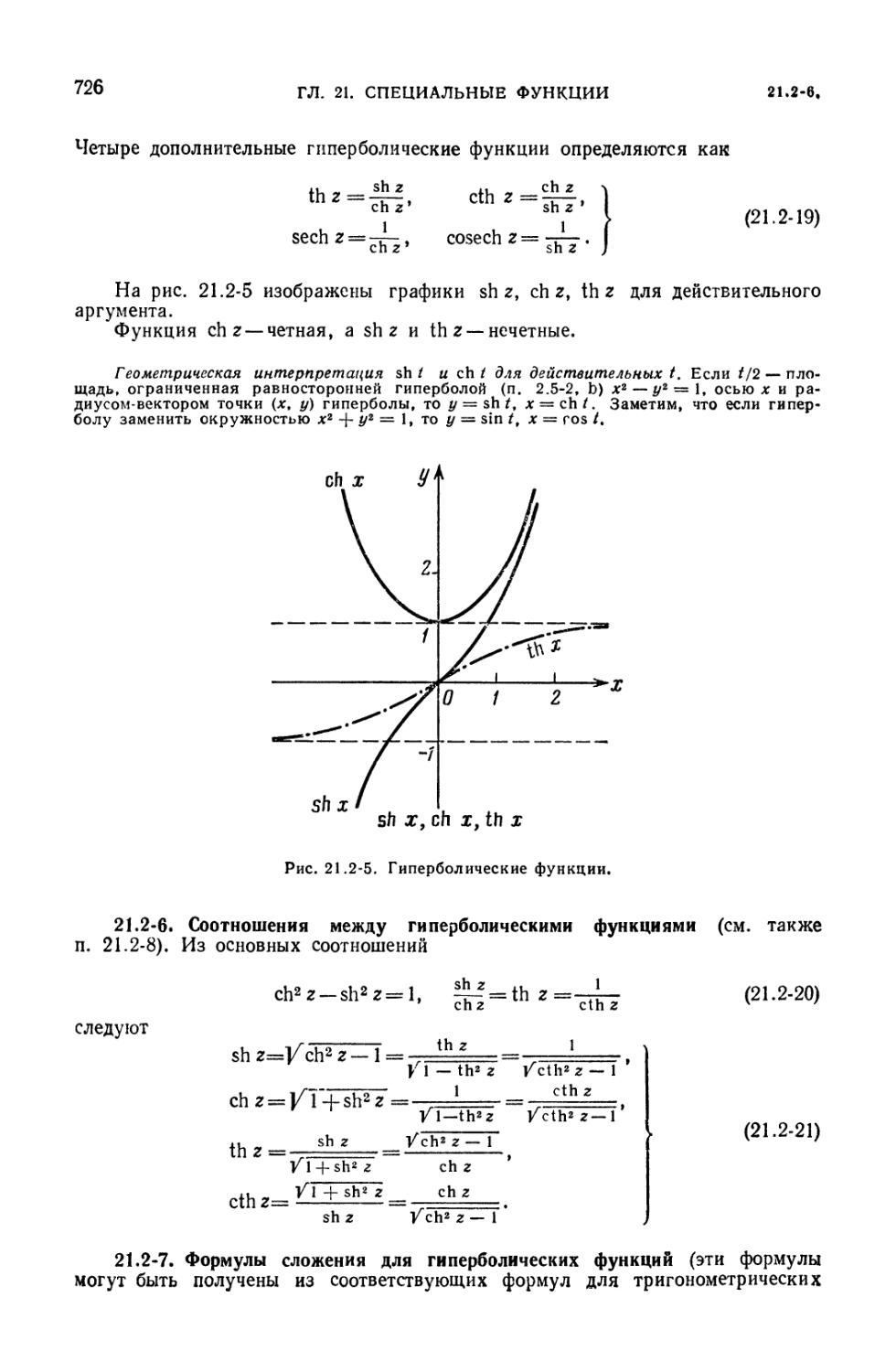
для кратных углов (723). 21.2-4. Обратные тригонометрические функции
(724). 21.2-5. Гиперболические функции (725). 21.2-6. Соотношения между
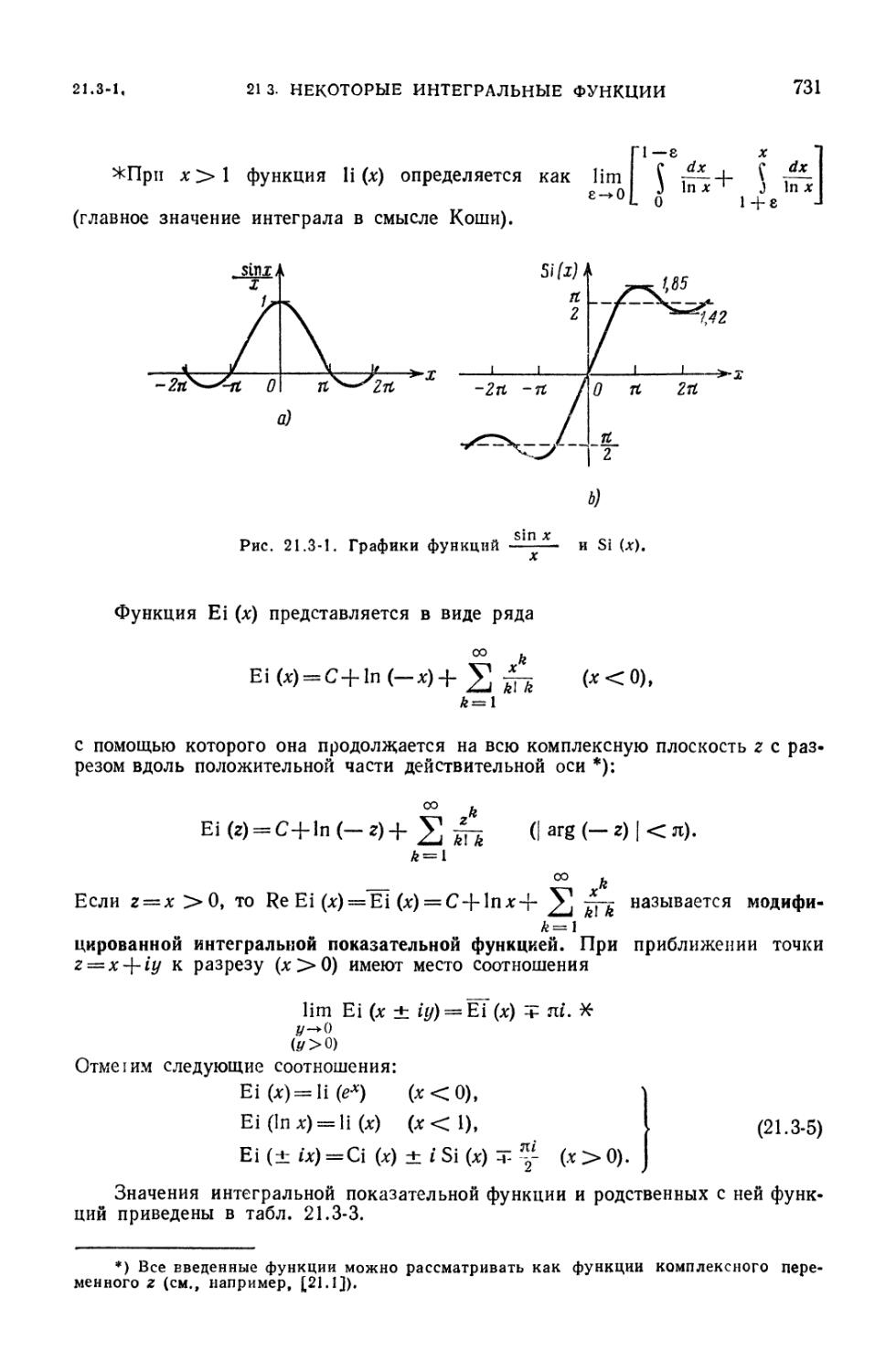
гиперболическими функциями (726). 21.2-7. Формулы сложения для
гиперболических функций (726). 21.2-8. Обратные гиперболические функции
(727). 21.2-9. Соотношения между показательной, тригонометрическими и
гиперболическими функциями (728). 21.2-10. Определение логарифма (728).
21.2-11. Соотношения между обратными тригонометрическими, обратными
гиперболическими и логарифмической функциями (729). 21.2-12.
Разложения в степеннйе ряды (729). 21.2-13. Разложения в бесконечные
произведения (730). 21.2-14. Некоторые полезные неравенства (730).
21.3. Некоторые интегральные функции 730
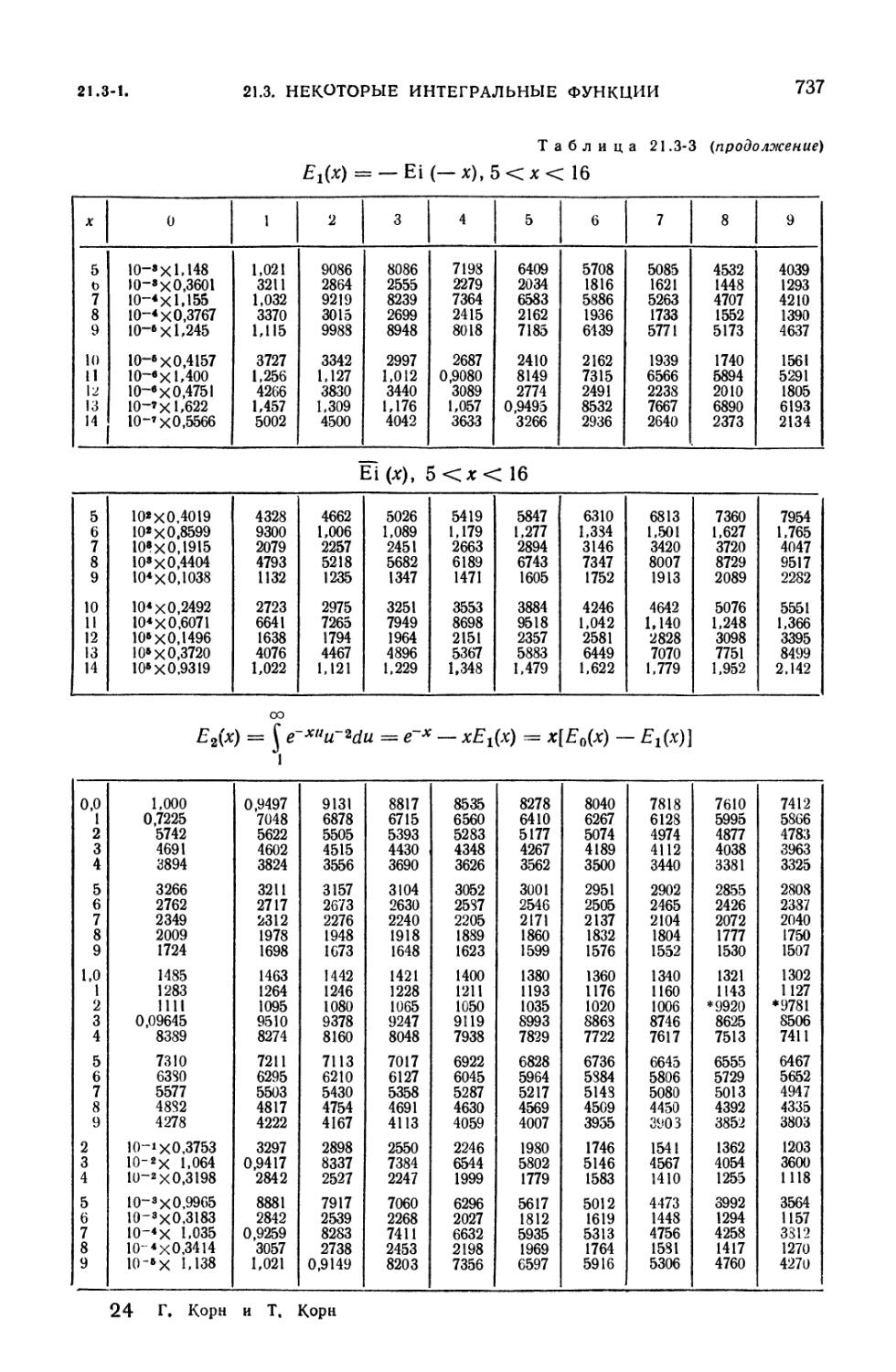
21.3-1. Интегральные синус, косинус, логарифм и показательная
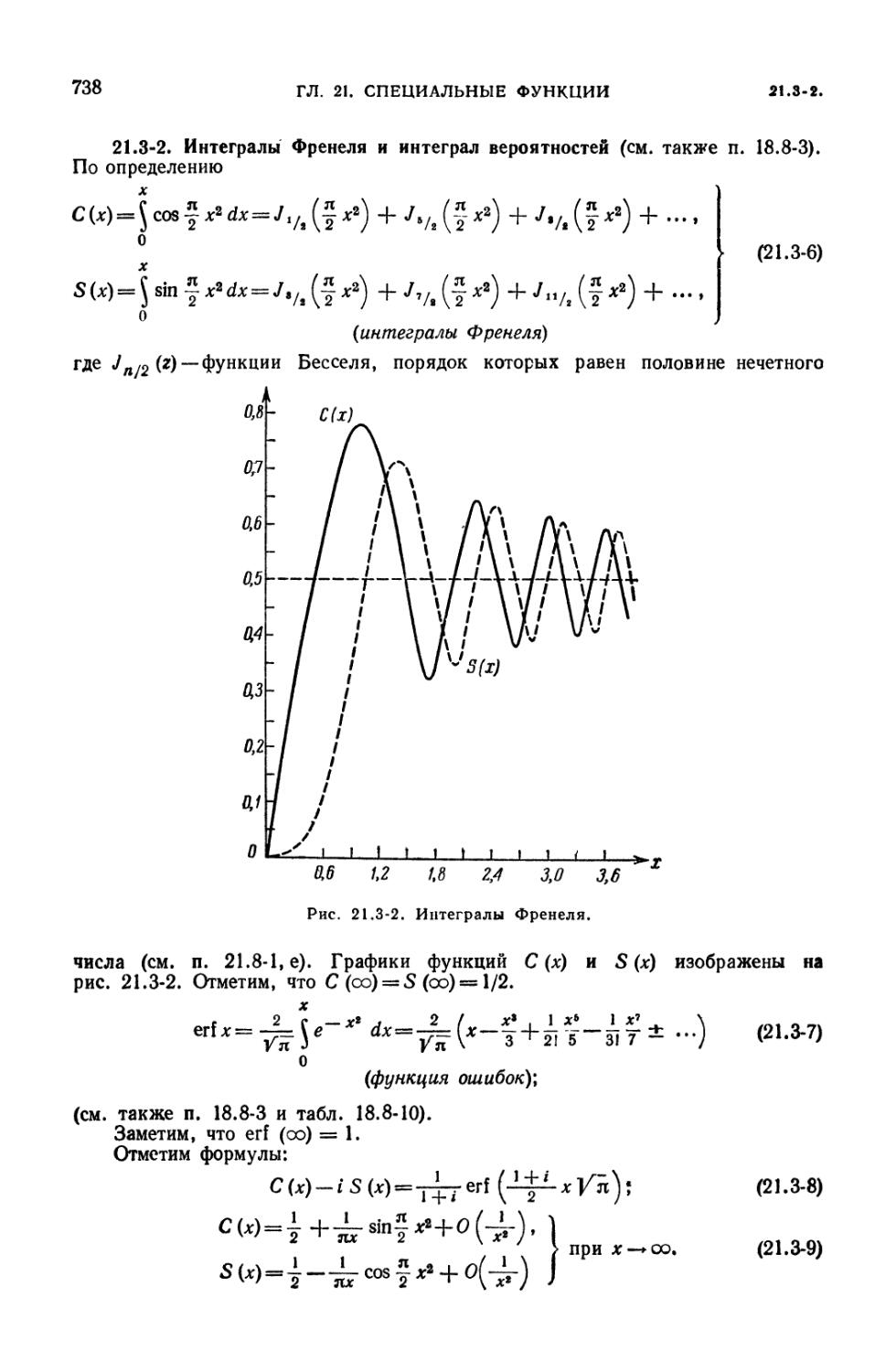
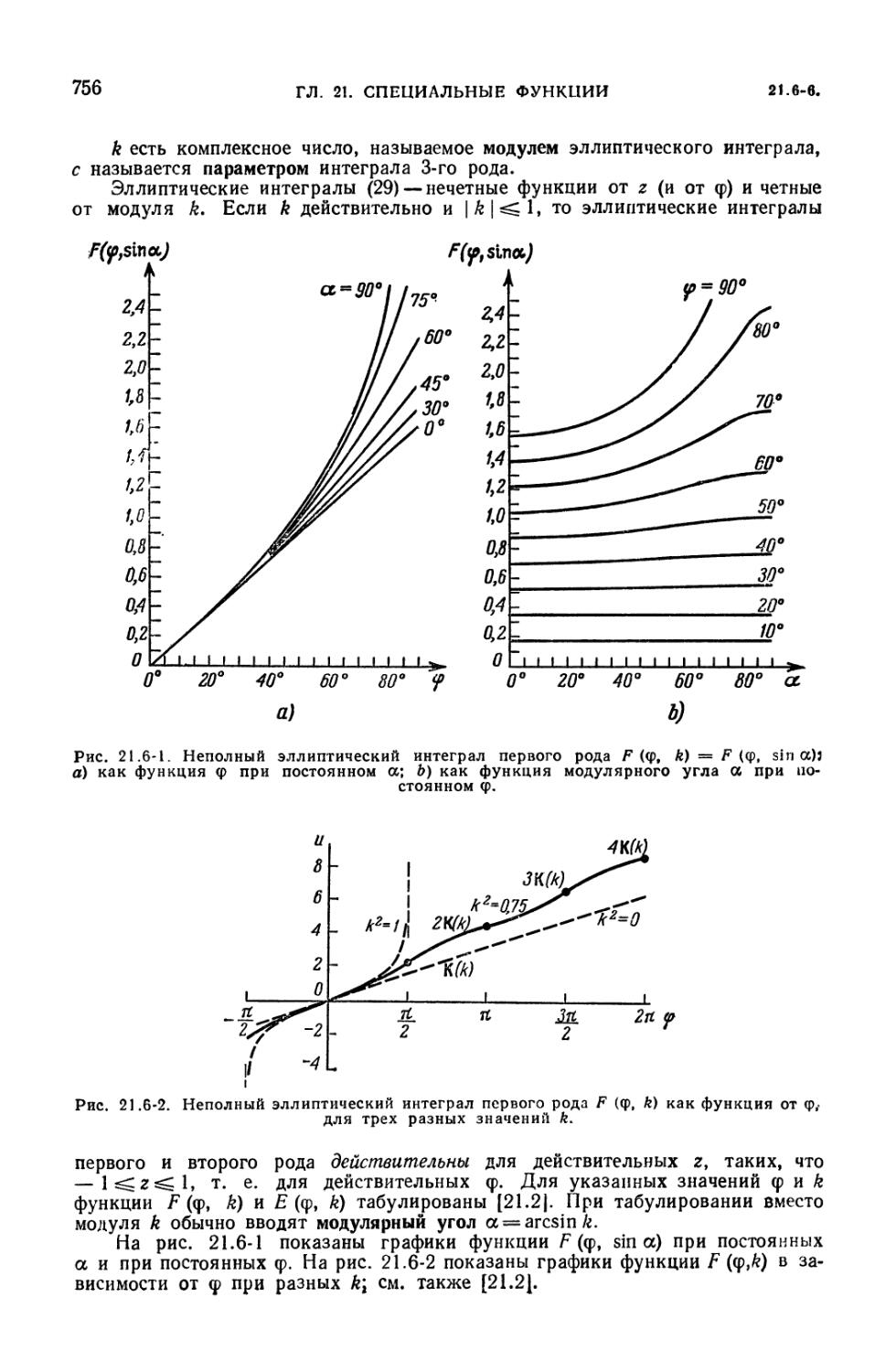
функция (730). 21.3-2. Интегралы Френеля и интеграл вероятностей (738).
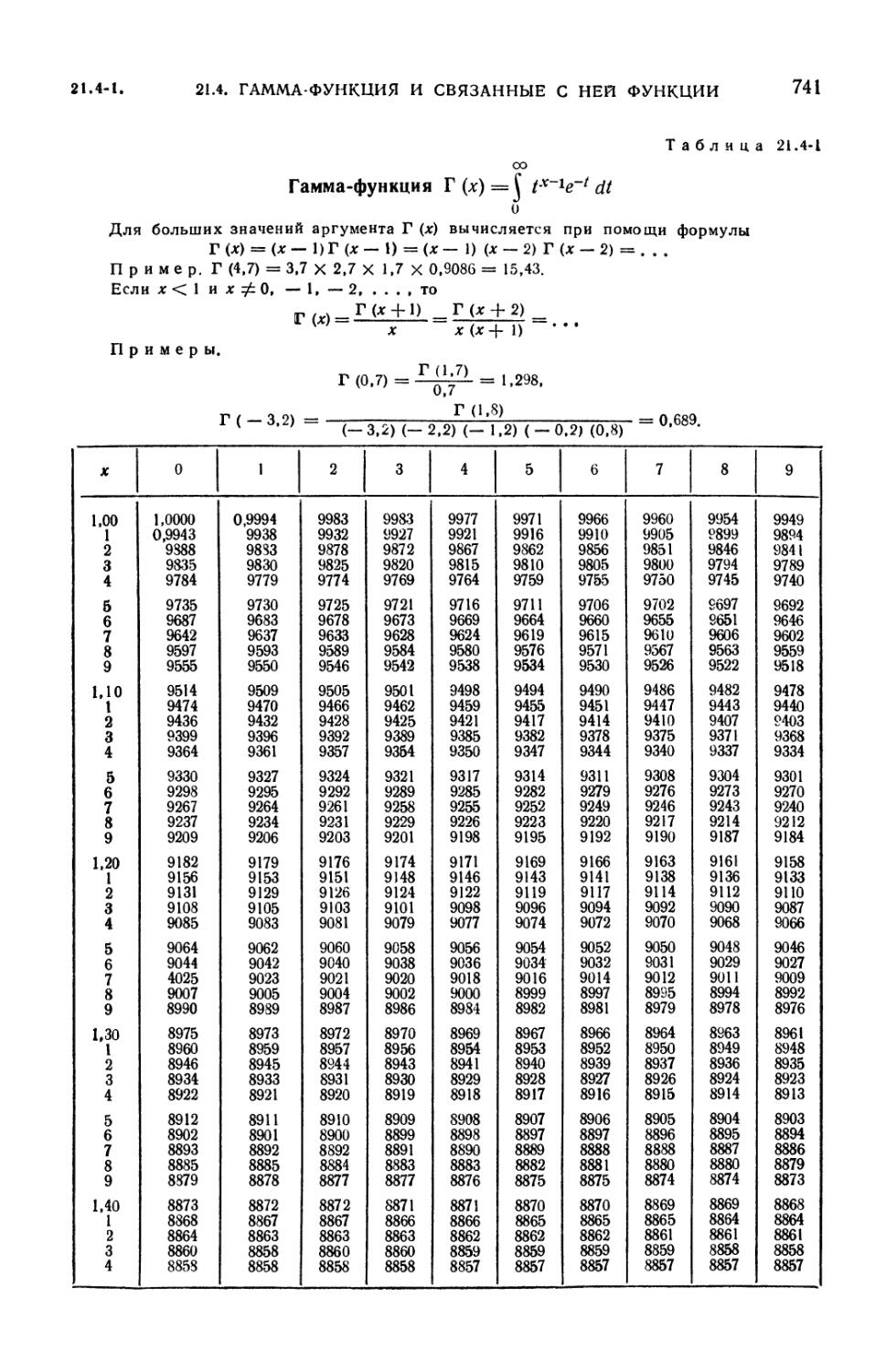
21.4. Гамма-функция и связанные с ней функции 739
21.4-1. Гамма-функция (739). 21.4-2. Асимптотическое разложение Стирлинга
для Г (г) и п\ (743). 21.4-3. Логарифмическая производная гамма-функции
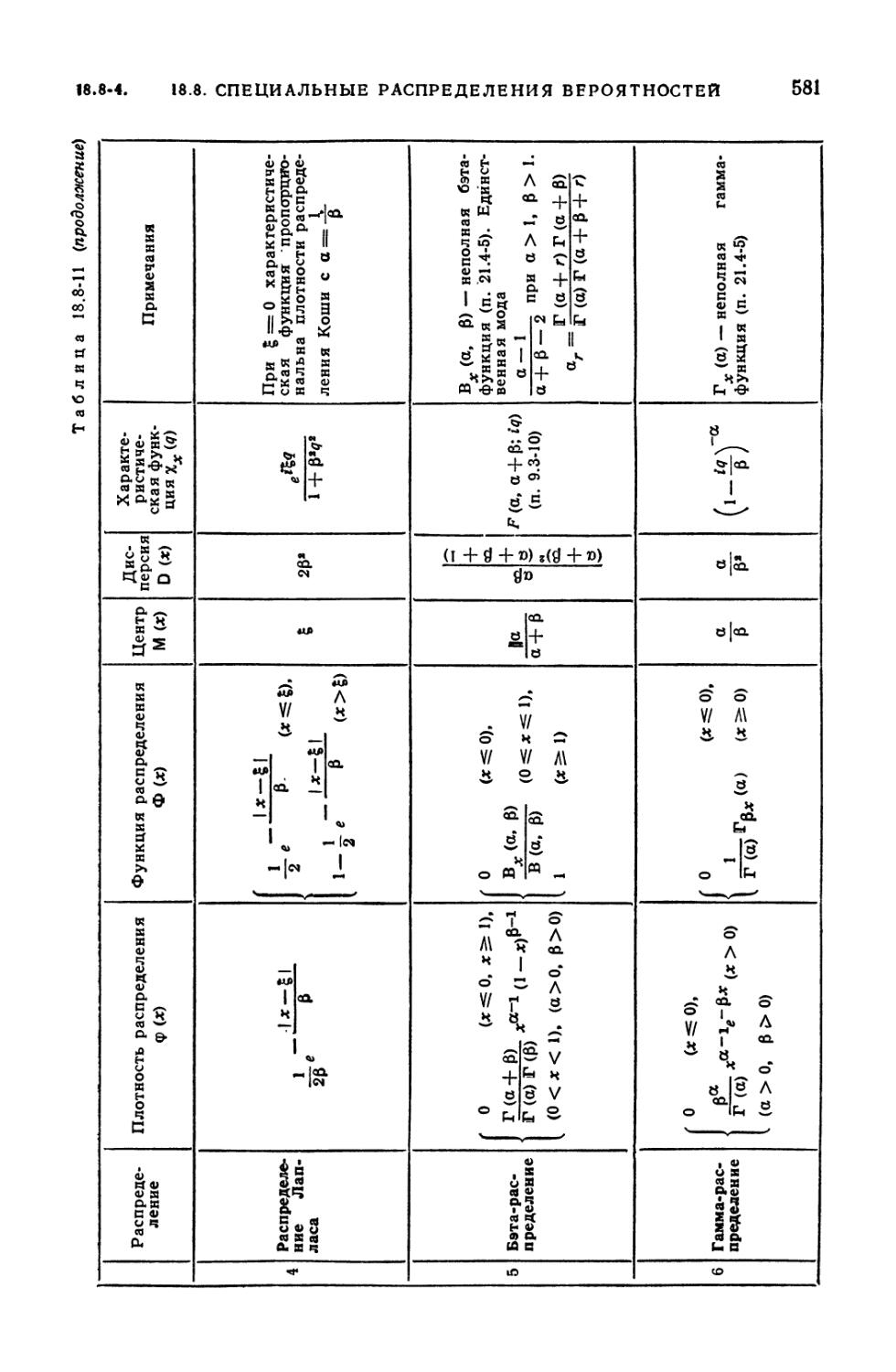
(743). 21.4-4. Бета-функция (743). 21.4-5. Неполные гамма- и бета-функции
(744).
21.5. Биномиальные коэффициенты и факториальные многочлены. Многочлены
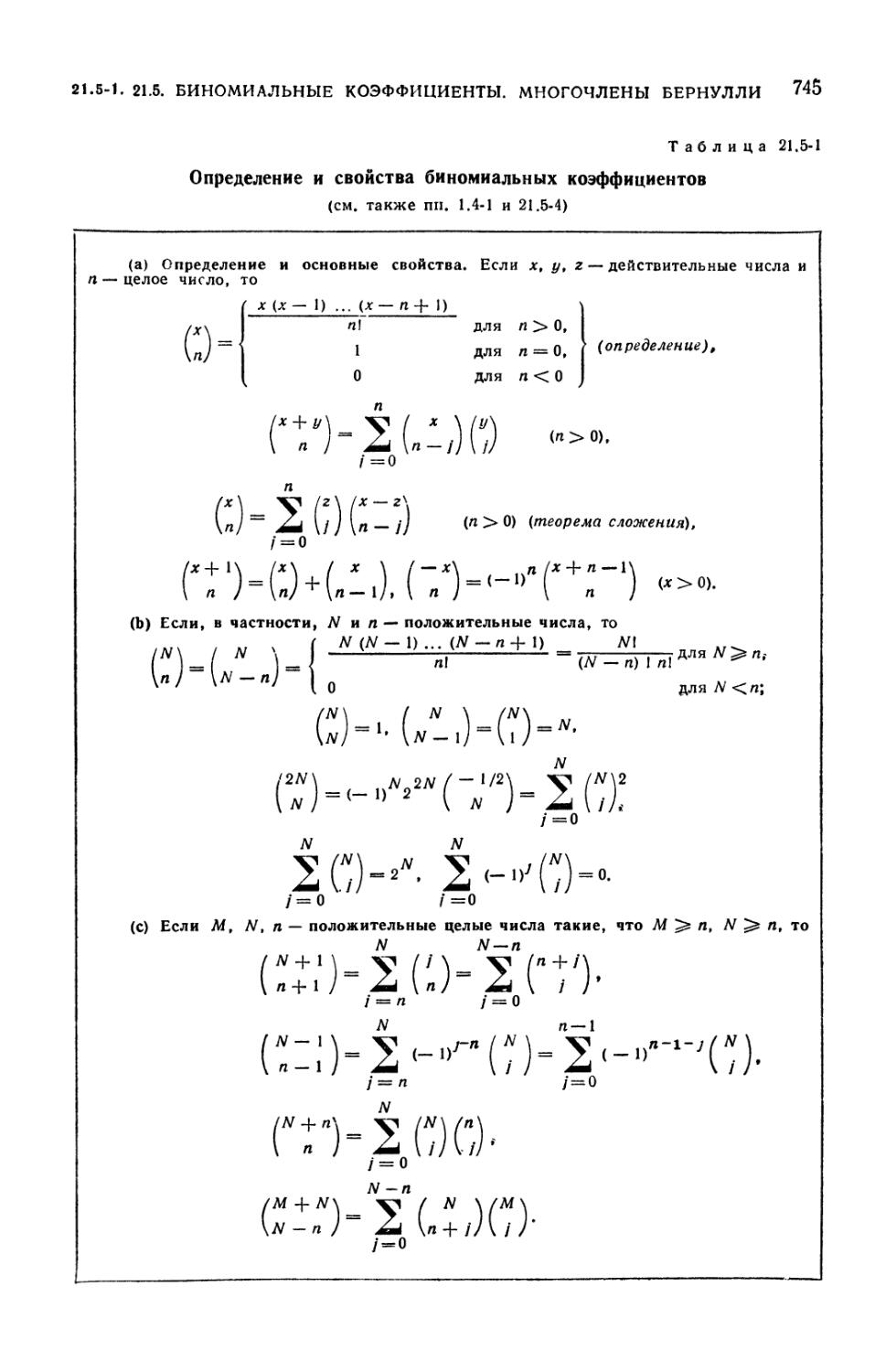
и числа Бернулли 744
21.5-1. Биномиальные коэффициенты и факториальные многочлены (744).
21.5-2 Многочлены и числа Бернулли (746). 21.5-3. Формулы,
связывающие многочлены Бернулли и факториальные многочлены (747). 21.5-4.
Приближенные формулы для ( 1 (747).
21.6. Эллиптические функции, эллиптические интегралы и связанные с ними
функции 748
21.6-1. Эллиптические функции; общие свойства (748). 21.6-2. #>-функция
Вейерштрасса (748). 21.6-3. £- н а-функции Вейерштрасса (750). 21.6-4.
Эллиптические интегралы (751). 21.6-5. Приведение эллиптических интегралов
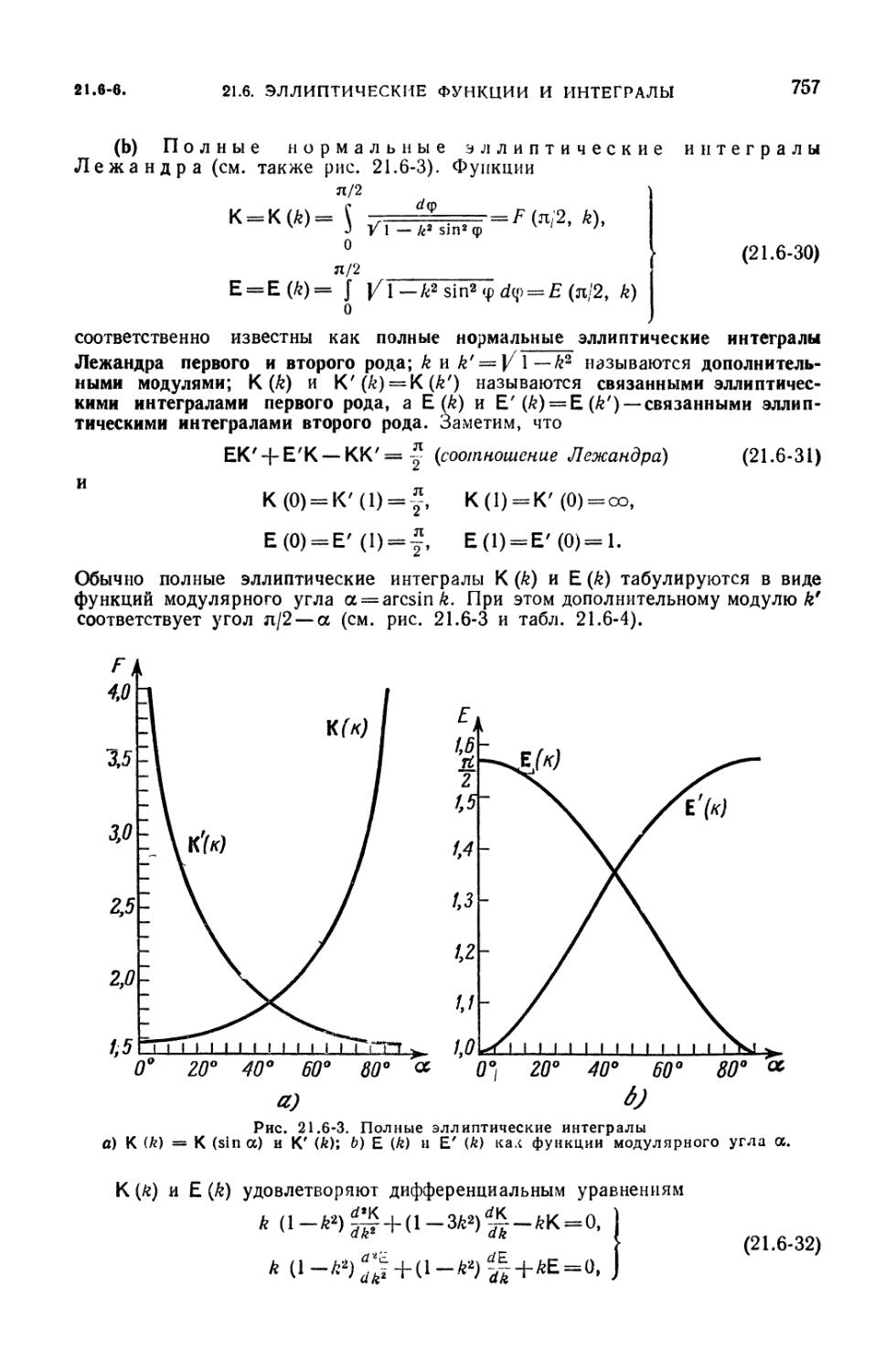
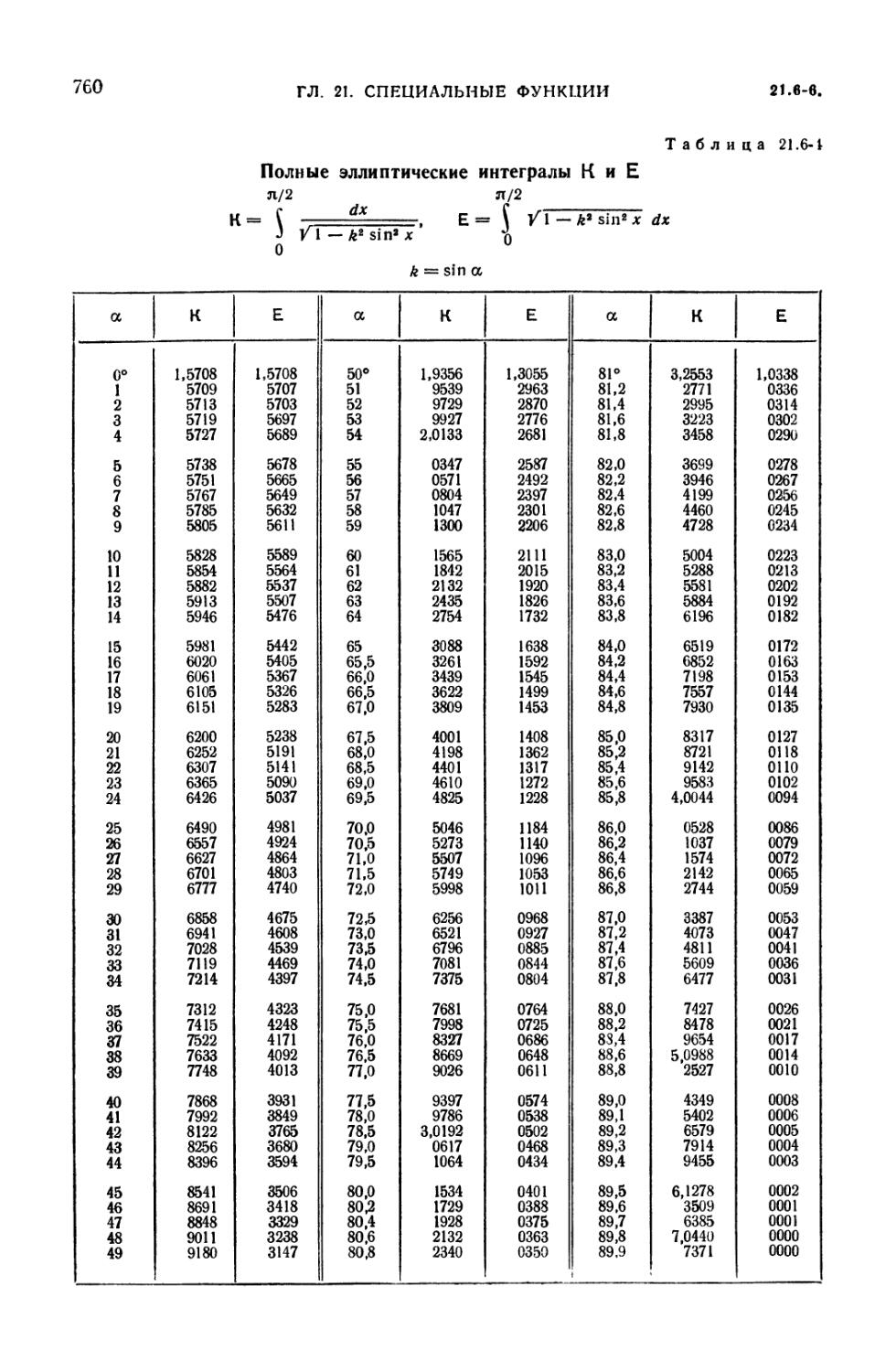
(751). 21.6-6 Нормальные эллиптические интегралы Лежандра (753). 21.6-7.
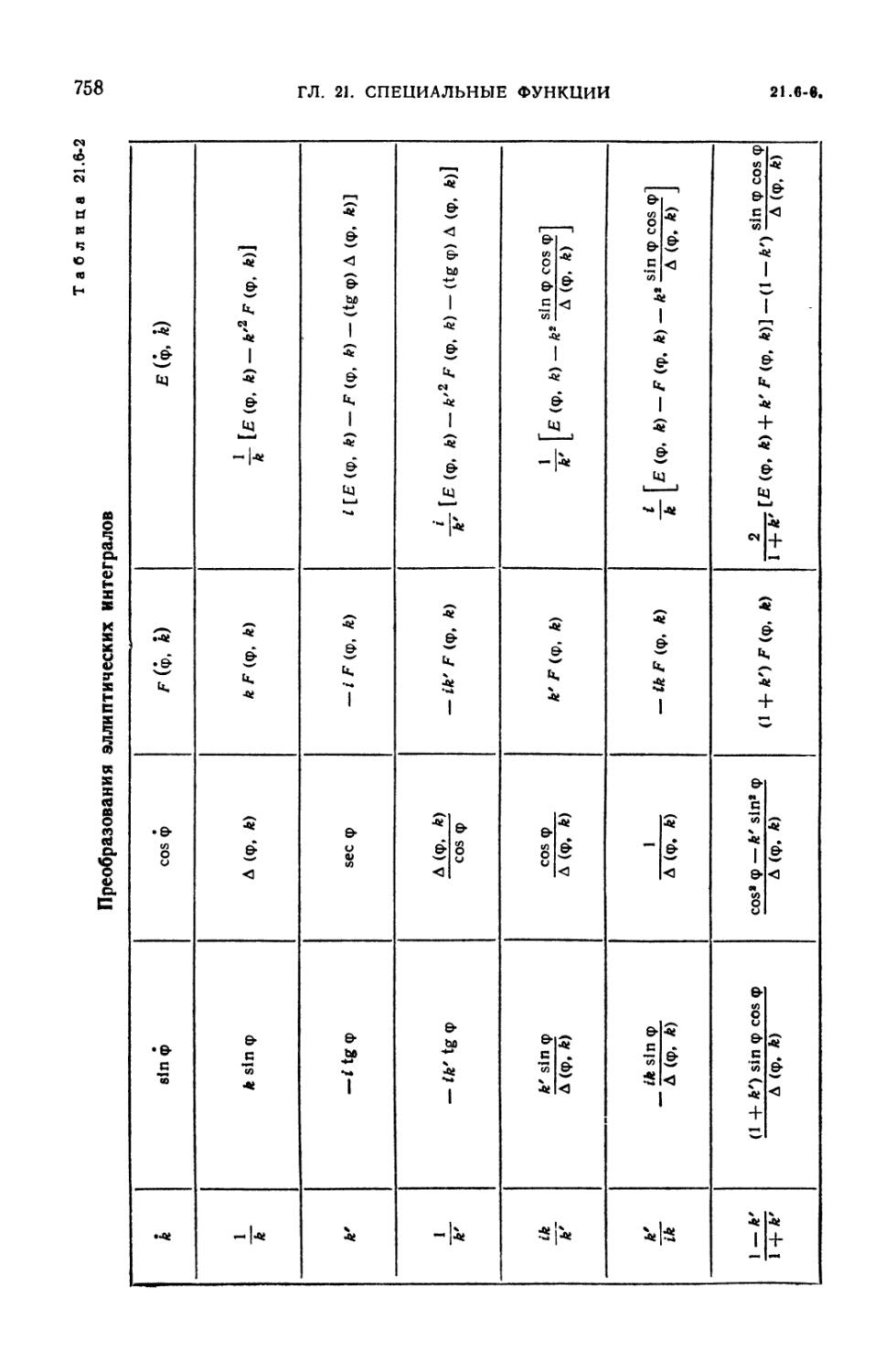
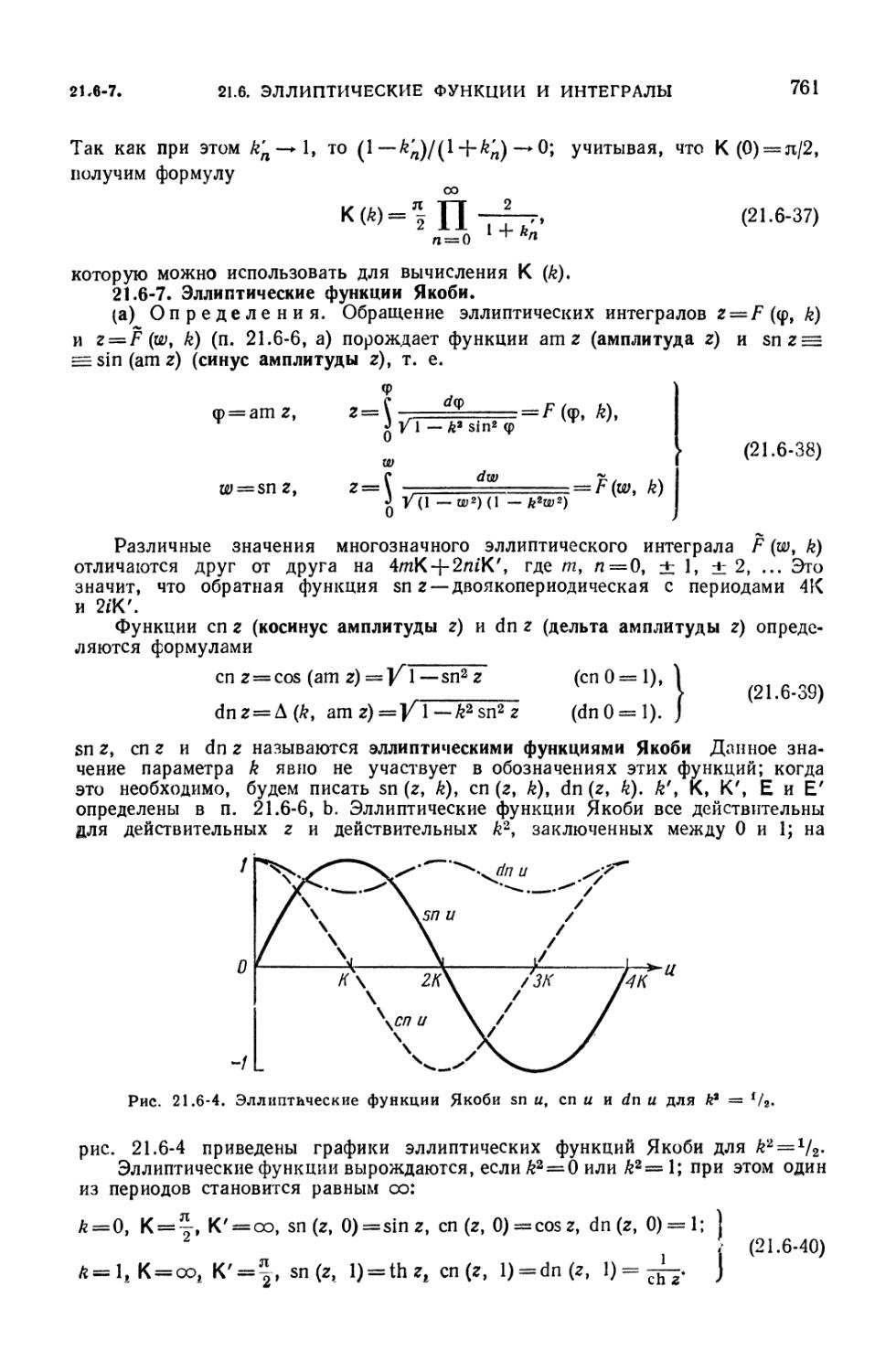
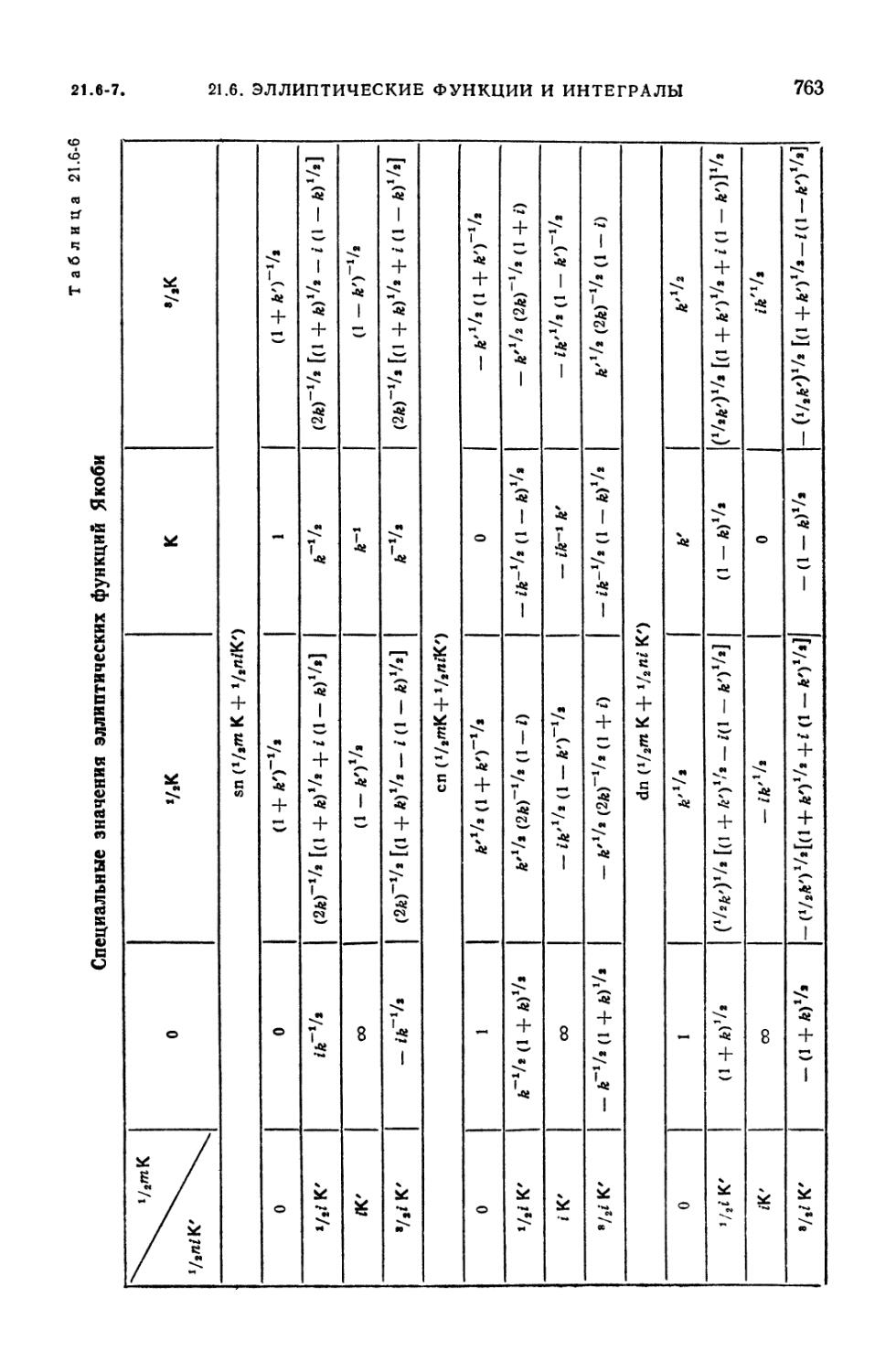
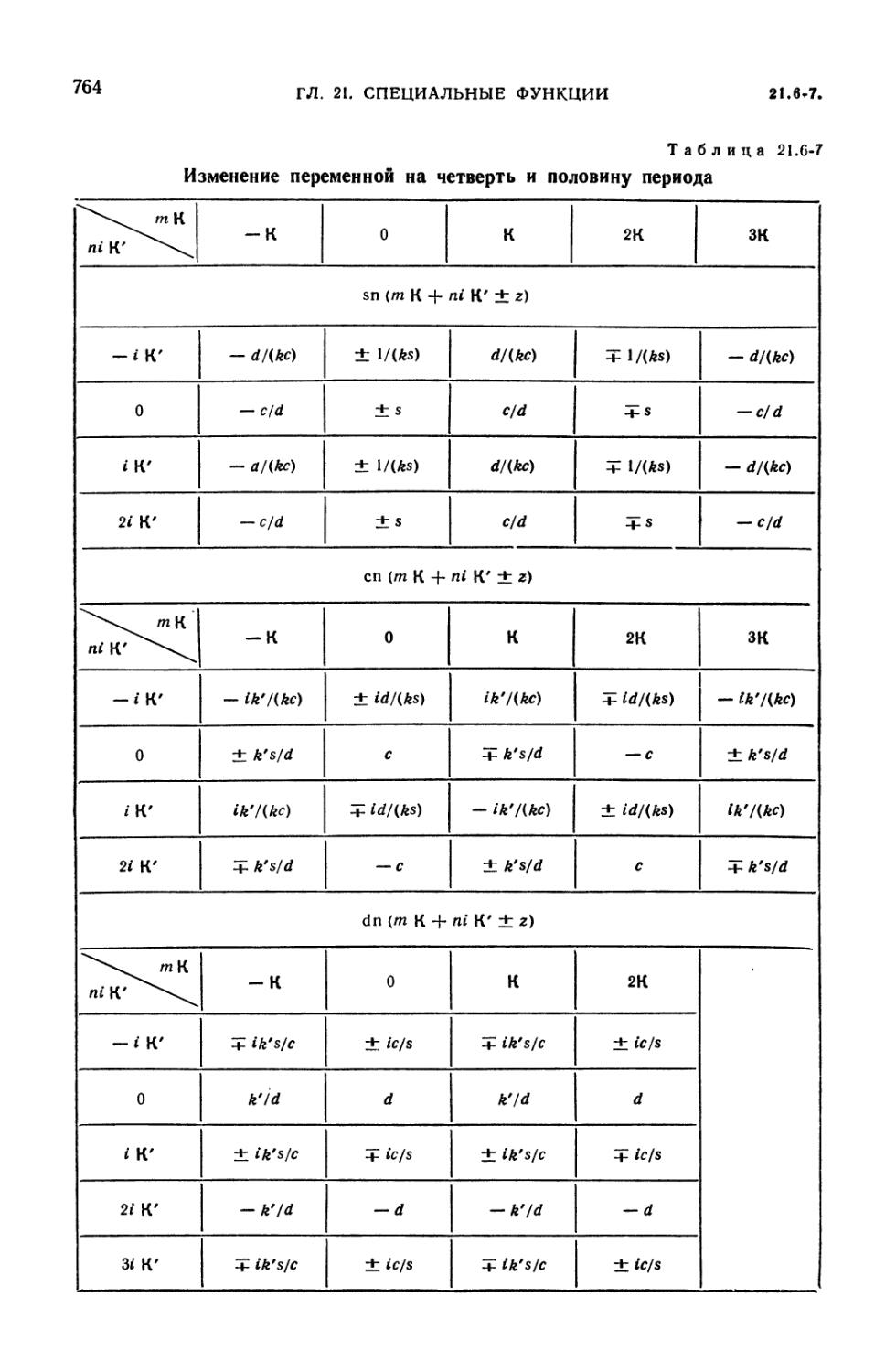
Эллиптические функции Якоби (761). 21.6-8. Тэта-функции Якоби (765).
21.6-9. Соотношения между эллиптическими функциями Якоби,
Вейерштрасса и тэта-функциями (767).
21.7. Ортогональные многочлены 767
21.7-1. Введение (767). 21.7-2. Действительные нули ортогональных
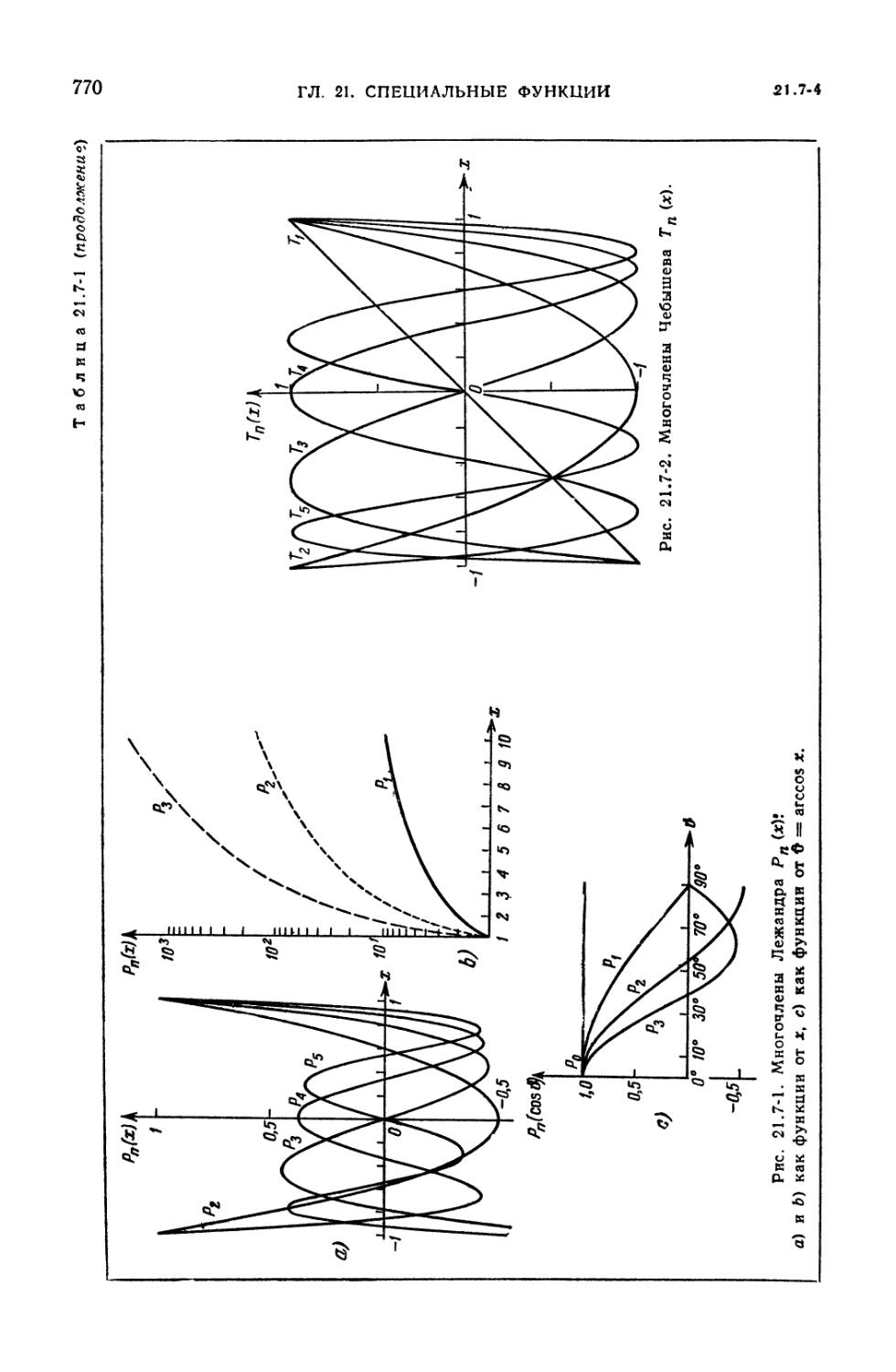
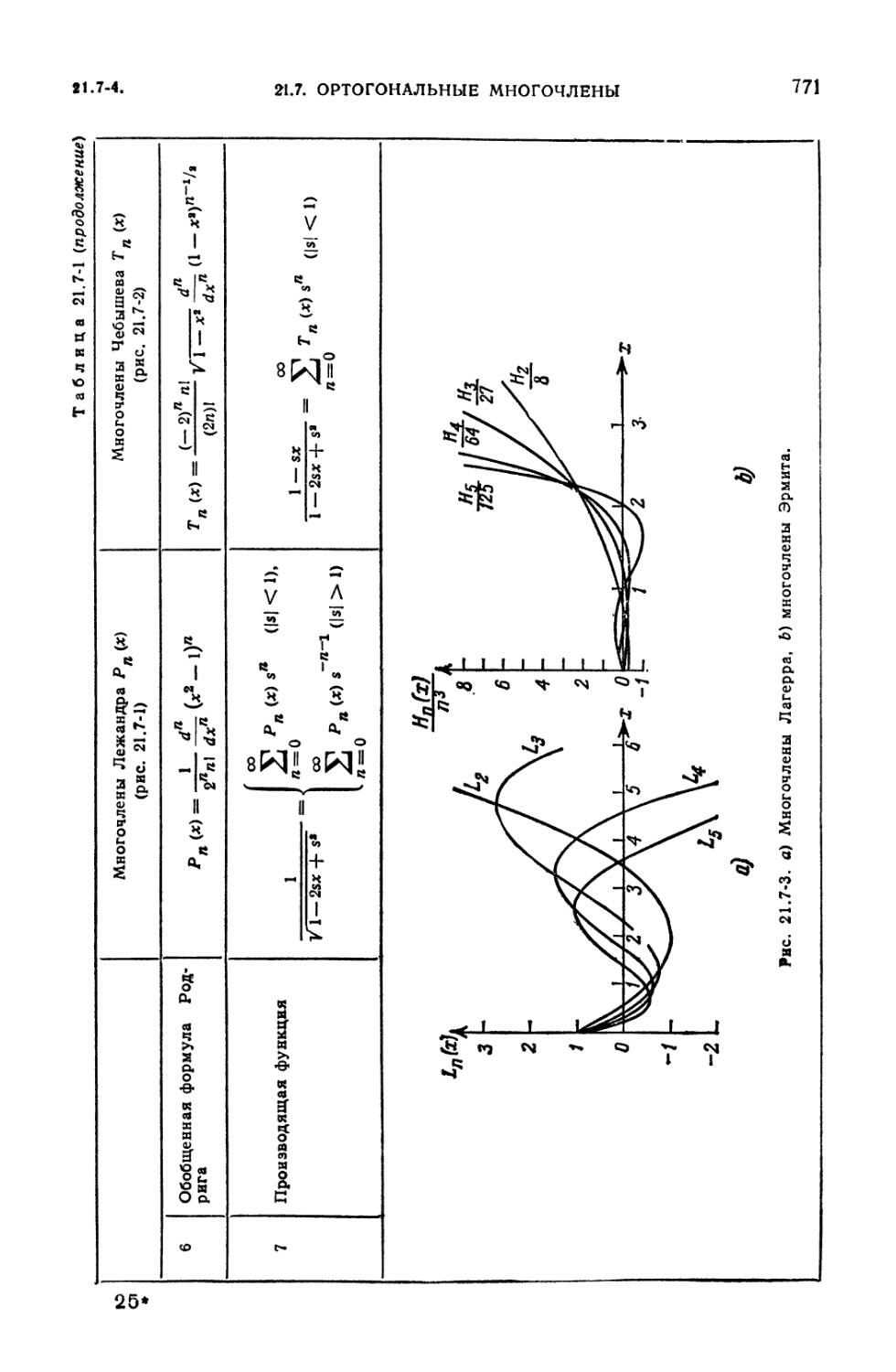
многочленов (768). 21.7-3. Функции Лежандра (768). 21.7-4. Многочлены Чебы-
шева первого и второго рода (768). 21.7-5. Обобщенные многочлены и
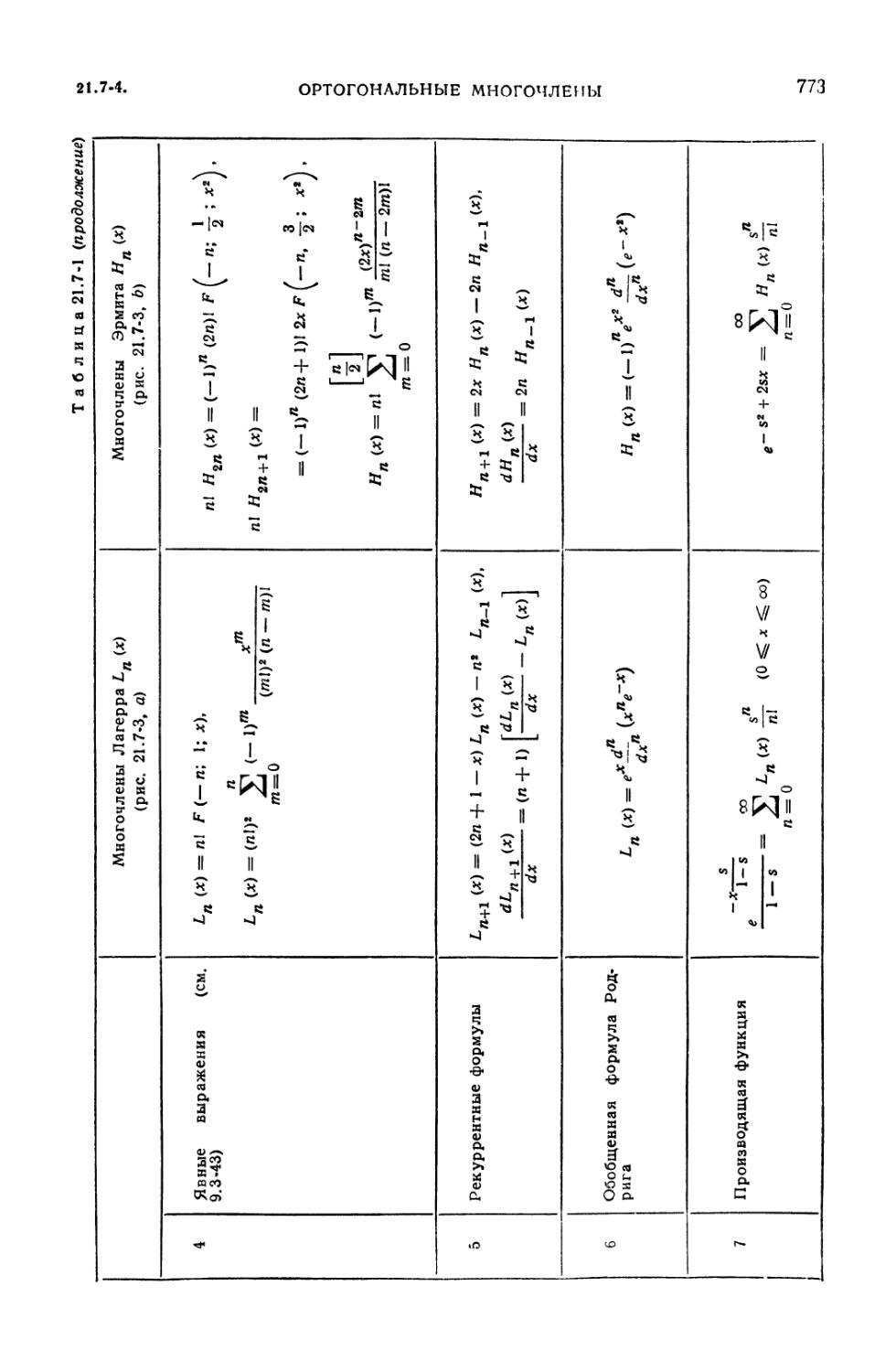
присоединенные функции Лагерра (774). 21.7-6. Функции Эрмита (775). 21.7-7.
Некоторые интегральные формулы (776). 21.7-8. Многочлены Якобн и
Гегенбауэра (776).
21.8. Цилиндрические функции, присоединенные функции Лежандра и
сферические гармоники 777
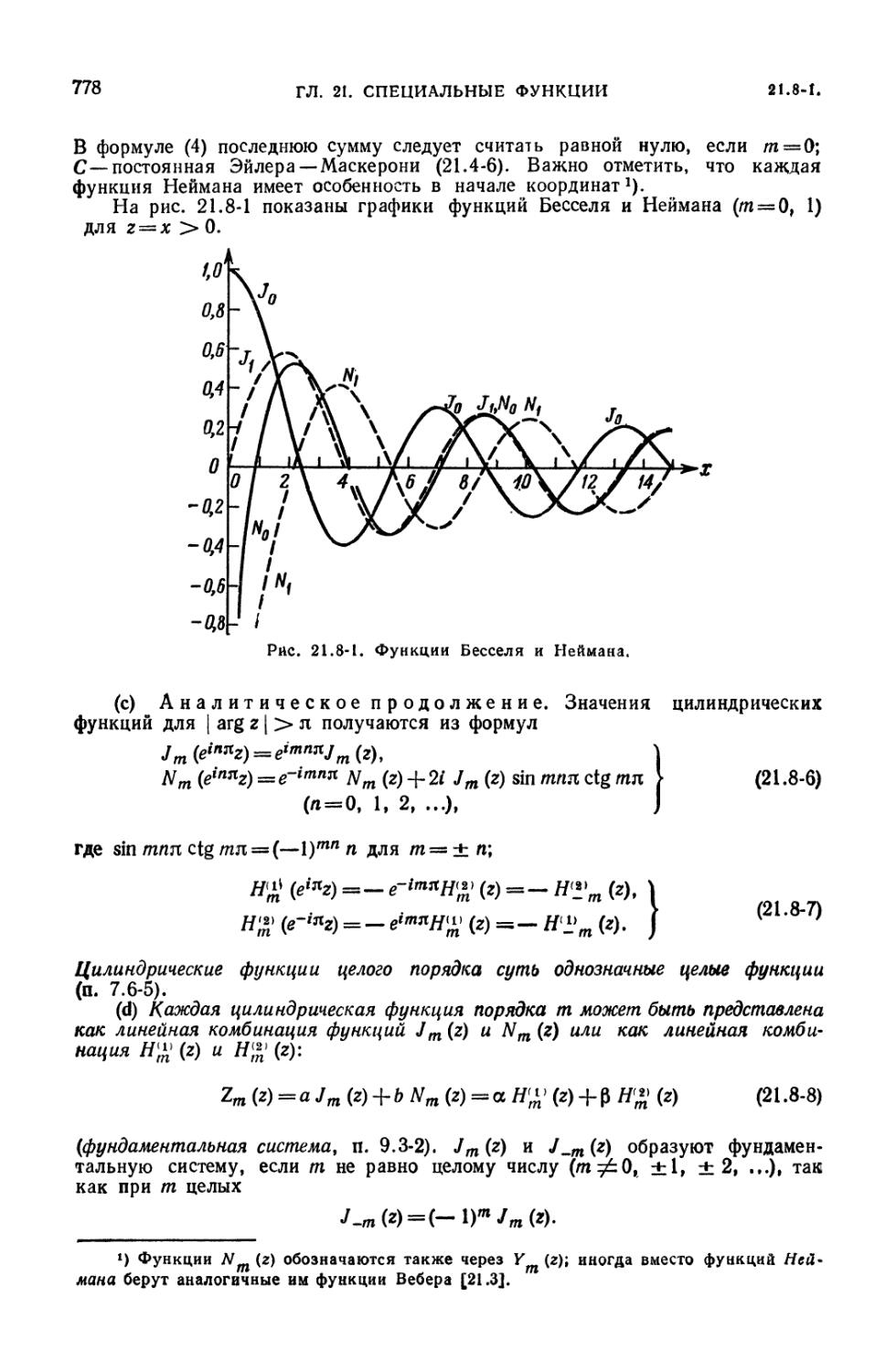
21.8-1. Функции Бесселя и другие цилиндрические функции (777). 21.8-2.
Интегральные формулы (779). 21.8-3. Нули цилиндрических функций
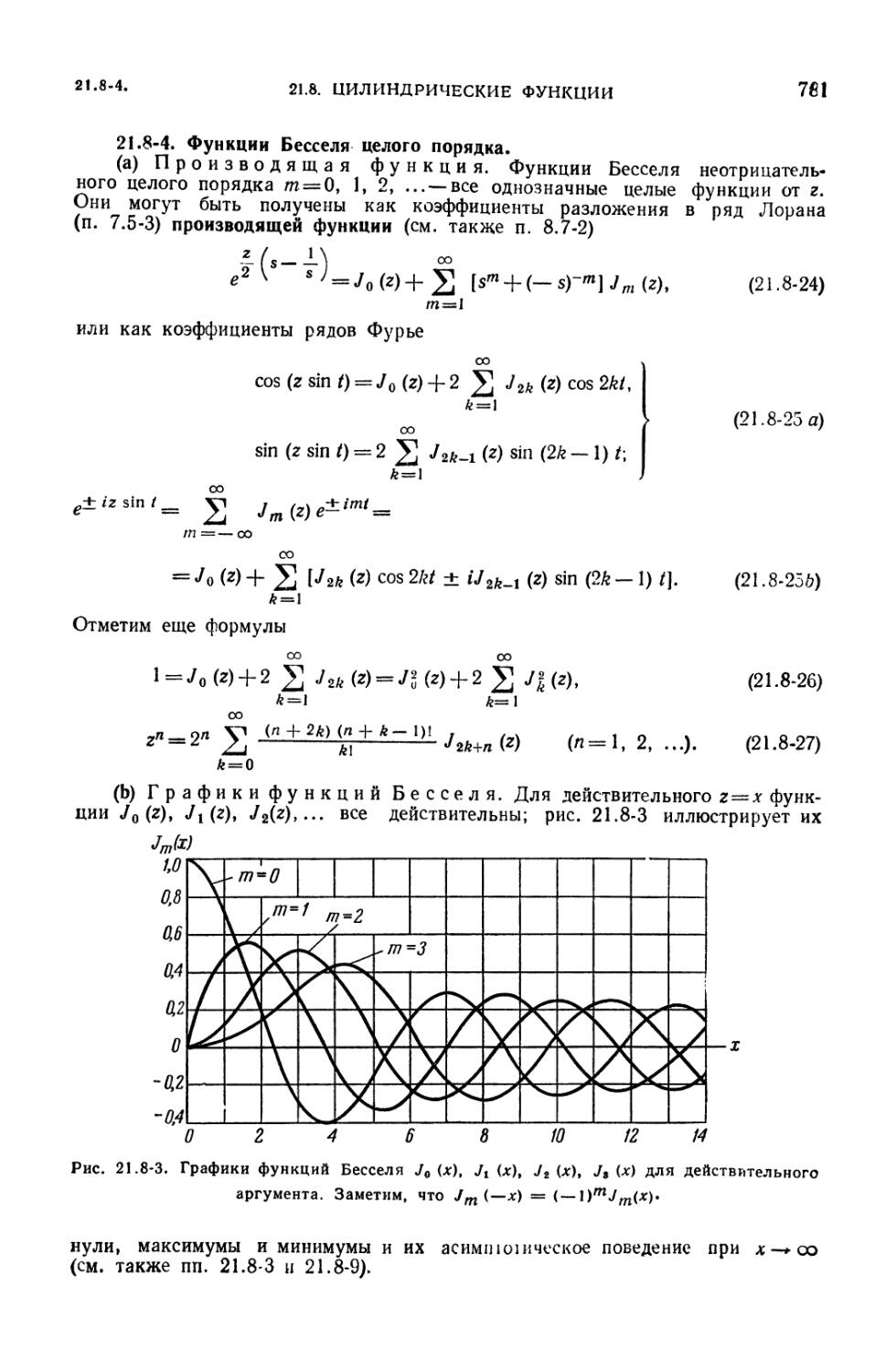
(780). 21.8-4. Функции Бесселя целого порядка (781). 21.8-5. Решение
дифференциальных уравнений при помощи функций Бесселя и связанных
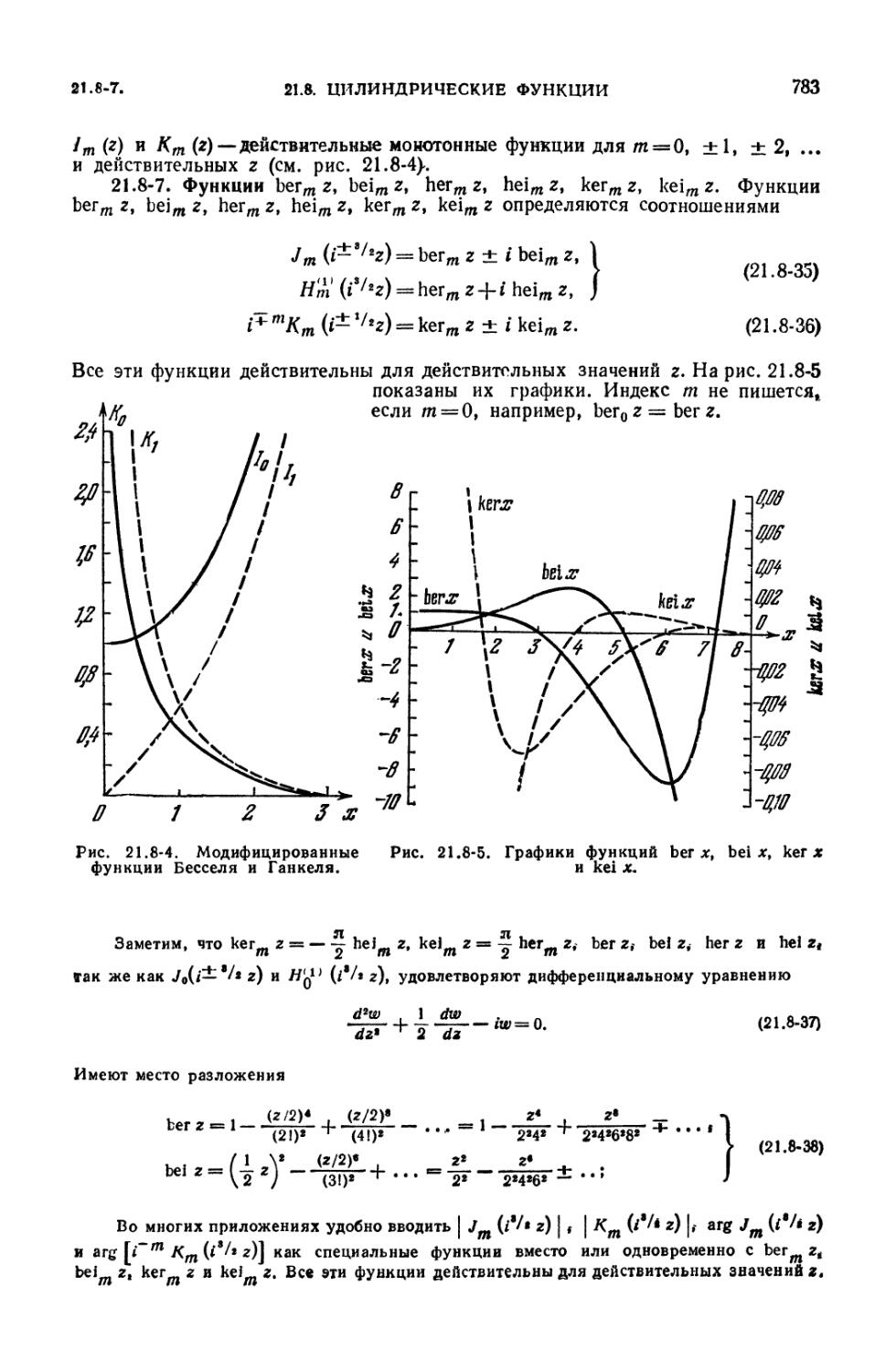
с ними функций (782). 21.8-6. Модифицированные функции Бесселя и Ган-
келя (782). 21.8-7. Функции bermz, beimz, hermz, heimz, kermz, keimz (783).
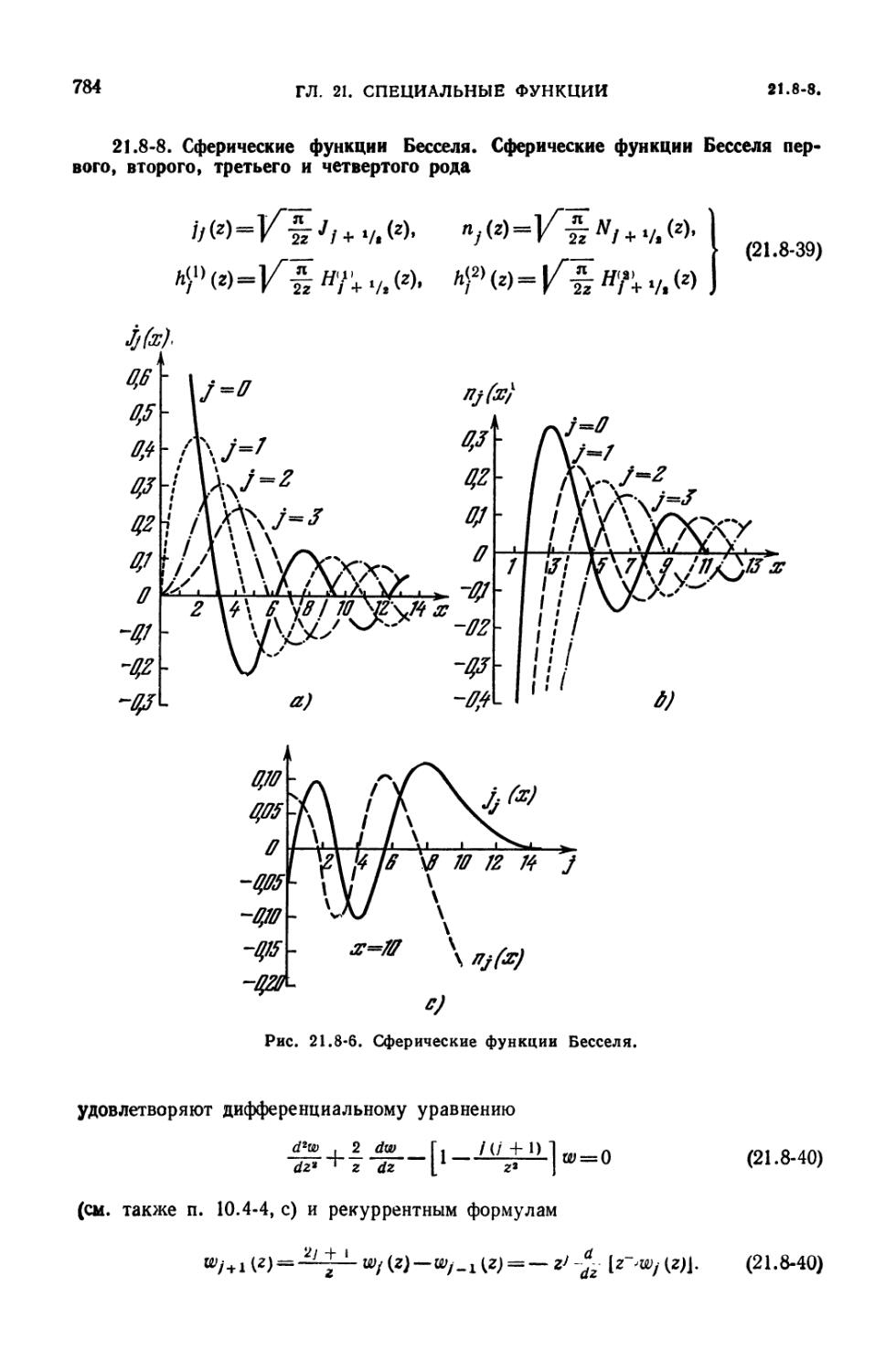
21.8-8. Сферические функции Бесселя (784). 21.8-9. Асимптотические раз-
20
ПЕРЕЧЕНЬ ТАБЛИЦ
ложения цилиндрических функций и сферических функций Бесселя для
больших значений \г\ (785). 21.8-10. Присоединенные функции и
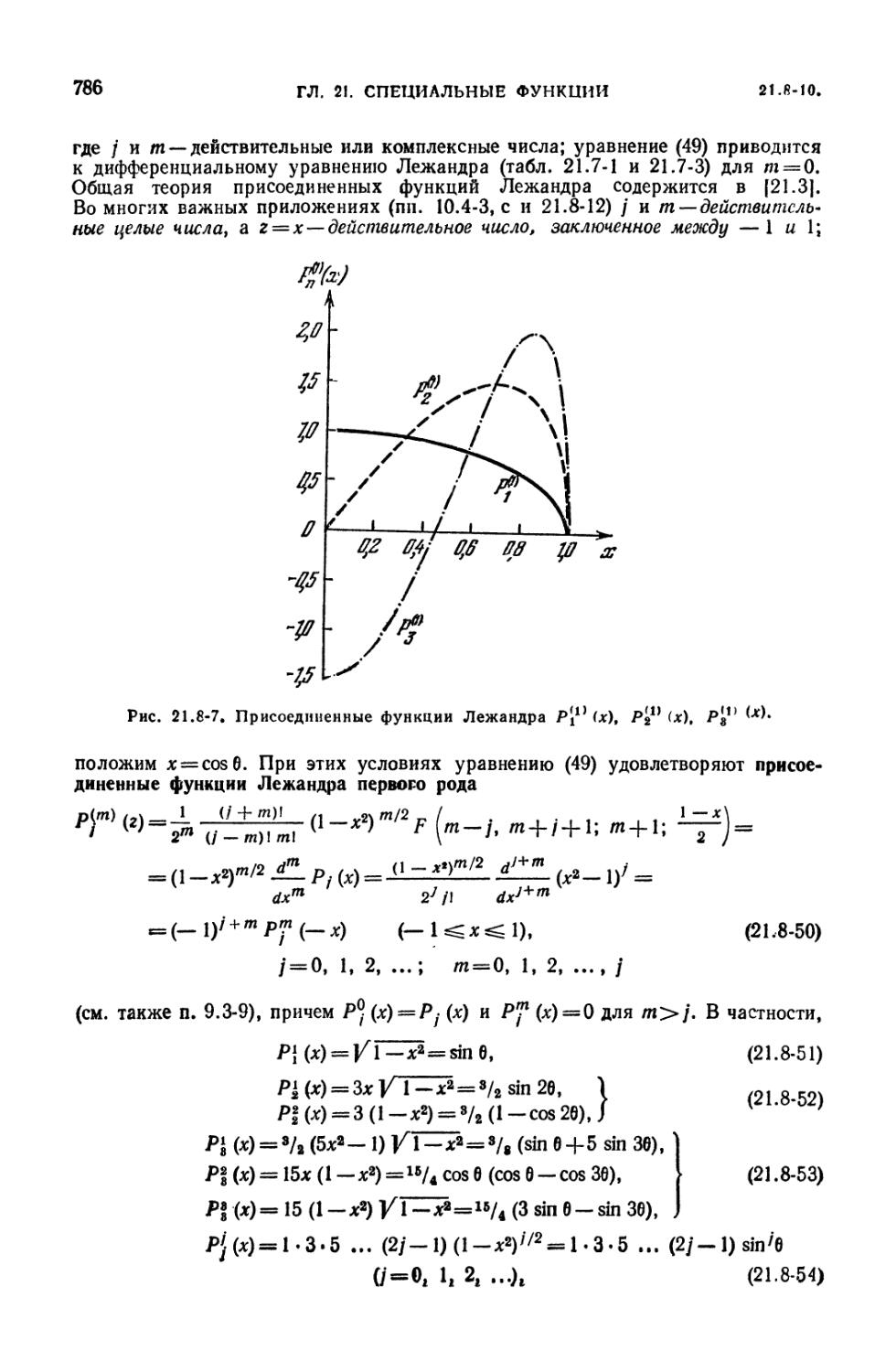
многочлены Лежандра (785). 21.8-11. Интегральные свойства присоединенных
функций Лежандра (787). 21.8-12. Сферические гармоники.
Ортогональность (787). 21.8-13. Теоремы сложения (789).
21.9. Ступенчатые функции и символические импульсные функции 790
21.9-1. Ступенчатые функции (790). 21.9-2. Символическая дельта-функция
Дирака (792). 21.9-3. Производные ступенчатых и импульсных функций
(793). 21.9-4. Аппроксимация импульсных функций (794). 21.9-5.
Представления интегралом Фурье (795). 21.9-6. Асимметричные импульсные
функции (795). 21.9-7. Многомерные дельта-функцин (795).
Литература 796
Указатель важнейших обозначений 801
Предметный указатель 804
ПЕРЕЧЕНЬ ТАБЛИЦ
Глава 1
1.10-1. Правильные многоугольники 47
1.10-2. Тела вращения 48
1.10-3. Пять правильных многогранников 49
1.11-1. Решение плоских треугольников 50
1.12-1. Решение сферических треугольников 54
Глава 2
2.4-1. Классификация кривых второго порядка 65
2.4-2. Касательные, нормали, поляры и полюсы кривых второго порядка ... 68
2.5-1. Эллипс, гипербола и парабола. Канонические уравнения и основные
формулы 72
Глава 3
3.5-1. Классификация поверхностей второго порядка 90
3.5-2. Стандартные (канонические) уравнения и основные свойства
невырожденных поверхностей второго порядка 94
Глава 4
4.5-1. Производные часто встречающихся функций 108
4.5-2. Правила дифференцирования 111
4.6-1. Свойства интегралов 114
4.7-1. Некоторые часто встречающиеся пределы 130
4.8-1. Суммы некоторых числовых рядов 135
4.10-1. Действия со степенными рядами 144
4.11-1. Коэффициенты Фурье и среднеквадратические значения периодических
функций 151
4.11-2. Свойства преобразования Фурье 154
4.11-3. Преобразования Фурье 155
4.11-4. Косинус-преобразования Фурье 158
4.11-5. Синус-преобразования Фурье 159
Глава 5
5.2-1. Свойства скалярного произведения 164
5.2-2. Свойства векторного произведения 165
5.3-1. Дифференцирование векторной функции скалярного аргумента 167
5.5-1. Правила действий с оператором V I72
5.5-2. Операции над скалярными функциями 174
5.5-3. Операции над векторными функциями 174
5.6-1. Теоремы, связывающие объемные и поверхностные интегралы 175
Глава 6
6.3-1. Соотношения между базисными векторами и координатами векторов в
различных локальных системах отсчета 181
ПЕРЕЧЕНЬ ТАБЛИЦ
21
6.4-1. Векторные соотношения в ортогональных координатах 184
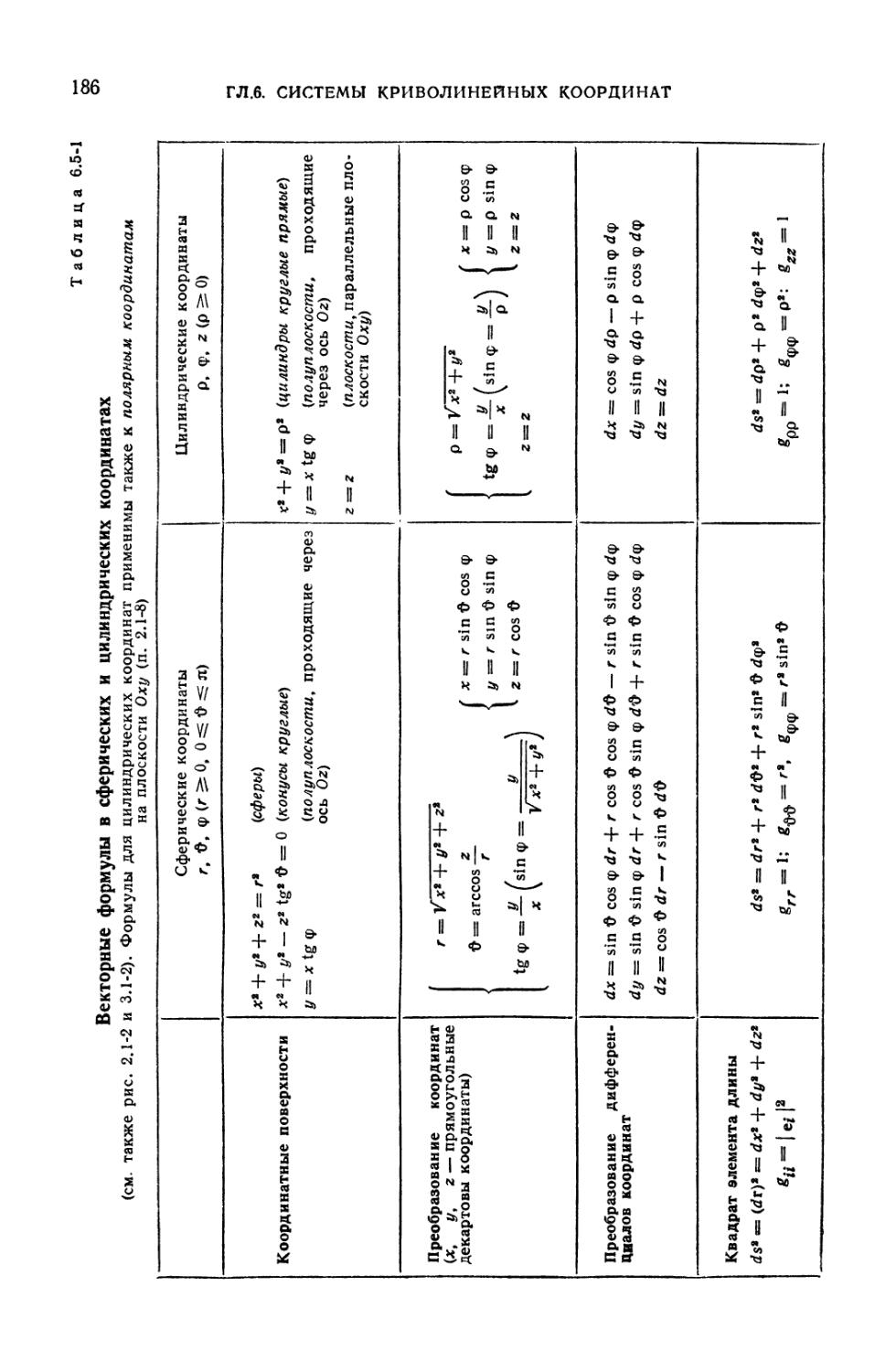
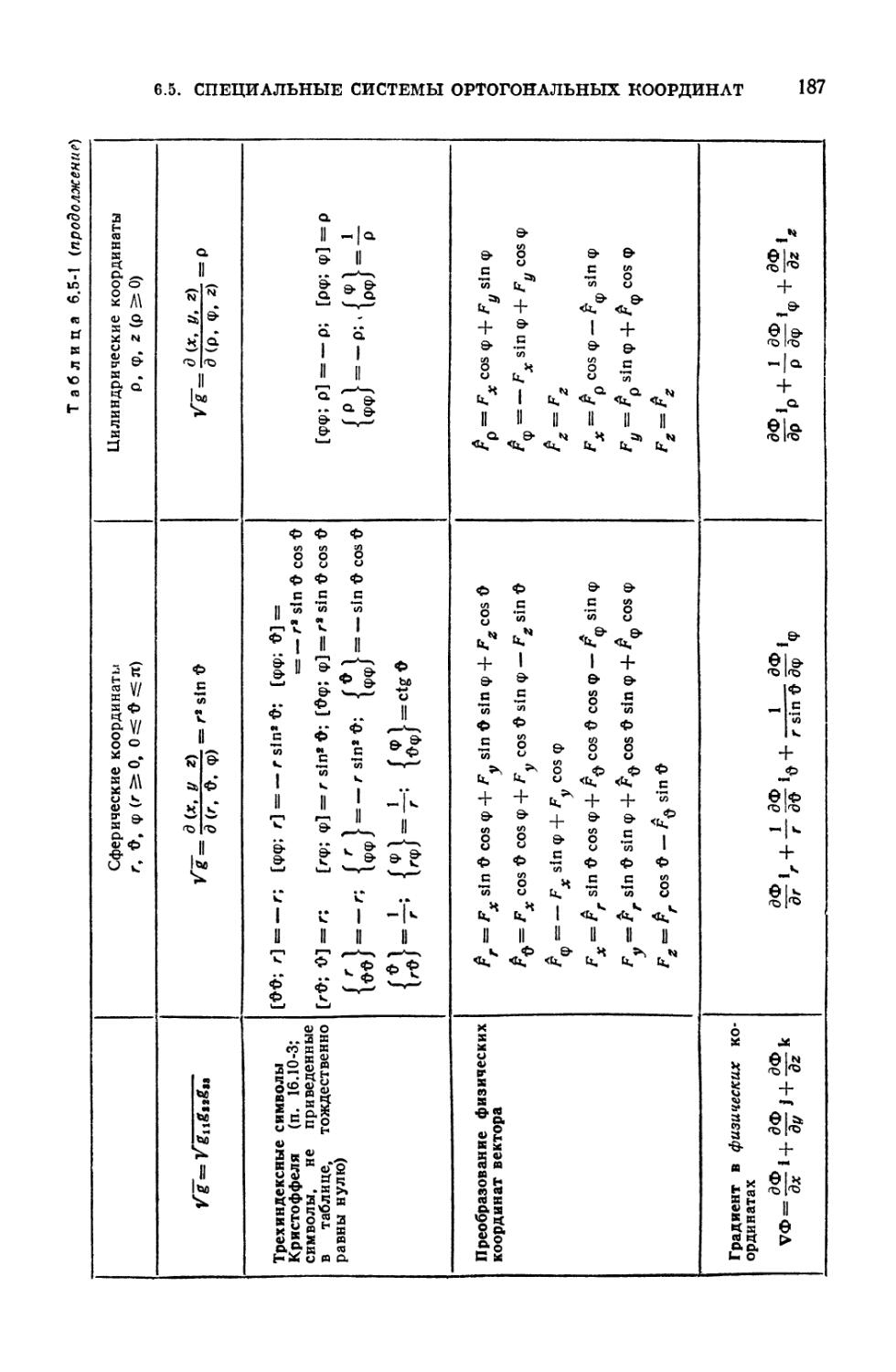
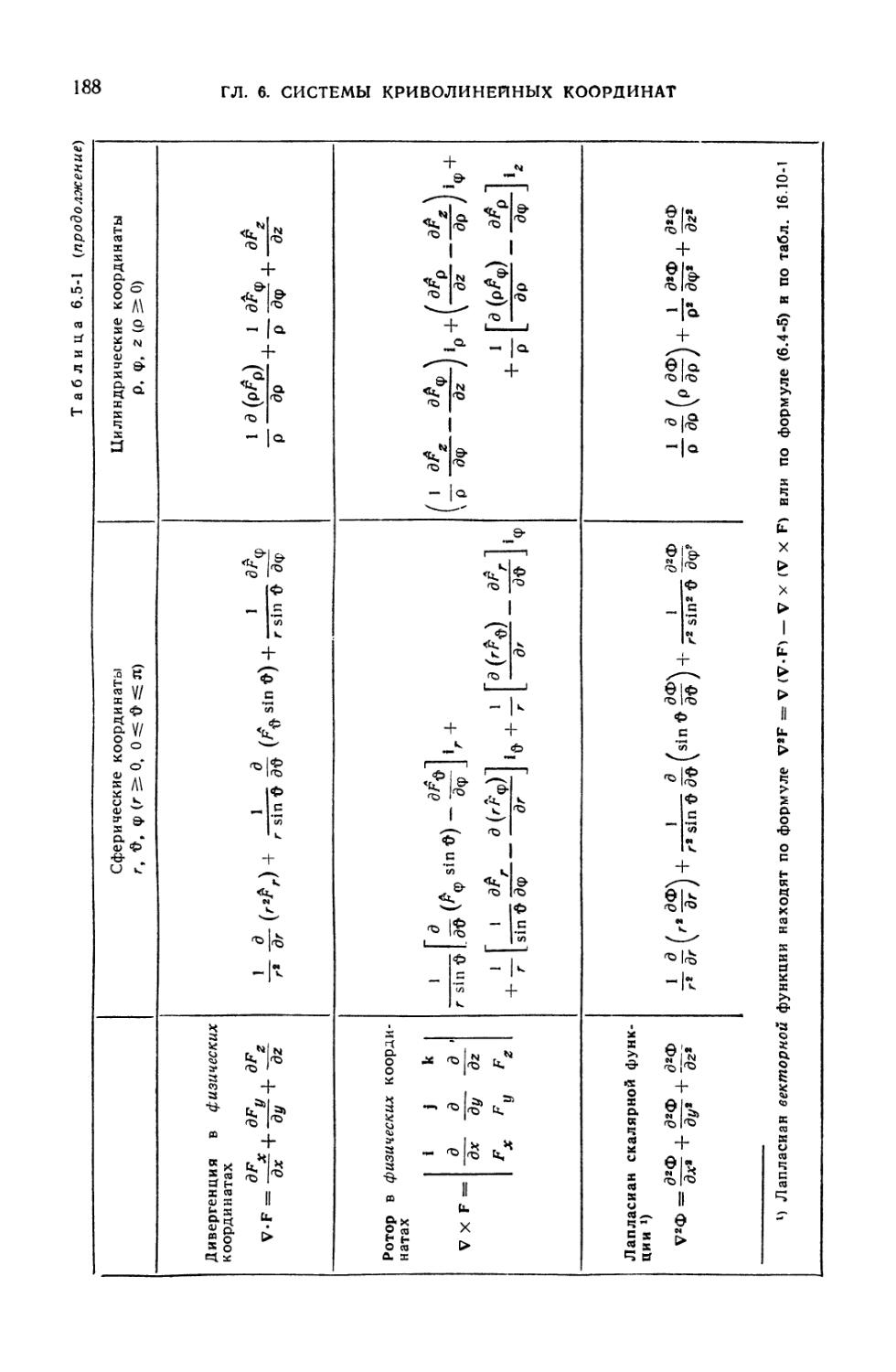
6.5-1. Векторные формулы в сферических и цилиндрических координатах . . . 186
6.5-2. Общие эллипсоидальные координаты А,, ц, v 189
6.5-3. Координаты о, т, Ф вытянутого эллипсоида вращения 190
6.5-4. Координаты о, т, Ф сплюснутого эллипсоида вращения 191
6.5-5. Координаты о, т, z эллиптического цилиндра 191
6.5-6. Конические координаты и, v, w 192
6.5-7. Параболоидальные координаты К, ц, v 192
6.5-8. Параболические координаты а, т, ф 193
6.5-9. Координаты 0, т, z параболического цилиндра 193
6.5-10. Бицилиндрические координаты о, т, z 194
6.5-11. Тороидальные координаты а, т, ф 195
6.5-12. Биполярные координаты о, т, Ф 195
Глава 7
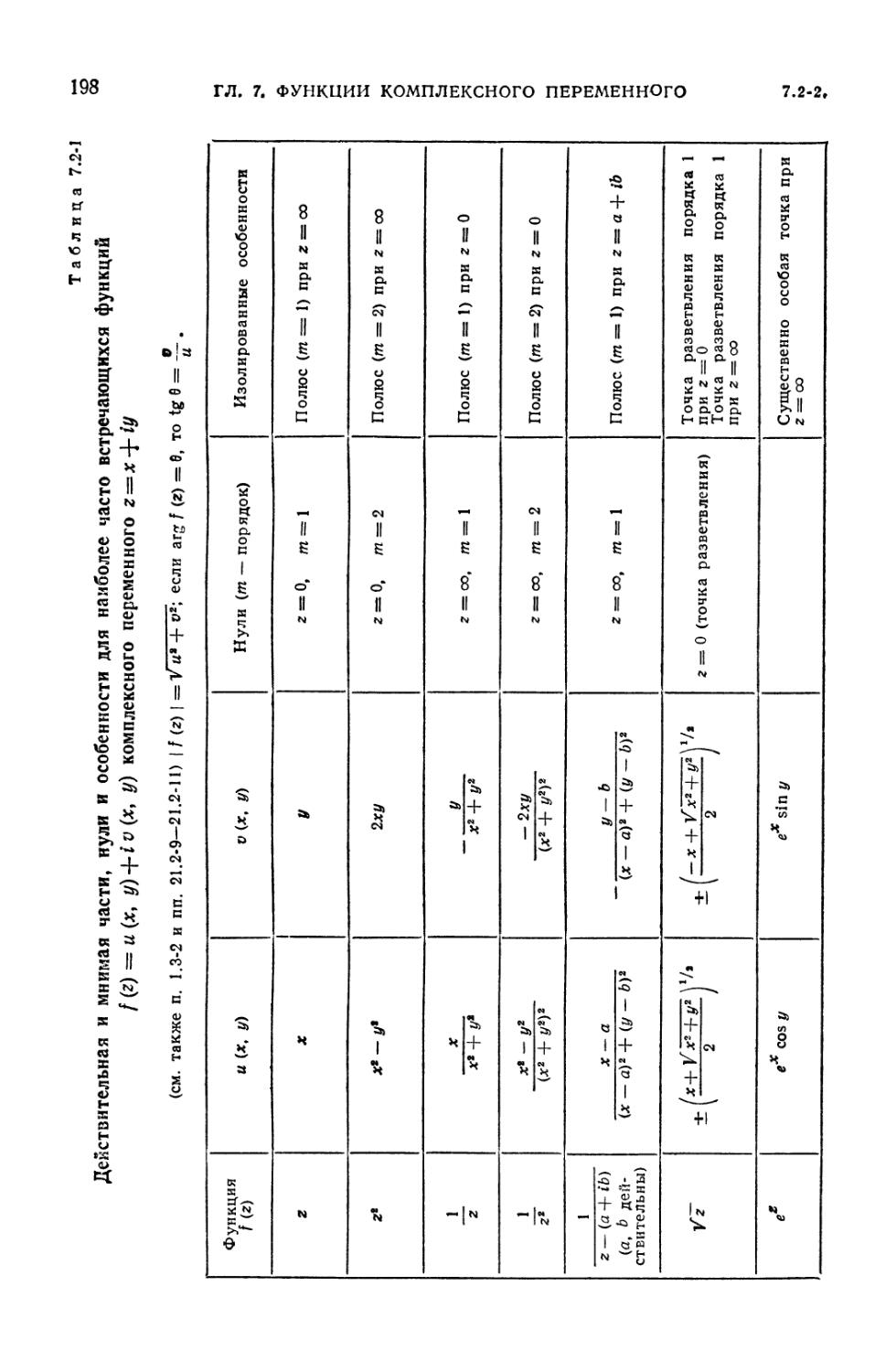
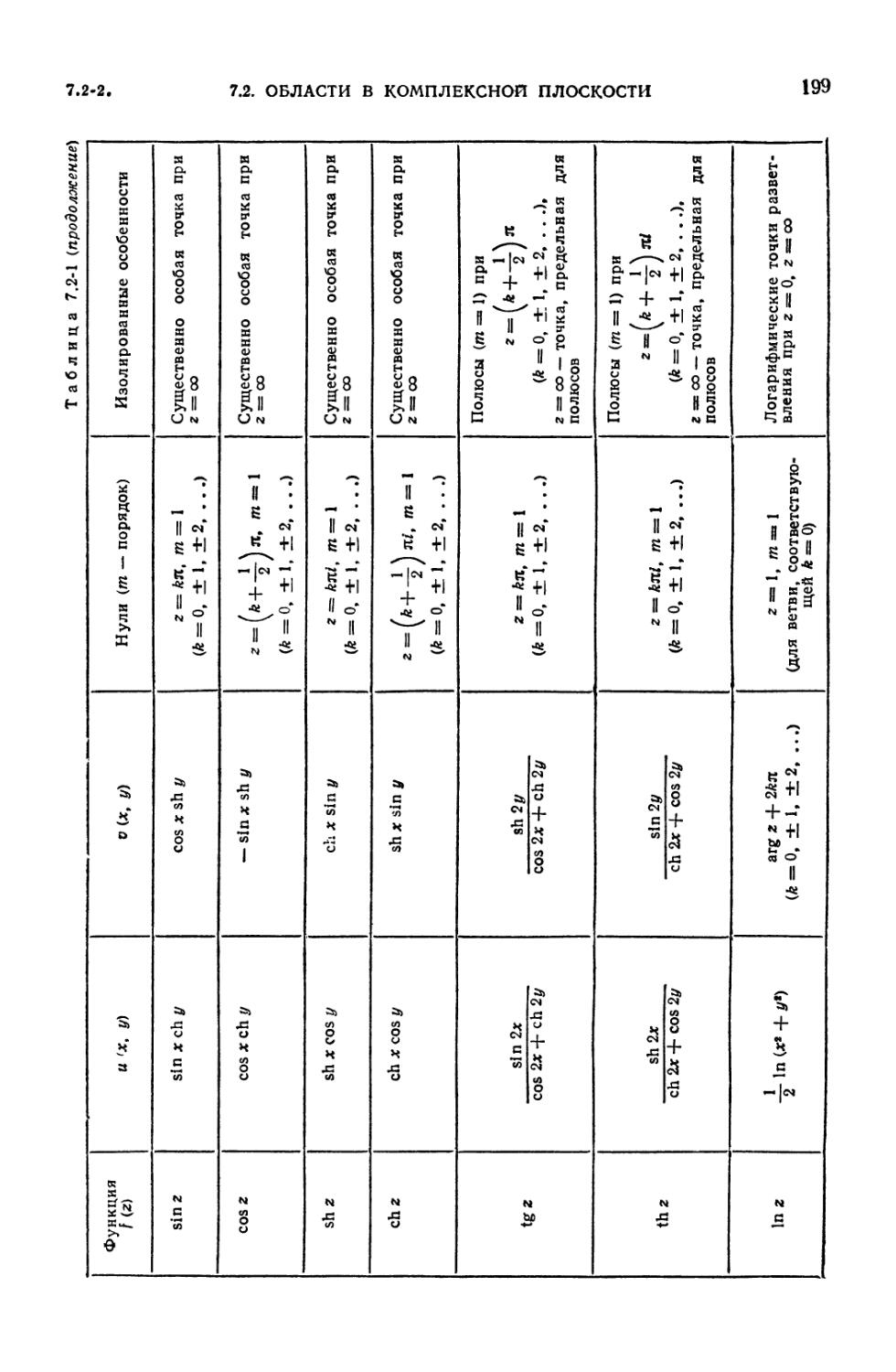
7.2-1. Действительная и мнимая части, нули и особенности для наиболее часто
встречающихся функций f (z) = и (х, у) + iv (x, у) комплексного
переменного z = х 4- iy 198
7.9-1. Свойства отображения w *=—(z -\ ) 218
7.9-2. Примеры конформных отображений 219
7.9-3. Конформные отображения некоторых областей D на единичный круг . . . 226
Глава 8
8.3-1. Теоремы соответствия операций над оригиналами и изображениями . . . 231
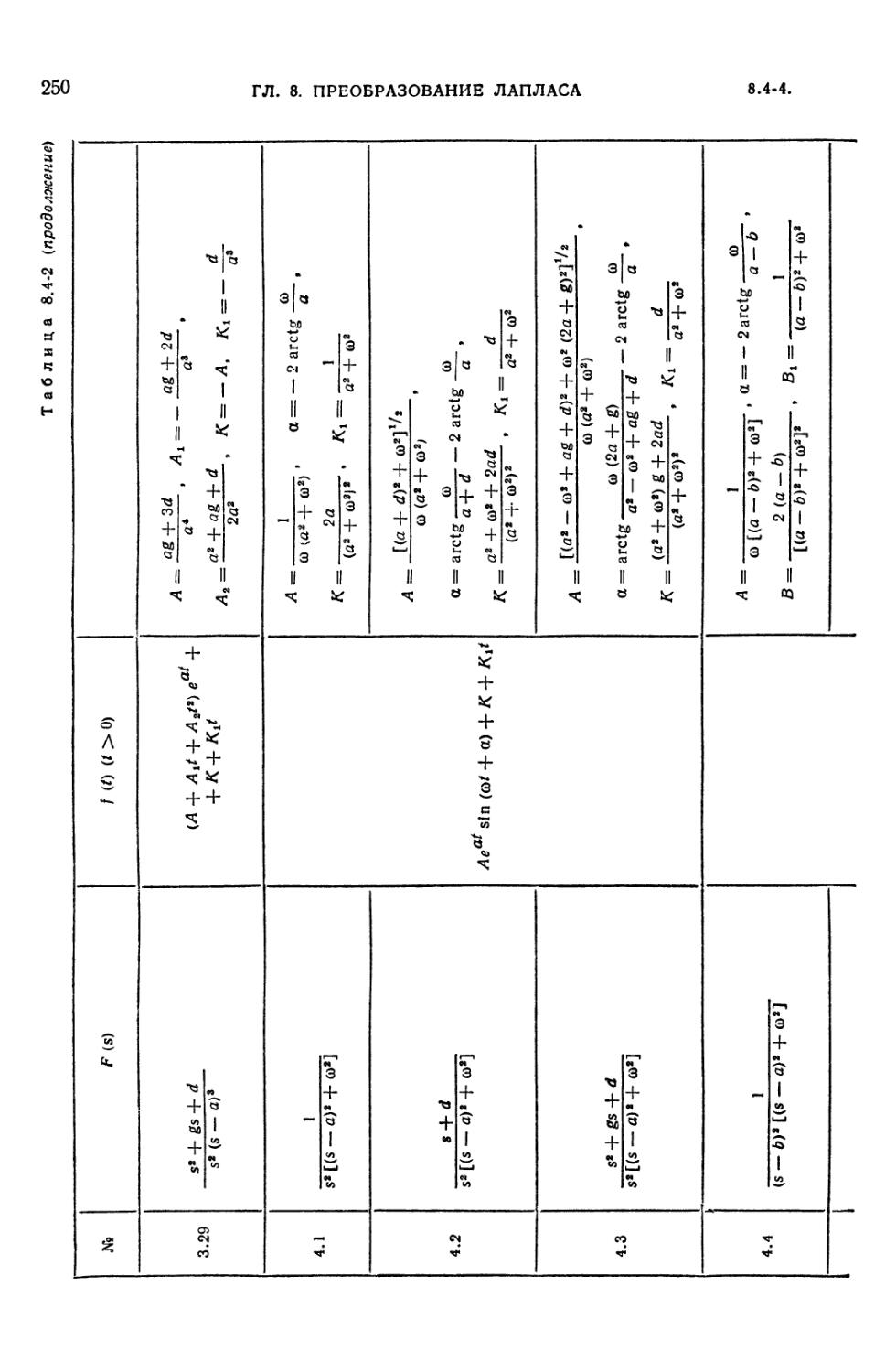
8.4-1. Таблица преобразований Лапласа 235
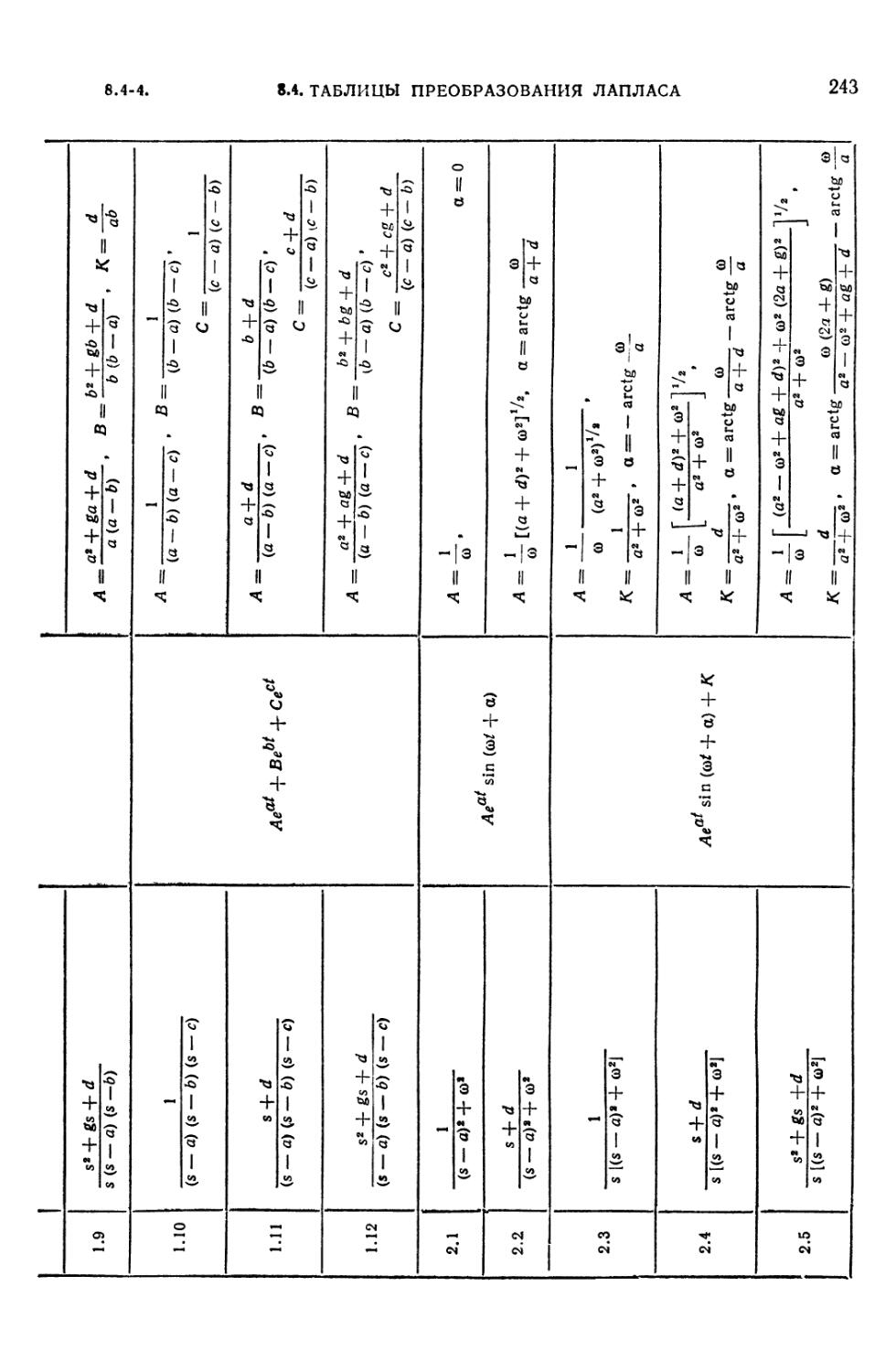
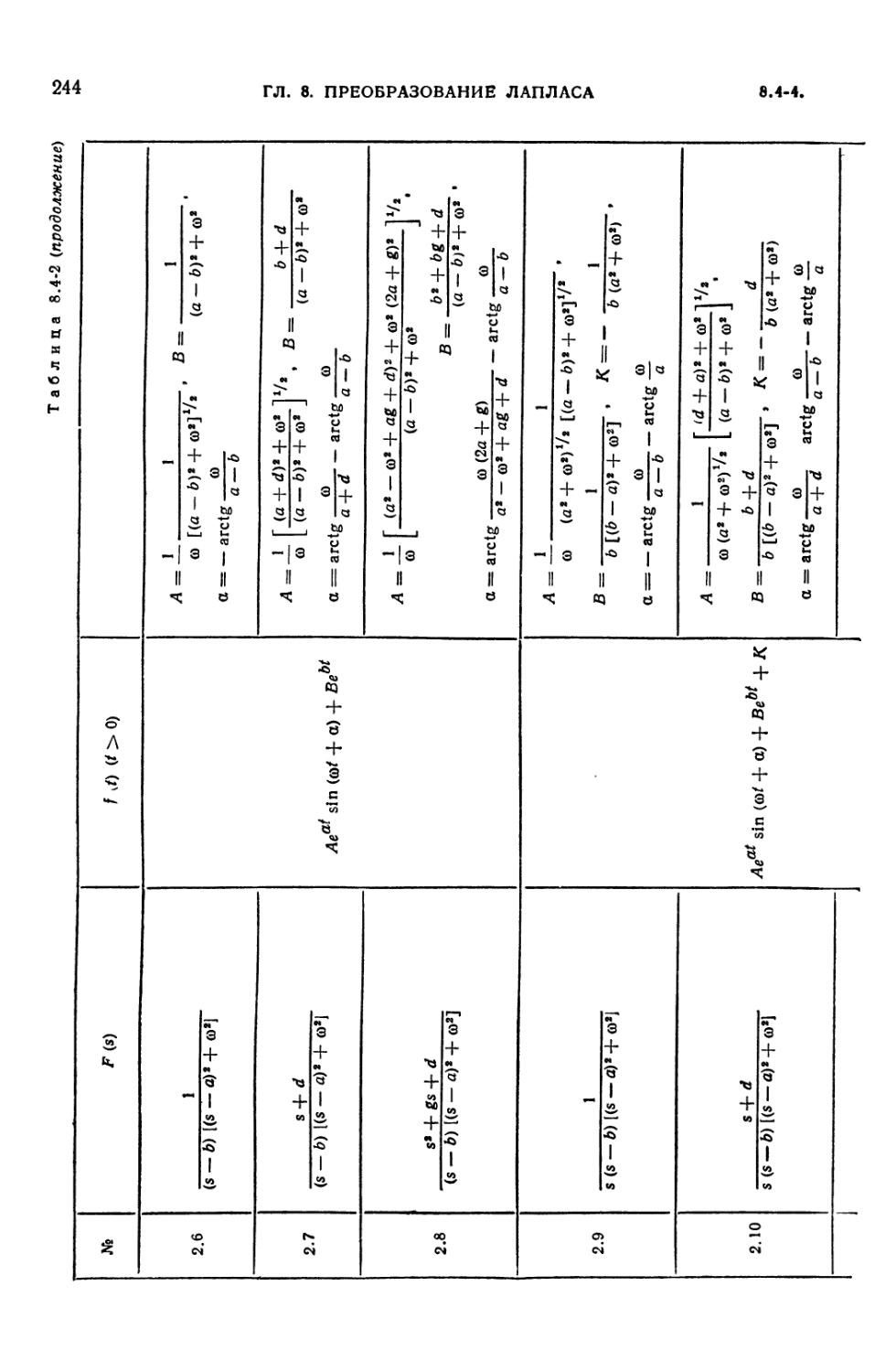
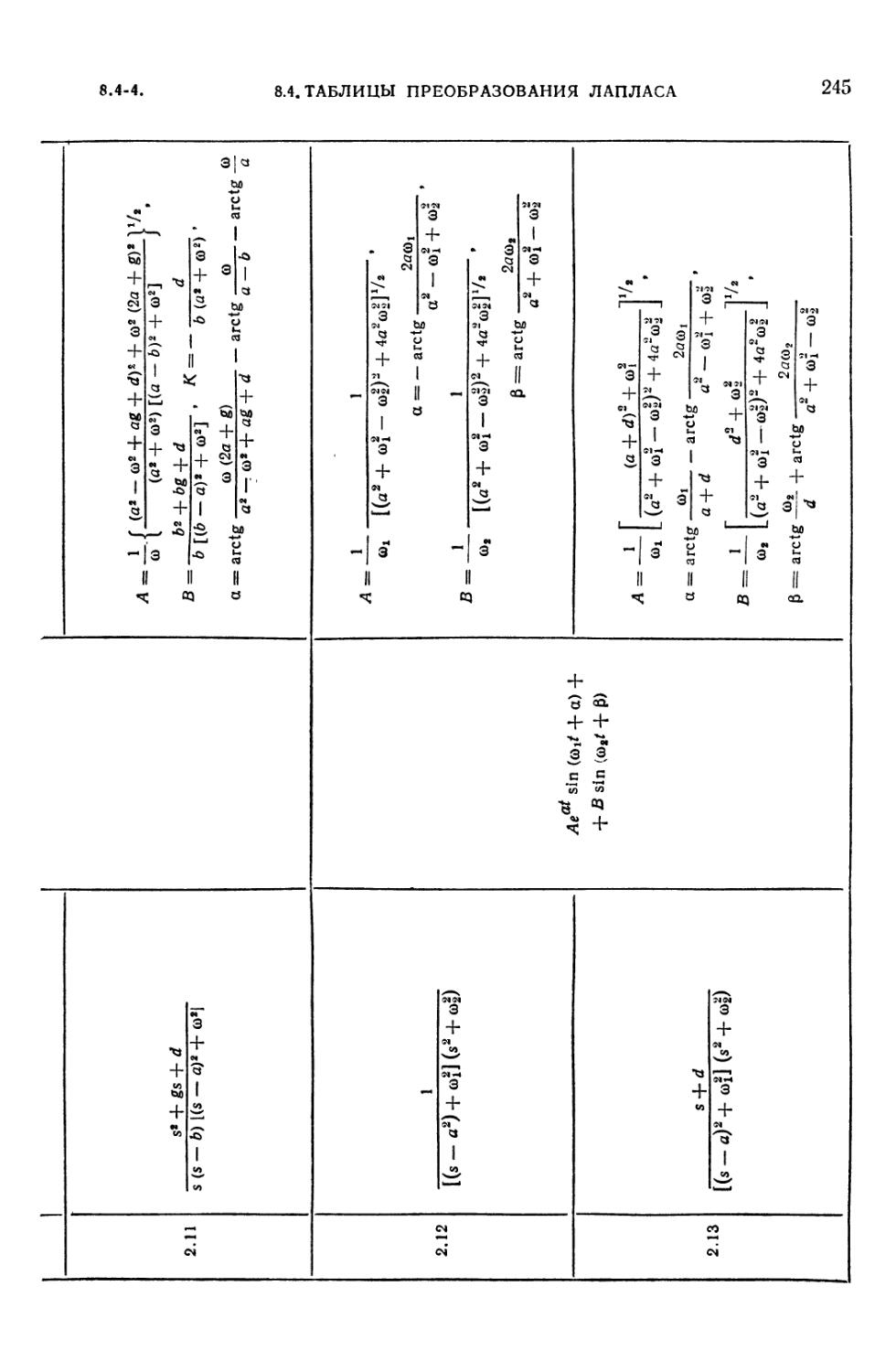
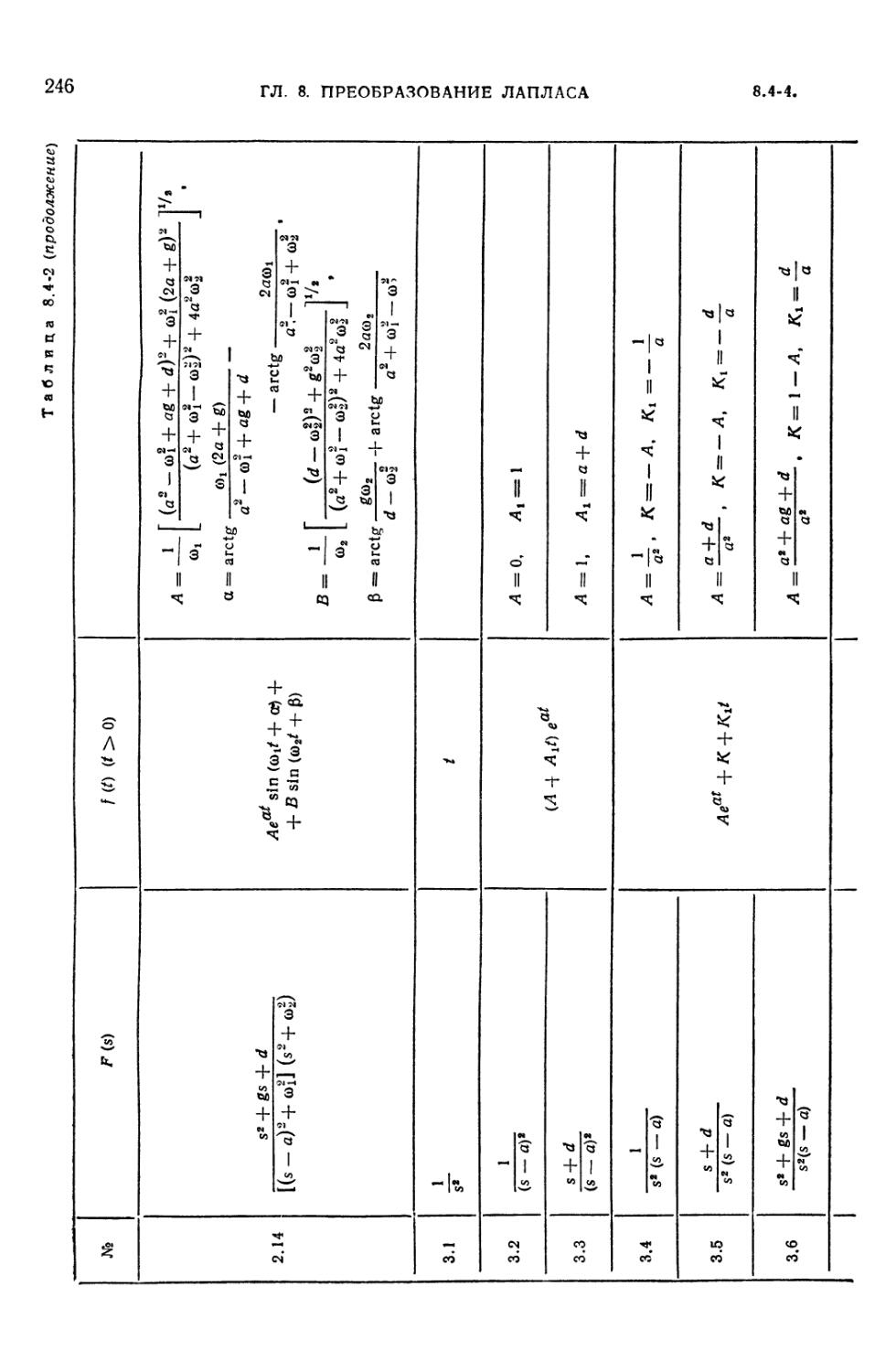
8.4-2. Таблица преобразований Лапласа для рациональных изображений F (s) =
= Dx (s)/D (s) 242
8.6-1. Некоторые линейные интегральные преобразования, связанные с
преобразованием Лапласа 257
8.6-2. Преобразования Ганкеля 259
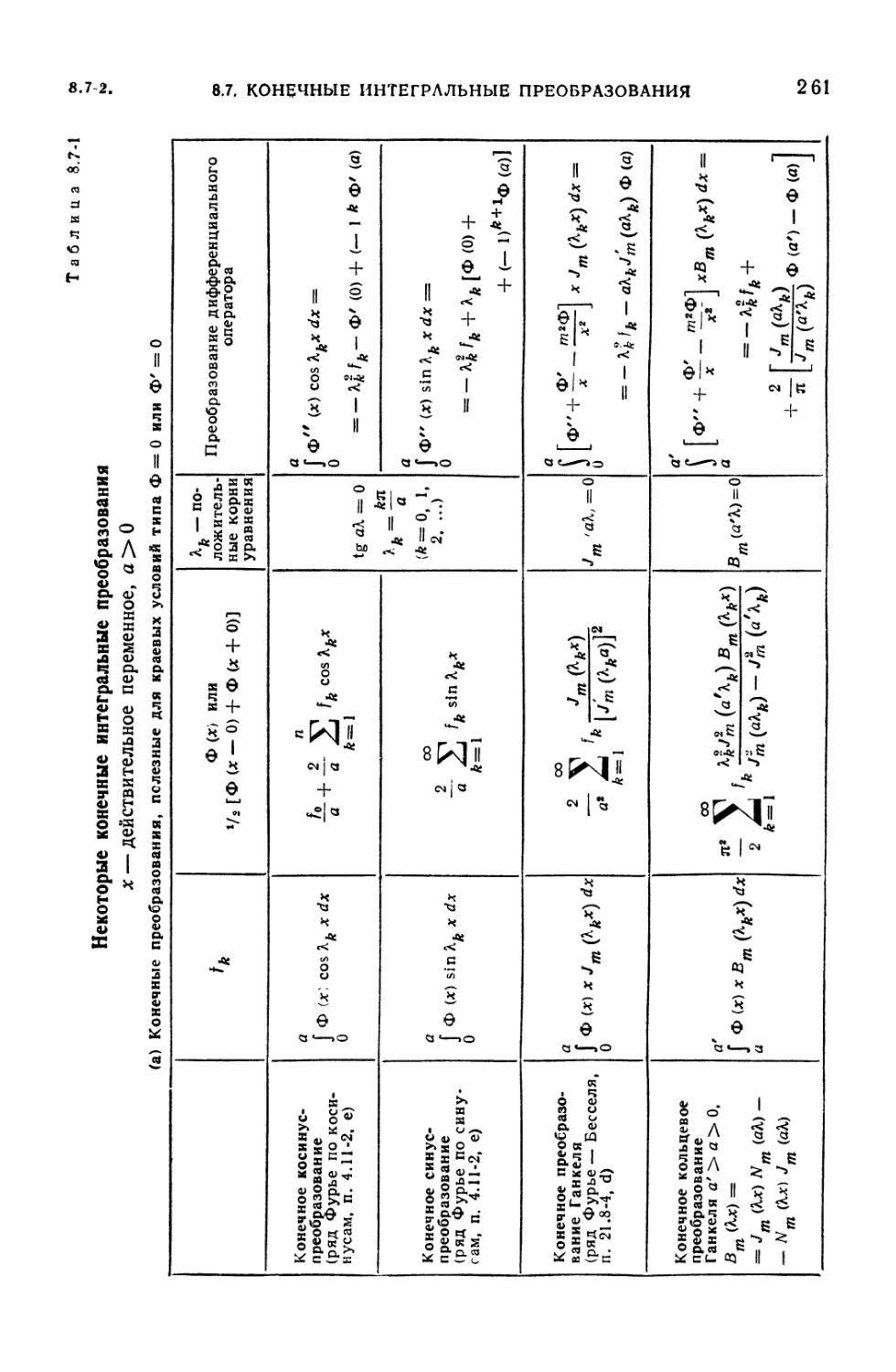
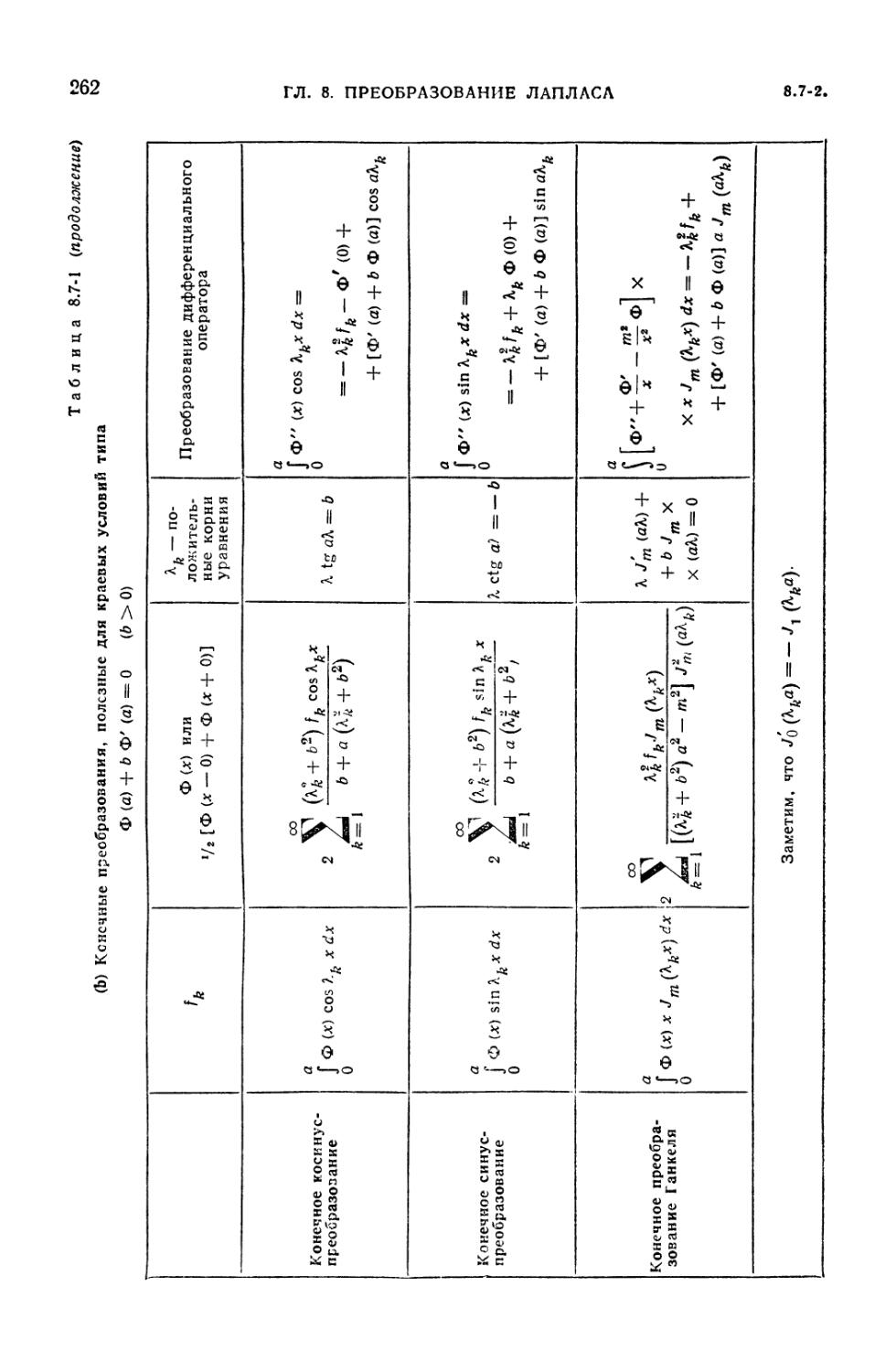
8.7-1. Некоторые конечные интегральные преобразования 261
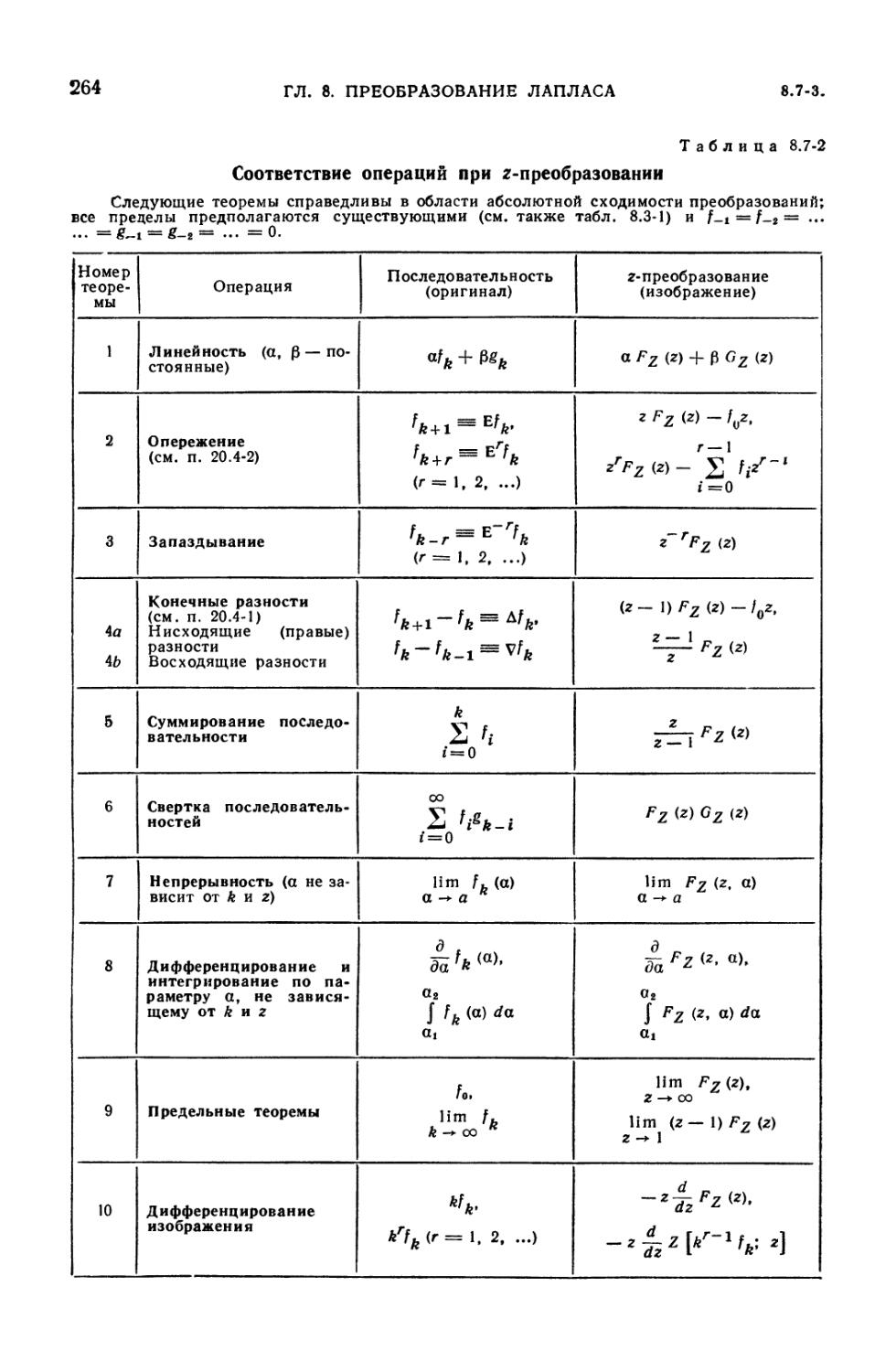
8.7-2. Соответствие операций при ^-преобразовании 264
Глава 9
9.3-1. Функции Грина для линейных краевых задач 274
9.3-2. Дополнительные формулы для гипергеометрических функций 281
9.3-3. Дополнительные формулы для вырожденных гипергеометрических
функций 283
Глава 10
10.2-1. Полные интегралы для некоторых специальных типов уравнений с
частными производными первого порядка 304
10.4-1. Важнейшие линейные дифференциальные уравнения математической
физики 320
Глава 12
12.5-1. Некоторые пространства числовых последовательностей 380
12.5-2. Некоторые пространства функций х (t), у (t) 381
12.8-1. Истинностная таблица для булевой функции 389
Глава 13
13.2-1. Некоторые нормы матриц 391
Глава 14
14.7-1. Сравнение различных обозначений скаляров, векторов и линейных
операторов 432
Глава 16
16.2-1. Определения тензорных величин наиболее распространенного типа,
основанные на законе преобразования их компонент 497
16.10-1. Дифференциальные инварианты, определенные в римановых
пространствах 516
Глава 18
18.2-1. Вероятности логически связанных событий 541
18.3-1. Числовые характеристики одномерных распределений вероятностей .... 545
22
ПЕРЕЧЕНЬ ТАБЛИЦ
8.7-1. Перестановки и разбиения 567
8.7-2. Сочетания и выборки 568
8.7-3. Размещения в ячейках или расположения 568
8.8-1. Вырожденное (причинное) распределение 571
8.8-2. Гипергеометрическое распределение 571
8.8-3. Биномиальное распределение 572
8.8-4. Распределение Пуассона 574
8.8-5. Геометрическое распределение 574
8.8-6. Распределение Паскаля 574
8.8-7. Распределение Пойа 575
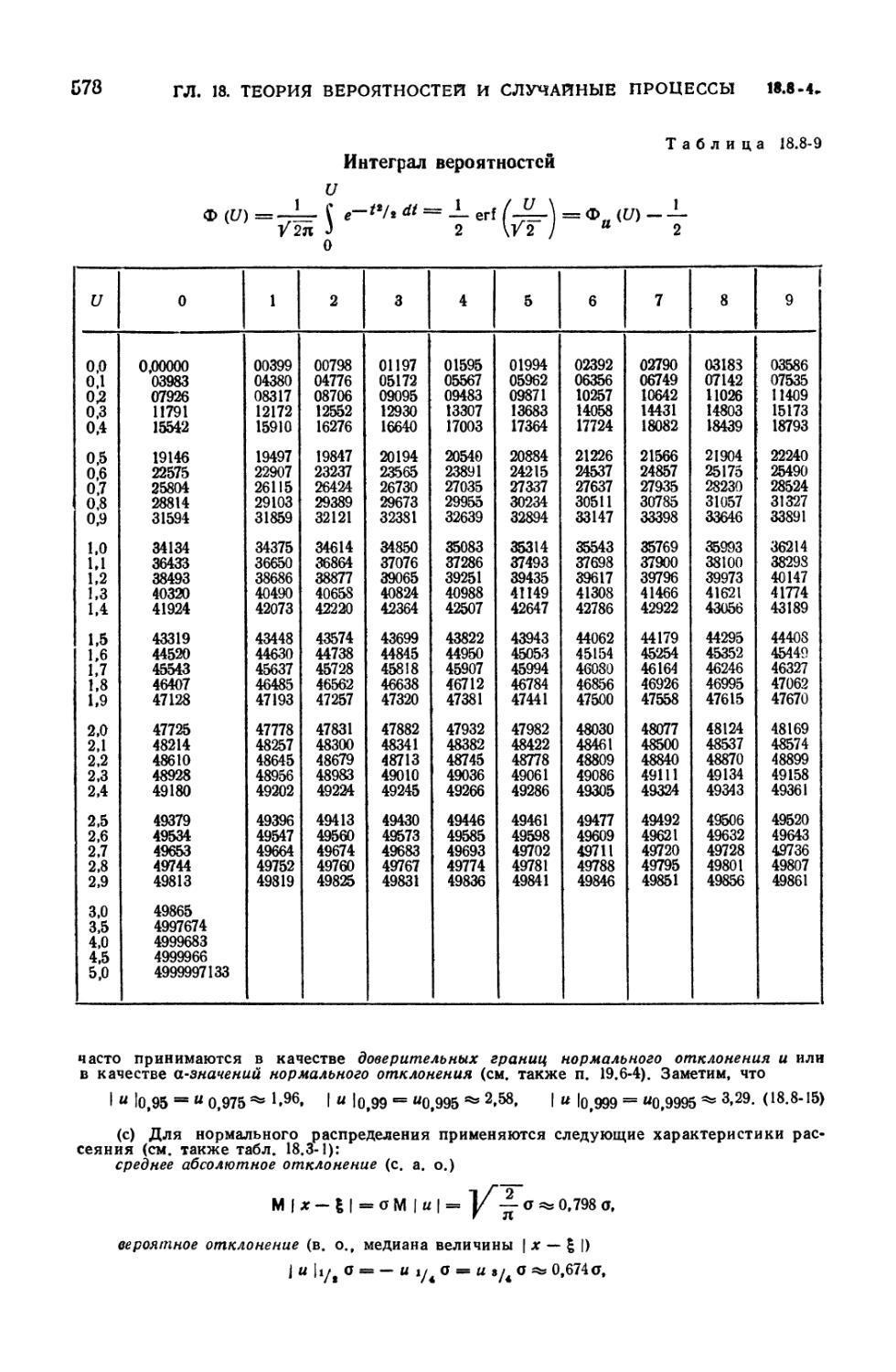
8.8-8. Плотность нормального распределения (стандартизованного) 577
8.8-9. Интеграл вероятностей 578
8.8.10. Функция ошибок 579
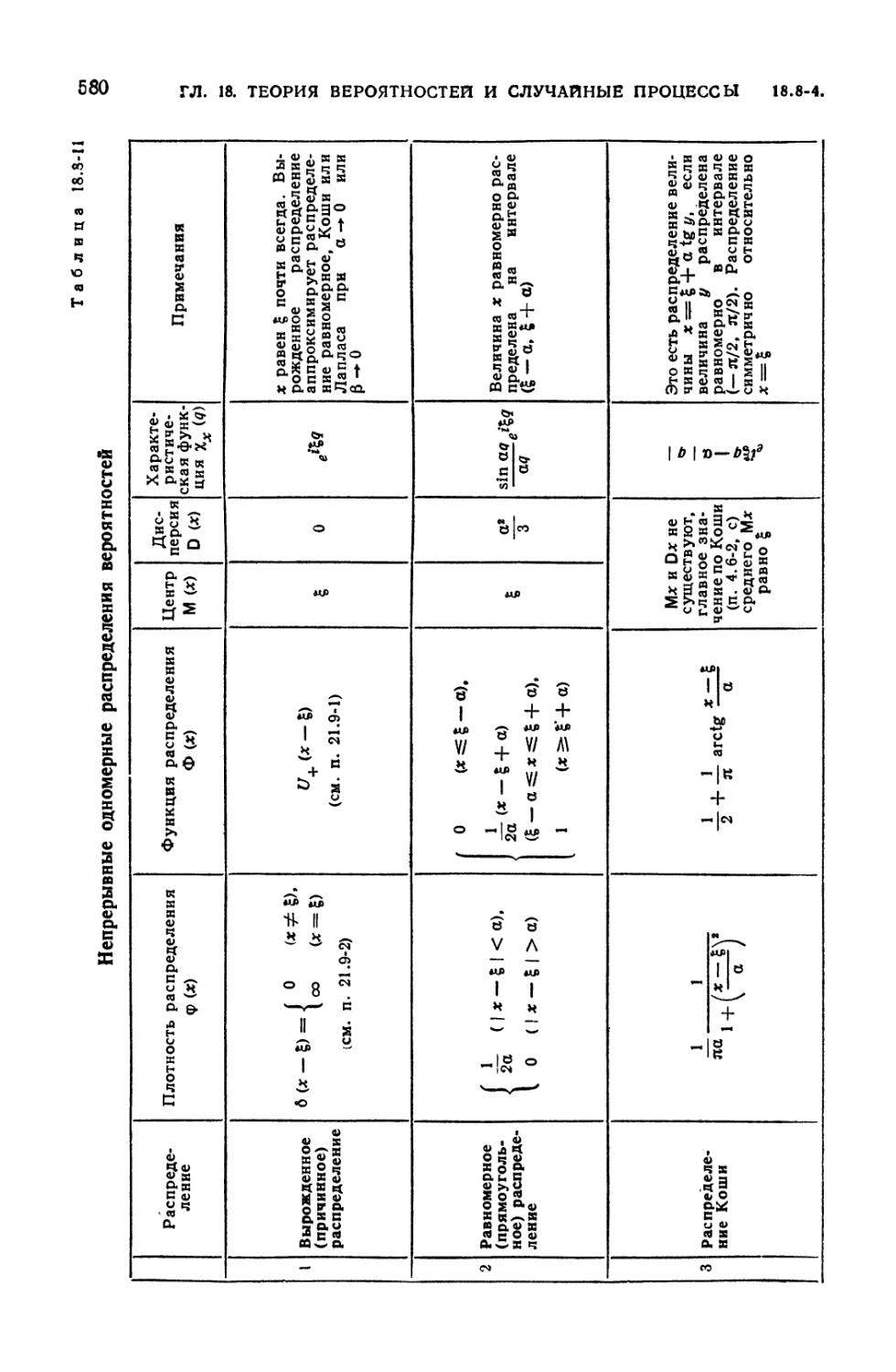
8.8-11. Непрерывные одномерные распределения вероятностей 580
Глава 19
19.5-1. х2-распределение с т степенями свободы 621
19.5-2. /-распределение Стьюдента с т степенями свободы 622
19.5-3. Распределение отношения дисперсий (^-распределение) и связанные с ним
распределения 623
19.5-4. ^-распределение 625
19.5-5. /-распределение Стьюдента 626
19.5-6. ^-распределение (распределение vz) 627
19.6-1. Некоторые критерии значимости, относящиеся к параметрам £, о2
нормальной совокупности 633
19.6-2. Доверительные границы для нормальной совокупности 634
19.6-3. Критерии значимости для сравнения нормальных совокупностей 636
19.8-1. Усредняющие фильтры 644
Глава 20
20.2-1. Таблица алгоритма разделенных разностей 657
20.4-1. Краткая таблица z-преобразований и преобразований Лапласа от
ступенчатых функций 673
20.5-1. Интерполяционные формулы с центральными разностями 678
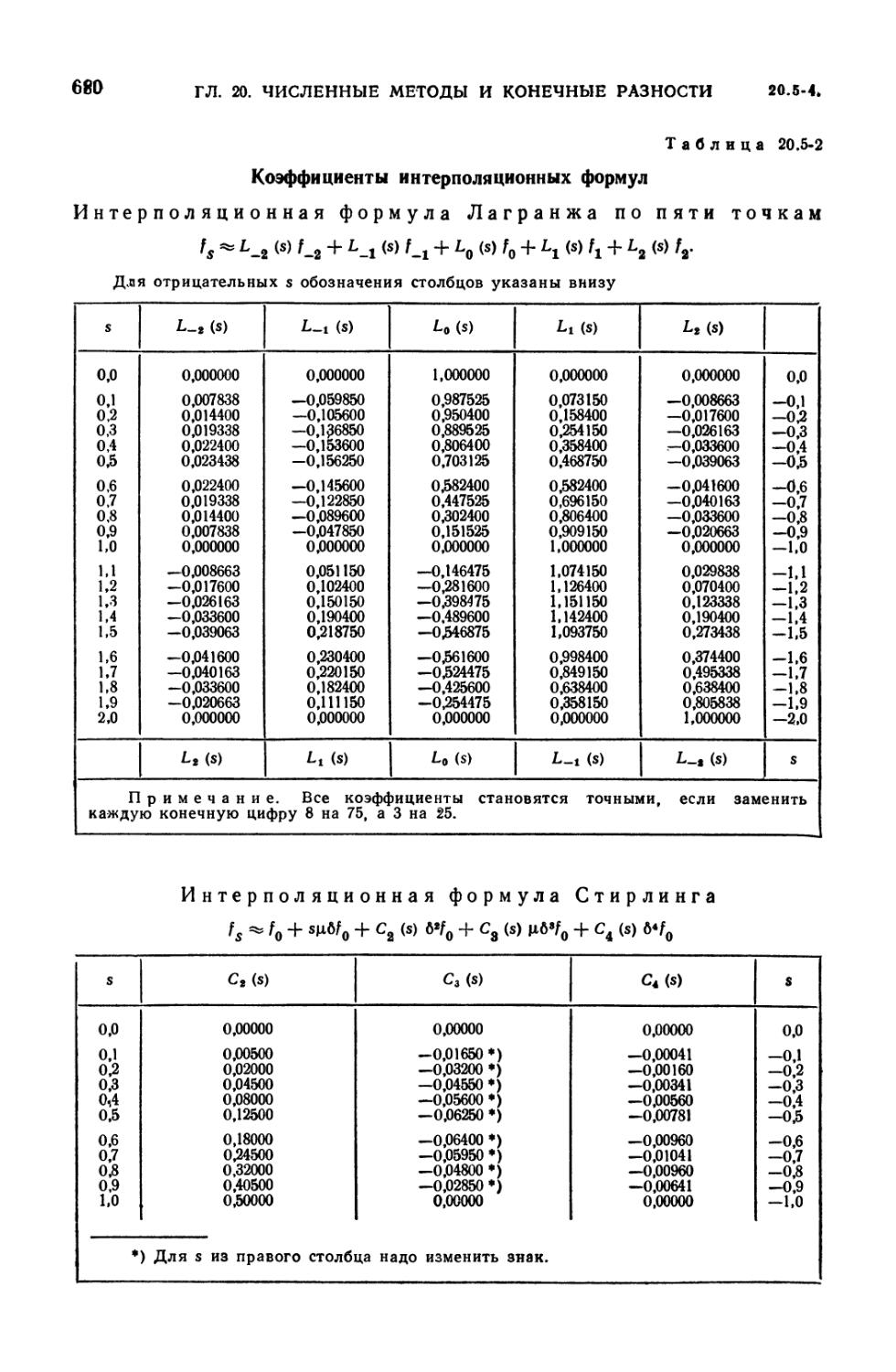
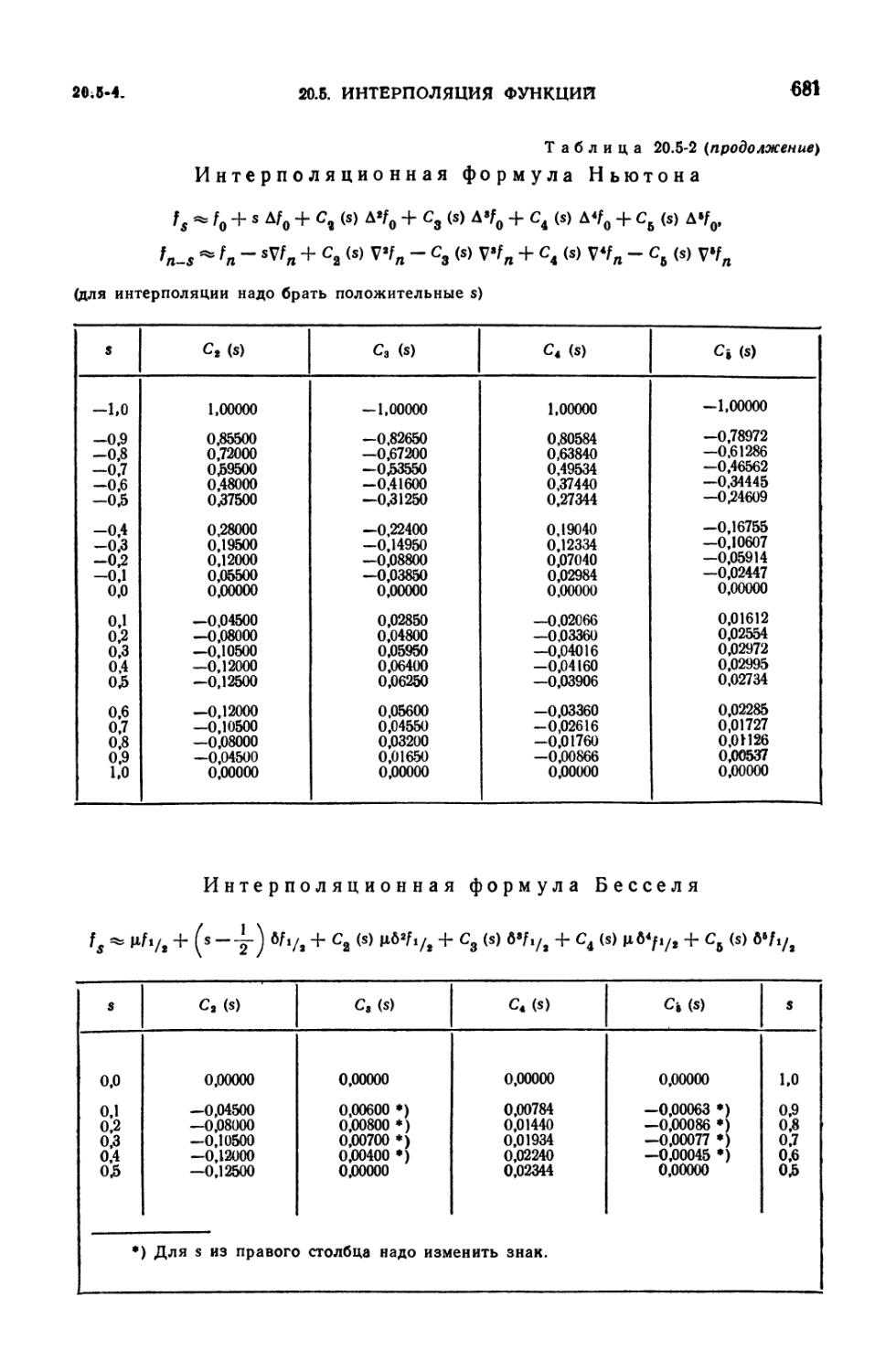
20.5-2. Коэффициенты интерполяционных формул 680
20.6-1. Многочлены Чебышева и степени х 687
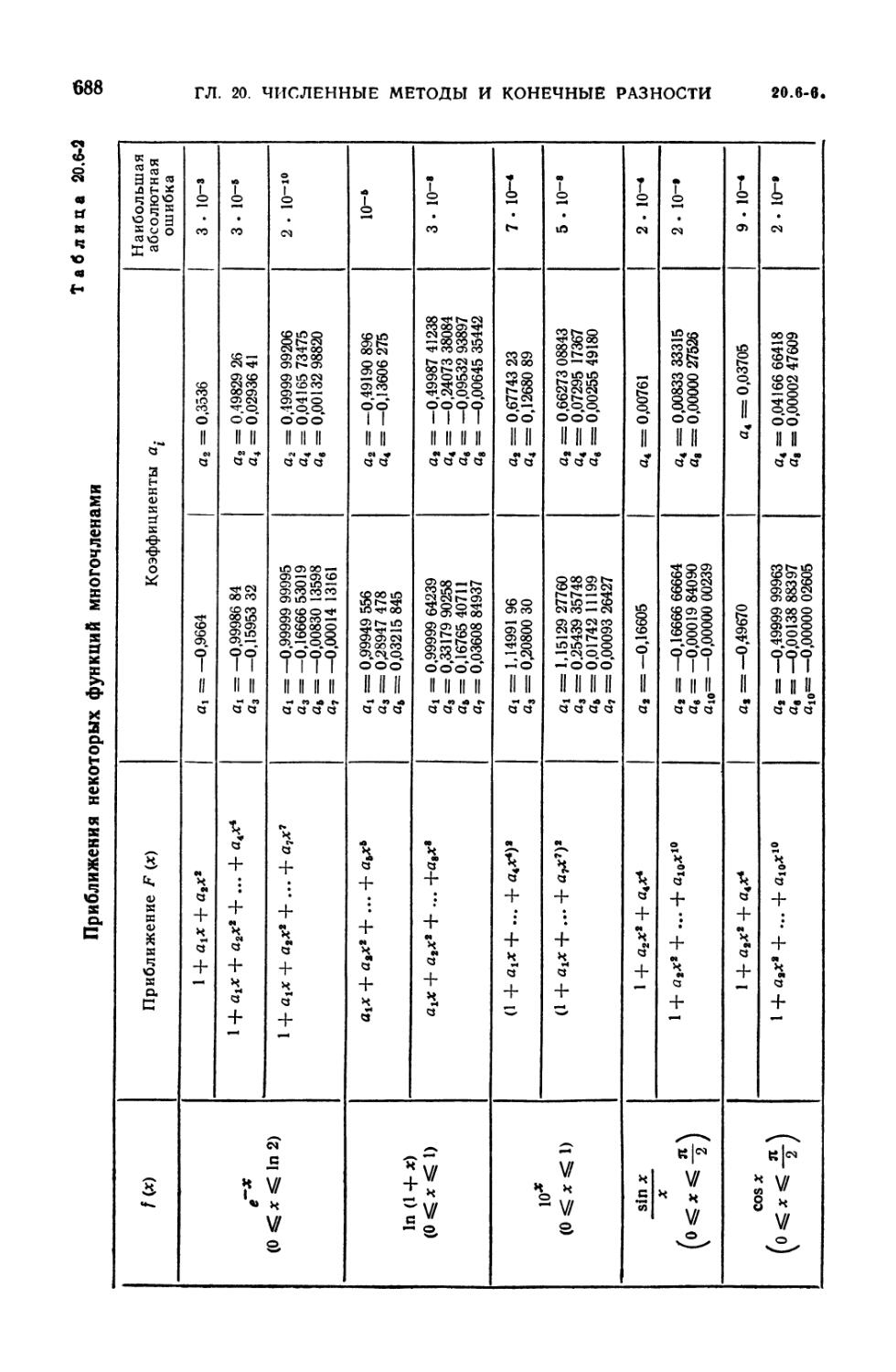
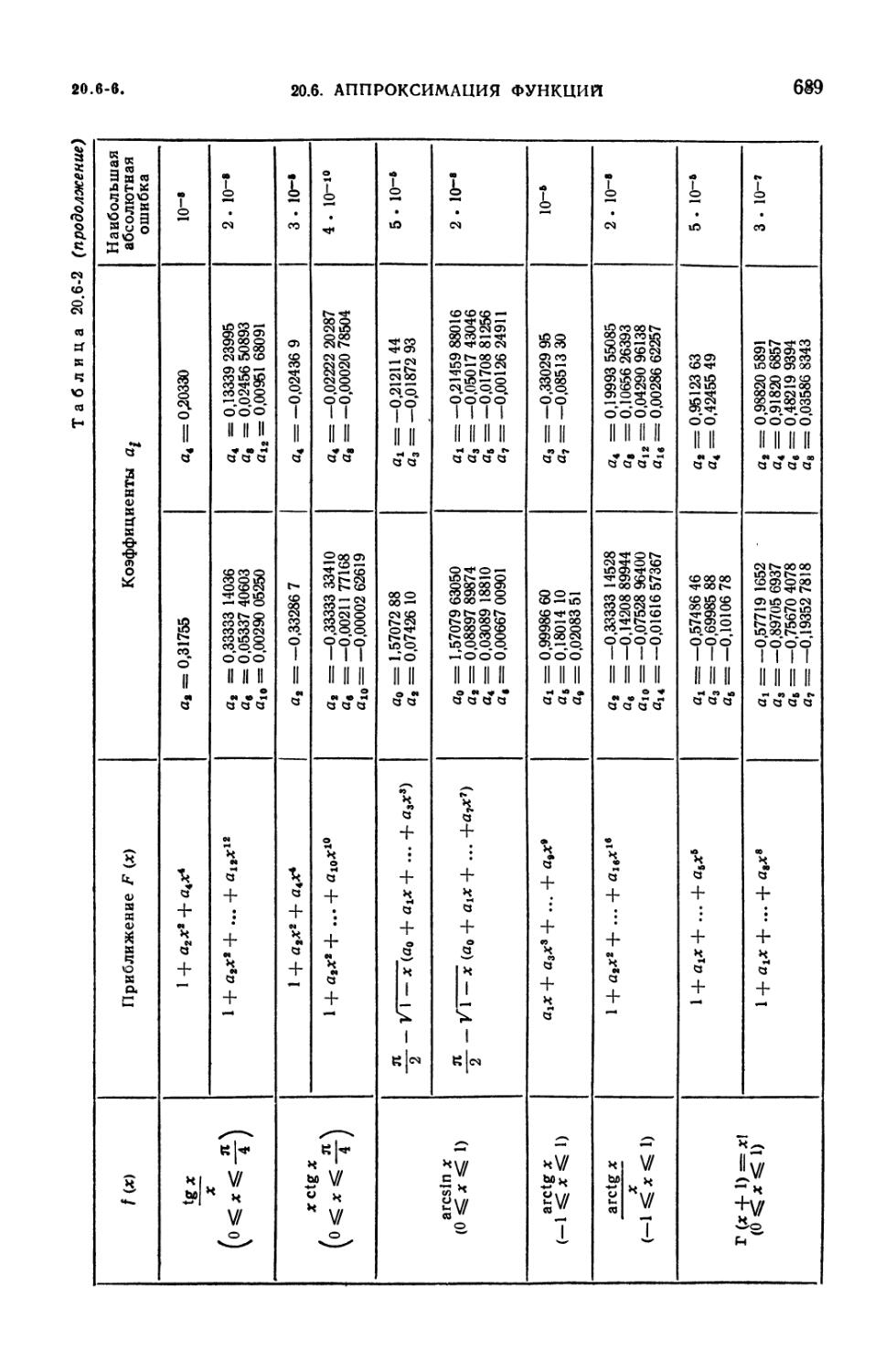
20.6-2. Приближения некоторых функций многочленами 688
20.6-3. Некоторые приближения цилиндрических функций 690
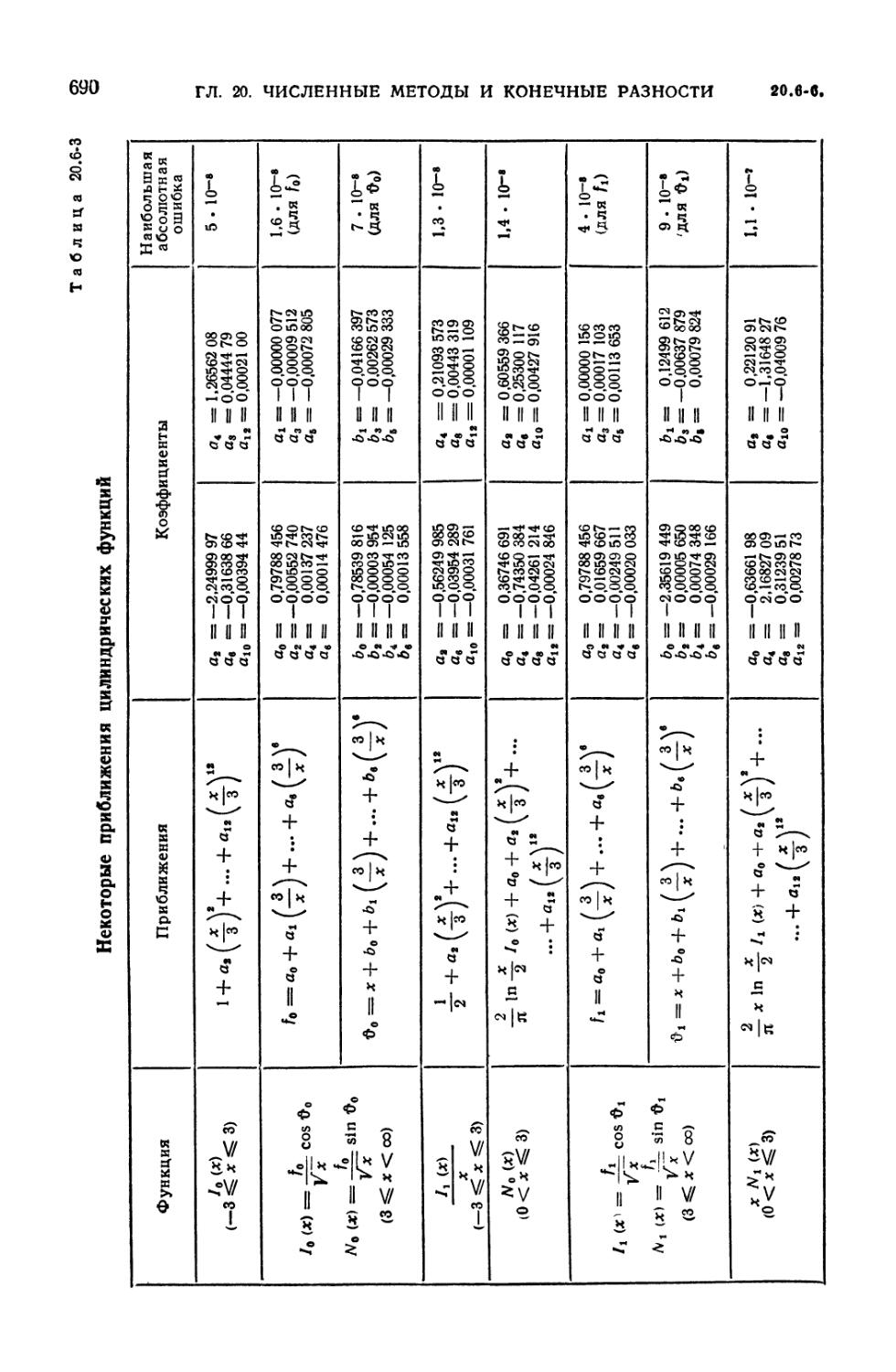
20.6-4. Приближения многочленами Чебышева 691
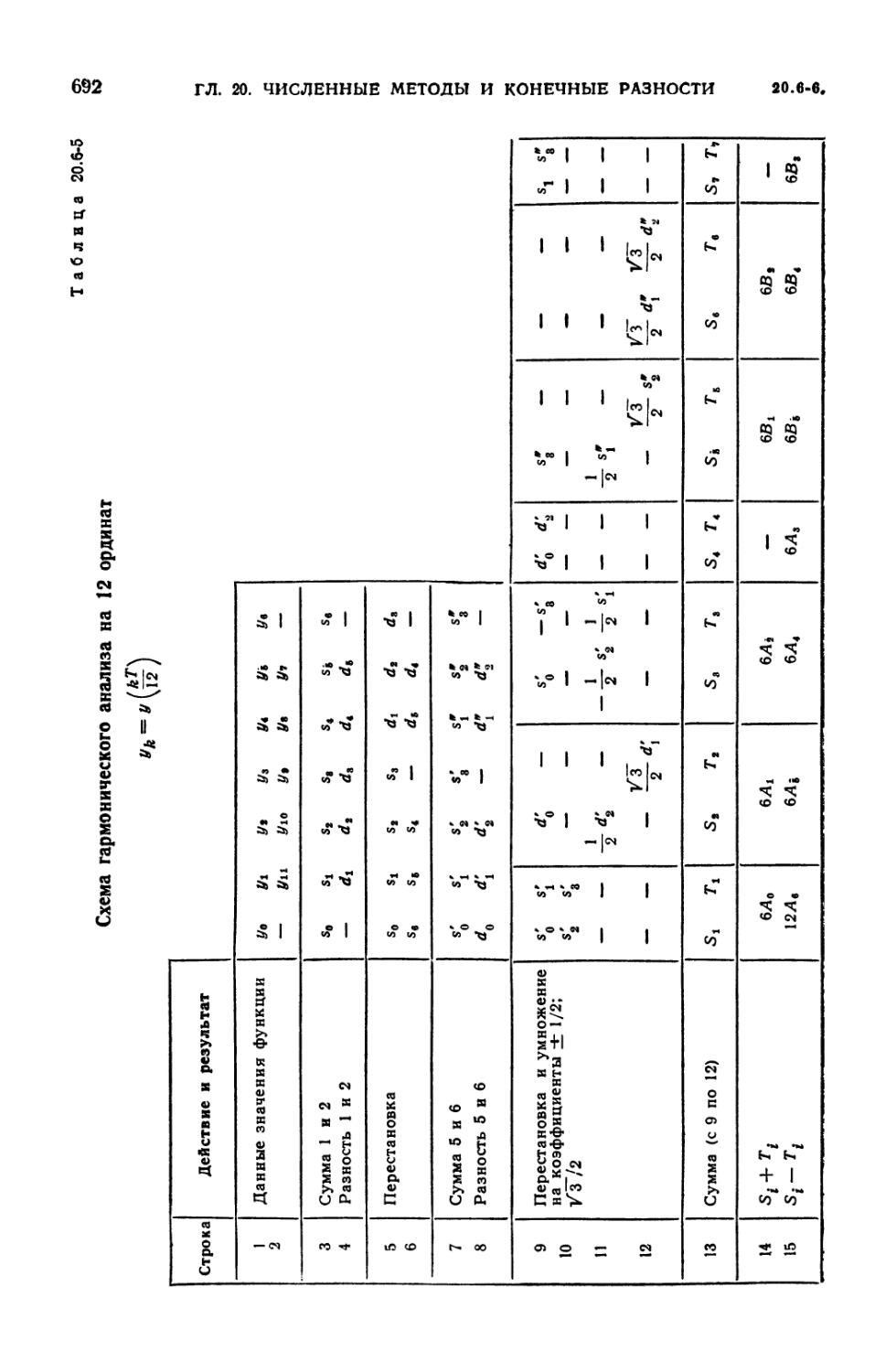
20.6-5. Схема гармонического анализа на 12 ординат 692
20.6-6. Разные приближения 694
20.7-1. Квадратурные формулы Ньютона — Котеса, замкнутый тип 697
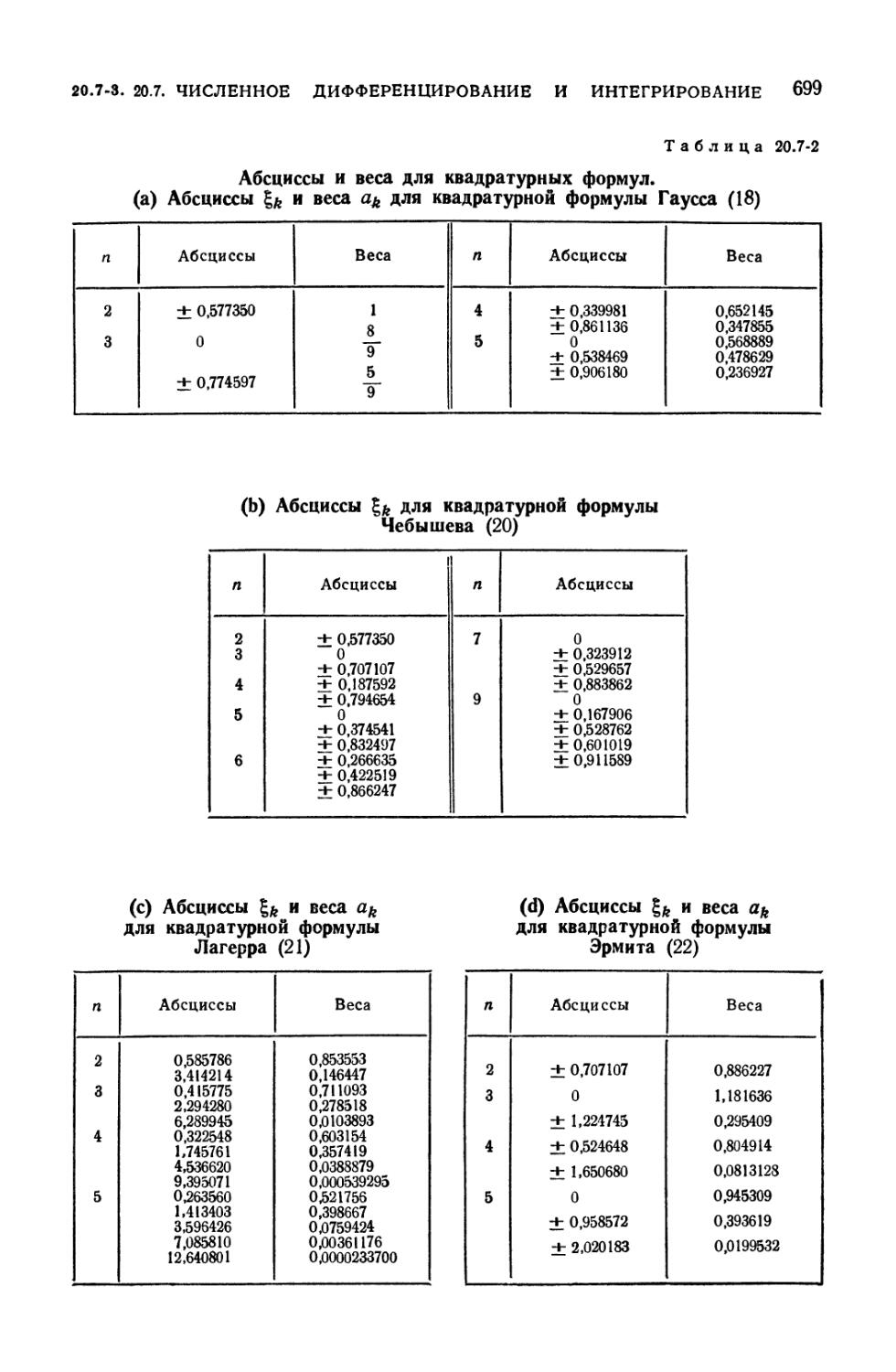
20.7-2. Абсциссы и веса для квадратурных формул 699
20.8-1. Некоторые методы Рунге — Кутта для обыкновенных
дифференциальных уравнений и систем таких уравнений 702
20.8-2. Некоторые методы четвертого порядка типа «предсказание —
коррекция» 705
Глава 21
21.2-1. Специальные значения тригонометрических функций 720
21.2-2. Соотношения между тригонометрическими функциями различных
аргументов 722
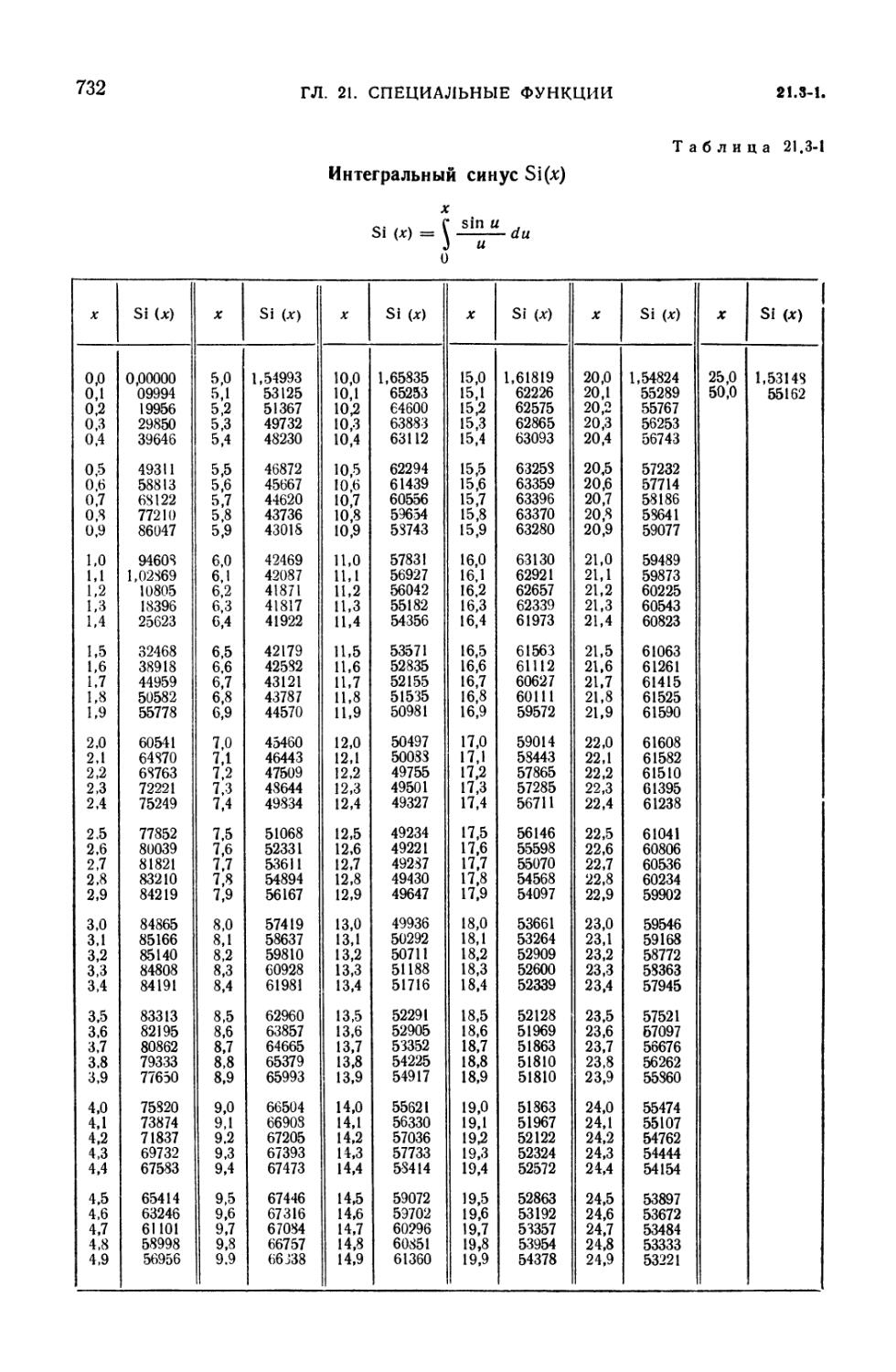
21.3-1. Интегральный синус Si (x) 732
21.3-2. Si (x) и интегральный косинус Ci (jc) 733
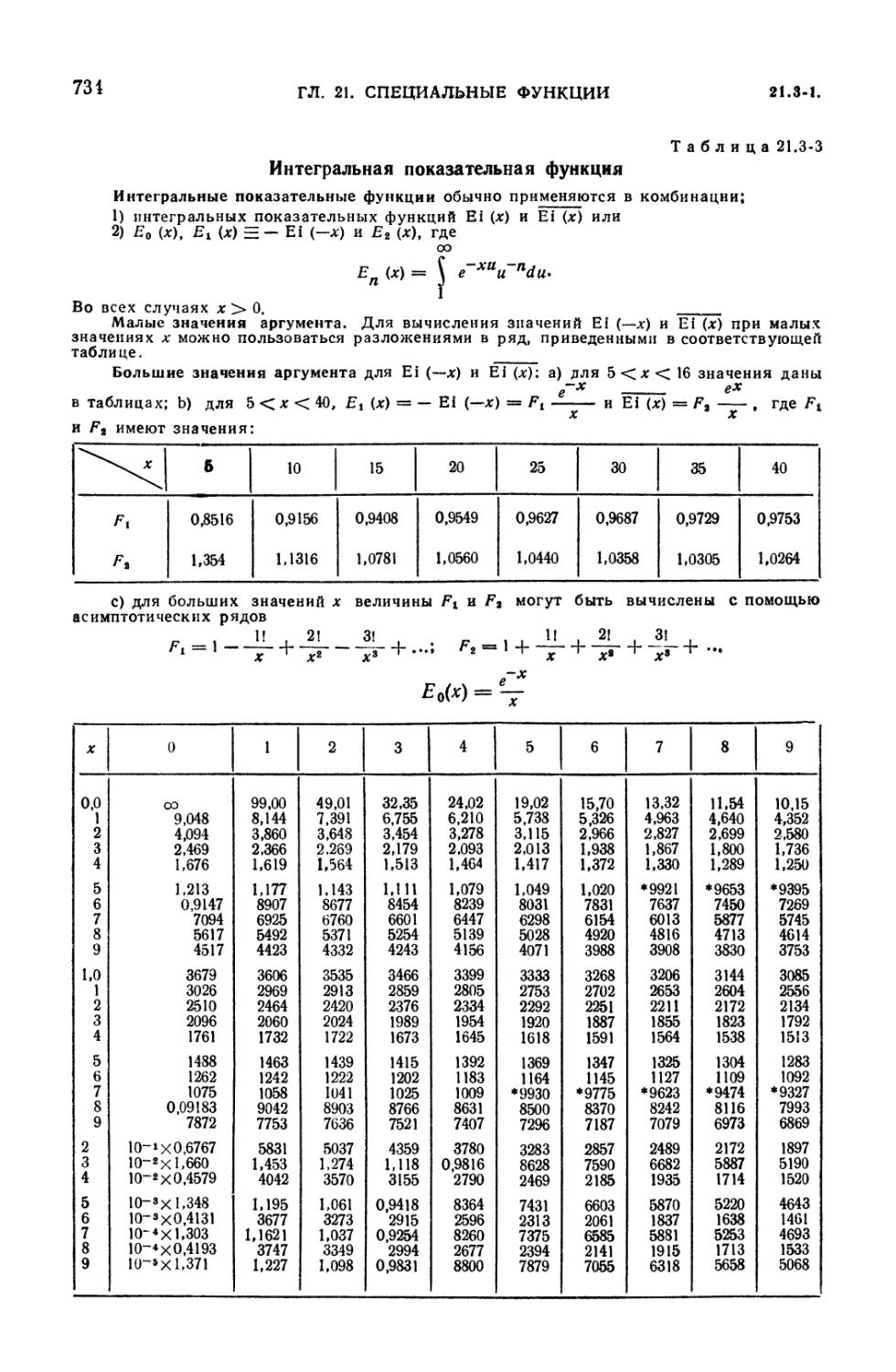
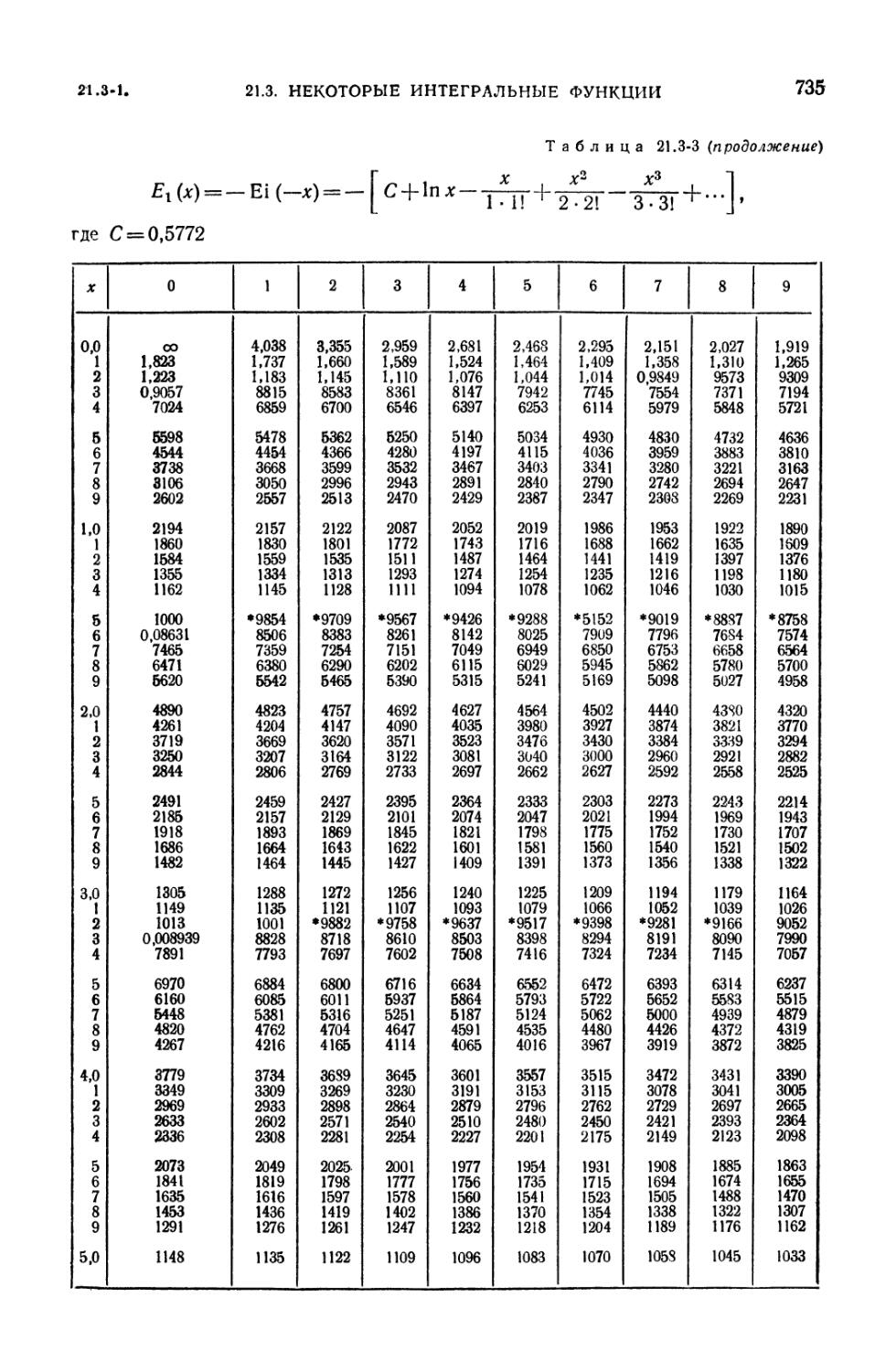
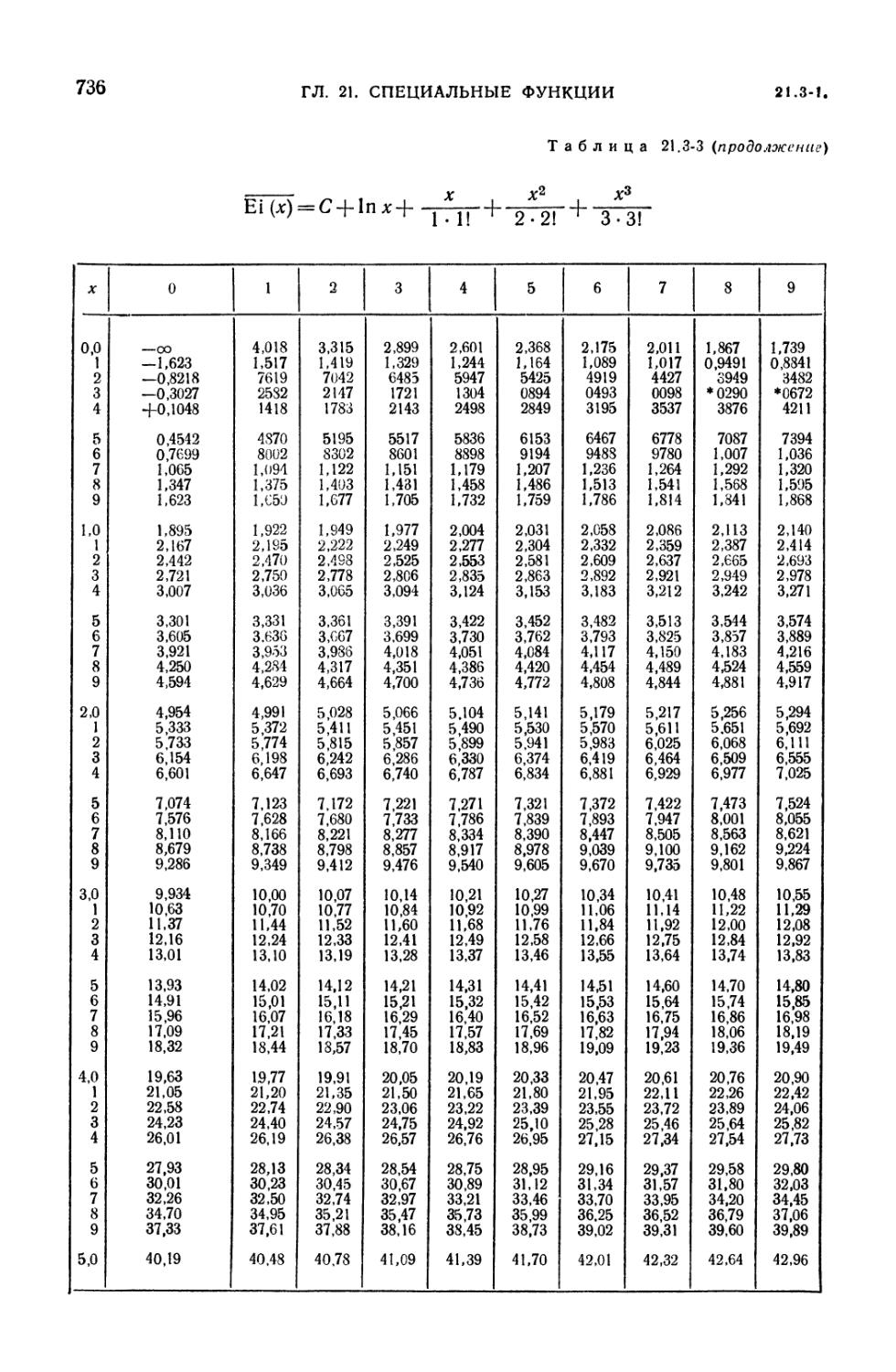
21.3-3. Интегральная показательная функция 734
21.4-1. Гамма-функция Г (х) 741
21.5-1. Определение и свойства биномиальных коэффициентов 745
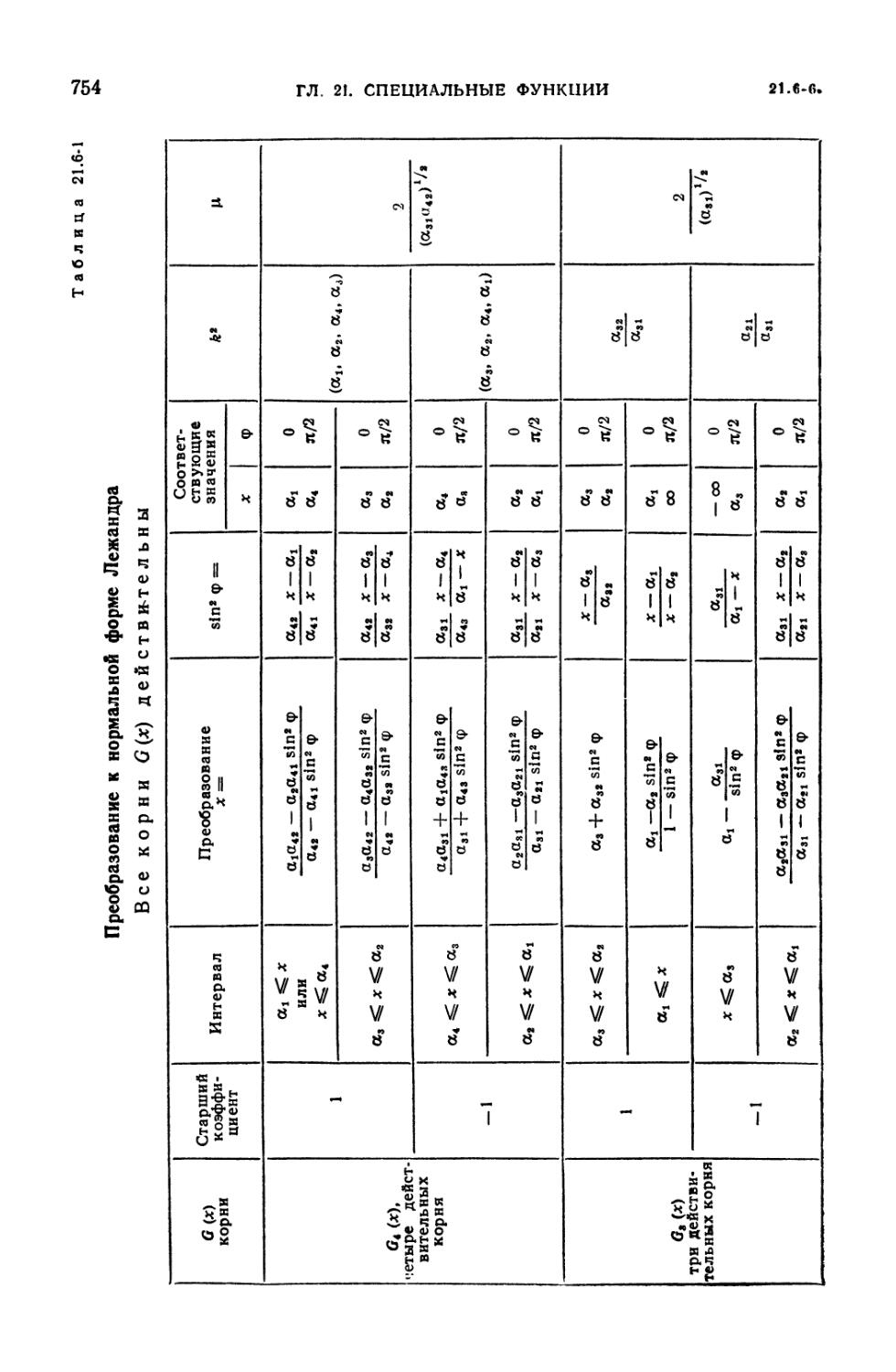
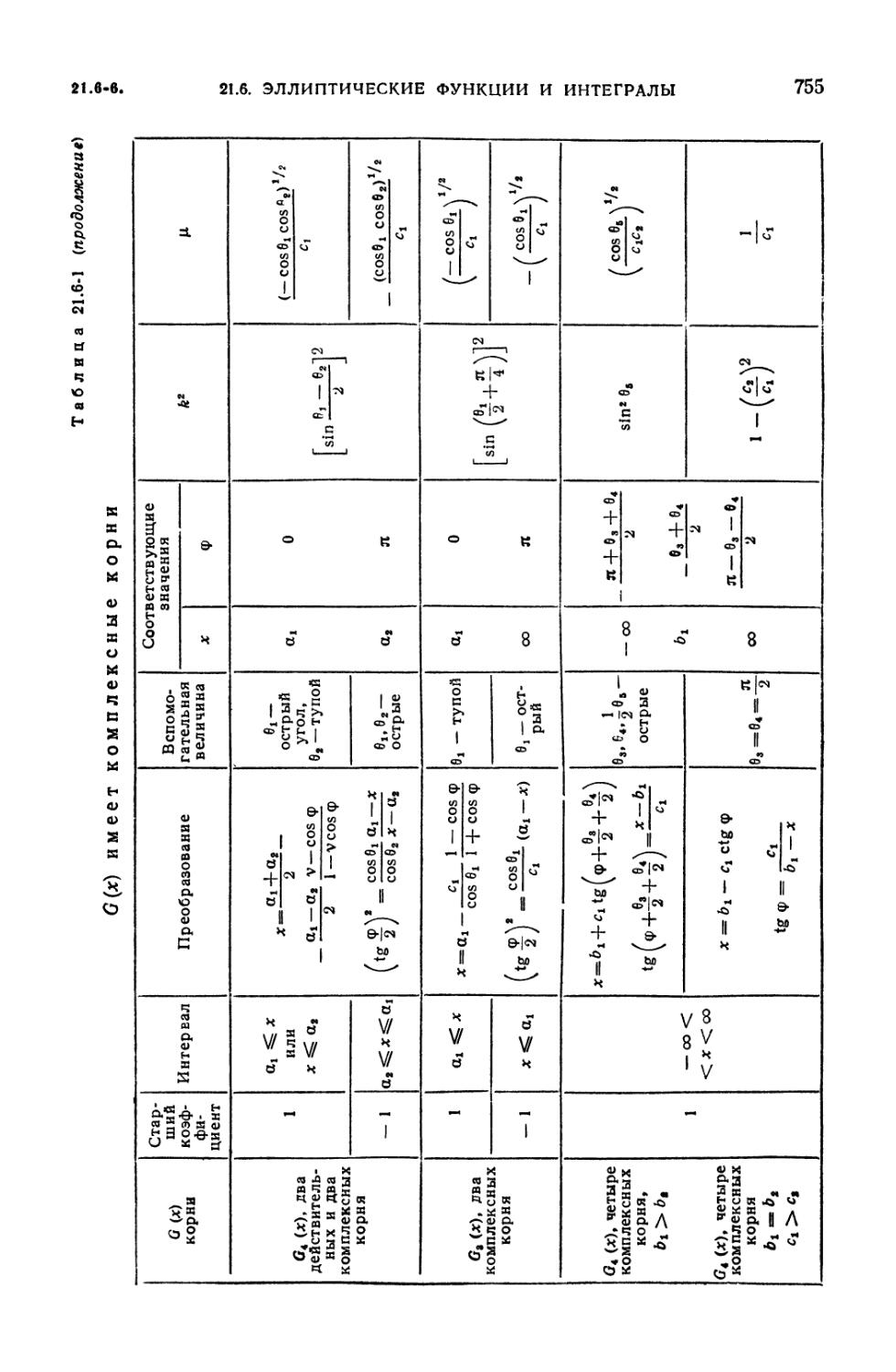
21.6-1. Преобразование к нормальной форме Лежандра 754
21.6-2. Преобразования эллиптических интегралов 758
21.6-3. Преобразования полных эллиптических интегралов 759
21.6-4. Полные эллиптические интегралы К и Е 760
21.6-5. Периоды, нули, полюсы и вычеты эллиптических функций Якоби 762
21.6-6. Специальные значения эллиптических функций Якоби 763
21.6-7. Изменение переменной на четверть и половину периода 764
21 6-8. Преобразования первого порядка эллиптических функций Якобм .... 766
21.7-1. Ортогональные многочлены Лежандра, Чебышева, Лагерра и Эрмита . . . 769
21.7-2. Первые ортогональные многочлены 774
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКОВ
Книгу Г. Корна и Т. Корн «Справочник по математике (для научных
работников и инженеров)» отличает весьма широкий охват материала. В ней освещаются
почти все вопросы как общего курса математики, так и большинства специальных
разделов, изучаемых во втузах с повышенной программой по математике
(векторный и тензорный анализ, криволинейные координаты, уравнения
математической физики, функции комплексного переменного и операционное исчисление,
вариационное исчисление, линейная алгебра, теория вероятностей и
математическая статистика и т. д.). Кроме того, в книгу включены главы, посвященные
современной алгебре, теории интегралов Лебега и Стилтьеса, римановой
геометрии, интегральным уравнениям, специальным функциям, а также целому ряду
других вопросов, далеко выходящих за рамки математической подготовки
инженеров, но постепенно становящихся необходимым орудием для научных
работников и инженеров-исследователей, работающих в самых разных областях. Много
внимания уделено связи рассматриваемых математических проблем с
прикладными дисциплинами (методы расчета и синтеза электрических цепей, линейные
и нелинейные колебания и др.).
В новом издании книга подверглась весьма существенной переработке.
Заново написаны главы 11 и 20 и значительная часть глав 13 и 18; и без того
обширный материал книги пополнился новыми разделами: дискретное преобразование
Лапласа (г-преобразование), конечные интегральные преобразования, матричные
методы решения систем дифференциальных уравнений, теория устойчивости
Ляпунова, математическое программирование, принцип максимума Понтрягина,
шаговые задачи управления и динамическое программирование — вот далеко не
полный перечень того, что добавлено авторами. Кроме того, из дополнений в книгу
включены справочные сведения по геометрии и сферической тригонометрии.
Конечно, можно иметь различные точки зрения на то, какой материал следует
включать в такого рода справочник; кроме того, в одной книге невозможно
изложить все разделы с одинаковой степенью полноты. Однако, как нам кажется,
ответы на вопросы, не нашедшие отражения в книге, следует искать уже либо
в монографиях, либо в специализированных справочных руководствах (типа
отдельных выпусков серии «Справочная математическая библиотека»,
выпускаемой Главной редакцией физико-математической литературы издательства
«Наука»).
В книге принята следующая рубрикация: глава, параграф, пункт; названия
всех пунктов указаны в оглавлении. Сплошная нумерация формул (и таблиц)
ведется в пределах одного параграфа; соответственно этому, если в тексте нужно
сослаться на формулу этого же параграфа, то указывается только ее номер. При
перекрестных ссылках указывается полностью номер главы, параграфа и пункта.
В конце книги приводится подробный предметный указатель, а также указатель
важнейших обозначений; во всех случаях читатель отсылается к соответствующему
пункту.
В процессе перевода был обнаружен ряд дефектов и неточностей; кроме того,
в некоторых случаях изложение не соответствовало принятому в нашей
отечественной литературе. Переводчики учитывали справочный характер книги, и для
удобства читателя большинство исправлений, замен и дополнений вносилось прямо
в текст. Принадлежащие переводчикам дополнения и подстрочные примечания
24
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКОВ
отмечены звездочками. Пункты, подвергшиеся значительной переработке, также
отмечены звездочками.
Нам пришлось в значительной мере заменить цитируемую литературу;
во многих случаях ссылки делались на неизвестные нашему читателю учебные
руководства. Приведенный в конце книги список литературы (ссылки на него
помещены в квадратные скобки) меньше всего претендует хотя бы на
относительную полноту; в него лишь включены наиболее известные издания (при этом мы
сочли возможным не указывать обычные втузовские курсы математики).
Значительной переработке подверглись дополнения в книге, включающие
разного рода таблицы. Ради уменьшения объема книги некоторые широко
распространенные таблицы были изъяты, а остальные помещены в соответствующие
разделы «Справочника». Перечень всех имеющихся в книге таблиц приведен после
оглавления на стр. 20—22.
Мы признательны всем читателям, обратившим наше внимание на те или иные
недочеты книги, и будем рады дальнейшим откликам на новое издание.
ИЗ ПРЕДИСЛОВИЯ АВТОРОВ
КО ВТОРОМУ АМЕРИКАНСКОМУ ИЗДАНИЮ
Новое издание «Справочника по математике» существенно расширено и
дополнено оригинальным материалом. Включены новые разделы, посвященные г-щеоб-
разованию, матричным методам решения систем дифференциальных уравнений,
теории устойчивости, представлению вращений, математи ческому
программированию, теории оптимального управления, случайным процессам и т. д. Глава
о численных методах почти целиком написана заново. Добавлены многие примеры
и таблицы.
Эту книгу можно рассматривать, во-первых, как достаточно полное собрание
математических определений, теорем и формул для научных работников,
инженеров и студентов. Ею могут пользоваться читатели, стоящие на разных уровнях
математического развития. Отсутствие доказательств и сжатость табличного
представления родственных формул сделали возможным объединение весьма большого
по объему справочного материала в одном томе.
Книга, однако, предназначена не только для наведения справок; в ней мы
пытались дать связное обозрение математических методов, применяемых в
различных приложениях. Каждая глава озаглавлена так, чтобы читатель мог быстро
ориентироваться в данном разделе математики. Такое изложение делает текст
удобным для пользования благодаря отсутствию доказательств; многочисленные
ссылки открывают доступ к более детальному изучению материала книги.
Особое внимание уделяется выявлению взаимосвязи различных разделов
и их роли в научных и инженерных приложениях; это достигается при помощи
соответствующих вводных замечаний и перекрестных ссылок.
Авторы пытались удовлетворить запросы разных кругов читателей, разделив
материал книги на три группы:
1. Наиболее важные определения и формулы, специально выделенные для
наиболее быстрого их обозрения.
2. Основной текст, состоящий из сжатого и связного обзора основных
результатов.
3. Более детальное обсуждение дополнительных вопросов, выделенное
мелким шрифтом. При таком построении включение этого материала не нарушает
структуры основного изложения.
Главы с 1 по 5 дают обзор основного курса колледжа *) по алгебре,
аналитической геометрии и анализу; глава 4 содержит также изложение интегралов Лебега
и Стилтьеса и рядов и интегралов Фурье, а глава 5 — векторный анализ.
Главы 6, 7 и 8 посвящены криволинейным координатам, функциям комплекс-
ного переменного и преобразованиям Лапласа. Добавлен новый материал по
конечным интегральным преобразованиям и г-преобразованию.
В главах 9 и 10 излагаются обыкновенные дифференциальные уравнения и
уравнения с частными производными, включая методы интегральных преобразований,
метод характеристик и теорию потенциала; проблемы собственных значений
трактуются в главе 15.
Глава 11 существенно изменилась; в дополнении к обычной теории экстремума
и классического вариационного исчисления здесь добавлены разделы по линейному
*) Это примерно соответствует общему курсу математики, изучаемому в наших
втузах. (Прим. ред.)
26 из ПРЕДИСЛОВИЯ КО ВТОРОМУ АМЕРИКАНСКОМУ ИЗДАНИЮ
и нелинейному программированию, теории игр, теории оптимального управления,
принципу максимума и динамическому программированию.
В главе 12 вводятся элементы современного абстрактного языка и описывается
конструкция математических моделей, таких, как группы, кольца, поля, векторные
пространства, булевы алгебры и метрические пространства. Изучение
функциональных пространств, продолженное в 14-й главе, позволяет расширить
применение методов функционального анализа к краевым задачам и проблемам
собственных значений в" главе 15.
Разделы, имеющие дело с более специальными темами, не претендуют на
полноту; их цель заключается в том, чтобы познакомить читателя с сущностью
определений и побудить его к чтению современной специальной литературы.
В главе 13 рассмотрены матрицы; здесь добавлены новые пункты по
матричным методам решения систем обыкновенных линейных дифференциальных
уравнений и по теории устойчивости Ляпунова. В главе 14 рассмотрены линейные
векторные пространства, линейные преобразования (линейные операторы), задачи
о собственных значениях и описывается применение матриц для представления
математических моделей. Дополнен материал по представлению вращений,
в связи с его важностью для физики.
Глава 15 содержит изложение разделов, связанных с проблемой собственных
значений, включая задачу Штурма — Лиувилля, краевые задачи для двумерных
и трехмерных областей и линейные интегральные уравнения.
Главы 16 и 17 соответственно касаются тензорного анализа и
дифференциальной геометрии и включают описание плоских и пространственных линий,
поверхностей и кривизны пространства.
В связи с возрастающей ролью статистических методов глава 18 представляет
довольно детальное изложение теории вероятностей и включает заново
написанное введение в теорию случайных процессов, корреляционных функций и спектров.
Глава 19 касается важнейших методов математической статистики и включает
подробные таблицы формул, описывающих специальные выборочные
распределения.
В новой главе 20 рассмотрены конечно-разностные методы и разностные
уравнения и изложены основные методы численного анализа. Глава 21 представляет
по существу собрание формул, описывающих свойства высших
трансцендентных функций.
Авторы надеются и верят, что эта книга даст читателю удобный повод детально
познакомиться с математическими методами и таким образом расширить свой
кругозор и взглянуть на свои специальные знания с более общей точки зрения.
ГЛАВА 1
ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ
И ТРИГОНОМЕТРИЯ (ПЛОСКАЯ И СФЕРИЧЕСКАЯ)
1.1. ВВЕДЕНИЕ. СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
1.1-1. ВВОДНЫЕ ЗАМЕЧАНИЯ. Эта глава посвящена алгебре1)
действительных и комплексных чисел, т. е. изучению тех соотношений между
действительными и комплексными числами, в которые входит конечное число
сложений и умножений. Уравнения, основанные на таких соотношениях,
рассматриваются здесь даже и в том случае, если при фактическом их точном
числовом решении нельзя обойтись конечным числом сложений и/или умножений*).
Определения и соотношения, изложенные в этой главе, служат основным
орудием во многих более общих математических моделях (см. также п. 12.1-1).
1.1-2. Действительные числа. Сложение и умножение действительных
чисел обладают следующими свойствами.
Если а и # —действительные числа (алгебраические,
рациональные, целые, положительные целые), то таковыми же являются
а-\-Ь и аЪ (замкнутость),
a-\-b — b-\-a, ab — ba (коммутативность),
* Т«ч/ ГГ i~~ ' [(ассоциативность),
a (be) = (ab) c = abc J v '
a- l=a (единица),
a(b-\-c)—ab-\-ac (дистрибутивность),
из a-\-c — b-\-c следует a — b,
из ca — cb, c^O, следует a — b (сокращение).
(i.i-i)
Действительное число 0 (нуль) обладает свойствами
я.0 =
-а, |
= 0 J
(1.1-2)
для каждого действительного числа а.
(Единственное) противоположное число —а и (единственное) обратное
число а~х — \\а для действительного числа а определяются соответственно так:
а + (— а) — а — а = 0,
(афО).
(1.1-3)
Делить на нуль нельзя.
Помимо «алгебраических» свойств (1), класс положительных целых, или
натуральных, чисел 1, 2, . . . обладает свойством упорядоченности (п. 12.6-2; п «больше, чем» т,
или м>т, если п = т-\-х, где х — некоторое натуральное число) и полной
упорядоченности (каждое непустое множество натуральных чисел имеет наименьший элемент).
Множество натуральных чисел, содержащее число 1 и для каждого из своих элементов п
следующий за ним элемент я + 1, содержит все натуральные числа (принцип
полной индукции).
Свойства натуральных чисел могут быть выведены из пяти аксиом Псано: 1) 1 есть
натуральное число; 2) для каждого натурального числа N существует единственное
следующее за ним натуральное число S(n); 3) S(n)^r\; 4) из S(n) = S(m) следует п — т
и 5) имеет место принцип полной индукции. (При его формулировке элемент, следующий
*) См. также подстрочное примечание к п. 12.1-2.
*) Термин «Л и/или В» (по английски «and/or») означает, что имеет место или А,
или В, или А и В вместе. Этот термин применяется в дальнейшем очень часто.
28 ГЛ 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.1-3.
за п, обозначается через S(n).) Сложение и умножение, подчиняющиеся правилам (1.1-1),
определяются «рекуррентными» соотношениями
п + 1 = S(n),
п -f S(m) = S(n -f m),
пЛ = n,
n • S (m) = m • m + n.
Целыми числами называются числа вида п,—п и 0, где п — натуральное число,
а рациональными — числа вида p/q, где р и q— целые числа и q фО.
Действительные числа можно ввести, исходя из множества рациональных чисел,
с помощью предельного процесса (см., например, [4.2]). Действительные числа, не
являющиеся рациональными, называются иррациональными.
Действительными алгебраическими числами называются действительные корни
алгебраических уравнений с целочисленными коэффициентами (п. 1.6-3), а действительными
трансцендентными числами — остальные действительные числа.
Класс всех рациональных чисел содержит корни всех линейных уравнений (п. 1.8-1)
с рациональными коэффициентами и включает в себя все целые числа. Класс всех
действительных алгебраических чисел содержит действительные корни всех алгебраических
уравнений (п. 1.6-3) с алгебраическими коэффициентами и включает в себя все
рациональные числа.
1.1-3. Отношение равенства (см. также п. 12.1-3). Из а — Ь следует Ь = а
(симметрия отношения равенства), а-{-с = Ь + с и ас = Ьс (вообще f(a)—f(b),
если / (а) обозначает некоторую операцию, приводящую к единственному
результату). Из а = Ь и b — с следует а = с (транзитивность отношения
равенства). Из аЬфО следует а^ЬО и Ь^ЬО.
1.1-4. Отношение тождества. Вообще говоря, уравнение относительно какой-либо
величины* или нескольких величин xlt х2, . . . будет удовлетворяться только при
некоторых специальных значениях х или специальных множествах значений xltxz, . . (см.
также п. 1.6-2). Если хотят подчеркнуть тот факт, что какое-нибудь уравнение
удовлетворяется при всех значениях х или xltx2, ... в известных представляющих интерес
пределах, то вместо символа = иногда пользуются символом тождества = (пример:
(х — 1) (* + 1) = х2 — 1), а пределы изменения рассматриваемых переменных иногда
указывают справа от уравнения. Символ а~Ь употребляется также в смысле: «а по
определению равно Ь».
1.1-5. Неравенства (см. также пп. 12.6-2 и 12.6-3). Действительное
число а может быть положительно (а>0), отрицательно (а<0) или равно
нулю (а = 0). Сумма и произведение положительных чисел положительны.
Действительное число а больше действительного числа Ь (а > Ь, Ь<а),
если а — Ь-{-х, где х — некоторое действительное положительное число.
Из а>Ь следует a + ob + ct aobc, если О О, и ас<Ьс, если с<0
(в частносги, — а< — Ь), 1/а<1/£, если ab>0 и 1/а>1/£, если ab<0.
Из а^Ь и Ь^с следует а ^ с. Из а ^ А и Ь^В следует а + Ь ^ А + В.
1.1-6. Абсолютные величины (см. также пп. 1.3-2 и 14.2-5). Абсолютная
величина \а\ действительного числа а по определению есть число, равное а,
если а ^ 0, и равное —а, если а < 0. Отметим:
а 1^0; из |а| = 0 следует а — ОЛ
|а|Ч6||^|а + *|^|а| + |Н} О-*"4)
|а|-|*И^|а-*1^И + 1П )
\ab\ = \a\ 1*1.
Из \а\^А и \Ь\^В следует
:Щ (ЬфО). (1.1-5)
a + b\^A + B и \ab\^AB. (1.1-6)
1.2. СТЕПЕНИ, КОРНИ, ЛОГАРИФМЫ И ФАКТОРИАЛЫ.
ОБОЗНАЧЕНИЯ СУММ И ПРОИЗВЕДЕНИЙ
1.2-1. Степени и корни. В случае, когда показатель степени п есть
натуральное число, /1-я степень произвольного действительного числа а (основания
степени) есть произведение п множителей, равных а. При а^О по
определению а°=1. Если а>0 и п — любое натуральное число, то арифметический
корень п-и степени из а есть единственное положительное решение уравнения
1.2-3. 1.2. СТЕПЕНИ, КОРНИ, ЛОГАРИФМЫ И ФАКТОРИАЛЫ 29
хп = а\ он обозначается символом a}/n = y/li. При а = 0, 01/л = У0 =0.
Если же а <С 0, то корень /г-й степени из а определяется лишь при нечетном п.
Именно, а1//г = -|/а есть в этом случае единственное действительное (на самом
деле отрицательное) решение уравнения хп = а. Пусть теперь а^О. Если
р = п/т, где п и т — натуральные числа, то по определению
aP = {p}lm)n = (an)Vm и а-Р=\/аР (а^О).
При любых натуральных пит
а'
,п/т_
0).
(1.2-1)
Степени с иррациональными показателями могут быть введены с помощью
некоторого предельного процесса (см. также п. 21.2-12). Соотношения
aP-a(l = aP+(i, (аР)Я = аРЯ (а >0), (1.2-2)
верные для рациональных показателей, остаются справедливыми и для любых
действительных р и q. Далее, для любых действительных ри</(о>0и^>0)
а~Р = ~,
ab)P = aPbP, (-Y
= аР-1,
аР
ЬР'
(1.2-3)
Замечание, у/а (квадратный корень из числа а^О) обычно
обозначается символом V а . О степенях комплексных чисел и корнях из них см. п. 1.3-3.
1.2-2. Формулы для уничтожения иррациональности в знаменателе дроби.
а а п /
Vb±Vc
Ь — с
Vb Ь
■ (VF+Vc
YF
V1
:=ТУ»Я
v\
(ур + уя + У*)-
~ Уф'-с) (b-Ych
(1.2-4)
(1.2-5)
(1.2-6)
1.2-3. Логарифмы. Логарифм x=logca числа а>0 при основании с>0
(с -ф 1) можно определить как решение уравнения
с*=а. (1.2-7)
В табл. 7.2-1 и в п. 21.2-10 приведены некоторые более общие сведения
о логарифмах. logca может быгь трансцендентным числом (п. 1.1-2). Отметим:
lOgfl
с *с =а, logcc=l, logccP = p, logc 1=0,
logc(0&) = logca+logc6 (основное свойство логарифмов),
' а
log,
= logc a — logc£,
log,, a = Jogca-logc,c«
*Vb-t
logc яр = Р 1обс <*, logc f >/"a j = — logc я;
1оз
(1.2-8)
««*,'"
loge,c =
i
log. c'
(замена основания). (1.2-9)
30 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.2-4,
Особый интерес представляют десятинные логарифмы с основанием 10 и
натуральные (неперовы) логарифмы с основанием
е= Hm U + ~)n =2,718281828... (1.2-10)
/г-*оо * '
е—трансцендентное число. Логарифм log^a обозначается символом In а,
a log10 а — символом lg а. Отметим:
1па = ^ = 1п 10.1ga=(2,30259...)lga, )
, { (1.2-П)
lg а = 1H1F = >g «• In а — (0,43429...) In а. J
1.2-4. Факториалы. Факториал п\ произвольного целого числа л^О
определяется формулами:
п
01 = 1, л! = Д *=Ь2.3...(л—1)л (л>0). (1.2-12)
k = i
В п. 21.4-2 приведены приближенные формулы для вычисления
факториалов п\ при больших п.
1.2-5. Обозначения сумм и произведений. Для любых двух целых чисел
(положительных, отрицательных или равных нулю) п и т ^ п
т
2 ak==an + an + l + ... + am_x+am (m— /i+l слагаемых), (1.2-13)
k — п
т
Д ak==anan + 1...am_mlam (m — n+\ множителей). (1.2-14)
k = п
Отметим:
mm' т' т т т' т' т
Л 2 %= S S ««. П П «/*- П П <v (1-2-15)
I = п k = я' k = п' i = п i = п k— n' k = n' i = /i
Бесконечные ряды см. в гл. 4.
1.2-6. Арифметическая прогрессия. Если а0 — первый член, а с?
—постоянная разность между следующим и предыдущим членами, называемая разностью
прогрессии, то
a^a^ + jd (/ = 0, 1, 2,...),
*п= 2 Я/^Ц^Рао + л^Ц^- (*0 + а„>. (1-2-16)
/ = о
1.2-7. Геометрическая прогрессия. Если а0 — первый член, ъг Ф 1
—постоянное отношение следующего члена к предыдущему, называемое знаменателем
прогрессии, то
а/=ао/-;(/ = 0, 1, 2,...),
JL Л. i — гл + 1 #ft — я„г
s* = S a/= S °orJ = a0—r^7~=-Vr7L-- О-2"17)
/ == 0 /==0
1.3-1.
1.3. КОМПЛЕКСНЫЕ ЧИСЛА
31
О бесконечной геометрической прогрессии см. п. 4.10-2.
1.2-8. Некоторые числовые суммы (см. также [4.6]).
п п
*=1 *=1
п
£ = 1 fc = l
л
^ ife8= я'(/14+|)', J! (2Л-1)3 = ла(2л»-1)
fc=i /fe = i
/г
(общую формулу для сумм 2 fcW см. в п. 4.8-5, d).
А; = 1
п
У !_=i !_=_^_,
Zj k(k+\) /г+1 /г + 1 '
6 = 1
V ! = 1U ! 1.
Бесконечные ряды см. в 4.8.
1.3. КОМПЛЕКСНЫЕ ЧИСЛА
1.3-1. Вводные замечания (см. также п. 7.1-1). Комплексные числа
(иногда называемые мнимыми числами) не являются числами в элементарном
смысле слова, применяемыми при подсчетах и измерениях. Они составляют
новый класс математических объектов, определяемый описанными ниже
свойствами (см. также п. 12.1-1).
Каждому комплексному числу с можно поставить в соответствие
единственную пару (а, Ь) действительных чисел а и Ь и обратно. Сумма и
произведение двух комплексных чисел сх++(аъ Ьг) и с2*-*(а2, Ь2) определяются
соответственно следующим образом: с1+-с2^-(а1 + а2» bx + b2) и c1c2^*(aia2 —
— b1b2faib2 + a2bi). Действительные числа а содержатся в классе комплексных
чисел в качестве пар (а,0). Мнимая единица i, определяемая условием
t*-*(0,l), удовлетворяет соотношению
/2 = — 1. (1.3-1)
Каждое комплексное число c*-*(ab,) может быть записано в виде суммы
с — a-\-ib действительного числа а++(а,0) и чисто мнимого числа /&*«-* (0,6).
Действительные числа a=Re си 6 = Im с соответственно называются
действительной частью и мнимой частью комплексного числа с. Два комплексных
числа с = а + ib и с = а — ibt имеющие одинаковые действительные и
противоположные мнимые части, называются сопряженными комплексными числами.
Два комплексных числа сг = аг +- ibi и с2 = а2 + ib2 равны в том и только
в том случае, если соответственно равны их действительные и мнимые части,
т. е. Ci = с2, лишь если аг = а2 и Ьг = Ь2* Из с = а + tb = 0 следует а = b = 0.
ГЛ 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.3-2,
Сложение и умножение комплексных чисел удовлетворяют правилам пп.
1.1-2 и 1.2-1, причем
*2 = — 1, /3 =
1, /*
J==—/, «4Я = 1 (л=о, 1, 2,...); )
С\ ± C2 = (ai ± a2) + i фх ± Ь2)у
схс2 = (а^ — bxb2) + / («!^2 + fl^i)»
rt __ at + /frt __ (g^z + frtfr2) -f / (a2fri — o^z)
c2 a2 + ib» ~~ a| 4- *>f
Ci + c2 = ci + c2, од = с^, (c1/c2)=c1/c2(c2^=0), 7=c,
с 4- с и т^, c — c
(ЪфО),
a = Re c=
6 = Im c=
2«
(1.3-2)
(1.3-3)
Класс всех комплексных чисел содержит корни всех алгебраических уравнении
с комплексными коэффициентами и включает в себя действительные числа.
1.3-2. Изображение комплексных чисел точками или радиусами-векторами.
Тригонометрическая форма комплексного числа (см. также п. 7.2-2).
Комплексное число z = x-\-iy удобно изображать точкой (г)=(х, у) или соответствующим
радиусом-вектором (пп. 2.1-2 и 3.1-5) на комплексной плоскости (рис. 1.3-1).
Оси Ох и Оу (в прямоугольной декартовой системе координат) называются
соответственно действительной и мнимой осью. Абсцисса и ордината каждой
точки (г) изображают соответственно
действительную часть х и мнимую часть у числа г.
Соответствующие полярные координаты (п. 2.1-8)
г = |г| = К*» + у» = ]Лг = |г|,
Дейстбительная ось
Рис. 1.3-1. Изображение
комплексных чисел точками
или радиусами-векторами.
Оси Ох и О у называются
соответственно
действительной и мнимой осью.
q; = Arg2, tgq>=-£
(хфО)
(1.3-4)
называются модулем и аргументом комплексного
числа г. Отметим:
х = г cos ф, у — г sin ф,
z=х + iy — г (cos ф+i sin ф)
.}
(1.3-5)
Модули комплексных чисел удовлетворяют
соотношениям (1.1-4) —(1.1-6). Если z—действительное число, то его модуль \г\
равен его абсолютной величине (п. 1.1-6).
* Аргумент комплексного числа z определяется с точностью до слагаемого
2&я, где k—любое целое число.
В качестве главного значения kvgz обычно выбирают значение,
определенное неравенствами —л < Arg г ^ я. Главное значение аргумента z
обозначают через arg2. При принятом условии arg2=—arg2. *
Для любых двух множеств (действительных или) комплексных чисел alt
а2, ..., ап и рх, р2, ..., ря
2 I а/'2 2 I P* I2 {нгРавенств0 Коши — Буняковского) (1.3-6)
2 OLfii
1=1
(см. также пп. 14.2-6 и 14.2-6, а).
1.3-3. Представление суммы, произведение и частного. Степени и корни.
Сумме комплексных чисел соответствует сумма соответствующих радиусов-
векторов (см. также п. п. 3.1-5 и 5.2-2). Если даны гх = гг (cos уг + i sin ф2)
1.4-1.
1.4. РАЗЛИЧНЫЕ ФОРМУЛЫ
33
и г2 = r2 (cos ф2 + i sin ф2), то
ггг2 = гхгг [cos (фх + ф2) + i sin (фх + ф2)],
■j-j = ^ [cos (ф, - ф2) + / sin (ф, - ф2)] (г2 Ф 0)
гп __ rn (C0S ф _|_ i sl-n ф)л __ rn (C0S Лф _|_ / sjn ^ф)
(/г —целое число) (формула Муавра).
Случай, когда показатели степени комплексны, см. в п. 21.2-9.
Если п—натуральное число и с—комплексное число, то у/"с
/1-й степени из с) есть решение уравнения гп=с. При сфО существует
различных корней л-й степени из с. Они определяются формулами
(1.3-7)
(корень
ровно п
У7-У&\ (cos*±^+i sin £±2**).
где f\c\ —арифметический корень из положительного числа \с\ (п. 1.2-1),
q) = argc и 6 = 0, 1, 2 л—1.
Отметим, что
(1.3-8)
В частности^
(1.3-9)
(1.3-10)
1.4. РАЗЛИЧНЫЕ ФОРМУЛЫ
1.4-1. Бином Ньютона и родственные формулы. Если a, b и
£—действительные или комплексные числа, то
(a±b)2 = a*±2ab + b2,
(а ± б)* = аЗ ± За2&+3а&а ± #»,
(а ± 6)* = а4 ± 4aty + 6a26a ± 4а#»+&*,
(а+6)" = 2J C'a"-'V (л = 1, 2,...),
/==о
где
п\
1 (л — /)
Г. Корн и Т. Кора
С^(7)-7м£=7)Г С/-©. 1* 2> ...««-О. 1, 2,...).
(14-1)
34 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА. ГЕОМЕТРИЯ II ТРИГОНОМЕТРИЯ 1.4-2.
(Бином Ньютона для целочисленных показателей п; см. также п. 21.2-12.)
Биномиальные коэффициенты Cfn подробно рассматриваются в п. 21.5-1
(a+b+c)* = a*+b*+c* + 2ab + 2ac+2bc; (1.4-2)
a*-b* = (a+b){a-~h), Л
a*+b* = (a + ib)(a—ib). J ( ' ' }
Если п —любое натуральное число, то
о»—6n«=(a—b)(an-i+a"-2b + ... + abn~*+bn-i). (1.4-4)
Если п —четное положительное число, то
а« — bn*=(a+b) (an-*~-an-4+.., + abn~*—bn-i). (1.4-5)
Если п — нечетное положительное число, то
ап + Ьп = (а+Ь) (а""1 — ап~Ч +... — abn~* + б""1).
Отметим также:
а* + а2^2 + б4 = (л2 + а& + б2) (а2 — аб + б2). (1.4-6)
1.4-2. Пропорции* Из a\b — c\d или ajb — cfd следует:
ТйЦ^-тЗё- <»/*«>«**« яромрцш,). (1.4-7)
В частности,
g±b с + d a—b g — d
(1.4-8)
1.4-3. Многочлены. Симметрические функции.
(a) Многочлен (целая рациональная функция) относительно х+, х2, ..., хп
есть сумма конечного числа членов вида аг11дг22..^лл, где каждое ki есть
неотрицательное целое число. Наибольшее значение суммы k1+k2 + ...+knt
встречающееся в каком-либо из членов, называется степенью многочлена.
Многочлен называется однородным, если все его члены имеют одну и ту же
степень (см. также п. 4.5-5).
(b) Многочлен относительно *-, х^, .... ^называется симметрическим, если для
любого множества значений^, х ...t x значение этого многочлена не изменяется при какой
угодно перестановке xv *2, .... хп (это определение распространяется и на любые
функции от xv х2, ..., хпу Элементарными симметрическими функциями от х~, х~, ...t х
называются многочлены S-, S„, ..., S определяемые следующим образом:
Si=*t-}-.K8-f ...-J-* 5,Е^Л + ^з + ..
п
S9z=zXix2xs-\-xtXtX4 -\-..., S —Х\Х%.
...}
(1.4-9)
где Sy — есть сумма всех Сп = ^ произведений, каждое из которых содержит *
сомножителей х, с несовпадающими индексами. Каждый симметрический многочлен
относительно хи ха, ... , хп может быть единственным образом записан как многочлен
относительно S-, S2, ... , S • коэффициенты этого нового многочлена являются
алгебраическими суммами целочисленных кратных заданных коэффициентов.
Каждый симметрический многочлен относительно xit xt, ... , xR может также
быть выражен как многочлен относительно конечного числа симметрических функций
п п п
s0~n, Si= 2 xi% sz~ 2 *f, ... tsh= ^ *?.-«. <1-4-10>
1.5-3.
1.5. ОПРЕДЕЛИТЕЛИ
35
Симметрические функции (9) и (10) связаны формулами Ньютона
(см. также п. 1.6-4). Заметим, что в соотношения (11) в явном виде не входит п.
1.5. ОПРЕДЕЛИТЕЛИ
U
=0 <*<«). 1
? 0.'
(*>л) J
1.5-1. Определение. Определитель (детерминант)
\ап а12 ... а1я
D = det[att]
a21 a22 ••• a2/l
Я/ll «Л2
(1.5-1)
квадратной таблицы (матрицы, п. 13.2-1) с л2 (действительными или
комплексными) числами (элементами) щь есть сумма п\ членов (—\Yaik 1(hk2-*• anknt
каждый из которых соответствует одному из п\ различных упорядоченных
множеств klt k2t ..., knt полученных г попарными перестановками
(транспозициями) элементов из множества 1, 2, ..., п. Число п есть порядок
определителя (1).
Фактическое вычисление определителя по его элементам упрощается с помощью
пп. 1.5-2 и 1.5-5,а. Отметим, что
п п
\D\*^ ТТ 5] \aik Г (неравенство Адамара). (1.5-2)
/==1 Аг=*Г
1.5-2. Миноры и алгебраические дополнения. Разложение определителя
по строке или по столбцу. (Дополнительный) минор D^ элемента сць в
определителе /1-го порядка (1) есть определитель (л — 1)-го порядка,
получающийся из определителя (1), если из него вычеркнуть /-ю строку и k-Pi
столбец. Алгебраическое дополнение Л# элемента а-^ есть коэффициент при а/й
в разложении определителя D, или
Aik = (-\)MDik=-£- (1-5-3)
Определитель D можно следующим образом выразить через элементы
произвольной его строки или столбца и их алгебраические дополнения:
п п
D = det [aik] = 2fl*/4r/e S fl/*4* С1-5"4)
* = 1 л=1
(/ = 1, 2,..., я) (разложение по столбцу или по строке).
Отметим также, что
п п
I] ацАи = 2 в/И/* = 0 (/ ф /). (1.5-5)
* = i k=l
1.5-3. Примеры. Определители второго и третьего порядка:
I ахх а 12 I
«2i «** =«11««-«1*«*ь (1.5-6)
= aii«82«38 —«ii«2e«82-f«i2«23«si--«i2a2i«33-T-«i3«2i«3i —
«it «« «is
Ott aM a8$
«si «es «»s
— «i»«88a»i— «li («в8«$$—«8s«»e) —«2i («i2«$$ — alsaSi) -f- a81 (atiaiS — «i8«88) =
= flH («««If — «»»^»2)~ «12 («21«»» —«2»^8l) + «l» («21«M — «M«Sl) И Т. Д. (1.5-7)
2*
36 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.5-4.
1.5-4. Дополнительные миноры. Разложение Лапласа. Определитель m-го порядка М9
получающийся из определителя п-го порядка D(tn^n), если из него вычеркнуть какие-
либо п—т строк и какие-либо п—т столбцов, называется минором m-го порядка
определителя D. Минор m-го порядка М и минор (п — т)-го порядка М' определителя D,
получающийся, если из D вычеркнуть строки и столбцы сохранившиеся в М, называются
дополнительными минорами: в частном случае m — nf М' = 1. Алгебраическое дополнение
М" минора М в D по определению равно (—1) 1 2 ' * ' * ' m1 i г2 ' * * ,п^ тМ',гд&
'xJ2f • • • »*т ~~ номеРа строк, a kvk2 km — номера столбцов, входящих в М. Пусть
заданы любые т строк (или столбцов) определителя D. Тогда D равен сумме
произведений ММ" всевозможных миноров m-го порядка М, расположенных в этих строках (или
столбцах), на их алгебраические дополнения М" (разложение Лапласа по нескольким
строкам или столбцам).
Определитель п-ro порядка D имеет Ст главных миноров m-го порядка,
диагональные элементы которых являются и диагональными элементами D.
1.5-5. Различные теоремы.
(а) Величина D определителя (1) не меняется при любой из следующих
операций:
1) замене строк столбцами и столбцов строками (перемене
местами индексов i и k в равенстве (1));
2) четном числе перемен местами любых двух строк или любых
двух столбцов;
3) прибавлении к элементам любой строки (или столбца)
соответствующих элементов какой-либо другой строки (или соответственно
столбца), умноженных на одно и то же число а.
Пример:
ап аХ2 ••• о>лп
а21 а22 ••• а2П
Я/л ап2
ян
012
a2i
а22
Я/11
ап2
ап + аах2 аХ2
а21 + аа22 #22
<*1П
а2п
апХ + аап2 an2
(1.5-8)
Чп а2п
(b) Нечетное число перемен местами любых двух строк или любых двух
столбцов равносильно умножению определителя на — 1.
(c) Умножение всех элементов какой-либо строки или столбца на
множитель а равносильно умножению определителя на а.
(d) Если элементы j-й строки (или столбца) определителя п-го порядка D
тп m m
представлены в виде сумм 2 *п» У] *т2» ••• > 2 Сгп* то 0пРе^елитель & Ра"
т
вен сумме J] Dr определителей п-го порядка. Все элементы каждого из on ре-
г = \
делителей Dr, кроме элементов j-й строки (столбца), совпадают с
соответствующими элементами определителя D, а в j-й строке определителя Dr стоят
элементы сгЪ сг2,..., сгп.
Пример.
аи + Ьи аХ2 + ЬХ2 ... а1п + Ьхп I
«21
а2ч
<*2П
<*п\
апч
пп
|Яц
\а21
\ат
ах2 .
а22 .
<*п
12
.. а>т
.. а2п
•• апп
+
hi hu •■
а21 а22 ..
ап1 ап2 .
• hn
• Я2Я
•• апп 1
(1.5-9)
1.6-3. 1.6. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ: ОБЩИЕ ТЕОРЕМЫ 37
(е) Определитель равен нулю, если
1) все элементы какой-либо его строки или столбца равны нулю,
2) соответствующие элементы каких-либо двух его строк или
столбцов равны или же пропорциональны.
1.5-6. Умножение определителей (см. также п. 13.2-2). Произведение двух
определителей п-ro порядка det [a/#] и det [b(k] равно
= det | %ajibkA
det [aik\ det [&/ft] = det ^ацЬ!к =
= det
л
2 я/А/
L/=i
= det ^ajibjk •
(1.5-10)
t.5-7. Изменение порядка определителей. Данный определитель можно следующим
образом записать в виде определителя более высокого порядка:
11
*21
12
а22
11
«21
*12
*22
1Л
°2Л
"/il
0
Л2
0
пп
0
(1.5-11)
где числа а. произвольны. Этот процесс можно повторять сколько угодно раз.
Порядок данного определителя иногда можно понизить с помощью соотношения
*11
*21
\1
0
0
0
«12
а22
аП2
0
0
0
•• аЫ
•• а2П
•• апп
... о
... о
.. о
«И «12 •
«21 «22 •'
«Л1«/12 •'
ЬЦ blt •
ЬП *22 '
Ьтх ьт2 •
• °im
• «2m
. «« —
пт
• ьш
•• *зт
•• Ьтт
11
*21
**1Я
а2П
*11 *!•
(1.5-12)
§ 1.6. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ: ОБЩИЕ ТЕОРЕМЫ
1.6-1. Вводные замечания. Решение алгебраических уравнений имеет особо важное
значение в связи с тем, что к этому виду относятся характеристические уравнения
систем линейных дифференциальных уравнений (см. также пп. 9.4-1, 9.4-4 и 14.8-5). Общая
задача отделения корней (возникающая, например, при исследовании устойчивости) может
быть изучена методами п. 1.6-6 и/или п. 7.6-9. Приближенное решение уравнений
рассматривается в пп. 20.2-1 —20.2-5.
.6-2.
:я в пп. 20.2-1 —20.2-5.
Решение уравнения. Корни. Решить уравнение (см.
f(x) = 0
также п. 1.1-4)
(1.6-1)
с неизвестным л; —значит найти значения х (корни уравнения (1), нули
функции / (л;)), удовлетворяющие этому уравнению. Решение можно проверить
подстановкой.
1.6-3. Алгебраические уравнения. Уравнение (1) вида
/ (х) ее a»xn + a1xn-i + ... + an_1x + an = 0 (а0 Ф 0), (1.6-2)
где коэффициенты at — действительные или комплексные числа,
называется алгебраическим уравнением степени п с неизвестным х\ / (я) — многочлен
38 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ !.*.4.
степени п относительно х (целая рациональная функция; см. также пп. 4.2-2, d
и 7.6-5). Коэффициент ап — свободный член многочлена (2).
Значение х=хг есть корень кратности (порядка) т (кратный корень, если
т> 1) уравнения (2) (нуль порядка т функции f (х)\ см. также п. 7.6-1) если
/ (х) =g(x) (х—Хх)™, где g (х) — многочлен и g (хг) Ф 0. Алгебраическое
уравнение степени п имеет равно п корней, если корень кратности т считать т
раз (основная теорема алгебры многочленов). Полное решение уравнения (2)
указывает все корни вместе с их кратностями.
Числа, являющиеся корнями алгебраических уравнений с целочисленными
коэффициентами, называются алгебраическими числами (вообще говоря, комплексными); если
коэффициенты — алгебраические числа, то корни все еще остаются алгебраическим» (см.
также п. 1.1-2). Общие формулы, выражающие корни алгебраических уравнений через
их коэффициенты и содержащие только конечное число сложений, вычитаний,
умножений, делений и извлечений корня, существуют только для уравнений следующих
степеней: первой (линейные уравнения, п. 1.8-1), второй (квадратные уравнения, п. 1.8-2),
третьей (кубичные уравнения, пп. 1.8-3 и 1.8-4) и четвертой (уравнения четвертой
степени, пп. 1.8-5 и 1.8-6).
1.6-4. Соотношения между корнями и коэффициентами. Симметрические функции Sk
и s^ (п. 1.4-3) корней хи х2 хп алгебраического уравнения (2) связаны с его
коэффициентами а0, at, .... ап следующим образом:
?-
1) kSk (k= 1. 2, ..., я),
. 2s* + — + aosk e ° <* = 1. 2, .
я).
(1.6-3)
(1.6-4)
Равенства (1.6-4) представляют собой другой вариант формул Ньютона (1.4-11). Отметим
также
(-D*
St 1
Si St
Ss S2
sk sk-
o . . .
2 0..
s, 3 0 .
1
.. 0 1
.. 0
.. 0
. «1
s*=
Kt)*
3aa a2
0 . .
a0 0
at a0 0
(£ = 1, 2, ..., n).
(1.6-5)
1.6-5. Дискриминант алгебраического уравнения. Дискриминант Д алгебраического
уравнения (2) есть произведение а2п — 2 и квадратов всех разностей (дг/ — х^ (/ > k)
корней xi уравнения (квадратные корня порядка т рассматриваются как т равных
корней с разными индексами):
д = а2п - 2 П <*/ - xk)2 = а\п - 2 [ W <*,. х2, .... хп) ]« =
0 i>k
2п-
= Q0
s/i-l
sn + 1
s2n-
п(п-\)
= (-1)
-i- R lf> /'). d.6-6)
a0
W
(xlt x2,
Мя
xt xt .
** X2 '
xn *2 ..
.. xn — *
1
n
-П 0Ч-xk)
i>k
1.6-6. 1.6. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ: ОБЩИЕ ТЕОРЕМЫ 39
(этот определитель называется определителем Вандермонда). s^ — суммы k-x степеней
корней многочлена f (x) (s0 = п) и R (f, f) — результант (п. 1.7-3) многочлена f (x) и его
производной (п. 4.5-1) f (х). Дискриминант А есть симметрическая функция корней xlt
х2, .... хп, обращающаяся в нуль в том и только в том случае, если f (x) имеет по
крайней мере один кратный корень (необходимо являющийся общим корнем f (х) и ? (х); см.
также п. 1.6-6, g).
1.6-6. Действительные алгебраические уравнения и их корни.
Алгебраическое уравнение (2) называется действительным, если все его коэффициенты
аь — действительные числа. Соответствующий действительный многочлен / (х)
при всех действительных значениях х принимает действительные значения.
Для отделения корней (действие, которое предшествует приближенному
решению уравнений, п. 20.2-1) полезны нижеследующие теоремы. В теоремах
(Ь) — (f) корень кратности т рассматривается как т корней.
(а) Комплексные корни. Комплексные корни действительного
алгебраического уравнения появляются парами комплексных сопряженных чисел
(п. 1.3-1). Действительное алгебраическое уравнение нечетной степени всегда
имеет хотя бы один действительный корень.
я
*Все корни уравнения (2) по модулю не превосходят числа N = \+-—г
где Л — наибольшее из чисел
\Ч\
|Оо1
I ап |; это правило справедливо
и для уравнений с комплексными коэффициентами.*
(Ь) Теорема Рауса — Гурвица. Число корней с положительной
действительной частью действительного алгебраического уравнения (2) равно числу
перемен знака в любой
отличны от нуля)
или
где
из последовательностей (в предположении, что Tt
(1.6-7)
т* тъ II,
?V т19 тхт
го = яо>0, 7\ =
Гз =
аг а0 0
а3 а2 ах
аь а4 а3
•
Т9
-_ -э • • •»
2» *2Тз, ..
<h, Тг =
тп
тп-\
Г'
• • ^Я-2 Тп-Ь
\а1 ай\
П =
аг а0
а3 Ч
аь а4
а7 а*
«л
0
«1
а3
аь
0
а0
а2
а*
(1.6-8)
(элементы а,-, отсутствующие в уравнении (2), полагаем равными нулю).
Если среди Tt есть равные нулю, то подсчет усложняется (см. [1.2]).
Критерий Рауса — Гурвица. Для того чтобы все корни
действительного уравнения (2) имели отрицательные действительные части,
необходимо и достаточно, чтобы выполнялись неравенства
Г0>0, TiX), Г2>0,... Гл>0.
Из положительности всех T-t следует положительность всех
коэффициентов ai уравнения (2).
Альтернативная формулировка. Все корни действительного
уравнения (2) п-й степени имеют отрицательную действительную часть
в том и только в том случае, если это верно для уравнения (п—\)-й степени
а^'1 + а[хп-*+alxn~* + а]хп~^ + ...==
s^^-1 + ^—28 а3) *л~2 + а3х»-* +( ««- -%Г<ь)*-* + ... = 0.
Эта теорема может применяться повторно и дает простую рекуррентную
схему, полезную, например, при исследовании устойчивости. Если один из
коэффициентов а^\ равен нулю, то метод усложняется.
40 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ »6-в.
«Критерий Льенара — Шипара. Для действительного уравнения (2)
с положительными коэффициентами все корни имеют отрицательную
действительную часть, если положительны или все Т{ с четными индексами, или
все Ti с нечетными индексами.
(Более общая формулировка этого критерия приведена в [1.2].)*
(c) Отделение действительных корней: правило знаков
Декарта. Число положительных корней действительного алгебраического
уравнения (2) либо равно числу N перемен знака в последовательности а0, аг..., ап
коэффициентов, причем коэффициенты, равные нулю, не учитываются, либо
меньше числа N на четное число.
Если перемен знака нет, то уравнение (2) положительных корней не имеет:
если есть одна перемена знака, то имеется в точности один положительный
корень. Применяя эту теорему к f (— x), получаем аналогичную теорему для
отрицательных корней.
(d) Отделение действительных корней: верхняя
граница действительных корней (пп. 4.3-3). 1) Если первые k
коэффициентов а0, аг,... ,аь_1 действительного алгебраического уравнения (2)
неотрицательны (ak — первый отрицательный коэффициент), то все
положительные корни уравнения (2) (если они есть) меньше, чем 1 + ^rqlaQ, где q —
наибольшая из абсолютных величин отрицательных коэффициентов.
Применяя эту теорему к f (—х), можно таким же образом получить
нижнюю границу отрицательных корней.
* 2) Если при х — с многочлен f (х) и его производные f (x), f"{x),...
..., fin) (x) (п. 4.5-1) принимают положительные значения, то с является верхней
границей действительных корней уравнения (2). *
(e) Отделение действительных корней: теорема Ролля
(см. также п. 4.7-10). Производная (п. 4.5-1) f (x) действительного многочлена
f (x) имеет нечетное число действительных корней между двумя соседними
действительными корнями многочлена f (x).
Пусть а и b — два соседних действительных корня уравнения f (х) = 0 и пусть f(a) zfiO
и f (b) -jz 0. Уравнение f (x) = 0 между а и b либо вовсе не имеет действительных корней,
либо имеет один действительный корень в зависимости от того, будут ли числа f (a)
и / (Ь) иметь одинаковые или противоположные знаки. Лишь один действительный
корень уравнения f (х) = 0 может оказаться больше наибольшего корня или меньше
наименьшего корня уравнения /' (*) =0.
(f) Отделение действительныхкорней: теорема Бюдана —
Фурье. Пусть N (х) — число перемен знака в последовательности значений
f (x), f (x), f" (я),..., fin) (х) для любого действительного алгебраического
уравнения (2). Тогда число действительных корней уравнения (2), заключенных между
двумя действительными числами а и 6 > а, не являющимися корнями уравнения
(2), либо равно N (a) — N (6), либо меньше N (а) — N (Ь) на четное число. При
подсчете N(a) члены последовательности, равные нулю, вычеркиваются. Если
при подсчете N (Ь) окажется, что f{i) (b) — 0 для k+\ ^i^l — 1, а / lftl(6) ф0
и fd) (b)^0, то$'и(Ь)заменяются на (— 1)/_/ sgn fll) (b).
Число действительных корней уравнения (2), заключенных между а и Ь, нечетно
или четно в зависимости от того, будут ли f (а) и f ф) иметь противоположные или
одинаковые знаки.
(g) Отделение действительных корней: метод Штурма.
Пусть для данного действительного алгебраического уравнения (2) без кратных
корней (п. 1.6-2) N (х) есть число перемен знака в последовательности
значений многочленов (члены, обращающиеся в нуль, не учитываются):
fo (x) = f (x) =£o (*) h (x)—f2 (*). h (x)=/' (x) =£x (*) /,(*)-f3(x)A
где при i > 1 каждый многочлен Д- (х) есть взятый с коэффициентом —1
остаток (п. 1.7-2), получаемый при делении Д_2 (*) на fi-i(x)\ многочлен fn(x)^bQ
1.7-3.
1.7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ
41
есть постоянная. Тогда число действительных корней уравнения (2),
заключенных между двумя действительными числами а и Ь>а, не являющимися
корнями уравнения (2), равно N (a) — N(b).
Метод Штурма применим и в том случае, если для. удобства вычислений какой-либо
из многочленов fi(x) в описанном выше процессе заменить многочленом Fj (x) =fj(x)/k (x),
где k (х) — положительная постоянная или многочлен относительно х, положительный
при а ^ х ^ Ь, а оставшиеся многочлены получить, исходя из F^(x), а не из fy (*).
Подобную же операцию можно вновь проделать над любым из многочленов F; (х) и т.д.
Если уравнение f (х) =0 имеет кратные корни, то f (х) и f'(x) имект общий делитель
(п. 1.7-3). В этом случае многочлен fn(x) не является постоянной, и N(a) — N (Ь) есть
число корней между а и Ь, причем каждый кратный корень считается только один раз.
1.7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
И ДЕЛЕНИЕ МНОГОЧЛЕНОВ. ЭЛЕМЕНТАРНЫЕ ДРОБИ
1.7-1. Разложение многочленов на множители (см. также п. 7.G-6). Если
многочлен F (х) может быть представлен в виде произведения многочленов^ (*),
/г (*)»•••» /s M. то эти многочлены называются множителями (делителями)
многочлена F (х). Если х—хг — корень кратности т произвольного множителя ft (x),
то он является и корнем кратности М^т многочлена F (х). Каждый
(действительный или комплексный) многочлен f (х) степени п относительно х может
быть единственным способом представлен в виде произведения постоянной
и п линейных множителей (х — ak), именно
п
f(x)==aQxn + a1xn-i + ...+an_1x+anEEa0TI(x-xk)1 (1.7-1)
где xk— корни многочлена f (х); корню xk кратности mk (п. 1.6-2)
соответствует mk множителей (x—xk) (теорема о разложении многочлена
на множители). Каждая пара множителей [х- (cik + mk)] и [х — (ak — mk)]y
соответствующая паре комплексных сопряженных корней х^ — ак-\-тк и
xk = ak — i(uk (см- также п. 1.6-6а), может быть объединена в действительный
квадратный множитель l(x — ak)2-\-a>k2]-
1.7-2. Деление многочленов. Остаток. Частное F (x)/f (x) от деления
многочлена F (х) степени N на многочлен f (x) степени n<N может быть
представлено в виде
F(X) _ A0xN + AlxN-1 +...+an _
fix) — a0xn+alXn-1 +... + *„ """
E=(b0x*>-n + b1xN-n-i+ ... +bN-n)+j±$-> (1.7-2)
где остаток гг (х) есть многочлен степени, меньшей, чем п. Коэффициенты Ъь
и остаток гг (х) определяются однозначно, например с помощью процесса
деления углом (алгоритма деления).
Остаток Гх (х) отсутствует в том и только в том случае, когда
многочлен f(x) является делителем (п. 1.7-1) многочлена F (х).
Остаток, получаемый при делении любого многочлена f (х) на (х — с),
равен f (с) {теорема Везу),
1.7-3. Общие делители и общие корни двух многочленов. Если многочлен g (x)
является общим делителем (множителем) многочленов F (х) и f (*), то его корни являются
общими корнями этих многочленов. Отношение (2), как и числовую Дробь, можно
сократить на любой общий множитель числителя и знаменателя.
Многочлены
F (х) = A0xN + AxN~* + ... + AN
а
f (x) = а0хп + atxn *+... +а
ГЛ. !. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.7-4.
имеют по крайней мере один общий корень (и, таким образом, общий делитель
ненулевой степени) в том и только в том случае, если определитель порядка N -f- я
(F,
\л.
0
0
Оо
0
0
f) =
А,
Ао
.
«1
а0
.
А2
At
.
0-2
Oi
.
.
Л2 ..
.
.
а2 ...
.
»
•
. .
ал-1
•
.
* t • •
. . .
0 А0 At A2
% ° • •
ап-1 "п ° •
. ...
AN^i AN О
^V-l
О
О
О
О
do cl\ а?
п-г
(результант многочленов F (х) и f (x)) равен нулю.
взаимно просты.
• Имеет место формула
R {F, f) = (- \)Nn R tf, F) =i4ja;
„tf
a
(1.7-3)
В противном случае F (*) и f (x)
N
П П (a.-0,)f
1 / = 1
где a4« и 0. — соответственно корни F (x) и f (#)• *
Наибольший общий делитель (общий множитель наибольшей степени) многочленов
F(x) и f (х) определен однозначно с точностью до постоянного множителя н может быть
найден следующим образом. Делим f (х) на rt (*), где rt (x) определен формулой (1.7-2);
получаем остаток г2 (х). Затем делим г, (*) на получившийся остаток г2 (х) и продолжаем
этот процесс до тех пор, пока некоторый остаток, скажем, rk (x), не окажется равным
нулю. Тогда остаток fu+ (*), умноженный на произвольный постоянный множитель, и
будет искомым наибольшим общим делителем. Если гх (х) = 0, то наибольшим общим
делителем будет сам многочлен f (x).
1.7-4. Разложение на элементарные дроби. Любое отношение g(x)/f(x)
многочлена g (х) степени т и многочлена / (я) степени п > т без общих
корней (п. 1.7-3) может быть следующим образом представлено в виде суммы п
элементарных дробей, соответствующих корням х^ (кратности т&)
многочлена / (я):
т.
bki
fix) ZjZj,x_XuV- Zj
k /=i
(*-**>'
wki
vk2
kmk
(x-xk) • (x-xrf
;}(1M)
Коэффициенты by можно найти одним из следующих методов или же
комбинацией этих методов:
1. Если mk=\ (яд —простой корень), то bkl=g (xk)/f (xk).
2. Умножая обе части равенства (4) на / (л;) и приравнивая
коэффициенты при одинаковых степенях х в обеих частях полученного
равенства.
3. Умножая обе части равенства (4) на f(x) и последовательно
дифференцируя полученное равенство. Пусть ср^ (лг)=/ (х)/(х — xk) k.
Тогда bkmk, bkmk_i, ... последовательно находятся из соотношений
g' (Xk) = bkmk4>k (**) + Ь*тел_1ф* (xk),
g" (xk) = bkmkq>Z (xk) + 2bkmk_ly'k (xk) + 2bkmk_2q>k (xk),
l)
(xk) = bkmk4>1
(mk-1)
(4) + mkbkmk_ ^k 2) (xk) +
+ Щ («*- 1) bkmk-&Tk 3) (**> + —+ W*!M>* (xk).
1.8-3. 1.8. ЛИНЕЙНЫЕ, КВАДРАТНЫЕ, КУБИЧНЫЕ УРАВНЕНИЯ &
Элементарные дроби, соответствующие произвольной паре комплексных
сопряженных корней а^+Шк и ak~~^t кратности т^, обычно соединяются в
Х + dkl X+dk2 XJ*~ dkmk
Ckl[(x-afc)*+<o*k] +€*[lx-akP + aiy+-+ [(x-a#+tii\m* ' 0'7'5)
Коэффициенты су и dy могут быть определены непосредственно описанным
выше методом 2. Если g(x) и / (я)—действительные многочлены (п. 1.6-6), то
все коэффициенты bkf, ckj, dkj в окончательном разложении на элементарные
дроби действительны.
Каждая рациональная функция от х (п. 4.2-2, с) может быть
представлена в виде суммы многочлена и конечного числа элементарных дробей (см.
также п. 7.6-8). Разложение на элементарные дроби играет важную роль
в связи с интегрированием (п. 4.6-6, с) и интегральными преобразованиями
(п. 8.4-5).
1.8. ЛИНЕЙНЫЕ, КВАДРАТНЫЕ, КУБИЧНЫЕ УРАВНЕНИЯ
И УРАВНЕНИЯ ЧЕТВЕРТОЙ СТЕПЕНИ
1.8-1. Решение линейных уравнений. Общее уравнение первой степени
(линейное уравнение)
ах = Ь или ах — Ь = 0 {афО) (1.8-1)
имеет решение
*=4- (1.8-2)
1.8-2. Решение квадратных уравнений. Квадратное уравнение
ax* + bx+c=0 (афО) (1.8-3)
имеет корни
*1,2 = 2Н » О-8"4)
где в случае, когда а, Ь и с—любые комплексные числа, ]/ б2 — Аас есть одно
из значений квадратного корня.
Если уравнение (3) действительно, то его корни хг и х2 либо
действительные различные, либо действительные равные, либо комплексные
сопряженные в зависимости от того, будет ли (п. 1.6-5) D = b2 — 4ac соответственно
положителен, равен нулю или отрицателен. Отметим, что
Xi+x2 = —b/a и дг|*2=с/а.
1.8-3. Кубичные уравнения: решение Кардано. Кубичное уравнение
x* + ax2 + bx+c=0 (1.8-5)
подстановкой х = у— ■»■ приводится к «неполному» виду
Корни ylf у2, Уз «неполного» кубичного уравнения (6) равны
я i d Л4-В..Л — В ^г~-
уг = А + В, у2,3 = f-±t —— Уз,
где
«-arm.
(1-8-7)
44 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА. ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.8-4.
причем в качестве А и В берутся любые значения кубичных корней из
соответствующих комплексных чисел, удовлетворяющие соотношению АВ=—р/3.
Если уравнение (6) действительно, то (в тех случаях, когда это возможно)
следует брать действительные значения этих корней. Если кубичное уравнение
(6) действительно, то оно имеет или один действительный корень и два
сопряженных комплексных корня, или три действительных корня, по крайней
мере два из которых равны, или три различных действительных корня в
зависимости от того, будет ли Q соответственно положительно, равно нулю или
отрицательно. В последнем случае («неприводимый» случай) можно
воспользоваться методом п. 1.8-4,а. Отметим, что дискриминанты (п. 1.6-5) уравнений
(5) и (6) равны —108 Q.
1.8-4. Кубичные уравнения: тригонометрическое решение. Пусть «неполное»
кубичное уравнение (6) действительно.
(а) Если Q<0 («неприводимый» случай), то /?<0 и
(Ь)
Если
<?>г0,
Р>0,
if.-г]
cos a = —
то
/ Р а
/__cosT.
2|/TZeos
Q
2У-(р/3)»'
№**>
(1.8-8)
yt = — 2Yp/3 ctg 2а. уг, 8 = V>/3 (ctg 2а ± i Y3 cosec 2a),
*.-а/£Т0«'<т). ^э=ц/(1У(,э,<1).
(1.8-9а)
(с) Если Q ^ 0, р < 0, то
У1 = — 2Y— plb cosec 2а, у2,ь = Y—p/Ъ (cosec 2а ± iYT ctg 2а), Л
*«=3/Я:(.«,^), ->-|УН7 ("»■<*). I а'8'96>
Во всех случаях берется действительное значение кубичного корня.
1.8-5. Уравнения четвертой степени: решение Декарта — Эйлера.
Уравнение четвертой степени
x* + ax*+bx2 + cx + d = 0 (1.8-10)
подстановкой х = у—J- приводится к «неполному» виду
У* + РУ* + ЯУ+г = 0- (1.8-11)
Корни уъ у2, у3, #4 «неполного» уравнения четверюй степени (11) равны
одному из выражений _
± Vzx±V4±Vz9y (1.8-12)
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие
УчУчУъ =-f, (1.8-13)
причем zv z2 и z3-— корни кубичного уравнения
*+|-*Ч^*-£-0. (1-8-14)
1.8-6. Уравнения четвертой степени: решение Феррари. Если уг —
произвольный корень кубичного уравнения
уЬ — Ьу* + (ас—Щ y — d*d-\-\bd —с2=0 (1.8-15)
1.9-3.
1.9. СИСТЕМЫ УРАВНЕНИЙ
45
(резольвенты уравнения (10)), то четыре корня уравнения (10) находятся как
корни двух квадратных уравнений
х2+тХ+Ч= ± ^(т- Ь+Уг) х*+(т У1-°) *+т -d> (L8-16>
где подкоренное выражение в правой части является полным квадратом.
Отметим, что дискриминанты (п. 1.6-5) уравнений (10) и (15) совпадают.
1.9. СИСТЕМЫ УРАВНЕНИЙ
1.9-1. Системы уравнений. Решением некоторого множества (системы) урав-
нений
Л(*1. х* -0 = 0 (/=1, 2,...) (1.9-1)
с неизвестными хг, х2,... называется множество значений неизвестных xv
х2,..., удовлетворяющих одновременно каждому из уравнений системы (1).
Система (1) решена полностью, если найдены все такие решения. Чисто можно
последовательно исключать неизвестные #у из системы (1), например разрешая
одно из уравнений относительно дсу и подставляя полученное выражение в
оставшиеся уравнения. Число уравнений и неизвестных таким путем
уменьшается до тех пор, пока не остается решить одно уравнение с одним
неизвестным После этого процесс повторяется в обратном порядке, для нахождения
второго неизвестного и т. д. Решения можно проверить подстановкой.
Чтобы исключить Xi, скажем, из двух уравнений \х (*ь *г) = 0 и f2 (xt, x2) = 0, где
ftixt, xz) и fz(xt, xz) — многочлены относительно xt и х2 (п. 1.4-3), рассматривают обе
эти функции как многочлены относительно xt и составляют их результант R (п.1.7-3).
Тогда х2 должно удовлетворять уравнению R — 0.
1.9-2. Системы линейных уравнений: правило Крамера. Рассмотрим систему
п линейных уравнений с п неизвестными хъ х2, ..., хп:
апхг + а12х2 +... + а1пхп = Ьъ д
а21хх+а22х2 +...+а2пхп = Ь2, или ^ aikxk = bi (/=1,2 /г). [(1.9-2)
ап1хг + ап2х2 + ... + апп»п = Ьп
Если определитель системы (2)
*=1
D = det [aik] =
ап a12...aln
021 а22 • • • а2П
(1.9-3)
I ат апг • • • апп I
не равен нулю, то система (2) имеет единственное решение
Db
xk = -j^ (&=1, 2,..., п) (правило Крамера), (1.9-4)
где Dk — определитель, получающийся из D при замене элементов alft, a2kl ...
...,ank k-TQ столбца соответствующими свободными членами bx, b2t...,bn, или
Д*=2 Aikbi (Л-1, 2,...,/г), (1.9-5)
/ = 1
где Aik — алгебраическое дополнение (п. 1.5-2) элемента aik в определителе
D (см. также пп. 13.2-3 и 14.5-3).
1.9-3. Линейная независимость (см. также пп. 9.3-2, 14.2-3 и 15.2-1, а).
(а) т уравнений fi(xlt х2, ..., хп)=0 (/ = 1, 2, ..., т) или т функций
fi (xi> x2* •••» хп)* определенных при всех значениях хг, х2, ..., хп, линейно
ГЛ. !. ЭЛЕМЕНТАРНАЯ АЛГЕБРА. ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.9-4.
независимы, если
т
из того, что У! kih (*i» хъ ••*» хп) ==0 ПРИ всех значениях .
/=i f (1.9-6)
ati, *2> •••» *я следует, что А1 = А,2 = ... = Ят = 0.
В противном случае эти т уравнений или функций линейно зависимы, т. е.
по крайней мере одно из них может быть представлено в виде линейной
комбинации остальных. Это всегда имеет место в тривиальном частном случае,
когда одно или более из уравнений //(*lf х2, ...хп) = 0 есть тождество.
п
п однородных линейных функций 2 aikXk ('=!» 2, ..., п) линейно незави-
симы в том и только в том случае, если det [а^] ф 0 (см. также п. 1.9-5).
п
Более общее утверждение: т однородных линейных функций V а;ьхъ (/ = 1,2 т)
А-1
линейно независимы в том и только том случае если {тхп)-матрица [а^1 имеет
ранг т (п. 13.2-7).
(Ь) т множеств, каждое из которых состоит из п чисел х\*\ х£\ ..., х£\
xf\ xf\ ..., х^\ ...; х\т), х^\ ..., *4т) (например, решения системы
уравнений или наборы компонент т штук /2-мерных векторов), линейно независимы,
если т
из 2 V4°=<> (/=1.2, .....п) следует ^ = ^ = ... = ^=0.(1.9-7)
Это выполняется в том и только том случае, если (/ихя)-матрица
\хЩ имеет ранг т (п. 13.2-7).
1.9-4. Системы линейных уравнений: общая теория (см. также п. 14.8-10).
Система т линейных уравнений с п неизвестными хг, х2, ..., хп
2 *!*** = *! <*-1. 2,..., т) (1.9 8)
имеет решение в том и только в том случае, если матрицы
lalx а12 ... aln \ /ап а12 ... а1п Ьг
а21 а22 ... а2п I а21 а22 ... а2п Ь2
/f I
\ат\ <*т2 ••• йтп \^т\ «т2 ••• <■
(1.9-9)
(матрица системы и расширенная матрица системы) имеют один и тот же
ранг (п. 13.2-7). В противном случае уравнения несовместны.
Единственное решение, о котором говорилось в п. 1.9-2, существует,
если г=т = п. Если обе матрицы (9) имеют ранг г^т, то уравнения (8)
линейно независимы при г = т и линейно зависимы при г</и (п. 1.9-3, а).
В случае г<т некоторые т — г уравнений можно выразить в виде линейных
комбинаций остальных г уравнений (независимых), и им удовлетворяют
решения этих г уравнений. Линейно независимые уравнения определяют
некоторые г^т неизвестных как линейные функции остальных /г — г неизвестных,
остающихся произвольными.
1.9-5. Системы линейных уравнений: п однородных уравнений с п
неизвестными. В частности, система п однородных линейных уравнений с п
неизвестными п
i>«***=0 (/ = 1, 2,..., п) (1.9-10)
А=1
1ЛФ-1. 1.10. ФОРМУЛЫ, ОПИСЫВАЮЩИЕ ПЛОСКИЕ ФИГУРЫ И ТЕЛА 47
имеет решение, отличное от тривиального (нулевого) решения дг1=лг2 = ...=
=*л=0, в том и только а том случае, если D = det [aik]=Q (см. также
п. 1.9-3, а).
В этом случае существует точно п — r линейно независимых решений х[*\
х{%.., х{»; х\*\ *<«..., 42);...; ^Гг), ЛЛ~Г),...,^(ГГ). Л r-ранг
матрицы системы (п. 1.9-4). Наиболее общим решением тогда является
п—г
ti^Cf/p (/=1,2 п)% (1.9-11)
/==1
гдг с/ — произвольные постоянные (см. также п. 14.8-10).
В важном частном случае, когда г = п—1,
Xi*=cAkl, x2 = cAk2, ..., xn=cAkn, (1.9-12)
где Akj —алгебраическое дополнение (п. 1.5-2) элемента ау в определителе D
(причем k выбрано так, что хотя бы одно из Ау (/=1, 2, ..., п) отлично
от нуля) есть решение при любой произвольной постоянной с. Это значит,
что все отношения Х{/хь определены однозначно; решения (12), получающиеся
при различных таких значениях k, тождественны (см. также п. 14.8-6).
1.10. ФОРМУЛЫ, ОПИСЫВАЮЩИЕ ПЛОСКИЕ ФИГУРЫ И ТЕЛА
1.10-1. Трапеция (стороны а, Ь, с, d; а и Ь параллельны; высота h есть
расстояние между а и Ь\ площадь 5):
S-f(a + ft)A. h=7±FVs(s-a+b)(s-c)(s-d), где s="-»+ g + " .
Трапеция является параллелограммом при а = 6 (тогда c = d) и ромбом
при a = b=c = d.
Таблица 1.10-1
Правильные многоугольники (длина стороны равна а)
Число
сторон
п
3
4
5
6
8
10
1
Правильный
многоугольник
Треугольник
Квадрат
Пятиугольник
Шестиугольник
Восьмиугольник
Десятиугольник
Радиус
описанной
окружности
я а
2 sin (я//г)
|/3
1 / 1 , ^5
" У 2 + Т0
а
f a+vw
Радиус
вписанной
окружности
— а
" tg (л/п)
2
|(l+^2)
•fl/5 + 2/5
Площадь
a»
j К 25+10 УЬ
2a' (1 + Y2)
5 ■ t
lQtVb + 2Yb I
48 ГЛ. I ЭЛЕМЕНТАРНАЯ АЛГЕБРА. ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.10-2.
1.10-2. Правильные многоугольники. В табл. 1.10-1 приведены выражения
для радиусов описанной и вписанной окружностей и для площади
некоторых правильных многоугольников.
1.10-3. Круг (радиус г).
(a) Длина окружности 2лг, площадь яг2.
(b) Центральный угол, равный ф радианам, определяет дугу длиной гф,
сектор с площадью г2ф/2, хорду длиной 2г sin (ф/2), сегмент с площадью
г2(ф —sin ф)/2.
(c) Площадь между окружностью радиуса гх и заключенной внутри нее
(не обязательно концентрической) окружностью радиуса г2 равна я^ + г*) X
Х(г1-г2).
1.10-4. Призмы, пирамиды, цилиндры и конусы.
(a) Объем призмы или цилиндра с основанием 5Х и высотой h равен hSv
(b) Объем пирамиды или конуса с основанием St и высотой h равен hSjZ.
(c) Объем усеченной пирамиды или конуса с основаниями 5t, S2 и
высотой h равен h (S1 + V~S^S2 + S2)IZ.
(d) Боковая поверхность прямого кругового конуса с радиусом
основания г и высотой h равна яг}/ r2 + /i2.
1.10-5. Тела вращения (см. табл. 1.10-2).
Таблица 1.10-2
Тела вращения
1
2
3
4
5
Тело
Сфера радиуса г
Сплюснутый эллипсоид
вращения (сфероид) (Ось
2а>26, e-]/"l-J£;
вращение вокруг малой
оси.)
Вытянутый эллипсоид
вращения (Ось 2а>26,
е—у 1 -; вращение
вокруг большой осн.)
Тор, образованный
вращением круга радиуса г
вокруг оси, отстоящей
на расстоянии R от
центра
Сферический сегмент
радиуса г, заключенный
между параллельными
плоскостями; h —
расстояние между
плоскостями; гх, г2 — радиусы
оснований
Площадь поверхности
4яг2
8 1—8
2лЬг + 2л — arcsin e
е
4л2/?/-
2ЛГЛ + Л (Г2+ Г2)
Объем
1-
х пагЬ
sпаЬ' 1
2n'Rr'
|ft (ЗГ2 + 31 +А»)
I.tt-I.
1.11. ТРИГОНОМЕТРИЯ НА ПЛОСКОСТИ
49
1.10-6. Правильные многогранники. В таблице 1.10-3 приведены основные
элементы всех правильных многогранников.
Таблица 1.10-3
Пять правильных многогранников
(Длина
Правильный
гогранник
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
*) Фо
ребра равна а; соответствующие числа F граней, Е вершин и
связаны формулой Эйлера Е -f- F — К = 2 *))
Число и тип
граней
4
равносторонних
треугольника
6 квадратов
8
равносторонних
треугольников
12
правильных
пятиугольников
20
равносторонних
треугольников
рмула Эйлера ci
Радиус
описанной
сферы
\уъ
\Yl
f/2
!(l+/5)/8
£Уз(б + /б>
праведлива для
Радиус
вписанной
сферы
тИ
а
2"
f/*
4 \ Уь
-4^(3+/б)
любого выпукл
Площадь
поверхности
a* V3
6 а*
2а2 V3
За*Х
XУ 5(5+2/5)
50*^3
ого многогранн
К ребер
Объем
a-Yu
а*
S"
^'(15+ 7/5)
ie'(3+/5)
ика.
1.11. ТРИГОНОМЕТРИЯ НА ПЛОСКОСТИ
1.11-1. Вводные замечания. Прямоугольные треугольники. Тригонометрия
на плоскости описывает соотношения между сторонами и углами плоских
треугольников в терминах тригонометрических функций (п. 21.2-1— 21.2-4);
заметим, что все плоские фигуры, ограниченные
прямыми линиями, можно рассматривать как
комбинации треугольников. Так как каждый плоский
треугольник можно разложить на прямоугольные треугольники,
то наиболее важными тригонометрическими
соотношениями являются соотношения между сторонами и углами
прямоугольных треугольников.
Прямоугольные треугольники. В каждом
прямоугольном треугольнике (рис. 1.11-1) с катетами а, Ь и
гипотенузой с:
Рис. 1.11-1.
Прямоугольный
треугольник.
А + В = 90е, а2 + Ь* = с2 (теорема Пифагора),
sin A = cos В =-
tg/4 = ctgB = -
sinB = cos Л=—,
с
tgB = ctgA = K
(111-1)
ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА, ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.11-2.
Рис. 1.11-2.
Косоугольный
треугольник.
1.11-2. Свойства плоских треугольников. В каждом плоском треугольнике
(рис. 1.11-2) сумма углов равна 180°. Сумма любых двух сторон больше
третьей сгороны, против большей из двух сторон лежит
больший угол.
Треугольник на плоскости единственным образом
определяется (с точностью до преобразования симметрии):
1) тремя сторонами,
2) двумя сторонами и углом, заключенным между
ними,
3) стороной и двумя прилежащими к ней углами.
В каждом плоском треугольнике три биссектрисы его углов
пересекаются в центре М вписанной окружности. Три
перпендикуляра к его сторонам, проходящих через середины этих
сторон, пересекаются в центре F описанной окружности, Три
медианы пересекаются в центре тяжести G треугольника. Три
высоты треугольника пересекаются в точке Н, лежащей на
одной прямой с точками Fw G, причем HG : ~GF = 2. Середины сторон, основания высот
и середины отрезков, соединяющих Н с каждой из вершин треугольника, лежат на
одной окружности (окружность девяти точек» окружность Фейербаха). Центр этой
окружности есть середина отрезка HF.
1.11-3. Формулы для решения треугольников. В нижеследующих
соотношениях А, В, С являются углами, лежащими соответственно против сторон
a, by с треугольника. Площадь треугольника обозначена через S; R и г
являются соответственно радиусами описанной и вписанной окружностей, ар =
= ~(а + Ь + с).
Таблица 1. 11-1
Решение плоских треугольников
(Все остальные случаи получаются циклической перестановкой.)
Случай
1
2
3
4
Даны
Три стороны а, Ь, с
Две стороны и угол
между ними Ь, с, А
Одна сторона и два
угла а. В, С
Две стороны и угол
против одной из них
Ь. с, В
Использованные формулы
(А + В + С = 180°)
А, В, С из (2) или (5)
—^— из (6) или (7), затем
В и С; или В, С из (3) и (4):
. _ b sin A
ь с — b cos A
а из (3) или (4)
Ь, с из (3);
А = 180° — В — С
из (3);
b sin A
Q ==: —
sin В
г „ С$\ПВ
sinC=-r-
А = 180° — В — С
Условия существования
решения
Сумма двух сторон должна
быть больше третьей
Задача имеет одно
решение, если b >: с, два
решения, если b<ic, csinB<ib; I
одно решение, если b <.c,
с sin В = Ь\ при Ь<с,
с sin В > 6 решения нет
1.12-1.
1.12. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
51
Для того, чтобы получить все формулы, необходимые для решения
треугольников, нужно произвести одновременную циклическую перестановку Л,
В, С и а, Ь, с. Табл. 1.11-1 позволяет вычислить все стороны и углы
треугольника по определяющим его сторонам и углам.
а2 = о2 + с2—2bc cos А = (Ь+с)2 — 46с cos2 -^-(теорема косинусов), (1.11-2)
2/? (теорема синусов), (1.11-3)
sin A sin В sin С
с=a cos В + Ь cos Л (теорема о проекциях) (1.11 -4)
sin 4 = + l^^^. cos^ + KH^E.
sin/l = + £•)/ P(p-a)(p-b)(p-c),
6+c 4* 2
tg-B-C '
2
Длина высоты ha= ^ (S=-^aha).
4Я
"27?
(1.11-6)
(b + c) sin^acos^-j^, (6-c)cos^ = asin^=^, (1. 11-7)
r=(p~a)tg4 = (p-6)tgf = (p-c)tg| =
= 4/? sin £ sinf sin | = p tg £ tgf tg?-, (1.11-8)
p=q + g+g=4/?cos4cosf-cos§, (1.11-9)
S == ~ ab sin С = -j be sin Л = -j ac sin £ =
= Vp(p-a)(p-b)(p-c) =
= 2#* sin Л sin В sin C= ?nr = pr. (1.11-10)
Длина биссектрисы wa=y^Ybc(a + b + c) (b+c—a).
Длина медианы та= jY2b2+2c2 — a2.
1. 12. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
1.12-1. Введение. Сферические треугольники. На поверхности шара
кратчайшее расстояние между двумя точками измеряется вдоль окружности
большого круга, т. е. окружности, плоскость которой проходит через центр
шара (геодезической, п. 17.3-12). Вершины сферического треугольника
являются точками пересечения трех лучей, выходящих из центра шара,
и сферической поверхности. Сторонами a, bt с сферического треугольника
52 ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА. ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.12-2.
1.12-1. Сферический
треугольник.
называют те углы между лучами, которые меньше 180° *). Каждой стороне
треугольника соответствует дуга большого круга на поверхности шара
(рис. 1.12-1). Углы Л, В, С сферического
треугольника, противолежащие сторонам а,
Ь, с соответственно, представляют собой, по
определению, меньшие, чем 180°, углы между
дугами больших кругов, соответствующими
сторонам треугольника, или углы между
плоскостями, определяемыми данными
лучами.
Сферическая тригонометрия занимается
изучением соотношений между сторонами и углами
сферических треугольников (например, на
поверхности Земли и на небесной сфере). Однако
физики и инженеры во многих задачах
предпочитают использовать преобразования вращения
(п. 14. 10-1), а не сферическую тригонометрию.
1.12-2. Свойства сферических
треугольников. Каждая сторона и угол
сферического треугольника по определению
меньше 180°.
Геометрия на поверхности шара
является неевклидовой (см. также п. 17.3-13);
в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°,
сумма углов заключена между 180° и 540°. В каждом сферическом
треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон
больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс
третий угол.
Сферический треугольник единственным образом определяется (с точностью
до преобразования симметрии):
1) тремя сторонами,
2) тремя углами,
3) двумя сторонами и заключенным между ними углом,
4) стороной и двумя прилежащими к ней углами.
Замечание. Для каждого сферического треугольника можно определить большие
круги, играющие роль перпендикуляров, проведенных через середины сторон, биссектрис,
медиан и высот. Плоскости трех больших кругов каждого типа пересекаются по прямой.
В полной аналогии с описанной окружностью плоского треугольника существует
описанный прямой круговой конус, содержащий три прямые линии, определяющие
треугольник; ось этого конуса есть прямая, по которой пересекаются плоскости
перпендикуляров, проведенных через середины сторон. Существует также вписанный прямой кру'
говой конусу касающийся трех плоскостей, соответствующих сферическому треугольнику;
ось этого конуса есть прямая, по которой пересекаются плоскости биссектрис. «Радиус»
описанной окружности и «радиус» вписанной окружности представляют собой углы,
равные соответственно половинам углов при вершинах первого и второго конусов.
Если R — радиус шара, то площадь S# сферического треугольника выражается
формулой
SR = R*e, (1.12-1)
где е—сферический эксцесс (избыток):
А + В + С — л,
(1.12-2)
измеряемый в радианах. Величина d — 2я — (а -\- b + с) называется сферическим дефектом.
Полярный треугольник, соответствующий данному сферическому треугольнику,
определяется тремя лучами, перпендикулярными к плоскостям, связанным со сторонами
данного треугольника. Если один сферический треугольник полярен относительно
другого, то и второй будет полярен относительно первого Стороны одного из полярных
относительно друг друга треугольников дополняют углы другого до 180°. Таким образом,
каждая теорема или формула, относящаяся к сторонам и углам треугольника, может
быть преобразована в теорему или формулу об углах и сторонах полярного треугольника.
*) Если один из этих углов равен 180°, то сферический треугольник вырождае1СЯ
в полуокружность большого круга.
1.12-4.
1.12. СФЕРИЧЕСКАЯ ТРИГОНСШЕТРИЯ
53
1.12-3. Прямоугольный сферический треугольник. В прямоугольном
сферическом треугольнике по меньшей мере один угол, например С, равен 90°;
противоположная сторона с называется гипотенузой. Соотношения между
сторонами и углами прямоугольного сферического треугольника могут быть
извлечены из следующих двух мнемонических
правил Непера:
В диаграмме на рис. 1.12-2 синус любого из
указанных в ней углов равен
1) произведению тангенсов двух углов,
прилежащих к нему на диаграмме,
2) произведению косинусов двух углов,
противолежащих ему на диаграмме.
Пример. Найти стороны и углы прямоугольного
сферического треугольника, зная гипотенузу с и сторону а.
Эта задача имеет решение только при условии
sui a ^ sin с, тогда
cos 6:
cos с
' cos a '
COS В as
tg a
igc*
sin A =
sin a
Замечай ие. Если а меньше, равно или больше Рис. 1.12-2. Правила Непера.
90°, то и Л соответственно меньше, равно или больше
90°. и наоборот.
Если даны а и Л, то задача имеет решение только
ь том случае, когда предыдущее условие выполнено и, кроме того, sin a =$ sin А; если
а ф А, то решений два.
Если даны А и В, задача имеет решение только при выполнении условий 90° < А -[-
Ч- В < 270° и — 90° < А — В <90° (см. п. 1.12-2).
Сферический треугольник со стороной, равной 90°, называется квадрантным
треугольником и может рассматриваться как полярный треугольник прямоугольного
сферического треугольника.
Ко всем задачам, включающим решение сферических треугольников
(прямоугольных или косоугольных), настоятельно рекомендуется делать эскиз,
ясно показывающий, будут ли различные углы и стороны меньше, равны
или больше 90°.
1.12-4. Формулы для решения сферических треугольников (см. также
рис. 1.12-1). В следующих ниже соотношениях Л, В, С являются углами,
противолежащими соответственно сторонам а, Ь, с сферического треугольника.
«Радиусы» описанного и вписанного конусов обозначены соответственно через
г и р. Формулы, не включенные в перечень, могут быть получены одновременной
циклической перестановкой Л, В, С и а, Ь, с. Таблица 1.12-1 позволяет
вычислять стороны и углы любого сферического треугольника пр трем подходящим
сбразом заданным сторонам и/или углам. Неравенства, отмеченные в начале
л. 1.12-2, должны быть приняты во внимание, для того чтобы исключить
посторонние результаты при решении треугольников.
sin a sin b sin с
sin A sinB sin С
{теорема синусов),
(1.12-3)
cos а — cos Ь cos с + sin Ь sin с cos А (теорема косинусов для сторон), (1.12-4)
cos А — — cos В cos С + sin В sin С cos а (теорема косинусов для углов), (1.12-5)
tg^cos£+iL=tgfcos^£,
А В+С Ь+с , А
tg ——^ cos ^- = ctg ~ cos
tg*-^sm^=ctg^sin
b — c
2 '
b — c.
(аналогии Непера) (1.12-6)
ГЛ. 1. ЭЛЕМЕНТАРНАЯ АЛГЕБРА. ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ 1.12-4.
Таблица 1. 12-1
Решение сферических треугольников
(см. формулы п. 1.12-4 и рис. 1.12-1)
Случай
1
2
3
4
5
6
Даны
Три стороны
а, Ь, с
Три угла
А, В, С
Две стороны и
заключенный между
ними угол
Ь, с, А
Два угла и
заключенная между ними
сторона
В, С, а
Две стороны и
противолежащий одной
из них угол
Ь, с, В
Два угла и
противолежащая одному из
них сторона
в, с, ь
Формулы для вычисления
А, В, С из (8) и
циклической перестановки
а, Ь, с из (8) и циклической
перестановки
В+С В-С
НН и —г-из (6)-
затем В и С; а из (7), (8)
или (4)
Ь + с Ь — с /Л.
Нп и т из (6)-
затем b и с; А из (7), (8)
или (5)
С из (3); А и а из (6)
с из (3); Л и а из (6)
Условия существования
решения
0 < a -f Ь + с < 360°
Сумма двух сторон должна
быть больше третьей
180° < А + В + С<540°;
Сумма двух углов должна
быть меньше 180° плюс
третий угол
Задача имеет одно или два
решения, если
sin с sin В :< sin b.
Сохраняются те из
величин С, для которых А — В \
и а — Ъ имеют одинаковый
знак;
A -f- В — 180°
и а + b — 180°
также должны быть одного I
знака I
Задача имеет одно или два
решения, если
sin Ь sin С < sin В. |
Сохраняются те из
величин с, для которых А — В 1
и а — b имеют одинаковый I
знак; I
A -f- В — 180°
иа + &- 180°
также должны быть одного 1
знака I
1.12-4.
1.12. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
55
. Л . Ь + с . а В —С \
sin -^ sin —~— = sin j cos —g—, I
. A b + c a B + C
sin- cos -±- = cos j cos -3L-,
Л . b — c . a . B — C
cos j sin -y- = sin j sm —y-,
A b—c a . B+C
cos у cos —2~ = cos ^ sm —y—»
i (аналогии Деламбра
и Гаусса)
a + b + c
с_ А + В + С \
Ъ _ _ f ,
sin
cos
sin
л
2
A
2
a
2"
a
-V
sin(s — b)s\n (s-
sinbsinc
sinssin(s—a)
sin fr sine
— cos 5 cos (5-
sinBsinC
cos (S — B)cos
-c)
»
-A)
»
(S-
C)
(формулы половинных
углов)
f sin С
. _ l/cos (5 —Л) cos (5 —В) cos (5—С)
Clg Г "" V - cos 5
. "l/ sin (s — a) sin (s — b) sin (s —c)
tg P ~~ V sin s
fxg* __s!n (s—a) ift a __ cos (S — Л)
Cl» 2 — tg p ' ё 2 ~~
ctg г
tS J- V 1ST Й ifi '8 -4^ '8
<■(
1У + 1Л^"^
(уравнение Люилье).
(1.12-7)
(1.12-8)
(1.12-9)
(1.12-10)
(1.12-11)
Некоторые тригонометрические соотношения становятся особенно удобными для
вычислений с помощью логарифмов, если в них использованы новые
тригонометрические функции
vers Л = 1 — cos Л, covers Л = 1 — sin Л, hav Л = у (1 — cos Л). (1.12-12)
Таким образом, если имеются в наличии таблицы функции hav, то для решения
сферических треугольников можно использовать следующие формулы:
hav Л = .sin (ST*? S!" (S~C) , hava = hav ф — с) + sin b sin с hav Л. (1.12-13)
sin b sin с
Другие аналогичные соотношения можно получить циклической перестановкой.
ГЛА ВА 2
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.1. ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
2.1-1. Вводные замечания (см. также п. 12.1-1). Геометрия занимается
изучением объектов, которые могут быть в том или ином смысле отождествлены
с точками, и представляет собой математическую модель, воспроизводящую
отношения между этими объектами. В основе каждой геометрической системы
лежат определенные аксиомы. Они могут быть выбраны таким образом, чтобы
соответствующая модель отражала свойства реального физического
пространства. Однако задачей геометрии является также логическое построение самых
разнообразных аксиоматических систем, в том числе и таких, которые
не всегда отвечают наглядным представлениям. В аналитической геометрии
точка определяется системой чисел (ее координат), и, следовательно,
геометрические факты записываются в виде соотношений между координатами.
Главы 2 (аналитическая геометрия на плоскости) и 3 (аналитическая
геометрия в пространстве) следуют тому способу изложения, который принят
в большинстве элементарных курсов: основные понятия геометрии
предполагаются известными и просто переводятся на язык алгебры, становящейся
вследствие этого средством исследования геометрических форм.
В гл. 17 кратко изложен и использован более глубокий метод,
состоящий в построении различных геометрических систем на основании заданных
аксиом. В пп. 17.1-1 —17.1-6 содержатся краткие
сведения из дифференциальной геометрии плоских
кривых, включая определения касательной,
нормали и кривизны.
2.1-2. Декартова система координат. Декартова
система координат связывает с каждой точкой Р
плоскости, на которой выбраны две
направленные прямые (оси координат) Ох и Оу,
пересекающиеся в начале координат О (рис. 2.1-1), пару
действительных чисел, абсциссу х и ординату
^ИСкосоуголГнРаяВсис?1м|Рко: У> ПРИ ЭТом ПИШУТ Р(х> У)- Прямая, проходящая
ординат. Отрезки OEt и через точку Р параллельно оси Оу, пересекает
ОЕ2 — единицы масштаба на ось Ох в точке Р'. Аналогично прямая, «проходя-
осях- щая через точку Р параллельно Ох, пересекает
Оу в точке Р". Величина направленного отрезка
ОР' = х (положительная, если направление ОР' совпадает с направлением
оси Ох, и отрицательная в противном случае) и определенная аналогичным
способом величина ОР"=у называются декартовыми координатами точки Р.
В общей (косоугольной) декартовой системе координат угол со между
осями Ох и Оу может принимать значения 0< со < гс(правая система) или
— я<со<0 (левая система). Если для измерения отрезков ОР' и ОР"
используются различные единицы длины, то система координат называется обще л
декартовой или аффинной.
Оси координат делят плоскость на четыре квадранта (рис. 2.1-1). Абсцисса х
положительна для точек (х, у), расположенных в квадрантах I и IV, отрицательна в
квадрантах // и 111, равна нулю для точек оси Оу; ордината у положительна для точек
2.1-4.
2.1. ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
57
в квадрантах / и II, отрицательна для точек в квадрантах /// и IV, равна нулю для
точек оси Ох. Началом координат служит точка (0, 0).
Замечание. Аналитическая геометрия на евклидовой плоскости постулирует
взаимно однозначное соответствие между точками прямой и действительными числами
(«координатная* аксиома, аксиома непрерывности, см. также
п. 4.3-1).
2.1-3. Правая декартова прямоугольная система
координат. В правой декартовой прямоугольной
системе координат направления осей выбираются так, что
поворот оси Ох на я/2 в положительном
направлении, т. е. в направлении, противоположном
вращению часовой стрелки, совмещает полуось
положительных х с полуосью положительных у. При этом условии
координаты х, у равны соответственно расстояниям
от координатных осей Ох и Оу до данной точки Р,
определенным по величине и знаку (рис. 2.1-2).
В этой главе, если не оговорено противное,
всегда применяется правая декартова прямоугольная система координат,
2.1-4. Основные формулы в декартовых прямоугольных координатах.
Рис. 2.1-2. Системы ко
ординат: правая
декартова прямоугольная
полярная.
и
1. Расстояние d между точками Рг (хъ ух) и Р2 (х2, */2)
d = V(x2-x1r + (y2-y1)\ ^
2. Угол у между двумя направленными отрезками Р±Р2 и Р3Р\
(х2 — xt) (*4 — х3) + (Уъ — Ух) (У* — Уз)
cos у —
V (Х2 - Xt)* + (у2 - Ух)* V(Xt - *3)2 + (У* - Уг)2'
(2.1-1)
(2.1-2)
Направляющими косинусами направленного отрезка PtP2 называются косинусы
углов а и а = — а образованных отрезком с положительными направлениями
х у 2 х*
координатных осей:
cos а = -
cos а = sin а
У
V(x2-xi)^ + (y2-yl)^
У2—У1
(2.1-3)
V(x2-x1)* + (y2-yl)*
3. Координаты *, у точки Р, делящей направленный отрезок PtP2 между
точками Рг (xlt ух) и Р2 (*2, Уг) в отношении РХР : РР2 = т : я=Х : 1,
определяются формулами
тх2 -\~ пхх *i + hx2
т + п
_ ту 2 + пух
1 +А,
. У\ + Ьу2
У~~ т + п 1 + А, '
Координаты середины отрезка PiP2:
_*1 + Х2
У =
-со< А,< + со.
Ух -Ь Уг
(2.1-4)
(2.1-5)
X При 0<А,<со точка Р лежит внутри отрезка РгР2, а при —1 <А,<0
и —со<А,<—1—вне его. При Х = 0 точка Р совпадает с точкой Р1% а при
X — ± со точка Р стремится к точке Р2.
Формулы (4) сохраняют смысл при X — — 1, если прямая дополнена
несобственной или «бесконечно удаленной» точкой, которая делит любой отрезок
этой прямой в отношении, равном —1.x
4. Площадь S треугольника с вершинами Рг (xlt yt), Р2 (х2, у2), Р3(х3, у3)
определяется формулой
*=г
Ч У\ 1
Ч Уг 1
хв Уз *
= о Iх* (^» ~ У*) + х* (Уз - Уг) Л- *з (У1 - У2)1 (2.1 -6)
58
ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.1-5.
В.частности, если x9 = y3 = 0t то
S = -
#1 Х2
2 I У1 У2
= -j(x1y2—x2y1).
(2.1-7)
П
#\
Значение S положительно, если направление обхода РхР2Рз совпадает с
положительным (против часовой стрелки) направлением вращения.
2.1-5. Преобразование декартовых координат при параллельном переносе
осей. Пусть х, у — координаты произвольной точки Р относительно декартовой
системы координат; пусть Jc, у — координаты
этой же точки Р относительно другой
декартовой системы координат, оси которой
соответственно параллельны осям первой системы и
направлены так же, как они, и начало
которой имеет относительно системы Оху
координаты х0, у0. Если на осях этих систем
выбраны одинаковые единицы масштаба, то коорди-
J наты х, у связаны с х, у следующими
формулами преобразования (рис. 2.1-3):
# %
Рис. 2.1-3. Параллельный
перенос осей координат.
'"*-'- ~У=ГУ0 1 (2.1-8)
х = х + х0, у = у + у0- )
Уравнения (8) допускают еще одно истолкование.
Если рассматривать х и у как координаты
относительно первоначальной системы координат (т. е. системы Оху), то точка (х, у) может быть
получена из точки (х, у) при помощи переноса на — х0 в направлении оси Ох и на — у0
в направлении оси Оу. Применение этого
преобразования к каждой точке некоторой пло- -. У а
ской кривой можно рассматривать как преоб- *\^п-А
разование переноса кривой.
2.1-6. Преобразование декартовых
прямоугольных координат при повороте осей.
Пусть х, # —координаты некоторой
точки Р относительно декартовой
прямоугольной системы координат. Пусть х>
у — координаты этой же точки
относительно новой прямоугольной системы
координат с тем же началом, расположенной
относительно системы Оху таким
образом, что угол хОх между осью Ох и
осью Ох равен б; угол отсчитывается в
положительном направлении (рис. 2.1-4).
При одинаковых единицах масштаба на осях координаты х, у связаны с
координатами х, у следующими формулами преобразования:
Рис. 2.1-4. Поворот осей координат.
x — xcosQ+y sin б,
x=xcosQ— у sin б,
y — — xsinQ+ycosb
y = xsin Ь+ycosQ
■}
(2.1-9)
Если рассматривать х, у и х, у как координаты двух различных точек относительно
одной и той же системы координат, то формулы (9) определят преобразование поворота
на угол —8 вокруг начала координат, переводящее точку (х, у) в точку (х, у)>
2.1-7. Одновременный перенос и поворот координатных осей. Если начало
координат системы Оху из п. 2.1-6 не совпадает с началом системы Оху и
2.1-8.
2Л. ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
59
имеет относительно последней координаты х0, у0, то уравнения
преобразования принимают вид
*= (*—*о) cos 6 + (у—у0) sin 6,
*/ = — (*—*о) sine + (у—у0) cose,
или _ _ f (2.1-10)
*=*0+*cos6 — # sine,
у = Уъ-}-х sinQ—y cosQ.
Формулы (10) позволяют найти зависимость между координатами точки
в любых двух правых декартовых прямоугольных системах координат с
одинаковыми единицами масштаба на осях.
Формулы (10) определяют также преобразования переноса и вращения, переводящие
точку (х, у) в точку (х ,у), где обе точки рассматриваются в одной и той же системе
координат.
Замечание. Преобразования (8), (9) я (10) не изменяют расстояния (1) между
двумя точками или величину угла, определяемую формулой (2). Соотношения,
составляющие содержание евклидовой геометрии, не изменяются при преобразовании переноса
и поворота, т. е. инвариантны относительно этих преобразований (см. также пп. 12.1-5,
14.1-4, 14.4-5).
2.1-8. Полярные координаты. Полярная система координат на плоскости
задается точкой О (полюс) и направленной прямой Ох (полярная ось). С
каждой точкой Р плоскости, на которой задана полярная система координат,
можно связать определенную пару чисел р, ф (полярные координаты).
Полярный радиус р есть длина отрезка ОР, а полярный угол <р — радианная мера
угла хОР, отсчитанная в направлении, противоположном вращению часовой
стрелки (см. рис. 2.1-2). Угол ф определен с точностью до слагаемого 2kn,
где k — любое целое число. Точка (р, ф) по определению совпадает с точкой
( —р, Ф ± л); это условие связывает определенную точку плоскости с
каждой парой чисел (р, ф) не только при положительных, но и при
отрицательных значениях р. Для полюса О величина ф не определена.
Замечание. В отличие от декартовой системы, полярная система координат
не устанавливает взаимно однозначного соответствия между парами чисел (р, ф) и
точками плоскости. Однако в большинстве приложений возникающая в результате этого
неопределенность может быть устранена.
Если полюс и полярная ось совпадают соответственно с началом О и
осью Ох прямоугольной системы координат (см. рис. 2.1-2), то при условии,
что для измерения г, х и у использованы равные единицы масштаба,
декартовы и полярные координаты связаны следующими формулами преобразования:
* = рС08ф, # = рБтф, \
p=V*+?, tg<p=^, хфо.) (2-М1)
Имеют место следующие формулы (р, <р — полярные координаты);
1. Расстояние d между точками (p!t ф!) и (р2, <р8):
d = l/pf -f- P| — 2pip8 cos (ф8 - фО. (2.1-12)
2. Площадь треугольника с вершинами Pt (рь ф£), Р8 (р8, ф8), Р9 (р8, фа):
S = 2 tPlp2 sin (ф* ~" ф1) + p8ps sin (ф» "~ ф2) + p'Pl s|n (ф* ~~ ф*^* (2.1-13)
В частности, если р8 = 0, то
с 1
2 [PiP* sin (ф8 — ф,)]. (2.1-14)
О знаке S см. п. 2.1-4.4.
О других криполинейных системах координат см. в гл. 6.
60
ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.1-9.
2.1-9. Способы задания кривых (см. также пп. 3.1-13 и 17.1-1).
(a) Уравнение кривой. Уравнение вида
Ф(*. */) = 0 или y = f(x) (2.1-15)
удовлетворяется координатами точек, принадлежащих определенному
точечному множеству. В большинстве случаев, представляющих интерес, это
точечное множество образует кривую (см. также п. 3.1-13). Обратно, заданную
кривую можно определить уравнением (15), которое должно удовлетворяться
координатами всех точек кривой и только этих точек. Возможен случай,
когда кривая имеет более одной ветви.
Кривые, определяемые уравнениями
ф(л:, г/) = 0 и Хср(л:, г/)=0,
где X — отличная от нуля постоянная, совпадают.
(b) Параметрическое задание кривых. Плоская кривая
может быть задана также двумя уравнениями
*=*(*), y=y(t), (2.1-16)
где / — переменный параметр.
(c) Пересечение двух кривых. Значения координат хну,
которые одновременно удовлетворяют уравнениям двух кривых
Фг(*. #) = 0, ф2(*, г/) = 0, (2.1-17)
определяют точку пересечения этих кривых. В частности, если уравнение
Ф (х, 0) = 0 имеет действительные корни, то они служат абсциссами точек
пересечения кривой ф (*, у) — 0 с осью Ох.
Если ф (х, у) — полином степени п (п. 1.4-3), то кривая <р (х, у) = 0 пересекает ось
Ох (как и любую прямую линию, п. 2.2-1) в п точках (кривая п-го порядка); однако
некоторые из этих точек пересечения могут совпадать или быть мнимыми.
Для любого действительного Я уравнение
Ф! (х, У) + Ь<р* (х, у) = 0 (2.1-18)
определяет кривую, проходящую через точки пересечения (действительные или мнимые)
двух кривых (17).
(d) Уравнение
Ф1 (х, У)-Щ(х, у)=0 (2.1-19)
удовлетворяется координатами точек, принадлежащих любой из кривых (17), и не
удовлетворяется координатами других точек.
2.2. ПРЯМАЯ ЛИНИЯ
2.2-1. Уравнение прямой линии. Каждое уравнение, линейное относительно
декартовых координат х и у, т. е. уравнение вида
Ах + Ву + С=0, (2.2-1)
где А и В не равны нулю одновременно, определяет прямую линию (рис. 2.2-1).
Обратно, каждая прямая линия может быть определена линейным
уравнением (1). При С —0 прямая проходит через начало координат.
Особенно важное значение имеют следующие виды уравнения прямой.
1. Уравнение прямой с угловым коэффициентом.
Прямая, образующая угол ф с положительным направлением оси Ох (рис. 2.2-1)
и пересекающая ось Оу в точке (0, Ь):
y = kx+b, ^ = tg ф.
Коэффициент k называется угловым коэффициентом прямой.
2.2-2.
2.2. ПРЯМАЯ ЛИНИЯ
61
2. Уравнение прямой в отрезках. Прямая линия, пересекающая
ось Ох в точке (а, 0) и ось Оу в точке (0, Ь) (см. рис. 2.2-1):
7 • ft
(а^О, Ь-фО).
3. Нормальное уравнение прямой. Пусть р —длина
перпендикуляра, опущенного из начала координат на прямую, а 0 —угол
(измеренный в положительном направлении) между положительным направлением
сси Ох и направлением перпендикуляра,
опущенного из начала координат на прямую
(см. рис. 2.2-1).
Тогда уравнение прямой имеет вид
х cos б + у sin 0— р — 0.
4. Уравнение пучка прямых
с центром в точке (xlt yi):
y—y\ = k(x—x1).
5. Уравнение прямой, проходящей
ные (несовпадающие) точки Рг (xlt yx) и Р2 (х2, УъУ-
Уравнение прямой,
через две дан-
У—У\
X — *i
Уг — Ух х2 — хх
X
Ч
Х2
у 1
Уг 1
У* 1
= 0.
Если прямая задана общим уравнением (1), то отрезки а и Ь, отсекаемые ею
на осях, угловой коэффициент &, расстояние прямой от начала координат р,
cos0 и sin 0 выражаются через коэффициенты Л, В и С следующим образом:
«=-^, ь=
"±/Л* + В2'
в1
COS0 =
= tgq) = -3,
А
'±YAt + Bj
sin 0 =
~±Va* + b*'
(2.2-2)
(2.2-3)
Во избежание неопределенности знак перед радикалом выбирается так,
чтобы соблюдалось условие р > 0.
В этом случае cos 6 и sin 0 являются направляющими косинусами положительной
нормали прямой — перпендикуляра, опущенного из начала координат на прямую
(см. п. 17.1-2). Если С = 0, то выбор положительного направления на нормали
произволен.
2.2-2. Другие способы задания прямой. Параметрические уравнения прямой
могут быть записаны в виде
при этом
x — axt-\-x0, y = avt+y0 (/ — переменный параметр);
аух0 — аху0 и аху0 — avx0
k =
а =
Ь = -
ыул
ахУо ~ ауХо
±V(ax)* + (°y)2
sin 0 = —
COS0 =
иУ
V(ax)*+(°y)*
±V(ax)*+W
(2.2-4)
(2.2-5)
(2.2-6)
Если знак корня выбран так, что р ;> 0, то начало координат будет лежать
справа от направления1 в котором точка (ху у) перемещается по прямой при
возрастании t.
62
ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.3*1^
= 0. (2.3-2)
Уравнение прямой в полярных координатах:
р (A cos ф + В sin ф) + С = 0 (2.2-7)
или
рсоз(ф—6) = р, (2.2-8)
где Л, В, С, р и б имеют тот же смысл, что и в п. 2.2-1; р, ф—полярные
координаты.
2.3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ
2.3-1. Точки и прямые. Расстояние 6 от точки Р0(х0, у0) до прямой
Ах-{-Ву+С = 0, определенное по величине и знаку, может быть найдено по
формуле
Ь=Ах. + Ву. + С (23_1}
Ya* + в* '
где знак перед радикалом противоположен знаку С. Иногда 6* называют
отклонением точки от прямой; отклонение положительно, если начало
координат и точка Р0 (х0, у0) лежат по разные стороны от прямой, и отрицательно,
если по одну сторону.
Три точки (#!, #,), (х2, у г) и (дг3, уд) лежат на одной прямой в том и
только в том случае, если (см. также п. 2.2-1)
I *\ Уг 1 I
Us У2 1 J
1*з Уз *
2.3-2. Две или несколько прямых.
(a) Две прямые
AtX + Btf+C^O или y^kxx+bt (2.3-За)
и
А2х + В2у + С2 = 0 или y = k2x+b2 (2.3-36)
пересекаются в точке
BiC2 — B2Ct fri — b2 CjA2 — C2At k2bj — ktb2 /n oa
X~~A1B2-A2B1 — k2-kS У A1B2^A2B1 k2-ki ' K'-°mV
(b) Угол у12 между двумя пересекающимися прямыми (За) и (36)
определяется формулой
tg Vl2- yi^. + B.B,- 1+ *,*," ^"d 5)
X Под углом Yi2 ПРИ этом понимается угол, на который нужно повернуть
прямую (За) вокруг точки пересечения прямых против часовой стрелки до
первого совмещения с прямой (36). Поменяв местами kx и k2, получим
тангенс смежного угла 721 = л—Yi2-#
(c) Прямые (За) и (36) параллельны, если
АХВ2 — ^2^ = 0 или k2 = kv (2.3-6)
и перпендикулярны, если
ЛИ2 + #1#2=0 или k2=—~. (2.3-7)
(d) Уравнения прямых, проходящих через точку (*1г уг) под углом у
к прямой (За):
2.3-3. 2.3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ &*
В частности, нормаль к прямой (За), проходящая через точку {х1% уг),
определяется уравнением
*/-*/i = ^(*-*i) или у-У1 = — ±-(х-хх). (2.3-9)
(е) Уравнение любой прямой, параллельной (За):
А1х+В1у + С=0. (2.3-10)
Расстояние б между параллельными прямыми (За) и (10):
а Ct — c
±V a\+b\
(2.3-11)
Если в (11).знак перед радикалом противоположен знаку Съ то б будет
положительным, когда начало координат и прямая (10) лежат по разные
стороны от прямой (За).
(f) Уравнение любой прямой, проходящей через точку пересечения прямых
(За) и (36), имеет вид
(А1х + В1у + С1) + Х(А2х + В2у + С2)^01 (2.3-12)
где X —постоянная (см. также п. 2.1-9, с). Обратно, каждое уравнение вида
(12) определяет прямую, проходящую через точку пересечения данных
прямых. Если (За) и (36) параллельны, то (12) определяет прямую, которая
в свою очередь им параллельна. Совокупность прямых, определяемых
уравнением (12) при различных значениях параметра А,, называется пучком
прямых, а точка их пересечения — центром пучка. Если базисные прямые (За)
и (Щ пучка заданы нормальными уравнениями (п. 2.2-1), то (—X) равно
отношению расстояний от любой точки прямой (12) до базисных прямых; при
А,= | и X ——1 полученная прямая служит биссектрисой угла между
базисными прямыми пучка.
(g) Для того чтобы три прямые
Alx + Bly + Cl = 01 А2х + В2у + С2 = 0, А3х + Взу + С3 = 0 (2.3-13)
пересекались в одной точке или были параллельны, необходимо и достаточно,
чтобы
= 0, (2.3-14)
Mi
\А2
\А3
Bi С,|
#2 ^2
#з Сз |
т. е. чтобы левые части уравнений (13) были линейно зависимы (п. 1.9-3, а).
2.3-3. Тангенциальные координаты. Уравнение
Zx + v\y+l = 0 (2.3-15)
определяет прямую линию (£, г\). Числа £ и г) называются ее тангенциальными
(линейными, плюккеровыми) координатами. Если точечные координаты х, у фиксированы, а |,
т] рассматриваются как переменные, то (15) становится уравнением точки (х, у), т. е.
точки пересечения всех прямых (15). Симметрия уравнения (15) относительно точечных и
тангенциальных координат влечет за собой соответствие (двойственность) между
теоремами, относящимися к взаимному расположению точек и прямых (пп. 2.3-1 и 2.3-2).
Уравнение F (|, tj)=0 определяет семейство прямых, которое, вообще говоря, имеет
огибающую, зависящую от вида функции F (£, tj) (п. 17,1*7).
64
ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 2.4-1.
2.4. КРИВЫЕ ВТОРОГО ПОРЯДКА (КОНИЧЕСКИЕ СЕЧЕНИЯ)
2.4-1. Общее уравнение второй степени. Кривые второго порядка (конические
сечения) определяются уравнениями второй степени относительно декартовых
прямоугольных координат. Общее уравнение второй степени относительно х,
у имеет вид
где
аих2 + 2а12ху + а22у2 + ?ai3x + 2а2Яу + а33 = О
(anx+a12y+a13)x + (a2^x+a22y + a23)y + (a3lx + a32y + a33)==0t
aik=ciki (i, &=1, 2, 3).
2.4-2. Инварианты. Для любого уравнения (1) три величины
аи а12 а13
/ = 011 + 022. 0==Л33 =
аи а12
#21 ^22 I
021 022 023
031 032 033
(2.4-1)
(2.4-2)
являются инвариантами относительно переноса и поворота осей (2.1-8),
(2.1-9) и (2.1-10). Эти инварианты определяют свойства кривой второго
порядка, не зависящие от ее положения на плоскости.
Инвариант Л, а также иногда Д=8Л, называют дискриминантом уравнения (1).
2.4-3. Классификация кривых второго порядка. Табл. 2.4-1 содержит
классификацию кривых второго порядка, основанную на их инвариантах (2.4-2);
в этой таблице
Л' =
022 023
032 033
+
0ц 013
31
0.ч
(2.4-3)
А' является инвариантом относительно поворота осей (семиинвариантом).
2.4-4. Условие подобия невырожденных кривых второго порядка. Две
невырожденные кривые второго порядка (А ФЩ, заданные уравнениями вида (1), подобны, если
/)=0 для каждого из уравнений (т. е. если обе кривые — параболы) или если £> ^ о
для каждого из уравнений и отношения ац'.ац.ац для этих уравнений совпадают.
2.4-5. Характеристическая квадратичная форма и характеристическое уравнение.
Многие важные свойства кривых второго порядка могут быть изучены при помощи
характеристической квадратичной формы
F0 (х, у) = апх* -4- 2ai2xy + а2гу*,
(2.4-4)
соответствующей уравнению (1). В частности, невырожденная кривая второго порядка
(АфО) оказывается действительным эллипсом, мнимым эллипсом, гиперболой или
параболой з зависимости от того, будет ли F0 (л:, у) положительно определенной,
отрицательно определенной, неопределенной или полуопределенной квадратичной формой, что
устанавливается по корням Яь Я2 ее характеристического уравнения
аи — Я
aia
#23 — ^
= 0 или К2 — A + D=0.
(2.4-5)
Корни Яь К2 являются собственными значениями действительной симметрической
матрицы [а.. ] (пп. 13.4-5, 13.5-2) и, как следствие этого, всегда действительны.
>1< Заметим, что инварианты / и D кривой второго порядка следующим образом
выражаются через корни характеристического уравнения (5):
/ = Х, + Я,, D = A,iA,8.
Отсюда следует, что если один из корней к(, К2 равен нулю, то D = 0f а если A,g= — %и
т. е. /=0, то D<0 (см табл. 2.4-1). *
2.4-6. Центры и диаметры кривых второго порядка.
(а) Диаметром кривой второго порядка называется прямая, являющаяся
геометрическим местом середин параллельных хорд. Говорят, что диаметр
сопряжен хордам (а также направлению хорд;, которые он делит пополам.
2.4-6. 2.4. КРИВЫЕ ВТОРОГО ПОРЯДКА (КОНИЧЕСКИЕ СЕЧЕНИЯ)
65
Таблиц 2.4-1
Классификация кривых второго порядка
Центральные
кривые второго порядка
DjbQ
Нецентральные
кривые второго порядка
(без центра или с
неопределенным
центром)
D = 0
D>0
D<0
D =0
Невырожденные кривые
А ф0
i<o
т>0
Действительный
эллипс
(окружность, если
/2 = 4D или
«11 = а22, ахг = 0)
Мнимый эллипс
(ни одной
действительной точки)
Гипербола
Парабола
Вырожденные
(распадающиеся) кривые i
Л = 0
Действительная точка
пересечения двух мнимых
прямых (эллипс, выродившийся
в точку)
Пара действительных
пересекающихся прямых
(выродившаяся гипербола)
Л'>0
Л'<0
Л' = 0
Пара мнимых
параллельных прямых
(ни одной
действительной точки)
Пара
действительных параллельных
прямых
Одна
действительная прямая (пара
совпавших прямых)
Диаметр, сопряженный хордам, образующим угол б с положительным
направлением оси Ох, определяется уравнением
(апх+а12у + а13) cos Ь-\-(а21х+а22у + а23) sin 6 = 0. (2.4-6)
(b) При D Ф 0 все диаметры кривой второго порядка пересекаются
в одной точке —центре кривой (другое определение см. в п. 2.4-10). При
/) = б все диаметры параллельны или совпадают. В случае йФО кривая
второго порядка называется центральной.
Координаты центра (х0, Уо) определяются уравнениями
ацХ0-\-а12у0 -f at3 — 0, a2lx0 + а22у0 -J- a2s = 0, (2.4-7)
откуда следует, что
tfis al2
I я*а #22
_Ч аи ai» I
0\a2i а»« I
(D^O).
(2.4-8)
Если кривая центральная, то перенос (2.1-8) начала координат в ее центр (8) приводит
уравнение кривой к виду
aitx* + 2а12ху + а22у* + ~ = 0, (2.4-9)
где х, у — координаты относительно новой системы.
(с) Каждый из двух сопряженных диаметров центральной кривой второго
порядка делит пополам хорды, параллельные другому диаметру (см. также
п. 2.5-2, е).
3 Г. Корн и Т. Корн
66
ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 2.4-7.
2.4-7. Главные оси. Диаметр, перпендикулярный к сопряженным ему
хордам, называется главной осью кривой второго порядка и является осью
симметрии кривой. Каждая центральная кривая второго порядка (D Ф 0) либо
имеет две взаимно перпендикулярные главные оси, либо каждый диаметр
является главной осью; в последнем случае кривая является окружностью.
При D = 0 кривая имеет одну главную ось (см. табл. 2.4-1). Точки
пересечения кривой второго порядка с ее главными осями называются вершинами
этой кривой.
Главные оси имеют направление собственных векторов матрицы \a-k] (i, k = \, 2)
(см. п. 14.8-6). Иначе говоря, направляющие косинусы cos б, sin б нормалей к главным
осям (п. 2.2-1) удовлетворяют уравнениям
(а1;
- Я) cos 0 + а12 sin 6 = 0, а21 cos 6 + (а22 — I) sin S = О,
(2.4-10)
где Я —отличный от нуля корень уравнения (5). Направления главных ocefi и
сопряженных им хорд называются главными направлениями кривой второго порядка. Угол
между положительным направлением оси Ох и каждым из двух главных направлений
кривой определяется формулой
Од
tg 2<p = tg26 = 12—; (2.4-11)
ои — а22
только окружность имеет неопределенные главные направления.
2.4-8. Приведение уравнения кривой второго порядка к стандартному
(каноническому) виду. Если ввести новую систему координат, совершив
поворот осей на угол, удовлетворяющий уравнению (11), и подходящий перенос
начала (п. 2.1-7), то уравнение (1) любой невырожденной кривой второго
порядка может быть приведено к следующему стандартному (или
каноническому) виду (параметры а2, Ъ2 и р, встречающиеся в канонических
уравнениях, весьма просто выражаются через корни ^ :> Я2 характеристического
уравнения (5) и инварианты A, D, /):
if. + fr^1 (эллипс),
J_ A
' U D'
А
0 Л, D
А
~— ^=1 (гипербола),
J_ А
Я, D'
Ь2 = ±^-
А
Л1Л2
у2 = 2рх (парабола),
P=7V-l=iV4>°> Ь-0.
(2.4-12а)
(2.4-126)
(2.4-12с)
Уравнения вырожденных (распадающихся) кривых второго порядка анааогичным
способом приводятся к виду
х2 и2
— + ^ = 0 (точка),
х2 у2
— — = 0 (пересекающиеся прямые), ■
х2 ■
— = 1 (параллельные прямые),
х2 = 0 (одна действительная прямая).
Замечание. Поворот координатных осей (2.1-9) на угол, удовлетворяющий
уравнению (11), приводит к диагональному виду матрицу [а^] характеристической
квадратичной формы (4) (см. также п. 14.8-6). Изменение б на угол, кратный я/2,
соответствует некоторой перестановке переменных х, у, —х и — у. Канонические уравнения
(12, а), (12, Ь), (12, с) соответствуют такому выбору 6, при котором фокусы (п. 2.4-9)
кривых второго порядка лежат на оси Ох,
2.4-10. 2.4. КРИВЫЕ ВТОРОГО ПОРЯДКА (КОНИЧЕСКИЕ СЕЧЕНИЯ) 67
2.4-9. Геометрическое определение невырожденной кривой второго
порядка. Каноническое уравнение любой невырожденной кривой второго
порядка (12) может быть при помощи подходящего преобразования начала
(п. 2.1-5) приведено к виду
#2 = 2р* —(1—е»)** (р>0). (2.4-14)
В этом случае кривая проходит через начало координат новой системы; ось
Ох является осью симметрии кривой. Уравнение (14) выражает тот
факт, что невырожденная кривая второго порядка является геометрическим ме*
стом точек, отношение расстояний которых е^=0 (эксцентриситет) от
данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кри*
вая есть эллипс при е <с 1 и, в частности, окружность при е = 0,
гипербола при е>1 м парабола при е = 1.
Уравнение директрисы кривой (14):
*=—FTTTI)' <2-4-15>
координаты фокуса:
* = rqb У = 0. (2.4-16)
Директриса перпендикулярна к оси симметрии, проходящей через фокус и
вершину кривой (фокальная ось). Расстояние между фокусом и директрисой
равно р/е. Если кривая второго порядка центральная (эллипс или
гипербола), то прямая
является осью симметрии кривой и, следовательно, кривая имеет два фокуса
и две директрисы.
Фокальным параметром невырожденной кривой второго порядка
называется половина длины ее хорды, проходящей через фокус и
перпендикулярной к фокальной оси (фокальная хорда); фокальный параметр равен р.
Замечание. Все типы кривых второго порядка, вырожденных и
невырожденных, могут быть получены как плоские сечения прямого кругового конуса при различных
положениях секущей плоскости относительно конуса. Если кривая распадается на пару
параллельных прямых, то следует считать, что конус вырождается в цилиндр.
2.4-10. Касательные и нормали к кривым второго порядка. Полюсы и
поляры. Уравнение касательной (п. 17.1-1) к кривой второго порядка (1) в ее
точке (xlt yt) имеет вид
апхгх + а12 (угх + хгу) + а2,у1у + ai3 {хг + х) + а23 (yt + у) + а33 = 0 л
или \ (2.4-18)
(яц*1 + апУ1 + Я1з) х + (a2lxt+a22yt+а23) у + (а31хг+а32ух+а33) = 0. )
Уравнение нормали (п. 17.1-2) к кривой второго порядка (1) в точке
(хъ У1) имеет вид
х ~х1 у — У\ (2 4-19)
ailx1-\-a12y1 + а13 а2Ххх -f а22у± + а23 ' i • /
Уравнение (18) определяет прямую, называемую полярой точки (хъ ух)
относительно кривой второго порядка (1), независимо от того, лежит ли
точка (xl9 yt) на кривой или нет; точка (xlf ух) называется полюсом
прямой (18). Поляра точки кривой есть касательная к кривой в этой точке.
3*
Таблица 2.4-2
Касательные, нормали, поляры и полюсы кривых второго порядка
Кривая
Уравнение кривой
Уравнения
касательных к кривой,
проходящих через
точку (хи ух)
Уравнения
касательных к кривой,
имеющих данный
угловой
коэффициент k
Уравнение
поляры точки (хх, ух)
или уравнение
касательной к кривой
В ТОЧКР (Хх, Ух)
Координаты хи У\
полюса прямой
Ах + By + С = 0 с
относительно
кривой
Уравнение
нормали к кривой в точке
(хи Ух)
Уравнение,
которому
удовлетворяют «линейные
координаты» £, 1]
любой касательной
1х + цу + 1 = 0
к кривой
Окружность радиуса R
с центром в начале
координат
** + */* = R*
У — У\ _
X — Хх
-*1*1±*К**1+ *!-*»
Я* — х\
у = kx ± R V 1 + к2
xix -f уху = R*
AR*
*i—-—.
BR2
Ух= —
XX
£*+n* = ^r
Парабо.»а с фокусом
f-|-. Oj и
директрисой *«--f
y* = 2px
У — У\^
X— Хх
Ух±У У\-2рхх
2*i
y = kx + JL
УхУ = P (x -f Xx)
С
*i«X.
Bp
У— Ух Ух_
x — Хх Р
л—-§■ Б
Эллипс с центром в начале
координат; большая ось
2а на оси Ох, малая
ось 26
f + $-u.>b
У — Ух
х— Хх
-ХхУх±У^х\ + а2у\-а2Ь2
— а2 — х*
у = kx±V k2a* + Ь*
ххх ухУ ,
а2 "Т" ь2
а*А
хх = - —
Ь2В
У1=~ —
У—Ух ^а2Ух
х — Хх Ь2Хх
а2|2 _|_ &*Г|2 = 1
Гипербола с центром
в начале координат;
действительная ось на оси 2а,
мнимая ось 2Ь
х2 У2 _ 1
а* ъ2
У — Ух =
X — Хх
- ХхУх±У - Ь2х\ + а*у\ + а2Ь2
~~ а2 — *|
г/ = kx ± V k*a2 — Ьг
Ххх УхУ , |
а2 Ъ2
а?А
Х* = —с"-
^1 = "^"
У — У1^ a2Vi
х — Хх Ь2Хх
а*1* — 6*л2 = 1
2.4-11. 2.4 КРИВЫЕ ВТОРОГО ПОРЯДКА (КОНИЧЕСКИЕ СЕЧЕНИЯ) 69
Уравнения касательных, поляр и нормалей для кривых второго
порядка, заданных каноническими уравнениями (п. 2.4-8), приведены в
таблице 2.4-2.
Замечание (теоремы о полюсах и полярах).
1. Если прямая, проведенная через полюс Р, пересекает поляру в точке Q, а
кривую второго порядка — в точках Rt и R2, то точки Р и Q гармонически разделяют
n p R О
Ri и Rz, т. е. * = —р~ (новое определение поляры).
2. Если точка лежит на некоторой прямой, то ее поляра проходит через полюс
этой прямой. Если прямая проходит через некоторую точку, то ее полюс лежит на
поляре этой точки.
3. Диаметр кривой второго порядка есть поляра бесконечно удаленной точки,
через которую проходят сопряженные ему хорды; центр кривой второго порядка
есть полюс бесконечно удаленной прямой (новое определение диаметра и
центра).
4. Фокус кривой второго порядка есть центр пучка, обладающего тем свойством,
что полюс любой его прямой принадлежит перпендикулярной к ней прямой пучка.
Директриса есть поляра фокуса (новое определение фокуса и дирек-
т р и с ы).
Из 1—4 следует, в частности, что:
(a) Если через точку можно провести две касательные к кривой, то поляра этой
точки проходит через точки касания.
(b) Касательные к кривой в концах диаметра параллельны сопряженным ему
хордам.
(c) Точка пересечения касательных к кривой в концах любой ее хорды, проходящей
через фокус, лежит на директрисе.
(d) Каждая хорда, проходящая через фокус, перпендикулярна к прямой,
проведенной через фокус и точку пересечения касательных в концах хорды.
2.4-11. Другие способы задания кривых второго порядка.
(а) Кривая второго порядка вполне определяется пятью своими точками,
если никакие четыре из них не лежат на одной прямой (п. 2.3-1). Уравнение
кривой второго порядка, проходящей через пять точек (хъ уг), (х2, у2)*
(Ч> Уз), (*4. Уа)> (*б. УьУ-
X*
х\
х\
х\
х\
х\
ху
ЧУг
ЧУ*
ЧУз
ЧУ\
ЧУь
У2
У\
У1
У\
А
У\
X
ч
ч
ч
ч
ч
Кривая второго порядка вырождается в том и только в том случае, когда
три из заданных точек лежат на одной прямой.
Замечание. Построение кривой второго порядка, проходящей через пять
данных точек, осуществляется при помощи теоремы Паскаля: точки пересечения
противоположных сторон шестиугольника, вписанного в кривую второго порядка, лежат на
одной прямой (или являются бесконечно удаленными).
Кривая второго порядка также вполне определяется пятью касательными, если
никакие четыре из них не пересекаются в одной точке. Построение касательных
к этой кривой производится при помощи теоремы Брианшона: диагонали, проходящие
через противоположные вершины шестиугольника, описанного около кривой второго
порядка, пересекаются в одной точке (или параллельны).
(Ь) Если фокус невырожденной кривой второго порядка принят за полюс,
а ось симметрии — за полярную ось, то уравнение этой кривой в
полярных координатах р, ф будет иметь вид
У
У\
Уъ
Уз
У*
Уь
(2.4-20)
р
Р 1 + е cos ф •
(2.4-21)
70 ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 2.5-1.
2.5. СВОЙСТВА ОКРУЖНОСТЕЙ, ЭЛЛИПСОВ, ГИПЕРБОЛ И ПАРАБОЛ
2.5-1. Окружность: формулы и теоремы (см. также табл. 2.4-2).
(a) Общее уравнение окружности в декартовых прямоугольных
координатах:
Х2+У2 + Лх + Ву + С = 0, |
или I
(x-xtf + (y-y0)* = R\ \ (2.5-1)
где
2х0 = — Л, 2у0^—В, 2R = VA* + B*-4C. )
Точка (х01 г/0) — центр окружности, R — ее радиус. Окружность (1) касается
оси Ох, если 4С—А2, и оси Оу, если 4С = В2.
Уравнение окружности с центром в начале координат:
x* + y* = R*. (2.5-2)
(b) Уравнение окружности, проходящей через три точки (xlt у{), (х2, у2), (х3, у3)>
\х* -\- у2 х у 1
Uf + ^f *i У1 1
Uf + i'l х2 у2 1
Ьгё + ^i *з У г 1
=0. (2.5-3)
(c) Длина L каждой из касательных, проведенных из точки (xt, yi) к окружности (1):
L = V(xt - *0)2 + (yt - г/о)2 -R*. (2.5-4)
(d) Две окружности
Х2 + У2+а1Х + Вху -f d = 0, ** + *■ + Л2* + В2у + С2 = 0 (2.5-5)
являются концентрическими в том и только в том случае, когда Ах —А2 и Bt = B2.
Необходимое и достаточное условие ортогональности окружностей имеет вид
АХА2 + ВхВг = 2 (Ct + С2).
(e) Все окружности, проходящие через действительные или мнимые точки
пересечения двух окружностей (5), определяются уравнением
*2 + У + Ахх + Bty +• С4 + Я (д:2 + i/2 + Л2* + В2# + С2) = 0, (2.5-6)
где А,— параметр. Кривая (6) существует и в том случае, когда окружности (5) не имеют
действительных точек пересечения.
(f) При А, = — 1 уравнение (6) превращается в уравнение прямой
(А1-Аш)х+ (Bt -B2)y+ (Ct - Сш) = 0, (2.5-7)
которая называется радикальной осью двух окружностей (5). Радикальная ось является
геометрическим местом точек, из которых могут быть проведены касательные равной
длины к двум данным окружностям. Если две окружности пересекаются (касаются), то
радикальная ось является их общей хордой (касательной к окружностям в общей точке).
Радикальной осью двух концентрических окружностей служит бесконечно удаленная
прямая. Три радикальные оси, связанные с тремя попарно взятыми окружностями,
пересекаются в одной точке (радикальный центр). Этот факт используется при построении
радикальной оси двух непересекающихся окружностей. Если центры трех окружностей лежат
на одной прямой, то их радикальным центром служит бесконечно удаленная точка.
(g) Уравнение окружности радиуса R с центром (р0, Фо) в полярных координатах:
pa — 2pp0cos (ф — ф0) + р20 = Д2. (2.5-8)
2.5-2. Эллипс и гипербола: формулы и теоремы (см. рис. 2.5-1,
а также п. 2.5-3, табл. 2.4-2 и 2.5-1).
(а) Длины большой и малой осей эллипса (2.4-12, а) т. е. отрезков,
отсекаемых эллипсом на его осях симметрии (рис. 2.5-1, а), равны
соответственно 2а и 2Ь. Сумма фокальных радиусов гг и г2 (табл. 2.5-1,6)
постоянная {и равна 2а) для каждой точки эллипса.
2.5 3. 2.5. СВОЙСТВА ЭЛЛИПСОВ, ГИПЕРБОЛ И ПАРАБОЛ 71
(b) Гипербола имеет две асимптоты (п. 17.1-6), пересекающиеся в ее
центре. Для гиперболы (2.4-12 £) уравнения асимптот:
у = ^-хи y=z——x. (2.5-9)
Угол ф между асимптотами гиперболы определяется из уравнения tg (q>/2) =
= bla; если a = bt то ф = я/2 (равносторонняя гипербола).
(c) Длина действительной оси гиперболы, т. е. расстояние между ее
вершинами (рис. 2.5-1, Ь), равна 2а. Мнимой осью называется главная ось,.
а) Ъ) с)
Рис. 2.5-1. а) эллипс, Ь) гипербола, с) парабола; каждая из кривых задана
каноническим уравнением относительно изображенной на рисунке системы координат. Пока*
заны фокусы, оси и фокальный параметр.
перпендикулярная к действительной оси. Касательная к гиперболе в ее
вершине пересекает асимптоты в точках, расстояние между которыми равно 2Ь
(рис. 2.5-1, Ь). Разность между фокальными радиусами rt и г2 гиперболы
(табл. 2.5-1,6) постоянна: она равна 2а для правой ветви и — 2а для левой.
(d) Если dt и di —длины любых двух сопряженных диаметров (п. 2.4-6, с) эллипса
или гиперболы, то
dkd2 sin (arctg k2 — arctg ki) = 4ab, (2.5-10)
где ki, k2 — угловые коэффициенты диаметров.
(e) Для пересечения гиперболы (2.4-12 6) со своим диаметром у = kx необходимо
и достаточно выполнение условия k2 < 62/а2. Асимптоту можно рассматривать как
хорду, встречающую гиперболу в бесконечно удаленной точке и совпадающую с
сопряженным ей диаметром (а также как поляру бесконечно удаленной точки кривой).
(f) Отрезки секущей заключенные между гиперболой и ее асимптотами, равны между
собой. Точка касания делит отрезок касательной, заключенный между асимптотами,
пополам. Произведение расстояний от точки гиперболы до асимптот постоянно.
(d) Площадь треугольника с вершинами в центре эллипса и в концах любой пары
его сопряженных диаметров постоянна. Площадь треугольника, заключенного между
асимптотами гиперболы и любой ее касательной, постоянна.
2.5-3. Построение эллипсов и гипербол, их касательных и нормалей.
(а) Построение эллипса по его осям 2а и 2Ь.
1. Пусть О — точка пересечения двух взаимно перпендикулярных прямых. На одной
из них строим отрезок Р'ОР = 2а, а на другой — отрезок Q'OQ = 2b. Тем самым уже
построены 4 вершины эллипса: Р, Р\ Q, Q'. Проводим через точку О произвольную
наклонную, откладываем на ней отрезки OR = b и OS = а, затем проводим через точку R
прямую, параллельную Р'Р, а через точку 5 — прямую, параллельную Q'Q. В пересечении
получим точку искомого эллипса.
2. Из точки Q как из центра раствором циркуля, равным ОР = а, делаем на
отрезке Р'ОР засечки F' и F (фокусы эллипса). На отрезке Р'Р выбираем произвольную
точку Т. Окружности радиусов Р'Т и РТ с центрами соответственно F* и F пересекутся
в двух точках искомого эллипса.
72
ГЛ. 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.5-3.
Таблица 2.5-1
Эллипс, гипербола и парабола. Канонические уравнения
и основные формулы
(см. также пп. 2.4-9, 2.5-2 и рис. 2.5-1)
1
2
3
4
5
6
7
8
9
Стандартное
(каноническое) уравнение
Эксцентриситет
Фокусы
Уравнения
директрис
Фокальный
параметр (см. п. 2.4-9)
Фокальные радиусы
(расстояния от
фокусов до произвольной
точки (х, у) кривой)
Уравнение
диаметра, сопряженного
хордам с угловым
коэффициентом k
Площадь сегмента
между дугой,
выпуклой влево, и хордой,
проходящей через
точки (хи у±) и (х1г
-Ух)
Уравнение в
полярных координатах (ср.
с уравнением (2.4-21))
Эллипс
х2 и2
— -4- — = 1
а2 ^ Ь2
(рис. 2.5-1, а)
— V-£<«
(08, 0),
(— 08, 0)
а _ а
~ е' ё~
Ь2
ri = а + еде,
г2 == а — ех
-^паЪ +
h I
+ -£- [хх у а* - х* +
-4- о2 arcsin —- )
Ь2
р 1-е2 cos2 ф
Гипербола
х2 У* .
а2 Ь2
(рис. 2.5-1, Ь)
8 =
-v«+^>.
(08, 0),
(— ае, 0)
_а __ а
~ е ' ~~ ~~ е
Ь2
г t = а -\- ех,
г 2 = — а + ех
Ь2
Х1У1 —
— Чт + т)
„.- -**
к 1-е2 cos2 ф
Парабола
^/2 = 2рх
(рис. 2.5-1, с)
е= 1
(f-«)
—■i
р
r = * + i
*=£
TXiyi
Чр cos ф
1 — COS2 ф
Построение гиперболы. Пусть Р'ОР — действительная ось гиперболы, F и
F' — ее фокусы. На действительной оси выбираем произвольную точку Т так,
чтобы соблюдалось условие ОТ>ОР. Окружности радиусов Р'Т и РТ с центрами
F и F' пересекутся в точках гиперболы (см. табл. 2.5-1, соотношения между
OF— OF', а и Ь).
(Ь) Для построения касательных и нормалей к эллипсам и гиперболам оказываются
полезными следующие свойства этих кривых:
1. Касательные к эллипсу (2.4-12 а) в произвольной его точке (Х\, ух) пересекают
ось Ох в той же точке, что и касательные к окружности х2 + уг = а2 в точках
(«1 + Ya* - хр.
2.6-1.
2.6. УРАВНЕНИЯ НЕКОТОРЫХ ПЛОСКИХ КРИВЫХ
73
2. Касательная и нормаль к эллипсу в любой его точке делят пополам углы между
прямыми, соединяющими эту точку с фокусами («фокальное свойство» эллипса);
аналогичным свойством обладает гипербола.
3. Произведение расстояний от фокусов до любой касательной к эллипсу или
гиперболе постоянно и равно б2. Основания перпендикуляров, опущенных из фокуса на
касательные, лежат на окружности, построенной на большой оси (на действительной оси)
как на диаметре; эта теорема может быть использована для построения эллипса или
гиперболы, как огибающей касательных к этим кривым.
(с) Эллипс или гипербола могут быть приближенно построены при помощи
соприкасающихся окружностей в их вершинах (п. 17.1-4). Центры кривизны эллипса или
гиперболы, соответствующие вершинам, лежащим на фокальной оси, также лежат на
этой оси; радиусы кривизны в этих точках равны Ь2/а. Центры кривизны для вершин,
лежащих на малой оси эллипса, также лежат на малой оси, радиус кривизны в каждой
из этих точек равен а2/Ь.
2.5-4. Построение параболы, ее касательных и нормалей.
(a) Если заданы ось параболы, ее фокус и расстояние между фокусом и
директрисой, то для построения параболы могут быть использованы следующие ее свойства:
1. Расстояние между фокусом и любой точкой Р параболы равно
расстоянию между директрисой и той же точкой Р (см. также п. 2.4-9).
2. Прямая, перпендикулярная к оси параболы и делящая пополам
отрезок перпендикуляра, опущенного из фокуса на директрису, касается параболы
в ее вершине. Перпендикуляр, восставленный в любой точке Q этой прямой
к отрезку, соединяющему Q с фокусом, касается параболы. Обратно, любая
касательная и перпендикуляр к ней, проврденный через фокус, пересекаются
в точке, лежащей на касательной к параболе в ее вершине.
(b) Для построения касательных и нормалей к параболе оказываются полезными
следующие ее свойства:
1. Расстояние между любой точкой Р параболы и фокусом равно
расстоянию между фокусом и точкой пересечения оси параболы с касательной в Р.
2. Касательная и нормаль к параболе в любой ее точке Р делят пополам
углы между проходящими через Р диаметром параболы и прямой,
соединяющей Р с фокусом-, заметим, что все диаметры параболы параллельны ее оси.
Эта теорема заключает в себе фокальное свойство параболы.
3. Нормаль к параболе в любой ее точке Р и перпендикуляр, опущенный
из Р на ось, пересекают последнюю в точках, расстояние между которыми
постоянно и равно р.
4. Директриса параболы есть геометрическое место точек пересечения
взаимно перпендикулярных касательных.
(c) Для уточнения формы параболы можно использовать соприкасающуюся
окружность кривой (п. 17.1-4) в ее вершине. Центр этой соприкасающейся окружности лежит
на оси, радиус равен р.
2.6. УРАВНЕНИЯ НЕКОТОРЫХ ПЛОСКИХ КРИВЫХ*)
2.6-1. Примеры алгебраических кривых (см. рис.2.6-1):
(a) Парабола Нейля (полукубическая парабола): у = ах^ .
(b) Локон Аньези: х2у = 4а2 (2а — у).
(c) Конхоида Никомедэ: (х2 + У2) (х — я)2 = х2Ь2.
(d) Циссоида Диоклеса:
у* (й _ х) = хв или р — а (•^•^ — cos ф).
(e) Лемниската Бернулли:
(х2 + у2) — а2 (х2 — у2)=0 или р2 — a2 cos 2ф = 0.
(f) Овалы Кассини: (х2 -\- у2 -\- а2)2 — 4а2х2 = с4 (геометрическое место
точек, для которых произведение расстояний до точек ( — а, 0) и (а,0) равно с2).
(g) Строфоида: х3 + х (а2 + у2) = 2а (у2 + х2).
(h) «Крест» (Cruciform):
Х2у2 = а2 {Х2 + у*) или р = -jg-.
(i) Кардиоида:
(х2 + у2 — ах)2 = а2 (х2 + у2) или р = а (1 + cos ф).
*) Наиболее подробным справочником по плоским кривым служит книга [2 3].
74
ГЛ. 2, АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
2.Ь
(j) Трисектриса:
2 _ х* (За - х) или /4 1__
у а + х v \ Y cos ф
Парабола Нейля
a. J я
а>Ь
а<Ь
Улитка Паскаля
Рис. 2.6-1. Некоторые алгебраические кривые,
(к) Астроида:
д.з/3 _|_ ^2/з _ а2/з или х _ а С08з t,y — a sin3 Л
(1) Декартов лист:
я3 -f- г/3 = Заху или х :
За/
0 = ;
За/г
( — оо ^ * ^ + оо).
' t* + 1 ' * -— f s -I-1
(ш) Улитка Паскаля:
(д;2 + г/2 —ад;)2 = ^2(д;2 + г/2) или p = £ + acos(p,
(на рисунке обозначены декартовы координаты точек пересечения кривой с осями).
2.6-2. Примеры трансцендентных кривых (см. рис. 2.6-2).
(a) Цепная линия: f/=-f (ех/а + е~х/а) =ach-£.
(b) Спираль Архимеда: р = шр.
(c) Параболическая спираль: р2 = 2р(р.
(d) Логарифмическая спираль: р = ае^.
2.6-2.
2.6. УРАВНЕНИЯ НЕКОТОРЫХ ПЛОСКИХ КРИВЫХ
75
(е) Циклоида (кривая, описанная точкой, отстоящей на расстоянии аг от
центра круга радиуса а, катящегося без скольжения по оси абсцисс):
х = at — ах sin /, у = а — аг cos /.
(2.6-1)
Замечание. При aA<ia циклоида называется укороченной, при аг > а —
удлиненной. Если а1 = а, то получается обычная циклоида (именно она
изображена на рис. 2.6-2).
\
ЮЛ/
2rta £
Ут
-^
Спираль Архимеда Логарифмическая шраль
Рис. 2.6-2. Некоторые трансцендентные кривые.
(2.6-2)
(f) Эпициклоида (кривая, описанная точкой, отстоящей на расстоянии аг
от центра круга радиуса а, катящегося без скольжения по окружности
x2-\-y2=zb2 и находящегося вне этой окружности):
х = (а + Ь) sin -£- / — ах sin —£— *»
/ir\ # j a Л- Ь j.
у — (а-{-b) cos-r-1 — ах cos —£— /
(см. замечание к (е)).
(g) Гипоциклоида (кривая, описанная точкой, отстоящей на расстоянии at
от центра круга радиуса а, катящегося без скольжения по окружности
х2-{-у2~Ь2 и остающегося внутри нее):
Ь-а .
х = (Ь-
-а) sm-^-t-
-cix sin
y=z(b — a) cos-у / + 0i <
/
(см. замечание к (е)).
(h) Трактриса:
* = afcos/ + ln tg-g-) 2/ = a sin/.
(2.6-3)
(2.6-4)
ГЛАВА 3
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
3.1. ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
3.1-1. Вводные замечания (см. также п. 2.1-1). Глава 3 посвящена
аналитической геометрии трехмерного евклидова пространства. Точки задаются
радиусами-векторами или системами
действительных чисел (своими
координатами).
3.1-2. Декартова система координат
(см. также п. 2.1-2). Декартова
система координат позволяет связать с
каждой точкой Р пространства, в
котором выбраны три не лежащие в одной
плоскости направленные прямые Ох,
Оу, Oz (оси координат), пересекающиеся
в начале О, три вполне определенных
действительных числа (декартовы
координаты) #, у, z\ при этом пишут Р (x,y,z).
Рис
угольная
ОЕи ОЕ2
Правая декартова косо-
система координат. Отрезки
и ОЕ3 — единицы масштаба
на осях.
Пусть задана (в общем случае
косоугольная) система осей Ox, Оу, Oz (рис. 3.1-1);
тогда плоскость, проходящая через точку Р
и параллельная плоскости Oyz, пересекает
ось Ох в точке Р'. Аналогично плоскости,
проходящие через Р и параллельные
соответственно Oxz и Оху, пересекают ось Оу в точке Р" и ось Oz в Р'". Длине каждого из
направленных отрезков ОР', ОР" и ОР'" приписывается знак плюс, если направление
отрезка совпадает с направлением
соответствующей оси, и знак минус в противном случае. Числа
х=ОР'. у=ОР", z=OP"' называются декартовыми
координатами точки Р (х, у, z) относительно
данной системы координат, образованной осями Ох,
Оу, Oz и выбранными на осях единицами
масштаба.
3.1-3. Правая система осей. Оси Ох,
Оу, Oz могут образовывать правую или
левую систему. Для правой системы (см.
рис. 3.1-1) поворот от оси Ох к оси Оу на
угол, меньший я, совершается в
направлении против часовой стрелки, если смотреть
на плоскость Оху из какой-либо точки
положительной полуоси Oz (положительная
сторона плоскости Оху).
3.1-4. Правая декартова прямоугольная
система координат. В прямоугольной системе
координат оси взаимно перпендикулярны
(рис. 3.1-2). Координаты х, у> z точки Р
равны направленным расстояниям от
начала координат О до плоскостей, проведенных
координатным плоскостям Oyz, Ozx, Оху.
1
Z
\о_
,
г
\
5>
уГ У
/£х
'Ч
P*(x,yyzMr)
- \р»
г / у
/х
/
/р'
г/
Рис. 3.1-2. Системы координат:
правая декартова прямоугольная,
цилиндрическая и сферическая.
через точку Р параллельно
3.1-7.
3.1. ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
77
В настоящем справочнике, если не оговорено противное, всегда
применяется правая декартова прямоугольная система координат, причем для
измерения х, у, г применяется одна и та же единица масштаба.
3.1-5. Радиус-вектор. Каждая точка Р (х, у, z) = Р (г) может быть задана
своим радиусом-вектором
^ r=*i + */j-fzk=={*, у, г}; (3.1-1)
этот вектор г = 0Р определяет преобразование переноса, переводящее точку
из начала координат О в точку Р. Базисные векторы i, j, k суть единичные
векторы, направление которых совпадает соответственно с направлением осей
Ох, Оу и Ог дннной декартовой прямоугольной системы координат (см. также
5.1 и п. 5.5 2).
3.1-6. Цилиндрическая и сферическая системы координат. На рис. 3.1-2 показаны
также цилиндрические координаты р, ф, z и сферические координаты г, 0, <р (полярный
радиус, широта и долгота), связанные с декартовыми прямоугольными координатами
следующими формулами преобразования:
Р =
tg<P
-Yxz-{-yz, jc = p coscp, \
^Ц. #=psincpt >
x' 2 = 2; J
(3.1-2)
r= Vx2 -\-yz + 22, x=r sin S coscp,
- 2
cosS = -
• r „ , . , ' # = Г Sin 6 Sill ф, I /Q 1 o\
vx*-\- y2 + z2 > (3.1-3)
tg<p=—, 2= Г COS 0.
Дальнейшие сведения об этих, а также о других криволинейных координатах см.
в гл 6.
3.1-7. Основные формулы в декартовых прямоугольных координатах и
в векторной форме. Имеют место следующие формулы (операции над
векторами см. в гл. 5).
1. Расстояние d между точками
^i (*i. Уъ *i) = Pi (i*i)
и
Ла (*2. Уъ г2) == Р2 (г2):
rf = /fe-^l)2+(^2~^l)2 + (Z2~21)2 = /(r2-r1).(r2-r1)==|r2-r1|. (3.1-4)
2. Угол у между прямыми РХР2 и Р3Р4» направление которых
определяется векторами PjPg и ^Л:
cos v __. (*2 — Art) U4 — х3) + (j/2 — У у) (У* — j/») + (22 — *i) (г4 — *»> __.
/йг ~ * i)2 + (У 2 -У1)2+ (22 - 2i)2 /(*4 - АГз)2 + (^/4 - У г)2 + <*« - 23)2
^ (rt-nHr.-r,), (ЗЛ.5)
| г, — гж | |г4 — г3 | v
3. Координаты х, у, г и радиус-вектор г точки Р, делящей
направленный отрезок РХР2 в отношении Р^Р : РР2 = т : /г = Я : 1, определяются
формулами:
/mra-f./i*i __х±-\-\хш
х~ т + п ~~ 1-J-A, '
^ m + л 1+А, '
m22 + fl*i 2i + Az2
Z~ т + п ~~ 1 + Я '
ИЛИ
mr2 -f /irt п + Ахг
(3.1-6)
73
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
3.1-8.
См. замечание к аналогичным формулам для геометрии на плоскости
в п. 2.1-4, 3.
Координаты и радиус-вектор середины отрезка РгР2:
_Хх+Х2
У
_У\ + У2
2 '
. П+Га
(3.1-7)
3.1-8. Направляющие косинусы.
(а) Направляющими косинусами cos <хХ1 cos <xy, cos az направленного
отрезка Р1Р2 называются косинусы углов между РгР2 и положительными
направлениями осей Ох, Оу, Ог соответственно:
cos ах
cos a
cos az
X
У
Y(x2
V(xt~-
-*i)
-*i)"
xz-
2 + {Уг
У2'
+ (У2-
Zjj-
-Xi
-Ух)
-Ух
-Ух)
2 + (22-
' + (22-
-Zi)2
^xl>'
У (X* ~Х1)* + {у2 -Уг)2+ (22 - 2l)2
cos2 ах + cos2 а у + cos2 az = 1.
(3.1-8)
(3.1-9)
cos a 0
Направляющие косинусы направленного отрезка Р2РХ суть
— cos <Ху, — cos <х2.
(Ь) Направление прямой может быть также определено любыми тремя
числами аХУ ау, az> пропорциональными направляющим косинусам cos a^f
cos ау, cos az\ в этом случае
cos ax
cos a.
cosa^
v>
к<
'l+«l+4'
av
2 i 2 i 2 '
4+ay + 4
az
Yax + al + al
(3.1-10)
Знак перед корнем должен быть одинаковым во всех трех равенствах; его
выбор определяет положительное направление на прямой. Роль этих чисел
могут играть координаты любого вектора а (п. 5.2-2), совпадающего по
направлению с РХР2 или P2PV (Пример. ax = x2 — xlt ay = y2 — y1, az = z2 — z1.)
Направляющие косинусы являются координатами единичного вектора,
совпадающего по направлению с Р±Р2 (п. 5.2-5).
(с) Угол у между двумя направленными отрезками, направляющие
косинусы которых равны соответственно cos axt cos ayt cos az и cos ax, cos a'
cosa^ или направления которых определяются тройками чисел аХ1 ау, az и
а'х, а', аг, находится по формуле
cos y = cos ах cos а'х + cos ay cos a' + cos az cos a'z =
axax+ayay+aza'z
v*x+**y+*iV*-x+*-;+*-;'
(3.1-11)
2.1-12.
3.1. ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
79
3.1-9. Проекции. Проекции направленного отрезка РХР2 на оси Ох, Оу и Oz равны
соответственно
l-xl = dcosax
dx + dy + dz
--У2~УЛ
-d cosa ,
dZ=Z2-Zl = dC0Saz
■}
(3.1-12)
где cosa , cosa,., cosct — направляющие косинусы (8), d — длина отрезка (4).
•* У fc z , f ,
Проекция РХР2 на прямую с направляющими косинусами cosa^, cos a^, cosa2
(п. 3.2-1, b) равна dcosy, где cosy определяется формулой (11). Проекции РХР2 на
плоскости Oyz, Oxz и Оху равны соответственно
d0 = d sina,,,
* У
d0 =d sin a.
(3.1-13)
Проекция PXP2 на плоскость, нормаль которой имеет направляющие косинусы cosa^,
cos a'y, cos a'z (п. 3.2-1, b), равна dsinv, где cosy определен формулой (11).
3.1-10. Вектор площади. Площадь плоской фигуры в трехмерном пространстве
может быть задана вектором А, модуль которого равен площади А фигуры, а
направление совпадает с направлением положительной нормали (п. 17.3-2) к плоскости фигуры
A = i4N, (3.1-14)
где N — единичный вектор положительной нормали. Каждая из декартовых
прямоугольных координат вектора А равна площади проекции фигуры на координатную плоскость,
перпендикулярную к соответствующей оси. Площадь параллелограмма, построенного на
векторах а и Б, может быть задана вектором А=ахЬ (см. также п. 5.2-7).
Площадь А треугольника с вершинами Plt Р2, Р3 определяется формулой
Л2=-
У\ zx
Уг z2
Уз *з
Л= —
Хх Ух
Х2 Уг
*з Уз
Zx Xx
z2 х2
z3 х3
Zx
z2
Zz
+
Хх Ух
х2 у2
*з Уз
2р
[г^гГз],
(3.1-15)
(3.1-16)
1
6
*1 Ух
Хг Уг
X, Уз
хх Ух
Zx 1
z2 1
*3 1
Zx 1
где р — расстояние от начала координат до плоскости треугольника (п. 3.2-16). Площадь
А положительна, если вращение правого винта в направлении РХР2Р3 сообщает винту
поступательное движение в направлении положительной нормали к плоскости
треугольника (п. 3.2-1, Ь).
3.1-11. Вычисление объемов (см. также п. 5.2-8).
(а) Объем V тетраэдра с вершинами Рх, Р2, Ра, Р4
= j [(г, - г,) (г, - 14) <г4 - г,)]. (3.1-17)
Знак V зависит от того, в каком порядке рассматриваются вершины тетраэдра.
(Ь) Объем V параллелепипеда, построенного на векторах а, Ь и с,
V = [abc]. (3.1-18)
Иногда объем считают только положительным; тогда V = |[abc]|.
3.1-12. Преобразование декартовых прямоугольных координат при
параллельном переносе и повороте осей.
(а) Перенос осей. Пусть х, у, 2 —координаты произвольной точки Р
относительно декартовой прямоугольной системы координат; пусть X, у, z —
координаты той же точки Р относительно другой декартовой системы
координат, оси которой направлены так же, как оси первой системы, и начало
которой имеет относительно системы Охуг координаты х0, yQt z0. Если
80
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.1-12.
единицы масштаба на осях этих систем совпадают, то координаты х> у, z
связаны с х, у, г следующими формулами преобразования:
Х = Х— Xq, Xz==: X -\-Xq, J
У=у — Уо, У = У + Уо> \ (3.1-19)
z = z — z0, z = z + z0. J
(b) Поворот осей. Пусть х, у, г и х> г/, z — координаты одной и той
же точки Р относительно двух различных правых декартовых прямоугольных
систем координат с общим началом О; пусть вторая из них расположена
относительно системы Охуг таким образом, что
ось Ох имеет направляющие косинусы /n, /21, ^зи
ось Оу имеет направляющие косинусы /12, /22, ^32»
ось Oz имеет направляющие косинусы /13, /2з» ^зз-
Тогда относительно системы Oxyz
ось Ох имеет направляющие косинусы tn, t12, tl3t
ось Оу имеет направляющие косинусы t21, /22, /2з»
ось Oz имеет направляющие косинусы t31t t32t t33.
Если для измерения х, у, г, х, у, z применяются одинаковые единицы
масштаба, то формулы преобразования, связывающие координаты х, у, z с
координатами х, у, z, имеют вид
x = t11x + t21y + t3lz, x = t11X + t12g + t13z, 1
y=t12x + t22y + t32z, или y = t21x + t22y-\-t23zt > (3.1-20)
z = t13x + t23y + t33z z = t3lx-\-t32y + t32z. J
Замечание. Преобразования (20) называют ортогональными (пп. 13.3-2 и 14.4-5);
каждое t,. равно своему алгебраическому дополнению в определителе
det[^] = l </, ft = 1,2,3) (3.1-21)
(п. 1.5-2); при этом
ду*,=ду,*=и !!;2". (31-22)
(c) Одновременный перенос и поворот осей. Если начало
системы координат Oxyz не совпадает с началом системы Oxyz и имеет
относительно последней координаты х0, у0, z0, то формулы преобразования
принимают вид:
X = tu (x — x0) + t21 (y—y0) + t31 (z — z0)t
g = t12 (x — x0) + t22 (y — y0) + t32 (z — z0),
г = 'is (x — *0) +123 (y — y0) +133 (z — z0),
или \ (3.1-23)
X — t1±X -f- t12y + t13Z + XQ,
y = t2lx + t2tg+t2Zz+y0,
Z = t3lX + t32g + ^332 + Z0,
где направляющие косинусы tik удовлетворяют соотношениям (21) и (22).
Уравнения (23) связывают координаты относительно любых двух правых
декартовых прямоугольных систем с одинаковыми единицами масштаба на осях.
Более общие преобразования координат рассмотрены в гл. 6.
(d) Другое истолкование формул преобразования.
Уравнения преобразования (23) (частными случаями которых служат (19) и
(20)) могут быть истолкованы еще как соотношения, определяющие новую
точку Р с координатами jc, r/, z относительно той же самой системы
координат Oxyz. Преобразование, в котором точка Р соответствует точке Р с
координатами xl у, г, состоит в последовательном выполнении параллельного
переноса и поворота пространства (см. также пп. 14.1-3 и 15.5-1).
3.1-14.
3.1 ВВЕДЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ
81
Замечание. Расстояния между точками, углы между направленными отрезками
и, следовательно, все соотношения между векторами, составляющие содержание
евклидовой геометрии, сохраняются при повороте и параллельном переносе (23), т. е. они
инвариантны относительно этих преобразований (пп. 12.1-5 и 12.1-4).
3.1-13. Аналитическое задание кривых (см. также пп. с 17.2-1 по 17.2-6).
Непрерывной кривой трехмерного пространства называется множество точек
Р (*» У* z) = P(r)> координаты которых удовлетворяют системе
параметрических уравнений
x = x(t), л
y = y(t), илиг = г(0, | (3.1-24)
Z = z(t) (—•OD^t1^t^t2^OD), J
где x(t), y(t)t z (0 —непрерывные функции действительного параметра t
в замкнутом интервале [tlt t2] (параметрическое задание кривой). С другой
стороны, кривая может быть определена равносильной системой уравнений
<Pi(*. #. z) = 0> <М*. У. *) = 0- (3.1-25)
Кривая может иметь более чем одну ветвь.
Кривая (24) называется простой кривой (простой дугой, простым отрезком кривой)
или, точнее, простой кривой в смысле Жордана, если функции х (/), у (/), z (t)
однозначны, непрерывны и в замкнутом интервале [/,, /2] нет таких двух различных
значений т4 и т2, для которых справедливы все три равенства:
х(Тг) = х(т2), у(т1) = у(х2), 2(т1) = 2(т2). (3.1-26)
Заметим, что термин простая дуга часто употребляется для обозначения геометрического
места точек, координаты которых х, у, z в некоторой декартовой прямоугольной системе
координат удовлетворяют уравнениям у = f (x), z = g (х), а ^ х ^ Ь, где функции f {x),
g(x) однозначны и имеют непрерывные производные в интервале [а, &]. Простая жорда-
нова кривая состоит из одной ветви и не имеет кратных точек, т. е. точек самопересечения.
Простой замкнутой кривой называется непрерывная кривая, единственными кратными
точками которой являются ее начальная и конечная точки; это значит, что единственным
решением уравнений (26) в интервале [/,, /2] служит т, = ttl т2 = t%. Кривая (24)
называется регулярной дугой, если при некотором параметрическом задании этой кривой
функции x(t)t у (t), z (t) имеют в каждой точке кривой непрерывные производные
первого порядка (п. 4.5-1) по параметру t, по меньшей мере одна из которых отлична от
нуля; точка кривой (24) с координатами х (/<>), У (*о), z (t0) называется ее регулярной
(обыкновенной) точкой, если для значений t, достаточно близких к /0, кривая
представляет собой регулярную дугу. Регулярная кривая есть простая кривая или простая
замкнутая кривая, составленная из конечного числа регулярных дуг.
Все эти определения переносятся на кривые в двумерных пространствах (пп. 2.1-9 и
7.2-1), а также на кривые в пространствах, размерность которых больше трех (п. 17.4-2).
3.1-14. Способы задания поверхностей (см. также пп. 17.3-1—17.3-13).
Множество точек Р (х, у, z) = P(r), координаты которых удовлетворяют
системе уравнений
х = х(и, v), у = у(и, v), z = z(u, v) (3.1-27)
при подходящих значениях действительных параметров ut v, называется
непрерывной поверхностью, если правые части уравнений (27) являются
непрерывными функциями параметров. Поверхность может быть определена также
уравнением
ф(*, «Л г) = 0 или z = /(jc, у). (3.1-28)
Поверхность может иметь более чем одну полость.
Поверхности, определяемые уравнениями
Ф(*, у, z) = 0 и А,ф(*, у, г)=0, (3.1-29)
совпадают, если только постоянная X отлична от нуля.
Простой поверхностью называется непрерывная поверхность, состоящая из одной
полости и не имеющая самопересечений (кратных точек). При этом подразумевается, что
простые поверхности являются двусторонними (односторонние поверхности, такие, как
лист Мёбиуса, исключаются).
82
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.1-15.
Точка поверхности (27) называется регулярной точкой, если при некотором
параметрическом задании поверхности функции (27) имеют в достаточной близости к
рассматриваемой точке непрерывные частные производные первого порядка и по меньшей мере
один из определителей.
I дх_ д,у I I ду_ dz I I dz дх 1
\ ди ди \ \ ди ди \ ди ди
L I , (3.1 -30)
\ дх_ дУ \ \ ду dz dz дх
J dv dv I I dv dv | \ ди dv \
отличен от нуля. Простой кусок поверхности, ограниченный регулярной замкнутой
кривой, называется регулярным, если все его внутренние точки регулярные. Регулярной
поверхностью называется двусторонняя простая (замкнутая или незамкнутая) поверхность,
составленная из конечного числа регулярных кусков с общими регулярными дугами
и точками.
3.1-15. Специальные типы поверхностей. Линейчатой поверхностью называется
поверхность, образованная движением прямой линии (ее образующей). Цилиндр есть
поверхность, образованная движением прямой, остающейся параллельной некоторой
данной прямой и пересекающей данную линию (направляющую). В частности, уравнения
вида f (х, у) —0, f (х, z) = 0, f (у, z) = 0 определяют цилиндры, образующие которых
параллельны соответственно осям Oz, Oy, Ох. Конус есть поверхность, образованная
движением прямой, проходящей через данную точку (вершину конуса) и пересекающей
данную линию (его направляющую). Поверхностью вращения называется поверхность,
образованная вращением плоской кривой вокруг неподвижной оси, лежащей в плоскости
кривой. Так, уравнение z = f (Yx- -\~ у2) определяет поверхность, описанную вращением
f z = f (х),
кривой \ _п вокруг оси Oz.
3.1-16. Поверхности и кривые.
(a) Линия пересечения двух поверхностей
Уг(х, У, z) = 0, <M*, у, г)=0 (3.1-31)
представляет собой кривую, точки которой (я, у, г) удовлетворяют каждому
из уравнений (31) (см. также п. 3.1-13). Линия пересечения может иметь
более одной ветви. Уравнения (31) могут также определять лишь одну или
несколько изолированных точек, принадлежащих обеим поверхностям, или
не определять ни одной точки.
Кривые
Г Ф (0, у, z) = 0, / ф (х, 0, z) = 0, Г ф (х, у, 0) = 0,
I д: = 0;1 У = 0', \ z=0
представляют собой линии пересечения (если они существуют) поверхности ф (д:, у, z)=0
с плоскостями Oyz, Oxz и Оху соответственно.
(b) Для любого действительного значения X уравнение
<Pi(*. У, г)+Ху2(х, у, z) = 0 (3.1-32)
соответствует поверхности, проходящей через линию пересечения
поверхностей (31), если последняя существует.
(c) Уравнение
<Pi(*> У> *)-(p2(*, #> г) = 0
соответствует поверхности, образованной точками обеих поверхностей (31) и не
содержащей никаких других точек.
(d) Уравнение проекции кривой (31) на плоскость Oyz (или Oxz, Оху) может быть
получено исключением из уравнений (31) переменной х (соответственно у, z).
(e) Координаты х, у, z точек пересечения кривой (31) с поверхностью (28) должны
удовлетворять всем трем уравнениям (31), (28). Для любых действительных kit K2 уравнения
Ф (х, У, z) + А,! ф! (л:, у, z) = 0, ф (л:, у, z) + А,2 Фз (*, У, г) = 0 (3,1-33)
определяют кривую, проходящую через все эти точки пересечения.
(f) Кривая однопараметрического семейства
Ф! (*, У, z, К) =0, ф2 (л:, у, z, Я) =0 (3.1-34)
описывает поверхность, уравнение которой может быть получено путем исключения
параметра К из (34).
3.2-1.
3.2. ПЛОСКОСТЬ
83
3.2. ПЛОСКОСТЬ
3.2-1. Уравнение плоскости.
(а) Уравнение, линейное относительно декартовых прямоугольных
координат, т. е. уравнение вида
Ax + By + Cz + D = 0 или A-r + D = 0
(3.2-1)
где Л, В и С не равны нулю одновременно, определяет плоскость; обратно,
каждую плоскость можно определить уравнением первой степени относительно
декартовых прямоугольных координат.
Коэффициенты А, В, С равны проекциям вектора А = {Л, В, С},
перпендикулярного к плоскости, на оси Ох, Оу, Oz соответственно (п. 3.1-8, Ь); вектор А имеет
направление положительной или отрицательной нормали к плоскости (см. ниже) и называется
нормальным вектором плоскости. При D = 0 плоскость проходит через начало координат.
(Ь) Особенно важное значение имеют следующие виды уравнений
плоскости:
1. Уравнение плоскости в отрезках. Плоскость,
пересекающая ось Ох в точке (а, 0, 0), ось Оу в точке (0, Ь, 0) и ось Oz в точке
(0, 0, с), имеет уравнение
4+-
-Нг=1.
2. Нормальное уравнение плоскости. Пусть р>0 — длина
перпендикуляра, опущенного из начала координат на плоскость; пусть cos a^,
cos ayt cosoc^ — направляющие косинусы (п. 3.1-8) этого направленного
перпендикуляра, началом которого служит начало координат, а концом точка
плоскости (положительная нормаль к плоскости). Тогда уравнение плоскости
имеет вид
л; cos ах+у cos ay + z cos аг — p = 0.
3. Уравнение плоскости, проходящей через данную
точку. Если плоскость проходит через точку Рг (xv yv zl) = P1 (rx), а
направление нормали к плоскости задано проекциями Л, В, С вектора нормали А
на оси декартовой прямоугольной системы координат, то уравнение плоскости
имеет вид
Aix-xJ + Biy-yJ + Ciz-zJ^O или А-(г-г1)=0.
4. Уравнение плоскости, проходящей через три
данные ТОЧКИ Р1(Х11 yl9 Z^EEEPfo), Р2 (х2, #2, Z2) == Р (Г2), Рв (х3, */3, Z3) =5
= Р(г3), не лежащие на одной прямой (п. 3.4-3, а) имеет вид
или
х у
г
1
хг ух zx 1
#2 Уъ Ч 1
*з Уз Ч 1
Ух Ч 1
Уг Ч 1
Уз
Ч 1
х +
= 0,
ч хг 1
z2 х2 1
Ч
Ч 1
или [(r-r1)(r~r2)(r~r3)]=0>
У +
*i Уг 1
х2 Уг 1
*з Уз 1
г —
*i Ух
х2 Уг
хз Уз Ч I
84
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.2-2.
(с) Если плоскость задана уравнением общего вида (1), то введенные
выше величины a, bt с, р, cos а*, cos а^, cos <xz выражаются через Л, В, С, D
следующим образом:
cos ax =
cos a
А* и— В* "~~ С1
А
cos a?
= В
С
±VA* + B2-f С2 ' ± /Л* + Б2 + С* '
(3.2-а)
где знак перед корнем выбирается так, чтобы соблюдалось условие р>0.
Если D = 0, то выбор положительного направления на нормали к плоскости
произволен.
3.2-2. Параметрическое задание плоскости. Любая плоскость может быть задана
следующими параметрическими уравнениями (п. 3.1-14):
: = xt -f axu + bxv, у = у1 + ауи + byV, z = zl + azii + &2i\
г = rt + ил + vb.
3.3. ПРЯМАЯ ЛИНИЯ
| (3.2-4)
3.3-1. Уравнения прямой.
(а) Два независимых линейных уравнения
ц>г(х, */, z)==A1x + Biy+CiZ + D1 = 0,
cp2(*, у, z)==A2x + B2y+C2z + l
-D2 = 0 J
(3.3-1)
или
Аг. r + D1==0, А2 • r + D2 = 0
(Ахх А2^0; см. также пп. 1.9-3, а, 5.2-2 и 5.2-7) определяют прямую как
пересечение двух плоскостей (п. 3.1-16, а). Обратно, каждая прямая может
быть определена уравнениями вида (1). При D1 = D2 — 0 (и только в этом
случае) прямая проходит через начало координат.
(Ь) Особенно важное значение имеют следующие виды уравнений прямой:
1. Уравнения прямой, проходящей через две точки
^i (*i> Уъ *i) и ^2 (*2. У* *2):
x — xt __ y—yi _ z — zt
*2 — xt y2 — Ух z2 — zt'
2. Уравнения прямой, проходящей через данную точку
в данном направлении (канонические уравнения прямой).
Если прямая проходит через точку Рх (xv уъ г^^Р^г) и параллельна
вектору a = {axt ау, аг\ (направляющий вектор прямой; см. также п. 3.3-2),
то ее уравнения могут быть приведены к виду
*_ZL?±=y_ZLVi = L=lit или r-r^a/.
(с) Вектор а = Ах х А2 является направляющим вектором прямой (п. 3.1-8, Ь),
заданной как линия пересечения двух плоскостей (уравнения (1)); его
проекции на оси декартовой прямоугольной системы координат равны
соответственно
о^^Са —#2C1( ау = СгА2 — C2Alt аг = АХВ2 —A2BV (3.3-2)
8.4-!. 3 4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ И ПРЯМЫХ
Направляющие косинусы прямой и, следовательно, углы axt ayt az между
прямой и осями Ох, Оу и Ог определяются по формулам
cos «* = -! (BxCa-^Ci), cos «</ = ^ (C^-C,^),
cosaz = ±(A1B2-A2Bl)t
м = [(ад-ад)2+(си2-с2л1)2+ИА-л2в1)^. (З.з-з)
Тот или иной выбор знака перед корнем определяет положительное
направление на прямой.
Уравнения (2) и (3) являются условиями того, что прямая с
направляющими косинусами cos axt cosa^, cos аг или с направляющим вектором А
перпендикулярна к двум векторам Кх и А2, заданным своими проекциями А1%
Blt Сх и Л2, В2, С2 на оси декартовой прямоугольной системы координат.
(d) Уравнения плоскостей, проектирующих прямую (1) на плоскости Оху, Oxz и Оуг
соответственно (т. е. плоскостей, проходящих через прямую и перпендикулярных к
соответствующим координатным плоскостям), таковы:
(CtA2 — C2At) х + (CtBt — C2Bt) у + {CtD* — СгОх) = О, \
(BtA2 - B2At) х + (BtC2 - ВгСх) у + {BXD* - B2Dt) = О, I (3.3-4)
(AtB2 - A2Bt) x + (AtC2 - A2Ct) y+ (A^D* - A2Dt) = 0. J
Любые два из уравнений (4) определяют прямую (1).
3.3-2. Параметрические уравнения прямой. Декартовы прямоугольные
координаты (х, у, г) произвольной точки прямой удовлетворяют параметрическим
уравнениям (п. 3.1-13):
x = xl+axtt y = yi + aytt z — zx + aztt или г = г1 + /а, (3.3-5)
где а —направляющий вектор, Р1(а:1, yv zx) = Pi (гх) — некоторая
фиксированная точка прямой.
3.4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧЕК,
ПЛОСКОСТЕЙ И ПРЯМЫХ
3.4-1. Углы.
(a) Угол Yi между двумя прямыми с направляющими косинусами cos aXf
cos a», cos az и cos aXt cos ayt cos az определяется по формулам (см. также
п. 3.1-8, с):
cos Yi = cos ax cos ax + cos ay cos ay+cos az cos az t (3.4-1)
sin2 Yi = (cos а у cos az — cos az cos ay)2 + (cos az cos ax — cos a^ cos az)2 +
+ (cos a* cos a'y — cos a^ cos ai)2. (3.4-2)
Если прямые заданы параметрическими уравнениями (п. 3.3-2) r=rt-{-ta и r = ri -f-
-f/а', то
а • а' . | а X а' | ,..л
Прямые параллельны, если cos Yi = 1. и взаимно перпендикулярны, если cos Yi = 0.
(b) Угол Y2 между двумя плоскостями Ax + By+Cz + D = 0 и Л'л: + £'г/4-
+ C'z + D' = 0, или A-r + D = 0 и A'-r + D' = 0 (угол между их нормалями),
определяется по формуле
АА'-\-ВВ'+ СС А • А' /о л л\
cosy2=-r- - л ■ = • (3.4-4)
Кл» + Д8 + С«/Л/2-}-В,2 + С'2 |А||А'|
Если плоскости заданы параметрическими уравнениями (п. 3.2-2) г = rt-{-иа-{-vb и
г = 1*1 -j- «а' -j- t/b'f то
(а X b) • (а' х Ь') ,, . _w
86
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.4-2.
(с) Угол уз между прямой
х — хх_у-
"х "у "z
и плоскостью Ax+By+Cz~\-D = 0 (угол между прямой и ее проекцией на
плоскость) определяется по формуле
Aax + Bay+Caz
sin 7з = г . (3.4-6)
V А* + В*+С*Уа* + а1+а1
В частности, прямая параллельна плоскости, если sin Уз = О (лежит на плоскости,
если, кроме того, Axt + Byt -j- Czt + D = 0); прямая перпендикулярна к плоскости, если
sin уз = 1. Угол между прямой и нормалью к плоскости равен л/2 — у3.
X (d) 1. Условия параллельности двух прямых
*=*l=K^J!i = l=li9 или г = Г1 + /а,
имеют вид
X — Xi __ У — У1 _ Z—Zj
а
, или г = г| + /а',
ах ау
—=—, или а' = ^а, или аХа' = 0.
Если, кроме того, прямые имеют общую точку, то они совпадают.
2. Прямая x~x^==y — ^iz=iz — z* t или г = Г! + /а, и плоскость Ах+Ву +
ах ау az
+Cz + D = 0 или А-г + D — O взаимно перпендикулярны, если прямая
параллельна нормали к плоскости (и сама служит нормалью), т. е. если
-^ = -^=-^., или а = ХА, или а х А = 0.
3. Две плоскости
Ax + By + Cz+D = 0, или A-r + D = 0
И
A'x + B'y + C'z + D'^Q, или A'-r + D' = 0
параллельны, если параллельны их нормали, т. е. если
A==^.===^Jt или А = ЯА', или АхА' = 0.
Если плоскости, кроме того, имеют общую точку, то они совпадают.^
3.4-2. Расстояния.
(а) Расстояние 6 от точки Р0 (х0, у0, z0) = Р0 (г0) до плоскости Ах +
-\-By+Cz-{-D = 0 или А-г + £> = 0 (определенное по величине и знаку):
Axo + Byo + Czo+D At0 + D
о== —== ; («3.4-7)
У A* +S2 + C2 + | А |
знак перед корнем противоположен знаку D. Иногда б называют
отклонением точки от плоскости. Отклонение положительно, если начало координат
и точка Р0 (xQ, y0t z0) лежат по разные стороны от плоскости, и отрицательно,
если по одну сторону.
Если плоскость задана параметрическим уравнением (п.3.2-2) г =ri + wa -\- vb, то
axb
б = (г-го)-Г
axb |
(3.4-8)
3.4-3. 3.4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ И ПРЯМЫХ
(Ь) Расстояние d от точки PQ (xQ, yQ, z0) = Р0 (г0) до прямой
'-У1 Z—Zt
у "z
— | аХ (г°~ Г1^ __,
|а| —
или г = г1 + /а:
у\
У
У1—Уо
+
* I
+
-Х0
У
Ух—У о
V4 + °u + 4
(с) Кратчайшее расстояние dx между прямыми
- xt
(3.4-9)
-г-1, или r = r1 + te, r = ri + te':
Vax + ay+az Yax + a'y + ai2 sin Yi
a;
^1 — ^1 ^l — 2!
или ^1=liLi LI—IL , где sin Yx определяется равенством (2). Если
>(3.4-10)
| аха1
прямые параллельны (sinv1 = 0), то dx определяется равенством (9). J
Замечание. Если в определителе, стоящем в правой части равенства (10),
заменить *i, yVt zx переменными х, у, z и приравнять его к нулю, то полученное уравнение
определит плоскость, проходящую через вторую прямую параллельно первой. Если
прямые пересекаются, то плоскость проходит через обе эти прямые.
(d) Расстояние d2 между параллельными плоскостями Ax-\-By-\-Cz-\-D=*
= 0, A'x + B'y + C'z + D' = 0:
I d-d'|
V A* -f B* -f C2
(3.4-11)
(e) Расстояние d3 от плоскости до параллельной ей прямой определяется
по формуле (7).
3.4-3. Специальные случаи взаимного расположения точек, прямых и плоскостей.
(а) Т о ч к и. 1. Три точки Pt (xlt ylt zt), P2 {x2, y2, 28) и P, (*3, y%, 2S) лежат на
одной прямой, если (необходимое и достаточное условие)
Xi — *i
Уз — Ух ;
Уг— У\
Xz — Xi
или (см. также равенство (3.1-15))
_zs — zx
'z2 — zt
, или rs — fi = % (г8 — ft),
У1
Уг
Уз
Zx 1
z2 1
г* 1
=
ZX Xx 1
z2 x2 1
z3 x3 1
Xx У1 1
xz y2 1
*з Уя 1
= 0,
(r3 — r,)X(r2 — r,) = 0.
(3.4-12)
(3.4-13)
(3.4-14)
вие)
2. Четыре точки лежат в одной плоскости, если (необходимое и достаточное усло-
Хх Ух Zt 1
Xi У2 Z2 1
*з Уя гь 1
Хх Ух 24 1
= 0, или [(г8 — Хх) (г8 - гО (г4 -Г!)] = 0.
(3.4-15)
(Ь) Плоскости. 1. Если три плоскости Ах -f- By + Cz + D = 0, А'х -f- В'у -f- C'z -}-
4- D' = 0, А"х + В"у -f C'z -f- D" = 0 проходят через одну и ту же прямуюг то
Д =
А
А'
А"
В
В'
В"
с
с
С"
= 0.
(3.4-1G)
88
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.4-4.
2. Если четыре плоскости Ах -\- By -\- Cz -\» D — 0, А'х -f- В'у -\- C'z -j- D' = О, А"х -f-
. ^..- . ~„ „ - . ~... . ^... . ~,„ q проходят через одну и ту же точ-
(3.4-17)
+ В"у -f C'z + D" = 0, Л"'* + В"'у + С
к#, то
А В
А' В'
Л" В"
А'" В'"
'z + D"e
С D
С D
С" D
С" D
т. е. левые части их уравнений линейно зависимы (п. 1.9-3, а).
(с) Прямы е. Две прямые лежат в одной плоскости (т. е. пересекаются или
параллельны), если (необходимое и достаточное условие) четыре определяющие их
плоскости удовлетворяют условию (17). Если прямые заданы параметрическими уравнениями
г = г -j- /а, г = г' + /а', то условие (17) принимает вид
[('
г;>
= 0.
(3.4-17а)
3.4-4. Тангенциальные координаты плоскости и принцип двойственности. Уравнение
£*+TU/ + £z+l =° <3-4-18)
определяет плоскость (|, т|, £)• Числа |, т|, £ называются ее тангенциальными
(линейными, плюккеровыми) координатами. Если точечные координаты х, у, z фиксированы,
а £» "Л, £ рассматриваются как переменные, то (18) становится уравнением точки (х, у, г),
т е. точки пересечения всех плоскостей (18).
Симметрия уравнения (18) относительно точечных и тангенциальных координат
приводит к следующему принципу двойственности (см. также п. 2.3-3): наряду с каждой
теоремой о взаимном положении точек, прямых и плоскостей справедлива другая теорема,
которая получится, если в формулировке первой теоремы поменять местами термины
«.точка» и «плоскость».
3.4-5. Некоторые дополнительные соотношения.
(a) Если фх (х, у, г) = 0 и ф2 (х, у, г) = 0 — уравнения двух плоскостей,
то уравнение
<Pi(*> У, z) + h(p2(x, у, z) = 0 (3.4-19)
определяет плоскость, проходящую через линию пересечения данных
плоскостей (или параллельную им обеим, если они параллельны). Уравнение (19)
называется уравнением пучка плоскостей. Если обе плоскости заданы
нормальными уравнениями (п. 3.2-1,2), то (—X) равно отношению расстояний от
любой точки плоскости (19) до заданных (базисных) плоскостей; при А,= 1 и
% = — 1 полученные плоскости являются биссекторными плоскостями
двугранных углов между данными плоскостями.
Если плоскости ф1 = 0 и ф2 = 0 параллельны, то все плоскости (19) также
им параллельны.
(b) Уравнения прямой, перпендикулярной к плоскости Ax + By+Cz +
+ Z) = 0 и проходящей через точку Р0 (х0, у0, z0):
(3.4-20)
(c) Направляющий вектор и направляющие косинусы линии пересечения
двух плоскостей определяются по формулам (3.3-2) и (3.3-3).
(d) Точка пересечения трех плоскостей Ax + By-\-Cz + D = 0, A'x+B'y +
4- С'z + D'= 0 и A"x + B"y + C"z + D" ~0 имеет следующие координаты:
х = -
2 =
1
л
1
л
D
D'
D"
А
А'
А"
В
В'
В"
В
В'
В"
С
С
С"
D
D'
£>"
1
, А =
A D
С
A' D' С
A" D" С
ABC
А' В' С
А"
В" С"
.
(3.4-21)
3.5-4.
3.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
39
3.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
3.5-1. Общее уравнение второй степени. Поверхности второго порядка
(квадрики) определяются уравнениями второй степени относительно
декартовых прямоугольных координат. Общее уравнение второй степени относительно
переменных х, у, z имеет вид
«и*2 + «22#2 + «зз*2 + ^а12ху + 2al3xz + 2a23yz + 2аих + 2аиу + 2auz + «44 = О
или
(апх + а12у+a13z + аи) х + (а21х+а22у + a23z + аи) у +
+ (c3iX + a32y + a33z + a3i)z + ailx + ai2y + aMZ + au==0, (3.5-1)
где aik = aki; I, k=\, 2, 3, 4.
Уравнение (1) можно записать в векторной форме
(Аг) • г + 2а . г + о44 = 0, (3.5-2)
где А — аффинор с координатами А1.=а.^, а—вектор с координатами а- = а^ (см.
также п. 16.9-2).
3.5-2. Инварианты. Для любого уравнения (1) четыре величины
/=«11 + «22 + <
D = /U
«и
«гз |
«2:
«31 «32 «33 I
21 "22
«12
До,
У =
>л==
«11
«21
«П
«21
«31
«41
«12
«22
«12
«22
«32
«42
+
«22
«32 <
«13 «14
«23 «24
«33 «34
«4
3 «44
«23
+
«33
«13
«31
(3.5-3)
являются инвариантами относительно параллельного переноса и поворота
осей (3.1-19), (3.1-20), (3.1-23). Эти инварианты определяют свойства
поверхности, не зависящие от се положения в пространстве. Детерминант А
называется дискриминантом уравнения (1).
3.5-3. Классификация поверхностей второго порядка. Табл. 3.5-1 содержит
классификацию поверхностей второго порядка, основанную на их
инвариантах, определенных в п. 3.5-2. В этой таблице
А' = Ап + А22 + А3з,
Aik обозначает алгебраическое дополнение элемента а^ в определителе
A = det\ajk\t см. п. 1.5-2,
Л" =
«и
«41
«14
«44!
+
«22
«42
«44
+
«33
«34
«44
(3.5-4)
А' и А'
риантами).
3.5-4. Характеристическая квадратичная форма
При помощи характеристической квадратичной формы
являются инвариантами относительно поворота осей (семиинва-
и характеристическое уравнение.
^о (х, у, z) = аххх* + аггУ2 + a33z2 + 2at2xy + 2a13xz + Чаггуг,
(3.5-5)
соответствующей уравнению (1), могут быть изучены важные свойства поверхностей
второго порядка. В частности, невырожденная центральная поверхность второго порядка
(А ф 0, D ф0) оказывается действительным эллипсоидом, мнимым эллипсоидом или
гиперболоидом в зависимости от того, будет ли F0 (x, у, z) соответственно положительно
определенной, отрицательно определенной или неопределенной квадратичной формой, что
устанавливается по корням Кх, Я2, Я3 ее характеристического уравнения (п. 13.4-5, а)
an- >
«21
«31
<• «12 «13
«22 Л #23
Аза #зз
= 0 или К9 — /Я2 Н- JK — D = 0.
(3.5-6)
90
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.5-4.
Корни Ль Л2,
матрицы [Я/il]
Л8 являются собственными значениями действительной симметрической
(п. 13.4-2) и, как следствие этого, всегда действительны. Имеем:
' — Ли -f- ^2 ~Ь Я-3| J == Л1Л2 ~Ь Л2Л3 ~Ь А-з^-ь ^) — ЛгЛгЛз-
Таблица 3.5-1 (а)
Классификация поверхностей второго порядка
Центральные
поверхности
DjtO
Нецентральные
поверхности
D=0
D/, J
оба больше
нуля
DI, J
не оба
больше нуля
Невырожденные поверхности
А >0 Л <0
Мнимый
эллипсоид
Однополостный
гиперболоид
Гиперболический
параболоид
Эллипсоид
Двуполостный
гиперболоид
Эллиптический
параболоид
Вырожденные
поверхности |
А = 0
Точка
(действительная вершина
мнимого конуса)
Действительный
конус
Цилиндры (см. табл.
3.5-1 (б), А'фО>)
Пары плоскостей
(см. табл. 3.5-1 (б),
Л' = 0)
Л =0, D = 0, У>0
Л = 0. D = 0, У < 0
Л = 0, D = 0, У = 0
Ранг квадратной
матрицы [я,ь] 4-го
порядка (п. 13.2-7)
*) Пара совпавш
признаков: (а) ранг Га
Цилиндры
А'фО
Эллиптический
цилиндр (мнимый
эллиптический
цилиндр, если Л'/>0;
действительный, если
Л'/<0)
Гиперболический
цилиндр
Параболический
цилиндр
3
их плоскостей характс
ik] равен 1, (б) А = D
Т
а б л и ц а 3.5-1 (Ь)
Пары плоскостей
Л'=0
Пара мнимых
плоскостей,
пересекающихся по действительной
прямой
Пара действительных
пересекающихся
плоскостей
Пара параллельных
плоскостей (мнимых,
если Л">0;
действительных, если
/1"<0)
2
физуется любым из (
= J = Л'= Л" =0, / :
Пара
действительных
совпадающих
плоскостей *)
1 '
следующих двух
£0.
3.5-6.
3.5 ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
91
(3.5-7)
3.5-5. Диаметральные плоскости, диаметры и центры поверхностей второго
порядка.
(a) Для любой поверхности второго порядка (вырожденной или
невырожденной) геометрическим местом середин параллельных хорд служит
плоскость, которая называется диаметральной плоскостью поверхности,
сопряженной этим хордам (или направлению этих хорд). Диаметральная плоскость
поверхности (1), сопряженная хордам с направляющими косинусами cosav,
cos ayi cos az, определяется уравнением
(anx + a12y + a13z + a14) cos ax + (a21x + a22y + a23z + a24) cos ay +
+ (a31x + a32y + a33z + a34) cos a2 = 0.
(b) Прямая, по которой пересекаются две диаметральные плоскости,
называется диаметром, сопряженным семейству плоскостей, параллельных
сопряженным хордам этих диаметральных плоскостей. С другой стороны, диаметр
является геометрическим местом центров кривых второго порядка, по
которым пересекают поверхность параллельные между собой плоскости семейства.
Уравнения диаметра, сопряженного семейству плоскостей с заданными
направляющими косинусами нормалей cos аХ1 cos ay, cos a2:
«U* + «12# + «13Z+ «14 «21* + «22# + «23* + «24 «31* + «32# + «33^ + «34 /ОСОЧ
cos a^ cos a cos az • l0**0"6/
(c) При Dz^zO все диаметры поверхности второго порядка пересекаются
в одной точке, центре поверхности (другое определение см. в п. 3.5-8). При
D = 0 все диаметры параллельны или лежат в одной плоскости. В первом
случае, т. е. при D^jtO, поверхность называется центральной.
Координаты х0, у0, г0 центра определяются системой уравнений
«11*0 + «12#0 + «13*0 + «14 = 0.
«21*0 + «22^0 + «23*0 -
«31*0 + «32#0 + «3320 '
откуда
, + «14 = 0, \
) + «24 = 0, К
, + «34 = 0, J
(3.5-9)
1
D
«14 «12
«24 «22
«34 «32
«13
«23
«33
, Уо=~
1
D
«и
«21
«31
«14 «13
«24 «23
«34 «33
, *0=—
1
D
«и
«21
«31
«12
«22
«32
«14
«24
«34
(3.5-10)
Если поверхность центральная, то перенос (3.1-19) начала координат в ее центр (10)
приводит уравнение поверхности к виду
«и* + «22# + «зз22 + 2а12ху + 2a13*z + 2a23yz + — «= 0,
(3.5-11)
где хУ у у г — координаты относительно новой системы.
(d) Три диаметра центральной поверхности второго порядка называются
сопряженными диаметрами, если каждый из них сопряжен плоскости двух
других диаметров.
3.5-6. Главные плоскости и главные оси.
(a) Диаметральная плоскость, перпендикулярная к сопряженным ей
хордам, называется главной плоскостью поверхности второго порядка и является
ее плоскостью симметрии. Каждая поверхность второго порядка имеет по
меньшей мере одну главную плоскость и по меньшей мере две плоскости
симметрии. (Пример: параболический цилиндр имеет одну главную плоскость.)
Только цилиндры имеют плоскости симметрии (перпендикулярные к
образующим), которые не являются главными плоскостями. Каждая невырожденная
поверхность второго порядка имеет по меньшей мере две взаимно
перпендикулярные главные плоскости. Каждая центральная поверхность (п. 3.5-5) имеет
по меньшей мере три главные плоскости (ровно три, если она не является
поверхностью вращения), среди которых всегда существуют три взаимно
перпендикулярные.
(b) Диаметр, являющийся линией пересечения двух главных плоскостей,
называется главной осью поверхности и является ее осью симметрии. Если
92
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
3.5-7.
поверхность имеет две главные оси, то она имеет и третью, перпендикулярную
к ним обеим. Каждая невырожденная поверхность имеет по меньшей мере
одну главную ось. Центральная поверхность имеет по меньшей мере три
(ровно три, если она не является поверхностью вращения) взаимно
перпендикулярные главные оси, представляющие собой нормальные к ее главным
плоскостям диаметры (сопряженные как этим плоскостям, так и между собой,
см. п. 3.5-4, а); среди главных осей центральной поверхности всегда имеются
три взаимно перпендикулярные.
Нормали к главным плоскостям имеют направления собственных векторов
матрицы [а/£], /, k==l, 2, 3 (см. п. 14.8-6). Направляющие косинусы этих нормалей
cos a^, cos ау, cos az определяются системой уравнений
(ахх — Я) cos ах + ах2 cos ау -f- ахь cos az = 0, \
а2х cos ах + (о22 — ^) cos ау + а2з cos az = О, J. (3.5-12)
o3i cos ах-\- аз2 cos ау + (а33 — Я) cos az = О, J
где А, — отличный от нуля (заведомо действительный) корень характеристического
уравнения (6). -КЕсли все корни Кх, Я2, Я3 уравнения (6) отличны от нуля, то система (12)
определяет для каждого из этих корней направляющие косинусы главной оси. В том
случае, когда Я —0 является простым корнем характеристического уравнения (6), ему
соответствуют направляющие косинусы единственной главной оси. Если же л = 0 —
кратный корень, то поверхность является параболическим цилиндром или парой
параллельных плоскостей. В этом случае система (3.5-12) содержит только одно независимое
уравнение. Если дополнить ее уравнением
ахх cos ах -f- а42 cos ау + а43 cos az — О,
то новая система определит направление образующих цилиндра.-&
3.5-7. Приведение уравнения поверхности второго порядка к стандартному
(каноническому) виду. Если ввести новую систему координат, осуществив
1) поворот координатных осей (п. 3.1-12, Ь), в результате
которого нормаль к каждой из взаимно перпендикулярных плоскостей
а) Ь)
а> е)
Рис. 3.5-1. Невырожденные поверхности второго порядка: а) эллипсоид, Ь) однополост-
иый гиперболоид, с) двуполостный гиперболоид, d) эллиптический параболоид, е)
гиперболический параболоид.
симметрии поверхности станет параллельной одной из новых осей
(преобразование к главным осям, см. п. 14.8-6);
3.5-8.
3.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
93
2) подходящий перенос начала (п. 3.1-12, а),
то уравнение (1) любой невырожденной поверхности второго порядка может
быть преобразовано к одному из видов, перечисленных в табл. 3.5-2. Эти
поверхности изображены на рис. 3.5-1. Каждое из полученных уравнений
называется стандартным (или каноническим) уравнением соответствующей
поверхности. В табл. 3.5-2 приведены также основные свойства
поверхностей и соотношения, позволяющие определить параметры я2, б2, с2, р и q по
инвариантам Л, D, J и / уравнения (1).
Уравнения вырожденных поверхностей (см. табл. 3.5-1) аналогичным образом
приводятся к следующему стандартному виду:
У2
Ь*
У2
z2
- -- = 0 (точка),
- = 0 (действительный конус; круговой, если а2 = Ь2),
х2 у2
—2 + п = 1 (эллиптический цилиндр; круговой, если а2 = Ь2),
х2 и2
— — -г- = 1 (гиперболический цилиндр),
а2 1
х2 у2
~ =0 (прямая).
(3.5-13)
, - = 0 (пара пересекающихся плоскостей),
а2 о*
у2—2рх (параболический цилиндр),
х2
- = 1 (пара параллельных плоскостей),
а2
х2 = 0 (одна действительная плоскость).
Направления новых осей Ох, Оу, Oz определяются уравнениями (12) с точностью до
поворота на угол, кратный Jt/2, вокруг любой из новых осей; этому преобразованию
соответствует перестановка переменных х, —х, у, — у, г. —z в канонических
уравнениях табл. 3.5-2.
3.5-8. Касательные плоскости и нормали поверхности второго порядка.
Полюсы и поляры.
(a) Определение касательных плоскостей и нормалей поверхности, а также
условия их существования приведены в п. 17.3-2. Уравнение касательной
плоскости к поверхности (1) в точке Рг (xv yv zt) имеет вид
апхгх+а22угу+а33гхг+а12 (угх+хгу)+а13 (ггх+хгг) +
+ «23 [У& + ЧУ) + «14 (*1 + *)+ «24 (У1 +У) + «34 (*1 + *) + «44 = 0
или | (3.5-14)
(«ii*i + «i2#i + «13*1 + «i4> х + (021*! + а22у1 + а23гг + а2Х) у +
+ («31*1 + «32#1 + «33*1 + «3l) 2 + (a4i*! + «42^1 + «43*1 + «44> = 0.
(b) Уравнения нормали к поверхности (1) в точке (xv yv zt) (см. также
п. 3.3-16, Ь):
X— Хх
У —Ух
ОцХх + а12У1 + «13-21 + «14 «21*1 + «22#1 + «23*1 + «24 "
Z — Zt
«31*1 + «32#1 + «33*1 + «34 '
(3.5-15)
(с) Уравнение (14) определяет плоскость, которая называется полярной
плоскостью точки (*], уъ zt) относительно поверхности второго порядка (1)
независимо от того, лежит ли точка (xlt уъ zt) на поверхности или нет; точка
(*i» #i» ^i) называется полюсом плоскости (14). Полярная плоскость точки,
Таблица 3.5-2
Стандартные (канонические) уравнения и основные свойства невырожденных поверхностей второго порядка
(см. также табл. 3.5-1; уравнения касательных и полярных плоскостей см. в п. ,
Поверхность (см. также
рис. 3.5-1)
Действительный
эллипсоид (эллипсоид вращения
(сфероид), если два главных
диаметра равны и либо (а)
1 меньше, чем третий (вытя-
1 нутый сфероид), либо (Ь)
больше, чем третий
(сплюснутый сфероид); сфера, если
а2 = 62 = с2)
Однополостный гипербо-
1 лоид (гиперболоид вращения,
! рсли аг = Ьг)
Стандартное
(каноническое)
уравнение
х* у* г* ,
аг ~т~ ь2 "*" С*
(рис. 3.5-1, а)
Х2 у* гг
а» ~т" Ь* с*
(рис. 3.5-1, Ь)
Сечение
плоскостью
Действительный
или мнимый эллипс;
точка (касательная
плоскость)
Гипербола,
парабола или эллипс в
зависимости от того,
параллельна секущая
плоскость двум,
одной или ни одной
прямолинейной
образующей
асимптотического конуса; пара
пересекающихся
прямых (касательная
плоскость)
Замечания
Вершины в точках (■+- а,
0, 0), (0, ± Ь, 0), (0, 0, ± с);
длины главных диаметров
равны соответственно 2а,
2Ь, 2с
Линейчатая поверхность
с двумя семействами
прямолинейных образующих
т+-г-Ч, + *>1
/(т--?-)--*)
"т+т-'Ы-).}1
>(т--9-+* 1
Геометрическое место
прямых, пересекающих три
данные прямые.
Асимптотический конус (внутри
поверхности):
** J-У% Z% 0
аг "Г Ь2 С2
3.5-8)
Параметры а, Ь, с,
выраженные через
инварианты A, D
И Ai, А>2» A3
1 А
a==z-%;~D'
b^-L.A.
л2 D '
c2 = -J-A
Ьх D9
D ^ Ai Л»2 Л»з
2 Х А
а "" л2 D '
1 ^
К > К > о > л*,
/^ = Лх Л-я Л»з
Таблица 3.5-2 (продолжение)
Поверхность (см. также
рис. 3.5-1)
Двуполостный
гиперболоид (гиперболоид
вращения, если Ъг — с2)
Эллиптический
параболоид (параболоид
вращения, если р = q)
Гиперболический
параболоид
Стандартное
(каноническое)
уравнение
хг у2 г2
а2 Ь2 с2 ~
(рис. 3.5-1, с)
Х- + »- = 2г
Р Я
(рис. 3-5-1, d)
(р > 0, q > 0)
*-'-' = &
Р Я
(р > 0, q > 0)
(рис. 3.5-1, е)
Сечение
плоскостью
Гипербола,
парабола или эллипс в
зависимости от того,
параллельна секущая
плоскость двум, одной
или ни одной
прямолинейной образующей
асимптотического
конуса; пара
пересекающихся прямых
(касательная плоскость)
Парабола
(диаметральная плоскость);
действительный или j
мнимый эллипс;
точка (касательная
плоскость)
Парабола
(диаметральная плоскость);
гипербола; пара
пересекающихся
прямых (касательная
плоскость)
Замечания
Вершины в точках (± а,
0, 0); расстояние между
вершинами равно 2а.
Асимптотический конус (вне
поверхности): |
х* у2 г*_0
аг Ъг сг
Вершина в начале
координат
Седловая точка в начале
координат. Линейчатая
поверхность с двумя
семействами прямолинейных
образующих
Vp Yq 1
_£-__*- = ?* j
Yp Yq K )
и
х у \
Yp Vq"11, I
* _1_ У _ 2Z 1
Yp ' Yq И
Параметры a, b, c, p, q,
выраженные через
инварианты A, D
и Ai,. Л2, A3
2 ] A h2 l A
Q ~ AXD' Ь ~%ZD1
2 l A
° -~A2D'
Ai > 0 > A2 > Ae,
D = Ai %2 A3
1 -if A
Ai ^ %2 ^> Л3 == 0» J = A1A2
p = i"J/-7-
1 1/ A
Ai ^> Л2 = 0 > Л3, J = AiA3
96
ГЛ. 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 3.5-9.
принадлежащей поверхности второго порядка, если касательная плоскость
поверхности в этой точке.
(d) Полярная плоскость р любой точки В данной плоскости а проходит
через полюс А этой плоскости а.
(e) Центр поверхности второго порядка есть полюс бесконечно удаленной плоскости.
Диаметральная плоскость есть полярная плоскость бесконечно удаленной точки, через
которую проходят хорды, сопряженные этой диаметральной плоскости.
(f) Полярные плоскости всех точек данной прямой пересекаются по одной прямой; эта
последняя прямая содержит полюсы всех плоскостей, проходящих через данную прямую.
Две полученные прямые называют парой полярно сопряженных прямых.
(g) Диаметр поверхности второго порядка есть прямая, полярно сопряженная
бесконечно удаленной прямой пространства.
(h) Полярная плоскость допускает геометрическое определение, аналогичное
определению поляры (см. п. 2.4-10).
3.5-9. Некоторые дополнительные формулы и теоремы.
(а) Уравнение сферы радиуса г с центром в точке Рх (xif ylt zt) = Pt {rt):
(x — *t)2 + {y — yt)2 + (z — zt)* =r2 или | r — Г! | = r.
(b) Общий вид уравнения сферы:
А (х2 + у* + z2) -f 2B* +2Су + 2Dz -f £ = 0, А ф 0.
(3.5-16)
(3.5-17)
(с) Пусть Рх и Р2— точки пересечения сферы с прямой (секущей), проходящей через
данную точку Р0 (х0, Уо, z0). Тогда произведение величин направленных отрезков P0Pi
и P0Pz постоянно для всех секущих, проходящих через Р0, причем
РоРх • PoPz = xi + Уо + 4 -
(3.5-18)
Теорема остается справедливой и в том случае, когда Рх и Pz совпадают (если
рассматривать вместо секущей ее предельное положение — касательную к сфере в точке Рх == Р2.
проходящую через точку Р0).
(d) Для половик трех сопряженных диаметров эллипсоида (п. 3.5-5):
1. Сумма квадратов равна a2 -j- b2 + с2.
2. Объем построенного на них параллелепипеда равен abc.
(e) Диаметральная плоскость поверхности второго порядка
х2
а2'~
.V*
с2 ''
I
(3.5-19)
(эллипсоид, однополостный гиперболоид или двуполостный гиперболоид, см. также табл.
3.5-2), сопряженная диаметру с направляющими косинусами cos a cos а , cos a2,
определяются уравнением
х cos a
у cos а
У
z cos а_
- Ь*
= 0.
Направляющие косинусы трех сопряженных диаметров cos a , cos о.
cos ft, cos ft; cos у , cos у cos у удовлетворяют соотношениям
cos а^ cos $x cos а cos ft cos a2 cos R^
a2
cos a^ cos yx
cos ft^ cos yx
—2
cos a„ cos y„ cos a_ cos y*
У У * *
'■ £i — £i
cos ft cos у
cos ft cos у
У
с2
= 0.
(3.5-20)
cos a ; соь ft
(3.5-21)
Знаки в уравнениях (20) и (21) должны совпадать со знаком соответствующих членов
в уравнениях (19).
■#(!) Уравнение диаметра поверхности (3.5-19), сопряженного плоскости с
направляющими косинусами нормали cos a , cos a , cos a , имеет вид
У
± a2 cos a
± b2 cos a„ ± c2 cos a„
У z
.*
3.5-10.
3.5. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
97
3.5-10. Параметрическое задание поверхностей второго порядка (см. также пп.3.1-14):
х = a sin и cos v, у = b sin и sin v, z = c cos и (эллипсоид), (3.5-22)
x = a ch и cos v, у = b ch и sin v, г = с sh и (однополостный гиперболоид),(3.5-23)
х =± a ch и, у — b sh и sin у, г = с sh m cos d (двуполостный гиперболоид), (3.5-24)
(знаки + и — соответствуют двум полостям),
х= Vp и cos v, у — Yq и sin v, z = у и2 (эллиптический параболоид), (3.5-25)
х = Vp и ch v, у — Yq и sh v, г = — и* (гиперболический параболоид), (3.5-26)
х = аи cos v, у = bu sin v, z —си (действительный конус). (3.5-27)
Возможны также многие другие параметрические задания этих поверхностей.
4 Г. Корн и Т, Корн
ГЛАВА 4
ФУНКЦИИ И ПРЕДЕЛЫ. ДИФФЕРЕНЦИАЛЬНОЕ
И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
4.1. ВВЕДЕНИЕ
Эта глава посвящена главным образом числовым функциям действительных
переменных. Введение пределов функций (пп. 4.4-1—4.4-7) позволяет определить
новые математические операции (предельные процессы), такие, как сложение
и умножение бесконечного числа членов, дифференцирование и интегрирование.
Определения и теоремы, изложенные в этой главе, применимы как к
действительным, так и к комплексным функциям и переменным, если специально не
оговорено, что речь идет лишь о действительных величинах. Аналитические
функции комплексного переменного рассматриваются в гл. 7.
4.2. ФУНКЦИИ
4.2-1. Функции и переменные (см. также п. 12.1-4).
(a) Если дано правило соответствия, относящее каждому данному
действительному или комплексному числу х из множества Sx действительное или
комплексное число
У = /(*), (4.2-1)
то у называется (числовой) функцией
y = U(x) = f(x)
аргумента х. Равенство (1) указывает значение (или значения) y = Y — f(X)
переменной у, соответствующее каждому допустимому значению х = Х
переменной х\ при этом х называется независимым переменным, а (/—зависимым
переменным.
Термин «переменное х», в сущности, отсылает к множеству значений X, а равенство (1)
символизирует множество соответствий, связывающих значения X переменного х и
значения Y = f (X) переменного у. В согласии с обозначениями, применяемыми в
большинстве учебников, символом х мы будем обозначать и переменное х и значение этого
переменного, если только это не сможет привести к путанице.
Если х и у рассматривать как декартовы координаты на плоскости (п. 2.1-2),
то действительная функция y = f(x) действительного переменного х часто
изображается кривой (графиком функции у от х, см. также п. 2.1-9).
(b) Подобным же образом функция
У = /(*!. *2. .... *л) (4.2-2)
п переменных х1% х2, ..., хп относит упорядоченному множеству значений
(независимых) переменных хъ х2, ..., хп значения (зависимого) переменного у.
Функция может быть определена таблицей своих значений или правилом вычисления
такой таблицы с помощью известных операций (конструктивные определения). Функция
может также быть определена неявно (п. 4.5-7) или с помощью определяющих свойств,
описываемых функциональными, дифференциальными или интегральными уравнениями,
экстремальными свойствами (п. 11.4-2), поведением при некоторых значениях аргумента
и т. д. Каждое неконструктивное определение нуждается в доказательстве сущее твованияг
устанавливающем, что функция, обладающая указанными свойствами, существует,
4.3-1. 4.3. ТОЧЕЧНЫЕ МНОЖЕСТВА, ИНТЕРВАЛЫ И ОБЛАСТИ 99
(c) В большинстве приложений переменные х, у или xv х~ х у
обозначают физические объекты или величины, так что соответствующие соотношения (1)
или (2) описывают физические закономерности. (Пример, у — х^2, если xt, x2 и у
соответственно обозначают напряжение, силу тока и мощность в простом электрическом
контуре.)
(d) Множество Sx значений х (или множество значений xlt x2, ..., хп),
для которых определены- соотношения (1) или (2), есть область определения
функции f (х) или f\x1% x2, ..., хп). Соответствующее множество Sy значений у
есть множество значений функции.
(e) Последовательность действительных или комплексных чисел s0, s±t
s2, ... представляет функцию sn = s(n), определенную на множестве
неотрицательных целых чисел п.
4.2-2. Функции со специальными свойствами (см. также пп. 1.4-3, 7.3-3,
7.6-5 и 7.6-7).
(a) Функция однозначна, если каждому значению аргумента
соответствует единственное значение функции х). Функция многозначна, если хотя бы
одному значению аргумента соответствует два или более значений функции.
В дальнейшем всюду в этой главе рассматриваются только однозначные
функции, и это всякий раз специально не оговаривается. Функция у (х) имеет
обратную функцию х (у), если из у = у (х) следует х = х (у).
(b) Функция / (х) действительного или комплексного переменного * четна,
если /(—*)=/(*), нечетна, если /(—х)=—/(#); является периодической
с периодом Г, если f(t-{-T) = /(/).
Каждая функция f (x), область определения S которой вместе с каждым входящим
в него числом х содержит и число — х, может быть представлена в виде суммы четной
функции (1/2) [f (х) -f- / (— *)] и нечетной функции (1/2) [f (x) — f (— *)]. Периодическая
функция / с периодом Т называется антипериодической, если f (t + Т/2) =— f(t). Каждая
периодическая функция / (/) с периодом Т может быть представлена в виде суммы
антипериодической функции (1/2) [jF (t) — / (t -f- Г/2)] и функции (1/2) [/ (/) + f (f + Т/2)],
периодической с периодом Т/2.
(c) y = f(x) есть алгебраическая функция от х, если хну удовлетворяй:т
соотношению вида F (х,у) = 0, где F (х,у) — многочлен относительно хну
(п.1.4-3). В частности, y = f(x) есть рациональная (рациональная алгебраическая)
функция от х, если / (х) есть многочлен (целая рациональная функция) или
частное двух многочленов (дробная рациональная функция), у есть линейная
функция от х, если у = ах-\-Ь.
4.3. ТОЧЕЧНЫЕ МНОЖЕСТВА, ИНТЕРВАЛЫ И ОБЛАСТИ
4.3-1. Вводные замечания. При рассмотрении свойств функции / (х)
действительного переменного х часто требуется указать множество значений х, для
которых значение / (х) определено и удовлетворяет данным условиям. Заметим,
что подобным образом могут быть описаны и функции, и множества. Обычно
о значениях 2) действительного переменного х (или объектов, которым
соответствуют значения х) говорят как о точках (х) прямой, а о множествах таких
действительных чисел —как о линейных точечных множествах.
Свойства функции / (xlt x2t..., хп) действительных переменных xlt x2, ..., хп
подобным же образом связывают с множеством «точек» (xlt x2, ..., хп) в /г-мер-
ном «пространстве», включающем все рассматриваемые точки (xlt x2t ..., хп)
(п. 14.1-2).
Использование геометрического языка подсказывается аксиомой непрерывности
Кантора — Дедгкинда, постулирующей существование взаимно однозначного соответствия
*) Многие авторы категорически настаивают на том, что по определению каждая
функция должна быть однозначна, так что, например, две ветви -\-Yх и —-У^для -±У х
всегда следует рассматривать как две функции.
2) См. также п. 4.2-1.
4*
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.3-2.
между действительными числами и точками прямой. Эта «координатная аксиома» (п. 2.1-2)
совместима как со свойствами действительных чисел, так и с постулатами,
определяющими евклидову и другие геометрии.
В пп. 4.3-2 — 4.3-6 рассматриваются главным образом те свойства точечных множеств,
которые непосредственно применяются в теории функций действительных
переменных. В пп. 7.2-2—7.2-4 рассматриваются области на комплексной числовой плоскости.
Вообще говоря, о любом множестве (классе) объектов (в частности, объектов,
соответствующих значениям действительного переменного или переменных) можно
говорить как о точечном множестве. Свойства таких множеств рассматриваются ниже, в
пп. 12.5-1 — 12.5-4.
4.3-2. Свойства множеств.
(a) Алгебра множеств (классов). Объект (точка) Р, содержащийся
в множестве (классе) 5, есть элемент множества S(Pe 5). Множество 5Х
является подмножеством другого множества S2 (Si содержится в S2, 5Х cz 52), если
каждый элемент множества Sx является элементом и множества S2. Множества
Sx и S2 равны (Si = S2), если они содержат одни и те же элементы, т. е. если
5Х с: 52 и S2 с: Sv Пустое множество ф по определению есть подмножество
каждого множества 5. Собственное подмножество (собственная часть) множества
5 есть непустое подмножество S, не равное 5. Объединение (логическая сумма)
Si U S2 (или St + S2) есть множество всех элементов, содержащихся либо в
Sv либо в 52, либо и eSv ивS2. Пересечение (общая часть, логическое
произведение) 5Х П S2 (или Si S2) множеств 5Х и S2 есть множество всех элементов,
содержащихся ив Slt и в S2. Дополнение множества 5 до множества /,
содержащего S, есть множество всех элементов из /, не содержащихся в S.
Подмножества любого множества (класса) I с операциями логического сложения и
умножения составляют булеву алгебру (п. 12.8-1).
(b) Кардинальные числа и счетность. Два множества Sx и S2
имеют одну и ту же мощность (кардинальное число), если существует взаимно
однозначное соответствие между этими множествами. 5 есть бесконечное
множество, если оно имеет ту же мощность, что и хотя бы одно из его
собственных подмножеств; в противном случае 5 — конечное множество.
Бесконечное множество S счетно, если можно установить взаимно
однозначное соответствие между ним и множеством натуральных чисел. Каждое
кардинальное число конечного множества тождественно с числом его элементов.
Каждое бесконечное подмножество счетного множества счетно. Объединение
счетного множества счетных множеств есть счетное множество.
Кардинальные числа, соответствующие бесконечным множествам, называются
бесконечными кардинальными числами. Кардинальное число каждого счетного множества
совпадает с кардинальным числом множества натуральных чисел и обозначается
символом jj$0. Множество всех действительных чисел (или множество точек прямой, п. 4.3-1)
несчетно; соответствующее кардинальное число обозначается символом ft.
4.3-3. Границы.
(a) Действительное число М есть верхняя граница или нижняя граница
множества Sy действительных чисел у, если для всех у е Sy соответственно
у^М или у^М. Множество действительных или комплексных чисел
ограничено (имеет абсолютную границу), если множество абсолютных величин (модулей)
этих чисел имеет верхнюю границу; в противном случае множество не ограничено.
Каждое (непустое) множество Sy действительных чисел у, имеющее верхнюю
границу, имеет точную верхнюю границу (наименьшую верхнюю границу) sup Sy,
а каждое (непустое) множество Sy действительных чисел, имеющее нижнюю
границу, имеет точную нижнюю границу (наибольшую нижнюю границу) inf Sy.
Если множество Sy конечно, то его точная верхняя граница sup Sy необходимо
равна наибольшему числу, принадлежащему Sy: max Sy (максимуму 5V),
а точная нижняя граница inf Sy равна минимуму min Sy.
Пример. Множество всех действительных чисел, меньших 1, имеет точную верхнюю
границу 1, но не имеет максимума.
(b) Действительная или же комплексная функция y—f(x) или же у =
= / (хх,х2,..., хп) ограничена на множестве 5 «точек» (х) или (xv x2l..., хп), если
4.3-6. 4.3. ТОЧЕЧНЫЕ МНОЖЕСТВА, ИНТЕРВАЛЫ И ОБЛАСТИ Ю1
ограничено соответствующее множество Sy значений функции у. Точно так же
действительная функция у = [(х) или */ = / (хи х2, ..., хп) имеет верхнюю
границу, нижнюю границу, точную верхнюю границу, точную нижнюю границу,
(абсолютный) максимум и/или (абсолютный) минимум на множестве 5 «точек»
(х) или (xlt x2t ..м хп), если это верно для соответствующего множества Sy
значений функции у.
(с) Действительная или комплексная функция f (х, у) или f (л: х2 х ; у)
равномерно ограничена на множестве 5 «точек» (л:) или /дг х2 *л), если абсолютная
величина (модуль) функции f как функция от у имеет верхнюю границу, не зависящую от х
или от хг х2 хп на 5. Равномерные верхние границы и равномерные нижние границы
определяются аналогично.
4.3-4. Интервалы (см. также пп. 4.3-3 и 4.3-5). Пусть х—действительное
переменное. Множество всех значений х (точек), удовлетворяющих условиям:
1) а<.х<. Ь, есть ограниченный открытый интервал (а,Ь),
2) а<Сх, есть неограниченный открытый интервал (а, +оо),
3) #<а, есть неограниченный открытый интервал (—оо, а),
4) а^х^Ь, есть ограниченный замкнутый интервал [а, Ь].
Замкнутый интервал называют также отрезком, или сегментом, или
замкнутым промежутком. Множества точек (х), удовлетворяющих условиям
а^х < 6, а<.х^Ь, а^х, х^а, можно называть полуоткрытыми
интервалами. Каждый интервал /х, содержащийся в другом интервале /2, есть
частичный интервал интервала 12.
4.3-5. Определение окрестностей.
(a) Пусть а —любое действительное число. (Открытая) б-окрестность
точки (а) в пространстве действительных чисел есть любой открытый интервал
вида (а — 6, а + б), содержащий точку х — а, иными словами, множество
всех точек (л:), удовлетворяющих условию | х — а | < б, где б —некоторое
положительное число. Окрестность точки х — а есть любое множество, содержащее
некоторую б-окрестность этой точки.
(b) Множество (М, +°°) всех точек (х), для некоторого действительного
числа М удовлетворяющих условию х> М, есть (открытая) окрестность «точки»
плюс бесконечность (+ оо) в пространстве действительных чисел; множество
(—со, /V) всех точек (л:), для некоторого действительного числа N
удовлетворяющих условию x<N, есть (открытая) окрестность «точки» минус
бесконечность (—оо) в пространстве действительных чисел.
(c) В пространстве, «точки» которого суть (описываются как)
упорядоченные множества (хъ лг2, ..., хп) действительных чисел, (открытую) о-окрест-
ность точки (аъ а2, ..., ап), где аъ а2, ..., ап конечны, можно определить как
множество всех точек (хъ х2, ..., хп), удовлетворяющих условиям \х1 — а1 | < б,
I *2— fl21 *< о\ •••» | хп~~ап I < о\ гДе б —некоторое положительное число.
Окрестность точки (а1% а2, ..., ап) есть любое множество, содержащее некоторую
б-окрестность этой точки.
Замечание. Определения окрестностей, подобные тем, которые были даны
выше, нельзя считать самоочевидными; они подчиняются постулатам, определяющим
«топологические» свойства рассматриваемого пространства (см. также п. 12.5-1). В
частности, для неограниченных значений переменных (как выше в (Ь) ) окрестности можно
определить различными способами (так, + оо и — оо можно рассматривать как одну и
ту же точку или же как две разные точки; см. также п. 7.2-2). В прикладной
математике выбор таких определений будет зависеть от характера тех объектов, которые
«представлены» точками (х) или (л^, х2 х ). Определение окрестностей тесно
связано с определением открытых множеств (п. 4.3-6), областей (п. 4.3-6) и пределов
функций на рассматриваемом пространстве (п. 4.4-1; см. также п. 12.5-3).
4.3-6. ^Открытые и замкнутые множества и области. Все нижеследующие
определения зависят от того, каким образом определены окрестности в
пространстве С, содержащем рассматриваемые множества и области (от топологии
этого пространства, см. также пп. 12.5-1 — 12.5-4).
(а) Точка Р есть предельная точка (точка конденсации, точка
накопления) множества S аС, если каждая окрестность точки Р содержит точки
102 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.4-1.
множества S, отличные от Р. Точка Р есть внутренняя точка множества S,
если Р имеет окрестность, целиком содержащуюся в S. Точка Р£С, не
являющаяся внутренней точкой ни множества S, ни его дополнения до С, есть
граничная точка множества S. Точка Р множества S есть его изолированная
точка, если у нее есть окрестность, не содержащая других точек множества S.
Точечное множество S есть:
открытое множество, если оно состоит только из внутренних точек;
замкнутое множество, если оно содержит все свои предельные точки;
конечное множество замкнуто;
дискретное (изолированное) множество, если оно содержит только
изолированные точки; дискретное множество на евклидовой плоскости или в
евклидовом пространстве конечно или счетно; конечное множество дискретно;
связное множество, если его нельзя представить в виде объединения
двух непересекающихся множеств, каждое из которых не содержит
предельных точек другого. (См. также п. 12.5-4.)
(Ь) Множество на евклидовой плоскости или в евклидовом пространстве ограничено,
если ограничено множество декартовых координат всех его точек. Область (открытая)
есть открытое связное множество. Объединение открытой области и ее граничных точек
(границы области) есть замкнутая область.
Область D на евклидовой плоскости называется односвязной, если любая простая
вамкнутая кривая (п. 3.1-13), целиком принадлежащая D, может быть стянута в точку
с помощью непрерывной деформации, не выходя из области D. Область не односвязная
называется многосвязной.
Область V в евклидовом трехмерном пространстве называется:
поверхностно-односвязной, если любую простую замкнутую кривую, лежащую в V,
можно с помощью непрерывной деформации стянуть в точку, не выходя из V;
пространственно-односвязной, если любую простую замкнутую поверхность типа
сферы, лежащую в V, можно с помощью непрерывной деформации стянуть в точку, не
выходя из V.
Например, шар односвязен с точки зрения обоих определений, шаровое кольцо —
только с точки зрения первого определения, а тор («баранка») — только с точки зрения
второго.
4.4. ПРЕДЕЛЫ, НЕПРЕРЫВНЫЕ ФУНКЦИИ И СМЕЖНЫЕ ВОПРОСЫ
4.4-1. Пределы функций и последовательностей (см. также пп. 4.8-1 и
12.5-3; см. примеры в табл. 4.7-1).
(a) Функция f (х) имеет (необходимо единственный) предел \imf(x) = L при
х-*а
х, стремящемся к конечному значению х = а (предел в точке а\ f(x)-+L при
х—*а), если для каждого положительного числа е существует такое
положительное число 6, что при 0<|* — а|<6 функция f(х) определена и
|/(*)-! |<в.
Функция f (х) действительного переменного х имеет (необходимо
единственный) предел lim f(x) = L при х, стремящемся к плюс бесконечности
х-+ + оо
(когда х неограниченно возрастает; f(x)-*L при *—+ оо), если для каждого
положительного числа е существует такое действительное число N, что при
х > N функция / (х) определена и | / (х) — L | < е.
Если функция f(x) "имеет предел L, то говорят, что она стремится к L.
(b) Последовательность чисел (п. 4.2-1) s0, slt s2, ... (=s (n)) имеет
(необходимо единственный) предел lim sn — S (сходится к S), если для каждого
л-+оо
положительного числа е существует такой номер N, что при п> N
выполняется неравенство \ sn — S | < е. Критерий сходимости последовательности
см. в п. 4.9-1, где рассматриваются признаки сходимости бесконечных рядов.
(c) Действительная функция f (x) неограниченно возрастает (стремится к плюс
бесконечности):
1. При х, стремящемся к конечному значению х — а (/ (л:) -*> -f- оо при х -*■ а\
некоторые авторы пишут lim / (х) — -f- оо), если для каждого действительного числа М суще-
х->а
4.4-3
4.4. ПРЕДЕЛЫ, НЕПРЕРЫВНЫЕ ФУНКЦИИ
103
ствует такое положительное число 6, что при 0< J х — а | <б функция f (x) определена
Hf(jr)>Af.
2. При х, стремящемся к плюс бесконечности (f (х) -+■ -+- оо при х -*- -+- оо; некоторые
авторы пишут lim / (х) = + оо), если для каждого действительного числа М сущест-
*-*-{-оо
вует такое действительное число N, что при д:> N функция f {x) определена и f(x)>M.
Аналогичное определение дается в случае последовательности. Действительное
переменное х или f (х) стремится к минус бесконечности (х — — оо или f (х) -+ — оо), если
соответственно — х —■ + оо или —f (*)-* +оо. В (Ь) и (с) устанавливается математический
смысл символов +оэ и —- оо в системе действительных чисел (см. также пп. 4.3-5 и
7.2-2).
Если f (х) -> -f- °° или f (х) -> — оо при х -*■ а (при х -*- -f оо; при х -+ — оо), то
говорят, что функция f (х) является бесконечно большой при х -+ а (соответственно при
х -> + оо; при х -* — оо). Если f (х) -+ О при х -*• а (при х -* -f со; при х — — оо), то
функция f (х) называется бесконечно малой при х —■ а (соответственно при х -* -\- со; при
х -> — оо).
4.4-2. Операции над пределами (см. также пп. 4.4-6,с и 4.8-4). Если
пределы в правой части нижеследующих равенств существуют, то существуют
пределы и в левой части равенств и
lim [f(x)+g(x)] = lim f(x)+ lim g(x),
x -*■ a x -+a x -»a
lim [af (x)] = a lim / (x)t
x -*a x —■ a
hm[f(x)g(x)]=limf(x) lim g(x), \ (4.4-1)
x-+a x-+a x -+a
lim f{x)
где а может быть как конечным, так и бесконечным; эти правила применимы
и к пределам последовательностей (п. 4.4-1), а также к пределам функций
нескольких переменных (п. 4.4-5).
4.4-3. Асимптотические соотношения между двумя функциями (см. также
п. 4.8-6). Если даны две действительные или комплексные функции f(x), g(x)
действительного или комплексного переменного х, то пишут
1. f(x) = 0[g(x)\ (f (x) есть 0[g(x)]); f(x) есть функция не низшего
порядка малости чем g (х) при х —► а, если существует окрестность точки а,
в которой при х Ф а отношение f(x)/g(x) ограничено.
2. f(x) = 0*[g(x)]; f(x) и g(x) имеют один и тот же порядок (функция
f(x) асимптотически пропорциональна g (xj) при х-+а, если предел
lim [f(x)/g(x)\ существует и отличен от нуля.
X-+CL
3. f(x)~g(x); f(x) и g(x) эквивалентны (функция f (х) асимптотически
равна g(x)) при х—>а, если lim [/ (x)/g (x)] = 1; отсюда следует, что отноше-
х-»а
ние разности f(x) — g(x) к g(x) (или к f (х)) стремится к нулю при х—+а.
4. f(x) = o[g(x)] (/ (x) есть o[g(x)]); f(x) есть функция более высокого
порядка малости чем g(x) при х-+а, если lim [/ (x)/g (x)] = 0. Это иногда
х-+а
читают и так: «функция f(x) пренебрежимо мала по сравнению с g(x)* при
х—-а.
В каждом из этих определений а может быть как конечным, так и
бесконечным. Бесконечно малыми порядка 1, 2, ... при х—*0 называются
функции того же порядка, что и соответственно функции xt x2t ... при х—*0.
Бесконечно большими порядка 1, 2, ... при х—>+оо называются функции того
же порядка, что и соответственно функции х, х2, ... при х —*-f-oo.
Асимптотические соотношения часто позволяют оценивать или приближать функцию
/ (х) с помощью g (х) в некоторой окрестности точки х = а.
Пишут
/ (х) => ф (*) + О [g (*)], если f(x) — Ф (х) = О [g (x)l%
I {х) = ф {х) + о [g (*)], если £ С*) — Ф (*) =» о [g (*>].
104 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.4-4.
4.4-4. Равномерная сходимость.
(a) Функция / (хг, х2) сходится равномерно на множестве 5 значений х2:
1. К функции \im f (xlt x2) = L(x2), если для каждого положительного
xt -*• а
числа е существует такое положительное число б, что при О^!^ — а\<д
и при всех x2^S функция f (xlt x2) определена и выполняется неравенство
I / (*i> x2) — L (х2) | < е (6 не зависит от х2).
2. К функции lim f (xv x2) — L(x2), если для каждого положитель-
д^ + оо
ного числа е существует такое действительное число N, что при хг> N и
при всех х2 е 5 функция f (хъ х2) определена и выполняется неравенство
l/(*i. x2) — L(x2)\<e.
(b) Последовательность функций s0(x), s2 {x), s2(x)t ... равномерно
сходится на множестве S значений х к функции
lim sn (x) = s (x),
П-+СО
если для каждого положительного числа 8 существует такой номер N, что
при п> N и при всех xeS выполняется неравенство | sn (х) —s (л:) | <С е (см.
также пп. 4.6-2 и 4.8-2).
4.4-5. Пределы по совокупности переменных и повторные пределы.
(a) Если термин «окрестность» понимать в смысле, указанном в п. 4.3-5,с, то
функция f (Xi, х2) имеет (необходимо единственный) предел lim f (*i, x2) = L, если для
xt -* at
xz -+аш
каждого положительного числа е существует такая окрестность D точки (alt а2), что
для всех точек (хх, x2)^D, исключая, быть может, точку (alt a2), функция f (xlt х2)
определена и I f (xXt х2) — L | < е. При этом а, и/или а2 могут быть как конечными, так
и бесконечными.
Двойная последовательность s00, s10, ... имеет предел lim s =s (сходится к s),
т -*• со тп
п -*• со
если для каждого положительного числа 8 существуют такие два номера М и N, что
при т > М и п> N выполняется неравенство I s — s I < 8. Пределы функций более
чем двух переменных определяются аналогично.
(b) Если существует такое положительное число б, что
lim f (хи x2) = f (aXt x2) при 0< | x2 — a2 | < 6,
xx -»at
lim f {xlt x2) = f {xlt a2) при 0 < | xt — at | < 6
x2-*a2
и по крайней мере в одном из этих предельных процессов сходимость на указанном
множестве равномерна, то все три предела
lim f (*i, x2), lim Г lim / Ult *2)1
*i — at xt-+ ax [x2 -*• a2 I
x2 -* a2
и
lim | lim f (xXt х2)Л
x2 -* a2 [xt -* at \
существуют и равны друг другу. Аналогичные теоремы справедливы и в случае, когда
at и/или а2 бесконечны.
4.4-6. Непрерывные функции.
(а) Функция f(x), определенная в некоторой окрестности точки х = а,
непрерывна при х = а (в точке а), если предел lim f (x) существует и ра-
х -* а
вен /(а), т. е. если для каждого положительного числа е существует такое
положительное число б, что при \х — а|<6 выполняется неравенство
|/М-/(в)1<в.
(4.4-2)
4.4-7.
4.4. ПРЕДЕЛЫ, НЕПРЕРЫВНЫЕ ФУНКЦИИ
105
Точно так же функция f(xlt х2, ..., хп), определенная в некоторой
окрестности точки (аъ а2, ..., ап), непрерывна в точке (а1% а2, ..., ап)> если
lim f(xl9 х2, ..., хп) = f(alt а2, ..., ап).
хх -> ах
х2-»а2
Функция f (xt, х2 *„) непрерывна в точке (at, a2, ... , ап) по хи если
функция f (xt, az ап) непрерывна в точке xt = at. Функция, непрерывная в точке
(tfi, az ап) по каждой из переменных хх, х2 хп в отдельности, может не быть
непрерывной в точке (а,, а2 ап).
(b) Функция непрерывна на множестве точек (например, в интервале или
в области), если она непрерывна в каждой точке этого множества.
Действительная функция f (x), непрерывная на ограниченном замкнутом
интервале [а, Ь], ограничена на [а, Ь\ и хотя бы по одному разу принимает
каждое значение, заключенное между ее точной верхней и точной нижней
границами на [а, Ь] (п. 4.3-3), включая и эти границы. Аналогичная теорема
верна и для действительной функции двух и большего числа переменных,
непрерывной в ограниченной замкнутой области.
Функция f (x) равномерно непрерывна на множестве 5, если для каждого
положительного числа е существует такое положительное число б, что для всех х *= S и ^£5
при | х — X | < б выполняется неравенство \ f (х) — f (X) | < е. Функция, непрерывная на
ограниченном замкнутом интервале [а, Ь], равномерно непрерывна на [а, Ь].
(c) Если две функции fug непрерывны в данной точке х или (хх, х2, ... , хп\, то
непрерывны в этой точке и функции f -f- g, f — & и fg\ если функция g не обращается
в этой точке в нуль, то в этой точке непрерывна и функция f/g. Если дано, что
lim у. (х) = А£ (/— 1, 2, ...) и что функция F (уи у2, ... , уп) непрерывна в точке
х-+а v
(Ах% А2 Ап), то
lim F [yt (х), у2 (х), ... , уп (х)] = F (Аи А2 Ап) (4.4-3)
х-*а J
(см. также п. 4.4-2). В частности, если каждая из функций у- (х) непрерывна при х = а,
то это верно и для F [yt {x), у2 (х) уп (*)].
Предел s (х) равномерно сходящейся на множестве S значений х последовательности
функций s0 (х), sx (x) непрерывных на S, есть функция, непрерывная на S.
4.4-7. Односторонние пределы. Односторонняя непрерывность.
(а) Функция / (х) действительного переменного х имеет (необходимо
единственный) предел
lim /(*)= lim /(*)=/(a + 0) = I+
jc -»- a-f-0 *->a +
в точке а справа, если для каждого положительного числа е существует такое
положительное число 6, что при 0<л: — а<6 функция f (х) определена и
выполняется неравенство | / (х) — L+ | <е. Функция / (х) имеет в точке а
предел слева
lim /(*)= Ит /(*) = /(a —0) = L_,
х-*- а —0 x->a —
если для каждого положительного числа е существует такое положительное
число б, что при 0<а — *<6 функция / (х) определена и выполняется
неравенство |/ (*) — £- I <е. Если существует предел lim / (x)t то пределы
х-+а
lim / (х) и lim f (x) существуют и
*-»а + 0 х-*а — 0
lim / (х) = lim / (х) = lim / (х).
х-+а-\-0 х-*-а — 0 х-*-а
ЮЗ ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.4-8.
Обратно, если lim f(x) = ^im f(x)> то предел lim / (x) суще-
х — а — 0 х — а + 0 х-»а
ствует.
(b) Функция / (х) непрерывна в точке а справа или слева, если
соответственно / (а + 0) = / (а) или f(a — 0) = /(а). Точка разрыва первого рода
действительной функции / (х) есть точка а, в которой функция / (х) разрывна (т. е.
не непрерывна) и существуют пределы /(а + 0) и f (а — 0); наибольшая
разность между двумя из чисел / (а), / (а + 0) и / (а — О) есть скачок функции / (л:)
в такой точке разрыва *). Точки разрыва первого рода функции f (х) образуют
конечное или счетное множество (п. 4.3-6,а).
(c) Функция / (л:) кусочно-непрерывна на интервале /, если она
непрерывна в / всюду, за исключением конечного числа точек разрыва первого
рода.
Функция f (xlt x2, ... , хп) кусочно-непрерывна в области V «-мерного
пространства, если она непрерывна в V всюду, за исключением, быть может, некоторого
множества регулярных гиперповерхностей (регулярных кривых при /1 = 2, регулярных
поверхностей при п = 3, пп. 3.1-13 и 3.1-14), разбивающих V на конечное число подобластей,
в каждой из которых функция f (xlt x2 хп) имеет единственный односторонний
предел при приближении к любой граничной точке подобласти изнутри этой подобласти.
4.4-8. Монотонные функции и функции ограниченной вариации.
(a) Действительная функция / (л:) действительного переменного х строго
монотонна на интервале /, если она на нем определена и если для любых
двух точек хг и х2 интервала / либо из хх < х2 всегда следует / (хг) < / (х2)
(возрастающая функция), либо же из хх<.х2 всегда следует / (л^) > / (х2)
(убывающая функция). Функция / (л:) нестрого монотонна на /, если она
определена на / и если для любых двух точек хг и х2 интервала / либо из
хх<.х2 всегда следует / (xt) ^ / (х2) (неубывающая функция), либо же из
х1<Сх2 всегда следует / (х{) ^ / (х2) (невозрастающая функция). Аналогичные
определения даются для монотонных последовательностей (п. 4.2-1).
(b) Действительная функция / (лг) действительного переменного х есть
функция ограниченной вариации на интервале [а, Ь]9 если существует такое
положительное число М, что для всех разбиений а = х0 <хх < х2 < ...<хп — Ь
интервала [а, Ь] выполняется неравенство
2 I/to)-/(*/-i) К м.
/= 1
Функция / (л:) есть функция ограниченной вариации на [а, Ь] в том и только
в том случае, если она может быть представлена в виде f (x) ^f1(x)—f2(x),
где /t (л:) и /2 (д:) ограничены и не убывают на [а, Ь].
Если / (л:) и g(x) —функции ограниченной вариации на [а, Ь], то и
f(x)-{-g(x) и f (x) g (х) — функции ограниченной вариации на [а, Ь]. Функция
f (х) есть функция ограниченной вариации на каждом конечном интервале
[а, Ь]9 на котором она ограничена и имеет конечное число относительных
максимумов и минимумов (п. 11.2-1) и точек разрыва первого рода (условия
Дирихле).
Функция ограниченной вариации на [а, Ь] ограничена на [а, Ь] и имеет
только точки разрыва первого рода (п. 4.4-7).
В физических приложениях условие, чтобы f (x) была функцией ограниченной
вариации на каждом ограниченном промежутке, выражает тот факт, что функция f (x)
ограничена и что компоненты очень высокой частоты не могут существенно влиять на ее
интенсивность (п. 18.10-9).
*) Часто скачок функции f (х) в точке а определяют как разность f (а + 0)— /(а — 0).
Для монотонной функции это определение и данное в тексте совпадают.
4.5-2.
4.5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
107
4.5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
4.5-1. Производные и дифференцирование.
(a) Пусть у ==/ (х) — действительная функция действительного
переменного х, определенная в некоторой окрестности точки х. Первая производная
(производная первого порядка) функции / (л:) по * в точке х есть предел
^oU£±^iCusjta^sgs^/Ws/.W^. (4.5-1)
В каждой точке х, в которой предел (1) существует, производная -р =/'(#)
есть мера скорости изменения у относительно х. Производная /' (л:) есть
угловой коэффициент касательной (п. 17.1-1) к графику функции у=/ (л:) (см.
п. 4.2-1, а) в точке х.
Соответствующие односторонние пределы (п. 4-4-7,а) называются левой производной
V- (х) и правой производной /' (л:) функции f (х) в точке х.
(b) Вторая, третья, ..., /i-я производные (производные второго, третьего, ...
..., /i-го порядка) функции y = f(x) по л: в точке х определяются
соответственно формулами
(4.5-2)
d_ (1, ,„ч = d*y = (,„ /<л й_ ,,„_!, ,„ч _ d"y __ t
dxn
„,-Г М = я? = /'"(*) s^'W^^^'W,
если соответствующие пределы существуют.
(с) Операция отыскания производной /' (х) данной функции f (x)
называется дифференцированием функции / (л:) по х. Функция / (л:) дифференцируема
при тех значениях х или на том множестве значений х, при которых
существует производная /' (л:). Функция / (х) непрерывно дифференцируема, если
производная /' (х) существует и непрерывна. Функция f (х) называется
кусочно-гладкой на промежутке /, если функция / (х) непрерывна на /, а ее
производная /' (х) кусочно-непрерывна (п.4.4-7, с) на /. Дифференцируемая
функция непрерывна.
Производные большого числа часто встречающихся функций приведены
в табл. 4.5-1. Производные от комбинаций этих функций могут быть найдены
с помощью правил дифференцирования из п. 4.5-4.
4.5-2. Частные производные.
(а) Пусть y=f(xv x2, ..., ^ — действительная функция переменных хъ
х2, ..., хп, определенная в некоторой окрестности точки (хг, х2, ..., хп).
Частная производная (первого порядка) функции / (xv х2, ..., хп) по хх в точке
(xlt х2, ..., хп) есть предел
f (ХХ -f Д*1, Х2, Х3, ... , Хп) — / (Хи Х2 Хп)
hm — =
Ал:!
Ахх
^J = §!-=rXl(xl9Xt9...9x^ (4.5-3)
Производная dx\ — {E[)xi.x2 xn^fxx(xi> *2' *' хл) в кажД°й ™чке
(Хх, х2> ..., хп), в которой существует предел (3), есть мера скорости
изменения у относительно хх при фиксированных значениях остальных
независимых переменных. Частные производные -^~, -—-, ..., ~ определяются
аналогично. Каждая частная производная ~- может быть найдена посредством
k
дифференцирования функции f (xv x2, ..., хп) по xk, если остальные п — 1
независимых переменных рассматривать как постоянные параметры.
108 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.5-2.
(см.
Таблица 4.5-1
Производные часто встречающихся функций
также в гл. 21 производные некоторых специальных функций)
(а)
Пх)
ха
ех
а*
In х
logax
sin x
cos x
f (X)
axa~l
ex
ax In a
1
X
1
x In a
cos x
— sin x
f <n (x)
a (a — 1) (a —2) ... (a — r -f- 1) xa~r
cx
ax (In af
(- 1Г1 (r -W~
л: In a
sln(* + rT)
cos(* + r |-)
(b)
f <*)
tg*
ctg x
sec a:
cosec x
sh x
ch *
thjc
cth x
Г U)
1
cos2 x
I
sin2 x
sin л
cos2 *
cos x
sin2 x
ch x
sh *
1
ch* x
1
sh2*
f (*)
arcsin x
arccos x
arctg *
arcctg x
arsh jc
arch x
arth дг
arcth *
xx
f (x)
1
/l —X*
1
У1 - x*
1
1 + *8
1
1 + лг*
1
утм^т
V*8 —1
1
1 —JC2
1
i — x*
х*(\ -h In x)
(b) Частные производные более высокого порядка функции y=f(xi, ...j#w)
определяются формулами
fry —с» _^ д _ ду
— ix^X*. дх. дх. *
fry
дх\ —,xkxk dxk dxk dxi dxk " 'Xi*k ~ dxk dxi
d a#
dx^dXjdx^
c;
ГГЛ
_ d d*y
дх. дх: дх
k ил1 ил/
И Т. Ач
4.5-3.
4.5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
№
если соответствующие пределы существуют. В каждом случае число
произведенных дифференцирований есть порядок соответствующей частной
производной. Отметим, что
ё$ггък {1фк)' (4-5"4)
если: 1) производная дх Удх существует в некоторой окрестности точки
(xlt x2t ..., хп) и непрерывна в точке (хъ хъ ..., хп) и 2) производная ^—|—
существует в точке (хъ х2% ... , хп).
4.5-3. Дифференциалы.
(а) *Пусть функция y = f(x) определена в некоторой окрестности точки х
и пусть d* —приращение независимого переменного х (дифференциал
независимого переменного х). Функция y—f(x) имеет в точке х (первый)
дифференциал, если ее приращение в этой точке может быть представлено в виде
Ly=zf(x + dx) — f{x) = Adx+o[dx)%
где А не зависит от dx. В этом случае (первым) дифференциалом функции
y = f(x) называется главная линейная часть приращения функции dy = Adx.
Функция y = f(x) имеет в точке х дифференциал в том и только в том
случае, если она имеет в этой точке (первую) производную; ее дифференциал
равен dy = df=^dx^f (x) dx. Так что
Ay=Ef(x + dx)-f(x) = f (x)dx + o(dx) = dy + o(dx).
Подобным же образом пусть функция y = f(xlt х2, ..., хп) переменных хи
х2, ...» хп определена в некоторой окрестности точки (хъ х2, ..., хп) и пусть
dxlt dx2y ..., dxn — приращения независимых переменных- (дифференциалы
независимых переменных) хъ х2, ..., хп. Функция y = f(xlt x2t ..., хп) имеет
в точке (xlt хъ ..., хп) (первый) дифференциал (полный дифференциал), если
ее приращение в этой точке может быть представлено в виде
Ду ==/(*,+ </*i, x2+dx2l ..., xn + dxn) — f(xl9 х2, ..., хп) =
=Aidx1 + A2dx2 + ... + Andxn+o(p),
где р = у dx\ + dx\ +... + dx\ и Alt A2, ..., Ап не зависят от йхъ dx2i ...
..., dxn. В этом случае (первым) дифференциалом (полным дифференциалом)
функции y = f(xlt x2, ..., хп) называется главная линейная часть приращения
фуНКЦИИ dy = A1dx1 + A2dx2 + ... + Andxn.
Отметим: 1) Если функция y = f(xlt x2t ..., хп) имеет в точке (хъ х2, ..., хп)
дифференциал, то она непрерывна в этой точке и имеет в ней все частные
производные первого порядка. 2) Если функция y = f(xlt x2, ..., хп) имеет
в точке (хъ x2i ..., хп) все непрерывные частные производные первого порядка,
то она имеет в этой точке (первый) дифференциал. (Из одного факта
существования всех частных производных еще не следует существования полного
дифференциала.) Дифференциал функции y=f(xlt x2, ..., хп), если он
существует, имеет вид
dy=df^dx1 + ^dxt + ... + -^dxnt (4.5-5)
где производные берутся в рассматриваемой точке.
Функция y — f(xly x2, ..., хп) дифференцируема в точке (хъ х2> ..., хп)>
если она имеет в этой точке (первый) дифференциал. В этом случае
Ду ==/(#! + <&!, x2-+-dx2, ... , xn + dxn) — f(xi* *2> ••• .»я) —
= dxtdXl+дъ dx2 + -~ + щ^dxn+o(p) = dy + o(p).
ПО ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.5-4.
Функция y=zf(xlt а?2,..., хп) дифференцируема на множестве точек
(хъ х2у ..., хп), если она дифференцируема в каждой точке этого множества.
Функция y = f(xlt x2t ..., хп) непрерывно дифференцируема на некотором
множестве, если на этом множестве все частные производные jr-y-t -—-,..., ~-
ОХ\ ОХ% п
существуют и непрерывны. Функция y = f{x1% x2,..., хп) называется кусочно-
гадкой в области V t если она непрерывна в V, а ее частные производные
1f/'/- -/-,..., ~~ кусочно-непрерывны в V (п. 4.4-7, с).
OXi ОХ2 ft
(b) Дифференциал каждого независимого переменного рассматривается
как постоянная, так что d2x = d (dx) = d3x ^ d (d2x) = ... = 0. Дифференциал
зависимого переменного есть функция от независимого переменного или
переменных. Второй, третий, ...дифференциалы нужное число раз
дифференцируемой функции находятся последовательным дифференцированием первого
дифференциала, например, если х, хг и х2 — независимые переменные, то
#/ (х) == d (df) = d [f- dx) = -^f dx\ (4.5-6)
d*f (xv x2) = d (df) == Ц dx\ + 2 ggj- dx,dx2 + gj dxl (4.5-7)
<T/ (xlf *2) = ^ C* ^~ ^Г" ^2* (4.5-8)
Отметим также
d2/ К (*). «2 (*) ил (*)] s rf (#) =* % dx* =^(d (щ) duk +-d~d4k) ==
(с) Все функции от da^, dx2, ..., da^ того же порядка, что и dx'i dx'* •.•dxrn
при da^ —0, dx2 —* 0,... , dxn—»0, суть бесконечно малые порядка гх + г2 -{-
-+-••• + гл (п- 4.4-3). В частности, г-й дифференциал dr/функции/ (xv x2, ...хп),
если он существует и не равен нулю в данной точке, есть бесконечно малая
порядка г.
4.5-4. Правила дифференцирования. В табл. 4.5-2 перечислены наиболее
важные правила дифференцирования. Формулы из табл. 4.5-2, а и b
применимы и при вычислении частных производных, если в каждом случае вместо
-J— писать j-. Так, если
ui = ui(xlt х2,..., хп) (i = l, 2 т),
то
Умножая каждую формулу из табл. 4.5-2, а и b на dx или на dx2, получаем
аналогичные правила для вычисления полных дифференциалов (см. также п.4.5-3); так,
d(u + v) = du + dv, d (uv) = v du+ud v. (4.5-11)
Правила дифференцирования интегралов указаны в табл. 4.6-1, а
дифференцирования бесконечных рядов — в п. 4.8-4, с.
4.5-4. 4.5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Ш
Таблица 4.5-2
Правила дифференцирования
(п. 4.5-4; в каждом случае существование соответствующих производных
предполагается)
(a) Основные правила *):
d df dux df du2 df dum
d* L ' ' rn dtix dx * du2 dx ^ ^ dum dx *
(b) Сумма, произведение и частное. Логарифмическое дифференцирование:
d г / v i / . 1 du , dv d _ , ._ dM
d r , v /41 rfw . dv d I « (*) 1 I f du dv \ _ , . . лп
d* * |/ (л;)
Замечание. Чтобы продифференцировать функцию вида у = 1 —? " ,
^1 (*) ^2 (X) ... '
может оказаться полезным найти сначала ее логарифмическую производную.
г
d^
dx
Г , ^ a^ dru ^&drv dr , ч \ ~k dr~k U dkv
fc = 0
(c) Обратная функция. Если функция у — у (х) имеет обратную функцию
х = х{у)**) я4М- = у'хфО,то
(d) Неявная функция (см. также п. 4.5-7). Если функция задана неявно
должным образом дифференцируемым соотношением F (х,у) = 0, где Fy ф О, то
*М-.. -£. *!?- = - JL(F* F''_2/r, ^ + /?, F'2\
dx F' * dx2 F>* \ xx у ху х у ^ yy x).
y У
(e) Функция, заданная с помощью параметра t. Если даны х = х (/), У = у (0 и
;« = £*.>, iW = £.sw = <*. *« = &.»
^ = уЖ **у в * (0 /у (О - * (t) у (О
*) В первой формуле (а) при m > 1 следует предполагать дифференцируемость
функции f (их, и2, ... , и \ в соответствующей точке, для чего достаточно
непрерывности в этой точке всех ее первых частных производных: см. п. 4.5-3.
**) Если функция у (х) на интервале а ^ х ^ b строго монотонна и непрерывна,
то на замкнутом интервале с концами у (а) и у (Ь) она имеет обрати у/о функцию х (у),
также непрерывную. Если, кроме того, функция у (х) в точке х0, где а < х0 < Ь,
имеет производную у'(х0)фО, то функция х (у) в соответствующей точке у0 = у (х0)
также имеет производную и справедлива первая из нижеследующих формул. Если
функция у (х) имеет вторую производную, то имеет место и вторая из этих формул.
ГЛ. 4 ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.5-5.
4.5-5. Однородные функции. Функция f!(*i, х2,..., хп) есть однородная функция степени
г относительно аргументов xlt х2 хп. если f (axlt ax2t ..., ахп) = arf (xt,x2 xn) (см.
также п. 1.4-3, а). Если/" (xit х2 хп) —непрерывно дифференцируемая однородная
функция степени л, то
"' £ +х> & + •" +х" ЪТп = т f <*"** яп) <4-5"|2>
(теорема Эйлера од однородных функциях).
4.5-6. Якобианы и функциональная зависимость (см. также пп. 4.6-12,
6.2-3, b и 16.1-2). Если функции
y«=2/i(»i. *2> •••> хп) (*'=1. 2,..., п) (4.5-13)
непрерывно дифференцируемы в некоторой области гс-мерного пространства
и если якобиан или функциональный определитель
д (Уи Уг Уп)
т
det U-i- (4.5-14)
д (xltx2 хп)
отличен в ней от нуля, то уравнения преобразования (13) (см. также п. 14.1-3)
в достаточно малой окрестности каждой точки области определяют взаимно
однозначное соответствие этой окрестности и множества точек (ylt уъ ..., уп),
образованных значениями функций (13), принимаемыми в этой окрестности.
Если дифференциалы
п
^- 25^ (i==1,2"-"*) (4-5"i5)
линейно зависимы в данной области (п. 1.9-3), то якобиан (14) в этой
области тождественно равен нулю. Если в V нет точки, в которой все элементы
якобиана (14) одновременно обращаются в нуль, то якобиан (14) тождественно
равен нулю в области V в том и только в том случае, когда у каждой точки
этой области существует такая окрестность, в которой функции yt связаны
некоторым непрерывно дифференцируемым соотношением Ф (уъ у2, ..., 2/я) = 0,
где производные ~ не все одновременно равны нулю. В этом случае говорят,
что функции (13) функционально зависимы в этой окрестности (см. также
п. 4.5-7, с).
4.5-7. Неявные функции.
(a) Если функция у = у(х) задана неявно должным образом
дифференцируемым соотношением F (х, г/) = 0, то
17 = - >; ' S = - Vf(F~ F'y ~ 2F*yF'*F'y + W <F'y * °>- <4-5"16)
(b) Если т функций y1 = yx (xlt x2, ... , xn), y2 = y2(xi, x2, ..., xn), ...,ym=z
= ym (xlt x2, ... ,xn) от п независимых переменных xlf x2, ..., xn заданы неявно
m соотношениями
Fi{yi*y* — >ym* xltx2,...,xn) = 0 (/ = 1,2, ...,m), (4.5-17)
где Fi — непрерывно дифференцируемые функции в рассматриваемой области, то
1. Дифференциалы dy, и dxt связаны т линейными уравнениями dFi = 0.
ду,-
2. Для каждого значения Аг ===== 1, 2,..., п все т производных . '
oxk
могут быть получены по правилу Крамера (п. 1.9-2) из т линейных уравнений
1
/==1
or: oys or J
4.6-1.
4.6 ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
113
если только
д (Fi. Ft Fm)
д {у и Уг
• Ут)
S4-Sr]*°
(4.5-19)
для рассматриваемых значений xt, x2, ..., хп. Дифференцируя уравнения (18),
получаем соотношения, дающие производные более высокого порядка
функций yj.
В частности, два непрерывно дифференцируемых соотношения F (х, #, г) = О
и G (х, у, г) = 0 дают
dx : dy : dz =
Fy. Fi
a'y a'z
P'z F'x
°z °'x
F'xFy
°x ay\
(4.5-20)
■Х- Если, например, первый из определителей справа отличен от нуля, то данные
соотношения определяют у и z как функции от х (см. (с)) и уравнения (20) позволяют
dy dz
найти производные-—- и •—?—. X
(с) Теорема существования неявныхфун кций (см. также п. 4.2-1, Ь). Пусть дана
точка Р — (Xi, xz хп; yt, y2 ут), в которой выполняются соотношения (17) и (19).
Если все Fi и dFi/dyj непрерывны в некоторой окрестности D точки Р, то т
соотношений (17) в некоторой окрестности точки (xlf x2 хп) определяют у: как непрерывные
функции от хх, х2, ... , хп. Если, кроме того, в D непрерывны и все производные dF^/dx^
то в указанной окрестности точки (хх, х2, ... , хп) существуют и непрерывны
производные dyjfdxfe. Если якобиан (19) в D тождественно равен нулю, то левые части
соотношений (17) в некоторой окрестности точки Р функционально зависимы (п. 4.5-6), так
что у,- не определены однозначно.
4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
4.6-1. X Определенные интегралы (интеграл Римана).
(а) Пусть действительная функция / (х) определена и ограничена на
ограниченном замкнутом интервале [а, Ь]. Разобьем этот интервал на п частичных
интервалов точками
а — х0 <х1<х2<...<хп — Ь.
Выберем в каждом из частичных интервалов по произвольной точке g; (x^ ^
п
^h^xi) и составим сумму (интегральная сумма) £/ (&) (л^ — xi_t).
Если существует предел интегральной суммы при стремлении к нулю
длины наибольшего частичного интервала разбиения: max (xi — х^) —► 0, то
функция f (х) называется интегрируемой в смысле Римана на интервале [а, Ь\.
Предел этой суммы
/ = Hm S / (Ь) ta - Xi_x) = J / (*) dx, (4.6-1)
max (jct- — X{_\\-+0 /=1 a
называется определенным интегралом от / (л:) по интервалу [а, Ь] в смысле
Римана (интеграл Римана). Это определение означает, что для любого
положительного числа е существует такое число б > 0, что при любом разбиении
интервала [а, Ь] на частичные интервалы, длины которых меньше 6:
max (xi — xi_x) < б,
и при любом выборе промежуточных точек £/ выполняется неравенство
t=i
Функция / (х) называется подынтегральной функцией, а а и Ь — пределами
интегрирования. В табл. 4.6-1 перечислены важнейшие свойства
определенных интегралов.
1H ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-1.
Таблица 4.6-1
Свойства интегралов
(a) Элементарные свойства. Если интегралы существуют, то
b a b с b
\f {x)dx = -\f (x) dx *), J f(x) dx == J f (x) dx + J f (x) dx.
a b а а с
b b b b b
J [u (x) + v (x)] dx = J и (x) dx + J v (x) dx, J а и (x) dx = a J и (х) dx.
a a a a a
(b) Интегрирование по частям. Если функции и (х) и v (х) непрерывно
дифференцируемы на интервале а ^ х ^о, то
b ъ b
J и (х) vf (x) dx = и (х) v (х) | — J v (х) и' (х) dx
а а а
или
Ъ ь Ь
J и dv = uv | — J vdu.
а а а
(c) X Замена переменного (интегрирование подстановкой). Если функция х = х (и)
непрерывно дифференцируема на интервале a =< и ^ (3, а функция J (x) непрерывна
на интервале т ^ х ^ М, где т —■ точная нижняя, а М — точная верхняя граница
функции х (и) на интервале а ^ и ^ {3, то
* О) Э
* (a) a
(d) X Дифференцирование по параметру. Если функция f {x, Я) и ее частная
производная -д— f (х, Я) непрерывны на множестве а ^ * ^ Ь, Я0 ^ Я ^ Яь а функции и (Я) w
у (Я) дифференцируемы на интервале Я0 ^ Я ^ Я1 и удовлетворяют на нем условиям
а < и (Я) < Ь, а < и (Я) < 6, то яры Я0 ^ Я < Я4
Ь Ь
d Г , , nv , С а
^ f (дг, Я) </* = ^ / (*, Я) </х,
dk ,
а а
v (Я) v (Я)
A J f(x.X)dx= j |-М*,ЯМ* + ММЯ), Я)^-,(к(Я), Я)^_
w (Я) ы (Я)
(правило Лейбница).
Первая формула остается в силе и для несобственных интегралов, если предполо-
b b -
жить, что интеграл J f (jc. Я) d* сходится, а интеграл J 3jrM*t А,) <*•* равномерно схо-
а а
дится на интервале Я0 ^ Я < Xt. {При этом функция f (x, Я) и ее производная
—- f {х, Я) предполагаются непрерывными лишь на множестве а ^х<Ь, Я0 ^ Я ^ Я1
с/Я
или на множестве a < * ^ Ь, Я0 ^ Я ^ Яь)
Ь
*) Зто равенство следует рассматривать как определение интеграла J f (x) dx
а
а
при b ^ а. Из него также вытекает, что J / (x) dx = 0.
4.6-2. 4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ И5
Таблица 4.6-1 (продолжение)
Второй случай часто можно свести к первому подходящей заменой переменных.
Отметим также, что
Я % |
\ а а
(е) Неравенства (см. также п. 4.6-19). Если интегралы существуют, то (при
а<Ь)
из f (х) :< g (х) на {а, Ь] следует
Ь Ь
\t(x)dx^\g (х) dx.
а а |
Если | f (х) | ^ М на ограниченном интервале [а, Ь], то из существования инте-
Ь Ь
грала J f (х) dx вытекает и существование интеграла J | / (х) \ dx и
а а
Ь
\ f (х) dx
а
b
^\\f(x)\dx^M(b-a).
а
ь
Если функция у = f (х) на интервале [а, Ь] неотрицательна, то интеграл J f (x) dx
а
выражает площадь, ограниченную кривой y = f(x), осью абсцисс и двумя прямыми х= а
и х— Ь. Если f (x) ^ 0, то интеграл выражает эту площадь, взятую со знаком минус.
(Ь) Функция f (х), ограниченная на ограниченном замкнутом интервале [а, Ь],
интегрируема на нем в смысле Римана в том и только в том случае, если она непрерывна
почти всюду на [а, Ь] (п. 4.6-14, Ь). Это, в частности, верно: 1) если функция f (x)
непрерывна на [а, Ь"\; 2) если функция f (х) ограничена на [а, Ь] и имеет на [а, Ь] конечное
или счетное множество точек разрыва; 3) если функция f (x) монотонна на [а, by,
4) если f (х) есть функция ограниченной вариации на [а, Ь] (см. также п. 4.4-8). Если
функция f (х) интегрируема на [а, Ь], то она интегрируема и на каждом интервале,
содержащемся в [a, by
4.6-2. Несобственные интегралы
(а) Если функция / (х) ограничена и интегрируема на каждом
ограниченном интервале, содержащемся в (а, Ь), то понятие определенного интег-
ь
рала lf(x)dx (п. 4.6-1) можно расширить так, что оно станет применимым
а
и когда
1. Функция f (х) не ограничена в любой окрестности одного из пределов
интегрирования а или Ъ (см. также п. 4.6-2, Ь).
2. Интервал (а, Ъ) не ограничен.
Так, если функция / (х) ограничена и интегрируема на каждом конечном
интервале [а, X], где а<.Х<.Ъ, то по определению полагают
ь х
U(x)dx= lim \f{x)dx (4.6-2a)
i х-+ь-о Ja
и, в частности, при & = -|-oo
+oo X
f / (x) dx = lim \ f (x) dx. (4.6-26)
a X-H-oo i
Точно так же
ь ь ь ь
\f(x)dx= lim \f(x)dx, [f(x)dx= lim \ f (x) dx. (4.6-2<>)
i X-*a+0i _k X --со*
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-2.
Каждый несобственный интеграл, определенный таким образом,
существует или сходится, если существует предел в правой части равенства.
Несобственный интеграл от функции / (х) сходится абсолютно, если сходится
соответствующий несобственный интеграл от |/(*)|. Из абсолютной сходимости
следует сходимость (см. также пп. 4.6-15, е и 4.9-3). Несобственный интеграл,
который сходится, но не абсолютно, называется условно сходящимся.
(Ь) ■# Правила интегрирования из табл. 4.6-1 применимы к должным
образом сходящимся несобственным интегралам. Если функция / (х) определена
в ограниченном или неограниченном интервале (а, Ъ) или [а, Ь], за
исключением, быть может, конечного числа точек а^ сг < с2 <С ... <. сп ^ Ь, не
ограничена в любой окрестности щ каждой точки * = £,•(« = 1, 2, ...,и), а вне
объединения окрестностей и1% и2,»..,ип ограничена, то несобственный интег-
ь
рал С / (х) dx можно определить как сумму несобственных интегралов вида (2).
а
Например, если сх = а и с2 = Ь и пределы в правой части равенства
существуют, то
ъ d х2
[ f (x) dx = lim [ f (x) dx + lim [ f (x) dx, (4.6-3)
J Xt-a+0 x\ X2-+b-0 i
где d — произвольная точка интервала (a, b).
Если a = — со и 6 = -|- со, то
со d X2
\ f (x) dx = lim \ f (x) dx + lim [f (x) dx. (4.6-4)
_£, X^-co £ X2->+oo /
Если f (л:) не ограничена в окрестности тачки с, лежащей внутри
интервала (a, b)% то
ь *t ь
U(x)dx= lim f/(*)d*+ lim U (x) dx (a<c<b). (4.6-5)
a X^c~0a Хг-+с+0Х2
В случае, если интегралы (4) и (5) не существуют, могут все же существовать
соответствующие главные значения интеграла по Кош и
X Гс — б Ь 1
lim J f (x) dx и lim J f (x) dx -f J /(*)</*; (4.6-6)
X— +oo — X 6-» + 0L a с-J-6 J
если какой-либо из интегралов (4) и (5) существует, он необходимо равен своему
главному значению.
Ь
(c) Несобственный интеграл С / (х, у) dx равномерно сходится на множе-
а
стве 5 значений у, если соответствующий определенный интеграл сходится
ь
к своему пределу (пп. 4.6-2, а и Ь) равномерно на S (п. 4.4-4). Если ^f(x, y)dx
а
при каждом у из интервала Уо<у <Уг есть интеграл вида (2а) и если
функция f (x, у) непрерывна на множестве a^x<b, #o<#<#i» a интеграл
\ f (*» У) dx равномерно сходится в интервале у0 < у < уъ то \f (x, у) dx есть
а а
непрерывная функция от у в этом интервале (теорема о
непрерывности). Аналогичные теоремы верны и для интегралов вида (2Ь) и (2с).
(d) Признаки сходимости и равномерной сходимости перечислены
в пп.4.9-3 и 4.9-4.
4.6-6.
4.6 ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
117
1.6-3. Среднее значение. Среднее значение функции / (л:) на интервалах
[a, b], [0,-j-oo) и (— оо,+оо) по определению соответственно равно
ь х х
lim IffMWv « l«ni
a 0 —X
если эти величины существуют.
4.6-4. Неопределенные интегралы. Функция / (х) имеет в интервале [а, Ь]
неопределенный интеграл <{f(x)dxy если существует такая функция F (*), что
/"(*)=/(*) на [а, 6]. В этом случае функция F (х) однозначно определена
в [а, Ь] с точностью до произвольной аддитивной постоянной С (постоянной
интегрирования); любая такая функция F (х) называется первообразной
(примитивной) функции / (х) на [а, Ь]. Полагают
$f(x)dx = F(x)+C (а^х^Ь). (4.6-8)
Заметим, что разность F (x)—F (a) = F (х) |* при а^х^Ь определена
однозначно.
Отметим также, что
J [а и (х) + 3 v (х)} dx = а J и (х) dx -f 3 J v (x) dx, (4.6-9)
J и (x) v' (x) dx ~ и (x) v (x) — J u' (x) v (x) dx, (4.6-10)
если эти неопределенные интегралы существуют (см. также табл. 4.5-2 и 4.6-1).
4.6-5. Основная теорема интегрального исчисления. Если f (х)—функция,
ограниченная и интегрируемая на интервале [а, Ь\, и если существует
первообразная F (х) функции f (х) на [а, Ь], то
х \х
J/ffi)«*S==^W =F(x)-F(a) (a^x^b). (4.6-П)
а \а
В частности, это верно, если функция f (х) непрерывна на [а, Ь\. При этом
X
Л $/©«-/(*) (а^х^Ь). (4.6-12)
а
Более общее утверждение: если функция f (x) ограничена и интегрируема на [а, Ь],
х
то интеграл Jf (£) d| является функцией ограниченной вариации на [а, Ь], и для почти
а
всех х из [а, Ь] (п.4.6-14, Ь) имеет место равенство (12).
Замечание. Основная теорема интегрального исчисления дает возможность
вычислять определенные интегралы, обращая процесс дифференцирования.
4.6-6. Методы интегрирования.
(а) Интегрирование есть операция отыскания (определенного или
неопределенного) интеграла от данной подынтегральной функции f (x). Определенные
интегралы можно вычислять непосредственно как пределы интегральных сумм
(численное интегрирование, пп.20.6-2 и 20.6-3) или путем вычисления
вычетов (п.7.7-3). Чаще пытаются найти неопределенный интеграл и затем
пользуются формулой (11). Чтобы найти неопределенный интеграл, данную
подынтегральную функцию / (х) нужно с помощью «правил интегрирования»,
перечисленных в табл. 4.6-1, а, Ь, с, представить в виде суммы известных
производных.
В дальнейшем перечисляются методы интегрирования, применимые к
некоторым специальным типам подынтегральных функций. Существуют разной
П8 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-G.
степени полноты таблицы определенных и неопределенных интегралов (см.,
например, [4.6]).
(Ь) Интегрирование многочленов:
l(an + an-iX + an-2X2 + -.' + a0xn)dx =
= апх + -тап_1х* + -тап_2х3 + ...
м + 1
а0хп+1 + С.
(4.6-13)
(с) Интегрирование рациональных функций. Методы,
описанные в пп. 1.7-2 и 1.7-4, сводят интегрирование каждой рациональной
функции к интегрированию суммы многочлена (п.4.6-6, Ь) и некоторого числа
элементарных дробей (1.7-5) и/или (1.7-6). Элементарные дроби последовательно
интегрируются с помощью следующих формул:
\ dX т={ {m-l){x-Xl)m-l~
•><*-*!) [ ln|jT —АГХЦ-С
■а)2 + ю2! со
С d£
-С (тф\)%
(т=1);
arctg -
-С;
2т — 1
2та)2 [(х — а)2 + со2]"
2пки
-_1 Г dx
2 J [(* — а)2 + о2]
J- (4.6-14)
х dx
С х d)
©»]т+1
а (* — а) — со2
2та)2 [(* — а)2 + о2]"
(2т — 1) а
2та)
1) а Г d£
1 * [(* —а^+й)2]"
(d) Функции, интегрирование которых с помощью
замены переменных сводится к интегрированию
рациональных функций.
1. Если подынтегральная функция f (x) есть рациональная функция от sin x
и cos*, то полагают H = tg-~-, так что
sin* =
2ц
1 +и»
1 — к2
1 -f W2'
dx =
2 du
1 + w2*
(4.6-15)
2. £слы подынтегральная функция f (x) есть рациональная функция от sh x
и ch*, то полагают w = th-|-, так что
sh* =
2w
l — w2'
спл: =
l + ц2
1 — w2'
dx —
2du
1 — w2'
(4.6-16)
Замечание. Если f (x) — рациональная функция от sin2 x, cos2 x, sin д: cos* и tg дг
(или от соответствующих гиперболических функций), то вычисления упростятся, если
сделать замену и = tg х (или и — th x).
3. £слы подынтегральная функция f (x) есть рациональная функция от х
и либо от У\—х2, либо от yrx2—\J либо от yrx2+\J то задача сведется к
случаю 1 или 2, если соответственно сделать подстановку # = cosp, или * = chi>,
или * = sh v.
4. Если подынтегральная функция f (x) есть рациональная функция от х
и либо от У х2 +1, либо от \rx2 — \t то можно положить соответственно
и~х+Ух2 ± 1; тогда
* = i(«+TT> l^±T=I(«±i). ^ = i(l±1i)rfu. (4.6-17)
4.6-8.
4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
119
5. Если подынтегральная функция f (х) есть рациональная функция от х
и от \/rax2-{-bx-\-c, то задача сведется к случаю 3 (или 4), если сделать
подстановку
У\ *ас — Ь* \* 2а
6. Если подынтегральная функция f (x) есть рациональная функция от х
и от и=у а*хТ_ ну пРичем ad — ЬсфО, то в качестве новой переменной берут и.
7. Если подынтегральная функция f (x) есть рациональная функция от х,
Yax-\-b и Ycx-\-d, где а ф О, то в качестве новой переменной берут и =
= Vax + b.
В различных специальных случаях применяют многочисленные другие
подстановки.
(e) Интегралы от функций вида
хпеах, хп In х, хп sin x, xn cosx (пф—1);
sin" х cosm х (п-\-тфО), еах sin" x, eax cosn x
вычисляют с помощью интегрирования по частям (табл. 4.6-1, Ь), применяя
его, если нужно, несколько раз.
(f) Многие интегралы нельзя выразить в виде конечных сумм, содержащих только
алгебраические, показательные и тригонометрические функции и функции, им обратные.
В этом случае подынтегральную функцию можно разложить в бесконечный ряд (пп. 4.10-4,
4.11-4, 15.2-6) или же прибегнуть к численному интегрированию. В гл. 21 можно найти
х Ь
примеры «новых» функций от х, определяемых как интегралы вида \ f (£) d\ или \ f (x, ч\)йц.
а а
4.6-7. Эллиптические интегралы. Если / (х) — рациональная функция от х
ь
и от VЯо*4 + а1х3 + а2*2 + аз* + 04» то )f(x)dx называется эллиптическим ин-
а
тегралом; можно исключить тривиальный случай, когда уравнение
ао*4 + агх3 + а2х2 + а3х + а4 = 0
имеет кратные корни. Каждый эллиптический интеграл можно выразить через
элементарные функции и нормальные эллиптические интегралы (п. 21.6-5);
значения последних приведены в таблицах.
4.6-8. Кратные интегралы (см. также пп. 4.6-11, 4.6-12 и 4.6-13).
(а) Пусть функция f(x, у) кусочно-непрерывна (п. 4.4-7) в ограниченной
замкнутой области D, определяемой как условиями a^xz^b, gi(x)^y^g2(x)t
так и условиями а^г/^р, уг (у)^х^у2(у), где ^(я), g2(x), y1(y)t y2Q) —
кусочно-непрерывные функции в указанных интервалах. Тогда
)dy ) f(x,y)dx=U ) f(xty)dx\dy = }dx ] f(x,y)dy =
а У i (У) а1уг(у) J a gt(x)
= $f(x,y)dxdy. (4.6-19)
D
Аналогичные теоремы справедливы для тройных, четырехкратных и т. д.
интегралов.
Пример. Если D — область, ограниченная окружностью х2 -f- у2 = \г и функция
t {х, у) = с постоянна, то
1 Y\ Тх* \
И ^ **' y)dxdy = A \ dx \ cdy = 4с \ Vi —х2 dx = пс.
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-9.
(Ь) Если функция f (х, у) непрерывна на множестве а ^ х <-\- оо, а ^ у ^0, и интег-
+ CQ
рал \ / (л:, у) dx равномерно сходится на интервале а ^ у ^ 0, то
а
0 4- оо -f оо 0
§dy j f (х, у) dx = j dx j f (x, y) dy. (4.6-20)
а а а а
Аналогичные теоремы верны для несобственных интегралов других типов.
4.6-9. * Длина дуги спрямляемой кривой (см. также пп. 6.2-3, 6.4-3 и 17.2-1).
Пусть С —дуга непрерывной кривой, лежащая в конечной части плоскости
или пространства. Длиной s(C) этой дуги называется предел длины ломаной,
вписанной в эту дугу, при условии, что длина наибольшего звена этой ломаной
стремится к нулю. Если указанный предел существует, то дуга называется
спрямляемой.
Для регулярной кривой на евклидовой плоскости или в евклидовом
пространстве, описываемой в прямоугольных декартовых координатах уравнениями
или * = *('). У = УЦ) на плоскости \ r4 fi 2П
или х==х^ y = y(t), z = 2(t) в пространстве f К*-*-*1)
(п. 3.1-13), длина бесконечно малой дуги, соответствующей промежутку [t,t+dt]t
есть элемент дуги
I на плоскости,
s=\vw+dy>+^vm+m+m^dt
[ в пространстве.
(4.6-22)
Знак корня выбирается обычно так, чтобы производная s' (t) была ^ 0. Длина
дуги s (С) кривой, соответствующей конечному интервалу [/0, /], равна
s = s(C) = $ ds = \ ~dt = s(t). (4.6-23)
С t0
Длина дуги s (С) есть геометрический объект, не зависящий от системы
координат и от выбранного для описания кривой параметра t. В пп. 6.2-3 и 6.4-3
приведены формулы, выражающие ds (а значит, и .s' (t)) в криволинейных
координатах.
Длина дуги s (С) существует, если функции (21) являются на [tQ, t] функциями
ограниченной вариации; в этом случае элемент ds определен почти всюду (п. 4.6-14, Ь) на С.
Каждая регулярная кривая спрямляема.
4.6-10. Криволинейные интегралы (см. также пп. 5.4-5, 6.2-3 и 6.4-3, где
введены векторные обозначения и используются криволинейные координаты).
Для данной спрямляемой дуги С, описываемой при a^t^b уравнениями (21),
криволинейный интеграл §f(x, У, z)ds от ограниченной функции / (х, у, г) по
С
определению равен
т
\ f (х, у у z) ds= lim J)f[x (т,-), у (т*), z (т;)] Asit
г max As. -* 0 /_i
где
Asi = V[x(ti)-x(ti_l)]* + [y(ti)--y(ti_1)}* + lz(ti)-z(ti_l)]z
(fl = f0</1</2<...</III = 6; ti_1^Ti^th 1 = 1, 2 от), (4.6-24Я)
4.6-11
4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
121
если предел существует (см. также п. 4.6-1). Криволинейный интеграл (24а)
можно вычислить (или непосредственно определить) как интеграл по /:
ь
$/(*, у, z)ds = \f[x(t), y(t), z(t)]§dt, (4.6-246)
С а
где элемент дуги ds находится из (22). Опуская в (24) члены, относящиеся
к z, получаем криволинейный интеграл для кривой, расположенной на
плоскости Оху. Несобственные криволинейные интегралы определяются по
способу п. 4.6-2.
4.6-11. Площади и объемы (см. также пп. 5.4-6, 5.4-7, 6.2-3, 6.4-3 и
17.3-3, где введены векторные обозначения и используются криволинейные
координаты).
(a) Пусть S — ограниченная замкнутая область на евклидовой плоскости.
Если точная верхняя граница множества площадей всех многоугольников,
содержащихся в S, и точная нижняя граница множества площадей всех
многоугольников, содержащих S, равны, то область S называется квадрируемой
(измеримой по Жордану), а общее значение этих границ называется площадью
А области S. В частности, область S ограниченная простой замкнутой
регулярной кривой, квадрируема. Объем U ограниченной замкнутой области V в
трехмерном евклидовом пространстве определяется аналогично.
Площадь А ограниченной регулярной поверхности 5 (п. 3.1-14)
определяется следующим образом. Разобьем 5 на конечное число частей; в каждой
части выберем по произвольной точке и ортогонально спроектируем эту часть
на касательную плоскость к поверхности в выбранной точке (п. 17.3-2).
Площадь поверхности А есть предел (если он существует) суммы площадей
полученных таким образом проекций, когда диаметр наибольшей из
рассматриваемых частей стремится к нулю.
* Диаметром множества Е в метрическом пространстве С (п. 12.5-2),
в частности, в евклидовом пространстве, называется точная верхняя граница
расстояний между любыми двумя точками множества Е. ■#
(b) Площади и объемы можно вычислять (или даже непосредственно
определять) как двойные или тройные интегралы в соответствующих
координатах:
Л = ( dA = \\dxdy в евклидовой плоскости, (4.6-25)
U.= \ dv=\\\dxdy dz в евклидовом пространстве. (4.6-26)
V V
Площади и объемы не зависят от выбора системы координат. В криволинейных
координатах х1, х2, х3 (п. 6.2-1) *)
u = \dv " №affi£V*'dx2 dxi (4-6"27)
v v
(см. также пп. 4.6-13, 6.2-3 и 6.4-3).
В криволинейных координатах и, v на плоскости или поверхности (п. 3.1-14)
А = J dA = \\Ya (и v) du dv, (4.6-28)
где а (и, v) — функция, определяемая в п. 17.3-3, с.
(c) Простые частные случаи. Площадь плоской области, ограниченной
прямыми х = а и х = Ь, где а<.Ь, и двумя кривыми у = gt (х) и у = g2 (x), причем
b
gt (x) < g2 (х) при а ^ х ^Ь, равна J [g2 (x) — gt (x)] dx (A > 0). Площадь плоской
а
Ч Здесь 1, 2, 3 — не показатели степени, а индексы.
122 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-12.
области, ограниченной простой замкнутой кривой С, описываемой уравнениями х =
= x(t),y = y(t) или уравнением г = г (<р) (п. 2.1-8), где функции удовлетворяют
должным условиям, равна
A==T§{x^~y^j)dt или Лвт5г1(ф)*ф' (4-6"29)
С С
где символ ф указывает, что интегрирование производится по замкнутой кривой; А > О,
если обход кривой С совершается против часовой стрелки.
Площадь поверхности А, образованной вращением кривой у = f (х) ^ 0 (а ^ х ^ Ь)
вокруг оси Ох, и объем U, ограниченный этой поверхностью, равны
Ь г тт-ст Ь
А = 2л J f (x) у 1 + (jg Г dx, U = n\[f (*)]« dx. (4.6-30)
а ' а
4.6-12. Интегралы по поверхности и по объему (см. также пп. 5.4-6,
5.4-7, 6.2-3 и 6.4-3, где введены векторные обозначения и рассматриваются
криволинейные координаты). Интегралы по поверхности и интегралы по объему
можно определить как пределы сумм по способу пп. 4.6-1 и 4.6-10. Их можно
также ввести непосредственно как двойные и тройные интегралы g помощью
элементов площади и объема, определенных в п. 4.6-1 L
Интеграл по поверхности от кусочно-непрерывной функции / (и, v) по
удовлетворяющей должным условиям поверхности 5 с криволинейными
координатами и, v равен
$/(«, v)dA=^f(u, v) Va (и, v) du dv. (4.6-31)
Сюда в качестве частных случаев входят и интегралы по плоским областям
(где, в частности, возможен и случай u = xt v = y, Va(u, t>) = l).
Интеграл по объему от кусочно-непрерывной функции
/(*, у, z)=f[x(xl, х*, *3), y(xit x2, x*)t z(x\ x2, a:3)]
по ограниченной области V равен
[f(x> У'> z) dV = \[\f (x, y, z)dxdydz =
£=$$$/[*(*!, x2, *з), y(x\ x2, хз), z(x\ x\ *3)l/(ff; % Z)x3)dxidx*dx*.
(4.6-32)
Несобственные интегралы по поверхности или по объему (неограниченные
функции или области) определяются по способу п. 4.6-2.
Формулы, связывающие интегралы по поверхности и интегралы по объему,
рассматриваются в пп. 5.6-1 и 5.6-2. Отметим частные случаи этих формул,
связывающие криволинейные интегралы и интегралы по плоской области
(С —граница области S; обход С совершается против часовой стрелки):
где
цао^,_ая^)|^=фр(х> y)dx+Q(Xt y)dy
s с
(формула Грина),
\ (iiV*-*V»«) dA = §(u£- v£) ds
s с
(двумерная 2-я формула Грина), J
V2v(x и) = —4-— — ds = —du — —dx
v v (х, у) _ дх2 -f- д , дп as _ дх ау ду ах.
(4.6-33)
4.6-14.
4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
123
4.6-13. Замена переменных в интегралах по объему и по поверхности.
Если с помощью непрерывно дифференцируемого преобразования координат
Х1==Х1(Х11 X2, X*), х* = Х*(Х1, X2, *3), Х9=Х3(Х1г X2, X3),
La О?1. Т», IF») ^ J
ввести новые координаты х1, х2, X3 (см. также п. 6.2-1), то интеграл по
объему (32) можно переписать в новых координатах:
\ f (х, у, г) dV = Щ ф (х1, х2, л:3) dx1dx2dx9 =
v v
= Ш Ф (** №' *2> Х3)> Х* (-*1' ^2» ^' ^ ^' *2' ^ arl,-|,-a) dXldX%d&.
(4.6-34)
Интегралы по поверхности преобразуются аналогично (см. также
п. 17.3-3).
4.6-14. Мера Лебега. Измеримые функции.
(a) Мера точечного множества. Внешняя мера Лебега те (S)
произвольного ограниченного точечного множества S на прямой есть точная
нижняя граница (п. 4.3-3) суммы длин конечного или счетного множества
интервалов, покрывающих S. Внутренняя мера Лебега m,- [S] множества 5
есть разность между длиной b — а любого ограниченного интервала [а, Ь),
содержащего 5, и внешней мерой дополнения множества 5 до [а, Ь] (п. 4.3-2, а).
5 есть измеримое множество с мерой Лебега m[S], если me[S] = mi[S] = m[S]
(конструктивное определение меры Лебега). Неограниченное множество 5
на прямой измеримо, если для всех Х> О измеримо пересечение (— Х> X)[\S.
При этих предположениях по определению полагают
m[S]= lim m[(—X, X)()S];
X-+ + oo
мера т [S] может быть как конечной, так и бесконечной.
Рассматривают и более общее определение: мера М [S], определенная на подходящем
классе (вполне аддитивной булевой алгебре, п. 12.8-4) точечных множеств 5, есть
функция множества со свойствами
М [S] >0, М [ф] = 0, (4.6-35)
и для каждого конечного или счетного множества попарно непересекающихся точечных
множеств Si, S2, ...
M[S1US,U...] = -M [Srf + Af [S2] + ... (4.6-36)
Мера Лебега т [S] точечного множества на прямой обладает дополнительным свойством
т[(а, b)] = b — a (4.6-37)
для каждого ограниченного интервала (а, Ь); таким образом, мера Лебега является
обобщением длины интервала (аксиоматическое определение меры Лебега; см. также
пп. 12.1-1, 12.8-4 и 18.2-2).
Мера Лебега точечных множеств в пространствах двух, трех, ... измерений
определяется (либо конструктивно, либо аксиоматически) с помощью аналогичных обобщений
площади и объема.
(b) Каждое ограниченное открытое множество (п. 4.3-6, а) измеримо.
Можно высказать более общие утверждения. Борелевское множество на прямой
есть множество, полученное посредством конечной или счетной
последовательности объединений, пересечений и/или взятия дополнений интервалов и
получающихся в результате комбинаций. Класс борелевских множеств есть вполне
аддитивная булева алгебра измеримых множеств. Каждое измеримое множество
есть объединение некоторого борелевского множества и множества лебеговой
124 ГЛ. 4 ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-15.
меры нуль. Каждое конечное или счетное множество измеримо и имеет лебегову
меру нуль. Аналогичные теоремы справедливы и в многомерном случае.
Если какое-либо свойство выполняется для каждой точки данного
интервала, области или множества, исключая, быть может, лишь множество
лебеговой меры нуль, то говорят, что это свойство выполняется на данном
интервале, области или множестве почти всюду (или почти во всех точках
этого интервала и т. д.).
(с) Измеримые функции. Функция / (х), определенная на интервале
[а, Ь]!), измерима на [а, Ь], если для каждого действительного числа с
множество точек х интервала [а, Ь], в которых f(x)^c, измеримо.
В этом определении условие f(x)^.c можно заменить любым из условий f (х)<.с,
f{x)>c, f(x)>c.
Функция, непрерывная на [а, Ь], измерима на [а, Ь]. Если на [а, Ь] измеримы
функции ft(x), f2(x) то на [а, Ь] измеримы и функции ft (x) + fz (x), afx(x), fi(x)f2(x),
а также и lim f„(x), если этот предел на [а, Ь] существует (и даже если этот пре-
/г —оо
дел существует на [а, Ь] лишь почти всюду).
Аналогичные определения и теоремы справедливы и для измеримых функций
f (х х х ), определенных на пространстве точек (л: х ... ,х ), допускающем
определение меры Лебега.
4.6-15. Интеграл Лебега (см. также пп. 4.6-1 и 4.6-2).
(а) Интеграл Лебега от ограниченной функции. Пусть
действительная функция y = f(x) измерима и ограничена на ограниченном
интервале [а, Ь] и А и В — соответственно ее нижняя и верхняя точные
границы. Разобьем интервал [Л, В], содержащий множество значений функции
/ (х) на [a, 6J, на п частей:
А = Уо<У1<У*< — <Уп = й*
(4.6-38)
и обозначим через Si множество точек х интервала [a, b]t в которых yt_x <
</ (Х)^У1- Составим две суммы (интегральные суммы Лебега):
2 yuimlSi] и J] ytmlSi].
i = i
Обе интегральные суммы стремятся к одному и тому же пределу, не
зависящему от выбора значений yi, если только наибольшая из разностей yi — yt_x
стремится к нулю. Число
п ь
1= lim У) yitn[Si] = \f(x)dx (4.6-39)
есть определенный интеграл от функции / (х) по интервалу [а, Ь] в смысле
Лебега (интеграл Лебега).
Это определение означает, что, каково бы ни было положительное число е,
можно указать такое число б>0, что при любом разбиении интервала [Л, В]
на части такие, что max (yi — yi_x) < б, будут справедливы неравенства
'-2 yi-imlSi)
i = \
<8 И
/-S yifnlSi]
<е,
а значит, и неравенство
/-2 4i*[Sd
/ = 1
<е,
») Функция / (х) может быть определена на [а, Ь] не всюду, а лишь почти всюду.
4.6-15.
4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
125
гДе yi-i ^ Л* ^ Vi интеграл Лебега можно определить и как предел суммы
Ц mmlSt)
i = i
(b) Интеграл Лебега от неограниченной функции. Если
функция / (х) измерима и не ограничена на ограниченном интервале [а, Ь],
то интеграл Лебега определяется как
ь ь ь
[f(x)dx= lim [fA (x) dx+ lim [fR(x)dxt
где
B-*-col
О, если f(x)^0t
/*(*) = ] /W. если 0 </(*)*=£ Д,
Л, если f(x)>A\
0, если f(x)^0,
fB(x) = l f(x)t если 0>f(x)^B,
В, если / (*) < В.
(4.6-40)
Если интеграл \f(x)dx существует, то функция / (х) интегрируема по Лебегу
а
(суммируема) на интервале [а, Ь].
(с) Интеграл Лебега по неограниченным интервалам.
х
Если для всех X > а существует интеграл \ f (x) dx, то интеграл Лебега
а
-\- оо
f / (x) dx определяется условием
Ч-оо Xt X2
\ f(x)dx= lim \ h(x)+ lim f f2(x)dx,
*i-* + oo £
X8-* + oo
где
-{°'
(4.6-41)
+s°
если / (л:) ^ 0,
если f(x) >0,
если / (x) ^ 0,
:(*), если /(*)<0.
Интеграл [ f (x) dx определяется аналогично, а интеграл \ f(x) dx — равен-
— 00 —OO
ством (4) на стр. 116.
(d) Интеграл Лебега по точечному множеству. Кратные
интегралы Лебега. Интеграл Лебега J f (х) d х по произвольному измеримому
множеству точек 5 определяется без изменения так же, как и в пп. 4.6-15, а и Ь.
Кратный интеграл Лебега по области или измеримому множеству точек (* дг ..., х \
определяется аналогично.
(e) Существование и свойства интеграла Лебега.
Сравнение интеграла Лебег г и интеграла Римана. Каждая
126 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-16.
ограниченная измеримая функция на любом ограниченном измеримом множестве
суммируема. Функция, суммируемая на измеримом множестве S, суммируема
и на каждом измеримом его подмножестве.
Из определений пп. 4.6-15 а, Ь, с и d следует, что интеграл Лебега
\ f (х) dx существует в том и только в том случае, если существует интеграл
s
Лебега \ I / (лг) | dx. Если любой собственный или несобственный, простой или
s
кратный интеграл Римана существует в смысле абсолютной сходимости
(п. 4.6-2, а)!), то соответствующий интеграл Лебега существует и равен
интегралу Римана.
Теоремы из табл. 4.6-1 и пп. 4.6-5 и 4.7-1, с, d справедливы и для
интеграла Лебега.
Для каждого конечного или счетного множества попарно непересекающихся
измеримых множеств Sit S2, ...
J f (x) dx = J f (x) dx + J f (x) dx + ..., (4.6-42)
SiUSzl) ... St S2
если интегралы существуют. Интеграл Лебега по любому множеству (лебеговой) меры
нуль равен нулю.
Замечание. Лебеговское интегрирование поименимо к более общему классу
функций, чем римановское интегрирование, и упрощает формулировки многих теорем.
Многие теоремы, высказанные в терминах интеграла Лебега, непосредственно применимы
к абсолютно сходящимся несобственным интегралам Римана (см. также пп. 4.6-16 и 4.8-4, Ь).
4.6-16. Теоремы о сходимости (теоремы о непрерывности; см. также п. 12.5-1).
(a) Если последовательность функций s0 (x), st (х), sz (x) каждая из которых
ограничена и интегрируема в смысле Римана на ограниченном интервале [а, 6], равно-
b
мерно сходится на [а, Ь] к функции s (х), то предел lim \sn (х) dx существует и равен
п-+соа
Ь
интегралу \ s (х) dx.
а
(b) Следующая более общая теорема формулируется специально для интеграла
Лебега: пусть s0 (х), st (x), s2 (х), ... и неотрицательная функция сравнения А (х) суммируемы
на измеримом множестве S, и пусть I sn (х) I ^Л (х) при всех п и при почти всех х £ S
(п. 4.6-14, Ь). Тогда из того, что lim sn (х) — s (х) для почти всех х £ 5, следует, что
п -+ оо
предел lim J sn (х) dx существует и равен J s (лг) dx (теорема сходимости Лебега; см.
п-+со s s
также п. 4.8-4, Ь).
4.6-17. Интеграл Стилтьеса.
(а) Интеграл Римана — Стилтьеса. Интеграл Римана—Стилтьеса
от функции / (л:) с интегрирующей функцией g (x) по ограниченному интервалу
[а, Ь] по определению есть
b m
\ f (х) dg (x) = lim 2 / <Ь> IS (*i)-g (*/-i)b (4.6-43)
i max (xi - xt _ j) -* 0 i = {
где
a = xQ < xt < x2 < ... < xm = b
*) Отметим, что функция
,/4_tf/„. 1\_0 . 1 2 1
не суммируема на интервале (О, 1), несмотря на то, что несобственный интеграл Римана
1 1
Г f (х) dx = lim \ f (x) dx==sin 1
0 X-W
существует.
4.6-17.
4.6. ИНТЕГРАЛЫ И ИНТЕГРИРОВАНИЕ
127
<Ь). )
и xi^^li^Xi (об определении предела см. п. 4.6-1). Если g (x) — функция
ограниченной вариации (п. 4.4-8, b), a f (х) —непрерывная функция на [а, 6],
то предел (43) существует.
Несобственные интегралы Римана — Стилтьеса определяются, как и в п.
4.6-2.
(b) Интеграл Лебега —Стилтьеса. Каждая функция g (x), неубывающая и
непрерывная справа (п. 4.4-7, Ь) на ограниченном интервале [а, Ь], с помощью
соотношений (35), (36) и
М [а < х < Р] = g (j5) — g (а) (а < а < J5 < Ь), (4.6.44)
где в квадратных скобках указано множество значений х, определяет меру (меру Лебега—
Стилтьеса) М [S] каждого борелевского множества (п. 4.6-14, Ь) на интервале [а, Ь].
Отметим, что
М [а < х < р] = g (Р) — g (а — 0), М [а < х < р] = g (P — 0) — g (а),
М [а < Jf<P] = g(P — 0) — £(а-0), M [x = a] = g (а) - g (а — 0) (а < а < Р <
(4.6-45)
Отправляясь от меры Лебега—Стилтьеса ограниченных интервалов по способу п. 4.6-14, а,
вводят меру М [S] Лебега—Стилтьеса произвольного измеримого множества как общее
значение внутренней и внешней меры.
Если задана функция у = f (x), ограниченная и измеримая на интервале [a, b], то
интеграл Лебега—Стилтьеса по [а, Ь] от функции f (x) с интегрирующей функцией g (x)
по определению есть
b т
Г / (х) dg (х) = lim £ Ч/Л* [S/1 (4.6-46)
для произвольного разбиения (38) интервала, содержащего множество значений функции
f (x); Si и здесь есть множество значений х, в которых у; __ j < / (х) ^ #/ (об
определении предела см. п. 4.6-15, а).
Интеграл Лебега—Стилтьеса от ограниченной или неограниченной функции f (x) по
любому измеримому множеству можно теперь определить по способу пп. 4.6-15, Ь, с и d,
предполагая, что функция g (x) ограничена на каждом рассматриваемом ограниченном
множестве. В многомерном случае функция g (x) заменяется функцией, неубывающей по
каждому аргументу. Можно, далее, применяя равенство (48) к сумме двух монотонных
Ь
функций (п. 4.4-8, Ь), определить интеграл Лебега—Стилтьеса J f (x) dg (x) с любой интег-
а
рирующей функцией g (x) ограниченной вариации. Если интеграл Римана — Стилтьеса
существует в смысле абсолютной сходимости, то соответствующий интеграл Лебега—
Стилтьеса ему равен.
(c) Свойства интеграла Стилтьеса (см. также табл. 4.6-1).
Если (а, Ь) — ограниченный или неограниченный интервал, для которого
существуют рассматриваемые интегралы, то
\fdg--lfdg1), ]fdg=lfdg+]fdg, (4.6-47)
а Ь а а с
Ь Ь Ъ Ъ Ь Ь
$tfi+/i)<te = $/i<te+$/i*. $/dtei + Si) = $M*i + $M&. (4.6-48)
а а а а а а
ь ь ь
5 («/)*=$/* (ад)=a \ fd^ (4.6-49)
а а а
Ь Ь
\tdg = ig\a-\gdl (4.6-50)
а а
*) См. сноску на стр. 114.
128 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.6-18.
Если g(x)—неубывающая функция на (at b)t то
Ь ь
|$/«te|^$l/l* (a^b). (4.6-51)
а а
Если g (х) — неубывающая функция и f(x)^F(x) на (at b), то
ь ь
\fdg^\Fdg (a^b). (4.6-52)
а а
Интегралы Стилтьеса часто имеют «наглядный» смысл (криволинейные
интегралы, интегралы по поверхности, по объему; интегралы по
распределению массы, заряда и вероятности, п. 18.3-6). Заметим, что интеграл
Стилтьеса в качестве частных случаев включает в себя обычные интегралы и суммы:
ь ь
\ f (х) dg (*)=»$/ (х) g' (x) dx, (4.6-53)
a a
если функция g (x) непрерывно дифференцируема на (a, b) и
4.6-18. Свертки. Свертка Стилтьеса двух функций f (х) и g (х) по интервалу (а, Ь)
есть по определению функция
Ь Ь
ЧГ (0 = J / (t - л:) dg (x) =: J g (/ - x) df (x) (4.6-55)
a a
для всех значений t, для которых эти два интеграла существуют и равны. Классическая
свертка f (х) и g (x) по (а, Ь) подобным же образом определяется как
Ь Ъ
ЧГ (0 = J / (( - х) g (x) dx = J g (/ — л:) f (x) dx. (4.6-56)
a a
В литературе и (55) и (56) часто просто называют сверткой функций f (х) и g (х) по (а, Ь)
b
и любую из этих функций (55) и (56) обозначают символом f ■*■ g или f X g; точный смысл
а
обычно очевиден из контекста (см. также пп. 4.11-5, 8.3-1, 8.3-3 и 18.5-7).
Если имеют место равенства (55) и (56), то
g*f = f*g. f * (g * h) = (f * g) * h = f * g * h, fx(g + h)=fXg + f*h. (4.6-57)
При a= — oo и/или b — -j- oo, если интегралы существуют, то равенства (57)
справедливы.
Свертка двух конечных или бесконечных последовательностей а (0), а (1), и (2), ... и
Ъ (0), b (1), b (2), ... есть последовательность
а * ь = S а (/ — k) b № <* = 0, 1, 2, ...). (4.6-58)
4.6-19. Неравенства Минковского и Гельдера.
(а) Если {а, Ь) — ограниченный или неограниченный интервал, для которого
интегралы в правой части существуют, то
Vb 11/р Vb -\\/р Vb 1\/р
Nlfi-ff2|p<*£ ^MIMP^ + Jlf. 1"<*« 14.6-59)
(1 ^ Р < + оо) (неравенство Минковского),
Ь Vb ll/p Vb l(p - \)/р
| J f if. dg | ^ J I f, P dg\ U\f2 \PttP - 1) </g
(1 < p < -{- со) {неравенство Гельдера). (4.6-60)
4.7-1.
4.7. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
129
Эти неравенства справедливы, в частности, для обычных интегралов Римана и Лебега и,
более общо, для многомерных интегралов. При р = —^—г = 2 неравенство (60)
превращается в неравенство Коши — Шварца (15.2-3) *).
(Ь) Из неравенств (59) и (60) вытекают соответствующие неравенства для сумм и для
сходящихся бесконечных рядов. Если суммы справа существуют, то
[21 ч+bk |р],/р < [21 «* 1"],/р+[| 16* 1"],/р w-6-бь
(1 ^ р < -f- оо) {неравенство Минковского),
11 «*»* | « [2 I «* \")UP [| I »* СЛР ~ " f ~ Ш" (4.6-62,
(1<р<-г-оо) (неравенство Гельдера).
При р» ^_ =s2 hi
(см. также п. 1. 3-2).
Прир = —-—г = 2 неравенство (62) превращается в неравенство Коши — Буняковского
4.7. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ. РАСКРЫТИЕ
НЕОПРЕДЕЛЕННОСТЕЙ. ТЕОРЕМЫ ВЕЙЕРШТРАССА О ПРИБЛИЖЕНИИ
4.7-1. Теоремы о среднем значении (см. также п. 4.10-4).
Нижеследующие теоремы полезны для оценки значений и пределов действительных
функций, производных и интегралов.
(а) Если функция f (х) непрерывна на [а, Ь] и дифференцируема на (а, Ь),
то в интервале (а, Ь) существует такое число X, что
t(b)-f{a)=f'(X)(b-a) (4.7-1)
(теорема Лагранжа; теорема о конечном приращении). Число X часто
записывают в виде X = a+Q (b — a)(0<6 < 1). При f (a) =/(b) эта теорема
называется теоремой Ролля (см. также (п. 1.6-6, е).
Если функция t (Ху х2, .... *п) непрерывна при <*^Х;^Ь. и дифференцируема при
Of < х- < b. (/ = 1, 2, . . ., п), то существует набор таких чисел Х„ Х%, • • •* ^л- ч,по
а. < Xj < Ь. Ц = \,2 п) и
2л дх.
/ (V Ь9 . . .,*„) - f (av а, «я) - 2i 25J L . * <*' ~ fli) <4-7"2>
/=1 "Xlt Лй Хп
(b) Ясли 1) функции и (х) и v (х) непрерывна на [а, Ь], 2) v (b) ф v (а) и 3)
производные и' (х) и и' (х) существуют в интервале (а, Ь) и одновременно не обращаются в нуль,
то в интервале (а. Ь) существует такое число X, что
и ф) - и (а) и' (X) ? 3
v (Ь) - v (a) v' (X) х ' '
(теорема Коши).
(c) Если функция f (х) непрерывна на [а, Ь\, то в интервале (а, о) сущест*
вует такое число X, что
ь
\f(x)dx = f{X)(b-a). (4.7-4)
а
(d) Если функции f(x)ng(х) непрерывны на [а, Ь] и g(x)^0 на [а, Ь]
(или g(x)^0 на [at b]), то в интервале (а, Ь) существует такое число X,
что ъ b
]f(x)g (x) dx=f (X) ] g (x) dx. (4.7-5)
*) В отечественной литературе это неравенство называют неравенством Коши — 1>у-
, няковского
5 Г. Корн я Т. Корн
130 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.7-2.
Если функции f (х) и g (х) непрерывны на [а, Ь] и функция g (х) в этом интервале
не возрастает (или не убывает), то в интервале (а, Ь) существует такое число X, что
Ь X Ь
\t ix) g (x).dx = g (a) j f (x) dx + g (b) j f (x) dx. (4.7-6)
a a X
Если, кроме того, g (x) ^ 0 на (a, b), то в интервале (a, b) существует такое число X, что
X
g (a) j f (x) dx, если g (x) не возрастает,
ft (4.7-7)
g (b) \ f (x) dx, если g (x) не убывает.
b
§f(x)g(x)dx= ]
a
4.7-2. Раскрытие неопределенностей (примеры см. в табл. 4.7-1).
1{Х)
>(х)
(а) Пусть функция / (*) вида £|5, и (х) v (*), [и (x)]v '•*> u(x) — v (x)
в точке х=а не определена и принимает вид -jp ^, 0 • оо, 0°, со0, I00 или со—сю.
Это значит, что /(я) = ^-~, где lim u(x) = 0 и lim v(x)=0 в первом
v \Х) х-*-а х-+ а
случае; /(*)=^-|, где lim и (х) = со и lim v (x) = со — во втором;
f(x) = u(x) v(x), где lim и(х) = 0 и lim t>(*) = co — в третьем, и т.д. Термин
*-*a x-*a
«раскрытие неопределенностей» означает, что отыскивается предел lim/(#). Если
х-* а
этот предел существует, то часто по определению полагают /(я) = lim f(x).
х-+а
Таблица 4.7-1
Некоторые часто встречающиеся пределы (п. 4.7-2)
11т Л +-Y1 = е =fe 2,71828, lim (1 -f x)ll* = *, lim * = In с, О 0,
*. х , ,, sin* .. tg x ., sh* tl th* ,
lim jc = l. lim = lim -s—= lim = lim = l,
*-»0-f x-+Q x *-»>0 x *-»>0 x *-»>0 X
,. sin our , ^ ^ ,
lim = ю (— oo < © < -I- oo),
x-+0 *
lim *aln.v= lim jc"aln * = lim xae~x = 0 (a>0).
*-*0-{- *-*--j-oo *-* + оо
(b) Случаи 0/0 и со/со. Пусть lim a(*) = lim г>(*) = 0. £&«" сущест-
x-*-a x-+a
eyem окрестность точки х=а, в которой при xyta: I) у(х)фО и 2) лргж>
eodwwe и' (х) и v' (х) существуют и v' (x)zfiO, то
лг-+а w *-ю w
*&ш предел в правой части равенства существует (правило Лопиталя).
Пусть lim и (х)= lim v (x)= со. Если существует окрестность точки
х-*а х-*а
х = а, в которой при хфа производные и' {х) и v' (x) существуют и v' (*)^£0,
4.8-1.
4.8. БЕСКОНЕЧНЫЕ РЯДЫ И ПРОИЗВЕДЕНИЯ
131
то равенство (8) справедливо, если предел в правой части этого равенства су-
ществует (эта теорема также называется правилом Лопиталя).
Если само отношение и, ,* представляет собой неопределенность, то
указанный метод может быть в свою очередь применен и к " '*} , так что
Ит fi<4 = Hm ffl^-= lim ^f; (4.7-9)
этот процесс, если необходимо, может быть продолжен и дальше.
(с) С л у ч а и 0 • со, 0°, со0, 1°° и со—со. Выражения и (х) v (х), [и (x)]ViXi
и и(х) — v(x) с помощью какого-либо из соотношений
u(x)v(x) = ^^^^
■ l/v (х) — 1/« (дг)'
_J 1_
u(x)-v(x)=v^ uJ*==\ng(x) ^(х)=£Щ
и (х) V (х)
(4.7-10)
часто можно привести к виду ~~, и тогда к ним становятся применимыми
методы п. 4.7-2, Ь.
(d) При вычислении пределов иногда бывает полезно воспользоваться
формулой Тейлора (п. 4.10-1).
(e) Методы пп. 4.7-2, а, Ь, с и d применимы и для отыскания одно-
сторонних пределов lim f (x) и lim f(x) (п. 4.4-7). Пользуясь тем, что
*-*а—о х^>а+о
lim /(*) = \imf(\/y), находят lim f (x).
4.7-3. Теоремы Вейерштрасса о приближении (см. также пп. 4.10-4, 4.11-7
и 12.5-4).
1) Пусть f (х)—действительная функция, непрерывная на ограниченном
замкнутом интервале [а, Ь]. Тогда для каждого заданного положительного числа е
(максимум погрешности приближения) существует такой действительный
п
многочлен Р(х)== J] akxk, что \ f (х)—Р (х) | < е при всех х <= [а, Ь].
£ = 0
2) X Пусть функция f (х) удовлетворяет дополнительному условию f (Ь) =
— f (а) и со = 2л/(Ь — а). Тогда найдется такой действительный тригонометри-
т
ческий многочлен Т (х) = 2 (ak cos kwc+fik sin Ых), что \ f (x) — Т (х) | < е
при всех х е [а, Ь].
Аналогичные теоремы справедливы и для функций двух и большего числа
переменных. Теоремы Вейерштрасса о приближении позволяют различные свойства
непрерывных функций выводить из соответствующих свойств многочленов или
тригонометрических многочленов.
4.8. БЕСКОНЕЧНЫЕ РЯДЫ, БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
И НЕПРЕРЫВНЫЕ ДРОБИ
4.8-1. Бесконечные ряды. Сходимость (см. также п. 4.4-1). Бесконечный
ряд а0 + а1 + а2+ ... действительных или комплексных чисел (членов) а0, aif
а2> ... сходится, если последовательность s0, slf s2, ... его частичных сумм
5*
132 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.8-2.
п
sn= 2 ak имеет предел s, т. е. в том и только в том случае, если после-
*=о
довательность остатков /?n+1 = s — sn сходится к нулю. В этом случае s =
= lim sn называется суммой ряда, и разрешается писать
Я-*°° ОС П
а0 + аг + а2+...= 2 а* = Hm ]£ ak=\imsn = s. (4.8-1)
fc=0 «-^oo^=0 л-юо
Ряд а0 + а! + а2+... (необходимо сходящийся) называется абсолютно
сходящимся, если сходится ряд | а0 | + | ах | + | а2 | + ... Если ряд не сходится, то
он называется расходящимся (он расходится; см. также п. 4.8-6). В пп. 4.9-1
и 4.9-2 приводятся некоторые признаки, позволяющие исследовать сходимость
заданного бесконечного ряда
4.8-2. Ряды функций. Равномерная сходимость (см. также п. 4.4-4). Ряд
функций а0(х) + а1(х) + а2(х) + ... сходится к функции (сумме) $(*) при
каждом значении х, при котором
п
lim 2 ak(x) = 8(x).
Ряд равномерно сходится к s (x) на множестве 5 значений х, если на
множестве S к функции s (х) равномерно сходится последовательность его частич-
п
ных сумм sn(x)= 2 ak(x)' В п. 4.9-2 приведены некоторые признаки рав-
л=о
номерной сходимости.
4.8-3. Операции иад сходящимися рядами.
СО 00
(a) Сложение и умножение на число. Если 2 ak и 2 ^k ~"
*=0 Jfe=0
сходящиеся ряды с действительными или комплексными членами и
а—действительное или комплексное число, то
2 ч+ 21 **= 21 (fl*+w. a 2 **= 2 «*• <4-8-2>
J9 каждом из этих случаев из сходимости или абсолютной сходимости рядов
в левой части вытекает сходимость или соответственно абсолютная сходимость
ряда в правой части.
(b) Перестановка членов. Коммутативно сходящийся ряд есть
ряд, который сходится и имеет одну и ту же сумму при любой перестановке
его членов; это имеет место в том и только в том случае, если ряд
абсолютно сходится. Каждый ряд, получающийся из такого ряда, если из него
выбросить какие угодно члены, также абсолютно сходится.
Сходящийся, но не абсолютно сходящийся ряд называется условно сходящимся.
Члены каждого условно сходящегося ряда с действительными членами можно переставить
так, что: 1) последовательность его частичных сумм станет сходиться к данному
пределу, 2) последовательность его частичных сумм станет неограниченно возрастать, 3)
последовательность его частичных сумм станет неограниченно убывать и 4)
последовательность его частичных сумм станет колебаться между двумя любыми данными числами
{теорема Римана).
со со
(с)Двойныеряды. Двойной ряд 21 2 aik СХ°ДИТСЯ к s (имеет сумму
|=0*=0
•). если т п
Нт 2 2 а** = 8
т-+ оо/==ол==0
л-* со
4.8-4. 4.8. БЕСКОНЕЧНЫЕ РЯДЫ И ПРОИЗВЕДЕНИЯ 133
(п 4.4-6). Отметим, что
оо оо оо/оо \ оо/оо \
2 2 а<*= 2 2 4= 2 21 «4 <4-8-3>
если все три ряда сходятся (теорема Прингсгейма о суммировании по
столбцам и по строкам). В частности, если рассматриваемый двойной ряд
оо оо оо оо
2 2 aik сходится абсолютно, т. е. если сходится ряд 2 2 1а**1» то этот
1 = 0 Л = 0 / = 0Л = 0
ряд имеет одну и ту же сумму при любом порядке суммирования.
оо
(d) Произведение двух бесконечных рядов. Если 2 ak
оо
и 2 Ьь—абсолютно сходящиеся ряды с действительными или комплексными
*=о
00 00
членами, то двойной ряд 2 2 а1^ь есть абсолютно сходящийся ряд с сум-
/=ofe = o
мой ( 2 ал ] ( 2 ьь ) • Более общо:
(s*)(s
ОО \ / 00 \ 00 П
2 а** 2 ^ = 2 2 аЛ_л (правило Коши), (4.8-4)
^=0 /\k=0 J п = 0/г=0
если ami/ три ряда сходятся.
4.8-4. Операции над бесконечными рядами функций.
(a) Сложение и умножение наограниченнуюфункцию.
00 ОО
Если ряды ^ ak M и 2 ^k № сх°дятся равномерно (п. 4.8-2) на множестве
5 значений х, то равномерно на множестве 5 сходятся и ряды
оо оо
2 [а* м + ьь wi" 2 ф w <** w.
г&> ф (л;) — произвольная ограниченная на S функция.
(b) Пределы, непрерывность и интегрирование (см. также
00
п. 4.4-5). Пусть ряд 2 ak (*) равномерно сходится на ограниченном откры-
том интервале (а, 6), х = х0 и x=Xi—dee любые точки этого интервала. Тогда
00 ОО
1. lim 2 а*(*)= 2 lim а*М»
00 00
lim 2 **(*>=■ 2 Ит ak(x)f
*->*oH-Ofc=o Л==0*->.к0 + 0
ОО 00
lim 2 «*(*)=■ 2 lim fl*W«
134 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.8-Б.
если при /г = 0, 1, 2, ... существуют соответствующие пределы
lim ak (х), lim a# (x), lim ak (x).
*-**о х-**0 + 0 х-*>*0—О
00
2. Сумма ряда 2 ^W непрерывна в точке x = x0t если в этой точке
непрерывен каждый член ряда ak (x).
00
3. Ряд 2 ak (x) равномерно сходится на замкнутом интервале [л*0, хг] и
k = o
Хх Г 00 "? 00 Jfj
*о1_£ = 0 J Л = 0*0
гели каждый член ak (x) непрерывен на [x0t xt]. Из сделанных предположений
вытекает сходимость ряда в правой части каждого из этих равенств.
Нижеследующая теорема формулируется специально для интеграла Лебега. Она
может применяться и к должным образом сходящимся несобственным интегралам Римана
со
(см. также п. 4.6-15). Если ряд \j a^ (х) функций, суммируемых на (ограниченном
Л=0
или неограниченном) измеримом множестве (в частности, на интервале) S, сходится на S
почти всюду, то
1 °°
Г*" 2 \akW*** <4-8"5)
k = 0 S
\\ 2e*w r
sU=o J
если существует такое действительное число А (или функция А (х), суммируемая на S,
I n I
п. 4.6-16), что J^] л^(х)\<А для всех п и почти для всех х £ S. Заметим, что равно-
\k = 0 I
мерная сходимость не предполагается.
со
(с) X Дифференцирование. Пусть ряд 2 ak (*) сходится по край-
k = o
ней мере в одной точке с е (а, Ь). Тогда, если производные а'0 (х), а\ (*),
00
а'2 (х),... существуют на (а, Ь) и ряд 2 ak(x) равномерно сходится в интер-
>fe=о
00
вале (а, Ь), то ряд ^У] а# (х) сходится в (а, Ь) и
00 00
s S e*w- S a'k w (a <*< «• (4-8-6>
/г = 0 Л = 0
4.8-5. Улучшение сходимости и суммирование рядов. Суммы некоторых рядов
(см. также пп. 7.7-4 и 20.4-3).
(а) Преобразование Эйлера. Если ряд в левой части равенства
2<-1>ч- 2(-,)/г^т' (48-7)
Л = 0 £ = 0 2
сходится и разности А ав определяются, как в п. 20.4-1, а, то 5то равенство
справедливо. Ряд в правой части равенства часто сходится быстрее, чем ряд слева.
4.8-5.
4.8. БЕСКОНЕЧНЫЕ РЯДЫ И ПРОИЗВЕДЕНИЯ
135
(Ь) Преобразование Куммера. Если для сходящихся рядов
оо оо
• - 2** и s= 23'*
k=0 k=0
существует предел у= lim (a /b ) jtOt то
п-*оо п п
оо
s
Л = О Л=*(Л Л/
Если сумма S известна, то преобразование Куммера может оказаться полезным при
числовых выкладках.
В таблице 4.8-1 приведены суммы некоторых числовых рядов (наиболее подробные
таблицы такого рода см. в [4.6]).
Таблица 4.8-1
Суммы некоторых числовых рядов
оо
*=1
оо
оо
£=1
00
vi 1 я*
*=1
00
VI 1 Я4
Zj Л«™90'
* = 1
2 4^—.
fc=l
оо
2j гсг+тг"1,
*=i
00
2j *(*+!)<* + 2)
£=1
оо
У А* ! |£
Zj a "l-a' ,£
1
_±_ — оЬ 1.
! s— ch 1
оо
2j (2k - 1)*
Л-1
оо
VI 1 Я*
Zj k* ** 945*
£ = 1
Zj 2k - 1
£=1
оо
£=1
оо
Л-1
оо
23
k = \
я»
"* 8'
я
в4'
00
Zj (2*- 1) (2Л+ 1) 2'
(-1)* I
(- D*
Т5!)Г-см1'
(-О*"1
VI (- 1)*+! Я*
Zj a2 "12'
А=-1
оо
VI 1 Я»
Zj A» ~ 9450' !
k = \ I
VI (- 1)* Х Я»
Zj ■ (2k - i)« 32' 1
*=i
oo
VI 1 3
Zj (k-i) (k + \) 4*
k = 2
оо 1
4 ' Zj k (k + 1) ... (Л +m> e mm! (W ' Л —J'
A = l 1
11 < 1 (бесконечно убывающая геометрическая прогрессия)
(с) Формула суммирования Пуассона. Если ряд V / (2я£ -f /)
Л = —оо
равномерно сходится на интервале О < t < 2я /с функции, разлагающейся в ряд Фурье
(см. п. 4.11-4), то
оо оо +оо
2 f (2яЛ) я ^ 2 $ f (T) f"" '*ТrfT* (4-8*9)
д» = — оо & =— оо—оо
если интеграл в правой наста равенства существует.
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.8-6.
(d) Формула суммирования Эйлера — Маклорена. Если
производная №т "Ь 2) (дс) существует и непрерывна при 0 < х ^ п, то
2/<»-5 tmdt+MtUM2 +
*=о
т d
* = 1
"В*
+ 2р cf{2к~г){п)-'(2*_1)(0)] + (2^rlfr'(2т+2)(0л)
(т,л = 1,2, . . . ; 0 < в < 1),
(4.8-10)
еде Вj — числа Бернулли, определяемые в п. 21.5-2.
Формула (10) часто позволяет дать замкнутое выражение для приближенного пред-
п
ставления конечной суммы V f (*) или представить ее в виде сходящегося или полу-
сходящегося (п. 4.8-6, а) ряда. Эта формула применяется также для численного
интегрирования (п. 20.7-2, с).
Отметим следующие формулы для сумм специального вида (частные случаи этих
формул приведены в п. 1.2-8 и табл. 4.8-1):
п
А = 1
п
k —
1_
!w + i
n
2 4 + 1(Я-Ы)
N + \-k
Bft,
1_
k2N-
2
*=1
оо
2
2 (2W) ! ~2^,
(-1)*+» <-!)" + ! (22"-!-1) я2"
*,2W
(2*-1)2^
(2ЛГ)1
(~1)^+1(22^-.1)я2^
2 (2W) I
*2#»
52W.
(4.8-11)
(4.8-12)
(4.8-13)
В формулах (11) — (13) N == 1, 2, . . .
(е) Лемма Абеля. Следующая лемма иногда оказывается полезной для оценки
частичных сумм Пусть последовательность а0, at. а8, . . положительных действитель-
п
них чисел удовлетворяет условиям а0 ^ at ^ а8 ^ . . . ^ а ^... Тогда a«S^ \J akak^
^ aeS't где S u 5' — соответственно наименьшая и наибольшая величина из последователь^
г
нести сумм 2_i аъ пРи Г == 0» *» 2* • • • » п-
/г
Отсюда следует, что если для любого п справедливы неравенства М ^ \j а^^ЛГ,
Л=0
/г
то aeM ^ Yj afeafe^a0Af' также для любого п.
4.8-6. Расходящиеся бесконечные ряды (см. [4.2], т. II, гл. XII, § 6).
(а) По л у схо д и мость. Расходящийся ряд а0+а1+а2 + *.. может быть
полезен для приближения величины s, если абсолютная погрешность |s — sn\ =
I n I
в j—2 ak » прежде чем вновь начинает возрастать, убывает до некоторо-
I *=о I
го достаточно малого минимума, достигаемого при определенном значении /ц
номера п (полусходящийся ряд).
4.8-7.
4.8. БЕСКОНЕЧНЫЕ РЯДЫ И ПРОИЗВЕДЕНИЯ
137
п
Если при этом последовательные частичные суммы ^] «л поочередно то
больше, то меньше величины s, то ряд называется обвертывающим. Соседние
члены такого ряда обязательно имеют разные знаки (знакочередующийся ряд).
оо
(Ь) Асимптотические ряды. Расходящийся ряд 2 ak М есть
асимптотический ряд, описывающий поведение функции f(x) при х-*х0
оо
(/(*)"*- 2 аь(х) ПРИ х~*хо)> если существует такой номер N, что при лю-
бом фиксированном п > N
lm,„F^[^w-Joa*w]=a (4-8",4>
lim
х
Расходящийся ряд 2 fl*M есть асимптотический ряд, описывающий
л=о
оо
поведение функции / (х) при #-» + со (f(x)^ 2 а*М ПРИ *""** +°°)> если СУ*
ществует такой номер N, что при любом фиксированном п> N
lim *»/(*)- J «*(*)==<>. (4.8-15)
*- + «> L *=о J
Асимптотический ряд дает полусходящиеся приближения функции /(#),
причем при х -* дг0 или * -> + оо номер л0 -► со (см. также пп. 4.4-3 и 8.4-9).
(е) Суммирование средними арифметическими. Сходящийся
или расходящийся ряд а0-\- at-\- аг-\- . . . суммируем средними арифметическими
(суммируем по методу Чезаро средними первого порядка, суммируем Си суммируем (С, \)У
к Ci-сумме Su если последовательность o0t otl otl ... средних арифметических
я —1 / k \
сходится к St. Каждый сходящийся ряд суммы-
а«-1=1 I] S* Где sk= S */
* = 0 \ /»0 /
р^ел средними арифметическими и 5t = s. Ряд с положительными членами суммируем
средними арифметическими в том и только в том случае, если он сходится (см. также
п. 4.11-7).
4.8-7. Бесконечные произведения,
(а) Бесконечное произведение
(l+a0)(l+al)(l+a2)..^f[(l+ak)
k = Q
действительных или комплексных множителей Х-^а^ФО сходится к числу
оо
P = JJ (1+аь)ф0 (значению бесконечного произведения), если
л-*о°Л±о
со
Это имеет место в том и только в том случае, если ряд 2 "i(l +fl*) сходится
А=0
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.8-8.
п
к одному из значений In р (см. п. 21.2-10). Если 1'т ТТ (1 + ал) = 0,
то говорят, что бесконечное произведение расходится к нулю.
(Ь) Бесконечное произведение ТТ (1+а^) (необходимо сходящееся) сходится абсо-
00
лютно, если сходится произведение ТТ (I-f-J a^ f ); для этого необходимо и достаточно,
оо
чтобы абсолютно сходился ряд \j а.. Бесконечное произведение сходится коммута-
тивно (т. е. его значение не зависит от порядка множителей) в том и только в том
случае, если оно сходится абсолютно (см. также п. 4.8.-3, Ь).
оо
(с) Бесконечное произведение ТТ [1+в£ (*)] равномерно сходится на множестве S
значений х, для которых при всех k выполняется условие 1 + я^ (*) ^0, если последова-
п
тельность функций ТТ [I+я^С*)] равномерно сходится на S к функции, не
принимало
кицей на S значения, равного нулю. Это, в частности, имеет место, если на S равно»
00
мерно сходится ряд \\ \ а^ (х) \.
4.6-8. Непрерывные (цепные) дроби. Последовательность вида
So = &o; Si = &„ + ТТ". s8 = b0 "\ ^г*
ь2
St = b0 + ^
*х +
а*
t* i а»
Ь* + "7Г~
(4.8.-16)
называется последовательностью, определяющей данную непрерывную дробь; n-ft
знаменатель равен Ьп^+ап1Ьп.
■К Сокращенно непрерывная дробь обычно записывается так:
°+ Ьг + Ьг + Ь% + ...+ 6Я + ...
ал
Дробь -т— называют л-л» звеном непрерывной дроби. Непрерывная дробь называется
°п
конечной, если она имеет конечное число звеньев, и бесконечной, если она имеет их
бесконечное число. X
Разложение некоторых функций в непрерывную дробь сходится быстрее, чем
соответствующее разложение в степенной ряд, и оказывается полезным в некоторых
приложениях (расчет электрических сетей; см. также п. 20.5-7).
■К Примеры. Приведем разложения некоторых функций в непрерывную дробь
(следует иметь в виду, что такое разложение не единственно);
х . , X X X X X X X
** = ! + - -
1 - 2 + 3- 2 + 5 - ... - 2 + 2я + 1 -...
1 X X X X
1 _ i + 2-З + ...+ 2 —2/1 + 1 +..,
(—оо<*<оо).
, ,. . . х х х 2х 2х пх пх / ^ iv
1п(1+*) = т + 1Г+1Г+ -5-+ _+_ + _+_|+eee о-о.
(хфп/2 + kn),
(-00<*<00). *
* л:2 **
tgJf==T- Т- Т"-...
* *8 4дг8
**
— 2л + 1
.. + 2я + 1
+
4.9-1.
4.9. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ И ИНТЕГРАЛОВ
139
4.9. ПРИЗНАКИ СХОДИМОСТИ И РАВНОМЕРНОЙ СХОДИМОСТИ
БЕСКОНЕЧНЫХ РЯДОВ И НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
4.9-1. Признаки сходимости бесконечных рядов (п. 4.8-1).
(a) Необходимое и достаточное условие сходимости.
Последовательность действительных или комплексных чисел s0, slt s2t ...
(например, последовательность частичных сумм некоторого ряда, п. 4.8-1)
сходится в том и только в том случае, если для каждого положительного числа е
существует такой номер N, что из m>N -и п > N следует \ sn — sm | < в
(критерий Коши сходимости последовательностей или рядов),
(b) Признаки сходимости рядов с положительными
членами (эти признаки полезны и как признаки абсолютной сходимости
рядов с произвольными действительными или комплексными членами, пп. 4.8-1
и 4.8-3). Ряд fl0 + ai + «2 + "* с положительными членами сходится, если
существует такой номер N, что при п > N выполняется хотя бы одно из
следующих условий:
1. ап^Мп и\или^^-^ *+1 , где М0 + Мг + М2 +... — схо-
ап мп
дящийся ряд сравнения с положительными членами (признак сравнения).
2. По крайней мере одна из величин
аП+1-,^п, -<аП+Х
ап
1+2*
[•(■f¥-1)+1]1"+f
(4.9-1)
имеет точную верхнюю границу А < 1.
Четвертый из этих четырех признаков сильнее третьего (признака Раабе),,
который в свою очередь сильнее двух первых (признака Даламбера и
«радикального* признака Коши).
3. an^f (/г), где f (х) — положительная невозрастающая функция,
+ °°
для которой сходится (несобственный) интеграл \ f (x) dx (инте*
гральный признак сходимости Коши; см. также п. 4.9-3, Ь).
Ряд а0 + я1 + а2 + ... PacX0^umcHf если существует такой номер N, что
при п > N выполняется хотя бы одно из следующих условий:
я t d f
1. an^dn и/или —z±±^~~7T^t ^e dQ + d1 + dг-{-...—pacxoдщuйcя
an n
ряд сравнения с положительными членами (признаки сравнения
для расходимости).
2. По крайней мере одна из величин условия 1 имеет точную
нижнюю границу А ^ 1.
3. CLn^f (n)t где f (x)— положительная невозрастающая функция,
для которой интеграл \ f(x)dx расходится.
Замечание. В качестве ряда сравнения часто бывает полезен ряд N #
*=1 *
который при действительном к сходится, если Я > 1, и расходится, если % ^ 1.
(с) Ряд а0 + а1 + а2 + ... с действительными членами сходится:
1. Если соседние его члены имеют разный знак (знакочередующийся
ряд), его общий член ап не возрастает по абсолютной величине и
11т я„ = 0 (признак Лейбница).
п -+ оо
ИО ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.9-2.
2. Если последовательность s0, sx, s2, ... его частичных сумм
ограничена и монотонна', эта последовательность монотонна, лишь если
члены ряда имеют один и тот же знак. См. в этом случае признаки
из (Ь).
(d) Пусть а0, а1% а2, ... — невозрастающая последовательность
положительных чисел. Ряд а0ао + а1а1 + а2а2 + --- сходится:
1. Если сходится ряд а0-\-ах + а2-\-... (признак Абеля; см. также
п. 4.8-5, е).
п
2. Если lim ал=0ц сумма У] ал яяк функция от п ограничена
п-+со k==0
(признак Дирихле).
4.9-2. Признаки равномерной сходимости бесконечных рядов (п. 4.8-2).
(a) Необходимое и достаточное условие равномерной
сходимости. Последовательность s0 (x), sx (x), s2(x), ... действительных
или комплексных функций (например, последовательность частичных сумм
некоторого ряда функций, п. 4.8-2), определенных на множестве S значений х,
равномерно сходится на множестве S в том и только в том случае, если
для каждого положительного числа е существует такой номер N, не зависящий
от х, что из m>N и п> N для всех xeS следует \ sn (x)— sm(x) | <е
(критерий Коши равномерной сходимости последовательностей или рядов).
(b) Ряд а0 (х) + ах (х)+ а2(х) + ... действительных или комплексных
функций равномерно и абсолютно сходится на каждом множестве S значений х,
на котором функции ап (х) определены, и при всех п выполняется неравенство
\ап (х) | =^Мл» zde M0-\-M1+M2 + ...—сходящийся ряд сравнения с
положительными членами, мажорирующий ряд (признак Вейерштрасса). Сходимость ряда
сравнения может быть исследована с помощью признаков п. 4.9-1, Ь.
(c) Пусть а0, av а2, ...—невозрастающая последовательность
положительных чисел. Ряд а0ао (х) + а1а1 (*)+а2а2 (х)-{-... равномерно сходится на мно-
охестве S значений х:
1. Если ряд а0(х) + а1(х) + а2(х) + ... равномерно сходится на S
(признак Абеля, см. также п. 4.9-1, d)
2. Если lim an=0 и существует такое число Л, что
П-+СЮ
п |
2 flftW ^^ пРи всех п и пРи всех *^S (признак Дирихле).
|*=о I
X Признаки Абеля и Дирихле часто полезно применять и в более общей
форме, рассматривая вместо последовательности ocq, ах, ... последовательность
функций. См., например, [4.21, т. II, стр. 451. #
4.9-3. Признаки сходимости несобственных интегралов (см. также п. 4.6-2).
В пп. 4.9-3 и 4.9-4 приводятся признаки сходимости несобственных интегра-
+ оо b X
лов вида \ f(x)dx и \f(x)dx= lim ^ f (x) dx. Несобственные инте-
а а х —& —оа
гралы других типов сводятся к интегралам этого вида (п. 4.6-2).
Предполагается, что действительная функция / (х) ограничена и
интегрируема на каждом ограниченном интервале [а, X], не содержащем верхний
предел интеграла.
(а) Необходимое и достаточное условие сходимости
(критерий Коши). Несобственный интеграл \ f (x) dx сходится в том и
а
только в том случае, если для каждого положительного числа е существует
I Xj
такое число М>а, что из Х2 > Хг > М следует
\ f (х) dx
<е.
4.9-3. 4.9. ПРИЗНАКИ СХОДИМОСТИ РЯДОВ И ИНТЕГРАЛОВ HI
ь
Аналогично интеграл \ f (x) dx сходится в том и только в том случае, если
а
для каждого положительного числа е существует такое число 6 (0 < 6 < 6 — а),
1 Xt
что из Ь — Ь<.Х1<Х2<.Ь следует
i
f (х) dx
(b) Признаки сходимости несобственных интегралов
от неотрицательных функций (эти признаки полезны и как
признаки абсолютной сходимости несобственных интегралов от произвольных
действительных или комплексных функций; заметим, что из абсолютной сходимости
следует сходимость). Если функция f (x) ^ 0 в интервале интегрирования, то
-boo Ь X
несобственный интеграл \ \{x)dxuAu {f(x)dx = lim \f (x) dx сходится
a a X-+& — Oo
x
в том и только в том случае, если интеграл \ f (x) dx как функция от X
а
ограничен в интервале интегрирования. В частности, если интервал
интегрирования содержит такое число М, что при х > М (соответственно при М <
< х < Ь) выполняется неравенство f (x)^g (х), где g (x) — функция сравнения,
для которой сходится интеграл j g (x) dx I или соответственно \ g (x)dx ,
то первоначальный интеграл сходится (признак сравнения).
+ оо Ь
Аналогично, если g (х) ^ 0 и интеграл J g (x) dx или J g (x) dx расходится, то
М М
из f (x) ^ g (х) следует, что расходится и соответствующий интеграл от / (х).
Замечание. Интеграл V -г-, где а>0, сходится при Х>1 и расходится
а
Ь
при Я < 1, а интеграл \ г- сходится при Х<1 и расходится при А,^1. Если
J (Ь — х)к
а
Ъ
f (х) = О (l/xty (К > 1) при х-* + со, то интеграл J f (x) dx сходится абсолютно. Если
а
Ъ
f (х) = О fl/ ф — х)Ц (К < 1) при х-*Ь — о, то интеграл J f (x) dx сходится абсолютно
(см. также п. 4.4-3).
-г-со Ъ
(c) Если несобственный интеграл \ f (x) dx или С / (х) dx сходится абсо-
а а
лютно, а сс(х)—функция, ограниченная на интервале интегрирования и
интегрируемая на каждом конечном интервале [а, X], не содержащем верхнего пре-
4- со
дела интеграла, то несобственный интеграл \ a(x)f(x)dx или соответст-
а
ь
венно \a(x)f (x) dx сходится (абсолютно),
и
(d) Пусть функция а (х) ограничена и монотонна на интервале а^х< + оо.
Ц- со
Несобственный интеграл \ а (х) / (х) dx сходится:
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.9-4.
1. Если интеграл \ f (x) dx сходится (аналог признака Абеля,
а
п. 4.9-1, d) или
х
2. Если интеграл f / (x) dx как функция от X ограничен на
а
интервале а ^Х< + оо и lim а(х) = 0 (аналог признака Дирихле,
Х-+ + 00
п. 4.9-1, d).
(е) В п. 8.2-4 см. ряд приложений.
4.9-4. Признаки равномерной сходимости несобственных интегралов
(см. также п. 4.6-2, с).
(a) Необходимое и достаточное условие равномерной
сходимости. Критерий сходимости Коши из п. 4.9-3, а превращается
00
в критерий равномерной сходимости несобственного интеграла [f(x, y)dx
а
Ь
или [ f (x,y) dx на множестве S значений у, если дополнительно указать, что
а
число М или б, находимое по этому критерию при каждом у е S для любого
положительного числа г, не зависит от у (см. также п. 4.9-2, а).
-)-оо Ь
(b) Несобственный интеграл J f (х, у) dx или J / (х, у) dx равномерно и
а а
абсолютно сходится на каждом множестве S значений у таком, что при
любом у е S и любом х из интервала интегрирования выполняется
неравенство \f(x, y)\^g(x), где g(x) —функция сравнения, интеграл от которой
4-оо Ь
\ g(x)dx (или соответственно \g(x)dx) сходится (аналог признака Вейер-
а а
штрасса, п. 4.9-2, Ь).
(c) Несобственный интеграл \ а (х, у) f (x, у) dx равномерно сходится
а
на множестве S значений у, если при любом у е 5 функция а (х, у) не
возрастает на интервале а^#< + со и равномерно стремится на S к нулю
Iх I
огра-
при х-+ +оо и если при х^а и y&S абсолютная величина
$/(*, y)dx
ничена константой Л, не зависящей ни от х, ни от у (аналог признака
Дирихле, п. 4.9-2, с).
4.10. РАЗЛОЖЕНИЕ ФУНКЦИЙ В БЕСКОНЕЧНЫЙ РЯД
И ПРЕДСТАВЛЕНИЕ ИХ ИНТЕГРАЛОМ. СТЕПЕННЫЕ
РЯДЫ И РЯД ТЕЙЛОРА
4.10-1. Разложение функций в бесконечный ряд и представление их
интегралом. Функцию f (x) часто разлагают в соответствующий бесконечный ряд
оо
2 ak Фл (*) ввиду того, что
1. Последовательность частичных сумм (или средних
арифметических, пп. 4.8-6, с и 4.11-7) этого ряда может давать полезные
для вычислений приближения функции /(*).
4.1U-2.
4.10. СТЕПЕННЫЕ РЯДЫ И РЯД ТЕЙЛОРА
143
2. Операции над функцией / (х) может оказаться возможным
описать в терминах более простых операций над функциями фЛ (х)
или над коэффициентами ak (методы преобразований см. также
пп. 4.11-5, b и 8.6-5). Функция щ(х) и коэффициенты а^ могут
иметь какой-либо наглядный (физический) смысл (п. 4.11-4, Ь).
Подобные же преимущества может давать представление функций в виде (обычно
Ь
несобственного) интеграла J а (Я) <р (х, К) dx (см. также пп. 4.11-4, с, 4.11-5, с и гл.8).
а
Возможность реализации одного или обоих преимуществ, перечисленных выше,
часто нуждается в сходимости или же равномерной сходимости ряда или интеграла
(отсюда — важность признаков сходимости из пп. 4.9-1—4.9-4), но это относится не
ко всем случаям (пп. 4.8-6, 4.11-5 н 4.11-7).
4.10-2. Степеннйе ряды.
(a) Степенной ряд относительно (действительного или комплексного)
переменного х есть ряд вида
оо оо
2 я* (*—Q)h или а0 + а1х + а2х2 + ...= 2 akxk ПРИ Д = 0, (4.10-1)
k= о k = о
где коэффициенты я0, alt a?, ...—действительные или комплексные числа.
Для любого степенного ряда (1) существует такое действительное число
Гс(0^гс^ + оо), wrco этот ряд сходится абсолютно при \х\<гс и расходится
при | х | > гс. Число гс называется радиусом сходимости данного степенного
ряда. Каково бы ни было число q, удовлетворяющее условию 0 <С q <C гс,
степенной ряд (1) равномерно сходится при \х \^q (на интервале, если #
—действительное переменное, и в круге, если х—комплексное переменное).
Из сходимости степенного ряда (1) при х—х0 вытекает его сходимость и при |*f<
<|*of, а из его расходимости при х=х0 вытекает его расходимость и при |лг|>|лг01.
(b) Сходящиеся степенные ряды можно складывать в соответствии с
равенством (4.8-2) и перемножать в соответствии с правилом Коши (4.8-4). При
| х | < гс сумма степенного ряда (1) есть непрерывная и сколько угодно раз
дифференцируемая функция х. Степенной ряд (1) можно почленно
дифференцировать при \х\<гс и интегрировать на любом замкнутом интервале,
содержащемся в интервале (—гс, гс). Получающиеся в результате почленного
дифференцирования или почленного интегрирования от 0 до х ряды имеют тот же
радиус сходимости гс.
Некоторые правила действий со степенными рядами приведены
в табл. 4.10-1.
(c) Если существует такое положительное число г, что при всех х, удов-
оо оо
летворяющих условию \ х | < г, два степенных ряда 2 akxk u 2 bkxk имеют
одну и ту же сумму f (х), то а0 = 60, а1 = &1, а^ — Ь^ ... (теорема
единственности).
Пример. Бесконечная геометрическая прогрессия
оо
a0 + aQx + a0x* + ... z= а0 % xk =s а0 -г-— (| х | < 1), (4.10-2)
£ = 0
(см. также пп. 1.2-7 и 1.7-2) сходится абсолютно при | х | < 1 и расходится при \х\^\.
Для любого qt удовлетворяющего условию 0 < q < 1, прогрессия равномерно сходится
при | х j ^ q.
Действия со степенными рядами
st = 1 4- ахх 4- агх* -+. a3*8 4- я**4 + ••• .
s2 = 1 4- btx + ^x* 4- bzx* 4- *U*4 + ... .
s3 — 1 4- cxx 4- c2x2 4- c3x3 4- c4x4 4- ...
Операция
$9^8Т1
h = S-2
к—У-
k-T1''
s3~s7
SS = SiS2
S3 = Si/Sj
ss = exp (s, — 1)
s-, = 1 4- In s,
Cl
— a,
-2a,
1
1
/iaj
Qi + *>i
fli — bt
ax
at
c2
flI-*2
3a2-2a2
Ta2~Tal
3 о 1
TflT-Tfl2
— (л — 1) c,a, + na2
b2 4- atbt 4- a2
at — (&i*i 4- b9)
fl2+Ta!
1
a2 —2~ aic,
*3
2fllfl2-°3-a!
6ага2 - 2a3 - 4a3
1 1 , 1 .
T fl3 ~ T вЛ + Те ai
3 1 5 ,
TfllG2--2-fl3--T6"fll
cxa% (n — 1) 4-
+ T *la! (n - 0 (л — 2) + na3
*з -f axb2 4- a*6i 4- a«
ая — (tic, 4- fciCi 4- bj
fl3 + V2+Tai
я., — у (a2c, 4- 2a,c2)
C*
2аЛ-3а?а2-а4+а1+а!
ба^д 4- 3a| — 2a4 — 12a2a2 4- 5a}
Ta4-rflifl3-Tfli + i6-fl!a2-i28flf
3 . 3 a 1 15 ft , 35 4
T "A + Т "J"»" fl4-l6 flffl2 + 128 Q\
na4 4- cxaz (л — 1) 4- -у л (л — I) a| 4-
4- y (« — 1) (n — 2) r,a,a2 4-
4- ^ (n - 0 (n - 2) (л - 3) схаь
b* 4- a,&3 4- a2b2 4- a3&i + «4
a* — (bic8 4- btc2 4- bs^i 4- b4)
a4 + Vs + T fll+ T fl2fl? + "ST Gt
e4 — -j- (a3c, 4- 2a2c2 4- Zatcz)
4.10-4.
4.10. СТЕПЕННЫЕ РЯДЫ И РЯД ТЕЙЛОРА
145
4.10*3. X Теоремы Абеля и Таубера.
(a) Пусть г > 0. £сла ряд ^ аьг сходится и имеет сумму s; то ряд 2 ak*
со
в замкнутом интервале [0, г] сходится равномерно и lim V яьх » s
x-*r-0 k^o *
(теорема Абеля).
со
(b) Пусть г > 0. £сл« ряд JjTj а. ж* сходится в интервале [0, г), причем
ft=0
оо с»
Um 2 аь** —s и lim ^afcr*e °» mo ряд S а£г * сходится и его сумма
равна s (теорема Таубера).
Замечание. Особы
4.10-4. Ряд Тейлора (см. также п. 7.5-2).
(a) Пусть f (x) — действительная функция, имеющая в интервале а^х<.Ь
п-ю производную рП) (х). Тогда
t(x) = f(a)+f'(a)(x-a)+y"(a)(x-a)*+...+
+Т£±1Т1Гп-1) (я) (х-аГ^+Яп (х) (а^х< Ь), (4.10-3)
где | Rn (х) | ^ u~".a| sup | /(Л) (£) I (формула Тейлора). Rn (x) называется
т а<\<х
остаточным членом формулы Тейлора.
Более точно, существует такое число Х = а+6 (я — а), что а<Х<я
(или 0<6< 1) и
Rn(x)^\dl\dl...\f^(l)dl = y^(X)(x--ar (a^x<b) (4.10-4)
а а а
п раз
(Остаточный член формулы Тейлора в форме Лагранжа), X и б зависят от я,
х и п (см. также п. 4.7-1). Формулы (3) и (4) остаются справедливыми и
если функция f (х) имеет я-ю производную в интервале — Ь <.х^ а, причем
здесь Ь < х < X < а.
(b) Пусть функция f(x) имеет в интервале (а—г, а+r) все производные
и пусть для нее в этом интервале lim Rn (jt) = 0. Тогда
п-+ао
со
К*,в 2] д/'*'(*)(*-*)*. |*-а|<г (4.10-5)
и ряд равномерно сходится к f (х) на любом промежутке | # — a\^qt где q<Zr
(разложение функции f (х) в ряд Тейлора в окрестности точки а). Здесь по
определению положено 0! = 1 и /(0) (a)—f(a).
Если в (5) вместо а написать х. а вместо х—а написать Адг, то соотношение (5)
со
можно переписать в виде f (х + Ах) = VJ - fik) (х) Дж* (пп. 4.5-3 и 11.2-1). При а = 0
со
ряд Тейлора (5) \j — fik) (0) х* называется рядом Маклорена.
k = 0
(c) Каждое разложение функции f (х) в ряд по степеням (ж — а), сходящийся при
a— r <*<а-{- г, необходимо тождественно с (5) (п. 4.10-2, с). Если f (x) —
рациональная функция, то ее разложение по степеням х или по степеням \/х часто получают,
неограниченно продолжая процесс деления (п. 1.7-2, см. также равенство (2)). Примеры
разложения в степенной ряд см. в п. 21.2-12.
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.10-5.
Разложения в степенной ряд допускают почленное дифференцирование и
интегрирование (см. 4.10-2, Ь) и, таким образом, оказываются полезными для интегрирования
функции / (х) и для решения дифференциальных уравнений (п. 9.2-5). Заметим, однако, что
п
п-я частичная сумма \j — f ) (а) (х — а) ряда Тейлора не обязательно будет наилуч-
шим приближением функции f (х), являющимся многочленом я-й степени (см. также
п. 20.5-1).
Функция f (x), которая может быть разложена в степенной ряд, сходящийся в
некоторой окрестности точки а, называется аналитической в этой окрестности (см. также
п. 7.3-3).
4.10-5. Кратный ряд Тейлора.
(а) Пусть f txu *2t ... t x \ — действительная функция, имеющая все непрерывные
частные производные порядка ^ т в некоторой окрестности D точки а. Тогда
п
' (*Г Х2 *п) = f («Г «. %) + X ST L a a) (** ~ °i) +
i = \ 1 Л V 2 ип)
п п
+ ъТ>2±'Шж\(а a aA*i-ai)(xf-aj)+-+«m(xv*V-'xn)
/ = 1 у = 1 * I K"l' a2 °п)
((*г х2 хп) е D) (формула Тейлора). (4.10-6)
Остаточный член R (хЛ% хЛ, ... , хЛ удовлетворяет соотношению, аналогичному
ПЪ VI 2 ТЫ
равенству (4).
Формулу (6) можно записать при помощи дифференциалов
/ (a, + dxv а2 + dxr а„ + <**„) - f (av a2 a„) =
-*t+±W + ...+ jsj^jji "т'Ь + Я„ (4.10-7,
где все дифференциалы вычисляются в точке (av а2 ал), а
1
""'Vr *! Хп)
Rm = mdm,\iv у V4 М-Ч + Чх,. 0<«<1. /=1.2 я). (4.П-Я)
(Ь) Если функция / (xt, xit ..., хп) имеет в D все непрерывные частные производные
и lim R (xt, х2. ..., х ) = 0 в D, то равенство (6) приводит к разложению функции
f (Xt, x2, .... *л) в кратный степенной ряд {кратный ряд Тейлора), Если функция
f (*lt x2, ... , хп) может быть разложена в степенной ряд, сходящийся в некоторой
окрестности точки (а а , ... , а ), то она называется аналитической в этой окрестности.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
4.11-1. Вводные замечания. Ряды Фурье и интегралы Фурье используются
для представления и/или приближения функций (п. 4.10-1) во многих важных
приложениях. Разложение в ряд Фурье есть частный случай разложения в ряд
по ортогональным функциям (см. пп. 15.2-3—15.2-6).
4.11-2. Ряды Фурье.
(а) Если задан интервал разложения —• я < / < я, то ряд Фурье,
порожденный действительной функцией /(/), для которой существует интеграл
я
\ I / (т) I ^T x)t есть бесконечный тригонометрический ряд
— я
оо оо
\<h + 2 (akcoskt + bksmkt)~ 2 ***'*'« (4.1 Ma)
k=\ /e=—оо
i) Во многих приложениях достаточно рассматривать интегралы в этом параграфе
как интегралы Римана (п. 4.6-1), но использование интеграла Лебега (п. 4.6-15) делает
теорию значительно шире применимой. См. в пп. 15.2-3— 15.2-6 ряд теорем,
формулируемых специально для интеграла Лебега.
4.11-2.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
147
коэффициенты которого определяются по формулам Эйлера —Фурье
ak~h \ f (*) cos to dT, Ьь = ^ \ f (т) sin to dT,
—я —я
я
\
(6 = 0, 1,2, ...). (4.11-16)
Здесь ak и ^—действительные, a cft —вообще говоря, комплексные числа
(п. 4.11-2, d).
(b) Если задан интервал разложения — Г/2 < / < Г/2, то ряд Фурье,
порожденный действительной функцией /(/), для которой существует инте-
грал \ {/ (тг) | dx% есть бесконечный тригонометрический ряд
-'Г/2
+ 00
«о + 51 <e* C0S to°' + h sin ОД) я 2 с**'*®*' (cd0 = ^), (4.11 -2a)
где
/e = 1 A = — oo
Т/2 Т/2
2 f г /_ч *. j «. 2
a^ = у J ^T) cosk(d°T dTt bh—j \ f (T) sin ^G)oT ^»
-Г/2
—T/2
T/2
ck=-c_k = ±(ak-ibk) = ± $ f(T)e-ik°»xdx.
— T/2
(4.11-26)
В частном случае, когда Г — 2я, равенства (2) превращаются в равенства (1). Если
в качестве интервала разложения выбрать интервал (a, a -f* Г), то интегралы в (2b)
следует брать не между — Т/2 и Г/2, а между а и а+Г.
Г/2
(с) х £"дш существует интеграл \ [/ (т)]2 dx, то средняя квадратиче-
--772
екая погрешность
Т/2
Т $ [/СО-Л. OOP*,
— Г/2
п
где Рп (0=2 ао+ 2 (а* cos ^ "т" + Рл sin ^ -jr)-—произвольный тригонометри-
*=1
ческий многочлен, яры каждом п принимает наименьшее значение, когда в
качестве коэффициентов akt j3ft многочлена Рп (t) берутся соответствующие
коэффициенты Фурье (26) ak и bk функции f (t)t т. е. когда тригонометрический
многочлен Рп (t) есть частичная сумма
п
sn (0 -1 «о + 2 (afccosfe 2^+ bk sin ft Щ
ряда Фурье функции f (t) (см. также п. 15.2-6).
148 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.11-3.
Если тригонометрический ряд (2а) сходится к f (t) в интервале (— Т/2, Т/2)
равномерно, то его коэффициенты необходимо являются коэффициентами Фурье (2b)
функции f (t) (теорема Эйлера).
(а) -Х- Если абсолютная величина \ f (t) I интегрируема на интервале разложения, то
коэффициенты Фурье а^ и bk функции f (t) при & -* оо стремятся к нулю (теорема
Римана — Лебега). Если функция f (t) на всем замкнутом интервале разложения имеет
непрерывные производные до (т — \)-го порядка включительно, причем каждая из этих
производных в концах этого интервала имеет одно и то же значение, и если т-я
производная кусочно-непрерывна, то коэффициенты Фурье ak и Ь^ функции f (t) при k -* со
убывают не медленнее, чем k~m, т. е.
№
km*
где С — постоянная.
(е) Действительные коэффициенты а. и Ь. и комплексные коэффициенты с^
связаны формулами
ak=ck + c-k> Ьк = 1(ск-с-к)
ck = T (ak ~ ibk)> c-k - T (e* + tbh)
\ (k - 0
, 1. 2, ...),
(4.11-3)
где bQ = о. Ряд Фурье (2) четной или же нечетной функции / (f) (п. 4.2-2, Ь) сводится
соответственно к ряду Фурье по косинусам и к ряду Фурье по синусам.
4.11-3. Интеграл Фурье и преобразование Фурье (примеры см.
в табл. 4.11-3 — 4.11-5).
(а) Интеграл Фурье, порожденный действительной функцией /(/),
абсолютная величина |/(/) | которой интегрируема на интервале —оо<^<+со
(интервал разложения) *), по определению есть
-]-СО -f-OO
+ 0О
~- $ d<0 $ /(T)COSG)(/-T)dTEEE $ С (V) е2*1™ ** Е=
+ оо
+ 00
J= \ С(ъ)ешдп = ± \ Q(co)*lfi)/dco, (4.11-4а)
У*2я
где
-1-со
c(v)= \ I;(т) e"2mvx dx,
+ оо
С(<й)=тк $ w^^m'te)'
+ оо
fi((o)~ $ /(т)г'«Л = сЩ(вВ82яу).
(4.11-46)
Функция c(v) называется преобразованием Фурье с (v) = & [/ (/)] функции /(/).
Заметим, что преобразованием Фурье функции / (/) называют не только с (v),
но и С (со) или же Q (со).
») См. сноску к п. 4.11-2.
4.11-4.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
149
(Ь) Косинус- и синус-интегралы Фурье, порожденные действительной
функцией /(/), абсолютная величина |/(/)| которой интегрируема на
интервале разложения 0</<+оо, определяются соответственно как
где
-{-00 -[-00
2 \ сс (со) cos 2nvt d\ = уA i Сс (со) cos со/ dco,
о о
-{-00 -{-00
2 J cs (v) sin 2jiv/ dv = уi- J Cs (со) sin со/ dco,
cc (v) = 2 \ / (t) cos 2rcvr dx9
+ 00
Cc(co) = |/T J /(T)coscoTflfT = ^cc(v),
(4.11-5a)
cs (v) = 2 С / (t) sin 2jivt dxt
о
Cs (со) = j/iL $ / (t) sin сот di == -^=r cs (v) (со = 2nv).
> (4.11-56)
Действительные функции cc (v) = &'c [/ (/)] и cs (v) = ^"s [/ (/)] называются
соответственно косинус-преобразованием Фурье и синус-преобразованием Фурье
функции f (t). Часто косинус- и синус-преобразованием Фурье называют вместо
этого Сс (со) и Cs (со).
4.11-4. Функции, разложимые в ряд Фурье и представиМые интегралом Фурье.
Гармонический анализ (примеры см. в табл. 4.11-1).
(а) Ряд Фурье или интеграл Фурье, порожденный действительной
функцией f(t), абсолютная величина которой интегрируема на соответствующем
интервале разложения /,
1) сходится к ~ "о" на каж^ом открытом интервале,
где функция f(t) и ее производная f (t) кусочно-непрерывны (п. 4.4-7, с);
при этом на каждом замкнутом интервале, в котором функция
непрерывна, ряд Фурье равномерно сходится к /(/);
2) сходится равномерно к f (/) на каждом таком интервале (а, Ь) с:
cz (а—6, b + Ь) с/, где 6 > 0, что на (а —6, b + Ь) функция f (t)
непрерывна и имеет ограниченную вариацию (п. 4.4-8, Ь);
3) сходится к
f (t - 0) + f(t + 0)
на каждом открытом интервале,
содержащемся в /, на котором функция f (t) имеет ограниченную
вариацию (признак Жордана).
Напомним, что функция f (t), ограниченная и имеющая конечное число
относительных максимумов, относительных минимумов и точек разрыва первого
рода на некотором конечном интервале (условия Дирихле, п. 4.4-8, Ь), является
на этом интервале функцией ограниченной вариации.
(Ь) Гармонический анализ периодических функций.
Пусть f (t)—действительная периодическая функция с периодом Г (п. 4.2-2, Ь),
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.11-4,
Т/2
для которой существует интеграл \ | / (т) | dr. Тогда
— Т/2
со
/ (0 = 4 ^ + И (а* cos Ы*1 + Ь* sin teo*> = I] ckeik^f=
fc=l £ = —00
00
= co + 2 2 lc*i cos ^^ + ar£ c*).
fc=l
Г/2
a* = f 5 /(*) cos fa»0T</т fa)0 = y-, 6 = 0, 1, 2, ...V
— 772
Г/2
2 Г
bk — f \ f (T) s*n £<*>oT ^»
-7-/2
Г/2
(4.11-6)
— T/2
на каждом открытом промежутке, на котором / (/) и /' (/) кусочно-непрерывны,
если в каждой точке разрыва /(/) по определению положить
/(0 =
f (t - 0) + f(t + 0)
(см. также п. 4.4-8, Ь). Таким образом, функция / (t) представлена в виде
суммы
1) постоянного члена (а0/2)=Со (среднего значения функции /(/),
см. также пп. 4.6-3 и 18.10-9) и
2) некоторого множества синусоидальных членов (синусоидальных
компонент) с частотами v0=l/T (основной частоты), 2\0 = 2/Т (2-й
гармонической частоты), 3v0 = 3/r (3-й гармонической частоты),...
k-я гармоническая компонента 2 | с^ | cos [k -y- + argCfc) имеет частоту kv0 =
= k/T, круговую частоту кщ = 2nkv0 = 2nk/Tt амплитуду 21 сь \ = V ak + Н и
«фазу> arg ck = — arctg (bk/ak).
Нечетные гармонические члены в разложении (6) описывают антипериодическую
часть функции / (/) (п. 4.2-2).
Отметим, что
Т/2 со со
</"> = Jr $ [Мх)]-Л—1-eJ + i 2 («1 + *©- 2 |<*|2, <411-7>
— Г/2 fc=l /?=—со
«глы интеграл в левой части равенства существует {теорема Парсеваля, см. также
п. 15.2-4). В табл. 4.11-1 приведены коэффициенты Фурье и средние значения квадрата (7)
некоторых периодических функций. По поводу численного гармонического анализа см.
п. 20.6-6.
4,11-4.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
151
Таблица 4.11-1
Коэффициенты Фурье и среднеквадратические значения
периодических функций
Периодическая функция,
f (О = f{t + Т)
Коэффициенты Фурье
Среднее
значение.
<f> =
2
Среднее
квадрати*
ческое
значение,
</2>
Прямоугольный
импульс
йа
•--»$•№)•
2 2
&-=0
'"£-
Симметричный
треугольный
импульс
Ёкк.
2 2
ап=А
п
fnT0
К2Т
2Т
ЗГ
лЬ±Ьх
Симметричный
цеидальный
импульс
'Jffift
X s
Г/i (Го- 7\)
2 2 2 2
X s
2Т ] Х
To-hTt
,.27-0 + 7'
27"
ЗГ
Полусину
соидаль-
ный
импульс *)
■#EUL
ад = Л-/-Х
■MiPP-O]
+
чн"-+ф
л Л 7"
& =0
Л*
2Г
*) При Гв= L. = IL.f (/)= -1 А [~ + ~- cosa)/-b j cos2u)r- 1 cos 4со* +
4-^cos6a)/
-•)
«детектированная» синусоида.
При Т0 = Т » -~, f (0 - -1 Л (i- + 4" cos 2со* - ~ cos 4й)* + -^ cos бсо/ — ..Л
«выпрямленная» синусоида.
№2 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.11-4.
Таблица 4.11-1 (продолжение)
Периодическая функция,
fW = /H T)
Коэффициенты Фурье
Среднее
значение,
2
(П =
Средне-
квадрати-
ческое
значение,
<f2)
Срезанная
синусоида
4h
II
тт/К
Ж±2.2&у2
Ал ' о
[(Я+ !)-£-] _
х
+ S
— 2 cos
X
2^
£J от
wo
w tti
со|со ^
+
Треугольная форма
сигнала
II
л ля* J
j4_
2
3
(с) Функции, представим ые интегралом Фурье.
Пусть /(^—действительная функция, для которой существует интеграл
+ 00
j |/(T)|rfT. Тогда
+ со
+ с»
/(/)= [ c(v)e2nivtdv = ~ [ С (со) <?*«>'Жо =
+ со
= ^ J Q(G))<?l4o'dfG>,
+ со
c(v)= J / (т) e-M«ivT dx,
+ 00
С(ш)=тУ S 'w^'lS-
>л2л
+ 00
Q(cd)= J /(T)^G)tdT = c(-|i) (g> = 2jiv)
(4.11-8)
на каждом открытом интервале, на котором / (/) и /' (г) кусочно-непрерывны,
если в каждой точке разрыва / (t) по определению положить
/(0-/(,-°> + /(, + °>.
4.11-4.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
153
Функция /(/), имеющая преобразование Фурье c(v), называется обратным
преобразованием Фурье .F"1 [с (v)] функции с (v); при данных предположениях,
если функция / (/) непрерывна, равенство (8) определяет ^_1 [с (v)] однозначно.
Равенство (8) можно переписать в различных формах, например:
-|- со -{-со -f-°°
/ (/) = -— \ d<o [ f (х) cos о (/ — т) dx = ]/ £. С | с (©) | cos [©/ + arg С (©)] d® =
— со — со О
+ со
«2 V [Л (v) cos 2nv/ + В (v) sin 2nvt] dv (о = 2nv). (4.11-9)
О
Действительные функции А (V) и В (V) в (9) соответственно являются
косинус-преобразованием четной части (п. 4.2-2) функции f (/) и синус-преобразованием нечетной
части функции f(t):
+ 00
^(v)=g(V>+2g<-V)^yc[/(0+2f(-/)]^ J "Deo.*™*.
-В(1)-^^-У,[
У (Q - / (- о
— со
+ 00
■]-J
> (v^O) (4.11-10)
f (т) sin 2лvt dx,
с (v) = с (— v) = A (v) — /В (v).
А (V) = 0, если функция f (t) нечетна, а В (v) == 0, гели функция f (t) четна (см. также
п. 4.11-3, Ь).
Представление интегралом Фурье описывает функцию / (t) как сумму бесконечно
малых синусоидальных компонент с частотой v или круговой частотой (О = 2nv (v ^ 0);
функции 2 | с (v) j nargc(v) соответственно определяют амплитуду и фазу этих
синусоидальных компонент.
Отметим, что с (— v) = ~c (v), С (— ©) = С (о) и что
+ СО +00 + СО
J [f (т)]8 dx = J | с (v) I* dv - J |C (o) I* do,
— CO — CO — CO
(4.11-11)
если интеграл в левой части равенства существует (теорема Парсеваля; см. также
табл. 4.11-2).
(d) Функции более общего типа могут быть представлены в виде суммы функции (8)
и некоторого множества периодических функций (6), так что у них существуют как
сдискретный спектр», так и «непрерывный спектр» (см. также п. 18.10-9). Рассмотрение
рядов Фурье и интегралов Фурье может быть формально унифицировано с помощью
введения обобщенного преобразования Фурье (п. 18.10-10).
(e) Теорема Пэли — Винера. Пусть <р (о) — действительная неотрицательная функ-
со
ция, определенная при — со< © <со, и J <р2 (о) d® существует. Для того чтобы суще-
— со
ствовала действительная или комплекснозначная функция f (t), равная нулю при t ^ О
и такая, что ее преобразование Фурье С (о) удовлетворяет условию
I С Ш I =
Y2n
О
5'
(t)e
-Ш
dt
=» Ф (о).
необходимо и достаточно, чтобы интеграл \
I 1пф((о) 1
1 +о2
da> был сходящимся.
Примечание. Теорему Пэли — Винера для преобразования Фурье в комплексной
области см. в п. 7.6-5.
Таблица 4.11-2
Свойства преобразования Фурье
<см. также п. 4.11-3 и табл. 8.3-1)
Пусть
+ оз __
JT (f (/)] === J / (t) e" 2nivt dt=c (v) = /2я С (2jw),
— 00
+ 00 + 00
— 00 —00
+ co
У с Cf (0] =2 J f(t) cos 2nv/ A = cc (v),
0
4-00
Л1/01-2 J /<0sin2nv*<rt=*s(v)
0
и предположим, что рассматриваемые преобразования Фурье существуют.
(a) SF [a h (О + Э f» (01 - а У Ifi CO] + 3 У U* <0] <лы«еи«остб).
■^[TTOJ-M-vh
^" [f (аО] e "JT * ("Тг) Са>0) (теорема масштаба, теорема подобии),
У U (* + *)3 = e2JUVTc (v) (теорема о сдвиге).
(b) Если функция f (t) непрерывна, то из у [/ (t, а)] -+ У [f (*)] при а -* а
следует f (t, а) -* f (/) (теорема непрерывности). Аналогичные теоремы справедливы
и для косинус- и синус-преобразований Фурье.
(c) У ft <0] ^ [ft tf>] = У ft <*) * f, (/)].
где
1 (01 У ft (')] = У if 1 0) * fi (01. 1
У ft (0 f, (О] - jr ft (0] X jr ft (0] J (wwwie fi w" ° wm" >•
+ oo -J- oo
/l (/) # f8 (0 - J f 1 (t) f, (/ - T) <*T a J ft (* - T) f, (T) rfT
+ 00 +00
ci (v) X *a (V) = J c, (A,) c2 (v — k)dk= J ^ (v — A,) *8 (X) dA,
— oo —oo
(n. 4.6-18).
p if (t) cos 2nv„/] = i- [c (v - v0) + с (v + Vo)],
^ [f (/) sin 2JIV./] = i- [C (V - V0) - С (V + Vo)]
> (теорема о модуляции).
(d) ^ l(f(n(t)] » <2n/v)r ^ [f (/)] (r = 0, 1. 2. ...)
(теорема о дифференцировании),
если предположить, что производная f(r) (0 существует при всех t и что все
производные меньшего порядка при 11 | -*> + оо стремятся к нулю.
+ оо +оо
(e) Если интегралы J | ft (t) |8 dt и J | ft (t) Iя Л существуют, то
— оо — оо
+ оо + оо
J У ft (01 У ft (01 dv = J Л (О ft (О Л (теорема Парсеваля).
— 00 — 00
4.11-4.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ 155
Таблица 4.11-3
Преобразования Фурье
00
f(/)==_J_ С C((0)emtd(0
V2n J
~ 00
1 fit)
^ (а>0)
etat, p<t<g,
0, t<p, t>q
0, / < 0
«—Р'я (Rep>0),
<f-'2/s
cos a/», (a > 0)
sin a/2
l/f* (0<Res<l).
11 j-Vt
«-«I'l
Г7— <a > 0)
ch at
sh a/ ^ ^ v
5П5 -*<«<«
— 00
C(0))
0, 1 (0 | > a
/ eiq (a-©) ^'p (a-©)
i ' i / • w ^a»
(2л) /» © — a
1 4 — P
\ -—fr. © = a
(2Я) V»
! * I
(2л)1/* (a — © + /c)
(2p)—Vte—®f/4pt
e-©V2
У©2 я \
(2a)-Vte Va 4J(
(i)I/fr (1 - ^.Ш (i-.я)|«|«
1 ю l-Vt
[(a*-j-(Q2)1/g+ <*]'/*
(a2-b(02)1/8
/_2_Y/* cos (a/2) ch (©/2) I
\ я / ch © + cos a
/_LV/t sin a
\ 2я/ ch © + cos a
l56 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.11-5.
Таблица 4.11-3 (продолжение)
00
f (t) = -L^ [ С (О) ***</©
Y2n J
— оо
/(0
ch at , ^ _ v
ЯП? (-я<а<я)
££ <-*<«<*>
(в» _<■)-«/.. |<|<0.
0, | ' 1 > а
sin [ft (a8+<2)'/«l
(О2— **)'/•
0, | / | > а
0, 1 * 1 > а
рп (0, m < 1,
0, | t\ > 1
оо
C((o) = -i^ f f(t)e4<otdt
Y2n J
— 00
С (о)
/ I y/i shu)
\2я/ i (ch о + cos a)
/2 y/2sin (a/2)ch ((0/2)
\ я / Mch о + cos a)
(л/2)1/! 7в (a©)
0, | о | > 6,
<n/2)Vt ,/0(aV&» — ©*J, Ко К 6
(я/2)1/! «MVc^-f^)
(Я/2)1/! У0 (|/(02_^2)
iV" Vi yn + 1/f (a»
4.11-5. Некоторые свойства коэффициентов Фурье и преобразования Фурье
(см. также пп. 4.10.1 и 8.3-1).
(a) Теорема единственности. Должным образом интегрируемая
функция /(/) однозначно определяет свои коэффициенты Фурье (26) или свое
преобразование Фурье. Обратно, полный набор коэффициентов Фурье или
преобразование Фурье однозначно определяет соответствующую функцию f(t)
почти всюду (п. 4.6-11, Ь) в интервале разложения; в частности, функция f (t)
однозначно определена в каждой точке непрерывности в интервале разложения.
Эта теорема единственности сохраняет силу даже в том случае, если ряд
Фурье или интеграл Фурье не сходятся (см. также п. 4.11-7).
Заметим, что не каждый тригонометрический ряд (даже не каждый сходящийся
тригонометрический ряд) является рядом Фурье и не каждая функция с (v) является
преобразованием Фурье (см. также п. 4.11-2, с).
(b) Операции над рядами Фурье. Пусть f(t) — функция с
коэффициентами Фурье a^, big, с ft и ф (t) — функция с коэффициентами Фурье ailt
4.11-в.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
157
Рл» Ук для одного и того же интервала разложения, и пусть X и \i —
действительные числа. Тогда функция X f (t) + \i cp (/) имеет коэффициенты
Фурье Xak-\-\iak, Xbk + V$k> ^л + МУл (почленное сложение и умножение
на число).
Почленное интегрирование ряда Фурье (2) по интервалу (/0, /), содержаще-
муся в интервале разложения, дает ряд, сходящийся к \ f (т) di. Если / (/) —
периодическая функция с периодом 7\ то эта теорема справедлива для любых
значений t0 и t.
Заметим, что эти теоремы не требуют сходимости данных рядов Фурье. По поводу
дифференцирования бесконечных рядов см. п. 4.8-4.
(с) Свойства преобразования Фурье. Наиболее важные
свойства преобразования Фурье перечислены в табл. 4.11-2 (см. также п. 8.3-1).
Примеры преобразований Фурье приведены в табл. 4.11-3—4.11-5. Значительно
более подробная таблица преобразований приведена в [8.2) и [8.7].
Отметим также, что
Ус if (О cos 2rtv0f] = ~ [сс (v + v0) + сс (v - v0)J,
Ус U (0 sin 2nv0t] - i- [cs (v + v0) - cs (v - v0)],
У& a (t) cos 2rtv0f] = -i- [c& (v + v0) + cs (v - v0)]f
Ув U (0 sin 2rtV] = 1 [cc (v - v0) - cc (v + ve)J,
Ус lfi2n (t)] = (- i)' (2nv)*r Ус U (0] - 2 Г2 (- »' (2«v)^ f'^-t/-l) <+ 0).
/=0
^c[f,2r + 1,(OJ = ("l)r(2«v)2r+15rs[/(0]-2 S (-1)/(2«у^//(1г"щЛ(+^
^[Г)(0]-2яг5Гс[Г"1,(/)]
при г = 0, 1,2, .... предполагая, что производные в левых частях равенств
существуют при 0< / < + со и что все производные меньшего порядка при t -* -J- со стремятся
к нулю.
4.11-в. Интегралы Дирихле и Фейера (см. также п. 4.11-7). Частичные суммы
п
so (0 = -g flo. sn (О — -j «• + 2 (аЛ cos * "у" ~Ь 6* sin k ~Т)
** (л-1,2,...) (4.11-12)
л— 1
и соответствующие средние арифметические о г(() = — У] «д (О (п. 4.8-6, с) ряда Фурье
п л«о
158 ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.11-в.
Таблица 4.11-4
Косинус-преобразования Фурье
00
1 / (t) = у — ^ Сс (0)) cos tot d®
\ °
1 МО
1, 0 < t < a,
0, t>a
t~s (0 < Re s < I)
cos /, 0 < / < a,
0, t > a
Г'
'""
cos(t<2)
sin (| /.)
(1-*2>\ 0</<l,
0, t > 1
(Rev>-1)
00
Сс (со) = |/ — J f (0 cos at dt
0
Cc (a»
/ 2 y/8 sin «a
\ Я / 0)
(#)V*r<l-.>.ln (-«.««),.« |
/ 1 y/2 [sin a (1 - со) sin a (1 -f- ©)]
\2лУ L 1-й) + 1 + 0) J
\ Я J 1 + CD* |
J_ g-0)2/4
/0)2 Я \
. / Л й>* \
51П(т--у)
2vr (v + 1) 0) - v - V» jv + i/2 (со)
Примечания.
1) Если Сс (со) — косинус-преобразование Фурье для f (t)t то f (со) — косинус-
преобразование для CQ (t).
2) Если ПО — четная функция в интервале (—со, оо), то
косинус-преобразование Фурье для f (t) (0 < / ^ оо) есть С (со).
3) Косинус-преобразование Фурье для f (t/a), где a>0, есть а С (aco).
4.п-е,
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ 169
Таблица 4.11-5
Синус-преобразования Фурье
оо
f (t) = 1/ — J Cs (to) sin to/ dto
0
fit)
1, 0</<<z,
0, *>a
t~s (0 < Re s < 2)
e~t
tn~xe~at {a > 0)
te-ty*
sin /
t
0, 0 < / < a.
(/2 _ ai)Vtt t > a
/ (1 - /»)\ 0 < l < 1.
(Rev>-1)
Примечания.
1) Если Cs (о) — синус-преобразо
образование для Cs (t).
2) Если / (/) есть нечетная фуню.
зование Фурье для / (/) (0</<оо) ест
3) Синус-преобразование Фурье ДJ
оо
Cs (to) = y^- ) f (0 sin to/ dt
0
Cs (to)
(—У/* 1 — cos ato
\ я j to
(±y/.r<l-.)cos(4«.)»«
/ 2 y/, to
\я/ 1 + to2
f-—V/f (n - 1)! (a* + to8)- "/2 X
x sin (n arctg co/a)
to*-*>2/2
(2я)~1/2 1п|-1±^|
1 1 — to 1
(-£)■'• j.<a»>
2vr(v+ l)to-v-1/8yv+8/a((o)
вание Фурье для f (/), то / <co) —сннус-пре- !
;ия в интервале (— оо, со), то синус-преобра- 1
ь iC (to).
1я f (//а), где а > 0, есть a Cs (ato). j
ГЛ. 4. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 4.11-7.
(2) можно записать в виде
к го
— Г/2 sin "f 0 sin -уг
(-?<'<£: »=о.1.2....).
(4.11-13)
/*. я ?V 2 Г/. /(<_т) + п< + т) /s,„ я f I
rfT
(4. И-14)
- Г/2 \ sm Т / 0 \ S,"T
(_I<r<I:«-i.s....)
(см. также интегральную формулу Дирихле, п. 21.9-4, Ь).
4.11-7. Суммирование средними арифметическими.
(а) Частичные суммы ряда Фурье функции / (/) могут не представлять собой
полезных приближений функции / (/). Это, в частности, может случиться, если
ряд расходится или если эти частичные суммы «отходят» от функции /(/)
вблизи ее точки разрыва (неравномерная сходимость вблизи точки разрыва,
явление Гиббса). В этом случае можно прибегнуть к суммированию средними
арифметическими (п. 4.8-6, с).
Каждый ряд Фурье (2) суммируем средними арифметическими к функции
f(t) при всех t в интервале ( — Г/2, Г/2), для которых функция f (t), непрерывна;
в точках разрыва первого рода средние арифметические сходятся к
2 (теорема Феиера). Средние арифметические сходятся к / (/)
почти всюду в интервале разложения; они сходятся к / (/) равномерно на
каждом таком интервале (a, b) cz (а — 6, Ь-\-Ь) с: ( — Г/2, Г/2), где 6>0, что
функция /(/) на (а —б, Ь + д) непрерывна.
(в) Точно так же% если существует интеграл \ \ f (т) | d % и функция
— оо
/(/) непрерывна всюду, то средние арифметические
ТШ№ S C^)e^d^l ] f(t + T)bjL\dx (4.11-15)
О -| -со \ Т /
равномерно сходятся при X -> + оо к функции f (t) на каждом ограниченном
интервале. Если функция / (/) равномерно непрерывна на всем интервале
(—со, +оо), то и равномерная сходимость распространяется на интервал
(—со, +со).
4.11-8 Кратные ряды и интегралы Фурье.
(а) Если задана /г-мерная область разложения, определяемая неравенствами
aj<tj<aj+T/, /=1, 2, ... пУ то кратный ряд Фурье, порожденный
функцией f (tlt /2, ..., /„), для которой существует интеграл
■l+rIel+ri
S I ••
аг °*
ап+Тп
■ ] 1/(т„
"п
т2, ..
,., д-Л,^, .
.. uint
4.11-8.
4.11. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ
161
по определению есгь
ОО ОО 00
ck k ...* ехр
2ш / kf -zr
/=1
2 2-2
2==_oo *„=-
<
ья = т т !.. тп S $ ••• J /(Ti. T2 Tn) X 1(4.11-16)
Й1+Г1а2+Г2 *Л+ГЛ
X exp
-2ш У
^ kfT,
/ = i
rfxi ^/t2 ... di„
(b) Кратный интеграл Фурье, порожденный функцией / (flt t2t..., /,,),
для которой существует интеграл
+00 -{-СО -г°°
J J ... j |/(ть т2(...,тл) idin й(т2...а(тл,
—оо —оо —оо
по определению есть
I -j-oo -|-oo -f*°°
п/Ш $ J - J C(u)l* "*•-• Шл)ехр
i 2©^/
L /-i
flfa),du)2... flf(on,
i +oo -f-co -f-oo
С(а)1(С02, ...,(0„)= (i/KZ\n J J — J /(Ti, Та,...,Тл)
X
X exp — г ^ ®/T/ dTidx2... dxn.
[(4.11-17)
Как и в равенстве (4), можно ввести vy=©y/(2n). Для областей
интегрирования, определяемых неравенствами 0 < /у < + оо или — оо < /у < 0, по аналогии
с п. 4.11-3 получают кратные синус-и косинус-интегралы Фурье.
(с) Если задана область разложения — оо < tx < + со, а2 < /2 < л2 + ?Y
то для функции / (/1( t2) можно получить «смешанное» разложение Фурье:
. -j-oo -j-oo ./ 2я*2\
j +оо Ог+Гг _ / 2лт2\
^(0)!)=—/=- J J /(ть та)* \lTl т* ) dxxdx»
1 2Г *Л _'оо о.
-оо а2
} (4.11-18)
Аналогично можно скомбинировать интегралы Фурье и ряды Фурье (а также
синус- и косинус-интегралы Фурье) и в случае более чем двух измерений,
(d) Показательные функции в (16), (17) и (18) с помощью равенств (21.2-28)
могут быть представлены в виде суммы синусов и косинусов. Все теоремы
пп. 4.11-2 — 4.11-7 могут быть обобщены на случай кратных рядов и интег*
ралов Фурье.
6 Г. Корн и Т. Кора
ГЛАВА 5
ВЕКТОРНЫЙ АНАЛИЗ
5.1. ВЕКТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
В каждом классе векторов (например, перемещений, скоростей, сил, нап-
ряженностей магнитного поля) можно определить операции, известные как
сложение векторов и умножение их на (действительные) скаляры (п. 5.2-1),
а также как скалярное умножение векторов (п. 5.2-6). Классы векторов,
встречающиеся в геометрии и физике, чаще всего связаны с двух- или
трехмерным евклидовым пространством.
1. Векторы любого класса допускают однозначное представление
в виде перемещений (т. е. направленных отрезков) в геометрическом
пространстве. Это представление сохраняет соответствие между
суммами векторов, произведениями их на скаляры и скалярными
произведениями векторов (см. также пп. 12.1-6 и 14.2-1 — 14.2-7).
2. В большинстве приложений векторы появляются как функции
точки в геометрическом пространстве (вектор-функции точки, п. 5.4-1).
Такие векторы, как скорости и силы, обычно впервые определяются на
геометрическом языке как «величины, обладающие длиной и направлением»,
или, несколько точнее, как величины, которые могут быть представлены
в виде направленных отрезков, складывающихся по «правилу
параллелограмма». Такой геометрический подход, общий для большинства
элементарных курсов, использован в пп. 5.2-1 и 5.2-8 при введении основных
операций над векторами. Рассмотрение векторов с более общей точки зрения дано
в п. 12.4-1 и в гл. 14.
Векторный анализ изучает векторные (и скалярные) функции. Любой
вектор может быть задан набором числовых функций (координат вектора) в
соответствующем базисе (пп.5.2-2, 5.2-3, 5.4-1 и 6.3-1).
Замечание. Описание физического состояния векторными величинами следует
рассматривать не только как способ сокращенной записи системы координатных
уравнений одним уравнением, но и как пример математической модели, элементы которой не
ограничиваются числами. Заметим также, что класс объектов, допускающих взаимно
однозначное соответствие с классом направленных отрезков, может и не являться
векторным пространством, если у него нет описанных выше алгебраических свойств.
5.2. ВЕКТОРНАЯ АЛГЕБРА
5.2-1. Сложение векторов и умножение вектора на (действительный)
скаляр. Векторная сумма а + b двух векторов а и b одного класса есть вектор,
соответствующий геометрической сумме соответственных направленных
отрезков (правило параллелограмма). Произведение вектора а на действительное
число (скаляр) а есть вектор, соответствующий направленному отрезку,
в | а | раз более длинному, чем отрезок, соответствующий вектору а, и
направленному в случае отрицательного а в сторону, противоположную вектору а.
Нулевой вектор О каждого класса векторов соответствует перемещению
нулевой длины; и а -\- 0 = а.
5.2-4.
5.2. ВЕКТОРНАЯ АЛГЕБРА
163
Определенные таким образом сложение векторов и умножение их на
скаляры удовлетворяют соотношениям:
a + b = b + a; а + (Ь + с) = (а + Ь) + с = а + b + с; )
а (ра) = (аР) а; (а + Р) а = аа + pa; a (a-f b) = aa + ab; У (5.2-1)
la = a; (—l)-a = —a; 0a = 0; a —a = 0; a + 0 = a. J
Обобщение векторной алгебры см. пп. 14.2-1 — 14.2-4.
5.2-2. Разложение векторов по базисным векторам, т векторов ах, а2, ..., ат
линейно независимы, если из
Mi + Мг + ••• + hm*m = О
следует
A-i =: А-2 == • • • == А^| = U.
В противном случае эти векторы линейно зависимы (см. также пп. 1.9-3
и 14.2-3). Любой вектор а трехмерного векторного пространства может быть
разложен по трем линейно независимым векторам е^ е2, е3, т. е. представлен
в вцде их линейной комбинации
а = axet + а2е2 + а3ез- (5.2-2)
Коэффициенты аъ а2, а3 называются координатами вектора а по отношению
к базису, определенному базисными векторами ех, е2, е3 (см. также п. 14.2-4).
Если базисная система задана, то векторы а, Ь, ... представляются
упорядоченными тройками (аъ а2, а3), (Рь р2, Рз)» ••• их координат; при этом
а + b и оса представляются соответственно тройками (аг -\- рх, а2 + Р2, а3 + Рз)
и (аах, аа2, аа3). Соотношения между векторами могут быть выражены через
соответствующие системы соотношений между их координатами.
Векторы, принадлежащие двумерному векторному пространству (например,
плоские перемещения), представляются подобным образом упорядоченными
парами координат.
Для разложения векторов, определенных в данной точке пространства (п. 5.4-1),
обычно выбирают базис, связанный с используемой координатной системой. В гл б
специально рассматривается разложение векторов по векторам локального базиса,
направленным по координатным линиям криволинейной системы координат в каждой точке
и перпендикулярно к ним; величины и направления векторов локального базиса, вообще
говоря, различны в различных точках. Формулы преобразования координат вектора,
заданных в различных базисах, даны в табл. 6.3-1 и в п. 14.6-1.
5.2-3. Декартовы прямоугольные координаты вектора. Если в пространстве
задана правая прямоугольная система декартовых координат (п. 3.1-4), то
единичные векторы (п. 5.2-5) i, j, k осей Ох, Оу и Oz соответственно
образуют удобную систему базисных векторов. Координаты ах, ау, а2 вектора
a — axi-±-ayj-\-a2k (5.2-3)
называются декартовыми прямоугольными координатами вектора а.
Заметим, что эти координаты
ах = а • i, Qy = а • j, a2 = a-k
(п. 5.2-6) являются проекциями вектора а; координаты м- \, u «j, и • к любого единичного
вектора и являются его направляющими косинусами (п. 3.1-8).
5.2-4. Векторы и физические размерности. Векторы можно умножать не только на
безразмерные скаляры (например, постоянный вектор скорости умножают на интервал
времени, чтобы получить вектор перемещения). Если физическая величина есть вектор (2)
или (3), то ее физическую размерность целесообразно приписать координатам вектора,
а не базисным векторам. При этом последние рассматриваются как безразмерные
величины и могут быть использованы в качестве общей базисной системы для различных
классов векторов, имеющих различные физические размерности (например^ перемещения,
скорости, силы и т. п.; см. также п, 16.1-4).
6*
164
ГЛ. 5. ВЕКТОРНЫЙ АНАЛИЗ
Б.2-5.
5.2-5. Модуль (норма, абсолютная величина, длина) вектора. Модуль
| а | вектора а в евклидовом пространстве есть скаляр,
пропорциональный длине перемещения, соответствующего вектору а (п. 5.1-1; абстрактное
определение см. пп. 14.2-5 и 14.2-7). Модуль вектора удовлетворяет
соотношениям (1.1-4). Вектор, модуль которого равен 1, называется единичным
вектором или ортом. (Попарно перпендикулярные) базисные векторы i, j, k
(п. 5.2-3) являются единичными, так что
I a J I = I Ду 1 > I gj/i 1 = I ау I ♦ I в Л = I «* I.
|a| = V4 + eJ + eS.
5.2-6. Скалярное (внутреннее) произведение двух векторов. Скалярное
произведение а • b [другое обозначение (а, Ь)] двух векторов а и b есть
скаляр
а -Ь= | а | |b|cosv, (5.2-5)
где у — угол между векторами а и b (абстрактное определение см. пп. 14.2-6
и 14.2-7).
Если а и b — физические величины,то физическая размерность скалярного
произведения а • b должна быть указана (см. также п. 5.2-4). В табл. 5.2-1
Таблица 5.2-1
Свойства скалярного произведения
(а) Основные соотношения:
ab = Ьа; а(Ь + с)
а-а — а2 = | а |2 ^ 0;
= a-b -f- a
lab К
c;
|a|
(aa)
• |Ы;
b = a (a-b)
cos Y =
(Ь) Выражение в прямоугольных декартовых координатах (п.
U = j.j =kk = 1; 4 =
a'b = (V + v + ^k)'W
ax = ai> at/ = a^ аг
jk = k.i =
+ ty + b
= ak.
= 0;
,k) =
= a b
X X
+ вЛ +
'•
ab
/a2b2 '
5.2-3):
a b :
uz z'
приведены основные соотношения для скалярного произведения. Два
ненулевых вектора а и b взаимно перпендикулярны тогда и только тогда, когда
а-Ь = 0.
5.2-7. Векторное произведение двух векторов. Векторное произведение
а X b (другое обозначение [а, Ь]) двух векторов а и b есть вектор, модуль
которого равен
| а X b | = [ а | | b | sin у; (5.2-6)
его направление перпендикулярно к обоим векторам а и b и совпадает с
направлением поступательного движения правого винта при его повороте от а к b
на угол, меньший я. Два вектора линейно зависимы (п. 5.2-2) тогда и толькв
тогда, когда их векторное произведение равно нулю. В табл. 5.2-2 приведены
основные соотношения для векторного произведения. Более общее
определение векторного произведения см. п. 16.8-4; в пп. 3.1-10 и 17.3-3 даны
представления площади области как вектора.
(5.2-4)
5.2-8.
5.2. ВЕКТОРНАЯ АЛГЕБРА
Свойства векторного произведения
165
Таблица 5.2-2
<а) Основные соотношения:
а х b — — b x а; а х (Ь + с) = а х b + а х с; (аа) х b = а (а х Ь);
а К а = 0; а • (а х Ь) = b . (а х Ь) = 0.
Ь) Выражение в любом базисе et, е2, е3:
| а = a^t + а2е8 + а3е3; b = 3^ + fl2ef -f- 03e8,
a x b =
e2 x ей ai |3i
e3 X e, a8 |32
oi X e2 a3 08
с) Выражение в прямоугольных декартовых координатах:
i х 1 = j х j = к х к = 0, I x j = к, j x к = i, к x i = 1;
л X Ь =
i i к
ax Qy Qz
b b b
x у z
a a a a a a
"y uz z x x у i
=
i +
1 J +
b b
z x 1
b b
x у
k =
= (aybz - azby) ' + («A ~ axbz) J + (°xby ~ ayhx) k'
5.2-8. Смешанное (векторно-скалярное) произведение.
а • (b X с) == [abej = [bca] = [cab] = — [bac] = — [cba] = — [acb], (5.2-7)
fabc]2 = [(a X b) (b X c) (c X a)j = a2b*c2 - a2 (b • c)2 — b2 (c . a)2 — c2 (a . b)2 +
■f- 2 (a- b) (b-c)(c- a) =
a • a a • b a • с
b« a b- b b- с
с • a c« b с • с
(определитель Грама, см.
п. 14.2-6),
[abc; [def] =
ad a • е а • f
bd b-e b-f
c« d c«e c« f
(5.2-8)
(5.2-9)
В любом базисе elf е2, е3 (п. 5.2-2, см. также пп. 5.2-3 и 6.3-4)
labc]=
«i Pi Yi
<*2 P2 Y2
«з h Ys
[e, e2 e3].
(5.2-10)
В правой системе декартовых прямоугольных координат
labcj
tty Ьу Су
az bz cz
(> 0, если векторы a, b, с
образуют правую тройку).
(5.2-И)
166
ГЛ. 5. ВЕКТОРНЫЙ АНАЛИЗ
5.2-9.
5.2-9. Другие произведения, содержащие Солее двух векторов.
а х (Ь х с) - Ь (а . с) - с (а . Ь) - | (а *Ь) (a ^ | (5.2-12)
(двойное векторное произведение),
(а х Ь) • (с X d) = (а • с) (Ь . d) — (а • d) (b . с) =1 * '* * '* |> (5.2-13)
I а • с b • d 1
(а X b)2 = a2b2 — (а • b)2t (5.2-14)
(а х Ь) X (с х b) = [acd] b — [bed] a = [abd] с — [abc] d. (5.2-15)
5.2-10. Разложение вектора а по направлению единичного вектора и и ему
перпендикулярному:
а = u (a . u) + ux(axu). (5.2-16)
5.2-11. Решение уравнений ([abc] ф 0).
(а)
(сха)
[abc]
(b) x • а = р, \
х.Ь = <7, К Х=^Р (Ьхс) + Я (сха) + г (axb).
х • с = г, J
(c) ах + Ъу + сг + d t= о,
Ldbc]. [adc]. labd].
(5.2-17)
(5.2-18)
(5.2-19)
(5.2-20)
* [abc]'* У [abc]; Z [abc]'
(d) (bxc) x + (cxa) 0 + (axb) г + d = 0,
— d ♦ a t __ d • b d • с
x~~ [abc]'* ^~ [abc]1 г e [abc]'
5.3. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА
5.3-1. Векторные функции и их пределы. Векторная функция v = v(t)
скалярного аргумента t ставит в соответствие каждому значению аргумента t из
области определения (см. также п. 4.2-1) одно (однозначная функция) или
несколько (многозначная функция) «значений» вектора v. В прямоугольных
декартовых координатах
v = v (0 = 0* (0 \ + vy (t) i + v2 (t) k. (5.3-1)
Вектор-функция v (0 ограничена, если ограничен ее модуль |v(/)|. Она
имеет предел vx= lim v (0, если для каждого положительного числа е суще-
ствует такое число б, что из 0 < 11 — tx | < б следует | v (0 — vx | < е (см. также
пп. 4.4-1 и 12.5-3). Если lim v(t) существует, то
lim v (0 = i lim vx(t) + \ lim vv(f) + k ^m M0- (5.3-2)
t-*tt t-+tt t-*tt y t->tt
Предел суммы векторов, скалярного и векторного произведений находится по
формулам, аналогичным формулам п. 4.4-2.
Вектор-функция v (0 непрерывна при t — tlt если lim \{t) = \(t{) (см. также
пп. 4.4-6 и 12.5-3).
5.3-2. Дифференцирование. Векторная функция v (0 дифференцируема при
данном значении ?, если существует конечная производная (см. также п. 4.5-1):
*W_lim vtf + ^-vtf). (5.з.з)
Если производная d?v/dt2 от dv/dt существует, она называется второй
производной от v(0, и т. д. Табл. 5.3-1 содержит основные правила
дифференцирования.
5.3-3. 5 3. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА 167
Таблица 5.3-1
Дифференцирование векторной функции скалярного аргумента
(а) Основные правила:
d r „v . ,.,v, dv , dvt
-rfr[v(0±w(/)]--5r±-sr
-jf Ca v (/)] = a —- (a = const);
-^f U (0 v </)] - -|f v (0 + f (t) -£f ; -jf [v (t) . w (/)] =
rfv
w +v
d r ,. ,. n dv , dw
-Ж fv «> x w ('>1 = "ЗГ x w + v x 7Г
d r. .... dv df
4[v.()»«)M0] = [|™] + [v|.] + [vwl].
(b) В прямоугольных декартовых координатах
dv {t) dvr (t) dv.. it)
•4—^7-J +
dt
dt
dt
dw
dt ;
(с) Если базисные векторы et (t), e8 (0. e3 (0 — функции от/и v (t) =ax (0 et (t) +
+ a, (0 e2 (0 + a3 (0 e3 (/), то
dv (/) / dat . da* . da3 \ , f det . de2 . de3 \
Аналогичные правила применимы к вычислению частных производных dv/dtlt
dv/dt2t ... векторной функции v = v(^, t2t ...) от двух или более скалярных
аргументов t1% t2, ...
Замечание. Если v° (0 *- орт вектора v (t):
v (/) - | v (0 J v° (/).
dv° . dv d | v | . . . . dv° d \ v \
v° -f a) XV,
(5.3-4)
где вектор w направлен (по правилу правого винта) вдоль оси, вокруг которой
поворачивается вектор v (0, и имеет длину, равную угловой скорости поворота вектора v(0 по
отношению к t. (Пример: вектор угловой скорости в физике; см. также п. 17.2-3).
В формуле (4) первое слагаемое характеризует изменение длины вектора v (t), а второе
слагаемое — изменение его направления. Если | v (/) | = const, то векторы v (t) и dv/dt
перпендикулярны.
5.3-3. Интегрирование и обыкновенные дифференциальные уравнения.
Неопределенный интеграл V (/) = J v (t) df от векторной функции v (t) определяется как решение
векторного дифференциального уравнения (см. также п. 9.1-1):
d
dt
V (О = v <f).
(5.3-5)
которое можно заменить системой дифференциальных уравнений для координат вектора
V(0- Другие обыкновенные дифференциальные уравнения, содержащие производные от
векторной функции скалярного аргумента, трактуются подобным же образом.
Определенный интеграл
Г у (t) dt = lim
a 6-0
n
/=1
ЛИ'*-*l-l).
где
a = t0<tt </2<... <tn = b
и tt_± < xt < t.; d = max | ti — t._t \
(см. также п. 4.6-1), может быть выражен через координаты
Ъ Ь Ь b
J v (0 dt = i J vx (0 dt + j J v (0 tf/ + k J ^ (0 tff.
(5.3-6)
(5.3-7)
168
ГЛ. б. ВЕКТОРНЫЙ АНАЛИЗ
5.4-!.
5.4. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
5.4-1. Вводные замечания. Конец этой главы посвящен скалярным и
векторным функциям точки в евклидовом пространстве. Если не оговорено
противное, скалярные и векторные функции предполагаются однозначными,
непрерывными и дифференцируемыми достаточное число раз. Соотношения
между скалярными и векторными функциями устанавливаются:
1) в инвариантной форме (независимо от системы координат) и
2) в координатной форме по отношению к правой прямоугольной
декартовой системе координат (п. 5.2-3), так что1)
F(r)==F(*, у, z)==Fx(x, уу z)\+Fy(xt у, z)\+F2(x, у, г) к. (5.4-1)
Соотношения в пп. 5.4-2—5.7-3 не зависят от выбора системы координат
в пространстве. Запись векторных соотношений в локальных базисах систем
криволинейных координат рассматривается в гл. 6.
5.4-2. Скалярные поля. Скалярное поле есть скалярная функция точки
Ф(г) = Ф(*, у, z) вместе с областью ее определения. Поверхности
Ф(г)==Ф(лг, у, 2) = const (5.4-2)
(п. 3.1-14) называются поверхностями уровня поля; они позволяют
представить поле геометрически.
5.4-3. Векторные поля. Векторное поле есть векторная функция точки
F(r)=F(*, у, z) вместе с областью ее определения. Векторные линии (линии
тока) в каждой точке (г) имеют направление вектора поля F (г) и
определяются дифференциальными уравнениями
drxF(r) = 0 или тг-т-^ г=__^ - = —*!—_ (5.4-3)
v ' ?х(х, у, z) Fy(x, у, z) F2{x, у, z) v '
Векторное поле F (г) может быть представлено геометрически своими
векторными линиями, относительная плотность которых в каждой точке (г)
пропорциональна .модулю | F (г) |.
5.4-4. Векторный элемент линии и длина дуги (см. также п. 4.6-9).
(a) Векторный элемент линии (дифференциал радиуса-вектора) dv вдоль
кривой С, описываемой уравнениями
г=г(0 или J y = y(f)% (5.4-4)
1 z = z(t\
определяется в каждой точке (г) = [*(/), y(t), z(i)\ формулой
dr = dxi+dy} + dzk = (£i+%] + §k)dt=%^dt. (5.4-5)
Вектор dv направлен по касательной к кривой С в каждой регулярной точке
(см. также п. 17.2-2).
(b) Длина дуги s спрямляемой кривой (4) (п. 4.6-9) выражается формулой
s = ids,
Г.
где
А.уЛ.+^+Л._У(^)'+(й1+(?)1л-
=£d<=K5FTdF=-j/fTf<« (5.4-6)
в каждой регулярной точке (г) = [х(1)» У (0» 2 (01 кривой С.
*) Всюду в гл 5 и 6 индексы в обозначениях F F F ... не указывают на
дифференцирование по х% у, г, ...
5.4-6.
5 4 СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
169
5.4-5. Криволинейные (линейные) интегралы (см. также п. 4.6-10). Для
спрямляемой дуги С, заданной уравнением (4), скалярные интегралы
$Ф(г)£Й= $Ф(*, у, z)ds=\Q>\x(t), y(t)t 2(0] jjj-Л.
С С С
\F(T)-dv= ^Fx(x, у, z)dx + Fy(x, у, z)dy + Fz(x, yt г) dz =
с с
(5.4-7)
можно определить непосредственно как пределы сумм тем же способом, что
и в п. 4.6-10; однако более удобно подставить функции х (/), у (/), г (/)*,
dx/dt, dy/dt, dz/dt из формул (4) в формулу (7) и интегрировать по /.
Подобным же образом определяются и векторные криволинейные интегралы:
J Ф (г) dx — i J Ф {xt у, г) dx + j J Ф U, #, z) dy + k J Ф (*, #, г) dz =
С С С С
= § Ф (г) -L dt = ^ I Ф <*, ^/, z) ~ I + Ф (дс, |/, 2) ^ j + Ф (*, у, г) ~ к\ dt, (5.4-8)
С С
\ F (r)xdr= ^ F (г)Х^у <// =
С С
ei ]iry<"-r,*V) + il(r£dx-Fxdz) + k \(Fxdy-Fydx) =
с
Значение скалярного или векторного криволинейного интеграла зависит
от пути интегрирования С, если только не выполнены специальные условия
п 5.7-1.
Применение криволинейных координат см. пп. 6.2-3 и 6.4-3.
Замечание. Часто оказывается полезным в качестве нового параметра в
выражения (7), (8), (9) ввести длину дуги s с помощью формулы (6).
5.4-6. Поверхностные интегралы (см. также пп. 4.6-12 и 17.3-3,с).
(а) В каждой регулярной точке двусторонней поверхности, заданной
уравнением r=r(w, v) (п. 3.1-14), можно определить векторный элемент
поверхности (вектор площадки)
«-(£х&)*«*-
-[ai-£fe)'+(e^-w^)i+(w#-*e)k] *"»■ (5.4-ю)
В случае замкнутой поверхности координаты ы, v на поверхности обычно
упорядочивают так, чтобы направление вектора dS (направление
положительной нормали к поверхности, п. 17.3-2) было внешним по отношению к телу,
ограниченному данной поверхностью.
Элемент площади поверхности в точке (и, v) определяется так:
dS--
1^4 ^£1*1 do.
(5.4-11)
В частности, при u — xt v=y, z = z(x, у)
170
ГЛ. 5. ВЕКТОРНЫЙ АНАЛИЗ
5.4-7
(Ь) В дальнейшем предполагается, что площадь \ dS (п. 4.6-11) рассма
1'
триваемой поверхности S существует; в этом случае формула (10) определяет
элемент d$ почти всюду на 5 (п. 4,6-14,Ь). Скалярные поверхностные
интегралы
j<D(r)dS и JF(r).dS (5.4-13)
и векторные поверхностные интегралы
$(D(r)dS и JF(r)XtfS (5.4-14)
от функций Ф (г) и F (г), заданных на поверхности, могут быть определены
непосредственно как пределы сумм так же, как в пп. 4.6-1, 4.6-10 и 5.3-3.
Однако удобнее применить формулу (10), чтобы выразить каждый
поверхностный интеграл через двойной интеграл по координатам и, v (см. также
п. 6.4-3,Ь). Иногда в формулах (13) и (14) вместо одного знака интеграла
пишут два, например ((ф(г)^. Скалярный поверхностный интеграл
F (г) • dS называется потоком вектора F (г) через поверхность S. Заметим,
i
что
J F(*, t/, 2).dS = ^Fx\x(y, 2), у, z]dydz +
+ $$М*- У1*> 2)' z\dxdz + [[Fg[x9 у, z(x, y)]dxdy. (5.4-15)
В первом интеграле независимые переменные и = у, v = z, во втором
интеграле u — z, v — x и т. д. (см. также формулу (12)).
Формально к такому же результату приводит запись dS = dy dz i -f-
-\-dzdx \-\-dx dyk, но она требует специальных оговорок относительно смысла
dx, dyt dz.
5.4-7. Объемные интегралы (см. также п. 4.6-12). Если дана область V
в трехмерном евклидовом пространстве, то скалярный объемный интеграл
\<b(r)dV = ^<b(xt у, z)dxdydz (5.4-16)
и векторный объемный интеграл
\?(T)dV = l\l[Fx(x, у, z)i + Fy(x9 у, z))+F2{x, yy z)k]dxdydz (5.4-17)
могут быть определены как пределы сумм тем же способом, что и в п. 4.6-1;
они могут быть также выражены непосредственно через тройные интегралы
по х, yt z. О применении криволинейных координат см. пп. 6.2-3,b и 6.4-3,с.
5.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
5.5-1. Градиент, дивергенция и ротор; инвариантные определения.
Градиент скалярной функции точки Ф(г)==Ф(*, у, z) есть векторная функция
точки, определяемая формулой
I Ф (го dS
grad Ф (г) = УФ == lim ^— , (5.5-1)
6-»>0 J dV '
Б.5-2.
5.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
171
где Ух — область, содержащая точку (г), 5х —замкнутая поверхность,
ограничивающая область Vi, 6 —наибольшее расстояние от точки (г) до точек
поверхности Si.
Дивергенция векторной функции точки F (г) есть скалярная функция
точки, определяемая формулой
div F (г) == V • F = lim Zi—
б-о Jdv
(5.5-2)
Ротор векторной функции точки F (г) есть векторная функция точки,
определяемая формулой
J dSxF(Tl)
rot F (г) ее VXF= limii_ . (5.5-3)
6-0 J dV
Замечание. В каждой точке, где существует вектор grad Ф (г) ф 0, его модуль
IVOI
vm+m+m
(5.5-4)
равен наибольшей производной по направлению dO/ds в этой точке, а его направление
совпадает с направлением, в котором эта наибольшая производная достигается (п. 5.5-3,с).
Векторные линии поля grad Ф определяются уравнениями
</гХУФ = 0 или dx\dy\dz-
дФ t дФ ф дФ
" дх * ду * дг'
(5.5-5)
Линии градиента, определяемые этими уравнениями, перпендикулярны к
поверхностям уровня (5.4-2).
5.5-2. Оператор V. В прямоугольных декартовых координатах линейный
оператор V (набла) определяется формулой
di+£i+T*b-
'дх
(5.5-6)
Его применение к скалярным и векторным функциям точки формально
соответствует некоммутативной операции умножения на вектор с декартовыми
координатами д/дх, д/ду, д/дг:
VO(*. у, z) = grad(D(*, у. *) = ^i+gj+*fk,
dFv dFu dF9
V-F(*, у, z) = divF(*, ^, *) = _*+ " + -^,
dy
VxF(jc, y, z)==rot F(jc, y, z) =
(dFz dFy\ (dFx dFz\ (dFy dFx\
^ \dy~~~~dz~) i +\Tz IT J i + \d7~w)k==
(O.V)<D-0,g+0,S + 0.g.
(o.v)p-e,^+ofj£.+e.S-
дх ду дг
Fx Fy Fz
дх
Jydy
= (G • \FX) i + (G • VF„) ] + (G • VFZ) k.
В таблице 5.5-1 приведены правила действий с оператором V.
(5.5-7)
172 ГЛ. 5. ВЕКТОРНЫЙ АНАЛИЗ 5.5-3.
Таблица 5.5-1
Правила действий с оператором V
(а) Линейность (а = const)
V (Ф + ЧГ) = VO + V^; V (аФ) = а УФ;
V . (F + G) = V • F + V • G; V • (aF) = а V • F;
V X (F + G) = V X F + V х G; VX (aF) = a V x F.
(b) Действия с произведениями
V (ФЧО = W УФ + Ф V4P";
V (F . G) = (F • V) G + (G • V) F -f F X (V X G) -f- 0 X (V X F);
V • (OF) = Ф V • F + (УФ) • F;
V • (F X G) = G • V X F — F • V X G;
(G • V) OF = F (G . УФ) + Ф (G • V) F;
V x (OF) = OV X F + УФ x F;
V x (FxC) = (G • V) F - (F • V) G + F (V • G) - G (V • F);
(G . V) F = ~ [V x (F x G) -f V (F . G) - F (V . G) + G (V • F) -
- Fx(VXG) -
- G X (VXF)].
Заметим, что векторные соотношения, содержащие уФ, V-F_h VXF, не зависят от
ора системы координат. Вырал - — - —
координат см. в гл. 6 и п. 16.10-7.
выбора системы координат. Выражение операций УФ, V'F и VXF в различных системах
'6.10-7
5.5-3. Полный дифференциал, полная производная и производная по
направлению.
(a) Полный дифференциал йФ скалярной функции точки Ф (г),
соответствующий перемещению точки dv ~dxi-\-dy j + dzk, есть
dO = ^dx + ^dy + ?£dz = dr.grad<b = idr'V)<l> (5.5-8)
(см. также п. 4.5-3,а).
(b) Полная производная d(fr/dt функции Ф(г) вдоль кривой г = г(/) есть
скорость изменения функции Ф (г) по отношению к параметру /, когда г
изменяется как функция от / (см. также табл. 4.5-2,а):
йФ дФ dx . дФ dy , дФ dz (dx „\m /с с Q\
где г = г(/) или x = x(t), y = y(t), z = z(t).
Замечание. Если функция Ф явно зависит от /, т. е. Ф = Ф (г, /), то
£-(£•*)•+£•
(c) Производная по направлению dO/ds от скалярной функции точки Ф (г)
есть скорость изменения функции по отношению к величине перемещения s
точки (г) вдоль выбранного направления. Если направление задано единичным
вектором u = cos ax i+ cos ay j + cos <хг к с направляющими косинусами cos <xx,
cos ay, cos az (п. 3.1-8, а), то производная по этому направлению равна
йФ дФ , дФ , дФ . г-7\ лч /г г 1, \
^■ = -gFC0sajc+ а7 cosa</ + ~dj cos az = (u . V) Ф; (5.5-11)
d(b/ds есть полная производная от функции Ф (г) по длине дуги s кривой,
касающейся вектора u = dr/ds.
5. Б-в.
Б.5 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
173
(d) Полный дифференциал, полная производная и производная по
направлению от векторной функции точки F (г) определяются аналогично:
dF*=(dr -\) F = (dr -\) Fxi+ (dr -\) Fy l + (dr -V)Fgk =
= dFxl + dFyl + dF£k,
di
i +
dF dFz
d¥
ds _(u • V) F = (u • V) Fx i + (u • V) Fy j + (u . \)FZ k =
ds
ds
(5.5-12)
5.5-4. Производные высших порядков по направлению. Ряд Тейлора. Производные
порядка п от функций Ф и F по направлению единичного вектора и определяются
формулами
dn dn
dsh ф (г) = (и ' V)/* ф (г) и din F (Г) = (U ' ЮП F (гК (5.5-13)
Если рассматриваемые ниже ряды сходятся, то (см. также п. 4.10-5)
Ф (г + Аг) = Ф (г) + (Аг • V) Ф (г) Н--^- (Аг • V)2 Ф (г) + . . . =
= е(Лг' V) Ф(г) = Ф (г) -|- Аг ^ Ф (г) + i (Ar)2 AL ф (г) + .... (5.5-14а)
F (г + Дг) = F (г) Н- (Аг . у) F (г) + — (Аг . V)2 F (г) +
= е(Аг • V) F (г) = F (г) + Аг £- F (г) + ~ (Аг)2 — F (г) +
(5.5-НЬ)
(5.5-16)
где все производные по направлению берутся в точке (г) в направлении Аг, а Дг = | Аг|.
5.5-5. Оператор Лапласа. Оператор Лапласа (лапласиан) V2 = V«V
(обозначаемый иногда через А) выражается в декартовых прямоугольных
координатах формулой
^•^£+£+5 (5.5.15)
(другие выражения см. гл. 6 и п. 16.10-7). Этот оператор может быть
применен к скалярным и векторным функциям точки с помощью
некоммутативного скалярного «умножения»:
™=(£+£+£) ф <*.»..И
V2F = \2FX i + 4*Fy j + V2FZ k. J
Заметим, что
У2(аФ + Р^)==а V2(D + p V2^ (линейность), (5.5-17)
V2 ((!>¥) = ¥ У2Ф+2 (V<D) • (VY) + <D V2¥. (5.5-18)
5.5-6. Операции второго порядка. Отметим следующие правила
повторного применения оператора V:
div grad Ф = V • (\Ф) = V2<D,
graddiv F = V (V • F) = V2F + Vx(VxF),
rot rot F = Vx(VxF) = V(V-F)-V2F, £ (5.5-19)
rot grad Ф = V x (\Ф) = О,
divrotF = V-(VxF) = 0.
174
ГЛ. 5. ВЕКТОРНЫЙ АНАЛИЗ
5.5-7.
5.5-7. Операции над простейшими функциями от г. В табл» 5.5-2 и 5.5-3
приведены результаты применения дифференциальных операций к
некоторым простейшим скалярным и векторным функциям от радиуса-вектора г.
Таблица 5.5-2
Операции над скалярными функциями
(/•е=|г|, а = const, п = 0, ± 1, ± 2, ...)
ф
а • г
, гп
VO
а
/1-2
пг г
г
7*
У2Ф
0
п {п + 1) гп~*
1
г2
Операции над векторными функциями
Таблица 5.5-3
1 F
г
а X г
агп
vrn
alnr
V • F
3
0
nrn~2 (r • a)
(n + 3) rn
г • a
Г
V X F
0
2а
nrn~2 (rxa)
0
rxa
r2
(G • V) F
G
a X G
nrn~2 (r • G) a
+ nrn~*X
X (r • G) г
(G • г) а
r2
V2F
0
0
л (л+ 1) X
X rn~2 a
л (/г + 3) X
X rn~2 r
a
7»
V (V • F)
о
0
nrn~2a + j
+ л (л-2) rn~4 X
X (r • a) r
л (л -f 3) /-n-2r
a 2 (r • a) r
r2~ r*
Дополнительные формулы могут быть получены с помощью табл. 5.5-1. Отметим
еще формулы {F (r). v} r==F (r)> (5 5.20)
V^-=-Vx^ при a = const. (5.5-21)
5.5-8. Функции от двух и более радиусов-векторов» В типичном случае двух
радиусов-векторов г =3 (х, у, z) и о == (£, т|, £) к функциям вида Ф (г, Q )==Ф (л:, #, z\ |, tj, £),
F (г, Q) == F (*, у, z; |, Т), £) могут быть применены два различных оператора у:
В частности, имеем
ф (г - о) = - v0 Ф (г — о), -j
F(r-Q) = -VQF(r-o), I
<F(r-o)=-VQXF(r-o). j
(5.5-22)
Б.6-1.
5.6. ИНТЕГРАЛЬНЫЕ ТЕОРЕМЫ
175
5.6. ИНТЕГРАЛЬНЫЕ ТЕОРЕМЫ
5.6-1. Теорема о дивергенции *) и связанные с ней теоремы.
(а) В табл. 5.6-1 собраны важнейшие теоремы, связывающие объемные
интегралы по области V и поверхностные интегралы по границе S этой
области. Область V предполагается ограниченной и пространственно-односвяз-
ной (п. 4.3-6), поверхность 5-— замкнутой и регулярной (п. 3.1-14), функции —
однозначными и непрерывными в V и на 5, причем все частные производные,
Таблица 5.6-1
Теоремы, связывающие объемные и поверхностные интегралы
1. Теорема о дивергенции
2. Теорема о роторе
3. Теорема о градиенте
| 4. Теоремы Грина
5. Частные случаи
J V • F (г) dV = J dS • F (г)
V S
JVXF(r)dV=JdSxF(r)
V S
\ J V Ф (r) dV = J dS Ф (r)
V S
J V<D • VW dV -j- \ЧГ V20 dV = J dS . (W V<D) =
V V S
s !
J OF V2<D — Ф V240 dV = J dS - (ЧГ VO - Ф V4T) =
-1 (»&-£)«
5
\ \2Ф dV = \ dS • VO = [ -|~ dS (теорема Гаусса),
V S S
J , VФ I8 <*V 4- J Ф У2Ф d7 == J dS • (Ф УФ) =
V V S
S
встречающиеся в объемных или поверхностных интегралах, предполагаются не-
прерывными соответственно в V или на S. Все теоремы остаются справедливыми
и для неограниченной области, если подынтегральные функции в поверхностных
интегралах имеют порядок 0(\/г3) при г—"со (п. 4.4-3). Формулы для
поверхностных и объемных интегралов в системах криволинейных координат см. гл. 6
и п. 17.3-3; приложения см. пп. 15.6-5 и 15.6-10.
Словесная формулировка теоремы о дивергенции (теоремы Гаусса-Остро-
градского) такова. Поток вектора через замкнутую поверхность (п. 5.4-6) ра-
вен интегралу от дивергенции по объему, ограниченному этой поверхностью.
(Ь) Замечание о нормальной производной. Нормальная
производная от скалярной функции Ф (г) в регулярной точке поверхности S
*) Эта теорема в отечественной литературе называется теоремой Гаусса — Остро»
градского.
176
ГЛ. 5 ВЕКТОРНЫЙ АНАЛИЗ
5.6-2.
есть производная по направлению положительной нормали, т. е. dS (если
поверхность замкнута, то обычно берут внешнюю нормаль, п. 17.3-2).
Нормальная производная обозначается обычно через дФ/дп, так что
a^-rfS==(rfS.V)<I>.
5.6-2. Теорема о роторе и связанные с ней теоремы. Если векторная
функция F (г) однозначна и имеет непрерывные частные производные всюду в
конечной поверхностно-одиосвязнон области V и если лежащая в области V
поверхность S односвязна, регулярна и ограничена регулярной замкнутой
кривой С, то
\ dS • |VxF (г)] =ф dv • F (г) {теорема Стокса), (5.6-1)
т. е. криволинейный интеграл от F (г) по замкнутому контуру С равен по-
току ротора VxF через поверхность, натянутую на контур С. Ориентация
вектора площадки dS должна быть согласована с ориентацией контура С по
правилу правого винта. (Точнее, такая ориентация производится у края
поверхности, а затем продолжается по непрерывности.)
При тех же условиях, что и выше,
J (dSxV)XF (r)=&drxF (г), (5.6-2)
S С
и для любой однозначной скалярной функции Ф (г) с непрерывными частными
производными в области V
WSxVO(r) = &tfr Ф(г). (5.6-3)
Формулы (1), (2), (3) остаются справедливыми и для неограниченной области V, если
подынтегральная функция в криволинейном интеграле справа имеет порядок О (1/г*) при
г —• оо (п. 4.4-3).
5.6-3. Поля с разрывами на поверхностях (см. также п. 15.6-5, Ь). Пусть скалярная
функция Ф (г) или координаты векторной функции F (г) непрерывно дифференцируемы
по обе стороны от регулярной поверхности 5Ь но разрывны на Si, причем существуют
предельные значения как на одной (положительной) стороне поверхности
Ф+ (г) или F+ (г),
так и на другой (отрицательной) стороне поверхности
Ф_ (г) или F_ (г).
В каждой точке (г) поверхности St определим функции
п° (г) [Ф+ (г) — Ф._ (г)] (поверхностный градиент)» \
п° (г) • [F+ (г) — F_ (г)] (поверхностная дивергенция), К (5.6-4)
n° (r)x[F+ (г) — F_ (г)] (поверхностный ротор), J
где п° — орт положительной нормали к поверхности St в точке (г) (п. 17.3-2). Тогда ин-
тегральные теоремы табл. 5.6-1 останутся в силе и для таких функций, если в точках
поверхности St заменить в объемных интегралах градиент, дивергенцию и ротор на их
поверхностные аналоги.
5.7. ОТЫСКАНИЕ ВЕКТОРНОГО ПОЛЯ ПО ЕГО РОТОРУ
И ДИВЕРГЕНЦИИ
5.7-1. Безвихревое векторное поле. Векторное поле F (г) называется
безвихревым в обласги Vy если в каждой точке этой области
VxF(r) = 0,
т. е.
°!jL JH = dFi J'lL = -*_^£ =о
дг ду дх дг ду дх
(5.7-1)
5.7-3.
5.7. ОТЫСКАНИЕ ВЕКТОРНОГО ПОЛЯ
177
Поле F (г) является безвихревым тогда и только тогда, когда —F (г) есть
градиент \Ф (г) некоторой скалярной функции точки Ф (г) в каждой точке
области V (см. также формулу (5.5-19)); в этом случае выражение
F (г) -dr==Fx (*, у, z) dx + Fy (х, у, z) dy+F2 (*, у, z) dz =s
гЕЕ — flfr • \Ф (г) == — dQ) (5.7-2)
есть полный дифференциал (п. 4.5-3, а). Функцию Ф (г) часто называют
скалярным потенциалом безвихревого векторного поля.
Если область V псверхностно-односвязна (п. 4.3-6. Ь), то Ф (г)—
однозначная функция, определяемая по F (г) с точностью до аддитивной постоянной,
и криволинейный интеграл от F (г) по кривой С, лежащей в области V, не
зависит от пути интегрирования:
$Р(р).</р = -[Ф(г)-Ф(а)]. (5.7-3)
а
В этом случае указывают только нижний и верхний пределы интегрирования.
Криволинейный интеграл $F(p)«flfp по любому замкнутому пути С
(циркуляция вектора F (г) вдоль С) в области V равен нулю. Если область V
многосвязна, то функция Ф (г) может быть многозначной.
В частности, условие
dFx dFy
W—Ш-^О (5-7-4)
необходимо и достаточно для того, чтобы криволинейный интеграл
1 Р* <*'
у) dx + Fy (x, у) dy
не зависел от пути интегрирования, т. е. чтобы подынтегральное выражение было
полным дифференциалом 1)
5.7-2. Соленоидальные (трубчатые) векторные поля. Векторное поле F (г)
называется соленоидальным в области V, если в каждой точке этой области
dF dF dF
V.F(r)=0, т.е. —+-^ + — = 0. (5.7-5)
Векторное поле является соленоидальным тогда и только тогда, когда
F (г) есть ротор V х А (г) некоторой векторной функции точки А (г) (см. также
формулы (5.5-19)), которая называется векторным потенциалом векторного
поля F (г).
5.7-3. Отыскание векторного поля по его ротору и дивергенции.
(а) Пусть V —конечная открытая область пространства, ограниченная
регулярной поверхностью 5 (п. 3.1-14), положительная нормаль которой
однозначно определена и непрерывна в каждой точке поверхности.
Если дивергенция и ротор поля F (г) определены в каждой точке (г)
области V, то всюду в V функция F (г) может быть представлена в виде суммы
безвихревого поля ?г (г) и соленоидального поля F2 (г):
F(r) = F!(r) + Ft(r)
ГА6 VxF!(r)=0; V-F2(r)
(теорема разложения Гельмгольца).
=о } (5-7"6)
1) См. сноску к п. 5.4-1.
178
ГЛ. 5. ВЕКТОРНЫЙ АНАЛИЗ
Б.7-3.
Функция F (г) определяется однозначно при дополнительном условии
задания нормальной составляющей F (г) • -r^sP ФУнкЧии *ЧГ) в каждой точке
поверхности S (теорема единственности).
Эффективное отыскание функции F (г) по этим данным сводится к решению
дифференциальных уравнений с частными производными при некоторых краевых условиях.
Важный частный случай, в котором
V.F(r)=0, VXF(r)=0,
и, значит, всюду в V
F (г) = — VO (г), У2Ф (г) =s О,
рассматривается в теории потенциала (пп. 15.6-1—15.6-10).
(Ь) Если в каждой точке (г) пространства заданы функции
V . F (г) = 4я Q (г); V X F (г) = 4я I (г), (5.7-7)
то формулы (6) определяют ?г (г) и F2 (г), а следовательно, и F (г),
однозначно с точностью до такого слагаемого F0 (г), для которого V2F0(r) = 0.
Имеют место следующие формулы:
Fi(r) = -V<D(r),
F2(r) = Vx A (r),
0{r) = l-2M-idvt \ (5.7-8)
где интегралы справа (скалярный и векторный потенциалы) предполагаются
существующими (см. также п. 15.6-5); интегрирование производится по всем
точкам (р) пространства.
ГЛАВА 6
СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
6.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
В главе 6 дается описание скалярных и векторных функций точки
(см. также пп. 5.4-1—5.7-3) в криволинейных координатах (п. 6.2-1).
Векторы будут разложены по направлениям координатных линий или
перпендикулярно к ним (пп. 6.3-1—6.3-3). Применение криволинейных координат
упрощает многие задачи; например, можно выбрать такую систему координат,
чтобы на координатной поверхности рассматриваемая функция была
постоянной (пп. 6.4-3 и 10.4-1, с).
Основное внимание в гл. 6 уделяется ортогональным системам координат
(пп. 6.4-1—6.5-1), как наиболее важным для физических приложений.
Представление векторных соотношений в неортогональных координатах
рассмотрено более подробно в тензорном анализе (гл. 16).
6.2. СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
6.2-1. Криволинейные координаты. Система криволинейных координат,
заданная в области V трехмерного евклидового пространства, ставит в
соответствие каждой точке (*, у, г) упорядоченную тройку действительных чисел
я1,-*2, х31). Криволинейные координаты х\ х2, х3 точки (х, у, г) ~ (я1, х2, х3)
связаны с ее прямоугольными декартовыми координатами х, у, г формулами
x1=x1(xt у, г), x2 = x2(xt у, г), *» = *»(*, у, г), (6.2-1)
где функции (1) всюду в V однозначны и непрерывно дифференцируемы,
д (х1 х2 х3)
причем якобиан -^р—'—^ Ф 0 {допустимые преобразования, см. также пп.
4.5-6 и 16.1-2).
Система координат х1, х2, Xs будет декартовой (п. 3.1-2; но, вообще говоря, не
прямоугольной) в том и только в том случае, когда все уравнения (1) линейны.
6.2-2. Координатные поверхности и координатные линии. Условие xi =
— х1(х, у у 2) = const определяет координатную поверхность. Координатные
поверхности, соответствующие различным значениям одной и той же координаты
х\ не пересекаются в V. Две координатные поверхности, соответствующие
различным координатам х\ xJ, пересекаются по координатной линии,
соответствующей третьей координате xk. Каждая точка (х, у, z) = (л:1, х2, х3) из V
может быть представлена как точка пересечения трех координатных
поверхностей или трех координатных линий.
6.2-3. Элементы длины дуги и объема (рис. 6.2-1; см. также пп. 6.4-3
и 17.3-3).
(а) Элемент длины дуги ds между двумя «соседними» точками (х, у, z) =
= (**, х2у х3) и (x + dx, y + dyt z + dz) = (xi + dxl, x2 + dx2, x3 + dx3) задается
*) Значки 1, 2, 3 в обозначениях xlt х2к х* не являются показателями степени;
см. также пп. 16.1-2 и 16.1-3.
180 ГЛ. 6. СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ в.3-1.
квадратичной дифференциальной формой
з з
ds2 = dx2 + dy2 + dz2 = J? 2 £'* (**» *2» **)dx% d*k> (6-2~2)
/ = i k = l
где
(/, /г=1, 2, 3).
Функдии giki*1* x2, x3) — компоненты метрического тензора (п. 16.7-1).
Рис. 6.2-1. Элементы координатных линий, поверхностей и объема в системе
криволинейных координат.
(Ь) Шесть координатных поверхностей, соответствующих точкам (х1, х2, х3)
и (x1 + dx1, x2 + dx2, x3 + dx3) (рис. 6.2-1), ограничивают элемент объема
(параллелепипеда)
dv=дд£: £ %)dxi ^ d*> <6-2-3)
где
(см. также пп. 5.4-7, 6.4-3, с, 16.10-10). Система координат называется
правой в области V, если касательные векторы к координатным линиям х1, х2,
х3, ориентированные в сторону возрастания соответствующих координат (что
определяет положительные направления координатных линий), образуют
правую тройку (как и орты i, j, k правой декартовой системы координат). Для
правой системы координат якобиан д (х> у> z)/d (x1,x2,x3) = \fg > 0.
Описание векторных элементов линий и поверхностей в криволинейных
координатах см. пп. 6.4-3, 17.3-3 и 17.4-2.
6.3. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ ВЕКТОРА
6.3-1. Координаты вектора и локальный (местный) базис. В гл. 5
векторные функции точки были разложены по базису i, j, k системы декартовых
координат; модуль и направление каждого вектора этого базиса одни и те же
в каждой точке. Если векторная функция F (г) описывается в
криволинейных координатах х1, х2, х3, то удобнее применять локальный базис из
векторов, касательных к координатным линиям в каждой точке (х1, х2, х3) или
перпендикулярных к ним. Такие базисные векторы сами являются векторными
функциями точки. В каждой системе криволинейных координат можно
указать три способа выбора локального базиса (пп. 6.3-2 и 6.3-3).
6.3-t.
6.3. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ ВЕКТОРА
181
Таблица 6.3-1
Соотношения между базисными векторами и координатами
векторов в различных локальных системах отсчета
(а) Соотношения между i, j, k и векторами локальных базисов i., е-, е1 системы
криволинейных координат х1, х2, л:3:
X !_е.- е -—-i + -^-i + -2 к-
' VTa V 1~дх< +dxii + dxlK
дх1 . дх' дх1 .
е* = -~~ i -f- /- j + ~- к (' = 1.2, 3),
дх * ду * дг • • " |
3 3 3
1- уд*1 i^r.i.- у -а*ч= у дх.*к
jLi дх у *" l Ld дх l jL дх'
/ = 1 1 = 1 1 = 1
3 3 3
<-2f^=2^-2£"- \
/=i / = i ;=1
3 3 3
"2^'.-2^--2S--
/=1 /=1 /=1
(Ь) Соотношения между F F F физическими координатами F-, контрава-
риантными координатами F. и ковариантными координатами F1 в системе
криволинейных координат х1, х2, х3:
ri У g" ' дх х^ ду У^ дг г*
Р .= *LFx +Д^+Др (/ = 1.2,3).
1 дх' х дх' У дх' г
Р _ \^А__\ dX-F'- X^F
х jL dxi V*u jL dxi jL dx lt
/=i /=i /=i
3 A 3 3
F - X дУ Fl - \ ^ Fl - X ^ F
у 2ddxi VTa 2d dxi 2d дУ l'
/ = 1 1 = 1 1 = 1
з л з з
V* dz Fi \У dz i \i dx
г ~ 2d ^ v^ii ~~ 2d ^ ~~ 2L ~э*~l
/=1 i = l i = l
182
ГЛ. 6. СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
6.3-2.
Таблица 6.3-1 (продолжение)
(с) Соотношения между векторами локальных базисов и координатами векторов
в двух системах криволинейных координат (базисные векторы и координаты векторов
для системы хх, х2, х3 отмечены чертой сверху, см. также п. 16.2-1);
3 3
i, = -
1
Vi
efc; e
&kk
/=i *=i
1. 2, 3),
з
k-vt;^: ^=2#f<: ?*-2-ё-"'(*-,'2-8)-
/=i
- = у V дх] дхН
Zik £ ^ d-i d~k
gJh
a, k = \, 2, з).
/=1 Л = 1
6.3-2. Физические координаты вектора. В качестве векторов
локального базиса в каждой точке (х1, х2, х3) = (г) выберем единичные векторы
\г (х1, х2, х3), i2 (л:1, x2t x3)t i3 (х1, x2t х3), касательные к координатным
линиям х1, х2, х3 (см. также п. 16.8-3).
Каждая векторн_ая функция
F (г) == F (х1, х2, х3) может быть
однозначно представлена в виде
F(r) = F(*i, *2, *з) =
-Aii+Ali+^A (6.3-1)
в каждой точке (г) = (л:1, х2, х3).
Физические координаты
Р1 = Р1(х\ х\ х3),
F2 = F2(x\ х\ х3), Н6-3-2)
Р* = Рь(х\ х\ х3)
Координ. линия х 2
Координ. линия х1
Рис. 6.3-1. Разложение вектора F по
единичным векторам ilf i2, i3; физические
координаты Flt F2, F3 вектора.
вектора F и локальные базисные
векторы \г (х1, х2, х3), \2 (х1, х2, х3), i3 (х1, х2, х3) могут быть выражены
непосредственно через координаты Fx, Fyt Fz того же вектора и орты i, j, k
прямоугольной декартовой системы координат (см. табл. 6.3-1).
Заметим, что функции -J= —. Г7== ^т. Г7== ~^Т являются
направляющи а*" У^ид/' V^udx1
щими косинусами орта ц (т. е. i-й координатной линии) по отношению
к осям Ох, Оу> Ог (см. также рис. 6.3-1).
в.3-3. Контравариантные и ковариантные координаты вектора. В качестве
локального базиса можно также выбрать либо тройку векторов
ei (х1, х2, х$) £з YJTi ill «* (**, х\ х*) s= V17i
е, (х\ х*, хя) =з YlTs is,
направленных по координатным линиям, либо тройку векторов
'I
(6.3-3)
е1 (*», х2, х3) ==
etxe8<
[eie2e8]'
е* (л:1, х2г хя) гэ
е» X et .
[eie8e83'
е3(^ х2'х9)^Ь^г (6-3-4)
в.4-1. 6.4. СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ 183
направленных перпендикулярно к координатным поверхностям. Каждый вектор F (г)
может быть представлен в одной из следующих форм:
F (г) = F (*i, х2, хя) = F*et + F2e2 + F*ea = /^е1 -j- F2e2 + F9e* (6.3-5)
в каждой .точке (г) == (Jt1, х2, х3). Как модули, так и направления базисных
векторов е, и е1 меняются от точки к точке, за исключением того случая, когда х1, х*,
Xs — декартовы координаты (п. 16.6-1,. а). .
Контравариантные координаты F1 =з F1 (х1, х2, х3) == F • е1 и ковариантные
координаты F. == F; (х1, х2, хя) == F • е. (/ = 1, 2, 3) в системе координат хх, х*, х* и
соответствующие базисные векторы е. и е1 могут быть выражены непосредственно через
F , F , F и орты i, j, k прямоугольной декартовой системы координат (табл. 6.3-1).
Отметим еще формулы (см. также пп. 16.6-1 и 16.8-4):
е2 X е3 __ ез X е1 _ е* X е».
Cl ~ [е^е*] ' е* ~ [е^е*]' е* ~ [е^е^"]' (6,d"6)
[eie2e3] = [е^е»]-1 » [М,!,] У gng2,g,8 = ± /"И (6.3-7)
/— ь ( 1 при i ==■ k,
«* •е* = «i*; I ч I = Кг,-,-; Vе = { 0 при (. Ф k_ (6.3-8)
В частном случае прямоугольных декартовых координат х1 = х, х2 ^ у, *3 =г г имеем:
et = е* = lj = I; еа = е* = i2 == ]; е3 = е* = 13 = к. (6.3-9)
Главное преимущество представления векторов в контравариантных и
ковариантных координатах заключается в относительной простоте соотношений, связывающих
эти координаты в различных системах координат (табл. 6.3-1; см. также п. 6.3-4).
6.3-4. Запись векторных соотношений в криволинейных координатах.
Каждое векторное соотношение, записанное в гл. 5 в прямоугольных
декартовых координатах, может быть записано в криволинейных координатах с
помощью табл. 6.3-1. Если рассматриваемое соотношение содержит производные
или интегралы, то следует учитывать, что базисные векторы в системе
криволинейных координат сами являются функциями точки.
Многие практически важные задачи допускают применение системы
ортогональных координат (п. 6.4-1). В этом случае формулы пп. 6.4-1—6.4-3 и
табл. 6.4-1—6.5-11 дают сравнительно простое выражение для векторных
соотношений непосредственно в физических координатах. В тех случаях,
когда такие специальные методы непригодны, целесообразнее применять не
физические координаты векторов, а контравариантные и ковариантные координаты;
формулировка соотношений еекторного анализа в контравариантных и ковариантных
координатах изложена подробно в гл. 16 как частный случай более общих
соотношений тензорного анализа.
В частности, применение формул пп. 16.8-1—16.8-4 для вычисления
скалярного и векторного произведений и прямой метод ковариантного дифференцирования
(пп. 16.10-1 — 16.10-8) дают выражения для дифференциальных операторов типа УФ,
V • F. V X F.
6.4. СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ. ВЕКТОРНЫЕ
СООТНОШЕНИЯ В ОРТОГОНАЛЬНЫХ КООРДИНАТАХ
6.4-1. Ортогональные координаты. Система криволинейных координат
х1, х2, х3 (п. 6.2-1) называется ортогональной, если функции gik (х\ х2, х3)
удовлетворяют соотношениям
gik№, x\ х3) = 0 при 1фк (6.4-1)
в каждой точке (я1, х2, х3). Координатные линии, а значит, и векторы
локального базиса i1( i2, i3, будут при этом перпендикулярными друг к другу
184
ГЛ. б. СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
в.4-2.
в каждой точке; каждая координатная линия перпендикулярна ко всем
координатным порерхностям, соответствующим постоянным значениям
рассматриваемой координаты.
6.4-2. Векторные соотношения.
(а) В табл. 6.4-1 приведены наиболее важные векторные соотношения в
ортогональных координатах. Функции gn=ga(x1, x2, *3) = |е,-|2 для каждой
системы ортогональных координат получают из формулы (6.2-2). В этих
формулах знаки плюс и минус относятся к правой и левой системам координат.
Таблица 6.4-1
Векторные соотношения в ортогональных координатах
(Знаки плюс и минус относятся к правой и левой системам ортогональных
координат.)
(а) Скалярное и векторное произведения
F.G = A6,+£,&, + £,&,: |F !
Из X i3 A Gi
F X G = i, X ii A Gt
Mi X it A Gz
|A бг Нг
[FGH]= F2 G2 H2
I ^8 G3 ^3
(b) Дифференциальные операторы х) (g
Vrf + FI+F*,
i2 i
«i
А А А
Gt G2 6,
A Gt Hx
A G2 H2
A G3 H9
&U&22§33)
[IlltW =±
[Ygix dxX Yg22 dx*
Yg33 дх*
"-ММ>У&)+М>-У£)+М>У1)\'
V X F ==± -—
Yg
(F-V) Ф=±
Ygxt i,
_a_
dxl
A YJTx A YIT* A YITz
А, дФ
Yg„ \2
_д_
дх*
У 5зз *з
А.
дх*
Ft дФ , F2 дФ .
\Yg7i дх* Yg22 дх* Yg33 дх*/
™<ъ = _!_ \JL l^L dJb\j>A_(YX д_ф\ _д_ (Yf_ дф\\
Ye L^1 \ «i« дх*' дх* \ *••" дхУ дх* \ ^зз дхЧУ
*) Выражение для V8F получают из формулы V2F == V (V*F) — V X (V X F) или
из правил п. 16.10-7. Выражение для (F«V) G получают из табл. 5.5-1 или из правил
п. 16.10-7.
Примечание. Формулы для VO, V • F hV X F могут быть получены и
непосредственно и? инвариантных определений п. 5.5-1, примененных к элементарному объему,
изображенному на рис, 6.2-1.
6.4-3. 6.5 СПЕЦИАЛЬНЫЕ СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ 185
(Ь) Для любой системы ортогональных координат:
'*'1* I 0 при *=^/г; I i, X ix = i2 X i2 = i3 X i3 = 0; [iii2i3J = ± 1; J
b^TFF^bVzii* Pi = VtriF* = ± -r=Fi (/ = 1, 2, 3); (6.4-3)
[eie2e3] = [eWJi = [1х1я13] К £п£22£зз = ± V~g\ (6.4-4)
Ue2 \-t3 —= ± [ r__ и н i2 h-T= Ц —
dx* dx2 dx* tySu dxi Vg™ dx* Vg™ dx*
Ч='1~+*~+*3^=±(77=*1^Л^=Ч^+^=**^). (6-4-5)
6.4-3. Криволинейный интеграл, поверхностный интеграл и объемный
интеграл (см. также рис. 6.2-1).
(a) Для спрямляемой кривой С векторный элемент линии dr имеет
физические координаты dsx — Yg\\ dx1, ds2 = V gw dx'2, ds3 = \fg33 dx3, т. е.
dr = ^ dt = dx\ + dy j + dzk = cfs1 \1 + ds2 \2 + ds3 i3 =
= Vthi dx1 \t + V&2 dx* i2 + Vg^s dx3 i3. (6.4-6)
Подходящее выражение (6) для dr должно быть подставлено в криволинейный
интеграл, определенный в п. 5.4-5. Для ортогональных координат х1, х2, х3
^Р-^^^Л^ + ЛЛ. + ^^^^Л^ + Л^+Л^Л (6.4-7)
С С С
Заметим что для любой системы криволинейных координат
dr = ei dx1 + е2 dx2 -J- e3 dx3
(см. также п. 17.2-1; для ортогональных координат х1, х2, х*
J F • dr = J Ft dx* + F2 dx2 + Fa dx» = J g^F* dx* + g22F* dx* + gisF* dx».
С С С
(b) Описание площади поверхности S и векторного элемента поверхности
dS в координатах на поверхности дано в пп. 5.4-6 и 17.3-1, В частности,
если система ортогональных координат выбрана так, что поверхность S есть
часть координатной поверхности xk = const, то координаты xi и xJ образуют
на этой поверхности систему ортогональных поверхностных координат, и
dS = Vgugjj dx1 dxi \k = dst dsf \k = ~- dx1 dxJ tk
(1Ф1ФкФг, Л = 1, 2, 3). (6.4-8)
Относительная простота получающихся отсюда выражений для поверхностных
интегралов (5.4-13) и (5.4-14) часто служит основным поводом для введения
системы криволинейных координат (см. также и. 10.4-1, с). Знак квадратного
корня в формуле (8) определяется выбором положительного направления
нормали (п. 17.3-2): знак + соответствует правой системе координат.
(с) Элемент объема dV, появляющийся в выражениях (5.4-16) и (5.4-17)
для объемного интеграла, дается формулой (6.2-3) или
dV^^ yx;z)xi) dx1 dx*dx*=± \Tgdx* dx* dx* = ± Vg11g22g^ dx1 dx* dx3^
= ± dsx ds2 ds3. (6.4-9)
Если система координат правая в формуле (9) берется знак плюс.
6.5. ФОРМУЛЫ ДЛЯ СПЕЦИАЛЬНЫХ СИСТЕМ ОРТОГОНАЛЬНЫХ
КООРДИНАТ
В табл. 6.5-1—6.5-12 даны формулы для некоторых специальных систем
ортогональных координат. В частности, для каждой такой системы
табулированы функции ga (xlt x2t х3) = | е,-12.
Таблица 6.5-1
Векторные формулы в сферических и цилиндрических координатах
(см. также рис. 2.1-2 и 3.1-2). Формулы для цилиндрических координат применимы также к полярным координатам
на плоскости Оху (п. 2.1-8)
1 Координатные поверхности
Преобразование координат
(х, у, г — прямоугольные
декартовы координаты)
Преобразование
дифференциалов координат
Квадрат элемента длины
ds* « (dr)* = dx* + dV* + dz2
Сферические координаты
r, ft, Ф (г ^ 0, 0 =< ft < я)
x* 4- У2 + 22 — г* {сферы)
х2 -\- у2 — z* Xg2 ft = 0 (конусы круглые)
у = х tg q> (полуплоскости, проходящие через
ось Oz)
•
г = ^а:* -f-^-f-2*
2 ( x = r sin ft cos ф
ft = arccos — 1
t l у = r sin ft sin ф
te © - v fsin <p y \ w = г cos ft
x \ Vx* + y2J
dx = sin ft cos <p dr -\- r cos ft cos ф dft — r sin ft sin ф dip
dy = sin ft sin ф dr -f- г cos ft sin ф tfft -\- r sin ft cos ф dq>
dz = cos ft dr — r sin ft db
ds2 = dr* -f- r2 dft2 + r* sin* ft dq>*
Цилиндрические координаты
p, ф, 2 (p > 0)
v2 + y2 = P2 (цилиндры круглые прямые)
у = л' tg ф (полуплоскости, проходящие
через ось Oz)
z = z (плоскости, параллельные
плоскости Оху)
•
' f x — p cos ф
tg<P = — fsin ф = -£-J <# = р5Шф
I 2 = 2
V 2 2
dx = cos ф dp — p sin ф </ф
d# = sin ф dp -f- p cos ф */ф
</2 = dz
flf = 1; g = о2: £ =s 1
6pp * 6фф м йгггг
Таблица 6.5-1 (продолжение)
Vg^Vgligt2S»S
Трехиндексные символы
Кристоффеля (п. 16.10-3;
символы, не приведенные
в таблице, тождественно
равны нулю)
Преобразование физических
координат вектора
1 Градиент в физических ко-
1 ординатах
дх ду ' { дг
Сферические координаты
г, ft, ф (г >: 0, 0 =< ft ^ я)
О (Г, 'О', ф)
[ft ft; г] •= — г; [фф; г] = — г sin2 ft; [фф; О] =
= — г* sin ft cos Ф
[/"&; О] = г; [гф; ф] = г sin* О; [Фф; ф] = г* sin fl cos ft
Ш = -Г: {фф} = -Г8|П**: {<р*ф} -'"«cos*
ш--^ шч= ш-*«
£„ = F^ sin 'б' cos ф -f F„ sin 0 sin ф -f- F^ cos ft
r x у я
Ра= F cos ft cos ф -f- F cos О sin ф — F£ sin О
i £ф = — F^ sin ф -f ^y cos ф
F *=F sin Ф cos ф + F^, cos 0 cos ф — F sin ф
F ев Р sin Ф sin ф 4- F^, cos ft sin ф + ^ф cos ф
F2 •= £ cos ft — F,§ sin О
дФ. 1 ЭФ . 1 дФ.
dr г + г dfl О "*~ г sin О Эф Ф
Цилиндрические координаты
P, ф, 2 (р>0)
'* d(p, ф, 2) Р
[ФФ; р] = — р; [рф; ф] = р
1фф) 1Рф] Р
Рр = Fx cos ф 4- Fy sin ф
^ф = — Fx sin ф 4- Fy cos ф
Fx = Fp cos ф — £ф sin ф
Fy = ^p sin ф 4- £ф cos ф
F = £
Г г г
дФ j , 1 дФ { дФ f
ар р+р аф Ф+а2 ^
Таблица 6.5-1 (продолжение) ►—
Сферические координаты
г, #, ф (г > 0, 0 < ф < л)
Цилиндрические координаты
р, ф, z (р > 0)
Дивергенция в физических
координатах
VF =
дх
3F
J Кл.
^ ду ^
dz
дК
■7*-w(r2pr)+ Г^Гъй (/^sin0) + 71hT5"a^
1 a(PFp) i а»ф а^
Р ^Р р dq> dz
Ротор в физических
координатах
V X F =
i j k
д д д
дх ду dz
F F F
х у г
1 \д /л ч **ъ\
г Lsin О дф dr J d+r L д^ дф J Ф
\ р дф dz / Р "*" \ dz dp / Ф
4t
а (р/ф)
йр
±5»
dф
}
Лапласиан скалярной
функции *)
V2<D =
д2Ф д*ф д*Ф
: d** ~*~ ду2 + dz*-
г* drV dry
1
г* sin fl dO
(sin*ff
1
д*Ф
'\
У п r2 sin2 ft дф?
_d_ / dO\ 1 д*Ф
dp VP dp J + p* dф* +
д*Ф
dz»
l) Лапласиан векторной функции находят по формуле V2F = V (V-F^ — V у (V х F) или по формуле (6.4-5) и по табл. 16.10-1
6.5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ 189
Таблица 6.5-2
Общие эллипсоидальные координаты X, [л, v
(а) Координатные поверхности (к > — сг > jn > — b2 > v > — а2)
*** f/2 Z2
• -f -г—- h —г— = 1 {однополостные гиперболоиды),
a2 -h jn ' b2 + [x. с2 + jn
Jt2 /У2 22
-—-■ 1- 7~l h -—-:— = 1 {двуполостные гиперболоиды).
(b) Преобразование к эллипсоидальным координатам
(a2 -f Я) (а2 + jn) (а2 + V).
(а2 — б2) (а2 — с2)
. _Ф2 + Ь) Ф* + ») ib2 + \).
У ф2 — с2) ф2 — а2)
_ (с2 + Я) (с2 + Ю (с» + у)
(с2 — а2) (с2 — Ь2) '
(c) Специальная система эллипсоидальных координат и, v, w вводится
формулами
Я - 4$> (и)
Ц = 4#> (v)
V = 4#> (ш) —
так что (см. п. 21.6-2)
dX . du dv
du = , dv -• ^
a2 + b2
3
a2 + b2
3
a2 + b2
3
d[i
+ c2
+ c*
+ c2
dw
УШ' УШ)' v7~(vj'
где f (/) = (a2 + /) (ft2 + /) (c2 + /).
mi a - А-ЮА-у) - _ pi - v) (ix - Я) _ (v - Я) (v - ц)
w SU - ~ 4/ (Ji) ' *W Af (jx) ' svv 4/ (v)
guu = 4 C#4") - #> (f)] [IP (и) - iP <«»)].
«ww = * HP <»> - P <«)] [p (w) - ip (v)].
(e) Лапласиан скалярной функции
V-Ф =7Г-^Г7Г1-^ "ST I ^<*> ^rl +
(Я — д) (я — v) ая
+ _J_£M
(JX — V) (JX -
= J_ Г 1 д*Ф 1 д^Ф
4 \{1Р (и) - р (v)] [IP (и) - IP (в>)] ди* + [р (с) - IP (w)] [ip (v) - ip (и)] dv2 +
, 1 д2Ф\
+ ИР («О - JP («)] ИР («») - JP (»)] dw*)'
190
ГЛ. б. СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
Таблица 6.5-3
Координаты а, т, <р вытянутого эллипсоида вращения
(ось Ог — ось вращения; см. также рис. 6.5-1)
Рис. 6.5-1. Ортогональная система софокусных эллипсов и гипербол с фокусами F, F'.
Эти кривые определяют систему эллиптических координат на плоскости и порождают
координатные поверхности в следующих системах координат:
1) вытянутого эллипсоида вращения (если эти кривые вращаются вокруг оси Р'ОР;
табл. 6.5-3);
2) сплюснутого эллипсоида вращения (если эти кривые вращаются вокруг оси Q'OQ\
табл. 6.5-4);
3) эллиптического цилиндра (если эти кривые смещаются перпендикулярно к
плоскости рисунка; табл. 6.5-5).
(а) Координатные поверхности (о ^ 1 >: т ^ — 1)
1 {вытянутые эллипсоиды вращения),
х* + у* z*
а* (а8— l)^afof "
Х2 -4- «2 22
2 g _2 Н—2~8 я * (двуполостные гиперболоиды вращения),
у «= х tg ф (полуплоскости, проходящие через ось Ог).
Все эллипсоиды и гиперболоиды имеют общие фокусы (0, 0, а) и (0, 0, — а);
сумма и разность фокальных радиусов в любой точке (х, у, г) равны соответственно
2ао и 2ах.
(b) Преобразование к координатам вытянутого эллипсоида вращения
х* = а* (о2 — 1) (1 — т2) cos2 <р, у2 = а2 (а2 — 1) (1 — т2) sin2 <p, z — аох.
(c) Специальная система и, v, <p вводится формулами
а =« ch и, T = cost>, Ф = Ф (0:< и < оо, 0=5 v < я, 0^ф<2я)$
при этом
х = a sh и sin и cos ф, # = а sh и sin и sin ф, 2 = a ch и cos v.
а2 — т8
(d) g — а2 -
w еаа а2 — Г
в»
, а2—т8
£фФ в °2 <°2 - О О - т2);
■*„
(е) Лапласиан скалярной функции
1
a2 (sh8 и + sin21>), g — а8 sh8 и sin2 и.
V8<D
а2 (а2 — т2)
/ д Г/л2 1. аф1 . д Г/1 ^ dV] . а*-т8 д2Ф1
{с* [<а2 - *> WJ + St L(1 - Т8) "grj + (а8 - 1) (1 -18) a^-}
6.5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ 191
Таблица 6.5-4
Координаты а, т, ф сплюснутого эллипсоида вращения
(ось Oz — ось вращения; см. также рис. 6.5-1)
(а) Координатные поверхности (о ^ 0; —1 ^ т^ 1)
Х2 _1_ ц2 22
—- -\—г—г = 1 (сплюснутые эллипсоиды вращения)
а2 (1-Ьа2) ' а2 о2
Х2 л. ц2 гг
2 __ —- = 1 (однополостные гиперболоиды вращения),
у = х tg ф (полуплоскости, проходящие через ось Oz).
(b) Преобразование к координатам сплюснутого эллипсоида вращения
х2= а2 (1 -f о2) (1 — т2) cos2 <р, у2 = а2 (1 -f а2) (1 — т2) sin2 ф; г = аат.
(c) Специальная система и, v, ф вводится формулами
о = sh и, т = cos t>, ф = ф (0^ы<оо, 0^и<я, 0^ф<2я);
при этом
х ==в о ch и sin и cos ф, # = a ch и sin и sin ф, г = a sh и cos t».
(d) R —а2 я. = а2 5 = а2 (1 + а2) (1 — т2)*
w *аа 1 -|- а2' тт 1 — т2' ФФ
5йи = gvv = а2 (sh2 " + cos2 tr)' 5фф = а* ch2 " sin2 v'
(e) Лапласиан скалярной функции
Таблица 6.5-5
Координаты а, т, 2 эллиптического цилиндра
(применяются также как (софокусные) эллиптические координаты
на плоскости Оху; см. также рис. 6.5-1)
(a) Координатные поверхности (о >: 1; —-1 ^ т :< 1)
х2 у2
~2^г + a (g2_ i\=== 1 (эллиптические цилиндры),
х2 и2
аЧ2 ^~ а2 (т2 — 1) ~ 1 (гипеРболические Цилиндры),
г = г (плоскости, параллельные плоскости Оху),
(b) Преобразование к координатам эллиптического цилиндра
х = аат, у2 = а2 (о2 — 1) (1 — т2), z = г.
(c) Специальная система и, v, г вводится формулами
о = ch и, т = cos v (0 ^ и < оо; 0 ^ с :< я);
при этом
х = а ch и cos t», # = а sh а sin v, г— г.
(d) g = а2 °2~х2 а ==& а2~~т2 g = 1:
vu/ sgg a2 — 1 ' tt 1-х2' **
*«« = 2™ = fl2 <sh2 ы + sin2 ">• *« = Ь
(e) Лапласиан скалярной функции
1 /д*Ф д2Ф\ д*Ф
~~ a2 (sh2 и + sin2 v) \ди* ~*~ di>2 J + дг*
192 гл. 6. системы криволинейных координат
Таблица 6.5-6
Конические координаты a, v, w
(a) Координатные поверхности (с2 > v2 > Ь2 > ад*)
*8 -f ^2 -(- 22 = ы2 (сферы),
х2 у2 г2
~~Т ^—г _ h2 "^—» t — 0 {конусы, ось которых совпацает с осью 02),
** и% z2
~~Т "1—21- />г "^ 2 _ г ~ ° (конусы, ось которых совпадает с осью Ох).
(b) Преобразование к коническим координатам
_^_uvw , ц» (у2 — б2) (ад2 — Ь2) , ц» (а* — с») (ад» — с»)
х ~" — 6с ' ^ б8 Ь2 — с2 * 2 с2 с2 — Ь2
(c) s =, - tf»(i;»-a»') а - «' (»' ~ »')
l/ s«tf • бг>» (а2 — £2) (2* __ сгу bww (w2 — b2) (ад2 — с2)*
Таблица 6.5-7
Параболоидальные координаты X, \х, v
(а) Координатные поверхности (А,<£<ц<Л<у)
х2 и2
* _ v + л __ д = 2г Н- Л (эллиптические параболоиды),
Н £—5 = 2г + jn (гиперболические параболоиды).
М- — Л jn — В
———г- И _ • = 2z + v (эллиптические параболоиды).
(Ь) Преобразование к параболоидальиым координатам
2 = М-Я)И-ц) (Л-у) = (Д - Я) (Д - ц) (В - у)
Я—Л ' ^ Л —S
г = i- (Л + В — X - ц - v).
(с\ о 1 Он- Я) (у- X) 1 (у - jn) (Я - jn)
1 ' ЬАЛ 4 (Л — Л) (В - ХУ ё|ЫМ 4 (Л - ц) (В — ц)'
1 (X - V) (ц — у)
gvv 4 (Л — v) (В - у)-
6.5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ 193
Таблица 6.5-8
Параболические координаты а, т, <р
(ось Oz — ось вращения; см. также рис. 6.5-2)
(а) Координатные поверхности
( (софокусные параболоиды
о*
х*+у*
-- — 2z + т»
вращения; фокусы в начале координат),
у = jc tg ф (полуплоскости, проходящие
через ось Oz).
(b) Преобразование к параболическим
координатам
л: = от cos ф, у = ox sin ф.
(т2 — а8).
(d) Лапласиан скалярной функции
_i__a_/ зф\ / 1 1 \ д2Ф|
Рис. 6.5-2. Ортогональная си*
стема софокусных парабол с
фокусом F. Эти кривые
определяют систему параболических
координат на плоскости и
порождают координатные
поверхности в следующих системах
координат;
1) параболических (если эти
кривые вращаются вокруг оси
PfFP'\ табл. 6.5-8);
2) параболического
цилиндра (если эти кривые смещаются
перпендикулярно к плоскости
рисунка; табл. 6.5-9).
Таблица 6.5-9
Координаты о*, т, z параболического цилиндра
(применяются также как параболические координаты на плоскости Оху,
см. также рис. 6.5-2)
= 2у + о"2,
(a) Координатные поверхности
Ъ2
t } (софокусные прямые параболические цилиндры),
■£-—**+*• j
2 = 2 (плоскости, параллельные плоскости Оху).
(b) Преобразование к координатам параболического цилиндра
(с) *л
--8Г
X = ОТ,
r-0* + T2, g
"во &тт
(d) Лапласиан скалярной функции
1
у=4- <т2 - °2>'
: 1.
у2Ф =
а2 + т2
/а2Ф агф\
W2 + ат2;+
dz*
7 Г. Корн и Т. Корн
194 гл. 6. системы криволинейных координат
Таблица 6.5-10
Бицилиндрические координаты С, т, z
(применяются также как биполярные координаты на плоскости Оху;
см. также рис. 6Л>-3)
(а)
Координатные поверхности
** + (У — а ctg а)2 = а2 (ctg2 a + 1) (прямые круглые цилиндры).
(х — а cth т)2 + #2 = а2 (cth2 т
— 1) (прямые круглые
z = 2 (плоскости, параллельные плоскости
Для каждой точки (л:, у) плоскости Оху о есть угол.
идущими из полюсов А (—а, 0) и В (а,
радиусов точки (*, у).
1 (Ь) Преобразования
(с)
a sh т
~~ ch т — cos a* —
а sin а
^ ch т — cos а*
а2
°<мг °хх (ch т — cos а)2* °2г,г
0) в точку (*, у)\ е1
1 x*+(y-ta)*
2 x* + (y+ia)*
1 (* + а)2+^
2 (jf _ а)2 + г/2'
«^.^--«vCS+^+S-
цилиндры),
Оху).
образованный
лучами,
— отношение полярных 1
Z = Z,
а1
Рис. 6.5-3. Семейство окружностей с двумя полюсами А, В и семейство окружностеГг,
ортогональных к ним. Эти кривые определяют биполярную систему координат на
плоскости и порождают координатные поверхности в следующих системах координат:
1) бицилиндрических (если эти кривые смещаются перпендикулярно к плоскости
рисунка; табл. 6.5-10);
2) тороидальных (если эти кривые вращаются вокруг оси Q'OQ; табл. 6.5-11);
3) биполярных (если эти кривые вращаются вокруг оси Р'ОР\ табл. 6.5-12).
6.5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ ОРТОГОНАЛЬНЫХ КООРДИНАТ
Таблица 6.5-11
Тороидальные координаты а, т, ф
(ось Oz — ось вращения; см. также рис. 6.5-3)
(a) Координатные поверхности
*2 + у2 -f- (г — a ctg о)2 =» -sin8 g {сферы),
(Yx* + V*— a cth t)8 + 2* = —^ (торы),
у = x tg ф (полуплоскости, проходящие черкез ось Ог).
(b) Преобразования
a sh т __ — JL 1 *' + У' -f (? — fo)f
а 2 х* + #» + (г + ia)«*
ch т —- cos а
а sh x
ch х — cos а
а sin а
cos
sin
Ф,
Ф.
ch т — cos а*
— я=<а^я, 0^х<оо, о^ф<2я.
. . __ а^ а2 sh8 т
w gacr— ёхх — (ch т — cos а)8* ёФФ (ch x — cos о>2'
(d) Лапласиан скалярной функции
*7*<Ь — <ch т — C0S а)8 \Л / Sh Т дФ\
"~ а2 sh х [do \ch x — cos а да /
д / shx дФ\ 1 д*ф-\
"~ дх \ch х — cos а дх ) sh т (ch х — cos а) дф2 J
Таблица 6.5-12
Биполярные координаты о, т, ф
(ось Ог — ось вращении, см. также рис. 6.5-3>
(a) Координатные поверхности
хг + У* + (2 — a cth х)2 = ^^ (сферы),
а8
(У* г 4- у2 — а ctg о)2 + 22 = . 2 (поверхности, полученные при вращении дуг
а2 I
окружностей (у — а ctg о*)2 -f г2 = . вокруг оси Ог; так как | ctg а | < — -,
sin о | sin о ]
то окружности пересекают ось Oz),
у = * tg ф (полуплоскости, проходящие через ось Ог).
(b) Преобразования
a sin a cos ф 1_ . х2 + У2 + (2 + Q)2
* e ch х — cos а* Т " 2' П х2 +- */2 + (г — а)2*
а sin а sin ф J . [Yx2 + (/2 — *а]2 -{- г»
у = — л: о1 =—in— • ■ -—'
ch х — cos а' 2 [/** -|- у2 + *а]2 + 22
а sh х . у
Z е- _- tg ф = -£-,
ch х — cos а * *
— со < х < со, 0 ^ а < я, 0^ф<2я.
а8 __ fl2s:n2a
с) «тт — goa — (ch т — cos а)2' ФФ ~~~ (ch x — cos a)2*
(d) Лапласиан скалярной функции
_ (ch х— cos а)ж Г д ( sin a дФ\ d / sin о дФ\ 1 д2Ф~|
~~ a2sina [ дх \chx~cos а дх / da\ch x—cosa da/~*~sina(ch x—cosa) дф2]
7*
196
ГЛ. б. СИСТЕМЫ КРИВОЛИНЕЙНЫХ КООРДИНАТ
Примечание. Семейство координатных поверхностей
хх = л:1 (х, у, z) = const, х2 = х2 (х, у, z) = const, х9 = х* (х, у, z) = const
является в то же время семейством координатных поверхностей и для всех систем
координат
71 = 71 (^), 72 = 72(*2), 73 = -Р(*3).
■К В таблицах 6.5-2 — 6.5-12 не приведены выражения для
дифференциальных операторов V<D, V«F и VxF в соответствующих системах координат.
Их легко получить, пользуясь общими формулами табл. 6.4-1 (Ь), так как
для всех систем координат даны выражения для функций цц.
Полные таблицы выражений для дифференциальных операторов приведены
в [5.2]. Отедует отметить, что применяются различные обозначения для
координат; поэтому необходима осторожность при пользовании разными
источниками.
Формулы п. 6.4-3 позволяют получать выражения для векторных
элементов линии dx и поверхности dS и элемента объема dV.
Различные дополнительные формулы (например, символы Кристоффеля)
могут быть получены с помощью соотношение приведенных в пп. 16.10-1 —
— 16.10-8. X
ГЛАВА 7
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
7.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Теория аналитических функций комплексного переменного доставляет
инженерам и исследователям много полезных математических моделей. Многие
математические теоремы упрощаются, если рассматривать действительные
переменные как частный случай комплексных переменных. Комплексные
переменные употребляют для описания двумерных векторов в физике; аналитические
функции комплексного переменного описывают двумерные скалярные и
векторные поля (п. 15.6-8 и п. 15.6-9), Наконец, аналитические функции
комплексного переменного реализуют конформные отображения одной плоскости на
другую (пп. 7.9-1 — 7.9-5).
7.2. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ОБЛАСТИ
В КОМПЛЕКСНОЙ ПЛОСКОСТИ
7.2-1. Функции комплексного переменного (см. также п. 1.3-2 и п. 4.2-1 и
табл. 7.2-1; отсылаем к гл. 21 для дополнительных примеров). Комплексная
функция
w = f(z) = u(xt y)+iv(x, y) = \w\e* (7.2-1)
(z = x + iy = \z\ei<P)
каждому значению независимой комплексной переменной z из некоторой
области определения ставит в соответствие одно или несколько значений
зависимой комплексной переменной до.
Однозначные, многозначные и ограниченные, функции комплексного
переменного определены в пп. 4.2-2, а и 4.3-2, Ь. Пределы комплексных функций и
последовательностей и непрерывность комплексных функций, а также сходимость,
абсолютная сходимость и равномерная сходимость комплексных рядов и
несобственных интегралов были определены в гл. 4; теоремы гл. 4 применимы к
комплексным функциям и переменным, если они не сформулированы специально
для действительных количеств.
оо
В частности, каждый комплексный степенной ряд ^] а^ (z — a)k имеет
действительный радиус сходимости гс (О ^ rc ^ оо) такой, что ряд сходится
равномерно и абсолютно при \z — a\ <гси расходится при \ г — а | > гс (п. 4.10-2, а).
7.2-2. z-плоскость и до-плоскость. Окрестности. Бесконечно удаленные
точки (см. также п. 4.3-5). Значения независимой переменной
z = x + iy
ставятся в соответствие единственной точке (х, у) комплексной плоскости г.
Значения w—u + iv таким же образом ставятся в соответствие точкам (ut v)
плоскости w.
Окрестность (открытая) точки z = a, лежащей в конечной части плоскости,,
определяется как совокупность точек z таких, что |г —а|<6, где 6>0.
Таблица 7.2-1
Действительная и мнимая части, нули и особенности для наиболее часто встречающихся функций
f(z) = u(x, y) + iv(x, у) комплексного переменного z=*x-\-iy
(см. также п. 1.3-2 и пп. 21.2-9—21.2-11) | f (z) \ =У и* + о2; если arg f (г) = В, то tg В = -- .
Функция
f (г)
2
28
Z
Z2
1
z — (а + И>)
(а, Ь
действительны)
/Г
ег
и (х, у)
X
х*-у*
X
х* + у*
х* -у*
(х2 + г/2)2
* — а
U - а)* + (у- ЪУ
^(х+Ух*+у* \1/ш
ех cos у
v (х, у)
У
2ху
У
х* + У2
— 2ху
(*2 + */2)2
У-Ь
(х - а)2 + (У - Ь)*
+ (-х+Ух* + у*У1*
ех sin у
Нули (т — порядок)
2 = 0, т = 1
2 = 0, m = 2
г = оо, m = 1
г = оо, т = 2
г = оо, m = 1
г = 0 (точка разветвления)
Изолированные особенности
Полюс (т = 1) при 2 = оо
Полюс (т = 2) при z в= оо
Полюс (т = 1) при 2 = 0
Полюс (т = 2) при 2 = 0
Полюс (т = 1) при 2 = а 4- #
Точка разветвления порядка 1
при 2 = 0
Точка разветвления порядка 1
при z = со
Существенно особая точка при
2 = СО
Таблица 7.2-1 (продолжение)
Функция
М2>
sin 2
cos z
sh г
chz
tgz
thz
In z
« '*. #)
sin xchy
cos * ch #
sh x cos */
ch x cos #
sin 2*
cos 2x 4- ch 2#
sh2jc
ch 2x + cos 2#
-1 In <*■ + *■)
о U. #)
cos x sh у
— sin * sh у
ch * sin у
sh * sin i/
sh2#
cos 2x + ch 2y
sin 2^
ch 2jc -f cos 2#
arg z -f 2/гл
(& = 0, ± 1, ±2, ...)
Нули (m — порядок)
2 ass &Я, Ш = 1
(& = 0, ± 1, ±2, . . .)
(£ = 0, ± 1, ±2, . . .)
г == &ji/, m = 1
(fc = 0, ± 1, ±2, . . .)
2 = (* + ~)я/, m-1
(& = 0, ± 1, ± 2, . . .)
z = kn, m = l
(£—0, ± 1, ±2, . . .)
2 = kni, m = 1
(fe = 0, ± 1, +2, ...)
2 = 1, m ав 1
(для ветви,
соответствующей A = 0)
Изолированные особенности
Существенно особая точка при
г = оо
Существенно особая точка при
2 = ОО
Существенно особая точка при
2 = ОО
Существенно особая точка при
2 =sOO
Полюсы {т =s 1) при
(* = 0, ± 1, ±2, . . .),
г = со — точка, предельная для
полюсов
Полюсы (т = 1) при
2в(* + т)я/
(£ = 0, ± 1, ± 2, . . .).
г =в со — точка, предельная для
полюсов
Логарифмические точки
разветвления при 2 = 0, 2 « со
200 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.2-3.
Бесконечно удаленная точка (z — оо) определяется как точка z,
соответствующая началу координат (г = 0) при преобразовании г=\/г. Окрестностью
точки г = оо является внешность любого круга.
7.2-3. Кривые и контуры (см. также п. 2.1-9 и п. 3.1-13). Непрерывная
кривая в z-плоскости есть последовательность точек z = x-{-iy таких, что
г = z (t) или х = х (/), y = y(t)
(— со ^ tx ^ / ^ t2 ^ со), (7.2-2)
где х (t) и у (/) — непрерывные функции действительного параметра t.
Непрерывная кривая (или ее часть) есть простая кривая (жорданова дуга), если
она состоит из единой ветви и не содержит кратных точек; это значит, что
функции х (t) и у (t) однозначны и в замкнутом интервале [/t, t2] нет таких
двух различных значений %г и т2, для которых справедливы оба равенства
x(ti) = x(T2) и y(Tj) = y(x2).
Простая замкнутая кривая (замкнутая жорданова кривая) есть
непрерывная кривая, состоящая из единой ветви без кратных точек, кроме
совпадающих начальной и конечной точек.
Простая кривая или простая замкнутая кривая называется (простым)
контуром, если она спрямляема (п. 4.6-9)2). Элемент расстояния между
соответствующими точками г и z-\-dz контура (2) есть
ds = \dz\ = Vdx* + dy*.
7.2-4. Границы и области (см. также пп. 4.3-6, 7.9-16 и 12.5-1). Геометрия
комплексной плоскости (включая определение расстояния и угла) тождественна с геометрией
евклидовой плоскости точек (л:, у) или векторов г = xi -f- у) для конечных значений х и
у, кроме определения точки z = оо (п. 7.2-2)*). Точки комплексной плоскости z
представляют гомеоморфное (п. 12.5-1) отображение точек сферы с долготой arg z и широтой
-0 2 arctg —— (стереографическая проекция); при этом точки 2 = 0 и z = оо
соответствуют противоположным полюсам. Точки каждой простой замкнутой кривой С разделяют
плоскость на две связные открытые области: каждая непрерывная кривая, содержащая
точки обеих областей, содержит точку их общей границы (теорема Жордана).
Если С не содержит точку г = оо, то одна из двух областей ограничена (т. е.
находится целиком в конечной части плоскости, где | z | ограничен), а другая не ограничена;
если С содержит точку z = оо, то обе области не ограничены.
В более общем случае граница С области D может быть множеством
непересекающихся простых кривых (многосвязная область, см. также п. 4.3-6). В этом случае
положительное направление (положительный обход) граничной кривой определяется как
оставляющее область D (внутренность граничной кривой) слева (против часовой стрелки
для наружной компоненты границы, см. также ниже рис. 7.5-1). Открытое множество
точек по одну сторону от граничной кривой С есть открытая область; добавляя к этому
множеству точки, лежащие на самой границе, получаем замкнутую область.
В дальнейшем, если область D дополняется ее граничными точками, то
получившуюся замкнутую область будем обозначать D.
7.2-5*. Комплексные контурные интегралы (см. также п. 4.6-1 и 4.6-10).
По определению
\ f (г) dz = lim 2 / (W (*f- **-i). (7.2-3*)
i max \zi—zi^ , |-0/a,
где точки г0, zu ..., zn расположены одна за другой вдоль контура С; a = z0 —
*) Некоторые авторы применяют термин контур только к регулярным кривым
(п. 3.1-13).
*) В комплексной плоскости вводится только одна бесконечно удаленная точка.
В проективной плоскости, т. е. в евклидовой плоскости, дополненной несобственными
элементами (бесконечно удаленными точками) любая совокупность параллельных прямых
определяет свою бесконечно удаленную точку; эти точки образуют бесконечно
удаленную прямую.
7.3-2.
7.3. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
201
то
начальная точка контура, Ь = zn — конечная. Каждая из точек & лежит на
участке кривой [z;_x, zt] и может совпадать с одним из его концов.
Из определения интеграла (За) следует, что
\f(z)dz=\u(x, y)dx-v(x, y)dy + i\v(x, y)dx + u(x, y)dy, (7.2-36)
С С С
где действительные криволинейные интегралы берутся по тому же контуру,
что и комплексный интеграл. Свойства интегралов табл. 4.6-1 переносятся
на рассматриваемые интегралы; в частности, изменение направления
интегрирования на контуре С изменяет знак интеграла.
Если вдоль контура С функции и {х, у) и v (х, у) непрерывны (т. е.
непрерывны функции и [х (0, у (01 и v Iх (0. У (01» гДе х (0. У (0 — параметрические
уравнения контура (см. (7.2-3)), то интеграл (За) существует.
Если при этом длина контура С равна L и на контуре
\f(z)\^M,
\^f(z)dz\*cML. (7.2-4)
Если контур С содержит точку z = oo или если f (z) не ограничена на С,
то интеграл (3) может быть определен как несобственный интеграл в смысле
п. 4.6-2.
7.3. АНАЛИТИЧЕСКИЕ (РЕГУЛЯРНЫЕ, ГОЛОМОРФНЫЕ) ФУНКЦИИ
7.3-1. Производная функция (см. также п. 4.5-1). Функция w = f(z)
называется дифференцируемой в точке z = a, если предел
*!=/'(*)= lim Hz + Az)-f(z) (7.3-1)
dz Az - 0 Az
(производная / (z) no z) существует при z = a и не зависит от способа
стремления Az к нулю. Функция может быть дифференцируема в точке (например,
| z |2 при z = 0), на кривой и во всей области.
7.3-2. Уравнения Коши —Римана. Для того чтобы функция f(z)—u (х, у) +
+ / v (х, у), определенная в некоторой области, была дифференцируемой в
точке z этой области, необходимо и достаточно, чтобы функции и (х, у) и v (x, у)
были дифференцируемы *) в той же точке и чтобы, кроме того, выполнялись
условия
Ш = 1%, £--|i (уравнения Коши-Римана). (7.3-2)
Тогда
~Ш~дх^1 ~дх~~ду~~1 ду~дх 11Й}~!Й}~т~1Тх\ \1Л'6)
■X При переходе к полярной системе координат х —г cosy, y = rsmy, где
r = |z| и (p = argz, уравнения Коши —Римана принимают следующий вид
(ГФ0):
dt£ _ 1 dv dv __ 1 ди
дг ~~ г дф» дг г дф«
Производная /' (z) равна
ff /-\ Г (dtl I , dt)\ l (dtl I • dt)\ vy
/ М=Т\д? + 1И7) "ЛЗф + 'Зф)-*
*) Т. е. имели полные дифференциалы; для этого достаточно, чтобы частные
производные их, Uy^ vx, Vy были непрерывны в рассматриваемой точке (см. п. 4.5-3).
202 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.3-3.
7.3-3. Аналитические функции.
(a) Однозначная функция / (z) называется аналитической (регулярной,
голоморфной) в точке z = a, если она дифференцируема в некоторой
окрестности точки а.
f (г) — аналитическая в точке а тогда и только тогда, когда она предста-
оо
вима степенным рядом /(z) = JJ ak(z—~a)k> сходящимся в некоторой окрест'
k = o
ности точки г —а (равносильное определение).
Функция называется аналитической в открытой области D, если она
аналитическая в каждой точке этой области.
Отсылаем к пп. 7.4-1—7.4-3 для расширения этого определения
применительно к многозначным функциям.
(b) / (г) называется аналитической в бесконечности, если функция F (г) =
= /(1/*) — аналитическая в точке z = 0.
Функция f (г) аналитична в бесконечности тогда и только тогда, когда
оо
она может быть представлена рядом f (г) = 2 ^kz~k n0 отрицательным
стекло
пеням г, сходящимся для достаточно больших значений | z | (см. также п. 7.5-3).
Термины дифференцируемая, аналитическая, регулярная и голоморфная
применялись в одном и том же смысле разными авторами.
7.3-4. Свойства аналитических функций. Пусть f (z) — аналитическая в от-
крытой области D. Тогда во всей области D:
1) уравнения Коши — Римана (2) удовлетворяются (верно и
обратное утверждение);
2) u(xt у) и v(x, у) —сопряженные гармонические функции
(п. 15.6-8);
3) все производные функции f (z) существуют и являются
аналитическими функциями (см. также п. 7.5-1);
2
4) в односвязной области D интеграл { f (£) а\ не зависит от конту-
а
ра интегрирования, если только этот контур имеет конечную длину и
целиком лежит в области D; производная интеграла есть f(z) (см.
также п. 7.5-1);
5) значения f (z) на линии или в подобласти, целиком лежащих в
области D, определяют f(z) единственным образом всюду в D.
Все обычные правила дифференцирования и интегрирования (пп. 4.5-4 и
4.6-1) применимы к аналитическим функциям комплексного переменного.
Если функция w = f(z) аналитична в точке г==а и 1'(а)ф0, то f (z)
имеет аналитическую обратную функцию z(w) (п. 4.2-2, а), определенную
в окрестности точки w=f(a).
Если W—F{w) и w=f(z) — o6e аналитические, то W есть
аналитическая функция от г.
Если последовательность (или ряд, п. 4.8-1) функций /> (г),
аналитических в открытой области D, сходится равномерно к пределу f (z) всюду в D,
то f (z) — аналитическая функция и последовательность (или ряд) производных
f'k (z) сходится равномерно к /' (z) всюду в D {теорема Вейерштрасса).
■Х- Если функции ffr (г) — аналитические в области D и непрерывны в D, то
равномерная сходимость последовательности (или ряда) fk (z) во всей замкнутой области 15
будет следовать из равномерной сходимости на границе этой области. При этом можно
гарантировать сходимость последовательности производных только в открытой области
7.4-2.
7.4. МНОГОЗНАЧНЫЕ ФУНКЦИИ
203
В условии теоремы Вейерштрасса последовательность (или ряд) контурных
интегралов i fk(z)dz, где контур С—конечной длины и лежит в D, сходится
Ь
равномерно к \f(z)dz.
с
7.3-5. Теорема о максимуме модуля. Абсолютное значение \f(z)\
функции f (z), аналитической в открытой ограниченной области D, не может дости*
гать максимума ни в одной точке области D, если только f (z) не_ константа.
Если, кроме того, функция f(z) непрерывна в замкнутой области D и |/(z)|^M
на границе, то j/(z)|<M всюду внутри D при условии, что f(z)^t const.
* Если функция / (z) при приведенных условиях не обращается в нуль
в области D, то и минимум | / (z) j не может достигаться внутри области. X
7.4. МНОГОЗНАЧНЫЕ ФУНКЦИИ
7.4-1. Ветви. Обобщением теории аналитических функций является
рассмотрение ветвей fx (z), /2 (z), ... многозначной функции / (z), которые
определяются как однозначные непрерывные функции в области их определения.
Каждая ветвь принимает некоторое множество значений функции /(г) (см.
также п. 7.8-1).
7.4.-2. Точки разветвления и разрезы.
(а) Пусть многозначная функция / (z) определена всюду в окрестности D
точки z — a, исключая, быть может, саму точку а. Тогда точка а называется
точкой разветвления (точкой ветвления) функции / (z), если f (z) переходит
от одной своей ветви к другой, когда переменная точка z описывает в
окрестности D замкнутую кривую вокруг точки а. Если после m-кратного обхода
этой кривой в одном и том же направлении мы снова впервые вернемся к
первоначальной ветви, то число т—1 называется порядком точки
разветвления. Если / (z) определена в точке разветвления, то значение / (а) есть общее
для всех ветвей, полученных при указанном обходе. (Примеры.
Функция У г имеет точку разветвления порядка 2 при z = 0; все три ветви равны
нулю в точке разветвления. Функция l/|/"z также имеет точку разветвления
порядка 2 при z = 0; все три ветви в этой точке не определены (см. п. 7.6-2, Ь).)
•# Если z=a — точка разветвления порядка /и—1, то функция ф (£) =
= /(£т + я) однозначна в окрестности точки £ = 0; если эту окрестность
разбить на т секторов лучами arg£ = 2jifc/m (& = 0, 1, ..., т — 1), то значения
функции Ф (£) в каждом из таких секторов совпадают с соответствующими
значениями одной из ветвей /(z).
Если, описывая кривую вокруг точки z — a сколько угодно раз в одном
и том же направлении, мы каждый раз будем получать новые ветви, то
точка а называется точкой раззетвления бесконечного порядка или
логарифмической точкой разветвления. (Пример: w = \nz при z = 0.) X
Точка z = oo есть точка разветвления функции /(z), если начало
координат есть точка разветвления для функции /(1/г) (см. также п. 7.6-3).
Пусть для функции f (z) обратная функция Ф (w) существует и однозначна всюду
в окрестности точки w = f (а). Тогда z = а ф со является точкой разветвления порядка т
для f (2), если Ф' (w) имеет нуль порядка т (п. 7.6-1) или полюс порядка т -f 2 (п. 7.6-2)
при w —f (а). (Пример: w = Vz и w = \/Vz, a = 0.)
Подобным образом, если Ф (w) существует и однозначна всюду в окрестности тон-
ки w — f (оо), то точка z = оо является точкой разветвления порядка т функции f (z),
если <&'_\w) имеет нуль порядка т -j- 2 или полюс порядка т при w = f (оо). (Пример}
w = Vz и w = \IYz.)
X Если точка а является точкой разветвления функции f(z), то в ее
окрестности функция f(z) может иметь несколько различных групп ветвей,
а также ветви, аналитические или не аналитические в точке а и для которых
204 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.4-3.
эта точка не является точкой разветвления. Каждая группа ветвей или
отдельная ветвь определяются выбором начального значения функции / (г) (элемента
функции /(z), см. п. 7.8-1). При обходе точки а ветви выбранной группы
переходят друг в друга; все ветви этой группы имеют одно и то же значение
в точке а, или они в ней не определены.
Если в окрестности точки разветвления z=a функция f (г) имеет несколько
разных групп ветвей, то говорят, что функция f (г) имеет над точкой а разные
точки разветвления. На римановой поверхности функции f (г) (см. п. 7.4-3)
им соответствуют разные точки. Для каждой точки а функция / (г) может
иметь не более счетного множества различных групп ветвей.
Пример. Функция w = У 1 -j- Yz имеет четыре ветви. В окрестности точки z = 0
эти ветви распадаются на две группы, по две ветви в каждой. Ветви первой группы
объединяются значением w \2_0= 1, а ветви второй группы значением w |^_0 = — 1. Для
каждой группы точка z — 0 является точкой разветвления первого порядка.
В окрестности точки z = 1 ветви распадаются на три группы. Две ветви, образующие
первую группу, объединяются условием Yz Lj = — 1 (тогда w = 0); для этой группы
точка z = 1 служит точкой разветвления первого порядка. Вторая и третья группы,
получающиеся при условии Yz |г_1=1, состоят каждая из одной аналитической в точке г=1
ветви, соответственно принимающей значения w \g_i-V2 и w \гшт-± = — V"2.
Более сложные примеры см. в [7.7]. -Х-
(Ь) Отдельные однозначные ветви функции / (z) определены в областях,
ограниченных разрезами, которые являются простыми кривыми, выбранными
так, что ни одна замкнутая кривая, окружающая точку разветвления, не лежит
в области определения какой-либо однозначной ветви. Выбор ветвей и
разрезов для заданной функции / (z) не единствен, однако точки разветвления и
число ветвей определяются единственным образом.
Примеры. Для функций w = -*/~z и w = In z разрезом может служить любая
простая кривая, соединяющая точки разветвления г = 0и z — oo, например,
положительная или отрицательная части действительной оси.
Для функций w = Yl — z2 и w — Arcsin z разрезом может служить любая простая
кривая, соединяющая точки разветвления — 1 и 1, например, отрезок действительной
оси (проходящий через точку 2 = 0 или через точку г = оо).
Для функций w = Yl Н- z2 и w = Arctg z разрезом может служить, например,
отрезок мнимой оси, соединяющий точки разветвления — / и /.
Все ветви моногенной аналитической функции могут быть последовательно получены
аналитическим продолжением ее элемента (п. 7.8-1).
7.4-3. Римановы поверхности. Часто бывает полезно представить
многозначную функцию как однозначную, определенную на римановой поверхности.
Такая поверхность состоит из некоторого числа z-плоскостей, или «листов»,
соответствующих ветвям функции / (г) и соединенных вдоль соответствующим
образом выбранных разрезов. О способах построения римановых поверхностей
см. [7.2], [7.4]. Заметим, что конструкция римановых поверхностей для
произвольных функций может быть весьма сложной и требовать большой
изобретательности при построении.
Если функция ш = /(г) и ей обратная обе многозначны, то z-плоскость
и w плоскость можно заменить соответствующими римановыми поверхностями;
при этом функция ш = /(г) будет определять взаимно однозначное
соответствие между точками обеих римановых поверхностей, исключая точки
разветвления.
Замечание. Риманова поверхность для моногенной аналитической функции
(полученной аналитическим продолжением, п. 7.8-1) будет связной; таким образом,
многозначная функция f(z)=±l, несмотря на аналитичность каждой ветви, не является
моногенной аналитической функцией.
■Х- Более сложный пример представляет многозначная функция w = In ez,
распадающаяся на бесконечное множество различных однозначных ветвей w = z -j- 2kni (k — 0, 1,
2, . . .). Эта функция не имеет точек разветвления. -^
7.5-1. 7.5. ИНТЕГРАЛЬНЫЕ ТЕОРЕМЫ И РАЗЛОЖЕНИЯ В РЯДЫ 205
Всюду в этой книге, исключая специальные утверждения, применимые
к многозначным функциям, речь идет только об однозначных аналитических
функциях или об однозначных ветвях аналитических функций (см. п. 7.8-1).
7.5. ИНТЕГРАЛЬНЫЕ ТЕОРЕМЫ И РАЗЛОЖЕНИЯ В РЯДЫ
7.5-1. Интегральные теоремы. Пусть / (г)—функция, аналитическая в
некоторой области, С —замкнутый контур, принадлежащий этой области вместе
со своей внутренностью D, и г — любая точка из D. Тогда
\f(QdZ> = 0 (интегральная теорема Коши),
с
/(z) ~ы i F~Zd%> (интегральная формула Коши),
с
(С-
(7.5-1)
С
-_L
Z2ni
С
f"(Z) = 24 f (D dt
С
(7.5-2)
Рис. 7.5-1 иллюстрирует применение интегральной теоремы Коши к
многосвязной области (см. также п. 7.7-1).
Равенства (2) выражают функцию с
f (z) и ее производные через граничные
значения /(z). В частности,
= 2ш.
(7.5-3)
Интегральная теорема Коши
обобщается на тот случай, когда на
контуре С функция / (г) перестает быть
аналитической, оставаясь непрерывной:
если функция / (г) аналитична в одно-
связной области D и непрерывна в
замкнутой области D, то интеграл (1),
взятый по ее границе С, равен нулю.
# Интеграл вида JL { -^-^ dt,t где
С
С —замкнутый или незамкнутый
контур и <р (£)—функция, непрерывная на контуре С, называется интегралом
типа Коши. Интеграл типа Коши представляет функцию F (z), аналитическую
в каждой области, не содержащей точек контура С. При этом Fln) (z) =
= ~. \ —Ф n+i <%>• О свойствах и приложениях интегралов типа Коши см.
[7.1], гл. 3, § 3. *
Если функция f (z) непрерывна в односвязной области D и равенство (1)
имеет место для любого замкнутого контура С, лежащего в D9 то / (z) —
аналитическая в этой области (теорема Морера).
Рис. 7.5-1. Теорема Коши для
многосвязной области (пп. 7.2-4 и 7.5-1).
Область D ограничена внешним контуром
С и внутренними контурами Си С2, ...
..., Cfci направления обхода контуров
указаны на рисунке;
г * г
с i=i ct
206
ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
7.5-2.
7.5-2. Разложение в ряд Тейлора (см. также п. 4.10-4).
(а) Если f (г) аналитична внутри окружности К радиуса г с центром в
точке г=а(афоо), то существует единственный ряд по степеням (г —а),
равномерно сходящийся к f (z) при | z — a\^r' < г:
оо
/(2)= 2 <*(*-*>*■ (7-5-4>
еде
^-^Ю-^-Ш-.*
и /С' —окружность \z—a\ = r'.
Наибольший круг /Сс (| z—- а | =^гс), все внутренние точки которого
лежат внутри области, в которой / (z) аналитична, является кругом сходимости
степенного ряда (4); гс есть радиус сходимости (п. 4.10-2, а). Наиболее
важные разложения функций в степенные ряды приведены в п. 21.2-12.
(b) Если М (г') — верхняя граница \f(z)\ на /С', то
| ая | = 11 /<»> (а) | ^ ^Цр- (неравенства Коти). (7.5-5)
(c) Если в ряде Тейлора (4) отбросить все члены, стоящие заап_х (z —а)л-1,
то остаточный член Rn (z) равен
J?.W-fiE=fl»!S "О* |^(2)|^fiiZ^\"_I^l_. (7.5.6)
2ш* *'(£-<*)" (£-2)' ЛЧ/' \ г' У г'_|2-в|
(Если положить \z — a\ = kr't где &<1, то Rn (z) ^ ^yzTp-.)
7.5-3. Разложение в ряд Лорана.
(а) ££ли / (z) аналитична в кольце между двумя концентрическими
окружностями К\ и /С2 с центрами в точке г = а(афсо) и радиусами гг и r2 < rlt
то существует единственное разложение в ряд по положительным и
отрицательным степеням (z —a)
оо оо
/(2)= Ц ak(z-a)*+ ^ Mz-a)-*(r2<|z-a|<ri), (7.5-7)
£ = 0 k = l
где
K[—окружность | z—a | = r| < гг и К'^ — окружность \ z—a \ =r'2 > r2.
Первая сумма в равенстве (7) равномерно сходится для | z—a | ^г; и a«a-
литична внутри Къ вторая сумма (главная часть разложения для f (г))
равномерно сходится для \z—a\^r'2 и аналитична во внешности окружности /С2.
Замечание. Случай а = оо приводится к предыдущему при помощи
преобразования z= 1/2, переводящего г = оо в начало координат.
■К Ряд (7.5-7) можно записать в виде
оо
где Г —любая окружность, расположенная между Кг и /С2. *
7.6-2.
7.6. НУЛИ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
207
(Ь) Если в первой сумме равенства (7) ограничиться членами по
Ял-i (z —а)л-1 включительно, то остаточный член Rn(z) будет равен
Если во второй сумме равенства (7) последним слагаемым взять
fyt-i (2—a)~(/,~1}, то остаточный член /?* (z) будет равен
tf*(2)== If <С-«)"/<Р^
л 2ш (г - а)я К; g - г
(7.5-9)
Ж (г^) и ЛЦгз) — верхние границы для |/(z)| на К[ и /CJ соответственно.
7.6. НУЛИ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
7.6-1. Нули (см. также п. 1.6-2). Точки г, для которых f(z) = 0t
называются нулями функции /(г) (корнями уравнения / (z) = 0). Функция /(г),
аналитическая в точке г = а, имеет нуль порядка т, где /п — целое
положительное число, если в точке z = a первые т коэффициентов а0, alt а2,..., am_t
разложения функции / (г) в ряд Тейлора (7.5-4) равны нулю. При этом / (г) =
= (г — а)отф (z), где ф (г) аналитична в точке а и ф (а) ф 0.
Нули функции f (z), аналитической в области D, все изолированы друг от друга
(т. е. каждый нуль имеет окрестность, внутри которой f (z) ф 0, исключая сам нуль), или
/ (z) тождественно равна нулю в области D.
X Иначе говоря, нули функции f (z), не равной тождественно нулю, не могут иметь
предельной точки в области D. В то же время они могут иметь предельную точку на
границе области D. Например, пусть D — круг | z | < 1 и f (z) = sin __ . Нули z — 1 — —
имеют предельную точку г = 1. X
Если fi (z) и /2 (г) — аналитические в сдносвязной ограниченной области D
и на ее контуре С и если | /2 (г) | < | /г (г)\ф0 на С, то функции fx (г) и
/i(z)+/2(z) имеют одинаковое число нулей в области D (теорема Руше).
Каждый многочлен степени п имеет п нулей с учетом их кратности
(основная теорема алгебры, см. также п. 1.6-3).
7.6-2*. Особые точки.
(а) Особые точки однозначных аналитических
функций. Особой точкой или особенностью функции /(г) называется точка,
в которой /(г) не аналитична. Точка г = а называется изолированной
особенностью / (г), если существует действительное число 6 > 0 такое, что f (z)
аналитична при 0<|г — а|<б, но не в самой точке z = a. Изолированные
особенности для г — афоо могут быть такими:
1. Устранимая особенность, если функция /(г) ограничена в
некоторой окрестности z — at исключая, возможно, саму точку а,
т. е. когда все коэффициенты Ь^ разложения в ряд Лорана (7.5-7)
функции / (г) в точке а равны нулю.
Пример. w=*^-Z имеет устранимую особенность при г=0.
В дальнейшем устранимые особые точки обычно не считаются
особыми.
2. Полюс порядка m(m=l, 2,...), если в разложении Лорана
(7.5-7) функции /(г) по степеням (г —а)
^^°г &т+1 = ^л+2 = ... = 0
208 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.6-2.
(главная часть разложения содержит лишь конечное число членов).
В этом случае Пт/(г) = со при любом стремлении г к а. При этом
2-*00
функция F (г)=1// (г) будет аналитична в некоторой окрестности
точки а (если положить F (а) = 0) и иметь в этой точке нуль
порядка т. Функцию f (г) в окрестности точки а — полюса порядка
т —можно представить в виде /(г) = —, где лр (г) аналитична и
(г — а)т
Примеры. w=- 5— имеет полюс 3-го порядка при г = 2;
w=igz имеет полюсы 1-го порядка в точках z— ~ + kn (& = 0, нн 1,...).
3. Существенно особая точка, если в разложении Лорана (7.5-7)
функции / (г) имеется бесконечное число членов, содержащих
отрицательные степени {z — a)\ при этом не существует ни конечного,
ни бесконечного предела функции /(г) при г, стремящемся к а.
Примеры. Функции sin (1/г) и е i/z имеют существенно особую
точку при 2 = 0.
^ (Ь) Особые точки многозначного характера. Особые
точки многозначного характера являются точками разветвления
многозначной функции f (г). Определение точки разветвления конечного порядка и
логарифмической точки разветвления дано в п. 7.4-2.
Пусть точка разветвления z = a имеет конечный порядок, равный т—1,
т. е. объединяет группу из т^2 ветвей функции / (г). Если все эти ветви
имеют конечный или бесконечный предел при г —*■ а, то точка а называется
алгебраической точкой разветвления. В этом случае однозначная функция
(см. п. 7.4-2)
F(Q=f(Zm+a) (7.6-1)
имеет при £ = 0 правильную точку или полюс.
Если ветви функции /(г) не имеют предела при г—-а, то точка а
называется трансцендентной точкой разветвления *). В этом случае однозначная
функция F (t) имеет при £ = 0 существенно особую точку.
Разложение функции F (£) в окрестности точки £ = 0 в ряд Лорана
порождает представление многозначной функции / (г) в окрестности точки
разветвления конечного порядка
оо
/1 = —-ОО
Если а —алгебраическая точка разветвления, то лишь конечное число
коэффициентов сп с отрицательными индексами отлично от нуля; в противном
случае а —трансцендентная точка разветвления.
Примеры. Функция |/ z — 1 имеет алгебраическую точку разветвления порядка 2
при z= 1; эта точка есть нуль для всех трех ветвей.
Для функции \l\fz— 1 точка z = 1 также является алгебраической точкой
разветвления порядка 2; предел любой ветви при z -*■ 1 равен оо. Соответствующая однозначная
функция Ф (g) = 1/g имеет в точке £ = 0 полюс.
Функция sin (\1'Уz ) имеет трансцендентную точку разветвления порядка 2 при z=0.
Соответствующая функция Ф (£) = sin (1/£) имеет при £ = 0 существенно особую точку.
Если в окрестности точки а функция / (г) имеет несколько разных групп
ветвей, т. е. если над точкой а лежат разные точки разветвления (см. п. 7.4-2),
то поведение каждой такой группы ветвей нужно рассматривать независимо
*) Логарифмические точки разветвления относят к числу трансцендентных,
7.6-5.
7.6. НУЛИ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
209
друг от друга; для каждой такой группы строится своя однозначная
функция F(£). *
7.6-3. Нули и особенности в бесконечности. Функция /(г) аналитична
в бесконечности, если / (1/2) —аналитическая в начале координат (п. 7.3-3, Ь).
Точка 2 = оо есть нуль или особенность одного из типов, указанных в п. 7.6-2,
если / (1/2) имеет соответственный характер в начале координат. Поведение /(г)
в бесконечности может быть исследовано с помощью разложения /(1/г) в ряд
Лорана в окрестности 2 = 0.
7.6-4. Теоремы Вейерштрасса и Пикара. Пусть / (г) —однозначная
функция, имеющая изолированную существенно особую точку при z — a. Тогда
1) для любого комплексного числа А (включая А = со) существует
последовательность точек z^-> а такая, что lim / (zk) = А (теорема
£-*оо
Вейерштрасса *));
2) для любого комплексного числа Афоо, за исключением, быть
может, одного значения А = А0, каждая окрестность точки а содержит
бесконечное множество точек z таких, что f(z) = A (теорема Пикара)*
^Примеры. Функция e^z имеет существенно особую точку z = 0.
Уравнение eVz—A имеет в каждой окрестности этой точки бесконечное число корней для
любого А фсо, кроме А = 0. Для функции sin (I/z), также имеющей существенно особую
точку z = 0, исключительных значений для А нет. -Х-
7.6-5. Целые функции.
(а) Целой функцией / (г) называется однозначная аналитическая функция,
не имеющая особых точек в конечной части плоскости. Она представляется
всюду сходящимся степенным рядом f (г) = а0 + а1г + ... + апгга + ...
Таким образом, целая функция может иметь единственную особую точку при
z = со. Если эта особенность есть полюс порядка т, то f(z) — многочлен (целая
рациональная функция) степени т. Если г = со—существенно особая точка,
то /(г) называется целой трансцендентной функцией. Если, наконец, г = со —
правильная точка (т. е. / (г) — аналитическая для всех значений z), то f (z)
есть константа (теорема Лиувилля).
Целая трансцендентная функция принимает любое значение до, исключая,
возможно, одно значение, в бесчисленном множестве точек г.
■# (Ь) Характеристики роста целых функций. Пусть / (z) —
целая функция и М (r)= max |/(г)|. В силу теоремы о максимуме модуля
|z|=r
(п. 7.3-5) М (г)— возрастающая функция от г и lim М (г) = со, если только
г -*> оо
f(z) — не константа. Если М (г) = 0(г&), то / (г) — многочлен степени не выше
f[x] (целая часть \i).
Пусть / (г) — целая трансцендентная функция. Если существует число Р>0
такое, что М (г) < ег для всех достаточно больших г, то f (г) называется
функцией конечного порядка. Число р= inf P^0 называется порядком целой
функции.
г 2 ez
Примеры, е , sin г, cos z — функции порядка 1, ez — функция порядка 2, е
не имеет конечного порядка (целая функция бесконечного порядка).
Если функция f (2) имеет порядок р и существует число К > 0 такое, что
М (г) <еКг , то f(z) называется функцией конечного типа. Число a = inf K^0
называется типом целой функции.
*) Эта теорема была ранее доказана русским математиком /О. Сохоцким и
итальянским математиком С. Казоратти.
Отметим, что теорема справедлива для неизолированной особой точки, являющейся
предельной для полюсов.
210
ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
7.6-6.
Если а>0, то /(г)— функция нормального типа, если а = 0, то
минимального типа. Для функции бесконечного (максимального) типа
полагают а=оо.
Если пределы справа существуют, то
Р= lim in in м (г) а== lim in м (г)
Г-+СО 1П Г ' Г-+СО Гр
Целая функция /(г) называется функцией экспоненциального типа, если она
первого порядка и конечного типа (р=1, о < оо), а также если р<1.
(с) Преобразование Фурье и целые функции (см. п. 4.11-3).
Пусть функция /(/) обращается в нуль при \t\"^a. Тогда ее преобразование
Фурье
а
Q(s)= J f(t)e"istdt
— а
есть целая аналитическая функция от s экспоненциального типа ^а (р=1 и
а^а, или р < 1).
Теорема Винера — Пэли. Пусть г|? (s) — целая функция экспонен-
со
циального типажа и такая, что { | г|? (х) |2 dx < оо (интеграл берется
— оо
по действительной оси). Тогда существует функция f (t), равная нулю при
|f| ^а, преобразование Фурье которой равно ty(s). x
7.6-6. Разложение целой функции в произведение. Для каждой
последовательности точек 20, zlf z2, ..., не имеющих предельной точки (п. 4.3-6,а) в
конечной части плоскости (т. е. имеющих z = oo своей единственной предельной
точкой), существует целая функция /(г), которая своими единственными нулями
имеет нули порядка mk, в точках z=zk. Пусть Zo = 0, г^фО (fc>0); если
г0 = 0 не является нулем, то т0 = 0. Функция /(г) может быть представлена
в виде
оо
'^"fl.Hl-'^^K» "•6-2>
где g(z) — некоторая целая функция, а целые числа /> выбираются так,
чтобы бесконечное произведение равномерно сходилось в любой ограниченной
области (теорема Вейерштрасса; примеры см. в п. 21.2-13).
00
>fc Если последовательность ги г2, ... такова, что ряд у — сходится для неко-
*mi | гп \Р
п = 1
торого целого положительного числа р, то все числа г^ можно положить равными р — 1.
Если последовательность {zk} произвольная, то можно взять r^ «= [In k] (целая часть
In Л). X
7.6-7. Мероморфные функции. Однозначная функция / (z) называется меро-
морфной в области D, если ее единственными особенностями в D являются
полюсы. Число этих полюсов в каждой конечной замкнутой части D
обязательно конечно. Полюсы могут иметь предельную точку на границе области D.
В частности, D может совпадать со всей конечной комплексной
плоскостью (исключая z = oo); тогда в любой конечной части плоскости имеется
только конечное число полюсов, и единственной предельной точкой для
полюсов может быть бесконечно удаленная точка.
7.7-1.
7.7. ВЫЧЕТЫ И КОНТУРНЫЕ ИНТЕГРАЛЫ
211
Каждую функцию, мероморфную в конечной плоскости, можно представить в виде
отношения двух целых функций, не имеющих общих нулей, и, следовательно, в виде
отношения двух произведений вида (7.6-2).
Функция, мероморфная в конечной плоскости и имеющая в бесконечности
правильную точку или полюс, есть рациональная алгебраическая функция, представимая в виде
отношения двух многочленов (см. также п. 4.2-2, с).
7.6-8. Разложение мероморфных функций на простейшие дроби (см. также п. 1.7-4).
Пусть f (z) — функция, мероморфная в конечной плоскости и имеющая полюсы с задан-
mk
ными главными частями (п. 7.5-3) ^ b^j (z — zk)~~ ' в т0ч-кс^х z = zk* чисЛ0 которых
конечно или бесконечно и которые не имеют предельных точек в конечной части пло*
скости. Тогда можно найти такие многочлены рх (z), p2 (z), ... и целую функцию g (z),
что
f(*)-2
-/ 1
2 bkf <*-V ! -Pk <г> + g<2>- <7-6-3)
k L/=
Ряд равномерно сходится в каждой ограниченной области, в которой f (г) аполитична
(теорема Миттаг-Леффлера).
7.6-9. Нули и полюсы мероморфных функций. Пусть f (z) — мероморфная
функция в некоторой области G и С—замкнутый контур, принадлежащий
вместе со своей внутренностью области G и не проходящий ни через нули,
ни через полюсы функции f (z). Пусть N — число нулей и Р — число полюсов
f (z), лежащих внутри G, причем нуль или полюс порядка т считается т раз.
Тогда
с
если Р = 0, то формула (4) дает число нулей
ArAvg f (z)
W = -^-^ > (7.6-5)
еде Дс Arg / (г) обозначает изменение аргумента f (z) при обходе точкой z
контура С в положительном направлении (принцип аргумента).
Формула (5) означает что w — f (z) отображает движущуюся точку z, описывающую
один раз контур С, на движущуюся точку w, окружающую в ш-плоскости начало
координат столько раз, сколько нулей имеет функция f (z) внутри контура С в г-плоскости.
Формулы (4) и (5) играют важную роль для определения положения нулей и полюсов
f (z) и лежат в основе геометрических критериев устойчивости (см. [7.1]).
7.7. ВЫЧЕТЫ И КОНТУРНЫЕ ИНТЕГРАЛЫ
7.7-1. Вычеты. Пусть в точке z = a функция / (лг) или аналитична или
имеет изолированную особенность. Тогда вычетом Res/ (а) г) функции / (z)
в точке а называется коэффициент при (z— а)"1 в разложении Лорана (7.5-7),
или
Resf(a) = ±-[f(Odb (7.7Ла)
с
где С —контур, окружающий точку а и не содержащей внутри себя
особенностей / (z), отличных от а.
*) Вычеты обозначаются также Res [f (г); а] или Res f (z).
z — a
212 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.7-2.
Вычет Res/ (со) функции / (г) при z = co определяется как
Res/(со) =^ $ /(0<*Е, (7.7-16)
-с
где интегрирование производится в отрицательном направлении по контуру
С (в этом случае внешность контура С остается слева), заключающему
внутри себя все особые точки /(z), лежащие в конечной части плоскости.
Это значит, что z = oo является для функции / (г) пли правильной, или
изолированной особой точкой.
Res/(со) равен взятому со знаком минус коэффициенту при z-1 в
разложении Лорана в окрестности бесконечно удаленной точки. Отметим, что
Res/(co)=lim [— zf(z)l (7.7-2)
z-*oo
если этот предел существует.
Если f(z) или аналитична, или имеет устранимую особенность при
г = афоэ, то Res/(a)=0 (см. также формулу (7.5-1)). Если г=аФ со есть
полюс порядка т, то
Res/(a)= ' Ит J^^fr - а)* f (г)]. (7.7-3)
(m — 1)1 z-+a dzm l
В частности, пусть z=a Фсо — простой полюс и f (z)—p (z)/q (z), где
p (z) и q (z) — аналитические функции в точке а и р(а)Ф0. Тогда q(a) = 0,
Я' (а)фО и
•ХЕсли бесконечность —правильная точка для функции f (z), то вычет
Res/ (со) может и не равнятся нулю. Например, если /(z) = l/z, то z = co
есть нуль, а Res/(со) = —1.*
7.7-2. Теорема о вычетах (см. также п. 7.5-1). Пусть однозначная
функция f (z) аналитична в области D, за исключением изолированных особых
точек, а замкнутый контур С принадлежит вместе со своей внутренностью
области D, содержит внутри себя конечное число zv z2, ..., zn особых точек
и не проходит ни через одну из них. Тогда
п
2^7 \ f (0 <%>— 2 Res^(z^ {теорема о вычетах). (7.7-5)
с k = \
С особой осторожностью нужно следить, чтобы контур С не пересекал
разрезы для f (z) (см. также п. 7.4-2).
■КЕслн функция f (z) однозначна и аналитична во всей комплексной плоскости, за
исключением только изолированных особых точек (необходимо конечного числа, так как
иначе существовала бы конечная или бесконечно удаленная предельная точка множества
особых точек), то сумма всех ее вычетов (включая вычет Res Moo)) равна нулю.*
7.7-3. Вычисление определенных интегралов.
(а) Часто можно вычислять действительный определенный интеграл
ь
\f(x)dx, рассматривая его как часть комплексного контурного интеграла
а
[ f (z) dz при условии, что контур С включает интервал (a, b) действитель-
с
ной оси. Теорема о вычетах (5) может помогать в таких вычислениях и
может, в частности, сводить неизвестные интегралы к уже известным.
7.7-4.
7.7. ВЫЧЕТЫ И КОНТУРНЫЕ ИНТЕГРАЛЫ
213
(Ь) Для вычисления некоторых интегралов вида { f(x)dx следует при-
— 00
менить формулу (5) к контуру С, состоящему из интервала (—R, R)
действительной оси и дуги Сц окружности \z\ = R в верхней полуплоскости.
Следующие леммы часто позволяют отбросить интегралы по дуге С„ при R—*оо:
1. lim f/(z)dz = 0, если f (z) аналитична при |z|>#0 "
z f (z) стремится к нулю при \ z | —*■ оо, когда у^0\ последнее, в
частности, выполняется, если |/(г)|<—т—.— где а>0, при всех
| z\l "га
достаточно больших \г\.
2. Лемма Жордана. Если F (z) аналитична в верхней
полуплоскости, исключая, возможно, конечное число полюсов, и стремится к
нулю при | z | —* оо, когда у^О, то для любого действительного
положительного числа т
lim \ F (Q eimZ dZ = 0.
Метод контурного интегрирования может давать главное значение интеграла по
оо
Коши (см. п. 4.6-2) для J f (х) dx, когда сам интеграл в обычном смысле не существует.
— оо
Лемма Жордана бывает особенно полезна для вычисления несобственных интегра-
оо
лов вида J* F (х) е^тх dx и, согласно формуле Эйлера, интегралов вида
— оо
оо оо
J F (x) cos mx dx и J F (x) sin mx dx
— оо —оо
эти интегралы встречаются при преобразовании Фурье п. 4.11-3 и в формуле
обращения для преобразования Лапласа, п. 8.2-6).
(c) Если s — какая-либо полуокружность круга \ z — а | = е, где точка 2 = а —
простой полюс функции f (z), то
lim ff ft) </£ = я/Res f (a).
e-*Os
Это используется, во-первых, при вычислении интегралов по контурам, когда прихо-
С eiz
дится «огибать» простой полюс (например, при вычислении \ — dz по контуру,
состоящему из отрезка (— R, R) действительной оси и полуокружностей | z J = R и f z | = r
при Л-*оо и г -*- 0) и, во-вторых, для вычисления главного значения по Коши
некоторых несобственных интегралов.
(d) Теорему о вычетах можно применять к интегралам вида
2я
J R (cos ф, sin ф) d(pf
О
где R — рациональная функция от cos ф и sin ф, если совершить подстановку
z = «'Ф, 4ф 1
cos ф = — ^z + —J, sin
Р = — dz^ \
'], ,, (7.7-6)
* = 27(г-¥>]
7.7-4. Применение вычетов к суммированию рядов. Пусть контур С окружает точки
z = m, z — т -f- 1, z = т + 2, ... , z = п, где т — целое число, и пусть f (z) аналитична
214 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.8-1.
внутри С, за исключением, быть может, конечного числа полюсов а^, а2 а^, из
которых ни один не совпадает с точками z = т, z = т -+- 1, z = т -f- 2, .... z = п. Тогда
п N
2 f<*> = 2^ WQctgJlU:~.S Res *(*/)» (7'7'7)
£=m С /=1
где Res g (аЛ — вычет функции g (z) = я f (z) ctgnz в точке z = as
n N
2 (- 1) k f{k) = .1. ^ я f (g) cosec Jig </C - 2 Res gl (*/)» (7,7"8)
£ = m С / = 1
где gj (2) = л f (z) cosec яг. Иногда бывает возможно выбрать контур С так, что интеграл
в правой части формулы (7) или (8) исчезает.
7.8. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
7.8-1. Аналитическое продолжение и моногенные аналитические функции
(см. также пп. 7.4-1—7.4-3).
(a) Пусть однозначная функция /х (z) определена и аналитична всюду
в области Dx\ функция /2 (г), определенная и аналитическая в области D2,
есть аналитическое продолжение /х (г), если существует пересечение областей Dx
и D2, содержащее открытую область Dc, в которой функции fx (z) и /2 (z)
совпадают.
Аналитическое продолжение /2 (г) определяется единственным образом по
значениям /х (z) в Dc (см. также п. 7.3-3). Сверх того, аналитические
продолжения ft (z) удовлетворяют каждому функциональному уравнению и, в
частности, каждому дифференциальному уравнению, которому удовлетворяет fx (z)
(принцип консерватизма функциональных уравнений). Можно также
воспользоваться функцией /2 (z) для расширения области определения Д (z) и обратно:
рассматривать /х (z) и /2 (г) как элементы единой аналитической функции / (г),
определенной всюду в Dx и D2.
fi (z) и/или /о (z) могут допускать дальнейшее аналитическое
продолжение, ведущее к другим элементам функции f(z).
(b) Многозначные функции. Заметим, что /х (z) и /2 (z) не
обязательно совпадают во всем пересечении областей их определения. /2 (z)
может иметь аналитическое продолжение /3 (z), определенное в Dlt но не
совпадающее с /х (z). Аналитическое продолжение может производить элементы,
принадлежащие к различным ветвям многозначной аналитической функции f(z)\
два значения / (z0), полученные при аналитическом продолжении fx (z) вдоль двух
различных путей С и Съ совпадают, если С и Сг не окружают точку
разветвления f(z).
(c) Возможные аналитические продолжения данного элемента образуют
моногенную аналитическую функцию / (z), определенную, исключая
изолированные особенности, во всей плоскости или в связной области с
естественными границами. В то время как выбор последовательности элементов,
определяющих / (z), не является фиксированным, принцип консерватизма
функциональных уравнений применим ко всем элементам и каждый такой один
элемент единственным образом определяет все ветви, изолированные особенности
и естественную границу f (z).
7.8-2. ^Методы аналитического продолжения.
(а) Стандартный метод аналитического продолжения отправляется от
функции /(г), определенной степенным рядом (7.5-4), сходящимся в круге
\z — a\<r. Для каждой точки z = b этого круга значения f(b), /'(&),...
известны и определяют разложение в ряд Тейлора в окрестности z — b.
Новый степенной ряд сходится внутри круга |z — b\<.r't который может иметь
7.9-1.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
215
часть, расположенную вне первого круга. Тогда мы получаем аналитическое
продолжение функции f (z) в часть круга с центром в точке Ъ, лежащую вне
круга с центром в точке а. Этот процесс может быть продолжен вплоть до
естественных границ функции; каждый степенной ряд есть элемент / (г).
Замечание. Функция, определенная степенным рядом с конечным радиусом
сходимости, имеет по крайней мере одну особую точку на границе круга сходимости.
(b) Пусть даны две односвязные области Dt и D2 без общих точек такие,
что их границы имеют один общий кусок у. Если функции Д (г) и f2 (z)
аналитичны соответственно в областях Dx и D2, непрерывны в Dx + Y и ^2+Y
(т. е. вплоть до линии у) и совпадают во всех точках кривой у, то функции
/i (z) и /2 (z) являются аналитическими продолжениями друг друга.
(c) Принцип симметрии. Пусть /(г) определена и аналитична
в области D, граница которой содержит отрезок у оси Ох, непрерывна в D+y
и принимает на у действительные значения. Тогда функция /* (г),
определенная в области D*, симметричной с областью D относительно действительной
оси, соотношением
/*(*) = /(*), (7.8-1)
является аналитическим продолжением / (z) в области D*. Более общо, пусть
f(z) определена и аналитична в области D, граница которой содержит дугу
окружности или прямолинейный отрезок S2, на котором f (г) непрерывна и
принимает значения, лежащие на некоторой дуге окружности или
прямолинейном отрезке Sw в плоскости w. Тогда функция f (г) может быть аналитически
продолжена в область D *, симметричную с областью D относительно Szt
причем ее значения в точках, симметричных относительно S2, будут
симметричны относительно Sw.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
7.9-1. Конформное отображение.
(а) Функция w = f(z) отображает точки z-плоскости (или римановой
поверхности, п. 7.4-3) в соответствующие точки до-плоскости (или римановой
поверхности). В каждой точке г такой, что / (г) аналитична и /' (г) ф О,
отображение w = f(z) конформно, т. е. угол между двумя кривыми,
проходящими через точку г, переходит в равный по величине и по направлению
отсчета угол между соответствующими кривыми в плоскости w.
Бесконечно малый треугольник около такой точки z отображается в подобный
бесконечно малый треугольник до-плоскости; каждая сторона треугольника «растягивается»
в отношении \ f (z) | : 1 и поворачивается на угол argf (z). Коэффициент искажения
(локальное отношение малых площадей) при отображении w = f (z) = и (х, у) + i v (x, у)
равен
|f»W|..|l«L4_|- 7 | (7.9-1)
д (х, у) ' л" я" '
в каждой точке z, где отображение конформно. Конформное отображение преобразует
линии х = const, у = const в семейство ортогональных траекторий в су-плоскости. Обратно,
линии и (х, у) = const, v (х, у) = const соответствуют ортогональным траекториям в
z-плоскости (см. также табл. 7.2-1).
Область z-плоскости, отображающаяся на всю до-плоскость функцией f (z), называется
фундаментальной областью функции f (z). Точки, где f (z) = 0 называются критическими
точками отображения w = f(z)1). Отображение, которое сохраняет величину, но не
направление отсчета угла между двумя кривыми, называется изогональным или
конформным отображением второго рода (пример изогонального, но не конформного
отображения: w = z)>
I ди
дх
dv
дх
ди
ду 1
dv
ду 1
*) Некоторые авторы называют особые точки, где l/f/ (z) =0, также критическими
точками f (z).
216 ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.9-2.
(Ь) Отображение w = f(z) конформно в бесконечно удаленной точке, если
функция
W = f(l/2) = F(2)
отображает начало г —0 конформно в w-плоскость.
Две кривые пересекаются под углом у в точке 2 = со, если
преобразование 2=1/2 переводит их в две кривые, пересекающиеся под углом у в точке
2 = 0. Аналогично w=f(z) отображает точку г = а конформно в точку ш = оо,
если w=\/f(z) отображает г —а конформно в точку w = 0 (см. также п. 7.2-3).
7.9.2. Дробно-линейное отображение (преобразование).
(а) Дробно-линейное отображение
W = ^T^ (bc-ad)?b0 (7.9-2)
устанавливает взаимно однозначное соответствие между точками 2-плоскости
и точками w-плоскости. Оно имеет две инвариантные точки
2 = ^ [(a-d) ± V(a-d)*+4bc] (7.9-3)
(которые могут и совпадать), отображающиеся сами в себя. Отображение
конформно всюду, исключая точку 2 = —d/Cy которой соответствует ш = оо.
Прямым и окружностям 2-плоскости соответствуют прямые или
окружности до-плоскости и обратно; в этой связи можно прямые рассматривать как
окружности с бесконечным радиусом, проходящие через бесконечно удаленную
точку. Для каждого дробно-линейного отображения, отображающего четыре
точки 2t, 22, 23, г соответственно в wly w2, w3, w,
Zi — Z . Zt -- Z2 Wx — W tWx —W2
z3 — z * z3 — z2 ~~ wA — w * w3 — w2
(7.9-4)
(инвариантное двойное отношение или ангармоническое отношение1)).
Равенство (4) определяет единственное дробно-линейное отображение, переводящее
три данные точки zv г2, 23 соответственно в три данные точки wv w2, w3.
Существует дробно-лине иное отображение, которое преобразует заданную
окружность или прямую в г-плоскости в заданную окружность или прямую
в w-плоскости (см. также табл. 7.9-2 и п. 7.9-3).
Частные случаи. Отображение
w = Az-\-B, (7.9-5)
где А и В — произвольные комплексные числа, соответствует вращению на угол arg A,
растяжению в | А | раз и параллельному сдвигу на вектор В. Линейное отображение (5)
есть самое общее конформное отображение, которое сохраняет подобие геометрических
фигур.
Отображение
w = - (7.9-6)
z
представляет геометрически инверсию точки z относительно единичной окружности
с центром в начале координат с последующим симметричным отображением относительно
действительной оси. Отображение (6) преобразует:
1) прямые, проходящие через начало координат, в прямые, также
проходящие через начало координат;
2) окружности, проходящие через начало координат, в прямые, не
проходящие через начало координат, и наоборот (прямые, не проходящие через
начало координат, в окружности, проходящие через начало);
3) окружности, которые не проходят через начало координат, в
окружности, также не проходящие через начало координат.
*) Двойное отношение (4) действительно, если точки ztt z2t z9t г (и следовательно,
точки wlt w2, wif w) лежат на окружности или прямой.
7.9-4.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
217
(b) Дробно-линейные отображения (2) образуют группу; обратные
преобразования и произведения дробно-линейных отображений также являются
дробно-линейными (п. 12.2-7). Каждое дробно-линейное отображение (2)
может быть представлено как результат (произведение) трех последовательных
простейших дробно-линейных отображений:
г' = г + — (параллельный перенос), (7.9-7а)
г" = — (инверсия и симметрия), (7.9-76)
w= °~~2а г"-\-— (вращение и растяжение с последующим
параллельным переносом). (7.9- 1с)
7.9-3. Отображение w = -^-(z^"j) *)• Отображение
w = ±(z+ -L) (7.9-8а)
эквивалентно следующим:
= (±=-^\9 или z = w + VuP^l (7.9-86)
w — 1
w+ 1
или
Преобразование (8) конформно, за исключением критических точек
z=l
и
z = — 1.
И внешность, и внутренность единичной окружности
1*1=1
отображаются на всю плоскость до, из которой удален прямолинейный отрезок
соответствующий единичной окружности
1*1=1.
Некоторые важные свойства преобразования (7.9-8а) приведены в табл. 7.9-1.
7.9-4. Интеграл Шварца —Кристоффеля. Интеграл Шварца —К ристоф-
феля
до = Л \ (г — *!)06!-» (г — дгаЛ-1... (z-xnfn~l dz + B,
2 а/=/г-2
(7.9-9)
отображает верхнюю полуплоскость #:>0 конформно во внутренность
многоугольника в до-плоскости; контур многоугольника соответствует действительной
оси, вершины дох, до2,..., wn соответствуют различным точкам xit x2,.*.,xn оси Ох
и внутренний угол многоугольника в вершине доу равен ауд (/=1, 2,..., /г). Для
каждого данного многоугольника в до-плоскости три из точек xj могут быть
*) Это отображение обычно называют отображением Жуковского.
218
ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
7.9-6.
Свойства отображения w = -у fz+ -^Л
(см. также табл. 7.9-2 и 7.9-3)
Таблица 7.9-1
г = х + 1у = I 2 ! <?1<Рг о; = и -\- iv •-
JQ
Точка, кривая (ые) или
область в ,г-плоскости
Окружности с центром в 0
| 2 | = еа = const ф 1
Прямолинейные лучи,
выходящие из начала координат
ф = const ф 0
Единичная полуокружность
1*1 = 1, у^О
Единичная полуокружность
|2| = 1, У<0
Прямолинейные отрезки
действительной оси у == 0,
соответствующие интервалам
-оо<*< — 1,
- К х < 0,
0<*<1,
1 <* <0О
Линии тока для течения,
обтекающего единичный
круг со скоростью V2 в оо
Соответствующие линии
постоянного потенциала ско-
1 ростей
Точка кривая (ые), или
область в и>-плоек ости
Эллипсы с фокусами + 1
1 — 1
ch2 a * sh2 а
Гиперболы с фокусами + 1
и2 vz _
cos2 ф sin2 ф
Прямолинейный отрезок
- 1 < и < 1
Прямолинейный отрезок
- 1 < и < 1
Прямолинейные отрезки
действительной оси v = 0
— со< и <— 1,
— 1 > и > — со,
со> и> 1,
1 < н<со
v = const
и = const
Замечания
Если ф возрастает, то 6
возрастает для | z | > 1 и
убывает для | z | < 1
Если ф возрастает, то и
убывает
Если ф возрастает, то и
возрастает
выбраны произвольно; остальные точки Xj и параметры А и В определяются
единственным образом.
Если одной из вершин многоугольника соответствует бесконечно удаленная
точка, например, хп = оо, то формула (9) приводится к виду
z
w = A' J (Z-x\fi-1 (z-д:;)a2-1...(z-^_l)a«~l-"1^z + Б^ (7.9-10)
А' и В' — постоянные параметры и х\9 x'2t ,
лп — \
— новые точки оси Ох.
Фактическое определение точек х, или X: весьма сложно, за исключением
некоторых вырожденных случаев и когда один или несколько углов а я обращаются в нуль
1см. [7.6]).
Приложения формулы Шварца — Кристоффеля к отображению параллелограммов и
прямоугольников в су-плоскости приводят к эллиптическим функциям (п. 21.6.-1).
Отображения 26 — 30 в табл. 7.9-2 суть частные случаи формулы Шварца —
Кристоффеля.
7.9-5. Таблица отображений. Табл. 7.9-2 иллюстрирует некоторые
отображения, часто встречающиеся в различных приложениях.
7.9-5.
7,9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
Примеры конформных отображений
219
Таблица 7.9-2
Рис. 1. w = 28.
В'
«
§§
\д'
В'
Рис. 2. w — г2.
т.
D С>
Рис. 3. w = г2.
Рис. 4. о; — 1/г
220
ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.9-5.
Таблица 7.9-2 (продолжение)
ДШ
В'\
%-*
Рис. 5. w = 1/2.
тС1
С
С
\1
А В П' Е'А' В
Рис. 7, w — ег.
— и
У
iff
F
А
Е
Р
ш
t
0
С
3
2
W-x
ТВ' \С В'А
—и
Рис. 9. w = sin z.
7.9-5.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ 22*
Таблица 7.9-2 (продолжение)
2
С'\
В'
-и
Рис. 10. w = sin z.
и
2
У
■
г"
г
с
ш
J3
г
в
;
и
Ж
Л' V Г
УШ\
/Г В'
Рис. П. w = s\nz\ BCD ; у = k. B'C'D' есть полуэллипс
Рис. 12. иу =
г- 1
2+1
Рис. 13. w ■■
i-z
l-f 2
222
ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.9-5,
Таблица 7.9-2 (продолжение)
*1 + *2
az —
*i - *2
(а > 1 и R0 > 1, если — 1 < хг < atj < 1).
-X
Рис. 15. с^ 2-Q : g-'+^, + VW-l)(xj- I) ;
az — 1
Яо =
*i + х2
xtx2 - 1 - V(xi - l) (jcJ- l)
(*2 < а < *t и 0 < /?0 < 1, если 1 < х2 < xt).
£' В'
Рис. 16. до — г -\
7.9-5.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ 223
Таблица 7.9-2 (продолжение)
Рис. 18. w = z -f
V k2 + l J ^ U2 - i J
У'
B'C'D' есть полуэллипс
2
7-H
Рис. 20. ш = In
; ЛВС есть дуга
2+1
окружности *2 -f- У2 ~ %У ctg & = 1.
U=7t
и=-тс
z + 1
Рис. 21. су = In _ t •; центры окружностей
2-1
в точках z = cth с^, радиусы —г—
(/г= 1, 2).
224
ГЛ. 7. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.9-5.
Таблица 7.9-2 (продолжение)
Рис. 22. w = k In
V " F
+ In 2 (1 - fc) + nl - k In (2+1)-
— tf
1 —Л
— (1 - Л) In (2 - 1); *! = 2k - 1.
Рис. 23. w = tg» -
1 + COS 2
2 И 4- 1
Рис. 24. w = cth — = —~-—
Рис. 25. w = In cth — .
7.9-5.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ 225
Таблица 7.9-2 (продолокение)
В ■ С В Е Л'
Рис. 26. w = ni -f г — In z.
'•шж?
'С
В'
ж.
в с1в
Рис. 27. w = 2 (2 + 1)V« -f In
(2+ l)'/i-l
rfi 27'
«щ
ЛI F\A В С к
Рис.28.ш==^1пЬЦ^+1п1±1; U
—и
k I - ikt ' 1 - /
V г + л» У
л' /Г
5 ■ С 2J
Рис. 29. w = — [(z* — l)1/* -f Arch z].
я
€ ЛА BCD" С В'
Рис. 30. w = Arch ;— - Arch -—' .
8 Г. Корн и Т. Корн
226 ГЛ. 7, ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 7.9-5.
1
Конформные отображения некоторых областей D
на единичный круг (| w | ==с 1)
Таблица 7.9-3
г = х + iy = | z | е*^, к; = и + if = |
J9
1
2
3
4
5
6
7
^ 8
9
10
11
Область D
в ^-плоскости
Верхняя полуплоскость
У>0
Правая полуплоскость
х^О
Единичный круг
|*|<1
Полоса шириной я
0 < х < я,
— оо <#<со
Сектор единичного круга
|Z|<1
0 ^ ф ^ па
z-плоскость с разрезом
от z = 0 до z = оо вдоль
положительной части
действительной оси
Внешность эллипса
02 "I" £2
Внешность параболы
| z | cos* -|- = 1
Внутренность параболы
| г | cos2 -|- = 1
Полукруг
|*|<Д, *>0
Область, ограниченная
прямыми линиями
(многоугольник)
Преобразование
1 iX z — а
w = е =
z — а
{"К действительно)
2 + а
(к действительно)
ik z — а
w ~е'
1 \ - CLZ
(Я действительно)
w-\ {г
w -j- 1
(1+^1/а)1_,(,_г1/а)«
(1+г1/а)2+/(1_г1/а)2
Vz — i
w =
Vz + i
.-4[(а-Ь,- + ^]
-■-( 2 Y
*-W + w
w = tg* (± Vz"}
. z2 + 2Rz — /?*
Комбинация отображения
Шварца — Кристоффеля
(п. 7.9-4) с отображением 1
Замечания
z = a
преобразуется
в точку
w — 0
z = a преоСразуется
в точку ш = 0
Частный случай
преобразования
Шварца — Кристоффеля
(7.9-9)
См. также п. 7.9-3
7.9-6.
7.9. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
227
7.9-6. Функции, отображающие специальные области на единичный круг.
(a) Теорема Римана об отображении. Для каждой односвязной
области D в г-плоскости, кроме всей г-плоскости и г-плоскости, из которой
удалена одна точка, существует конформное отображение w = f (z), которое
устанавливает взаимно однозначное соответствие между всеми точками области D
и внутренними точками единичного круга |ш|<1. Аналитическая функция
f (z) определена единственным образом, если задан образ точки а области D
и угол поворота любой кривой, проходящей через эту точку, /п. е.
f (a) = w0 и argf (a) = a,
где w0 и а-—заданные величины.
Если D ограничена регулярной кривой (п. 3.1-13) С, то функция /(г)
непрерывна на С и устанавливает взаимно однозначное соответствие между
всеми точками С и точками единичной окружности |ш| = 1.
Замечания. 1) Отображение задается определенной аналитической функцией / (г);
2) за исключением отмеченных выше тривиальных случаев, каждую область D,
ограниченную простым контуром, можно отобразить конформно на другую область D*, также
ограниченную простым контуром.
Проблема конформного отображения области D на единичный круг тесно связана
с решением краевой задачи Дирихле для области D (п. 15.6-9). Часто требуемое
конформное отображение может быть получено последовательным применением простых
преобразований.
(b) В табл. 7.9-3 приведены некоторые конформные отображения заданных
областей D на единичный круг.
ГЛАВА 8
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ДРУГИЕ
ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
8.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Преобразование Лапласа (п. 8.2-1) связывает однозначную функцию F (s)
комплексной переменной s (изображение) с соответствующей функцией /(/)
действительной переменной t (оригинал). Это соответствие, по существу,
взаимно однозначное для большинства практических целей (п. 8.2-8);
соответствующие пары / (/) и F(s) часто определяются при помощи таблиц.
Преобразование Лапласа характерно тем, что многим соотношениям и операциям
над оригиналами / (/) соответствуют более простые соотношения и операции
над их изображениями F (s) (пп. 8.3-1—8.3-4). Оно применяется, в частности,
для решения дифференциальных и интегральных уравнений; метод решения
заключается в преобразовании данного уравнения, содержащего оригиналы / (/),
в эквивалентное уравнение относительно соответствующих изображений
Лапласа F (s). (Операционное исчисление, основанное на преобразовании
Лапласа, пп. 9.3-7, 9.4-5 и 10.5-2.)
8.2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.2-1. Определение. Преобразование Лапласа (одностороннее)
оо
F(s) = £[f(t)\ = ]f(t)e-Stdt (8.2-1)
ставит в соответствие каждой однозначной функции (оригиналу) / (t) (t
действительно), для которой несобственный интеграл (1) сходится, единственную
функцию F (s) (изображение) комплексной переменной s — o-\-ia).
Интеграл (1) называется интегралом Лапласа, а функция F (s) —
преобразованием Лапласа (односторонним) функции / (/). Часто употребляются записи
F(s) = X{f(t)ts] или F(s) #/(/).
8.2-2. Абсолютная сходимость. Если интеграл Лапласа (1) абсолютно
сходится при о = о0, /п. е. существует предел
Ь оо
lim \ \f(t)\e~0oi dt=\ \f(t)\e-0otdt, (8.2-2)
то он сходится абсолютно и равномерно для о^о0 и изображение F (s) —
аналитическая функция (п. 7.3-3) при Res = a^a0. Точная нижняя грань оа
действительных чисел а0, для которых это условие соблюдается, называется
абсциссой абсолютной сходимости преобразования Лапласа Jg [/(/)]'» в
полуплоскости Res>aa изображение F (s)—- функция аналитическая.
Хотя некоторые теоремы, относящиеся к преобразованию Лапласа, нуждаются только
в существовании преобразования (простой сходимости), существование абсциссы
абсолютной сходимости будет предполагаться во всем дальнейшем изложении. Там, где
необходимо специально отмечать область абсолютной сходимости, связанную с соотношением,
включающим преобразование Лапласа, будем писать 0 > о" справа от исследуемого
соотношения, как в формуле (3).
8.2-в.
8.2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
229
8.2-3. Область определения. Область определения аналитической функции
F(s) = XlfW] (°>°a) (8.2-3)
обычно расширяется при помощи аналитического продолжения (пп. 7.8-1 и
7.8-2) до полной s-плоскости, за исключением особых точек (см. п. 7.6-2),
расположенных слева от прямой о = оа.
Такое расширение области определения всегда подразумевается.
8.2-4. Достаточные условия существования преобразования Лапласа.
Преобразование Лапласа % [f (t)), определенное формулой (1), существует в смысле
абсолютной сходимости (п. 8.2-2; см. также п. 4.9-3):
оо
1) для а^О, если [ \f(t)\dt существует;
2) для о>оа, если интеграл (возможно, несобственный)
I=\\f(()\dt
существует для каждого конечного tx>0 и \f(t)\^Ke a для f>t2^
^0 (/(/) имеет экспоненциальный порядок или f(t) — 0\e a ) при
/ —оо, п. 4.4-3);
3) для о > 0 или о>оа (какая из границ больше), если X [/' (01
существует (не обязательно в смысле абсолютной сходимости) для
о>оа.
8.2-5. Обратное преобразование Лапласа. Обратное преобразование Лапласа
^6~X[F (s)] функции Г (s) комплексной переменной s = o + i(d есть функция
/(/), для которой преобразование Лапласа (1) есть F (s). He каждая функция
F (s) имеет обратное преобразование Лапласа.
8.2-6. Теорема обращения. Пусть F (s) = JS [/ Ml» a > aaJ гпогда в каждом
открытом интервале, где f (t) ограничена и имеет конечное число точек
максимума, минимума и точек разрыва (или, более общо, / (/) имеет
ограниченную вариацию (п. 4.4-8, Ь)),
Oi + iR
tiW=m*to J F(s)e«d8 =
[[/('-0)+/(/ + 0)] для />0,
*=f {/(0 + 0) для /==0, \(°1>°а)- (8.2-4а)
0 для t<0 )
Б частности, для каждого t > 0, где f (t) непрерывна,
Oi + iR
/7(/) = 2Й lim \ F(s)e*d8 = f(f) (o^Oa). (8.2-46)
R^0Oal-iR
Путь интегрирования в формулах (4) лежит справа от всех особых точек
аг -f- /оо
F (s). Интеграл приводится к интегралу ^-. \ F(s)estds, если последний
существует; в противном случае fj (t) есть главное значение интеграла по Коши
(п. 4.6-2, Ь).
230
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.2-7,
8.2-7. Существование обратного преобразования Лапласа. Особо следует обратить
внимание на то. что существование предела (4) еще не достаточно для того чтобы F (s)
имело обратное преобразование Лапласа. (Пример: F (s) = ) Существование
Jg~l [F (s)] должно быть проверено Для каждого применения теоремы обращения.
Следующие теоремы дают достаточные (но не необходимые) условия для существования
jg-i if (s>].
1. Если F (s) аполитична для а^ о и имеет порядок < — 1 (п. 4.4-3), то
Jg~l [F <s)] существует-, оно непрерывно для всех t и f (t) = О \е а ) при t->oo
и соответствующая абсцисса абсолютной сходимости есть а Заметим, что
при этих условиях формула (4Ь) справедлива и
^-i[F(s)] = 0 для t^O.
2) Пусть F (s) =ф [Ft (s), F2 (s), .... FR (s)], так что <р (zv z2 zn)
аполитична относительно каждого z. и равна нулю для ^1=z2 = ■•• —zn — О. u
Fk{s)=<%Vk{t)] «*>%: * = 1. 2 п):
тогда £fi~l[F(s)] существует и соответствующее преобразование Лапласа имеет
абсциссу абсолютной сходимости
8.2-8. Единственность преобразования Лапласа и его обращения.
Преобразование Лапласа (1) единственно для каждой функции f (t), имеющей такое
преобразование. Обратно, две функции ft(t) и f2 (t), имеющие одинаковые
преобразования Лапласа, совпадают для всех t > 0, за исключением, возможно,
множества меры нуль (п. 4.6-14); fi(t) = f2(t) для всех t>Q, где обе функции
непрерывны (теорема Лерха). f (t) определяется единственным образом по
преобразованию Лапласа для почти всех /> 0 (п. 4.6-14, Ь); данная функция F (s)
не может иметь более одного обратного преобразования Лапласа,
непрерывного для всех t > 0.
Различные разрывные функции могут иметь одинаковое преобразование Лапласа.
В частности, единичная функция (см. также п. 21.9-1) /(0=0 для *<0 и f (t) = 1 для / >0
имеет преобразование Лапласа 1/s независимо от значения, принимаемого f (/) при / =0.
8.3. СООТВЕТСТВИЕ МЕЖДУ ОПЕРАЦИЯМИ НАД ОРИГИНАЛАМИ
И ИЗОБРАЖЕНИЯМИ
8.3-1. Таблица соответствия операций. Табл. 8.3-1 содержит некоторые
теоремы, устанавливающие соответствие между операциями над оригиналами
/ (t) и операциями над их изображениями F ($) и обратно. Эти теоремы
составляют основу применения преобразования Лапласа (операционного
исчисления, основанного на употреблении преобразования Лапласа).
8.3*2. Преобразования Лапласа периодических функций и произведений
оригиналов на синус или косинус.
(а) Если /(/) —периодическая функция с периодом Т (п. 4.2-2, Ь) и
т
\ I / (0 I & существует, то
Т
X If (01=—-гт; $ f W e"stdt <a > °>- (S-3-1)
1 — е 0
Замечание. Интеграл в правой части равенства есть целая функция (п. /.6-5),
так что jf [f (t)] не имеет особенностей для конечных s, за исключением простых полюсов
на мнимой оси.
Таблица 8.3-
Теоремы соответствия операций над оригиналами и изображениями
Следующие теоремы все справедливы, если преобразование Лапласа существует в смысле абсолютной сходимости
(см. также пп. 8.3-2 и 20.4-5)
Номер
теоремы
1
2а
2Ь
2с
3
4
5
Операция
Линейность (а, 3 — постоянные)
Дифференцирование оригинала *), если /' (0
существует при всех t > 0
если fir) (t) существует при всех / > 0
если f (t) ограничена при / > 0 и f (0
существует при t > 0, исключая точки t = t\,
t2, ..., где f (t) имеет односторонние пределы
Интегрирование оригинала
Изменение масштаба
Сдвиг аргумента у оригинала, если / (/) = 0
для t ^ 0
*) Абсцисса абсолютной сходимости для J2? [/ {П (
Оригинал
аЫО-ЬРМ/)
<г= I, 2, ...)
V (t)
t
I f (T) dx
0
f (at) (a > 0)
f{t-b) (b> 0)
/)] равна О или Ga в зависимости
Изображение
a Fx (s) + 0 Fz (s)
s F (s) - / (0 -f 0)
srF (s) - sr_1 / (0 + 0) -
-Г2/'(о + о)-...-Г1' (0 + 0) |
s F (s) - / (0 + 0) - ^ *~ (S X
s
т'Ш
«Г** F (s)
от гого. что больше.
Таблица 8.3-1 {продолжение)
Номер
теоремы
6
7
8
9а
9Ь
10
11
1)
ной сз
1 ' '"* 1 1 1 111 III..
Операция
Свертка оригиналов *)
Соответствие пределов оригиналов и
изображений (теорема непрерывности; а не зависит
от / и s)
Дифференцирование и интегрирование по
параметру а, не зависящему от / и s
Дифференцирование изображения
со
Интегрирование изображения, если J F (s) ds
s
сходится (путь интегрирования расположен
справа от абсциссы абсолютной сходимости)
Сдвиг аргумента у изображения
Существование ft -Х- f2 предполагается; абсолю
одимости Л5 [ft X f2]. См. также п. 8.3-3.
Оригинал
fi*f2 = Jfi(T)M*-T)dT =
0
lim f(t, a)
a-» a
a2
a)dafit* a)' b) \ fit' a) da
-tf(t)
(-\)rtrf(t)
-ffCO
e^fit)
гная сходимость JS [ft (/)] и JS [f2
Изображение
^i (s) F2 (s)
Hm F(s, a)
a-»- a
a2
a) -^— F (s, a), b) ^ F (s,
a,
a) da
F' (s)
F'n (s)
CO
J F (s) ds
s
F{s-a)
(0] есть достаточное условие для абсолют-
8.3-4.
8.3. СООТВЕТСТВИЕ МЕЖДУ ОПЕРАЦИЯМИ
233
(Ь) Если f (0 — антипериодическая функция (п. 4.2-2, Ь) с периодом Г, т. е. f (t-\- Т[2) =
(0-
Г/2
= — / (0*) " J \f(t)\dt существует, то
0
Г/2
-gPW-, '.Г/2 S П,)'-~$<
1 "г е о
(с) Если f(t) — антипериодическая функция, положительная для 0</< Т/2, и
функция ф! (t) получена в результате ее детектирования, т. е.
dt
(а > 0).
(8.3-2)
Ф1 (0 ■■
f(t) при f(t)>0,
О при f (0 < О,
X ГФ1 (0] = _sr/2 ,S? tf (01 (с > 0).
(8.3-3)
(d) Если f (t) — анти периодическая функция, положительная для О < / < Т/2г и
функция Ф2 (0 получена в результате ее выпрямления, т. е.
Ф2(0
-{-';
f(t) при f(/)>0,
(О при f(/)<0.
sT
J? ГФ2 (О] = cth ^- ^ [f (/)] (а > 0).
(8.3-4)
(е) Преобразование произведений оригиналов на синус
или косинус. Если F (s) —преобразование Лапласа для f (t). то
%\f(t) sin ©/]«=-£ [F (s-m)-F (s + i
X [/ (0 cos cot] = 4 iF (s-ia>) + F (s + i
8.3-3*. Преобразование произведения (теорема о свертке). Пусть
Fi (s) = # [/i (01 (а > aj, F2 (s) =«S? [/2 (01 (a > a2).
■HI. )
-1(D)]. J
(8.3-5)
cS? [/l(0/2(0] =
Тогда
Я -f- /00
2й/ § Fl(z)F2(s-z)dz (l>o1)t (8.3-6)
Я — /oo
К + /00
^ \ F2(z)Fx(s-z)dz (X>a2). (8.3-7)
Я — /оо
В обеих формулах следует считать, что Res>a1-f-a2; это значит, что
изображение произведения МО МО — аналитическая функция в полуплоскости
a = Res>ai-f-a2.
8.3-4. Предельные теоремы. Если F (s) — преобразование Лапласа для /(О
" «5? [/' (0J существует, то
lim sF(s)=f (0 + 0).
s -* 00
£слм, кроме того, существует предел f (t) при t—>co, то
lim sF(s) = lim /(/).
s -*• 00 / -> 00
(8.3-8)
(8.3-9)
*) Такую функцию называют еще «функцией с зеркально сдвинутыми полуволнами».
234
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-1.
8.4. ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
И ВЫЧИСЛЕНИЕ ОБРАТНЫХ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА
8.4-1. Таблицы преобразования Лапласа. Таблицы преобразования Лапласа
имеются во многих справочниках, например, [8.2] [8.7]. В табл. 8.4-1 и 8.4-2
приведены наиболее часто встречающиеся преобразования.
8.4-2. Вычисление обратных преобразований Лапласа. В пп. 8.4-3—8.4-9
описываются различные приемы отыскания оригинала / (/), соответствующего
заданному изображению F (s) (см. также пп. 9.3-7, 9.4-5 и 10.5-2).
Замечание. Если существование Зи~х [F (s)] заранее неизвестно, то результаты,
полученные применением теоремы обращения (8.2-4), должны быть проверены с помощью
формулы (8.2-1).
Особая осторожность рекомендуется при применении разложения в ряды для
получения Su г [F (s)]; по-видимому, непосредственное асимптотическое или даже сходящееся
разложения могут не привести к правильному результату, если F (s) и f (/) не
удовлетворяют специальным ограничительным условиям.
Некоторые достаточные (но не необходимые) условия для справедливости разложения
в ряд <5?_1 [F (s)] приведены в пп. 8.4-6—8.4-9. Во многих случаях, где функция / (/)
подозревается как об l [F (s)], это может быть проверено подстановкой в исходное
дифференциальное уравнение; поэтому эвристический метод отыскания JU 1 \F (s)] может
оказаться весьма полезным.
8.4-3. Применение контурного интегрирования. Значение контурного
интеграла (8.2-4) часто удается получить при помощи теоремы о вычетах (пп. 7.7-1—
7.7-3) и леммы Жордана (п. 7.7-3, Ь).
Если F (s) — многозначная функция, то контуры не должны, конечно,
пересекать разрезы для F (s) (п. 7.4-2).
8.4-4. Обратное преобразование Лапласа для рациональных алгебраических
функций: разложение Хевисайда»
(а) Если F (s)—рациональная алгебраическая функция, выраженная
отношением двух многочленов
F (*)=%$ (8.4-1)
причем степень многочлена D (s) выше степени многочлена Dx (s), то X"1 [F (s)]
равно сумме вычетов (п. 7.7-1) функции F (s) est no всем особым точкам
(полюсам) F(s). Для вычисления обратного преобразования Лапласа 56~х [F (s)]
сначала находим корни S/, уравнения D (s) = 0 (которые определяют полюсы F (V))
методами, описанными в пп. 1.8-1—1.8-6 или 20.2-2—20.2-3; тогда:
1. Если D(s) = aQ(s — Si)(s — s2) ... (s — sn) (все корни уравнения
D(s) = 0 простые), то
Х^ [F (s)] = <5?"1 [^] = 2 Т?Щ) Л' (t > 0)' (8А'2а)
2. Если D(s) = a0(s—sl)mi (s—s2)m2 ... (s — sn)m,l9 то
где
l dj-i
Hkj=-
i!-l)\(mk-i)\d*>-
(t > 0), (8.4-26)
('-'*) kDl
D{s)
Ml)| ^
Js = Sh
8.4-4.
8.4 ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
235
Таблица 8.4-1
Таблица преобразовании Лапласа
(а, Ь и с — различные постоянные)
F(s)
fit) <*>0)
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1/s
1/5»
\/sn (/i = l, 2, . . .)
1/VT
*-*/■
5— (л+ V2)(,i= 1,2, . . .)
Г (ft)
5*
1
s — а
]
(k>0)
(s - a)"
Г (ft)
(n = 1, 2 )
(s - a)'
(ft>0)
1
(s -a) (s- b)
s
(s -a) (s- b)
1
(s - a) (s - b) (s — c)
1
s2 + a2
s
s* + a*
s2 — a2
s
s2 — a2
1
s (s2 + a2)
1
S2 (S2 _j_ a2)
(s2 + a2)2
(n - 1)1
1
/я/
2 /f/я
2ntn—1/i
1 .3- 5 ... (2л-1) Vn
tk-l
J*
и*
1 tn-
(n - 1)1
Z*"1^
a — о
-ica/
-,w)
-Ц- (aeat - bebl)
a — b
(b - c) eat + jc-a) ebt + (a - b) ect
(a -b){b- с) (с - a)
1 .
— sir
a
cos at
1
sh at
ch at
J_
a
J.
a'
— (1 — cos at)
— (at — sin at)
jr—r- (sin a/ — at cos a/)
2a8
236
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 8.4-4.
Таблица 8.4-1 (продолжение)
F(s)
f (0 (/ > 0)
22 |
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
(S2 _|_ a2)2
S2
(S2 + О2)2
s2 — а2
(s2 + а2)2
s
(82 + а2) (52 + &2)
1
(S — Л)2 + Ь*
s — а
(s — а)2 + Ь*
За2
s3 -{- а*
4а»
s* + 4а4
s
s4 + 4а*
1
s4 — а*
s
s*— а*
8a*s2
(s2 + a2)»
-Н^Т
s
(s — а)3/г
j/s —a —Vs — b
1
/s + a
Vs
s — a2
Vs
s + a*
I
/s (s — a2)
I
Vs (s + a2)
-77— sin at
2a
-g— (sin a/ -f a/ cos a/)
/ cos at
cos a/ — cos bt
b*-a*
-r- ea si n 6/
6
*af cos bt
fat _ ea//2
( at
(cos —
VT
■o-, fl'W
- /3 sin
sin a/ ch a/ — cos at sh a/
1
2a2
si n at sh a/
■я—r (sh a/ — sin a/)
2a8
г—г (ch a/ — cos a/)
(1 -J- a2/2) sin a* — at cos a/
n\ dtn n\ n
1 eat(\+2at)
(ebt-eat)
Ynt
2 Vnf1
—Lr- - aea2/ erfc (а /Г)
/я/
_L=- + аеаЧ erf (а V7)
/я/
aVt
0
Ynt Vn
1 a2/
*e,erf(a/f)
aVt
dA,
«.4-4.
8.4.ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 237
Таблица 8.4-1 (продолжение)
F (si
fit) (t>0)
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
6*-а*
(s - а2) ( b + Vs )
1
Vs {Vs + a)
1
is + a) V7+b
bz — a*
Vs (s — a2) (Vs 4- b)
d-s)n
sn + Vi
(1 - s)n
sn + V*
Vs + 2a
Vs
Y7+aVs + ь
Г (k)
(s + a)A (s + b)b
(k>0)
(s + a)1^ (S + b)*/*
Vs + 2a — Vs
Vs + 2a + /s
(а — &)&
(Vs + a + Vs + b)2k
(V7T~a + Vs )~2V
Vs Vs + a
1
(v > - 1)
Vs* + a2
(Vs2 + e2 — s)v
Vs2 + a2
(v>-l)
(£>0)
(s2 -f a2)*
(V^MP-s)* (£>0)
(s - Vri2^^2)v
y^nr^
(v>-l)
*a2/ [b — a erf (a V7)] - te6*' eric (d /F)
*a2' erfc (а V7)
—= Г* erf (V^=^ y7)
У b — a
еаЧ ГА. erf (а У7) - 11 +Vf< erfc (ft У7)
л!_
(2л)! 1/яГ "2Л
н.ЛтП)
n\
Vn (2л + 1)!
H2n+i(Vt)
ae~at Vi (at) + /0 (a/)]
/я (_-L-)*-v.,_i/f(e+6)/ x
^'i-v,[t')
-f e^h(at)
^-''-"Чт")
Jo (at)
Vn ( t \*-Vf
Г (Л)
ш
Jk-*/*(«»
•*-Jkm
avIv (at)
238
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 8.4-4.
Таблица 8.4-1 {продолжение)
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74 |
75
76
77
F (s)
■ (h ^ъ ()\
(S* _ fl2)fc
e~*s
s
e~ks
s2
1 p-bs
/ii -v. ГЛ
S*1
1 - e~ks
s
1 l+cth(-Ifcs)
s (l -e~ks) 2s
1
s (eks - a)
— thfts
s
1
s(l+6-£s)
^i-thfts
1
s sh fts
1
s ch ks
— cihks
s
s-iqp^rcth-2T
l
<s»+i)(i-r**)
s
_L-e-(*/s)
/s
1 **/*
V7
f (0 {t > 0)
1Ая / / \ft-»/t/ ,лЛ 1
j "TWV2TJ 7A-«/.<e/>
J 0, если 0 < / < ft,
I 1, если / > k
i 0, если 0 < / < k, j
\ t — k, если />ft
Г 0, если 0 < t < ft,
\-ч^-—>• !
J 1, если 0<t <k,
\ 0, если t>k
1 -f [//ft] = n, если (л - 1) k < / < «Л
(л = 1, 2, ...) (рис. 8.4-1, а)
( 0, если 0<t<k,
< 1+в + а2 + ...-Мл~\
( если лЛ < f < (л + 1) Л (л = 1, 2, ...)
Af (2ft, 0 = (- l)"""1,
если 2ft (л — 1)< * < 2kn (л = 1, 2, ...)
(рис. 8.4-1, Ь)
если (л — 1) ft < / < nk
Н (2ft, 0 (рис. 8.4-1, с)
F (t) = 2 (л - 1),
если (2л — 3) ft < t < (2л — 1) ft (/ :> 0)
Л* (2ft, f+ 3ft) + 1«1 -f (- 1)л,
если (2л - 3) ft < t < (2л - 1) ft (* > 0)
/?(0=2л-1,
если 2ft (л — 1)<* <2ftл
| si n ft/1
J sin *, если (2л — 2) я< / < (2л — 1) Я,
(0, если (2л — 1) n<t <2ля
Л (2 Vkl)
■ рпч 2 l/"]b?
/я/
* лЬ 9 т/Т?"
" СИ Z У fil 1
/я/
8 .4-4.
8.4.ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 239
Таблица 8.4-1 (продолжение)
F(s)
f(t) (t>0)
78
79
80
81
82
83
84
85
як
1 _— (ft/s)
,v, €
-4-ek/i
S /2
e—*VT
s
. 1 h V~
e л i s
Vs
e-v. е-*/»
0*>0)
<H>Q)
(ft>0)
<ft>0)
(Л>0)
(ft^O)
/ь ь> m
87
89
90
91
92
93
s (a + Vs)
e-kYs
Vs (a + Vs)
e-kVs(s + a)
Vs (s + a)
— ft V"s* -f fl2
/s2 + a2
— kVs2 — a2
e
Vs2 - a2
(ft>0)
s
vjmt^ v" "
,-As-.-*^
» + a8
e-kVs*-a\-ks
Vnk
l
sin 2 Vkt
sh2Vkf
Vnk
-±= exp (_ *L)
Vnt> \ it J
(tw)
(-*)
2
erfc
1_
Vnt
exp I
_eaft eaMtertc(aYt + *
f
+
2 vry"
+ ыс(т?г)
eak ea2t erfc /a y, _| b\
\ 2Vt J
{:-
{
l°-
I /o (a //" ~ ft2) ,
0f если 0<*<ft,
1/2 a//° (4" a T//2"~^2) • если / > k
0, если 0</ <ft,
Jo (a Vt2 - k2). если t > ft
0, если 0 < / < ft,
если / > ft
Л (a Vt* + 2kt)
( 0, если 0 < t < ft,
{ — ak ■ A (a Vt1 — ft2), если * > ft
\ W2-ft*
Г 0, если 0 < t < ft,
J aft
V/2-ft2
/i (a//« — ft1), если *>ft
240
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 8.4-4.
Таблица 8.4-1 (продолжение)
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
ПО
111
112
ИЗ
114
F{s)
a*t-kir*T« (v
Vs* -f a2 (Vsz -f a2 + s)v
— In s
s
~ Ins (k> 0)
s*
———— In ^ (\\
- — v« -> uj
s — a
In s
s2 + i
s In s
s2 -f 1
-y-ln (1 + ks)(k>0)
. s — a
In z
s — b
-i-ln(l + *2s«)
— In (s2 + a2) (a > 0)
s
-i- In (s2 + a2) (a > 0)
sz
s2+a2
ln—~
. s2 — a2
arctg —
1 . k
— arctg —
s ь s
ek4* erlc(ks) (k>0)
1 h242
— e erfc (£s) (fc>0)
s
eks erlcV'ks (k>0)
-±r erfc (VFs)
Vs
—L ekS erfc (У*5) (£ > 0)
-te) 1
f (*> С > 0)
Г 0, если 0 < f < /г.
\\jTkj J^{aVtz~k2)t если'>*
Г'(П —In* [Г'(1) = - 0,5772]
-Л-1 Г Г' (k) In М
ЦГ <*)]2 Г (Л) J
; еа' [In a- Ei (-а/)]
cos/Si * —sin/Ci/
— sin / Si / — cos t Cit
-EiK)
! -\-(ebt-e°<)
-°й
2 In а — 2 Ci (aO
— [a/ ln a + sin a/ — a/ Ci (aO]
2
— (1 — cos at)
~ (1 — ch a/)
-J- sin tt
Si <#)
1 ex / /2 \
kVn * [ 4k*J
-(*)
УТ
яУ7 (/-ffc)
f 0, если 0 < / < k
\ (я/)""1/2, если />£
1
/я (* -f- b)
-—- sin (2* V7)
8.4-4.
8.4 ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 241
Таблица 8.4-1 (продолжение)
115
116
117
118
119
120
121
122
123
124
125
F(s)
Ys \ Vs I
Ко (ks)
Ко (k Ys)
~eksKt(ks)
-±=rKx(kYs)
Ys
■к** (*■)
ne~ksh (ks)
ne~ksIt (ks)
— eas Ei (—as)
1 as
h se Ei (— as)
(y- — Si s\ cos s H- Ci s sin s
f (t) (t > 0)
1 --2*tT
f 0, если 0<t <k,
\ (t2 — k2)~l/*. если / > k
1 / k2 \
i _
--Vt(t + 2k)
1 / k* \
Texprir)
—jL- Ко (2 ^2*7")
( [t (2k - 0]""1/e, если 0 < / < 2k,
I 0, если t->2k
l С k — t
1 - если О -г" t -f" 2£
< A V7(2A - 0
I 0, если *>2A
т^Ьг (a>0)
/л ^ (\\
</ + a)» {a^0)
1
t2 + l
1+
a)
(0,1
U,o)
М(сД
(ОД
(2c,0)
\T
(2c,0)
Рис. 8.4-1. Графики оригиналов к изображениям 65, 67 — 69, 71.
Таблица 8.4-2
Таблица преобразований Лапласа для рациональных изображений F (s) = -—
Dt (s)
(s)
Каждая формула справедлива для многочленов Dt (s) и D (s) как с комплексными, так и с действительными коэффициентами.
Наибольший практический интерес представляет последний случай; при этом корни многочленов действительны и/или комплексно
сопряженные, а функции f (t) —действительные.
Заметим, что
(s — а)2 -j-©2c= [s — (а + ш)] f-з — (а — /©)] и Kt sin at -f K2 cos <at = |//Cf-f /<2 sin (ю* -f а), где a = arct^ (KJKJ
№
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
F(s)
s
1
s — a
,
s (s — a)
s + d
s (s — a)
1
(s - a) (s - 6)
s + <*
(s — a) (s — 6)
1
s (s — a) (s — b)
s + d
s (s — a) (s — b)
f if) V > 0)
1
J*
АеЫ + К
Aeat + Bebt
Aeat + BsM + Я
*-!•«—ir
-(■+4).*~£
4 _ 1 в ■ ■ '
a — b ' b — a
A = a-±±, B = b-±±
a — b * b — a
A- l В l К Х
a {a — b) * b ф — a) * *x aft
fl + rf fc + d rf |
a (a — ft) ' ft (ft — a) * ab
8.4-4.
8.4. ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
243
48 h
II
43
+
од
+
<*
Q
"а
+
+
^
<
'о
1
•q
о
1
£*
1
о
и
^
•а
+
од
+
СО
1
|
1
со
1 со
а>
-
С
"С
1
& 1
а* С.
^
о
1
'а'
1
>
1
S-
1
1
з
1
з
II
^
-
1
1
3"
1
со
"о"
1
со
О
43
+
•а
+
*°
а
43
+
^
•О
1
'о'
It? I
1 1^
в II
1
S-
1
3
"^
1
з
1
з
II
^
Ъ
«
О
+
<и
CQ
+
*
"а
+
со
CJ
1
1
1
со
о4
|
_
«
43
+
од
. +
+
од
+
•^
а
4з
+
од
+
"а
^
•о
1
'о
It? Т, М
1 |^
S ||
1
*S
5
t?
1
з
1
з
II
Ч
чз
+
од
+
Q0
1
1
со
1
"в"
1
«о
CN
~*
о
"
в
-|Э
II
Ч
'а
3
+
'З'
1
w
•^
СЧ*
43
31+
1 °
и*
СО
11
е
3
+
1 ^
! +
о
1—1
-|3
И
ч
в
-ь
3
с
<л
<*»
*
4з
+
3
+
"о"
|
>2-
oi
oi
8;в
Jbp
—
о
со
я I
Ъ II
3 в
+ .
3 |з
- +
3
О
II If
•<: х
_
ST
3
+
я
1
со
СО
со
oi
3|<з
°
со
1
1 1
143
>' 3
3
+
4?
+
з
+
<3
"о
3 я
—I I3
-3
"о
II II
«* *
*
+
'в
+
Ж»
3,
с
"53
43
+
И
;р
3
+
1
"*
CN
з!сз
! '
1 ьо
* т» 1
од
+
см
3
_1_
[
4Т
+
+
3
1
3
СО 1
|43
ОД
+
см^
% 3
3
+
+
ОД
+
3
1
<->
СО
II '
в
3
-1 ^ +
Нз Ы
и II
■* *
43
+
ОД
+
5Г
3
+
1
со
СО 1
Ю 1
oi I
244
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-4.
1 **
А
с-
1 "*-■
1
^
-,
-
3
+
|
3
1
i ~
—
N
3
+
2. 3
1
>2- о
1 I U.
СО
3 1
и к
ч в
4-
«о
3
+
3"
1
1
CQ
' е," 3
3
+
+
о
1
la
8 1
t■
1 s
<3
9
+
-|в й
II II
ч в
•с
с»
CQ
+
*3
н-
3
с
"в
3
+
еа 1
1
w 1
1
1 СО I
*°.
of 1
43
со
3
+
ea 1
1
CO I
1
IWJ, 1
г»
oi
> •*
M
So
+
CM
3
+
4?
+
tifl
+
еа
3
1
еа
Г1 +
+
о
3
+
•о
1
1
1 •
еа
3*
1
з
.—.
-Is
||
Ч
+
+
**
со
3
+
еа
1
со
1
00
oi
3
,1
"о
СО
1
3
•о
+
+
3
1
£Р
сО
II
в
-
—
^
3
Z
.
3
м
з
1
i
i
•? *
1
з
еа
3
3
II 1
3
+
1
1—J
«о
Ч CQ
a
CN
3
1
1
СО
1
СО
со
3|о
ЬД
й
ев
1
|«о
3 1
ьд
1
II
в
^
*4
+
'о
+
•а
еа
3
+
3
1
з
3
з
3
II
^
!еа
43
3
з
1
II
43
+
г—»
3
+
1
W
о
II
CQ
*
+
+
е*
+
3,
.S
"от
в
•в
+
со
3
+
еа
о"
I
1
со
1
1 со
О
•"■*
ci
3|о
"о
«0
1
|*°
3 1
1 <3
"о
со
з +
|<3
2?
1?
со
II
в
1
8.4-4.
8.4. ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
245
~ I
Я
сз
ем
«1
3
+
•«
+
+
3
1
1
^$
г-, "^
3
+
3
+ у
•О
1
3
3 ы
•О о
1 •-.
<м j сз
7 и !
it *
3
о
+
v—J—/ •«>
Нэ
St
+ ^
5L 3
о
1
43
+
+
3
1
<3
^ "о
*° се
1! II II
«3
: а
3 5
3
II
+
3
1 +
"а
я —
3
+
171
У
+
а
м-м
У
СЗ
+
3
1
1
3
+
я
см
3
+
Я-ч
3
1
2?
сз
1
3
Чз
+
р__
е.»
+
ет
*«
<М(Я
3
Ф4
+
»1
*W
1
3
+
«1
з
Сз
CN
Ф1<М
Я
1
3
+
а
ьд
о
СЗ
+
3
-
3 Й
+
+ +
я
с
И
«>
Ч
3
с
05
+
3
1 +
+
246
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-4.
о
А
S
^
*tn
к
*
^
г———I
34
toe
+
О
CN
з
1 +
^
+
t»e
+
©I—i
3
1
3
'Ф
+
51
7з
1
3
+
■ *
-|з
1 ^
II
^
3
Q
<м
1 X
+
cn,
3
«I'M
3
+
«- е. *
3 >
1
*1 *
и) 3
■в г "«.
+ 7 +
«ад ' SL
«1-4 |
3 •*
1 w
*о
(MCI
3
+
S1
<М»1
3
1
+
О!
>—*
ьл ' '
2 -1 э"
03 1
II II
в cq
+ _
^аз.
'si
w с
в -a
w 05
^
IX—«ч
*«
+
(л
tie
+
ел
ям
3
+
(л
w-t
3
+
х—ч
1
W'
^
—'
см*
3
а
CN
IW>
3
1
1
м<з
bn
1
с
J
3
3
L
3
1
•«
Jar
"о
СО
II
са
-1-
1 w
~* 1
со
I
"?
о
II
^
+
•X
«—«
II
^
^
^
-1-
5
^
м
а4
1
(Л
CN
СО
+
оо
«
"о"
1
<л
СО
со
1
1
II
1
II
*
~\%
1°
II
^
-
'о'
1
(л
в)
>*
со
41 Iе
1
II
*
1
II
*
•«
+
Q
3
II
^
"»*,
*<
+
Ч>
^
•«
+
"о
1
1
(Л
(л
Ю-
СО
■**|в
II
*
^f
|
II
+1
tie
а
+
о
О
II
^
•«
+
оо
tie
+
*j
"о"
1
(л
СО
со*
8.4-4.
8.4. ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
247
I
II
+
•«
+
tx>
+
«о
в
|
W»
I
■у
+
-И
*°
I
II
•«
+
Ой
+
о
.о
1
о
•«
+
tlfl
•с
+
•о
+
+
Г +
II
_ +
I ■*
3 +
II
•О М|"сз
•«
+
W)
о
+
а
•о
|
a
о
S
+
w
•«
+
abg
3 7 «
248
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-4.
II
II
И
Л
I
+ ■
+ '
о
СМ
1
v>
+
•о
•» 1
V) 1
1
о
S"
1
о
II
+
+
+ '
II
+ :
4-
•**
•С)
+
+
II
II
см|о
I
8.4-4.
8.4. ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
249
*
+
1
1! II
"? к?
.
43
<N
<3
*о
^
к I
II II
^ *
^
*
+
*
+
в
<а
Я;
^
+
S
+
«л
е»
9
1
ьо
ьо
CN
(N
СО
43
+
ад
+
о
*
1
II И
<? X
.
•«
<N
э
со
"С
\ 1
II II
•ч; а<
•«
+
ад
+
to
е»
'о
1
ьо
ьо
СО
(N
СО
—
^
1 ""
2,
1
3*
|
1
^ CQ
со
<N
|
3 ^
1 1
И II
^ 0Q
•"*
S"
1
'в
1
ьо
•*г
(N
СО
•«
+
«3
5 "*
| +
3 *°
1
5*
1
1
Ч «Э
.
см
+
+
а
со
5"
1
3
^
1 1
II II
■ч: cq
^5
С
CQ
+
CQ
+
4^
^
+
•«
+
5*
1
1
"о1
1
ьо
ю
(N
СО
•а
+
ад
а
+
•«
2L +
ад
1 *°
3 +
54
1
1
з
II 11^
^ CQ
^
+
з
(N
+
ад
+
з
3
1
з
if
l I
II II
■Ч; CQ
•«
+
(О
ад
+
(О
5*
1
1
а*
1
ьо
СО
°1
СО
^
1
1
| |
II II
^ ^
.
*~"
S
1 -
4—
^5
1
1
з
сч
II К
^ <f
43
+
•о
*^
1
1
1
II II
<е ^
"tt
+
£ ■*
it
|
1
з
<м
II II'
^ ^ 1
<*>
CQ
+
^
*—
•о
1
1
(Л
"9
1
со
t^
°i
СО
<и
"i
^
+
*t,
^
чэ
+
-о
1
1
(О
^
1
(О |
1
СО 1
°1 1
СО j
250
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-4.
4-
I
II
+ +
+ '
W1 I
3 Q
Зв
3
+
3
•«
+
а
с
3
"«
«
CSJ
+
3
+
а
II
За
ад
+
сч
3
•«
+
ад
+
04
3
1
^3
ьл
и
СО
1
!<
*
43
+
йв
3
+
w
w
£
ч
^
+
43 ,
з
-Ь
3 I
II
3
+ ^
& '
I ^
3
3
+
8.4-4.
8.4 ТАБЛИЦЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
251
3 ьо
+1
И
05
+
3 ~
+ 3
з з
I +
г з
Я I—J
II I
в в
II
4-
а
4-
3
с
"со
я:
ч>
С4
CQ
+
CQ
+
~ 3
- 3
3
+
+1
«о I
tuO
з
|+
I
3
н-
3
■ +
3
+
252
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-6.
(b) Иногда удобно получать обратное преобразование Лапласа в случае кратных
корней уравнения D (s) = 0 прямо предельным переходом, ведущим к совпадению
различных простых корней (см. также табл. 8.3-1, 7). Пример:
X'1 Гг-Ц-Л- Пт «5Г1 U ^ 1 - Urn I [e<a + h>' - eat] = teat (t > 0)
L(s-a)2J ft-o l(s — a-h) (s — a)] h^0 hl K^ '
и, более общий случай:
cST1 Г—!—Л - —I— /*-V </>о).
L(s-a)mJ (m-1)!
(c) Комплексные корни. В формулах (2) пары членов, соответствующих
комплексно сопряженным корням s = а± ш, можно преобразовать следующим образом
(см. также п, 8.4-5):
{А + iB) f^a + Ш) t + {А _ ,В) ,/ya-ifi» / e 2Л,/уг/ cos ш/ _ 2В/г^ sin ^ e
= flfV*' sin (со/ + а) = Rtreat cos (со/ + а'), I (8 4-3)
i? = 2/A2-h В8, а = — arctg-^-, а'= arctg-^-;
Л, В, /?, а и а' все действительны, если коэффициенты многочленов Dt (s) и D (s)
действительны; <5f_1 [F (s)] есть тогда действительная функция от /.
(d) Если один нз корней sk уравнения D (s) — 0 будет также корнем уравнения
£>i (s) =0, то один или несколько членов разложения (2) исчезают. Вообще же в случае
общих корней многочлены D (s) и Dt (s) имеют общие множители, на которые их следует
сократить.
8.4-5. Обратное преобразование Лапласа для рациональных алгебраических
функций: разложение на простейшие дроби. Вместо применения формул
разложения Хевисайда (2) можно воспользоваться разложением F (s)=D1(s)/D (s)
на сумму простейших дробей методом, описанным в п. 1.7-4.
Если D (s) и Dx (s) не имеют совпадающих корней, то каждому
действительному корню sk = a уравнения D(s) = 0 отвечает mk простых дробей вида
Ь1 Ь* Ьтг.
s — a (s — a)2> (s — a)mb
где т^ — кратность корня Sk = a. Каждой паре комплексно сопряженных
корней sk = a ± /со отвечает mk простых дробей вида
s + dt s + d2 s -f dmk
Co
1(s — a)2 + u)2' 2[(s —a)2 + co2]2 mk \{s — a)2 + со2]т&'
где mk — кратность корней sk — a± /со, %~г [F (s)\ находится как сумма
обратных преобразований Лапласа таких слагаемых (табл. 8.4-2).
8.4-6. Разложения в ряды. Если функция F (s) сложная или если F (s)
задана неявно, например, как решение дифференциального уравнения (п. 9.4-5),
то иногда возможно находить %~х [F (s)j, раскладывая F (s) в сходящиеся
ряды и беря обратное преобразование Лапласа последовательных членов ряда.
Этот процесс можно также применять для аппроксимации d6~l[F(s)\. Часто
метод разложения в ряды опирается на следующую теорему.
Пусть функцию F (s) можно представить в полуплоскости Re s ^ a в вида
ряда
со
f(s)= S Fk(a),
ft=0
8.4-8.
8.4. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
253
Пусть далее все интегралы \ \fu(t)\e °<*1 dt существуют и сходится ряд
о
сю со оо
2 \ \fkif)\ е~°а* dt. Тогда ряд 2 fk (0 сходится абсолютно к функции f (t)
£=00 k=0
почти для всех t (п. 4.6-14, Ь) и
Г оо ~| сю оо
Xi/«i = cS? 2 МО = 2 «S?[/*(0J= S f*W-^W (a>aa).(8.4-4)
L*=o J fc = o fc=o
8.4-7. Разложения по степеням /. Если изображение F (s) может быть
разложено в ряд по отрицательным степеням s
Fls) = bi + b$+..., (8.4-5)
сходящийся при | s | > г > 0, то при всех / > 0
fV) = J^lFls)\ = b1 + b%t + b£t*+ ...+-^_/*-i+... (8.4-6)
(Ряд справа сходится при всех значениях /.)
Разложение (8.4-5) часто можно получать как разложение Лорана (п. 7.5-3)
в окрестности точки s==oo или, в случае рациональных алгебраических
функций типа рассмотренного в п. 8.4-4, простым делением.
Если F (s) при | s | > г представляется сходящимся рядом
оо
1
/г = 0
/г = 0
В частности, если ряд слева сходится, то
со
зет
/7(s) = _a У ~% (Rea>0)» <8-4"7>
/г = 0
оо
<Se~1[F(s)] = la-1 ^ Г (М-a)'* {t>0)' {8A'8)
/г = 0
ряд слева сходится, то
1 V ck I { Г Г» с* с* 1
VT 1 7Ц = тс' + 1 {2') + Гг&)'+7175<2'>' + -J «><»• *8-4"9»
L £ = 0 J
8.4-8. Разложения по многочленам Лагерра. Каждая функция
^ (s) = х У (01 (а>%),
аналитическая в точке s = co, может быть разложена в абсолютно сходящийся ряд по
степеням
Z = s-oaa+4i <8-4-10>
для a>aa; соответствующий ряд Тейлора сходится для | z |<1. В частности, для о" ==0
изображение F (s) можно представить в виде
/>w-u-*> 2 v*-rFr, 21с*Стй)* <0>а*>' (М-И
— -... — 'Mj
254
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.4-9.
где
R
Vе 2 с'*Т™(ъ) ел —о. 1. 2. ...>.
/«о
Если условия п. 8.4-6 выполняются, то для почти всех t^O
MO-jp-^e.)]-*-'/2 f] Ц^. (8.4-12)
где L. (О — полиномы Лагерра, определенные в п. 21.7-1.
8.4-9. Разложения в асимптотические ряды. Аппроксимацию X [/(/)] и
jf"1 [F (s)] иногда удается получить при помощи асимптотических рядов
(п. 4.8-6, Ь).
* (а) Асимптотическое разложение изображения. Пусть
F (s) =£g[f(t)] и оригинал f (/) может быть разложен $ окрестности точки
( = 0 в абсолютно сходящийся ряд вида
00
/(/)= 23 Ф? (— К Хо < X, < ... — со). (8.4-13)
/=о
Тогда F (s) имеет при s —*> со асимптотическое разложение
^(s) ~ 2j ^у "^ТТГ • (8'4"14)
/ = о s
Ряд справа формально получается почленным переходом из ряда (13)
путем преобразования Лапласа.
(Ь) Асимптотическое разложение оригинала. Пусть
F(s) = %[f(t)) (o>oa)
и выполняются следующие условия
1) F (s) имеет лишь изолированные особые точки — полюсы и
алгебраические точки разветвления,
2) F (s) в полуплоскости Re s < 0 стремится к нулю при | s | —> со,
3) число особых точек s = Sk с наибольшей действительной частью
конечно (6=1,2,...,/) и разложение F (s) в окрестности каждой
такой точки дастся рядом
оо x{k)
/==о
Тогда оригинал f (/) имеет при t—*co асимптотическое представление
Г(^2^2т-^й^' (8-4',6)
где , * /^ч=0» «лм МЛ) = 0, 1, 2, ...
г (_ *j*>) '
Следующий частный тип асимптотического разложения важен в связи
с решением некоторых дифференциальных уравнений с частными
производными (п. 10.5-2).
8.5. ФОРМАЛЬНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
255
Если функцию F (s) в окрестности точки s = 0 можно разложить в
сходящийся ряд вида
00
F (s) = i (a0 + a1si'* + a2s + a3s*'*+ ...) = 1 % afs"2 , (8.4-17)
/=о
а все остальные особые точки F (s) (если они имеются) расположены в
полуплоскости Res<0, то оригинал f(t) имеет при t — oo асимптотическое
представление
оо
/W-«o+-77 Ц (- П^+1 Г(7У/2). (8.4-18)
(При переходе от формулы (16) к формуле (18) учтено, что
ro/t-Л л \J^ 2/' /
Более тонкие достаточные условия для справедливости асимптотических
разложений приведены в [8.3].
8.5. ФОРМАЛЬНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИМПУЛЬСНЫХ
ФУНКЦИЙ
(a) Заметим, что в формуле (8.4-13) и в аналогичных разложениях в ряды
обратное преобразование Лапласа отдельных слагаемых, равных a, asl/2,ast
as$/2, ... , строго говоря, не существует, так как эти функции не стремятся
к нулю при s —► оо. Во многих приложениях члены такого вида могут
появляться под знаком суммы или интеграла, несмотря на то, что сама сумма или
интеграл имеют обратное преобразование Лапласа.
(b) Если применить преобразование Лапласа (8.2-1) к определениям
импульсных функций 6(0 и 6+(t) г) и их «производных» (пп. 9-4-3 и 21.9),
то получим формальные результаты:
J?[e(Ol=1/., cS?[6+(/)]=i, «s?[6;(/)j=s, J?[б;(/)]=А ... , )
J?[6(/-fl)J = «S?[6+(/-fl)] = e-^ (a>0), I (8.5-1)
X Wk){t — a)] = «3?l6Cfe>(/ — a)] = e-*ss* (fl>0, /fe = 1 f 2, ...) J
и, если /(/) непрерывна для t = a^О,
X [6+ (/-а)/ (/)] = в-«*/ (а). (8.5-2)
Равенства (1) и (2) употребляются во многих приложениях, хотя нельзя
забывать, что эти соотношения не имеют строгого математического смысла.
Новые результаты, полученные применением равенств (1) и (2), должны
всегда проверяться с точки зрения законности математических действий *)
(см. также п. 8.2-7 и 21.9-2, а).
*) Односторонняя импульсная функция б (t) более подходит для употребления
в связи с односторонним преобразованием Лапласа, чем симметрическая импульсная
функция б (/)
*) В настоящее время большое развитие получила теория «обобщенных» функций,
включающая в себя затронутые здесь вопросы (см. [8.6], [13.6], [21.6]).
256
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.6-1.
8.6. НЕКОТОРЫЕ ДРУГИЕ ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
8.6-1. Вводные замечания. Преобразование Лапласа (8.2-1) есть
функциональное преобразование, связывающее «точки» F (s) в пространстве
изображений с «точками» f (t) в пространстве оригиналов (см. также пп. 12.1-4 и
.15.2-7). Табл. 8.6-1 и пп. 8.6-2 — 8.6-4 знакомят с некоторыми другими
функциональными преобразованиями (см. также п. 4.11-5).
8.6-2. Двустороннее преобразование Лапласа.
(a) Двустороннее преобразование Лапласа
оо
сВД(01= ^ / (0 «"*' dt = X [f it); s] + X\f(- t); -s], (8.6-1)
— 00
есть заманчивое q6o6iueHne преобразования Лапласа, применимое, подобно
преобразованию Фурье (пп. 4.11-3 — 4.11-7), к задачам, где участвуют
значения / (t) для / < 0. j£B [f (0; s] сходится абсолютно тогда и только тогда,
когда оба интеграла %[f(t)\ s] и <5f [/(—/); —s] абсолютно сходятся, так
что область абсолютной сходимости, если она существует, есть полоса в s-пло-
скости, определенная двумя абсциссами абсолютной сходимости. Многие
свойства двустороннего преобразования Лапласа просто получаются из
соответствующих свойств одностороннего преобразования Лапласа. В частности,
%B[f (01 = £ [/(/)], если /(0 = 0 для /^0, (8.6-2)
<%Blf (*)] = <% If (*)]-j , если f(t) = c для t^O. (8.6-3)
(b) Значения обратного преобразования j£^ l [F ($)] не обязательно равны
нулю для /<0, так что £~£Х [F (s)\ существует для более широкого класса
функций F (s), чем X'1 [F (s)].
Если дано изображение
F(s)=XB[f(t)] (oat«y«,aJt
то для каждого значения t, имеющего окрестность, в которой f (t)—функция
ограниченной вариации,
Qi + iR
fl « = 2^ lim $ F W eSt ds = \ V <*-0)+/ (f+ 0)] (8.6-4)
R-*coal-iR
(теорема обращения).
Теорема обращения для одностороннего преобразования Лапласа (п. 8.2-6)
может рассматриваться как частный случай формулы (4).
Двустороннее преобразование Лапласа и его приложения детально
рассматриваются в [8.3].
8.6-3. Преобразование Лапласа в форме интеграла Стилтьеса. Преобразование
Лапласа в форме интеграла Стилтьеса
оо
<#5[<Р(0]= $ estdq>{t) (8.6-5)
0
дает возможность сформулировать в более общем виде многие теоремы обыкновенного
преобразования Лапласа (см. также п. 4.6-17).
Другие функциональные преобразования, приведенные в табл. 8.6-1, также могут
быть записаны в форме интегралов Стилтьеса.
Заметим, что F (s) = se~bs можно представить в форме (5), не употребляя
импульсных функций (п. 8.5-1). Преобразование Лапласа — Карсона (табл. 8.6-1,1) иногда
употребляется для подобных целей.
Таблица 8.6-1
Некоторые линейные интегральные преобразования, связанные с преобразованием Лапласа
(см. также пп. 4.11-3 — 4.11-5, 8.6-1 —8.6-5, 10.5-1, 15.2-7, 15.3-1, 18.3-8 и 20.4-5)
1
2
3
4
5
Преобразование
Преобразование
Лапласа — Карсона
Двустороннее
преобразование
Лапласа
Преобразование
Фурье
Преобразование
Меллина
Преобразование
Гильберта
(употребляется главное
значение
интеграла)
*) Предполагается,
Определение
оо
s J f(t) e~stdt
0
oo
J fit,e-stdt
— oo
f f(t)e-™ivtdt
— oo
oo
J / it) ts~ldt
0
oo
л J s — t
— 00
что преобразование с}
Формула обращения
Ox + l 00
Oj — tOO
Oj -f- i oo
m \ F«)eS'ds
Ot — too
f F (v) e23tI'v/rfv
— oo
ox -f- i oo
Ш \ *«r'*0>o)
Oj — tOO
i- Г ?^U
Л J t — S
— 00
гществует.
Связь с односторонним
преобразованием Лапласа х)
злим: s]
^?В [ПО: s] =
= J? [f (/); s] +
+ «a? if <-/); -s]
«*?в [f </); 2nfv]
^В [f(*0; -si
~J??{j??[f (-/); s']; s}-
Примечание
п. 8.6-2
пп. 4.11-3 — 4.11-5
п. 20.4-5
fit) и F(s)
таковы, что если
оо
f it) = — С [а (со) cos (ot -f
0
4- 6 (со) sin со/] dco,
TO
oo
F is) = — \ [b (со) cos cos —
0
— а (со) sin cos] da>
258
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.6-4.
8.6-4. Преобразования Гаикеля и Фурье —Бесселя.
(a) Определение и теоремы обращения. Интегральное
преобразование
/»=^m[/(0] = ^m[/(0; *] = ]f(t)t Jm(st)dt (8.6-6a)
(преобразование Ганкеля порядка т),
где /(^ — действительная функция и Jm (z) — функция Бесселя порядка т
00
(п. 21.8-1), существует в смысле абсолютной сходимости, когда [ \f(t)\dt
существует. Если, кроме того, f (t)—функция ограниченной вариации в
окрестности точки t, то имеет место формула обращения
00
fI(t)=\f(s)s Jm(st)ds = ± [/(/_0)+/(/+0)] (8.6-66)
(m:>—1/2) (теорема обращения Ганкеля),
которая определяет обратное преобразование единственным образом в точке
непрерывности.
(b) Свойства преобразований Ганкеля. Отметим следующие
соотношения
Жт If (at); в] = ±Жт [/ (0; ~\ (8.6-7)
Жт [}/(0] = ^ {SVm-ilfm + SVm+ilf (t)}}> (8-6-8)
Жт\Г (01 = 2^ {И- 1) Жт+l U (t)]-(m+ 1) Жт-lU Ш, (8.6-9)
Xm[f" (t) + \f'(t)-%f(t) ]=-з*Жт [/(/)], (8.6-10)
ls3Vm[f(t)]eVm[g(t)]ds=]tf(t)g(t)dt (m^-1/2) (8.6-11)
(теорема Парсеваля для преобразования Ганкеля),
Примеры преобразований Гаикеля см. в табл. 8.6-2.
(c) Преобразования Фурье—Бесселя (см. также пп. 21.8-1 и 21.8-2).
Следующие парные интегральные преобразования связаны с интегральным
преобразованием Ганкеля (6):
Ms) = J / (О U (st) dt.
О
f/ (0 = $ /<s) sJm(st) ds = A [f{t - 0) + f (t + 0)]
0
oo
(m«=0, 1, 2, ...), (8.6-12)
0
oo
f/ «)=[ f (s) — Jmt , / <s/> s« rfs - A [/ (/ - 0) + f (/ +
0)]
}• (m = 1, 2, ...). (8.6-13)
Оба интегральных преобразования относятся к парным преобразованиям Фурье — Бесселя;
для т = 0 формулы (13) сводятся к синус-преобразованию Фурье.
8.6-4. 8.6. ДРУГИЕ ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 25Э
Таблица 8.6-2
Преобразования Ганхеля
f (/) = J sf (s) J (st)ds,
0
f(s) = J tf (t) Jm (st) dt
0
fit)
tm, 0<t<a
0, t > a
1, 0</ <a
0, / > a
(a2 — t2), 0</<a
0 t>a
&-*е-Р**
tme— P*-
p~le-Pt
fli-1
г"
p
г-*
t
е-*
m
>- 1
0
0
>- 1
>- 1
> —1
>- 1
0
0
1
1
I
f(s) [
°m+1y
s m + l ^
-£■ * («>
4a 2a2
-^ ./t (sa) — — J0 (sa)
sv Г (m/2 + Ц/2) / m д
2m + y/H'»/2r(i+m) * 42t2' "*" '
S с 4р
(2p)m + 1
2^sm Г (jn/2 + m/2 + V2) Г (1 + д/2 + т/2)
/ ц m 1 m ц s» \
/ч ^4 2 ' 2 ' 2 • 2 2 ' ! ' m' s' + W
—^
4P/
2^Г('/а + ц/2 + т/2)
sl* + l Г (7.-Д/2 +m/2)
(s» + p*)—Vt
P(S2-|- p*)—Va
<s* + /?2)1/2-P
s
I p
s s (s*-J-p8)Va
s (s* -f- /у*)- 8/?
9*
260 ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 8.7-1.
Таблица 8.6-2 (продолжение)
fit)
а
(02 _{_ /2)3/2
sin at
t
sin at
t
sin /
m
0
0
1
0
Ms)
e~as
(a2 — s2)~ '/2>
0,
о,
a
s (S2 —a2)72'
л/2,
arcsin —,
s
0<s <a
s> a
s < a
s > a
S<1
s> »
8.7. КОНЕЧНЫЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ, ПРОИЗВОДЯЩИЕ
ФУНКЦИИ И ^-ПРЕОБРАЗОВАНИЕ
8.7-1. Ряды как функциональные преобразования. Конечные
преобразования Фурье и Ганкеля. Конечная сумма или сходящийся ряд
ФМ= S fk4{x*k) (8.7-1)
k = — 00
представляет функциональное преобразование функции (последовательности)
ffc=/ (&), определенной на дискретном множестве значений & = 0, ± 1, ± 2,...
Заметим, что для некоторых fk и Y (л:, &) этот ряд можно записать как
интегральное преобразование в форме интеграла Стилтьеса (п. 4.6-17)
оо
ф(х)= j ¥(*, k)dq(k).
— оо
Ряды (1) и формулы типа (4.10-5), (4.11-6), (7.5-4) и (7.5-7),
определяющие коэффициенты fk по функции Ф (л:), составляют соответствующие взаимно
обратные функциональные преобразования. В табл. 8.7-1 приведены
соотношения для коэффициентов рядов Фурье и рядов Фурье-—Бесселя,
рассматриваемых как интегральные преобразования с конечным интервалом
интегрирования (конечные интегральные преобразования). В каждом случае приведено
преобразование подходящего линейного дифференциального оператора
второго порядка в связи с применением метода интегральных преобразований
для решения краевых задач (см. пп. 10.4-9, 10.5-3, 15.2-4, 21.8-4, d и [8.5]).
8.7-2. Производящие функции. Если функциональное преобразование (1)
имеет вид сходящегося степенного ряда
со
V(s)=2/*s*e (8-7-2)
Таблица 8.7-1
Некоторые конечные интегральные преобразования
х — действительное переменное, а > О
fa) Конеяные преобразования, полезные для краевых условий типа Ф = 0 или Ф' = О
Ф (х) или
Ч2[Ф(х-0)+Ф(х + 0)}
Л^-по-
ложитель-
ные корни
уравнения!
Преобразование дифференциального
оператора
Конечное косинус-
преобразование
(ряд Фурье по
косинусам, п. 4.11-2, е)
J Ф (х) cos lk x dx
a
+ T 2 f* cos V
J ф" (х) cos Xkx dx =
*=1
Конечное синус-
преобразование
(ряд Фурье по
синусам, п. 4.11-2, е)
J Ф (х) sinhk х dx
Т 2 fAslnV
*=1
tg aX
А* =
(А=0
2, .
= 0
kn
а
1
.)
' *! ^- Ф' (0) + (-1*Ф/ (о)
J Ф" (*) sin Ял * rf* =
0
в - ЛА '* + Ял [Ф (0) +
+ (- 1)* + 1Ф(а)]
Конечное
преобразование Ганкеля
(ряд Фурье — Бесселя,
п. 21.8-4, d)
J Ф (*) х Jm (Kkx) dx\
a2 jLi
*=1
I'm (V)]2
J 'ok, = 0
m '
H*"+T-^]"-^ —
= - Ф* - я Vm (a?^) Ф (a)
Конечное кольцевое
преобразование
Ганкеля а' > а > 0,
J°W'Bm(V)H
Z*'S..
(аЧ) Вт (V)
*=1
к*) - Jm («Ч)
Вт(а'Я)=0|
Таблица 8.7-1 (продолжение) £g
(b) Кснсчные преобразования, полезные для краевых условий типа ^
Ф (а) + Ь Ф' (а) = О (Ь > 0)
Конечное косинус-
преобразозание
Конечное синус-
преобразование
Конечное
преобразование Ганкеля
h
а
J Ф (х) cos ?.^ л: tf*
0
а
j О (*) sin \kx dx
0
I<blx)xJm(hx)dx
0
Ф (*) или
«/. [Ф(х-0) + Ф(д:+0)]
2 V (4 + OffecosV
со
2 у (>4Jrb2)fksinbkx
■Ьяк Ь + а(к£ + Ь2,
со
„ \ *K'm(V)
" лЦ [(4 + б2) а2 - т2] У2„, (aXft)
& = 1
Xk ~ ПО"
ложитель-
ные корни
уравнения
К tg aX = b
% ctg a) = — b
К Ут (аК) +
+ bJmX
X (ак) = 0
Преобразование дифференциального
оператора
а
J Ф" (х) cos K^x dx =
0
--фА-ф'«»4-
+ [Ф' (а) + Ъ Ф (а)] cos аЯ^
а
\ Ф" {x)s\r\'Kkxdx =^
0
+ [Ф' (а) + Ь Ф (a)] sin a%k
и
**JmMd* Ф* +
+ [Ф' (а) + ЬФ (а)] а 7т (<aft)
Заметим, что Jq (к.а) =— У- (^я)-
8.7-3. 8.7. КОНЕЧНЫЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 263
то у (s) называется производящей функцией для последовательности
коэффициентов fk = f(k). Функция
?*<*>= f] Ti$fc <8-7-з>
k = 0
называется экспоненциальной производящей функцией. Применения и
свойства производящих функций см. в пп 18.3-8 и 18.7-2.
Пример. Числа Фибоначчи определяются рекуррентными
соотношениями
/o=/i=l. fk=h-i+fk-2 (* = 2, 3,...). (8.7-4)
Для них производящая функция
(8.7-5)
8.7-3. ^-преобразование. Определение и формула обращения,
^-преобразованием последовательности fk называется функция комплексного переменного
Z[fk'> z] = Fz(z)t определенная рядом
Z [/*; z] = Fz (z) = /0 + 7 + ii + - (I z I > '«)> (8-7'6)
сходящимся (абсолютно и равномерно) вне некоторого круга радиуса га,
зависящего от данной последовательности.
Так, если | fk \ ^Ме^, то ряд (6) сходится при | г | > еа.
Подразумевается, что область | г | > га определения функции F z (z)
расширена с помощью аналитического продолжения, как и в п. 8.2-3.
Соответствующая формула обращения имеет вид
'*в55 $ rz W гк~Х dz (k = °> J. 2* •••). (8-7"7>
с
где С —любой замкнутый контур, окружающий все особые точки функции
Fz(z), в частности, любая окружность | г | > га.
Значение интеграла (7) часто удается получить с помощью теоремы о
вычетах (пп. 7.7-1—7.7-3). Если Fz (z) — рациональная функция, то можно
пользоваться разложением на простейшие дроби (как в п. 8.4-5). Обращение
особенно просто, если Fz(z) может быть разложено по степеням 1/г.
В табл. 8.7-2 собраны важнейшие свойства z-преобразования. Их
приложения к решению разностных уравнений и к анализу систем управления
по выборочным данным приведены в п. 20.4-6; там жэ обсуждается связь
между z-преобразованием и преобразованием Лапласа ступенчатых функций.
В табл. 20.4-1 приведены некоторые z-преобразования.
z-преобразования связаны с преобразованием Меллина из табл. 8.6-1. Заметим, что
связь между степенными рядами и преобразованием Меллина аналогична связи между
00
рядами Дирихле V fbe~ и преобразованием Лапласа.
* = 0 *
пласа
■^Замена переменной г = е% приводит к дискретному преобразованию Ла«
л = 0
264
ГЛ. 8. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
8.7-3.
Таблица 8.7-2
Соответствие операций при ^-преобразовании
Следующие теоремы справедливы в области абсолютной сходимости преобразований;
все пределы предполагаются существующими (см. также табл. 8.3-1) и f_t=f_2= ...
... =£,-1 = 2-2= ... =0.
Номер
теоремы
1
2
3
4а
4fc
б
6
7
8
9
10
Операция
Линейность (а, 0 —
постоянные)
Опережение
(см. п. 20.4-2)
Запаздывание
Конечные разности
(см. п. 20.4-1)
Нисходящие (правые)
разности
Восходящие разности
Суммирование
последовательности
Свертка
последовательностей
Непрерывность (а не
зависит от k и z)
Дифференцирование и
интегрирование по
параметру а, не
зависящему от k и г
Предельные теоремы
Дифференцирование
изображения
Последовательность
(оригинал)
«'fc + Wft
C = l, 2, ...)
<r= !, 2, ...)
k
i = 0
i."*-«
Hm f. (a)
a -* a R
a2
J fk (a) da
0.1
kfk.
krfk(r== 1. 2, ...)
г-преобразование
(изображение)
a Fz (z) + p Gz (г)
2 Fz <*> - f0z.
i=0
*~rFz&
(z~\)Fz(z)-I0z,
lhP^
Fz (z) Gz (z)
lim Fz (z, a)
a-y a
o2
J Fz (г, a) da
lim Fz(z)t
Z-+CO
lim (2— 1) F7 (2)
2-1
ГЛАВА 9
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
9.1. ВВЕДЕНИЕ
9.1-1. Вводные замечания. Дифференциальные уравнения позволяют
выразить соотношения между изменениями физических величин, и потому они
имеют большое значение в приложениях. В §§ 9.1, 9.2 и 9.3 дано
классическое введение в теорию. В § 9.4 рассматриваются линейные
дифференциальные уравнения с постоянными коэффициентами, причем упор делается на
решение их методом преобразования Лапласа. В § 9.5 речь идет о
нелинейных уравнениях второго порядка. В § 9.6 приведены дифференциальные
уравнения Пфаффа, хотя они и не являются обыкновенными
дифференциальными уравнениями.
Некоторые вопросы, относящиеся к дифференциальным уравнениям,
рассматриваются в других главах: преобразование Лапласа —в гл. 8, краевые
задачи и задачи о собственных значениях —в гл. 15, дифференциальные
уравнения, определяющие специальные функции, —в гл. 21.
Применяемые далее обозначения выбраны так, чтобы облегчить ссылки на общие
учебники. Поэтому действительные переменные обозначаются через х, у=у(х)\
комплексные переменные, встречающиеся в общей теории линейных дифференциальных
уравнений, обозначаются через z, w = w(z). Независимое переменное в §§ 9.4 и 9.5, обычно
представляющее время, обозначено через t,
9.1-2. Обыкновенные дифференциальные уравнения. Обыкновенным
дифференциальным уравнением порядка г называется уравнение
Fix, У(х), у'(х), ..., */(Г,(*)] = 0, (9.1-1)
которое связывает независимое переменное х, искомую функцию у = у (х) и ее
производные у' (х), ..., yir)(x). Решение (интегрирование) дифференциального
уравнения (1) заключается в отыскании функций (решений, интегралов) у (*),
которые удовлетворяют этому уравнению для всех значений х в определенном
конечном или бесконечном интервале (а, Ь). Заметим, что решения могут
быть проверены подстановкой в уравнение.
Общее решение обыкновенного дифференциального уравнения порядка г
имеет вид
у = у(х; С„ С2, ..., Сг), (9.1-2)
где Съ С2, ...» С г —произвольные постоянные (постоянные интегрирования,
см. также п. 4.6-4). Каждый частный выбор этих постоянных дает частное
решение. В задаче Коши (начальной задаче) требуется найти частное решение,
удовлетворяющее г начальным условиям
У1хо) = у0, У' (*o) = 0i. ••.. У{Г~1} Ы=У(оГ-1), (9.1-3)
по которым определяются г постоянных Clt C2, ...» Сг. В краевой задаче на
у (х) и ее производные накладываются г краевых условий в точках х — а и
х = Ь (см. также п. 9.3-4) *).
•) Строго говоря, начальные и краевые условия относятся к односторонним
производным (п. 4.5-1).
266 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.1-3.
График каждого частного решения называется интегральной кривой; совокупность
всех таких графиков образует г-параметрическое семейство интегральных кривых.
Обратно, если дано г-параметрическое семейство достаточное число раз
дифференцируемых функций (2), то, исключая постоянные Сх, С2, ..., Сг из г -f- 1 уравнений
yW =yl» (*; Си Ct Сг) (/ - 0, 1. 2 г),
получим дифференциальное уравнение r-го порядка, описывающее это семейство.
Некоторые дифференциальные уравнения имеют еще дополнительные решения —
особые интегралы, которые не включаются в общее решение (2) (см. также п. 9.2-2,Ь).
9.1-3. Системы дифференциальных уравнений (см. также пп. 13.6-1—13.6-7).
Система обыкновенных дифференциальных уравнений
Л(*; у» № ...; у[. yl, ...)=о 0 = 1, 2, ...) (9.1-4)
связывает одно независимое переменное х и несколько искомых функций
У\=Уг(х)* Уъ — Уъ(х)> ••• и их производных. Порядком г,- каждого
уравнения (4) называется наивысший порядок входящей в него производной. Вообще
говоря, требуется п уравнений (4) для отыскания п искомых функций yk (x)\
общее решение . * . ч
должно содержать r = r1 + r2 + ...-\-rn произвольных постоянных.
Интегрирование системы (4) часто можно свести к интегрированию
одного обыкновенного дифференциального уравнения порядка г путем
исключения п— 1 переменных yk и их производных. Гораздо важнее, что каждую
систему (4) можно свести к равносильной ей системе г уравнений первого
порядка путем замены высших производных вспомогательными неизвестными
функциями.
9.1-4. Существование решений. Для корректности постановки начальной
или краевой задачи требуется доказательство существования решения,
указывающее иногда и путь его построения. Существование физического явления,
описываемого данным дифференциальным уравнением, может лишь
подсказать, но не доказать существование решения; доказательство существования
проверяет состоятельность математической модели (см. также пп. 4.2-1,Ь и
12.1-1; примеры теорем существования см. в пп. 9.2-1 и 9.3-5).
Правильно построенная математическая модель должна допускать
решения в виде непрерывных функций от параметров, начальных значений и т. п.
9.1-5. Общие указания.
(a) Подстановка ряда Тейлора (п. 4.10-4) или других рядов для у (х) в данное
дифференциальное уравнение может дать уравнения для неизвестных коэффициентов (см. также
пп. 9.2-5,Ь и 9.3-5). Некоторые дифференциальные уравнения могут быть упрощены
заменой переменных (пп. 9.1-5,Ь, 9.2-3, 9.3-8,с). Каждое дифференциальное уравнение или
система таких уравнений могут быть сведены к системе уравнений первого порядка,
к которым применимы методы п. 9.2-5.
(b) Следующие типы неполных дифференциальных уравнений легко сводятся к урав~
нениям низших порядков (см. также пп. 9.2-3, 9.5-6):
F (х. ут\ у'п+1> у(п+т) = 0 (подстановка у =у1П>),
г (у. у'. у'\ ...
I подстановка х = у, ~у = у';
Если дифференциальное уравнение F (х, у, у^
там у, у\ ..., у{Г> в смысле п. 4.5-5, то вводят у^у'/у.
9.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
9.2-1. Существование и единственность решений.
(а) Дифференциальное уравнение первого порядка вида
%Ч(*.У) (92-1)
,«"). 0
огда у" =
F (х, у,
dy'
" dx
У\ -
_ dy' dy
dy dx'
..*(n) =
dy-
= ~~y и т. д.
dx
0 однородно
)•
no
аргумен-
9.2-2.
9.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
267
имеет решение у — у(х), удовлетворяющее условию у(х0)=у0, если f (х, у)
непрерывна в некоторой окрестности точки (x0t y0). Более определенно, если
f(x, у) непрерывна в открытой области D и удовлетворяет в этой области
условию Липшица
\f(x, y)-f(x9 Ч)\^М\у-ц\, (9.2-2)
еде М —некоторая положительная постоянная, то дифференциальное
уравнение (1) при любом начальном условии y(x0)=y0t где точка (х0, у0)
принадлежит области D, имеет единственное решение у = у(х). Кажцое решение
может быть продолжено до границы области D.
Геометрическая формулировка теоремы такова: через каждую точку
области D проходит единственная интегральная кривая.
Условие Липшица (2) удовлетворяется» в частности, если f (х, у) имеет в D
ограниченную производную dffdy.
(Ь) (см. также п. 9.1-3). Аналогичная теорема существования справедлива и для
систем дифференциальных уравнений первого порядка в нормальном виде:
J? - U (х: Уг.Уг *„) V - 1. 2 П), (9.2-3)
если условие Липшица (2) заменить на
IU С *i уп) ~ U С- "1 %) I < м 2 I «и - ч I- <9-2-">
k==\
Условие (4) соблюдается, в частности, если все df./ду* ограничены.
9.2-2. Геометрическое толкование. Особые интегралы (см. также пп.
с 17.1-1 по 17.1-7).
(a) Если х, (/—декартовы прямоугольные координаты точки, то
дифференциальное уравнение первого порядка
F(x,y,p) = 0 {р = Тх) (9-2"5>
описывает поле направлений или поле линейных элементов (*, у, р),
проходящих через точку (х, у) с угловым коэффициентом p = dy/dx = f (х, у). Каждый
линейный элемент касателен к некоторой интегральной кривой однопарамет-
рического семейства решений
у = у(х, X) или ф(*, у, Х) = 0. (9.2-6)
Поле направлений позволяет приближенно графически построить интегральные
кривые; общий характер семейства интегральных кривых может быть исследован
методом п. 9.5-2 При построении интегральных кривых могут оказаться полезными изоклины
F (х, у, pi) = 0 или f (xt у) = pi, на которых интегральные кривые имеют фиксированный
угловой коэффициент рх. Кривая ^—|- —- f = О дает геометрическое место точек
возможного перегиба.
(b) Особые интегралы (см. также п. 9.1-2). Пусть F (х, у, р)
непрерывно дифференцируема. Исключение р из уравнений
F(x,y9p) = Ot g = 0 (9.2-7)
дает дискриминантную кривую данного дифференциального уравнения
(геометрическое место особых линейных элементов). Кривая, определяемая ypah3-
нениями (7), есть особая интегральная кривая, если на этой кривой
-д +--/? = О, причем обе производные df/dx и dF/dy не обращаются в нуль
одновременно. Огибающая семейства интегральных кривых (6) всегда является
особой интегральной кривой; она может быть найдена по общему интегралу
методом п. 17.1-7.
268 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.2-3.
9.2-3. -XПреобразование переменных (примеры см. в п. 9.2-4).
(a) Замена переменных (точечное преобразование)
х=Х(х, д), y = Y(x, у) gij^^o], j
д-^ + д-1Ъ f ' I (9.2-8)
P-dx д_Х.+д_Х- \Р-<Гх)
дх ду )
преобразует данное уравнение (1) или (5) в новое дифференциальное
уравнение относительно х и д> которое может оказаться проще исходного. Найдя
решение д = д(х), мы получаем искомое решение в параметрическом виде:
х = Х(х, д(х)), y — Y(xt g(x)). Если решение преобразованного уравнения
получено в неявном виде и (х, #) = 0, то искомая связь между у и х может
быть найдена исключением х и д из трех уравнений:
x=X(xt g), y = Y(x, g) и и(х, д)=0.
(b) Контактные преобразования (см. также пп. 10.2-5, 10.2-6 и 11.6-8).
Замена переменных
при условии
х = х (х, у, р), у=у (х, у. р) (р = ^ (9.2-9а)
определяет контактное преобразование, сопоставляющее линейные элементы х, у, р и
- - - dy _ дх ' ду _ dp
dx дх_ d* dx
дх+дуР 1р
таким образом, что линейные элементы, образующие гладкую Дугу, отображаются на
гладкую дугу и касание дуг сохраняется.
Контактное преобразование может быть задано формулами
х = х х, у, р), у = у (х, у. р), р = р (х, у, р) [у(^ ^ у ф Oj, (9.2-9с)
при условии
dy-pd~x = g (х, у, р) (dy - р dx) [g (х, у, р) ф 0]. (9.2-9tf)
При этом формулы р == dy/dx ир= dy/dx эквивалентны.
В частности, g (х, у, р) ~ — 1 дает легко обратимое контактное преобразование Ле-
жандра
х = р, У = рх — у, р = х, (9.2-10)
которое преобразует данное дифференциальное уравнение (5) в
F(p, рх-у. *) = 0. (9.2-11)
Уравнение (11) может оказаться более простым, чем исходное. Если его решение будет
найдено, то решение исходного уравнения получится обращением формул (10).
9.2-4. Решение специальных типов уравнений первого порядка.
(а) Следующие уравнения интегрируются в квадратурах:
1. Уравнение с разделяющимися переменными y' = fi (x)/f2 (у)»
Общий интеграл f f2 (у) dy=\fx (x) dx+C.
2. «Однородное» уравнение первого порядка: y'=f(y/x). Замена
у — у/х приводит уравнение к типу 1: д''= ~ У*
0.2-4.
9.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
269
3. Уравнение в полных дифференциалах есть уравнение вида
Р (х, у) dx+Q (х, у) dy = 0, (9.2-12)
где левая часть представляет собой полный дифференциал dq>\ это
значит, что выполнено условие -^-^~ (п. 5.7-1). Общий интеграл
х у
Ф (*, у) = \ Р (х, у) dx+^Q (xQ, у) dy = C. (9.2-13)
Хо Уо
Если левая часть уравнения (12) не является полным дифференциалом
(-0-ф-^\ то можно найти интегрирующий множитель jn = jut (xt у) такой, что
произведение \х (Pdx+Q dy) будет полным дифференциалом. Интегрирующий
множитель jji (xt у) удовлетворяет дифференциальному уравнению с частными
производными
•С-&Н£-*8- (9-2-14)
4. Линейное уравнение первого порядка у'+а(х) y—f (x) (см.
также пп. 9.3-1 и 9.3-3) допускает интегрирующий множитель
Г а(х) dx
Общее решение
^=ТГ73о~ [S f(*)P(*)dx + c\- (9.2-15)
Некоторые уравнения первого порядка можно привести к одному из указанных
типов заменой переменных (п. 9.2-3). В частности, уравнение у' = f (ax + fiy) приводится
к типу 1 заменой ~у — ах + $у. Уравнение у' = f ( а** ; \.хУ , Vl ) при at$2 — а2р\ ф 0
_ _ \ <*2Х -+- РгУ -г Уг /
приводится к типу 2 заменой х = х — х0, у = у — у0 (параллельный перенос осей
координат), где х0, у0 — точка пересечения прямых atx + р\# -f- yt = 0 и а2х + &2У -Ь Ya = 0.
Если же с^Эз — a2Pi = 0, то это уравнение приводится к типу 1 заменой ~у=* а±х + р\#.
_ Уравнение у' =■ ft (x) у -\- f2 (x) уп (уравнение Бернулли) приводится к типу 4 заменой
У = УХ~п(пф\).
(b) X Если уравнение первого порядка дано в виде
y=h(x, у'), (9.2-1G)
то иногда оказывается удобным продифференцировать обе его части по х и получить
дифференциальное уравнение относительно у* (х):
,-**+£.& (92.|7
дх ' ду' dx
Если последнее уравнение удается решить и найти у' == у' (х), то подстановка этого
результата в данное уравнение (16) позволяет найти искомую функцию у (х). Если
решение уравнения (17) получается в виде и (х, у') = U, то соотношение между х и у дается
в параметрической форме через параметр р = у':
и(х, р) = 0, у = h (x, р).
Аналогично уравнение х = Л (у, у') дифференцированием по у приводится к уравнению
—т- = -д г- -г—;——- с независимой переменной у и искомой функцией у' (у).
Примеры. Дифференциальное уравнение Клеро у == у'х + f (У') имеет общее
решение y=Cx + f (С) и особый интеграл (в параметрической форме) х =— /' (р), y=—pf (p) -j-
4- f (P).
Дифференциальное уравнение Лагранжа y — xf (у') -\-g (у') приводится к уравнению
У' = f (У') + [*/' (У') +&' (У')] -jj", записав последнее в виде tf (у') — у'] -~- -f V (у') х +
-J-g' (У') —0, получаем линейное дифференциальное уравнение относительно х (у').
(c) Уравнение Риккат и. Общее уравнение Риккати
у' = а (х) у2 + Ь(х)у + с (х) (9 2-18)
270 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.2-5.
иногда упрощается подстановкой у = \/у . Замена
~У~'
х — х, у = — -
а(х) у
приводит к однородному линейному уравнению второго порядка относительно у—у (х):
V" - [~^ + Ь <*>] I1 + а (х) с (х)у~= 0. (9.2-19)
Если известно одно частное решение yt (x) уравнения (18), то подстановка
У = Ух (х) + —
У
приводит к линейному дифференциальному уравнению. Если известны два частных
решения уи у% или три частных решения уи у2, у%, то имеем соответственно
у = ух + у'-у* у = У1 {У* - У^ + Cj/2 <*» - *з) (9.2-20)
1 + С exp J а (х) (у2 — #,) dx » (#2 — #,) 4- С (#i — #3) '
Для любых четырех частных решений уи у2, у$, у* двойное (ангармоническое) отношение
J!L^vL.ju^1vL постоянно.
l/t — У г У* ~ Уз
Специальное уравнение Риккати
у' 4 ау* = Ьхт (9.2-21)
4k
при т = 0 относится к типу 1, а при т = - — (k = ± 1, +2, ... ) приводится к этому
1 — 2k
типу путем ^-кратного повторения одной из указанных ниже подстановок. При k > О
подстановка
\_
x==Jm+Z, yTSSJL+ JL
х2у ах
даст __
J^_. + ^jJ=F7m, (9 2-22а)
где
т + 3* т + 3 т -f 3
При Л < 0 подстановка
JC
=- т+\> у = —--
х (Ь х у+т+\)
дает уравнение (22а) с
-5__ _» Т- « S = -2S±i. (9.2-22.)
m + 1 m-f 1 m 4 1
■Х- Наконец, при m = — 2 уравнение (21) приводится к типу 2 подстановкой у=\/ у*
Многочисленные примеры специальных типов дифференциальных уравнений
приведены в [9.4]. #
9.2-5. Общие методы интегрирования.
(а) Метод последовательных приближений Пи к ар а.
Для интегрирования дифференциального уравнения г/'= /(*, у) при данном
начальном условии у (х0) =у0 выбирают некоторую начальную функцию у^ (х)
и вычисляют последовательные приближения искомого решения:
yU+lUx)=Vo+ lf[x,y[n(x)]dx (/ = 0,1,2,...). (9.2-23)
Этот процесс сходится при выполнении условий п. 9.2-1. Метод Пикара
особенно удобен, если интегралы в формуле (23) могут быть вычислены в
замкнутой форме, хотя в принципе можно применять и численное интегрирование.
9.3-2. 9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 271
Вполне аналогичный метод применяется к системам (3) дифференциальных
уравнений первого порядка.
(Ь) Разложение решения в ряд Тейлора (см. также п. 4.10-4).
Если данная функция / (л:, у) дифференцируема достаточное число раз, то
коэффициенты у(ТП)(х0)\т\ ряда Тейлора
У(х) = у (*о) + У' (*о) (* - *о) + 4" у" (хо) (х - *0)2 +. -. (9.2-24)
можно получить последовательным дифференцированием данного
дифференциального уравнения:
У' (*) = /(*. У)*
»" w-£•+■2-»'--Й-+#/(*.»).
и последующей подстановкой x = x0l у = у{х0)=у0.
Аналогичный метод применяется к системам дифференциальных
уравнений первого порядка.
9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
9.3-1 Линейные дифференциальные уравнения. Принцип наложения (см.
также пп. 10.4-2, 14.3-1 и 15.4-2). Обыкновенное линейное дифференциальное
уравнение порядка г, связывающее действительные или комплексные
переменные z и w = w(z)y имеет вид
lw = a0(z)^L + at(z)££- + ... + ar(z)w=f(z). (9.3-1)
dz dz A
Общее решение уравнения (1) есть сумма какого-либо его частного решения
и общего решения соответствующего однородного линейного дифференциального
уравнения
Lw = a0(z)^r + ai(z) J^ + ... + ar(z)w = Q. (9.3-2)
dz dz L
По отношению к неоднородному уравнению (1) уравнение (2) называется
приведенным.
Если wt (z) и w2 (z) — частные решения линейного дифференциального
уравнения (1) для правых частей f (z)~f1(z) и /(z)^/2(z) соответственно, то
a wx(z) 4-р w2(z) будет частным решением уравнения (1) для правой части
f (z) = afx (z) -f- P /2 (z) (принцип наложения, суперпозиции). В частности, каждая
линейная комбинация решений однородного линейного дифференциального
уравнения (2) также является его решением.
■# Очевидное решение w = 0 уравнения (2) называется нулевым или
тривиальным.
В дальнейшем предполагается, что все функции aQ (z), аг(г),..., ar(z)
и / (z) непрерывны в некоторой области D изменения независимого
переменного, причем в точках этой области коэффициент а0 (z) не равен кулю. Точки,
в которых a0(z) = 0, являются особыми для уравнения (1). ■#
9.3-2. Линейная независимость и фундаментальные системы решений
(см. также пп. 1.9-3, 14.2-3 и 15.2-1).
(а) Пусть wx (z), w2(z),..., wr (z) суть г— 1 раз непрерывно
дифференцируемые решения линейного однородного дифференциального уравнения (2).
г
г решений w^ (z) называются линейно независимыми в D, если ^ ^k wk (z) = 0
272 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 0.3-3.
в D только при %i = %2 = ... = %rz=0 (п. 1.9-3). Это имеет место тогда
и только тогда, когда определитель Вронского (вронскиан)
W[wvw2f...,wr]==
w\ (z)
w2(z)
w'2(z)
wr(z)
w'r{z)
w\r-[>
,,ir-D
(г).
„c-l>
(*)
(9.3-3)
отличен от нуля всюду в D. Равенство W = 0 в какой-либо точке z из D
влечет за собой тождество W = 0 для всех z из D1).
(b) Однородное линейное дифференциальное уравнение (2) порядка г имеет
не больше г линейно независимых решений. Любые г линейно независимых
решений wx (z), w2 (z)t ..., wr(z) составляют фундаментальную систему реше-
г
ний, линейные комбинации которых 2 ak wk(z) Дают все частные решения
А = 1
уравнения (2).
(c) ^Использование известных частных решений для
понижения порядка. Если известно одно нетривиальное решение wL однородного
уравнения (2), то преобразование w = wt J v dz приводит это уравнение к однородному
линейному дифференциальному уравнению порядка г—\, т. е. понижает его порядок на
единицу. Указанное преобразование эквивалентно двум последовательным преобразованиям
w ==wtu и и' = v.
Если известно т линейно независимых решений w., до», ... , wm уравнения (2), то
можно понизить его порядок до г—т последовательным применением следующего
процесса. Преобразование w = ю J v dz приводит к уравнению порядка г — 1 с известными
линейно независимыми решениями
V,
wt
V /w* Y ( wm-\ V
Повторяя
этот процесс т раз, придем к линейному однородному уравнению порядка
9.3-3. Решение методом вариации постоянных. Функции Грина.
(а) Если функции wx (z), w2 (z), ... , wr (z) представляют г линейно
независимых решений однородного линейного дифференциального уравнения (2), то
общее решение неоднородного уравнения (1) есть
w = Cx (z) wt (z) + C2 (z) w2 (z) +... + Cr (z) wr (z), (9.3-4)
где
2 C'k(z)wM(z)=0 (/=0, l,...,r-2),
S^wir-'M.)»^
k=\
(9.3-5)
Решив систему г уравнений (5) относительно неизвестных производных
C'k (z), простым интегрированием находим затем
В принципе этот метод сводит решение любого линейного дифференциального
уравнения к решению однородного линейного дифференциального уравнения.
1) Заметим, что эта теорема неприменима к любому множеству г — 1 раз
непрерывно дифференцируемых функций w^ (z); они должны быть решениями подходящего
дифференциального уравнения (2), коэффициенты которого удовлетворяют условиям,
сформулированным в п. 9.3-1.
»&-*. 9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 27<*
(Ь) В случае действительных переменных z = x и w^w(x) частное
решение неоднородного уравнения (1) часто бывает удобнее представить в виде
w = I G (х, I) f (I) d% (a<x< Ь), (9.3-6)
а
где G (х, £) есть функция Грина (п. 9.4-3), дающая «фундаментальное»
решение. При этом общее решение уравнения (1) есть
" = JG(*,E)/(E)dE+ E Akwk(x).
а /г = 1
(9.3-7)
где u>k (х) — линейно независимые решения уравнения (2), а А^ —
произвольные постоянные, определяемые по начальным или краевым условиям.
Функцию Грина G(xt !•) можно выразить через любые г линейно
независимых решений w/g (x) однородного уравнения (2):
G(x>t)=m zc'k®wk(x)U(x-t),
(9.3-8)
где C'k (х) получаются из уравнений (5), a U (/) — единичная функция, опре-
деленная в п. 21.9-1 ^(/)={?:^;<5;)
Для линейных дифференциальных уравнений порядка г = 2 общее решение
дается формулой (4) или (7), где
с;(*) = -
Сш (х) =
f(x)
W2 (X)
w1 (x) w'2 (x) — w2 (x) w[ (x)
a>i (x)
a0 (x)
fix)
aQ (x) w1 (x) w;2 (x) - w2 (x) w\ (x) »
_J m (x) w2 (I) — wz (x) wt (l) и ( >v
do (I) wt (|) w't (I) - w2 (|) w\ (I) u ** 5'*
(9.3-9)
(c) x В то время как общее решение (7), получающееся с помощью
функции Грина (8), есть только другой способ записи формулы (4), часто
оказывается возможным построить функцию Грина G (х, £) так, чтобы частное
решение (6) удовлетворяло определенным начальным или краевым условиям.
Если краевые условия линейны и однородны относительно w (x) и ее
производных, то искомая функция Грина G (х, !•) должна удовлетворять
следующим условиям:
1. G(x, £) при фиксированном значении £ является непрерывной
функцией от х и удовлетворяет заданным однородным краевым
условиям.
2. Производные до r-го порядка включительно от G(xt £) по х
непрерывны для х £ [а, Ь], за исключением точки * = £; в этой точке
непрерывны производные до (г —2)-го порядка, а (г —1)-я
производная имеет разрыв первого рода со скачком
дГ-*а
д/-
dr'1G
1
r-t, - (a<l<b). (9.3-10)
3. G (x, £) как функция от х всюду в [а, Ь], за исключением
точки лг = £, удовлетворяет уравнению
LG(x, E)=0 (*^6). (9.3-11)
Функцию Грина G (*, g) можно определить условием LG (x, £) =
= б (л: — |), где 6(0 — функция Дирака, определенная в п. 21.9-2.
ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ».3-3.
Отсюда следует, что
LG(*,6) = 0 (хфЪ) HjLG(*,E)dE = l.
(9.3-1 la)
Существование и свойства таких функций Грина рассматриваются с более
общей точки зрения в гь 15.5-1; см. также п. 9.4-3. В табл. 9.3-1 приведены
функции Грина для некоторых краевых задач.
Таблица 9.3-1
Функции Грина для линейных краевых задач
b
Каждая приведенная ниже краевая задача имеет решение w (х) = Г G (xt £) f (£) d\.
а
Формула (9.3-7) позволяет получить решение при других начальных или краевых
условиях (см. также пп. 9.3-3, 9.4-3, 10.4-2, 15.4-8, 15.5-1). Решения для других интервалов
(a, b) получаются из табличных с помощью линейного преобразования координат.
№
п/п
la
lb
\с
\d
1 U
2
3a
Zb
4a
\b
Дифференциальное
уравнение
dzw е . х
d'w . , ,
d2w
—+k>W=f(X)
d2w
*) Это есть обобщен*
ряет уравнению (9.3-10)
Интервал
{a, b)
a = 0
b = 1
a = - 1
b = 1
a = — oo
b = oo
a = 0
b = 1
a = — 1
b= 1
a = 0
b = 1
a = — 1
b = 1
гая функци
Краевые условия
w (0) =ш (1) = 0
w (0) = 0
w' (1) = 0
w (Q) = — w (1)
a>' (0) = — w' (1)
ay (— 1) =w (1) = 0
w(— 1) =oy (1)
Of' (—1 ) =W' (1)
a) конечна
в (— oo, oo)
w (0) =w (1) = 0
w (— 1) = a> (1)
a;' (— 1) =oy' (1)
w (0 ==ш (1) = 0
w (— 1) = a> (1)
a>' (— 1) = w' (1)
я Грина в смысле п. 1
G (jr. 1) (x^D
G (5. *) <* ^ £)
-(1-6)*
— x
-}"-«-!
-у <*-Е-*&+|)
-4-<*-i>*-
-±<"1
sin £.v sin Л (1 — ^)
~~ k sin Л
cos k ix — £ + 1)
J>fcsin£
sh /г* sh 6 (1 — I)
*sh£
ch *(*-*+!>
2£ sh £
5.5-l,b; она не удовлетво-
9.3-5.
9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 275
Таблица 9.3-1 {продолжение)
п/п
5
6
7
Дифференциальное
уравнение
dx \ ах J
— — w = / (*)
(неоднородное
уравнение Бесселя)
(неоднородное
уравнение Лежандра)
d4w . . .
3F—'W
Интервал
а = 0
Ь = 1
а = —1
Ь= 1
а = 0
6 = 1
Краевые условия
су (0) конечно
оу (1) = 0
W (—1), ОУ (1)
конечны
w (0) = «;' (0) =
= ш (1) = ш' (1) = 0
G (х, £) (* < £)
G (6. дс) <х ^ £)
In g (m = 0)
-i[(f г-«>1
(m = 1, 2, ...)
-L in a-*) (i+6)-
1 - In 2 + -A- (m = 0) «)
1 /l+дс 1-5W2
2m\\—x'\-\-t)
(m= 1, 2, ...)
*2 (£ _ П2
- 6 (2д?6 + др-36)
9.3-4. Приведение двухточечных краевых задач к задачам Коти. Общая теория
краевых задач и задач о собственных значениях, включающая и обыкновенные
дифференциальные уравнения, рассмотрена в пп. с 15.4-1 по 15.5-2 (см. также п. 9.3-3).
В связи с методами численного решения часто бывает полезен следующий прием.
Если дано линейное дифференциальное уравнение r-го порядка Lw = f (z) с г
краевыми условиями, наложенными на w (z) и ее производные в двух точках z = a, z — b,
то решение задачи записывается в виде
w = w0 (z) + Е ak wk (z)f
(9.3-12а)
где функции w. (z) находятся из (г + 1)-й задачи Коши\
LwQ (z) » / (*) при wU) (a) = 0 (/ = 0, 1, ... , г - 1), )
ч п </>,* f 0 С/ ^Ь л — 1> I (/ = 0, 1,...,г-1;[ (9.3-126)
Подставляя заданные краевые условия в общее решение (12а), получают систему г
уравнений с г неизвестными коэффициентами а.
Примечание. Если краевая задача не линейна* например,
d2w
dz2
■■ t (2, wt w') при w (a) = w w (b) = w^f
(9.3-13)
то часто можно вычислить значения w (b) для двух или трех выбранных значений
неизвестного начального условия о/' (а) и затем исправить значение w' (а) с помощью
интерполяции.
9.3-5. Линейные дифференциальные уравнения в комплексной области.
Тейлоровские разложения решения и влияние особенностей.
(а) Линейное дифференциальное уравнение
£+M,)f£=+...+M*)»=-/<*>
dz dz
имеет аналитическое решение w=w(z) в каждой регулярной точке z, где
функции аь (z) и f (z) аналитичны. Если эти функции однозначны и если
276
ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ».3-в.
область D односвязна и состоит только из регулярных точек, то заданные
начальные значения w(z0), w' (z0), ..., w{r~l) (z0) в любой точке z0eD
определяют единственное решение w(z) в D.
Чтобы получить это решение в виде ряда Тейлора (см. также п. 4.10-4),
надо подставить
w(z) = w(z0) + w'(z0)(z-z0) + ±w''(z0)(z-z0)*+... (9.3-14)
и
/(2)=/(г0) + //(2о)(2-г0)+^/"(г0)(г-г0)2 + ...,
вл(г) = ^(2о) +a,k(zQ)(z-z0) + llavk(z0)(z-z0)2 + .t. (£ = 1, ... , г)
в данное дифференциальное уравнение; сравнение коэффициентов получающихся
степенных рядов даст рекуррентные соотношения для неизвестных
коэффициентов -rfWlk)(z0) {k = r, r+1, ...). (Значения производных w{k) (z0) для
k = 0, 1, ..., г—1 заданы в виде начальных условий.) Ряды (14) сходятся
абсолютно и равномерно в каждом круге |z —z0|</?, лежащем в D.
(Ь) Аналитическое продолжение любого решения w(z) линейного
дифференциального уравнения вокруг особых точек одного или нескольких
коэффициентов а^ (z) даст, вообще говоря, различные ветви некоторого
многозначного решения (см. также пп. 7.4-2, 7.6-2, 7.8-1).
В частности, полный обход вокруг особой точки преобразует фундаментальную
систему решений w (z), w2 (z), • • • , w (z) однородного линейного дифференциального
уравнения в новую фундаментальную систему а^ (z), w2 (г), • • • . w (z). Эти две
фундаментальные системы обязательно связаны невырожденным линейным
преобразованием
г
w. (г) = ^ aikwk (z) (i = 1.2, .... г).
k = \
Собственные значения матрицы [а^] (п. 13.4-2) не зависят от частного выбора
фундаментальной системы wx (z), w2 (z), • • • , wr (z).
9.3-6.* Решение однородных уравнений путем разложения в ряд в
окрестности правильной особой точки.
(а) Особая точка z = zt одного или нескольких коэффициентов а^ (г)
называется изолированной особой точкой однородного линейного
дифференциального уравнения
^+а1(г)^ + ...+аг(2)ш = 0, (9.3-15)
dz dz x
если в некоторой ее окрестности нет других особых точек. Изолированная
особая точка z = zt называется правильной (слабо особой), если, все
коэффициенты ak(z) имеют в этой точке полюсы порядка не выше k, т. е. а& (z) =
= —- £, где все pk (г) аналитичны в некоторой окрестности Dx точки Zx1).
В этом случае уравнение (15) можно записать в виде
<*-*,)'$+(*-*i)'-1ft(*)4?r + ...
dzr * dz'
... + (z-z1)Pr_l(Z)d£ + pr(z)w=0. (9.3-16)
l) Если некоторые р. (z) имеют нули в точке zit то соответствующие
коэффициенты a. (z) будут иметь полюсы порядка меньшего чем k\ они могут даже быть
регулярными функциями в окрестности точки г±.
«.3-7.
9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
277
Остальные изолированные особые точки называются существенно особыми.
Если z = Zi есть правильная особая тонка (или регулярная точка), то
однородное линейное дифференциальное уравнение (15) допускает решение вида
оо
» = («-*!)■* 2 **(*-*i)*- (9.3-17)
Если |х — не целое число, то (z — z^v означает какую-либо однозначную
ветвь многозначной функции, регулярную в комплексной плоскости с
разрезом вдоль некоторого луча, выходящего из точки z, (см. п. 7.4-2).
Показатель \i должен удовлетворять алгебраическому уравнению степени г
—определяющему уравнению
|1(|А-1) ... (,1-Г+1) + |А(|*-1) - (H-' + 2)Pi(Zi)+...
... + ^Pr-i(*i) + Pr(*i) = 0. (9.3-18)
Коэффициент а0фО может быть выбран произвольно, остальные
коэффициенты аь определяются последовательно из рекуррентных соотношений,
получающихся при подстановке ряда (17) в уравнение (15) или (16). Ряды
в (17) сходятся абсолютно и равномерно в каждом круге \z — z1\<cR,
лежащем в Dv
Различные корни |А = |xlt fx2, ..., [ir определяющего уравнения (18) дают
линейно независимые решения (17) данного дифференциального уравнения,
за исключением тех случаев, когда некоторые из них отличаются на целое
число. В таких случаях, а также в случае равных корней определяющего
уравнения можно использовать известные решения для понижения порядка
данного дифференциального уравнения (п. 9.3-2, с) или отыскивать решения
по методу Фробениуса (см. также п. 9.3-8, а).
Показатели jx^ связаны с собственными значениями Х^ матрицы
преобразования (а1к) п. 9.3-5,Ь для одного обхода правильной особой точки zx соот-
ношением Afc = e * •
(b) Правильные особые точки на бесконечности (см.
также пп. 7.2-1 и 7.6-3). z = co называется правильной особой тонкой
уравнения (15), если преобразование
w (z) = w f—\=w (z),
Kzl \ (9.3-19)
dw -2 dw_ d2w -4 d2w , o~3 dw_ x
dz~~ dz* dz2 ~~ dz* d~z y
приводит к дифференциальному уравнению с правильной особой точкой z =
= 0. В этом случае решение преобразованного уравнения можно получить,
как показано выше.
(c) Обобщение. Если z = Zi не является правильной особой точкой, причем
функции Pfo(z) имеют полюсы в z = zt, то все же можно искать решение в виде,
аналогичном (17), заменяя степенной ряд рядом Лорана (п. 7.5-3) по положительным
и отрицательным степеням (z — zt).
9.3-7. Методы интегральных преобразований. Если в линейном дифференциальном
уравнении (1) коэффициентами служат многочлены aft (z) = 2 ahkz » т0 ег0 интегРи-
h
рование при начальных условиях а/(-^ (0) — а;(/) часто упрощается применением
преобразования Лапласа, как в п. 9.4-5. Применяя формулу
J?lzV*'W; »]-(-«*-^ Ь*#[ш(*); •] -% sk~^w'^ (0 + 0)1,
(9.3-20)
г
278 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.3-8.
можно получить новое и, можят быть, более простое дифференциальное уравнение
для изображения *g [w (г); s] решения.
Более общие интегральные преобразования (табл. 8.6-1) могут быть подобным
образом применены в различных специальных случаях (см. также п. 10.5-1 и [10.4]).
9.3-8. Линейные уравнения второго порядка (см. также пп. 15.4-3,с
и 15.5-4).
(a) Результаты общей теории применимы, в частности, к линейным
уравнениям второго порядка. Главный интерес представляет здесь однородное
уравнение
L» ==£?+<!, <*)£+«• (*)»-<>. (9.3-21)
Уравнение (21) равносильно уравнению
p(z) = exp^al(z)dzt q (z)=a2(z) p (z). J
Если известно одно решение wt(z) уравнения (21) или (22), то общее
решение есть
ш(г) =ш1(г) [C1 + C,$¥ff?77)]. (9.3-23)
(b) Разложение решения в ряд (см. также пп. 9.3-5, 9.3-6,
9.3-9 и 9.3-10). В важном частном случае уравнения второго порядка, пред-
ставимого в виде
(z-*i)2 d^ + (2-zl)pl(z)d-^+p2(z)w = 0t (9.3-24)
где pt (z) и p2(z) аналитичны в 2 = 2!, определяющее уравнение (18) сводится к
I*1 + ^ lPi (*i) -11 + Pi (*i) = 0. (9.3-25)
Это уравнение имеет два корня. Корень \i-\ii с большей действительнол
частью приводит к решению вида
оо
а^а*! (*) = (*-г,)* 2 e*(*-«i)*. (9.3-26)
*=о
Второй корень \i2 приводит к линейно независимому от wx (г) решению
подобного вида, если \i2 не совпадает с \1г или не отличается от него на це^оз
число. В противном случае линейно независимое от wx (z) решение может
быть записано в виде
00
w = Aw1(z)\n(z-zl) + {z-zl)»* 2 bk(z-z1)K (9.3-27)
/fe = 0
Подставляя каждое из решений (26) или (27) в данное дифференциальное
уравнение (24), получаем рекуррентные соотношения для коэффициентов.
(c) Преобразование переменных. Следующие преобразования
могут иногда упростить данное дифференциальное уравнение (21) или
привести его к дифференциальному уравнению с известным решением.
1. Подстановка w — wexp \ ф (z) dz дает
-d~ + [*i (*) + 2ср (г)] ^ + [а2 (г) + а, (г) Ф (г) + <р' (г) + у* (г)] Ш = 0.
(9.3-28)
Надо попробовать выбрать ф (z) так, чтобы получить более простое
новое дифференциальное уравнение; в частности, выбор ф(г) =
».3-9. 9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 279
= — -g ах (г) исключает коэффициент при ~. Подходящая
подстановка z — z(z) также может дать некоторое упрощение
дифференциального уравнения.
2. Подстановка
w = Ae^(z)dz; © = ^ (9-3-29)
W
преобразует уравнение (21) в дифференциальное уравнение первого
порядка типа Риккати (п. 9.2-4, с).
(d) Существование решения и его нули при
действительном аргументе. Пусть х — действительное переменное. Однородное линейное
дифференциальное уравнение
U а £| + «1 (*> ddY + a2(x)w=0 (9.3-30)
имеет решение w = о/ (х) в каждом интервале [а, Ь], где at (x) и а2 (х) действительны
и непрерывны; решение однозначно определяется начальными значениями w (x0), W (х0)
для любого значения х0 € [а, Ь]. w (x) может иметь лишь конечное число нулей в любом
конечном интервале [а, Ь], в котором w (x) =£ 0; нули двух линейно независимых решений
перемежаются в [а, Ь].
9.3-9. Гипергеометрическое дифференциальное уравнение Гаусса и Р-урав-
ненне Римана (см. также пп. 9.3-5 и 9.3-6). -
(а)-* Гипергеометрическое дифференциальное уравнение
z(l-z)d-^ + [c-(a + b+l)z]%-abw = 0 (9.3-31)
имеет правильные особые точки z = oo (с показателями \х — а, |1 = 6), г—\
(с показателями и = 0, \х — с — а — Ь) и 2 = 0 (с показателями |х = 0, |х = 1 — с)
и не имеет других особых точек. Решения уравнения (31) содержат в
качестве частных случаев многие элементарные функции и специальные функции,
рассмотренные в гл. 21.
Разложение в ряд вблизи z = z, =0 дает гипергеометрическую функцию
вида (17) при |х = 0 и |lx = 1 — с с
п — (fl + ** + *4fr + и + *) я
При |и = 0 получаем специальную гипергеометрическую
функцию—гипергеометрический ряд
w = F(a, Ь; с, г) = 1 +а± г + ^ " (п +Д*Д+ " г' + - <9-3"32)
(с не должно равня!ься нулю или целому отрицательному числу). Этот ряд
сходится абсолютно и равномерно при |z|<l; сходимость распространяется
и на единичную окружность, если Re (a-\-b—с) < О1). Ряд (9.3-32)
сводится к геометрической прогрессии при а=1, Ь — с и к многочленам Якоби
(п. 21.7-8),если а равно целому отрицательному числу. Ясно, что F (a, b\ c\ z) =
= F (Ь, а; с; г).
Второе (линейно независимое) решение уравнения (31) может быть получено
способом, указанным в п. 9.3-S,b; в частности, гипергеометрическая функция второго
рода
Ф (а, Ь; с, z) ===
_ Г (а — с + 1) Г ф— с + 1) Г (с — 1)
"~ Г (а) Г ф) Г (1-0
является решением уравнения, если с отлично от целого числа
F(a— с+\, Ь — с+\\ 2 — с\ г) (9.3-33)
>) При 0 <; Re (а -\- Ь — с) < 1 ряд условно сходится во всех точках единичной
окружности, кроме точки 2=1.
280 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.3-0.
Отметим следующие соотношения ( | z | < 1):
F (а,Ь; с, г) =
1
Г (с)
Г (а) Г
^~Г \ Са_1 (1 - 0С"а~1 (J - 2D'* dt [Re с > Re a > 0],
(9.3-34)
^ = y-F(a+l, Ь+U c+U 2); ^ = ^- Ф (а + 1; 6+1: с+1; 2), (9.3-35)
^ <«. * « » " Г^а)Г(г1Й [Re (а + 6 - ,)< 0]. (9.3-36)
F (а, Ь; с; г) = (1 — z)c~a~b F (с — а, с—6; с; 2).
Приведем некоторые линейные преобразования F (а, 6; с; 2) (полный перечень
таких преобразований приведен в [21.3]):
F(a, Ъ; с; г) = (1 — z)~a F (а, с — Ь; с; ~Г\) = (1 — *)~Ь F (ъ. с — а; с; jzT\\
(9 3-37)
Формулы (37) позволяют аналитически продолжить F (а, Ь\ с, г) в полуплоскость
I 2
• < 1, т. е. Re 2 < 1/2.
*<«• b^^)-r^)Th=T)F^ *S a + 6-c+ls 1-.) +
+ (1 - zf-*-b Г (ОгГ (а + Ь-с) ^ (g_ q> с_Ь; с_в_ь+1. ,_2) (93.38)
[ | arg (1 — 2) I < л; а + 6 — с ф 0, ±1, ± 2, •. • ].
С помощью формулы (38) гипергеометрическую функцию можно продолжить
в круг |2—1 |<1 с разрезом по отрезку [1, 2], а также выявить характер ее
особенности в точке 2 = 1.
[ | arg (— г) | < л; а — ЬфО, ±1, ±2, • • • ].
Формула (39) позволяет продолжить F(a, Ь\ с; z) во внешность единичной
окружности |2|>1 с разрезом по лучу [1, оо].
В табл. 9.3-2 приведены дополнительные формулы.
(b) P -у равнение Римана. Уравнение (31) является частным случаем
Р-уравнения Римана
d*w /1 — а— а7 1 — Р — Р^ 1 — у — у" \ dw
dz2 ' \ 2 — zt •" 2 — г2 •" z — 23 ) dz~^
_l_ Гац/ (^1 — 2t) (?1 — гз) , РЕ' (22 — 23) (22 — Zt)
+ L F=^ + 7=Tt +
+ УУ/(гз-г1)(23-22)1 » = 0
2— Z3 J (2 — 2,) (2 — 22) (2 — гя)
которое имеет три различьые правильные особые точки: z = zt (с показателями а, а7)»
2 = г2 (с показателями 0, 0') и z — zz (с показателями у, у'); здесь
а + а' + 0 + 0' + у + у' = 1.
Решение уравнения (40) обозначается так:
W (2)
Одним из решений служит функция
/г — гЛа /2
Г 2, 22 28 ^
= *>< а р у г V.
U' 0' у' J
V, - J' (l^)V *<. + • + *. + >'-*:. + .-«': glSS-S> (9-3"4I)
Это решение сводится к (32) при 21=0> 22 = оо, 28 = 1 и
a = 0, 0 = а, у = 0; а' = 1 — с, 0' = 6, у7 = с — а — &.
9.Э-9. 9.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 28*
Таблица 9.3-2
Дополнительные формулы для гипергеометрических функций
1. Формулы приведения Гаусса.
с F (а, Ь — \; с; г) — с F (а — \, Ь; с; г) + (а — Ь г F (а, Ъ,
c(a — b)F(a, Ь; с; z) — а (с — Ь) F (а + 1, Ь; с + 1; z) +
+ Ь (с — a) F (а, Ь + 1;
с (с + 1) [F (а, Ь\ с; z) — F (а, Ъ\ с + 1; 2)] — abz F (а + 1, 6 + 1;
cF(a, 6; с; z) — (с — a) F (а, Ь + 1; с + 1; z) — а (1 — z) F (а + 1, 6 + 1;
cF(a, 6; с\ z) + (6 — с) F (а + 1, Ь\ с + 1; z) — Ь (1 — z) F (а + 1, 6+ 1;
с (с — 6z — a) F (а, Ь; с; z) —с (с — a) F (а — 1, 6; с; z) +
+ abz(l — z) F(a + 1, 6+ 1;
с (с — az — b) F (a, b; c; z) — с (c — b) F {a, b — 1; c; z) +
+ obz (1 — z) F (a+1, 6+1
с F (a, b; c; z) — с F (a, b + 1; c; z) + az F (a + 1, 6 + 1;
cF (a, b\ c; z) — с F (a + 1, b; c; z) + bz F (a + \, b + 1;
с [a — (c — b) 2] F (o, 6; c; z> — a<? (1 — z) F (a + 1, 6; c; z) +
4- (c — a) (c — b) z F (a, b;
c[b — (c — a) z] F (a, b\ c\ z) — be (1 — z) F (a, 6+1; c; z) +
+ (£-0)^-6)2/? (a, 6;
c(c + 1) [F (a, 6; <?; z) — F (a, b + 1; с + 1; z)] +
+ a(c — b)zF (a + 1, 6+ 1;
с (с + 1) [F (о, b; c\ z) — F (a + 1, 6; с + 1; z)] +
+ b {c — a) z F (a + 1, 6 + 1;
cf(fl, 6; c; z) — (c — b)F(a, b\ c + 1; z)--b F (a, 6 + 1;
с F (a, 6; c; z) — (c — a) F (a, b; с + 1; z) — a F (a + 1, 6;
2. Разные формулы.
<1+«)«*(«. а+-1-&:*+±;г>) = ф, 6; 26; jjJLjJ.
/i _L »\2a f f 9/7 9/7 4- 1 r' r' 9\ — Fin n -4 —• r*
I1 Tz/ r ^"» zu г * — ^i ^i z> — r ". " ПГ ^T* c* /j i v2 •
F^a, 6; a+6+-^-; sin2 ф) = F (2a, 26; a + 6 +-L; sin*-~Y
«+1
^+1
с + 2;
с+ 1;
с+\\
с+1
с+1
с+1
с+1.
с+ 1;
c+U
с + 2,
с+2;
с+1;
с+1;
2)
г)
г)-
z)-
z)-.
г)
; г)
г)
г)-
2):
2) =
2)
2) =
«) =
Z) =
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
3. Выражение некоторых элементарных функций через гипергеометрические
(см. также таблицу 21.7-1).
(1 +х)п = F (—я, 1; 1; —х).
In (1 +x) = xF (1, 1; 2; — х),
arcsin* = *F(i-, -~; ~; x^j.
arctgf X = X F (-L 1; -|_; - ^
282 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.3-10.
Таблица 9.3-2 (продолжение)
n пх — n sin х F (—'-—, —-—; —; sin2 jc К
«л*-*(-£-,--£-: i-: sin**)~
„ (\ + л 1 —л 1 х . \
= COS*/^--X-, _—; _; sin* *j =
Л 1 —Л 1
= cos" х F
2 ' 2 ' 2 '
tg2 *),
9.3-10. Вырожденные гипергеометрические функции. Особую точку z—1
гипергеометрического дифференциального уравнения (31) можно передвинуть
в z = b заменой г на zfb\ тогда при Ь->со особая точка z = b будет
стремиться к уже имеющейся особой точке z = oo (вырождение особой точки). Это
приводит к дифференциальному уравнению вырожденной гипергеометрической
функции (Куммера)
г*£ + (с-г)%х-т=0. (9.3-42)
которое имеет од я у правильную особую точку 2 = 0 и одну существенно
особую точку z = oo. Многие специальные функции являются решением
уравнения (42) при частном выборе значений а и с (гл. 21).
Разложение решения в ряд в точке z = 0 дается формулой (17) при jx = 0
ии = 1 —с, где
a + H + k
Uk+1 {с + ц + k) <1 + Щ-*> "**
При jut = 0 получаем вырожденную гипергеометрическую функцию Куммера —
вырожденный гипергеометрический ряд (см. п. 21.7-5):
B, = F(e;c;j)»l+£z + ^£g±»Jri+... <|г|<оо). (9.3-43)
Второе (линейно независимое) решение можно получить тем же способом, что и
в п. 9.3-8, Ь; в частности, вырожденная гипергеометрическая функция второго рода
.Г (а— с+ 1)Г(с— 1)
Г (а) Г (1 - с)
является решением, если только с — не целое.
Отметим следующие соотношения:
1
F (С; С' Z) = Г (ayrt - а) I ^ ° ~ Я*''™'* *$ Re с> Re а > 0; (9.3-45)
0
*L = - F (а + 1; с + 1: *): ^ = - Ф (а + 1; с + 1; г); (9.3-46)
F (а; с; г) = ezF (с — а; с: — z). (9.3-47)
В табл. 9.3-3 приведены дополнительные формулы.
8.4-1. 9.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 283
Таблица 9.3-3
Дополнительные формулы для вырожденных гипергеометрических функций
'(а:2а;2г)=2а *е ' " (в 2 ) г ^ + _^ Л 2 ey ^ ( (2/ "2 ),
a F а 4- 1; с Н- 1; z) = (а — с) F (а; с + 1; 2) + с F (а; с; 2),
а F (а + 1; с; 2) = (z + 2а — с) F (а; с; 2) + (с — a) F (а — 1; с; z),
(л = 0, 1, 2, ...),
(0 < Re a < Re с).
Г(а+ 1)
0
[Re (а + v -Ь 1) > 0; | arg z | < л/2].
9.3-11. Обобщенные гипергеометрические ряды. Степенные ряды (32) и (43)
являются частными случаями рядов
mFn{al% я2, ..., ат\ съ с2, ..., сп\ z) ==
-Ей i'tio*'"^*'* (т. «=1, 2,...), (9.3-48)
ГДе (*) ^ = х (х + 1) • • • (х + k — 1). 5 этих обозначен иях гипергеомгт р ические
ряды (32) и (43) запишутся соответственно как 2FX (а, Ъ\ с; z) и XFX (a; c\ z).
9.4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
9.4-1. Однородные линейные уравнения с постоянными коэффициентами
(см. также п. 9.3-1)
(а) Уравнение первого порядка
*о^+ад = 0 (Оо^О) (9.4-1)
имеет решение
у = Се а« [С=</(0)]. (9.4-2)
При я0/а, > 0 (а0/й1 называется иногда постоянной времени)
У (°o/ai)=y (0) e-i «= 0,37</ (0), у (4с?0/а,) =« 0,02j/ (0).
ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.4-1.
(Ь) Уравнение второго порядка
*о^ + аЛ+а2у = 0 (яо^О) (9.4-3)
имеет решение
у^С^ + С^, \
*/ = (d + C20* 2а° (а?-4а0а« = 0). (9.4-46)
Если а0, аъ а2 действительны, то при а\ — 4я0а2<0 корни slf s2 будут
комплексными; в этом случае формулу (4а) удобнее представить в виде
у=fit (л cos to/ _|_ в sin w/) __ #eot sin ((,)/ _|_ а) t (д. 4-4с)
где величины
называются соответственно постоянной затухания и собственной круговой
частотой. Постоянные Сг, С2, Л, Б, /?, а определяются по начальным или
краевым условиям (см. также п. 9.4-5, а).
Если а0, аг > 0, то величина £ = называется коэффициентом затухания; при
С > 1. £ = 1, 0<£<1 получаем соответственно апериодическое затухание (4а),
критическое затухание (4Ь), затухающие колебания {4с). В последнем случае логарифмический
декремент 2яа/со есть натуральный логарифм отношения последовательных максимумов
решения у (t).
Уравнение (3) записывают иногда в безразмерном виде
_L **+2-£-**+«,-0
o1l±(o1Vli-V*
при слабом затухании (£2 < 1) имеем й)х = У а2/а0 ^ й).
(с) Для интегрирования уравнения порядка г
Lv-<h%r+a1£p% + ... + afy=0 (а^фО) (9.4-5)
надо найти корни характеристического уравнения — алгебраического уравнения
степени г:
a0sr+a^-1 + ... + ar^s + ar = 0. (9.4-6)
Если все корни slt s2, ..., sr этого уравнения различны, то общее решение
дифференциального уравнения (5) есть
у = с/1' + С2е$2' +... + Сгг* . (9.4-7а)
Если некоторый корень sk имеет кратность т#, то соответствующие члены
в (7а) надо заменить на
[Ck + Cklt+Ck^ + ... + Ck{mk^xf^iy^. (9.4-76)
Различные члены в решении (7) называются собственными колебаниями, г
постоянных Ck и Cty определяются по начальным или краевым условиям (см.
также п. 9.4-5, а).
9.4-2. 9.4. ЛИНЕЙНЫЕ УРАВНЕНИЯМ ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 285
Если коэффициенты уравнения (5) действительны, то комплексные корни
характеристического уравнения встречаются сопряженными парами о ± т.
Соответствующие пары членов в решении также будут комплексно
сопряжены и могут быть заменены действительными членами:
tmCe<o+to) t + tmceio-m)t = tmeot (А cos ^t+B sin со/) = Rtmeot sin (to/ + a), (9A-7c)
где А и В или R и a— новые (действительные) постоянные интегрирования,
(d) Если дана система п однородных линейных дифференциальных
уравнений с постоянными коэффициентами
Ф/1(й)у1+Ф/1(й)у2 + -.. + Ф/1.(ЙУ|.-0 (/=1, 2, .... /г), (9.4-8)
где cp/fe (d/dt) — многочлены от d/dt> то каждая из п функций, составляющих
решение yk—yk(t) (k — \, 2, ... , /г), имеет вид (7); показатели s,- будут теперь
корнями характеристического уравнения системы
D(s)-det[V/*(s)] = 0. (9.4-9)
Подставляя выражения вида (7) в уравнения (8), мы получаем соотношения
между коэффициентами; коэффициенты, оставшиеся произвольными
(постоянные интегрирования), определяются по начальным или краевым условиям
(см. также п. 9.4-5, b и п. 13.6-2).
9.4-2. Неоднородные уравнения (см. также п. 9.3-1).
(a) Методы, изложенные в пп. 9.3-1—9.3-4, применимы ко всем линейным
дифференциальным уравнениям. Поэтому общее решение неоднородного
уравнения
l-y^a0d^r+al^+... + ary = f(t) (9.4-10)
можно представить в виде суммы общего решения (7) приведенного
уравнения (5) и какого-либо частного решения уравнения (10).
Если, как это часто бывает в приложениях, /(/) = 0 при /^О1), то
частное решение y = yN (t) уравнения (10) такое, что yN = y'N = ... = y(£J— ^ = 0
при / ^ 0, называется нормальной реакцией на внешнюю нагрузку / (/).
Решение уравнения (10) при заданных начальных значениях величин у, у\ ..., у{Г"1}
есть сумма решения соответствующей начальной задачи для однородного
уравнения (5) и нормальной реакции yN (t).
Во многих приложениях (устойчивые электрические цепи, колебания) все корни
характеристического уравнения [(6) или (9)] имеют отрицательные действительные части,
и общее решение уравнения (5) исчезает более или менее быстро (устойчивый
«переходный процесс»). В таких случаях главный интерес представляет обычно «установившийся
процесс» y — ygs {t) —частное решение, вызванное данной нагрузкой f (t). В других
случаях yssU) определяется не только данным дифференциальным уравнением, но и
начальными условиями. Нормальная реакция #дг (t) может как содержать, так и не содержать
переходные члены.
(b) Всякое решение Ук — УкУ) (6 = 1, 2, ..., л) неоднородной системы
линейных дифференциальных уравнений
^(л)У1+Ф/»Й)й + -+Ф/«(д)*«-//С) (/-1.2...., я) (9.4-11)
есть сумма частного решения этой системы и общего решения
соответствующей однородной системы (8). Нормальная реакция системы (11) на множество
внешних нагрузок /у (/), равных нулю при / ^ 0, есть частное решение, в
котором при /^0 все функции yk вместе со своими соответствующими
производными равны нулю.
') Это означает, что рассматриваются правые части только вида / (/) а / (/) С/+ (/),
где U+ (t) — единичная функция, определенная в п. 21.9-1.
286 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.4-3.
(с) Если правая часть содержит периодический член, частота которого совпадает
с частотой незатухающего синусоидального члена в общем решении соответствующего
однородного уравнения или системы, то данное уравнение или система не будет иметь
ограниченного решения (резонанс).
9.4-3. Свертки и функции Грина (см. также пп. 9.3-3, 9.4-7 и 15.5-1).
(a) Физически реализуемые задачи Кош и. Применение
метода функции Грина (п. 9.3-3, Ь) к дифференциальному уравнению (10)
позволяет представить нормальную реакцию на внешнюю нагрузку f (t) в виде
интеграла Дюамеля или свертки
t t
У=Ух (0 = j К С-т)/ (т) d% = [h+ (т)/ (/-т) </т, (9.4-12)
о о
если предположить, что /(/) = 0 при /^0 и h+(t — т) = 0 при t^i, так что
«будущие» значения /(/) не могут воздействовать на «более ранние» значения
у (t) и «мгновенные» влияния исключаются {физически реализуемые системы).
При этом
/ т
о*
если существуют производные в правой части. Функция h+(t—т) есть
частный случай функции Грина и определяется условиями
со
U+(/ —т) = 0 (/>т); \"U+(f —T)dx = l V > °)i (9.4-14a)
А+(/ —т) = Л+(/ — т)==... = /г<Г- ° (/ — т) = 0 С^т). (9.4-146)
h+(t — т) есть нормальная реакция на единичный импульс б+(/ — т) (п. 21. 9-6);
уравнение (14а) можно записать в символической форме
U+(/ — т) = 6+(/ —т). (9.4-14с)
Заметим, что \h+(t — %) dx есть нормальная реакция на единичную нагрузку
U+(t — т) (п. 21.9-1), т. е. Л+(/—т) есть производная от нормальной реакции
на единичную нагрузку. Символическое дифференциальное уравнение (14с)
часто легко решается операторным методом п. 9.4-5; другой путь
нахождения h+(t) заключается в интегрировании однородного дифференциального
уравнения
LM/) = 0 (/>0) (9.4-Ш)
при начальных условиях
Л+(0 + 0)=Л;(0 + 0)=... = /^-2)(0 + 0)=0,
/^-«(О + О)-^
Пример. Для Ly = a^ + y имеем: /i+(/) = l e""//e (/>0).
(b) При аналогичных условиях нормальная реакция системы линейных
дифференциальных уравнений (11) может быть представлена в виде
п 1
Vk= 2 1<Л+>*/ <*-*>'/ (T)rfT <*-!. 2 я>. (9.4-15)
/ = 1 0
где (Л+)^/ (* — т) —решения системы (II), соответствующие правым частям /у (f) =0
(9.4-14с)
0.4-4. 9.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 287
Ифк), ffc(t) = 6+ (t — т). Матрица функций [(h+)kj (t —т)] есть частный случай матрицы
Грина.
(c) Свертка (12) дает нормальные реакции также и в том случае, когда f (t) и у (/)
связаны дифференциальным уравнением вида
"•S-+-.^f+■■■+'--b3^-S*+-+'-'■ •"•
Такие соотношения могут получиться, в частности, когда система (11) приводится к
одному уравнению путем исключения (п — 1) искомых функций.
Некоторые (h+)kj (t), а значит, и /ц. (0, в случае соотношений типа (16) могут
содержать особенности типа дельта-функции (обобщенные функции Грина, п. 15.5-1, Ь). Если
при этом
h+ (t) = ct6+ (t - tt) + c26+ (t -U) + ... + h0 (/),
то формула (12) сводится к
У = »n <*> - V (*-'i) + c2f (' - 'г) + - + J Ло <' - x> ' <x) Л (' > 0)'
0
(d) Более общие задачи. «Симметрические» и
«асимметрические» функции Грина. В случае, когда правая часть при
/^0 отлична от нуля, можно ввести «симметрическую» функцию h(t—T),
определяемую уравнением (см. п. 21.9-2)
L/i(/-t) = 8(/-t) (9.4-17)
и подходящими начальными или краевыми условиями. Решение
00 00
у= ^ /1(/-т)/(т)4т= $ h(T)f(t—T)dT (9.4-18)
— 00 —ОО
будет, в частности, удовлетворять уравнению (10) при /^0 и
У (0-0) = */' (0-0) = ... = #"-1> (0-0) = 0,
если f(t)==f(t)U(t) (п. 21.9-1) и если
h(t-i) = h' (/-T) = ... = /i^-i'(/~T) = 0 (*<т). (9.4-19а)
«Асимметрические» функции h+ (t) удобнее применять вместе с
преобразованием Лапласа, а «симметрические» h(t) — с преобразованием Фурье. В
обычных физических приложениях сохраняют условия (19а), так как «.будущие*
значения функции не могут влиять на решение; при этом hv(t) и h (t)
совпадают в точках непрерывности. Часто внешняя нагрузка не может оказать
мгновенного действия на решение, так что h(t — i) удовлетворяет более
сильным условиям
h(t-T) = h'(t—t) = ... = /i"-i>(/-t) = 0 (/^т) (9.4-196)
и h (/) совпадает с h+ (t).
Пример. В электрической цепи, содержащей только сопротивление R, сила тока
у (/) и напряжение f (t) связаны соотношением у (t)=f (t)/R, так что здесь h (t) = б ,(t)/R
и h (t) а б {t)/R. Но для Ly sa а ^ + У имеем /t+ (/) в Л (0 ян -i- Г"'/а.
9.4-4. Устойчивость. Линейное дифференциальное уравнение (10) или
система (11) устойчивы, если все корни соответствующего характеристического
уравнения (6) или (9) имеют отрицательные действительные части; тогда малое
изхменение начальных условий не может вызвать больших изменений решения
(более общее определение устойчивости см. п. 9.5-4, а). Характер корней может
быть исследован методами пп. 1.6-6 и 7.6-9 (критерии устойчивости для
электрических цепей и систем управления). Дифференциальное уравнение (10)
288 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.4-5.
устойчиво тогда и только тогда, когда существует \ | Н+ (т) | di I или соответ-
? \
ственно j | h (т) | di . Аналогичные условия для каждой функции hkj(i)
— оо '
системы (11) (п. 9.4-3, Ь) являются необходимыми и достаточными для
устойчивости этой системы.
9.4-5. Операторный метод решения (см. также п. 8.1-1, 8.4-1—8.4-5, 9.3-7,
10.5-2 и 13.6-2, с).
(a) Для интегрирования линейного дифференциального уравнения (10)
с начальными значениями у (0 + 0), у'(0 + 0) у1г~1} (0+0) применяют
преобразование Лапласа (8.2-1) к обеим частям уравнения, полагая X[y(t)]^
^ У (s) и X U (t)] = F (s)' Получающееся линейное алгебраическое уравнение
(вспомогательное уравнение)
(aoSr + alS^+ ... +ar)Y (s) = F (s) + G (s)t
G(s) = y(0 + 0) (a0s>~i + aiS>~* + ... + ar_x) +
+ y'(0 + 0)(aosr-* + alSr-*+ ..+ar_2)+ } (9-4-20)
+
+ У{Г~2> (0 + 0) (аФ + ах) + а0у^ (0 + 0)
легко разрешимо относительно изображения искомого решения:
Y(s) = — ££> + — ^ . (9.4-21)
Здесь первый член есть изображение Y w (s) нормальной реакции yN (t) (п. 9.4-2, а),
а второй член представляет влияние ненулевых начальных значений функции
у (t) и ее производных. Решения у (t) и yN(f) находятся по своим
изображениям с помощью табл. 8.4-1 или 8.4-2 или по правилам пп. 8.4-2 — 8.4-9.
В частности, каждый из г членов разложения функции ;— ^ -
(а#г+а18Г1+...+ог)
на простейшие дроби (п. 8.4-5) дает соответствующий член в решении (7).
Этот метод решения применяется без существенных изменений и к
дифференциальным уравнениям вида (16).
(b) Применение преобразования Лапласа к системе дифференциальных
уравнений (11) приводит к системе линейных алгебраических уравнений
Ф/1 (s) Уг (s) + Ф/2 (s) У2 (s) + ... + Ф/я (s) Уп (s) = Ff (s) + Gj (s)
(/=1, 2, ..., я), (9.4-22)
где функции Gj (s) зависят от начальных условий. Решая полученную систему
по правилу Крамера (1.9-4), находят изображения искомого решения
VI Ajk <s> V AJk (s)
yki*)= 2^ "^r^(s)+2i ^"G/(s) {k==u 2t""n)t (9,4'23)
где Ajk (s) — алгебраические дополнения элементов фу^ (s) в определителе системы
D (s) = det [фу^ (s)] (см. также п. 1.9-2). Первая сумма в формуле (23) есть
изображение нормальной реакции, а вторая представляет влияние начальных
условий.
Искомое решение уь (t) находится путем обращения преобразования
Лапласа.
9.4-6. 9.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 289
В задачах, содержащих неустойчивое дифференциальное уравнение
(п. 9.4-4) или импульсные внешние нагрузки, решение может иметь
особенности типа дельта-функций (см. также пп. 8.5-1 и 21.9-6).
9.4-6. Периодические внешние нагрузки и решения.
(a) Синусоидальные внешние нагрузки и решения.
Синусоидальные установившиеся решения. Любая система
линейных дифференциальных уравнений (11) с действительными
коэффициентами и синусоидальными внешними нагрузками одной частоты
ff(t)=EBfun(G>t + fy) (/=1, 2, ..., п) (9.4-24 а)
допускает единственное частное решение вида
yk(t) = Aksm(<i>t+ak) (£=1, 2, ..., п) (9.4-24 Ь)
(если нет резонанса, т. е. если со/ не является корнем характеристического
уравнения). В частности, если все корни характеристического уравнения (9)
имеют отрицательные действительные части (устойчивая система, п. 9.4-4),
то синусоидальное решение (24 Ь) будет единственным установившимся
решением (п. 9.4-2).
(b) Метод комплексных амплитуд. Синусоидальные внешние
нагрузки и решения (24) можно поставить во взаимно однозначное
соответствие комплексным числам (комплексным амплитудам)
V2 Y2 /rz
Аи их. А
у|*'в* —р|/5Е* (А=1. 2, ...,/!).
(9.4-25)
Абсолютная величина каждой комплексной амплитуды равна среднему квадра-
тическому значению соответствующей синусоиды, а ее аргумент равен началь*
ной фазе синусоиды. Комплексные амплитуды (25) связаны (комплексными)
линейными алгебраическими уравнениями
9/i(^)Y1 + 9/2(/(o)Y2+...+9y„(t(o)Yn = F/ (/=1, 2 /г), (9.4-26)
которые отвечают системе (11) и могут быть решены относительно неизвестных
комплексных амплитуд (ср. п. 9.4-5, Ь):
п
-г
Ajk (/со)
(6 = 1, 2, ..., л). (9.4-27)
D (/со)
/=1
В случае резонанса (п. 9.4-2, с) выражение (27) может не иметь смысла.
(с) Синусоидальные величины (24) удовлетворяют данной системе дифференциальных
уравнений (11) тогда и только тогда, когда этим оке свойством обладают комплексные
гармонические функции
' ' ' ^ (9.4-28)
(/=1, 2 п), \
(* = 1. 2 я), J
yA(o-v/(el+eik)-V^
которые часто более удобны в расчетах, чем сами синусоиды (24).
(d) Более общие периодические внешние нагрузки
(см. также пп. 4.11-4, 4.11-5 и 9.4-5, Ь). Если дана устойчивая система (11)
с периодическими внешними нагрузками вида
00
/ (t) = Ц + 2 (ah cos НШ + bh sin Ш)г (9.4-29)
Л=1
10 Г. Корн а Т. Корн
290 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.4-7.
то метод комплексных амплитуд можно применить к каждому
синусоидальному члену отдельно и затем путем наложения получить установившееся
периодическое решение. Этот метод может оказаться более удобным, чем
метод преобразования Лапласа, если в решении надо найти только небольшое
число гармоник.
9.4-7. Передаточные функции и частотные характеристики.
(а) Передаточные функции. Передаточной функцией называется
функция
1 Укг (s)
#(*) = —^ т=г-. — = -7гтт- (9-4-3°)
a„sr + a,sr *■+ ... -J-a
F(s)
(см. формулу (21)). Передаточная функция представляет некоторый линейный
оператор (п. 15.2-7), который преобразует внешнюю нагрузку на входе в
нормальную реакцию на выходе (рис. 9.4-1).
Рис. 9.4-1. Представление линейных дифференциальных уравнений с постоянными
коэффициентами с помощью передаточных функций. Если y^(t) становится внешней
нагрузкой для второго дифференциального уравнения с нормальной реакцией гц ((), то две
передаточные функции перемножаются, т. е.
ZN (s)
F(s)
. = Нх (s) H% .
Более общо, каждая функция
D(s)
в формуле (23) есть передаточная
функция, относящая нормальную реакцию yk (t) системы (11) на выходе
внешней нагрузке /у (/) на входе, когда все остальные внешние нагрузки
отсутствуют. Эти передаточные функции образуют передаточную матрицу.
Передаточная функция для уравнения (16) есть
H(s)-
Vp+V
iP-i
+ — +*«
.^-l -
+ ar
(9.4-31)
(b) Частотные характеристики (см. также п. 9.4-6, а). Частот-
Ajk (ш)
ные характеристики Н (ко) и D связывают комплексные амплитуды,
представляющие синусоидальные внешние нагрузки, и установившиеся решения
с одной и той же частотой со. В частности, абсолютная величина и аргумент
частотной характеристики связывают амплитуды и фазы синусоид на входе
и выходе: если /(/) = £ sin (со/ + Р)> y(t) = A sin (со/ + а), то
IЯ №»)! = -
arg# (ко) = а — р.
(9.4-32)
Для схемы, представленной на рис. 9.4-1, амплитудные характеристики
| Н (/со) | перемножаются, а фазовые характеристики arg H (ico) складываются.
(с) Соотношения между передаточными функциями,
частотными характеристиками и функциями Грина (см.
также п. 9.4-3 и теоремы о свертках в табл. 8.3-1). Передаточная функция
И (s) есть преобразование Лапласа от асимметрической функции Н+ (/}:
Н{*) = ] h+(t)e~stdt.
(9.4-33)
9.4-8. 9.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 291
Частотная характеристика Н (ш) есть преобразование Фурье от
симметрической функции h (t):
оо
Я(/о))= J h(t)e~iaitdt. (9.4-34)
— оо
Формулы (33) и (34) указывают возможность получения функций h+ (t) и h (t)
как обращений преобразований Лапласа или Фурье для рациональных функций.
9.4-8. Нормальные координаты и собственные колебания.
(а) Свободные колебания. Малые незатухающие колебания
механических или электрических систем часто описываются системой п линейных
дифференциальных уравнений второго порядка
п
2 {bfk& + a,k)yk = 0 (/ = 1, 2, ..., /г), (9.4-35)
в которой обе матрицы [а^\ и [bjk] симметричны, положительно определены
(п. 13.5-2) и таковы, что характеристическое уравнение (9) имеет 2/г различных
ненулевых чисто мнимых корней ± кох, ± /ш2, ... , ± i'cort • Такие п пар корней
соответствуют свободным синусоидальным колебаниям с п собственными часто-
ТаМИ 2jt » 2л » ••', 2л #
Для данной системы (35) можно ввести нормальные координаты уъ у2, ...
..., уп с помощью линейного преобразования
п
Ун= 2 thhSh (* = 1. 2, ..., п) (9.4-36)
с такими коэффициентами t^, чтобы привести одновременно обе матрицы [aJk]
и [bjk\ к диагональному виду (пп. 13.5-5 и 14.8-7); преобразованная система
будет иметь простой вид:
Получающиеся здесь свободные синусоидальные (собственные) колебания
yh = Ahsin((dht+'ah) (Л=1, 2, .../г) (9.4-38)
не влияют одно на другое (разъединены). Нормальные координаты могут иметь
непосредственное физическое истолкование.
Пример. Для системы
~Г = - <ulyt — a2 (yt — у%)\ ^- = — ©0^2 - а3 (У* — £i)
нормальными координатами являются 9t = У1 + У9, $ъ = У\ — Уъ- При начальных условиях
#i = i, г/»==0, -Jr =» -^ — 0 ПРИ ' = ° уравнения для нормальных координат
££i в _ tt« J ; £!?» в _ ( «2 + 2а*) £3
дают
& = cos ©о *: Л = cos V «о + 2а2 t,
и следовательно.
2
10*
jf.-IWi + yj-co.J—u2L o,cosL_jl_ о/<(
■ ro й. ... К^Т2а^ - (00 l/Si+lSi + а>0
Уг = -к\У1 — У2) = Sin 5 ' Sin 9 '•
292
ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ «.В-!.
При а2 < ©2 (слабая связь) эти решения описывают так называемое явление резонанса.
(Ь) Вынужденные колеба-
Рис. 9.5-1. Изоклины, направления поля и
некоторые решения дифференциального
уравнения
dy у
соответствующего уравнению Ван дер Поля
н и я. Соответствующая
нужденных колебаниях
задача о вы-
(/ = 1, 2 п) (9.4-39)
может быть решена в принципе
методом п. 14.8-10 путем разложения
внешней нагрузки f, (t) по собственным
функциям. Обычно более удобен
операторный метод п. 9.4-5.
9.5. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
ВТОРОГО ПОРЯДКА
9.5-1. Вводные замечания.
В пп. 9.5-2 — 9.5-5 вводится общая
терминология и наиболее простой
метод приближенного решения из
теории нелинейных колебаний.
Для дальнейшего изучения
рекомендуются [9.6], [9.7]. Многие
методы решения тесно связаны со
специфическими приложениями.
Метод возмущений из п. 10.2-7, с
часто применяется для упрощения
нелинейных задач, особенно в небесной
механике. Численные методы решения
см пп. 20.7-4 и 20.7-5.
9.5-2. Представление на
фазовой плоскости. Графический метод
решения (см. также п. 9.2-2).
Дифференциальное уравнение второго
порядка
да-'('.*£) (9-5-')
равносильно системе уравнений
первого порядка
U-i; #=/('. у, у)-
dt
dy
dt
d*y
dt*
=»-H-l* (W) -|f.
^ (9.5-2)
Общее решение y = y(t), y—y(t)
уравнений (1) или (2) может быть
представлено геометрически
семейством ориентированных фазовых
траекторий на фазовой плоскости
Оуу. Такое представление
полезнее всего в том случае, когда
данная функция /(/, у, у) не содержит явно независимого переменного t.
В этом случае система (2) относится к системам вида
Qiy/y) Р-5-3)
=*у>
М- = 1. Показана лишь правая
полуплоскость.
%=P(y,yh
dt
0.5-3. 9.5. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА ^93
(9.5-4)
(автономная система) и фазовые траектории удовлетворяют
дифференциальному уравнению первого порядка
dt/ = Q(y, у)
dy р(у. у)'
которое каждой точке (у, у) ставит в соответствие наклон проходящей через
нее интегральной кривой. Получающееся поле направлений («изображение»
дифференциального уравнения на фазовой плоскости) позволяет сделать
набросок у (у) и отсюда у (t) по заданным начальным значениям у и у> можно
начать с построения геометрического места точек постоянного наклона dy/dy — m
(изоклин, рис. 9.5-1).
9.5-3. Особые точки и предельные циклы (см. также п. 9.5-4).
(а) Обыкновенные и особые точки фазовой плоскости.
Точка (у, у) фазовой плоскости системы (3) "называется обыкновенной точкой,
если Р (у, у) и Q (у, у) дифференцируемы и не обращаются одновременно
в нуль; через каждую обыкновенную точку проходит единственная фазовая
траектория. Точка (у0, у0) называется особой точкой, если
Р (ft. У о) = 0; Q (*/о, У о) = 0. (9.5-5)
Особые точки классифицируются по характеру фазовых траекторий в их
f)
Рис. 9.5-2. Фазовые траектории в окрестности особых точек шести типов (пп. 9.5-3 ш
9.5-4).
а) Устойчивый узел; Ь) неустойчивый узел; с) устойчивый фокус; d) неустойчивый фокус;
е) седло; f) центр.
окрестности; наиболее важные типы особых точек изображены на рис. 9.5-2.
Физически особые точки есть точки покоя (равновесия), допускающие
устойчивые или неустойчивые положения равновесия #=#0 (п. 9.5-4),
294 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.5-4.
(Ь) Периодические решения и предельные циклы.
Периодические решения y — y(t) соответствуют замкнутым фазовым траекториям,
и обратно. Замкнутая фазовая траектория С называется предельным циклом,
если она имеет окрестность из обыкновенных точек, в которой все фазовые
траектории спиралевидно приближаются к С (устойчивый предельный цикл)
а) Ь)
Рис. 9.5-3. а) Устойчивый предельный цикл, заключающий неустойчивую особую точку
в начале. «Мягкое» самовозбуждение колебаний при произвольно малых начальных
значениях у и у. Ь) Устойчивый предельный цикл, заключающий устойчивую особую точку
в начале и неустойчивый предельный цикл (показанный пунктиром). «Жесткое»
самовозбуждение колебаний при начальных значениях вне неустойчивого цикла.
или удаляются от С (неустойчивый предельный цикл) или приближаются к С
с одной стороны и удаляются от нее с другой (полуустойчивый предельный
цикл). Примеры см. пп. 9.5-4, с и 9.5-5 (см. также рис. 9.5-3).
(с) Индекс Пуанкаре и теоремы Бендиксона. Во многих приложениях
представляет интерес существование предельных циклов (устойчивых колебаний). В
дополнение к аналитическому критерию п. 9 5-4 полезна иногда следующая теория.
Индексом замкнутой кривой С, состоящей из обыкновенных точек фазовой плоскости,
называется число полных оборотов вектора, задающего направление поля, при обходе
точкой (у, у) контура С. Индексом изолированной особой точки Р называется индекс
любой замкнутой кривой, охватывающей точку Р и не содержащей других особых точек.
При этом:
1. Индекс замкнутой кривой С равен сумме индексов всех (изолированных)
особых точек, лежащих внутри С; если внутри С все точки обыкновенные, то
ее индекс равен нулю.
2. Индекс узла, фокуса или центра равен 1; индекс седла равен — 1
(см. рис. 9.5-2).
3. Индекс любой фазовой траектории равен 1; следовательно, предельный
цикл должен содержать по крайней мере одну особую точку помимо седла (рис.
9.5-3).
* ~ ^ л. Л дР , &Q
Внутри любой области фазовой плоскости, где 1 г сохраняет знак, сущест-
ду ду
вуют незамкнутые фазовые траектории (первая теорема Бендиксона). Траектория, кото*
рая остается внутри ограниченной области и не приближается ни к какой особой точке
при 0 :< t < оо, либо является замкнутой, либо асимптотически приближается к
некоторой замкнутой траектории (вторая теорема Бендиксона).
9.5-4. * Устойчивость решений по Ляпунову*) (см. также пп. 13.6-5 —13.6-7).
(а) Решение yi — yi(t) (i=\, 2, ..., п) системы обыкновенных
дифференциальных уравнений вида
§ вМ': Уъ У* -. Уп) (<•=!, 2, ..., /г), (9.5-6)
соответствующее начальным условиям f/j (^o) = ^*o» называется устойчивым по
Ляпунову, если для любого е>0 можно найти такое б = б(е)>0, что из
системы неравенств | xi0 — у^ | < 6 будут следовать неравенства | х( (/)—щ (t) | < е
для всех / ^ /в, где к% (t) — решение, определяемое начальными условиями
*) Теория устойчивости по Ляпунову изложена во многих руководствах; см.,
например, [9.1], [9.3].
9.5-4. 9.5. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 295
Xi (to)—xiQ. Это значит, что малое изменение начальных условий не может
вызвать больших изменений решения.
Устойчивое решение у( (t) называется асимптотически устойчивым, если
можно указать такое число г, что из неравенств |*;0 — У to I <-r будут
следовать соотношения lim | jc,- (t)—yi (t) |=0 (/=1, 2, ..., n). Асимптотически ус-
t-*<x>
тойчивое решение называется асимптотически устойчивым в целом (вполне
устойчивым), если г = оо, т. е. если при любых начальных условиях xi0 решение
Xi (0 — yi (0 при t — со.
В частности, все решения устойчивой системы линейных дифференциальных
уравнений с постоянными коэффициентами асимптотически устойчивы в целом
(все корни характеристического уравнения такой системы имеют
отрицательные действительные части, см. п. 9.4-4).
(Ь) Устойчивость положения равновесия автономной
системы. Пусть
Ъ=П <Уг. й. -. Уп) ('=1. 2 п) (9.5-7)
— автономная система дифференциальных уравнений (все функции fi не
зависят явно от /) и (у10, #20» •••» #ло) —какая"либо ее точка покоя, т. е.
Л (#ю> #20» •••> #ло) = 0 (**=1» 2, ..., /г). Тривиальное «равновесное» решение
yi(t) = yio (г = 1, 2, ..., л),
соответствующее данной точке покоя, является асимптотически устойчивым,
если линеаризованная система (система первого приближения)
п
W=2 (§)0 С**-*») (<*= 1. 2. .- п) (9.5-8)
устойчива (все частные производные берутся в исследуемой точке покоя
(#ю» #20» *..» Упй))- Эт° имеет место тогда, когда все корни s характеристического
уравнения
det[(§)0-sS*]=° <9-5-9)
имеют отрицательные действительные части. Тривиальное решение будет
неустойчивым, если уравнение (9) имеет хотя бы один корень с положительной
действительной частью; если нет корней с положительной действительной
частью, но среди корней есть чисто мнимые, то требуется дополнительное
исследование (см. п. 13.6-7).
В частности, для системы (3) характеристическое уравнение есть
s4dT+f) s+lTT-d-ff) -о- <9-510>
\ду ду/о \ду ду ду ду/о
где все частные производные берутся в точке покоя (у0, yQ).
Для уравнения второго порядка y=f (у, у) и точки покоя (у0, у0)
(значит, / (у0, £/0) = 0) характеристическое уравнение можно записать, не переходя
к системе (3):
*-(«) ,-(*.) =0.
\ду Jo \ду]о
Точка покоя системы (3) есть (см. рис. 9.5-2)
—устойчивый или неустойчивый узел, если оба корня sx и s2 уравнения
(10) действительны и соответственно отрицательны или положительны^
— седло, если sx и s2 действительны и имеют разные знаки^
296 ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.5-5.
—устойчивый или неустойчивый фокус, если st и s2 комплексно
сопряжены и имеют соответственно отрицательную или положительную
действительную часть.
Если корни уравнения (10) чисто мнимы, то для линеаризованной системы
точка покоя является центром. Выяснение характера точки покоя данной
нелинейной системы требует, как уже отмечалось, дополнительного исследования.
(с) Устойчивость периодических решений. Устойчивость
периодического решения у — у It) =£ 0, у = у (t) системы (3) зависит от устойчивости такого
же решения линеаризованной системы
dt ду ду
*ь'у dQ* +dQ*- I <9-5'U>
dt ду ду
которой удовлетворяют малые вариации (п. 11.4-1) 6у, 6у периодического решения.
(Здесь все частные производные берутся в точке (yp(t), Ур(?))т) Это — система
линейных дифференциальных уравнений с периодическими коэффициентами, имеющими тот
же период Т, что и данное решение; уравнения (11) допускают два линейно независимых
решения вида
бу = Ли (0. бу = Л„ (t); by = № Л„ (0, Ьу = еМ hi2 </), (9.5-12)
где h-k (t) — периодические функции, а
Периодическое решение устойчиво при Х<0 и неустойчиво при % > 0; случай А, = 0
требует дополнительного исследования.
Пример. Дифференциальное уравнение Ван дер Поля
^JT + y-»U-yz) ^f = 0 (ц>0) (9.5-14)
имеет устойчивый предельный цикл в окрестности приближенно периодического решения
у = у (t) яа» 2 cos /; у =у (t) s& — 2 sin / и X = —■ \х [1 -J- О (ц,)] (см. также п. 9.5-5)-
9.5-5. Приближенный метод Крылова и Боголюбова.
(а) Первое приближение. Эквивалентная
регуляризация. Решение дифференциального уравнения вида
%+W + Vif{y,U) = 0, (9.5-15)
где ц — малая постоянная, так что последний член представляет малое
нелинейное возмущение, ищут в виде
y=r (/) cos ф (/). (9.5-16)
Пренебрегая ошибкой порядка jli2, находим «амплитуду» г (t) и «полную фазу»
Ф (/) из дифференциальных уравнений первого порядка
2я
Ш^ШЬ \ /(rcos Я, — г© sin Я) sin ЯdX = — jax (г),
о
2Я
^"эс=а)+ 2яг© \ / (г cos ^» — г® sin ^) cos Я dX = К«2 (О-
о
При данном начальном значении г(0) = г0 решение эквивалентного
линейного дифференциального уравнения
(9.5-17)
9.5-0. 9.5. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 297
аппроксимирует решение данного дифференциального уравнения (15) с
ошибкой порядка ц2. Для периодического решения типа предельного цикла
(п. 9.5-3, Ь) приближенная амплитуда rL находится из a (rL) = 0, а круговая
частота приближенно равна |/а2 (г^). Этот предельный цикл устойчив, если
-^-г==г^>0, и неустойчив, если ~~ L ==/.^<0. Для самовозбуждения из
состояния покоя должно быть % (0) < 0.
Указанное первое приближение представляет интерес в связи с периодическими
нелинейными колебаниями. В таких случаях эквивалентное линейное дифференциальное
уравнение (18) дает то же накопление и рассеяние энергии по циклу, что и данное
нелинейное уравнение (15). Поэтому эквивалентное линейное уравнение может применяться
в исследованиях явления нелинейного резонанса.
(Ь) Улучшенное первое приближение. Улучшенное приближение
первого порядка дается формулой
y = r(t) cos
ф(0 + ^| ^"+ 2 [«Л(г>С08Л(Р(/) + Рл(г)51пА(Р(/>])
, (9.5-19)
где г (0 и <р (0 определяются из уравнений (17), а
2я
1
л
( __ { \ f (r cos К, — ra> sin К) cos k% d% (k = 0, 2, 3, . .
0
2я
Р* <г) = (ьг—\\ \ * (Г C0S ^ ~~ Г(0 Sin ^ Sin k^ d^ U = 2, 3, . . .).
(9.5-20)
)
Пример. В случае дифференциального уравнения Ван дер Поля (И) уравнения
(17) дают
"._£(,_£), ,<„-_, />'** . (9.5-2|)
fitf
V
14-
го \е
&
0
При г = г^ = 2 имеется устойчивый предельный цикл. Все коэффициенты (20) исчезают,
за исключением pY, улучшенное первое приближение есть
г8 (Л
= г(/) cos (i -f Фо) — М- —т£г sin 3 (/ -f Фо).
(9.5-22)
Приближение Крылова — Боголюбова (19) есть улучшение более простого метода
Ван дер Поля, который строил приближения вида
у — а (/) cos Ш + b (t) sin ©Л
Метод Крылова — Боголюбова может быть распространен на случай периодической
внешней нагрузки в правой части дифференциального уравнения (15) (нелинейные
вынужденные колебания, субгармонический резонанс).
9.5-6. Интеграл живых сил. Дифференциальное уравнение вида
d2y
(9.Б-23)
представляющее значительный интерес в динамике, может быть приведено к уравнению
первого порядка умножением на dyjdt и интегрированием;
*V2lf[y)dif + Cl
+ C„
(9.5-24)
(9.5-25)
298
ГЛ. 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 9.6-!.
9.6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПФАФФА
9.6-1. Дифференциальные уравнения Пфаффа (см. также пп. 3.1-16 и
17.2-2). Дифференциальное уравнение Пфаффа
Р(х9 у, z)dx + Q(x, у, z)dy + R(x, у, z)dz = 0 (9.6-1)
с непрерывно дифференцируемыми коэффициентами Р, Q, R может быть
истолковано геометрически как условие ортогональности интегральных кривых
(с касательным вектором (dx> dy, dz)) заданному полю направлений (Р, Q, R).
Чтобы найти интегральную кривую, лежащую на произвольной (регулярной)
поверхности
/(*, у, z) = 0, (9.6-2)
надо решить обыкновенное дифференциальное уравнение, получающееся при
исключении z и dz из уравнения (1) и df (x, у, z)=0 При этом
интегральные кривые будут описываться двумя уравнениями f (х, у, z) = 0, g (x, у, z, С) =0,
где С—постоянная интегрирования.
9.6-2. Вполне интегрируемый случай (см. также п. 9.2-4).
Дифференциальное уравнение Пфаффа (1) вполне интегрируемо, если существует
интегрирующий множитель \i — \x(xt yt z) такой, что \i (P dx+Qdy + R dz) есть полный
дифференциал dcp (*, у, z); это имеет место тогда и только тогда, когда
'(§-£)+Q(£-£)+*(f-£H- (9-6-3)
В этом случае каждая линия на интегральной поверхности
ф(*, у9 z) = C, (9.6-4)
ортогональной семейству кривых, описываемых системой
dx__dy dz /оасч
является интегральной кривой. Отсюда следует, что решения, найденные
методом п. 9.6-1 по подходящим образом выбранному семейству поверхностей
(обычно плоскостей)
/(*, у, *) = /(*, у% г\ Х)-0, (9.6-6)
лежат на некоторой интегральной поверхности (4), получающейся путем
исключения А, из решения / (х, у, z; A,) = 0, g (*, у, z, С; А,)=0 (метод Майера).
Другой метод нахождения интегральной поверхности (4): считая z
постоянным, находят решение обыкновенного дифференциального уравнения
Pdx-\-Qdy = 0b виде и(х, у, z)—-K = Q. Тогда интегральная поверхность
описывается уравнением
Ф(*. у, z)e=u(x, у, г)-г|?(г) = С, (9.6-7)
где ф (г) — решение обыкновенного дифференциального уравнения,
получающегося путем исключения х и у из
ldu_\_du_\_/da_d^\
Р дх~~ Qdy~ R\dz dz)' ^.b-»J
Заметим, что общее значение отношения в (8) есть упомянутый
интегрирующий множитель fx (xt yt z).
Приложения в термодинамике: адиабатическое условие 6? = 0 имеет вид (1),
интегрирующим множителем служит \/Тх где Г — абсолютная температура, bq/T —
(полный) дифференциал энтропии.
ГЛАВА 10
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
10.1. ВВЕДЕНИЕ И ОБЗОР
10.1.1. Вводные замечания. Пункты 10.2-1—10.2-7 посвящены
дифференциальным уравнениям с частными производными первого порядка и их
геометрической интерпретации и включают элементы теории Гамильтона—Якоби
канонических уравнений.
В пп. 10.3-1—10.3-4 изучаются характеристики и краевые задачи для
гиперболических, параболических и эллиптических уравнений второго порядка.
В пп. 10.4-1—10.5-4 представлены решения наиболее важных линейных
дифференциальных уравнений математической физики (уравнение
теплопроводности, волновое уравнение и т. д.) с эвристической точки зрения и
простейшие применения метода интегральных преобразований. Более усложненная
теория линейных краевых задач и проблемы собственных значений
описываются в гл. 15.
10.1-2. Дифференциальные уравнения с частными производными (см.
также п. 9.1-2).
(a) Дифференциальное уравнение с частными производными г-го порядка
есть функциональное уравнение вида
т* ( ~ дФ дФ дФ д*Ф Д л „л , <v
/?(*!, хъ ..., хп\ Ф;^, ^,...,^-;-^-, ...J=0, (10.1-1)
включающее по меньшей мере одну частную производную г-го порядка от
неизвестной функции Ф (xlt х2 хп) двух или более независимых
переменных хъ х2, ..., хп.
Функция Ф (хг, х2, ...,хп), удовлетворяющая данному уравнению (1) в
некоторой области точек (хг, х2, ..., хп), называется решением или интегралом
дифференциального уравнения с частными производными*
Общее решение (общий интеграл) данного уравнения г-го порядка (1)
содержит, как правило, произвольные функции. Выделение частных
интегралов производится путем задания соответствующих дополнительных условий,
т. е. условий, налагаемых на функцию Ф и / или ее производные, на кривой,
поверхности и т. д. в пространстве точек (xv x2, ..., хп) (краевые условия,
начальные условия).
Многие дифференциальные уравнения с частными производными допускают
дополнительные решения (особые интегралы), которые не могут быть
получены из общего интеграла ни при каком выборе произвольных функций
(п. 10.2-1, с).
(b) Дифференциальное уравнение с частными производными называется
однородным, если произведение аФ любой постоянной а на решение Ф также
является решением.
Дифференциальное уравнение (1) называется линейным*, если F — линейная
функция от Ф и ее производных (см. также пп. 10.4-1 и 10.4-2).
(c) Система дифференциальных уравнений с частными
производными. Условия совместности. Система дифференциальных
уравнений
Fi(*v *»• - • V фг фа- - • gff • -) -° « = '• 2- •••> «»•»-*>
300 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.1-3.
Ц + М*1, **)=о,
[ИМ
д*Ф dft
dxt dxs ~~ дхг*
дФ
д*Ф _ dft
дх2 дхх """ дхх
содержит несколько неизвестных функций Ф^^х^ *2, ... , хп), Ф2 (xv x2 хп), ... и
их частные производные.
Каждое дифференциальное уравнение (1) или систему дифференциальных уравнений
(2) можно свести к системе дифференциальных уравнений первого порядка, принимая
подходящие производные за новые неизвестные функции (см. также п. 9.1-3).
Система дифференциальных уравнений (2) допускает решение Ott Ф2, ... только
тогда, когда заданные функции F. и их производные удовлетворяют условиям
совместности (условиям интегрируемости), которые гарантируют, что дифференцирование двух
или более уравнений (2) приводит к совпадению производных высшего порядка от
функций Ф|Ч
Условия совместности получаются исключением функций Ф. и их производных из
последовательности уравнений, полученных дифференцированием данных
дифференциальных уравнений системы (2).
Пример. Дана система
Дифференцируя, получим
dft df2
так что данная система уравнений совместна, если ^— = ■=—.
(d) Существование решений. Как для обыкновенных дифференциальных
уравнений (п. 9.1-4). фактическое существование и единственность решений для данного
дифференциального уравнения с частными производными или системы таких уравнений
требуют доказательства в каждом случае, даже если условия совместности соблюдаются.
См. [10.5], где приведены некоторые теоремы существования.
10.1-3. Решение дифференциальных уравнений с частными производными;
разделение переменных (см. также пп. 10.4-2—10.4-9). Во многих важных
случаях попытка найти решение в виде
Ф = Ф(*1, *2 *rt) = <Pl(*l)<Po(*2» *9> •••» Хп) (10.1-3)
позволяет записать данное дифференциальное уравнение (1) в разделенной
форме
Firm d4>1 ^2ф1 \ = F fir v v • m • дЩ д®9 \
*i\xv <Pi. ^-» -щ* —J = r%[xtt x9 xnt ф0, ^-, ^-, ...J.
Неизвестные функции фг {xx) и ф0(*2» *з» •••» хп) должны удовлетворять
дифференциальным уравнениям
F%(x* *э *п> Фо; % g, ...) = C, (10.1-46)
где С—константа разделения, которая определяется в соответствии с
заданными краевыми условиями или другими присоединенными условиями.
Заметим, что уравнение (4а) — обыкновенное дифференциальное уравнение
относительно неизвестной функции фх (хг)\ для уравнения (4Ь) иногда возможно
повторение процесса разделения.
Разделение переменных с успехом применяется при решении многих
линейных однородных уравнений с частными производными математической
физики; иногда разделение становится возможным после соответствующей
замены переменных (в качестве примеров см. пп. 10.4-3—10.4-9).
10.2-1.
10.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
301
проходящей через фиксированную
10.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ
ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
10.2-1. * Уравнения с двумя независимыми переменными. Геометрическая
интерпретация (см. также пп. 9.2-2 и 17.3-11).
(а) Возьмем дифференциальное уравнение с частными производными
первого порядка относительно неизвестной функции г = г(х, у):
F(x, у, г, р, <?) = 0 (p = g, <7=g, F*p+Fl*0), (10.2-1)
где данная функция F дважды непрерывно дифференцируема, и рассмотрим х,
у, г как декартовы прямоугольные координаты. Тогда каждое решение г =
= z(#, у) уравнения (1) представляет поверхность (интегральную поверхность).
Для любой интегральной поверхности,
точку М (х, у, 2), уравнение
касательной плоскости имеет вид
Z-z = p(X-x) + q(Y-y),
где р и q связаны уравнением (1), в
котором х, у и г рассматриваются как
постоянные. Огибающей семейства
касательных плоскостей является конус
(конус Монжа). Касательная плоскость
к любой интегральной поверхности
касается также конуса Монжа вдоль
одной из его образующих. Линии на
интегральной поверхности, касающиеся
в каждой своей точке соответствующей
образующей, называются
характеристическими линиями или характеристиками.
Вдоль характеристик выполняются
соотношения
dx _dy
dz
'PFp + «Fq'
Рис. 10.2-1. Начальная полоса и одна
характеристическая полоса на
интегральной поверхности. / — конус
Монжа в точке Р0.
Р q
Последовательность значений (х>
Уу z, p, q), как говорят, описывает
плоский элемент, связывающий угловые коэффициенты р и q касательной
плоскости с точкой (х, у, г). Данное уравнение (1) определяет поле плоских
элементов (х, yt z, p, q), касательных к конусам Монжа (рис. 10.2-1).
Если Fp и Fq явно не зависят от р и q (квазилинейное уравнение первого
порядка), то каждый конус Монжа вырождается в прямую (ось Монжа).
(Ь) Полосы и уравнения характеристик. Совокупность
дифференцируемых функций
*=*(/), y = y(t), z = z(t), p = p(/), q = q(t) (10.2-2)
представляет плоские элементы (точки и касательные плоскости) вдоль полосы
регулярной поверхности, если функции (2) удовлетворяют условию полосы
— = п — 4-а^-
dt p dt^4 df
Для данного уравнения с частными производными (1) каждая
совокупность функций (2), удовлетворяющая системе обыкновенных
дифференциальных уравнений
dy_
£ = pFp + qFgt
Ж = ^р* Ш = ^я* 1 (характеристические у рае*
нения, связанные с
уравнением (1))8
:,
(10.2-3)
302 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.2-2.
описывает вместе с уравнением (1) характеристическую полосу.
Характеристическая полоса касается конуса Монжа в каждой точке (х, у, г);
соответствующая кривая
*=*(/), y = y(t), z = z(t)
лежит на интегральной поверхности и является характеристикой.
Интегральные поверхности могут касаться друг друга только вдоль характеристик.
(с) Особые интегралы (см. также пгг. 9.2-2,Ь, 10.1-2,а и 10.2-3,с). Решения
2 = г (х, у) уравнения (1), полученные исключением р и q из уравнений
dF dF
F (х, у, z, p, q) = 0, ^- = 0, -^ = 0, (10.2-4)
являются особыми интегралами. Они не удовлетворяют условию Fp + F^^zO и не могут
быть получены из общего интеграла уравнения (1).
10.2-2. Задача с начальными условиями (задача Коши). Требуется найти
решение z — z(x> у) уравнения (1), удовлетворяющее начальным условиям
{граничным условиям типа Коши)
*=*о(т)> У=Уо(*)* z = z0(t), р = р0(т), <7 = <70(т), (10.2-5д)
где
f[*oW. УоСО. z0(T), РоОО. 9оМ] = 0, \
dz0_n dx0 dy0. > (10.2-56)
эти условия задают начальную полосу, т. е. точки и касательные плоскости
к искомой интегральной поверхности вдоль регулярной кривой С0; проекция
С0 на плоскость Оху есть простая кривая (п. 3.1-13). Чтобы решить задачу
Коши, надо найти решение
x = x(t, т), */ = */(/, т), z = z(t, т), р = р(/, т), q^q(t,x) (10.2-6)
системы характеристических уравнений (3), удовлетворяющее начальным
условиям (5) при / = 0. Результирующие функции (6) удовлетворяют уравнению (1);
решение z — z(xt у) или в неявном виде ф(л, у, z) = 0 находим, исключая
параметры /ит.
Задача с начальными условиями имеет единственное решение, если из данных
начальных условий (5) следует
',£-'.£*« PMUH- «»■">
J3 противном случае задача имеет решение только тогда, когда данные начальные
условия (5) описывают характеристическую полосу; при этом имеется бесчисленное множе-
ство решений.
>< При постановке задачи можно было бы сначала считать заданной только
начальную кривую С0, а величины р0 и q0 определить из двух соотношений (56). Если эти
уравнения имеют несколько решений, то кривая С0 может принадлежать различным
начальным полосам, для каждой из которых задача Коши решается отдельно.
Пример. Найти решение уравнения pq — z = 0, удовлетворяющее начальным
условиям: х0 = \, у0 = х, 20 = т2 (т. е. найти интегральную поверхность, проходящую
через заданную кривую). Система уравнений (3) имеет вид
dx dy dz _ ft dp dq
di = q- ji~p- ж-2""-**- ж=р- м=ч-
Ее решение, принимающее при t = 0 значения (xQ, yQr z0, p0, q0):
P = Рое*, Я = Qoe , z =» z0e2 , x = qj -f- xQ — qQ, y = pj -f y0 — p0.
Начальные значения р0 и q0 связаны условиями p0q0 = та и q0 = 2х, откуца </<> = 2т,
р9 =5 т/2. Следовательно,
10.2-3.
10.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
303
Здесь **' У) — 2т ф 0. Исключая параметры /их, получаем единственное
решена + х - 1)'
16
Если ищется решение данного уравнения pq— z = 0, удовлетворяющее начальным
условиям *0 = т, #0 = т2, г0 = т3, то уравнения (5Ь) принимают вид p0q0 = т3 ир0 +
-f- 2т<7о = Зт2 и имеют две системы решений р' = т2, <?' = т и р'' = 2т2, q" =т/2.
Соответственно этому надлежит решать две задачи Коши. Для первой из них х = те , # = %2е ,
z = т3е2 , откуда z = xy
Для второй * = т (<Г + 0/2, # = Т* (2* — 0, г = тЛ?2'.
В обоих случаях условие единственности выполняется.-^
10.2-3. Полные интегралы. Общие, частные, особые интегралы; решения
характеристических уравнений.
(a) Полный интеграл уравнения с частными производными первого
порядка (1) есть двупараметрическое семейство решений
-. лч / i \ / д2Ф д2Ф д2Ф д2Ф ,гЛ /1Л 0 Q4
г=Ф(*, у, Я, fi) (__-^_^Q), (10.2-8)
причем функция Ф и ее производные
H = p(*, у, X, ц) = р, ^ = <7(*. ^ *<> Р) = Я
в некоторой области пространства х> у, X, \х должны иметь непрерывные
частные производные по х> у, X, \i. Данная последовательность значений
(ху у, 2, р, а), удовлетворяющая уравнению (1), должна определять
единственные значения параметров X, jji.
Полный интеграл (8) производит общий интеграл, если ввести
произвольную функцию jji = jjl (Л,) и исключить X из уравнений
г-Ф[х, у, X, ц(\)]=0, !£+^f=0 (10.2-9)
(огибающая однопараметрического семейства интегральных поверхностей,
п. 17.3-11).
(b) Получение частных интегралов из общего. Для
получения частного интеграла, соответствующего заданным начальным
условиям (5), надо найти соответствующую функцию \х (X), входящую в общий
интеграл, определенный в п. 10.2-3,а.
Функцию jji (X) находим, исключая х, у и т; из соотношений
аФ(^,я,ц)=ро(т)) аФ(^,я,ц)=(?о(т)) х=ч(х)> у=Ыт) (102.Ю)
(c) Отыскание особых интегралов. Исключая К и jn из уравнений
г-Ф^у.КМ-0. *»(*.д.ЫО-0, <>Ф(х,у,Кч)=0> (Ш2.П)
можно получить особый интеграл (огибающую двупараметрического семейства
интегральных поверхностей).
(d) Решение характеристических уравнений. Каждый
полный интеграл (8) уравнения с частными производными первого порядка (1)
производит решение системы обыкновенных дифференциальных уравнений (3).
Функции x = x(t)t y = y(t) получаются из соотношений
дФ(х-£К »>=<, аф(*^->"'*) = р;, (10.2-12)
где X, \1 и р — произвольные постоянные интегрирования; z = z(/), p*=p(t)t
q = q(t) получаются подстановкой x = x(t, X, \i, Р) и y*=y(t, X, jji, Р) в
равенства
*=«>(*,</,*, ц), Р=аФ(^^', g»£?Ji^Aii). (Ю.2-13)
304 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.2-4.
(е) Специальные случаи. Табл. 10.2-1 содержит полные
интегралы для некоторых часто встречающихся типов уравнений с частными
производными первого порядка и позволяет применять методы п. 10.2-3 ко
многим задачам.
Таблица 10.2-1
Полные интегралы для некоторых специальных типов уравнений
с частными производными первого порядка *)
ЛГо
1
2а
2Ъ
2с
3
4
Тип уравнения
х, у. z явно не
содержатся в
уравнении
Содержится только
одна из переменных
X, У. 2
Переменные
разделены
Обобщенное
уравнение Клеро (см.
также п. 9.2-4)
*) Многие другие сп
F (р, q) = 0
p = f(xt q),
Q =f (У, P)
p=f (г, q)
P = f(z)
Ft (x, p) = F% (y, q)
(=Л. п. 10.1-3)
или
P=h(x. Я),
Я = h (У, Я)
г = рх + яу 4- f (P* я)
ециальные типы уравнен]
Полный интеграл
2 = Ф (X, у, к. Ц)
г = %х 4 \'у 4 [х,
где F (к, X') = 0
2 = J М*. &) dx -f by 4 Д.
z = lf(y.k)dy + hx+)i
(* dz
Х { Ку J ф (г. Я) ' M,f ГДС ф (2t '
есть решение уравнения
р = f (2; Яр)
*+^ = $rS+*
2 = J f 1 (Jr. Я) d* 4-
+ J ft (1/. tody + ц
z=*Xx + ny + f(K, fx)
ift приведены в [10.8]
10.2-4. Уравнения с п независимыми переменными.
(а) Задача с начальными условиями (см. также пп. 10.2-1
и 10.2-2). Требуется найти решение
г=Ф(*1, х2, ..., хп)
уравнения с частными производными первого порядка
/4*1» хг* •••» *п* г> Pi* Рг* •••» Ря)=0 )
(10.2-14)
10.2-4.
10.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
305
(10.2-15а)
удовлетворяющее начальным условиям
2 = 20(Т1, Т2, ..., T/j_i), #i = #fo(Tl» T2, ..., ТЛ_Х),
Pi = Pio(4> Ъ> •••. Ч-i) С = 1. 2» •••» п),
где система уравнений #t=*;0(Ti» T2» •••»T«-i) представляет
гиперповерхность, не имеющую кратных точек, и
F (х10, x2q, . • • , #ло» 2о'» Рю> Р2о» • • •» Рпо)= 0»
л
ОЛГ. .
■1). (10.2-156)
e-i>»^ «-». 2 »■
=i
7
Чтобы получить соотношение между хи х2, ..., хп и г, надо найти решение
системы обыкновенных дифференциальных уравнений
dz \\ dxk
dt~ 2j Ph dt *
k=i
dx: dF
i
dt др.*
dP,
dF
dF
(t = l, 2, ..., n) (характеристические уравнения), удовлетворяющее
начальным условиям (15) при / = 0, и исключить п параметров тх, т2 ..., тп_х и /.
■#Как и в случае /г = 2 (см. п. 10.2-2), можно в качестве начальных
условий задать только функции г0 и *,-0, а функции р,-0 определить из
уравнений (156).*
Задача с начальными условиями имеет единственное решение, если данные
начальные условия (15) приводят к тому, что
dF
dp±
дх±
дхл
dF
dxt
dx9
dF
dxt
dx„
d%„
dx.
n-1
fo„
[d 1хл, хл x\ I 1
(10.2-17)
(b) Полные интегралы и решение характеристических
уравнений (см. также п. 10.2-3). Полный интеграл дифференциального
уравнения (14) есть л-параметрическое семейство решений
*=.<D(xlf *2, ..., хп\ аи а2, .... ап) {det [щщ] ^°}' (Ю-2-18)
причем функция Ф и ее производные
дФ _ .
Q- —Pi (*i> Х2, ..
Xfi'i ^1» ^2»
-. «л)
должны иметь непрерывные частные производные по всем xi и а/. Данная
последовательность значений (х1% #2, ..., хп\ г; р1% р2, ..., рп),
удовлетворяющая уравнению (14), должна определять единственные значения
параметров ах, а2, ..., ап.
Полный интеграл (18) производит общий интеграл, если ввести п
произвольных функций ад=»ад(А,1, ^2» •••» K-i) (* = 1. 2» •••» л) и исключить
л —1 параметров Я/ из п уравнений
г = Ф[*!, *2, ..., хп\ о^Я*, Ь2, ..., &„_!),
а2 (Xi, Аг2, ..., АгЛ-1), ..., ал (Я»1э А,2, • .•»ЯЛ_1)],
А 0Ф 0аь
2е:ж=0 .(/-1.2,....n-1).
*»1 * '
(10.2-19)
306
ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
10.2-5.
Каждый полный интеграл (18) производит решение системы обыкновенных
дифференциальных уравнений (16). Функции *,= #*(0 (/ = 1, 2, ..., п)
получим из соотношений
!£ = РЛ/ (*=1, 2, ..., /1-1), i£ = /, (10.2-20)
где alf a2, ..., art; plf p2, ..., (3rt_j — (2/г — 1) произвольных постоянных
интегрирования; функции z = z(t) и pi = pi(t) (i=l, 2, ..., /г) найдем,
подставляя *£ = *,•(/; alf a2, ..., art; (Jlf |э2, ..., prt-1) в выражения
z = (D(*1, *2, ..., хп\ al9 a2, ..., a„), Р, = 4~ rt=l, 2, ..., /г).
/
(с) Особый интеграл (см. также пп. 10.2-1,с и 10.2-3,с). Особый интеграл
дифференциального уравнения (14) есть решение z — Ф (* х , .... * ), получающееся
исключением р- из я -+- 1 уравнения
F(*i-*i *»: г: "i- "г "п) = 0- )
£-» «-.. «>• J
Из данного полного интеграла особый интеграл получается, если исключить параметры
av a2 ап из п + 1 уравнения
2 - Ф (*Г Х2 V aV % %) - °. )
£->-* <*='•* ->• }
10.2-5. Преобразования соприкосновения (см. также п. 9.2-3,6). Некоторые
задачи, содержащие уравнения с частными производными первого порядка,
могут быть упрощены введением дважды дифференцируемого преобразования
Xi = %i \Xi, Х2, ... , Хп\ Z\ р^ р2, ... , рп), |
p=pi(xlt x2t ..., хп\ г\ р19 ря, ..., рп)9 > (£ = 1, 2, ..., /г),
г = г (*lf х2, ..., хп; г; plf р2, ..., рп) J
где
а(*гЛ V» * ^г ?2 ^-^о
d(*i< *2 xn'z' Pv ?2 Рп) '
(10.2-23)
?-]£P*d** = g(*i. x2t ..., хп\ z\ plt p29 ..., ря)[Л—2 P*d*J
/г = 1 \ £=1 /
выбранного таким образом, что
[g(*i, **...» -V. 2; рх, р2 рп)^0]. (10.2-24)
л
При этом условии полный дифференциал dz = J] Рл^*л преобразуется также
£=1
в полный дифференциал dz= У\рий%к> где pi — -?- (/ = 1, 2, ..., /г).
Такое преобразование называется преобразованием соприкосновения;
преобразование соприкосновения необходимо сохраняет каждое условие полосы
и будет также сохранять касание регулярных элементов поверхности для
л = 2 (см. также п. 10.2-1).
10.2-6.
10.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
307
Преобразование соприкосновения (23) преобразует данное
дифференциальное уравнение (14) в новое дифференциальное уравнение
?(*i, Хг, ...» *п\ 2; р19 ръ ..., Рп) = Р(х1у х2, ..., хп\ г; plt р2, ..., рЛ) = 0
Л=|р '=1. 2. -. ") (10.2-25)
с решениями 2 = 2 (Xlt x2, ..., ХЛ). Иногда случается, что новое уравнение
(25) не содержит р( и не является тогда дифференциальным уравнением.
Пример, n-мерное преобразование Лежандра (см. также п. 9.2-3,b и 11.6-8);
^i^Pv~Pi^xi 0* =1.2 п),
п } (10.2-26)
10.2-6. Канонические уравнения и канонические преобразования.
(а) Канонические уравнения. Для уравнения с частными
производными первого порядка
G(xu др., .... хп\ р19 рг рп) = 0 (Р( = щ> 1 = 1. 2, .... /г), (10.2-27)
которое явно не содержит искомую функцию г, характеристические
уравнения (16) имеют особенно простой вид
/г=1
dXf дО dp, дО
1Г=Щ- ЧТ=-Щ (' = !. 2 ») (Ю-2-29)
(канонические уравнения).
Замечание. Решение каждого дифференциального уравнения (14) может быть
сведено к решению дифференциального уравнения простого вида (27) относительно л-{-1
независимых переменных xv x^, ... , хп, г; каждое решение
"ЯВ('Г Х2 ХП-*)
Дифференциального уравнения
F\xt. х»
такое, что и (*г *2 хп; z) = 0.
ди ди
дхг дх2
п* ' ~~ ди ' ~~ ди ' '
дг дг
>ешение 2=2 (х~, х , ...
ди \
... аГ =° О0.2-30)
, *д) данного уравнения (14),
(Ь)# Канонические преобразования (см. также п. 11.6-8).
Дважды непрерывно дифференцируемое преобразование
Pi
где
i=Xi(xv х2,..., хп\ ръ р2,..., Рп)Л 2
't = Pi (*i> % •••» *л'» Pv Рг. •••» Рл) J
d(*tt *g xn: Pl, p2 pn)
~~ д {xlt xif ... t xn\ px, p2. ... , Pn) ^ '
(10.2-31)
308
ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
10.2-в.
называется каноническим преобразованием, если оно преобразует канонические
уравнения (29) в новые канонические уравнения
dxt д ___
~7Г*=~"Ц$7с(хь *2.-... хп\ Pi» ря. —. Рл).
dp[ __ д _ _ _
"~^"~ ~ ~^7 G (xi> *2»---» хп* Pi» Рг»---» Р/г)
(i=l, 2 п). (10.2-32)
Это должно иметь место для произвольной дважды дифференцируемой
функции G (xlt #2,..., хп\ Pi» Рг»"-» Рл)- Преобразование (29) будет канони-
ческим, если выражение 2 (р* ^л — Pk dxk) будет полным
дифференциале
лом для производящей функции Q = Q (хъ х2,...» хп; ръ р2,..., pw),
т. е.
2 (Pk dxk - рА (ЙЛ) = d Q *) (10.2-33)
(имеется в виду, что р^ и *Л выражены по формулам (31)).
При соблюдении условия (33) функция G (xlt х2,..., хп\ plt р2,..., Рп)
получается из функции G путем подстановки вместо *,- и р/ их выражений
через xi и р,-.
Каноническое преобразование может быть выражено в терминах
производящей функции Q (xlt *2, ..., xn\ plf p2, ..., рп)\ последняя часто задается
как функция xi и х-% или pi и р/. В частности, каждая дважды
дифференцируемая функция Q = W(xv х2,..., xn; xlt х2,..., #„) определяет каноническое
преобразование такое, что
J^. - - d\F - d\F
2j (Pkdxk-pkdxk)=(№ или Pi=-^r, p; = _._
/г = l */
(/ = 1, 2,..., /г); (10.2-34)
чтобы получить формулы (31), нужно от независимых переменных х-ь и xt
перейти KJfj И Pi.
dpi dp и
Из формулы (34) следует, что -^— = =т—. Если записать соотноше-
axk dxi
ние (34) в виде
п
S <Р* ^+** <**> = d (¥ + Е **?*)'
то получатся формулы -к— = —г—. Аналогично получаются еще две группы
oxk dpi
формул
dxi dxk dPi dxk ,. , , 0 ,
^Л dp i dPk dxt v ' '
*) Иногда такие канонические преобразования называют унивалентными; в
дальнейшем речь идет только о них. Более общие канонические преобразования рассмотрены
в книге [Ю.9].
10.2-в.
10.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
309
Отметим, что для рассматриваемого канонического преобразования определитель
матрицы Якоби Д=1.
Канонические преобразования (31) образуют группу (см. также п. 12.2-8).
Заданное дифференциальное уравнение первого порядка (27) с
каноническими уравнениями (29), новыми каноническими уравнениями (32) связано
с дифференциальным уравнением
G(xlt x2t..., ~хп\ ~pv р2,..., ~рп) = 0 (р£=-#-, /=1, 2 п). (10.2-35)
Решение z = z(xv *2»».«» xn) преобразованного уравнения (35) связано
с решением z—z(xv x2t ..., хп) исходного уравнения (27) соотношением
* = z-Q (xlt x2t ..., хп; plt p2,..., рп). (10.2-36)
Уравнения (31) и (36) совместно составляют преобразование
прикосновения (п. 10.2-5).
(с) ■# С к о б к и Пуассона. Данная пара дважды непрерывно
дифференцируемых функций g (xlt x29..., хп\ pv р2,..., pn)t h (xv x2t... ,хп; plt p2 рп)
определяет скобку Пуассона
Л = 1
Скобки Пуассона обладают следующими свойствами:
[h, g] = -[g, Л], [g, g] = 0, [g,const] = 0, (10.2-38)
tei+A. h] = [gv h] + [g2t h], [glg2t h]=g2 [glt h]+gl [g2, h], (10.2-39)
[/. [g> h]] + [g* №, f]] + [h> If* g]]=0 (тождество Пуассона). (10.2-40)
Заметим, что из [/, g] = 0, [f, h] = 0 следует [g, h]—0.
Дано преобразование (31) и пусть
g(xv x2t...,xn; pv p2 Pn)=g(xv 4 xn\ pv p2t ..., pn),
h (xv x2t ..., xn\ pv p2t..., ~pn) = h (xlt x2t ..., xn\ plt p2t ..., pn)
n
dg dft dh dg \
_ ъъ-щъг (10-2-41)
(Первые два равенства означают, что функции g и h получены из функций g и h
путем замены переменных *,-, р^ через Х(, pi с помощью преобразования,
обратного к преобразованию (31).)
Данное преобразование (31) есть каноническое преобразование тогда и только
тогда, когда оно сохраняет скобки Пуассона, т. е. если [gt h] = [gt h] для
всех дважды непрерывно дифференцируемых функций g, h.
Любое каноническое преобразование (31) удовлетворяет условиям
[**. ч] = 0> [Ри Pk\ = 0> \
r_ _ 1 J0, если i^bk,
(*,fc = l, 2, ..., п). (10.2-42)
Условия (42) необходимы и достаточны для того, чтобы
преобразование (31) было каноническим.
310 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.2-7.
Если [g, Л] = 1, то функции g и h называются канонически сопряженными;
в частности, из (42) следует, что любая пара функций xkt fk(k—\, 2,..., п)
является канонически сопряженной. Часто приходится рассматривать
преобразование вида (31), зависящее от параметра /:
** = *,-(/; *i, х2 хп\ р1% р2% ..., pn)t \ 2
Pi = Pi it\ хъ Ч *п\ Л. Р2 Рп)- )
43)
Это преобразование будет каноническим (т. е. сохраняющим канонические
уравнения (29), если соотношения (42) выполняются для любого значения t
(см. п. 10.2-7, с)).
Отметим, что если Xi и p-t являются функциями параметра /, так что
совокупность канонических уравнений (29) удовлетворяется, то для каждой
дифференцируемой функции f{t\ xly x2> ---,хп\ р1% р2,..., рп) имеем:
-д- = [/.01 + ж- (10*2-44)
В частности, из^ =0 и [Д G] = 0 следует, что /=const.
10.2-7. Уравнение Гамильтона — Якоби. Решение канонических уравнений.
(а) Важным приложением теории уравнений с частными производными
первого порядка является решение системы обыкновенных дифференциальных
уравнений, которые могут быть записаны как канонические уравнения,
связанные с дифференциальным уравнением специального вида
#1» Х2, ...» Xn\
Pi. Pt. .... Pn>=0, (10.2-45)
(p = -~\ pf-=—; i = l, 2,..., n) (уравнение Гамильтона—Якоби).
Заметим, что уравнение содержит /г+1 независимых переменных х и Х(.
Из уравнений (29) следует, что dxjdt=\\ это можно записать как x=t
(принимая х = 0 для / = 0); 2/г канонических уравнений (29) для *,- и p-t имеют
вид х)
dxi д гг \
-— = ■^7-^^. xlt *а, ..., хп\ р19 р2, ..., рп),
an ' а <10-2-46>
-4Г= — -дх~Гн& *i» х* •••» хп* Pi. Рг. «... Рп) ('. = 1. 2, ..., /г). J
Система обыкновенных дифференциальных уравнений, имеющая
приведенную форму (46), играет важную роль в вариационном исчислении (п. 11. 6-8),
а также в аналитической динамике и оптике.
Если удалось найти п-параметрическое решение
z = 0>(/, xl9 x2l ..., хп\ av a2, ..., ап) (10.2-47)
уравнения Гамильтона — Якоби (45), для которого det Г д *—1 ф0, то
решение Xi=Xi(t), pi — pi(t) (/=1, 2, ..., п) системы 2п обыкновенных
дифференциальных уравнений (46) получается из соотношений
-^-Ф(Л хъ хъ ..., хп\ аъ а2, .,., ая) = Р; (i = l, 2, ..., л), (10.2-48)
где ak и Р/ суть Ъг постоянных интегрирования', после отыскания функции
Pi находятся подста
также п. 10.2-4, Ь).
xi(t, аъ a2,..., ОС/Г, Pi, Рг» •••. Ря) функции pt находятся подстановкой х\ в
соотношения pi = dQ)ldxi (i = l, 2, ..., п) (см. тг
1) Остающееся каноническое уравнение есть dpjdt =■ — dHJdt,
10.2-7.
10.2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
311
(Ь) Применение канонических преобразовании (см. также
п. 10.2-6, Ь). Если полный интеграл (47), дающий решение уравнений (46), неизвестен,
то можно пытаться ввести каноническое преобразование, связывающее 2п + 2
переменных х = /, р, X;, р, с 2л + 2 новыми переменными х = 7, р, х., р., так что р -f- Я =
-р + Я. и
dx{ дН dp. дН
d~t "" др( ' dt ~ dx. ""
В этом случае выражение
л / л _ - - \
2 Р/Л - ЯЛ - [ У] pfe d*fe - ЯЛ = rfQ (10.2-50)
Л--=1 \* = 1 /
*»• ^2 *Л;
|)ференцируемая
I d2W 1
должно быть полным дифференциалом производящей функции Q (t, xit xz, ... , *Л;
Pi, p% p ). В частности, пусть t = t. Тогда каждая дважды дифференцируемая
функция Q = 4T(t, хи х2, .... хп\ Xi, x2
определяет каноническое преобразование такое, что
Р.=» Р: =» — « = 1. 2 ... , я),
1 а*. » ' ад:.
(10.2-51)
— дЧ?
Иногда возможно так выбрать это преобразование, что Я уже не зависит явно от х.
(преобразование к циклическим переменным Xj), тогда соответствующие уравнения (49)
интегрируются непосредственно: р. = const.
(с) Теория возмущений. Дано решение (47) уравнения Гамильтона —
Якоби (45); производящая функция Ч?" = Ф(/, хи х2, ... , хп; xt, х2, ... , хп) определяет
каноническое преобразование v5l), дающее постоянные значения преобразованным
переменным
*l = ai> Pi^-h (* e *» 2 п)- (Ю.2-52)
Как пэказано в п. 10.2-7,а 2в уравнений (52) дают решение х^ —х^ (/), p. = p.(t)
канонической системы (46).
Данное решение «невозмущенной» канонической системы (46) часто позволяет
решить канонические уравнения
dx. OK dpx дК
~1Г=др--' ~dt -^ (*« 1.2. ...,*),
W } (10.2-53)
К = Я (t, хи х21 ... ,- хп; ри р2, ... , рп) +
+ еЯ4 (/, хи х21 ... , хп; ри р2, ... , рп)
и гИх — малый дополнительный член {возмущение, т. е. эффект малого отклонения тела
1 небесной механике). Применение извзстного решения (47) для «невозмущенного»
уравнения Гамильтона — Якоби (45) вводит новые переменные х,, р. каноническими
преобразованиями (51) о производящей функцией
ЧГ= Ф (/, хи х2, ... i xn; хи х2, ... , хп).
Теперь уравнения (46) заменены уравнениями (53); 1с. и р. уже не являются
постоянными и удовлетворяют преобразованным каноническим уравнениям
dx, дНЛ dpt дНЛ
-~-»е—ri., _Le_e-^ (i-1, 2, ...,яь (10.2-54)
dt др. dt dx.
которые, возможно, легче решить, чем данную систему (53). Если записать
Ъ « а, + е X. (/), р. « - ^ + е Р. (О (/ — 1. 2 п),
то поправки е X. (t), е P^ (t) к константам (52) производят соответствующие поправки
к решениям невозмущенной системы (46).
312 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.3-1.
10.3. ГИПЕРБОЛИЧЕСКИЕ, ПАРАБОЛИЧЕСКИЕ И ЭЛЛИПТИЧЕСКИЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ
ПРОИЗВОДНЫМИ. ХАРАКТЕРИСТИКИ
10.3-1. Квазилинейные уравнения с частными производными второго
порядка с двумя независимыми переменными. Характеристики.
(а) Уравнение с частными производными г-го порядка называется
квазилинейным, если оно линейно относительно производных г-го порядка от
неизвестной функции Ф. Квазилинейное уравнение второго порядка с двумя
независимыми переменными х и у имеет вид
д2Ф . 0 д2Ф . д*Ф . г> к /1л г» ,v
где allf a12, a22 и В — функции от х, */, Ф, ^- и -^-. Предполагается, что все
встречающиеся функции и их производные непрерывны.
(Ь)* Характеристики. Дана кривая С0 (в плоскости Оху),
описываемая уравнениями
х = х(т), у = у(т), ХЮ-З^а)
и последовательность краевых условий типа Коти1)
ф-W. S-PM. S-«W (£-р£+«2) (Ю.з-26)
(эти условия в п. 10.2-2 назывались начальными).
Кривая С0 вместе с функциями (2Ь) образует полосу первого порядка Сг.
Заданная совокупность функций (2) единственным образом определяет
значения
д*Ф . . д*Ф ,. д*Ф , v
д*=иЮ> Wdy = vW> W=W(T)
(и также значения производных высшего порядка от Ф) на кривой (2а) в
каждой точке Р0, где функции (2а) не удовлетворяют обыкновенному
дифференциальному уравнению
ап(Э2-2а12^ + а22 = 0 |
dx atx
(10.3-4)
В самом деле, производные a, v, w от Ф на Сх должны удовлетворять
уравнению (1) и условиям полосы второго порядка
dp dx , dy da dx , dy /mo r*
так что, например,
Qn dy dp + a2t dx dq + В dx dy ш g fi
u~~ an dp - 2att dx dy + a22 dx* " uu.o-oj
*) Если заданы граничные значения нормальной производной дФ/дп (п. 5.6-1)
дФ 1_
/(£)'+Ш
г('Тт-р©=Р(т)- (10-3-3)
то решая уравнение (3) вместе с условием ^ = Р "^ + <7 т^. найдем р (т) и <? (т).
10.3-2. Ю.З. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 313
Уравнения (4) выполняются в точке Р0, если С0 есть дуга
характеристической кривой (называемой часто характеристикой) у — у (*),
удовлетворяющей уравнению (4), или если С0 касается такой кривой в точке Р0.
Собственно говоря, характеристики связывают с дифференциальным уравнением
(1) кривые х — х(х), у — у (т), z = z (т) на интегральной поверхности г = Ф(х, у), так
что у = у (х) удовлетворяет уравнению (4). Если уравнение (1) линейно, т. е. а1Ь
«12, Д22 и В не зависят от z, р и д, то характеристики определяются независимо
от выбора z, р и д, т. е. независимо от интегральной поверхности.
Основная задача Коши для уравнения (1) ставится следующим образом. Дана
полоса первого порядка d; надо найти решение Ф (х, у) уравнения (1) такое, чтобы
поверхность Ф (*, у) содержала полосу Ct. (Решение ищется в некоторой малой
окрестности кривой С0; см. также п. 10.3-4.) Если полоса Ct целиком состоит из точек,
в которых уравнения (4) соблюдаются (характеристическая полоса), то, чтобы на ней
можно было построить полосу второго порядка, должно соблюдаться дополнительное
условие. Так как на интегральной поверхности выражение (6) должно быть
конечным, то
дФ дФ
Р = 1Гх И Я = ~Гу
должны удовлетворять обыкновенному дифференциальному уравнению
аи dy dp + ai2 dx dg + В dx dy = 0
или
'«_ аъ±Уа\г-ача* В ldy\
_ — (10.3-7)
dp a22 a22 \dp)
на каждой характеристике, определенной уравнением (4) с соответствующим знаком
плюс или минус. В этом случае полоса второго порядка определяется не однозначно.
Эго означает, что на характеристических полосах возможно ветвление интегральной
поверхности, т. е. имеются различные интегральные поверхности, для которых вдоль
характеристики значения Ф, р и g совпадают, а некоторые производные высших
порядков оказываются различными.
Замечание. Производные второго порядка от Ф могут быть разрывны (но
обязательно конечны) на характеристике, так что различные решения могут быть
соединены вместе вдоль характеристик.
(с) Гиперболическое, параболическое и
эллиптическое уравнения. Данное квазилинейное уравнение с частными
производными (1) является на выбранной интегральной поверхности:
1) гиперболическим, если апа22 — af2<0 во всех точках
поверхности; тогда уравнение (4) описывает два различных семейства
характеристик;
2) параболическим, если апа22 — af2 = 0; тогда существует одно
семейство характеристик;
3) эллиптическим, если апа22—о\2 > 0; тогда действительных
характеристик не существует.
Следовательно, тип квазилинейного уравнения зависит от того, какое
решение рассматривается, и может быть разным для разных решений.
10.3-2. Решение гиперболических уравнений методом характеристик (см. также
п. 10.3-4). В гиперболическом случае (апа22 — а\2 ^ °) одновременное решение
четырех обыкновенных дифференциальных уравнений (4) и (7) выражает р — дФ/дх и q =
г= дФ/ду на интегральной поверхности как функции хну, так что Ф = Ф (х, у)
может быть получена дальнейшим интегрированием. Во многих приложениях дФ/дх
и дФ/ду более важны, чем Ф (х, у) (компоненты скорости); этот метод образует
основу для многих аналитических и численных методов решения в теории сжимаемой
жидкости.
Вычисления значительно упрощаются в специальном случае. Если В=0, то
ашх—• ш,®),--'-
где индекс означает, что в уравнениях характеристик (4) и (7) выбираются
соответственно знаки плюс или минус. Если в дополнение atl, at2 и а22 зависят только от
дФ/дх и дФ/ду, то нужно решать только уравнение (7) для получения характеристик
(двумерное устойчивое сверхзвуковое течение жидкости). Напротив, если aiu а1г и а22
8ависят только от х и у, то нужно решать только уравнение (4)*
314 гл. ю. уравнения с частными производными ю.з-з.
10.3-3. Преобразование гиперболических, параболических и эллиптических
уравнений к каноническому виду. Пусть а1Ъ а12 и а22 — функции только от
х и у, так что обыкновенное дифференциальное уравнение (4) разделяется на
два уравнения первого порядка
Л — %1(х1 у) с решениями hx (xt y) = alt (10.3-9a)
^f = ^2 (*> У) с решениями h2(x, y)==a2t (10.3-96)
где аь а2 —произвольные константы.
В зависимости от знака функции апа22 — а\2 в рассматриваемой области
значений х> у1) возможны три случая.
1. Гиперболическое дифференциальное уравнение
(апа22 — яЬ <0). Xi (x, у) и Х2 (х, у) действительны и различны. Существуют
два однопараметрических семейства действительных характеристик (9а) и (9Ь)\
через каждую точку рассматриваемой области проходит одна кривая каждого
семейства. Вводя новые координаты
* = М*. У). 7=М*. У)> (10.3-10)
преобразуем данное уравнение (1) к канонической форме
Система координат
--/(*».*£?).
дх ду
х — у
" 2
(10.3-12)
производит вторую каноническую форму
W~~W=e\1' * Ф' W "Si)' (Ю.3-13)
2. Параболическое дифференциальное уравнение
(flne2a-"#j2 = 0). Ях (*, #) и А,2 (х, у) действительны и тождественны.
Существует одно однопараметрическое семейство действительных характеристик (9);
через каждую точку (х, у) рассматриваемой области проходит одна
характеристика. Вводя новые координаты
x = h1(x, y)t у = Н0{х, у)у (10.3-14)
где h0(x, у) есть произвольная дифференцируемая функция такая, что
|*' у'- Ф<д, преобразуем уравнение (1) к каноническому виду
Щ=1 (х, 9, Ф, f, f). (10.3-15)
дхй \ дх ду )
3. Эллиптическое дифференциальное уравнение
(апа22 — а|3>0). А* (я, у) и %2 (х> у) и, следовательно, пх (х, у) и Л2 (х, у) —
комплексно сопряженные; действительных характеристик не существует. Вводя
% — hi (*. У) + h2 (х, у) п— hl (*' у) ~~ Нг (*' ^ (10.3-16)
*) В обычных случаях дискриминант а^а—а| не меняет знака в
рассматриваемой области. Заметим, что знак Дпа22 — а\2 есть инвариант относительно
непрерывно дифференцируемых преобразований координат х = х (х, у), у = у (х, у) с
ненулевым якобианом.
-X В последнее время большое значение получили задачи смешанного типа, когда
дискриминант си«22 — «|2 меняет знак в рассматриваемой области (см. £10.7]),-К
10.3-4.
10.3. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
315
преобразуем уравнение (1) к каноническому
виду
дФ дФ\
> дФ\
"' д'у]'
(10.3-17)
Эти три типа уравнений с частными производными существенно
отличаются друг от друга заданием краевых условий, обеспечивающих
существование и единственность решения (пп. 10.3-4 и 15.6-2).
10.3-4. Типичные краевые задачи для уравнений второго порядка.
(а) Гиперболические дифференциальные уравнения.
В задаче Коши (задача с начальными условиями) в п. 10.3-1, b требовалось
•const
у = const
ОЬласть ВР
ОЬласть В,
const
'(/■= const
Рис. 10.3-1. Краевые задачи для гиперболических дифференциальных уравнений.
найти решение гиперболического дифференциального уравнения (1), задавая Ф,
-г^ и 0— на дуге С0 регулярной кривой, которая не является
характеристикой (4) и не касается характеристик. Такая кривая пересекает каждую
характеристику не более чем в одной точке; заданные начальные значения
определяют Ф в треугольной области D0, ограниченной С0 и характеристиками
каждого семейства (рис. 10.3-1, а). Более точно, значения Ф в каждой точке Р
области D0 определяются значениями Ф и ее производных на части Ср дуги
С0, которая ограничена характеристикам^ проходящими через точку Р.
316 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.3-5,
Второй тип краевой задачи задает только линейное соотношение
а-^ + |ЗФ = &(*, у) на дуге С0, определенной выше; в дополнение Ф задана
на характеристике Сс, проходящей через конечную точку дуги С0 (рис. 10.3-1, Ь).
Третий тип краевой задачи задает Ф на двух пересекающихся дугах
характеристик Сс и С'с (рис. 10.3-1, с) (задача Гурса).
Комбинации этих трех типов задач могут указывать допустимые краевые
условия для более сложных границ. Так, на рис. 10. 3-1, d Ф, дФ/дх и дФ/ду
могут быть заданы на С0, а соотношения вида a-j- -\- $Ф = Ь (х, у) —на
каждой из дуг С() и CJ. Решения в разных областях, показанных на рис. 10.3-1,
«склеиваются» вдоль характеристик так, что Ф непрерывна, а дФ/дх и дФ/ду
могут быть разрывными. Заметим, что замкнутые границы в плоскости Оху не
допускаются.
Пример. Начальные задачи для гиперболического одномерного волнового
уравнения, п. 10.3-5.
(Ь) Параболические дифференциальные уравнения.
Здесь существует только одно семейство характеристик. Хотя задача Коши
может опять быть разрешима для соответствующей дуги С0, однако
обычно задается Ф на характеристике х(=/) = 0 и линейная комбинация
а -к- + РФ на двух кривых, которые не пересекают и не касаются друг
друга или характеристик. Замкнутые границы в плоскости Оху не допускаются.
П р и м е р. Допустима следующая краевая задача для параболического
уравнения диффузии ^-2 + —г -дТ ~ 0: задано Ф (*, t) = Ф0 (*) на характеристике *=0
Y дФ
алгз
(начально; условие) и а (х, t) -^- + 0 (х, t) ф на кривых * = а и х =» р (краевые условия).
(с) Эллиптические дифференциальные уравнения (см.
также пп. 10.4-1 и 15.6-2). Действительных характеристик не существует;
краевые условия типа Коши не допускаются. Типичные задачи: задают
линейную комбинацию а(х, у) j- + $(x, у) Ф на кривой С, окружающей
ограниченную область или
неограниченную область (корректная
краевая задача).
10.3-5. Одномерное волновое
уравнение (см. также пп. 10.3-4, а
10.4-8, а и 10.4-9, Ь).
Гиперболическое дифференциальное уравнение
д*Ф (х, t)
дх*
1 д*Ф (х
" с* dt2
t)
= 0
Рис. 10.3-2. Характеристики для одномерного
волнового уравнения
дгф 1 д2ф
"die* ~c* dt*
■•0.
(одномерное волновое уравнение)
(10.3-18)
имеет общее решение
Ф(*. 0 = Ф1(*-сО + Ф2(* + <*),
(10.3-19)
которое представляет пару
бегущих волн, распространяющихся соответственно вправо и влево вдоль оси Ох
с постоянной скоростью с. Характеристики x±ct = const есть геометрическое
место, точек постоянной фазы (рис. 10.3-2). В пп. 10.3-5, a, b и с приведены
решения для трех типов задач с начальными условиями. На практике метод
to.з-e. ю.з. уравнения с частными производными 317
Фурье (п. 10.4-9) может быть предпочтительнее, особенно в приложениях к
неоднородным дифференциальным уравнениям (вынужденные колебания).
(a) Начальные условия
Ф (*, 0) = Ф0 (*), д-§ I Q = v0 (х) (- со < х < со) (10.3-20)
представляют корректную задачу Коши (пп. 10.3-1 и 10.3-4, а; см. также
рис. 10.3-1, а и 10.3-2). Решение есть
x+ct
Ф(^0 = |[Фо(*-сО + Ф0(*+сО] + £ \ ve©dE. (Ю.3-21)
x-ct
(решение Даламбера),
Возмущение начальных условий, произведенное на заданном интервале а<х<Ь.
затрагивает решение в интервале а — ct <* < 6 + ct. Разрывность Ф0 (х)
распространяется в оба направления.
(b) Начальные условия
Ф(*. 0) = Ф0(*), Щ^^о(х) (Х^0) (10.3-22)
и краевое условие
ф(0, /) = 0 (t^O) (10.3-23)
представляют смешанный тип краевой задачи (см. также п. 10.3-4, а
и рис. 10.3-1, d и 10.3-2). Решение
x + ct
Olx,f) = {-[P(x-c0 + P(x + d)] + ± $ Q(E)«, (10.3-24)
x-ct
*М"{-Фо<-*> (*<o), «<*>-{-*<-*> (,<o> (10'3-25>
представляет суперпозицию прямой и отраженной волн.
(c) Начальные условия
Ф(*. 0) = Ф0(*), ^|, = 0 = v0W (Q^x^L) (10.3-26)
и краевые условия
Ф(0, t) = <S(L, 0=0 (/^0) (10.3-27)
определяют другую смешанную задачу (см. также рис. 10.3-1, d, и 10.3-2).
Решение дается формулой (24), где Р (х) и Q (х) интерпретируются как
периодические функции с периодом 2L и соответственно равные Ф0 (х) и v0 (x) для
O^x^L и — Ф0( — х) и—v0(— х) для — L^x<0.
10.3-6. Метод Рима на — Вольтерра для линейных гиперболических уравнений
(см. также пп. 10.3-4 и 15.5-1). Метод позволяет иногда получать решение
задачи Коши (п. 10.3-1) для действительного гиперболического
дифференциального уравнения
1ф(*' У)=Ш1+аЬ* У)ъ+Ь1х' У)1§+с1х' *>фв='<*' *>• (10-3-28>
где Ф и -^, -j- заданы на граничной кривой С0, удовлетворяющей условиям
п. 10.3-1. В соответствии с рис. 10.3-1, а решение в каждой точке Р с
координатами * = |, у = Ц выражается в зависимости от начальных значений
318 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.3-7.
х
Gо = exp \b (*, г]) dx (у = г\)
Ф (*» у), дФ/дх, дФ/ду на сегменте граничной кривой Ср, ограниченном
характеристиками, проходящими через точку Р 1):
ФЙ, Л) = С*Фи- $ G^(ady-bdx) +
СР
+ $ [^dy + GRd-Txdx)+SS Grfdxdy^G^^-
Ср Dp
-$ GRQ>(ady-bdx)- \ {<bdJ£dx + GRd-^dy)+\\GRfdxdy, (10.3-29)
Ср Ср Dp
где так называемая функция Римана — Грина G^(xt у; g, tj) непрерывно
дифференцируема внутри области Dp, ограниченной Ср и характеристиками,
проходящими через точку Р, и удовлетворяет условиям простой краевой задачи
LG«=S -i(a°/?)-i(ftG«)+cG«=° (*• у внутри °р).
GR = exp 5 а (Е, у) «у (* = g). j (10.3-30)
X
^ = ехр J 6 (л:,
Примеры. Для а = 6 = с = 0 функция G/^= 1. Для а = b = 0, с = const
функция G^= У0 [/4?1^^Г(£Г-^лТ1. где JQ (z) — функция Бесселя первого рода порядка
нуль (п. 21.8-1). Для многих практических применений, в которых встречаются
линейные гиперболические дифференциальные уравнения с постоянными коэффициентами,
предпочтительнее метод интегральных преобразований (п. 10.5-1).
10.3-7. Уравнения с тремя и более независимыми переменными.
Действительное уравнение с частными производными вида
п п
2 2 а* (*!» ** •" • **) дх. дхь +
+ b(Xi,x2, ..., хп; Ф; ||, ..., |^) = 0, (10.3-31)
где Ф = Ф(*1, хъ ..., хп), называется эллиптическим дифференциальным
уравнением, если матрица [а^] положительно определена (п. 13.5-2) всюду в
рассматриваемой области.
Во многих задачах рассматриваются неэллиптические дифференциальные
уравнения с неизвестной функцией Ф, зависящей от п пространственных
координат хъ х2, ..., хп и временной координаты /.
Дифференциальные уравнения вида
%-££ '» <£k + B' ^= 2 2 сш ^Г+В, (10.3-32)
/ = 1£=1 ' k f«l* = l l k
где матрица [с^] = [с,-^ (хъ хъ ..., хп\ f)\ положительно определена и В есть
функция от *;, /, Ф и дФ/дх^ являются соответственно примерами уравнений
гиперболического и параболического типов [10.7J.
1) См. также формулу (10.3-4).
10.4-1. 10.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 319
Характеристики более общих дифференциальных уравнений (31) и (32) суть
поверхности или гиперповерхности, на которых краевые условия типа Коши не позволяют
определить производные высших порядков искомого решения. Эллиптические
дифференциальные уравнения не имеют действительных характеристик. Понятие характеристик
может быть распространено на уравнения с частными производными порядка высшего,
чем два, и на некоторые системы уравнений с частными производными [10.5].
10.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ.
ЧАСТНЫЕ РЕШЕНИЯ
10.4-1. Физические основы и обзор.
(a) Многие проблемы классической физики приводят к отысканию
решения Ф (х, t) или Ф (г, /) линейного уравнения с частными производными
в заданном интервале или области V (табл. 10.4-1). Неизвестная функция Ф
и/или ее производные должны, кроме того, удовлетворять заданным
начальным условиям при / = 0 и линейным краевым условиям на границе 5 области V'.
Аналогичные задачи возникают в квантовой механике.
Каждое дифференциальное уравнение, приведенное в табл. 10.4-1, является
однородным (п. 10.1-2, Ь), если / = 0. Заданное краевое условие также
однородно, если наряду с каждой функцией Ф, которая удовлетворяет краевому
условию, ему удовлетворяет и функция аФ. Неоднородности возникают
в результате действия внешних влияний (силы, источники тепла,
электрические заряды или токи) на рассматриваемую физическую систему. Для
эллиптических уравнений типично описание стационарных процессов (стационарные
температурные и электростатические поля, упругая деформация).
Параболическое и гиперболическое дифференциальные уравнения описывают переходные
процессы (свободные колебания, возникающие вследствие заданных начальных
возмущений) или, если имеются неоднородности, зависящие от времени
(«вынуждающие» функции в дифференциальных уравнениях или краевых условиях),
описывают процессы распространения возмущений (вынужденные колебания,
излучение).
Можно связать каждую задачу обсуждаемого типа со своей аппроксимирующей
системой обыкновенных дифференциальных уравнений, заменяющей каждую
пространственную производную разностным коэффициентом в смысле п 20.8-3 (метод разностно
дифференциальных уравнений). Этот метод применим не только для численного решения;
аналогия с дискретными проблемами типа, описанного в пп. 9.4-1 —9.4-8, может
приводить к интересным физическим аналогиям.
(b) Конструкция реше н и я м ето до м с у п е р п о з и ци и.
Многие важные методы решения линейных дифференциальных уравнений
основываются на фундаментальных теоремах суперпозиции, сформулированных
явно в пп. 9.3-1 и 15.4-2. Метод наложения (суперпозиции) разумно
выбранной последовательности основных функций дает возможность получать
решения, удовлетворяющие заданным краевым условиям и/или заданным начальным
условиям, а также получать решения неоднородных уравнений. Разложения по
собственным функциям (пп. 10.4-2 и 15.4-12) и методы интегральных
преобразований (пп. 9.3-7, 9.4-5 и 10.5-1 —10.5-3) представляют систематические
схемы для конструирования таких решений. Методы функций Грина (пп. 9.3-3,
9.4-3, 15.5-1 —15.5-4, 15.6-6, 15.6-9 и 15.6-10) являются суперпозиционными
схемами, которые сводят решение соответствующих задач к задачам с простыми
вынуждающими функциями или краевыми условиями.
Общая теория линейных краевых задач содержится в гл. 15. Пункты
10.4-3—10.4-8 представляют применение частных методов с эвристической
точки зрения элементарного курса.
(c) Выбор системы координат. Система координат х1, х2 или
х1, х2, х3, определяющая точку г, обычно выбирается так, что, во-первых,
возможно разделение переменных (п. 10.1-3) и/или, во-вторых, заданная
граница S представляет координатную линию или поверхность или пару
координатных линий или поверхностей.
Таблица 10.4-1
Важнейшие линейные дифференциальные уравнения математической физики
со
8
Тип
Параболический
Гиперболический
Эллиптический
Уравнения 4-го
порядка
Физический смысл
Уравнение
теплопроводности, диффузии
Волны (струны, мембраны,
течение жидкости),
затухающие волны. Телеграфное
уравнение
Статический случай
Упругие колебания
Статический случай
Одномерное уравнение
д*Ф 1 дФ . , Л
д*ф 1 д2ф _, „
д*Ф д*Ф дФ
д*- "" а° а/г~ ах ~дГ~~
— а2Ф = / и, о
д2ф « / ч
с)4ф 1 д*Ф , , ,
д4ф * , ,
Многомерное уравнение
РФ-^-5-/(г.О
у8ф _ ао _ _
"" ai Ж "" а*ф ^'(г' ^
V>0 = /(r)
1 д2Ф
V*V*<X> = f(r)
Дополнительные
условия
Краевые условия;
начальное условие для Ф
Краевые условия;
начальные условия для Ф
дФ
и St
Только краевые условия
Краевые условия;
начальные условия для Ф
дФ
И «"
Только краевые условия
tO.4-2. 10.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 321
10.4-2. Линейные краевые задачи (см. также пп. 15.4-1 и 15.4-2).
(a) Пусть V —заданная трех- или двумерная область точек (г) и пусть 5 —
граничная поверхность или граничная кривая области V. Требуется найти
решение данного дифференциального уравнения
LO(r)=/(r) (r si/), (10.4-la)
удовлетворяющее последовательности краевых условий
В|Ф(г) = Мг) ('-1. 2, ..., N\ rsS), (10.4-16)
где |_Ф и В/Ф —линейные однородные функции от неизвестной функции Ф (г)
и ее производных. Каждое решение этой линейной краевой задачи можно
записать в виде суммы Ф = ФА + Фв решений простых краевых задач
|_ФА(г)=0 (г el/), (10.4-2а)
В,ФА(г) = 6|.(г) (i = l, 2, ..., N; rsS) (10.4-26)
LOB(r) = /(r) (r el/), (10.4-За)
В,Фв(г) = 0 (/ = 1, 2, ..., N; rsS), (10.4-36)
Заметим, что уравнение (2) является однородным дифференциальным
уравнением, в то время как уравнение (3) имеет однородные краевые условия.
(b) Однородные дифференциальные уравнения с
неоднородными краевыми условиями. Частные решения, приведенные
в пп. 10.4-3 — 10.4-6, обычно позволяют представить Фд (г) как сумму ряда
или определенный интеграл:
фа м -2] «и** м или фа о*) = $ а м % (■*) ^ <10-4-4)
от подходяще выбранных частных решений Ф^ (г) уравнения (2а).
Коэффициенты ofy или a(\i) выбираются так, чтобы удовлетворялись краевые
условия (26). Часто функции Ф^ (г) образуют полную ортоноржированную систему
(п. 15.2-4; например, ряды Фурье, интегралы Фурье); тогда возможно
представить данные функции 6/ (г) в виде (4) и найти неопределенные коэффициенты а^
или а(\х) методом сравнения коэффициентов (п. 10.4-9).
(c) Неоднородные дифференциальные уравнения
с однородными краевыми условиями: разложения по
собственным функциям (см. также пп. 15.4-5—15.4-12). Для
важного класса дифференциальных уравнений (1) решение Фв (г) уравнения (3)
можно получить простой суперпозицией решений ЧГ (г), соответствующих
однородным дифференциальным уравнениям
UF (г) = VF (г) (г €= V) (10.4-5а)
для различных возможных значений X, при которых Т (г) удовлетворяет
однородным краевым условиям
B|Y(r) = 0 (i = l, 2, ..., N; г es S). (10.4-56)
Вообще такие решения (ненулевые) существуют только при специальных
значениях параметра X (собственные значения); решения ¥ = 4^ (г),
соответствующие каждому собственному значению, называются собственными функциями
краевой задачи (5).
В пп. 10.4-3—10.4-8 приводятся частные решения ЧГ(г) для некоторых
дифференциальных уравнений вида (5а). Эти функции позволяют при помощи
11 Г. Корн и Т. Корн
322 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.4-3.
метода наложения получать решения соответствующих неоднородных
уравнений (3). Собственные функции, соответствующие дискретной
последовательности собственных значений, часто образуют удобные ортонормированные
системы (п. 15.2-4) для представления правых частей и решений в виде
/ (0 = 2/Л (г), ФВ = Ц РЛ (г). (10.4-ба)
Я, К
Непрерывная совокупность (непрерывный спектр) S^ собственных значений X
приводит к интегральным представлениям
/ (г) = J F (X) Тя. (г) dk, Фв = j Р (X) Ъ (г) dX. (10.4-66)
Подстановка выражений (6а) или (66) в уравнение (3) позволяет найти
неизвестные коэффициенты р^ или р (X). Отсылаем к пп. 10.5-1 и 15.4-12 для
общей теории этого метода решения и его области применения. Важный
альтернативный метод решения уравнения (3), так называемый метод
функций Грина, трактуется в пп. 15.5-1 — 15.5-4.
(d) Задачи, включающие зависимость от времени.
В задачах, в которых искомые функции зависят и от пространственных
координат и от времени, решается линейное дифференциальное уравнение
LO>(r, t) = f(rt t) (reV,/>0) (10.4-7a)
при соответствующих линейных начальных условиях
Л;Ф(г, 0) = ру(г) (/=1, 2,..., M; ге= V) (10.4-76)
и линейных краевых условиях
В;Ф(г, *) = Мг. *) (* = 1, 2,.... W; re=S; *>0). (Ю.4-7с)
Так как начальные условия (76) есть просто краевые условия на
координатной поверхности / = 0, то применимы методы пп. 10.4-2, а и b (п. 10.4-9).
Следующие методы позволяют упростить решение задач с начальными
условиями:
\.Фв = Фв(т, t) может быть представлено в виде суммы
функций, соответственно удовлетворяющих однородным начальным
условиям и однородным краевым условиям.
2. Разделение переменных (пп. 10.1-3, 10.4-7, b и 10.4-8).
3. Преобразование Лапласа по переменной t (пп. 10.5-2 и
10.5-3, а).
4. Метод Дюамеля (п. 10.5-4).
10.4-3. Частные решения уравнения Лапласа: трехмерный случай (см.
также табл. 6.5-1, пп. 10.1-3 и 15.6-1 — 15.6-9; решения в других
координатных системах приведены в [10.7]).
(а) Прямоугольные декартовы координаты^, у, г:
*2ф=!£+г-+1£-=0- <10-4-8>
Допустимы частные решения
G>ktk9ks (х, у, z) = ekix+foy + k»z (£x> k2t £3__любые комплекс- )
ные числа, удовлетворяющие условию £i + £| + &l = 0),
Фом, <*• *• z>= (*+**>еНшУ+к* <« + Ч = °)' ( (Ш,4"9)
Фооо (*. У, г) = (а + Ьх) (а + fy) (А + Вг)ь )
10.4-3. 10.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 323
которые образуют различные произведения действительных линейных,
показательных, тригонометрических и/или гиперболических функций.
(Ь) Цилиндрические координаты р, ф, г. Пусть Ф = и (ф) X
Xv(z)w(p) (п. 10.1-3). Тогда
V20>e
1 д
р
JLI <Ць\л 1 д2ф.гд2ф — п
(10.4-10)
Разделение переменных приводит к трем обыкновенным дифференциальным
уравнениям:
^М(ф)+т^(ф) = 0, (10.4-11)
d*
d^v(z)-K*v(z) = 0K
(10.4-12)
(10.4-13)
где функция и (ф) удовлетворяет условию периодичности: и (ф+2я) = и (ф);
это будет, когда т=0, ±1, ±2,...; К — произвольная константа
(константа разделения, п. 10.1-3), которая определяется по данным краевым
условиям. Уравнение (10) допускает частные решения (цилиндрические гармоники)
вида
Ф± Кт (р, ф, 2) = е-Кг Zm (Щ (a cos тф + р sin /жр),
Ф±*0(Р» <Р> г) = ?±Л2о(/Ср)(а+Рф),
фот(Р» Ф» 2) = (а + ^)^Лрт + ^(асозтф+р8ттф),
Фоо(р, ф, г) = (а + ^)(Л+В1пр)(а + рф)(т = 0, 1,2,...),
1
(10.4-14)
где Zm(£) — цилиндрическая функция (п. 21.8-1); в частности, если данная
задача требует ограниченности решения Ф при р = 0, то Zm (£) должна быть
функцией Бесселя первого рода Jm(Q (п. 21.8-1).
Если в последнем случае положить K=iX9 то комбинации комплексно
сопряженных решений Ф+цт образуют действительные решения вида
(a cos Kz + b sin Xz)Im (Xp) (a cos пкр + p sin /яф),
где Im(kp) = i~mJm(iXp)—модифицированная функция Бесселя (п. 21.8-6).
Заметим, что в случае осевой симметрии, т. е. когда Ф не зависит от ф,
т = 0.
(с) Сферические координаты г, 0, ф. Пусть <b = u(y)v(cose)w(r).
Тогда
г2^ф^±(г2дЛ\ + -l—±(sinbd-^\4- —!—^ = 0 ПО 4-151
Разделение переменных дает
5ги(ф) + т«м(ф) = 0, (10.4-16)
0-W^ о (Й-2С ^»«) + [/(/+O-r^giJoCJ-O (£ = cos6), (10.4-17)
^HrJ+ff.HO-^HrK (10.4-18)
11*
324 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.4-4.
Функция v (£) = v (cos б) должна быть непрерывна при 6 = 0 и б = я; это
означает, что т=0, ± 1, ±2, ...,±:/ и / = 0, 1, 2... Уравнение (15)
допускает частные решения вида
9/т(г» в, ф) = ^Л^+-^7)/э7г(со8е)(асо8тф + Р$1птф)
(/ = 0, 1, 2, ...; т-0, 1, 2, ..., /), (10.4-19)
где Р? (Q —присоединенная функция Лежандра первого рода порядка j
(п. 21.8-10). Комбинация таких решений производит более общие частные
решения
Фу (г, 6, ф)в(лг' + -7|т)1'/<в' ф) (/ = 0, 1, 2,...), (10.4-20)
где
/
*"/(0, Ф)= S ^/г(со8е)(атсо8тф+рт8ттф) =
т==0
/
= 2 ymP\ml(cosb)eimq> (/-=0,1,2,...). (10.4-21)
т=-/
Функции (21) удовлетворяют уравнению (15) для г = const и называются
поверхностными сферическими гармониками степени / (см. также п. 21.8-12).
Имеется 2/ + 1 линейно независимых поверхностных сферических гармоник
степени /. Для разложения в ряд по ортогональным решениям заметим, что функции
У*£-Ш- р7 <- °> ~ -. УШШР? **• 9> - -
(/ = 0, 1, 2, ...; т = 0, 1, 2 /)
или более удобные функции
{У^ттШ plim'(cos в) е*"ф и=°- '•2- -: т="■ - '■± 2 ± л
образуют ортонормальную систему в смысле п. 21.8-12. Эти функции называются тессе-
ральными сферическими гармониками (секториальными сферическими гармониками для
т == /; см. также пп. 10.4-9, 15.2-6 и 21.8-11). Ортонормальные функции
2££!jycoi4
называются зональными сферическими гармониками.
Если допускаются решения с особенностями для 0=0, 6 = я, то появляются
аналогичные решения, содержащие ассоциированные функции Лежандра второго рода [21.3].
10.4-4. Частные решения для трехмерного уравнения Гельмгольца (см.
также п. 10.3-5). Дифференциальное, уравнение
V2<D + A:2(D = 0 (уравнение Гельмгольца) (10.4-22)
встречается при разделении переменных в трехмерном волновом уравнении
(п. 10.4-8, Ь) и в уравнении теплопроводности (п. 10.4-7, Ь). Коэффициент к2
может быть отрицательным (А: = £х, пространственный вид уравнения Клейна —
Гордона).
Для заданного однородного линейного краевого условия (например, Ф = 0
на границе S ограниченной области V) уравнение (22) допускает решения
только для соответствующей дискретной последовательности значений к2
(проблема собственных значений, п. 15.4-5).
(а) Прямоугольные декартовы координаты х, yt z.
Уравнение (22) имеет частные решения;
Фо*2*3 (х, у, z) = (а + Ъх) еИк*У+к*Я (Щ + к% = А2), \ (№.4-23)
Фоол (*. у, г) = (а + Ьх) (а + fly) eikz, J
V-
10.4-5. 10.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 325
которые можно представить в виде различных произведений действительных
линейных, показательных, тригонометрических и/или гиперболических функций.
(Ь) Цилиндрические координаты р, ф, z (см. также п. 10.4-3, Ь).
Пусть Ф = и (ф) и (г) w (р); тогда уравнение (22) разделяется на
уравнения (11), (12) и
w* w (р) + т т* w (р) + И2+к2) - 'йw (р)=°* (10-4_24)
где m = 0, ± 1, ±2,... и К — произвольная константа разделения,
определяемая краевыми условиями. Уравнение (22) допускает решения вида
ф± Кт(Р> Ф> z) = e±KzZm (p j/*2 + К2) (a cos ту + р sin тф) ]
(m = 0, 1,2,...).
Если Z = i%, то
ф±am (Р» Ф» z) = ^±аг2^(р V^2 — ^2) (а cos ™Ф + Р sin тф),
Фоо (Р, Ф, *) = (« + &*) Z0 (ftp) (а + рф).
(10.4-25)
(10.4-27)
Заметим, что для осевой симметрии т = 0.
(с) Сферические координаты г, б, ф (см. также п. 10.4-3, с).
Пусть Ф = и (ф) v (cos б) w (г). Тогда уравнение (22) разделяется на уравнения
(16), (17) и
^Ю(г)+^^ю(г) + [л«-^±^]ю(г)=0. (Ю.4-26)
Уравнение (22) допускает частные решения вида
Ф4/ (г, 9, Ф) = ^ Z/+1/2 (Ar) К/ (в, Ф) (/ = 1, 2,...),
e±ikr
Фдо(г> в, ф) = (центральная симметрия),
где К/(б, ф) — сферическая поверхностная гармоника (21). В частности, если
данная задача требует непрерывности решения для г = 0, то Z, , 1/2 (kr)lY~r~
есть сферическая функция Бесселя первого рода (п. 21.8-8).
10.4-5. Частные решения двумерных задач (см. также пп. 15.6-7 и 15.6-10, Ь).
(a) Уравнение Лапласа
уаф = i!«L 4- i!<L = i_ JL (r 1±\ 4- — -^- = 0 ПО 4-28)
допускает частные решения
Ф^ (*, у)=е±К{х + Ч Ф0 (*,у) = (а + to) (a + fy), (10.4-29)
Фш (г, Ф) = (Аг™ + ^) (а cos/пф + Р sin тф) (т=0, 1,2,...),!
Ф0(г, ф) = Л+В1пг, )
где /С, а также а, 6, а, р, Л, Z? — произвольные постоянные, определяемые
краевыми условиями.
(b) Двумерное уравнение Гельмгольца. Двумерное
уравнение вида (22) допускает частные решения
Ф*Л <*• У) = «"**+** (*? + Ч=*). у (Ю 4.31)
Фол (*, у) = (а + to) <?«Ч
ф*т(г» ф) = 2Ш (&r) (a cos тф-f p sin тф) (т = 0, 1, 2,...),
Ф0(г, ф) = Z0 (fcr) (а + М-
| (10.4-32)
326 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.4-в.
(с) Комплексно сопряженные решения (29) и (31) образуют различные
произведения действительных линейных, показательных, тригонометрических
и/или гиперболических функций.
10.4-6. Уравнение Шредингера. Трехмерное дифференциальное уравнение
V* Ф + (Ц. _ %г \ф в 0 (10.4-33)
(/ = 0, 1, 2, ...), (10.4-34)
допускает частные решения
фЛ/</1 б, ф) = Л~^2/ + 1 (2Xr) Y. (6, ф),
т+'
Фх, - / <г* б> ф) = -^jT L72/~1 {2Хг) у/(в' ф)
где L^ (Z) — функции Лагерра (п. 21.7-5). Если Ф нормировано (п. 15.2-16), то оно
образуется решениями первого типа (34). Нормированные решения существуют только для
собственных значений (п. 15.4-5) № таких, что с/% = я = 0, 1, 2, ... В этом случае
функции Лагерра сводятся к присоединенным полиномам Лагерра и решения (34) образуют
ортогональную систему в смысле пп. 21.7-5 и 21.8-12.
10.4-7. Частные решения для уравнения теплопроводности и диффузии
(см. также пп. 10.3-4, Ь, 10.4-9, 10.5-3, 10.5-4 и 15.5-3).
(a) Одномерное уравнение диффузии
т£~^-%-=° (10-4-35)
допускает частные решения
<Dfe (х, 0 = «* '** ~ *'**', Ф0 (*. t) = a + Ьх,
Ф(*. t) = ^e 4v' (t>0),
где k — произвольная константа разделения, определяемая краевыми условиями.
(b) Двух- или трехмерное уравнение диффузии
V2Q-^-^r=° (la4-37>
допускает частные решения
ф (г, t) = Ф* (г) е-***4 , (10.4-38)
где <bk (г) — частное решение соответствующего уравнения Гельмгольца (22)
(пп. 10.4-2 и 10.4-5, b); k — произвольная константа разделения,
определяемая краевыми условиями. Уравнение (37) также допускает частное решение
г2_
\_е Ауч (двумерный случай),
ф(г, 0*= { ' __^ (10.4-39)
1 е 4ч2* (трехмерный случай).
Y1*
10.4-8. Частные решения для волнового уравнения. Синусоидальные волны
(см. также пп. 4.11-4, Ь, 10.3-5, 10.4-9, 10.5-2 и 15.6-10).
(а) Одномерное волновое уравнение
ii*._JLj?f*_ = o (10 4-40)
а** с* dt* и KlKJt*w'
допускает частные решения вида
ф (х, 0 = е±1Мхе±ш = в±'*<*±<*> (а) = kc), (10.4-41)
где k — произвольная константа, определяемая краевыми условиями. Функ-
10.4-8. 10.4. ЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 327
ции (41) и соответствующие значения k2 образуют собственные функции
и собственные значения (пп. 10.4-2 и 15.4-5).
Решения вида (41) образуют следующие действительные решения:
Ф (х, t) = С соэ (со/ + Vi) cos (kx + Y2)
(синусоидальные стоячие волны),
ф (х, t) = a cos (at T kx) + b sin ((at + kx) =
= A cos (cot + kx-{-y)
(синусоидальные волны, распространяющиеся
в положительном и отрицательном направлении оси х)
Круговая частота со, частота v = a)/(2rc), волновое число k, длина волны
А, = 2я/£ и фазовая скорость с синусоидальной волны связаны соотношениями
(о) = £с). (10.4-42)
Xv = 4- = c.
(10.4-43)
Суперпозиция синусоидальных волн (42) в виде рядов Фурье или интегралов
Фурье образует более общие волны.
(Ь) Двух- или трехмерное волновое уравнение
1 д*ф
с2 dt*
:0
(10.4-44)
?2ф
допускает частные решения вида
ф(г, t) = <&k(r)e±i(ot (a> = kc), (10.4-45)
где <bk (r) — частное решение соответствующего уравнения Гельмгольца (22)
(пп. 10.4-4 и 10.4-5, b); k — произвольная константа разделения,
определяемая краевыми условиями. Решения вида (45) образуют решения, содержащие
действительные тригонометрические функции; в частности, отметим следующие
решения:
Ф (*> У у z; t)=aAcos [<ot чй (kxx + k2y + k3z) + y]
(k\ + k\ + k\ = k* <» = ьс)
(синусоидальные плоские волны, нормаль к фронту
которых имеет направление {kv k2, k3}),
Ф (р, Ф, г; t) = Zm (р У& - К2) cos (at + Кг + тф + у)
(т = 0, 1, 2, ... ; со = kc)
(синусоидальные цилиндрические волны),
Ф(г, 0, ф;/) = -^=- Zj+x/2(kr)Y(b, <p)coe(arf + V)
(/ = 0, 1, 2,...; (d = kc)
(синусоидальные сферические стоячие волны),
А
Ф (г, б, ф, t) = — cos (Ш +
(излучение точечного источника)
kr + y) |
гка), J
Ф (', 0, ф, t)=A (—- cos (mt + &r) + ~ sin (со/ + &r)l cos 0
(излучение диполя), I
Ф (/*, ф; 0 = Zm Фг) (a cos тф + Р sin тф) (а cos Ы + 6 sin atf) ^
(т = 0, 1, 2, ...; а)=&?)
(двумерные синусоидальные круговые стоячие волны). )
(10.4-46)
(10.4-47)
(10.4-48)
(10.4-49)
(10.4-50)
(10.4-51)
328 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.4-9.
Цилиндрические волны (47) распространяются в положительном и отрицательном
направлении оси Oz с фазовой скоростью с' = ы/К = kc/K, которая, как видно, зависит
от о и К (дисперсия). Групповая скорость в направлении оси Oz равна
did/dK = Kc/k.
(с) Общее одномерное затухающее волновое уравнение (телеграфное уравнение).
Уравнение передачи по линии
д*Ф д*Ф дФ _
(10.4-52)
Jkxest%
допускает частные решения вида
Ф (*. t) •■
где s » a -J- ш есть корень квадратного уравнения
a0s* + ats + (a2 + Л2) ■
(10.4-53)
.0. (10.4-54)
Комплексно сопряженные решения (53) образуют затухающие синусоидальные волны,
в смысле п. 9.4-6; в случае кратных корней уравнения (54) следует поступать так, как
в п. 9.4-1, Ь. Уравнение (52) включает уравнения (35) и (40) как частные случаи.
Аналогичные обобщения имеют место в многомерном случае.
10.4-9. Решение краевой задачи резложением в ортогональные ряды. Примеры (см.
также п. 10.5-3). Следующие примеры иллюстрируют применение частных решений,
приведенных в пп. 10.4-3— 10.4-8.
(а) Задача Дирихле для сферы (см, также пп. 10.4-3, с, 15.6-2, а и 15.6-6, с).
Требуется найти функцию Ф (г, б, <р), которая удовлетворяет уравнению
Лапласа у2Ф = 0 внутри данной сферы г < R и принимает заданные краевые значения
Ф (/?, в, ф) = Ь (б, ф) на сфере. Ясно, что следует применять сферические координаты г,
в, ф (п. 10.4-1, с).
Записываем неизвестную функцию в виде суммы решений (19), которые необходимо
конечны при г — 0 (J3 = 0);
со /
ф = Ф (г, G, ф) = ^j JVj r Pj (cos б) (afm cos тф -f- 0ym sin mq>y
/=0m=0
Неизвестные коэффициенты aym» 0ym вычисляются по заданным краевым условиям
Ф (R, б, Ф) = 2 2 * РТ (cos S) (aJ'm cos m<P + P/m sin m<P) = b (0. Ф)*
/=0m=0
Согласно условиям ортогональности п. 21.8-12
2я я
вуо*
w/m-
2/4-1 1
4я
-т С ^ф С 6 (б, ф) Pj (cos б) sin б d6,
2/4-l(/-m)! 1
2я
i dq>\b {В, q>) Pm (cos 6) cos /лф sin б dB,
2я (/ + m)! д/ .
0 0
2я я
p, = HL±i U-fn)\ ±_ p £/ф С 6 (в, ф) P™ (cos 6) sin /пф sin б dB
11 2я (/ + m)! d/ J 3 /
0 0
(/ = 0, 1, 2, . . .; m= 1, 2 /).
(10.4-55)
(b) Свободные колебания упругой струны (см. также п. 10.3-5).
Поперечные смещения Ф (х, t) упругой струны удовлетворяют одномерному волновому
уравнению
д*Ф _ 1 д*Ф>
дх* с* dt*
начальным условиям
дФ I
Ф (*, 0) :
и краевым условиям
= Фо(*),
dt / = 0
= v0 (х)
(0 < *< L)
Ф (°. 0 в фа (/>» ф <L» '> в ФЬ <'>•
10.5-1. 10.5. МЕТОД ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ 329
Рассмотрим частный случай Фа (t) — Фь (t) = 0. Стоячие волны (42) одномерного
волнового уравнения удовлетворяют заданным краевым условиям, когда Y2 =—я/2 и
половина длины волны Я/2 = Л/k целое число раз укладывается в длине струны L;
k =» -ц, (0 = kc =» -£- (я =s 0, 1 ,2, . . .).
Записываем решение в виде ряда из частных решений
л = 1
и определяем коэффициенты ап и &л из начальных условий, пользуясь формулами для
коэффициентов Фурье (п. 4.11-4, Ь):
L
2
о
L
Ji-5fSv»w-DTlto (« = 1.2,...).
о
Решение представляет сумму гармонических стоячих волн, возбужденных
заданными начальными условиями.
(с) Свободные колебания круглой мембраны. Поперечные
смещений Ф (г) мембраны, закрепленной по окружности г = 1, удовлетворяют волновому урав~
1 д2Ф
нению у*Ф j -^jT"я0 <r < l)t краевому условию Ф = 0приг=1и начальным условиям
дФ
Ф«Ф0(г), — =v0(r) при г = 0(г<1).
Применим полярные координаты г, <р. Так как Ф непрерывна при г^О, то образуем
суперпозицию решений (51), содержащих только функции Бесселя первого рода, т. е.
^m^kr^~Jm^kr^ ^n 21.8-I). Такие решения образуют характеристические колебания,
удовлетворяющие заданному краевому условию, если
k = — = ь (л, т = 0, 1, 2, . . .),
с тп * lit /t
где kmn есть л-й действительный положительный нуль функции J (£); эта задача есть
задача о собственных значениях.
Решение представляется в виде суммы характеристических колебаний
со оо
Ф (г. <р. О - 2 2 '* < W) <em» C°S m<P + Р»
ш = 0 л = 0
v /ял тп ' /ял /яп ''
где неизвестные коэффициенты определяются как обыкновенные коэффициенты Фурье
при подстановке заданных начальных условий.
10.5. МЕТОД ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
10.5-1. Общая теория (см. также пп. 8.2-1, 8.6-1, 9.3-7, 9.4-5, 10.4-2, с
и 15.4-12). Требуется найти решение Ф = Ф (xlt х2, ..., хп), удовлетворяющее
заданным краевым условиям действительного линейного дифференциального
уравнения с частными производными
дх% дхп
= /(**, ^, ..., хп), (10.5-1)
где L2 —линейный однородный дифференциальный оператор с производными
и коэффициентами, содержащими хъ х2, ..., хп_ъ но не хп.
330 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 10.5-2.
Для простоты примем хп изменяющимся в некотором ограниченном или
неограниченном интервале (а, Ь) для всех хъ х2, ..., xn-i так» что граница S
области решения состоит из двух координатных поверхностей (см. также
п. 10.4-1, с). Уравнение (1) можно часто упростить, применяя линейное
интегральное преобразование
Ь
ф(*1, *я. •••. хп-ъ s) = \К(хПУ s)y(xlt х2, ...txn)dxn. (10.5-2)
а
Если ядро преобразования К(хп, s) выбрано так, что
LfK(xni s) = ^(a0V--r-l<hK) + aEK=k(8)K. (Ю.5-3)
дхп дхп
(Lf —оператор, сопряженный с Lx (п. 14.4-3)), то интегрирование по частям
(обобщенная формула Грина, п. 15.4-3) приводит к возможно более простому
дифференциальному уравнению
\xn = b
Хп = а
— I \ХЪ x2t ..., Хп-Ъ s) — Р \ХЪ x2* •••» ХП> S)
Р (х19 х2, ..., хп; s) = ao (к^-фЩ + ^-а^ФК j
(10.5-4)
относительно неизвестной функции Ф (xlt x2, ..., xn_i, s), являющейся
интегральным преобразованием искомого решения. Заметим, что новое
дифференциальное уравнение включает в себя краевые значения Фи дФ/дхп, заданные для
х^ — а, хп — Ь и переменных х1у хъ ..., xn_v Метод интегрального
преобразования предполагает существование интегралов (2) и сходимость формулы
обращения
Э
Ф (*!, x2t ...,*„) = $ Я (xn, s) Ф (xlt х2у ..., xn_i, s) ds, (10.5-5)
а
(см. также п. 15.3-7). Табл. 8.6-1 на стр. 257 содержит некоторое число
употребительных интегральных преобразований и формул обращения.
Заметим, что в решениях преобразованного дифференциального уравнения (4)
константы интегрирования следует рассматривать как произвольные функции от s.
Метод интегральных прео5разований можно обобщить на дифференциальные
уравнения, содержащие производные высших порядков от х; кроме того, интегральное
преобразование можно применять по двум переменным х, х , одновременно. Если в
выражении Н (х s) допускается б-функция, то формула (5) может приводить к
разложениям в ряды для Ф в конечном интервале (а, Ь) (конечные интегральные
преобразования [8.5]).
10.5-2. Преобразование Лапласа по временной переменной (см. также пп.
8.2-1, 8.3-1, 9.3-7 и 9.4-5). Задача с начальными условиями для
гиперболических и параболических дифференциальных уравнений часто упрощается
введением одностороннего преобразования Лапласа
ф(*)=$ Ф(0в"в/Л,
о
которое преобразует каждое линейное дифференциальное уравнение с
частными производными с постоянными коэффициентами
V2® " "о "J£ - «1 ж - «аФ =/ (г, 0 (Ю.5-6)
10.5-3. Ю.5. МЕТОД ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИИ 331
в новое и, возможно, более простое дифференциальное уравнение
у2ф_(я052 + а15 + а2)Ф = /(г, 8)-[(вв8 + а1)Ф + авДв0+0 (10.5-7)
для неизвестного интегрального преобразования Ф (г, s) решения Ф (г, /).
Краевые условия преобразуются подобным же образом; заметим, что
уравнение (7) включает в себя заданные начальные условия.
10.5-3. Решение краевых задач методом интегральных преобразований. Примеры
(см. также п. 10.4-9). Следующие примеры иллюстрируют простейшие применения
интегральных преобразований к решению краевых задач (см. также [8.5]).
(а) Одномерное уравнение теплопроводности в случае
фиксированной температуры на концах: применение
преобразования Лапласа. Теорема Дюамеля (п. 10.5-4) сводит важный класс одномерных
задач теплопроводности к виду
Ф (*. 0 + 0) = Ф0 (х) (начальное условие),
Ф (a, t) = Ф = const, Ф (b, t) — Ф^ = const (t > 0) (краевые условия).
Дифференциальное уравнение преобразуется к виду
**£Д_£*Л ,,__£*« ia<x<b).
Если, в частности, Ф0 (х) = Ф0 = const, то
Ф (х, s) = Ct (s) ех У*/У + С8 (s) в" * V7/Y + 5t ,
s
где функции Ct (s) и С2 (s) должны быть выбраны так, чтобы выполнялись
преобразованные краевые условия
Ф Фи
Ф (х, t) получается как обратное преобразование Лапласа методами пп. 8.4-2 — 8.4-9.
х Vs
В частности, для а = 0, Ф =0, Ф0 = 0 имеем
Фь sh Y
Ф (х, s) = — Чт . Ф (х, t) = Ф
bVs
vb
sh
Y
^iJfc^rWWhlnf
/=1
Заметим, что эта задача может быть решена методом п. 10.4-9.
еплопроводности
ниесинус-и коси]
ке применимы, если а —
д*Ф (х, t) 1 дФ (х, г)
(Ь) Задача теплопроводности в случае бесконечного
интервала. Применениесинус-и косину с-п реобразованнй Фурье.
Методы п. 10.5-3, а также применимы, если а = 0, b = со:
—а* у* —ы—=° <*>»•.'> о).
Ф (х, 0 + 0) = Ф0 (х) (х > 0) (начальное условие)*
Ф (0. t) « Фа (О,
со
f | Ф (х, t) |2 dx существует
Применяя синус-преобразование Фурье
(t > 0) (краевые условия)»
Ф (s, t) =r у — \ ф (х, t) sin s* dx
0
(п. 4.11-3), можно, как в п. 4.11-5, с, получить преобразованное дифференциальное
уравнение _
1 дФ (s, О , ,-=- .. т/2 _ ,,.
-,—^-£+1»Фв(.. t)=y -вФа«)
332 ГЛ. 10. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ Ю.5-4
и преобразованное начальное условие Ф (s, 0 -f 0) = Фо (s). Преобразованная задача
имеет решение
Ф (s. /) - Ф0 (s) е" y2s2t + У~ y2s $ Фа (О *- Y8s2 « -т> dx.
откуда
ф (х, t) = у $- \ Ф (s, 0 sin s* ds.
Если, в частности, задано Ф (t) = const « Ф и Ф0 (д:) ==з 0, то <Dft (s)=0h
Ф (s, 0 = Ф
1 _ е- У2*4
Vh Ф<*.<> = Фа(>-ег .-JL-).
Если задано краевое условие
дФ (х, t)
дх \х = 0 + 0 "
(теплоизолированный конец), то применяется косинус-преобразование Фурье
V>0)
Ф (s, t) = 1/ — \ ф (*, /) cos s* dx.
10.5-4. Формулы Дюамеля (см. также п. 9.4-3).
(а) Пусть U —однородный линейный оператор с производными и
коэффициентами, не содержащими переменную t. Пусть Ф(*, /) есть решение задачи
с начальными и краевыми условиями
1Ф + А0(х)д-^- + Аг(х)д-£==0 (0<*<L; />0),
ф(лг, 0 + 0) = 0, ^|0 + 0 = 0 (0<*<L),
а^ + Рф = М0
(* = 0, />0),
(10.5-8)
и пусть ¥(*, £) —решение этой задачи для b(t) = \ (/>0). Тогда
t t
Ф(*, t) = V(x, t)b(0 + 0)+\ ¥(*, t-x)b'(%)d% = ^T\^(xt t-x)b(T)dx
о о
(0<x<L; />0).
(b) Решение Ф (г, t) общего уравнения диффузии
V tk (г) V] Ф + а (г) Ф - ^ —■ = f (г, t) (reV, t> 0),
Ф (г, 0) = Ф0 (г) (г е V), } (10.5-10)
(10.5-9)
дФ
а -~ + ЭФ = b (г, О
(res, />0)
с зависящими от времени возмущающей функцией f (r, t) и краевым условием b (r, t)
связано с решением 4f (г, /; А,) более простой задачи
1 дФ
V-[*(r)v]V+a(r)V- ^-^=Пг, Я) (reV, *>0),
W (г. 0; Я) = Ф0 (г) (г е V),
(res, />0),
(10.5-11)
где f (г, К) н b (г. А,) зависят от параметра Я и не зависят от времени t. Решение Ф (г, t)
получаем из формулы
Ф (г, t) = ~ [у (г, / - Ь; К) dK. (10.5-12)
ГЛАВА 11
МАКСИМУМЫ И МИНИМУМЫ
1Ы. ВВОДНЫЕ ЗАМЕЧАНИЯ
Очень широкий класс задач составляют экстремальные задачи, в которых
требуется найти значения параметров или функций, реализующих максимум
или минимум некоторой зависящей от них величины. Во многих инженерных
задачах, например, желательно найти максимум меры выполнения или минимум
стоимости. Кроме того, можно по крайней мере приблизить решения многих
задач, выбрав неизвестные значения параметров или функций так, чтобы они
давали минимум ошибки в пробных решениях; иногда такой прием позволяет
применить для решения данной задачи мощные методы численных приближений.
Примеры: решение задач о собственных значениях в теории колебаний и
квантовой механике (пп. 16.4-7 и 15. 4-8, Ь); принципы Гамильтона и Якоби в динамике.
11.2 ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
11.2-1. Локальные максимумы и минимумы (см. также п. 4.3-3).
Действительная функция f (*), определенная при х = а, имеет в точке а (локальный)
максимум или (локальный) минимум /(а), если существует такое
положительное число 6, что при всех Ах = х — а, для которых выполняются неравенства
О < | А* | < 6 и существует значение / (а+Адг), соответственно г)
Д/ = /(а+Д*)-/(а)<0
или
Д/ = /(а + Д*)-/(а)>0.
Если в каждом из этих случаев выполняются нестрогие неравенства (^ или ^), то
говорят, что функция f (x) имеет в точке а нестрогий максимум (минимум).
Локальный максимум (минимум) называется внутренним максимумом
(внутренним минимумом) или граничным максимумом (граничным минимумом),
если соответственно точка а является внутренней точкой или граничной точкой
области определения функции f(x) (п. 4.3-6, а)2).
11.2-2. Условия существования внутренних максимумов и минимумов.
(a) Если существует производная f (а), то функция f (x) может иметь
в точке а внутренний максимум или минимум лишь в том случае, когда
при * = а
Г(а) = 0 (11.2-1)
(необходимое условие экстремума).
(b) Если существует вторая производная f" (а), то функция f (x) имеет
в точке а
максимум при f (а) = 0 и /" (а) < О,
минимум при f (а) = 0 и /" (а) > 0.
») Af есть приращение- данной функции f (х), соответствующее приращению А*
независимого переменного х. Приращение Af есть функция от а и от Аде; его не следует
смешивать с вариацией 6f, вводимой в п. 11.4-1.
2) В формулировке задачи должна быть точно указана область определения функции
f (х). Например, функция ft (x) — х (— оо < х < + оо) не имеет максимума, а функция
ft (х) = х (х ^ 1) имеет при х = 1 граничный максимум.
334
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.3-1.
(с) Более общее утверждение: если существует производная f(n) (а) и если
f (а)=/"(а) = ...=/<я-1> (а) = 0, то функция f(x) имеет в точке а
максимум при п четном и /(л) (а) <0,
минимум при п четном и /(л,(а)>0.
Если п нечетно, то функция f (х) в точке а не имеет ни минимума,
ни максимума, а имеет точку перегиба (п. 17.1-5).
(Условия, сформулированные в b и с, являются достаточными условиями
экстремума.) Если /' (а) = 0, то во всех случаях говорят, что функция f(x)
при х=а имеет стационарное значение.
Примеры. Каждая из функций х2. дг4, хЛ, . . . имеет при х = 0 минимум, а каждая
из функций x*t jc5, х7, . . . имеет х = О точкой перегиба.
11.3. ЭКСТРЕМУМЫ ФУНКЦИЙ ДВУХ И БОЛЬШЕГО ЧИСЛА
ДЕЙСТВИТЕЛЬНЫХ ПЕРЕМЕННЫХ
11.3-1. Локальные максимумы и минимумы1). Действительная функция
/C*i, х2,..., хп)> определенная при xt = av я2 = а2,..., хп = ал, имеет в точке
(#i> а2, ..., ал) (локальный) максимум или (локальный) минимум f(av а2,..., ап),
если существует такое положительное число 6, что при всех А*!, А*2, •».» А*л.
для которых выполняются неравенства 0 < ]/*A*f + Д*| +... + Д*л < 6 и
существует значение /(ях+Д*!, а2 + Д*2, ..., ал + Д*л), приращение функции
А/==/(<*! +А*!, а2 + Д*2,..., ал + Д*л) —f(alt а2,..., ал), (11.3-1)
соответственно меньше нуля или больше нуля. Локальный максимум (минимум)
называется внутренним максимумом (внутренним минимумом) или граничным
максимумом (граничным минимумом), если точка (alt a2,..., ап) является
соответственно внутренней точкой или граничной точкой области определения
функции /(*!, х2, ..., хп) (п. 4.3-6, а).
Определение строгого и нестрогого экстремума аналогично п. 11.2-1.
11.3-2. Формула Тейлора для приращения функции. Приращение функции
А/, определяемое соотношением (1), является функцией от ах, а2,..., ап и
от A*x, Д*2,..., Д*л. Если функция f(xv x2,..., хп) имеет в некоторой
окрестности точки (alt a2,..., ап) непрерывные частные производные до второго
порядка включительно, то
а/=Е^
«=1
Axt+
ап)
+■
п п
JL V V d2f
2 Zl Zj дх. дх.
i = \ k=l l R
Алг;Д** + о(р2), (11.3-2)
(ai. % ..., an)
где p = VA*f + Д*| +... -j- Ax% (локальная формула Тейлора, см. п. 4.10-5). Члены
порядка 1 и 2 относительно Дд^ в этой формуле соответственно составляют
первый дифференциал df и половину второго дифференциала d2f функции
/(*i. *2» •••» хп) в точке (а1% а2,..., ап) (см. также п. 4.5-3, Ь).
11.3-3. Условия существования внутренних максимумов и минимумов.
(а) Если функция f(xlt x2,..., хп) дифференцируема в точке (alt a2, ..., ап),
то она может иметь в точке \ах% а2>..., ап) внутренний максимум или минимум
') См. сноски к п. 11.2-1.
П.3-4. н.э. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ 335
лишь в том случае, когда ее первый дифференциал df обращается в этой точке
в нуль, т. е. когда
-^ — 0 -^- — 0 ^- — 0 т 1-Ъ
дхх —и' ад:2 —и' ••"' д*л кп.бб)
при xt = av x2 — a2i..., *л = ял (необходимые условия экстремума),
(Ь) Если функция f (х1у х2, ..., хп) имеет в некоторой окрестности точки
(alt а2,..., ап) непрерывные вторые частные производные и если в этой точке
выполняются необходимые условия (3), то в случае, когда второй дифференциал
«2/=2 2
d*f
дх, дх.
*—1А=1 ' k
bxfixk (11.3-4)
ап)
есть отрицательно определенная квадратичная форма (п. 13.5-2), функция
!(хц х2, ..., *л) имеет в точке (а1% а2,..., ал) максимум, а в случае, когда
этот дифференциал есть положительно определенная квадратичная форма,
функция f(xlt x2t..., хп) имеет в этой точке минимум (достаточные условия
экстремума).
Если условия (3) выполняются в точке (av a2,..., ал), то во всех случаях
говорят, что функция f (xlt x2,..., хп) имеет в этой точке стационарное значение;
сама точка называется стационарной.
Пример. Найти максимумы и минимумы функции
г == Злг» — х + у* — Ъу* — 1.
Необходимые условия
g = 9*3-l=0 и 1=3^-6^ = 0
удовлетворяются здесь при
*=1/3, 0 = 0; jc = — 1/3, 0с=О; *=1/3, # = 2; * = —1/3, у = 2.
Но, рассматривая характеристическое уравнение квадратичной формы (4) (см. пп. 13.4-5
и 13.5-6)
(18* — ц) (6^ —6 —[А) = 0,
видим, что единственными экстремальными значениями являются максимум (ц* — — 6,
jn2 = — 6) z — — 7/9 при * = — 1/3 и у = 0 и минимум (fXi =6, jx2 =6) z =— 47/9 при
*= i/з и 0 = 2.
(с) Если первый дифференциал df достаточное число раз непрерывно
дифференцируемой функции f (xv x2t ,,м хп) обращается в точке (а^ а^ ,,м ад) в нуль, а второй
дифференциал d2f есть полуопределенная квадратичная форма (п. 13.5-2), то характер
стационарного значения зависит от дифференциалов более высокого порядка. Если же
dzf есть неопределенная форма, то функция f (х~ *2> ., #f хп) не имеет в точке (ах> о2>.. м ап)
ни максимума, ни минимума.
Если из уравнений (3) получена система значений х1 <= alf x2~a2t ..., хп~ат т0
характер квадратичной формы (4) можно определить любым из методов, перечисленных
в п. 13.5-6. Можно также исследовать функцию на максимум и минимум, фактически
рычислив значения f (ol + Д*- a„ + Д*2> t# #f a + &хп) Для разумным образом выбранных
комбинаций приращений Д*1? Д*2> ,,м Д*л.
11.3-4. Условные экстремумы. Метод множителей Лагранжа. Максимумы
и минимумы действительной функции f (xlt х2, ..., хп) переменных xv x2, ..., хп,
подчиненных достаточно гладким дополнительным условиям в виде т < п
уравнений связи
<Pi(*i» *2»---» хп) = 0, (р2(хг, *2. •••, *л) = 0,..., фт (ДС1, лг2,..., *л) = °. (Н.3-5)
в принципе можно найти по способу п. 11.3-3, исключив т из п переменных
*и х2,..., хп с помощью уравнений (5). Если непосредственное исключение
336
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.3-5.
т переменных невозможно или нецелесообразно, то применяют следующее
необходимое условие максимума или минимума функции при ограничениях (5):
**-«*...= **=<), (11.3-6)
dxt дхг д*п
где
т
Ф(*1. *2. ••.. *л)=/(*1» *2> .... */*) + 2 */Ф/(*1» *«»••" *«)•
m параметров Xj называются множителями Лагранжа; п + т неизвестных
xi — ai и Xj находят из п+т уравнений (5) и (6).
Заметим, что уравнения (6) представляют собой необходимые условия экстремума
функции Ф (xi, x2 хп), если xlt x2, .... хп считать независимыми переменными.
Пример. Найти стороны прямоугольника максимальной площади, вписанного
в окружность:
*2 _|_ у2 = Г2.
Площадь А прямоугольника можно записать в виде
А = 4ху.
Тогда
Ф (х, у) = 4ху + к (*« + у* - г2).
Необходимые условия экстремума дают
дФ дФ
так что искомый максимум дают значения К — — 2 и * = # = г/У2.
11.3-5. Численные методы. Если, как это часто бывает, при отыскании
максимумов и минимумов функций многих переменных получают сложную
систему уравнений или если явное дифференцирование затруднено или
невозможно, то экстремумы находятся при помощи последовательного применения
метода проб. Некоторые важные численные методы для решения такого рода
задач описаны в пп. 20.2-6 и 20.3-2.
11.4. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ, ИГРЫ
И СМЕЖНЫЕ ВОПРОСЫ
11.4-1. Задача линейного программирования.
(а) Постановка задачи. Задача линейного программирования
заключается в нахождении г переменных Xlt X2t..., Хп минимизирующих
данную линейную функцию (целевую функцию)
z = F(Xlt X2,..., Хг)эСА + СА + ... + СЛ (11.4-1а)
(или максимизирующую — г) при линейных ограничениях-равенствах
aiiX1 + aitX2 + ... + airXr=Ai (t = l, 2,..., п) (ПАЛЬ)
и линейных ограничениях-неравенствах
Aj1X1 + Aj2X2 + ...+AjrXr^Bj (/ = 1, 2, ..., m). (11.4-lc)
Заметим, что не каждая задача указанного типа имеет решение. Рис. 11.4-1
иллюстрирует один простой пример.
В типичных приложениях это — задача о нахождении необходимо положительных
величин Хи Х2, ...» Хп т. е. г видов сырьевых материалов («входные» данные), мини-
11.4-1. 11.4. ЛИНЕЙНОЕ ПРОГРАММИРОВ., ИГРЫ И СМЕЖНЫЕ ВОПРОСЫ
мизирующих общую стоимость F (Хи Х2 Xr) (la) соответствующих величин т
«выходных» продуктов
q{ssAilXl + Ai2X2 + u„ + AirXr </- 1, 2 т)
с нижними уровнями Ви Вг, .... Вт. Имея в виду г условий Xk ^ 0 (k— 1, 2, ..., г) и
m ограничений qi>B^ (С = 1, 2 т), мы получаем п — г-{-т ограничений-неравенств.
Большое количество примеров, рассмотрено в [11.1], [11.2].
Рис. 11.4-1. Множество решений а) на плоскости (Xlt Х2), и Ь) в пространстве (xlt x2, х3)
для задачи линейного программирования
z = ЪХХ + 2Х8 = min
при условиях
*t = Xt ^ 0, хг = Х2 > 0, *3 = 5Xi + Х2 — 5 ^ О
или
z = 3*! + 2лг2 = min
при условиях
5** + *2 — *з = 5, xt > 0, *2 > 0, *$ > 0.
(b) Задача линейного программирования в стандартной форме. Допустимые
решения. Задача линейного программирования, сформулированная в п. 1,
может быть путем введения в случае необходимости вспомогательных
переменных сведена к стандартной форме (основная задача линейного
программирования):
Требуется минимизировать целевую функцию
z=f(xv х2,..., xn)ssc1x1 + c^ct + ... + cnxn (11.4-2а)
при т<.п линейных ограничениях-равенствах
^iiXi + ai2x2 + ... + ainxn = bi (i = l, 2,..., т) (11.4-26)
и п линейных ограничениях-неравенствах
xk^0 (£=1, 2,..., /г). (11.4-2с)
Допустимое решение (план) задачи линейного программирования, данной
в стандартной форме, есть упорядоченное множество чисел (xv x2,..., хп),
удовлетворяющих ограничениям (2Ь) и (2с); это — точка в л-мерном пространстве.
338 ГЛ. Н. МАКСИМУМЫ И МИНИМУМЫ п.4-1.
Допустимое решение, минимизирующее целевую функцию (2а), называется
оптимальным решением (оптимальным планом).
Чаще всего оптимальное решение, если оно существует, единственно*
однако возможны случаи, когда оптимальных решений бесчисленное множество.
Для существования допустимого решения необходимо (но не достаточно!),
чтобы система (2Ь) была совместна. В дальнейшем считается, что это
выполняется; ранг матрицы системы г^т<п. Тогда г линейно независимых
уравнений системы (2Ь) определяют некоторые г неизвестных как линейные
функции остальных /г— г неизвестных—свободных неизвестных (см. п. 1.9-4).
Фактически выражая все переменные через свободные неизвестные, можно
прийти к задаче линейного программирования, содержащей п—r переменных
и п линейных ограничений-неравенств, выражающих неотрицательность
исходных п переменных.
Допустимое решение, соответствующее нулевым значениям свободных
неизвестных, называется базисным допустимым решением (опорным планом),
невырожденным, если все остальные переменные положительны, и
вырожденным, если среди них есть хоть одно нулевое.
Если существует какое-либо допустимое решение для задачи линейного
программирования, то существует и базисное допустимое решение. Если, кроме
того, целевая функция имеет нижнюю границу на множестве решений, т. е.
существует оптимальное решение, то существует и оптимальное базисное
решение.
Множество всех допустимых решений данной задачи линейного
программирования есть выпуклое множество в /г-мерном пространстве решений; это
значит, что каждая точка (glf £2, •••» £л) прямолинейного отрезка,
соединяющего два допустимых решения \х1% *2,..., хп) и (*'ь х'ъ •.., х'пУ-
lk = *Xk + (l-*)x'k (0^а-^1; *=1, 2,..., п)
см. также п. 3.1-7), есть также допустимое решение.
Более точно, множество допустимых решений есть выпуклый
многоугольник или многогранник в плоскости или гиперплоскости, определяемый
уравнениями (2Ь) с граничными линиями, плоскостями или гиперплоскостями (2с),
как это указано в простом примере на рис. 11.4-1, Ь.
Если существует конечное оптимальное решение, то задача линейного
программирования либо имеет единственное оптимальное решение в одной из
вершин многогранника решений, либо минимальное значение z достигается на
всем выпуклом множестве, порождаемом двумя или более вершинами
(вырожденное решение).
(с) Двойственность. Задача минимизации
z=F(Xlt Х2,..., Xr) = C1X1 + C2X2 + ... + CrXr=mm
с ограничениями
AtlX1 + AbX% + ... + AirXr-Bi^O (t = l, 2,..., m),
Xk^0 (*=1, 2,..., r)
и соответствующая задача максимизации
*> = G(Yl9 К2,..., Y„J-B1Yl + B%Y% + ... + BmYm = max
с ограничениями
AikYi + A*kYt + ... + AmkYm-Ck^O (Л = 1, 2,..., г),
Г^О (i=l, 2,..., т)
называются двойственными задачами линейного программирования.
Если одна из задач (3) или (4) имеет конечное оптимальное решение, то
то же имеет место для второй задачи, причем
mine = maxi0. (11.4-5)
(11.4-3)
(11.4-4)
11.4-2. 11.4. ЛИНЕЙНОЕ ПРОГРАММИРОВ., ИГРЫ И СМЕЖНЫЕ ВОПРОСЫ 339
Если одна из задач имеет неограниченное решение, то вторая задача не имеет
допустимых решений.
Теорема двойственности позволяет заменить данную задачу линейного
программирования другой, имеющей меньшее количество неизвестных или
меньшее количество ограничений-неравенств, и поэтому используется в
некоторых численных методах решений.
11.4-2. * Симплекс-метод.
(a) Задачи линейного программирования могут быть решены численными
методами наискорейшего спуска, указанными в п. 20.2-6, однако симплекс-
метод извлекает выгоду из линейности выражений (1) и (2).
В дальнейшем предполагается, что система уравнений (2Ь) линейно
независима, т. е. что г = т. Если решение задачи линейного программирования
существует, то оно достигается в одной из вершин многогранника решений;
последние могут быть найдены совместным решением т линейных уравнений
(26) и каких-то п — т уравнений *£ = 0. Очевидно, что при большом числе
переменных и ограничений этот процесс практически неосуществим ввиду
крайне большого числа возможных вершин многогранника решений; симплекс-
метод доставляет вычислительную схему перехода от вершины к вершине
(от одного базисного решения к другому) в направлении наименьшего значения 2.
(b) Применение симплекс-метода начинается с выбора какого-либо
допустимого базисного решения. В принципе это можно сделать так: выбираются
п—т свободных переменных (свободных неизвестных), а остальные т
переменных (базисные переменные) с помощью последовательного исключения
переменных (п. 1.9-1 и 20.3-1) выражаются через них. Если базисные
переменные обозначены через хъ х2,..., хт, то уравнения (2а) и (26) в
результате исключения могут быть записаны в следующей канонической форме:
х\ + (а1, т+1хт+1 + • • • + ainxn) — Pi»
х2 + (а2, m+ixm+i + • • • + а2пхп) — Рг»
хт + (ат, т+1хт+1 + • • • + атпхп) = Рт»
* = (Ym+l*m+l + • • • + Упхп) + *о-
Если все $( неотрицательны, то
Чо' •=1\2,,"',Г; с-4-7>
^ 0, i = m+l, т + 2, ..., п
образуют базисное допустимое решение.
Произведенный выбор свободных и базисных переменных далеко не
очевиден; процедура, облегчающая выбор начального решения, будет описана в (d).
Если в выражении для целевой функции z в (6) все у* неотрицательны,
то решение (7) есть оптимальное решение (никакое допустимое изменение
свободных переменных не может уменьшить z). Это оптимальное решение
единственно, если все yk положительны.
(c) Рассмотрим теперь случай, когда решение (7) является невырожденным
базисным допустимым решением (т. е. plf р2, ..., рт>0, см. п. 11.4-1),
которое не оптимально, т. е. среди ул естъ отрицательные.
Пусть, для определенности, Y/c"~наибольшее по абсолютной величине
из отрицательных yk. Для получения улучшенного базисного допустимого
решения в следующий итерационный цикл в качестве базисной переменной
вводится хк, заменяющее предшествующую базисную переменную xIt которая
в соответствии с уравнениями
xi = $i-<*iKxK (/ = 1, 2, ..., m)
(11.4-6)
первой убывает до нуля, когда хк возрастает от нулевого значения (это
340
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.4-2.
возможно тогда, когда среди aiK есть положительные). Значит, индекс /
ассоциируется с наименьшей возможной величиной (обязательно положительной)
К а1К-
Улучшенное базисное решение дается равенством (8а) и
$i~~aiKxK^® (*=!» 2» •••» m» заметим, что *7=0),
(i = m+l, m + 2, ..., п, 1ФК).
.-{.
'"Ю
При этом
Теперь введение
(11.4-8я)
(11.4-86)
*e «e+Vjrtc- го+УкТ^ < V
*«,=
Э/
а//С а1К
(11.4-9)
в систему (6) приводит ее к канонической форме относительно новых базисных
переменных.
Замечание. Симплекс-метод не реализуем, если все aJK
неположительны] тогда целевая функция г не имеет нижней границы на множестве
решений.
Полный симплекс-алгоритм можно удобным образом табулировать в виде
симплекс-таблицы и осуществить с помощью электронных вычислительных
машин; обычно оптимальное решение достигается за конечное число шагов.
Минимальное ,
допустимое '
решение ,
' / 2 3 4 ^6/7 8
Рис. 11.4-2. Множество решений в пространстве (Xtt -^2).
Если в процессе вычислений базисные переменные соответствуют выро-
ждающемуся базисному допустимому решению (т, е, одна из базисных
переменных возвращается к нулевому значению, см. п. 11.4-1, Ь), дальнейшее уточнение
значения целевой функции, в принципе, прекращается; однако в практических
задачах это встречается редко.
Можно распространить симплекс-метод на случаи вырождения посредством
малых изменений данных коэффициентов (метод возмущений).
Пример (рис. 11.4-2). Задача минимизации функции
z = ~ Xt+-g ХЛ
11.4-2. Ц.4 ЛИНЕЙНОЕ ПРОГРАММИРОВ., ИГРЫ И СМЕЖНЫЕ ВОПРОСЫ 341
с, ограничениями-неравенствами
5Х1 + Х2 — 5^0, *i>0.
2Х!-|-5Х2 — 10^0, Х»>0
путем введения вспомогательных переменных
xl = Xl, x2=5Xi + X2-5, x$=2Xt + bX2-lO, *4 = *i
преобразуется к стандартной форме
z~=—*1 + --*4=т1п,
5*i — х 2 + *4 = 5,
2*i — *s + 5jc4 = 10,
*1, *2, *3, *4>0.
Отправляясь от *i и *2 как базисных переменных (первая вершина справа на
рис. 11.4-2), получаем каноническую форму задачи:
1 5
*i — -J ^з + -2"^4 = 5>0.
*2-|-*3 + f *4 = 20>0,
24z = 3*3 —7*4 + 30.
Коэффициент при *4 в последнем выражении отрицателен, целевая функция убывает
при возрастании *4. При этом возрастании первой обращается в нуль переменная х2.
Таким образом, *4 заменяет базисную переменную *2, д = 4, / = 2 и
20 40 15 _
^^-гТ^-гз"' *1 = ^з~« *2-*,-о.
2
Новая каноническая форма задачи относительно хх, *4 есть
5 1 _ 15
Д:1~23ДГ2Н"23ДГз~23>0'
.2 5 40
*4+2~3*2~~23 *3==23>0'
12- 23z = 7*2 +17*з + 205.
В целевой функции коэффициенты при свободных переменных *2, *3 положительны;
значит, получено единственное оптимальное решение
__ 205 205
2min— 12. гз^ 276*
(d) Использование искусственных переменных для начала
симплекс-процедуры. Симплекс-метод, как описано, предполагает, что подходящий выбор
начальных базисных переменных xlt х2, ..., хт образует некоторое базисное
допустимое решение с plf р2, •••» Рт^О-
Указанный выбор не очевиден. Нижеследующая процедура может быть
применена для начала решения; она же позволяет установить существование
допустимых решений.
Рассмотрим задачу линейного программирования в стандартной форме (2)
и будем считать, что уравнения (2Ь) записаны так, что все 6/^0. Введем т
искусственных переменных хп+1, хп+2, ..., хп+т и решим вспомогательную
задачу о минимизации линейной формы
«'=в*я+1+*я+2 + -••+*«+»! (11.4-10а)
при условиях
апхг + а12х2 +... + а1пхп + *я+1 = Ьг ^ 0,
021*1 + <*22*2 + ... + С12пХп + Хп+2 = Ь2 ^ 0,
^тгЧ + 0^2*2 +... + атпхп+хп+т = Ьт ^ 0,
xk^0 (6=1, 2, ..., п+т).
(11.4-106)
342
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.4-3.
Принимая хъ х2, ..., хп за свободные переменные, a xn+i, *л+§, ..., хп+т —
за базисные, получаем базисное допустимое решение вспомогательной задачи:
xi = 0 для l^i^n и xn+J—bj для 1^/^m. Применяя симплекс-метод,
находим оптимальное решение вспомогательной задачи. Если это решение
таково, что wmin = 0, т. е. все хп+1, ..., хп+т равны нулю, то оно определяет
допустимое решение исходной задачи. Если же для оптимального решения
t<ymin>0, то исходная задача не имеет допустимых решений.
11.4-3. Нелинейное программирование. Теорема Куна — Такера. Если
линейная целевая функция и/или одно или более линейных ограничений в задаче
линейного программирования (1) заменены нелинейными относительно
переменных Xk, то имеет место задача нелинейного программирования. Такая задача
возникает, например, если границы множества решений и/или линии уровня г
на рис. 11.4-1, а заменены кривыми.
Задачи нелинейного программирования представляют практический
интерес, но, за малым исключением, поддаются лишь численным методам решения
(п. 20.2-6).
Необходичое (но не достаточное) условие максимума функции
2 = /^, *2,
*п)
(11.4-11)
при условиях-неравенствах
хп)^0 (/=1,2,
т)
заключается в существовании т +1 неотрицательных множителей Лагранжа
Я0, А*, ..., %т (см. п. 11.3-4), не равных одновременно нулю и таких, что
%i^0 (i = 0, l, ..., го),
МР/ = 0 (i = 1, 2, ..., m),
л- tn л
*«^+2>Ж- = 0 <*-1. 2,..., и).
k i = i k
(11.4-12a)
{Теорема Ф. Джона; функции / и cpt- предполагаются дифференцируемыми.)
В условиях (12а) Х0 положительно и может считаться равным единице всякий
раз, когда существуют п действительных чисел (уъ у2, ..., уп) таких, что
для рассматриваемых значений xv x2, ..., хп
дЦ>1
2
k=i
t = l, 2,
ЩУ*
т
*^0, если ipi— линейная
функция в некоторой окрестности
(*i. *2> •••» хп)>
<0 в остальных случаях
(11.4-126)
(формулировка Эйбеди теоремы Куна —Такера).
11.4-4. Введение в конечные игры двух партнеров с нулевой суммой.
(а) Игры с чистыми стратегиями. Конечная игра двух
партнеров с нулевой суммой есть модель конфликтной ситуации, характеризуемой
конечной матрицей выигрышей
ап а12 ... а1т
021 а22 ••• а2Ш
(11.4-13)
. ап\ ап2 • • • ап\
где а^ —(положительные или отрицательные) выигрыши игрока А у игрока В,
если А выбирает t-ю из п чистых стратегий Slt S2, ..., Sn, удобных для
него, а В выбирает k-ю из т чистых стратегий Sj, Sg, ..., S'm, возможных
для него. Ни один из игроков не знает выбора другого.
П.4-4. Ц.4. ЛИНЕЙНОЕ ПРОГРАММИРОВ., ИГРЫ И СМЕЖНЫЕ ВОПРОСЫ
Заметим, что сумма выигрышей обоих игроков равна нулю при каждом
ходе (отсюда и название —игра с нулевой суммой). Игра симметрична, когда
т — п и аы^х—аиг для всех t, k.
Для выигрыша максимизирующий игрок А выбирает f-ю строку матрицы
выигрышей с тем, чтобы максимизировать min a^, тогда как минимизирующий
k
игрок В должен минимизировать max a^. Для каждой заданной матрицы (13)
i
max min а\ь ^ min max a^. (11.4-14)
ik k i
Если обе величины в (14) равны для (не обязательно единственной) пары
i = /, k = K> то говорят, что игра имеет седловую точку или решение /, К
и (единственную) цену aJK.
Оптимальные стратегии для такой игры не имеют смысла, если игрок А
знает предстоящий ход J5, и обратно.
(Ь) Игры со смешанными стратегиями. Смешанные стратегии определяются
с помощью вероятностей (п. 18.2-2) р1% р2, -.., рл, приписываемых игроком А
его п возможным стратегиям Sv S2, ..., Sn, и вероятностей р[, р'2, ...., р'т%
приписываемых игроком В его стратегиям S[, S^, ~ч Sm
п т \
./=1 / = 1 /
В игре со смешанными стратегиями А стремится максимизировать минимум
математического ожидания (п. 18.3-3)
п т
, min ,22 aikPtPk
Р\,Р2 Рщ iz==l *=1
посредством выбора plt p2» •••» Рл» тогда как В стремится минимизировать
п т
max ^ 2 WiP'k
pvp2 Pni = ik = i
путем выбора р\, р'2, ..., р'т.
Для любой заданной матрицы выигрышей (13)
max I min 2 § aikpiP'k\=*
PV P2 pnLp\. P2 pm / = 1 * = 1 J
Г n m 1
= min max 2 2 <W^6 (П.4-15)
pj. P2 PmLPV p2 Pni = lk = \ J
(теорема минимакса для конечной игры двух партнеров с нулевой суммой
выигрыша). Общая величина (15) называется ценой v игры.
Каждая конечная игра двух партнеров с нулевой суммой имеет по меньшей
мере одно решение, определяемое оптимальными стратегиями plt p2, ..., рп\
P'v P* •••' Р'т-
Возможны и несколько решений, но цена игры необходимо единственна.
Безобидная игра двух партнеров с нулевой суммой имеет цену, равную нулю.
Пример. Известная игра «герб-решка» имеет матрицу выигрышей
344
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.5-1.
в которой стратегия 1 для каждого игрока есть решка-герб, а стратегия 2 — герб -решка.
Игра симметричная, безобидная и не имеет седловых точек.
Решение: р1=р^ = 1/2, р2=^=1/2.
(с) Связь с линейным программированием. Игры со
смешанными стратегиями привели к развитию некоторых приближенных методов,
однако наиболее важные приложения связаны с линейным программированием.
Решение данной матричной игры не изменяется от прибавления ко всем а^
одной и той же положительной константы а, так что не будет ограничением
рассматривать игры с положительной ценой v > 0. В этом случае
оптимальные стратегии р±, р2, ..., рп и pj, p'2, ..., р'т и цена v конечной игры двух
партнеров с нулевой суммой с заданной матрицей выигрышей (13) есть
Pi = vXi (/=1, 2 п),
p'k=*vYk (* —1, 2, ..., m),
о-:1
'min
(И.4-16)
е^е emin» ^max» ^i* * k определяются как решения двойственных задач
линейного программирования (п. 11,4-1):
2 = X1 + X2 + ... + X„ = min
с ограничениями
%Л + я2А + ." + ялА^1 № = 1, 2, ..., т)%
Xt^O (i = l, 2, ..., л),
w=Y1+Y2 + ...+ Ym = max
с ограничениями
<4iYi + abYt + ... + almYm^l (i = l, 2 п)(
Yk^0 (fc=l, 2, ..., m).
11.5. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ. МАКСИМУМЫ И МИНИМУМЫ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
11.5-1. Вариации.
(a) Вариация ду функции у (х) переменного х есть функция от х,
определяемая при каждом значении х как разность ду зз Y (х)—-у (х) новой
функции Y (х) и функции у (х).
Вариацию ду, вызывающую изменение функционального отношения между
у и х, не следует смешивать с приращением Ку значения данной функции у(х),
вызываемым приращением Ах независимого переменного х (п. 11.2-1).
(b) Если дана функция F[yx (*), у2 (*)> ..., уп (х)\ х], то ее приращение,
соответствующее вариациям дуъ ду2, ..., дуп функций уг(х), у2(х), ...» Уп(х)>
есть
AFaF^+J^, #2+fy/2, ..., Уп+ЬУп\ x)—F(ylt уъ ..., */л; *). (11.5-1)
Если функции у (х) и 6# дифференцируемы, то вариация ду' производной
у' (*), вызываемая вариацией ду, есть
ду' в б g я £ (6*/) в У (*) - */' (*). (11.5-2)
Если дана функция F [*/,(*), у2(х), ..., */„ (*); */,' (*), у£ (*), —. Ул (*)*. *Ь
то ее приращение, соответствующее вариациям 6^, ду2, ..., дуП1 есть
AF^F(y1 + dy11 уъ + Ъуг> ..., Уп + ЬУп\ yl + fyl, У'* + Щ, •••» 0п + ^л*. *> ""
— ^(^1. %» •••» Ул". 01» Й» '••' 0я"» *)• О1-5"3)
11.5-2.
11.5. ЗАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
345
(c) Если функция F имеет в некоторой области непрерывные частные
производные второго порядка, то ее приращение, определяемое равенством (3),
можно представить в виде
+ *|1/(S{iSi*'**+'^i*.*l+^V,<«}+.W».OIJH)
где
Р = У6У\+ЬУ\Ш + ЬУ2+ЬУ22 + --- + ЬУ%+ЬУпг (п. 4.10-5).
Члены степени 1 и 2 относительно ду и by' в формуле Тейлора (4)
соответственно составляют первую вариацию 6F функции F и половину второй ее
вариации б2/7.
(d) Определения и формулы пп. 11.5-1.a, b и с без изменений
переносятся на функции yt yi и F двух и большего числа независимых
переменных xv хъ ...
11.5-2. Максимумы и минимумы определенных интегралов. В то время как
теория обыкновенных максимумов и минимумов (пп. 11.2-1 — 11.3-5) имеет дело
с неизвестными значениями независимых переменных х или #;,
соответствующими максимумам и минимумам заданных функций, предметом вариационного
исчисления является отыскание неизвестных функций у (х) или yi (х)у
реализующих максимум или минимум определенных интегралов вида
XF
l=$F[y(x), у'(х), x]dx (11.5-5a)
Х0
ИЛИ
Хр
/= S^[0i(*). Уг(*)> •••» Уп(х)\ у[(х), у'2(х), ..., уп(х)\ x]dx, (11.5-56)
Хо
где F—данная функция, причем заданы конечные пределы интегрирования
xQ, xF и граничные значения у (*0), у{хр) или */г-(*0), #;(*/?)• в других
задачах пределы интегрирования и/или граничные значения также неизвестны и
нуждаются в определении. / есть функционал (п. 12.1-4), определенный на
соответствующем множестве функций.
Определенный интеграл (5) имеет сильный максимум или сильный минимум
для данной функции у (х) или данной системы функций у-г (#), если существует
такое число е > 0, что
xF xF
М = Ь $Fdx~ §&Fdx<0 или A/>0 (11.5-6)
Xq Xq
для всех вариаций by или для всех систем вариаций 6#/, для которых
соответственно 0<|&/|<еили 0<|/"б#| + 6#! + ... + 6^4<8 при x0^x^xF.
Интеграл / имеет слабый максимум или слабый минимум, если
неравенство (6) выполняется для всех вариаций by или Ьу^ для которых
соответственно 0<j/V + 6#'2<e или 0<У~Ъу\ + Ьу[2 + ... + Ьу% + Ьу^<& при
Xq^X^ Хр.
Условия слабого экстремума сужают множество допустимых функций
сравнения; поэтому сильный максимум (или минимум) является в то же время и
слабым максимумом (или минимумом).
346
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.5-3
Пусть область значений допустимых функций у (х) или у^ (х) удовлетворяет
неравенствам типа
У (х) < a, f (yv y2 уп) > 0.
Тогда, если значения функций у (х) или у. (х), реализующих экстремум интеграла /,
лежат внутри области значений, то говорят о внутреннем экстремуме; если же эти
значения полностью или частично лежат на границе области значений, то говорят о граничном
экстремуме.
В большинстве приложений функции у (х) или yi (x), дающие максимум
или минимум интегралу (5), должны выбираться не среди множества всех
возможных функций от х, а лишь среди множества функций определенного класса.
В дальнейшем всюду, где это необходимо, предполагается, что рассматриваемые
интегралы существуют и что 1) функции, дающие максимум или минимум
интегралу, выбираются среди множества всех функций, имеющих на рассматриваемом
промежутке или области непрерывные вторые производные, и 2) каждая
подынтегральная функция F имеет непрерывные вторые производные.
11.5-3. Решение вариационных задач. Функции у (х) или у-г (#),
реализующие максимум или минимум данного определенного интеграла, могут быть
найдены 1) как решения дифференциальных уравнений, получающихся из
условия б/г = 0 (пп. 11.6-1 — 11.6-7), или же 2) «прямыми» методами, описанными
в пп. 11.7-1 — 11.7-3.
Нетривиально замечание, что задача рассматриваемого здесь типа может
не иметь решения. Для каждого решения, полученного с помощью
необходимых (но не достаточных) условий пп. 11.6-1 — 11.6-7, должно быть проверено,
действительно ли оно обладает свойствами максимума или минимума.
Некоторые достаточные условия существования экстремума определенных
интегралов рассмотрены в п. 11.6-9.
11.6. ЭКСТРЕМАЛИ КАК РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ: КЛАССИЧЕСКАЯ ТЕОРИЯ
11.6-1. Необходимые условия максимумов и минимумов.
(а) Необходимым условием существования максимума или минимума
определенного интеграла
xF
1=$ F [У (х), y'M,x]dx (11.6-1)
Х0
при фиксированных х0 и хр является равенство
xF
б/ =
Х0
xF xF
\ K(S)-SW^=°
Х0
для произвольно малой вариации ду. Поэтому каждая функция у (х),
реализующая максимум или минимум этого интеграла, должна удовлетворять
дифференциальному уравнению
d (dF\ dF d*F . , d*F „, , d*F dF n /u fi 9\
Тх\ду-')---ду-^дуЪУ +Wd?y +дГдР^Ту==0 (U.b'Q
(уравнение Эйлера).
Общее решение уравнения (2) содержит две произвольные постоянные
(если Fy, , ф 0); они определяются из того, что функция у (х) либо принимает
заданные граничные значения у (х0) и/или у (xf), либо же удовлетворяет
каким-либо другим условиям, определяющим ее граничные значения (п, 11.6-5).
11.6-t. 11.6. ЭКСТРЕМАЛИ КАК РЕШЕНИЯ ДИФФЕРЕНЦ. УРАВНЕНИЙ 347
Приведенное условие является необходимым условием слабого экстремума, а
значит, и сильного. Отметим, что достаточные условия слабого экстремума менее
ограничительны, чем сильного (п. 11.6-10).
(b) Точно так же каждая система из п функций yi(x), у2 (*), •••> Уп(х)>
реализующая максимум или минимум определенного интеграла
XF
/== \Р[УЛ*)> У*{х), .... УпМ\ у'Лх), ИМ, ..., уп(х)\ x]dx, (11.6-3)
должна удовлетворять системе п дифференциальных уравнений
~ (j-l\ — ~ = 0 (i = 1, 2,..., п) (уравнения Эйлера) (11.6-4)
и некоторым заданным граничным условиям (см. также п. 11.6-1, с).
Функции у (х) или уг (х), удовлетворяющие уравнению или уравнениям
Эйлера для данной вариационной задачи, называются экстремалями
рассматриваемой задачи; они образуют 2/г-параметрическое семейство.
(c) Дальнейшим необходимым (но не достаточным) условием максимума или
минимума I является то, что на экстремали матрица Г 1 соответственно неположи-
[d*F I
dyfly'k J
тельна или неотрицательна (п. 13.5-2) (условие Лежандра). В одномерном случае эти
dzF dzF
условия сводятся соответственно к - ■ ^0 или - .. ^ 0 (см. пп. 11.6-7 и 11 6-10).
ду'2 ду'2
Вообще говоря, необходимые условия п. 11.6-1, а иЬ предполагают, что функции у (х)
или yi (х) дважды непрерывно дифференцируемы, однако это не является каким-либо
дополнительным ограничением. Если интегрируемая функция F имеет непрерывные
вторые производные, то все непрерывно дифференцируемые функции у (х) или yi (х),
реализующие экстремум интеграла I, необходимо имеют непрерывные вторые производные во всех
точках интервала (хл, хр), в которых д2Р/ду'2фО или соответственно матрица I -— I —
I. dvfiVk J
положительно или отрицательно определенная (п. 13.5-2) (теорема Дюбуа — Реймона).
(d) Получение условий (2) и (4) из б/ = 0 основано на фундаментальных леммах
вариационного исчисления:
XF
1. Если f (х) непрерывна на замкнутом интервале [хо, хр] и \ f (x) g (х) dx — О для
х0
любой функции g (х), имеющей непрерывную производную и такой, что g (х0) = g (хр) = 0,
то f (х) == 0 на [х0, xF].
XF
2. Если f (х) непрерывна на [*о, хр] « ( f (х) g (х) их = 0 для любой непрерывной
Хо
XF
функции g (х) такой, что V g (x) dx = 0, то f (x) является константой.
хо
Примеры приложений, в которых рассматриваются
вариационные задачи: геодезические в римановых пространствах (п. 17.4-3); вывод
уравнений Лагранжа из принципа Гамильтона. См. также п. 15.4-7.
Пример. Брахистохрона в трехмерном пространстве. Если в трехмерном
пространстве задана прямоугольная декартова система координат, причем ось Ох направлена
вертикально вниз, то эта классическая задача состоит в определении пространственной
кривой у — у(х), z = z (х), для которой материальная точка, скользя по этой кривой
без трения под действием силы тяжести из начала координат, достигает некоторой заданной
точки [хр>0, у (хр), z (хр)] за наименьшее время. Так как в силу закона сохранения
енергии
их-
7-г[(£)Ч»)Ч£)1'
348
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.0-2,
где g—ускорение силы тяжести, то нужно найти минимум интеграла
хр
tY2g= \-L Vl + {у')2 + U')2 <**•
и
Уравнения Эйлера имеют вид
dl У \ = ± 1 *' \ = о
dX U1/2 Y\ 4- (У')2 + (z')V dX \дс1/в Vl + <^>2 + (г')2 /
*V2 /i 4_ (У')2 + (г')2 *V2 ]/ТТТ7Й + (z')2
= £*,
где ct и с2 — константы. Так как ~ = —, то кривая должна лежать в вертикальной
плоскости, которая, если задать граничные условия
У (хр) = ур, г (хр) = 0,
будет плоскостью Оху. В этом случае / = 0и -——У =сь Положив, у' = tg(//2),
найдем
* = а (1 — cos 0, где а = -^-в
Далеэ
d# — y'dx — tg (//2) a sin t dt = а (1 — cos 0 </*
y = a(t — sin 0 -f£.
Поскольку ^ = 0 при х = 0, постоянная Л должна быть равна нулю. Постоянная я будет
зависеть от значений хр и ^. Искомая кривая является циклоидой (п. 2.6-2, е) с
основанием на оси Оу и точкой возврата в начале координат.
Замечание. Задача о брахистохроне, как и задача из п. 11.6-3, представляет
пример задачи на минимум криволинейного интеграла (п. 4.6-10). Задачи этого типа всегда
можно свести к случаю, когда интегрирование производится лишь по одной независимой
переменной
11.6-2. Условные экстремумы. Метод множителей Лагранжа. Требуется
найти систему функций ух (х), у2(х) уп (х), реализующую максимум или
минимум определенного интеграла (3) и, кроме того, подчиняющуюся т<п
достаточно гладким дополнительным условиям или уравнениям связи
Ф/(^1. ^2. •••» Уы *) = 0 (/ = 1, 2, ...;m<n). (11.6-5)
Если невозможно непосредственно исключить т из п переменных у(,
воспользовавшись соотношениями (5), то искомую систему функций уг (л:),
У2 (*). •••» Уп (х) получают как решение системы дифференциальных
уравнений (уравнений Эйлера)
=(*г)-ё-0 (,=1,2 n)t (1К6'6)
подчиненное условиям (5), где
т
Ф==/^ + 21М*)Ф/- (П-6-7)
/=1
Неизвестные функции X/ (х) называются множителями Лагранжа (см. также
п. 11.3-4). Если задача имеет решение, то л + m функций yi и к/ определи-
П.6-3. 11.6. ЭКСТРЕМАЛИ КАК РЕШЕНИЯ ДИФФЕРЕНЦ. УРАВНЕНИЙ 349
ются из л+m уравнений (6) и (5) и из заданных граничных условий.
Дифференциальные уравнения (6) являются необходимыми, но не достаточными
условиями максимума или минимума.
Метод множителей Лагранжа можно применять и в случае достаточно гладких
неавтономных условий вида
Ф/ (Уи Уг УП\ у[, у[ у'п\ х) =0 (/=1, 2 т). (11.6.-8)
11.6-3. Изопериметрические задачи. В изопериметрической задаче
требуется найти систему функций yi(x), у2 (х), ..., уп (х), реализующую максимум
или минимум определенного интеграла (3) и подчиняющуюся условиям
*F
$ V* (У1. .У* — i .Уя'. ?v У*> •••' Уп* x)dx=ck (k=l, 2,..., г), (11.6-9)
где Ck — заданные постоянные. Если функции Ч^ достаточно гладкие, то
применим метод множителей Лагранжа: неизвестные функции yi (л:), подчиненные
условиям (9), должны удовлетворять системе дифференциальных уравнений (6),
где в этом случае
(De=F+ 2 щТ*. (11.6-10)
г множителей Лагранжа \ik являются постоянными и их вместе с п
неизвестными функциями yi(x) находят из г + п уравнений (9) и (6) и заданных
граничных условий.
Пример. Площадь плоской области, ограниченной кривой x=x(t)t y==y(f)t
можно найти с помощью формулы
2я
~ \ lx^-y~\dt.
И-*-*)'
О
где t — подходящим образом выбранный параметр. Чтобы найти максимум площади / при
дополнительном условии
2л
О
тоянная, положим
о
где R — отличная от нуля постоянная, положим
Уравнения Эйлера (6) имеют вид
М 4-2U — -0 ^+2ц^-0
dt +^ dt* — °« dt + ** dt* ~ °'
Заданное дополнительное условие и эти уравнения удовлетворяются при
^ + х0, y — Rsm^
x = Rcos -^-\-x0, y^ — Rsin-^+Уо, где ц=|/у,
т. е. искомая кривая есть окружность радиуса /? (см. также п. 11.7-1).
Замечание. Чтобы найти максимум или минимум интеграла (3), подчиненного т
дополнительным условиям (5) и г условиям (9), пользуются уравнениями (6), где
т г
/=1 4=1
350
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.6-4.
11.6-4. Решение вариационных задач в случае, когда подынтегральная
функция содержит производные высших порядков. Чтобы найти максимум или
минимум определенных интегралов вида
xF
/==$ р(У1>Уг ~->Уп> У\>У2> ••-> Уп> У\>У2 y"n\...;x)dxt (И.6-11)
можно все производные выше первого порядка ввести в качестве новых
независимых переменных, связав их друг с другом и с у. условиями yi=dy]/dx,
y'l' — dylldx, ... В результате необходимые условия максимума и минимума
интеграла (14) принимают вид
й-т,{щ+т)-%т+~-° "=''2 «(и-б-12)
при этом предполагается, что подынтегральная функция является достаточно
гладкой. Для того чтобы решить задачу полностью, следует еще задать
граничные значения всех производных до (/г— 1)-го порядка включительно
каждой из функций yi, входящих в F.
11.6-5. Вариационные задачи с неизвестными граничными значениями и
неизвестными пределами интегрирования.
(a) Даны пределы интегрирования, неизвестны
граничные значения. Чтобы найти максимум или минимум определенного
интеграла (3) в случае, когда одно или несколько граничных значений yi (лг0)
и/или yt(xF\ не заданы и не связаны какими-либо условиями (см. п. 11.6-5с),
каждое отсутствующее условие заменяется соответствующим естественным
граничным условием
—1 = 0 (х = хп и/или x — xF). (11.6-13)
dyt \ и г/
Общее число условий по-прежнему равно 2/г и позволяет найти 2л
произвольных постоянных, содержащихся в общем решении уравнений Эйлера.
(b) Даны граничные значения, неизвестны пределы
интегрирования. Если один из пределов интегрирования, например, хР%
не дан, но граничные значения у. (xF) даны, то экстремаль yi (x) должна
удовлетворять соотношению
п
dF~y'k-F = 0 (x = xp). (11.6-14)
2L ьУк
(с) Общее условие трансверсальности. Часто один из
пределов интегрирования, например, хр и/или одно или несколько значений у((хру
не даны явно, но известно, что «точка» [д:^ у±(хр), у2(хр), ..., yn(xF)]
удовлетворяет п непрерывно дифференцируемым соотношениям
Gj[x; Уг(х)9 ..., уп(х)] = 0 (/=1, 2, ..., п^п). (11.6-15)
Предел интегрирования хр и неизвестные функции у1(х)1 ..., уп(х),
максимизирующие или минимизирующие интеграл (3), удовлетворяют уравнениям
Эйлера (4), граничным условиям (15) и условиям трансверсальности.
дУ1 ^ 3 дУ1
/=1
dF \Л dGf
П.в-в. 11.6. ЭКСТРЕМАЛИ КАК РЕШЕНИЯ ДИФФЕРЕНЦ. УРАВНЕНИЙ 351
для каждого значения у. (xF), не заданного явно, и
г п 1 п
U=i
/=1
если Хр неизвестно. Л. суть /гх множителей Лагранжа, подлежащие
определению вместе с /г+1 неизвестными уЛхр) и/или хр из /г + /г3 + 1
соотношений (15) и (16).
Заметим, что уравнения (13) и (14) являются частными случаями
уравнений (16а) и (166).
В простейшем частном случае /г=1 и G (л:, у) = у — ф (л:) = 0 условие
рансверсальности имеет вид
F(xt у, y,) + W(x)^y']Fyt(xi у,.у') = 0 (x = xF).
(d) Аналогичные методы используются в случае, когда заданы не все
граничные условия, соответствующие х = х0.
Пример. Минимизировать интеграл
<F
I = J G [* (О, У (0, г (/)] is =
-(«<*«.,«. .ю>/($Ч($Ч(£)'*
[G (x, у, z) > 0],
где (*0, yQ, z0) и (jc/г, ур, zp) лежат на двух подходящих (выпуклых) непересекающихся
регулярных поверхностях SQ и Sp, определенных уравнениями
В* (х, у, z) = 0, Вр (х, у, z) = 0.
Здесь условия трансверсальности имеют вид
dх . dу . dz _ I
d/ " atf " dt ~~ ^
dB0 tdBot dB0
~дГш by ""ЗГ (Г-Го)'
dBF ^ ав/г e dBF
"ST : Ty~: "аГ С = ip)*
т. е. экстремаль пересекает поверхности $0 и 5/? ортогонально.
Если, в частности, G (х, у, z) = 1, то / есть расстояние между поверхностями и
экстремаль есть прямая.
Существование минимума зависит от специальных свойств (выпуклости) данных
поверхностей.
11.6-6. Задачи Больца и Майера. Функционал вида
Хр
J e S F [у1 {х)> у2 {х) уп {х); у\ {х)> у* {х) v'n <*>'■ *] dx +
+ h [Уг (*F)' у2 (XF)> •" . Уп (XF)> xf], (l 1.6-17)
который максимизируется на некотором классе функций у. (х) (задача Больца).
удовлетворяющих заданным граничным условиям (15), может быть записан в виде
хр
J = $ {F + Уп + \) d*> (П.6-18)
х0
352
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.6-7.
гДе Уп + \
нию-связи
дополнительная функция, удовлетворяющая дифференциальному уравне-
п
*«+>- Sfi£*i + e (*o«*«v) (,1-6-19)
и граничным условиям
уп+1 (*о) - °. Уп+\ (xf) =h [У1 (*f), н (xf), -. *Л (м; *rt; (1! •6"20)
^ удовлетворяют уравнениям Эйлера для интеграла (18), составленным с учетом
наложенных связей (см. п. 11.6-2). Аналогичная процедура используется, если
дополнительно даны условия, связывающие граничные значения на конце лг = х0.
Если у. (х) удовлетворяет заданным дифференциальным связям, но F = О, так что
минимизируется или максимизируется только граничная функция п, то такая задача
называется задачей Майера, которая будет рассмотрена в пп. 11.8-1 — 11.8-6, посвященных
теории управления.
11.6-7. Ломаные экстремали. Отражение, преломление и односторонние экстремумы.
Функции у (х) или у, (х), максимизирующие или минимизирующие определенный
интеграл (1) или (3), могут предполагаться принадлежащими классу непрерывных функций,
обладающих кусочно-непрерывной производной (п. 11.5-2).
d2F
Они могут иметь угловые точки для значений х, таких, что - = 0 или матрица
Г_4!^]_п
L дУ1 дУк J
олуопределенная для некоторых у, у или yv y2,
или же когда F имеет разрывы (п. 11.6-1 и 13.5-2).
Угловые точки, в частности, могут встречаться:
1. Для некоторых х на интервале значений
рис. 11.6-1, а.
2. На кривой, поверхности, гиперповерхности
5 (*, у) = 0 или 5 (*; yv у2,
Уп
как это показано на
Уп)'
••о.
(11.6-21)
пересекаемых экстремалями («преломление» экстремалей, рис. 11.6-1, Ь).
3. На границе некоторой области, из которой экстремали исключены
посредством ограничений-неравенств
S (дг, у)^0 или 5 (*; yv уу ..., уп) 5=0 (11.6-22)
(рис. 11.6-1, с и d).
В каждой «свободной* угловой точке [xv у (*х)] или [Ху у1 (xj, y2 (xj, . . ., Уп (Д^)]
(см. рис. 11.6-1, а, но не Ь, с, d) экстремали должны удовлетворять соотношениям
Гу> <*! - 0) = Fy. (хг + 0), [Fy,y -F]x = Xi_0 = [Fy,y> - F]x = x± + 0;
или
F
(X - 0) :
1
F
:F '{X +0).
Vi 1 '
'—1. 2.
Ac = 1
tf — F
•\t F»'/k-p]
•■Xt + 0
(условия Вейерштрасса— Эрдмана)»
(11.6-23)
Разбор примеров, соответствующих рис. 11.6-1, а — d, см. [9.3].
В случае отражения (рис. 11.6-1, Ь) и преломления (рис. 11.6-1, с) экстремалей линия,
поверхность или гиперповерхность, определенные уравнениями (21) или (22), являются
промежуточными границами, в точках пересечения с которыми экстремали должны
удовлетворять угловым условиям
ty<*i + °>-fy<*i-°>e-Al!^l ~-|f I \ , )
У l y 1 l^k + ° ^Ui-0)/=l, 2 п I
п
«П dF
k = l
dF
дУк
I ^»>-F
:1
dv'k
Ук
Jjc = xt + 0
где постоянная Л — множитель Лагранжа.
х = хх — 0
(dS\ _*S| \ I
I дх \xt + 0 дх |*1 — 0J» J
(11.6-24)
11.6-8. 11.6. ЭКСТРЕМАЛИ КАК РЕШЕНИЯ ДИФФЕРЕНЦ. УРАВНЕНИЙ 353
В каждом случае угловые условия дополняют заданные граничные условия для
нахождения угловых точек.
В случае граничного (одностороннего) экстремума, показанного на рис. 11.6-1, йь
экстремум может достигаться лишь на кривых, состоящих из дуг экстремалей и частей
границы указанной выше области, причем в точках перехдда экстремалей на границу они
имеют общую касательную (см. также п. 11.8-5).
tF
Замечание. В частном случае / = \ G (х, у, z) ds, ds2 = dx2 + dy* + dz2, угло-
вые условия соответствуют законам отражения и преломления в оптике, если G (х, у, г)
интерпретировать как величину, обратную скорости распространения света.
S(x у)=0
(Хг-Уг) (xF>yr)
руют
х,у)=0
d)
Рис. 11.6-1. Экстремали с угловыми точками.
а) Две бесконечные последовательности кусочно-линейных экстремалей минимизи-
2
О
■ У')2 у'2 dx, у (0) = 0, у (2)
Уравнение Эйлера — Лагранжа определяет семейство экстремалей у = ах -f* b, где а
и b находятся из граничных условий и условий Вейерштрасса — Эрдмана, откуда следует^
что а равно либо 0, либо 1. Заметим, что
d2F
^=\2у»-\2у> + 2
d2F
не может обращаться в нуль на (0, 2) и
ду"<
->0 каждой минимизирующей экстремали.
Заметим также, что не существует гладкой экстремали, доставляющей наименьшее зна*
чение /.
b) Преломление экстремалей.
c) Отражение экстремалей от граничной линии.
d) Экстремаль, частично совпадающая с граничной линией.
11.6-8. Канонические уравнения и уравнение Гамильтона — Якоби.
(а) п уравнений Эйлера (4), соответствующих вариационной задаче п. 11.6-1, Ь, экви-
нтны 2/1 уоавнениям пеового пооялка:
валентны 2/г уравнениям первого порядка:
дН „, дН
y'iSSW
Р'^~щ
3—. * = 1,2. ...,д
(И.6-25а)
12 Г. Корн и Т. Корн
354
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.6-9.
относительно 2/г функций щ и p-t = dFJdy-it где
и(УгЧ V PV P2> -. V *) =
/г
- 2 Piy'i-F(yr у2 v v ^ v *)'
1 = 1
(11.6-256)
(контактные преобразования, см. также п. 10.2-6 и 10.2-7). Система (11.6-25 а) называется
канонической системой уравнений Эйлера или кратко каноническими уравнениями.
Заметим, что условия трансверсальности (13), (14), (16) и угловые условия (23), (24)
значительно упрощаются введением функций р^ и Я. В классической динамике
канонически сопряженные или присоединенные переменные р- интерпретируются как
обобщенные моменты, а гамильтонова функция И имеет размерность энергии. В пп. 11.8-1 — 11.8-6,
в связи с теорией управления, задачи вариационного исчисления переформулированы в
терминах канонических уравнений.
Иногда можно упростить решение задачи введением 2п -\- 1 новых переменных Уир1
Н (9v Уъ> ••• » Уп'* Ръ Ръ ••• » Рп* х) посредством канонических преобразований (п. 10.2-6),
из которых следуют новые канонические уравнения
#-*£. *; — £?. <1 = 1.2 г».
dPi дУ(
(Ь) Предполагая, что минимум
XF
min / = min J F (у у у ; у' \f у\' • х) dx ==
*tW. *|W VnM xo '
s 5 ['с yi (xo)> у2 (xo) vn (xo)' Ул. (xf)> у2 (xf) Уп (*f)\ =
- s [*o. Уг (хо)' у* (*o) Уп (xo)} - 5 (*. У г. У2 Уя)
определяет единственную экстремаль при фиксированных хр, у- (хр) и переменных
xQ = X, у. (*0) = Yi (i = 1, 2 п), функция S (X, Yv Y2 Уя) удовлетворяет
уравнению в частных производных первого порядка
Ш + " i*v Y* Yn- щ. Щ §? х)" ° <11-6-26'
(уравнение Гамильтона — Якоби).
Обыкновенные дифференциальные уравнения (25а) являются уравнениями
характеристик для (26) (см. также п. 10.2-7).
11.6-9, Вариационные задачи в случае нескольких независимых переменных;
максимумы и минимумы кратных интегралов. Часто требуется найти систему п
функций уг(х1% х2,..., хт)у y2(xlt х2,..., хт), ..., yn(xv х2, ..., хт) от т
независимых переменных х1у х2, ..., хт, реализующую максимум или
минимум кратного интеграла
I = \\...[F dx1dx%...dxm% (11.6-27)
где F—данная функция п + т-\-тп переменных уи xk и yitk — dyddxk* При
этом граница 5 области интегрирования V и граничные значения функций
yi могут быть как заданы, так и не заданы. Предполагается, что функции yi
выбираются среди множества всех функций, имеющих в V непрерывные
вторые частные производные (см. также п. 11.5-2).
Если подынтегральная функция F является достаточно гладкой, то
каждая система функций уъ у2> ...^ уп, реализующая максимум или минимум
11.6-10. 11.6. ЭКСТРЕМАЛИ КАК РЕШЕНИЯ ДИФФЕРЕНТ!. УРАВНЕНИЙ 355
интеграла (18), должна удовлетворять системе уравнений с частными
производными
т
2 4(0-f=° ('=1,2 п) (11-6"28)
и надлежащим граничным условиям. Для решения вариационных задач с
уравнениями связи применим метод множителей Лагранжа, описанный в пп. 11.6-2
и 11.6-3.
Если граничные значения одной или нескольких неизвестных функций у. не заданы,
то следует с помощью условия 6/ = 0 получить естественные граничные условия,
аналогичные уравнениям (13). Пусть, например, в случае двух независимых переменных
xv хп граница 5 есть регулярная замкнутая кривая, задаваемая уравнениями *, = х± (s),
х2 =^3 (s), где s —длина дуги. Тогда естественные граничные условия имеют вид
__dF dx%__dF_d>b_0 (,_1§2 я)в (1L6.29)
дУЬ1 ds dyi.2
ds
Пример. Малые смедения струны длины L могут быть описаны функцией у (х, t)
координаты х, измеряемой вдоль струны, и времени i. Кинетическая и потенциальная
энергия всей струны соответственно равны
г-=-$„-* "-Ц4*.
0
где т — масса единицы длины, a Q — натяжение струны. Чтобы интеграл
tp tp L
J (Г -t/) dt - i- [ \ (my'f - Qy'l ) dx dt
to U 0
имел минимум (принцип Гамильтона), должно выполняться соотношение
.. Q ..
ltt^~m Ухх%
являющееся уравнением колебаний струны.
*11.6-10. Достаточные условия для максимума и минимума в простейшей
задаче. Пусть функция
*-*<*) (я--") (11-6-30>
является экстремалью интеграла
XF
l=\F(x, у, y')dx (11.6-31)
Хо
при заданных x0,xF и У(х0)=у0, у (х F) = у р.
Дифференциальное уравнение второго порядка
S (р«'Уг') + (тхFy«>-F««) г=0' ("-6-32)
где вместо у и у' подставлены их выражения из (30), называется уравнением
Якоб и.
Если существуем решение уравнения Якоби, равное нулю при х=х0 и не
обращающееся в нуль при x0<x^xF* оговорят, что экстремаль (30)
удовлетворяет условию Якоби.
Геометрически это означает, что существует однопараметрическое
семейство экстремалей^ включающее данную экстремали выходящих из точки
12*
356
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.7-1.
(л-0, г/0) и не пересекающихся при xQ < х ==с Хр, — поле экстремалей с центром
в точке (х0, г/о)-
Если для экстремали (30) условие Якоби выполняется и функция
£(*, У, у'. Р)-/="(*, У> y')~F(x, У, p)-to'-p)Fy.(x, у, р) (11.6-33)
(функция Вейерштрасса)
неположительна во всех точках (х, у), близких к точкам экстремали у = у (х),
и при значениях у', близких к p = dy/dx на той же экстремали, то эта
экстремаль реализует слабый максимум интеграла (31). Это, в частности,
выполняется, если вдоль выбранной экстремали
Fy>y><Q (усиленное условие Лежандра). (11.6-34)
Если экстремаль удовлетворяет условию Якоби и функция Е
неположительна при всех (х, у), близких к точкам экстремали, и при всех у', то эта
экстремаль реализует сильный максимум.
Достаточное условие минимума получается при выполнении неравенства
Е ;>: 0 (соответственно Fy,y, > 0).
Достаточные условия экстремума в многомерном случае приведены в
[11.12], [11.13].*
11.7. РЕШЕНИЕ ВАРИАЦИОННЫХ ЗАДАЧ ПРЯМЫМИ МЕТОДАМИ
11.7-1. Прямые методы. В каждом из так называемых прямых методов
нахождения максимума или минимума данного определенного интеграла
XF
/= ] F[y{x), y'(x), x\dx (11.7-1)
Х0
искомую функцию у (х) пытаются приблизить последовательностью функций
ui М> "г W» ••• » выбираемых так, чтобы все они удовлетворяли граничным
условиям, наложенным на у (х). Каждая функция иг (х) должна быть
дифференцируемой функцией от * и г параметров аг1, аг2, ... , агг. Последние
определяются так, чтобы они давали максимум или минимум функции
Хр
1г(ъги аГ2 «„)= j F[ur(x), u'r(x), x]dxt (11.7-2)
Xo
(г. е. удовлетворяли уравнениям
£^ = 0 (/=1, 2,..., г; г=1, 2,...) (11.7-3)
(см. п. 11.3-3, а].
Для каждой функции у (х), полученной таким путем в качестве предела
последовательности приближающих функций иг(х), и2(х),..., требуется еще
доказать у что она действительно реализует максимум или минимум
определенного интеграла (1).
Аналогичными методами можно решать вариационные задачи и в случае
нескольких неизвестных функций (п. 11.6-1, Ь) и/или нескольких
независимых переменных (п. 11.6-9). Если заданы уравнения связи (пп. 11.6-2 и
11.6-3), "то им подчиняют каждую приближающуюся функцию; максимумы
и минимумы приближающих интегралов можно тогда находить с помощью
метода множителей Лагранжа из п. 11.3-4 (см. пример).
Прямые методы могут давать числовые приближения и/или точные
решения. Так как при условиях, перечисленных в п. 11.5-2, решения вариацион-
11.8-1. 11.8. ЗАДАЧИ УПРАВЛЕНИЯ И ПРИНЦИП МАКСИМУМА 357
ных задач должны удовлетворять дифференциальным уравнениям,
выражающим условие б/ = 0, то каждый прямой метод решения вариационной задачи
является также приближенным методом решения дифференциальных уравнений.
Пример. Решить изопериметрическую задачу, рассмотренную в качестве примера
в п. 11.6-3, приближая х (t) и у (t) соответственно последовательностями
ur (t) = af + 2 (ak cos *' + bk sin kt),
£=1
vr(t == ^- + 2 (<** cos kt + $k sin kt) (r = 1, 2, ...),
k = \
так что
2л
О k=\
найти максимум интеграла lf при дополнительном условии
Од г
\ [Ш + (Чг7] <"=* 2 »М + »* + «1 + эЭ-*.
О £=1
применим метод множителей Лагранжа из п. 11.3-4 и найдем
* ' * * * f (Л = 1. 2 г)
~ aAr + 2V^6Ar =0' " bk + 2Kkak '■
'-0,
}
при r=l, 2, ... Начиная с & =- 1, получим %г = 1/2, pt = —at ax = bt; при k > 1
a, = b. = a^ = p\ = 0. В этом примере прямой метод дает точное решение
х = ~ 4 01 cos / -{- bx sin *, у = ~ — bt cos / 4 ai s^n '.
где аз + Ьз^^г.
11.7-2. Метод Релея—Ритца. В этом методе искомое решение у (х) пытаются
разложить в ряд по полной системе функций Ч?. (x) (п. 15.2-4) так, чтобы приближающие
функции
г
иг (х) == 2 v ^/ w
/ = 0
удовлетворяли заданным граничным условиям. Как правило, функции ЧЛ (х)
ортогональны, и таким образом, параметры a . = а у не зависят от г (п. 15.2-4), в точности
так же, как в примере п. 11.7-1.
Метод Релея — Ритца оказывается полезным для численных решений некоторых
задач о собственных значениях в теории колебаний и квантовой механике (см. также
п 15.4-7).
11.7-3. Приближение// (л:) полигональными функциями. Решение у (х) можно
приблизить полигональными функциями иг (х), каждая из которых определяется, например,
г своими значениями arl = uf (х0 + &х), аг2 = иг (х0 + 2Дх) агг = иг (х0 -{- гДх) =*
= иг (хр — А*) В этом случае условия (3) дают дифференциальное уравнение (п. 20.4-3),
приближающее уравнение Эйлера (11.6-2) данной вариационной задачи.
11.8. ЗАДАЧИ УПРАВЛЕНИЯ И ПРИНЦИП МАКСИМУМА
11.8-1. Постановка задачи.
(а) Уравнения состояния, управления и критерий.
В задачах управления состояние динамической (механической, электрической,
химической и т. д.) системы характеризуется п переменными
состояния (фазовыми переменными) Xi(t)t х2 (4>. •••! хп (0? удовлетворяющими п
358
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.8-1.
дифференциальным уравнениям первого порядка
dx.
-jf = fi(xi>x2>-"* xn\ иъ u2,...t ип) (уравнение состояния). (11.8-1)
Типичные переменные состояния-—обобщенные координаты и скорости в
механике, электрические токи и напряжения, концентрации в химии (п. 11.8-3);
независимая переменная t обычно является временем.
Задача состоит в определении г управляющих переменных (управления)
uk — uk(t) (& = 1, 2, ..., г) как функций от t в интервале t0^t z^tp, мини
мизирующих заданный критерий-функционал (критерий качества)
Xo(tF)= \ M*i. *2. •••» хп\ "и иъ •••» ur)dt (11.8-2)
(например, цену, среднеквадратическую ошибку, время достижения цели
и т. д.) и удовлетворяющих неравенствам
Q/(ult u2t ..., ur)^0 (/ = 1, 2, ..., N), (11.8-3)
определяющим замкнутую область допустимых управлений V.
Возможные ограничения фазовых координат (xlt x2i ..., хп) будут
рассмотрены в пп. 11.8-1, d и 11.8-5.
Оптимальное управление uk (f) определяет оптимальную траекторию
Xi — Xi(t) в /г-мерном фазовом пространстве. Решение такой задачи
управления требует задания подходящих граничных условий для определения
начальных и конечных значений х-г (t0)t x-t (t^)\ начальное и конечное время t0t tp
могут быть неизвестными (п. 11.8-1, с).
(Ь) Задача оптимального управления и вариационное
нечисление. Методы пп. 11.8-2 — 11.8-5 могут рассматриваться как
обобщенное вариационное исчисление, применяемое для решения важного класса
задач, поставленных в п. 11.8-1. На языке предыдущих пунктов x-t (t) и uk(t)
являются неизвестными переменными.
Например, все задачи пп. 11.6-1 — 11.6-7, связанные с максимизацией или
минимизацией интегралов
хр
1 = \ F[yi <*>. У* <*> Уп {х)> у[ {х) у'п W? *] dx
при соответствующих ограничениях и/или граничных условиях, формулируются кан
задачи оптимального управления, если произвести замену
X == t, Хо = t0, Хр == tp,
dx.
1 = х0 (tp), у. (х) S3 х. (О, -~ ззш, (0 as yt (х) (/ = 1,2 л).
В этом частном случае теория п. 11.8-2 приводит к классическим каноническим
уравнениям п. 11.6-8; этот подход иногда может упростить данную задачу.
Уравнения состояния (1) являются дифференциальными связями,
переменные pi, определяемые в п. 11.8-2, суть соответствующие множители Лагранжа.
Сопряженные уравнения и принцип максимума, введенный в п. 11.8-2,
образуют необходимые (но не достаточные) условия для оптимальных и^ х\
и в существенном эквивалентны уравнению Эйлера (11.6-4) вместе с
условием £ $=Ю (п. 11.6-10), когда последние применимы.
Принцип максимума устанавливает условия оптимизации в элегантной,
удобной и наиболее общей форме, позволяющей непосредственное
исследование систем с разрывными управлениями (п. 11.8-3).
11.8-1. 118. ЗАДАЧИ УПРАВЛЕНИЯ И ПРИНЦИП МАКСИМУМА 359
(c) Многообразия начальных и конечных состояний.
Во многих задачах управления вместо задания начального момента времени tQ
и начальных значений х± (t0), Н (*<>)» ••• » хп (t0) указывается, что начальное
состояние [*i(W> *2 (*о)» •••»*/i(*o)] принадлежит (/г—/г0)-мерному многообразию
начальных состояний (гиперповерхность, линия или точка в пространстве
состояний), задаваемому уравнениями
Bj [*i (0. Ч (0. • • • >*п (01 = 0 (/ = 1, 2, ... ,л0 < п). (11.8-4а)
Конечное состояние \хг (tF), x2(tp), ..., хп (/^)] аналогичным образом)
принадлежит (/г — /г^-мерному многообразию конечных состояний
GJ[x1(t)1 x2(t), ..., *я(0] = 0 (/=1,2,...,л^л) (11.8-46)
В дополнение могут быть даны ограничения-неравенства, определяющие
соответствующие области в каждом многообразии (4).
Заметим, что каждое неравенство
G[*, (О, x2(t) хп </)]<0, (11,8-5)
содержащее, например, конечные состояния внутри данной «-мерной области
пространства состояний, в существенном эквивалентно соответствующему ограничению-равенству,
так как каждая траектория, входящая в область конечных состояний, должна пересечь
ее границу.
(d) Непрерывность, дифференцируемость и условия
независимости (см. также п. 11.5-2). Если не оговорено противное, то
относительно *,-, и& и / предполагается:
1. Данные функции /0, flt ..., fn непрерывно дифференцируемы
по переменным состояния x-t и непрерывны относительно переменных
управления uk.
2. Функции Qj непрерывно дифференцируемы и имеют
ненулевые градиенты.
3. nQ функций £j и tip функций G. определяющие многообразия
начальных и конечных состояний, непрерывно дифференцируемы;
их функциональная независимость выражается в том, что ранги
(п. 13.2-7) матриц [дВ Jdxt (tQ)] и ^dQJdxi (/F)] соответственно равны
п0 и nf.
Все допустимые управления uk (t) принадлежат классу функций с
ограниченной вариацией на интервале (tQt tF\ (односторонние пределы существуют
почти всюду; п. 4.4-8) и кусочно-непрерывно дифференцируемы там, где они
непрерывны.
Соответствующие xi (t) кусочно-непрерывно дифференцируемы. Возможны
менее ограничительные предположения, однако результирующие теоремы
становятся более громоздкими.
(e) Обобщения (см.также пп. 11.8-4 и 11.8-5). Оптимизационные методы,
введенные в пп. 11.8-1 — 11.8-5, могут быть применены к более общим задачам.
В частности,
1. Если одна или несколько данных функций f., Qj, фу, \Ру явно зависят от
независимой переменной t («неавтономные» системы), то можно свести задачу к более простой
посредством введения новой переменной состояния / =* х „,-,, Для которой
dx„ li
-Ж1-1 ='« + !■ *« + lPo)-'o. *«+1М='Л <П-8-6>
Этот же способ применим и в случаях, когда некоторые В ■ или G, зависят явно
соответственно от t и /-.
2. Если заданы непрерывно дифференцируемые ограничения-равенства, содержащие
переменные состояния
q>j(*v *2 хп) = 0 Wel» 2' ■"' т) (11-8'7>
360
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.8-2.
и изопериметрические условия
*F
\^j{XV X2 Xn)dt = Cf ^ = 1' 2 т,) <И-8"8)
с кусочно-непрерывно дифференцируемыми 47., то задача может изучаться с помощью метода
множителей Лагранжа (пп. 11.6-2, 11.6-3). При этом функция f0 в критерии-функционале
(2) заменяется на
т т'
F0zzsf0+ 2 \-е>ф/+ 2^\ о1-8-9)
/=i k=\
где %* (t) и ри суть соответственно переменные и постоянные множители Лагранжа.
Ограничения на переменные-состояния, включающие также и управление,
рассматриваются в п. 11.8-5.
3. Критерий-функционал
*F
f<fF)~\ F(XVX2 V uv U2 ur)dt + hlxl(tF) xn(fF)] <l,'8-I0>
h
приводится к простейшей форме (2), если ввести
'о (*Г Х2 V UV Ч Ur)=F + h (t) - h (/0), *
гДе п
dh
■Л
к «)^£h [xt (0. *2 (0 хп Щ я J] -°± f.
(11.8-11)
(см. также п. 11.6-6).
4. Если ограничения (4) на управляющие переменные и. явно зависят от
переменных состояния х- (включая, возможно, / = х А, то эту зависимость обычно можно
исключить путем введения новых управляющих переменных.
Пример. Ограничение (4) вида
\Uk\<«(Xl- Х2 Xtl)
приводится к форме
1*| <1,
если ввести новую переменную управления v, полагая u.—vq (х^ х„ х ).
11.8-2. Принцип максимума Понтрягина.
(а) Сопряженные переменные и оптимальный
гамильтониан. Удобно трактовать критерий-функционал (2) как конечное
значение xQ (tF\ дополнительной переменной состояния х0 (/), удовлетворяющей
уравнению
^Г = /о(*1. х* *••' **> "!' "2' -•» ^ (11.8-12)
и начальному условию
*0('о) = 0. (11.8-13)
Необходимое условие оптимального управления выражается принципом
максимума Понтрягина. Определим п-\-\ сопряженных переменных р0 (/),
рг (/), ..., pn(t) как решения (л+1) дифференциальных уравнений первого
порядка
п
dp. ^r\ df.
-^г = — У ^- Pk (* = 0, 1, 2, ..., п\ tQ<:t <tF)t (сопряженныеуравнения),
k=o
(11.8-14)
причем
Ро (0 = const ^0. (11.8-15)
П.8-2. 11 8. ЗАДАЧИ УПРАВЛЕНИЯ И ПРИНЦИП МАКСИМУМА 361
Тогда оптимальное управление, минимизирующее функционал (2), реала-
зуется допустимыми управляющими переменными uk — uk (t), которые
максимизируют гамильтонову функцию
п
Н(ХЪ Х2, ..., Хп\ Ро. Pi. .... Рп\ "1. «2. .... «a)= 2 Pifi' О1-8"16)
для каждого t между tQ и tF; более того,
М (xlt х2, ..., хп\ р0, ръ ..., />„)==
max
= ("г иъ .... ur)cu Н(хъ хъ ..., хп\ р19 р2, ..., рп; ии и2, ..., иг) = 0
(tQ*s£t^tF). (11.8-17)
Кроме того, оптимальные x-t (t) и uk (t) должны удовлетворять данным
условиям (1) и (4) и условиям трансверсальности
п0
Р|+^Л/^7=0 if = t0\ /=1,2, ..., п), (11.8-18А)
/=1
/г
р<+2
ас,
Л/ — = 0 (/ = />; /=1, 2, ...,/г), (11.8-186)
7=1
соответствующим условиям (4); Лу, Л;- — неизвестные константы (см. также
пп. 11.6-5, 11.6-8, 11.8-2, Ь).
В предположениях, указанных в п. 11.8-1, с, сопряженные переменные
pi (t) должны быть кусочно-непрерывно дифференцируемыми функциями. Они
остаются непрерывными и тогда, когда f0 и/или flt /2, ..., fn претерпевают
разрывы на гиперповерхности S, определенной уравнением
g(*i, х2, ..., *„) = 0,
где g —непрерывно дифференцируемая функция и f-t имеют односторонние
производные по хх, х2> ..., хп с каждой стороны S («отражение» оптимальных
траекторий, см. также п. 11.6-7).
При этих условиях оптимальный гамильтониан остается непрерывным
на S.
(Ь) Краевая задача. Условия принципа максимума имеют своим
следствием соотношения, выражающие каждую управляющую переменную
через Xi И Pf.
uk = uk(x0t xlt ..., хп\ Ро, plt ..., рп) (k = l, 2, ..., т). (11.8-19)
Эти соотношения могут быть получены посредством решения задачи на
максимум [возможно, с ограничениями-неравенствами (3)] для каждого /.
Задача оптимального управления сводится к решению 2/2 + 2
дифференциальных уравнений (1), (12) и (14) или
dx, дН dp. дН
ИГ~Щ> !Г=-Ц С^0'1 »)• (И-8-20>
следующих из уравнения (17), при указанных выше краевых условиях. Так
как сопряженные уравнения (14) однородны относительно р/, можно
произвольным образом выбрать константу в уравнении (15) так, что
М0=-1 Со^'^'/г). iii.e-2i)
362
ГЛ. И. МАКСИМУМЫ И МИНИМУМЫ
11.8-3.
Таким образом, имеется точно 2/i +/iQ +/г^ + 2 краевых условий (4), (13),
(18) и (21) для определения 2/1+2 неизвестных постоянных интегрирования,
n0 + n>F неизвестных множителей Л'., Л, и неизвестного интервала tF—tQ.
Недостающие краевые условия получаются подстановкой t = tF в
уравнение (17). Если tQ или tF не даны явно, то вводится дополнительная
переменная состояния лгл+1:
dxn+\
jf~ — *» xn+i (to)== ^o
(см. также п. 11.8-1, е).
Замечание. Если некоторое краевое условие (4), например Gj = 0, позволяет
явно выразить или исключить какое-либо краевое значение, например, xj (tp), то р/ (tp\
не определяется из (4) и (18). В этом случае У-е уравнение (46) (и, следовательно,
ЛЛ и /-е уравнение (186) просто пропускаются. Если, с другой стороны, краевое
условие переменной состояния, например, х/ (tp), остается «свободным» или
неопределенным посредством соотношений (4Ь), то /-е уравнение (186) влечет соответствующее
«естественное условие» — pj (tp\ = 0 (см. также п. 11.6-5).
Аналогичные частные случаи связаны с уравнениями (4а) и (18а).
(с) Так как принцип максимума выражает лишь необходимые (но не
достаточные) условия оптимальности управления (по этому вопросу см. [11.17]), то
метод Понтрягина может давать несколько кандидатур оптимального решения,
либо же решения не существует.
Решение двухточечной краевой задачи обычно достигается численными
итерационными методами (см. также п. 20.9-2 и 20.9-3). Помимо этого
получение максимизирующих функций (19) может быть достигнуто
последовательными приближениями.
11.8-3. Примеры.
(а) Навигационная задача Цермел о. В стационарном поле скоростей
v {vt (*i. x2), v2 (jcb x2)}, где хх и х2 — прямоугольные декартовы координаты, движется
точка с постоянной по величине скоростью V (v% -f- v| = V2). Дано; xt (0) =0, х2 (0) =0;
требуется минимизировать время
tF
М'/О ='!>-$ dt (f0^1)'
0
необходимое для достижения заданной конечной точки (^/?. *2/г) посредством выбора
и (0 угла между направлением скорости V точки и осью xt.
Уравнения состояния (| v | = У);
~f = *i <*i. хж) + V cos и, ~ff = v2 (xlt x2) + V sin и. ~£- =» 1 1*0 = t).
Отсюда
Н == рх (vt + V cos и) + р2 (v2 -f- V sin и) — 1,
где принято ро =— 1.
Для максимума Н необходимо выполнения равенств
cos и = Pl sinH = — — *
Vp\ +р% ' Ур\ + Pi'
опряженным уравнениям
Г —("'SS + p*5f!)' "ЗГ {*Щ + РшдГ.)
pt и /?1 должны удовлетворять сопряженным уравнениям
EEl
dt
и
М = max Н = р1и1 + Р2^2 - V ]А>| + р| - 1 =0,
Если, в частности, vt и v2 постоянны, то таковы же pL, р2, и; их значения, вместе
с tpt удовлетворяют условиям
^(0)=0, *a(0)=0t *X(V) =*1/?. x2{tp) = x^F.
11.8-3.
11.8. ЗАДАЧИ УПРАВЛЕНИЯ И ПРИНЦИП МАКСИМУМА
363
(Ь) Простейшая задача регулирования по быстродействию
Даны Xi (0), х2 (0) = xt (0) и уравнения состояния
dxx **_к-иа) (т е —'
~df X2' dt ~U(t) V dt*
Требуется минимизировать время
= и </)).
'('*)-
dt (f0 — 1).
необходимое для достижения заданного конечного состояния хх (//г) = *2 (//г) = ^(^==0.
посредством оптимального управления такого, что
IMOK1.
Максимизация гамильтониана
И == Р!*2 -f р2и — 1
при условии | w | ^ 1 приводит к управлению
1 (Р2>0).
.<0)
и
: Sign p2 ■■
f 1 (р2:
Л -1 (Р2-
dp
dt
= Pi(0), Р*
^- = — pt — const,
= Pt(0)-*Pi<0).
Оптимальные траектооии в плоскости хи xt суть дуги парабол, соответствующих
и _ J и и __ i# эти дуги 'пересекают «кривую переключений», соответствующую рг = 0,
и каждая траектория продолжается к началу координат вдоль этой кривой (рис. 11.8-1).
Каждая траектория зависит от параметров pt (0), р2 (0), которые должны
выбираться так, чтобы удовлетворялись заданные граничные условия д^ (//?) = х2 (tp) = 0.
Сила тяга
О
Цель на
врйите
Рис. 11.8-1. Траектории на фазовой
плоскости для простейшей задачи
регулирования.
Рис. 11.8-2. Геометрия задачи
перевода ракеты с одной орбиты на
другую.
(с) Простейшие задачи о переходе с одной орбиты
недругу ю и о встрече за минимальное время. Соответственно рис. 11.8-2
движение ракеты в вертикальной плоскости в предположении постоянства ускорения силы
тяжести (— g) и отсутствия сопротивления воздуха задается четырьмя уравнениями
состояния
dt
dt
dx_
dt
di_
dt
T cos и
тц + т (t — tQ)
T sin и
— g.
x==xlt x =
m0 -+- m (t — t0)
z x2, у ss *3, у =*4 — переменные состояния; g, T (тяга), m0 (масса ракеты
на старте), m<0 (постоянная скорость расхода горючего) — данные постоянные.
Требуется перевести ракету с данной горизонтальной стартовой орбиты
х (t0) ■■
У Со) =
= Voto,
-Уо*
X (t0) = v0l
364
ГЛ. II. МАКСИМУМЫ И МИНИМУМЫ
It.8-4.
на заданную горизонтальную орбиту некоторой цели так, чтобы
х (fF) = vF tF + а, х (tF) = vF;
V(tF)=*F- i(^) = °-
Таким образом, решение задачи завершается программированием управляющей
переменной — угла и — и (t) так, чтобы минимизировать общий расход горючего in (tF — t{))
<F
или просто V dt.
h
Так как многообразия начальных и конечных состояний зависят явно от t и tF, то
полагаем хь = /, dxjdt = UB (*0) = tQt xQ (tF) = tF.
Максимизация гамильтониана
.. • , T cos и • , Г Т sin и Л . .
Н = PtX + p2 : Ь pay -f р4 : g + р6 — 1
m0 + m(t —10) lm0 + m(t — t0) J
дает
ая/а« =
Сопряженные
дают
pi
Рз
= 0
или
COS W
уравнения
(0
(0
dpi
df
==Pi (to).
=- Pa Co),
dp3
df/
P2
P4
— P2 J
P_2_
3i n и 4- p4 cos и = 0
VpT+pI
dpb
' df
(/)=-
<0=-
= 0t
-Pi
-Рз
sin " = —
dp 2
df
(to) (t -
(to) (t -
= — Pu
- to) + P*
- to) 4- P*
P±
Vn+^i'
dp*
df
(to).
(to).
= — P%
Рь (t) =
Pb
(to).
Так как начальные и конечные значения х, у, у фиксированы, то представляют
интерес лишь условия трансверсальности (18). Имеем
*('o)-Vo = °- x(tF)-VFtF-a = Q.
М'о) + л;=°- Pi('f) + A1=0.
или
*5 Со) - Л; *0 = 0. Pt(tF)- AtvF = 0.
Учитывая, что pi и ръ постоянны, получаем pi = ръ = 0. Кроме того, максимальное
значение гамильтониана равно нулю при t — tF:
- Z la м W Со) + 1 Со) + "1 Со) «F ~ 'о)2 ~ 2"з Со) "4 Со) С?" 'о)1 V. +
Wo — т \i — То)
+ sp3Co)CF-g-sp4Co)-1=°-
Последнее, вместе с восемью данными начальными и конечными условиями,
определяют девять величин tQ, tF, x (tQ), x (tQ), у (tQ), y\tQ), p2(tQ), p3(tQ), p4 (tQ) и тем
самым все решение.
11.8-4. Матричные обозначения в задачах управления. Для задач управления
удобно использовать матричные обозначения п. 13.6-1 (а также соответствующие
тензорные обозначения, п. 14.7-7).
Введем:
х = х (t) == {*0, хг . . ., хп} — матрица-столбец (п -\- l)Xl,
представляющая вектор состояния,
и = и (t) == |«t, u2, . . ., urj — матрица-столбец rXl,
представляющая вектор управления,
р = р (t) ~ (p^, pv . . ., рп) — матрица-строка \х(п + 1),
представляющая сопряженный вектор
(см. также п. 14.5-2). Соотношения п. 11.8-1 и 11.8-2 можно записать теперь в болееком-
df Г df. ]
пактной форме; заметим, что v~ = ^-- есть матрица размера (л 4- 1)Х(л 4~ *)•
11.8-5. 11.8. ЗАДАЧИ УПРАВЛЕНИЯ И ПРИНЦИП МАКСИМУМА 365
В частности, имеем
dx . , ч дН
— = г (х,и) =-з— (уравнения состояния),
dp df дН , v } (11.8-22)
—■ = — р -к— = — ^— (сопряженные уравнения), ■ '
Н (р, х, и) == pf (гамильтониан).
Критерий-функционал (2) может рассматриваться как матричное произведение
(внутреннее произведение п. 14.7-1) х0=сх матрицы-столбца х и матрицы-строки с=(1, 0, 0, ... , 0)
размера 1 X (п + 1).
В [11.14] рассмотрен случай, когда критерий-функционал определен как сх с более
общей матрицей-строкой с.
11.8-5. Ограничения-неравенства для переменных состояния. Угловые условия
(см. также п. 11.6-6).
(a) Если область X допустимых систем состояний (* * ... , хп) ограничена
неравенствами
Sj(xQ, xv ... , хп; uv u2 иг) <0 (/=1, 2, ... , т), (11.8-23)
ЬГ
зования оптимальной траектории (см. также п. 11.8-1, е), то теория п. 11.8-2 остается
без изменения для траекторий или их частей, находящихся внутри замкнутой области
X, определенной уравнениями (23).
Для траекторий и частей траекторий, находящихся на границе X, по меньшей
мере одно из ограничений (23) превращается в равенство. Для простоты рассмотрим
граничную область D$, определенную единственным уравнением
S(xQt xv ... , хп; uv ... , "г) = 0. (11.8-24)
В этой области применим метод множителей Лагранжа пп. 11.6-2 и 11.8-1,е; таким
образом, каждая оптимальная траектория удовлетворяет уравнению (24) и соотношениям
п. 11.8-2,а с заменой f0 на
"о - 'о + * W s- f(V *v - • хп) е DS]. О'-8-25>
где Я — множитель Лагранжа.
Аналогично f0 может быть заменена вО^ одним из следующих выражений:
JL ло(& 1)
f0 s/o + и (0 s<*> =■ и + n <o 2j —dx~.— h
*=0 l
[(*0, *! xn)GDS- k=\,2 n], (11.8-26)
где
n
St0i-S = Q, S(1' = i^== V ^ ^=0, ... (11.8-27)
i = 0 *
Hi (t) — множитель Лагранжа.
(b) Если sW есть первая из функций (27), содержащая управляющую
переменную и явно, то неравенство 5^0 называют ограничением-неравенством /С-го порядка.
В этом случае оптимальная траектория, входящая в граничную область D$,
определенную уравнением (24), изнутри X в момент / = tt должна удовлетворять угловым
условиям (условиям скачка)
к~2 — I , ,, as<*-'>!
+ (v/c-i + *) —^г
\t~ti
/ = /4 J (11.8-28)
k = 0 l
(/ = 1, 2 л), I
где постоянные v^ — множители Лагранжа, b — произвольная постоянная.
Оптимальная траектория, покидающая граничную область состояний в момент / = ^
в первый раз после вхождения в нее при t = tt, должна удовлетворять угловым условиям
dSlK-\)
М',-°)-М', + о)-». dXt
w.('-''2 ">'}
U 1.8-29)
Збб
ГЛ. 11. МАКСИМУМЫ И МИНИМУМЫ
11.8-6.
Произвольную постоянную bt встречающуюся в обоих уравнениях (28) и (29), обычно
полагают равной нулю, так что p. (t) непрерывны в точке выхода. Если оптимальная
траектория преломляется в граничной области D§, соответствующей единственному
ограничению (24), то tt = t2 и угловое условие (28) выполняется с b = о.
Если единственное ограничение (24) заменяется двумя или более такими
ограничениями, члены, соответствующие новым ограничениям (с дополнительными множителями),
прибавляются к каждой сумме в уравнениях (25), (26), (28) и (29). Случаи явной
зависимости от времени изучаются способом п. 11.8-1,е.
Замечание. Относительно угловых условий (28), (29) в специальных случаях
см. [11.14].
11.8-6. Метод динамического программирования (см. также п. 11.9-2).
Если задача оптимального управления, поставленная в п. 11.8-1, определяет
единственную оптимальную экстремаль для фиксированных xi (tF) и переменных
xt(t*) = Xi (i = l, 2, ..., л),
то минимум критерия-функционала
min \ f0(xlt x2t ...j хп; ult w2, ..., ur)dt=a
«i«>. V> V>7.
E=S(Xlt Хъ ..., Xn) (11.8-30)
удовлетворяет уравнению с частными производными первого порядка
М fxv Х2 Хп; ^f-.^f» •••»^г) =° (Уравнение Гамильтона—Якоби),
(11.8-31)
где М — оптимальная (максимизированная) функция Гамильтона из
уравнения (17) (см. также п. 11.6-8).
Обыкновенные дифференциальные уравнения (20) суть соответствующие
уравнения характеристик, и способ получения их решений из полного
интеграла уравнения (31) известен (п. 10.2-4).
Динамическое программирование «погружает» данную задачу
оптимального управления в класс аналогичных задач с различными начальными
координатами.
Уравнение с частными производными (31), которое дает решение для
всего указанного множества задач, выражает тот факт, что каждая часть
оптимальной траектории оптимизирует критерий-функционал для соответ*
ствующих начальных и конечных точек (принцип оптимальности Беллмана).
Из принципа оптимальности можно получить цельную теорию
оптимального управления при весьма общих предположениях.
Вообще же численное решение уравнения (31) при л>2 затруднительно
(см. [11.16] [11.17], где динамическое программирование рассмотрено в более
общем виде).
11.9. ШАГОВЫЕ ЗАДАЧИ УПРАВЛЕНИЯ И ДИНАМИЧЕСКОЕ
ПРОГРАММИРОВАНИЕ
11.9-1. Постановка задачи. Важный класс оптимизационных задач,
включающих шаговое управление (что содержит управление непрерывными системами
посредством вычислительных машин) или шаговую оптимизацию ресурсов,
может быть сформулирован следующим образом:
Система описывается множеством переменных состояния х~(хг, х2, ..., хп),
образующих последовательность °х, гх, tt.t nxt ..§1 так что каждое изме-
It.9-2.
11.9. ШАГОВЫЕ ЗАДАЧИ УПРАВЛЕНИЯ
367
нение состояния дается уравнениями состояния (в этом случае
конечно-разностными, см. также п. 20.4-3)
или
*+ч=
«управляющая
h (**i.
кх2, ..
('* =
*+!* =
переменная»
kX
1, 2,
7<**,
*+ltfE
; л+1«1,
..., п)
*+1«),
={k+l"l
k+1u2
, k+4
МУ
ur)
(11.9-1)
J
где «управляющая переменная» k+1u = {k+1uv k+1u2, ..., k+1ur\ определяет
последовательность решений (стратегий), изменяющих k-ю систему состояний
в (&+1)-ю.
Если задано начальное состояние °х (и, возможно, некоторое множество
ограничений-равенств или неравенств для переменных состояния и
управления), то задача заключается в нахождении оптимальной стратегии хы, 2ы, ...
... tMut минимизирующей данный критерий
N—1
"*о= 2 h(*x. k+1u)+h(Nx) = NxQ(ox), (11.9-2)
k = 0
где N=\, 2, ... — количество рассматриваемых шагов (динамическое
программирование). Как и в случае непрерывных задач оптимального управления,
начальные и конечные состояния могут быть либо заданными, либо не
заданными, возможно также обобщить постановку задачи способом,
указанным в п. 11.8-1, е.
11.9-2. Принцип оптимальности Беллмана (см. также п. 11.8-6).
Если lut 2ut ..., Nu—некоторая оптимальная стратегия для
последовательности состояний °х, гх Nx в некоторой задаче динамического
программирования с начальным состоянием °х, то 2и, Зи Nu есть оптимальная
стратегия для тех же критерия-функции и конечного состояния Nx, но с начальным
состоянием гх. Если обозначить min^*0(X) через NS(X), то принцип опти-
и
мальности выражается рекуррентным соотношением (уравнением с частными
конечными разностями, п. 20.4-3, Ь)
NS (X) = min {/о (X, ]u) + N ~lS [f(XS)]\ (N=2, 3, ...),
iS(X) = minf0(X,iu),
(11.9-3)
где минимум определяется в соответствии с заданными ограничениями.
Численное решение этого функционального уравнения с неизвестными
функциями NS (X) заключается в шаговой конструкции класса оптимальных
стратегий для некоторого класса начальных состояний.
Ожидаемая оптимальная стратегия «погружена» в этом классе.
Решение обычно использует вычислительные устройства, но даже в этом
случае решение задачи с более чем двумя или тремя переменными состояния Xi
практически возможно лишь в частных случаях. Ряд примеров и
приближенных методов содержится в [11.16], [11.17] в [11.20] рассмотрено шаговое управ-
лениеа аналогичное принципу максимума.
ГЛАВА 12
ОПРЕДЕЛЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ:
СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА И АБСТРАКТНЫЕ
ПРОСТРАНСТВА
12.1. ВВЕДЕНИЕ
12.1-1. Математические модели. Физические процессы, вообще говоря,
описываются в терминах операций (наблюдений, экспериментов), связывающих
физкческче объекты.
Сложность подлинных физических ситуаций требует упрощенных
описаний с помощью словесных, символических и даже физических моделей,
которые «абстрагируют» подходящим образом выбранные «существенные» свойства
физических объектов и ситуаций.
Математика в самом общем смысле слова имеет дело с определением
и использованием символических моделей. Математическая модель охватывает
класс неопределяемых (абстрактных, символических) математических объектов
таких, как числа или векторы, и отношения между этими объектами.
Математическое отношение — это гипотетическое правило, связывающее
два или более символических объекта (см. также пп. 12.1-3 и 12.8-1). Многие
отношения могут быть описаны при помощи математических операций,
связывающих один или несколько объектов (операнд, операнды) с другим объектом
или множеством объектов (результатом операции). Абстрактная модель с ее
объектами произвольной природы, отношениями и операциями определяется
непротиворечивым набором правил (определяющих аксиом), вводящих
операции, которыми можно пользоваться, и устанавливающих общие отношения
между их результатами (аксиоматическое определение математической модели
с помощью ее свойств; примеры см. в пп. 12.2-1, 12.3-1, 12.4-1, 12.5-2, 12.6-1,
12.8-1 и 1.1-2). Конструктивное определение вводит новую математическую
модель, пользуясь уже известными математическими понятиями (например,
определение сложения и умножения матриц в терминах сложения и
умножения чисел, п. 13.2-2).
Непротиворечивость аксиоматического определения должна быть доказана
конструктивным построением примера, удовлетворяющего определяющим
аксиомам (доказательство существования, см. также пп. 4.2-1 и 9.1-4). Кроме того,
обычно проверяют взаимную независимость определяющих аксиом.
Математическая модель будет воспроизводить подходящим образом
выбранные стороны физической ситуации, если можно установить правила
соответствия, связывающие специфические физические объекты и отношения с
определенными математическими объектами и отношениями. Поучительным и/или
интересным может также быть и построение математических моделей, для
которых в физическом мире аналогов не существует. Наиболее общеизвестными
математическими моделями являются системы целых и действительных чисел
(п. 1.1-2) и евклидова геометрия; определяющие свойства этих моделей
представляют собой более или менее непосредственные абстракции физических
процессов (счет, упорядочение, сравнение, измерение).
Объекты и операции более общих математических моделей часто
ассоциируются с множествами действительных чисел, которые могут быть соотнесены
с результатами физических измерений. Получающиеся таким образом
представления математических моделей с помощью числовых операций специально
рассматриваются в главах 14 и 16.
12.1-4.
12.1 ВВЕДЕНИЕ
369
12.1-2. Обзор. Современная (абстрактная) алгебра1) имеет дело с
математическими моделями, определяемыми в терминах бинарных операций
(«алгебраических» операций, обычно представляющих собой различные
типы «сложения» и «умножения»), которые связывают пары математических
объектов (операнды или оператор и операнд) с соответствующими
результатами операций. В пп. 12.2-1 — 12.4-2 вводятся некоторые из наиболее
общеупотребительных моделей такого рода, именно: группы, кольца, поля, векторные
пространства и линейные алгебры, булевы алгебры отдельно рассматриваются
в пп. 12.8-1-12.8-6.
Важный вопрос о линейных преобразованиях (линейных операторах) и их
собственных векторах и собственных значениях излагается в гл. 14. Представление векторов
и операторов с помощью числовых компонент и матриц подробно обсуждается в
главах 14, 15 и 16.
Пункты 12.5-1 —12.6-3 служат кратким введением к теории
математических моделей, позволяющих определить предельные процессы и порядок, в
частности, в пп. 12.5-2—12.5-4 рассматриваются метрические пространства.
В пп. 12.7-1 — 12.7-5 указаны простые схемы комбинирования математических
моделей (прямые произведения и прямые суммы).
12.1-3. «Равенство» и отношения эквивалентности.
(a) Предполагается, что аксиоматическое определение каждого класса
математических объектов, рассматриваемых в этой главе, влечет за собой
существование правила, устанавливающего, являются ли два данных
математических объекта а и Ъ «равными» (эквивалентными или неразличимыми с tohkli
зрения модели, а = 6) или нет; это правило должно быть таким, что:
1) а —а (рефлексивность отношения равенства),
2) из а — Ь следует Ь — а (симметрия),
3) из а = 6, Ь = с следует а = с (транзитивность).
В пп. 13.2-2 и 16.3-1 приводятся примеры определения равенства в конструктивно
определяемых моделях.
(b) Вообще любое отношение а ~ b между двумя объектами а, Ь класса С называется
отношением эквивалентности в том и только в том случае, если оно рефлексивно (а ~ а),
симметрично (из а ~ b следует b ~ а) и транзитивно (из а ~ b, b ~ с следует а ~ с).
Любое отношение эквивалентности определяет разбиение класса С, т. е. подразделение
класса С на подклассы без общих элементов. Элементы одного и того же такого
подкласса эквивалентны в смысле свойств, определяющих отношение эквивалентности.
Примеры. Равенство, тождественность функций (п. 1.1-4), равенство и подобие
треугольников, изоморфизм (п. 12.1-6).,
12.1-4. Преобразования, функции, операции (см. также пп. 4.2-1, 14.1-3
и 14.3-1). Набор правил х-+х', ставящих каждому объекту х класса С
в соответствие некоторые объекты х' класса С, называется преобразованием
(отображением) класса С в класс С; х' есть функция
X'=x'(x) = f(x) (12.1-1)
аргумента х с областью определения С и множеством значений, содержащимся
в С Классы С и С могут быть различными, но могут и совпадать.
Соотношение^) можно рассматривать как операцию над операндом х, дающую результат х'.
Если в классах С и С даны удовлетворяющие нужным условиям
определения равенства (п. 12.1-3), то операция (преобразование, функция) (1)
определена корректно, если из х — у следует х'=у. Предполагается, что если
специально не будет оговорено противное, это условие всегда будет выполняться.
Отображение (1) называется однозначным [f (x) — однозначная функция я],
если каждому объекту х соответствует единственный объект х'. Все отобра-
*) Слово алгебра имеет три слабо связанных между собой значения: 1) общий
предмет, как в данном случае (абстрактная алгебра, элементарная алгебра); 2) теория
алгебраических операций, используемая в связи со специфической моделью (матричная
алгебра, тензорная алгебра); 3) тип математической модели (линейная алгебра, булева
алгебра).
370 ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.1-5.
жения в дальнейшем всегда предполагаются однозначными, и это специально
не оговаривается. Отображение класса С на класс С называется взаимно
однозначным (взаимно однозначным соответствием классов С и С), если оно
отображает класс С на весь класс С и определяет однозначное обратное
отображение (обратное преобразование) х' —* х. Многие авторы категорически
настаивают на том, что каждое отображение по определению должно быть
однозначно (см. также сноску к п. 4.2-2). Множество пар (х, х) называется
графиком функции f (х). Каждый объект х в равенстве (1) может сам быть множеством
некоторых объектов х1% х2, ... ; таким путем можно определить функции
x' = f (xi> х2> •••) ДВУХ и более аргументов.
Числовая (действительная или комплексная) функция, определенная на
некотором множестве функций, называется функционалом (например, интеграл
[ Ф (х) dxt наибольшее значение функции ф (х) на [а, Ь] и т. д.).
и
Сами преобразования (функции, операции) можно рассматривать как новые
математические объекты (см., например, п. 14.3-1).
12.1-5. Инвариантность (см. также пп. 12.2-8, 13.14-1, 14.4-5, 16.1-4
и 16.4-1). Если дано преобразование (1) класса (пространства) С в себя,
то любая функция F (х, у, ...) такая, что F[f(x), f (у), ...] = F(x, */,...)
для всех х, у, ... из С, и любое соотношение О (х, у, ...) = Л такое, что
О [/ (х), f (у), ...] = А для всех х, у, ... из С, называются инвариантными
относительно преобразования (1).
12.1-6. Представление одной модели другой: гомоморфизмы и изоморфизмы.
Пусть М — математическая модель (п. 12.1-1), состоящая из объектов а, 6, ...
и включающая операции О, Р, ..., результаты которых О (а, 6, ...),
Я (а, 6, ...), ... являются элементами модели М1), и М' — вторая модель
с операциями О' (а'', Ь\ ...), Р'(а\ Ъ\ ...), ... Отображение а —+ d множества
элементов модели М в множество элементов модели М' называется
гомоморфизмом модели М в модель М (относительно указанных операций), если при
этом отображении О (а, 6, ...)-* О' (а\ Ь\ ...), Р (а, Ъ, ...)—*Р'(а', Ь\ ...), ...
Гомоморфизм сохраняет все отношения, основанные на рассматриваемых
операциях, т. е. каждое таког отношение между элементами а, Ь> ... модели М
порождает соответствующее отношение между элементами а\ Ь\ ... модели М\
Гомоморфизм, отображающий модель М в себя, называется эндоморфизмом.
Если гомоморфизм отображает модель М на всю модель ЛГ, то М'
называется гомоморфным образом модели М.
Изоморфизм—это взаимно однозначный гомоморфизм. Если существует
изоморфизм модели М на модель М', то модели М и ЛГ называются
изоморфными относительно рассматриваемых операций; в этом случае как отображение
М —* ЛГ, так и обратное отображение ЛГ —> М являются гомоморфизмами.
Изоморфизм, отображающий М на себя, называется автоморфизмом модели М.
Понятие гомоморфизма и родственные с ним понятия изоморфизма и
автоморфизма имеют огромное практическое значение, так как они позволяют
представлять одну модель другой моделью. Можно, в частности, представлять
математические объекты некоторыми множествами действительных чисел
(аналитическая геометрия, матричное и тензорное представления). Заметим, что
изоморфизм есть отношение эквивалентности (п. 12-1-3, Ь) между моделями:
свойства целого класса изоморфных моделей можно выводить из (или
рассматривать на примере) свойств любой модели этого класса.
Некоторые авторы требуют, чтобы каждый гомоморфизм М -*- М' отображал М
на всю модель ЛГ. В этом случае гомоморфизм определяет изоморфизм между моделью,
состоящей из непересекающихся классов элементов модели М, и моделью ЛГ.
1) Элементы a, bt ... не обязательно должны принадлежать одному классу
математических объектов (например, они могут быть векторами и скалярами, п. 12.4-1).
12.2-2.
12.2. ГРУППЫ
371
12.2. АЛГЕБРА МОДЕЛЕЙ С ОДНОЙ ОПРЕДЕЛЯЮЩЕЙ
ОПЕРАЦИЕЙ: ГРУППЫ
12.2-1. Определение и основные свойства группы.
(a) Класс G объектов (элементов) а, 6, с, ... называется группой,
если определена бинарная операция, которая каждой паре элементов а, Ь
класса G ставит в соответствие некоторый объект (результат операции) а 0 Ь
так, что:
1) aQb является элементом класса G (замкнутость по
отношению к определяющей операции);
2) а 0 (Ь 0 с) = (a Q Ь) 0 с (ассоциативный закон);
3) G содержит (левую) единицу Е такую, что для каждого
элемента а из (?, EQa = a;
4) для каждого элемента а из G в G существует (левый)
обратный элемент а'1 такой, что аГ1 © а = Е.
Два элемента а, Ь некоторой группы перестановочны, если a Qb = b Qa.
Если все элементы а, Ь группы G перестановочны, то определяющая операция
называется коммутативной, а группа G — коммутативной или абелевой группой.
Группа (?, содержащая конечное число g элементов, называется конечной
группой (группой порядка g); в противном случае G — бесконечная группа.
В этом последнем случае группа G может быть счетной или несчетной.
(b) Каждая группа G имеет единственную левую и единственную правую
единицу, и эти единицы равны (Е Qa — aQE = а). Каждый элемент а имеет
единственный левый и единственный правый обратный элемент, и эти элементы
равны (a'1 Qa = aQa~1 = E).
Отсюда
из cQa — cQb следует а = Ь, }
л , _ , } (законы сокращения). (12.2-1)
из aQc = b 0 с следует а = Ь )
Группа G содержит единственное решение х любого уравнения cQx = b или
xQc = b, т. е. в группе возможны однозначно определенные правое и левое
«деление».
(c) Операцию, определяющую группу, часто называют (абстрактным)
умножением (см., однако, п. 12.2-10); тогда ее результат записывается как
произведение ab, а элемент, обратный элементу а, —как а'1. Это соглашение
свободно используется в следующих пунктах.
Кратные произведения аа, ааа, ... записывают в виде целых степеней а2, а8, ... t
причем (а~г)п =га~п, а° = Е. Заметим, что
(а"1)"1 = а, атап = ат+п, (ат)п = атпt (а*)"1 = Ь^а'1. (12.2-2)
12.2-2. Подгруппы. Подмножество Gx группы G называется ее подгруппой,
если Gx является группой в смысле определяющей операции группы G. Это
справедливо в том и только в том случае, если 1) множество Gt содержит все
произведения принадлежащих ему элементов и все элементы, обратные его
элементам *), или 2) для любой пары элементов at b из G± множество Gx
содержит и произведение аЬ~г.
Пересечение (п. 4.3-2, а) двух подгрупп группы G есть подгруппа группы G. Сама
группа G и Е называются несобственными подгруппами группы G; все остальные
подгруппы—собственные. Если G—группа конечного порядка g (п. 12.2-1), то порядок gt
любой ее подгруппы Gt является делителем порядка группы (теорема Лагранжа);
число g/gx называется индексом подгруппы Gt (в группе G).
*) В случае конечной группы второе требование излишне^ так как оно следует из
первого.
372 ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.2-3.
12.2-3. Циклические группы. Порядок элемента группы. Циклическая группа состоит
из степеней а°=Е, а, а2, ... одного элемента а и обязательно коммутативна. Любая
группа простого порядка и любая подгруппа циклической группы являются циклическими.
Каждый элемент а любой группы G порождает в G циклическую подгруппу,
состоящую из всех его степеней. Порядок этой подгруппы называется порядком элемента а;
если он конечен, то он равен такому наименьшему натуральному числу т, что ат = Е\
в противном же случае а называется элементом бесконечного порядка.
12.2-4. Произведения подмножеств. Смежные классы.
(a) Произведение *) CtC2 двух подмножеств Ct и С2 группы G есть множество,
состоящее из всех (различных) произведений аха2 элементов ах из Сх и элементов а9
из С2. Произведение СХС2 двух подгрупп группы G является подгруппой в G в том и
только в том случае, если GtG2 — GZGX.
(b) Левым смежным классом xGt в группе G по ее подгруппе Gx называется
множество всех произведений хах данного элемента х из G и любых элементов ах из Gx.
Аналогично правый смежный -класс Gxx есть множество всех произведений вида а^х.
Смежный класс по подгруппе Gx сам является подгруппой в том и только в том случае
если х есть элемент из Gx; при этом условии xGx = Gtx = Gt. Два левых смежных класса,
по Gx либо совпадают, либо не имеют ни одного общего элемента; то же самое
справедливо и для двух правых смежных классов. Каждая подгруппа Gx группы G определяет
разбиение (п. 12.1-3) группы G на конечное или бесконечное число пх левых смежных
классов и разбиение G на пх правых смежных классов', если G — группа конечного
порядка g, то п± равняется индексу g/gx подгруппы Gx (п. 12.2-2). Два элемента a, b
группы G принадлежат одному и тому же левому смежному классу по подгруппе GXt
если Gx содержит а~1Ь одному и тому же правому смежному классу по Gx, если Gx
содержит Ьа~х.
12.2-5. Сопряженные элементы и подгруппы. Нормальные делители.
Фактор-группы.
(a) Два элемента х и х' группы G называются сопряженными, если они
связаны преобразованием (п. 12.1-4)
х'=сГ1ха (или х = ах'а~1)у (12.2-3)
где а —некоторый элемент группы G. Тогда говорят, что х' является
результатом трансформирования элемента х элементом а. Сопряженность
является отношением эквивалентности (п. 12.1-3) и определяет разбиение
группы G на классы сопряженных элементов.
(b) Преобразование (3) переводит кажцую подгруппу Gt группы G
в сопряженную подгруппу С^аГ^а. Подгруппа Gx отображается сама
на себя (G[ — GJ для любого элемента а из G в том и только в том случае,
если 1) элементы ах подгруппы Gx перестановочны с любым элементом а
группы G(aGi — Gia) или 2) подгруппа Gx содержит все элементы,
сопряженные с ее элементами. Подгруппа, отличающаяся этими свойствами, называется
нормальной подгруппой (нормальным делителем, инвариантной подгруппой)
группы G.
Любая подгруппа индекса 2 (п. 12.2-2) является нормальным делителем группы G.
Простая группа не содержит никаких нормальных делителей, кроме себя самой и Е.
(c) Левые смежные классы (п. 12.2-4, Ь) по нормальному делителю
совпадают с соответствующими правыми смежными классами и образуют группу
по отношению к операции умножения, определенной в п. 12.2-4, а; эта группа
называется фактор-группой G/Gx группы G по нормальному делителю Gx.
Если G—группа конечного порядка, то порядок фактор-группы G/G± равен
индексу g/gx подгруппы Gx (п. 12.2-2).
12.2-6. Нормальный ряд. Композиционный ряд. Для любой группы G нормальным
рядом называется такая (конечная) последовательность подгрупп G —G, Gv G2,
... , G —Е, что каждая подгруппа Q. является нормальным делителем подгруппы G .
Нормальный ряд называется композиционным рядом группы G, если G. при любом i
есть собственный нормальный делитель подгруппы G._j и если между G-^ и G. нельзя
вставить никакого другого нормального делителя, т. е. если каждый композиционный
1) Произведение СХС2 Двух подмножеств не следует смешивать с их пересечением
{логическим произведением, п. 4.3-2) Сх О С2, а также с прямым произведением (п. 12.7-2).
12.2-9.
12.2. ГРУППЫ
373
фактор G^JG. — простая группа (п. 12.2-5). Между любыми двумя композиционными
рядами одной и той же группы G существует такое взаимно однозначное соответствие,
что соответствующие их элементы являются изоморфными группами {теорема Жорда-
на — Гельдера). Группа G называется разрешимой, если все ее композиционные факторы
являются циклическими группами (п. 12.2-3).
12.2-7. Центр. Нормализаторы.
(a) Множество всех элементов группы G, перестановочных с любым элементом этой
группы, является нормальным делителем группы G\ он называется центром группы G.
(b) Множество всех элементов группы G, перестановочных с данным элементом а
из G, является подгруппой группы G (нормализатором элемента а), которая содержит
циклическую подгруппу, порожденную элементом а (п. 12.2-3), в качестве своего
нормального делителя.
Множество элементов группы G, перестановочных с каждым элементом данной
подгруппы Gi группы G, является подгруппой группы G (нормализатором подгруппы G^,
которая содержит Gx в качестве нормального делителя.
Число различных элементов или подгрупп группы G, сопряженных (п. 12.2-5) с
некоторым ее элементом или подгруппой, равно индексу (п. 12.2-2) нормализатора этого
элемента (или соответственно этой подгруппы) в группе G.
12.2-8. Группы преобразований или операторов (см. также пп. 12.1-4,
14.9-1 — 14.10-7 и 16.1-2). Множество G всех взаимно однозначных
преобразований х' = f (х) любого класса С на себя образует группу, определяющей
операцией в которой является последовательное применение двух
преобразований (умножение преобразований или операторов).
Если Gx — произвольная подгруппа группы преобразований G, то два объекта
х, х', связанные каким-либо преобразованием х' = f (x) из подгруппы Glt называются
эквивалентными относительно подгруппы G\. Это отношение есть отношение
эквивалентности (п. 12.1-3), так что каждая подгруппа Gx определяет разбиение
(классификацию) множества С. Каждое свойство, инвариантное (п. 12.1-5) по отношению к Gt
(ко всем преобразованиям из Gi), присуще всем объектам х, эквивалентным
относительно Gi. Множество (обычно числовых) функций Fx (x), F2 (x), ... , инвариантных по
отношению к Gx, называется полной системой инвариантов группы Gt, если множество
значений этих функций однозначно определяет класс эквивалентности любого данного
объекта х из С.
Примеры групп преобразований: все п\ подстановок из п элементов
(симметрическая группа степени п)\ все п\/2 четных подстановок, соответствующих
четным числам транспозиций из п элементов (знакопеременная группа степени п). Любая
подстановка счетного множества объектов S может быть выражена как произведение
циклических подстановок некоторых подмножеств множества S так, что никакие два
таких цикла не действуют на одни и те же элементы из S.
12.2-9. Гомоморфизмы и изоморфизмы групп. Представление групп
(см. также пп. 12.2-4, 12.2-5 и 14.9-1 — 14.10-7).
(a) Гомоморфизм или изоморфизм (по отношению к определяющей
операции, п. 12.1-6) переводит элементы а, Ь, ... данной группы G в элементы
а', Ъ\ ... некоторой группы G' так, что (ah)' -+a'b'. Единица группы G
переходит в единицу группы G'\ обратные элементы переходят в обратные.
При каждом гомоморфизме группы G на группу G" множество элементов группы G,
отображающихся в единицу группы G', есть нормальный делитель Gg группы G, а
множество элементов, отображающихся в произвольный элемент группы G', есть
некоторый смежный класс по G^; фактор-группа G/Gg изоморфна группе G'. Нормальный
делитель Gg называется ядром гомоморфизма. Каждый нормальный делитель Gx группы G
является ядром гомоморфизма, переводящего G в фактор-группу G/Gt.
Класс всех автоморфизмов любой группы G образует группу; класс всех
преобразований вида (3) группы G (внутренних автоморфизмов группы G) есть подгруппа группы
автоморфиз мое.
Сопряженные подгруппы обязательно изоморфны.
(b) Всякая группа G изоморфна некоторой подгруппе (может быть
представлена такой подгруппой, реализована в виде такой подгруппы) группы всех
взаимно однозначных преобразований некоторого класса объектов на себя
(теорема Кэли, см. также п. 12.2-8). В частности, каждая конечная группа
изоморфна некоторой группе подстановок (регулярное представление конечной
группы, п. 14.9-1,а). Представления групп с помощью линейных
преобразований и матриц см. в пп. 14.9-1 — 14.10-7.
374
ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.2-10.
12.2-10. Аддитивные группы. Классы вычетов и сравнимость.
(a) На определяющую операцию в коммутативной группе (абелевой группе,
п. 12.2-1, а) часто смотрят как на (абстрактное) сложение. Ее результат можно
записывать в виде суммы а-\-Ь, а единицу и элемент, обратный данному элементу а,
соответственно как 0 (нуль или нулевой элемент) и — а; при этом пишут
а+(- Ь) =а — Ь.
Группу в этом случае называют аддитивной (группой по сложению), а выражения вида
a -f- а, а-\-а-\-а, —а—а, ... обозначают символами 2а, За, —2а, ...
(b) Каждая подгруппа коммутативной группы есть нормальный делитель.
Смежные классы по подгруппе Gx аддитивной группы G называются классами вычетов по
модулю Gt; два элемента а, Ь группы G, принадлежащие одному и тому же классу
вычетов (т. е. для которых Gx содержит а — Ъ; см. также п. 12.2-4,Ь), называются
сравнимыми по модулю Gx [а == b (G\)]. Сравнимость есть отношение эквивалентности
(п. 12.1-3, см. также п. 12.2-4, Ь). Фактор-группа G/Gi аддитивной группы G является
группой классов вычетов по модулю Gx и может быть обозначена символом G [mod G{].
Два целых числа тип сравнимы по модулю г \т = п (mod г)], где г — целое
число, если разность т — п делится на г; это значит, что т и п при делении на г дают
одинаковые остатки.
12.3. АЛГЕБРА МОДЕЛЕЙ С ДВУМЯ ОПРЕДЕЛЯЮЩИМИ ОПЕРАЦИЯМИ;
КОЛЬЦА, ПОЛЯ И ОБЛАСТИ ЦЕЛОСТНОСТИ
12.3-1. Определения и основные теоремы.
(a) Класс R объектов (элементов) а, Ь, с, ... называется кольцом, если
определены две бинарные операции, обычно называемые (абстрактными)
сложением и умножением, такие, что
1) R есть коммутативная группа по сложению (аддитивная
группа, п. 12.2-10), т. е. R замкнуто по отношению к сложению, и
a-\-b = b-\-a, a + (b-\-c) — (a + b)-\-c,
а + 0 = а, а + (~а) = а —а = 0;
2) произведение ab есть элемент R (замкнутость по отношению
к умножению)',
3) a(bc) = (ab)c (ассоциативный закон для умножения)*);
4) а (Ь + с) = ab + ас, (b-\-c)a — ba-\-ca (дистрибутивные законы).
Заметим, что а-0 = 0-а = 0 для любого элемента а кольца R. Два
элемента рФО и q=£Q кольца R, для которых рд = 0, называются
соответственно левым и правым делителями нуля. В кольце без делителей нуля из ab — 0
следует либо а = 0, либо 6 = 0, либо а = Ь — 0 и действуют законы
сокращения (12.2-1).
Целочисленные «кратные» элементы а кольца, например, 2а, За, ... (п. 12.2-10,а),
вообще говоря, не являются произведением элементов кольца. Целые степени элементов
кольца определяются, как в п. 12.2-1, с.
(b) Если кольцо R содержит левую единицу, т. е. такой элемент Е, что
Еа = а для всех а (см. также п. 12.2-1,а), и правую единицу, т. е. такой
элемент Е', что аЕ' — а для всех а, то Е' = Е и Е обязательно является как
единственной левой» так и единственной правой единицей. В этом случае Е
называется кольцом с единицей.
Могут быть и такие кольца, в которых существует одна или несколько правых
единиц, но нет ни одной левой единицы, или наоборот.
Если а —произвольный элемент кольца с единицей Е> то его левым
обратным (мультипликативным) элементом называют такой элемент aj~ , что
аТ~1а = Е. Аналогично, а~1 называется правым обратным элементом, если
aaJl = E.
*) Иногда также рассматривают неассоциативные кольца, в которых ассоциативный
закон не соблюдается.
12.4-1. 12.4. ЛИЫЕЙН. ВЕКТОРНЫЕ ПРОСТРАНСТВА И ЛИНЕЙН. АЛГЕБРЫ 375
Если элемент а обладает как левым, так и правым обратным элементом,
то они равны между собой: aj~l = a~ =а~~1; в этом случае элемент а
обладает единственным обратным элементом.
Заметим, что не все элементы кольца обязаны иметь обратные элементы.
(c) Поле есть кольцо с единицей, которое содержит: 1) по крайней мере
один элемент, отличный от нуля, и 2) для каждого элемента афО
мультипликативный обратный элемент а"1. Ненулевые элементы поля F образуют
группу по умножению.
Если а и с—произвольные элементы поля F, причем сфО, то уравнения
сх = Ь и хс = Ь
имеют в F решения; эти решения единственны (однозначно определенные левое
и правое деление, см. также в п. 12.2-1, Ь). Делителей нуля в поле нет.
(d) Кольцо или поле коммутативны, если
ab = ba
для всех а и Ь. Коммутативное поле иногда называют просто полем, в отличие
от тела или некоммутативного поля. Полем Галуа называют конечное
коммутативное поле. Область целостности — это коммутативное кольцо с единицей и без
делителей нуля. Любая конечная область целостности является полем Галуа.
В любой области целостности все ненулевые элементы аддитивной группы имеют
один и тот же порядок (п. 12.2-3). Его называют характеристикой этой области
целостности.
(e) Краткие сведения об упорядоченных полях см. в п. 12.6-3.
Примеры полей: рациональные числа, действительные числа, комплексные
числа.
Примеры областей целостности: целые числа, комплексные числа
с целой действительной и мнимой частью, многочлены с действительными или с
комплексными коэффициентами.
Примеры коммутативных колец: четные целые числа (кольцо без
единицы), непрерывные функции на конечном интервале (кольцо имеет делители
нуля).
12.3-2. Подкольца и подполя. Идеалы.
(a) Подмножество Rt кольца R называется его подкольцом, если Rt является
кольцом в смысле определяющих операций кольца R. Это имеет место в том и только
в том случае, если Rt для любой пары своих элементов а и Ь содержит а — Ь и ab.
Аналогично подмножество Fx поля F называется его подполем, если Fx есть под-
кольцо кольца F, имеющее по крайней мере один ненулевой элемент, и если для
каждой пары элементов а и 6^0 множества FL оно содержит и ab~l. Ненулевые
элементы подполя Ft образуют подгруппу мультипликативной группы поля F.
(b) Подмножество It кольца R называется идеалом в R, если
1) It есть подгруппа R по сложению;
2) It содержит все произведения аЬ (левый идеал), или все
произведения Ъа (правый идеал), или все произведения ab и Ьа (двусторонний
идеал), где а — любой элемент из Ilt а Ь — любой элемент из R.
Пример. В кольце всех целых чисел числа, кратные некоторому числу р,
составляют двусторонний идеал.
12.3-3. Расширения. Коммутативное кольцо или поле часто оказывается
возможным включить в качестве подкольца или подполя в «более широкое» поле (поле
отношений, алгебраическое расширение и т. д.; см. также пример в п. 12.4-2). Теория
полей, включающая так называемую теорию Галуа, занимается вопросом о
существовании таких расширений. (Приложения: исследование возможности построения
с помощью циркуля и линейки, или решения алгебраических уравнений с помощью
радикалов, или построения латинских квадратов.)
12.4. МОДЕЛИ, ВКЛЮЧАЮЩИЕ В СЕБЯ БОЛЕЕ ОДНОГО КЛАССА
МАТЕМАТИЧЕСКИХ ОБЪЕКТОВ: ЛИНЕЙНЫЕ ВЕКТОРНЫЕ
ПРОСТРАНСТВА И ЛИНЕЙНЫЕ АЛГЕБРЫ
12.4-1. Линейные векторные пространства. Пусть R — кольцо (с
мультипликативной) единицей 1 (п. 12.3-1); элементы а, |3, ... кольца R будем
называть скалярами. Класс U объектов (элементов) а, Ь, с, ... называется
(линейным) векторным пространством над кольцом R, а элементы класса U
376 ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.4-2.
называются векторами, если определены две бинарные операции — векторное
сложение и умножение вектора на скаляр такие, что 1)
1) U есть коммутативная группа по векторному сложению: для
каждой пары элементов a, b e U пространство U содержит их
векторную сумму а + b и
a + b = b + a, a + (b + c) = (a + b) + c,
а + 0 = а, а + (— а) = а — а = 0,
где 0 —аддитивный нулевой элемент (нулевой вектор) пространства //,
а —а — элемент, аддитивный обратный элементу а (п. 12.2-10);
2) если а —любой вектор из U и а —любой скаляр из R, то U
содержит вектор аа, произведение вектора а на скаляр а
(замкнутость по отношению к умножению на скаляр);
3) (оф) а = афа) (ассоциативный закон для умножения на скаляр);
4) а (а + Ь) = аа + ab, (а + р) а = аа + ра (дистрибутивные законы);
5) 1а = а.
Заметим, что
0а = 0, (— 1)а = — а, (—а)а = —(аа). (12.4-1)
Линейные векторные пространства исключительно важны для прикладной
математики; они 6v^yT детально рассмотрены в гл. 14 (см. также главы 5, 6,
15, 16 и 17).
12.4-2. Линейные алгебры. Пусть R — кольцо скаляров с единицей. Класс
X называется линейной алгеброй (линейной ассоциативной алгеброй,
системой гиперкомплексных чисел) над кольцом R, если определены три бинарные
операции (сложение и умножение в X и умножение элементов из X на
скаляры) такие, что
1) X есть кольцо,
2) X есть линейное векторное пространство над кольцом
скаляров R.
Рангом линейной алгебры называется ее размерность как векторного
пространства (п. 14.2-4). Если линейная алгебра есть поле, то она называется
алгеброй с делением (п. 12.3-1). Матричное представление линейных алгебр
см. в п. 14.9-7.
Элемент А ф 0 линейной алгебры называется идемпотентным, если А2= At и ниль-
потентным, если существует такое натуральное число т > 1, что Ат = о. Эти
определения, в частности, применимы к матрицам (п. 13.2-2) и к линейным операторам
(п. 14.3-6).
Примеры (см. также пп. 13.2-2 и 14.4-2). 1) Поле комплексных чисел —
коммутативная алгебра с делением ранга два над полем действительных чисел. 2) Поле
кватернионов а, Ь, ••• является единственным расширением (п. 12.3-3) поля
комплексных чисел, которое образует некоммутативную алгебру с делением над полем
действительных чисел. Каждый кватернион а может быть представлен в виде
а = а0 + iat + /а2 + ka3 = (а0 + шх) + (а2 + ш3) /, (12.4-2)
где а0, cti, а2, а3 — действительные числа, а /, / и k — специальные кватернионы
(вместе с 1 они являются элементами базиса), подчиняющиеся следующим правилам
умножения:
1 к l* I (12.4-3)
jk = —kf=i, ki=—ik = f, ij = — }i = k. J
i) Некоторые авторы требуют, чтобы U содержало не только сумму любых двух
векторов, но и всякую бесконечную сумму at -f- а2 И , сходящуюся в некотором
специальном смысле; определенные таким образом векторные пространства не
относятся к алгебре в собственном смысле слова (см. также п. 14.2-1).
12.5-1.
12.5. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
377
Если положить а = а0 — tai — /аз — ka3, то
| а ;2 = аа = ad = а© + af -f а| -f а*! (12.4-4)
а"1 = а/| а |«, а ^ 0 (12.4-5)
(см. также п. 14.10-4).
12.5. МОДЕЛИ, ДОПУСКАЮЩИЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНЫХ
ПРОЦЕССОВ: ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
12.5-1. Топологические пространства (элементарные свойства точечных
множеств см. в п. 4.3-2).
(a) Класс С объектов (точек) х называется топологическим пространством,
если он может быть представлен как объединение некоторого семейства / своих
подмножеств, которое содержит:
1) пересечение любой пары своих множеств,
2) объединение любого множества своих множеств.
Элементы семейства / и пустое множество называются открытыми множествами
пространства С, а семейство открытых множеств —топологией пространства С.
Некоторое семейство <$ открытых множеств называется базой пространства С,
если каждое множество из / есть объединение каких-либо множеств из $>.
Пересечения любого подмножества Сх топологического пространства С
с открытыми множествами этого пространства задают топологию в Сх
(относительная топология подпространства Сх).
Одно и то же множество может допускать несколько топологий (и при этом
получаются различные топологические пространства); всякое множество С допускает
тривиальную топологию, при которой открытыми множествами считаются только С и пустое
множество, и дискретную топологию, когда открыто любое подмножество пространства С
(b) При данной топологии окрестностью точки х е С называют любое
множество в С, которое содержит открытое множество, содержащее х. Часто под
окрестностью точки х понимают только открытое множество, содержащее х.
Коль скоро определены окрестности, точно так же как в п. 4.3-6, а, можно
определить предельные точки, внутренние точки, граничные точки и
изолированные точки множеств; топологические пространства очевидным образом
обобщают и абстрагируют некоторые свойства системы действительных чисел.
В любом топологическом пространстве С множество является открытым
в том и только в том случае, если оно содержит только внутренние точки;
множество S замкнуто; 1) если S есть дополнение в С некоторого открытого
множества или 2) если S содержит все свои предельные точки (равносильные
определения). Множество S всюду плотно в С, если в каждом открытом
множестве пространства С содержится хотя бы одна точка из S. Топологическое
пространство называется сепарабельным, если оно содержит счетное всюду
плотное множество. Если в пространстве С существует счетная база, то С
сепарабельно.
Топологическое пространство С называется компактным, если всякая
бесконечная последовательность его точек имеет в нем хотя бы одну предельную
точку; это имеет место в том и только в том случае, если каждое счетное
семейство открытых множеств, покрывающее С (т. е. объединение которого
равно С), содержит конечное подсемейство, покрывающее С (см. также п. 12.5-4).
Множество точек S топологического пространства С называется
относительно компактным (компактным в С), если всякая бесконечная
последовательность точек множества S имеет предельную точку в С. Множество S
компактно (компактно в себе), если каждая бесконечная последовательность его
точек имеет предельную точку в S.
Топологическое пространство С называется бикомпактным, если каждое
семейство открытых множеств, покрывающее С, содержит конечное
подсемейство, покрывающее С. Бикомпактное пространство компактно.
378 ГЛ, 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.5-2.
Бикомпактность и компактность являются обобщением понятия ограниченности
и замкнутости множества (п. 4.3-6) в конечномерных пространствах, где имеют место
теоремы Больцано — Вейерштрасса и Гейне — Бореля (п. 12.5-4).
(c) Предельные и граничные точки множества S соответственно образуют его
производное множество S' и его границу. Замкнутое множество 5 U S' называется замыканием
множества 5. Два множества отделены, если никакое из них не пересекается с
замыканием другого. Множество называется связным, если оно не может быть представлено
в виде объединения двух отделенных собственных его подмножеств (пример: область
в евклидовом пространстве, п. 4.3-6, d).
(d) Непрерывность. Гомеоморфизмы. Отображение
(преобразование, соответствие, функция, операция)* —>x' = f (х) топологического
пространства С в топологическое пространство С называется непрерывным в точке
аеС, если для каждой окрестности V точки / (а) в С существует такая
окрестность U точки а в С, образ которой содержится в U'. Отображение / (л:)
непрерывно в С, если оно непрерывно в каждой точке пространства С; для
этого необходимо и достаточно, чтобы множество всех точек, отображающихся
в любое открытое множество V пространства С (полный прообраз
множества (/'), было открыто в С.
Непрерывное взаимно однозначное отображение, имеющее непрерывное
обратное отображение, называется гомеоморфизмом или топологическим
отображением; соответствующие топологические пространства называются гомео-
морфными или топологически эквивалентными.
(e) Топология — наука о свойствах и величинах, инвариантных относительно
топологических отображений (топологические инварианты; см. также п. 12.1-5). Весьма
существенно, что подходящие топологические пространства служат моделями,
допускающими определение сходящихся предельных процессов с помощью понятия окрестности
(см. также пп. 4.3-5, 4.4-1 и 12.5-3) *). В конкретных случаях топология часто
вводится прямо путем определения окрестностей или сходимости.
Примеры. Определение окрестностей, данное в п. 4.3-5, устанавливает в системе
действительных чисел «обычную» топологию и позволяет ввести пределы,
дифференцирование, интегрирование, бесконечные ряды и т.д. Подобным же образом в п. 5.3-1 дается
определение топологии для пространства евклидовых векторов (см. также пп. 12.5-3
и 14.2-7).
12.5-2. Метрические пространства. Класс С объектов (точек) х, у, z, ..,
называется метрическим пространством, если для каждой упорядоченной пары
точек ху у из С определено действительное число d (х, у) (расстояние между х
и у, метрика) такое, что
1) d(x, y) = 0 в том и только в том случае, если х—у,
2) d(x, y)^d(xt z)-\-d(yy г) (неравенство треугольника) для
любых ху у, г из С.
Из этого определения вытекает
d(xt у)^0, d(y, x) = d(x, у) (12.5-1)
для всех х и у из С.
Два метрических пространства называются изометричными, если между ними
существует взаимно однозначное соответствие, сохраняющее расстояние (изометрия).
Свойства, общие для всех метрических пространств, изометричных данному, называются
метрически инвариантными.
Примеры. Действительные и комплексные числа образуют метрические
пространства с метрикой d (х, у) == | х — у | . Вообще любое нормированное векторное
пространство (п. 14.2-5) допускает метрику d {х, у) = || х — у || (см. также пп. 14.2-6, 14.2-7
и 15.2.-2).
12.5-3. Топология, окрестности и сходимость в метрическом пространстве.
(а) Если а — любая точка метрического пространства С, то множество
точек х е С, для которых d (а, х) < б, называется открытым шаром радиуса 5
с центром а. Открытые шары конечных радиусов составляют базу в
пространстве С (п. 12.5-1). Открытые множества в С — объединения любых
множеств открытых шаров. Окрестностью точки а в С называется любое множество,
содержащее открытый шар с центром а. Множество точек х е С, для которых
*) Целиком за пределами этого справочника остается алгебраическая топология^
12.5-4.
12.5. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
379
d (а, х) ^ б, называется замкнутым шаром радиуса Ь с центром а. Множество
в пространстве С называется ограниченным, если оно содержится в
некотором замкнутом шаре этого пространства.
(Ь) Последовательность точек х0, хъ х2, ...метрического пространства С
сходится к пределу аеС, если
d(xni а)—>0 при п—>со
(см. также п. 14.2-7).
Если переменная точка х (£) пространства С является функцией действительного
переменного £, то говорят, что функция х (£) сходится к пределу а 6 С при % -+ а,
если d [*(£), fl]-*■ 0 при £ -► а. Функция x'=f(x), связывающая точки х
метрического пространства С^ и точки х' метрического пространства Сд|, непрерывна в точке
а £ СМ* если
d [f (*), f {а)] -+ 0 при d {х, а) -* 0.
12.5-4.* Метрические пространства со специальными свойствами. Теория
точечных множеств.
(a) Метрическое пространство С называется:
полным, если любая последовательность xl9 x2, ... точек
пространства С, для которой lim d (xm, xn)—0 (последовательность
т-+со
п -*оо
Кош и, фундаментальная последовательность), сходится к некоторой
точке из С (см. также пп. 4.9-1, а, 4.9-2, а, 4.9-3, а, 14.2-7 и 15.2-2);
компактным, если любая бесконечная последовательность точек
пространства С содержит подпоследовательность, сходящуюся к
некоторой точке из С. Компактное метрическое пространство называется
также компактом (см. п. 12.5-1, Ь);
вполне ограниченным, если для любого 6 > 0 пространство С
есть объединение конечного числа открытых шаров радиуса 6;
локально компактным, если у каждой его точки есть окрестность,
замыкание (п. 12.5-1, Ь) которой компактно.
Множество S в полном метрическом пространстве С является полным метрическим
подпространством С (см. также п. 12.5-1, а) в том и только в том случае, если S
замкнуто. Для того чтобы метрическое пространство С было компактно, необходимо и
достаточно, чтобы оно было полным и вполне ограниченным, а для того чтобы оно было
вполне ограниченным, необходимо и достаточно, чтобы любое бесконечное его
подмножество содержало последовательность Коши.
Всякое конечномерное нормированное пространство является сепарабельным и полным
(см. также п. 14.2-7). Любой замкнутый шаре нем компактен, и потому такое пространство
локально компактно.
(b) Понятия, введенные в пп. 12.5-2 — 12.5-4, а, дают удобную терминологию для
многих задач, касающихся приближения произвольного элемента х подходящего
класса С последовательностью элементов х0, хи х2, ... из С. В таких случаях
d (x х\ измеряет погрешность приближения.
Примеры. Важные приложения имеет приближение функции f (t)
последовательностью функций s0 (Of si (Of $2 (Ot • • • (частичные суммы бесконечного ряда). Если
дано пространство С функций f (t), g (0. .... непрерывных в интервале 0 ^ t ^ 1,
то можно использовать метрики:
dt(f, g)= max If (О-в (0 1
0</^l
(максимальная погрешность — ведет к определению равномерной сходимости, и 4.4-4);
1
d2 (f. g) = J I f (x) - g (т) |» dx
0
{средняя квадратическая погрешность — ведет к определению сходимости в среднем с
показателем 2 и к приближениям по методу наименьших квадратов) и другие. С
топологией, определяемой метрикой dt (f, g), С есть полное и сепарабельное пространство;
счетное множество 5 многочленов с рациональными коэффициентами всюду плотно
в С и годится, таким образом, для приближений (см. также п. 4.7-3).
380.
ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.5-5.
(с) Компактное метрическое пространство бикомпактно (см. п. 12.5-1, Ь).
В любом компактном метрическом пространстве С:
1) всякое бесконечное множество имеет по крайнзй мере одну предельную
точку;
2) если S — произвольное замкнутое множество и А — произвольное
семейство открытых множеств пространства С, объединение которых содержит S
(покрытие множества S), то уже некоторое конечно? число множеств из
семейства А образует покрытие множества S.
Всякое ограниченное замкнутое подмножество евклидова пространства компактно.
Поэтому теоремы 1 и 2, в частности, применимы к ограниченным замкнутым
множествам действительных и комплексных чисел и к таким же множествам в двух- и
трехмерном евклидовом пространстве. Они называются в этом случае соответственно тео*
ремой Больцано — Вейерштрасса и теоремой Гейне — Бореля о выделении конечного
покрытия.
12.5-5. Примеры: пространства числовых последовательностей и функций.
Понятия, введенные в пп. 12.5-2—12.5-4, обеспечивают четкую и
стимулирующую терминологию для многих задач, касающихся приближения
произвольного элемента подходящего класса С некоторой последовательностью
элементов xv х2, ... из С. В таком случае расстояние d (хп, х) измеряет
погрешность приближения или степень того, насколько система, характеризуемая
последовательностью xv х2, ..., отклоняется от требуемого результата х.
В таблицах 12.5-1 и 12.5-2 приведено несколько примеров топологических
пространств. Особенно важные приложения касаются приближения некоторой
функции / (/) последовательностью функций s1(/), s2 (/), ..., являющейся,
например, последовательностью частичных сумм какого-либо бесконечного
ряда (см. также пп. 4.7-3, 5.3-11, 13.2-1, 13.2-11, 14.2-7 и 15.2-2).
Таблица 12.5-1
Некоторые пространства числовых последовательностей
x=(llt l2, ...), y = (r\lt ть ...)
Обычное
обозначение
т
с
/2
/Р
Определение
Ограниченные
последовательности
действительных чисел
Сходящиеся
последовательности
действительных чисел
Последовательности
комплексных чисел, для
которых сходится ряд
оо
2 l^l2
Последовательности
комплексных чисел, для
которых сходится ряд
2 1**1
<р= 1. 2. . . .)
Расстояние d (x, у)
&uP\h~%\
S£P 1 Ч ~ Ч1
Г оо
оо "
Л \h-**\p\
_Ar = I J
IV*
Up
Замечания
Полное, не
сепарабельное
Все полные и
сепарабельные
12.5-5.
12.5. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
381
Таблица 12.5-2
Некоторые пространства функций х (t), у (t)
Сем. также пп. 14.2-7, 15.2-2 и 18.10-9; определения легко распространяются
на функции двух или более переменных)
Обычное
обозначение
Определение
Расстояние
Замечания
F[0, 1]
Действительные
функции, определенные на
[0, Ц
Метрики не существует. Топология
определяется поточечной сходимостью
С[0, 1]
Непрерывные
действительные функции,
определенные на [0, 1]
sup
0</<1
1*<0-* (О I
Полное; сепара-
бельное
(п. 4.7-3);
равномерная
сходимость
V- (а, Ь)
Комплексные функции,
для которых интеграл
Ь
Г I х (t) |« dt
существует в смысле
Лебега (п 4.6-15)
I x(t)-y (/) |t dt
Lp (a, b,
Комплексные функции,
для которых интеграл
Ь
J I * (О lP dt
а
существует в смысле
Лебега (р = 1, 2, . . .)
Полные
(п. 15.2-2); сепа-
рабельные, даже
когда интервал
(а, Ь) не
ограничен; сходимость
в среднем
$ | х {t) -у (О \Р dt
1/р
Комплексные функции,
для которых существует
предел
1
lim
Т/2
J Iх (О
- 7/2
lim J- [ ]X(t)-
Г-^+оо
2 dt,
Т/2
I
- 7/2
-yQ)\%dt
Полное, не сепа-
рабельное
причем интегралы
понимаются в смысле
Лебега 1)
/г
*) Точками пространств L (a, b), lP (a, b) и L являются не сами функции,
а классы функций; в каждый такой класс входят функции, совпадающие почти
всюду (см. п. 4.6-14, Ь).
382 ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.5-6.
12.5-6. Теорема Банаха о сжатых отображениях и последовательные
приближения. Пусть x' = f(x) — любое отображение замкнутого множества S полного
метрического пространства С в себя, удовлетворяющее для всех х, у из S условию
dlfW, f(y)]^«,d(x, у), (12.5-2)
где а— некоторое положительное число, меньшее, чем единица («сжатог
отображение»). Тогда множество S содержит единственную неподвижную точку
xj отображения f, для которой
f(Xj) = Xj. (12.5-3)
Кроме того, решение xj уравнения (3) является пределом всякой
последовательности точек
xn+i = f(*n) (л = 0, 1. 2, ...) (12.5-4)
для произвольной начальной точки х0 из S. Скорость сходимости
приближающей последовательности оценивается по формуле
*(*«. */) ^Т^ d{xl9 х0) (л = 0. 1, 2, ...). (12.5-5)
Теорема Банаха (принцип сжатых отображений) служит мощным методом
установления сходимости в обширной области применения аппарата
приближений (пп. 20.2-1, 20.2-6 и 20.3-5).
12.6. ПОРЯДОК
12.6-1. Частично упорядоченные множества.
(а)# Порядок. Класс S объектов (элементов) а, Ь, с, ... называется
частично упорядоченным множеством, если между некоторыми парами его
элементов а, Ь определено отношение порядка (правило предшествования) а^Ь
такое, что
1) из а^Ь и Ь^с следует а^с (транзитивность), ^
2) а^а (рефлексивность). )
Если а ^ Ъ и афЬ, то пишут а < Ь. Часто, кроме того,
предполагается, что
3) из а^Ь и ЪНаследует а — b1) (антисимметричность). (12.6-1а)
Для любого подмножества частично упорядоченного множества, так же как в
п, 4.3-3, можно определить понятия верхней границы, нижней границы, точной нижней
границы, точной верхней границы, наибольшего и наименьшего элементов. Если
частично упорядоченное множество удовлетворяет условию 3), то точная верхняя (точная
нижняя) граница любого его подмножества, если она существует, единственна.
Частично упорядоченное множество называется полным (полной структурой), если
в нем выполяется условие 3) и если каждое непустое его подмножество имеет
точную верхнюю и точную нижнюю границы. Частично упорядоченное множество
называется условно полным, если в нем выполняется условие 3) и если каждое непустое
его подмножество, имеющее верхнюю границу (ограниченное сверху), имеет и
точную верхнюю границу. Последнее условие выполняется в том и только в том
случае, если каждое непустое его подмножество, имеющее нижнюю границу
(ограниченное снизу), имеет и точную нижнюю границу.
(Ь) Структуры. Частично упорядоченное множество называется структурой, если
в нем выполняется условие 3) п. 12.6-1, а и если у каждой пары а, Ь его элементов
имеется (необходимо единственная) точная верхняя граница sup (a, b) и (необходимо
единственная) точная нижняя граница inf (a, b). В каждой стргктуре можно
определить «сумму» а -f- b = sup (a, b) и «произведение» ab = inf (a, b) любых двух
элементов. Так определенные сумма и произведение обладают свойствами 1, 2, 3, 5, 6 булевых
алгебр, перечисленными в п. 12.8-1.
12.6-2. Линейно упорядоченные множества. Класс S элементов а, Ь, с, ...
называется линейно (просто, совершенно) упорядоченным множеством (цепью),
если в нем определено отношение порядка, удовлетворяющее условиям 1), 2)
*) Некоторые авторы это условие формулируют в виде: «а<£ исключает Ь <, а».
12.7-3.
12.7. КОМБИНАЦИИ МОДЕЛЕЙ
383
и 3) п. 12.6-1, и, кроме того, условию, что для любой пары а, Ь различных
элементов множества 5 либо а < 6, либо Ь < а.
Линейно упорядоченное множество 5 называется вполне упорядоченным
множеством, если всякое непустое его подмножество имеет наименьший элемент.
12.6-3*. Упорядоченные поля (см. также пп. 1.1-5 и 12.3-1).
(a) Коммутативное поле К называется упорядоченным полем, если некоторые его
элементы называются положительными (> 0) и если выполняются условия:
1) для всякого элемента а £ К имеет место одно и только 1
г 1\1 6-2^
одно из трех отношений: а > 0, а =■ 0, — а > 0; J
2) из а > 0 и Ь>0 следует a -f- b>0 и ab > 0.
Если — а > 0, то элемент а называют отрицательным и пишут а < 0. Если
положить а~>Ь, когда а — b > 0, то поле становится линейно упорядоченным множеством
(п. 12.6-2).
(b) Всякое условно полное (п. 12.6-1, а) упорядоченное поле изоморфно {по сложению
и умножению) полю действительных чисел. Любая упорядоченная область целостности,
множество положительных элементов который вполне упорядочено (п. 12.6-2), изоморфна
кольцу целых чисел.
12.7. КОМБИНАЦИИ МОДЕЛЕЙ: ПРЯМОЕ ПРОИЗВЕДЕНИЕ,
ТОПОЛОГИЧЕСКОЕ ПРОИЗВЕДЕНИЕ И ПРЯМАЯ СУММА
12.7-1. Декартово произведение. Пусть Съ С2, ...—-некоторые классы
объектов. В пп. 12.7-1 — 12.7-5 рассматривается новый класс С, элементы
которого представляют собой всевозможные упорядоченные множества {aJt а2, ...}
объектов аъ а2, •••» взятых соответственно из классов С1% С2, ... По
определению {аъ a2t ...} = {&i, b2, ..♦} втом и только в том случае, если а1 — Ь1,
а2 = Ь2, ... Класс С называется декартовым произведением классов Съ С2, ...
Этот метод комбинирования математических объектов в более сложные мате-
матические объекты ассоциативен:
{аъ {a2t a3}} = {{av а2}у а3} == {%, а2, а3\. (12.7-1)
Остается связать операции в С с операциями в Clt C2, ...
12.7-2. Прямое произведение групп (см. также п. 12.2-1). Прямым
произведением (? = (?! (х) (?2 двух групп Gx и д2 называется группа, образованная
всеми упорядоченными парами {аь а2}, где аг — любой элемент группы G1%
а а2 — любой элемент группы G2 с умножением, определяемым формулой
К, а2\ {Ь19 Ь2} == \aiblt a2b2}. (12.7-2)
Порядок группы G равен произведению порядков групп G± и G2. Группа G
имеет единицу E = \EV Е2}, где Ех и Е2 —единицы соответственно в Gx и в G2.
Если у групп С?! и G2 нет общих элементов, то {av a2\ можно записывать как
внешнее произведение ага2, причем а1Е2 = а1, Еха2^а2 и Gx и G2 —
подгруппы в G.
Примеры. Любая скалярная величина в физике является внешним произведением
числа и единицы измерения. Выражения вида работа = массе х ускорение х перемещение
— тоже внешние произведения.
12.7-3. Прямое произведение действительных векторных пространств (см.
также пп. 12.4-1, 14.2-1 и 14.2-4). Прямым произведением U = U1®U2 двух
действительных векторных пространств Ux и U2 называется действительное
векторное пространство, образованное всеми упорядоченными парами (внешними
произведениями) {аь а2} = а!а2, где &1 — любой элемент из 21ъ а а2 — любой
элемент из U2 с векторным сложением и умножением векторов на скаляры,
определяемыми формулами
аПаз + Ь^ЕЕЕа^а + а!^, (a^bj) a2 = а^ + Ь^, \ 9
ааха2 = (аах) а2 = ах (аа2). J
384
ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.7-4.
Линейная размерность векторного пространства U равна произведению
линейных размерностей пространств Ux и U2.
Пример. Построение тензоров как внешних произведений векторов приведено
в пп. 16.3-6, 16.6-1 и 16.9-1.
12.7-4. Топологическое произведение (см. также п. 12.5-1). Топологическое
произведение двух топологических пространств Сг и С2 есть их декартово
произведение с топологией (семейством открытых множеств), определяемой
следующим образом: открытое множество есть декартово произведение любых двух
множеств S± и S2, где St — открытое множество в Cl% a S2 — открытое
множество в С2.
12.7-5. Прямая сумма.
(a) Прямой суммой W = Ux ф U2 двух векторных пространств 21г и U2t
взятых над одним и тем же кольцом скаляров R, называется векторное
пространство, образованное всеми парами [alt a2], где ах —любой элемент из 11х,
а а2 —любой элемент из U2, с векторным сложением и умножением векторов
на скаляры а из R, определяемыми формулами
[ai> aaJ-Hbi, Ъ2] = [&1 + Ъ1, a2 + b2], a [av a2] = [аа^ аа2]. (12.7-4)
Размерность пространства W равна сумме размерностей пространств Ux и U2,
Если Ux и U2 не имеют общих элементов, то можно писать [ах, а2] = ах+а2
и пространства UY и U2 являются тогда подпространствами W. Каждое линей-
ное векторное пространство размерности большей, чем единица, может быть
представлено в виде прямой суммы его непересекающихся подпространств.
(b) Прямой суммой R' = Rx ф R2 двух колец Rx и R2 называется кольцо,
образованное всеми упорядоченными парами (часто называемыми прямыми
суммами) [аъ а2] со сложением и умножением, определяемыми формулами
[av а2] + [Ьъ Ь2\ = [а1 + Ьъ а2 + Ь2], [аъ a2][blt Ь2] = [афъ а2Ь2] (12.7-5)
(c) Прямая сумма двух линейных алгебр (п. 12.4-2) есть линейная алгебра
из упорядоченных пар со сложением, умножением и умножением на скаляр,
определяемыми формулами (4) и (5).
12.8. БУЛЕВЫ АЛГЕБРЫ
12.8-1. Булевы алгебры. Булевой алгеброй называется класс § объектов Л,
В, С, ..., в котором определены две бинарные операции, обозначаемые как
(логические) сложение и умножение, со следующими свойствами:
(a) Для всех Л, В, С из 8
1) $ содержит А-\-В и А В (замкнутость);
2) А + В = В + А, \
> (коммутативные законы);
3) А + (В~^-С) = (А + В) + С, I
А (ВС) = (АВ)С J ^ассо^иатитые Зак<>ны)\
4) А(В + С) = АВ + АС,
А + ВС = (А + В)(А + С),
5) А-\-А — АА—А (свойства идемпотентности);
6) А+В = В в том и только в том случае, если
А В —А (свойство совместимости).
(b) Кроме того,
7) $ содержит элементы / и 0 такие, что для всякого
элемента А из §
Л + 0 = Л, AJ=At Л0=0, Л + /=/;
> (дистрибутивные законы);
12.6-2,
12.8. БУЛЕВЫ АЛГЕБРЫ
385
8) для каждого элемента Л класс 8 содержит элемент А
(дополнение элемента Л, часто обозначаемое символами А или /—А) такой,
что
Л + Д=/, ЛЛ=0.
В каждой булевой алгебре
А(А + В)~А + АВ^.А (законы поглощения), (12.8-1)
(А + В)ее<
)~А + ВJ
^двойственность, законы де Моргана), (12.8-2)
(ляЬ - -
Аее-А, 7=0, б=/, (12.8-3)
А+АВ — А+В, АВ + АС+ВСе=АС + ВС. (12.8-4)
Если Л + В = В, то вместо ЛВ можно писать В — А (дополнение А до В).
Элементы А, В, С, ... булевой алгебры называются дизъюнктными, если попарные
произведения любых элементов этого множества равны 0.
Символы U и П, используемые в пп. 4.3-2, а, 12.8-5, b и 18.2-1 для обозначения
объединения и пересечения множеств и событий, часто употребляются и для
обозначения логического сложения и умножения в любой булевой алгебре, причем вместо Л + В
пишут А У В, а вместо АВ пишут А ("| В.
12.8-2. Булевы функции. Приведение к каноническому виду. Если даны п
булевых переменных Х1% Х2, ...,Хл, каждое из которых может быть равно
любому элементу данной булевой алгебры, то булевой функцией
Y = F(Xl9 Х2, .... Хп)
называется выражение, получаемое из Xlt X2, ..., Хп путем сложения,
умножения и взятия дополнения.
В каждой булевой алгебре существует ровно 2(2Л) различных булевых
функций п переменных. Из соотношений п. 12.8-1 следует
F(X, Y, ..., + 9.)==F(X,Y, ...r,+), (12.8-5)
F (X, X, К, ...) = XF(I, 0, Y, ...) + XF(0, J, Y, ...) =
= [X + F(09 I, Y, ...)][x + F(I9 0, Y, ...)], (12.8-6)
XF(X, X, Y, ...) = XF(I,
X+F(X, X, Y9...)==X + F\
1. 0, Y, ...), \
7(0, I, Y, ...). J
(12.8-7)
(b) Всякая булева функция лцбо тождественно равна 0, либо может быть
единственным образом представлена в виде суммы одночленов ZXZ2 ...Zn,
где Zi равно или Х^ или Xi (канонический вид булевой функции,
геометрическую иллюстрацию см. на рис. 12.8-1). Булеву функцию Y = F (Xlt X2t..., Хп)
можно привести к каноническому виду следующим образом:
1) пользуясь равенством (2), разложить дополнения к суммам и
произведениям;
2) с помощью первого дистрибутивного закона свести функцию
F (Хъ Х2, ..., Хп) к сумме произведений;
3) с помощью тождеств Х/Х; = Х/ и XiXi = Q и равенств (4)
упростить полученное выражение;
4) если какой-либо член / не содержит одной из переменных,
например Xi, то переписать / в виде fX't-\-fXi.
13 Г. Корн и Т. Корн
386
ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА
12.8-3
Во многих приложениях может оказаться полезным опустить шаг 4) и,
продолжив шаг 3), как можно больше упростить каждый член разложения.
Ввиду законов де Моргана (2) каждую булеву функцию, не равную
тождественно нулю, можно также единственным образом представить в виде
I XfX2^
X/ Х2 Х3
X/XzXsSf \
/XfX2XJ Xf Х2 Х3\
'XfX2X^/ XfX2X3
XfXgXJ
Рис. 12.8-1. Диаграмма Венна (диаграмма Эйлера). Диаграммы этого типа
иллюстрируют отношения в алгебре классов (п. 112.8-5;. Если прямоугольник, круг, квадрат и
треугольник обозначить соответственно через /, Xi, X2, Х3, то диаграмма показывает,
что всякая булева функция от Xi, X2, Х3 может быть представлена как объединение
минимальных многочленов от Xlt Х2, X, (п. 12.8-2). Заметим, что имеется 23 = 8
различных одночленов.
произведения сумм Z\ + Z2 + ... + Zn, где Zi равно либо Xit либо Xt. Всего имеется
2п таких сумм.
Примеры:
(AB + CD)= (А+Ъ) (C + D) = AC+AD + BC + BD,
(аТвисЧ^)=а^
12.8-3. Отношение включения (см. также п. 12.6-1).
(а) Равенство А + В = В, или АВ = А, эквивалентно рефлексивному
отношению частичного упорядочения А^В [или В^А\ (логическое) отношение
включения].
+ BD, )
с)(в+5). J
(12.8-8)
(b) Во всякой булевой алгебре изА^ВиВ^А следует А = В и
А + В == sup (А, В), АВ =* inf (А, В),
(12.8-9)
где границы определяются отношением включения. Каждая булева алгебра является
структурой (п. 12.6-1, Ь).
(с) Если А — произвольный элемент булевой алгебры $, то элементыХА ^ А
алгебры g образуют булеву алгебру, в которой А играет роль I.
12.8-4. Алгебра классов. Подмножества (подклассы) А, В, ... любого
множества (класса) / образуют булеву алгебру (алгебру классов) по
отношению к операциям логического сложения (объединения), логического
умножения (пересечения) и взятия дополнения, определенного в п. 4.3-2, а. Пустое
множество (или любое множество, не содержащее ни одного элемента из /)
обозначают символом 0. Отношение ^ (п. 12.8-3) превращается в логическое
отношение включения cz.
12.8-5. Изоморфизм булевых алгебр. Диаграммы Венна. Две булевы
алгебры с конечным числом элементов изоморфны {по отношению к сложению,
умножению и взятию дополнения, п. 12.1-6) в том и только в том случае,
если они имеют одно и то же число элементов. Всякая булева алгебра
изоморфна некоторой алгебре классов (п. 12.8-4). Диаграммы Венна (диаграммы
Эйлера), подобные диаграмме, изображенной на рис. 12.8-1, наглядно
иллюстрируют свойства булевых алгебр с помощью алгебры классов.
12.8-6.
12.8. БУЛЕВЫ АЛГЕБРЫ
387
12.8-6. Алгебры событий и символическая логика. Алгебры событий
служат моделями для комбинирования событий (должным образом определенных
исходов идеализированных экспериментов; см. п. 18.2-1). Если Еи Е2, ...—
такие события, то
£i U Е2 — событие (предложение) Ег или Е2 (или и то, и другое,
не исключающее или),
Eif\E2 — событие (предложение) Ег и £2,
Ё — событие (предложение) не Е>
I — достоверное событие (объединение всех возможных исходов,
п. 18.2-1),
О — невозможное событие.
В двузначной (аристотелевой) логике алгебра гипотетических событий
(логических высказываний, утверждений) Е связана с более простой булевой
алгеброй значений истинности Т[Е], равных или 1 (Е истинно) или О
(Е ложно), гомоморфизмом (п. 12.1-6):
Г[/] = 1, Г[0] = 0,
Т[ЕгUЕ2{ = Т(£х) + Т(£2), TVh(]E2] = T[Ег] Т[£,],
Т[Ё] = Т[Е]- (12.8-10)
На основании этих предложений высказывание Е либо истинно, либо ложно
(закон исключенного третьего), и значение истинности любого высказывания Е,
fi А
А
00 01
А
и to
В В
во
В1
А
0
А
1
СО
с t
А
00 Of
^
//
А
10
»\*
а)
В В
00
01
и
ю
00
в
01
1
ft
?
to
в
в
в
в
с)
„00
с
01
11
с
10
/
000
в
V
001
А
ОН 010
в
А
too tot
в в
А
111 110
в
В
j
в
п
В
й)
С 0
С 1
А
0
1
/
/
А
Г1Г1Р
1
0
* '
0
1
в
е)
Рис. 12.8-2. Карты Карно а) — d) соответственно для двух, трех, четырех и пяти
булевых переменных и с) карта для функции из табл. 12.8-1 от трех переменных.
представимого как булева функция F(E1% E2, ...) от множества событий Еи
Е2, ... (логически связанного с этим множеством), дается формулой
T[E] = T[F (Elt E2t ...)W(n£ibn£2h ."), (12.8-11)
где
0 + 0 = 0, 0+1 = 1, 1 + 1 = 1,
0-0 = 0, 0-1=0, Ы = 1,
0 = 1, 1=0.
(12.8-12)
13*
388 ГЛ. 12. СОВРЕМЕННАЯ (АБСТРАКТНАЯ) АЛГЕБРА 12.8-в.
А А
а)
Ь)
щ
щ
А
4
ш
'{
i
ш
п
В ^ В
ABC
\
(
1
1
1
1
1
1
/
;
N
м
щ
в$
1
ABB
ABB
d)
О
F - ABC +ABC + AQC^. .
- BC+ABC= (B + C)(A+B+C)
Рис. 12.8-3. Логическое упрощение с помощью карты Карно.
12.8-8.
12.8. БУЛЕВЫ АЛГЕБРЫ
389
12.8-7. Представление булевых функций истинностными таблицами. Карты Карно.
Если задана система булевых переменных Х^, Х^, ... , X каждая из которых может
принимать значения 0 или 1 (п. 12.8-6), то всякая из 2*2 / булевых функций
У-F (X,. *,.... JT„)
однозначно определяется соответствующей истинностной таблицей (таблица 12.8-1), в
которой указаны значения данной функции для всех возможных аргументов. В таблице
Таблица 12.8-1
Истинностная таблица для булевой функции
F = XYZ + XYZ + XYZ + XYZ + XYZ = (X + Y + Z) (X + Y + Z) (X + Y+ Z)
X
0
0
0
0
Y
0
0
1
1
z
0
1
0
1
F
0
1
1
1
Соответствующий
одночлен
X YZ = m0
X YZ = mt
XYZ = m2
XYZ = m,
X
1
1
1
1
Y
0
0
1
1
z
0
1
0
1
F
0
1
1
0
Соответствующий
одночлен
XYZ = mA
XYZ = m6
XYZ = m9
XYZ = m,
12.8-1 указано также обычное расположение соответструющих одночленов (п. 12.8-2);
каждому одночлену ставится в соответствие двоичное число, определяемое порядком
нулей и единиц относительно X, Y, Z. Функция F равна булевой сумме тех
одночленов, для которых в этой таблице указано значение функции 1.
Карта Карно — это диаграмма Венна (п. 12.8-5), состоящая из правильно
расположенных квадратов, каждый из которых соответствует одному из 2п одночленов,
порожденных п переменными (рис. 12.8-2). Значения данной функции F из истинностной
таблицы вносят в нужные квадраты; тогда функция F равна сумме всех одночленов, для
которых в соответствующих квадратах стоит единица. Для функций, пожалуй, до шести
переменных карта Карно позволяет удобным образом перегруппировать эти одночлены
в объединения и пересечения так, чтобы минимизировать, скажем, число логических
сложений, умножений и/или взятия дополнений. Это полезно для экономного
конструирования схем электронных вычислительных машин (рис. 12.8-3).
12.8-8. Полная аддитивность. Алгебры меры (см. также пп. 18.2-1 и 18.2-2). Многие
алгебры классов и алгебры событий требуют распррстранения определяющих
постулатов на объединения и пересечения бесконечного множества членов (т. е., строго говоря,
выхода за пределы собственно алгебры, п. 12.1-2).
Булева алгебра g называется вполне аддитивной, если каждая бесконечная сумма
^i + ^! + - единственным образом определена как элемент §, Вполне аддитивная
булева алгебра $ называется алгеброй меры, если существует действительная функции
(мера) М (А), определенная для всех элементов Де^и такая, что
1) М (А) > О,
2) М (0) = 0,
3) М (Л, 4 А2 •+- ...) = М (At) + М (А2) •+-... для любого конечного или
счетного множества элементов At, Аг, ... , удовлетворяющего условию:
A-Ak = 0 при i ф k.
Примеры мер: Мощность конечного множества (п. 4.2-3), длина, площадь, объем,
меры Лебега и Стилтьсса (пп. 4.6-14, 4.6-17), значение истинности (п. 12.8-6), вероятность
<п. 18.2-2).
ГЛАВА 13
МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ
J3.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Аппарат матриц позволяет более просто представлять различные
математические и физические операции с помощью числовых операций над
элементами матриц.
Для большей легкости ссылок в пп. 13.2-1 — 13.4-7 алгебра матриц и
матричное исчисление вводятся как независимый объект, а в гл. 14
описывается применение матриц для представления векторов, линейных
преобразований (линейных операторов) и скалярного произведения.
В пп. 13.5-1 — 13.5-6 подобным же образом квадратичные к эрмитовы
формы вводятся с точки зрения алгебры; их значение для представления
скалярного произведения выясняется в пп. 14.7-1 и ХАЛ-2.
13.2. АЛГЕБРА МАТРИЦ И МАТРИЧНОЕ ИСЧИСЛЕНИЕ
13.2-1. Прямоугольные матрицы.
(а) Если собираются воспользоваться какой-либо из «матричных
операций», определяемых в п. 13.2-2, то таблицу
Mi flu ... Ахл \
4 = 1*21 fl22 ... Ам \^[aik] (13.2-1)
\ami am2 ••• amn/
«скаляров» #/£, взятых из коммутативного поля F (п. 12.3-1), называют
(прямоугольной) матрицей размера т х п над полем F. Элементы а;/, называются
элементами матрицы; элемент aik расположен в f-й строке и в k-м столбце
матрицы (1); т есть число строк, а /г — число столбцов. Матрица конечна,
если она имеет конечное число строк и конечное число столбцов; в против-
кОхМ случае она бесконечна.
Матрица (1) над полем комплексных чисел ограничена, если она имеет
конечную норму. Вот типичное определение нормы матрицы
= stip
т п
2 2] aiklfl\k
1=1 /5=1
т п \
S l^i2=2] 1^1а=Ч 03.2-2)
V-i *=1 /
(см. также табл. 13.2-1 и п. 14.4-1). Конечная матрица над полем
комплексных чисел всегда ограничена.
В этом справочнике все матрицы предполагаются конечными матрицами
над полем комплексных чисел *). Матрица A s= [a(k] называется действительной,
если все ее элементы #;# — действительные числа.
*) Бесконечные матрицы рассматриваются, например, в [13.1].
13.2-1. 13.2. АЛГЕБРА МАТРИЦ И МАТРИЧНОЕ ИСЧИСЛЕНИЕ 391
Таблица 13.2-1
Некоторые нормы матриц
(п и/или т могут быть и бесконечными; см. также пп. 12.5-5 и 14.4-1)
(а) Прямоугольные матрицы размера т х п А == [Д^] (т, п > 1)
II Л II = sup
т п
2 2 в^л
i=i k=i
1 т п
2 l*'!1- Si4*!""1
\/=1 4=1
т п
|| A ||IS sup 2 \aik\t II Л ||И ^ sup 2] la. 1
£ /== 1 * *« i
1 т п \\/р
V=i£=i /
m л
па\u-21 2 ie»i
*=i*=i
1 т п \t/f
" Л ''2 s 2 2 1 °*А I2 I (евклиД°ва норма).
(b) Столбцы * = 1 В или строки х г (git Ё2' • • • » S )
uJ
ii*np-iisiip= 2 \ьк\*\ (p-i.2,...)
j|X|ll»ll*lll = 2 |^|
£=1
/л \ Vt
|| * ||, == || * ||2 == [ 2 | Sfe |2 1 (евклидова норма)
ll*lloo = l|S|loo = snp|6A|.
(с) Соотношения. Для каждой нормы выполняются соотношения
II Л + В || < || А || + || В || , || схЛ || = | а | || А || , || АВ ||< || Л || ||
3 частности,
II Л* ||, < || Л ||, 1| дс||,.
)
в\\.
392 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.2-2.
(b) Матрица размера лх1 называется столбцом, а матрица размера
1 X п — строкой. Будут применяться следующие обозначения:
/ЕЛ
ь )^{ы=х, fl; fr¥rx'* I <13'2-3>
'" / (bl> Ь2» • • • » Ъп) = lfe/гJ — х » J
\ln/
где ^ — комплексное число, сопряженное с gft (см. также пп. 13.3-1, 14.5-1
и 14.5-2).
(c) Матрица размера пхп называется квадратной матрицей порядка /г.
Квадратная матрица А = [а^] называется:
треугольной (наддиагональной), если из / > к следует aift = 0,
строго треугольной, если из i^k следует aift = 0,
диагональной, если из 1Фк следует аг/г=0,
мономиальной, если в каждой ее строке и в каждом столбце
имеется лишь один элемент, отличный от нуля.
13.2-2. Основные операции. Операции над матрицами определяются с
помощью операций над их элементами.
1. Две матрицы А = [aik] иВ= [bik] размера тхп равны друг
другу (А=В) в том и только в том случае, если aik — bik для всех
i и к (см. также п. 12.1-3).
2. Сумма двух матриц А = [alk\ иВ = [bik] размера тХп есть
матрица размера тХп
А + В^ [aik] + [bik] шт [aik + bik].
3. Произведение матрицы A ss [alft] размера шХл на скаляр а
есть матрица размера тХп
aA = a[aik]==[aaik].
4. Произведение матрицы A ss [ay] размера тхп на матрицу
Bz=[bjk] размера пХг есть матрица С = [сцД размера тхг
C = AB^[aij][bfk\^[cik]t
где
п
/ = 1
Таким образом, элемент C(k матрицы С = АВ есть сумма произведений
элементов i-й строки матрицы А на соответствующие элементы jfe-ro столбца
матрицы В. В каждом произведении матриц АВ число п столбцов матрицы А
должно равняться числу строк матрицы В (форма матриц А и В должна быть
согласованной). Из существования произведения АВ вовсе не следует
существование произведения ВА. Если существуют оба произведения АВ и В А (это,
в частности, будет всегда, если А и В — квадратные матрицы одного и того
же порядка), то, вообще говоря, ВА Ф АВ (см. также п. 13.4-4). Отметим, что
А + В = В + А, А + (В + С) = (А + В) + С,
а(рЛ) = (ар)Л, а (ЛЯ) =(аЛ)В = Л (аВ),
А(ВС) = (АВ)С,
а(Л-ЬВ) = аЛ + аВ, (а + Р) Л = аЛ + рЛ,
(13.2-4)
А(В + С) = АВ + АС, (В + С)А = ВА + САУ
]Л + Б||^!|Л|| + ||В|!,||аЛ|| = |а|||Л||,||ЛВ||^||Л||||В||. (13.2-5)
13.2-6. 13 2. АЛГЕБРА МАТРИЦ И МАТРИЧНОЕ ИСЧИСЛЕНИЕ 393
13.2-3. Нулевая и единичная матрицы; обратные матрицы. Отметим
следующие определения:
1. Нулевая матрица [0] размера тхп есть матрица этого
размера, все элементы которой равны нулю. Тогда
Л + [0]=Л, 0Л = [0], [0]В = С[0] = [0],
где А — произвольная матрица размера тхп, В — произвольная
матрица, имеющая п строк, и С—произвольная матрица, имеющая т
столбцов.
2. Аддитивно обратная (противоположная) матрица —А для
матрицы A~[aik\ размера тхп есть матрица размера тхп
-Л = (-1М = [-«*];
тогда Л + (-Л) = Л-Л = [0].
3. Единичная матрица / порядка п есть диагональная матрица
размера пхп с единичными диагональными элементами:
г ее г „„^ с (0, если i=£k,
/ = №*[, где в,л = |,; если iz==k;
Тогда
/В = Я, С1 = С,
где £ — произвольная матрица, имеющая п строк, а
С—произвольная матрица, имеющая п столбцов; для любой же квадратной
матрицы А порядка п
1А = А1 = А.
4. Квадратная матрица А называется неособенной
(невырожденной), если она имеет (необходимо единственную) мультипликативно
обратную или npocT&v6pamHyio матрицу Л-1, определяемую условиями
ЛЛ~1 = Л"М = /. В противном случае Л —особенная (вырожденная)
матрица.
Квадратная матрица А = [aik] порядка п является невырожден-
пдй в том и только в том случае, если det (A) = det [aik] Ф 0; в этом
случае А~г есть квадратная матрица того же порядка п:
где Aik — алгебраическое дополнение элемента а^ в определителе
det[a^] (см. также пп. 1.9-2 и 14.5-3).
Квадратная матрица не вырождена в том и только в том
случае, если ее строки (столбцы) линейно независимы.
Произведение двух невырожденных матриц и матрица, обратная
невырожденной матрице, не вырождены; если А и В не вырождены и а^=0, то
(ЛВ)-1 = Я-М-1, (аЛГ1 = а-М-1, (Л"1Г1 = Л. (13.2-6)
13.2-4. Целочисленные степени квадратных матриц. По определению А0 = /,
А1 = А, А2 = А А, А* — AAA и если А — невырожденная матрица,
А*? = (А~г)Р = UT1 <" = »• 2. ->•
Применимы обычные правила действий со степенями (см. также п. 14.3-6).
13.2-5. Матрицы как строительные блоки математических моделей. Из
определений пп. 13.2-2 и 13.2-3 (конструктивные определения, п. 12.1-1) вытекают следующие
результаты:
1. Для любой пары натуральных чисел тип класс всех матриц размера
тхп над полем F есть тп-мерное векторное пространство над F (пп. 12.4-1
и 14.2-4). В частности, строки или столбцы из п элементов образуют n-мерные
векторные пространства (см. также п. 14,5-2).
394 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.2-6.
2. Класс всех квадратных матриц данного порядка п над полем F есть
линейная алгебра порядка п2 над F; вырожденные матрицы являются
делителями нуля (п. 12.4-2).
3. Класс всех невырожденных квадратных матриц данного порядка п над
полем F образует мультипликативную группу (п. 12.2-1) и вместе с нулевой
матрицей размера пхп — алгебру с делением порядка п2 над полем F (п. 12.4-2).
Аналогичные теоремы справедливы и для ограниченных бесконечных матриц над
полем действительных или комплексных чисел.
13.2-6. ■)£ Умножение на матрицы специального вида. Матрицы перестановки. Пусть
А — произвольная квадратная матрица порядка п. Тогда
1. Если В — матрица, полученная из единичной матрицы л-го порядка
заменой числа 1 в i-Ъ. строке на комплексное число а, то матрица АВ
получается из матрицы А умножением всех элементов С-го столбца на а.
Матрица В А получается из матрицы А умножением всех элементов
1-й строки на а.
2. Если С — матрица, полученная из единичной матрицы л-го порядка
заменой недиагонального элемента 6.fe—О на 1, то матрица АС получается
из матрицы А заменой k-го столбца на сумму k-го и i-го столбцов. Матрица С А
получается из матрицы А заменой i-й строки на сумму i-й и k-й строк.
3. Если D — матрица перестановки, получающаяся из единичной матрицы
перестановкой каких-либо ее двух столбцов (или, что то же самое, двух ее
строк с теми же номерами), то матрица AD получается из матрицы А
перестановкой соответствующих столбцов, а матрица DA перестановкой
соответствующих строк.
13.2-7. Ранг, след и определитель матрицы (см. также п.14.3-2). Ранг
данной матрицы А есть такое число г =э гА, что по крайней мере один
определитель г-го порядка (п. 1.5-1), получаемый из этой матрицы при удалении
некоторых строк и/или столбцов, отличен от нуля, а все определители (г +1)-го
порядка равны нулю. Ранг матрицы равен наибольшему числу линейно
независимых строк (или столбцов). Квадратная матрица А порядка п является
невырожденной в том и только в том случае, если ее ранг г = п, т. е. det (А) ф О
(п. 13.2-3).
*Ранг суммы двух матриц не больше суммы их рангов: rA B^rA + rB.
Если матрица А имеет размеры тхя, а матрица В — размеры п X q, то
для ранга матрицы АВ имеют место неравенства
гА + гв — п ^ rAB ^ min (гА,гЛ (неравенства Сильвестра). X
След (шпур) матрицы А за [а^] размера п X п есть сумма
Тг(Л)=|] а»
/ = 1
ее диагональных элементов *).
Для двух квадратных матриц А и В одного и того же порядка
Тг(Л+#) = Тг(Л) + Тг(В), Тг(аЛ) = аТг(Л), \ m 2 ?.
Тг(ВЛ) = Тг(ЛЯ), Тг(АВ-ВА)=0. ( \M.t-t)
det (АВ) = det (ВА) = det (A) det (В). (13.2-8)
13.2-8. Разбиение матриц. Матрица, имеющая более чем одну строку и
столбец, прямыми, проведенными между строками и/или столбцами, может
быть разбита на меньшие прямоугольные подматрицы. Две соответствующим
образом разбитые матрицы А и В размера пхп можно перемножить,
пользуясь входящими в них прямоугольными подматрицами как элементами в
обычной формуле произведения матриц (п. 13.2-2); получающиеся таким путем
элементы произведения являются подматрицами матрицы А В размера пхп.
Эта теорема бывает полезна при некоторых выкладках (п. 20.3-4).
*) Иногда след матрицы обозначают $р(Л).
13.2-12. 13.2. АЛГЕБРА МАТРИЦ И МАТРИЧНОЕ ИСЧИСЛЕНИЕ 395
13.2-9. Клеточные матрицы. Прямые суммы (см. также пп. 13.4-6, 14.8-2
и 14.9-2). Клеточная матрица есть квадратная матрица Л, которую можно
разбить так, чтобы получилась диагональная матрица (п. 13.2-1, с), вдоль
диагонали которой идут квадратные подматрицы Лх, Л2, ...:
^ j[0]j...
Л =
[0]j A2\... U (13-2-9)
V
Клеточную матрицу часто рассматривают как прямую сумму
л^елзе...
квадратных матриц, идущих вдоль ее диагонали (см. также п. 12.7-5).
Отметим, что Ap=Af? ©Л£@... при р = 0, 1, 2, ... (а если Л— невырожденная
матрица, то и при р=— 1, — 2, ...) и
Тг(Л) = Тг(Л1) + Тг(Л2) + .
det(A) = dei(Al)dei(A2)...
-}
(13.2-10)
13.2-10. Прямое (внешнее) произведение матриц (см. также п. 12.7-3). Прямое
(внешнее) произведение А®В матрицы А а \а;ь 1 размера тхп и матрицы В=Г6^£'| размера
т'хп' есть матрица
А <8> В »[cjh\ (cjh = aikbVk.) (13.2-11)
размера тт'Хпп', где индекс /означает порядковый номер пары (/, /') в
последовательности (1, 1), (1, 2) (1, т'), (2, 1), (2, 2) (т, т'), а индекс h — порядковый номер пары
(&, k') в аналогичной последовательности. Отметим, что
(А ®В) (C®D)—AC®BD, (13.2-12)
Тг (А ® В) = Тг (А) Тг (В). (13.2-13)
■X В (12) предполагается, что число строк матрицы С равно числу столбцов матрицы А
и число строк матрицы D равно числу столбцов матрицы В, а в (13) — что А и В —
квадратные матрицы. -Х-
13.2-11. Сходимость и дифференцирование.
(a) Последовательность матриц S0, St> S2, ..., имеющих одно и то же
число строк и одно и то же число столбцов, называется сходящейся к такой же
матрице S, если при я —*оо каждый элемент матрицы Sn сходится к
соответствующему элементу матрицы S, т. е. если lim || S — Sn |J — 0. Подобным же
п -*со
образом определяется предел матричной функции A = A(t) скалярного
аргумента t (см. также п. 12.5-3).
(b) Если элементы матрицы А = [aik] являются дифференцируемыми
функциями a-lk (t) скалярного аргумента t, то пишут
da^ ^[***(01 = -^(0- (13.2-14)
L dt J —
Частные производные и интегралы от матриц определяются аналогично.
13.2-12. Функции матриц. Матричные многочлены и алгебраические
функции матриц определяются с помощью элементарных матричных операций.
оо
Теорема Кэли — Гамильтона (п. 13.4-7) каждый сходящийся ряд 2 akAk
k = 0
по степеням квадратной матрицы Л порядка п (аналитическую функцию
матрицы Л) сводит к некоторому многочлену л-й степени от Л.
396 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.3-1.
J3.3. МАТРИЦЫ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ СИММЕТРИИ
13.3-1. Транспонированная и эрмитово сопряженная матрица (см. также
пп. 14.4-3 и 14.4-6, а). Если Л = [aik\ — произвольная матрица размера тхп
над полем комплексных чисел, то
Матрица, транспонированная по отношению к Л, есть матрица
A' = [aki] размера пхт. Матрица, эрмитово сопряженная с А (просто
сопряженная, присоединенная, ассоциированная)*), есть матрица
A* = \aki] размера пхт.
Отметим следующие соотношения:
(А + В)' = А' + В', (аЛ)' = аЛ\ (ЛВ)' = В'Л',
(А-У-И'Г1. (А')' = А || Л' || = || Л ||, } (13.3-1)
[0]' = [0], /'=/;
'•I
(Л + В)* = Л* + В*, (аЛ)* = аЛ*, (АВ)*=В*А*, \
(Л-1)* = (Л*)-1, (А*)* = А, ||Л*|| = ||Л||, 1 (13.3-2)
[0]* = [0], /* = /. J
Матрицы Л, А' и Л* необходимо имеют один и тот же ранг.
Для каждой квадратной матрицы А
Тг (Л') = Тг (Л), det (A') = det (Л); (13.3-3)
Тг(Л *) = Т~г~(Л), det(i4*) = det(4). (13.3-4)
13.3-2. Матрицы со специальными свойствами симметрии (см. также
пп. 14.4-4 —14.4-6). Квадратная матрица А = [щ^] называется
симметрической, если А'— А, т. е. если а/^ = а^,
кососимметрической (антисимметрической), если Л' = —Л, т. е.
если aik = —akh
эрмитовой (самосопряженной), если A* = At т. е. если a^==fl^/,
косоэрмитовой (альтернирующей), если Л* =—Л, т. е. если
ортогональной, если Л'Л = ЛЛ' = /, т. е. если А' = А 1,
унитарной, если A*A = AA* = It т. е. если А*=А~Х.
Эрмитова матрица является симметрической, косоэрмитова — кососимметрической и
унитарная — ортогональной в том и только в том случае, если все их элементы
действительны. Диагональные элементы эрмитовой, косоэрмитовой и кососимметрической матрицы
соответственно действительны, чисто мнимы и равны нулю.
Определитель эрмитовой матрицы действителен. Определитель косоэрмитовой
матрицы размера п X л является действительным, если п четно, и чисто мнимым, если
п нечетно. Определитель кососимметрической матрицы нечетного порядка равен нулю.
Определитель унитарной матрицы по модулю равен \, а определитель ортогональной
матрицы равен -4- 1 или — 1.
13.3-3. Правила комбинирования (см. также п. 14.4-7).
(а) Если А—симметрическая матрица, той АР (р — О, 1, 2, ...), Л-1, TAT
и а А—симметрические матрицы.
1) Термины сопряженная, присоединенная и ассоциированная употребляются в
различных смыслах (см. также пп. 12.2-5, 14.4-3. 16.7-1 и 16.7-2); некоторые авторы называют
присоединенной к А матрицу Л-1 det (А) (состоящую из алгебраических дополнений
с переставленными индексами). Символы А', А* и Л=[а.,1 =(Л')*, обозначающие
соответственно матрицу транспонированную, эрмитово сопряженную и комплексно
сопряженную с данной матрицей А, также варьируются; некоторые авторы матрицу, эрмитово
сопряженную с А, обозначают символом л+.
13.3-4. 13.3. МАТРИЦЫ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ СИММЕТРИИ 397
Если Т — произвольная невырожденная матрица, то матрица ТAT будет
симметрической в том и только в том случае, если симметрической будет и
матрица А; поэтому для любой ортогональной матрицы Т матрица Т~1АТ
будет симметрической в том и только в том случае, если симметрической
будет и матрица А.
Если А и В—симметрические матрицы, то и А-\-В —симметрическая
матрица. Произведение А В двух симметрических матриц А и В есть
симметрическая матрица в том и только в том случае, если ВА = АВ.
■Х- Произведение АВ двух кососимметрических матриц А и В есть симметрическая
матрица в том и только в том случае, если В А = АВ, и кососимметрическая, если В А =
= -АВ.Х
(b) Если А —эрмитова матрица, то и АР(р = 0, 1, 2,...), А'1 и Т*АТ-~
эрмитовы матрицы; а А — эрмитова матрица, если а —действительное, и косо-
эрмитова матрица, если а —чисто мнимое.
Если Т' — произвольная невырожденная матрица» то матрица Т*AT будет
эрмитовой в том и только в том случае, если эрмитовой будет и матрица А;
поэтому для любой унитарной матрицы Т матрица Т~гАТ будет эрмитовой
в том и только в том случае, если эрмитовой будет и матрица А.
Если А и В—эрмитовы матрицы, то и Л + В — эрмитова матрица.
Произведение АВ двух эрмитовых матриц А и В есть эрмитова матрица
в том и только в том случае, если ВА — АВ.
■X Произведение АВ двух косоэрмитовых матриц Л и В есть эрмитова матрица в том
и только в том случае, если В А = АВ, и косоэрмитова, если В А =— АВ. #
(c) Если А—ортогональная матрица, то и АР(р — 0> 1, 2, ...), Л-1, А'
и —А—ортогональные матрицы. Если матрицы А и В ортогональны, то и
матрица АВ ортогональна.
Если А—-унитарная матрица, то « ^(р=0, 1, 2, ...), Л-1, А* и аА
при | а | = 1 — унитарные матрицы. Если матрицы А и В унитарны, то и
матрица АВ унитарна.
13.3-4. Теоремы о разложении. Нормальные матрицы (см. также л п.
13.4-4, а и 14.4-8).
(a) Для каждой квадратной матрицы А над полем комплексных чисел
1 1
1. у (Л + Л') = Si есть симметрическая, а у (Л — Л') = 52 —
кососимметрическая матрица, Л = 51+52 есть (единственное)
разложение данной матрицы Л в сумму симметрической и кососимметрической
матриц.
2. — (А-\-А*) = Н1 и gT (Л — Л*) = Н2 — эрмитовы матрицы;
матрица Ш2—косоэрмитова; Л = #1 + Ш2 есть (единственное)
разложение данной матрицы Л в сумму эрмитовой и косоэрмитовой
матриц (аналогичное разложению комплексного числа на
действительную и мнимую части).
3. АА* и А*А есть эрмитовы неотрицательные (см. п. 13.5-3)
матрицы.
4. Существуют полярные разложения матрицы Л
A=QU и A = UxQlt
где Q и Qx —неотрицательные эрмитовы матрицы, однозначно
определяемые условиями Q2 = AA* и Qf—A*At a U и 01 —унитарные
матрицы, однозначно определяемые в том и только в том случае,
если Л — невырожденная матрица (полярные разложения матрицы
аналогичны представлению комплексного числа в тригонометрической
форме z = г (cos ф + i sin ср)).
(b) Квадратная матрица Л называется нормальной матрицей, если А*А =
= АА* или, эквивалентно, если Н2Н1 = Н1Н2-
398 ГЛ. 13. МАТРИЦЫ. КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.4-Ь
13.4. ЭКВИВАЛЕНТНЫЕ МАТРИЦЫ, СОБСТВЕННЫЕ ЗНАЧЕНИЯ,
ПРИВЕДЕНИЕ К ДИАГОНАЛЬНОМУ ВИДУ И СМЕЖНЫЕ ВОПРОСЫ
13.4-1. Эквивалентные и подобные матрицы (см. также пп. 12.2-5, 13.5-4*
13.5-5 и 14.6-2).
(a) Две прямоугольные матрицы А и В эквивалентны, если существуют
такие две квадратные невырожденные матрицы 5 и Г, что А и В связаны
преобразованием
B = SAT. (13.4-1)
Каждая матрица В, эквивалентная данной матрице А, имеет столько же
строк и столько же столбцов, сколько и матрица А, и может быть получена
из А с помощью последовательного применения шести операций, определенных
в п. 13.2-6. Эквивалентные матрицы имеют один и тот же ранг; две
матрицы размера тхп, имеющие один и тот же ранг, эквивалентны.
Если B — QA или B = AQ, где Q —невырожденная матрица, то А и В
эквивалентны.
(b) В частности, две квадратные матрицы А и А подобны (иногда их на*
зывают просто эквивалентными), если существует такая невырожденная
матрица Т (преобразующая матрица), что Л и Л связаны преобразованием подобия
Л = Г-МГ или Л=ГЛГ-1; (13.4-2)
А, А и Т необходимо являются квадратными матрицами одного и того же
порядка.
При каждом преобразовании подобия (2) сохраняется результат сложения
матриц, умножения матриц и умножения матрицы на скаляр (см. также
п. 12.1-6). Две подобные матрицы имеют один и тот же ранг, один и тот
оке след и один и тот же определитель (см. также п. 13.4-2, а).
(c) Две квадратные матрицы А и А, связанные преобразованием
Л = Г'ЛГ, (13.4-3)
где Т — невырожденная матрица, называются конгруэнтными. Две квадратные матрицы
А и А, связанные преобразованием
Л = ГМГ, (13.4-4)
где Т — невырожденная матрица, называются соединенными. В каждом из этих случаев
А, А и Т необходимо являются квадратными матрицами одного и того же порядка.
(d) Эквивалентность, подобие, конгруэнтность и соединенность матриц являются
отношениями эквивалентности; каждое из них определяет разбиение
класса'рассматриваемых матриц (п. 12.1-3, Ь). В большинстве приложений две или несколько подобных
матриц дают различные представления некоторого линейного преобразования
(линейного оператора) А (п. 14.6-2). В этой связи представляет интерес: 1) нахождение
преобразования подобия, дающего особенно простое представление оператора А (приведение
данной матрицы к диагональному или какому-либо иному «каноническому» виду), и 2)
нахождение свойств матриц, инвариантных относительно преобразований подобия и, таким
образом, общих для каждого класса подобных матриц (к числу таких свойств, например,
относятся ранг, след, определитель, собственные значения).
13.4-2. Собственные значения и спектры квадратных матриц (см. также
п. 14.8-3).
(а) Собственными значениями (собственными числами, характеристическими
числами) квадратной матрицы А = [а^] называются те значения скалярного
параметра X, для которых матрица А —XI является вырожденной. Спектр
(спектр собственных значений) матрицы А есть множество всех ее собственных
значений.
Собственные значения квадратной матрицы А можно определить и
непосредственно как собственные значения линейного оператора,
представляемого матрицей А (п. 14.8-3); подобные матрицы имеют один и тот оке спектр.
13.4-4. 13.4. ЭКВИВАЛЕНТНЫЕ МАТРИЦЫ, СОБСТВЕННЫЕ ЗНАЧЕНИЯ 399
(Ь) Если нормальная матрица А (А*А = АА*, п. 13.3-4, Ь) имеет
собственное значение X, то матрица А* имеет собственное значение X, матрица
И1=-^(А + А*) имеет собственное значение Re X и матрица Н2 = тр (А •— А*)
имеет собственное значение Im X (см. также, п. 13.3-4, а).
Все собственные значения данной нормальной матрицы являются
действительными в том и только в том случае, если эта матрица подобна
некоторой эрмитовой матрице (см. также п. 14.8-4). В частности, все собственные
значения эрмитовых и действительных симметрических матриц действительны.
Все собственные значения унитарной матрицы по модулю равны 1; в частности,
действительные собственные значения действительных ортогональных матриц
равны +1 или —1, а их комплексные собственные значения появляются парами
е—1Ч. Квадратная матрица невырождена в том и только в том случае, если
все ее собственные значения отличны от нуля. О вычислении собственных
значений см. пп. 13.4-5, а, 14.8-5, 14.8-9 и 20.3-5.
13.4-3. Приведение квадратной матрицы к треугольному виду.
Алгебраическая кратность собственного значения (см. также п. 14.8-3, е).
(a) Для любой квадратной матрицы А существует такое преобразование
подобия А = Т~гAT, что А есть треугольная матрица (п. 13.2-1, с).
Диагональные элементы каждой треугольной матрицы, подобной матрице А,
являются собственными значениями матрицы А, и каждое собственное значение X/
матрицы А встречается в качестве диагонального элемента во всякой такой
треугольной матрице одно и то же число т'- ^ 1 раз; число т'* называется
алгебраической кратностью данного собственного значения А,.
Замечание. Алгебраическая кратность т: собственного значения "К, может не
совпадать с его геометрической кратностью т,, определяемой в п. 14.8-3, Ь.
(b) След Тг (А) равен сумме всех собственных значений матрицы А,
причем каждое собственное значение считается столько раз, какова его
алгебраическая кратность. Определитель det (А) (п. 13.2-7) равен точно таким же
образом подсчитанному произведению собственных значений (см. также п. 13.4-5).
13.4-4. Приведение матриц к диагональному виду (см. также п. 14.8-5).
(a) Квадратная матрица А может быть преобразованием подобия при»
ведена к диагональному виду (т. е. существует такая невырожденная
преобразующая матрица Т, что матрица А — Т~ХАТ диагональна, п. 13.2-1, с)
в том и только в том случае, если А подобна некоторой нормальной
матрице (п. 13.3-4, Ь). Более конкретно, данная матрица А может быть
преобразованием подобия с унитарной преобразующей матрицей Т (или, если
матрица А действительна,—с действительной ортогональной преобразующей
матрицей) приведена к диагональному виду в том и только в том случае,
если А—нормальная матрица (Л*Л=ЛЛ*, п. 13.3-4, Ь). В любом случае
диагональные элементы матрицы А являются собственными значениями
матрицы Л; каждое собственное значение матрицы А встречается в качестве
диагонального элемента матрицы А ровно столько раз, какова его
алгебраическая кратность. Метод, дающий преобразующую матрицу Т с нужными
свойствами, описан в п. 14.8-6.
Частные случаи матриц, приводимых к диагональному
виду. Эрмитовы и унитарные матрицы (а потому действительные и симметрические
или ортогональные матрицы) представляют собой частные случаи нормальных матриц.
Каждая матрица, имеющая собственные значения только алгебраической кратности 1,
подобна некоторой нормальной матрице.
(b) Две эрмитовы матрицы А и В могут быть приведены к
диагональному виду одним и тем же преобразованием подобия (и, в частности, одним
и тем же преобразованием подобия с унитарной преобразующей матрицей Т)
в том и только в том случае, если ВА = АВ (см. также пп. 13.5-5 и 14.8-6, е)*
400 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.4-6.
(с) Для любой эрмитовой матрицы А существует такая невырожденная
матрица Т, что матрица А = Т*АТ диагональна; диагональные элементы
матрицы А в этом случае действительны. В частности, существует такая
невырожденная матрица Т, что диагональные элементы матрицы А
принимают только значения +1, —1 и/или 0.
Для любой действительной симметрической матрицы А существует
такая действительная невырожденная матрица 7\ что матрица А —Т'АТ
диагональна. В частности, существует такая действительная невырожденная
матрица Т, что диагональные элементы матрицы А принимают только
значения + 1. —1 и/или 0.
Матрицы Т с искомыми свойствами получают из соотношения Т = DU, где U —
унитарная (или действительная ортогональная) матрица, для которой матрица U~XAU
диагональна, a D — действительная диагональная матрица; матрицу U находят по
методу п. 14.8-6 (см. также п. 13.5-4, d).
13.4-5. Собственные значения и характеристическое уравнение матрицы.
(а) Спектр собственных значений квадратной матрицы А = [Щь\ порядка
п совпадает с множеством корней алгебраического уравнения п-й степени
Fa(X)== det (A - XI) == det [aik - X6ik] =
\ап — X а12 ... а1п
#21 ^22 — X
.-*
= 0 (13.4-5)
(характеристическое уравнение или вековое уравнение матрицы А).
Кратность (порядок, п. 1.6-2) каждого корня Xj этого уравнения равна
его алгебраической кратности т- как собственного значения, так что т\ +
+ т'2 +... = п.
Подобные матрицы размера пхп имеют одни и те же
характеристические уравнения; коэффициенты уравнения (5) являются симметрическими
функциями п корней %lt Х2, ..., Хп (п. 1.6-4). В частности, коэффициент при
Я/1-1 и свободный член уравнения (5) соответственно равны
{-1)п-1(Х1 + 12 + ... + Хп) = (-1)п-1Тг(А), \
№...** = <** (А). I {16АЬ)
Коэффициент при Хп~г равен взятой с множителем (— 1)г сумме всех ( )
главных миноров г-го порядка (п. 1.5-4) определителя det (Л).
(Ь) (См. также п. 14.8-3). Для любой квадратной матрицы А с
собственными значениями Xj матрица аА имеет собственные значения aXf, а матрица
АР—собственные значения X? (р = 0, 1, 2, ..., а если А — невырожденная
матрица, то р = 0, ± 1, ± 2, ...).
Каждый многочлен или аналитическая функция f (А) (п. 13.2-12) имеет
собственные значения f (kj).
ОО
Матричный степенной ряд У] ak&k сходится (п. 13.2-1, а) в том,
со
и только в том случае, если степенной ряд У] akrf годится для каждого
собственного значения Xj матрицы А. Если две квадратные матрицы А и В
имеют соответственно собственные значения Xf и ji/j, то спектром
собственных значений прямого произведения А® В (п. 13.2-10) является множество
всевозможных произведений ЯдИд.
13.5-2.
13.5. КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ
401
13.4-6. Собственные значения клеточных матриц (прямых сумм, п. 13.2-9).
Спектр клеточной матрицы (прямой суммы), А = А±® Л2©, ... есть
объединение спектров матриц А1У А2, ...; алгебраические кратности складываются.
Вклад в спектр каждой подматрицы Аь может быть найден с помощью ее
характеристического уравнения.
13.4-7. Теорема Кэли—Гамильтона и смежные вопросы.
(a) Каждая квадратная матрица А удовлетворяет своему собственному
характеристическому уравнению (п. 13.4-5, а), т. е.
FA (А) = 0 (теорема Кэли — Гамильтона). (13.4-7)
(b) Теорема Кэли—Гамильтона позволяет каждую целочисленную степень, а потому
и каждую аналитическую функцию квадратной матрицы А порядка п представлять в виде
линейной функции от п различных положительных целочисленных степеней матрицы А
(см. также п. 13.2-12). Точнее,
п
'<А>-т2 А»-*АЛ~*. (13-4-8)
*=i
где А — определитель Вандермонда (п. 1.6-5) det [A,* I, а Ду — определитель,
получаемый, если в Д вместо }J, XL ... , кп подставить f (Xj, f (К ) f (kn).
Если все собственные значения Я^, Xg, ... , X матрицы А различны, то равенство (8)
можно переписать в виде
п П (Л — 'ki I)
^■Hf^ 'nV-V (13'4-9)
(теорема Сильвестра).
13.5. КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ
13.5-1. Билинейные формы. Билинейная форма от 2п действительных или
комплексных переменных glf |2, ..., |n, r\lt т]2, ..., г\п есть однородный
многочлен второй степени (п. 1.4-3)
х'Ау= 2 2 аш1м, (13.5-1)
t = l fc = i
х'~[%ь\—матрица-строка, у = [%] — матрица-столбец (п. 13.2-1, Ь).
13.5-2. Квадратичные формы. Квадратичная (однородная) форма от п
действительных или комплексных переменных glf g2> •••» in есть многочлен
Л4*=2 2^Ш = ^х^ (13.5-2)
/ = 1 k = \
где Лх = (-2-J (Л + Л') —«симметрическая часть» (п. 13.3-4) матрицы А = [а^].
Выражение (2) тождественно равно нулю в том и только в том случае,
если А—кососимметрическая матрица (а^ — —а^, п. 13.3-2). Квадратичная
форма (2) называется симметрической, если А — симметрическая матрица (я&/ =
= Я|й, п. 13.3-2), и действительной, если А — действительная матрица (и таким
образом, каждый элемент aik—действительное число, п. 13.2-1)*).
*) Каждой квадратичной форме можно поставить в соответствие бесконечно много
различных матриц А, для которых эта форма равна х'Ах. Среди них одна матрица
(матрица А и о которой шла речь выше) является симметрической. Обычно квадратичную
форму записывают именно с помощью этой матрицы и, таким образом, всякая
квадратичная форма является симметрической. Квадратичная форма называется
'действительной, если действительной является эта симметрическая матрица. Например, форма
Si ~\- 'iila*~"^tSi + &i действительна, так как ее симметрическая запись имеет вид ii + Sa*
402 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.5-3.
Действительная симметрическая квадратичная форма (2) (а также
соответствующая действительная симметрическая матрица А) называется
положительно определенной, отрицательно определенной, неотрицательной или
неположительной, если соответственно х'Ах > 0, х'Ах < 0, х'Ах ^ 0 или х'Ах ^ 0
для каждого набора действительных чисел glf g2, ..., £л, не все из которых
равны нулю. Все остальные квадратичные формы являются неопределенными
(т. е. знак х'Ах зависит от выбора чисел glf g2, ..., |л) или тождественно
равными нулю.
Действительная симметрическая квадратичная форма (2) (а также соответствующая
действительная симметрическая матрица А) называется положительно полуопределенной
или отрицательно лолу определен ной, если соответственно она неотрицательна или
неположительна и если х'Ах = 0 для некоторого набора |1# |2, ... , | действительных чисел,
не все из которых равны нулю.
13.5-3. Эрмитовы формы. Эрмитова форма от п действительных или
комплексных переменных |1э |2> •••» 1» есть многочлен
х*Ах= 2 21 "ikhlk, (13.5-3)
где А ==[а^]— эрмитова матрица {aik = aki), а матрица х* е= [£i, |2 Lb
Форма (3) принимает действительные значения для каждого набора комплексных
чисел £х, £2, ..., |д в теш и только в том случае, если А—эрмитова матрица
(см. также п. 14.4-4).
Эрмитова форма (3), а также соответствующая эрмитова матрица A = [a^J,
называется положительно определенной, отрицательно определенной,
неотрицательной или неположительной, если соответственно х*Ах>0, х*Ах<0,
х*Ах ^0 или х*Ах^ 0 для каждого набора комплексных чисел glf Е2, ..., £л,
не все из которых равны нулю. Все остальные эрмитовы формы (или
эрмитовы матрицы) являются неопределенными (т. е. знак х*Ах зависит от выбора
чисел £2, |lf ..., £п) или тождественно равными нулю.
Эрмитова форма (3) (а также соответствующая эрмитова матрица А) называется
положительно полуопределенной или отрицательно полу определенной, если соответственно
она неотрицательна или неположительна и если х*Ах = и для некоторого набора
комплексных чисел £i, £2. ••• . £rt« не все иэ которых равны нулю
13.5-4. Преобразование квадратичных и эрмитовых форм. Приведение
к сумме квадратов.
(а) Линейная подстановка
п
?;= У tiklk (/ = 1, 2 П)
b £{ Ж \ (det[tik]^0) (13.5-4)
х = Тх
(невырожденное однородное линейное преобразование координат вектора,
«пассивная» точка зрения, п. 14.6-1) переводит каждую квадратичную форму (2)
в квадратичную форму от новых переменных 1г, {£, ..., %п:
п
х'Ах== 2 2 ^ikhL^x'Axy
где
п
Qik= 2 2j a0n{hk (h /2 = 1, 2, ..., n)
ИЛИ /=-1 /1 = 1
А = Т'АТ.
(13.5-5)
13.5-4.
13.5. КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ
403
Если А — симметрическая матрица, то и А — симметрическая матрица, если
А и Т — действительные матрицы, то и А—действительная матрица.
Линейная подстановка (4) переводит каждую эрмитову форму (3) в новую
эрмитову форму:
где
п п
х*Ах~ 2 S ~aiklilk>
п п
/= 1 Л=1
А=Т*АТ.
(13.5-6)
(b) Для каждой данной действительной симметрической квадратичной
формы (2) существует такое линейное преобразование (4) с действительными
коэффициентами //#, что новая матрица А в (5) является диагональной
(см. также п. 13.4-4, с), так что
п
х'Ах~х'Ах=в 2 «//Р- (13.5-7)
Точно так же для каждой эрхмитовой формы (3) существует такое
линейное преобразование (4), что
п
х*Ах = ~х*Ах= 2 2и|1*|«. (13.5-8)
Число г отличных от нуля коэффициентов в равенствах (7) или (8) не
зависит от выбора преобразования* приводящего матрицу А к диагональному
виду, и равно рангу матрицы А; число г называется рангом данной квадратичной
или эрмитовой формы. Для любой данной действительной симметрической
квадратичной формы (2) разность между числом положительных и числом
отрицательных коэффициентов ац в равенстве (7) не зависит от выбора
преобразования, приводящего матрицу А к диагональному виду (закон инерции квадратичных
форм); это число называется сигнатурой данной квадратичной формы. В
точности такое же утверждение справедливо и для эрмитовых форм (закон инерции
эрмитовых форм).
(c) В частности, для каждой действительной симметрической квадратичной
формы (2) существует действительная ортогональная матрица Г, а для каждой
эрмитовой формы (3)—унитарная матрица 7\ приводящая матрицу А к
диагональному виду (см. такл^е п. 13.4-4). Получающееся в результате
преобразование к главным осям (преобразование к нормальным координатам |lf |2,..., |л,
см. также п. 9.4-8) дает нормальный вид данной квадратичной или эрмитовой
формы
п п
х'Ахееех'Ахее.^ %В или х*Ах Е=~х*~Ах =е ^J U I Ь |2, (13.5-9)
/=1 /=1
где множество действительных чисел Ki составляет спектр собственных значений
данной матрицы А (п. 13.4-2).
(d) Добавочное преобразование £/= £//К| X/1 (i = l, 2, ..., п) приводит
выражение (9) к каноническому виду
п п
х'Ах шш J\ ег tf или х*Ах - 2 е* I Ь I2* (13.5-10)
404 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.5-5.
где каждый коэффициент ег- равен +1, — 1 или 0, если соответствующее
собственное значение X-t положительно, отрицательно или равно нулю.
(е) Вопрос о нахождении подходящих матриц, приводящих данную
матрицу А к диагональному виду, рассмотрен в п. 14.8-6.
13.5-5. Одновременное приведение двух квадратичных или эрмитовых
форм к сумме квадратов (см. также пп. 13.4-4, b и 14.8-7). Если даны две
действительные симметрические квадратичные формы х'Ах и х'Вх, причем
х'Вх —положительно определенная форма, то можно найти действительное
преобразование (4), одновременно приводящее к сумме квадратов формы х'Ах
и х'Вх. В частности, существует такое действительное преобразование (4)
к новым координатам flf |2, ..., |Л, что
п п
х'Ах = х'А x=z 2 ftl* , х'Вх ев ?5bJ] it . (13.5-11)
i = \ /=l
Точно так же, если даны две эрмитовы формы х*Ах и х*Вх, причем х*Вх —
положительно определенная форма, то существует такое преобразование (4)
к новым координатам |lf |2, ..., £л, что
п п
х*Ах^ х*Ах=~ 2 Rllii2, х*Вх== х*Вх=~ J] ||£]2. (13.5-12)
В любом случае множество действительных чисел \ilf jjl2, ..., \in состав-
ляет спектр собственных значений матрицы В~гА, получаемый как
множество корней алгебраического уравнения л-й степени
det {А — \iB) == det [aik — ixbik] = 0. (13.5-13)
Искомую матрицу преобразования Т можно найти по методу п. 14.8-7 или же
с помощью равенства T = UT0, где Т0 — матрица преобразования, приводящего форму
х'Вх или х*Вх к каноническому виду (п. 13.5-4, d), at/ — унитарная матрица,
приводящая форму х'Ах или х*Ах к сумме квадратов (п. 13.5-4, с).
Замечание. Две действительные симметрические квадратичные формы х'Ах
и х'Вх или две эрмитовы формы х*Ах и х*Вх Можно одновременно привести к сумме
квадратов с помощью одной и той же унитарной матрицы преобразования Т в том
и только в том случае, если ВА «= АВ (см. также пп.13.4-4, b и 14.8-6, е).
13.5-6. Признаки положительной определенности, неотрицательности и т. д.
(a) Действительная симметрическая квадратичная форма, или эрмитова
форма, является положительно определенной, отрицательно определенной,
неотрицательной, неположительной, неопределенной или тождественно равной
нулю (пп. 13.5-2 и 13.5-3) в том и только в том случае, если (необходимо
действительные) собственные значения Xj матрицы А = [а^] соответственно
все положительны, все отрицательны, все неотрицательны, все неположительны,
имеют различные знаки или все равны нулю.
Действительная симметрическая квадратичная форма, или эрмитова форма,
является положительно полуопределенной или отрицательно определенной в том и только
в том случае, если она соответственно неотрицательна или неположительна и если по
крайней мере одно собственное значение А,, матрицы А == [а^] равно нулю.
Заметим, что числа К- являются корнями характеристического уравнение (13.4-5);
знаки этих корней часто можно исследовать одним из методов п. 1.6-6.
(b) ■# Для того чтобы эрмитова матрица А = [а^] (и соответствующая
эрмитова форма, или действительная симметрическая квадратичная форма)
была положительно определена, необходимо и достаточно, чтобы каждый
из определителей
I а1\ а\2 I I Яц «12 «13 I
Ш \Ч\ ^22 Г U2i «22 Ягз . •••• det[a,-*J (13.5-14)
«31 «32 033 I
13.6-1. 13.6. ВОЗМУЩЕНИЯ И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА 405
был положителен. Для того чтобы эрмитова матрица А = [aik] (и
соответствующая эрмитова форма или действительная симметрическая
квадратичная форма) была неотрицательна, необходимо и достаточно, чтобы все
главные миноры определителя det [aik\ (т. е. все миноры, получающиеся из этого
определителя вычеркиванием строк и столбцов с одними и теми же номерами
или, иначе говоря, миноры, симметричные относительно главной диагонали
этого определителя) были неотрицательны.
Отметим, что для неотрицательности эрмитовой матрицы неотрицательность
только угловых миноров (14) недостаточна.
(c) Эрмитова матрица А (и соответствующая эрмитова форма или
действительная симметрическая квадратичная форма) отрицательно определена,
неположительна или отрицательно полуопределена в том и только в том
случае, если матрица — Л соответственно положительно определена,
неотрицательна или положительно полуопределена.
(d) Матрица А является неотрицательной эрмитовой матрицей в том
и только в том случае, если существует такая матрица В, что А=В*В
Действительная матрица А является неотрицателной симметрической
матрицей в том и только в том случае, если существует такая действительная
матрица В, что А=В'В. В любом из этих случаев матрица А положительно
определена, если В, а значит и А, —невырожденная матрица.
(e) Если эрмитовы матрицы А и В положительно определены или
неотрицательны, то это же верно и для матрицы АВ. Каждая положительно
определенная эрмитова матрица А имеет единственный квадратный корень Я,
определяемый условиями, что Н2 — А и что Н — эрмитова положительно
определенная матрица (см. также п. 13.3-4).
13.6. МАТРИЧНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ (ДИНАМИЧЕСКИХ СИСТЕМ). ВОЗМУЩЕНИЯ И ТЕОРИЯ
УСТОЙЧИВОСТИ ЛЯПУНОВА
13.6-1. Системы обыкновенных дифференциальных уравнений. Матричные
обозначения. Как мы заметили в п. 9.1-3, если подходящие производные
ввести в качестве новых переменных, общую систему обыкновенных
дифференциальных уравнений (9.1-4) можно свести к системе уравнений первого порядка
■$■=/! ft Уъ 2/2, ...,!fo) (* = 1,2, ...,п). (13.6-1а)
Систему (1а) записывают в виде одного матричного дифференциального уравнения
fh(t\ 2/i. 2/2. •••» Уп)^
' Ы'; Уъ 2/2. •••» Уп)
dt —~dt
/Уг (t)\
I 2/2 (t)
\Уп (t)l
\~f(t, y) (13.6-16)
\fn (ЬУи 2/2. •••. Уп)/
(см. также п. 13.2-11), где у (/) и f(t, у) — матрицы размера п X 1 (столбцы).
Если функции fi в интересующей нас области непрерывны и удовлетворяют
условию Липшица (9.2-4), то решение у (t) уравнения (16) однозначно
определяется начальным условием
/!/i(0)
y(0)JV,<P) | = | *" |=j/e- (13.6-lc)
\Уп (0),
406 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.6-2.
Если / в явном виде не зависит от независимой переменной /, то система (1)
называется автономной (стационарной).
Помимо того, что матричные обозначения удобны, они, как мы увидим, позволяют
распространить интуитивные представления, возникающие при изучении простых
дифференциальных уравнений первого порядка, на системы уравнений первого порядка.
Кроме того, матричные операции, нужные для решения линейных систем (п. 13.6-2),
легко выполняются электронными вычислительными машинами.
В большинстве важных приложений / обозначает время, а у. (t) —фазовые
переменные (переменные состояния), описывающие состояние некоторой механической системы.
В таком случае система (1) называется динамической системой (см. также п. 11.8-4) *).
13.6-2. Линейные дифференциальные уравнения с постоянными
коэффициентами.
(а) Однородные системы. Нормальная форма решения.
Решение однородной линейной системы
dt
ИЛИ
= 2 *«'***• </i(°> = ^o 0 = 1, 2, ..., п) (13.6-2а)
% = Ау% у(0) = у0 (A = [aih]) (13.6-26)
с постоянными коэффициентами щк (см. также пп. 9.3-1 и 9.4-1, d) имеет вид
y(t) = eA'y0 (f^O), (13.6-3)
где матричная функция eAi является матрицей размера п X п, определяемой
в соответствии с пп. 13.2-12 и 13.4-7. Разложение функции eAi по формуле
(13.4-8) требует громоздких перемножений матриц, но если данная матрица А
имеет п различных собственных значений, то разложение функции eAi по
теореме Сильвестра (13.4-9) дает нормальную форму решения из п. 9.4-1.
Часто можно упростить решение задачи (2) путем введения п новых фазовых
переменных у* с помощью такого невырожденного линейного преобразования:
п
Vi = 2 Uhh (/ = 1» 2 п) или у = Т~у> <13-6_4)
Л=1
чтобы получающаяся в результате система
где Ш = А!" *(0)=^ > (13.6-5)
А == Т~гАТ.
Уо'<
- 1
стала проще, чем первоначальная (см. также пп. 14.6-1 и 14.6-2). Если, в частности,
существует преобразование (4), приводящее данную матрицу системы А к
диагональному виду (пп. 13.4-4 и 14.8-6), то новые переменные у. называются нормальными
координатами рассматриваемой линейной системы (см. также п. 9.4-8). Они
удовлетворяют системе уравнений с «разделенными» переменными
-Л = xhyh (Л = 1, 2, . . . , п), (13.6-6)
где %v А,2, •••, ^ — собственные значения матрицы А. Если матрица А имеет п
различных собственных значений, то решение первоначальной системы (2) на
основании (4) имеет вид
Уп = yh^Kfli (h = 1. 2 п). (13.6-7)
*) Во многих технических книгах столбец у (t) называют вектором состояния.
Правильней было бы сказать, что элементы у.% (t) матрицы у (t) (переменные состояния)
описывают вектор состояния в некоторой определенной системе координат (в смысле
тензорного анализа, гл. 16).
13.6-3. 13.6. ВОЗМУЩЕНИЯ И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА 407
Комплексно сопряженные члены в решении (7), а также совпадающие и
нулевые собственные значения можно рассмотреть подобно тому, как это сделано
в п. 9.4-1. В общем случае с помощью преобразования (4) можно получить
треугольную матрицу А (п. 13.4-3), так что функции у^ (t) можно последовательно вычислить
одну за другой.
(Ь) Неоднородные уравнения. Матрица Грина. Линейная
система
dt
= 2 aikyk + fi(t), yi(0) = yio (*=l, 2, ..., n) (13.6-8a)
или
§ = Ay + f (0, у (0) = t/0 (A = [aik])9 (13.6-86)
dt
где f(t) — матрица размера лх 1 (столбец), описывает реакцию линейной
системы на внешние нагрузки fi(t). Как и в пп. 9.3-1 и 9.4-2, решение у (t)
получается в результате сложения решения (3) соответствующей однородной
системы и некоторого частного решения (нормальной реакции) yN(t):
y(t) = eAtyQ+yN(t)
где
yN{t) = \h+(t-x)f{%)d%J\h+(l)f(t--Z)dt. I
(/^0) (13.6-9)
Матрица Грина h+(t—т) = [{h+(t—т)}^] размера п X п для задачи
Коши (8) является обобщением одномерной функции Грина в п. 9.4-3 и
удовлетворяет уравнению
^±P-=Ah+(t) (/>0). А+(0) = /, (13.6-10)
так что
h+(t) = eAt (/^0). (13.6-11)
Матрица /ц. (/) является реакцией на набор (асимметричных) единичных
импульсов f.(t) = 6+{t) {С=\, 2, .... я; см. также п. 9.4-3, d). Заметим, что решение (9)
полностью аналогично решению одномерной задачи dy/dt = ay + f (/), у(0)=у0.
(с) Операторное решение (см. также п. 9.4-5). Применяя
преобразование Лапласа к элементам матрицы данной системы уравнений (8)
с постоянными коэффициентами, получаем
sY(s)-y0 = AY(s) + F(s)
или
Y (s) = (sI-A)-iy0 + (s /- A)-*F (s), (13.6-12)
где Y (s) и F (s) соответственно обозначают изображения функций у (t) и / (/).
Члены равенства (12) являются изображениями членов равенства (9).
Обратное преобразование Лапласа каждого элемента Y\ (s) матрицы Y (s) дает y-t (t).
13.6-3. Линейные системы с переменными коэффициентами (см. также
пп. 9.2-4, 9.3-3).
(а) Самая общая линейная система (1) имеет вид
§ = A(t)y + f(t)t (13.6-13)
где А (0 ==[aik(t)]~-матрица размера п X л, а /(0~матрица размера п X 1
(столбец) (система линейных дифференциальных уравнений с переменными
408 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.6-4.
коэффициентами и внешними нагрузками). Решение снова можно записать
в виде
y(t) = w+(t, 0)yo + $w+{t, X)f{X)dX (*^0), (13.6-14)
где ш+(/, А,) —матрица Грина размера п х п, определяемая при /^А,как
решение задачи
dw+ (i, к)
w.
>±£-±L=A(t)w+(ttX) </>*), | (13.6.15)
+ (Я, X) = I J
или как реакция на набор (асимметрических) единичных импульсов /; (t) =
= 6+(/ — Я), где i=l, 2, ..., /г; см. также п. 9.4-3, d. Для системы с
постоянными коэффициентами w+ (/, X) == h+ (t — X).
(b) Для любой действительной или комплексной матрицы A (t) с непрерывными
элементами решение однородной линейной системы
& = А«)у (13.6-16)
имеет вид Y (t) у (0), где Y = Y (/) — матрица размера п X п, являющаяся
единственным решением матричного дифференциального уравнения
^ = Л(/)У, У(0) = 7. (13.6-17)
at
Матрица Y (t) является невырожденной; ее столбцы образуют п линейно независимых
решений системы (16) (фундаментальная матрица решений, см. также п. 9.3-2).
Матрица U (t) == [У"1 (/)]* служит единственным решением уравнения
-*E = A*(t)U, (У <0) =» J. (13.6-18)
at
Уравнения (17) и (18)~называются сопряженными линейными уравнениями ').
Матрица Грина w+{t, X) из п. 13.6-3, а равна
w+ (t, A,) ss Y (/) У-* (X) ss Y (О U* (к) (t > А,), (13.6-19)
так что решение (14) соответствует матричной форме решения из п. 9.3-3 методом
вариации постоянных.
13.6-4. Методы возмущений и уравнения в вариациях.
(а) Пусть задана система дифференциальных уравнений
-J = /C У\ <*), у(0)-Уо. (13.6-20)
зависящая от набора (столбца) {аъ а2, ..., ат\ т параметров о^, и пусть
у{1, (t)—известное ее решение %яя значений параметров а = а, зг {ап, а12, ...
••• » ашЬ Возмущенное решение yl\)(t) + by(t)i соответствующее
возмущенному столбцу параметров а = а1 + 8а, может оказаться легче найти путем
решения системы
j-tby = f(t, y{ll + by\ о, + ва)-/(/, уп); а,), бг/(0) = 0 (13.6-21)
') * -77 — ^ (0 и — I ~г А* (О являются сопряженными операторами в
простое»
рэнстве матричных функций и (t) размера п х 1, для которых интеграл J и* (t) и (О dt
0
существует и и (0) = 0, если скалярное произведение двух таких функций и и v
оо
определить формулой (и, у) = J и* {t) v (/) <# (п. 14.4-3; см. также п. 15.4-3).
13.6-6. 13.6. ВОЗМУЩЕНИЯ И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА 409
для возмущения (вариации, п. 11.5-1) ду9 чем с помощью непосредственного
решения системы (20). Система (21) является точной. Однако для должным
образом дифференцируемой матричной функции f(t, у; а) можно, пренебрегая
всеми членами разложения правой части (21) в ряд Тейлора, кроме членов
первого порядка, найти приближение для ду (возмущение первого порядка),
решая линейную систему
ЪТЬУ = ТуЬУ + ЪаЬа' бУ(°) = 0. (13.6-22)
где элементы матрицы df/dyzs [dfi/dyk]u== а==а размера п X п и матрицы
df/da == [dfi/dak] п размера п х /я, вообще говоря, зависят от ВЫбран-
tZ у{1и и иг
ного решения yiV (t), а потому и от /. Если возмущения бу,- малы по
сравнению с \yt\t то можно пренебречь ошибками, возникающими от замены
точной системы приближенной.
(b) Зависимость решения у (t) от параметров си часто описывают
коэффициентами чувствительности, т. е. производными решения по параметрам ^. «= ду-/да^9
образующими матрицу Z = ду/да ss [d^j/da^] размера п X т. Для каждого
данного решения у - (t) коэффициенты чувствительности являются функциями от t
и удовлетворяют тп линейным дифференциальным уравнениям (уравнениям в
вариациях по параметрам или уравнениям чувствительности)
(c) При изучении зависимости решения от начальных значений #. (0) = ^ эти
вначения можно рассматривать как параметры. В этом случае начальные условия
бу(0)—0 в системах (21) и (22) можно заменить условиями
Ьу (0) = у (0) - у(1) (0) = бу0. (13.6-24)
Для уравнения (23) в вариациях по начальным значениям г^. = ^У:/дуь0 начальные
условия следует взять в виде
ЪЮ-*^| _J° <^«. ,, ,_,., „, (13.0-25)
1к °Уко \у=у{1) U « = *>
13.6-5. Устойчивость решений: определения (см. также п. 9.5-4).
Различные виды устойчивости решения y — y{i)(t) системы
^Не. у) (^« (13.6-26)
можно определить с помощью того эффекта, который вызывают возмущения
параметров (п. 13.6-4). Нижеследующая теория относится к устойчивости
в смысле Ляпунова, которая определяется эффектом от малого изменения
начального значения
на получающееся в результате возмущение
при t > t0<
Решение y = y,i}(t) системы (26) называется:
Устойчивым в смысле Ляпунова, если для каждого е > 0
существует такое Д (е, /0) > 0, что из || 6y(t0) || < А (г, *0) следует, что
||fy/(0ll<8 пРи всех t^t0. В противном случае решение
называется неустойчивым.
Асимптотически устойчивым в области Dx (/0) фазового
пространства, состоящего из точек y=s{ylt y2 уп}, если решение
410 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.6-6.
У a) if) устойчиво и если из того, что у (t0) принадлежит области
Ог(/0), следует, что lim 6#(/) = 0 (т. е. \\by(t)\\-+0 при /-*со,
t-+CQ
п. 13.2-11).
Асимптотически устойчивым в целом (вполне устойчивым,
глобально асимптотически устойчивым), если областью асимптотической
устойчивости является все фазовое пространство.
Замечание. В приведенных выше определениях норма \\ бу \\ матрицы
размера п X 1 (столбца) бу = {6ylt Ьу2у .... буЛ определяется в соответствии с
равенством (13.2-2) формулой
II бу II = sup | %гЪУ1 + Ъ26у2 + ... + ЪпЪул | (13.6-27Д)
Если это удобно, ее можно заменить одной из норм (таблица 13.2-1)
11 ЬУ 118 = [(6^i)2 + (б^2)2 + 1" (6уп)2]1/2 (евклидова норма) (13.6-276)
или
II ЬУ "l = I Ч I + I б*2 I + — + I 4t I- (L3.6-27C)
Заметим, что в этих определениях речь идет об устойчивости решений,
а не систем (см. также ,пп. 9.4-4 и 13.6-7). Если решение устойчиво в смысле
Ляпунова, то достаточно малые изменения начальных значений не могут
привести к большим изменениям решения за какой угодно промежуток времени.
Для асимптотически устойчивого решения эффект от конечного изменения
начальных значений в указанных границах ставет сколь угодно малым после
того, как пройдет достаточно большой промежуток времени. Если решение
асимптотически устойчиво в целом, то даже сколь угодно большое изменение
начальных значений в конце концов вызовет пренебрежимый эффект.
Асимптотическая устойчивость является требованием для практических
контрольных систем.
13.6-6. Функции Ляпунова и устойчивость.
(а) Устойчивость равновесия автономных систем (см.
также п. 9.5-4, Ь). Точка покоя y(t) = ya) (t^O) автономной системы
%=!(У) 00) (13.6-28)
определяется условием
/(*/<1>) = 0. (13.6-29)
Достаточно рассматривать точки покоя у (t) = y{V = 0, так как другие точки
покоя t/ = t/(i, в фазовом пространстве можно перевести в начало "координат
с помощью простого преобразования координат.
Функцией Ляпунова для решения y(t) — 0 данной системы (28) называется
любая такая действительная функция V (у) == V (ylt у2, ..., уп)> что в
некоторой окрестности D точки у = 0 в фазовом пространстве, состоящем из точек
у == {ylt y2, ..., уп}, функция V (у) непрерывно дифференцируема и
1/(//)>0 при уФО, I/ (0)=0,
d и t ч V av dyk V dv t
(13.6-30)
■— V (y) === -— V [y (t)] — производная функции V, вычисленная в силу системы
(28), т. е. вдоль интегральных кривых.
i3.6-7. 13.6. ВОЗМУЩЕНИЯ И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА 411
Решение (точка покоя) у (t) == 0 устойчиво в смысле Ляпунова в том
(и только в том) случае, если существует соответствующая функция Ляпунова
(теорема Ляпунова об устойчивости).
Решение y(t)==0 асимптотически устойчиво в окрестности D, если
существует функция Ляпунова V (у), удовлетворяющая в D строгому неравенству
dV/dt<cO для всех уфО (теорема Ляпунова об асимптотической
устойчивости).
Решение г/(/) == О асимптотически устойчивое целом, если функцию
Ляпунова V (у) можно определить для всего фазового пространства так, что
выполняются условия теоремы об асимптотической устойчивости и V (у) ~> со при
|| у || -> со (теорема Лассаля).
Решение у(/) = 0 уравнения (28) неустойчиво, если существует область Du
содержащаяся в некоторой окрестности D точки у = 0, и действительная
функция U (у) такие, что
1. Функция U (у) непрерывно дифференцируема в Dx и
UW>0> I Wj*>0
п
dU_
<V
для всех у ф О в Di,
2. U (у) = 0 во всех граничных точках области Dv лежащих
внутри D;
3. у —0 есть граничная точка области Dx (теорема Четаева
о неустойчивости).
В частности, решение неустойчиво, если условие 1) выполняется
во всей окрестности D точки у = 0 (теорема Ляпунова о
неустойчивости).
(Ь) Неавтономные системы. Каждое решение у (t) = y(1) (t) системы
-fo— fif, у) (t^O) при помощи замены х (t) — y (t) — ya) (t) можно
преобразовать в решение х (t) s= 0 новой системы
§ = /(/, x + yn))-f(t, ylv)-F(t, x) (t^-0). (13.6-31)
При этом F(t, 0) = 0 для всех t^O.
Функция V (t, x) е= V (t, xx, х2, ..., хп) называется функцией Ляпунова
для системы (31), если
1. V (t, x) непрерывно дифференцируема в некоторой
окрестности Q точки х = 0 в фазовом пространстве (хх, х2, ..., хп) при всех
2. V (t, 0) = 0 при всех t^O.
3. V (t, x)^W (x) для всех точек х, принадлежащих Q, и при
всех / ^ 0, где функция W (х) такова, что W (х) > 0 для всех
^Ои W (0) = 0.
п
4- чт=д-ж+ 2 wkFk^° для всех *eQ и /^°-
k = \
При таком определении функции Ляпунова теорема п. (а) об
устойчивости переносится на неавтономные системы без всяких изменений. В теореме
об асимптотической устойчивости нужно дополнительно потребовать
выполнения неравенства -rr^ — W1(x) для всех х е Q и /^=0, где функция
№\(л:)>0 при хфО и 1^(0) = 0.
13.6-7. Приложения н примеры (см. также п. 9.5-4).
(а) Приложения такие, как проектирование контрольных систем,
мотивируют поиск функций Ляпунова, позволяющих установить асимптотическую
412 ГЛ. 13. МАТРИЦЫ, КВАДРАТИЧНЫЕ И ЭРМИТОВЫ ФОРМЫ 13.6-7.
устойчивость в рассматриваемых областях фазового пространства или же
в возможно больших его областях («прямой метод» исследования устойчивости
по Ляпунову). Функции Ляпунова для частных решений не являются
единственными, и практические методы поиска являются скорее искусством, чем
наукой.
Рис. 13.6-1. Область асимптотической устойчивости для уравнения Дуффинга
J£jL + а~^ + у + Ьу* = 0 при а = 1, Ь = -0,04.
(Ь) Как мы отметили в п. 9.5-4, а, решение у (t) = 0 линейной однородной системы
с постоянными коэффициентами
~7 = Ау (13.6-32)
(п. 13.6-2, а) асимптотически устойчиво в целом (вполне устойчиво) в том и только
в том случае, если эта система устойчива в смысле п. 9.4-4, т. е. если все собственные
значения матрицы А имеют отрицательные действительные части. Это выполняется
в том и только в том случае> если для произвольной положительно определенной
симметрической матрицы Q существует такая положительно определенная симметрическая
матрица Р, что
А'Р + РА =-<?. (13.6-33)
13.6-7. 13.6. ВОЗМУЩЕНИЯ И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА 413
Тогда V(y) ^y'Py есть функция Ляпунова для решения у = 0 (// — транспонированная
матрица для у).
(с) Уравнение Дуффинга
описывает нелинейные колебания пружины. Полагая у — уи у = y2l получаем
нелинейную систему первого порядка
Теория п. 13.6-6 показывает, что
v (Ух, t'•) - \ (М + Ч + Щ), ъ- - " ауЪ
есть функция Ляпунова для решения ух (/) = у2 (/) = 0 при а >0 и 6>0 («сильная
пружина»); это решение асимптотически устойчиво в целом.
При о>0 и 6<0 («слабая пружина») решение #i (0 = #2 (0 = О асимптотически
устойчиво, но не в целом (рис. 13.6-1).
ГЛАВА 14
ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И ЛИНЕЙНЫЕ
ПРЕОБРАЗОВАНИЯ (ЛИНЕЙНЫЕ ОПЕРАТОРЫ).
ПРЕДСТАВЛЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
МАТРИЦАМИ
14.1. ВВЕДЕНИЕ. СИСТЕМЫ ОТСЧЕТА И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
14.1-1. Вводные замечания. В этой главе дается обзор теории линейных
векторных пространств (см. также п. 12.4-1) и линейных преобразований
(линейных операторов). Векторы и линейные операторы представляют
физические объекты и операции во многих важных приложениях.
Большинство практических задач требует описания (представления)
математических моделей (п. 12.1-1) с помощью упорядоченных наборов
действительных или комплексных чисел. В частности, понятия гомоморфизма и
изоморфизма (п. 12.1-6) позволяют многие математические модели «представлять»
соответствующими классами матриц (п. 13.2-1; см. также п. 13.2-5), так что
абстрактным математическим операциям соответствуют числовые операции
над элементами матриц. (Примеры: матричные представления операторов
квантовой механики и электрических преобразователей.) В пп. 14.5-1 — 14.10-7
описывается применение матриц для представления векторов, линейных
операторов и элементов групп.
14.1-2. Числовое описание математических моделей: системы отсчета (см.
также пп. 2.1-2, 3.1-2, 5.2-2, 6.2-1, 12.1-1 и 16.1-2). Система отсчета (система
координат) есть схема правил, описывающих (представляющих) каждый объект
(точку) некоторого класса (пространства, области некоторого пространства) С
соответствующим упорядоченным набором (действительных или комплексных)
чисел (компонент, координат) хъ х2% ... Число координат, требуемых для
определения каждой точки (хи х2, ...), называется размерностью
пространства С (см. также п. 14.2-4). Во многих приложениях значения координат
связаны с системами физических мер.
14.1-3. Преобразования координат (см. также пп. 2.1-5 — 2.1-8, 3.1-12,
6.2-1 и 16.1-2). Преобразование координат хи х2, ... есть множество правил
или соотношений, ставящих каждой точке (х19 х2, ...) в соответствие новый
набор координат. Преобразование координат допускает две интерпретации:
1. «Активная» точка зрения, или точка зрения «alibi»:
преобразование координат
х[ = х\(хъ х2% ...), х'2 = х:2 (хъ х2, ...), ..., (14.1-1)
описывает операцию (функцию, отображение, п. 12.1-4), относящую
каждому данному математическому объекту (точке) (х1% х2, ...)
некоторую новую точку (х[% *2» •••)•
2. «Пассивная» точка зрения, или точка зрения «alias»:
преобразование координат
хх=\ (хъ х2% ...), х2 = х2(хъ х2, ...),... (14.1-2)
вводит новое описание (новое представление) каждой точки (xlt x2, ...)
посредством новых координат xlt x2, ...
Преобразования координат позволяют абстрактные математические отношения
представлять числовыми соотношениями («активная» точка зрения) и заменять системы
14.2-1.
14.2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА
415
отсчета («пассивная» точка зрения). Замена системы отсчета часто упрощает данную
задачу. (Примеры: приведение к главным осям, пп. 2.4-8, 3.5-7, 9.4-8 и 17.4-8;
контактные преобразования, пп. 10.2-5 и 11.6-6, обобщенные координаты в динамике )
14.1-4. Инвариантность (см. также пп. 12.1-5 и 16.2-1; для более
подробного рассмотрения отсылаем к пп. 16.1-4 и 16.4-1). Функция координат,
поставленных в соответствие некоторому объекту или объектам, инвариантна
относительно данного преобразования координат (1) или (2), если значение этой
функции не меняется при подстановке вместо каждой координаты *,- функции
х\ (xlt x2, ...) или xi(xlt x2, ...). Соотношение между значениями координат
инвариантно, если оно сохраняет силу при любых подстановках такого рода.
Инвариантность относительно преобразования координат «активного» типа
интерпретируется в духе п. 12.1-5. Функции и соотношения, инвариантные
относительно какого-либо класса преобразований координат «пассивного» типа,
можно рассматривать как функции от реальных объектов (инвариантов),
представляемых различными наборами координат в различных системах отсчета
или соответственно как соотношения между ними. Полная система инвариантов
/i (хъ х2> •••)» M*i» х2> •••)> ••• однозначно характеризует все свойства объекта
(хг, дг2, ...), инвариантные относительно данного класса (группы)
преобразований координат (см. также п. 12.2-8).
14.1-5. Системы мер. Представление модели, включающей два или более
класса объектов, требует, вообще говоря, системы отсчета для каждого класса
объектов; получающееся в результате множество систем отсчета называется
системой мер. Изменение системы мер включает в себя преобразование
координат «пассивного» типа для каждого класса объектов; обычно эти
преобразования связывают таким образом, чтобы обеспечить инвариантность
некоторых важных функций и/или соотношений (см. также пп. 16.1-4, 16.2-1 и 16.4-1).
14.2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА
14.2-1. Определяющие свойства. Как уже говорилось в п. 12.4-1,
линейное векторное пространство U, состоящее из векторов а, Ь, с, ... , над
кольцом (с единицей, п. 12.3-1) R, состоящим из скаляров а, |3, ... , допускает
сложение векторов и умножение векторов на скаляры, обладающие
следующими свойствами:
1. U есть коммутативная группа относительно сложения
векторов: для каждой пары векторов a, b из U пространство U
содержит их сумму а + b, причем
a + b = b+a, a + (b + c) = (a + b) + c.
Кроме того, U содержит нулевой вектор 0 и для каждого вектора
а противоположный вектор —а такие, что
a-f-0 = a, а + (—а) = а — а = 0.
2. U содержит произведение оса каждого вектора аЕ^на любой
скаляр осе/?, причем
(оф)а = афа), 1а = а,
a(a + b) = aa + ab, (а+Р)а = оа + ра,
где 1—единица кольца R.
Отметим, что
0.а=0, (— 1)а = — а, (—а)а = — (аа). (14.2-1)
Если специально не оговорено противное, то подразумевается, что все
линейные векторные пространства, рассматриваемые в этом справочнике, явля-
416 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.2-2,
ются действительными векторными пространствами или же комплексными
векторными пространствами, соответственно определяемыми как линейные
векторные пространства над полем действительных чисел и над полем
комплексных чисел.
В случае векторных пространств, допускающих определение сходимости
(п. 14.2-7, Ь), некоторые авторы называют совокупность векторов,
обладающую описанными выше свойствами, линейным многообразием, а термин
векторное пространство резервируют для замкнутых линейных многообразий,
т. е. линейных многообразий, содержащих все свои предельные точки
(п. 12.5-1, Ь); в случае конечномерных многообразий эти два понятия
равносильны (п. 14.2-4).
14.2-2. Линейные многообразия и подпространства в 11. Подмножество Ux
линейного векторного пространства U есть линейное многообразие в U, если
Ux есть линейное многообразие над тем же кольцом скаляров, что и U\ Ux
называется подпространством пространства И, если оно является замкнутым
линейным многообразием в U (см. также п. 14.2-1). Собственное
подпространство пространства U есть его подпространство, отличное от 0 и от самого U.
Любое данное множество векторов ех, е2, ... пространства U порождает
(определяет) линейное многообразие, содержащее всевозможные линейные
комбинации векторов ej, e2, ...
Пример: прямые линии и плоскости, проходящие через начало координат в
трехмерном евклидовом пространстве.
14.2-3. Линейно независимые и линейно зависимые векторы (см. также
пп. 1.9-3, 5.2-2 и 9.3-2).
(a) Конечное множество векторов alf a2, ... линейно независимо, если
из Л1а1 + А,2аа + ... = 0 следует, что А,1 = А,2 = ... = 0. (14.2-2)
В противном случае векторы аг, а2, ... линейно зависимы и по крайней мере
один из них, например аА, может быть выражен в виде линейной комбинации
afe = ^ \kj2Li остальных векторов а; этого множества. Это, в частности, верно
i
в том тривиальном случае, когда а^ — нулевой вектор.
(b) Определения п. 14.2-3, а применимы и к бесконечным множествам векторов alt
аа, .... если можно приписать смысл условию (2). Вообще говоря, для этого требуется,
чтобы, помимо алгебраических постулатов из п. 14.2-1, векторное подпространство
допускало определение сходимости (пп. 12.5-3 и 14.2-7, Ь).
14.2-4. Размерность линейного многообразия или векторного пространства.
Базисы и системы координат (системы отсчета).
(а) Базис (линейный) линейного многообразия U есть такое множество
линейно независимых векторов еь е2, ... многообразия U, что каждый вектор
а <= U может быть представлен в виде линейной формы
а = а1е1 + а2е2 + ... (14.2-3)
относительно базисных векторов е,-. Каждое множество линейно независимых
векторов образует базис линейного многообразия, состоящего из
всевозможных линейных комбинаций данных векторов.
(Ь) В конечномерном линейном многообразии или векторном пространстве,
порожденном п базисными векторами:
1) каждое множество из п линейно независимых векторов
является базисом;
2) никакое множество из т<Сп векторов не является базисом-,
3) каждое множество из т> п векторов необходимо линейно
зависимо.
Число п называется (линейной) размерностью данного векторного
пространства. Бесконечномерное векторное пространство не допускает никакого
конечного базиса.
14.2-6. 14.2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА 417
(c) В каждом действительном или комплексном векторном пространстве
размерности п числа ах, а2, ... , ап являются единственными координатами
вектора а = а^ + • • • + апеп в системе координат (система отсчета),
определяемой базисными векторами ех, е2, ... , еп. Отметим, что вектор а + b имеет)
координаты а,- + р,-, а вектор оса — координаты аа,- (/ = 1, 2, ..., п; см. п. 5.2-2).
(d) Два линейных векторных пространства U и W над одним и тем же
кольцом скаляров а, р, ... изоморфны (п. 12.1-6) в том и только в том
случае, если между ними можно установить взаимно однозначное соответствие
а^-*а', b«-*b', ... , при котором a + b^a' + b' и аа^аа'. В случае
конечномерных векторных пространств для этого необходимо и достаточно, чтобы
U и W имели одну и ту же линейную размерность.
В частности, каждое «-мерное действительное или комплексное векторное
пространство изоморфно пространству матриц-столбцов, имеющих п строк, соответственно над
полем действительных или комплексных чисел (матричное представление, п. 14.5-2).
14.2-5. Нормированные векторные пространства. Действительное или
комплексное векторное пространство U называется нормированным векторным
пространством, если для каждого вектора а£2( существует такое
действительное число || а || (норма, абсолютная величина, модуль вектора а), что из
а = Ь следует ||а|| = [|Ь[| и что для всех a, b из U:
(|а|)^0, из||а|| = 0 следует, что a=0, |] aa j| = | а |[] а(], }
|| а + b |] ^ [| а [| +1| b Ц (неравенство Минковского). )
Единичный вектор есть вектор с единичной нормой (см. также п. 5.2-5).
Отметим, что |] —а || = 1 а || и ||0|| = 0.
14.2-6. Унитарные векторные пространства.
(a) Действительное или комплексное векторное пространство U
называется унитарным (эрмитовым, предгильбертовым) векторным пространством,
если можно определить бинарную операцию, ставящую каждой паре a, b
векторов из U в соответствие скаляр (а, Ь) — скалярное, или внутреннее,
произведение а и Ь, причем:
1) (a, b) = (b, а) (эрмитова симметрия);
2) (а, Ь + с) = (а, Ь) + (а, с) (дистрибутивный закон);
3) (a, ab) = a(a, b) (ассоциативный закон)1);
4) (а, а):>0; из (а, а) = 0 следует а = 0 (положительная определенность).
Отсюда следует, что в каждом унитарном векторном пространстве
(b + c, a) = (b, a) + (c, a), (aa, b) = a(a, b), (14.2-5)
| (а, Ь)|2^(а, a) (b, b) (неравенство Коши — Шварца). (14.2-6)
Неравенство Коши —Шварца (6) (см. также п, 1.3-2) превращается в
равенство в том и только в том случае, если au b линейно зависимы (см. также
пп. 1.3-2, 4.6-19 и 15.2-1, с).
т векторов ах, а2, ..., ат пространства U линейно независимы в том и
только в том случае, если определитель det [(at-, ал)] т-порядка (определитель
Г рама, см. также 5.2-8 и 15.2-1, а) отличен от нуля.
(b) Если унитарное векторное пространство действительно, то все ска-
лярные произведения (а, Ь) действительны, и скалярное умножение векторов
коммутативно, так что
(a, b) = (b, a), (aa, b) = a(a, b). (14.2-7)
Замечание. Используемые в теории относительности пространства с
внутренним произведением с неопределенной метрикой являются действительными или
комплексными векторными пространствами, допускающими определение скалярного произведения
х) Некоторые авторы вместо этого требуют, чтобы (аа, Ь) = а (а, Ьь что сводится
к перестановке а и b в определении произведения (а, Ь); тогда (a, ab) = а (a, b).
14 Г, Корн и Т. Кори
418 ГЛ. И. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.2-7.
(а, Ь), удовлетворяющего условиям (I) — (3), ио не удовлетворяющего условию (4) из
п. 14.2-6, а. Все векторы такого пространства могут быть подразделены на векторы с
положительным, отрицательным или нулевым квадоатом (а, а). Полагают ||а || = У||(а, а)||.
См. также пп. 14.2-5 и 16.8-1.
14.2-7. Норма, метрика и сходимость в унитарных векторных
пространствах. Гильбертовы пространства.
(a) Каждое нормированное векторное пространство (п. 14.2-5) является
метрическим пространством с метрикой d (a, b) = i|a —Ь(| (п. 12.5-2) и в нем
(как и в п. 12.5-3) можно определить окрестности и сходимость (см. также
п. 5.3-1). В этом смысле ряд а0-|-а1 + а2-f-... сходится, и его сумма равна
п со
вектору s= lim ^^ а/г— У) а/г пространства U в том и только в том слу-
п-юо & = 0 & = 0
II п II
чае, если lim s — У] ал =0.
я —со|| k = Q II
Нормированное векторное пространство является полным (п. 12.5-4)
в том и только в том случае, если каждая послеловательность векторов
s0» sb s2, ... пространства U, удовлетворяющая условию
lim ||srt-sm|] = 0
/г-* со
m->co
{последовательность Коиш, фундаментальная последовательность, см. также
п. 4.9-1), сходится к некоторому вектору sg^.
Полное нормированное векторное пространство называется банаховым
пространством. Каждое конечномерное нормированное векторное пространство
является полным.
(b) Каждое унитарное векторное пространство позволяет формулами
d(a, b) = Ца — b|| = V(а — b, a-b), j (14.2-8)
ввести норму (абсолютную величину, модуль) (|а|| каждого вектора а,
расстояние d (а, Ь) между двумя «точками» a, b из U и угол у между любыми
двумя векторами а и Ь. Функции ||а|| и <i(a, b), определенные в (8),
удовлетворяют всем условиям пп. 14.2-5 и 12.5-2.
Если U — действительное унитарное векторное пространство, то cos у —
действительное число для всех а и b и в силу неравенства (6) Коши — Шварца — 1 ^ cos у ^ 1.
(с) Конечномерные действительные унитарные векторные пространства
называются евклидовыми векторными пространствами. Они являются сепара-
бельными, полными и локально компактными (п. 12.5-4) и служат моделями
для /г-мерных евклидовых геометрий (см. также главы 2 и 3 и пп. 5.2-6
и 17.4-6).
Полное унитарное векторное пространство называется гильбертовым
пространством х). Все полные пространства последовательностей и функций,
перечисленные в табл. 12.5-1, являются гильбертовыми (а потому и
банаховыми) пространствами.
х) Некоторые авторы раньше требовали, чтобы каждое гильбертово пространство
было не только полным, но и сепарабельным (п. 12.5-1, Ь); иногда гильбертовым
называют только бесконечномерное полное унитарное пространство.
14.3-2. 14.3. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ (ЛИНЕЙНЫЕ ОПЕРАТОРЫ) 419
Гильбертовы пространства сохраняют многие свойства евклидовых
пространств. В частности, каждое сепарабельное (п. 12.5-1) бесконечномерное
действительное или комплексное гильбертово пространство изоморфно и изомет-
рично пространству /2 соответственно действительных или комплексных
бесконечных последовательностей (gx, |2, ...), для которых сходится ряд
II(5i. ёг» •••)ll2 = Uil2 + l£2l2 + --. (табл. " 12.5-1). Поэтому каждому вектору
из сепарабгльного бесконечномерного гильбертова пространства можно
поставить в соответствие счетное множество координат.
Каждое подпространство гильбертова пространства является полным его
подпространством (см. также п. 14.2-2) и, таким образом, и само является гильбертовым
пространством.
14.2-8. Теорема о проекции. Если заданы произвольный вектор х
унитарного векторного пространства U и полное его подпространство 1СЪ то
существует единственный вектор у — хр из иъ реализующий минимум расстояния
|| х—у || для всех у из Uv Кроме того, хр является единственным вектором
у из Ux, для которого разность х — у ортогональна каждому вектору хх
из Ult т. е.
(х—хр, Хх) = 0 (хх из UX) (14.2-9)
(см. также п. 14.7-3). Отображение х—»хр есть ограниченный линейный
оператор (п. 14.4-2), называемый ортогональной проекцией пространства U на Ux.
Теорема о проекции чрезвычайно важна для практики, потому что
условие (9) определяет оптимальное приближение вектора х вектором у из «более
простого» класса Ult если погрешность приближения измеряется числом ||х — у|)2.
Примеры: Проекция точек на плоскость в евклидовой геометрии, ортогонапь-
ные приближения (пп. 15.2-3, 15.2-6, 20.6-2 и 20.6-3), средняя квадратическая регрессия
(п. 18.4-6)
14.3. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ (ЛИНЕЙНЫЕ ОПЕРАТОРЫ)
14.3-1. Линейные преобразования векторных пространств. Линейные
операторы. Пусть U и W—линейные векторные пространства над одним и тем
же полем скаляров ее, |3, ... Тогда (однородное) линейное преобразование
пространства U в пространство 1С есть отображение
х' = /(х)==Ах, (14.3-1)
ставящее каждому вектору хе2( в соответствие некоторый вектор х' е W
так, что при этом сохраняются «линейные» операции сложения векторов и
умножения векторов на скаляры:
f (x + y) = f (х) + f (у), f (ax) = а f (x). (14.3-2)
Каждое линейное преобразование может быть записано как умножение
вектора на линейный оператор А (линейную операцию), причем
А (х + у) == Ах +Ау, А (ах) = а (Ах). (14.3-3)
Линейное преобразование {оператор), отображающее линейное векторное
пространство U в себя, называется линейным оператором в пространстве U,
Функция f (х) = Ах + а' называется линейной векторной функцией. При задании
каждого линейного оператора должна быть указана область его определения. В физике
первое из соотношений (3) часто называют принципом суперпозиции для данного класса
операций.
14.3-2. Множество значений, ядро и ранг линейного преобразования
(оператора). Множество значений линейного преобразования А (образ при
преобразовании А, п. 12.1-4) линейного векторного пространства U в линейное
14*
420 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.3-3.
векторное пространство W есть линейное многообразие (п. 14.2-2) в W'.
Ядро линейного преобразования А есть многообразие в U, состоящее из всех
векторов, отображающихся в нулевой вектор пространства W. Ранг г и
размерность ядра г' линейного преобразования А —это соответственно
линейные размерности (п. 14.2-4, Ь) множества его значений и его ядра. Если U
имеет конечную размерность я, то множество значений и ядро любого линей-
ного преобразования А являются подпространствами, и г-\-г' = п.
14.3-3. Сложение н умножение на скаляры. Нулевое преобразование.
(a) Пусть А и В — линейные преобразования (операторы), отображающие
U в 1С. Тогда по определению А ± В и аА —линейные преобразования
пространства U в W, при которых
(А ± В)х = Ах± Вх, (аА)х = а(Ах) (14.3-4)
для всех векторов хе2/.
(b) Нулевое преобразование О пространства U в W определяется условием
Ох= 0для всех векторов хе^, где 0 —нулевой вектор пространства #'.
14.3-4. Произведение двух линейных преобразований (операторов).
Тождественное преобразование.
(a) Пусть А —линейное преобразование (оператор), отображающее U в U\
и В-—линейное преобразование, отображающее W (множество значений
преобразования А) в U". Произведение ВА есть линейное преобразование
пространства U в U", получающееся, если последовательно произвести
преобразования А и В (см. также п. 1*2.2-8):
(BA)xeeB(Ax). (14.3-5)
(b) Тождественное преобразование I любого векторного пространства U
переводит каждый вектор х е U в себя:
Ixeeex, l'A = AI = A, (14.3-6)
где А-—линейное преобразование пространства U в W, а I и Г—
соответственно тождественные преобразования этих пространств.
14.3-5. Невырожденные линейные преобразования (операторы). Обратные
преобразования (операторы). Линейное преобразование (оператор) А
называется невырожденным (неособенным), если оно взаимно однозначно отображает
пространство U на все пространство W (пространства U и W в этом случае
необходимо изоморфны, п. 14.2-2). Преобразование А является
невырожденным в том и только в том случае, если оно имеет единственное обратное
преобразование (обратный оператор) А-1, отображающее W на U так, что
из х' = Ах следует х = А~1х/, и наоборот, или
AA"1 = I/, A^A^I, (14.3-7)
где I и Г —тождественные преобразования соответственно в U и в W,
Произведения и обратные преобразования невырожденных преобразований
(операторов) являются невырожденными; если А и В не вырождены и а^£0, то
(AB)-1 = B-iA~1, (аА)-1 = а-1А~1, (А~1Г1 = А. (14.3-8)
Невырожденные линейные преобразования (операторы) сохраняют линейную
независимость векторов, а потому и линейные размерности отображаемых
многообразий (пп. 14.2-3 и 14.2-4).
Линейное преобразование (оператор) А, определенное на конечномерном
векторном пространстве, невырождено в том и только в том случае, если
из Ах = 0 следует х = 0, т. е. если г = п и г'—0 (п. 14.3-2).
14.3-6. Целые степени операторов. Пусть А —линейный оператор в
линейном векторном пространстве U. По определению А° = 1, АХ = А, А2—АА,
А3=ААА, ... и, если А —невырожденный, А~р = (А~1)р = (АР)~1 (р = 1,2, ...)
Справедливы обычные правила действий со степенями (см. также п. 12.4-2).
14.4-3. 14.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В НОРМИРОВАННОМ ПРОСТРАНСТВЕ 421
14.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В НОРМИРОВАННОМ ИЛИ ГИЛЬБЕРТОВОМ
ПРОСТРАНСТВЕ. ЭРМИТОВЫ И УНИТАРНЫЕ ОПЕРАТОРЫ
14.4-1. Ограниченные линейные преобразования (см. также п. 13.2-1, а).
Линейное преобразование А нормированного векторного пространства
(п. 14.2-5) U в нормированное векторное пространство W называется
ограниченным, если А имеет конечную норму
||АЦ = sup i~f- sup (|Ax(|.
x€=# l|x|1 ||x||=l (14.4-1)
x^O
Отметим, что
|]АЦ^0, (|аА[Н|а|(|А(|, ЦА + ВЦ ^|| A|] + || ВЦ, \
|AB||^||A||||B[|,||Ax||^||A||||x[|.
(14.4-2)
Каждое линейное преобразование (оператор), определенное на конечномерном
нормированном векторном пространстве, ограничено.
^Линейное преобразование А нормированного векторного пространства
U в нормированное векторное пространство W непрерывно, если оно
непрерывно как отображение метрического пространства U в метрическое
пространство W (см. пп. 14.2-7 и 12.5-3, Ь). Линейное преобразование одного
нормированного векторного пространства в другое непрерывно в том и только
в том случае, если оно ограничено.*
Если U — унитарное векторное пространство (п. 14.2-6) и А — линейный
оператор в U, т. е. оператор, отображающий U в себя (п. 14.3-1), то
A«=s%JwL=l|xsi;pI»Axii=
хфО
I (x Av) I
= ДР0Т7Р7Г = 1|Х|1=5;Р|,= 11(Х>АУ)'- (14.4-3)
14.4-2. Ограниченные линейные операторы в нормированном векторном
пространстве.
(a) Ограниченные линейные операторы А, В, ... в нормированном
векторном пространстве U составляют линейную алгебру (п. 12.4-2), операции
в которой определены в пп. 14.3-3 и 14.3-4, причем нулем служит нулевой,
а единицей тождественный оператор. Вырожденные операторы являются
в этой алгебре делителями нуля (п. 12.3-1, а), а невырожденные образуют
мультипликативную группу и вместе с нулевым оператором — алгебру с
делением (п. 12.4-2). Если U — пространство конечной размерности /г, то алгебра
линейных операторов имеет ранг п2.
Алгебра операторов, вообще говоря, не коммутативна (см. также п. 12.4-2).
Оператор АВ —ВА называется коммутатором операторов А и В.
(b) Ограниченные линейные операторы в гильбертовом пространстве
(п. 14.2-7, Ь) позволяют, как в пп. 13.2-11 и 13.2-12, определить с помощью
метрики || А —ВЦ сходящиеся последовательности и аналитические функции
операторов (п. 12.5-3).
14.4-3. Сопряженный оператор. Каждый ограниченный линейный оператор А
в гильбертовом пространстве U имеет единственный сопряженный оператор А*,
определяемый условием
(х, Ау) = (А* х, у) для всех х и у из U, (14.4-4)
422 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.4-4.
При этом
(А + В)* = А* + В*, (аА)* = аА*,
(АВ)* = В*А*, (А-1)* = (А*Г1, (А*)* = А, [ (14.4-5)
1|А*||Н|А||, ||А* А||=||А||2, 0* = 0, 1* = 1;
(Ах, By) == (х, A* By) a (В* Ах, у). (14.4-6)
(см. также пп. 14.2-6, а, 14.2-7, b и 14.4-9).
14.4-4. Эрмитовы операторы. Линейный оператор А в гильбертовом
пространстве U называется эрмитовым (самосопряженным), если
А*==А, т. е. (х, Ау) = (Ах, у) для всех х и у из U. (14.4-7)
Если U— комплексное гильбертово пространство, то оператор А является
эрмитовым в том и только в том случае, если скалярное произведение (х, Ах)
для всех х действительно, или
(х, Ах) = (Ах, х) = (Ах, х) для всех х £ U. (14.4-8)
Всякий эрмитов оператор в комплексном гильбертовом пространстве является
ограниченным. Оператор А, удовлетворяющий условию А* =—А, называется
косоэрмитовым.
Эрмитовы операторы играют важную роль в тех приложениях, где требуется, чтобы
скалярное произведение (х, Ах) было действительным числом (теория колебаний,
квантовая механика). Эрмитов оператор А называется соответственно положительно
определенным, отрицательно определенным, неотрицательным, неположительным, положительно
полуопределенным, отрицательно полуопределенным, неопределенным или нулевым, если
это же верно для скалярного произведения (эрмитовой формы) (х, Ах) (см. также пп.
13.5-3 и 14.7-1).
14.4-5. Унитарные операторы. Линейный оператор А в гильбертовом
пространстве U называется унитарным, если
А*А = АА* = 1, т. е. А* = А"1. (14.4-9)
Каждый унитарный оператор является невырожденным и ограниченным
и ||А|| = Ь Каждое унитарное преобразование х' = Ах, где А —унитарный
оператор, сохраняет скалярное произведение:
(*'» У') = (Ах, Ау) = (х, у) для всех х и у из U, Л
||х'|| = ||Ах|| = ||х|| для всех х £ U. ) { ' ' U'
Если пространство U конечномерно, то каждое из соотношений (10) влечет за
собой унитарность оператора А.
Унитарные операторы сохраняют скалярное произведение векторов, а также
сложение векторов и произведение векторов на скаляры; таким образом, при унитарных
преобразованиях норма векторов, расстояния, углы, ортогональность и ортонормированность
(пп. 14.2-7, а и 14.7-3) инвариантны (п. 12.1-5).
14.4-6. Симметрические, кососимметрические и ортогональные операторы
в действительных унитарных векторных пространствах.
(а) Оператор А*, сопряженный (п. 14.4-3) с линейным оператором А
в действительном гильбертовом пространстве U, часто называется
транспонированным оператором (преобразованием) и обозначается символом А'; он
удовлетворяет соотношениям
(х, Ау) = (Ау, х) = (А'х, у) = (у, А'х) для всех х и у из 11. (14.4-11)
Если рассматриваемое векторное пространство действительно, то во всех
соотношениях из п. 14.4-3 вместо А* можно писать А'.
14.4-8. 14.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В НОРМИРОВАННОМ ПРОСТРАНСТВЕ 423
(Ь) Линейный оператор (преобразование) А в действительном
гильбертовом пространстве U называется симметрическим, если
А' = А, т. е. (х, Ау) = (у, Ах) для всех х и у из U, (14.4-12)
кососиммстрическим (антисимметрическим), если
А' = — А, т. е. (х, Ау) = — (у, Ах) для всех х и у из U, (14.4-13)
ортогональным, если
А'А = АА' = 1, т. е. А'^А"1. (14.4-14)
Ортогональные операторы в действительном гильбертовом пространстве
являются унитарными, так, что для них верны утверждения из п. 14.4-5.
14.4-7. Правила комбинирования (см. также п. 13.3-3).
(a) Если А—эрмитов оператор, то это же верно и для операторов
А^(р=0, 1, 2, ...), А"1, Т*АТ и, если а —действительное число, для
оператора аА. Если а —чисто мнимое, то оператор аА — косоэрмитов.
Если Т — любой невырожденный оператор, то оператор Т*АТ является
эрмитовым в том и только в том случае, если эрмитовым является оператор А;
поэтому для любого унитарного оператора Т оператор Т-1АТ является
эрмитовым в том и только в том случае, если это же верно для оператора А.
В частности, если рассматриваемое гильбертово пространство действительно
и А — симметрический оператор, то такими же будут и операторы А^ (р = 0, 1, 2, ...),
А-1, Т'АТ и аА. Если Т — любой невырожденный оператор, то оператор Т'АТ
является симметрическим в том и только в том случае, если симметрическим является и А;
для любого ортогонального оператора Т оператор Т_1АТ является симметрическим
в том и только в том случае, если это же верно и для А.
(b) Если А и В — эрмитовы (или симметрические) операторы, то это же
верно и для суммы А + ЕЗ. Произведение А В двух эрмитовых (или
симметрических) операторов А и В является эрмитовым (или симметрическим)
оператором в том и только в том случае, если ВА = АВ (см. также п. 13.4-4, Ь).
(c) Если А — унитарный оператор, то это же верно и для А** (р = О,1, 2,...),
А-1, А*, а если |а| = 1, то а для аА. Если А и В —унитарные операторы,
то и АВ — унитарный оператор.
Если А — ортогональный оператор, то это же верно и для Ар (/? = 0, 1,
2, ...), А-1 = А' и —А. Если А и В—ортогональные операторы, то АВ —
ортогональный оператор.
14.4-6. Теоремы о разложении. Нормальные операторы (см. также пп.
13.3-4 и 14.8-4).
(а) Для каждого ограниченного линейного оператора А в гильбертовом
пространстве U операторы у (А + А*) = Иг и ^- (А — А*) = Н2 являются
эрмитовыми. Представление А = Н1 + /Н2 есть (единственное) разложение данного
оператора А на эрмитову и косоэрмитову части (ср. с разложением
комплексного числа на действительную и мнимую части).
Если пространство U действительно, то это разложение превращается
в (единственное) разложение оператора А на симметрическую часть -у (А + А')
и кососимметрическую часть у (А — А').
Для каждого ограниченного линейного оператора А в гильбертовом
пространстве операторы АА* и А*А являются эрмитовыми и неотрицательными.
Существует разложение A = QU оператора А в произведение
неотрицательного эрмитова оператора Q и унитарного оператора U. Оператор Q однозначно
определяется условием Q2 = AA*, а оператор U определяется однозначно
в том и только в том случае, если А — невырожденный оператор. Аналогично
A = U,Q1, где Qf = A*A (ср. с п. 13.3-4, а).
424 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.4-9.
(Ь) Оператор А в гильбертовом пространстве U называется нормальным
оператором, если А*А = АА*.или, что эквивалентно, если Н2Н1 = Н1Н2.
Ограниченный линейный оператор А нормален в том и только в том случае, если
|| Ах || ==|| А || • || х || для всех хе^, Эрмитовы и унитарные операторы
нормальны.
14.4-9. Сопряженные векторные пространства. Более общее определение
сопряженных операторов.
(a) Ограниченные линейные преобразования А нормированного векторного
пространства U в произвольное полное нормированное векторное пространство
(банахово пространство, п. 14.2-7) образуют полное нормированное векторное
пространство, сложение и умножение в котором определяются формулами (14.3-4),
а нормой служит || А ||. В частности, множество ограниченных (в смысле п.
14.4-1) линейных (и однородных) скалярных функций ф (х) (линейных
функционалов), определенных на нормированном векторном пространстве U, составляет
полное нормированное векторное пространство U*, сопряженное (дуальное,
двойственное) к пространству U.
Пусть
х' = Ах
— ограниченное линейное преобразование пространства U в какое-либо другое
нормированное векторное пространство W. Тогда условие
ф' (х') г ф' (Ах) » ф (х) (14.4-15а)
определяет ограниченное линейное преобразование
Ф = А*ф' (14.4-15/?)
пространства #'*, сопряженного к U\ в пространство #*, сопряженное к U.
Оператор А* называется сопряженным оператором к оператору А; имеем
II А* || = || А ||. (14.4-16)
Заметим, что (А*)*, вообще говоря, не совпадает с А.
(b) Каждую ограниченную линейную (однородную) скалярную функцию ф (х)
(линейный функционал), определенную на гильбертовом пространстве U, можно
представить в виде скалярного произведения
Ф(х) = (и, х), (14.4-17)
где и —некоторый вектор из U. Соответствие между векторами ф из U*
и векторами и из U является изоморфизмом, и на основании п. 14.4-1
|ф(х)||- sup ф(х)^||и||, (14.4-18)
II х || = 1
и следовательно, это соответствие является изометрией (пп. 12.5-2 и 14.2-7).
Поэтому гильбертово пространство является самосопряженным, т. е. оно
изоморфно и изометрично сопряженному к нему пространству. Определение
оператора, сопряженного к линейному оператору в гильбертовом пространстве,
можно тогда свести к простому определению сопряженного оператора,
приведенному в п. 14.4-3.
14.4-10. Бесконечно малые линейные преобразования (см. также пп.4.5-3
и 14Л0-5).
(а) Бесконечно малое линейное преобразование (бесконечно малый
линейный оператор) в нормированном действительном или комплексном векторном
пространстве имеет вид
А = 1 + еВ, (14.4-19)
где В —ограниченный оператор, а | 8 |2 пренебрежимо мало по сравнению с 1
(обычно е —скалярный дифференциал), т. е. |е|2^0.
14.5-1.
14 5, МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ВЕКТОРОВ
425
(b) Для бесконечно малых линейных преобразований
А=1 + еВ, А1 = 1 + 81В1, А2 = 1 + 82В2
имеем
А-1^ —еВ, А1А2 = 1 + (81В1 + 82В2) = А2А1. (14.4-20)
Бесконечно малые линейные преобразования (операторы) перестановочны.
(c) Бесконечно малое линейное преобразование А = 1 + еВ в унитарном
векторном пространстве является унитарным в том и только в том случае,
если оператор еВ косоэрмитов. Бесконечно малое линейное преобразование
А = 1 + еВ в действительном унитарном векторном пространстве является
ортогональным в том и только в том случае, если оператор еВ кососиммет-
ричен.
14.5. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ВЕКТОРОВ И ЛИНЕЙНЫХ
ПРЕОБРАЗОВАНИЙ (ОПЕРАТОРОВ)
14.5-1. Преобразование базисных векторов и координат векторов:
«активная» точка зрения (см. также п. 14.1-3). Рассмотрим конечномерное1)
действительное или комплексное векторное пространство Un с системой координат,
определяемой п базисными векторами ех, е2, ..., ел (п. 14.2-4). Каждый вектор
п
«^а+Еа+.-.+Ьа- 2 Е*е* ^14-5"1)
описывается своими координатами glf |2, ..., £л. Линейное преобразование
(оператор) А в пространстве Un (п. 14.3-1) переводит каждый базисный
вектор eft в соответствующий вектор
п
е'А = Аел = в1*е1 + а2Лев + ...+аяЛея= 2 aikti (k = l, 2, ..., л), (14.5-2)
/ = i
а каждый вектор х £ Un — в соответствующий вектор х' £ Un\
п п п
х'с=Ах = А 2 tk4= 2 ^е;= 2 £&. (14.5-3)
£ = 1 *=l / = i
Координаты gj вектора х' и координаты %k вектора х отнесены к одному
и тому же базису elf e2, ..., еп и связаны п линейными однородными
соотношениями преобразования
Ei—flu5i + fli26» + —+ в1л6л» \
Ei==fl»b + fl2eE2 + —+ д«л£я1 (преобразование коорди-
> «am векторов, «активная» (14.5-4)
I точка зрения).
Ъ'п = ап1Ъ1 + ап212+... + апп1п I
1) Теория пп. 14.5-1 — 14.7-7 применима и к некоторым бесконечномерным векторным
пространствам (пп, 14.2-4 — 14.2-7, Ь). Такие пространства должны допускать определение
счетных базисов (п. 14.2-4), а также ортонормированных базисов (п. 14.7-4) и сходимости^».
14.2-7), так что суммы вроде той, которая рассматривается в (1), превращаются в сходящиеся
бесконечные ряды. В частности, это справедливо для всякого сепарабельного гильбертова
пространства (п. 14.2-7, с). Векторные пространства, не допускающие счетных базисов,
могут быть представлены подходящими пространствами функций (п. 15.2-1).
426 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.5-2.
14.5-2. Матричное представление векторов и линейных преобразований
(операторов). Для каждого данного базиса et, e2, ..., ел в пространстве Un\
1) векторы х = £iei + £2e2 + --- + 5/ie/i B %п взаимно однозначно
представляются матрицами-столбцами { \ь } (п. 13.2-1);
2) линейные преобразования (операторы) в Un взаимно
однозначно представляются квадратными матрицами A =s [at-ft] порядка /г,
определяемыми в (2) или (4).
Соответствие между векторами и операторами и указанными матрицами
есть изоморфизм (п. 12.1-6): суммы и произведения, содержащие скаляры,
векторы и операторы, переходят в аналогичные суммы и произведения
матриц. Тождественный оператор переходит в единичную матрицу, а обратный
оператор —в обратную матрицу; невырожденным операторам соответствуют
невырожденные матрицы, и наоборот.
В частности, бескоординатное векторное равенство
х' = Ах
представляется в базисе ех, е2, ..., еп матричным равенством
(14.5-5)
= Ллг,
(14.5-6)
которое эквивалентно п соотношениям (4); произведение линейных
преобразований А и В представляется произведением соответствующих матриц А и В.
векторное пространство Цт можно подобным же образом представить матрицами
размера т х п. Преобразования, связывающие два действительных векторных пространства,
всегда можно представить действительными матрицами.
14.5-3. Матричные обозначения для систем линейных уравнений (см. также
пп. 1.9-2—1.9-5). Система линейных уравнений
1] aikxk = bi
(i = l, 2, ..., т)
(14.5-7)
эквивалентна матричному уравнению
Ах = Ь или
Ягл
(14.5-8)
Неизвестные Я& мож.но рассматривать как координаты неизвестного вектора,
для которого преобразование (8) дает вектор с координатами 6/. Если, в
частности, матрица [а^] не вырождена (п. 13.2-3), то матричное уравнение (8) имеет
единственное решение
* = Л-1&; (14.5-9)
Формула (9) эквивалентна правилу Крамера (1.9-4).
14.6-1.
14.6. ЗАМЕНА СИСТЕМЫ КООРДИНАТ
427
14.5-4. Диадическое представление линейных операторов. Линейный оператор А
в «-мерном векторном пространстве может быть выражен в виде суммы /2 внешних
произведений пар векторов (п диад) по способу п. 16.9-1. Соответствующая матрица А
размера п х п может быть аналогично выражена в виде суммы внешних произведений пар
матриц-строк и матриц-столбцов (см. также п. 13.2-10).
14.6. ЗАМЕНА СИСТЕМЫ КООРДИНАТ
14.6-1. Преобразование базисных векторов и координат векторов:
«пассивная» точка зрения (см. также п. 14.1-3).
(а) Если дан координатный базис elf e2, ..., еп в конечномерном х) векторном
п
пространстве ?/п, то т векторов ал = 2 а,-^(^=1, 2, ..., т) линейно неза-
i=l
висимы (п. 14.2-3) в том и только в том случае, если матрица [а^] имеет
ранг т (см. также п. 1.9-3).
В частности, для каждого координатного базиса elf e2, ..., ел в Un
*k = tik*i + hk4 + — + tnk*n=* 2 Uk*i (£=1, 2, .... л), (14.6-1)
*=i
где det [///?] ф 0 (преобразование базисных векторов).
Матрица Т = [tik] представляет (необходимо невырожденное)
преобразование Т, связывающее старые базисные векторы е; и новые базисные
векторы tk — Ttk (в смысле равенства (14.5-2)).
(Ь) Теперь каждый вектор х £ Un может быть выражен как через
координаты \{ относительно системы е,-, так и через координаты |^ относительно
системы е^:
п п
х= 2 ^е',== 2 £***•
i=l /г = 1
(14.6-2)
Координаты li и %k одного и того же вектора х связаны п линейными
однородными соотношениями преобразования
li = *ii£i + ^£2 + • • • + tinln>
£__/ti/ti Л-t f (преобразование коорди-
fe2 — 2ibi i- *22b2 T- • • • -г hn<=>n> Ham векторов: «пассивная»
точка зрения)
In — tmli + ^2^2 + • • • + tnnin
или в матричной форме
//ц /la • •• tin
х=
и
41 42
t2l t22
U
lni 1пй
= Тх.
(14.6-3)
Смысл соотношений преобразования (3) следует отличать от смысла формально
аналогичных соотношений (14.5-4) и (14.5-6).
*) См. сноску к п. 14.5-1,
428 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.6-2.
Отметим также обратные соотношения, именно
: 1, 2 п)\ (14.6-4)
det[tikl к
ft = 1
/г
Ь-^-агпщ* «-•» "> j
или "** I
* = Т \ )
где Г^ алгебраическое дополнение элемента /^ в определителе det [fy^] (п. 1.5-2).
14.6-2. Представление линейного оператора в различных базисах.
(a) Рассмотрим линейный оператор А, представляемый матрицей А в базисе
elt е2,..., еп (п. 14.5-2) и матрицей А в базисе е^, е~2, ..., еп так, что для
каждого вектора
х' = Ах, х' — Ах, х —Ах* (14.6-6)
Если дана матрица преобразования Г, связывающая базисы е,- и ед, так что
х = Тх, х=Тх' (14.6-7)
(п. 14.6-1), то матрицы А и А связаны преобразованием подобия (п. 13.4-1)
Д=Г-ЧГ или А^ТАТ-1. (14.6-8)
Наоборот, каждая матрица А, связанная с матрицей А преобразованием
подобия (8), представляет тот же самый линейный оператор А в координатном
базисе ех, е2,..., ел.
Если линейный оператор А в базисе ел и линейный оператор В в базисе
tk = Ttk представляются одной и той же матрицей, то В = ТАТ~1.
(b) Все матрицы (8), представляющие один и тот же оператор А, имеют
один и тот же ранг г, равный рангу оператора А (п. 14.3-2). След и
определитель матрицы А также являются общими для всех матриц (8) и
называются следом Тг (А) и определителем det (А) оператора А (см. также пп. 14.1-4
и 13.4-1, Ь).
(c) Матричная запись преобразования базисных векторов.
Если разрешить рассматривать строки и столбцы, состоящие из векторов, то
соотношения (1) и (6) можно соответственно записать в виде
(е\ ё, ...) = (е1 е2 ...) Т, (14.6-9)
W e2-..)=<ci е*"->Л. (14.6-10)
где
x = (et ef...)x = (ei.e2...)i, \ (146.и
.«*« x' = (et е2...) *'=(е! е2...) х )
(см. также п. 16.6-2).
14.6-3. Последовательное применение операторов (см. также пп. 14.5-2 и
14.10-6).
(а) Пусть даны два невырожденных линейных оператора А и В,
представленных в базисе еь е2,..., ert матрицами A^[atk\ и £ = [6^]. Их
последовательное применение
х' = Ах, х" = Вх' = ВАх (14.6-12)
14.7-1. M.7. ПРЕДСТАВЛЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ 429
представляется соотношениями
х' = Ах, х" = Вх' = ВАх, x^iBAYW, (14.6-13)
где ,е={Ь, е„..., и, *Щ1'х9 б;,..., ?„} и *"в={е;, ?;,..., ед-
столбцы из компонент соответствующих векторов относительно базиса е,-.
В частности, последовательное применение операторов А и В к базисным
векторам tk приводит к новым системам базисных векторов
п
i = 1
(Л = 1, 2,..., /г). (14.6-14)
Следует обратить внимание на то, что оператор В, вообще говоря,
отличается от оператора, определяемого преобразованием базисных векторов tV
с помощью матрицы В:
п
ek= £ ^-Л = АВА"1ел = АВеь (14.6-15)
i = 1
и следовательно,
х'" = АВх, х'" = АВх, (14.6-16)
так как матрица £ = [&/£] относительно базиса t'k представляет оператор
ABA"1, г не В (см. п. 14.6-2, а). _
(Ь) Столбцы x=E\llt ga,..., £„}, x = {Ii, |2»--»I/i} H^^lli, £2,..., £„},
представляющие один и тот же вектор
п п п _
х= 2 Ел— 2 6ле*= 2 1*«ь О4'617)
1 = 1 Л=1 £=1
связаны преобразованиями пассивного типа
х = А~1ВА~х, х = Ах = ВАх, И =(ВА)~1х. (14.6-18)
Еще раз отметим, что, вообще говоря, ХфВх.
14.7. ПРЕДСТАВЛЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ.
ОРТОНОРМИРОВАННЫЕ БАЗИСЫ
14.7-1. Представление скалярного произведения (см. также пп. 14г2-6,
п п
14.7-6 и 16.8-1). Пусть векторы а= 2 а*е* и ь== 2 РФ в конечномерном *)
унитарном векторном пространстве # соответственно представляются
матрицами-столбцами а = {а;} и & = {£,•} по способу п. 14.5-2 (см. также п. 13.2-1, Ь).
Тогда
(a, b)= J] 2 лЛРл = а*06, (14.7-1)
<— 1 ik — 1
где
О = to*l. gik = («/. *а) (*, k = 1, 2,..., п)
*) См. сноску к п. 14.5-1.
430
ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.7-3.
и а * ^(ах, а2,..., ал) — матрица-строка. Матрица G = \gik] необходимо
является эрмитовой (gik = gki) и положительно определенной (п. 13.5-2); если U —
действительное унитарное векторное пространство, то G—действительная и
симметрическая матрица.
Соотношение (1) позволяет описать через числовые координаты векторов нормы, углы,
расстояния, сходимость и т. д.в U (см. также п. 14.2-7). В частности, для каждого вектора
х = 2 ^в и
i =r I
п хц» = 2 2 ***«&=*•**• <14-7-2)
< — 1 Л — 1
Эрмитова форма (2) (см. п. 13.5-3) называется основной формой пространства U
относительно базиса е,. еа е„
1» 2» • • •» л*
14.7-2. Замена системы координат (см. также пп. 14.6-1 и 16.8-1). Если ввести новые
базисные векторы е^, для которых а = Tat b = Tb (п. 14.6-1), то из инвариантности
(14.1-4) скалярного произведения
п п п п
(a, b) = a*Gfc= 2 2 gik*fik= 2 2 *iJfe5Ak = S*8S (14-7"3)
/=16=1 i=i6=1
следует, что
8 =p,J = [(?,, ?4)] = Г«вГ. <14.7-4)
14.7-3. Ортогональные векторы и ортонормированные системы векторов.
(a) Два вектора а и b унитарного векторного пространства U (взаимно)
ортогональны, если (a, b)=0 (cos 7 = 0, п. 14.2-7, Ь). Ортонормированная
(ортогональная нормированная) система векторов есть система попарно
ортогональных единичных векторов u1( u2,... так, что
<■*.,)-«»-{?• Г \Ф1'\ (.-.^1.2....). (14.7-5)
I 1, если i=k )
Каждая система попарно ортогональных ненулевых векторов (и, в частности,
каждая ортонормированная система) линейно независима. Таким образом,
наибольшее число векторов в любой такой системе (ортогональная
размерность пространства U) не может превышать линейную размерность
пространства U (см. также пп. 14.2-3 и 14.2-4, Ь).
(b) Неравенство Бесселя (см. также п. 15.2-3, Ь). Если даны
конечная или бесконечная ортонормированная система u1( u2, ... и любой
вектор а <= U, то
т
2 I (Uk* a)l2^l!all2 (неравенство Бесселя). (14.7-6)
А = 1
Знак равенства имеет здесь место в том и только в том случае, если
вектор а принадлежит линейному многообразию, порождаемому данной орто-
нормированной системой (см. также п. 14.7-4); т может быть как конечным, так и
бесконечным; неравенство Бесселя часто используется для доказательства
сходимости бесконечных рядов.
14.7-4. Ортонормированные базисы (полные ортонормированные системы).
(а) В конечномерном унитарном векторном пространстве размерности п
каждая ортонормированная система из п векторов образует базис (ортонор-
мированный базис). Вот более общее утверждение. В каждом гильбертовом
пространстве U (п. 14.2-7, Ь) ортонормированная система векторов. ult u2,...
14.7-5. J4.7. ПРЕДСТАВЛЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ 431
образует ортонормированный базис (полную ортонормированную систему) в том
и только в том случае, если она удовлетворяет следующим условиям:
1. Каждый вектор аЕ^ может быть записан в виде
a = a1u1 + a2U2 + --M где ал = (ил, а) (&=1, 2,...).
2. Для любого вектора а = а1и^ + а2и2 + ...
|j а ||2 == | a! |2 +1 а2 |а +... (равенство Парсеваля).
3. Для любой пары векторов a = a1u1 + a2u2 + ... и b = p1u1 +
+ P2u2 + ...
(а, b) = a1J31 + a2fU + ...
4. Ортонормированная система ult u2,... не содержится ни
в какой другой ортонормированной системе пространства U. Для
любого вектора а <= U из (и^, а) = 0(&=1, 2,...) следует, что а = 0.
Из каждого из этих четырех условий следуют остальные три условия.
Сравнительная простота выписанных выше выражений для ||а||2 и (а, Ь)
делает ортонормированные базисы особенно удобными в качестве
координатных базисов. Заметим, что если а и а' — два вектора с одними и теми же
координатами ak, то ||а — а'|| = 0 (теорема единственности).
(Ь) Построение ортонормированной системы векторов.
Если elf e2,... — любая конечная или счетная система линейно независимых
векторов в гильбертовом пространстве, то существует ортонормированная
система иг, и2,... порождающая то же самое линейное многообразие.
Такую ортонормированную систему можно построить с помощью
следующих рекуррентных формул (процесс ортогонализации Г рама—Шмидта, см.
также п. 15.2-5):
vi
Vi = е1э v/+1 = е/+1 - 2 (u*> е;+1) uk
(1 = 1, 2,...). (14.7-7)
14.7-5. Матрицы, соответствующие сопряженным операторам (см. также
пп. 14.4-3-14.4-6, 13.3-1 и 13.3-2).
(a) Если линейный оператор А в конечномерном пространстве
представляется в некотором базисе матрицей А, то сопряженный оператор А*
представляется в этом же базисе матрицей G~1A*G1) (см. п. 14.7-1).
(b) Для ортонормированного базиса и19 и2, ... имеем G = / (см. п. 14.7-3) и
A ss [aik] = Цщ, Аи/г)].
(14.7-8)
Значит, сопряженным операторам соответствуют сопряженные матрицы, и
наоборот. Таким образом, в случае ортонормированного базиса эрмитовым,
косоэрмитовым и унитарным операторам соответствуют матрицы тех же типов,
и наоборот. В частности, симметрическим, кососимметрическим и
ортогональным операторам в действительных векторных пространствах соответствуют
симметрические, кососимметрические и ортогональные матрицы.
Верно и более общее утверждение. В случае ортогонального (но не
обязательно ортонормированного) базиса унитарным или ортогональным
операторам соответствуют матрицы того же типа.
*) Заметим, что во взаимном базисе (п. 14.7-6) оператор А* представляется
матрицей А*,
432 гл. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.7-6.
14.7-в. Взаимные базисы.
(a) Для каждого базиса е-, е е в конечномерном векторном пространстве
существует единственный взаимный (дуальный) базис el, e2, .... ея, определяемый
симметричными соотношениями
(е*. eft) - ЬШ = { °- еСЛ".' * Н <«. * _ .. 3 .). (И.7-90,
v «' ,л I 1, если i = Л J
так что каждый вектор е* ортогонален всем е. с k ф i n
[(е*. е*)] = G-l = [(е., e^)]-l, (14.7-96)
/г
eft= 2 «^е* <* = 1. 2 л). (14.7-10)
/=!
(b) Векторы а, Ь, ..., представляемые в базисе е. матрицами-столбцами a, b, ...f
в базисе е» представляются матрицами-столбцами Ga, Gb 1) и
(а, Ь) = a*Gb = a* (Gb) =* (Ga)*b = (Ga)*G-* (G6). (14.7-11)
Таблица 14.7-1
Сравнение различных обозначений скаляров, векторов
и линейных операторов
Бескоординатные
(инвариантные)
обозначения
а (скаляр)
<е/- ek)
U. е*)
а (вектор)
у = Ах
А (линейный
оператор)
Матричные
представления
а
[(е., efe)]^G
Ке\ e*)J - С"1
а
Ga
у = Ах
А
GA
AG~l
GAG~l
Координаты (элементы матриц) 1
условные
обозначения
а
««•*
Нет специального
символа
ai
Нет специального
символа
п
aik
Нет специальных
символов
тензорные
обозначения
а
««•»
«'*
а1
в/ = *•*"*
**-*'***
А'
*
Aik = hiAi
Aik = Aigik
**-«</4«'*
*) Векторы a, b можно также представить матрицами-строками (Ga)*, (Gb)*, . . или
{Ga)\ (Gby что соответствует представлению их ковариантными компонентами
(гш. 16,2-1 и 16.7-3).
14.8-2. 14.8. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ 433
В частности, если
п
а — ^ а^.. то (е*, а) = а£-.
/ = 1
Линейный оператор А, задаваемый в базисе е^. матрицей А, в базисе е*
представляется матрицей GAG~l.
(с) Базис еА, е2 ел, взаимный другой системе базисных векторов
п
задается формулами
е„= 2 ',Л. r*det[/.ft]*0.
e* = S 'rfee'- (14,7-12)
/=1
Говорят, что базисные векторы е* и е. преобразуются контраградиентно (см. также п. 16.6-2).
Аналогично
из х = Тх следует G* = Г (Gx). (14.7-13;
(d) Каждый оргпонормированный базис (п. 14.7-4, а) совпадает со взаимным к нему
базисом (является самодуальным), так что е' = е. = u. (i — 1, 2, .... п) и
G = /. G*==*, СЛ0-1===Л. (14.7-14)
14.7-7. Сравнение обозначений. Для того чтобы облегчить ссылки на
стандартные учебники, в гл. 12-14 координаты векторов помечаются только
нижними индексами, В усовершенствованной системе обозначений, применяемой
в тензорном анализе и описываемой в п. 16.1-3, употребляются не только
нижние, но и верхние индексы. В табл. 14.7-1 дается обзор различных
обозначений, применяемых для описания векторов и линейных операторов; ею можно
пользоваться для перевода одних обозначений в другие (см. также п. 16.2-1).
14.8. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ
ЛИНЕЙНЫХ ОПЕРАТОРОВ
14.8-1. Вводные замечания. Изучение собственных векторов и собственных
значений представляет исключительный практический интерес ввиду того, что
1) многие соотношения, в которые входит некоторый линейный
оператор, радикально упрощаются, если в качестве координатных
базисных векторов взять его собственные векторы (приведение
матриц к диагональному виду, квадратичных форм к сумме квадратов,
решение операторных уравнений в спектральной форме; см. также
п. 15.1-1);
2) собственные значения линейного оператора выражают важные
свойства этого оператора без ссылки на какую бы то ни было
конкретную систему координат.
Во многих приложениях собственные векторы и собственные значения
линейных операторов имеют прямей геометрический или физический смысл;
обычно они могут быть интерпретированы на языке задачи о максимуме и
минимуме (п. 14.8-8). Наиболее важные приложения относятся к эрмитовым
операторам, имеющим действительные собственные значения (пп. 14.8-4 и 14.8-10).
14.8-2. Инвариантные многообразия. Разложимые линейные преобразования
(линейные операторы) и матрицы. Многообразие Ux в линейном векторном
пространстве U называется инвариантным относительно данного линейного
оператора А в пространстве U, если А переводит каждый вектор x^Ux в
некоторый вектор Ах£#г Если U конечномерно и ех, е2, ...А ew, em+1, ...t tn —
434 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.8-3.
координатный базис в U, обладающий тем свойством, что векторы ех, е2, ..., ет
порождают Ult то оператор А представляется матрицей А, которую можно
подразделить следующим образом:
[0]
А
(14.8-1)
А,"
где Af—матрица размера тхт, представляющая оператор А$ в
пространстве U1% «индуцированный» оператором А. Может случиться, что оператор Af
можно подвергнуть дальнейшему приведению.
Линейное преобразование (линейный оператор) А в векторном
пространстве U называется разложимым (приводимым, вполне приводимым 1)), если
пространство U есть прямая сумма U = U1 0 U2 @ ... (п. 12.7-5, а) двух или более
подпространств U1% 11ъ ..., каждое из которых инвариантно относительно А.
В этом случае оператор А записывают как прямую сумму А = Л10Л20 ...
линейных операторов Ai, A2, ..., индуцированных оператором А соответственно
в Ub #2, ...
Квадратная матрица А представляет разложимый оператор А в том и
только в том случае, если матрица А подобна клеточной матрице (прямой
сумме матриц Аъ Л2, •••, соответствующих операторам Ах, А2, ..., см. также
п. 13.2-9). Матрица Л, обладающая этим свойством также, называется
разложимой (приводимой, вполне приводимой).
14.8-3. Собственные векторы, собственные значения и спектр (см. также
п. 13.4-2).
(a) Собственный вектор (характеристический вектор) линейного оператора
(линейного преобразования) А в линейном векторном пространстве U есть
такой вектор у£#, что
Ау=Яу (У =5*0), (14.8-2)
где А, —некоторый скаляр, называемый собственным значением
(характеристическим значением) оператора А, соответствующим собственному вектору у.
(b) Если у—собственный вектор оператора А, соответствующий
собственному значению X, то это же верно для любого вектора ау Ф 0. Если ух, у2, ...,ys —
собственные векторы оператора А, соответствующие собственному значению X,
то это же верно и для каждого вектора а^ + а2у2 + ...+а$У$ Ф 0; эти
векторы порождают линейное многообразие, инвариантное относительно А
(п. 14.8-2; см. также п. 14.8-4, с).
Эта теорема также справедлива для сходящихся бесконечных рядов
собственных векторов в гильбертовых пространствах.
Если собственному значению X соответствует ровно т :> 1 линейно
независимых собственных векторов, то т называется геометрической кратностью
собственного значения X.
Собственные векторы, соответствующие различным собственным значениям
одного и того же линейного оператора, линейно независимы.
Линейный оператор в /г-мерном векторном пространстве имеет не более п
различных собственных значений. Каждое собственное значение
невырожденного оператора отлично от нуля.
(c) Если ограниченный линейный оператор А имеет собственное значение X,
то оператор аА имеет собственное значение аХ, а оператор АР имеет
собственное значение А,^(р = 0, 1, 2, ..., a если А — невырожденный оператор, то
р=0, ±1, ±2, ...). Каждый многочлен /(А) (п. 14.4-2, Ь) имеет собственное
значение f (X) (см. также п. 13.4-5, Ь). Все эти функции от А имеют те же
собственные векторы, соответствующие указанному собственному значению,
что и А.
*) См. сноску к п. 14.9-2, Ь.
14.8-4. 14.8. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ 435
(d) Спектр линейного оператора. Спектром ограниченного
линейного оператора А в банаховом пространстве (полном нормированном
пространстве, п. 14.2-7, a) U называется множество всех комплексных чисел
(спектральных значений, собственных значений*)) А,, для которых векторное
уравнение
Ах—Xx=f
не имеет для каждого вектора f единственного решения х = (А— AI)_1f
(см. также п. 14.8-10). Оператор (A—AI)"1 (резольвентный оператор,
резольвента) для множества значений Я, не принадлежащих спектру оператора А,
определен и ограничен на всем пространстве U. Спектр можно подразделить на
1) дискретный спектр (точечный спектр), определяемый
равенством (2) с собственными векторами у Ф 0;
2) непрерывный спектр, состоящий из тех спектральных
значений к, для которых оператор (А — Я1)-1 имеет область определения,
плотную в #, и неограничен;
3) остаточный спектр, состоящий из тех спектральных значений X,
для которых оператор (А —Я!)"1 имеет область определения, не
плотную в U, и неограничен.
Спектр ограниченного линейного оператора А содержит его предельный
спектр, определяемый как множество всех комплексных чисел Х> для которых
существует такая последовательность единичных векторов ulf u2, ..., что
|| (А — XI) ип || ^ 1//г (п = 1, 2, ...). Предельный спектр содержит дискретный
и непрерывный спектр (см. также п. 14.8-4).
Остаточный спектр ограниченного линейного оператора А в гильбертовом
пространстве содержится в дискретном спектре оператора А*.
(e) Спектр линейного оператора А в конечномерном нормированном
векторном пространстве совпадает со спектром каждой матрицы Л, представляю-
щей оператор А, как в п. 14.5-2. Алгебраической кратностью m'j любого
собственного значения Xj оператора А называется алгебраическая кратность
числа Xj как собственного значения соответствующей матрицы {п. 13.4-3, а).
Алгебраическая кратность т', больше или равна геометрической кратности т.-
собственного значения Xj (см. также п. 14.8-4, с).
Для каждого линейного оператора в конечномерном нормированном векторном
пространстве след Тг (А) оператора А равен сумме всех его собственных значений, каждое
из которых считается столько раз, какова его алгебраическая кратность, а определитель
det (А) равен таким же образом подсчитываемому произведению всех собственных значений
(см. также п. 13.4-3, Ь).
Характеристическое уравнение Рд(к)—0, соответствующее классу подобных
конечных матриц (п. 13.4-5, а), называется характеристическим уравнением представляемого
этими матрицами оператора А; оно дает его собственные значения вместе с ик
алгебраическими кратностями. Теорема Кэли — Гамильтона (Fд (А) =0, п. 13.4-7, а) и теоремы из
п. 13.4-7, b применимы и к линейным операторам # конечномерных нормированных
векторных пространствах.
(f) Если А—ограниченный линейный оператор в гильбертовом пространстве
то из Ау = Ху и A*z = jxz следует, что либо jx= А, либо (у, z)=C (см. также
п. 14.8-4).
14.8-4. Собственные векторы и собственные значения нормальных и
эрмитовых операторов (см. также пп. 13.4-2, 13.4-4, 14.4-6, 14.8-8, 15.3-3, Ъ,
15.3-4 и 15.4-6).
(а) Если А —нормальный оператор в гильбертовом пространстве (А *А =
= АА*, п. 14.4-8, Ъ), то А и А* имеют одни и те же собственные векторы;
соответствующие собственные значения операторов А и А* являются
комплексными сопряженными числами. Спектр каждого нормального оператора совпадает
с его предельным спектром; остаточный спектр пуст (см. также п. 14.8-3, d).
*) Некоторые авторы называют собственными значениями все спектральные
значения, а другие пользуются этим термином только для дискретного спектра.
ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.8-5.
Для каждого нормального оператора А с собственными значениями X эрмитовы
операторы Hi —-у (A -f* A *), Н8 — -к^ (А — А*) и А*А имеют те же собственные
векторы, что и А, и соответственно собственные значения Re Я», Im К и | X |2.
(b) Все спектральные значения любого эрмитова оператора действительны.
Обратное верно не всегда, но каждый нормальный оператор, имеющий действительный
спектр, является эрмитовым.
(c) Следующими важными спектральными свойствами нормальных
операторов, в частности, обладают эрмитовы операторы:
1. Ортогональность собственных векторов. Собственные векторы,
соответствующие различным собственным значениям нормального
оператора, попарно ортогональны.
2. Свойство полноты собственных векторов. Каждый ограниченный
нормальный оператор А в гильбертовом пространстве U вполне
приводим (п. 14.8-2). При этом U есть прямая сумма подпространства,
порождаемого ортонормированной системой собственных векторов
оператора А (п. 14.7-4), и подпространства, состоящего из векторов,
ортогональных каждому собственному вектору оператора А. В
конечномерном случае ортонормированная система собственных векторов
порождает U.
Каждый нормальный оператор А в конечномерном унитарном векторном пространстве
21 разложим в прямую сумму (п. 14.8-2) нормальных операторов Аь А2. • • •. определенных
в соответствующих подпространствах Цъ #2> ••• пространства U таких, что каждый
оператор А;- имеет единственное собственное значение %,. В каждом подпространстве Ut
существует полная ортонормированная система собственных векторов уЧ',
Если собственное значение X нормального оператора имеет алгебраическую
кратность т, то геометрическая кратность значения X также равна т, и наоборот.
(d) * Спектральное представление. Следующими свойствами
нормальных операторов обладают, в частности, эрмитовы операторы. Если у1(
Уг»"-» Ул~"ортонормированная система собственных векторов нормального
оператора А в конечномерном пространстве ^их-любой вектор вида х =
= iiyi+l»yi + —+1яУя (1л = (У*. х) п. 14.7-4, а), то
Ах = Х111у1+Яв|8ув + ... + Я,я|яуя,
(спектральное представление оператора А),
(х, Ax)=x1ii1|2+^li2l2+...+^lirtl2J
(14.8-3)
где Xk — собственное значение, соответствующее yk (см. также п. 13.5-4, Ь).
X Вопросу о спектральном представлении операторов в произвольном гильбертовом
пространстве (спектральный анализ операторов) посвящена обширная литература; см.,
например, [13.4], [13.6]. #•
14.8-5. Определение собственных значений и собственных векторов:
конечномерный случай (см. также пп. 13.4-5 и 13.5-5; численные методы см. в п. 20.3-5).
Если А = [atk] — матрица размера пхп, представляющая линейный оператор А
относительно базиса е1( е2 ея, то собственные значения X и собственные
векторы у = r]iei+Л2е2 + • • • + i)n*n оператора А определяют следующим образом:
1. Собственные значения находят как корни алгебраического
уравнения я-й степени (характеристического уравнения)
det(A-M)=5det(i4-W)s=
ац —X аи ... а1я
#21 а22—Я...а2я
14.8-6. 14.8. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ 437
2. Координаты г|(/)( *](/), ..., т|(/) всех ту линейно независимых
собственных векторов
у(/)« ци^ + Л(/)е2 +... + 1|(/>ел,
соответствующих каждому отдельному собственному значению А,/,
получают, решая систему п однородных линейных уравнений
(ап - к,) r\U) + а12ц(П +... + ami\U) = 0,
(hiЛ<>> + («22 - V) Л(£ + • • • + <*an Л(£ = 0.
атЦ^+ anir\lj) + ... + (ann — Kf) т)</> = 0,
матрица которой имеет ранг n — rrif (п. 1.9-5).
, Л(/) .
т/ матриц-столбцов у(У) = ( 2 | называются модальными столбцами (или
просто собственными векторами) данной матрицы А, соответствующими
собственному значению К/. Каждый модальный столбец можно умножить на
произвольную постоянную, отличную от нуля.
14.8-6. Приведение и диагонализация матриц. Преобразование к главным
осям (см. также п. 14.8-2).
(а) Каждая конечная система линейно независимых собственных
векторов yv y2 у5, соответствующих одному и тому же собственному
значению линейного оператора А, порождает подпространство 11ъ инвариантное
относительно А (п. 14.8-3, Ь). Если уг, у2, ..., ys взять в качестве пер-
Уи У|. ....
А будет щ
вых s базисных векторов, то оператор А будет представляться матрицей вида
А~\ : I (14.8-4)
\[0]М/
(Ь) Пусть, в частности, А —нормальный оператор в конечномерном
векторном пространстве размерности п. Тогда метод п. 14.8-5 дает ровно п линейно
независимых собственных векторов
уф = л(/)е1 + л(/)е2 +... + г)(Пеп.
Соответствующие п модальных столбцов образуют невырожденную модальную
матрицу
ТН'*]> где **-*?• <14-8-5>
причем каждому отдельному собственному значению К/ соответствует пг/
соседних столбцов; /г = /тгг-+-лтг2 + •.. столбцов имеют индексами последовательные
значения &=1, 2,».., п. Преобразование координат пассивного типа
х = Тх (14.8-6)
(п. 14.6-1) вводит в качестве координатного базиса п собственных векторов y(J>
нормального оператора А. Преобразование подобия
А = Т1АТ (14.8-7)
438 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.8-6.
дает матрицу А, представляющую оператор А в новой системе координат J
А есть клеточная матрица
*=1йК£|. (,4-8-8)
где каждая подматрица А/ соответствует собственному значению %j оператора А,
отличному от других его собственных значений, и имеет ровно т}- строк и ту
столбцов (см. также п. 14.8-4, с).
(c) Если п собственных векторов, определяющих столбцы модальной
матрицы (5), попарно ортогональны, то преобразование подобия (7) дает
диагональную матрицу А (приведение данной матрицы А к диагональному виду,
диагонализация, п. 13.4-4, а). Чтобы получить матрицу Т преобразования,
приводящего данную матрицу Л, представляющую нормальный оператор А,
к диагональному виду, поступают следующим образом:
1. Если все собственные значения Xj—простые (это верно, если
характеристическое уравнение не имеет кратных корней), то
матрицу А диагонализирует каждая модальная матрица (5).
2. Если существуют кратные собственные значения Xj, то с
помощью процесса Грама — Шмидта (п. 14.7-4, Ь) ортогонализируем
каждое множество т;- собственных векторов у(/) =!H(/)e1 + i4/)e2 + ««-
••• + л{/Чг п модальных столбцов у(/)== I ^2 I, представляющих по-
№/
лучающиеся в результате m1+m2+... = /i попарно ортогональных
собственных векторов
составляют тогда искомую Матрицу преобразования 7\
(d) Во многих приложениях первоначальный координатный базис ех, е2,...
...,ел является ортонормированным (прямоугольные декартовы координаты),
так что
(х, Ах)~*М*ее 2 2J а,Л& (Н.8-9)
/ = U=*1
(п. 14.7-4, а), а в качестве нового координатного базиса берется ортонорми-
рованная система собственных векторов у(/) (получаемая, если нужно, с
помощью процесса Грама —Шмидта). Тогда каждая модальная матрица 7\
образованная из v^^, является унитарной матрицей. Унитарное преобразование
координат (6), вводящее в качестве базисных векторов п ортонормированных
собственных векторов, называется преобразованием к главным осям для
оператора А (см. также пп. 2.4-7 и 3.5-6).
Преобразование к главным осям для эрмитова оператора А приводит
соответствующую эрмитову форму (9) к ее нормальной форме (13.5-9) (см. также п. 13.5-4).
(e) Два эрмитовых оператора А и В могут быть в одном и том же
базисе представлены диагональными матрицами в том и только в том случае,
если ВА = АВ (см. также пп. 13.4-4, b и 13.5-5).
14.8-8. 14.8. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ 430
14.8-7. «Обобщенная» задача о собственных значениях (см. также пп. 13.5-5
и 15.4-5).
(a) В некоторых приложениях требуется найти «собственные векторы» у
и «собственные значения» \х, определяемые соотношением вида
Ау = ^Ву (уФО), (14.8-10)
где В — невырожденный оператор. Векторы у и числа jji обязательно являются
собственными векторами и собственными значениями оператора В_1А; если
В — тождественный оператор, то задача сводится к задаче, определяемой
равенством (2). Если А и В — эрмитовы операторы и В положительно
определен (п. 14.4-4), то
1) все собственные значения jx действительны;
2) можно ввести новое скалярное произведение
(a, b)BE=(a, Bb) (14.8-11)
(см. также п. 14.2-6, а). По отношению к этому новому скалярному
произведению оператор В_1А оказывается эрмитовым, и к нему
применимы теоремы об ортогональности и о полноте из п. 14.8-4, с.
В частности, собственные векторы у, соответствующие различным
собственным значениям ц, попарно ортогональны относительно
скалярного произведения (11) (см. также п. 14.7-3, а).
(b) Рассмотрим конечномерное унитарное векторное пространство и орто-
п
нормированную систему координат ulf u2, ..., ип, так что (a, b)= 2 ak$k
k = l
(п. 14.7-4, а). Пусть А и В представляются эрмитовыми матрицами А = [а^]
и B = [bik\t причем матрица В является положительно определенной. Тогда
собственные значения |л, определяемые равенством (10), совпадают с корнями
алгебраического уравнения /г-й степени
det (Л - \хВ) = det \aik — \ibik] = 0 (14.8-12)
(характеристическое уравнение для «обобщенной» задачи
о собственных значениях).
Для каждого корня jjy кратности /я/ существует ровно mj линейно
независимых собственных векторов y(/) = 'ni/)u1"bTl2/)u2 + "*+ <Пл">ия» координаты т^7)
этих векторов получаются из системы линейных однородных уравнений
2 (*£А-ЮЫПЬЛ=° 0е1' 2' "•' *)• (Н.8-13)
k = \
Применяя к mt~\-mt -{-... = л собственным векторам процесс Грама—Шмидта
(п. 14.7-4, Ь), находим полную ортонормированную систему векторов относительно нового
скалярного произведения
п п
(а,Ь)в-а*Б^« 2 2 *'*"** (14.8-14)
Если в качестве координатного базиса взять эту ортонормированную систему собственных
векторов, подобно тому как это было сделано в п. 14.8-6, с, то эрмитовы формы (х, Ах) =
= х*Ах и (х, Bx)»jc*B* примут вид (13.5-12) (одновременное приведение двух эрмитовых
форм к сумме квадратов, п. 13.5-5).
(c) Аналогичная «обобщенная» задача о собственных значениях для случая
бесконечномерных векторных пространств рассматривается в п. 15.4-5.
14.8-8. Задачи о собственных значениях как задачи о стационарных
значениях (см. также п. 15.4-7).
440 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.8-8.
(а) Рассмотрим эрмитов оператор А в конечномерном унитарном
векторном пространстве U и выберем в U ортонормированный координатный базис,1)
ulf u2, ..., un, так что А представляется эрмитовой матрицей Л = [а;д].
Важная задача нахождения собственных векторов у(;)=Л1/)и1 + Лг^г + •••"+"Л^^ил
и соответствующих собственных значений А,/ оператора А в точности
эквивалентна каждой из следующих задач:
1. Найти каждый вектор у ф0 (т. е. его координаты т|,-), для
которого
(У, Ау) у*Ау 2 2 aikWk
__ t = 16=l
п
(У, У) У* У 2 **№
5=1
(частное Релея) (14.8-15)
принимает стационарное значение. Эти стационарные значения у — y{J)
(у(/) Ау</>)
определяют А,/ как отношение / п) \})\ •
2. Найти каждый вектор у, для которого форма
(у, Ау) ее у*Ау ее % 2 а1кчт (14.8-16)
t = \ k=\
принимает стационарное значение при условии, что
(у,у)ЕЕ^=2 I -П* Iе— 1- О4.*-")
/=1
Эти стационарные значения у = у(-/) определяют А,у = (у(/), Ау(/)).
3. Найти каждый вектор у^О, для которого скалярное
произведение (у, у) принимает стационарное значение при условии, что
(У» Ау) = 1. Эти стационарные значения у(^ дают А,/= ; ~л
(y(/)f у(/)) '
Пусть собственные значения оператора А занумерованы в порядке
возрастания, причем собственное значение кратности т повторяется т раз: Хг ^
=<: А^^... ^А,п. Наименьшее собственное значение Хг равно минимальному
значению частного Релея (15) для произвольного вектора у е U. г-е собственное
значение Хг в этой последовательности подобным же образом меньше или
равно частному Релея для всех ненулевых векторов, ортогональных ко всем
собственным векторам, соответствующим собственным значениям A,lf X2,..., Kr__v
Число %г есть максимум минимума min (у, Ау)/(у, у) для произвольных
У€Е#Г
(г —-1)-мерных подпространств Ur пространства U {принцип минимакса
Куранта).
Последние теоремы можно высказать и для задач 2 и 3, и для максимумов вместо
минимумов; заметим, что минимум в задачах 1 и 2 соответствует максимуму в задаче 3,
и наоборот. Эрмитова форма (у, Ау) обычно имеет прямой физический смысл. Задача 3
собственным значениям оператора А ставит в соответствие главные оси некоторой
поверхности второго порядка (см. также пп. 2.4-7 и 3.5-6).
(Ь) Обобщения. Теория п. 14.8-8, а может быть распространена на
«обобщенную» задачу о собственных значениях, определяемую условием Ау =
») В большинстве приложений для удобства берут ортонормированный базис; в общем
случае, нужно только в равенствах (15) — (17) сделать замену (у, Ay)^y*GAy и (у, у)=з
14.8-9.
14.8. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ
441
= цВу, где А —эрмитов, а В —положительно определенный эрмитов
оператор (п. 14.8-7). Нужно только в формулировке каждой задачи из п. 14.8-8, а
заменить (у, у) на (у, у)в = (у, By). При этом частное Релея (15) заменяется
отношением
п п
(У, Ay) у*Ау ^ S aikWk
= ES-^fi (14.8-18)
(У, By) у*By ^ S btkWk
i = l k = \
(частное Релея для «обобщенной» задачи о собственных значениях).
Аналогичные теоремы справедливы и для подходящих классов операторов в
гильбертовых пространствах; в этом случае формы (у, Ау), (у, у) и (у, By) могут оказаться не
суммами, а интегралами, так что задачи о стационарных значениях из п. 14.8-8, а
превращаются в вариационные задачи (п. 15.4-7).
14.8-9. Границы для собственных значений линейных операторов (см.
также п. 15.4-10). Для исследования собственных значений часто оказываются
полезными следующие теоремы.
(а)Х Для каждого собственного значения X линейного оператора А,
представляемого матрицей А = [щи\ размера п X п,
|a,|^min(P, Q), (14.8-19)
где
п п
Р= max 2 1***1. Q= max S la*/l-
Для действительной и мнимой частей характеристических чисел имеют место
оценки:
min [Яеац~ РЦ^ЯеК^ max [Rea^ + P,],
1 as i :< n 1 =S i' =5: n
min [lmau — Pi]^\m%^ max [Imau + Pi],
l=^i<M l^i^n
n n
где Pi= 2 \aij\' ^ этих °^eHKax ?l можно заменить на Qt= Yj | ayt |.
/=1 /=i
Если дополнительно предположить, что | я/; | > Pj для « = 1, 2, ..., /г, То
|Х|^ min [\au\-Pi].
1 =s i < п
(Величины Pi могут быть заменены на Qt-.)
Действительная часть Re К лежит между наименьшим и наибольшим собственными
значениями матрицы Ht~ —(А-{-А*), а мнимая часть Im А,— между наименьшим и
наибольшим собственными значениями матрицы Я2=— (Л — А*) (см. также п. 13.3-4, а).
(b) Для эрмитовых матриц и операторов
Ibf^ESl*'*!1' 1*КНА||. (14.8-20)
i k
(c) Теоремы сравнения. Пусть \ц ^ ц2 ^ ... ^ цп —
последовательность (с учетом кратностей) собственных значений конечномерной задачи о
442 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.8-10.
собственных значениях (10), где А и В —эрмитовы операторы, причем В является
положительно определенным. Тогда:
1) прибавление положительно определенного эрмитова оператора
к к не может уменьшить ни одно из собственных значений \ir в зтой
последовател ьност и;
2) прибавление положительно определенного эрмитова оператора
к В не может увеличить ни одно из собственных значений |хг;
3) если векторы у рассматривать только в некотором (п —
т)-мерном подпространстве пространства U, то п — т собственных
значений \ь\ ^ \л'2 ^ ... ^ [in _ m задачи, получаемой при таком
ограничении, будут удовлетворять соотношениям
IV^IV^IVhh (' = 1, 2, .... п-т). (14.8-21)
Эти ограничения обычно принимают вид т независимых линейных
уравнений, связывающих векторные координаты щ.
Эти теоремы применимы к операторам в гильбертовых пространствах, если А и В —
положительно определенные операторы, дающие дискретную последовательность \лх ^\i2^ ...
с конечными кратностями.
14.8-10. Неоднородные линейные векторные уравнения (см. также пп. 1.9-4,
15.3-7 и 15.4-12).
(a) Если А —ограниченный линейный оператор в гильбертовом
пространстве, то векторное уравнение
Ax-JU=f (14.8-22)
имеет для каждого данного вектора f единственное решение х в том и только
в том случае, если скаляр X не принадлежит спектру оператора А (п. 14.8-3, с!).
Если X есть собственное значение Xt оператора А в смысле равенства (2),
то уравнение (22) имеет решение только в том случае, если данный вектор f
ортогонален каждому собственному вектору оператора А*, соответствующему
собственному значению Хг. В этом последнем случае существует бесконечное
множество решений: решением является каждая сумма любого частного
решения и произвольной линейной комбинации собственных векторов,
соответствующих собственному значению Kv
(b) В важном частном случае
Ax = f, (14.8-23)
где А —ограниченный нормальный оператор, единственное решение х для
каждого данного вектора f существует в том и только в том случае, если
из Ах = 0 следует х = 0, т. е. если А — невырожденный оператор. Если А —
вырожденный оператор, то уравнение (23) имеет решение только в том случае,
если вектор f ортогонален каждому собственному вектору оператора А*,
соответствующему собственному значению нуль.
(c) Для эрмитова оператора А = А*, имеющего ортонормированную систему
оо
собственных векторов у^, для которых f == 2 (Уь 0 У&> решение уравнения
(22) дается формулой
k = \ k
где Xk — (не обязательно различные) собственные значения^ соответствующие
каждому вектору ул.
14.9-2. 14.9. ПРЕДСТАВЛЕНИЯ ГРУПП И СМЕЖНЫЕ ВОПРОСЫ 443
14.9. ПРЕДСТАВЛЕНИЯ ГРУПП И СМЕЖНЫЕ ВОПРОСЫ
14.9-1. Представления групп.
(a) Каждая группа (п. 12.2-1) может быть представлена гомоморфизмом
(п. 12.1-6), отображающим ее в группу невырожденных линейных
преобразований некоторого векторного пространства (представляющего пространства,
пространства-носителя) и, следовательно, в некоторую группу невырожденных
матриц (это —одна из форм теоремы Кэли, сформулированной в п. 12.2-9, Ь).
Представление степени или размерности п группы G в поле F есть группа
матриц Л, В, ... размера пХп над полем F, связанная с элементами а, 6, ...
группы G гомоморфизмом А=А(а), В = В(Ь), ..., так что из ab = c для всех
а и Ь из группы G следует, что А (а) В (Ь) = С (с) (условие представления).
Число п равно линейной размерности представляющего пространства.
Представление называется точным (истинным), если оно взаимно однозначно
(и, таким образом, является изоморфизмом, п. 12.1-6).
Каждая группа допускает в качестве представляющего пространства
некоторое комплексное векторное пространство, т. е. каждая группа имеет
представление в поле комплексных чисел. Такое представление позволяет
описать определяющую операцию произвольной группы в терминах сложения
и умножения чисел (см. также пп. 12.1-1 и 14.1-1). В большинстве
приложений речь идет о группах преобразований (п. 12.2-8; примеры см в п. 14.10-7).
Каждая группа а„ а2, .... а конечного порядка g допускает точное представление,
содержащее g линейно независимых матриц перестановки (п. 13.2-6) А- (аА^\а;ь ( а/)1»
определяемых условиями
( 1, если а~;Ха.а.—Е,
К 0 в противном случае
где Е — единичный элемент данной группы (регулярное представление конечной группы).
Таким образом, каждая конечная группа изоморфна некоторой группе перестановок (см.
также п. 12.2-8).
(b) Два представления (М ъ <М группы G называются подобными или
эквивалентными, если все пары матриц А (а) представления <^$ и А (а)
представления & связаны одним и тем же преобразованием подобия (п. 13.4-1, Ь)
А =Г~М7\ В этом случае говорят, что матрицы А (а) и А (а) описывают
одно и то же линейное преобразование А (а) представляющего пространства,
общего для <& и е^ (см. также п. 14.6-2).
Представление ^ называется ограниченным, унитарным и/или
ортогональным, если соответствующим свойством обладают все его матрицы. Каждое
представление конечной группы и каждое унитарное представление ограничено.
Для каждого ограниченного представления существует эквивалентное
унитарное представление.
(c) Ранг любого представления <& есть наибольшее число линейно
независимых матриц1) в off.
14.9-2. Приведение представлений.
(а) Представление <р%? группы G называется приводимым 2), если
представляющее пространство U имеет собственное подпространство 11г, инвариантное
относительно <^, т. е. относительно каждого линейного преобразования,
*) Так как матрицы можно рассматривать как векторы, линейная независимость
матриц определяется точно так же, как в п. 14.2-3.
2) Определения в этом пункте применимы и к любому множеству линейных
преобразований в векторном пространстве или к соответствующему множеству матриц (не
обязательно группе).
</. /, А = 1
.... g).
(14.9-1)
444 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.9-3,
описываемого матрицей из <о^ (п. 14.5-2). Это верно в том и только в том
случае, если существует преобразование подобия
Д=Г-1Л7\
одновременно переводящее матрицы А (а), В (6), ... представления <$* в
соответствующие матрицы вида
АЛа) \ А(а)\ I Bt(b) \ В ф)
Л(а)~[ : , В(Ь) = { ;■ ), ..., (14.9-2)
[0] \А%(а) J у [0] \Bt(b)
где Ах(а), Вг(Ь), ... — квадратные матрицы одного и того же порядка.
Матрицы А! (а), В1(Ь)1 ... — образуют представление <J%X данной группы G
с представляющим пространством Uv Представление, которое не является
приводимым, называется неприводимым.
(Ь) Представление (ffl называется разложимым1), если его представляющее
пространство U является прямой суммой U = U1®U2@... (п. 12.7-5, а)
подпространств Mlt #2> ..., инвариантных относительно <&. Это имеет место
в том и только в том случае, если существует преобразование подобия
А = Т~1АТ, одновременно переводящее матрицы А (а), В (Ь), ...
представления q%? в соответствующие клеточные матрицы
Аг(а) \ [0] J ...\ / B,(b) \ [0]
Л(а)~\ [О] ! A2(d)")"Г . S(6) = j [0] \ Bt"(b) I ... I (14.9-3)
(прямые суммы матриц, п. 13.2-9), где соответствующие подматрицы имеют
один и тот же порядок. Каждое множество матриц А{ (а), £;(&), ... 0 = 1, 2,...)
образует представление <э^/ данной группы G с представляющим
пространством Ui. Представление ^ записывается как прямая сумма e^ = e^i©
(c) Представление ^% называется вполне приводимым, если оно разложимо
на неприводимые представления (неприводимые компоненты) <$?{1\ е^?(2\ ...
(d) Условия приводимости (см. также п. 14.9-5, Ь). Каждое
ограниченное представление (и, в частности, каждое представление конечной
группы) либо вполне приводимо, либо неприводимо.
Группа G имеет разложимое представление в том и только в том случае, если она
является прямым произведением (п. 12.7-2) простых групп (п. 12.2-5, Ь).
Ограниченное представление &Z вполне приводимо в том и только в том случае, если
существует матрица Q, не имеющая вида а/, перестановочная с каждой матрицей из<$?.
Неприводимые представления коммутативных (абелевых) групп необходимо одномерны.
Если все соответствующие матрицы А, А двух неприводимых представлений <$1 и
&1 связаны одним и тем же преобразованием QA = A Q, то либо (Ж и G/t эквивалентны,
либо Q = [0] (лемма Шура).
14.9-3. Неприводимые представления группы.
(а) Разложение <& = d%!,li © g^(2) © ••• данного вполне приводимого
представления $£ некоторой группы на неприводимые компоненты единственно
с точностью до эквивалентности и перестановки порядка слагаемых. Каждое
*) Термины приводимое, разложимое и вполне приводимое различными авторами
переставляются по-разному. В действительности в случае ограниченных матриц,
преобразований и представлений, а значит, для всех представлений конечных групп, они
эквивалентны (п. 14.9-2).
14.9-5. 14.9. ПРЕДСТАВЛЕНИЯ ГРУПП И СМЕЖНЫЕ ВОПРОСЫ 445
вполне приводимое представление однозначно определяется (с точностью до
эквивалентности) своими неприводимыми компонентами. Если e%(J) — одно из /яу
имеющихся взаимно эквивалентных неприводимых компонент представления
е^(/ = 1, 2, ...), то можно писать
(b) Для каждой группы G конечного порядка g
1) число т различных неэквивалентных неприводимых представлений конечно
и равно числу различных классов сопряженных элементов (п. 12.2-5, а);
2) если л, — размерность 1-го неприводимого представления, то его ранг
равен л у {теорема Бернсайда); ранг каждого представления <$£ группы G равен
сумме рангов Лу различных неприводимых компонент q%\
3) каждое число л • является делителем g и
n\+n\+... + n*m=g\ 04.9-4)
4) регулярное представление группы G (п. 14.9-1, а) содержит j-e
неприводимое представление группы G ровно л • раз.
(c) Нахождение полного множества неприводимых представлений группы G
операторов представляет особый интерес как ключ к решению некоторых задач о собственных
значениях. Если Н —эрмитов оператор, перестановочный с каждым оператором из группы G,
то между различными собственными значениями К- оператора Н и неэквивалентными
неприводимыми представлениями &1И) группы G существует взаимно однозначное
соответствие, и геометрическая кратность каждого собственного значения %^ равна размерно-
emu e%(J) (классификация собственных значений в квантовой механике из соображений
симметрии [13.7]).
14.9-4. Характер представления.
(a) Характер представления & есть функция
Х(а)==Тг)А(а)), (14.9-5)
определенная на элементах а группы G, представляемой <э^. Сопряженные
элементы группы (п. 12.2-5, а) имеют равные значения характера.
Для каждого ограниченного представления
Х(а"1) = 5сЙ. (14.9-6)
Два вполне приводимых представления одной и той же группы G эквивалентны
в том и только в том случае, если их характеры совпадают.
(b) Характеры неприводимых представлений называются простыми или
примитивными характерами, а характеры приводимых
представлений—составными характерами. Из <э^ = <J%X © е^2 ©... следует % (а) == Xi (a) + %2 («) + •••,
где %(a)t %i(a), %2 (я), ...—характеры соответственно представлений <&,
(Мъ е%*2» •••
14.9-5. Соотношения ортогональности (см. также п. 14.9-6).
(а) Примитивные характеры %{1) (а), %12) (а), ..., соответствующие
неэквивалентным неприводимым представлениям S£ll\ e^(2), ••• конечной группы (?,
удовлетворяют соотношениям
средн. ap. {xW(a)x{n(a)} = ± £ X^Wx^W-
а £ G
446 ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.9-6.
Для каждого вполне приводимого представления dffi *>* nii<$!11' © m2<2^(2) © ...
группы G
X (а) ss mt%W (a) + m2X(2) (а) + ... . (14.9-8)
mf = средн. ар. {х</> (ф X (а)} = i ^ Х(/) (а) X (а), (14.9-9)
средн. ар. {ЙП^Гх <<*)}==£- ^] I X (a) I8 = mj + m| + ... ^ 1. (14.9-10)
Если q^ неприводимо, то средн. ар. {| Х<Д) I8} "= 1-
(Ь) Каждое из m неэквивалентных неприводимых представлений effi1^ конечной
группы G эквивалентно соответствующему унитарному неприводимому представлению,
содержащему матрицы |и}£' (а)\ (см. также п. 14.9-1, Ь). Элементы этих унитарных
матриц удовлетворяют соотношениям
средн. ар. |ii<J> (a) u\Q, (а)} - j ^j "^ <а> "/'2' (а) = ^7 6IJ'6K'6bk' (14.9-11)
flGG '
(/, /' « 1, 2 m; *, £ = 1, 2 у, t\ Л' в 1, 2 лу).
14.9-6. Прямые произведения представлений.
(a) Если e^i — /Zi-мерное, а <э^2 —^-мерное представления одной и той
же группы О, то матрицы размера п^Хп^, получаемые как прямые
произведения (п. 13.2-10) матриц из ^г на матрицы из <&2% образуют п1п2-мер-
ное представление группы G — прямое (кронекеровское) произведение e^i ® е^г
представлений ^г и е^2 (см. также п. 12.7-2). Его представляющее
пространство является прямым произведением представляющих пространств для
e^i и g^2 (п- 12.7-3). Характер % (а) представления & = <МХ ® е^2 решен
произведению характера %г (а) представления ^г и характера %2 (а)
представления е^2:
XW-XiWXiW- (14.9-12)
Если (&i и е^2 ограничены или унитарны, то это же верно и для <^%г (х) <э^2.
(b) Прямое произведение е^(1) ® е%*(2) двух ограниченных неприводимых
представлений <&11) и <М{<2,) группы G неприводимо, если размерность
представления <М{1) и/или е^(2) равна 1; в противном случае <М(Х) ® е^?(2) вполне
приводимо, С помощью этого последнего факта можно из данного
неприводимого представления группы G получать новые ее неприводимые представления.
(c) Неприводимые представления прямого произведения Gt ® G2 двух групп Gt и G9
(п. 12.7-2) являются прямыми произведениями R(J) ® R^'^ неприводимых представлений
R(J) группы Gt и Я*/') группы G8.
14.9-7. Представления колец, полей и линейных алгебр (см. также п. 12.3-1
и 12.4-2). Кольца, поля и линейные алгебры также могут быть представлены
подходящими классами матриц или линейных преобразований. В частности,
линейная алгебра порядка п2 над полем F, имеющая единицу, изоморфна
алгебре матриц порядка пХп над полем F (регулярное представление линейной
алгебры, см. также пп. 14.9-1, а и 14.10-6).
14.10. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВРАЩЕНИЙ
14.10-1. Вращения в трехмерном евклидовом векторном пространстве.
(а) Каждое ортогональное линейное преобразование
х' = Ах (А'А = ДА' = 1) (14.10-la)
в трехмерном евклидовом векторном пространстве (п. 14.2-7, а) сохраняет
14.10-2. 14.10. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВРАЩЕНИИ 447
модули векторов и углы между векторами (пп. 14.4-5 и 14.4-6). Такое
преобразование называется (собственным) вращением, если det (А) = 1, т. е. если
это преобразование, кроме того, сохраняет относительную ориентацию любых
трех базисных векторов (и потому правую и левую системы координат,
векторное произведение двух векторов и смешанное произведение трех векторов).
Преобразование (1а) с det(A) = —1 называется несобственным вращением
или вращением с отражением.
(Ь) Пусть iij, u2, u3 — любой ортонормированный базис (п. 14.7-4), и
пусть
Каждое преобразование (1а) задается формулами
£2 = a2i5i +я22£2+ я2з?з. f (14.10-16)
£з = Яз1|1 + Яз2£2 + Язз£з J
или в матричной форме
х'^Ах, (14.101с)
где для собственных вращений
det[a£ft] = det(^) = l. (14.10-2)
Так как рассматриваемая система координат является ортонормирозанной,
действительная матрица A =s [a^], описывающая каждое вращение,
ортогональна (А'А = АА'=1, см. также п. 14.7-5), т. е.
о о
2w-2<W*-{J; если \tkk) С*-1. 2.3), (Н.10-3)
и каждый коэффициент од равен алгебраическому дополнению элемента aki
в определителе det [од]. Любые три из коэффициентов агь определяют все 9.
Геометрически коэффициент aik есть косинус угла между базисным век-
з
тором щ и повернутым базисным вектором и^ = Аил= 2 a/kuf (см« также
п. 14.5-1):
alk = ul-uk=utm(Ank) <'• * = 1» 2» 3>- (14.10-4)
14.10-2. Угол поворота. Ось вращения.
(а) Вращение (1) поворачивает радиус-вектор х каждой точки
трехмерного евклидова пространства на угол поворота б вокруг направленной оси
вращения, точки которой инвариантны. Угол поворота 6 и направляющие
косинусы Ci, c2, с3 положительной оси вращения определяются формулами
cos6 = i[Tr(A)-l] = |[Tr(^-l]=i(ali + aS2 + a33-l),
cl~~ 2 sin 6 » °2~ 2 sin 6 » Cs"~~ 2 sin 6 »
так что б > 0 соответствует вращению правого винта, вворачиваемого в
направлении положительной оси вращения. Либо знак угла б, либо направление
оси вращения могут выбираться произвольно.
Направление положительной оси вращения — это направление собственного вектора
6-1 и4 -\-с2и2-{■ csus, соответствующего собственному значению -+- 1 оператора А и
находимого путем приведения матрицы А к диагональному виду (п. 14.8-6) Остальными
собственными значениями оператора А являются cos 6 ± i sin 6 «е^Ч
(14.10-5)
448
ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.10-3.
(Ь) Матрица преобразования Л, соответствующая данному вращению,
описываемому числами б, съ c2t с3, есть
/«11 «12 «1з\
А ^|я21 «22 «23 =
\«31 «32 «33/
/1 0 0\ (с\ сгс2 Clc3\ f 0 -с3 с2\
= cos6 0 1 0 +(1— cos6) Ua с% с2с3 +sin6 с3 0 —сх ]. (14.10-6)
\0 0 1/ Wx с3с2 с% I \—с2 сг 0/
14.10-3. Параметры Эйлера и вектор Гиббса.
(a) Четыре симметричных параметра Эйлера
A^CxSin y> ^ = c2sin 2~, v=c3sin у, p=cos |- (14.10-7)
(A,2 + fx2 + v2 + pa=l)
однозначно определяют вращение, так как из равенства (6) следует:
A2_M,2_V2 + P2 2(^-vp) 2(vb + |xp)\
А = ( 2(^ + vp) jx2_v2_x2 + P2 2(H,v-^p) J, (14.10-8)
\4 2(vA,-jJip) 2(|xv + A,p) V2 —А,2 —|и2 + р2/
параметры X, |i, v, p и — A,,— fi,— v,— p представляют одно и то же
вращение.
(b) Вектор Гиббса
G = GxUj + <j2u2 + G3u3,
где
(14.10-9)
такжз однозначно определяет вращение. Повернутый вектор х' можно
записать в виде
x' = Ax = cos22-[(l-|G|2)x + 2(G.x)G + 2G Хх]. (14.10-10).
14.10-4. Представление векторов и вращений спиновыми матрицами и
кватернионами. Параметры Кэли — Клейна.
(а) Если задан ортонормированный базис ux, u2, u3, то каждый
действительный вектор х = g^x + ^2U2 + 1зЩ может быть представлен (вообще говоря,
комплексной) эрмитовой матрицей размера 2x2
н=(\3 ?l"tSl) = EiSi+E.Si+E»s.. (14.10-и)
где эрмитовые спиновые матрицы Паули
ч: i). ч: !■ ч; J) —>
соответствует базисным векторам ulf u2, u3. Соответствие (И) является
изоморфизмом, сохраняющим результат сложения векторов и умножения векторов
на (действительные) скаляры.
Для каждого вращения (1) вектор вращения
14.10-5. 14.10. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВРАЩЕНИЙ 449
представляется матрицей
где V — (вообще говоря, комплексная) унитарная матрица с определителем,
равным 1 (унимодулярная матрица):
где
|a|2 + |&|2=^2 + |X2 + V2 + p2
= l } (14.10-15)
Комплексные числа а, 6 определяют соответствующее вращение
однозначно, но a, b и —а, —6 (a nojoMy матрицы U и —U) описывают'одно
и то же вращение. Числа a, b,—b, а или числа б, /6, —ib, а называются
параметрами Кэли — Клейна данного вращения.
Геометрически комплексные параметры a, b определяют преобразование комплексной
плоскости
сш — Ь
" 7—Г= (1а;2 + |&|*=1)
bu -f a
(дробно-линейное преобразование, п. 7.9-2), переводящее стереографическую проекцию и
точки (£ь gf, £3) сферы на комплексную плоскость (п. 7.2-4) в стереографическую
проекцию н' повернутой точки (£' £' £').
(Ь) Линейные комбинации матриц /, iSlt iS2 и iSs с действительными
коэффициентами образуют представление алгебры кватернионов (п. 12.4-2),
скаляры которой соответствуют действительным кратным матрицы /, а
образующие соответствуют матрицам iSlt iS2, /S3, причем
Sf = S! = Si = /,
S2S3 = — S3S2 = iSlt SaS^—SiSs^iSz, \ (14Л0-16)
О1О2 = — «->2*5>1 = iSs-
Каждая комплексная матрица размера 2x2 может быть представлена в
виде такой линейной комбинации; в частности,
U = р/ — / (XSx + [iS2 + v53), ^ (представление вращения
и* = р/ + * (^5i +1^52 + v53) J кватернионами).
Снова матрицы U n —U определяют одно и то же вращение однозначно.
14.10-5. Вращения вокруг осей координат. Следующие матрицы
преобразования описывают правые вращения вокруг положительных координатных
осей:
Л1(г|?)= JO cosi|? — sin яр ) (вращение на угол ^ вокруг щ), (14.10-18 а)
0
р
—
0 0 ^
cos я|? — sin i|?
sin i|? cos i|?y
cos ф 0 sin \|A
0 10
sint|) 0 cosi|?y
i42(i|))= 0 10 (вращение на угол г|? вокруг u2), (14.10-186)
(cos -ф — sin -ф o\
sin ip cosip 0 j (вращение на угол ip вокруг u3). (14.10-18 с)
0 0 1
15 Г. Корн и Т. Корн
450
ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.10-в,
Заметим, что
лу'(*)==ли+) = 4(-+)
(t'=l,2,3).
(14.10-19)
14.10-6. Углы Эйлера.
(а) Каждая матрица Лее|я^], описывающая собственное вращение в
трехмерном евклидовом пространстве, может быть различными способами
представлена в виде произведения трех матриц (18), и, в частности, так:
А==А3(а)А2ф)А3(у)==
/cos а — sin а 0'
е= sin а
\0
cos а
0
• sin у 0\
cosy 0
0 1
(cos а cos р cos у —
— sin а sin у)
(sin а cos P cos Y +
+ cos а siny)
\— sin p cos у
= ^32 (а> Р. ?)•
— (cos а cos p sin у +
+ sin а cos y)
(— sin а cos P sin y +
+ cos a cos y)
sin P sin y
cos a sin |
sin a sin |
cosP
(14.10-20)
Три угла Эйлера а, р, у однозначно определяют вращение; в свою
очередь, они однозначно определяются данным вращением с точностью до
целочисленного кратного 2я, за исключением случая, когда р = 0 («карданов
подвес», п. 14.10-6,(1).
Оси *', У, г' прямоугольной декартовой системы координат
(рассматриваемые как твердое тело), вначале направленные вдоль векторов u1( u2, u3,
можно повернуть так, чтобы они стали
направлены вдоль векторов u[t u'2t u's с
помощью трех последовательных вращений (18)
(см. рис. 14.10-1; обратите внимание на п.
14.6-3, где объясняется, казалось бы,
обратный порядок матриц в равенстве (20)):
1) Поворот вокруг оси г' на угол
Эйлера а,
2) поворот вокруг оси у' на угол
Эйлера р,
3) поворот вокруг оси г' на угол
Эйлера у.
Обратное вращение А""1 (переводящее
вектор х' в исходный вектор х)
представляется матрицей
Л-* = Л'= Л3 (-YM2 (-РМз (-a) ^
= Лз2(— y, — P, — а)==
ее Л8а(я-у. P, я —а). (14.10-21)
Рис. 14.10-1. Углы Эйлера а, 0, \.
Ось OL второго вращения (на угол
Э) часто называют линией узлов.
Заметим, что а и 0 — сферические
координаты вектора и' в системе
Ul. U2, U3.
Существует шесть способов, которыми
матрицу вращения (1) можно выразить в виде произведения
A — Ai^AkWJAi^^AikW!, fc, if,) (J,*-1,2,3; i*k), (14.10-22)
вращений вокруг двух различных осей координат. Из других получающихся
14.10-в. 14.10. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВРАЩЕНИЙ 451
в результате систем углов Эйлера часто пользуются той, которая
определяется произведением
А == А3 (a') At т А3 (у') == А31 (а', р\ у*). (14.10-23)
Она связана с системой (20) соотношениями
а' = а + л/2, Р' = р, y'=Y~Jt/2- (14.10-24)
(b) Кроме того, существует шесть способов представления матрицы
вращения Л в виде произведения
А=А1(Ьг)А,М AkM = Aifk(blt б2, е3)
(/, /, fc=l, 2, 3; 1ф/, \Ф\ }фк)
(14.10-25)
вращений вокруг трех различных осей координат. В частности, матрица
А = Аг(ч>)Аг(Ь)А9®) =
(cos 6 cos яр — cos б sin г|э sin б
sin ф sin б созгр + cosq) sin \|э — sin ф sin б sin г|э + cosq) cosi|) — sin ф cos б ] з
— cos ф sin б costp + sin ф sin \|) cos ф sin б sin г|э + sin ф cos\|) cos ф cos б у
^Л123(ф, б, ф) (14.10-26)
часто используется для описания положения самолета или космического
корабля, совершившего последовательно поворот на угол крена ф, угол
u'z (ось тангажа)
u'f (ось крена)
и '3 (ось скольжения)
Рис. 14.10-2. Подвижные оси самолета.
тангажа 9 и угол курса гр вокруг осей, проходящих через его центр тяжести и
направленных соответственно вперед, в сторону его правого борта и к его
дну (рис. 14.10-2).
(с) И без того большой набор, состоящий из 12 систем углов Эйлера, определенных
выше, еще увеличивается из-за того, что некоторые авторы один или несколько из углов
Эйлера берут с обратным знаком и что иногда в литературе пользуются левыми
системами координат. Кроме того, нужно предостеречь читателя, что ему необходимо
проверять, определено ли данное преобразование с помощью углов Эйлера как оператор
(«активная» интерпретация, п. 14.5-1) или как преобразование координат («пассивная»
интерпретация, п. 14.6-1), так как можно спутать матрицы А и A~l — Af. В частности,
матрица х = j£i» |2. |я} координат вектора х в неподвижной системе и^ и матрица
# = lit, 1г. 1з} еГ(> координат в повернутой системе u^ связаны отношениями
* = Ах%
•• А~*х = А'х,
(14.10-27)
15*
452
ГЛ. J4. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.10-7.
а матрицы из базисных векторов (п. 14.6-2) преобразуются по формулам
(u;^a;)=^iu2u8)^ или ("и"*'("•)• <|4-,0"28)
См. также п. 14.6-3.
(d) Параметры си с2, cs, 6 и А,, ц, v, p легко выразить через углы Эйлера с
помощью равенств (5) и матрицы углов Эйлера. Таким образом1),
% — сх sin
-i„v=J!.i„If
9^ в
a = е z coS "о" *
.6 a —v , Э
ц = c2 sin -r = cos —j- sin -^,
Y = c8 sin — = sin —-i cos -| ,
6 = e
(14.10-29)
Заметим, что прибавление 2я к одному из углов Эйлера меняет знак всех
параметров (29) и не меняет матрицы вращения А.
Если -ф2 = 0 в равенстве (22) или б2 = я/2 в равенстве (25) (например, |5=0, $' = 0
или б = я/2), то два остающихся угла Эйлера уже однозначно не определяют данное
вращение («карданов подвес»). Таким образом, углы Эйлера можно применять для
описания вращений лишь при известных ограничениях.
14.10-7. Бесконечно малые вращения, непрерывное вращение и угловая
скорость (см. также пп. 5.3-2 и 14.4-9).
(а) Бесконечно малое трехмерное вращение на бесконечно малый угол
db вокруг оси вращения с направляющими косинусами съ с2, с3 описывается
соотношением
x' = x + dx'=(l+dA)x. (14.10-30)
\-\-dA есть ортогональное бесконечно малое преобразование, так что
преобразование dA кососимметрично (п. 14.4-10). В ортонормированном
координатном базисе ulf u2, u3 преобразование dA описывается кососимметрической
матрицей
/ 0 — с3 с2
dA = [A aik\6_Q] db = l c3 0 -п ] db, (14.10-31)
\— с2 Ci 0
получаемой дифференцированием соотношения (6). Отметим, что
rfx' = (dA)x = (cXx)c(6,
(14.1032)
где c = c1u1+c2u2-f-c,3U3 — единичный вектор в направлении
положительной оси вращения.
Вот более общее утверждение. Если W — любой кососимметрический
линейный оператор в трехмерном евклидовом векторном пространстве U, пред-
*) а и b определены в п. 14.10-4. Заметим, что иногда употребляются несколько
другие определения параметров Кэли — Клейна.
14.10-7. H.IO. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВРАЩЕНИЙ 453
ставляемый в ортонормирдванном координатном базисе uv u2J u3 кососимме-
трической матрицей
I 0 —w3 wt\
W={ w3 0 —wA
\—w2 w1 0 /
то для каждого вектора х (= U
x' = Wx = w X x,
где w=waii,+w2u2+WgU3 (см. также п. 16.9-2).
(b) Для непрерывного трехмерного вращения, описываемого соотношением1)
*'(') = А (Ох,
где х — постоянный вектор, формула (32) дает
dJ^ = dMl х==(о W х х' (0 -со (ОХ [А (0 х]. (14 10-ЗЯа)
Вектор со (0, выражающийся через неподвижные и вращающиеся
базисные векторы но формулам
со (0 = Щ (0 Uj+о)2 (0 и2 + со3 (/) и3 ==
= щ (0 пг' (0 + ю2 (0 Щ' (0+ »з (0 и3' (0, (14.10-336)
направлен вдоль мгновенной оси вращения (оси вращения х' ->x'-}-dx'), a
| со (0 | есть мгновенная скорость вращения относительно t. Если параметр t
есть время, то вектор со(0 называется угловой скоростью вращения.
Из равенств (33) получаем
^-в(0А«. (14.10.34»
где Й —-кососямметрический оператор, описываемый в системах координат uXf u2f u,
и it* (/), u^ (/), и' (0 соответственно матрицами
/ 0 — о>з (0 ©t(0\
G (/) = 1 ш» (0 0 ' — со, (t) ,
\- (o2 (/) со, (t) 0 /
/ 0 _£,</) ®f(/)\ i (14.10-35)
Q(0=( wa(/) 0 -©i(/)
\ - co2 (/) w, (/) 0
Пользуясь соотношениями (14.6-8) и тем, что A-1 = А', находим
^=-ЙА = АЙ, Qs^A'. QssA'^. (14 10.36)
1) Здесь, как и ранее, х' — ш производная, а вектор, получающийся из х в
результате вращения.
454
ГЛ. 14. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ПРЕОБРАЗОВАНИЯ 14.10-8.
Подставляя (8), (20) или (26) в (36), получаем соотношения между компонентами
угловой скорости и элементами матриц (направляющими косинусами), параметрами Эйлера
и углами Эйлера. В частности,
Hi ss d'f \aik\ = I «3^22 — oi^fj Oi023 — «Г3а21 «>2a2i — ©1^11 J, (14.10-37)
^(Оз^зг — (02°зз (Oia33 — (03а31 (Da^si — <0ia»s
o, (/) г 2 (ip — Xp — jiv + Hv) г
= — sina -37 4* cos a sin 0
<o2 (0 == 2 (Др — [Ар — vX + vi) ==
2= cos a -± + sin a sin p -~;
at at
(D3 (0 == 2 (vp — vp — A,JLi -f % Д) 2=5
a*a , a dy
"©! (0 = 2 (lp — Xp 4- Av — JLIV) S= )
=-sin Pcos Y -^+ sin y -^ =
s= cos б cos tj?-^? 4- sin t|) -^;
£T8 (0 ==s 2 (Др — ЦР 4- vX — vb) га
.da
Л ' ™ л dt
(компоненты со (0
в неподвижной
системе координат)
===sin р sin у -ji 4- cos Y -^- ss 4
-cos 6 sint|? -^ 4- cos t|? —;
©3 (t) 2=£ 2 (vp — Vp 4- ^ — &Д)J
„ n da . dy
4ф , rftj?.
™*^+:3--|пв5г+!^
A ' <tf
d*
(компоненты о (0
во вращающейся
системе координат)
^-cSl(»i *"*-»• d"*)'
== ©i sin -ф 4- «2 cos t|3,
ss (o2 sin t|? — «h cos \|?) tg 6 4- (o8.
(11.10-38)
(14.10-39)
(14.10-40)
14.10-8. Группа трехмерных вращений и ее представления (см. также
пп. 12.2-1—12.2-12 и 14.9-1—14.9-6).
(а) Ортогональные преобразования (1) трехмерного евклидова
векторного пространства в себя необходимо ограничены и невырождены и
образуют группу трехмерных вращений-отражений Rj-. Собственные вращения
(det (А)= 1) образуют нормальный делитель группы R^1, группу трехмерных
вращений R$. Ни группа Rj1, ни группа R$ не коммутативны.
Вращения, имеющие один и тот же по абсолютной величине угол
вращения |6|, принадлежат к одному и тому же классу сопряженных элементов.
Вращения вокруг произвольной фиксированной оси образуют коммутативную
подгруппу группы R+ (двумерные вращения).
±
#з является подгруппой группы всех невырожденных линейных преобразований
евклидова векторного пространства на себя (полная линейная группа, ПЛГ). Заметим,
что каждое преобразование из ПЛГ является произведением собственного или несобст-
14.10-8. 14.10. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВРАЩЕНИЙ 455
венного вращения и неотрицательного симметрического преобразования (аффинного
преобразования, сжатия или растяжения; см. также пп. 14.4-8 и 13.3-4).
(Ь) Неприводимые представления группы /?+. Матрицы
(20) образуют неприводимое унитарное двукратное представление группы /?£
в поле комплексных чисел, т. е. группа трехмерных вращений R+
представляется группой унитарных преобразований с определителем 1 двумерного
унитарного векторного пространства на себя (двумерная унимодулярная
унитарная группа, специальная унитарная группа, СУ Г).
Справедливо и более общее утверждение. Группа трехмерных
вращений R+ имеет ограниченные неприводимые представления размерностей п = 2,
3, 4, ... Полную систему унитарных неприводимых представлений удобно
обозначить символами <э^1/2), <э^(1), <з^*/2), •••, где е^' имеет размерность
л = 2/+1, а матрица размера (2/+Ох(2/+1), представляющая вращение
с параметрами Кэли—Клейна а, Ь, —о, а (п. 14.10-4) или углами Эйлера а,
Р, у (п. 14.10-6), имеет вид
И(о. (J. Y)]s
[оо h -|
V (-0 У (/+m)l (/-M)H/ + g)H/-g)» (uvj-m-haj+q-h /JM+m-g h* =
[oo h
V НГУ(/ + т)1 (j-m)\ </ + ?)! U-Q)l 4,
Zj (/—m—Л)! U + Q — h)\ (h — q + m)\ h\ A
/i = 0
x^lcm»W, (С08|)2/-т+<7-2Л(8т I^-^+^j (14.10-41)
Считается, что 1/(7V!) = 0 при N<0, и поэтому каждая сумма имеет только
конечное число членов. Представление <&1^ является точным {взаимно одно*
знанным) при /=1, 2, ... и двукратным при / = 1/.2» 3/г» ••• (см« также
п. 14.10-4). Характером (п. 14.9-4) представления е^(;) служит функция
** (а, р, у) s Тг [^ (а, р, у)]^51"^^6 (14.10-42)
(/ = 0, V2, 1, 3/2, .-.).
где б —угол поворота, определенный в п. 14.10-2.
Особые индексы /, т и q, применяемые для <$?<Л и £/^»— это как раз
индексы, связанные с сферическими функциями степени j (п. 21.8-12). Для
целочисленных значений / эти функции образуют (2/+1)-мерное
представляющее пространство для e^(-/} с функциями (21.8-66) в качестве ортонормиро-
ванного базиса.
ГЛАВА 15
ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ,
КРАЕВЫЕ ЗАДАЧИ И ЗАДАЧИ О СОБСТВЕННЫХ
ЗНАЧЕНИЯХ
15.1. ВВЕДЕНИЕ. ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
15.1-1. Вводные замечания. Функциональный анализ рассматривает
подходящим образом выбранные классы функций как множества «точек» в
топологических пространствах (гл. 12) и, в частности, классы функций, состоящих
из многомерных векторов, допускающих определение скалярного произведения
(п. 15.2-1) и разложения по ортогональным функциям (базисным векторам,
см. п. 15.3-4). Изящные и богатые геометрическими аналогиями выводы теории
линейных преобразований, введенной в гл. 14, распространяются на широкий
класс операций, включающий линейные интегральные преобразования и
дифференцирование. Решения линейных дифференциальных уравнений,
обыкновенных и с частными производными, и линейных интегральных уравнений
находятся путем более или менее простого обобщения решения систем
линейных уравнений, в частности, сюда могут быть включены задачи о собственных
значениях (пп. 14.8-3 и 15.4-5).
В пп. 15.3-1—15.3-10 рассматриваются линейные интегральные
уравнения, в пп. от 15.4-1 до 15.4-12 вводятся линейные краевые задачи и задачи
о собственных значениях для дифференциальных уравнений. Остальная часть
главы содержит различные методы решения линейных краевых задач, а именно:
1. Разложения по собственным функциям (п. 15.4-12); этот метод может
быть расширен включением различных методов интегральных преобразований
(и. 10.5-1).
2. Функции Грина (пп. 15.5-1, 15.5-3, 15.6-6, 15.6-9).
3. Сведение к интегральным уравнениям (п. 15.3-2).
4. Вариационные методы (п. 15.4-7, см. также пп. 11.7-1—11.7-3). В
частности, в пп. 15.6-1—15.6-10 рассматриваются краевые задачи для уравнений
Лапласа и Пуассона (теория потенциала) и пространственная форма волнового
уравнения.
Несмотря на то, что многие практические задачи поддаются лишь
численному решению (п. 20.9-4), общая и интуитивно наглядная точки зрения
функционального анализа предоставляют возможность далеко идущего
проникновения в теорию поведения колебательных систем, атомных явлений и т. д.
15.1-2. Обозначения (см. также п. 15.4-1). На всем протяжении пп.
с 15.2-1 до 15.5-4 Ф (х), /(*), F (х), ... обозначают или функции одной
независимой переменной х или, для краткости, функции нескольких переменных а1,
л:2, ..., хп (см. также пп. 6.2-1 и 16.1-2). В одномерном случае dx есть просто
дифференциал, в многомерном случае
dx = dx1 dx2.., dxn.
Интеграл
/= J/(E)*E (15.1-1)
v
представляет в одномерном случае определенный интеграл
ь
а
15.2-1. 15.2. РАЗЛОЖЕНИЯ ПО ОРТОГОНАЛЬНЫМ ФУНКЦИЯМ 457
по ограниченному или неограниченному интервалу V = (a, b), а в /г-мерном
случае — я-кратный интеграл
/ = $$..-{/(P. £2> -.. ln)d?dl*...dt» (15.1-2)
по области V в /г-мерном пространстве. Как правило, возможно ввести эле-
мент объема dV (g) = Y\g(£>) I ^ так» что каждый интеграл (2) приобретает
вид объемного интеграла (пп. 6.2-3, 15.4-1,b и 16.10-10).
15.2. ФУНКЦИИ КАК ВЕКТОРЫ. РАЗЛОЖЕНИЯ
ПО ОРТОГОНАЛЬНЫМ ФУНКЦИЯМ
15.2-1. Квадратично интегрируемые функции как векторы. Скалярное
произведение и нормирование1).
(a) Действительная или комплексная функция, определенная на
измеримом множестве Е «точек» (х) или (х1, х2, ..., хп), квадратично интегрируема
на Е, если существует в смысле Лебега интеграл \\f(l)\2d^ (п- 4.6-15).
Е
Класс L2 (более точно L2(V)) всех действительных или комплексных
квадратично интегрируемых функций на некотором интервале или в некоторой
области соответственно образует бесконечномерное действительное или
комплексное унитарное векторное пространство (п. 14.2-6), если рассматривать
функции /(*), h{x)y ... как векторы и определить
вектор-сумму функций /(*•) и h (x) как f(x) + h(x)\
произведение вектора f (х) на скаляр а как af(x);
скалярное произведение векторов f(x)nh (x) как
(/, h)= JY(E)7(i)A(E)dE. (15.2-1)
где у (х)—данная действительная неотрицательная функция (весовая функция),
квадратично интегрируемая на V. Замене весовой функции соответствует
замена независимой переменной; во многих приложениях y (*) = * или
У (£)<%> есть элемент объема (п. 15.4-1, Ь).
Линейная независимость множества функций (векторов) в L8 определяется способом
п. 1.9-3 (см. также п. 14.2-3). Квадратично интегрируемые функции f^x), f2(x), ..., fm(x)
линейно независимы тогда и только тогда, когда определитель Грама det Uf.f f.\]
отличен от нуля (см. также п. 14.2-6, а).
(b) Как и в п. 14.2-7, норма функции (вектора) f (х) в L2 есть число
m=vwT)=\^®\t <&)?<&'*' (15-2"2)
Функция f(x) (необходимо квадратично интегрируемая) нормируема тогда и
только тогда, когда ||/[| существует и отлична от нуля. Умножение на 1/||/(|
нормируемой функции f (х) доставляет функцию f(x)/\\f\\ с единичной нормой
(нормирование /(*)).
(c) Скалярное произведение, определенное равенством (1), имеет свойства,
перечисленные в п. 14.2-6. В частности, если /(*), Н(х) и действительная
неотрицательная весовая функция у (х) квадратично интегрируемы на V, то
имеет место неравенство Коши —Шварца
\(f, h)\* = \\y}hdt\2^[y\f?dt\y\h\2dZ = (f,f)(ht h) (15.2-3)
I v Iv V
*) Обозначения см. п. 15.1-2.
458 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.2-2.
и неравенство Минковского
1/+АН
— (^ v I /+л |« €*б У/я «^ (J v I / 1*^Б У/я -Ь( 5 v I л I* ^bY7- ^ НЯ1 Ч-П л И- 05.2-4)
15.2-2. Метрика и сходимость в 12. Сходимость в среднем (см. также
пп. 12.5-2—12.5-4, 14.2-7 и 18.6-3).
(a) Как унитарное векторное пространство, L2 допускает введение
расстояния между функциями (метрика, п. 12.5-2)
d(f% Л) = [|/~Л[| = Г^ 7 (5) I /(S) - ^ (g) I2 rfgT/2. (15.2-5)
Корень (5) из среднего квадратичного разности между f(x) и п(х) равен
нулю (метрическая эквивалентность f (x) и h (x)) тогда и только тогда, когда
f(x) — h(x) для почти всех х в V (п. 4.6-14, Ь).
(b) Сходимость в среднем. Метрика (5) порождает следующее
определение сходимости по метрике в L2. Для данного интервала или
области V последовательность квадратично интегрируемых функций s0(jc), s1(x), ...
сходится в среднем (с индексом 2) к пределу s (x) (sn (х) в среднем s (*) ПРИ
п -* со), если
d*(snis)==\\sn-s\\*=~ $y(t)\sn(l)-s(t)\*d%-+0 при п -со. (15.2-6)
В этом случае последовательность определяет ее предел в среднем:
1. i. m. sn(x) = s(x), единственным образом почти всюду в V и, в частности,
я-*оо
в каждой точке непрерывности s(x). Сходимость в среднем не обязательно
имеет своим следствием обычную сходимость последовательности s0 (*)»
st(x)t ... в каждой точке, а обычная сходимость последовательности в каждой
точке области V не имеет следствием сходимость в среднем. В частности,
бесконечный ряд квадратично интегрируемых функций а0(х) + а1(х) + а2(х)-\-...
сходится в среднем к пределу s(x), если
п
5 fl*Wrq555iM SW ПРИ л-00-
6 = 0
В этом случае пишут
ао(х) + а1(х) + а%(х) + ... = s (x).
в среднем
(c) Полнота L§. Теорема Рисса —Фишера. Пространство L2»
ассоциированное с данным интервалом или областью V, является полным
(п. 12.5-4, а). Именно, каждая фундаментальная последовательность
квадратично интегрируемых функций s0(x), sr (х), s2(x) т. е.
последовательность, для которой lim d(smi sn) = 0, сходится в среднем к квадратично
т-+ оо
п-юо
интегрируемой функции s (х) и определяет s (х) однозначно для почти всех х
в V (теорема Рисса—Фишера).
Замечание. Свойство полноты, выраженное теоремой Рисса — Фишера,
превращает L8 в гильбертово пространство (п. 14.2-7, с); в нем можно ввести ортонормирован-
ный базис со всеми свойствами, указанными в пп. 14.7-4 и 15.2-4. Это является важным
обстоятельством для использования интегрирования по Лебегу и сходимости в среднем.
(d) По определению, / (х, а) в средне? F (*) ПРИ а — а> если
lim (/(*, o)-FW|=0.
a-Ki
15.2-4. 15.2. РАЗЛОЖЕНИЯ ПО ОРТОГОНАЛЬНЫМ ФУНКЦИЯМ 459
15.2-3. Ортогональные функции и ортонормированные последовательности
функций (см. также п. 14.7-3).
(a) Две квадратично интегрируемые функции f (*), h (x) называются
взаимно ортогональными (ортогональными относительно действительной
неотрицательной весовой функции YM1))» если
(/, А)= ЫБ>ША(Е)<*Е = 0. (15.2-7)
v
Последовательность функций иг (х)> и2(х), ... называется ортонормированной,
если
(ul,uk)=^yBtuk^ = 6№~\0, "*" '*Н (i, * = 1, 2, ...). (15.2-8)
1/ ^i, если i — к j
Каждое множество нормируемых взаимно ортогональных функций (и, в
частности , каждая ортонормированная последовательность) является линейно
независимым .
(b) Неравенство Бесселя. Для любой конечной или бесконечной
ортонормированной последовательности и1(х)1 и2(х), ... и любой квадратично
интегрируемой на V функции f (х) выполняется неравенство Бесселя
Si (и*. f)l2^ (/>/)• (15.2-9)
k
Знак равенства возможен тогда и только тогда, когда f (x) принадлежит
линейному многообразию, натянутому на иг(х), и2(х), ... (см. пп. 14.2-2,
14.7-3 и 15.2-4).
15.2-4. Полные ортонормированные последовательности функций.
Ортонормированные базисы (см. также п. 14.7-4). Ортонормированная
последовательность их(х), u2(x)t ... в L2(V) является полной ортонормированной
последовательностью (ортоиормированным базисом) тогда и только тогда, когда
выполняются следующие условия:
1. Каждая квадратично интегрируемая функция может быть
представлена в форме f(x) = /i"i(*) + 'ft"2 (*) + •••» гДе fk =
в среднем
= («*. /) (*=1. 2, ...).
2. Для каждой квадратично интегрируемой функции / (х) такой,
что fiUt(x)+f2u2 (*) + ... = f(x)t имеет место тождество Пар-
в среднем
севаля или соотношение полноты (см. также п. 14.7-3, b и 15.2-3, Ь)
(A/) = l/il2+|/a|a+...
3. Для каждой пары квадратично интегрируемых функций /(*),
h(x) таких, что
fi"i М + /2"2 (*) + ••• = / W.
в среднем
Л^х (х) + /l2H2 (*) + ... = h (x)t
в среднем
имеет место соотношение
*) Некоторые авторы называют f (х) и Л (дг) взаимно ортогональными только в
случае у (х) г 1, т. е. если j* /Л </£ = 0.
V
460 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.2-5.
4. Ортонормированная последовательность их (х), и2(х), ... не
содержится в какой-либо другой ортонормированной
последовательности в L2(V); каждая квадратично интегрируемая функция /(*),
ортогональная к каждой uk (х), равна нулю почти всюду в V.
Каждое из этих четырех предложений имеет следствиями три
остальных. Если на интервале или в области V дана полная ортонормированная
последовательность функций ut (х), и2(х), ... и некоторая последовательность
оо
комплексных чисел flt /2, ... такая, что ^ \fk\2 сходится, то существует
квадратично интегрируемая функция f (х) такая, что fxux (x)-\-f2u2 (*) + ...
сходится в среднем к f(x) {теорема Рисса —Фишера, см. также п. 15.2-2, с);
fk определяют f(x) однозначно почти всюду в V и, в частности, если f (х)
непрерывна, то всюду в V (теорема единственности, см. также п. 4.11-5).
15.2-5. Ортогонализация и нормирование последовательности функций (см.
также п. 14.7-4, Ь). Пусть дано счетное (конечное или бесконечное) множество
линейно независимых (п. 1.9-3) функций q>i(x), <jp2M» •••» нормируемых на V;
тогда существует ортонормированная последовательность функций иг (х),
и2(х), ..., порождающая то же самое многообразие функций. Эта
последовательность может быть построена посредством следующих рекуррентных
формул (процесс ортогонализации Г рама —Шмидта):
иМ... D'W --. VlW I
| •>,(*> J Yfvt. v.)' I
' \ (15.2-10)
Vl (X) = <Pl (X), Vl+1 (x) = <p,-+1 (X) - 2j ("ft. <Pi+l) "ft (X),
ft=l
0 = 1.2,...). j
См. также п. 21.7-1, примеры.
15.2-6. Аппроксимации и разложения в ряды по ортогональным функциям
(см. также пп. 4.11-2, с, 4.11-4, Ь, 15.4-12,20.6-2,20.6-3,20.9-9,21.8-12).
Пусть дана квадратично интегрируемая функция f (x) и ортонормированная
последовательность иг(х), и2(х), ... Аппроксимация f(x) в форме
sn(x) = a1u1(x) + a2u2(x) + ... + anun(x) (/г=1, 2, ...) (15.2-11)
доставляет наименьшее значение средней квадратической погрешности
\ I sn (х) -/ (х) |2 dx% если ak = (uk, f).
V
Заметим, что выбор коэффициентов ak не зависит от п. Это свойство
вместе с относительной простотой формул, указанных в п. 15.2-4, делает
очень важными разложения в ряды
f(x) = /гМ*)+/2"2 (*) + ..-> где fk = (uk, f) (k = \, 2, ...)
в среднем
по подходящим образом выбранной последовательности ортонормированных
функций.
15.2-7. Линейные операции над функциями. В пп. 8.2-1, 8.6-1—8.6-4, 15.3-1, 15.4-1,
20.4-2 введены различные линейные операции (п. 14.3-1)
<р(х) = 1Ф(Ъ), (15.2-12)
связывающие функцию <р (х) с данной функцией Ф (£) так, что
L [Oi (£) + Ф8 <£)] = LOt (%) + 1.Ф, (£).
L [а Ф (£)] = а 1.Ф (I). (15.2-13)
15.3-1. 15.3, ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И УРАВНЕНИЯ
461
Ф (£) и ф (*) могут принадлежать одной или различным областям. Как и в п. 14.1-3,
существуют две различные интерпретации функционального преобразования (12):
1. Уравнение (12> описывает операцию над функцией (точка зрения «alibi» или
«активная»).
2. Ф (|) и ф (х) представляют один и тот же абстрактный вектор (в том же смысле,
как две матрицы, п. 14.6-1, Ь), и уравнение (12) описывает замену представления (точка
зрения «alias» или «пассивная», особенно используемая в квантовой механике, см. также
п. 8.1-1).
15.3. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ЛИНЕЙНЫЕ
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.3-1. Линейные интегральные преобразования1).
(a) В пп. 15.3-1 —15.3-10 рассматриваются линейные интегральные
преобразования
К/(Е>- $ *<*• l)nt)dt = F (*), (15.3-1)
связывающие пары функций / (£) и F (х). Функция /£(*, £) называется ядром
линейного интегрального преобразования. Все интегралы предполагаются
существующими в смысле Лебега (п. 4.6-15).
Области, которым принадлежат функция-объект / (£) и результирующая
функция F (х) в уравнении (1), не обязательно тождественны (см., например,
преобразования Лапласа, п. 8.2-1). В пп. 15.3-1, b — 15.3-10 предполагается,
что х и g изменяются в одном и том же интервале или в одной и той же
области. «Символическое» интегральное преобразование
5 в (*. в/о <<е-/м
представляет единичное преобразование (см. также пп. 15.5-1 и 21.9-2).
Линейное интегральное преобразование (1) может быть трактовано или с точки
зрения «alibi», или с точки зрения «alias» (п. 15.2-7). Каждое ядро представляет линейный
оператор в том же смысле, что и матрица (п. 14.5-2, см. также п. 15.3-1, с).
(b) Для данного ядра К (х, £), К (х, £) === К (5, х) называется
транспонированным ядром, К* {х, £) =я К (£, х) называется сопряженным (эрмитово
сопряженным) ядром (см. также п. 14.4-3). Данное ядро К (х, £) называется
симметричным, если /С (%, х) == /С (х, £);
эрмитовым, если К (£, х) = К (х, £);
нормируемым, если С \ \ К (х, £) j2 d£ dx существует и отличен
v v
от нуля;
непрерывным в среднем на V, если
11т [ \K(x + Axt t)-K(x, Ю12^ = 0
(см. также п. 12.5-1, с);
вырожденным (разделяющимся), если К (х, £) может быть пред-
т
ставлено в виде конечной суммы К (х, £)= 2 fi(x)^i(l)-
i = i
Нормируемое ядро представляет ограниченный оператор (п. 14.4-1) так, что F (х)
нормируема, если f (|) нормируема (п. 15.2-1, Ь). Вырожденные ядра представляют
операторы конечного ранга (п. 14.3-2). Если К (х, £) эрмитово, нормируемо и непрерывно
в среднем на V и f (\) квадратично интегрируема на V, то F (х) непрерывна в V.
1) Обозначения см. п. 15J-2, см. также п. 15.4-1, Ь.
462
ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.3-2.
(с) Матричное представление. Произведение двух
интегральных преобразований. Дано нормируемое ядро К (х, |) и ортонормиро-
ванный базис (п. 15.2-4) их (*), и* (х), ... в пространстве функций f (х). Пусть
(15.3-2)
f <*> = 2 fkuk&). F (x) = £ Fkuk (x)
в среднем £~j л л в среднем ^Tlj
оо оо
в среднем /Si ^=1
Г**Л = I I "Г<^ * <*• &> uk ® dx d^\ •
Тогда уравнение (1) эквивалентно матричному уравнению
Заметим, что произведение матриц [я**. 1 [Л;ь], соответствующее ядру
J М (х, л) К (л, S) *Л.
представляет произведение двух последовательных интегральных преобразований (1),
ядра которых К (х, £), М (х, |) соответствуют [&^], [т;ь]. Если К {х,Ъ) — вырожденное
ядро, то возможен выбор и. (х) такой, что матрица [k-y] будет конечной.
15.3-2. Линейные интегральные уравнения. Обзор. Интегральное
уравнение есть функциональное уравнение (п. 9.1-2), включающее интегральное
преобразование над неизвестной функцией Ф (х) (если функциональное
уравнение включает также производные от Ф (х), то говорят об
интегро-дифференциальном уравнении). Интегральное уравнение называется однородным, если
каждое кратное аФ(д:) некоторого решения Ф (х) также есть решение.
В пп. 15.3-2 — 15.3-10 рассматриваются линейные интегральные уравнения
в общей форме
Р(*)Ф(*)-Х| *(*, l)0(t)d'Z = F(x), (15.3-3)
где ядро К (х, £) и функции р (х), F (х) являются заданными. Область
интегрирования V может быть фиксированной (интегральные уравнения типа фред-
гольмовых) или переменной (интегральные уравнения типа вольтерровых,
п. 15.3-10). Назовем три важных типа задач.
1. Линейные интегральные уравнения первого рода (р (х) ss 0,
Я = — 1; п. 15.3-9), в которых надо найти неизвестную функцию Ф (х)
по данному ее интегральному преобразованию F (х).
Соответствующее операторное уравнение КФ = /7 аналогично матричному
уравнению [Ы{Ф*} = {^Ь
2. Однородное линейное интегральное уравнение второго рода
(F(*)==0, Р(*)==1, X неизвестно; пп. 15.3-3 — 15.3-6) представляет
задачу о собственных значениях. Соответствующее операторное
уравнение ЖФ = Ф аналогично матричному уравнению X [ktk] {Ф^} = {Ф/}.
3. Неоднородное линейное интегральное уравнение второго
рода (Р (*)=== 1, А, задано; п. 15.3-7) может быть записано в виде
Ф — ХКФ — F и представляет задачу, тип которой был обсужден
в п. 14.8-10.
Если 3 (х) — действительная положительная функция всюду в V, то можно свести
общее линейное интегральное уравнение (3) посредством преобразования
Ф<*)
Ф <лг) = -^L. F (х) = F (х) Vfi (х), К (х. & = К (х, l)Yfi {х) 0 <£), (15.3-4)
/0 (х)
к линейному интегральному уравнению второго рода.
15.3-4. 15.3. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И УРАВНЕНИЯ 463
15.3-3. Однородное интегральное уравнение Фредгольма второго рода.
Собственные функции и собственные значения (см. также п. 14.8-3 и 15.4-5).
(a) Функция i|) = i|)(*), не равная тождественно нулю в V и
удовлетворяющая однородному интегральному уравнению Фредгольма второго рода
Ж*(Е)«Х $/С(*. £)*(£) <£ = *(*) (15.3-5)
v
при определенном значении параметра X, называется собственной функцией
(характеристической функцией) линейного интегрального уравнения (5) или
ядра /С (х, Q. Соответствующее значение X есть собственное значение
интегрального уравнения.
Если г|?х (х) и г|?2 (х) — собственные функции, соответствующие одному и
тому же собственному значению X, то то же самое относится к их линейной
комбинации аЛ (х) + а2г|)2 (х). Число т линейно независимых собственных
функций, соответствующих некоторому собственному значению, называется
рангом X; если К(х, £) —нормируемое ядро, то каждое т конечно.
Собственные функции, соответствующие различным собственным значениям линейного
интегрального уравнения (5), линейно независимы. Общее количество линейно
независимых собственных функций конечно только в том случае, когда
К (х, £) — вырожденное ядро.
Если линейный оператор К, описываемый линейным интегральным преобразованием
(б), имеет единственный обратный L = К-1, то i|) (*) и А, суть собственная функция и
собственное значение неособенного оператора L (см. также п. 15.4-5) и все собственные
значения отличны от нуля. Во многих приложениях L является дифференциальным
оператором, а К (х, £) —функцией Грина (п. 15.5-1).
(b) Собственные функции и собственные значения
эрмитовых ядер (см. также пп. 14.8-4 и 15.4-6). Если К(х, £)—
эрмитово ядро, то имеют место следующие свойства:
1. Все собственные значения интегрального уравнения (5) дей-
ствительны.
2. Собственные функции, соответствующие различным
собственным значениям, взаимно ортогональны (с весом 1, п. 15.2-3).
3. Если ядро К (х, £) нормируемо, то все собственные значения
отличны от нуля.
4. Существует по меньшей мере одно собственное значение,
отличное от нуля; собственные значения образуют дискретную
последовательность, содержащую не более конечного числа собственных
значений в каждом конечном интервале, и каждое собственное значение
имеет конечный ранг.
15.3-4. Теоремы разложения.
(а) Теоремы разложения для эрмитовых ядер. В
соответствии с определениями скалярного произведения (п. 15.2-1) и сходимости
в среднем (п. 15.2-2) с у(х)=\ каждое нормируемое эрмитово ядро К (*, £)
обладает ортонормированной последовательностью собственных функций tyi(x),
\|?2 (х), ... так, что для каждой функции F (х), представимой в форме F (х) =
= [ К (х, £) / (£) d% (интегральное преобразование (1) функции f (£) или шетоко-
образное» представление F (х)), справедливо разложение
F(x) = 2 F,#k(x) (*esV),
в среднем k==l
^=(4>ft.f)=Uft(i)f (i)rfi (*=i,2, ...)•
(15.3-6)
464
ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.3-5.
Ряд (6) сходится абсолютно и равномерно к F (х) для всех х е V, если f (£)
кусочно-непрерывна в V или если f (g) квадратично интегрируема, а ядро
К (х, g) непрерывно в среднем. Эрмитово ядро К (х, £) называется полным,
если каждая квадратично интегрируемая функция F (х) может быть
представлена в форме (1) или (6), так что собственные функции t|)fe (x) образуют
полную ортонормированную последовательность (п. 15.2-4); это имеет место,
например, если /((*, £) — положительно или отрицательно определенное
(п. 15.3-6).
Каждое нормируемое эрмитово ядро К (х, £) может быть разложено в ряд
оо
К (х, I) = У* J- %W% (х) (х, I e= V). (15.3-7)
в среднем ^{Kk
Ряд сходится равномерно к К (х, £) для всех х, \ е V, если К (х, £) непрерывно
в среднем или если V есть ограниченный интервал или ограниченная область, так что
К (х, £) непрерывно для всех х, £ е V и интегральное уравнение (5) имеет конечное число
положительных или отрицательных собственных значений (теорема Мерсера).
(Ь) Вспомогательные ядра и теоремы разложения для
неэрмитовых ядер. Пусть К (х, |) — нормируемое ядро и nk > 0 — положительные
числа, для которых существуют ненулевые решения системы уравнений
Vk J К (х, I) vk (I) d\ = wk (x), »k J K* (x, I) wk (I) dl = vk {x). (15 3-8)
Тогда числа jn| являются собственными значениями вспомогательных эрмитовых ядер
J К* (х, т|) К (л, 6) dx\ и J К (х, г\) К* (л, I) dx\.
V V
Любая функция F (х), представимая как интегральное преобразование (1) с ядром
К или К*, может быть разложена в ряды
оо
F(x) - V b.wk(x), где Ь. = (w., F) (хе V), <15.3-9а)
в среднем ff~l
или
оо
F(x) = У. a.v.(x), где а. »(v., F), (15.3-96)
в среднем ^^j к к к \ к t
Эти ряды сходятся абсолютно и равномерно к F (х) для всех х в V, если f (|)
кусочно-непрерывна в V, или f (\) квадратично интегрируема, а К (х, £) непрерывно в"среднем; весовая
функция равна 1 (п. 15.2-1). Для каждого нормируемого ядра К (х, |)
оо
К(х,Ъ) = У -1ЕГЦУ w. (х) (х, I с= V). (15.3-10)
в среднем *-*. ^k
к = \
Если ядро К (х, £) самосопряжено, то vk (x) — w^ (x), и формула (10) превращается
в фврмулу (7).
15.3-5. Итерированные ядра. Итерированные ядра определяются
соотношениями
КН*. 6)-*(*,©, Кр^(х,1)^]Кр{х,х\)К{%1)с1ц (р=2, 3, ...)
(15.3-11)
и представляют степени К^ линейного оператора К уравнения (1). Линейное
интегральное уравнение
ЖРф (£) - X j Кр (*, I) Ц (I) rfE=ip (х) (15.3-12)
15.3-7. 15.3. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И УРАВНЕНИЯ 465
имеет те же собственные функции го (#), что и уравнение (5), с
соответствующими собственными значениями А? (см. также п. 14.8-3, d). Обратно,
каждое решение ty(x) уравнения (12) является решением уравнения (5). Если
ядро К (х, I) эрмитово и нормируемо, то
оо
*,<*.Е)- 2 -V**©**(*). p-2,3,...;x,5eV (15.3-13)
и эти ряды сходятся абсолютно и равномерно в V.
15.3-6. Эрмитовы интегральные формы. Задача о собственных значениях как
вариационная задача (см. также пп. 11.1-1, 13.5-2, 13.5-3, 14.8-8, а, 15.4-7).
(a) Пусть дано нормируемое эрмитово ядро К (х, |); скалярное произведение
(необходимо действительное)
(Ф, КФ) = \ \~Ф (х) К (х, I) Ф (|) dx d\ (15.3-14)
V V
называется эрмитовой интегральной формой или, в частности, действительной квадра-
тической интегральной формой, если К (х. £) — действительное и симметричное1).
Эрмитова интегральная форма (14) (а также эрмитово ядро К (х, £)) называется
положительно определенным, отрицательно определенным, неотрицательным или
неположительным, если выражение (14) соответственно положительно, отрицательно, неотрицательно
или неположительно для каждой функции Ф (х), не равной тождественно нулю в V и
такой, что интеграл существует. Интегральная форма (14) положительно определена или
отрицательно определена в том и только в том случае, когда все собственные значения %^
соответственно положительны или отрицательны.
(b) Проблема нахождения собственных функций ч|э (х) и собственного значения Я.
нормируемого эрмитова ядра может быть сформулирована как задача о стационарных
значениях, способом, подобным изложенному в п. 14.8-8, а.
Найдем квадратично интегрируемую функцию Ф (х) такую, что эрмитова
интегральная форма (14) имеет стационарное значение при условии
(Ф, Ф) = $ I Ф<6)1§ <*6 = 1.
V
Функция 0 = ty. (х) доставляет указанное стационарное значение форме (14), причем
V V
Здесь также приложимы все другие теоремы п. 14.8-8, а. Следует лишь вспомнить,
что оператор К, представимый данным ядром К(х, £), имеет собственные функции 1|з^ (|)
и собственные значения 1ДА. Часто бывает возможно решить интегральное уравнение
вида (5), точно или приближенно, методами вариационного исчисления.
15.3-7. Неоднородное уравнение Фредгольма второго рода (см. также
п. 14.8-10).
(а) Существование и единственность решения. Фредтоль-
мово линейное интегральное уравнение второго рода
Ф (*)-*, jj/C(*. l)®(t)dl = F(x) (15.3-16)
v
имеет следующее «альтернативное» свойство:
1. Если данный параметр X не является собственным значением,
ядра К (х, I), то уравнение (16) имеет единственное решение Ф(х).
1) Заметим, что в матричных обозначениях, введенных в п. 15.3-1, с,
оо оо
<ф, КФ) = 2 2 к1Ь?1фк- (15.3-15)
<=1А=1
466
ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.8-7,
2. Если А, равно одному из собственных значений Xj уравнения
(5), то «союзное» однородное интегральное уравнение
й ]ТЩГх)х(1)^^%(х) (15.3-17)
v
имеет решение % (х), не равное тождественно нулю в V, и данное
интегральное уравнение (16) имеет решение Ф (х), лишь если F (х)
ортогональна (с весовой функцией \) каждому решению %(х)
уравнения (17). Заметим, что уравнения (17) и (5) идентичны для
эрмитовых ядер.
При указанных выше условиях решения существуют, в частности, когда
К (х, £) кусочно-непрерывно и нормируемо, a F (х) непрерывна и квадратично
интегрируема на V. Если во втором случае решение Ф (х) существует, то
уравнение (16) имеет бесконечное количество решений, так как каждая сумма
некоторого частного решения и линейной комбинации собственных функций
г|? (*), соответствующих Кг, является решением; в частности, существует
единственное решение Ф (х), ортогональное ко всем этим собственным функциям.
(Ь) Сведение к интегральному уравнению с
эрмитовым ядром. Если К (х, £) нормируемо, то каждое решение Ф (х)
уравнения (16) есть решение интегрального уравнения
OW-|X|^(^E)0(E)^«FW-X5T(|7T)F(E)dE, (15.3-18а)
где Н (ху £) есть эрмитово ядро, определяемое формулой
H(x,t)E=eiarzxK + e-UrsKK*-\K\ \К (i\, x)K (i\, Q *r\. (15.3-186)
V
Вследствие этого достаточно изучить методы решений для эрмитовых ядер.
Замечание. Н (х, £) и К (х, |) имеют тождественные собственные функции,
соответствующие собственным значениям I %. I и %..
(с) Резольвентное ядро. Решение Ф(х) линейного интегрального
уравнения (16) удобно писать в форме
<D(x) = F (х) + Х $Г (x,t;K)F (t)d%. (15.3-19)
v
Функция Г (*, £; Я) называется резольвентным ядром (иногда она называется
взаимным ядром) для интегрального уравнения (16); уравнения (16) и (19)
представляют взаимно обратные линейные преобразования.
Когда резольвентное ядро Г (*, |; X) существует, оно удовлетворяет интегральным
уравнениям
Г (jr. I; К) - К \ К {х, t) Г (t, |; X) dt = К <*, t), )
Г (х,1; К) - К J К </. I) Г (х, t; К) dt = К (х, I), | (Jg
Г (х, |; К) — Г (*, I; V) = (ЯГ—V) \ Г (х, t\ X) Г (t, g; V) dt
для произвольных X, А/, не являющихся собственными значениями К (х, £).
15.3-8. 15.3. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И УРАВНЕНИЯ
15.3-8. Решение линейного интегрального уравнения (16) (см. также п.
20.8-5, численные методы).
(а) Решение последовательными приближениями.
Ряды Неймана. Полагая
ф£°] (*) = /?(*),
вычисляют последовательные приближения
<l>V + ll(x) = F(x) + X J/C(*. £)фС/](£)</£ (/ = 0, 1,2, ...) (15.3-21)
v
искомого решения Ф(х) уравнения (16). Функции (21) можно рассматривать
как частичные суммы бесконечного ряда (называемого рядом Неймана)
F(x) + X \ К(х, t)F (t) dl + W \к2(х, t)F(I) dt + ...==
= (\+XK + X*K* + ...)F (x). (15.3-22)
Если К (х, |) нормируемо, F (х) квадратично интегрируема на V, то
существует действительное число
^l\K(x,l)?dxdfT^
такое, что ряд Неймана (22) сходится в среднем к решению (19) при | X | < гс.
Если, кроме того,
$|/C(*,E)lf<JE и $|К(?,*)|2^
равномерно ограничены в V, то степенной ряд (22) и соответствующий ряд
для резольвентного ядра
Г (*, 1\ X) = К (х, 1) + ХК2 (х, I) + V /С3 (*,© + .-• (15.3-23)
сходятся равномерно к указанным пределам при xt £ е V и \ X | < гс.
Функция (23) в таком случае является аналитической функцией от X
при | X | < гс и может быть аналитически продолжена (п. 7.8-1), давая тем
самым резольвентное ядро для других возможных значений X. Ряд (23), как
и ряд (22), известен под названием ряда Неймана.
Если нормируемое ядро К(х, £) эрмитово, то радиус сходимости (или
сходимости в среднем) гс дается формулой ^с = |\|» гДе \ есть наименьшее
по абсолютной величине собственное значение ядра.
(Ь) Формула Г и л ьбе рта—Шмидта для резольвентного
ядра (см. также п. 14.8-10). Для каждого нормируемого и эрмитова ядра
К (х, g) решение линейного интегрального уравнения (16) дается формулой
(19) с резольвентным ядром
(формула Гильберта—Шмидта), (15.3-24)
где г|)Л — ортонормированные собственные функцииг) ядра К (х, £). Ряд
сходится равномерно для х, 1^ V и X^:Xk.
1) Если %. есть собственное значение, имеющее ранг т (п. 15.3-3, а), то пишут
А^+1 = ... = А,. т_1 —^i, и таким образом, ряд (24) имеет т членов, содержащих
собственные функции tfy (*). ф|+1 (*), ..., t|), j (*), соответствующих А^.
468
ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.3-9.
Г (х, £; ^) есть мероморфная функция Я, в конечной части Х-плоскости; вычеты
Г(дг, £; К) в ее полюсах связаны простыми соотношениями (пп. 7.6-8 и 7.7-1) с собствен?
нымн функциями ^>k (х).
Формула Гильберта — Шмидта для решения, когда X равно собственному значению А,..
Если параметр А, равен некоторому собственному значению %> данного ядра К (х, £), то
из суммы (24) (не являющейся теперь резольвентным ядром) исключаются члены,
содержащие X., и к правой части (19) прибавляется произвольная собственная функция \|?(лг).
соответствующая %.. Результирующая функция Ф (х) является решением данного
интегрального уравнения (16) при ограничениях случая 2 в п. 15.3-7, а.
(с) Формулы Фредгольма для резольвентного ядра.
Если К (х, |) нормируемо, резольвентное ядро Г (*, £; К) может быть
выражено в виде отношения двух целых функций (см. также п. 7.6-7)
Т(х,1;К)--
где
D(X)
(15.3-25)
D(X)=2
(-1)*
ckxk,
k=o
0(д:,Е;Я)=21Цг-0*^Е)^
(15.3-26)
с
C0=l, D0(x,l) = K(x,#
и для fc = l, 2, ...
сл«$оЛ-1(Е,Е)«.
V
Dk (x, э-с* К(*-Б)-л 5 *(*' ^D*-i(ть 5) *ь
Оба степенных ряда сходятся для всех конечных V, степенной ряд для
О (х, \\ А,) сходится равномерно в V. Полюсы Г (х, |; А,) совпадают с
нулями D (X).
Отметим аналогию между функциями D (х, |; К), D (А,) и определителями,
используемыми для нахождения решения xk аналогичной конечномерной задачи, по правилу
п
Крамера (1.9-4) ]£[ («,-* -~X6ik) xk = bi <' = *» 2 ">•
Л=1
(d) Сингулярные ядра. Если данное ядро К (*, £) не ограничено в
окрестности х =£, тогда как итерированное ядро /С* (*, |) остается ограниченным, решение
Ф (л:) уравнения (16) находят посредством решения интегрального уравнения
Ф (*) - Я» J К% (х, I) Ф (6) </g = F (*) + X $ /( (*. |) F (|) <£. (15.3-27)
Уравнение (27) получено подстановкой
Ф (х) = F (х + Я $ /С (л.6) Ф (|) <£
V
в левую часть уравнения (16). Эта процедура может быть использована, если первым
итерированным ядром, остающимся ограниченным, является /С3 U, £). К4 (*, I), ..
15.3-9. Решение линейного интегрального уравнения Фредгольма первого
рода (см. также пп. 14.8-10, Ь, 15.4-12, 15.5-1). Если линейное интегральное
уравнение
$К(х,$Ф®(% = Р(х) (15.3-28)
V
15.3-10. 15.3. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И УРАВНЕНИЯ 469
с нормируемым ядром К (х, £) имеет решение Ф(лг), то теорема разложения
п. 15.3-4, b дает
00
Ф(*) = 2l»*(w*.'r)i>*M + <P(*). (15.3-29)
в среднем &=1
где vjt (a:), wk (х) и \ik определены в п. 15.3-4, b и ф (х) — произвольная
функция, ортогональная ко всем v^ (х).
Если vк (х) образуют полную ортонормированную последовательность в L9 (V)
(п. 15.2-4), то ф (д:) = 0 для почти всех х в V и решение (29) единственно почти всюду
в V. Если w. (х), как и v. (x), образуют полную ортонормированную последовательность
в L9(V), то интегральное преобразование (28) является неособенным и допускает
однозначное обращение
\ = Ф (х).
где
\К-г(х, |)F(i)rf| = 0(
*_i <*. £> = 2 Н wk <*> vk {х)'
(15.3-30)
K-i (x, |) называется взаимным ядром, ассоциированным с К (х, |), и представляет
линейный оператор К-1. Для эрмитовых ядер К (х. |) имеем v^ {х) = wk (х), nk — | %k |.
15.3-10. Интегральные уравнения Вольтерра.
(а) Пусть х и £—одномерные действительные переменные. Тогда
1. Интегральное уравнение Вольтерра второго рода
Ф(*)-Х$Я(*,Е)Ф(Б)<*Б==/Ч*) (15.3-31)
о
сводится к интегральному уравнению Фредгольма (16) на интервале
V = (0, оо), если ввести новое ядро
К(х, Взй(г, t)U+(*-l)={ "iX' 1) %?я f J* } (15-3-32)
2. Интегральное уравнение Вольтерра первого рода
5я(*,£)ф(0<*Е=/Ч*)
(15.3-33)
посредством дифференцирования сводится к виду (31), где
дН (х, I) dP(x)
Н (х, х) '
^w=«
dx
Н (х, х)
(15.3-34)
(Ь) Следующий пример иллюстрирует метод решения для одного класса
интегральных уравнений Вольтерра, имеющих неограниченные ядра Для нахождения решения
уравнения
[ Ф(1)п dt = F(x) <0<а<1)
J (x — £)a
(*-|)
(15.3-35)
умножают обе его части на (у — х)а ~~ 1 и интегрируют по х в пределах от а до у.
Получаемое при этом интегральное уравнение имеет ограниченное ядро. Его решением
является
Ф (х) = -
F(a)
F' (I) d\
(х-
a)l~a J(A._|)1—а
(15.3-36)
В частном случае при а = 1/г уравнение (35) известно под названием интегрального
уравнения Абеля.
470 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.4-1.
15.4. ЛИНЕЙНЫЕ КРАЕВЫЕ ЗАДАЧИ И ЗАДАЧИ О СОБСТВЕННЫХ
ЗНАЧЕНИЯХ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
15.4-1. Линейные краевые задачи. Постановка задачи и обозначения (см.
также пп. 9.3-1, 10.3-4, 15.1-2, 15.2-7).
(a) Линейную однородную функцию от функции Ф (х) и ее производных
будем записывать в виде произведения L<D (x) функции Ф (х) и линейного
дифференциального оператора L, например, вида djdx или—-V2 — q(x19 х2> х3).
Требуется найти неизвестную функцию Ф (*), удовлетворяющую линейному
дифференциальному уравнению
LO>(x)=f(x) (xe=V) (15.4-1а)
внутри открытого интервала или области V, и N линейным краевым
условиям
Bi<S>(x) = bi(x) (/ = 1, 2, ..., N; xeS), (15.4-1/?)
где S —граница области V; каждая из В/Ф(*) есть линейная однородная
функция от Ф (х) и ее производных.
(b) Обозначения. Объемные интегралы и скалярные
произведения (см. также пп. 4.6-12, 15.1-2, 15.2-1, 16.10-10). В
одномерном случае х есть действительная переменная, уравнение (1а) есть
обыкновенное дифференциальное уравнение, V есть ограниченный или
неограниченный открытый интервал, концы которого х = а, х = Ь образуют границу S.
В n-мерном случае х обозначает «точку» (х1у *2, ..., хп) в /г-мерном
пространстве, уравнение (la) есть уравнение с частными производными.
Предполагается возможным ввести объемный элемент
dV (х) = У \g(х1, х*> ... ,хп) | dx1 dx* ... dxn = V\g (x) \ dx
тем же способом, что в пп. 6.2-3, b и 16.10-10; K|g(*)| действителен и
положителен всюду в V. Тогда С ф (£) dV (£) есть л-мерный объемный интеграл
по V и можно определить скалярное произведение двух функций и (x)t v (x),
как в п. 15.2-1,
(и, v)=[y0 (I) T® v (I) dl = $ й|) v (I) dV (I). (15.4-2)
Заметим, что у0 (х) = У\ g(x)\ зависит от системы координат. Аналогично можно
предположить существование соответствующего элемента поверхности dA (x)
(х в S) на границе гиперповерхности S; тогда \ <р(£)а\4 (I) — интеграл по
поверхности в /г-мерном пространстве (см. также п. 4.6-12 и 6.4-3, Ь).
В частности, при /*=3 V есть ограниченная или неограниченная открытая
область пространства с граничной поверхностью S; S есть регулярная
поверхность (п. 3.1-14). При п=2 V есть соответственно плоская область с
(регулярной) граничной линией S.
15.4-2. Дополнительное дифференциальное уравнение и краевые условия
для линейной краевой задачи. Теоремы о суперпозиции (см. также пп. 9.3-1,
10.4-2, 14.3-1, 15.2-7). С каждой линейной краевой задачей (1) можно
связать однородное дополнительное или приведенное дифференциальное уравнение
1.Ф(л:) = 0 (*e=V) (15.4-За)
и совокупность однородных «дополнительных краевых условий»
В,Ф(д:) = 0 (t = l, 2, ..., N\ л: £= S). (15.4-36)
15.4-3.
15.4. ЛИНЕЙНЫЕ КРАЕВЫЕ ЗАДАЧИ
471
Следующие важные теоремы устанавливают связь между решениями Ф (лг)
данной линейной краевой задачи (1) и функциями, удовлетворяющими более
простым условиям вида (3).
1. Решение каждой линейной краевой задачи (1) может быть
сведено к линейной краевой задаче с тем же оператором L и
краевыми условиями (3) (см. также п. 15.5-4)х).
2. Наиболее общий вид функции, удовлетворяющей линейному
дифференциальному уравнению (1л), может быть записан в виде
суммы некоторого частного решения уравнения (la) и наиболее
общего решения дополнительного уравнения (За).
3. Однородному линейному дифференциальному уравнению
удовлетворяет любая линейная комбинация его решений.
4. Пусть Фх (л:) и Ф2 (л:) удовлетворяют соответственно
дифференциальным уравнениям £фг (x)=f1 (х) и L<D2 (л:) = f2 (х) с
одинаковыми линейными однородными краевыми условиями В;Ф(л:) = 0.
Тогда аФх (л:) + РФг (х) удовлетворяет уравнению LO (х) = а/х (л:) +
+ Р/г (х) пРи указанных краевых условиях.
5. Пусть Фх (л:) и Ф2 (л:) удовлетворяют однородному линейному
дифференциальному уравнению 1.Ф(л:) = 0 с соответственными
линейными краевыми условиями В^Ф]. (x) = bii (x) и В;Ф2 (x) = b2i (х).
Тогда аФх (л:) + РФ2 (х) удовлетворяет заданному уравнению и
краевым условиям В,Ф (л:) = abu (х) + $b2i (x).
15.4-3. Эрмитово сопряженные и сопряженные краевые задачи. Эрмитовы
операторы (см. также пп. 14.4-3, 14.4-4, 15.3-1, Ь).
(а) Данная однородная линейная краевая задача (3) и определение
скалярного произведения (2) порождают эрмитово сопряженную краевую задачу
L*x(*) = 0 (jteV), (15.4-5я)
BfxW=0 (i = h 2 N\ xsS) (15.4-56)
посредством условия
(v, U)-(L*t>, и)=Л [vLu + uTFv]dV=0, (15.4-6)
где и—и(х), v = v(x) — пара соответственно дифференцируемых функций,
причем и (х) удовлетворяет заданным краевым условиям (36), v (x)
удовлетворяет эрмитово сопряженным краевым условиям (56); и и v могут
рассматриваться как принадлежащие сопряженным векторным пространствам (14.4-9).
Два линейных дифференциальных оператора второго порядка L и L* являются
эрмитово сопряженными тогда и только тогда, когда функция vLu — uL*v имеет форму
я-мерной дивергенции
п
■ У —- \У | g (х) | pk\ (табл. 16.10-1), где каждая pk есть функция от и, v,
VI & (х) | *-*, дх*
и, v и их производных первого порядка 8).
При этом становится возможным представить объемный интеграл J [vLu — uL*v]dV
V
через интеграл по границе S; формулы такого типа известны как обобщенные формулы
*) Если записать Ф (х) — Ф (х) -{- v (х), где v (x) — соответствующим образом
выбранная функция, удовлетворяющая граничным условиям (1), то Ф (х) есть решение линейной
краевой задачи
1.Ф (х) =f (х) - Lv (x) (*<= V); В,Ф (х) = 0 (/ = 1, 2 N; x ъ S); (15.4-4)
Lv (x) определяется выбором v (x) и может содержать члены с б-функциями; часто
возможно найти о (х) так, что Lv (х) = 0 (см. также п. 10.4-2).
*) Верхние значки kt как и в гл. 6 и 16, не являются показателями степени.
472 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.4-3.
Грина (см. также п. 15.4-3, с). Эрмитово сопряженные краевые условия В^м = О,
В* v <= 0 (х в S) определяются из условия обращения в нуль интеграла по границе, т. е.
выполнения условия (6).
В случае действительных функций и операторов эрмитово сопряженные задачи,
операторы и краевые условия обычно называются взаимно сопряженными.
(Ь) Эрмитовы операторы. Дифференциальный оператор L
называется эрмитовым (самосопряженным), если
(о, Lu)-(Lv, и) = \ [vLu — uLv] dV = 0
(15.4-7)
для каждой пары соответственно дифференцируемых функций и = и (х), v = v (х),
удовлетворяющих одинаковым однородным краевым условиям, определяющим
некоторое линейное многообразие функций. Эрмитово сопряженные краевые
задачи с эрмитовыми операторами, имеющие одинаковые краевые условия,
тождественны (самосопряженные краевые задачи).
(с) Частные случаи. Действительные операторы
Штурма — Лиувилля и обобщение теоремы Грина (см. также пп. 5.6-1
и 15.5-4). В одномерном случае уравнения (За) и (5а) являются
обыкновенными линейными дифференциальными уравнениями с заданными краевыми
условиями на концах интервала (a, 6)==V. Если скалярное произведение
ь
определено формулой (и, v) = ^uvdx (п. 15.2-1), то для действительных диф-
а
ференциальных операторов второго порядка имеем
■ , \ dzu . / \ du , / \
1и^а0(х)-г-г+а1(х) -г- + а2(х) и,
dx*
dx
vLu — uL*v =
dT lQ0 (*) "]—й7 ial (*) »1 + a2 (*) ».
dx
dP(x)
dx
P (x) = a0 (x) (w' — uv') + [ax (x) — a0 (x)] uv.
(15.4-8)
P (x) иногда называют конъюнкцией и (х) и v(x) относительно оператора L.
Условие ах (х) == а0 (х) превращает L в самосопряженный оператор
Штурма — Лиувилля
L—£[*<*>£]-*<*>• 05.4-9)
где р (х) = — а0 (х) и q(x) = — a2(x) (см. также п. 15.4-8); интегрирование
по частям приводит к обобщенной формуле Грина
\(vLu — uLv) a\ — — p(x) (vuf — uv')
(15.4-10)
В трехмерном случае определим скалярное произведение формулой (2),
а оператор V2 —так же как в табл. 6.4-1 или 16.10-1. Тогда, считая ц —
= q(x1i x2t xs) действительной дифференцируемой функцией, будем иметь,
что действительный дифференциальный оператор
L==_V2 — q(xi, x2, x3) (15.4-11)
является самосопряженным и удовлетворяет обобщенной формуле Грина
J (vLu-uLv)dV = -\ (vVu-u Vy).dA = -$ U^—u^jdA (15.4-12)
15.4-5.
15.4. ЛИНЕЙНЫЕ КРАЕВЫЕ ЗАДАЧИ
473
(см. также табл. 5.6-1). Аналогичная формула может быть написана для
двумерного случая.
15.4-4. Теорема Фредгольма об альтернативе (см. также пп. 14.8-10,
15.3-7,а, 15.4-12). Линейная краевая задача, определяемая дифференциальным
уравнением
L<S(x) = f(x) (x<=eV) (15.4-13a)
с однородными краевыми условиями
В/Ф(*) = 0 (/=1, 2, ..., N\ *esS), (15.4-136)
имеет единственное решение тогда и только тогда, когда эрмитово
сопряженная (сопряженная) краевая задача (5) имеет лишь решение %(х), тождественно
равное нулю, % (х) = 0. Если же однородная краевая задача (5) имеет решения
%(х), отличные от нуля, то данная задача (13) разрешима, лишь если f(x)
ортогональна к каждому %(х), т. е.г)
(X. f)=\ifdV=0. (15.4-14)
V
Если последнее условие выполнено, то данная задача (13) имеет бесчисленное
множество решений.
Замечание. Во многих приложениях L есть эрмитов оператор, и эрмитово
сопряженная задача (5) совпадает с данной задачей (13).
15.4-5. Задачи о собственных значениях для линейных дифференциальных
уравнений (см. также пп. 10.4-2,с, 14.8-3, 15.1-1).
(a) Для заданной совокупности линейных краевых условий собственной
функцией (характеристической функцией) линейного дифференциального
оператора L называется решение ф (#), не равное тождественно нулю в V,
дифференциального уравнения
L^(x) = %^(x) (*e=F), (15.4-15)
где X есть соответствующим образом определенное число, называемое
собственным значением (характеристическим числом) оператора L, связанным
с собственной функцией ф (лг).
(b) Более общие задачи о собственных значениях приводят к нахождению
собственных функций ^(х)ф0 и собственных значений X, удовлетворяющих
линейному дифференциальному уравнению
L^(x) = XB{x)ip(x) (xzeV) (15.4-16)
и заданным линейным однородным краевым условиям; В (х) есть
действительная и положительная функция в V.
(c) Если ф(л:) есть собственная функция, принадлежащая собственному
значению X, то это оке самое можно сказать о а ф (х) ф 0. Если г^ (*), ф2 (*)» • • •
... , ф5 (х) суть собственные функции, принадлежащие собственному значению X,
то то же самое имеет место для любой функции
«1*1 М + «2*2 (*) + ". + «А (*) Ф 0.
Эта теорема приложима также к равномерно сходящимся рядам по
собственным функциям.
Собственные функции, принадлежащие различным собственным значениям,
линейно независимы (пп. 1.9-3, 9.3-2). Если собственному значению X
принадлежат т > 1 линейно независимых собственных функций, то число т
называется рангом собственного значения.
') В одномерном случае dV совпадает с их.
474 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.4-6.
(d) Спектр линейной задачи о собственных значениях.
Непрерывный спектр и обобщенные собственные функции (см. также
пп. 14.8-3, d и 15.4-12). Для заданных однородных линейных краевых условий и В (х) > О
спектр линейной задачи о собственных значениях (16) есть множество комплексных
чисел X таких, что дифференциальное уравнение
L Ф (х) — К В (х) Ф (х) = / (х) (х <= V) (15.4-17)
с заданной нормируемой «возмущающей» функцией f (x) не имеет единственного
нормируемого решения, удовлетворяющего заданным краевым условиям. Спектр может быть
непрерывным и остаточным, а также дискретным, который определен уравнением (16)
с нормируемыми собственными функциями г|)(*).
В частном случае, когда В (*) = 1, говорят о спектре дифференциального оператора L.
Если L — эрмитов оператор и В (х) > 0, то дискретный и непрерывный спектр
задачи (16) включается в предельный спектр (п. 14.8-3, d). Часто можно получить
предельный спектр приближением задачи о собственных значениях последовательностью
задач о собственных значениях, имеющих лишь дискретный спектр. В процессе таких
предельных переходов собственные функции заменяются множеством функций, зависящих
от непрерывно изменяющегося параметра %; такие функции известны под названием
обобщенных собственных функций; они удовлетворяют уравнению (16).
Пример. Обыкновенное дифференциальное уравнение
dzO (х) = _ % ф (х) с у в ^ то)
dx*
при краевых условиях
со
Ф (0) = 0. J | Ф (£) |» dl < оо
О
имеет непрерывный спектр 0 ^ % < оо. Этот спектр аппроксимируется дискретным
спектром % = (kn/a)2 (& = 0, 1, 2, ...) задач о собственных значениях
d*Oa (х)
dx*
-.-КФа(х) с V =г (0, а), Ф (0) = Ф (а) = О
Jlk
при а -* оо. Собственные функции sin х (& = 0, 1, 2, ...) последней задачи
аппроксимируют обобщенные собственные функции sin Yh x при а-* со (переход от рядов Фурье
к интегралам Фурье).
15.4-6. Собственные значения и собственные функции эрмитовой задачи
© собственных значениях. Полные ортонормированные множества собственных
функций (см. также пп. 14.8-4, 14.8-7, 15.2-4, 15.3-3, 15.4-3, Ь).
(а) Если оператор L в уравнении (15) эрмитов, то
1. Все значения % спектра действительны.
2. Нормируемые собственные функции if/, \fft, соответствующие
различным собственным значениям, взаимно ортогональны:
i*
Если L — эрмитов оператор, имеющий чисто дискретный спектр, то имеет
место следующая теорема разложения:
3. Существует ортонормированная последовательность
собственных функций tyi(x), г|)2 (*)» •••» доставляющая разложение в ряд
ф(*) = а1^1(х) + а2УЗр2(х) + ...
в среднем
(e* = $*k<pdy. *=1. 2» •••) (15.4-18д)
v
каждой квадратично интегрируемой функции ф (х), удовлетворяющей
краевым условиям задачи и такой, что L ф (х) существует почти
всюду в V.
(Ь) Эти же теоремы распространяются на «обобщенную» задачу о
собственных значениях (16), где L — эрмитов оператор и В(х)>0 в предположении,
15.4-7.
15.4. ЛИНЕЙНЫЕ КРАЕВЫЕ ЗАДАЧИ
475
что ортогональность и нормированность переопределены посредством
скалярного произведения *)
(и, v)B=yuvBdV.
Таким образом, разложение (18 а) заменяется более общим разложением
Ч>(х) = а1Ц>1(х) + а2Ц>2(х) + ... (я*в$*кфД<*У, *=1, 2> •••)• (15.4-18 6)
Ортонормированность собственных функций \|?л (а:) определена как
J йЫЛЛ^вй- { °' КЛЯ 1фк' } (i, ft^ 1, 2, ...). (15.4-19 а)
^ 1,1, если t = k )
Эти соотношения содержат как частный случай соотношения, полученные для
задачи (15).
(с) Для эрмитовой задачи с (необходимо действительным) непрерывным спектром,
обладающим обобщенными собственными функциями (см. п. 15.4-5, d), существует
множество обобщенных собственных функций ^ (х, К), для которых
J * (6. А,) Ф (6. V) ^ (S) rf V(6) = 6 (А, - X'). (15.4-19 6)
15.4-7. Эрмитова задача о собственных значениях как вариационная задача
(см. также пп. 11.7-1 — 11.7-3, 14.8-8, 15.3-6, Ь, 15.4-10).
(a) Задача о собственных значениях (16) для эрмитова дифференциального
оператора L с дискретными собственными значениями Xlt %2> ••• эквивалентна
каждой из следующих вариационных задач г).
1. Найти функцию г|э(*)^0 в У, удовлетворяющую данным
краевым условиям и обращающую вариацию (пп. 11.5-1 и 11.5-2)
функционала
0|?, гл» у (частное Релея) (15.4-20)
0|>,-£t|>) | |t|>|*£</V
V
в нуль.
2. Найти функцию гр (л:), удовлетворяющую данным краевым
условиям и обращающую вариацию функционала
(г|>, b|?) = J^b|?d7 (15.4-21)
в нуль при условии, что
(я|), Вг|?)= CH>|*fldF = l. (15.4-22)
В каждом из этих случаев функция г|э = г|?£ (*) доставляет функционалу
стационарное значение %k.
Таким образом, возможно использовать прямые методы вариационного
исчисления, в частности, метод Релея — Ритца (п. 11.7-2), при решении задачи
о собственных значениях для обыкновенных дифференциальных уравнений
и уравнений с частными производными.
(b) Пусть дан эрмитов оператор L с дискретным спектром, содержащим
не более конечного числа отрицательных собственных значений (пп. 15.4-8,
15.4-9), и пусть собственные значения расположены в порядке их возрастания,
>) В одномерном случае dV = dx.
476
ГЛ 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.4-8.
причем собственные значения ранга т повторены т раз: Kt ^ Х2 ^... Наи*
меньшее собственное значение \А равно минимуму частного Релея (20) для
произвольных «допустимых» функций я|н*)» т- е- Для произвольных
нормируемых г|?(*), которые удовлетворяют данным краевым условиям и таких, что
частное Релея существует.
Аналогично г-е собственное значение Хг указанной выше последовательности
не превосходит частного Релея для всех «допустимых» функций г|? (х) таких, что
\qkq>BdV = 0 (15.4-23)
для каждой собственной функции я|^, соответствующей %г, \2, ..., \г_г
(принцип минимакса Куранта).
15.4-8. Одномерная задача Штурма —Лиувилля о собственных значениях.
(а) Рассмотрим одномерную действительную переменную х и пусть V —
ограниченный интервал (а, Ь). Тогда наиболее общий действительный эрмитов
дифференциальный оператор второго порядка L имеет вид (9). Действительное
дифференциальное уравнение {однородное дифференциальное уравнение
Штурма — Лиувилля)
L*--{£[pi*)£]+*(x)}*-
— [pW-fr+P'W Til+*(*> *]=**(*>* (15.4-24a)
определяет самосопряженную задачу о собственных значениях, если это
уравнение дополнить однородными линейными краевыми условиями
Bi ф = ах г|/ (а) + Pi г|з (а) = 0, В2я|? в а2 я|?' (b) + fo я|? (6) = 0, (15.4-246)
или условиями периодичности
Bi^)e^(flf) —^(6) = 0, В2я|?^я|)'(я) —я|?'(6) = 0. (15.4-24с)
Здесь предполагается, что р (х), q(x) и В (х) дифференцируемы в [а, Ь], р(х)
и В(х) положительны в [а, Ь] и не существует собственных функций,
отвечающих числу А,=0. Эти предположения обеспечивают дискретность спектра.
-Х-При условии (24£) все собственные значения имеют ранг 1. При
условиях периодичности (24с) ранг может равняться двум. Например, уравнение
ф'/ + Я'ф = 0 с условиями (24с) при а = 0 и & = 2я имеет собственные числа
"к = п2 и собственные функции cos nx и sin nx.
Больше двух ранг быть не может.
Если в задаче (24 а, Ъ) р (х) > 0, В (х) > 0, q (х) ^ 0, а^ ^ 0, а2р2 ^ 0,
а? + Р!>0» а1 + Р1>0, то все собственные значения положительны, за
исключением случая, когда <7(*)==0, р, = р2 = 0, в котором А,0 = 0. ■#
Если собственные значения расположить в порядке возрастания Xt ^
^Х2^ то Кп асимптотически пропорционально п2 при п—-со (п. 4.4-3).
В пп. 9.3-4—9.3-10, а также в пп. 21.7-1—21.8-12 изучены различные упрощающие
преобразования и методы решения однородных дифференциальных уравнений типа (24).
Задачи Штурма — Лиувилля возникают, в частности, при разделении переменных в
краевых задачах для линейных дифференциальных уравнений с частными производными
(см. пп. 10.4-3—10.4-9) и имеют важное значение в квантовой механике. Заметим, что
каждое дифференциальное уравнение вида
а° {Х) Ч^ + Qi {Х) Ж + °2 {Х) * = % k {X) * (15.4-25)
можно привести к виду (24а) посредством умножения обеих частей его на
f fliU)--ао (х) dx
J а0(х)
(см. также п. 9.3-8, а). Отсюда следует, что примеры пп. 10.4-3—10.4-9 могут
рассматриваться как задачи Штурма —Лиувилля.
J5.4-10.
15.4. ЛИНЕЙНЫЕ КРАЕВЫЕ ЗАДАЧИ
477
(Ь) Если в формуле (9) положить q (*) = ?i (x) — q-2 (х), то
Ъ Ь ъ
\ uLu d%=\ [(pit'2 + 2qtuW + <72w2) d| — (puW + QiU2)]^
a a
b b
J ulv d\ = J [pw'u' + <7i ("'» + «f') H- <72wo] d£ — [(pf — <7it>) "]Q.
(15.4-26)
Интегралам (26) во многих приложениях (см. также п 15.4-7) можно придать физический
смысл.
(с) Обобщения и родственные задачи. Многие общие задачи связаны
с рассмотрением неограниченного интервала V s (0, оо) или V = (— со, со) с краевыми
условиями, в которых указывается асимптотическое поведение i|) (*) на бесконечности или
другие ограничения. Далее, могут допускаться особенности в точке х—а или х = Ь
у функций р(х), q (х) или В(х). В случае, когда функции р (х), q (х) или В (х) имеют
особенности на концах ограниченного интервала (а, Ь), спектр может оставаться чисто
дискретным.
Неоднородная краевая задача, включающая оператор Штурма—Лиувилля L, может
быть решена методами пп. 9.3-3, 9.3-4, 15.4-12, 15.5-1.
15.4-9. Задача Штурма — Лиувилля для уравнений с частными
производными второго порядка (см. также п. 15.4-3, с).
(a) Пусть х = (хх, х2 хп). Определим скалярное произведение фор-
мулой (2) с dV = dx1dx2...dxn. Тогда действительное уравнение с частными
производными (многомерное однородное уравнение Штурма -— Лиувилля)
с функциями р = р(хг, х2 дсл)>0, В (х1, х2, ... , *л)>0, q = q(x1tx2, ..., xn)t
дифференцируемыми на V и 5, определяет самосопряженную задачу о
собственных значениях при однородных краевых условиях вида а-—+ ря|? = 0.
Если заданная область ограничена, то спектр собственных значений указанной
задачи дискретен и содержит не более чем конечное число отрицательных
собственных значений. Если расположить собственные значения в порядке их
возрастания A,j ^ %2 ^ • ••» то &п ~" °° ПРИ п ~~* °°-
(b) В трехмерном случае последняя теорема приложима к задаче о собственных
значениях для дифференциального уравнения
— v2t|3— q(xl, х*, х$) ф = ЯВ (х1, х2, л:*) г|э
с краевыми условиями вида a -~- -j- рф = 0, В>0 и q, дифференцируемыми в V и на S.
Из обобщенной формулы Грина (12) следует
fuLudV=* J [(vw)2 — qu*]dV— J (и yw) • d\. (15.4-28)
V V S
Интегралу (26) во многих приложениях (см. также п. 15.4-7 и табл. 5.6-1) можно придать
физический смысл
15.4-10. Теоремы сравнения (см. также п. 5.6-1, Ь, 14.8-9, с и 15.4-7).
Нижеследующие теоремы сравнения имеют место для дифференциальных
уравнений Штурма—Лиувилля как обыкновенных, так и с частными
производными, определенных в пп. 15.4-8—15.4-9.
Пусть дано некоторое дифференциальное уравнение (24а) или (27) и интер*
вал или область V с краевыми условиями (246) или (24с) ф/a^O); тогда:
1. Возрастание р и q и/или убывание В влечет возрастание
собственных значений К^; аналогично убывание р и q и/или возрастание
В влечет убывание собственных значений.
478 гл. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.4-11.
2. Расширение интервала или области V влечет убывание
собственных значений Хь, порождаемых условиями
г|?(а) = г|?(&) = 0 или ^(xlt х2 хп)=0 на S, (15.4-29а)
и убывание собственных значений %ь> порождаемых условиями
(15.4-296)
аф
яр' (а) = г|?/ (6) = 0 или -^- = 0 на S
3. Каждое собственное значение Хь, порождаемое краевыми
условиями оы|>' (a) + Pt|)(a)==at|)'(&) + Pt|)(6) = 0 или а-Ц-+Рг|э = 0 на
S с (З/а^О, есть неубывающая функция от Р/а. В частности,
условия Неймана (296) не увеличивают собственных значений
сравнительно с условиями Дирихле (29а).
4. Модификации задачи о собственных значениях, усиливающие
ограничения (присоединение условий) на г|э, влекут неубывание
собственных значений.
Теоремы сравнения имеют важное значение для теории колебаний (эффект масс,
жесткость, геометрия натуральных частот).
Примеры (см. также п. 10.4-9): t|)"=—%•$ (х) {колебания струны) и у*Ф (*, У, z) =■
= —Ад|)(*. У, г) (колебания мембраны).
15.4-11. Решение дискретных задач о собственных значениях методами возмущений.
Даны собственные значения %. и ортонормированные собственные функции г|). эрмитовой
задачи
Иэ = Лл|э. (15.4-30)
Требуется аппроксимировать собственные значения Х^ и собственные функции $£
«возмущенной» эрмитовой задачи
L$4-eL'$=ȣ$ (15.4-31)
при неизменных краевых условиях; 8L'$ — малый возмущающий член (г < I).
(а) Р а н г Х- равен 1. Для каждого собственного значения %> невозмущенной
задачи имеем
где
кфС 1
**-*! + « ^ *F^
кф1
+ ..
■*>* +
« = i, 2,...),
Цк-1+№к*У
(/, Лр= 1, 2, .. .).
(15.4-32)
(15.4-33)
(b) P а н г K'L p аве н т. Для каждого собственного значения к* ранга т с
собственными функциями *фх, t|)2, ...t t|?m существуют m различных собственных значений
возмущенного оператора. Соответствующие значения АЛ = (к — А,у)/е аппроксимируются
корнями векового уравнения m-й степени
Lf|-AX L|f
l\ l' — да,
.. L
21
2»
1/Л
b2m
^mm "~ АЯ.
!0,
(15.4-34)
которые могут быть и совпадающими. Собственная функция или собственные функции,
соответствующие каждому значению X = Х* -f* АЛ,, аппроксимируются выражением
4 = 1
15.4-12.
15.4. ЛИНЕЙНЫЕ КРАЕВЫЕ ЗАДАЧИ
479
где ak получены из уравнений
т
V ak (L'ik — 6ik M) = 0, /=1,2 m. (15.4-35)
fe=l
Заметим, что не существует других т собственных функций, кроме указанных
выше, доставляющих аппроксимации Я и гр для случая ранга, большего чем единица;
полученные аппроксимации для ф имеют «нулевой порядок» и не пропорциональны 8.
Относительно приближений высшего порядка см. [5.2].
(с) Изучение непрерывного спектра см. [10.6].
15.4-12. Решение краевых задач посредством разложений в ряды по
собственным функциям (см. также пп. 10.4-2, с, 14.8-10, 15.4-4, 15.5-2; примеры
см. п. 10.4-9).
(a) Очень важный класс физических краевых задач (например, упругие
колебания, электромагнитная теория) относится к действительным линейным
дифференциальным уравнениям — обыкновенным или с частными производными
L Ф (х) — X В (х) Ф (*) = / (х) (х €= V), (15.4-36)
L—-эрмитов оператор (см. п. 15.4-3, Ь), В (х) > 0 в V при заданных однородных
краевых условиях. Если f(x) = 0 в V (нет приложенных сил, токов и т. п.),
то уравнение (36) сводится к дополнительному уравнению
L ф (х) = X В (х) ф (х) (х е= V), (15.4-37)
которое удовлетворяется только собственными или обобщенными собственными
функциями ф (х) со спектральными значениями X. В неоднородном случае (36)
(например, вынужденные колебания) X является заданным параметром.
Рассмотрим сначала задачу (36), при условии, что задача о собственных
значениях (37) имеет чисто дискретный спектр (не обязательно различных)
собственных значений А*, А,2, ... с соответствующими ортонормированными
функциями фх (х), ф2 (х), ... (п. 15.4-6, Ь). Предполагая, что «вынуждающая
функция» может быть разложена в ряд
оо
f(x) = B(x) J] fk%(x) (fk=\qkfdV, *=1, 2, ...\ (15.4-38)
k=\ \ V J
для почти всех х е V, можно ожидать, что решение уравнения (36) имеет
вид «разложения по главным колебаниям»
оо
фМ = ХтГ^Г+'М- (15.4-39)
в среднем *d Nk л
k=i I
Ряд (39) определяет решение Ф (х) однозначно в каждой точке непрерывности,
если только параметр X не равен некоторому собственному значению Xk
(резонанс!). В последнем случае решение существует, лишь когда f(x)
ортогонально ко всем собственным функциям, принадлежащим Xk, так что /^ = 0.
Тогда существует бесконечное количество решений, состоящих из ряда (39)
плюс линейная комбинация собственных функций, принадлежащих Xk.
(b) Если краевая задача (37) обладает чисто непрерывным спектром DA
с обобщенными собственными функциями ф (х, X), имеющими свойство
ортогональности (\9Ь) (например, оператор Штурма — Лиувилля имеет особенности
в V, или же V неограничена), то возможно представить решение Ф (л:) как
«обобщенный интеграл Фурье» по (необходимо действительному) спектру DA,
430 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.5-1.
Имеем тогда почти для всех х е V
Ф(*)= \ Я(ЛЖ*. Л)<*Л, //(Л)--^ \^TK)f(l)dV (15.4-40)
(см. также п. 10.5-1, методы интегральных преобразований).
Если задача о собственных значениях (37) имеет как дискретный, так и
непрерывный спектр, то решение будет содержать члены вида (39) и
интеграл (40); оба типа членов могут быть объединены в интеграл Стилтьеса по
спектру.
(с) Методы решений пп. 15.4-12, а и 15.4-12, b могут быть применены
и тогда, когда данный оператор L не эрмитов, если только доказано
существование соответствующих ортонормированных разложений по собственным
функциям.
15.5. ФУНКЦИИ ГРИНА. СВЯЗЬ КРАЕВЫХ ЗАДАЧ И ЗАДАЧ
О СОБСТВЕННЫХ ЗНАЧЕНИЯХ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ
15.5-1. Функции Грина для краевой задачи с однородными краевыми
условиями (см. также пп. 9.3-3, 9.4-3, 15.4-4; примеры см. в табл. 9.3-1, пп. 15.6-6,
15.6-9).
(а) Линейная краевая задача
LQ)(x) = f(x) (*€=!/), (15.5-1а)
В;Ф(л:) = 0 (i=l, 2, ..., N; xezS) (15.5-16)
представляет данную функцию f (х) как результат линейной операции над
неизвестной функцией Ф (х), удовлетворяющей заданным краевым условиям.
Если возможно записать соответствующую обратную операцию в форме
линейного интегрального преобразования (п. 15.3-1)1)
Ф(*)= $<?(*. t)f(t)dV(t) (15.5-2)
для каждой возможной функции f(x), то ядро G(x, £) называют функцией
Грина для данной краевой задачи (1).
G(x, £) должна удовлетворять однородным краевым условиям (Щ вместе
с условиями
LG(x, £) = 0 (*, l<z=V; хф%), \
\LG(x, I) dV (I) =1 (х €= V) \ (15.5-За)
или
LG(x, 6) = в(*. I) (*, £е= V), (15.5-36)
где 6 (х, £) есть дельта-функция в системе координат, в которой поставлена
краевая задача (п. 21.9-7).
Формула (2) представляет решение Ф (х) краевой задачи (1) как суперпозицию
элементарных решений G (х, £)/(£), имеющих особенность при * = |. Эти элементарные
решения могут быть интерпретированы как эффект импульсных сил, точечных зарядов
и т. д., f (Ъ) 6 (х, |) в точке * = £ (см. пп. 9.4-3, 15.5-4, 15.6-6, 15.6-9). Функция Грина
часто может быть найдена непосредственно интегрированием «символического
дифференциального уравнения» (ЗЬ) с данными краевыми условиями методами, указанными
в пп. 9.4-5, 10.5-1, 15.4-12. См. табл. 9.3-3, пп. 15.6-6 и 15.6-9, где даны примеры функций
Грина.
1) В одномерном случае dV =dx.
15.5-2.
15.5. ФУНКЦИИ ГРИНА
481
(b) Модифицированная функция Грина (см. также п. 15.4-4). Краевая
задача (1) не имеет функции Грина, удовлетворяющей уравнению (3), если эрмитово
сопряженная краевая задача
L*X(*) = 0 (x*=V). B/XW = 0 U£S)
(15.5-4)
имеет решение %{х), отличное от % {х) г= 0 (см. п. 15.4-4). В этом случае тем не менее
возможно построить модифицированную функцию Грина G (х, £), доставляющую
представление (2) для всех f (*). ортогональных к х (*)• G (х, I) должна удовлетворять уравнению
L G (х,1) = 6 U, I) - ^ *0Л <S) X0k <*>
/е=1
(15.5-5)
и краевым условиям (\Ь). Здесь х0ь (*) есть полная ортонормированная
последовательность решений задачи (4). В рассматриваемом случае результирующее решение (2) не
может быть единственным, однако существует единственная модифицированная функция
Грина, которая удовлетворяет дополнительным условиям ортогональности
J Х0Л (6) С (ж, l)dV(l)=0 (/e = l, 2.
.)•
(15.5-6)
Если L — эрмитов оператор, то % . суть просто его собственные функции для к == 0.
(с) Функции Грина для эрмитово сопряженных краевых задач (п. 15.4-3, а)
являются эрмитово сопряженными ядрами (п. 15.3-1, Ь). Для каждой функции
Грина G(x, £), принадлежащей эрмитову оператору L (п. 15.4-3), G(f, х)~
= <?<*.£)-
15.5-2. Связь краевых задач и задач о собственных значениях с
интегральными уравнениями. Резольвента Грина.
(а) Если существует функция Грина G(x, £) краевой задачи (1), то из
формулы (2) следует, что общая краевая задача
LG>(x)-\B(x)0(x) = f(x) (x€EV), J
BiQ)(x) = 0
(t=l, 2,
N\ jce5)
эквивалентна линейному интегральному уравнению
Ф(*)-Х$/С(*. t)®(l)dl = F(x), }
(15.5-8)
Заметим, что интегральное уравнение включает в себя заданные краевые
условия. В одномерном случае dV (£) = dl и | g (g) | ~ 1.
Полученное интегральное уравнение распространяет теорию пп. 15.3-1 —
15.3-9 и численные методы п. 20.9-10 на линейные краевые задачи и задачи
о собственных значениях. В частности, можно использовать ряды Неймана
(15.3-23) и аналитическое продолжение для введения резольвентного ядра
(п. 15.3-7, с) Г (х, £; X) так, что решение принимает форму
(15.5-9)
<t>(x) = F(x) + X lF(x, l\ X)F(E)d£-
Г (*; £; X) называют резольвентой Грина; она является ядром линейного
преобразования, представляющего резольвентный оператор (L — X)"1 (п. 14.8-3, d).
Г (х, £; К) часто можно построить методами п. 15.3-8; следует отметить, что
ядро К (х, £) не необходимо должно быть нормируемым. Множество особых
точек X функции Г (х, |; К) совпадает со спектром оператора L(n. 15.4-5, d),
который может включать и непрерывный спектр. В частности, полюсы Г (х, £; X)
соответствуют дискретным собственным значениям L, тогда как точки
разветвления указывают на наличие непрерывного спектра (см. 15.2).
16 Г. Корн и Т. Корн
482
ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
15.5-3,
(Ь) Задачи для эрмитовых операторов. Разложение
функции Грина по собственным функциям (см. также п. 15.3-3,
15.3-4, 15.4-6, 15.4-12).
В важном частном случае, когда L —эрмитов оператор и В (х)
действительна и положительна в V, можно ввести новую неизвестную функцию
Ф(*)-Ф(*)/Д (*)]/]*(*) |
(15.5-10)
и заменить уравнение (8) линейным интегральным уравнением с эрмитовым
ядром
Ф(х)-%{К(х, I) <Б(Э<*Б-/Ч*).
R(x, E)«G(*. l)V B(x)B(t)V\g(x)g&)\,
F(x) = Vb(x)V\7(xT\JG(x9 Df{l)dV(l). J
(15.5-11)
Эрмитова задача о собственных значениях
L -ф (х) = X В (х) г|) (*) (*е V),
B,i|>(*)-0 </-!, 2, ..., N; *<
IS) )
и интегральное уравнение
9 (х) - X \К (х, I) $ (£) d\
V
(15.5-12а)
(15.5-12&)
имеют идентичный спектр; соответствующие собственные функции ф (х) и tf (x) связаны
соотношением tj? (х) =г|) (х) V В (х) Y | g (x) \ • Если спектр собственных значений чисто
дискретный, то существует полная последовательность собственных функций ify (x) и
ф,« (л:) так, что
(15.5-13)
В этом случае /С (х, £) есть нормируемое ядро и
оо
1
G (х, I) - V т- *А (&> ** <*> (АГ» S S V).
в среднем .", Л
(15.5-14)
Последнее выражение не содержит явно В (х) или g (x). В случае задачи Штурма—Лиу-
вилля с чисто дискретным спектром (пп. 15.4-8, а и 15.4-9) ряды (14) сходятся абсолютно
и равномерно в V (см. также теорему Мерсера п. 15.3-4).
(с) Если данная краевая задача (7) выражается в терминах дифференциальных
инвариантов (п. 16.10-7), то G (х, |), К{х, I) и К (х, |) являются функциями точки,
инвариантными относительно преобразований используемой системы координат.
15.5-3. Приложение метода функций Грина к задаче с начальными условиями:
обобщенное уравнение диффузии (см. также пп. 10.4-7, 10.5-3, 10.5-4). Требуется найти
решение Ф ■■ Ф (х, t) задачи
V dt ' Л"' '" \ (*€=V) (15.5-15)
"fix,*), \
} {Xi
Ф (*, 0) — Ф» (х)
с заданными константами а*, Ь и однородными краевыми условиями Ф = 0 или дФ/дл = 0
иа границе данной я-мерной области V, л = 1,2 или 3. Имеем
t
Ф t*, О - J J 0 {х, t; I, т) / (1, т) dx dV (1) - a* J G (*, t; g. 0) Ф0 (|) dV (I) (/ > 0),
OV V
(15.5-16)
15.5-4.
15.5. ФУНКЦИИ ГРИНА
483
где G (х, t\ \, х) — функция Грина, удовлетворяющая заданным краевым условиям,
v,0 _ а> ™ _ bG - 6 U. *,« , - .„ . ^ VK (l5>5_l7)
>(*, |)6<*-T), \
G=*0 (/ < т)
Если фЛ (jc) hL- соответственно собственные функции и собственные значения
пространственного волнового уравнения
V2t|) (х) + Лд1> (*) =0 (х£ V) (15.5-18)
при заданных краевых условиях (пп. 10.4-4 и 10.4-5, Ь), то
G (jr. /; 6, T) - - -^ 2j ' Я ** <6> *A (*> (' > T)* (15.5-19)
k
Если l/ совпадает со всем пространством, то
G {x, t; I, x) =
-1Л/2 j
=-[^^Г^-[-т^^-^<—] о*-.».*.
(15.5-20)
где | г — о I — расстояние между точками (х) = (г) и (£) = (о).
Результирующее решение (16) известно как интегральное решение Пуассона задачи
о диффузии.
15.5-4. Метод функций Грина для неоднородных краевых условий (см.
также п. 15.4-2).
(а) Решение Ф (х) трехмерной линейной краевой задачи
LO(*)«0 (*еУ). ВО(*) = &(*) (*e=S) (15.5-21)
часто может быть записано в форме поверхностного интеграла
0(*)-JGs(*. l)b(l)dA(l) (15.5-22)
для каждой заданной функции Ь (х), интегрируемой на S. Gs(xt £) должна
удовлетворять данному дифференциальному уравнению при х е V, £ e 5 и
BGs(x, £) = 0 (х, |eS; хФ1)9)
:1# f (15.5-23)
\BGs(x, t)dA(D-
Gs (x, £) называют либо функцией Грина второго рода, либо просто функцией
Грина (см. также п. 15.6-6). Аналогичные соотношения имеют место и в
двумерном случае (см. также п. 15.6-9). Линейные краевые задачи для
неоднородных дифференциальных уравнений, так же как и при неоднородных
краевых условиях, могут быть часто решены суперпозицией объемного (2) и
поверхностного (22) интегралов.
(Ь) Как указано в п. 15.4-2, каждая краевая задача (21) может
рассматриваться как краевая задача типа (1). Отсюда следует, что Gs(xt £)
может быть выражена через обычную функцию Грина G(x, £), определенную
способом п. 15.5-1 для задачи с «дополнительными» однородными краевыми
условиями. В частности, рассмотрим двумерную и трехмерную краевую задачу
для действительного самосопряженного дифференциального уравнения вида
LO (х) = -[V*+q] О (*)=0 (х е У), (15.5-24)
где q~q (х) — действительная дифференцируемая функция. Если G (л:, £) —
функция Грина, удовлетворяющая уравнению
-PH-dOl*! Е)-в(др, |) (15.5-25)
16*
484
ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
16.6-1.
при заданных однородных краевых условиях (п. 15.5-1), то формула Грина
(15.4-12) дает
Ф<*) = $ [<?(*, Й^-Ф©^]^Й) (*esV), (15.5-26)
где символ d/dv обозначает производную по нормали. Отсюда для краевых
условий вида
B(D(*)^<I>U) = M*) (*e=S) (15.5-27)
(т. е. для условий Дирихле) решение (22) приводит к соотношению
Gs(x, E) = -2£^i> ffieS)t (15.5-28)
где G (#, £) удовлетворяет в V уравнению (25) и обращается в нуль на 5.
Для краевых условий (задача Неймана)
ВФ(х)-°£ = Ь(х) (*e=S) (15.5-29)
решение (22) дифференциального уравнения (24) сводится к использованию
«функции Неймана»
Gs(xt E) = G(*. I) ffi e= 5), (15.5-30)
где G(x, l) удовлетворяет уравнению (25) в V и dG (x, g)/d/i = 0 на 5.
В пп. 15.6-6 и 15.6-9 указаны приложения этих соотношений при решении краевых
задач для эллиптических дифференциальных уравнений. В п 10-3-6 показан сходный
метод при решении задач с начальными значениями для уравнений гиперболического типа
(см. также п. 10.3-5).
15.6. ТЕОРИЯ ПОТЕНЦИАЛА
15.6-1. Введение. Дифференциальные уравнения Лапласа и Пуассона (см.
также п. 5.7-3, 10.4-3 и 10.4-5). Многие важные приложения связаны с
решением Ф (г) линейных уравнений с частными производными:
уравнения Лапласа
?2ф(г) = 0, (15.6-1)
уравнения Пуассона
V2 0(r) = — 4nQ(r), (15.6-2)
где Ф(г) и Q (г) — функции точки в трехмерном точечном евклидовом
пространстве (г) == (л:, у, z) =• (л:1, х2, х3) или двумерном точечном евклидовом
пространстве (г) =s (л:, у)&=(х1% х2), Ф (г) часто интерпретируется как
потенциал безвихревого векторного поля
Р(г) = ?Ф(г),
порождаемого распределением зарядов или масс, так что V • F (r) = 4rcQ (г)
(пп. 5.7-2, 5.7-3, 15.6-5). Изучение таких потенциалов и, в частности,
решений дифференциального уравнения Лапласа (1) известно как теория
потенциала.
15.6-2. Трехмерная теория потенциала. Классические краевые условия задачи.
(а) Задача Дирихле. Ограниченная область V, допускающая
решение краевой задачи (Дирихле)
У2ф(г) = 0 (ге1/), Ф(г) = Ь(г) (rsS) (15.6-3)
для всякой заданной непрерывной функции Ь (г), называется областью
Дирихле. Если решение существует, то оно необходимо единственно. Если V —
неограниченная область, то должно быть указано асимптотическое поведение
15.6-4.
15.6 ТЕОРИЯ ПОТЕНЦИАЛА
4Я5
решения на бесконечности, скажем, ф(г) = 0(1/г) (при г—* оо; последнее
условие влечет единственность решения в случае его существования. В п. 15.6-6, d
обсуждаются вопросы существования решения.
Решение Ф (г) задачи Дирихле (3) доставляет стационарное значение интегралу
Дирихле | {yQ>)*dVt где Ф (г) предполагается дважды непрерывно дифференцируемой в V
V
и на 5 и удовлетворяющей данным краевым условиям (см. также п. 15.4-7, а). Задача
Дирихле имеет особую важность для электростатики (см. п. 10.4-5).
(Ь) Задача Неймана. Для второй классической краевой задачи
(Неймана)
ГФ(г) = 0 (resV), ^ = М0 (rsS), (15.6-4)
где Ь (г) — данная непрерывная функция; существование решения требует
выполнения условия \b (r)dA—0 (см. также теорему Гаусса, табл. 5.6-1).
S
Если V — неограниченная область, то для существования решения необходимо
ф (г) = 0(1 /г) и дФ/дп = 0(\/г2) при г—* со. Решение задачи Неймана в
ограниченной области V единственно с точностью до аддитивной постоянной.
Задача Неймана возникает, в частности, при изучении течения несжимаемой
жидкости (см. п. 10.4-5).
15.6-3. Теорема Кельвина об инверсии. Если Ф (г) есть решение дифференциального
уравнения Лапласа в некоторой области V, лежащей внутри сферы | г — а | == R, то
функция
• <г> - тг=тт ф [n^TF(r -а> +а] <15-6'5)
есть решение уравнения Лапласа в соответствующей области, лежащей вне сферы, и
обратно.
В сферических координатах г. б, <р это означает, что если Ф (г, 0, ш) есть решение
R / R2 \
при '<#, то — Ф( —, б, ф) есть решение при г > R, и обратно.
Отсюда следует, что так называемая внешняя краевая задача
V2 Ф (г) = 0 (г вне V),
а ~ + РФ = Ь (г) <re=S).
Ф(г) = 0(—-) при г -* со
(15.6-6)
для ограниченной области V может быть преобразована в соответствующую краевую
задачу для внутренней области V, полученной из V посредством преобразования
инверсии
?- а = ! г *\ [« <г - а>- <15-G-7>
15.6-4. Свойства гармонических функций.
(а) Теоремы о среднем значении и максимуме
модуля. Решения Ф(г) уравнения Лапласа (1) называют гармоническими
функциями. Каждая функция Ф (г), гармоническая в открытой области V,
аналитична (п. 4.10-5, Ь) и имеет в V гармонические производные любого
порядка. Каждое значение Ф (гг) равно среднеарифметическому (п. 4.6-3)
значений Ф (г) на поверхности (а отсюда и по объему) сферы с центром в точке
г = гх в предположении, что сфера содержится внутри области V (теорема
о среднем значении). Обратно, непрерывная функция Ф (г) является
гармонической в каждой открытой области, в которой выполняется свойство среднего
значения.
Функция Ф(г), гармоническая внутри ограниченной области V и на ее
границе S, не может иметь максимума или минимума внутри V (теорема
486 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.6-Б.
о максимуме модуля, см. также п. 7.3-5). Если Ф (г) —гармоническая в V,
непрерывна в V и на 5 и равна нулю на S, то Ф(г) = 0 в V. Если Ф (г) —
гармоническая в V, непрерывно дифференцируема в V и на 5 и дф/дл = 0
на S, то Ф (г) постоянна в V. Теорема об инверсии п. 15.6-3 доставляет
аналогичные теоремы для неограниченной области V вне S.
(Ь) Теоремы Гарнака. Следующие ниже теоремы интересны в связи с
аппроксимацией гармонических функций.
Если последовательность s0 (г), st (г), s2 (г), ... функций, гармонических в V и
непрерывных на границе S области V, равномерно сходится на S, то эта
последовательность сходится равномерно в V к некоторой функции s (г), гармонической в V и такой,
что s (г) = lim s (г) на S. Последовательность частных производных от функций s (г)
п-+со п п
сходится равномерно к соответствующей частной производной s (г) в каждой замкнутой
подобласти V (первая теорема Гарнака).
Пусть дана последовательность функций s0 (г), st (г), s2 (г), .... гармонических в V
и таких, что s0 (г) ^ st (г) ^ s2 (г) ^ ... для всех г в V. Из сходимости этой
последовательности в некоторой точке V следует сходимость последовательности всюду в V и
равномерная сходимость в каждой замкнутой подобласти V; предел данной
последовательности есть функция, гармоническая в V (вторая теорема Гарнака).
15.6-5. Решения уравнений Лапласа и Пуассона как потенциалы.
(a) Потенциалы точечного заряда, диполя имульти-
п о л я. Следующие ниже частные решения уравнения Лапласа имеют
особенно простую физическую интерпретацию:
потенциал единичного точечного заряда в точке (р) ss (|, г], £):
фо(г-р)^ . 1 . шв— 1 (г^Ёр); (15.6-8)
потенциал единичного диполя, направленного вдоль единичного вектора их
в точке (р):
<Pi(r-p) ^-(Ui • V) Фо (r-р) (г Ф р). (15.6-9)
Более общо, потенциал мультиполя порядка / в точке р = 0:
Oy(r) = (-iy(pyV)(py^.V)...(p1.V)^(r)-
i+k+i=/ ox oy oz
где так называемые компоненты момента мультиполя Qfj^ суть константы,
определяемые посредством / векторов pl9 p2 ру, образующих мультиполь.
В сферических координатах г, б, ф имеем
ф/(г)=7^МЯ=7^7>(ф' 6) (г^0)' (15'6"П)
где Уу(ф, б) —сферическая функция /-го порядка (п. 21.8-12). Мультиполи
второго и третьего порядков известны под названием соответственно квадри-
поля и октиполя.
(b) Потенциалы распределений зарядов. Соотношения
для разрывов. Другие частные решения уравнения Лапласа получаются
линейной суперпозицией (или интегрированием) простых потенциалов и
потенциалов диполей. В частности, представляют интерес объемные потенциалы
распределений зарядов и диполей
$С(р)Фо(г-р)^(р)=5т^т^1/(р), (15.6-12)
- $ [р (Р) • V] фо (r-р) dl/ (P) = — J [Р (Р)' V] —±—dV(9) (15.6-13)
V V
15.6-5.
15.6. ТЕОРИЯ ПОТЕНЦИАЛА
487
и потенциалы поверхностных распределений зарядов и диполей (потенциалы
простого и двойного слоев)
\o(9)^(r-9)dA(p)=\-^jdA(9), (15.6-14)
-Jp(p)[rfA(p).VJ4)0(r-p) = -Jp(p)^£M(pH
— S^(P)K(7r=oT)**(P)- <15(М5>
о
Потенциалы одномерных распределений зарядов (линейные интегралы) представляют
интерес главным образом в двумерной теории потенциала (п. 15.6-7).
Если плотность зарядов Q (г) ограничена и интегрируема в V, то простой объемный
потенциал (12) и все его производные существуют и равномерно непрерывны при всех г;
производные могут быть получены дифференцированием под знаком интеграла.
Потенциал удовлетворяет уравнению Пуассона (2), если Q (г) ограничена и непрерывно
дифференцируема. Если функции поверхностной плотности а (г) и р (г) дважды
дифференцируемы на 5, то:
1. Потенциал простого слоя (14) непрерывен в каждой регулярной точке г0
поверхности 5. То же самое имеет место для производной оФ/ot в некотором направлении,
касательном к S в точке г0; однако производная дФ/дп вдоль нормали к S в точке г0
претерпевает разрыв, причем
дФ~\ дФ1
!*J+—«г]-"-4"0™' <15-6-16)
Здесь индексы + и — указывают соответствующие односторонние пределы, когда г -*> г»
по положительной или отрицательной стороне нормали к S.
2. Разрывы потенциала двойного слоя (15) и его касательных производных
удовлетворяют соотношениям
Ф+ (го) - Ф (Го) - Ф (го) - Ф- (Го) = 2яр (г0), (15.6-17)
дФ]
dt
1 дФ1 дФ1 дФ1 _ др „** .л
J+-wJr=r.= arUr.-*i-2"ar (15<И8>
в каждой регулярной точке г0, принадлежащей £, в которой нормальная производная
дФ/дп непрерывна.
Замечание. В частном случае, когда р (г) = р, потенциал двойного слоя (15)
равен умноженному на р телесному углу с вершиной в точке (г); этот угол принимается
положительным, если точка (г) расположена на положительной стороне нормали к 5.
Для замкнутой поверхности S потенциал равен —4лр, если (г) внутри 5, и равен нулю,
если (г) находится вне 5.
(c) Разложение по мультиполям и теорема Гаусса.
Рассмотрим потенциал Ф (г), порождаемый некоторой комбинацией распределений зарядов,
заключенных в ограниченной сфере j г | ^ R; пусть Q-р — конечный общий заряд. Ф (г)
является линейной комбинацией потенциалов типа (12)—(15); для | г | > R можно
разложить Ф (г) в ряд Тейлора (5.5-4) с членами (10) или в ряд по сферическим функциям (11).
Для достаточно больших г потенциал таким образом последовательно аппроксимируется
потенциалом точечного заряда Qf, расположенного в начале, потенциалом точечного
заряда плюс потенциал диполя и т. д. (разложение по мультиполям). Для каждой
регулярной поверхности, заключающей внутри себя распределение зарядов, теорема Гаусса
(табл. 5.6-1) принимает специальный вид
^ dA-уФ = J ^ dA = - 4я<?7\ (15.6-19)
(d) Общие решения уравнений Лапласа и Пуассона
как потенциалы. Пусть V — односвязная, ограниченная или
неограниченная трехмерная область с регулярной граничной поверхностью 5, и пусть
Ф(г) дважды непрерывно дифференцируема в V и непрерывно дифференци-
4S8 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.6-6.
руема на 5; Ф(г) = 0(1/г) при г —оо. Тогда теорема Грина (табл. 5.6-1 или
п. 15.4-3, с) позволяет представить Ф(г) в форме
Ф («-) = 47Г $ 1Ф» (г-Р) ?р Ф (Р)] • <** (р) -^ J [Ф (р) Vp Фо (r-p)j • d\ (p)-
~ш W» <Г_Р)va ф (р> dK (Р> (г е V)' (15-6-20а)
q'oCr-pJ^jT^T. (15.6-206)
где Vp означает дифференцирование по компоненте р; заметим, что Vp(p0(r—р)=
= ^фо(г — р). Формула (20) выражает любое решение Ф (г) уравнения
Пуассона (2) как потенциал, порожденный тремя распределениями:
1. Распределения простого слоя (14) с плотностью
1 уФ0-^А _ 1 0Ф
4я </Л 4я д/г*
2. Распределения двойного слоя (15) с плотностью
3. Объемного распределения (12) с плотностью
-4^*Ф = <2(Г).
Последний потенциал равен нулю, если Ф (г) удовлетворяет в V
уравнению Лапласа (1).
Замечание. Выражение (20а) обращается в нуль, если точка г находится вне V,
и равно Ф (г)/2 для точек г, принадлежащих поверхности 5.
15.6-6. Решение трехмерных краевых задач посредством функций Грина.
Метод функций Грина пп. 15.5-1 и 15.5-4 позволяет выразить решение Ф (г)
задачи Дирихле (3) и задачи Неймана (4) для подходящих областей V в форме
поверхностных интегралов
Ф(г) = $С5(г, 9)b(9)dA(p). (15.6-21)
В п. 15.5-4,b указана связь между «поверхностной» функцией Gs(r, p)
Грина и обычной функцией Грина С? (г, р), доставляющей решение
ф(г) = 4л $ О (г, p)Q(p)dV(p) (15.6-22)
V
уравнения Пуассона (2) при «дополнительных» однородных условиях Дирихле
или Неймана. Суперпозиция решений (21) и (22) доставляет решение
уравнения Пуассона с заданными граничными значениями Ь (р) функции Ф или
дФ/дп (п. 15.4-2). Заметим, что G (р, г) == G (г, р) (п. 15.5-1). Функции Грина
легко найти в следующих частных случаях (заметим, что положительное
направление нормали идет вне замкнутой поверхности).
(а) Функция Грина для всего пространства. Если V
есть все трехмерное пространство, то формула (20) доставляет единственное
решение (22) уравнения Пуассона при «краевом условии» Ф(г) = 0(1/г) при
г —* со. Соответствующая функция Грина есть
G(r'P) = iS^l = 4Uo(r-p) О5'6"23*
(см. также п. 5.7-3).
15.6-в.
15 6, ТЕОРИЯ ПОТЕНЦИАЛА
489
(b) Полупространство с условиями Дирихле. Если V —
полупространство г > О, то функции Грина для условий Дирихле имеют вид
(?(г'Р) = г(г-4т-Т7^Тт) = ^'(")»(г-Р)-Ч'о(г-р)], (15-6-24)
G (г, p) = -^ = |£"L = * —, (15.6-25)
где точка (р) = (|, т], —£) есть зеркальное отражение точки (р) s g, r\, £)
в граничной плоскости. Решение (22) может быть интерпретировано как
объемный потенциал, порождаемый данным зарядом и индуцированным им
зарядом в точке (р); решение (21) выражает влияние неоднородных условий
Дирихле в виде потенциала двойного слоя, расположенного на границе.
(c) Сфера с условиями Дирихле. Интеграл Пуассона.
Если V есть внутренность сферы |г| = /?, то функции Грина при условиях
Дирихле имеют вид
6(г* Р) = 4я ГГ^^Т~7Г^
Г2
= ^[фо(г-р)-7Фо(^г~р)]( (15.6-26)
J г» — R*
4я R {Г2 + д2 _ 2Rr cos y)3/j '
Г l \— d-G — д&\ — J га — fl2 ПК К 97\
где у ~ Угол между г и р, или
cos y=cos 6 cos 6' +sin б sin 6'cos((p — ф'), (15.6-28)
если сферические координаты точек (г) и (р) обозначены соответственно
через г, б, ф и р', б', ф'. Второй член в формуле (26) можно рассматривать
как эффект индуцированного заряда, симметричного данному относительно
сферы в соответствии с теоремой Кельвина об инверсии (п. 15.6-3). Решение
(21) задачи Дирихле
V2(D(r, 8, ф) = 0 (r<R)t Ф|г = я = &(е, <р)
имеет вид
Ф(г, б, ф) =
2я
(Д2 + Г2 _ 2Rr cos y)3/2 Пуассона)
R (R* — г*) с ,, с Ь (9', <р') sin 6" dv {интегральная формула /1К ~ огл
3 d(p i rp.4.r.-2i?rco^V, Пуассона) {15Л-23)
и может быть интерпретировано как потенциал двойного слоя.
Выражение (27) может быть разложено по сферическим гармоникам в
соответствии с (21.8-68) (разложение по мультиполям, п. 15.6-5, с, см. также
п. 10.4-9). Формулы (26) —(29) доставляют решения для внутренности сферы
(r<R). Если V—внешность сферы (/->/?), С? (г, р) также дается формулой
(26), однако теперь
G (г о) *G<r.Q)_aO(rtQ)1
^Sl^PJ — dv - dp Jp=*'
так что знаки правых частей формул (27) и (29) должны быть изменены на
обратные.
(d) Теорема существования. Функция Грина G (г, Q) уравнения Пуассона
с условиями Дирихле и, следовательно, решение задачи Дирихле с разумными краевыми
условиями существует для каждой об гости, ограниченной конечным числом кусков
регулярных поверхностей, каждая точка которых может быть вершиной тетраэдра,
расположенного вне V»
490 ГЛ 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 1S.6-7.
15.6-7. Двумерная теория потенциала. Логарифмический потенциал.
(a) Во многих трехмерных задачах теории потенциала функция Ф (х, у, г)
не зависит от координаты г и V есть прямой цилиндр, граничная
поверхность 5 которого пересекает плоскость Оху по некоторой линии С (например,
потенциал и течение вблизи бесконечного цилиндра, плоские границы). Эти
задачи составляют содержание двумерной теории потенциала.
Теорема о дивергенции и теорема Гаусса принимают вид (4.6-33);
используя прямоугольные декартовы координаты дг, у или плоские полярные
координаты г, ф, можно записать уравнение Лапласа в виде
™-E+S-7*('S)+£S-0' О5-6'*»
уравнение Пуассона —
m-a*+1F"7*Vr ■д7) + 7*-д& = -2л(1> (15.6-31)
где Ф = Ф (г), Q = Q (г), г =з (х, у) в (г, ф).
На двумерные гармонические функции полностью переносятся теоремы
п. 15.6-4; следует только в теоремах о среднем значении заменить сферы на
окружности. Формула Кельвина (5) имеет место для каждой окружности
|г — а|=/?; таким образом, если Ф (г, ф) есть решение для /■<#, то
7'Ф(т"» ^J есть Решение Для г>/?, и обратно.
(b) Двумерное уравнение Лапласа (30) имеет элементарное решение,
называемое логарифмическим потенциалом точечного источника в г = р,
t|?0 (r-p) = In г—Цг7 —In l , (15.6-32)
которое описывает потенциал равномерно заряженной прямой линии в
направлении оси г. Функция (32) играет роль функции (8) в двумерной теории так,
что потенциалы (12), (14) и (15) из п. 15.6-5 заменяются соответствующими
логарифмическими потенциалами
$ Q(p)*>(r-p) A4(p)-$ Q(9)\nj^—dA (p), (15.6-33)
D D
$ a(p)*i(r-p)rfe(p)-Ja(p)lnfF437*(P). (15.6-34)
с с
— $Р(Р)Ж Л <р)— $Р (Р)^InT77iT[ ds(p). (15.6-35)
с с
Уравнение (20) заменяется на
С
Заметим, что
Д^лад..*^^--^*. (15.6-37)
15.6-8. Двумерная теория потенциала; сопряженные гармонические функции
(см. также пп. 7.3-2 и 7.3-3).
(а) Плоскость Оху может рассматриваться как комплексная числовая
плоскость с точками г—x+iy. Пара (необходимо гармонических) функций
15.6-8.
15.6. ТЕОРИЯ ПОТЕНЦИАЛА
491
Ф (*, у) и W (х, у) называются гармонически сопряженными в области D
плоскости Оху тогда и только тогда, когда функция
5 = Ф(*, y) + (V{x9y)
есть аналитическая функция от z=x+iy в области D.
Сопряженные гармонические функции связаны уравнениями Коши —Ри-
мана
и определяют одна другую всюду в D с точностью до аддитивной постоянной.
Если дана функция Ф (х, у), гармоническая в D, то ¥ (*, #) выражается
криволинейным интегралом
*(*.*)= У (-|f^+^^> (15.6.39а)
где *0 и ^ — произвольные постоянные, а путь интегрирования расположен
внутри D. Если дана ЧГ (#, #), то имеем
(х, у)
ф <*•*>= 5 UF^-W^)' (15.6-396)
Линии Ф(#, #) = const и Y (#, #) = const образуют взаимно ортогональные
семейства. Эти линии имеют важную физическую интерпретацию
{эквипотенциальные линии и линии градиента в электростатике, линии уровня
потенциала скоростей и линии тока для несжимаемых течений).
Н часто называют комплексным потенциалом.
(b) Каждое преобразование
z=z(z) (z=x + iy, z = x+iy), (15.6-40)
аналитическое в V и такое, что dz/dz Ф 0 в V (конформные отображения,
п. 7.9-1), преобразует сопряженные гармонические функции Ф(#, у), ЧГ (х, у)
в сопряженные гармонические функции Ф (х, у), ЧГ (х, у) с взаимно
ортогональными линиями уровней. Эта теорема позволяет упрощать граничные
линии и линии уровня посредством конформных отображений (см. также
п. 15.6-9).
(c) Пусть Ф (х, у) есть решение задачи Неймана
V2¥= 0 (в Я), -—■ »Ь (*, у)=Ь (s) (на С) (15.6-41)
так, что Ф(*, у) и ее производные непрерывны на С и, следовательно, в D. Тогда
функция (396), комплексно сопряженная функции W (jc, #), есть решение задачи Дирихле
у8Ф =» 0 (в D), Ф (*, у) = В (jc, #) = В (s) (на С), (15.6-42)
где
1~ » — ^ (на С) или В (s) — — \ Ь (s) ds -f const. (15.6-43)
Решение Ф (*, у) задачи Дирихле (42) аналогичным образом доставляет решение (39а)
задачи Неймана (41), если только
- ф Ь (s) ds = § Щ- ds = 0. (15.6-44)
С С
так, что теорема Гаусса выполняется (см. также табл. 5.6-1 и п. 15.6-5, с).
492 ГЛ. 15. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 15.6-9.
15.6-9. Решение двумерных краевых задач. Функции Грина и конформные
отображения (см. также пп. 15.5-1, 15.5-4, 15.6-6). Методы функций Грина
пп. 15.5-1 и 15.5-3 позволяют выразить решение Ф (г) уравнения Пуассона (31)
с однородными линейными краевыми условиями в виде
Ф (г) = \G (г, р) Q (р) dA (p) (15.6-45)
D
и решение Ф(г) уравнения Лапласа (30) с данными краевыми значениями
Ь (г) функции Ф или дФ/дп в виде
Ф (г) = $ Gs (г, р) Ь (р) ds (p). (15.6-46)
G
Решение уравнения Пуассона при неоднородных линейных краевых условиях
может быть получено суперпозицией интегралов вида (45) и (46). Заметим,
что С? (г, р) = (?(р, г).
Функции Грина легко находятся в нижеследующих специальных случаях.
(a) Функция Грина для всей плоскости. Если D — вся
плоскость, то формула (36) доставляет единственное решение (45) уравнения
Пуассона при «краевом условии» Ф(г)—* 0 при г-* со. Соответствующая
функция Грина есть
G(r>p)=JrlnlT^J. (15.6-47)
(b) Полуплоскость с условиями Дирихле. Если D —
полуплоскость *>0, то функции Грина для условий Дирихле имеют вид
г^(Г-р,_^(г-р)]-±1„ glg + glg, (15.6-48)
где точка (р) == (— £, г\) есть зеркальное отражение точки (р) === (£, х\) в
граничной линии.
(c) Окружность с условиями Дирихле. Интегральная
формула Пуассона. Если D есть круг г < /?, то функции Грина для
условий Дирихле имеют вид
. R* + ГА£г - 2rp cos «p - <р')
°<г. р>=^1п г.+;;.-»рсо,(ф-ф')' (15-6-5°)
"Sl^P/—"av др\р =R~2nR fl2+r'-2tfr cos«p—q>') • I10-0"131)
где p', ф'—-полярные координаты точки (р).
Решение (45) задачи Дирихле
?2ф(г ф) = 0 (r<R), ФГж/? = 6(ф), (15.6-52)
принимает вид
2я
* с <р)= 4 j «.+,.-*«•;£.<,-»■> ь w) w %ZZTM *°myM <15-653)
и может быть разложено в ряд Фу рве по ф.
Уравнения (50) — (53) доставляют решения для круга /•</?. Если D есть
область г>/?, то G(r, p) также выражается формулой (50), но в этом случае
0'5(г, р) =— "я"— лП = r так» что янак в правых частях формул (51) и
(53) должен быть изменен на обратный.
:~2я'
15.6-10.
15.6. ТЕОРИЯ ПОТЕНЦИАЛА
493
(d) Существование функций Грина и конформные
отображения. Из п. 15.6-9,с и теоремы Римана об отображениях
(п. 7.9-6) следует существование функции Грина (а отсюда и решения задачи
Дирихле) для некоторой области D, которая вместе со своей границей может
быть отображена конформно на единичный круг. Более точно, пусть w — w(z)—
аналитическая функция, отображающая точки z=x-\-iy замкнутой области D
в точки единичного круга так, что точка £ = £ + /т] области D переходит
в начало, или
w(z)=\ (2 на С), w(Q = 0. (15.6-54)
Тобда задача Дирихле для области D имеет функцию Грина
G(x, у, Е, л)«<?(г. 0-ln^-. (15.6-55)
15.6-10. Распространение теории на более общие дифференциальные
уравнения. Запаздывающие и опережающие потенциалы (см. также п. 10.4-4).
Теория пп. 15.6-5, 15.6-7 и 15.6-9 позволяет конструировать решения
уравнения Лапласа и Пуассона посредством суперпозиции точечных и диполь-
ных потенциалов. Эта теория легко обобщается на более общие
дифференциальные уравнения
V2(D + fc2(D = 0, (15.6-56)
V20> + £2Ф = — 4я<7 (г), (15.6-57)
которые включают пространственную форму волнового уравнения (&
—действительно, п. 10.4-4) и пространственную форму уравнений Клейна —Гордона,
используемого в ядерной физике (k — iy). Дифференциальное уравнение (57)
принадлежит к типу, изученному в п. 15.5-4, Ь.
(a) Трехмерный случай. Трехмерное уравнение (56) имеет
элементарное частное решение
p±ik(r—q)
Фо(г-р)=* ,r_Qj (г#р). (15.6-58)
Для действительных k положительный знак соответствует уходящим волнам,
отрицательный знак —приходящим волнам; при мнимых к = Ы представляет
большой интерес только отрицательный показатель — |и|.
Подстановка выражения (58) вместо ф0 (г — р) = ___ в формулы (8) —
(15), (23), (24) доставляет решения дифференциальных уравнений (56) и (57)
вместо соответствующих решений уравнений Лапласа и Пуассона.
Результирующие решения волнового уравнения (п. 10.4-8) суть частные случаи
запаздывающих потенциалов (положительный знак в формуле (58)) и опережающих
потенциалов (отрицательный знак в формуле (58)).
В частности, если Ф (г) — дважды непрерывно дифференцируемое решение
однородного дифференциального уравнения (56), формула (20) заменяется по теореме Гельм-
еольца на
•»- i J (*£Zr- v»4"—i i К **№)■« " «"-
о о
(г е= V).
(b) Двумерный случай. В случае двумерных дифференциальных
уравнений вида (56) и (57) элементарные частные решения (32) заменяются на
( — Ц-Н{01)(1г\г — р\) (уходящие волны),
Фо(г, p)=i л] (15.6-60)
( -у Н{02) (k | г — р |) (приходящие волны),
где Н[г) (г) — функции Ганкеля (п. 21.8-1).
ГЛАВА 16
ПРЕДСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. ТЕНЗОРНАЯ
АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ
16.1. ВВЕДЕНИЕ
16.1-1. Вводные замечания. В тензорном исчислении рассматриваются
специальные математические объекты (см. п. 12.1-1), тензоры, задаваемые обычно
в каждой точке пространства и меняющиеся от точки к точке. Эти объекты
представляют собой, следовательно, функции точки; роль «точек» могут играть
элементы различной природы, определяемые системами чисел — координат
этих точек. Предполагается, что каждый тензор может быть аналитически
охарактеризован упорядоченной системой функций от координат точки
(компонент тензора); эти функции могут выбираться по-разному, но так, чтобы
введенные с их помощью математические соотношения между тензорами не
зависели от конкретного выбора аналитической характеристики.
Тензорная алгебра является обобщением теории векторных пространств (пп. 12.4-1
и 14.2-1 — 14.2-7), линейных алгебр (пп. 12.4-2 и 14.3-5) и их представлений
(п. 14.1-2). Тензорный анализ занимается изучением тензоров как функции точки
(тензорное поле) и применяется в основном для описания пространства с кривизной (гл. 17)
и в теории поля в физике. Тензорные методы часто позволяют проследить на
относительно простой математической модели изменение сложных количественных
характеристик при переходе от одной системы отсчета к другой.
16.1-2. Системы координат и допустимые преобразования. Рассмотрим
множество объектов, которые будем называть точками. Предположим, что
каждой точке множества отнесена по определенному правилу упорядоченная система
л<оо действительных чисел х}% х2> ..., хп (ее координат), причем точки
множества взаимно однозначно соответствуют точкам некоторой области л-мер-
ного арифметического пространства переменных х) х1, я2, ..., хп.
Преобразование координат («пассивная» точка зрения на формулы преобразования, см.
п. 14.1-3), допустимое в смысле последующего изложения, состоит в том, что
каждой точке относятся п новых координат х1, х2, ..., хп, связанных
следующими формулами преобразования с координатами относительно исходной
системы:
Хк=*Хк(х\ х2у ..., хп) (£=1, 2, ..., п). (16.1-1)
Уравнения (1) должны удовлетворять в рассматриваемой области
следующим двум требованиям:
1) функции xk (я1, х2, ..., хп) непрерывно дифференцируемы,
2) якобиан (п. 4.5-5) det [dxk / дх1] отличен от нуля.
Множество допустимых преобразований образует группу (п. 12.2-1) относительно
«умножения», т. е. последовательного выполнения преобразований (см. также п. 12.2-8).
Якобиан произведения двух преобразований равен произведению якобианов этих преобразовав
ний. Каждое допустимое преобразование (1) имеет единственное обратное
преобразование, якобиан которого равен обратной величине якобиана данного преобразования.
16.1-3. Компоненты объектов. Индексные обозначения. В тензорном анализе
рассматриваются объекты, связанные с точками (х1, х2, ..., хп) пространства
п измерений (п < оо, п. 14.1-2) и представляющие собой функции точек (п. 5.4-1),
определенные в некоторой области пространства. Каждая такая функция,
») Здесь и дальше верхние индексы не являются степенями,
16.1-4.
16.1. ВВЕДЕНИЕ
495
обозначим ее Qfc1, x2, ..., хп)> может быть, по предположению, определена
(координатное представление объекта Q) системой п1* < со скалярных функций
QO'ii /2» •••» Уд! х1, х2, ...» хп) ее компонент (координат) (см. также п. 14.1-2);
индексы jv /2, ..., /^ пробегают целые значения от 1 до п. В зависимости от
типа объекта (пп. 16.2-1 и 16.2-2) некоторые из индексов записываются в каждой
компоненте наверху, другие — внизу. Например, объект Q может определяться
nr+s компонентами Q Н ' ,Г'(хг, х2> ..., хп), где все индексы принимают
/j h .. • 's
значения от 1 до п. Эти обозначения позволяют сокращенно записать суммы
вида
п
2 AikBk=Cl (1 = 1, 2, ..., п) как AikBk = C\
А = 1
2 2 AkiBkcih->DJh (/,А=1, 2, .... л)как А*к!В*Ън = От
* = 1 л = 1
а также суммы, содержащие векторы:
л
2 я*ед = а как аЛеЛ = а.
А = 1
Сокращенная запись суммы основана на следующих соглашениях:
1. Соглашение о суммировании. Суммирование от 1 до п
производится по каждому немому индексу, встречающемуся дважды, один
раз внизу и один раз наверху.
Обозначение любого немого индекса может быть изменено, так как немые
индексы «взаимно уничтожаются» при суммировании. (Пример: А Ву=*
= A JB.=Al #д.) При перемножении сумм следует использовать
различные индексы суммирования.
2. Соглашение о ранге. Все свободные индексы, встречающиеся
только внизу или только наверху, пробегают значения от 1 до л, там
что уравнение с R свободными индексами является сокращенной
записью п^ уравнений:
Как верхние, так и нижние индексы из различных частей уравнения
должны совпадать.
3. В производных вида да*1дхк индекс k считается нижним.
В настоящей главе немые индексы в соответствии с соглашениями 1), 2)
всегда используются для обозначения суммирования. Так, выражения вида
AikBk следует рассматривать как суммы, если специально не оговорено
противное, например AikBk (не суммировать^.
Во многих приложениях индексные обозначения оказываются более совершенными,
чем матричная запись, использованная в гл. 13 (см. табл. 14.7-1 для сравнения
обозначений).
16.1-4. Системы отсчета и индуцированные преобразования. Геометрические
объекты (см. также пп. 14.1-5 и 16.2-1). Рассмотрим класс объектов,
являющихся функциями точки. Говорят, что для этого класса или для множества
классов задана система отсчета (координатная система), если каждому объекту
по некоторому правилу соответствует (взаимно однозначно) система
действительных чисел — компонент (координат) объекта.
Каждый объект должен определяться во всех системах отсчета одним и тем же
числом компонент. В физике значение каждой компоненты представляет собой обычно
результат физического измерения.
496 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.2-1.
Полезно считать, что с каждой системой координат х1% х2, ..., хп
связана своя система отсчета (система отсчета х). Тогда компоненты
Q.1'*'" '(х1, x2t ..., xf1) объекта Q(дг1, х2 хп) в системе отсчета х и ком-
lllV-ls
— k k ...k
поненты Q.M S(Xlt x2t ... , Xn) того же объекта в системе отсчета X свя-
запы индуцированным преобразованием
-«$1^; №":::'<*• *2 *Л)> •••• QS2:::S^- *г *">!• <161-2)
которое порождается каждым допустимым преобразованием координат (1).
Класс С объектов Q (jc1, *2, ..•лт/г), определяемых в системе отсчета х скалярными
iJ ... i
компонентами Q/ / / (х1 х2 .... хп)> называется классом инвариантных или геоме-
txi2 ... *s * • • '
трических объектов (иногда называемых тензорами в наиболее широком смысле слова),
если математические свойства объектов этого класса могут быть описаны в терминах
операций, не зависящих от системы отсчета (см. также пп 12.1-1 и 16.4-1). Это значит,
что индуцированные преобразования (2) следующим образом связаны с операциями,
заданными в С:
1. Соответствие между допустимыми преобразованиями координат (1)
и соответствующими индуцированными преобразованиями (2) есть
гомоморфизм (п. 12.1-6), сохраняющий произведение двух индуцированных
преобразований.
2. Каждое индуцированное преобразование является изоморфизмом,
сохраняющим операции, определенные в С (см. также п. 16.4-1). Если
определены операции, связывающие элементы двух или более классов Сх, С2, ...
(например, скаляры и векторы), то они также сохраняются при
преобразованиях, индуцированных в Си С2, ...
Можно рассматривать также классы объектов, инвариантных лишь относительно
подгруппы множества допустимых преобразований (п. 12.2-8).
16.2. АБСОЛЮТНЫЕ (ИСТИННЫЕ) ТЕНЗОРЫ
И ОТНОСИТЕЛЬНЫЕ ТЕНЗОРЫ (ПСЕВДОТЕНЗОРЫ)
16.2-1. Определение абсолютных и относительных тензоров, основанное
на законе преобразования их компонент (см. также табл. 16.2-1 и п. 6 3-3).
В настоящем справочнике, а^также в большинстве приложений
рассматриваются действительные (абсолютные или относительные) тензоры, т. е. тензоры
с действительными компонентами. В основу определения тензора можно
положить соотношения, связывающие компоненты тензора в различных
координатных системах. При переходе от одной координатной системы к
другой компоненты тензора подвергаются линейному однородному
преобразованию (4) или (5), различному для абсолютных или относительных тензоров
различного типа; тип тензора определяется законом преобразования его
компонент.
Если задано пространство точек (х1, х2, ... , хп) и группа допустимых
преобразований координат (16.1-2), то
1. Скаляром (абсолютным скаляром; тензором ранга 0) а
называется объект, который в координатной системе х определяется
функцией а(х1, х2, ... , хп) и в координатной системе X функцией
а (х1, X2, ... , Хп), связанной с а (я1, х2, ... , хп) в каждой точке
пространства соотношением
ос = а.
(16.2 1)
16.2-1. 16.2. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ТЕНЗОРЫ 497
Таблица 16.2-
Определения тензорных величин наиболее распространенного типа,
основанные на законе преобразования их компонент
(п. 16.2-1; п. 16.1-3, система индексных обозначений)
Тип тензорной
величины
1. Абсолютный скаляр
(тензор ранга 0)
(Я = г = s = 0)
2. Абсолютный контра-
вариантный вектор а
(Я = г= 1, s = 0)
3. Абсолютный кова-
риантный вектор а
(R = S= 1, Г = 0)
1 4. Абсолютный контра-
вариантный тензор А
ранга 2
(# = г = 2, s = 0)
5. Абсолютный кова-
риантный тензор А
ранга 2
(# — s = 2, г = 0)
6. Абсолютный
смешанный тензор А ранга 2
(Я = 2, r = s = 1)
Компоненты в системе
координат
*\ х2 хп
а(х\х2, ...,*")
аЧх\ х2 хп)
а{{х\х\ ...,хп)
Aik(x\ х2 хп)
Aik(x\x* хп)
А^х1, х2 хп)
Компоненты в системе
координат
?. х2 хп
аСх1, х2 хп) =
= а{х\ х2 хп)
дх'
дх'
* dxk '
jjh ^ Jh^Jbc*_ Aik
дх1 дх*
- дх1 дхк
jh~~dxJ dlch ik
-д/ _ dxj dxk Ai
h dx( dxh k !
2. Контравариантным вектором (абсолютным
контравариантным вектором; абсолютным контравариантным тензором ранга 1)
называется объект, который в координатной системе х
определяется п упорядоченными числами или функциями (компонентами) *)
а* (х1, х2, ... , хп) и в системе хопределяется п упорядоченными
компонентами a* (Jc1, х2> ... , Хп), связанными с а* (х1, х2 хп) в
каждой точке пространства преобразованием
nk =
дхк
17
(16.2-2)
3. Ковариантным вектором (абсолютным ковариантным вектором;
абсолютным ковариантным тензором ранга 1) называется объект,
который в координатной системе х определяется п упорядоченными
компонентами я/Ос1, х2, ... , хп) и в системе х определяется п
упорядоченными компонентами ui(x1t х2, ... , хп), связанными с
Щ(х1* х2, ... , хп) в каждой точке пространства преобразованием
(16.2-3)
*> В векторной алгебре (гл. 5) компоненты вектора назывались координатами
вектора Отметим, что термины компоненты тензора а координаты тензора
применяются взаимозаменяемо.
498 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.2-2.
4. Тензором А, г раз контравариантным и s раз ковариантным
(истинным тензором, абсолютным тензором, г раз контравариантным
и s раз ковариантным), называется объект, который в координатных
системах х и X определяется соответственно nr+s компонентами
aW2 •" %Л (х1, x2t..., хп) и nr+s компонентами А*?*'" ^(Х1, X2 X"),
связанными с А \2"' ft (х1, х2, ... , хп) в каждой точке преобразо-
iiii — 's
ванием
Vy..*r^cftfti to* ^^_L±1 ...J>*L а*1**-*г. (16 2 4)
АкЩ...Ц dxit dxi2 •" dxir d-xk'v &-к'ш д-к'8ЧЧ-*ш
Общее число индексов r+s называется рангом (валентностью)
тензора А.
5. Относительным тензором (псевдотензором) А веса W, г раз
контравариантным и s раз ковариантным, называется объект, определяемый в каждой
координатной системе nr\s упорядоченными компонентами, которые при
переходе к новой системе координат преобразуются по закону
kfa.-.k,. _Q-Xkx dxbj dxkr Qxri дх*'*
*iAi...*i dx't dx** '" bxlr dxkl dxk2 '"
где W — целое число. При W = -{- 1 относительный тензор называется
тензорной плотностью, при W = — 1 —тензорной емкостью.
Уравнение (5) включает (1), (2), (3) и (4) как частные случаи, соответствующие
W = 0.
'А-'г
Тензор с компонентами А.,., ., называется смешанным тензором, если ни г, ни s
не равны нулю. Преобразование (5), характеризующее любую тензорную величину,
является линейным и однородным относительно компонент тензора. Преобразование,
обратное преобразованию (5), имеет вид
Ц2-{г^дх^дх^ аЛа^а^ dik* -АУ-ЛГаС?. х2 ~xn)W
'W-'J дГх^ дхЪ '" &*г дЛ дхГ2 "' d/s 4*4-4 Ь(Л х2 Л J •
(16.2-6)
Замечание. Для того чтобы не вводить новых символов, компоненты тензоров
иногда различают относительным положением верхних и нижних индексов. Так, A*k и
A J обозначают различные системы компонент (см. пп. 16.7-2 и 16.9-1).
16.2-2. Инфинитезимальное перемещение. Градиент скалярного поля (см. также
пп. 5.2-2, 5.7-1, 6.2-3, 16.10-7). Дифференциалы координат dxl определяют контравариант-
ный вектор, который называется вектором инфинитезимального перемещения dr. Если
скаляр а задан дифференцируемой функцией от координат х1, то да/дх служат
компонентами ковариантного вектора — градиента v« скаляра а. Ковариантный вектор,
заданный компонентами а-, является градиентом скаляра в том и только в том случае, если
да* dak
—тс f в ° Для всех '• Ь> ПРИ 9Т0М предполагается, что все частные производные
дхн дх1
непрерывны.
16.3-5.
16.3. ТЕНЗОРНАЯ АЛГЕБРА
499
16.3. ТЕНЗОРНАЯ АЛГЕБРА: ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ОПЕРАЦИЙ
16.3-1. Равенство тензоров. Два тензора А и В одного и того же типа,
ранга и веса называются равными (А = В) в точке (х1, х2% ... t хп)% если в
этой точке равны соответствующие компоненты тензоров относительно
некоторой координатной системы
AW" -Ч*1, jc2, ..., хП)=*В}У" fix1, х\ ... , хп) \ (равенство тензоров).
(16.3-1)
Отсюда следует, что соответствующие компоненты тензоров А и В равны в
каждой координатной системе (см. также п. 16.4-1). Равенство тензоров
обладает свойствами симметрии, рефлексивности и транзитивности (п. 12.1-3).
Замечание. В тензорной алгебре не определяются никакие соотношения между
значениями тензоров в различных точках пространства. Некоторые из этих
соотношений для частного случая тензоров в римановых пространствах рассматриваются в
п. 16.10-9.
16.3-2. Нуль-тензор. Нуль-тензором 0 любого заданного типа, ранга и
веса называется тензор, обладающий тем свойством, что все его компоненты
в некоторой координатной системе равны нулю. Условие того, что А = 0 в
точке (х1, х2, ... , *л), имеет вид
А.1.*'" Ц (х1, х2, ... , *л)=0 (нуль-тензор). (16.3-2)
'i'a ••• *s
Все компоненты нуль-тензора А равны нулю в любой координатной системе,
16.3-3. Сложение тензоров. Если задан класс тензоров одного и того же
типа, ранга и веса, то суммой С = А + В двух тензоров А и В называется
тензор, компоненты которого в некоторой координатной системе (и,
следовательно, в каждой координатной системе) равны суммам соответствующих
компонент тензоров А и В:
a i a i a i \
С И - !> = А}.2 '" f+B}* '" / \ (сложение тензоров). (16.3-3)
Сумма тензоров A -f В является тензором того же ранга, типа и веса, что и каждое
из слагаемых. Сложение тензоров коммутативно и ассоциативно.
16.3-4. Умножение тензора на абсолютный скаляр. Произведением В = аА
тензора А на скаляр а называется тензор, компоненты которого в каждой
координатной системе равны произведениям компонент тензора А на скаляр а:
i i i it i \
В}}'" f=aA}*'" f \ (умножение на скаляр). (16.3-4)
пн... h чъ ...h) v '
аА является тензором того же ранга, типа и веса, что и А. Умножение на скаляр
коммутативно, ассоциативно и дистрибутивно относительно сложения как тензоров, так
и скаляров. В частности, (— 1) A s — А есть тензор, противоположный тензору А.
т. е. А-И-А) = 0.
16.3-5. Свертывание смешанного тензора. Свертывание—-операция,
которая может быть применена к смешанному тензору. Рассмотрим смешанный
тензор А с компонентами A}2"' f. Если выбрать какой-нибудь верхний
индекс и какой-нибудь нижний индекс и просуммировать все компоненты
с совпадающими значениями этих индексов, то полученные nr+s~2 суммы
будут компонентами нового тензора того же веса, что и А, г—1 раз контра-
вариантного и s —1 раз ковариантного. Смешанный тензор может бытц
500 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.3-6.
вообще говоря, свернут различными способами; кроме того, свертывание
может быть повторено несколько раз.
Пример. Свертывание абсолютного или относительного смешанного тензора А
ранга 2 с компонентами А1, порождает абсолютный или относительный скаляр А1. «л| +
+ Д* + ... АгАпп (след А).
16.3-6. Произведение (внешнее) двух тензоров (см. также п. 12.7-3).
Произведением С = АВ (внешним) двух тензоров А и В веса W и W соот-
ветственно, определяемых компонентами А}.2"'/ иБ J ? ••• Ч называется
тензор с компонентами
i i i k k k i r i k k k ч
ci2... r i 2 ... ptsssA\t... rB л 2... p I (внешнее умножение). (16.3-5)
*1*2 ... tsfei/?.2 ... A<7 i\H ... »s *1^2 ... *<7 J
Произведение АВ является тензором веса № -f W\ r + P раз контравариантным и
s-f^ раз ковариантным. Умножение тензоров ассоциативно и дистрибутивно относи^
тельно сложения. Однако оно, вообще говоря, не коммутативно, так как порядок
следования индексов в формулах (5) является существенным.
Примеры. а1Ь = А1 , а*Ь^ = А1,, a,bk = Л^. Произведение (4) является
частным случаем внешнего произведения тензоров.
16.3-7. Внутреннее произведение. Если произведение двух тензоров А
и В, определяемое формулами (5), можно свернуть (п. 16.3-5) таким образом,
что в каждом из слагаемых один или несколько верхних индексов компоненты
*Л *
А-*'" Сбудут совпадать с одним или несколькими нижними индексами
1 k k k
компоненты В**"'р,. то полученные суммы будут служить компонентами
Л|Ло ... Rq
нового тензора, который называется внутренним произведением тензоров А и В.
В общем случае можно образовать несколько таких внутренних произведений.
Каждое внутреннее произведение тензоров А и В является тензором того же веса,
что и АВ. Ранг внутреннего произведения равен разности между рангом АВ и числом
попарно взятых индексов, по которым производилось суммирование. Внутреннее
умножение дистрибутивно относительно сложения тензоров. Иногда внутреннее умножение
тензоров называют свертыванием этих тензоров.
Примеры. а*Ь. = Y. А^ак= с1, А1кЬ{ = Dft, Bikb.t = fkt С .ftafe = hv
16.3-8. Признак тензора. Пусть в координатной системе х заданы /г#
компонент Q(/r /2, .... \р\ х1, х2, ..., хп) объекта Q и пусть X —тензор»
i i i
описываемый компонентами X}}'" ,г-(х1, х2, ..., хп). Как и в п. 16.3-6,
Ч1ъ... ls
внешнее произведение QX будет определяться /z/*+r+s компонентами
i i i
Q (/',, /«.•••» ip) X} . '" .r>. Внутреннее произведение Q и X определяется сумма-
ми, образованными таким свертыванием (п. 16.3-5) объекта QX, при
котором один или несколько индексов каждой компоненты Q(jv /2, ..., /«)
совпадает с одним или несколькими индексами (верхними или нижними)
компоненты X}?'" / , входящей в то же слагаемое. Для того чтобы объект Q
ЧЧ ... *s
был тензором, необходимо и достаточно, чтобы для каждого тензора X
некоторого определенного (фиксированного) ранга, типа и веса внешнее
произведение QX или какое-нибудь внутреннее произведение объекта Q и тензора X
было тензором Y определенного (фиксированного) ранга, типа и веса.
1С.4-1. 16.4. ИНВАРИАНТНОСТЬ ТЕНЗОРНЫХ УРАВНЕНИЙ 501
Можно получить аналогичную теорему, заменив X внешним произведением R
различных произвольных векторов определенных фиксированных типов и весов. Ранг и тип Q
могут быть в каждом случае определены на основании подсчета верхних и нижних
индексов Вес Q равен разности весов Y и X.
Примеры. 1)Q является абсолютным тензором, г раз контравариантным и s раз
ковариантным. если для каждого абсолютного вектора а с компонентами а1
'r+s~~l
где правые части служат компонентами абсолютного тензора, зависящего от а.
2) Q является абсолютным тензором, г раз контравариантным и s раз ковариантным,
'Л \
если для каждого абсолютного тензора А с компонентами А > t ' >
ЧЧ ... »V
п
S X - S в(/г /, iw)A/
Vt.
>, = l/2 = ' 'r + S =
r+s> Ws+t ... W
где а — абсолютный скаляр, зависящий от А.
#3 амечание. Объект Q, определяемый п* компонентами Qik. является
абсолютным ковариантным тензором ранга 2 в том и только в том случае, если
для каждых двух абсолютных контравариантных векторов с компонентами а1 и b .
Объект О., является тензором, если
есть абсолютный скаляр для каждого абсолютного контравариантного вектора а с
компонентами а1, и Qik = Qki*
16.4. ТЕНЗОРНАЯ АЛГЕБРА. ИНВАРИАНТНОСТЬ
ТЕНЗОРНЫХ УРАВНЕНИЙ
16.4-1. Инвариантность тензорных уравнений. При любом допустимом
преобразовании координат (16.1-1) компоненты тензоров преобразуются по
законам, сохраняющим результаты сложения, свертывания и внешнего
(следовательно, и внутреннего) умножения, а также равенство тензоров. Каждое
соотношение между тензорами, которое можно выразить через эти операции
(и операцию предельного перехода), инвариантно относительно группы
допустимых преобразований координат. Если соотношение, записанное в виде
уравнений между компонентами, имеет место в одной координатной системе,
то оно справедливо во всех координатных системах (см, также пп. 12.1-6
и 16.1-4)
Пример. Из
следует
'i'a...'g V,...*. 'i'a...'.f
и обратно; это соотношение может быть символически записано в виде А 4- В = С.
Следовательно, о тензорах и тензорных операциях можно говорить
безотносительно к координатным системам (системам отсчета). Каждую подобранную
502 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.5-1.
подходящим образом систему тензорных величин можно рассматривать как
класс инвариантных объектов с определенными в этом классе и вполне
определяющими его (с точностью до изоморфизма, п. 12.1-6) абстрактными
операциями, не связанными с координатным представлением объектов.
Так, классы абсолютных тензоров ранга 0, 1 и 2 представляют собой
соответственно скалярные поля (п. 12.3-1, с), векторные прострагнства (п. 12.4-1), линейные
алгебры (п. 12.4-2; см. также п. 16.9-2) или кольца линейных операторов (пп. 14.5-2,
14.6-2, 16.3-8). Классы тензоров ранга 2, 3, • • • можно рассматривать как прямые
произведения векторных пространств (п. 12.7-3; см. также п. 16.6-1, с).
16.5. СИММЕТРИЧНЫЕ И АНТИСИММЕТРИЧНЫЕ ТЕНЗОРЫ
18.5-1. Симметричные и антисимметричные объекты. Объект О с/
компонентами Q(lv /2t ..., ]'%), каждая из которых снабжена упорядоченной
системой из R"индексов ]v /2, ..., jRt называется
1. Симметричным по какой-нибудь паре индексов, например
/i и /2, если
Q (/! = '. /2=*. h — /*) = «(/i = *. /i = '. /a- - • //?)•
2. Антисимметричным (кососимметричным) по какой-нибудь паре
индексов, например jt и /2, если
для всех значений i, k% /3, ..., /^ от 1 до п.
Объект Q называется симметричным (абсолютно симметричным) или
антисимметричным (абсолютно антисимметричным) относительно всех индексов,
если он соответственно симметричен или антисимметричен по любой паре
индексов.
Симметричность (антисимметричность) тензора или псевдотензора
относительно некоторой пары верхних или нижних индексов является свойством,
инвариантным относительно группы допустимых преобразований координат.
16.5-2. Символы Кронекера. Обобщенным символом Кронекера ранга 2г
(6-объектом ранга 2г) называется абсолютный тензор, л27* компонент которого
6 * 2 '' /"определяются следующим образом:
1) б'1'2'"/ = + 1 или —■ 1, если все верхние индексы ilt it, ...
..., ir различны и система нижних индексов kv k2t ..., kr получена
соответственно четным или нечетным числом транспозиций из системы
верхних индексов.
2) Ьк11*'Улкг = 0 для всех других комбинаций верхних и
нижних индексов.
Особенно важную роль играют б-символы Кронекера ранга 2,
определяемые следующими условиями:
•и? ?:*
Свертывание любого смешанного тензора Д по верхнему индексу I и нижнему
it
индексу *' (п. 16.3-5) равносильно внутреннему умножению (п. 16.3-7) А на fy •
Каждый символ Кронекера абсолютно антисимметричен (п. 16.5-1) как по верхним, та»
и по нижним индексам. Все символы Кронекера ранга 2г > 2п равны нулю.
16.5-4. 16.5. СИММЕТРИЧНЫЕ И АНТИСИММЕТРИЧНЫЕ ТЕНЗОРЫ 503
1г п\
ir (п - г) 1 >
(16.5-5)
(16.5-6)
4V-- v
Если Л .' / ,' симметричен по любой паре верхних индексов, то
'1*2 .. • *s
AV'-Wiy-Л-О. (16.5-2)
't '• . . . 'г
Если Л .' 3 .» симметричен по любой паре нижних индексов, то
*1 ** . . . h
«^'••••'mV? •••'r-o. (16.6-9
Л Л ... Л
Если Л г абсолютно антисимметричен, то
*М* ' ' '^ЛА * " *' = г! Л Vi ' ' * 'г. (16.5-4)
Следует также отметить, что
*!*.•••*, (*-г)1 АЛ...АГ /r + 1...// Vi'
а** *'
16.5-3. X е-объекты (символы Леви-Чивита) (см. также п. 16.7-2). е-сим-
волы
о'1'*---1"=№:::'»" * ч<а...<л=Ч<2,'-'-л (165-7)
определяют абсолютно антисимметричные относительные тензоры (е-объекты)
ранга п и веса + 1 и — 1 соответственно. Из (16.5-7) следует:
1. е 1 2" п = е{ { . = 0, если среди индексов il9 t2, ..., in
имеется хотя бы два одинаковых.
2. е 1 2'" п ~е, f , =1, если упорядоченная система ин-
lil2 — - 1п
дексов ilt i2,..., in отличается четным числом транспозиции от
системы 1, 2, ..., п.
3. е12'**л = е. . , =—1, если упорядоченная система
111г • •• ln 4 л
индексов ilf /2, ..., in отличается от 1, 2, ..., п нечетным числом
транспозиций.
Следует также отметить, что
^I'i-'-'r'r+i"-'^ (я_г)!в'Л--Л (16.5-8)
е*1**'"**е1 , , =n\, (16.5-9)
12"' Я
g'iV"W л2, лл =. /^!м!а A^=detUH. (16.5-10)
16.5-4. Альтернированное произведение двух векторов (см. также пп. 16.3-4
и 16.10-6). Альтернированным произведением двух контравариантных или двух кова-
риантных векторов (иногда бивектором) называют антисимметричный тензор ранга 2
с компонентами
K'y = aV-aV или v.f = a.^ - аД. (16.5-11)
Вес альтернированного произведения равен сумме весов его сомножителей.
504 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.6-1.
16.6. ЛОКАЛЬНАЯ СИСТЕМА БАЗИСНЫХ ВЕКТОРОВ
(ЛОКАЛЬНЫЙ БАЗИС)
16.6-1. Выражение векторов и тензоров через векторы локального базиса.
(a) Если задана координатная система х, то каждый (абсолютный или
относительный) контравариантный вектор с компонентами а1 (я1, х2, ..., хп)
может быть представлен в виде инвариантной формы
а = а* (х1, х2, ... , Xя) ^(х1, х2, ..., хп). (16.6-1)
Эта форма линейна относительно п абсолютных контравариантных векторов
е, (л:1, х2, ..., хп), е2(х1> *2» •••» хП)> •••» е/г (**» *2» •••» Xя)* последние
называются контравариантными локальными базисными векторами координатной
системы х (о значении немых индексов см. п. 16.1-3). Компоненты i'-го
базисного вектора е* равны б}, 6?, ..., 6" (см. также п. 14.2-3).
(b) Аналогично каждый (абсолютный или относительный) ковариант-
ный вектор b с компонентами bi (x1, х2, ..., хп) может быть следующим
образом выражен через п абсолютных ковариантных локальных базисных
векторов
е1 (х1, х2, ..., хп)у е2 (х1, х2, ..., хп), ..., еп (х1, *2, ..., хп)
координатной системы х:
h = bi (х1, х2, ..., хп) ё (х1, х2, ..., хп). (16.6-2)
Компоненты 1-го базисного вектора е' равны 6\, 6^, ..., 6^. Следует отметить,
что векторы (1) и (2) принадлежат, вообще говоря, различным векторным
пространствам.
(c) Каждый абсолютный или относительный тензор А с компонентами
А } У" .С может быть представлен в виде инвариантной формы
'Л
I } 3
А = ^М;.\\;*<Л ".e;eV2...e4 (16.6-3)
Эта форма однородна относительно локальных базисных векторов е,- и е'\
16.6-2. Преобразование локального базиса при преобразовании координат.
2/г локальных базисных векторов е^х1, л:2, ..., хп) и е'(х1, х2, ..., хп),
связанных с системой координат х1, *2, ..., хп, позволяют получить
аналитическое представление любого тензора в виде системы его компонент (п. 16.1-4).
Новые локальные базисные векторы tk (х1, х2, ..., хп) и е (jc1, x2> ..., хп),
связанные с системой координат X1, ..., Хп, имеют в этой системе компоненты,
равные соответственно 6^ и 6*.
Векторы локального базиса системы X1 выражаются через векторы
локального базиса системы х1 следующим образом:
ik (х1, x\ ..., **) = ^е*(*1, х\ ..., **),
ох
ё* рс1, х2, ..., jc") = ^er" (х1, х2, ..., х^).
дх1
(16.6-4)
Необходимо помнить, что е* (х1, х3 Xй) и е. (^l, pt # #> yi) являются,
вообще говоря, различными векторами (одного и того же векторного пространства), а не
одним и т;>м же вектором, заданным различными способами Вектор.и е- преобразуются
формально так же, как компоненты абсолютного ковариантного вектора (когредиентно
16.7-1. 16.7. ТЕНЗОРЫ В РИМАНОВЫХ ПРОСТРАНСТВАХ 505
этим компонентам); закон преобразования е совпадаете законом преобразования
компонент контравариантного вектора. Компоненты а абсолютных контравариантных
векторов и компоненты 6. абсолютных ковариаитных векторов (и, как следствие, контра-
вариантные и ковариантные базисные векторы е. и е*) преобразуются контрагредиентно,
т. е. таким образом, что внутреннее произведение alb* является инвариантом (см.
также п. 16.4-1).
16.7. ТЕНЗОРЫ В РИМАНОВЫХ ПРОСТРАНСТВАХ.
АССОЦИИРОВАННЫЕ ТЕНЗОРЫ
16.7-1. Риманово пространство и фундаментальные тензоры. В каждом
римановом пространстве может быть определено скалярное произведение,
а вместе с ним длины и углы (п. 16.8-1; см. также п. 14.2-7); эти
определения приводят в свою очередь к полезным обобщениям евклидовой геометрии
(см. также пп. 17.4-1—17.4-7).
Пространство конечного числа измерений, точки которого определяются
упорядоченными системами п действительных1) чисел (координат) х1, х2, ...
..., хп, называется римановым пространством, если в нем задан абсолютный
ковариантный тензор ранга 2 (п. 16.2-1) с компонентами gikix1, х2> ..., хп),
удовлетворяющими в рассматриваемой области пространства следующим трем
требованиям:
1) Каждая компонента gikix1, х2, ..., хп) является
действительной функцией координат и имеет непрерывные частные производные;
2) gik(x\ х2у ..., x*) = gki(x\ х2, ..., *»);
3) Я = det [#*(**, *2, ..., х*)\ФЪ.
Квадратичная форма, соответствующая матрице [g-k (лг1, х2, ..., jcn)], часто
предполагается положительно определенной (п. 13.5-2), хотя это не является необходимым;
случай неопределенной формы представляет интерес для теории относительности
(см также пп. 16.6-1 и 17.4-6).
Все перечисленные свойства тензора gik инвариантны относительно
допустимых (п. 16.1-2) преобразований координат. Тензор (см. также п. 17.4-2)
с компонентами giklx1, x2, ... , хп) (метрический тензор) и абсолютный
симметрический тензор ранга 2, компоненты которого gtk (x1, х2, ..., хп)
определяются соотношениями
Л/=б/ или ^=^г' о6-7-1)
где Gik — Gki есть алгебраическое дополнение (п. 1.5-2) g-tk в определителе
det [gik\ (ассоциированный метрический тензор), называются
фундаментальными тензорами риманова пространства.
X Компоненты каждого из фундаментальных тензоров определяют дифференциал
длины дуги ds (или линейный элемент ds*) и, следовательно, всю внутреннюю
геометрию риманова пространства (п. 17.4-1—17.4-7). Так как при любом преобразовании
координат g — det [g^] преобразуется по формуле
я Г*1, i2 ?*) - «(А >? *") (aU1' *' У>) ^
то естественно принять, что
д(х\ х\ ....х*).
а (л:1, х2, ...,*")
г) Теория, изложенная в пп. 16.7-1—16.10-11, применима к векторам и тензорам
с действительными компонентами, определенными в действительных римановых
пространствах (последнее означает, что координаты точек действительны), а также в
римановых пространствах теории относительности, где мнимые координаты используются,.
в сущности, лишь как форма записи.
606 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.7-2.
При этом допущении выбор знака перед У \ g (х1, x2, ... , х*1) | в одной системе коор*
динат однозначно определяет соответствующий знак для любой системы. Система
координат х1, х2. ... , хп называется правой, если в этой системе координат скалярная
плотность У \g (х1, х2, ... , хп) | положительна, и левой, если она отрицательна (см. также
пп. 6.2-3, b и 6.4-3, с). #
16.7-2. Ассоциированные тензоры *). Поднятие и опускание индексов.
Контравариантный (абсолютный или относительный) вектор с компонентами а1
и ковариантный вектор с компонентами а*, заданные в римановом пространстве,
называются ассоциированными, если их компоненты связаны в каждой точке
следующими соотношениями:
ak = aigik и, следовательно, cii=gikafc. (16.7-2)
Аналогично, для того чтобы получить тензор, ассоциированный данному тензору
с компонентами А££"\% , следует, по определению, поднять индекс k пос-
1 2 s ki
редством внутреннего умножения на g или опустить индекс t посредством
внутреннего умножения на gjf, можно также совершить несколько операций
этого рода. Тензор, ранг которого больше единицы, имеет несколько различных
ассоциированных тензоров. Поскольку компоненты всех тензоров,
ассоциированных данному тензору А, целесообразно обозначать одной и той же буквой Л,
необходимо принимать во внимание порядок, в котором верхние индексы
расположены по отношению к нижним (см. также п. 16.2-1). Так, результат
поднятия индекса k2 в А} У" г. записывается следующим образом:
Я1Я2 ••• S
a'aAV.s-^&~V (16Л-3)
Поднятие ранее опущенных или опускание ранее поднятых индексов
возвращает к компонентам первоначального тензора.
Замечание. Контравариантные и ковариантные е-символы (п. 16.5-3) связаны
соотношениями
h ъ h 1 h i h i hi I (lb.7-4)
и не являются ассоциированными относительными тензорами.
16.7-3. Эквивалентность ассоциированных тензоров. Соответствие между
ассоциированными тензорами в римановом пространстве устанавливает между
ними отношение эквивалентности, разбивающее множество всех тензоров
на классы эквивалентных тензоров, не имеющие общих элементов (п. 12.1-3, Ь).
Поэтому в римановом пространстве компоненты всех тензоров, ассоциированных
тензору А, рассматриваются как различные аналитические представления
тензора А (см. также п. 16.9-1).
В частности, компоненты, ak и а;, связанные соотношениями (2), можно
интерпретировать как контравариантные и ковариантные составляющие одного
и того же вектора а относительно локального базиса, связанного с данной
системой координат. В обозначениях п. 16.6-1
а=а*ел = а;е*\ (16.7-5)
Следовательно, базисные векторы е1( е2 еп и е1, е2 еп в случае рима-
нова пространства можно рассматривать как два различных базиса одного
*) См. также сноску в п. 13.3-1.
16.8-2. 16.8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 507
и того же векторного пространства; их называют взаимными базисами (см.
также п. 16.8-2). Зависимость между векторами взаимных базисов совпадает
по форме с зависимостью между компонентами ассоциированных векторов:
e* = gikeh ei=gikek. (16.7-6)
Подстановка выражений (6) для некоторых из е^ и е^ в (16.6-3) соответствует
поднятию или опусканию индексов тензора А (см. также п. 16.9-1).
16.7-4. Операции над тензорами в римановых пространствах. В римановом
пространстве;
1). Любые два тензора одного ранга и веса можно сложить, согласно
определению, приведенному в п. 16.3-3, для чего в случае необходимости нужно
предварительно поднять или опустить индексы таким образом, чтобы
компоненты слагаемых приобрели одинаковую структуру, т. е. одинаковое
расположение верхних и нижних индексов.
2). Тензор может быть свернут по любой паре индексов согласно правилу
п. 16.3-5, для чего в случае необходимости один из этих индексов должен быть
предварительно поднят или опущен. Свертывание по двум верхним
индексам I, k соответствует внутреннему умножению на g^; свертывание по двум
нижним индексам /, & соответствует внутреннему умножению на gl .
3. Внутреннее произведение двух тензоров А и В определяется как
свертка их внешнего произведения АВ по некоторому индексу (или индексам) А
и соответствующему индексу (или индексам) В согласно правилу (2).
16.8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И СВЯЗАННЫЕ
С НИМ ПОНЯТИЯ
16.8-1. Скалярное (внутреннее) произведение двух векторов в римановом
пространстве. В соответствии с содержанием п. 16.7-4 в римановом
пространстве можно определить скалярное (внутреннее) произведение (см. также пп.
5.2-6, 6.4-2,а, 14.2-6) а • b для любых абсолютных или относительных
векторов а и b с действительными компонентами а1 или а^ и Ь1 или Ь^\
n-b^gikix1, х* хп)а*(х1, х2 xn)bk(xl, х* хп) =
= а^ = а^/ = ^Ч^ = Ь.а. (16.8-1)
Длиной (модулем) | а | абсолютного или относительного вектора а с
компонентами (действительными) а1 или а^ называется соответственно абсолютный
или относительный скалярный инвариант
| а | == + }/7?, а2 = а • а = gikalak = а1а{ = gikaiak. (16.8-2)
Если квадратичная форма g^a1 ak является положительно определенной,
то длину вектора а можно рассматривать как норму || а || (см. п. 14.2-5).
Единичным вектором называется абсол^пый вектор, длина которого
равна 1. Косинусом угла у (определение угла) между двумя абсолютными или
относительными векторами называется абсолютный скалярный инвариант
С08?=т£птг (16-8'3)
Формулы (2) и (3) обобщают элементарное определение скалярного
произведения.
i k
Замечание. Если квадратичная форма g^a а не является определенной
(неопределенная метрика, см. также п. 17. 4-4) в точке (ж1, х2 я71), то скалярный
квадрат а • а абсолютного или относительного вектора а в этой точке может быть
положительным, отрицательным или равным нулю в зависимости от знака выражения йц^а\
причем из равенства | а | =в 0 не следует, вообще говоря, что а = 0.
16.8-2. Скалярные произведения локальных базисных векторов.
Ортогональная система координат (см. также пп. 6.3-3, 6.4-1, 17.4-7, а). Длины
локальных базисных векторов elt e2, .,.i e„; е^е^ ...е* и углы между ними
508 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.8-4.
в каждой точке (х1, х2, ..., хп) (п. 16.6-1) определяются соотношениями
e.tk=gik {х\ х2 х»)9 I (16.8-4)
Векторы е- направлены по касательным к соответствующим координатным линиям,
k k
с имеют направления нормалей к координатным гиперповерхностям. Каждый е
перпендикулярен ко всем е^, кроме е^. Система координат а^, х2, ... , хп называется
ортогональной, если g-k (х1, х2, ... , хп) si 0 для i ф k: в этом случае е. (а также е ) попарно
ортогональны. Не каждое риманово пространство допускает введение ортогональной системы
координат.
Две системы базисных векторов е. и е', связанные соотношениями е • е. = 6', на-
« k
зываются взаимными оазисами рассматриваемого риманова пространства (см. также
п 14.7-6).
16.8-3. Физические компоненты тензора (см. также п. 6.3-4) Локальные единичные
векторы и;, каждый из которых имеет направление координатной линии, соответствующей
индексу вектора, следующим образом выражаются через e-j и е :
: gifte*. e. = vH1^7u,. e* = g''fte.. (16 8.5)
]„ тензора А (в частности, физическими компонен-
1
Y\ ги i
у\ «и I
Физическими компонентами А: ;
12
тами q вектора а) называются величины, определяемые уравнениями
п
а= ^ «/> «у-*Г1*/;1вУ. (16.8-6)
А - .£ £ ... £ А, , . fR U/iU/2... „ . (16.8-7)
/j = 1 /2 = 1 /fl=l
для определения А, / ... , достаточно внести в (16.8-7) вместо А его выражение (16.6-3)
'1/2 1ц
и заменить и. по формулам (16.8-5). Физическая компонента вектора а в направлении
вектора b определяется как а • b/| b |.
16.8-4. Векторное произведение и смешанное произведение (см. также
пп. 5.2-7,5.2-8, 6.3-3, 6.4-2). Векторным произведением а X b двух абсолютных
или относительных векторов а и b трехмерного риманова пространства (п = 3)
называется вектор с компонентами (см. также п. 16.5-3)
Y\g\ l J 2 Y\g\ v ' ' J "
VWi *ijk а*Ь' = -i- Y\T\eijk (ctbJ-aJb1).
Отсюда следует, что
axb =
Y\g\
ej e2 e3
% a2 a3
b\ b2 63
Полезно отметить, что
eg X c3
[ete2e3] '
e2 x e8
= £e»efc»J '
=V\g\
_ e» x et
"[eie«e,] •
e1 x e'
= £e»e*e»] '
e1 e2 e3
a1 a2 a3
{b1 b2 b3
= _
ca _ e, x e2 \
[eie2ea] ' |
e> x
3 £e1ef<
e2 I
(16.8-8)
(16.8-9)
(16,8 10)
16.9-1. 16.9. ТЕНЗОРЫ РАНГА 2 В РИМАНОВОМ ПРОСТРАНСТВЕ 509
где смешанное произведение [abcj определяется, как и в п. 5.2-8, следующим
образом:
I #i ^i ci I
[abcl=a.(bxc)=^=
а2 Ь2 с2
а3 Ь3 с3
а1 Ь1 с1
Ф Ь* с*
& Ь* сз
YTJ
е**щЬрк =V\ g | em<*Vc*\ (16.8-11)
в частности,
[CiCA]=K|*|f [eWJss_j_
(16.8-12)
Формулы табл. 5.2-2 и п. 5.2-9 остаются в силе.
Замечание. Определение векторного произведения (8) охватывает элементарное
соотношение (5.2-6) и определяет векторное произведение двух абсолютных векторов как
абсолютный вектор. Некоторые авторы опускают множитель Y\ g I в определении (8),
вследствие чего векторное произведение Двух абсолютных векторов становится
«аксиальным» вектором (в отличие от «полярного» или абсолютного вектора), который можно
рассматривать либо как относительный контравариантный вектор веса + U либо как
относительный ковариантный вектор веса — 1.
16.9. ТЕНЗОРЫ РАНГА 2 В РИМАНОВОМ ПРОСТРАНСТВЕ
16.9-1. Диадные произведения. Абсолютные (истинные) или относительные тензоры
ранга 2 А, В, ... , риманова пространства, определенные, например, своими смешанными
компонентами А* В1. ... (см. также п. 16.7-2, замечание о порядке индексов), представляют
интерес для многих приложений. С ними иногда связывают особую систему обозначений,
краткое описание которой дано в следующих пунктах.
Каждый тензор А (ранга 2) может быть представлен в виде суммы п диадных
произведений (диад), т. е. тензорных (внешних) произведений двух векторов:
A-P/I'-(,}.,) (,/.*). A'k-p'f9
(16.9-1)
Либо левые множители pJ, либо правые множители q^ могут быть выбраны произвольно,
если только они являются линейно независимыми (п. 14.2-3). В частности.
A = Alket ek - A(k e'e* - A**pk - At Ve,.
(16.9-2)
A = е;А* = Akek, A* = Alkek, Ак = А\*{. (16.9-3)
Используя физические компоненты А., (п. 16.8-3), можно представить тензор А в виде
1=1k=\
Aik = Atk Y\ &u&kk I (не сУммиРовать '),
A =g Aj.
(16.9-4)
В случае ортогональных координат (п. 16.8-2)
2l;*. = A"h |/ -— (не суммировать!).
\ -Ai.~l/~-iL
(16.9-5)
^Замечание. Иногда диадой называют произвольную сумму диадных произведений,
т. е. произвольный тензор ранга 2. ^
510 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.0-2,
16.9-2. Умножение тензоров ранга 2 и векторов и связанная с ним система
обозначений. Для обозначения внутреннего произведения, образованного из (действительных)
тензоров ранга 2 и векторов риманова пространства (см. также п. 16.8-1), используются
следующие обозначения:
А • а = р ,(q^ . а) — вектор с компонентами A1 a f (16.9-6)
а . А = (а • рЛ q^ — вектор с компонентами А1 а^, (16.9-7)
А • В = РЛя? • р!) Я ~ тензор с компонентами A1 BL (16.9-8)
где B=p,V; = Я^е*.
Благодаря принятым обозначениям алгебра тензоров ранга 2 в точности совпадает
с алгеброй линейных операторов (аффиноров), изложенной в пп. 14.3-1 — 14.3-6, так как
тензор ранга 2 связывает с каждой точкой (х1, х2, ... t xn) некоторое линейное
преобразование. В табл. 14.7-1 осуществляется сравнение тензорных обозначений, «классических»
обозначений гл. 14 и матричных обозначений тензоров и векторов.
Определения симметричного и антисимметричного тензора ранга 2 аналогичны
соответствующим определениям из п. 16.5-1, Именно, -тензор А называется симметричным,
если Aki = А . или А,у = Л^., или Л» «= А*£ но отсюда не следует с необходимостью,
что Л,- = А £, так же как это соотношение не означает, что А симметричен (см. также
п. 14.7-5).
След матрицы [Л .*], т. е. Тг (Л) = р,. q^, называется первым скаляром тензора (1).
3 ' 3
Скаляр А"Вя ^ 2 (^i * ^IK4 *ч ) называется двойным скалярным произве-
дением. При п~3 можно определить векторное произведение
а х А = (а Xpy)q;, А X a-Py(q^X а), А X В - Py (q/ X Р^) я'Л. (16.9-9)
Вектор уд = Ру х q^ называется вектором тензора (1). v^ = 0 в том и только в том
случае, если А симметричен. Если А антисимметричен, то для любого вектора а
а . A^-g-v^ х а = —А • а, (16.9-10)
т. е. векторное умножение эквивалентно внутреннему умножению на антисимметричный
тензор ранга 2.
16.9-3. Собственные векторы и собственные значения (см. также п. 14.8-3).
Собственные значения и собственные векторы тензоров ранга 2 определяются в каждой точке
{х1, х2, ... , хп) так же, как в п. 14.8-3. Коэффициенты характеристического уравнения
(п. 14.8-5), соответствующего тензору, являются абсолютными или относительными
скалярами.
Симметричный тензор ранга 2 А в трехмерном евклидовом пространстве может быть
геометрически интерпретирован при помощи семейства поверхностей второго
порядка (3.5-1) с коэффициентами а^. =Л.^(/. k— 1, 2, 3) (см. также п. 3.5-1).
16.10. АБСОЛЮТНОЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.
КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
16.10-1. Абсолютные дифференциалы.
(а) Ни для определения бесконечно малого приращения тензорной
величины, ни для определения ее дифференциала не может быть использовано
понятие разности между «значениями» тензора в точках (x1+dx1, ..., xn+dxn)
и (х1, х2 ..., хп), так как тензорная алгебра в римановом пространстве
(пп. 16.3-1 —16.3-7) не определяет соотношений между «значениями» тензора
в различных точках пространства. Вместо этого в тензорном анализе
формулируются следующие требования (постулаты), определяющие абсолютные
дифференциалы da, da, db, dA, rfB, ... скаляров, векторов и тензоров *) (компо-
*) Рели це оговорено противное» имеются в виду абсолютные скаляры» векторы
и тензоры,
16.10-1. 16J0. АБСОЛЮТНОЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ 511
ненты скаляров, векторов и тензоров риманова пространства предполагаются
дифференцируемыми):
1. Абсолютные дифференциалы da, da и dA являются тензорами
того же ранга и типа, что а, а и А.
2. Абсолютный дифференциал da скаляра а определяется в
соответствующей координатной системе выражением
В частности,
3. Имеют место следующие правила дифференцирования:
rf(a -b)=a- rfb+b. da, )
d(A + B) = dA+dB,
d(AB) = AdB + BdA,
d(aA) = Ada+adA. )
(16.10-1)
(16.10-2)
d(a + b) = da + db, d (a&) = a da+a dz;
отсюда следует, что
da = d (а*е() = e^ da1+a1 dtt = a^ (x1, x*t ..., xn) dx^t =
«= d {ate) = e' dat + at dtl = a{ j (jc1, x2t ..., xn) dxJe*t
т. е. компоненты вектора da равны
(16.10-3)
Da1 = a!* dxJ или Dat = a^ . dxK
Постулаты, перечисленные выше, определяют инвариантные операции
(пп. 16.4-1 и 16.10-7) и приводят к независимому обобщению векторного
анализа, изложенного в гл. о; постулаты удовлетворяются, если положить
a>5+iV' ъу-Э-г&в*-«*"?/- (,6Л(М)
Функции Г^. (х1, х29 ..., хп) представляют собой трехиндексные символы Крис-
тоффедя 2-го рода, определенные в п. 16.10-3.
Замечание. Формулы (3) и (4) определяют каждую компоненту абсолютного
дифференциала da как сумму «относительных дифференциалов» da или da^ и членов,
вызванных изменением базисных векторов при переходе от точки к точке (и,
следовательно, изменением метрики при этом переходе).
Производные da/dx* вектора а можно определить соотношением
da = ~~ dxf. (16.10-5)
дх!
При этом
да д , da1 t д^ д да. .
= —г (aUs) =—т е. 4- а -Л = а1 л; = —7 (а:ег) = —V е' +
dxf dxl K l) dxf l dxl -Г* dxiKl ' dxl
+ ai^7 = <*,**, (16.16-6)
dxi •»/
de, . L dtt de* . .
—4 = Г*е -Г.. .e*- —f, —т=-Г< e* (16.10-7)
dxi it k if; k dxl f dxf Ы
{Tn^ ь — символы Кристоффеля первого рода (см. п. 16.10-3)).
(Ь) Из постулатов п. 16.10-1, а следует, что абсолютный дифференциал
любого тензора А, заданного в римановом пространстве дифференцируемыми
51?
ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ
16.10-2.
компонентами А 4 ? '" f,,
/|'2 уЛ
его компоненты £Л * ?"
Ф2 ••
является тензором того же ранга и типа, причем
К определяются следующим уравнением:
(16.10-8)
dk^d
<Л •
DAtt.
1 2
1л / i ... /:еае'2
\ 1 2 S
.. i iJn ... /
• — А ' ? '
где (символы Кристофф(
/X ...
А }}
4*2-
V ^Лл'зУ
Ч/ д*7 11*2 •
dxl 4*2-'
...е/ге
</*',
*ля Г
л=
•*'s
г рЛ
s
+ г
V2...e'^
ила ...
1»
определены
i. kin ... t'
1Л ' ' '
ki i\i2 ... «s
['еп{
s
В П.
—..
+ ..
5/2...e<ve 'e2
16.10-3)
..e s
.. i's_
r-\n
ь +
(16.10-9)
X Иногда для обозначения абсолютного дифференциала вместо da, dA
пишут Da, DA. #•
16.10-2. Абсолютный дифференциал относительного тензора. Абсолютный
дифференциал относительного тензора (п. 16.2-1) определяется по аналогии с абсолютным
дифференциалом тензора (п. 16.10-1). В частности, абсолютный дифференциал а относительного
скаляра а веса W определяется в соответствующей координатной системе выражением
да
Da = a.dxf, гдес^Д- №гу*а.
(16.10-10)
При W = 0 формула (10) переходит в (1). Абсолютный дифференциал dA любого
относительного тензора веса W (с дифференцируемыми компонентами) определяется
выражением (8) с дополнительным слагаемым вида
WT
ffc
Vi-'r
А: .
Hl2
(16.10-11)
_ АV? - *r _ Y\T\W — Г—5 V& - Ч.
/ Aixi2 ... *s - м s ' dxi Yy\T\w hh ... h J ■
(16.10-12)
в правой части формулы (9), так что
dxi
dA является относительным тензором, ранг, тип и вес которого совпадают с рангом,
типом и весом А.
16.10-3. Символы Кристоффеля.
(а) Если риманово пространство отнесено к координатам х1, х2у ..., хпу то
его символами Кристоффеля первого рода [ij\ k] = Г;у; к(хгу х2у ..., хп) и
символами Кристоффеля второго рода {/*/} =Г*;. (я1, *2,...,*л) (трехиндексными)
называются следующие функции координат х1, х2у ..., хп:
1 * 2\ dxf ^ дх1 dxk )'
(16.10-13)
где gik и gik — компоненты фундаментального тензора риманова пространства.
16.10-4.
16.10. АБСОЛЮТНОЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
513
Символы Кристоффеля*) не являются, вообще говоря, тензорами и при
переходе к новой системе координат преобразуются по закону:
г — **L dxf dxS г
lhk:>— d-xhd-xkd-xr 4fi
. d2xl dxi
5i" Ъ&Ъх* дУ gih
j^r ox- ox' ox- ps i d2xs dxr u
hk~ dxh dxk dx1* if dxhdxb dxs *
(16.10-14)
функции Thk. r si Thk. r (x1, x2,..., xn) и Yrhk s Yrhk (л:1, x2 ..., xn) суть символы
Кристоффеля, связанные с системой координат х1, х2, ..., х .
(Ь) Символы Кристоффеля удовлетворяют следующим соотношениям;
Г =Г
i/'.k j(;k'
if,k hk if
tf Ji
k =gkhr
1t] tj\h
dxk ik\i^ ik\i &hj ik^*ih jk*
dgij и \
JL-inYiTi-itb
g^det [gik].
dei
Гц = —г • ек
4 dxf
dei de& . dei
_4- . ek = г • eS Tif.k = -4 -eft.
dxl dxi 4tk dxi
(16.10-15)
(16.10-16)
(16.10-17)
(16.10-18)
(16.10-19)
(16.10-20)
(с) В важном случае ортогональных координат **, х2, •••, хп (пп. 6.4-1 и 16.8-2),
который характеризуется условием gik = g^fi^, предыдущие соотношения принимают вид
ri/;k = ri
= 0
___ 1 dgn
rii'.k- 2 dxk
{1ф1фкф i).
r£/:.--r/«*'
1 dm
2 dxf '
r^ == —
a 2g
i to,,
kk
Tk ==r^ =
ik ~~ ki '
dx*
1 dg}
ИФк).
kk .
1 ding.
kk
2 dxl
(16.10-21)
16.10-4. Ковариантное дифференцирование. Вследствие аналогии между
выражениями (4), (9) и обычными частными производными операцию образо
— Л А* .' по компонентам тензора А.- ■
вания функций А}2 Г'
Ч12~-%/ dxi 4l2 — *s "М*2 — *s
называют ковариантным дифференцированием по метрике, определяемой
тензором gik.
*) В математической литературе символы Кристоффеля предпочтительно
обозначаются 1\у.£, Г,у. Однако во многих руководствах для них сохраняется обозначение
скобками [*/; k]. {t k /}.
17 Г. Корн и Т. Корн
514
ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 16.10-5.
Если АЬ}' Г' являются компонентами абсолютного тензора А, то ком-
«1*2». н
Li ... i
поненты А.>.> :* также определяют абсолютный тензор
1[12 ••• ls,j
VA =А& '" *Г- е^е,. ... eire'ie'2 ... eW, (16.10-22)
г раз контравариантный и s + 1 раз ковариантный. Тензор VA (а иногда
также каждую отдельную его компоненту) называют ковариантной
производной тензора А; для компонент тензора А используют также обозначение
da}2- f> ,
«1*2 ""'s л11*2-1г
' И'9 ... «я /)*/
\12 ••• »s д*/ М»2 ••• %j
д 'Л-"'г
Следует иметь в виду, что ни частные производные—7 Л. у ^, «« «от-
носительные» дифференциалы йАУ}> "* 5 не являются, вообще говоря, компо-
t\t2 ... *s
нентами тензора.
16.10-5. Правила ковариантного дифференцирования (см. также п. 16.10-7).
Применение тензорного анализа часто упрощается благодаря тому, что
обычные правила дифференцирования суммы и произведения (табл. 4.2-5) остаются
справедливыми для ковариантного дифференцирования:
г
дх/ \ *\12-~Н Н*2 — 18/ 4*2 —%/ n^ — hj
dxi \ hl2 — ls k\k2 ••• ksj \„„ ,л «m
= A iJ2 ... lr BkiS '" \ <BkiS - \ a h fr- lr \ (16.Ю-23)
Hl2 ... ls k\k2...ksj ~t~ k\k2...ks k\k2...k'sj'
n iJ ...k ... i iJ ...k ... i
—гЛ.'.' . /=A.'J . / (правило для свертки).
Последние два правила применяются также для ковариантного
дифференцирования внутреннего произведения (пп. 16.3-7 и 16.8-1).
Важное значение имеют соотношения
gik.j=gik,j=0 (теорема Риччи), | (16.10-24)
Si/
Уравнения (24) показывают, что фундаментальные тензоры ведут себя
относительно ковариантного дифференцирования как константы.
Ковариантная производная тензора, ассоциированного тензору А, является
тензором, ассоциированным VA (см. также пп. 16.7-2 и 16.7-3).
Ковариантные производные ^-символов Кронекера и е-объекта (пп. 16.5-2
и 16.5-3) равны нулю.
16.10-6. Ковариантные производные высших порядков. Если компоненты
данного тензора и компоненты метрического тензора gik имеют производные
достаточно высокого порядка, то можно рассматривать ковариантные произ-
LL ... /
водные высшего порядка с компонентами А}* .- . . . . Полученные
4*2 ••• HJ\i2 —/m
при этом тензоры, вообще говоря, не симметричны по нижним индексам /';
ковариантная производная не зависит от последовательности
дифференцирования в том и только в том случае, если риманово пространство является
le.tfr-fc, 16.10. АБСОЛЮТНОЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ 515
плескам (локально евклидовым) (п. 17.4-6, с). Для любого вектора с
компонентами ai
ai.jk-ai,k/=Rrijbar> (16.10-25)
где R[lk — компоненты смешанного тензора кривизны (п. 17.4-5) риманова
пространства.
16.10-7. Дифференциальные операторы и дифференциальные инварианты
(см. также пп. 5.5-2 и 5.5-5).
(а) Если рассматривать выражение
—г А.*.? .- tittu ...е; е »е 2 ... es гз
дх! «1*2 ... 's Х 2 г
как результат «умножения» тензора
д*;/2...£е'1е'2
...е,ге'«е'2...е/«
.е s
на символ V/==—г, то ковариантную производную (22) тензора А можно
' дх*
записать в виде внешнего «произведения» (п. 16.3-6) тензора А и
(инвариантного) «вектора»
V за е>-^ s e^V/, (16.10-26)
который называется дифференциальным оператором набла; его «компоненты»
—-v=V/ преобразуются, как ковариантные компоненты вектора (п. 16.2-1).
Для любого преобразования координат в римановом пространстве
%-%-Ь или *-£*/• <16Л0-27>
(Ь) Соотношения между компонентами тензоров, полученные в результате
ковариантного дифференцирования, а также сложения и умножения тензоров,
инвариантны относительно группы допустимых преобразований координат
(см. также пп. 16.4-1 и 16.10-1). Тензорные величины, образованные
посредством внешнего и внутреннего умножения других тензорных величин на
инвариантный оператор (26), называются дифференциальными инвариантами»
В табл. 16.10-1 указаны важнейшие дифференциальные инварианты.
16.10-8. Абсолютные (внутренние) производные и производные по
направлению (см. также п. 5.5-3). Если в римановом пространстве задана
регулярная кривая
** = *'(/) (ti^t^t2), (16.10-28)
то компоненты dx*/dt определяют контравариантный вектор dr/dt,
«направленный» по касательной к данной кривой (п. 17.4-2) Абсолютной (внутренней)
производной dA/dt истинного или относительного тензора А (с
дифференцируемыми компонентами) по параметру t вдоль данной кривой называется
следующий тензор того же веса, ранга и типа, как А:
компоненты тензора -^ равны
ЭгЖу-^Жу-1.! 4-. (16.10-29)
dt i{t2 ... *s ф2 ... tSJ- dt
17*
516 ГЛ. 16. ТЕНЗОРНАЯ АЛГЕБРА И ТЕНЗОРНЫЙ АНАЛИЗ 36.10-8.
Таблица 16.10-1
Дифференциальные инварианты, определенные
в римановых пространствах
[V=e/ -==e/'v. см. также пп. 16.2-2, 16.10-1 — 16.10 7, табл. 6.4-1 — 6.5-11 )
\ дх* ' }
(a) Градиент (абсолютного) скаляра а есть (абсолютный) вектор
у да п да
Va = еу г == е}gJl г .
dxl 1 дх!
(b) Ковариантная производная уа (абсолютного) вектора а называется
градиентом или локальным аффинором вектора а. Дивергенция (абсолютного) вектора а
является (абсолютным) скаляром у • а; она равна
i Da1 да1 , ьЛ 1 д
+ л**~7=г-£г^Л
1 дх1 dxi kl Y\g\ дх1
Замечание. Соответствующие формулы табл. 5.5-1 могут применяться
к градиенту и дивергенции в римановых пространствах (см. также п. 16.10-5).
(с) Оператор Лапласа у2 ~^ V • V является инвариантным скалярным
оператором gl : — ==gl^V;Vi,. В частности, лапласиан v2a (абсолютного) скаляра a
дх1 dxk l к
имеет вид
gi* _D_ Ja gik Ja __ gik ,__Ща _ _/;
дх1 дх^ dxk \ dxldxb
(d) Если (абсолютный) вектор а задан компонентами а-, то
антисимметричный (абсолютный) тензор с компонентами
Dai Daj dQi da;
c == . 2_ == v a _. v a, == : r—
lJ dxl dxl J l l ' dxl dxl
тождественно обращается в нуль в том и только в том случае, если а является
градиентом (абсолютного) скаляра.
Замечание. При п — 3 можно определить ротор (абсолютного) вектора а
как (абсолютный) вектор v x а с компонентами
1 Da; ... 1
Y \g\ дх1 Y\g\ l ;
7 V/fc =- y.aJlk
_ ■_ /__ ___N //t _ ._ ^j__ J_\ /M
2 /| g ! \ ддт' d*/ У 2 /| g | \ d*« d*/ /
(см. также п. 16.8-4). К (абсолютным) векторам трехмерного риманова пространства
могут применяться формулы табл. 5.5-1 и уравнения (5.5-19).
Если компоненты тензора А зависят от I не только через координаты х1, х2, ..., хп
но и явно, то
</А дА
DAM Г> дА
dt ~ dt +
©-)*•
1*2 - V
¥2 — 's _ ¥2 — *'s _ ^ V'2 - lr __f
<i<2
-7 = -j + л.М !> .—. (16.Ю-30)
Производной по направлению dA/ds тензора А в направлении данной
кривой №=7-0, п. 17.4-2) называется абсолютная производная тензора А по
длине дуги s вдоль кривой.
ie.10-11. 16.10. АБСОЛЮТНОЕ ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ 517
16.10-9. Тензоры, постоянные вдоль кривой. Уравнения параллелизма.
Тензор А является по определению постоянным вдоль регулярной кривой (28)
(т. е. его «значения» в соседних точках кривой «равны»), если его
абсолютная производная (30) (и, следовательно, также его абсолютный дифференциал
dA = -j-dsJ вдоль кривой равны нулю. Суммы и произведения таких
тензоров также постоянны вдоль рассматриваемой кривой, так что, например,
модули постоянных векторов и углы между ними постоянны. Каждый вектор а,
компоненты которого а* (х1, х2, ..., хп), щ(хг% х2, ..., хп) удовлетворяют
дифференциальным уравнениям
Оа' = 0 или Da/ = 0 (уравнения параллелизма) (16.10-31)
при условии, что дифференциалы координат х1, х2, ..., хп определяют
смещение вдоль кривой (28), подвергается «параллельному переносу» вдоль
кривой.
Замечание. Вектор, полученный в результате «параллельного переноса»
данного вектора а вдоль замкнутой кривой, не совпадает, вообще говоря, с этим вектором
по возвращении в исходную точку (см. также п. 17.4-6).
16.10-10. Интегрирование тензорных величин. Элемент объема. Интегралы от
тензорных величин вдоль кривых в римановом пространстве могут быть определены при
помощи скалярных интегралов по параметру так же, как это сделано для векторов
в пп. 5.4-5 и 6.2-3, а.
Элемент объема dV определяется (см. также пп. 6.2-3, b и 6.4-3, с) следующим
выражением:
dV = YYT\ dx1 dx2 ... dxn. (16.10-32)
■Х-Если в выражении для dV опустить множитель Y\ g\, то элемент объема
оказывается псевдоскаляром веса —1, т. е. скалярной емкостью (п. 16.2-1); так как V\ g \ —
скалярная плотность, то (16.10-32) определяет dV как инвариант.^
Интегралы по объему от скалярных инвариантов являются скалярными
инвариантами, но интегралы по объему от тензоров ранга R > 0 не являются, вообще говоря,
тензорами. Элемент объема может быть определен также для подпространства; он
является аналогом элемента площади в трехмерном пространстве. Существуют обобщения
интегральных теорем, приведенных в пп. 5.6-1 и 5.6-2 (см. п. 16.10-11).
16.10-11. Дифференциальные инварианты тензоров ранга 2; интегральные теоремы
(см. также п. 16.9-1). Дивергенцией тензора А ранга 2 (с дифференцируемыми
компонентами), определенного в римановом пространстве, называется вектор v*A; оператор v
(п. 16.10-7) действует как ковариантный вектор. Следует отметить соотношения
V-(aA) = av-A -f A-va, (16.10-33)
v.(a-A) = (va)--A + (v A)-a, v-(A-a) = (va)- -A + (V A)-a, (16.10-34)
где тензор А получен транспонированием А (^ь~^« )• Тензор уа называется
градиентом а (табл. 16.10-1).
Для функций, кривых и поверхностей, удовлетворяющих известным условиям,
имеют место интегральные теоремы, аналогичные теоремам пп. 5.6-1 и 5.6-2:
J v-A dV = J JA-A, (16.10-35)
V S
j*VadV= JfifAa; J (vxA) dV = J (tfAxA), (16.10-36)
V S V S
J V-(A-a) dV = J dA.(A-a), (16.10-37)
V S
J"<*A.(VXA)= Jdr-A. (16.10-38)
S С
ГЛАВА 17
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.1. КРИВЫЕ НА ЕВКЛИДОВОЙ ПЛОСКОСТИ
17.1-1. Касательная к плоской кривой. Пусть кривая С задана (п. 2.1-9)
уравнениями
* = *(/), У = У(!) (17.1-lfl)
или
Ф(ж, </) = 0, (17.1-16)
или
* = /(*)• (17.1-lc)
Касательной к кривой С в ее точке Рх (xlt ух) ss Рг [х (/х), у (tx)\ называется
прямая, являющаяся предельным положением секущей, проходящей через Рх и
через отличную от нее точку Р2 этой кривой при стремлении Р2 к Pv
Кривая (1) имеет единственную касательную с уравнениями
х=(§\(1-Ь)+Х1, у = (%\а-и)+ух, (17.1.2а)
или
Шх-^ + (^\(У-У^0, (17.1-26)
или
у-у^{тХ{х-Х1) (17-ь2с)
в каждой регулярной точке (xv y{) кривой; регулярная точка характеризуется
либо тем, что а) при некотором выборе параметра функции x(t)> y(t) будут
иметь в достаточной близости от tx непрерывные производные первого
порядка, не равные одновременно нулю, либо тем, что Ь) для некоторого
уравнения ф(#, у) = 0 кривой С функция ф(#, у) имеет в достаточно малой
окрестности точки (х19 ух) непрерывные частные производные первого порядка,
из которых по меньшей мере одна отлична от нуля. Из Ь) всегда следует а);
условия а) и Ь) эквивалентны, если (xv уг) не является кратной точкой
кривой С, что заведомо имеет место для той дуги кривой, на которой хотя бы
одна из производных х' (/), у' (t) сохраняет знак.
Угловой коэффициент касательной (2) равен
•«•-(а-(й№-(йА <17л-з>
17.1-2. Нормаль к плоской кривой. Нормалью к кривой (1) в регулярной
точке Рг (хх, уг) называется прямая, проходящая через Рх и
перпендикулярная к касательной в точке Рг:
у-у^-щщ:^-^- о™-*)
Положительное направление нормали может быть тем или иным способом
согласовано с положительным направлением касательной; последнее совпадает
с положительным направлением кривой. Положительное направление кривой
определяется некоторым дополнительным условием (возрастание t,
возрастание х и т. д.; см. также п. 2.2-1).
17.1-4. 17.1. КРИВЫЕ НА ЕВКЛИДОВОЙ ПЛОСКОСТИ 519
17.1-3. ^Особые точки. Всякая точка кривой, не являющаяся регулярной,
называется особой. Пусть кривая (\Ь) обладает тем свойством, что все
производные от ф(лг, у) до (п — 1)-го порядка включительно равны нулю в точке
Рх(хг, г/х), в то время как производные /i-го порядка непрерывны в
некоторой окрестности (xlf ух) и не равны одновременно нулю в этой точке. Тогда
кривая имеет п касательных в Pt; некоторые из них могут совпадать или
оказаться мнимыми (последних будет четное число). Так, если все
производные первого порядка от ф (х, у) равны нулю в точке PL (хъ ух), а
производные второго порядка не все равны нулю, то угловые коэффициенты dy/dx
двух касательных в точке Рх являются корнями квадратного уравнения
Э(Й)'+2A-S+S-o <*-*. '-*>• <™>
Корни уравнения (5) и, следовательно, две касательные, могут быть
действительными и различными (двойная точка, узел), совпадающими (точка
возврата либо точка самоприкосновения) или мнимыми (изолированная точка);
во всех этих случаях точка (хъ ух) является особой.
Свойства кривой в особой точке могут быть описаны также в терминах
производных от х (t) и у (t).
17.1-4. Кривизна плоской кривой. Соприкасающейся окружностью (кругом
кривизны) плоской кривой С в ее точке Рх называется предельное положение
окружности, проходящей через Рх и две соседние точки кривой Р2 и Р3, ПРИ
стремлении Р2 и Р3 к Рх.
Центр этой окружности (центр кривизны кривой С, соответствующий
точке Pj) лежит на нормали к С, проведенной в точке Pv Координаты центра
кривизны равны
все производные вычисляются при x — x1(t = t1)\ точками обозначено
дифференцирование по t. Радиус pk круга кривизны (радиус кривизны кривой С
в точке Р,) равен обратной величине кривизны k кривой С в точке Рх;
кривизну можно определить как предел отношения угла поворота касательной
к длине соответствующей дуги As кривой С при стремлении As к нулю:
b — J- — dJL — d9V'
. _ _ './\V\+№)']*= *S~"* •• (17.1-7)
все производные подсчитываются при х=хх (t = t1)1). Данная кривая С
является соответственно вогнутой или выпуклой в положительном направлении
оси Оу в зависимости от того, будет ли производная d2y/dx2 и, следовательно,
кривизна k положительной или отрицательной. Многие авторы называют
кривизной, как это и сделано в п. 17.2-3, не k> a \k\.
В полярных координатах р, ф (п. 2.1-8) дифференциал длины дуги ds и
угол \х между касательной к кривой р = р(ф) и полярным радиусом-вектором
определяется формулами
d* = dp* + p»*p», tg|i = p/g-, (17.1-8)
откуда следует, что
, 1 _d* dq> ,dn_P ^Z\d<t>) P dq>* (]7 . q.
•) Правые части формул (6) и (7) можно выразить через частные производные от
левой части уравнения кривой <р (*, у) = 0 при помощи формул (4.5-16).
520
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.1-6.
17.1-5. Порядок касания плоских кривых. Говорят, что кривые y—f(x) и
y=g(x) имеют в точке Pi(xlt yt) касание п-то порядка, если
/<*i) = *(*i). /'(*i)=*'(*i). ...,fin)(xi)=g{n)(xi)> fin+1>(Xi)^g(n+1)(XiY>
(17.1-10)
это определение предполагает, что f (х) и g (x) имеют в точке хг производные
до (/г + 1)-го порядка включительно.
■КПри соблюдении условий (10) разность f(x-\-Ax)— g(x-\-Ax) является
бесконечно малой (/г+1)-го порядка относительно А*.*
В точке касания касательные к кривым совпадают.
Одна из кривых лежит по разные стороны от другой в достаточной
близости от точки касания, т. е. кривые пересекаются в этой точке в том и
только в том случае, если п четно. Точка, в которой кривая и касательная
к ней имеют касание второго порядка (или любого четного порядка),
называется точкой перегиба. В точке перегиба кривая пересекает свою
касательную. Кривизна в точке перегиба равна нулю.
17.1-6. Асимптоты. Прямую линию называют асимптотой данной кривой С,
если расстояние от точки Р (*, у) кривой до прямой стремится к нулю при
х2+у2~► оо; говорят также, что кривая С асимптотически приближается к этой
прямой. Предельное положение касательной к регулярной кривой есть
асимптота; обратное утверждение неверно.
■ХЕсли кривая задана уравнением у = f (x) и пределы
lim LW. = а и lim [/ (х)-ах] = Ь
Х-+СО Х Х-+СО
существуют, то прямая у = ах -f- Ь является асимптотой кривой.>|<
17.1-7. Огибающая семейства плоских кривых. Огибающей однопараметри-
ческого семейства кривых
<р(*. у, Х) = 0 (17.1-11)
называется кривая, касающаяся в каждой своей точке одной из кривых
семейства. Иногда к огибающей относят также точки, которые принадлежат
одновременно всем кривым семейства. В дальнейшем имеется в виду именно
это последнее определение. Уравнение огибающей можно получить, если
исключить параметр X из уравнений (11) и уравнения
аф(уХ)=Фх(*, у, Ь) = 0; (17.1-12)
такое исключение параметра возможно и заведомо приводит к огибающей,
если в рассматриваемой области значений х, у и X выполняются условия
Т^Г^О, ЪхФО- (17.1-13)
В общем случае уравнения (11) и (12) определяют А,-дискриминантную
кривую, т. е. геометрическое место точек, в которых пересекаются бесконечно
близкие кривые семейства (предельное положение точек пересечения кривых
ф(*, у, Х1) = 0 и ф(*, у, Х2) = 0 при X2-+Xi). Наряду с огибающей А,-дискри-
минантная кривая содержит и особые точки кривых, принадлежащих
семейству.
17.1-8. Изогональные траектории. Семейство кривых, пересекающих все
кривые однопараметрического семейства ф(*, у, Х) = 0 под данным углом у,
определяется дифференциальным уравнением
(Ё C0SV-f «nV)^+g sin y + 5 cosy) dy = 0; (17.1-14)
при y = jt/2 уравнение (14) определяет ортогональные траектории.
17.2-2. 17.2. КРИВЫЕ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 521
17.2. КРИВЫЕ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
17.2-1. Вводные замечания (см. также п. 3.1-13). В пп. 17.2-1—17.2-6
рассматриваются геометрические свойства кривой С, определяемой
уравнениями г==г//\ \
или I (/i^/^/2) (17.2-1)
*-*(*). y=yV), z=z(t) J
(tx и t2 могут равняться соответственно —оо и + со). Функции (1) имеют
непрерывные производные по /, и dr/dt Ф О для всех значений / из
промежутка /х^/^/2» т* е- С—регулярная дуга, В случае необходимости будет
предполагаться существование производных более высокого порядка.
Удобно принять за новый параметр длину дуги
t*
s= $ds= J V dx. dx = \ Vdx*+dy*+dz* = $ V&+$* + Pdt
(n. 5.5-4); знак ds выбирается произвольно и определяет положительное на-
правление на кривой и касательной (см. также пп. 17.2-2 и 17.2-3).
Производные по s будут обозначаться штрихами, так что, например,
, __ , __ dx_ dx ids
X — Xs — ds— dtjdt .
Уравнения кривых в криволинейных координатах (гл. 6) кратко рассмотрены
в п. 17.4-1.
17.2-2. Подвижной трехгранник (см. также пп. 17.2-3 и 17.2-4).
(a) Касательная к кривой. Касательной к кривой С в точке Рг (гх) sa
ss Рг (хи уъ гг) называется прямая, являющаяся предельным положением
секущей, проходящей через Рх и отличную от нее точку Р2 кривой при
стремлении Р2 к Рг. Кривая (1) имеет единственную касательную в каждой
точке, в которой существует dr/dt Ф 0. Положительное направление
касательной соответствует положительному направлению на кривой.
(b) Соприкасающаяся плоскость и соприкасающаяся окружность. Главная
нормаль. Соприкасающейся окружностью или кругом кривизны кривой С
в точке Рг называется предельное
положение окружности, проходящей через
Рх и две соседние точки Р2 и Р3 кривой
при стремлении Р2 и Р3 к Pv Плоскость
этой окружности называется
соприкасающейся плоскостью кривой С в точке Рг\
она содержит касательную к С в точке
Pv Направленная прямая, идущая из
точки Рх в центр соприкасающейся
окружности, называется главной нормалью
кривой С в точке Рг\ главная нормаль
перпендикулярна к касательной.
(c) Бинормаль. Нормальная и
спрямляющая плоскость. Бинормалью кривой С
в точке Рг называется направленная
прямая, проходящая через точку Рх и
образующая вместе с положительной
касательной и главной нормалью правую
систему декартовых прямоугольных осей
(п. 3.1-3). Плоскости, определяемые
осями этого «подвижного трехгранника»,
называются: нормальной (плоскость, перпендикулярная к касательной),
спрямляющей (плоскость, перпендикулярная к главной нормали), соприкасающейся
(плоскость, перпендикулярная к бинормали) (см. рис. 17.2-1).
Касательная
'Бинормаль
Рис. 17.2-1. Подвижный трехгранникя
связанный с пространственной
кривой С.
522
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17,2-а.
(d) Единичные векторы t, n и Ь, направленные, соответственно вдоль
положительной касательной, главной нормали и бинормали, следующим
образом выражаются через производные от функции г —r(s) no s; здесь и далее
производные по s обозначаются штрихами:
t = r' (единичный вектор касательной),
г- г" (единичный вектор главной нормали),
! г" j
b = txn (единичный вектор бинормали)
(17.2-2)
Вектор &п = г" называется вектором кривизны; через k обозначена кривизна,
рассмотренная в п. 17.2-3.
17.2-3. Формулы Френе — Серре. Кривизна и кручение пространственной
кривой (см. также пп. 17.2-4 и 17.2-5).
(a) Единичные векторы (2) удовлетворяют в каждой точке кривой
соотношениям
t' = £n, п' = — &t + Tb, b' = —тп (формулы Френе —Серре),
где
* = р^ = 1 *' 1 = 1 г" I» т=р^=в-*г 1Г'Г"Г"'Ь О7-2"3)
При возрастании s точка Рх движется по кривой С; при этом:
1. Касательная вращается вокруг мгновенного положения
бинормали с положительной угловой скоростью k (кривизна кривой С
в точке Рх).
2. Бинормаль вращается вокруг мгновенного положения
касательной с угловой скоростью т (кручение кривой С в точке Рх);
т положительно, если вид кривой напоминает правую винтовую
нарезку.
3. Трехгранник вращается как твердое тело вокруг мгновенной
оси, направление которой определяется вектором Дарбу Q — Tt+kb,
с угловой скоростью (положительной), равной | й | = J/"t2+&2 (полная
кривизна кривой С в точке PJ.
Механический смысл производных от базисных векторов трехгранника Френе
становится более очевидным, если переписать формулы Френе в виде
t'= Q xt = (A:b) Xt, n' = QXn, \ ,17 9 4*
b'=Qxb = (xt)xb; J KU'*'*}
Pfr—X/k есть радиус кривизны кривой С в точке Pt (радиус соприкасающейся
окружности); рт= 1/т называется радиусом кручения.
(b) Скалярные функции k — k(s) и t = t(s) определяют кривую с точностью до
положения в пространстве (естественные уравнения кривой). С является плоской кривой в том
и только в том случае, если ее кручение тождественно равно нулю; аналогично С —
прямая линия, если ее кривизна тождественно равна нулю, и только в этом случае.
(c) При произвольном выборе параметра t
p7~ 1Я» ' T-Pt-|fx?|»- °-25)
«очками обозначено дифференцирование по /. Полезно отметить, что
г = s t Н—5— s»n = st + ( —Ь) X? (17.2-6)
Qk \ pft 1
(разложение ускорения движущейся тонки на тангенциальную и нормальную составляю*
щае; см. также п. 5.3-2).
17.2-Б. 17.2. КРИВЫЕ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 523
17.2-4. Уравнения касательной, нормали и бинормали; уравнения соприкасающейся,
нормальной и спрямляющей плоскостей.
(a) Касательная, главная нормаль и бинормаль кривой С в точке Рх (rt) =
E^i (*i, Vu 2i) определяются соответственно следующими векторными уравнениями:
r — ti + ut, r = rt-|-wn, r — Tt-^ub, (17.2-7)
где и— переменный параметр.
Векторные уравнения соприкасающейся, нормальной и спрямляющей плоскостей
имеют соответственно следующий вид:
(г — г1).Ь = 0, (г — rO-t^O, (r —rt)-n = 0. (17.2-8)
(b) Координаты единичных векторов (2) относительно правой декартовой
прямоугольной системы координат равны:
* =*' t = у* tm = г' (направляющие косинусы касательной), (17.2-9а)
х у z
п — — х", nt, __ -г- у", я ==-ir z" (направляющие косинусы главной нормали), (17.2-96)
■* к У к * к
Ъх=\(у'г"-у"г'), Ьу = ±(г'х"-г"х'\ bg = I (x'y"-x"tf) (17.2-9c)
(направляющие косинусы бинормали).
Кривизна и кручение выражаются формулами
Qk рт R
Подстановка направляющих косинусов <9) в
X — Xi _ У--Ух _ Z —
у' г'
У" Z"
у... Z,.t
(17.2-10)
(17.2-11)
приводит к уравнениям касательной, нормали и бинормали в декартовых прямоугольным
координатах; уравнение
(х —хг) cos а^ -+• (У — Уг) cos ау + (г — zj cos ag = 0 (17.2-12)
определяет соприкасающуюся, нормальную, спрямляющую плоскости.
17.2-5. Дополнительные замечания.
(a) Центр кривизны кривой С, связанный с ее точкой Pit определяется радиусом-
вектором
г* = г1 + о*п- (17.2-13)
(b) Предельное положение сферы, проходящей через четыре различные точки Рь
Р±, Р$ и РА кривой, при стремлении Р2, Р3 и Р4 к Р, называется соприкасающейся
сферой кривой в точке Яь Ее центр лежит на прямой, проходящей через центр кривизны
и имеющей направление бинормали. Радиус-вектор tq центра соприкасающейся сферы
и ее радиус р^ таковы:
PQ= У Л + (PtP*)2 . rQ = Tk + pTp*b = ri + p*n + Ptp^b« (17.2-14)
Кривая С лежит на сфеое радиуса R, если qq == R (необходимое и достаточное
условие).
Полярными прямыми кривой С называются касательные к ее полярной кривой;
последняя определяется как геометрическое место центров соприкасающихся сфер
кривой С. Полярная поверхность кривой С есть линейчатая поверхность (п. 3.1-15),
образованная касательными к полярной кривой.
(с) Эвольвенты и эволюты. Касательная к кривой С описывает линейчатую
поверхность, состоящую из двух полостей, касающихся вдоль данной кривой.
Эвольвентами (развертками) кривой называются кривые, лежащие на этой поверхности и
ортогональные ее образующим, т. е. касательным к кривой С. Если известно уравнение г = г (s)
кривой С, то уравнения эвольвент имеют вид
р = р (s) = r(s) + (d-s)t(s). (17.2-15)
Каждой эвольвенте соответствует свое значение d, представляющее собой постоянную
сумму длины дуги s и отрезка касательной PqpI от точки Pq кривой С до точки Р f
эволюты. Кривая С называется эволютой кривой С, если касательные к С являются
нормалями к С, т. е. если С есть эвольвента кривой С, Эволюты кривой С лежат на ее
полярной поверхности.
524
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.3-1.
17.2-6. Порядок касания (см. также п. 17.1-5). Пусть кривые r = f (s) и г —g(s)
проходят через точку Pt (rt), где г, =f (st) =g(St). Если расстояние между точками этих
кривых | f (st + As) — g(si + As) | является бесконечно малой (я+1)-го порядка
относительно As, то говорят, что кривые имеют касание л-го порядка в точке Pt.
Необходимым и достаточным условием того, что регулярные кривые r = f(s) и
r = g(s) имеют касание я-го порядка в точке Pt {хи уи z^^Piiri), являются
соотношения
f(S|)=g(Si) = ra, i>(st)=g'(St) f(«> (S1)=g(")(S1), f(/l+1)(Si)^g<,l+1)(S1)i
(17.2-16)
которые должны выполняться при подходящем выборе начала отсчета и направления на
каждой из кривых.
Для кривой, заданной уравнениями z — z(x)t у — у(х), условия касания л-го порядка
принимают вид, аналогичный (17.1-10).
17.3. ПОВЕРХНОСТИ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
17.3-1. Вводные замечания (см. также п. 3.1-14, примеры см. в п. 3.5-10).
В пп. 17.3-1 — 17.3-14 рассматривается геометрия регулярного куска
поверхности 5, определяемого векторным уравнением
г = г(ы, v), (17.3-1а)
или уравнениями
х=х(и, i>), y=y(u, v), z = z(u, v), (17.3-16)
или
Ф(*, У, z) = 0, (17.3-lc)
для некоторой области изменения параметров (криволинейных координат на
поверхности) и, v (п. 3.1-14). Предполагается, что функции (1) имеют
непрерывные частные производные первого порядка, и ранг матрицы
(17.3-2)
равен 2 (п. 13.2-7), т. е. три функциональных определителя д (х, у)/д (и, v)
д (у, г)/д (и, у), д (z, х)/д (ut v) не обращаются в нуль одновременно, или
г„хг,^0 (г.з£. г„ = £). (17.3-3)
В случае необходимости предполагается существование производных более
высокого порядка.
Условия, перечисленные выше, обеспечивают существование и линейную
независимость векторов г и г , направленных соответственно по касательным к координатным
линиям и== const и v = const на поверхности, проходящим через точку (и, v). Точки
поверхности, в которых три определителя существуют, но обращаются в нуль при любом
выборе параметров и, v, называются особыми точками', им соответствуют ребра, вершины
и т. д.
17.3-2. Касательная плоскость и нормаль к поверхности.
(а) В каждой точке поверхности Рг (гх) = Рг (xt yl9 zx) = {ult v{),
удовлетворяющей условиям п. 17.3-1 {регулярная точка поверхности), существует
единственная касательная плоскость, которая определяется как предельное
положение плоскости, проходящей через три различные точки поверхности Ръ
^2» ^з ПРИ стремлении Р2 и Р3 к Рг\ при этом Р2 и Р3 перемещаются вдоль
кривых, имеющих различные касательные в точке Pv Эта плоскость содержит
дх
ди
дх
dv
ду
ди
ду
dv
дг
ди
дг
dv
17.3-3. 17.3. ПОВЕРХНОСТИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 525
касательные ко всем регулярным кривым поверхности, проходящим через Рг.
Касательная плоскость определяется уравнением
[г —гх, гй, 14,] = 0 или
*—*i У — У1 * — Ч
дх ду дг
ди ди ди
дх ду дг
dv dv dv
= 0,
(17.3-4)
где все производные берутся при u=uv v = vv
(b) Нормалью к поверхности 5 в ее регулярной точке Рг называется
прямая, проходящая через Рг и перпендикулярная к касательной плоскости в этой
точке. Уравнение нормали имеет вид
г —rlS=/N,
где
N =
г„ х г„
д (У, z) . д (г, х) д(х, у)
д(и, v) "*" д(и, v) Ji~ д(и, v)
1/ Г д (у, z) I» [а (г, х) 1» Г д(х, у) у
У L д (и, v) J "*" L а (и, v) J ч" L а <«, и) J
(17.3-5)
(17.3-6)
есть единичный вектор нормали к поверхности 5 в точке Рг\ все производные
берутся при и = иъ v=vv Направление вектора N называется направлением
положительной нормали в точке Рг\ положительное направление линии и
(направление вектора гя)4 положительное направление линии v (направление
вектора г^,) и положительная нормаль образуют правую систему осей (п. 3.1-3).
17.3-3. Первая основная квадратичная форма поверхности. Дифференциал
длины дуги и элемент площади.
(а) Дифференциал радиуса-вектора г вдоль кривой
г = г [u(t)t v(t)] или u = u(t), v = v(t),
лежащей на поверхности 5, имеет вид
dr = rttdu + rvdv
(17.3-7)
(17.3-8)
и, следовательно, квадрат дифференциала длины дуги ds=\dt\ на
поверхности (1) в точке (и, v) равен
ds2=\dr |2 = £(и, v)du2 + 2F(u, v)dudv+ G (и, v) dv2
(первая основная квадратичная форма поверхности),
^(«.-)—.-(5-),+(*),+(*),«
О(*«0-г^.-(£)'+(&)' + (£)'.
где
(17.3-9)
В каждой регулярной точке поверхности (1), отнесенной к (действительным)
координатам и, v, квадратичная форма (9) является положительно
определенной (п. 13.5-2), т. е.
£>0, (?>0, £(?-F2>0. (17.3-10)
(b) Угол v между двумя регулярными кривыми на поверхности}
r = R,(0 или « = £/,(0, v=Vi(t)
и
r=Ra(/) или ы = С/8(0. v=-Vt(th
52в ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ 17.3-4.
приходящими через точку (и, v), определяется формулой
cos v = dR*'dR* = E du* dU* +F (dUt dVt + dUidVJ + QdVid Vj ^
l«ill«tl Ye dU\+ 2F dUv dVi + G dv\ V E dU% + 2F dU2 dV% + G dV%
ds ds ' \ ds ds ~ ds ds J ' ds ds
В частности, угол Vi между координатными линиями и — const и v = const, проходящими
через точку (и, v), определяется формулами
F V EG — F8
cosvi = -7t=rr. sin Yi= X— . (17.3-12)
Veg Yeg
Условие ортогональности координатных линий и, v имеет вид FssO (см. также пп. 6.4-1
и 16.8-2).
(с) Векторный элемент площади d\ и элемент площади dA в регулярной
точке поверхности (и, v) определяются выражениями
d\ = (ru xrv)dudv=N\dA\,
dA= ± | dА | = Va{u, v) du dv,
где
«(«, v)4rnXrvl^EG-F^[I^Y+[l^f+[l^]\ (17.3-13)
Знак dA может быть выбран произвольно (см. также пп. 4.6-11, 5.2-7, 6.4-3, Ь).
17.3-4. Геодезическая и нормальная кривизна кривой на поверхности.
Теорема Менье.
(a) В каждой точке (и, v) регулярной кривой С
r = r[u(s), v(s)] или u = u(s), v = v(s), (17.3-14)
лежащей на поверхности S, вектор кривизны г"=£п (п. 17.2-2, d) может
быть единственным образом представлен в виде суммы двух векторов, один
из которых (вектор геодезической или тангенциальной кривизны) лежит в
касательной плоскости, а другой (вектор нормальной кривизны) направлен вдоль
нормали к поверхности 5, т. е.
r"=kn = kQ(N X r') + ^N; (17.3-15)
N—единичный вектор нормали к поверхности. В каждой точке [u(s)> v{s)]
величина
&G = [6r'nN] = [r'r"N] (геодезическая кривизна кривой С в точке (ut v))
(17.3-16)
является кривизной проекции кривой С на касательную плоскость (см. также
п. 17.4-2, d) и
^ = Aj(n.N) = r".N = — r'-N'
(нормальная кривизна кривой С в точке («, v)) (17.3-17)
является кривизной нормального сечения (сечение поверхности плоскостью,
содержащей нормаль к поверхности, плоскость которого проходит через
касательную к С; см. также п. 17.3-5).
(b) Теорема Менье. Кривизна k кривой, лежащей на поверхности,
равна, кривизне kN нормального сечения, плоскость которого проходит через
касательную к кривой в данной ее точке, деленной на косинус угла а между
соприкасающейся плоскостью кривой в этой точке и плоскостью нормального
сечения, т. е.
£ = |_1*Ч (17.3-18)
17.3-Б. 17.3. ПОВЕРХНОСТИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ Ь21
Уравнение (18) выражает кривизну любого наклонного сечения через
кривизну нормального сечения с той же касательной.
17.3-5. Вторая основная квадратичная форма. Главные кривизны,
гауссова кривизна и средняя кривизна.
(а) Для того чтобы записать выражения для kN (формула (17)) в
криволинейных координатах и, v, рассматриваем dN = Nudu + Nvdv и вводим
обозначения
—dx • dN =L (и, v) du* + 2 M (uy v) du dv + N(u, v) dv*
(вторая основная квадратичная форма поверхности),
где
L(u, v) = —ru.
М(и, v) = —ra-
N(u, i>) = — iv
N« =
VEG — F*
■Ne«*
™v~Yeg
v "u~~Yeg-f*'
/Г2
(17.3-19)
Все производные берутся в точке (и, v)\ подробные выражения для
смешанных произведений можно написать по формуле (5.2-11).
Кривизна нормального сечения в точке (и, v) поверхности S, плоскость
которого проходит через бесконечно близкую точку этой поверхности (u + du9
v-\-dv), равна
du2 + 2М dudv-\- N dv*
E du2 + 2F dudv + G dv* '
(17.3-20)
'l—^ff-Lffi + MSZ + lffi-i
■^ Из формулы (8), записанной в виде dr = du
( , dv
следует, что
отношение dv/du вполне определяет направление касательной к рассматриваемому
нормальному сечению. •&
(Ь) Точка поверхности, в которой kN имеет одно и то же значение для всех
нормальных сечений (L: М : N = E : F : G), называется омбилической. В
каждой неомбилической точке (ut v) существует два нормальных сечения
(главные нормальные сечения), которым соответствуют наибольшая величина k±
и наименьшая величина k2 кривизны kN (главные кривизны поверхности S
в точке (ut v)). Плоскости главных нормальных сечений взаимно
перпендикулярны] для любого нормального сечения в точке (и, v), плоскость которого
образует угол 6 с плоскостью первого главного нормального сечения,
kN = kx cos2 0 + k2 sin2 б (теорема Эйлера).
(17.3-21)
Величины kt и k2 являются корнями характеристического уравнения *)
L-kE M-kF
M-kF N-kG
= 0.
(17.3-22)
*) Иначе говоря, kx и k9 есть собственные числа обобщенной задачи о
собственных значениях матрицы A — kB, где
\М NJ* \F С/
в матрица В положительно определена (п. 14.8-7).
А =
528
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.3-6»
Симметрические функции
H(ut v)^~(kx+k2) и К (и, v)^kxk2
называются соответственно средней и полной (гауссовой) кривизной
поверхности 5 в точке (ы, v); они следующим образом выражаются через коэффициенты
основных квадратичных форм:
Я г 1 (kx + k2) ■■ \ EN~G2!LMFt* °L (средняя кривизна), (17.3-23)
/Caft^sa EG~L Fi (гауссова кривизна) (17.3-24)
(см. также пп. 17.3-8 и 17.3-13). Значения функций klt k2t H и К не зависят
от выбора криволинейных координат.
В зависимости от того, будет ли квадратичная форма (19) определенной,
полуопределенной или неопределенной (п. 13.5-2) в точке (и, у), эта
последняя является
эллиптической точкой, в которой /С = ^2 > 0 (нормальные
сечения все выпуклы или все вогнуты; поверхность не пересекает
касательную плоскость; пример: любая точка эллипсоида);
параболической точкой, в которой Kz=k1k2 = 0 (например,
любая точка цилиндра);
гиперболической точкой (седловой точкой), в которой K^kxk2 <0
(имеются как выпуклые, так и вогнутые нормальные сечения;
поверхность пересекает касательную плоскость; пример: любая точка
однополостного гиперболоида).
Омбилическая точка (&t=&2, п. 17.3-5, Ь) необходимо является либо
эллиптической, либо параболической.
17.3-6. Некоторые направления и кривые на поверхности. Минимальные
поверхности.
(а) Линией кривизны на поверхности называется кривая, в каждой точке которой
касательная принадлежит плоскости главного нормального сечения в этой точке. Через
каждую неомбилическую точку (и, v) поверхности 5 проходят две линии кривизны
v = v (и), которые являются взаимно перпендикулярными; их дифференциальное
уравнение имеет вид
I dv* — du dv du21
С. (17.3-25)
dv9
E
L
— du dv
F
M
du
G
N
(b) Асимптотической линией поверхности называется кривая, нормальная кривизна
(20) которой р каждой точке равна нулю; асимптотические линии определяются
дифференциальным уравнением
L du2 + 2M dudv + N dv2 = 0. (17.3-26)
(Пример: любая прямая линия на поверхности.) Направления касательных к
асимптотическим линиям называются асимптотическими направлениями поверхности.
•# В эллиптической точке поверхности асимптотические направления являются
мнимыми.
В гиперболической точке имеются два различных асимптотических направления.
Линии кривизны делят пополам угол между ними.
В параболической точке имеется одно асимптотическое направление, которое
совпадает с направлением касательной к главному нормальному сечению, имеющему нулевую
кривизну. >fc
(с) Направления двух регулярных дуг поверхности
и = Ut (t), v=Vx (t) и и = U2 (t) v=Vt (t)
называются сопряженными в точке их пересечения (и, v), если касательная к одной из
17.3-7. 17.3, ПОВЕРХНОСТИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 529
этих дуг в точке (и, v) является предельным положением прямой, по которой
касательная плоскость поверхности в точке (и, v) пересекается с касательной плоскостью
поверхности в некоторой точке второй дуги при стремлении этой точки к (и, v). Условие
сопряженности имеет вид
L dUt dU2 + M (dU1 dV9 4- dUt dVt) + N dVt dV2 = 0.
(17.3-27)
(Пример: направления линий кривизны.)
Отношение сопряженности является взаимным.
(d) Координатные линии и — const, v = const являются
ортогональными, если F = 0,
сопряженными, если М =0,
линиями кривизны, если F == 0, М s 0,
асимптотическими, если L == 0, N == 0.
Все приведенные условия необходимы и достаточны.
(e) X Минимальной поверхностью называется поверхность, у которой Н (и, v) = 0,
т. е. k2 = — ki (формула (23)). Это имеет место в том и только в том случае, когда
асимптотические линии образуют ортогональную сеть. X
Пусть дана поверхность в виде односвязной области, ограниченной замкнутым
контуром. Если оставить неизменным контур и менять натянутую на него поверхность (как
меняется упругая пленка), то поверхность, имеющая наименьшую площадь, будет
обязательно минимальной; отыскание минимальной поверхности по заданному контуру
называется задачей Плато.
Физическим аналогом минимальной поверхности может служить мыльная пленка,
натянутая на изогнутый в пространстве проволочный контур.
17.3-7. Поверхности как римановы пространства. Трехиндексные символы Кристоф-
феля и параметры Бельтрами. Регулярный кусок поверхности 5 с первой основной
квадратичной формой (9) является двумерным римановым пространством, отнесенным
к координатам и, v, метрический тензор которого имеет компоненты: gli = Et £i2—
= £2i=/\ gj2 = 0 (пп. 16.7-1 и 17.4-1; см. также п. 17.3-12); а (и, v) = EG — F* есть on-
редилитель метрического тензора (п. 16.7-1). Если рассматривать поверхность как
риманово пространство, то на ней можно определить векторы, тензоры, скалярное
произведение и ковариантное дифференцирование (п. 16.2-1, 16.8-1 и 16.10-1). Трехиндексные
символы Кристоффеля второго рода (п. 16.10-3) имеют для поверхности S следующий вид *):
.0E„-2FFa + FEv
U.
tl 2jS=\2 1J5^
12 2j,
2 (EG — F2)
GEv-FGn
2 (EG — F*)
-FG7t + 2GF7t-GG„
2 (EG — Fz)
{,\}s-
-FEu+2EFu-
■££..
U 2J5 \2 lj,
12 2J5
2 (EG — F*)
EG„-
FE„t
2 (EG — F*)1
-2FF7+FGn.
2 (EG — F2)
(17.3-28)
обозначение «5» использовано для того, чтобы отличить символы Кристоффеля
поверхности от символов Кристоффеля ■! . Л объемлющего пространства.
Для функций Ф (и, v), Ч? (и, v), имеющих непрерывные частные производные
нужного порядка, могут быть составлены дифференциальные инварианты
Vc (Ф, W) sb
— EG — F2
(первый дифференциальный параметр Бельтрами),
д GO„ — FOv д ЕФ„ — FO
V EG — F2L
ди YEG — F* dv YEG — F
{второй дифференциальный параметр Бельтрами),
г"]
(17.3-29)
вполне аналогичные уф.^Р* и у2Ф. определенным в табл. 16.10-1. Так как двумерное
риманово пространство «погружено» в трехмерное евклидово пространство, ковариантное
дифференцирование на поверхности можно интерпретировать при помощи
действительного сравнения векторов поверхности в соседних ее точках; оцнако при этом должно
рассматриваться не приращение вектора, а его ортогональная проекция на касательную
плоскость.
*) См. сноску на стр, 513.
530
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
J 7.3-в.
17.3-8. Уравнения с частными производными, связывающие коэффициенты
основных квадратичных форм. Theorema Egregium Гаусса.
(а) Изменение линейно независимых векторов г г N («локальный базис») при
смещении вдоль координатных линиий поверхности описывается следующими
соотношениями:
ruv = {il2}sra + {i22}srv + M,i-
rW = {212}sr« + {222}sr* + A'N- J
(уравнения Гаусса), (17.3-30)
N« = * г, \(FM — GL) г + (FL — EM) r 1 1 t
UEG — F*V k^v vh I (уравнения /j7 3.3П
1 ( Вейнгартена)
(b) Условия совместности системы дифференциальных уравнений (17.3-30) (условия
ruuv =
имеют вид
L* + {i\}sM + {i2i}sN = Mu + {l\}sL + {i\}sM- \1ГненТ „„,»
\ Маинарди — (17.3-32)
M* + {l\}sM + {l\}s» = N» + {22}sl' + {2\}sM' ) ^^^
Т[дй \ 1 2JS~dv{\ l/S + ll 2JS11 2JS~U l)s\2 2jsj = EG — F* в *#
(17.3-33)
(с) Уравнения (33) выражают К только через Е, F, G и их производные, откуда
следует, что гауссова кривизна К(и, v) поверхности является инвариантом изгибания,
т. е. не меняется при таких деформациях поверхности, при которых сохраняется ее
первая квадратичная форма (Theorema Egregium Гаусса).
17.3-9. Определение поверхности коэффициентами ее основных
квадратичных форм. Три функции Е(и, v), G(u, v) и F (uy v), удовлетворяющие
условиям Е(иу v)>0, G(u, a)>0, EG — /Г2>0, определяют метрику
(внутреннюю геометрию) поверхности. Шесть функций Е, F, G, L, M, N,
удовлетворяющих указанным выше неравенствам и условиям совместности (32) и (33),
однозначно определяют действительную поверхность г = г(ы, v) с точностью до
ее положения в пространстве (основная теорема теории поверхностей).
17.3-10. Отображения.
(а) Взаимно однозначное преобразование (отображение)
5-й(и, о), 5-йи. v), [4&-3*0] (17.3-34)
ставит в соответствие каждой точке (и, v) данного регулярного куска
поверхности г = г(и, v) определенную точку (и, v) регулярного куска другой
поверхности г = г(ы, v). В дальнейшем символы с чертой сверху будут относиться
ко второй поверхности. Функции и (и, v), v(u, v) предполагаются
дифференцируемыми достаточное число раз. Отображение называется
изометрическим (сохраняет все метрические величины на
поверхности), если
£ (й, v) в Е (и, v)9 7 (й, i)sf (и, v)y G (й, v) = G(и, v);
*) В отечественной литературе уравнения (17.3-32), основываясь на хронологической
последовательности, в которой они рассматривались, называют уравнениями Петерсона —
Кодацци.
17*3-1Ъ 17.3. ПОВЕРХНОСТИ D ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 531
конформным (сохраняет углы), если
^ (uyv) :T(utv):~G(iitv)^E(uy v):F(u, v):G(u,v);
эквиареальным (сохраняет площади), если
д(й, у) _-\/~EG — F*
д(и, v) "" " £G — F2'
(Ь) Для получения конформного отображения (34) каждая из поверхностей конформно
отображается на плоскость, а затем одна плоскость отображается на другую при помощи
аналитической функции комплексного переменного (п. 7.9-1).
Для того чтобы отобразить конформно поверхность r = r(w, v) на плоскость с декар-
то вы ми прямоугольными координатами £ (и, v), т) (w, v), решается дифференциальное
уравнение
Е («, v) du2 -f 2F (и, i>) dudv + G {и, v) dv2 = 0 (17.3-35 a)
или, что то же,
*j_-£(_F + i/£C-l™) и f£ = -i(-F-,/EG-F'). (17.3-35 6»
Интегралы этих уравнений определяют мнимые кривые (изотропные или
минимальные «кривые» на поверхности, которые характеризуются условием ds2 = 0)
U (и, v) = const, V (и, v) = const.
Тогда первая квадратичная форма поверхности в действительных ортогональных
координатах
Ци. v) = jlU + V). г\(и, 10 = 1 <1Г-У) (17.3-36)
(изотропные или изотермические координаты) принимает вид
</s» = iM&. г» (</£» +</T|«J (17.3-37)
и становится пропорциональной первой квадратичной форме d%z-{-dr\2 плоскости с
декартовыми прямоугольными координатами |, г|.
17.3-11. Огибающие (см. также пп. 10.2-3 и 17.1-7). Пусть уравнение
Ф(*. </, 2, А,)=0 (17.3-38)
определяет однопараметрическое семейство поверхностей, для которого
УФХУФ^О, ф'и^О (17.3-39)
в некоторой области V пространства. Тогда в области V существует поверхность
(огибающая данного семейства), которая касается каждой из поверхностей (38) вдоль кривой
(характеристики), определяемой уравнениями
Ф (*, у, z, Я) =0 ср£ (х, у, z, X) = 0, (17.3-40)
т. е. имеет с поверхностью семейства общую касательную плоскость в каждой точке
характеристики.
Если, кроме того, в области V выполняется условие Г УФУФА,УФЯл] ^ 0» то
огибающая имеет ребро возврата, т. е. кривую, которая касается каждой характеристики (40);
точка касания ребра возврата и характеристики называется фокусом. Координаты фокуса
определяются уравнениями
Ф (х, у, z, X) =0, ф{ (х, у, z, %) =0, фм (х, у, 2, к) = 0. (17.3-41)
Исключение К из уравнений (41) приводит к уравнениям ребра возврата.
Уравнения (40) определяют при фиксированном значении К =^КХ кривую, являющуюся
предельным положением линии пересечения поверхностей
Ф (х, у, z, kt) =0 и ф (х, у, z, Х2) =0 при Кг -*Яг,
если А. произвольно, то уравнения (40) определяют геометрическое место таких кривых.
Это геометрическое место (Я-дискриминантная поверхность) содержит, наряду с
огибающей, все особые точки поверхностей семейства (ребра, узловые точки и-т. д.).
Ребро возврата является, аналогично, геометрическим местом точек пересечения
трех бесконечно близких поверхностей (38).
17.3-12. Геодезические линии поверхности (см. также п. 17.4-3).
Геодезической линией регулярного куска поверхности 5 называется регулярная
дуга, геодезическая кривизна которой (п. 17.3-4, а) тождественно равна нулюз
532 ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ 17.3-13.
геодезическая либо является прямой линией, либо ее главная нормаль
совпадает с нормалью к поверхности в каждой точке. Для любой геодезической
и —и (s), v — v(s) или v — v(u)
соответствующие функции и (s), v (s) и v (и) удовлетворяют дифференциальным
уравнениям
"</*■ +U lis U) +2(l 2Js<fcrfs + l2 2Js U) ~0, I
~^+U llsW +2{l 2)s^dJ + \2 2)s\^) ==°
(17.3-42a)
или
du* -\2 2\s \du) +[2{l 2)5 (2 2JsJ W +
+
[{.'.b-'WJs-l,',}.- <«•"•»
Эти соотношения определяют единственную геодезическую, проходящую через
каждую данную точку в каждом данном направлении. Геодезические линии
кривой поверхности имеют много свойств, аналогичных свойствам прямых
линий на плоскости (см. также п. 17.4-3). Если на поверхности существует
кривая наибольшей или наименьшей длины, соединяющая две данные точки
поверхности, то она является геодезической. Вопрос о существовании
геодезической, проходящей через две данные точки поверхности, требует специального
исследования в каждом отдельном случае.
17.3-13. Геодезические нормальные координаты. Геометрия на поверхности (см.
также п. 17.4-7).
(a) -X Система геодезических нормальных координат и, v (полугеодезические
координаты) характеризуется тем, что координатные линии v = const являются геодезическими
линиями, а координатные линии и = const — их ортогональными траекториями. X
Всегда можно так выбрать систему полугеодезических координат, что вдоль каждой
из геодезических координата и играет роль длины дуги s и длина отрезка геодезической
между линиями u = ut и и — и2 равна иг — их. Тогда семейство линий w = const
называется геодезическими параллелями, так как заключенные между любыми двумя из таких
линий отрезки ортогональных к ним геодезических имеют равные длины.
Первая основная квадратичная форма поверхности, отнесенной к полугеодезическим
координатам, принимает вид
ds* = du* + G (и, v) dv*. (17.3-43)
В полугеодезических координатах полная (гауссова) кривизна
1 d2V~G G\-2GGUU
К = = — —. (17.3-44)
VG ди2 4G*
(b) В специальном случае геодезических полярных координат геодезические v = const
пересекаются в одной точке (полюсе), a vt есть угол (п. 17.3-3, Ь) между геодезическими
v = 0 и v = vt. Каждая линия «=const есть «геодезическая окружность» радиуса и,
пересекающая все линии v = const под прямым углом. «Дуга окружности радиуса ы»,
соответствующая центральному углу dv, равна
YG(u, v) dv = \и — ~ К0и* + о («3)1 dv, (17.3-45)
где Ко — гауссова кривизна в полюсе. Величина (45) меньше, равна или больше чем udv,
если соответственно /С0>0. /Со=0 или /С0<0.
Длина окружности Cq (и) и площадь Aq {и) геодезического круга малого радиуса и
с центром в полюсе связаны с длиной окружности 2ли и площадью ли2 круга того же
радиуса на плоскости следующими соотношениями:
3 2ли-С0(и) 12 nu*-AG(u) nn.fi.
_ Jim - = — lim т = /C0. (17.3-46)
17.4-2.
17.4. ПРОСТРАНСТВА С КРИВИЗНОЙ
533
(с) Для любого геодезического треугольника на поверхности постоянной гауссовой
кривизны К разность я — (Л + В + С), где А, В, С — углы треугольника (дефект
треугольника), связана с его площадью Sf соотношением
А + В + С — n = KSTt (17.3-47>
Как следствие, геометрия на поверхности постоянной кривизны является евклидовой при
К = 0, гиперболической при К<0 и эллиптической при /С> 0. Поверхности
постоянной равной гауссовой кривизны изометричны (теорема Миндинга).
Примеры. Для сферы радиуса R гауссова кривизна К = 1//?8. Поверхность
постоянной отрицательной кривизны К может быть получена вращением трактрисы
х= . sin/, у — /in tg —+ cos/)
Y=k V-K\ 2 /
вокруг ее асимптоты (псевдосфера).
17.3-14. Теорема Гаусса —Бонне, Пусть гауссова кривизна К (и, v)
непрерывна в замкнутой односвязной области поверхности S, граница которой С
состоит из п регулярных дуг с геодезической кривизной KQ (и, v). Тогда сумма в
всех п внешних углов границы связана с интегральной кривизной \\ KdA области
s
S следующей формулой:
j KQ ds + ЭД К dA = 2n — & (теорема Гаусса —Бонне), (17.3-48)
с б
Первый из интегралов обращается в нуль, если область ограничена геодезическими;
формула (47) является частным случаем теоремы Гаусса—Бонне.
17.4. ПРОСТРАНСТВА С КРИВИЗНОЙ
17.4-1. Вводные замечания. Теория, изложенная в пп. 17.4-2—17.4-7,
посвящена изучению в криволинейных координатах таких геометрических
понятий, как длина, угол, кривизна, и обобщению их на некоторый класс
многомерных пространств, а именно римановых пространств, введенных в гл. 16.
17.4-2. Кривые, длины и направления в римановом пространстве (см. также
пп. 4.6-9, 5.4-4, 6.2-3)1).
(a) Метрические свойства, связанные с /г-мерным точечным римановым
пространством, отнесенным к координатам х1, х2, ..., xnt задаются
компонентами его метрического тензора gik(xlt х2, ..., хп) (п. 16.7-1), который
определяет скалярное произведение и, следовательно, модули и направления
векторов в каждой точке (п. 16.8-1).
(b) Регулярная дуга С определяется п параметрическими уравнениями
xl=xl(t) (tx^t^t2) (17.4-1)
с непрерывными производными dxl/dtt не обращающимися одновременно в нуль.
Дифференциалы dx( = (dxl/dt) dt служат компонентами вектора, который можно
рассматривать как направляющий вектор dx касательной к кривой С в ее
точке (xlt х2 хп)\ элемент расстояния ds между двумя соседними точками
кривой (х1, х2, ..., хп) и (xl + dxlt x2+dx2 xn-\-dxn) определяется
следующим образом:
ds = Vgik(x\ х2 x")dxidx*=zygik{xi9 X2 xn)d£d£dt. (17.4-2a)
Знак ds выбирается так, что ds > 0 для dt>0 (положительное направление на
х) Уравнения (4)—(6) могут применяться непосредственно лишь в случае ds^/ЬО.
Изотропные направления и линии нулевой длины (dr ф0, ds=\dr \=0) в римановых
пространствах с неопределенной метрикой кратко рассмотрены в п. 17.4-4.
534
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.4-3.
кривой С в случае положительно определенной квадратичной формы g(k dtfdx*).
В некоторых случаях ds определяется соотношением
ds == V\ gik (xx, х2 хп) dxl dxk | . (17.4-26)
Длина дуги s кривой С от точки кривой, соответствующей значению параметра
t — t0i определяется интегралом
..jd.sjV^^A (17.4-3)
to t0
Величина интеграла (3) не зависит от выбора параметра t на кривой.
(c) Под направлением кривой (1) в каждой ее точке (х1,х2 Xя)
понимается направление вектора dr; иными словами, угол у между любым
вектором а, заданным в точке (х1, х2, ♦ .., хп), и кривой определяется формулой
cos у = , а i, w (п- 16.8-1). В частности, угол у между двумя регулярными
I а | i as j
дугами xl — Xi (t) и xi = Xt (t) находится по формуле
dxi dxk
^y^gik-ar-aT' (17.4-4)
Общие точки (л —1) из п координатных гиперповерхностей* = const (/ = 1, 2, .... п),
проходящих через данную точку (д:1. х2, .... хп), лежат на координатной линии,
соответствующей л-й координате (см. также п. 6.2-2). Косинус угла между r'-й и fc-й
координатными линиями в точке (дг1, х2, .... хп) равен &1ъ1^&ц&ъь.
(d) Единичный вектор dr/ds (с компонентами dxl/ds) является единичным
вектором касательной к кривой С в точке (х1, х2 хп). Первый вектор
кривизны d2r/ds2 (с компонентами y~\T~P перпендикулярен к кривой
(направление главной нормали, см. также п. 17.2-2, Ь); его абсолютная величина
^=т=у^тш) (i7-4-5)
называется первой кривизной кривой С в точке (дг1, х2,..., хп) (см. также
п. 17.3-7).
17.4-3. Геодезические линии в римановом пространстве (см. также
п. 17.3-12).
(а) Геодезической линией риманова пространства называется регулярная
дуга, геодезическая кривизна которой равна нулю в каждой точке кривой
или, чтэ то же, единичный касательный вектор которой dr/ds сохраняет
постоянное значение (в смысле параллельного перенесения, п. 16.10-9) вдоль
кривой:
йЧ л „ D Ых1\ (fix* , \i\dxidxk л ,л-7 л *\
-^=0 или _^_Js_ + |/^__ = 0. (17.4-6)
Дифференциальные уравнения (6) (п уравнений второго порядка) определяют
единственную геодезическую xi = xi(s)9 проходящую через данную точку
\х* = х1 (Si)] в любом данном направлении (соответствующем заданным
значениям dx{jds при s-=s^).
Геодезические линии могут определяться также уравнениями более обще! о вида,
а именно, дифференциальные уравнения
+ {/' 1^5^-МО^ (17.4-7)
т I/ *J dt dt dt
7Л-5.
17.4. ПРОСТРАНСТВА С КРИВИЗНОЙ
535
(с заданными начальными значениями хг и dx4dt) определяют геодезическую л' = х* (t)\
вид функции
^-£/(2)'
связан с выбором параметра t на геодезической, но не меняет кривую как таковую.
(Ь) Геодезические линии обладают многими свойствами прямых
евклидовой геометрии (см. также п. 17.4-6). Если существует кривая наименьшей
или наибольшей длины (3), соединяющая две данные точки риманова
пространства, то она является геодезической. Дифференциальные уравнения
геодезической (6) или (7) можно рассматривать как уравнения Эйлера (пп. 11.6-1
и 11.6-2), выражающие тот факт, что первая вариация длины дуги (3),
соединяющей данные точки, равна нулю. Вопрос о существовании геодезической,
соединяющей две данные точки риманова пространства, требует в каждом
отдельном случае специального исследования.
17.4-4. Римановы пространства с неопределенной метрикой. Изотропные
направления и геодезические нулевой длины. Если фундаментальная форма
gik{xx, х2, ..., хп) dxldxk
риманова пространства является неопределенной (п. 13.5-2) в точке (**, *2, ..., xn)t
то квадрат I а | * — g^a'a* вектора а может быть положительным, отрицательным или
равным нулю, и из | а | = 0 не следует, вообще говоря, что а = 0. В любой точке
(**, jc2, ..., хп) направление вектора а^:0, удовлетворяющего условию | a|2 = g/^a* = 0*
называется изотропным направлением. Для вектора элементарного перемещения dr фЪ%
имеющего изотропное направление, ds = \ dx \ = 0; при этом точки (xlf х2у ,.м хп) н
(дг -f- dx^» •••» хп -J- dxn)t связанные таким изотропным перемещением, различны.
Кривая х1 = х1 (/), удовлетворяющая условию
«<*££-о. ом*
имеет изотропное направление в каждой своей точке (кривая нулевой длины,
изотропная кривая, см. также п. 17.3-10, Ь).
Кривая х1 = х1 (0, удовлетворяющая одновременно уравнениям (7) и (9),
называется геодезической линией нулевой длины. Каждое изотропное направление определяет
единственную геодезическую линию нулевой длины, проходящую через данную точку в этом
направлении (одно из применений — траектории светового луча в римановом пространстве
теории относительности).
17.4-5. Тензор кривизны риманова пространства.
(а) Тензором кривизны (тензором Римана — Кристоффеля) данного
риманова пространства называется абсолютный тензор ранга 4 со следующими
смешанными компонентами (здесь г —немой индекс):
или с ковариантными компонентами
%*/.-£>*/*/,- j~k № <]- -^ № «]+ {fk} lih; r]-{/h) [Ik; r\^
2 \_dxidx* dx'dxh dxidxh дх1дх^.\
+8rs {№ s] [ili; r\-[jh; s] \ik; /•]}. (17.4-П)
X Иногда пользуются также обозначениями
Riikh =RU. kh и R№ = R-i,kh^Rhk, /.'*
536
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.4-6.
Компоненты тензора кривизны удовлетворяют следующим соотношениям:
Я/** — */**"*"*'/**. Riikh+RM+Xhjk = °- <17-4"12>
%kh -Rkhii Ritkh —Rim* RUkh +Rikhi +Kih/k -°: ('7.4-13)
вторые соотношения в формулах (12) и (13) столбца называются тождествами Риччи.
Тензор кривизны n-мерного риманова пространства имеет — существенных
компонент, через которые выражаются остальные его компоненты. Абсолютные
производные тензора кривизны удовлетворяют тождествам Бианки (Бианки — Падова)
>' ' °' * D* .и u-v. I
(тождества Бианки). (17.4-14)
Rfkh,r + R)hr.k +Rjrk,h'ss0' \
Rijkh,r + Rijhr, k + Rijrk. h - ° J
(b) Тензором Риччи данного риманова пространства называется
абсолютный тензор ранга 2 с ковариантными компонентами
«.-«.-«j.-£=fiFI-=.W-Ws.-»Tii+vlH(*4
(17.4-15)
или со смешанными компонентами Rlj ss ^kRkj Тензор Риччи в п-мерном рима-
новом пространстве является симметричным и имеет п *" "*" существенных
компонент.
Собственные направления тензора Риччи (п. 14.8-3) называются
главными направлениями Риччи; они определены в каждой точке риманова
пространства.
(c) Скалярным инвариантом или скалярной кривизной риманова
пространства называется скалярный (абсолютный) инвариант
R в /?{ в J%k в fSkR{kj (17.4-16)
(d) Тензором Эйнштейна данного риманова пространства называется
абсолютный тензор ранга 2 с компонентами
°*1-#1-тЩ или S-*»0/-^/-!-^!/. (17-4-17>
Дивергенция (п. 16.10-7) (?'• t тензора Эйнштейна тождественно равна нулю.
17.4-6. Геометрическое истолкование тензора кривизны. Плоские
пространства и евклидовы пространства.
(a) Параллельное перенесение вектора вдоль
замкнутого контура. Параллельное перенесение вектора a (Da' =0, п. 16.10-9)
вдоль бесконечно малого замкнутого контура
(х\ х\ ..., *") — (x1 + dx1t x* + dx2,..., xn + dxn)-+
— (л:1 + dx1 + dl1, x2 + dx2 + rfg2,..., xn + dxn + d\n) —
-*(x1 + dl11 x* + dl2,..., xn + dln) — (x11 л:2,..., хп)
вызывает изменение каждой компоненты а1 вектора а на
Ьа! = —R)kh afdxkdlh (17.4-18)
(см. также уравнение (16.10-25)).
(b) * Геодезически параллельные линии. Пусть х1 =
= х1 (s, A,)1) — уравнения однопараметрического семейства геодезических, где
*) Принятое здесь обозначение лр* = xl (s, К) исключает геодезические нулевой длины.
17.4-7.
17.4. ПРОСТРАНСТВА С КРИВИЗНОЙ
537
s —длина дуги геодезической, X — параметр семейства. Ортогональные
траектории семейства (геодезические параллельные) отсекают на геодезических
линиях дуги равной длины. Следовательно, эти ортогональные траектории
можно при подходящем выборе начала отсчета на каждой из геодезических
определить уравнением s = const. Вектор с компонентами
будет иметь направление нормали к геодезической К — const, касаясь в то же
время двумерной поверхности риманова пространства *' = a;'(s, Я) (s, Я
—переменные параметры). Вектор т|' меняется при перемещении вдоль любой из
геодезических семейства таким образом, что
l£r=-*/*fc4Vp*. (17.4-19)
где pi—координаты единичного вектора касательной к данной геодезической
линии.
(с)* Плоские пространства. Риманово пространство называется
плоским, если в окрестности каждой его точки существует такая система
координат g1, £2, ..., £Л (декартовы прямоугольные координаты), что в этой
окрестности
ds2 = 8l(|i)2 + e2 (|«)» + ... + в/, СТ> (17.4-20)
где 8/ постоянны и равны либо +1, либо — 1.
Риманово пространство является плоским в том и только в том случае,
если все компоненты его тензора кривизны RLh или R^^ равны нулю в
каждой точке пространства, так что в плоском пространстве смешанные кова-
риантные производные не зависят от последовательности дифференцирования,
и параллельное перенесение тензора вдоль замкнутого контура оставляет все
компоненты тензора неизменными (пп. 16.10-9 и 17.4-6, а)1).
В любой декарто.вой координатной системе все символы Кристоффеля тождественно
равны нулю; ковариантное дифференцирование сводится к обычному дифференцированию и
любая геодезическая определяется линейными параметрическими уравнениями £* =alt-{-bl.
Фундаментальная форма (20) может быть дополнительно упрощена посредством
введения координат £* = |/"в.£*; £* является мнимым, если е- — — 1 (это последнее
обстоятельство имеет место в теории относительности).
*(d) Плоское риманово пространство с положительно определенной
метрикой (все е,- в (20) равны+1) называют локально евклидовым. Топология
(п. 12.5-1) локально евклидова пространства может отличаться от «обычной»
топологии евклидова пространства элементарной геометрии (гл. 2 и 3); иногда,
впрочем, локально евклидово пространство также называют евклидовым
независимо от его топологии. С другой стороны, плоское пространство иногда
называют локально евклидовым независимо от того, является ли его
фундаментальная форма положительно определенной, а в случае положительно
определенной формы (17.4-20) употребляют термин «собственно евклидово
пространство»; если же форма (20) не является положительно определенной, то
пространство называют псевдоевклидовым. ■#
17.4-7. Специальные координатные системы. Благодаря инвариантности
тензорных уравнений (п. 16.1-4, 16.4-1, 16.10-7, Ь) часто удается упростить
математические рассуждения путем использования одной из специальных
координатных систем.
1) При этом предполагается, что контур может служить границей поверхности, все
точки которой принадлежат плоскому пространству.
538
ГЛ. 17. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
17.4-7.
(a) Не каждое риманово пространство допускает ортогональные координаты
(gik==0 для i ФИу п. 16.8-2), но всегда возможно выбрать одну из координат,
пусть для определенности это будет хп, так, что ее координатные линии будут
ортогональны ко всем остальным координатным линиям, вследствие чего
фундаментальная квадратичная форма принимает вид
^2=2 flgikdx*dx*+gnn(dx?)* (17.4-21)
£ ===== 1 Лг = 1
в каждой точке (л:1, л:2, ..., хп). При этом всегда можно выбрать систему
координат так, что будет выполняться одно'из дополнительных условий gnn = l
или £/1/17=— Н хп является тогда длиной s дуги каждой из координатных
линий xl = const (i = l, 2, ..., /г—1), представляющих собой геодезические,
ортогональные ко всем гиперплоскостям хп = const (нормальные геодезические
или полугеодезические координаты, см. также п. 17.3-13).
(b) # Каждое риманово пространство допускает такую систему координат
fc1, i2y ..., §л, что его фундаментальная квадратичная форма будет иметь
вид (20) в одной наперед заданной точке пространства. Более того, система
координат может быть выбрана таким образом, что в этой точке компоненты
тензора gik и частные производные первого порядка dgik/dxJ будут совпадать
соответственно с компонентами метрического тензора псевдоевклидова
пространства и их частными производными; оно называется соприкасающимся
псевдоевклидовым пространством риманова пространства в данной его точке. В
окрестности каждой своей точки риманово пространство с точностью до бесконечно
малых высшего порядка изометрично соприкасающемуся псевдоевклидову
(собственно евклидову, если метрика положительно определенная) пространству.
(c) Римановыми (нормальными) координатами с началом О называются
числа xl — sp\ где р*: — компоненты единичного вектора касательной в точке О
к геодезической линии, соединяющей О с точкой (л:1, л:2, ..., хп), a s
—геодезическое расстояние между О и точкой (л:1, л:2, ..., хп). Каждое риманово
пространство допускает геодезические координаты с любым началом О; при этом
символы Кристоффеля обращаются в точке О в нуль.
ГЛАВА 18
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
18.1. ВВЕДЕНИЕ
18.1-1. Вводные замечания. Вероятностями называются значения некоторой
действительной функции, определенной на классе идеализированных событий,
которые представляют собой результаты испытания (опыта или наблюдения).
Вероятности вводятся посредством определенных аксиом (п. 18.2-2; см. также
п. 12.1-1), абстрагируемых из основных свойств статистических относительных
частот (п. 19.2-1). Практически понятие вероятности проявляется в том, что
обычно относительная частота случайного события в каждой
последовательности независимых повторных испытаний приближается к соответствующей
вероятности (п. 19.2-1) х).
Теория вероятностей занимается определением и описанием моделей,
связанных с понятием вероятности. В частности, здесь рассматриваются методы
вычисления вероятности некоторого события по известным или заданным
вероятностям других событий, которые с ним логически связаны. Многие
приложения теории вероятностей относятся к области случайных процессов (пп. с 18.8-1
18.2. ОПРЕДЕЛЕНИЕ И ПРЕДСТАВЛЕНИЕ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ
18.2-1. Алгебра событий, связанных сданным испытанием. Каждая
вероятностная модель описывает некоторый идеализированный опыт (или
наблюдение), обладающий тем свойством, что для класса $+ его возможных исходов
(событий) имеют смысл следующие определения.
1. Объединение (логическая сумма) fiU^U ••• (или ^i + ^2+««-)
конечной или бесконечной последовательности событий Е\, Е2,...
есть событие, состоящее в осуществлении хотя бы одного из
событий Ev Е2, ...
2. Совмещение (логическое произведение) Ег (] Е2 (или ЕХЕ2) двух
событий Et и Е2 есть событие, состоящее восуществлении и Ег и Е2.
3. Дополнение (логическое отрицание) Е события Е есть событие,
состоящее в неосуществлении события Е (событие Е называют
«противоположным» событию Е).
4. Достоверное событие / состоит в осуществлении хотя бы
одного из событий класса $+.
5. Невозможное событие О состоит в том, что не осуществляется
ни одно из событий класса $+.
Класс 8 событий, состоящий из класса $+ и О, образует вполне
аддитивную булеву алгебру (пп. 12.8-1 и 12.8-4) —алгебру событий, связанных с данным
испытанием.
Любое из соотношений Е1[}Ег = Е1 или Ег(]Е2 = Е2 заключает в себе
логическое отношение включения E2czE1 (Е2 влечет Ег). Отметим, что 0аЕс/.
События Et и Е2 называются несовместными, если Е1(]Е2 = 0. Множество $t
*) До тех пор, пока это положение имеет место, оно может рассматриваться как закон
природы; не надо смешивать это положение с математическими теоремами типа теоремы
Бернулли или закона больших чисел (п. 18.6-5).
540 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.2-2.
совмещений E(]Ei образует алгебру событий, связанных сданным испытанием
при дополнительном условии, что имеет место событие Ех\ Е1(]Е1 = Е1 есть
достоверное событие в $г (см. также п. 12.8-3).
18.2-2. Определение вероятности. Условные вероятности. Пусть с данным
испытанием связан класс % событий Е (п. 18.2-1). Вероятностью Р {Е}
события Е называется определенная на «§ однозначная действительная функция,
удовлетворяющая трем условиям (аксиомам вероятностей):
1) Р {£}:>: 0 для любого события Е из $;
2) р]/} = 1 для достоверного события /;
3) P{£1U£2U...} = P{£i} + P-{£2}+ ••• для любой (конечной
или бесконечной) последовательности попарно несовместных
событий £|, Е2 ...
Из аксиом 1), 2), 3) следует, что 0^Р{£}^1; в частности, если 0—
невозможное событие, то Р {0} = 0. Важно отметить, что из равенств Р{£} = 1
или Р{£}=0 не следует, что Е является достоверным или соответственно
невозможным событием.
Вводимая далее аксиома 4) связывает «абсолютную» вероятность Р {Е},
относящуюся к данному испытанию, и «условную» вероятность Р {Е | Ех),
относящуюся к испытанию, ограниченному дополнительным условием
осуществления события Ev Условная вероятность Р {Е \ Ег\ события Е при условии
осуществления события Ег определяется аксиомой
4) Вероятность совмещения событий Е(]Ег равна
P{£fl£i} = P{£i} P{£ l^i} (правило умножения вероятностей);
вероятность Р {£* | £"i} не определена, если Р {Е^ — О.
По отношению к указанному выше «ограниченному» испытанию все величины
Р ■[£ I ЕЛ являются обычными вероятностями, именно вероятностями совмещенных
событий E{]Elf образующих алгебру $, исходов этого испытания (п. 18.2-1). На практике
каждая вероятноть может быть истолкована как условная вероятность, соответствующая
некоторым условиям, наложенным при проведении испытания
18.2-3. Независимость случайных событий. Два события Ег и Е2
называются независимыми (независимыми по вероятности), если
P{El(\Et} = P{E1}P{Et}t (18.2-1)
так что Р{£1|£2} = Р{£1}, если Р{Е2}фО, и Р {Е2\ Ег} = Р {Е2}> если
Р{Ег}фО.
События Ev Ev ..., EN называются независимыми в совокупности, если
выполняются все указанные ниже соотношения:
Р {Ei(\E,} = P{Ei} Р {£/} (1 <i < / ^ N),
(18.2-2)
Р{Е,ПЕ,ПЕк}=Р{Ег}Р{Е,}Р{Ек} (l^i<j<k^N),
р{£1п^п.".п'4}=р"{^}*р{£2} :.: ру^}.
18.2-4. Сложные испытания. Независимые испытания и повторные независимые
испытания. Часто испытание можно расчленить на отдельные частичные испытания (см.
также пп. 18.7-3 и 18.8-1). Результаты первого, второго, ... частичных испытаний
обозначим через Е', Е", ... Результат Е сложного испытания может быть описан как
совмещение событий Е = Е'[\Е"[\ ...; в общем случае их вероятности будут зависеть от природы
и взаимодействия частичных испытаний.
Два (или более) частичных испытания называются независимыми, если независимы
их результаты Е', Е" полученные в процессе сложного испытания. Если некоторое
частичное испытание независимо от остальных, то вероятность осуществления любого его
исхода при проведении сложного испытания равна соответствующей вероятности при
самостоятельном проведении частичного испытания.
Повторными независимыми испытаниями называется последовательность
независимых испытаний, каждое из которых имеет один и тот же набор возможных исходов Е и
их вероятностей Р {£}• Вероятность получения определенной последовательности
результатов Ev E ..., Еп при проведении п повторных независимых испытаний равна
Р iEv Ег Еп) -Р {Ei} р {Ч - р {*„}• (1В-2'3'
18.2-5. 18.2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ 541
18.2-5. Правила сочетаний (см. также пп. 18.7-1 — 18.7-3). Каждая из
теорем табл. 18.2-1 выражает вероятность некоторого события через вероятности
других событий, логически связанных с ним.
Таблица 18.2-1
Вероятности логически связанных событий
(а) Вероятность неосуществления
события Е
Вероятность осуществления хотя
бы одного из двух событий Ei и Е2
(Et или £2 или обоих)
Вероятность совмещения всех собы-
тий Ev E2 EN
(b) Вероятность осуществления хотя
бы одного из N независимых в
совокупности событий £ Е2 £дг
Вероятность совмещения событий
Ev E .... Ej\j, независимых в
совокупности
р {е} = 1 -р{е}
Р {£, U Е2\ =
= Р {Е1} + Р{е2}-Р{е1 П Et]
Р {Е1П Е2 П ... П EN} =
= P{Ei}p{E,|Ei} ...
...P{EN\E1<\E2<\ ...П%-1}
P{E1\)El\)...\}EN} =
= l-(l-P{El})X
Р{£1П£2П...П%} =
= P{El}P{E2}...P{EN}
Вероятности осуществления не менее т и точно т из N (не обязательно
независимых) событий Ev E2, ... , Eft равны соответственно
?т= S <-»'-т(Г_11)5/: *м- 2! <-1>/~т(У5/
/=т / = т '
(т = 1, 2 ЛГ), (18.2-4)
где
Заметим, что
N N
Если £x, E ... , £^у независимы r совокупности, то величины (5) приводятся к
симметрическим функциям (1.4-9) от Р{£;} (табл. 18.2-1, Ь).
Примеры. Если вероятность выпадения каждой стороны игральной кости
равна 1/6, то
вероятность выпадения или 1 или 6 есть 1/6-f 1/6= 1/3,
вероятность невыпадения 6 есть 1 — 1/6 = 5/6,
вероятность выпадения 6 хоть один раз за два бросания кости есть 1/6 + 1/6 —
— 1/36=11/36,
вероятность выпадения 6 точно один раз за два бросания кости есть 1/3—2/36=5/18,
вероятность выпадения 6 дважды за два бросания есть 1/36.
642 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 1.&.2-G.
18*2*6. Теоремы Байеса (см. также п. 18.4-5, Ь). Пусть Н1У Нъ ... — после*
довательносщь попарно несовместных событий, образующих полную группу,
т. е. #х (J #2 U ... = /. Тогда для каждой пары событий Я/, Е имеет место
формула Байеса
Р frt|£},pWn*> P{H<}P{B|Hrf
piE\ 2р {",■}р iE I »i\
i
Формула (7) позволяет вычислять «апостериорные» вероятности Р SH- I Е\ через
«априорные» вероятности Р {ЯЛ «гипотез» #..
18.2-7. Представление событий как множеств в пространстве выборок.
Каждый класс § событий Е может быть представлен как множество g попарно
несовместных событий ЁфО так, что каждое событие Е есть объединение
некоторого подмножества событий из g. g называется пространством выборок
или множеством элементарных событий, связанных с данным испытанием.
Каждое множество элементарных событий Ё из g соответствует некоторому
событию Е. В частности, само g соответствует достоверному событию, а пустое
множество из g — невозможному событию. Вероятности Р {Е} могут
рассматриваться при этом как значения некоторой аддитивной функции множества,.
вероятностной функции, определяющей распределение вероятностей в
пространстве выборок.
Таким образом, алгебра событий 8 изоморфно отображается на алгебру измеримых
множеств (см. также пп. 4.6-17, b и 12.8-4). Множество элементарных событий,
соответствующее условным вероятностям Р IE I ЕЛ, есть подмножество, составляющее событие Et.
Обратно, множество элементарных событий, связанное с некоторым испытанием, может
рассматриваться как подмножество в пространстве выборок, связанном с более общим
испытанием.
18.2-8. Случайные величины. Случайная величина есть любая (не
обязательно численная) переменная х, «значения» которой х = Х образуют множество
элементарных событий {х = Х} или, другими словами, обозначают точки в
пространстве выборок. Соответствующее распределение вероятностей называется
распределением случайной величины х.
Каждая измеримая функция (п. 4.6-14, с) х, определенная на некотором множестве
элементарных событий, есть случайная величина; ее распределение задается
вероятностями событий — измеримых подмножеств значений х.
18.2-9. Описание вероятностных моделей на языке случайных величин и
их функций распределения. Во многих задачах элементарные события Е бывают
отмечены значениями X действительной случайной величины х. Таковы,
например, результаты измерения. Сложные события, скажем, {х^а}, {sin*>0,5)-
или {* = arctg2}, соответствуют измеримым множествам значений величины х.
Более общим образом каждое случайное событие может быть отмечено
упорядоченным набором X = (Xlt X2, ...) действительных чисел Xv X2, ..-,
который дает «значение» многомерной случайной величины х = (xv x2, ...)•
Каждая из действительных величин хъ хъ ... сама является случайной
величиной.
Если множество элементарных событий, связанное с данным испытанием,
отмечено случайной величиной х или х, то вероятности случайных событий
однозначно описываются распределением вероятностей этой случайной величины.
В настоящем справочнике все действительные случайные величины считаются
заданными в интервале (—оо, +оо); значения случайной величины, не
соответствующие элементарным событиям Ё, трактуются как невозможные события
и им приписывается вероятность 0.
18.3-2. 18.3. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ Б43
Распределение действительной случайной величины х задается ее функцией
распределения *)
Фх (X) = Ф (X) = Р {х < X}. (18.2-8)
Распределение многомерной случайной величины x = (#!, х2, ...) задается
функцией совместного распределения
ФХ(ХГ Хг ...)зФ(*х> Xr ...) = P{xl<Xv x2<X2, ...}. (18.2-9)
Обратно, функция распределения определяется по данному распределению
вероятностей однозначно для всех значений случайной величины, за возможным исключением
множества меры нуль (п. 4.6-14). Функция распределения всегда определена однозначно
в точках непрерывности. Каждая функция распределения является неубывающей
функцией от каждого из своих аргументов и
Фл:(-оо) = 0, Ф^(+оо) = 1, (18.2-Ю)
Фх(-оо, Хг Х9, ...)-Фж(*г -со, Х3, ...) = ... =0, Л ^ ^
Фх (4-оо, +оо, +оо, ...) = 1. J
18.3. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
18.3-1. Дискретные одномерные распределения вероятностей (примеры см.
в табл. 18.8-1 — 18.8-7). Действительная случайная величина * называется
дискретной, если вероятности
Рх(Х) = Р{Х)ееР{х = Х} (18.3-1)
отличны от нуля только для счетного множества спектральных значений Х =
— Х{1), Х{2), ... (спектр дискретной случайной величины). Каждое дискретное
распределение вероятностей описывается или функцией (1) или функцией
распределения
Фх(Х)~Ф(Х)==Р{х<Х}= 2 Р(Х*)- (18.3-2в)
Функцию распределения удобно записывать с помощью единичной функции 1/+ </)
такой, что U+ (О == О при t =< О, U+ (/) = 1 при t > 0 (п. 21.9-1):
Ф (X) = р (Х{1)) U+ (X - Х{1)) + р (Х(2)) U+ (X - Х(2)) + ... (18.3-26)
В настоящем справочнике символ ^]у(х) обозначает сумму значений функ-
X
ции у(х) по всем спектральным значениям дискретной случайной величины х.
Заметим, что
2р(*) = Ф(+оо) = 1. (18.3-3)
X
18.3-2. Непрерывные одномерные распределения вероятностей (примеры см.
в табл. 18.8-11). Действительная случайная величина х называется
непрерывной, если ее функция распределения ФХ(Х) = Ф(Х) непрерывна и имеет
кусочно-непрерывную производную —плотность распределения вероятностей
величины х:
Р IXz~x<X + AX\ ёФ
<ЫХ) = Ф(Х)= lim -J ^JL L= (18.3-4)
*) В некоторых руководствах функция распределения определяется несколько
иначе: Ф (X) ss Р {л: ^ X},
544 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.3-3.
Дифференциал йФ = ср (X) dX
вероятности. Отметим формулы
Р {X^x<.X + dX} называется элементом
Р{*<Х}е=Ф(Х) =
а ^ х < Ь} = Ф (Ь)-Ф (а)= J ср (*) cfc, (18.3-5)
X
5 ф (*)<&,
J ф(лг)^ = Ф(оо) = 1.
(18.3-6)
Если х — непрерывная случайная величина, то каждое событие |*=XJ. имеет
вероятность нуль, но не обязательно является невозможным. Спектром непрерывной
случайной величины х называется множество значений х = X, в которых <р (X) ^0.
18.3-3. Математическое ожидание и дисперсия. Числовые характеристики
одномерного распределения вероятностей (см. также п. 18.3-6).
(а) Математическое ожидание (среднее значение) функции у (х) от
дискретной или непрерывной случайной величины х есть
Му(х) =
^У(х)р (х)
(х дискретна),
\ У (х) Ф (*) dx (x непрерывна),
(18.3-7)
если эти выражения существуют в смысле абсолютной сходимости (см. пп. 4.6-2).
(Ь) В частности, математическое ожидание (среднее значение, центр
распределения) М*=£ и дисперсия Dx = o2 дискретной или непрерывной случайной
величины х определяются по формулам
М* = £ =
Dx = o* = M(*— £)2 =
%хр(х)
X
оо
J xy(x)dx
— сю
2(*-s)2p«
х
со
\ (х-1?ч(х)*х
(х дискретна),
(х непрерывна),
(х дискретна),
(х непрерывна).
(18.3-8)
Для вычисления дисперсии можно применять формулы
D* = a2 = M*2 — £2 = М*(*-1) —g(g — 1).
(18.3-9)
Если существуют \Ах и Da:, то средний квадрат отклонения М(дг— Х)2 = о2-|-(£ — X)2
случайной величины х от данного числа X будет наименьшим (и равным о2) при X = |.
(c) М* и Dx не являются функциями от х\ это — функционалы (п. 12.1-4),
описывающие свойства распределения случайной величины х: ЬЛх характеризует
положение величины х, а D* —ее рассеяние. Определения других числовых
характеристик одномерного распределения вероятностей даны в табл. 18.3-1
и в пп. 18.3-7 и 18.3-9. Заметим, что некоторые параметры типа ЬЛх, Dx,
М|*—-£|, ... могут не существовать у данного распределения вероятностей.
(d) Табл. 18.8-1 —18.8-7 и 18.8-11 дают математические ожидания и
дисперсии некоторых часто употребляемых распределений.
18.3-3. 18.3. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 645
Таблица 18.3-1
Числовые характеристики одномерных распределений вероятностей
(см. также пп. 18.3-3, 18.3-7, 18.3-9)
(a) Квантили. Квантиль порядка Р одномерного распределения есть такое
значение хр случайной величины х, для которого
Р {X < Хр } = Ф {Хр ) ша Р (0 < Р < 1).
*i/2 есть медиана распределения. Квартили xi/±, *у2, xs/±, децили xQ л, xQ 2, ..., xQ ft
и процентили *0 Q1, *0 02, .... xQ 99 делят область изменения х соответственно на 4,
10 и 100 интервалов, попадания в которые имеют равные вероятности.
Квантили существуют у каждого распределения вероятностей, но они не
обязательно однозначно определены. Таблицы квантилей широко используются в
статистике (пп. 19.5-3, 19.5-4).
(b) Характеристики положения.
1. Центр распределения (математическое ожидание) Мл: = £ (п. 18.3-3).
2. Медиана x\j2 (см. выше).
3. Мода непрерывного распределения есть точка максимума плотности
распределения вероятностей <р (*). Мода дискретного распределения есть такое спектральное
значение £ что предшествующее и следующее за ним спектральные значения
имеют вероятности, меньшие чем р (£т).
Распределения, имеющие одну, две или более мод, называются соответственно
одномодальными, двухмодальными или многомодальными.
(c) Характеристики рассеяния.
1. Дисперсия а» — D* (п. 18.3-3).
2. Среднее квадратическое отклонение (стандарт) 0 = VOx.
3. Коэффициент вариации а/£.
4. Среднее абсолютное отклонение М | х — \ |.
5. Интерквартильная широта x*j — *i/4 и (10—90)-процентильная широта
*0,9 ~" *0,Г
в. Размах (разность между наибольшим и наименьшим спектральными
значениями).
7. Полуширота одномодального непрерывного распределения есть полуразность
двух значений величины х, в которых
Ф (х) =-2~ max ф (*) = — ф (£т).
(d) Характеристики асимметрии и эксцесса. Первые две из вводимых ниже
характеристик определяются через моменты (см. пп. 18.3-7 и 18.3-9).
и,, и,
1. Коэффициент асимметрии Yi =—jt—~~
2. Коэффициент эксцесса у2 = —- 3 = —г—.
Ц§ к!
3. Пирсоновская мера асимметрии для одномодального распределения
= ~ (см. также п. 19.3-5).
а
Вместо величин у, и у2 употребляются также Yf и y2 ~Ь 3 или — (у^ + 3).
18 Г. Корн и Т. Корн
646 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.3-4.
18.3-4. Нормирование. Если известно, что функция г|) (х) ^ 0 пропорциональна
вероятности р (х) дискретной случайной величины х (п. 18.3-1), то
£ У (х) t|> (*)
PW=^W° *iX) l My(x)=~ (18.3-10)
Если функция г|) (д:) ^s 0 пропорциональна плотности <р (*) распределения
непрерывной случайной величины х (п. 18.3-2), то
} y(x)^(x)dx
— оо
00
Фи)=^^ = -^ • М #(*) = —^- . (18.3-11)
Аг оо оо
-оо
В обоих случаях \/k называется нормирующим множителем. Подобный метод
применим и в случае многомерных распределений.
18.3-5. #■ Неравенство Чебышева и связанные с ним формулы. Неравенство
Чебышева дает оценку сверху для вероятности того, что абсолютное
отклонение | jc — g | случайной величины х от ее центра распределения £ = М#
превзойдет данное число
Р{|*-£|^а}^£ (а>0). (18.3-12)
Если все значения я^О, то имеет место оценка
Р{*^я}^|- (я>0). (18.3-13)
Если х имеет непрерывное одномодальное распределение, то справедлива
более сильная оценка
Р{|*-£|^4^{ ' + %, (18.3-14)
где s — пирсоновская мера асимметрии (табл. 18.3-1); заметим, что s = 0, если
распределение симметрично относительно моды.
18.3-6. Единое описание распределений вероятностей с помощью интеграла
Стилтьеса. Изучение дискретных и непрерывных распределений вероятностей
можно объединить, если представить вероятность каждого события {а^х<.Ь}
как интеграл Лебега —Стилтьеса (п. 4.6-17)
Ь
Р {а ^ х < Ь) = J б(Ф (х), (18.3-15)
а
где Ф (х) see Р {я < X} — функция распределения случайной величины х
(пп. 18.2-9, 18.3-1, 18.3-2). В случае непрерывного распределения интеграл
(15) приводится к интегралу Римана. В случае дискретного распределения
функция Ф(х) определяется формулой (2) и интеграл (15) приводится
к сумме 2 р(х).
а^х<Ь
С помощью интеграла Стилтьеса мы получаем единые выражения
00 ОО ОО
М*= 5 xdO(x); M */(*)= J у(х)йФ(х)\ Dx= $ (x -1)2 dQ) (x)
— оо —оо —оо
(18.3-16)
как для дискретного, так и для непрерывного распределений. Интеграл
18.3-7. 18.3. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 547
Стилтьеса применим также и к более общим распределениям, в частности,
к распределениям, которые частично дискретны, а частично непрерывны.
Аналогичные понятия применяются в случае многомерных распределений
(пп. J8.4-4 и 18.4-8).
18.3-7. Моменты одномерного распределения вероятностей.
(a) Моментом порядка г^О случайной величины х относительно числа X
называется математическое ожидание М (х — Х)г.
(b) В частности, начальный момент порядка г (^относительно Х = 0) есть
ar = M*r= J хгйФ{х) =
I 2*^ м {* дискРетна)»
X
(18.3-17)
J xr(p(x)dx (# непрерывна).
Центральный момент порядка г (относительно центра распределения
g = M*) есть
2 (* — IV Р (*) (* дискретна),
X
оо
(х—IY ф (х) dx (x непрерывна).
Иг = М (*-£)'=$ (x-lYdO(x) =
U
(18.3-18)
Если существует величина txr или \i , то существуют все моменты ak и ц. порядков
k ^ г; если интеграл (или ряд) для аг или |i расходится, то расходятся все интегралы
(ряды) для ak и [х^ порядков k ^ г.
Если распределение вероятностей симметрично относительно своего центра, то все
(существующие) центральные моменты цг нечетного порядка г равны нулю.
(с) Факториальным моментом порядка г случайной величины х относительно X = 0
называется
a[r] »М*И «м* (*—1) ... (jc— r-f- 1). (18.3-19)
Центральным факториальным моментом порядка г называется М (* —£)[г^«
Абсолютным моментом порядка г относительно X = 0 называется 0 =М | х |г.
Отметим формулы
М (дс - X)* = |i, + Й - *)2 > Д>:
«о = >*о = af°3 в Эо e f-
(18.3-20)
(d) Одномерное распределение вероятностей однозначно определяется своими момен-
тами a0, ab a2 если все они существуют и если ряд > •—^ сходится при «е-
*=0
котором s > 0 (см. также соотношение (28) и сноску на стр. 548).
(e) Примеры приведены в табл. 18.8-1 — 18.8-7; в п. 18.3-10 указана связь
между ar, pf и а[г].
18*
548 ГЛ 18 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.3-8.
18.3-8. Характеристические и производящие функции (примеры см. в табл.
18.8-1 — 18.8-8).
(а) По распределению вероятностей одномерной случайной величины х
однозначно определяется (в общем случае комплексная) характеристическая
функция
j^^sM^'a $ *Ч* <№>(*)*
(2eiqxp (*) (* дискРетна)>
X
оо
^ elQx(p (х) dx (x непрерывна),
(18.3-21)
где ^ — действительная переменная, изменяющаяся от —со до +со.
(Ь) По распределению вероятностей случайной величины х однозначно
определяются производящая функция моментов
Мх (s) == Uesx ss $ esx d<S (x) ■•
[ S eSXp W (x ДискРетна)
X
00
\ esxq> (x) dx (x непрерывна)
(18.3-22)
и производящая функция факториальных моментов
I 2 s*p w (x дискРетна)»
€0
ух (S) == Ms* a $ S* </Ф (*) =
J s^O*)^* (х непрерывна),
(18.3-23)
где s — любое комплексное число, для которого приведенные интегралы или
ряды сходятся абсолютно.
(с) Характеристическая функция Хх(я) однозначно определяет
распределение вероятностейх). Это же справедливо и для каждой из функций Мх (s) и
ух (s), если они существуют в смысле абсолютной сходимости в некотором
интервале действительной оси, включающем точку s — О в случае Mx(s) или
точку s—l в случае yx(s). В частности, для дискретной или непрерывной
случайной величины х имеем
Q
р(*)= lim «5 \ e"iqxXx (Я) dq (x дискретна),
(18.3-24)
УМ = Ш \ e~iqxXx{q)dq (* непрерывна).
Формула (24) дает также выражение р (х) или ф (х) через Мх (s), так как
Mx(iq) = Xx(q). (18.3-25)
(d) Во многих задачах бывает значительно легче описать распределение
вероятностей через %х (g), M (s) или ух (s), чем вычислить непосредственно Ф (х), р (х) или <р(л:)
(пп. 18.5-3, 18.5-7 и 18.5-8). Методы п. 18.3-10 позволяют просто вычислять
математическое ожидание, дисперсию и моменты через % (д), М (s) или у (s). Линейные инте-
J) Ф (*) определяется однозначно, за возможным исключением множества точек
меры нуль; если Ф (*) непрерывна, то она определяется однозначно (см. также п. 18.2-9).
18.3-10 18.3. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 549
тральные преобразования с (21) по (24) можно осуществлять с помощью таблиц
преобразования Фурье или Лапласа.
(е) Производящая функция y^ (s) применяется, в частности, в задачах, содержащих
дискретные распределения со спектром 0, 1, 2, .... для которых
оо
Ух (s) = 2 skp (k), р (Л) = -1. у*** (0) (k = 0, 1, 2. ...)•
Л = 0
18.3-9. Семиинварианты (см. также п. 18.3-10). Если для одномерного
распределения вероятностей существует момент г-го порядка аГ1 то
существуют семиинварианты хь к2, ..., хг, определяемые разложением
lnx*(<7)= S *kiJ%r+o((T)- (18.3-26)
При условиях п. 18.3-7, d все семиинварианты существуют и однозначно
определяют распределение вероятностей.
18.3-10. Вычисление моментов и семиинвариантов через %х(я)> Mx(s) и
yx(s). Соотношения между моментами и семиинвариантами. Многие
характеристики распределения могут быть вычислены непосредственно по %x(q),
Mx(s) и ух (s) без предварительного нахождения Ф(лг), р (х) или ф (л:). Если
рассматриваемые далее выражения существуют, то
ar = i-rxW(0) = M¥(0); 0^ = 7^ (1),
кг = Гг—г\пхх(я).
Заметим, что
=-^lnAMs) . (18.3-27)
д = 0 ds |s = 0
оо оо оо ^
мх <s> = Цa* sw- ln ** <s> = 1>* ж; Y*(s+1} - 2] aw *r (18-3-28)
k = 0 k=\ Дг==0
если только стоящие слева функции (производящая функция моментов, производящая
функция семиинвариантов и производящая функция факториальных моментов
соответственно) аналитичны в окрестности точки s = 0.
Из формул (28) можно получить М* и Dx:
Мх = Б = аг = 0С|
= g = a1 = a[1] = K \
14 \ (18.3-29)
= а* = ^ = а2-^ = а[2]--£(£-1) = к2. J
В табл. 18.3-1 указаны и другие характеристики, которые могут быть
выражены через моменты.
Следующие формулы связывают моменты и семиинварианты
д = £ (-l)ft(r)ar_/; ar= £ (ЦК-*** ('-0.1.2....). (18.3-30)
6 = 0 ч/ £ = 0 ч '
г —1
airj = 2] Sfcar-k (г == °' *' 2 См' также п- 21-5-3), (18.3-31)
6=0
e«-a[2] + «[l]=B*i + *i, 1
a3 = a[3] + 3a[2] + ct[{] = *3 + Зк^ + к{; I (18.3-32)
«4 = a[4] + 6a[3] + 7a[2] + a[l] = *4 + 6*f*2 "+* 4*l*3 + 3*l "+* *?» J
JLi3 = x3; jn4 = x4 + 3*2, (18.3-33)
«4 = ^4 - 3|ij, кб = д6 - 10дЛ, кв = H - 15^4 - Юда + 30J4J. (18.3-34)
550 ГЛ 18 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.4-1.
18.4. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
18.4-1. # Многомерные случайные величины (см. также п. 18.2-9). Если
случайное событие описывается упорядоченным набором действительных чисел
Xlf Х2, ... , Хп, то этот набор представляет значение д-мерной случайной
величины х = (д:1, х2, ... , хп). Можно также говорить о системе случайных
величин или о /г-мерном случайном векторе. Каждое элементарное событие
может рассматриваться как результат сложного испытания, состоящего в
измерении всех величин хъ х2, ... , хп и интерпретироваться как точка
/i-мерного пространства (xlt х2, ... , хп) или как вектор х {хъ х2, ... , хп\.
Каждая из величин хх% х2, ... , хп является случайной величиной
(одномерной). Если говорят, что х —случайный вектор (или /г-мерная случайная
величина), то величины xlt х2, ... , хп называют его случайными
координатами.
18.4-2. Двумерные распределения вероятностей. Распределения координат
случайной величины. Распределение системы двух случайных величин хъ х2
или двумерного случайного вектора х {хъ х2) задается функцией совместного
распределения
Ф, (Хъ Х2) в Ф (Xlt X2) ^ Р {*, < Хх\ х2 < Х2}. (18.4-1)
Каждая из случайных величин хг и х2 (координаты случайного вектора)
определяется соответствующей функцией распределения (одномерной)
<ЪЛХ1)шшР{х1<Х1\шшР{х1<Х1\ лг2<оо} = Ф(Х1, оо), л as 4 2)
ф2 (Хя) s Р {х2 <Х2} ^P{Xl< со; х2 < Х2] = Ф (со, Х2). J ' " }
Отметим, что функция (1) полностью определяет функции (2). Наоборот,
функции (2) определяют функцию (1) только при условии, что случайные
величины хг и х2 независимы (см. п. 18.4-11).
18.4-3. Дискретные и непрерывные двумерные распределения вероятностей.
(а) Двумерная случайная величина х ss (xv x2) называется дискретной
(имеет дискретное распределение вероятностей), если совместная вероятность
выполнения условий д:1 = Х1, *2 = Х2
рх(Хи Хг)ш*р(Х1% X2)^P{xx = Xi; х2 = Х2\ (18.4-3)
отлична от нуля только для счетного множества (спектра) точек (Хъ Х2),
т. е. если и хг и х2 являются дискретными случайными величинами (п. 18.3-1).
Распределения случайных координат хг и х2 определяются вероятностями
pl(X1)^P{x1^Xl} = ^iP(X11 Xt),}
р2(Х2)^Р{х2 = Х2}^р(Хи Х2).
(18.4-4)
(Ь) Двумерная случайная величина х ==(*,, х2) называется непрерывной
(имеет непрерывное распределение вероятностей), если функция
распределения Ф (Х1ч Х2) непрерывна всюду и если двумерная плотность распределения
вероятностей
Фх (Хи Х2) _ <р №, Х2) ^^^fa) (18.4-5)
существует и кусочно-непрерывна. Дифференциал q>(xv x2)dx1dx2 называется
элементом вероятности. Спектр непрерывного двумерного распределения
вероятностей есть множество точек, в которых плотность распределения (5) от-
18.4-4. 18.4. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 551
лична от нуля. Распределения координат хх и х2 определяются плотностями
распределения
q>i'.*i)«
. dOt (Xt)
dX
йФг (X2)
bi= $ <p(Xlf x2)dx2,
-oo
oo
dX
фг №)
(с) Отметим формулы
2j2jp(xlt x2) = 2jp1(x1)=2jp2(x2)=lt
Р= J q>(*lf X2)^i.
(18.4-6)
oo oo
J J ф(*ь *2)rf*id*2= J Ф!^)^!— J ф2(лг2)с(л:2 = 1.
— oo —00
(18.4-7)
18.4-4. Математическое ожидание, моменты, ковариация и коэффициент
корреляции.
(а) Математическое ожидание (среднее значение) функции у (хъ х2) двух
случайных величин хъ х2 определяется через их совместное распределение
формулой
оо оо
Щ(хи х2) = J J y(xlt х2)йФ(хъ *2) =
= J
для дискретного
распределения,
хх х2
Т Т и(г у\п(х x\dx dx Для непрерывного
) ) У(хц х2) q>(*lf x2)dxxdx2 распределения,
(18.4-8)
I —оо —оо
если эти выражения существуют в смысле абсолютной сходимости.
Замечание. Если у есть функция только одного xt, то среднее значение (8)
совпадает со средним значением, определенным по распределению величины xt.
(b) Средние значения (математические ожидания) Мд:1 = ^1, Млг2 = £2
определяют точку (glf £2), называемую центром совместного распределения
вероятностей (центром рассеяния). Величины М (xl — XlYi (x2-—X2)r* называются
моментами порядка гх-\-г2 относительно точки (Хъ Х2). В частности, моменты
порядка rt + r2 относительно начала (начальные моменты) и относительно
центра распределения (центральные моменты) определяются соответственно
формулами (см. также п. 18.3-7):
*'■• |1Г1Г§ = М to-g,)" (x2-l2)rK (18.4-9)
rtrt
= ЬЛхГ1х'
1 -1
(с) Центральные моменты второго порядка представляют особый интерес
и имеют специальные названия и обозначения
^12 = A,2i = M(a:1 — gi) (лг2 — ?2) = cov{a:1, x2\
(ковариация xt и дг2, корреляционный момент,
смешанный момент второго порядка),
Р12 = Р21 = Р(*Ь Х2) =
"12
=м
Xi— Si X2 — It
(коэффициент корреляции между xt и х2).
(18.4-10)
652 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ I8.4-&.
Заметим, что
-l^Pi2^1,
= MxiX2 — £i£2 = P12040Y
(18.4-11)
18.4-5. Условные распределения вероятностей, связанные с двумя
случайными величинами.
(а) Распределение системы двух случайных величин хъ х2 определяет
условное распределение величины хх при лг2 = Х2, и условное распределение
величины х2 при лг1 = Х1. В случае дискретного совместного распределения
эти условные распределения также являются дискретными и описываются
условными вероятностями (п. 18.2-2):
Р\ ;г№-1 ^а) = Р {х1 = Хг | х2 — Х2\ р2\х2) ■
р2 , (х21 хх) - р {*2=х21 ^=xt} = ^Л#-
(18.4-12)
В случае непрерывного совместного распределения условные распределения
величин *! и х2 также являются непрерывными и описываются условными
плотностями распределений:
q>(Xlt Хл) /v.vx ф(Х" *2>
Ф1|2(Л1|Л2)- ф2(Х2) > Ф2|1(Л2|Л1)=а Ф1(Х1)
(Ь) Отметим формулы
Ep42(*i|*2) = S>2|i(*iFi)=1.
(18.4-13)
J Ч>1 ! 2 (*1 \Ч) Лх\=\Ъ\ 1^2^1)^2=1,
р„ф№|^3.р'(х')р»|'(х'1х0,
1|2^ '' 2> S"l(*l)"2ll(*2|*,)
21 ц 2| " 2M*2)'.i2(xi|*2)
J»l(*l)»2|l(X2|*l)rf*l
—с»
(формулы
Байеса,
см. также
п. 18.2-6)
(18.4-14)
(18.4-15)
(с) Если дано дискретное или непрерывное распределение вероятностей
системы двух случайных величин хг и лг2, то условное математическое
ожидание функции у (xlt x2) при *i = Xi есть
2г/(Хр *2)02|i (*2|*i) Для Дискретного
М{,<*. *>!*>={ 5 распределения,
J г/ (Хр д:2) ф2| j (*2|^i) dx2 Для непрерывного
-с» распределения,
если эти выражения существуют в смысле абсолютной сходимости. Заметим^
что М {у(хъ х^\Хх} есть функция от Хг.
18.4-7. 18.4. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 553
*2Ь 1
Пример. Условные дисперсии величин xt и х2 равны соответственно
D \xt\XM}-M {(xt-M {xt\XE\)*\Xt}t
D \х21 Xt\ - М {(*2 - М {х21 Xt})21 Xt\,
18.4-6. Регрессии (см. также пп. 18.4-9 и 19.7-2).
(a) Если дано распределение системы двух случайных величин хг и х2,
то регрессией х2 на хг называется любая фунция g2 (хг), приближенно
представляющая статистическую зависимость х2 от xv При этом величина х2
представляется как сумма двух случайных величин
*2 = g2(*i) + M*i. x2), (18.4-18)
где h2(xv х2) рассматривается в качестве поправочного члена (остатка).
В частности, средняя квадратическая регрессия х2 на хг
12*2 ^211(^21*0 для Дискретного
х2 распределения,
? / . v. (18.4-19)
J ^2 Ф211 (*2 *i) dx2 Для непрерывного
—с» распределения
минимизирует средний квадрат отклонения
М [х2--ё2 (*i)]2 = M [Ля (*i. Ъ)]2- (18.4-20)
Соответствующая кривая л:2 = М {л^лгЛ называется кривой средней квадрати-
ческой регрессии величины х2.
(b) Часто оказывается достаточным аппроксимировать регрессию (19)
линейной функцией
g2(*i) = g(2*(xi)==l2 + $2i(xi — £1); £21 = Pi2^ (линейная регрессия х2 на хх).
(18.4-21)
Уравнение (21) описывает прямую линию —прямую регрессии величины х2;
p2i есть коэффициент регрессии х2 на хг. Формула (21) представляет линейную
функцию axx + b, коэффициенты которой a=P2i и ^ = 1г — P21S1 минимизируют
средний квадрат отклонения
М \х2 - (ахг + b)}* = ol + а*в\ - 2ар12а1а2 + Ц2 - (<& + Ь)]К
Наименьший средний квадрат отклонения (остаточная дисперсия) равен
°1 О—р?2); таким образом, коэффициент корреляции р12 измеряет качество
«наилучшего» линейного приближения.
(c) Регрессия (19) может быть аппроксимирована более точно с помощью многочлена
степени т > 1 (параболическая регрессия порядка т) или с помощью других функций*
коэффициенты которых выбираются так, чтобы минимизировать отклонение (20).
(d) Если рассматривать в качестве независимой переменной величину х2, то мы
получим подобным образом среднюю квадратическую регрессию xt на х2:
gi(*2) = M{*i!*2}, (18.4-22)
и линейную регрессию хх на х2:
2(}Ч*2)=|1 + (312(*2-|2); Pl2 = Pl2^-. (18.4-23)
1 о-2
Заметим, что в общем случае ни функции (19) и (22), ни функции (21) и (23)
не являются взаимно обратными. Все линии регрессии проходят через центр (£i, £2)
распределения вероятностей.
18.4-7. л-мерные распределения вероятностей.
(а) Распределение системы п случайных величин xlt x2t..., хп или /г-мер-
ного случайного вектора х задается функцией совместного распределения
ФХ(ХЬ Х2)..., Хп) = Ф (Л,, Х2)..., Х„) = Р {*! <Хих2<Х2г ...,хп<Хп}
(18.4-24)
654 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.4-7.
(п. 18.2-9). Распределение подсистемы т<п величин xlt х2,..., хт есть т-мер-
чое распределение, получаемое из исходного распределения (маргинальное
распределение). Соответствующая т-мерная функция распределения
(маргинальная функция распределения) получается из /г-мерной функции распределения
(24) подстановкой Ху = оо для каждого из п—т аргументов Ху, которые не
входят в выбранную подсистему, например,
Фц(*1. Х«) = Ф(*1. Xt, со со);
Ф2(*2) = Ф(о°» *2» ОО СО), И Т. Д.
(b) /i-мерная случайная величина x = (xlt х2,..., хп) называется дискретной
(имеет дискретное распределение вероятностей), если совместные вероятности
М*1, *2,— *п)=Р(Х1. *2,-. *«) = Р{*1=*1, *2 = *2,- *п = *п}
(18.4-25)
отличны от нуля лишь для счетного множества (спектра) точек (Хь ..., Хп),
т. е. если каждая из величин xlt х2 хп дискретна (см. также пп. 18.3-1 и
18.4-3, а).
Распределения подсистем случайных величин и условные распределения
определяются так же, как в пп. 18.4-3,а и 18.4-5,а, т. е.
*3 хп
*1 *3 *п *\
Pi|2(*il*2) = p"**!: *,}; рц2з(*1|*2. ^3)=^%-%^;
*23|l(*2. Х3|Х1)==^з(^,^, Х3) и ^ ^
(c) /i-мерная случайная величина x = (xlt х2 хп) называется
непрерывной (имеет непрерывное распределение вероятностей), если функция
распределения Ф (Хи Х2 Хп) непрерывна всюду и если плотность
распределения вероятностей
дпФ(Хи Х2, .... Х\
Фж(*ь Х2 Хв) = ф(Х1| Xtt ...,*„) = дх,х дХ п) (18.4-26)
существует и кусочно-непрерывна. Дифференциал
<p(*it x2, ..., xn)dx1dx2 ... dxn
называется элементом вероятности (см. также пп. 18.3-2 и 18.4-3, Ь). Спектр
непрерывного распределения вероятностей есть множество всех точек
(Xit X2, ..., Хп), в которых плотность распределения (26) отлична от нуля.
(d) Отметим формулы
22 — 2р(*1» ** •••'я)*1»
(18,4-27)
— 00 —00 —00
18.4-8. 18.4. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 655
(е) Плотности т-мерных маргинальных распределений и условных распределений,
получаемых из непрерывного n-мерного распределения вероятностей, определяются так
же, как в пп. 18.4-3, b и 18.4-5, а, например,
оо оо
»»<**• х')"а*Рал&,*')- S - $ ф (xi- *•• *« хп) dxs - ■**«•
— 00 —00
_ /V > V \ Ф12 (-^1. Х2) ^ /V | V V \ Ф123 (-^1. Х2, Хл).
»1!2(Х, , X.) = фг(Хг) ■ <РЦ23<^. I Хщ. X,) = фаз (Л§> л>) ■
„ /У Y I Y \ Ф123 (^1. Х2, Х9)
Ф12,3 (Х„ Х2 | Х3) ^-j .
(!) Распределение системы двух или более многомерных случайных величин х =э
^ (*i, *г. •••). У ss (уь #2, ...), ... есть совместное распределение всех величин
хч х2, ...; Уи Уг, ...; ...
Замечание. Совместное распределение может оказаться дискретным по одной
или нескольким случайным величинам и непрерывным по другим; кроме того, каждая
случайная координата может быть частично дискретной и частично непрерывной.
18.4-8. Математические ожидания и моменты (см. также п. 18.4-4).
(a) Математическое ожидание (среднее значение) функции y = y(xlt... ,хп)
от п случайных величин xv х2> ..., хп определяется формулой
со оо оо
My(xvx2, ..., хп)= J J ... Ij y(xv x2, ..., xn)dO(xl9 хъ ..., xn) =
— oo—oo —со
f SS-S^fe x* •••> xn)p(xv x2, ..., xn) (для дискретного
хг х2 хп распределения),
оо оо со (18.4-28)
) J •" J ^^i» X2> ••" *»)<P(*i» ** •••» xn)dxxdxt ... <iA:n
— C30 —00 —00
(для непрерывного распределения),
если эти выражения существуют в смысле абсолютной сходимости.
Замечание. Если у есть функция только m < я из п случайных величия
*-, *2 хп, то математическое ожидание (28) совпадает с математическим ожиданием у
по отношению к m-мерному распределению только рассматриваемых т величин.
(b) п математических ожиданий Мх1 = £)1, М*2 = Е2> • ••» Млгл = ^л
определяют точку (gx, £2, ..., £л), которая называется центром распределения
вероятностей. Величины М (хг — Хг)Г1 (х2 — Х2)г* ... (хп — Хп)п называются
моментами порядка r1 + r2 + ... + rn относительно точки (Xv X2> ..., Хп). В
частности, моменты относительно начала (начальные моменты) и относительно
центра распределения (центральные моменты) определяются формулами
а
= Мл:г1/2.../л,
W*~"n * * " \ (18.4-29)
IV г9... г =М ta-E/1 (x2-U)r*... (*„-bt)r».
1 2 /j
(с) Центральные моменты второго порядка представляют особый интерес
и имеют специальные названия и обозначения:
*/л = *** = м (Ъ — Ь) (** — Ел) =
[ Ох(=о* при i = k (дисперсия)
(/, * = 1,2, .... л). (18.4-30)
cov{*,-, Xk) при t:^& (ковариация)
Эти моменты определяют матрицу моментов [Л#]. Ее определитель det [kik]
w) J
556 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.4-9.
называется обобщенной дисперсией /г-мерного распределения. Коэффициенты
корреляции
Pik = P(xi> ^) = -7=^ = M^^^p^ (/, *=1, 2, ..., п) (18.4-31)
определяют корреляционную матрицу [р,-л] /г-мерного распределения, если
только все Gt ф. 0. Величину
гшт=Ш<>1
иногда называют коэффициентом разброса.
Матрицы [hfc] и [Р^] действительны и симметричны. Их общий ранг (п. 13.2-7) г
есть ранг /z-мерного распределения вероятностей.
■^Распределение называется собственным или несобственным в зав#симости от того,
будет ли г = п или г < п. В случае собственного распределения матрицы [ky] и Гр.. 1
являются положительно определенными (п. 13.5-2).-К
Эллипсоидом рассеяния для собственного л-мерного распределения вероятностей
с центром в начале координат называется л-мерный «эллипсоид»
п п
X 2 АдЛ-ДЪ-я + 2. (18.4-32)
/=1 /5=1
где [Л ««Л — f^/fc]-1 есть матрица, обратная матрице моментов.
Эллипсоид рассеяния обладает тем свойством, что при равномерном распределении
вероятностей в нем матрица моментов такого распределения совпадает с ГА,., 1.
Эллипсоид рассеяния иллюстрирует распределение вероятностей по различным направлениям.
«Объем» этого эллипсоида пропорционален корню квадратному из обобщенной
дисперсии. Для несобственного распределения вероятностей (при г < п) спектр (п. 18.4-7)
сосредоточен на некотором r-мерном линейном многообразии (прямой, плоскости,
гиперплоскости) в л-мерном пространстве точек tx„ х2, ... , хЛ и там же расположен его
эллипсоид рассеяния. Так, например, спектр двумерного распределения вероятностей
при г = 1 лежит на прямой, а при г = 0 находится в одной точке.
18.4-9. Регрессия. Коэффициенты корреляции (см. также пп. 18.4-6 и
19.7-2).
(a) Если дано совместное распределение п случайных величин xv х2, ...
.,., хп, то зависимость одной из этих величин, например хъ от остальных
п— 1 величин можно изучать с помощью формулы
*i=£i(*2. х3, ..., хп) + Нг(хъ х2, ..., хп)у (18.4-33)
где hx (хъ х2, ..., хп) рассматривается как поправочный член.
(Средняя квадратическая) регрессия хг на х2, х3, ..., хп есть функция
gl(*2> Х3> •.., Хп) = М \Х1 I Х2> *3> ••> *Я} =
( 2*iPil23 — n(xi\x2> хз> •••» хп)> если хх дискретна,
" (18.4-34)
3 ^1фИ28"' п (*il*2» хз> •••» хп) йхъ если хг непрерывна,
— оо
которая минимизирует средний квадрат отклонения
M[*i—gi(x2, х3, ..., л:л)]а = М[(Л1(л:1, х2, ..., л:л)]а.
М {хг\Х2, Х3 , ... ,Хп} есть условное среднее значение величины хг при х2 = X2t
х8 = Х3, ..., хп = Хп (см. также п. 18.4-5).
(b) Регрессия величины х% на остальные п— 1 величин часто
аппроксимируется линейной функцией—линейной регрессией
d'^ + SM'A-e*), р<*=-4Ь t18-4-35*
18.4-11. 18.4. МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 557
где [Л^] = [кцг]'1 есть матрица, обратная матрице моментов. Коэффициенты
регрессии |3,л определяются единственным образом, если распределение —
собственное (п. 18.4-8). Сводный коэффициент корреляции
р(*,. «{'>)= У 1-тпг (18-4-36)
является мерой корреляции между х% и остальными п— 1 величинами.
(c) Случайная величина hW = #/—gj1* (разность между xi и ее «линейной
оценкой» g\ ) при Л^^О) называется остатком xi относительно остальных
п— 1 величин. Заметим, что
cov ih\l\ *Л} = 0 (i=£k), D Л}1) = -~— (остаточная дисперсия). (18.4-37)
(d) Коэффициент корреляции величин х% и х9 по отношению к величинам *_, ...,*•
Р12|34...Я=Р(Й(^4...Я. 4734...„) Г== <18-4-38>
измеряет корреляцию между xt и х2 после устранения линейных изменений, вызванных
влиянием величин #3, х^, .... х . В частности, при л = 3;
Р12~ Р13Р23
Pl2l3==
V('-P?3)(1-PI3)
18.4-10. Характеристические функции (см. также п. 18.3-8). Совместное
распределение вероятностей л-мерной случайной величины x = (xv х2 хп)
однозначно определяет характеристическую функцию
ЭСх(Ч) = Хх(<?1.<72>-"-<7я)ЕнМ ехр(' 2 »***) =
= 1 I - I ехр(' 2 V**)*M*i.*,. -.*»). (18-4-39)
— оо —оо — оо \ k=\ I
Для непрерывного распределения имеет место формула обращения
Фх(*Г XV -• *«) =
1
(2Я)Я
оо оо оэ / п \
$ $ " \ exp -t ^ <?Л Хх (Яг Ч Яп) dqidq2 ... dqn.
— оо — оо — оо \ k=\ J
(18.4-40)
Характеристическая функция, соответствующая m-мерному маргинальному
распределению т из п величин *г *2 хп, находится путем подстановки в формулу (39)
значений qk — Одля всех тех х<, которые не входят в m-мерное распределение; так,-
например, х12 (<7Г <72) = ХХ (<7Г Яг 0 0).
Моменты и семиинварианты многомерных распределений могут быть получены как
коэффициенты разложений в степенные ряды функций хх и *п Хх подобно тому, как это
сделано в п. 18.3-10.
18.4-11. Независимость случайных величин (см. также п. 18.2-3).
(а) Случайные величины х1% х2, ..., хп называются (взаимно)
независимыми, если независимы в совокупности события {^eSJ, {х2 e S2}, ...
..., {х„ е S„} для любого набора множеств Slt S2t ..., Sn действительных
чисел. Для этого необходимо и достаточно, чтобы
Ф(*1, *а. •••! хп) = Ф1(х1)Ф2(х2) ... Фп(хп) (18.4-41)
558 ГЛ. !8. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.4-12.
или в случаях дискретных и непрерывных случайных величин соответственно,
чтобы
Р (*ь *я, ... , Хп) ~ Pl (Xl) р2 (х2) ... рп (Хп)у Л
Ц>(хъ х2, ..., *„) = <pi(*i)<pa(*a) ... фл(*л). /
Распределение системы независимых случайных величин вполне
определяется их индивидуальными распределениями. Независимые случайные
величины не коррелированы, т. е. р^ = 0 при всех I ф k (п. 18.4-8, с), но обратное
утверждение не всегда справедливо.
(b) Независимость многомерных случайных величин х1( х2, ... определяется
формулами вида (41) или (42), в которые вместо xlt x2t ... надо подставить
Xi, х2, ...
Пример. Многомерные случайные величины (xit х2) и (х3, х4, хй) независимы тогда
и только тогда, когда
Ф12345 (*Ь Х2, Х3, X*, ^)ЭФ„ (Xit Х2) Ф345 (*з. *4. Хй). (18.4-43)
Заметим, что формула (43) влечет за собой независимость х2 и хй, xt и (xs, xA), (xlt х2) и
(х3, хь) и т. д.
(c) Если в распределении дискретной или непрерывной л-мерной случайной
величины (*г х х ) m-мерная величина (х х , .... х ) независима от (п — от)-мерной
(18.4-44)
8Ф12...т(*г V --iXm)-
(d) Случайные величины xt и х2 независимы тогда и только тогда, когда
характеристическая функция двумерной случайной величины (xlt xz) равна произведению
индивидуальных характеристических функций координат хх и х2 (п. 18.4-10), т. е.
Xi2 (<7i, Q2) == Xi (<7i) Хг (<7г). (18.4-45)
Аналогичная теорема верна для многомерных случайных величин.
(e) Если случайные величины xlt x2, ... невависимы, то независимы и случайные
величины уг (xt), у2 (х2), ... Аналогичная теорема верна и для многомерных случайных величин.
18.4-12. Энтропия распределения вероятностей.
(а) Энтропия распределения вероятностей для одномерной случайной вели*
чины х с дискретным или непрерывным распределением определяется
соответственно формулами
величины (хт j, . .
^12 ... т[(т+ 1) .
или
<*>12 ... mi(m+ 1). .
. , хЛ, то
. . п (хг хг •
. п (*г хг ' '
х \х
= Р\2 .
'XJ&
.. , т(х\
"я)-
Я(*) =
М bg2 -^щ- = — £р(х) log2 р (х),
X
оо
- $ ф (х) log2 ф (х) dx.
1__
ф(*)
(18.4.46)
Н (х) есть мера априорной неопределенности измерения величины х. В случае
дискретного распределения вероятностей Н (х) ^ 0, причем Я (лг) = 0 тогда
и только тогда, когда х имеет вырожденное (причинное) распределение
(табл. 18.8-1). Непрерывное распределение, имеющее наибольшую энтропию при
данной дисперсии о2, является нормальным распределением (п. 18.8-3) с Н (х) =
= loga |/2яеа2.
(Ь) Для дискретного или непрерывного распределения вероятностей
двумерной случайной величины (xlt x2) энтропия определяется соответственно
следующими формулами:
Г — М l0g2 p (ХЪ Х2), ПЛАА7\
Н (*i. Ч) = i .., , ч (№4-47)
i — Mlog^fo, л:2).
18.5-i. 18.5. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАМЕНА ПЕРЕМЕННЫХ 559
Условная энтропия Нх (хЛ определяется соответственно как
^■W-t-Miog.w.w*) (184'48)
(это не условные математические ожидания). Переставляя индексы 1 и 2,
получим условную энтропию Нх (*2). Имеют место соотношения
Н (xv х,) = Н (Xl) + HXi (х,) = Н (х2) + HXt (х,) ^ Н (хх) + Н (х,). (18.4-49)
Равенство в правой части достигается тогда и только тогда, когда величины
хг и х2 независимы (п. 18.4-11).
Неотрицательная величина
J (xv х2)« Н (хг) + Н (х2) - Н {xv х2) - Н (хг) - НХ2 (х,) = Н(х2) - HXi (*2)
(18.4-50)
может служить мерой зависимости между хг и х2.
Функционалы (46) —(48) и (50) играют важную роль в статистической
механике и теории информации.
18.5. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАМЕНА ПЕРЕМЕННЫХ
18.5-1. Вводные замечания. Ниже даются соотношения, позволяющие
рассчитывать распределения вероятностей функций от случайных величин.
18.5-2. Функции (или преобразования) одномерной случайной величины.
(a) Распределение вероятностей функции у — у(х) вполне определяется
распределением вероятностей случайной величины х (см. также п. 18.2-8).
(b) Пусть случайные величины х и у связаны взаимно однозначным
соотношением y — y(x)t x—x(y). Тогда:
1. Если у (х) — возрастающая функция, то
Фу{У) = Фх[х (V)], ®х{Х) = <йу\у{Х)\, Л
Ур = У(хр), хР=х(Ур) (0<P<\).f V*-5'1»
Заметим, что соотношение ух,=у (*i/2). связывающее медианы Xi/ и f/i/a,
справедливо как для возрастающей, так и для убывающей функции у (*).
2. Если х и у — непрерывные случайные величины, то
Vy(Y)\dy\ = vx[x(Y)]\dx\ или <py(Y) = <px[x(Y)]\-%.\^Y (18.5-2)
для всех значений Y величины г/, при которых производная dx/dy существует
и непрерывна.
Замечание. Если функция х (у) многозначна, то
Ч>у(У) = Ч>1(У) + Я>2(У)+ ....
где ф4 (У), ф2 {У), . . . —плотности распределения, получаемые из формулы (2) для
соответствующих однозначных ветвей xt (у), х2 (У). . . . функции х (у).
Пример. Если у~хг, то хх =-\-Yy, x2 — — Yy и
f0 при У<0,
фОО = { _1_ю ,,,^ ,__!__ш ,_ 1/ха ПШ1 у>0. <18>3)
(YY) + jy~<Px(-VY) пРа У>°-
660 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.5-3.
(с) Для сложной функции f[y{x)\ согласно п. 18.3-6 имеем
Mf(y) = Mf[y(x)]= J f[y(x)]d<J)x(x). (18.5-4)
—оо
Заметим, что ни существование однозначной обратной функции х(у), ни диф-
фсренцируемость у (х) не предполагаются. В частности, для /(#) = е5^
получаем производящую функцию моментов My(s) = Mesyt а для /(у) = е^ —
характеристическую функцию %y(q) = \Aei(iy (п. 18.3-8).
Пример. Пусть y = sin {х-\-а), где а = const, а случайная величина х распределена
равномерно в (0, 2л). Тогда
2л я/2 1
У 2Л J Л J/0 Л J, ^1—^
откуда, согласно формуле (18.2-21 )♦
0 " — л/2 " — 1 ' * у
f ±—1—
У I о
при |#|<1,
при | у | > 1 (см. также п. 18.11-1, Ь).
(д) С помощью теоремы о свертке (п. 8.3-3) для двустороннего преобразования
Лапласа (п. 8.6-2) формулу (4) можно записать в виде
Oi 4-too
ММ^)=~2лГ S Mx(s)ds J f [y(x)]e"sx dxf (18.5-5)
0\ -—100 ~ OO
где внешнее интегрирование проводится по такой вертикальной прямой, чтобы интеграл
абсолютно сходился. Этот комплексный интеграл иногда легче вычислить, чем
интеграл (4).
(е) Заметим, что вообще М у (х) ф. у (М*) (см. также п. 18.5-3).
18.5-3. Линейные преобразования одномерной случайной величины.
(a) Если х — непрерывная случайная величина и y = ax+bt то
<РИП=т^ТФ,(-^). (18.5-6)
(b) Если рассматриваемые ниже средние существуют, то
М (ах+Ь)=*а Mx+b, D (ах+Ь) = а* Dx, (18.5-7)
M(ax + by = a'-ar + (KrlS)a'"1bar_1+ ... + Ы%
1ах+ъ{я) = еМя1х{аЯ), Max+b(s) = ebsMx(as), yax(s) = yx(sa).
(18.5-8)
Семиинварианты х. для х (п. 18.3-9) связаны с семиинвариантами к* для у = ах-\-Ь
соотношениями
xf = ащ + bi к* = агхг (г > 1).
(c) Особый интерес представляет линейное преобразование к стандартному
виду (нормирование):
*'=JL=T- с М*' = 0, D*' = l. (18.5-9)
х' называется стандартизованной (нормированной) случайной величиной.
(d) Если функцию у=у(х) на большей части спектра величины х можно
представить приближенно линейной функцией (линеаризация), то
*^0(»+y'(B(*-E). My (*)*** (g)t Dy(x) = [y'(l)l*Dx. (18.5-10)
18.6-4. 18.5. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАМЕНА ПЕРЕМЕННЫХ 561
18.5-4. Функции (или преобразования) многомерных случайных величин.
(a) Если случайные величины
У\ = У\(*ь *2> •••> *л). У2 = У2(*1> х2, ..., хп\ ... (18.5-11)
представляют функции п случайных величин xlt x2t ..., хп, то распределение
вероятностей каждой случайной величины у{ однозначно определяется
распределением вероятностей системы величин хъ х2, ..., хп\ то же верно для каждого
совместного или условного распределения любого конечного числа случайных
величин у(
Например, функция распределения величины у. и функция распределения системы
величин у. и у. определяются соответственно формулами
ФУ, (Yi) - I J • • • J «фх (х1> V • • - Хп)> <18'5-12)
»i (xl> ••"xn)<Yl
ФУ{Ук iYV Yk)^ J J • • • J «фх (*г *,.... • *„). 08.5-13)
Ук (*i< ••"xn)<Yk
(b) Если x ==(*!, x2, ..., xn) и у=(Уи y2, ..., yn)—-непрерывные п-мерные
случайные величины, связанные взаимно однозначным невырожденным
преобразованием (11), то их плотности распределения фх (Хъ Х2, ... , Хп) и
фу (Уъ Уъ ..., Уп) связаны соотношением
%(YV У2 ^«Л^^-^п^Фх^Г *Г "•- Xn)\axidx2-dXn\
ИЛИ
la(*l *„) I
b(Yi'-'Yn) = <PAXl Хп)
•(^•••7^)1. <18-5'14>
где Х/- = д:/(К1, ..., Kn) (t = l, 2, ..., /г), для всех Уъ У2, ..., Кл, для
которых якобиан существует и непрерывен.
Если функция х (у) многозначна, то фу (Ух, У2, .... У ) может быть вычислена
способом, аналогичным указанному в п. 18.5-2, Ь.
(c) Для функции f (ylt у2, — , ут)> где ^ = #(*lf*a, ...,*„) (/=1, ...,m),
00 ОО ОО
М/(у„ у2 </m) = j $ — $ f*M*i. *«• -• *»). (18-5-15)
— оо— оо —оо
Как и в п. 18.5-2, с, здесь не предполагается дифференцируемость функций
У{(хъхъ ...,*„) (/=1,2, ...,т). Для f ^exp(s1t/1 + s2t/2+ ••• +sm#m) получаем
совместную производящую функцию моментов величин ylt y2, ..., ут, а для
/ =ехр (iq-iух + ЩъУъЛ--••+ ЩтУт) —совместную характеристическую функцию.
Преобразование, подобное формуле (5), применяется в некоторых задачах для
случайных процессов (п. 18.12-5).
(d) Для любых двух случайных величин хх и х2
Mxtx2 = MjciMjc2 + cov (*,, х2), (18.5-16)
если эти средние существуют. Если *,, *., ... , х взаимно независимы, то
Мхгх2 ... хп = MjtjMjtg ... М*л
при условии существования этих средних.
(е) Если у = ХуХ2 и ф^ (хЛ = 0 при х± < 0, то (п. 18.5-4, Ь)
662 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.B-S.
*у(у)-Iф*ь *(xi-y)dxi-$ф*». *>(xv £)|£|dxi- <185-17>
Подобным образом можно рассматривать и другие подходящие функции у = у (*,, xt).
18.5-5. Линейные преобразования (см. также пп. 14.5-1 и 14.6-1). Для каждого
невырожденного линейного преобразования
»i - ъ + 2 «»(** - е») « -1.2 п) \
(в матричной форме # = Л + А (х — £)) /
(18.5-18)
распределения л-мерных случайных величин (*r *2> ..., *л) и (yv yv ..., # ) имеют
одинаковый ранг (п. 18.4-8, с), причем
М#; = т^ (/= 1. 2, .... л) (в матричной форме М# —Т)), (18.5-19)
л я
^=м(*.-п.)(^-пл)= 2 2 *mv
/=1 h=]
(/, ftsl, 2, ... , л) (в матричной форме
7*V*A I
5 Л' = АЛЛ'). J
(18.5-20)
если рассматриваемые средние существуют. Здесь Л = [Л.^] и Л' = [Л/fcl — матрицы
моментов (п. 18.4-8, с) для (xv x2, .... хп) и (уг, у2, ..., #л) соответственно.
Методы п. 13.5-5 позволяют найти:
1) такое ортогональное преобразование вида (18), чтобы матрица новых
моментов Kfo (а значит, и новая корреляционная матрица) была диагональной
(приведение к некоррелированным случайным величинам у.\*
2) такое преобразование вида (18), чтобы т^ = п2 = ... = Т). = 0 и Я/д »
е= 6ik (приведение к некоррелированным стандартизованным случайным вели'
чинам у.у
18.5-6. Математическое ожидание и дисперсия суммы случайных величин.
(а) Для любых двух (не обязательно независимых) случайных величин
*1» *2
М (*i ± *2) = M*i ± Мд:2 = б1 ± Ег>
D (*! ± x2) = Dx1 + Dx2 ± 2 cov {хъ х2} =а?+а| + 2р12ого2
(закон сложения дисперсий),
если рассматриваемые средние существуют.
(Ь) Более общие формулы:
(18.5-21)
\ /=1 / /»i
(л \ п л
; = 1 / /=1 /c=l
(18.5-22)
(с) Если функцию у — у (*lt *2, .... *л) на большей части спектра л-мерной
величины (xv х~, ... , х \ можно приближенно представить линейной функцией, то
С*"**)
л ъп
и средние М# и Оу можно приближенно вычислять с помощью формул (19) и (20).
18.5-7.18.5. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАМЕНА ПЕРЕМЕННЫХ 563
18.5-7. Суммы независимых случайных величин (примеры см. п. 18.8-9).
(а) Если хх и х2 — независимые случайные величины, то
00 ОО
s J Ф2 (X - хх) d<S>x (хг) в $ Фх (X - х2) <1Ф« {x2)t
—оо —оо
x*i + *,WsasXi(«xato).
Pxt + x2 W = Pl (X) * р2 (X) - £р2 (X -хх) р± (хг) -
= 2^1(^ — Л:2)Р2(^2) (*1. *2 ДИСКретНЫ),
*2
(18.5-23)
Ф^ + ^С^Ф^^Фг**)83 J 4>2(X-x1)(p1(x1)dx1^
— оо
оо
5=3 3 Ф*^"""*а) Фа(*г) dx% (хъ х2 непрерывны),
j
где индексы 1 и 2 относятся соответственно к распределениям хх и #$•
(Ь) В более общем случае, если х = х1 + х^-{- ...+*я есть сумма фиксированной»
, (?). (18.5-24I
ф^ (X) =» Фг (X) * Ф2 (х) * ... X Фл (X), Хд: (?) = %г (Я) Х2 (?) ... Хп (Q).
и если существуют рассматриваемые выражения, то
Рх (X) = рх (X) X Р2 (X) # ... * рл(Х), <рх (X) = фх (X) * ф2 (X) * ... * Ф„ <*).
М^ (s) = М x (s) M2 (s) ... Mn <s), yx (s) = Yl (s) Y2 (s) ... Y„ (s);
/г /г /г /г
М* = £ = V Mjc.= ^ 6». D* = o-* = £ D^= £ ab
i=l /=1 /=1 i=l
л
M (* - 6)» = £ M (AT. - |.)3;
i = l
i=l
(18.5-251
<18.5-2в|
(18.5-27)
(18.5-281
(18.5-29)
н<'>-<
Формулы (24) и (26) позволяют вычислять моменты высших порядков с помощь»
соотношений, приведенных в п. 18.3-10.
Распределение суммы х = х1~\- х~-\- ... -т"<*л взаимно независимых случайных
величин хj, х, ..., х с математическими ожиданиями | £2, ... , %п и дисперсиями а*
а|, .... ал даже для небольших п иногда можно удовлетворительно аппроксимирован»
нормальным распределением (п. 18.8-3) с поправочным членом.
Пусть |=»М* = ^ + £2+ ... + £„, a* = Djf=xa24-a|-b ...+ал = м2. а д3, ц4 —
центральные моменты третьего и четвертого порядков суммы х. Тогда плотность ф^ (*)
можно аппроксимировать рядом Грама — Шарлье (п. 19.3-3), если ф^ =* 0 при | х | > т
для некоторого а > 0. В этом случае формулы (18.8-6) и (19.3-3) дают
1 —-
х а у 2п
[l b~YiU*- ^т^^-в*'2 + 3) + ...].
564 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 15.5-8.
где х' = ——2, Yi =Гз~ и Y2 ~7^ — 3 ~~ коэффициенты асимметрии и эксцесса для х
(табл. 18.3-1). Нормальное приближение можно считать удовлетворительным тогда,
когда каждая величина х- распределена симметрично относительно ^, так что у1 — Ь
(см. также п. 18.6-5, центральная предельная теорема).
(с) Распределение суммы z = (zlt z2, ...) = х-(-У двух независимых многомерных
случайных величин х » (дгь лг2, ...) и у = (#ь #2t ..Дописывается формулами
СО 00 00
Oz(Zv Z2, ...) = J J ... J Oy(Z^-xv Z2-x2, ...)dOx(xv xv ...), (18.5-30)
— OO—OO —00
M?r *2' "O^M^r ?2« -)Xy(*r V -)• (18.Б-31)
18.5-8. Распределение суммы случайного количества случайных величин. Пусть хи
xz, ... — независимые случайные величины с одним и тем же распределением
вероятностей, и пусть k — дискретная случайная величина со спектральными значениями О, 1,
2, ... , причем величина к независима от xit x2, ... Если производящие функции ух (s)
и Yt (s) существуют, то распределение суммы х = х1 + х -J- ... -f- х. Дается
производящей функцией
Y*(s)=Y*[Y*i(s)l- (18.5-32)
18.6. СХОДИМОСТЬ ПО ВЕРОЯТНОСТИ И ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
18.6-1. Последовательность распределений вероятностей. Сходимость по
вероятности. Последовательность случайных величин ylt y2t ... сходится по
вероятности к случайной величине у, если вероятность того, что уп
отличается от у на любое конечное число стремится к нулю при п —* оо:
yn^Zy при п—*со, если lim Р {| у—уп |>е} = 0 для любого е>0. (18.6-1)
я-*оо
m-мерная случайная величина у сходится по вероятности к m-мерной случайной
величине у, если каждая координата величины у сходится по вероятности к
соответствующей координате величины у.
Если случайные величины упъ уп2, ..., упт сходятся по вероятности
соответственно к постоянным alt а2 ат при п—>со, то любая рациональная
функция g(ynlt уп2, ..., Упт) сходится по вероятности к g(alt a2f ..., ат),
если только g(alt a2, ... t ат) конечно.
18.6-2. Пределы функций распределения, характеристических и
производящих функций. Теоремы непрерывности.
(a) уп сходится по вероятности к у при п—+со тогда и только тогда,
когда последовательность функций распределения Фу (Y) сходится к пределу
Фу (Y) во всех точках Y, где Фу (V) непрерывна (сходимость в основном).
(b) Уп сходится по вероятности к у при п—>оо тогда и только тогда,
когда последовательность характеристических функций %у (q) при любом q
сходится к предельной функции %(q), непрерывной при <7=0; в этом случае
^y(q) = ^(q)=z lim %у (q) (теорема непрерывности для характеристических
П-+СО П
функций).
(c) Последовательность дискретных случайных величин yit y2, ... сходится по
вероятности к дискретной случайной величине у при я-*оо тогда и только тогда, когда
lim pu (Y) = PtJ (Y). (18.6-2)
я-*оо уп У
Если все случайные величины уи у2, ... имеют целые неотрицательные спектральные
значения О, 1, 2, ... и обладают производящими функциями yyi (s), yyz (s), ... то
формула (2) справедлива тогда и только тогда, когда lim ytl (s) = уп (s) при 0 ^ s < 1
п->оэ уп У
(теорема непрерывности для производящих функций).
18.6-5. 18.6. СХОДИМОСТЬ ПО ВЕРОЯТНОСТИ И ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 565
Заметим, что последовательность дискретных случайных величин может сходиться
по вероятности к случайной величине, которая не будет дискретной (см. например,
табл. 18.8-3).
(d) Аналогичные теоремы применимы, если у (п) сходится как функция непрерывного
параметра п.
(e) Аналогичные теоремы применимы к многомерным случайным величинам.
18.6-3. Сходимость в среднем, (см. также п. 15.2-2). Последовательность
случайных величин ylt у2 имеющих конечные начальные моменты Myj
(и, следовательно, конечные математические ожидания и дисперсии (п. 18.3-7)),
сходится в среднем (квадратичном) к случайной величине у (М#а<со), если
lim М(уп-у)* = 0. (18.6-3)
я-*оо
Отсюда следует, что и М (уп — у) "тг^О-
Сходимость в среднем влечет за собой сходимость по вероятности.
Обратное, вообще говоря, неверно; более того, из сходимости уп —- у не следует
даже, что ЬАу и Dy существуют.
18.6-4. Асимптотически нормальные распределения вероятностей (примеры
см. в табл. 18.8-3 и п. 19.5-3). Случайная величина уп с функцией
распределения Фу (Y) распределена асимптотически нормально, если существует
последовательность пар действительных чисел у\п, ап таких, что случайные
величины (уп — Цп)/°п сходятся по вероятности к стандартизованной
нормальной величине (п. 18.8-3). Это имеет место тогда и только тогда, когда для
всех а и Ь > а
lim Р{г)п + сЮп<Уп<Чп + Ьоп}=Фа(Ь)-фи(а), (18.6-4)
п-+оо
где Фи (х) — нормальная функция распределения.
Формула (4) позволяет аппроксимировать распределение вероятностей
величины уп для достаточно больших п нормальным распределением с центром
цп и дисперсией о\ь
Заметим, что из формулы (4) не следует ни то, что т\п и о2л являются математическим
ожиданием и дисперсией величины у , ни то, что последовательность у сходится по
вероятности, ни то, что пределы Муп и х\п или Dyn и ал совпадают. На самом деле эти
пределы могут даже не существовать.
18.6-5. Предельные теоремы.
(a) Пусть \хп —число появлений события Е в п независимых испытаниях
и р {Е} =%—вероятность появления события Е в каждом из испытаний. Тогда
1) последовательность относительных частот hn = \in/n появления
события Е за п независимых повторных испытаний при п —► оо
сходится в среднем и, следовательно, по вероятности к Р {£}=&
(теорема Бернулли);
2) hn имеет асимптотически нормальное распределение с
центром Цп = Ь и дисперсией о2п = — ft(l — ft) (см. также табл. 18.8-3).
Заметим, что
Р(Рп) = (1п)ъ1Ч1-Ъ)П~'1п (И« = 0, 1,2 Я),
(b) Пусть xv х2, ... — последовательность взаимно независимых случайных
величин, имеющих одно и то же распределение вероятностей с конечным
математическим ожиданием £. Тогда при п—>со имеем:
(18.6-5)
566 ГЛ. 18 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.7-1.
1) случайная величина хп = — (х1+х2 + ...+хп) сходится по веро-
ятности к £ (теорема Хитина, закон больших чисел);
2) случайная величина хп имеет асимптотически нормальное рас*
пределение вероятностей с центром х\п — 1 и дисперсией Оп = о2/п при
условии, что существует общая дисперсия о2 величин xv х2, ...
(теорема Линдеберга—Леви, центральная предельная теорема).
(с) Пусть Х-^, Х2, • • • — последовательность взаимно независимых случайных
величин, имеющих конечные математические ооюидания \v £2* ••• " дисперсии
о\, of, ... Тогда при п-^со:
1) из о2п—+0 следует, что хп — 1п^?0\
п
1
2) из lim — У]°1 — ® следуе
i=l :=\ /=1
(закон больших чисел, теорема Чебышева);
п
3) случайная величина ^ xi имеет асимптотически нормальное
* = 1
п п
распределение с центром Цп= ^jh и дисперсией Оп= 2 а* пРи
t=l i=1
условии, что для любого положительного числа е
п ( п
О 2 г* *i. если (Xi-ЪР^* S а!»
im -4г—— = 1, где г; = { ' * (18.6-6)
п -+ оо
/•= 1
О, если (xt — £/)2>е ^ о!
i = 1
(центральная предельная теорема, условия Линдеберга).
■X Условия Линдеберга удовлетворяются, в частности, если существует такое
положительное число а, что при п -* оо
-72^2М|*,-£,|«+в-0,
ал i=l
л
где oJ= У| of (условия Ляпунова). X
i= I
18.7. СПЕЦИАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ
18.7-1. Вводные замечания. Многие задачи теории вероятностей сводятся
к нахождению распределения случайной величины х (или системы случайных
величин) по данному распределению других случайных величин хг, х2,...
Как правило, простые события, отмечаемые значениями величины х,
оказываются сложными событиями по отношению к значениям величин xv х2,...
Первый шаг в решении любой такой задачи должен состоять в четком
определении множества элементарных событий, отмеченного каждой случайной
величиной. Тогда вероятности сложных событий могут быть вычислены методами
18.7-2. 18.7. СПЕЦИАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ 567
пп. 18.2-2—18.2-6 и 18.5-1 — 18.7-3. Формулы (18.3-3), (18.3-6), (18.4-7) или
(18.4-27) могут применяться для контроля вычислений.
18.7-2. Задачи с дискретным распределением вероятностей: подсчет
событий и комбинаторный анализ. Следующие соотношения (каждое в отдельности
или в сочетании с соотношениями пп. 18.2-2—18.2-6) помогают вычислять
вероятности сложных событий по данному множеству элементарных событий.
(a) Если множество элементарных событий конечно (состоит из N «случаев»)
и все элементарные события равновероятны, то вероятность сложного события
(«успеха»), определяемого как объединение Nx элементарных событий
(«благоприятствующих» случаев), можно вычислить по формуле
г,л«~„™, „~ ~ „« число благоприятствующих случаев N. /1Q - , v
вероятность успеха = л —— - = -±т (18.7-1)
г J общее число всех случаев N у '
(b) Если множество элементарных событий счетно (конечно или бесконечно)
и событие Е состоит в объединении Nx элементарных событий с
вероятностями pt и N2 элементарных событий с вероятностями /?2» • ••» то
P{E} = NiPl + NEp% + ..., (18.7-2)
причем N1 + M2 + ... не обязано быть конечным.
(c) Во многих задачах рассматриваемые элементарные события
представляют собой различные возможные расположения данного множества или
множеств элементов, так что числа Nlt N2, ... в приведенных выше
соотношениях являются количествами перестановок, сочетаний и т. п. Наиболее важные
определения и формулы для них приведены в таблицах 18.7-1 — 18.7-3.
Свойства факториалов и биномиальных коэффициентов приведены в п. 1.2-4 и
табл. 21.5-1. Для приближенных вычислений применяется формула
Стерлинга (п. 21.4-2). Дополнительный материал содержится в книге [18.10].
Таблица 18.7-1
Перестановки и разбиения
1
2
3
Число различных перестановок из п различных
объектов
a) Число различимых последовательностей из N
объектов, содержащих п ^ N неразличимых
объектов типа 1 и N — п неразличимых объектов типа 2,
или
b) Число различимых разбиений
последовательности из N различных объектов на два класса из
п ^ N и N — п объектов соответственно
a) Число различимых последовательностей из
;V = N% -f- N + . . . -f Nr объектов, содержащих Nx
неразличимых объектов типа 1, N2 неразличимых
объектов типа 2, ... и N неразличимых объектов
типа г, или
b) Число различимых разбиений
последовательности N = N^ + N2 -{- . . . -f- N различных объектов
на г классов из Nv N .... N объектов
соответственно
п\
(N\ Nl
\п J~ (N — п)\ п\
(биномиальные
коэффициенты, п. 21.5-1)
ЛП
Nx\ N%\... Nr\
(мультиномиальные
коэффициенты)
568 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.7-2.
Таблица 18.7-2
Сочетания и выборки
Каждая формула справедлива для М<л, N = п и N > л
1
2
Число различимых неупорядоченных
сочетаний из N объектов различного типа
по п в каждом:
a) объект каждого типа может
встречаться не более одного раза в любом
сочетании (сочетания без повторений)
b) объект каждого типа может
встречаться 0, 1,2, ... или п раз в любом
сочетании (сочетания с повторениями)
c) объект каждого типа должен
встречаться по крайней мере один раз в каждом
сочетании
Число различимых выборок
(размещений, упорядоченных рядов) объема п из
совокупности N различного типа объектов:
a) объект каждого типа может
встречаться не более одного раза в любой
выборке (выборки без возвращения,
размещения без повторений)
b) объект каждого типа может
встречаться 0, 1, 2, . . . или л раз в каждой
выборке (выборки с возвращением,
размещения с повторением)
С)
Г.—М";::')
(;:а
N (N - 1) . . . (N - п + 1) = f ] л!
Nn
Пример. Дано множество N =3 различного типа элементов а, Ь, с. Для л = 2
существуют 3 сочетания без повторения (ab, ас, be), 6 сочетаний с повторениями (аа,
ab, ас, bb, be, се), 6 различимых выборок без возвращения (ab, ас, ba, be, ca, cb)t 9 разли*
чимых выборок с возвращением (аа, ab, ас, ba, bb, be, ca, cb, се).
Таблица 18.7-3
Размещения в ячейках или расположения
Каждая формула справедлива для N < п, N = п и N > п
1
2
Число различимых размещений из л
неразличимых объектов в N различных
ячейках (положениях):
a) нет ячейки, которая содержит более
одного объекта
b) каждая ячейка может содержать 0, 1,
2, . . . или п объектов
c) каждая ячейка должна содержать хотя
бы один объект
Число различимых размещений из л
различных объектов в N различных ячейках:
a) нет ячейки, которая содержит более
одного объекта
b) каждая ячейка может содержать 0, 1,
2, . . . или п объектов
0
Г.-'ЬП-Т')
с::)
N(N- 1). . .(N-n+ \) = ljn\
Nn
18.7-3. 18.7. СПЕЦИАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ВЕРОЯТНОСТНЫХ ЗАДАЧ 569
18.7-3. * Применение производящих функций. Теорема Пойа.
(а) Сочетания из п различных объектов Аъ А2, ..., Лп по k без
повторений могут быть получены как коэффициенты а^ производящей функции
F(s)= 2 aks* = (l+A1s)(l+A#)...(l+Ans).
£ = 0
Число таких сочетаний равно коэффициенту ал = (£) перечисляющей
производящей функции (энумератора)
M*)=S aksk = (\+s)n.
k = 0
Более общая модель описывает сочетания с повторениями. Если какой-
либо объект Af может повторяться 0, гъ г2, ... или гд раз, то в выражении
для F (s) множитель \-\-AjS следует заменить на 1 + Л/-15 1 + ... + Л,^ ?.
Соответственно, в выражении для F* (s) один множитель 1+s заменяется на
l+sri+...+sr9.
Если повторяются и другие объекты, то подобным же образом
заменяются другие множители.
Если каждый из объектов может повторяться любое число раз, то
,-• * 'S-
F, (s) = (l +s + *+..y = (T±7) =2 (""
*=o v
Если при этом каждый из я объектов должен встретиться хоть один разе
I', (.)-(•+- + ...)•-(г^г)"- 2 (Jl»V-
(b) Число размещений из п различных объектов по k без повторений
равно коэффициенту Ъь перечисляющей производящей функции
п
G.w=2£?s*=(1+syi; bk=zkl{nk)-
Если один из объектов может повторяться 0, г1( г2, ... или rq раз, то
г
S
Если допустимо любое число повторений каждого объекта, то
G,(s) = (l+s+£+...)" = ««
Если при этом каждый из п объектов должен встретиться хоть один раз,
С.<«) = ^+7? + ... + ^)(1+»)я-1.
О. (s)=»(s+|f-+...)" = («•-!)«.
(с) Теорема Пойа о подсчете. Пусть конечное множество D состоит из п
элементов (точек) рис каждой точкой р сопоставлен определенный элемент
(объект) / из другого конечного множества R; при этом с несколькими
570 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.7-3.
разными точками р может быть сопоставлен один и тот же объект /. Это
отображение D в R можно представить в виде конфигурации (схемы) (рис. 18.7-1).
1^ Конфигурация
Рис. 18.7-1. Два примера конфигураций. Конфигурация 2 получена из конфигурации /
перестановкой точек рх и р2. Две такие конфигурации могут быть эквивалентными при
соответствующем соглашении о симметрии точек множества D и неразличимости двух
(или более) символов в R (для примера fx и f3).
Пусть G —группа подстановок (перестановок) элементов множества D
(п. 12.2-8). Две конфигурации Сх и С2 называются эквивалентными по
отношению к группе G, если некоторая перестановка в G переводит Сх в С2;
эквивалентные конфигурации обязательно содержат одни и те же объекты.
Каждая перестановка Р из G разбивает точки р на определенные
подмножества (циклы) так, что в каждом подмножестве перестановка будет
циклической (п. 12.2-8). Обозначим через bk число таких циклов длины k для
некоторой перестановки (b1-\-2b2 + .*.-\-nbn = n). Тогда циклический индекс
Zg группы G определяется как многочлен
Zg^> s* *»)*-}■ 2^ ь2...ьп '№...«'«.
где g — общее число перестановок в G (т. е. порядок группы G), ^^2... ъп —
число перестановок, содержащих bt циклов длины 1, Ь2 циклов длины 2, ...
... , Ьп циклов длины п (сумма берется по всем перестановкам Р из (?).
Сопоставим далее с каждым объектом f из R неотрицательное целое число w
(вес объекта) и обозначим через aw число различных объектов f веса ш. Весом
конфигурации назовем сумму весов входящих в нее объектов. Обозначим
через Aw число неэквивалентных конфигураций веса ш.
Теорема Пой а. Производящие функции
ОО 00
a(s)= 2 а^ и A (s)= 2 Aw^
ш=0 ад=0
связаны соотношением
A(s) = ZG[a(s)t a(s% ..., a(s»)].
ОО
В частности, общее число конфигураций А (1)= 2 &w связано с общим
ОО
числом объектов я(1)=2 aw соотношением
ш=о
A(l) = ZG[a(\)t а(\) а(\)].
» обобщена на с
теризуются двумя или более весами U8
Теорема может быть обобщена на случай, когда объекты I и конфигурации харак«.
"МО].
18.8-1. 18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 671
18.7-4. Задачи с дискретным распределением вероятностей: успехи и
неудачи в составляющих испытаниях. Часто рассматриваются такие составляющие
испытания, которые допускают только два возможных исхода («успех» и
«неудача»). Вероятности различных сложных событий при этом могут быть
подсчитаны методами пп. 18.2-2 — 18.2-6 через вероятности ftlf ft2, ... успехов в
первом, втором, ... составляющих испытаниях.
Для применения методов пп. 18.5-6—18.5-8 следует связать с &-м составляющим
испытанием дискретную случайную величину х^ со спектральными значениями 1 и О,
соответствующими событиям «успех» и «неудача»; для этой величины имеем;
Рхк0)=*ь ^<°) = >-^. (18-7-3)
Mxk =Ok, Dxk =0Л (1 - 0Л). (18.7-4)
Х*л<*>в 0-<>*>+V'*' Mxj? =0 ~^>+VS • Y*ft<s> = 0-**>+<V- (18.7-5)
Успехи в двух или более независимых испытаниях будут по определению
независимыми событиями (п. 18.2-4). Повторные независимые испытания, каждое из которых
имеет лишь два возможных исхода, называются испытаниями по схеме Бернулли (,61 =
*=Ф2= ••• =&)■ Вероятность появления точно х = xt + х2 + ... -f* xn успехов в п
испытаниях по схеме Бернулли дается биномиальным распределением (табл. 18.8-3).
18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
18.8-1. Дискретные одномерные распределения вероятностей. Таблицы
18.8-1 — 18.8-7 описывают некоторые дискретные одномерные распределения,
представляющие интерес в связи с выборочными обследованиями, теорией
Таблица 18.8-1
Вырожденное (причинное) распределение
(см. также табл. 18.8-11)
1 при х = £,
(а) р (х) ^ '
( 1 при * = Б, )
= 62=1 \ (* = 0, ± 1, ±2, . . . ; £ —целое).
6 К 0 при х ^l J
(b) Ы\х = £, Dx = О, Y.V (s) = si
Гипергеометрическое распределение
Таблица 18.8-2
(а) р (х) = /N\~X {X e °* Ь 2 п; N>n>0; N>:N1 = VN> 0).
(b) Ш = -~ = п&: Dx —
N ' " N*
(c) Типичное толкование, р (х) есть вероятность того, что случайная
бесповторная выборка объема п (п. 19.5-5) содержит точно х элементов типа 1, если эта
выборка производится из генеральной совокупности N элементов, среди которых
Nt = ftN элементов принадлежат типу 1.
(d) Приближения. Если N -*• со, в то время как п и* = NtfN остаются
фиксированными, то гипергеометрическое распределение стремится к биномиальному
распределению (табл. 18.8-3; бесповторные выборки мало отличаются от повторных
выборок, если отношение n/N мало). Аппроксимация биномиальным распределением
применима, если n/N < 0,1.
572 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.8-1
Таблица ia.8-3
Биномиальное распределение
(рис. 18.8-1; см. также п. 18-7-3)
р(Х)
0,25\
р(х)
0,25\
\РМ
, ■ I I
1^
О 12 3 4x0 1 2 ЗлО 1 234 т-1 т пи- / л-/ n х
а) Ь, с)
Рис. 18.8-1. Биномиальное распределение:
а) п = 4, Ф = 0,4; Ь) п = 3, Ф = 0,8; с) п = 16, Ф = 0,7; т — мода.
(а)
р (х) = (П)®х (1 — Ф)" х (х = 0, 1, 2, ... , л; 0 < Ф < 1).
Вероятность р (х) имеет наибольшее значение, когда х равен целой части числа
(л -f 1) Ф (если это число целое, то р [(л + 1) Ф] = р [(л + 1) Ф — 1]). Яри Ф >
л+1
она
последовательность р (0), р (1), р (2), ... монотонно возрастает, при Ф < ——г
л -+- 1
монотонно убывает, в остальных случаях биномиальное распределение одномодально
(рис. 18.8-1). Заметим также, что
**«- i:fi*i*i-^"i=i-^(f-f)=i-<^(m,mJ,er^)
/ = 0
с т, = 2 (* + 1), тг = 2 (л — х) (см. пп. 19.5-3 и 21.4-5).
(Ь) М* = п^, Dx = лФ (1 - Ф), у* (5) = № + 1 - Ф)л,
а2 = лФ + л (л — 1) Ф2, а3 = л (л — 1) (л — 2) Ф8 + Зл (л — 1) Ф2 + лФ,
|ха = «^ (1—Ф) (1 -2Ф), |х4 == /г^ (1 — ф) [1 +3(л —2)Ф(1 — Ф)],
1 _ 6Ф(1 — Ф)
Yi!
1 —2Ф
УмФ (1 — Ф) '
Y«=-
лФ (1 — Ф)
(с) Типичное толкование, р (х) есть:
1) вероятность того, что повторная случайная выборку объема л
(п. 19.5-5) содержит точно х элементов типа 1, если генеральная
совокупность объема N содержит ftN элементов типа 1;
2) вероятность появления события точно х раз в п независимых
испытаниях по схеме Бернулли (п. 18.7-3) при условии, что вероятность события
в каждом испытании равна Ф.
18.8-2. 18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 573
Таблица 18.8-3 (продолжение)
(d) Приближения. Биномиальное распределение при п -*• оо является
асимптотически нормальным с центром п& = £ и дисперсией /гФ (1 — ф) = о2 (предельная
теорема Муавра — Лапласа, частный случай центральной предельной теоремы,
п. 18.6-5). При 0 < •& < 1
когда
когда
Р{Хг:
(*-е\-Ф (х+^~ъ)
U)'T«l о )
О*
/x. + i—6\
-'W ~ф«\ а /
(At-6)» , 0 (X.-6)»
о4 • а4
рН^^Ь®,»)-
-ф«
■фи
-» 0;
-ф«
('"
\
\
(Х"
\
(а),
1
" 2
а
1
2
а
i
/■
-S
).
когда п -*- со при фиксированных а, 6.
Приближения, основанные на этих соотношениях, применимы при
а* = пЪ (1 — fl) >: 9.
Об исследовании ошибок приближения см. [18.8]. Аппроксимацию биномиального
распределения распределением Пуассона см. в табл. 18.8-4.
игр и т. п. В первую очередь табулированы производящие функции ух (s),
так как по ним легко найти характеристические функции и производящие
функции моментов по формулам
Xx(q) = y.x(eig)\ Mx(s) = yx(es)
(см. также п. 18.3-8). Моменты, не приведенные в таблице, можно вычислить
методами п. 18.3-10.
18.8-2. Дискретные многомерные распределения вероятностей (см. также
п. 18.4-2).
(a) Полиномиальное распределение описывается формулой
(хи *2 *»«=0, 1. 2, ...; x1+x2+...+xn = N),
где Ъ1г Ь2 $>„—положительные числа, сумма которых
»i+»t + -+»» = l-
Если испытание имеет п попарно несовместных исходов Е-, Е , ... , Е с
вероятностями "&г ^2, ... , #п, где dj-j-dg-f-... +^п = К то выражение (1) дает вероятность того,
что события Е Е2, ... , Е произойдут соответственно *-, х ... , х раз за 7V
повторных независимых испытаний (см. также п. 18.7-3).
В классической статистической механике xv *2, ... , хп~-числа замещений п
независимых состояний с априорными вероятностями <к, Ь , ... , & соответственно.
(b) Многомерное распределение Пуассона описывается формулой
(xlt х2, ..., *Л = 0, 1, 2, ...; £Л > 0, 6 = 1, 2 п).
(18.8-2)
674 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.8-2.
щ
Pfx)
0.5
{-Д/ 0,3\
0J\
О 1 2 х
я)
Распределение Пуассона
(рис. 18.8-2)
Р(1)
0,Н0\
0J20\-
0,Ю0\
ОЩ
0Щ-
Q,№r
««/
0,020}-
О
0 12 3 4 2
Ь)
JL
Таблица 18.8-4
В, = Ю
I i
0 1 2345678910 12 14 16 18 20 х
О
Рис. 18.8-2. Распределение Пуассона.
(а) р (х) = е
_.-е_£
х\
(b) M.t = DJc = |,
<лг = 0. 1, 2, ... ; I >0),
ct-t
а2=££-Ь 1),
«4 = S(S3 + 6Б1 + 7БН-1),
a-=6(S» + 3g+ l),
(с) Распределение Пуассона аппроксимирует гипергеометрическое распределение
(табл. 18.8-2) и биномиальное распределение (табл. 18.8-3), когда ftN -* оо, п -+ оо,
ft-> О при условии, что ft/2 имеет конечный предел £ (закон малых чисел). Это
приближение применяется при О < 0,1. Наиболее важные приложения распределения
Пуассона, связанные со случайными процессами, см. п. 18.9-3.
Геометрическое распределение
Таблица 18.8-5
(а) р (х) = ft (I — ft)* (х = 0, 1, 2, ... ; 0 < ft < 1),
1 -ft ^ 1 —ft . , Ф
(b) М*=-
ft
Dx-
Уг (s)
1 -(1 -ft) !
(с) Типичное толкование, р (х) есть вероятность появления события («успеха»)
в первый раз после точно х испытаний по схеме Бернулли при вероятности успеха ft.
ф (х) = 1 — (1 — ft)* + i (* = 0, 1, 2, ...) есть вероятность того, что первый успех
появится самое большее после х испытаний (см. также табл. 18.8-6).
Распределение Паскаля
Таблица 18.8-6
р (х) =(т + * 1\$т (1 -ft)* (* = 0, 1, 2, ... ; т= I, 2, ... ; 0< ft < I).
(Ь) Ы\х = т
Ох
1 - ft , ч / ft \т
=m-w vs>=4i-(i-o)s) •
(с) Типичное толкование, р (х) есть вероятность появления события («успеха»)
в т-й раз после точно т -+- х—1 испытаний по схеме Бернулли при вероятности
успеха ft. Ф (х) есть вероятность того, что m-й успех наступит самое большее после
т + х— 1 испытаний. При m = l распределение Паскаля сводится к
геометрическому распределению (табл. 18.8-5).
18.8-8.
•18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
575
Распределение Пойа
Таблица 18.8-7
(а)^ЧтТТГ|)
I \*l (1 + P) - п-н*- »)Р]
*!
Р(0)
(др = 1, 2, ...),
р <0) = <1 + № Р <£ > о, Э > 0).
— JL
(b) М* = I, Ох = | (1 + К), у* (s) = (1 + К - №) Р .
(c) Распределение Пойа сводится к распределению Пуассона (табл. 18.8-4) при
3 = 0 и к геометрическому распределению (табл. 18.8-5) при 0 = 1. О толковании
на языке случайных процессов (процесс размножения) см. [18.8].
18.8-3. Непрерывные распределения вероятностей: нормальное
распределение (Гаусса). Непрерывная случайная величина х распределена нормально
с математическим ожиданием (центром) £ и дисперсией а2 (или нормальна
с параметрами |, о2), если
*«",!%• 'ч " '-Х-^).
(18.8-3)
<D(JT)--p= \ е 2 \ ° 1 dx =
ay 2я J
— оо
-M^-tI'X^-)]- ]
Распределение стандартизованной нормальной величины (нормального
отклонения) w = ^~ (см. также п. 18.5-3,с и п. 18.8-4) дается формулами
(рис. 18.8-3):
1
9*
-ти>
' Y2n V2n \ 2 /
(плотность нормального распределения; см. табл. 18.8-8),
*.W-^jr^*-i[i+d(i)]
— 00
(нормальная функция распределения; см. табл. 18.8-9),
М« = 0, Du = l.
erf z — функция ошибок (см. также п. 21.3-2 и табл. 18.8-10):
} (18.8-4)
erf
zs-erf(-z)s--|=-fe-C«dE = 20B(zVr2)-l.
у я J
(18.8-5)
<Ры(Я) имеет точки перегиба при X = £ ± о. Заметим, что
где Я- (г) — многочлен Эрмита степени k (п. 21,7-1).
(18.8-6)
576 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.8-4.
Каждое нормальное распределение симметрично относительно центра |; g есть
медиана и единственная мода. Коэффициенты асимметрии и эксцесса равны нулю;
H2k = 1 • 3 ... (2k - 1) o2k, ц2к1 -0 (k =* 1, 2, ...),
«l = g. x2 = а2, и3 = и4 = ... = 0,
(18.8-7)
(18.8-8)
Xx (Q) = exp {- -^- q* + /£?). (18.8-9)
Моменты a относительно начала можно вычислить способом, указанным в п. 18.3-10.
г(Щ
0J5/6
0,4/6
0,3/6
0,2/6
0,1/6
\г*м
-0,5
-0,4
-0,3
-0,2
-0,1
о £-Зб Ыбх'Ьб i Ьб №в t+Зб х
1 I tiii i i >.
-з -г -1 о 1 z з и
о 1тьТи*Ъ^м№ &6ЩГ*
-z -/
о
з и
Рис. 18.8-3. а) Плотность нормального распределения
b) Нормальная функция распределения
ФИ<1/). U:
Ф(Х)=
1 х Jl(JL=JL\2
i_ J e 2 V о J flfx =
О У"2я —оо
Фи{и), U-
х-Ъ
18.8-4. Нормальные случайные величины: распределение отклонений от центра,
(а) Для любой нормальной случайной величины х с центром | и дисперсией о»
р {.<*<»> =*в(^)-*в(а-^)
(18.8-10)
16.8-4. 18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 577
Таблица 18.8-8
Плотность нормального распределения (стандартизованного)
и
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1.6
1,7
1.8
1,9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
0
0,39894
39695
39104
38139
36827
35207
33322
31225
28969
26609
24197
21785
19419
17137
14973
12952
11092
09405
07895
06562
05399
04398
03547
02833
02239
01753
01358
01042
00792
00595
1
39892
39654
39024
38023
36678
35029
33121
31006
28737
26369
23955
21546
19186
16915
14764
12758
10915
09246
07754
06438
05292
04307
03470
02768
02186
01709
01323
01014
00770
00578
2
39886
39608
38940
37903
36526
34849
32918
30785
28504
26129
23713
21307
18954
16694
14556
12566
10741
09089
07614
06316
05186
04217
03394
02705
02134
01667
01289
00987
00748
00562
3
39876
39559 !
38853
37780
36371
34667
32713
30563
28269
25888
23471
21069
18724
16474
14350
12376
10567
08933
07477
06195
05082
04128
03319
02643
02083
01625
01256
00961
00727
00545
4
39862
39505
38762
37654
36213
34482
32506
30339
28034
25647
23230
20831
18494
16256
14146
12188
10396
08780
07341
06077
04980
04041
03246
02582
02033
01585
01223
00935
00707
1 00530
5
39844
39448
38667
37524
36053
34294
32297
30114
27798
25406
22988
20594
18265
16038
13943
12001
10226
08628
07206
05959
04879
03955
03174
02522
01984
01545
01191
00909
00687
00514
6
39822
39387
38568
37391
35889
34105
32086
29887
27562
25164
22747
20357
18037
15822
13742
11816
10059
08478
07074
05844
04780
| 03871
03103
02463
01936
01506
01160
00885
00668
00499
7
39797
39322
38466
37255
35723
33912
31874
29658
27324
24923
22506
20121
17810
15608
13542
11632
09893
08329
06943
05730
04682
03788
03034
02406
01888
01468
01130
00861
00649
00485
8
39767
39253
38361
37U5
35553
33718
31659
29430
27086
24681
22265
19886
17585
15395
13344
11450
09728
08183
06814
05618
04586
03706
02965
02349
01842
01431
01100
00837
00631
00470
9
39733
39181
38251
36973
35381
33521
31443
29200
26848
24439
22025 I
19652
17360 |
15183 I
13147
11270
09566
08038
06687
05508
04491
03626
02898
02294
01797
01394
01071
00814
00613
00457
и при У>=0;
Р {\x~t\<Yo} = P{l-Yo<x<l+Yo}=*
Y _ul
-Ж S* 2 ^=2Фл(К)-1=ег£^^)=Ф1а1<К). (18.8-11)
-У
oo u2
P { l*-£|>Ka} = —-J в 2 Л|-2[1-Фв<у)]-
= 1
(b) Квантили
"■егГ(тг)=1~ф|ы1(УМ,м'
12)
| и | p = <g + p=» I и |1-a = и _ a_.
2 2
определяемые формулой
Р{|*-6К1«1р*}-*-1-о,
19 Г. Корн и Т. Корн
(18.8-13)
(18.8-14)
578 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.8-4.
Таблица 18.8-9
Интеграл вероятностей
и
Ф (U) = JL, С ,-*•/. dt = JL erf ММ = ф (С/) _ _L
Y2n 3 2 \/2 У а 2
О
С/
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
1 0,8
0,9
1.0
1.1
1,2
1.3
1.4
1.5
1,6
1.7
1.8
1.9
2.0
2,1
2,2
2,3
2.4
2,5
2,6
2,7
2,8
2,9
3,0
3,5
4,0
4,5
5,0
0
0,00000
03983
07926
11791
15542
19146
22575
25804
28814
31594
34134
36433
38493
40320
41924
43319
44520
45543
46407
47128
47725
48214
48610
48928
49180
49379
49534
49653
49744
49813
49865
4997674
4999683
4999966
4999997133
1
00399
04380
08317
12172
15910
19497
22907
26115
29103
31859
34375
36650
38686
40490
42073
; 43448
44630
45637
46485
47193
47778
48257
48645
48956
49202
49396
49547
49664
49752
49819
2
00798
04776
08706
12552
16276
19847
23237
26424
29389
32121
34614
36864
38877
40658
42220
43574
44738
45728
46562
47257
47831
48300
48679
48983
49224
49413
49560
49674
49760
49825
3
01197
05172
09095
12930
16640
20194
23565
26730
29673
32381
34850
37076
39065
40824
42364
43699
44845
45818
46638
47320
47882
48341
48713
49010
49245
, 49430
; 49573
49683
49767
49831
4
01595
05567
09483
13307
17003
20540
23891
27035
29955
32639
35083
37286
39251
40988
42507
43822
44950
45907
46712
47381
47932
48382
48745
49036
49266
49446
49585
49693
49774
49836
5
01994
05962
09871
13683
17364
20884
24215
27337
30234
32894
35314
37493
39435
41149
42647
43943
45053
45994
46784
47441
47982
48422
48778
49061
49286
49461
49598
49702
49781
49841
6
02392
06356
10257
14058
17724
21226
24537
27637
30511
33147
35543
37698
39617
41308
42786
44062
45154
46080
46856
47500
48030
48461
48809
49086
49305
49477
49609
49711
49788
49846
7
02790
06749
10642
14431
18082
21566
24857
27935
30785
33398
35769
37900
39796
41466
42922
44179
45254
46164
46926
47558
48077
48500
48840
49111
49324
49492
49621
49720
49795
49851
8
03183
07142
11026
14803
18439
21904
25175
28230
31057
33646
35993
38100
39973
41621
43056
44295
45352
46246
46995
47615
48124
48537
48870
49134
49343
49506
49632
49728
49801
49856
9
03586
07535
11409
15173
18793
22240
25490
28524
31327
33891
36214
38298
40147
41774
43189
44408
45449
46327
47062
47670
48169
48574
48899
49158
49361
49520
49643
49736
49807
49861
часто принимаются в качестве доверительных границ нормального отклонения и или
в качестве а-значений нормального отклонения (см. также п. 19.6-4). Заметим, что
I " 1о,95 в м 0,975 **» !.96. I " 1о,99 = "0,995 *» 2&, I и |0#999 = "0,9995 ^ 3«29- <18-8" 15>
(с) Для нормального распределения применяются следующие характеристики
рассеяния (см. также табл» 18.3-1):
среднее абсолютное отклонение (с. а. о.)
М|*-1|=оМ|ы|=]/ — ад» 0,798 о.
вероятное отклонение (в. о., медиана величины | х — £ |)
j и 1у8 о = — и ij о » и «д о ^ 0,674а,
18.8-4. 18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 579
Таблица 18.8-10
Функция ошибок
г
я J
о
г
0.00
1
2
з
4
&
6
7
8
9
10
1
2
з
4
5
6
7
8
9
20
1
1 2
1 з
1 4
1 ^
6
7
8
9
30
1
2
з
4
5
6
7
8
9
40
1
2
з
4
5
i 6
1 7
8
9
50
0
0.0000
0113
0226
0338
0451
0564
0676
0789
0901
1013
1125
1236
1348
1459
1569
1680
1790
1900
2009
2118
2227
2335
2443
2550
2657
2763
1 2869
| 2974
3079
3183
3286
3389
3491
3593
3694
3794
3893
3992
! 4090
4187
4284
4380
4475
4569
4662
4755
4847
4937
5027
5117
5205
1
ООП
0124
0237
| 0350
0462
0575
0688
0800
0912
1024
1136
1247
1359
1470
1581
1691
1801
1911
2020
2129
2238
2346
2454
2561
2668
2774
2880
2985
3089
3193
3297
3399
3501
3603
3704
3804
3903
4002
4100
4197
4294
4389
4484
4578
4672
4764
4856
4946
5036
5126
5214
2
0023
0135
0248
0361
0474
0586
0699
0811
0923
1035
1147
1259
1370
1481
1592
1702
1812
1922
2031
2140
2249
2357
2464
2572
2678
2784
2890
2995
3100
3204
3307
3410
3512
3613
3714
3814
3913
4012
4110
4207
4303
4399
4494
4588
4681
4773
4865
4956
5045
5134
5223
3 |
0034
0147
0260
0372
0485
0598
0710
0822
0934
1046
1158
1270
1381
1492
1603
1713
1823
1933
2042
2151
2260
2368
2475
2582
2689
2795
2901
3006
3110
3214
3317
3420
3522
3623
3724
3824
3923
4022
4119
4216
4313
4408
4503
4597
4690
4782
4874
4965
5054
5143
5231
4
0045
0158
0271
0384
0496
0609
0721
0834
0946
1058
1169
1281
1392
1503
1614
1724
1834
1944
2053
2162
2270
2378
2486
2593
2700
2806
2911
3016
3120
3224
3327
3430
3532
3633
3734
3834
3933
4031
4129
4226
4322
4418
4512
4606
4699
4792
4883
4974
5063
5152
5240
5
0056
0169
0282
0395
0507
0620
0732
0845
0957
1069
1180
1292
1403
1514
1625
1735
1845
1955
2064
2173
2281
1 2389
2497
1 2604
2710
2816
2922
3027
3131
3235
3338
3440
3542
3643
3744
3844
3943
4041
4139
4236
4332
4427
4522
4616
4709
4801
4892
4983
5072
5161
5249
6
0068
0181
0293
0406
0519
0631
0744
0856
0968
1080
1192
1303
1414
1525
1636
1746
1856
1966
2075
2184
2292
2400
2507
2614
2721
2827
2932
3037
3141
3245
3348
3450
3552
3653
3754
3854
3953
4051
4149
4245
4341
4437
4531
4625
4718
4810
4901
4992
5081
5170
5258
7
0079
0192
0305
0417
0530
0643
0755
0867
0979
1091
1203
1314
1425
1536
1647
| 1757
' 1867
1977
2086
2194
2303
2411
2518
2625
2731
2837
2943
3047
3152
3255
3358
3461
3562
3663
3764
3864
3963
4061
4158
I 4255
4351
4446
4541
4634
4727
4819
4910
5001
5090
5179
5266
8
0090
0203
0316
0429
0541
0654
0766
0878
0990
1102
1214
1325
1436
1547
1658
1768
1878
1988
2097
2205
2314
2421
2529
2636
2742
2848
2953
3058
3162
3266
3369
3471
3573
3674
3774
3873
3972
4071
4168
4265
4361
4456
4550
4644
4736
4828
4919
5010
5099
5187
5275
9
0102
0214
0327
0449
0553
0665
0777 1
0890
1002
1113 j
1225
1336 i
1448
1558 1
1669
1779 1
1889 i
1 1998 l
1 2108 |
2216 j
2324 j
2432 ;
2540 j
2646
2753
2858
2964 i
3063 i
3172 i
3276 1
3379 j
3481
3583 i
1 3684 !
3784 j
3883 !
3982 I
4080 j
4178
4274
4370 1
4465
4559
4653 !
4746
4837
4928
5019
5108
5196
5284
1S*
Таблица 18.8-
Непрерывные одномерные распределения вероятностей
8
1
2
з
Распределение
Вырожденное
(причинное)
распределение
Равномерное
(прямоугольное)
распределение
Распределение Коши
Плотность распределения
Ф(*)
1 со (х = 1)
сем. п. 21.9-2)
ih <1*-61<а).
1 0 ( | х - % | > а)
1 1
»I + (._=iy
Функция распределения
ФС*)
£/+(*-&)
(см. п. 21.9-1)
«
0 (*<£-а).
1 <*^6'+a)
^-f^arctglzJ
Центр
М <*>
S
1
Дисперсия
D (х)
0
а2
3
Мх и Dx не
существуют,
главное
значение по Коши
(п. 4.6-2, с)
среднего ЬЛх
равно |
ристическая
функция %х (<7)
Я*
sin аисЦд
ад
е
1
<*>
Примечания
х равен 1 почти всегда.
Вырожденное распределение
аппроксимирует
распределение равномерное, Коши или
Лапласа при a -*• 0 или
Величина х равномерно
распределена на интервале
(S - a, I + а)
Это есть распределение
величины х =*= £ + a tgу, если
величина # распределена
равномерно в интервале
(—я/2, я/2). Распределение
симметрично относительно
Таблица 18.8-11 (продолжение)
Распределение
Плотность распределения
Ф(х)
Функция распределения
Ф(х)
Центр
М(х)
Дисперсия]
D (х)
ристическая функ-
Примечания
Распределение
Лапласа
-U-6I
W
{
1
1 2
1-
е
1 "
2е
X-
Э
-i£
1\
<*^1).
-II
20*
*«&
1 + 0*<72
При g = 0
характеристическая функция
пропорциональна плотности
распределения Коши с а = -5-
Р
Бэта-распределение
О (х < 0, х > 1),
Г (а 4-0) д^х р-1
Г (а) Г О) u X)
(0<х< 1), (а>0. 0>О)
0 (х ^ 0),
В„<а, 0)
В (а, 0)
1
(О^х^ 1).
(х>\)
На
а 4-0
F(a, а+ 0; i<7)
(п. 9.3-10)
В^ (а, 0) — неполная бэта-
функция (п. 21.4-5).
Единственная мода
аТ"р"-2 ПРИ а>1' Э>К
Г (а + г) Г (а + 0)
а/- ~ Г (а) Г (а 4- 0 4- ')
Гамма-распределение
0 (х =5 0),
jLLxa-ie-fix(x>0)
I (а > 0, 0 > 0)
|1 Г (а)
(^^0),
Гй)%(а) (х =
0)
а
о-«"
Г^ (а) — неполная
функция (п. 21.4-5)
Б82 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.8-5.
половина полушироты У2\п 2 о ^ 1,177а,
нижний и верхний квартили х i/4 = £ -j- и 1д о « £ — I и | i/4 а, # •д = | -f- и зд »
- 6 + I и I V, °- ,
жгра точности h =—-=—
а/2
18.8-5. Различные непрерывные одномерные распределения вероятностей.
Табл. 18.8-11 описывает некоторые непрерывные одномерные распределения.
18.8-6. Двумерные нормальные распределения.
(а) Двумерное нормальное распределение задается плотностью
распределения
1 ._ С 1
ц>(хъ *2)= \ exp f 1 чК~2р1&Ц1ц2 + ц1)\ (18.fi
aroF^Fi-p^ \ 2(1-р22) J'
«1=^^-. "2 = -^^ (ai>0, a2>0, |p12|^ 1).
Распределения координат хх и *2 являются нормальными с центрами \^
£2 и дисперсиями af, af соответственно; pi2 — коэффициент корреляции между
хг и х2. Пять параметров glf £2, af, of, р12 вполне определяют распределение.
Условные распределения хг и х2 тоже нормальны с
М{х1|дг2}=|1 + р12^-(х2-|2); D{^1|Ar2}=c7f (1 —pf2), (18.8-17)
M{x2\Xl}=l2 + 9l2 -^(^-Ei); D{^2|^} = ai(l~pf2), (18.8-18)
так что кривые средней квадратической регрессии совпадают с прямыми
регрессии (п. 18.4-6). хг и х2 независимы тогда и только тогда, когда они
не коррелированы (pi2 = 0, см. также п. 18.4-11). Заметим, что
4 ^ [ (18.8-19)
Р{*1^£ь *2^£2} = P{*i^£i; *2^£2} = i—^arcsinp12. J
(b) Каждое двумерное нормальное распределение (16) может быть описано
стандартизованными нормальными величинами ил, и2 с коэффициентом корреляции р}2 или
независимыми стандартизованными нормальными величинами и' и' (п. 18.5-5), а именно:
Ф (хи хг) dxt йхг =
~ 2пуТ^г ехр["Н^й)(Ы?"2р1г"Л + U|)]"°Л =
=<ta (ui) 9„ («э d«i *«;=<р« («;> <»» Сг)du; ds, <l8-8-20>
где
Ul = £LZiiL( «,-.*t=ls., и> »i-p«.». , ц,= «,-Р..«. , ,18.8.m
х °« 2 "• ' i^-pj, ! К1 - р;,
(c) Распределение (16) можно представить графически с помощью эллипсов равной
вероятности <р (xit х2) = const или
22)
Вероятность того, что точка (хи хг) лежит внутри эллипса (22), равна
Р-ФХ.<2)С^»).
что означает Я2 = хр (2) (табл. 19.5-1). Две прямые регрессии, определенные
уравнениями (17) и (18), делят пополам все хорды эллипса равных вероятностей, идущие в
направлениях осей *j и х% соответственно (см. также п. 2.4-6).
18.8-0. 18.8. СПЕЦИАЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ Б83
18.8-7. Круговое нормальное распределение. Формула (16) определяет
круговое нормальное распределение с центром (|х, £2) и дисперсией а2, если pi2=
= 0, а1 = сг2 = о\ При этом эллипсы равных вероятностей сводятся к
окружностям, соответствующим квантилям радиального отклонения (радиальной ошибки)
Распределение г дается формулами (см. также табл. 19.5-1)
<M')=j,qv<2)(£)
г»
' 2а»
(г^О),
Фг(*) = Р {(*1-?1)2 + (*2-У2^#2}= $ Ф, (0^= Фх2(2) (£).
Отметим формулы
rVteVx"/i<2) а^1.1774(У
(круговая вероятная ошибка),
{средняя радиальная ошибка).
Mr
-VI-
1,2533а
(18.8-23)
(18.8-24)
(18.8-25)
18.8-8. /г-мерные нормальные распределения. Распределение /г-мерной
случайной величины (xv х2, ..., #„) называется /г-мерным нормальным
распределением, если оно является непрерывным с плотностью распределения
"V il rxi еХрМ^ 2 A/*(*/-W(**-w| (18.8-26)
V (2я)л det [bjk] I *f±xj£x J
где
fyft = **/ И [Л;А] = [^Г1.
Нормальное распределение вполне определяется своим центром (£lf g2» ••• > 5л)
и матрицей моментов [hjk] = [Ajk]~1 или дисперсиями и коэффициентами
корреляции (п.18.4-&). Характеристическая функция равна
[п п п -I
* Ц iw -4 2 S v*w* • <18-8-27>
/=1 7=16=1 J
Каждое m-мерное маргинальное или условное распределение, получаемое из
нормального распределения, является нормальным. Все гиперповерхности средней квадра-
тической регрессии совпадают с соответствующими гиперплоскостями регрессии
Ш. 18.4-9).
п случайных величин *-, *2, ..., хп, имеющих нормальное n-мерное распределение,
взаимно независимы тогда и только тогда, когда они не коррелированы (см. также
п. 18.4-11). Каждое л-мерное нормальное распределение может быть описано как
распределение системы п взаимно независимых стандартизованных нормальных величин,
связанных с исходными величинами линейным преобразованием (п. 18.5-5).
18.8-9. Теоремы сложения для специальных распределений (см. также
п. 18.5-7 и табл. 19.5-1).
(а) Биномиальное распределение (табл. 18.8-3), распределение Пуассона
(табл. 18.8-4) и распределение Коши (табл. 18.8-8) устойчивы
(«самовоспроизводятся») при сложении независимых величин. Если случайная величина х
является суммой
* = *i + *2 + ... + *m
S84 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.9-U
т взаимно независимых случайных величин xv x2, ..., хтг то
из Р|(*,)-(2)^(1-*)я*-** следует рх (*) = Q 0*0-ФУ1"*
(/г = /г1 + /г2 + ... + /гт), (18.8-28)
tf л:
из Р1\хй = &Щ следует рх W = rf|"(6*Ei + b + --- + bii). (18.8-29)
<Б = Е1 + Ы-- + Бт)- (18.8-30)
(b) Сумма х=хг+х2 + ...+хп взаимно независимых случайных величин xv
х^ х,г имеет нормальное распределение тогда и только тогда, когда
все они нормально распределены, В этом случае
l = I1+l2+-+in; a*=a*+a|+...+a*. (18.8-31)
Если случайные величины *р х0, ... t xR (не обязательно независимые) имеют
нормальные распределения, то величина х = а^ + а2*2 + ... + апхп имеет нормальное
распределение с центром и дисперсией, определяемыми формулами (18.5-22).
18.9. ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
18.9-1. Случайные процессы. Случайный процесс есть случайная функция
x(t) от независимой переменной t. Каждое испытание дает определенную
функцию X(t), которая называется реализацией процесса или выборочной
функцией. Случайный процесс можно рассматривать либо как совокупность
реализаций- процесса X (/), либо как совокупность случайных величин,
зависящих от параметра /. При этом должны быть заданы распределения
вероятностей систем случайных величин Xi—x(ti)t x2=x(t2)t ... (выборочных
значений) для любого конечного множества значений t1% t2, ... (выборочных
моментов). Случайный процесс дискретен или непрерывен, если дискретно или
непрерывно распределение величин x(ti), x(t2)% ... для каждого конечного
множества tl9 t2% ... Процесс называется случайной последовательностью
(процессом с дискретным временем), если независимая переменная может
принимать только счетное множество значений.
Более общо случайный процесс может описываться многомерной случайной
величиной х (/) = [х (/), y(t), ...].
В большинстве приложений независимой переменной t служит время, а величина
х (t) или х (t) означает состояние физической системы.
Примеры: результаты последовательных наблюдений, состояния динамической
системы в статистической механике Гиббса или квантовой механике, сообщения и шумы
в системах связи, временные ряды в экономике,
18.9-2. Описание случайных процессов.
(а) Для описания случайного процесса надо задать распределение
величины x(ti) и совместные распределения систем величин [#(/i), x(t2))%
[*(*i), ^ft)» *(*з)1» ••• Для каждого конечного множества значений tl% t2% t3t...
(первое, второе, ... конечномерные распределения вероятностей случайного
процесса). Эти распределения описываются функциями распределения
соответственно первого, второго, ... порядков (см. также п. 18.4-7):
Фа,(*1. fi)-P{*(fi)<Xib \
Ф<2, (Хи tx\ X2, t2) ^P{x ft) < Хг\ х (t2) < Х2}, \ (18.9-la)
18.9-3.
18.9. ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
585
Дискретные и непрерывные случайные процессы описываются
соответственно вероятностями или плотностями распределения:
Pt»(Xu t» Xt, f,)-P{*(*i)-Xi; *(«-*,},
дФ(]\ д2Ф/>
Феи (*i. « = -^, Ф(2, №, fc *.. «-aj^ft. •
(18.9-16)
Замечание. Последовательность функций распределения (1а) описывает
случайный процесс с возрастающей подробностью, так как каждая функция распределения
Ф(п> вполне определяет все предыдущие функции распределения Ф(т) (т < п) (п. 18.4-7).
Это же справедливо и для каждой из последовательностей (\Ь). Каждая из функций (1)
симметрична относительно перестановки пар Х^ t. и X k, t^.
(b) Условные распределения вероятностей для случайного процесса
получаются из функций (\Ь) так же, как в п. 18.4-7, например
P(XU hi •••» Хщ* tm\Xm+i, tm+ъ •••» Хп, **)=*
(18.9-2а)
(18.9-26)
pin-m>(Xm+V *m+V '" ; Хп> *п)9
ф№» ^i» •••» ^m» *m I ^ш+i» Wi» •••; хп% W=
Ф,Я1(*г 'г ■■■-.*»■'и)
ф(я-ш)(^я1+Г Wl: •" ; Хп* *п)
Замечание. Функции (2), вообще говоря, уже не будут симметричными
относительно перестановки пар Х^ ^ и Х^, t^, отделенных вертикальной чертой.
(с) Многомерный случайный процесс, порождаемый, например, парой
функций x(t), y(t), определяется подобным же образом с помощью совместных
распределений выборочных значений *(//), y(tk)- В частности,
Ф2 (*i. h\ K2, /2) = Р{ х ft) < Х1% у (t2) < Y2\. (18.9-3)
18.9-3. Средние по множеству наблюдений. Корреляционные функции.
(a) Общие определения. Для функции f[x(ti)t ...,x(tn)] от д
выборочных значений *(/х), ..., x(tn) (статистик, см. п. 19.1-1) формула
М/-М/[*(/,), ...,*(/„)] =
= $...$ f(Xlt .... Хя)йФ1Я)<Х19 tt; ...; Xnt tn) (18.9-4)
— СХ> —00
определяет среднее по множеству наблюдений (предполагается, что стоящий
справа интеграл сходится абсолютно). В формуле (4) интегрирование
производится по Х1% ..., Хп\ М/ есть функция от tlt ..., tn.
Аналогично для многомерного процесса, описываемого функциями
*('). У(0,
М/И/х), y(t2);x(t3)t yd,); ...]==
СО 00
= $ ... $ f(Xu Y2; X3, yt; ...)d<D{Xu h; Y2, t2; X3, t3; Yt,.tti...). (18.9-5)
— CO —00
(b) Корреляционные функции. Особый интерес представляют
средние М *(/) = £(/), bAx2(t) и корреляционные функции;
автокорреляционная функция
R,*('i. W«M [*(/!)*(/,)] (18.9-6в)
586 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.9-4.
«■(0-R**('.Q. 1
'■W-Rxxi*. О-16 (OP. \ (18.9-7)
v [х (h), у (t2)] = R^ {tlt tt) -1 ft) n (/,), J
и взаимная корреляционная функция
Rxy &. У = M [ж (h) у Ш (18.9-6*)
Они выражают важнейшие свойства случайного процесса и часто
представляют все, что известно о данном процессе; заметим, что
m*2(o=r**c о.
D*
cov |л v*i/> у игл = *^ху \
где л(^2) = М^(/2). Формулы (18!9-б) и (18.9-7) относятся только к действие
тельным случайным процессам.
ХЗ амечание. Во многих руководствах введенные функции R и R называют
ковариационными. Автокорреляционная функция вводится соотношением Кхх(\> U) ^
= М [х 0i)x(t2)], где х (0 =s х (/) — £ (/> — центрированная случайная функция. Легко
проверить, что
Аналогично, взаимная корреляционная функция определяется как
**j,<'r'i)-M[J('i)*('i)]-
При таком определении корреляционных функций
Dx 0) - ^ </. /> и cov [* (tl)t у (у ] = *,, рг у #.
Если x(t) и у(/) являются комплексными случайными процессами
(фактически двумерными случайными процессами), то корреляционные
функции определяются соотношениями
которые содержат соотношения (6) как частный случай.
Заметим, что и для действительных и для комплексных х и у
R**ft 0 = M|*(0|2, (18.9-9)
I R^ Л. У I2 ^ М | * (tt) |> М | у (/,) |i, (18.9-10)
причем из существования математических ожиданий в правой части вытекает
существование корреляционных функций в левой части.
(с) Характеристические функции, л-мерная
характеристическая функция, соответствующая функции распределения я-го порядка для
случайного процесса, есть (см. также п. 18.4-10)
%(п)(Яъ *ъ Й2> к\ .... <7л. /я) = Мехр f У. qkx(tk)
Г'2-
L *=i
(18.9-11)
Аналогично определяется совместная характеристическая функция для х (/),
y(t), ... Дифференцирование характеристических функций позволяет находить
моменты Mx(ti), Mjc2(/j), Rxx(tlt t2), ..., так же как в пп. 18.3-10 и 18.4-10.
18.9-4.* Интегрирование и дифференцирование случайных функций.
(а) Пусть #(/) — случайная функция, а/(/) —заданная не случайная
функция. Интеграл
y = \fif)x{t)dt (18.9-12)
а
18.9-4.
18.9. ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Б87
ь
есть случайная величина, значения которой суть §f(t)X(f)dt, где Х(/) —
а
какая-либо реализация x(f) (предполагается, что интегралы существуют для
всех реализаций X (/)). Справедлива формула
ь ь
My=M$f(t)x{t)dt=*$f (t) M* (0 dt (18.9-13)
а а
Далеко идущим обобщением является определение интеграла (12) как предела
в среднем (п. 18.6-3) соответствующих интегральных сумм" (стохастическнй интеграл).
Интеграл существует в среднем тогда и только тогда, когда существует
Ь Ь
J f <*i> dtt J f (t2) Rxx ( tit (2) dt2 = M\V Iя. (18.9-14)
a a
Несобственный интеграл (а = — со и/или b = со) определяется обычным образом, как
предел собственных интегралов.
(Ь) Пусть случайная функция x(t) такова, что все ее реализации Х(/) —
дифференцируемые функции. Тогда производная случайной функции
*(0 = ^ (18.9-15)
будет представлять собой случайную функцию, возможные реализации
которой суть производные соответствующих реализаций X (/).
Математическое ожидание и корреляционные функции для производной
определяются формулами
Мх(/)=—sr-^SW.
p. r/ м dR**(/l' 'g)
(18.9-16a)
Если существуют производные от X (t) высших порядков, то формулы
(16а) обобщаются следующим образом (р и а —целые числа, порядок
производной):
М*<РЧ0-Е(Р,Ю. К^р>,«,<*!. ЦддР+*а,Т^ /g)- <W-9-«&>
Случайный процесс х (/) непрерывен в среднем в смысле п. 18.6-3, если
Urn М1*« + А0-*(0|" = 0.
Дг-»-0
Это имеет место тогда и только тогда, когда R^ (/lf /2) непрерывна при / =в / = /.
Случайный процесс ж (О называется производной в среднем от случайного процесса
х (/), если
1К.«|аиЦ8=г*-*«Г-»
Для существования производной в среднем от случайного процесса х (/) необходимо
и достаточно, чтобы существовала производная л. *—— при *i ~ *8 = /.
OTi Of;
Если производная в среднем существует при всех t, то для нее справедливы
формулы (16).
Можно также определить интеграл и производную в смысле сходимости по
вероятности (п. 18.6-1).
588 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.9-5.
Важные соотношения этого пункта применяются, в частности, для вывода
соотношений между входными и выходными сигналами в п. 18.12-2.
18.9-5. Процессы, определяемые случайными параметрами. Иногда
случайный процесс можно представить как неслучайную функцию x=x(t; r\lt %,...)
от t и случайных параметров г\ъ rj2, ... При этом случайный процесс вполне
определяется совместным распределением параметров rj1( rj2, ... и
м/[*(&,..., *tti)] =
00 00
= $-$ '[*('г Чг % -) хС»'- \> % •••)] *»4l4l ... (Пг% •••)•
— 00 —00
(18.9-17)
В частности, каждое распределение вероятностей для такого случайного
процесса однозначно определяется его характеристической функцией (п. 18.4-10)
Ъп)(Яъ h; ...; qn, tn)=*
оо оо Г п 1
= $ •••$ «p'Svfciri,-)^,..^^-). <18-9-18>
— 00 —00 L k = l J
18.9-6. Разложение по ортонормированной системе. Если действительный или
комплексный случайный процесс х (/) с конечным математическим ожиданием М * (О и
непрерывной корреляционной функцией R^ (tlf f ) задан на замкнутом интервале [а, Ь], то
существует полная ортонормированная система функций Ju^ (/)} (п. 15.2-4) такая, что
оо Ь
* W e 2 ckuk (/)' cft = I "Л (/) * ('> л (ft = 1. 2. ...), (13.9-19)
ft = l а
где интегралы и ряд сходятся в среднем в смысле п. 18.6-3 (см. также п. 18.9-4, а).
Таким образом, случайный процесс представляется множеством случайных
коэффициентов {сЛ\ первые п коэффициентов могут дать подходящее приближенное
представление. В частности, существует такая полная ортонормированная система Uy (t) г t|u (/),
что все величины с^ будут некоррелированными стандартизованными случайными вели"
чинами, т. е.
Mck = 0, М cick" bik (/' * - 1, 2, ...) (18.9-20)
(теорема Карунена—Лоэва). А именно, упомянутые функции tyk it) будут собственными
функциями интегрального уравнения
Ь
а
(см. также п. 15.3-3). Соответствующие собственные значения Я^ неотрицательны и могут
иметь кратность не более конечного порядка (по теореме Мерсера, п. 15.3-4), причем
Ь Ь оо
М \ | х (t) |» dt = J R^ (/, 0 tf » 2 J-. (18.9-22)
a a ft = l k
Теорема Карунена—Лоэва обобщает теорему п. 18.5-5.
Примеры. Периодический случайный процесс (п. 18.11-1), щум с ограниченной
полосой частот (п. 18.11-2, Ь). Несмотря на то, что явное аналитическое решение
интегрального уравнения (21) редко возможно, эта теорема применяется в теории
обнаружения сигналов.
18.10-2. 18.10. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ 589
18.10. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ.
КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ И СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ
18.10-1. Стационарные случайные процессы. Случайный процесс x(t)
называется стационарным, если все его конечномерные распределения вероятно*
стей инвариантны относительно сдвига по параметру t:
Фш>(Хь h+to; Х2, ь+ь\...; Xnt tn+t0) шш
■■Фся>(*1. h\ Х2, /2; ...; Xnt tn) (-со</0<со; /t-1, 2, ...), (18.10-1)
т. е. если распределение вероятностей л-го порядка зависит только от п— 1
разностей
Ti=/2-'i» t2 = /s-'i -гл-1 = 'л-'1 (18.10-2)
выборочных моментов tk. Аналогично, два или более случайных процессов
х (t)> y(t)t." называются совместно стационарными, если все их совместные
распределения вероятностей инвариантны относительно сдвига по параметру t.
Для стационарных и совместно стационарных случайных процессов
каждое среднее по множеству наблюдений (п. 18.9-3) зависит только от л-—1
разности (2); например,
М/[*(«, *(« *(«]«М/И0), х(тг) х(чп_г)] (18.10-3)
для всех ti (см. также п. 18.10-2).
18.10-2. Корреляционные функции по множеству наблюдений (см. также
п. 18.9-3).
(a) Для действительного или комплексного стационарного процесса х (t)
[и совместно стационарных процессов x(t)t y(t)] средние значения
Мх (/) = М* (0) = М* = £; М | х (t) |* = М | х (0) |а = М | х |2;
м*,(о=л. м\у{*)\*=Щу\*
постоянны, а корреляционные функции зависят только от запаздывания т =
= /2 — tv В этом случае*)
*xxM=M\xJf)x{t+T)] = Rxx(-T), \ (18.10-4)
Rjrir СО - М [Щ У (t+т)] = R^ (- т), j
I Яхх W I ^ R** (0) - М | * |а, (18.10-5)
I Rxy W la ^ R** (0) Ryy (0) = М | х |2 М | у |2. (18.10-6)
В последних формулах из существования математических ожиданий справа
вытекает существование корреляционных функций слева. Если корреляционная
функция Rxx(t) непрерывна при т=0, то она непрерывна при всех т.
Матрица [Rxx (^ — ^)] является эрмитовой и положительно полу определен ной
(п. 13.5-3) для любого конечного множества значений /-, /„, ... , t .
Случайные процессы называются стационарными (или совместно
стационарными) в широком смысле, если для них средние tAx(t), My(t) постоянны и
корреляционные функции зависят только от т, как в формулах (4),
(b) Нормированные корреляционные функции определяются формулами
о (T)-R**(T)-|SI*. о (т)-- *ху™~У* (18Ю-7)
ухх ' м | х |« -111»' vxy /м | * j» -1 & I» Ум | * |» -1 я I»
При этом | р„ (т) | ^ 1, | р^ (т) | < 1.
■•) См. замечание к п. 18,9-3, Ь.
690 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.10-3.
(с) Для действительных стационарных процессов x(t) и y(t)
корреляционные функции действительны и
Ъхх W - Rxx (- т), Rxy (т) - R^ (- т).
(18.10-8)
Нормированные корреляционные функции р**(т) и рху(т) являются дей*
ствительными коэффициентами корреляции (п. 18.4-4).
18.10-3. Спектральная плотность по множеству наблюдений. Для
стационарного случайного процесса x(t) и совместно стационарных случайных
процессов х (0, у (0 спектральная плотность Фхх (со) и взаимная спектральная
плотность Ф^ (со) по множеству наблюдений (по множеству реализаций)
определяются с помощью соотношений Хинчина—Винера
ф**(®)= $ ^М^л=Ф«М,
— 00
оо
Ф*!/Н= $ R*i,(т)*-^dт = Фi,.к(co).
(18.10-9)
Спектральная плотность Фхх (со) всегда действительна, даже для
комплексного процесса х (t); но взаимная спектральная плотность Ф^ (со) может
быть комплексной даже при действительных х (t) ну (t).
При соответствующих условиях сходимости имеют место формулы
обращения
оо
— оо
— оо
(18.10-10)
Преобразования Фурье (9) вводятся обычно для упрощения соотношений
между корреляционными функциями входного и выходного сигналов в
линейной стационарной системе (п. 18.12-3). Существование преобразований (9)
требует, кроме существования М | х |2 и М | у |2 (п. 18.9-3), еще и достаточно
быстрого стремления к нулю величин R^ (т) и R^ (т) при т —* оо. В случае
периодического процесса для возможности применения спектральных
плотностей приходится вводить члены с дельта-функциями (п. 18.10-9).
18.10-4. Корреляционные функции и спектры действительных процессов.
Если x(t) и y(t) действительны, то действительны и корреляционные
функции Яхх(х)г RxyW't B этом случае (см. также формулы (8))
ф^ (со) = 2 С R^ (т) cos сот dx = Ф^— со), (18.10-11)
RjwW-
: (со) cos сот dco = R-^ (— т),
<*>ху (<*) =Фух (— ©) = ®ХУ (- со).
(18.10-12)
(18.10-13)
18.10-5. Спектральное разложение средней «мощности» действительных
процессов. Для действительного процесса x(t) подстановка т=0 в
соотношение (12) дает
М | * I2 = Яхх (0) = -i- f Фхх (со) dco = ^ f Фхх (со) dco. (18. Ю-14)
0 —оо
18.10-7. 18.10. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ 691
Это можно толковать как спектральное разложение средней «мощности»
М | х |2 по частотам со в (0, со) или (— оо, со). Второй интеграл дает
разложение по всем положительным и отрицательным частотам со спектральной
плотностью ФХх(®) (размерность Ф^(со) есть (единицы х)21герц)у первый
интеграл —по неотрицательным («действительным») частотам с «односторонней»
спектральной плотностью 2ФХХ (со).
Взаимная спектральная плотность ФХу (со), вообще говоря, комплексная,
не может быть истолкована так просто, для действительных процессов х (/)>
у (t) подстановка т=0 в соотношение (10) дает
— оо 0
Величину Re Ф^ (со) иногда называют взаимной спектральной плотностью
мощности. Мнимая часть 1тФ^(со) не дает вклада в среднюю мощность (15).
18.10-6. Другие виды спектральной плотности по множеству наблюдений.
В литературе спектральная плотность записывается еще в следующих видах:
S**(v) = <D**(2*v) с М|х|'» f Sxx(S)dvt (18.10-16)
— со
где v=~, размерность S^(v) есть (единицы х)2/герц,
&*И = 2ЙФ**И с МИ2=5 Й**И*». (18.10-17)
— 00
размерность gxx (со) есть (единицы х)2/радиан в секунду.
Для односторонней плотности применяются обозначения
Г^ (v) = 2S^ (у) = 2Ф« (2rev) (v ^ 0), (18.10-18)
G^ (со) = 2g« (со) == -i Фхх (со) (со ^ 0). (18.10-19)
Аналогично записываются также и взаимные спектральные плотности.
Большое количество различных обозначений требует внимания при работе
с литературой.
18.10-7. Средние по времени и эргодические процессы.
(а) Средние по времени. Для любого процесса x(t) среднее по
времени (по параметру t) от функции /[*(*i)» x(t2}> ••• » x(tn)] определяется
так:
</[*(«. *(«, ...,*(Ш =
т
r-S!»^ S /[*('i+0.*('i+0 x(*n+t)\dt, (18.10-20)
— Г
если этот предел существует *). Если х U) описывает случайный процесс, то
(f) есть случайная величина для каждого данного множества значений ttf t2, ...
... , /Л. Заметим, что
М(/) = М/, (18.10-21)
если соответствующие интегралы существуют.
*) Вместо обозначения <f>, так же как и вместо Mf, иногда применяют f; но
последнее обозначение лучше сохранить для эмпирического среднего
f-.1(1/+«,+...+»/>,
где Л есть значение / для yfe-й выборки х (О =* kx (/) (k = 1, 2, ... , п) (см. также п. 19.8-4).
592 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.10-8.
(Ь) Эргодические процессы. Стационарный случайный процесс
x(t) обладает эргодическим свойством, если для любой функции f [xfa), ..., х (tn)]
с вероятностью 1 среднее по времени (20) совпадает со средним по множеству
наблюдений (18.9-4), т. е.
Р{(/) = М/} = 1 (18.10-22)
(при условии, что эти средние существуют). При этом каждая реализация
x(t) определяет случайный процесс однозначно с вероятностью 1, например,
через характеристическую функцию (18.9-11), вычисляемую по x(t) с помощью
формулы (21). Каждое среднее по времени t, например, {х), (х2) или RXx(x)
{п. 18.10-8) описывает с вероятностью 1 общее свойство всего множества
реализаций x(t).
Стационарный процесс эргодичен,
подмножества равна 0 или 1.
если вероятность любого его стационарного
Два или более совместно стационарных случайных процессов называются
совместно эргодическими, если эргодическое свойство имеет место для любых
выборочных средних.
18.10-8. Корреляционные функции и спектральные плотности по времени.
Для действительных или комплексных функций х (t)t у (t) (которые могут и
не быть реализациями .случайного процесса) с конечными средними
квадратами по времени
<|*(0)|«>- lim ± [ \x(t)\*dt,
Г->оо ll JT
Т
<|*/(0)|*>= lim i \ \y(t)\*dt
— Г
существуют корреляционные функции по времени
автокорреляционная функция
Т
1
(18.10-23)
#**(*) = <*(0)*(т)>= lim 2у \ x(t)x(t + T)dt (18.10-24)
Т—*со ___ j>
и взаимная корреляционная функция
т
Я*у(т)==<Д0)*/(т)> = lim ± \ 7{f)y(t+x)dt (18.10-25)
Г-*оо lL JT
(обращаем внимание на разницу в обозначениях корреляционных функций
по множеству наблюдений (R) и по времени (/?)).
Эти корреляционные функции удовлетворяют соотношениям, которые
получаются из соотношений п. 18.10-2, если каждое среднее по множеству
наблюдений (математическое ожидание) заменить соответствующим средним
по времени.
Спектральная плотность Фхх((д) и взаимная спектральная плотность
*Рх?(<*>) Для средних по времени вводятся с помощью соотношений Хинчина—
Винера
оо
— с»
Чху (») - $ Мт) е~'т dT== *r* (»)•
(18.10-26)
18.10-$. 18.10, СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ 693
Если эти спектральные плотности существуют (без формального допуска
членов с дельта-функциями), то, они удовлетворяют соотношениям,
аналогичным тем, которые приведены в пп. 18.10-3—18.10-5.
Другие виды спектральных плотностей вводятся так же, как в п. 18.10-6.
Если x(t)y у (/) — реализация совместно стационарного процесса, то
корреляционные функции (24), (25) и спектральные плотности (26) являются
случайными величинами, математические ожидания которых равны
соответствующим средним характеристикам по множеству наблюдений. Если x(t)t y(t)
совместно эргодичны, то с вероятностью 1 их корреляционные функции (24),
(25) и спектральные плотности (26) совпадают с соответствующими средними
характеристиками по множеству наблюдений.
Спектральные плотности можно ввести также с помощью формального соотношения
^v<u)>= lim oraT («>)bT «■». (18.10-27а)
где af ((a) к bf (со) —преобразования Фурье от «усеченных» функций Xf (t) и ур (t),
равных соответственно х (t), у (t) при | / | < Г и равных 0 при | t | > Г:
Г Г
ar(co) = J х (t) е~Ш dt; &г(со) = J У (О е~Ш dt. (18.10-276)
— Г —Г
Соответствующую спектральную плотность по множеству наблюдений можно при
этом определить как математическое ожидание: Oxv (со) = М\Р"v (со); тогда соотношения
Хинчина — Винера (26) будут следовать из теор"емы Бореля о свертке (табл. 4.11-2).
Однако формулы (27) имеют смысл только, если спектральные плотности не содержат
членов с дельта-функциями (п. 18.10-9 и 18.11-5; см. также п. 18.10-10).
18.10-9. Функции с периодическими компонентами (см. также п. 18.11-1). Так же
как и другие средние по времени, корреляционные функции и спектральные плотности
по времени представляют особый интерес, когда они с вероятностью 1 совпадают с
соответствующими характеристиками по множеству наблюдений (в случае эргодических
процессов, п. 18.10-7, Ь, это верно для всех средних по времени). Если это имеет место, то
простые интегралы (24), (25) обычно легче вычислить, чем двойные интегралы (4).
Таким образом, эргодическое свойство позволяет истолковать, например, Ф (со) как
«частотный спектр» одной «типичной» реализации х (t), так как Ф (со) ss Ч?хх (со)
с вероятностью 1.
Корреляционные функции и спектральные плотности по времени легко вычислить
для функций х (О. У (t), представимых в виде сумм периодических слагаемых. В
частности, для
х (/) = a cos ((dtt -f Ф). У (О = a cos (co8f -HW (18.10-28а)
имеем
а* л I -к аа cos (coil -4- "ф — ф) при со* = colt
Rxx (Т) = J cos u)lT; Rxv (T) = { (18.10-286)
V 0 (д2ф при C0i.
Более общо, пусть х (t) —действительная функция с ограниченной вариацией в
каждом конечном интервале (п. 4.4-8), имеющая конечный средний квадрат (среднюю
мощность) < | а: (0) |8). Тогда функция х (О может быть представлена почти всюду (п. 4.6-14, Ь)
как сумма ее среднего значения (х (0)> = с0, некоторого ряда периодических слагаемых
и апериодической компоненты р (t):
00 /со t °°
x(t)= 2 V k +P<0=*§+ 2 («лсо8«л/ + &л81пюл/) + р(0-
£ =—оо k = \
со
= *о+ £ Ллсо8(юл/ + фл)+/>(0. (18.10-29а)
* = 1
где
©о =» 0, со^ « — ©_£ > о,
ck = { ("к - ibk) " J V* = C"-ft (*=1.2, ...),
4 = 4+»!=" Ы2.
594 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.10-9.
При этом
Г
с0 при о « О,
ck==c-k при Q== °k
lim -у J *(Oe ШМ= { сь=с_ъ при со = ®b (£ = ± l.±2, ...)*
~^ I 0 для остальных значений
c0 при со = О,
^«5?
J x (/) cos at dt= | у а^ при со =сол (k « 1, 2, ...)«
— Г
О для остальных значений о;
lim
Г-оо
i ? х (О sin со* dt - < 2
- bk при о = со^ (k = 1, 2, ...)*
для остальных значений со;
Нт ;рр
S*«>
е~ШМ = 0.
(18.10-296)
(18.10-29с)
— Г
Пусть, далее, функция у (t) удовлетворяет тем же условиям, что и х (/). так что
00 fco t
У <*> e 23 4ke k +q {t) e
£==—CO
CO
«= Yo 4- S (aft cos юл/ + Эл sin a>k A + <7 (0 =
A=l
со
-=Yo+ 23 B* cos (V + %) + * (/): (18.10-30)
Jfe=l
круговые частоты coi, <o2. ... можно считать общими для обеих функций х (t) и у (О.
Тогда справедливы соотношения
k ——со
= 4 + 4 2 Л1СО5(0*Т + *рр<тЬ
Л = 1
со
^<©) = 2я 23 |^|2в(«-®Л) + ^рр(©)-
k = — со
со
со
**««- 23 W/e*T + *pa«-
(18.10-31)
Л = —со
: *о*0 + 42 KV* + W cos V + (вЛ - * A) sin <°* Я + Rpq <т> =
£=1
со
= с0?0 + Т 2 Л ftBft cos (<V + % ~ Ч) + Rpq «■
1"
8.10-32)
т w-a» S <***«(•-•*) + *'»«»>•
&=—со
18.10-10. 18.10. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ 595
Взаимная корреляционная функция R (тУ измеряет связь между х (/) н у (t) или
«сериальную корреляцию» между значениями функций х (t) иу(/ + т), разделенными
запаздыванием т. Функции х (t) и у (t) называются некоррелированными, если R (х) === 0.
Замечание. Функции х (/), у (t) принадлежат гильбертовому пространству со
скалярным произведением (и, v) => {и (0) v (0)} (п. 14.2-6). Отметим соотношения
ортогональности
lim
Г— оо
1
2Т
— Г
J \ 0 при <дф&;
lim
1
2Т
\ cos (о/ + a) cos (Q/ + 0) <#
-Г
-{
■V- cos (а — Р) при о =я G,
0 при о --£ Й.
(18.10-33)
(18.10-34)
18.10-10. Обобщенные преобразования Фурье и спектральные функции.
(а) Чтобы избежать затруднений с членами, содержащими дельта-функции в
преобразованиях Фурье и спектральных плотностях периодических функций, можно ввести
обобщенное преобразование Фурье X jn^ (to) от x(t) по формуле
со
с о— tof_ е— toot
Xlntm-Xint(i%)- \ x(t) -^ dt. (18.10-35)
Формула обращения здесь записывается с помощью интеграла Стилтьеса (п. 4.6-17);
с»
*(/) = J в*®* dX{nt(to). (18.10-36)
— со
Если существует обычное преобразование Фурье Xp(to), то
*lnt (/©) - Xlni (toQ) - -i- J *F ('•) *«K
X^ (to) = 2я -
(Oo
d*int (to)
did
(18.10-37)
Если функцию x (i) можно представить рядом 2 сье * (например,- в случае
k = — со
периодических функций, см. также п. 18.11-1), то обобщенное преобразование Xjnf (to)
будет ступенчатой функцией (п. 21.9-1).
(Ь) Обобщенная спектральная функция 0[nt to) для стационарного
или стационарного в широком смысле случайного процесса х (/) есть обобщенное
преобразование Фурье от его корреляционной функции;
ф1п1 <©) - «Dint <<°о) =
оо
е— tot _ р— to0T
R«« ияк «т=
,-Мф
2л J *
. ((d) </<D,
(Oo
причем
RjPjpW- J e^dOlnito).
(18.10-38)
Аналогичные соотношения имеют место для корреляционных и спектральных
функций по времени.
596 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.11-1.
(с) Для действительных стационарных или стационарных в широком смысле
процессов х (t) имеют место следующие обобщения соотношений Хинчина—Винера (9) и (26)5
2£* М | Xini U (о -f- е)] - XInt [/ ((о - е)] |» = JL [Oint «о -И) - Фш (ш - е)] =
-is-'f^w—5г I R«wTr^ft (I8J0-39)
о —е —со
со
2n\im~ $ |XJnt[/(©+e)]-XInt[*(e>-e)] |»со8©х</©-
— со
Т
- 11m -i. J *</)*(' +D Л-Я^СО. (18.10-40)
— Г
Отсюда при т = 0 получаем теорему Винера о квадратичном отклонении:
со Т
2л lim -J- \ |Х1п1[Мю + в)]-Х1п1[/(©-в)]|»</©= - »m w \ l*(«lf
e-»-0 ^e J ' Г-*со *l J-,
Л.
-Г
(18.10-41)
Если существует спектральная плотность по времени W (©), то соотношение (40)
приводит к соотношению Хинчина — Винера (26), причем
ЧГХХ «о) = 2П lim -^-1 X,nt [* (® + в)] - *lnt [/ (©-в)]|Я. (18.10-42)
18.11. ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ
18.11-1. Процессы с постоянными и периодическими реализациями.
(а) Постоянная выборочная фу н к ц и я (рис. 18.11-1, а). Если
каждая выборочная функция (реализация) х {t) тождественно равна постоянному
x(t)
Ь)
x(t) A
Т
г
-От
aku(t-tk)
h^JC
хпг
ч*^-*7
Рис. 18.11-1. Выборочные функции (реализации) для пяти примеров случайных
процессов. На рис. 18.11-1,* х (/) есть сумма показанных отдельных импульсов akv (t — t^).
случайному параметру а с определенным распределением вероятностей,
то этим вполне определяется случайный процесс. Такой процесс является
18.11-1. 18.11. ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ 597
стационарным, но не эргодическим. Если существует М а2, то
М*(/) = Ма, RA:A:(T) = Ma2, (18.11-1 а)
в то время как
<*(/)>«*, /?„(т) = А (18.11-16)
(Ь) Синусоидальный случайный процесс (рис. 18.11-1,6)
х (t) = a sin (со/ +а). (18.11-2)
Если амплитуда а постоянна, а фаза а — случайная величина с равномерным
распределением вероятностей в интервале (0, 2я), то процесс х (t) стационарен
и эргодичен с
Ф,1, [*(Q]~-,J— (1*1^*),
я Ya2— х*
Ш (0 = (х (/)> =0, R^ (т) = /?„ (т) = ^- cos сот
сот. j
(18.11-3)
Если амплитуда а —непрерывная случайная величина с плотностью фа (а),
не зависящая от фазы а, то процесс x(t) стационарен, но, вообще говоря,
не эргодичен. При этом
ф(1]
Л J v a2 — x2
|в|>|*|
1
Мх (0 = 0, R^ (т) = ~ Ma2. cos сот.
(18.11-4)
Ф (a) da
г ф {а) аа
■К (Здесь предполагается, что интеграл J -^—j— сходится.) X
В частности, если амплитуда а имеет распределение Релея с плотностью (п. 18.8-7)
(18.11-5)
Фв<а)
(ае-Та* <«><»•
"to <а<0)'
то случайный процесс х (/) будет гауссовским (п. 18.11-3).
Если фаза а распределена неравномерно на интервале (0, 2я), то процесс не будет
стационарным даже при постоянной амплитуде а.
(с) Общий периодический процесс (см. также п. 18.10-9).
Синусоидальный случайный процесс есть частный случай общего
периодического процесса со случайной фазой вида
со
x(t)=c0+ 2 [eftCoe*(©of + a) + bftSta*(<Do*+a)], (18.11-6)
k=\
где фаза а распределена равномерно в интервале (0, 2я) (предполагается, что
ряд сходится в среднем в смысле п. 18.6-3). Такой процесс стационарен и
эргодичен, причем
Mx(t) = (x(t))=cQ,
со
R^(T)=/?^(T) = C? + i J! (al + bl)Q0Sk%T*
k = l
со
=2яс*6(о>) + |- 2] (eJ + 4)[e(«-toe) + e(<D+toe)l-
4 = 1
(18.11-7)
598 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ ISA 1-2.
Более общий периодический процесс определяется рядом Фурье
x(t) = c0+ 2 (ал cos *©</ + *>£ sin Лй)0/),
k= 1
(18.11-8)
в котором все (действительные) коэффициенты eQI a., bk случайны, а ряд предполагается
сходящимся в среднем. Такой процесс будет стационарен в широком смысле при
выполнении следующих условий:
Mak=*Mbk=0,
MaJ-M*l,
т0а(. мс0ьк « шрк = о,
Ma.ak
: Mbibk = О
(18.11-9)
В этом случае формула (8) дает разложение процесса х (/) по ортогональной системе
в смысле п. 18.9-5, причем
Ш (О а №.
о»
R^(T) = Mc2 + i JJ M (aj + Ь%) cos *g>0*.
£=1
(18.11-10)
■Jf (d) Б е л ы й ш у м. Стационарный случайный процесс х (t) с постоянной
спектральной плотностью Ф (о) = Ф0 называется белым шумом.
Это название объясняется некоторой аналогией с белым светом: белый свет
представляет собой сумму всех спектральных составляющих, имеющих одну и ту же
интенсивность, белый шум представляет собой сумму гармонических колебаний всех частот, имею»
щих одну и туже дисперсию амплитуды.
Корреляционная функция для х(()
равна
оо
R^ (т) = -~ J Ф0*/й)Т da> = Фоб (т)
(см. формулу (21.9-25)). Величина Ф0
называется интенсивностью белого
шума. Белый шум представляет чисто
случайный процесс (см. п. 18.11-4, Ь). •)£
18.11-2. Процессы с
ограниченным спектром. Теорема Кстельни-
кова.
(а) Процесс x(t) имеет
ограниченный спектр или
ограниченную полосу частот, если его
преобразование Фурье XF(m)
(п. 4.11-3) равно нулю при
| со | > 2пВ; число В называется
шириной спектра процесса x(t) и
измеряется в герцах, если t
измеряется в секундах.
Теорема В. А. Котел fa-
ник о в а. Каждый процесс x(i)
Рис. 18.11-2. График функции
. 4 sin я/
sine / =в —.
я/
с ограниченным спектром может быть представлен в виде
00
sin 2лВ (t — ik)
:«- 2
*('*)■
(tk=k/(2B), k=0, +1, ±2, ...),
k = — oo
(18.11-11)
т. е. процесс x(t) для всех t однозначно определяется своими выборочными
значениями x(tk) в точках tkt разделенных промежутками \/(2В).
Функции (рис. 18.11-2)
,,— , sin 2nB(t — t.)
uk (0 - V2B si"C 2B {t - tk) = yiB 2nB \ t k' (A = 0, ±1, ±2, ,..) (18.11-12)
18.11-4. 18.11. ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ
599
образуют полную ортонормированную систему в пространстве функций х (t) с
ограниченным спектром ширины В; отметим «выборочное свойство» функции sine:
оо
xk^x (tk)=s2B I x{t)slnc2B(t — tk)dt (£ = 0, ± \i ±2,r...) (18.11-13)
— oo
(в точках tk непрерывности функции x (/)),
oo
J sine (I — 0 sine (A, — k)<Tk =
— 00
- 2BJ^ sine 2B (/ - /.) sine 2B (t - t,) dt = 6., = { \ <| J Jj' |
(/. Л = 0, ± 1, ±2, ...>. (18.11-14)
(b) Стационарный или стационарный в широком смысле случайный
процесс х (t) имеет ограниченный спектр ширины В тогда и только тогда, когда его
спектральная плотность по множеству наблюдений Ф^(со) равна нулю при
| ш | > 2я£* В этом случае разложение (11) сходится в среднем (п. 18.6-3), т. е.
Г со 12
М|*(0— JJ xksmc2B{t — tk) ,
I k — — oo J
и формула (II) представляет каждую реализацию x(t) через ее выборочные
значения Xk—x(k/(2B)) с вероятностью I.
Замечание. В частном случае стационарного процесса с «плоским» ограниченным
спектром частот:
I Фа ( I ю |< 2лВ),
=0 (18.11-15)
Ф^(«» = {
О ( | (0 | > 2пВ);
(18.11-16)
выборочные значения х.=х (k/(2B)) центрированы и некоррелированы.
18.11-3. Гауссовские случайные процессы (см. также пп. 18.8-3—18.8-8
и 18.12-6). Случайный процесс называется гауссовским, если все его
распределения вероятностей нормальны для всех tlt t2t •.. Каждый гауссовский
процесс однозначно определяется своим (обязательно нормальным) распределением
вероятностей второго порядка и, следовательно, корреляционной функцией
RxxWu h) — М*(/i)x(t2) вместе с l(t) = bAx{t). В частности, совместное
распределение каждого множества выборочных значений x1 = x(t^y x2 — x{t2), ...
..., xn — x(tn) является нормальным распределением, плотность которого дается
формулой (18.8-26) с
£у=М*(/,), hk = Rxx(tj, td-lfy (Л ^=1, 2 п), (18.11-18)
[Л/*] = 1Я/*П- (18.11-19)
Процессы, получаемые при сложении гауссовских процессов или при
линейных действиях над ними, являются снова гауссовскими (п. 18.12-2).
Коэффициенты разложения гауссовского процесса по ортонормированной
системе (п. 18.9-5) являются совместно нормальными случайными величинами.
18.11-4. Марковские процессы и процесс Пуассона.
(a) Случайный процесс порядка п. Случайный процесс имеет
порядок /г, если он вполне определяется своими функциями распределения Ф(Л)
порядка п (п. 18.9-2), но не определяется функциями распределения порядка
п-\.
(b) Чисто случайный процесс. Случайный процесс х(t)
называется чисто случайным, если случайные величины x(t{)} x(t2), ••• взаимно
600 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.11-4.
независимы для любого конечного множества tv t2t ••• Чисто случайный про-
цесс вполне определяется функцией Фт(Х19 tt), p(1) (Хг /t) или фа)(Х1 ti).
Примеры: последовательность независимых наблюдений, испытания по схеме Бер-
нулли, случайный выбор в статистике (п. 19.1-2) представляют чисто случайные
последовательности. Чисто случайный процесс с непрерывным параметрам предполагает
реализации с неограниченным спектром и, строго говоря, не может описывать действительные
физические явления.
(с) Марковские процессы. Дискретный или непрерывный
случайный процесс х (t) называется (простым) марковским процессом, если для любого
конечного множества t1<.t2 ... </n-i < tn
Р(ХЯ. tn\Xl9 tlt ...; Xn_1% tn^) = p(Xnt tn\Xn_l9 tn^) (18.11.20a)
или
Ф(ХЯ, tn\Xlf tl9 ...; Xn_lt tn^) = ip(Xnt tn\Xn_lt tn_x) (18.11-206)
соответственно. Если дано x(tn_1) = Xn_1, то знание x(tn_2), x(tn_9)> •••
не добавляет никакой новой информации о распределении х (tn).
Марковский процесс вполне определяется своим распределением
вероятностей второго порядка и, следовательно, может быть задан распределениями
вероятностей первого порядка и «вероятностей перехода»
p(X2,t2\x,t) или Ф (X,, t2 | *, t) (t<t2). (18.11-21)
Марковские случайные последовательности часто называются цепями
Маркова. Каждый чисто случайный процесс является марковским.
Многие физические процессы могут быть описаны как марковские.
Важный класс задач состоит в отыскании функций (21) по заданным их
((начальным значениям» при t = tv Из определяющего свойства (20) марковского
процесса вытекают уравнения Колмогорова—Смолуховского — Чепмена
Р(ХШ, t2\Xlt tJ=%p{X%, tt\x, t)p(x, t\Xlt у (h^t^t2)
x{t)
(18.11-22a)
или
Ф(4 t2\Xlt tj= J q>(Xt, t2\x% t)<p(x,t\Xlt tjdx {h^t^Q.
(18.11-226)
Уравнение (22) есть разностное уравнение первого порядка (п. 20.4-3),
которое может быть решено относительно неизвестной функции (21)
независимой переменной t, если задана р (х, t\ Хъ t±) или ф (х, t\ Xl9 t^). Если
Pn)(Xlt tx) или ф(1) (Xlt ti) известна, то марковский процесс вполне
определен при всех t > tv
(с!)Пуассоновский процесс. Во многих задачах со случайным
поиском, очередями, радиоактивным распадом и т. п. x\t) есть дискретная
случайная величина со спектральными значениями 0, 1, 2, ... (число
«успехов», телефонных вызовов, распадов и т. п.). Применяемые модели часто
предполагают выполнение марковского свойства (20а) и следующих свойств
переходных вероятностей:
[ 0 при Х2 < х,
I 1— аД/ + о(Д/) при Х2 = х, .
р{Х29 t2\x, 0 = | аМ + о(М) при Х2=*+1, (18.11-23)
I о (А/) при X2>x+l, I
где At=t2 — t; х, Х2 = 0, 1, 2, ..., а через о(Д/) обозначены такие члены,
что ^>->Q при А/-*0 (п. 4.4-3).
18.11-5. 18.11. ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ
601
Чтобы найти
P(Xft\Xltt1) = P(K1T) (/C = X-X1 = 0, 1,2,...; T^t-tJ
подставим переходные вероятности (23) в уравнение Колмогорова (22а) при
/2 = / + Д/ и получим разностное уравнение
Р{К, Г + А/)-Р<*. T)=_ap(1<t л + ар(^^1> Л + ПА£) (18П.24)
(/С=0, 1, 2, ...),
где Р (— 1, Т) = 0. При А/ —► 0 уравнение (24) приводится к дифференциально-
разностному уравнению
^Р(К, Г)=-аР(/С, T) + aP(K-U T) (К=0, 1, 2, ...). (18.11-25)
Решая уравнение (25) последовательно для /С = 0, 1, 2, ... при начальных
условиях
Р(0, 0) = p(Xi, /xlXi. У = 1, Р(К, 0) = р(Х1 + К, tt\Xu y = 0 (K>0)
(18.11-26)
получаем
P(/C, Г)«=б-аГ^^- (Г^О, /С = 0, 1, 2, ...). (18.11-27)
Таким образом, число К изменений состояния в любом интервале времени
длины Т имеет распределение Пуассона (табл. 18.8-4); а есть средняя
плотность числа событий за единицу времени или средняя скорость отсчетов
в процессе Пуассона.
Вероятность того, что не произойдет ни одного изменения состояния, равна
Р(0, Г) = е—аТ (Т^О); (18.11-28)
поэтому вероятность того, что состояние изменится по крайней мере один раз, равна
1 —Р(0, Г) = 1 — е—аТ (Г^О). (18.11-29)
Интервал времени 7\ между последовательными изменениями состояния есть
случайная величина с плотностью распределения
ф (TJ^ae— «ri (7\>0) (18.11-30)
* 1
и математическим ожиданием 1/а.
Внутри любого конечного интервала времени длины Т пуассоновский процесс
однозначно определен распределением множества взаимно независимых случайных величин К',
ty *2* ••• • *К* где ^ есть числ0 изменений состояния в течение времени Г, a tv *2, ... ,^_«
моменты времени первого, второго, ... , К-го изменения состояния в течение этого
интервала времени. При этом
РК(К)=*Р(К, Т) = е-*ТЩ^- </< = 0, 1, 2, ...). J
ф* \к(*ь\К)=*~Т <* =1. 2. ...; А=Н. 2 К),} (18.11-31)
к I
18.11-5. Некоторые случайные процессы, порождаемые процессом Пуассона.
(а) Случайная, телеграфная волна (рис. 18.11-1, с).
Функция *(/) принимает только значения +а или —а, причем последовательность
изменений знака представляет собой процесс Пуассона со средней скоростью
602 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.11-в.
отсчетов а (п. 18.11-4, d). Такой процесс стационарен и эргодичен, если он
начинается с /=—оо и для него
М*(/)=0,
R,
4а2а
хАх)=а*е-^
(о2 + 4а»
"1
(18.11-32)
(Ъ) Процесс, порождаемый пуассоновской выборкой
(рис. 18.11-1, d). Функция x{t) изменяет значение с каждым изменением
состояния некоторого процесса Пуассона со средней скоростью отсчетов а; между
изменениями состояния функция x(t) постоянна и принимает непрерывно
распределенное значение х с математическим ожиданием g и дисперсией о2.
Такой процесс стационарен и эргодичен, если он начинается ct=— со и для
него
Mx(f) = l,
2;*а } (18.11-33)
R*,«=62+oV-e'
Ф^(ю) = 2^6(со)-
о2 + а2#
"I
(с) Дробовой эффект и формулы Кемпбелла (рис. 18.11-1, е).
Функция х (t) есть сумма большого числа кратковременных импульсов:
* = l
форма которых дается функцией v = v(t) с
00
J ^(/)e-/(a^==yF(/(D),
(18.11-34)
(18.11-35)
в то время как амплитуда импульса ak есть случайная величина с конечной
дисперсией, а последовательность случайных моментов tk представляет
процесс Пуассона со средней скоростью отсчетов а. Такой процесс стационарен
и эргодичен, если он начинается с / =—оо; он аппроксимируется гауссовским
случайным процессом, если импульсы перекрывают друг друга достаточно
часто. Для этого процесса
00
М*(0 = 1 = аМал. j v(t)dt,
— 00
М*2(0 = |г + аМа|. I v2(t)dtt
— 00
00
(18.11-36)
R^(T)=i* + aMa2. J v(t)v(t+x)dtf
— 00
Фхх (со) = 2я*2 6 (со) + aMa|. | VF (ico) |2.
В частном случае, когда ak—фиксированные постоянные, формулы (36)
известны как формулы Кемпбелла.
18.11-6. Случайные процессы, порождаемые периодической выборкой.
Состояние некоторого стационарного и эргодического случайного процесса q (t)
измеряется периодически и результат фиксируется в течение постоянного
промежутка времени А/. Получаемый случайный процесс x(t) стационарен
и эргодичен, если момент начального измерения выбирается случайно и
распределен равномерно в интервале (О, АО- Реализация x{t) подобна
изображенной на рис. 18.11-1, d, но здесь изменения состояния отделяются
интервалами, кратными АЛ Если q — случайная величина, принимающая только два
18.12-1. 18.12. ДЕЙСТВИЯ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ 603
значения -f-а и — ас вероятностями х/г и х/г» то х(0 имеет вид случайной
телеграфной волны, как на рис. 18.11-1, с (с той же оговоркой, что и выше).
Если различные измерения величины q независимы, то
R^) = (M?)2 = (M*)2 = g2 при |т|>А/;
Rxx (т) = М (<72). Р (/, t + т — в одном промежутке А/) +
-Ь(М^)2 - Р(/, t+i — в разных промежутках At) = } (18.11-37)
= 0*.(1-Ш)+Б» при |т|^Д/
и, следовательно,
sin (О
да а
+ 2я£26((о).
(18.11-38)
На рис. 18.11-3 дано сравнение R**(t) и О** (со) для случайной
телеграфной волны и процесса жеребьевки с одинаковыми средними значениями
£ = 0, дисперсиями М*2 = а2 и средней скоростью отсчетов a = -x&t.
Рис. 18.11-3. Корреляционная функция и спектральная плотность для случайной
телеграфной волны (а) и процесса бросания монеты (Ь) с одинаковыми средними значениями
1 = 0, дисперсиями Мх2 = о2 и средней скоростью отсчетов а =-к- Д/ (на шкалах о в
случаях а) и Ь) приняты разные единицы масштаба).
18.12. ДЕЙСТВИЯ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
Пусть х (/), У (t) —
(18.12-1)
18.12-1. Корреляционные функции и спектры сумм.
случайные процессы. Для их линейной комбинации
z(t) = ax(t) + $y(t)
с действительными или комплексными коэффициентами а, Р корреляционные
функции Rxg(tlt /2), R**(*i. t2), RZ2(tlt t2) даются формулами
Rxz=<x>Rxx+$Rxy> R-г* — ^Rx*+PR#.*»
R«H «I2 R^+| p I2 R^ + apR^+apR
X* I
(18.12-2)
604 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.12-2.
Эти формулы остаются справедливыми и для корреляционных функций
R^OO» R**(T)» RwM B случае стационарных процессов; соответствующие
спектральные плотности равны
Фхг = аФ^ + $Фху\ Фгх = аФ^+$Фух,
Ф«= I а I2 Фхх+1 P I2 <&„„ + «№,„ + аРФу*.
(18.12-3)
18.12-2. Соотношения между входным и выходным сигналами для
линейных систем. Рассматривается действительная линейная система с
действительными входным сигналом x(t) и выходным сигналом
оо оо
у(/)- $ w(t, \)x(X)dk= $ A(f, 0*(/-OrfC. (18.12-4)
— 00 —00
где весовая функция до (функция Грина, п. 9.3-3 и п. 9.4-3) есть реакция
системы на единичный импульсный входной сигнал 6 (t—X) и h (/, £) зз
-«>(*, '-£)•
В наиболее важных приложениях / есть время и w (t, А,)=0 при t < А,, так как
физически реализуемые системы не могут реагировать на будущий импульс (см. также
п. 9.4-3).
Если #(/)—действительный случайный процесс и если средние квадраты
Мл:2 (/) и My2 (/) конечны, то
00
!%(/) = $ w (tt Я) Мх (X) dX; (18.12-5)
— 00
00
— 00
00
Щу ft» У = 5 w ft» и) Ry* ft. I*) rf|i
— 00
(обобщенные соотношения Винера—Ли);
00
М*/2(/) = J ю(Л V)RyxV. V)dp- (18.12-7)
(18.12-6)
£слм х (t) — гауссовский процесс, то у (t) —тоже гауссовский процесс и он
вполне определяется соотношениями (5)—(7).
18.12-3. Стационарный случай.
(а) Если входной сигнал x(t) стационарен и если линейная система
инвариантна во времени, т. е.
где
w(t, X) = h(t-X)t h(tt Q = h(Q=± I Я(*ю)в»«*Ао,
#(/cd)= $ Л (0 *-'««.
(18.12-8)
то выходной сигнал (реакция системы) y(t) тоже стационарен. Если при
этом x(t) зргодичен (п. 18.10-7, Ь), то и у (t) тоже эргодичен.
18.12-5. 18.12. ДЕЙСТВИЯ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ 605
Соотношения (4)—(7) для действительных x(t)t y{t) сводятся к следующим:
оо со
1,(0= \ h(t-X)x(k)dk= $ А(0*('-£К. (18.12-9)
— 00 —00
оо
Му = ЬЛх- J h®dl, (18.12-10)
—00
00 00
R*i,W-IW-T)- $ h(r-k)Rxx(K)dk= J /i(DR„(t-D4.
— 00 —00
00 00
JW*)= $ A(*-i»)R**(i*)«i|*= $ *«)R»*(»-0<t
— 00 —00
(соотношения Винера—Ли),
Щ2= f А(ОК**ЙК- (18.12-12)
(18.12-11)
Для физически реализуемых систем h(Q = 0 при £ < 0.
(Ь) Важные соотношения (11) значительно упрощаются, если их
представить через спектральные плотности (п. 18.10-3):
Фху (со) = Я (т) Фхх (со); Ф^ (о) = Я (/©) Ф^ (со),
Ф^ (со) = Я(/со) Ф^ (со) = Я (/©) Ф^ (со) = | Я (/со) рф^ (о>).
(с) Отметим также следующие соотношения:
оо
— 00
00 00
(18.12-13)
К (18.12-14)
В частном случае, когда входной сигнал есть стационарный белый шум с Rxx(*) =
= Ф0б (т) (п. 18.11-1, d):
**ИТ)==ФоЛ(т)'
К|/ИТ)=ФофЛЛ<т)'
00
My* - Ф0ФЛЛ (0) = Ф0 J А' (С) d£.
(18.12-15)
(18.12-16)
(18.12-17)
18.12-4. Соотношения для корреляционных функций и спектров по
времени. Соотношения (2), (4) и (10)—(17) справедливы и для соответствующих
средних по времени (п. 18.10-7—18.10-9), если они существуют.
18.12-5. Нелинейные операции. Если х (t) — случайный процесс, то
У = у{х) = у[х(Щ (18.12-18)
определяет новый случайный процесс; распределения и средние по множеству
наблюдений для процесса у находятся методами пп. 18.5-2 и 18.5-4. В
частности, корреляционная функция выходного сигнала у (t) для действительного
606 ГЛ. 18. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СЛУЧАЙНЫЕ ПРОЦЕССЫ 18.12-в
процесса находится по формуле
оо оо
Rw('i. «- $ $ уЫуЫч^Хь xjdx^x* (18.12-19)
— оо—'оо
где *i = *(?i), x2=x(t2).
Иногда удобнее формула
Rm Cv <•) - - <щг И * ** Ci. ••) y (si) y (Ч) dsi dh-
С С
где оо \ (18.12-20)
У (s) = J у (*) <Г** </дг (а4 < Re s < o2),
— 00
контуры интегрирования d и С8 параллельны мнимой оси и лежат в полосе
абсолютной сходимости интеграла.
18.12-6. Нелинейные операции над гауссовскими процессами.
(а) Теорема Прайса. Если даны две совместно нормальные
случайные величины хъ х2 с ковариацией %12 и если функция f (хъ х2) для некото*
рых действительных а > О, Ь < 2 допускает оценку
то
(л=1, 2, ...). (18.12-21)
Эта теорема позволяет находить средние и, в частности, корреляционные
функции по формулам вида
М/(*1( *,)= f М^х*,} dk12+C, (18.12-22)
о
где С есть среднее значение M/(xlf х2) при А,12 = 0, т. е. для
некоррелированных xlt х2.
Эта теорема приводит также к полезным рекуррентным соотношениям:
Мх?х? = тп $' Мх?~1х2~1 dku + Mx? Mx% (л, m=l, 2, ...). (18.12-23)
В частности,
Mxfxl = 2Xf2 + 4Х12Мх1 Мх2 + Мх* . M*f.
(18.12-24)
(b) Разложение в ряд. Если стационарный гауссовский процесс
x(t) имеет Мх = 0, ЯХх(Т) = °2Рхх(Т) И если для функции #(*) существует
Яуу (т), то
Щ = ад Rjrjr (т) = £ R** (т), Rw (т) = 2 <4Р** (т)>
*=0
где
^==^4= ^ y(°vV2)e-v2Hk(v)dv (* = 0, 1, 2, ...),
У 2^я/г!
Ял (с;) —многочлены Эрмита (табл. 21.7-1).
(18.12-25)
ГЛАВА 19
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.1. ВВЕДЕНИЕ В СТАТИСТИЧЕСКИЕ МЕТОДЫ
19.1-1. Статистики. Математическая статистика занимается как
статистическим описанием результатов опытов или наблюдений, так и построением и
проверкой подходящих математических моделей, содержащих понятие
вероятности. Ее методы расширяют возможности научного предсказания и
рационального принятия решения во многих задачах, где существенные параметры
не могут быть известны или контролируемы с достаточной точностью.
Статистическое описание и вероятностные модели применяются к
физическим процессам, обладающим тем свойством, что хотя результат
отдельного измерения физической величины х не может быть предсказан с
достаточной точностью, значение некоторой подходящей функции у=у (xlt x2, ..., хп)
от множества результатов хъ х2, ..., хп повторных измерений может быть
предсказано с существенно лучшей точностью. Такая функция называется
статистикой, а указанное свойство физического процесса —его
статистической устойчивостью. Статистическая устойчивость в каждой конкретной
ситуации есть эмпирический физический закон, который может быть п-роверен
юлько опытом.
Часто точность предсказания некоторой статистики возрастает с
возрастанием объема п выборки (xv х2, ..., хп) {физический закон больших чисел).
Наиболее известные статистики — относительная частота (п. 19.2-1) и
выборочные средние (п. 19.2-3).
19.1-2. Классическая вероятностная модель: статистики случайной
выборки. Понятие о генеральной совокупности.
(а) В классической модели наблюдаемая физическая величина х
рассматривается как одномерная случайная величина с подлежащей определению
или оценке плотностью ф(#). Каждая выборка (xlt х2, ..., хп) значений х
рассматривается как результат п независимых повторных измерений (п. 18.2-4).
При этом xlt х2, ..., хп представляют собой взаимно независимые случайные
величины с одинаковой плотностью вероятности ф (х). Такая выборка
называется случайной выборкой объема п и представляет собой /г-мерную
случайную величину (х1% х2, ••., хп). Плотность ее распределения называется
функцией правдоподобия:
L(xlt х2, ..., *л) = Ф(*1)ф(*2)...фО*/*)- (19.1-1)
Каждая статистика, определяемая как некоторая функция
У=У(хъ x2t ..., хп)
выборочных значений х1% х2, ..., хп% представляет собой случайную величину,
распределение которой (выборочное распределение статистики у) однозначно
определяется функцией правдоподобия, а следовательно, и распределением
величины х. Каждое выборочное распределение зависит, как правило, от
объема выборки п.
Кроме рассматриваемой модели, могут встречаться и другие: распределение х может
быть дискретным (игры, контроль качества), выборка может иметь бесконечный объем,
значения х. могут быть не одинаково распределены и не быть взаимно независимыми,
случайная величина х может быть многомерной.
608
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.1-3.
(Ь) Когда возрастает объем выборки (/г), многие выборочные статистики
сходятся по вероятности (п. 18.6-1) к соответствующим параметрам
теоретического распределения величины х\ в частности, относительные частоты
сходятся по вероятности (и даже в среднем; п. 18.6-3) к соответствующим
вероятностям (п. 19.2-1). Поэтому каждую выборку рассматривают как выборку
из теоретически бесконечной генеральной совокупности, распределение
признака в которой совпадает с теоретическим распределением вероятностей
величины х. Последнее называется распределением генеральной совокупности,
а его параметры —параметрами генеральной совокупности. Во многих
приложениях теоретическая генеральная совокупность есть идеализация
действительной совокупности, из которой получена выборка. О выборочном методе
для конечной совокупности см. п. 19.5-5.
19.1-3. Связь вероятностной модели с опытом: оценка и проверка.
(a) Оценка параметров. Статистические методы позволяют учесть
данные опыта (выборочные значения) для уточнения деталей вероятностной
модели, например, для оценки плотности вероятностей ф(#) случайной
величины х. Знание же вероятностной модели позволяет прогнозировать будущие
события, что важно для принятия решений. В большинстве приложений
относительные частоты (п. 19.2-1) применяются непосредственно только для
грубой качественной оценки распределения генеральной совокупности. Обычно
задаются определенным типом закона распределения генеральной
совокупности
Ф = Ф(*; %. ЧЪ •••) (19.1-2)
и по данным случайной выборки (xlt x2, ..., хп) оценивают лишь неизвестные
параметры %, %, ... В пп. 19.3-1—19.3-5 приведено некоторое количество
типовых законов распределения для подбора их в соответствии с физическими
предпосылками.
Параметры гц, т|2, ... обычно характеризуют определенное свойство
теоретического распределения величины х (например, генеральное среднее,
дисперсию, асимметрию, см. табл. 18.3-1). Для оценки значений этих параметров
по данным выборки (xlt x2t ..., хп) пользуются значениями таких статистик
УЛхг* х2> •••» *я)» Уг(хъ *2» •••» хп)> •••» которые характеризуют
аналогичные свойства выборки (например, выборочное среднее, выборочную дисперсию,
пп. 19.2-3—19.2-6). Выбор «подходящих» статистик не обязательно
однозначен; предпочитают оценки y(xlt x2, ..., хп), которые сходятся по вероятности
к х\ при п—+со (состоятельные оценки), у которых математическое ожидание
равно т| (несмещенные оценки) или у которых выборочное распределение
имеет наименьшую дисперсию (эффективные оценки) и/или которые легче
вычислить (пп. 19.4-1—19.4-5).
(b) Проверка статистических гипотез. Для проверки
статистических гипотез, устанавливающих некоторые свойства теоретического
распределения (например, значения параметров тц, т|2, ...), оценивается
правдоподобие (1) испытываемой выборки (х1% х2, ..., хп) при условии, что
для вычисления функции L(xlt x2t ... , хп) применяется предполагаемая
плотность распределения (2). Гипотеза отбрасывается, если испытываемая выборка
(*i. *2» •••» хп) попадает в область малого правдоподобия, т. е. если
найденное из опыта значение статистики у(хъ х2, ...» хп) маловероятно при
выбранной гипотетической функции правдоподобия. Выбор вероятности, которую
следует считать малой (уровня значимости критерия), зависит от условий
задачи.
Непараметрические критерии проверяют свойства гипотетического
распределения, которые не сводятся к значениям параметров (например,
идентичность двух распределений, независимость двух случайных величин, пп. 19.6-8
и 19.7-6); эти критерии удобны тем, что не требуют знания типа
распределения (2) генеральной совокупности.
19.2-2.
19.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ
609
Примечание. Некорректное применение статистических методов может
привести к неверным заключениям. Все (возможно, и не высказанные явно) предположения,
относящиеся к теоретическому распределению, должны быть проверены. Никогда не
следует применять одну и ту оке выборку для оценки и для проверки. Заметим, наконец,
что статистические критерии не могут доказать ни одной гипотезы: они могут лишь
указать на «отсутствие опровержения».
19.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ. ОПРЕДЕЛЕНИЕ
И ВЫЧИСЛЕНИЕ СТАТИСТИК СЛУЧАЙНОЙ ВЫБОРКИ
19.2-1. Относительные частоты.
(a) Определение. Пусть событие Е состоит в том, что значение
случайной величины х принадлежит некоторому множеству SE (обычно
некоторому классовому интервалу, п. 19.2-2, Ь), и пусть дана случайная выборка
(*i. *2» •••» хп) значений величины х. Частотой события Е в данной
случайной выборке называется количество пЕ выборочных значений #£, попадающих
в SE, а относительной частотой —отношение пЕ к объему выборки п:
А{£}=^. (19.2-1)
(b) Центр распределения и дисперсия. Так как случайная
выборка может рассматриваться как результат последовательности п
испытаний по схеме Бернулли (п. 18.7-3), то случайная величина пЕ имеет
биномиальное распределение (табл. 18.8-3), где 0 = Р{£} = f d<b (x) есть вероят-
ность события Е и
МЛ{£} = Р{£}, DM£} = P*E}(1,TP*£})- (19.2-2)
Относительная частота h{E) есть несмещенная состоятельная оценка
для соответствующей вероятности Р {Е}; при п -> оо эта оценка h{E)
асимптотически нормальна с параметрами (2) (пп. 18.6-4 и 18.6-5, а).
19.2-2. Распределение выборки. Группированные данные.
(a) Эмпирическая функция распределения. Для данной
случайной выборки (xv x2, ..., хп) эмпирическая функция распределения
F(X) = h{x<X} (19.2-3)
есть неубывающая ступенчатая функция с F(—оо) = 0, F(+oo)=l. Она
является несмещенной состоятельной оценкой для функции распределения
Ф(Х) = Р{х<Х\ (п. 18.2-9) и определяет частотное распределение выборки
(эмпирическое распределение).
(b) Классовые интервалы и группированные данные.
Пусть размах случайной величины х разделен на конечное (или бесконечное)
число подходящим образом выбранных классовых интервалов Xj—^ A-fy^
^х <Х/+у АХ/ (/=1,2,...), длины которых соответственно равны АХи
АХ2, ... (середины интервалов суть Хг<.Хг <...). Для данной случайной
выборки групповая частота nj есть число тех х^, которые попадают в /-й
классовой интервал (описание выборки через группированные данные).
Относительные частоты Ay=/i///i попадания в /-й классовой интервал
должны в сумме давать единицу; они являются несмещенными состоятельными
оценками для соответствующих вероятностей
*/-!дл/
20 Г, Корн и Т. Корн
610
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.2-3.
Накопленные частоты Nj и накопленные относительные частоты F/
определяются формулами
*/- 2 Л" F>= 2 Л*=4 53 "< = TW (*/+j-AX,). (19.2-4)
Для выборок достаточно большого объема при достаточно малых классовых
интервалах все выборочные статистики могут быть вычислены по относительным частотам h, =>
= nJn, точно так же как соответствующие параметры генеральной совокупности
вычисляются по вероятностям. Применение группированных данных дает экономию в
расчетах, если объем выборки п больше, чем 25. Кроме того, статистики F (X), п,, п*, N *
и F. дают различные графические представления выборочного распределения и.
следовательно, оцениваемого распределения генеральной совокупности (гистограмма, полигон
распределения и т. д).
(с) Выборочные квантили Хр определяются формулой (см. также табл. 13.3-1
и п. 19.5-2),
h{x<Xp} = F{Xp} = P (0<P<1). (192.5)
Эта формула определяет Хр неоднозначно, она лишь указывает границы выборочных
значений Ху\ X\i называется выборочной медианой, Xi/ t X\i и X»/ —выборочными
квартилями; аналогично определяются выборочные децили и процентили.
19.2-3. Выборочные средние (см. также пп. 18.3-3, 19.2-5 и 19.5-3).
(a) Выборочное среднее значение величины х. Пусть дана
случайная выборка (хъ х2, ...» хп)\ выборочным средним значением величины х
называется
п
*Нг(*1+*»+-"+*»>вТ 2 хк. (19.2-6)
k=i
Для выборочного распределения, заданного классовыми интервалами
с центрами х = Хи Х2, ..., Хт (п. 19.2-2), выборочное среднее X
аппроксимируется значением
т
*0 = Т<ЛЛ + *2Х2 + ...+Ят*т) = 4- 2 nfXf (19'2"7)
(выборочное среднее при группированных данных).
X есть характеристика положения для выборочного распределения.
Отметим моменты распределения величины X:
М* = £, 0х==1Г' (19.2-8)
М(*-|)3 = £, М^-ЕУ^**-1^^'. (19.2-9)
если величины справа существуют (ц3 и ^—центральные моменты
теоретического распределения величины х). Выборочное среднее X есть несмещенная
состоятельная оценка для генерального среднего £ = М#. Если а2 существует,
то X имеет асимптотически нормальное распределение с параметрами (8) при
л->со (пп. 18.6-4 и 19.5-2).
(b) Выборочное среднее для у(х). Выборочное среднее для
функции у (х) случайной величины х есть
п
9=jrly(x1)+y(xJ + ...+y(xn)]=± 2 У(*к) (19.2-10)
* = l
илих при группированных данных,
т
9а=Т Е п,у(Х,). (19.2-11)
/'=1
1».2-4.
19.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ
611
Оценки, основанные на формуле (И), иногда можно улучшить введением
поправочного члена (п. 19.2-5).
19.2-4. Выборочные дисперсии и моменты (см. также пп. 18.3-3, 18.3-7,
19.2-5, 19.4-2 и 19.5-2).
(а) Выборочные дисперсии
k = \
(19.2-12)
являются характеристиками рассеяния выборочного распределения; s
называется выборочным стандартным отклонением. Отметим формулы
Ms2 = 2-=-V; MS2 = aa, (19.2-13)
ds,-t(m*-^t°*> (19-2-14)
если величины справа существуют. S2 есть несмещенная состоятельная оценка
для генеральной дисперсии a2 = D#, и потому она чаще применяется, чем s2.
(b) Моменты выборки. Выборочные начальные моменты аг и
выборочные центральные моменты тг порядка г определяются формулами
л
1
ог = хГ=± 21 4; гпг^(х-ху=±- 2 (ХЬ-ХУ- (19.2-15)
Л=1 Л=1
Заметим, что
Mar = ar, Dar= n r, (19.2-16)
Mmr = ^r + 0(-i-),
D^ = 4-(^2r-2^r-i^+i-^ + ^2^^1) +0 (^). (19.2-17)
если величины справа существуют,, аг есть несмещенная состоятельная оценка
для соответствующего теоретического начального момента аг = М*г
генеральной совокупности. Если существует а2г, то аг имеет при я -> оо
асимптотически нормальное распределение с параметрами (16). тг есть состоятельная,
но смещенная оценка для теоретического центрального момента jxr = M (# — £)г.
Несмещенными и состоятельными оценками для jn, и ji4 будут соответственно
л2 л (л2 — 2л + 3) т4 — Зл (2л — 3) т\
т „
(л-1)(л-2)'"3 " <л-1)(л-2)(л-3)
(с) Характеристики асимметрии и эксцесса (см. также табл.
13.3-1 и п. 19.3-5). Статистики
«;/.. &г «;"
характеризуют соответственно асимметрию и эксцесс выборки и являются состоятельными
оценками асимметрии и эксцесса генеральной .совокупности (см. также п. 19.4-2). Грубо
говоря, gt > 0 указывает на длинный «хвост» в правой части распределения. Некоторые
авторы вводят g\ и ^ + 3 вмест0 ё1 и eZ-
20*
612
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.2-5.
19.2-5. Упрощенное вычисление выборочных средних и дисперсий. Поправка на
группировку.
(а) При вычислении удобно выбрать начало отсчета Х0 вблизи центра выборочного
распределения и считать по формуле
п
"^^о + }2 <?*"*•> <19'2-19>
/г = 1
или, при группированных данных*
/=1
(19.2-20)
(19.2-21)
(19.2-22)
(b) Выборочные дисперсии s8 и 5я могут быть подсчитаны по формуле
или, при группированных данных,
т
2 п — 1 2 __ 1 V „ v2 ^2
sG = -n—sGs=T 2j nixi""xG-
/=1
(c) Вычисления при группированных данных особенно упрощаются,- если все
классовые интервалы имеют одинаковую длину АХ и если за начало отсчета принята
середина одного из классовых интервалов, так что
Xi===tX0 + у/л*. (19.2-23)
где У. принимает только целые значения 0# + 1, + 2* ... Тогда
xG=X0 + yGbXt ~VG=\ 2 n1Yl>
/=1
(19.2-24)
(19.2-25)
Проверять вычисления можно,- выбирая другое начало отсчета, например, Х0 -f AX.
(d) Поправка Шеппарда на группировку. Пусть все классовые
интервалы имеют одинаковую длину АХ. Если для теоретического распределения
величины х оба «хвоста» имеют высокий порядок соприкосновения с осью х, то приближение
sq к истинной выборочной дисперсии s2 можно улучшить путем прибавления поправки
Шеппарда ——. Для выборочных моментов по группированным данным
12
flrG = 7 2 */*/» mrG = "7Г 2 ni (*/- *gY
/=1 /-1
(19,2-26)
можно ввести аналогичные поправки с помощью оценок
°; = aiG,
1
1
1 } (19.2-27)
«J = HG - Т alG (A*>2. m; - m3G(
а\ = а4<? - 4" °2<? (ЛХ)2 + 2^0 (ЛХ)4' mi = m4G —у m2G (ЛХ)8 + Ш (ЛХ)4*
Вообще
a'r= 2 (л)^1"*-1)Влв(/._Л)0(АХ)* (г =1,2, ...). (19,2-28)
где В^ — числа Бернулли (п, 21,5-2),
19.3-?. 19.3. ТИПОВЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 613
Приведенные оценки совпадают с оценками по негруппированным данным в том слу-
2л
чае, когда хх (Я) в 0 при | q \ ^ ^ — е (8 >0). Для нормально распределенной
величины х при ДХ :<2а
а1 ^ ai с точностью Д° 2»3 * 10~8 д* ПРИ S =£ 0.
а1 ^ ai "" —12 с Т0ЧН0СТЬК) до 3,1 • 10-8а* при £ = 0.
Примечание. Поправка Шеппарда часто применима в качестве оценки ошибки,
возникающей при округлении выборочных значений в точных формулах (12) и (15).
Например, средняя ошибка округления АХ/2 в значениях х^ воздействует обычно на s*
только как (ДХ)2/12.
19.2-6. Размах выборки (см. также п. 19.5-4). Размах w случайной выборки
(*i, #2, ..., хп) есть разность между наибольшим и наименьшим значениями
х^- Размах выборки имеет физический смысл (контроль качества) и служит
для грубой, но удобно вычисляемой оценки характеристик генеральной
совокупности. Размах выборки, наименьшее и наибольшее выборочные значения
дают примеры порядковых статистик.
19.3. ТИПОВЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
19.3-1. Вводные замечания. В качестве теоретического распределения
(генеральной совокупности) в статистических моделях могут служить
распределения вероятностей, описанные в пп. 18.8-1 — 18.8-9, в частности,
нормальное, биномиальное, гипергеометрическое и пуассоновское распределения.
Применимость тех или иных частных типов распределения (с подходящими
параметрами) может быть установлена как теоретически, так и по графику
эмпирического распределения.
Особенно удобно нормальное распределение. Каждое нормальное распределение
вполне определяется своим первым и вторым моментами. В случае нормальногЪ
распределения генеральной совокупности точно рассчитаны статистические критерии
выборочного распределения (пп. 19.6-4 и 19.6-6). Применимость нормального распределения часто
обосновывается центральной предельной теоремой (п. 18.6-5); в частности, ошибки
измерения часто рассматриваются как нормально распределенные суммы большого количества
независимых «элементарных» ошибок.
19.3-2. * Класс распределений Кэптейна. Часто оказывается желательным
сопоставить с опытными данными такое распределение случайной величины х
в интервале (а, Ь), чтобы некоторая функция g(x) имела нормальное
распределение, т. е. чтобы
^„.o.p^]. „и__$в«',Н[а^Ч,ЦЗ|. <'93"
Функция g(x) должна быть монотонной при а<.х<.Ь и изменяться от —со
до +со- После того как функция g(x) выбрана (например, из теоретических
соображений), остается оценить только два параметра jx = Mg(#) и agt что
для нормального распределения сделать нетрудно.
Случайная величина х, описываемая распределением (1), может рассматриваться
как предел последовательности случайных величин
xr+l e*r + zr+i h (xr) (г e °» U 2' ->'
кяждая из которых есть результат действия малых независимых импульсов г^, г^ ... t г
удовлетворяющих условиям п. 18.6-5, с, причем
«i+.,+...+«,-.2 Ц^-l w-fW-
614
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.3-3.
В частности, если h (xf= const = С, то ^ {х) = {л — х0)/С и р«и пределеиие (1»
нормальное. Если Л (д:) = х, т. е. эффект действия* импульса прбгторционален уже достигнутому
значению случайной величины, и х0 ~ 1, то g {*) = In x, и мы имеем логарифмически
нормальное распределение
•"-{Js-l-iVb^n*-
^0),
>0)
(19.3-2)
случайной величины х = г * (п. 18.5-5) часто удобно аппроксимировать
19.3-3. Ряды Г рама—Шар лье и Эджворта. Плотность стандартизованной
чайной величины
с помощью формулы
V* (*> а. Фо <*)-£ £ Ф;" (*) + [1 (£• - 3) Ф}«• <*)+$ (У <pj," W |. (19.3-Ча)
где а2 = ц.2, jj-з» Щ— параметры теоретического распределения величины г
(п. 18.3-7, Ь). Вводя коэффициенты асимметрии и эксцесса (табл. 18.3-1, d),
формуле (За) можно придать вид
ф*(*) ^ Фа W —j! Фа" W+[rf <Р« ' (*)+^f ф" " Wl' (19.3-36)
•^Формула (3) дает поправочные члены при замене плотности
распределения ф*(х) плотностью нормального распределения Ц)и(х). В частности,
формула (3) может применяться для приближенного пострюения плотности
распределения суммы я независимых случайных величин; в этом случае
коэффициент при фи имеет порядок 0(п~1'*), а коэффициенты при слагаемых,
объединенных квадратной скобкой, — 0(гГ1).х
Аналогичное выражение для функции распределения Фх (х) получается
из (3) заменой ер]** (х) на ф£) (х). Заметим, что для входящих в формулу (3)
производных от плотности нормального распределения фи (х) имеются широко
распространенные таблицы и что параметры (коэффициенты) могут быть легко
оценены как функции моментов (п. 19.4-3); все же расчет выборочных
распределений здесь не прост.
Для весьма ограниченного класса распределений формула (3) содержит первые
члены разложения в ряд Грама — Шарлье по ортогональным функциям (п. 15.2-6):
Ф^ <*> - Фи U) + у, Ф«" <*> + j] Oj?1 (х) + ... е (19.3-4а)
4>х (х) = фи (х) + Ш *«' (*> + Т\ ф"' {Х) + "' > (19.3-46)
где
со
ч*=(_ й-)* X"* Ш ф* w "*- <19-з"4с)
Я. (*)— многочлен Эрмита степени k (п. 21.7-1). В частности, Г)3 =— уь тц — Y2'
Ряд (4а) сходится к Ф __(*), если существуют все моменты \ilt jn2, ... и если
1 •*
? Т*2
J И </Ф (*) сходится; ряд (46) будет при этом сходиться к <р {х) во всех точках
— оо
непрерывности, если <р (х) есть функция ограниченной вариации (п. 4.4-8, Ь) в (— оо, оо).
Для очень большого класса распределений аппроксимация (3) может быть обоснована
асимптотическими рядами Эджворта [18.6].
19.3-4. Усеченные нормальные распределения и распределение Парето.
(а) Усеченные нормальные распределения. Если из нормальной
совокупности со средним ц и дисперсией а8 (п. 19.1-2) исключить все события {*<*о},
19.4-1.
19.4. ОЦЕНКИ ПАРАМЕТРОВ
615
то оставшаяся совокупность будет иметь одностороннее усеченное нормальное
распределение, для которого ф (х) = Ф (*) = 0 при х < ха и
•w-(MrW»*(£^Ji)' °W= 1-т Т <«>*>■ (I9-3-5)
где т = Фаf ° "Г ■) — степень усечения, равная вероятности Р J*< *0} в исходном
распределении.
Первые два начальных момента усеченного распределения равны
} (19.3-6)
а8 = ц* + сг»(й + *о) Ф Uo) + OK J l
Если заданы х0 и моменты а0 а2 (последние оцениваются выборочными моментами aif a2;
п. 19.2-4, Ь), то JJ. и О могут быть найдены с помощью таблиц Пирсона, дающих
численное решение уравнений (6) [18.5].
(Ь) Распределение Парето определяется формулами ф (х) = Ф (*) = 0 при х < х0 и
ф(*)=^(7°)а+1' Ф(^) = 1~Й)а {х>х°; а>0)' (19-3"7)
I = м* = ^~-j *0 (а > 1). *у8 =21/а*0. (19.3-8)
19.3-5. Типы распределений Пирсона. Плотность многих непрерывных
распределений вероятностей может быть определена как решение дифференциального уравнения
«Л = *+*Ь ф {x)t (19.з-9)
dx Tie + T)sJf + П^2
содержащего четыре параметра. Каждый параметр т^ может быть выражен через первые
четыре момента аг или \лг (п. 19.4-3), но расчет выборочных распределений, даже
в наиболее простых случаях, труден. Распределения, определяемые уравнением (9),
могут быть классифицированы в зависимости от характера корней уравнения ti2 -Ь Г)лх -j-
-+■ ти-*8 = 0* Эти распределения охватывают многие распределения, приведенные в табл.
18.8-11, пп. 18.8-3 и 9.5-3, как частные случаи.
Для распределений Пирсона вводится пирсоновская мера асимметрии (табл. 18.3-1):
^О— ~ 2(5Y2-6Y? + 6)' <19'3 10)
при малых Yi. Ye отсюда следует, что %т ^s I — -^ OYi.
19.4. ОЦЕНКИ ПАРАМЕТРОВ
19.4-1. Свойства оценок (см. также п. 19.1-3).
(a) Статистика y(xit х2, ..., хп) называется состоятельной оценкой для
параметра rj теоретической совокупности, если у сходится к г\ по
вероятности при увеличении объема выборки п* т. е. если вероятность любого
конечного отклонения \у — т)| стремится к нулю при я — со (п. 18.6-1).
(b) Смещением некоторой оценки у параметра х\ называется разность
М(/ — т|. Оценка у называется несмещенной оценкой параметра rj, если Му~ц.
(c) Асимптотически эффективные оценки и
эффективные оценки. Желательно применять такие оценки, выборочные
распределения которых возможно меньше рассеиваются около искомого значения
параметра, т. е. оценки с возможно меньшей стандартной ошибкой УЩ =
= о (у). Для важного класса оценок y(xlt x2, ..., хп), выборочные
распределения которых асимптотически нормальны со средней rj и дисперсией к/п
(см. также п. 19.5-2), постоянная X определяется формулой
h=}im_nDy^Xmia = _ I . (19.4-1)
*№)'
616
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.4-2.
Асимптотическая эффективность е^ {у} =—j~ такой оценки измеряет
рассеяние асимптотического распределения около параметра г\\ у называется
асимптотически эффективной оценкой параметра rj, если k = XmIn. Каждая
асимптотически эффективная оценка является состоятельной.
Более общо, «относительная эффективность» оценки у (*х, х2, ... , *л) параметра г|
по данной выборке объема п измеряется обратной величиной среднего квадрата
отклонения М (у — т])2. При достаточно общих условиях средний квадрат отклонения ЬЛ(у — ц)2
различных возможных оценок у данного параметра ц имеет конечную нижнюю граньй
определяемую формулой
(19.4-2)
где Ь (ц) = My — ц (см. [18.6]).
Для несмещенных оценок у выражение (2) сводится к
^min |_
Dy>—n /(Ппфу' 09.4-3)
Эффективность е (у) —— несмещенной оценки, удовлетворяющей соотношению (3),
измеряет рассеяние выборочного распределения около -г\ = ЬАу. В этом случае предел
lim е Jyl, если он существует, называется асимптотической эффективностью. Некото-
п-+со 1
рая (обязательно несмещенная и состоятельная) оценка // называется эффективной оцен-
кой параметра т], если Dy существует и равна нижней грани .
(d) Достаточные оценки. Оценка у(х1% х2, ...>хп) параметра^
называется достаточной оценкой, если функцию правдоподобия для выборки
(п. 19.1-2) можно представить в виде
L(Xlt Х2, ..., Хп; л)-М^ т|)МХь *i. .», Хп)9 \ Ал^
УшшУ(х19х%9...9хя)9 ) (19'4"4)
где L2 не зависит от rj. В этом случае условное распределение вероятностей
величины (*!, х2, ..., хп) при условии \y=Y\ не зависит от rj, так что
достаточная оценка у параметра г\ подытоживает всю информацию
относительно г], содержащуюся в выборке. Эффективная оценка обязательно является
достаточной.
(e) Обо бще н и я. Формулы (1) —(3) применимы и к дискретным
распределениям, если вместо плотности распределения у(х1у х2, ..., хп)
подставить в них р(хъ x2i ..., хп). Теория, изложенная выше, применима без
изменения к совокупностям, описываемым многомерными случайными величинами.
Совокупность т подходящих несмещенных оценок у , у ... , у называется
совместно эффективной оценкой т параметров х\ тц, ... , ч\ , если эллипсоид рассеяния
(п. 18.4-8, с) совместного выборочного распределения совпадает с «эллипсоидом минимального
рассеяния», аналогично минимуму дисперсии, определенному формулой (3). Совместные
асимптотически эффективные оценки определяются подобным образом через
асимптотические выборочные распределения. Обратная величина обобщенной дисперсии (п. 18.4-8, с),
соответствующей совместному выборочному распределению величин у у2, ... , у
является мерой относительной совместной эффективности этой совокупности оценок.
Чтобы определить совокупность т совместно достаточных оценок yv у2 у
надо только заменить случайную величину у в формуле (4) m-мерной случайной величи-
ной (yv yr ... . ут).
19.4-2. Некоторые свойства статистик, применяемых в качестве оценок
(см. также п. 19.2-4).
(а) Функции от моментов. Каждая статистика, представимая
в виде рациональной функции от выборочных моментов аг, является состоя*
19.4-4.
19.4. ОЦЕНКИ ПАРАМЕТРОВ
617
тельной оценкой той же самой функции от соответствующих моментов аг
генеральной совокупности при условии, что рассматриваемые моменты
существуют и что значение функции в них конечно (см. также п. 18.3-7).
Несмещенную состоятельную оценку часто удается получить из смещенной
состоятельной оценки путем умножения ее на подходящую функцию от п.
Аналогичная теорема применима к функции от выборочных моментов аг Г
для многомерных выборок. В частности, величины g1t got /.., rih и г (п. 19.7-2)
1 л ir ir 1а . 84 ### щ
являются состоятельными оценками соответствующих параметров Yi» Y2» ^/ь» Р;ь
и р генеральной совокупности.
12 * 34 ••• "*
(Ь) Для выборок из нормальной совокупности имеем:
1) Я—эффективная оценка для g.
2) х к s2— совместные асимптотически эффективные оценки для g и
а2, но s2—смещенная оценка; х и S2 = __ ] s2 — совместные
достаточные и асимптотически эффективные оценки для g и a2; S2 имеет
эффективность п~~ .
п
3) Если g известно, то s2 = (*—g)2 — эффективная оценка для а2.
4) Выборочная медиана х±/ имеет асимптотическую
эффективность 2/я.
Для выборок из биномиального распределения (табл. 18.8-3)
*-—эффективная оценка для g.
Для выборок из двумерного нормального распределения (п. 18.8-6) с
известным центром распределения выборочные центральные моменты /и, /12 и /22
(п. 19.7-2) являются совместными асимптотически эффективными оценками
ДЛЯ Ац, Л>12 ^ Л22.
19.4-3. Нахождение оценок. Метод моментов. Если распределение
генеральной совокупности описывается функцией
Ф(*; цъ Лг. •••). ф(*; Ль Лг. •••) или р(х; %, г]2, ...)
заданного вида с подлежащими определению параметрами %, т]2, ..., то
каждая числовая характеристика распределения ЬЛх, Dx, <xr и т. д. является
функцией параметров %, ц2, ... В частности,
«1 = 0! (Ль Лг, •••), а2 = «2 (Ль Лг, -..). — •
если эти моменты существуют. Метод моментов определяет (совместные)
оценки
У\ (ХЪ *2> •••» */l)> #2 (Xl* Х2* ••• » Xfl)> •••» Ут\ХЪ Х2* ••• » Хп)
для соответствующих параметров цъ г]2, ..., х\т посредством т уравнений
а>г(Уъ У2> •••» Ут) = аг(х19 х2, ..., хп) (г=1, 2, ..., т), (19.4-5)
получаемых путем приравнивания первых т выборочных моментов аг
соответствующим моментам аг генеральной совокупности. Получаемые при этом оценки
Ук будут функциями от выборочных моментов (см. также п. 19.4-2, а).
19.4-4. Метод наибольшего правдоподобия. Для любой данной выборки
(*i. х2> •••» хп) значение функции правдоподобия L(xlt х2, ..., хп) (п. 19.1-2)
есть функция неизвестных параметров х\ь %, ... По методу наибольшего
правдоподобия в качестве оценки каждого параметра щ выбирается такая
функция Ук(хъ х2* •••» хп)> которая придает возможно большее значение
величине L(xlt х2, ... , хп\ уъ у2, ...) для всех выборок (хъ х2, ..., хп). Для
получения совокупности т (совместно) наиболее правдоподобных оценок
2/l (*l> x2t •••! xn)t У2\х1> х2> •••! хп)* •••! Ут\ХЪ Х2г •••! Хп)
618
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.4-5.
решают систему т уравнений наибольшего правдоподобия *)
~\пЦхъ х2, ..., хп\ у1$ у2,..., ут)=0 (£=1, 2, .... т), (19.4-6)
которые выражают необходимые условия максимума функции правдоподобия,
если последняя дифференцируема (п. 11.3-3).
Хотя метод наибольшего правдоподобия часто приводит к более
сложным вычислениям, чем метод моментов, наиболее правдоподобные оценки
могут оказаться предпочтительнее, особенно в случае малых выборок, так как:
1) Если эффективная оценка (или совокупность совместно
эффективных оценок) существует, то она будет единственным решением
уравнения (или системы уравнений) правдоподобия (6).
2) Если достаточная оценка (или совокупность достаточных
оценок) существует, то каждое решение уравнения (или системы
уравнений) правдоподобия (6) будет функцией этой оценки (или оценок).
Кроме того, при достаточно общих условиях уравнения правдоподобия (6) цмеют
решения, дающие состоятельные, асимптотически нормальные и асимптотически
эффективные оценки [18.6].
Пример. Если величина х распределена нормально, наиболее правдоподобная
п
оценка X =*для £ является эффективной оценкой и минимизирует ^ (xi~~x)z (мет°д
i = \
наименьших квадратов в теории ошибок). Заметим, что метод наибольшего правдоподобия
применим также к многомерным совокупностям.
19.4-5. Другие методы нахождения оценок. Некоторые методы, обычно применяемые
в критериях согласия, могут быть использованы и для оценок параметров (п. 19.6-7,
см. также пп. 19.9-1 — 19.9-5).
19.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
19.5-1. Вводные замечания. Здесь рассматриваются распределения
статистик, часто применяемых в качестве состоятельных оценок для
соответствующих параметров генеральной совокупности. В п. 19.5-2 речь идет о
приближенном расчете выборочного распределения для больших выборок, в
пп. 19.5-3 и 19.5-4 — 0 распределении статистик, получаемых из нормальных
совокупностей.
19.5-2. Асимптотически нормальные выборочные распределения (см. также
п. 18.6-4). При достаточно большом объеме выборки выборочные
распределения многих статистик можно аппроксимировать нормальным распределением
с помощью следующих теорем, получаемых из п. 18.6-5.
(a) Пусть статистика у(х1% х2% ..., хп) представима в виде функции
y — f(mlt т2, ...) от выборочных моментов mk, и пусть f(mlt тъ ...) определена
и дважды непрерывно дифференцируема в окрестности точки т1 = ц1, m2 = \i2, ...
Тогда выборочное распределение статистики у при п—#-оо асимптотически
нормально с центром /(|лх, ji2» ...) и дисперсией вида -\-0 (—)• Эта
теорема применима, в частности, к выборочному среднему *, к выборочным
дисперсиям s3 и iS2 и ко всем выборочным моментам аг и тг (п. 19.2-4).
Аналогичная теорема применима к многомерным распределениям.
(b) Распределение каждой выборочной квантили Хр асимптотически нормально
р (1 р\
с центром Хр и дисперсией ~—г-, если только генеральная квантиль хр единст-
Г П ф2 (Хр) Г
венна и если производная <р' (х) существует и непрерывна в окрестности точки х = хр
Эта теорема применима, в частности, к выборочной медиане Xt/ . При аналогичных
условиях любое совместное распределение выборочных квантилей (и, следовательно,
например, выборочной интерквартйльной широты) также является асимптотически нормальным.
*) Функции L и In L дочитают максимума одновременно.
19.5-4.
19.6. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
619
19.5-3. Выборки из нормальной совокупности. Распределения %2, t и v2.
(a) В случае выборок из нормальной совокупности (нормальных выборок)
все выборочные значения являются нормальными случайными величинами
и многие выборочные распределения могут быть вычислены явно с помощью
пп. 18.5-7 и 18.8-9. Предположение о нормальности генеральной совокупности
часто опирается на центральную предельную теорему (п. 18.6-5; пример:
ошибки измерения).
Для любой выборки объема п из нормальной совокупности с центром £
и дисперсией а2
^ t
1)—г-г=г имеет стандартизованное нормальное распределение
olV п
(«-распределение, п. 18.8-4);
2) —r~=. = , ъ (отношение Стьюдента) имеет
/-распределение CR-1 степенью свободы (табл. 19.5-2);
оч (п — 1) S* ns2 1 ri , -Ч9 «
3)-—#г = -&- = & 2j{Xk-x)2 имеет ^распределение
с /г —1 степенью свободы (табл. 19.5-1);
4)—*—— имеет стандартизованное нормальное распределение;
xi — £ xi — £ l/л — l
5) -^—~ s— V ~7Г" имеет ^-распределение с л —1 степенью
свободы;
а\ xi — х Л/ ~ хй — х
о) у _ =— имеет г-распределение с т = и — 2
степенями свободы (п. 19.7-4);
л
7)-~- = — 2 (** —£)2 имеет ^-распределение с п степенями
свободы.
Дополнительные формулы см. ниже в табл. 19.6-1. Табл. 19.5-1 — 19.5-3
описывают распределения х2> t и v2\ квантили этих функций табулированы
(см. табл. 19.5-4-19.5-6).
(b) Выборочное среднее х и выборочная дисперсия s2 независимы тогда
и только тогда, когда рассматриваемая выборка получена из нормальной
совокупности.
Для каждой нормальной выборки х, s2 и тгт~ '2 взаимно независимы для
всех г; для g1 = m3m2 8/з, g2 = -^—3
имеем
Mgx = 0. Dgl = (ny-n2;3)- (19.5-1)
19.5-4. Распределение размаха выборки (см. также пп. 19.2-6 и 19.7-6).
(а) Если генеральная совокупность имеет непрерывное
распределение, то размах до случайной выборки объема п имеет плотность
распределения
00
фшИ = /г(л-1) $ [<b{x + w)-<I>(x)]n-2q>(x)y(x + w)dx. (19.5-3)
620
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.5-5.
Эта функция табулирована для некоторых видов распределений генеральной
совокупности [18.9].
(Ь) Для нормальной генеральной совокупности среднее значение и средне-
квадратическое отклонение размаха w пропорциональны среднему квадратичес-
кому отклонению о генеральной совокупности:
Mw = kno, Dw = c2no2\ (19.5-4)
kn, cn и cn/kn табулированы как функции от п\ w/kn есть несмещенная оценка
для а. Средний размах
_ wt + w2+ ...+w
w = —
для т случайных выборок объема п имеет при т -* со асимптотически нор-
мальное распределение с центром кпо и дисперсией ~—; w/kn является при
этом несмещенной состоятельной оценкой для а.
(c) Для равномерного распределения генеральной совокупности в
интервале (а, Ь)
M»-(ft-e)^f. D»Hb-«)»fr + S.fr% (19-5"5)
и w n х- есть несмещенная состоятельная оценка для Ь — а.
Заметим, что арифметическое среднее из наименьшего и наибольшего
выборочных значений есть состоятельная несмещенная оценка для М*.
(d) Для любого непрерывного распределения генеральной совокупности вероятность
того, что по крайней мере доля q всей совокупности расположена между крайними
значениями Jcmjn и хтах данной случайной выборки объема п, равна
i_/w*-i + <n-i>*'1- (19.5-6)
19.5-5. ^Выборочный метод для конечной совокупности. Пусть дана
конечная совокупность N элементов (событий, результатов измерений или
наблюдений) Ev Ev ... , ENy каждый из которых отмечен одним из М ^ N
различных спектральных значений Xv X2, ... , Хм некоторой дискретной
случайной величины х (п. 18.3-1). Функция р (х) определяется значениями
р (Xi) = Ni/N, где Ni — количество элементов, отмеченных спектральным
значением X/.
Математическое ожидание и дисперсия случайной величины х равны
м м
Mx=Z = W И "&> Ох = * = ± 2 NiiXt-t)*. (19.5-7)
i = i * = 1
Пусть (xlt x2, ... , хп)—бесповторная случайная выборка объема п. Здесь
Х\ рассматривается как случайная величина, соответствующая числовой
отметке первого случайно выбранного элемента, х2 — второго элемента и т. д.,
причем элементы выбираются без возвращения. Любая из случайных величин
xi имеет то же распределение, что и сама величина х, однако, в отличие от
выборки из бесконечной генеральной совокупности, величины x-t и х/ не
являются независимыми. Имеем
cov(*/t дс/)=—77~ГТ
a» , ч t | (19.5-8)
? to* *j) = — лПГТ- J
19.5-5.
19.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
621
Пусть Я^-^-^] Xi и ^2 == и _ 1 У) (**—«*)*— соответственно выборочное
1 = 1
* = 1
среднее значение и выборочная дисперсия. Тогда
М*-Е. D^-^TT. М52 = лГ^Т^
DS2 =
N {N - п)
а*
(N - 1)2 (Л^ - 2) (W - 3) я (л - 1) Х
X[2nN*-o(n+l)(N-l) +ln-l)(N-lYy&
где 72 — коэффициент эксцесса.
Эти формулы при N—+CQ приводятся к формулам пп. 19.2-3 и 19.2-4.
Если коэффициентом эксцесса можно пренебречь (уг ^ 0), то при больших N вели-
l/~(N — \)пх— £ . . гм(П-.\)-\
чина t = I/ __ ^-2- имеет в первом приближении /-распределение с —^ '-
числом степеней свободы.
Таблица 19.5-1
^-распределение с т степенями свободы
(рис. 19.5-1 и табл. 19.5-4; см, также пп. 18.8-7, 19.5-3 и 19.6-7)
0 Z 4 6 8 10 12 14
Рис. 19.5-1. %2-распределение для различных значений т.
1 (°
(а) <ру (К) =г <px* {т) (У) = { 1_
1 Г (т/2)
(b) My = т, Dy = 2т.
Мода т — 2 (т > 2).
Момент порядка г относительно // = 0:
m (m + 2) ... (т + 2г — 2).
при Y < 0,
т —2 У
157ГУ 2 . 2 приК>0.
Семиинвариант порядка г!
2r~l (r~l)\m.
Коэффициент асимметрии 2 Y2/m»
Коэффициент эксцесса 12/т.
Характеристическая функция
(1 - 2Wm/2
622
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19 5-5.
Таблица 19.5-1 (продолжение)
(с) Типичная интерпретация. Если т взаимно независимых стандартизованных
случайных величин и. = -
имеют нормальные распределения, то сумма их
квадратов %2 = 2 "I имеет %2-распределение с т степенями свободы.
k=i
т
Если ^ и% выражена в видг суммы от г квадратичных форм у, (и и , ... ,« )
k= 1
рангов соответственно т* (п. 13.5-4, Ь), то уг у2, ..., уг взаимно независимый
имеют %2-распределения с т^ т2, ... , тг степенями свободы тогда и только тогда,
когда m1 + m2 + ... + /»r»'n (теорема разложения).
Сумма г независимых случайных величин уг, у2, ... , у , имеющих
%2-распредгленив с т т2, .... тг степенями свободы соответственно, имеет %*-распределение
с т = т + mg -f*... + тг степенями свободы (теорема сложения или свойство
устойчивости, см. также п. 18.8-9).
(d) Квантили для у обозначаются через %р или %р (т). В таблицах часто
дается X* —. а (т) в зависимости от а.
(e) Приближения. При т -+ оо!
у распределена асимптотически нормально с центром т и
дисперсией 2т.
у/т распределена асимптотически нормально с центром 1 и
дисперсией 21 т.
V2y распределена асимптотически нормально с центром V 2т — 1
и дисперсией 1.
Из последнего свойства вытекает аппроксимация квантилей
1
Хр (т) ^ -у (^2т - 1 + ир)* (т > 30),
■ квантили стандартизованного нормального распределения (п. 18.8-4, Ь).
Эта аппроксимация не годится при значениях Р, близких к 0 или 1. Лучшая
аппроксимация дается формулой
где и г
^'""-('-^Г + 'рШ
Таблица 19.5-2
/-распределение Стьюдента с т степенями свободы
(рис. 19.5-2 и табл. 19.5-5; см. также пп. 19.5-3 и 19.6-6)
■■1—*"Т^ 1
0,5
0,4
у'
/S
/Л
/Аз
1
J) 02
* 0,1
"Ч Нормальное
"V/ распределение
" V
\\
\\
- U
\ i -распределен
V / Стьюдента
VZ (т*3)
1 _ . i ^^Т^ 1
'4
-2 -/
Рис. 19.5-2. f-распределение Стьюдента; сравнение со стандартизованным нормальным
распределением.
19.5-5. 19.5 ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ 623
Таблица 19.5-2 (продолжение)
(b) My = 0 (m > 1), Dj/= m^2 (m > 2).
Мода О. Коэффициент асимметрии 0.
3 ifji — 2)
Коэффициент эксцесса — __ (m > 4).
Моменты порядка 2г относительно # = 0:
1 -3 ... (2г — I)
■ тг (2г < т).
(т — 2) (ш — 4) . . (т — 2г)
(с) Типичная интерпретация. Распределению Стьюдента подчинено отношение
хо
* = / =
l^J-W + ^ + .-. + 'S.)'
г m
где дс0, л:-, *„, ... , * — взаимно независимые нормально распределенные случайные
величины с центрами 0 и дисперсиями о2. Заметим, что t от о2 не зависит.
(d) Квантили у для у обозначаются через /_; заметим, что *р= — t^_p.
Распределение величины | у \ — \ t \ связано с /-распределением формулами
P{\y\<Y} = P{-Y<y<Y} =
У
-_1уф/(«)(|*^-2Ф/(«)(У)-1вФ1'(«)1<У)-
с»
Р {I У I > У} = 2 J Ф/ (w) (У) ^ = 2 [1 - Ф, (т) (У)] = 1 - ф„ (т), (У).
У
Квантили | f lj _ а = t _ 2, определяемые соотношением Р {\ у \>]t lj_a} =» a,
табулированы; в некоторых таблицах значения i f L обозначены через t .
(е) Приближения. При m -*• оо распределение # асимптотически нормально
с центром 0 и дисперсией 1, так что (см. п. 18.8-4, Ь)
<ръ»р и mi_a = ^1_a/2^l«l1.a=«1_a/2 (m>30).
Таблица 19.5-3
Распределение отношения дисперсий (^-распределение)
и связанные с ним распределения
(табл. 19.5-6; см. также п. 19.6-6)
(а) «fy <Ю ss <р0. (m§ mt) (У) =
г 0 при У<0,
Г
(=4^)
V m'j Г(т/2)Г(т'/2) V ^ т' J р " •> "•
624 ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 19.5-5.
Таблица 19.5-3 {продолжение)
Момент порядка г относительно г/ = 05 г <т/2 + г)Г (mV2 — г) (тг/т)^
(с) Типичная интерпретация. Этому распределению подчинено отношение vz
двух случайных величин, имеющих х*"РаспРеделения с т и т' степенями свободы,
или
1 U±.8j. _i_ J* .
«*_ m' g2
-(*? + *! + ... + ***)
^ °2 _L / '2 '* '2 \ * m 1 —g2 •
т'\х\ + *а + ... + *m7
где все т-\- т величин *f и xk взаимно независимы и нормально распределены
с центрами 0 и дисперсиями о8. Заметим, что v2 от а2 не зависит.
(d) Преобразование переменных. Распределение отношения дисперсий V2
описывается также другими случайными величинами:
1) и с плотностью
ф1> (т, т') ( ' в
О при V < 0,
2(^)2 ,(1^ ^(if^v.) ' nP„v>o:
2) z = In t» =s — In t>2 с плотностью
т-\- т'
2
(распределение Фишера);
3) «•-■£«•
(е) Квантили
3) g2 = —- t;2 ( 1 -j r v2) с бета-распределением (табл. 18.8-11).
m \ т /
V| (m, m') = - , ot (m, m') иг. (m, m')
табулированы в функциях от а для различных значений т% т\
Специальные случаи
vp (1. т) = /f + p (mh f p (m, oo) - -L Хр (m), *J> (1, со) - u\ + p ,
2 2
*P/2(m) «X"_p<«) P «P/2
(f) Приближения. При m-*co, m'-»oo величина г распределена асимптотически
нормально с центром ■ t • и дисперсией —■—— . Эта аппроксимация пригодна
при т > 30, т' > 30.
19.6. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
525
t^ioooiQ^ *2Й1Й^22 ^ O)oocof- csjocsjqio t^oooco)© смсососм со
ад$ад з$фзд «ада®, задал вдв.-.З Щ&&Я &.
СМтГГ^ОООО COCSJOOO) — OO^CSJCOO) COlOCOr-O COO)00©CO COOO)CO CM
-HN«2flO COCSJCOt^CO — iOr--t^iO COOi^OOCSJ *Й(О^СО Ют*<—О) SS
TfOOOOCOCO ©CO —CO — COO^fOOCSJ Фб)(ОФО COCOO)CSJlO 00 —тт>СО O)
--1ЙО
<Jb-t^O)£- lOci
— ^н^н^н«« — (MCNCMCS! CSJCNCSJO
I
л
о
о
ft
о
?bgcs§
ЮОХМ^^ <MO>0>Tt"<M ifiCONCOC
f)CSJ^
h —CO
^.^.^Л <£l^'4<£i0l, cstu3.00..o*c'*i *^t*Z°lc>i^l <4.°Q.°i*dlc'2. ^^.^.Я.
2S5i
CSJO)CSJO)0> 00C0OCSJCSJ — <МЮ —— ifilCOOOO — — O)C0iO lOCSJt^O) О
ScJSoi.C^ 13oD©CSJtjh СО00,_СЛ- CO tJ^CO l>; O) ©_ -«„^t^iS CO. t^O>©—. CM.
см
**«CplAO)CO OCSjTt"00> 0>t^^ft^t^ CSJCSJt^COOO lOTt"t^<MO QCOOOlO Tt"
CO^OTt"^ t^CSJO)OOt^ OOOCOCOO lflOlfl«t^ т*« —OOCOtJ* CM©00f- CO
0 4.0CO«C ©OOlQCO — O>00COrFC0 — ©OOt^lO TFCO — OO) OOt^lOTt" CO
OO—— CM cocOTt"iO<o <0t^00 0>O >
0*00 —— csjcsjcOTt^ iO~co"r»"V-""c» С»00~-£см cO'&tfxfttO c^aoood) О
ОООгЛ 00Tt"C5Ot^ CSJiOiO —CO О — 00 О) CO <M tJ« O) 00 СП
S^Sfi t^OT^O)-* — OOCOuQtJ* T*Tj«Tj<iOf- O) —COCO 5)
т*< — 00 1ОСООГ-1О CO ©.00 CO TF CM © 00 CO •* CSJ — O) f- lO
cScOCSJ —lO lOt^COift© lOCQCO —CM CSJCSJOt^— —00 — 00— О) —0000 CO
8.28.РЛ 82S?Sji[ БД8БД №^=Л 8SJ8.2B3 fcLsAS. %
0*0*0*0*— —CSJ csj со со ^«if>\o«Ot^ г»00*оГо*О* —CSJ coco т£ 1гГсо*со*г»* 00*
OQlOCDCSJ ^^CMCSJO) O)00»Q00lO ^t" iO CO t^ t<- lO © CO CM f- O) lO t^ Tt" to
©TfOOCSlin COCOCOCOlO ©Г-СОСО00 — Й5©СОСО —00)0)0) OCSjTt<t^ О
©„©„—„^„o., — лоюо ^•"I'l^e», <RcslallJ3.csL слсосчслсо ^i"*^ со
0*0*0*0*0 ——CSJCSJCO co^tj*iOiO СО*г»*Г»*с»оГ O)*o*— — csj с6^^\Л CO*
OOlOh^ CMO)CO000O CO — t^OO) CMOOlOCOO t^CMCOCOTt" 00O)lOCO CO
8<N— 0)Ю t^CO^OOift lOt^OCOCSJ —Q—COCO 0)^0>iOCSJ CDt^COiQ Ul5
.Q.— «H.55. oq.см cqc>5$ ою-сосм, oo^©.cocsj. оо.ю—.oo.io ~<x>iJ5csji ел
0*o"o*©0* O— — csj csj co'co-^t^xo \tifOt^t^0O 00*0)0 0*— CM csj со •* rj*
-<NCOreiO COt-00O>© -CSICO^JO JO t- 00 £ g 5388S8 8&88 8
8 5
to£2 О 3 00 ЧФ СЛ £ CO fcO ~ Q (O 00 »4 C7> СЛ »* CO Ю ~
©©©p ©©©©© ©©©©© ©©©©© ©o©©© ©©©©© ©©©©©
шш ъъъъъ ¥$шж is is sis а здзди ииш м^г§
© © © ©
"? ]§ § "&
©©©©© ©©©©© © © © © © ©о©©© ©©©о© ©©о^-ь-
qo "go "oo "go "oo "oo oo "oo "oo "oo "bo "90 op "00 go <л" ^ ~~ ~~ "л- "л~ v~ ""~ "~ "л "л "л "л ^ --
-j 00 с» со о •— to 1
i © СО 0> ф СО S Ф Ф О^-00^-0>
1Й8Й «S2J222 S2 S2 SS й 8 £ to 8 83 со 2 £ & $ 8? S3 $ 8 £ £
i <р о> $3 © *- со 4* ел о со со *- со сп » о w ч - ся о со со to со ^i ел о
1§з1
OiOJ^J^J^J ^J^J^J^J
•<1 —J —3 ^3 -J -*J -<I^1^J^J^J OOi
s & 8 £ § £ S £ 2 8 8 гз!
to to to to о
о "s со «о "со
j- н jo м to to to to to to to to to to toto to to to to to to to to to to to to to to to c» 4> to
i> c§ 8 8 ^£^ся§ °> S §> 3 § So§ © ~ to co^o^S tSo^§?£ 2J ^3 5 ё ©
© © © »- u> ел oo to o> © »й- со rf> © o>co ~ © © *- ел © со ~ oo to $ Si м »- о й со о
to to to to
Co Co Ь ^
o> с© о со
to to to ьэ to
ч м ч со <o
to to to to to
h fe fe S S
to to to to to
fe Ss is s |s
oo to to -«а со
tototototo to to to to со со со *» <л *-
• *- СП 00 CO
i s;
to to to to
ел o> cj> ^-j
tototototo tototototo to to to to to to to со со со еосоеоеосо
lqlqlqi<|i<i ia ""J bo oo a со oo oo oo lo to b о р "►- L-to"
СЯ С7" C» ^1 4 00 CO © —* CO 4». О -J CO tO rfk^J — C7«© 0> СЛ i
о 5S со - «о iq^j^jco— ел ~ oo oo — ч ч мел о — it .
Sen со о
4л со -^1
^ 4^ СП (О СО
8 S "2 S8 8
со со со со
Mill
со со со со со
<Л CTi СТ> 0> —J
tt? 4J "^ "" ""
еосоеоеосо со со со со о>
,_._. , VjVjIoVjoo oo oo со со ©
4> 4> »р» »*. 4*. rf> 4* СП СП СП
Ъ ~ to со 1й- "ел ^ "о "^ "со
-д ^ м - w оо со .*». © ел
СО О ►— 00 -^J -«J *- — СЛ СО
ел со ел О)
— 4» СО •»*
О — 00 СО
19 5-5.
19.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
627
а*
я
ч
ж
ОС
^ *
в 5,
I *
-3 |
ж
X
& 6
- 3
с
о
2.
я
ь
•е-
я
О.
В
о»
я
4>
а
£
5
з а
я я
О) ST
а а
Ч Я
О 4)
о s
я я
a а
о о
о о
5 я
оГ ел оо «р io вГ^» сзГ
со оо^сЗ «о\л §£?■■ ео^л о£
со* со" со ifTcN* «**cn ^*cn ео*
"Ф,е© cq eo cn ^
cn ео cn eo*cN ео*
ЗДф28Д8оД
СТ>СЗ>ООСр10СО'ФСЗ>
со ё$ о» г-^сз? S t2 с. _. w.
со со со 1л см «<*cn «*Tcn ео"
т£ СО СО «Ф CN CN
cn* co*cn eo*cN ео"
ЗДВДВДЗД
слфооерюео'Фез*
cn eo*cN eo*cN eo"
t^ or» oo ift о ел «ф «*
ел вГоо* ееГ\л* ео*-Ф сзГ
со*г-соиГсоиГс*^с*ч(Г cn eo*cN ео*с* ео*
СЗ)еЗ>ООС0\ПОО^СЗ>
^•«•фОиП^СМСО^Г-
**". *V«1 ^Я. ^°Ч "i^ 1>
СО* гГсО И?СО lft*CN «<*CN ч**
I» 00 "Ф СО СО ^
cn ео*с* eo*cN ео*
•ф, S^co1 3^.. ooS, eS^
C3) С3)00 СО \П
адвдщадфгд
CO* Г« СО Ift СО lffcN «^CN ^<
uq ow; t^cq 5£
cn eo*cN eo*cN ео*
оГ «Too* ctTio* ео*-Ф сзГ
адздэад^д
CO* t^CO CO*CO* lf?CN «**CN «Ф*
— 2*©aOCN<3>
cq ©55 г^-ф i^
cn «**cn eo*cN eo"
ЗД8Д8Д26!£
о" езГоо* ер\о*^*«Ф сзГ
со* г^со со*со* иГс?" ^cn ^<
Ю©"Ф СО С© Г«
55 f^iQ оо^-Ф ср^
cn ^< cn ео^с" ео*
оГ сзГсо со\о* ^**ф ез?
°l "V*! ^154 *L?i ез^со и^
со гГсо coVo* lfTcN ^*cn «ф*
О ^QOO—«00
t^ С\Ф СЗ^Ю Г«
cn ^*cn eo*cN ео*
ЗД£££ДЗД
of вГоо* «Гкэ ^«ф сзГ
CO©CNlQCOePCN©CO©
ел 5>uq co^cn Mvq «5^00 Щ^
со* гГсо со*со* иГсо* lfTcN ^*
см *» cn ^» см ео*
еллоо^ю^^сз*
§CNt^r«00r-t^^— »ч
, f^lO ^CN СО^О *^СЛ t^
т1* гГсО СО'СО* ufcO* lfTcN ^*
CN* ^CN ^TcN во"
2 sf °°* й л ^** £
СОГ-СОСМ^еЧСОСвГ^Ю
о oo^cq cp^cq ao-; с^сл оо^
ti* fTco* cp^co* мГео mTcn ^*
oqu^t^eo^cq^
cn ^*cn ^Tcn ^*
OOOO—»#ОС0001Л
c»5 ео^оо, е\с5 сем^ ^
2 Sf°° й^40* ^^ ^
OUJOJlft
-ёо^осз^
т*<Г«С0С0С01ЛС0М5С0ч
8A$8|S?S
cn ^*cn ^*cn ^T
5^00 ^O 00^00 CN^
2 S °° CN^^* ^"^ ^
£Д£ДЗД8Д«5Д
ti* oo*co cp^co* co'eo иГсо и?
CN ^CN ^*CN ^
со ^ oo г- ел <£ 95 «3
с*э eo^oq со o.o^oq ^
О) сзГсо|Ссо*^*<фо> tj< od"co r^co со со 1л со 1Л
«А^8Д5Д8^Д 5ДД8Д^
CO 55 О^СЗ> —^CN С75 СО^
ел сзГоо* г^со'иГф о*
сЧЧ5о2Д^ЙДЯД
т1* 00*СО Г« СО СО СО* 1Л СО* 1Л
Or^-OCNCNCN
о с^о со^сл ер^
COlfTcO^CN^
С? вО^О CN^CN^Ift^O.C^
ел* езГсз* асТссГиГхО о
®А&А®.8Д8Д^
•Ф о6*СО* 1^ СО СО*СО СО СО* 1Л
ад=ДДА
СО* 1Л СО* 1Л СО* ^<
О) ел cn е*Гсо lfTio **
^ Of^l* Г« СО* Г« СО* СО СО* 1Л
сог*»со^ооо
cqcq^CN ^—CN^
со* iffco* иГсо* иь
сог«оососу>ез>—«ер
ст> езГсл езГсо*со \о см
<х>оо\ОЦ5^ез>соез> —и?
**: ""Vi Ч>°. "V00. «t*^ ^1
^* езГ*Ф об*^* г^со «Гсо со
eo*eoco*tf5co*iff
ад^^Д^А
сз> езГсз* «э'ео otTirt ео
2!Д^Д$8Д8л2Д
\г*о *Ф езГ^* о6**ф осТ«ф г-
оо о со ео о о
елс^обез^оог^
со* t*Tco «Гсо* «Г
ЕД2Д£Д1рД
w ^ ^
ю ео\о e>fio «^ л о «ф о
см «о «ф ю
coc^t^e^tqS
^* сз> *ф e3J *Ф ез)
-^ « «о
628
ГЛ 19 МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.5-5.
К
S
сперс
большей дк
ы для
еней свобод
о степ
Числ
8
200
о
о
о
S
8
CSJ
£
to
**
CSJ
о
О
00
t^
to
lO
rt"
CO
CSJ
-
252523 25352525 25333535 2335352533 253535 1
355535 35352555 25252525 2525252232 333525
312525 55255533 25252525 2225252325 353533
332333 21212222 25212525 25252-52522 252523
555333 33333333 21252525 2525252325 252225
535333 55535323 33333323 2525252225 352525
232323 53333353 53235323 2525252525 252525
232325 23232553 53552523 2323232325 252525
232323 23232323 25232325 5353335353 232525
232323 23255523 23232325 2525555333 555325
151515 23252523 23232525 2323252525 255553
531553 3533553515132523 2323252523 232525
335333 55531515 §51315151523252323 232323
333333 53333335 535355551515131315 335335
333333 35353353 33333333 3335151515 151555
331353 53335353 53533353 3155335335 553315
333335 33335353 33555333 3353555553 333353
333353 35355535 35333355 5533353533 535553
333553 ЗЗЗЭзЗД 53533333 5333333333111355
333333 33535351 ЗЗзЗзЗЗЗ 3533135533 551553
зЗЗЗЗЗ 55335333 §5333333 3533555553 533353
630
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.6-1.
19.6. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
19.6-1. Статистические гипотезы. Рассмотрим пространство выборок
(дг1( х2, ..., хп), где*!, ..., *л—действительные случайные величины. Каждое
непротиворечивое множество предположений, относящихся к распределению
n-мерной величины (хх, ... , хп), называется статистической гипотезой.
Статистическая гипотеза Я называется простой, если она однозначно определяет
распределение вероятностей; в противном случае она называется сложной.
Пусть распределение n-мерной величины (хг, х2, ... , хп) определено
одной из функций Ф(х19 х2, ... , хп; г\и г\2, ...), ф(дг1( х2, ... , хп\ г\г, т|2, ...)
или p(xlf х2, ..., хп\ %,г|2, ...), где r\lf г|2, ... — параметры (см. также п. 19.1-3).
Тогда простая статистическая гипотеза приписывает параметрам v\l9 т]2, ...
вполне определенные значения г|10, г^о, ••• («точка» в пространстве
параметров), тогда как сложная статистическая гипотеза ограничивает «точки»
T)t, т}2, ... некоторой областью в пространстве параметров. Класс допустимых
статистических гипотез (допустимых комбинаций параметров) ограничен
условиями рассматриваемой задачи.
Если случайная выборка (х^, *2, ... , *п) получена из одной теоретической
совокупности (т. е. если случайные величины х^ взаимно независимы и одинаково
распределены), то статистические гипотезы относятся к значениям параметров совокупности
или к отношениям между ними. Заметим, однако, что теория пп. 19.6-1 и 19.6-2
относится не только к таким выборкам, но и к выборкам из любого случайного процесса.
19.6-2. Критерии с фиксированной выборкой; определения. Пусть дана
некоторая фиксированная выборка объема п\ критерий статистической
гипотезы Я есть правило, позволяющее отвергнуть или не отвергнуть гипотезу
Я на основании выборки (Xv X2 Хп). Каждый критерий определяет
критическое множество (область) S «точек» (xlt х2 хп): гипотеза Я
отвергается, если выборка (Хъ X2t ... , Хп) принадлежит критическому множеству,
и не отвергается в противном случае.
Такое принятие или отбрасывание гипотезы не дает логического
доказательства ее или опровержения. Здесь возможны четыре случая:
1. Гипотеза Я верна и принимается согласно критерию.
2. Гипотеза Я неверна и отвергается согласно критерию.
3. Гипотеза Я верна, но отвергается согласно критерию (ошибка
первого рода).
4. Гипотеза Я неверна, но принимается согласно критерию
(ошибка второго рода).
Для любого множества (фактических) значений параметров %, г|2, ...
вероятность отвергнуть проверяемую гипотезу по данной критической
области 5 равна
nS (\* \> "•) в Р {(xv х2 хп) е S> \> %> ..•} =
= [dO(xlt х2 хп; rix, г)2, ...). (19.6-1)
Если с гипотезой Я конкурирует лишь одна альтернативная простая
гипотеза Ях = {г|1 = Г|11, г|2 = г|а1, ...}, то вероятность я5(т|и, г|21, ...)
отвергнуть гипотезу Я, когда верна гипотеза Я1( называется мощностью критерия,
определенного на S, по отношению к гипотезе Ях (см. также рис. 19.6-1, а).
График вероятности 1 — 0 правильного отбрасывания гипотезы Я в
зависимости от вероятности а ложного отбрасывания ее называется оперативной
характеристикой критерия (рис. 19.6-1, Ь; см. также п. 19.6-3).
19.6-3. Уровень значимости. Правило Неймана — Пирсона отбора
критериев для простых гипотез.
(а) Желательно применять такую критическую область S, чтобы
вероятность JWr^, г|а, ...) была мала, если проверяемая гипотеза верна, и велика
19 6-3.
19.6. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
631
в противном случае. Пусть критическая область S применяется для проверки
простой гипотезы #0зз {^i = Tlio- % = 'П2о» •••} («нулевая гипотеза»), и пусть
эта гипотеза верна. Тогда вероятность напрасно отвергнуть гипотезу Н0
Плотность вероятно-]
сти статистики у
при справедливости
нулевой гипотезы Н0\
Плотность вероятности статистики у
Вероятность ее
/южного отбрасывания
гипотезы Н0
выбрасывания /-/ЗСмощ-
ность критерия)
Плотность
вероятности статистики
у при
справедливости
конкурирующей гипотезы Н.
Статистика
Вероятность /3 область (при попадании
ложном пштатив Н« ° этУ область статистики
ложного принятия п0 у &потеза Hq отбрасывается)
Ф
Вероятность 1-J5
правильного
отбрасывания]
1
Ь)
Вероятность ее
/южного
отбрасыбания
Рис. 19.6-1.а) Проверка нулевой гипотезы Н0 по сравнению с простой конкурирующей
гипотезой Нх с помощью статистики у = у (xlt хг, .... х ). Ь) Оперативная
характеристика критерия.
(ошибки первого рода) есть ns (r]10, г]20, ...) = а; а называется уровнем
значимости данного критерия: критическая область 5 проверяет простую
гипотезу на уровне значимости а.
В случае дискретных случайных величин xv *2, ... хп нельзя задавать а
произвольным образом, можно лишь указать верхнюю границу для а. Критическая область,
применяемая для проверки сложной гипотезы Н ss {(Tit, Tb. ...)eD}, будет давать,
вообще говоря, различные уровни значимости для различных простых гипотез
(комбинаций параметров ть, ти, ...). допускаемых гипотезой Я; можно указать точную
верхнюю грань этих уровней значимости.
(Ь) Для каждой выборки объема п и данного уровня значимости а:
1. Наиболее мощный критерий для простой гипотезы Я0«
= {г]1 = г]10, Лг^Лго» •••} относительно простой альтернативной
гипотезы Я1 = {г]1 = т]11, 112 = 1121. •••} определяется такой
критической областью S, которая дает наибольшее значение вероятности
*5(Чц. Лаг •••)•
2. Равномерно наиболее мощный критерии есть наиболее
мощный критерий относительно всех допустимых альтернативных
гипотез; такой критерий не всегда существует.
632
ГЛ. !9. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.6-4.
3. Критерий называется несмещенным, если ns (rjjj, t]2£, ...)^а
для каждой простой альтернативной гипотезы Нг\ в противном
случае критерий будет смещенным. Наиболее мощный несмещенный
критерий относительно данной альтернативной гипотезы Нх и
равномерно наиболее мощный несмещенный критерий выделяются из
несмещенных критериев, как указано выше.
Критическая область 5 для наиболее мощного критерия строится так,
чтобы для всех выборочных точек {хъ х2, ... , хп) отношение правдоподобия
ф(*1. *2. ••• » ХП> Ли» Л20» •••)/ф(^Ь *2. '••» ХП> Лп> Л2Ь •••)
или
р(хъ х2, ... , хп\ г|10, г|20, ...)/р(^ь *2, ... , хп\ г|п, т]21, ...)
было меньше некоторого постоянного С; различные значения С будут давать
«лучшие» критические области при различных уровнях значимости а.
Равномерно наиболее мощный критерий представляет особый интерес при проверке
гипотезы Н0 по отношению к сложной альтернативной гипотезе. На практике
в отборе критерия решающим фактором может оказаться легкость вычисления.
Обычно можно увеличить мощность каждого критерия путем увеличения
объема выборки п (см. также п. 19.6-9).
19.6-4. Критерии значимости. Пусть проверяемое свойство генеральной
совокупности сводится к множеству значений параметров г]1 =г]10, Л2=Л2о» •••»
которые сравниваются с выборочными оценками этих параметров. В качестве
основы критерия пробуют построить такую статистику
У = у(хъ *2> ••• . хп\ г|10, г|20, ...)=*g(yi, y2> •••; Лю. Лго. ...). (19.6-2)
значения которой измеряют отклонения или отношения сравниваемых
параметров генеральной совокупности и выборки. При этом простая гипотеза
#0=5 {% = г|10, г)2 = г|2о» •••} отвергается с данным уровнем значимости а
(«отклонение» значимо), если выборочное значение у попадает вне допустимого
интервала {ур^у^Ур }, для которого
Р {УР1 ^y^yP2} = P2-Pi= 1-a. (19.6-3)
Таким способом определенные критерии часто называются критериями
значимости. Формула (3) определяет Ур ^Ур (Лю» Л2о' •••) " Ур =
— Ур (Лю» Л20» •••) тк квангпили выборочного распределения статистики
y(xlt х2, ... , хп\ г|10, г|20, ...). Часто оказывается возможным выбрать
статистику у так, чтобы ее квантили ур были независимы от г|10, г|20, ...
Важные примеры приведены в табл. 19.6-1 и в пп. 19.6-6 и 19.6-7.
В приложениях к контролю качества границы у и у , определенные формулой
Pi P2
(3), называются границами допуска при данном уровне значимости а, а интервал
(у , у ) называется интервалом допуска (см. также рис. 19.6-2).
19.6-5. Доверительная область.
(а) Пусть построено семейство критических областей 5а(г)г, г|2, ... ,) для
проверки множества простых гипотез (допустимых комбинаций параметров
Ль Лг» •••) ПРИ некотором заданном уровне значимости а х). Тогда для любой
фиксированной выборки (л:1 = Х1,... ухп = Хп) множество Da (Хъ Х2>..., Хп)
комбинаций параметров (%, г|2, ...) («точек» в пространстве параметров),
согласуемых с данной выборкой, есть доверительная область уровня а; 1 —а
называется доверительной вероятностью. Доверительная область содержит
все допустимые комбинации параметров, принятие которых на основе
1) В случае дискретного распределения критические области Sa (т^, л2» •••)
определяются для уровня значимости, не превосходящего <х.
19.6-5.
19.6. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
633
Таблица 19.6-1
Некоторые критерии значимости, относящиеся к параметрам g, a2
нормальной совокупности
(см. также пп. 19.5-3,а и 19.6-4). Выборки предполагаются случайными.
Квантили находятся по таблицам. При большом объеме выборки применимы
аппроксимации квантилей, данные в табл. 19.5-1 и 19.5-2 *)
№
1
2
3
4
5
6
7
8
9
Проверяемая
гипотеза
6 = 6о
(о
известно)
1^Ь
(о
известно)
(а
известно)
$ = to
l^h
l^lo
o» = oj
G^O-2
о2 >: аз
0
1) Во мне
2) Замети
1 дует внимател
a .«
as -не я
*w* о
s aj и а
н „ о н
со и
н " w о
О а> я к
* —So
alVn
* —go
S/Vn
S2
0
>гих таблиц
м, что в та
ьно провер
Критическая
область 5
отбрасывания
гипотезы при
данном уровне
значимости а
(^ а для
сложных
гипотез)
|у|>1«!1-а =
V>ui-a
У<иа =
1-а
r*i>i<ii_«-
(m = n — 1)
У>*1-а
{т = п — 1)
y<ta = -ti-a
(m = л — 1)
У < ЗСа/2 2)
(т = /г — 1)
£>Х* а
2
(т =л — 1)
(т = п — 1)
ах | / \1 обоз?
5лицах чаще да*
ять указания, к
Мощность
я5 (1, а)
*«Ы^)
Применяется
формула (19.6-1)
p{x'<2-xs4+
P{x2>jx2!-a}
Р |Х2 < a2"XaJ
гачено через f .
отся х| _ а, чем Э&:
таблицам.
Примечания
Простая гипотеза.
Наиболее мощный «#-
смещенный критерий;
разномерно наиболее
мощный критерий не
существует
Сложные гипотезы.
Если допустимые
гипотезы ограничены
условием £ >: £„ для
критерия 2 или£:<£0
для критерия 3, то
любой из этих
критериев будет
равномерно наиболее
мощным для простой
гипотезы g = £0
Простая гипотеза;
«двусторонний
/-критерий». См.
примечание к критерию 1
Сложные гипотезы;
«односторонний
/-критерий». См.
примечание к критериям
2 и 3
Простая гипотеза; не
существует
равномерно наиболее мощный
критерий
Сложные гипотезы;
если допустимые
гипотезы ограничены
условием о2 > аз для
критерия 8 или о2 :<
:<0"2 для критерия 9,
то любой из этих
критериев будет
равномерно наиболее
мощным для простой
гипотезы о2 = о"2
в каждом случае еле-
634
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.6-6.
Таблица 19.6-2
Доверительные границы для нормальной совокупности
При больших п применима аппроксимация, данная в табл. 19.5-1 — 19.5-3
№
1
2
3
Параметр гц
£ (а8 известно)
£ (а8 неизвестно)
а*
Доверительный интервал {Yi^ili^Ys}.
Доверительная вероятность 1 — а = Р8 — Pi
р* Vn pi Vn
РшУп РцПГ
x2 x2
Рг Pi
%t%)
данной выборки имеет вероятность Р {(Хг, Х2, ... , Хп) е Sa (гц, tj8, ...)} ^
^1 —а.
(b) Доверительные интервалы, построенные по
критериям значимости (см. также п. 19.6-4 и табл. 19.6-2). Чтобы найти
доверительные области, связывающие значения одного из неизвестных
параметров, скажем, %, с данным
выборочным значением Y = y(Xlt Х2, ... , Хп)
подходящей статистики у, обратимся
к рис. 19.6-2. Начертим нижнюю и
верхнюю границы допуска ур^ (тц) и
ур (г]1) в зависимости от тц для данного
уровня значимости а. Пересечение этих
граничных кривых с каждой прямой
y = Y определяет нижнюю и верхнюю
границы Yi = Yi(^)> Y2=Y2(*0
доверительного интервала Da = (ylt y2) уровня
а. Доверительный интервал содержит
такие значения параметра гц,
принятие которых на основе выборочного
значения y = Y имеет вероятность
19.6-6. Критерии сравнения
нормальных совокупностей. Дисперсионный анализ.
(а) Статистики объединенных выборок. Рассмотрим г взаимно
Доберительныц
интербал
Теоретические значения параметра 7jf
Рис. 19.G-2. Построение доверительных
интервалов.
независимых случайных выборок (хц, */2, ..., #mt)
купностей с центрами £,• и дисперсиями a?(t = l, 2,
объема щ имеет центр и дисперсию
из г генеральных сово-
..., г). Пусть i-я выборка
*=1
k=i
(i=l, 2, .... г).
(19.6-4)
!9.в-6.
19.6 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
635
Эти г выборок можни эассматривать как «объединенную» выборку, объем
которой, центр и дисперсия даются формулами
/=1k=l
--r=T[</l--r)Si.+(r-1)sji],
где
(19.6-6)
Статистики S8 (суммарная дисперсия) и S^ измеряют рассеяние внутри
выборок и между выборками соответственно.
(Ь) Сравнение нормальных совокупностей (см. также
табл 19.5 1 —19.5-3) Если имеется г независимых выборок из нормальных
совокупностей г центрами \i и одинаковыми дисперсиями о] = о2, то S2, Sa
и 5д являются состоятельными несмещенными оценками для дисперсии
генеральной совокупности а2 (как правило, неизвестной). Случайные величины
S2 S2a
(я —г)—j- и (г—1)--=р независимы и имеют х2_РаспРеДеления со степенями
свободы п — г и г—1 соответственно.
Отметим выборочные распределения следующих статистик:
(*i - xk) - (h - Ik)
1.
2.
мальное распределение
(xi-*k) — (h-h) \f nink
S0 f п. + nk
Щ + nk — 2 степенями свободы.
2
~ имеет v2-распределение,
имеет 2-распределение
4.
1п^
-^- имеет v2-распределение,
So
имеет стандартизованное нор-
имеет t-распределение с
(т = щ— 1, т' = /гл—1).
(m==r—1, т' = п—г).
In -^— имеет г-распределение
Оо
Таблица 19.6-3 показывает применение этих статистик в критериях
сравнения нормальных совокупностей. Доверительные границы для разности g,-—£$
можно вычислить из /-распределения. Случай нормальных распределений
с различными дисперсиями рассмотрен в [18.9].
(с) Дисперсионный анализ. В третьем критерии табл. 19.6-3
средние значения g,- сравниваются путем разбиения общей дисперсии S2 на
639 ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 19.6-6.
составляющие S2 и S2A, обусловленные соответственно статистической флук»
туацией внутри выборок и различием между выборками. Этот метод известен
как дисперсионный анализ; рассматриваемый здесь частный случай относится
Таблица 19.6-3
Критерии значимости для сравнения нормальных совокупностей
(см. также табл. 19.5-2 и 19.5-3)
№
1а
lb
2а
2Ь
3
Проверяемая гипотеза
(дано а\ — а|)
(дано <з\ — а%)
^1 ==%2== '" ==^Г
(дано а\ = а\ = ... = а2)
Критическая область, в которой гипотеза
отвергается при уровне значимости ^а
lflrl>2, а
Si
lns;>2i-a
SK *
или — > v{ _а
*i - *k -\f nink
„ (« = «1-1. т' = пЛ-1)
(критерий Фишера)
><1-а
(m="i+nft-2)
(/-критерий;
* отметим
специальный
случай я^ = 1)
| вд 1 (т = г—1, т' = п — г)
| *П S7 | Z\ a (критерий Фишера)
к группировке по одному признаку, соответствующему значению индекса L
Подобные критерии применяются в исследованиях эффекта различных методов
лечения, обработки почвы и т. п. [18.6], [18.9].
Дисперсионный анализ для группировки по двум признакам (случайные блоки).
Рассмотрим rq выборочных значений х-k, расположенных в таблицу
х11 *12 '' * xiq
*21 *22 ••• ХЩ
ХГ1 ХП • • • Xrq
и введем средние по строкам д^.* средние по столбцам х.^ и общее среднее х с помощью
формул
Я г г q
**•-{ 2 XW Х* = 7 2 ХШ> X=7j 2 2 Xik- <19'6"7>
19.6-7.
19.6. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
637
Общая дисперсия разбивается следующим образом;
1=1k=l
- rq-i [c--')(g-i)so3 + (r-i)g3; + r(g-i)5;I],
sl
" (г-!)'(«-1) I] Ё(*»-*'--*-* + ^
(дисперсия, обусловленная
i=\k=l
флуктуацией внутри
строк и столбцов).
Si =
S 1 =
г—I
V"! /- -\2 (дисперсия между строками).
i = \
Я
Я-*
£ С.*-*)
2 (дисперсия между столбцами).
(19.6-8)
Если случайные величины х.^ распределены нормально с одинаковыми дисперсиями,
то случайные величины SJj, Sf и S\\ взаимно независимы и имеют %2-распределения с0
степенями свободы (г — \) (q — 1), г—\ и q — 1 соответственно. Статистика «Sf/sj имеет
^-распределение с т = г—1, т' = (г—1)(^ — 1) и служит для проверки равенства
средних по строкам Мх(, =£/. тем же способом, что и в табл. 19.6-3. Аналогично «Sfj/S2 имеет
^-распределение с m — q — 1, т' = (г — 1) (? — 1) и служит для проверки равенства
средних по столбцам Mx.k = £.£.
19.6-7. Критерий согласия у2 (см. также табл. 19.5-1).
(а) Критерий %2 контролирует согласованность гипотетических
вероятностей Pk — P{Ek) случайных событий Elt Е2, ..., Ег с их относительными
частотами hk = h{Ek} = nkln в выборке из п независимых наблюдений. Во
многих приложениях каждое событие Е^ состоит в том, что некоторая случайная
величина х попадает в определенный классовый интервал (п. 19.2-2), так что
критерий %2 позволяет сравнивать гипотетическое теоретическое распределение
величины * с ее эмпирическим распределением.
Согласие измеряется с помощью статистики
<-»2^-2
(nk-ipk)2
ПРи
(19.6-9)
k = i
k = \
распределение которой при /г—► оо стремится к распределению %2 с т = г—\
степенями свободы. Если все прь > 10 (для этого при необходимости
объединяют некоторые классовые интервалы), то критерий %2 отвергает
гипотетические вероятности с уровнем значимости а при г/>%|__ а(т). Если т>30,
то вместо ^-распределения можно пользоваться нормальным распределением
величины У 2%2 с центром У2т— 1 и дисперсией 1.
(Ь) Критерий х2 с оцениваемыми параметрами. Если
гипотетические вероятности pk зависят от q неизвестных параметров т^, ц2, ...
..., x\qi то сначала находят совместные наиболее правдоподобные оценки этих
параметров по данной выборке (п. 19.4-4) и подставляют полученные
значения Pfc = PfcOli» Л2» •••» Щ) в формулу (9). При достаточно общих условиях.
(см. ниже) статистика у сходится по вероятности к %2 с m — r — q—\
степенями свободы и критерий %2 применим с m = r — q—\. Критерии этого типа
проверяют применимость нормального распределения, распределения Пуассона
и др. с параметрами, оцениваемыми по выборке.
638
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.6-8.
Указанная сходимость имеет место, если функции р^ (т^, т|а* ... ,- х\ А в некоторой
окрестности точки (т^, ти, . . . , 1\Л совместного максимума правдоподобия удовлетворяют
следующим условиям:
г
l- S pk(\'\ V"1-
k = \
2. Вероятности pk (r\v тц, .. . , r\ А имеют положительную нижнюю грань
и дважды непрерывно дифференцируемы, а матрица (др^/дг\Л имеет ранг д.
19.6-8. Непараметрическое сравнение двух совокупностей: критерий знаков.
Проверяемая гипотеза состоит в том, что две случайные величины х и у
независимы и одинаково распределены; последнее утверждение мы будем понимать
в следующем смысле:
Р {х-у>0}=Р {х-у <0} = j,
если известно, что Р {х=у}=0.
Рассмотрим случайную выборку п пар (xlt yt), (х2, у2)> •••, (*«» ynY ПРИ
вычислении объема выборки п пренебрежем парами, для которых xi = yi
(совпадения). Вероятность того, что более чем т разностей xi—yi
положительны, равна
Пусть теперь та есть наименьшее значение т, для которого р (т) ^ а.
Односторонний критерий знаков требует отвергнуть проверяемую гипотезу с
уровнем значимости ^ а, если число положительных разностей Xi—yi превосходит та.
Двусторонний критерий знаков требует отвергнуть гипотезу с уровнем
значимости 2а, если число положительных или число отрицательных разностей
превосходит т^; т^ табулировано в зависимости от а и п (см. [18.3], {18.5]).
Критерий знаков может применяться также для проверки: 1) симметрии
распределения вероятностей, 2) гипотезы о том, что значение х = Х является
медианой распределения.
19.6-9. Обобщения. Критерии, основанные на фиксированной выборке (пп. 19.6-1 —
19.6-7), допускают только две возможности: отвергнуть или не отвергнуть проверяемую
гипотезу на основании выборки. Последовательные критерии разрешают увеличение
объема выборки (дополнительные наблюдения) в качестве третьего возможного решения;
тогда можно уточнять оба уровня значимости и мощность критерия (относительно
некоторой альтернативной гипотезы), пока проверяемая гипотеза не будет в конце концов
принята или отвергнута.
Схемы критериев с фиксированной выборкой и последовательных критериев
представляют собой частные случаи решающих функций или правил поведения, связанных
с принятием гипотезы (решением) по каждой выборке некоторого наблюдаемого признака.
19.7. НЕКОТОРЫЕ СТАТИСТИКИ, ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
И КРИТЕРИИ ДЛЯ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
19.7-1. Вводные замечания. Здесь даются лишь некоторые часто
применяемые определения, формулы и критерии, не исчерпывающие исследования
многомерных статистик. Отметим, что многомерные статистики служат для
оценки н проверки стохастических связей между случайными величинами.
19.7-2. Статистики, получаемые на основе многомерных выборок.
(а) Пусть дана многомерная случайная величина x = (#i, х2, ..., *v)
(п. 18.2-9); по аналогии с пп. 19.1-2, 19.2-2, 19.2-4 определим случайную
выборку объема п:
(х1> Х2, ...j Хл) 2S (яи, ДГ21, ***t Хуь #12» #22» •••! XV2t •••» ХШ> Х1Ю •••! х\п)
19.7-3. 19.7. СТАТИСТИКИ ДЛЯ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ 639
и статистики: выборочное среднее от Х{
п
1
выборочное среднее от f (хъ х2, ..., xv)
п
1
f(xlt x2i ..., *v) = - 2 /C*i*. *2*. •••» *v*). (19.7-2)
выборочные дисперсии (при / = /) и ковариации (при i^/)
hf = (Xi—Xi)(Xi—xf) = ln (/, у = 1, 2, ..., v) (19.7-3)
и выборочные коэффициенты корреляции
I.
-гп (*, /=1, 2, ..., v). (19.7-4)
Точка x = (^i, -£2» ••• > *v) есть центр выборочного распределения, матрица
L == (hj) — матрица моментов выборки.
(b) Для двумерной случайной выборки (хп, х21\ х12, х22\ •••; х1п, х2п)
двумерной случайной величины (х1% х2) определяют выборочные коэффициенты
регрессии
bn^-r^f, bli=^ = rn^. (19.7-5)
Эмпирическая линейная средняя квадратическая регрессия х2 на хх
g2(xl)=X2+b21(x1-xl) (19.7-6)
представляет линейную функцию ахг + Ь, которая минимизирует средний
квадрат отклонения в выборке
п
[х2-(ахг + Ь)]*=± 2 Г*2*-(я*1*+*)]2 (19.7-7)
(см. также пп. 18.4-6, b и 19.7-4, с).
Для v-мерных совокупностей эмпирические сводный и частные
коэффициенты корреляции и коэффициенты регрессии получаются из выборочных
моментов lij по формулам, аналогичным формулам (18.4-35) —(18.4-38), и служат
для оценки соответствующих параметров генеральной совокупности. Полную
теорию см. в [18.6] и [18.9].
(c) Статистики (1) —(4) могут быть аппроксимированы оценками по
группированным данным по способу пп. 19.2-3 — 19.2-5. Оценки по группированным
данным likQ центральных моментов второго порядка %ik можно улучшить
поправками Шеппарда
'«=<«0---пг(дх.-)2; '«='»а <'**>•
где ДХ/ — длины классовых интервалов. Эти поправки часто сглаживают
ошибки, возникающие от группировки, если AXi не превосходит восьмой
части размаха величины x-t. Практические схемы вычислений даны в [18.9].
19.7-3. Оценки параметров (см. также п. 19.4-1). Теорема п. 19.4-2, а
применима к многомерным распределениям, и поэтому статистики (3) — (5),
так же как и выборочные средние хь, являются состоятельными оценками
соответствующих параметров генеральной совокупности. Среднее значение
640
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.7-4,
и дисперсия каждого выборочного среднего Xt и выборочной дисперсии /^=«*
даются формулами (19.2-8), (19.2-13) и (19.2-14); дополнительно отметим формулы
М///=^-Я//=^+0(1), (19.7-8)
«%-«■ [М (*<-?,)2(Xj-ljY-Щ+О (^), (19.7-9)
cov {/«, /„} -I [М(д:|-Ь)«(д:/-|/)»-ЯйЯ,/у1 + 0 (^-), (19.7-10)
cov {/й, /,,}=! [М (*,—&)3 (*/ —6/) —*-«М+° (lis-). (19-7-И)
Mr,/ = pv+0(i). (19.7-12)
Drif имеет порядок 1/л при возрастании п.
Для многомерных нормальных распределений (см. также п. 19.7-4)
М«ЫГЦ-<-' ><-п2> ••<"-> det^J,
(rt>V>2).
оdet[lyi-^;-lv^0 - — ;;v " detW
(19.7-13)
19.7-4. Выборочные распределения в случае нормальной совокупности
(см. также пп. 18.8-6 и 18.8-8). Для случайной выборки из многомерной
нормальной совокупности выборочные распределения и критерии, содержащие
только выборочные средние Хх и выборочные дисперсии /h = sJ, получаются
непосредственно из п. 19.5-3. Остается исследовать статистики, которые
описывают стохастические связи между случайными величинами я/, в частности,
выборочный коэффициент корреляции и коэффициенты регрессии.
(а) Распределение выборочного коэффициента
корреляции. Рассмотрим случайную выборку (хп, jrai; х12, х22\ ...; х1п, х2п) из
двумерной нормальной совокупности с плотностью распределения
где
*(Л* *г) = w.lrr=y ^{-Т^^-2^и, + иЦ, (19.7-14)
«1=J1i^-, "2=-£а^12- (oi>0, aa>0, -1<р=р12<1).
Плотность распределения выборочного коэффициента корреляции г1г=г
(п. 19.7-2) равна
(2рг)*
1
л_2 _Z=1„ _!L=1 f ^»-i <tf
= iL^£-(1~P2) 2 d"^ 2 } (i-PH»)"-'KI3p (-Kr<l) (19.7-15)
и равна 0 при | г | > 1; отметим формулы
Мг-р+0(1). Dr-JL=i^+0(^). (19.7-16)
Заметим, что фГ(Л)(г) не зависит от £lf g2» о~1э а2; /г^4.
Полезно ввести новую случайную величину
19.7-4. 19.7. СТАТИСТИКИ ДЛЯ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
которая при п> 10 распределена приблизительно нормально с центром и
дисперсией
Поведение статистик г и у при различных значениях рил представлено на
рис. 19.7-1.
/>=0 р=0,5 р=0,8
п=50 п =50 п=50
-1.0-0,8-0,6ЧИ-0,г 0 0,2 0,4 0,6 0,8 1,0 г
а)
Ь)
Рис. 19.7-1. Плотности распределения статистик г и у, применяемых для оценок
коэффициента корреляции р двумерных нормальных распределений.
Если у и у* — значения статистики (17), вычисленные для двух независимых
случайных выборок объемов п им' из одной и той же нормальной совокупности, то у — у*
имеет приближенно нормальное распределение с центром 0 и дисперсией ^ ^ 3 + п, _у
(Ь) /--распределение. Критерий некоррелированности
в ел и ч и н. В важном частном случае р=0 (гипотеза некоррелированности
величин!) плотность распределения (15) сводится к
фг(пЛО =
•№)
л-4
Уп
'Т^У'-"1
(-1<г<1). (19.7-19)
В этом случае величина t = Vn — 2 _,, , имеет t-распределение с п—2
степенями свободы (табл. 19.5-2). Статистика г Vn—l имеет г-распределение
с /г —2 степенями свободы, r-распределение табулировано; оно асимптотически
нормально со средним 0 и дисперсией 1 при п —► оо. Как t-распределение, так
и г-распределение дают критерии для гипотезы р=0.
(с) Проверка гипотетического значения коэффициента
регрессии (см. также п. 19.7-2). Если дана случайная выборка из
двумерной нормальной совокупности с плотностью (14), то гипотетическое значение
коэффициента регрессии $21 = -^=р12£- (п. 18А-6>Ъ) проверяют при помощи
статистики
/' =
01
•./i-Ъ
(&21 — P2l)»
(19.7-20)
21 Г. Корн в Т. Корн
642
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.7-5,
которая имеет t-распределение с п — 2 степенями свободы. Этот критерий
значительно более удобен, чем непосредственное применение распределения
выборочного коэффициента регрессии 621 [18.9].
(d) v-м ерные выборки. Для случайной выборки из v-мерной
нормальной совокупности с плотностью распределения (18.8-26) совместное
распределение выборочных средних xlt x2, ... , xv является нормальным со средними
значениями £lf £2> • • • * £v и матрицей моментов Л/я. Совместное распределение
величин xi не зависит от совместного распределения v 2 выборочных
моментов In (обобщенная теорема Фишера, см. также п. 19.5-3, Ь).
19.7-5. Выборочная средняя квадратическая сопряженность признаков.
Критерий независимости двух случайных величин, основанный на таблице
сопряженности признаков (см. также п. 19.6-7).
(а) Пусть дана двумерная случайная выборка (хъ уг\ х2, у2\ •••; Хл>Уп)
случайных величин х, у. В таблице сопряженности признаков эти п выборочных
пар размещены в г классовых ^-интервалах и s классовых (/-интервалах.
Пусть
щ. пар (хъ, yk) попадают в /-й классовый ^-интервал,
n.j пар (*fe, yk) попадают в /-й классовый «/-интервал,
щ-j пар (*£, yk) попадают в /-й классовый ^-интервал и /-Й классовый
(/-интервал.
Выборочная средняя квадратическая сопряженность признаков есть
статистика
г s (nij _^iLn-j\2 г s
(19.7-21)
которая измеряет зависимость между х и у. Величина f2 заключена между О
и min (г, s) — 1 и достигает последнего значения тогда и только тогда, когда
каждая строка (при r^s) или каждый столбец (при г ^s) содержит только один
элемент, отличный от нуля.
(b) Если х и у независимы, то при п —> оо статистика nf2 сходится
по вероятности к у} с m—(r — \)(s— 1) степенями свободы (табл. 19.5-1). Если
все ягу> 10 (при необходимости некоторые классовые интервалы объединяются),
то гипотеза о независимости отвергается с уровнем значимости а в
критической области nf2>%\_<x(m) (п. 19.6-3).
(c) Особый интерес представляет частный случай r=s = 2 (таблица
сопряженности признаков 2 X 2); в этом случае
>g (пцп22 — »i2^2i)*r П9 7 22^
П1'П2'ПЧП'2 '
(см. также [18.6]).
19.7-6. Порядковая корреляция по Спирмену. Непараметрический критерий
независимости. Пусть относительно случайной выборки п пар (xlf yx\..., xni yn)
известно только, что xk в порядке убывания величины занимает Л&-е место,
а уь в порядке убывания величины занимает Bk-e место (6=1, 2, ..., л).
Если величины х и у независимы, то при п—*оэ статистика (коэффициент
порядковой корреляции)
# = 1-г^п- 2 (Ak-Bk)* (19.7-23)
распределена асимптотически нормально с центром 0 и дисперсией \\(п — 1).
Для любого значения п > 1 гипотеза о независимости отвергается с уровнем
значимости ^ а (п. 19.6-3), если
R> = (односторонний критерий) (19.7-24)
Ул-1
19.S-I. 19.8. СТАТИСТИКИ И ИЗМЕРЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА 643
ИЛИ
\R| > ■ I~ct/2. (двусторонний критерий). (19.7-25)
У п — 1
nR
Примечание. Если двумерное распределение (х? у) нормально, то 2 sin—~- есть
о
состоятельная оценка для коэффициента корреляции р
19.8. СТАТИСТИКИ И ИЗМЕРЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА
19.8-1. Средние по конечному промежутку времени. Пусть
f(h, t2 tn)^flx(tt), x(t2), ..., x(tn); у ft), У ft) У (У; -J 09.8-1)
есть функция от выборочных значений *(/;)» УУд* ••• одномерного или
многомерного случайного процесса *(/), y(t)t ... (п. 18.9-1). Средние по конечному
промежутку времени вычисляются либо через выборочные значения, либо
путем непрерывного усреднения по конечному промежутку времени с помощью
формул
[/]л=4- S tih+m Ь+Ш tn + ktt) = ± 2 /(МО, (19.8-2)
т т
</>reT-J/ft+^'i+^-*'n+W^=-r J W^ О9-8-3)
Эти средние [/]п и (/)г представляют собой случайные величины,
распределение которых определяется данными случайными процессами.
Если случайный процесс х (/) стационарен, то
М[/]Л = М(/)Г = М/, (19.8-4)
т. е. средние по конечному промежутку времени [f]n и (f)T являются
несмещенными оценками центра распределения М/.
Дисперсия оценки [/]„ равна
отя-йг- s S cov [/('до. /(^)]=
= 4" °/ + 4 "Ё ( ! - "г) cov V (°)» / <Ш)1- (19*8-5)
£=1
Среднее (3), если оно существует, может быть получено предельным
переходом из среднего (2) при Д/ —*0, я =--ту-—*> со, &Д/ = А,. Такой
предельный переход приводит к дисперсии оценки (})Т:
т
D </>г -4" К! ^ 4") cov I/ (°). / W1 л- (19-8"6>
В зависимости от характера корреляционной функции
Kff(l)=cov[f(0), /(X)]-lvr[/(0)-M/I[/W~M/] =
-M/(0)/W~(M^2 = R//W-(M/)a (19.8-7)
дисперсии (5) или (6) могут убывать или не убывать при возрастании объема
выборки п или промежутка времени интегрирования Г.
21*
644
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
10.8-2.
19.8-2. Усредняющие фильтры. Усреднение по времени часто осуществляется
низкочастотным фильтром четырехполюсника или электромеханическим измерительным
прибором с инерцией и затуханием. Рассмотрим, в частности, фильтр, инвариантный
относительно сдвига времени, со стационарным входным сигналом f (t)—r(^ + Л ^"г*'» ••• • *л"^^'
ограниченной функцией влияния h (g) и частотной характеристикой Я (to) (п. 9.4-7).
Если входной сигнал действует от t =0 до t — Т (время усреднения), то выходной сигнал
фильтра будет
Т оо
г (Т) - J hT (Т - к) f (к) dK - J h г (0 / (Т - О </£. (19.8-8)
— с» 0
где
Таким образом,
Лт (О
-{
л С) (о < с < Г),
о С g <о. Г).
(19.8-9)
(19.8-10)
М z (Г) - М f J Л (t) </£ - а (Т) М f,
0
так что г (Т)/а (Г) есть несмещенная оценка для Mf.
Дисперсия этой оценки находится из соотношения
с»
D г (Т) = М [г (Т) - М г <Г)]« « J 4>hThT <*>[R// (X> ~ (M *>*] Л (19.8-И)
— с» * *
где (см. также п. 18.12-3)
с»
*hThT ®> e J ЛГ (S) ЛГ (£ + Х) «&• (19.8-12)
Г Г —оо
При Г-+оо дисперсия D г (Т) не стремится, вообще говоря, к нулю, а обычно
приближается к стационарной дисперсии выходного сигнала:
оо . оо
D г (оо) - J фЛЛ (X) [R/; (А,) - (М /)*] <& «^ J | Я (to) |« Ф (о) </© ^
-°° -оо
«ь 2 | Я (0) |« ф (0) В£(?> (19.8-13)
где Ф (о) — спектральная плотность (п. 18.10-3) функции f (t) — Ш, &EQ """ ширина
спектра эквивалентного «равномерного» низкочастотного фильтра с частотной характеристикой
HEq(to)
*«»- |
Я (0) при | (0 | < 2nB£Q(
О при | о | > 2ji££q.
^£0 есть мера приведенного рассеяния усредняющего фильтра. Табл. 19.8-1 дает
Я (to) и В£п для некоторых фильтров (с плоским спектром на входе).
Таблица 19.8-1
Усредняющие фильтры
Фильтр первого порядка
Фильтры второго порядка
с сильным затуханием
с критическим затуханием
со слабым затуханием
И (to)
1Л<А»Г1+1)(/©Га+1)]
l/(tort+l)»
a8 -f- ©2
(to + а)* -+- ©J
Бя<?
1/(4 Г0)
1^4(^4- Г,)]
1/(2 Т0)
а8 Н- ©J
2ю,
19.8-3* 19.8. СТАТИСТИКИ И ИЗМЕРЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА 645
л
19.8-3. Примеры.
(a) Измерение среднего значения. При измерении математического
ожидания М х = £ некоторого стационарного случайного напряжения х (t) с
Rxx <т) в аЧ~а'Г' + &*' фхх ((D) e J+'a» + 2я£26<о» (19.8-14)
(белый шум, проходящий через простой фильтр с шириной спектра а/(2я) герц, или
случайная телеграфная волна со средней скоростью отсчетов а/2, п. 18.11-5) дисперсия
оценки (x)f равна
в«г-¥|(1-г)'-,*-й^-1+'-,г)<й (19-8-,5)
и для усредняющего фильтра первого порядка из табл. 19.8-1 с Т > Т0
(практически Т>1Т0)
в. <г, «■ в. м - g X ит* +? с + -I - ДЙЛ < "А* <19-8-16>
(b) Измерение среднего квадрата. При измерении среднего квадрата
Mf = М*2 для гауссовского шума * (0. удовлетворяющего условиям (14),
R .. (т) = 2а*е~2а\ т1 И- (а2 -f £2)2,
8аа2 > (19.8-17)
Ф//(Ш) = ^Й2аТ2 + 2я<а2 + 52)б(£й)'
D(jc2>r=="(aTj-2 (2«7,-l+^-2a7')<^ <19-8"18>
и для усредняющего фильтра первого порядка с Г > Г0 и f = ^а
Вг(Г)^Вг<оо) = -^ГГ<-^7. (19.8-191
(c) Измерение корреляционных функций (см. также п. 18.9-3).
Дисперсия оценки корреляционных функций для совместно стационарных процессов х (О.
у (/) дается соотношениями (5), (6) и (11) при f (t) == х (/) у (t -j- т). К сожалению, эта
дисперсия зависит от момента четвертого порядка
М If (0) f (X)] = M[x(t)x(t + X)y(t + T)y(t + T + X)], (19.8-20)
который редко бывает известен. В частном случае совместно гауссовских и стационарных
сигналов х (/), у (/) с нулевыми средними значениями
М If (0) f (X)] = R^ (X) Ryy (X) + Rxy (т) + R^ (т -f- X) Rxy (т - X), (19.8-21)
но даже это выражение содержит неизвестную корреляционную функцию R (т) и,
следовательно, бывает полезным только в простых случаях.
Для стационарного гауссовского процесса х (t)
оо
D (х (О х (t + х))т < у- ^ R2XX (Я) dX (| Т |< Т). (19.8-22)
0
Зависимость оценки автокорреляционной функции
Т
(х (/) * </ + т)>г= -^$ х (X) х (X + т) <tt (19.8-23)
от ширины спектра сигнала и от запаздывания можно иллюстрировать на примере
гауссовского шума x(t), удовлетворяющего условиям (14). В этом случае
D(x(t)x\t-\rT))T =
«=2 в* {2аТ-\ +2e-2a7* + t(2aT+l)(2a7,-.l)--2(aT)2]6-2aT} (7*>т>0). (19.8-24)
646
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.8-4.
При т = 0 это выражение совпадает с (18). Если время наблюдения Т велико по
сравнению с обратной величиной ширины спектра сигнала (при аТ ^ 10е), то
£ < D (х (t) х (t + т)>г < 2~г (I Т | < Г). (19.8-25)
Для более общего случая стационарного гауссовского сигнала х (t) с
Rxx (т) = А"-« I * I cos ю ХТ + | Ых j« (19.8-26)
получается такое же неравенство
D (х (t) X(t + x))T^2£f (а Г > 10», | т |< Г). (19.8-27)
19.8-4. Выборочные средние. Через гх(f), 2x(t), ... здесь обозначены
различные реализации случайного процесса (рис. 19.8-1). Независимость
реализаций означает, что любое конечное множество выборочных значений lx(t{)9
Рис. 19.8-1. Четыре независимые реализации х Ц) = х (t) непрерывного случайного
процесса.
*x(t2), ... не зависит от любого множества выборочных значений другой
реализации kx (/).
Если в последовательности независимых опытов можно получить
некоторое множество реализаций xx{t)% 2x(t)> ..., nx(t), то выборочные значения
1x{t1)i 2х fa), ..., nx(tx) образуют классическую случайную выборку объема п,
т. е. kx(tx) — независимые случайные величины с одинаковым распределением
вероятностей. Аналогично, *х (*i), ^(/2). 2* d)> 2x (t2)> ..., пх (*i), л* (/2) или
M'i). ly{tJ> 2x(tx), 2y(tJ, ...2 nx ft), w*/ft) образуют двумерную случайную
выборку.
19.9-1. 19.9. ЗАДАЧИ СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ 647
Поэтому такие выборочные средние как
xlh) = ~l1x(t1) + 2x(t1) + ... + nx(t1)],
п п
л=1
л=1
(19.8-28)
являются статистиками в смысле классической статистической теории. Для
нахождения выборочных средних нужны повторные или множественные опыты,
но обычно проще получить дисперсии и распределения вероятностей для
выборочных средних, чем для средних по времени. В частности,
Dx (У-} Dx (у, D/=-±-D/,
D(x(/1)^(^)=~DA:(/1)r/(/2),
(19.8-29)
как и в п. 19.2-3 (см. также рис. 19.8-1).
19.9. ПРОВЕРКА И ОЦЕНКА В ЗАДАЧАХ СО СЛУЧАЙНЫМИ
ПАРАМЕТРАМИ
19.9-1. Постановка задачи. Практически важный класс ситуаций,
требующих принятия решения, может быть представлен на модели рис. 19.9-1.
Шум
Состояние
среды
(Внешние
ислобия,
Влияющие
на работу
системы)
Наблюдения,
измерения,
Восприятие
Данные
от органоб
чибстб или
оатчикоб
Решающий механизм,
содержащий а приор
ные знания о систе-\
ме и среде
9ЯЖХ)
Решения
(отбеты, упрабля-
ющая сила)
Дейстбия системы.
Включающие бзаимодейстбие
системы и среды
C(s,g) ^
Измерения
дейстбия
Рис. 19.9-1. Контекст для статистических решений (принятие гипотезы)
Цена С (риск) некоторого действия системы есть функция от состояния
среды, представленного m-мерной случайной величиной s ==s (slr % ..., sm)t
и решения, представленного г-мерной величиной y==(ylt yZt ...j уг):
C = C(s, у). (19.9-1)
648
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
10.9-2.
Человек, машина или система принимает решение у, основываясь на
данных, представленных я-мерной случайной величиной x*s(xlt х2, ...,#л),
которая связана с состоянием среды через совместное распределение s и х.
Принимающий решение образует у как решающую функцию (см. также
п. 19.6-9) от имеющихся данных *):
У=у(х). (19.9-2)
Если дано совместное распределение s и х вместе с функцией риска (1),
представляющей действие системы для каждой комбинации состояния среды
и решения, то задача состоит в минимизации ожидаемого риска
MC(s, y) = $$C[s, у(х)]<*Ф(в, х) (19.9-3)
S X
путем оптимального выбора решающей функции у(х). Величины s, x и у
могут быть как непрерывными, так и дискретными.
19.9-2. Оценка и проверка с помощью формул Байеса. Если параметры
состояния среды slf s2, ..., sm рассматриваются как параметры неизвестного
распределения вероятностей наблюдаемой выборки (х1% x2, ..., хп), то задача
похожа на классическую задачу оценки и контроля; существенное различие
состоит в том, что параметры slf s2 sm являются теперь случайными
величинами.
Для непрерывных величин s, x знание состояния системы на основе
полученной выборки х означает знание плотности условной вероятности ф (s | х).
Минимизация ожидаемого риска (3) или
М С (s, у) = \йФ (х) \ С [s, у (х)] йФ (s | х) (19.9-4)
X S
сводится при этом к минимизации условного риска
М С (s, у | х) = $ С [s, у (х)] йФ (s | х) (19.9-5)
S
для каждой выборки х путем выбора подходящей решающей функции у(х).
Если дано «априорное» распределение s и плотность условного
распределения q)(x|s), то «апостериорное» распределение вероятностей, нужное для
формулы (5), получается с помощью формул Байеса (пп. 18.2-6 и 18.4-5)
в виде
^Ф(81хНгф(х|8)'Ф(8) . (19.9-6)
J ф (х | s) dO (s)
s
Метод принятия решений, основанный на такой минимизации ожидаемого
риска, называется оценкой по Байесу.
Если, как это часто бывает, неизвестны функция риска C(s, у) или
«априорное» распределение величины s, то оценка по Байесу становится
невозможной. Иногда удается свести задачу к классическим методам оценок
наибольшего правдоподобия (п. 19.4-4) и критерию Неймана —Пирсона
(п. 19.6-3).
19.9-3. Случай двух состояний, проверка гипотез (см. также пп. 19.6-1—
19.6-4). Пусть существуют только два состояная среды: s = 0 (нулевая
гипотеза) и s=l (конкурирующая гипотеза). Допустим два возможных решения
*) Здесь не рассматривается случайный или частично случайный выбор решения
(как в играх со смешанной стратегией, п. 11.4-4, Ь).
19,9-3.
19.9. ЗАДАЧИ СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
649
#=0, #=1, которые соответствуют принятию или отбрасыванию нулевой
гипотезы на основе выборки наблюденных значений (xlt х2, ...,* л). Задача
сводится к установлению критической области (области отбрасывания) S
выборочных точек (Хц х2, ..., хп), которая дает минимум ожидаемого риска
MC(s, y) = C(s = Q,y=Q)p0^q>(xlt *2» •••• xn\s = 0)dx1dx2...dxn +
s
+ C(s = 0, */=1)р0 W(*i» X* •••» Xn \s = 0)dxldx2...dxn +
+C(s=l, #=0)(1—p0) $<P(*i» *2» •••> xn\s=\)dxxdx2...dxn +
s
-fC(s=l, */=l)(l—p0)W(*i, *2 xn\s=\)dxldx2...dxnt (19.9-7)
где p0 = P(s==0), a S—дополнение к S (область принятия гипотезы).
Ожидаемый риск М С (s, #) будет минимальным, если нулевая гипотеза отвергается
каждый раз, когда отношение правдоподобия
A^i» *2 *п) " Ф(*г *2 *„!* = <>) (19.9-8)
(см. также п. 19.6-3) превосходит критическое значение
А — Ро Cjs^O, y=\) — C(si=0t у = 0)^
С l-po C(s=l, 0 = O;-C(s=l, ^=1)
ро цена ложного отбрасывания (ложная тревога) /1Q Q Q\
1 — ро цена ложного принятия (промах) * \ • /
Заметим, что любая возрастающая или убывающая функция от
отношения правдоподобия (8) может заменить его в качестве статистики для
проверки гипотезы; само отношение правдоподобия является монотонной
функцией от «апостериорной» условной вероятности p(s\xv x2t ..., xn)t которая
тоже может служить в качестве такой статистики.
Пример. Обнаружение сигнала на фоне гауссовского шума с плоским спектром.
Надо решить, является ли принятый сигнал х (О с шириной спектра В чистым шумом
[s = 0 или х (0 = п (/)] или полезным сигналом с добавочным шумом [s = 1 или х (/) =
= s (0 + п (О]. Конечная ширина спектра позволяет описать и сигнал и шум с помощью
выборочных значений
xk = х (kAt), sk = s (kAt), nk = n (kAt),
где A/ = r^-; k=\, 2, ..., 2BT; T — время наблюдения (п. 18.11-2).
2B '
Отсюда
Г 2ВТ 1
, 2ВТ 1ВТ «
Л (*1- "г *2ВГ) = ехр I- ^ ^ S* + P^ 2 V») •
650
ГЛ. 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
19.9-4.
Так как величина
2ВТ 2ВТ Т
*fa х2 Х2ВТ) = -2^" 2 V* = S S {Ш) * (&А/) А/ * \ * (/) * {t) dt
А=1 Л=1 О
есть возрастающая функция от отношения правдоподобия A(xv xv ..., *2В7*)» то она
может быть использована как статистика для проверки гипотезы. Подсчитав эту
величину либо путем дискретного суммирования, либо путем интегрирования, сравнивают
ее с критическим значением zq% определяемым с помощью р0 и С (s, у); неравенство
г > zq соответствует решению у = I.
19.9-4. Оценки по методу наименьших квадратов. Пусть среда имеет
непрерывно распределенное множество состояний, представляемых значениями
величины sse^j, s2 sm), и пусть m компонент yk решающей функции
ys(^j, у2 ут) надо выбирать так, чтобы аппроксимировать
соответствующие значения s^ возможно лучше в некотором смысле, уточняемом
функцией риска С (s, у). В практически важном случае оценок по методу
наименьших квадратов функция риска задается в виде
т
C(s, y) = C(slt s2 sm\ ylt y2% ..., ym)= 2 isk-yk)\ (19.9-10)
В этом случае минимум М С (s, у) достигается, когда каждая компонента уь
равна условному математическому ожиданию величины sk для полученной
выборки (*!, х2 хп):
со
yk = M(sk\xlt х2 хп)= $ sk<p(sk\xlf х2, ...» xn)dsk (£=1, 2 т)
— 00
(19.9-11)
(см. также пп. 18.4-5, 18.4-6 и 18.4-9), где ф (s^ | xlt х2, ..., хп)
из ф(*1( #2, ..., xn\sit s2 sm) с помощью формулы Байеса
^sjx^i» •••» sm\xi> •••» хп)~
Фх | s fa - . хп I sr - » sm) <** fa " ' sm)
hx\s (*i *n I si sm) <*>s («! «т) Лх ». **m '
s
Пример. Измерение случайной величины на фоне гауссовского шума. Надо оценить
случайную величину s по выборке (xv *2, ..., х Л измеренных значений
если для величины s известна плотность априорного распределения вероятностей
а относительно величин п. известно, что они независимы между собой и от s, причем
** i»(хгх* хп Is) - (mrjff'2 ехр Г- ЩГ Jj, <**" SH •
Формула Байеса дает
получается
(19.9-12)
19.9-4. J9.9. ЗАДАЧИ СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ 651
где
' пх £
PN °'SI ,= 1
Поэтому оценка по методу наименьших квадратов (минимизация М (у — s)2)
приводит к значению
п
которое зависит от выборочных значений xk только через статистику х (выборочное
среднее) и является смещенной оценкой; смещение возрастает с возрастанием P^j и
убыванием объема выборки п. Для полученной оценки ожидаемый риск равен
s *~ п
ГЛАВА 20
ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ
20.1. ВВЕДЕНИЕ
20.1-1. Вводные замечания. Глава 20 содержит описание вычислительных
методов, причем упор делается на методику, а не на схемы или программы
расчета. В пп. 20.4-1—20.5-7 дается исчисление конечных разностей.
Разностные методы представляют интерес не только для численного интегрирования
дифференциальных уравнений, но также и в тех математических моделях, где
переменные изменяются дискретными шагами.
20.1-2. Ошибки. За исключением возможных промахов (грубых ошибок)
в приближенных вычислениях встречаются ошибки начальных данных, ошибки
округления, вызванные использованием конечного числа знаков, и ошибки
усечения, вызванные конечной аппроксимацией бесконечного процесса. Влия-
д*.
ние малых ошибок А*; или малых относительных ошибок —- на результат
xi
/(xv х2, ...) может быть оценено с помощью дифференциала (п. 4.5-3); так,
А (лг1+лг2) = А^1 + А^2> A (xiX2)=x1 hx2+x2 A*i, (20.1-1)
| A (*i — хг) I ^ 1 A*t I -Н А*2 I А (хгх2) _Axt . Ax2 (20 1-2)
I *i — хг \^" | *i — х2 | ' хххг xt *~ х2 \ • >
Возникновение и распространение ошибок в более сложных вычислениях
составляют предмет продолжающихся исследований; точные результаты
получены лишь в отдельных классах вычислений. Желательно своевременно
обнаруживать промахи и ошибки с помощью различных программ контроля
(например, подстановкой приближенного решения в исходное уравнение),
осуществляемых на каждом этапе расчета. В качестве весьма грубого
практического совета можно рекомендовать сохранять на две значащие цифры больше,
чем это оправдывается точностью исходных данных или требуемой точностью
результата. В сходящихся итерационных процессах (пп. 20.2-2, 20.2-4, 20.3-2,
20.8-3 и 20.9-3) влияние ошибки уменьшается, за исключением ошибок,
нарушающих сходимость.
Вычислительная схема называется устойчивой, если ошибки округления
(абсолютные или относительные) в исходных данных и при расчете не вызывают возрастающего
эффекта. Более точно, определение устойчивости вычислительной схемы часто
оказывается возможным связать с асимптотической устойчивостью решения разностного
уравнения (рекуррентного соотношения), как в п. 20.8-5.
Вместо слова «ошибка» часто применяют «погрешность».
20.2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
20.2-1. Вводные замечания. Численному решению уравнения
/(г)=0 (20.2-1)
должно быть предпослано хотя бы грубое исследование вопросов
существования и положения корней, их оценка и т. д. (см. также пп. 1.6-6 и 7.6-9).
Решения могут быть проверены подстановкой.
20.2-2.
20.2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
653
20.2-2. Итерационные методы.
(a) Данное уравнение (1) приводят к виду
z=cp(z). (20.2-2)
Выбирая некоторое начальное приближение z^, вычисляют последовательные
приближения
2[/+1]==ф(2[Л) (j==0t lf 2, ...). (20.2-3)
Сходимость таких приближений к искомому решению г требует отдельного
исследования.
Теорема о сжимающих отображениях п. 12.5-6 часто позволяет
установить сходимость и оценить быстроту сходимости. Итерации заканчивают
тогда, когда отношение , r-ч i становится достаточно малым.
UL/J|
Признак сходимости и оценка ошибки. Если существует такая область D в
комплексной плоскости и такое положительное число М < 1, что
| ф (Zt) — ф (Z8) | ^ М | Zt — Z8 | для всех Zu Zt из D,
и если D содержит и все точки zt удовлетворяющие неравенству
| , _ гШ | < _£_ | 2[/1 _ г[/ " 1] | (20.2-4)
для каждого значения />1, wo приближения (3) сходятся к некоторому решению г
уравнения (1); это решение удовлетворяет неравенству (4) и является единственным в D.
Заметим, что правая часть неравенства (4) дает верхнюю грань ошибки /-го
приближения гШ.
(b) Возможны различные способы приведения уравнения (1) к виду (2). Вот
некоторые итерационные формулы, основанные на специальном выборе
функции ф(г):
zU+^zM-tffeU]), (20.2-5)
z[/+i] = z[/]_d£^ (метод Ньютона), (20.2-6)
-r/-nW/i ;(«Ц) 1 {/(J/3)}»r(J/3) ,2027>
Эти итерационные формулы особенно удобны при вычислении действительных
корней. Для нахождения комплексных корней действительных уравнений надо выбирать
комплексное начальное приближение г'"]. Признак сходимости и оценка ошибки из
п. 20.2-2,а применимы во всех случаях.
Формула (6) есть частный случай общего метода Ньютона (п. 20.2-8). Если
производная f' (z) непрерывно дифференцируема в рассматриваемой области и если можно найти
такие положительные числа А, В, С, что
f («ГО)
^ В (20.2-8О)
|/"(2)1<С^^ (20.2-86)
при
| г — г[°] | ss -— (1 — V\ - 2АВС), (20.2-8с)
то искомый корень 2 удовлетворяет последнему неравенству и быстрота сходимости
метода Ньютона оценивается неравенством
| г _ г[П | < -Д- (2АВС)2'~1 (I = 1, 2, ...). (20.2-9)
27 1
Отметим, что здесь имеет место относительно быстрая сходимость.
654 Гл. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.2-2.
Примеры. Применение метода (6) к уравнениям 1/г — а «= 0, г* — а = 0,
1/г8 -1/с = 0и2Л-а = 0 дает итерационные формулы вычисления 1/а, Т^а и у^а (а > 0)3
при / -»- oof 0 <
2[0] <li (20.2-10)
г[/ +1] — y f «[Л + ~рт) •* ^«~ при / -* оо, zt°] > 0 (алгоритм Герона)( (20.2-И)
rf/+ 1] - rf/] [l + °-(22а[Л)2] -* У5 при / - оо, 0 < rfO] < /й, (20.2-12)
rf/ + Ц - (l -1) 2Г/3 + ^ J -» УЪ при /-.со. 2[0}>0. (20.2-13)
(с) ^Правило ложного положения (regula falsi, метод
секущих). Правило ложного положения отличается от приведенных выше
итерационных методов тем, что для определения нового приближения z^ + 1^
используют два предыдущих (возможны и более общие схемы, использующие
несколько предыдущих приближений, см. п. 20.2-4, Ь). Для решения
уравнения (1) выбирают два начальных приближения zt0], z^ и строят
последовательные приближения
#™-^-,w~-?w\im (/=1,2 >• (20-2"14а)
Для отыскания действительных корней действительных уравнений
приближение z^-7"^1^ обычно строят по z^ и z^, где k ==k (/)</ — наибольший
индекс,, такой, что / (z^) и / (sf-Щ имеют разные знаки:
гС/+1]=гС/]-1да^ш-^(гСЛ)- (20-2-Ш)
В частности, разные знаки должны иметь f(z^) и /(z^); при указанной
схеме обеспечена локализация корня между z^ и z^.
|А) Улучшение сходимости по Эйткеяу— Стеффенсену. Если
Ф (г) действительна и трижды непрерывно дифференцируема в окрестности
действительного корня z, причем <р' (z) ф\, то сходимость итерационного процесса (3) можно
улучшить с помощью следующей итерационной схемы;
гШ^фУО]), гГ2]~ф(*П)), )
:Г,1 , jm (zW-zlW
it^-фУ?]), *C6]-V(2[4])f
2С5]-22Н] + 2[ЗГ
(20.245)
Итерации заканчивают, когда один из знаменателей оказывается близким к нулю
(вообще говоря, желаемая точность достигается раньше этого, если последовательность
4Ш) сходится). Этот метод, подобно методу секущих, может применяться вместо быстро
сходящегося метода Ньютона, если вычисление значений fr(z) вызывает затруднения.
(е) Кратные корни. Итерационные схемы, опирающиеся на
формулы (6) (метод Ньютона) или (7), не будут сходиться в окрестности кратного
коряя уравнения* Заметим, что кратные корни функции / (г) являются
корнями ее производной /' (г); для алгебраических уравнений наибольший общий
делитель функций / (z) и /' (г) может быть получен методом п. 1.7-3.
20.24»
20.2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
655
(t) Мет® д проб. Если изолирвванный простой корень действительного
уравнения (1) лежит между 2 = а и г ** bt то вычисляют f fg "У ). Если f [ ~t ) имеет тот
же знак* скажем* что и f (b)g то далее вычисляют f \ -г- (а + а "^ ) L и т. д.
20.2-3. Вычисление значений многочлена.
(а) Последовательные умножения. Для применения
рассматриваемых далее итерационных методов надо уметь вычислять значения
многочлена
f (z) =з а0г*+axzn~l+...+ап_гг + ап. (20.2-16)
Для этой цели либо вычисляют последовательно aQz + alt z (a0z + ai) + a2»
2
либо предварительно находят величины /(с), f€ (с), — /" (с), ... по схеме Гор-
можно:
нера и затем пользуются формулой (17).
(Ь) Схема Горнера. Деление многочлена f(г) на (г—с) дает новый
многочлен fx(z) и остаток f(c) (п. 1.7-2); деление fx(z) на (z—с) дает
многочлен /2 (г) и остаток /' (с). Продолжая этот процесс, получаем
последовательно остатки /(с), /' (с), Y\f" (c)» ^Р" (c)i •••* которые являются
коэффициентами разложения многочлена
F(u)^f{u+c)=*
^f(c)+rWu+y"(c)u*+...+±f«>(c)u»^f(z). (20.2-17)
Схема Горнера для комплексного аргумента. Если /(г)—многочлен с
„действительными коэффициентами, а c = a+ib, to f(c)=Ac+B = (Aa+B) + iAbi
где Л z + B—действительный остаток от деления / (z) на (г2—2az + a2+62).
20.2-4. Численное решение алгебраических уравнений. Итерационные
методы.
(а) Общие метфды. Чтобы вычислить изолированный простой корень
алгебраического уравнения
/ (г) _ а02л+«12л-1 + ...+ал.12 + ад=0, (20.2-18)
1) применить метод Ньютона (6);<
2) применить формулу (5) с £=l/a„_i, вычисляя по схеме
Горнера последовательные значения многочлена
2[/+l]^2[/1__L f(2[/])e (20.2.19)
Если an-i=0, заменяют z на a = z—с и применяют формулу (17)$
чтобы привести уравнение (18) к виду F (ы) = 0;
3) применить метод секущих (п. 20.2-2, с).
Сходимость этих и излагаемых ниже других методов итерации зависит от выбора
начального приближения. Начальное приближение может быть получено или из
предварительного исследования, или из квадратичной интерполяции функции f (z)f или
методами п. 20.2-5. При отсутствии такой информации иногда можно выбирать в качестве
начального приближения нуль или малое действительное число. В случае комплексных
корней применима схема Горнера для комплексного аргумента, если только f (z) есть
многочлен с действительными коэффициентами; при этом в качестве начального
приближения можно испытать такое число a -j- lbt которое минимизирует величины \ А\ и \ В \
в указанной схеме. Как только найден один из корней zk, можно разделить многочлен
/ (г) на (г — г^) и затем в качестве начального приближения для следующего корня
можно выбирать г^ или zk (1 + i).
Для комплексных корней методы Мюллера и Бэрстоу упрощают вычисления и
обеспечивают более быструю сходимость^ чем метод Ньютона,^ если корни близки друр
к другу.
656 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.2-5.
(Ь) Метод Мюллера. Вместо линейной интерполяции метода
секущих здесь применяется квадратичная интерполяция, что приводит к итерации
вида
2С/
7 —. sign В/, (20.2-20а)
г[/+1]вг[/]_(г[Л_г[/-1]).
где
B/l+VB7-4iY7
C/ = (l+ ?/)//,
//-/tf/]). ^ j/^rJj7-21 (/ = 0,1,2,...).
(20.2-206)
Для начала решения можно положить
z[0] = _lt 2[1]==1| ,[2]==0
fo = an — an-i+an-2+ •
/2=ал.
Метод Мюллера распространяется также и на неалгебраические уравнения.
(с) Метод Бэрстоу. Пусть многочлен (16) содержит квадратный
множитель z2 — uz — v, определяющий два различных простых корня
уравнения (18), и пусть известны достаточно хорошие начальные приближения «£°1
и t/[°] для и и v. Тогда последовательность лучших приближений, сходящихся
к и я vt дается формулами
ИГ/+П = И[/Ц
„[/ + >]=: 0[/] +
#3^3-^i#L2
Л—1 П-—1
"WI.
(^«У-й-^а
(20.2-21а)
где величины
мулам
&5ь » с£ вычисляются последовательно для каждого / по фор-
&Ш = ak + «[/ЦЯ , + о^Л 2,
6M=ftm_c[/]_cm_0
ДЯ = ftW + и[/ЦЛ_ + „С/],
л5л }«*-°'!'2 п)'
°-Г
L-2"
(20.2-216)
Этот метод более удобен для многочленов четной степени.
20.2-5. Специальные методы решения алгебраических уравнений.
(а) Алгоритм разделенных разностей. Этот метод,
обобщающий классический метод Бернулли, может давать приближения ко всем
корням алгебраического уравнения (18) за один цикл расчета. Он применяется
также для получения начальных приближений в итерационных методах.
Вычисления располагают по схеме табл. 20.2-1, где
<(+l
((=1, 2, ...) (20.2-22)
Зв.г-5. 20.2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 657
Таблица 20.2-i
Таблица алгоритма разделенных разностей
<#] = -57
4П=
Qt'l
Е[П
4']
4']
Q[_2] = 0
.^1
Qt2]
Q[2]
EL2J-
421
£[2]
<?L3H°
Q[3]
<481
...£[«-»] =
2-n
••
.. £[«-П
3-я
... £[*-!]
4-я
q^-o
Q[«]
v2-rt
«89.
Вычисления становятся невозможными, если q[^j или обращается
в нуль. Тем не менее, метод разделенных разностей эффективен во многих
частных случаях. Например, если все п корней г1% г2, ..., гп уравнения (18)
положительны или если все корни являются простыми с различными
ненулевыми абсолютными величинами, то для каждого k имеем
lim Q[(k] = zk, (20.2-23)
lim £p] = 0, (20.2-24)
так что каждый столбец таблицы 20.2-1 дает приближение к корню.
Вообще, пусть | гг | ^ | г2 | ^... ^ | zn | > 0. Если алгоритм разделенных
разностей не отказывает, то формула (23) дает каждый корень zk, который
отличается по абсолютной величине от соседних с ним в указанной выше
последовательности, а формула (24) остается справедливой при \ г^ | > | zk+t \.
Это помогает указать корни с равными абсолютными величинами, например,
сопряженные комплексные корни.
(Ь) Метод Г р еффе —Л о б а чев ск о го. Если дано алгебраическое
уравнение с действительными коэффициентами
п
/(*)^ JI(z-zk)^zn + alzn-i + ...+an=Q,
то сначала находят коэффициенты а'Р многочлена
ДгШ-г)^(-1)" Д (z*-zl)^(-l)n(zr + a["(zzy-i + ... + a<,l>.
* = 1
658 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.2-5.
С помощью таблицы
\ k — n
ап
ап
4
п
k = n — l
an-i
~an-l
-4-1
+ 2ап°П-2
п — 1
£ = /1 — 2
ал-2
2
ап—2
-2an-ian-9
+ 2ап ал-4
е.
* = л — 3
ал-5
~an-S
-4-3
+ 2an-2an-4
-2ая_1ап_»
+ 2аяая-в
«й-з
(Номер
столбца) 1
...
...
••
Повторяя этот процесс, получают последовательно коэффициенты а\"
многочленов
(- 1)» Д («';-«*0 - <- ^ (*'0"+«i</) (^О"-1 + ...+а«>.
& = 1
При возрастании / столбцы в расчетных таблицах оказываются одного из трех
типов:
1) В некоторых столбцах удвоенные произведения становятся
пренебрежимо малыми, так что последовательные записи в этих
столбцах становятся квадратами с одинаковыми знаками (правильные
столбцы); если последовательные записи имеют одинаковые знаки,
а их абсолютные значения оказываются равными определенной доле
квадрата предыдущего значения, то мы имеем частично правильные
столбцы.
2) Записи столбцов могут иметь чередующиеся знаки (колеблю*
щиеся столбцы).
3) Некоторые столбцы могут не обладать указанной выше
правильностью.
Каждая пара правильных столбцов (например, k и k — r)t разделенная
г—1 неправильными столбцами, соответствует г корням г с равными
модулями такими, что
*Ф
а</)
/г — г
|г|2У+/—1 ПрИ /-*00.
(20.2-25)
Эти г корней все либо действительны, либо чисто мнимы, если г— 1
разделяющих столбцов частично правильны. В частности:
1. Два соседних правильных столбца (например, к и &-— 1)
определяют простой действительный корень г такой, что
при /~>оо.
20.2-в.
20.2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
659
2. Два правильных столбца (k и к — 2), разделенные одним
колеблют имея столбцом, определяют пару простых комплексно
сопряженных корней г таких, что
„</> ,
|г|2->+1 при /->со.
I ak — 2
На практике сначала находят действительные корни и чисто мнимые;
знаки определяют подстановкой или с помощью п. 1.6-6. Затем упрощают
уравнение делением на выделенные множители.
(c) Матричный метод. Корни алгебраического уравнения (18) п-й степени
са» = 1 можно вычислить как собственные значения (п X я)-матрицы
0 1 0 ... 0 0
о о 1 ... о о
^sl • • • • ) (20.2-26)
о о ... о 1
одним из методов, описанных в п. 20.3-5.
(d) Метод Горнера. Метод Горнера (для действительных корней) сводится
к последовательному вычислению коэффициентов многочленов Ft (и) =з f (и -f- Ci), ^2 (") =
г Fx (и + ct), ... по схеме Горнера, где clf ciy ... выбираются так, чтобы уменьшить
абсолютные величины остатков. Если удается получить F. (0) =& 0, то искомый корень
приближенно равен с^ -f* с2 ~Ь • • • Н~ ef.
20.2-6. Системы уравнений и экстремальные задачи (см. также пп. 11.1-1,
12.5-6, 20.2-2 и 20.2-3).
(а) Постановка задачи. Итерационные методы. Задача
решения системы п уравнений
fi (*i, *2* ..., */г) = 0 (I = 1, 2, ..., п) (20.2-27)
с п неизвестными xlt x2, ..., хп эквивалентна задаче минимизации функции
п
/4*1. *i. .... *«)- S l//(*i. *2, .... *л)|2 (20.2-28)
i=l
или какой-либо другой возрастающей функции от абсолютных величин | Д-1
невязок (ошибок) ff^fi(xlt хъ ..., хп), t = l, 2, ..., /г. Задача отыскания
минимума (или максимума) функции п переменных и сама по себе имеет
большое практическое значение.
Для решения этой задачи итерационными методами начинают с
произвольных значений *[°1 (/=1, 2, ..., п) и строят последовательные
приближения
хи+\]===х[П + 1иЦП (i«I, 2,..., л; /=0,1,2,...), (20.2-29)
которые сходятся к некоторому решению х-г при /->оо.
Различные методы отличаются выбором «направления» /-го шага, т. е.
выбором отношений vy^: v%]: ... : v\p. Величина шага определяется значением
параметра А,[/1, минимизирующим величину F (x\j+1], xl/+1], ...,л:^+1])
как функцию от А,^. Эту функцию обычно аппроксимируют ее тейлоровским
разложением или интерполяционным многочленом по трем —пяти выбранным
значениям А,^. Последний метод применим для отыскания max и min
таблично заданной функции F {хи х2 ,..., хп).
660 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.2-7.
Сходимость таких итерационных методов часто можно установить с помощью
теоремы о сжимающем отображении п. 12.5-6; при этом искомое решение рассматривается
как вектор с нормой у х\ + х\ -+- . . . -+- х\ или | х± | + | *2 | 4* . • • ■+■ | хп |.
(b) Изменение на каждом шагетолько одного
переменного. На каждом шаге изменяют только одно из xi, либо циклически,
либо так, чтобы уменьшить наибольшую по модулю невязку (см. также
п. 20.3-2, с, релаксация).
(c) Методы поиска. Чисто случайный поиск состоит в отборе
наибольшего (или наименьшего) из значений F (хг, *2»««., *л) Для некоторого
количества случайно выбранных точек (х\, х2, ...,#л); он применяется,
главным образом, при отыскании начальных приближений для итерационных
методов. В метсде случайных возмущенийначипают с некоторой точки (хъ х2,..., хп)
и вводят множество случайных возм ущений всех неизвестных Axlt Ax2t ...» А*л
для получения большего (или меньшего) значения исследуемой функции F.
Рассчитанная при этом точка дает следующее приближение, и поиск
продолжается. При этом методе, в отличие от метода чисто случайного поиска, можно
использовать свойство непрерывности исследуемой функции. Метод случайных
возмущений часто применяется в тех случаях, когда градиентные методы
отказывают из-за таких особенностей многомерной области, как «хребты», «ущелья»,
«плоскогорья» и кратные экстремумы. Дальнейшее1 развитие этого метода
приводит к стратегиям, включающим изменение шага и предпочтение
определенных направлений, зависящих от прошлых успехов или промахов.
(d) Условный экстремум (см. также пп. 11.3-4, 11.4-1 и 11.4-3). Задачи на
условный экстремум с уравнениями связей <pt- (*lf *2> .... *л) = 0 (С = 1, 2, .. . , г)
можно решать методом вспомогательных функций, добавляя к исследуемой функции
г г
F (xi, хъ • • •. хп)член вида 2 Ki I ь (хъ *2, • • хп) Iили 2 к&? (*i, • • • • V-
i=\ i = l
где каждый множитель К£ —некоторое большое положительное число при отыскании
минимума (отрицательное—при отыскании максимума), a m — четное положительное
число. Существуют программы по оптимизации на цифровых ЭВМ, включающие выбор
меняющейся стратегии поиска в случае медленной сходимости.
20.2-7. Градиентные методы.
(а) Метод наискорейшего спуска. Выбирают v№=— dF/dxiy
где все производные вычисляются при х{ = ху\ и уменьшают величину шага
)$Я по мере приближения к минимуму функции F (рис. 20.2-1).
Для аналитических функций F и малых значений /,- тейлоровское
разложение F (А,^) позволяет выбрать оптимальную величину шага
2Д)'
*М=— ±=1 0 = 0,1,2,...), (20.2-30)
d*F dF dF
ZZ
dxk dxh dxk dxh
где все производные вычисляются при х^х\^. Параболическая интерполяция
функции F (Х^) может оказаться более удобной.
(Ь) Спуск с вычислением координат градиента. Часто
вычисление координат вектора градиента dFjdxk> необходимых для метода
наискорейшего спуска, оказывается невозможным или непрактичным. Тогда
указанные производные заменяют разностными отношениями AF/Ax^, получаемыми
путем поочередного изменения только одного переменного х^. Так как при
этом на каждый шаг расчета в направлении градиента затрачивается п шагов
20.2-1
20.2. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
661
расчета координат градиента, то предпочитают продолжать расчеты в
вычисленном направлении до тех пор, пока больше нельзя уточнить исследуемую
функцию, и только после этого снова пересчитывать координаты градиента.
kFl*i>*i)
Минимум
Рис. 20.2-1. График исследуемой на минимум функции в случае двух независимых
переменных. Показано три минимума, линии уровня и линии наискорейшего спуска. В этом
примере все три минимума функции F (хи х2) имеют одно и то же нулевое значение.
20.2-8. Метод Ньютона и теорема Канторовича (см. также пп. 20.2-2
и 20.9-3).
(а) Метод Ньютона. Выбирая некоторое начальное приближение х\°^9
находят последовательные приближения *р~^ путем решения системы
линейных уравнений
л+2ё^/+11"^я>-° °'=1'2 п)-
(20.2-31)
где значения функций // и частных производных dfi/dx^ берутся при хъ = *ф
/ = 0, 1, 2,...
(Ь) Теорема Канторовичи о сходимости. Предположим,
что матрица [dfi/dxk] имеет обратную матрицу (п. 13.2-3) [dfildxk\~l =з
= l^ik (xi> х2* •••* хп)\ Для рассматриваемых значений х^.
Пусть А, В, С —такие положительные числа (нормы матриц, п. 13.2-1),
что в начальной точке xi = x\0^
max 2 I И* | ^ A, max £ | Yikfk \^Bt С ^ ^я (20.2-32я)
'$, I i I, I
fc=l
fe = l
Если fi(xit х2, ..., хп) дважды непрерывно дифференцируемы и удовлетворяют
условию
п
i. k = \
dx,dxk
(i=h 2 n)
для всех точек (xv x2t ... f n) в кубической области
тах|^_^о]
•AC
(1-К1-2Л^С),
(20.2-326)
(20.2-33)
662 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.3-1.
то система (27) имеет решение (хи х2, ..., хп) в той же области (33), и
скорость сходимости оценивается так:
max |*,-4Л I ^ "iFT l^BQ^'K (20.2-34)
Это указывает на относительно быструю сходимость.
20.3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И ОБРАЩЕНИЕ МАТРИЦ.
СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦ
20.3-1. Методы исключения.
(а) Решение системы линейных уравнений
0ii*i + «12*2 + • • • + а1пхп=bi9
Л21*1 + «22*2 + • • • + а2ПХП = ^2»
(20.3-1)
0/11*1 + 0/12*2 + • • • + ЯппХп = ЬП
по правилу Крамера (п. 1.9-2) требует слишком большого количества
умножений, если п :>: 4. Излагаемые ниже методы позволяют решить систему (1)
путем последовательного исключения неизвестных.
(b) Метод исключения по главным элементам (метод
Гаусса). Пусть ац—коэффициент, наибольший по абсолютной величине.
Чтобы исключить Xj из 1-го уравнения (t^=/), умножим 1-е уравнение на
ац1аи и вычтем из *-го уравнения. Затем повторяем этот процесс для
исключения другого неизвестного из оставшихся п — 1 уравнений и т. д.
(c) Компактная схема исключения. Находим xnt хп_г х%
в указанном порядке из уравнений
*1 + «12*2 + «13*3 + • • • + «1й*/1 = Pi»
*2 + а23*3 + • • • + &2ПХП = ?2»
(20.3-2)
*/1 = Р/1
после вычисления элементов следующей п X (/г+1)-матрицы:
Yn
Y2i
a12
а13
«23
а1Л
СС2П
Y/ii Y/i2 Y/i3
с помощью рекуррентных формул:
Pi
Р2
Pi.
Y/i = a/i (*=1. 2, ..., л); <*i* = ^f (*=2, 3, ...-, л),
/г — 1
4ik = <*ik— S Vf/а/л (*\ * = 2, 3, ..., n\ i^k)t
а*/г
^ = ^7 [a-ik— 2 Ту*/*] Р. * = 2, 3> •••» ^ *<■*)»
J (20.3-3)
20.3-2. 20.3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И ОБРАЩЕНИЕ МАТРИЦ 663
Вычисление определителя производится по формуле
det[a^]=YiiY22...Ymi.
(20.3-4)
Компактный метод требует меньшего количества промежуточных записей,
чем метод Гаусса, и становится особенно простым, когда матрица [а;&]
симметрична (aki = aik). В этом важном частном случае
«** = ?£ ('<*>•
(20.3-5)
(d) Матричная запись метода исключения. Метод Гауеса можно
толковать как преобразование данной системы (1) вида
к виду
п п—х 1 п п—1 1
с помощью последовательности неособенных матриц Г1§ Г2, ..., Т f выбираемых так
чтобы получающаяся матрица тптп_г ••• тгА была треугольной матрицей, как в
системе (2).
Кроме того, в компактной схеме речь идет об отыскании простой матрицы
преобразования Г такой, чтобы система Т Ах = ТЬ имела треугольную форму (2). Встречаются
и другие методы, в которых вместо умножения слева применяется умножение справа.
Некоторые из модифицированных схем, приведенных в литературе [20.5], позволяют
уменьшить накопление ошибок округления.
20.3-2. Итерационные методы (см. также пп. 20.2-6 и 20.2-7).
(а) Итерационные методы имеют преимущество перед методами
исключения для таких систем линейных уравнений, которые имеют достаточно
«разреженную» матрицу [ом], т. е. для которых многие из а^, особенно вдали
от главной диагонали, равны нулю. Такие системы (и притом очень большие)
встречаются в задачах численного интегрирования дифференциальных
уравнений с частными производными (п. 20.9-4).
Излагаемые ниже итерационные методы для системы линейных
уравнений (1) с действительными коэффициентами дают последовательные
приближения решения л^(1'=1, 2, ..., п) в виде (20.2-29). Невязки, получаемые
на каждом шаге итерации, будем обозначать через
(i = l, 2, ..., п; /=0, 1, 2, ...). (20.3-6)
Замечание. Для многих итерационных схем требуется, чтобы матрица
коэффициентов А = [вц,] была нормальна с положительно определенной симметричной
частью (п. 13.3-4) или чтобы матрица А была симметричной и положительно
определенной (п. 13.5-2). Если для данной матрицы коэффициентов это условие не выполнено, то
можно попробовать так переставить или преобразовать данные уравнения, чтобы
получить относительно большие диагональные коэффициенты, или можно решать
эквивалентную систему
п п п
2 2 ahiaikxk= 2 ahibi
1=1 £=1 t = l
(ft= 1, 2,
n),
(20.3-7)
матрица коэффициентов которой обязательно симметрична
если только матрица А не вырождена.
положительно определена,
(Ь) Простая итерация и итерация Зейделя.
Преобразуем данную систему (путем перестановки уравнений и/или умножения их
на постоянные) к такому виду, чтобы диагональные коэффициенты ац были
положительными и возможно большими. Начиная с произвольных значений
664 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.8-3.
д]°](/ = 1, 2, ..., /г), вычислим последовательные приближения по формуле
простой итерации
(i = l, 2 /г; / = 0, 1, 2, ...) (20.3-8)
или по методу Зейделя
»\л==1 ^ /
(/ = 1, 2 /г; / = 0, 1, 2, ...) (20.3-9)
Обе схемы просты, но могут сходиться медленно или не сходиться совсем. Положи»
тельная определенность матрицы [а-. 1 гарантирует сходимость.
(c) Методы релаксации позволяют ускорить сходимость
итерационного процесса при вычислении вручную. Начиная с произвольного
приближения *[.°] (обычно просто х\°]==\, х\£*]=х^ ==...== х\®]==0), пробуют
находить последовательные приближения х\^ таким образом, чтобы свести п
невязок (6) к нулю. На каждом шаге выписывают невязки ftp и
комбинируют следующие методы:
1. Координатная релаксация. На каждом шаге «ликвидируют»
наибольшую по абсолютной величине невязку ftp путем
исправления ОДНОГО ТОЛЬКО Xjl
fill
*[/+1] ^ х\П —+--\ *['+! W/1 (/ ф /). 120.3-10)
Для начальных шагов допустим грубый подсчет jfj^"1^
2. Блочная и групповая релаксации. В некотором множестве
(«блоке») координат хЦ^ придадим им равные приращения яр"*"1-' —
—ху] так, чтобы ликвидировать одну из невязок /[/~*~1-' или чтобы
свести к нулю сумму всех невязок. Этот последний метод
применяется, в частности, когда все начальные невязки ftp имеют
одинаковый знак.
При групповой релаксации для выбранного множества координат
х\^ приращения могут быть различными.
3. Сверхрелаксация. Иногда можно ускорить сходимость
релаксации, изменяя знак регулируемой невязки и уменьшая ее
абсолютную величину, вместо того чтобы полностью ликвидировать ее на
данном этапе.
Методы релаксации особенно удобны при решении вручную большого количества
простых линейных разностных уравнений, используемых обычно для приближенного
решения уравнений с частными производными (п. 20.9-3). Эффективность методов
релаксации во многом зависит от навыков и искусства вычислителя, а также от знания им
физического существа вопроса.
(d) Систематическая сверхрелаксация применяется при
решении «разреженных» систем, возникающих в задачах численного
интегрирования уравнений с частными производными. Рассмотрим систему уравне-
20.3-3* 20.3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И ОБРАЩЕНИЕ МАТРИЦ 665
ний (1), преобразованную так, чтобы все диагональные коэффициенты был**
равны 1(^7=1), и заменим итерацию (9) на следующую:
^[/+1]=Л[/]_Ш/ /'2 ^/+11+ J aikXW-b\
(/ = 1, 2 n; / = 0, 1, 2, ...),
где сверхрелаксационный множитель coy > 1 выбирается для ускорения
сходимости; Методы выбора множителей со/ описаны в [20.5J.
(е) Градиентные методы минимизируют некоторую
положительную функцию типа
/ = i / = i
способом, изложенным в п. 20.2-7. Если матрица коэффициентов [alk\
симметрична и положительно определена, можно вести расчет по формулам
XU+\)=XU].
™—f C-i t z. )• ,а'-з-")
2 2 '..'!" *'
Если сходимость имеет колеблющийся характер, то ее можно ускорить путем
умножения последнего члена формулы (11) на 0,9 при некоторых значениях /.
(f) Метод взаимных градиентов. Пусть дана система
линейных уравнений (1) с действительной, симметричной и положительно
определенной матрицей коэффициентов [а^]9 и пусть х\0^ — начальное приближение.
Положим v^=ffl и вычислим последовательно
,ГУ+П —ГГЛ k=\
ъ 4'Ч/]
| = д:1
*Ш
л п
ki{aikv[n>
2 2 ^РЧ"
<,[/+!] =;[/+П * = !*=!
»[/]
of/1
t = l, 2, ..., л,
/ = 0, 1, 2, ...
(20.3-12)
где т^= 2 2 алл°л^ °А^в Значения /[/] удовлетворяют формуле (6). При
Л = 1Л = I
отсутствии ошибок округления этот метод дает точное решение xi = x\n}
после п шагов; сверх того, этот метод имеет все преимущества итерацион*
ной схемы, но требует много умножений.
20.3-3. Обращение матриц* (см. также пп. 13.2-3 и 14.5-3).
(а) Методы пп. 20.3-1 и 20.3-2 непосредственно применимы для
численного обращения . данной невырожденной матрицы А = [я/лЬ а также для
вычисления det [а^].
666 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.3-4.
(Ь) Итерационная схема обращения матрицы. Чтобы для данной
(п X /2)-матрицы Л найти обратную матрицу А'1, начинают с произвольной (яХя)-матрицы
ДО]
X (скажем, X = Е) и вычисляют последовательные приближения
Л/ + 1].
ЛП |
Xй ^ АЛ = Xlji (2E — ЛХ[/]) (/ = 0, 1, 2, ...). (20.3-13)
Если эта последовательность сходится, ее пределом является Л-1 (см. также п. 20.2-2, Ь),
(с) (см. также п. 13.4-7). Для каждой невырожденной (лхя)-матрицы А
А~1 =
где
= - т (А"~1 + Vя _2+ - + W + ап-гЕ)-
п
ах = — Тг Л,
а. = - 1 [Д/1 Тг Л + дм Тг Л2 + ... + аг Тг Л^1 + Тг Л']
(/ = 2. 3 л).
(20.3-14)
20.3-4. Решение системы линейных уравнений и обращение матриц при
помощи разбиения на клетки (см. также п. 13.2-8).
(а) Система линейных уравнений (1) может быть записана в матричной
форме (п. 14.5-3):
fan а12 ... а1п\ /хЛ /Ь^
а21 а22 ... аш \[ х2 \==( Ь2 \^^
Axi
(20.3-15)
W/
Уравнение (15) можно преобразовать путем разбиения матриц на клетки:
Ахеее
Ац | Л18
)(Й)-Й)-*
где
Л*11 «12
Ли = (а21 «22
(*1
ХМ** ; ^ =
(т<л).
\атг ат2
(20.3-16)
Решение системы матричных уравнений
AuXt + AnXi^Bi, | (20.3-17)
А2\Х1-\'А22Х2^= В2 J
приводит к уравнению
(Ап-А12А£А21) Х1 = Б1-Л12Л^2, (20.3-18)
которое дает т линейных уравнений для первых т неизвестных лг^, дг2, ..., хт,
если только известна обратная матрица A^i порядка п—т. Этот метод
особенно удобен, если надо найти лишь первые т неизвестных.
(Ь) Обратная матрица А~г получается тоже разбитой на клетки
где
Сц = (Ац — А12А2£А21) 1, С2г — — А2£А2\Сц$
С22 = (А 22 — А 21-/4 ]fj Л12) , С12 = — A ilA i2C22»
(20.3-19)
так что обращение матрицы порядка п сводится к обращению двух матриц
меньших порядков (т и п—т).
20.3-5. 20.3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И ОБРАЩЕНИЕ МАТРИЦ 667
20.3-5. Собственные значения и собственные векторы матриц (см. также
пп. 13.4-2-13.4-6, 14.8-5 и 14.8-9).
(a) Характеристическое уравнение. Собственные значения
%k матрицы A = [aik] порядка п находят как корни характеристического
уравнения
FA (I) = det [aik-Mih] =0 (20.3-20)
одним из методов, описанных в пп. 20.2-1—20.2-3. Чтобы избежать
непосредственного развертывания определителя, можно вычислить FA (к) для /г+1
выбранного значения Я (скажем, Я=0, 1, 2, ..., я), после чего многочлен
п-и степени F А (к) находится по одной из интерполяционных формул п. 20.5-3.
(b) Итерационный метод. Пусть матрица Л—эрмитова, так что
все ее собственные значения действительны; во многих приложениях А
действительна и симметрична. Если наибольшее по модулю собственное значение
%м — простое, то, начиная с произвольного начального вектора х^> например,
-{1, 0, 0, ..., 0}, вычисляют последовательно произведения
хи+11 = а;АхМ (/=0, 1, 2, ...), (20.3-21)
где ау—подходящий множитель, выбираемый, например, так, чтобы
наибольшая по модулю координата вектора лг^'+П равнялась 1. При возрастании j
векторы х^ будут приближаться к собственному вектору, принадлежащему
доминирующему собственному значению Хм\ последнее можно вычислить по
формуле
п п
2 2 aikxixk
Этот метод сходится тем быстрее, чем значительнее отличается I %м I от
модулей всех остальных собственных значений матрицы А и чем ближе
направление начального вектора х^ к направлению искомого собственного вектора;
если х*- —{1, 0, 0, ..., 0} не удовлетворяет этому условию, то пробуют
{0, 1, 0, ..., 0} и т. д. Можно ускорить сходимость путем применения А2
или А3 вместо А в формуле (21).
Последующие собственные значения и собственные векторы находят после
приведения матрицы (п. 14.8-6). О других методах см. [20.5]", [20.9].
Если наибольшее по модулю собственное значение "Кщ имеет кратность т>1, то
последовательность векторов, определенных формулой (21), сходится к одному из
собственных векторов, принадлежащих Xjy. Выбирая различные начальные векторы дДЭД,
можно построить т линейно независимых векторов инвариантного подпространства,
принадлежащего А,д|,
(c) Метод вращений. Если дана действительная симметричная матрица А =
= Га..1 = лЕО], то начинаем с исключения недиагонального элемента еще, имеющего
наибольшую абсолютную величину, путем ортогонального преобразования
лШ = гГ'Л.. r,-(<tt).
где
Uk -б* V + (cos *i - *) (б/+б*)1+sin *i Wk - б'6*)
(/, £=1« 2 я),
2а1К
t2 2$! = — .
aII~aKK
(20.3-23)
668 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.4-U
(вращение на угол fti в плоскости, натянутой на е/ и eir, см. также пп. 2.1-6 и
ГП [2]
14.10-2, Ь). Применяя аналогичный прием к А , получают Лит. д. Произведение
матриц преобразования Tt Tt Ts ... сходится к некоторой ортогональной матрице,
которая приводит матрицу А к диагональному виду, даже если она имеет кратные
собственные значения.
20.4. КОНЕЧНЫЕ РАЗНОСТИ И РАЗНОСТНЫЕ УРАВНЕНИЯ
20.4-1. Конечные разности и центральные средние.
(a) Пусть у=у (*)— Функция действительного переменного х. Для данного
множества равноотстоящих значений аргумента
xk=x0+kAx (6=0, ±1, ±2, ...; Д* = Л>0)
и соответствующих значений функции ук=у (хк)=у (x0+k^x) определяют
нисходящие разности (для интерполяции вперед)
Д"Уа = ДУл+1 — Ьук = ук+г — tyk+i+Уь
д^=Д'-^+1-Д'-1^= 21 (~ lY[r,)y*+r-j I
/ = о w'
(г = 2, 3, ...; £=0, ±1, ±2, ...) ]
я восходящие разности (для интерполяции назад)
ЧУк = Ук—Ук-1 = Ьук_ъ \
(г = 2, 3, ...; >fe = 0, ±1, ±2, ...)• J
Число г называется порядком разности.
(b) Центральные разности определяются формулами
ЬУк = Ук + \/2-Ук - 1/2 =А^ - 1/2,
6^ = 6'-^+1/2-6'-^_1/2 = Д^_г/2 (r = 2, 3, ..
Центральные средние определяются формулами
Иг</* = | (^/*"1^- 1/2 +^"^ч-1/2) (г = 2» 3» •••)•
Если значения функции yk = y(x0 + kAx) известны лишь для целых
значений ky то центральные разности и центральные средние можно вычислить
для k=± Va» ± 3/г» •••, если порядок г нечетный, и
для 6=0, ±1, ±2, ...j если порядок г четный.
(20.4-1)
(20.4-2)
(20.4-3)
(20.4-4)
20.4-2. 20.4. КОНЕЧНЫЕ РАЗНОСТИ И РАЗНОСТНЫЕ УРАВНЕНИЯ 669
(с) Конечные разности удобно располагать в таблицы таких типов;
Х-х У-1
Х0
ХХ
*2
Хз
х-я
Х-2
Х-1
х0
х±
Х-2 У.
Х-1 У-
Хо Уо
ХХ Ух
Xt Уг
Уо
Ух
Уг
У»
У-
У-
У-
Уо
Ух
•2
-1
&У-х
Д|Л>
ЬУх
ьу*
■S
ЧУ-2
-2
ЧУ-х
■1
УУо
УУх
<*-•/,
6У-Чг
*УЧг
ьу*/г
Aty-i
Д2|/о
A2l/i
Ч2У-х
Ч2Уо
Ч2Ух
62*/-i
б2Уо
Ь*Ух
Ь*У-х
A4l/-i
Wo
«•y-l/f
Ь*Уо
6*y1/2
(20.4-5)
(20.4-6)
(20.4-7)
Заметим, что вычисление разности порядка г требует знания г+1
значения функции и что у многочлена п-й степени разности п-го порядка постоянны.
20.4-2. Операторные обозначения.
(а) Определения. Оператор смещения Е для функции у = у(х)
действительного переменного х и фиксированного приращения Ax = h определяют
формулами
Еу(х)=у(х+Ах), Е>-у(х)=у(х+гЬх), (20.4-8)
где г — любое действительное число.
Разностные операторы Д, V, б и оператор усреднения |х определяются так:
Л У (х)=У (х+Ах) — у(х), \
Чу(х)=у(х)-У(х — Ьх)> I (20.4-9)
6,w=(*+^)-H*-^).)
ру{х) = ±[у(х-^)+у(х+Щ]. (20.4-10)
Заметим, что при а^ = и (xQ + ЛД*), vk~v (*o "+" ЛДд0
AukAvk- )
Д ("* + vk) e b»k + Avk> Л (auk) = (
*= «ЛА»Л 4- t»^AwA + Aw
670 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.4-3.
Заметим также, что при А* = 1
ДдгИ = д [*<*-1) ... <*-г-{-1)] = /-*(*-1) ...<* —r + 2) = r*[r—l3i
(20.4-12)
(20.4-13)
(20.4-14)
Заметим
(20.4-15)
(b) Соотношения между операторами (см. также п. 14.3-1):
A = E-l=EV = E1/26, V = l-E~1 = E-1A = E-1/26,
6 = E1/2-E-1/2 = E-1/2A = E1/2V, ^ = |(E1/2 + E-1/2),
Е=1 + Д, VA = AV = 62.
Отметим для памяти
Дг = (Е-1)^2 (-iy(j)E'-' (г=1, 2, ...),
/=о w'
откуда легко получаются формулы для V = E~*IA и 6 = Е~1^,Д
также, что
Если г —целое и положительное, то ряд (15) конечен; в противном случае
его сходимость требует исследования.
(c) Для аналитической функции
Er = erA*D=l + rA*D+^r(rA*D)2+... (о = —) (20.4-16)
(операторное обозначение ряда Тейлора, п. 4.10-4).
20.4-3. Разностные уравнения,
(а) Обыкновенное разностное уравнение порядка г есть уравнение
G(*k> У к* Ук+ь •••» Ук+г)^0(хк, yk, Eyk% •♦., E^ft)=0
(&=0, ±1, ±2, ...? r=l, 2, ...), (20.4-17)
связывающее значения Ук=1У(хь)=у(хо + ^ А*) функции у=*у(х) на
дискретном множестве значений *=*£=л:04-& Д#> где А#—фиксированное
приращение. Часто бывает удобно ввести в качестве новой независимой переменной
*-*0--0, ± 1, ±2, ...
А*
величину к-
Обыкновенное разностное уравнение порядка г можно представить как
соотношение, связывающее значение уь и конечные разности ts}yki Vlyk или &уь
вплоть до порядка г. Разностное уравнение может также связывать уь и
раздал V *уь &иъ
ностные отношения —г , — или —— вплоть до порядка г.
д*' ajc' ^xi
Решением разностного уравнения (17) называется такая функция y=zy(x),
что последовательность \}ъ удовлетворяет данным уравнениям для некоторой
области значений к. Общее решение обыкновенного разностного уравнения
порядка г содержит, вообще говоря, г произвольных постоянных, которые
должны быть определены по начальным, краевым или другим дополнительным
условиям, налагаемым на уь- Решение разностного уравнения в любой
конечной области значений k сводится в принципе к решению системы уравнений.
Разностные уравнения применяются: 1) для аппроксимации дифференциальных
уравнений (пп. 20.9-2 и 20.9-3) и 2) для решения задач, прецставляющих модели с
дискретными переменными.
20.4-4. 20.4. КОНЕЧНЫЕ РАЗНОСТИ И РАЗНОСТНЫЕ УРАВНЕНИЯ 671
Пример: суммирование рядов. Задача решения разностного уравнения
первого порядка вида
А**-1 = ^л = аА или Ук=Ук_1 + ак (20.4-18)
С данным начальным значением у0 = а0 равносильна задаче суммирования ряда (п. 4.8-5)
k
yk = yk-l+ak = 2 af <* = 0' U 2' •••>• (20.4-19)
7=0
Эта задача аналогична интегрированию дифференциального уравнения y' = f(x).
Операторы 2 и V являются взаимно обратными. Отметим суммирование по частям
п п
2 "kAok = (un+lvn+l-umvm)- 2 »* + 1Л"*- <2О-4-20>
(b) Уравнение с частными разностями связывает значения
Ф.у ... =O(x0+iAx, yQ+jby ) (i. / =0, ±1. ±2, ...)
функции Ф = Ф (х, у, . . .); порядок уравнения с частными разностями есть наибольшая
разность между значениями i, значениями / встречающимися в этом уравнении.
В п. 20.9-3 приведены формулы, выражающие различные разностные операторы через
значения функции Ф-. .... и указано их применение для приближенного решения
дифференциальных уравнений с частными производными.
20.4-4. Линейные обыкновенные разностные уравнения.
(а) Структура общего решения (см. также пп. 9.3-1 и 15.4-2).
Линейное обыкновенное разностное уравнение порядка г имеет вид
ao(k)yk+r+<ti(k)yk+r-i+ ... +*г(Ь)ук**
-[0в(*)ЕЧ-М*)Е'-1+ .« +*ЛЬ)\Уы=№)> (20.4-21)
где at (k) и f(k)—данные функции от 6=0, ±1, ±2, ... Общее решение
уравнения (21) может быть представлено в виде суммы какого-либо его частного
решения и общего решения соответствующего однородного уравнения (триве*
денного* уравнения)
la0(k)E>'+a1(k)E>'-i+ ... +ar(k)]yk = 0. (20.4-22)
Любая линейная комбинация решений линейного однородного разностного
уравнения (22) является решением этого уравнения (принцип наложения).
Теория обыкновенных разностных уравнений во многом подобна теории обыкновенных
дифференциальных уравнений. В частности, однородное линейное разностное уравнение (22)
допускает не более г решений У(1)^ , У{%)ь » • • • » линейно независимых на множестве
k = 0, 1, 2, ... Линейная независимость г таких решений равносильна требованию, чтобы
определитель Казоратти
" УП) k У(2) k **• У1Г) k
yiv k+i ^(2) ft+i ••• yir) k+i
K [ya)k* yiz)kt • • • * ymk] s
y(V k + r-i yl2) k + r-i *•• yir) k + r-1
(20.4-23)
не был тождественно равен нулю при &=0, 1, 2, ... Этот определитель аналогичен
определителю Вронского в п. 9.3-2.
Если в неоднородном уравнении (21) правая часть представляет собой линейную
комбинацию f (k) = a ft (k) + 0^2 Ш, то решение^ этого уравнения есть подобная же
линейная комбинация решений, отвечающих правым частям ft (k) и f2 (k).
(b) Метод вариации произвольных постоянных (см. также
п. 9.3-3). Если известны г линейно независимых решений у{1) k, y(2) ^, ... ,~ y(r) k
«приведенного» уравнения (22), то общее решение неоднородного линейного разностного
уравнения (21) можно найти в виде
Vk - С1<*> »ал + С2 <» »<« *+-.+ Сг (*) ytnit (20.4-24*)
672
ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.4*5.
где
г
2 *<Л>А+/ДСА<*>=° (/=1. 2. .... г-1).
\ (20.4-246*
S/,A)fe + rACft <*>=М*>.
После решения системы г линейных уравнений (246) относительно АС* (Л) находим
каждое Сд (Л) путем суммирования, как в формуле (19).
20.4-5. Линейные обыкновенные разностные уравнения с постоянными
коэффициентами (см. также пп. 9.4-1—9.4-8). Общее решение линейного
однородного разностного уравнения
аоУк+г+^Ук+г-1 + ''' + агук^(а0Ег+а1Е^ + ...+аг)ук==0 (20.4-25)
с постоянными коэффициентами а0, alt ... , аг имеет вид
У к = Clki + C^t + • • • + СД*' (20.4-26)
где А*, А,2, ... , А,,. —корни характеристического уравнения
а0Кг+а1'кГ1 + ... + аг = 0, (20.4-27)
если только все его г корней различны. Если некоторый корень, скажем,
Xj, имеет кратность т, то соответствующий член в решении (26) составляет
(Cl + kC2 + ... + km-iCmy) №. Если все коэффициенты aj действительны, то два
члена, соответствующих простым комплексно сопряженным корням Х = ре—1ф,
можно заменить на рл (A cos£<p+£ sin fop). Коэффициенты С/, А, В, ... должны
быть определены по начальным или краевым условиям.
Решение неоднородного линейного разностного уравнения
o{y,i+r + a1yk+r.1 + ... + aryk^(a0Er+a1E^ + ...+ar)yk=f(k) (20.4-28)
можно находить общим методом п. 20.4-4, Ь, но более удобными могут
оказаться специальные методы, излагаемые ниже.
20.4-6. Методы преобразований для линейных разностных уравнений с
постоянными коэффициентами.
(а) Метод г-преобразования (см. также пп. 8.7-3 и 9.4-5). Подвергнем
обе части разностного уравнения (28) z-преобразованию с помощью теоремы
сдвига 2 из таблицы 8.7-2, обозначив через
Yz(z) = % [yk; z] шшу0+^+^.+... (20.4-29)
г-преобразование неизвестного решения —последовательности y0t уъ у2, ...Это
приводит к формуле
yz (г)» ЦЦ + , У2] , (20.4-30)
где первое слагаемое справа, как и в п. 9.4-5, представляет «нормальную
Реакцию» на заданное внешнее воздействие —последовательность / (0), / (1),
(2), ... , а второе слагаемое отражает действие г начальных значений у0, уи
&>. ... , Уг-i- Здесь
Gz (2) — У о (°о2г+tfiz'-1 +... + аг_гг) +
+yi(a0zr-i + a1zr-* + ...+ar_2z) + ...+yr_la0z. (20.4-31)
Неизвестные yk могут быть получены либо как коэффициенты при 1/2*
в разложении Y^(z) по степеням z, либо с помощью таблицы г-преобразова-
20.4-6. 20.4. КОНЕЧНЫЕ РАЗНОСТИ И РАЗНОСТНЫЕ УРАВНЕНИЯ &73
пия (таблица 20.4-1). Как и в случае преобразования Лапласа, обращение
У2 (г) можно упростить с помощью разложения на простейшие дроби,
которые представляют «собственные колебания», соответствующие корням
характеристического уравнения (27).
Таблица 20.4-1
Краткая таблица г-преобразований и преобразований Лапласа
от ступенчатых функций
1
2
3
4
5
6
7
8
9
10
Последовательность выбранных
значений
yk=y{k)
(k = 0, l. 2, ...)
1
k
(Э (*=0,1,2....)
«*
СУ"1
(n = 0, 1, 2, ...)
ak sin bk
ak cos bk
2-преобразование
% \«k- z\ =
00
/=o
z
z-\
z
(2- 1)*
г (г + 1)
(г- 1)в
2
<2-l)n+1
2
г — a
az
(z-a)*
2
<2-a>n+1
2
(z — a) (z-6)
аг sin 6
22 — 2oz cos 6 -f- a2
z (2 — a cos 6)
г2 — 2az cos b-\- a?
Преобразование Лапласа
ступенчатой функции
оо
JSP Г7. и И\Л — -...""".* ... ▼ f, /Л /~'5
«^ Х.Ц-У I'JJ s ^, У \\) е
/=о
s
1 1
s es — 1
s(e5-l)2
1
s (^ - \)n
es-l 1
s es — a
es — 1 a
s (es - a)2
** - 1 1
es-\ 1
, (**_a)(e*_ft)
*5 — I a sin 6
s <?2S — 2aes cos 6 + a2
£5 — 1 es — a cos 6 J
s *25 — 2aes cos 6 + a2
(b) Представление выборочные данных рядами
импульсных функций и ступенчатыми функциями. Метод
преобразования Лапласа. Если формально ввести асимметричную импульсную функцию
6+ (0. то последовательность выборочных значений у0. Ух* У2* ..• можно представлять
(и притом взаимно однозначно) рядом импульсных функций
У* (О - Уо 6+ (t) + yt6+ (t - Т) + уг&+ (t - 2Г) + ... (t > 0), (20.4-32)
где Т — положительная постоянная (выборочный интервал).
Если две последовательности выборочных значений у0, уи уц ... и f (0)t f (\)tf (2b ...
удовлетворяют разностному уравнению (28), то соответствующие функции у* (t) и f* (t)
удовлетворяют функциональному уравнению (разностному уравнению для функций):
а0У* (t + гТ) + агу* [t + (г - 1) Г] + ... + <у/* (0 - f* \f) {t > 0) (20.4-33)
с определенными начальными условиями.
22 Г, Корн и Т. Корн
674 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.4-7.
К уравнению (33) можно применить формальное преобразование Лапласа импульсных
функций (п. 8.5)
£ [у* it); s] в Я [У* </)] = Уо + Ухе" Ts + V*~ 2Ts + ... (20.4-34)
При этом
<% [у* (t + kT)] =ebTs {<£ [у* </)]-<*о + Уг е- Ts + ... +ук-\е-1Ь-1) Ts)}.
Изложенный метод преобразования аналогичен методу ^-преобразования с z = e's
(дискретное преобразование Лапласа; п. 8.7-3).
Вместо того чтобы применять обобщенные функции, можно представить
последовательность у0, уи Уг* ••• с помощью соответствующей ступенчатой функции (см. п. 21.9-1)
t
l+y(t) = f у* (X)dl = yk при kT<t < (k + 1) T (t>0; £ = 0, 1, 2, ...). (20.4-35)
0
Функции \^y(t) и j[ f (t) удовлетворяют тому же функциональному уравнению*
что и у* (/) и f* (t), так что снова допустимо преобразование Лапласа.
Отметим формулы
В табл. 20.4-1 приведены пары преобразований Лапласа для некоторых ступенчатых
функций; при этом принято, что Т = 1.
20.4-7. Системы обыкновенных разностных уравнений. Матричная запись.
Как и в случае дифференциальных уравнений, можно рассматривать систему
обыкновенных разностных уравнений, содержащую две или более неизвестных
функций y(Xk)=yk> z(xk) = Zk, ... Любое разностное уравнение (17) порядка
г можно привести к системе г уравнений первого порядка введением новых
переменных Е*уь или Alyk (i = l, 2, ... , г—1).
Так же, как в п. 13.6-1, система линейных разностных уравнений
первого порядка (рекуррентных соотношений)
Ук+i = аиУк + 012** + — + h(b), \
*Ы = аш1Ук + <Ь*к + -+Ы(Ь)' \ (20.4-36а)
с постоянными коэффициентами щ* может быть записана в матричной форме
(см. также п. 14.5-3):
Yk+1 = AYk + F(k), (20.4-366)
где Yksa{yk, гь, ...}, F(k)^{fx(k)t /2 (£)> ...} —векторы (матрицы-столбцы),
a Л == [а;у]. Если дано YQ ss {y0, z0, ...}, то решением является
k-i
Yk = AkY0+ 2 Ak~h-iF(h), (20.4-37)
л=о
где матрица Akt по аналогии с п. 13.6-2, Ь, называется матрицей изменения
состояния для системы (36). Степени матрицы Ак, нужные для решения,
могут быть вычислены с помощью теоремы Сильвестра (п. 13.4-7, Ь), так
что каждое собственное значение матрицы Л, т. е. корень
характеристического уравнения
det[i4-X£l = 0, (20.4-38)
снова соответствует собственным колебаниям (см. также пп. 13.6-2 и 20.4-5).
20.5-2.
20.5. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ
675
Этот метод применим, в частности, к решению линейного разностного
уравнения (28) порядка г, если оно сначала приведено к системе вида (36)
путем введения yk+l, yk+ъ ••• » Ук*г-\ в качестве новых переменных, так что
У к — {Ук+г-Ъ УА+г-2.
(*)-{£/(*), 0,0,
/ °1 а2
la, сц>
- : ;
••• > Ук\г
.., о},
аг-\
а0
0
0
а0 }
0
0
/•]
(20.4-39)
0 0 ... 1 0
20.4-8. Устойчивость.
(a) Аналогично п. 9.4-4, линейное разностное уравнение (28) или система
(36) с постоянными коэффициентами называется устойчивой, если все корни
соответствующего характеристического уравнения (27) или (38) по
абсолютной величине меньше единицы. При этом действие малых изменений
начальных условий затухает (стремится к 0) при возрастании k.
Имеется признак устойчивости, аналогичный условию Раусса —Гурвица
(п. 1.6-6, Ь) для корней с отрицательной действительной частью.
(b) Определение устойчивости и асимптотической устойчивости решений
по Ляпунову (п. 13.6-5) и соответствующие теоремы (п. 13.6-6) легко
распространяются на решения Y0t YXt Y2> ... линейных и нелинейных
автономных систем разностных уравнений
Yk+i^FWk) №==0, 1, 2, ...). (20.4-40)
d V
Условия типа -^ ^ 0 для функций Ляпунова V (у) непрерывного
аргумента просто превращаются в условия А1/(КЛ)^0 для функции Ляпунова
V (Yjg) дискретного аргумента.
20.5. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ
20.5-1. Вводные замечания (см. также пп. 12.5-4, b и 15.2-5).
Интерполяционная формула сопоставляет с функцией у (х) функцию известного класса
У (*) =н К (я; а0, ах, а2, ... , ал), зависящую от /г + 1 параметров а/,
выбранных так, чтобы значения Y (х) совпадали со значениями у {х) для данного
множества я+1 значений аргумента хь (узлов интерполяции):
У(хк)=У(Хк)=Ук-
В пп. 20.5-2 — 20.5-6 излагается параболическая интерполяция. Другие
интерполяционные методы рассматриваются в пп. 20.5-7 и 20.6-6.
Применение интерполяции (и, в частности, интерполяционных многочленов) не
всегда оправдано. В случае эмпирических функций может оказаться желательным сгла-
окивание колебаний у (^), вызванных случайными ошибками, например» посредством
аппроксимации по методу наименьших квадратов.
20.5-2. Общие формулы параболической интерполяции (значения
аргумента могут быть и неравноотстоящими). Интерполяционная формула п-го
порядка аппроксимирует функцию у (х) многочленом /г-й степени Y (х),
удовлетворяющим условиям Y(xk)=y(хь)—Ук в я+1 узлах
интерполяции—точках xk (k=0t 1, 2, ... 2 /г).
22*
676 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.Б-2.
(а) Интерполяционная формула Лагранжа
(х — хл) (х — хЛ ... (х — хЛ
Y (*) = ; _ у < sbii aL „. j.
■*»)...
1 (х
l(*i
(х«-хп)
-*«)(*-
-*о)(*1"
-1_-
-*а).
-*•>■
(*-
..(*-
...(*f
ч) (*
*п)
~*п)
-*!)■
</l+-
...(*-
••
"*«.
-l)
i'n - *о) (*„ - *i) ... ft, - *„-:) ^ (20'5'°
(b) Разделенные разности и интерполяционная
формула Ньютона. Разделенные разности определяются так:
(г = 2, 3, ...).
Интерполяционная формула Ньютона имеет вид
У (*) = Уо + (х—*b)M*o. *i) + (* —*о)(*—*1)Д2(*о» *i» *t)+...
— + Ц (* — *л) Ал (*ot *i» *2» ••• » */*>• (20.5-3)
В отличие от формулы (1), прибавление новой пары значений (xn+l9 yn+i)
сводится здесь просто к прибавлению одного нового члена. Разделенные
разности (2) для формулы (3) удобно записывать в таблицу того же типа, что (20.4-5).
Нахождение разделенных разностей есть линейная операция (п. 15.2-7) над у (*).
Каждая функция (2) вполне симметрична по всем своим аргументам.
(c) Итерационно-интерполяционный метод Эйткена.
Если требуется найти лишь значения интерполяционного многочлена У (х)%
а не его представление, то может быть применена следующая схема. Пусть
У if k- ••"— интерполяционный многочлен, определяемый парами (X(t yi)t (#/, #/),
(*а. Уь)>---> так что
Ут...п = У(х).
Интерполяционные многочлены возрастающих степеней могут быть получены
последовательно так:
х, 1
'-*о Уо\ Г12=—-—\*—Xi Уг\
*2 *o I X — *a *12l 8 ° I *— x9 ^ 123 I» • • •
Этот процесс можно закончить, когда у значений двух интерполяционных
многочленов последовательных степеней совпадет требуемое количество знаков,
(d) Остаточные члены. Если у (х) достаточное число раз
дифференцируема, то для интерполяционной формулы, базирующейся на п+\
значениях функции y0t ylt y2t..., уп, остаточный член (ошибка интерполяции)
может быть записан в виде
*•*(*)-* М-У М-7гТШУ(,1+1,Ю П (*-**)» (20.5-4)
т * = о
£0.5-4.
20.5. ИНТЕРПОЛЯЦИЯ ФУНКЦИИ
677
где I лежит в наименьшем интервале /, содержащем все точки х0, хъ х2, ..., хп
и х (см. также п. 4.10-4; вообще говоря, g зависит от х). Отсюда следует
оценка
п
1
I /?«+i м I ^ игтш ™*х} у(п+1) го IП I *-** I- (20-5-5>
20.5-3. Интерполяционные формулы для равноотстоящих значений
аргумента. Ромбовидные диаграммы. Пусть Ук = У (**)> xk=x0+k Ал: (6=0, ± 1,...),
где Д#—фиксированное приращение, как в п. 20.4-1; введем обозначение
(a) Интерполяционные формулы Ньютона. Если даны у0,
Уъ Уъ>'" или #о» У-ъ У-г>---> то из формулы (3) получаем соответственно
Y(x) = yo+jf А^ + ^2ГДА% + ..., |
\ (20.5-6)
Первая формула применяется для интерполирования «вперед», а вторая для
интерполирования «назад».
(b) Интерполяционные формулы с центральными
разностями. Табл. 20.5-1 дает наиболее употребительные интерполяционные
формулы для того случая, когда заданы значения у0, у1у у2,... и y_lt у_ъ ...
(см. также рис. 20.5-1). Заметим, что формулы Эверетта и Стеффенсена удобны
при работе с такими таблицами, для которых проще составлять таблицы
разностей только четного или только нечетного порядков.
Коэффициенты всех указанных выше формул приведены в табл. 20.5-2.
(c) Применение ромбовидной диаграммы. Многие
интерполяционные формулы можно получить с помощью ромбовидной диаграммы
(диаграммы Фрезера), приведенной на рис. 20.5-1. Некоторые более сложные
интерполяционные формулы (например, формулу Эверетта) можно получить,
усредняя несколько эквивалентных интерполяционных многочленов.
20.5-4. Обратная интерполяция.
(а) По данным значениям
xk = xq -f kAx, Ук^У^к) (A = 0, 1,2 л)
требуется найти заключенное между х0 и хх значение \ аргумента х, соответствующее
данному значению ч\ функции у (х); Ах предполагается настолько малым, чтобы f было
единственным. Можно применить общую формулу (1) или (3), меняя ролями хну. Вместо
этого можно применить одну из итерационных схем п. 20.2-2 для решения уравнения
К(£)-П = 0,
где Y (х) — подходящий интерполяционный многочлен, аппроксимирующий у (х); для
первого шага итерации применяют линейную интерполяцию, для второго шага —
квадратичную и т. д. Наиболее удобен итерационно-интерполяционный метод Эйткена
(п. 20.5-2, с), в котором надо поменять местами х и у.
(Ь) Обратная интерполяция с помощью обращения рядов.
Применяя любую подходящую интерполяционную формулу в виде степенного ряда
получаем
где
Y (х) == «о + atx + а2х* + ... ъ* у,
г^У-а° 4-Г (У-аА2 I
8 а19 5 «1 W»
(20.5-7)
Интерполяционные формулы с центральными разностями
Дано нечетное число п + 1 — 2т + 1 значений функции yk = у (дг0 + k Ax) (k = 0, ± 1, ± 2, ..
Таблица 20.5-1
где Ах — фиксированное приращение; и ■■
Х — Хр
Ах
со
№
Название
формулы
Интерполяционный многочлен Y (х)
Остаточный член 1)
Rn+l{x) ^R2m+i (x)
Стирлинга 2)
*>+ 2j U+lj 2 + Zj 2A^ 2*-1 )6 ^
k=0 fc=l
(2^+l)^2/7l+1><l)AjCH
Бесселя 8)
У о + ff i
2
m—1
m—l
>2*„ . a2^,
+ 2j 2ГГГ1 2* J6 "/.+ 2-1 1 2* J 2
£ = o
* = 1
f^"1)^^^
m — l
Эверетта »)
<>-*> ,.+*„+ 2 {(^к^(%+дт V4
*=i
("+;"')»lM"(|)4^
Стеффенсена
*=1
&й)',2т+1,е>^н
*) | лежит в наименьшем интервале, содержащем х и все применяемые узлы интерполяции.
,ч о /u + k\ и {и2— 1) (и2 — 2*) ... (и*—Л*)
*) Заметим, что („+,)- ^FFTji '
8) Модифицированная формула Бесселя дает простейший многочлен, учитывающий влияние разностей до 6-го порядка:
У U) = ,, + uty4t + U^ZJ1 Щ^ + "<«-V.>C-l) (б.,1/2 - ^ «•*,.) +
, (ы + 2) (и*- 1) и(Ь*уо + Ь*уг 191 6«у0 + 6«^
24
2 924 2
)•
y_4 (u+4), A2y_5 (u+5)3 A4y_6 (u+6)5 A6y-7 [u+lh
1 ^Ay.4 (u+4)2 A3y_5 (u + 5LA5y-6 (u+6)6 A7y.7
y-3to+3)i Azy^u+4)3 A\5^u+5)5 A6y.^6)7
1 Ay-3 {u+3)2 А3у-л (u+4UA5y-s ("+5)бА\$
y.2 te+2hA2y-3(u+3)3A4y.4^u+4)5A6y.5 (u+5)7
1 Ay-2 (u+2)2 A3y-3 {u+3)4 A5y,4 (u + 4)6 A7y.5
y-f ЬЩ#!ьЬ+2)3А%3Ь+3)сА*у-4Ык
i Ay-, (u+f)2A3y-2(u+2)4A5y-3(u+3)6 A7y.4
У01^(и)г+-А2^-{и+1)3у;А4у_г+^^^
1-^Ay^--(u)i"^"A3y-r (ti+tk r;JW*" №)б*А7У-з
yS "X S ^ч S \ у
yt (u-1), A\ (u)3 A4y-< lu+1)5 A6y-2 (u+2)7
\ S X. / \ , / \ 7
/ Ayf (u-1)2 A3yQ lu)4 Asy4U/+1)SA7y-2
y2 (u-2)f A2yf (u-l)3 A% (u)5 A6y4 (u+1)7
/ 4^2 Ы-ги A3yf (u-lL A5y0^luKA7y4
Уз^'3)^Л%^и'2)3^4У1 \^-';> ЛбУ0 ^U)7
1 Ay. (u-3h A% (u~2)4 A5yf(u-t)6 A7y0
yS \ У^ \ ^ \ /
У4 (u-4)f A2y3 (u-3)3 A% (u-2)5 A% (q-1)7
—*— Ньютона (бперед) Гаусса ff) * •••*••- Бесселя
-+*-Ньютона (назад) —►- Стирлинга (и+к)5*уи+к№
Рис. 20.5-1. Ромбовидная диаграмма для интерполяционных формул. Сокращенное
обозначение
(U + «s=i-(U + ft)M = (u + *).
Для получения интерполяционной формулы вдоль некоторого пути диаграммы
применяются следующие правила:
1. Когда столбец разностей пересекается слева направо, добавляется один член.
2. Если путь входит (слева) в некоторый столбец разностей с положительным
наклоном, то добавочный член равен произведению разности, стоящей на пересечении пути
и столбца, скажем, Ьгу^р, на коэффициент (и -J- р — 1)^ лежащий точно под этой
разностью.
3. Если путь входит (слева) в некоторый столбец разностей с отрицательным
наклоном, то добавочный член равен произведению разности, стоящей на пересечении пути
и столбца, скажем, Д^*/_р, на коэффициент (и -f* p)&. лежащий точно над этой разностью.
4. Если путь входит (слева) в некоторый столбец разностей горизонтально, то
добавочный член равен произведению разности, стоящей на пересечении пути и столбца,
скажем, ^у^р, на среднее арифметическое двух коэффициентов (м-J- р)^ и (и -J- p — 1)^,
лежащих соответственно точно над и под этой разностью.
5. Если путь пересекает (слева направо) столбец разностей между двумя
разностями, скажем, A*i/_(p_j_i) и Д*#_р, то добавочный член равен произведению среднего
арифметического этих двух разностей на коэффициент (и -J- р)^, стоящий на пересечении пути
и столбца.
6. Каждая часть пути, проходимая справа налево, вызывает те же самые члены*
что и при прохождении слева направо, но с противоположным знаком.
7. Со столбцом табличных значений функции можно обращаться, как со столбцом
разностей нулевого порядка, по тем же правилам, что и с остальными столбцами
разностей, если только ромб входит точно в этот столбец (левым концом). Таким образом,
атот столбец может пересекаться путем, образующим положительный, отрицательный
или нулевой наклон, как и с остальными столбцами.
680 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.5-4.
Таблица 20.5-2
Коэффициенты интерполяционных формул
Интерполяционная формула Лагранжа по пяти точкам
fs * L-2 <s) U + L-i <s> Li + Lo <s> fo + Li <s) fi + L2 <s) fr
Для отрицательных s обозначения столбцов указаны внизу
S
0.0
0.1
! 0,2
0,3
0,4
0.5
0,6
0,7
0,8
0.9
1,0
1,1
1.2
1.3
1,4
1,5
1,6
1.7
1,8
1.9
2.0
L-* (s)
0.000000
0.007838
0.014400
0.019338
0.022400
0.023438
0.022400
0.019338
0.014400
0.007838
0.000000
-0.008663
-0.017600
—0.026163
—0.033600
—0.039063
—0.041600
-0.040163
-0.033600
-0.020663
0.000000
L*(s)
L_i (s)
0.000000
-0.059850
—0.105600
-0.136850
-0.153600
-0.156250
-0.145600
—0.122850
—0.089600
-0.047850
0.000000
0.051150
0.102400
0.150150
0.190400
0.218750
0.230400
0.220150
0.182400
0.111150
0.000000
Lt (s)
Lois)
1,000000
0.987525
0.950400
0.889525
0.806400
0.703125
0.582400
0.447525
0.302400
0.151525
0.000000
—0.146475
—0,281600
-0.398475
-0.489600
-0346875
-0,561600
-0,524475
-0.425600
-0,254475
0.000000
Lo(s)
Li(s)
Iiiiiiiiil
L-t (s)
Lt(s)
iiiiiiiiil
L-t (s)
0.0
-0,1
—0,2
-0.3
-0.4
-0.5
-0.6
-0.7
—0.8
-0.9
-1,0
-1,1
-1,2
-1,3
-1,4
-1.5
-1,6
-1,7
-1,8
-1,9
-2,0
s
Примечание. Все коэффициенты становятся точными, если заменить
каждую конечную цифру 8 на 75, а 3 на 25.
Интерполяционная формула Стирлинга
fs*>f0 + sn6f0 + c2 (s) 6% + c8 (s) цб% + c4 (s) 6%
s
0.0
* 0.1
0.2
0.3
0,4
0.5
0.6
0.7
0.8
0,9
1,0
*
Ct(s)
0.00000
0.00500
0.02000
0.04500
0.08000
0.12500
0,18000
0,24500
0,32000
0.40500
0,50000
) Для s из правого столб
C3(s)
0.00000
-0.01650*)
—0.03200 *)
—0.04550 *)
-0.05600 *)
-0.06250 *)
—0.06400 *)
-0.05950 *)
-0.04800 *)
-0.02850 *)
0,00000
ца надо изменить знак.
C4(s)
0.00000
-0.00041
—0.00160
-0,00341
-0.00560
-0.00781
-0.00960
-0.01041
—0,00960
-0.00641
0,00000
S
0.0
-0.1
-0.2
-0.3
-0.4
—0.5
-0.6
-0.7
-0.8
-0.9
-1,0
20.B-4.
20.5. ИНТЕРПОЛЯЦИЯ ФУНКЦИИ
681
Таблица 20.5-2 (продолжение)
Интерполяционная формула Ньютона
fs^f0 + s AfQ + С, (s) А% + C3 (s) A»f0 + C4 (s) А% + Cfi (s) A»f0,
>л-* ~ 'и - s^„ + C2 (•) Vfя ~ C3 (s) V.fя + C4 (s) VVn - C6 (,) W|l
(для интерполяции надо брать положительные s)
s
-1,0
—0,9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
Ся is)
1,00000
0,85500
0,72000
0,59500
0,48000
0,37500
0,28000
0,19500
0,12000
0,05500
0,00000
—0,04500
-0,08000
—0,10500
—0,12000
-0.12500
-0,12000
—0,10500
-0,08000
—0,04500
0,00000
Cz (s)
-1,00000
-0,82650
—0,67200
-0,53550
-0,41600
—0,31250
-0,22400
-0,14950
—0,08800
-0,03850
0,00000
0,02850
0,04800
0,05950
0,06400
0,06250
0,05600
0,04550
0,03200
0,01650
0,00000
C4 (s)
1,00000
0,80584
0,63840
0,49534
0,37440
0,27344
0,19040
0,12334
0,07040
0,02984
0,00000
—0,02066
—0,03360
—0,04016
-0,04160
-0,03906
—0,03360
-0,02616
-0,01760
-0,00866
0,00000
С-ь (s) 1
-1,00000
-0,78972
—0,61286
-0,46562
—0,34445
—0,24609
-0,16755
-0,10607
-0,05914
-0,02447
0,00000
0,01612
0,02554
0,02972
0,02995
0,02734
0,02285
0,01727
О.0И26
0,00537
0,00000
Интерполяционная формула Бесселя
fs *> Hf*/f + (« ~4") 6fl/2 + C2 (S) »Ъ%Чш + C3 (S) 6*fi/2 + C4 (S> l*eVV» + C5 (S) ЬЧЧг
s
0,0
0,1
0,2
0,3
0,4
0,5
1 *
C2 (s)
0,00000
-0,04500
—0,08000
-0,10500
—0,12000
—0,12500
\ Для s из правогс
Ca(s)
0,00000
0.00600 *)
0,00800 *)
0,00700 *)
0,00400 *)
0,00000
> столбца надо изм
C<(s)
0,00000
0,00784
0,01440
0,01934
0,02240
0,02344
енить знак.
Ci(s)
0,00000
-0,00063 *)
-0,00086 *)
-0,00077 *)
-0,00045 *)
0,00000
s
1,0
0,9
0,8
0,7
0,6
0,5
682 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 26.5-5.
Таблица 20.5-2 (продолжение)
Интерполяционная формула Эверетта
fs ** О - s) fQ + с2 (s) 6Н0 4- с4 (s) 6<f0 + sft + с2 (1 - s) л»/х + с4 (1 - s) 6^
S
0,0
0,1
0.2
0,3
0,4
0,5
Ct(s)
0,00000
—0.02850
—0,04800
—0.05950
—0.06400
—0.06250
С4 (s)
0,00000
0,00455
0,00806
0,01044
0,01165
0.01172
s
0,6
0,7
0.8
0.9
1.0
C*(s)
—0.05600
—0.04550
—0,03200
—0.01650
0.00000
С4 (s)
0,01075
0.00890
0,00634
0,00329
0,00000
Интерполяционная формула Стеффенсена
fs^f0 + с! <s> #»/i + сз (s) 63fl/2- ci (~s) V-Vi " сз (~s) 68f-Vi
s
-0.5
-0,4
-0.3
-0.2
-0.1
0.0
C! (S)
—0.12500
—0.12000
-0,10500
—0.08000
—0,04500
0.00000
C3(s)
0.02344
0.02240
0.01934
0.01440
0.00784
0.00000
s
1 0.1
0.2
0.3
0.4
0,5
Ct (s)
0.05500
0,12000
0,19500
0.28000
0.37500
C9 (s)
-0.00866
—0.01760
—0,02616
—0.03360
—0.03906
20.5-5. Интерполяция с оптимальным выбором узлов (см. также п. 20.7-3).
Многочлен Y (х) степени я, который совпадает с у (х) вп-|-1 точках х = xj (/ = 0, 1, 2, ...* п)
I n I
на [а, 6] таких, что max П (х — хЛ будет иметь наименьшее значение, приб-
«<*<*|a-=o I
лиженно минимизирует максимум абсолютной величины ошибки интерполяции (4) на [а, Ь].
Такой многочлен Y (х) дается формулой
/2х-
-Ь — а\
-a )9
где
/ = о
(2/+ l)kn
2/1 + 2
Тk (£) — многочлен Чебышева степени k (п. 21.7-4),
*/=-
а + Ь
+ •
, (2/+D Я
' 2/1 + 2
(Л-0, 1, 2,..., л),
(/ = 0, 1, 2,...,- п).
(20.5-8а)
(20.5-86)
20.5-6. Интерполяция функций нескольких переменных. Для аппроксимации
функции z = г (*, у) многочленом Z (х, у), удовлетворяющим условию Z (х, у) = г (х, у) на
заданном множестве точек (х^ y^t можно сначала интерполировать по х функцию z (x, у^)
при фиксированных у^, а затем интерполировать относительно х, что даст Z (х, у).
Другой путь заключается в подстановке в интерполяционную формулу по у
интерполяционной формулы относительно х. Если Ах = Ау — h —- фиксированное приращение и
z (*„ + / А*. Уо + k Ay) = zik (/, k = 0, ± 1, ± 2, ...),
Ах
.У — Уо
(20.5-9)
20.6-2.
20.6. АППРОКСИМАЦИЯ ФУНКЦИЙ
683
то, дважды применяя интерполяционную формулу Бесселя из табл. 20.5-1, получаем
формулу Бесселя интерполяции по двум переменным;
2 (*, у) = -|- (*оо + *io + *oi + *ii) + T (" ~ т) (2l° ~"*00 + *u "~ *ol) +
+ 4" (°"" t) (*01 "" г°°+ г"""*lo) _l~ (""" т) v~" ~s~)(г"~"г"~"*oi + г°о) +'"
(20.5-10)
Аналогичные методы применяются для функций трех и более переменных. См. также
[20.1].
20.5-7. Обратные разности и интерполяция рациональными дробями. Пусть у (х£ =
«=#£ ф = 0, 1, 2, ...^ где xQt xlt x2t ...e — произвольные узлы интерполяции; определим
обратные разности:
Р1 <*e. *i> - *° ""*/ » Р2 <*о. *« *2) = ft ,у Д°~*2 |у—гт + Уи
УО — УХ Pi (*0t *l) — Pi (*lt *2/
pr (x0.xvxt, ...f *г) =
-"Б ГТ^Г^ хХ°7\-о 71х—х 7TT+Qr-2<xbx*' ••••*'-0
P/* - 1 (*0» *1 Г - I) Pr— 1 (*l, *2» •"• Г)
<r = 3, 4, ...).
(20.5-11)
Функция i/ (*) для узлов xit x*, x3l ... аппроксимируется рациональной функцией,
которая получается из разложения в непрерывную дробь вида
где
Pi (X, Xt) = P! (*lt X2) + n ,у V^ Г-'
Р2 (*t *1. Х2) —Ух
р2 (*» хи х2) =» р8 (*4, х2 х3) + - —Х±-
(20.5-126)
P8 (*, Хи Х2, Х9) —pi (*lt Xt) '
Если |/ (*) — рациональная функция, то непрерывная дробь обрывается.
20.6. АППРОКСИМАЦИЯ ФУНКЦИЙ ОРТОГОНАЛЬНЫМИ
МНОГОЧЛЕНАМИ, ОТРЕЗКАМИ РЯДА ФУРЬЕ
И ДРУГИМИ МЕТОДАМИ
20.6-1. Вводные замечания. Параболическая интерполяция на практике
хороша лишь для аналитических функций и только тогда, когда их значения
не искажены шумом (случайными ошибками). Случайные ошибки в значениях
функции сильно искажают интерполяционные многочлены высоких степеней,
а при интерполяции многочленами низких степеней теряется существенная
информация. Поэтому при наличии случайных ошибок предпочитают применять
«сглаживающую» аппроксимацию такими многочленами или рациональными
дробями, которые минимизируют либо взвешенную среднюю квадратическую
ошибку аппроксимации, либо максимум абсолютной ошибки на всем
выбранном интервале (а, Ь). Отметим, что разложения в ряд Тейлора
аппроксимируют аналитическую функцию лишь в непосредственной близости от одной
выбранной точки и поэтому редко применяются в численной аппроксимации
(только при условии сверхбыстрой сходимости).
20.6-2. Приближения функций многочленами по методу наименьших
квадратов на интервале (см. также п. 15.2-6). Для данной функции / (х) требуется
построить функцию F (х) вила
F М = а0 ф0 {х) + ах уг (*)-{-... + ал ф„ (х) (20.6-1)
684 Гл. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.В-3.
так, чтобы минимизировать взвешенную среднюю квадратическую ошибку на
интервале (а, Ь):
o* = ly(x)[F(x)-f(x)]*dxt (20.6-2)
а
где у(х) — заданная неотрицательная весовая функция.
Если функции щ (х) действительны и попарно ортогональны с Еесом у (х)
на интервале (а, Ь), т. е. если
Ь
\ У (х) Ф/ (х) ф/ (х) dx = 0 (/ Ф /), (20.6-3)
а
то искомые коэффициенты а/ определяются по формулам
ь
J Y <*) f <*) Ф* <*> d*
af = ^ (t=0, 1, 2,...). (20.6-4)
J Y (x) q>4 (x) dx
a
Аппроксимация ортогональными функциями, например, ортогональными
многочленами (пп. 20.6-2 — 20.6-4) или тригонометрическими полиномами
(п.20.6-6), имеет то замечательное преимущество, что улучшение аппроксимации
путем добавления нового члена ап+х фл + 1 (л:) не меняет ранее вычисленных
коэффициентов a0t ax, a2,...f ап.
Подстановка * = а2 + Р, dx = adz в формулах (1) —(4) позволяет изменить
масштаб или сдвинуть рассматриваемый интервал.
Заметим, что вычисление коэффициентов по формуле (4) требует знания
функции f(x) на всем рассматриваемом интервале (а, Ь).
20.6-3. Приближения функций многочленами по методу наименьших
квадратов на дискретном множестве точек. Если функция / (х) задана только на
дискретном множестве (т+1) точек х0, хъ х2,..., хт, то приближение (1)
по методу наименьших квадратов принимает другой вид. Здесь надо
минимизировать взвешенную среднюю квадратическую ошибку вида
т
а'2= 2 Vik^ta)-f(**)ft (20.6-5)
где yk — заданные положительные* веса. Это опять-таки проще всего сделать
в том случае, когда функции фг (х) представляют собой многочлены степени г,
попарно ортогональные с весами уц на заданном множестве точек, т. е. когда
т
2 ?*Ф*(**)Ф/(*а)-0 (1ФП. (20.6-6)
Такие многочлены можно получить из последовательности 1, х, х2,...
методом ортогонализации Шмидта, п. 14.7-4. Коэффициенты а* определяются
по формулам
т
fl>-£=^ У=0, 1, 2,..., п\ п^т). (20.6-7)
*«0
20.6-3.
20 6. АППРОКСИМАЦИЯ ФУНКЦИЙ
685
При п=т получающийся многочлен совпадает с интерполяционным
многочленом; если л<т, то добавление нового члена an + 1yn + i(x) оставляет
предыдущие члены без изменения. Особый интерес представляют указанные
ниже два частных случая.
(a) Многочлены Чебышева. Если значения аргумента xQ, хъ
*2»"-» хт можно свободно выбирать, скажем, в интервале (— 1, 1), то
целесообразно в качестве этих значений взять корни многочлена Чебышева Тт+1 (х)
(п. 21.7-4), т. е. положить
**всм1Ипя (/?==0, *•2 т)- (20,6"8)
Тогда при единичных весах 7^=1 ортогональные многочлены, определяемые
соотношением (6), совпадают с многочленами Чебышева 7\- (х) (см. также п. 20.5-5).
(b) Равноотстоящие точки. Если т+1 =2М+1 точек xk делят»
отрезок [а, Ь] на 2М равных частей, так что
x*=~t-£ +kbx (Д*=^=р, 6=0, ±1, ±2,..., ± М), (20.6-9)
то ортогональные многочлены щ (х), определяемые соотношением (6) при
единичных весах Yfc=l, имеют вид
(1 = 0, 1, 2 2М; М = 1, 2,...),
(20.6-10)
т
МвР|(Й-£^±А1,М|)
где
kr^0 (k\V(2M)W
*M-z(*-l)(z-2)...(*-*+l) (* = 1, 2,...), 1
*ГО«1 (*^0), 0^ = 0 (Л—1. 2,...); j
(20.6-1 la)
(20.6-116)
при этом
м
V 0i№ 2ЛЛ сал# + *+1)1 <дл# —pi
1л Pi\Rt *М)— <2f+l)[(2Af)!]»
(/ = 0, 1, 2,..., 2М;М=1, 2, ...)
(20.6-12)
(встречаются и другие нормировки ортогональных многочленов).
Ортогональные многочлены до пятой степени:
p0(tt 2M) = 1, Pl(tt 2М) = ±р
3**- М (М + 1)
Pi (Л 2М) =
Л (Л 2М) =
Л1 (2Л* - 1) '
5*»- (ЗАР + ЗА* ■
П*
p4(tt 2M)=-
М (М - 1) (2М - 1) '
35** - 5 (6Af* -f- 6Af - 5) ^ + 3Af (Af * -\)(М + 2)
2М (Л1 - 1) (2Af - 1) (2М - 3)
P.tt 2M) =
63/» - 35 (2ЛР + 2А* ~3)f» + (15Af«-f 3(M» — 35ЛР—50Л1 -f 12) t
— 2Л* (М- 1) (2Af- 1) (2Л* -3) (М-2) '
(20.6-13)
В частности, при М = 2 (пять точек):
Ро(0 = 1> Pi(0
U Р2(0=Т^2-2)'
Рз (0=4 («•-17/), р4 (*) = -^ (35^—155^ + 72),
.)
(20.6-14)
68G ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.G-4.
Если обозначить значения функции / (х^) через /л, то аппроксимация
многочленами до третьей степени при Л4 = 2 дает следующие сглаженные значения;
F-»-Jo (69/_s+4/.I-6/0+4/1-/2)=/_a-4*/*
F_t = ± (2U + 27f_i+l2fa-8f1 + 2M=U+± */„
F0—jL (_ 3/_2+ 12/_j +17/,+ 12/х —3fa)=/a—± 6*h, \ (20.6-15)
F i=i <2b-8/-i+ 12/o + 27/1 + 2/2)=/,+ I «•/„,
^2=4(-^+4/-I-%+4/1 + 69/2)=/8-^ 64/o. ^
20.6-4. Равномерные приближения.
(a) Равномерные приближения минимизируют наибольшее значение
абсолютной ошибки \F (x)—f(x)\ либо на всем отрезке fa, b], либо на дискретном
множестве точек. Вычисление коэффициентов а/ многочлена (1), дающего
равномерное приближение к функции / (#), весьма трудоемко.
На практике при использовании в формуле (1) в качестве $k (x)
многочленов Чебышева (возможно, с изменением начала отсчета и масштаба, см. также
п. 20.6-4, Ь) равномерные приближения оказываются близкими к
приближениям по методу наименьших квадратов. Это имеет место тогда, когда
приближение многочленами Чебышева
п
F(x)= 2 я* Tk (a*) [Tk (х)=cos £0, cos Ъ=х]
Jfe=0
имеет ошибку того же порядка, что и первый отбрасываемый членаЛ+1 ТЛ+1(а*)
для всех х е [а, Ь\. Так как многочлен Тп+^ (our) в рассматриваемом
интервале колеблется с амплитудой 1, то наибольшее значение абсолютной ошибки
приближенно равно | an+j |.
(b) Иногда удобно применять смещенные многочлены Чебышева Т*(дг),
определяемые на отрезке [0, 1] формулами
T*(x)=Tn(2x-l)=cosn$ (cosd=2*-l; /t=0, I, 2, ...) (20.6-16)
или
Ц(х)=1, 7f(*) = 2*-l, T* + l(x)=2(2x-l)T*(x)-T*_l(x)
(л=1, 2, ...). (20.6-17)
(c) Таблица 20.6-1 дает несколько первых многочленов Тп(х) и Т*(х),
а также разложения степеней 1, х, х2, ..., х* по этим многочленам (см. также
п. 21.7-4). Таблицы 20.6-2 — 20.6-4 дают некоторые полезные приближения
трансцендентных функций многочленами.
20*6-5. Экономизация степенных рядов. Если вычисление коэффициентов
разложения по ортогональным функциям значительно сложнее, чем
вычисление отрезков степенного ряда для функции / (я), то с небольшой потерей
точности можно понизить степени этих отрезков, выразив высшие степени х через
низшие степени и многочлены Чебышева. Например, из табл. 20.6-1 находим
**=^(-9*+120^-432д* + 576**)+^ Г9 (х).
Последний член на отрезке [—1, 1] колеблется с относительно малой
амплитудой ;^г. Отбрасывая этот член, мы получаем представление хд через
многочлен седьмой степени; далее эту процедуру можно повторить с я7 и т. д.
Вместо этого можно все степени выразить через многочлены Чебышева и
пренебречь тема из нихг которые будут иметь малые коэффициенты.
20.6-6.
20.6. АППРОКСИМАЦИЯ ФУНКЦИЙ
687
Таблица 20.6-1
Многочлены Чебышева Тп(х) и Г* (х) и степени х
1 гв=и
Тг=Х
Г* = 2** — 1
Г8 = 4*» —3*
Г4 == 8л:* — 8** + 1
Ть = Ш* - 20** + 5*
Гв = 32*« — 48** + 18а:2 — 1
Г* == 64л:' — 1 12л:5 + 5б*8 — 7х
Т8 = 128л:8 — 256*» + 160** — 32л:* + 1
Т9 = 256л-9 — 576л:7 -f 432*6 — 120*» -f 9*
Г*-1
Г*=2*—1
Г*=8** — 8л*+1
Г* = 32л:« _ 48** + 18* — 1
1 8
Г* = 128** — 256*8 + 160** — 32* + 1
1
1 = Г0 1
х -=7\
^=4(Гв+г*}
*з=-1(ЗГ1+Г8)
** = -1(ЗГ0 + 4Г8+Г4)
^ — -^(Ю^ + бГ.+ Г.)
*• =» -1 (ЮГ, + 15Га + 6Г4 + Гв)
*7 = -^ (357\ + 21 Ть + 7Г8 + Г#)
*8 = -щ (35Г0 + 56Г8 + 28Г4 + 8Гв + Ть)
Х$ = Уб (126Г1 + 84Г» + 36Гв + 9Г» + Гв)
1 " Г*о
*=4(г?+г?)
^ = -г(зго+4ГГ + г1)
*» = -±- (ЮГ* + 15Г* + 6Г* + Г*)
**в "Ж (35Г*+56Г* + 28Г* + 8Г* + ТЦ
20.6-6. Численный гармонический анализ и тригонометрическая интерполя-
ция (см. также пп. 4.11-4, b и 20.5-1).
(а) Даны m значений функции y{Xj,)=yk при xk = k— (& = 0, 1, 2, ...
... , т— 1); требуется аппроксимировать у (х) на интервале (0, Т)
тригонометрическим полиномом
п
KM^i-Ao+S^/cos/^ + B/sin/^) (n<f) (20.6-18)
/=i
m—1
так, чтобы минимизировать сумму квадратов отклонений ^ \У (xk) — yit\2»
л=о
Искомые коэффициенты Л/, В/ определяются по формулам
т — 1 т —1
*/-5 2 »*«/?. ^-iE»»*/? (0^/<f). (20.6-19)
/г=0 Ar = 0
В частном случае п — т/2 формулы (18) и (19) вместе с
т-1
лл = лт/2-=1 2 <— «>* ад <20-6-20>
* = 0
дают К (*.) =-» |/ (*ft) (тригонометрическая интерполяция) при произвольном Вп.
Аналогичные формулы для неравноотстоящих *Л» а также численные методы для
многомерного анализа и синтеза см. в [20.11].
Таблица 20.6-2
Приближения некоторых функций многочленами
fix)
в'*
(0 < х < In 2)
In (14- х)
(0 < х < 1)
10*
(0 ^ х < 1)
sin *
cos*
Приближение F (*)
1 4- at* 4- a2x*
1 + atx + a2*2 + — + а*х*
\ + atx + a2x* + ... + a7x7
axx 4- алх* 4- ... 4- аьхь
atx 4- a2x* 4- ... 4-ae*8
ОЧ-в^+.-. + о***)1
{I + atx + ... + a*')*
1 4- a2*2 4- a4x*
1 4- Я2*2 4- ... 4- al0x»
1 4- a2x* 4- я**4
1 + ашХш + ... + aio^io
Коэффициенты a.
a, = —0,9664
at = —0,99986 84
a3 = —0,15953 32
at = —0,99999 99995
a3 = —0,16666 53019
ab = —0,00830 13598
a7 = —0,00014 13161
ax = 0,99949 556
a3 = 0,28947 478
а6 = 0,03215 845
at = 0,99999 64239
a3 = 0,33179 90258
06 = 0,16765 40711
a7 = 0,03608 84937
a, = 1,14991 96
a3 = 0,20800 30
at = 1.15129 27760
a3 = 0.25439 35748
06=0,01742 11199
a7 = 0,00093 26427
a2 = -0,16605
a2 = —0,16666 66664
at = —0,00019 84090
a10= —0,00000 00239
at = —0,49670
a2 = —0,49999 99963
a. = —0,00138 88397
a10= —0,00000 02605
a2 = 0,3536
a2 = 0,49829 26
a4 = 0,02936 41
a2 = 0,49999 99206
a4 =0,04165 73475
ae =0,00132 98820
a2 = —0,49190 896
a4 = — 0,13606 275
a2 = —0,49987 41238
a4 = —0,24073 38084
ae = —0,09532 93897
a8 = —0,00645 35442
a2 = 0,67743 23
a4 = 0,12680 89
a2 = 0,66273 08843
a4 = 0,07295 17367
ae = 0,00255 49180
a4 = 0,00761
a4 = 0,00833 33315
a8 = 0,00000 27526
a4 = 0,03705
a4 = 0,04166 66418
a8 в 0,00002 47609
Наибольшая
абсолютная
ошибка
3 . Ю-з
з. ю-»
2 . Ю-10
Ю-*
з. ю-8
7 . 10-*
5 • Ю-8
2 • 10-*
2 • 10-»
9 . 10-*
2 • 10-»
Таблица 20.6-2 (продолжение)
fix)
ХА1
xctgx
arcsin x
(0 ^ x < 1)
arctg *
arctg *
(-1 i£x < 1)
Г (x + 1) = *!
(0 ^ x < 1)
Приближение F (x)
1 + a2x2 4- а4д^
1 + a2x* + ... + а12лг«
1 + a2x2 + a4x*
l + a2x*+ ... + аюдг10
-j- - V 1 - x (e0 + ai* + ... + a**3)
-j- - V 1 - x {a0 + alX + ... +a7x')
o.\X + а3л:8 + ... + a9x9
I + a2x* + ... + a19x>*
l + fli*+ ... + a6^
1 + atx + ... 4- a8*8
Коэффициенты а*
a, = 0,31755
a2 = 0.33333 14036
ae =0.05337 40603
a,в = 0.00290 05250
a2 = 0.33286 7
a2 =—0.33333 33410
ae =-0.0021177168
| a10=— 0.00002 62619
a0 = 1,57072 88
a2 = 0.07426 10
a0 = 1,57079 63050
a2 = 0.08897 89874
a4 = 0.03089 18810
a$ = 0.00667 00901
at = 0.99986 60
a6 = 0.18014 10
a9 = 0.02083 51
a2 = -0.33333 14528
ae =—0.14208 89944
a10=— 0.07528 96400
a14 = —0,01616 57367
at = —0.57486 46
a3 = —0,69985 88
a6=— 0.10106 78
^=-0,57719 1652
aa = —0.89705 6937
a6 = -0.75670 4078
a7 = —0.19352 7818
a4 = 0,20330
a4 =0.13339 23995
a. = 0.02456 50893
al2 = 0.00951 68091
a4 = —0.02436 9
a4 = —0.02222 20287
a9 = —0,00020 78504
at =-0.21211 44
a3 = —0,01872 93
at = —0.21459 88016
a3=—0,05017 43046
a6=-0.01708 81256
a7 = — 0,00126 24911
a3 = —0.33029 95
a7 = -0.08513 30
a4 =0.19993 55085
a9 = 0,10656 26393
a,2 = 0.04290 96138
al6 = 0.00286 62257
a2 = 0.95123 63
a4 = 0.42455 49
a2 = 0.98820 5891
a4 = 0.91820 6857 1
at = 0.48219 9394
a8 = 0.03586 8343
: Наибольшая
! абсолютная
ошибка
ю-*
2 . Ю-» 1
з. io-«
4 . 10-»°
5 • 10-»
2 . 10~8
ю-*
2 . 10-*
5 . 10-*
3 . 10-'
Таблица 20.6-3
Некоторые приближения цилиндрических функций
CD
ее
с
Функция
/о (X)
(-3 ^ х < 3)
/о (*) = -~ cos fl0
к*
7V0 (x) = -^= sin fl0
V7
(3 < х < оо)
Л (*)
(—3 ^ х ^ 3)
N0 (х)
(0 < х ^ 3)
Л (д^ = -Д= cos Oj
/V t <дг) = ~ sin ft,
/а:
(3 < х < оо)
д: Л^ (д:)
(0 < д: ^ 3)
Приближения
1 + а,(±)'+... + а„(±)"
f. _«, + «,(_)+.„+ «,(_)
«0 = лг + 6„ + 6. (4) + ... + Ь, (-1)
т + -(т) + -+в»(т)и
-1 Ш -|- /, (ж) + а» + а, (^)'+ ».
h = a0 + al(±) + ... + a,(±)'
Ъ1=х+Ь, + Ь1 {^j + ... + Ь. (4)'
н-*1"4/«(*)+в'+*(т),+ -
- + а"(т)"
Коэффициенты
а2 =—2.24999 97
ав =—0.31638 66
а10 = —0,00394 44
а0 = 0.79788 456
а2 = —0.00552 740
а4 = 0,00137 237
ав = 0.00014 476
60 = —0.78539 816
Ъ2 = —0.00003 954
64 = —0.00054 125
fce= 0.00013 558
ая =—0,56249 985
at =-0,03954 289
а10 = —0.00031 761
а0 = 0,36746 691
а. =-0,74350 384
а8 = —0,04261 214
а12= — 0.00024 846
аа = 0.79788 456
а2 = 0,01659 667
а4 = —0.00249 511
ав = —0.00020 033
bo = -2,35619 449
62 = 0.00005 650
64 = 0,00074 348
bo = -0.00029 166
а0 =-0.6366198
а4 = 2.16827 09
а8 = 0.31239 51
а12 = 0.00278 73
а4 =1.26562 08
as =0,04444 79
а12 = 0,00021 00
ах = —0,00000 077
а3 = -0,00009 512
а6 = —0,00072 805
6, = —0,04166 397
63 = 0.00262 573
Ь6 = —0,00029 333
а4 =0,21093 573
ав =0,00443 319
| а12 = 0,00001 109
ая =0,60559 366
а. =0,25300 117
а10 = 0,00427 916
at = 0,00000 156
а3 = 0,00017 103
а6 = 0,00113 653
bt = 0,12499 612
Ьа = -0.00637 879
Ь% = 0,00079 824
а8 = 0,22120 91
а, =—1,31648 27
а10 = —0,04009 76
Наибольшая
абсолютная
ошибка
5 . 10-8
1,6 • 10-е
(для f0)
7 . 10-е
(для Фо)
1,3 • 10~8
1,4 . Ю-»
4 . 10-е
(для ft)
9 . Ю-* 1
'ДЛЯ At)
1,1 . 10-»
20.6-6.
20.6. АППРОКСИМАЦИЯ ФУНКЦИИ
691
Таблица 20.6-4.
Приближения многочленами Чебышева Тп(х) = cos /iO, где cos О = 2л: — 1
fix)
е"х
(0 < х ^ 1)
ех
(0 < х < 1)
In (1 + х)
(0 < х < 1)
лх
со5~Г
<-1< х < 1)
Sln-2"
(—К х < 1)
1 arctg х
(-1 ^ х < 1)
1 arcsin *
Приближение
7
л = 0
л=0
11 i
л = 0
5
/2=0
5
* S AnT* <**>
/2=0
10
л=0
i При |лг|>
9
л = 0
Замечание:
При /272 < х <
arcsin х = arccos Vl
л
0
1
3
0
1
2
3
0
1
2
з
4
5
0
1
2
0
2
0
1
2
3
4
5
1 по
0
1
2
з
4
arc
— х
Ап
0,64503 5270
—0,31284 1606
0,03870 4116
-0,00320 8683
1,75338 7654
0,85039 1654
0.10520 8694
0.00872 2105
0,37645 2813
0,34314 5750
—0,02943 7252
0.00336 7089
—0,00043 3276
0.00005 9471
0.47200 1216
-0.49940 3258
0.02799 2080
1.27627 8962
—0,28526 1569
0.00911 8016
0,88137 3587
—0,10589 2925
0,01113 5843
—0,00138 1195
0,00018 5743
—0.00002 6215
лагают arctg х = -
1,05123 1959
[ 0,05494 6487
1 0,00408 0631
0.00040 7890
[ 0.00004 6985
я
rcos х = -^ arcsi
полагают
*'» arccos x = arcsin
л
4
5
6
7
4
5
6
7
8
6
7
8
9
10
11
3
4
5
3
4
5
6
7
8
9
10
ГС
2
5
6
7
8
9
п х.
^ l
0,00019 9919
—0,00000 9975
0,00000 0415
—0,00000 0015
0.00054 3437
0,00002 7115
0.00600 1128
0,00000 0040
0.00000 0001
—0,00000 8505
0,00000 1250
—0,00000 0188
0,00000 0029 1
—0,00000 0004
0.00000 0001
—0,00059 6695
0,00000 6704
—0,00000 0047
—0,00013 6587
0,00000 1185
—0.00000 0007
0,00000 3821
—0,00000 0570
0.00000 0086
—0,00000 0013
0.00000 0002
* 1
arctg —
X
0,00000 5881
0,00000 0777
0,00000 0107
0.00000 0015
0.00000 0002
VI-**.
(b) Схема на 12 ординат. Вычисление сумм (19) упрощается,
если m делится на 4. Удобная расчетная схема при т=12 приведена в
табл. 20.6-5.
Таблица 20.6-5
Схема гармонического анализа на 12 ординат
Vk = y(j2)
Строка
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Действие и результат
Данные значения функции
Сумма 1 и 2
Разность 1 и 2
Перестановка
Сумма 5 и 6
Разность 5 и 6
Перестановка и умножение
на коэффициенты ± 1/2;
/3/2
Сумма (с 9 по 12)
Si-Ti
Уо Ух У* Уа Уа Уь Уо
— Ун Ухо Уо Уо Уч —
So Si S2 Sg S4 Sj Sg
— d\ d2 <1я dA db —
S0 Sj S2 S3 й?1 й?2 ^8
s; s; s; s; sr n si
<*„ <*; *; - *• rfj -
s, r,
6A„
12A,
и -
So T2
6At
6Л5
s' — s'
0 3
2 S2 2 Si
S* Tt
6Ai
6A4
d' d'
S4 T4
6Л3
4
2 5Г
2 2
Si ГБ
6Bt
6B5
2 1 2 *
se re
6B,
6B4
sl SJ
S» Г»
6B,
to
3
s
о
ь
га
ж
я
Б
га
5:
га
н
о
fa
2
о
Я
га
я
S
га
"О
>
W
Я
о
о
ч
Я
20.B-7.
20.6. АППРОКСИМАЦИЯ ФУНКЦИИ
693
Отметим более простые формулы для случая, когда нужны гармоники не выше
третьего порядка:
6Л0 = Уо + У1 Н- Уг + ». + Уи* 6Л, = у0 — у2 -f. У* — Ун + У* — #ю.
4Л2=#о — #3 + #в — ^ 68,=»^ — £, + #5 — ^/7 +#»— #11. > /00 6-21)
> (20.6
^-Чт)-'(т)+*(£)-*(£>
Ах = у (#о — #в) + Лз.- Si = -- (ys — #») 4- Вз.
Четыре добавочных значения функции для формулы (22) часто можно снять
непосредственно с графика функции у (х).
(с) Отыскание неизвестных периодических компонент. Если
для функции вида
f (и) = At cos ©хи 4- #j sin ©хи 4- ^2 cos u>2« + #2 sin g>2« + ... + Вт sin й)щ«
известны из опыта N(N^3m-\- 1) значений
f0-f (0). ft = f(l). fa=f (2). .... f^_i = M^-l)„
то
, COS й)_
определяются как корни (алгебраического) уравнения
cos wo) — ах cos (m— 1) со — ... — am_i cos со — — а = 0,
коэффициенты которого а^ должны удовлетворять системе линейных уравнений
т-\
е,- = 2 С' + Ь - 1 + ^2т 4- i - Л - l) ak + ^m + / - l«m - f/ - 1 ~ hm 4 / - I = 0
(/=1, 2, ... , N — 2m).
Для нахождения m коэффициентов а^ по методу наименьших квадратов надо решить
систему т линейных уравнений
N — 2m
* /=1
После того как ©. найдены, относительно легко найти А. и В. методом, указанным в
п. 20.6-6, а.
20.6-7. Разные приближения.
(a) Более общие методы приближений не ограничиваются линейными агрегатами
вида (1), но используют рациональные или другие легко вычислимые аппроксимирующие
функции F (х) = F (*; с^, а2, ... , ад) с параметрами с^, а2, ... , ап, которые
определяются так, чтобы минимизировать взвешенную среднюю квадратическую ошибку или
наибольшую абсолютную ошибку аппроксимации.
(b) Метод П а д э дает приближения достаточное число раз дифференцируемой
функции f (х) с помощью рациональных дробей
а +алх + ... + а /*
/? (*) а ^ ^~- (т, п - 0, I, 2, ...). (20.6-23)
тп \+btx + ... + Ьпхп
коэффициенты которых определяются из тождества
[/ (0) + f (0) ж 4- ..„ + -L fШ) (0) хт] (1 + Ьхх + ... + Ьпхп) =з
= aQ 4- V + ... + атхт. (20.6-24)
Отсюда получается система т + /г -J- I линейных уравнений с m + л + 1 неизвестными
коэффициентами а- и Ъ^. Предполагается, что дробь (20.6-23) несократима. При п = 0
функция RmQ№ Дает просто отрезок ряда Тейлора (п. 4.10-4).
Таблица 20.6-6. <g
Разные приближения ^
/(*)
arctg x
(—1^*^=1)
X
erf x = -Д=- [ e—^dK
Yn 3
0
(0 ^ x < oo)
*2
e *
V2n
(— CO < X < CO)
л: Я*
У2Я J
1 —CO
J (0 =S x < со)
Приближение
ai' + a3*3, / = J^1
a^ + a3t* + ... + a,/»
*+l
д:
1 + 0,28ж*
1 — Ш + att* + a3/») e—x%
t }
1 -f px
1 - (ax* + ... + «J*) e-*2
t- l
* l + px
. 1
<1 + в1*+ ... +a.**)*
, 1
(l + aj*+ ... + ae*e)ie
(a0 + a2x» + a4x* + a6*e)-*
(a0 + «2*2 + ... + a10x^)-i
l--~d + ctx-b ... + c4**)-*
l-~(l + ctx+ ... +свдг»)-м
Коэффициенты
ex == 0,86304
at = 0,86859 1718
ag *= 0,17752 2071
a9 = 0,19133 7714
p = 0,47047
a2 = — 0,09587 98
p = 0,32759 11
at = — 0,28449 6736
a4 = - 1,45315 2027
ai = 0,278393
a& = 0,000972
at = 0,07052 3078
a3 = 0,00927 0527
ab = 0,00027 6567
a0 = 2,490835
a4 = — 0.024393
a0 = 2,50523 67
a4 = 0,22647 18
a8 = - 0,02024 90
ct = 0,196854
cs = 0,000344
Cx = 0,04986 7347
c3 = 0,00327 7626
cb = 0,00004 8891
a, = 0,36415
a3 = 0,28933 5524
a7 = 0,09437 6476
fli = 0,34802 42
a8 = 0,74785 56
a. = 0,25482 9592
a3 = 1,42141 3741
a6 = 1,06140 5429
a2 = 0,230389
a4 = 0,078108
a2 = 0,04228 2012
a4 = 0,00015 2014
ae = 0,00004 3064
a2 = 1,466003
ae = 0,178257
a„ = 1,28312 04
a« = 0,13064 69
a10 = 0,00391 32
c2 = 0,115194
c4 = 0,019527
c2 = 0,02114 1006
c4 = 0,00003 8004
c« = 0,00000 5383
Наибольшая
абсолютная
ошибка
6.10-*
ю-*
5.10-»
2,5-10-*
1.5.10-» 1
5.10-* 1
3.10-* 1
2,7.10-»
2,3.10-*
2,5-10-*
1 1,5-10-»
J
20.7-1. 20.7. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ 695
Пример. Для / (дг) = Г имеем R (х) = -^ —— i
Я4о (х) = 1 + х + ~ х* +1 х» + ~ *•.
Я82 <*) =
24 — 6*
12 — 6* -{- *2'
(с) В последние годы разработано много методов аппроксимации в связи с
цифровыми ЭВМ. Оптимальная форма аппроксимации выбирается в зависимости не только от
вида аппроксимируемой функции, но и от применяемой машины. Некоторое количество
примеров различных типов приведено в табл. 20.6-6.
20.7. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
20.7-1. Численное дифференцирование. Численное дифференцирование
чувствительно к ошибкам, вызванным неточностью исходных данных,
отбрасыванием членов ряда и т. д., и поэтому должно применяться с осторожностью.
(а) Применение таблицы разностей для
равноотстоящих значений аргумента (см. также п. 20.4-1). Для
дифференцируемой достаточное число раз функции у (х)
dxT'
£ = 0Ц^п(1+Д,]' = ^(д-1д*+1дз-...)', (20.7-.)
так что если д?^=д:0+Мдс (k—0, ±1, ±2, ...). то
y'k -у' (**)=°**-е (д^-1 ^Ук+j к*Ук -•••)•
tf-*"(**)-D,y*-ufe
/и * N \ (20-7-2)
Дифференцирование интерполяционных формул Стирлинга и Бесселя дает
соответственно
У'к =5i(^*—Я" Ь*Ук + -)' 1
(20.7-3)
(20.7-4)
Многие подобные формулы, а также и формулы для аппроксимации
производных высших порядков, могут быть выведены путем дифференцирования
подходящих интерполяционных формул (см. также рис. 20.9-1).
Приведем еще явные трехточечные формулы дифференцирования с остаточными
членами;
1 а***
"-1 - Ш (- 3"-i + Ч - Уг) + Т ""' ©•
*о = 2^ ("" *-1 + *l) - ^Г *'" (S)'
*i = 2^ C-l * 4"о + 3"l) + ^f *"' <*>•
где *_! < | <; хь
(20.7-5)
696 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.7-2.
(Ь) Применение разделенных разностей (см. также п. 20.5-2, Ь).
Дифференцирование интерполяционной формулы Ньютона (20.5-3) для произвольных
узлов интерполяции *0, xit х2, ... дает
У(Г)(Х)
/-1
Fj{x)wm S (x-xk)
(/=1, 2,
.).
(20.7-6)
(с) Численное дифференцирование после сглаживания.
Следующие формулы получаются путем дифференцирования многочленов наилучшего сред-
нек&адратического приближения, и поэтому на них меньше сказываются случайные
ошибки опытных данных
У к*
1
гто.2 /"*+/.
/=—п
' Ах п (п + 1) (2п ■
При п = 2 это дает
^ ^ ТоЬ (~ 2Ук-2 -Ук-1 + Ук + 1 + 2^ + 2).
Вот еще несколько формул:
(d) Численное дифференцирование по отрезку ряда
Фурье. Если функция у (*) аппроксимирована тригонометрическим полиномом Y (х)
(20.6-18), то для производной у' (х) можно получить оценку
(20.7-7)
(20.7-8)
(20.7-9)
У'(х)
~ 2я
(20.7-10)
20.7-2. Численное интегрирование для равноотстоящих узлов,
(а) Квадратурные формулы Ньютона — Котеса. Квадратурные формулы
Ньютона — Котеса замкнутого типа (табл. 20.7-1) основаны на аппроксимации
*0-f я д*
J у(х) dx^a0y0 + aly1 + a2y2 + ... + anyn,
Хо
где
_<-1У
л-к
аЬ ~~ k\ (n — k)\ )
О
Дл- С Л, (Л. — 1) (Л, — 2) ... (Я, — п)
a — k)
dX,
(20.7-11)
Уь=у(*к) —данные значения функции для л+1 равноотстоящих значений
аргумента Xk=x0-\-kAx (k = 0, 1, 2, ... , /г). Формулы являются точными, если
у (х) — многочлен степени не выше чем п. Вместо того чтобы применять зна-
20.7-2. 20.7. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ 697
Таблица 20.7-1
Квадратурные формулы Ньютона — Котеса, замкнутый тип
№
1
2
3
Правило трапеций
<л = 1)
Правило Симпсона
(п = 2)
Правило Уэддля
(л = 6) •)
х0 + п Ах
/' ** J y(x)dx=I
Хо
~2 (Уо + Уд
■у (Уо + 4^i + yt)
з
-jq Ах (у0 -f byt +Уг +
+ Ьуъ +У4 + ЬУь + У*)
Погрешность / — /'
(*о < 1 < х0 + я Ах)
- -L А* V (6)
--^A*V*'<S)
+ 9A*V8)(6')1
*) При выводе правила Уэддля точный коэффициент 41/140 при А*у0 заме-
1 нен на 3/10.
чения л>6, складывают т сумм вида (11) при л^б для последовательных
подынтервалов:
х0~\-тп Ах
J y(x)dx=*
Хо
Хо + /г А* *0 -f- 2л А* х0 + tnn Ax
= J y(x)dx + J #(*)<** + ...+ J */(*)<**• (20.7-12)
x0 х0-{-пАх х0-\-(т — \)пАх
(b) Формула Грегори. Симметричная квадратурная формула Грегори
х0 4- л д*
J у(ж)^^Дд:[(^Уо + У1 + ... + Уя-1 + 7Уя) + {(АУо--АУя-1)--
*0
—Я" (А1Уо + А1^1) + ^(А»Уо + А»Уя^)-1й(А4Уо + А4У||-«) + --.] (20.7-13)
дает поправочные члены к правилу трапеций (табл. 20.7-1). Если эта
формула доведена до разностей порядка 2т, то она является точной для
многочленов у (х) степени не выше (2m+l) (m=0, 1, 2, ...).
В частности, отбрасывание всех разностей дает правило трапеций
х0-\-п Ах
J yiX)dx*,&x(jy0 + v1 + yt + ...+vnmml + ± y^ (20.7-14)
Хо
точное для линейных функций. Отбрасывание разностей третьего порядка и выше дает
формулу
х0 4- « Ах
С / 9 28 23
^ у (ж) их ъ Ах ^ у0 + -£j- Ух + -я* У г +
+ *+...+ *„_, + ж *„_, + i^, + ¥ *-)• <20-7-,6>
точную для многочленов у (*) третьей степени.
698 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.7-3.
(с) Применение формулы Эйлера — Маклорена. Формула
суммирования Эйлера—Маклорена (4.8-10) дает ряд квадратурных формул, содержащих, кроме
значений у (х), также и значения ее производных у£=*у' (*jfe), У% = у" (*&)t...
Получающиеся квадратурные формулы
\ V{x)dx = ^ (у0 + У,)-~ (У[ - 10 + ~ W - У'й") - . .. (20.7-16)
Хо
дают поправочные члены к правилу трапеций (табл. 20.7-1).
20.7-3. Квадратурные формулы Гаусса и Чебышева
ь
(a) Интеграл \y(x)dx с помощью замены переменных
" *=Ц*Е+*±*. «,©_»=£ у М (20.7-17)
1
приводится сначала к виду \ r\ (£) d\. Квадратурная формула Гаусса:
-1
1 п
где л значений аргумента |^ являются корнями многочлена Лежандра Рп (£)
(п. 21.7-1). Абсциссы Ik и веса ал Для некоторых значений п приведены
в табл. 20.7-2.
Погрешность квадратурной формулы Гаусса (18) равна
(/it)4 (b-a)2n + 1 {2n) ta<x<b) (20.7-19)
(b) Квадратурные формулы Чебышева применяются тоже после
предварительной замены переменных (17); они имеют вид
1
$ Л®«^[Л ffii) + 4(b) + ... + 4(b.>] (я-2, 3, 4, 5, 6, 7, 9). (20.7-20)
— 1
Абсциссы £л приведены в табл. 20.7-2. Применение равных весов минимизирует
вероятную ошибку, если значения у (х) подвержены нормально
распределенным случайным ошибкам.
При л = 3 погрешность квадратурной формулы (20) равна ^ f J yv(X)
(a<X<b).
(c) Отметим еще квадратурную формулу Лагерра
21)
Где g —корни многочлена Лагерра Lff (£) (п. 21.7-1), и квадратурную формулу Эрмита
со п __
J rv ч ю « » J "^ <8*>. °*=ТШШ (п "''2' * *,к (20,7'22)
— 00 & = 1
где 6ь-" корни многочлена Эрмита Нп (|) (п. 21.7-1).
Абсциссы lk и веса ак для формул (21) и (22) приведены в табл. 20.7-2.
20.7-3. 20.7. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ 699
Таблица 20.7-2
Абсциссы и веса для квадратурных формул,
(а) Абсциссы Ik и веса ak для квадратурной формулы Гаусса (18)
п
со to
Абсциссы
± 0,577350
0
± 0,774597
Веса
1
8
9
5
9
п
4
5
Абсциссы
-*- 0,339981
+ 0,861136
0
+ 0,538469
+ 0,906180
Веса
0,652145
0,347855
0,568889
0,478629
0,236927
(Ь) Абсциссы Ik Для квадратурной формулы
Чебышева (20)
п
2
3
4
5
6
Абсциссы
-*- 0,577350
0
■+- 0,707107
■+- 0,187592
-*- 0,794654
0
■+- 0,374541
■+- 0,832497
■+- 0,266635
■+- 0,422519
■+- 0,866247
n
7
9
Абсциссы
0
-t- 0,323912
-t- 0,529657 1
-t- 0,883862
0 i
■+- 0,167906 j
-1- 0,528762
+ 0,601019
-1-0,911589 |
(с) Абсциссы Ik и веса ak
для квадратурной формулы
Лагерра (21)
п
2
3
4
5
Абсциссы
0,585786
3,414214
0,415775
2,294280
6,289945
0,322548
1,745761
4,536620
9,395071
0,263560
1,413403
3,596426
7,085810
12,640801
Веса
0,853553
0,146447
0,711093
0,278518
0,0103893
0,603154
0,357419
0,0388879
0,000539295
0,521756
0,398667
0,0759424
0,00361176
0,0000233700
(d) Абсциссы lk и веса а^
для квадратурной формулы
Эрмита (22)
п
2
3
4
5
Абсциссы
± 0,707107
0
± 1,224745
± 0,524648
± 1,650680
0
± 0,958572
+ 2,020183
Веса
0,886227
1,181636
0,295409
0,804914
0,0813128
0,945309
0,393619
0,0199532
700
ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.7-4.
Отметим также квадратурную формулу Гаусса — Чебышева
X п
j pft^SvU**), «*-7- ^ = С05?^"Я (* = 1'2 я)-
где lk — корни многочлена Чебышева Гд (*) (п. 21.7-4).
20.7-4. Построение и сравнение квадратурных формул.
(a) Коэффициенты ak и абсциссы xk квадратурной формулы
Ь
\V М У (*) dx^a0y (x0) + агу (хг) + ... + апу(хп) (20.7-24)
а
можно получить разными способами.
1. Можно потребовать, чтобы формула была точной для у (*) = 1, х, х2, ...
• .., хт (т<2/г). Это дает т+1 уравнений для неизвестных ал и *л:
j/vW^=fl/[| + Vi + ,,,+flX (' = 0, 1, 2, ..., m; т<2/г).
(20.7-25)
2. Можно предписать некоторые или все абсциссы х^ (формулы Ньютона —
Котеса, Грегори) или все ak (формулы Чебышева). При этом некоторые абсциссы
могут находиться вне области интегрирования.
3. Можно наложить на веса ak условия симметрии (формула Грегори)
или условия минимизации влияния ошибок округления. Для последнего условия
все веса ak должны быть положительны.
Относительная ценность этих требований зависит от области применения.
(b) Формулы интегрирования типа Гаусса, например, (18), точны для
многочленов степени ^2/г—1, в то время как формулы Ньютона —Котеса
точны лишь для многочленов степени ^ /г. В этом смысле формулы Гаусса
лучше для функций, имеющих производные высоких порядков. Если же
функция имеет только кусочно-непрерывную первую производную, то лучшей
может оказаться формула трапеций. Имеются обобщения квадратурных
формул Гаусса, которые оказываются точными для тригонометрических
полиномов и других специальных функций.
20.7-5. Вычисление кратных интегралов. Кратные интегралы можно вычислять
повторным применением методов, описанных в пп. 20.7-2 и 20.7-3. Для двойных
интегралов можно пользоваться формулами
h h
2h*
с с 2h2
) ) fix, у) dxdy*z— (2/00 + /10 + /01 + f_b0 + f0t _J (20.7-26)
-h—h
или (Симпсона)
h h
\ \ f(*. y)rf*^*^-[16f00 + 4(^IO + fol + f_li0 + fOi-1) +
+ fll + 'l.-l + '-Ы + Li. -lb (20.7-27)
где
fjk = f (/ Д*, k Ay), Ax=Ay = h (U=0,+ 1).
Для тройных интегралов:
h h h
\ \ \ f (*' y> z) dx dV*Zf*T h* (fioo + foio + fooi + Li,oo + fo.-i.o + foo,-i).
-h~H-h (20.7-28)
20.8-2. 20.8. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ УРАВНЕНИЙ 701
где
fyk » / (i Длг, / Ду, k Az), Лдс = Ay = Лг = Л (*, /, k — 0, ± 1).
При этом область интегрирования разбивают на части с помощью декартовой сетки
координатных линий или поверхностей.
Простейшая двумерная формула интегрирования гауссова типа есть
11 3 3
J J fU. y)dxdy<* £ £ V <\. \k),
— 1—1 * = lft = l
где t
X, = -/3/5, X2=0, ^ = ^3/5, ^
ax - 5/9, a2 = 8/9, a3 = 5/9; a.k = %. J (2°* 7'29)
Для многомерных интегралов больший интерес представляют методы Монте-Карло,
п. 20.10-1.
20.8. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
20.8-1. Вводные замечания. Численному интегрированию иногда
целесообразно предпослать грубое графическое решение (п. 9.5-2| для ориентировки.
Решение начальных задач (Коши) рассматривается в пп. 20.8-2 — 20.8-8,
решение краевых задач —в пп. 20.9-1 и 20.9-3.
При численном интегрировании дифференциального уравнения первого
порядка
y'=f(x,y) (20.8-1)
с данным начальным условием y(xQ)=yQ выберем фиксированное приращение
Дх=Л независимого переменного х и введем следующие обозначения:
xk=x0 + kAx (fc=0, 1, 2, ...);
вычисленные (вообще говоря, приближенные) значения решения у(х) и
производной у' (х):
Ук"*У(Хк)=У(Хо+ЬЬх)> \ /fe п 1 9 ч
(20.8-2)
Отвлекаясь от ошибок округления, разность Ук+i— y(xk+i) между
вычисленным и точным значениями решения назовем ошибкой усечения. Если в
формуле численного интегрирования заменить точные значения у (*л), f/(^_i), ...
на Ук> Ук-ъ •••» то разность yk+i—y(xk+i) Даст локальную ошибку усечения.
Полная ошибка усечения вызывается не только локальной ошибкой, но и
распространением ошибок от более ранних шагов интегрирования (п. 20.8-5).
20.8-2. Одношаговые методы решения задачи Коши. Методы Эйлера и
Рунге —Кутта.
(a) Метод Эйлера состоит в пошаговом применении простой формулы
Ук+1=Ук+!кЬ* (*=0, 1, 2, ...). (20.8-3)
Он дает хорошее приближение решения только при достаточно малом Д# = Л
и только для нескольких первых точек. Модификации этого метода
определяются формулами:
Й+1-Й+/(** + 7. Ук+fkTJ^ *20-8-4>
У*+1-У*+Т fo+/(**+i. Ук+fk А*)] А*. (20.8-5)
(b) Mетоды Рунге — Кутта различных порядков приведены в та0-
лице 20.8-1. Методы (а) и (Ь) называют методами третьего порядка, так как
702 гл. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.8-2.
Таблица 20.8-1
Некоторые методы Рунге — Кутта для обыкновенных
дифференциальных уравнений (п. 20.8-2)
и систем таких уравнений (п. 20.8-6)
I В каждой формуле k- = fk Ax = f (xk, y^ Ax, I
(a) Vk + t = yk + 4"(*l + 4*2 + *3>-
».-'(** +т-**+т) *«•
*3 = f Ck + ЛДГ- У к + 2*2 ~ *l) Д*!
<ь> ^+1 = ^ + т(*1 + 3*з)-
*2 ='(** +f<"* + f) **'
h =f {хк + т **- »к + Т **) **
<с> **+i = »* + Т (*i + 2** + 2*з + *«)•
*з ='(** + ¥• ** + т) д*'
<*> **+1 = ^ft + Т (*1 + 3*S + 3*3 + *<)•
*4='(Д:А + ДДГ' ^ + *1-*2 + *з)ДДГ:
(е) у к+1 = У к + Т К +(2 - ^2) *2 + (2 + ^2 ) *з + *«1-
** -'(** + Т-'ь + т) &х-
20.8-3. 20.8. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ УРАВНЕНИЙ 703
формулы для yk+l являются точными при /(*, #) = 1, *, х2, х3; для
достаточное число раз дифференцируемой функции f(x, у) локальная ошибка усечения
имеет порядок О (А*4) при А* —> 0 (п. 4.4-3). По аналогичным соображениям
методы (с), (d), (e) называют методами четвертого порядка. Из них метод (с)
является наиболее употребительным.
20.8-3. Многошаговые методы решения задачи Кош и.
(a) Начало решения. Сверх заданного начального значения у0
каждая из приведенных далее схем решения требует вычисления еще нескольких
значений функции уи у2, ..., что может быть сделано одним из методов
пп. 9.2-5, 20.8-2 или 20.8-4. Это «начало решения» должно быть вычислено
с большей точностью, чем требуется для всего решения, по крайней мере
в 10 раз. Если для начала решения применяется метод Рунге —Кутта, то
величину шага Ax — h для него надо брать меньшую, чем для последующей схемы
расчета.
(b) Простые экстраполяционные схемы. Если уже известны
#А» Ук-г> #л-2» •••» т0 Для аппроксимации последующего значения решения
xk+i
У(Ч+д^Ук + $ /(*, y)dx (20.8-6)
xk
интегрируют вместо f(xs у) какой-либо интерполяционный многочлен,
определяемый значениями /д, fk-ъ /ft-2» ••• (экстраполяция). Применяя вторую
интерполяционную формулу Ньютона (20.5-6), получают формулу Адамса
Обрывая общую формулу интегрирования (7) последовательно на разностях все
более высоких порядков, получаем формулу Эйлера (3), правило трапеций
*А+1-** + Т (3fA-fft-l)A*' <20-8-8>
формулу третьего порядка
"ft + i = Ч + Т2 (23f* - Шк-1 + Vk-2) Д* f20-8^
и формулу Адамса — Башфорта четвертого порядка, приведенную в табл. 20.8-2.
(c) Методы типа «прогноз — коррекция» и изменение
величины шага. Обозначая «предсказанное» (прогнозированное) значение
yk + j по формуле (7) через у^*\ и соответствующее значение функции /
через /£р_]!Др можно с помощью значения f^^\ = /(*£ + р #£p+fli) улучшить
аппроксимацию y(Xk + i)- При этом уточненное, скорректированное значение
yk+1 использует предсказанное значение fft+1B квадратурной формуле
замкнутого типа
(20.8-10)
Формула коррекции (10) усекается подобно формуле (7) на разностях
соответствующих порядков. Получающаяся разность #*^— Ук^Ч межДУ
скорректированным и предсказанным значениями может служить для оценки
локальной ошибки усечения; при подходящем выборе приращения Ax = h эту
ошибку можно сделать меньше заданного допуска.
704 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.8*4.
(20.8-11)
Чтобы уменьшить вдвое величину шага расчета Л = Д*, для формул
четвертого порядка применяются следующие интерполяционные формулы:
У. 1==Г2-8[45^ + 72^_1 + 11^_2 + (--9/л + 36/л_1 + 3/л.2)А^,
2
^+1 = 4[П^ + 72^_1 + 45^_2--(3/л + 36/л_1-9/л_2)Ал:].
Чтобы увеличить вдвое величину шага расчета, достаточно использовать
найденные значения решения через одно.
20.8-4. Улучшенные многошаговые методы.
(а) Более общие формулы интегрирования открытого типа (используемые
как предсказывающие) и замкнутого типа (используемые как формулы коррек-
пии) можно записать соответственно в виде
Ук+i = AQyk + A1yk_1 + А9ук-2 + АзУк-з +
+ (B0fk + B1fk_l + B2fk_2 + B3fk_3) Ах (предсказание), (20.8-12)
Ук + 1 = аоУк + <*1Ук-1 + а2Ук-* +
+ (Ь-ifk + i + Ык + bjk _ 1 + bjk _я) Ах (коррекция). (20.8-13)
Обычно не принято определять все коэффициенты из условия, чтобы
каждая формула была точной для функций /(х, у)=\, х, х2, ... Вместо этого
требуют согласования лишь до членов четвертого порядка (т. е. до х*
включительно), а остающиеся свободные коэффициенты выбирают так, чтобы
уменьшить распространение ошибок или чтобы упростить вычисления (п. 20.8-5).
В табл. 20.8-2 приведены некоторые наиболее употребительные формулы
четвертого порядка.
(b) Применение модификаций. В каждом методе
«предсказание—коррекция» разность у\°^\— y*jf+\ почти пропорциональна локальной
ошибке усечения. Поэтому можно уточнить решение с помощью следующей
модификации. До подстановки предсказанного значения у%*+* в формулу
коррекции к нему прибавляют поправку а (*/£орр — #£ред)» пропорциональную
указанной разности на предыдущем шаге расчета, а затем от скорректированного
значения у%0£*[ вычитают величину (1—а) (у™£р\ — У^+^) для получения
окончательного значения yk + i (табл. 20.8-2).
(c) В методе Димсдейла четвертого порядка производится итерация по
формулам
»*+i-4("*+i'*+i) + 7(,*-,*+i)A*' 1
, \ (20.8-14)
** + !-** +7 С*+ 4'* + l + '*4t)A*' )
начиная с некоторого выбранного значения Уьл.** например, Уи,2 ^ Vk ~^~ ^k ^х* ПРИ
этом метод допускает изменение величины шага путем простой подстановки нового
значения А*. Этот метод не требует специального расчета начала решения, но после того,
как решение начато, можно избежать итерации с помощью применения экстраполяции
для предсказания yk + 2-
20.8-5. Сравнение различных методов решения. Контроль величины шага
и устойчивость.
(а) Формулы интегрирования, выбранные из-за малой локальной ошибки
усечения, могут способствовать накоплению ошибок в последовательности
значений решения.
Выбор метода решения дифференциального уравнения требует некоторого
компромисса между учетом локальной ошибки усечения, устойчивостью и ере*
20.8-5. 20.8. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ УРАВНЕНИЙ 703
Таблица 20.8-2
Некоторые методы четвертого порядка типа «предсказание — коррекция»
Каждая схема может быть использована как с модификацией, так и без нее.
Модифицированные значения обозначены через 1/^од,, ^од, = f (xh , 1t 4^одУ Во всех
К-Г I Л-fl \ «+1 R+ 1 /
случаях величина уточнения в последней строке дает верхнюю грань локальной ошибки
усечения.
п о
(а)
Ад
(Ь)
(с)
малую
тельна
Предсказание по
амсу — Мултону и
„пред =
умод =
С+РГ
<W =
s yk + 2,4
,np? +
:^ + "24
=yKOpp _
yktl
Метод Хемминга
„пред^;
yk+\
,мод =
ср.р=
yk+l =
**-8 +
^KT +
"T(9yk
s|fKop|P.
Адамсу — Баш форту
модификацией
(86fA-59fft
!?! /-„корр _
270 \"ft
-1+37^-2"S'*
- ^рад)
•(nTi + 19f*-5/ft-i+fft-s
. 1?. Л ,к°РР
270^ft+l
T^k-fk-
ш№рр-
4_L 3
--?- fuK°PP
121 ГА + 1
_ ,/Пред\
-1 + 2^-»)Д*
- .</£Ред)
-(та+«*-'*
-*ет)
С К О
-з)л*
,)Д*
-l)A*
ррекцией
Метод Милна, модифицированный Хеммингом, имеет относительно
локальную ошибку усечения, но является неустойчивым, если df/dy отрица-
или представляет матрицу с отрицательными собственными значениями
//Пред =
ук+\
у мод =
,KOPf =
yk+l =
"A-3 +
«пред i
yk+\ ^
-yk-l +
. i/Kopp _
т (2f*";*-
йК0РР-
.1+ «*-•) А*
»пРе«)
|(fMO„+4,ft+,fti)Aj(
i(Cf
_,пред)
менем расчета. Сверх этого предпочтительнее те формулы, в которых
слагаемые имеют одинаковые знаки и не слишком отличаются по абсолютной
величине, так как при этом уменьшается влияние ошибок, вызванных округлением.
Окончательный выбор зависит от области применения и от применяемых
вычислительных средств. Часто применяется двойная точность вычисления значений
переменных.
Если данная функция f(x, у) очень сложная, то основное время расчета
связано с вычислением ее значений. Для задачи Коши с умеренно гладкой
функцией f (х, у) многошаговые схемы интегрирования требуют относительно
мало вычислений производных и допускают экономный автоматический
контроль величины шага по величине \у™*£ — #££е* |- Методы Рунге — Кутта
очень устойчивы (п. 20.8-5) и не требуют отдельной программы для начала
23 Г. Корн и Т. Корн
706 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.8-6.
решения; поэтому они предпочтительнее для задач, связанных с частым
изменением шага. Но методы Рунге — Кутта требуют относительно большого
количества вычислений производных на каждом шаге и для них весьма сложен
эффективный контроль величины шага.
Чтобы оценить локальную ошибку усечения для контроля величины шага в
методах Рунге — Кутта, можно сравнить результаты, полученные при разной величине шага
(используя, по возможности, уже накопленные значения производных), или же
исследовать подходящие функции от &.. Для часто применяемого метода Рунге — Кутта (с)
из табл. 20.8-1 величина
е =3^+1 /±x + kt — 2*з ~ 2/г4 (20.8-15)
дает грубую оценку локальной ошибки усечения.
(Ь) Устойчивость приближенного решения у0, уи у2,
ного с помощью многоточечной формулы
уравнения (1), вычислен-
Uk+1 = Aoyk + A1yk_1 + .
+ <В-Л+1 + B°fk + B^k-l + - + V*-r> А*«
(20.8-16)
зависит от устойчивости соответствующего линеаризованного разностного уравнения
для последовательности ошибок е0, elt e2, ... , а именно
9k+l
^ A0ek -f At
ду \х — х1
{В-1еШ + B*k + Biek-1 + - + Brek-r) Ax (20-8-17)
(п. 20.4-8). Отвечающее ему характеристическое уравнение
(— 1 + В_,Л/0 zm + (А0 -f B0Ah) zr -f- (At + BtAh) zr~l + ...
...+(Ar + BrAh)=0,
-A -= -fril.. . h = Ax,
df I
dy\
(20.8-18)
будет иметь корень zt ^ exp Ah при малых значениях | Ah |. Если А ■■
>0,
-~dy\x = xk
то соответствующее собственное колебание последовательности ошибок будет
неустойчивым; но таким же будет и точное решение у (х) вблизи * = *-, так что относительная
ошибка может оказаться и незначительной при малых Дат.
При г = 0 (простой одношаговый метод) корень гх будет единственным. При г > 0
уравнение (18) будет иметь дополнительные корни, отвечающие побочным колебаниям
в вычисленном решении, возникающим вследствие разностной аппроксимации высокого
порядка. Для относительной устойчивости вычисленного решения требуется, чтобы все
такие дополнительные корни при рассматриваемых значениях Ддг лежали внутри
единичного круга | z | < 1 (п. 20.4-8).
Наибольший риск существует при изменении шага (которое, подобно ошибкам
округления, может вызвать побочные колебания) и вблизи границ устойчивости
исходного дифференциального уравнения. Если есть подозрение в возникновении такой
ситуации, то его можно проверить путем искусственного введения малого возмущения.
Устойчивость схем «прогноз — коррекция» зависит и от предсказывающей формулы
и от формулы коррекции, но в большей степени от последней, если величина коррекции
мала.
20.8-6. Обыкновенные дифференциальные уравнения высших порядков и
системы дифференциальных уравнений.
(a) Каждое обыкновенное дифференциальное уравнение второго или более
высокого порядка равносильно системе уравнений первого порядка (п. 9.1-3).
Если записать последнюю в матричной форме п. 13.6-1, то кажый метод
решения из пп. 20.8-2 — 20.8-4 дает аналогичный метод численного интегрирования
системы.
(b) В частности, рассмотрим систему обыкновенных дифференциальных
уравнений первого порядка вида
*/' = /(*, у, г, ...), *'=£(*, у, г, ...),... (20.8-19)
с решением у=у(х), г = г(х),...
20.8-7. 20.8. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ УРАВНЕНИЙ 707
Интегрирование системы (19) методам последовательных приближений
Пикара или с помощью рядов Тейлора по существу уже описано в п. 9.2-5.
Метод Рунге — Кутта применяется по схеме, подобной п. 20.8-2, Ь:
где
(20.8-20)
Уш = Уь + е (^i + 2*2 + 2*з + *4).
4+1 = zk +• {- (тх + 2т2 + 2т3 + т4), ...,
Щ=ё{хк, yki zb...)A*
m2=£^+^,^+A, *+^,...)д*,...,
** = /(** +А*. Ул + *8. z*+m3, ...)Д*,
я«|я^(^ + ^. #л+*з. гл + /Я8....)Д*....
Любая разностная схема из п. 20.8-3 можег быть применена к каждому
из уравнений (19) с обозначениями
/(**. Уъ *kf •••)=/*. g(*k:
z(xk) = zk |
(20.8-21)
(с) Устойчивость точного решения y=y(x) системы в матричных
обозначениях
dy _
dx
= /(*. У)
зависит от матрицы (df/dy) (п. 13.6-5). Уравнение (17) становится матричным
разностным уравнением; при исследовании относительной устойчивости
собственные значения этого уравнения надо сравнивать с собственными значениями
матрицы (df/ду) \x = xk [20.12].
20.8-7. Специальные формулы для уравнений второго порядка. Ввиду
практической важности дилеренциальных уравнений второго порядка
представляют интерес приведенные ниже схемы численного интегрирования
дифференциального уравнения
#"=/(*. У, У')
(20.8-22)
при начальных условиях y(xQ)=yQ, у' (х0)=у'0', в этих схемах введены
обозначения:
xQ + kbx = xk9 y(xk) = yk, y'(xk) = yk> /(**» Ук> y'k)=fk
(k = 0, 1, 2,...). (20.8-23)
Приведенные ниже методы могут быть распространены на системы уравнений
второго порядка так, как указано в п.20.8-6.
23*
708
ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ
20.8-8,
где
(20.8-24)
(a) Метод Рунге-Кутта для уравнения (22):
Ук+1=*Ук + Ум*х + -ъ (ki + kz + h) A*.
У'к + l^y'k + J (kl + 2k2 + 2k3 + kd>
h = f(Xk, Ук> У$Ьх>
*2 = /(^+т- Уь + У'кТ* У'к + ъ)***
*» = / (xk+ т. **+# Т + 7 А*' У'к +f) **•
^4 = / /*а + А*, Ул + ^ А* + -у А*» #* + *з) А*.
(b) Интерполяционно-итерационная схема. Начиная с
некоторого пробного значения fk+1, итерируют
(20.8-25)
Ук +1 = 2Ук - 0*-i + (/* +12 *2 /*+i) А*2>
(с) Схема «предсказание — коррекция»
Ук+х^Ук-з + Ъ (2fk—fk-i + 2fk-2) Аде («предсказание»),
Ук+1=Ук~1 + ^(Ук + 1+4У'к + У'к-0Ах>
Й +! = Ул -1 + i C*+i + 4^ + ^*-*) Д* («коррекция»).
(20.8-26)
Если /(*, г/, у'), не содержит явно #', то можно применять в качестве
предсказывающей формулу
yll4 = 2yk_1-yk_3 + \ ifk+fk-i+fk-d Ьх\
а для уточнения формулу (Штермера)
УТ?! = 2ук -у^г + ^ (/"Р« +10/ft +/*-i) Л*2
(см. также п. 9.1-5, Ь).
(d) Метод Нумерова для линейных уравнений (см. [20.12]).
Линейное дифференциальное уравнение вида
(20.8-27а)
(20.8-27&)
У" = / (х) у + g (х)
(20.8-28)
можно решить с помощью одной лишь формулы коррекции (27Ь); подставляя в
уравнение (28), получаем
и*+1 = 2uk ~ uk-l + [ fk*k + Ч + Т2 (g*+l - 2gft + gA-l)] Д*2'
(20.8-29)
20.8-8. Анализ частотных характеристик. Если дана устойчивая формула
интегрирования (12), то синусоидальный ввод f.==e k вызовет синусоидальное решение
20.9-2. 20.9. КРАЕВЫЕ ЗАДАЧИ; ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 709
y.=z Ц (/о)) е k (так же как в п. 9.4-6). Подстановка дает частотную характеристику
И (/со) = G (*)=, , ?•£-*-£.£-... Л* («—'•**)• (20.8-30,
Здесь формулы интегрирования можно толковать как приближения к идеальному
оператору интегрирования — по амплитуде и фазе. Для уменьшения распространения
ошибок округления надо, чтобы ошибка Я (/со)—— убывала с частотой, см. [20.12].
I *со I
20.9. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ, КРАЕВЫЕ ЗАДАЧИ;
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
20.9-1. Вводные замечания. В пп. 20.9-2 — 20.9-5 описываются разностные
методы, применимые для численного решения краевых задач как для
обыкновенных дифференциальных уравнений, так и для уравнений с частными
производными, а также и для численного интегрирования гиперболических и
параболических уравнений с частными производными. Кроме описанных здесь
методов имеются еще следующие методы решения.
Приведение уравнения с частными производными к обыкновенным
дифференциальным уравнениям путем разделения переменных (пп. 10.1-3 и 10.4-9),
решения характеристического уравнения (пп. 10.2-2 и 10.2-4) или метода
характеристик (п. 10.3-2).
Приведение к вариационной задаче (пп. 11.6-9 и 15.4-7) и решение ее
прямыми методами, например методом Ритца (п. 11.7-2)
Приведение к интегральному уравнению (п. 15.5-2), которое можно решать
прямыми методами или с помощью методов аппроксимации п. 20.9-10.
Методы возмущений для решения задачи о собственных значениях описаны
в п. 15.4-11.
20.9-2. Двухточечная краевая задача для обыкновенных дифференциальных
уравнений (см. также пп. 9.3-3, 15.4-5 и 15.5-2). Двухточечная краевая задача,
т. е. задача нахождения решения обыкновенного дифференциального
уравнения, удовлетворяющего краевым условиям на границе интервала (at b)t может
быть сведена к задаче Коши методом п. 9.3-4. Более подходящим может
оказаться следующий разностный метод.
Разделим данный интервал (а, Ь) на равные промежутки точками
х0 = а, x1 = x0-\-hx, х2 = х0 + 2Длг, ..., хп—х0 + пАх = Ь
и заменим каждую производную и в дифференциальном уравнении и в
краевых условиях соответствующим разностным отношением того же порядка
(п. 20.7-1, а, рис. 20.9-1 и 20.9-6). Это позволяет аппроксимировать данное
дифференциальное уравнение разностным уравнением того же порядка.
Численное решение разностного уравнения сводится к решению системы уравнений
относительно неизвестных значений функции yk — у (х0 + kАх) (пп. 20.2-5 —
20.3-2). При расчетах вручную особенно удобны релаксационные методы
(п. 20.3-2, с).
dzu 1
Пример. Чтобы найти решение уравнения Tj + t^"' удовлетворяющее
краевым условиям #(0) = 1, г/ (1) = 0, целим интервал (0, 1) на п промежутков длины
&х=1/п и, заменяя -— ^s —^, получаем разностное уравнение
710
ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ
20.9-3.
с дополнительными условиями yQ = 1, Уп = 0. При п= 4 (k = 1, 2, 3) получаем следующую
систему относительно уи у2, у9:
( - 1,99^+ у2 = -1
< yt- 1,99^2-f- ^з = 0,
I г/2 — 1,99г/з =0.
20.9-3. Обобщенный метод Ньютона (квазилинеаризация). Хотя численные методы
пп. 9.3-4 и 20.9-2 применимы как к линейным, так и к нелинейным двухточечным
краевым задачам, эти методы легче применять к линейным задачам. Для решения важного
класса нелинейных двухточечных краевых задач вида
У" = fix. у. у') (a<x<b), \
4>[у(а), у'(а)]=0, Ц[у(Ь), y'(b)]=0 J ( •"'
часто применяется метод квазилинеаризации. Начиная с пробного решения yWl (x),
которое удовлетворяет заданным краевым условиям, получают последовательные
приближения у№](х), у№](х), ... путем решения линейных задач
,»[/+!] = f (x, у1П,?1П) +fy (x, уШ, ytfl) (у[/+1] -уШ) +
+ !у(х.уЫ.у1П){уи+И-у1П).
VylyMw.y'W (а)] [у[/+П (а)-уМ (а)] +
+ <Vy> ЫП (а), у'М (а)] [y'U+Ч (а) -у'Ш (а)] = 0,
% [уМ (Ь). yW (b)] lyU+lkb) -yM (b)] +
+ V ^[/] <*>• *'с/1<*> J1у'и+1]<*> -у,[п (*>] =°-
Этот метод без труда обобщается на системы дифференциальных уравнений с помощью
матричных обозначений п. 13.6-1 и является обобщением метода Ньютона п. 20.2-8: подобно
последнему, он может сходиться весьма быстро. Здесь можно сформулировать и общие
условия сходимости, но удобнее проверять сходимость методом проб.
20.9-4. Разностные методы численного решения уравнений с частными
производными для случая двух независимых переменных. Методы решения
задач для уравнений с частными производными аналогичны изложенным в
п. 20.9-2. Введем подходящую сетку значений координат Xi = x0-{-ikx, Ук =
= yQ + kky (i, 6 = 0, ±1, ±2, .*..); неизвестная функция Ф(*, у) будет
представлена дискретным множеством своих значений Ф(Х[, уь) —Oik-
Аппроксимируем каждый дифференциальный оператор соответствующим разностным
оператором того же порядка так, что любая производная будет
аппроксимирована соответствующим разностным отношением. Получаемое разностное
уравнение будет давать систему уравнений для неизвестных значений Ф^.
Наиболее важные задачи приводят к следующим ситуациям.
1. Краевая задача для эллиптического уравнения (например, задача Дирихле
для у2Ф = 0, п. 15.6-2) приводит к системе N линейных уравнений
относительно N неизвестных Ф^.
Большое число уравнений и неизвестных, связанное с такими
разностными методами, затрудняет решение задач даже на больших ЭВМ. С другой
стороны, характерные особенности разностных операторов, получающихся
для обычных линейных уравнений с частными производными второго и
четвертого порядков (табл. 10.4-1), приводят к системе линейных уравнений
с «разреженными» матрицами, которые имеют мало ненулевых членов вдали
от главной диагонали. Поэтому к таким задачам хорошо подходят
итерационные методы п. 20.3-2.
2. Линейная задача о собственных значениях (например, у2Ф = ХФ с под-
(ходящими краевыми условиями, п. 15.4-1) приводит к задаче о собственных
значениях некоторой матрицы.
3. Задача Коши для параболического или гиперболического уравнения
(п. 10.3-4) приводит к системе уравнений, если выбранная схема сведения к раз-
(20.9-2)
20.9-6, 20.9. КРАЕВЫЕ ЗАДАЧИ; ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 711
ностным уравнениям сопоставляет каждое неизвестное значение Ф^ с другим
неизвестным, так же как и с известным, значением функции (неявные методы
решения задач Коши).
4. Если для производных по времени в задаче Коши применяется
разностная аппроксимация (п. 20.7-1), то мы получаем рекуррентные формулы для
последовательных значений Ф^, начинающихся от заданных начальных
значений (явные методы решения задачи Коши).
Вообще говоря, явные методы решения задачи Коши требуют меньше
вычислений, чем неявные методы, но в рекуррентных схемах распространение
ошибок и вопросы устойчивости подобны тем, которые возникают при
численном интегрировании обыкновенных дифференциальных уравнений. Как и в
последнем случае, аппроксимация может быть улучшена с помощью метода
«предсказание — коррекция», аналогичного рассмотренному в п. 20.8-3
(см.также п. 20.9-8).
20.9-5. Двумерные разностные операторы. На рис. 20.9-1—20.9-6
приведены часто встречающиеся линейные разностные операторы. В частности,
каждая диаграмма на рис. с 20.9-1 по 20.9-5 дает центрально-разностное
выражение для центра «звездочки» через взвешенную сумму значений функции
«сверху», «снизу», «справа» и т. д. относительно центра; каждый весовой
коэффициент помещен в соответствующем узле сетки. Например, рис. 20.9-1 надо
понимать так:
h2^®\(xhyk)^®<<xi + h> Ук) + Щхг-Н% ук) + Щхь yk + b) + <l>(xi, Ик-А)-
-4Ф(*£, ул) = Ф* + 1.* + Ф*-1. * + Ф,-, * + 1 + Ф/, *-1-4Ф/л,
где ft = A* = A# есть шаг сетки по обоим переменным хну.
Рис. 20.9-1 применяется для сетки прямоугольных декартовых
координат при равных шагах по х и у. Рис. 20.9-3 применяется при изменении
шага сетки, либо чтобы приспособить ее к неправильным границам, либо
чтобы увеличить точность вычислений в некоторой области, представляющей
особый интерес. В любом случае используемая сетка может быть уточнена
после первых грубых подсчетов.
Рисунки 20.9-2, 20.9-4 и 20.9-5 демонстрируют разностные операторы
для сеток, отличающихся от прямоугольных декартовых. На рис. 20.9-6
приведены разностные операторы для интерполирования вперед и назад.
Для расчетных целей сетка точек (л^, yk) часто обозначается простой
последовательностью 1, 2, ...; соответствующие значения Ф^ обозначаются при
этом через Фь Ф2, ... (см., например, рис. 20.9-7). В расчетах
релаксационного типа (п.20.3-2) при решении линейных краевых задач вошло в обычай
применять крупный план области и записывать значения функции и невязки
непосредственно в каждой точке сетки. Значения функции и невязки от
предшествующих шагов релаксационного процесса просто вычеркиваются или
стираются.
Примечание. Дифференциальный оператор в линейных краевых задачах нельзя
заменять разностным оператором более высокого порядка, так как это может вызвать ложные
колебательные составляющие в решении получающегося разностного уравнения. С
другой стороны, в разностных схемах решения задач Коши для гиперболических или
параболических уравнений часто используют разностные операторы высших порядков, чем
соответствующие производные, подобно тому как это сделано в пп. 20.8-1—20.8-5.
20.9-6. Представление краевых условий (рис. 20.9-7). Аппроксимируем
данные границы линиями применяемой сетки; если нужно, вводим
градуированную сетку (рис. 20.9-3). Тогда:
1. Если заданы краевые значения искомой функции Ф, то
вписываем их в соответствующих точках границы (рис. 20.9-7, а).
2. Если заданы краевые значения производных (таких, как
дФ/дп, п. 5.6-1, Ь), то продолжаем сетку за границу области и
аппроксимируем краевые условия соответствующими разностными
7J2 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.9-6.
0—0 000 00—-00» 00000
2"1
дх'
ах'
п дх*
f?2V<
0-г0
б-кЬ
Zh2V2
0
•о
4h<
Щ
Рис. 20.9-1. Операторы для центрально-разностной аппроксимации (прямоугольная
сетка декартовых координат: Ах = Ay = h). Относительная погрешность имеет порядок h2.
3/i2V2
j§h<V<
16
h4V4
91)4 V4
Рис. 20.9-2. Центрально-разностная аппроксимация дли сетки из правильных
треугольников со стороной h. Относительная погрешность имеет порядок И1,
21).9-в. 20.9. КРАЕВЫЕ ЗАДАЧИ; ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 71<*
Рис. 20.9-3.
Центрально-разностный оператор, применяемый
для градуированной сетки или
для аппроксимации вблизи
границы. Относительная
погрешность имеет порядок h.
2A2h2sin2ilV2
Рис. 20.9-4. Центрально-разностный оператор*
применяемый для косоугольной сетки
декартовых координат. Относительная
погрешность имеет порядок №.
Рис. 20.9-5. Центрально-разностный оператор, применяемый для сетки полярных
координат г, ф. Относительная погрешность имеет порядок г АгАср. Удобна сетка,
градуированная соотношением Лг = /-Дф.
©-©-© О-^У-Q
(EKEWZHD ©4ZM2HD
JL
diz
fj2.
dx2
Рис. 20.9-6. Разностная аппроксимация для интерполирования вперед или назад
(прямоугольная сетка декартовых координат Ах == Ay = h). Относительная погрешность
имеет порядок h2.
714 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.9-7.
отношениями. Получающиеся уравнения, так же как и разностные
отношения, аппроксимирующие само дифференциальное уравнение в
точках вблизи границы, будут включать значения функции в точках,
лежащих вне области; но все такие значения можно исключить
алгебраическими преобразованиями.
*Д
Граница
Граница
*г
I
i
Прямоугольная сетка
а)
Треугольная сетка
ь)
Рис. 20.9-7. Представление краевых условий для у2Ф = 0 или у4Ф = 0. Сетка
продолжена влево от данной границы и введены «отраженные значения» <Е>2 = Фг. Ф* = Ф4 Для
представления условия дФ/дп = 0 на границе разностным отношением. Краевое
условие Ф = 0, V2<D = 0 (например, свободный край упругой пластины) представляется
подобным же образом через Фх = Ф3 = 0, Ф2 = —Фг. Ф4 = —®4-
Пример. На рис. 20.9-7, Ь показано, как аппроксимируются краевые условия
дФ/д/1 = 0 путем «отражения» значений функции в границах так, что Ф' —Ф2 = 0, Ф^ —
— ф = 0. Для дифференциального уравнения у2Ф = 0, применяя первый разностный
оператор рис. 20.9-2, получаем
Ф2 + Ф4 + Фб + Ф4 + Ф2 + Ф1 ~ 6ФЯ = °
или, так как из краевого условия вытекает ф^ = ф Ф'= Ф4,
2Ф2 4- 2Ф4 + Ф5 + Ф1 — 6Ф3 = 0.
Последнее уравнение содержит только точки, лежащие внутри области или на границе.
20.9-7. Задачи, содержащие более двух независимых переменных.
Аналогичные методы применимы к задачам, содержащим более двух независимых
переменных. В частности,
Л2у2Ф (*> У. *)**<*> (x + h, у, г) + Ф (x-h, у, г) + Ф (*, y + h, г) + Ф (*, y-h, г) +
+ Ф(х, у, г + Л) + Ф(*. у, г — К) — 6Ф(*, у, г). (20.9-3)
Число независимых переменных часто может быть уменьшено путем
разделения переменных (п. 10.1-3).
20.9-8. Пригодность разностных схем. Условия устойчивости. Пригодность решения,
полученного разностной аппроксимацией, требует исследования. Если
дифференциальное уравнение аппроксимируется двумя различными разностными уравнениями, то даже
при одном и том же шаге сетки мы можем получить значительное расхождение. Сверх
того, не всегда возможно улучшить аппроксимацию путем уменьшения шага сетки, даже
если разностное уравнение допускает точное решение. Пригодны только такие схемы,
в которых при уменьшении шага сетки решение разностного уравнения сходится к
решению рассматриваемого дифференциального уравнения. Для параболических и
гиперболических уравнений с частными производными такая сходимость имеет место только
тогда, когда шаги сетки по обеим координатам удовлетворяют некоторому условию
устойчивости. Так, решение разностного уравнения
Ф (дс+ Длг.О -
• 2Ф (лг, t) + Ф (х •
■ Длг, t)
_ 1 Ф (х, t + At)
' a* At
■Ф (х, t)
20.9-9. 20.9. КРАЕВЫЕ ЗАДАЧИ; ИНТЕГРАЛЬНЫЕ УРАВНЕНИИ
715
сходится к решению уравнения теплопроводности (п. 10.4-1)
д^Ф==± дФ
дх* a2 dt
при At -*• 0, Ах -* 0, если At <^-^ Ах2.
Решение разностного уравнения
Ф (*+ Ад:, /)~2Ф (л:, 0 + Ф (* — Д*. J) _ 1 Ф (х, t -f АО — 2 Ф (*, Q -f Ф (х, i — At)
А/а
сходится
к
решению
Ах2
волнового
уравнения
д2Ф
дх2
с2
_ 1 д2Ф
~~ с2' dt2
при At -* О, Дл: -* 0, если At < — Дл:.
с
Такие условия устойчивости обеспечивают также лучшую аппроксимацию при
конечном шаге сетки.
Заметим, что неявные методы (п. 20.9-4) не требуют таких ограничений, как явные
методы, приведенные выше. Например, неявный метод, основанный на аппроксимации
Никольсона
a2At
' Ах2
( a2At\
[Ф (х - Д*. / + ДО + Ф(х+ Ах, t + ДО] + [1 + д^г) ф (** * + А') ="
=О ~£^)ф {хг °+£^[ф {х ~**• °+ф {х+Ах> пь
дает приближенное решение уравнения теплопроводности, которое сходится к точному
решению, как только Ах -*> 0, А/ -•> 0.
20.9-9. Методы аппроксимирующих функций для численного решения
краевых задач.
(а) Аппроксимация функциями, точно
удовлетворяющими краевым условиям. Пусть переменное х одномерно или
многомерно, x = (xv x2y ..., хп) (п. 15.4-1). Требуется найти решение
дифференциального уравнения обыкновенного или с частными производными
LO (*) = /(*) (x£V)9 (20.9-4A)
удовлетворяющее краевому условию
В Ф (х) = 6 (x) (x £ S) (20.9-46)
на границе S данной области V (п. 15.4-1). Аппроксимируем искомое
решение Ф (л:) некоторой аппроксимирующей функцией
Ф = ф(г, а1( а2, ..., ат), (20.9-5а)
которая удовлетворяет краевым условиям и зависит От т параметров av a2, ...
..., ат. Во многих приложениях уравнения (4) линейны и функцию Ф (х)
аппроксимируют линейной комбинацией известных функций
т
Ф-2 «*Ф*М. (20.9-56)
где фх(л:) удовлетворяет краевому условию (4,6), а ф2 (л:), ..., ут(х)
удовлетворяют однородному краевому условию В Ф (х) = 0 (х £ S) (см. также п. 15.4-2).
Ошибка аппроксимации (5а) или (56) есть функция от <xv а2, ..., ат:
Е(х\ аъ а2, ..., am)==Lq(x\ ах, а2, ..., ат) — f(х). (20.9-6)
Неизвестные параметры ott, ot2, ..., ат выражения (5а) или (56) определяют
по одной из следующих схем.
716 ГЛ. 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.9-10.
1. Коллокация. быбирают ak так, чтобы ф (л:; alt ..., ат)
точно удовлетворяла данному дифференциальному уравнению (4а)
в т точках х — Хъ х = Х2, ..., х = Хт, т. е. чтобы
E(Xi\ ах, а2, ..., ат) = 0 (/ = 1, 2, ..., т). (20.9-7)
2. Средние квадратические приближения (см. также
п. 20.6-2). Выбирают ak так, чтобы минимизировать среднюю квадра-
тическую ошибку
J (о,, а2, ... ,a„)sJ|£ (£; alf a2, ..., am) | 2 dg (2o.9-8)
или величину
Л/
У (alf а2, ... , am) s ^ 6Л I £ (*а5 <*i. <*2> - , «т) 12, (20.9-9)
Л = 1
где 6h — подходящим образом определенные весовые коэффициенты,
приданные N точкам Хг, Х2, ..., XN из V. Например, можно взять
равноотстоящие точки и положить
b1 = b? = ... = bN = l.
Коэффициенты ak определяются из т условий
-^=0 или ~=0 (Ы,2 я»). (20.9-10)
k k
3. Метод Галеркина. Выбирают т линейно независимых
«весовых функций» г|?х (л:), if>2 (*), ..., if>m (л:) (часто применяют
г|эл = фл) и определяют а^ так, чтобы
Ф/(Б)£(5; «1. сс2, ...,aw)dg = 0 (/=1, 2, ..., m). (20.9-11)
Если данные уравнения (4) линейны (линейная краевая задача), то и
получающиеся при аппроксимации вида (56) уравнения (7), (10) или (11) будут ли-
нейны.
(Ь) Аппроксимация функциями, которые точно
удовлетворяют дифференциальному /равнению. Часто
предпочтительнее использовать аппроксимирующие функции (5), которые для всех х из V
точно удовлетворяют дифференциальному уравнению (4а), и подбирать
параметры ak по краевым условиям одним из указанных выше методов.
20.9-10. Численное решение интегральных уравнений (см. также п. 15.3-2).
(a) Решение Ф (л:) линейного интегрального уравнения
Ф(х)-Х\ К(х% l)Q>{l)dl = F(x) (20.9-12)
V
часто можно аппроксимировать итерационным методом п. 15.3-8, а, или
же можно аппроксимировать данное ядро К (х, £) многочленом или другим
вырожденным ядром (п. 15.3-1, Ь), чтобы упростить решение. Задача о
собственных значениях (F^0) часто может рассматриваться как вариационная
задача (п. 15.3-6).
(b) Метод аппроксимирующих функций п. 20.9-9 применим также
непосредственно к численному решению линейного интегрального уравнения (12).
Выберем аппроксимирующую функцию вида (56) и вычислим т функций
tk М = Фа М -Ц К (х, I) щ (I) d$ (* = 1, 2, ..., m). (20.9-13)
20.10-1.
20.10. МЕТОДЫ МОНТЕ-КАРЛО
717
Тогда
1. Метод коллокации дает т линейных уравнений
т
2 akfk(Xi) = F(Xi) (i = l, 2 т)
k = \
(20.9-14)
2. Метод наименьших квадратов приводит к системе линейных
уравнений
т ,
2 Aihak = h (/==1, 2, ..., m),
*=i
где
(20.9-15)
N
Aik= S bhh(Xh)fk(Xh)t
/t = l
Pi = S biJi{Xh)F{Zh)\
/i = i
6Л —весовые коэффициенты, определяемые так же, как в формуле (9).
3. Метод Галеркина приводит к системе линейных уравнений
Ш J
2 Alkak = h (/ = 1, 2, ...,m),
где
[ (20.9-16)
,л-$
A*=\ % (?) /* (I) С к=\ t« © f (?) dg.
'i*
— CO—CO -—CO
с помощью выборочного среднего значения
20.10. МЕТОДЫ МОНТЕ-КАРЛО
20.10-1. Методы Монте-Карло. Каждый расчет методом Монте-Карло
можно рассматривать как оценку некоторого интеграла
со со со
/== $ S - $ /ЛЛ Wd(1,(^ **. •••• М (20.Ю-1)
ia
f(*i, x2, ...,xN)= 4- 2 /(**ь **i. -. ЧЛ (20.10-2)
* = i
где (xlt x2, ..., хN) — некоторая (вообще говоря, многомерная, N>1)
случайная величина с известной функцией распределения Ф (хи х2, ..., xN).
Методы Монте-Карло широко применяются при исследовании явлений
в случайных процессах, слишком сложных для явного решения методами
теории вероятностей, а именно, в задачах диффузии нейтронов, задачах
детектирования и связи и в разнообразных исследованиях операций. Сверх этого,
часто имеет смысл преобразовать зддачи других типов, особенно содержащие
сложные многомерные интегралы, в такую форму, которая позволяет решать
их методами Монте-Карло.
718 ГЛ 20. ЧИСЛЕННЫЕ МЕТОДЫ И КОНЕЧНЫЕ РАЗНОСТИ 20.10-2.
Для простоты ограничимся рассмотрением оценки методом Монте-Карло
одномерного интеграла
со
/= J f(K)d<b(k) (20.10-3)
— со
с помощью среднего значения
Ш = 4-[/(1*Ж(2*) + -+/(л*)Ь (20.10-4)
Дисперсия этой оценки по случайной выборке (}х, 2х, ..., пх) равна
D/W--i-D/W, (20.10-5)
так что средняя квадратическая ошибка убывает только как 1/|ЛГ при
возрастании п (п. 19.2-3). Дисперсия оценки вызвана случайными флуктуациями
в распределении различных выборок, (}х, 2х> ..., пх).
20.10-2. Два метода уменьшения дисперсии оценки. Следующие методы
«подправляют» выборку (**, 2х, ... , пх) так, чтобы уменьшить дисперсию выборочной средней
при условии сохранения соотношения
MM*) = Mf <*) = /. (20.10-6)
т. е. без смещения оценки.
(а) Метод расслоенной выборки. Диапазон изменения случайной
величины х делят на некоторое число подходящим образом выбранных классовых интервалов
£, 1 < х ^ lf. и фиксируют число п, в остальном независимых выборочных значений х ==»
в= 'Xiг (/ = 1, 2, ... t n.)i попадающих в /-й классовый интервал. Предполагая заранее
известными вероятности
*V - р {б/., < * < в/} - * с*,) - ф aj-г) <20-10-7>
попадания в /-й классовый интервал, можно в качестве несмещенной оценки / применить
среднее по расслоенной выборке
1 nU „ ,
(20.10-8)
причем
Окрасе* - 2-^D'(4)- <20-,0-9>
Заметим, что повторные расслоенные выборки будут отличаться только внутри
классовых интервалов. Дисперсия (9) может оказаться меньше дисперсии случайной выборки
D f (х)/п при п = ^ nf если предварительная информация позволяет удачно выбрать
/
значения £ • и п,. Лучше всего было бы выбрать классовые интервалы с одинаковыми
дисперсиями
. S/ Г, *'
D f Cxj) = p-\ f'ft)#(W-Ы f (X) <?Ф №) |
и затем назначить теоретически точные числа выборок в каждом классовом интервале
по формуле
п. = пР, (20.10-11)
В этом идеальном случае будем иметь относительно малую дисперсию оценки
Dfi*Wj-TD'('*/)• (20Л0-,2)
При уменьшении величины классовых интервалов метод расслоенной выборки
приводит к результатам, аналогичным тем, которые дают квадратурные формулы. Но обычно
берут большие классовые интервалы; на практике особый интерес представляют
многомерные интегралы, где простые соотношения симметрии могут помочь удачному выбору
классовых интервалов.
(20.10-10)
20.10-4.
20.10. МЕТОДЫ МОНТЕ-КАРЛО
719
(b) Применение коррелированных выборок. Если выборочные
значения х не являются независимыми (как это бывает в чисто случайной выборке),
то выражение (5) для дисперсии оценки надо заменить на (см. также п. 19.8-1):
D Пйкорр = 4 D fix) + ~ 2 2 c°v {f (4 f (**) }. (20.10-13)
i<k
Разумно введенная отрицательная корреляция (т. е. корреляция с отрицательным
коэффициентом корреляции) между выбранными парами выборочных значений '*, х
будет приводить к отрицательным членам с ковариациями в формуле (13) и может
уменьшить дисперсию по сравнению с дисперсией случайной выборки D f (x)/n без смещения
оценки.
Приведем простой пример. Пусть величина х распределена равномерно в интервале
ех- 1
(0, 1) и пусть f (х) есть монотонная функция —__ Планируем выборку так, чтобы п
было четным и 2х = 1 — 1х, *х — 1 — Зх пх = 1 — п~1х; в остальном выборочные
значения независимы. Так как f (х) и f (1 — х) коррелированы отрицательно, то
дисперсия средней уменьшается:
так что средняя квадратическая ошибка уменьшается примерно в 5, 6 раз. Кроме того,»
коррелированная выборка требует генерирования меньшего количества случайных чисел.
С другой стороны, более интересны применения к многомерным задачам.
Заметим, что метод расслоенной выборки фактически также приводит к
отрицательной корреляции между выборочными значениями: значение гх не может попасть
в данный классовый интервал, если значение х его уже заполнило.
20.10-3. Использование предварительной информации. Метод значимой выборки.
Вычисления по методу Монте-Карло часто могут быть упрощены путем разумного
использования предварительной информации о возможном результате. В методе значимой
выборки пробуют оценить интеграл (1) с помощью выборочного среднего / (y)/g (у)*
где у — случайная величина с плотностью распределения вероятностей
<!>у(У)=ё(У) d°dyy) • (20.10-14)
Легко видеть* что такая оценка является несмещенной. Функция g (у) выбирается
так, чтобы дисперсия
От^мШ^-Л2 (20.10-15)
ё {у) U (у) J
00
была мала, при условии, что J <р (у) dy = 1.
— оо
В частности, выбор g (у) == f (y)/I уменьшает дисперсию (15) до нуля, но для этого
надо знать неизвестное значение /.
Значимая выборка позволяет «сконцентрировать» выбор вблизи нужных значений у$
например, там, где f (у) быстрее изменяется.
20.10-4. Некоторые методы генерирования случайных чисел. Проверка случайности.
В методах сравнения для генерирования псевдослучайных чисел х., меньших данного
положительного модуля т, начинают с некоторого неотрицательного числа х0 < т
и вычисляют последовательные значения
х. = [axUl + c]mod m (i - 1, 2, ... ; 0 < а < т, 0 < с < т), (20.10-16)
где сложение по модулю т определено в п. 12.2-10. В двоичной вычислительной машине
модуль т удобно Еыбирать равным 2 , где / —длина машинного слова (число разрядов).
При с = 0 генератор называется мультипликативным генератором сравнения, в
противном случае — смешанным генератором сравнения.
Последовательности, получаемые этим способом, не вполне случайны, но имеют
такие «псевдослучайные» свойства, как равномерное распределение в интервале (0, т)^
некоррелированность различных х., случайно выступающий ряд четных и нечетных
чисел и т. д. Равномерность распределения может быть проверена по критерию
согласия х2 (п. 19.6-7), а порядковая (сериальная) корреляция — так, как указано в п. 19.7-4.
Заметим, однако, что даже при отсутствии корреляции выборки (д^, *2 *п),
образованные при помощи последовательности псевдослучайных чисел, могут не быть неза-
висимыми, что может привести к неприятным сюрпризам. Может оказаться разумным
получить вполне случайные выборки с помощью цифрового преобразования белого шума.
Псевдослучайные числа с распределением, отличным от равномерного, легко
получить как функцию F (хЛ от равномерно распределенных случайных величин.
ГЛАВА 21
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.1. ВВЕДЕНИЕ
21.1-1. Вводные замечания. Глава 21 представляет по существу собрание
формул, связывающих специальные функции. Отсылаем к гл. 7 для связи
с теорией функций комплексного переменного и к гл. 9, 10 и 15 для
применений к дифференциальным уравнениям. Гораздо более подробное изложение,
а также сведения о реже встречающихся специальных функциях можно найти
в книгах [21.1] и [21.3]. В книгах [21.5] содержится перечень числовых
таблиц специальных функций.
21.2. ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
21.2-1. Тригонометрические функции (см. также табл. 7.2-1).
(а) Тригонометрические функции w — sinz, w==cosz могуг быть
определены при помощи степенных рядов (п. 21.2-12), как решения
дифференциального уравнения
d2w
dz2
+ ад = 0,
как z = arcsin ад, z = arccos w (интегральные представления, п. 21.2-4) или,
для действительных z, в геометрических терминах (гониометрия, рис. 21.2-1).
Остальные аригонометрические функции определяются как
tgz =
™± ctgz = Ti- =
"cos z *
1
COS Z
sin 2
cosecz = -
(21.2-1)
(21.2-2)
Таблица 21.2-1
Специальные значения тригонометрических функций
А
(градусы)
А
(радианы)
sin A
cos A
ч* л
ctg A
0°
360°
0
0
1
0
± оо
30°
л
6
1
"2
vt
2
vT
3
vT
45°
л
4
Y2
2
V2
2
I
1
60°
Л
3
/3"
2
1
2
Yz
з"
90°
л
2
1
0
-j: со
0
180°
л
0
-1
0
±oo
270°
Зл
2
-1
0
±oo
0
21.2-1.
21.2. ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
721
Рис. 21.2-1. Определения тригонометрических функций для данного угла фз
Ф = — (в радианах).
sin ф -
cos ф = —,
I/ sin ф , х cos ф
sec ф = — =
cos ф
1
COS ф '
у sin ф '
cosec ф = -^— =
у sin ф "
/
-SO9
Vr >
'/80° 270° 360°
J i l_
JL rt\ ЗтС /2rt tp
2 \ 2 '
syk
V -£>
Рис. 21.2-2. Графики тригонометрических функций для действительного аргумента
г = ф.
722
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.2-2.
(b) sin z и cos z —периодические функции с периодом 2я; tgz и ctg г
периодичны и имеют период я; sin z, tg z и ctg z — нечетные функции, a cosz—
четная функция.
На рис. 21.2-2 изображены графики sin z, cosz, tg z и ctg z для
действительного аргумента.
На рис. 21.2-3 показаны прямоугольные треугольники, которые облегчают
запоминание значений тригонометрических функций для г = я/6( = 30°), z =
= я/4( = 45°) и г = я/3( = 60°) (см.
также табл. 21.2-1).
(с) Соотношения
sin z = cos
Рис. 21.2-3. Специальные треугольники
■fi-M
cos z = sin (у —z)>
tg2 = ctg(*~-z),
ctgz = tgg-z), J
(21.2-3)
для вычисления значений
тригонометрических функций углов 30°, 45°. 60°
позволяют выражать значения
тригонометрических функций любого
действительного аргумента через значения
функций для аргумента, заключенного между 0 и я/2 рад( = 909) (табл. 21.2-2
и рис. 21.2-1).
Таблица 21.2-2
Соотношения между тригонометрическими функциями
различных аргументов
sin
cos
tg
ctg
-Л
—sin A
cos A
-tg Л
— ctg A
f±»
cos A
+ sin A
+ ctg A
+ tg A
n± A
ц: sin A
— cos A
±tgA
± ctg A
%-±л
— cos A
±sin A
ч= ctg A
+ tg A
2л ± А
± sin A
cos A
±tg A
± ctg A
21.2-2. Соотношения между тригонометрическими функциями (см. также
п. 21.2-6). Основные соотношения
sin2z + cos2z=l, s-£J==tgz==4-
1 ' COSZ & Ctg2
имеют следствиями формулы:
sin z—V\ —
!z =
tgz
cos z =Y 1 — sin2 z =
sin z Yl— cos2 z
/l + tg22 /l-fctg'2*
1 _ ctg z
tg Z =
CtgZ =
/l + tg22 /l+Ctg*2'
1
V\ — sin22
_Y\ — sin22_
sin 2
COS 2
COS 2
"Ctg 2 '
1
/l—COS22 {SZ*
(21.2-4)
(21.2-5)
21.2-3. 21.2. ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
723
21.2-3. Теоремы сложения и формулы для кратных углов.
(а) Из основного соотношения
sin (А + В) = sin A cos В + sin В cos A
следуют:
sin (А ± В) = sin A cos В ± sin В cos A,
cos (Л ± В) = cos Л cos В + sin Л sin В,
tg(A±B)=-
tg Л ± tg В
. tg Л tg В '
ctg(A±B) =
ctg A ctg В :
ctg В ± ctg A
sin 2Л = 2 sin Л cos Л,
соз2Л=со82Л —sin2 Л = 2со82Л —1 = 1—2 sin2 Л,
1б2Л= 2igA
lgZ/1 1-tgM»
Ctg 2Л :
ctg2 A — 1
2 ctg A
sin
._!/!
2
, A sin Л 1 — cos A
tg2"~"l-bcosi4 ~~
= ± (Ctg A-\g A);
cos A A "i/*14-cosj4
2—> C0St=K-4—
ctg£ =
sin A
1 — cos A
sin Л '
1 -f cos Л t
sin A
a sin Л + 6 cos A =/- sin (Л+£) = г cos (90°- — Л —Я),
(21.2-6)
(21.2-7)
(21.2-8)
(21.2-9)
(21.2-10)
Sin Л ;
. n 0 . Л + B A+B
smB = 2 sin —^— cos
cos Л + соз£ = 2 cos Z cos
2 '
л -в
2
Л
В
sin
2
Л
cos Л—cos В = — 2 sin «». 2
sin (Л ± Bl sin (В ± Л).
tg Л ± tg Я =
cos Л cos В
2 cos Л cos £ = cos (Л —В) +cos (Л + В),
2 sin Л sin В = cos (Л — В) —cos (Л + £),
2 sin Л cos В = sin (Л — B) + sin (Л + В),
2 cos2 Л = 1 +cos 2Л, 2 sin2 Л = 1 —cos 2Л.
(Ь) Если п — целое положительное число, то
sin пг = ( ) cos"-1 z sin z — ( % \ cos"-3 z sin3 z +
+ [ - j cos'1-5 z sin5 z +
COS A12 = C0S"2-
cos^z sin2 z +
•4- j A ) cos71 4 z sin4 z
i (21.2-11)
(21.2-12)
\ (21.2-13)
724
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.2-4.
Если /г —нечетное целое число, то
п — \
smnz = l—!^
j— J sin /гг — ( J sm (n
з)зт(/г-6)г + ... + (-1)
2)z + (2)sin(n-4)z-
я—1
2
п — 1 ) sin г
cos" z = (1)" х Tcos nz + ft] cos (n - 2) z + ft) cos (n - 4) z +
+ ft] cos (/г —6) г + ...+ я-i jcos г .
(21.2-14)
Если /г — четное целое число, то
sin" z =
-^L[COsm-[l)
»■
cos (/г —2) z + (0)cos(/i — 4) z —
л—2
-... + (-1)
п — 2
nz = (i)" 1[cosnz+(^cos(«-2)z + Qcos(«-4)z +
(21.2-15)
+ ... + [ n_l2)cos2z
21.2-4. Обратные тригонометрические функции (см. также табл. 7.2-1).
(а) Обратные тригонометрические функции
o> = arcsinz, wj = arccosz, w = arctgz; ay = arcctgz1)
определяются как обратные соответственно к функциям
z = sinw, z = cosw, z = tgw, z = c\gw
или как
arcsm z =
= \ -—===■, arccos z = — \
dz
= $rTF- arcctge = - \
V\ — z*
dz
1+z2
(21.2-16)
*) В английской литературе эти функции иногда обозначаются через sin"1 z, cos^z,
tg-1 Z, Ctg"1 2.
21.2-5. 21.2. ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ 725
На рис. 21.2-4 изображены графики обратных тригонометрических функций
для действительного аргумента; заметим, что arcsin z и arccos z действительны
только при z действительном и \г\^ 1. Все четыре обратные
тригонометрические функции бесконечнозначны, потому что тригонометрические функции —
периодические. Для действительного аргумента главные значения arcsin z и
arctgz заключены между —я/2 и я/2 (см. рис. 21.2-4); главное значение
arccos z и arcctgz заключено между 0 и я.
(Ь) Отметим формулы
arcsin a ± arcsin b = arcsin (a \r\ — b2 1 b Y\ — a2) —
= arccos (/1 —a2 Y\ — b2 + ab),
arccos a ± arccos b = arccos (ab 4/l — a2 V\ — b2) =
= arcsin (b V\ —a2 ± a Y\ —b2)>
a±b
arctg a ± arctg b — arct^
1 +ab
(21.2-17)
21.2-5. Гиперболические функции (см. также табл. 7.2-1).
Гиперболические функции ay = shz, ад = спг определяются степенными рядами (п. 21.2-12),
orcfg xk
Рис. 21.2-4. Графики обратных тригонометрических функций.
как решения дифференциального уравнения
d2w
dz*
-W=0,
или просто соотношениями
. ez-e~z . ег + е'г
sh2= - , спг =—75—.
(21.2-18)
726
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.2-6,
Четыре дополнительные гиперболические функции определяются как
ch z \
thz =
sech z --
_ sh z
" ch г'
1
= chz*
cth z--
cosech z -
shz '
l
" sh 2 '
(21.2-19)
На рис. 21.2-5 изображены графики shz, ch z, th z для действительного
аргумента.
Функция chz —четная, a sh z и th z —нечетные.
Геометрическая интерпретация sh / и ch t для действительных t. Если t/2 —
площадь, ограниченная равносторонней гиперболой (п. 2.5-2, Ь) х2 — у2 = 1, осью х и
радиусом-вектором точки (л:, у) гиперболы, то у = sh t, x = ch t. Заметим, что если
гиперболу заменить окружностью х2 -J- У2 = 1» то у = sin t, x = ros /.
sn x,ch x, th x
Рис. 21.2-5. Гиперболические функции.
21.2-6. Соотношения между гиперболическими функциями (см. также
п. 21.2-8). Из основных соотношений
следуют
ch2z-sh2z=l, ~f = th z=7TTTT
ch 2 cth 2
shz=yrch2z-l = T
th2
chz = Kl~+sh2Z:
thz==
sh 2
*A1 — th2 2 V^cth2 2~ 1 '
1 _ cth 2
/l—th22 ~"/cth2 г—Г
Vch2 z — 1
cthz=
Vl + sfcz ch 2
/l+sh2 2__ ch2
sh 2
/ch2 2 — 1
(21.2-20)
(21.2-21)
21.2-7. Формулы сложения для гиперболических функций (эти формулы
могут быть получены из соответствующих формул для тригонометрических
21.2-8. 21.2. ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
727
функций применением соотношений п. 21.2-9).
sh (Л ± В) = sh Л ch В ± ch Л sh В,
ch (А ± В) = ch Л ch В ± sh Л sh В,
,, ,. п, th Л ■+- th В ,, /л . m cth Л cth В -t- l
thH±fl)« 1±игли1Б, cth(d±fl)- cthB±cth^ ;
(21.2-22)
8Ь2Л = 2сЬЛ5ЬЛ,
2 th Л
Ш2Л =
1 -f thM '
сЬ2Л=сЬ2Л + 5Ь2Л,
,, п „ cth2 .
cth 2Л =
hM + shM, \
th2 Л + 1 . >
2cth Л » J
(21.2-23)
sh^jAi
thf
sh Л
ch Л — 1
"chi4-fl sh Л
, A 1/ch Л+ 1
с1Ь-2- = Ььл-1-
sh Л
(21.2-24)
shM ±shB = 2sh-^^-ch-^5-
ch Л + ch Б = 2 ch A±A Ch -^Ц=А
ch Л —chB =
thi4 ± thB =
cth Л ± clhB =
:2sh-l±^sh^
sh (Л ± B)
'' ch Л ch В '
sh (В ± Л),
sh Л sh В
(21.2-25)
2ch AchB = ch(A + B) + ch(A-B),
2sh A shB = ch (A+B)-ch (A-B),
2 sh A ch B = sh (A + B) + sh (А — Б),
2 ch2 Л == 1 + ch 2Л, 2 sh2 Л = 2 ch 2Л — 1.
(21.2-26)
21.2-8. Обратные гиперболические функции (см. также п. 21.2-4).
Обратные гиперболические функции 2) &y = arsh z, w — arch z, до = arth z определяются
соответственно как z — shw, г = спш, г = Шш.
Отметим соотношения
arsh а ± arsh Ь == arsh (a Vo2 + I ±b Ya2 -j- l) = arch (Ya2 -\- 1 Yb2 -f- 1 ± aft),
arch a ± arch ft = arch (ab ± Ya2 — 1 }/"ft2 — l) =
= arsh (b Ya2 — 1 ± a l/ ft2 — l), \ (21.2-27)
:ft
arth a ± arth 6 = arth
1 ±ab
') В английской литературе применяются также символы sh-1 z, chwl г, th"1 z (см.
сноску на стр. 724).
728
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.2-9.
21.2-9. Соотношения между показательной, тригонометрическими и
гиперболическими функциями (см. также пп. 1.2-3 и 21.2-12 и табл. 7.2-1).
е1г = cos z + i sin zt
ei2+e4z
cos z = —-~ , sin z =
2i
^^спг+shz, ez — chz — sh z;
aix-.
nZ 1 n~Z
cos z = ch /z,
sin z =— i sh iz,
tgz = — i th t'z,
ctg z = i cth iz,
= e'*lna = cos(A:lna)
shz = —y—;
ch z = cos /z,
sh z = — i sin iz,
th z = — / tg/z,
cth z = t ctg /z;
+ t sin (x In a),
x* = e'
•,4nj: = cos(ln*) + /sin (lnx),
ix = ex[n l = coSy + i sin у (главное значение),
^гяя»^^ в(2л+1)Я1 = __ J (/г = 0, ±1, ±2, ...),
1*=г'1п' = е~л/2 (главное значение).
(21.2-28)
(21.2-29)
(21.2-30)
(21.2-31)
(21.2-32)
(21.2-33)
Рис. 21.2-6. Показательная и логарифмическая функции.
21.2-10. Определение логарифма (см. также пп. 1.2-3 и 21.2-12, табл. 7.2-1
и рис. 21.2-6).
In z = ln | z | + i Argz;
In (/A-) = ln* + (?/i + y)nff
In (— x) = In x + (2/z -j- 1) ni
(л = 0, ±1, ±2 ...).
(21.2-34)
(21.2-35)
21.2-12. 21.2. ЭЛЕМЕНТАРНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ 729
21.2-11. Соотношения между обратными тригонометрическими, обратными
гиперболическими и логарифмической функциями.
arccos 2= i arch 2, arch z == i arccos 2,
arc sin 2 = — i arsh iz% arsh z = — i arc sin i2,
arctg 2 = — t arth /2, arth z — — f arctg t*2,
arcctg2 = f arcth fz, arcth z = i arcctg iz\
arccos 2 = — tin (г + i Kl—22), arch 2 = In (z + Yz2 — l),
arcsin г = — Пп (t'2 + Kl—z2), arsh 2 = In (г + Кг^+Т),
arct?2 = ~Alni±|,
arcctg 2 = -l In |^1,
(21.2-36)
„ 1,1+2
arcth 2 = iln^rj.
(21.2-37)
21.2-12. Разложения в степенные ряды (см. также пп. 4.10-1—4.10-4).
•j-^ = l+2 + 22 + ... (|г|<1; геометрическая прогрессия, п. 1.2-7); (21.2-38)
(l-r-z)^ = l+(^) z + (Л z2 + ... (|г|<1; биномиальный ряд, см. также
пп. 1.4-1 и 21.5-1); (21.2-39)
*=l+*+h+w+-
23 26
'3! "+"51
(|2|<оо); (21.2-40)
| 2 |< со; (21.2-41)
22 , 2* __
'2!+4! +
shz = z + £l+f] + ..., ch2=l+^ + ^ + ... |2|<co; (21.2-42)
arcsm z-
1п(1+г)=г-|- + г3"-^±...
~2!т1 4 5 ' 2 4 6 7 ' "
„„ , , 1 г» . 1 3 г» 1 3 5 г'
шьл г = г-т J + г • т ' б""2 ' 4 ' б * 7
(I г|< 1),
(I г |< 1);
(21.2-43)
(21.2-44)
23 26 1
arctg г = г —j + g-+ ...,
arthZ = Ilniii=2+f + f + ....
(|г|<1).
В терминах чисел Бернулли (п. 21.5-2)
о2* Л>2А_ j j ^
W 92Л (О'
,ег= 2 (_„*-i Ui
(21.2-45)
4=1
(24)1
-"й",-'+т*,+^+яг" + -
(...<*).
(21.2-46)
\ z /
ct-r2 = — V (— \)k ?A z2k = l —• i 2 -- г» — 26— ПгКл) (21.2-47)
ClZZ 2 Z-J < U (2*)! г 3 2 45 Z 945 Z "' (l 2' < '* К '
k = 0
Из разложений (46) и (47) можно получить разложения для функций th г и cth г с
помощью формул (32).
730
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.2-13.
21.2-13. Разложения в бесконечные произведения (см. также п. 7.6-6).
*'-«П[Чя),].с"'-ШЧгАт>],Ь |г1<ет- (2L2-48)
k=\
А: = 0
Аналогичные разложения для функций sh z и ch 2 могут быть получены с
помощью формул (32).
21.2-14. Некоторые полезные неравенства.
sin х < х < tg x (0 < х < я/2),
sin x > 2х/п (—я/2 < х < я/2),
cos х < ^^ < 1 (— я< * < я)}
ех>\+х,
л:
е 1""*< 1— *<<Г* (л:<1);
1-М
<ln(l+x)<*
(*>-!).
д:< —In (1—д:) <7-Ё^ (*<1).
| In (1 -л:) | < Злг/2 (0 < х < 0,5828).
Приведенные неравенства обращаются в равенства при х = 0.
(21.2-49)
(21.2-50)
(21.2-51)
(21.2-52)
(21.2-53)
21.3. НЕКОТОРЫЕ ИНТЕГРАЛЬНЫЕ ФУНКЦИИ
21.3-1. Интегральные синус, косинус, логарифм и показательная функция.
По определению
X 00
с- / \ Г sin х , я Г sin х , я . . / ч 1 х3 . 1 дг5 _
О х
(интегральный синус), (21.3-1)
Значения интегрального синуса приведены в табл. 21.3-1; см. также
рис. 21.3-1.
оо х
Qt ч С cos х , ,0,1 f 1 — cos дс , >о , 1 I л:2 , 1 ** __
W==~~J -т-^л:=С + 1пх-^ dx = C+\n x -^ -2- + Г] j + ...
* О
(л:>0) (интегральный косинус), (21.3-2)
где С *« 0,577216 — постоянная Эйлера — Маскерони, определенная в п. 21.4-1.
Значения интегрального косинуса находятся при помощи табл. 21.3-2.
Еi (л:) = \ — dx (л:<0) (интегральная показательная функция), (21.3-3)
—со
X
П (л:) = { —х~ (х > 0) (интегральный логарифм), (21.3-4)
21.3-1,
21 3. НЕКОТОРЫЕ ИНТЕГРАЛЬНЫЕ ФУНКЦИИ
731
*Прн лг>1 функция И (л:) определяется как lim
£->0
(главное значение интеграла в смысле Коши).
1—8 X "|
3 In х ' J In x\
0 1+8 J
n^-^z-rt
a)
1
-2rt
z
7
/ ^,«
0 Л in
it
г
Рис. 21.3-1. Графики функций и Si (x).
Функция Ei (л:) представляется в виде ряда
Ei(*) = C+ln(-*)+2I -^ (*<0),
Л=1
с помощью которого она продолжается на всю комплексную плоскость z с
разрезом вдоль положительной части действительной оси *):
Ei (z) = C+ln (-*)+ 2 Wk <l ar^ (~2> К")-
A = l
Если 2 = л: >0, то Re Ei (*) = Ei (л:) = С + 1пл: + 2j rf£ называется модифи-
k = \
цированной интегральной показательной функцией. При приближении точки
z — x-\-iy к разрезу (д:>0) имеют место соотношения
lim Ei (х ± i#) = Ei (л:) т т. Ж
(У>0)
Отмешм следующие соотношения:
Ei(*) = H(**) (*<0), \
Ei (In дг) = Н (лс) (х<\), [ (21.3-5)
Ei (± ix) =Ci (*) ± / Si (х) т я/ (л > 0). |
Значения интегральной показательной функции и родственных с ней
функций приведены в табл. 21.3-3.
*) Все введенные функции можно рассматривать как функции комплексного
переменного г (см., например, [21.1]).
732 ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ 21.3-1.
Таблица 21.3-1
Интегральный синус Si (я)
х
0. , . г sin и ,
О
#
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2.5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3.8
3,9
4,0
4,1
4,2
4.3
4,4
4,5
4.6
4,7
4.8
4.9
SiU)
0,00000
09994
19956
29850
39646
49311
58813
68122
77210
86047
9460S
1,02*69
10805
18396
25623
32468
38918
44959
50582
55778
60541
64870
68763
72221
75249
77852
80039
81821 !
83210
84219
84865
85166
85140
84808
84191
83313
82195
80862
79333
77630
75820
73874
71837
69732
67583
65414
63246
61101
58998
56956
X
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7.5
7,6
7,7
7,8
7,9
8.0
8,1
8.2
8,3
8,4
8.5
8,6
8,7
8.8
8,9
9,0
9.1
9.2
9,3
9,4
9.5
9,6
1 9,7
9,8
9.9
Si (x)
1,54993
53125
51367
49732
48230
46872
45667
44620
43736
43018
42469
42087
41871
41817
41922
42179
42582
43121
43787
44570
45460
46443
47509
48644
49834
51068
52331
53611
54894
56167
57419
58637
59810
60928
61981
62960
63857
64665
65379
65993
66504
66908
67205
67393
67473
67446
67316
67084
66757
66J38
1
X
10,0
10,1
10,2
10,3
10,4
10,5
10,6
10,7
10,8
10,9
11,0
11,1
11,2
11,3
11,4
11,5
11,6
11,7
11,8
11,9
12,0
12,1
12,2
12,3
12,4
12,5
12,6
12,7
12,8
12,9
13,0
13,1
13,2
13,3
13,4
13.5
13,6
13,7
13,8
13,9
14,0
14,1
14,2
14,3
14,4
14,5
14,6
14,7
14,8
14,9
Si (x)
1,65835
65253
64600
63883
63112
62294
61439
60556
5Э654
53743
57831
56927
56042
55182
54356
53571
52835
52155
51535 1
50981
50497
50083
49755
49501
49327
49234
49221
49287
49430
49647
49936
50292
50711
51188
51716
52291
52905
53352
54225
54917
55621
56330
57036
57733
58414
59072
5Э702
60296
60851
61360
X
15,0
15,1
15,2
15,3
15,4
15,5
15,6
15,7
15,8
15,9
16,0
16,1
16,2
16,3
16,4
16,5
16,6
16,7
16,8
16,9
17,0
17,1
17,2
17,3
17,4
17,5
17,6
17,7
17,8
17,9
18,0
18,1
18,2
18,3
18,4
18,5
18,6
18,7
18,8
18,9
19,0
19,1
19,2
19,3
19,4
19,5
19,6
19,7
19,8
19,9
Si (x)
1,61819
62226
62575
62865
63093
63258
63359
63396
63370
63280
63130
62921
62657
62339
61973
61563
61112
60627
60111
59572
59014
58443
57865
57285
56711
56146
55598
55070
54568
54097
53661
53264
52909
52600
52339
52128
51969
51863
51810
51810
51863
51967
52122
52324
52572
52863
53192
53357
53954
54378
X
20,0
20,1
20,2
20,3
20,4
20,5
20,6
20,7
20,8
20,9
21,0
21,1
21,2
21,3
21,4
21,5
21,6
21,7
21,8
21,9
22,0
22,1
22,2
22,3
22,4
22,5
22,6
22,7
22,8
22,9
23,0
23,1
23,2
23,3
23,4
23,5
23,6
23,7
23.8
23,9
24,0
24,1
24,2
24,3
24,4
24,5
24,6
24,7
24,8
24,9
Si (x)
1,54824
55289
55767
56253
56743
57232
57714
58186
58641
59077
59489
59873
60225
60543
60823
61063
61261
61415
61525
61590
61608
61582
61510
61395
61238
61041
60806
60536
60234
59902
59546
59168
58772
58363
57945
57521
67097
56676
56262
55360
55474
55107
54762
54444
54154
53897
53672
53484
53333
53221
X
25,0
50,0
Si (x)
1,53148
55162
21.3-1. 21.3, НЕКОТОРЫЕ ИНТЕГРАЛЬНЫЕ ФУНКЦИИ 733
Таблица 21.3-2
Si(x) и интегральный косинус Ci (x)
х
St(x) == In д: + С — CiCat) = J LLJ2LHdu.
о "
00
С1(л) = - J ^—p- du = In x -f С - S,(*)
(С «as 0,5772 — постоянная Эйлера — Маскерони)
X
0,0
0,1
0,2
i 0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1 Ы
! 1.2
ьз
1.4
1.5
1.6
1.7
1.8
1.9
2.0
! 2'1
1 2.2
2,3
2.4
2.5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
S» <*>
0,00000
00249
00998
02241
03973
06185
08866
12002
15579
19578
23981
28766
33908
39384
45168
51233
57549
64088
70820
77713
84739
91865
99060
1,06295
13540
20764
27939
35038
42035
48903
55620
62163
68511
74646
80552
86211
91613
96745
2,01600
06170
10449
14438
18131
21535
24648
27479
30033
32317
34344
36124
X
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5J
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7.5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
St (x)
2,37669
38994
40113 |
41044
41801
42402
42866
43210
43452
43610
43704
43749
43764
43766
43770
43792
43847
43947
44106
44335
44643
45040
45534
46130
46834
47649
48577
49619
50775
52044
53423
54906
56491
56171
59938
61786
63704
65686
J 67721
1 69799
71909
74042
76186
78332
80468
82583
84669
86713
88712
90651
X
10,0
10,1
10,2
10,3
10,4
10,5
10,6
10,7
10,8
10,9
11,0
11.1
11,2
11,3
11.4
11,5
11.6
11,7
11,8
11,9
12.0
12.1
! 12.2
12.3
12.4
12.5
12.6
12.7
12,8
12,9
13,0
13,1
13,2
13,3
13,4
13,5
13,6
13,7
13,8
13,9
14,0
14,1
14,2
14,3
14,4
14,5
14,6
14,7
14.8
14.9
Si (*>
2,92527
94327
96050
97688
99234
3,00688
02045
03300
04457
05514
06467
07323
08083
08749
09322
09814
10225 1
10561
10828
11038 i
11190
11301
11370
11412
11429
11436
11437
11438
11453
11484
11540
11628
11754
11924
12142
12414
12745
13134
13587
14104
14688
15338
16054
16835
17677
18583
19545
20564
21630
22746
X
15,0
15,1
15,2
15,3
15,4
15,5
15,6
15,7
15,8
15,9
16,0
16,1
16,2
16,3
16,4
16,5
16,6
16,7
16,8
16,9
17,0
17,1
17,2
17,3
17,4
17,5
17,6
17,7
17,8
17,9
18,0
18,1
18,2
18,3
18,4
18,5
18,6
18,7
18,8
18.9
19.0
19.1
19.2
19,3
19,4
19,5
19,6
19,7
19,8
19,9
5| (дс)
3,23899
25090
26308
27552
28814
30087
31363
32641
33911
35167
36401
37612
38790
39932
41032
42088
43096
44050
44947
45788
46568
47288
47945
48543
49077
49553
49969
50330
50639
50895
51107
51276
51404
51500
51568
51610
51633
51645
51648
51648
51660
51661
51685
51727
51790
51879
52002
52156
52348
52578
X
20,0
20,1
20,2
20,3
20,4
20,5
20,6
20,7
20,8
20,9
21,0
21,1
21,2
21,3
21,4
21,5
21,6
21,7
21,8
21,9
22,0
22,1
22,2
22,3
22,4
1 22,5
22,6
22,7
22,8
22,9
23,0
23,1
23,2
23,3
23,4
23,5
23,6
23,7
23,8
23,9
24,0
24,1
24,2
24,3
24,4
24,5
24,6
24,7
24,8
24,9
Si <*)
3,52853
53173
53535
53946
54402
54905
55456
56049
56687
57368
58085
58840
59629
60446
61288
62155
63037
63935
64842
65751
66662
67568
68465
69348
70216
71059
71879
72670
73427
74153
74838
75483
76089
76651
77170
77644
78072
78459
78801
79101
79360
79582
79767
79917
80036
80129
80197
80243
80271
| 80288
X
25,0
50,0
j
St (ДС)
3,80295
4,49486
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ 21.3-1.
Таблица 21.3-3
Интегральная показательная функция
Интегральные показательные функции обычно применяются в комбинации;
1) интегральных показательных функций Ei (л:) и Ei (л:) или
2) Е0 (х), Et (x) =- Ei (-*) и Е2 {х), где
оо
Еп (х) = \ е~хаи~пс1и.
Во всех случаях х > 0.
Малые значения аргумента. Для вычисления значений Ei (—x) и Ei (x) при малых
значениях х можно пользоваться разложениями в ряд, приведенными в соответствующей
таблице.
Большие значения аргумента для Ei (—х) и Ei (х): а) для 5<д:< 16 значения даны
е~х ех
в таблицах; Ь) для 5 < х < 40, Et (х) — — Ei (—л:) = Ft и Ei (л:) = F2 , где Ft
и F% имеют значения:
^s. а;
Ft
F,
б
0,8516
1,354
10
0,9156
1,1316
15
0,9408
1,0781
20
0,9549
1,0560
25
0,9627
1,0440
30
0,9687
1,0358
35
0,9729
1,0305
40
0,9753
1,0264
с) для больших значений х величины Ft и F2 могут быть вычислены с помощью
асимптотических рядов
/г -1 1! 4- 2! 3! Л- • F -14- U 4- 2! 4- 3! -4-
е~х
X
0,0
1
2
з
4
5
6
7
8
9
1.0
1
2
з
4
5
6
7
8
9
2
3
4
5
6
7
8
9
0
оо
9,048
4,094
2,469
1,676
1.213
0,9147
7094
5617
4517
3679
3026
2510
2096
1761
1488
1262
1075
0,09183
7872
10-1x0,6767
10-2Х1,660
10-2x0,4579
10-3Х 1,348
10-зХ0,4131
ю-*х ьзоз
10-4x0,4193
10-5x1,371
1
99,00
8,144
3,860
2,366
1,619
1,177
8907
6925
5492
4423
3606
2969
2464
2060
1732
1463
1242
1058
9042
7753
5831
1,453
4042
1,195
3677
1,1621
3747
1,227
2
49,01
7,391
3,648
2.269
1,564
1,143
8677
6760
5371
4332
3535
2913
2420
2024
1722
1439
1222
1041
8903
7636
5037
1,274
3570
1,061
3273
1,037
3349
1,098
3
32,35
6,755
3,454
2,179
1,513
1,111
8454
6601
5254
4243
3466
2859
2376
1989
1673
1415
1202
1025
8766
7521
4359
1,118
3155
0,9418
2915
0,9254
2994
0,9831
4
24,02
6,210
3,278
2,093
1,464
1,079
8239
6447
5139
4156
3399
2805
2334
1954
1645
1392
1183
1009
8631
7407
3780
0,9816
2790
8364
2596
8260
2677
8800
5
19,02
5,733
3,115
2,013
1,417
1,049
8031
6298
5028
4071
3333
2753
2292
1920
1618
1369
1164
♦9930
8500
7296
3283
8628
2469
7431
2313
7375
2394
7879
6
15,70
5,326
2,966
1,938
1,372
1,020
7831
6154
4920
3988
3268
2702
2251
1887
1591
1347
1145
♦9775
8370
7187
2857
7590
2185
6603
2061
6585
2141
7055
7
13,32
4,963
2,827
1,867
1,330
♦9921
7637
6013
4816
3908
3206
2653
2211
1855
1564
1325
1127
♦9623
8242
7079
2489
6682
1935
5870
1837
5881
1915
6318
8
11,54
4,640
2,699
1,800
1,289
♦9653
7450
5877
4713
3830
3144
2604
2172
1823
1538
1304
1109
♦9474
8116
6973
2172
5887
1714
5220
1638
5253
1713
5658
9
10,15
4,352
2,580
1,736
1,250
♦9395 ,
7269 I
5745 |
4614 1
3753 ;
3085
2556 1
2134
1792 |
1513
1283 !
1092 |
♦9327 1
7993 1
6869
1897
5190
1520
4643
1461
4693
1533
5068
21.3-1. 21.3. НЕКОТОРЫЕ ИНТЕГРАЛЬНЫЕ ФУНКЦИИ 735
Таблица 21.3-3 (продолжение)
£t (*) = _£! (-Jt) = -[c + lnJc—ffir+^r-^r + ...]f
где С = 0,5772
X
0,0
1
2
з
4
5
6
7
8
9
1.0
1
2
з
4
5
6
7
8
9
2,0
1
2
з
4
5
в
7
8
9
1 3,0
1
2
з
4
5
6
1 7
I 8
9
!4,0
1
2
1 з
4
5
1 6
1 7
з
i 9
5,0
0
оо
1,823
1,223
0,9057
7024
5598
4544
3738
3106
2602
2194
1860
1584
1355
1162
1000
0,08631
7465
6471
6620
4890
4261
3719
3250
2844
2491
2185
1918
1686
1482
1305
1149
1013
0,008939
7891
6970
6160
5448
4820
4267
3779
3349
2969
2633
2336
2073
1841
1635
1453
1291
1148
•
4,038
1,737
1,183
8815
6859
5478
4454
3668
3050
2557
2157
1830
1559
1334
1145
♦9854
8506
7359
6380
5542
4823
4204
3669
3207
2806
2459
2157
1893
1664
1464
1288
1135
1001
8828
7793
6884
6085
5381
4762
4216
3734
3309
2933
2602
2308
2049
1819
1616
1436
1276
1135
2
3,355
1,660
1,145
8583
6700
5362
4366
3599
2996
2513
2122
1801
1535
1313
1128
♦9709
8383
7254
6290
5465
4757
4147
3620
3164
2769
2427
2129
1869
1643
1445
1272
1121
♦9882
8718
7697
6800
6011
5316
4704
4165
3689
3269
2898
2571
2281
2025
1798
1597
1419
1261
1122
3
2,959
1,589
1,110
8361
6546
5250
4280
3532
2943
2470
2087
1772
1511
1293
1111
*9567
8261
7151
6202
5390
4692
4090
3571
3122
2733
2395
2101
1845
1622
1427
1256
1107
♦9758
8610
7602
6716
5937
5251
4647
4114
3645
3230
2864
2540
2254
2001
1777
1578
1402
1247
1109
4
2,681
1,524
1,076
8147
6397
5140
4197
3467
2891
2429
2052
1743
1487
1274
1094
♦9426
8142
7049
6115
5315
4627
4035
3523
3081
2697
2364
2074
1821
1601
1409
1240
1093
♦9637
8503
7508
6634
5864
5187
4591
4065
3601
3191
2879
2510
2227
1977
1756
1560
1386
1232
1096
5
2,468
1,464
1,044
7942
6253
5034
4115
3403
2840
2387
2019
1716
1464
1254
1078
♦9288
8025
6949
6029
5241
4564
3980
3476
3040
2662
2333
2047
1798
1581
1391
1225
1079
♦9517
8398
7416
6552
5793
5124
4535
4016
3557
3153
2796
2480
2201
1954
1735
1541
1370
1218
1083
6
2,295
1,409
1,014
7745
6114
4930
4036
3341
2790
2347
1986
1688
1441
1235
1062
♦5152
7909
6850
5945
5169
4502
3927
3430
3000
2627
2303
2021
1775
1560
1373
1209
1066
♦9398
8294
7324
6472
5722
5062
4480
3967
3515
3115
2762 |
2450
2175
1931
1715
1523
1354
1204
1070
7
2,151
1,358
0,9849
7554
5979
4830
3959
3280
2742
2308
1953
1662
1419
1216
1046
♦9019
7796
6753
5862
5098
4440
3874
3384
2960
2592
2273
1994
1752
1540
1356
1194
1052
♦9281
8191
7234
6393
5652
5000
4426
3919
3472
3078
2729
2421
2149
1908
1694
1505
1338
1189
1058
8
2,027
1,310
9573
7371
5848
4732
3883
3221
2694
2269
1922
1635
1397
1198
1030
♦8887
76S4
6658
5780
5027
43S0
3821
3339
2921
2558
2243
1969
1730
1521
1338
1179
1039
♦9166
8090
7145
6314
5583
4939
4372
3872
3431
3041
2697
2393
2123
1885
1674
1488
1322
1176
1045
9
1,919
1,265
9309
7194
5721
! 4636
i 3810
3163
2647
2231
1890
1609
1376
1180
1015
*8758
7574
6564
5700
4958
4320
3770
3294
2882
2525
2214
1943
1707
1502
1322
1164
1026
9052
7990
7057
6237
5515
4879
4319
3825
3390
3005
2665
2364
2098
1863
1655
1470 1
1307 1
1162
1033
736 ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ 21.3-1.
Таблица 21.3-3 (продолжение)
X
0,0
1
2
3
4
5
6
7
8
9
1,0
1
2
з
4
5
6
7
8
9
2,0
1
2
з
4
5
6
7
8
9
3,0
1
2
з
4
5
6
7
8
9
4,0 ■
1
2
з
4
51
6
7
8
9
5,0
0
—оо
—1,623
—0,8218
—0,3027
+0,1048
0,4542
0,7699
1,065
1,347
1,623
1,895
2,167
2,442
2,721
3,007
3,301
3,605
3,921
4,250
4,594
4,954
5,333
5,733
6,154
6,601
7,074
7,576
8,110
8,679
9,286
9,934
10,63
11,37
12,16
13,01
13,93
14,91
15,96
17,09
18,32
19,63
21,05
22,58
24,23
26,01
27,93
30,01
32,26
34,70
37,33
40,19
1
4,018
1,517
7619
2582
1418
4S70
8002
1,094
1,375
1,650
1,922
2,195
2,470
2,750
3,036
3,331
3.636
3,953
4,284
4,629
4,991
5,372
5,774
6,198
6,647
7,123
7,628
8,166
8,738
9,349
10,00
10,70
11,44
12,24
13,10
14,02
15,01
16,07
17,21
18,44
19,77
21,20
22,74
24,40
26,19
28,13
30,23
32,50
34,95
37,61
40,48
2
3,315
1,419
7042
2147
1783
5195
8302
1,122
1,403
1,677
1,949
2,222
2.498
2,778
3,065
3,361
3,667
3,986
4,317
4,664
5,028
5,411
5,815
6,242
6,693
7,172
7,680
8,221
8,798
9,412
10,07
10,77
11,52
12,33
13,19
14,12
15,11
16,18
17,33
18,57
19,91
21,35
22,90
24,57
26,38
28,34
30,45
32,74
35,21
37,88
40,78
3
2,899
1,329
6483
1721
2143
5517
8601
Ы51
1,431
1,705
1,977
2,249
2,525
2,806
3,094
3,391
3,699
4,018
4,351
4,700
5,066
5,451
5,857
6,286
6,740
7,221
7,733
8,277
8,857
9,476
10,14
10,84
11,60
12,41
13,28
14,21
15,21
16,29
17,45
18,70
20,05
21,50
23,06
24,75
26,57
28,54
30,67
32,97
35,47 !
38,16
41,09
4
2,601
1,244
5947
1304
2498
5836
8898
1,179
! 1,458
1,732
2,004
2,277
2,553
2,835
3,124
3,422
3,730
4,051
4,386
4,736
5.104
5,490
5,899
6,330
6,787
7,271
7,786
8,334
8,917
9,540
10,21
10,92
11,68
12,49
13,37
14,31
15,32
16,40
17,57
18,83
20,19
21,65
23,22
24,92
26,76
28,75
30,89
33,21
35,73
38,45
41,39
5
2,368
1,164
5425
0894
2849
6153
9194
1,207
1,486
1,759
2,031
2,304
2,581
2,863
3,153
3,452
3,762
4,084
4,420
4,772
5,141
5,530
5,941
6,374
6,834
7,321
7,839
8,390
8,978
9,605
10,27
10,99
11,76
12,58
13,46
14,41
15,42
16,52 1
17,69
18,96
20,33
21,80
23,39
25,10
26,95
28,95
31,12
33,46
35,99
38,73
41,70
6
2,175
1,089
4919
0493
3195
6467
9488
1,236
1,513
1,786
2,058
2,332
2,609
2,892
3,183
3,482
3,793
4,117
4,454
4,808
5,179
5,570
5,983
6,419
6,881
7,372
7,893
8,447
9,039
9,670
10,34
11,06
11,84
12,66
13,55
14,51
15,53
16,63
17,82
19,09
20,47
21,95
23,55
25,28
27,15
29,16
31,34
33,70
36.25
39,02
42,01
7
2,011
1,017
4427
0098
3537
6778
9780
1,264
1,541
1,814
2,086
2,359
2,637
2,921
3,212
3,513
3,825
4,150
4,489
4,844
5,217
5,611
6,025
6,464
6,929
7,422
7,947
8,505
9,100
9,735
10,41
11,14
11,92
12,75
13,64
14,60
15,64
16,75
17,94
19,23
20,61
22,11
23,72
25,46
27,34
29,37
31,57
33,95 I
36,52
39,31
42,32
8
1,867
0,9491
3949
♦0290
3876
7087
1,007
1,292
1,568
1,841
2,113
2,387
2,665
2,949
3,242
3,544
3,857
4,183
4,524
4,881
5,256
5,651
6,068
6,509
6,977
7,473
8,001
8,563
9,162
9,801
10,48
11,22
12,00
12,84
13,74
14,70
15,74
16,86
18,06
19,36
20,76 1
22,26 1
23,89
25,64
27,54
29,58
31,80
34,20
36,79
39,60
42,64
9
1,739
0,8841
3482
1 *0672
4211
7394
1,036
1,320
1,595
1,868
2,140
2,414
2,693
2,978
3,271
3,574
3,889
4,216
4,559
4,917
5,294
5,692
6,111
6,555
7,025
7,524
8,055
8,621
9,224
9,867
10,55
11,29
12,08
12,92
13,83
14,80
15,85
16,98
18,19
19,49
20,90
22,42
24,06
25,82
27,73
29,80
32,03
34,45
37,06
39,89
42,96
21.3-1. 21.3. НЕКОТОРЫЕ ИНТЕГРАЛЬНЫЕ ФУНКЦИИ 737
Таблица 21.3-3 (продолжение)
Ег(х) = — Ei (— х), 5 < х < 16
X
5
*>
7
8
9
10
11
12
13
14
0
10-» X 1.148
10-» X 0,3601
10-*х1,155
10-* X 0,3767
10-* X 1,245
Ю-*Х0,4157
10-е X Ь400
10-в X 0,4751
10-» X 1,622
10-'х0,5566
1
1,021
3211
1,032
3370
1,115
3727
1,256
4266
1,457
5002
2
9086
2864
9219
3015
9988
3342
1.127
3830
1,309
4500
3
8086
2555
8239
2699
8948
2997
1,012
3440
1,176
4042
4
7198
2279
7364
2415
8018
2687
0,9080
3089
1,057
3633
5
6409
2034
6583
2162
7185
2410
8149
2774
0,9495
3266
6
5708
1816
5886
1936
6439
2162
7315
2491
8532
2936
7
5085
1621
5263
1733
5771
1939
6566
2238
7667
2640
8
4532
1448
4707
1552
5173
1740
5894
2010
6890
2373
9
4039
1293
4210
1390
4637
1561
5291
1805
6193
2134
Ei(*), 5<*<16
5
6
7
8
9
10
И
12
13
14
10*Х0,4019
10* х 0,8599
10»х0,1915
10» X 0,4404
10* х 0,1038
10* х 0,2492
Ю*Х0,6071
10»х0,1496
106х 0,3720
10» X 0,9319
4328
9300
2079
4793
1132
2723
6641
1638
4076
1,022
4662
1,006
2257
5218
1235
2975
7265
1794
4467
1,121
5026
1,089
2451
5682
1347
3251
7949
1964
4896
1,229
5419
1,179
2663
6189
1471
3553
8698
2151
5367
1,348
5847
1,277
2894
6743
1605
3884
9518
2357
5883
1,479
6310
1,334
3146
7347
1752
4246
1,042
2581
6449
1,622
6813
1,501
3420
8007
1913
4642
1,140
2828
7070
1,779
7360
1,627
3720
8729
2089
5076
1,248
3098
7751
1,952
7954
1,765
4047
9517
2282
5551
1,366
3395
8499
2.142
оо
Е2(х) = J e-*atr*du = е~* — хЕг{х) = х[Е0(х) — Ег(х)]
1
0,0
1
2
з
4
5
6
7
8
9
1,0
1
2
з
4
5
6
7
8
9
2
3
4
5
6
7
8
9
1,000
0,7225
5742
4691
3894
3266
2762
2349
2009
1724
1485
1283
1111
0,09645
8389
7310
63S0
5577
4882
4278
10-1x0,3753
10-г х 1,064
10-2x0,3198
10-3хО,9965
10-Зх0,3183
10-*Х 1.035
10*х0,3414
10-»х Ы38
0,9497
7048
5622
4602
3824
3211
2717
2312
1978
1698
1463
1264
1095
9510
8274
7211
6295
5503
4817
4222
3297
0,9417
2842
8881
2842
0,9259
3057
1,021
9131
6878
5505
4515
3556
3157
2673
2276
1948
1673
1442
1246
1080
9378
8160
7113
6210
5430
4754
4167
2898
8337
2527
7917
2539
8283
2738
0,9149
8817
6715
5393
4430
3690
3104
2630
2240
1918
1648
1421
1228
1065
9247
8048
7017
6127
5358
4691
4113
2550
7384
2247
7060
2268
7411
2453
8203
8535
6560
5283
4348
3626
3052
2537
2205
1889
1623
1400
1211
1050
9119
7938
6922
6045
5287
4630
4059
2246
6544
1999
6296
2027
6632
2198
7356
8278
6410
5177
4267
3562
3001
2546
2171
1860
1599
1380
1193
1035
8993
7829
6828
5964
5217
4569
4007
1980
5802
1779
5617
1812
5935
1969
6597
8040
6267
5074
4189
3500
2951
2505
2137
1832
1576
1360
1176
1020
886S
7722
6736
5884
5148
4509
3955
1746
5146
1583
5012
1619
5313
1764
5916
7818
6128
4974
4112
3440
2902
2465
2104
1804
1552
1340
1160
1006
8746
7617
6645
5806
5080
4450
3903
1541
4567
1410
4473
1448
4756
1581
5306
7610
5995
4877
4038
3381
2855
2426
2072
1777
1530
1321
1143
•9920
8625
7513
6555
5729
5013
4392
3852
1362
4054
1255
3992
1294
4258
1417
4760
7412
5866
4783 1
3963
3325
2808
2387
2040 |
1750
1507
1302
1127 1
♦9781 1
8506 1
7411
6467
5652
4947 1
4335
3803
1203
3600 1
1118
3564
1157
3312
1270 i
4270
24 Г. Корн и Т. Корн
738
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
51.3-2.
21.3-2. Интегралы Френеля и интеграл вероятностей (см. также п. 18.8-3).
По определению
C(*) = $cosf *dx = Jt/t($ *■) + /./t(f *2) + Л/,("-*2) + -•
(21.3-6)
S{x)=\ sin f *dx = Jt/t (f *■) + У,/,(f *•) + ylt/, (f *■) + ...,
0
(интегралы Френеля)
где Jn,2 (г) — функции Бесселя, порядок которых равен половине нечетного
0,6 1,2 1,8 2,4 3,0 3,6
Рис. 21.3-2. Интегралы Френеля.
*~Х
числа (см. п. 21.8-1, е). Графики функций С (х) и S (х) изображены на
рис. 21.3-2. Отметим, что С (оо) = 5 (оо) = 1/2.
erf*= ikS'-* *-■£(*-?+й1-ят± -) (21-3-7)
о
(функция ошибок);
(см. также п. 18.8-3 и табл. 18.8-10).
Заметим, что erf (оо) = 1.
Отметим формулы:
C(x)-iS(x)=:j^Teri (±tLxVn):
5W = i~li7C0S^2 + ^)
при # —»oo.
(21.3-8)
(21.3-9)
21.4-1. 21.4. ГАММА-ФУНКЦИЯ И СВЯЗАННЫЕ С НЕЙ ФУНКЦИИ 739
Некоторые интегралы:
х
\ C(x)dx = xC(x)—^ sin ~ х**
О
х
[ S (х) dx = * S (л:) + ~ cos ~- ** — ~ t
J Я 2 Я
О
X
\ erf х dx =x erf х + -L- О?""** — l).
Интегралы
1 с sin х , х
■5-
2Vx J /*
О
_1_ ^ ,1 *»
3 7 3! 11 51
1 jj^^^l^l^L + iJi.J.^.^
2оЛс J /*
О
5 2! 9 4! 13 6!
также иногда называются интегралами Френеля.
Функция
erfcjc
2 г Л-**
= l-erf*=-M e-^dx
(21.3-10)
(21.3-11)
(21.3-12)
называется дополнительным интегралом вероятностей.
21.4. ГАЛША-ФУНКЦИЯ И СВЯЗАННЫЕ С НЕЙ ФУНКЦИИ
21.4-1. Гамма-функция.
(а) Интегральные представления. Гамма-функция Г (г) обычно
определяется как
или для Re 2 < 0
Г (г) = 5 e-'p-idt (Rez>0)
(интеграл Эйлера второго рода)
с
(интегральное представление Ганкеля),
(21.4-1)
(21.4-2)
где контур С идет из — со по отрицательной части действительной оси, обходит
начало координат в положительном направлении (против часовой стрелки)
и опять по отрицательной части оси х возвращается к исходной точке. Это
определение может быть расширено при помощи аналитического продолжения
(п. 7.8-1). Единственными особенностями Г (z) в конечной части плоскости
24*
740
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.4-1.
являются простые полюсы с вычетами -—j— при
г = — п (я=0, 1, 2, ...);
-=—■ есть целая функция. Рис. 21.4-1 представляет график Г (х) для
Рис. 21.4-1. График Г (я -+- 1) для действительных значений п. Последовательные
относительные максимумы и минимумы приближенно равны
Г (1,432) = 0,886; Г ( — 1,573) = М02;
Г (—0,5040) =- —3,545; Г (—2,611) = —0,888.
действительных х. Значения Г (х) приведены в табл. 21.4-1. Заметим, что
Г(1) = УЪ, Г(1)=1, \
Г(/г+1) = /г! (/г = 0, 1, 2, ...). j
(b) Другие представления для Г (г).
(21.4-3)
п\
Г(г)= lim 2(2+1)(2 + 2) ... (г + п)п* (определение Эйлера),
1
Г (2)
— 9PCz TT (\ л_1Л /~Т (бесконечное произведение
— ze 11 V' "**"*/ Вейерштрасса),
k = 1
С —постоянная Эйлера — Маскерони, определенная как
(/г v со 1
2 -[ — In/г) = —$ e-Mn/rf/ = — ^ In In ~rft^0,5772157
(21.4-4)
(21.4-5)
\/г = 1
(с) Функциональные уравнения
Г(г + 1) = гГ(г),
Г (г) Г (-2) = -
Г(г)Г(1-г)= .л ,
v ' х ' sin лг '
■■(WW-)-
(21.4-6)
(21.4-7)
(21.4-8)
п-)-/^п,г(г+;)г(г+^)...г(г+^)
(п = 2, 32 ...) (теорема умнооюения Гаусса). (21.4-9)
21.4-1. 21.4. ГАММА-ФУНКЦИЯ И СВЯЗАННЫЕ С НЕЙ ФУНКЦИИ 741
Таблица 21.4-1
оо
Гамма-функция Г (л:) = f tx~le4 dt
о
Для больших значений аргумента Г (д:) вычисляется при помощи формулы
Г (х) = (л: — 1) Г (л: — 1) = (д: — 1) (х — 2) Г (х - 2) = . . .
Пример. Г (4,7) = 3,7 X 2,7 X 1,7 X 0,9086 = 15,43.
Если х < 1 и х ф 0, —1,-2 то
1Г/г)_.Г(* + 1) _Т(х + 2) _
1 w *<*+ 1) -•••
Примеры.
Г (0,7) = Г (01,7?) = 1,298,
Г ( ~ 3>2) ~~ (-3,2)(-2,2)(-'l,2)(-0,2)(0,8) ~ °'689'
X
1,00
1
2
з
4
б
6
7
8
9
ЫО
1
2
з
4
5
6
7
8
9
1,20
1
2
з
4
5
6
7
В
9
1.30
1
2
з
4
5
6
7
8
9
1,40
1
2
з
4
0
1,0000
0,9943
9888
9835
9784
9735
9687
9642
9597
9555
9514
9474
9436
9399
9364
9330
9298
9267
9237
9209
9182
9156
9131
9108
9085
9064
9044
4025
9007
8990
8975
8960
8946
8934
8922
8912
8902
8893
8885
8879
8873
8868
8864
8860
8858
1
0,9994
9938
98S3
9830
9779
9730
9683
9637
9593
9550
9509
9470
9432
9396
9361
9327
9295
9264
9234
9206
9179
9153
9129
9105
9083
9062
9042
9023
9005
8989
8973
8959
8945
8933
8921
8911
8901
8892
8885
8878
8872
8867
8863
8858
8858
2
9983
9932
9878
9825
9774
9725
9678
9633
9589
9546
9505
9466
9428
9392
9357
9324
9292
9261
9231
9203
9176
9151
9126
9103
9081
9060
9040
9021
9004
8987
8972
8957
8944
8931
8920
8910
8900
8892
8884
8877
8872
8867
8863
8860
8858
3
9983
9927
9872
9820
9769
9721
9673
9628
9584
9542
9501
9462
9425
9389
9354
9321
9289
9258
9229
9201
9174
9148
9124
9101
9079
9058
9038
9020
9002
8986
8970
8956
8943
8930
8919
8909
8899
8891
8883
8877
8871
8866
8863
| 8860
8858
4
9977
9921
9867
9815
9764
9716
9669
9624
9580
9538
9498
9459
9421
9385
9350
9317
9285
9255
9226
9198
9171
9146
9122
9098
9077
9056
9036
9018
9000
8984
8969
8954
8941
8929
8918
8908
8898
8890
8883
8876
8871
8866
8862
8859
8857
5
9971
9916
9862
9810
9759
9711
9664
9619
9576
9534
9494
9455
9417
9382
9347
9314
9282
9252
9223
9195
9169
9143
9119
9096
9074
9054
9034
9016
8999
8982
8967
8953
8940
8928
8917
8907
8897
8889
8882
8875
8870
8865
8862
8859
8857
6
9966
9910
9856
9805
9755
9706
9660
9615
9571
9530
9490
9451
9414
9378
9344
9311
9279
9249
9220
9192
9166
9141
9117
9094
9072
9052
9032
9014
8997
8981
8966
8952
8939
8927
8916
8906
8897
8888
8881
8875
8870
8865
8862
8859
8857
7
9960
9905
9851
9800
9750
9702
9655
9610
9567
9526
9486
9447
9410
9375
9340
9308
9276
9246
9217
9190
9163
9138
9114
9092
9070
9050
9031
9012
8995
8979
8964
8950
8937
8926
8915
8905
8896
8888
8880
8874
8869
8865
8861
8859
8857
8
9954
9899
9846
9794
9745
9697
9651
9606
9563
9522
9482
9443
9407
9371
9337
9304
9273
9243
9214
9187
9161
9136
9112
9090
9068
9048
9029
9011
8994
8978
8963
8949
8936
8924
8914
8904
8895
8887
8880
8874
8869
8864
8861
8858
8857
9
9949
9894
9841
9789
9740
9692
9646
9602
9559
9518
9478
9440
9403
9368
9334
9301
9270
9240
9212
9184
9158
9133
9110
9087
9066
9046
9027
9009
8992
8976
8961
8948
8935
8923
8913
8903
8894
8886
8879
8873
8868
8864
8861
8858
8857
742 ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ 21.4-1.
Таблица 21.4-1 (продолжение)
1 х
5
6
7
$
9
1,50
1
2
з
4
6
6
7
8
9
1,60
]
2
з
4
6
6
7
8
9
1,70
1
2
з
4
5
6
7
8
9
1,80
1
2
з
4
&
6
7
8
9
1.90
1
2
з
4
&
6
7
8
9
2.00
j
0
8857
8856
8856
8857
885Э
0,8362
8866
8370
8876
8882
8889
88Э6
8905
8914
8324
8935
8947
895Э
8972
8986
9001
9017
9033
9050
906S
9086
9106
9126
9147
9168
9191
9214
9233
9262
9238
9314
9341
9368
9397
9426
9456
9487
9518
9551
9584
9618
9652
9688
9724
9761
9799
9837
9877
9917
9958
1,0000
1
8857
8856
8856
8858
8860
8863
8866
8871
8876
8882
8889
8897
8906
8915
8925
8936
8948
8961
8974
8988
9003
9018
9035
9052
9070
9088
9108
9128
9149
9170
9193
9216
9240
9265
9290
9316
9343
9371
9400
9429
9459
9490
9522
9554
9587
9621
9656
9691
9728
9765
9803
9841
9881
9921
9962
0004
2
8856
8856
8856
8858
8860
8863
8867
8871
8877
8883
8890
8898
8907
8916
8926
8937
8949
8962
8975
8989
9004
9020
9036
9054
9071
9090
9110
9130
9151
9173
9195
9218
9242
9267
9293
9319
9346
9374
9403
9432
9462
9493
9525
9557
9591
9625
9659
9695
9731
9768
9806
9845
9885
9925
9966
0008
3
8856
8856
8857
8858
8860
8863
8867
8872
8877
8884
8891
8899
8908
8917
8927
8939
8950
8963
8977
8991
9006
9021
9038
9055
9073
9092
9112
9132
9153
9175
9197
9221
9245
9270
9295
9322
9349
9377
9406
9435
9465
9496
9528
9561
9594
9628
9663
9699
9735
9772
9810
9849
9889
9929
9971
0013
4
8S56
8856
8857
8858
8860
8864
8868
8872
8878
8884
8892
8900
8909
8918
8929
8940
8952
8964
8978
8992
9007
9023
9040
9057
9075
9094
9114
9134
9155
9177
9200
9223
9247
9272
9298
9325
9352
9380
9408
9438
9468
9499
9531
9564
9597
9631
9666
9702
9739
9776
9814
9853
9893
9933
9975
0017
5
8856
8856
8857
8858
8861
8364
8868
8873
8879
8885
8892
8901
8909
8919
8930
8941
8953
8966
8979
8994
9009
9025
9041
9059
9077
9096
9116
9136
9157
9179
9202
9226
9250
9275
9301
9327
9355
9383
9411
9441
9471
9503
9534
9667
9601
9635
9670
9706
9742
9780
9818
9857
9897
| 9938
1 9979
0021
6
8856
8356
8857
8359
8361
8864
8869
8373
8879
8836
8893
8901
8910
8920
8931
8942
8954
8967
8981
8995
9010
9026
9043
9061
9079
9098
9118
9138
9160
9182
9204
9228
9252
9277
9303
9330
9357
9335
9414
9444
9474
9506
9538
9570
9604
9633
9673
9709
9746
9784
9322
9861
9901
994?
9983
0026
7
8856
8856
8857
8359
8361
8865
8869
8874
8830
8887
8394
8902
8911
8921
8932
8943
8955
8968
8982
8997
9012
9028
9045
9062
9081
9100
9120
9140
9162
9184
9207
9230
9255
9280
9306
9333
9360
9388
9417
9447
9478
9509
9541
9574
9607
9642
9677
9713
9750
9787
9826
9865
9905
9946
9987
| 0030
8
8856
8856
8857
8859
8862
8865
8369
8875
8880
8887
8895
8903
8912
8922
8933
8944
8957
8970
8984
8998
9014
9030
9047
9064
9083
9102
9122
9142
9164
9186
9209
9233
9257
9283
9309
9335
9363
9391
9420
9450
9481
9512
9544
9577
9611
9645
9681
9717
9754
9791
9830
9869
9909
9950
9992
0034
9
8856
8856
8857
8859
8862
8866
8870
8875
8381
8888
8896
8904
8913
8923
8934
8946
8958
8971
8985
9000
9016
9031
9048
9066
9084
9104
9125
9145
9166
9188
9211
9235 '
9260
9285
9311
9338
9366
9394
9423
9453
9484
9515
9547
9580
9614
9649
9684
9720
9757 1
9795
9834
9873
9913
9954
9996
0038
21.4-4. 21.4. ГЛММА ФУНКЦИЯ И СВЯЗАННЫЕ С НЕЙ ФУНКЦИИ 743
21.4-2. Асимптотическое разложение Стирлинга для Г (г) и п\ (см. также
пп. 4.4-3, 4.8-6, b и 21.5-4).
(| arg 2 | < я) (ряд Стирлинга), (21.4-10)
Ряд Стирлинга особенно полезен для больших значений | г |; для
действительных положительных г абсолютная величина ошибки меньше, чем абсолютная
величина последнего из взятых членов. Заметим, в частности, что
lim п-п'-— =1 или п\ % ппе~п У2лп при л-*со (21.4-11)
(формула Стирлинга).
Относительная ошибка формулы Стирлинга убывает с возрастанием п\
асимптотическая формула часто применяется при вычислении отношения двух
факториалов или гамма-функций.
Отметим более специальные формулы:
—я-| -—
ппе nV2nn<n\<nnV2nne l2n, (21.4-12)
я! - пя Y2Hh ехр (- п + -^ - -1-- + .. .) (21.4-13)
при п -* оо.
21.4-3. Логарифмическая производная гамма-функции.
оо
А = 0
ф (г) = Г U ~Tt] dt "* ~ ^ (~ + ~—) * (Re Z > 0)* (21-4"15>
о е о
Заметим, что
М> (1) = — С, я|?(2+ 1)=ф(2)+1 (21.4-16)
(С — постоянная Эйлера — Маскерони).
21.4-4. Бета-функция. Бета-функция (полная) определяется как
B(P,*)-£g£g-Bto,p) (21.4-17)
или при помощи аналитического продолжения интеграла
1
В(р, <j; = $'p~l(l-O*"l<0 (Rep>0, Re^>0) (21.4-18)
(интеграл Эйлера первого рода),
оо _ я/2
B(jp, <г) = ^ } '^p+g Я = 2 ^ 8ш«Р-1фСОб««-1ф(/ф. (21.4-19)
744
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.4-5.
Отметим формулы
В(р, q)B(p + q, r) = B(<7, r)B(q + r, р), (24.4-20)
-=т ' =/г (я, т=1 2,..,). (21.4-21)
В (л, т) \ т
ная бета-функция Б (р, <?) соответственно определяются аналитическим продолжением
интегралов
z
Гг(р)= ItP'h"1 dt (Rep>0), (21.4-22)
0
г
В(р, q)= f tp~l (\ -О^"1 dt (Rep>0, Re <? >0; 0<z< 1). (21.4-23)
2 о
Величина
В- (р, <?)
/Я(Р. <?)=-
В (р. <7)
называется отношением неполной бета-функции.
Большое число определенных и неопределенных интегралов, связанных с гамма-
функцией, содержится в [4.6], [21.3].
21.5. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ И ФАКТОРИАЛЬНЫЕ
МНОГОЧЛЕНЫ. МНОГОЧЛЕНЫ И ЧИСЛА БЕРНУЛЛИ
21.5-1. Биномиальные коэффициенты и факториальные многочлены (см.
также и. 1.4-1 и 21.5-3). В табл. 21.5-1 приведены определение и основные
свойства биномиальных коэффициентов I ). Выражение
' х\
хг" ■
L"] = ( Ы =Х(*— 1) ... (ДГ — /24-1) =
= S^xn + S\n)xn- ]+... +S^lxx (/г = 0, 1, 2, ...) (21.5-1)
называется факториальным многочленом степени п. Коэффициенты S^
называются числами Стирлинга первого рода и могут быть получены с помощью
рекуррентной формулы
S<" + i> = SW-"4-i- (2L5-2)
Заметим, что
п
(х + у)№= 2 (nk)x[kVn-kl (я = 0, 1, 2, ...) (21.5-3)
6 = 0
(биномиальная теорема Вандермонда)*
21.5-1. 21.5. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ. МНОГОЧЛЕНЫ БЕРНУЛЛИ 745
Таблица 21,5-1
Определение и свойства биномиальных коэффициентов
(см. также пп. 1.4-1 и 21.5-4)
(а) Определение и основные свойства. Если х, у, z — действительные числа и
п — целое число, то
( х (х — 1) ... (х— п + 1)
О'
о
для п > О,
для п = 0, } (определение),
для п < О
Г.')-2(.:,)ГО »>•>•
\я/ = ^ \/ J ^л _ I) (п > 0) (теорема сложения),
(ТКЫ.:,). Г.*)-'--т.*-') «>»..
ли, в частнс
С)--(/-.)-(?)-*■
(Ь) Если, в частности, N и п — положительные числа, то
N (N — 1) ... (JV-./1-f. 1) АЛ
/г!
(АГ — п) ! л!
для Af ^ /г,-
для А/ <л;
/=0 /=0
(с) Если Af, N, п — положительные целые числа такие, что М ^ п, N ^ п, то
N W — п
(7К.л»(-л-Ш
i (■)-*-■ 2<->'(;н
/=0 /=0
— положительные целые числа такие,
c:.')-i('.)-2"cr)-
/ = п / = 0
c::)-i'-^(;)=2'-""-'C).
/ = л
m-i(X).
/ = 0
(;*:)-2"(.:,)С)-
/=о
/-о
746
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.5-2.
21.5-2. Многочлены и числа Бернулли.
(а) Определения. Многочлены Бернулли В^ (х) порядка л = О, 1,2,...
и степени k определяются из разложения производящей функции (п. 8.6-5)
fnoXt
Tfbr = S Bin) М 4г <л = 0' >• 2- -)• Р1.6-4)
1в 1) л—о
Многочлены Бернулли порядка 1 обычно называются просто многочленами
Бернулли. Заметим, что
Bf(x) = x*, B[n+»x = -^-f~£il(x-l)(x-2)...(x-n)] (n>k). (21.5-5)
к к п\ dx
Числа В^ (0) = В^ называются числами Бернулли порядка л; имеем
^ = |/Г£ (-0,1,2,...);
В<"> = 1, В1Л> = —1д, В£я) = ^л(3Л-1), j
^я> — —g- я« (я — 1), Б|я) = дал(15л«-30л»+5я+2),
4л)=-^"2("-1)(3/г2--7л--2), !
Б6/1) = 4(Ж п (63^5 —315л4 + 315/гЗ + 91/га_42/г—16).
(21.5-6)
(21.5-7)
Числа Бернулли порядка 1 обычно просто называют числами Бернулли.
B^ — Bk, Bk = 0 для всех нечетных k> 1, и
В0 = 1, Z?i = —о~* ' В2= ■
ВА = -
зо'
^в—42"*
(21.5-8)
Числа Бернулли В2п положительны при л нечетном и отрицательны при
л четном. Числа Бернулли могут также быть получены с помощью
рекуррентной формулы
*о = 1. 1 + Ю^1 + (2)^ + ...+(л11)^1 = 0 ^ = 2,3,...) (21.5-9)
или в виде определителей (формула Лапласа)
0
I СМ 41
в„=(-1)«л!| 4 -4 „4- ... о
(П + 1)1 Л| (/I - 1)1
1
21
1
31
1
41
. . .
1
1
1
2!
1
3!
1
0
1
1
21
• • •
1
21.Б-4. 21.5. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ. МНОГОЧЛЕНЫ БЕРНУЛЛИ 747
(Ь) Некоторые свойства многочленов и чисел Бернулли.
± Bf w = k BW_x ,,,, jj BW ({(«-^[BW, W-*W, (в)], (21.5-10)
a
Д J3<JJ> (k)=mB <*-|> (k). bnB%\k) - m <m - 1) ... <m - л + 1) * m_rt
(£=0, ± 1, ±2, ... ; m^n) (см. п. 20.4-1), (21.5-11)
В%) {x + d =s(«> (JC) + * в («J 0 (jc), в<л)(1) _ B(«) + лв (я-1) ^ (2i.5-12)
$ e?)(6>^-rnAS*+i <*>-s*,'1)<x>'J^r^)*-^"0. <2l-5-i3>
Bk (n ~~ x) = (~ U*fi^(*) (теорема о дополнительном аргументе); (21.5-14)
£(-1)(1)-(.-А)в<"). J
m-1
£ У* (m*) =m*_1 VJ B^4x-\- —J (теорема умноокения)'.
(21.5-15)
-ii>M..H^M.2-=^,
r = l
Bjb»+1«-i<-.^'(«+.). 2S^-
r = l
(21.5-16)
21.5-3. Формулы, связывающие многочлены Бернулли и факториальные
многочлены. Многочлены и числа Бернулли связаны с факториальными многочленами
(п. 21.5-1) по степеням х\ эти связи используются при решении разностных
уравнений и, в частности, при суммировании рядов (п. 4.8-5, d).
XW = (xn) n\ =* (*-1)... (х-п + \) = В%+1) (х +1)==
= II (l-\)B™k х* (л==0' 1* 2* -)• (21-5"17>
5(g~l)(S-2)...(g-2r+l)^-f(£-l)[2r~13 «-
= w[Blr) M-Btr)] (г —1. 2. ...)- (21.5-18)
21.5-4. Приближенные формулы для (^j (см. также п. 21. 4-2). Если N — положи-
2 I N I !*/ПГ
тельное целое число игш— -— л < I/ JL , то
N-l , Nz* N-\ . , Nyb x
«-^""•^-^~" (■♦•-.♦-■) -*
19)
748
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6-1.
Если п < N, то
п2
При больших значениях N, п и N — я применяется формула Стирлинга
21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ, ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
И СВЯЗАННЫЕ С НИМИ ФУНКЦИИ
21.6-1. Эллиптические функции; общие свойства. Функция w=f(z)
комплексной переменной г называется эллиптической функцией, если:
1. f (z) является двоякопериодической функцией с двумя
конечными примитивными периодами (наименьшими периодами) щ и соа,
отношение которых не есть действительное число*), т. е.
!(г + тщ + п(д2) = }(г) (т, /1 = 0, ± 1, ± 2, ...; Im (^-j^O). (21.6-1)
Точки z плоскости, отличающиеся друг от друга на период,
называются конгруэнтными.
2. Единственные особенности f (z) в конечной части плоскости
суть полюсы (см. также пп. 7.6-7 — 7.6-9).
Двоякопериодическая функция повторяет значения, принимаемые ею в
параллелограмме периодов, определенном точками 0, со1( со2, щ+щ, причем две
стороны, соединяющие три последние точки, нужно исключить как
принадлежащие смежному параллелограмму. Порядком эллиптической функции
называется число полюсов в параллелограмме периодов, причем каждый полюс
считается столько раз, какова его кратность.
Двоякопериодическая функция, не имеющая полюсов в параллелограмме
периодов (целая двоякопериодическая функция), есть постоянная. Сумма вычетов
двоякопериодической функции в ее полюсах в параллелограмме периодов равна
нулю; отсюда следует, что простейшая нетривиальная эллиптическая функция
имеет порядок 2. Эллиптическая функция f (z) порядка г принимает каждое
значение w в точности г раз в каждом параллелограмме периодов, если это
значение считать столько раз, какова кратность корня уравнения f (z)—w=Q.
Разность между суммой всех нулей и суммой всех полюсов функции f (z),
расположенных в параллелограмме периодов, равна некоторому ее периоду.
Эллиптические функции обычно встречаются в связи с интегралами или
дифференциальными уравнениями, содержащими квадратные корни из многочленов третьей или
четвертой степеней (например, при вычислении длины дуги эллипса, при решении
уравнения колебаний маятника; см. также пп. 4.6-7 и 21.6-4.) Эллиптические функции Вейершт-
расса и нормальные эллиптические интегралы образуются из простых функций с известными
особенностями и просты для теоретических исследований (пп. 21.6-2, 21.6-3 и 21.6-5 Ь).
Для численных расчетов предпочтительнее эллиптические функции Якоби (п. 21.6-7),
которые могут рассматриваться как обобщение тригонометрических функций; нормальные
эллиптические интегралы Лежандра, тесно связанные с обратными функциями Якоби,-
также подробно табулированы (пп. 21.6-5 и 21.6-6).
21.6-2. ^-функция Вейерштрасса.
(a) jp (2)=jp (21 щ, со.,) есть четная эллиптическая функция порядка 2
с периодами со1( со2 и двукратными полюсами в точках z = mco1 + /zco2 (я, т =
= 0, ±1, ±2, ...). Функция jp (z) определяется как
f(3)=p(*i*i. °2)=4 + 2] [(,-т,! _»«.),-(„.,+,,»,). J н»(-«)
т, п
т* + п* ф0
11т(1г)>0]- (21-6-2)
*) Следует иметь в виду4 что во многих руководствах периоды обозначаются через
b(Di и 2(оа,
(21.5-20)
(21.4-11).
21.6-2. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ 749
Суммирование распространяется по всем целым значениям тип
(положительным, отрицательным и нулевым), за исключением одновременных нулевых
значений т и п. Функция w = ft(z) удовлетворяет дифференциальному
уравнению
где
(~-)2 = 4w*--g2w--g3 = 4 (а>-в1) (w-e2) (ш-е3), (21.6-3)
*1 = К^)' *~P(J4f2L> *з = Р(^> (21.6-4)
ei+e2+e3 = 0, е1е2+е1еа + е2еа = —-} g2t ехе2е3 = \ g^ (21.6-5)
Параметры g2, g3 определяют постоянные щ9 со9, связанные с каждой р-функ-
цией, и называются инвариантами %> (z) = p (z | a>lt (o2)=fP(z; g2, gs)', заметим,
что при любом t ф 0
P(tz\t(Dlt toJ-Г» Р (г | ©I, озз), p(fc; Г^2, r*g3)=r* f> (г\ g2> g3). (21.6-6)
Точки w=eu e2t e3 и до = ооесть точки разветвления обратной для
р (2 | о)1( о)2) функции
? J /4ш3
dw
V4w* — g2w — g3
(21.6-7)
(нормальный эллиптический интеграл Вейерштрасса первого рода).
Заметим следующие разложения в ряды:
Р (z; g,. g ) = — 4- — z2 4- 5з г* -{- -^- ze 4- Зё*ёя г» 4- =>
5 I*, *2. £>> 2f ^20 ^23 Г 1200 ^ 6160 ^'"
со
-i-+ 21 V2/2"2[0<|2|<min(l(o1|, lffl.1)],
(21.6-8)
m, n
£ = 1
йз=14оУ ! = (2-£lY (Л^-^У^
m, n
m2 + "2^0
л2&
/fe = l
^2* \U-e
> (21.6-9)
и теорему сложения
Ю)
(b) Каждая эллиптическая функция f(z) с периодами ыи щ может быть
представлена как рациональная функция от у (z; щ, щ) и %>' (z; а>и оа2). Более
точно, / (г) может быть записана в виде
f(z) = RiW(z)]+P'(z)R2[P(z)],
(21.6-11)
где Ri и /?2 — рациональные функции; р'(z) — нечетная- эллиптическая
функция порядка 3.
750
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6-3.
21.6-3. £- и а-функции Вейерштрасса.
(a) £- и а-функции Вейерштрасса не являются эллиптическими функциями,
однако могут быть использованы для построения эллиптических функций
с заданными особенностями. По определению
£(*) = £(z|o)1( o)2) =
~~ ~z "•" Zj [z — mcui — пщ"» mcDi + пщ ' (mcut + «cu2)2J ** '*
m, /г
a(2) = a(2|©lf (o2) =
= Z | j ^ 1 — OTfl)i + nu)J exP [wcui-j-ncue"•"2(mu)i + «Cu2)2j = ""■ a (""г)
m, n
m2-\-nzjt0
[ImO>0]' (21.6-12)
где сумма и произведение распространяются по всем целым (положительным,
отрицательным и нулевым) значениям т и /г, за исключением одновременных
нулевых значений т и /г. £ (z) имеет простые полюсы и a (z) имеет простые
нули в точках г = тщ-\-пщ, и
£'(*) —Р W, £$-£(*>• (21.6-13)
Формулы (8) и (13) позволяют получить разложения функций £ (г) и a (z)
в ряды Лорана в окрестности точки z = 0. Отметим, что
£ (г) = f ш . (нормальный эллиптический интеграл
const^4^*""^*^""53 Вейерштрасса второго рода).
(21.6-14)
Теорема сложения для ^-функции
е (л+д)-с и)+е (в)+{ ^-iu?- (21-6-15)
Если ввести обозначения*) 2g (шх/2) == т]г, 2^(со2/2) =г|2, то 1\1щ — г\2(о1=*2т и
£(z + ma)1 + /2(u2) = £(z)+mT]1 + «if]2 (m, /i=0, ±1, ±2, ...),\
a(z+mco1 + «u)2)= } (21.6-16)
в(_ 1)« + « + ™а(г)ехр [(тЦ1 + пц2) (г + т°» + п<»>)].
(b) -Х- Если эллиптическая функция f (г) имеет в параллелограмме
периодов только простые полюсы Ь^ с вычетами Аь (& = 1> 2, ..., г), то
г
/М- 2 Лл£(г-&*) + С (21.6-17 а)
fc = l
Если эллиптическая функция f (z) имеет в параллелограмме периодов
нули ak и полюсы &л(£=1, 2, ..., г), каждый из которых пишется столько
раз, какова его кратность, то
а (г — а,\ о (г — аЛ ... о (z — а Л
f («>-c,(,-^,;,-j...,;«-»;i' (21-6-17 6>
где &*= 2 а*""~ 2 ^Л""полюс Функции /(z), конгруэнтный полюсу bj. X.
fc=l fc = 2
-*) Если периоды обозначены через 2cd^ а 2й)4 (см. сноску на стр. 748), то полагает
til = £(©i). Tj2 = I (Сй2).
21.6-5. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ 751
21.6-4. Эллиптические интегралы (см. также п. 4.6-7). Функция
г
F(z) = $f(z)dz (21.6-18)
а
называется эллиптическим интегралом, если / (г) есть рациональная функция
от z и квадратного корня \^G (z) из многочлена
G(z) = a0zi + alz3 + a2z2 + a3z+ai = a0(z — al) (z — a2) (z — а3) (z—aj, (21.6-19)
не имеющего кратных корней; сюда включается случай многочлена третьей
степени G (z) = G3(z), который рассматривается как многочлен четвертой
степени G(z) = G4(z) при условии, что а4 = со и а0 = 0 так, что формально
a0(z — a^) = a1.
В формуле (18) считается, что нижний предел интегрирования а не
совпадает ни с одним корнем многочлена G (z).
Каждый эллиптический интеграл есть многозначная функция от z;
разные пути интегрирования производят бесчисленное множество значений
функции. Точки z = alf z = a2, г = схз, z = a4 являются точками разветвления.
Соединяя аъ <х2 и а3, а4 двумя соответствующим образом определенными
разрезами, можно получить связную риманову поверхность (п. 7.4-3),
подобную поверхности тора.
21.6-5. Приведение эллиптических интегралов. Следующие действия
приводят каждый эллиптический интеграл к сумме элементарных функций и
трех так называемых нормальных эллиптических интегралов (см. также [21.2|,
[21.3]; в [21.3] содержится очень подробная таблица явных формул,
выражающих эллиптические интегралы через нормальные эллиптические интегралы).
{а) Алгебраическое приведение. Заметим, что четные степени
У G (z) есть многочлены от г, и запишем
/ (~) = Р* <г> + р2 (*) VG~(z) ^(pi + Р* Vg) (р, - Р4 YG) в
Р8 (2) + Ра (2) YG~W) (Рз)2 - (Pa)2 G
=/?1(*)+Й%' (21-6"20)
где Pi (z)-— многочлены, а Rx (z) и R2 (z) -— рациональные функции.
Интегрирование Rt (z) приводит к элементарным функциям (п. 4.6-6).
Разлагая рациональную функцию R2 (z) на простейшие дроби (п. 1.7-4\
приведем вычисление \ 2 dz к интегралам вида
In=*[{zZJ?l dz (л=0, ±1, ±2, ...). (21.6-21)
* Yg (z)
Каждый такой интеграл может быть выражен через /0, /if /2 и /_х при
помощи рекуррентной формулы
(2л+6) Vn+4 + (2rt+5) Ww* + (2n + 4) V«+2+ j
+ (2n + 3) bBIn+l + (2n+2) b4In = 2 (z-c)"+i \TgW)
(n=0, ±1, ±2, ...), (21.6-22)
где коэффициенты b^ определяются из тождества
G (z) = a0z* + ciiZ3 + a2z2 + aHz+a4 ■=»
= &0 (z-<:)« + &! (z-c)3 + 62 (z-c)a + fc8 (z-c) + ^4. (21.6-23)
Формула (22) позволяет явно выразить /2 через У0, /х и /_и если aQ=»0
752
ГЛ. 21 СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6-5.
(т. е. bQ = 0) или если с есть корень уравнения О (z)=0 (т. е. 64 = 0). Пусть
с не является таким корнем; тогда можно записать /2 как
С Й^ЛяС<£^Л + аС *^+р С *£_ (21.6-24)
J YG (г) J T^G (2) J T^C (2) r Vtf (г)
где г=с' есть корень <j(z)=0. Следовательно, каждый эллиптический
интеграл (18) может быть выражен в виде суммы элементарных функций и трех
сравнительно простых типов эллиптических интегралов первого, второго и
третьего рода (п. 21.6-4):
г г г
с dz ? z dz с dz
1 VG (г),
Swk. ^z-o'vob. (2L6-25>
Первый из этих интегралов обычно рассматривают как нормальный
эллиптический интеграл первого рода; другие два интеграла (25) непосредственно
применяются редко, и чаще пользуются их линейными комбинациями
—нормальными эллиптическими интегралами второго и третьего рода (пп. 21.6-2,
21.6-3 и 21.6-6).
Эллиптический интеграл первого рода конечен для всех z; он аналитичен
всюду, за исключением алгебраических точек разветвления av a2, a3, a4.
Эллиптический интеграл второго рода аналитичен всюду, исключая те же
точки разветвления и полюс на бесконечности (если а^ = 0, то а4 = оо и
интеграл имеет на бесконечности точку разветвления и принимает в ней
бесконечное значение).
Эллиптический интеграл третьего рода помимо алгебраических точек
разветвления av а2> а3, а4 имеет еще логарифмическую точку разветвления
при z=c.
(b) Замена переменных. Нормальные формы Вейер-
штрасса и Римана. В процессе приведения можно ввести новую
переменную интегрирования z = z (z), преобразующую эллиптические интегралы
(21) или (25) в новые эллиптические интегралы, содержащие более удобные
многочлены G (г) и, возможно, более простую рекуррентную формулу (22).
В частности, дробно-линейное преобразование
г= А* + В (AD-ВСФО) (21.6-26)
Cz+D
(п. 7.9-2), выбранное так, что точки разветвления z = a1, a2, a3, a4
преобразуются в точки z = elt e2, e3t оо, приводит к эллиптическим интегралам в
нормальной форме Вейерштрасса, где &(z) = 4z3—g2z — £з- Эти интегралы
связаны с функцией Вейерштрасса jf> (п. 21.6-2). Напротив, преобразование (26),
отображающее точки z = alt a2, a3, a4 в z=0, 1, l/k, —\/kt где k есть
действительное число, заключенное между 0 и 1, приводит к эллиптическим
интегралам в нормальной форме Римана, где G (z) = z (l — z) (l — k2z2.)
(c) Приведение к нормальной форме Лежандра. Чаще
х
требуется преобразовать действительный интеграл \ f (x) dx к нормальной форме
а
Лежандра, где S(z) = (l— z2) (l— k2z2) и k есть действительное число,
заключенное между 0 и 1. Процесс приведения приводит к действительным
нормальным интегралам Лежандра (п. 21.6-6), для которых имеются подробные
таблицы.
21.6-в. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ 753
Пусть G (х) — действительный многочлен, положительный в интервале
X
(а, х)\ тогда \ f (x) dx принимает действительные значения, если интервал
а
интегрирования не содержит действительных корней уравнения (?(*)=0.
Табл. 21.6-1 содержит преобразования х=х((р), отображающие интервал
интегрирования (а, х) в соответствующий интервал действительного аргумента ф
между 0 и я/2, так что
"Х --VVf=n^ (0<*2<1) (21.6-27)
-УЩх!
Y\ —k2 sin2 ф
для различных возможных типов действительных многочленов четвертой
степени G (х) = <?4 (х) и третьей степени G (*) = <?3 (х). Соответствующие значения
постоянных параметров k2 и \х также табулированы.
Во всех случаях старшие коэффициенты (а0 или ах) многочленов G (х)
приняты равными 1 или —1. В случае действительных корней принимаем
«1 > «2 > аз > а4» комплексные корни обозначаем bx ± icx и b2 ± tc2, где
&i ^ Ьг, сг > О, с2 > 0. Иногда вводятся вспомогательные величины:
щк=^ак — щ (I, &=1, 2, 3, 4), ]
tge1 = ^-F^. tge2==
V
аг — b,
^з = ^. tge4 = ^f>
tg[(9o/2)2]==
bx — bt
cos 83
(21.6-28)
"cos 04'
v = tg[(e1-e1)/2Jtg[(81 + ea)/2J. J
21.6-6. Нормальные эллиптические интегралы Лежандра (см. также пп. 21.6-4
и 21.6-5).
(а) Определения. Нормальные эллиптические интегралы Лежандра
(неполные) определяются формулами
^2
/(1 —22) (1 —£2*2)
^(z, /г)
о о
(нормальный эллиптический интеграл Лежандра первого рода);
Ф z
£(Ф, k) = J /1 -*» sin* ф </Ф = $ l/^Tiri^ dz==£ <2' *>
о о
(нормальный эллиптический интеграл Лежандра второго poda)t
ф
с?Ф
1 — Дг2 sina ф
3(1 -\-cz*)V(
dz
= Я (Z, С, k)
(1—22) (1 — ^222)
и
(нормальный эллиптический интеграл Лежандра третьего poda)t
где г = sin ф, так что F (sin ф, &) = У7 (ф, /г) и т. д.
(21.6-29)
Таблица 21.6-1
Преобразование к нормальной форме Лежандра
G(x)
корни
G4 (х),
четыре
действительных
корня
G» (х)
три
действительных корня
Старший
коэффициент
1
-1
1
-1
Интервал
at < х
или
х <а4
а3 < х < а2
а4 < х < а3
а2 < х < at
а3 < х < а2
а, <*
*<а8
а2 ^ х ^ o&j
Все корни G(х) дей
Преобразование
* =
tti(X42 — (ZsGUi sin2 ф
a42 — сщ sin2 ф
a3a42 — a4a32 sin2 ф
a42 — a38 sin2 ф
ct4a3i + ttia43 sin2 ф
a3i + a4s sin2 ф
a2a3i —a3a2i sin2 ф
a3i — a2i sin2 ф
a3 -f a32 sin2 ф
at —a2 sin8 ф
1 — sin2 ф
a3i
O&2CC31 — 0C30C2i Sin2 ф
«si — a«t sin* ф
ств *ьте льны
Sin2 ф ass
О&42 X — Otj
a4i x — (x>2
a42 x — аз
a32 x — a4
(X31 д: — a4
a43 ai — *
a31 д: — a2
a2i * — a3
* — a8
a82
AT — (Xi
x — a2
«81
«1 — *
(X31 ДГ — (X>2
«21 * — 0t8
Соответствующие
значения
X
a,
a4
a3
a2
a4
a8
a2
at
a3
a2
a,
00
— 00
a3
a2
a,
Ф
0
я/2
0
Я/2
0
Я/2
0
Я/2
0
Я/2
0
Я/2
0
Я/2
0
Я/2
k*
(a„ a2, a4, a3)
(a3, a2, a4, aj
«82
a3i
«21
a3i
**
2
(a3i«42)1/s
2
<a*i)l/2
Таблица 21.6-1 (продолжение)
G (х)
корни
G4 (х), два
действитель-
1 ных и два
1 комплексных
1 корня
G, (дг). Два
комплексных
корня
<?4 (*)» четыре
комплексных
корня,
bt > Ьш
к?4 (дг), четыре
J комплексных
корня
bt=b*
Старший
фициент
1
— 1
1
— 1
1
Интервал
аг ^ х
или
х ^ а2
а2^^^а!
ai ^ х
х < at
— оо<
<*<00
G (х) имеет i
Преобразование
Ql-|-a2
Х 2
cti — а2 V —cos ф
2 1—vcosф
fttr^y cos81a1— x
\ b 2) cos82*-a2
д: = а с« 1 ~ cos ф
1 cos Bt 1 4- cos ф
(. ф\2 cos8, ,
д: = 6i — сх ctg ф
комплексные корни
Вспомогательная
величина
острый
угол,
82—тупой
острые
8i — тупой
8, —
острый
8з» е4.2^»~
острые
e.-e.~£
Соотв етств ующи е
значения
X
a2
оо
— оо
bt
00
ф
0
л
0
л
я + е3 +84
2
е8 + 84
2
я—83 — ©4
2
fe2
h^r
[-Й+ЙГ
sin» 88
-ЙУ
Д
(—£OS_8i£OS_S)1A
С,
(cosOj cos82)V2
(^ri)"
-(^Г
/ cos e6 \Vi
\ cxc2 )
1
Ct
756
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6-6.
k есть комплексное число, называемое модулем эллиптического интеграла,
с называется параметром интеграла 3-го рода.
Эллиптические интегралы (29) — нечетные функции от z (и от ф) и четные
от модуля k. Если k действительно и |&|^1, то эллиптические интегралы
f(y,sina,J
F(p,sir\&)
J
2,4
2,2
2,0
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0
I y> = 90°
I / /80°
- У^ У 70°
'^\^^^^ во*
I- """__ 50°
- w
30°
- 20°
: ю°
"i i » i i i i i i i i i i i i i i i >
0° 20° 40° 60" 80° ас
Ъ)
Рис. 21.6-1. Неполный эллиптический интеграл первого рода F (ф, k) = F (ф, sin a)}
а) как функция <р при постоянном а; Ь) как функция модулярного угла а при
постоянном ф.
Рис. 21.6-2. Неполный эллиптический интеграл первого рода F (ф, k) как функция от ф,-
для трех разных значений k.
первого и второго рода действительны для действительных z, таких, что
— l^z^l, т. е. для действительных ф. Для указанных значений ф и к
функции F (ф, k) и Е (ф, k) табулированы [21.2]. При табулировании вместо
модуля k обычно вводят модулярный угол a = arcsin/e.
На рис. 21.6-1 показаны графики функции F (ф, sin а) при постоянных
а и при постоянных ф. На рис. 21.6-2 показаны графики функции F (ф,&) в
зависимости от ф при разных k\ см. также [21.2J.
21.6-6. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ 757
(Ь) Полные нормальные эллиптические интегралы
Лежандра (см. также рис. 21.6-3). Функции
Я/2
О
31/2
Е = Е(£) = J Kl-/<2sin24)d({)==£(ji/2, k)
о
(21.6-30)
соответственно известны как полные нормальные эллиптические интегралы
Лежандра первого и второго рода; k и k' — V \—k2 называются
дополнительными модулями; К (k) и К'(&) = К(/г') называются связанными
эллиптическими интегралами первого рода, а Е (k) и Е' (/г) = Е (&') — связанными
эллиптическими интегралами второго рода. Заметим, что
ЕК' + Е'К — КК' = -=- {соотношение Лежандра)
(21.6-31)
К(0) = К'(0 = у, К(1) = К'(0) = со,
Е(0) = Е'(1) =
Е(1) = Е'(0)=1.
Обычно полные эллиптические интегралы К (k) и Е (k) табулируются в виде
функций модулярного угла a = arcsin£. При этом дополнительному модулю к'
соответствует угол л/2— а (см. рис. 21.6-3 и табл. 21.6-4).
Z0° 40° 60° 80° <*
а)
20° 40° 60°
6J
80° <*
Рис. 21.6-3. Полные эллиптические интегралы
а) К (/г) = К (sin а) и К' (/г); b) Е (/г) и Е' (k) кал функции модулярного угла а.
К (/г) и Е (k) удовлетворяют дифференциальным уравнениям
(21.6-32)
' dk2
dk
Таблица 21.6-2 rjj
Преобразования эллиптических интегралов
к
1
я
k'
~W
ik
k*
k'
ik
1 — Я'
1 + *'
sin ф
k sin ф
-^дф
— ik' tg Ф
я' sin ф
Д (Ф, k)
ik sin ф
А (Ф. k)
(1 + a') sin ф cos ф
А (ф. л)
COS ф
А (ф, k)
sec ф
А(ф, k)
COS ф
COS ф
А (Ф, k)
1
А (Ф. k)
cos8 ф — я' sin2 ф
А (ф, k)
F(v, k)
k F (ф, k)
-iF{q>, k)
— ik' F (ф, k)
k'F(q>, k)
— ikF (ф, k)
(1 + я') F (ф, «)
Я (i>, я)
-A- [£ (Ф, k) - k'2 F «p. k)]
i [£ (ф, я) - F (ф, я) - (tg ф) А (ф, я)]
-jr [E (ф, я) - я'2 F (ф, *) - (tg ф) А (ф, k)]
tK***-*5!^]
±[£(Ф, *,-,(,. *)-*.^^jp]
2 TE(W k) 1 Г/Чш ittl П /.^81ПфС08ф
1 -f Я' L£ 1ф' *' ' * ' (ф' *)J (1 Л ' Д «p, я)
21.6-6. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ
759
так что для действительных k2 < 1
K(*)-^(j. J; l;*)-f [1 + (1)V+(L±)V + ...], j
E(*,-|F(-I.i; !;*)-![,-ф'*-(ь§Н _...], j (2L6-33)
где Z7 (a, 6; с; г) —гипергеометрическая функция, определенная в п. 9.3-9.
(с) Преобразования. Нормальные эллиптические интегралы Лежан-
дра (29) с модулями k, \jk9 k\ \\k\ ik\V% k'\ik, (l—*')/(l +k')t 2j/"jfe/(l+fc)
связаны соотношениями, приведенными в табл. 21.6-2, где
]Л— £2sin2(p=A (ф, k)
(21.6-34)
(см. также п. 21.6-7, а). Табл. 21.6-3 содержит различные соотношения для
полных нормальных эллиптических интегралов (30), а табл. 21.6-4 — значения
этих интегралов.
Т а б л и да 21.6-3
Преобразования полных эллиптических интегралов
к
1
к
k'
1
k'
ik
k'
k'
ik
1 — *'
1 + A'
2Vk
1 i+л
K(i)
k (K + iK')
K'
A'(K'-MK)
A'K
Ж'
(1 + А) К
К'(»
Ж'
к
А'К
А'(К'Н-Ж)
k(K + Ж')
<!+*') К'
1 + *к,
Е(»
-L[E—*'«K-f (Е'-А2К')]
Е'
~[Е'-А»К'-*(Е-А'»К)]
±*
±*
Е+А'К
1 + А'
2Е-А"К
1+А
Е' (J)
^ |
Е
тИ
~ [Е'-А2К'-*(Е-А"К)]
~[E-A'2K-t(E'-A2K')]
2Е'-А2К'
1+А' |
Е' + АК'
1 + k
В частности,
кс*)-гттк(ттй-
Положим в (35) последовательно
2У^
k'0—k't ^/i4-i~~TTF
(я = 0, 1, 2, ...)
(21.6-35)
(21.6-36)
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ 21.6-в.
Таблица 21.6-1
Полные эллиптические интегралы К и Е
я/2 л/2
К = [ dX Е = \ Vl-k^sh^x dx
J Y\— 62 sin2* -A
£ = sin a
a
0°
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
К
1,5708
5709
5713
5719
5727
5738
5751
5767
5785
5805
5828
5854
5882
5913
5946
5981
6020
6061
6105
6151
6200
6252
6307
6365
6426
6490
6557
6627
6701
6777
6858
6941
7028
7119
7214
7312
7415
7522
7633
7748
7868
7992
8122
8256
8396
8541
8691
8848
9011
9180
E
1,5708
5707
5703
5697
5689
5678
5665
5649
5632
5611
5589
5564
5537
5507
5476
5442
5405
5367
5326
5283
5238
5191
5141
5090
5037
4981
4924
4864
4803
4740
4675
4608
4539
4469
4397
4323
4248
4171
4092
4013
3931
3849
3765
3680
3594
3506
3418
3329
3238
3147
a
50°
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
65,5
66,0
66,5
67,0
67,5
68,0
68,5
69,0
69,5
70,0
70,5
71,0
71,5
72,0
72,5
73,0
73,5
74,0
74,5
75,0
75,5
76,0
76,5
77,0
77,5
78,0
78,5
79,0
79,5
80,0
80,2
80,4
80,6
80,8
К
1,9356
9539
9729
9927
2,0133
0347
0571
0804
1047
1300
1565
1842
2132
2435
2754
3088
3261
3439
3622
3809
4001
4198
4401
4610
4825
5046
5273
5507
5749
5998
6256
6521
6796
7081
7375
7681
7998
8327
8669
9026
9397
9786
3,0192
0617
1064
1534
1729
1928
2132
2340
E
1,3055
2963
2870
2776
2681
2587
2492
2397
2301
2206
2111
2015
1920
1826
1732
1638
1592
1545
1499
1453
1408
1362
1317
1272
1228
1184
1140
1096
1053
1011
0968
0927
0885
0844
0804
0764
0725
0686
0648
0611
0574
0538
0502
0468
0434
0401
0388
0375
0363
0350
a
81°
81,2
81,4
81,6
81,8
82,0
82,2
82,4
82,6
82,8
83,0
83,2
83,4
83,6
83,8
84,0
84,2
84,4
84,6
84,8
85,0
85,2
85,4
85,6
85,8
86,0
86,2
86,4
86,6
86,8
87,0
87,2
87,4
I 87,6
87,8
88,0
1 88,2
83,4
88,6
88,8
89,0
89,1
89,2
89,3
89,4
89,5
89,6
89,7
89,8
89,9
К
3,2553
2771
2995
3223
3458
3699
3946
4199
4460
4728
5004
5288
5581
5884
6196
6519
6852
7198
7557
7930
8317
8721
9142
9583
4,0044
0528
1037
1574
2142
2744
3387
4073
4811
5609
6477
7427
8478
9654
5,0988
2527
4349
5402
6579
7914
9455
6,1278
3509
6385
7,0440
7371
E
1,0338
0336
0314
0302
0290
0278
0267
0256
0245
0234
0223
0213
0202
0192
0182
0172
0163
0153
0144
0135
0127
0118
0110
0102
0094
0086
0079
0072
0065
0059
0053
0047
0041
0036
0031
0026
0021
0017
0014
0010
0008
0006
0005
0004
0003
0002
0001
0001
0000
0000
21,6-7. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ 761
Так как при этом k'n-*\, то (1— ^)/(1+&«) ~"~*0» учитывая, что К(0) = я/2,
получим формулу
К(*)=ШтТ
(21.6-37)
гс = 0
которую можно использовать для вычисления К (/г).
21.6-7. Эллиптические функции Якоби.
(а) Определения. Обращение эллиптических интегралов z = F (ф, k)
и z = F (w, k) (п. 21.6-6, а) порождает функции am z (амплитуда г) и snz =
= sin(amz) (синус амплитуды z), т. е.
Ф = атг, 2= [- ф = ^(Т> W,
w = sn
J у(1-и»«)(1
(1 ~/г2Ш2)
= /="(», Л)
(21.6-38)
Различные значения многозначного эллиптического интеграла F (до, k)
отличаются друг от друга на 4тК + 2ш'К', где т, я = 0, ±1, ±2, ... Это
значит, что обратная функция sn 2 —двоякопериодическая с периодами 4К
и 2/К'.
Функции en z (косинус амплитуды z) и dn г (дельта амплитуды г)
определяются формулами
en z = cos (am z) = ]A — sn2z (en С _,, ,
r ' } (21.6-39)
dnz = A(/?, amz) = y\—k2sn2z (dn ~ *v
sn z, en г и dn z называются эллиптическими функциями Якоби Данное
значение параметра k явно не участвует в обозначениях этих функций; когда
это необходимо, будем писать sn (z, /г), en (г, /г), dn (z, k). k'', К, К', Е и Е'
определены в п. 21.6-6, Ь. Эллиптические функции Якоби все действительны
для действительных z и действительных /г2, заключенных между 0 и 1; на
сп 0 = 1), 1
in 0=1). j
f^U
Рис. 21.6-4. Эллиптические функции Якоби sn и, спы и dn и для k2 = f/2.
рис. 21.6-4 приведены графики эллиптических функций Якоби для k2==1/2.
Эллиптические функции вырождаются, если &2 = 0 или k2= 1; при этом один
из периодов становится равным со:
/г = 0, K = y» к' = °°, sn(z» 0) = sinz, cn (z, 0)=cosz, dn (z, 0) = 1; ]
/г=1,К = оо2 K' = |, sn(z, l) = thz, cn (z, l) = dn(z, 1) = ^-r. ]
(21.6-40)
762
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6-7.
Эллиптические функции Якоби могут быть также определены в терминах
р-( £-, а- или б-функций соотношениями п. 21.6-9.
(Ь) Различные свойства и специальные значения. Все
эллиптические функции Якоби имеют порядок 2 (п. 26.1-1); их периоды,
нули (простые) и полюсы (простые) приведены в табл. 21.6-5. snz есть нечетная
Таблица 21.6-5
Периоды, нули, полюсы и вычеты эллиптических функций Якоби
Функция
sn (2, к)
en {z, к)
dn(z, к)
Примитивные
периоды
4К
21 К'
4К
2К + 2/ К'
2К
4/К'
Нули
2т К + 2ш К'
(2т + 1)К + 2л/К'
(2т + 1)К4-
4-<2я+1)/К'
Полюсы
2т К + (2л + 1) / К'
Вычеты
(- \)т
(_ 1)Я*+Л
/л
(.!)«+!/
функция, а сп 2 и dn г —четные функции от z. В табл. 21.6-6 приведены
специальные значения функций. Табл. 21.6-7 показывает эффект изменения
аргумента на четверть и половину периода; при этом используются удобные
обозначения
sn (г, k) = s, en (2, &)=с,. dn (z, k)=d
(например, ks=ksn(z, k)).
Отметим еще соотношения:
Sna2 + cna2 = £2Sn22 + dn22==l, dn2 2 — k2 СП2 2 = £'2;
sn(— z) = — sn2, en (— 2) = en 2, dn (— z) = dnzj
sn (2K —z) = sn г, sn (2/K' —z)=—snz, I
en (2K — z)= — en 2, en (2tK' —z) = — en 2, >
dn(2K —z) = dnz, dn(2/K' —z) = —dnz; i
z
Ё (Sn 2, &) = ? dn2 2 dz.
0
(с) Теоремы сложения:
sn Л en В dn В -f sn Д en Л dn Л
1 — Л2 sn2 Л sn2 В '
$П (А + В) =
сп(Л + В) =
ёп(Л + Я) =
сп Л сп В — sn Л dn Л sn Б dn Б
1 — k* sn2 Л sn2 В '
dn Л dn В — &2 sn Л сп Л sn В сп В
I — Л2 sn« Л sn* В
(21.6-41)
(21.6-42)
(21.6-43)
(21.6-44)
(21.6-45)
(21.6-46)
(d) Дифференцирование:
d (sn z)
dz
d (en z)
= cnzdn z,
dz
d (dn z)
flfz
= — snzdnz,
= — &2sn zen z.
(21.6-47)
Таблица 21.6-6 ю
ЧгШК' ^\^
Специальные значения эллиптических функций Якоби
0
V.K
К
•/•к
[ sn (V»m К + Vti'K')
0
1 WK'
1 Ж'
1 ■/•* К'
0
/*-*/.
00
- /*-v.
0 4- Л')"1/»
tfjfefVi [(1 + *)V* + ' (1 - Л)1/»]
(I-*')1/*
(2Л)""1/. [(1 -|- *)*/• — / (1 — А)1/.]
1
А-*/-
Л-1
*-*/.
(l + ik')"1/»
(2Л)_1/2 [(i 4_ Л)»/1 - / (l - «Vi]
(1 - А'Г,/в
(2ikr,/i[(i+ik)Vi + /(i-ik)1/il
ciKViroK-fViiflC')
0
1 V.* К'
1 /К'
1 -А' К'
1
Л"1/» (1 4- *)*/•
оо
- к'Чш (1 + k)lt*
Jfe'VtO-ffc'f1/»
Л'1/* (2Л)~*/« (1 — 0
-fV^Mi-^r1/»
-Л/1/2(2^)~1/2(1 _{_/)
0
— /А-1/» (1 -k)1!*
— ik-* V
-ibrxl*{\ - k)1'*
— A'1/» (1 + А')"1/я 1
— А*1/» (2А)~*/« (l 4-/) 1
-/*''/■ <1 -k')'1!*
v'/i (2jfe)"~Vt (i - /)
dn(VamK+Va««KO
0
V,*K'
/К'
•/•/ К'
1
(1 + A0V*
оо
- о + *>1/в
А'1/.
(1/^о1/.[(1+ло,'/--/(1-*')*/.]
-/г1/.
- (Vi*')x/»[(1 + АОж/« -И 0 - ^)1/*J
k*
(1 - *)'/•
0
- (1 - Jk)Vt |
*'V. 1
(v.*-)1/. [(i+nVt + zci-r)]v. 1
/A'1/.
- {Чшк'УЬ [(1 +ik'),/»-/(l-ik')1/>]|
764
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6.7.
Таблица 21.6-7
Изменение переменной на четверть и половину периода
-К
0
К
2K
3K
sn (m К + ni К' + г)
-i К'
0
*К'
2i К'
- <*/<**)
— c/d
- tf/(ifc)
— c/d
± l/(*s)
±s
± 1/Us)
±s
d/<to)
c/d
d/(kc)
c/d
+ l/(ks)
+ s
+ l/(*s)
+ s
- d/<to)
— c/d
- d/(*c)
— c/rf
сп (т К -f ni К' ± г)
- i К'
0
/К'
2* К'
-К
- Ik'l(kc)
± £'s/d
ik'l(kc)
+ £'s/d
0
± id/(ks)
с
+ *tf/(£s)
— с
К
ik'/(kc)
+ £'s/d
- *Л7(Лс)
± £'s/d
2K
+ *d/(£s)
— с
± id/(ks)
с
3K
— ik'/(kc)
± fc's/d
tk'/ikc)
+ fc's/d
dn(mK + ni К' ± г)
— * К'
0
/К'
2i К'
3* К'
-K
+ ifc's/c
k'ld
± *£'s/c
- *7<*
+ ik's/c
0
± *c/s
d
+ ic/s
— d
± ic/s
К
+ ik's/c
k'ld
± i£'s/c
— k'/d
+ ^'s/c
2K
± fc/s
d
+ /c/s
— d
± ic/s
21.6-8. 21.6. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ И ИНТЕГРАЛЫ 765
(e) Преобразования. Табл. 21.6-8 показывает соотношения между
эллиптическими функциями Якоби с модулями k и ik\k\ k\ \jkt \\k't k'lik
(см. также п. 21.6-6, с).
(f) Разложения в ряды:
Sn2=2-(l+^)|i + (l + 14^ + /j4)|i_..M
СП 2 = l-|L + (l+4*2)ff-(l +44*2+16*4) Ц-+...,
|*|<min(|K'|, |2К + /К'|, |2K-iK'|).
(21.6-48)
21.6-8. Тэта-функции Якоби.
(а) Даны комплексная переменная v и комплексный параметр q = ei:ix
такой, что т имеет положительную мнимую часть. Четыре тэта-функции1)
01(0) = ^1(0|Т)==2 2 (— \)пя{п + 1/2)Ш sin (2/г+1) nv =
/i = 0
00
«»/ 2 (-oV-^V™)2""1,
Я= — 00
оо
^2 (о) =<>2 (»|т)=2 2 ^(Л + 1/2>2 cos <2/г + !> лу==:
я = 0
л = — оо
оо
^з(у) = 03(^|т) = 1+2 2 <7rt8cos2/uw =
л = 0
= S fie*™)**,
П "—00
fl4 (о) = ^4 (о I т) = 1 +2 2 (— О" ^ cos 2ши> =
я=0
- 2 (-DVfe"10)1
(21.6-49)
— все периодические целые функции от v соответственно с периодами 2, 2,
1,1. Четыре тэта-функции (49) имеют нули соответственно в точках
о = т + лт, m+/iT + V2» /w + fa+VjT + V*. 'H + fo + VJ*,
где m, я = 0, ±1, ±:2, ...; эти нули позволяют представить тэта-функции
в виде бесконечных произведений (7.6-2) [21.3].
1) Иногда 0"4 (и) обозначают через й0 (у) или Ф 4i>).
766
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.6-8.
Таблица 21.6-8
Преобразования первого порядка эллиптических функций Якоби
образование
А
! в
с
D
Е
z
k'z
— iz
kz
-ik'z
— ikz
к
ik
k'
k'
1
k
1
k'
k'
ik
k'
1
k'
k
k'
ik
k
ik'
1
k
k
k'K
K'
/f(K-ftK')
*'(K'+iK)
kK'
k'
k' (K' + iK)
к
kK'
k'K
/MK-MK')
sn (г, k)
sn {г, k)
dn (z, k)
sn (г, k)
en (г, k)
k sn (z, k)
_,ft,sn£ft)
en (г, k)
sn (г, k)
dnJzTk)
en (г, к)
СП (2, Л)
dn (2, Л)
I
СП (2, k)
dn (2, Л)
dn (2, *)
СП (2, Л)
dn (2, Л)
Mi. i)
1
dn (2, Л)
dn (2, Л)
en (2, /г)
СП (2, Л)
1
СП (2, *)
сп (2, /г)
dn (2, Л)
Тэта-функции «е являются эллиптическими функциями. 0«екб хорошая сходимость
рядов (49) позволяет вычислять различные эллиптические функции и эллиптические инте-
гралы с помощью соотношений п. 21.6-9; тэта-функции являются решениями
дифференциального уравнения с частными производными
д«Ф Л .дФ Л
-г— Am -г— = О,
dv2 дх
которое связано с уравнением диффузии (п. 10.3-4, Ь).
(Ь) Отметим соотношения:
. <*).
Ol (° + у) - ^2 (»). Ф8 (v + 4") - - *1 <*>•
^3 (» + у) - ^4 (»), ^4 (v + 4) " <>. <">.
^ (Р + 1) в ^ 1Я ^^ ^ (t,)' ^ (^ + I) ~ ^ Я ^ (t,)* J
(с) Для отыскания •&. (—ТГпГ х 4- В ) пРименяются формулы}
*! (о | х + 1) - е'я/4*! (о | т). ф, <» | т + 1) - в^Ц, (и | х)
(21.6-50)
(21.6-51)
(21.6-52)
Ф» (0 | т + 1) - <>4 <* | т), 0« <» I * + 1) - Ф, <о| т)
Чт НИ K?<iwVT»« <*'*>•
}
(21.6-53)
(21.6-54)
21.7-1.
21.7. ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ
767
(d) Значения четырех тэта-функций и их производных при v = О для краткое™
обозначают так:
fl. (0) = fl;, flj- (0) = 0], ... (/ = 1, 2, 3, 4).
оти значения удовлетворяют соотношениям
0'/' 0«
0;=я020304. &~
■ + :
■ + х*-
(21.6-5Я|
21.6-9. Соотношения между эллиптическими функциями Якобн, Вейер*
штрасса и тэта-функциями. Если различные параметры, входящие в опреде»
ления snz, enz, dn z, p (z), £(z), a (z) и fy (z) (nn. 21.6-2, 21.6-3, 21.6-6 —
21.6-8), связаны соотношениями
то
ь-vtt-m-
K-^Vei-e,=%<H,
k
tK
У e,-e, V«J
= ^Ке,-е3=тК,
*=£=2! (ImT>°>
до =
' V^i — ^з = 2Ку, а=
Cui
до
= 2К'
dnw =
У
*1 —
Р<г>-
#><2)
*3
- «1
- <*s
— *2
0*
02
^4
02
-**
01
04
02
04
0»
(f)
(f)
(f)'
<*>.
J? (2) - e, 03 #, <t.) •
Р(Ф
■-ei+(ei-e3)-— = e2 + (e1-e3)-—--
ei — e9
sn2 до
(21.6-56)
(21.6-57)
(21.6-58)
(21.6-59)
(21.6-60)
21.7. ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ
21.7-1. Введение. Ортогональные многочлены, рассматриваемые в пп. 21.7-1—
21.7-8, являются специальными решениями линейных однородных
дифференциальных уравнений второго порядка, связанных с гипергеометрическим
уравнением (9.3-31) (многочлены Лежандра, Чебышева и Якоби) или с
вырожденным гипергеометрическим дифференциальным уравнением (9.3-42)
(многочлены Лагерра и Эрмита). Эти специальные решения порождаются
специальными однородными краевыми условиями; каждый класс ортогональных
многочленов есть последовательность собственных функций для проблемы
собственных значений типа Штурма —Лиувилля. Для большинства приложений
важны только действительные значения аргумента z = x*).
Многочлены i|?0(jc), i|?i (*), t|)2 (*), ... каждого типа определяются с
точностью до постоянных множителей, которые обычно (но не всегда) выбираются
так, что коэффициент при хп в многочлене /г-й степени г|)л (х) равен единице.
Последовательные многочлены каждого типа могут быть определены
1) в терминах соответствующих гипергеометрических рядов
(п. 9.3-9, а) или вырожденных гипергеометрических рядов (п. 9.3-10);
2) с помощью рекуррентных формул, получающихся из
дифференциальных уравнений;
*) Ортогональные многочлены в комплексной области рассматриваются в [7.1], [21.3J.
768
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.7-2.
3) последовательным дифференцированием производящей
функции Ф (х, s) (см. также п. 8.7-2);
4) процессом ортогонализации Г рама — Шмидта степеней 1,
х, х2, ... с соответствующим весом у(х) на некотором интервале
(п. 15.2-1, а, 15.2-5);
5) из интегральных представлений (п. 21.7-7), которые обычно
связаны с интегральными преобразованиями решений
дифференциальных уравнений или с коэффициентами рядов Тейлора или Лорана
производящих функций.
В табл. 21.7-1 приведены основные соотношения для многочленов
Лежандра, Чебышева, Лагерра и Эрмита. В табл. 21.7-2 приведены выражения для
первых семи многочленов (многочлены Чебышева приведены в табл. 20.6-1);
одновременно даны выражения для степеней х через многочлены Лежандра.
Выражения для последующих многочленов см. в [21.4].
Подчеркнем, что единой системы нормировки ортогональных многочленов
нет; поэтому необходима осторожность при пользовании разными источниками.
Разложения в ряды по ортогональным многочленам производятся в смысле
п. 15.2-4 и дают важные приближения с минимальной соответственно
определенной средней квадратической ошибкой (п. 15.2-6; см. также пп. 20.5-1, 20.6-3).
21.7-2. Действительные нули ортогональных многочленов. Все нули каждого
из ортогональных многочленов, рассмотренных в пп. 21.7-1—21.7-8, простые.
Два последовательных нуля tyn (x) разделяются одним нулем tyn+1 (х) и по
меньшей мере одним нулем i|?m (x) для каждого т> п. Таблицы нулей
многочленов приведены в [21.4].
21.7-3. Функции Лежандра (см. также пп. 21.8-10, 21.8-11 и 21.8-13).
Дифференциальному уравнению (дифференциальному уравнению Лежандра) и рекуррентным формулам
для многочленов Лежандра (табл. 21.7-1) удовлетворяют не только многочлены Лежандра
первого рода Р (г) (табл. 21.7-1), но также и функции Лежандра второго рода Q (г);
для z = x и — 1 < *< 1 они равны
Qo(,) = J_lnl±£ QlW-£i„i±£-if
Q* (x) = ~ (Зх* - 1) In ~±~* ~JX> - (21.7-1)
Более общо, метод п. 9.3-8, b позволяет получить линейно независимые решения Р (z),
Qa (z) дифференциального уравнения Лежандра (функции Лежандра первого и второго
рода) для нецелых положительных и отрицательных, а также для комплексных
значений п = а; решения для п — а и м = — а — 1 тождественны.
21.7-4. Многочлены Чебышева первого и второго рода. Дифференциальному
уравнению и рекуррентным формулам для многочленов Чебышева (табл. 21.7-1)
удовлетворяют не только многочлены Чебышева первого рода (табл. 21.7-1)
Тп (х) = cos (n arccos х) (п = 0, 1, 2, ...), (21.7-2)
но также функции Чебышева второго рода
U0 (х) — arcsin х,
Un (х) = sin (n arccos *) = ~ *' ^ Тп (х) (п = 1, 2, ...). (21.7-3)
1 dTn+i
Функции Uп (х) не являются многочленами от х; функции—;—- —у* - есть много-
п л -f- 1 ах
члены; их обычно называют многочленами Чебышева второго рода. Отметим формулы
Тп {х) =- п*% ЪЧ Un <*> (л = °' *• 2' •••>• <21-7~4>
1
I
— 1
С Un {X) Um {x) dx = [ 0 при пфт или п = т = 0, \ (217-5)
J у\ — х* I я/2 ПРИ п = тф0. ) '
ю
СП
Ортогональные многочлены Лежандра, Чебышева, Лагерра и Эрмита
(см. также пп. 21.7-1—21.7-7)
Таблица 21.7-4
1
2
3
4
5
Дифференциальное
уравнение
Вес и интервал ортогонали-
зацни
Ортогональность и
нормировка
Явные выражения1)
(см. 9.3-32)
Рекуррентные формулы
Многочлены Лежандра Р (х)
(рис. 21.7-1)
d2w dw
0 ~~ х2) Ж* - 2х ~Тх + п (л + ° ш = °
ав-1, 6=1
1 f 0 (тфп).
-1 12ТП(т-га)
Рл(*)=р(-л, п+1; 1; Ц^).
Ря(*)-
-2-«V (_n m (2л-2т)1 «-«m
Zj ' ml (л - m)! (л — 2m)!
m=0
**-l </P_
*= x P„ (x) -\ —r -~
,ч Vп"1 п л — 1
' 1 "21 Равно "о" » если п — четное» и —-— , если л — нечетное.
Многочлены Чебышева Гя (х)
(рис. 21.7-2)
d2w dw
0 — х2)~-х ^ + n2w = 0
d*2 dx
v (*) —
e—1, ft-1
1 \ я m- = <л/2 (т = пфО),
_}' V 1 - x* ^ я (m = „ = o)
Гл(*)=р(л, -л; i; Ц-^),
Гд (*) = cos (л arccos x) =
■iS'-"-':,;'--j«"
m=0
rw«-uir»W-TM«
770 ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ 21.7-4
Таблица 21.7-1 {продолжение)
Многочлены Лежандра Р (х)
(рис. 21.7-1)
(рис. 21.7-2)
Обобщенная формула Род-
рига
ptx) = -J- ±-
п 2пп\ dxn
(*2-l)"
'.»-*&*т=*$*-«™
Производящая функция
2] Pn(x)sn (|s|<l),
= 1 л = 0
2 P»<*>s (1*1 >»
1—sx
1 — 2sx +
1Г= S r*(*)S" ««К»
/г = 0
0
-/
-2
_
. ? 4
м/
'/• У
/2'
' 1
3/
л ' ^
ЛЛ
Д
1 i >-^
\5 £*■
V
*~х
а)
Ь)
Рис. 21.7-3. а) Многочлены Лагерра, Ь) многочлены Эрмита.
Таблица 27.1-Х {продолжение)
(рис. 21.7-3, а)
Многочлены Эрмита 2) Н (х)
(рис. 21.7-3, Ь)
Дифференциальное
уравнение
d2w dw
dx*
dx
d2w _ dw , . A
—r-r- — 2* -r- + 2nw = 0
dx2 dx
Вес и интервал ортогонали-
зации
Y (X) = e ~
a = 0, b =oo
YW
= s— x*.
oo, b = со
Ортогональность и
нормировка
— а:2
-{
О (m ф п),
2п п\ Yn (m = п)
1) Иногда многочлены —j LR (x) обозначают через Ln (x).
*) Иногда рассматривают многочлены Нел (х) = 2"~'г/2 Hn(x/Y~2), которые удовлетворяют дифференциальному уравнению
d2w dw ,
-j-i — х —г- + nw = 0.
dx2 dx ^
Т а б л и ц а 21.7-1 (продолжение)
4
5
6
7
Явные выражения (см.
9.3-43)
Рекуррентные формулы
Обобщенная формула Род-
рига
Производящая функция
Многочлены Лагерра Ln (x)
(рис. 21.7-3, а)
Ln (x) = nl F(-n\ 1; х),
Ln (x) = (п\)* V <- \)т ^
/тП^О {т\)Цп-т)1
L/z+l (*} = {2п + l ~ х) Ln {х) ~ n* Ln-l ix)>
dLn + iM \dLnW 1
Ln(x) = e*£n(x»e-*)
s
1 —s oo n
\ 1 / iv\ s (ft ^ r ^* rn\
1 - s ~ 2j я ( ' n! (° ^ A ^ CO)
л = 0
Многочлены Эрмита HR (x)
(рис. 21.7-3, 6)
nl^W = (-l)"(2n)IF(-«;i;^(
= (~l)n (2n+l)!2A:F^-ra, -|; xA ,
[-1
я v ' 2.Л ml (a — 2m)!
m = 0
dH (х)
ип w-<- dV2 4 (,-*•>
oo
n = 0
774
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.7-5.
Таблица 21.7-2
Первые ортогональные многочлены (см. также табл. 20.6-1)
(Po(x) = L0(x) = Ho(x) = l)
(а) Многочлены Лежандра Рп (х)
Pi (х)=х х7 = Ш <16Р' + 88Р» + 182Р» + 143Р'>
Р2 (х) = -i <3*» - 1) x9==W\ (16Pe + 72Р* + 110Р2 + ЗЗРо)
^з (х) = у (5** - Здс) *» = 1 <8Р5 + 28Р3 + 27Pt)
^4 (*) « j <35*4 - 30*» + 3) ** = 1 <8Р4 + 20Р2 4- 7Р0)
J>e <*) = -g- (63*» - 70*» + 15*) ** » -g- (2P3 + 3Pi)
P# (*) = 1 (231** - 315** H- 105*2 - 5) *2 = -i- <2P, + P0)
P7(*)= 1(429*'-693*» +315*»-35*) * = P4
lb
(b) Многочлены Чебышева см. в табл. 20.6-1.
(c) Многочлены Лагерра Ln (*)
It <*) = -*+ 1
I8 (jc) = *2 - 4* -f 2
£3 (дг) == - x9 4- 9*2 - 18* 4- 6
I4 (*) = ** — 16*» 4- 72*2 _ 96* + 24
I, (*) = - *» + 25** — 200*» 4- 600*2 — 600* 4- 120
U (*) = *• — 36*» 4- 450*4 — 2400*» 4- 5400*2 __ 4320* -f- 720
L7 (*) = - *' 4- 49** - 882*» 4. 7350** __ 29400*» 4. 52920*2 — 35280* 4. 5040
(d) Многочлены Эрмита Нп (*)
Ht (*) = 2*
H2 (*) = 4*2 — 2
Я3 (лг) = 8*» — 12*
//< (*) = 16** — 48*2 4- 12
Нь (*) = 32*» — 160*» 4- 120*
Н, (*) = 64** — 480** 4- 720*2 — 120
Н1 (*) = 128*' — 1344*» 4- 3360*» — 1680*
21.7-5. Обобщенные многочлены и присоединенные функции Лагерра (см.
также пп. 9.3-10 и 10.4-6).
(а) Обобщенные многочлены Лагерра степени л—/г и порядка k
I* (*)=£* Ln (*) = (- 1)* п\ Q F (k-n; k+ 1; x) (21.7-6)
(л=1, 2, ...; k = 0t 1, 2 n),
где F(k — n\ k + l; л:) —вырожденная гипергеометрическая функция,
удовлетворяют дифференциальному уравнению
*S+(*+l-*)^ + («-A)a< = 0 (21.7-7)
21.7-в.
21.7. ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ
775
для целых значений я=1, 2, ...; 6 = 0, 1, 2, ..., п. Уравнение (7)
приводится к дифференциальному уравнению для многочленов Лагерра (табл. 21.7-1)
при & = 0. Производящая функция для обобщенных многочленов Лагерра
SX
Условия ортогональности и нормировки
со
\ x*e-*L* (х) Lkm (x) dx=J^LF6a,m. (21.7-9)
О
* (b) Обобщенные многочлены Лагерра L^ (x) обычно определяются с
помощью обобщенной формулы Родрига
L^ (х) = e*jr* -^ (е-^дг^+а).
Если a = k — целое число, то Lrt*> (л:) = JzJ2_ £*+^ (*), где
L*,(a:)—многочлены, определенные формулой (6). (Часто L^ (x) называют просто
многочленами Лагерра и обозначают /,"(*).)
Многочлены L^ (x) удовлетворяют дифференциальному уравнению
d*w , , , « v dw . л
имеют явное выражение
^«--E^t:)'
m=0
s
и производящую функцию ^j-.
При а>—1 многочлены /,^а) (лг) ортогональны на интервале (0, оо) с ве-
оо
сом y М =е~хха; они нормированы: J г""*^ [l{,0) (a:)]2 dx = n\ Г (л -f- a+1). х-
о
(с) Функции ф . (х) = лЛ~ */2^„7++/ (*) (« = 1. 2. ••• *. / = О, Ь 2, ...» я — 1),
которые часто называются присоединенными функциями Лагерра, удовлетворяют
дифференциальному уравнению
*^+2^ + [n-T-MfiL]a'-0('* = 1'2--":/=0'1'2'-"'m-,)(21-7-10)
и условию
о
(см. также п. 10.4-6).
- х*/2
21.7-6. Функции Эрмита. Функции ф (*) = е Яя (лг) (л =0* Ь 2* ...)# обычно
называемые функциями Эрмита, удовлетворяют дифференциальному уравнению
и условию
^_ + (2л+1-*2)ш=0 (л = 0. 1,2,...) (21.7-12)
00
J % <*> Фт (*) dx = 2ял1 /я о . (21.7-13)
— 00
776
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.7-7.
21.7-7. Некоторые интегральные формулы.
п
р (cos 6) = — \* (cos б -J- i sin б cos t)n dt (n = 0, 1, 2, ...) (21.7-14)
0
{интеграл Лапласа);
Pn <*» - ТИТ Ф 2Ut~^n+1 " (" = "' '* 2' •") <21-7"'5)
(интеграл Шлефли),
контур интегрирования в формуле (15) окружает точку z = х:
г—— °°
Hnix)-y*±\ (xY2+ii)»e
/*
2 dt (л=0, 1, 2, ...);
(21.7-16)
(/г!)з
$А-[<>>]'^ = <^
W
S^-^wr—T^ir <•-*+'>.
о
со
\ (21.7-17)
^ д^+V* [l* (а:)]2 tf* = (/|(1')^)| (6«2 - бп/fe + Л» + 6/1 - ЗА + 2)
0
(п= 1, 2, ... ; А = 0, 1, 2 п - 1);
оо
J xe-*2 Hn(x)Hm(x)dx = 2n~1n\ Уя6п,т-1 + 2П(п + 1)1 /л 6п.т+1- (21.7-18)
— 00
21.7-8. Многочлены Якоби и Гегенбауэра.
(а) Многочлены Якоби (гипергеометрические многочлены) есть специальный случая
гипергеометрических функций
Ч>„ (х) = F (— п, а + п\ у; х) = -
л:1—Y (1 - д:)У-а
[хУ+п-1 {{_х)а-у+П] (21.7-19)
Y(Y + D ... (Y+4-D dxn
(п. 9.3-9); они удовлетворяют условиям ортогональности *)
1
J ХУ 1 (1 _ х)* У у>п {х) ф^ {х) dx =
О
Г(у)Г(а-у+П (а- у + 1)(а-у-1-2) ... (а - у-j-/i) nl
Г (а)
(Ь) Функции
а(а+1).. (а + п - 1) V (Y+ О ... (Y + л — 1) a + 2/i л»ю
(Rey>0; Re (a - у) > — D. (21.7-20)
■ Z5, (л -J- 2a, — n; a -f-
1 1 -*\
-a m = Г <" + 2a>
'и1 ' Г (л + 1)Г(2аГ V" ' ~~* '" " ' 2 ' 2
(21.7-21)
называются многочленами Гегенбауэра (ультрасферическими). Они представляют
обобщение многочленов Лежандра (табл. 21.7-1), к которым и приводятся при а — 1/2.
Многочлены Гегенбауэра удовлетворяют дифференциальному уравнению
d2w dw
(х2 - 1) -j^ + (2a + 1) x -d- - n (n + 2a) w =0
(21.7-22)
*) Многочлены, определенные формулой (21.7-19), ортогональны на интервале [0, 1].
Чаще рассматриваются многочлены Якоби, ортогональные на интервале ].— 1, 1J; одни
сводятся к другим заменой переменной.
21.8-1.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
777
и условиям ортогональности
1
\ (1 - ,.)<»-'/' С« (х) С° (х) dx = л Г (2а + я)
Многочлены Гегенбауэра могут быть получены как коэффициенты разложения в
степенной ряд производящей функции
со
(, -2sx + s*)~a= Jjcjjws". (21.7-24)
м = 0
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ, ПРИСОЕДИНЕННЫЕ ФУНКЦИИ
ЛЕЖАНДРА И СФЕРИЧЕСКИЕ ГАРМОНИКИ
21.8-1. Функции Бесселя и другие цилиндрические функции.
(а) Цилиндрическая функция (круговая цилиндрическая функция) порядка т
есть решение w = Zm(z) линейного дифференциального уравнения
^y+j-^ + П—^-)ш = 0 (дифференциальное уравнение Бесселя), (21.8-1)
где т — действительное число; цилиндрические функции Zm(z) удовлетворяют
рекуррентным соотношениям
Zm+i(2)=?fLZm(2)-Zm_1(2) =
(21.8-2)
при m = 0 получим Z1(z) — —Z'0(z). Функции ekze-im^Zm(K^) суть решения
уравнения Лапласа в цилиндрических координатах р, ф, z (цилиндрические
гармоники, п. 10.4-3, Ь). Цилиндрические функции нецелого порядка
многозначны (п. 9.3-5, Ь); их главная ветвь определяется условием |argz|<ji
(разрез от 2 = 0 до 2 = —со; п. 7.4-2).
(Ь) Наиболее часто встречаются следующие цилиндрические функции
порядка т\
■ м-ЙГ2
2/ ^J k\T(m + k+U
k=0
Й
;
(| arg г | < я)
Nm(z) = -
(функции Бесселя первого рода)\
[Jm(z)cosmn — J_m(z)] (тфО, ±1, ±2, ...),
(21.8-3)
NM (г) = (-1Г #_m (*) = | /*, (г) (lnf + С)-
оо . I k m-f-r \
я\2У Zj Л!(т + Дг)! \2 / Zj / "**" Zj / J
* = 0 \/=l /=1 /
m-\~k
— ±(±Ym V ^LZ-iZlilL f £\2*
(m = 0, 1, 2, ...; | arg 2 | < я)
(функции Бесселя второго рода или функции Неймана);
Hm(z) = Jm(z) + i NM(z), H%(z) = Jm(z)-i Nm(z)
(функции Ганкеля первого и второго рода).
(21.8-4)
(21.8-5)
778
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.8-1.
В формуле (4) последнюю сумму следует считать равной нулю, если т = 0;
С—постоянная Эйлера —Маскерони (21.4-6). Важно отметить, что каждая
функция Неймана имеет особенность в начале координат1).
На рис. 21.8-1 показаны графики функций Бесселя и Неймана (т = 0, 1)
для z = x >0.
0,8
0,6
0,4
0,2
0
0,2
0,4
■0,6
0,8
~ 1 Л
/ /\
' / V
L-JLJj
0 1 2
/ 1
г!
1 /»,
j /
V ^
\ \А6
/ 8/\ 40\ /12 / 14/ "
Г / VXX-/
Рис. 21.8-1. Функции Бесселя и Неймана.
(с) Аналитическое продолжение. Значения цилиндрических
функций для | arg 21 > я получаются из формул
Jm(einnz) = eim™Jm(z),
Nm (einnz)=e-imnn Nm (z) + 2i Jm (z) sin mnn ctg тк
(я = 0, 1, 2, ...),
]
(21.8-6)
где sin mnn ctg /лл = (— \)mn n для m = ± «;
Д# (el*z) =-е-^Н^' (г) =- Н<?т (г),
^(г)=-Я'1'т(г), \
Цилиндрические функции целого порядка суть однозначные целые функции
(п. 7.6-5).
(d) Каждая цилиндрическая функция порядка т может быть представлена
как линейная комбинация функций Jm (z) и Nm (г) или как линейная
комбинация W» (z) и Я«' (г):
Zm(z)=aJm(*)+bNm(z)=aH^(z) + fiH%(z)
(21.8-8)
(фундаментальная система, п. 9.3-2). Jm (г) и J_m(z) образуют
фундаментальную систему, если т не равно целому числу (тфО% ±1, ±2, ...), так
как при т целых
J.m(z)=(-irJm(z).
1) Функции N' (г) обозначаются также через Y (г); иногда вместо функций
Неймана берут аналогичные им функции Вебера [21.3].
21.8-2.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
779
Вронскианы (п. 9.3-2) указанных систем равны
W{Jm(z), Nm(z)}=-^, W{W»{z)% tf,->(2)}=-l|Lf
Первые два вронскиана не зависят от т. Отметим, что
Jm <*) = у [И% (г) + Н% (г)], Nm (г) = 1- [Я£ (г) - Н% (г)], (21.8-9)
'-« (*) = у [*'тя Я# (г)+е-'«я ЯД' (г)]. (21.8-10)
(е) Цилиндрические функции, порядок которых равен половине нечетного
целого числа (т=± 1/2, ± 3/2, ...)» выражаются через элементарные функции
(см. также п. 21.8-8):
21.8-2. Интегральные формулы (см. п. 8.6-4).
(а) Интегральные представления для J0 (г), Ух(г), 72(2)» •••
л
J m(z)=-^\ cos (mt-zsmt)dt (m = 0, 1, 2, ...) (21.8-16)
о
{интегральная формула Бесселя);
(т = 0, 1, 2, ...); (21.8-17)
Jm (z) = {-=£-\eizcost cos mtdt (m=0, 1, 2, ...); (21.8-18)
о
^т(2)=2„т(4)т^Г'»-^ 4<<И (| argг | <л; т=0, 1, 2, ...) (21.8-19)
(интеграл Сонина — Шлефли),
где контур интегрирования начинается в точке 7 = 00, идет по отрицательной
Jim
J*m+l
(г) =
(г) =
2
" Я
2
"я~
/
я/2
0
л/2
0
„. л
(а яп 0
(z sin /)
]
cos 2mt dt,
i
sin(2m + l)/<«
780
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.8-3.
части действительной оси, окружает в положительном направлении начало
координат и возвращается по отрицательной части действительной оси в
бесконечность.
(Ь) Формулы Зоммерфельда и Пуассона. Комплексный
интеграл (рис. 21.8-2)
Zm (*) =— ) & <2 cos' + mt>> di (21.8-20)
с
(интеграл Зоммерфельда)
равен Н[т} (г) для контура С\, Н{™ (г) для
контура С2 и 2Jm(z) для контура С3. Эти
контуры могут быть деформированы при
условии, что начало и конец каждого из
них стремятся к точке t=co в указанных
заштрихованных областях; / = 0 и t = K
могут быть использованы как седловые точки
(точки перевала) для Сг и С2 при
вычислении Zm (z) для больших значений г (см.
также п. 21.8-9).
Отметим еще формулу
я/2
Рис. 21.8-2. Контуры
интегрирования для интегралов
Зоммерфельда; t = у Н- *Л.
Jm(*)-
Yn
2 (2/2) *— [ cos (z cos t) sin2m * d/
Г(ш-Н/2) 0J
(m>-Vi) (21.8-21)
(интегральная формула Пуассона),
(с) Некоторые интегральные формулы, содержащие
цилиндрические функции (см. также п. 21.8-4, с).
х
I Jm {ах) Jm ®х) xdx==
- oT^pi PV-i <&*> 'm «**> " «'rn-l (a*> ym <&*>] «*2 " &2 * °>;
J Km <«*>]• ***~T V'rn «**>]2 + -y (*2 -5?) Km <a*>]2 («>-!>
(интегралы Ломмеля); )
\ x~m+njm {ax) dx = 2/l"mam~/l"1 /
0
(21.8-22)
■(-"-г4)
(—1<я<2»1+ 1).
(21.8-23)
21.8-3. Нули цилиндрических функций.
(a) Все нули цилиндрических функций простые, за исключением, быть
может, z = 0. Последовательные положительные или отрицательные
действительные нули двух линейно независимых действительных цилиндрических
функций порядка т перемежаются; z — О есть единственный возможный общий
нуль.
(b) (См. также рис. 21.8-3). Функция Jm(z) имеет бесконечное число
действительных нулей; для т">—1 все ее нули действительны. Для т=0, г/2,
1, з/2, 2, ... и п=1, 2, ..., Jm (z) и Jm+n(z) не имеют общих нулей.
Для т = 1, 2, ... последовательные положительные или отрицательные
действительные нули Jm (z) разделяются единственными действительными
нулями Jm+\(z) и единственными действительными нулями J'm{z).
21.8-4.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
781
21.8-4. Функции Бесселя целого порядка.
(а) Производящая функция. Функции Бесселя
неотрицательного целого порядка т = 0, 1, 2, ... — все однозначные целые функции от г.
Они могут быть получены как коэффициенты разложения в ряд Лорана
(п. 7.5-3) производящей функции (см. также п. 8.7-2)
(-1
= Л(2)+2 lsm + (-syn]Jm(z),
или как коэффициенты рядов Фурье
оо
cos (z sin t) = J0 (z) + 2 2 J2k (2) cos 2kt,
fc=l
i (z sin 0 = 2 j>] J2k_t (z) sin (2k — 1) t\
(21.8-24)
(21.8-25 a)
k=\
e± iz sin /в Ц jm(2)e±imtss
ЛИ =—00
со
= «/о (2) + 2 [«^ (2) cos 2/г/ ± tV2/j_! (z) sin (2fc - 1) t].
Отметим еще формулы
со со
ft=i *=1
со
z —z 2j k\ J2k+n(z) (л=1, 2, ...).
£ = 0
(21.8-256)
(21.8-26)
(21.8-27)
(b) Графики функций Бесселя. Для действительного z=x
функции J0(z), Jx(z), J2(z),... все действительны; рис. 21.8-3 иллюстрирует их
Jo,®
W \
0,8
0,6
0,4
П2\
О
-0,2
-0,4
л
\
....
-/77-0
\ У
.,
/m=f т=2
^/77=3
О
10
12
14
2 4 6 8
Рис. 21.8-3. Графики функций Бесселя J0 (x), Jt (х), J2 (x), J9 (x) для действительного
аргумента. Заметим, что Jm(—x) = (~-\)mJm(x).
нули, максимумы и минимумы и их асимшотческое поведение при jc-^co
(см. также пп. 21.8-3 и 21.8-9).
782
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.8-5.
(с) Условия ортогональности (см. также пи. 15.2-3 и 21.8-2, с).
Если |Х/ и fifc—два нуля функции Jm (г) (необходимо действительные), то
имеют место условия ортогональности
{О, если {фк
? V'm О*/)]1 —Г Г/яи-1 Ш\2> ^ЛИ i = k. (2l*8'28)
#(d) Ряды Фурье —Бесселя. При достаточно общих условиях
функцию / (х) можно разложить в ряд
00
f (*) = 2 aft ^m (№) (P*d Фурье— Бесселя), (21.8-29)
k=\
где \ilt fi2» ...—положительные нули функции Jm(z), расположенные в
порядке их возрастания, а коэффициенты ak равны
1
ak =
^\tf(t)Jm(»kt)dt.
lJm+i v «/i 0
Разложение (29) имеет место для любого действительного т > — V*. если f (x)
кусочно-непрерывна и имеет ограниченную вариацию в (О, 1), и интеграл J Vx \ f (x) \ dx
О
существует. В точках разрыва функции f (x) сумма ряда (29) принимает значение
Vttf <*-0) + Н* + 0)].*
21.8-5. Решение дифференциальных уравнений при помощи функций
Бесселя и связанных с ними функций. Линейное дифференциальное уравнение
^ + Ц^^ + [(^-1)»+а-^^]а^0 (21.8-30)
имеет решение вида
w = zaZm(bzc). (21.8-31)
Многие специальные случаи уравнения (30) представляют значительный
интерес (пп.. 21.8-6 — 21.8-8; см. [9.4]).
21.8-6. Модифицированные функции Бесселя и Ганкеля.
Модифицированные цилиндрические функции порядка т:
I (z) = i~m Jm (iz) (модифицированные функции Бесселя),
Кт (г) = у im+1 Н1£ (iz) (модифицированные функции Ганкеля) * к ' ' '
\ (21.8
определяются с помощью формул (3) —(5); определения могут быть расширены
с помощью формул (6) и (7). Функции (32) суть линейно независимые
решения дифференциального уравнения
(модифицированное дифференциальное уравнение Бесселя)
(см. также п. 10.4-3, Ь) и удовлетворяют рекуррентным формулам
/щ+1 М - /щ-1 W -2-T^m(2)^2^Im (Z) - 1т_х (2),
W М = /Cm-i « +2J~ Km W — 2 £ Кт (z)-Km^ (z)\
(21.8-34)
21.8-7.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
783
/m (г) и Кт (г)—действительные монотонные функции для т = 0, ±1, ±2, ...
и действительных z (см. рис. 21.8-4}.
21.8-7. Функции bermz, beim z, herm z, heim z, kermz, keim z. Функции
berm z, beim г, herm z, heim z, kerm z, keim z определяются соотношениями
•/m (i±3/2z) = berm z ± * beim z,
tfJA'(ji/i*) = herlflz + /
t i beim z, 1
-ihei^z, j
*T mK« (t- V*z) = кегш z ± / keim z.
(21.8-35)
(21.8-36)
Все эти функции действительны для действительных значений z. На рис. 21.8-5
показаны их графики. Индекс т не пишется,
если т = 0, например, ber0z=berz.
/
#
^
#•
#
V
0,4
Ко
1 \Ki I I
А//,
-1 i / /
i / /
1 i / /
Л » / /
1 1 / /
- \ \ / /
\\ / *
- \ \/ /
^Jt^ /
\ \ /
- V
- As
/ n^.
V—- i i ^«fc. т
о
3 х
Рис. 21.8-4. Модифицированные Рис. 21.8-5. Графики функций ber x, bei x, ker*
функции Бесселя и Ганкеля. и kei jc.
Заметим, что ker_ z — — — hei^ z, keJ^ z = — her^ 2, ber 2,- bei 2, her 2 и he! zt
«■ак же как J0(i—bl* z) и Я^1} (ia/« г), удовлетворяют дифференциальному уравнению
■£-+*■£--*-•■ <21-8-37>
Имеют место разложения
224» ""*" 22486888 "*"
(2!)* ^ (4!)
DC1 2 \ 2 У (3!)* + • • • " а> 2*4*6* £ " '
)
(21.8-38)
Во многих приложениях удобно вводить | Jm (/a/e г) | f | /Cm (/ /* 2) |,- arg 3m \i h г)
и arg [Г"т /Cm(i8/* г)] как специальные функции вместо или одновременно с berm 2в
beim г, ker z и kei^, г. Все эти функции действительны для действительных значений г.
784
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.8-8.
21.8-8. Сферические функции Бесселя. Сферические функции Бесселя
первого, второго, третьего и четвертого рода
(21.8-39)
Ц2
О
-о/
\/-0
■I W-'
0,3
У Л \^УХх*> 'i
it/. 1 ЛлА/х.л уГ, > -#г
\I\NL/ ^" -BZ\
-4У|
\fj]!№s
6)
Рис. 21.8-6. Сферические функции Бесселя.
удовлетворяют дифференциальному уравнению
<te* ^ г dz [1 z* J ш и
(см. также п. 10.4-4, с) и рекуррентным формулам
(21.8-40)
«7+1 ^z)^lLrL wi W-»/-i W = — *; ^ I2"'»/ WJ-
(21.8-40)
21.«-10.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
785
Для целых значений / сферические функции Бесселя суть элементарные
трансцендентные функции (см, также п. 21.8-1):
/.<*>=
sin г
Cw-
.и
А'„2'(г)='е
-и
(21.8-42)
1 sin г
Л/(*) —(— 1)/+1/-у-1 W- (21.8-43)
Графики функций //(z) и nj(z) для г=#>0 показаны на рис. 21.8-6
а) и б); на рис. с) показана зависимость jj(x) и лу (х) от индекса / при х = 10.
21.8-9. Асимптотические разложения цилиндрических функций и
сферических функций Бесселя для больших значений | z | (см. также пп. 4.4-3, 4.8-6).
При г—*оо
-Bm(2)sin(z-^-£)],
iV« W ~ 1/^ [**(*) sin (г - ^-- ±) +
+ Bffl(2)cos(Z-if—£)] J
где Ат (г) и Вт (z) имеют асимптотические разложения
Лт(г)=1-(4т8-,)(4т'-9)^
(i argz| <л), (21.8-44)
Вт(г) =
4т2 — 1
2! <82)2 '
■ (4т2 — 1) (4т2 — 9) (4т» — 25) (4та — 49) __
""*" 4! (82)* ~*~
<<1т2 — 1) (4т2 —9) (4та — 25)
8z
3! (82)3
(21.8-45)
Подставляя разложения (44) и (45) в формулы (5), получим соответствующие
асимптотические разложения для Н^ (г) и Н$ (г). Из разложений (44) и (45)
следует, что для | z | > т при z —► со
J mi?)
.(9 rrm £t\ I
/m + VtW^l/"^sin(z-f) (m=0, 1, 2, ...),
//(2)^4cos(2-i±ln), Яу(г)^1в|п(г-1±1п), 1
л/ (*)^i(—o/+1*te.
ajtw<
f/+le-te.
} (21.8-46)
(21.8-47)
(21.8-48)
21.8-10. Присоединенные функции и многочлены Лежандра.
(а) Присоединенные функции Лежандра степени / и порядка т есть
решения дифференциального уравнения
(!-*)$-& f- + [/(/+i)_T^rJffl,=0, (21.8-49)
786
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.8-10.
где / и т —действительные или комплексные числа; уравнение (49) приводится
к дифференциальному уравнению Лежандра (табл. 21.7-1 и 21.7-3) для т = 0.
Общая теория присоединенных функций Лежандра содержится в [21.3].
Во многих важных приложениях (пп. 10.4-3, с и 21.8-12) / и т —
действительные целые числа, а г = х — действительное число, заключенное между —1 и 1;
2,0
я
-10
Рис. 21.8-7. Присоединенные функции Лежандра Р[1) (х), Р(21} (х), Р{9г) <«*)•
положим х = cos б. При этих условиях уравнению (49) удовлетворяют
присоединенные функции Лежандра первого рода
%2 № ф ffff у? х
/
S
/
-(i-*r*j£-PiM= <'-**>т/2 dJ+m (**-i/ =
dxm 2J j\ dxJ+m
(21,8-50)
«=(— l)' + m/>?*(— x) (— l^x^\)t
/ = 0, 1, 2, ...; m=0, 1, 2, ..., /
(см. также п. 9.3-9), причем P°j (x) = Pj (x) и PJ1 (x) = 0 для m>/. В частности,
Р}(д;) = КГ=Г^=япе, (21.8-51)
Pi (x) = 3* уТ^ЗЗ = 8/2 sin 26, \
P22 (x) = 3 (1 - x2) = 8/2 (1 - cos 26), J
P\ (*) = 8/г (5л:2— 1) VHT=T2==8/8 (sin 6 +5 sin 36), ]
p\ (x) = 15* (1 — x2) = 16/4 cos 6 (cos 6 — cos 36), |
pj (jr)= 15 (l-*2) VT^j?="/4 (3 sin 6-sin 36), j
р>(*)=ьз.5 ... (2/-i)(i-*2)'/2 = b3.5 ... (2y-i)sm'e
(7 = 0, 1, 2f ...), (21.8-54)
(21.8-52)
(21.8-53)
21.8-12.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
787
где cos0=* (см. также п. 21.8-12). Соответствующие графики показаны на
рис. 21.8-7.
(b) Присоединенные функции Лежандра, определенные формулами (50),
удовлетворяют следующим рекуррентным соотношениям (— 1 <дг< 1):
W + 1) хР? (x)-(j-m+\)P?+{(x)-(j+m)P'fl_l (х)=0
(0^т^/-1); (21.8-55)
(x*-\)-^P?(x)-(j--m+\)P^{(x) + (i+\)xPT(x)=0
(О^т^/); (21.8-56)
Р? + 2(х)-2(т+\) у±_ Pf+lW + [/(f+l)-g»(«+l)l^ (x)=0
(0^т^/-2); (21.8-57)
Я7*+ 1 М-р7-1 М = <2'+ !) У^-1*?РТ"! W (0^т ^/-1); (21.8-58)
(/+m)(/ + m+l)Pf_1W-(/-m)(/-m+l)Pf+1W-
= (2/+1)КГ=^Р/т+1(лг) (0^т</—1). (21.8-59)
(c) Асимптотическое поведение. При /-*оо
(0<8<я). (21.8-60)
21.8-11. Интегральные свойства присоединенных функций Лежандра (см. также
П. 21.7-7).
я
р ? {х) = (_ 1) m/2 <i+«>] f (л: + yii—J cos /)' cos m* <tf
/ /I я J
0
(/ = 0, 1, 2, ... ; т = 0, 1, 2, ...,-/) (интегральная формула Гейне); (21.8-61)
J Py {x)Pr (x)dx- 2/+1 (/_т)!б/,г
(/, r = 0, 1, 2, ... ; m = 0, 1. 2, ...); (21.8-62)
rr w w l </+m>! e 1РГ(ДС)]2 * (/+т)!
ЦР, (*>J rfjf-j-^——, ^ ___*, = _ __
о о
(/ = 0,1.2,...; m=l, 2, ...,-/) (21.8-63)
21.8-12. Сферические гармоники. Ортогональность (см. также пп. 10.4-3, с,
14.10-7rb и 15.2-6).
(а) Решения Ф (г, 9, ср) уравнения Лапласа в сферических координатах
(10.4-15) называются сферическими гармониками. Сферические поверхностные
гармоники степени / суть решения дифференциального уравнения с частными
производными
-S-4-ctge 4г+!Шй> %г + 1 (/+1) У-0. (21-8-64)
полученного разделением переменных в уравнении (10.4-15). Если потребовать,
чтобы решения были регулярны при 0^0 ^я, 0^ ср^2я и удовлетворяли
условию Yf (0, ф+2я) = Ку(0| <р)& то мы приходим к проблеме собственных
788
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.8-12.
значений (п. 15.4-5), допускающей решения только при целых значениях /.
Можно не касаться отрицательных значений /, так как — / — 1 и / дают
одинаковые значения /(/ + 1). Действительные собственные функции
V
V
2/+1 U-m)\ рт
</ + «)! */
2Я
(COS 6) COS Шф,
2/ + 1 U-m)\
2я
(/+m)!^r(sin0)sinmcP
(/ = 0, 1, 2,
m = 0, l, 2,
(21.8-65)
называются тессеральными сферическими гармониками степени ; и порядка т\
они периодичны на поверхности сферы и меняют знак вдоль узловых линий
~Щ
120°Щ180У
130°
Рис. 21.8-8. Узлы функций Р% (cos e)sin3<p на развернутой поверхности сферы.
Функция отрицательная в заштрихованной части.
б = const и ф = const (рис. 21.8-8); на самих этих линиях они рачны нулю.
При m = i функции (65) называются секториальными сферическими гармониками
и при т = 0 — зональными сферическими гармониками. Обе функции (65) и белее
часто встречающиеся комплексные функции
l/"2£±i (/Tl,m!)l! Pim' (cos 6) *<«ф
(/ = 0, 1, 2, ...; т = 0, ± 1, ± 2,
/)
(21.8-66)
образуют ортонормированную последовательность собственных функций в смысле
скалярного произведения
2п я
(/, /i) = $ dtp $ / (6, ф) h (8, ф) sin 0 db
о о
(21.8-67)
(п. 15.4-6, Ь). (/, Л) = 0 для каждой пары функций (65) или функций (66),
если \ФК если же f = h, то скалярное произведение равно единице: (/, /)= 1.
Существует 2/+1 линейно независимых сферических поверхностных гармоник
степени /.
(Ь) Каждая дважды дифференцируемая действительная функция
Ф(6, ф)(О^0^л, 0^ф^2л), Ф(6, ф + 2я) = Ф(б, ф),
21.8-13.
21.8. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
789
определенная на поверхности сферы, допускает разложение в абсолютно и
равномерно сходящийся ряд
ф (9. ф) = 2 [ ^ а/о Р/ (cos 6) + 2 pf (cos 0) (a/m cos тф + p/m sin пир)] —
/ = 0 т = 1
т /
= 22 Vfm^lmKcos0)^4>, (21.8-68а)
/=0т=-/
где
2я я
ам=тзг #гёг $ ^С08 тф $ф (0, ф) РГ(cos 0) sin е dd>
о
2я
О
Я
Р/тв ТЗГ UT^T S <*ф Sin тф S Ф (9' ф) РТ (C°S 9) Sin 9 ^
О О
> (21.8-686)
2/ + 1 </-т)!
2я
2я
4я
g-^gj J <*ф в^Ф J Ф (0, ф) Pf (COS 0) Sin 0 dQ,
(/ = 0, 1, 2, ...; m = 0, 1, 2 /).
Разложения вида (68) физически интерпретируются как разложения
потенциалов по мультиполям (пп. 15.6-5, а и с).
21.8-13. Теоремы сложения.
Wfin
s(fl2>9>2)
/Ъ**Я>
Рис. 21.8-9. Геометрическая иллюстрация к теоремам сложения.
(а) Теоремы сложения для цилиндрических функций.
Пусть Рг и Р2 — две точки плоскости с полярными координатами (рх, фх),
(р.,, фг). Согласно рис. 21.8-9, а пусть pi>p2, так что 0^|г|э| <j и
d2 = Pf + Pi ~2p!p2 cos (фх - ф2),
^2/ф = р,-р^(Ф1-Ф1)
(21.8-69)
Р1_Рг^(Ф1-Ф8) ' J
Тогда для каждой цилиндрической функции Zm (z), удовлетвоярющей
790
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.9-1.
уравнению (1), ^
Zm(ad)eim* = J] Zm+k(a9l)Jk(ap2)eik^-^ (21.8-70)
k= — оо
(теорема сложения для цилиндрических функций),
где а —произвольное комплексное число. В частности, если <рг — ф2 = я, то
со
Zm[a(Pi + p2)]= 2 zft(«Pi)^m-ft(ap2). (21.8-71)
£=—оо
(Ь) Теоремы сложения для сферических функций
Бесселя и многочленов Лежандра. Пусть Рх и Р2 ~~~ Две точки
пространства со сферическими координатами (rv 8lf cp!), (r2, 02, ф2). Согласно
рис. 21.8-4, b пусть 61 + 02<я; тогда
d2 = r\ + г1 — 2гггъ cosy,
cos y = cos 0Х cos 02+ sinGx sin 02 cos ($>x
и
/o(«^) = "= 2 (S^+lJ/n^/Ha^P^cosY),
Р1-Ф2) i
(21.8-72)
Kv №) = Ш = Ц <2* + О л*п (a'i) /* (ar2) ^л (cos Y) (ft >r ,)
*=o
(теорема сложения для сферических функций Бесселя
порядка нуль).
Pj (cos у) = Р/ (cos 00 Pj (cos 02) +
/
+2 И 17^^яГ(С08в1)рГ(С08е2)С08Л1(ф1~^
т = 1
(теорема сложения для многочленов Лежандра).
(21.8-73)
(21.8-74)
21.9. СТУПЕНЧАТЫЕ ФУНКЦИИ И СИМВОЛИЧЕСКИЕ ИМПУЛЬСНЫЕ
ФУНКЦИИ
21.9-1. Ступенчатые функции (см. также пп. 4.6-17, с, 18.3-1 и 20.4-6).
(а) Ступенчатой функцией действительной переменной х называется
функция, которая изменяет свои значения только в дискретной последовательности
точек разрыва (необходимо первого рода, п. 4.4-7, Ь). Значения функции
в точках разрыва могут быть как определены, так и не определены. Наиболее
часто применяются ступенчатые функции х)
0 при х <0,
V2 при *=0, (симметричная единичная функция),
1 при х > О
и-{Х) \ 1 при *^0,
п ' (асимметричные единичные функции)
(21.9-1)
1 при *>0
(см. также рис. 21.9-1).
*) Система обозначений различных единичных функций не является общепринятой;
поэтому необходима осторожность лри пользовании разными источниками.
21.9-1.
21.9. СТУПЕНЧАТЫЕ И ИМПУЛЬСНЫЕ ФУНКЦИИ
791
Заметим, что
£/(0-0)=0, [/(0+0) = 1, £/(<?*) = М (21.9-2)
U[(x-a)(x — b)]=U[x — max (a, b)] + U [min (а, 6)— *]. (21.9-3)
Каждая ступенчатая функция может быть представлена (за исключением,
возможно, ее значений в точках разрыва *=#*) как сумма вида
^akU(x-xk)t 2 я* 6L (*-**) или %akU+(x-xk).
k k k
(Примеры: sgn x = 2U (х) — 1; функции скачков в п. 20.4-5).
кё'М
j=fe
h + 0
'h .XT h 7с
М
\КШ
т
h+0
A h
U
4
Р
Рис. 21.9-1. Единичные ступенчатые функции С/ (дг) и U+ (х) и аппроксимации
импульсных функций б (*), 6+ (ж), б' (*) и б+ (х).
(Ь) Аппроксимация ступенчатых функций
непрерывными функциями
£/(*) = lim fi+iarctgowl. (21.9-4)
(21.9-5)
{/(*) = lim -L[erf(a*) + 1],
a-*oo *
£/(*) = lim 2^"ал?,
a-» oo
ax
а-*со " J
(21.9-6)
(21.9-7)
792
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.9-2.
(с) Представления интегралом Ф у р ье (см. также п. 4.11-6).
1 Т еш
Комплексный контурный интеграл ^-т \ —— dot соответственно равен U (t)
— со
или — U (— t) в зависимости от того, огибает ли контур интегрирования
начало координат против часовой стрелки (т. е. по полуокружности,
расположенной в нижней полуплоскости) или по часовой стрелке (по
полуокружности в верхней полуплоскости). Главное значение интеграла по Коши
(п. 4.6-2, Ь) равно U (t) — х/2. Отделяя действительную и мнимую части,
получим
оо
и®=к S ^^ + 7- (21-9-8)
—ОО
Отметим также формулу
оо
(/(1-/)=1 $ sin (o^cos Ш d(u ((^0) (2199)
—00
21.9-2. Символическая дельта-функция Дирака*).
(а) Симметричная единичная импульсная функция или функция Дирака
6 (х) действительной переменной х определяется условием
$/(i)6(E-x)<^=
при Х<а или Х>Ь>\
(а<Ь), (21.9-10а)
0
Vt/W
f(X)
при Х<а или Х>6,
при Х = а или Х = Ь,
при а< X < 6
где / (х) — произвольная функция, непрерывная в точке х = Х.
Более общее определение функции о (х):
Ь
'О при Х<а или X>bt
\i/tf(X + 0) при Х = а,
1/2f(X-0) при Х = Ь,
ki/2[/(X_0)+/(X+0)] при а<Х<Ь
\(а<Ь), (21.9-106)
где /(^ — произвольная функция ограниченной вариации в окрестности точки
х — Х. 6(х) не является функцией в обычном смысле; из определения (10)
следуют несовместимые условия
00
6(*)=0 (хфО), $ б(|)^=1; (21.9-10с)
— 00
6(х) есть символическая (обобщенная) функция, позволяющая формально
представить функциональное преобразование / (£) — / (х) как интегральнее
преобразование (п. 15.3-1, а). Формальное применение 6 (х) приводит к удобным
обозначениям, подсказывающим обобщения многих математических соотношений
(см. также пп. 8.5-1, а, 15.5-1 и 18.3-1). Хотя функций, обладающих в точ-
*) В настоящее время широкое развитие получила теория обобщенных функций,
играющая важную роль при изучении дифференциальных уравнений математической
физики, б-функция Дирака может рассматриваться/как один из примеров обобщенных
функций. По этому поводу см., например, [13.6J.
21.9-3.
21.9. СТУПЕНЧАТЫЕ И ИМПУЛЬСНЫЕ ФУНКЦИИ
793
ности свойствами (10), не существует, возможно в некотором смысле
рассматривать 6 (*) как пределы обычных функций (п. 21.9-4).
Математические предложения, в которых применяются импульсные
функции, следует рассматривать как эвристические и нуждающиеся в строгих
обоснованиях.
Можно избежать применения импульсных функций, вводя интегралы
Стилтьеса (п. 4.6-17); тогда
ь ь
\f(l)b{l-X)<% = \f{l)dV&-X).
а а
При этом возможно ввести обобщения понятий «функции» и «дифференциала»
(теория распределений Лорана Шварца) *).
(Ь) Формальные соотношения, содержащие 6 (*).
6(ал:) = 1б(*)(а>0), 6 (— *) = 6 (х), (21.9-11)
f(x)6(x-a) = ±[f(a-0)+f(a + 0)]d(x-a)t * 6 (*)=(), (21.9-12)
&(х2-а*) = ±-а[6(х-а) + д(х + а)] (а > 0), (21.9-13)
00
$ b(a-x)b(x-b)dx = b(a-b). (21.9-14)
— оо
21.9-3. Производные ступенчатых и импульсных функций (см. также
п. 8.5-1). Формулы (10) приводят к соотношению (а>0)
00
%[b(t-a)]=\ 6 (t-a) в'** dt = e~as = s X [U (t -a)],
о
откуда следует символическое равенство
6W==^£/W (21.9-15)
(это равенство формально можно получить также из формулы (19) п. 21.9-4, Ь).
Производные 6' (х), 6" (х),... импульсной функции 6 (х) определяются условиями
b
Sf(l)^(l-X)d^^
а
[О при Х<а или Х>Ь/
V2(-l)r/(r,(X+0) при х = а, \tn^h\
|V2(-l)r/(r)(^-0) при х = Ь, (Ка<.о),
11/2(— 1)г[/(г) (X —0)+/(Г)(Х+0)] при а<Х<Ь
(21.9-16)
где /(^ — произвольная функция такая, что односторонние пределы /(Г) (X — 0)
и /(Г) (Х+0) существуют. Функции 8(Г)(£ — X) есть ядра линейных
интегральных преобразований (п. 15.2-1), представляющих повторные дифференцирования.
Отметим символическое соотношение
б "-1 (а:) = (— IK r! AS£L. (г = 0, 1, 2, ...), (21.9-17)
*) См. сноску на стр. 792.
794
ГЛ. 21. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
21.9-4.
21.9-4. Аппроксимация импульсных функций (см. также рис. 21.9-1).
(a) Аппроксимация 6 (*) непрерывно
дифференцируемыми функциями. Возможно аппроксимировать б (х) непрерывно
дифференцируемыми функциями
а<*'а>=я<а£ + в при а-*°°* (21.9-18а)
6(*, а) = ~е~а*х* при а —оо, (21.9-186)
у я
Ь(х, а) = ^-^~ при а —оо (21.9-18с)
в том смысле, что lim b(x, а)=0 (х^£0) и
а-*оо
00
lim \ f®b(x-t, а)^==у[/(*-0)+/(* + 0)]
а-°°-Ло
при условии, что f(x —0) и /(*+0) существуют; заметим еще, что
lim Т 6 ft, a)dl = \.
а-оо^
Интегрирование аппроксимирующих функций (18) приводит к соответствующим
аппроксимациям ступенчатых функций (формулы (4) и (5)). <5? [6 (* — а, а)] {а > 0)
сходится к е [6 (х — а)] при а-*оо для каждой функции (18) (см. раздел 8.5).
(b) Аппроксимация б(дг) разрывными функциями, б (л:)
часто аппроксимируется центральной конечной разностью (п. 20.4-3)
6(*. h)=V« + h)-mx-h) при л_0 (21.9-19)
Отметим также, что
00
Нт 1 С Ш si™<*-£> rfg = |[/(X-0)+/(X+0)l (-oo<X<oo)
© -* 00 " ^J1 Л * *
{интегральная формула Дирихле) (21.9-20)
и
(—я<Х<д), (21.9-21)
если f(x)— функция ограниченной вариации в окрестности точки х = Х
(см. также п. 4.11-6).
(c) А п п р о к с и м а ц и я ф у н к ц и й б' (*), 8" (*), ..., Ь(п (х).
Последовательное дифференцирование формулы (18а) приводит к аппроксимирующим
функциям
6' <*, «)=»-£ (а^+и. при a - со, (21.9-22)
t_(-irriSIn[(r+1)aretg|-1
*"(,, Р)=П у ^ + |И)(г + 1)/2 ' ПРИ Р-00 ('=0' Ь2. ...)• (21.9-23)
Заметим также, что
Ь>Ь ц„и « + »-* W + UI*-* при А_о. (21.9-24)
21.9-7. 21.9. СТУПЕНЧАТЫЕ И ИМПУЛЬСНЫЕ ФУНКЦИИ 795
21.9-5. Представления интегралом Фурье. Отметим формальные соотношения
оо
6(х-Х)=-1- I e-ie>xeie>xd<*, (21.9-25)
— 00
ОО
1
6"> (х-Х) =~ \ (ш)ге- ^хеШх da, (21.9-26)
— оо
00
[6 (х — X) + б (х + X)] = ^ $ cos coX cos ш did. (21.9-27)
21.9-6. Асимметричные импульсные функции (см. также пп. 8.5-1 и 9.4-3).
(а) Асимметричные импульсные функции б+ (х), Ъ+(х) 6^г) (л:)
определяются соотношениями
(21.9-28)
г х *ч с ~ „ч ~ С 0 при Х<а или Х^М
до/<|)б+(1-*)<и/(х+о) прри ^х<ь }(.<«.
(21.1
До Ю + 6 \(-1)'/">(Х+0) при а^Х<* /
(а<6; г=1, 2, ...). (21.9-29)
Можно записать
6+ (х) = 26 (*) U (х) = -A U+ (х). (21.9-30)
Чтобы получить аппроксимирующие функции для б+(лг), нужно подставить
аппроксимирующие функции п. 21.9-4 в соотношения (30), например,
6+0c.k)-Uix)-%tx-h) при А^О. (21.9-31)
6;(x,/,)=4t;W-2t;%ft/2) + t;^-ft» при /^0. ,21.9-32,
(Ь) Можно ввести 6+(—х) — 6-(х) как вторую асимметричную импульсную
функцию, соответствующую «производной» асимметричной ступенчатой функции U- (х)
(п. 21.9-1).
21.9-7. Многомерные* дельта-функции (см. также п. 15.5-1). В я-мерном пространстве
точек (к1, jc2, ... , хп) с элементом объема
dV = dV (л:1, Л ... , хп) = V\g (Д А ... хп) \ dx1 dx2 . . . dxn
(п. 16.10-10) n-мерная дельта-функция б (я1, fc1; *2, £2; .. . ; *л, £п) должна удовлетворять
условию
$ / (I1. ?, . .. , 1П) б (X1, I1; X2, ?• ... ; Хп, ln) dV fe1. £2. . . . .- £Л) -
= /(^. А ... , хп) (21.9-33)
для каждой точки (х1, X*, .. . ,- Хп) в Vt где f (xv x2 *Л) непрерывна. Заметим*
что определение б (х1, £*; х2, £2; . . . ; *Л, £Л) зависит от выбора системы координат и
теряет смысл, если dV = 0. В частности, для прямоугольной декартовой системы
координат *« |/« г имеем dV = ate d# ate и
6 (*, 6; 1/. Л? ^ t) = б (ж - |) б 0/ - х\) б (г - О (21.9-34)
ЛИТЕРАТУРА
К главе 1
1.1. К у р о ш А. Г., Курс высшей алгебры, «Наука», 1971.
1.2. Мишина А. П. и П р о с к у р я к о в И. В., Высшая алгебра, СМБ, «Наука»,
1965.
1.3. П о г о р е л о в А. В., Элементарная геометрия, «Наука», 1972.
1.4. С т е п а н о в Н. Н., Сферическая тригонометрия, ОНТИ, 1936.
1.5. К е м е н и Д., Введение в конечную математику, «Мир», 1965.
1.6. К о к с т е р X., Введение в геометрию, «Наука», 1966.
1.7. Л а н д а у Э., Основания анализа, ИЛ, 1947.
1.8. Феферман С, Числовые системы. Основания алгебры и анализа, «Наука»,
1971.
1.9. Строй к Д., Краткий очерк истории математики, «Наука», 1964.
К главам 2 и 3
2.1. А л е к с а н д р о в П. С, Лекции по аналитической геометрии, дополненные
необходимыми сведениями из алгебры, «Наука», 1968.
2.2. Ильин В. А. и П о з н я к Э. Г., Аналитическая геометрия, «Наука», 1971.
2.3. П о г о р е л о в А. В., Аналитическая геометрия, «Наука», 1968.
2.4. Ефимов Н. В., Квадратичные формы и матрицы, «Наука», 1972.
2.5. С а в е л о в А. А., Плоские кривые. Систематика, свойства, применения
(справочное руководство), Физматгиз, 1960. См. также [1.6].
К главе 4
4.1. Смирнов В. И., Курс высшей математики, в пяти томах, «Наука», 1967.
4.2. Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления,
тт. I —III, «Наука», 1969.
4.3. Колмогоров А. Н. и Фомин С. В., Элементы теории функций и
функционального анализа, «Наука», 1972.
4.4. Кудрявцев Л. Д., Математический анализ, тт. 1, 2, «Высшая школа», 1970,
1971.
4.5. Никольский С. М., Курс математического анализа, тт. 1, 2, «Наука», 1973.
4.6. Градштейн И. С. и Рыжик И. М., Таблицы интегралов, сумм, рядов
и произведений, «Наука», 1971.
4.7. Ильин В. А. и П о з н я к Э. Г., Основы математического анализа, ч. 1, 2,
«Наука», 1971.
4.8. Б у д а к Б. М. и Фомин С. В., Кратные интегралы и ряды, «Наука», 1967.
4.9. Натансон И. П., Теория функций вещественной переменной, Физматгиз, 1957.
4.10. Дьедонне Ж-, Основы современного анализа, «Мир», 1964.
4.11. Руди н У., Основы математического анализа, «Мир», 1966.
К главам 5 и 6
5.1. К о ч и н Н. Е., Векторное исчисление и начала тензорного исчисления, Изд-во
АН СССР, 1961.
5.2. Маделунг Э., Математический аппарат физики (справочное руководство),
«Наука», 1968.
6.3. Шилов Г. Е., Лекции по векторному анализу, Гостехиздат, 1954.
5.4. X а л м о ш П., Конечномерные векторные пространства, Физматгиз, 1963.
К г л а в е 7
7.1. Лаврентьев М. А. и Шабат Б. В., Методы теории функций
комплексного переменного, «Наука», 1965.
7.2. Маркушевич А. И., а) Краткий курс теории аналитических функций,
«Наука», 1966.
б) Теория аналитических функций, тт. 1, 2, «Наука», 1967.
7.3. Свешников А. Г. и Тихонов А. Н., Теория функций комплексного
переменного», «Наука», 1970.
7.4. Евграфов М. А., Аналитические функции, «Наука», 1965.
7.5. Уиттекер Э. Т. иВатсои Дж. Н., Курс современного анализа, тт. I,
II, Физматгиз, 1962 — 1963.
ЛИТЕРАТУРА
797
7.6. Коппенфельс В. и Штальман Ц., Практика конформного
отображения, ИЛ, 1963.
7.7. М ы ш к и с А. Д., Математика для втузов. Специальные курсы, «Наука», 1971.
7.8. Привалов И. И., Введение в теорию функций комплексного переменного,
«Наука», 1967.
7.9. Ф и л ь ч а к о в П. Ф., Приближенные методы конформных отображений, «Нау-
кова думка», 1964.
7.10. Л а в р и к В. И. и Савенков В. Н., Справочник по конформным
отображениям, «Наукова думка», 1970.
7.11. Г у р в и ц А. и К у р а н т Р., Теория функций, «Наука», 1968.
7.12. Ш а б а т Б. В., Введение в комплексный анализ, «Наука», 1969.
К главе 8
8.1. Дёч Г., Руководство к практическому применению преобразования Лапласа и
z-преобразования, «Наука», 1971.
8.2. Диткин В. А. и Прудников А. П., Интегральные преобразования и
операционное исчисление, СМБ, Физматгиз, 1961.
8.3. Ван-дер Поль Б. и Г. Бреммер, Операционное исчисление на основе
двухстороннего преобразования Лапласа, ИЛ, 1952.
8.4. Снеддон И., Преобразования Фурье, ИЛ, 1955.
8.5. Т р а н т е р Д., Интегральные преобразования в математической физике, Гостех-
издат, 1956.
8.6. 3 е м а н я н А., Интегральные преобразования обобщенных функций, «Наука»,
в печати.
8.7. Бейтмен Г. и Эрдейи А., Таблицы интегральных преобразований в двух
томах, СМБ, «Наука»:
т. 1. Преобразования Фурье, Лапласа, Меллина, 1969;
т. 2. Преобразования Бесселя. Интегралы от специальных функций, 1970.
См. также [7.1], [7.4], [7.7].
К г л а в е 9
9.1. П о н т р я г и н Л. С, Обыкновенные дифференциальные уравнения, «Наука»,
1970.
9.2. Петровский И. Г., Лекции по теории обыкновенных дифференциальных
уравнений, «Наука», 1970.
Э л ] " ~ "
9.3. Э л ь с г о л ь ц Л. Э., Дифференциальные уравнения и вариационное исчисление,
«Наука», 1969.
9.4. Камке Э., Справочник по обыкновенным дифференциальным уравнениям,
«Наука», 1971.
9.5. Б е л л м а н Р., Теория устойчивости решений дифференциальных уравнений,
ИЛ, 1954.
9.6. Андронов А. А., В и т т А. А., X а й к и н С. Э., Теория колебаний,
Физматгиз, 1959.
9.7. Боголюбов Н. Н. иМитропольский Ю А., Асимптотические методы
в теории нелинейных колебаний, Физматгиз, 1963.
9.8. Боголюбов Н. Н. и Крылов Н. М., Введение в нелинейную механику,
Киев, 1937.
9.9. Стокер И., Нелинейные колебания в механических и электрических системах,
ИЛ, 1952.
9.10. Степанов В. В., Курс дифференциальных уравнений, «Наука», 1966.
9.11. Коддингтон Э. и Л е в и н с о н Н., Теория обыкновенных
дифференциальных уравнений, ИЛ, 1958.
9.12. Лефшец С, Геометрическая теория дифференциальных уравнений, ИЛ. 1961.
9.13. С а н с о н е Д., Обыкновенные дифференциальные уравнения, тт. 1, 2, ИЛ, 1953.
9.14. Т р и к о м и Ф., Дифференциальные уравнения, ИЛ, 1962.
9.15. Хартман Ф., Обыкновенные дифференциальные уравнения, «Мир», 1970.
К главе 10
10.1. Петровский И. Г., Лекции об уравнениях с частными производными,
Физматгиз, 1961.
10.2. Соболев С. Л., Уравнения математической физики, «Наука», 1966.
10.3. Тихонов А. Н., Самарский А. А., Уравнения математической физики,
«Наука», 1966.
10.4. Курант Р. и Гильберт Д., Методы математической физики, т. 1, Гос-
техиздат, 1951.
10.5. Курант Р., Дифференциальные уравнения с частными производными, «Наука»,
1965.
10.6. Морс Ф. М. и Ф е ш б а х Г., Методы теоретической физики, тт. I, 11, ИЛ,
1958.
10.7. Линейные уравнения математической физики, СМБ, «Наука», 1964.
10.8. Камке Э., Справочник по дифференциальным уравнениям в частных
производных первого порядка, «Наука», 1966.
10.9. Г а н т м а х ер. Ф. Р., Лекции по аналитической механике, «Наука», 1966.
798
ЛИТЕРАТУРА
10.10. Владимиров В. С, Уравнения математической физики, «Наука», 1971.
10.11. Годунов С. К., Уравнения математической физики, «Наука», 1971.
10.12. Зоммерфельд А., Дифференциальные уравнения в частных производных
физики, ИЛ, 1950.
10.13. Ф р а н к Ф. и М и з е с Р., Дифференциальные и интегральные уравнения
математической физики, ОНТИ, 1937.
К главе 11
11.1. В е н т ц е л ь Е. С, Исследование операций, «Советское радио», 1972.
11.2. Г е р м е й е р Ю. Б., Введение в теорию исследования операций, «Наука», 1971,
11.3. Вайда Ф., Теория игр и линейное программирование, в сборнике «Линейные
неравенства и смежные вопросы», ИЛ, 1959.
11.4. Г асе С, Линейное программирование, Физматгиз, 1961.
11.5. Гей л Д., Теория линейных экономических моделей, ИЛ, 1963.
11.6. Данциг Г., Линейное программирование, «Прогресс», 1966.
11.7. Дрешер М., Стратегические игры, «Советское радио», 1964.
11.8. К а р л и н С, Математические методы в теории игр, программировании я
экономике, «Мир», 1964.
11.9. Ль юс Р., Р а йф а X., Игры и решения, ИЛ, 1961.
11.10. Нейман Д., Моргенштерн О., Теория игр и экономическое поведение,
«Наука», 1970.
11.11. Хедли Д., а) Линейная алгебра (для экономистов), «Высшая школа», 1966;
б) Нелинейное и динамическое программирование, «Мир», 1967.
11.12. Гельф. анд И. М. и Фомин С. В., Вариационное исчисление,
Физматгиз, 1962.
11.13. Б лисе Г., Лекции по вариационному исчислению, ИЛ, 1950.
11.14. Понтрягин Л. С, Болтянский В. Г., ГамкрелидзеР. В.,
Мищенко Е. Ф., Математическая теория оптимальных процессов, «Наука»,
1969.
11.15. Болтянский В. Г., а) Математические методы оптимального управления,
«Наука», 1969.
б) Оптимальное управление дискретными системами, «Наука», 1973.
11.16. Беллман Р., Динамическое программирование, ИЛ, 1960.
11.17. Беллман Р. и Дрейфус С, Прикладные задачи динамического
программирования, «Наука», 1965.
11.18. Уайльд Д., Методы поиска экстремума, «Наука», 1967.
11.19. Фан Лянь-цень и Вань Г у-с е н, Дискретный принцип максимума,
«Мир», 1967.
11.20. Л е й т м а н Д., Введение в теорию оптимального управления, «Наука», 1968.
11.21. Мерриэм К., Теория оптимизации и расчет систем управления с обратной
связью, «Мир», 1967.
11.22. Моисеев Н. Н., Численные методы в проблемах синтеза оптимальных систем,
«Наука», 1972.
См. также [7.7], [9.3], [Ю.4].
К г л а в е 12
12.1. Ван-дер Варден Б., Современная алгебра, ч. 1, 2, Гостехиздат, 1947.
12.2. К у р о ш А. Г., Лекции по общей алгебре, Физматгиз, 1962.
12.3. К У р о ш А. Г., Теория групп, «Наука», 1967.
12.4. Александров П. С, Комбинаторная топология, Гостехиздат, 1947.
12.5. Понтрягин Л. С, Основы комбинаторной топологии, Гостехиздат, 1947.
12.6. К е л л и Д., Общая топология, «Наука», 1968.
12.7. Новиков П. С, Элементы математической логики, «Наука», 1973.
12.8. Мендельсон Э., Введение в математическую логику, «Наука», 1970.
12.9. Владимиров Д. А., Булевы алгебры, «Наука», 1969.
К главам 13 и 14
13.1. Г а н т м а х е р Ф. Р., Теория матриц, «Наука», 1966.
13.2. Гельфанд И. М., Лекции по линейной алгебре, «Наука», 1971.
13.3. Мальцев А. И., Основы линейной алгебры, «Наука», 1970.
13.4. Ахиезер Н. И. иГлазманИ. М., Теория линейных операторов в
гильбертовом пространстве., «Наука», 1966.
13.5. Люстерник Л. А. иСоболев В. И., Элементы функционального анализа,
«Наука», 1965.
13.6. Функциональный анализ, СМБ, «Наука», 1972.
13.7. Беллман Р., Введение в теорию матриц, «Наука», 1969.
13.8. Банах С, Курс функционального анализу, «Радяньска школа»* Ки1в, 1948.
13.9. В у л и х Б. 3., Введение в функциональный анализ, «Наука», 1967.
13.10. Данфорд Н. и Шварц Л., Линейные операторы, ИЛ, 1962.
13.11. Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу,
ИЛ, 1954.
13.12. Э д в а р д с Р., Функциональный анализ, «Мир», 1969,
ЛИТЕРАТУРА
799
13.13. Ван-дер Варден Б., Методы теории групп в квантовой механике, ДНВТУ,
1938.
13.14. В е й л ь Г., Классические группы, их инварианты и представления, ИЛ, 1947.
13.15. В и г н е р Е., Теория групп, ИЛ, 1961.
13.16. В и л е н к и н Н. Я., Специальные функции и теория представлений групп,
«Наука», 1965.
13.17. К и р и л л о в А. А., Элементы теории представлений, «Наука», 1972.
13.18. Мурнаган Ф., Теория представлений групп, ИЛ, 1950.
13.19. Б а р б а ш и н Е. А., Введение в теорию устойчивости, «Наука», 1967.
13.20. Красовский Н. Н., Некоторые задачи теории устойчивости движения,
Физматгиз, 1959.
13.21. Л е т о в А. М., Устойчивость нелинейных регулируемых систем, Физматгиз,
1962.
13.22. Л а - С а л л ь Ж., Л е ф ш е ц С, Исследование устойчивости прямым методом
Ляпунова, «Мир», 1964.
13.23. Желобенко Д. П., Компактные группы Ли и их представления, «Наука»,
1970.
См. также [4.3], [4.4], [5.4], [9.3], [10.4].
К г л а в е 15
15.1. Петровский И. Г., Лекции по интегральным уравнениям, «Наука», 1965.
15.2. Т р и к о м и Ф., Интегральные уравнения, ИЛ, 1960.
15.3. Интегральные уравнения, СМБ, «Наука», 1968.
15.4. Ахиезер Н. И., Лекции по теории аппроксимации, «Наука», 1965.
15.5. Бохнер С, Лекции об интегралах Фурье, Физматгиз, 1962.
15.6. М и х л и н С. Г., Лекции по линейным интегральным уравнениям, Физматгиз,
15.7. Мусхелишвили Н. И., Сингулярные интегральные уравнения, «Наука», 1968.
См. также [4.3], [4.10], [5.2], [10.5], [10.6], [13.4], [13.5], [13.8] — [13.12].
К главам 16 и 17
16.1. П о г о р е л о в А. В., Дифференциальная геометрия, «Наука», 1969.
16.2. Р а ш е в с к и й П. К., Дифференциальная геометрия, Физматгиз, 1956.
16.3. Р а ш е в с к и й П. К., Риманова геометрия и тензорный анализ, «Наука», 1967.
16.4. Сокольников И. С, Тензорный анализ (теория и применения в геометрии
и в механике сплошных сред), «Наука», 1971.
16.5. Стернберг С, Лекции по дифференциальной геометрии, «Мир», 1970.
16.6. Эйзенхарт Л., Риманова геометрия, ИЛ, 1948.
Кглавам 18 и 19
Колмогоров А. Н., Основные понятия теории вероятностей, ОНТИ, 1936.
Г н е д е н к о Б. В., Курс теории вероятностей, «Наука», 1967.
Боровков А. А., Курс теории вероятностей, «Наука», 1972.
Арлей Н. и Б у х К., Введение в теорию вероятностей и математическую
статистику, ИЛ, 1951.
Ван-дер Варден Б., Математическая статистика, ИЛ, 1960.
Крамер Г., Математические методы статистики, ИЛ, 1948.
Л о э в М., Теория вероятностей, ИЛ, 1962.
Феллер В., Введение в теорию вероятностей и ее приложения, ИЛ, 1952.
X а л ь д А., Математическая статистика с техническими приложениями, ИЛ,
1956.
Р и о р д а н Д., Комбинаторный анализ, ИЛ, 1963.
Большее Л. Н., Смирнов Н. В., Таблицы математической статистики,
«Наука», 1965.
Прохоров Ю. В. иРозановЮ. А., Теория вероятностей, СМБ, «Наука»,
1973.
Дуб Д., Вероятностные процессы, ИЛ, 1956.
Розанов Ю. А., Случайные процессы, «Наука», 1971.
У и л к с С, Математическая статистика, «Наука», 1967.
Саати Т. Л., Элементы теории массового обслуживания и ее приложения,
«Советское радио», 1971.
К г л а в е 20
20.1. Б е р е з и н И. С. и Ж и д к о в Н. П., Методы вычислений, тт. 1, 2, «Наука»,
1966.
20.2. Бахвалов Н. С, Численные методы (анализ, алгебра, обыкновенные
дифференциальные уравнения), «Наука», 1973.
20.3. Гельфонд А. О., Исчисление конечных разностей, «Наука», 1967.
20.4. Канторович Л. В. и Крылов В. И., Приближенные методы высшего
анализа, Физматгиз, 1962.
20.5. Фаддеев Д. К. и Ф а д д е е в а В. Н., Вычислительные методы линейной
алгебры, Физматгиз, 1963.
18.1.
18.2.
18.3.
18.4.
18.5.
18.6.
18.7.
18.8.
18.9.
18.10.
18.11.
18.12.
18.13.
18.14.
18.15.
18.16.
800
ЛИТЕРАТУРА
20.6. МихлинС. Г. иСмолицкий Х.Л., Приближенные методы решения
дифференциальных и интегральных уравнений, СМБ, «Наука», 1965.
20.7. Милн В. Э., Численный анализ, ИЛ, 1951.
20.8. Милн В. Э., Численное решение дифференциальных уравнений, ИЛ, 1955.
20.9. Хаусхолдер А. С, Основы численного анализа, ИЛ, 1956.
20.10. О с т р о в с к и й А. М., Решение уравнений и систем уравнений, ИЛ, 1963.
20.11. Уиттекер Э. и Робинсон Г., Математическая обработка результатов
наблюдений, ОНТИ, 1935.
20.12. X е м м и н г Р. В., Численные методы, «Наука», 1972.
20.13. К о л л а т ц Л., Функциональный анализ и вычислительная математика, «Мир»,
1969.
20.14. Метод статистических испытаний (метод Монте-Карло), СМБ, Физматгиз, 1962.
20.15. Е р м а к о в С. М., Методы Монте-Карло и смежные вопросы, «Наука», 1971.
20.16. В а з о в В., Форсайт Д., Разностные методы решения дифференциальных
уравнений в частных производных, ИЛ, 1963.
20.17. Уилкинсон Д., Алгебраическая проблема собственных значений, «Наука»,
1970.
К г л а в е 21
21.1. Л е б е д е в Н. Н., Специальные функции и их приложения, Физматгиз, 1963.
21.2. Янке Е., Эмде Ф., Леш Ф., Специальные функции (формулы, графики,
таблицы), «Наука», 1968.
21.3. Бейтмен Г. иЭрдейи А., Высшие трансцендентные функции, в трех томах,
СМБ, «Наука»:
т. 1. Гипергеометрическая функция и ее обобщения. Функции Лежандра, 1967;
т. 2. Функции Бесселя, функции параболического цилиндра, ортогональные
многочлены, 1968;
т. 3. Эллиптические и автоморфные функции, функции Ламе и Матье, 1969.
21.4. Математический анализ (вычисление элементарных функций), СМБ, Физматгиз,
1963.
21.5. Ахи ез ер Н. И., Элементы теории эллиптических функций, «Наука», 1970.
21.6. Г е л ь ф а н д И. М. и Ш и л о в Г. Е., Обобщенные функции и действия над ними,
Физматгиз, 1959.
21.7. 1) Л е б е д е в А. В. и Ф е д о р о в а Р. М., Справочник по математическим
таблицам, Изд-во АН СССР, 1956.
2) Б у р у н о в а Н. М., Справочник по математическим таблицам (дополнение),
Изд-во АН СССР, 1959.
См. также [4.6], [5.2], 17.1], [7.5], [8.6], [8.7], [10.4], 113.16].
УКАЗАТЕЛЬ ВАЖНЕЙШИХ ОБОЗНАЧЕНИЙ
Скаляры и матрицы
а, 0 ... скалярные (числовые) величины —
главы 5, 6, 12 — 16.
а комплексно сопряженная с а 1.3-2
| а | абсолютная величина а, модуль а,
1.3-2
А, В, ... ; А = [а^] матрицы (чаще всего
__ квадратные) 13.2-1
А —[а^] матрица комплексно
сопряженная с А 13.3-1
А' г [a^i] матрица, транспонированная
с A J3.3-1
А* = [в^] матрица эрмитово
сопряженная с А 13.3-1
4-4-4)
матрица-столбец 13.2-1
Ниже указаны главы или пункты, в которых вводятся или определяются
обозначения, используемые в книге
| а | == (а.а)1/2 абсолютная величина
(норма) а 5.2-5, 16.8-1
(а, Ъ) общее скалярное произведение 14.2-8
И a j| = (а, а)1/2 норма а 14.2-5, 14.2-7
(jF, h) скалярное произведение функций
15.2-1
|| f || = (f, f) 1/2 норма функции 15.2-1
axb векторное произведение векторов а,
Ь, 5.2-7, 16.8-4
[abc] смешанное произведение векторов
5.2-8, 16.8-4. См. также 16.1-3 по поводу
немых индексных обозначений и 14.7-7
для сравнения обозначений.
Линейные операторы
и тензоры
А, В ... линейные операторы — главы 14,
15 и 20 или тензоры диадика — глава 16
L, В линейные дифференциальные
операторы 9.3-1, 10.4-2, 15.2-7, 15.4-1
К линейный интегральный оператор 15.3-1
А', В', ... ; L\ К', транспонированные
к А, В, ... ; L, К 14.4-6, 15.3-1, 15.4-3
А*, В*, ... ; L*. К* сопряженные и
эрмитово сопряженные с А, В, ... ; L, К
14.4-3, 15.4-3
D оператор дифференцирования 20.4-2
V (набла) векторный дифференциальный
оператор 5.5-2, 16.10-7
V* s= V*V оператор Лапласа 5.5-5, 16.10-7
Ё оператор смещения 20.4-2
V оператор восходящих разностей 20.4-2
Л оператор нисходящих разностей 20.4-2
Латинский алфавит
arcsin z, arccos г, aretg г обратные
тригонометрические функции арксинус,
арккосинус, арктангенс 21.2-4
arg г аргумент г 1.3-2
arsh г, arch г, arth г обратные
гиперболические функции ареасинус, ареакоси-
нус, ареатангенс 21.2-8
В., В^ числа Бернулли 21.5-2
В У1' (х) многочлены Бернулли 21.5-2
Ьег„, г, beim 2 21.8-7
т т
С (s, у) цена (риск) действия системы 19.9.1
С° (х) многочлена Гегенбауэра 21.7-8
Спт или {™\ биномиальные коэффициенты
21.5-1
С {х) интеграл Френеля 21.3-2
ch 2 гиперболический косинус 21.2-5
Ci x интегральный косинус 21.3-1
*' ^[ЭД33^». ^2» '••) матрица-строка
13.2-1
Векторы и координаты
векторов
а, Ь, ... и х, у, ... векторы 5.2-1, 12.4-1,
14.2-1, 16.2-1
и единичный вектор 5.2-5, 14.2-5, 16.8-1
i, j, k правый прямоугольный декартов
базис 5.2-3
е., е1 базисные векторы 6.3-3, 14.2-4, 16.6-1
!• и и- единичные базисные векторы 6.3-2,
16.8-3; ортогональные единичные
базисные векторы 6.4-1, 14.7-4
радиусы-векторы в
г — XI -{- у} -{- 2к, | трехмерном
евклидовом простр!
вы 5, 15, 17
О — £i + Tjj
4-2k, \
вом пространстве гла-
а = агех + а2е* -f- ... вектор,
представленный в виде линейной формы
относительно базисных векторов 14.2-4
а = aiti! + a2u8 + ... вектор, выраженный
через ортонормированный базис
векторов 14.7-4
а = akek = а1^ -fa2e2 -f ... + апеп контра-
вариантный вектор (функция) с
координатами а 6.3-3, 16.6-1
а = akek = а^1 + а2е2 + ... -f апеп кова-
риантный вектор (функция) с
координатами ak 6.3-3, 16.6-1
а = агиг + a2u2 -f ... + апип вектор,
выраженный посредством физических
координат ak 6.3-2, 16.8-3
a«b скалярное произведение векторов а и
Ь 5.2-6, 16.8-1
26 Г. Корн и Т. Корн
802
УКАЗАТЕЛЬ ВАЖНЕЙШИХ ОБОЗНАЧЕНИЙ
en z (косинус амплитуды) эллиптическая
функция 21.6-7
cos г косинус 21.2-1
ch-1 г гиперболический ареакосинус (arch z)
21.2-8
dn г (дельта амплитуды) эллиптическая
функция 21.6-7
det [азу] определитель 1.5-1
' (vv %
Уп)
д(ху
якобиан 4.5-6
erf х функция ошибок 21.3-2
erfc х дополнительная функция ошибок
21.3-2
Е (ф, k) нормальный эллиптический
интеграл Лежандра второго рода 21.6-6
Ei x, 1Й* экспоненциальный интеграл 21.3-1
Е (k) полный нормальный эллиптический
интеграл Лежандра второго рода 21.6-6
</> среднее по времени (случайной величины)
18.10-7
[/] , (f)f среднее по конечному
промежутку времени 19.8-1
F (а, Ь; с; z) == tFx (a, b; с; z)
гипергеометрическая функция 9.3.9, 9.3-11
F (а; с; г) == 1F1 (а; с; г) вырожденная
гипергеометрическая функция 9.3-10,
9.3-11
F (ф, k) нормальный эллиптический
интеграл Лежандра первого рода 21.6-6
F* (?) = F% (e^) дискретное преобразование
Лапласа 8.7-3
[/(01 преобразование Фурье 4.11-3
& с U (О]. &"s V (О] косинус- и
синус-преобразование Фурье 4.11-3
g (со), g (со) спектральные плотности
по множеству наблюдений 18.10-6
hy' (z), ft\ ' (2) сферические функции
Бесселя третьего рода 21.8-8
h (£) функция влияния 19.8-2
И (i(o) частотные характеристики 9.4-7
Н (s) передаточные функции 9.4-7
И (2) многочлены Эрмита 21.7-1
*<1>,
/(2)
(2) функции Ганкеля 21.8-1
i = V—1 мнимая единицы 1.3-1
/ (2) модифицированная функция Бесселя
21.8-6
12 (p. Q) отношение неполной
бета-функции 21.4-5
Im 2 мнимая часть z 1.3-1
inf x точная нижняя грань 4.3-3
ix (/) реализация случайного процесса!9.8-4
/. (2) сферическая функция Бесселя
первого рода 21.8-8
J' (2) функция Бесселя первого рода 21.8-1
К (k) полный эллиптический интеграл
Лежандра первого рода 21.8-1
Кт (2) модифицированная функция
Ганкеля 21.8-6
Кхх ('г У' Кху (*V *г)
автокорреляционная и взаимная корреляционная
функции соответственно 18.9-3
ker
keim2 21.8-7
L% класс действительных или комплексных
квадратично интегрируемых функций
15.2-1
Lniz) многочлены Лагерра 21.7-1
LJJ (*), L^"' (x) обобщенные многочлены
Лагерра 21.7-5
L [f (/)] зз L U (О, S] преобразование
Лапласа 8.2-1
И (2) интегральный логарифм 21.3-1
Нт 2 предел 4.4-1
1. i. т. х предел в среднем 15.2-2
logc 2 логарифм 1.2-3, 21.2-10
М {#} =! математическое ожидание 18.3-3,
18.4-4, 18.4-8, 18.9-2
max х, min x максимальное и минимальное
значения 4.3-3
Nт (г) цилиндрическая функция Неймана
второго рода 21.8-1
п\ факториал 1.2-4
п. (г) сферическая функция Бесселя
второго рода 21.8-8
О [g (x)], о [g (x)] асимптотические
соотношения 4.4-3
Р п (2) многочлены Лежандра первого рода
21.7-1
Р*? (2) присоединенные функции Лежандра
первого рода 21.8-10
Qn (z) функции Лежандра второго рода
21.7-3
R^-, R£ группа трехмерных вращений-
отражений и вращений соответственно
14.10-8.
^хх W* ^хи № соответственно
автокорреляционная и взаимная корреляционная
функция по времени 18.10-8
R«(*r У- RxxM- R*j,('r У- «*„«
автокорреляционные и взаимные
корреляционные функции по множеству
наблюдений 18.9-3, 18.10-2
Re г действительная часть z 1.3-1
Res f (а) вычет функции f (z) в точке 2 = а
7.7-1
S (х) интеграл Френеля 21.3-2
SJ^ ' числа Стирлинга 21.5-1
sgn х функция-сигнум (знак) 21.9-1
Si (x) интегральный синус 21.3-1
sin 2 синус 21.2-1
sin-1 2 арксинус (arcsin z) 21.2-4
sin я/
sincf= , 18.11-2
ш
5 (v), S (v), спектральные плотности
по множеству наблюдений 18.10-6
sh 2 гиперболический синус 21.2-5
sh~* 2 гиперболический ареасинус (arsh z)
21.2-8
sn 2 (синус амплитуды) эллиптическая
функция 21.6-7
sup х точная верхняя граница 4.3-3
Т (2) многочлен Чебышева первого рода
21.7-1
tg 2 тангенс 21.2-1
tg-1 2 арктангенс (arctg z) 21.2-4
th 2 гиперболический тангенс 21.2-5
th-1 z гиперболический ареатангенс (arth z)
21.2-8
Тг (А) или Sp (А) след матрицы 13.2-7
УКАЗАТЕЛЬ ВАЖНЕЙШИХ ОБОЗНАЧЕНИЙ
803
Un (2) функции Чебышева второго рода
21.7-4
U векторное пространства 12.4-1
* ~ п (Х1 ~*~ *2 + ••• "+* хп) выборочное
среднее значение 19.2-3
A^int ('©) обобщенное преобразование
Фурье 18.10-10
У/ (^» Ф) сферическая поверхностная
гармоника 21.8-12
г [ftf 2] = Z^ (2) Z — преобразование
последовательности fy 8.7-3.
Z(j циклический индекс группы G 18.7-3
Zm(z) цилиндрическая функция 21.8-1
Греческий алфавит
В (р, q) бета-функция 21.4-4
В (р, q) неполная бета-функция 21.4-5
Г (2) гамма-функция 21.4-1
Г (р) неполная гамма-функция 21.4-5
Г (V) односторонняя спектральная
плотность по множеству наблюдений 18.10-в
6ifi, 6^ — символ Кронекера 13.2-3, 16.5-2
о (х), 6+ (х), 6- (х) импульсные функции
21.9-2
6 (х, |) многомерная дельта-функция 21.9-7
Ayk нисходящие разности 20.4-1
V#il восходящие разности 20.4-1
£ (г) дзета-функция Вейерштрасса 21.6-3
Ъ, (z) тэта-функция Якоб и 21.6-8
\ку. центральное среднее 20.4-1
Р х (тЬ Р w, (t) нормированные
корреляционные функции 18.10-2
а (г) сигма-функция Вейерштрасса 21.6-3
<D|nt (со) обобщенная спектральная
функция 18.10-10
Фхх ^' ®ху ^ соответственно
спектральная и взаимная спектральная
плотности по множеству наблюдений 18.10-3
%Х(Я) характеристическая функция 18.4-10
*(«) (qV *v qr f2> - ' V <n) «-мерная
характеристическая функция 18.9-3
ф(2) пси-функция 21.4-3
Ч?хх (ю), Ч?ху (со) соответственно
спектральная и взаимная спектральная
плотности по времени 18.10-8
IP (2) IP — функция Вейерштрасса 21.6-2
Специальные
математические знаки
J y(t) функция скачка 20.4-5
© прямая сумма 12.7-5, 13.2-9, 14.8-2,
14.9-2
прямое произведение 12.7-2, 13.2-10
логическое умножение 12.8-1, 18.2-1
логическое сложение 12.8-1, 18.2-1
Et U £2 — событие Ei или Е2 12.8-6
Е± П ^2 — событие Ei и Е% 12.8-6
Е — событие не £ 12.8-6
/ — достоверное событие 12.8-6
0 — невозможное событие 12.8-6
^ — символ свертки 4.6-18
2 суммирование 1.2-5
произведение 1.2-5
k — m
п
п
k — m
= символ равенства 1.1-3, 12.1-3
г символ тождества 1.1-4
=^ приближенно равно
~ асимптотически равно 4.4-3
<, >, ^, ^ символы неравенства
12.6-1
е принадлежность элемента 4.3-2
Э так, что
[ц] целая часть ц (наибольшее целое число,
не превосходящее ц)
1-5,
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
(Цифры указывают номера пунктов, например 14.2-5 означает п. 5 нз § 2 гл. 14)
А
Абсолютная величина вектора 5.2-5, 14.2-5
— — действительного числа 1.1-в,
Абсцисса 2.1-2
— абсолютной сходимости преобразования
Лапласа 8.2-2
Автоморфизм 12.1-в
— группы внутренний 12.2-9
Аксиома координатная 2.1-2
— непрерывности 2.1-2
— — Кантора — Дедекинда 4.3-1
Аксиомы вероятностей 18.2-2
— определяющие 12.1-1
— Пеано 1.1-2
Алгебра 12.1-2
— булева 12.8-1
— — значений истинности 12.8-6
— гипотетических событий 12.8-6
— классов 12.8-4
— линейная ассоциативная 12.4-2
— — над кольцом 12.4-2
— меры 12.8-8
— операторов линейная 14.4-2
— с делением 12.4-2, 14.4-2
— событий 12.8-5, 18.2-1
— утверждений 12.8-6
Алгебраическая кратность собственного
значения 13.4-3
Алгебраическое дополнение 1.5-2
Алгоритм Герона 20.2-2
— разделенных разностей 20.2-5
Амплитуда 4.11-4, 21.6-7
— комплексная 9.4-6
Аналитическая функция матрицы 13.2-12
Аналитическое продолжение функции 7.8-1
Аналогии Дел амбр а и Гаусса 1.12-4
— Непера 1.12-4
Ангармоническое отношение 7.9-2
Аппроксимация импульсных функций
21.9-4
— Никольсона 20.9-8
— см. также Приближение
— функции 15.2-6
Аргумент комплексного числа 1.3-2
— — —, главное значение 1.3-2
Асимметрия табл. 18.3-1, 19.2-4
Асимптота 17.7-6
— гиперболы 2.5-2
Асимптотические соотношения между
функциями 4.4-3
Астроида 2.6-1
Аффинор 16.9-2
— локальный вектора табл. 16.10-1
Б
Базис 5.2-2
— дуальный взаимный 14.7-6
— линейного многообразия 14.2-4
— локальный 6.3-1, 17.3-8
Базис ортонормированный 14.7-4, 15.2-4
Базисная переменная 11.4-2
Базисные векторы 3.1-5
Базисы взаимные 16.7-3
— — риманова пространства 16.8-2
Белый шум 18.11-1
Бесконечное произведение 4.8-7
Бесконечный ряд 4.8-1
Бета-распределение вероятностей 18.8-5
Бета-функция неполная 21.4-5
— полная 21.4-4
Бивектор 16.5-4
Билинейная форма 13.5-1
Бином Ньютона 1.4-1
Биномиальные коэффициенты 1.4-1, 21.5-1,>
табл. 18.7-1
— —, приближенные формулы 21.5-4
— —, свойства 21.5-1
— —, теорема сложения 21.5-1
Бинормаль 17.2-2, 17.2-4
Биссектриса 1.11-3
Борелевское множество 4.6-14
Брахистохрона 11.6-1
Булева алгебра 4.3-2, 12.8-6
— — вполне аддитивная 12.8-8
— функция 12.8-2
— —, канонический вид 12.8-2
Булевы алгебры изоморфные 12.8-3
В
Валентность тензора 16.2-1
Вариационное исчисление 11.5-2
Вариация 11.4-1
Вектор 5.1, 12.4-1
— аксиальный 16.8-4
— бинормали единичный 17.2-2, 17.2-3
—, выражение через векторы локального
базиса 16.6-1
— Гиббса 14.10-3
— главной нормали единичный 17.2-2,
17.2-3
— Дарбу 17.2-3
— диадика 16.9-2
— единичный 5.2-5, 14.2-8, 16.8-1
— — локальный 16.8-3
— инфинитезимального перемещения
16.2-2
— касательной единичный 17.2-2, 17.2-3,
17.4-2
— ковариантный 16.2-1
— — абсолютный 16.2-1
— контравариантный 16.2-1
— — абсолютный 16.2-1
— кривизны 17.2-2
— — геодезической 17.3-4
— — нормальной 17.3-4
— — первый 17.4-2
— — тангенциальной 17.3-4
—, матричное представление 14.5*2
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
805
Вектор нормали единичный 17.3-2
— нормальный плоскости 3.2-1
— нулевой 5.2-1
— площади 3.1-10
— площадки 5.4-6
— полярный 15.8-4
—, представление комплексными
матрицами 14.10-4
— случайный многомерный 18.4-1 18.4-7
— собственный 14.8-5
— сопряженный 11.8-4
— состояния 11.8-4
— угловой скорости 5.3-2
— управления 11.8-4
Векторная линия 5.4-3
— сумма 5.2-1
— функция линейная 14.3-1
Векторное двойное произведение трех
векторов 5.2-9
— поле 5.4-3
— произведение двух векторов 5.2-7
— пространство 14.2-1
— — бесконечномерное 14.2-4
— — евклидово 14.2-7
— —, линейная размерность 14.2-4
— — линейное 14.2-1
Векторное пространство линейное над
кольцом 12.4-1
— —, матричное представление 14.2-1
— — нормированное 14.2-5
— — полное 14.2-7
— — предгильбертово 14.2-6
— — унитарное 14.2-6, 14.2-7
— — эрмитово 14.2-6
Векторно-скалярное произведение трех
векторов 5.2-8
Векторные уравнения 5.2-11
— функции поля 5.5-1
Векторный анализ 5.1-1
— элемент линии 5.4-4
— — поверхности 5.4-6
Вектор-сумма функций 15.2-1
Вектор-функция 5.3-1
—, правила дифференцирования 5.3-2
Векторы ассоциированные 16.7-2
— базисные 5.2-2, 6.3-1
— — локальные 6.3-2
— — — контравариантные 16.6-1
— линейно зависимые 5.2-2, 5.2-7
— — независимые 5.2-2
— ортогональные 14.7-3
—. условие перпендикулярности 5.2-8
Величина случайная см. Случайная
величина
Вероятности событий, правило умножения
18.2-2
Вероятностная функция 18.2-7
Вероятность неосуществления события
18.2-5
— осуществления т событий из N 18.2-5
— — хотя бы одного события 18.2-5
— события 18.1-1, 18-2-2
— — апостериорная 18.2-6
— — априорная 18.2-6
— — сложного 18.7-2
— — условная 18.2-2
— совмещения событий 18.2-2, 18.2-5
Вершина конуса 3.1-15
Вершины кривой второго порядка z.4-7
Вес конфигурации 18.7-3
— объекта 18.7-3
Ветвь функции 7.4-1
Возмущение 10.2-7, 13.6-4
— первого порядка 13.6-4
Волна приходящая 15.6-10
— синусоидальная круговая 10.4-3
Волна синусоидальная круговая
сферическая 10.4-8
— — стоячая 10.4-8
— — цилиндрическая 10.4-8
— уходящая 15.6-10
Волны 10.4-1
— затухающие 10.4-1
Восьмиугольник 1.10-1
Вращение 14.10-1
Вращение вокруг осей координат 14.10-5
— двумерное 14.10-8
— на бесконечно малый угол 14.10-7
— несобственное 14.10-1
—, представление комплексными
матрицами 14.10-4
— с отражением 14.10-1
Время усреднения 19.8-2
Вронскиан 9.3-2
Выборка без возвращения табл. 18.7-2
— с возвращением, табл. 18.7-2
— случайная 19.7-2
— — многомерная 19.7-4
Выборки из нормальной совокупности
19.5-3
Выборочная дисперсия 19.2-4, 19.7-2
— медиана 19.2-2
— средняя квадратичная сопряженности
признаков 19.7-5
— функция 18.9-1
Выборочное значение 18.9-1
— —, представление рядом импульсных
функций 20.4-6
— —, — ступенчатыми функциями 20.4-6
— среднее 19.7-2, 19.8-4
— — при группированных данных 19.2-3
— — случайной величины 19.2-3
— —, упрощенное вычисление 19.2-5
— — функции случайной величины
19.2-3
— стандартное отклонение 19.2-4
Выборочный интервал 20.4-6
— квантиль 19.2-2
— квартиль 19.2-2
— коэффициент корреляции 19.7-2
— — регрессии 19.7-2
— момент 18.9-1
— — начальный 19.2-4
— — центральный 19.2-4
Вырождение особой точки 9.3-10
Высота 1.11-3
Вычет функции 7.7-1
Вычисление значений многочлена 20.2-3
Г
Гамма-распределение вероятностей 18.8-5
Гамма-функция 21.4-1
—, асимптотическое разложение Стирлин-
га 21.4-2
— —, бесконечное произведение Вейер-
штрасса 21.4-1
—, интегральное представление Ганкеля
21.4-1
—, интегральные представления 21.4-1
—, логарифмическая производная 21.4-3
— неполная 21.4-5
—, определение Эйлера 21.4-1
—, теорема умножения Гаусса 21.4-1
—, функциональные уравнения 21.4-1
Гамильтониан 11.8-4
Гармоника сферическая зональная 10.4-3
— — поверхностная степени / 10.4-3
— — секториальная 10.4-3
— — тессеральная 10.4-3
Гармоника цилиндрическая 10.4-3
Гармоническая компонента 4.11-4
806
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Гармонический анализ периодических
функций 4.11-4
— — численный 20.6-6
Генеральная совокупность 19.1-2
Генератор сравнения мультипликативный
20.10-4
— — смешанный 20.10-4
Геодезическая линия 17.3-12
— окружность 17.3-13
— параллель 17.3-13
Гильбертово пространство 14.2-7
Гипербола 2.4-8, 2.4-9
—, построение 2.5-3
—, — касательных и нормалей 2.5-3
— равносторонняя 2.5-2
Гиперболоид двуполостный 3.5-7,
3.5-10
— однополостный 3.5-7, 3.5-10
Гипергеометрическая функция см.
Функция гипергеометрическая
Гипергеометрические многочлены см.
Многочлены гипергеометрические
Гипергеометрический ряд см. Ряд
гипергеометрический
Гипотеза конкурирующая 19.9-3
— некоррелированности величин 19.7-4
— нулевая 19.9-3
— статистическая 19.6-1
Гипоциклоида 2.6-2
Главная линейная часть приращения
функции 4.5-3
— ось кривой второго порядка 2.4-6
— — поверхности второго порядка
3.5-6
— плоскость поверхности второго порядка
3.5-6
Главные направления кривой второго
порядка 2.4-7
Гомеоморфизм 12.5-1
Гомоморфизм 12.2-9
Градиент вектора 16.10-7, 16.10-11
— поверхностный 5.6-2
— скаляра 16.2-2, 16.10-7
— скалярной функции точки 5.5-1
Граница множества 12.5-1
— — абсолютная 4.3-3
— — верхняя 4.3-3
— — нижняя 4.3-3
— — точная 4.3-3
— области 4.3-6
— функции верхняя 4.3-3
— — нижняя 4.3-3
— — точная 4.3-3
Границы допуска 19.6-4
График функции 4.2-1, 12.1-4
Группа 12.2-1
— абелева 12.2-1
-— аддитивная 12.2-10
— бесконечная 12.2-1
Группа вращений двумерных 14.10-8
— вращений-отражений 14.10-8
— вращений трехмерных 14.10-8
— вращений-отражений трехмерных
14.10-8
— знакопеременная степени п 12.2-8
— коммутативная 12.2-1
— конечная 12.2-1
— линейная полная (ПЛГ) 14.10-8
-— по сложению 12.2-10
— простая 12.2-5
— разрешимая 12.2-6
— симметрическая степени п 12.2-8
— унитарная специальная (СУГ) 14.10-8
— — унимодулярная двумерная 14.10-8
— циклическая 12.2-3
Группированные данные 19.2-2
Д
Двойное отношение инвариантное 7.9-2
Двойственность 12.8-1
Двойственные задачи линейного
программирования 11.4-11
Действительная ось 1.3-2
— часть комплексного числа 1.3-1
Действительные числа, свойства 1.1-2
Декартов лист 2.6-1
Деление левое, правое 12.2-1
— многочленов 1.7-2
— отрезка 2.1-4
Делители многочлена 1.7-1
Делитель многочленов общий 1.7-3
— нормальный 12.2-5
— нуля левый, правый 12.3-1
Дельта амплитуды 21.6-7
Дельта-объект ранга 2г 16.5-2
Дельта-окрестность 4.3-5
Дельта-символ Кронекера ранга 2 16.5-2
Дельта-функция 21.9-2
— многомерная 21.9-7
Десятиугольник 1.10-11
Детектирование функции 8.3-2
Детерминант 1.5-1
Дефект треугольника 17.3-13
Дециль 18.3-3
Диагонализация матриц 14.8-6
Диаграмма ромбовидная 20.5-3
— Фрезера 20.5-3
Диаграммы Венна 12.8-5
— Эйлера 12.8-5
Диада 14.5-4, 16.9-1
Диадное произведение 16.9-1
Диаметр кривой второго порядка 2.4-6
— множества 4.6-11
—-, сопряженный семейству плоскостей
3.5-5
Диаметральная плоскость поверхности
второго порядка 3.5-5
Диаметры (сопряженные) поверхности
второго порядка 3.5-5
— — центральной кривой второго порядка
2.4-6
Дивергенция вектора 16.10-7
— векторной функции точки 5.5-1
— поверхностная 5.6-2
— тензора ранга 2 16.10-11
Динамическое программирование 11.8-6,
11.9-1
Директриса 2.4-9
Дискретное преобразование Лапласа 8.7-3
Дискриминант алгебраического уравнения
1.6-5
— общего уравнения второй степени 2.4-2,
3.5-2
Дискриминантная кривая 9.2-2
Дисперсионный анализ 19.6-6
— — для группировки по двум признакам
19.6-6
Дисперсия между столбцами 19.6-6
— — строками 19.6-6
— обобщенная 18.4-8
—, обусловленная флуктуацией внутри
строк и столбцов 19.6-6
— остаточная 18.4-9
— случайной величины 18.3-3
— суммарная 19.6-6
— суммы случайных величин 18.5-6
— условная 18.4-5, 18.4-8
Дифференциал абсолютный вектора 16.10-1
— — относительного скаляра 16.10-2
— — — тензора 16.10-2
— — скаляра 16.10-1
— — тензора 16.10-1
предметный указатель
807
Дифференциал дуги в полярных
координатах 17.1-4
— независимого переменного 4.5-3
—- относительный скаляра 16.10-1
—- полный векторной функции точки 5.5-3
— — скалярной функции точки 5.5-3
— — функции 4.5-3
— функции второй, третий, ... 4.5-3
— — первый 4.5-3
Дифференциальная форма квадратичная
6.2-3
Дифференциальное исчисление 4.1-1
— уравнение Бернулли 9.2-4
Бесселя 21.8-1
— — — модифицированное 21.8-6
— — неоднородное 9.3-3
— — Ван дер Поля 9.5-4, 9.5-5
— — вырожденной гипергеометрической
функции Куммера 9.3-10
«— — гипергеометрическое Гаусса 9.3-9
— — для многочленов Гегенбауэра 21.7-8
— — — — Лагерра 21.7-5
Дифференциальное уравнение для
многочленов Чебышева 21.7-4
— — — присоединенных функций
Лежандра,21.8-10
— — — сферических функций Бесселя
21.8-8
— — — функций Эрмита 21.7-6
— — дополнительное 15.4-2
— — Клеро 9.2-4
— — Лапласа 15.6-1
— — Лежандра 9.3-3, 21.7-3
— — линейное в комплексной области
9.3-5, 9.3-6, 9.3-7
— -— — второго порядка 9.3-8
— — —, метод вариации постоянных
9.3-3
— — — неоднородное с постоянными
коэффициентами 9.4-2
— — —, нулевое (тривиальное) решение
9.3-1
— — — однородное, понижение порядка
9.3-2
— — — — с постоянными
коэффициентами 9.4-1
— — —, операторный метод решения
9.4-4
—- — —, особые точки 9.3-1
— — — первого порядка 9.2-4
—- — — порядка г 9.3-1
— — — приведенное 9.3-1
— — —, принцип наложения 9.3-1
— — —, — суперпозиции 9.3-1
— — — устойчивое 9.4-4
— — —, фундаментальная система
решений 9.3-2
— —, метод последовательных
приближений Пикара 9.2-5
— — нелинейное 9.5-2
—- — неполное 9.1-5
— —• обыкновенное 9.1-2
— — однородное 9.2-4
— —, преобразование контактное 9.2-3
— —, — Лежандра 9.2-3
— —, — точечное 2.2-3
— — приведенное 15.4-2
—- — Пуассона 15.6-1
— — Пфаффа 9.6-1
— — — вполне интегрируемое 9.6-2
— —, разложение решения в ряд Тейлора
9.2-5
— —, решение с помощью функций
Бесселя 21.8-5
— — Риккати общее 9.2-4
— — — специальное 9.2-4
Дифференциальное уравнение Риккати о
разделяющимися переменными 9.2-4
— — с частными производными см.
Уравнение с частными производными
— —, теорема существования и
единственности решения 9.2-1
— — устойчивое 9.4-4
— —- Штурма—Лиувилля 15.4-8
— — — — многомерное 15.4-9
Дифференциальные инварианты 16.10-7
— — тензора ранга 2 16.10-11
— параметры Бельтрами 17.3-7
Дифференциальный оператор набла 16.10-7
Дифференцирование вектор-функции 5.3-2
— ковариантное 16.10-4
— матриц 13.2-11
— по параметру 4.6-1
— случайных функций 18.9-4
—- функции 4.5-1
—- функциональных рядов 4.8-4
— численное 20.7-1
— — по отрезку ряда Фурье 20.7-1
Длина вектора 5.2-5, 16.8-1
— дуги 4.6-9, 5.4-4, 17.4-2
— интервала, обобщение 4.8-14
— касательной к окружности 2.5-1
Доверительная вероятность 19.5-5
— область 19.6-5
Доверительный интервал 19.6-5
Додекаэдр 1.10-6
Долгота 3.1-6 ,
Дополнение Л до В 12.8-1
— множества 4.3-2
— события 18.2-1
— элемента 12.8-1
Допустимое решение см. Решение
допустимое
Дробь непрерывная см. Непрерывная
дробь
— элементарная 1.7-4
Дуга жорданова 7.2-3
— простая 3.1-13
— регулярная 3.1-13, 17.2-1, 17.4-2
— спрямляемая 4.6-9
Б
Единица 12.2-1
3
Задача Больца 11.6-6
— вариационная, методы решения 11.6-4,
11.6-5, 11.6-9, 11.7-1, 11.7-2
— взаимно сопряженная 15.4-3
— Гурса 10.3-4
— Дирихле 15.6-2
— — для сферы 10.4-9
— изопериметрическая 11.6-3
— Коши 9.1-2, 10.2-2, 10.2-3
— — корректная 10.3-5
—- —, метод решения Милна
«предсказание коррекция» 20.8-3
— —, — — Эйлера 20.8-3
— —, методы решения многошаговые
20.8-3, 20.8-4
— —, — — одношаговые 20.8-2
, Рунге—Кутта 20.8-2, 20.8-4,
20.8-5, 20.8-6, 20.8-7, табл. 20.8-1
— —, — — типа «предсказание —
коррекция» 20.8-3, табл. 20.8-2
— —, схемы решения интерполяционно-
итерационные 20.8-3
— —, — — разностные 20.8-3
— —, — — экстраполяционные 20.8-3
— — физически реализуемая 9.4-3
808
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Задача Коши (г + 1)-я 9.3-4
— краевая см. Краевая задача
— линейного программирования 11.4-1
— — — в стандартной форме 11.4-1
— — — основная 11.4-1
Задача Майера 11.6-6
— навигационная Цермело 11.8-3
— начальная 9.1-2
— —, метод решения одношаговый 20.8-2
— —, — — Рунге—Кутта 20.8-2
— Неймана 15.6-2
— нелинейного программирования 11.4-3
— о встрече за минимальное время 11.8-3
— о диффузии, интегральное решение
Пуассона 15.5-3
— о переходе ракеты с одной орбиты на
другую 11.8-3
— о собственных значениях дискретная
15.4-11
— — — — для линейных
дифференциальных уравнений 15.4-5
— — — — для эрмитовых операторов
15.5-2
— — — — обобщенная 14.8-7
— — — — эрмитова 15.4-6, 15.4-7
— оптимального управления 11.8-1
— Плато 17.3-6
— регулирования по быстродействию
11.8-3
— с начальными условиями 10.2-2, 10.2-4
— управления 11.8-1
— Штурма—Лиувилля для уравнений с
частными производными второго
порядка 15.4-9
— — — о собственных значениях 15.4-8
Задачи линейного программирования
двойственные 11.4-1
— на условный экстремум 20.2-7
— управления шаговые 11.9-1
Закон ассоциативный 12.2-1
— — для умножения 12.3-1
— больших чисел 18.6-5
— дистрибутивный 12.3-1
— инерции квадратичных форм 13.5-4
— — эрмитовых форм 13.5-4
— исключенного третьего 12.8-6
— малых чисел 18.8-1
— сложения дисперсий 18.5-6
Законы де Моргана 12.8-1
Замкнутость 12.2-1
— по отношению к умножению 12.3-1
Замыкание множества 12.5-1
Затухание апериодическое 9.4-1
— критическое 9.4-1
Звено непрерывной дроби 4.8-8
Знаменатель прогрессии 1.2-7
Значение функции наибольшее 4.3-3
— — наименьшее 4.3-3
И
Игра безобидная 11.4-4
— конечная двух партнеров с нулевой
суммой 11.4-4
— с чистой стратегией 11.4-4
— симметричная 11.4-4
— со смешанной стратегией 11.4-4
Игрок максимизирующий 11.4-4
— минимизирующий 11.4-4
Идеал 12.3-2
— двусторонний 12.3-3
— левый 12.3-2
— правый 12.3-2
Излучение диполя 10.4-8
— точечного источника 10.4-8
Изображение 8.2-1
Изображение, асимптотическое
разложение 8.4-9
Изоклина 9.2-2,9.5-2
Изометрия 12.5-2
Изоморфизм 12.1-6
— булевых алгебр 12.8-5
Икосаэдр 1.10-6
Импульс полусинусоидальный 4.11-4
— прямоугольный 4.11-4
— трапецеидальный симметричный 4.11-4
— треугольный симметричный 4.11-4
Инвариант 14.1-4, 16.2-1
— изгибания 17.3-8
— скалярный 17.4-5
Инвариантность относительно
преобразования координат 14.1-4
— преобразований 12.1-5
Инварианты кривой второго порядка 2.4-2
— общего уравнения второй степени 3.5-2
— топологические 12.5-1
— функции Вейерштрасса 21.6-2
Инверсия точки 7.9-2
Индекс группы циклический 18.7-3
— замкнутой кривой 9.5-3
— изолированной особой точки 9.5-3
— подгруппы 12.2-2
— свободный 16.1-3
Индексные обозначения 16.1-3
Интеграл вероятностей 18.8-3, 21.3-2
— — дополнительный 21.3-2
— Дирихле 4.11-6
— дифференциального уравнения с
частными производными общий, частный,
особый, полный 10.1-2,10.2-3
— Дюамеля 9.4-3
— живых сил 9.5-6
— Зоммерфельда 21.8-2
— Лапласа 21.7-7
— Лебега кратный 4.6-15
— — от неограниченной функции 4.6-15
— — от ограниченной функции 4.6-15
— — по неограниченным интервалам
4.6-15
— —, свойства 4.6-15
— —, сравнение с интегралом Римана
4.6-15
— —, условие существования 4.6-15
— Лебега—Стилтьеса 4.6-17
— несобственный 4.6-2
— —, признаки сходимости 4.9-3
— особый 9.1-2, 9.2-2
— — по Коши, главные значения 4.6-2
— по объему 4.6-12
— — —, замена переменных 4.6-13
— по поверхности 4.6-12
— — —, замена переменных 4.6-13
— Римана 4.6-1, 4.6-15
— Римана—Стилтьеса 4.6-17
— случайной функции 18.9-4
— Сонина—Шлефли 21.8-2
— Стилтьеса 4.6-17
— стохастический 18.9-4
— типа Коши 7.5-1
— Фейера 4.11-6
— Фурье 4.11-3
— Шварца—Кристоффеля 7.9-4
— Шлефли 21.7-7
— Эйлера второго рода 21.4-1
— — первого рода 21.4-4
— эллиптический см. Эллиптический
интеграл
Интегралы Ломмеля 21.8-2
— Френеля 21.3-2
Интегральная кривая 9.1-2
— поверхность 10.2-1
— показательная функция 21,3-1
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
809
Интегральная сумма 4.6-1
— форма квадратичная действительная
15.3-6
— — эрмитова 15.3-6
— — — неотрицательная 15.3-6
— — — отрицательно определенная
15.3-6
— — — положительно определенная
15.3-6
Интегральное исчисление 4.1-1
— преобразование Ганкеля 8.6-4
— — единичное 15.3-1
— — конечное 8.7-1, 10.5-1, табл. 8.7-1
— — линейное 8.6-1,15.3-1
— —• —, матричное представление
15.3-1
— — символическое 15.3-1
— — Фурье 4.11-3
— — — обратное 4.11-4
— — —, свойства 4.11-5
— — Фурье—Бесселя 9.6-4
— уравнение 15.3-2
— — Абеля 15.3-10
— — Вольтерра второго рода 15.3-10
—- — — первого рода 15.3-10
— — линейное неоднородное второго рода
15.3-3
— — — однородное второго рода 15.3-2
— — — первого рода 15.3-2
— — общее 15.3-2
— — однородное 15.3-2
— — с эрмитовым ядром 15.5-2
— — типа Вольтерра 15.3-2
— — — Фредгольма 15.3-2
— — Фредгольма линейное второго рода
15.3-7, 15.3-8
— — — — первого рода 15.3-9
— — — однородное второго рода 15.3-2
Интегральные суммы Лебега 4.6-15
— теоремы 5.6-2, 16.10-11
— уравнения, численные методы решения
20.8-5
Интегральный косинус 21.3-1
— логарифм 21.3-1
— синус 21.3-1
Интегрирование 4.6-6
— вектор-функции 5.3-3
— дифференциальных уравнений 9.1-2
— многочленов 4.6-6
— неравенств 4.6-1
— по частям 4.6-1, 4.6-6
— подстановкой 4.6-1
— рациональных функций 4.6-6
— случайных функций 18.9-4
— тензорных величин 16.10-9
— функционального ряда 4.8-4
— численное см. Численное
интегрирование
— элементарных дробей 4.6-6
Интегрирующий множитель 9.2-4
Ичтегро-дифференциальное уравнение
15.3-2
Интенсивность белого шума 18.11-1
Интервал допуска 19.6-4
— неограниченный открытый 4.3-4
— ограниченный замкнутый 4.3-4
— — открытый 4.3-4
— полуоткрытый 4.3-4
— частичный 4.3-4
Интерквартильная широта 18.3-3
Интерполяционная формула 20.5-1
— — Бесселя 20.5-3
— — — модифицированная 20.5-3
— — — по двум переменным 20.5-6
— — Лагранжа 20.5-2
Интерполяционная формула Ньютона
20.5-2
— — Стеффенсена 20.5-3
— — Стирлинга 20.5-3
—- — Эверетта 20.5-3
— — л-го порядка 20.5-2
Интерполяционные формулы Ньютона
20.5-3
— — с центральными разностями 20.5-3
Интерполяционный многочлен 20.5-3
Интерполяция обратная 20.5-4
— — с помощью обращения рядов 20.5-4
— параболическая 20.5-2
— рациональными дробями 20.5-7
— с оптимальным выбором узлов 20.5-5
— тригонометрическая 20.6-6
— функций нескольких переменных 20.5-6
Испытание сложное 18.2-4
Испытания независимые 18.2-4
— — повторные 18.2-4
— по схеме Бернулли 18.7-4
Истинностная таблица 12,8-7
Итерационно-интерполяционный методЭйт*
кена 20.5-2
Итерационные методы численного решения
уравнений 20.2-2, 20.2-4
— формулы численного решения
уравнений 20.2-2
Итерационный процесс, оценка ошибки
20.2-2
— —, признак сходимости 20.2-2
— —, улучшение сходимости по Эйтке-
ну—Стеффенсену 20.2-2
Итерация Зейделя 20.3-2
— простая 20.3-2
К
Каноническая система уравнений Эйлера
11.6-8
Карданов подвес 14.10-6
Кардинальное число 4.3-2
— — бесконечное 4.3-2
Кардиоида 2.6-1
Карта Карно 12.8-7
Касание м-го порядка 17.1-5, 17.2-6
Касательная к кривой плоской 17.1-1
— — — пространственной 17.2-2, 17.2-4
—, направляющие косинусы 17.2-4
— плоскость 17.2-2
— — к поверхности второго порядка 3.5-8
Квадрант 2.1-2
Квадрат 1.10-1
Квадратичная форма 13.5-2
— — действительная 13.5-2
— — неопределенная 13.5-2
— — неотрицательная 13.5-2
— — неположительная 13.5-2
— — отрицательно определенная 13.5-2
— — — полуопределенная 13.5-2
— — поверхности вторая основная 17.3-5
— — — первая основная 17.3-3
— — положительно определенная 13.5-2
— — — полуопределенная 13.5-2
— — симметрическая 13.5-2
— — характеристическая 2.4-5, 3.5-4
Квадратурная формула Гаусса 20.7-8
— — Гаусса—Чеоышева 20.7-3
— — Грегори 20.7-2
— — двумерная 20.7-5
— — Лагерра 20.7-3
_ _ Чебышева 20.7-3
— — Эрмита 20.7-3
Квадратурные формулы Ньютона— Котеса,
замкнутый тип 20.7-2
810
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Квадратурные формулы, построение и
сравнение 20.7-4
Квадрика 3.5-1
Квадриполь 15.6-5
Квазилинеаризация 20.9-3
Квантиль порядка Р 18.3-3
Квартиль 18.3-3
Кватернион 12.4-2
Класс вычетов по модулю 12.2-10
— геометрических объектов 16.1-4
— инвариантных объектов 16.1-4
— распределений Кэптейна 19.3-2
— смежный левый, правый 12.2-4
— сопряженных элементов 12.2-5
Ковариация 18.4-4, 18.4-8
Колебание вынужденное 9.4-8
— затухающее 9.4-1
— свободное 9.4-8
— собственное 9.4-1
Колебания круглой мембраны свободные
10.4-9
— упругие 10.4-1
— упругой струны свободные 10.4-9
— характеристические 10.4-9
Коллокация 20.9-9
Кольцо 12.3-1
— без делителей нуля 12.3-1
— коммутативное 12.3-1
— с единицей 12.3-1
Коммутатор операторов 14.4-2
Компакт 12.5-4
Комплексная плоскость 1.3-2, 7.2-4
Комплексные числа сопряженные 1.3-1
Комплексный контурный интеграл 7.2-5
Композиционный ряд 12.2-6
— фактор 12.2-6
Компонента 14.1-2
Компоненты вектора физические 16.8-3
— метрического тензора 6.2-3, 16.7-1
— момента мультиполя 15.6-5
— тензора 16.2-1
— — физические 16.8-3
— функции 16.1-3
Конические сечения 2.4-1
Контур 7.2-3
Конус 1.10-4, 3.1-15
— действительный 3.5-7, 3.5-10
— Монжа 10.2-1
Конфигурация эквивалентные по
отношению к группе 18.7-3
Конформное отображение 7.9-1
Конхоида Никомеда 2.6-1
Конъюнкция 15.4-3
Координата 14.1-2
Координатная гиперповерхность 17.4-2
— линия 6.2-2, 17.4-2
— поверхность 6.2-2
Координатные линии на поверхности 17.3-1
— плоскости 3.1-2
Координаты биполярные 6.5-10
— бицилиндрические 6.5-10
— вектора 5.2-2
— — декартовы прямоугольные 5.2-3
— — ковариантные 6.3-3
— — контравариантные 6.3-3
— — физические 6.3-2
— геодезические нормальные 17.4-7
— — полярные 17.3-13
— декартовы 2.1-2, 3.1-2
— — прямоугольные, общее
преобразование переноса и поворота 3.1-12
— — —, одновременное преобразование
переноса и поворота 2.1-7
— — —, преобразование параллельного
переноса 2.1-5, 3.1-12
— — —-, — поворота 2.1-6, 3.1-12
Координаты декартовы, связь о
полярными 2.1-8
— изотермические 17.3-10
— изотропные 17.3-10
— конические 6.5-6
— криволинейные на поверхности 17.3-1
— — ортогональные, векторное
произведение в.4-2
— — —, векторный элемент линии 6.4-3
— — —, дифференциальные операторы
6.4-2
— — —, криволинейный интеграл 6.4-8
— — —, площадь поверхности 6.4-3
— — —, символы Кристоффеля 6.5-1
— — —, скалярное произведение 6.4-2
—- — —, элемент объема 6.4-3
— — точки 6.2-1
— —, элемент длины дуги 6.2-3
Координаты линейные 2.3-3, 3.4-4
— неподвижной системы 14.10-5
— нормальные 9.4-8, 13.6-2
— ортогональные 17.4-7
— параболические 6.5-8, 6.5-9
— параболического цилиндра 6.5-9
— параболоидальные 6.5-7
— плюккеровы 2.3-3, 3.4-4
— повернутой системы 14.10-7
— полугеодезические 17.3-13, 17.4-7
— полярные 2.1-8, 6.5-1
— —, связь с декартовыми 2.1-8
— римановы с началом О 17.4-7
— середины отрезка 2.1-4, 3.1-7
— сферические 3.1-6, 6.5-1
— —, связь с декартовыми 3.1-6
— тангенциальные 2.3-3, 3.4-4
— тензора 16.2-1
— тороидальные 6.5-11
— точечные 2.3-3
— точки 2.1-1, 16.1-2
— —, делящей отрезок в отношении к
2.1-4, 3.1-7
— — пересечения трех плоскостей 3.4-5
— фокуса 2.4-9, 17.3-11
— функции 16.1-3
— центра кривизны 17.1-4
— — поверхности второго порядка 3.5-5
— цилиндрические 3.1-6, 6.5-1
— —, связь с декартовыми 3.1-6
— эллипсоида вращения вытянутого
6.5-3
— — — сплюснутого 6.5-4
— эллипсоидальные общие 6.5-2
— эллиптического цилиндра 6.5-5
Корень алгебраического уравнения 1.6-2
— — — кратный 1.6-3
— арифметический из действительного
числа 1.2-1
— — л-й степени 1.2-1
— из комплексного числа 1.3-3
Корректность определения операции 12.1-4
Корреляция отрицательная 20.10-2
— ранговая по Спирмену 19.7-6
Косинус амплитуды 21.6-7
Косинус-интеграл Фурье 4.11-3
Косинус-преобразование конечное табл.
8.7-1
— Фурье 4.11-3
Коэффициент асимметрии 18.3-3
— вариации 18.3-3
— затухания 9.4-1
—- искажения 7.9-1
— корреляции 18.4-4, 18.4-8, 18.4-9
— — сводный 18.4-9
— — ранговой 19.7-6
— разброса 18.4-8
— регрессии 18.4-6, 18.4-9
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
811
Коэффициент регрессии, проверка
гипотетического значения 19.7-4
— чувствительности 13.6-4
— эксцесса* 18.3-3
Коэффициенты алгебраического уравнения
1.6-3
— биномиальные, см. Биномиальные
коэффициенты
— мультиномиальные табл. 18.7-1
— Фурье 4.11-1
Краевая задача 9.1-2
— — двумерная, решение посредством
функции Грина 15.6-9
— — двухточечная, приведение к задаче
Коши 9.3-4
— — для уравнения гиперболического
10.3-4
— — — — параболического 10.3-4
— — — — эллиптического 10.3-4
— — корректная 10.3-4
— — линейная 10.4-2, 15.4-1, 15.4-2
— — общая, связь с интегральным
уравнением 15.5-2
— —, решение 15.4-12
— —, — методом интегральных
преобразований 10.5-1, 10.5-3
— —, — разложением в ортогональные
ряды 10.4-9
— — самосопряженная 15.4-3
— — трехмерная, решение посредством
функции Грина 15.6-6
— — эрмитово сопряженная 15.4-3
Краевые условия 15.4-1
— — взаимно сопряженные 15.4-3
— — дополнительные 15.4-2
— — Неймана 15.5-7
— — эрмитово сопряженные 15.4-3
Крамера правило 1.9-2
Кратность собственного значения
алгебраическая 14.8-3
— — — геометрическая 14.8-3
Кратные интегралы, вычисление 20.7-5
«Крест» 2.6-1
Кривая, асимптотически приближающаяся
к прямой 17.1-6
— вогнутая 17.1-4
— второго порядка 2.4-1
— — —, инварианты 2.4-2
— — — невырожденная, геометрическое
определение 2.4-9
— — — центральная 2.4-6
— выпуклая 17.1-4
— жорданова замкнутая 7.2-3
— изотропная 17.3-10, 17.4-4
— минимальная 17.3-10
— непрерывная 3.1-13, 7*2-3
— нулевой длины 17.4-4
—, параметрическое задание 2.1-9
— простая 7.2-3
— — в смысле Жордана 3.1-13
— -г замкнутая 3.1-13, 7.2-3
— регулярная 3.1-14
— средней квадрэтической регрессии
18.4-6
— характеристическая 10.3-1
— л-го порядка 2.1-9
Кривизна 17.1-4, 17.2-3
— гауссова 17.3-5
— геодезическая 17.3-4
— нормальная 17.3-4
— нормального сечения 17.3-5
— области интегральная 17.3-14
— первая 17.4-2
— полная 17.2-3, 17.3-5
— скалярная 17.4-5
— средняя 17.3-5
Кривизна, формула 17.2-4
Кривизны главные 17.3-5
Криволинейные координаты см.
Координаты криволинейные
Криволинейный интеграл 4.6-10
— — векторный 5.4-5
— — скалярный 5.4-5
— —, условие независимости от пути
интегрирования 5.7-1
Кривые второго порядка вырожденные
2.4-8
— плоские алгебраические, примеры 2.6-1
— — трансцендентные, примеры 2.6-2
Критерии непараметрические 19.1-3
Критерий знаков односторонний,
двусторонний 19.6-8
— значимости 19.6-4
— качества 11.8-1
— Коши равномерной сходимости
несобственных интегралов 4.9-4
— — — — последовательностей или
рядов 4.9-2
— — сходимости несобственных
интегралов 4.9-3
последовательностей или рядов
4.9-1
— Льенара—Шипара 1.6-6
— некоррелированности величин 19.7-4
— Рауса—Гурвица 1.6-6
— с фиксированной выборкой 19.6-9
— статистической гипотезы 19.6-2
— — — наиболее мощный 19.6-3
— — — несмещенный 19.6-3
— — — равномерно наиболее мощный
19.6-3
— — — смещенный 19.6-3
— х8 с оцениваемыми параметрами 19.6-7
— — согласия 19.6-7
Критерий-функционал 11.8-1, 11.8-4
Критическая область 19.6-2
Критическое множество 19.6-2
Круг 1.10-3
— кривизны 17.1-4, 17.2-2
— сходимости степенного ряда 7.5-2
Кручение 17.2-3
—, формула 17.2-4
Куб 1.10-6
Л
Лапласиан 5.5-5, 5.5-6
— скаляра 16.10-7
Лемма Абеля 4.8-5
— Жордана 7.7-3
— основная вариационного исчисления
11.6-1
— Шура 14.9-2
Леммы фундаментальные вариационного
исчисления 11.6-1
Лемниската Бернулли 2.6-1
Линейная алгебра над кольцом 12.4-2
— функция 11.4-1
Линейное многообразие 14.2-1
— —, линейный базис 14.2-4
— программирование 11.4-1
Линейные дифференциальные уравнения
сопряженные 13.6-3
— ограничения-неравенства 11.4-1
— ограничения-равенства 11.4-1
Линейный интеграл 5.4-5
— функционал 14.4-9
Линии градиента 5.5-1
— пересечения поверхности с
координатными плоскостями 3.1-16
Линия асимптотическая 17.3-6
812
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Линия геодезическая 17.3-12, 17.4-3
— — нулевой длины 17.4-4
— кривизны 17.3-6
— пересечения двух поверхностей 3.1-16
— тока 5.4-3
— узлов 14.10-6
— характеристическая 10.2-1
Логарифм 21.2-10
— действительного числа 1.2-3
— — —, свойства 1.2-3
— десятичный 1.2-3
-— натуральный (неперов) 1.2-3
Логарифмическая точка разветвления
7.4-2
Логарифмический декремент 9.4-1
Логика Аристотелева 12.8-6
— двузначная 12.8-6
— символическая 12.8-6
Локон Аньези 2.6-1
Ломаная Эйлера 20.8-2
Х-дискриминантная кривая 17.1-7, 17.3-11
М
Максимум внутренний 11.2-1, 11.3-1
— граничный 11.2-11, 11.3-1
— кратного интеграла 11.6-9
— локальный 11.2-1, 11.3-1
— нестрогий 11.2-1
— определенного интеграла 11.5-2
— — — внутренний 11.5-2
— — — граничный 11.5-2
_ __ _ сильный 11.5-2
— — — слабый 11.5-2
— условный 11.3-4
— функции абсолютный 4.3-3
Математическая операция 12.1-1
— статистика 19.1-1
Математическое ожидание случайной
величины 18.3-3
— — суммы случайных величин 18.5-6
— — условное 18.4-5, 18.4-9
— — функции от случайной величины
18.3-3, 18.4-4, 18.4-8
Матрица аддитивно обратная 13.2-3
— альтернирующая 13.3-2
— антисимметрическая 13.3-2
— ассоциированная 13.3-1
— бесконечная 13.2-1
— , вековое уравнение 13.4-5
— вращений 14.10-6
— выигрышей 11.4-4
— Грина 9.4-3, 13.6-2
— действительная 13.2-1
— диагональная 13.2-1
— единичная порядка п 13.2-3
— изменения состояния 20.4-7
— квадратная вполне приводимая 14.8-2
— — невырожденная 13.2-3
— — неособенная 13.2-3
— — порядка п 13.2-1
— —, приведение к диагональному виду
13.4-4
— — — к треугольному виду 13.4-3
— — приводимая 14.8-2
— — разложимая 14.8-2
— —, собственные значения 13.4-2
— —, — числа 13.4-2
— —, условие невырожденности 13.2-3,
13.4-2
— —, характеристические числа 13.4-2
— —, целочисленные степени 13.2-4
— клеточная 13.2-9
— —, собственные значения 13.4-6
— —, спектр 13.4-6
— комплексно сопряженная 13.3-1
Матрица конечная 13.2-1
— корреляционная 18.4-8, 18.10-2
— кососимметрическая 13.3-2
— косоэрмитова 13.3-2
— модальная 14.8-6
— моментов 18.4-8
— — выборки 19.7-2
— мономиальная 13.2-1
— над полем комплексных чисел
ограниченная 13.2-1
— наддиагональная 13.2-1
— неотрицательная 13.5-2
— неположительная 13.5-2
— нормальная 13.3-4
— нулевая 13.2-3
— ортогональная 13.3-2
— отрицательно определенная 13.5-2
— — полуопределенная 13.5-2
— передаточная 9.4-7
— перестановки 13.2-6
— положительно определенная 13.5-2
— — полуопределенная 13.5-2
—, правила комбинирования 13.3-3
— присоединенная 13.3-1
— противоположная 13.2-3
— прямоугольная размера т х п над
полем 13.2-1
—, разбиение на клетки 20.3-4
— решений фундаментальная 13.6-3
— самосопряженная 13.3-2
— симметрическая 13.3-2
— системы 1.9-4
— — расширенная 1.9-4
—, соответствующая сопряженному
оператору 14.7-5
— сопряженная 13.3-1
—, спектр собственных значений 13.4-2
— строго треугольная 13.2-1
—, теоремы о разложении 13.3-4
— транспонированная 13.3-1
— треугольная 13.2-1
— унимодулярная 14.10-4
— унитарная 13.3-2
—, характеристическое уравнение 13.4-8
— эрмитова см. Эрмитова матрица
— эрмитово сопряженная 13.3-1
Матрица-столбец 13.2-1
Матрица-строка 13.2-1
Матрицы конгруэнтные 13.4-1
— подобные 13.4-1
— просто эквивалентные 13.4-1
—, равные друг другу 13.2-2
—, связанные преобразованием подобия
13.4-1
— соединенные 13.4-1
— эквивалентные 13.4-1
Медиана 1.11-3
— распределения 18.3-3
Мера 12.8-8
— асимметрии пирсоновская 18.3-3
— Лебега в пространствах двух, трех,...
измерений 4.6-14
— — внешняя 4.6-14
— — внутренняя 4.6-14
— —, определение аксиоматическое 4.6-14
— —, — конструктивное 4.6-14
— Лебега — Стилтьеса 4.6-17
— точности 18.8-4
Метод Бэрстоу решения алгебраических
уравнений 20.2-4
— взаимных градиентов 20.3-2
— вращения 20.3-5
— вспомогательных функций решения
задачи на условный экстремум 20.2-6
— Галеркина. 20.9-10
— Гаусса 20.3-1
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
813
Метод градиента 20.2-4, 20.3-2
— Горнера 20.2-5
— Греффе — Лобачевского 20.2-5
— Димсдейла 20.8-4
— динамического программирования 11.8-6
— Зейделя 20.3-2
— значимой выборки 20.10-3
— исключения, матричная запись 20.3-2
— — по главным элементам 20.3-1
— исследования устойчивости по
Ляпунову 13.6-7
— итерационный отыскания собственных
значений и собственных векторов
матрицы 20.3-5
— квазилинеаризации для решения
нелинейных двухточечных краевых задач
20.9-3
— коллокации 20.8-4, 20.8-5
— Крылова — Боголюбова
приближенного решения дифференциальных
уравнений 9.5-5
Майера решения дифференциального
уравнения Пфаффа 2.6-2
— матричный численного решения
уравнений 20.2-5
— Милна «предсказание — коррекция»
20.8-3, табл. 20.8-2
— моментов для отыскания оценок 19.4-3
— Мюллера решения уравнений 20.2-4
— наибольшего правдоподобии для
отыскания оценок 19.4-4
— наименьших квадратов 20.9-10
— — — дискретный 20.5-1
— наискорейшего спуска 20.2-7, 20.3-2
— Нумерова решения линейных
дифференциальных уравнений 20.8-7
— Ньютона численного решения
уравнений 20.1-2, 20.2-8, 20.9-3
— Падэ 20.1-7
— Пикара последовательных
приближений 20.8-6
— преобразования Лапласа 20.4-6
— проб 20.2-2
— простой итерации 20.3-2
— расслоенной выборки 20.10-2
— секущих 20.2-2
— случайных возмущений 20.2-6
— средних квадрэтических приближений
20.9-9
— функций Грина для неоднородных
краевых условий 15.5-4
— — —, приложение к задаче с
начальными условиями 15.5-3
— Хемминга «предсказание — коррекция»
20.8-2
— чисто случайного поиска 20.2-6
— Штурма 1.6-6
— Эйлера решения задачи Коши 20.8-2
— г-преобразования для линейных
разностных уравнений 20.4-6
Методы аппроксимирующих функций
20.9-9, 20.9-10
— возмущений 11.4-2, 13.6-4
— генерирования случайных чисел 20.10-4
— исключения 20.3-1
— итерационные численного решения
системы уравнений 20.2-6, 20.3-2
_____ __ уравнения 20.2-2, 20.2-4
— многошаговые решения задачи Коши
20.8-3
— — улучшенные 20.8-4
— Монте-Карло 20.10-1
—- одношаговые решения задачи Коши
20.8-2
— поиска 20.2-6
— релаксации 20.3-2
Методы Рунге-Кутта решения задачи Коши
20.8-2, 20.8-4 — 20.8-7, табл. 20.8-1
— типа «предсказание— коррекция» 20.8-3
табл. 20.8-2
— третьего порядка 20.8-2
— уменьшения дисперсии оценки 20.10-2
— четвертого порядка 20.8-2
Метрика 12.5-2
— в пространстве L2 15.2-2
Метрическая эквивалентность функций
15.2-2
Минимум внутренний 11.2-1, 11.3*1
— граничный 11.2-1, 11.3-1
— кратного интеграла 11.6-9
— локальный 10.2-1, 11.3-1
— нестрогий 11.2-1
Минимум определенного интеграла 11.5-2
— — — внутренний 11.5-2
— — — граничный 11.5-2
—- — — сильный 11.5-2
— — — слабый 11.5-2
— условный 11.3-4
— функции абсолютный 4.3-3
Минор 1.5-2
— главный 1.5-4
— дополнительный 1.5-4
— ш-го порядка 1.5-4
Мнимая единица 1.3-1
— ось 1.3-2
— часть комплексного числа 1.3-1
Многогранник решений задачи линейногв
программирования 11.4-1
Многогранники правильные 1.10-6
Многообразие начальных и конечных
состояний 11.8-1
Многообразия инвариантные 14.8-2
Многоугольники правильные 1.10-1, 1.10-2
Многочлен 1.4-3, 7.6-5
—, алгоритм деления 1.7-2
—, разложение на множители 1.7-1
— симметрический 1.4-3
— тригонометрический 4.11-2
Многочлены Бернулли 21.5-2, 21.5-3
— — порядка п 21.5-2
— Гегенбауэра 21.7-8
— гипергеометрические 21.7-8
— Лагерра обобщенные 21.7-5
— Лежандра первого рода 21.7-3
— —, теорема сложения 21.8-3
— ультрасферические 21.7-8
— Чебышева первого, второго рода 20.6-3^
21.7-7, табл. 20.6-1
— — смещенные 20.6-4, табл. 20.6-1
— Якоби 21.7-8
Множества отделенные 12.5-1
Множество бесконечное 4.3-2
— векторов линейно зависимое 14.2-3
— — — независимое 14.2-3
— вполне упорядоченное 12.6-2
— всюду плотное 12.5-1
— выпуклое 11.4-1
— дискретное 4.3-6
— допустимых значений задачи линейного
программирования 11.4-1
— замкнутое 4.3-6, 12.5-1
— значений функции 4.2-1
— измеримое с мерой Лебега 4.6-14
— компактное 12.5-1
— — в себе 12.5-1
в С 12.5-1
— конечное 4.3-2
— линейно упорядоченное 12.6-2
— неограниченное 4.3-3
— ограниченное 4.3-3, 4.3-6, 12.5-3
— открытое 4.3-6, 12.5-1
— относительно компактное 12.5-1
814
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Множество полное 12.6-1
— производное 12.5-1
— просто упорядоченное 12.6-2
— пустое 4.3-2
— связное 4.3-6, 12.5-1
— собственное 4.3-2
— совершенно упорядоченное 12.6-2
— счетное 4.3-2
— топологического пространства
открытое 12.5-1
— точечное линейное 4.3-1
— условно полное 12.6-1
— частично упорядоченное 12.6-1
— элементарных событий 18.2-7
Множители Лагранжа 11.3-4, 11.6-2
— многочлена 1.7-1
Множитель левый 16.9-1
— многочленов общий 1.7-3
— нормирующий 18.3-4
— правый 16.9-1
Мода распределения дискретного 18.3-3
— — непрерывного 18.3.3
Модели изоморфные 12.1-6
Модель 12.1-1
— математическая 12.1-1
— термоэлектронного тока 18.11-4
Модули дополнительные полного
нормального эллиптического интеграла Ле-
жандра 21.6-6
Модуль 12.2-10
— вектора 5.2-5, 14.2-5, 16.8-1
— действительного числа 1.3-2
— комплексного числа 1.3-2
—■ нормального эллиптического
интеграла Лежандра 21.6-6
Модулярный Угол нормального
эллиптического интеграла Лежандра 21.6-6
Момент выборочный 18.9-1
— корреляционный 18.4-4
— случайной величины 18.3-7, 18.4-4,
18.4-8
— — — абсолютный 18.3-7
— — — начальный 18.3-7, 18.4-4, 18.4-8
— — — факториальный 18.3-7
— — —- — центральный 18.3-7
— центральный 18.3-7, 18.4-4, 18.4-8
— — — —- второго порядка 18.4-4,
18.4-8
Мощность критерия 19.6-2
— множества 4.3-2
Н
Направление асимптотическое 17.3-6
— главное Риччи 17,4-5
—- главной нормали 17.4-2
— изотропное 17.4-4
— кривой 17.4-2
—- координатных линий положительное
6.2-3
— положительное 7.2-4
— положительной нормали 17.3-2
Направления сопряженные 17.3-6
Направляющая конуса 3.1-15
— цилиндра 3.1-15
Направляющие косинусы 2.1-4, 3.1-8
— — вектора 5.2-3
— — прямой 3.3-1
Направляющий вектор прямой 3.3-1
Натуральные числа, принцип полной
индукции 1.1-2
Невязка 20.2-4
Нелинейное программирование 11.4-3
Неопределенный интеграл 4.6-4
— — от вектор-функции 5.3-3
Непрерывная дробь 4.8-9
Непрерывность суммы функционального
ряда 4.8-4
— функции 4.4-6
— — равномерная 4.4-6
Неравенства 1.1-5, 12.6-2, 12.6-3
Неравенство Адамара 1.5-1
— Бесселя 14.7-3, 15.2-3
— Гельдера 4.6-19
— Коши 1.3-2
— Коши — Буняковского 4.6-19
— Коши — Шварца 4.6-19, 14.2-6, 15.2-1
— Минковского 4.6-19, 14.2-5, 15.2-1
— Сильвестра 13.2-7
— треугольника 12.5-2
— Чебышева 18.3-5
Несобственный интеграл 4.6-2
— — сходящийся 4.6-2
— __ __ абсолютно 4.6-2
— — — равномерно 4.6-2
— — — условно 4.6-2
Норма вектора 14.2-5, 15.2-1, 16.8-1
— матрицы 13.2-1
— — евклидова 13.6-5
—- оператора конечная 14.4-1
— функции 15.2-1
Нормализатор подгруппы 12.2-7
— элемента 12.2-7
Нормаль главная 17.2-2, 17.2-4
— —, направляющие косинусы 17.2-4
— к кривой 17.1-2
— к поверхности 17.3-2
— — — второго порядка 3.5-8
Нормальная плоскость 17.2-2, 17.2-4
— производная от скалярной функции
5.6-2
— реакция на внешнюю нагрузку 9.4-2
— — на единичный импульс 9.4-3
Нормальное сечение 17.3-4
Нормальные сечения главные 17.3-5
Нормальный делитель 12.2-5
— ряд 12.2-6
Нормирование 18.3-4
— последовательности функций 15.2-5
— случайной величины 18.5-3
— функции 15.2-1
Нормы матриц табл. 13.2-1
Нули ортогональных многочленов 21.7-2
— цилиндрических функций 21.8-3
Нуль 1.1-2
— функции 1.6-2, 7.6-1
— — порядка m 7.6-1
Нуль-тензор 16.3-2
О
Область 4.3-6
—- Дирихле 15.6-2
— допустимых управлений 11.8-1
— замкнутая 4.3-6
— измеримая по Жордану 4.6-11
— квадрируемая 4.6-11
— многосвязная 4.3-6
— ограниченная 7.2-4
— односвязная 4.3-6
— определения 4.2-1
— с естественными границами 7.8-1
— отбрасывания 19.9-3
— принятия гипотезы 19.9-3
— функции фундаментальная 7.9-1
— целостности 12.3-1
Образ модели гомоморфный 12.1-6
Образующая линейчатой поверхности 3.1-15
Обращение матриц 20.3-3, 20.3-4
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
815
Обращение преобразования Лапласа 8.2-5,
8.2-6, 8.2-8
Обход положительный 7.2-4
Объединение 4.3-2
— событий 18.2-1
Объект абсолютно антисимметричный по
всем индексам 16.Б-1
— — симметричный по всем индексам
15.6-1
— антисимметричный по паре индексов
16.5-1
— — по всем индексам 16.5-1
— кососимметричный по паре индексов
16.5-1
—- симметричный по паре индексов 16.5-1
— — по всем индексам 16.5-1
Объем выборки 19.1-1
— области 4.6-11
— параллелепипеда 8* 1-11
— тетраэдра 3.1-11
Объемный интеграл векторный 5.4-7
— —, связь с поверхностным 5.6-1
— — скалярный 5.4-7
Овалы Кассини 2.6-1
Огибающая поверхность 17.3-11
— семейства интегральных кривых 9.2-2
— — плоских кривых 17.1-7
Ограничение-неравенство К-го порядка для
переменных состояния 11.8-4
Одночлен 12.8-2
Окрестность точек -{-со, —оо 4.3-5
—точки 4.3-5, 7.2-2, 12.5-1, 12.5-3
Окружности концентрические 2.5-1
—, условие ортогональности 2.5-1
Окружность 1.10-3, 2.5-1
— девяти точек 1.11-2
— Фейербаха 1.11-2
Октаэдр 1.10-6
Октиполь 15.6-5
Операнд 12.1-1
Оператор антисимметрический 14.4-6
— взаимно сопряженный 15.4-3
— кососимметрический 14.4-6
— косоэрмитов 14.4-4
— Лапласа 5.5-5, 16.10-7
—- —, правила повторного применения
5.5-6
— линейный 14.3-1
— — бесконечно малый 14.4-10
— — вполне приводимый 14.8-2
— — невырожденный 14.3-5
— — несобственный 14.3-5
— — ограниченный 14.4-1
— —, отыскание собственных векторов
14.8-5
— —, — — значений 14.8-5
— —, представление в различных
базисах 14.6-2
— —, — диадическое 14.5-4
— —, — матричное 14.5-2
— — приводимый 14.8-2
— разложимый 14.8-2
— —, характеристическое уравнение
14.8-3
— набла (V) 5.5-2, 5.5-8
— —, свойства 5.5-2
— нормальный 14.4-8
— —, спектральное представление 14.8-4
— обратный 14.3-5
— ортогональный 14.4-6
—, правила комбинирования 14.4-7
— резольвентный 14.8-3
— самосопряженный 15.4-3
— — Штурма — Лиувилля 15.4-3
— симметрический 14.4-6
— смещения 20.4-2
Оператор сопряженный 14.4-3, 14.4-9
—, теоремы о разложении 14.4-8
— транспонированный 14.4-6
— унитарный 14.4-5
— усреднения 20.4-2
—, целые степени 14.3-6
— эрмитов 14.4-4, 15.4-3
— — неотрицательный 14.4-4
— — неположительный 14.4-4
— — отрицательно определенный 14.4-4
— — — полуопределенный 14.4-4
— — положительно определенный 14.4-4
— — — полуопределенный 14.4-4
— — самосопряженный 14.4-4
— —, спектральное представление 14.8-4
Операторы дифференциальные эрмитово
сопряженные 15.4-3
—, последовательное применение 14.6-3
— разностные 20.4-2
— — двумерные 20.9-4
—, соотношения между ними 20.4-2
Операции над векторными функциями 5.5-1
— — скалярными функциями 5.5-7
Операция 12.1-1
— коммутативная 12.2-1
— корректная 12.1-4
— линейная 14.3-1
Опорный план 11.4-1
Определение аксиоматическое 12.1-1
— конструктивное 12.1-1
Определенный интеграл в смысле Римана
4.6-1
— —, важнейшие свойства 4.6-1
— —, вычисление с помощью теоремы
о вычетах 7.7-3
от вектор-функции 5.3-3
Определитель 1.5-1
— Вандермонда 1.6-5
— Вронского 9.3-2
— Грама 5.2-8
—, изменение порядка 1.5-7
— Казоратти 20.4-4
— метрического тензора 17.3-7
— оператора 14.6-2
—, разложение Лапласа 1.5-4
—, свойства 1.5-5
— системы линейных уравнений 1.9-2
Оптимальное решение 11.4-1
Оптимальный план 11.4-1
Ордината 2.1-2
Оригинал 8.2-1
—, асимптотическое разложение 8.4-9
Орт 5.2-5
Ортогонализация последовательности
функций 15.2-5
Ортогональная проекция пространства
14.2-8
Ортогональные многочлены 21.7-1. 21.7-2
Оси координат 2.1-2, 3.1-2
Основание степени 1.2-1
Особая точка вырожденная 9.3-10
— — функции 7.6-2
Особенность функции 7.6-2
— — изолированная 7.6-2
— — устранимая 7.6-2
Остаток 1.7-2
— ряда 4.7-1
Остаточный член 20.5-2
— — ряда Лорана 7.5-3
-— — — Тейлора 7.5-2
— — формулы Тейлора 4.10-4
— — — — в форме Лагранжа 4.10-4
Ось вращения 14.10-2
— гиперболы действительная 2.5-2
— — мнимая 2.5-2
— эллипса большая, малая 2.5-2
816
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Отклонение вероятное (в. о.) 18.8-4
— от точки до прямой 2.3-1
— радиальное 18.8-7
— среднее абсолютное (с. а. о.) 18.3-3
— — квадр этическое 18.3-3
— точки от плоскости 3.4-2
Отношение включения логическое 12.8-3,
18.2-1
— неполной бета-функции 21.4-5
— порядка 12.6-1
— равенства, симметрия 1.1-3, 12.1-3
— —, транзитивность 1.1-3, 12.1-3
— Стьюдента 19.5-3
— тождества 1.1-4
— эквивалентности 12.1-3
Отображение взаимно однозначное 12.1-4
— дробно-линейное 7.9-2
— Жуковского 7.9-3
— изогональное 7.9-1
— изометрическое 17.3-10
— класса в класс 12.1-4
— конформное 7.9-1, 17.3-10
— — второго рода 7.9-1
— непрерывное в топологическом
пространстве 12.5-1
— — в точке 12.5-1
— обратное 12.1-4
— однозначное 12.1-4
— сжатое 12.5-6
— топологическое 12.5-1
— эквиареальное 17.3-10
-а,=т(г + т)7-9-3
Отражение экстремалей от граничной
линии 11.6-7
Отрезок 4.3-4
Отрицание логического события 18.2-1
Оценка асимптотически эффективная 19.4-1
— достаточная 19.4-1
— несмещенная 19.1-3, 19.4-1
— ошибки приближения 20.2-2
— по Байесу 19.9-2
— по методу наименьших квадратов 19.9-4
— совместная асимптотически
эффективная 19.4-1
— совместно достаточная 19.4-1
— — эффективная 19.4-1
— состоятельная 19.1-3, 19.4-1
— эффективная 19.1-3, 19.4-1
Ошибка 20.2-4
— вероятная круговая 18.8-7
— второго рода 19.6-2
— квадратичная средняя взвешенная
20.5-1
— начальных данных 20.1-2
— округления 20.1-2
— первого рода 19.6-2
— радиальная 18.8-7
— — средняя 18.8-7
Ошибка, см. также Погрешность
— усечения 20.1-2, 20.8-1
— — локальная 20.8-1
П
Пара полярно сопряженных прямых 3.5-8
Парабола 2.4-8,. 2.4-9
Нейля 2.6-1
— полукубическая 2.6-1
—, построение 2.5-4
—, — касательных и нормалей 2.5-4
Параболоид гиперболический 3.5-7, 3.5-10
— эллиптический 3.5-7, 3.5-10
Параллелограмм периодов 21.6-1
Параллельность прямых 2.3-2
Параллельные геодезические 17.4-6
Параметр генеральной совокупности 19.1-2
— нормального эллиптического
интеграла Лежандра третьего рода 21.6-6
Параметрическое задание кривой 3.1-13
— — плоскости 3.2-2
Параметры Кэли — Клейна 14.10-4
— Эйлера 14.10-3
Первообразная 4.6-4
Переменная зависимая 4.2-1
— канонически сопряженная 11.6-8
— независимая 4.2-1
— присоединенная 11.6-8
— состояния 11.8-1, 13.6-1
— управляющая 11.8-1, 11.9-1
— фазовая 11.8-1, 13.6-1
Переменные сопряженные 11.8-2
Пересечение 4.3-2
Период примитивный 21.6-1
— функции 4.2-2
Перпендикулярность прямых 2.3-2
Пирамида 1.10-4
План задачи линейного
программирования в стандартной форме 11.4-1
— опорный 11.4-1
— оптимальный 11.4-1
Плоскость 3.2-1
Плотность распределения вероятностей
18.3-2, 18.4-3
— — нормального 18.8-4
— — случайных величин 18.5-4
— — условная 18.4-5
— спектральная взаимная по множеству
наблюдений 18.10-3, 18.10-6
— — мощности взаимная 18.10-5
— — по времени 18.10-8
— стандартизованной случайной величины
19.3-3
Площадь области 4.6-11
— параллелограмма 3.1-10
— поверхности 4.6-11
— треугольника 2.1-4, 2.1-8, 3.10-10
Поверхности второго порядка,
классификация 3.5-3
— — —, параметрическое задание 3.5-10
Поверхностный интеграл векторный 5.4-6
— —, связь с объемным 5.6-1
— — скалярный 5.4-6
Поверхность вращения 3.11-15
— второго порядка 3.5-1
— — — центральная 3.5-5
— как риманово пространство 17.3-7
— линейчатая 3.1-15
— минимальная 17.3-6
— непрерывная 3.1-14
— простая 3.1-14
— регулярная 3.1-14
— уровня 5.4-2
Погрешность квадратной формулы Гаусса
20.7-3
— — — Чебышева 20.7-3
— максимальная 12.5-4
— приближения 12.5-4, 12.5-5
—, см. также Ошибка
— средняя квадратическая 12.5-4
Подвижный трехгранник 17.2-2
Подгруппа 12.2-2
— инвариантная 12.2-5
— несобственная 12.2-2
— нормальная 12.2-5
— собственная 12.2-2
— сопряженная 12.2-5
Подкольцо 12.3-2
Подматрица 13.2-8
Подмножество 4.3-2
Подполе 12.3-2
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
817
Подпространство 14.2-2
— собственное 14.2-2
Покрытие множества 12.5-4
Поле 12.3-1
— векторное 5.4-3
— — безвихревое 5.7-1
— — соленоидальное 5.7-2
— —, теорема единственности 5.7-3
— Галуа 12.3-1
— кватернионов 12.4-2
— коммутативное 12.3-1
— линейных элементов 9.2-2
— направлений 9.2-2
— некоммутативное 12.3-1
— отношений 12.3-3
— скалярное 5.4-2
— упорядоченное 12.6-2
— экстремалей 11.6-10
Полоса 10.2-1
— характеристическая 10.2-1
Полуширота 18.3-3
Полюс 2.1-8, 2.4-10, 17.3-13
— касательной плоскости к поверхности
второго порядка 3.5-8
— функции порядка т 7.6-2
Поляра точки 2.4-10
Полярная кривая 17.2-5
—- ось 2.1-8
— плоскость точки относительно
поверхности второго порядка 3.5-8
— поверхность 17.2-5
— прямая 17.2-5
Полярные координаты 2.1-8
Полярный радиус 2.1-8, 3.1-6
— угол 2.1-8
Поправка Шеппарда на группировку 19.2-5
Порядок 12.6-1
— группы 12.6-1, 18.7-3
— дифференциального уравнения 9.1-3
— определителя 1.5-1
— разности 20.4-1
— точки разветвления 7.4-2
— целой функции 7.6-5
— частной производной 4.5-2
— элемента 12.2-3
— эллиптической функции 21.6-1
Последовательность 4.2-2
— двойная сходящаяся 4.4-5
— квадратично интегрируемых функций,
сходящаяся в среднем 15.2-2
— Коши 12.5-4
— матриц сходящаяся 13.2-11
— случайных величин, сходящаяся в
среднем 18.6-3
— случайных величин, сходящаяся в
среднем 18.6-3
— — —, — по вероятности 18.6-1
—- сходящаяся 4.4-1
—, — к пределу 12.5-3
— фундаментальная 12.5-4
— функций ортонормиоованная 15.2-3
— — — полная 15.2-4
— — равномерно сходящаяся 4.4-4
Постоянная времени 9.4-1
— затухания 9.4-1
— интегрирования 4.6-1
— Эйлера — Маскерони 21.3-1, 21.4-1
Потенциал безвихревого векторного поля
15.6-1
— векторный векторного поля 5.7-2
— двойного слоя 15.6-5
— диполя 15.6-5
— запаздывающий 15.6-10
— комплексный 15.6-8
— логарифмический точечного источника
15.6-7
Потенциал мультиполя 15.6-5
— опережающий 15.6-10
— простого слоя 15.6-5
—, разложение по мультиполям 15.6-5
— скалярный безвихревого векторного
поля 5.7-1
— точечного заряда 15.6-5
Потенциалы распределений зарядов и
диполей объемные, поверхностные 15.6-5
Поток вектора через поверхность 5.4-6
Почти всюду 4.6-14
Правила дифференцирования 4.5-4
— — ковариантного 16.10-5
— Непера 1.12-3
Правило Коши умножения рядов 4.8-3
— Крамера 1.9-2
— Лейбница 4.6-1
— ложного положения 20.2-2
— Лопиталя 4.7-2
— параллелограмма 5.2-1
— Симпсона 20.6-2
— соответствия 4.2-1, 12.1-1
— трапеций 20.6-2
— Уэддля 20.6-2
Предел в среднем квадратично
интегрируемых функций 15.2-2
— вектор-функции 5.3-1
— двойной последовательности 4.4-5
— матричной функции 13.2-11
— последовательности 4.4-1
— — производящих функций 18.6-2
— — характеристических функций 18.6-2
— суммы функционального ряда 4.8-4
•— функции 4.4-1
— — по совокупности переменных 4.4-5
— — распределения 18.6-2
— — слева 4.4-7
— — справа 4.4-7
Пределы интегрирования 4.6-1
—, операции над ними 4.4-2
Предельный цикл 9.5-3
— — неустойчивый 9.5-3
— — полуустойчивый 9.5-3
устойчивый 9.5-3
Представление алгебры кватернионов
14.10-4
— вращение кватернионов 14.10-4
— групп 12.2-9
— группы вполне приводимое 14.9-2
— — гомоморфизмов 14.9-1
— — истинное 14.9-1
— — конечной регулярное 14.9-1
— — неприводимое 14.9-2, 14.9-3
— —, неприводимые компоненты 14.9-2
— — ограниченное 14.9-1
— — ортогональное 14.9-1
— — приводимое 14.9-2
— — разложимое 14.9-2
— — размерности 14.9-1
— — степени п 14.9-1
— — точное 14.9-1
— — унитарное 14.9-1
— —, условия приводимости 14.9-2
Представления группы подобные 14.9-1
— — эквивалентные 14.9-1
Преломление экстремалей 41.6-7
Преобразование антисимметрическое 14.4-6
— аффинное 14.10-8
— базисных векторов 4.5-1, 14.6-1
— — —, матричная запись 14.6-2
— Ганкеля конечное табл. 8.7-1
— — — кольцевое табл. 8.7-1
— Гильберта 8.6-1
— допустимое 6.2-1
— инвариантное 12.1-5
— индуцированное 16.1-4
818
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Преобразование интегральное см.
Интегральное преобразование
— к главным осям 14.8-6
— каноническое 10.2-6
— — уиивалентное 10.2-в
— квадратичных форм 13.5-4
— класса в класс 12.1-4
— когредиентное 16.6-2
— контрагредиентное 16.6-2
— — базисных векторов 14.7-6
— координат 14.1-3
— —, активная и пассивная точки
зрения 14.1-3
— — векторов, активная и пассивная
точки зрения 14.5-1, 14.6-1
— кососимметрическое 14.4-6
— Куммера 4.8-5
— Лапласа, абсолютная сходимость 8.2-2
— —, абсцисса абсолютной сходимости
8.2-2
— — в форме интеграла Стилтьеса 8.6-3
Преобразование Л'апласа дискретное 8.7-3
— — двустороннее 8.6-1, 8.6-2
— — для произведений оригиналов на
синус или косинус 8.3-2
— —, достаточные условия
существования 8.2-4
— — импульсных функций 8.5-2, 20.4-6
— — обратное 8.2-5
— — — для рациональных функций 8.4-4,
8.4-5
— — —, достаточные условия
существования 8.2-7
— — —, приемы вычисления 8.4-3, 8.4-9
— — —, условие единственности В.2-8
— — одностороннее 8.2-1, 10.5-2
— — периодических функций 8.8-2
— —, предельные теоремы 8.3-4
— — ступенчатой функции 20.4-5
— —, таблица соответствия операций
8.3-1
— —, таблицы 8.4-1
— —, теорема обращения 8.6-2
— —, теоремы соответствия операций
8.3-1
— — условие единственности 8.2-8
— Лапласа — Карсона 8.6-1
— Лежандра я-мерное 10.2-5
— линейное бесконечно малое 14.4-10
— — вполне приводимое 14.8-2
— —, матричное представление 14.5-2
— — невырожденное 14.3-5
— — несобственное 14.3-5
— — ограниченное 14.4-1
— — приводимое 14.8-2
— — разложимое 14.8-2
— Меллина 8.6-1
— нулевое 14.3-3
— обратное 12.1-4, 14.3-5
— ортогональное 3.1-12, 14.4-6
— подобия 13.4-1
— пространства линейное однородное
14.3-1
— симметрическое 14.4-6
— случайной величины 18.5-2
— — — линейное 18.5-3
— соприкосновения 10.2-5
— тождественное 14.3-4
— транспонированное 14.4-6
— функциональное 8.7-1
— Фурье 8.6-1
— — и целые функции 7.6-5
— — обобщенное 4.11-4, 18.10-10
— Эйлера 4.8-4
— эрмитовых форм 13.5-4
г-преобразование 8.7-3
Приближения многочленами Чебышева
табл. 20.6-4
— равномерные 20.6-4
— — функций многочленами табл. 20.6-2
и табл. 20.6-3
— рациональными дробями 20.6-7
— см. также Аппроксимация
— функций многочленами по методу
наименьших квадратов на интервале 20.6-2
— — — — — — — — дискретном
множестве 20.6-3
Приведение матриц 14.8-6
Призма 1.10-4
Признак сходимости, см. Сходимость
— устойчивости решений системы
линейных разностных уравнений' 20.4-8
Примитивная 4.6-4
Принцип аргумента 7.6-9
— Гамильтона 11.5-7
— двойственности 3.4-4
— консерватизм функциональных
уравнений 7.8-1
— максимума Понтрягина 11.8-2
— минимакса Куранта 14.8-8, 15.4-7
— наложения 20.4-4
— оптимальности Беллмана 11.8-6, 11.9-2
— сжатых отображений 11.5-6
— симметрии 7.8-2
— суперпозиции для класса операции
14.3-1
Приращение функции 11.4-1
Программа контроля 20.1-2
Программирование динамическое 11.9-1
— линейное 11.4-1
— нелинейное 11.4-3
Прогрессия арифметическая 1.2-6
— геометрическая 1.2-7, 21.2-12
бесконечная 4.10-2
Проективная плоскость 7.2-4
Проекции направляющего вектора на
координатные оси 3.3-1
Проекция вектора на подпространство
14.2-7
— направленного отрезка на ось 3.1-9
— — — на плоскость 3.1-9
— — — на прямую 3.1-9
— пространства ортогональная 14.2-8
— стереографическая 7.2-4
Произведение 12.2-1
— бесконечное 4.8-7
— вектора на диадик 16.9-2
— — на скаляр 5.2-1, 15.2-1
— векторное 16.8-4
векторов альтернированное 16.5-4
— — скалярное 15.2-1
— внешнее 12.7-2
— внутреннее 16.8-1
— групп вращений прямое 14.10-8
— — прямое 12.7-2
— действительных векторных пространств
прямое 12.7-3
— диадика на вектор 16.9-2
— диадиков 16.9-2
— — векторное 16.9-2
— диадное 16.9-1
— интегральных преобразований 15.3-1
— классов декартово 12.7-1
— комплексных чисел 1.3-1, 1.3-3
— линейных операторов 14.3-4
— — преобразований 14.3-4
— логическое 4.3-2
— матриц 13.2-2
— — внешнее 13.2-10
— — прямое 13.2-10
— матрицы на скаляр 13.2-2
— подмножеств 12.2-4
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
819
Произведение представлений кронекеров-
ское 14.9-6
— — прямое 14.9-в
— рядов 4.8-3
— скалярное 16.8-1
— смешанное 16.8-4
— событий логическое 18.2-1
— тензора на скаляр 16.3-4
*— тензоров внешнее 16.3-6
— — внутреннее 16.3-7
— топологическое 12.7-4
Производная абсолютная истинного тензора
16.10-8
— — относительного тензора 16.10-8
Производная в среднем от случайного
процесса 18.9-4
— вектора 16.10-1
— вектор-функции 5.3-2
— импульсной функции 21.9-3, 21.9-4
— ковариантная 16.10-4
— неявной функции 4.5-4, 4.5-7
— нормальная от скалярной функции 5.6-2
— обратной функции 4.5-4
— по дуге, обозначение 17.2-1
— по направлению высшего порядка 5.5-4
— — — от векторной функции точки 5.5-3
— — — от скалярной функции точки
5.5-3
— по нормали 15.5-4
— полная векторной функции вдоль
кривой 5.5-3
— — скалярной функции вдоль кривой
5.5-3
— случайной функции 18.9-4
— — —, математическое ожидание 18.9-4
— — —, корреляционные функции 18.9-4
— ступенчатой функции 21.9-3
— тензора по направлению 16.10-8
-— функции вторая, третья, ... (второго,
третьего, ... порядка) 4.5-1
— —, заданной параметрически 4.5-4
— — левая 4.5-1
— — первая (первого порядка) 4.5-1
— — правая 4.5-1
— функция 7.3-1
— частная см. Частная производная
Производные ковариантные высших
порядков 16.10-6
Производящая функция 8.7-2
— — многочленов Лагерра табл. 21.7-1
— — — Лежандра табл. 21.7-1
— — — Чебышева табл. 21.7-1
— — — Эрмита табл. 21.7-1
— — моментов 18.3-8
— — обобщенных многочленов Лагерра
21.7-7
— — семиинвариантов 18.3-10
— — сочетаний и размещений 18.7-2
— — факториальных моментов 18.3-8
— — экспоненциальная 8.7-2
Промах 20.1-2
Промежуток замкнутый 4.3-4
Прообраз множества полный 12.5-1
Пропорции производные 1.4-2
Пропорция 1.4-2
Пространства гомеоморфные 12.5-2
— изометричные 12.5-2
— функций, примеры табл. 12.5-2
— числовых последовательностей,
примеры, табл. 12.5-1
Пространство банахово 14.2-7
— бикомпактное 12.5-1
— векторное линейное 14.2-1
— — — над кольцом 12.4-1
— выборок 18.2-7
— гильбертово 14.2-7
Пространство гомеоморфное 12.5-1
— двойственное 14.4-9
— дуальное 14.4-9
— компактное 12.5-1
— локально евклидово 17.4-6
— метрическое 12.5-2
— — вполне ограниченное 12.5-4
— — компактное 12.5-4
— — локально компактное 12.5-4
— — полное 12.5-4
— представляющее 14.9-1
— псевдоевклидово 17.4-6
— — соприкасающееся 17.4-7
— риманово 16.7-1
— — плоское 17.4-6
— с внутренним произведением с
индефинитной метрикой 14.2-6
— сепарабельное 12.5-1
— собственно евклидово 17.4-6
— сопряженное 14.4-9
— топологически эквивалентное 12.5-1
— топологическое '12.5-1
Пространство-носитель 14.9-1
Процентиль 18.3-3
Процентильная широта 18.3-3
Процесс гауссовский 18.11-3, 18.12-6
— марковский 18.11-4
— ортогонализации Грама — Шмидте
14.7-4, 15.2-5
— переходный 10.4-1
—, порождаемый пуассоновской выборкой
18.11-5
— пуассоновский 18.11-4
— —, средняя скорость отсчетов 18.11-4
— распространения возмущений 10.4-1
— случайный 18.9-1
— — дискретный 18.9-1
— — многомерный 18.9-2
— — непрерывный 18.9-1
— — — в среднем 18.9-4
— — общий периодический 18.11-1
— —, порождаемый периодической
выборкой 18.11-6
— —, — пуассоновским процессом 18.11-1
— — порядка п 18.11-4
Процесс случайный,разложение по ортонор-
мированной системе 18.9-6
— — с дискретным временем 18.9-1
— — с ограниченным спектром 18.11-2
— — с периодическими реализациями
18.11-1
— — с постоянной реализацией IS. 11-1
— — синусоидальный 18.11-1
— — стационарный 18.10-1
— — — в широком смысле 18.10-2
— стационарный 10.4-1
— чисто случайный 18.11-4
— эргодический 18.10-7
Процессы случайные, действия над ними
18.12
— — совместно стационарные 18.10-1
— — — — в широком смысле 18.10-2
— — — эргодические 18.10-7
Прямая 3.3-1
— регрессии 18.4-6
Прямоугольный треугольник 1.11-1
Псевдосфера 17.3-13
Псевдотензор 16.2-1
Псевдоэкспонента 21.5-1
Пучок прямых 2.3-2
Пятиугольник 1.10-1
Р
Равенство 12.1-3
— матриц 13.2-2
820
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Равенство множеств 4.3-2
— Парсеваля 14.7-4
— тензоров 16.3-4
Радикальная ось двух окружностей 2.5-1
Радикальный центр 2.5-1
Радиус кривизны 17.1-4, 17.2-3
— кручения 17.2-3
— сходимости степенного ряда 4.10-2,
7.5-2
Радиус-вектор середины отрезка 3.1-7
— точки 3.1-5
— —, делящей отрезок в отношении к
3.1-7
Разбиение класса С 12.1-3
— матриц 13.2-8
Размах 18.3-3
— выборки 19.2-6
Размерность векторного пространства
линейная 14.2-4
— пространства 14.1-2
— — ортогональная 14^7-3
— ядра линейного преобразования 14.3-2
Размещения без повторений 18.7-3, табл.
18.7-2
— с повторениями 18.7-3, табл. 18.7-2
Разности разделенные 20.5-2
Разностное отношение 20.4-3
— уравнение линейное 20.4-4
— — — с постоянными коэффициентами
20.4-5
— — обыкновенное 20.4-3
Разность восходящая 20.4-1
— нисходящая 20.4-1
— обратная 20.5-7
— прогрессии 1.2-6
— центральная 20.4-1
Разрез 7.4-2
Ранг квадратичной формы 13.5-4
— линейного преобразования 14.3-2
— линейной алгебры 12.4-2
— матрицы 13.2-7
— многомерного распределения
вероятностей 18.4-8
— представления 14.9-1
— произведения матриц 13.2-7
— собственного значения 15.3-3, 15.4-5
— суммы матриц 13.2-7
— тензора 16.2-1
— эрмитовой формы 13.5-4
Раскрытие неопределенностей 4.7-2
Распределение вероятностей 18.2-7
— — асимптотически нормальное 18.6-4
— — биномиальное 18.7-4, 18.8-1
— — — Пуассона обобщенное 18.7-4
— — вырожденное (причинное) 18.8-1,
18.8-5
— — геометрическое 18.8-1
— — гипергеометрическое 18.8-1
— — Коши 18.8-5
— — Лапласа 18.8-5
— — маргинальное 18.4-7
— — многомерное 18.4-7
— — непрерывное 18.8^3
— — несобственное 18.4-8
— — нормальное двумерное 18.8-6
— — — круговое 18.8-7
—- — — усеченное 19.3-4
— —, описание с помощью интеграла
Стилтьеса 18.3-6
— — Парето 19.3-4
— — Паскаля 18.8-1
Пойа 18.8-1
— — полиномиальное 18.8-2
— — Пуассона 18.8-1
— — — многомерное 18.8-2
— — равномерное 18.8-5
Распределение вероятностей случайного
процесса 18.9-2
— — случайной величины 18.5-4
— — собственное 18.4-8
— — условное 18.4-5
— выборки частотное 19.2-2
Распределение выборочного коэффициента
корреляции 19.7-4
— выборочное асимптотически
нормальное 19.5-2
— генеральной совокупности 19.1-2
— логарифмически нормальное 12.3-2
— нормального отклонения 18.8-4
— нормальное (Гаусса) 18.4-3
— — многомерное 18.8-8
— одномерное, числовые характеристики
18.3-3
— одномодальное, двумодальное,
многомодальное 18.3-3
— отношения дисперсий 19.5-3
— размаха выборки 19.5-4
— случайной величины 18.2-8
— стандартизованной нормальной
величины 18.4-3
— статистики выборочное 19.1-2
— Стьюдента 19.5-3, 19.7-4
— суммы случайных величин 18.5-7,
18.5-8
— Фишера 19.5-3
— эмпирическое 19.2-2
— г 19.7-4
— t 19.5-3
— и 19.5-3
— X2 19.5-3
Расстояние 12.5-2
— между параллельными плоскостями
3.4-2
— — — прямыми 2.3-2
— — прямыми кратчайшее 3.4-2
— — точками 2.1-4, 2.1-8, 3.1-7
— от плоскости до параллельной ей
прямой 3.4-2
— от точки до плоскости 3.4-2
— — — до прямой 2.3-1, 3.4-2
Расходимость ряда, признаки сравнения
4.9-1
Расширение алгебраическое 12.3-3
Реализация процесса 18.9-1
Ребро возврата 17.3-11
Регрессия 18.4-6, 18.4-9
— линейная 18.4-6
— параболическая 18.4-6
— средняя квадратическая 18.4-6, 18.4-9
— — — линейная эмпирическая 18.7-2
Резольвента 14.8-3
— Грина 15.5-2
— уравнения четвертой степени 1.8-6
Резонанс 9.4-2
Результант 1.6-5
— многочлена 1.7-3
Результат операции 12.1-1
Релаксация блочная 20.3-2
— групповая 20.3-2
— координатная 20.3-2
Рефлексивность 12.1-3
Решающая функция 19.6-9
Решение алгебраического уравнения 1.6-2
— — — полное 1.6-3
— — — численное 20.2-4, 20.2-5
— асимптотически устойчивое в области
13.6-5
— в целом 13.6-5
— — — глобально 13.6-5
— вполне устойчивое 13.6-5
— вырожденное 11.4-1
— Даламбера 10.3-5
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
821
Решение дифференциального уравнения
общее 9.1-2
— — — приближенное, метод Крылова —
Боголюбова 9.5-5
— — — с частными производными общее,
частное 10.1-2
— — — частное 9.1-2
Решение допустимое 11.4-1
— — базисное 11.4-1
— — — вырожденное, невырожденное
11.4-1
— игры 11.4-4
— неустойчивое 13.6-5
— оптимальное 11.4-1
— устойчивое по Ляпунову 13.6-5
— разностного уравнения 20.4-3
— системы дифференциальных уравнений
асимптотически устойчивое, устойчивое
в целом 9.5-4
— — — — вполне устойчивое 9.5-4
— — — — неустойчивое 9.5-4
— — — — периодическое устойчивое,
неустойчивое 9.5-4
— — — — тривиальное устойчивое,
неустойчивое 9.5-4
— — — — устойчивое по Ляпунову 9.5-4
— — уравнений операторное 13.6-2
Решения линейного дифференциального
уравнения линейно независимые 9.3-2
Риманова поверхность 7.4-3
Риманово пространство, операции над
тензорами 16.7-4
Риск 19.9-1
— ожидаемый 19.9-1
— условный 19.9-2
Ротор вектора 16.10-7
— векторной функции точки 5.5-1
— поверхностный 5.6-2
Ряд 4.8-1
— асимптотический 4.8-6
—- биномиальный 21.2-12
— гипергеометрический 9.3-9
— — вырожденный 9.3-10
— — обобщенный 9.3-11
— двойной 4.8-3
— импульсных функций 20.4-6
— как функциональное преобразование
8.7-1
— композиционный 12.2-6
— Лорана 7.5-3
— —, главная часть 7.5-3
— Маклорена 4.10-4
— Неймана 15.3-8
— нормальный 12.2-6
— обвертывающий 4.8-6
— полусходящийся 4.8-6
—, признаки сходимости 4.9-1
— расходящийся 4.8-1
— степенной 4.10-2
— — комплексный 7.2-1
— —, свойства 4.10-2
— Стирлинга 21.4-2
—, суммируемый по методу Чезаро 4.8-6
—, — средними арифметическими 4.8-6
—, — Ct 4.8-6
—, — (d l) 4.8-6
— сходящийся 4.8-1
— — абсолютно 4.8-1
— — коммутативно 4.8-3
— —, перестановка членов 4.8-3
— — равномерно 4.8-2
— — —, свойства 4.8-4
— —, свойства 4.8-3
—, — условно 4.8-3
— Тейлора 4.10-4, 5.5-4, 7.5-2
— — кратный 4.10-5
Ряд Тейлора, операторное обозначение
20.4-2
— тригонометрический 4.11-2
— функциональный 4.8-2
— —, признаки сходимости 4.9-2
— —, условие интегрируемости 4.8-4
— Фурье 4.11-2
— — кратный 4.11-8
— —, операции над ним 4.11-5
— Фурье —Бесселя 21.8-4
С
Самосопряженность гильбертова
пространства 14.4-9
Свертка 9.4-3
— двух последовательностей 4.6-18
— — функций 4.6-18
— Стилтьеса 4.6-18
Свертывание смешанного тензора 16.3-5
— тензоров 16.3-7
Сверхрелаксационный множитель 20.3-2
Сверхрелаксация 20.3-2
— систематическая 20.3-2
Свободное неизвестное 11.4-1, 11.4-2
Свободный член многочлена 1.6-3
Свойства метрически инвариантные 12.5-2
Сегмент 4.3-4
Седло 9.5-4
Седловая точка игры 11.4-4
Семейство интегральных кривых 9.1-2
Семиинвариант 18.3-9, 18.4-10
Семиинварианты (инварианты
относительно поворота осей) 2.4-3, 3.5-3
—, связь с моментами 18.3-10
Сигнал, треугольная форма 4.11-4
— фильтра выходной 19.8-2
Сигнатура квадратичной формы 13.5-4
Символ Кронекера обобщенный ранга 2г
16.5-2
Символы Кристоффеля второго рода 16.10-3,
17.3-7, табл. 6.5-1
— — первого рода 16.10-3, табл. 6.5-1
— Леви —Чивита 16.5.3
Симметрия 18.1-3
Симплекс-метод, введение искусственных
переменных 11.4-2
— решения задачи линейного
программирования 11.4-2
Синус амплитуды 21.6-7
Синус — интеграл Фурье 4.11-3
Синусоида выпрямленная 4.11-4
— детектированная 4.11-4
— срезанная 4.11-4
Синус—преобразование Фурье 4.11-3
— — конечное табл. 8.7-1
Система алгебраических уравнений 1.9-1
— векторов ортонормированная 14.7-3
— — — полная 14.7-4
— — —, построение 14.7-4
— геодезических нормальный координат
17.3-13
— гиперкомплексных чисел 12.4-2
— дифференциальных уравнений 2.1-3
— — — автономная 9.5-2, 9.5-4, 13.6-1
— — — динамическая 13.6-1
— — —, матричные обозначения 13.6-1
— — — линеаризованная 9.5-4
— — — неавтономная 13.6-6
— — — с частными производными 10.1-2
— — — стационарная 13.6-1
— — —, теорема существования и
единственности решения 9.2-1
— инвариантов полная 12.2-8, 14.1-4
Система криволинейных координат 6.2-1
_ — —. ортогональная 6.4-1
822
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Система криволинейных координат правая
6.2-3
— координат 14.1-2, 16.1-4
— — аффинная 2.1-2
— — декартова 2.1-2, 3.1-2
— — — общая 2.1-2
— — — прямоугольная правая 2.1-3,
3.1-3, 3.1-4
— — левая 2.1-2, 16.7-1
— — ортогональная 16.8-2
— — полярная 2.1-8
— — правая 2.1-2, 16.7-1
— — сферическая 3.6-6
— — цилиндрическая 3.1-6
— линейных дифференциальных
уравнений, операторный метод решения 9.4-4
— — — —, периодические внешние
нагрузки 9.4-6
— — — — устойчивая 9.4-4
— —- однородных дифференциальных
уравнений с постоянными коэффициентами
9.4-1
— — уравнений 1.9-2
— — — несовместная 1.9-4
— — —, общая теория 1.9-4
— — — однородных 1.9-5
— — —, правило Крамера 1.9-2
— мер 14.1-5
— отсчета 14.1-2, 16.1-4
— разностных уравнений, матричная
запись 20.4-7
— — — устойчивая 20.4-8
— случайных величин 18.4-1
— уравнений Эйлера каноническая 11.6-8
— физически реализуемая 9.4-3
Скаляр 5.2-1, 12.4-1, 16.2-1
— абсолютный 16.2-1
— диадика первый 16.9-2
Скалярное поле 5.4-2
— произведение векторов 5.2-6
— — двойное 16.9-2
Скачок функции 4.4-7
Скобка Пуассона 10.2-6
Скорость вращения мгновенная 14.10-7
— — угловая 14.10-7
— средняя отсчетов в процессе Пуассона
18.11-4
След матрицы 13.2-7, 13.4-3
— оператора 14.6-2
Сложение абстрактное 12.3-1
— векторное 12.4-1
— векторов 5.2-1
— комплексных чисел 1.3-1
— логическое 12.8-1
— рядов 4.8-3, 4.8-4
— тензоров 16.3-3
Случайная величина 18.2-8
— — двумерная дискретная 18.4-3
дискретная 18.3-1, 18.4-3
— — многомерная 18.4-1
— — — дискретная 18.4-7
— — — непрерывная 18.4-7
— — непрерывная 18.3-2, 18.4-3
— — нормированная 18.5-3
— — стандартизованная 18.5-3
— выборка 19.8-4
— — двумерная 19.8-4
— — объема 19.1-2
— последовательность 18.9-1
— телеграфная волна 18.11-5
— функция, дифференцирование 18.9-4
— —, интегрирование 18.9-4
Случайные блоки 19.6-6
—- величины независимые 18.4-11
— — некоррелированные 18.4-11
— —» условие независимости 18.4-11
Случайные координаты 18.4-1
Случайный вектор многомерный 18.4-1,
18.4-7
— процесс см. Процесс случайный
Смешанное произведение трех векторов
5.2-8
Смещение оценки 19.4-1
Собственная функция интегрального
уравнения 15.3-3
— — краевой задачи 10.4-2
— — линейного дифференциального
оператора 15.4-5
— — обобщенная 15.4-5
— — эрмитова ядра 15.3-3
— — ядра 15.3-3
Собственное значение 10.4-2
— — диадика 16.9-2
— — интегрального уравнения 15.3-3
— — линейного дифференциального
оператора 15.4-5
— — оператора 14.8-3, 14.8-4
— — эрмитова ядра 15.3-3
Собственный вектор диадика 16.9-2
— — оператора 14.8-3, 14.8-4
Событие 18.2-1
— достоверное 18.2-1
— невозможное 18.2-1
— противоположное 18.2-1
События, независимые в совокупности
18.2-3
—, — по вероятности 18.2-3
— несовместимые 18.2-1
Совмещение событий 18.2-1
Соотношение Лежандра 21.6-6
Соотношения Винера—Ли 18.12-2, 18.12-3
— Хинчина — Винера 18.10-3, 18.10-10
Соприкасающаяся окружность 17.1-4,
17.2-2
— плоскость 17.2-2, 17.2-4
— сфера 17.2-5
Состояние конечное 11.8-1
— начальное 11.8-1
Сочетания без повторений 18.7-3, табл.
18.7-2
— с повторениями 18.7-3, табл. 18.7-2
Спектр дифференциального оператора
15.4-5
— линейного оператора 14.8-3
— — — дискретный 14.8-3
~ — — непрерывный 14.8-3
Спектр линейного оператора остаточный
14.8-3
— — — предельный 14.8-3
— — — точечный 14.8-3
— линейной задачи о собственных
значениях 15.4-5
— матрицы 13.4-2
— непрерывный 15.4-5
— случайной величины дискретной 18.3-1
— — — непрерывной 18.3-2, 18.4-3, 18.4-7
— собственных значений 10.4-2
Спектральная функция, см. функция
спектральная
Спектральное значение 18.3-1
Спектры действительных случайных
процессов 18.10-4
Спиновые матрицы Паули 14.10-4
Спираль Архимеда 2.6-2
— логарифмическая 2.6-2
— параболическая 2.6-2
Спрямляющая плоскость 17.2-2, 17.2-4
Среднее выборочное 19.8-4
— значение случайной величины 18.3-3
— — функции 4.6-3
— — — от случайной величины 18.3-3,
18.4-4, 18.4-8
предметный указатель
823
Среднее по времени 18.10-7
— по конечному промежутку времени
19.8-1
— по множеству наблюдений 18.9-3
— по параметру 18.10-7
— по расслоенной выборке 20.10-2
— эмпирическое 18.10-7
Статистика 19.1-1
— объединенных выборок 19.6-6
— порядковая 19.2-6
Статистическая гипотеза 19.6-1
— —, проверка 19.1-3
— — простая 19.6-1
— — сложная 12.6-1
— устойчивость 19.1-1
Стационарное значение 11.2-2, 11.3-3
Степень многочлена 1.4-3
— усечения 19.3-4
— целая 12.2-1
— числа действительного 1.2-1
— — комплексного 1.3-3
Столбец колеблющийся 20.2-3
— матрицы 13.2-1
— модальный 14.8-5
— правильный 20.2-3
— — частично 20.2-3
Стратегия 11.9-1
— оптимальная 11.4-4, 11.9-1
— смешанная 11.4-4
— чистая 11.4-4
Строка матрицы 13.2-1
Строфоида 2.6-1
Структура 12.6-1
— полная 12.6-1
Ступенчатая функция 20.4-6
Сумма комплексных чисел 1.3-1, 1.3-3
— логическая 4.3-2
— — событий 18.2-1
— матриц 13.2-2
—- прямая векторных пространств 12.7-5
— — колец 12.7-5
— — линейных алгебр 12.7-5
— ряда 4.8-1
— — из обратных степеней целых чисел
4.8-5
— степеней натуральных чисел 1.2-8, 4.8-5
— тензоров 16.3-3
—, сокращенная запись 16.1-3
Суммирование по частям 20.4-3
— рядов, применение вычетов 7.7-4
— —, связь с решением разностного
уравнения 20.4-3
— — средними арифметическими 4.8-6
— —, формула Пуассона 4.8-5
— —, — Эйлера — Маклорена 4.8-5
Сфера 1.10-5, 3.5-9
Сферические гармоники 21.8-12
— — зональные 21.8-12
— — поверхностные 21.8-12
— — секториальные 21.8-12
— — тессеральные 21.8-12
Сферический дефект 1.12-2
— сегмент 1.10-5
— треугольник, см. Треугольник
сферический
— эксцесс (избыток) 1.12-2
Сфероид 1.10-5
Схема Горнера 20.2-3
— — для комплексного аргумента 20.2-3
— исключения компактная 20.3-1
Сходимость в среднем в пространстве L2
15.2-2
— — — последовательности случайных
величин 18.6-3
— неравномерная вблизи точки разрыва
Сходимость несобственных интегралов,
признак Абеля 4.9-3
— — —, — Дирихле 4.9-3
— — —, — сравнения 4.9-3
— — — равномерная, признак Вейер-
штрасса 4.9-4
— — — —, — Дирихле 4.9-4
— по вероятности 18.6-1
— последовательности 12.5-3
— последовательных приближений 20.2-2
— ряда 4.8-1
— —, признак Абеля 4.9-1
— —, — Даламбера 4.9-1
— —, — Дирихле 4.9-1
— —, — Коши интегральный
«радикальный» 4.9-1
— —, — Лейбница 4.9-1
— —, — Раабе 4.9-1
— —, — сравнения 4.9-1
— — равномерная, признак Абеля 4.9-2
— — —, — Вейерштрасса 4.9-2
— функции 12.5-3
— — равномерная 4.4-4
Т
Таблица истинностная 12.8-7
— отображений 7.9-5
— сопряженности признаков 19.7-5
Тела вращения 1.10-5
Тело 12.3-1
Тензор 16.1-4
— абсолютный ковариантный ранга 1
16.2-1
— — контравариантный ранга 1 16.2-1
— — г раз контравариантный и s раз
ковариантный 16.2-1
—, аналитические представления 16.7-3
— ассоциированный данному 16.7-2
— выражение через векторы локального
базиса 16.6-1
— истинный 16.2-1
— кривизны 17.4-5
— метрический 16.7-1
— — ассоциированный 16.7-1
— относительный веса W, г раз
контравариантный и s раз ковариантный 16.2-1
— постоянный вдоль кривой 16.10-9
— ранга 0 16.2-1
2 16.9-1
— — — антисимметричный 16.9-1
— — —, дивергенция 16.10-11
— — —, дифференциальные инварианты
16.10-11
— — —, интегральные теоремы 16.10-11
— — — симметричный 16.9-2
— Римана — Кристоффеля 17.4-5
— риманова пространства
фундаментальный 16.7-1
— Риччи 17.4-5
— смешанный 16.2-1
— Эйнштейна 17.4-5
Тензорная емкость 16.2-1
— плотность 16.2-1
Тензорные уравнения, инвариантность
16.4-1
Тензоры, равные в точке 16.3-1
Теорема Абеля для степенных рядов
4.10-3
— Банаха о сжатых отображениях 12.5-6
— Безу 1.7-2
— Бендиксона первая, вторая 9.5-3
— Бернсайда 14.9-3
— Бернулли 18.6-5
— Больцано — Вейерштрасса 12.5-4
— Брианшона 2.4-11
824
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Теорема Бюдана 1.6-6
— Вандермонда биномиальная 21.5-1
— Вейерштрасса 7.3-3, 7.3-4, 7.6-4, 7.6-6
— Винера о квадратичном отклонении
18.10-10
— Винера — Пэли 4.11-4, 7.6-5
— Гаусса 5.6-1, 15.6-5
— умножения гамма-функций 21.4-1
— Гаусса — Бонне 17.3-14
— Гаусса — Остроградского 5.6-1
— Гейне — Бореля о выделении
конечного покрытия 12.5-4
— двойственности в линейном
программировании 11.4-1
— Джона 11.4-3
— Дюбуа — Реймона 11.5-2
— единственности векторного поля 5.7-3
— — для степенного ряда 4.10-2
— — преобразования Фурье 4.11-5
— — ряда Фурье 4.11-5
— — сходимости в среднем 15.2-4
— Жордана 7.2-4
— Жордана — Гельдера 12.2-6
— Канторовича о сходимости решения
системы алгебраических уравнений
20.2-8
— Карунена — Лоэва 18.9-6
— Кельвина об инверсии 15.6-3
— косинусов 1.11-3
— — для сторон сферического
треугольника 1.12-4
— — для углов сферического
треугольника 1.12-4
— Котельникова 18.11-2
— Коши 4.7-1
— — интегральная 7.5-1
— Куна — Такера 11.4-3
— Кэли 12.2-9, 14.9-1
— Кэли — Гамильтона 13.4-7
— Лагранжа 4.7-1
— — о порядке подгруппы 12.2-2
— Лассаля об асимптотической
устойчивости 13.6-6
— Лебега о сходимости 4.6-16
— Лерха 8.2-8
— Линдеберга — Леви 18.6-5
— Лиувилля 7.6-5
— Ляпунова о неустойчивости 13.6-6
— — об асимптотической устойчивости
13.6-6
— — об устойчивости 13.6-6
— Менье 17.3-4
— Мерсера 15.3-4
— Миндинга 17.3-13
— минимакса для конечной игры двух
партнеров с нулевой суммой выигрыша
11.4-4
— Миттаг—Леффлера 7.6-8
— Морера 7.5-1
— непрерывности для производящих
функций 18.6-2
— — для характеристических функций
18.6-2
— о выборе 18.10-6
— о вычетах 7.7-2
— о градиенте 5.6-1
— о дивергенции 5.6-1
— о дополнительном аргументе
многочленов Бернулли 21.5-2
— о конечном приращении 4.7-1
— о максимуме модуля 7.3-5
— — — — для гармонических функций
15.6-4
— о непрерывности определенного
интеграла, зависящего от параметра 4.6-2
— о проекциях 1.11-3, 14.2-8
Теорема о разложении многочлена на
множители 1.7-1
— о роторе 5.6-1
— о свертке преобразования
произведения 8.3-3
— о среднем для гармонических функций
15.6-4
— обращения Ганкеля 8.6-4
— — для одностороннего преобразования
Лапласа 8.6-2
— — преобразования Лапласа 8.2-6
— основная алгебры 7.6-1
— — интегрального исчисления 4.6-5
— — теория поверхностей 17.3-9
— Парсеваля 4.11-4
— — для преобразования Ганкеля 8.6-4
— Паскаля 2.4-11
— Пикара 7.6-4
— Пой а о подсчете 18.7-3
— Прайса 18.12-6
— предельная Муавра — Лапласа 18.8-1
— — центральная 18.6-5
— Прингсгейма о суммировании по
столбцам и строкам 4.8-3
— разложения 19.5-3
— — Гельмгольца 5.7-3
— Рауса — Гурвица 1.6-6
— Римана об отображении 7.9-6
— — об условно сходящихся рядах 4.8-3
— Римана — Лебега 4.11-2
— — — о тригонометрических рядах
4.11-2
— Рисса — Фишера 15.2-4
— — — о свойстве полноты 15.2-2
— Риччи 16.10-5
— Ролля 1.6-6, 4.7-1
— Руше 7.6-1
— Сильвестра 13.4-7
— синусов 1.11-3, 1.12-4
— сложения 19.5-3
— — для биномиальных коэффициентов
21.5-1
— — для многочленов Лежандра 21.8-й
— — для сферических функций 21.8-3
— — для цилиндрических функций 21.8-13
— Стокса 5.6-2
— существования неявных функций 4.5-7
— — функции Грина 15.6-6
— Таубера для степенных рядов 4.10-3
— Умножения для многочленов Бернулли
21.5-2
— Фейера 4.11-7
— Фишера обобщенная 19.7-4
— Фредгольма об альтернативе 15.4-4
— Хинчина 18.6-5
— Чебышева 18.6-5
— Четаева о неустойчивости 13.6-6
— Эйлера 17.3-5
о коэффициентах тригонометрического
ряда 4.11-2
— — о тригонометрических рядах 4.11-2
— — об однородных функциях 4.5-5
Theorema Egregium Гаусса 17.3-8
Теоремы Байеса 18.2-6
— Вейерштрасса о приближении 4.7-2
— Гарнака о гармонических функциях
15.6-4
— Грина 5.6-1
— Лиувилля об эллиптических функциях
21.6-1
— о непрерывности 4.6-16
— о нормальном распределении суммы
случайных величин 18.8-9
— о полюсах и полярах 2.4-10
— о разложении операторов 14.4-8
— о среднем 4.7-1
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
825
Теоремы о суперпозиции 15.4-2
— о сходимости 4.6-16
— предельные теории вероятностей 18.6-5
— разложения для эрмитовых ядер 15.3-4
— сложения для эллиптических функций
Якоби 21.6-7
— соответствия операций над оригиналами
и их изображениями 8.3-1
— сравнения для уравнений Штурма —
Лиувилля 15.4-10
Теория вероятностей 18.1-1
— возмущений 10.2-7
— потенциала 15.6-1
— — двумерная 15.6-7
— распределений Лорана Шварца 21.9-2
Тета-функции см. Тэта-функции
Тэтраэдр 1.10-6
Тип целой функции 7.6-5
Тождества Бианки 17.4-5
Тождество Пуассона 10.2-6
— Риччи 17.4-5
Топология 12.5-1
— дискретная 12.5-1
— пространства 12.5-1
—- — относительная 12.5-1
— — тривиальная 12.5-1
Тор 1.10-5
Точка 16.1-2
— бесконечно удаленная 7.2-2
— внутренняя 4.3-6
— возврата 17.1-3
— гиперболическая 17.3-5
— граничная 4.3-6
— двойная 17.1-3
— дифференциального уравнения особая
изолированная 9.3-6
— — — — правильная 9.3-6
— — — слабо особая 9.3-6
— — — существенно особая 9.3-6
— изолированная 4.3-6, 17.1-3
— инвариантная 7.9-2
— конденсация 4.3-6
— накопления 4.3-6
— омбилическая 17.3-5
— особая 17.1-3, 17.3-1
— — многозначного характера 7.6-2
— отображения критическая 7.9-1
— параболическая 17.3-5
— перегиба 17.1-5
— пересечения кривых 2.1-9
— — прямых 2.3-2
— покоя 9.5-3, 13.6-6
— предельная 4.3-6
— равновесия 9.5-3
— разветвления (ветвления) 7.4-2, 21.6-4
— — алгебраическая 7.6-2
— — бесконечного порядка 7.4-2
— — конечного порядка 7.4-2
— — логарифмическая 7.4-2
— — трансцендентная конечного
порядка 7.6-2
— — функции 7.6-2
— разрыва первого рода 4.4-7
— регулярная 3.1-13, 3.1-14, 17.1-1
— самоприкосновения 17.1-3
— седловая 17.3-5
— существенно особая 7.6-2
— угловая 11.6-7
— — свободная 11.6-7
— фазовой плоскости обыкновенная
9.5-3
— — — особая 6.5-3
— эллиптическая 17.3-5
Точки конгруэнтные 21.6-1
Траектория изогональная семейства
кривых 17.1-8
Траектория ортогональная семейства
кривых 17.1-8
Трактриса 2.6-2
Транзитивность 12.1-3
Трансформирование элемента 12.2-5
Трапеция 1.10-1
Треугольник 1.10-1
— квадратный 1.12-3
— плоский, свойства 1.11-2
— —, формулы для решения 1.11-3
— полярный 1.12-2
— сферический, вершины, стороны, углы
1.12-1
— — прямоугольный 1.12-3
— —, свойства 1.12-2
— —, формулы для решения 1.12-4
Трехгранник Френе 17.2-3
Тригонометрия на плоскости 1.11-1
— сферическая 1.12-1
Трисектриса 2.6-1
Тэта-функции Якоби 21.6-8
У
Угловая точка свободная 11.6-7
Угловой коэффициент 2.2-1
Углы Эйлера 14.10-6
— —, геометрическая интерпретация
14.10-6
Угол между асимптотами гиперболы 2.5-2
— между векторами 16.8-1
— между дугами 17.4-2
— между координатными линиями 17.4-2
— между кривыми на поверхности 17.3-3
— между направленными отрезками 2.1-4,
3.1-8
— между плоскостями 3.4-1
— между прямой и плоскостью 3.4-1
— между прямыми 2.3-2, 3.1-7, 3.4-1
— поворота 17.10-2
Узел 17.1-3
— интерполяции 20.5-1
— неустойчивый, устойчивый 9.5-4
Улитка Паскаля 2.6-1
Умножение абстрактное 12.2-1, 12.3-1
— вектора на скаляр 5.2-1, 12.4-1
— вероятностей 18.2-2
— комплексных чисел 1.3-1
— логическое 12.8-1
— операторов 12.2-8
— определителей 1.5-6
преобразований 12.2-8
— ряда на число или ограниченную
функцию 4.8-3, 4.8-4
— тензора на скаляр 16.3-4
— тензоров внешнее 16.3-6
— — внутреннее 18.3-7
Управление оптимальное 11.8-1
— шаговое 11.9-1
Управления 11.8-1
Управляющая переменная 11.8-1
Уравнение алгебраическое действительное
1.6-6
— — —, отделение корней 1.6-6
— — —, свойства корней 1.6-6
— — степени п 1.6-3
— —, численные методы решения 20.2-4,
20.2-5
— асимптотической линии 17.3-6
— бинормали 17.2-4
— в полных дифференциалах 9*2-4
— вековое матрицы .13.4-5
— векторное линейное неоднородное
14.8-10
— волновое двумерное, частные решения
10.4-8
826
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Уравнение волновое одномерное 10.3-5
— — — затухающее, частные решения
10.4-8
— — —, частные решения 10.4-8
— — трехмерное, частные решения 10.4-8
— второй степени общее 2.4-1, 3.5-1
— Гамильтона — Якоби 10.2-7, 11.6-8
— Гельмгольца двумерное, частные
решения 10.4-5
— — трехмерное 10.4-4
— — —, прямоугольные декартовы
координаты 10.4-4
— — —, сферические координаты 10.4-4
— цилиндрические координаты
10.4-4
— геодезической линии 17.4-3
— главной нормали 17.2-4
— диаметра конического сечения,
сопряженного хордам 2.4-6
— — поверхности второго порядка,
сопряженного семейству плоскостей 3.5-5
— диаметральной плоскости поверхности
второго порядка 3.5-5
— директрисы 2.4-9
— дифференциальное см.
Дифференциальное уравнение
— диффузии 10.4-1
— — двумерное, частные решения 10.4-7
— — обобщенное 15.5-3
— — одномерное, частные решения 10.4-7
— — трехмерное, частные решения 10.4-7
— Дуффинга 13.6-7
— интегральное см. Интегральное
уравнение
— касательной к кривой второго порядка
2.4-10
— — — — плоской 17.1-1
— — —- — пространственной 17.2-2,
17.2-4
— — плоскости 17.3-2
— — — к поверхности второго порядка
3.5-8
— квадратное 1.8-2
— Клейна — Гордона 10.4-4
— конического сечения в полярных
координатах 2.4-11
— — —, проходящего через пять точек
2.4-11
— кривой 2.1-9
— — второго порядка, приведение к
каноническому виду 2.4-8
— кубическое 1.8-3
— — неполное 1.8-3
— —, неприводимый случай 1.8-4
— —, решение Кардана 1.8-3
— —, — тригонометрическое 1.8-4
— Лапласа двумерное 15.6-7
— — —, частные решения 10.4-5
— — трехмерное, прямоугольные
декартовы координаты 10.4-3
— — —, сферические координаты 10.4-3
— — —, цилиндрические координаты
10.4-3
— линейное 1.8-1
— — однородное, матричное обозначение
14.5-3
— линии кривизны 17.3-6
— Люилье 1.12-4
— нормали к кривой второго порядка
2.4-10
— — — — плоской 17.1-2
— — к поверхности 17.3-2
— — к прямой 2.3-2
— нормальной плоскости 17.2-4
— огибающей семейства плоских кривых
17.1-7
Уравнение окружности в полярных
координатах 2.5-1
— — общее 2.5-1
— —, проходящей через точки
пересечения двух окружностей 2.5-1
— —, — через три точки 2.5-1
— — с центром в начале координат 2.5-1
— определяющее 9.3-6
— плоскости в отрезках 3.2-1
— — нормальное 3.2-1
— — общее 3.2-1
— — , проходящей через данную точку
3.2-1
— —, —через три точки, не лежащие на
одной прямой 3.2-1
— поверхности второго порядка,
приведение к каноническому виду 3.5-7
— —, проходящей через линию
пересечения поверхностей 3.1-16
— проекции кривой на координатную
плоскость 3.1-16
— прямой в отрезках 2.2-1
— — в полярных координатах 2.2-2
— — нормальное 2.2-1
— — общее 2.2-1
— —, параллельной данной 2.3-2
— —, проходящей через данную точку
перпендикулярно плоскости 3.4-5
— —, — через две точки 2.2-1
— —, — через точку пересечения прямых
2.3-2
— —,—. — — под углом к прямой 2.3-2
— — с угловым коэффициентом 2.2-1
— Пуассона двумерное 15.6-7
— пучка плоскостей 3.4-5
— — прямых 2.2-1
— с частными производными 10.1-2
— — — — гиперболическое 10.3-1 —
10.3-3, 10.3-6, 10.3-7
— — — — квазилинейное 10.2-1, 10.3-1
— — линейное 10.1-2
—.—.___, метод разделения
переменных 10.1-3
_________ однородное 10.1-2
— — — — параболическое 10.3-1, 10.3-3,
10.3-7
— — — — первого порядка 10.2-1
— — — — эллиптическое 10.3-1, 10.3-3,
10.3-7
— — — разностями 20.4-3
— связи 11.3-4
— соприкасающейся плоскости 17.2-4
— спрямляющей плоскости 17.2-4
— сферы 3.5-9
— телеграфное 10.4-1
— —, частные решения 10.4-8
— теплопроводности 10.4-1
— — одномерное, преобразование
Лапласа 10.5-3
— — —, синус- и косинус-преобразования
Фурье 10.5-3
— функциональное 20.4-6
— характеристики 17.3-11
— характеристическое 10.2-2, 10.2-4
— — квадратичной формы 2.4-5, 3.5-4
— — матрицы 13.4-5
— четвертой степени 1.8-5
— — — неполное 1.8-5
— — —, решение Декарта — Эйлера 1.3-5
— — —, — Феррори 1.8-6
— Шредингера, частные решения 10.4-6
— Эйлера 11.6-1
— Якоби 11.6-10
Уравнения асимптот гиперболы 2.5-2
— в вариациях по параметрам 13.6-4
— Вейнгартена 17.3-8
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
627
Уравнения Гаусса 17.3-8
— геодезической линии 17.3-12
— канонические 10.2-6
— канонических поверхностей второго
порядка 3.5-7
— Колмогорова — Смолуховского —
Чепмена 18.11-4
— Коши — Римана 7.3-2
— кривой естественные 17.2-3
— —, проходящей через точки
пересечения кривой с поверхностью 3.1-16
— кривых второго порядка канонические
2.4-8, 2.4-9
— линейно зависимые 1.9-3
— — независимые 1.9-3
— Майнарди — Кодацци 17.3-8
— нормали к поверхности второго порядка
3.5-8
— параллелизма 16.10-9
— Петерсона — Кодацци 17.3-8
— плоскостей, проектирующих прямую на
координатные плоскости 3.3-1
— преобразования 4.5-6
— прямой как пересечения двух
плоскостей 2.3-1
— — канонические 3.3-1
— — параметрические 2.2-2, 3.3-2
— —, проходящей через данную точку в
данном направлении 3.3-1
— —, — через две точки 3.3-1
— ребра возврата 17.3-11
— сопряженные 11.8-2, 11-8-4
— состояния 11.8-1, 11.8-4
— — конечно-разностные 11.9-1
— чувствительности 13.6-4
— эвольвент 17.2-5
— Эйлера 11.6-1
Уровень значимости критерия 19.1-3,
19.6-3
Ускорение движущейся точки, разложение
на тангенциальную и нормальную
составляющие 12.2-3
Условие граничное естественное 11.6-5
— Лежандра усиленное 11.6-10
— Липшица 9.2-1
— необходимое максимума функции при
условиях-неравенствах 11.4-3
— параллельности плоскостей 3.4-1
— — прямой и плоскости 3.4-1
— — прямых 2.3-2
— пересечения трех прямых в одной точке
2.3-2
— перпендикулярности прямой и
плоскости 3.4-1
— — прямых 4.3-2, 3.4-1
— представления 14.9-1
Условие того, что две прямые лежат в
плоскости 3.4-3
— —, — три плоскости проходят через
одну прямую 3.4-3
— —, — — точки лежат на одной
прямой 2.3-1, 3.4-3
—- —, — четыре плоскости проходят
через одну точку 3.4-3
— —, — — точки лежат в одной
плоскости 3.4-3
— трансверсальности 11.6-5, 11.6-8
— — общее 11.6-5
Условия Вейерштрасса — Эрдмана для
экстремалей 11.6-7
— граничные типа Коши 10.2-1
— Дирихле 4.4-8, 4.11-4
— интегрируемости 10.1-2
— краевые 9.1-2
— Линдеберга 18.6-5
— Ляпунова 18.6-5
Условия начальные 9.1-2, 10.2-1
— параллельности прямых 3.4-1
— периодичности 15.4-8
— полосы 10.2-1
— скачка 11.8-5
— совместности 10.1-2
— трансверсальности 11.8-2
— угловые 11.6-7, 11.6-8, 11.8-5
— Якоби 11.6-8
Устойчивость дифференциального
уравнения 9.4-4
— — — асимптотическая 9.5-4
— периодических решений системы
дифференциальных уравнений 9.5-4
— по Ляпунову решений системы
дифференциальных уравнений 9.5-4, 13.6-5
— равновесия автономных систем 13.6-6
— равновесного решения системы
дифференциальных уравнений 9.5-4
— решений автономной системы 9.5-4
— — системы линейных разностных
уравнений 20.4-8
— статистическая 19.1-1
Ф
Фаза 4.11-4
Фазовая переменная 11.8-1
— плоскость 9.5-2
— траектория 9.5-2
Фактор композиционный 12.2-6
Фактор—группа группы по нормальному
делителю 12.2-6
Факториал 1.2-4
Факториальный многочлен степени п
21.5-1, 21.5-3
Фильтры усредняющие 19,8-2
Фокальная ось 2.4-9
— хорда 2.4-9
Фокальный параметр 2.4-9
Фокус 2.4-9, 17.3-11
— устойчивый, неустойчивый 9.5-4
Форма билинейная 13.5-1
— квадратичная 13.5-2
— однородная 13.5-2
— пространства основная относительно
базиса 14.7-1
— эрмитова см. Эрмитова форма
Формула Адамса 20.8-3
— Адамса — Башфорта четвертого
порядка 20.8-3, табл. 20.8-2
— Бессели интегральная 21.8-2
— Гильберта — Шмидта для
резольвентного ядра 15.3-8
— Грина для окружности с условиями
Дирихле 15.6-9
— — обобщенная 15.4-3
— Дюамеля 10.5-4
— интегральная Гейне 21.8-11
— — Дирихле 21.9-4
— — Коши 7.5-1
Пуассона 15.6-6, 15.6-9, 21.8-2
— интерполяционная см.
Интерполяционная формула
— квадратурная, см. квадратурная формула
— Лапласа для чисел Бернулли 21.5-2
— Муавра 1.3-3
— обращения 10.5-1
— Родрига обобщенная 21.7-5, табл. 21.7-2
— Стирлинга 21.4-2
— Тейлора 4.10-4, 4.10-5
— — локальная 11.3-2
— третьего порядка 20.8-3
— Штермера 20.8-7
— Эйлера для выпуклых многогранников
1.10-6
828
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Формула Байеса 18.2-6, 18.4-5
— Грина 4.6-12
— дифференцирования 4.5-1
— для уничтожения иррациональности в
знаменателе 1.2-2
— квадратурные см. Квадратурные
формулы
— Кемпбелла 18.11-5
— Ньютона 1.4-3, 1.6-3
— параболической интерполяции 20.5-2
— половинных углов 1.12-4
— приведения Гаусса для
гипергеометрических функций табл. 9.3-2
— разложения Хевисайда 8 4-4
— Фредгольма для резольвентного ядра
15.3-8
— Френе — Серре 17.2-3
— Эйлера — Фурье 4.11-2
Функции асимптотически
пропорциональные 4.4-3
— — равные 4.4-3
— асимптотические соотношения 4.4-3
— бесконечно большие порядка 1, 2, ...
4.4-3
— — — экспоненциального порядка
4.4-3
— — малые порядка 1,2, ... 4.4-3
— Бесселя сферические 21.8-8
— — —, асимптотические разложения
21.8-9
— — —, теорема сложения 21.8-3
— —.условия ортогональности 21.8-4
— — цилиндрические, асимптотические
разложения 21.8-9
— — — второго рода 21.8-1
— — —, интегральные представления
21.8-2
— — —, — формулы 21.8-2
— — — модифицированные 21.8-6
— — — нецелого порядка 21.8-1
— — — первого рода 21.8-1
— — — целого порядка 21.8-1, 21.8-4
— Вебера 21.8-1
— Вейерштрасса 21.6-2, 21.6-3, 21.6-9
— взаимно ортогональные 15.2-3
— Ганкеля, асимптотические разложения
21.8-9
— — второго рода 21.8-1
— — модифицированные 21.8-6
— — первого рода 21.8-1
— гармонически сопряженные 15.6-8
— гиперболические 21.2-5, 21.2-6, 21.2-7,
21.2-9
— —, геометрическая интерпретация 21.2-5
— —, разложение в степенной ряд 21.2-12
— единичные асимметричные 21.9-1
— импульсные асимметричные 21.9-3
— канонически сопряженные 10.2-6
— корреляционные действительных
случайных процессов 18.10-4
— — для линейной комбинации
случайных процессов 18.12-1
— Лагерра присоединенные 21.7-5
— Лежандра второго рода 21.7-3
— — первого рода 21.7-3
— — присоединенные 21.8-10
— — —, интегральные свойства 21.8-11
— — — первого рода 21.8-10
— линейно зависимые 1.9-3
— — независимые 1.9-3
— Неймана 21.8-1
— —, асимптотические разложения 21.8-9
— некоррелированные 18.10-9
— неявные, теорема существования 4.5-7
— обратные гиперболические 21.2-3,
21.2-11
Функции обратные гиперболические,
разложение в степенной ряд 21.2-12
— — тригонометрические 21.2-4, 21.2-11
— — —, главные значения 21.2-4
— — —t разложение в степенной ряд
21.2-12
— одинакового порядка 4.4-3
— от многих радиусов-векторов 5.5-8
—, отображающие специальные области на
единичный круг 7.9-6
— симметрические элементарные 1.4-3
— случайные величины одномерной 18.5-2
— случайных величин многомерных 18.5-4
— тригонометрические 21.2-1, 21.2-2,
21.2-3, 21.2-9
— —, разложение в бесконечные
произведения 21.2-13
— —, — в степенной ряд 21.2-12
— функционально зависимые 4.5-6
— цилиндрические, теорема сложения
21.8-13
— Чебышева второго рода 21.7-4
— эквивалентные 4.4-3
— элементарные, выражение через
гипергеометрические табл. 9.3-2
— эллиптические см. Эллиптические
функции
— Эрмита 21.4-6
— berm2, beim2, hermz, helmz, kermz,
keim2 21.8-7
Функционал 12.1-4
— линейный 14.4-9
Функциональное уравнение 20.4-6
Функциональный анализ 15.1-1
— определитель 4.5-6
Функция автокорреляционная 18.9-3,
18.10-8
— алгебраическая 4.2-2
— аналитическая 4.10-4
— — в бесконечности 7.3-3
— — в открытой области 7.3-3
— — в точке 7.3-3
— —, интегральные теоремы 7.5
— — моногенная 7.4-2
— — — с естественными границами 7.8-1
— —, разложение в ряд 7.5-2, 7.5-3
-— —, свойства 7.3-4
— антипериодическая 4.2-2, 8.3-2
— аппроксимирующая 20.8-4
— аргумента х 4.2-1
— бесконечно большая 4.4-1
— — малая 4.4-1
— бесконечного порядка 7.6-5
— — типа 7.6-5
— Вейерштрасса 11.6-10
— векторная линейная 14.3-1
— — точки 5.4-3
— вероятностная 18.2-7
— весовая 15.2-1
— взаимная корреляционная 18.9-3,
18.10-8
— влияния 19.8-2
— возрастающая 4.4-8
—, выпрямление 8.3-2
— Гамильтона 11.6-8
— гармоническая 15.6-4
— гипергеометрическая 9.3-9
— — второго рода 9.3-8
— — вырожденная второго рода 9.3-10
— — —, дополнительные формулы табл.
9.3-3
— — — Куммера 9.3-10
— —, формулы приведения Гаусса табл.
9.3-2
— голоморфная 7.3-3
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
829
Функция Грина 9.3-3
— — асимметрическая 9.4-3
— — второго рода 15.5-4
— — для краевой задачи с однородными
краевыми условиями 15.5-1
— — для линейных краевых задач 9.3-3
— — для плоскости 15.6-9
— — для полуплоскости с условиями
Дирихле 15.6-9
— — для полупространства с условиями
Дирихле 15.6-6
— — для сферы с условиями Дирихле
15.6-6
— — модифицированная 15.5-1
— — обобщенная 9.3-3
— — разложение по собственным
функциям 15.5-2
— — симметрическая 9.4-3
— двоякопериодическая 21.6-1
— —, детектирование 8.3-2
— — целая 21.6-1
— Дирихле S (х) 21.9-2
— дифференцируемая 7.3-1
— —- в точке 4.5-1, 4.5-3
— — на множестве 4.5-3
— дробная рациональная 4.2-2
— единичная симметричная 21.9-1
— измеримая 4.6-14
— —, свойства 4.6-14
— импульсная, аппроксимация
непрерывно дифференцируемыми функциями
21.9-4
— —, — разрывными функциями 21.9-4
— — единичная симметричная 21.9-2
— —, представления интегралом Фурье
21.9-5
— интегральный синус, интегральный
косинус и т. д. см. Интегральный синус
и т. д.
—, интегрируемая в смысле Римана 4.6-1
—. — по Лебегу 4.6-15
—, квадратически интегрируемая 15.2-1
— комплексная 7.2-1
— конечного порядка 7.6-5
— — типа 7.6-5
— координат, инвариантная относительно
преобразований координат 14.1-4
— корреляционная 18.9-3
— — нормированная 18.10-2
— — по времени 18.10-8
— — по множеству наблюдений 18.10-2
— кусочно-гладкая 4.5-1, 4.5-3
— кусочно-непрерывная 4.4-7
— линейная 11.4-1
— логарифмическая 21.2-10, 21.2-11
— —, разложение в степенной ряд 21.2-12
— Ляпунова 13.6-6
— матрицы 13.2-12
— мероморфная 7.6-7
— —, разложение на простейшие дроби
7.6-7
—- минимального типа 7.6-5
— многих переменных 4.2-1
— — — аналитическая 4.10-5
— — —, разложение в кратный ряд
Тейлора 4.10-5
— многозначная 4.2-2
— монотонная строго 4.4-8
— — нестрого 4.4-8
— невозрастающая 4.4-8
— Неймана 15.5-7
— неограниченно возрастающая 4.4-1
— непрерывная в точке 4.4-6
— — — — слева 4.4-7
— — —•—- справа 4.4?7
Функция непрерывная на множестве 4.4-6
— непрерывно дифференцируемая 4.5-3
— неубывающая 4.4-8
— нечетная 4.4-2
— нормального типа 7.6-5
— нормируемая 15.2-1
— обратная 4.2-2
— ограниченная 4.3-3
— ограниченной вариации 4.4-8
— однозначная 4.2-2, 12.1-4
— однородная степени г 4.5-5
— ошибок 18.8-3
— передаточная 9.4-7
— периодическая 4.2-2, 8.3-2
— подынтегральная 4.6-1
— показательная 21.2-9
— —, разложение в степенной ряд 21.2-12
— полигональная 11.7-3
— правдоподобия 19.1-2
— представление интегралом 4.10-1
—, — — Фурье 4.11-4
— производящая см. Производящая
функция
— равномерно непрерывная на множестве
4.4-6
— — ограниченная 4.3-3
— — сходящаяся 4.4-4
—. разложение в непрерывную дробь
4.8-8
—, — в ряд 15.2-6
—, — — — степенной 4.10-1
—, — — — Тейлора 4.10-4
—, — — — Фурье 4.11-4
— распределения 18.2-9
— — вероятностей случайного процесса
18.9-2
— — двумерного случайного вектора
18.4-2
— — маргинальная 18.4-7
— — многомерная 18.4-7
— — нормальная 18.3-3
— — эмпирическая 19.2-2
— рациональная 4.2-2
— —, разложение на элементарные дроби
1.7-4
— регулярная 7.3-3
— результирующая 15.3-1
— решающая 19.9-1
— Римана — Грина 10.3-6
— с зеркально сдвинутыми полуволнами
8.3-2
— скалярная точки 5.4-2
— случайная, см. Случайная функция
— собственная краевой задачи 10.4-2
— спектральная обобщенная 18.10-10
—, среднее значение 4.11-4
—, стремящаяся к пределу 4.4-1
—, — к + оо, — оо 4.4-1
— ступенчатая 21.9-1
— —, аппроксимация непрерывными
функциями 21.9-1
— —, представления интегралом Фурье
21.9-1
— суммируемая 4.6-15
—, сходящаяся к пределу 12.Б-3
— точек 16.1-3
—- убывающая 4.4-8
—, условие аналитичности в точке 7.3-3
—, условие дифференцируемости 7.3-2
—- характеристическая 18.3-8, 18.4-10
—- — д-мерная 18.9-3
—- — совместная 18.9-3
— целая 7.6-5
— —, разложение в произведение 7.6-6
— — рациональная 1.4-3, 4.2-2, 7.6-5
— — трансцендентная 7.6-5
830
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функция целевая 11.4-1
— цилиндрическая 21.9-1
— — круговая 21.8-1
— четная 4.2-2
— экспоненциального типа 7.6-5
— эллиптическая см. Эллиптическая
функция
Функция-объект 15.3-1
X
Характер представления 14.9-4
— — примитивный 14.9-4
— — простой 14.9-4
— — составной 14.9-4
Характеристика 10.2-1, 10.3-1, 10.3-7,
17.3-11
— области целостности 12.3-1
— оперативная критерия 19.6-2
— частотная 9.4-7, 20.8-8
Характеристическая функция 18.3-8,
18.4-10
— — интегрального уравнения 15.3-3
— — линейного дифференциального
оператора 15.4-5
— — ядра 15.3-3
Характеристический вектор оператора
14.8-4, 14.8-7
Характеристическое значение оператора
14.8-3, 14.8-4
— уравнение оператора 14.8-3
— число линейного дифференциального
оператора 15.4-5
Ц
Целевая функция 11.4-1
Цена действия системы 19.9-1
— игры 11.4-4
Центр выборочного распределения 19.7-2
— группы 12.2-7
— кривизны 17.1-4, 17.2-5
— кривой второго порядка 2.4-6
— окружности 2.5-1
— поверхности второго порядка 3.5-5
— пучка 2.3-2
— распределения вероятностей 18.3-3,
18.4-4, 18.4-8
— рассеивания 18.4-4
— соприкасающейся сферы 17.2-5
Цепная линия 2.6-2
— дробь 4.8-8
Цепь 12.6-2
— Маркова 18.11-4
Цикл 18.7-3
Циклоида 2.6-2
— удлиненная 2.6-2
— укороченная 2.6-2
Цилиндр 1.10-4, 3.1-15
— гиперболический 3.5-7
— параболический 3.5-7
— эллиптический 3.5-7
Цилиндрическая функция см. Функция
цилиндрическая
Цилиндрические гармоники 21.8-1
Циркуляция вектора 5.7-1
Циссоида Диоклесса 2.6-1
Ч
Частичная сумма ряда 4.8-1
Частная производная вектор-функции 5.3-2
— — функции 4.5-2
— — — более высокого порядка 4.5-2
Частное 1.7-2
— комплексных чисел 1.3-3
Частное Релея 14.8-8, 15.4-7
— — для обобщенной задачи о
собственных значениях 14.8-8
Частота круговая 4.11-4
— — собственная 9.4-1
— основная 4.11-4
— — гармоническая вторая, третья 4.11-4
— попадания относительная в /-й
классовый интервал 19.2-2
— события 19.2-1
— — групповая 19.2-2
— — накопленная 19.2-2
— — относительная 19.2-1
— — — накопленная 19.2-2
Частотная характеристика 9.4-7
Числа алгебраические 1.1-2
— Бернулли 21.5-2, 21.5-3
— — порядка п 21.5-2
— —, рекуррентная формула 21.5-2
— —, формула Лапласа 21.5-2
— иррациональные 1.1-2
— натуральные 1.1-2
— —, полная упорядоченность 1.1-2
— —, свойства 1.1-2
— —, упорядоченность 1.1-2
— Стирлинга 21.5-1
— трансцендентные 1.1-2
— Фибоначчи 8.7-2
— целые 1.1-2
— —, сравнимые по модулю 12.2-10
Численное дифференцирование 20.7-1
— интегрирование дифференциальных
уравнений 20.8-2
— — — — второго порядка 20.8-7
— — — — высших порядков 20.8-6
— — для равноотстоящих узлов 20.7-2
— — систем дифференциальных
уравнений 20.8-6
— — уравнений с частными
производными 20.9-1, 20.9-4
Численное решение алгебраических
уравнений 20.2:4
— — двухточечной краевой задачи для
дифференциальных уравнений 20.9-2
— — краевых задач, методы
аппроксимирующих функций 20.9-9
— — интегральных уравнений 20.9-10
Число алгебраическое 1.6-3
— действительное 1.1-2, 1.3-1
— комплексное 1.3-1
— мнимое 1.3-1
— обратное 1.1-2
— противоположное 1.1-2
— чисто мнимое 1.3-1
— Эйлера е 1.2-3
Числовые ряды 4.8-5
— суммы 1.2-8
Ш
Шар конечного радиуса замкнутый 12.5-3
__ — __ открытый 12.5-3
Шестиугольник 1.10-1
Ширина спектра случайного процесса
18.11-2
Широта 3.1-6
Э
Эвольвента 17.2-5
Эволюта 17.2-5
Экстремаль 11.6-1
— ломаная 11.6-7
— с угловыми точками 11.6-7
Экстремум, достаточные условия 11.2-2,
11.3-3
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
831
Экстремум, необходимые условия 11.2-2,
11.3-3
— односторонний 11.6-7
— определенного интеграла, необходимое
условие 11.6-1
— — — условный 11.6-2
— условный, необходимое условие 11.3-4
Эксцентриситет 2.4-9
Эксцесс 19.2-4
Элемент булевой алгебры дизъюнктивный
12.8-1
— вероятности 18.3-2, 18.4-3, 18.4-7
— группы 12.2-1
— — обратный левый 12.2-1
— дуги 4.6-9
Элемент кольца с единицей левый
обратный, правый обратный 12.3-1
— линейной алгебры идемпотентный 12.4-2
— — — нильпотентный 12.4-2
— матрицы 13.2-1
— множества 4.3-2
— объема 6.2-3, 16.10-10
— плоский 10.2-1
— площади 17.3-3
— — векторный 17.3-3
— — поверхности 5.4-6
— расстояния 17.4-2
Элементы группы перестановочные 12.2-1
— — сопряженные 12.2-5
— —, сравнимые по модулю 12.2-10
— определителя 1.5-1
—, эквивалентные относительно
подгруппы 12.2-8
Эллипс 2.4-8, 2.4-9
—, построение касательных и нормалей
2.5-3
—, — по осям 2.5-3
Эллипсоид вращения вытянутый 1.10-5
— — сплюснутый 1.10-5
—- действительный 3.5-7, 3.5-10
— рассеяния 18.4-8
Эллипсы равной вероятности 18.8-6
Эллиптическая функция 21.6-1, 21.6-2
Эллиптические функции Якоби 21.6-7,
21.6-9
— — —, дифференцирование 21.6-7
— — —, разложения в ряды 21.6-7
— — —, теорема сложения 21.6-7
Эллиптический интеграл 4.6-7, 21.6-4
— —, алгебраическое приведение 21.6-5
— — Вейерштрасса нормальный второго
рода 21.6-3
— — — — первого рода 21.6-2
— — Лежандра нормальный неполный
21.6-6
— — — — ПОЛНЫЙ 21.6-6
— —, нормальная форма Вейерштрасса
21.6-5
— —, — — Римана 21.6-5
— — нормальный первого, второго,
третьего рода 21.6-5
Эллиптический интеграл первого, второго,
третьего рода 21.6-4, 21.6-5
— —, приведение к нормальной форме
Лежандра 21.6-5
— — связанный 21.6-6
Эндоморфизм 21.1-6
Энтропия распределения вероятностей
18.4-12
— условная 18.4-12
Энумератор 18.7-3
Эпициклоида 2.6-2
Эргодический процесс 18.10-7
Эргодическое свойство 18.10-7
Эрмитова матрица неопределенная 13.5-3
— — неположительная 13.5-3
— — неотрицательная 13.5-3
— — отрицательно определенная 13.5-3
— — — полуопределенная 13.5-3
— — положительно определенная 13.5-3
— — — полуопределенная 13.5-3
— форма 13.5-3
— —, линейная подстановка 13.5-4
— — неопределенная 13.5-3
— — неотрицательная 13.5-3
— — неположительная 13.5-3
— _ отрицательно определенная 13.5-3
— — — полуопределенная 13.5-3
— — положительно определенная 13.5-8
— — — полуопределенная 13.5-3
Эффект дробовой 18.11-5
Эффективность оценки 19.4-1
— — асимптотическая 19.4-1
Я
Явление Гиббса 4.11-7
Ядро взаимное 15.3-7, 15.3-9
— вырожденное разделяющееся 15.3-1
— гомоморфизма 12.2-9
интегрального преобразования 15.3-1
— итерированное 15.3-5
— линейного преобразования 14.3-2
— непрерывное в среднем 15.3-1
— нормируемое 15.3-1
— резольвентное 15.3-7
— симметричное 15.3-1
— сингулярное 15.3-8
— сопряженное 15.3-1
— транспонированное 15.3-1
— эрмитово 15.3-1, 15.3-2
— — вспомогательное 15.3-4
— — неотрицательное 15.3-6
— — неположительное 15.3-е
— — отрицательно определенное 15.3-6
— — полное 15.3-4
— — положительно определенное 15.3-в
— —, разложение в ряд 15.3-6
— — сопряженное 15.3-1
— —, теоремы разложения 15.3-4
Якобиан 4.5-6
Г. Корн, Т. Корн
СПРАВОЧНИК ПО МАТЕМАТИКЕ
Для научных работников
и инженеров
М., 1973 г., 832 стр. с илл.
Редактор Н. X. Розов
Техн. редактор С. Я. Шкляр
Корректор //. Б. Румянцева
Сдано в набор U/VII 1972 г. Подписано к
печати 23/1II 1973 г. Бумага 60x90Vtc. тип. № 1.
Физ. печ. л. 52. Условн. печ. л. 52.
Уч.-изд. л. 70,72. Тираж 100 000 экз.
Цена книги 3 р. 89 к. Заказ № 414.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 1 «Печатный Двор»
имени А. М. Горького Союзполиграфпрома при
Государственном комитете Совета Министров
СССР по делам издательств, полиграфии и
книжной торговли, г. Ленинград, Гатчинская ул., 26