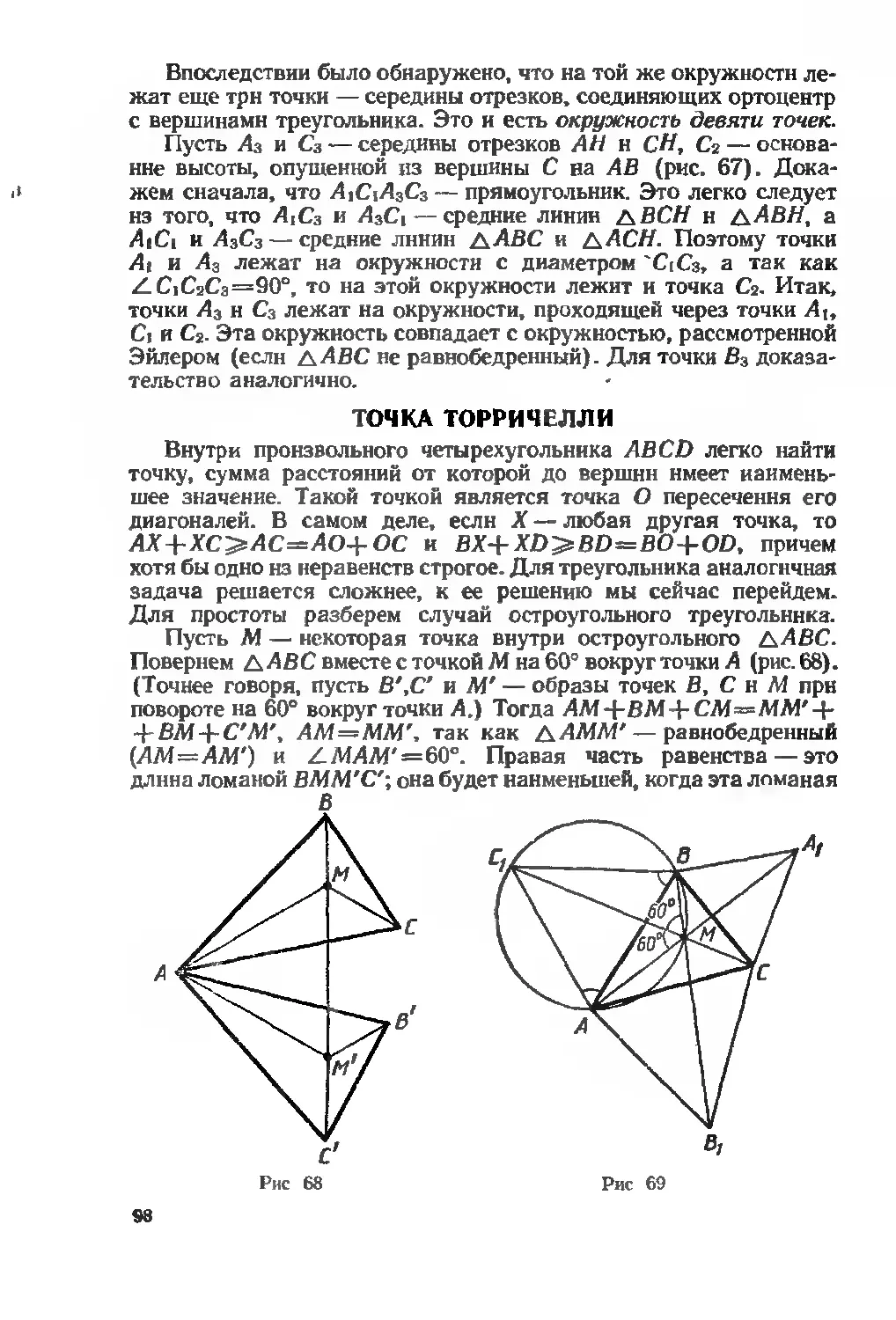
Автор: Никольская И.Л.
Теги: физико-математические науки математика учебное пособие
ISBN: 5-08-001287-3
Год: 1991
Текст
ФАКУЛЬТАТИВНЫМ
КУРС
ПО МАТЕМАТИКЕ
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ 7—9 КЛАССОВ
СРЕДНЕЙ ШКОЛЫ
Составитель И. Л. НИКОЛЬСКАЯ
Рекомендовано
Главным учебно-методическим
управлением общего среднего
образования Госкомитета СССР
по народному образованию
МОСКВА «ПРОСВЕЩЕНИЕ» 1991
Б БК 22.1я72
Ф18
Рецензенты:
кандидат физико-математических наук В. М. Уроев-
кандидат физико математических наук Д. А. Митькин',
учитель средней школы № 5 г. Люберцы В. В. Гузеев
Факультативным курс по математике: Учеб, пособие для
Ф18 7—9 кл. сред. шк./Сост. И. Л. Никольская.— М.: Просвеще-
ние, 1991.—383 с.: ил.—ISBN‘5-09-001287-3.
Книга содержит статьи по всем темам программы факультатива «За
4. • страницами учебников математики». Наряду с теоретическим материалом
. в пособие включенье примеры решения задач и упражнения для самостоя-
* тельной работы учащихся.
ф ИКФ' письмо ~ 89> доп- м 1 ББК 22-,я72
ISBN 5-08-001287-3
© Составитель Никольская И. Л., 1991
ОБРАЩЕНИЕ К ЮНЫМ ЧИТАТЕЛЯМ
Эта книга адресована тем, кто интересуется математикой и хо-
чет узнать о ней больше, чем можно прочитать в учебнике- или
услышать на уроке. Возможно, она окажется полезной и тем,
кто безразличен к математике и даже питает к ией неприязнь.
Ведь, чтобы узнать вкус яблока, надо его попробовать. На уроках
учитель разжевывает вам «математическое яблоко», а эта книга
дает возможность, опираясь на первоначальные, «азбучные» зна-
ния, полученные на уроках, самостоятельно илн с помощью учите-
ля «вгрызться» в математику и ощутить вкус к ней.
Каждый ли зиает, к какой деятельности ои способен, какой
заложен в нем талант, а может быть, гений? Известно, что путь
Ломоносова к вершинам Науки начался со знакомства с «Арифме-
тикой» Магницкого, и, кто знает, что было бы, ие попади она ему
в руки.
Предлагаемую вам книгу написалн людя, любящие математику
и избравшие ее своей профессией, с целью увлечь вас этой наукой,
помочь почувствовать ее красоту, обнаружить в себе математи-
ческие способности (а оии есть у многих!), наконец, пробудить
интерес к математике у тех, кто его до снх пор не испытывал.
Ведь владение математикой необходимо во всякой технической,
инженерной профессии, в любой отрасли естественнонаучного
знания, а без интереса к предмету по-иастоящему овладеть им
невозможно.
Чтение этой книги ни в коем случае не должно быть пассивным,
с ней надо работать. В каждой нз двенадцати статей, помещенных
в книге, приведены задачи, которые необходимо решить, чтобы как
следует понять и усвоить содержание статьи.
Содержание статей (одних в большей степени, других в мень-
шей) связано с содержанием основного курса математики, и оин
соответственно распределены по классам. К каждой статье дается
список литературы, обращаясь к которой вы сможете расширить
знания,по интересующему вас вопросу. (При ссылке на рекоменду-
емую книгу номер ее в списке литературы пишется в квадратных
скобках, например [2].) Хорошим помощником в факультативных
занятиях по математике вам послужат и следующие книги:
Энциклопедический словарь юного математика.— М.: Педаго-
гика, 1985.
Энциклопедия элементарной математики.— М.: Наука, 1966.
Детская энциклопедия.— М., 1972.— Т. 2.
Математика в понятиях, определениях и терминах.— М.: Про-
свещение, 1978.— Ч. 1.
Математика в понятиях, определениях и терминах.— М.: Про-
свещение, 1982.— Ч. 2
Советуем также регулярно читать журнал «Кваит».
Желаем успеха!
з
7 КЛАСС
СИСТЕМЫ СЧИСЛЕНИЯ
Язык математики — ее основные понятия и обозначения — вы-
рабатывался на протяжении многих столетий. Остаются в употреб-
лении, распространяются и постепенно становятся общепринятыми
наиболее универсальные, лаконичные, удобные в обращении сред-
ства этого языка. Это относится и и самому основному понятию,
возникшему при зарождении математики,— понятию числа. Спо-
собы записи чисел называются системами счисления.
Конечно, прежде всего речь идет о записи натуральных, т. е.
целых положительных чисел 1, 2, 3, 4, .... а затем —о записи
рациональных (дробных) и других чисел.
Мы привыкли пользоваться десятичной системой счисления.
Записывая число, скажем, 256, мы обычно не задумываемся,
что означает каждая цифра: ясно, что последняя цифра 6 — это
число единиц, 5 — число десятков, 2 — сотеи, так что 256 — это
короткая запись числа 2-1004-5-10 + 6. Десятичная система стала
сейчас общепринятой повсюду в мире. Но в глубокой древности
у многих народов складывались свои традиции записи чисел н
действий с иимн — они возникали и развивались вместе с практи-
ческими потребностями, такими, как подсчет и нумерация пред-
метов, измерение различных величии, торговля. И сейчас наш мир
вовсе не стал однообразно-десятичным. Многие предметы оби-
хода — ложки, чашки, стулья — обычно считают ие десятками, а
шестерками или дюжинами. Традиция измерять время (а также уг-
лы и дуги) в минутах и секундах — делить целое не иа 10, а на 60
частей — восходит к древневавилонской шестидесятеричной сис-
теме.
Разнообразие систем счисления имеет не только исторический
интерес. Хотя свойства чисел не зависят, конечно, от способа запи-
си, но в некоторых задачах удобнее представлять числа не в деся-
тичной, а в другой системе. Особенно многочисленны применения
двоичной системы, использующей всего две цифры — 0 и 1. Глав-
ное из этих применений — современные электронные вычисли-
тельные машины (ЭВМ) и системы передачи информации, в ко-
торых используются миниатюрные элементы с двумя устойчивыми
состояниями.
4
РАЗВИТИЕ СИСТЕМ СЧИСЛЕНИЯ
Простейшая система записи натуральных чисел rpeoyei лишь
одной цифры, скажем «палочки» |, которая изображает единицу.
Повторяя этот знак, мы можем записать числа два ||. три Щи т. д.:
каждое число п записывается просто п «палочками». Таким спо-
собом первобытный человек мог записать небольшие числа с по-
мощью зарубок на дереве (или, как индейцы Америки, узелком
и а веревке). В такой системе счисления очень удобно складывать
числа — достаточно просто приписать одно к другому:
III IIIII-IIIIIIII
3 + 5=8
Столь же легко вычесть из большего числа меиьшее. Нетрудно
и умножить одно число а на другое b — можно записать а рядов
no Ь палочек в каждом, а потом при желании выписать их в строку:
7
fiiiiiii
з{|||11|| -> IIIIIIIIIIIIIIIIIIHI
Innin
3-7=21.
Но, конечно, подобный способ записи очень неэкономен и для
больших чисел неизбежно приведет к ошибкам в счете. Возни-
кает естественная идея упрощения записи: разбить ее иа одинако-
вые группы и каждую группу заменить специальным знаком;
затем из этих знаков можно опять составить группу, придумать
для нее новое обозначение и т. д. По-видимому, примерно такую
эволюцию прошли иа протяжении сотеи н тысяч лет способы счета
и нумерации у разных народов.
В древнеегипетских иероглифических записях использованы
знаки [для единицы. для десятка. С для сотни (и некоторые
НИ
другие); скажем, 127 записывалось как С ^т0 пРимеР
дативной системы (от латинского additio — складывание): чтобы
узнать, какое число записано, нужно просто сосчитать сумму всех
входящих в запись чисел, порядок расположения знаков учиты-
вать ие нужно.
В Древией Греции постепенно сложился другой способ обо-
значения чисел — здесь однозначные числа 1, 2,.... 9 и несколько
следующих за ними «круглых» чисел (10, 20..... 90, 100, ...)
обозначались последовательными буквами алфавита с чертой иад
ними: а, 0. у, . Эта традиция через Византию пришла и в
древ неславянскую письменность.
5
В Древнем Риме в качестве «ключевых* чисел использовались
1, 5, 10, 50, 100, 500 н 1000— они обозначались соответственно I,
V, X, L, С, D н М.
Конечно, не случайно у многих народов «ключевыми» числами
оказались 5 и 10: это объясняется тем, что счет велся на паль-
цах (одной или двух рук). Вероятно, отсюда произошли и обозна-
чения римских цифр V (одна «пятерня») и X (две «пятерни»).
Знаки С, М и D — это просто первые буквы латинских слов centum
(сто), ntille (тысяча) и demimille (полутысяча), a L=50 можно
запомнить как «половнику от С—100», хотя настоящее его проис-
хождение, видимо, иное. Римские цифры можно увидеть иа цифер-
блатах часоа, часто нм и пользуются для обозначения веков, нуме-
рации глав в книге. Изредка иа старом доме можно увидеть н боль-
шое римское число — год постройки.
Числа 2, 3, 4, 8, 9, 14, 19, 20, 40, 1989 в этой римской записи
выглядят так:
II, III, IV, VIII, IX, XIV, XIX, XX, XL, MCMLXXXIX.
Как видно, здесь используется не только сумма, но и разность
двух «ключевых» чисел — для этого перед большим из них ставится
меньшее; благодаря этому вместо длинной аддитивной записи,
скажем LXXXXIIII, получается более короткая XCIV. Интересно,
что наиболее древние тексты использовали длинную, аддитивную
запись — «правило разности» появилось позднее.
У римской, как и у аддитивных систем, есть очевидные недостат-
ки: с числами, записанными по такой системе, трудно опериро-
вать — складывать их, вычитать, умножать. Чтобы использовать
очень большие числа (или дроби), приходится вводить новые циф-
ры или дополнительные знаки, новые правила обращения с инми.
Замечательная идея, позволяющая использовать немного цифр
для обозначения даже очень больших чисел,— переход к позицион-
ной системе счисления. В такой системе значение каждой цифры в
записи зависит от места — позиции, которую она занимает; так, в
десятичной системе одна и та же цифра может означать число
единиц, или десятков, или сотеи и т. д. в зависимости от разряда,
где она стоит.
Самая древияя позициоииая система известна нам по клино-
писным табличкам вавилонян, найденным в долине между Тигром
и Евфратом, возраст некоторых более 2 или даже 3 тысячелетий.
Все иероглифы жителей Древнего Вавилона составлялись из уз-
ких вертикальных и горизонтальных клинышков, эти два значка
» н hi m ш -пг =7
’ П * HI
J 2 3 4 5 в Д 34 59
Рис. 1
в
Т-П
72-
=60+12
TH
-« г
144=
=2-60+2*
-
*тп "
1600=
=26-60+40
Рис 2
т ТП 3-'
1 УТТ
4001=
=60г+6-60 + 41
П
т
использовались и для записи чисел. Одни вертикальный клинышек
обозначал единицу, горизонтальный — десятку. Как записыва-
лись числа от 1 до 59, ясно из рисунка 1 (это простая аддитивная
запись). Эти группы значков служили «цифрами» шестидесятерич-
ной системы: если требовалось записать число, большее 60, то сле-
ва от количества «единиц» записывалась еще одна такая же
«цифра», означавшая уже число следующего, второго разряда,
в 60 раз большего, затем еще левее — «цифра» третьего разряда,
в 602=3600 раз большего, чем простая «единица», и т. д. (рис. 2).
Таким образом, древневавилонскую систему можно назвать шести-
десятеричной позиционной системой: «ключевыми» числами в ией
служат степени числа 60, т. е. 1, 60, 602, 603, ... .
Вначале эта система использовалась в основном для записи
денежных единиц (1 мииа серебра равнялась 60 шекелям, 1 та-
лант— 60 минам). Но постепенно ее стали употреблять и для
расчетов календаря, записей астрономических наблюдений, изме-
рения площадей и урожая.
В более поздних записях появился еще один знай, игравший
роль нуля (прежде его заменял пробел, что, конечно, могло при-
водить к путанице). Таким же образом обозначались и «шестиде-
сятеричные дроби», н «смешанные» числа. Например, число
ёб’+ёбг+бб5 или 60а+6+^_> где а, Ь, с— «цифры» от 0 до 59,
записывалось так же, как и целое число 602а+60Ь 4-с. (Почему-то
не принято было ставить знак, отделяющий целые и дробные доли
числа; видимо, ошибиться в 60 или 3600 раз было трудно.)
Похожая система с «составной» записью цифр возникла и в
противоположном конце света — у индейцев племени майа; здесь
основными значками были точки (единицы) и черточки (пятерка),
а «ключевыми» числами 1,20, 18-20, 18-202 нт. д. (рнс. 3). Интерес-
но, конечно, чем был вызван выбор единицы третьего разряда
18-20 = 360 вместо 202=400? Может быть, тем, что 360 (как и вы-
бранное вавилонянами число 60) имеет очень много делителей?
12 18 128=
=6-20+8
450= 4001=
=360+4-20+10 =11-360+2-20+1
Рис. 3
У числа 60 их, каи нетрудно проверить, 12 (включая 1 и само это
число), это числа I, 2, 3, 4, 5, 6 н «дополнительные к ним» 10, 12,
..60; а у 360, конечно, еще больше делителей. Возможно, что
360 было выбрано просто потому, что оио близко к числу дней в
году.
Заметим, что у некоторых древиих народов вычисления не запи-
сывались, а проводились с помощью различных счетных досок
(греческий абак, китайские счеты и т. п.), иа которых по существу
возникало позиционное представление числа. Их потомки — рус-
ские счеты еще нередко помогают продавцам, ведь далеко не всюду
есть калькуляторы и электронные весы, автоматически умножающие
массу товара иа его цену.
Современная десятичная запись чисел возникла в Индии;
именно здесь привычный во многих странах счет — десятками,
сотнями, тысячами и т. д. — соедииилси с древневавилонской
позиционной записью. Позднее индийским искусством счета овла-
дели арабы, а от них начиная примерно с X в. его стали перенимать
в Европе. Система короткой записи даже очень больших чисел,
простые правила арифметических действий для чисел с любым
количеством цифр — этн преимущества обеспечили ее распростра-
нение, постепенное введение метрической системы измерения раз-
личных величин, переход от «шестидесятеричных» дробей к деся-
тичным, С XVII в. вошла в употребление современная алгебраи-
ческая символика (например, знаки « = », «4~» и др.). Позднее
для компактной записи очень больших и очень малых чисел все
чаще стали использовать степени 10, положительные и отрица-
тельные Например, 4 500000=45«10Б=4,5«106,
0,00037 =3,7-10 4. Здесь используется тот факт, что умножение
числа иа 10п — это просто сдвиг иа п разрядов (и, если нужно,
добавление нулей).
n-значное число с цифрами ап-\, ая—2, - •До мы будем
обозначать через an-ian-2- - -во- Решая задачи про цифры в деся-
тичной записи числа, полезно использовать представление ab=
= 10а4~^ и вообще
. .aiao=a,-i!O"_,+a,_,lO"-2+.. -+0110+00.
Аналогично для любого «смешанного» числа, состоящего из
целой части и десятичной дроби'
вл—ia„-2-. .Go. bibi. • .bm~an~110"—'-f-an_jIO”-2-f-..
4-ao-HilO-’ +Ы(Г2-Н. .+М(Гт.
Задачи
1. Докажите, что у квадрата любого целого числа одна нз двух
последних цифр четна.
Решение. Последние две цифры квадрата зависят только от
последних двух цифр а, b самого числа. Возведем число 10a-f-b
в квадрат: (10а 4-= 100а24-20а6 4-й2.
Если Ь четно, то последняя цифра этого числа тоже четна. А ес-
ли Ь нечетно, то четность предпоследней цифры этого числа такая,
как и предпоследней цифры числа Ь2 (к ней прибавляется четное
число 2аЬ). Остается проверить, что у квадратов всех нечетных чи-
сел 1, 3, 5, 7, 9 предпоследняя цифра четная (в частности, 0).
2. Найдите два девятизначных числа, в запись каждого из ко-
торых входят все девять цифр 1, 2, .... 8, 9, из которых одно
меньше другого в 8 раз.
У к а з а и не. Попробуйте умножить на 8 наименьшее нз та-
ких чисел 123 456 789. Если взять какое-то другое число х, большее
этого, то 8х будет больше, чем 987 654 321.
3. Расшифруйте следующие примеры иа сложение, умножение
и деление чисел (разным буквам в них соответствуют разные
цифры) в десятичной системе счисления:
а) .УДАР "•УДАР ДРАКА б) .ШАЙБУ + ШАЙБУ ХОККЕЙ в) .SEND 'MORE MONEY
г) АНТОН | ОН АНЯ ТОН ТО “ня д) ..АВС ХВАС ♦ * * * * * 1* * * * * * # # 1 x 1* jl V
ЛОИ АОН * **в ***** AAAAA
ж) *** X *** *6** **66 6*6 3) ab=c-d aabb—cc • cd aaabb b=ccc • ccd aaaabbbb=cccc 'Cccd
4. Найдите двузначное число х, если:
а) сумма его цифр в 3 раза больше, чем сумма цифр числа х-Н;
б) первая цифра числа 2х иа 3 больше, а вторая — иа 3 меньше,
чем у числа х.
5. Докажите следующее правило возведения в квадрат дву-
значных чисел 10а 4-5 (где а — любая цифра): «Найти произведе-
ние а (а 4-0 н приписать к нему справа 25». (Например, 752=5625.)
6. а) Шестизначное число оканчивается цифрой 6. Если пере-
ставить ее в начало, то число увеличится в 4 раза. Найдите это
число.
9
б) Найдите пятизначное число, которое от перестановки первой
цифры в конец уменьшается в 9 раз.
7. а) Один из играющих загадывает три натуральных числа
х, у, 2, ие больших 9. Второй называет любые три натуральных
числа а, Ь, с и узнает от первого сумму ax-}-by-}-cz. Какие числа
а. Ь, с нужно назвать, чтобы угадать все три загаданных числа?
б) Та же задача, если числа х. у, z могут быть любыми, меньши-
ми 1000.
в) Докажите, что даже если на натуральные х, у, z нет никаких
ограничений, то второй сможет отгадать их, задав последовательно
два таких вопроса.
8. а) Запишите римскими цифрами числа 98, 988, 1799.
б) Каково наименьшее число, для записи которого требуется
семь римских цифр?
8. Как записали бы числа 88, 988, 1988 в Древнем Вавилоне?
10. Найдите: а) двузначные; б) трехзначиые; в) четырехзнач-
ные числа, квадрат которых в десятичной записи оканчивается
самим этим числом. (Например, 7б2=5376.)
d-ИЧНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Пусть d — некоторое натуральное число, большее 1. Примем
это число за основание d-ичной системы. Для записи любого
натурального числа в такой системе требуется всего d цифр —
ими обозначаются нуль и первые d—1 натуральных чисел — от
1 до d — 1. Пусть запись натурального числа а в d-ичной системе —
строка из п цифр an-ian-2,. .ajOo. Тогда
a~an-ian-2.. .aiOo—an-id"~l +an-2(tn~2+.. .4-Cid-f-ao. (1)
Как правило, мы будем указывать индексом возле записи осно-
вание системы счисления (если оно отлично от 10).
Проверьте следующие равенства:
1324 = 1 -42 4-3.4+2=30,
10023=1.33+2=29,
7778=7.83+7.82+7=84-1=4095.
Числа d, d2, d3, ... в d-ичиой системе записываются как 10,
100, 1000...Ниже в таблице показаны записи чисел от 1 до 10
в некоторых системах.
d=10 1 2 3 4 5 6 7 8 9 10
d=8 1 2 3 4 5 6 7 10 11 12
d—5 I 2 3 4 10 11 12 13 И 20
rf—3 I 2 W 1! 12 20 21 22 100 101
d=2 1 10 11 100 101 no 111 1000 1001 1010
10
Если основание d не превосходит 10, мы используем в качестве
цифр первые d цифр десятичной системы; скажем, для d=3 это
цифры 0. I, 2; для d—8 — цифры 0, 1, 2, ..7. Если же d> 10,
то нужны еще специальные знаки для «цифр» 10, 11,.... d — 1; на-
пример, при d—16 для новых цифр (от 10 до 15) будем использо-
вать буквы А, В, С, D, Е, F. Тогда
1Е16—1 16+14=30: FFFj6= 15-162 +15-16+15=4095.
Из формулы (1) мы видим, что подсчет числа по его d-ичной за-
писи — это просто вычисление значения многочлена
Р (x)=an_ix"~1 +ая_2х”-2+-. -+fliX-rao (2)
при x=d, где цифры играют роль коэффициентов этого много-
члена.
Если нужно перевести много чисел нз какой-то одной, скажем
восьмеричной, системы в десятичную, удобно заранее подсчитать
степени основания системы: 1=8°, 8, 82, 83 и т. д. Но если речь
идет о подсчете одного какого-то числа, то проще действовать так:
3175в=3-83 + Ь82+7-8+5=((3-8 + 1) 8+7)8+5 = 1661
Этот способ требует меньше действий: вычисление значения много-
члена по схеме
Р (х)=(.. .(ця„]х+дп_2) х+.. .+aj) х+по
требует всего n— 1 умножений; а если считать его «в лоб» сна-
чала найти все степени х2, х3, ,хя~‘|, а потом уже а(х, ..
fln-ix”-1, потребуется 2п —3 умножений (да к тому же придется
запоминать промежуточные результаты вычислений).
Итак, мы видели, что очень просто перейти от d-нчной записи
числа к его обычной, десятичной записи.
Покажем теперь, как сделать обратную операцию: для задан-
ного (в десятичной записи) числа найти все цифры его d-ичной
записи.
Перевод числа из десятичной в d-ичную систему
1-й способ: «от младших разрядов к старшим».
Напомним, что разделить число а на Ь с остатком — это значит
представить его в виде a—bq-^-r, где (а, 5. q и г — целые
числа); г называется остатком, a q — неполным частным при деле-
ния а иа Ь.
Пусть aa-tan~z.. ,aia0 — d-ичнаЯ запись числа а. Тогда а =
=(cfl_ldn'2+...+a1)d+a0.
Отсюда видно, что последняя цифра По — это остаток от деле-
нии а на d, т. е. a = ^d+«o.
11
При этом неполное частное q будет равно числу ал_|...<*»«
т. е. числу а с отброшенной последней цифрой. Разделив q на а,
мы получим в остатке следующую цифру и т. д.
Рассмотрим два примера.
1. Найдем 7-ричную запись числа 1989. Последовательные де-
ления удобно записать так:
Ответ: 1989=55417.
Заметим, что остатки от деления на число 7 подчеркнуты
двойной чертой (последнее неполное частное, меньшее 7, есть,
конечно, и последний остаток). Проверим ответ:
55417=((5-7+5) 74-4) 74-1 = 1989.
2 Найдем двоичную запись числа 241. Здесь можно сразу
выписывать в два столбика неполные частные и остатки — делить
на 2 очень просто.
частные
241
120
60
30
15
7
3
1
остатки
1
0
0
о
1
1
1
1
Ответ: 241 = 111100012.
Проверка:
1111001s=2’+26+2s+24 +1 =2* (23+2’+2+1)+1 =
=2,(2, — 1)+1 = 16-15+1=241.
Наш первый способ отыскания d-ичных цифр числа а можно
сформулировать так:
(1) младшая цифра равна остатку от деления а на d;
(2) чтобы найти следующую цифру, надо а заменить полу-
ченным (неполным) частным и вновь применить (1); этот
шаг повторяется, пока последнее частное не станет мень-
ше d — это будет старшая цифра числа а.
12
2-й способ: «от старших разрядов к младшим».
Прежде чем описывать этот способ, обсудим, сколько цифр
будет содержать d-ичная запись числа а (здесь, конечно, подра-
«умевается, что старшая цифра a„_i этого числа ап-гап~2 ... а0 ие
равна 0). Самое большое п-зиачное число — то, у которого все п
цифр равны d— 1. Оно равно
(d-l)d”~l +(d-\)dn-2 + ...+(d-\)d+(d-l)=
=dn-~dn-l+dn-i—dn-2-\-. ..+d2-d+d-l=dn-lt
т. e. на единицу меньше, чем самое меньшее («+ 1)-значное
число 100 ... Orf—dn.
п
Например, наибольшее 4-значное число в троичной системе
равно
2222з=2.33 + 2 - 32Ч-2-ЗЧ-2=80=34- 1.
Таким образом, в записи числа а будет п цифр, если 100... 0</=
‘ ' -V-
я—1
=d"“,^a<d". Выделим его старший разряд:
а=ап_\ dn~1 zd.n~2+-. .4-oo)
Второе слагаемое ал_2.. .По — это (n-—1)-значков число — будет
меньше dn~i. Таким образом, чтобы найти первую цифру а,
нужно разделить а на d"-1 (с остатком). Частное будет равно
старшей цифре ал-ь Затем с остатком о„_2.. -Оо надо повторить
ту же операцию: разделив его на d"~2, мы найдем следующую
цифру ал_2 и т. д.
Конечно, чтобы использовать этот способ, удобно заранее
составить табличку «ключевых» чисел — степеней d, d2, .
dn~'^a<Zdn.
Рассмотрим два примера. Первый нам уже знаком.
1. Найдем 7-ричную запись 1989. Заметим, что 72=49,
73=343 <1989, 7'>1989.
1989 1 343
1715
274 | 49~
~~245
29 | 7
”28 X
1
' Ответ: 1989=^=5541,.
is
2. Найдем троичную запись числа 180. Заметим, что 3*=
=81 < 180<35.
180 181
162 2
-18LF
18 X
0
Ответ: 180=202003.
Обратите внимание иа то, что после деления иа 81 = 34 мы про-
пустили деление на 27—З3, а при делении на 9 = 32 остаток
сразу равен 0. Поэтому в разрядах, соответствующих З3, 3 и 3°=1,
стоят нули.
Сформулируем теперь второй способ отыскания d-ичных цифр
числа а несколько иначе. Будем, как это принято, через [х]
обозначать целую часть числа х» т, е. наибольшее целое число,
не превосходящее х. «Остаток» х—[х] называется дробной частью
числа х. Ясно, что для натуральных а н b целая часть нх отно-
шения^-J равна неполному частному от деления а на Ь. Например,
Пусть п — наименьшее натуральное число, для которого dnZ> а.
Положим вначале • Тогда
(1) старшая цифра а равна [xd];
(2) чтобы найти следующую цифру, надо заменить х на
xd—[xd]—дробную часть числа xd— и вновь приме-
нить (1)
Действуя по этому правилу, мы за п шагов найдем все п цифр
числа а.
Проиллюстрируем это иа последнем из рассмотренных выше
примеров: d=3, а =180, «=5. Вначале
[^•3]=[^42f]=2, «„ерь
[f-3]=[i-]=0'теперь х=т-
|д-з]=[2]=2, теперь х=0,
и поэтому последние две цифры равны 0. Итак, 180—202003.
Второй способ интересен тем, что позволяет сразу находить
старшие, самые «важные» цифры числа. Он применим не только к
целым числам а: с его помощью можно дробную часть числа пред-
14
ставить в виде d-ичной дроби. Такие дроби записываются так
же, как десятичные: d-ичной дробью с цифрами bt, Ьг, .... Ьт
(O^bi^d — 1) называется число
£+>+..-+>=0, М2...6„.
Правило отыскания цифр bi, b2, - -. для данного числа Ь, такого,
что 0<6<1, состоит в следующем:
(1) цифра Ь\ находится как целая часть числа bd: bi=[bd%
(2) для отыскания следующей цифры нужно применить (1),
заменив b «остатком» bd—[bd]— дробной частью чис-
ла bd.
Найдем, например, разложение в двончиую дробь чис-
и, наконец, [^-2 ]=[!]= 1—уже «без остатка». Итак, Ц-=
=0,011012.
Конечно, можно было бы просто найти разложение 13 = 11012
в двоичную систему, а затем результат 234-224-1 разделить на
32=25. Получилось бы то же самое разложение-
13 1101s _234-2г+1_ 1 | 1 I 1
32 25 25 22 ' 23 2s
Вот еще два примера разложения в 6-ричную дробь чисел
Т«^=03:
а) [5'-6]=[3т]==3> [т’6]=И=2 Ответ: |-=0.32»
(Проверка: f+|-=^=^=f.)
б) &е]=[1 f]=1- [f-6]44f ]=4-"снова [т-б]-
=[4-|-]=4, .... Ответ: -^=0,1444.. ,6
В последнем примере бесконечно повторяется одни и тот же
4 Е
«остаток» —; если, скажем, нас интересуют первые 5 разрядов,
то ответом будет 0,3 » 0,1444(поскольку остаток больше -%-,
мы округлили цифру 4 в большую сторону).
15
На этом примере мы видим, что число 6<С1 не всегда пред-
ставляется в виде конечной d-нчной дроби: для этого необходимо,
чтобы b можно было представить в виде дроби с некоторыми
целыми q и т. В противном случае всегда получается (для рацио-
нального числа Ь) бесконечная периодическая d-нчная дробь.
Может возникнуть вопрос: почему способ перехода от d-ич-
ной записи числа к обычной, десятичной, очень прост — сводится
кподсчету значения многочлена an~.idn~l +.. ,4-aid4-flo, а обрат-
ный переход сложнее? Конечно, и обратный переход можно было
бы осуществить точно так же: если иам известны десятичные циф-
ры числа с=ст-1- - -CiCo, то нужно просто подсчитать сумму
-Ч-й’Ю+й), ио все действия надо будет выпол-
нять в d-нчной системе.
Действия с d-ичными числами
Нам хорошо известны правила четырех арифметических дейст-
вий с многозначными десятичными числами: сложение, вычитание
и умножение столбиком, деление углом.
Точно такие же правила годятся и для d-ичной системы
с любым основанием d>l
Разумеется, при каждом d будут свои таблицы сложения и
умножения. Они отличаются от десятичных в тех клетках, где
стоят числа, большие или равные d, а именно d заменятся на 10,
d-J- 1 — на 11 и т. д. Приведем таблички сложения и умножения
в 8-рнчной и 3-ичиой системах счисления и несколько примеров
действий в этих системах.
+ 1 2 3 4 5 6 7
1 2 3 4 5 6 7 10
2 3 4 5 6 7 10 11
3 4 Б 7 10 11 12
4 5 6 10 11 12 13
Ь 6 7 ' И 12 13 14
6 7 10 1! 12 13 14 15
7 10 11 12 13 14 15 16
X 1 2 3 4 5 6 7
1 1 2 3 4 5 6 7
2 2 J 6 10 12 14 16
3 3 6 11 ]4 17 22 25
4 4 10 14 20 24 30 34
5 5 12 17 24 31 36 43
6 6 14 22 30 36 44 52
7 7 16 25 34 43 52 61
+ 0 1 2
0 1 2 0 1 2 1 2 10 0 10 11
, 1234
4 6544
1(ЮоО
v37
а52
133
тж
X 0 1 2
0 1 2 0 0 0 0 1 2 0 2 11
,11112
~*~11112
100001“
122
12
тшт
122
тотт
16
Таким же образом можно действовать с ti-ичнымн целыми
числами и дробями, а также смешанными числами вида
|вд—2- . .Оо, Ь\. . .6m = On — id',~l-|-Ол—2^”~2 + - • •4“До +
-г d -г..
Особенно просто выглядят правила действий в двоичной
системе:
0+1 = 14-0=1» 1 + 1 = 10, 0-1 = 1-0=0, 1-1 = 1.
Умножение столбиком сводится просто к сложению нескольких
одинаковых чисел, отличающихся только сдвигом:
X
10111
пою
ШП-
ЮН 1
10111
100101011
Двоичная система оказалась наиболее удобной для конструи-
рования электронных вычислительных машин. Дело в том, что наи-
более надежные н миниатюрные элементы, запоминающие и пере-
рабатывающие информацию, имеют два устойчивых состояния;
им соответствуют цифры 0 и 1
Строчками из 0 н 1 «кодируются» не только числа, но н вся
информация, которая передается машине: номера команд и ячеек
памяти, куда нужно поместить то или иное число, буквы текста,
которые нужно напечатать нли выдать на экран, н т. п.
Еще не так давно — в 60-х годах — всю информацию нужно
было вручную (илн с помощью перфокарт) вводить в машину в
готовом двоичном виде. Но записывали ее не двоичными, а 8-рнч-
ными цифрами. Дело в том, что перевод чисел нз одной системы
в Другу10 очень прост. Двоичную запись достаточно разбить на
группы по 3 цифры и каждое 3-значиое двоичное число заменить
8-ричной цифрой:
11 000 101 110 010 0012=305621
В самом деле, если oq, at, ... — двоичные цифры числа а, то
а—(ao~\-Qi -2+о2-22)+(пз+с< - 2+os-22) 8 +
+(ае+в7-2+ов-22)82+...,
где в каждой круглой скобке стоит цифра 8-ричиого представления
числа а.
. Сейчас с развитием языков программирования переработка
текста программы и числовых данных, вводимых с клавиат) I,
|Завм>1зьлТ обласяж I 17
788432
|3аивр1зь^а облагав
616 л lore ка
j »м. О- М. Горькаго
осуществляется автоматически, самой ЭВМ, так что пользователь
не замечает ее «двоичного» устройства: с ним имеют дело конст
рукторы машины н составители заложенных в нес вспомогатель-
ных программ, системные программисты.
Но всем, кто имеет дело с ЭВМ, известна единица количества
информации (памяти ЭВМ) — бит (от английских слов binary
digit — двоичная цифра). Например, для указания одного из
2® =64 полей шахматной доски требуется 6 бит. Восемь бит состав-
ляют более крупную единицу — байт. Таким образом, в байте
памяти можно поместить любое из 256=4008 чисел (от ООО до
377e— 1111111Ь); одного байта достаточно, например, чтобы
запомнить любой знак, вводимый с клавиатуры (включая цифры,
русские и английские буквы и ряд других вспомогательных зна-
ков).
Память ЭВМ измеряется обычно в килобайтах н мегабайтах
Интересно, что греческие приставки в «двоичном» мире ЭВМ озна-
чают не «тысяча» и «миллион», как обычно, а близкие к ним круг-
лые двоичные числа: 1024 =2’° И (1024)2=22°.
Различные позиционные системы (самые простые нз них — дво-
ичная и троичная) помогают разобраться во многих задачах про
взвешивание, «кодирование», отгадывание задуманных чисел; не
сколько таких задач помещено ниже. Об одной интересной игре
(«ним»), где выигрышная стратегия загадочным образом нахо-
дится лишь с помощью двоичной системы, можно узнать из кни-
ги [3] или статьи [11].
Задачи
11. Найдите десятичную запись чисел: 12з, 1010102. 2020б,
17778, 12345б, 1989|2, 12560.
12. а) Запишите числа 16. 25, 36, 64. 100 в системе счис-
ления с основанием d=8
б) То же для d=4; d~3; d—2; d=16.
13. В математической олимпиаде участвовало 13 девочек н
54 мальчика, а всего 100 человек. В какой системе записаны
этн сведения?
14. Найдите основание системы счисления d, если:
a) 15 = 30d; б) 50=303rf; в) 90=10100d; г) 150=2112,;
д) 500=200112^.
15. Какую цифру надо поставить на место ♦, чтобы число
21*10213 было четным?
16. Составьте таблицу сложения и умножения в 6-ричной сис
теме и выполните с ее помощью действия: а) 2146 + 3556,
б) 253б-301в- Проверьте результат, переведя все числа в десятич-
ные.
17. Добавив две цифры А н В вместо 10 и 11, составьте
таблицу умножения иа А и В всех цифр 1,2,3,...»9, А, В в 12-рич-
иой системе счисления.
18
18. Запишите в виде 6-ричиых дробей числа ~; -Ц-;
19. Каково самое большое 5-значное число:
а) в троичной системе; б) в 8-ричной системе? (Найдите де-
сятичные записи этих чисел.)
20. Сколько всего существует:
а) 5-значиых; б) п-зиачиых чисел в d-ичной системе?
Ответ: б) dn—(Г~*.
Заметим, что если бы мы подсчитывали все не более чем п-зиач-
иые числа, включая 0. от 00.. .0 до (d— l)(d—1), ,.(d—1), то
ответ получился бы другим: таких чисел dn
21. а) Запишите числа 45в, 77s, 5038 в двоичной системе.
б) Запишите числа IOIOIO2, 1101101г, 111 111 Ills в 8-ричной
и 16-ричной системах.
22. Найдите 3-значные числа (с цифрами 0, I, 2, 3, 4), которые
в любой d-нчиой системе при d^5 являются точными квадратами
Указание. Одно нз таких чисел 441; например, 44 U— 169
23. В любой d-ичной системе число 11.. .1 делится на 11.. .1,
k k
если п делится на k. Докажите это и запишите соответствующее
тождество для многочленов от d. Рассмотрите примеры: а) п—6,
d=2; б) «=12, d=3,
24 (Уравновешенная троичная система.) Укажите правило,
позволяющее записать любое натуральное число в «троичной сис-
теме с цифрами 1,0 и — 1», т. е. в виде а=Зп-’ 4-ай_23"-24~.. .4-
4-П13+со. где каждое а, равно 1, 0 или —1. (Например, 7 —
=3®—34-1 •4 Н 17=4 0—.) Представьте в таком виде
числа: а) 40; б) 80; в) 1991.
Указание. Можно предложить два таких правила. Вот
одно «от младших цифр к старшим»: будем делить число (а затем
получающиеся неполные частные) на 3, ио если остаток ра-
вен 2, то заменим его иа —1, а к частному добавим 1:
18 6 [3
^1 6 2 13
3 I
Чтобы сформулировать другое правило — «от старших цифр
к младшим», надо выяснить, в каких пределах заключены
гг-значные числа в такой системе (т. е. числа а = 3"“*4*-- •)•
25. а) Какие 6 гирь нужно выбрать, чтобы ими можно было
уравновесить любой груз, масса которого выражена целым числом
граммов от 1 до 64? (Гири кладутся иа одну чашку весов.)
19
б) Укажите 4 гири, с помощью которых можно взвесить любой
груз, масса которого выражена целым числом граммов от 1 до 40,
если гири можно класть на обе чашки весов.
в) Сколько нужно гирь, чтобы взвесить таким образом груз
от 1 до 100 г?
У к а з а и и е к б), в). Воспользуйтесь уравновешенной троич
ной системой.
26. Сколько вопросов нужно задать, чтобы угадать натураль-
ное число от 1 до 10 000, если иа каждый вопрос можно получить
только ответ «да» или «нет»?
Указание. Последовательность ответов «да», «нет» можно
записать в виде строчки нз двух цифр О и 1. Получив п ответов,
мы запишем «двоичный» код задуманного числа. Общее количест-
во таких rt-значных кодов (от 00 ... 0 до 11 ... 1) равно 2". Если
для любых двух из 10000 чисел нх коды различны, то 2П2> 10000.
27. (Троичный фокус.) Фокусник просит загадать одну из 27
карточек, сложенных в стопку. Затем он трижды проделывает та-
кую операцию: раскладывает карточки, снимая нх по одной, в три
стопки (левую, среднюю, правую — по очереди), спрашивает, в ка
кую стопку попала загаданная карточка, н вновь, не тасуя, соби-
рает три стопки в одну. Получив три ответа, ои сразу достает
загаданную карточку. Объясните, как ои это делает.
Указание. Представьте себе, что карточки занумерованы в
троичной системе числами 000, 001, 002, 010, 222. Тогда
каждый нз трех ответов позволяет угадать одну из трех цифр но-
мера загаданной карты. Чтобы в этом разобраться, удобно проде-
лать такие операции с З2 —9 карточками 00, 01, 02, 10, 11, .... 22:
для угадывания одной из них достаточно двух операций.
28. (Из задач Г. Дьюдени.) Объясните следующий способ ум-
ножения, требующий (кроме сложения столбиком) только умения
умножать и делить на 2. Пусть, например, нужно умножить
241 иа 23. Составляем два столбика чисел:
241 23
120 (46)
60 (92)
30 (184)
15 368
7 736
3 1472
1 2944
5543
В левом столбике мы просто последовательно делим числа на 2,
отбрасывая остаток, а в правом умножаем на 2. Если оставить в
правом столбике лишь те числа, которые стоят против нечетных
чисел левого (остальные взяты в скобки), то их сумма дает пра-
вильный ответ: 241-23 = 5543.
20
Указание. Представьте мысленно левое число в двоичной
системе.
29- Сформулируем правило сложения двух d-ичных чисел стол-
биком. (Для переносов из одного разряда в другой мы используем
переменную х как «ячейку памяти».)
Чтобы найтн цифры Cg. щ, С2, ... суммы, нужно:
положить х=0 и повторять для /=0, 1, 2, .. . следующие
операции:
сложить х н цифры i-ro разряда данных чисел;
положить d равным последней цифре этой суммы;
положить х равным первой цифре этой суммы (а если сумма
меньше d, то х=0).
Вычисления заканчиваются, когда исчерпаны все разряды
данных чисел и х=0. (Здесь подразумевается, что разряды зану-
мерованы, начиная с самого правого: 0-й, 1-й н т. д.)
Годится ли это же правило для сложения любых г чисел в
d-ичиой системе, г>2? Если нет, что следует исправить?
Ответ: правило годится для любых г чисел, только если r^d.
В общем случае «запоминать» приходится иногда и число, большее
илн равное d2, т. е. х нужно положить равным сумме с отброшенной
последней цифрой, а не «первой цифре суммы».
Указание. Сложите три или больше двоичных чисел из
одних единиц.
30. (Задача Иосифа.) По кругу стоят несколько ребят. Чтобы
выбрать водящего, оин выходят из круга через одного в следующем
порядке: первый — тот, с кого начинается счет — остается в круге,
следующий за ннм — второй — выходит, третий остается, четвер-
тый выходит и т. д. (против часовой стрелки). Определите, кто
останется последним — водящим (иа каком месте ои стоял, считая
от первого против часовой стрелки), если первоначально в круге
было: а) 16; б) 30; в) 100 человек.
Указание, а) Сначала из круга выйдут 8 человек с чет-
ными номерами. После этого останется тоже 8 человек, причем
первый вновь остается в круге. Точно то же повторится и после
второго оборота (когда в круге останется 4 человека), и после
третьего (когда останется двое). Поэтому водящим будет первый.
Аналогичное рассуждение показывает, что если вначале в кру-
ге 2fe ребят, то прн любом k водящим окажется первый
Чтобы угадать ответ для любого количества п ребят в круге,
полезно сначала проделать «эксперимент» дли небольших и.
Особенно красиво будет выглядеть ответ, если п и соответствую-
щий ему ответ 1п — номер водящего — записывать в двоичной сис-
теме: оказывается, 1п получается из п переносом первой цифры 1
в конец! (Если за этой цифрой стояли нули, их нужно от-
бросить.)
. Чтобы обосновать ответ, представим себе, что, выводя ребят
из круга, мы остановимся в момент, когда впервые количество
21
оставшихся в круге равно степени 2. Тот, кто стоит сразу за по-
следним выведенным нз круга, н будет водящим.
31. Для d = 4, 5, б, .. найдите два (d—1)-значных d-ичных
числа, в записи каждого из которых встречаются все цифры,
кроме 0, и одно получается из другого умножением на d—2.
Указание. Сравните эту задачу с задачей 2.
32. а) На трех одинаковых рисунках, изображающих доску
8X8 клеток, нужно раскрасить клетки 4 красками (белой, чер-
ной, красной и голубой) так, чтобы для любой из 64 клеток дос-
ки — одной и той же на всех рисунках — по набору ее цветов мож-
но было узнать, что это за клетка.
б) Та же задача для 4 рисунков доски 9X9 клеток и 3 красок
Л и тератур а
1. Берман Г. И. Число н наука о ием.— М.: Физматгиз, 1980.
2. Г л е й з е р Г. И. История математики в школе: VII—
VIII классы.— М.: Просвещение, 1982.
3. Фомин С. В. Системы счнслеини.— М_: Наука, 1980
4. Факультативный курс: Избранные вопросы математики.— М.
Просвещение, 1978.
5. К а с а т к и и В. Н. Новое о системах счисления.— Киев:
Вяща школа, 1982
6. Коврнженко Г. А. Системы счисления н двоичная ариф-
метика.— Киев: Радянска школа, 1984.
7. К у ж е л ь О.В. Развитой понятия про число. Ознаки подьль-
hocti. Доскональю числа.— Киев: Вища школа, 1974.
8. Нагибин Ф. Ф., Канин Е. С. Математическая шка-
тулка.— М.: Просвещение, 1988
9. Гарднер М. Математические досуги.— М.: Мир, 1974
10. Кнут Д. Искусство программирования для ЭВМ.— М.: Мир,
1974.—Т. 2.
II. Я г л о м И. М. Две игры со спич ками//Квант — 1971 — № 4,
Системы счисления//Квант.—1970.— № 6.
ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА
СОСТАВНЫЕ ЧИСЛА
Как вы знаете, натуральное число называется составным,
если его можно представить в виде произведения двух множите-
лей, каждый нз которых больше 1
Примеры составных чисел строить очень легко. Для этого нуж-
но взять какие-нибудь два числа, отличные от 1, и перемножить
их. Так, 2-3=6, 23-47=1081, 101-110011 = 11111111. Поэтому
числа 6, 1081, 1ШНП составные. Можно умножать по трн или
по четыре множителя. Произведение всегда будет составным чис-
лом. Самое маленькое составное число —это 4-2-2. Натураль-
ные числа 1, 2, 3 составными не являются. Не будет составным
и число 5, следующее по величине за 4 составное число есть
2-3=6>5.
А как узнать, будет заданное число составным илн нет?
Будут ли составными, например, числа 1009, 1517 илн число
11.. .1 4 11.. .1, записываемое 65 десятичными знаками?
32 32
Попробуем ответить на некоторые из этих вопросов. Заметим,
что каждый из множителей, в произведение которых раскладыва-
ется составное число, является его делителем. Поэтому можно
сказать:
Правило 1. Натуральное число составное, если оно делится
иа некоторое меньшее его число, отличное от 1.
Так, все четные числа, большие чем 2, делятся на 2 н по-
этому являются составными. А число 7 не делится ни на одяо из
чисел 2, 3, 4, 5, 6 и, следовательно, составным не является.
Чтобы проверить, пользуясь указанным правилом, будет
составным число 1009 или нет, иужио проверить, делится ли оно
на все числа из ряда 2,3, 4,..1007, 1008, т. е. совершить 1007 де-
лений. Это — утомительное занятие. Его можно значительно со-
кратить, если воспользоваться следующим правилом:
Правило 2. Каждое составное число N имеет делитель,
больший 1 и такой, что квадрат его не превосходит N.
По этому правилу делители составного числа N следует искать
среди чисел, квадраты которых не больше чем N. Из соотноше-
23
иия 312=961 <1009 <1024 = 322 следует, что если число 1009
составное, то у него есть делитель, содержащийся среди чисел
2, 3, 4, ..31. Таким образом, количество делений при проверке,
является число 1009 составным или нет, может быть сокращено
с 1007 до 30. Разделив 1009 на каждое из чисел 2, 3, ..31
(особенно просто это можно сделать с помощью калькулятора),
убеждаемся, что 1009 не делится ни иа один из делите-
лей. Такой исход означает, что число 1009 составным ие яв-
ляется.
Задачи
1. Количество делений можно сократить еще примерно в два
раза. Как это сделать?
2. Будет ли составным число 11111?
Попробуем теперь объяснить, почему выполняется правило 2.
Если N — составное число, то в соответствии с определением
его можно разложить в произведение двух множителей, скажем а
и Ь, т. е. N=a-b, где а>1, h>l.
Пусть Q — меньший из множителей, т. е. Ь^а Тогда
W=Q’6^a-o=a2, и составное число N имеет делитель а>1,
квадрат которого не превосходит N.
Задачи
3. Будут ли составными числа 622— 1; 421 — 1 и 421 + 1?
В 6-рнчной системе счисления число 622 записывается в виде
1 о^д.
22
В этой системе счисления имеем.
1 1 ^55. . .5 =5-11. г .1.
22 22 22
Таким образом, число 622—1 делится на 5.
Аналогично, пользуясь системой счисления по основанию 4,
находим:
(42,-1)10=1
р. ;.0 — 1 =33., .3—3-11 .1,
21 21 21
т. е. число 421 — 1 делится на 3.
В той же системе счисления имеем
(421 +1)|0= 1 0.. .0.1=11 -.303.. .031.
it
1 (оследнее равенство очень легко проверить умножением столби-
ком. Действительно,
19
v303 . 031
х 11
4 зоз.: .w
3030.. .031
10000. Г.000 г
20
Но (11)4 в десятичной записи есть 5. Итак, число 4214~ 1 делится
па 5.
Задание. Попробуйте доказать таким же способом, что чис-
ло 622—1 делится на 7.
4, Разложите число 21W4-1 на два множителя, каждый из ко-
торых больше, чем 250.
Так как 2106=2-2-.. ,-2~4. -4=453, то 2,w4~l =4534-1 и,
106 53
пользуясь системой счисления по основанию 4, как и ранее, легко
доказать, что это число делится на 5. Но нам нужно найти дели-
тели этого числа, большие, чем 250. Воспользуемся двоичной
системой счисления. В этой системе число 2,w4-1 записывается
в виде 10., .01. Перемножим столбиком два числа, которые в
105
двоичной системе имеют вид И.. .1 0.. .0 1 и 1 0.. .0 1 0.. -0> 1.
26 ' '~26 ' 25 26
Имеем:
1.
ТОГ
1.
.ио.
.000.
I...1IV.. -U1
10.. .010.. .01
“I“.ITO. “01
..1100 01
..001
: .0000.. .000.. .01
X
105
Таким образом, произведение этих двух чисел равно 2,06+1« По-
скольку
(1 Q.^.0,1 Рч. .01 )2 = 2s3 -Ь 2е7 4-1,
25 26
(-1.. .11.0.. .01)г=(10. -0)2-(1.0.. -Q);+1 =253-2" +1,
26 26 53 27
получаем следующее разложение:
2,сб 4-1=(2Ы - 227 4-1) (2s3 4-227 4- 0-
Sb
Клждый сомножитель записывается в двоичной системе более
•и-м !>! цифрой и потому больше, чем 260. Точно так же могут быть
разложены на множители числа 264*Ь 2|04-1, 2й 4-1 и т. д.
Задание Проверить, пользуясь указанными системами
счисления, иные разложения для чисел из задачи 3:
62!-1 =(S5^)6=(&5^)6.(10_01)6=(6" -1) (6" +1).
22 II 10
42' —1 =(33.. .3>=(33.. .3)4.(1а. -0 10- • 01)4=
21 7 6 6
=(47-1)(4,4 + 47 +1),
421 +1 =(io_gt)4=(3_j Q^i)4.(io^gi)4=
20 '~7 ’ (F* 6
=(4|*-47+1)(47+1)
5. Если число N может быть представлено в виде разности
квадратов двух чисел а2—Ь2, то разложение его на множители
получается немедленно:
Л'= а2—d2 =(а2—db)+(а&—Ь2)=
=а (а— Ь) 4-Ь (а—Ь) — (а 4- Ь) (а— Ь).
Способ разложения чисел на миожнтелн, основанный на этой
идее, был предложен французским математиком П. Ферма
(1601—1665).
Будем последовательно строить числа вида c?—N н прове-
рять, являются они квадратами или нет. Как только разность
a2—N станет равной квадрату целого числа Ь2, мы будем иметь ра-
венство N=cr— b2 и, значит, разложение числа А' на множители.
Из тождества (а-Н)2—а2=(о4-1+п)(п+1— а)=2а-М полу-
чается, что следующее число (а-{-1)2 — N может быть построено
из предыдущего а2—А' добавлением числа 2а4-1. Это упрощает
вычисления.
Попробуем таким способом разложить на миожители число
N=2077. Так как 452<2077< 462, то начальное значение а рав-
но 46 н первый член в нашей последовательности есть 462—2077=
=39. Числа, которые нам следует прибавлять для получения
следующих членов, равны 2-464-1=93, 934-2 = 95, 954-2=97,
974-2=99 н т. д. В итоге получаем последовательность
39, 394-93=132, 1324-95= 227, 2274-97=324= 182
Таким образом, (464-3)2—2077= 182 и
2077 = 492—182=(49 4-18) (49—18)=67-31
Задание. Попробуйте разложить иа множители с помощью
метода Ферма числа 1333, 1517, 9271.
26
Существует много других приемов разложения чисел иа мно-
жители. Большинство из них требуют знаний, выходящих за рамки
школы, и потому здесь не могут быть описаны. Заметим только,
что задача разложения на множители очень трудоемкая. Вы сами
это уже почувствовали. Конечно, затраты времени зависят от
величины разлагаемого числа. Например, в 1905 г. было доказано,
что так называемое число Ферма с номером 7
F?=22? 1 =2126 -h 1 =340282366920938463374607431768211457
составное. Лишь в 1970 г. с использованием ЭВМ было найдено
его разложение на множители:
Л=59649589127497217 -5704689200685129054721,
причем оба миожителя далее разложены быть не могут.
Число Fe=22'4-1 =2266+1 составное. Ойо может быть разло-
жено в произведение двух множителей, меныпнй из которых
равен 1238926361552897, а больший записывается 62 цифрами
десятичной системы. Ни один из множителей дальше ие разлага-
ется.
Известно, что
F9=22’+l=25,24-1 =2424833-A=(37-2J6 4- !)• А.
где А — некоторое составное число. Но даже с помощью самых
совершенных ЭВМ до сих пор ие удается разложить А на множи-
тели.
Приведем еще несколько любопытных разложений:
11111=41-271,
1111111=239-4649,
11111111111=21649-513239,
Н...1=53-79-265371653,
И.. .1 = 2071723-5363222357.
10001=73-137,
100000001 = 17-5882353.
Задачи
6. Если умножить число 777 на число 143, то получится шес-
тизначное число, записываемое одними единицами: 777-143 =
= 111111. Если же число 777 умножить на 429, то получится чис-
ло 333333, записываемое шестью тройками.
27
Найдите, на какие числа надо умножить число 777, чтобы
получить шестизначные числа, записываемые одними двойками,
одними четверками, одними пятерками и т. д.
7. Возьмем какое-нибудь двузначное число, например 12.
Удвоим его и припишем справа 0. К результату (240) прибавим
исходное число. Получится 252. Умножим это число на 481
В записи произведения трижды повторяется число 12:
252-481 ==121212.
Возьмем другое двузначное число, например 23. Проделаем с ним
те же операции:
23-2 =46, 4604-23 =483, 483-481=232323
Опять результат есть шестизначное число, в записи которого триж-
ды повторяется исходное двузначное число 23.
Можете проделать еще несколько экспериментов, взяв, напри-
мер, числа 34, 19, 70 и т. д. Опять в записи результата будет
трижды повторено исходное двузначное число.
Задание. Попытайтесь объяснить этот удивительный факт,
связанный со свойствами числа 481.
ПРИЗНАКИ ДЕЛИМОСТИ
Для проверки того, является данное число составным или нет,
требуется выполнить достаточно большое количество делений
его иа меньшие числа. Для некоторых делителей существуют
признаки, позволяющие устанавливать делимость на них без вы-
полнения самого деления значительно проще. Такие признаки
называются признаками делимости. Будем считать в дальней-
шем, что все рассматриваемые здесь числа записываются в деся-
тичной системе. Пусть аяап_|.. .щао—десятичная запись чис-
ла Л', т. е.
А= а„- 10я4-0—1-10“-’ + . - .+«!• 104-оо,
Вам, конечно, знакомы признаки делимости на 10, 5 н 2.
Признак делимости на 10. Число N делится иа 10 только в том
случае, если его младшая цифра «о равна 0.
Признак делимости на 5. Число N делится на 5 только в том
случае, если его младшая цифра ао делится на 5, т. е. равна 0 или 5.
Признак делимости на 2. Число Л' делится на 2 только в том
случае, если его младшая цифра ао делится на 2.
Каждый из этих признаков следует из того, что разность
N—ao делится на 10, т. е. делится на числа 10, 5 и 2, а,
значит, числа N и ао одновременно делятся или не делятся
на 10, 5 или 2.
28
Признак делимости на 4. Число Л' делится на 4 только в том
случае, если на 4 делится 2ai+«o, т. е. сумма его последней
и удвоенной предпоследней цифр.
Для обоснования признака делимости на 4 заметим, что раз-
ность
JV—(2ai4-ao)=(JV—(Wai +«o))+((10ai+n0)—(2ai +«о))
делится на 4 (число (N— lOai + <zo) делится даже иа 100, а остав-
шееся слагаемое равно 8а>). Поэтому числа N и 2ai+cio одновре-
менно делятся или не делятся на 4.
Каждый может придумать множество примеров иа применение
указанных выше признаков.
Перейдем теперь к признакам делимости иа 9 и 3. Справедли-
во следующее свойство делимости иа 9:
Разность между натуральным числом и суммой его цифр всегда
делится на 9.
Проверим это, например, для числа 1234.
1234—(1 +24-34-4)= 1224=9-136.
Можно попытаться выполнить проверку указанного свойства н на
других числах. Для того чтобы понять его причину, попробуем
вычисления с числом 1234 представить иначе:
1234— (1+2 + 3 + 4)=(1000—1) + (200—2)+(30— 3) =
=(1000—1) + 2 (100—1)+3 (10- 1)=999 + 2-99 + 3-9 —
= 9(111 + 2-11+3).
Как видим, дело в том, что числа 10—1, 102— 1, 103—1 делятся
иа 9. Эта делимость имеет место и для любого числа вида 10й—1.
Дей ств ите л ьно,
10* —1 = 10...0—1=99. ..9=9-11.. .1.
В общем случае разность между числом . .aio^ и
суммой его цифр равна
ая~ 10"+сл—1 • 10“—1 +.. .+«1 •1О+«о—(Пл+«л—] +.. +
+о»+ао)=ал (10й- O+^-i (10"“*-1)+... +oi (10-1).
Как мы только что установили, все разности в скобках делятся
на 9. Поэтому делится на 9 и разность между числом N и сум-
мой его цифр. Иначе свойство делимости на 9 можно высказать
так: натуральное число и сумма его цифр имеют одинаковые остат-
ки при делении на 9.
Оно дает также признаки делимости на 9 и 3.
Решение многих интересных задач основано иа использовании
признаков делимости.
29
Задачи
8. (Фокус.) Возьмем какое-нибудь число, большее чем 10, на-
пример 5647. Переставим произвольным способом цифры этого
числа. Например, так: 7456. Вычтем меньшее число из большего:
7456—5647 = 1809. В получившемся числе зачеркнем какую-
нибудь ненулевую цифру, а остальные цифры сложим. Так, если за-
черкнуть цифру 1, то сумма оставшихся цифр равна 17. Не зная
исходного числа и числа с переставленными цифрами, по этой
сумме легко определить зачеркнутую цифру. Для этого достаточ-
но сумму незачеркнутых цифр разделить на 9 и остаток вычесть
нз 9. Разность всегда равна зачеркнутой цифре. В рассматривае-
мом примере остаток от деления 17 на 9 равен 8 и разность 9—8=
= 1, т. е. равна зачеркнутой цифре. Если зачеркнуть цифру 9,
то сумма цифр 1+8+0 имеет нулевой остаток при делении на 9
н разность 9—О опять равна зачеркнутой цифре.
Какое бы число ни выбрать сначала, это свойство всегда вы-
полняется. Если вы попросите своего товарища, не знающего этот
секрет, написать на листке бумаги тайно от вас какое-нибудь
число, проделать с ннм указанные выше операции и сообщить сум-
му незачеркнутых цифр, то вы сможете немало удивить его,
указав зачеркнутую цифру
Объясним теперь этот фокус. Разность любого числа и числа
с переставленными цифрами делится иа 9. Действительно, оба этн
числа имеют одинаковую сумму цифр, и, значит, по свойству дели-
мости на 9, они имеют одинаковые остатки при делении на 9.
Рассмотрим разность двух чисел, отличающихся друг от друга
перестановкой цифр. Как мы установили, эта разность делится на
9 и по признаку делимости сумма ее цифр также должна делиться
на 9. Если от этой суммы отнять какую-нибудь ненулевую цифру,
то получившееся число при делении на 9 будет, очевидно, иметь
остаток, равный 9—а. В разобранном выше примере сумма всех
цифр разности равна 1 + 8+9=18. Отнимая от 18 цифры 9, 8, 1,
получим числа 9, 10, 17, имеющие при делении на 9 остатки 0, 1,8.
Эти остатки дополняют до 9 отнятые цифры. Фокус можно всячески
разнообразить. Вот еще несколько вариантов, основанных на той
же идее:
а) Предложите вашему товарищу написать какое-нибудь чис-
ло, сосчитать сумму его цифр и вычесть ее из написанного чис-
ла. В получившемся числе пусть он зачеркнет любую ненулевую
цифру, а сумму оставшихся цифр сообщит вам. По этой сумме
легко определить зачеркнутую цифру.
б) Пусть кто-нибудь из ваших знакомых напишет произволь-
ное натуральное число. Припишите к нему слева или справа не-
сколько цифр так, чтобы сумма всех цифр получившегося числа
делилась иа 9. У этого числа вы опять сможете угадать любую
зачеркнутую ненулевую цифру.
30
в) Напишите на листке бумаги произвольное число, напри-
мер 1234. Пусть кто-то вычтет из этого числа тайно от вас какое
ему захочется число, а затем припишет вычтеииое число к раз-
ности слева или справа. Если к найденному числу прибавить 8,
то, как легко проверить, получится число, делящееся на 9, т. е.
фокус может быть продолжен так же, как и ранее. Вместо 8 можно
взять любое число, сумма которого с 1234 делится иа 9.
9. Напишите какое-нибудь целое число. Сосчитайте сумму
его цифр н напишите ее. Затем сосчитайте сумму цифр получив-
шегося числа и действуйте так же до тех пор, пока не получится
однозначное число. Это однозначное число всегда равно остат-
ку от деления первоначального числа на 9.
Возьмем, например, число 123454321. Сумма его цифр равна 25.
Сумма цифр числа 25 равна 7. Делением числа 123454321 иа 9
легко убедиться, что его остаток также равен 7.
Это правило нахождения остатка числа при делении иа 9 легко
понять, если заметить, что по свойству делимости на 9 все числа
в последовательности сумм цифр (в разобранном примере это
123454321, 25, 7) имеют одинаковые остатки при делении иа 9.
10. (Старинный способ проверки арифметических действий.)
Перемножим какие-нибудь два числа, например 257 и 362. Имеем
257-362=93034. Найдем остатки при делении на 9 обоих множите-
лей и произведения. Особенно легко это сделать с помощью прави-
ла из задачи 9. Число 257 имеет остаток 5, второй множитель
362 имеет остаток 2, а остаток произведения равен 1. В средние
века был принят такой способ записи. Нарисуем две пересекаю-
щиеся черты. Слева и справа от получившегося креста запишем ос-
татки множителей, а вверху — остаток произведении (рис. 4).
Перемножим числа, стоящие слева и справа от креста, и за-
пишем под крестом остаток от деления этого произведения иа 9.
В нашем случае записать нужно 1 (рис. 5), так как 5-2=10=
=9+1.
Совпадение чисел над и под крестом ие случайно. Так будет
всегда, если произведение исходных чисел вычислено правильно.
Если же выше н ниже креста записаны различные числа, то в вы-
числения вкралась ошибка.
Так же можно действовать и при проверке правильности сло-
жения чисел. Нужно только под крестом записывать остаток от де-
ления иа 9 суммы чисел, стоящих слева и справа от креста. На-
пример, проверку равенства 763+1142=1905 дает рисунок 6.
\ 6 Z
7 >< в
\ 7 /
5 2
\ J /
5 7
Рис. 4
7
Рис. 5
6
Рис. 6
31
Объясним эти правила на примерах. Числа 763 — 7, 1142—я
1905—6 делятси на 9. Поэтому и разность (1905—6)—(763 —
—(1142—8)=7-f-8—6 делится на 9, т. е. остаток от деления иа
суммы чисел, записанных слева и справа от креста, должен С-
равен числу, записанному выше креста.
В случае произведения из равенств
93034 — 5-2 =257-362 —5-2 =257(362 — 2)4-2(257 —5)
находим, что
(93034 —1)=257 (362-2)4-2 (257—5)4- 5-2 — 1.
Все разности в скобках делятся иа 9. Поэтому и разность 5-2—1
должна делиться на 9, т. е. разность произведения остатков н ос-
татка произведения должна делиться иа 9
Правило, проверенное нами для двух слагаемых или множите-
лей, верно и в случае, если складываются илн перемножаются три,
четыре илн более чисел.
Найдем, иапрнмер, сумму трехзиачных чисел:
123 6
456 6
789 6
101 2
112 4
1581 24
Справа столбиком записаны остатки слагаемых. Их сумма рав-
на 24, а остаток ее от делении на 9 равен 6, т. е. остатку от деления
1581 на 9, так как 14-54-84-1 = 15 н 14-5=6.
Отметим, что совпадение чисел, записанных выше и ниже крес-
та, не означает, что вычисления выполнены правильно, хотя и дает
некоторую уверенность в их справедливости. Может случиться,
что ошибка прошла через нашу ловушку незамеченной.
11. Найти целое число, которое, будучи умножено иа 99, дает
62**427. К сожалению, кто-то замазал две цифры, обозначенные
звездочками. Как же все-таки найти ответ задачи?
Обозначим замазанные цифры буквами 62а6427 н попробуем
нх найти, пользуясь тем, что число 62а6427 должно делиться иа 99.
Имеем:
62а&427 =6 • 10^ 4-2 • 105 4-а • Ю4 4-Ь - Ю3 4-4 • 102 4-27 =
=6 (9999994- 1)4-20 (99994-1) 4-« (99994-1)4- Ю6 (994-1)4-
4-4 (994-1)4-27
Так как каждое из чисел 999999, 9999, 99 делится на 99, то
должна делиться на 99 и сумма
6 4-204-я4-1064-44-27=106 4-а 4-57.
32
Сумма 106 4-а 4*57 положительна и меньше, чем 994*57=156.
На промежутке от 1 до 156 есть только одно число, делящееся
на 99, а именно 99. Поэтому 106 4* а 4* 57—99, 106 4- а=42 н,
находим замазанные цифры а=2, 6=4. Наконец, разделив чис-
ло 6224427 на 99, получим ответ: 62873.
Задание. Попробуйте найти цифры, которые нужно поста-
вить вместо звездочек, чтобы число 32*35717* разделилось на 72.
(Ответ: 322357176.)
12. Напишите какое-нибудь число. Вычтите из него сумму
цифр, стоящих иа нечетных местах, если считать справа налево.
Затем прибавьте сумму цифр, стоящих на четных местах. Резуль-
тат всегда будет делиться на 11.
Например, если написано число 239765, то сумма его цифр,
стоящих иа нечетных местах, равна 5 4-7 4-3= 15, а иа четных
местах 64*94-2—17. Проделав указанные вычисления, найдем
239765-154-17 - 239767=11-21797.
Попробуйте объяснить это свойство. На нем основан признак
делимости на 11. Вычислим сумму цифр данного числа, стоящих
на нечетных местах, если считать справа налево, а затем вычис-
лим сумму остальных цифр. Из большей суммы вычтем меньшую.
Данное число делится на 11 только в том случае, если делится на 11
полученная разность.
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
Числа 6665 н 11395 делятси иа 5, т. е. число 5 есть их общий
делитель. Еще одним общим делителем является 43, ведь
6665-43-155, 11395-43-265.
/
Оба эти числа делятся также на 215. Последнее число 215 будет
самым большим нз общих делителей и называется наибольшим
общим делителем чисел 6665 и 11395.
Если а н Ь — целые неотрицательные числа, делящиеся иа
некоторое натуральное число d, то говорят, что d есть общий
делитель а и Ь.
Единица есть общий делитель любых двух целых чисел. При
а=Ь—0 любое натуральное число будет общим делителем а и b
Если О 0, то каждый делитель числа а ие превосходит а
по величине, и, значит, среди общих делителей чисел aub имеется
самый большой. Этот самый большой из общих делителей чи-
сел а н b называется их наибольшим общим делителем.
Для наибольшего общего делителя чисел а и b имеется
специальное обозначение (а, 6).
Так, например, наибольший общий делитель чисел 2 и 4 равен 2,
т. е. (2, 4)=2. Числа 5 и 6 ие имеют общих делителей, кроме 1,
поэтому их наибольший общий делитель равен 1.
Для любого натурального числа а имеем (а, 1)=1 (ведь 1 не
может делиться ии на какое натуральное число, отличное от I).
2 Заказ 775 ^3
Для любого натурального числа а справедливо равенство (а, 0)=а.
Действительно, оба числа а и О делятся на а. Но никакое число,
большее а, не может быть делителем а.
Очень полезно уметь находить наибольший общий делитель
двух чисел. Например, это может пригодиться, если мы захотим
представить какое-нибудь рациональное число в виде дроби,
имеющей по возможности меньшие числитель и знаменатель^ Так,
6665 _ 215-3! ^31
11395 215-53 53 '
С другими случаями, когда важно знать наибольший общий де
литель двух чисел, мы познакомимся в дальнейшем.
Как же следует поступать, чтобы найти наибольший общий
делитель двух заданных чисел? Такой способ придумали древне-
греческие ученые более двух тысяч лет тому назад. Он носит назва-
ние «алгоритм Евклида». О жизни греческого математика Евк-
лида достоверные данные не известны. Считается, что он жил
в III в. до н. э. в г. Александрии. Евклиду принадлежит вы-
дающееся научное произведение,, называемое «Начала». Оно со-
стоит из 13 книг и излагает основы всей древнегреческой матема-
тики: элементарной геометрии, арифметики, методов определения
площадей, объемов тел. Арифметике посвящены 7, 8 и S-я книги
«Начал». Именно здесь и описывается алгоритм Евклида (алго-
ритм нахождения наибольшего общего делителя).
Прежде чем перейти к его изложению, напомним некоторые оп-
ределения.
Пусть b — натуральное число. Бесконечный ряд чисел О, Ь,
2b, 36, 46 неограниченно возрастает и включает в себя все на-
туральные числа а, делящиеся иа Ь. Если а не делится на Ь, то оно
расположено между какими-то двумя соседними членами qb~
и («74-1)6 этого ряда, т. е. удовлетворяет неравенствам
qb<a<(q + \}b, q^O.
Вычитая из этих неравенств b*q, получаем 0<с—bq,<b.
Обозначим теперь разность a— bq буквой г, тогда 0<r<g.
Если число а делится иа Ь, то a=bq при некотором целом q
и имеем г—а—bq=O.
Итак, для любого целого неотрицательного числа а можно
найти целые числа q н г, такие, что
a—bq-\-r, С^г<.Ь. (1)
Число г называется остатком от деления а на Ь, число q —
неполным частным. Эти понятия хорошо вам известны. Мы уже
встречались с ними, когда обсуждали признаки делимости
Для нахождения чисел q и г можно воспользоваться делением
столбиком. Если у вас есть калькулятор, то с его помощью вы-
числения можно проводить намного быстрее. Разделим на кальку-
34
ляторе число а на Ь. Если а делится иа Ь, то на индикаторе вы-
светится целое число, равное q. В этом случае г=0. Если же а
ие делится иа 6, то на индикаторе появятся два числа, разделенные
точкой. Число, предшествующее точке, н есть q. Зная q, вычисляем
при помощи калькулятора г —а—bq.
Ну а теперь сформулируем алгоритм.
Алгоритм Евклида. Если 6 >-0 и г — остаток от де-
ления а н Ь, то
(а. *)=(*. г).
(2)
Другими словами, наибольший общий делитель двух натураль-
ных чисел равен наибольшему общему делителю меньшего из них
и остатка от деления большего на меньшее.
Сначала мы поупражняемся в применении алгоритма Евклида,
а затем попробуем найти его обоснование.
Вычислим (11395. 6665) —наибольший общий делитель чисел
11395 и 6665. Из равенства 11395—I-6665+ 4730 следует, что
4730 есть остаток от деления 11395 и 6665. Поэтому
(11395, 6665)=(.6665, 4730).
Остаток от деления 6665 на 4730 равен 1935, поэтому
(6665, 4730)=(4730, 1935).
Остаток от деления 4730 на 1935 равен 860, поэтому
(4730, 1935)=(1935, 860).
Остаток от деления 1935 иа 860 равен 215, поэтому
(1935, 860)=(860, 215).
Остаток от деления 860 на 215 равен 0» 860=4-125, поэтому
(860, 215)=(215, 0).
Выше мы отмечали, что для любого натурального числа а спра-
ведливо равенство (а, 0)=а. Значит, (215, 0)=215, н из приве-
денных выше равенств следует, что (11395, 6665)=215.
Рассмотрим еще один пример. Вычислим (1234, 9091). Спра-
ведливы следующие равенства:
9091 = 1234 - 74-453,
1234= 453- 24-328,
453= 328- 14-125,
328= 125 - 2 + 78,
125= 78- 14- 47,
78= 47- 14 31,
47= 31-14 16,
31= 16- 14- 15,
16= 15- 14- I.
15= 1-154- 0.
35
Так как (1234, 9091)—(9091, 1234), то находим (1234, 9091)=
=(9091, 1234)=(1234, 453)=(453, 328)=(328, 125)=(125, 78)=
=(78, 41)=(41, 31)=(31, 16)—(16, 15)—(15, !)=(!, 0)=1.
Итак, числа 1234 и 9091 не имеют общих делителей, кроме 1.
Чтобы привыкнуть к алгоритму Евклида, попробуйте самостоя-
тельно проверить, что
(525,231)=21,(38,105)= 1,
(6188,4709)= 17, (76501, 297191=113
В процессе применения алгоритма Евклида необходимо после-
довательно находить остатки от деления некоторых чисел. Про-
смотрите повторно разобранные выше примеры, а также ваши
собственные вычисления и попробуйте объяснить, почему наи-
больший общий делитель двух чисел равен последнему ненуле-
вому остатку при выполнении делений в алгоритме Евклида.
Выясним теперь, в силу чего выполняется равенство (2), т. е.
найдем обоснование алгоритма Евклида. Обозначим для этого
и=(а, Ь) н v=(b, г). Так как числа b и г делятся на о, то нз равен-
ства (1) следует, что а делится на и. Поэтому v является общим
делителем чисел а н Ь. Но и есть наибольший из общих делителей
чисел а н Ь, следовательно, v а. С другой стороны, числа а и Ъ
делятся иа и. Из равенства г=a—bq получается, что на и
делится и число г. Таким образом, и есть общий делитель b и г
и ие превосходит их наибольшего общего делители о, т. е. и^и.
Из неравенств и получается u=v, т. е. нужное
иам равенство (2). Справедливость алгоритма Евклида теперь
не вызывает сомнений.
ИЗМЕРЕНИЕ ОТРЕЗКОВ
Если есть два отрезка н меньший нз ннх укладывается на боль-
шем целое число раз, например 3 раза (ркс. 7), то говорят, что
больший отрезок равен утроенному меньшему. Если в результате
откладывания меньшего отрезка на большем получается остаток,
то можно попробовать откладывать на этом остатке половину,
третью часть илн какую-либо другую долю меньшего отрезка.
Так, иа рисунке 8, отложив один раз меньший отрезок CD на
большем АВ, получим точку D\ и остаток D\B. Третья часть
отрезка CD укладывается на отрезке дважды и, значит, иа от-
А V, В
С
Рис 7
D
Рис 8
36
резке АВ 5 раз. В таком случае говорят, что отрезок АВ ра-
вен отрезка CD
Два произвольных отрезка АВ и CD называются соизмеримы-
ми, если можно найти такой третий отрезок, который укладыва-
етси целое число раз как на отрезке АВ, так и на отрезке CD.
Если этот отрезок укладывается а раз иа отрезке АВ и b раз на
отрезке CD, то говорят, что отрезок АВ равен ~ отрезка CD.
Так, на отрезке длиной 2 м 32 см укладывается 232 раза отре-
зок, равный части отрезка, названного 1 м. Имея линейку с сан-
тиметровыми и даже с более мелкими миллиметровыми делениями,
легко определить, чаще всего приближенно, сколько раз н
доли метра укладываются на заданном отрезке, другими сло-
вами, измерить его.
Но как быть, если заданы два отрезка и требуется, ие исполь-
зуя лииейку с делениями, найти их общую меру, т. е. такой отрезок,
который укладывается целое число раз как в первом, так и во вто-
ром из данных отрезков. Способ нахождения общей меры приду-
мали древнегреческие математики; он излагается в «Началах»
Евклида и имеет много общего с алгоритмом нахождения наиболь-
шего общего делителя двух целых чисел.
Алгоритм Евклида. Будем откладывать меньший отре-
зок АI на большем Ао до тех лор, пока возможно. Если при этом от
большего отрезка ничего не останется, то общая мера заданных
отрезков равна меньшему из иих. Если же остается некоторый от-
резок Д2, то будем откладывать его иа меньшем из заданных от-
резков Ль пока не останется отрезок Аз, меньший, чем А2. И так
будем продолжать, пока не получим отрезок At, укладываемый иа
предыдущем Ak-i целое число раз. Этот отрезок А* и будет общей
мерой заданных отрезков Ао и Аь
Например, если Ао есть больший из отрезков, изображенных
иа рисунке 9, а А/ — меиьший из них, то, откладывая отрезок Aj
на До один раз, получим остаток А2. Этот остаток также один раз
помещается на отрезке Alt и остается от-
резок А3, который дважды и без остатка
укладывается иа отрезке Д2. Следователь-
но, Аз и есть общая мера отрезков Ао и
А|. Легко проверить, что он 5 раз уклады-
вается в большем н 3 раза в меньшем.
Поясним теперь, почему алгоритм Евк-
лида находит общую меру отрезков. Для
этого допустим, что некоторый отрезок С
может быть отложен без остатка а раз
. иа Ао и Ь раз иа А>.
Аа
A3 Аз
Рис. 9
37
Если принять С за единицу измерения, то получим, что дли-
на До равна а единицам, длина At — b единицам. Предположим,
что отрезок At укладывается q раз иа отрезке До и остается
Д2. Тогда длина равна a—qb=r отрезков С (где 0 <><6).
Аналогично количество отрезков С, помещаемых в Аз, равно
остатку от деления b иа г и т. д. Мы видим, что длины отрезков
До, А1, Аг выраженные в единицах С, образуют последователь-
ность остатков в алгоритме Евклида нахождении наибольшего
общего делителя чисел а и Ь, причем длина отрезка Д* будет
равна наибольшему общему делителю.
Следует отметить, что в «Началах» Евклида алгоритм нахож-
дения наибольшего общего делителя чисел излагается именно в
такой геометрической форме.
Мы познакомимся сейчас с одним нз величайших математи-
ческих открытий: существуют отрезки, для которых нельзя найти
общую меру. Этот удивительный факт был обнаружен древнегре-
ческими учеными и содержится в книге «Начала». Точнее, его
можно сформулировать так:
Теорема. Сторона и диагональ квадрата не имеют общей ме-
ры, т. е. несоизмеримы.
Это значит, что если взять квадрат со стороной 1 м, то длину
его диагонали невозможно выразить никаким дробным числом.
Можно, конечно, находить все лучшие приближенные значения:
I 3.7 17 .
1 м,тм,— И, — м,
но точное значение при этом не получится никогда.
Указанную цепочку приближенных значений можно про-
должить и дальше по следующему правилу:
2-174-7 _ 41 2-41 + 17 _ 99
2-12+5 29 ’ 2-29+12 3 70* ’
Если каждую из этих дробей представить в виде десятичной дроби,
то вы увидите, что у них становятся одинаковыми сначала первые
цифры, потом вторые, третьи и т. д.:
1 = 1,0000000. .
-|-= 1,5000000.
+=1,4000000...;
1,4166666..
+=1,4137931...;
+=1,4142857..
При этом получается последовательность цифр
1,4142135623730950488016887242096980785697..
38
дающая все более точное представление длины диагонали в виде
десятичной дроби. Вспомним, как называются десятичные доли
метра:
j|^m=10 2 м — сантиметр (см);
м=10~3 м — миллиметр (мм);
10”6 м —микрон (мк);
10“10 м ангстрем (А).
Если длина стороны квадрата равна 1 м, то приближенное с точ-
ностью до 1А значение длины диагонали есть
1 м 41 см 4 мм 213 мк 5623 А.
Самая мелкая нз десятичных долей — ангстрем используется в
физике для измерения некоторых очень маленьких величин. На-
пример, размер молекулы кислорода — ЗА.
Тем ие меиее мы умеем вычислять длину диагонали с любой
точностью. Правило построения дробей, дающих все лучшие зна-
чения ее, было открыто Теоном Смирнским во II в.
Вернемся к теореме о несоизмеримости стороны и диагонали
квадрата. Попробуем реализовать для этих двух отрезков алго-
ритм Евклида нахождении общей меры и покажем, что ои ни-
когда не завершит своей работы.
Пусть BCDE — некоторый квадрат (рнС. 10). Прежде всего
мы должны отложить меньший из отрезков — сторону CD иа диа-
гонали СЕ. Это можно сделать только один раз. Затем остаток
от диагонали будем откладывать на стороне квадрата и т. д.
Представим, что наш квадрат нарисован на листе бумаги.
Согнем лист и совместим точку В с точкой Db лежащей на диаго-
нали СЕ, так, что DiE=BE. Тогда DiE=CD. Разгладив линию
сгиба, получим отрезок ЕЕ». Чуть позже мы докажем равенст-
во BE}=DtC, означающее, что Ei есть конец отрезка, равного
остатку диагонали и отложенного на стороне квадрата ВС. Этот
остаток, действуя по алгоритму Евклида, f р
нужно отложить от точки Е| еще раз. Но
мы остановимся на некоторое время и рас-
смотрим возникшую картинку. Оказыва-
ется, и это будет установлено ниже, что
треугольник CDiE\ есть половинка квад-
рата CDiEiBi, отсеченная его диагональю
CEi. Значит, наш следующий шаг — от-
кладывание на EiG отрезка DiC есть
откладывание стороны некоторого квад-
рата иа его диагонали. Р.ч 19
39
Рис. 12
Мы находимся в ситуации, с которой начинали. Отложив отре-
зок DiC иа £|С, получим точку D?, затем опять квадрат
CD2E2B2 и т. д. (рис. 11). Этот процесс ие будет иметь конца,
и, значит, мы никогда не сможем найтн общую меру отрезков
CD и СЕ.
Осталось только объяснить равенство BE[=DjC н почему
треугольник CDiEt есть половина квадрата. Сгибая лист бумаги
по прямой Е£(, мы совместили дВ£|Е н ADiEjE. Поэтому
B£i=£iDi и Z.£jDi£ — прямой угол.
Перегнем лист бумаги по прямой E1D1. Линии сгиба пере-
сечет отрезок CD в точке F (рнс. 12). Углы EtDiE и EiDtC пря-
мые, поэтому после перегибания отрезок DiC ляжет на отрезок
DiE, а точка С попадет в некоторую точку Н, лежащую иа отрез-
ке О\Е. Это, в частности, будет означать, что
CF^FH и CEi = FaH. (1)
Если теперь перегнуть квадрат по диагонали СЕ, то, по-
скольку углы EiDiH н FDfH прямые, отрезок DjEi ляжет на от-
резок D\F. Но тогда точка £j совпадет с точкой F, ведь отрез-
ки СВ и CD совместятся. Отсюда получается, что совпадут отрез-
ки С£1 и CF, EiH и FH, т. е. CEi = CF н EXH~FH. Вместе с (1)
это приводит к равенствам CEi=CF=FH=EiH. Итак, в че-
тырехугольнике CFHE\ все стороны равны и угол FCEi прямой.
Но тогда CFHE\ — квадрат. Как известно, в квадрате диагонали
равны н, пересекаясь, делятся пополам. Поэтому отрезки E\D\
и CD\ равны между собой, и, значит, BEt=EtDi = C[h. Нужное
равенство отрезков доказано. Кроме того, ясно, что, если, напри-
мер, треугольник CFDi приложить к треугольнику CEiDt извне
квадрата BCDE и так, чтобы отрезки СЕ| н CF совпали, получится
квадрат, обозначенный на рисунке 11 буквами С, Dt, Е\,
Этим завершается доказательство теоремы о невозможности
точно измерить диагональ квадрата, если известна длина его
стороны.
40
РЕШАЕМ УРАВНЕНИЯ
Мы укажем здесь одно интересное применение алгоритма Евк-
лида.
Рассмотрим следующие задачи:
Задача 1. Как с помощью монет в 3 и 5 к., заплатить в ма-
газине кассиру 13 к.?
Ответ легко угадывается: нужно взять одну монету в 3 к.
и 2 монеты по 5 к., ведь
3-1+5-2=13
А как быть, если у вас есть только монеты по 5 к.?
Задача 2. В некотором царстве в обращении ходили монеты
достоинством в 12 и 19 к. Солдат пришел в лавку купить одну ко-
робку спичек стоимостью 1 к. Как он должен расплачиваться с тор-
говцем? Смог бы ои купить булку стоимостью 4 к., если бы в стране
обращались монеты по 12 и 18 к.?
Попробуем теперь ответить на поставленные вопросы. Рассмот-
рим сначала первый из них. Если обозначить через х количество
монет по 3 к. и через у количество монет по 5 к., которые необхо-
димо уплатить за покупку, то по условию должно выполняться
равенство
3x+5i/=13. (1)
Числа х= 1 и у=2 удовлетворяют этому уравнению и дают угадан-
ный выше ответ. Вместе с ними уравнению (1) удовлетворяют так-
же числа х=—4, у=5 или х=6, у—— 1 и вообще числа
х=1+5г^ у—2—Зл при любом целом п.
Действительно,
3 (1+5п)+5 (2—Зл)—3+15п+10—15л= 13.
Указанные выше пары чисел получаются при п= —1 и п=1.
Как же следует понимать отрицательные зиачеиия х и у? Упла-
та (—4) монет достоинством 3 к. означает, что кассир должен
вернуть вам 4 монеты по 3 к. В самом деле, если вы дадите кассиру
5 монет по 5 к., ои вернет вам 4 монеты по 3 к., то уплаченная
сумма будет равна
5-5-4-3=13 к.
При наличии же только трехкопеечных монет можно отдать
кассиру 6 монет по 3 к. и получить сдачу 1 монету в 5 к.
(3-6-5-1 = 13).
41
Теперь обратимся ко второй задаче. Если солдат отдаст тор-
говцу х монет по 19 к. н у монет по 12 к., то уплаченная сумма будет
равна 19*4- 12у копеек, и, значит, должно выполняться равенство
19*4-12^1. (2)
Ясно, что при этом одно из чисел х и у должно быть положитель-
ным, а другое — отрицательным, т. е. торговец должен возвра-
тить солдату некоторую сумму денег.
Аналогично второй вопрос этой задачи приводит к уравнению
18*4-121/=4. (3)
Уравнения, в которых неизвестные величины выражаются це-
лыми числами, называются диофантовыми по имени математика
Диофанта, жившего в III в. н. э. В своем научном труде
«Арифметика*, из которого до нас дошли только шесть книг
(общее же число их неизвестно), Диофант рассматривает разно-
образные уравнения с целочисленными и рациональными неиз-
вестными н указывает способы их нахождения.
Пусть теперь а. Ь и с — целые числа, Рассмотрим
уравнение
(4)
где неизвестные х и у есть целые числа. Обозначим d=(o, Ь) —
наибольший общий делитель а н Ь. Если х0, уо — целочисленное
решение уравнения (4), то из равенства ах0-^Ьуо=с (так как а и b
делятся иа d) следует, что с также должно делиться иа d. Значит:
Правило 1. Если с не делится на наибольший общий дели-
тель (а, Ь), то уравнение (4) не имеет решений в целых числах.
Рассмотрим уравнение (3). Легко сосчитать, что (18, 12)=6.
Поскольку 4 не делится иа 6, мы можем смело утверждать, что
уравнение (3) не имеет решений в целых числах, т. е. солдату не
удастся заплатить 4 к. монетами по 12 и 18 к.
Сосчитав наибольший общий делитель коэффициентов урав-
нения (2):
19= 12-14-7,
12= 7-14~5,
7= 5-14-2,
5= 2-24-1,
2= 1-24-0,
(5)
получим (12, 19) — 1. Условие из правила 1 выполняется. Но име-
ет ли уравнение (2) решение в целых числах? А если имеет, то
как его найти? И как поступать, если задано произвольное уравне-
ние вида (4), например:
231* 4-525у«210?
(6)
42
Полезно иметь в виду следующее правило:
Правило 2. Если с делится иа наибольший общий дели-
тель (а, ^'коэффициентов уравнения (4), то прежде всего следует
упростить это уравнение, разделив обе его части на (а, Ь).
Ранее вы нашли, что (231,525)= 21. Поскольку 231 = 21-11,
504=21-24, 210=21-10, то уравнение (6) можно упростить, за-
менив его иа
lU+25y=10. (7)
Заметим, что (11, 25) =1. Так будет и в общем случае, ведь мы
делим коэффициенты уравнения (4) на наибольший общий дели?
тель а и Ь. Значит, нужно научиться решать уравнение (4) в слу-
чае, когда (а, Л)=1 или, как говорят, если числа а и b взаимно
просты.
Допустим, что и и v— два натуральных числа, u>v и для
некоторых чисел Xt, yt, хг, у2 выполняются равенства
axt+by2=u, (8)
ахя+ by 2—v, (9)
т. е. пары чисел (xj, у}) и (Х2, Уг) есть решения уравнения (4) при
с=и и c=v. Разделим и иа v с остатком:
0^г<у.
Если обе части равенства (9) умножить на а и вычесть нз (8),
получится
a (xi — №)+b (yi—qyi)=r,
т. е. числа xi — qxz и yt—qyz образуют решение уравнения
ax+by=r, (10)
Зная решения уравнений ax-^by=v и ах±Ьу=г, точно так же
можно получить решение уравнения (4), где вместо v стоит оста-
ток от деления v иа г. Этот процесс можно продолжать н дальше.
Мы будем находить решения уравнений (4), где справа будут сто-
ять все меньшие и меньшие натуральные числа.
Для упрощения записи можно опустить коэффициенты а и Ь,
ведь они у всех уравнений будут одинаковыми, а также знаки 4- и
=. Тогда наши вычисления будут выглядеть так:
Xi—qx2
У\—ду2
43
Есть два уравнения
ах-^Ъу=а.
ax-^by=b.
(И)
для которых решения очевидны. Первое из них имеет решение
Х) = 1,1/1=0, а второе х2—О,1/2=1. Начав с этих решений и вы-
полняя указанные действия, получим, например, в случае уравне-
ния (2) такую последовательность таблиц:
1 1 0 0 1 10 12 1 0 1 1 — 1 12 7
1 1 1 — 1 — 1 — 1 2 7 7 5 2 — 1 — I 2 2 2 —3 5 5 2
2 —3 2 —5 8 1
Числа —5 и 8, получившиеся в последней таблице, удовлетворяют
уравнению (2). Действительно, 19-(—5)4~ 12-8—-95-^96= I.
Все вычисления удобно свести в одну таблицу. Отметим, что
Я X У г
1 0 19
1 0 1 12
1 1 — 1 7
1 — 1 2 5
2 2 —3 2
-5 8 1
столбцы этой таблицы, обозначенные буквами г и q, составляют
последовательность остатков и неполных частных в алгоритме
Евклида. Будем называть нх столбцом остатков и столбцом част-
ных. В общем случае, если числа а и b взаимно просты, последний
44
ненулевой остаток в алгоритме Евклида равен (а, Ь), т. е. равен 1.
Значит, в таблице обязательно встретится строка с 1 иа месте ос-
татков и мы можем утверждать, что справедлива следующая:
Теорема. Если а и Ь — взаимно простые числа, то уравне-
ние ах-^Ьу—1 имеет решение в целых числах х и у-
Найти это решение можно, пользуясь следующим правилом:
Правило 3. Напишем две строки чисел (1, 0, а) и (0, 1, Ь),
соответствующие уравнениям (11). Первой следует писать строку
для большего коэффициента. Каждую новую строку получаем из
двух предыдущих следующим образом. Вычисляем частное q от де-
ления остатка предпоследней строки на остаток последней строки.
Это число q записываем в последнюю строку на месте частных.
Все остальные элементы этой строки умножаем на q и вычитаем из
соответствующих элементов предпоследней строки. Так образуют-
ся трн элемента новой строки. Продолжаем выписывать новые
строки, пока не получится строка с остатком, равным 1. Числа, за-
писанные в этой строке в столбцах неизвестных, дают решение
уравнения ах+Ьу=\.
Для уравнения (7) таблица начинается строками
и имеет вид: 0 1 25 1 0 11
У г
Ч X
0 1 25
2 1 0 11
3 —2 1 3
1 7 -3 2
-9 4 1
25=11-2+3,
11=3-3+2,
3=2-1 + 1
Числа х = — 9иу=4 составляют решение уравнения Их+25#=1.
Действительно, 11 9)+25-4 = 1. Умножив их на 10, получим,
что числа
л=—90 и #=40
(12)
удовлетворяют уравнению (7).
Так же следует поступать н в общем случае:
46
Правило 4. Чтобы найти решение уравнения (4) при взаим-
но простых а и Ь, нужно сначала иайтн решение (х0; уо) уравнения
ох-|-6у=1; числа схс и суо составят решение уравнения (4).
Вместе с числами (12) уравнению (7) удовлетворяют и числа
л= -904-25п и у=40—1 In, (13)
где п может принимать любое целое значение. Действительно,
11 -(—90 +25^)4-25 (40— 11п)= 11 (—90)4-25*40=10.
Из формул (13), например, для п=4 получаем еще одно решение
уравнения (7): х= 10, у= — 4.
Подобное рассуждение верно и в общем случае: если (х« yi) —
некоторое решение уравнения (4), то при любом целом п числа
x=xi4-6n и y=yi — ап (14)
также будут его решением.
Мы получаем таким способом бесконечное множество решений
уравнения (4). В случае уравнении (7) ими будут, например, па-
ры чисел (—90; 40), (—65; 29), (-40; 18), (-15; 7), (10;-4),
(35; —15).....Но, может быть, существуют еще какие-то реше-
ния, которые нельзя получить с помощью формул (14)? Нет, это
неверно.
Правило 5. Если коэффициенты а и b уравнения (4) взаим-
но просты, то все решения уравнения (4) получаются по формулам
(И).
Чтобы объяснить это правило, понадобится следующее важное
свойство делимости целых чисел: пусть а, Ь — натуральные взаим-
на простые числа и с — такое, что произведение Ьс делится иа а.
Тогда с делится иа а.
Действительно, по теореме найдутся целые числа х0 и уо, такие,
что 1 =ахо-}-Ьуо. Умножая это равенство на с, получим с—а~сх0+
+ Ьс-уо. Отсюда, так как а и Ьс делятся иа а, получаем, что с де-
лится иа а. Свойство доказано. Если а и b не взаимно просты,
утверждение может нарушаться: 4*3 делится иа 6, но ни 4, ни 3 на
6 не делится.
Пусть (xi; у,) и (х2; у2) — решения уравнения (4),
ах, + fey, = с
axi-^by2=c,
причем коэффициенты а и & взаимно просты. Вычитая первое
равенство (15) из второго, получим
а (Л2—X])+fe (у2—у,)=0
или
a(x2—Xi)=Ь((/2—^). (16)
46
По сформулированному выше свойству делимости заключаем,
что разность у\ —у2 делится на а, т. е. при некотором целом п вы-
полняется равенство у,— у2~ап нли y2>=yi—an. Подставляя ап
вместо разности у\ — у2 в правую часть (16) и сокращая иа а,
приходим к равенству х2—xt=bn или x2=xi-^bn. Итак, любое
решение (х2; у2) уравнения (4) может быть получено с помощью
формул (14). Правило 5 получило обоснование.
Решим теперь следующую задачу:
Задача 3. Найти все натуральные числа в пределах от 1 до
100000, делящиеся иа 73 и оканчивающиеся цифрами 001.
Решение. Каждое такое число имеет вид 73х при некотором
натуральном х, н оно же может быть представлено в виде 1000*/ -f-1.
где у — натуральное число. Имеем уравнение
73х=1000у+1,
или
73х-1000^=1. (17)
Обозначим у— — Z. тогда уравнение примет вид:
73x4-10002—1. (fS>
Решая его я находим: X Х=137, z У = — 10 (см. таблицу). г
0 1 1000
13 I 0 73 1000 = 73-134-51, 73 = 51-14-22, 51=22-2+7, 22=7-3+1.
1 — 13 0 51
2 14 -1 22
3 -41 3 7
137 — 10 1
Решения уравнения (18) имеют вид
х=!37+1000п, 2=—10—73л.
Находим теперь все решения уравнения (17): х=137+1000я,
у= 104-73п, где п — любое целое число. Искомые числа имеют
вид:
73х—73 (137+1000л) = 10001+73000л (19)
47
н должны по условию задачи удовлетворять следующим не-
равенствам
I < 10001 +73000/2 < 100000.
При л=0 и 1 находим числа 10001 и 83001. Следующее число,
получающееся при /1=2, есть 156001. Оно больше чем 100000.
При /2=3, 4, ... будут получаться еще большие числа. Если же
п отрицательно, то по формуле (19) будут получаться отрицатель-
ные числа х. Итак, условию задачи удовлетворяют два числа:
10001 и 83001.
Прием с заменой у на — z можно использовать всегда, когда
коэффициенты а н Ь уравнения (4) имеют разные знаки.
Есть еще одни полезный прием, упрощающий решение, если
с — большое число. Рассмотрим, иапрнмер, следующую задачу:
Задача 4. В машину погрузили некоторое количество дета-
лей, упакованных в ящики двух размеров. Большой ящик с дета-
лями весит 24 кг, а малый 19 кг. Сколько было больших и сколько
малых ящиков, если известно, что общий вес груза равен 826 кг?
Решение. Обозначим количества больших и малых ящиков
буквами хну. Согласно условию должно выполняться равенство
24х+19^=826. (20)
Решая уравнение 24х+ 19г/— 1, находим х0=4, у0= — 5- Если
в соответствии с указанными ранее правилами умножить эти
числа иа 826, то получатся большие числа.
24
19
5
4
1
Поступим иначе. Разделим 826 на 19 с остатком: 826=19-43+9.
Пользуясь этим равенством, уравнение (20) можно перепи-
сать в виде 24х+19 (у—43)—9. Если теперь обозначить z—у—43,
получится уравнение 24*+ 19z=9. Ему удовлетворяют числа х( =
=4-9=36 и Zi=(—5)-9= — 45. Теперь находим yi=Zi+43=
— —2. Итак, числа Х|=36, yi = —2 составляют решение уравне-
ния (20), а любое его решение может быть получено по формулам
х=36+19/2, у=—2—24«, где п — произвольное целое число.
Числа х и у одновременно будут положительны только при п= — 1.
Итак, находим х=36—19=17, у= —2+24=22.
Ответ: 17 больших и 22 малых.
48
Задачи
13. Школьник купил несколько тетрадей, простых и цветных
карандашей. Тетрадь стоит 1 к., простой карандаш 4 к., а цвет-
ной 6 к. Всего было куплено 20 предметов и уплачено 40 к. Сколько
тетрадей, простых и цветных карандашей купил школьник?
От вет: 14, 5, 1.
14. Тринадцать пиратов добыли некоторое количество золотых
монет. Они пытались разделить их поровну, ио оказалось, что оста-
ется 8 штук. Когда они снова стали поровну делить монеты, после
того как два пирата упали за борт и были съедены акулами, ока-
залось, что остается 3 монеты. Потом в перестрелке погибли еще
3 пирата, но, когда 8 пиратов стали делить монеты, оказалось, что
остается 5 монет. Сколько всего было монет?
Ответ: наименьшее количество равно 333.
15. Женщина несла для продажи корзину яиц. Встретившийся
прохожий по неосторожности так толкнул ее, что корзина упала
иа землю и все яйца разбились. Прохожий захотел уплатить жен
шине стоимость разбитых яиц н спросил, сколько их всего было.
<Я не помню этого,— сказала женщина,— знаю только хорошо,
что когда я перекладывала яйца по 2, то осталось одно яйцо. Точно
так же всегда оставалось по одному яйцу, когда я перекладывала
их по 3, по 4, по 5, по 6. Когда же я перекладывала их по 7. то не ос-
талось ии одного яйца». Сколько было яиц?
Ответ: наименьшее количество равно 301.
16. (Игра.) Покажите трем участникам игры три предмета,
присвоив этим предметам номера 1, 2 и 3- Пусть каждый из играю-
щих, после того как вы отвернетесь, возьмет один из предметов и
спрячет его. Затем пусть первый человек умножит номер своего
предмета на 3, второй — иа 10, а третий — иа 12. Сложив получен-
ные произведения, пусть кто-либо из троих участников игры
объявит сумму. Зная сумму, вы можете узнать, кто из троих чело-
век взял какой предмет.
Как это сделать? Кто взял какой предмет, если сумма равна,
например, 41? Попробуйте объяснить следующее правило: нужно
вычесть из 72 объявленную сумму, затем разность разделить на 9 с
остатком, частное покажет номер предмета, взятого первым чело-
веком, а половина остатка даст номер предмета, взятого вторым
человеком.
17. Аналогичная игра для четырех человек. В этом случае номе-
ра предметов нужно умножать на 2, 21,25 и 26. Попробуйте объяс-
нить следующее правило угадывания-, чтобы определить, кто взял
какой предмет, надо нз 260 вычесть объявленное число н разность
разделить с остатком на 24, тогда частное покажет номер предме-
та, взятого первым человеком; если остаток разделить на 5 с остат-
ком, то частное от второго деления покажет номер предмета,
взятого вторым человеком, а остаток — номер предмета, взятого
третьим человеком.
49
ПРОСТЫЕ ЧИСЛА
Некоторые отличные от 1 числа натурального ряда могут быть
разложены в произведение меньших множителей. Например:
6=2-3, 8=2-2-2, 111=3-37.
Ранее мы назвали их составными. Составные числа ие исчерпы-
вают весь натуральный ряд. Нельзя разложить иа меньшие множи-
тели 2 и 3,5 и 7 (что было нами установлено ранее), а также числа
239, 701 и многие другие. Подобные числа, т. е. числа, которые
нельзя разложить в произведение меньших мио жителей, называ-
ются простыми.
Самое маленькое натуральное число I, конечно, ие расклады-
вается в произведение еще меньших множителей. Но 1 находится
иа особом положении, ведь она делит каждое натуральное число.
Считают, что 1 не есть простое число.
Таким образом, 1 ие относится ии к простым, ин к составным
числам. Любое же большее 1 натуральное число является или
простым, или составным. Среди четных чисел имеется единственное
простое — 2. Все остальные простые числа нечетны.
Интерес к простым числам, возникший в глубокой древности,
вероятно еще в школе Пифагора (V в. до и. э.), объясняется
тем, что из них с помощью умножения можно построить все нату-
ральные числа. С другой стороны, простые числа обладают рядом
загадочных свойств, в течение тысячелетий побуждавших иссле-
дователей на многочисленные и часто безуспешные попытки про
иикновения в их тайны.
Среди первых 1000 чисел, записываемых одними единицами,
простыми будут только
11, 11. .1, 11...1, II...1.
19 23 317
Будет простым число
11...1 4 11...1,
--v—« .——«
32 32
а также числа
2' + 1 = 3, 2! + 1=5, 2’ + 1 = 17,
2® +1 =257, 216 +1 =65537,
22—1 = 3, 2®-1=7, 2s—1=31,
2’—1 = 127, 213 —1=8191
Но
2ЗЕ 1 =4294967297 = 641 *6700417 и 2" —1=2047=23*89
— составные числа.
50
Примерами простых являются числа
99990001, 999999000001, 9999999900000001,
9091, 909091, 9091, 9091, 9091, 9091,
8 раз 14 раз 26 раз 32 раза
900900900900990990990991.
В начале XVII в. было установлено, что 2’7—1 и 2,9~ 1 прос-
ты. В 1722 г. Л. Эйлер после многолетних безуспешных попыток
доказал, что 231 — 1 — простое число. К началу нашего века стало
известно, что простыми являются числа 261 — 1 н 2127— 1. Вскоре к
ним были добавлены 2м — 1 и 2107 —1. Нужно сказать, что все Вы-
числения с этими числами проводились вручную и требовали не
только аккуратности, но и большой изобретательности, ведь, на-
пример, число 2127—1 записывается 39 цифрами.
С появлением в 50-е годы нашего века ЭВМ наступила новая
эпоха в поисках простых чисел. Было найдено еще 18 простых чисел
вида 2"—1. Самые большие из них и вообще самые большие из из-
вестных простых чисел — это
213204®-—1 и 22,и9‘-1.
Они были открыты в 1983 и 1985 гг. Может случиться, что, пока
наша книга выйдет из печати, этот рекорд будет побит.
Простые числа ведут себя совершенно непредсказуемо. Онн мо-
гут собираться группами, как, например,
17 и 19, 41 и 43, O-^'il. 156-5202±1, 291 -2,553±1.
Такие пары соседних простых чисел называются близнецами.
Предполагается, что их бесконечно много. Среди 150000 последо-
вательных чисел, первое из которых есть 10й, имеется 601 пара
близнецов. В натуральном ряде есть скопления по 3 числа, напри-
мер 3163, 3167,3169 или 32713, 32717,32719, а вместе с тем и сколь
угодно длинные отрезки, не содержащие простых чисел вообще.
Л. Эйлер обнаружил многочлен х2—х+41, который прн всех
х—0, 1,2,..., 40 принимает только простые значения. Но н сейчас
никто не знает формул, по которым можно было бы вычислять все
новые простые числа. Йх поиск напоминает поиск новых звезд на
ночном небе, прн этом роль телескопов исполняют самые мощные
и совершенные нз современных ЭВМ
Л. Эйлер (1707—1783)—велнкий ученый-математнк, ро-
дился н учился в Швейцарии. В возрасте 20 лет, получив пригла-
шение от только что созданной Петербургской академии наук, он
переезжает а Россию, где прожил в общей сложности более 30 лет
и-сделал необычайно много для развития‘науки. Ему принадлежат
труды по математние, механике, теории движения Луны н планет,
1 5
7 11
13 17
19 23
25 29
31 35
по географии и кораблестроению, теории музыки. Умер Эйлер в
1783 г. в Петербурге.
Как же узнать по заданному числу N, можно его разложить
на меньшие миожители или оно простое? В начале первого разде-
ла мы далн правило, позволяющее получить ответ на этот вопрос,
и там же доказали, что число 1009 является простым.
По этому правилу следует перебрать все числа, квадрат кото-
рых не превосходит N. Если N не делится ни на одно из них, то
N — простое число, в противном случае М составное.
Такой метод определения простоты чисел, по-видимому, первым
опубликовал а 1202 г. Леонардо Пизанский в книге,
названной «Кинга абака». Абак — это древний вычислительный
инструмент, подобный русским счетам. Леонардо родился в италь-
янском городе Пнзе около 1170 г. в семье городского писаря. Отец
его имел прозвище Бокаччо (добродушный), имя Фибоначчи
(сын Бокаччо) закрепилось за Леонардо и получило широкую
известность. Как купец, Леонардо много путешествовал по стра-
нам Востока, где и расширил свои математические знания. «Кинга
абака» содержала огромное количество сведений, почерпнутых из
трудов греческих и арабских ученых, задач и методов их решения,
придуманных самим Леонардо Пизанским, н послужила важным
средством распространения математических знаний в Европе.
Количество испытываемых делителей можно значительно со-
кратить. Например, если N не делится на 2, то незачем испыты-
вать в роли делителей Д' четные числа, а если М ие делится на 3,
то числа, делящиеся на 3. В результате мы исключим из испытыва-
емых делителей все числа, которые при делении иа 6 дают остатки
0,2, 3,4, т. е. останутся только числа вида бАг-J-1 я 6fe~|-5. Получа-
ется следующий усовершенствованный метод пробных делений:
1. Проверить, делится ли число М на 2 илн 3. Если делится, то
Д' — составное число.
2. Иначе составить таблицу пробных дели-
телей. В ней пераая строка имеет вид 1, 5, а
каждая последующая получается нз предыду-
щей добавлением числа 6. При появлении каж-
дой новой строки проверить, делится N на
входящие в нее числа илн нет. В результате мы
или найдем делитель АГ, и в этом случае N со-
ставное, илн доберемся до такого элемента таб-
лицы, квадрат которого превосходит N по ве-
личине. В последнем случае нужно прекратить
работу и можно утверждать, что N — простое.
Метод пробных делений позволяет также
находить и небольшие делители больших со-
ставных чисел.
Пользуясь этим методом при-1009, до-
статочно сделать только 10 пробных делений
на числа таблицы от 5 до 31 и предвари-
Б2
тельно проверить делимость 1009 на 2 н 3 с помощью признаков
делимости.
Можно добавить к первоначальным делителям 2, 3 еще и чис-
ло 5. Тогда таблица пробных делителей будет содержать 8 столбцов:
1 7 11 13 17 19 23 29
31 37 41 43 47 49 53 59
В первой ее строке будут стоять все числа из отрезка от 1 до 30=
=2-3-5, взаимно простые с 30, а каждая следующая строка получа-
ется из предыдущей добавлением 30 к ее элементам. Эта таблица
содержит еще меньше пробных делителей.
Метод пробных делений используется и на современных ЭВМ
Первоначальными делителями выбирают числа 2, 3, 5, 7, 11, 13.
При этом таблица содержит 5760 столбцов. Каждая новая ее
строка получается из предыдущей добавлением
30030=2-3-5-7-11-13
Числа, записываемые 14 десятичными знаками, проверяют-
ся на простоту за считанные секунды. Время, конечно, зависит
от величины числа и мощности используемой ЭВМ
Изменим немного рассматриваемую нами задачу. Предполо-
жим, что нам требуется найти все простые числа, лежащие на
отрезке натурального ряда от 1 до некоторого числа N, например
от 1 до 100. Способ исключения из этого промежутка всех состав-
ных чисел был известен еще древнегреческому математику Эра-
тосфену (276—194 гг. до и. э.) и иосит название решето Эра-
тосфена. Мы приведем его в несколько усовершенствованном виде:
1. Выписать все нечетные числа от 3 до N.
2. Вычеркнуть З2 и далее каждое третье число, затем вы-
черкнуть 52 и далее каждое пятое число.
3. Продолжать этот процесс, пока возможно, выбирая всякий
раз первое оставшееся невычеркнутым число, следующее за тем.
кратные которому были вычеркнуты последними.
4. Числа, которые остались иевычеркнутыми, составляют мно-
жество всех нечетных простых на отрезке от 1 до N.
Для ^=100 имеем следующую таблицу:
3 5 7 9 11 13 15 17 19 21
23 25 27 29 31 33 35 37 39 41
43 45 47 49 51 53 55 57 59 61
63 65 67 69 71 73 75 77 79 8£
- 83 85 87 89 91 93 95 97 99
S3
Для ясности мы не вычеркивали, а лишь подчеркивали нужные
числа. Прн этом числа, которые необходимо было вычеркнуть при
первом проходе по «просеиваемому» отрезку натурального ряда,
подчеркнуты одной чертой, прн втором проходе — двумя чертами,
при третьем — тремя чертами. Все заканчивается после трех прохо-
дов, так как первое, оставшееся невычеркнутым число, следующее
за 7, есть 11 и П2== 121 :> 100. Числа, оставшиеся неподчеркнуты-
ми, и есть нечетные простые, меиьшие или равные 100. Соберем их
в таблицу, добавив еще число 2:
2 3 5 7 11
13 17 19 23 29
31 37 41 43 47
53 59 61 67 71
73 79 83 89 97
Имеется всего 25 простых чисел на отрезке натурального ряда
от 1 до 100.
Чтобы объяснить метод решета, мы сначала проверим, что
наименьший отличный от 1 делитель любого натурального числа
k> 1 есть простое число.
Действительно, если бы этот делитель (обозначим его q) был
составным числом, то он должен был бы раскладываться на
меньшие множители q=uv, и> 1, v> 1. Число и, меньшее, чем q,
также является делителем k. Но это невозможно, ведь q — наи-
меньшее из делителей k. Итак, q — простое число.
Вернемся теперь к решету Эратосфена. Совершая проходы по
натуральному ряду, мы вычеркиваем только составные числа. В
первый раз числа, делящиеся на 3, во второй — те яз оставшихся,
которые делятся на 5, в третий — на 7 и т. д. Допустим, что среди
невычеркнутых осталось составное число а. Обозначим наимень-
ший отличный от 1 делитель числа а буквой р. Тогда а—р*Ь н,
как мы это проверили ранее, р — простое число. Раз р — простое
число, то оно также осталось невычеркнутым; кроме того,
pz^.pb=a^.N.
Это означает, что в какой-то из проходов ио натуральному ряду
были вычеркнуты, начиная с р2, все числа, делящиеся на р, в том
числе и а. Но ведь мы предположили, что а не вычеркнуто. Полу-
чившееся противоречие означает простоту числа а. Итак, все чис-
ла, оставшиеся иевычеркнутыми, просты.
В начале раздела мы привели множество примеров простых
чисел. Ученые открывали их постепенно, все большие н большие.
Но, может быть, когда-нибудь будет построено последнее, самое
большое из возможных простое число? Ответ на этот вопрос полу-
чили еще древние греки. В 9-й книге «Начал» Евклида содержится
следующее утверждение:
54
Теорема. Множество простых чисел бесконечно.
Докажем эту теорему. Предположим, что утверждение неверно,
т. е. простые числа образуют конечное множество н Р — самое
большое из них.
Рассмотрим число.
где в произведении участвуют все простые числа. Число N при
делении иа 2, на 3, на 5 н вообще на любое простое число имеет
остаток 1. В то же время наименьший, отличный от 1 делитель q
числа JV, как указывалось выше, есть простое число. Но число N
не может одновременно делиться на q и иметь при делении на q
остаток 1. Полученное противоречие означает, что самого большо-
го простого числа не существует.
Количество простых чисел на отрезке натурального ряда от 1 до
N очень быстро возрастает с увеличением N:
Количество простых чисел %
10" 25 25
10* 1229 12.3
10* 78498 7,8
10" 5 761 455 5,8
10“ 455 052 511 4.6
10” 37 607 912 018 3.8
10'* 3 204 941 750802 зя
10" 279238341 033 925 2.8
Третий столбец этой таблицы показывает, какую долю а процентах
составляют простые числа средн всех натуральных не превосходя-
щих N. Доля эта с ростом N снижается, хотя, как показывает
второй столбец таблицы, общее количество простых чисел стреми-
тельно нарастает. Если вы умножите показатель п числа N— 10л на
отвечающую ему долю простых чисел в процентах, то увидите, что
произведение с увеличением п приближается к некоторому числу.
К сожалению, в настоящее время приведенную таблицу нельзя
продолжить далее, тем не менее в 1896 г. было доказано, что это
число есть
43,429448190325182765... ,
причем его можно вычислить с любой нужной точностью.
Рассмотрим составленную нами таблицу простых чисел и рас-
пределим эти числа на группы в соответствии с тем, какой остаток
они имеют при делении на 10, т. е. по последней цифре:
55
Остатки Простые числа
0 -
1 11, 31. 41, 61, 71
2 2
3 3, 13, 23, 43, 53, 73, 83
4 -
5 5
6 -
7 7, J7, 37, 47, 67, 97
8 -
9 19, 29, 59, 79, 89
Средн четных чисел есть только одно простое число — 2. По-
этому группы, соответствующие остаткам 0,4,6,8, вообще не будут
содержать ни одного простого числа, а в группе с остатком 2 со-
держится единственное простое число 2. Целые числа, оканчиваю-
щиеся на 5, все делятся на 5, значит, группа с остатком 5 будет
содержать единственное простое число 5. А вот между остальными
группами, отвечающими остаткам 1, 3, 7, 9, простые числа распре-
делятся примерно поровну. Оказывается, что справедливо следую-
щее утверждение, уточняющее теорему Евклида о бесконечности
количества простых чисел:
Теорема. Для любых натуральных взаимно простых uub,
а>Ъ, существует бесконечное множество простых чисел, дающих
при делении на а остаток Ь.
Эта теорема была доказана в 1839 г. немецким математиком
Г. П. Дирихле (1805—1859).
Еще одно наблюдение над таблицей простых чисел: существу-
ет довольно много простых р, для которых р— 1 есть квадрат
натурального числа: 2, 5, 17, 37, 101, 197, 257, ... .Но доказать,
что таких чисел бесконечно много, до сих пор ннкто не смог, как н
бесконечность множества простых чисел вида 2"—1.
56
Задачи
18. Укажите все пары простых чисел-близнецов, расположен-
ные на отрезке натурального ряда от 1 до 100.
19. Докажите, что для любых целых чисел а и b среди значе-
ний многочлена х® 4-ах4- b прн х=0, 1,2,... имеется бесконечное
множество составных чисел.
20. Докажите, что: а) число 2"4-! может быть простым,
только если п—2к — степень двойки.^ Такне числа называются
числами Ферма и обозначаются 2s*4*1; б) число 2Р— 1 может
быть простым, только если р — простое число. Такие числа при
простом р называются числами Мерсенна и обозначаются Мр.
21. Докажите, что множество 3, 7, 11, 19, 23, . .. простых чи-
сел, имеющих остаток 3 при деления на 4, бесконечно.
ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ
Возьмем некоторое число N> 1. Его наименьший отличный от 1
делитель есть, как указано выше, простое число. Обозначим этот
делитель рь тогда N=Pi *й|. Если «|> 1,то наименьший отличный
от 1 делитель числа п( также будет простым числом. Обозначив его
/?2, найдем П1=р2‘П2, где Пг — натуральное число и
/V=pi-p2«n2.
Продолжая этот процесс, мы получим убывающую цепочку состав-
ных чисел
П1>П2>«3>.. (1)
и последовательность простых чисел рь р2, Рз, ..., таких, что
^=pi’p2’...*pk‘nk, k = l, 2, 3, ... . (2)
Ясно, что убывающая цепочка (1) натуральных чисел не может
быть бесконечной. Райо нли поздно наступит момент, когда очеред-
ное число nk станет равным 1. Тогда равенство (2) примет вид:
JV=Pl-p2‘. ..-р*. (3)
Итак, мы доказали, что каждое натуральное число, отличное
от 1, может быть представлено в виде произведения простых чисел.
Прн этом, конечно, допускаются представления, состоящие нз
одного множителя (в равенстве (3) k — 1). Так будет всегда, если
N — простое число.
А теперь давайте познакомимся с одной сказочной историей.
В то давнее время, когда мнр наполнен был лешнмн, ведь-
мами да русалками, когда реки текли молочные, берега были ки-
сельными, а по полям летали жареные куропатки, в то время жил-
был царь по вмени Горох н была у него дочь-царевна. Царевна бы-
57
ла ленива, у окна любила сидеть, в зеркальце глядеться. Много мук
претерпел царский министр, обучая ее арифметике. Но безуспешно.
Однажды царь зашел в горницу к дочери и застал ее в слезах.
Оказалось, что царевна на уроке не смогла ответить иа вопрос.
Министр отобрал у нее зеркальце н велел книжку читать.
— Батюшка, я уж целый час в книгу гляжу и понять не могу,
что это за пакость такая — нечетные числа.
— Не плачь, доченька,— отвечал ей царь,— не плачь родная.
Экое чудо — нечетные числа. Я тоже про них ничего не знаю, жнву
и царствую спокойно. Вот издам указ, отменю их вовсе, не будет
больше мучить тебя министр ненужными вопросами.
И издал царь указ: отменить нечетные числа, вычеркнуть нз
книг всякие упоминания о них и вообще всем про них забыть.
Пришлось царским мудрецам книги переделывать, новую науку
придумывать. Вот что писалось в «Царской арифметике» — новом
учебнике царевны:
1) «Натуральными» называются числа
2,4,6,8,10,12,14,16,.... (4).
2) «Натуральное» число называется «составным», если его
можно представить в виде произведения меньших «натуральных»
чисел; в противном случае оно называется «простым». Примеры:
4=2-2, 12=2-6, 60=6-10 — «составные» числа;
2. 6. 10. 30 «простые» числа.
ведь каждое из них нельзя представить в виде произведения
даух чисел нз ряда (4).
Царевна обрадовалась, ведь ненавистные ей нечетные числа
в книге больше не упоминались. Но еще больше обрадовался цар-
ский министр. Свое восхищение новым указом он выразил такими
словами:
— Мудрость Вашего величества не знает пределов. Уж сколько
лет я и многие достойные мужн бились над старинной научной
проблемой, пытаясь найти число, которое двумя разными спосо-
бами раскладывается на простые множители. Вы, государь, раз-
решили ее с гениальной простотой. Число 60 имеет нужное свойст-
во. Вот два различных его представления:
60=2-30=6-10,
ведь все множители 2, 6, 10, 30 — «простые» числа.
«Все к лучшему»,— подумал царь Горох н велел наградить мн- •
нистра медалью.
Вот и закончилась история. Трудно сказать, упростился ли от
царского указа учебник царевны. Вот некоторые новшества. Ока-
залось, что:
58
1. «Натуральное» число не делится само на себя, ведь частное
1 отменено.
2. Некоторые числа совсем не имеют общих делителей, на-
пример 2 н 6.
3. Появились неразрешимые в «целых» числах уравнения с ко-
эффициентами без общих делителей, например 4х-ф6</=2.
4, Пришлось отменить школьное правило нахождения наиболь-
шего общего делителя, согласно которому числа 60=2-30 н
60=6-10, состоящие из различных «простых» множителей, долж-
ны быть взаимно просты.
5. Появилось новое правило: произведение двух различных
простых чисел может быть квадратом «натурального» числа, на-
пример 2-50=102.
Подумайте сами, что еще могло измениться в «Царской ариф-
метике».
А теперь вернемся к привычным нам натуральным числам и
разберемся с проблемой, которую решал царский министр.
Легко проверить, например, с помощью калькулятора или вы-
числяя на бумаге, что справедливо равенство
989-1147 = 851-1333. (5)
Могут ли в этом или в другом подобном равенстве все четыре
множителя быть простыми числами?
Если число 1333 простое, то оно должно быть взаимно просто
с 989, ведь никакой делитель числа 989, кроме 1, ие может быть
делителем простого числа 1333. По свойству делимости заключаем,
что тогда 1147 должно делиться на 1333. Но ведь большее число не
может быть делителем меньшего. Это противоречие означает, что
1333 — составное число и даже, что 1333 не может быть взаимно
просто с 989. Действительно, вычисляя наибольший общий дели-
тель, находим
(1333, 989) =43 и 989=23-43, 1333=31 -43.
Теперь равенство (5) принимает вид:
23-43-1147 = 851-31-43.
Сокращай обе его части на 43, получаем:
23-1147 =31-851.
Рассуждая точно так же, заключаем, что числа 1147 и 851 не могут
быть взаимно простыми, н находим
(1147,851)—37, 1147 —31-37, 851=23-37.
69
Итак,
851 = 23-37 1147 — 31.37
989=23-43 1333=31-43
и равенство (5) можно переписать в виде
(23'43).(31 -37)=(23.37).(31 -43).
Все числа 23, 31,37 и 43 простые. Это можно проверить по таблице
из предыдущего раздела. Таким образом, левая и правая части
равенства (5) состоят нз одних и тех же простых множителей,
только расположенных в разном порядке.
Справедливо следующее утверждение, называемое основной
теоремой арифметики:
Теорема. Каждое отличное от 1 натуральное число может
быть разложено в произведение простых чисел. Такое разложе-
ние единственно, если не обращать внимания на порядок мно-
жителей.
Первую часть теоремы мы уже доказали в начале этого па-
раграфа.
Теперь докажем аторую.
Допустим, что существуют числа, представимые в виде произ-
ведения простых чисел разными способами. Выберем средн ннх са-
мое маленькое н обозначим его буквой N. Для числа N возмож-
ны два различных представления
N—pi-p2-.. .-pr=(j\*q2’• • -'Я*, (6)
где pi, р2, р„ Яъ Яг, - -qs — простые числа. Все числа qi, q2,
.... q£ отличные от pi. Действительно, если, например, qi=pi, то.
разделив равенство (6) на рь получим
М=р2 .. .•рг=Яг*.. -‘Я*
н число М, меньшее, чем N, представляется различными способами-
в виде пронзведення простых чисел. Но мы обозначили буквой W
самое маленькое число с этим свойством. Значит, действительно,
все числа q\, q2, .. qs отличны от pi н, следовательно, взаимно
просты с pi, т. е.
(<7i. Pi)=(<?2, Pi)=.. =(<?s, Pi)=l.
Произведение q^(qr.. ^qJ—N делятся на р, н (qit pi)=l. По .
свойству делимости заключаем, что на pi делится произведение
Я2'Яз'- • .’Яз~Я2 (яз--• ^qs)- Но множитель q2 также взаимно
прост с pi. Опять, пользуясь свойством делимости, заключаем,
что произведение qs-.. .-qs делится на pi н т. д. В конце концов
60
придем к заключению, что qt делится на pi. Но ведь qs и pi —
различные простые числа н такого быть не может. Это означает,
что наше первоначальное допущение неверно н равенство (6) воз-
можно, только если r=s н правая часть (6) получена перестанов-
кой сомножителей из левой части. Основная теорема арифметики
доказана.
В «Началах» Евклида эта теорема отсутствует. И впоследствии
она, вероятно, воспринималась как сам собой разумеющийся
факт. Первая точная ее формулировка и доказательство приводят-
ся в книге «Арифметические исследования» известного немецкого
математика К. Ф- Гаусса (1777—1855), изданной в 1801 г. Эта
важная теорема вскрывает структуру натуральных чисел по отно-
шению к операции умножения. Она показывает, что все натураль-
ные числа, кроме 1, получаются нз простых с помощью всевозмож-
ных умножений, причем в результате различных умножений полу-
чаются различные числа.
Средн множителей в произведении (3) могут, конечно, быть и
одинаковые простые числа. Переставим множители, упорядочив их
по возрастанию, а затем сгруппируем одинаковые среди ннх. Так.
имеем:
540=9.6-10=3-3-2-3-2-5=(2-2)-(3-3-3)-5=22-33-5.
В общем случае получаем разложение
. .*рг', pi<p2<. - -<ро (7)
где ki, ki, ..., kr — натуральные числа. Из основной теоремы
арифметики следует, что, как бы мы ни раскладывали число W на
простые множители, окончательное разложение (7) будет одним н
тем же; оно называется каноническим разложением
Поговорим теперь о делителях числа N. Если
d=pi'.. .р1;, где 0<Zi ()</,<&, (8)
то, как легко видеть, N делится на d, т. е. d является делителем N.
При этом в случае Z—0 считается, что соответствующее простое
число в разложении d отсутствует. Верно н обратное. Пусть D —
некоторый делитель /V. Тогда N—D-L, где L — натуральное число.
Раскладывая в этом равенстве числа D и L на простые миожители,
получим некоторое разложение для числа N. Так как N расклады-
вается в произведение простых чисел единственным образом,
заключаем, что все простые множители числа D входят в разло-
жение (7) и в степенях не больших, чем в N. Значит, D представи-
мо в виде (8).
Итак, все делители N имеют вид (8).
6]
Выпишем для примера все делители числа 540 = 2!-33-5:
1, 5, 3. 3-5, З2, 32-5, З3, 33-5, 2, 2-5, 2-3,
2-3-5, 2-32, 2-32-5, 2-33, 2-33-5, 22, 22-5, 22-3,
22-3-5, 22-32, 22-32-5, 22-33, 22-33-5.
Всего имеется 24 делителя.
Иногда бывает удобно разрешать в равенстве (7) показателям
степени k принимать нулевые значения, считая, что прн k~0 соот-
ветствующее простое число отсутствует. Например, можно запи-
сать:
10=2-5=2-3°. 5. 12=22-3=22-3-5°.
Прн таком соглашении любые два числа N и М можно записать
в виде
N=pi..... рк,\ М=р?' ...-р?'
(9)
с неотрицательными показателями.
Если d — общий делитель чисел N и М, то должно выполнять-
ся (8), а кроме того, неравенства
....
ведь d делит и М. Значит, 1\ не превосходит меньшего нз чисел
fet н zrn, /2, не превосходит меньшего из чисел k? и и т. д. Общий
делитель будет самым большим, если каждый показатель /ь ..1Г
принимает наибольшее возможное значение. Отсюда получается
известное правило вычисления наибольшего общего делителя.
Если
W=3132=2!-33-29 и М=7200 = 23-32-52,
ТО
(3132,7200)= 22 • З2 • 5° • 29°=36.
Наименьшее общее кратное двух чисел N и М есть, как извест-
но, наименьшее из натуральных чисел, делящееся на N н на М.
Пусть Af и Л1 имеют вид (9), где показатели k и т неотрицательны,
а натуральное число
Е=рК. .•Р,А /|>0...../г>0.
делится иа N и на М. Тогда по доказанному выше справедливы
неравенства
71>fci. /2>k2, .... jr>kr,
(Ю)
№
Общее кратное будет наименьшим, если каждый показатель / при-
нимает наименьшее возможное значение, т. е. /| равен большему из
чисел k\ н mi, /2 — большему нз чисел и т2 и т. д. В соответствии
с этим правилом находим:
НОК (3132,7200)=25-33-52-29=626400
Точно так же можно вычислять наибольший общий делитель и
наименьшее общее кратное трех и более чисел, но удобнее все-такн
несколько раз применять правило, указанное в задаче 22. д) к это-
му разделу.
Задачи
22. Докажите, что:
а) число N из равенства (7) имеет 1) (Ла1) - - -(fcr-Fl)
различных делителей;
б) справедливо равенство
(а-6, а-с)=а«(Ь, с) и, в частности,
наибольший общий делитель двух чисел делится на любой их об-
щий делитель;
в) если (а, с)=1, то имеет место равенство
(а-b, е)—(Ъ, с);
г) из формул, доказанных в п. б) ив), можно вывести следую-
щий, иногда более удобный, чем алгоритм Евклида, метод вычисле-
ния наибольшего общего делителя двух чисел а н Ь:
1) если а н b оба четны, то (a, b)=2- 1
2) если а четно и b нечетно, то (а, Ь)=^-^-, 0 ;
3) если а и b оба нечетны и a^tb, то (а. Ь)=(а—Ь, Ь).
Вот как, например, вычисляется с помощью этих правил наи-
больший общий делитель чисел 1978 и 2666. Имеем:
(1978, 2666)=2-(989, 1333)=2-(989, 344)=2-(989,172)=
—2-(989, 86)=2-(989, 43)-2-(946, 43)=2-(473, 43)=
= 2-(430, 43)=2-(215, 43)=2-(172, 43) = 2-(86,43)= 2-(43,43)=
=2-43=86.
Иногда можно комбинировать алгоритм Евклида и этот так
называемый бинарный алгоритм;
,д) если наибольший общий делитель двух чисел N н М умно-
жить на их наименьшее общее кратное, получится произведение
63-
N-Mtr. e. наименьшее общее кратное чисел N н М • Эта
формула позволяет вычислять наименьшее общее кратное, не
раскладывая числа на множители.
23. Найдите все пары натуральных чисел (х; у), удовлетворяю-
щие равенствам:
а) х2—1/2=®5, ответ: (3;2),
б) ху —х 4-у 4-6, ответ: (2; 8) и (8; 2).
24. а) Если А =2Л-г, где г — простое число, то сумма всех де-
лителей А равна (г-f-1)-(2'’+1 — 1).
б) Пусть Мр— 2Р—1 —простое число (число Мерсениа с но-
мером р). Докажите, что сумма всех собственных делителей чис-
ла т. е. делителей, меньших самого N, равна N.
Проверьте это для W=6 и N—28.
Такие числа называются совершенными. Предполагают, что
онн были известны уже в Древнем Вавилоне и Древнем Египте.
Сформулированное утверждение доказывается в «Началах»
Евклида. При р= 132049 и р=216091 получаются очень большие
совершенные числа. Эйлер доказал, что такой вид имеют все
четные совершенные числа. До сих пор неизвестно ии одного не-
четного совершенного числа.
25. а) Проверьте, что сумма собственных делителей числа 220
равна 284, а сумма собственных делителей числа 284 равна 220.
Древние ученые называли такие числа дружественными. О них
знал уже Пифагор.
б) Докажите, что если B=2a-p-q, где р, q — простые числа,
то сумма всех делителей В равна (p-f-1)-(2',+1 —1).
в) Докажите, пользуясь результатом п. б), а также п. а) за-
дачи 24, что если три числа
р=3-2',-|-1, ?=3-2"—1 и г=9-2!"-‘-1
простые, то числа
А = 2п-г и B=2n-p.q
дружественные.
Этот способ построения дружественных чисел указал в V в.
арабский математик Сабит ибн Корра. При п=2 получаем числа
Д —284 и В=220, при п=4 находим Д — 18 416 и В=17 296, при
п=7 Д = 9437 056 и fi=9 363 584. Этими тремя случаями исчер-
пываются все значения 20 000, при которых метод Сабита дает,
дружественные числа. Вот еще одна пара нечетных дружественных
чисел; 32«7-13-107 и 34-5-11 *2699, открытая Эйлером. В настоя-
щее время известно свыше 1000 пар дружественных чисел. Все
они достаточно большие по величине.
64
Литература
1. Берман Г. Н. Число и наука о нем. М.: Наука, 1976.
2. Воробьев Н. Н. Признаки делимости.—М.: Наука, 1980.
3. ГельфондА. О. Решение уравнений в целых числах.— М.:
Наука, 1983.
4. Дэвенпорт Г. Высшая арифметика.— М.: Наука, 196Б.
5. Курант Р., Роббинс Г. Что такое математика?— М.:
Просвещение, 1967.
6. Оре О. Приглашение в теорию чисел.— М.: Наука, 1980.
7. Радемахер Г., Теплиц О. Числа и фигуры.— М.:
Физматгиз, 1962.
8. Стро и к Д. Краткий очерк истории математики.— М.: Наука,
1984.
9. Юшкевич А. П. История математики в средние века.— М.;
Физматгиз, 1961.
3 Заказ 775
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
О ЦИРКУЛЕ И ЛИНЕЙКЕ
Если у вас сегодня в школе урок геометрии, то, собираясь в
школу, вы положите в портфель циркуль и линейку, некоторые
захватят н транспортир. Эти инструменты помогут вам рисовать
в тетради грамотные и аккуратные чертежи. Эти же инструменты
вы увидите и на столе инженера-конструктора, хотя уже появились
во многих конструкторских бюро приборы-графопостроители, ра-
ботающие вместе с электронно-вычислительными машинами и поз-
воляющие за несколько секунд получить сложнейший чертеж
(рис. 13, с).
Но, хотя машина рисует чертежи в течение секунд, математик
должен потратить довольно много времени, чтобы иа языке, по-
нятном машине, объяснить ей то, что оиа должна сделать —
написать программу и ввести ее в машину. Поэтому конструк-
торы нередко предпочитают работать с простейшими и древнейши-
ми инструментами — циркулем и линейкой.
Действительно, что может быть проще? Гладкая дощечка с
ровным краем — это линейка, а две заостренные палки, связанные
на одном конце, — циркуль. Сейчас и циркуль и лннейка стали
ииымн, чем они были 2—3 тыс. лет назад. 200—300 лет назад нх
старались украшать различными узорами и фигурами (рис. 13 б, в
и рнс. 14). Но прн этом назначение предметов осталось прежним:
по линейке мы проводим прямые (точнее, отрезки прямы*), а
циркулем рисуем окружности.
На вашей линейке нанесены сантиметровые и миллиметровые
деления. С их помощью можно откладывать на прямых отрезки
любой заданной длины, ио с помощью циркуля это можно делать
точнее. Поэтому уговоримся ие пользоваться шкалой иа линейке
Кроме этого, запретим себе пользоваться второй стороной линейки.
Итак, у нас в руках односторонняя линейка без делений и цир-
куль — приборы, с помощью которых проводили свои построения
еще древнегреческие математики 3000 лет назад.
Этих простейших инструментов оказывается достаточно для
выполнения огромного множества различных построений. Древним
грекам даже казалось, что любое разумное построение можно
совершить этими инструментами, пока они не наткнулись иа три
знаменитые задачи древности: «квадратуру круга», «трисекцию уг-
66
Рис. 13
ла» и «удвоение куба». Подробнее об этих задачах мы поговорим
позже, а сейчас убедимся в великолепных возможностях этих
инструментов.
Но сначала совершим подмену инструментов: чертежные
инструменты заменим иа математические. «В чем разница?»—
Рис. 14
67
спросите вы. А в том, что математические инструменты — это
ие реальные инструменты, а воображаемые; они могут проводить
математические прямые и окружности, которые, как говорил
Евклид, «не имеют толщины», а чертежные инструменты вместо
математической прямой изобразят полоску, ширина которой зави-
сит от степени отточенности карандаша. Окружность, изображен-
ная чертежным циркулем, будет черным колечком, а точка — не-
большим кружочком
Итак, построения мы будем проводить идеальными инструмен-
тами. Ну, а если то же самое построение мы затем произведем
чертежными инструментами, то получим приближенное решение,
которое будет тем точнее, чем аккуратнее мы совершим все
действия.
В учебнике геометрии рассказывается о том, как:
1) построить треугольник с данными сторонами;
2) отложить от данной полупрямой в данную полуплоскость
угол, равный данному углу;
3) построить биссектрису данного угла;
4) разделить данный отрезок пополам;
5) построить перпендикуляр к данной прямой, проходящий
через данную точку.
Эти построения встречаются чаще других, более того, они
входят как кирпичики во многие построения. Будем считать, что
вы отлично знаете, как проводятси эти построения, и если нам
по дороге встретится то или иное из них, то будем считать,
что его мы уже провели.
Решаем задачу на построение
Давайте подробно решим одну из задач на построение. Скажем,
такую:
Построить треугольник по высоте, биссектрисе и медиане,
выходящим из одной вершины
Для удобства будем обозначать длины данных отрезков че-
рез h, b и m соответственно. Начнем с того, что нарисуем какой-
нибудь треугольник АВС, проведем его высоту АН, биссектрису ДА
и медиану AM, после чего начнем размышлять о том, как связаны
эти его элементы с другими элементами треугольника. Эти раз-
мышления будут продолжаться до тех пор, пока мы не дога-
даемся описать вокруг треугольника окружность и провести ее
диаметр DE, проходящий через точку М — основание медианы
(рис. 15).
Тут мы замечаем, что продолжение биссектрисы АК пересе-
кает проведенную окружность в точке D, поскольку эта точка делит
дугу ВС пополам. Осталось заметить, что диаметр DE перпенди-
кулярен хорде ВС (так как проходит через ее середину), а центр
окружности — точка О лежит как на диаметре DE, так и на сере-
динном перпендикуляре к хорде AD (рис. 16).
68
Рис. 15
D
Рис. 16
На этом заканчивается первая часть решения задачи, которая
обычно называется анализом. Она, как правило, самая трудная
часть решения: увидеть связи между элементами фигуры, которые
позволят совершить построение,— это трудно. Здесь нет рецептов,
по которым можно было бы отыскивать такие связи
Следующая часть решения — построение состоит из описания
рецепта, осуществляющего нужное построение.
1. Проведем прямую I (иа ней будет лежать основание ВС
искомого треугольника) и отметим на ней точку Я.
Точка А находится на расстоянии h от примой /, причем отре-
зок АН перпендикулярен этой прямой. Построение точки А прове-
дем в два приема:
2. Проведем прямую через точку Н перпендикулярно пря-
мой Z.
Это можно сделать с помощью третьего школьного «кирпи-
чика», рассматривая прямую I с точкой Н на ней как развернутый
угол с вершиной Н (рис. 17)
3. Отложим от точки И отрезок АН длиной h.
Для этого достаточно провести окружность с центром в точке Н
и радиусом h (рис. 18). Точка пересечения этой окружности
с прямой /1 и даст искомую точку А.
Рис. 17
Рис 18
Рис. 19
69
Теперь мы можем на прямой I построить точки К н М. Для
этого:
4. Проведем окружность с центром в точке А радиусом b и
отметим точку К ее пересечения с прямой I (рис. 19).
5. Проведем окружность с центром в точке А радиусом т н от- '
метим точку М ее пересечения с прямой I (рис. 20).
Теперь проведем диаметр DE, для этого:
6. Проведем прямую h через точку М перпендикулярно пря-
мой I. Эта операция аналогична операции 2 (рис. 21).
Построим точку D. Для этого:
7. Проведем через точки А н К прямую h и отметим точку D
ее пересечения с прямой /з (рис. 22).
Построение близится к завершению. Появилась возможность
найти точку О — центр окружности, описанной вокруг искомого
треугольника.
8. Проведем серединный перпендикуляр Ц к отрезку AD н отме-
тим точку О его пересечения с прямой /з (рис. 23).
Теперь уже можно найти остальные вершины В н С искомого
треугольника, поскольку они лежат на прямой I и на описанной
вокруг треугольника АВС окружности, у которой мы уже знаем
центр О и радиус АО.
9. Проведем окружность с центром в точке О радиусом АО
и отметим точки В и С ее пересечения с прямой I (рнс. 24)-
Рис 23
Рнс 24
Рис 25
70
Рис. 26
Рнс 27
Осталось лишь закончить формальное построение треугольника
10. Проведем отрезок АВ (рис. 25).
11. Проведем отрезок АС (рис. 26).
Итак, мы имеем А АВС. Нужно проверить, что он искомый, т. е.
что его высота, медиана и биссектриса, проведенные из вершины А,
имеют длины h, Ь и т соответственно. Этот шаг решения назы-
вается доказательством
На рисунке 27 проведены отрезки АН, АК и AM, имеющие
длины h, Ь н т. Если мы докажем, что они являются высотой,
биссектрисой и медианой дЛВС, то тем самым мы докажем, что
ДЛВС искомый.
То, что отрезок AM — медиана дЛВС, следует нз того, что
дВОС равнобедренный по построению (ВО=ОС\ а ОМ— его
высота, а следовательно, и медиана, т. е. ВМ—СМ.
То, что отрезок АН — высота А АВС, следует из построения
прямой АН: она перпендикулярна прямой /, иа которой лежит
основание ВС.
Осталось показать, что АК— биссектриса дЛВС. Но прямая
АК, на которой лежит этот отрезок, пересекает окружность,
описанную около А АВС в точке D — середине дуги ВС, так как
диаметр DE делит пополам дугу, стягиваемую перпендикулярной
к нему хордой. Значит, ДВЛ/)= Д£)ЛС.
Наверное, теперь можно с полным основанием заявить, что
задача до конца решена? Оказывается, еще нет. Осталось вы-
яснить, всегда ли (т. е. при всех ли наборах отрезков h, b и т) за-
дача имеет решение. Сколько различных решений она может
иметь? Этот шаг решения задачи носит название исследование.
Во-первых, заметим, что при построении мы неявно использо-
вали соотношение между длинами заданных отрезков h<b<m.
которое следует из теоремы:
Биссектриса угла треугольника лежит между медианой и высо-
той, проведенными из той же вершины.
Если при этом учесть, что наклонная, проведенная нз точки А,
расположенной вне прямой I, к этой прямой тем больше, чем
71
дальше точка ее пересечения с этой прямой от проекции точки А
иа эту прямую, то мы и получим указанные неравенства. Исклю-
чение составляет лишь случай h=b=m.
Итак, либо h=b=m, либо h<b<.m, в остальных случаях
задача решения ие имеет.
В первом случае задача имеет бесконечно много решений —
годится любой равнобедренный треугольник, имеющий данную
высоту.
Рассмотрим второй случай. Очевидно, что от выбора прямой / и
точки Н иа ней форма треугольника не зависит. Точку А мы можем
выбрать (п. 3) в той или другой полуплоскости, но и от этого
форма треугольника не изменится. При построении точек К и М
(п. 4 и 5) мы обязаны брать их по одну сторону от точки Н (в силу
теоремы). Это можно сделать двумя способами. В зависимости от
выбора получим два решения, симметричные относительно высо-
ты АН. Прямая 13 (п. 6) проводится однозначно, точка D иа ней
(п. 7) также определяется однозначно. Несложно проверить одно-
значность и остальных построений (п. 8—11)
Итак, при соотношении длин h<b<m искомый треугольник
строится однозначно с точностью до расположения на плос-
кости.
Вот теперь задача решена полностью. Напомним шаги ее реше-
ния: анализ, построение, доказательство и исследование. Часто
школьники забывают об этом и решение сводят лишь к построе-
нию. Но это всего лишь «рецепт» или, как принято сейчас говорить,
алгоритм построения — последовательность действий, приводя-
щая к требуемому результату. А основа всего решения заклады-
вается на первом шаге — анализе. И хотя мы говорили, что здесь
нет четких правил, приводящих к результату, несколько советов
можно предложить.
МЕТОД ПОДОБИЯ
В ряде задач возникает следующая ситуация: если исключить
одно из условий, то остальным условиям будет удовлетворять
бесконечное множество подобных фигур. Построив фигуру, по-
добную данной, можно затем увеличить или уменьшить ее в нуж-
ном отношении так, чтобы получилась искомая фигура.
Проиллюстрируем этот метод, называемый методом подобия,
иа следующей задаче:
Построить окружность, касающуюся сторон данного угла и
проходящую через данную точку внутри этого угла.
Анализ здесь прост (учитывая подсказку о применении
метода подобия). Если откинуть требование прохождения окруж-
ности через данную точку, то условию будет удовлетворять лю-
бая окружность, касающаяся сторон данного угла.
Пусть искомая окружность имеет центр в точке О, а точка М,
лежащая на ней,— заданная в условии точка (рис. 28). Пусть
72
с
некоторая другая окружность касается сторон данного угла. Тогда
ее центр Oi лежит на биссектрисе I данного угла, как и точка О.
Проведем луч BD через точку М и отметим точку М। ее пересече-
ния с выбранной окружностью. Заметим, что треугольники ВОМ и
BOiM\ подобны, поскольку они гомотетичны с центром гомотетии
в точке В. Поэтому отрезок ОМ параллелен отрезку OiMi. Этого
замечания оказывается достаточно для построения требуемой ок-
ружности. Опишем построение.
1. Проводим биссектрису I данного угла.
Это третий нз школьных «кирпичиков». Теперь нужно построить
какую-нибудь окружность, касающуюся сторон угла.
2. Выбираем на построенной прямой I точку О\ и опускаем из
нее перпендикуляр O\Ki на прямую В А.
Конечно, построение перпендикуляра к данной прямой, прохо-
дящего через данную точку, состоит из нескольких шагов, но
мы ие будем их- описывать, поскольку очень похожее построение
встречалось в предыдущей задаче.
3. Проводим окружность с центром в точке Oj радиусом OiKt.
Эта окружность, очевидно, будет касаться сторон угла АВС.
4. Проводим прямую ВМ и отмечаем иа ней точку М} ее пере-
сечения с построенной окружностью.
Теперь нужно провести прямую МО.
5. Откладываем от полупрямой MD в ту сторону, где лежит
точка О], угол, равный углу OiM^D, и отмечаем точку О пересече-
ния построенной стороны угла с прямой I.
Точка О — центр искомой окружности. Теперь нужно построить
саму окружность, а для этого повторить п. 2 и 3, взяв вместо
точки Oj точку О.
6. Опускаем из точки О перпендикуляр ОК на В А.
7. Проводим окружность с центром в точке О радиусом ОК.
Построение закончено. Приступим к доказательству.
По построению эта окружность касается сторон угла; покажем,
что она проходит через точку М. Заметим, что A ВМ}ОУ со Л ВМО,
а также Д B/GAfi со Д ВКМ. Отсюда OtMr.BMt = OMzBM и
OiKr.BM^OK’.BM, или OM^(OiMi‘BM):BMi и OK=(OtKtX
73
XBM):BMt. Ho MiOi=OiKi, поэтому в этих равенствах одинако-
вы правые части, следовательно, одинаковы и левые, т. е. ОМ =*
= ОК. А это и означает, что окружность с центром в точке О и
радиусом ОК проходит через точку М.
Осталось провести исследование. Доп. 4 все построение
идет однозначно. Но в п. 4 появляются две возможности, по-
скольку луч ВМ пересекает окружность с центром в точке Oi в двух
точках: Mi н Мг (рис. 29). И мы получаем два решения задачи.
Рассмотренное построение неосуществимо в том случае, если
точка лежит на биссектрисе угла. В этом случае можно предложить
несколько другое построение, связанное с подобием /\M\OiKi
и Л МОК. Идею такого построении можно увидеть из рисунка 30.
МЕТОД ГЕОМЕТРИЧЕСКИХ МЕСТ
Основная идея метода подобия — временно отказаться от одно-
го из условий задачи — применяется в другом методе — методе
геометрических мест.
Рассмотрим какую-нибудь характерную точку фигуры и по-
думаем, где она сможет находиться, если отбросить одно из усло-
вий задачи. Эту совокупность точек обозначим через Fi. Теперь
вернем отброшенное условие и отбросим некоторое другое условие.
Посмотрим на совокупность Гг точек, в которых сможет находить-
ся выбранная нами характерная точка фигуры. Те точки, которые
принадлежат как совокупности точек Flt так и совокупности
Гг, и будут искомыми положениями этой характерной точки, а по
ией, как правило, восстанавливается и вся фигура.
Вспомним некоторые известные геометрические места точек.
1. Геометрическое место точек, равноудаленных иа расстоя-
ние К от заданной точки О, — это окружность с центром а точ-
ке О и радиусом R.
74
2. Геометрическое место точек, равноудаленных от двух то-
чек А и В,— перпендикуляр к отрезку АВ, проходящий через его
середину.
3. Геометрическое место точек, удаленных от заданной прямой
иа расстояние h,— пара прямых, параллельных данной прямой и
находящихся от нее иа расстоянии h.
4. Геометрическое место точек, равноудаленных от двух пере-
секающихся прямых,— биссектрисы углов, образованных этими
прямыми (рис. 31).
5. Геометрическое место точек, из которых данный отрезок
виден под данным углом,— дуги двух окружностей одинакового
радиуса, у которых этот отрезок является хордой (рис. 32).
В дальнейшем мы их будем обозначать ГМТ-1, ГМТ-2, ...,
ГМТ-5.
Применение метода геометрических мест рассмотрим на сле-
дующей задаче:
Построить треугольник по основанию, углу при вершине и вы-
соте, опущенной на это основание.
Как и раньше, проведем анализ задачи. Пусть ДЛВС ис-
комый. Если отбросить условие, что угол А задай, то вершина А
лежит иа ГМТ-3 — в точках пары прямых, отстоящих на задан-
ное расстояние h от основания треугольника (рис. 33). Если же
отбросить условие заданности величины высоты, то точка А
сможет лежать на ГМТ-5 — дугах двух окружностей, из которых
отрезок ВС вндеи под заданным углом а. Точка А может теперь
находиться в одной из четырех точек: Ль Л2. Л3 или Л<.
Отсюда построение искомого треугольника следует про-
водить в таком порядке:
1. На произвольной прямой откладывается отрезок ВС задан-
ной длины — основание треугольника.
2. Параллельно этой прямой проводятся прямые, отстоящие от
нее на расстояние h (ГМТ-3).
3.. Строится ГМТ-5 по заданному основанию и противолежа-
щему углу.
4. Соединяем одну из точек пересечения ГМТ-3 с ГМТ-5 от-
резками с концами отрезка ВС.
Рис 31
Рис. 32
75
Полученный треугольник искомый. Доказательство
этого довольно просто. По построению основание равно задан-
ному отрезку, высота также равна заданной величине н угол при
вершине равен заданному углу
Исследуя полученное построение в зависимости от величин
a, h н а, получаем, что прямые ГМТ-3 будут касаться дуг ГМТ-5
в том случае, если h—q=~ctg-~- (рис. 34). Если же h<.q, то
получаем четыре решения, а в случае касания — два. Если же
h > q, то решений нет. Четыре решения в первом случае на самом
деле дают вСего два симметричных треугольника, а два треуголь-
ника во втором случае равны.
Метод геометрических мест не является универсальным, по-
скольку с помощью циркуля и линейки можно вычерчивать лишь
прямые и окружности, в то время как геометрическое место то-
чек, получаемых в результате отбрасывания одного из условий
задачи на построение, может быть и более сложной кривой.
Когда я был школьником, мне кто-то предложил задачу, похо-
жую иа предыдущую: построить треугольник по основанию, углу
при вершине и биссектрисе этого угла. Построив ГМТ-5 по осно-
ванию и углу при вершине, я отметил точку D иа окружности,
через которую должна проходить биссектриса (рис. 35). Но что де-
лать дальше? Если отбросить условие, что конец биссектрисы ле-
жит на основании, то, проводя через точку D всевозможные
прямые и откладывая иа них от построенной окружности отрезки,
равные заданной величине биссектрисы, получим красивую петле-
образную кривую (рис. 36), которую, как я узиал позже, называют
«улиткой Паскаля» в честь выдающегося французского математи-
ка и физика XVII в. Если менять величину откладываемого отрез-
ка, то форма кривой меняется. Если эта величина станет равной
диаметру круга, то петля исчезает и возникает кривая, носящая
название кардиоида — сердцеобразная. Оиа получается также
при обкатывании порождающего круга равным ему кругом, если
следить за траекторией какой-либо точки иа границе катящегося
круга (рис. 37).
Ну, а если откладывать отрезки иа этих прямых ие от окруж-
ности, а от прямой, иа которой лежит основание треугольника?
Рис. 33 Рис. 34 рис. 35
Попробуйте сами это проделать. В результате получается кривая,
состоящая из двух кусков, которая называется конхоидой — ра-
ковиновидной (рис. 38). С помощью конхоиды, как я узнал позже,
греки еще в древности умели делить угол иа три равные части. Опи-
шем, как оин это делали (рис. 39).
Проведем прямую зафиксируем на ней вершину О и по-
строим угол, который хотим разделить на три равные части. На
втором его луче отложим некоторый отрезок ОА, величина кото-
рого пусть равна а. Из точки А проведем прямую I, параллельную
прямой /1. Теперь по примой I, точке О и отрезку а построим кон-
хоиду. Проведем далее .окружность с центром в точке А радиусом
ОА=а. Пусть С — точка пересечения этой окружности с кон-
хоидой. Проведем еще прямую ОС и отметим точку В ее пересе-
чения с прямой /. Поскольку АО=Ас=а и ВС—о, то треугольник
АВС равнобедренный и в нем углы А и В равны. Поэтому внешний
его угол ЛСО вдвое больше угла В, но Z.4C0= Z. АОС (равенства
сторон АО и АС). Осталось заметить, что Z_BOD= £АВС, таким
образом, Z_BOD=~ ЛАОО.
Подведем итог. Задачу мы не решили, ио познакомились с
двумя симпатичными кривыми.
Рнс. 40
Рис. 41
Следует заметить, что задачи на описание геометрических
мест точек сами по себе бывают очень интересными. Рассмотрим,
например, такую задачу:
Дан равносторонний треугольник ЛВС. Найти геометрическое
место точек М, для которых дАВМ и дАСМ равнобедренные.
Хотя эта задача не очень сложна, ио... Нужно иметь в виду,
что каждый из треугольников АВМ и АСМ может быть равно-
бедренным тремя способами. Так, для ДАВ/И может быть либо
АВ—ВМ, либо АВ=АМ, либо АМ^=ВМ.
В первом случае это— ГМТ-1, точка лежит иа окружности с
центром в точке В и радиусом АВ. Аналогично во втором случае
точка М лежит иа окружности того же радиуса с центром в точ-
ке А. В третьем случае это — ГМТ-2, серединный перпендикуляр
к отрезку АВ (рнс. 40). Аналогичное множество изображено
иа рисунке 41. Это точки М, для которых Д АСМ равнобедренный.
Если теперь наложить рисунок 40 на рисунок 41 я отметить
общие точки, то это будет окружность с центром в точке А и
еще 6 точек (рис. 42): Mi, М2, М$, М4, Ms, М& Осталось заметить,
что точки В, С, Вt и Ci из окружности следует выбросить, так как
в этих случаях возникают вырожденные треугольники. Итак,
ответом иа поставленный вопрос является окружность без четырех
точек и еще 6 точек
78
Конечно, это ГМТ довольно экзотично, ио если вы начнете рас-
сматривать приходящие вам в голову ГМТ, то не всегда вам удаст-
ся описывать их с помощью прямой и окружности. Эти линии прос-
тейшие среди сотен кривых, которые интересовали математиков и
инженеров. Лишь они среди плоских кривых «устроены» одинако-
вым образом в каждой своей точке, что позволяет нм двигаться «по
себе». Свойства окружности хорошо знали древние греки, они
считали ее венцом совершенства.
о возможных И НЕВОЗМОЖНЫХ ПОСТРОЕНИЯХ
Именно при изучении окружности древние наткнулись иа за-
дачу, ставшую затем символом неразрешимой проблемы. Это зада-
ча квадратуры круга, т. е. построения квадрата, равновеликого
данному кругу, с использованием лишь циркуля и лииейки. Эту
задачу не могли решить математики на протяжении более двух
тысячелетий. Лишь в XIX в. усилиями нескольких выдающихся
математиков — Ламберта, Лиувилля, Эрмита и Вейерштрасса —
была установлена неразрешимость этой задачи, невозможность
такого построения. Было предложено много приближенных реше-
ний. Одно из них изображено на рисунке 43. Неразрешимыми
оказались и задача трисекции угла — деления данного угла на три
равные части с помощью циркуля н линейки (рассмотренный выше
метод использует, кроме этих инструментов, еще н конхоиду), и за-
дача удвоения куба — построения ребра куба, объем которого
вдвое больше объема данного' куба.
Неразрешимой оказалась в рассмотренная нами задача о по-
строении треугольника по основанию, углу при вершине и биссект-
рисе этого угла, в то время как, заменяя слово «биссектриса» на
«медиана» или «высота», получаем задачу, имеющую несложное
решение. Нельзя построить треугольник, зная величины его бис-
сектрис, но можно построить его по медианам н можно построить
по его высотам.
Очень интересна история исследования задачи о построении
при помощи циркуля и линейки правильных многоугольников.
Древние греки умели строить правильный треугольник, квадрат,
правильные пятиугольник и пятнадцатиугольник, а также те мно-
гоугольники, которые получаются из ннх удвоением сторон, и
только их.
Новый шаг в этой области был сделан лишь
в 1801 г. великим немецким математиком
К- Ф- Г а у с с о м. Он указал способ построе-
ния циркулем и линейкой правильного сем-
надцатиугольника и все те натуральные л, для
которых построение правильных многоуголь-
ников с таким числом сторон возможно цирку-
лем и линейкой. Эти числа оказались связан-
ными с так называемыми числами Ферма.
Рис. 43
79
Их ввел в математику французский математик и юрист П. Ф е р-
м а. Это числа вида Fll=22‘+1. Ферма заметил, что первые пять
таких чисел: FO=22° 4-1=3, Fi=22'4-1=5, Fs=28* 4*1 = 17,
F3=22’4-1 =257, F4=22*4*l =65 537 — простые числа, и был
абсолютно уверен, что и все остальные числа такого вида простые.
Но Л. Эйлер показал, что Еб=4 294 667 297 =641*6 700 417
и, следовательно, не является простым числом. Более того, до
сих пор не найдено больше ни одного нового значения п, для
которого число Fn было бы простым, но и ие доказано, что
таких чисел больше нет.
Так вот, Гаусс показал, что циркулем и линейкой можно по-
строить только такие правильные многоугольники с нечетным чис-
лом сторон, у которых число сторон является либо простым
числом Ферма, либо произведением нескольких различных простых
чисел Ферма. Соответствующие правильные многоугольники с чет-
ным числом сторон получаются нз описанных нами последователь-
ным удвоением количества сторон. Таким образом показано, что
невозможно с помощью циркуля и линейки построить правильные
многоугольники с числом сторон, равным 7, 9, II, 13, 18, 21,
22, 23 н т. д.
Интересно, что здесь окончательное решение геометрической
проблемы сводится к решению арифметической проблемы. Заме-
тим, что и в остальных случаях, когда доказывалась невозмож-
ность построений с помощью лишь циркуля и линейки, это дела-
лось средствами алгебры.
В заключение немного поговорим о задачах, которые можно
решить с помощью только одного из двух рассматриваемых нами
инструментов. И тут нас ждет неожиданность. Оказывается, что
любая задача, которая решается с помощью циркуля и линейки,
может быть решена с помощью только одного циркуля! Это
кажется невероятным, ио это так. Соответствующая теорема была
доказана датчанином Мором и итальянцем Маскерони более
200 лет назад.
Конечно, если в формулировке задачи содержится требование
«провести прямую», то это требование без линейки ие выполнить,
но если требуется найти ту или иную точку, скажем построить
вершины треугольника по..то здесь линейка оказывается уже
ненужной.
Для чего нужна линейка в задачах иа построение? Если вни-
мательно подумать, то становится ясным, что она нужна лишь в
двух случаях:
1. По данным точкам А, В, С и D найти точку пересечения
прямых АВ н CD.
2. По данной окружности S и двум точкам Л и В найти
точки пересечения прямой Ав с окружностью S- Центр окружности
считается заданным.
Теорема Мора — Маскерони утверждает, что эти задачи мож-
но решить, используя только циркуль. В это уже можно поверить,
во
А какие задачи можно решить, используя лишь одну линейку?
Оказывается, что далеко не все те, что можно решить с помощью
обоих инструментов. Например, нельзя найти центр нарисованной
окружности. Но если в плоскости уже нарисована некоторая
окружность и указан ее центр, то с ее помощью можно выпол-
нить любое построение лишь одной линейкой, если такое построе-
ние возможно с помощью циркуля и линейки.
Задачи
1. Около правильного треугольника опишите квадрат, имею-
щий с треугольником общую вершину.
2- Даны три отрезка длинами а, b н с. Постройте отрезок
длиной -\/а2+Ь2+с2
3. С помощью линейки с делениями постройте биссектрису
данного угла.
4. Постройте окружность, касающуюся двух данных парвл-
лельных прямых и данной окружности.
5. Постройте прямоугольный треугольник по высоте, опущен-
ной нз вершины прямого угла и разности острых углов.
в. В данную трапецию впишите окружность, если боковая сто-
рона трапеции равна а и расстояние от центра окружности до
точки пересечения диагоналей трапеции равно d.
7. Постройте треугольник по серединам двух сторон н пря-
мой, на которой лежит биссектриса угла между этими сторонами.
8. Даны угол и точка внутри его. Постройте отрезок с кон-
цами на сторонах данного угла так. чтобы его середина находи-
лась в данной точке.
9. Постройте треугольник по вершине, середине противопо-
ложной стороны н точке пересечения высот.
10. Постройте треугольник по основанию, углу прн вершине
и радиусу вписанной окружности.
11. Даны окружность н точка вне ее. Постройте секущую,
проходящую через эту точку так, чтобы отрезок секущей вне ок-
ружности равнялся высекаемой хорде
12. Даны прямая, окружность н точка. Постройте правильный
треугольник, одна нз вершин которого лежит в данной точке, вто-
рая — иа данной прямой, третья — на данной окружности.
Указания к решениям задач
1. Угол а (рнс. 44) равен (90°—60°):2 = 15°. Построить угол
в 15° несложно, разделив угол в данном равностороннем тре-
угольнике пополам, а полученный еще раз пополам. Вторую сто-
рону квадрата можно построить, например, по углу 0, дополни-
тельному к углу а до 90°.
2. Построим прямоугольный треугольник с катетами а н Ь.
Его гипотенуза равна Далее построим прямоугольный
81
Рис. 44
треугольник с катетами а2^Ьг н с, гипотенуза которого —
искомый отрезок.
3. На каждой стороне от вершины отложим отрезки длиной
I и 2, концы которых соединим отрезками так, чтобы они пере-
секлись во внутренней точке. Прямая, проходящая через эту точку
и вершину угла, искомая.
4. Пусть расстояние между данными параллельными прямыми
равно h. Очевидно, что искомая окружность имеет радиус
и ее центр будет лежать на прямой, равноудаленной от двух дан-
ных. Построим эту прямую и проведем две окружности, концентри-
ческие с данной, радиусами г4—-- н | г—1-| . Точки пересечения
этих окружностей с построенной прямой будут центрами искомых
окружностей.
5. Пусть а н р — острые углы прямоугольного треугольника,
тогда у=а—₽ — данный угол. Так как а+0—90°, то, из этих
90°4-м 90° v
равенств находим, что а =—. Эти углы нетрудно
построить. Поскольку высота треугольника разбивает его на
два подобных ему треугольника, то каждый из инх можно по-
строить по катету н углам.
6. Угол между диагоналями трапеции (которая обязана быть
равнобочной) измеряется дугой окружности, стягиваемой боковой
стороной, поэтому точка пересечения диагоналей лежит на ок-
ружности, проведенной через концы боковой стороны н центр О
искомой окружности. Кроме того, она лежит н на окружности
радиуса d с центром в точке О,- т. е. в точке пересечения этих
окружностей. По точке Oi данная трапеция полностью восста-
навливается.
7. Заметим, что точка D пересечения биссектрисы треуголь-
ника MBN (рнс. 45) н серединного перпендикуляра к отрезку MN
лежит на окружности* описанной около &MBN. Построив точку D,
82
а затем указанную окружность, находим точку В, а по ней н точ-
ки А н С.
8. Если отложить на луче ОМ (рис. 46) отрезок ОС, вдвое
больший отрезка ОМ, н через точку С провести прямую, парал-
лельную стороне данного угла, до пересечения с другой его
стороной в точке А и вторую аналогичную прямую СВ, то полу-
ченная фигура О АС В — параллелограмм. Точка М делит отре-
зок АВ пополам.
9. Здесь, как н в других задачах, возможны несколько реше-
ний. Самое короткое опирается на тот факт, что точки, симметрич-
ные точке пересечения высот относительно сторон треугольника,
лежат на окружности, описанной вокруг этого треугольника. По-
рядок построения таков (рис. 47): строим прямую ВН (на ней ле-
жит высота треугольника). Через точку М — середину основания
проводим прямую, перпендикулярную прямой ВН. На этой пря-
мой I будет лежать основание треугольника. Находим точку L,
симметричную точке Н относительно прямой I. Точка О — центр
окружности, описанной около ДДВС, лежит на серединном пер-
пендикуляре к отрезку BL н на перпендикуляре, восставленном
из точки М к прямой /. Проведем окружность с центром в точ-
ке О радиусом ОВ, найдем точки А и С как точки пересечения
этой окружности с прямой I.
10. Если в Д ЛВС угол А при вершине равен а, то сумма
углов при основании ВС равна 180°—а, а сумма Z.OBC и Z.OCB
(рис. 48) вдвое меньше. Поэтому Z.ВОС =180°—
=90°Таким образом, точка О — центр окружности, вписан-
ной в д ДВС, лежит на дуге сегмента, вмещающего угол 90°-|-
+~, и на расстоянии г от основания, т. е. на прямой, параллель-
ной основанию н отстоящей от него на расстояние г. Следователь-
но, точка О находится в точке пересечения этой окружности
и прямой. По точкам В, С н О находится н точка Д
11. Решение этой задачи опирается на следующую теорему:
если нз точки М проведены к окружности секущая, пересе-
Рис. 46
Рис. 47
83
кающая ее в точках А и В, и касательная, касающаяся окружности
в точке С, то АМ‘ВМ—СМ2. Обозначим ВМ — х. тогда AM— 2х
и по теореме 2г2 —СМ2, т. е. х=СМ^.
Построение таково. Строим касательную СМ, затем прямо-
угольный равнобедренный дМСО с гипотенузой СМ (рис. 49).
Катет MD этого треугольника равен СМ —. Проведем окружность
радиусом MD с центром в точке М, точки В\ и В2 пересечения
ее с данной окружностью искомые. По ним находятся точки At и А2.
12. Повернем данную окружность на угол 60° вокруг данной
точки М и отметим точки пересечения полученной окружности
с данной прямой (точки At н Л2). Если повернуть данную пря-
мую на 60° в противоположную сторону, то получим соответствен-
но точки Bi н В2 пересечения образа этой прямей с данной окруж-
ностью. &MAiBt н дМЛ2В2 искомые.
Литер атур а
1. Глейзер Г. И. История математики в школе: VII—VIII клас-
сы.—М.: Просвещение, 1982
2. Костовскн й А. Н. Геометрические построения одним цир-
кулем.— М.: Наука, 1984.
3. Курант Р., Роббинс Г. Что такое математика? — М.:
Просвещение, 1967.
4. П р а с о л о в В. В. Задачи по планиметрии.— М.: Наука.
1986,—Ч. 1.
5. Радемахер Г., Теплиц О. Числа и фигуры: Опыты ма-
тематического мышления.— М.: Физматгиз, 1962.
6. Смогоржевскнй А. С. Линейка в геометрических пост-
роениях.— М.: Наука, 1984.
ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ В ТРЕУГОЛЬНИКЕ
Геометрия начинается с треугольника. Вот уже два с по-
ловиной тысячелетия треугольник является как бы символом гео-
метрии; но он не только символ, треугольник — атом геометрии.
Да и сегодня школьная геометрия становится интересной и
содержательной, становится собственно геометрией только с по-
явлением треугольника. Предшествующие понятия — точка, пря-
мая, угол — представляются расплывчатыми абстракциями, а на-
бор теорем и задач, с ними связанный, просто скучным.
Уже с первых шагов своего развития человек, а особенно
современный человек, сталкивается со всевозможными геометри-
ческими объектами — фигурами и телами. Известны случаи, когда
человек в юном, если не сказать в младенческом, возрасте увле-
кается геометрией и даже делает самостоятельные геометрические
открытия. Так, маленький Блез Паскаль придумал «игру в геомет-
рию», в которой участвовали «монетки» — круги, «треуголки» —
треугольники, «столы» — прямоугольники, «палочки» — отрезки.
Его отец, основательно знавший математику, на первое время
решительно исключил математику нз числа предметов, которым он
обучал своего сына, поскольку маленький Блез не отличался хо-
рошим здоровьем. Однако, обнаружив увлеченность сына, он кое-
что рассказал ему о таинственной геометрии, а застав Блеза в
момент, когда тот обнаружил, что углы треугольника составляют
в сумме два прямых, растроганный отец открыл своему 12-лет-
нему сыну доступ к математическим книгам, хранившимся в до-
машней библиотеке.
Треугольник неисчерпаем — постоянно открываются его новые
свойства. Чтобы рассказать о всех известных его свойствах, не-
обходим том, сравнимый по объему с томом Большой энциклопе-
дии. О некоторых нз них, а точнее говоря, о некоторых
замечательных точках, связанных с треугольником, мы и хотим
рассказать.
Поясним сначала смысл выражения «замечательные точки тре-
угольника». Все мы знаем, что биссектрисы внутренних углов тре-
угольника пересекаются в одной точке — центре вписанной в этот
треугольник окружности. Точно так же в одной точке пересекают-
ся медианы, высоты треугольника, серединные перпендикуляры к
85
его сторонам. Получающиеся при пересечении перечисленных тро-
ек прямых точки, конечно же, замечательны (ведь три прямые,
как правило, пересекаются в трех различных точках). Возможны
и замечательные точки других типов, например точки, в которых
достигает экстремума какая-либо функция, определенная для всех
точек треугольника. С другой стороны, понятие «замечательные
точки треугольника» следует толковать скорее на литературно-
эмоциональном уровне, чем на формально-математическом. Извес-
тен софизм, «доказывающий», что все натуральные числа «инте-
ресные». (Допустив, что есть «неинтересные» числа, возьмем средн
них наименьшее. Бесспорно, это число «интересное»: оно интересно
уже тем, что оно наименьшее среди «неинтересных».) Подобное
рассуждение, «доказывающее», что все точки треугольника «за-
мечательны», можно сконструировать н в нашем случае. Поэтому
мы не станем углубляться дальше в нюансы терминологии, а пе-
рейдем к рассмотрению некоторых примеров.
ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ
Докажем, что существует точка, равноудаленная от вершин
треугольника, илн, иначе, что существует окружность, приходя-
щая через три вершины треугольника. Геометрическим местом то-
чек, равноудаленных от точек А а В, является перпендикуляр к
отрезку АВ, проходящий через его середину (серединный перпен-
дикуляр к отрезку АВ). Рассмотрим точку О, в которой пересе-
каются серединные перпендикуляры к отрезкам АВ и ВС. Точка О
равноудалена от точек А н В, а также от точек В н С. Поэтому
она равноудалена от точек А и С, т. е. она лежит н иа середин-
ном перпендикуляре к отрезку АС (рнс. 50).
Центр О описанной окружности лежит внутри треугольника,
только если этот треугольник остроугольный. Если же треуголь-
ник прямоугольный, то точка О совпадает с серединой гипотенузы,
Рис. 50
Рис. 51
86
а если угол при вершине С тупой, то прямая АВ разделяет точ-
ки О н С.
Если в & А ВС угол прн вершине С острый, то сторона АВ
видна из точки О под углом, равным 2Z. С; это следует из того,
что Z.AOB в два раза больше вписанного Z-ACB, опирающегося
на ту же дугу. Если же С тупой, то сторона АВ видна из точ-
ки О под углом, равным 360°—2 Z. С. Воспользовавшись этим,
легко доказать теорему синусов: AB=2/?sinC, где Z? — радиус
описанной окружности Л АВС. В самом деле, пусть Cj — середина
стороны АВ. Тогда АС\=АО sin Z_AOC\—R sin С, поэтому
AB=2AC\=2R sin С. Теорему синусов можно сформулировать и
по-другому: «Проекция диаметра описанной окружности, пер-
пендикулярного первой стороне треугольника, на прямую, содер-
жащую вторую сторону, равна третьей стороне». Проверьте сами,
что это столь громоздкое утверждение является на самом деле
просто теоремой синусов.
В математике часто бывает так, что объекты, определенные
совсем по-разному, оказываются совпадающими. Покажем это на
примере.
Пусть Л |, Bi и Ci — середины сторон ВС, СА н АВ. Можно до-
казать, что окружности, описанные около AABiCi, ДА1ВС1 н
ДЛ1В|С, пересекаются в одной точке, причем эта точка — центр
описанной окружности &АВС (рис. 51). Итак, у нас есть две,
казалось бы, совсем разные точки: точка пересечения серединных
перпендикуляров к сторонам дАВС и точка пересечения описан-
ных окружностей дЛВ|С1, aAiBCi н &А1В1С. А оказывается,
что эти две точки почему-то совпадают!
Проведем, однако, обещанное доказательство. Достаточно до-
казать, что центр О описанной окружности A AS С лежит на ок-
ружностях, описанных около дАВ1Сь aAiBC( н aAjBsC. Углы
OBtA и OCiA прямые, поэтому точки Bi и Ci лежат на окружности
диаметром ОА, а значит, точка О лежит на окружности, описан-
ной около ДЙВ|С|. Для ДА1ВС] н ДЛ1В|С доказательство
аналогично.
Доказанное утверждение является частным случаем весьма
интересной теоремы: если на сторонах АВ, ВС н СА треугольни-
ка АВС взяты произвольные точки Clt Ai и Вь то описанные
окружности aABiCi, AAiBCj н aAiBiC пересекаются в одной
точке. Попробуйте доказать эту теорему самостоятельно.
Сделаем последнее замечание по поводу центра описанной
окружности. Прямые Л1В| и АВ параллельны, поэтому OCj_LA|B|.
Аналогично OBi -LAtCi н OAt -LBiClt т. е. О —точка пересечения
высот треугольника AiBiCi-.. Постойте, постойте! Мы пока еще
не доказывали, что высоты треугольника пересекаются в одной
точке. Нет ли здесь пути к доказательству? К этому разговору
мы еще вернемся.
87
ЦЕНТР ВПИСАННОЙ ОКРУЖНОСТИ
Докажем, что биссектрисы углов дЛВС пересекаются в од-
ной точке. Рассмотрим точку О пересечения биссектрис углов
А нВ. Любые точки биссектрисы Z. А равноудалены от прямых АВ
и АС, а любая точка биссектрисы Z.S равноудалена от пря-
мых АВ и ВС, поэтому точка О равноудалена от прямых АС и ВС,
т. е. она лежит на биссектрисе Z.C. Точка О равноудалена от
прямых АВ, ВС и С А, значит, существует окружность с центром О,
касающаяся этих прямых, причем точки касания лежат на самих
сторонах, а не на их продолжениях. В самом деле, углы при
вершинах А н В дАОВ острые, поэтому проекция точки О на пря-
мую АВ лежит внутри отрезка АВ. Для сторон ВС н СА дока-
зательство аналогично.
Пусть Л |, Bi и Ct — точки касания вписанной окружности тре-
угольника со сторонами ВС, СА и АВ (рис. 52). Тогда ABi =АС/,
BCi = BAt и CAj=CBi. Кроме того, Z.BiA|C> равен углам при
основании равнобедренного ДЛВ1С1 (по теореме об угле между
касательной н хордой) н т. д. Для Z.B1C1A1 н Z.AiBiCi доказа-
тельство аналогично.
Углы при основании любого равнобедренного треугольника ост-
рые, поэтому л A iBiCi остроугольный для любого Д АВС.
Если х=АВ), у=ВС\ н z=CAt, то х+у—с, y-±-z=a н
z-^x=b, где а, b и с — длины сторон дАВС. Складывая первые
два равенства и вычитая из них третье, получаем у=-+-~-. Ана-
логично и 2—. Следует отметить, что для че-
тырехугольника подобные рассуждения не привели бы к желаемо-
му результату, потому что соответствующая система уравнений
РйС. Б2
Рис 53
88
либо вообще не имеет решений, либо имеет их бесконечно много.
В самом деле, если х-\-у—а, y+z=b, z-\-t=c и t+x=d, то
у=а—х, z=b—у=Ь-а-\-х и t—C—b+a — x, а нз равенства
t^x—d следует, что a+c=b+d. Поэтому если a-^-c^b-^-d, то
система решений не имеет, а если a-^-c—b-^-d, то х можно вы-
бирать произвольно, а у, 2, t выражаются через х.
Вернемся снова к единственности решения системы уравнений
для треугольника. Используя ее, можно доказать следующее ут-
верждение: пусть окружности с центрами А, В н С касаются внеш-
ним образом в точках Ль Bi и Ci (рис. 53). Тогда описанная
окружность AABjCi вписана в дЛВС. В самом деле, если х, у
н 2—радиусы окружностей; а, b и с — длины сторон дЛВС,
то х-\-у—с, y+z=a, y-j-x—b.
Докажем три свойства центра О вписанной окружности А ЛВС.
1. Если продолжение биссектрисы угла С пересекает описан-
ную окружность дЛВС в точке М, то МА=МВ~МО (рнс. 54).
Докажем, например, что в ДЛМО равны углы при вершинах
Л н О. В самом деле, Z-OAM— Z.OAB~l~ Z.BAM и Z-AOM=
= ЛОАС+£лСО, ^OAB=Z.OAC н /_ВДМ = ЛВСМ=
—/LACO. Следовательно, AM—МО. Аналогично ВМ—МО.
2. Если Л В —основание равнобедренного ДЛВС, то окруж-
ность, касающаяся сторон Z.ACB в точках Л и В, проходит через
точку О (рнс. 55).
Пусть О' — середина (меньшей) дуги АВ рассматриваемой
окружности. По свойству угла между касательной н хордой
(см. [1]) Z-CAO'— Z-O'BA—Z-О'ЛВ, т. е. точка О' лежит на
биссектрисе Z-Л. Аналогично можно показать, что она лежит н на
биссектрисе Z.B, т. е. О'—О.
3. Если прямая, проходящая через точку О параллельно сто-
роне АВ, пересекает стороны ВС и СА в точках Л] и Вь то
Л 1В|=Л |В ЛВ[.
м
Рис. 54
Рис. 55
89
Докажем, что ДЛВ|О равнобедренный. В самом деле,
Z.B1OA = Z. О АВ — Z-BjAO (рис. 56). Поэтому ABi^BtO. Ана-
логично A[B—AiOt а значит, AlBl=AiO-^OBi=AiB-[-ABi.
* * *
Пусть в дАВС углы при вершинах А, В н С равны а, ₽, у.
Вычислим величину угла, под которым сторона АВ видна нз точ-
ки О. Так как углы дЛОВ при вершинах Л и В равны
f И А то Z.4OB = 180°—2±0 = 18О°—|80°~т =90°+-|-. Эта
формула бывает полезна при решении многих задач.
Выясним, например, в каком случае четырехугольник, образо-
ванный сторонами АС н ВС и биссектрисами ЛЛ( н BBi, являет-
ся вписанным. Четырехугольник OAfCBi вписанный тогда и толь-
ко тогда, когда Z.AtCBi + Z_AtOBi = 180° (см. [1]), т. е.
V+(90°-|—= 180°, а значит, у=60°. В этом случае хорды ОЛ1
и OBi описанной окружности четырехугольника ОА}СВ\ равны,
так как на них опираются равные углы ОСА у и ОС В,.
Вписанная окружность ДЛВС касается его сторон во внут-
ренних точках. Выясним, какие вообще бывают окружности,
касающиеся трех прямых АВ, ВС н С А. Центр окружности, ка-
сающейся двух пересекающихся прямых, лежит на одной нз двух
прямых, делящих пополам углы между исходными прямыми.
Поэтому центры окружностей, касающихся прямых АВ, ВС н С А,
лежат на биссектрисах внешних или внутренних углов треугольни-
ка (или же их продолжениях). Через точку пересечения любых
двух биссектрис внешних углов проходит биссектриса внутреннего
угла. Доказательство этого утверждения дословно повторяет дока-
зательство соответствующего утверждения для биссектрис внут-
ренних углов. В итоге получаем 4 окружности с центрами О, Оа, Оь
н Ос (рис. 57). Окружность с центром Оо касается стороны ВС и
Рис. 56
Рис. 57
90
продолжений сторон АВ и АС; эта окружность называется вневпи-
санной окружностью дЛВС. Радиус вписанной окружности тре-
угольника обычно обозначается через г, а радиусы вневписанных
окружностей — через га, *ъ н гс. Между радиусами вписанной и вне-
вписанной окружностей имеют место следующие соотношения:
и ггс=(р—а)(р—6), где р — полупериметр Д/ШС. До-
кажем это. Пусть /( н L — точки касания вписанной н вневписанной
окружностей с прямой ВС (рис. 58). Прямоугольные треугольники
СОК и COcL подобны, поэтому =7х’* ^аиее было доказа-
но, что СК— а+ь~с —р—с. Остается проверить, что CL—p.
Пусть М и Р — точки касания вневписанной окружности с пря-
мыми АВ н АС. Тогда
_ CL + CP CB+BL+CA+AP СВ+ВМ+СА+АМ _
сь----- - - - - р.
Для доказательства соотношения ггс=(р—а)(р—Ь) рассмот-
рим прямоугольные треугольники LOCB и КВО, которые подобны,
так как
Z ОВК4- Z OeBL = ^ВЛ + ЛЛВ1 =90с
Значит,, т. е. rr,—KO-LOc—BK-BL. Остается за-
метить, что ВК=а+2~ь =р—Ь в BL=CL—CB=p—a.
Отметим еще одно интересное свойство (попутно уже факти-
чески доказанное). Пусть вписанная и вневписанная окружности
касаютсн стороны АВ в точках N а М (рнс. 58). Тогда AM=BN.
В самом деле, BN—p—b и АМ=АР—СР—АС=р—Ь.
Соотношения ггс—(р—а)(р—Ь) и гр—гс(р—с) можно исполь-
зовать для вывода формулы Герона S2—p(p—а)(р—Ь)(р—с),
где S — площадь треугольника. Перемножая эти соотношения, по-
лучаем г2р=(р—а)(р—Ь)(р—с). Остается проверить, что S—pr.
Это легко сделать, разрезав ДЛВС на дДОВ, дВОС н ДСОЛ.
&1
ТОЧКА ПЕРЕСЕЧЕНИЯ МЕДИАН
Докажем, что медианы треугольника пересекаются в одной точ-
ке. Рассмотрим для этого точку М, в которой пересекаются медиа-
ны A Ai н ВВ\. Проведем в дВВ[С среднюю линию А [Аг, парал-
лельную ВВ\ (рнс. 59). Тогда AiM:AM=BiA2:ABi — BiA2:B]C==
=ВА[’.ВС= 1:2, т. е. точка пересечения медиан ВВ[ н АА[ делит
медиану АА[ в отношении 1:2. Аналогично точка пересечения ме-
диан CCi н AAi делит медиану ДА 1 в отношении 1:2. Следователь-
но, точка пересечения медиан AAt н ВВ[ совпадает с точкой пере-
сечения медиан АА[ и CCi.
Если точку пересечения медиан треугольника соединить с вер-
шинами, то треугольник разобьется иа три треугольника равной
площади. В самом деле, достаточно доказать, что рели Р — любая
точка медианы ЛА| в дАВС, то площади дАВР й дАСР равны.
Ведь медианы AAi и PAi в дАВС и ДРВС разрезают их на тре-
угольники равной площади.
Справедливо также н обратное утверждение: если для некото-
рой точки Р, лежащей внутри ДАВС, площади ДАВР, ДВСР
и Д САР равны, то Р — точка пересечения медиан. В самом деле,
из равенства площадей Д АВР н /\ВСР следует, что расстояния от
точек А и С до прямой ВР равны, а значит, ВР проходит через
середину отрезка АС. Для АР и СР доказательство аналогично.
Равенство площадей треугольников, на которые медианы раз-
бивают треугольник, позволяет следующим офазом найти отно-
шение площади s треугольника, составленного из медиан дАВС,
к площади S самого Д АВС. Пусть М — точка пересечения медиан
ДАВ С; точка А' симметрична А относительно точки Л! (рнс. 60).
С одной стороны, площадь дА'МС равна у-. С другой стороны,
этот треугольник составлен из отрезков, длина каждого из которых
2
равна — длины соответствующей медианы, поэтому его площадь
равна -у . Следовательно, s=~.
Рис. 59
Рис. 60
92
Весьма важным свойством точки пересечения медиан является
то, что сумма трех векторов, идущих из нее в вершины треугольни-
ка, равна нулю. Заметим сначала, что АМ=-|-(лВ4-Лс) , где
М — точка пересечения медиан ДЛВС. В самом деле, если
—* —> —► —* ।
АВА'С — параллелограмм, то АА'=АВ-\-АС и ЛМ=—АА'. По-
этому лЙ+МВ+Л^=-1-(а4+СД+Яв + СВ + 4С + Й) = 0.
Ясно также, что этим свойством обладает только точка пересече-
ния медиан, так как если X — любая другая точка, то
хл+хв4-хс-схм4-лй)+(хм+л7в)4-(хм+мс)=зхм.
Воспользовавшись этим свойством точки пересечения медиан
треугольника, можно доказать следующее утверждение: точка пе-
ресечения медиан треугольника с вершинами в серединах сторон
АВ, CD и EF шестиугольника ABCDEF совпадает с точкой пере-
сечения медиан треугольника с вершинами в серединах сторон
ВС, DE и FA. В самом деле, воспользовавшись тем, что если,
например, Р — середина отрезка АВ, то для любой точки X спра-
ведливо равенство ХЛ4- ХВ=2ХР, легко доказать, что точки пере-
сечения медиан обоих рассматриваемых треугольников обладают
тем свойством, что сумма векторов, идущих из них в вершины
шестиугольника, равна нулю. Следовательно, эти точки совпадают.
Точка пересечения медиан обладает одним свойством, резко
выделяющим ее- иа фоне остальных замечательных точек тре-
угольника: если Ь.А'В'С' является проекцией ДДВС на плос-
кость, то точка пересечения медиан к А’В'С' является проекцией
точки пересечения медиан ДДВС на ту же плоскость. Это легко
следует нз того, что при проектировании середина отрезка пере-
ходит в середину его проекции, а значит, медиана треугольника
переходит в медиану его проекции. Ни биссектриса, нн высота
таким свойством не обладают.
Нельзя ие отметить, что точка пересечения медиан треугольни-
ка является его центром масс, причем как центром масс системы
трех материальных точек с равными массами, находящихся в вер-
шинах треугольника, так н центром масс пластинки, имеющей
форму данного треугольника. Положением равновесия треуголь-
ника, шарнирно закрепленного в произвольной точке X, будет та-
кое положение, прн котором луч ХМ направлен к центру Земли.
Для треугольника, шарнирно закрепленного в точке пересечения
медиан, любое положение является положением равновесия. Кро-
ме того, треугольник, точка пересечения медиан которого опира-
ется на острие иглы, также будет находиться в положении равно-
весия.
93
ТОЧКА ПЕРЕСЕЧЕНИЯ ВЫСОТ
Чтобы доказать, что высоты &АВС пересекаются в одной
точке, вспомним путь доказательства, наметившийся в конце
раздела «Центр описанной окружности». Проведем через вершины
А, В и С прямые, параллельные противоположным сторонам;
этн прямые образуют ДЛ1В1С1 (рис. 61). Высоты А ЛВС являют-
ся серединными перпендикулярами к сторонам aAiSiCi. Следо-
вательно, онн пересекаются в одной точке — центре описанной
окружности ДД1В1С1. Точка пересечения высот треугольника на-
зывается иногда его ортоцентром.
Легко проверить, что если Н— точка пересечения высот
А ЛВС, то Д В н С — точки пересечения высот &ВНС, л СНА н
& АН В соответственно.
Ясно также, что Z-ABC+ Z_AHC= 180°, потому что Z_BA\H=
— Z.BCiB=90° (А| н Ci — основания высот). Если точка Н\ сим-
метрична точке Н относительно прямой АС, то четырехуголь-
ник ABCHi вписанный. Следовательно, радиусы описанных ок-
ружностей А АВС и Д.АНС равны и этн окружности симметричны
относительно стороны АС (рнс. 62).
Теперь легко доказать, что
АН—a |ctg А |, где а—ВС.
В самом деле,
AH=2Rsin Z_ACH~2R |cos А| |ctgA|.
Предположим для простоты, что А ЛВС остроугольный н рас-
смотрим АЛ1В|Сь образованный основаниями его высот. Оказы-
вается, что центром вписанной окружности АЛ1В1С1 является
точка пересечения высот А ЛВС, а центры вневписанных окруж-
Рис, 61
Рис 62
ностей AABiCi являются вершинами ДЛВС (рис, 63). Точки
Л1 и Bi лежат на окружности с диаметром СН (так как углы НВ^С
и HAiC прямые), поэтому Z.//CB1. Аналогично
AHAiCi^ £HBCi. А так как ^HCBt « Z_HBCi. то А,А — бис-
сектриса Z.B»A|C|.
Пусть Я — точка пересечения высот AAit BBi и CCi тре-
угольника АВС. Точки At н Bi лежат на окружности с диамет-
ром АВ, поэтому AH‘AiH~BH-BiH (см. [1]). Аналогично
BH-BiH^CH-CiH.
Для остроугольного треугольника справедливо также обратное
утверждение: если точки Аь Bi и Ci лежат на сторонах ВС, СА н
АВ остроугольного А АВС и отрезки AAt, BBi и CCi пересекаются
в точке Р, причем АР-А^Р—ВР* BiP~CP-CiP, то Р —точка пе-
ресечения высот. В самом деле, нз равенства
AP-AiP=BP*BtP
следует, что точки А, В, Л и Bt лежат на одной окружности
с диаметром АВ, а значит, Z.ABiB= Z-BAiA=y. Аналогично
Z.ACiC= Z.CAiA = pH ZCBjfl==ZBCiC=a (рис. 64). Ясно так-
же, что a-|-p=Z-BCiC4-Z-CCiA —180°, 0+т=18О° и
==180°. Следовательно, а==р=у=90°.
Точку пересечения высот треугольника можно определить еще
и другим весьма интересным способом, но для этого нам потребу-
ются понятия вектора и скалярного произведения векторов.
Пусть О — центр описанной окружности А АВ С. Сумма векто-
ров О А ОВ + ОС является некоторым вектором, поэтому сущест-
вует такая точка Р, что ОР—ОА-{-ОВ-\-ОС. Оказывается, что
Р—точка пересечении высот дДВС!
95
Докажем, например, что АР Л. ВС. Ясно, что ЛР—ЛО-Ь
+6р=АО+(ОА+ОВ+ОС)=ОВ+ОСнВС«- ОВ+ОС. По-
этому скалярное произведение векторов АР н ВС равно ОС2—
— ОВ2=/?2—Я2=0, т. е. эти векторы перпендикулярны.
Это свойство ортоцентра треугольника позволяет доказывать
некоторые далеко не очевидные утверждения. Рассмотрим, напри-
мер, четырехугольник ABCD, вписанный в окружность. Пусть
На, Нь, Нс и На — ортоцентры &BCD, &CDA, &DAB и дЛВС
соответственно. Тогда середины отрезков АНа, BHb, СНс, DHa
совпадают. В самом деле, если О — центр окружности, а М — се-
редина отрезка АНа, то ОМ=~{ОА-\-ОН^)=~(ОА-\-ОВ-\-
4-OC+OD). Для середин трех других отрезков получаем точно
такие же выражения.
ПРЯМАЯ ЭЙЛЕРА
Самым удивительным свойством замечательных точек тре-
угольника является то, что некоторые из них связаны друг с дру-
гом определенными соотношениями. Например, точка пересечения
медиан М, точка пересечения высот Н н центр описанной окруж-
ности О лежат на одной прямой, причем точка М делит отре-
зок ОН так, что справедливо соотношение ОМ*.МН=^1:2. Эта
теорема была доказана в 1765 г. Леонардом Эйлером, который
своей неутомимой деятельностью значительно развил многие об-
ласти математики н заложил основы многих новых ее разделов. Он
родился в 1707 г. в Швейцарии. В 20 лет Эйлер по рекомендации
братьев Бернулли получил приглашение приехать в Санкт-Петер-
бург, где незадолго перед этим была организована академия. В
конце 1740 г. в России в связи с приходом к власти Анны Леополь-
довны сложилась тревожная обстановка, и Эйлер переехал в
Берлин. Через 25 лет он снова вернулси в Россию, в общей слож-
ности в Петербурге Эйлер прожил более 30 лет. Находясь в Берли-
не, Эйлер поддерживал тесную связь с русской академией и был
ее почетным членом. Из Берлина Эйлер переписывался с Ломоно-
совым. Их переписка завязалась следующим образом. В 1747 г.
Ломоносова избрали в профессоры, т. е. в действительные члены
академии; императрица это избрание утвердила. После этого
реакционный чиновник академии Шумахер, яро ненавидящий Ло-
моносова, послал его работы Эйлеру, надеясь получить о ннх
плохой отзыв. (Эйлер был старше Ломоносова всего на 4 года,
ио его научный авторитет был к тому времени уже очень высок.)
В своем отзыве Эйлер писал: «Все сии сочинения не токмо хоро-
ши, ио н превосходны, ибо он изъясняет физические и химические
96
материн самые нужные н труд-
ные, кои совсем неизвестны н
невозможны были к истолкова-
нию самым остроумным н уче-
ным людям, с таким основатель-
ством, что я совсем уверен о
точности его доказательств...
Желать надобно, чтобы все про-
чие академии были в состоиннн
показать такие изобретения, ко-
торые показал господин Ломо-
носов».
Перейдем к доказательству
теоремы Эйлера. Рассмотрим
AAtBtCi с вершинами в сере-
динах сторон дЛВС; пусть Hi
нН — их ортоцентры (рис. 65). Точка Hi совпадает с центром О
описанной окружности дАвС. Докажем, что Д CiHiMoo д СНМ.
В самом деле, по свойству точки пересечения медиан С\М\СМ~
— 1:2, коэффициент подобия Д/hBiCi н дАВС равен 2, поэтому
С1Я,: СЯ = 1:2, кроме того, Z.HiCiM = Z.НСМ (Citfi || СН). Сле-
довательно, Z-C\MHi = Z-CMH, а значит, точка M лежит на
отрезке HiH. Кроме того, HiM‘.MH= 1:2, так как коэффициент
подобия /\C\HiM и £±СНМ равен 2.
ОКРУЖНОСТЬ ДЕВЯТИ ТОЧЕК
В 1765 г. Эйлер обнаружил, что середины сторон треугольника
н основания его высот лежат на одной окружности. Докажем и мы
это свойство треугольника.
Пусть Й2 — основание высоты, опущенной из вершины В на
сторону АС. Точки В н Въ симметричны относительно прямой A iCi
(рис. 66). Следовательно, дАВгС^ дЛ1ВС(« aABiCi, поэто-
му Z.AiB^Ci = Z-AiBiCi, а значит, точка лежит на описанной
окружности ДЛ1В1С1. Для остальных оснований высот доказа-
тельство аналогично. _ „
D D
4 Заказ 775
Рис. 66
Рис. 67
97
Впоследствии было обнаружено, что на той же окружности ле-
жат еще трн точки — середины отрезков, соединяющих ортоцентр
с вершинами треугольника. Это и есть окружность девяти точек.
Пусть Аз и Сз — середины отрезков АН н С’Я, Сг — основа-
ние высоты, опушенной из вершины С на АВ (рис. 67). Дока-
жем сначала, что AtCiA3C3 — прямоугольник. Это легко следует
нз того, что AfC3 и Л3С1 — средние линии дВСН н &АВН, а
Д|С1 и А3С3 — средние лннин дАВС и £±ЛСН. Поэтому точки
At и А3 лежат на окружности с диаметром 'С(Сз, а так как
ZCjCaCg^QO0, то на этой окружности лежит и точка С2. Итак,
точки А3 н Сз лежат на окружности, проходящей через точки А^
Cj и С2. Эта окружность совпадает с окружностью, рассмотренной
Эйлером (если А АВС не равнобедренный). Для точки Вя доказа-
тельство аналогично.
ТОЧКА ТОРРИЧЕЛЛИ
Внутри произвольного четырехугольника ABCD легко найти
точку, сумма расстояний от которой до вершин имеет наимень-
шее значение. Такой точкой является точка О пересечения его
диагоналей. В самом деле, если X — любая другая точка, то
АХ+ХС^АС=АО+ОС и ВХ+ XD^BD=BO+OD, причем
хотя бы одно нз неравенств строгое. Для треугольника аналогичная
задача решается сложнее, к ее решению мы сейчас перейдем-
Для простоты разберем случай остроугольного треугольника.
Пусть М — некоторая точка внутри остроугольного ДАВС.
Повернем Д АВС вместе с точкой М на 60° вокруг точки А (рис. 68).
(Точнее говоря, пусть В*,С’ и М’ — образы точек В, С и М прн
повороте на 60° вокруг точки А.) Тогда AM +ВМ4-СЛ1==ММ/4-
4-ВЛГ4~С*Л1', AM—ММ', так как Д.АММ' — равнобедренный
(АМ=АМ') и X-МАМ'=60°. Правая часть равенства — это
длина ломаной ВММ'С'-, она будет наименьшей, когда эта ломаная
98
совпадает с отрезком ВС'. В этом случае /_ЛЛ1В = 180о —
-ДЛЛШ'^120° н А.АМС= Z.AM'С' — 180°- zLAM'M — 120°,
т. е. стороны АВ, ВС и СА видны нз точки М под углом 120°.
Такая точка М называется точкой Торричелли треугольника АВС.
Докажем, впрочем, что внутри остроугольного треугольника
всегда существует точка М, из которой каждая сторона видна под
углом 120°. Построим на стороне АВ треугольника АВС внешним
образом правильный ДЛВС1 (рис. 69). Пусть М — точка пересе-
чения описанной окружности ДЛВС1 и прямой СС|. Тогда
Z.AMCi — AABCi —60° и Z BMCi — A BACf =60°. Поэтому сто-
роны ДЛВС видны из точки М под углом 120°. Продолжая эти
рассуждения немножко дальше, можно получить еще одно опреде-
ление точки Торричелли. Построим правильные треугольни-
ки А (ВС и ABiC еще и на сторонах ВС и АС. Докажем, что точка М
лежит также и на прямой ААь В самом деле, точка Л4 лежит на
описанной окружности /\А}ВС, поэтому ALAiMB— АЛ1Св=60°,
а значит, AAiMB-j- АВМА= 180°. Аналогично точка М лежит
и на прямой ВВ( (рис. 69).
Внутри дЛВС существует единственная точка М, из которой
его стороны видны под углом 120°, потому что описанные окруж-
ности дЛВСь дЛВ]Си ДЛ|ВС не могут иметь более одной об-
щей точки
Приведем теперь физическую (механическую) интерпретацию
точки Торричелли. Закрепим в вершинах ДАВС колечкн, про-
пустим сквозь ннх трн веревкн, одни концы которых связаны, а к
другим концам прикреплены грузы равной массы (рнс. 70). Ес-
ли х=МА, у=МВ, 2—МС на — длина каждой нити, то потенци-
альная энергия рассматриваемой системы равна mg(x—&)+
4- mg (у—a) A-mg (z—с). В положении равновесия потенциальная
энергия имеет наименьшее значение, поэтому сумма x-[-y+z тоже
имеет наименьшее значение. С другой стороны, в положении
равновесия равнодействующая сил в точке М равна нулю. Силы
эти по абсолютной величине равны, поэтому-попарные углы между
векторами сил равны 120°.
99
Остается рассказать, как обстоят дела в случае тупоугольно-
го треугольника. Если тупой угол меньше 120°, то все предыдущие
рассуждения остаются в силе. А если тупой угол больше илн равен
120°, то сумма расстояний от точки треугольника до его вершин
будет наименьшей, когда эта точка — вершина тупого угла.
ТОЧКИ БРОКАРА
Точками Брокара А АВ С называются такие его внутренние
точки Р и Q, что ЛАВРОВ SLBCP— Z.CAP н Z_QAB= Z_QBC=
= Z_ QCA (для равностороннего треугольника точки Брокара сли-
ваются в одну точку). Докажем, что внутри любого А АВС сущест-
вует точка Р, обладающая требуемым свойством (для точки Q до-
казательство аналогично). Предварительно сформулируем опреде-
ление точки Брокара в другом виде. Обозначим величины углов
так, как показано на рисунке 71. Поскольку Z.APB—180° — а+
4-х—У, равенство х=у эквивалентно равенству Z.APB = 180° —
— Л. А. Следовательно, Р — точка А АВС, из которой стороны АВ,
ВС и СА видны под углами 180°— Z.А, 180°— Z.B, 180° — Z.С.
Такую точку можно построить следующим образом. Построим на
стороне ВС треугольника АВС подобный ему треугольник СА|В
так, как показано на рисунке 72. Докажем, что точка Р пересече-
ния прямой AAi и описанной окружности A^jBC искомая. В са-
мом деле, АВРС= 180° —р н ААРВ= 180°-А Л|РВ = 180° —
— Z.AiCB = 180°—а. Построим далее аналогичным образом по-
добные треугольники на сторонах АС н АВ (рис. 73). Так как
Z. АР В = 180°—а, точка Р лежит также и на описанной окружнос-
ти А АВС\. Следовательно, Z_BPCX — Z.BAC, —р, а значит, точка
Р лежит на отрезке CCi. Аналогично она лежит н на отрезке BBt,
т. е. Р — точка пересечения отрезков ААЬ ВВ} и СС|.
Точка Брокара Р обладает следующим интересным свойством.
Пусть прямые АР. ВР и СР пересекают описанную окружность
Рис. 73
Рис. 74
ДЛВС в точках Ait Bi и Ci (рис. 74)н Тогда лАВС— ДВ1С1Л1.
В самом деле, Z..4jBiCi = Z.4iBiB4-Z.BBiCi==Z..Ai.4B-|-
+ Z.BCCj=sZ.i4i4B + Z.i4ii4C— Z.BAC, по свойству точки Бро-
кара дЛВС углы BCCi и AiАС равны, а значит, AiCj=BC. Ра-
венство остальных сторон ДЛВС и ДВ|С(Л| проверяется анало-
гично.
В 1984 г. на Всесоюзной олнмпнаде по математике предлага-
лась задача, в которой требовалось доказать, что для любого
треугольника существует не более шести точен, отличных от то-
чек Брокара, обладающих этим свойством. Точнее говоря, задача
имела следующую формулировку: «Дан ДЛВС. Через точйу Р
провели прямые РА, РВ н PC, которые пересекли описанную около
этого треугольника окружность в точках Л|, В( и Ci, отличных от
вершин треугольника. Оказалось при этом, что ДЛ1В1С1 конгру-
энтен (равен) Л АВС. Докажите, что существует не более восьми
точек Р с указанным свойством». (Автор задачи И. Ф. Шарыгин.)
Решение этой довольно трудной задачи можно прочитать в статье
Н. Б. Васильева «Задача о восьми точках» (Квант.— 1985.—
№ 3.—С. 39—40).
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
Мы рассмотрели далеко не все замечательные точки треуголь-
ника. Дадим определение еще трех точек, не доказывая соответст-
вующих теорем о пересечении троек прямых в одной точке.
Точка Лемуана — точка пересечения прямых, симметричных
медианам относительно соответствующих биссектрис.
Точка Жергонна — точка пересечения прямых, соединяющих
вершины треугольника с точками, в которых вписанная окруж-
ность касается противоположных сторон.
Точка Нагеля — точка пересечения прямых, соединяющих вер-
шины треугольника с точками, в которых вневписанные окруж-
ности касаются противоположных сторон (этн прямые делят попо-
лам периметр треугольника).
Во всех рассмотренных нами случаях Доказательство того,
что соответствующие тройки прямых пересекаются в одной точке,
можно провести с помощью теоремы Чееы. Мы сформулируем
эту теорему, но не будем ее доказывать.
Теорема. Пусть на сторонах Л В, ВС н СА треугольника АВС
взяты точки Ci, Ai и соответственно. Прямые AAit BBi и CCi
пересекаются в одной точке тогда н только тогда, когда
AC, в А, СВ,
С,В ‘ А,С ' В,А
Доказательство этой теоремы можно прочитать в книгах [3]
и Н].
Задачи
1. В равнобедренном треугольнике АВС угол А равен 100°.
О — центр описанной около дДВС окружности, J — центр впи-
санной окружности, И — точка пересечения высот. Найдите углы
треугольника: a) AOJ; б) АОН; в) AJH.
2. Докажите, что если для данного треугольника любые две
из следующих четырех точек:
а) центр описанной окружности;
б) центр вписанной окружности;
в) точка пересечения медиан;
г) точка пересечения высот —
совпадают, то треугольник правильный
3. Найдите углы треугольника, если известно, что одна из
биссектрис этого треугольника разбивает его на два равнобедрен-
ных треугольника.
4. Пусть М — точка на стороне АС треугольника АВС. Обозна-
чим через Ri н /?2 радиусы окружностей, описанных около тре-
угольников АВМ и СВМ соответственно. Докажите, что •
5. Даны окружность н точка А вне ее. АВ н АС — касательные
к окружности (В и С — точки касания). Докажите, что середины
двух дуг, на которые данная окружность разделена точками В н С,
являются центром вписанной н центром вяевписаниой окружности
треугольника АВС
6. Пусть / — центр окружности, вписанной в треугольник АВС,
Ja — центр вневписанной окружности (касающейся стороны ВС
и продолжений сторон АВ н АС). Докажите, что точки В, С, J, 1а
расположены на одной окружности.
102
7. Пусть J — центр окружности, вписанной в треугольник АВС.
Докажите, что прямая AJ проходит через центр окружности,
проходящей через точки В, С и J.
8. Пусть Ja — центр вневписанной окружности Найдите
Z.AJaC, если Z_ABC=$.
9. Три окружности радиусами 1, 2 и 3 попарно касаются друг
друга внешним образом. Найдите радиус окружности, проходящей
через точки касания этих окружностей.
10. Может ли радиус окружности, описанной около треуголь-
ника, все стороны которого меньше 1, быть больше 100?
11. Может ли площадь треугольника, все высоты которого
меньше 1 см, быть больше 1м2?
12. Биссектрисы треугольника меньше 1. Докажите, что его
площадь меньше .
13. Всегда лн из высот некоторого треугольника можно постро-
ить треугольник?
14. Всегда ли из биссектрис некоторого треугольника можно
построить треугольник?
15. Про две высоты треугольника известно, что каждая нз них
не меньше стороны, на которую она опущена. Найдите углы
треугольника
16. Стороны треугольника АВС связаны неравенствами
АВ<ВС<СА. Пусть / — центр вписанной в АВС окружности.
К какой нз вершин этого треугольника ближе всех расположен J?
17. Стороны треугольника связаны соотношениями АВ <ВС<
< СА. Пусть М — точка пересечения медиан этого треугольника
К какой нз сторон ближе всего расположена точка ЛР К какой из
вершин ближе всего расположена точка М? Ответьте на те же
вопросы для точки пересечения высот этого треугольника.
Литература
1. Киселев А. П. Элементарная геометрия.— М.: Просвеще-
ние, 1980.
2. Коксетер Г. С., Грейтцер С. Л. Новые встречи с гео-
метрией.— М.: Наука, 1978.
3. П р а с о л о в В. В. Задачи по планиметрии. — М.: Наука,
1986.—Ч. 1.
4. Ш а р ы г и и И. Ф. Задачи по геометрии: Планиметрии.— М.:
Наука, 1986.
8 КЛАСС
ЧИСЛОВЫЕ МНОЖЕСТВА
ПОНЯТИЕ МНОЖЕСТВА
Мнр чисел удивительно богат и разнообразен. Недаром ве-
ликий немецкий математик К. Ф. Г аусс '(1777—1855) писал:
«Математика — царица наук, теория чисел — царица матема-
тики». Трудно сказать, согласятся лн с этим высказыванием
физики, бнологи, историки... Но с тем, что теория чисел — одна
нз важнейших областей математики, согласятся все ученые,
работающие в ней. Во многих частях школьного курса вы изучали
большое количество различных фактов, теорем, методов, отно-
сящихся к числовой системе. Наша задача здесь — суммировать
эти знания, уточнить и обобщить известные вам представления.
При этом удобно будет пользоваться понятием множества.
Обычно говорят о множестве, составленном нз некоторых элемен-
тов, если этн элементы имеют общее свойство. Вместо слова
«множество» употребляются также слова «набор», «совокупность»
и др. Слово «множество» выделяется среди них тем, что считается
математическим термином. Как правило, множества обозначают
большими латинскими буквами и говорят: «множество А» и т. д.
Для обозначения особенно важных, часто встречающихся мно-
жеств вводятся специальные символы. Вот некоторые из них:
N— множество натуральных чисел, Z — множество целых чисел,
Q — множество рациональных чисел, R — множество действитель-
ных чисел. Особое место занимают множества, называемые число-
выми промежутками. Например:
[а; б]— множестве чисел, удовлетворяющих неравенствам
а^.х^Ь\
[а; Ь) — множество чисел, удовлетворяющих неравенствам
а^х<Ь;
(ц;4-оо) — множество чисел, удовлетворяющих неравенству
а<х н т. д.
Чтобы указать, что некоторый элемент а является элементом
множества А, применяется запись А. Она читается: «а принад-
лежит множеству А». Если а не принадлежит множеству А, то
используется запись а$А.
Рассмотренные выше множества состоят из чисел. Такие мно-
жества называются числовыми. Например, множество [а; £»] на-
зывается числовым отрезком, множество (о; Ь) — числовым интер-
104
валом и т. д. Однако множество может состоять и нз других эле-
ментов. Так, в геометрии изучаются множества, элементы кото-
рых — точки, например прямая, отрезок, окружность и т. д. При-
ведем определение окружности с использованием термина «мно-
жество»: «Окружностью радиуса г с центром в точке О называется
множество точек плоскости, расстояние от которых до О равно г».
Рассмотрим примеры.
1. Каждое целое число рационально. Значит, множество целых
чисел — часть множества рациональных чисел.
2. Каждая точка отрезка МК (рис. 75) принадлежит отрез-
ку MN. Значит, отрезок МК — часть отрезка MN. В математике
для указания того, что одно множество — часть другого, исполь-
зуется термин «подмножество».
Пусть А, В — множества. А называется подмножеством В, если
каждый элемент из А принадлежит В. Таким образом, можно
сказать, что Z — подмножество множества Q, отрезок МК — под-
множество отрезка MN.
Для обозначения того, что А — подмножество В, используется
запись Л с В, т. е. символ «с» обозначает слово «подмножество».
Эта запись читается: «Д — подмножество множества В» или «мно-
жество А содержится в множестве В». Если А не является подмно-
жеством В, то используется запись А(£В. Примеры: ZczQ,
KN с MN.
Исследуем вопрос: могут лн одновременно выполняться ут-
верждения ЛсВ и ВсД, где А, В — некоторые множества? По
определению Лей означает, что каждый элемент из А принадле-
жит В. Запись Вс А означает, что каждый элемент нз В принад-
лежит А. Сравнивая эти условия, видим, что множества Д и В со-
стоят нз одних и тех же элементов. Такие множества называются
равными. Для обозначения равных множеств используется запись
Д=В. Запись Ду=В обозначает, что множество А не равно мно-
жеству В.
Примеры.
1. Обозначим через В множество тех рациональных чисел,
которые можно представить в виде конечных десятичных дробей.
Очевидно, что ZczD. Верно лн, что D=Z? Нет, потому что не вся-
кая конечная десятичная дробь служит записью целого числа.
105
2. Очевидно, что DcQ. Верно ли, что D=Q? Нет, потому что
не всякое рациональное число может быть представлено конечной
десятичной дробью
3. Самостоятельно докажите, что
Множества бывают конечные и бесконечные. Например, в мно-
жестве корней уравнения (х—1)(х—2)=0 два элемента (числа 1
и 2), а в множестве N бесконечное количество элементов. Мно-
жество А, элементы которого можно пересчитать, называется
конечным. Число элементов конечного множества обозначает-
ся |Л|.
Чтобы задать конечное множество, можно записать друг за
другом все его элементы, разделяя нх точкой с запятой, а потом
заключить эту запись в фигурные скобки. Например, {1;2;3}
обозначает конечное множество, состоящее из элементов 1, 2 и 3.
В нем три элемента. Порядок записи элементов множества роли
не играет. Например, {1; 2; 3 }={2; 3; 1).
Отметим важное свойство: подмножество конечного множества
само конечно. Действительно, если В — конечное множество н
Ас В, то можно пересчитать элементы множества В в таком
порядке: пересчитаем сначала все элементы из А, потом оставшие-
ся элементы нз В. Ясно, что вместе с пересчетом элементов мно-
жества В получен и пересчет элементов А. Из проведенного рас-
суждения видно, что число элементов в подмножестве не превосхо-
дит числа элементов в множестве, которое его содержит, а если
|А1 = |В|, то и А=В.
Следствие. Если множество В содержит бесконечное под-
множество, то В бесконечно.
Для доказательства допустим, что В конечно н АсВ. Тогда А
должно быть конечным по приведенному выше свойству. Но это
противоречит условию. Значит, В — бесконечное множество.
Конечное множество можно задать двумя способами:
— указанием иа некоторое свойство, которому удовлетворяют
его элементы;
— перечислением его элементов.
При первом способе задания может оказаться, что данному
свойству не удовлетворяет вообще никакой элемент. Например,
уравнение х{х— 1)(хф-1)=(х~2)(х24-2х+3) не имеет корней
(докажите). Если некоторое свойство не выполняется ни для како-
го элемента, то будем говорить, что оно определяет пустое мно-
жество. Используя это понятие, можно сказать, что множество
корней приведенного выше уравнения пусто. Пустое множество
обозначается символом 0; оно считается конечным. Очевидно,
в пустом множестве 0 элементов: I 0 I =0_ Каждое множество А
содержит пустое подмножество. Поясним это свойство. Чтобы за-
дать подмножество данного множества, нужно указать условие,
которому удовлетворяют его элементы. Но условие может оказать-
106
ся противоречивым, т. е. таким, которому не будет удовлетворять
никакой элемент множества А. Значит, это условие определяет
пустое подмножество, т. е. 0cz А.
Задачи
1. Запишите с помощью фигурных скобок множество корней
уравнения:
а) х2—1,21=0; б) (х-1)(х-2)=(х-1)(х+3);
. ____________________________1_______
В) (к—1)(*—2)(х—3) (х—1)(х—2)(х—3)
2. Запишите с помощью фигурных скобок множество, состоя-
щее из:
а) целых чисел, таких, что — 3,7] ^х<4;
б) натуральных делителей числа 12; числа 30;
в) общих натуральных делителей чисел 12 и 30;
г) целых делителей числа 6.
3. Докажите, что:
а) EQ; б) Л®е(2,8; 2,9).
4. Пусть Е — множество, состоящее из таких чисел х, что
4^х2^9. Проверьте, что [2; 3]cz£. Верно ли, что [2; 3]—£?
5. Докажите, что множества Z, Q, R бесконечны.
6. а) Пусть а, b — целые числа, а<Ь. Обозначим через Л мно-
жество целых чисел отрезка [а; Ь} Найдите |А|.
б) На координатной плоскости расположен квадрат ABCD, где
А (10; 10), В (-10; 10), С (—10; —10), 0(10; -10). Сколько точек
с целыми координатами, расположено иа сторонах квадрата или
внутри его?
в) Докажите, что иа окружности х2-|-х/2= 102 лежит конечное
множество точек с целыми координатами (см. рнс. 76).
ОПЕРАЦИИ С МНОЖЕСТВАМИ
Определим операции, позволяющие по данным множествам
строить новые множества.
I. Если даны два множества, то можно образовать новое
множество, составленное из их общих элементов. Например,
общая часть множеств (1;2;3) и (2; 3; 4} — это множество {2; 3}.
Общая часть множеств называется нх пересечением. Пересечение
множеств А н В обозначается при помощи знака «f)> (знака пе-
ресечения). Например:
(1,2;3}П{2; 3; 4}={2; 3}.
107
Если заданы два множества, то можно образовать новое мно-
жество, включив в него, во-первых, элементы первого множества
н, во-вторых, элементы второго множества, не совпадающие с
элементами первого. Например, из множеств {1; 2; 3) н {2; 3; 4} при
этом получается множество (1; 2; 3; 4). Построенное таким образом
множество называется объединением первых двух. Объединение
обозначается знаком «U*- Например:
{1;2;3}U(2; 3;4)={1;2; 3; 4}.
Приведем примеры использования операций пересечения и
объединения множеств.
а) Пусть а(х) н b (х) — многочлены н А, В — множества кор-
ней уравнений а(х)=О, fe{x)=0 соответственно. Тогда множест-
во С корней уравнения а (х)-Ь (х)=0 равно объединению множеств
А и В. Докажем это свойство. Пусть хобС, т. е. а(хо)-Ь (хо)=О.
Известно, что произведение двух чисел равно нулю только тогда,
когда хотя бы одни нз множителей равен нулю: с(х0)—О или
й(хо)=О. Значит, х0 — корень одного из уравнений fl(x)—О илн
1>(х)=0, т. е. Хо принадлежит хотя бы одному нз множеств: А
или В. Наоборот, если известно, что а (хо)=О илн b (хо)=О,
то н fl (хо)-6 (хо)=О. Значит, множество С составлено из элементов
множеств А н В\
С=А[)В.
б) Операция пересечения множеств применяется там, где тре-
буется найти элементы, удовлетворяющие сразу двум условиям.
Например, множество общих натуральных кратных чисел 3 и 5 —
это пересечение множества натуральных кратных числа 3 и мно-
жества натуральных кратных числа 5.
Множества называются непересекающимися, если у них нет об-
щих элементов, т. е. нх пересечение пусто, н пересекающимися,
если у них имеются общие элементы. Наглядно представить рас-
положение множеств в различных случаях можно при помощи
точечных множеств; на рисунке 77, fl-e множества А, В изображе-
ны частями плоскости, ограниченными некоторыми овалами. Такой
способ изображения получил название диаграмм Эйлера — Вениа
(по именам двух ученых — Л. Эйлера (1707—1783) н англий-
ского логика Дж. Венна (1834—1923), изучивших и описавших
свойства этого способа изображения операций с множествами).
в<=Л ДПВ=0
О) Ф „ &)
' Рис. 77 '
А В
А\В
г)
108
Операции объединения н пересечения могут быть определены
не только для двух, но н для трех, четырех и т. д. множеств.
Смысл операций остается прежним: объединение нескольких мно-
жеств состоит из элементов, принадлежащих хотя бы одному из
данных множеств, а пересечение — общая часть данных множеств.
2. Введем еще одну операцию с множествами. Множество,
состоящее нз элементов, принадлежащих множеству Л, но не при-
надлежащих множеству В, называется разностью А н В, обозна-
чается А\В. Диаграмма Эйлера — Венна разности множеств при-
ведена на рисунке 77, г.
Разность множеств используется прн решении уравнений.
Пусть а (х), b (х) — многочлены. Л, В — множества норией урав-
нений а (х)=0, Ь (х)= 0 соответственно. Покажем, что множество С
корней уравнения =0 равно Л\В. Действительно, дробь
равна нулю, если ее числитель равен О, а знаменатель не равен 0.
Поэтому если Хо — корень уравнения а (х)=0, то а (хо)=0, b (хо)У=
#=0. Но это н значит, что х0€Л\В. Наоборот, если о(х0)=0 н
6 (Xo)¥=O, т. е. хь€Л\В, то х0 — корень уравнения =0. Значит,
С=Л\6.
Приведем пример использования операций с множествами прн
решении задач. Прежде всего предлагаем вам самостоятельно до-
казать такие свойства конечных множеств: а) если А(]В=0, то
|ЛиВ| = |Л 1+ |В|; б) если АсВ, то |В\А | = |В| — |Л|. В свойст-
ве а) связываются операция объединения множеств н нахождение
суммы числа элементов непересекающихся множеств.
Что же получится, если множества Л, В пересекаются? Тогда
прн пересчете-объединения некоторые элементы будут учтены
дважды; это те элементы, которые принадлежат АП В. Поэтому
для нахождения численности A(JB нужно из суммы ]А|-ЦВ|
вычесть |Л ПВ], т. е. верна формула
1Либ| = 1Л| + |В| - |ЛГ)В|,
которая называется формулой Грассмана в честь немецкого ма-
тематика Г. Грассмана (1809—1887). Эта формула часто
используется при нахождении числа элементов множества, за-
данного несколькими условиями.
Пример. Среди чисел первой тысячи (т. е. натуральных
чисел от 1 до 1000) найти количество чисел, не делящихся ни иа
3, нн иа 5.
Решение. Пусть Е — множество натуральных чисел
х^ 1000, Со — подмножество £, состоящее из чисел, делящихся на
заданное натуральное число а. Найдем | Са\- Натуральные числа,
делящиеся на а, — это числа а, 2а, За, ..., т. е. числа вида ka,
где k£N. Поэтому |Св| равно наибольшему натуральному k,
такому, что k -а^. 1000. В частности, |Сз1 =333, I Cs I =200. Кроме
109
того, |Е| = 1000. Пользуясь формулой Грассмана, получаем
|E\(C3UС5)| = |Е| -1C3UС6| = |Е| -(|С3| + |С5| - |СзПС5|)=
= 1000 - 333 - 200+ |СзПС6|.
Осталось найти |СзГ)Св1- Множество С3ПС5 состоит из чисел,
делящихся на 3 и на 5, т. е. делящихся иа 15. Значит, ] Сзf| С&1 =
= |Ci5|=66. Окончательно получаем, что в искомом множестве
1000-200—333+66=533 числа.
Прн решении уравнений с двумя неизвестными и их систем
нужно учитывать, что каждое решение есть пара чисел. Поэтому
возникает необходимость рассматривать множества, элементами
которых служат пары чисел. Пара чисел an b записывается так:
(а; Ь). Число а называется первой координатой пары, число Ь —
второй координатой. Пару (а; Ь) удобно изображать точкой М (а; Ь)
на координатной плоскости.
Произведением числовых множеств А н В называется множест-
во пар чисел (а; Ь), где а£Аг Ь£В. Произведение множеств обозна-
чается А ХЕ- Если хотя бы одно из множеств А, В пусто, то А ХЕ
также считается пустым множеством.
Теорема. Если А, В — конечные множества, то множество
А%В конечно и число его элементов равно произведению |А| и
IEI-
Доказательство. Пусть А=(at; а2; - - •; a*}, B={bt; b2;
. ..; Ьр). Зафиксируем первую координату х в паре (х; у), а вторая
пусть пробегает множество В. Например, прн x=ai получаем пары
(«Г, Ь|),..(gi; Ьр). Их столько, сколько элементов в В, т. е. р. Име-
ется k возможностей выбора первой компоненты нары, т. е. столь-
ко, сколько элементов в множестве А. Всего получается пар k-p,
т. е. |АхЕ1 = |А|-|Е|.
Замечание. В приведеииом доказательстве предполагает-
ся, что оба множества А, В непусты. Докажите, что результат
остается верным и в случае, когда одно нз множеств А, В пусто.
Задачи
7. Решите уравнение:
а) (х!-1)(л!-Зх+2)=0; б) -^1^=0.
8. На координатной плоскости даны три множества: А —
множество точек А (х; у), у которых |х| 1; В — множество точек
В (х; у), таких, что Ц/1 1; С — множество, равное графику функ-
ции у~2х. Изобразите множества: a) Af)B; б) AJE; в) Ар С;
г) ВрС; д) АрЕрС.
9. Пусть А — множество четных чисел из промежутка
[100; 1000], а В — множество чисел, кратных 5, из того же про-
межутка. Сколько чисел в множестве: а) Ар В; б) AJB?
ПО
10. Многие из вас любят журнал «Квант». Все читатели его-
интересуются хотя бы одной из областей знания — математикой
илн физикой. По данным одного из опросов, математикой интере-
суются 84% читателей, физикой — 64%. Какой процент читателей
«Кванта» интересуется и той н другой наукой?
II. На рисунке 78 изображены два множества точек коорди-
натной плоскости. Каждое из ннх представьте в виде произведения
двух множеств.
12. Докажите, что если А н В — непустые множества, Ас=В
н А бесконечно, то В — бесконечное множество.
13. Сколько различных множеств можно составить из чисел
1, 2, 3, 4, 5, 6, если для образования множества разрешается ис-
пользовать некоторые (необязательно все) нз них?
14. Операции с множествами обладают разнообразными
свойствами; докажите некоторые из них: a) Af)A=A и A|JA =А;
б) если АсВ,тоАПВ=А и в) А\А= 0; г) если
= 0, то А\В=±А-, д) AUB=(Af]B)U(B\A)U(A\B).
15. Верно ли, что если A—B\JCt то В=А\С?
16. а) Произведение множеств не обладает переместительным
свойством (в отличие от переместительного свойства умножения
чисел). Проверьте, например, что {1; 2}Х(0; 1}Х{Ъ 2}.
б) Объединение, пересечение и разность множеств обладают
распределительным свойством относительно произведения. Про-
верьте, например, что (AUB)XC=(AxC)U(BXC). в)’ Докажите,
что множество {(0; 0); (0; 1); (I; 0)} нельзя представить в виде произ-
ведения двух множеств.
ОПЕРАЦИИ НА ЧИСЛОВОМ МНОЖЕСТВЕ
1. Рассмотрим свойства, которыми могут обладать операции
с числами. Сначала уточним понятие операции.
Алгебраической операцией на числовом множестве М называ-
ется соответствие, прн котором любой заданной паре (a; fe) элемен-
тов нз М сопоставляется ровно одни элемент множества М.
П р н м е р ы. а) Известно, что сумма двух натуральных чисел
снова натуральное число и сумма целых чисел тоже целое число.
Hi
Значит, сложение на множестве N н сложение иа множестве 2 —
алгебраические операции. Мы привыкли считать, что сложение
н на N, и на Z — «одна и та же операция». Однако сложение на
множестве N и сложение на множестве Z имеют разные свойства:
уравнение х+8—5 имеет корень, если искать решение в/, и не
имеет, если искать решение в Л/. Замечание. Прн решении
упражнений, в которых встречается алгебраическая операция,
важно отмечать, на каком множестве рассматривается данная
операция.
б) Произведение двух натуральных чисел — натуральное
число. Произведение двух положительных рациональных чисел —
положительное рациональное число. Значит, умножение иа N и ум-
ножение иа множестве А положительных рациональных чисел —
алгебраические операции. Эти операции обладают различными
свойствами. Например, уравнение 2х=1 не имеет корней на
множестве N, но имеет иа множестве А.
Несмотря на то что одноименные операции на различных
множествах обнаруживают различные свойства, они все же могут
быть согласованы как сложение на N н Z илн как умножение на N
н А
Пусть на множестве М определена алгебраическая операция
и Вс^М. Если для любых элементов из В результат операции
вновь принадлежит В, то множество В называют замкнутым
относительно этой операции. Например, N замкнуто относительно
сложения как подмножество Z. Аналогично N замкнуто относи-
тельно умножения как подмножество А.
Примеры, а) Разность двух целых чисел — целое число
Значит, вычитание алгебраическая операция на Z. Будет ли она
алгебраической операцией также на N? Нет. Например, 5G2V,
б£Л/, но 5—V. Значит, N не замкнуто относительно вычитания
б) Является ли деление алгебраической операцией на Q? Нет,
потому что результат алгебраической операции должен быть
определен для любой пары элементов, а в данном случае это не
так: деление на нуль не имеет смысла. Тем не менее и такие дейст
вня, как деление, в математике изучаются. Их называют частич-
ными операциями. Частичная операция дает результат не для лю-
бой пары, ио в случае, когда результат можно найти, он опреде-
ляется однозначно.
Иногда множество удобно записывать в виде А={х|Р(х)},
где Р (х) — свойство, которому удовлетворяют все элементы мно-
жества А (н только они). Запись читается так: «Множество А
состоит из элементов х, для которых выполняется свойство Р(х)>.
Например, множество четных чисел можно записать в виде (х|х=
=2fe, k£Z}, т. е. «множество, состоящее из чисел вида 2k, где k —
целое число». Множество нечетных чисел можно записать в виде
{х1х=2*+1. kez}.
Иногда для записи множества приходится использовать два
или даже больше параметров, а ие одни, как в рассмотренных слу-
112
чаях. Например, множество А={х1х—а4-6 д/2, a, b 6Q} состоит нз
чисел вида а 4-6 д/2, где а, b — рациональные числа. В частности,
1£А,таккак 1 = 14-0-\/2. Аналогично О G А,-\/2£Л ит. д. (Докажи-
те, что А замкнуто относительно сложения и умножения. Замкнуто
ли это множество относительно вычитания?)
2. В математике рассматривают много разных операций. Одна-
ко мы ограничимся известными из школьного курса операциями
сложения, вычитания, умножения и деления. Эти операции наибо-
лее употребительны как в математике, так н на практике.
Все вычисления в алгебре производятся с использованием
свойста операций. Таких свойств очень много. Для их изучения
применяется та же идея, что и в геометрии, где небольшое коли-
чество фактов считается аксиомами, а другие доказываются на их
основе. В алгебре также выделяется набор основных свойств, ак-
сиом числовых операций. Приведем список этих аксиом:
1. Для любых чисел а, Ь:
а) а-\-Ь=Ь-\-а-, б) a-b—b-a.
(Переместительное свойство сложения и умножения.)
2. Для любых чисел а, Ь, с.
а) (а4-^)4-с = а-Ь(^4-с); б) (а*6)’С=а*(6«е)
(Сочетательное свойство сложения и умножения.)
3. Для любых чисел а, 6, с:
(а 4- Ь)-с~а-с 4- b 'С.
(Распределительное свойство сложения относительно умноже-
ния.)
4. Для каждого числа а:
а) «4-0—0-}-а=а; б) а*1 = 1-а—а.
(Основное свойство нуля и единицы.)
5. Для каждого числа а имеется только одно число 6, такое,
что а4-6=0; оно обозначается —а. (Основное свойство числа,
противоположного данному.)
6. Для каждого числа имеется ровно одно число Ь,
такое, что а • b — 1; оио обозначается а ~1 или . (Основное свойст-
во числа, обратного данному.)
7. Равенства а-)-Ь—с и с—а—Ь равносильны. (Основное
свойство вычитания.)
8. Если ау=0, то равенства а-Ь=с и —-=6 равносильны.
(Основное свойство деления.)
Свойства 1,2,4 подчеркивают сходство сложения и умножения.
С другой стороны, этн операции имеют н различия: у сложения нет
из
ограничений на указанные в свойствах 5 н 7 равенства, а для ум-
ножения такое ограинчеиие (а=/=0) есть в «параллельных» свойст-
вах 6 и 8.
На основе свойств действий формулируются правила преобра-
зований уравнений и выражений. Например, свойство 7 позволяет
указать правило переноса члена уравнения из одной части урав-
нения в другую с изменением знака. Впервые такие правила были
указаны в трактате замечательного арабского математика Мухам-
меда аль-Хорезм и «Краткая книга об исчислении аль-джсбр и
аль-мукабалы», написанном в 820 г. в Багдаде, одном из крупней-
ших центров науки того времени. Одно нз таких правил — «аль-
джебр» (по-русски — восстановление) — состояло в переносе чис-
ла из одной части уравнения в другую, причем слагаемое следова-
ло вычесть, а вычитаемое прибавить. Арабское слово «аль-джебр»
при переводах иа европейские языки превратилось в слово «ал-
гебра». Правило «аль-мукабала» нам также известно: это приведе-
ние подобных членов в выражении, его упрощение.
Приведем пример доказательства одного нз свойств операций.
На множестве действительных чисел выполняется распредели-
тельный закон умножения относительно вычитания:
(а—Ь)-с=а*с—Ь'С.
Доказательство. По свойству 2 запишем {а— b)+b=a.
Умножим это равенство иа с и по свойству 3 получим {а—Ь)*с-\-
~\-Ь'С~а-с. Если перенести слагаемое b-с в правую часть ра-
венства с противоположным знаком, то получим искомое ра-
венство.
Аналогично, используя основные свойства 1—8 и ранее дока-
занные теоремы, можно вывести все свойства арифметических
операций, например свойство нуля при умножении (а-0—0 для
любого числа а), правило знаков (а-(—b)=—a-b, (—«)-(—£>)=
=а-Ь для любых чисел а, Ь) и т. д.
В дальнейшем мы будем свободно пользоваться всеми извест-
ными из школьной алгебры свойствами арифметических действий.
Задачи
17. Даны множества: Ai={—1;0; 1}, Д2={— 1; 1}, Аз==[х\х=
=3t, A6Z). Л«=!х|*=ЗА + 1. As—|х|х—a^z] , Ae=
-R\Q. А,=[0; ЛЕ=(0; +<х>).
Исследуйте замкнутость каждого из них относительно сложения и •
умножения.
18. а) Докажите, что (a-f-6):c=a:c-f-6:c для любых чисел а,
b и любого с=#0.
б) Верно ли, что а:(^4-с)=а:6+а:с (при &4-с=^0; 6=#=0;
*¥=0)?
114
1ft. Простейшее тождество
x+(—x)—О
удивительно часто помогает решать
задачи, а) Пусть cti, а2, .
найдите сумму
(d— о2)+(а2—аз)4-.. at).
б) Докажите, что
_Lj_ J. l ~1------!—
1-2 ' 2-3 *+’
( Воспользуйтесь тождеством —-
в) Докажите, что +... + (24_,)^+0
(Воспользуйтесь тождеством —------— — . )
X X-J4, /
г) Докажите, что
(a—fc)(ab-,+afc-2fc+«ft~3^ + -.-+bt~,)=«ft—bk.
(* 11) •)
20. а) Проверьте, что площадь заштрихованной на рисунке
79 фигуры равна fe3.
б) Докажите, что 1Э+23+.. .-f-fc3=(l 4-2+ +^)2
(Используйте формулу из задачи 19, а.)
21. Упростите выражение
(х+о)(хг+а!)(х’+о,)(х'+а8)(х,6+а16).
(Указание. Умножьте н разделите это выражение на двучлен
(х—а).)
22. а) Про числа Xi и х2 известно, что х>-|-х2=5, xi«x2=6.
Пользуясь только этой информацией, найдите, чему равно х?+
+xl; a'i+xj. ,
б) Про числа X) и х2 известно, что xi+x2=a, Xi-x2—b. Дока-
жите, что каждое из этих чисел служит корнем уравнения x2+fe=
=ах.
ПОНЯТИЕ О ЧИСЛОВОМ КОЛЬЦЕ И ЧИСЛОВОМ ПОЛЕ
1. Арифметические операции изучаются в тесной связи друг
с другом. В математике выделено два наиболее важных набора
операций. Первый состоит из сложения, вычитания и умножения.
Второй, сверх того, включает деление. С этими наборами связаны
два важнейших понятия современной алгебры.
Определение 1. Непустое множество KcJ? называется
числовым кольцом (или просто кольцом), если К замкнуто отно-
сительно сложения, вычитания и умножения.
115
Определение 2. Множество Kczl? называется числовым
полем (или просто полем), если К содержит число 1 н замкнуто
относительно сложения, вычитании, умножения и деления (на лю-
бое не равное нулю число).
Примеры. Множество целых чисел 1 — кольцо. Множества
Q и К — поля. Очевидно, что любое поле является кольцом. Но
обратное неверно: кольцо Z полем не является (почему?). Мно-
жество А четных чисел также является кольцом, потому что
сумма, разность н произведение четных чисел — четные числа. Мы
видим, что одно числовое кольцо может содержаться в другом;
аналогично для полей. Это замечание служит основанием для вве-
дения следующего понятия.
Определение 3. Пусть А, В —- кольца иZA<=B. Тогда А
называется подкольцом кольца В. Пусть Л, В — поля и А с: В. Тог-
да А называется подполем поля В.
Пусть k — некоторое натуральное число. Легко показать, что
множество всех кратных числа k, т. е. множество {x\x—a-k, a{Z},
является кольцом, при этом подкольцом Z. Оказывается, что такой
вид имеет любое подкольцо Z. Исключение составляет кольцо,
состоящее из единственного числа — нуля; такое кольцо называет-
ся нулевым.
Теорема. Пусть В — подкольцо (ненулевое) Z. Тогда най-
дется натуральное число k, такое, что B={xlx—k^a, a£Z}.
Доказательство. Поскольку В — ненулевое кольцо; в
нем имеется некоторое натуральное число н Ь^В. Тогда
(—6) также принадлежит В и нз двух чисел Ь, —b одно натураль-
ное. Обозначим теперь через k наименьшее натуральное число в
кольце В. Для доказательства теоремы достаточно показать, что
любое число Ь£В делится на k. Для этого разделим b на k с остат-
ком: b=k-y-\-ct где y^Z и O^c^k— 1. Ясно, что с£В, потому
что —k-y. Если бы с было натуральным, то в В нашлось бы
натуральное число, меньшее, чем k, — противоречие с выбором k.
Значит, с=0, откуда b=k*y, y£Z. Теорема доказана.
Интересным примером кольца служит множество D конечных
десятичных дробей (проверьте, что D — кольцо). Это кольцо не
замкнуто относительно деления (мы знаем, что-y-gO, хотя 1 и 3 —
элементы D). Одиако в D имеется много примеров таких чисел,
обратные к которым также принадлежат D. Например, 260 и
1060 и -руб О....Попробуйте доказать, что если х£О,
60, то х имеет вид x=2fc5₽, где k, р целые числа. Этот пример
показывает, что изучение колеп тесно связано с теорией делимости
целых чисел
Все рассмотренные выше кольца были подмножествами Q (кро-
ме R). Вот пример кольца, содержащего иррациональные числа.
116
Обозначим через А множество {xJx=G-|-b a,b€Z\. Множество
А — кольцо, это легко проверить по определению.
Приведенный пример служит частным случаем общей конструк-
ции, которая называется расширением кольца. Пусть а — некото-
рое нецелое число. Какие числа необходимо присоединить к мно-
жеству Z, чтобы полученное множество образовало кольцо, содер-
жащее а? Ясно, что в искомом кольце должны содержаться все
числа вида 1, а, а2, а3, . и все суммы вида . .-Ь
-t-kpap, где р — целое неотрицательное число и k0, ki, ..., kp—
целочисленные коэффициенты.
Множество, состоящее из всевозможных таких выражений, —
кольцо. Ойо называется расширением Z при помощи числа а н
обозначается Z [а]. Рассмотренное выше кольцо А — расширение Z
прн помощи д/2; в данном случае достаточно использовать лишь
выражения вида потому что уже бД)2— целое число.
Теперь рассмотрим множество B={x\x=a + b-yfii, a, b£Q] и
докажем, что В — поле. Замкнутость относительно сложения, вы-
читания н умножения проверяется без труда. Чтобы доказать
замкнутость В относительно деления, достаточно проверить, что
если х£В и ху=о, то х~’СВ. Рассмотрим цепочку равенств:
1 _____а—Ь у/2_______ а—Ь ~\2 а —Ь
a+bfi (a + tV2)(a-*V2) a£-2fc2 a2—2fes **
В итоге x представлено в виде «рациональное число плюс рацио-
нальное число, умноженное на -у/2», т. е. В замкнуто относительно
деления, поэтому. В — поле.
Заметим, что в рассмотренной последовательности преобразо-
ваний мы домножали числитель и знаменатель дроби иа не равное
нулю число а—(действительно, если допустить, что
а—Ь-у/2—0, то либо -Д—рациональное число, либо а=Ь=О.
Использованный нами пример носит название исключение ир-
рациональности е знаменателе. При этом нужно домножить числи-
тель н знаменатель данной дроби иа такой множитель, чтобы у
полученной дроби знаменатель был бы уже рациональным числом.
Здесь удобно использовать формулы сокращенного умножения.
2. Многие числовые кольца связаны с алгебраическими уравне-
ниями. Напомним, что алгебраическим иазываетси уравнение вида
а (х)= b (х), где а (х) и Ъ (х) — многочлены. Алгебраическое уравне-
ние можно записать в виде с(х)—0, где с(х)—многочлен стан-
дартного вида. Особенно интенсивно в алгебре и теории чисел
изучаются алгебраические уравнения, коэффициенты которых —
рациональные числа. Дадим основное определение:
Число х0 называется алгебраическим, если оно является корнем
алгебраического уравнения с рациональными коэффициентами,
степень которого больше или равна 1.
117
Роль условия рациональности коэффициентов уравнения со-
стоит в следующем. Для любого числа х0 совсем просто указать
(алгебраическое) уравнение, корнем которого служит это число:
х—х®=0; можно указать н аналогичное уравнение любой степени:
(х—хо)*=О. Смысла в таких уравнениях немного. С другой сторо-
ны, указанное условие выделяет очень интересный и важный
класс уравнений.
Применяя к рациональным числам арифметические операции и
извлечение корней, мы всегда получаем алгебраические числа. По-
кажем, например, что число д/2-j—\/3 алгебраическое. Обозначим
его х0. Тогда x2=(’\^+^l3)2=54-2-\/б, значит, Хо—5=2-\/б.
Возведя это равенство в квадрат, получим (х®—б)2=24, т. е. хо —
корень уравнения х4— 10х24-1 =0.
Верно н гораздо более общее утверждение: множество алгеб-
раических чисел замкнуто относительно всех арифметических опе-
раций, т. е. является полем. Легко доказать, например, что если
Хо — алгебраическое число, то число х0-Ь 1 н вообще любое число
вида xo-}-fc, k£Q, алгебраическое. Точно так же xo’k алгебраичес-
кое. Мы не будем доказывать сформулированную теорему. Однако
в связи с ней возникает вопрос: быть может, каждое действитель-
ное число алгебраическое? Оказывается, что ответ на него отрица-
тельный. Существует неалгебранческие (трансцендентные) числа.
Мы вернемся к этому вопросу в заключительном разделе.
Задачи
23. Докажите следующие утверждения:
a) N— не кольцо; 2 — не поле;
б) если К —кольцо н а€Л, то и —
в) 0 содержится в любом кольце (верно ли, что 1 содержится
в любом кольце?);
г) если К — поле н а5^0, а£К, то а~1£К;
д) если К— кольцо и то 2 ст/С.
24. Докажите, что множество Д={х|х=6а4-156; a, b^Z\—
подкольцо в Z, и найдите c£N, такое, что
Д=(х|х=с«р; y£Z).
25. Кольцо 2 [-\/2|=(х|х=а+6 д/2; а, 6€Z} — не поле. Для до-
казательства достаточно найти такой элемент x6Z[y/2J, что
х~‘£2[-^2]. Покажем, например, что число х=2 обладает этим
свойством, т. е.
26. Исключите иррациональность в знаменателе каждой из
дробей:
1—^2 1 1
14-^2 ’ V2+V5 * V54-V6+V7
118
27. Докажите, что каждое число поля В=^(х\х=а-^Ь -у/2; а,
b^Q} служит корнем квадратного уравнения с рациональными
коэффициентами.
28. Найдите уравнение, корнем которого служит число /3—
—v2-
29. Пусть хс — корень уравнения 2;г-|-хЧ-1=0. Найдите
уравнение с корнем: а) б) Ло—1; в) г) —.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
1. При решении уравнений приходится постоянно сталкиваться
с тем, что их корни не принадлежат тем множествам, из которых
берутся коэффициенты. Например, корни квадратного уравнения
с рациональными коэффициентами могут быть иррациональными.
Это послужило важной причиной расширения области рациональ-
ных чисел. Рассмотрим еще одну, в практическом отношении
намного более важную причину, приведшую в конце концов к
построению множества действительных чисел: рациональных чисел
ие хватает для того, чтобы выражать результаты измерения. Рас-
смотрим этот вопрос иа примере измерения длины отрезка.
Определение. Отрезки АВ и CD называются соизмери-
мыми, если найдется отрезок XY, который в каждом из иих укла-
дывается целое число раз. XY называется общей мерой АВ и CD.
Ясно, что отрезки соизмеримы тогда и только тогда, когда,
взяв один нз них в качестве единицы измерения, мы получим в
качестве Длины другого отрезка рациональное число. На заре
возникновения математики в Вавилоне, Древнем Египте, Древней
Греции принималось как само собой разумеющееся, что результат
измерения будет рациональным числом в любом случае. В этом
ученых убеждал опыт практических измерений: все отрезки в пре-
делах достигаемой точности оказывались соизмеримыми. Но в VI в.
до н. э. древнегреческие математики (по преданию, первым
это сделал Пифагор) подвергли процесс измерения внимательному
анализу и, к своему изумлению, пришли к парадоксальному
результату, диагональ квадрата и его сторона несоизмеримы.
Действительно, пусть XY — общая мера АВ и АС в квадра-
те ABCD, т. е. AB=>p-XY, AC~k*XY. Применяя к равнобедрен-
ному прямоугольному Д АВС теорему Пифагора, получаем р2-)-
-)-р2=А2, т. е. 2=(-^-) . Но число 2 не может служить квадра-
том рационального числа (именно это и смог доказать Пифагор).
Значит, общей меры у АВ и АС нет. С современной точки зрения
теорему можно выразить так: -^2 — иррациональное число. Но для
древнегреческого математика слова «число» и «рациональное чис-
ло» были синонимами. Других чисел он не мог и не желал пред-
ставить.
119
Для полного признания иррациональных чисел потребовалось
более двух тысячелетий. Помимо общего прогресса науки, этому
способствовало развитие и распространение позиционной десятич-
ной системы счисления. Напомним ее основные положения: а) чис-
ла записываются с помощью специальных знаков — цифр, обозна-
чающих числа первого десятка; б) изменение места цнфры на одни
разряд вправо уменьшает ее числовое значение в 10 раз. Заметим,
что аналогичную идею можно использовать и при построении
системы единиц измерения длины: выбрать основную единицу,
для более точных измерений взять ее десятую часть, для еще более
точных — сотую и т. д. Именно так построена десятичиая система
мер, принятая сейчас во всем мире. Достоинство ее в том, что
результат измерения некоторой величины (например, длины) очень
удобно выразить числом в десятичной позиционной системе счис-
лении.
Подведем некоторые итоги: 1. Необходимость во введении
иррациональных чисел связана с тем, что прн выбранной единице
нзмереиня не у всякого отрезка длина выражается рациональным
числом. 2. Длина отрезка при использовании позиционного деся-
тичного принципа измерения имеет внд конечной или бесконечной
десятичной дроби.
Сопоставим эти факты с одним нз важнейших свойств длины:
длина отрезка — положительное действительное число. Мы при-
ходим к выводу, что каждое положительное действительное число
может быть представлено в виде конечной илн бесконечной деся-
тичной дроби. Для записи отрицательного числа в виде десятич-
ной дроби следует, конечно, поставить знак «—» перед записью
модуля этого числа.
2. Соответствие между положительными числами и длинами
отрезков можно расширить до соответствия между множеством
действительных чисел и множеством точек координатной прямой.
Вот небольшой «словарик перевода», пользуясь которым можно
переходить от некоторых числовых и алгебраических понятий к
геометрическим (а также и в обратную сторону):
М (х) — точка координатной х — координата точки М
прямой
М(х)еОх
М (xj) правее Р (х2)
отрезок МР
длина отрезка МР
x£R
Х»>Х2
числовой отрезок [х^ х2]
|Х|— х2|
Пользуясь геометрическими представлениями и их переводом
на язык алгебры, выведем теперь одно из основных свойств мно-
жества действительных чисел. Сначала введем нужные для этого
понятия. Заметим, что иногда вместо записи используют
запись В^>А (читается: «Множество В содержит множество Л»),
имеющую тот же смысл.
120
' 'Вл
Рнс. 80
О,25® 99... * 0,25®
Последняя не рабная О цифра
дггфзд... - о,25(^
Рис 81
Определение. Отрезок АВ называется вложенным в отре-
зок CD, если АВ с. СО. Бесконечная последовательность отрезков
AiBi - .=>Л*В{.=>... называется стягивающейся, если
при возрастании номера отрезка его длина неограниченно умень-
шается, приближаясь к нулю. (На рисунке 80 каждый отрезок по-
казан на своей прямой, хотя это одна н та же прямая.)
Наглядно очевидно, что у стягивающейся последовательности
отрезков имеется точка, общая всем ее отрезкам; ясно также, что
такая точка может быть только одна. При помощи «словарика
перевода» легко преобразовать это свойство в утверждение о
действительных числах. Мы получаем основное свойство стягива-
ющихся числовых отрезков: существует ровно одно число, принад-
лежащее всем отрезкам данной стягивающейся последовательнос-
ти числовых отрезков.
Приведем пример использования этого свойства. Покажем, что
1=0,999... . Для доказательства построим стягивающуюся по-
следовательность числовых отрезков, которым принадлежат оба
эти числа. Нужными свойствами обладает, например, последова-
тельность
[0,9: 1,1]=э[0,99: 1.01]:э [0.999: 1.001]о... _э[1 —10 1 + НГ*]:х.
Проверьте справедливость утверждений: а) каждый отрезок этой
последовательности содержится в предыдущем; б) длины отрезков
неограниченно уменьшаются, приближаясь к нулю; в) числа 1 н
0,999... содержатся во всех отрезках этой последовательности.
Этот пример служит иллюстрацией к полезному замечанию:
можно доказать, что каждое действительное число изображается
ровно одной бесконечной десятичной дробью, не содержащей
«хвоста» девяток. Мы всегда, пользуясь этим фактом, будем заме-
нять бесконечные дроби с «хвостом» девяток на дроби с нулями
иа конце (рис. 81). С учетом этого замечания имеется полное
соответствие чисел x£R, бесконечных десятичных дробей н точек
координатной прямой.
Пользуясь координатной прямой, легко придать наглядность
характеру расположения в множестве В целых и рациональных
чисел. Вспомним, что каждое действительное число можно с любой
121
точностью приблизить рациональным. Это означает, что точки с ра-
циональными координатами расположены иа прямой «густо». С
другой стороны, точки с целыми координатами встречаются «ред
ко». Уточним математическое содержание нашего представления о
том, что такое «густо» и что такое «редко».
Числовое множество называется дискретным, если его пересе-
чение с любым числовым отрезком конечно, н плотным, если его
пересечение с любым числовым отрезком непусто.
Множество Z целых чисел — дискретное множество, а мно-
жество Q рациональных чисел — плотное множество. Несложное
доказательство дискретности Z найдите самостоятельно (см. зада-
ние 6, а).
Теорема. Множество рациональных чисел плотно.
Доказательство. Заметим, что если длина отрезка, рас-
положенного на координатной прямой, больше или равна 1, то ему
обязательно принадлежит хотя бы одна точка с целой координатой.
Пусть теперь [а; Ь] — данный отрезок. Наряду с ннм рассмотрим
отрезки [2а; 2b], [За; 3bJ .... Длины этих отрезков равны (Ь—а),
2 (Ь—а), 3 (Ь—а),... . Ясно, что для некоторого натурального чис-
ла k длина отрезка [ka; kb] больше 1, т. е. k (b—а)> 1. Поэтому ему
будет принадлежать некоторое целое число р. Имеем: ka С kb,
откуда a^J~^b. Следовательно, рациональное число -^-принад-
лежит [о; /?], и, значит, [а; Ь]П 0-
Аналогичными рассуждениями можно доказать плотность мно-
жества D конечных десятичных дробей, множества дробей со зна-
менателями вида 2*. где k — неотрицательное целое число, и т. д.
Следствие. Пусть а, b(a<b)— иррациональные числа.
Тогда между инмн расположено некоторое рациональное число.
Действительно, подсказанному на отрезке [о; Ь]есть рациональное
чнсло с, такое, что а с Ь. Но с не равно ин а, ии b (так как ан b
иррациональны, а с рационально). Значит, а<с<Ь, т. е. с лежит
между а и Ь.
3. Рассмотренные иамн свойства действительных чисел можно
использовать при изучении уравнений н неравенств. Известно, что
решить уравнение — значит найти все его корни (т. е. найтн мно-
жество его корней). Но что означает слово «найти» в этом пред-
ложении? Мы увнднм, что возможно несколько подходов к зада-
нию «иайти корни уравнения». Исторически наиболее ранним был
подход, состоящий в поиске выражений длн нахождения корней, в
состав которых входили коэффициенты данного уравнения. Таким
образом, с этой точки зрения решить уравнение — значит найти
формулу, выражающую его корни через коэффициенты уравнения.
Например, формулы корней линейного и квадратного уравнений
нам известны, следовательно, мы умеем их решать. Такое понима-
ние задачи решения уравнений сыграло огромную роль в развитии
алгебры; иа протяжении нескольких веков эта задача считалась
122
главной в этой науке. Вот отрывок нз трактата замечательного пер-
сидского ученого (и поэта) Омара Хайяма (XI в.):
«.. .Искусство алгебры н аль-мукабалы есть научное искусство,
предмет которого составляют ... величины, являющиеся неизвест-
ными, но отнесенные к какой-либо известной вещи, по которой их
можно определить... Цель этого искусства состоит в нахожде-
нии соотношений, связывающих его предмет с указанными дан-
ными».
Напряженные поиски привели математиков к открытию формул
корней уравнений 3-й и 4-й степени (XVI в., Италия), в дальней-
шем были сделаны и другие замечательные открытия. Однако в
большинстве случаев полученные формулы были малопригодны
для проведения расчетов. Приведем, например, формулу корней
уравнения 3-й степени, полученную итальянскими учеными С ц н-
пионом дель Ферро (1456—1526) и Николо Тар-
таль е й (1500—1557): корнем уравнения х3-|-рхЧ-/7=О служит
число
Пользоваться этой формулой для приближенного нахождения кор-
ней затруднительно. Таковы и другие формулы корней. Вспомним
о наглядном н практически удобном, хотя и дающем небольшую
точность, графическом методе решения уравнений и неравенств.
Для нахождения корней уравнения а (х)=0 изобразим график
функции у=а(х) и найдем точки пересечения его с осью абсцисс.
Абсциссы полученных точек есть приближенные значения корней
уравнения. При решении неравенства а(х)>0 изобразим график
функции у=а(х), затем найдем ту часть графика, которая распо-
ложена в верхней полуплоскости, и возьмем абсциссы точек этой
части (рис. 82, а). Для неравенства я(х)<0 есть аналогичное
правило (рис. 82, б). Из рисунков видно, что корни уравнения
а(х)=0 разбивают область определения функции у=а(х) на ин-
тервалы, в которых она сохраняет знак. Чтобы узнать этот знак,
достаточно выбрать в интервале точку и найти знак функции в ией.
Таким образом, решение неравенства сводится к решению уравне-
ний.
{х|ед»о} = (с.-Ц и (£;+«) {x|fCx)<O}=f-~;o)U(«;c)
а)
В)
Рис 82
123
Мы видим теперь, что уравнения решаются по-разному. Однако
имеется одно непременное условие поиска корней: мы должны
быть уверены в том, что искомый корень существует. Возникает
поэтому проблема нахождения признаков существования корней
уравнений. Для квадратных уравнений такой признак нам извес-
тен. Приведем один нз признаков существования корня, пригодный
для алгебраических уравнений более высоких степеней (и для
многих других классов уравнений): если многочлен а (х) принимает
в точках x=xi и х=х2 значения разных знаков, то иа отрезке
[Xi;x2] уравнение а(х)=О имеет (хотя бы один) корень. Доказы-
вать эту теорему мы не будем. Одиако необходимо пояснить ее. За-
метим длн этого, что многочлен принимает близкие значения прн
близких значениях аргумента. Например, многочлен а(х)=х4 —
—2х34-Зх2—2х-|-2 при х—3 и х=3,01 принимает соответственно
значения о(х)=50 и а(х)=50,7. Если взять значение аргумента
еще блнже к х=3, то соответствующее значение многочлена будет
приближаться к а(3)==50. Поэтому график многочлена — плав-
ная, неразрывная линия; ее можно изобразить, не обрывая каран-
даша от листа бумаги. (Именно этим свойством графика мы поль-
зуемся, когда стронм его по точкам). Но теперь становится нагляд-
но ясным, что для того, чтобы перейти от значений одного знака
к значениям другого знака, многочлену необходимо «по дороге»
принять значение, равное нулю, т. е. в некоторой промежуточной
точке х0 между Х| н х2 значение а (х0)—0.
Опишем теперь прием приближенного решении уравнений, на-
зываемый методом деления отрезка пополам. Он состоит в построе-
нии последовательности вложеииых отрезков (начиная с отрезка
[xj;x2]), причем каждый следующий отрезок — одна из двух по-
ловин предыдущего. Какая именно половина, определяется следу-
ющим образом: левая половина выбирается тогда, когда значения
многочлена в левом конце отрезка и в его середине разных знаков;
правая половина выбирается тогда, когда значения многочлена
в правом конце отрезка и в его середине разных знаков. (Если же,
производя деление отрезка, мы наткнемся иа корень, то процесс
прекращается — задача решена.) Таким путем получается стяги-
вающаяся последовательность отрезков; общая точка этих отрез-
ков, как можно доказать, является корнем многочлена; концы
же его могут служить приближенными значениями корня. Легко
понять, что таким путем можно найти корень многочлена (т, е.
уравнения а(х)=0) с любой степенью точности (рнс. 83).
Следующий, отрезок
Рис. 83
124
Теорема. Уравнение а (х)—0, где а (к) — многочлен нечет-
ной степени, имеет корень.
Доказательство. Достаточно проверить, что многочлен
нечетной степени принимает как пложительные, так и отрицатель-
ные значения. Пусть дан конкретный многочлен а(х)=х34-лл:а+
+6*4-с (в общем случае рассуждения такие же). Рассмотрим
выражение
-2^ = l+f+>+^-
При больших по модулю значениях к трн последних слагаемых
в правой части мало отличаются от нуля. Поэтому выражение,
стоящее в правой части равенства, мало отличается от 1, т. е. оно
положительно. Значит, найдется такое число Хо, что числа
—и положительны. Отсюда получаем, что а(хо)>0,
*о (—*0/
а (—Хо)<0. По сформулированной выше теореме получаем, что иа
отрезке [—хо;хо] уравнение а(х)=0 имеет корень.
Уравнения четной степени разрешимы не всегда. Например,
квадратное уравнение х2-}-1 =0 не имеет корней, потому что для
любого х£/? многочлен x2-f-1 принимает положительные значения.
Вообще можно доказать, что многочлен четной степени с положи-
тельным старшим коэффициентом не имеет корней тогда и только
тогда, когда его можно представить в виде суммы квадратов
некоторых многочленов в положительного числа Напрнмер, урав-
нение х4—2х34-Зх2—2х-}-2=0 не имеет корней, потому что его
левая часть может быть преобразована к виду
(х2—xf'+x’-Hx—1)2+1.
Подведем некоторые итоги. Для этого приведем отрывок из
широко распространенного во второй половине XIX в. курса ал
гебры (его автор Ж. А. Серре — известный французский матема-
тик): «Алгебра, по существу говоря,—анализ уравнений...
С этой точки зрения алгебра может быть разделена иа трн части:
1. Общая теория уравнений. 2. Решение численных уравнений, т. е.
определение точных или приближенных значений корней уравне-
ния. 3. Алгебраическое решение уравнений, т. е. определение выра
жения, составленного из коэффициентов данного уравнения, кото-
рое, будучи в него подставленным вместо неизвестного, тождест-
венно ему удовлетворяет».
Сравните этот отрывок с приведенным выше высказыванием
Омара Хайяма. Прошло восемь веков активного развития алгебры,
но взгляд на предмет науки не изменился! И в настоящее время ре-
шение уравнений — одна из главных задач в алгебре. Конечно,
за последние два века в ней возникло н интенсивно развивается
много новых идей. Одна из них (кстати, успешно применяющаяся к
125
решению уравнений) — изучение свойств различных операций на
множестве.
Пример. Определим в кольце Z [-\/2] операцию: если х=п+
+ Ь ~у2 — даииое число, то положим х=а—b ^2; число х называ-
ется сопряженным к х. Легко доказать свойства операции сопря-
жения: х+у=х-±-у; Х'у-х-у; если k^N, то х*=(х)*; х~х тогда
и только тогда, когда xgZ. Пользуясь этими свойствами, докажем
удивительный результат, связывающий два, казалось бы, совер-
шенно разных вопроса: решение уравнений в целых числах и на-
хождение таких чисел в кольце Z [д/2], обратные к которым вновь
принадлежат Z [-^2]. Число х=а4-6 д/2 кольца Z [д/2] имеет в этом
кольце обратное число тогда и только тогда, когда я2—2&2 равно 1
илн —1. Действительно, если У—~, x£Z[-\j2], тох«у=1, откуда,
пользуясь свойствами операции сопряжения, x^y—l. Перемножая
последние два равенства, получаем (х-х)(у-у)~\. Но х«х=а2—
—2Ъ2\ если y~c~\-d -у/2, то y*y—ci—2d2, следовательно, (а2 —
-2fc2)(c2~2d2)=l, т. е. а2-2Ь2==±1.
Использование связей, подобных той, которая приведена в этом
примере, играет большую роль в современной алгебре н теории
чисел.
4. В заключение этого раздела изучим вопрос о количестве
корней алгебраического уравнения а(х)=О, где а (х)=а*х*-|-.. . +
+а(х4-ао— многочлен степени k. Предварительно докажем ут~
верждение (оно называется теоремой Безу): если х0 корень
уравнения а(х)=0, то многочлен а(х) можно представить в ви-
де а (х)=(х—Хо)-Ь (х), где Ь (х) — многочлен степени k— 1. Дейст-
вительно, поскольку о(хо)=0, то многочлен а(х) можно предста-
вить в следующем виде:
а(х)=а(х)—a(x0)~a>(xft—x^4-aA_j (x^’—xg
-)-ai(x—xo).
В каждом из этих слагаемых содержится множитель (х—Хо), вы-
нося который за скобку получаем выражение о(х)=а=(х—Хо)6(х).
Теорема. Количество корней уравнения а(х)=Ь, где
а(х) — многочлен степени k, не превосходит k.
Доказательство. Пусть Хь ..., хр—корни данного
уравнения. По теореме Безу (для корня Xi) имеем a(x)=(x—Xi)X
ХЬ(х), где Ь(х) — многочлен степени k—1. Числа х2, ...» хр,
очевидно, служат корнями уравнения £>(х)=0. Для корня х2, в
частности, получаем b (х)—(х—х2)-с (х), где с(х)—многочлен
(степени k—2), так что а(х)=(х—Х])(х—х2)-с(х). Повторяя это
рассуждение, придем в конце концов к равенству
а (х)=(х—Х1)(х—х2)-.. .-(х—xp)-d (х),
126
где d(x)— некоторый многочлен. Поскольку степень многочлена
равна сумме степеней множителей, получаем, что степень прои.з-
ведения всех множителей, кроме последнего, равна р, а следова-
тельно, степень а{х) больше или равна р. Теорема доказана
Отсюда в качестве следствия получаем, что множество реше-
ний неравенства а(х)>0, где а (х) — многочлен степени k, либо
пусто, лнбо состоит нз одного или нескольких промежутков.
Действительно, вспоминая связь решения уравнения а (х)=0 и не-
равенства а (х)>0, отметим на оси абсцисс все корни Xi, Ха,..хр
уравнения а(х)=О. Они разбивают ось на (р+1) промежутков,
в каждом нз которых многочлен а(х) сохраняет знак. Теперь
следует отобрать те из них, в которых а(х) положителен. Если
уравнение а(х)=0 не имеет корней, то многочлен с(х) сохра-
няет знак на всей оси, поэтому множеством решений неравенства
а(х)>0 будет все множество или пустое множество.
Задачи
30. Пользуясь переводом задачи на геометрический язык, ре-
шите уравнения: а) |х—3| —1; б) |х—1| + |х—2| = 1.
31. а) Пусть А (о), В(Ь), С (с), D(d)— точки на координат-
ной прямой. Докажите, что отрезок CD вложен в АВ тогда н
только тогда, когда a^.c^d^.b.
б) Последовательность (числовых) отрезков [0,7; 0,8}
[0,77; 0,78], [0,777; 0,778], — — стягивающаяся. Какое число
принадлежит всем этим отрезкам?
32. Пусть X — подмножество множества Y. Докажите, что:
а) если Y дискретно, то н X дискретно; б) если X плотно, то н У
плотно; в) если X плотно нА — конечное подмножество X, то
Х\А плотно (например, множество не равных нулю рациональ-
ных чисел плотно).
33. а) Найдите какое-нибудь число, расположенное между
числами 0,1234 и 0,12345; 0,(78) н 0,(789).
б) Докажите, что между двумя любыми рациональными числа-
ми содержится иррациональное.
34. Докажите, что неравенство 1а—b д/2| имеет бесконеч-
ное множество целочисленных решений. Указание. Восполь-
зуйтесь тем, что i/2—1<0,5 и (д/2—l)*€Z[-\/2] для любого нату-
рального числа k.
35. Решите графически неравенства: а) (х—1)(х—2)(х—3)3>0;
6) -^++^->0; в) -<0.
36. а) Придумайте какое-нибудь алгебраическое уравнение с
корнями 1; 2; 3.
б) Придумайте неравенство, имеющее множество решений;
(-«>; 1)U(2;3); (1;2)U(3; + «>); (1;2)U(2;3).
127
БЕСКОНЕЧНЫЕ ЧИСЛОВЫЕ МНОЖЕСТВА
1. Мы рассматривали числовые множества с точки зрения
числовых операций. Взглянем теперь на них иначе: нас будет ин-
тересовать сравнение множеств по количеству элементов. В каком
смысле множества могут быть бесконечны, но «равночисленны»?
Рассмотрим сначала очень важный класс бесконечных мно-
жеств, так называемые счетные множества. Множество назы-
вается счетным, если любому его элементу присвоено натуральное
число, номер этого элемента. При этом в качестве номеров должны
выступать все натуральные числа, каждое ровно одни раз. Прави-
ло присваивания номера называется нумерацией. Скажем теперь
иначе: бесконечное множество счетно, если его элементы можно
перенумеровать.
Пример. Покажем, как можно перенумеровать все целые
числа. Рассмотрим пары вида (—k; k), где k^N. расположим их
одну за другой по возрастанию k, на первое место поставим нуль.
Получим последовательность чисел: 0; — 1; 1; —2; 2;... , которая,
как нетрудно догадаться, содержит все целые числа. (Неотрица-
тельные целые числа стоят в ней на нечетных местах, а отрица-
тельные — иа четных.) Таким образом, можно сказать, что мно-
жество целых чисел счетно (рис. 84).
. . . Jj)-(j) О 2 3 . . .
О -1 1-2 2—3 3 . . .
Рис 84
В качестве упражнения заполните следующую таблицу:
Число 0 -3 2000
Номер числа 2 1001
Пример. Покажем, что множество Di=(0; 1)П^ правильных
десятичных дробей может быть занумеровано. Это кажется еще
поразительнее предыдущего: ведь Dt заполняет интервал (0; 1)
плотно, а множество номеров — дискретно. Тем не менее ...
Будем считать, что в записи дроби нз Di последняя цифра ие равна
нулю. Правило присвоения номера: записать все цифры в обратном
порядке и зачеркнуть стоящие иа конце запятую и нуль (рис. 85).
0,0305 ~’-'*-5030,0 ^^-—5030
Рис. 85
128
Напрнмер, данное число 0,0305. Тогда зеркально отраженное чис-
ло — 5030,0 и номер данного числа — 5030. Следовательно,
множество правильных десятичных дробей счетно.
Приведенные удивительные результаты наводят на мысль о
том, что любое бесконечное множество счетно. В дальнейшем мы
увидим, что это не так: существуют бесконечные несчетные мно-
жества; в таких множествах элементов «еще больше», чем нату-
ральных чисел. Но пока что будем изучать счетные множества.
Теорема. Бесконечное подмножество множества натураль-
ных чисел N счетно.
Действительно, пусть Л — бесконечное подмножество мно-
жества N. Найдем в А наименьший элемент (то, что такой эле-
мент найдется, является важнейшим свойством натурального ряда
чисел, это свойство называется принципом наименьшего эле-
мента). Этот элемент будет первым элементом в нашей нумера-
ции, обозначим его Оь Ясно, что множество А =Л\{Д|} бесконечно
(почему?). Найдем наименьший элемент в А и обозначим его аз.
Это будет второй элемент нашей нумерации. И т. д. Этот процесс
приводит к присвоению номера каждому элементу из А, потому что
на каком-то шаге каждый элемент из А станет наименьшим в
очередном множестве А и получит номер (fej-l) (см. рнс. 86).
Определение. Обобщенной нумерацией множества назо-
вем правило, которое каждому его элементу сопоставляет нату-
ральное число, причем разным элементам соответствуют разные
числа.
Из доказанной теоремы следует, что для установления счетнос-
ти множества достаточно найти его обобщенную нумерацию и
убедиться в бесконечности множества номеров.
2. Понятие множества было выделено как самостоятельное ма-
тематическое понятие только в последней трети XIX в. Вначале
теория множеств считалась очень абстрактной наукой, частью
«чистой математики». В дальнейшем, уже в XX в., она стала
успешно применяться и в приложениях математики. Приведем
пример, имеющий большое значение для использовании ЭВМ.
Чтобы произвести математическую обработку данных в ЭВМ,
нх необходимо преобразовать в форму, доступную для введения
в память ЭВМ, или, как говорят, закодировать. Каждый изучае-
мый объект получает условное обозначение — код. Закончив обра-
ботку кодов, можно вернуться к исходным объектам, совершив
t- • © • • ® ©...............
Наименьший элемент б А
• • X • •©• • © ©...............
^-Наименьший элемент 6 А}
••«••»••©©................................
^-Наименьший элемент б Аг
Рис. 86
5 Заказ Т75
129
обратное преобразование — декодирование. Удобно выбранный
способ кодирования помогает выявить те или иные особенности
изучаемых объектов.
Применим описанную ндею для доказательства счетности раз-
личных множеств. Начнем с множества рациональных чисел. Вве-
дем новый способ запнси рациональных чисел. Для этого рас-
смотрим следующую таблицу, пользуясь которой любую дробь
можно записать в виде цепочки цифр О, I, ... 9.
0 1 2’34 56789/-
10 11 12 13 14 15 16 17 18 19 20- 21
Правило кодирования: сначала записывается код минуса «—>
(если дробь отрицательна), затем коды цифр числителя, потом
код черты дроби «/» и, наконец, коды цифр знаменателя. Напри-
мер, код 2/3 равен 122013, а код (— 2/35) равен 2112201315. Оче-
видно, дробь можно однозначно восстановить по ее коду, т. е. по-
лучена обобщенная нумерация множества дробей. Теперь можно
доказать, что множество рациональных чисел счетно. Действитель-
но, представим нуль дробью 0/1, а остальные рациональные чис-
ла — несократимыми дробями с целыми числителями н натураль-
ными знаменателями. Пользуясь описанной кодировкой множества
дробей, получаем обобщенную нумерацию для Q. Следовательно,
Q счетно, потому что оно бесконечно и имеет обобщенную нуме-
рацию.
Пример счетного множества в геометрии. Множество точек
иа координатной плоскости с рациональными координатами счет-
но. Докажем это. Каждая точка иа координатной плоскости пол-
ностью определена парой (а; Ь) координат. Воспользуемся теперь
идеей кодирования, а для этого продолжим таблицу кодов, доба
вив трн столбца
( ) ;
22 23 24
Пользуясь этими таблицами, можно закодировать любую пару
рациональных чисел. Следовательно, для данного множества име-
ется обобщенная нумерация. Поскольку множество бесконечно,
оно счетно.
Покажем, наконец, что множество многочленов степени
от переменной х с рациональными коэффициентами счетно. Будем
записывать многочлены в стандартном виде — по убывающим
степеням неизвестного. Поскольку обозначение переменной (бук-
ва х) фиксировано, многочлен полностью определяется последо-
вательностью своих коэффициентов (вместо отсутствующих сла-
гаемых — одночленов с нулевыми коэффициентами — иа соответ-
ствующее место необходимо внести нуль). Например, для мно-
гочлена 2х44-х—1 последовательность коэффициентов такова:.
2; 0; 0; 1; — 1. Поэтому задача свелась к доказательству счетности
множества всех конечных последовательностей рациональных чи-
130
сел. Вот правило кодирования: берем код первого числа, потом
код точки с запятой, потом код второго числа и т. д. Таким обра-
зом, для данного множества указана обобщенная нумерация;
множество бесконечно, значит, оно счетно.
Приведем пример применения идеи кодирования в изучении
конечных множеств. Покажем, что количество всех подмножеств
fc-элемеитного множества равно 2fe. Определим прием кодирования
для подмножеств конечного множества. Пусть A={fli. az, -.а*)
и BczA. Кодом подмножества В будем считать цепочку из k цифр,
которая строится так: если а^В, то первый член цепочки равен 1,
если Gi $ В, то положим его равным 0. Аналогично по az строим
второй член цепочки н т. д. Очевидно, что у разных подмножеств
разные коды. Значит, подмножеств в А-элементном множестве А
столько, сколько имеетси цепочек длиной k, состоищих из нулей и
единиц. Таких последовательностей 2fe (докажите это), значит, и
подмножеств в ^-элементном множестве 2fe.
Чтобы помочь читателю освоиться с кодированием подмно
жеств, приведем пример для множества А=(аь а2, а3, сц, as, а&}
(см. задачу 13).
Подмножество (а,, а2} {аь а3} М 0 А
Код 110000 101000 001000 000000 111111
Заметим, что среди подмножеств имеются такие, которые
состоят из одного элемента, они называются одноэлементными. Их
полезно иногда рассматривать по той же причине, по которой
введено пустое множество: заранее не всегда известно, сколько
в данном множестве может быть элементов.
Таким образом, количество подмножеств конечного множества
само конечно. Будет ли счетно количество подмножеств счетного
множества? В п. 4 вы сможете убедиться, что нет.
3. В качестве последнего примера счетного множества при-
ведем множество алгебраических чисел. Напомним, что алгебраи-
ческое число — это корень алгебраического уравнения степе-
ни 1 с рациональными коэффициентами. Счетность множества
алгебраических чисел была доказана в 1874 г. выдающимся
немецким математиком Г. Кантором (1845—1918), основате-
лем теории множеств. Для доказательства этого утверждения
достаточно вспомнить, что множество многочленов с рациональны-
ми коэффициентами счетно и что у каждого многочлена степени
п 1 конечное множество корней. Пусть ai (к), а2 (х), ... — нуме-
рация многочленов степени больше или равной 1 с рациональными
коэффициентами, Alt А2,... — множества корней первого, второго
н т. д многочлена. Нумерацию множества алгебраических чисел
легко получить так: перенумеруем все числа в А], потом все числа
в Аг н т. д. Поскольку одно и то же число может быть корнем
сразу нескольких многочленов, следует устранить повторное при-
своение номера такому алгебраическому числу, которое уже
131
получило иомер; для этого можно просто, прежде чем присваивать
иомер очередному алгебраическому числу, посмотреть ие встрети-
лось ли оно нам раньше. Мы получили нумерацию множества
алгебраических чисел, это множество бесконечно <почему?),
следовательно, оно счетно.
4. Обратимся к такому важному вопросу: всякое лн дейст-
вительное число является алгебраическим? Удивительный от-
вет на него был получен Г. Кантором (а той же статье, где он
доказал счетность множества алгебраических чисел): он сумел
доказать, что числовой промежуток (0; 1) не является счетным
множеством. Из этого сразу следует нужный нам результат:
на промежутке (0; 1) существуют трансцендентные числа. Дейст-
вительно, если бы (0; 1) состоял только из алгебраических чисел,
то этот интервал был бы счетным множеством в противоречие со
сформулированной теоремой Г. Каитора.
Как быть с указанием конкретных трансцендентных чисел?
Способ доказательства, который будет приведен, ие дает ответа
на этот вопрос. Первые примеры конкретных трансцендентных
чисел были приведены французским математиком Жозефом Лну-
виллем в 1851 г. Он показал, например, что такое число, как
0,10010000001000. . .000100..трансцендентно.
2-3 2.3-4
нуля нулей
В конце XIX в. была доказана трансцендентность числа л. Зна-
чительные достижения в изучении трансцендентных чисел имеет
отечественная математика. В начале 30-х годов советский матема-
тик А. О. Гельфонд доказал, что любое число вида а6, где а, b —
алгебраические числа (а>0, fl#=l, b£Q), трансцендентно. Эта
задача стояла в математике почти 30 лет.
Приведем доказательство теоремы Г. Кантора. Будем пред-
ставлять числа бесконечными десятичными дробями. Допустим,
что множество (0; 1) удалось перенумеровать. Рассмотрим эту
нумерацию и, пользуясь ей, построим число, принадлежащее
(0; 1), ио не имеющее номера. Это и будет противоречием, дока-
зывающим сформулированную теорему.
Первое число: 0, aia2a3 .. .ak . ..,
второе число: 0, bib2b3 . .. bk ...
третье число: 0, С1С2С3 .. Сь ...
Построение искомого числа осуществим поразрядно. В качестве
цифры десятых возьмем цифру не равную ни 0, ни 9, ни а(.
В качестве цифры сотых возьмем цифру х2, не равную ын 0, ни 9,
ни Ь2. В качестве цифры тысячных возьмем цифру Хз, не равную
132
ни 0, ни 9, ни Сз. И т. д. Получим дробь О, Х1Х2Х3 ... Xk -.. . Она,
очевидно, не может быть равна нн нулю, ни единице (почему?), т. е.
изображенное этой дробью число принадлежит интервалу (0; 1).
Это число отличается от каждого числа нумерации. Действительно,
от k-того числа в нумерации это число отличается по меньшей
мере своим /г-тым разрядом. Таким образом, предположение счет-
ности множества (0; 1) привело к противоречию, следовательно,
оно несчетно.
Открытие несчетности континуума (так в теории множеств на-
зывается промежуток (0; 1) — от латинского слова, обозначающе-
го «непрерывный», «связный») имело для математики такое же
огромное значение, как и открытие несоизмеримых отрезков.
Изложенный метод доказательства, называемый диагональным
методом Кантора, имеет многочисленные применения в различных
разделах математики.
Задачи
37. Докажите, что (0; l)f)Z> и (0; 10] f|Z> счетны.
38. Докажите счетность множества: а) объединения конечного
и счетного множества; б) разности счетного и конечного множест-
ва; в) объединения конечного семейства счетных множеств;
г) объединения счетного семейства счетных множеств (см. рис. 87).
39. Докажите, что бесконечное подмножество счетного мно-
жества счетно.
40. Докажите счетность множеств: а) множества многочленов с
целыми коэффициентами от двух переменных х и у, б) множества
интервалов на координатной прямой с рациональными концами;
в) множества параллелограммов на координатной плоскости с
вершинами в рациональных точках.
Схема маршрута
\ш
^2° уР J3 °
В30 О О
В^ о о о о
Рис. 87
133
41. Пусть А — несчетное множество и ВсА- его счетное
подмножество. Докажите, что А\В несчетно. Пользуясь этим
фактом и теоремой Кантора, докажите, что множество иррацио-
нальных чисел несчетно; множество трансцендентных чисел не-
счетно.
42. Пользуясь диагональным методом Кантора, докажите, что
семейство всех бесконечных подмножеств натурального ряда чи-
сел несчетно.
43. Пользуясь подходящим кодированием, докажите, что се-
мейство всех конечных подмножеств натурального ряда чисел
счетно.
Литература
1. В и л е Н к и Н Н. Я- Рассказы о множествах.— М.: Наука, 1969.
2. К о р д е м с к и й Б. А. Увлечь школьников математикой.— М.:
Просвещение, 1981.
3. Курант Р., Роббинс Г. Что такое математика?—М.:
Просвещение, 1967.
4. Нивеи А. Числа рациональные и иррациональные.— М.:
Мир, 1966.
5. Петер Р. Игра с бесконечностью.— М.: Просвещение, 1968.
6. Р а д е м а х е р Г., Теплиц О. Числа и фигуры.— М.:
Физматгиз, 1962.
7. берлинский В. О теории множеств.— М.: Просвещение,
1966.
МЕТОД КООРДИНАТ
Вы уже знакомы с координатами на прямой н на плоскости.
Введение координат позволяет определять положение точки с по-
мощью чисел — координат этой точки. На прямой для этого нуж-
но лишь одно число (х), на плоскости — два (х; у), в простран-
стве — три (х; у, г). Метод координат дает возможность записы-
вать геометрические фигуры на языке арифметики, указывая
координаты точек этих фигур, или же иа языке алгебры с помощью
уравнений, решениями которых являются координаты точек дан-
ных фигур. Это позволяет применять алгебраические методы при
решении геометрических задач и, наоборот, исследовать уравнения
с помощью обращения к их графической интерпретации.
Идея координат зародилась в науке Вавилона и Грсции d свя-
зи с потребностями географин, астрономий и мореплавания. Еще
во И в. до и. э. греческий ученый Гиппарх предложил опреде-
лять положение точки на земной поверхности с помощью геогра-
фических координат — широты н долготы, выражаемых числами.
В XIX в. француз О р е с м (1323—1382) перенес эту идею в мате-
матику, предложив покрывать плоскость прямоугольной сеткой
и называть широтой и долготой числа, характеризующие положе-
ние точки на этой сетке. Наконец, в XVII в. французский ма-
тематик и философ Р. Декарт (1596—1650) первым увидел
и реализовал возможность записи геометрических фигур — линий
на координатной плоскости с помощью алгебраических уравнений,
связывающих координаты точек этих линий, что послужило осно-
вой создания новой отрасли математики — аналитической гео-
метрии.
Мы надеемся, что, прочитав эту главу н прорешав предложен-
ные в ней задачи, вы глубже поймете возможности метода коор-
динат и будете обращаться к его помощи в соответствующих
ситуациях.
КООРДИНАТЫ НА ПРЯМОЙ
Если иа прямой выбрать начало отсчета некоторую точку О) ,
направление, которое будет считаться положительным (его обычно
указывают стрелкой), и единицу масштаба (некоторый отрезок е),
135
то положение любой точки М на этой прямой будет определяться
одним числом (координатой), а именно расстоянием от точки М
до начала О, измеренным в единицах масштаба н взятым со зна-
ком «+»» если направление от О к М совпадает с положитель-
ным, и со знаком «—» в противном случае. Прямую с выбранным
иа ией началом, положительным направлением н единицей масш-
таба называют координатной прямой.
С помощью координатной прямой устанавливается, как говорят
математики, взаимно однозначное соответствие между числами и
точками иа прямой. А именно каждому действительному числу х
соответствует одна и только одна точка М (х) иа координатной
прямой, имеющая координату х; каждой точке на координатной
прямой соответствует одно н только одно число — координата
этой точки.
Имея в виду такое соответствие, говоря о числах, математи-
ки широко используют геометрическую терминологию, а само мно-
жество всех действительных чисел R называют нередко числовой
прямой или числовой осью. Так, например, вместо «возьмем чис-
ло х» говорят «возьмем точку Л?(х) на числовой оси», вместо
«множество всех действительных чисел х, удовлетворяющих ус-
ловию а^х^Ь» говорят кратко «отрезок [а; Ь]» н т. д. Указывая
точку М (а) с координатой, равной числу а, ее часто называют
просто «точка о», а на координатной прямой вместо М (о) пишут а
Модуль и расстояние на прямой
Модуль, нлн абсолютная величина числа, приобретает на коор-
динатной прямой наглядный смысл. А имение |х| есть не что иное,
как расстояние от точки М (х) до начала О координатной прямой,
а модуль разности двух чисел Xi и хг есть расстоииие между
точками Xi и Х2 иа координатной прямой. Такая интерпретация
позволяет легко решать ряд уравнений и неравенств, содержащих
модули, иа основе их геометрического смысла.
Так, например, уравнение |х—21=3 с геометрической точки'
зрения означает, что точка х находится на расстоянии, равном 3,
от точки 2, и потому решением его служат две точки х=5 н х= — 1.
Неравенство |х| означает, что точка х удалена от начала
координатной прямой не более чем на 2 единицы, и потому множе-
ство всех его решений есть отрезок [—2; 2].
Неравенства вида |х—а|<6 особенно часто используются
математиками. С геометрической точки зрения условие |х—е| <6
означает, что точка х удалена от точки М (а) менее чем иа 6 и мно-
жество всех точек, ему удовлетворяющих, есть промежуток
от а — 6 до a-f- 6, серединой которого является точка а. Промежу-
ток вида (а—б; а-|-б) называют 6-окрестностью точки а Аналогия
ное условие на плоскости задает, круг, а в пространстве — шар
радиуса б с центром в данной точке (которые называют б-окрест-
ностями точки иа плоскости и в пространстве соответственно).
136
Пример 1. Решим неравенство ]х—11^5.
Решение. Геометрически данное неравенство означает, что
точка х удалена от точки I не более чем на 5 единиц. Совокуп-
ность всех таких точек на координатной прямой есть отре-
зок [—4; 6].
Обратите внимание на то, что центром окрестности |лг-|-а|<б
является точка —а (а не fl), поскольку |x+a| = fx—(—a)|,
и, значит, |х-|-с| есть расстояние от точки к до точки —а
Пример 2. Решим неравенство |х-|-2|> 3.
Решение. Геометрически это неравенство означает, что точ-
ка к удалена от точки —2 более чем иа 3. Совокупность всех
таких точек на координатной прямой состоит нз двух бесконечных
промежутков (—со; —5) и (1; + со).
Задачи
1. Известно, что точка М, расположенная на координатной
прямой, в два раза ближе к точке А (2), чем к точке В (—10).
Найдите координату точки М. Сколько решений имеет эта зада-
ча? Запишите условие задачи с помощью модулей.
2. Решите, опираясь на геометрический смысл, следующие
уравнения и неравенства:
а) |х| >4; б) |х+П=2; в) |х-3|<4; г) |%+2| = |х-4|,
Д) 1<И<2;е) 2<|х-2|<4; ж) |х+3| =2|х-2|;
з) |х|+|х—2|—2.
3. Дайте геометрическую интерпретацию следующих нера-
венств и уравнений:
а) ]х—о| = |х—Z>|;6) |х—«|—3|л—Ь|; в) |х—а|< |х—Ь|;
г) |х—сЦ-|х—b[=d-, д) 1х—аЦ-|х—s^d; е) |х—с|—
— |х—Ь| — d.
Исследуйте влияние значений параметра d прн фиксированных
а и b (fl<b) на решение в случаях г) —е).
4. Задайте неравенством с модулем каждое из данных число-
вых множеств:
а) [-5; 5); б) (0; 2]; в) 2)U(2; + «>); г) (0; 2]U[4; 6);
Д) (-«>; 0]U[4; +«>); е) (-2; 2); ж) [0; +«>);
з) (—оо; —2).
Неравенство треугольника и свойства модуля
Каковы бы нн были три точки, расстояние между любыми двумя
из этих точек не больше суммы расстояний от них до третьей точки.
Таково одно из основных свойств расстояния, известное под наз-
ванием «неравенство треугольника». Это свойство выполняется и
на плоскости, и в пространстве, и на прямой. Если две точки
J37
а и b иа координатной прямой фиксировать, а третью х считать
переменной, то из неравенства треугольника следует, что при лю-
бом х
\х— а| 4- |х—6| > |а—Ы,
т. е. сумма расстояний от точки к до точек а и Ь не меньше, чем
расстояние между точками а и Ь. При этом равенство в (1)
достигается лишь в случае, когда х лежит между а и b (т. е. при-
надлежит отрезку [а; &]).
Полагая х=0 в неравенстве (1) и заменив b на — Ь, получим,
что
1а+Ы < Jal + 1Ы
(2)
при любых значениях а и Ъ, т. е. модуль суммы двух чисел всег-
да не больше суммы их модулей. Согласно сказанному ранее ра-
венство в соотношении (2) будет достигаться лишь в том случае,
когда точка х=0 (т.е. начало координатной прямой) принадлежит
отрезку с концами ан —Ь, а значит, числа а и b имеют одинаковые
знаки или хотя бы одно нз них равно нулю.
Аналогично из (1) можно получить, что la—Ь| |а| — |fe|
при любых а и Ь, т. е. модуль разности двух чисел не меньше
разности модулей этих чисел. Проделайте это самостоятельно.
Какое аналогичное неравенство, связанное с треугольником, вы
знаете? Когда в указанном неравенстве достигается равенство?
Задачи
5. Какое множество точек на координатной прямой задается
уравнением:
а) |х—21 + |х-6|=4; б) |х-2| 4-|х-6| = 10; в) |х-2| -J-
+ |х—6|=3?
6. Сколько решений (в зависимости от значений d) может
иметь уравнение:
a) |х+3|+ |х—5| =d; б) |х-2| — |х-4| =d;
в) l|x+l|-lx+3||-^d?
7. На координатной прямой задано п точек; At (х>),..Ап (х„),
причем xi<2x2<. . .<xft, Найдите на этой прямой такую точку М,
для которой сумма расстояний от иее до асех заданных точек
была бы наименьшей. Решите задачу для случаев л=2, 3, 4, 5.
Каким будет решение в общем случае?
8. Найдите наименьшее возможное значение для каждой из
данных сумм:
а) |х—2|1х—-4|; О |%4-2| 4-|х| + |х—3|; в) 1х—2| +
+ 1x4-41 + |xl + |x+8|; г) |х+31 + 1х+П + 1х-2| + |х-4| +
+ 1х—5|.
138
Деление отрезка в заданном отношении
При решении многих вопросов механики, физики, да н самой
математики возникает задача деления данного отрезка Д1Л2 в за-
данном отношении т. е. нахождение такой точки А отрез-
ка AtA2, для которой
ЛЛа As
Пусть точки Ai и Аз расположены иа координатной прямой
и имеют координаты Xi к хг соответственно. Найдем координату
точки А (х), расположенной между At и Аг и делящей отрезок
[xi; Хг] в отношении , Координата искомой точки должна, оче
видно, удовлетворять уравнению
|х—Х]| __Х|
lx—xd 12
(3)
и условию Х1<£х<Хз. Последнее условие позволяет раскрыть
модули так: {х—Xi | =х—Xi, lx—хг\ =хг—х. В результате прихо-
дим к уравнению решая которое получаем-
^2X14-11X2
Xj+12 ’
(4)
В частности, когда ki=l2=l, получаем знакомую формулу для
нахождения координаты середины отрезка
(5)
Формула (4) применяется в физике для нахождения центра
масс системы материальных точек. Если в точках Ai и Аг сосре-
доточены массы mt н Юг, то центр масс — это та точка отрезка
А]А2, которая делит его в отношении ~ . Если считать отре
зок Л1Д2 расположенным горизонтально и нагруженным на кон-
цах массами т} и тг, то центр масс — это та самая точка, в ко-
торую нужно поместить опору, чтобы «нагруженный отрезок»
находился в равновесии. В самом деле, условие равновесия опре-
деляется правилом рычага, установленным еще Архимедом: рычаг
находится в равновесии, когда силы, действующие иа него, обрат-
но пропорциональны плечам этих сил. Поэтому для точки равно-
весия А (рис. 88) должно выполняться условие AiA-mig=
"AAs-m^g, или 4—=—, и, значит, точка А есть не что иное,
° ЛЛ2 т> '
как центр масс материальных точек А» и Аз. Если Xt н х2-
координаты точек А\ и Аг, то координатой центра масс будет
ffliXi-j-fflgX; /g\
т1-Ьт2 ' '
139
AM A(x) Аг(хг)
О------Г------------------------------------Ъ
\р,-гп:д
Гг=чп2д
Рис. 88
Центр масс для большего числа материальных точек опреде-
ляется на основе правила: центр масс не меняется, если любые
две точки А и В данной системы заменить одной, расположенной
в центре масс точек А и В и имеющей массу, равную сумме масс
точек А и В.
Задачи
9. Найдите координаты точек, делящих отрезок [2; 14] коорди-
натной прямой в отношении: а) 2: 1; б) 1:3.
10. Сколько решений имеет уравнение , если не
требовать, чтобы точка х находилась между xi и *2? Найдите нх.
11. Если в формулу х=х‘1^^г для координаты точки, деля- .
щей отрезок [jn; х2] в отношении -у-, подставить отрицательное
1=#= — 1, то что за точку мы получим? Рассмотрите числовые
примеры.
12. Докажите, что центр масс системы нз трех материальных
точек, расположенных на координатной прямой и имеющих коор-
динаты xt, хц, хз н массы mi, т%, т$ соответственно, определяется
по формуле
y mtxl+mzX2+тзх3
Проверьте независимость результата от того, какие именно из
двух данных точек вы заменяете одной согласно правилу нахож-
дения центра масс.
13. Получите формулу для нахождения центра масс системы
из четырех материальных точек, расположенных на координатной
прямой. Какой вид будет иметь формула для общего случая
п точек?
14. Какое множество на прямой образуют все точки, коорди-
наты которых вычисляются по формуле x=ha-\-(l—tyb (где
а<СЬ), а случае, когда параметр X пробегает все значения из
промежутков: а) [0; 1]; б) [0; 0,5]; в) [0,5; 1]; г) (—оо; 0);
Д) (1; +°о); е) [0; 2]; ж) (-1; 0)?
140
КООРДИНАТЫ НА ПЛОСКОСТИ
Для определения положения точек на плоскости с помощью чи-
сел на ней проводят две взаимно перпендикулярные координатные
прямые с общим началом в точке их пересечения. Одну из этих пря-
мых (горизонтальную) называют осью абсцисс, другую (верти-
кальную) — осью ординат. Теперь положение любой точки М
плоскости можно задать, указав два числа — координаты проек-
ций Мх и Му этой точки на ось абсцисс и ось ординат соответст-
венно. Первую из указанных координат называют абсциссой
точки М, а вторую — ее ординатой.
Всюду далее мы будем предполагать, что масштабы по осям
абсцисс и ординат одинаковы. В этом случае говорят о прямоуголь-
ной декартовой системе координат.
Введение декартовой системы координат позволяет установить
взаимно однозначное соответствие между токами плоскости и упо-
рядоченными парами чисел — координатами точек. А именно каж-
дой паре (ж; у) действительных чисел соответствует точка М (х; у)
на координатной плоскости с абсциссой, равной х, и ординатой,
равной у, каждой точке на координатной плоскости соответству-
ет единственная пара чисел — координаты этой точки. Имея это
в виду, математики говорят о совокупности всех упорядоченных
пар действительных чисел как о числовой плоскости. При этом
каждой фигуре на координатной плоскости однозначно соответст-
вует некоторое множество пар чисел (координат точек данной
фигуры), т. е. некоторое множество точек числовой плоскости.
Формула расстояния
Если на плоскости введена система координат, то решение
многих вопросов существенно упрощается. Например, можно на-
ходить расстояние между двумя точками с известными координа-
тами Xi (хг, yi), Azfe; у-А не выполняя измерений, а с помощью
простой формулы:
d=V(x2—Х|)г+(|/2—У1)2. (1)
Напомним, что вывод этой формулы основан на теореме Пифагора.
В частности, если обе точки лежат на оси абсцисс или имеют оди-
наковые ординаты и, значит, находятся на прямой, параллельной
осн абсцисс, то из формулы (1) получается d=^(x2—Xif=
= |ха—Х||,т. е. знакомая уже формула расстояния иа координат-
ной прямой. Аналогично для точек с одинаковыми абсциссами
(т. е. лежащих на прямой, параллельной осн ординат) получаем
д=V0/2—IУ2 — yi I -
Последние формулы позволяют находить и расстояния от то-
чек до прямых, параллельных осям координат. Так, расстояние
от точки М (х; у) до прямой у=а равно \у—а|, а до прямой х—Ь
141
равно |х—6|. Так же легко находится и расстояние между двумя
прямыми, параллельными осям координат: если х==аь х=ач
(или у~аи У=а2)—уравнения таких прямых, то расстояние
между ними равно |os—Oi l.
Используя формулу расстояния, можно решать уже немало гео-
метрических задач на вычисления и доказательства, составлять
уравнения кривых, свойства которых описываются с помощью рас-
стояния. Так, например, даже уравнение прямой можно вывести с
помощью этой формулы (что и делается в учебнике геометрии
А. В. Погорелова), заметив, что прямая есть геометрическое место
точек, равноудаленных от двух фиксированных точек (в качестве
которых можно взять любые две точки, симметричные относитель-
но этой прямой).
Решение геометрических задач методом координат
В качестве примера, иллюстрирующего применение метода
координат для решения геометрических задач, докажем с его по-
мощью следующую теорему: «Сумма квадратов всех сторон парал-
лелограмма равна сумме квадратов его диагоналей».
Основой успешного применения метода координат является
удачный выбор осей и начала координат, делающий алгебраичес-
кие выкладки возможно более простыми. В нашем случае «свя-
жем» систему координат с параллелограммом ABCD так. как
показано на рисунке 89. Тогда в обозначениях, приведенных иа
рисунке, получим А (0; 0) В (Ь; с), C(b-]-a; с), D(a; 0) (тот факт,
что в указанных условиях точка С имеет координаты х—fr-pa,
у—с, мы предлагаем вам обосновать самостоятельно)
Итак, требуется доказать справедливость равенства
2АВ2+2А D2=АС1 + BD2.
Запишем аналитический эквивалент этого равенства в нашей сис-
теме координат, выразив длины соответствующих отрезков через
известные координаты их концов по формуле расстояния. Полу-
чим. что нужно доказать справедливость равенства
2 (Ь2 + (?)+2а2=(Ь+а)2+с2-Ц6-af+c*
Рис. 89
Раскрыв скобки в правой части
этого рввенства и приведя подоб-
ные слагаемые, получим 26г+
4- 2с2+2а2, что тождественно рав-
но выражению, стоящему в левой
части равенства. Тем самым тео-
рема доказана.
142
Задачи
15. Решив избавиться от Иванушки-дурачка, царь дал ему та-
кое поручение: --Пройдешь 200 верст на север, затем 150 на вос-
ток, далее 160 верст на юг, после чего повернешь на запад и
пройдешь еще 120 верст. Там найдешь родник с живой водой, на-
берешь ведро н мигом обратно — не вернешься завтра к обеду,
велю казнить». Может ли Иван выполнить поручение царя, если
будет идти со скоростью 5 верст в час, имея в своем распоря-
жении лишь одни сутки? (1 верста = 500 саженей = 1,0668 км.)
16. Докажите, что треугольник с вершинами в точках А (2; 2),
В(1; 5), С(3; 3) является прямоугольным.
17. Составьте уравнение прямой, проходящей через точку
Л(—2; 1) и перпендикулярной прямой x-|-2i/=0.
18. Найдите центр окружности, описанной около ДЛВС,
если Л(—3; 6), В (—5; 4), С (9; —10). Чему равен радиус этой
окружности?
19. Докажите, что отрезок, соединяющий середины диагоналей
трапеции, параллелен основаниям и равен их полуразности.
20. Докажите, что сумма квадратов сторон любого четырех-
угольника равна сумме квадратов его диагоналей плюс учетверен-
ный квадрат отрезка, соединяющего середины диагоналей.
21. Середины сторон АВ и CD, ВС и DE выпуклого пятиуголь-
ника ABCDE соединены отрезками. Докажите, что отрезок,
соединяющий середины полученных двух отрезков, параллелен
стороне АЕ и равен Д£. Указание. Ось Ох направьте по
стороне АЕ.
22. Докажите, что сумма квадратов диагоналей четырехуголь-
ника равна удвоенной сумме квадратов отрезков, соединяющих
середины его сторон.
23. Докажите, что сумма квадратов диагоналей трапеции рав-
на сумме квадратов ее непараллельных сторон, сложенной с удво-
енным произведением оснований.
24. Докажите, что суммы квадратов расстояний от любой точ-
ки плоскости до противоположных вершин прямоугольника равны
(т. е. для прямоугольника ABCD и любой точки Л1 справедливо
равенство МЛ2 + МС2 = МВ2+М£>2).
25. Докажите, что для любой точки М, взятой на основании
АС равнобедренного дЛВС, справедливо равенство ВС2 —ВМ2 =
=АМ-СМ.
26. Докажите, что расстояние от любой точки окружности,
описанной около равностороннего треугольника, до одной из его
вершин равно сумме расстояний от этой точки до двух других
вершин. Указание. Поместите начало координат в центре опи-
санной окружности, а ось Ох направьте параллельно одной из
сторон треугольника.
143
Деление отрезка в заданном отношении
Мы уже умеем решать такую задачу для отрезка, расположен-
ного на координатной прямой. Рассмотрим теперь отрезок 4i42
на координатной плоскости, где Л((хь у\), Уг) (рис. 90).
Если точка А делит этот отрезок в отношении —-, т. е.
то в силу обобщенной теоремы Фалеса точки Ах и Ау,
являющиеся проекциями токи А (х; у) на осн Ох и Оу соответствен-
но, делят отрезки этих осей [xj; X2J и (t/i; у?] в том же отноше-
нии у- и потому, воспользовавшись выведенной ранее формулой,
получаем:
—i,+fe ’ у~ h+>.,
Таким образом, и иа плоскости сохраняется та же формула,
причем абсцисса точки деления зависит только от абсцисс концов
отрезка, а ордината — только от ординат. В частности, при
Л|=Х2=1 получаем знакомые вам из курса геометрии формулы
для нахождения координат середины отрезка:
х=21±*-, (/=Л±Й.. (3)
Воспользуемся формулами (2) для доказательства того фак-
та, что все три медианы треугольника пересекаются в одной точ-
ке и делятся этой точкой в отношении 2:1, считая от вершины.
Введем систему координат, и пусть вершинами треугольника
являются точки A (xg yi), В (х2; Уъ), С (хз; уз)- Пусть L, М, N — се-
редины сторон АВ, ВС, АС соответственно. Согласно формуле (3)
найдем координаты точки Р(х; у), делящей медиану AM в отно-
шении 2: 1, с помощью формул (2). Получим:
1 . *- I 9 А 2+*3 1 . «. । Q
.. __ 1_____2 _ Xi+xs+хз _______ •______2 _ У1+У2+У3
1+2 3 ’ У 1 |-2 3
Из симметрии этих формул (равноправности вхождений Xi (f/i),
х2 (У2), хз (1/з)) ясно, что те же самые координаты будет иметь
Рве. 90
и точка, делящая в отношении
2:1 медиану CL, и точка, деля-
щая в том же отношении медиа-
ну ВIV. Но это означает, что
точка Р является общей для всех
трех медиан, т. е. точкой их пе-
ресечения. Заметим, что формулы
для координат точки пересече-
ния медиан треугольника ока-
зались очень простыми.
144
Формулы (2) могут быть применены для нахождения коорди- ,
пат х, у центра масс системы материальных точек, расположенных
на плоскости. Для двух точек A i (jq; yi\ А2 (№; £fe) с массами mi, m2
получаем:
___ miyi +тгуа .4»
В случае п точек Xt(xi; yt), Лг(х2; Уъ), .. > Ап(хп; уп) с масса-
ми mi, ..тп соответственно имеют место общие формулы
х т |Xi /и 2X2 -г. - - +тпхп __ mtyi+tnsya+‘“+i»Kyn _
mi + nt2+.-+'пп ’ У т,+т2+.. .-}-тп ’ ' f
Понятие о центре масс оказывается полезным при решении
некоторых геометрических задач. При этом существенно, что
центр масс любой системы материальных точек единствен (не
зависит от способа его нахождения). Так, например, сосредото-
чив в вершинах треугольника одинаковые массы, легко понять из
правила нахождения центра масс (возможности замены двух точек
их центром масс с сосредоточенной в нем суммарной массой этих
двух точек), что центр масс треугольника должен принадлежать
каждой из трех его медиан и, значит, все онн пересекаются в од-
ной точке. При этом сразу становится ясным, почему точка пере-
сечения медиан делит их в отношении 2:1, т. е. получаем новое
обоснование рассмотренного нами ранее геометрического факта.
Задачи
27. Отрезок АВ разделен на три равные части точками Л71 (1; 2),
Л^2(3; 4). Найдите координаты точек А и В.
28. Точка К — середина стороны АВ квадрата ABCD, а точ-
ка М делит диагональ АС в отношении АМ:МС=^3:1. Докажите,
что угол KMD прямой.
29. Точки Л(3; — 5), В (—3; 3) и С(— 1; —2) являются вер-
шинами треугольника. Найдите длину биссектрисы этого тре-
угольника, проведенной из вершины Л.Указание. Используйте
утверждение о том, что биссектриса делит сторону треугольника
на части, пропорциональные прилежащим к ннм сторонам, т. е.
для биссектрисы AM треугольника АВС справедливо ВМ’.МС=
=АВ:АС.
30. Докажите, что биссектриса угла при вершине А треуголь-
ника АВС со сторонами АВ—с, ВС=а, АС—b может быть вы-
числена по формуле I=-V6£.(L£.cс. t где I — биссект-
риса. Указание. Поместите начало координат в точку А, а ось
абсцисс направьте по стороне АС н воспользуйтесь указанием
к предыдущей задаче.
31. Найдите биссектрису прямого угла треугольника с кате-
тами а и Ь.
145
32. Докажите, что середина отрезка, соединяющего середины
диагоналей выпуклого четырехугольника, совпадает с точкой пере-
сечения прямых, проходящих через середины противоположных
сторон этого четырехугольника.
33. Докажите, что координаты центра квадрата ABCD можно
найти по формулам , у=У«+^+ис+Вв
34. Предложите и обоснуйте формулу для нахождения центра
правильного «-угольника с вершинами в точках (xi; у;),
Аз (х2; уз), .... Ап (хп, уп).
35. Докажите, что, каковы бы нн были положительные числа
Xi, Ха, Х3, точка с координатами ***» t и—
—находится внутри треугольника с вершинами
Л1 +Х2-|-Аз
л (xi; у,), В(х2; у2), С(х3; у3).
36. Выясните, что представляет из себя множество точек плос-
кости с координатами AiXi-f-Wa-btaXa; где
числа Xj, Х2, Хз принимают все неотрицательные значения, удов-
летворяющие условию Х1-|-Х2+Хз=1, а числа Х|, х2, х3, yi, у2, у3
фиксированы.
Составление уравнений линий
по их геометрическим свойствам
Характерным для геометрии способом задания линий являет-
ся определение их как геометрических мест точек, обладающих
заданными свойствами. Так, например, окружность определяется
как геометрическое место точек, равноудаленных от некоторой
фиксированной точки. Если ввести на плоскости декартову систе-
му координат и выразить на языке алгебры характеристическое
свойство, которым должна обладать точка М(х; у), чтобы при-
надлежать данному геометрическому месту точек, то мы тем самым
получим уравнение этого геометрического места точек. В разных
системах координат уравнеиия одной и той же линии будут
различными. Обычно оси координат стараются расположить так,
чтобы уравнение линии оказалось наиболее простым, а характе-
ристическое свойство точки, принадлежащей этой линии, легко
переводилось иа алгебраический язык. Так, если линия обладает
взаимно перпендикулярными осями симметрии, то их и прини-
мают за координатные оси; если у нее есть центр симметрии, то
начало координат помещают в этот центр и т. п. В частности,
как вы знаете, уравнение окружности приобретает наиболее
простой вид, если начало координат помещено в ее центр:
В некоторых случаях геометрическое место точек, обладаю-
щих заданным свойством, оказывается хорошо известной фигу-
146
рой — окружностью, прямой, отрезком и т. п. Этот факт бывает
весьма непросто установить геометрически, но легко обнаружить,
анализируя полученное уравнение. Проиллюстрируем сказанное
примерами.
Задача. Найдите геометрическое место точек, сумма квадра-
тов расстояний которых от двух заданных точек А и В есть ве-
личина постоянная, равная 2d2.
Решение. Поместим начало координат в середину отрез-
ка АВ, а ось абсцисс направим по прямой АВ. В этом случае
точки А и В будут иметь координаты А{—а; 0), В (а; 0), где
а—^-АВ. Пусть М (х; у) — некоторая («текущая») точка искомой
фигуры. Согласно характеристическому свойству для нее должно
выполняться равенство
МА 8+МВ2=2d2.
С помощью формулы расстояния это равенство легко перевести
на язык алгебры. Сделаем это. Поскольку МА2—(х+а)2+у2,
МВ2=(х—а)2±у2, то последнее равенство запишется в виде
(x+a)24-^+(x-a)8+i/2=2^.
После очевидных преобразований получаем уравнение искомого
геометрического места точек в виде
x*+yZ=d*-a*.
Но последнее уравнение вам хорошо знакомо. Оно задает не
что иное, как окружность радиуса -фр—а* с центром в начале
координат (т. е. в середине отрезка ДВ). Значит, искомое геомет-
рическое место точек и есть указанная окружность. (Сказанное
относится к случаю d>a. Если d=a, то получаем лишь одну
точку — середину отрезка АВ\ при d<a искомое ГМТ и вовсе
пусто.)
В то время как составление уравнения искомого геометричес-
кого места не потребовало от нас каких-либо «хитростей» (рас-
положение осей координат было вполне естественным), установле-
ние обнаруженного факта геометрически требует определенного
искусства. Для того чтобы оценить сказанное, попробуйте дока-
зать его без привлечения метода координат.
Задача. Отрезок длиной а-^-b скользит концами по осям
координат. Составьте уравнение кривой, которую опишет точка М
лого отрезка, делящая его на части а и Ь.
Решение. Пусть А (0; у'}, В (х*; 0) — положение концов от-
резка в некоторый момент (рис. 91). Ясно, что всегда (x'^+G/*)2 —
~(а-^Ь)2, поскольку гипотенуза дОДВ есть данный отрезок дли-
ной а+b. Выразим координаты точки М, упомянутой в усло-
вии, через х* и у*. Из подобия треугольников легко находим, что
147
Рис. 9i
Рис. 92
(можно воспользоваться и формулой деления
отрезка в заданном отношении). Но. значит, х'=а+Ь х. у'=
а-1-b
~ ‘ н потому должно выполняться равенство
После очевидных упрощений получаем окончательно уравнение
кривой, описываемой точкой М, в виде
Задачи
37. Составьте уравнение геометрического места точек, рав-
ноудаленных от двух данных точек А (2; I) и В (—1; 3).
38. Докажите, что геометрическое место точек, отношение
расстояний которых от двух данных точек А и В постоянно и
равно есть окружность (окружность Аполлония). Где на-
ходится центр и чему равен радиус этой окружности при k=2?
39. Найдите геометрическое место точек, разность квадратов
расстояний которых от двух данных точек А и В есть величина
постоянная, равная d2.
40. Составьте уравнение геометрического места точек, раз-
ность квадратов расстояний которых от точек А (0; 2) и В (2; 0)
равна 2.
41. Найдите геометрическое место точек, сумма квадратов
расстояний которых от вершин квадрата ABCD постоянна и рав-
на 4d2. Указание. Направьте оси координат по диагоналям
квадрата.
42. Найдите геометрическое место точек, сумма квадратов
расстояний от которых до сторон прямоугольника ABCD постоянна
и равна 2d2.
43. Составьте уравнение геометрического места точек, про-
изведение расстояний которых от двух данных точек Л (—а; 0)
и В (а; 0) есть величина постоянная и равна а2 (лемниската
Бернулли).
44. Составьте уравнение геометрического места точек, равно-
удаленных от точки А (0; 2) н оси Ох.
45. Составьте уравнение геометрического места точек, сумма
расстояний которых от двух данных точек А (—с; 0) и В (с; 0) по-
стоянна и равна 2а (эллипс). Покажите, что уравнение приводит-
ся к виду —1, где 62—а2—с2
46. Составьте уравнение геометрического места точек, раз-
ность расстояний которых от двух данных точек Л (—с; 0) и
В (с; 0) постоянна и равна 2а (гипербола). Покажите, что урав-
нение приводится к виду —-~=1. где Ь2—с2—а2
В поисках клада
Искателям сокровищ попала в руки записка следующего со-
держания: «На острове подойдите к березе и от нее идите в на-
правлении на сосну, измеряя расстояние. У сосны поверните на-
право и пройдите такое же расстояние. В конечной точке поставь-
те вешку. Затем, вернувшись к березе, идите в направлении иа
дуб, также измеряя расстояние. У дуба поверните налево и прой-
дите такое же расстояние. Снова отметьте конечную точку вешкой.
В середине отрезка, соединяющего поставленные вешки, находится
клад».
Приплыв на указанный остров, искатели сокровищ к велико-
му огорчению обнаружили, что ни березы, ни каких-либо ее сле-
дов иет, хотя сосна и дуб налицо. Несмотря на это, один из иих,
большой знаток математики, после недолгих расчетов сказал, где
следует искать клад, и вскоре клад был действительно найден.
Попробуем и мы определить местонахождение клада в указан-
ной ситуации. Воспользуемся методом координат. Обозначим
точки, в которых находятся береза, сосна и дуб, соответственно
буквами В, С, D, причем С — начало координат, а ось Ох напра-
вим по прямой CD (рис. 92). Координаты точки В (х; у) нам пока ие
известны. Координаты сосны (0; 0), дуба (d; 0), где d — расстоя-
ние от него до сосны. Найдем в этих условиях координаты точ-
ки К (на рисунке отмечена ♦), в которой зарыт клад.
Выполнив на чертеже построения, предусмотренные найденной
запиской, получим точки В\ и В2, в которых должны быть постав-
лены вешки. Их координаты легко находятся из равенства соответ-
ствующих прямоугольных треугольников: А СВ'В~ С,
ABB'D — &DB2B2. А именно В\ (—у; х), B2(d~^y, d—х). По-
скольку точка К служит серединой отрезка BiB2, то ее координаты
149
, x.-j-jco Wi 4-w? d
находятся по формулам x—— . y~ -p-. откуда x=~f
d „
н, значит, положение точки д не зависит от положения
исчезнувшей березы. Вместо указанных в записке замысловатых
построений достаточно найти сначала середину отрезка, соединяю-
щего сосну с дубом, а затем пройти от найденной точки по перпен-
дикуляру к указанному отрезку расстояние, равное половине рас-
стояния от сосны до дуба, так, чтобы сосна при этом движении ос-
тавалась слева, а дуб — справа.
Задачи
47. Кладоискателям лопала в руки старинная карта со следую-
щей инструкцией: «От места пересечения северной и восточной
дорог идите на север. Сначала вы увидите большую сосну, а за-
тем клен. Вернитесь к пересечению дорог. У восточной дороги,
если идти по ней на восток, стоит ель, а если идти на запад — дуб.
Поставьте первую вешку иа пересечении прямой дуб — сосна
и прямой ель — клен, а вторую — иа пересечении прямой ель —
сосна и прямой дуб — клеи. Там, где прямая, проведенная через
две поставленные вешкн, пересекает восточную дорогу, и зарыт
клад». Прибыв на место, кладоискатели обнаружили лишь упо-
мянутые в инструкции дуб, находящийся в четырех километрах от
пересечения дорог, и ель — в двух километрах от этого пересече-
ния. Однако никаких следов сосны и клена кладоискатели, как ни
старались, обнаружить не смогли. И тем не менее с помощью
метода координат клад был найден. А вы смогли бы это сделать
в описанной ситуации?
48. Лестница длиной /, поставленная вертикально к стене,
начинает падать, соскальзывая по полу, так, что ее основание
отходит от стены. Какую кривую опишет центр лестницы в процес-
се ее падения? Ответьте на тот же вопрос для произвольной
фиксированной точки лестницы.
49. Дцкажите, что в любом треугольнике квадрат стороны,
лежащей против острого угла, равен сумме квадратов двух других
сторон минус удвоенное произведение одной нз этих сторон на
проекцию второй стороны на эту сторону (т. е. требуется дока-
зать, что AC2~AB2-f-BC2—2AB-AD, где D — проекция верши-
ны С иа сторону АВ).
50. Окружность касается одной из сторон прямого угла в точ-
ке, находящейся на расстоянии а от его вершины, и проходит
через точку, находящуюся на другой стороне этого угла, на
расстоянии b от его вершины. Найдите радиус этой окружности
и длину отрезка, отсекаемого ею иа стороне угла.
150
ГРАФИКИ И УРАВНЕНИЯ
Если на плоскости введена система координат, то появляется
возможность задавать различные геометрические фигуры с по-
мощью формул, связывающих координаты точек этих фигур. Го-
ворят, что фигура Ф задается уравнением F(x; у)—0, если она со-
стоит нз всех тех и только тех точек плоскости, координаты
которых удовлетворяют данному уравнению. Такую фигуру Ф на-
зывают также графиком уравнения F(x; у)—0. Сказанное можно
символически выразить так:
М(х- у)бФч>Т(х; у)=0.
Аналогично можно говорить н о фигуре, задаваемой неравенством
с двумя переменными (т. е. о графике неравенства).
В связи с отмеченным соответствием между фигурами и урав-
нениями возникают следующие задачи:
— составить уравнение заданной тем или иным образом гео-
метрической фигуры в некоторой системе координат;
— по имеющемуся уравнению с двумя переменными изучить
геометрическую фигуру, им определяемую, выяснить ее характер-
ные свойства, установить возможную ее идентичность известной
фигуре;
— выяснить влияние тех илн иных преобразований уравнения
на форму определяемой им фигуры.
С первой нз упомянутых задач вы уже достаточно знакомы.
Отметим только, что одну и ту же фигуру н даже в одной и той
же системе координат можно задать различными н порой весьма
внешне непохожими уравнениями (хотя все они оказываются
равносильными).‘Для наиболее важных и хорошо изученных кри-
вых выделяют их специальные, стандартные, илн, как нх назы-
вают математики, канонические, уравнения, получаемые в опреде-
ленным образом связанной с данной кривой системе координат.
Так, например, каноническое уравнение окружности имеет вид
х2+«г=/?г.
В этом разделе будут рассмотрены некоторые вопросы, свя-
занные со второй н третьей из упомянутых выше задач.
Задачи
51. Задайте уравнениями фигуры, изображенные иа рисун-
ке 93.
52. Какая связь между графиками уравнений Ft (х; i/)=0,
Гз(х; у)=0 и графиком уравнения F| (х; y)*F^{x\ у)—0? Ответьте
на тот же вопрос для уравнения F? (х; y)4-F2(x; у)—0.
151
Особенности уравнений, обеспечивающие симметрию графиков
Не видя графика уравнения F(|x|; у)=0, можно с уверен-
ностью утверждать, что он симметричен относительно оси орди-
нат, поскольку если некоторая точка М (х; у} принадлежит этому
графику, то и симметричная ей относительно оси Оу точ-
ка М' (—х; у) также ему принадлежит, ведь х содержится в урав-
нении под знаком модули, а | — х| = |х|, и потому если F (1х|; у)=
=0, то н А(|—х|; у)=0. Аналогично график уравнения
F (х; I у!)=0 обладает симметрией относительно оси абсцисс, а фи-
гура, задаваемая уравнением вида F(|x|; |i/|)=0, симметрична
относительно обеих координатных осей, а значит обладает и
центральной симметрией относительно начала координат.
Из сказанного можно извлечь пользу при построении графиков
уравнений, содержащих одну или обе переменные под знаком мо-
дуля. Так, например, график уравнении lx| +1«/| = 1 (рнс. 94, с)
строится моментально, если учесть его симметрию относительно
осей координат,— достаточно изобразить лишь часть графика, ле-
жащую в первой четверти, задаваемую уравнением х+у—1 (т. е.
отрезок прямой у—1 —х, заключенный между координатными ося-
ми), н выполнить необходимые отражения. Для построения
графика уравнения х— 1«;1 = 1 достаточно построить его часть,
лежащую в верхней полуплоскости, где уравнение принимает вид
х—у— 1, а затем дополнить отражением полученной полупрямой
относительно оси абсцисс (рис 94, б).
Рис. 94
152
Задачи
53. Постройте, используя соображении симметрии, графики
уравнений:
а) |х| — |у| = 1; 6) x+|i/| = 1;b) х2—2|»1+»2=0;
г) Jf+2l!/l = I
Внесение модулей в уравнение позволяет изменять его график
в соответствии с весьма простыми правилами. На рисунке 95
показано получение графиков уравнений Р(|ж|; f/)=0, F (х; I */!)=
=0, F(|x|; |t/|)=0, F{— |х|; lyl)—0, F {х; — |у1)=0 по графику
исходного уравнения F (х; y)=G. Здесь важно обнаружить ту чет-
верть илн полуплоскость, в которой график совпадает с исходным.
Для уравнения F(|х|; |i/l)=0 таковой является первая четверть,
в которой |х|=х, )у| —у, а график уравнения F(x; — lyl)—0
совпадает с графиком исходного уравнения F(x; у)=0 в нижней
полуплоскости, поскольку именно в ней — 1у1~у.
Задачи
54. По графику уравнения F(x; yJ-O (рнс. 96, а) постройте
графики уравнений:
a) F(U1; </)=0; б) F(|x|; Ы)=0; в) F(x; -|j/l)=0;
г) д) f(|xl; -Ы)=0.
55. Внося модули в исходное уравнение, график которого
изображен на рисунке 96, а, задайте графики, приведенные на
рисунке 96, б — г.
Рис. §5
153
56. Покажите, что график уравнения Г(|х—а|; у}—0 сим-
метричен относительно прямой х=а. Укажите осн симметрии
графиков F(x; \у—£»f)==sO, F(U—а|; \у— Ы)=0.
Конечно, не только присутствие модулей в уравнении вызыва-
ет симметричность его графика. Так, например, если уравнение
содержит лишь четные степени переменной х, то график его сим-
метричен относительно оси Оу, а наличие только четных степеней
переменной у гарантирует симметрию графика относительно
оси Ох
Симметричное вхождение в уравнение переменных х и у га-
рантирует симметрию его графика относительно биссектрисы у =х
первого и третьего координатных углов, поскольку в этом
случае F (х; y)=F (у; х) (заметьте, что точки М (х; у) и М' (у; х) сим-
метричны относительно прямой у—х}. Примером может служить
график уравнения х3+у— 3x^—0 (декартов лист), изображен-
ный на рисунке 97.
Задачи
57. Какими нз следующих свойств: 1) симметрия относитель-
но осн Ох; 2) симметрия относительно оси Оу; 3) симметрия отно-
сительно начала координат; 4) симметрия относительно прямой
у—х; 5) симметрия относительно прямой у—— х — обладает
график уравнения:
ДекартоБ лист
Рнс 98
х3+у3-Зху=*0
Рис. 97
154
a) x4-y4=4xV; 6) x6+i/5=x^; в) x (x2+&s)=x’-/;
г) (x2-f-^)2=xp; Д) /-x*+x«=O; e) x4+i/4=x2+y2?
Указание. В случае 5 (отражение относительно прямой
у— __х) точка М (х; у) переходит в точку М' (—у; —х) (рис. 98).
58. На рисунке 99 изображены графики уравнений х2 —f>x2y=
= !6х2—25^; i/W-/; У4+х4=Зх3 —4х*; х'+у^хр. Какой
из графиков соответствует каждому из этих уравнений?
ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ И ИХ УРАВНЕНИЯ
В предыдущем разделе речь шла о некоторых общих связях
между уравнениями н графиками, выяснялось влияние некоторых
особенностей уравнений на вид задаваемых имн кривых. Однако
настоящий интерес для математики и ее приложений представляют
некоторые специальные кривые, обладающие примечательными
геометрическими свойствами, кривые, возникающие из практи-
ческих задач. В курсе геометрии вы познакомились с двумя такими
кривыми — прямой (заметим, что понятие «кривая» в математике
не противопоставляется понятию «прямая», а включает его в ка-
честве частного случая) и окружностью, знаете и нх уравнении.
Напомним, что именно с помощью уравнений в учебнике доказы-
вался ряд утверждений о пересечении окружностей н прямых. Это
характерный подход прн исследовании кривых. Метод координат
дает возможность, переведя геометрическую фигуру иа язык ал-
гебры, устанавливать затем ее свойства аналитически. Еще матема-
тикам Древией Греции были известны замечательные кривые:
парабола, эллипс и гипербола, о которых поговорим ниже.
155
Парабола
Хотя этот термин н известен вам из курса алгебры как на-
звание графика квадратичной функции у=ах2+^х-|-с, геомет-
рические свойства параболы вы вряд ли знаете. Дадим определе-
ние этой кривой, принятое в геометрии.
Параболой называется геометрическое место точек, равноуда-
ленных от некоторой точки, называемой фокусом, и некоторой
прямой, называемой директрисой.
Расположим ось абсцисс параллельно директрисе- параболы
на равном расстоянии от директрисы и фокуса, а ось ординат
пусть проходит через фокус F (рис. 100). Если р — расстояние
от фокуса F до директрисы, то в указанной системе координат
фокус есть точка F^O; а директриса задается уравне-
нием у= — Условие MF—MP (где МР— расстояние от точ-
ки М до директрисы) принадлежности точки М(х; у) данной
параболе в переводе на алгебраический язык даст равенство
Возведя обе части этого равенства в квадрат и выполнив очевид-
ные преобразования, получим уравнение параболы в виде х2=
=2ру. Уравнение такого вида называют каноническим уравнением
параболы. Если систему координат расположить иначе, то и урав-
нение получится другим. Каноническое уравнение параболы хо-
рошо тем, что оио просто н по нему легко определить и фокус,
и директрису параболы.
Слово «фокус» в переводе с латинского означает «очаг»,
«огонь»; оно оправдывается следующим замечательным свойством
параболы.
Если изогнуть узкую полоску хорошо отполированного метал-
ла по дуге параболы и направить на нее пучок световых лучей,.
Рис. 100
Рис. 101
156
параллельный оси симметрии параболы, то после отражения от
такой полоски все лучи пройдут через фокус. Наоборот, лучи
точечного источника света, помещенного в фокусе, отразившись от
полоски, пойдут параллельно осн параболы.
Указанное свойство параболы используют, изготовляя пара
болнческие отражатели для автомобильных фар и прожекторов
Если зеркало с поверхностью, образованной вращением параболы
около ее оси симметрии, направить иа Солнце, то в фокусе пара-
болы действительно будет очаг, н котором при достаточном разме-
ре зеркала можно даже плавить сталь. Согласно легенде А р-
х и м е д из Сиракуз (287—212 гг. до и. э.) сжег флот римлян,
обороняя свой город с помощью подобных зеркал.
Задачи
59. Составьте уравнение параболы с данными фокусом н ди-
ректрисой: a) F(0; 5), i/4-2=0; б) F(0; О), х+4=0; в) F(l; 2),
у—0. Изобразите эти параболы в системе координат.
60. Найдите фокус и директрису параболы, заданной урав-
нением: а) у—х2; б) у=х2-(-4х; в) х=уг-, г) х2+2х+у+2=0.
Указание. Заметьте, что фокус лежит на оси симметрии
параболы, а директриса перпендикулярна этой оси и удалена от
вершины параболы на то же расстояние, что и фокус.
61. Докажите, что точки, выделенные иа рисунке 101, лежат
на одной параболе. Составьте уравнение этой параболы. Предло-
жите способ построения параболы, основанный на полученном ре-
зультате.
62. Даны угол и точка А внутри его. Найдите геометрическое
место точек, для которых расстояние до точки А равно расстоя-
нию до ближайшей стороны угла.
Эллипс
Эллипсом называется геометрическое место точек, сумма рас-
стояний которых от двух фиксированных точек, называемых фоку-
сами, есть величина постоянная, большая, чем расстояние
между фокусами.
Пусть фокусами эллипса являются точки Ft, F2, причем FiF2=
—2с, а упомянутая в определении сумма расстояний равна 2а,
где 2а>2с. Из определения очевидна симметрия эллипса отно-
сительно примой, проходящей через фокусы, и серединного
перпендикуляра к отрезку FiF2. Указанные прямые примем за
оси Ох и Оу соответственно. При этом фокусами будут точки
Ft (—с; 0), F2(c; 0). Условие принадлежности точки М(х; у) эл-
липсу MFl -4-AfF2=2a запишется в такой системе координат в виде
V(^+^)2+i/2 +V(*—=2а-
157
Упростим это уравнение. Для этого перенесем один нз ради-
калов вправо. Возведем обе части полученного равенства в
квадрат:
(х+с)2+t?=4а2—4fl уКх—с)2+у2+(х—cf+tf,
откуда
a V(*—с)2+‘/2 = о2—сх.
После повторного возведения обеих частей равенства в квадрат
получаем:
а2 ((х—с)2+У1)=а*—2(?rx -j- eV
После приведения подобных слагаемых приходим к равенству*
х2 (fl2-c2)4-aV=c4-cV,
откуда j-J-И наконец, обозначив Ь2=а2—с\ прихо-
дим к каноническому уравнению эллипса:
+^=‘-
Из этого уравнения ясно, что эллипс пересекает оси коорди-
нат в точках А (—а; 0), В (а; 0), С(0; Ь). £>(0; — Ь). Эти точки
называют вершинами эллипса, отрезки АВ—2а, CD=2b— его
осями, а отрезки ОВ—а н ОС=Ь — полуосями (большой и малой
соответственно). Весь эллипс оказывается вписанным в прямо-
угольник со сторонами, лежащими на прямых х=—а, х=а,
у=—Ь, у=Ь (рнс. 102).
Каноническое уравнение эллипса напоминает уравнение окруж-
х2 и1
ностн, записанное в виде Если в последнем урав-
нении заменить у на -~у, то и придем к уравнению эллипса,
т. е. этот эллипс получается из окружности путем равномерного
У1 Ул
Рис. 102
Рис. 103
158
сжатия в -у- раз вдоль оси ординат. Так, например, эллипс
получается из окружности ^-+^-=1 путем заме-
ны у на 2у в ее уравнении, а значит, уменьшением в два раза
модуля ординаты каждой точки этой окружности. Подобный
способ построения эллипса с помощью равномерного сжатия ок-
ружности часто используется иа практике.
Расстояния от точки М (х\ у), лежащей на эллипсе, до его фо-
кусов F\ н Fa называют фокальными радиусами г\ и г г этой точ-
ки. Получим формулу для вычисления г2, т. е. формулу длины
отрезка AfF2, где Ft (с; О):
r2=V(x—с)2+(/5=У(х—Va2—Ь4)2+^=
=д/хг-2хл^г=-6г+а2—Ь!+62-^-х2=
—2леп+О2 =-^/(а—exf—a—ex
(мы заменили с на xfa?—b2, подставили вместо у2 его выраже-
ние через х из уравнения эллипса и, наконец, обозначили отно
шенне —, илн, что то же самое, через е). Итак, г2=
—а—ех. Аналогично показывается, что гг=«+«х (последнее
можно получить и из того, что л+г2=2а согласно определению
эллипса). Величину е=— называют эксцентриситетом эллипса
Заметим, что формулу г2^=а—ех можно переписать в виде
г2=е^-^—но —* есть не что иное, как расстояние d
от точки М(х; у) эллипса до прямой *=— (рнс. 103). Поэтому
r2=ed, илн -у=«, т. е. отношение расстояний любой точки эллнп
са от фокуса Р2(с; 0) и от прямой х=^- постоянно н равно е
Прямая х—~ называется директрисой эллипса.
Директрисой эллипса является и прямая х — —Для любой
точки эллипса отношение расстояния ее от «левого» фокуса
Fi (—с; 0) и «левой» директрисы постоянно н равно е. Для дока-
зательства можно повторить те же рассуждения, но можно обосно-
вать это и из симметрии эллипса.
159
Эллипс также обладает интересным оптическим свойством, а
именно если изогнуть зеркальную полоску по эллипсу, то лучи
света, выходящие нз источника, расположенного в одном фокусе
эллипса, отразившись от такой полоски, пройдут через второй
фокус
Задачи
63. Изобразите в координатной плоскости эллипсы, заданные
уравнениями:
' 9 ~ 4 * ' 25~16 *
Найдите фокусы, эксцентриситет и директрисы указанных эллин-
сов. Проверьте измерениями и вычислениями описанные выше
свойства эллипса для нескольких взятых на нем точек. Ука-
зание. Для более точного построения эллипса воспользуйтесь
приемом «сжатия» окружности.
64. Где расположены фокусы эллипса, заданного уравнением
Ь в случае, когда Как проходят директрисы
такого эллипса?
65. Предложите простой «веревочный» способ построения
эллипса с заданными фокусами и суммой фокальных ра-
диусов.
'36. Вернитесь к задаче, рассмотренной на с. 147. Предло-
жите прибор для вычерчивания эллипса с полуосями а н b на ос-
нове решения указанной задачи (эллипсограф Леонардо да Вин-
чи).
67. Докажите, что геометрическое место точек, отношение рас-
стояний от которых до точки Ft (с; 0) и до прямой ^=у(а>с)
постоянно и равно е, где е=“, есть эллипс |ё+-^г=1» если
принять Ь2—о2—с2.
68. Составьте уравнение геометрического места точек, отноше-
ние расстояний которых от точки F(2; 0) н оси Оу постоянно
и равно В какой системе координат можно получить кано-
ническое уравнение соответствующего эллипса?
69. Обоснуйте способ построения эллипса, показанный на
рисунке 104. Указание. Проверьте, что координаты выделен-
ных точек, образованных пересечением соответствующих отрезков,
удовлетворяют уравнению
Гипербола
Гиперболой называется геометрическое место точек, разность
расстояний которых от двух фиксированных точек, называемых
фокусами, есть величина постоянная, меньшая, чем расстояние
между фокусами.
Пусть фокусами гиперболы являются точки Fi и Fs, FiF2 = 2c,
а упомянутая в определении разность расстояний равна 2а,
где 2а<2с. Расположив оси координат точно так же, как это
было сделано ранее для эллипса, н проведя совершенно аналогич-
ные выкладки (сделать которые мы предоставляем читателю са-
мостоятельно) , получим каноническое уравнение данной гипербо-
лы в виде
где в отличие от эллипса Ь2==с2—о2
Для построения гиперболы, заданной этим уравнением, сна-
чала изображают так называемый основной прямоугольник ги-
перболы, стороны которого лежат иа прямых х— —а, х=а,
у— —Ь, у~Ь. Затем проводят диагональные прямые через проти-
воположные вершины этого прямоугольника. Эти прямые служат
асимптотами гиперболы — к ним неограниченно приближаются
ветви гиперболы, удаляясь от начала координат (греческое слово
«асимптота» буквально означает «несовпадающий», «несливаю-
щийся»). Асимптоты гиперболы чертил еще Архимед, однако
сам термин появился впервые у Аполлония (260—170 гг.
до и. э.). Своими вершинами гипербола касается сторон основного
прямоугольника,- лежащих иа прямых х~—а, х=а (рис. 105).
Заметим, что для любой точки М, лежащей иа правой кет- *
ви гиперболы, AfFi — MFz—2a, а для точки Л1, лежащей на ле-
вой ветви, MFz—MF\—2a, илн MFj—MFs=—2а. (Этн случаи
„2 .Д
объединились в уравнении -5—-^-=1 в результате возведения
в квадрат равенства MFi—AfF2==2a.)
6 Заказ 776
Рис. 104
Рис. 105
Число в—-—, где а — расстояние от центра гиперболы до ее
вершины, называется эксцентриситетом гиперболы. Очевидно, для
любой гиперболы е>1 (в то время как для эллипса е<1)
Аналогично тому, как это было сделано для эллипса, можно
показать, что фокальные радиусы Г|=Л1ГЬ любой точ-
ки М (х; у), лежащей на правой ветви, вычисляются по формулам
rt~ex-^a, г2—ех~а,
а фокальные радиусы точек левой ветви — по формулам
Г1——ех—а, г2——ех~ра.
Прямые х= —х=— называются директрисами гиперболы.
Для любой точки гиперболы отношение расстояния г до неко-
торого фокуса к расстоянию до односторонней с этим фокусом ди-
ректрисы есть постоянная величина, равная эксцентриситету
гиперболы:
У гиперболы тоже есть любопытное оптическое свойство: лу-
чи, исходящие от источника света, помещенного в фокусе гипербо-
лы, отражаясь от ее ветви, идут так, как будто они были выпуще-
ны из другого фокуса гиперболы.
Задачи
70. Изобразите гиперболы, задаваемые следующими уравне-
ниями, и найдите их фокусы:
a) Xs—в) в) 4*2=4
Указание. Фокусы гиперболы в) лежат на оси Оу.
71. Найдите фокусы гиперболы xt/= 1, знакомой вам из курса
алгебры. Чему равна разность фокальных радиусов точек этой
гиперболы?
72. Найдите геометрическое место точек, равноудаленных от
двух непересекающихся окружностей, радиусы которых Ri И
где
73. Будем считать, что волк и пантера бегают одинаково
быстро, но пантера всегда настигнет жертву, если сумеет прибли-
зиться к ней иа расстояние d решающего прыжка, волку же необ-
ходимо приблизиться к добыче вплотную. В какой части плоскости
пантера будет иметь преимущество в охоте, если она и волк уви-
дели добычу одновременно, находясь в точках Л и В?
74. Докажите, что геометрическое место точек, отношение
расстояний которых от некоторой точки (фокуса) и некоторой пря-
мой (директрисы) постоянно и равно е, есть парабола при е«1,
эллипс при е<1 и гипербола при е>1.
162
ЗАДАЧИ, СВЯЗАННЫЕ С УРАВНЕНИЕМ ПРЯМОЙ
Уравнения примой
Как вы знаете из курса геометрии, любая прямая на координат
ной плоскости может быть задана уравнением вида
ах+Ьу 4-с=0. (1)
Подобные уравнения называют линейными. Уравнение вида (1)
называют также общим уравнением прямой на плоскости.
Если ax-\-by-\-c=Q — уравнение некоторой прямой I, то урав-
нение ах+Ьу+с~р, где р^О, задает прямую I', параллельную /.
Это следует из того, что данные два уравнения не имеют общих
решений, а значит, прямые не имеют общих точек. Пусть точ-
ка Л1о(х0; уо) не принадлежит прямой (1). Тогда уравнение
ox4-6f/4-c=ax04-6t/o4-r (2)
гудет задавать прямую, проходящую через точку и параллель-
ную прямой I.
Пример 1. Составим уравнение прямой, проходящей через
точку М (2; —3) и параллельной прямой Зх—4#-}-5=0.
Решение. Подставляя координаты точки М в левую часть
энного уравнения, получим значение 23. Значит, искомым урав-
нением прямой будет Зх—4у-|-5=23, или окончательно Зх —
-4$/—18=0.
Пусть известны координаты двух точек л!< (хд yi) и М2 (х2; у2),
южащих на дайной прямой. Как составить ее уравнение? Легко
проверить, что таковым будет уравнение
(х—х,)(</2—^1)—(у—!/|)(*!—Х|)=0. (3)
Действительно, во-первых, это уравнение линейное и, значит, за-
дает некоторую прямую н, во-вторых, координаты двух данных то-
чек ему удовлетворяют, н, значит, это и есть та самая прямая,
о которой шла речь.
Пример 2. Составим уравнение прямой, проходящей через
точки Mi (2; 6) н М2(—4; 2).
Решение. По формуле (3) можно записать уравнение
(х—2) (2—6)—(t/—6)(—4—2)=0,
откуда после очевидных преобразований получим:
2х—3//Д-14=0.
Если известны координаты (а; 0) н (0; Ь) точек пересечения
прямой с осями Ох и Оу, то для этой примой проще всего запи-
сать уравнение в отрезках: в справедливости кото-
рого мы предоставляем вам убедиться самостоятельно.
163
Задачи
75. Составьте уравнения прямых, иа которых лежат стороны
ДЛВС с вершинами Л (5; —4), В(—1; I), С(0; —3). Составьте
уравнения прямых, проходящих через вершниы Д АВС параллель-
но его сторонам, н найдите координаты вершин треугольника,
образованного пересечением этих прямых.
76. Составьте уравнения в отрезках для прямых, проходящих
через заданные точки: а) Л (1; 0), В (0; 1); б) А (2; 0), В(0; 3);
в) Л (-2; 0), В (0; 4).
Расстояние от точки до прямой
Прн подстановке в уравнение ах-{-Ьу-\-с=0 некоторой прямой I
координат лежащих на ней точек значение выражении
ах4*by+с равно нулю. Если же точка Мо(хо;уо) не принад-
лежит прямой /, то указанная подстановка даст некоторое зна-
чение р=ахо4-6(/о+с. отличное от нуля. Каков геометрический
смысл этого значения?
Поскольку уравиеине ах-]~Ьу-рс—р определяет прямую Г,
параллельную исходной и проходящую через точку Мо (х0; у0), то
во всех точках примой Г значение ax+by+с также равно р.
Воспользуемся этим и, проведя прямую Г\\1 на чертеже (рис. 106),
выберем на ней наиболее удобную для вычислений точку,
а именно точку ее пересечения с осью Оу. В точке х=0,
а значит, Ьу+с=р, откуда t/=£— - Для исходной же прямой /
ордината точки В пересечения ее с осью Оу равна —. Поэтому
длина отрезка BMi равна | —0| = | ^-| .
Итак, отношение | -£-| дает длину отрезка, параллельного
оси Оу и заключенного между прямыми I и Г. Зная это, легко-
найти и расстояние между указанными прямыми (равное рас-
стоянию от точки Мо до прямой /),
а именно
d—BP—BM, sin а
Рис. 106
(4)
164
Вспомнив, что р есть значение левой части уравнения
исходной прямой в точке Л1 (хо‘, t/o), получаем окончательно
следующую важную формулу расстояния от точки до прямой:
,__\ахп±Ьуй±с\
(5)
Формула оказалась весьма простой — достаточно вычислить
модуль значения левой части уравнения прямой в дайной точке
н поделить его на
Пример. Расстояние от точки М (4; 7) до прямой 3x4-41/4-
4-10=0 находится согласно полученной формуле так:
13.4+4-7+101. 10
Задачи
77. Найдите высоту дДВС, опущенную нз вершины А, если
А ( — 12; 10), В (2; 2), С(—2; 5).
78. Докажите, что формула d остается справед-
-уа*+^г
лнвой и в случаях, когда данная прямая параллельна оси Ох или
оси Оу. Запишите ее для этих случаев в более простом виде.
79. Докажите, что расстояние между параллельными прямыми
ax+by+ci—Q и ах4-6$/4-С2=0 равно
ув*+^
80. Составьте уравнение прямой, равноудаленной от двух
параллельных йрямых х—21/4-5=0 н х-~2у—3=0.
81. Докажите, что уравнение
задает прямые, которые делят пополам углы, образованные при
пересечении прямых aix4'tij/4’Ci =0 и агх-^Ь2У-{-С2=0. Составь-
те уравнения прямых, содержащих биссектрисы углов, образо-
ванных прямыми 3x4*4t/—5=0, 4х—31/4-10=0.
Отклонение точки от ирямой
Если убрать знак модуля в формуле (5), то получим величину,
называемую отклонением точки от прямой. С точностью до знака
отклонение равно расстоянию до прямой. Но что означает сам
этот знак?
Из рисунка 106 ясно, что для всех точек М01 лежащих вы-
ше прямой ах+Ьу+с~0, точка М| оказывается «выше» точ-
ки В (О; -у-) и потому -у-» откуда ^->0. Последнее оз-
начает, что знак р (т. е. результата подстановки координат точ-
165
ки в левую часть уравнения прямой) одинаков для всех точек, ле-
жащих в верхней полуплоскости, определяемой примой. Во всех же
точках нижней полуплоскости знак р также, очевидно, оказывает-
ся одинаковым, но противоположным тому, который был в верхней
полуплоскости. Сказанное справедливо, разумеется, и в случае,
когда прямая параллельна оси ординат, если только слова «верх-
няя» и «нижняя» заменить на «правая» и «левая» (полуплос-
кости) .
Знак отклонения точки от прямой ах-\-Ьу-\-с=О изменится,
если умножить левую часть уравнения прямой на отрицательное
число. Существенно, однако, то, что знаки отклонений точек, ле-
жащих в одной н той же полуплоскости, одинаковы, а лежащих в
разных полуплоскостях различны. Заметим, что при решении ря-
да задач существенны именно знаки отклонений точек от прямой,
а не величины отклонений.
Линейные неравенства и полуплоскости
Согласно предыдущему прямая ах+Ьу+с=0 разбивает всю
координатную плоскость на две полуплоскости, в одной из кото-
рых ах-\-Ьу-\-с>0, а в другой ах by+с СО. Это можно трак-
товать м так:
линейное неравенство с двумя переменными ах-\-Ьу ]-с>0
задает одну из полуплоскостей, на которые плоскость ху разбива-
ется прямой ах+Ьу+с=*О.
Для того чтобы узнать, какая именно из полуплоскостей за-
дается данным неравенством, следует изобразить прямую ах+
-}-Ьу+с=О и, взяв любую не лежащую на ней точку Мо(х<>; Уо),
проверить выполнимость неравенства ax-j~by-j-c>-0. Если это
неравенство истинно в точке Мо, то им задается та самая полу-
плоскость, в которой лежит точка Мо. а если нет, то противопо-
ложная полуплоскость.
Пример. Изобразим множество решений неравенства
2х—z/+2<0.
Решение. Проводим прямую 2х—$/+2=0 в плоскости ху
(рис. 107). Берем в качестве контрольной точки начало координат
О (0; 0). Поскольку в этой точке не-
равенство не выполняется, то усло-
вие 2х—р+2<0 задает ту полу
плоскость, в которой начало коор-
динат ие лежит. Заштриховываем иа
чертеже эту полуплоскость.
Из сказанного выше ясно, что
система линейных неравенств с дву
мя переменными задает пересечение
полуплоскостей, определяемых каж-
дым из неравенств системы. В каче-
стве иллюстрации иа рисунке 108
166
Рис. 108
изображены множества решений следующих
неравенств:
систем линейных
а) Л х—
{ х+^^2.
2х— j/JsO,
х—2j/C0,
*+ «/<3;
2х— y^D,
х—2у^.О,
x-f- у^З,
*+ ^<6.
Задачи
82. Определите, пересекает ли отрезок с концами в точках
.4(1; —2), В(—1; 18) прямую 14% +у4~6=0.
83. Две прямые 2*4-3i/—5=0 п 5х—4i/4-2=0 при пересече-
нии образуют 4 угла. Определите, принадлежит лн точка М (8; 6)
тому же углу, что и начало координат, а если нет, то принадлежит
ли она смежному или вертикальному с ним углу.
84. Докажите, что любой выпуклый многоугольник в плоскос-
ти ху можно задать некоторой системой линейных неравенств.
Предложите способ аналитического (т. е. без использования
изображений на плоскости) выяснения того, лежит ли точка
М (х; у) внутри выпуклого многоугольника с вершинами в задан-
ных точках At (xf; у{), А2{х2-, у2), ..Ап(хп; уп).
85. Установите аналитически, лежит ли точка М (—2; 2) внут-
ри А АВС, если А (5; -4), В(~1; 5), С(-3; 1).
86. Задайте с помощью систем линейных неравенств множест-
ва, изображенные на рисунке 109.
87. Определите координаты центра окружности, вписанной в
треугольник с вершинами А (0; 3). В (4; 0), С (0; 0). Составьте
уравнение этой окружности.
88. На острове, берега которого лежат на прямых 3x-f-4y—
—625=0,4х—3у—0,t/=0, Робиизои хочет построить дом в таком
месте, наименьшее расстояние от которого до береговой линии
острова было бы максимальным. Определите координаты точки,
в которой следует строить дом.
167
89. Составьте уравнение биссектрисы того угла между пря-
мыми 3x-f-4i/4-5—0 и 4*4-3»/4-7=0, в котором находится точка
Д(1; -3)
90. Составьте уравнение окружности с центром в точ-
ке М (—2; 4), касающейся прямой х4*У—4=0.
Формула площади треугольника
Рассмотрим иа координатной плоскости ху треугольник
с вершинами в точках А (кг, yt), В (xs; Уг), С (хз; Уз)- Уравнение
прямой, на которой лежит сторона АВ этого треугольника, мож-
но, как вы знаете, записать в виде
(х—*1)(у2—Ум)—(у~У1)(х2—*i)=0.
Подставив координаты третьей вершины С (хз*, Уз) в левую часть
этого уравнения, получим некоторое значение
q =(х3 - х.) (у2—У»)—(f/з—УI) (х2 -х»). (6)
Чтобы понять геометрический смысл числа q, заметим, что
уравнение (х—Х|)(у2—У»)—(у—У\){х2—xt)=q задает прямую,
параллельную стороне АВ данного треугольника. Поэтому для
Рис. 110
каждой точки этой прямой резуль-
тат подстановки ее координат в
левую часть уравнения тот же.
что и для точки С (хз; уз), и дает
число q. Значит, то же значение
получится и для точки Ci (х4; у»)
пересечения упомянутой прямой
с прямой y=ylt параллельной оси
абсцисс и проходящей через вер-
шину А треугольника (рис. 110).
Но в этой точке (х—xi)(y2—у»)—
168
—(У—yt)(xs—*1)=(*4“-Х1)(у2—yi). Геометрический смысл послед-
него выражения понять уже несложно: |(х4—xi)(x/2—t/i)l есть ие
что иное, -как площадь параллелограмма со сторонами АВ и ЛС\.
Длина стороны АСх равна |х4—xt|, а длина высоты параллело-
грамма, опущенной из вершины В иа эту сторону, есть ие что иное,
как |^2—j/i|. Поэтому есть площадь дЛВСь но она такая
же, что и у дЛВС, с которого мы начали рассмотрение. (Ведь
вершина С| получилась в результате «скольжения» вершины С
по прямой, параллельной стороне треугольника, а основание ос-
талось неизменным!) В результате приходим к следующей заме-
чательной формуле дли площади треугольника:
S=-|-l(w—Х|)(02~01)“ (03—01)(х2 —Х1)|. (7)
Любопытен тот факт, что для целочисленных координат вер-
шин треугольника его площадь оказывается либо целым числом,
либо дробью со знаменателем 2.
Конечно, мы могли бы получить формулу для площади тре-
угольника и использун формулу расстояния от точки до прямой
(сделайте это сами), но наш вывод дает и другой путь нахождения
формулы расстояния, по которому мы советуем вам пройти самос-
тоятельно.
Уравнение треугольника
Если мы возьмем произвольно точку Л! внутри дЛВС,
или на его сторонах, то сумма площадей ДАВЛ4, ДВСЛ4, Д4СЛ1
даст нам площадь данного ДДВС и ие будет поэтому зависеть
от положения точки М. Если же мы возьмем точку М вне тре-
угольника, то упомянутая сумма площадей будет всегда больше
площади треугольника. Если наш треугольник задан в декартовой
системе координат и имеет своими вершинами точки 4(xi; У\),
В (х2; у$\ С (хз; уа), то с учетом сказанного и полученной только
что формулы для площади треугольника мы можем задать его
(как часть плоскости) уравнением
|(х—Х|)(02 —0|)—(0 —0i)(X2—Х01 +
+ 1(х—х2) (уз—уг)—(0—0г) (хз—х2) I +
+ 1(х—хз) (01—Уз)—(У—Уз) (х, —х3)| —2S, где
S=-|-KX3 —Х0(02—01)—(03—01)(Х2 —х,)|. (8)
График этого необычного уравнения состоит, очевидно, из
всех точек, лежащих внутри ДЯВС и на его сторонах.
Пример 1. Составим уравнение треугольника, изображен-
ного на рисунке 111. Для этого составляем уравнения его «сторон»
по формуле (3), задающей уравнение прямой по двум ее точкам:
169
Рис 111
(X - Xi) (t/2 - y() - (у—у,) (х2—Xi) = О
При этом (обратите внимание) до-
пустимым считаем раскрытие скобок
и приведение подобных слагаемых
и недопустимым — умножение обеих
частей уравнении иа некоторое число
(за исключением — 1). Полученные
таким образом уравнении сторон
имеют видх—у 4-1=0, х+у—1=0,
2i/~0. Сложив модули левых частей
этих уравнений н приравняв полу-
ченное выражение к удвоенной пло-
щади ДЛВС, равной в нашем случае 1, приходим к искомому
уравнению |х—у+ И + 1*4-0—11 +2Ы =2.
Имея такое уравнение, легко выяснить, принадлежит точка
данному треугольнику или нет.
Описанный метод дает возможность получить и уравнение лю-
бого выпуклого многоугольника (как части плоскости), координа-
ты вершин которого известны. (Ведь и для любого выпуклого мно-
гоугольника сумма площадей всех треугольников, которые полу-
чаются в результате соединения взятой внутри многоугольника
точки М сего вершинами (рис. 112), равна площади этого много-
угольника, а для точки вие его такай сумма всегда больше пло-
щади многоугольника.) В случае правильного многоугольника
можно воспользоваться и тем (вытекающим из отмеченного)
фактом, что сумма расстояний от любой из его точек до сторон
многоугольника есть величина постоянная.
Пример 2. Составим уравнение квадрата, изображенного на
рисунке 113. Воспользуемся тем, что сумма расстояний от точки
М{х; у), лежащей внутри квадрата (нлн на его границе), до
его сторон равна удвоенной длине стороны квадрата. Расстояние
от точки М(х; у) до прямых, параллельных осям координат,
х4-с=0 или #+с=0 находится особенно просто: d = |х4~с| или
Отсюда получаем искомое уравнение квадрата в виде
U+ll + ljH-H + lx-il + l!/-ll=4
Рис. 112
170
Рис 114
Заметим, что граница рассмотренного только что квадрата
тоже может быть задана простым уравнением с модулями:
|x+f/l+lx-J/l=2.
Убедиться в этом можно, раскрывая модули в четвертях, на ко-
торые координатная плоскость делится прямыми х-^у—О и
х—у=О.
Задачи
91. Докажите, что неравенство Ix-fj/l 4- lx— yl 4-2lx— 11 3>2
выполняется при любых значениях х и у.
92. Найдите наименьшие возможные значения следующих
выражений: а) |х| + |x+f/| + If/—1|; б) |х-|-2|+ 1х—3|+
4-lf/-2|+lf/|.
93. Найдите площадь треугольника с вершинами в точках
4(—3; 2), В (4; 10), С(3; 6) и составьте уравнение этого тре-
угольника. Выясните, воспользовавшись полученным уравнением,
лежит ли точка Л1(—1; 4) внутри этого треугольника.
94. Составьте уравнения многоугольников, изображенных на
рисунке 114.
Литература
1. Васильев Н.Ь., Гутенмахер В. Л. Прямые и кри-
вые — М.: Наука, 1976.
2. В и л е н к и и Н. Я. Множества на координатной плоскости//
Факультативный курс: Избранные вопросы математики 7—8.—
М.: Просвещение, 1978.
3. Гельфанд И. М., Глаголева Е. Г., К и р и л л о в А. А.
Метод координат.— М.: Наука, 1973.
4. Маркушевич А. И. Замечательные кривые — М.: Наука,
1978.
5. П о н т р я г и н Л. С. Знакомство с высшей математиком:
Метод координат.— М.: Наука, 1977.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
ЛОГИКА ВЫСКАЗЫВАНИИ
1. Классическая логика. Умение правильно рассуждать не-
обходимо в любой области человеческой деятельности: науке и
технике, юстиции и дипломатии, планировании народного хозяй-
ства и военном деле. Но, хотя умение это восходит к древней-
шим временам, логика, т. е. наука о том, какие формы рассуж-
дений правильны, возникла лишь немногим более двух тысяч лет
тому назад. Она была развита в IV в. до и. э. в работах вели-
кого древнегреческого философа Аристотеля (384—322 гг.
до н. э.), его учеников и последователей. Аристотель исследовал
различные формы суждений и их комбинаций, ввел понятие силло-
гизма, т. е. рассуждения, в котором из заданных двух суждений
выводится третье. Примером силлогизма может служить такое
рассуждение: «Все млекопитающие имеют скелет. Все киты —
млекопитающие. Следовательно, все киты имеют скелет». Ту же
форму имеет силлогизм «Все квадраты — ромбы, все ромбы — па-
раллелограммы. Следовательно, все квадраты — параллелограм-
мы». В общем виде этот силлогизм имеет форму: «Все а суть Ь, все
b суть с. Следовательно, все а суть с». А вот пример силлогиз-
ма неправильной формы: «Все квадраты — ромбы. Некоторые ром-
бы имеют острый угол. Некоторые квадраты имеют острый угол*.
Хотя оба утверждения, из которых был сделан вывод, истинны,
сам вывод о существовании квадратов с острым углом ложен.
Значит, силлогизм, имеющий форму: «Все а суть Ъ, некоторые b
суть с. Значит, некоторые а суть с», может привести и к ложным
выводам. Аристотель выделил все правильные формы силлогиз-
мов, которые можно составить из суждений вида: «Все а суть 6»,
«Некоторые а суть Ь», «Все а не суть Ь» н «Некоторые а не
суть Ь». Логика, основанная на теории силлогизмов, называется
классической.
Доказано, что общее число силлогизмов, которые можно
составить из суждений указанного вида, равно 256. Из ннх пра-
вильными являются лишь 24. Для проверки правильности силло-
гизмов можно использовать метод геометрической иллюстрации
логических рассуждений, который был предложен великим матема-
тиком XVIII в., петербургским академиком Л. Эйлером
(1707—1783) и широко применялся английским математиком
172
Дж. Венном (1834—1923). Согласно этому методу логические
рассуждения изображаются геометрически. Например, рису-
нок 115, а поясняет, что если все а суть Ь, а все b суть с, то
все а суть с. Рисунок 115, б поясняет силлогизм «Если все а
суть b и нн одио b не является с, то ни одно а не является с».
А рисунок 116,0 поясняет, почему не годится силлогизм «Все а
суть Ь, некоторые b суть с. Значит, некоторые а суть с». Впрочем,
иа рисунке 116,6 показан случай, когда некоторые а суть С. Это
показывает, что неправильно построенное рассуждение необяза-
тельно приводит к ложному выводу: случайно может оказаться
и так, что вывод будет истинным. Но логика считает допусти-
мыми только такие формы рассуждений, которые гарантируют
истинный результат во всех случаях, когда исходные утверждения
истинны. Такие рисунки называют диаграммами Эйлера — Венна.
Однако использование этих диаграмм затруднительно в сложных
случаях.
Как известно, в конце XVI в. в алгебре словесная форма
запнси алгебраических выражений стала тормозить развитие нау
ки и, чтобы облегчить выполнение алгебраических преобразований,
была создана’ буквенная символика, позволяющая выполнять
этн преобразования по строго определенным правилам. Точно так
же, чтобы облегчить проверку и преобразование сложных цепочек
рассуждений, было создано особое буквенное исчисление. Оно
получило название алгебры логики нли математической логики
Основы математической логики были заложены в XVII в. великим
иемецкнм математиком Г. Лейбницем (1646—1716). В се-
редине XIX в. ирландский математик и логик Дж. Буль
(1815—1864) своими трудами положил начало формированию
0
9
Рис. 116
173
математической логики как научной дисциплины. В обычной
алгебре буквы обозначают числа, а операции над ними символи-
зируют соответствующие операции над числами; в алгебре логики
буквы (обычно прописные латинские) обозначают высказывания,
а операции над ними символизируют операции над высказывания-
ми. В математической логике, как и в обычной алгебре, есть
тождества, верные для любых высказываний. Сначала познако-
мимся с основными операциями над высказываниями.
Упражнения
1. Нарисуйте диаграммы Эйлера — Венна, иллюстрирующие
суждения:
а) «Все х являются у»;
б) «Некоторые к являются у»;
в) «Ни одно х не является у»;
г) «Некоторые х не являются у*.
2. Докажите, что из предложения «Некоторые х являются у»
следует предложение «Некоторые у являются х».
3. Докажите, что если ни одно х не являются у, то ни одно
у не является х.
4. Изобразите диаграммы Эйлера — Венна, для которых
ложны оба высказывания: «Все л являются у» и «Ни одно х не
является у».
5. Следует ли нз того, что «Все х являются у и некоторые
у явлиютси z»t утверждение «Некоторые х являются z»?
6. Правильно ли рассуждение, имеющее форму: «Все х яв-
ляются у, и некоторые у являются z; значит, некоторые z яв-
лнются х»?
7. Правильно лн рассуждение, имеющее форму: «Все к яв-
ляются у, и некоторые у не являются z; значит, некоторые х
не являются z>?
8. Правильно ли рассуждение, имеющее форлу: «Ни одно х
не является у, и некоторые у являются z; значит, некоторые z
не являются ж»?
9. Правильно ли рассуждение, имеющее форму: «Все х явля-
ются у, н ни одно х не является z; значит, все у не являют-
ся z>?
10. Правильно ли рассуждение, имеющее форму: «Если неко-
торые х являются у, а некоторые у являются z, то некоторые х
являются z>?
II. Правильно ли рассуждение, имеющее форму: «Если не-
которые у являются х, некоторые у являются z и некоторые г
являются х, то некоторые х одновременно являются и у, и г»?
2. Высказывания. Основным понятием математической логи-
ки является высказывание. Так называют любое повествователь-
ное предложение, относительно которого известно, что оно либо
174
истинно, либо ложно. Высказывания могут быть выражены с по-
мощью слов, а также математических, химических и прочих
знаков. Примеры:
а) «Марс дальше от Солнца, чем Венера» (истинное выска
зывание);
б) «24~6>8» (ложное высказывание);
в) «II + VI>VIII» (ложное высказывание);
г) «Сумма чисел 2 и 6 больше числа 8» (ложное высказыва-
ние);
д) «В пределах нашей Галактики существуют внеземные циви-
лизации* (несомненно это высказывание либо истинно, либо лож-
но, но пока неизвестно, какая из этих возможностей выполнена)
Ясно, что высказывания б), в) и г) означают одно и то же,
ио выражены различными знаками и словами. Мы не будем
сейчас анализировать смысл исследуемых высказываннй, ограни
чась выяснением того, истинны они или ложны.
Не всякое предложение является высказыванием. Например,
восклицательные и вопросительные предложения высказываниями
ие являются («Какого цвета этот дом?», «Пейте томатный сок!*,
«Стоп!» и т. д.). Не являются высказываниями и определения
например: «Назовем медианой отрезок, соединяющий вершину
треугольника с серединой противоположной стороны» — здесь
лишь устанавливается название некоторого объекта; с тем же
успехом можно было бы дать это название иному объекту, скажем
лучу, делящему пополам угол при вершине треугольника, или
дать тому же объекту иное название. Таким образом, определе
ння не могут быть истинными илн ложными, они лишь фиксируют
принятое использование терминов.
Не являются высказываниями и предложения «Он сероглаз»
или «х2—4х 4-3=0»— в них не указано, о каком человеке идет
речь или для какого числа х верно равенство х2—4x4-3=0.
Такие предложения с переменными называют высказывательными
формами. Мы обсудим их в следующем разделе. Отметим, что
предложения «Некоторые люди сероглазы» и «Для всех х спра
ведливо равенство х2—4х4-3--0» уже являются высказывания
ми (первое из них истинно, а второе ложно).
Упражнения
12. Укажите среди следующих предложений высказывания:
а) «Луна — спутник Земли»;
б) «Все учащиеся любят математику»;
в) «Принеси мне, пожалуйста, книгу»;
г) «Некоторые люди имеют голубые глаза»;
д) «Окружностью называется множество всех точек плоскости,
расстояние которых до данной точки этой плоскости имеет за-
данную величину»;
е) «Вы были в театре?»
175
13. Установите, какие нз следующих предложений являются
истинными, а какие — ложными высказываниями:
а) «Число —2 меньше числа О»;
б) «Частное от деления числа 7 на 5 равно О»;
в) «Сумма чисел 5 их равна 10»;
г) «Существует такое действительное число х, что 2x45 = 15»;
д) «(13—2.7).4 = -4»;
е) «Все треугольники равнобедренные»;
ж) «Медианой треугольника называется перпендикуляр, опу-
щенный из вершины треугольника на противоположную сторону».
14. Выделите среди следующих записей высказывания н оп-
ределите, истинны они или ложны:
. 1917 9
а) *852 4 **
б) «6754-872 > (63 4 73 4 53)4 (83 4 73 4 23)»;
в) «8833<8824332»;
г) «(4 4 7) (4—7)=32»;
д) «х2—8x415=0»;
е) «(х4у)3=х343х2у48^24'1/3»'.
ж) «Всегда (х4«/)3=х343х2«/43х£/24!/2».
3. Простые и сложные высказывания. Некоторые высказыва-
ния можно разложить на отдельные части, при этом каждая та-
кая часть будет самостоятельным высказыванием. Например, вы-
сказывание «Сегодня в 4 часа дня я был в школе, а к 6 часам вече-
ра пошел иа каток» состоит нз двух частей: «Сегодня в 4 часа
дия я был в школе» и «Сегодня к 6 часам вечера я пошел на ка-
ток». Высказывание может состоять и из большего количества
частей.
Высказывание, которое можно разложить на части, будем
называть сложным, а неразложимое далее высказывание — прос-
тым. Подобно тому как из заданных чисел можно получить дру-
гие числа с помощью операций сложения, вычитания, умножения
и деления, а также операций перехода к противоположному или.
обратному числу, из заданных высказываний получаются новые
с помощью операций, имеющих специальные названия: конъюнк-
ция, дизъюнкция, импликация, эквиваленция и отрицание выска-
зывания. Хоть названия эти звучат непривычно, они означают
лишь хорошо нзвестное соединение отдельных предложений
связками «и», «илн», «если .... то ..«тогда и только тогда,
когда ...» и присоединение к высказыванию частицы «ие». Одиако
если в обыденной речи употребление этих связок н частиц не под-
чинено строгим правилам, из-за чего возможны разные толкования
одного и того же предложения, то в математической логике
смысл каждого слова четко определен, а чтобы обыдеииое толко-
вание слов ие влияло на их употребление, сами связки заменяются
особыми знаками.
176
Упражнения
15. Даны высказывания:
А: «Земля вращается вокруг Солнца»;
В: «Земля имеет форму шара».
Образуйте из даииых высказываний сложные и подчеркните
слова, при помощи которых они образованы.
16. Среди приведенных ниже высказываний укажите слож-
ные; выделите в иих простые, обозначив каждое из иих буквой.
Запишите с помощью букв каждое сложное высказывание:
а) «На уроке математики учащиеся отвечали иа вопросы учи-
теля и писали самостоятельную работу»;,
б) «Мы пойдем кататься на коньках или на лыжах»;
в) «Если в данном четырехугольнике диагонали имеют равную
длину, то этот четырехугольник — ромб»;
г) «—17^0»;
д) «Число 15 делится иа 3 тогда и только тогда, когда
сумма цифр этого числа делится на 3».
4. Отрицание. Рассмотрим следующие высказывания:
А: «Сегодня в 12 часов дия я был иа катке»;
В: «Сегодня я был на катке ие в 12 часов дня»;
С: «Я был на катке в 12 часов дня ие сегодня»;
D: «Сегодня в 12 часов дня я был в кино»;
Е: «Сегодня я был на катке в 3 часа дня»;
F: «Сегодня в 12 часов дня я не был на катке».
На первый взгляд высказывания В — F отрицают высказыва-
ние А. На самом деле это не так. Если внимательно вчитаться
в смысл высказывания В, то можно заметить, что оба высказыва-
ния А и В могут одновременно оказаться ложными — так бу-
дет, если сегодня я совсем ие был иа катке. То же самое от-
носится и к высказываниям А и С, А и D, а высказывания А и Е
могут оказаться и одновременно истинными (если, например, я
катался иа коиьках с И до 4 ч дня), и одновременно ложными
(если сегодня я совсем не был на катке). И только высказывание F
обладает следующим свойством: оно истинно в том случае, когда
высказывание А ложно, и ложно в том случае, когда выска-
зывание А истинно. Его называют отрицанием высказывания А.
Вообще отрицание высказывания А ложно, если А истинно,
и истинно, если А ложно. Отрицание высказываиня А обознача-
ют А или (не Д) (читается: «Не Д» или «Неверно, что Д>).
Следующая таблица показывает связь между А и Д:
А
И
Л
А
Л
И
177
Буквы «И» и «Л» — сокращения слов «истина» и «ложь» соответ-
ственно. Эти слова в логике называют значениями истинности
высказываний.
Обычно для построения отрицания данного высказывания на-
до присоединить к сказуемому частицу «не» или, если она уже есть,
опустить ее. Например, для высказывания «Сейчас небо синее»
отрнцанне будет «Сейчас небо не синее» или «Сейчас небо не яв-
ляется синим». А отрицанием высказывания «Гремучая змея не
имеет позвоночника» является высказывание «Гремучая змея
имеет позвоночник».
В математике отрицание высказывания, записанного с по-
мощью тех илн иных знаков, часто выражают, перечеркивая
соответствующий знак или опуская перечеркивающую линию.
Например, отрицанием высказывания «24-3=5» является «2-Б
4-3^5», а отрицанием высказывания aflb является й||Ь (где а и
b — прямые на плоскости). Иногда применяются иные обозначе-
ния: отрицанием высказывания а<Ь является а^Ъ — неравенст-
во а<Ъ истинно в том и только в том случае, когда а^Ь ложно.
Упражнения
17. Постройте отрицания приведенных ниже высказываний.
Определите значения истинности этих высказываний и их отри-
цаний.
а) «Число 5 — делитель числа 542»;
б) «Автомобиль ие имеет права ехать вперед иа красный
свет»;
в) «Существуют параллелограммы с прямыми углами»;
г) «Уравнение 2х2—3x4-1—О имеет целый корень»;
д) «Все корнн уравнения 2х2—3x4-1 =0 — целые»;
е) «Все натуральные числа делятся иа 2»;
ж) «Не существует натурального числа, делящегося на 2»;
з) «Существует целое число, делящееся иа все целые числа».
18. Средн следующих высказываний найдите отрицание выс-
казывания «Существуют четные простые числа»:
а) «Существуют нечетные простые числа»;
б) «Существуют четные составные числа»;
в) «Любое простое число иечетио»;
г) «Не существует четных простых чисел».
19. Определите, какие из предложений в следующих парах
являются отрицаниями друг друга н какие нет; объясните почему
а) «4<0; 4>0»;
б) «5-<0; 5^0»;
в) «ДАВС прямоугольный; дАВС остроугольный»;
г) «Натуральное число 6 четно; натуральное число 6 нечетно»;
д) «Он мой друг; ои мой враг»;
е) «Все простые числа четны; все простые числа нечетны»;
178
ж) «Человеку известны все виды животных, обитающих на
Земле; на Земле существует вид животных, неизвестный чело-
веку»;
з) «Ои мой друг; он друг моего брата».
20. Докажите или опровергните следующие предложения, об-
разовав нх отрицания:
а) 2С2; б) 3^5; в) все простые числа нечетны; г) ни одно
русское слово не содержит более двух одинаковых гласных подряд.
5. Конъюнкция и дизъюнкция высказываний. Высказывание
«Число 2 четное н простое» является сложным: оно состоит
из двух высказываний «Число 2 четное» н «Число 2 простое»,
связанных союзом «н». Оба эти высказывания истинны. Считают,
что и сложное высказывание «Число 2 четное и простое» тоже
истинно. Высказывание «Число 12 четное и простое» считается
ложным; оно состоит из высказывании «Число 12 четное» и «Чис-
ло 12 простое», из которых истинно только первое. Ложным
считают и высказывание «Число 12 нечетное и составное», и,
конечно, высказывание «Число 12 нечетное и простое», которое
состоит из двух ложных простых высказываний «Число 12 нечет-
ное» н «Число 12 простое», соединенных союзом «и».
Вообще если два высказывания Л, В связаны друг с другом
союзом «и», то полученное сложное высказывание «Л и В» счи-
тают истинным лишь в том случае, когда оба исходных выска-
зывания истинны. Если же хотя бы одно из иих ложно, то слож-
ное высказывание «А и В» считают ложным.
Высказывание «А и В* истинное, если истинны оба высказы-
вания Аи В, и ложное, если хотя бы одно из них ложное, назы-
вают конъюнкцией этих высказываний и обозначают А /\ В. Таким
образом, таблица истинности высказывания А/\В (читают: «А
1' В») имеет вид:
А в А Л В
И и И
И л л
Л и л
л л л
В школьной математике примером конъюнкции высказываний
может служить двойное неравенство, например 3<6<7. Такое
неравенство считают истинным лишь в том случае, когда истин-
ны оба входящие в него неравенства, в нашем случае это Зеб
и 6<7. Двойное же неравенство 3<6<4 ложно, так как хотя
3<6 истинно, но 6<4 ложно. Конъюнкцией является н выска-
зывание «Диагонали любого ромба перпендикулярны и делят углы
ромба пополам».
179
Высказывания можно связать друг с другом не только сою-
зом «и», ио и союзом «или», например: «На следующем уроке
будет контрольная или самостоятельная работа» (подробнее:
«На следующем уроке будет контрольная работа или на следую-
щем уроке будет самостоятельная работа»). «Если последняя циф-
ра числа равна О или 5, это число делится иа 5» (подробнее:
«Если последняя цифра числа равна 0, то это число делится иа 5,
илн если последняя цифра числа равна 5, то это число делит-
ся на 5»).
В обыденной речи союз «или» имеет два различных значения:
разделительное и неразделительиое. Например, если сказать:
«Завтра в 12 ч дня я буду в клубе нлн на катке», то не может
быть, чтобы оба обещания оказались выполнены: человек не может
быть одновременно в двух местах. Здесь союз «или» разделитель
иый. Но если сказать: «Я буду в клубе завтра в 12 ч дня или
в 6 ч вечера», то не исключено, что сбудется и то и другое: чело-
век может посетить клуб дважды в одни н тот же день. Здесь
тот же союз понимается в неразделительном смысле.
Чтобы устранить эту неопределенность, условились в мате-
матической логике использовать лишь неразделительное «илн»
Таким образом, в математической логике считают, что высказы-
вание А или В истинно, если истинно хотя бы одно из этих выс-
казываний, и ложно лишь в одном случае — когда оба эти выска-
зывания ложны. Высказывание «4 или В» называют дизъюнкцией
этих высказываний и обозначают А\/В (читают: «4 или В»). Та-
ким образом, таблица истинности для высказывания А V В имеет
следующий вид:
в
А V В
л
и
л
И
И
И
Л
В математике примером дизъюнкции высказываний может слу-
жить нестрогое неравенство, например 3^7. Такое неравенство
считается истинным, если истинно хотя бы одно из входящих в не-
го высказываний 3<7,3=7. Поэтому высказывания 3^7 и 3<ГЗ
истинны. Неравенство же 7^3 ложно, так как ложны оба выска-
зывания 7<3 и 7=3. Является дизъюнкцией и высказывание:
«Данный четырехугольник является прямоугольником или ром-
бом». Здесь могут оказаться истинными оба высказывания
(если четырехугольник является квадратом).
180
Упражнения
21. Среди следующих сложных высказываний выделите конъ-
юнкции и дизъюнкции и определите, ложиы онн или истинны:
а) «Число 27 кратно 3 и 9»;
б) «17<42с18»;
в) «Число 2 простое или четное»;
г) «АЛВС является остроугольным^ прямоугольным или ту-
поугольным»;
д) «Диагонали любого параллелограмма перпендикулярны и
делят друг_ друга пополам»;
е) —4, но — 4#=(—
ж) «72 = 49 и (—7)2 = 49»;
з) «Если треугольник равнобедренный, то ои равносторон-
ний»;
и) «21<21»;
к) «21 18».
22. Даны высказывания: А) «Я купил велосипед»; В) «Я
участвовал в соревнованиях по велоспорту»; С) «Я путешество-
вал по СССР». Сформулируйте высказывания, соответствующие
следующим выражениям:
а) А/\В; б) AVB; в) А/\В-, г) AVBVC;
д) А/\В‘, е) AVC; ж) А\/С, з) (А/\В)\/С.
6. Импликация и эквивалеиция высказываний. Рассуждения
чаще всего представляют собой цепочки высказываний. Эти выс-
казывания имеют обычно условный характер, т. е. утверждают,
что некое высказывание истинно при условии, что истинно дру-
гое, например: «Если у данного треугольника боковые стороны
равны, то равны и углы при основании». В общем виде такие
высказывания записываются так: «Если истинно А, то истинно В»,
или короче: «Если А, то В». Такое высказывание называют им-
пликацией высказываний А и В и обозначают А В. Высказыва-
ние А называют условием, а В — заключением. Например, пусть
А: «Сейчас хорошая погода» — и В: «Я пойду гулять». Тог-
да А -► В означает: «Если сейчас хорошая погода, то я пойду
гулять». Ясно, что если сейчас плохая погода, то сказавшего это
предложение нельзя назвать лжецои ии в случае, если он пойдет
гулять, ни в случае, если ои откажется от прогулки. Поэтому
импликацию с ложным условием надо считать истинной как при
истинном, так и при ложном заключении. Говорит, что такая имп-
ликация истинна тривиальным образом. Истинно высказывание
Л —>• В и в случае, когда А к В истинны. Единственным ва-
риантом, когда импликация А —*- В ложна, ивляется истинность
условия и ложность заключения.
Итак, импликацией высказываний А и В называют высказыва-
ние А—* В (если А, то В), ложное лишь в случае, когда А
181
истинно, а В ложна. Таблица лЛ#нностн для импликации имеет
следующий вид:
А в А-^В
И И И
И л Л
л и И
л л И
Высказывание «А тогда и только тогда, когда В» называют
зквиваленцией высказывании А и В и обозначают А-*-* В. Счи-
тают, что эквивалент* я двух высказываний истинна в том и только
в том случае, когда оба эти высказывания истинны нли оба ложны.
Таблица истинности для эквивалентен высказываний А и В
имеет следующий вид:
А в
И И Л л и л и л и л л и
Упражнения
23. В следующих составных высказываниях выделите состав-
лнющие их элементарные высказывания; укажите истинные имп-
ликации:
а) «Если число 48 кратно 8, то оно кратно 4»;
б) «Если — 3<— 1. то 32=6»;
в) «Если 1g 100=10, то у собаки четыре иогн»;
г) «Если 2-2=5, то существуют ведьмы».
24. Даны высказывания:
А: «Четырехугольник MNPQ — параллелограмм»;
В: «Диагонали четырехугольника MNPQ в точке пересечения
делятся пополам».
Сформулируйте словами высказывания и установите, нстиииы
они или ложны
а) А^В; б) В ->А; в) А -> В; г) В^А\
д) А-*В; е) В —А; ж) А—В;
з) (А-*В)Л(В->А).
25. Определите значении истинности высказываний:
а) «Если 16 делится иа 4, то 16 делится иа 2»;
б) «Если 17 делится иа 4, то 17 делится на 2»;
в) «Если 18 делится иа 4, то 18 делится иа 2»;
г) «Если 18 делитси иа 2, то 18 делится иа 4»;
142
д) «Если 2-2=5, то 83#=500»;
е) «Если 2-2=4, то 72=81»;
ж) «Если телепатия существует, то некоторые физические
законы требуют пересмотра»;
з) «16 делится иа 4 тогда и только тогда, когда 16 делит-
ся на 2»-
и) «17 делится на 4 тогда и только тогда, когда 17 делится
на 2»;
к) «18 делится иа 4 тогда и только тогда, когда 18 делится
на 2»;
л) «15 делится иа 5 тогда и только тогда, когда 15 делит-
ся иа 10».
26. Определите значение истинности Л и В при условии, что
высказывание:
а) «Если 2 — простое число, то А» истинное;
б) «Если В, то 2 — составное число» ложное;
в) «Если 2 — простое число, то В» ложное;
г) «Если А, то 2 — составное число» ложное;
д) «Д-*->(2<3)> истинное;
е) «В**(2>3)> истинное;
ж) «Д-w (2 >3)» ложное;
з) «В **(2<3)> ложное.
7. Алгебра логики. Из данных конкретных высказываний А,
В, С, D можно с помощью логических операций составить различ-
ные составные высказывания, например: (А VВ) —► (СЛ D). Ал-
геброй логики, называют раздел математической логики, в кото-
ром изучают общие свойства выражений, составленных из данных
высказываний. В алгебре логики мы будем использовать буквы
не только для обозначения конкретных высказываний, ио и для
обозначения логических переменных. Тогда буква будет означать
переменную, которая может принимать лишь два значения И и Л.
Если составить из логических переменных выражение, свя-
зав их по определенным правилам символами Д. V, и зна-
ками отрицания, получится логическое выражение, которое при
одних значениях истинности переменных истинно, а при других
ложно (например, Д ДВ истинно, если Д = И н В=И, и ложно,
если Д=И и В=Л). Вычисляя значения истинности выражения
при различных комбинациях значений истинности входящих в него
логических переменных, получаем таблицу истинности данного
логического выражения. Например, для выражения А ДВ таблица
истинности имеет такой вид:
А в л Ллв
И и л л
И л л л
л и и и
л л и л
де
Может случиться, что для двух внешне различных логичес-
ких выражений таблицы истинности одинаковы. Например, сос-
тавим таблицы истинности для выражений А V В н А —*- В:
Л\/В
Л
и
и
л
л
и
л
и
л
л
л
и
и
и
л
и
и
и
л
и
и
Последние два столбца здесь совпадают. В алгебре логики
принято называть такие два логических выражения логически эк-
вивалентными и писать X о У. В нашем случае
А->В&А\/В.
(1)
Отметим различие между эквивалеицией и эквивалентностью.
Эквиваленция является логической операцией, позволяющей по
двум заданным высказываниям А и В построить новое высказы-
вание А В\ эквивалентность же является отношением между
двумя составными высказываниями, состоящим в том, что нх зна-
чения истинности всегда одни и те же. Связь между этими
понятнями выражается следующим утверждением:
Логические выражения X и У эквивалентны в том и только
в том случае, когда эквиваленция X -♦* У нстиииа при всех зна-
чениях логических переменных.
Например, доказанную выше эквивалентность (1) можно сфор-
мулировать так: эквиваленция
(лув)~(Л->й)
(2)
истинна при любых предположениях об истинности Л и В.
Логические выражения, истинные при любых значеинях истин-
ности входящих в них переменных, называют тавтологиями (от
греческого тауто — то же самое и логос — слово).
Подобно тому как вся буквенная алгебра основана и а не-
скольких основных равенствах (a-$-b=b+a, а-|-(& + £)=(«+6)4
+с, ab=ba н т. д.), выражающих основные свойства арифме-
тических операций, алгебра логики осиоваиа на нескольких экви
валентностях. Приведем список основных эквивалентностей.
Начнем с эквивалентностей, содержаших лишь одну операцию
дизъюнкции или конъюнкции:
Л VBo BV/1
ЛДВоВДЛ
HVB)VCo^V(BVC)
ИАВ)ЛС-»-ЛЛ(ВЛС)
(3)
(Ч
(5)
(6)
1Ы
Эти эквивалентности показывают, что свойства операций
конъюнкции и дизъюнкции напоминают свойства операций сложе-
ния и умножения чисел. В то же время для чисел, вообще гово-
ря, соотношение a-^bc~(a-\-b)(a-{-c) неверно, т. е. сложение
не является дистрибутивным относительно умножении. Для
высказываний же верны обе эквивалентности:
4A(BVC)^(4AB)VHAC),
4V(BAC)o(4VB)AHVC>
(?)
(8)
т е. дизъюнкция дистрибутивна относительно конъюнкции,
а конъюнкция относительно дизъюнкции.
Прн операциях над числами особую роль играют О и 1: для
любого числа а верны равенства а4-0=а, 0«а=0 н а-1=а.
Подобную роль играют в алгебре логики высказывания И и Л,
где через И обозначено заведомо истинное высказывание и че-
рез Л — заведомо ложное высказывание. Легко проверить, что
для любого высказывания А справедливы соотношения
ИА^оА, И\/Ач>И, ЛЛАоЛ, Л\/АоА. (9)
Отметим еще, что для любого высказывания А имеем:
ААА^>А\/АоА.
(Ю)
Выведем теперь эквивалентности, содержащие операцию отри-
цания высказывания. Отрицанием высказывания А (обознача-
ют Д) является исходное высказывание А. т. е
А<^Д. (11)
Из соотношения (11) вытекает, что Д-оД и т. д. Это поз-
воляет упрощать выражения, содержащие знак отрицания.
С помощью таблицы истинности доказывается, что
ААВ-*>А\/в. (12)
Точно так же доказывают, что
AVBoAAB. (13)
Легко доказать, что
ААА^>Л. (14)
Применив к эквивалентности (14) правило (12) и учитывая
что ЛоИ, получаем, что ДАА^И. т. е. Д\/А-<ф-И. Иными
словами,
Л\/4оИ. (15)
185
Теперь рассмотрим эквивалентности, содержание операции
импликации и эквиваленции. Мы уже доказали раиее, что
А —* В -& А \/ В. Иными словами, сказать; «Если А, то В» — все
равно что сказать: «Не А или В». Применяя к этой эквивалентности
правило (13), получаем, что А -+ ВоА\/В<&А/\ВоАЛВ.
Таким образом,
Л — Вч^ЛДВ. (16)
Это равенство показывает, что опровергнуть импликацию мож-
но лишь единственным образом — доказав, что ее условие истинно,
а заключение ложно (впрочем, мы и так зиаем, что лишь в этом
случае импликация ложна).
Импликацию В —* А, полученную из Л-»-В перестановкой
условия и заключения, называют обратной для Л —* В. Другую
импликацию можно получить из Л —>- В, заменив и условие, н за-
ключение их отрицаниями. Ее называют противоположной данной.
Импликации Л —В и В —А либо одновременно истинны,
либо одновременно ложны. Таким образом, справедлива эквива-
лентность
АВ о В—* А. (17)
Доказанные эквивалентности позволяют преобразовывать ло-
гические выражения, содержащие логические переменные, подоб-
но тому как тождества обычной алгебры позволяют преобразо-
вывать буквенные выражения.
Упростим, например, выражение А /\В\/(В ДС). По правилам
отрицания дизъюнкции и конъюнкции и равенству (11) имеем:
Зт\В) V (В АС) о (ДАВ) А(ВДО о (Л АВ)Л(В V С).
А теперь, используя соотношения (5) и (7), получим (Л А В) А
А (В V С) <Ч(Л А В)А В] VKA А В) д С] о [А Д (В Д В)] V
\/[(ЛДВ)ДС].
Так как ВДВ о Л, ЛДЛо.П, то
(АДВ) Д(В\/С)о Л V[(A ДВ)ДС].
Наконец, согласно (9) наше выражение эквивалентно Л ДВДС,
т. е. оно истинно лишь в одном случае, когда Л и В нстнииы,
а С ложно (мы опустили скобки в окончательном выражении, так
как в силу свойства ассоциативности конъюнкции они несущест-
венны) . К тому же ответу можно было прийти путем логического
анализа выражения (оно истинно лишь в случае, когда ложно вы-
ражение А/\В\/(В/\С), а это имеет место лишь прн условии,
что ЛДВ истинно, а ВДС ложно и т. д.
186
Упражнения
27. Из простых высказываний
А: «Завтра будет дождь»;
В: «Мы пойдем в театр»;
С: «Завтра будет солнечно»;
D: «Завтра занятия начнутся раньше обычного» — образова-
ны следующие составные высказывания:
а) «Если завтра будет дождь, то занятия начнутся раньше
обычного и мы пойдем в театр»;
б) «Завтра будет солнечно или будет дождь и занятия нач
нутся раньше обычного»;
в) «Завтра занятия начнутся раньше обычного и мы пойдем
в театр тогда и только тогда, когда ие будет дождя и будет сол-
нечно».
Запишите данные сложные высказывания, используя символы
алгебры логики.
28. Каждое из простых высказываний, входящее в приве-
денные ниже сложные высказывания, обозначьте буквой и запи-
шите эти составные высказывания в символической форме.
а) Если прямая АВ перпендикулярна прямым CD и KL, то
прямые CD и KL параллельны.
б) Четырехугольник является параллелограммом тогда и толь-
ко тогда, когда его противоположные стороны попарно парал-
лельны, или тогда, когда его диагонали равны.
в) Я сделаю зарядку н, если будет хорошая погода, поеду
за город.
г) Четырехугольник является квадратом тогда н только тогда,
когда все его стороны и его углы равны.
д) Две плоскости параллельны тогда и только тогда, ког-
да они не имеют общих точек нлн совпадают.
е) Если Оа, с>Ь и с25^а2+62, то неверно, что треуголь-
ник со сторонами а, Ь, с прямоугольный.
29. Для каждого из следующих выражений придумайте по два
предложения соответствующей логической структуры:
Л->В; лдв-^(л\/я); Л\/В*>(ЛДВ).
30. Докажите, что следующие выражения являются тавтоло-
гиями:
а) (Л->Л)-»Л, б) (Л^Л)->_Л;
в) (И—»-Л)—>Л; г) [(Л->В)АВ]->Д;
д) е) Л-*(Л->С);
ж) [(Л —В)А(В-*С)]->(Л-»С)
31. Докажите следующие эквивалентности.
а) (ЛАВДМоЛ; б) (Л\/В)ДЛоЛ; в) (AVBhMo
^ЛДВ; г) 0AB)VAoBVA; д) (ЛМ)У(А№)^А;
е) (AVB)A0VB)^A
187
32. Упростите выражения:
а) ИЛДЛС)УИЛДЛ£>)У(ЛЛДЛС)У(ЛЛО)-^В;
б) (ДЛВ)УЛ^В;
в) (AABACA4)V(DABAD)V(BAC)
33. Согласно инструкции капитан должен находиться на суд-
не всегда, за исключением случаев, когда с судна выгружают
груз; если же груз не выгружают, то рулевой никогда ие отсутст-
вует, если не отсутствует и капитан. В каких случаях рулевой
обязан присутствовать иа судне?
34. В каждой из приведенных ниже импликаций выделите ус-
ловие н заключение. Сформулируйте импликацию, противополож-
ную данной и обратную противоположной. Определите, истинны
оии или ложны.
а) Если вы находитесь в Африке, то вы находитесь южнее
Москвы.
б) Если я учусь в школе, то мне больше чем два года.
в) Если последняя цифра числа 17 равна 5. то оно делится
на 5.
г) Если сумма цифр числа 25 делится на 3, то это число
делится на 3.
д) Если сумма цифр числа 23 делится на 5, то это число
делится на 5.
8. Логическое следование. Важную роль в алгебре логики
играет отношение логического следования. Мы знаем, например,
что если истинно А, то независимо от истинности или ложности
В дизъюнкция А V В истинна. В этом случае говорят, что А V В
логически следует из А. Если же истинна конъюнкция А/\В, то
истинно и А. Говорят, что А логически следует из А/\В.
В общем виде отношение логического следования определя-
ют так: логическое выражение У следует из логического выра-
жения X, если У истинно во всех случаях, когда X истинно. От-
ношение логического следования обозначают так: X => У (из X
логически следует У).
Так же как надо различать эквнвалеицню и эквивалент-
ность, ие следует путать импликацию с логическим следованием.
Импликация — это логическая операция, позволяющая по двум
заданным высказываниям А и В строить третье высказывание
А —*. а логическое следование — отношение, имеющее место
между двумя логическими выражениями. Связь между импли-
кацией и логическим следованием дается таким утверждением:
Логическое выражение У следует из логического выражения
X в том и только в том случае, когда импликация X Y истин-
на при всех значеииих переменных (т. е. является тавтологией).
Не составляет труда показать, что если X => У и У => X, то
X У (если У логически следует из X, а X логически следует
из У, то X и У логически эквивалентны).
188
Рассуждения, которыми обычно пользуются при доказатель-
ствах теорем, основаны на понятии логического следования —
из некоторых высказываний логически выводятся другие выска-
зывания. При этом можно быть уверенным, что при всех значе-
ниях логических переменных, при которых истинны исходные выс-
казывания (так называемые посылки), истинны и полученные
следствия (или, как говорят, заключения). Разумеется, чтобы га-
рантировать истинность заключений, надо быть уверенным в ис-
тинности посылок. Здесь можно повторить слова, сказанные анг-
лийским естествоиспытателем Гексли о математике: «Математи-
ка, подобно жериову, перемалывает лишь то, что в него засы-
пают. И как великолепнейшая в мнре мельница ие доставит пше-
ничной муки нз лебеды, так и страницы формул не доставят
истинного результата по сомнительным данным». Точно так же
самые логичные рассуждения, основанные на неверных посыл-
ках, ие гарантируют истинности заключений.
Рассуждение называется правильным, если из конъюнкции
формализованных посылок следует формализованное заключение.
Упражнения
35. Проверьте, какие из следующих высказываний истинны:
а) ХДУ=>Х; б) Х=^ХДУ; в) Х\/У=>Х; г) Х=>Х\/У;
Д) _(Х-> У)=>Х Д У; е) (Х_-> У)=> (У Х); _ж) _(ХУ)=>
=>(Х-*-У); з) (X-► У) => (У-> X); н) (X - У) Д X => У.
36. Запишите в формализованном виде нижеприведенные
рассуждения и проверьте, правильны ли они:
а) Если четырехугольник ABCD — ромб, то его диагонали
взаимно перпендикулярны. Четырехугольник ABCD — ромб. Сле-
довательно, его диагонали взаимно перпендикулярны.
б) Если 10 делится на 3, то 100 делится на 3. Число 10
делится на 3. Следовательно, 100 делится на 3.
в) Если 10 делится иа 2, то 100 делится на 2. Число 100
делится на 2. Следовательно, 10 делится на 2.
г) Если множество простых чисел конечно, то существует
наибольшее простое число. Наибольшего простого числа ие суще-
ствует. Следовательно, множество простых чисел бесконечно.
37. Ответьте иа приведенные ниже вопросы:
а) Что можно утверждать о правильности двух рассуждений,
которые в формализованном виде выглядят одинаково?
б) Может ли правильное рассуждение иметь ложное заклю-
чение? Может ли неправильное рассуждение иметь истинное за-
ключение?
в) Что можно утверждать о заключении правильного рассуж-
дения, если все его посылки истинны?
г) Что можно утверждать о посылках правильного рассужде-
ния, если его заключение ложно?
189
д) Что можно утверждать о рассуждении, все посылки кото-
рого истинны, а заключение ложно?
38. Можно ли на основании посылок «Если предмет интере-
сен, то ои полезен» н «Предмет неинтересен» заключить, что пред-
мет бесполезен? Почему?
39. Можно ли, исходя из посылки «Если ученик много за-
нимается, то ои успешно сдает экзамены», сделать заключение,
что ученик, провалившийся иа экзамене, занимается мало? Всегда
ли такое заключение истинно? Почему?
9» Переключательные схемы. Алгебра логики кажется на пер-
вый взгляд очень далекой от практических приложений. Но это
ие так. Во многих технических проблемах большую роль играют
переключательные схемы. Современные методы анализа и кон-
струирования таких схем широко используют понятия и формулы
алгебры логики.
Разберем простейшие примеры. Пусть цепь состоит из источ-
ника тока /, соединенного с лампой L посредством проводов
с ключом Р (рнс. 117, а). Ключ Р может быть либо включен,
либо выключен, и в соответствии с этим цепь будет лнбо замк-
нута, либо разомкнута. Сопоставим ключу Р переменную X, а
двум состояниям ключа — «включен», «выключен» — значения
«И» и «Л» переменной X соответственно; значение «И» при этом
будет соответствовать также состоянию цепи «замкнута», а «Л» —
состоянию цепи «разомкнута».
Если между источником тока и лампой поместить два ключа
Р и Q (рнс. 117,6), соединенные последовательно, то цепь будет
замкнута, когда оба ключа включены, и разомкнута, когда хотя
бы один из иих выключен. Конъюнкция переменных X и У, по-
ставленных в соответствие ключам Р и Q, истинна (цепь замкну-
та) , когда обе переменные X и Y истинны (т. е. Р н Q включены),
и ложна (цепь разомкнута), когда хотя бы одна нз переменных
ложна (хотя бы один ключ выключен). Таким образом, выра-
жение ХДУ описывает работу цепи, изображенной иа рисун-
ке 117, б.
Если два ключа Р и Q соединены с источником тока / н пот-
ребителем L параллельно (рис. 117, в), то цепь замкнута, когда
Рис. 117
КЮ
хотя бы один из ключей включен, н разомкнута, когда оба
они выключены. Работу такой цепи описывает дизъюнкция XV У
переменных, соответствующих ключам Р и Q. Выражение X\/ У
истинно (цепь замкнута), когда хотя бы одна из переменных ис-
тинна (хотя бы одни из ключей включен),*и ложно (цепь разомк-
нута), когда обе переменные ложны (оба ключа выключены).
Установленные соответствия дают возможность описать ло-
гическим выражением любую цепь с последовательно илн парал-
лельно соединенными ключами. С другой стороны, любое логичес-
кое выражение можно смоделировать в виде соответствующей
цепи.
Упражнения
40. Нарисуйте схему цепи, соответствующей выражению:
a) (X\/Y)A(Z\/X)AZ; б) ХУ(ХАУ)А(У->2)
41. Составьте выражение, соответствующее схеме, изобра-
женной на рисунке 118, и упростите его. Сформулируйте условия,
при которых цепь замкнута. Начертите схему, соответствующую
упрощенному выражению.
42. Начертите схему простейшей цепи, условия работы ко-
торой заданы следующей таблицей истинности:
и
и
И
и
Л-
л
и
л
и
л
и
л
и
л
л
и
л
л
и
л
Указание. Составьте выражение, соответствующее этой
таблице; выполните всевозможные упрощения.
Рис. 118
43. Комитет, состоящий из трех членов, выносит решение
большинством голосов при тайном голосовании. Составьте такую
схему, чтобы голосование каждого члена «за» производилось
нажатием кнопки (включением ключа) н в случае принятия реше-
ния (и только в этом случае) загоралась сигнальная лампочка.
ВЫСКАЗЫВАТЕЛЬНЫЕ ФОРМЫ И ОПЕРАЦИИ НАД НИМИ
1. Высказыввтельные формы. Предложение, содержащее пере
менную х, которое при подстановке вместо переменной ее зна-
чения становится высказыванием, называют высказывательной
формой и обозначают Р(х). Примерами высказывательных форм
могут служить предложения:
а) число х больше семи;
б) натуральное чнсло х больше семи;
в) река х впадает в Каспийское море;
г) протекающая в европейской части СССР река х впадает
в Каспийское море.
Из этих высказывательных форм можно получить различные
высказывания, придавая переменной х те или иные значения.
Например, заменяя в предложении в) букву х словом «Волга»,
получаем истинное высказывание «Река Волга впадает в Каспий
ское море». А заменяя в том же предложении букву х словом
«Дунай», получаем ложное высказывание «Река Дунай впадает в
Каспийское море».
Совокупность Т значений переменной х, при которых высказы-
вательиая форма Р (х) истинна, называется множеством истин-
ности этой формы. Например, для высказывательной формы
«Поэма х написана Лермонтовым» множеству Т принадлежат
«Демой», «Мцыри», но не принадлежит «Хорошо».
Уравнения, а также неравенства, содержащие переменную,
являются высказывательными формами.
Упражнения
44. Из следующих предложений выберите высказывательные
формы и укажите их множества истинности:
а) «х2—2х—15=0»;
б) «Для всех чисел х выполняется равенство х2—2х—15=0»;
в) «Существует такое отрицательное чнсло х, что х2—2х—
— 15=0»;
г) «Если чнсло х делится иа 3, то оио делится и на 9»,
д) «Все числа, делящиеся на 9, делятся иа 3»;
е) «Сушествуют числа, делящиеся на 9. но не делящиеся
иа 3»;
ж) «Неверно, что число 17 делится иа 5»;
з) «В прямоугольнике х диагонали равны»;
н) «В любом прямоугольнике диагонали равны».
192
45. Найдите множество истинности высказывательной фор-
мы «Число х четно», заданной на множестве
Х={0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
46. Найдите множества истинности следующих высказыватель-
ных форм:
a) V7+2-1; б) V*+2>1:
в) х3—Зх’+Зх—1>0; г) х>— 10х2+9=0:
Д) (х-1^=х3-3х2+3х-г, е) v?=«
ж) V?=W; '>) V?=—х;
и) V*7— — |х|; к) д/?= —1.
2. Операции иад высказывательными формами. Пусть выска-
зывательные формы Р(х), Q (х),... заданы на одном и том же мно-
жестве X. С помощью логических операций из этих форм можно
составить различные выражения, например:
Р(х)Д<?(х), P(x)-4Q(x)V*(x))ht. д.
Заменяя в каждом нз таких выражений переменную х каким-то ее
значением а, получаем сложное высказывание, составленное
из высказываний Р(а), Q(a) н т. д. Поэтому такие выражения
сами являются высказывательными формами. Они истинны при
тех а£Х, при которых истинно соответствующее высказывание.
Например, высказывательнан форма (3<х)Д(х<6) истинна при
х=4, так как высказывания 3<4 и 4<6 истинны, а потому
истинна и их конъюнкция.
Если известны множества истинности для высказывательных
форм Р (х) н Q (к), заданных на X, то легко найти множества ис-
тинности для форм P(x)/\Q(x), PJix)\/Q(x), P(x)—*Q(x),
P(x)++Q (x), а также для P x) и для Q (x). Форма P (x) истинна
для тех и только тех значений х, для которых Р (х) ложна. Поэтому
множество истинности для Р (х) — дополнение в X к множеству ис-
тинности для Р(х). Это можно записать такой формулой:
^=(Тр)'. (1)
Форма P(x)AQ(x) истинна для тех х, для которых истин-
ны н Р (х) н Q (х). Это значит, что множество истинности для
Р (х)Д Q (х) — пересечение множеств истинности дли Р(х) н для
<?(*):
(2)
(Таким образом, не случайно обозначения для операций конъюнк-
ций высказываний н пересечения множеств походят друг на дру-
га.) Точно так же убеждаемся, что
TP^TPl)TQ. (3)
193
7 Заказ 775
''числа/"''
делящиеся
'^на 4^
Числа,
делящиеся
на 2 .
Рис. 119
Если высказывательные формы Р(х) и Q (х) имеют одинаковые
множества истинности, т. е. если 7^=Т0, то их называют экви-
валент иымн или равносильными и пишут: Р (х) <> Q (х). В этом
случае эквиваленция Р (а) ** Q (а) истинна для всех X.
Высказывательные формы Р (х): «Натуральное чнсло х делит-
ся на 4» — и Q (х): «Натуральное чнсло х делится иа 2» — тако-
вы, что для всех натуральных чисел Q истинна импликация
Р (а) —* Q (а). Говорят, что Q (х) — следствие из Р (х)
Множество чисел, делящихся на 4,— подмножество в множе-
стве чисел, делящихся иа 2. Иными словами, в нашем примере
Т₽С2 TQ. Это ие случайно — всегда, когда импликация Р (а) Q (а)
истинна для всех а из X, т. е. когда Q (х) следует нз Р(х}, имеет
место соотношение TPtr.Tg (рис. 119). Верно и обратное утверж-
дение: если ТрС=70, то Р (х) —*- Q (х). Итак, Q(x) следует из Р(х)
в том и только в том случае, когда Tp<zTq. В этом случае
говорят, что Р(х)— достаточное условие для Q(x), a Q(x) —
необходимое условие для Р(х) или что <2(х)— следствие Р(х),
н пишут: Р (х) => Q (х).
Если и Р(х)=> Q(x), и Q(x)=> Р(х), то TpgcTq и TQccTP.
В этом случае Tp—Tq, т. е. Р(х) н Q(x) имеют одно и то же
множество истинности. Поэтому P(x)oQ(x). Эту же мысль
выражают ниаче, говоря, что Р (х) — необходимое н достаточное
условие для Q (х), a Q (х) — необходимое и достаточное условие
для Р(х\
Упражнения
47. Пусть X — множество треугольников. Постройте диаграм-
мы Эйлера — Венна, изображающие связи между следующими
высказывательиыми формами:
а) Р(х): «Треугольник х равнобедренный»; Q(x): «Треуголь-
ник х равносторонний»;
б) Р(х): «Треугольник х равнобедренный»; Q(x): «Углы при
основании треугольника х равны»;
в) Р(х): «Треугольник х прямоугольный»; Q(x): «В треуголь-
ник х можно вписать окружность».
Установите, какие из следующих импликаций истинны для!
всех х в каждом нз случаев а), б), в):
Р (х) Q (х), Р (х) -> Q (х), Р (х) Q (х), Р (х) — Q (х),
Q(x)—»-Р(х), Q(x)->P(x), Q(x>->P(x), Q(x)-^P(x).
194
48. Пусть Р(х): «Натуральное число х делится иа 5»; Q(x):
«Последняя цифра десятичной записи числа х равна нулю».
Какие из следующих импликаций истинны для всех х нз Л?
Сформулируйте их с помощью слов «необходимо» и «достаточно».
Для импликаций, истинных не для всех натуральных чисел, найди-
те множества истинности:
a) PW—0(х);
в) Р(х)-»(?(х);
д) <2 (*)—»₽(*):
ж) QW-*PW;
б) _Р«—QW;
г) — Q(x);
е) Q(x) —Р(х);
з) QW--PW-
49. В приведенных ниже предложениях проставьте вместо
многоточия слова «необходимо, но не достаточно», «достаточно,
но не необходимо», «необходимо и достаточно», чтобы получи-
лись предложения истинные для всех значений х:
а) Для того чтобы число х делилось на 5, ..чтобы его
десятичная запись кончалась цифрой 0.
б) Для того чтобы число х делилось на 9, ..., чтобы сумма
цифр его десятичной записи делилась на 3.
в) Для того чтобы треугольник х был равнобедренным
чтобы углы при основании были равны.
г) Для того чтобы параллелограмм х был ромбом, ..., чтобы
диагонали делили пополам его углы.
д) Для того чтобы параллелограмм х был квадратом,..что-
бы его стороны были равны.
50. Определите, равносильны лн следующие высказыватель-
ные формы, если переменные принимают значения нз множества:
1) натуральных чнсел N; 2) целых чисел Z; 3) рациональных
чисел Q- 4) действительных чнсел R:
а) |х|<0, лЧ-0г=О;
В) (x-t/2)(x—i-)(x+l)=0, x*=I;
д) х=у, ^Х=у[у;
е) х^у, |х| = |р|.
51. Выясните, следует ли хотя бы одна из данных высказы-
вательных форм из другой
а) |х|<3, х1—Зх 4-2=0;
б) х4=16, х2=4;
в) х2 4-х—6=0, (х-1)(х-2)(х-3)=0;
г) х—1>0, (х—2)(х—5)=0;
д) ха4-5х=0, х+1 = 14-х.
195
52. Выясните, являются ли следующие высказывательные
формы эквивалентными, если x£R:
а) |х|>0, (х+ 1)2=х24-2х
б) |х]>3, х2 —9>0;
в) ]х|<0. х24-4<3;
г) х>0, х2>0;
д) х=х,
е) х>2, х<2;
ж) х>2, х<2.
53. Найдите множество значений о, при которых данные
высказывательные формы эквивалентны:
а) ах4-1=0, х=1;
б) |х|>а, (х—3)2=х — 6x4-9;
в) |х|<о, 3;
г) х24-а2=0, |х|.
3. Кванторы. Чтобы получить из высказывательной формы
Р(х), х£Х, высказывание, можно заменить х одним из значе-
ний а£Х. Но существует другой способ получении высказываний
из высказывательных форм — навешивание кванторов. Для этого
перед высказывательной формой пишут квантор — слово, описы-
вающее ее множество истинности, например: «Для всех х
из X истинно, что ...» или «Существует такое х из X, что ...».
Так, из высказывательной формы «Человек х синеглаз» получают-
ся высказывания «Все люди синеглазы» (ложное высказывание)
илн «Существуют синеглазые люди» (истинное высказывание).
Поскольку в математической логике стараются заменять слова
знаками, то вместо слов «Для всех х нз X истинно ...» усло-
вились писать ух£Х, а вместо «Существует такое х из X, что ...»
пишут Эх£Х. Здесь V—перевернутая буква А, первая буква
английского слова all — все, а 3 — перевернутая буква Е, первая
буква английского слова exist — существует. Эти символы явля-
ются обозначениями соответственно для квантора всеобщности и
квантора существования. Таким образом, квантор всеобщности оз-
начает, что множество истинности Т высказывательной формы
совпадает со всем множеством X, а квантор существования озна-
чает, что Т непусто.
Возможны и другие прочтения записей (ух£Х) Р(х) и (эх£Х) Р (х),
соответственно равнозначные между собой; приведем наибо-
лее употребительные из них (слова в квадратных скобках иногда
опускаются):
1. (ух£Х) Р (х) читается так:
а) для любого (всякого, каждого) [значения] х нз X Р(х)
[истинно];
б) всякий (любой, каждый) элемент х множества X (где X -г-
миожество значений переменной х) обладает свойством Р;
в) каково бы ни было х, Р(х) истинно.
196
2. читается так:
а) существует [значение] х из X, такое, что Р(х) [истинно];
б) для некоторых (значений] х из X Р (х) [истинно];
в) по меньшей мере (хотя бы) одно [значение] х из X таково,
что Р(х) [истинно];
г) существует элемент х множества X, обладающий свойст-
вом Р\ по крайней мере (хотя бы) одни элемент х множества X
обладает свойством Р; некоторые элементы множества X облада-
ют свойством Р;
д) найдется такое х из X, что Р (х) истинно.
Иногда для краткости мы будем опускать указание множества
значений х и писать ухР(х) илн ЭхР(х).
Приведем примеры записи высказываний с помощью кванто-
ров и высказывательных форм. Пусть Р (х) означает «Число х чет-
ное». Тогда запись (ух 6 #) Р (х)' читается так: «Все натуральные
числа четны» (ложное высказывание), а запись (3x6#) Р(х):
«Существуют четные натуральные числа». Кратко пишут:
УхР(х), ЗхР(х)-, x£N.
Упражнения
54. Сформулируйте следующие высказывания, пользуясь обыч-
ным языком; установите их истинность нлн ложность:
а) (VA-e/г) (х— 1=х); б) 0х6Я) (х—1=х);
в) (VX6J?) (х-1^х); г) Йхея) (х-1^=х).
55. На множестве N всех натуральных чисел заданы выс-
казывательные формы Р (х): «Число х четное» — и Q (х): «Число
х кратно 4». Сформулируйте следующие высказывания, пользуясь
обычным языком, и укажите среди них истинные:
а) (Ух£#)Р(х); б) 0х6#)Р(х);
в) 0x6#) <?(*); г) (УхЕ#)0(х).
56. Введите обозначения для высказывательных форм н за-
пишите в символической форме следующие высказывания:
а) существует такое действительное чнсло х, что х2==4;
б) любое натуральное число четно;
в) существует такое действительное число х, что 5х=х—1;
г) не существует рационального числа х, такого, что х2=2.
57. Прочтите следующие записи, заменив обозначения кван-
торов общности и существования их словесными выражениями, и
определите значения истинности данных высказываний:
a) Vx((x+1)2=x*+2x+1); б) Зх(х + 1=2);
в)Эх(|х|<0); г) Vx(|x|>0);
' д) **(^Г=х+1): е> 3»fa2+s-5<0).
197
58. Свяжите переменную квантором так, чтобы получить ис-
тинное высказывание (переменные х, у, z в а) — г) принадле-
жат R):
а) |х| =—х; б) х2^0;
в) t/2-|-2^0; г) sin z#:2;
д) число букв в слове х равно 4;
е) все дороги из пункта х ведут на юг;
ж) в треугольнике у сумма внутренних углов равна 180°.
4. Многоместные высказывательные формы. До сих пор мы
рассматривали высказывательные формы, в которые входит лишь
одна переменная. Обычно такие формы связаны со свойствами
элементов множества X. Если же речь идет о соответствиях между
элементами различных множеств или одного и того же множества,
то приходится использовать высказывательные формы, содер-
жащие несколько переменных. Примерами таких форм могут слу-
жить: «Человек х живет в городе у», «Человек х — отец челове-
ка у», «Сумма чнсел х и у больше числа г» и т. д. Если высказы-.
вательная форма содержит две переменные, то ее называют
двухместной, если три — трехместной н т. д. Двухместную форму
записывают в виде Р(х; у), х£Х, y£Y, указывая множества значе-
ний для каждой переменной.
Множеством истинности двухместной высказывательной фор-
мы Р(х;у), х£Х, у£¥, называется совокупность пар (а; Ь), где
а£Х, b£Y, для которых Р (а; Ь) — истинное высказывание. Напри-
мер, если Р (х; у) означает «Река х впадает в море у», то к множе-
ству истинности этой формы принадлежат пары (Волга, Каспий-
ское море), (Дунай, Черное море), но не принадлежит пара (Ени-
сей, Азовское море). Множество всех пар (х; у), где х£Х, y£Y,
называется декартовым произведением множеств х и у (по вме-
ни выдающегося французского математика н философа Р. Д е-
карта (1596—1650) — творца метода координат) в обозначает
ся ХХУ- Таким образом, множество истинности двухместной
высказывательной формы является подмножеством декартова про-
изведении XX У-
Из каждой многоместной высказывательной формы можно по-
лучить высказывание, «навесив» на каждую переменную свой
квантор. Эти кванторы могут быть как одноименными (например,
кванторами всеобщности), так и разноименными. Поэтому из
двухместной высказывательной формы Р (х; у) получается восемь
высказываний (запишите нх!).
Например, если Р (х; у) означает «Река х впадает в море у», то
эти высказывания читаются так:
1) «Все рекн впадают в любое море»;
2) «В любое море впадают все реки»;
3) «Для любой реки есть море, в которое она впадает»;
4) «Для любого моря есть впадающая в него река»;
5) «Существует река, впадающая в любое море»;
-198
6) «Существует море, в которое впадает любая река»;
7) «Существует река, впадающая в некоторое море»;
8) «Существует море, в которое впадает некоторая река».
Легко видеть, что высказывания 1 и 2 равносильны, так же
как и высказывания 7 и 8: если все реки впадают в любое море,
то в любое море впадают все реки, и обратно; а если существует
река, впадающая в некоторое море, то существует море, в ко-
торое впадает некоторая река, и обратно. Вообще высказывания
V*WP(x; у) и V!/VxP(x; у) равносильны: они утверждают, что
множеством истинности для Р(х; у) является все декартово про-
изведение X%Y. Точно так же н %х^уР(х; у) означает, что
множество истинности для Р (х; у) непусто.
Высказывания у у g х Р (х; у) н g х у у Р (х; у) неравносильны. В
нашем примере первое нз них означает, что для каждого моря
есть впадающая в него река (это, по-видимому, истинно), а вто-
рое — что есть река, впадающая в каждое море (это наверняка
ложь). Таким образом, одноименные кванторы можно перестав-
лять, а разноименные переставлять нельзя. Поэтому на самом
деле получается не восемь, а лишь шесть различных высказыва-
ний. Легко доказать, что следующая импликация всегда истинна:
WyP(x,y)~>\fy3xP(x,y)
(если бы была река, впадающая во все моря, то уж наверняка
в любое море впадала бы хоть одна река).
Упражнения
59. Пусть X, У, 1 — множества прямых на плоскости. Проч-
тите следующие -высказывания и укажите среди них истинные:
а) ухэ9(х||9); б) в)
г) VxV!/Vz ((х||1/Л!/1|г)—>-x||z);
д) Wiflz ((x-Lj/AS-Lz) —>-x||z);
е) VxVWz ((x||zAy||z)—x||s);
ж) VxVyvz ((x-Li/A!/-Lz)—>-x-Lz).
60. Запишите в символической форме высказывания:
а) «Если х и у — натуральные числа, произведение кото-
рых делится иа простое число р, то хотя бы один из миожителей
делится иа р»;
б) «Для каждой прямой х иа плоскости и каждой точки этой
плоскости найдется прямая, проходящая через эту точку и па-
раллельная прямой х».
61. Приведите пример высказывательной формы Р(х; а! та-
кой, что Р(х; а) — нстниное высказывание.
62. Эквивалентны ли высказывания «Каждую задачу решил
по крайней мере один ученик» и «По крайней мере один ученик
решил все задачи»? Следует ли хотя бы одно из них из другого?
Почему?
199
Указание. Запишите данные высказывания символически,
обозначив через Р (х; у) высказывательную форму «Ученик к ре-
шил задачу у».
Поскольку уравнения и неравенства, содержащие переменную,
являются высказывательнымн формами, все сказанное выше для
таких форм применимо к уравнениям н неравенствам. Например,
два уравнения (соответственно два неравенства) называются
эквивалентными, если их множества истинности совпадают, или,
что то же самое, если они имеют одно и то же множество кор-
ней. Так, уравнение №—8x4-12=0 эквивалентно уравнению
3№—24x4-40=4— для обоих множество корней состоит из чи-
сел 2 и 6, Т={2; 6}. Неравенство 2х>8 эквивалентно неравен-
ству Зх>12— для обоих неравенств множеством решений (т. е.
множеством истинности) является промежуток (4; 4-°°)
При решении уравнений н неравенств нх заменяют эквива-
лентными уравнениями и неравенствами, т. е. преобразуют, не
изменяя их множеств истинности. В этом случае можно ие прове-
рять полученное решение, поскольку иа каждом шагу оно не из-
менилось и потому совпадает для заданного уравнения н уравне-
ния, получившегося в ходе преобразований. Но не всегда уда-
ется решить уравнение таким способом. Иногда приходится пере-
ходить от данного уравнения ие к эквивалентному, а лишь к его
следствию. Если, преобразуя уравнение
b W=gi W.
мы приходим к уравнению
h W=g2 W.
(1)
(2)
которое является следствием уравнения (I), то множество кор-
ней уравнения (2) содержит множество корней уравнения (1).
Поэтому, решив уравнение (2), надо еще проверить, удовлет-
воряют ли этн корни исходному уравнению (1).
Рассмотрим теперь уравнении с двумя переменными. Множе-
ство истинности такого уравнения изображается совокупностью
точек ЛЦх; у) координатной плоскости, прн подстановке ко-
ординат которых уравнение обращается в истинное высказывание.
Например, для уравнения №4-j/2=25 этим множеством являет-
ся окружность радиуса 5 с центром в начале координат.
Так как множество истинности для уравнения f(x; у)=0
обычно бесконечно, рассматривают системы двух таких уравнений,
т. е. конъюнкции вида
(f> (*; g)=0)A(fs(x; »)=0).
В школе конъюнкции обычно записывают в виде
h (*; »)=о,
(4)
(5)
200
Рис. 120
Рис. 121
Как мы уже знаем, множество истинности для конъюнкции
(4) (т. е. решение системы уравнений (5)) является пересечением
множеств истинности входящих в нее уравнений. На этом осно-
ван графический метод решения систем уравнений: изображают
иа плоскости множество истинности каждого нз уравнений систе-
мы и находят пересечение получившихся линий.
Пример. Решим графически систему уравнений
р2+/=25,
(Зу=4х.
Так как — уравнение окружности с центром О (0; 0) и
радиусом 5, а Зу—4х— уравнение прямой, то достаточно найти
точки пересечения прямой и окружности (рис. 120). Находим две
точки: Л(3; 4) и В(—3; —4). Значит, 1=1(3; 4), (—3; —4)}.
При решении систем уравнений их обычно заменяют эквива-
лентными системами уравнений. Иными словами, входящие в сис-
тему уравнении заменяют другими так, что при этом не нзменяетсн
пересечение множеств истинности (хотя сами множества истиннос-
ти для отдельных уравнений могут и меняться).
Все сказанное выше относится и к решению неравенств. На-
пример, решить систему неравенств
( х+Р>0
все равно что найти множество истинности конъюнкции
(х2+{/2<4)Л(х+р>0).
Для этого надо найти пересечение областей, задаваемых этими
неравенствами (рнс. 121).
Теперь рассмотрим понятие тождества. В школе обычно тож-
деством называют равенство, содержащее переменную н истинное
длн всех значений переменной, например х?+2х+ 1=(х-|-1)2-
201
Запись (Vx£I?)(x2+2x4-I=(x4-1)2) показывает, что равенство
выполняется для всех значений х.
5. Отрицание высказываний, содержащих кванторы. Отрица-
ние высказывания «Все волки серы» отнюдь не является пред-
ложением «Все волки не серы». На самом деле достаточно увидеть
хотя бы одного белого волка, чтобы убедиться в ложности того,
что все волкн серы. Таким образом, для того чтобы высказывание
(Ух£Х) Р(х) оказалось ложным, достаточно, чтобы нашелся хотя
бы один элемент а из X, для которого Р (а) ложно, т. е. Р (а) истинно.
Но в этом случае истинно высказывание $х£Х) Р (х). Обратно:
если $х£Х)Р(х) истинно, то (Ух£Х)Р(х) ложно. Мы доказали
таким образом, что
(Vx€A)P(x)o0x€A)P(x). (6)
Если обозначить здесь Р (х) через Q (х) н взять отрицания обеих
частей равенства (6), то получим, что
(VxEX)Q(x)^ ЭхбХ)(2(х)
(7)
Если высказывание содержит несколько кванторов, то с каждым
нз них поступают по указанному правилу, например:
ОС*) (VS/€ Y) Р (*; У) *>(V хЗД &УЕ Y)P(*; У)- (8)
Упражнения
63. Пусть Р (х) — высказывательная форма «Число х делится
на 5», a Q (х) означает «Число х четно». Прочтите высказывание
&*€A/)(P(x)AQ(x)) и постройте его отрицание.
64. Пусть Р (х; у) — высказывательная форма «Окружность х
вписана в треугольник у». Прочтите высказывания:
a) V*WP(x;p); б) ЗхурР(х;у); в) у/хЗу Р{х\ у);
г) х/уэх Р(х;у); д) ЭуухР(х; у)-, е) ЗхЭуР(х;у)
и постройте их отрицания.
65. Докажите илн опровергните следующие предложения, об-
разовав нх отрицания:
а) «Все простые числа нечетны»;
б) «Всякий четырехугольник, диагонали которого взаимно
перпендикулярны, — ромб»;
в) «Все корни уравнения |х| = —-1— рациональные числа»;
г) «Все элементы пустого множества принадлежат множест-
ву М»\
д) «Любое решение неравенства х2<0 является решением
уравнения х2—9=0»;
202
е) «Всякое квадратное уравнение имеет действительный ко-
рень».
66. Запишите символически следующие высказывания и их от-
рицания, определите значения истинности данных высказываний н
нх отрицаний:
а) «Для всякого рационального числа х найдется рациональное
число у, такое, что х-}-у=*х»\
б) «Существует натуральное число х, такое, что для всякого
натурального числа у выполняется равенство х+у=у»;
в) «Существует целое чнсло х, такое, что для любого целого у
справедливо равенство х4-^=0»;
г) «Всякое целое число имеет противоположное»;
д) «Каково бы нн было натуральное число х, найдется нату-
ральное число у, такое, что ху—хъ;
е) «Существует такое целое чнсло х, что произведение его с лю-
бым целым числом равно х»;
ж) «Для вснкого числа, ие равного 0. найдется число, даюшее
в произведении с ним 1»;
з) «Существует такое число, что произведение его с любым
другим не равным 0 числом равно 1».
67. Сформулируйте отрицания следующих высказываний в ут-
вердительной форме (т. е. так, чтобы отрицание данного выска-
зывания не начиналось со слов «не» или «неверно, что»):
а) «В каждом городе есть район, в каждой школе которого
есть класс, все ученики которого учатся без троек»;
б) «Существует город, в каждом районе которого есть футболь-
ная команда, все игроки которой не старше 18 лет»;
в) «В каждом городе есть улица, на которой по крайней мере
в одном доме, все окна выходят на юг»;
г) «Существует книга, иа каждой странице которой есть не ме-
нее чем одна строка, в которой буква «ы» встречается по меньшей
мере два раза»;
д) «В каждом городе хотя бы одна улица застроена только та-
кими домами, в которых есть однокомнатные квартиры».
6. Строение математической теоремы. Большинство математи-
ческих теорем формулируется так: на некотором множестве X из
высказывательной формы А (х) следует В (х). Такие формы можно
записать в виде
(Ух€Х)(Д(х)^В(х)).
Эти теоремы состоят из трех частей; описания множества X, к эле-
ментам которого эта теорема относится, формы А (х) (условия
теоремы) и формы В(х) (заключения теоремы).
П р и м е р. В теореме «Если диагонали параллелограмма рав-
ны, то ои является прямоугольником» X — множество всех парал-
лелограммов, А (х) — форма «Диагонали параллелограмма х рав-
203
ны» и В (х) — форма «Параллелограмм х является прямоугольни-
ком».
Теорема может содержать и формы от нескольких переменных.
Например, теорема «Большей дуге окружности соответствует боль-
шан хорда» записывается в виде VЛ'У у (А (х; у)-*- В (х; у)). Здесь
хну — дуги окружности, А (х; у)означает «Дуга к больше дуги у»,
В (х; у) — «Хорда, стягивающая дугу х, больше хорды, стягиваю-
щей дугу у».
По аналогии с понятиями обратной и противоположно^ импли-
каций введем понятия прямой, обратной и противоположной тео-
рем. Для теоремы
(*х€Х)(Л(х)->В(х))
(О
обратной назовем теорему
(V*6X)(B(x)-*4WX
противоположной — теорему
(V zgX)(A(x)-^B(z))
и обратной к противоположной — теорему
(v *ех)(в«-л<х)).
(2)
(3)
(4)
Теоремы (2) н (3) равносильны друг другу, равно как и теоре-
мы (П и (4).
Упражнения
68. Запишите символически аксиому параллельности (через
каждую точку проходит не более одной примой, параллельной
данной прямой) н ее отрицание. Дайте словесную формулировку
отрицания.
69. Запишите символически:
а) определение четной функции (функция f называется четной,
если вместе с каждым значением переменной х из ее области
определения значение — х также входит в область определения
этой функции и для любого х нз области определения f выпол-
няется равенство f (—x)=f(x));
б) определение нечетной функции (функция / называется не-
четной, если вместе с каждым значением переменной х из ее об-
ласти определения значение — х также входит в область опреде-
ления этой функция и для любого х нз области определении f вы-
полняется равенство f (—х)= — f (х));
в) необходимое и достаточное условие истинности утвержде-
ний: «Функция f не является четной», «Функция f не является не-
четной».
204
70. Запишите приведенные ниже теоремы в символической
форме и найдите для них обратные, противоположные и обратные
противоположным. Для этих теорем постройте отрицания. Укажи-
те, какие из теорем истинны.
а) Если в треугольнике АВС угол В прямой, то АВ2+ВС2~АС2.
б) Если четырехугольник A BCD — параллелограмм, то его диа-
гонали делят друг друга пополам.
в) Во всяком параллелограмме есть центр симметрии
г) Если сумма цифр десятичной записи натурального числа
делится на 5, то это чнсло делится на 5.
д) Если прямая а параллельна прямой Ь, а прямая b парал-
лельна прямой с, то прямая а параллельна прямой с.
е) Если прямая а перпендикулярна прямой Ь, а прямая b па-
раллельна прямой с, то прямые а и с перпендикулярны.
Л итература
1. Гжегорчнк А. Популярная логика.— М.: Наука, 1979.
2. К у т а с о в А. Д. Элементы математической логики.— М.:
Просвещение, 1977.
3. Никольская И. Л. Математн ческа н логика.— М.: Высшая
школа, 1981.
4. Столл Р. Р. Множества, логика, аксиоматические теории.—
М.: Просвещение, 1968.
5. С т о л я р А. А. Как мы рассуждаем.— Минск: Вышэйшая
школа, 1968.
6. С т о л я р А. А. Как математика ум в порядок приводит.-—
Минск: Вышэйшая школа, 1982.
7. Фрейденталь X. Язык логики.— М.: Наука, 1969.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ПЛОСКОСТИ
ВВЕДЕНИЕ
В морозный день хорошо видны изящные шестиугольные
узоры снежинок. Каждый узор имеет несколько осей симметрии.
Кроме того, он совмещается с самим собой прн повороте вокруг
центра на 120°.
Симметричность творений природы (морских звезд, жуков,
бабочек, кристаллов н т. п.) оказывает большое влияние и на
художественное творчество человека. Например, орнаменты, ко-
торыми издавна украшаются архитектурные сооружения, часто
имеют симметричные, повторяющиеся части. Симметрия играет
важную роль в творчестве дизайнеров, придающих техническим
конструкциям современную красивую форму.
Осевая симметрия, поворот, параллельный перенос являются
движениями. Понятие движения — одно нз основных в геометрия.
Оно позволяет по-иному взглянуть на школьный курс, с новой
точки зрения осмыслить теоремы и задачи, с которыми мы встре-
чаемся на уроках геометрии.
Еще Евклид определял равные фигуры как такие, которые
могут быть «совмещены» друг с другом. Под этим он понимал
перемещение фигуры как твердого целого — то, что мы теперь
называем движением. Например, доказывая признаки равенства
треугольников, Евклид говорил: «Наложим один треугольник на
другой так, чтобы...» Но поскольку свойства наложений (т. е.
движений) не были нм четко сформулированы, это предложение
является лишь обращением к нашим опытным представлениям,
а не математическим доказательством.
Наиболее последовательно идея о связи понятия равенства
фигур с движениями (и вообще о роли движений в геометрии)
была высказана выдающимся немецким математиком Феликсом
Клейном (1849—1925). В своей речи прн вступлении на долж-
ность профессора кафедры геометрии в университете города Эр-
ланген (1872 г.) ои призывал переосмыслить геометрию на основе
рассмотрения групп движений. Эта точка зрения (называемая
теперь эрлангенской программой) очень важна в геометрии.
Применение движений и других геометрических преобразова-
ний плоскости к доказательству теорем н решению задач на по-
строение, а также более подробный рассказ об идеях Клейна
и составляют предмет этого факультативного курса.
206
ПОНЯТИЕ ДВИЖЕНИЯ
В курсе алгебры вы познакомились с понятием функции,
Например, функция f (х)=2*4-5 числу х=3 ставит в соответствие
число f (х)=2-34-5= 11 —значение этой функции прн х=3. В
геометрии рассматриваются функции иного рода, называемые гео-
метрическими преобразованиями. В отлнчне от числовых функций
геометрические преобразования каждой точке ставят в соответст-
вие точку.
В качестве примера возьмем два плана одного и того же участ-
ка местности в разных масштабах (рис. 122). Каждому населен-
ному пункту, каждой точке первого плана однозначно соответству-
ет точка иа втором плайе. Этим осуществляется геометрическое
преобразование первого плана местности на второй.
Если при геометрическом преобразовании / точка А переходит
в точку А] или, как говорят, отображается на точку Ai, то пишут
А-*-А] (нлн А -4-Л]) и точку А называют образом точки А. Каж-
дая фигура отображается на некоторую другую фигуру — ее об-
раз. Так, при преобразовании одного плана на другой (рнс. 122)
имеем А—►Ль В—AB—*AtBt, Z\ABN-+&AiBiNi.
Определение. Геометрическое преобразование называет-
ся движением, если оно сохраняет расстояние между точками (т. е.
нз А—В—>В| следует AB=AiBi}.
Чтобы получить наглядное представление о движении, возьмем
лист бумаги с изображенной на нем фигурой F, наложим сверху
кальку и обведем на кальке фигуру F. После этого сдвинем произ-
вольным образом лист кальки (рис. 123) или наложим его на лист
бумаги обратной стороной (изнанкой, рис. 124). Тогда мы увидим
первоначальную фигуру F и ее образ Fi. Прн этом расстояния
между двумя произвольными точками фигуры F сохраняются:
ЛВ=Л1ВЬ ВС—В\С\, ДС=Д1С1 и т. д.
Заметим, что при геометрическом понимании движения мы
обращаем внимание лишь на начальное положение фигуры и ее
конечное положение (образ), отвлекаясь от траекторий движе-
ния отдельных точек, от времени, скорости и т. д. Этим геомет-
рическое понимание движения отличается от физического.
В результате движения прямая переходит в некоторую прямую,
луч переходит в луч, отрезок — в отрезок, угол — в угол, окруж-
ность — в окружность н т. д.
Рис. 122
207
Рис. 123
Рис. 124
Прн решении задач н доказательстве теорем часто пользуются
тем, что движение отображает пересечение двух фигур на пересе-
чение их образов. Иными словами, если F—>F|, то образом
пересечения фигур F и Н является пересечение фигур Fi и Их.
Аналогично объединение двух фигур отображается на объединение
нх образов.
Определение. Две фи1уры называются равными, если су-
ществует движение, отображающее одну из них на другую.
Так как движение сохраняет расстояние между точками,
то равные отрезки имеют одинаковую длину. Обратно: если два
отрезка имеют одинаковую длину, то они равны, т. е. существует
движение, отображающее одни из ннх на другой.
Аналогично две окружности равны в том и только в том случае,
если они имеют одинаковые радиусы. Два угла равны в том и толь-
ко в том случае, если они имеют одинаковую величину (т. е. содер-
жат одинаковое число градусов).
Задачи
1. На координатной плоскости осуществляется геометрическое
преобразование, при котором каждая точка смещается иа три еди-
ницы вправо (вдоль осн абсцисс) н затем еще на две единицы
вверх. Какая точка является образом точки А (—1; 1) прн этом
преобразовании? Образом какой точки является точка И (3; 1)?
Отметьте точки А(1;—1), /?(—!;—1), 0(1; 1), Р(0; —1),
М(—2; —1). Какая фигура является образом отрезка ДА? от-
резка АВ? отрезка СР? &АМК?
2. Проектирование отрезка АВ на отрезок CD из точки О
(рнс. 125) представляет собой геометрическое преобразование,
которое можно описать следующим образом: в точке О помещает-
ся источник света и образом каждой точки М отрезка АВ является
ее тень на отрезке CD. Какая точка является образом точки Л?
208
точки В? точки /С? Какая фигура является образом отрезка А К?
отрезка КВ?
3. Прн некотором движении точка А переходит в точку В. В ка-
кую фигуру переходят при этом движении окружность с центром А
и радиусом 2 см?
4. Прямые I и т пересекаются в точке А. При движении f этн
прямые переходят соответственно в прямые Ц и пересекающие-
ся в точке В. В какую точку переходит точка А при движении f?
Б. Известно, что расстояние между любыми двумя точками фи-
гуры F не превосходит 5. Справедливо ли то же самое для фигу-
ры G, которая равна фигуре В?
6- Три точки А, В, С удовлетворяют условию АВ+ВС—АС.
В результате движения f они перешли в точки Вь С|. Рас-
положены лн точки Л|, Bi, Ci на одной прямой? Какан нз них рас-
положена между двумя другими?
7. Докажите, что образом отрезка при движении f является
отрезок. Докажите, что образом прямой является прямая.
$ ПОВОРОТ
j Одним нз видов движений является поворот. Наглядное пред-
ставление о повороте можно получить следующим образом. Возь-
мем лист бумаги с изображенной на нем фигурой F, наложим
кальку и обведем фигуру F. Теперь закрепим кальку кнопкой в
некоторой точке О н повернем. На рисунке 126 поворот кальки
вокруг точки О выполнен иа угол 60°. Фигура Fj, изображенная
на повернутом листе кальки, — образ фигуры F при этом повороте.
В математике направление поворота против движения часовой
стрелки считают положительным, а по часовой стрелке отрицатель-
ным. Таким образом, на рисунке 126 фигура F| получается из
фигуры F поворотом вокруг точки О на угол -{-60°.
Рис. 125
209
Задача 1. Построить отрезок, являющийся образом отрезка
АВ при повороте вокруг точки О на угол —70°.
Решение. Проведем луч ОЛ и построим луч Z, получающийся
нз луча О А поворотом на угол —70°. На луче I построим такую
точку Л |, что ОЛ1 =ОЛ (рнс. 127). Точка Л1 является образом точ-
ки А прн рассматриваемом повороте. Аналогично построим точ-
ку В] — образ точки В прн этом повороте. Отрезок с концевыми
точками Ль В] и является образом отрезка АВ.
Рассмотренная задача показывает, что для построения образа
фигуры F при некотором повороте достаточно найти образы
характерных точек этой фигуры. В случае отрезка такими харак-
терными точками являются его концы. Для ломаной (или много-
угольнику) характерными точками являются вершины. А чтобы
найти образ окружности, надо построить образ ее центра и про-
вести окружность того же радиуса (рнс. 128).
Задача 2. Внутри прямого угла дана точка Л. Построить
равносторонний А АВС, вершины В н С которого лежат на сторо-
нах этого угла.
Решение. Прн повороте на 60° вокруг точки А (рнс. 129)
точка В переходит в точку С. Следовательно, прямая I, являющая-
ся образом прямой ОМ при этом повороте, содержит образ точки В,
т. е. содержит точку С. Из этого вытекает, что С есть точка пере-
сечения прямых ON н I. Так как прямую I можно построить,
то это позволяет найти точку С, а затем построить и искомый
ДЛВС.
Задача 3. Даиы окружность s с центром О н точка Л. Про-
вести в окружности хорду MN дайной длины так, чтобы нз точки А
она была видна под углом 40°.
Решение. Отбросим на времн требование о том, чтобы хорда
MN была видна из точки Л под углом 40°, и построим какую-
нибудь хорду НК, имеющую требуемую длину. Далее построим
Рис 128
д.
какую-нибудь точку Т, нз которой хорда НК видна под углом 40°
(рис. 130). Окружность п, описанная вокруг &НКТ, обладает тем
свойством, что нз любой точки дуги НТК (содержащей точку Г)
хорда НК видна под углом 40°; обозначим эту дугу через d. Теперь
ясно, что нужно повернуть эту дугу d вокруг точки О на такой угол,
чтобы повернутая дуга прошла через точку А. Для того чтобы опре-
делить, на какой угол нужно осуществить поворот, проведем ок-
ружность с центром О, проходящую через точку А, и обозначим
через В точку пересечения этой окружности с дугой d (рис. 131).
Прн повороте вокруг точки О на угол ВОА дуга d перейдет в ду-
гу dj, проходящую через точку Д, а хорда НК перейдет в хорду MN,
которая видна из точки А под углом 40°. Это и дает решение зада-
чи. (Возможно до четырех решений.)
211
Задачи
8. Отметьте две точки О к А. Осуществите поворот точки А
вокруг точки О на угол: а) 30°; б) —80°.
9. Начертите ломаную ABCD и отметьте точку О, не принадле-
жащую этой ломаной. Выполните поворот ломаной ABCD вокруг
точки О на угол -—ИО”.
10. Отметьте две точки О, Q и начертите окружность с цент-
ром О. Выполните поворот этой окружности вокруг точки Q на
угол 70°.
11. Дано:/.ЛЮМ=а, 0M=0N; кроме того, даны прямые
MPJ-OM, NQ.LON. Докажите, что прямая МР получается из
прямой NQ поворотом на угол а (илн на угол —а).
12. Отрезок Л1В1 получается нз отрезка АВ поворотом на
угол а (рис. 127). Докажите, что &ОАВ = Д ОА цвь Выведите от-
сюда, что АВ=Л]В1 (т. е. поворот является движением).
13. Отрезок A |Bi — образ отрезка АВ при повороте вокруг
точки О на угол а, М — точка пересечения прямых АВ н АцВ|.
Докажите, что: а) угол между прямыми АВ и AtBi равен |а|;
б) точки М, О, А, А1 лежат на одной окружности; в) точки М, О, В,
Bi лежат на одной окружности.
14. На сторонах дАВС построены вне его равносторонние
треугольники АВР, АСН, ВСМ. Докажите, что: а) отрезки ДМ, ВН,
СР равны; б) отрезки AM, ВН и СР пересекаются в одной точке.
15. Начертите две окружности, пересекающиеся в точке А.
Проведите в ннх равные хорды ABi и ABS, составляющие угол а.
16. Через точку А, данную внутри окружности, проведите хор-
ду, вдвое меньшую своего расстояния от центра.
17. Даны: а) трн параллельные прямые; б) трн концентри-
ческие окружности. Постройте равносторонний треугольник с вер-
шинами на этих прямых (окружностях).
18. Постройте равнобедренный прямоугольный треугольник с
вершиной прямого угла в заданной точке, у которого одна нз
вершин острых углов лежит иа данной прямой, а другая — на
данной окружности.
19. В данную окружность впишите прямоугольный треуголь-
ник, зная его острый угол и точку, через которую проходит один
из катетов.
20. Около данной окружности опишите равносторонний тре-
угольник, одна нз сторон которого проходит через данную точку.
21. Через данную точку проведите прямую, отрезок которой
между данными концентрическими окружностями виден из центра
под данным углом.
22. В данной окружности проведите хорду заданной длины так,
чтобы данная прямая отсекала от нее третью часть.
23. Через данную точку проведите окружность данного радиу-
са, которая пересекает данную окружность по хорде, имеющей
заданную длину.
212
24. Даны окружность s и две точки А, В. Постройте в окруж-
ности s такую хорду MN заданной длины, что прямые AM и BN:
а) параллельны; б) образуют заданный угол а.
25. На сторонах дАВС построены вне его квадраты ABMN,
BCPQ. Докажите, что: а) отрезки AQ и СМ равны и перпендику-
лярны; б) прн повороте на 90° вокруг центра квадрата ABMN
отрезок ВС переходит в отрезок МТ, равный н параллельный
отрезку BQ-, в) отрезок Л4<2 перпендикулярен медиане ВК. в Л АВС
и вдвое длиннее ее.
26. Внутри квадрата ABCD взята точка Р. Проведены перпен-
дикуляры: нз вершины А к прямой ВР, из вершины В к СР, из С к
DP, нз О к АР. Докажите, что все четыре перпендикуляра (илн их
продолжения) пересекаются в одной точке.
27. Внутри отрезка АЕ взята точка С и построены (по одну
сторону прямой АЕ) равносторонние треугольники АВС и CDE,
точки М и Р — середины отрезков AD и BE. Докажите, что Д СРМ
равносторонний.
28. Внутри отрезка АВ взята точка С и построены (по одну сто-
рону прямой АВ) квадраты ACMN и CBPQ, точки К и L — середи-
ны отрезков AQ и ВМ. Докажите, что CKL— равнобедренный
прямоугольный треугольник
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Поворот вокруг точки О иа 180° называют центральной симмет-
рией или, более подробно, симметрией относительно центра О. При
этом движении каждый луч с началом О переходит в противопо-
ложный ему луч (рис. 132). Если А — произвольная точка, отлич-
ная от О, а А> — ее образ при симметрии относительно центра О,
то точка О является серединой отрезка АЛь Это позволяет лег-
ко построить точку Ai, симметричную точке А относительно
центра О.
Напомним, что две прямые в том и только в том случае
параллельны, если они симметричны относительно некоторой
точки.
Далее, четырехугольник в том и только в том случае является
параллелограммом, если ои обладает центром симметрии. При
этом центром симметрии параллелограмма является точка пере-
сечения его диагоналей.
Задача 1. На сторонах параллелограмма ABCD построены
вне его равносторонние треугольники ABM, BCN, CDP, ADQ. До-
казать, что MNPQ — параллелограмм
А,
0
Рис. 132
Решение. Обозначим через О центр симметрии параллело-
грамма ABCD (рис. 133). Так как отрезки АВ и CD симметричны
относительно точки О, то &АВМ и CDP симметричны относитель-
но этой точки. Следовательно, точки М и Р симметричны относи-
тельно О, т. е. О — середина отрезка МР. Аналогично О — середи-
на отрезка NQ. Из этого и вытекает, что MNPQ — параллело-
грамм.
Задача 2. Внутри угла, меньшего чем развернутый, дана
точка А. Построить такую прямую, проходящую через точку А,
что ее отрезок, заключенный внутри угла, делится в точке А попо-
лам.
Решение. Пусть К н Т — точки пересечения искомой прямой
со сторонами данного угла MON (рис. 134). При симметрии от-
носительно А точка К переходит в точку Т. Следовательно, пря-
мая являющаяся образом прямой ОМ прн этой симметрии, со-
держит образ точки К, т. е. точку Т. Поэтому Т есть точка пересе-
чения прямых ON н п.
Построение осуществляется следующим образом. Построим
точку В, симметричную точке О относительно центра А, и про-
ведем через В прямую, параллельную ОМ. Это и будет прямая п, а
точка ее пересечения с ON — искомая точка Т.
Задача 3. В окружности проведены непересекающиеся хор-
ды АВ и МК. На хорде АВ задана точка О. Найти на окружности
такую точку Р, что угол МРК отсекает от хорды АВ отрезок, имею-
щий точку О своей серединой.
Решение. Обозначим искомый отрезок, отсекаемый от хорды
АВ, через НТ (рис. 135). Точки НнТ симметричны относительно О.
Следовательно, точка Т лежит иа отрезке NQ, являющемся обра-
Рис. 135
зом отрезка МР при симметрии относительно О. Точку N можно
считать известной — это образ точки Л4 прн симметрии относи-
тельно О. Далее, Z-PTN также известен (он равен вписанному
Z. МРК, опирающемуся на дугу МКу, обозначим этот угол через а
Тогда Z~KTN= 180°—а. Итак, точка Т обладает тем свойством,
что КЛУ=180°—а. Значит, построив какой-нибудь /LK.SN, рав-
ный 180° — а, и проведя описанную окружность KSN, мы получим
дугу s (изображенную жирно на рисунке 136), на которой лежит
точка Т. Итак, Т есть точка пересечения прямой АВ с дугой s, н это
позволяет построить точку Т, а затем Р.
Задачи
29. Отметьте точки О, А, В, ие лежащие иа одной примой
Постройте образы точек А и В при симметрии относительно цент-
ра О. Постройте образ отрезка АВ.
30. Начертите Л АВС я отметьте точку О вне его. Постройте
образ этого треугольника прн симметрии относительно точки О
31. Начертите окружность s и возьмите точку О вне ее. По-
стройте образ окружности s прн симметрии относительно точки О
32. Докажите, что если ABCD и ABtCDt — параллелограммы,
имеющие общую диагональ АС, причем точки В, Blt D, Dt ие лежат
иа одной прямой, то BB\DD\ — параллелограмм.
33. Докажите, что если два равных отрезка параллельны, то
существует точка О, относительно которой онн симметричны.
34. Через точку пересечения диагоналей параллелограмма
проведены две прямые. Докажите, что точки пересечения этих пря-
мых со сторонами параллелограмма являются вершинами нового
параллелограмма.
35. Докажите, что в параллелограмме ABCD вершины А и С
находятся на одинаковом расстоянии от прямой BD.
36. Через точку пересечения двух окружностей проведите се-
кущую, определяющую в этих окружностях равные хорды.
215
37. Через данную точку А проведите прямую, часть которой
между данной прямой и дайной окружностью делилась бы в точке
А пополам.
38. Постройте параллелограмм, две противоположные верши-
ны которого находятся в данных точках, третья — на данной ок-
ружности, четвертая — на данной прямой.
39. Даны две концентричные окружности и точка Л на мень-
шей из ннх. Проведите в большей окружности хорду, проходя-
щую через точку А, так, чтобы эта хорда делилась окружностями
иа три равные части.
40. Постройте параллелограмм ABCD, центром которого явля-
ется данная точка О. а вершины А. В. С. D лежат на данных
прямых а, Ь, с, d.
41. Постройте ДАВС, зная длину медианы ВМ и радиусы
окружностей, описанных около ДАВМ и дСВМ
42. Постройте дАВС, зная длины стороны АВ, медианы AM и
высоты ВН.
43. Постройте А А ВС, зиая длины стороны АВ. медианы AM и
высоты СВ.
44. В дАВС проведены медианы АК и СЕ. Докажите, что:
а) если Z. СА К = Z. А СВ—30°, то аАВС равносторонний;
б) если ZLBAK— А ВСЕ=30°, то дАВС равносторонний.
45. В выпуклом многоугольнике для каждой стороны имеется
равная и параллельная ей сторона. Докажите, что этот много-
угольник имеет центр симметрии.
46. Докажите, что если выпуклый многоугольник можно разре-
зать иа параллелограммы, то этот многоугольник имеет центр
симметрии.
47. Две равные окружности касаются в точке А. Окружность
вдвое большего радиуса содержит одну из ннх, касаясь ее в точ-
ке В, и пересекает другую в точках Р н Q. Докажите, что одна
из точек Р, Q лежит на прямой АВ.
48. На сторонах параллелограмма взяты такие четыре точки
(по одной на каждой стороне), которые также являются вершинами
параллелограмма. Докажите, что оба параллелограмма имеют
общий центр.
49. Докажите, что выпуклый шестиугольник АВCDEF с попарно
параллельными сторонами в том и только в том случае является
центрально-симметричным, если треугольник, образованный пря-
мыми АВ, CD, EF, и треугольник, образованный прямыми ВС,
DE, FA, имеют одинаковую площадь.
50. Внутри выпуклого п-угольиика с попарно непараллельными
сторонами взята точка О. Докажите, что ие существует п-\-1 пря-
мых, проходящих через О, каждая из которых делит площадь
многоугольника пополам.
51. Даны точка А, прямая р и иа ней точка Р. Постройте
такой угол с вершниой А, имеющий заданную величину, что отре-
зок, высекаемый им на прямой п делится в точке Р пополам.
216
ОСЕВАЯ СИММЕТРИЯ
Возьмем на плоскости две точки А и В. Существуют два движе-
нии, прн которых эти две точки остаются неподвижными. Одно из
этих движений — тождественное преобразование, которое не толь-
ко точки А и В оставляет неподвижными, ио и любую точку плос-
кости оставляет на месте. Другим движением, оставляющим точ-
ки Л и В неподвижными, является симметрия относительно прямой
АВ (осевая симметрия). Наглядное представление об осевой сим-
метрии можно получить следующим образом: надо перевернуть
плоскость в пространстве вокруг осн АВ «другой стороной»
(рис. 137). При этом каждая точка прямой АВ останется на месте,
а любая точка X, не принадлежащая прямой АВ, перейдет в точку
X», лежащую по другую сторону прямой АВ.
Построение точки, симметричной точке М относительно пря-
мой /, осуществляется следующим образом. Пусть точка М не ле-
жит на прямой /. Проведем через М прямую, перпендикулярную
прямой I, и обозначим через О точку пересечения этих прямых
(рнс. 138). Далее на луче, противоположном лучу ОМ, отложим
отрезок ON, равный отрезку ОМ. Тогда N и будет образом точки М
при симметрии относительно прямой I, т. е. при этой симметрии
M—+N (н в то же время N—*~M). Если же точка Р принадлежит
оси симметрии /, то Р—
Еще одно свойство осевой симметрии состоит в том, что она
меняет ориентацию. Поясним, что это означает. На рисунке 139
изображены две окружности, симметричные относительно пря-
мой I. На левой окружности указаны стрелки, задающие положи-
тельное направление обхода (против движения часовой стрелки),
а на правой — симметричные им стрелки. Видно, что на правой
окружности стрелки задают отрицательное направление обхода
(по движению часовой стрелки). Таким образом, при осевой сим-
метрии направление обхода (ориентация) меняется иа противопо-
Рис 137
Ряс. 138
217
I
Рис. 140
ложное. В отлнчие от осевой симметрии поворот (в частности,
центральная симметрия) не меняет ориентацию.
Напомним еще один важный факт, известный нз курса гео-
метрии. Пусть I — ось симметрии точек А и В, т. е. перпендикуляр
к отрезку АВ, проходящий через его середину. Если точка М при-
надлежит прямой /, то АМ—ВМ; если же М не принадлежит пря-
мой I, то АМфВМ. Иначе говоря, точка М в том н только в том
случае принадлежит осн симметрии точек А и В, если АМ=ВМ.
Задача 1. Даны две окружности типе центрами А и В,
пересекающиеся в точках М и Р (рис. 140). Доказать, что точки М
и Р симметричны относительно прямой АВ.
Решение. Обозначим через t образ точки М при рассмат-
риваемой симметрии. Мы пока ие знаем, совпадает ли Mi с Р. Но
ясно, что АМ=АМ\ (ведь точка А остается неподвижной, а рас-
стояния сохраняются). Это означает, что ЛЬ принадлежит окруж-
ности т. Точно так же ВМ=ВЛЬ, т. е. точка ЛЬ принадлежит
также окружности п. Таким образом. Mi есть одна из точек пере-
сечения окружностей тип. Следовательно, ЛЬ должна совпа-
дать с точкой Р, т. е. М—*~Р
Рнс. 141
218
Задача 2. Доказать, что нз всех треугольников с данным ос-
нованием н данной площадью наименьший периметр имеет равно-
бедренный треугольник.
Решение. Рассмотрим все треугольники с данным основа-
нием АВ и данной площадью, расположенные по одну сторону пря-
мой АВ. Их третьи вершины лежат иа одной прямой /, параллель-
ной АВ (рнс. 141). Обозначим через Bi образ точки В прн симмет-
рии относительно прямой I. Тогда для любого нз рассматриваемых
треугольников его периметр равен длине ломаной BACBi. Так
как отрезок АВ фиксирован, то наименьшим периметр дДВС
будет в том случае, если наименьшей будет длина ломаной АСВ\.
Но это будет в том случае, если эта ломаная превращается в отре-
зок ДВ|, т. е. если в качестве С берется точка пересечения этого от-
резка с прямой I. Но тогда Z. 1 = Z.2 и Z.2= Z.3 (в силу симмет-
рии), и потому Z. I = Z.3, т. е. &.АВС равнобедренный.
Задачи
52. Начертите прямую Z и постройте образ фигуры F прн сим-
метрии относительно этой прямой, если фигура представляет со-
бой: а) отрезок, не пересекающий прямую I; б) отрезок, пересекаю-
щий эту прямую; в) треугольник; г) окружность.
53. Две хорды окружности проходят через одну и ту же точку
радиуса н одинаково наклонены к этому радиусу. Докажите,
что хорды равны.
54. Докажите, что биссектриса угла между продолжениями
двух равных хорд окружности проходит через ее центр.
55. Отрезок АВ пересекает прямую р в точке К. Прн симметрии
относительно этой прямой Д—В—*-Bi. Докажите, что отрезок
Д|В] проходит через точку К.
56. Докажите, что еслн в треугольнике медиана совпадает с
биссектрисой, то этот треугольник равнобедренный
57. Прямые т, п не параллельны. Сколько осей симметрии
имеет фигура, представляющая собой объединение этих прямых?
58. Через точку А внутри данного угла проведите прямую, от-
секающую от сторон угла равные отрезки.
59. Даны прямая I н две точки Д, В по разные стороны от нее.
Найдите иа этой прямой такую точку О, что прямая I делит Z.AOB
пополам.
60. Даны две окружности и между ними прямая р. Постройте
равносторонний треугольник, две вершины которого находятся
на окружностях, а одна нз высот лежит на прямой р.
61. Даиы прямая I и точки А, В по одну сторону от нее. Найдите
на прямой / такую точку X, что лучи ХА, ХВ образуют равные углы
с прямой I.
62. Даны прямая р и две точки А, В по одну сторону от нее.
Найдите на прямой р точку X, для которой сумма ее расстояний
от точек Д н В наименьшая.
219
63. Даны прямая р и точки Л, В по разные стороны от нее. Най-
дите на прямой р точку X, для которой разность ее расстояний от
точек А и В наибольшая.
64. На данной прямой АВ найдите точку X, соединив которую
сданными точками М, N, получим /.МХА н jLNXB, первый нз ко-
торых вдвое меньше второго.
65. Постройте ромб ABCD с данной длиной диагонали АС,
у которого точки А и С лежат и а данной прямой, точка В —
на другой данной прямой, а точка D — на данной окружности.
66. Постройте четырехугольник ABCD, зиая его стороны, если
известно, что диагональ АС делит угол А пополам.
67. Постройте окружность, касающуюся дайной окружности н
касающуюся данной прямой в данной точке.
68. На прямой I найдите такую точку, что касательные, про-
веденные из нее к двум данным окружностям, составляют с пря-
мой I равные углы.
69. Постройте л АВС, если известны: а) Л.А, с, а-\-Ь\ б) Z-Л,
с, Ъ—а\ в) Z.S—Z.C, Ь, с\ г) Z.B—Z.C, a, ha\ д) ha, hc, hb.
70. Внутри данного угла отмечена точка М. Найдите на сторо-
нах угла такие точки А и В, чтобы треугольник АВМ имел наи-
меньший периметр.
71. Даны прямая с, точка С на ней н точки А, В по разные сто-
роны прямой с. Найдите на прямой с точку, из которой отрезки
АС и ВС видны под равными углами.
72. На прямой р дана точка Р, а по разные стороны от нее —
точки А и В. Постройте на прямой р такую точку X, что Z_AXB=
= 3 ЛВХР.
73. Равные окружности Si н s2 касаются окружности s внутрен-
ним образом соответственно в точках А и В. Произвольная точка
С окружности s соединена отрезками с точками А н В; этн отрезки
пересекают окружности si н S2 в точках С и D. Докажите, что пря-
мые АВ и CD параллельны.
74. Даны точка А, прямая р н на ней точка Р. Постройте
такой угол с вершиной А, имеющий заданную величину, что отре-
зок, высекаемый .им на прямой р, делится в точке Р пополам.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Представление о параллельном переносе мы получаем, выдви-
гая ящик письменного стола: все предметы, находящиеся в ящике,
перемещаются в одном и том же направленнн на одинаковое рас-
стояние. Можно предложить и другую модель параллельного пе-
реноса: начертим на листе бумаги прямую, наложим лист кальки и
проведем на нем эту же прямую, а затем сдвинем кальку так, чтобы
прямая перемещалась по себе (рис. 142).
Дадим математическое определение параллельного переноса.
Пусть а — некоторый вектор. Параллельным переносом на вектор
2ео
а называется геометрическое преобразование, которое произволь-
ную точку А переводит в такую точку Ai, что выполняется
равенстно AAi=a (рис. 143).
Параллельный перенос является движением. В самом деле,
пусть A—*Ai, B—^Bi, т. е. AAt—BBi—a. Тогда
+ВВ7= — с+ЛВ+а==ДВ,
и потому т. е. параллельный перенос сохраняет рас-
стояния.
Отметим, что если при параллельном переносе Л—>£) и В-*-С,
причем точки А, В, С, D не лежат на одной прямой, то ABCD —
параллелограмм (рис. 144).
Задача 1. Пункты А и В расположены по разные стороны
реки. Требуется построить дорогу наименьшей длины от Л к В, ко-
торая включала бы мост N1N2, перпендикулярный берегам.
Решение. Обозначим через а вектор, перпендикулярный бе-
регам, длина которого равна ширине реки. Тогда при па-
Рис. 143
Рис. 144
221
раллельном перенесена вектора (рис. 145). Образ точки А обозна-
чим через Ai. Тогда AA^TVi — параллелограмм. Следовательно,
длина пути ANiN^B равна длине ломаной AA\NzB. Но точка А]
иам известна. Поэтому путь будет кратчайшим при наименьшей
длине ломаной A iN?B, т. е. в случае, если N? — точка пересечения
отрезка AiB с дальним (от А) берегом. Это позволяет построить
искомый путь АМ'М^В.
Задача 2. Основания двух равнобедренных треугольников
расположены иа одной прямой (рис. 146). Провести прямую, па-
раллельную основаниям, которая высекает в треугольниках рав-
ные отрезки.
Решение. Обозначим вектор MN через а. Тогда при парал-
лельном переносе иа вектор а имеем М—*-N, P-+Q. Следова-
тельно, при этом параллельном переносе /\АВС перейдет в
AAjBiCi, который пересекается с &DEF по искомому'отрезку
NQ. Далее, обозначая через К, L середины искомых отрезков,
а через S, Т середины оснований треугольников, имеем K—+L,
S—^T. Но точки S и Т нам известны. Следовательно, известен и
вектор а. Это и позволяет построить ДА1В1С1» затем точки N, Q и
искомую прямую NQ.
Рис. 146
222
Задачи
75. Начертите вектор а и фигуру F, которая представляет
собой: а) угол; б) ломаную; в) окружность. Постройте образ
фигуры F при параллельном переносе на вектор а
76. Начертите две параллельные прямые а и Ь. Укажите вектор
параллельного переноса, переводящего прямую а в прямую Ь.
Сколько таких векторов существует?
77. Окружности с центрами А и В имеют равные радиусы.
Докажите, что при мая, параллельная АВ н пересекающая эти ок-
ружности, высекает в иих равные хорды
78. На плайе имеются река и ее приток, по разные стороны
от которых расположены селения А и В (рис. 147). Требуется
построить дорогу наименьшей длины от Я кВ, которая включала
бы перпендикулярные берегам мосты через реку и через приток.
79. Докажите, что если отрезок, соединяющий середины двух
противоположных сторон четырехугольника, равен полусумме двух
других сторон, то этот четырехугольник является трапецией (или
па ра л л елогр а м м ом ).
80. Через точку, расположенную между двумя данными па-
раллельными прямыми, проведите окружность, касающуюся этих
прямых.
81. Постройте параллелограмм, две смежные вершины которо-
го находятся в данных точках, а две другие лежат: а) на данной
окружности; б) одна на данной окружности, а другая иа данной
прямой.
82. Через данную точку проведите прямую так, чтобы ее от-
резок между двумя данными параллельными прямыми имел за-
данную длину. -
83. Проведите касательную к данной окружности так, чтобы
ее отрезок между двумя данными параллельными прямыми имел
заданную длину.
84. Постройте отрезок заданной длины с концами на двух
данных параллельных прямых так, чтобы он был виден из дайной
точки под заданным углом.
85. Постройте прямую, параллельную дайной прямой, которая
высекала бы из двух данных окружностей равные хорды.
86. Проведите прямую, параллельную данной прямой и высе-
кающую из двух данных окружностей такие хорды, что сумма (раз-
ность) длин этих хорд имеет заданную величину.
Рис. 147
223
87. В квадрате со стороной 1 расположена фигура, рас-
стояние между любыми двумя точками которой не равно 0,001. До-
кажите, что площадь этой фигуры меньше 0,34.
88. Постройте прямую, параллельную данной прямой, так, что-
бы данный угол высекал иа ней отрезок заданной длины.
89. Через данную точку проведите две прямые, которые обра-
зуют между собой данный угол и высекают на данной примой
отрезок заданной длины.
90. В окружности проведены две хорды АВ и МК. Найдите
иа окружности такую точку Р. что угол МРК отсекает от хорды АВ
отрезок заданной длины.
91. Даиы такие четыре прямые а, Ь, с н d, что а|| b, c ||d. Прове-
дите через данную точку А прямую, отрезок которой между прямы-
ми а, b равен ее отрезку между прямыми с, d.
композиция ДВИЖЕНИЙ
Пусть f, g — два движения плоскости. Возьмем произвольную
точку А, и пусть Д-Л-Д,, Л|-£-Дг. Результат последовательного
выполнения движений называется их композицией. Композицию
движений/, g (первым выполняется/, затем g) принято обозначать
записью g ° /. Это результирующее отображение переводит точку
А сразу в Л 2 (рис. 148), т. е.
Например, если /, g — повороты вокруг одной и той же точки О
соответственно на углы 30° и —70°, то g о [ — поворот вокруг той
же точки О на угол 30° 4-(—70°)= —40°. В этом случае компози-
ция движений обладает свойством коммутативности (перемести-
тельности), т. е. g ° f—f ° g- В общем же случае композиция
движений свойством коммутативности ие обладает. Например, ес-
ли / — перенос вправо (вдоль оси абсцисс) иа трн единицы, a g —
поворот вокруг начала координат на —90°, то композиция go f
переводит точку Д (0; 1) в точку В(1; —3), а композиция / о g пе-
224
реводит Д в другую точку С (4; 0), т. е. g ° f ие совпадает
С fog.
Легко видеть, что композиция любых двух движений также яв-
ляется движением. В самом деле, пусть
лЛд,, ВЛ-Вь А,-!>-Аг, Bi-St-Bt.
Так как f— движение, то AB—AtBi. Точно так же А1В)=А2В2
(поскольку g— движение). Следовательно, АВ=А2В2, т. е. ре-
зультирующее отображение g of сохраняет расстояния и потому
является движением.
Отметим, что если каждое нз движений f, g сохраняет ориента-
цию (или если каждое меняет ориентацию), то композиция g°f
является движением, сохраняющим ориентацию. Если же одно из
движений f, g сохраняет, а другое меняет ориентацию, то компо-
зиция g с f будет движением, меняющим ориентацию.
Сформулируем теперь свойство подвижности плоскости, кото-
рое играет важную роль при дальнейшем изучении движений: если
иа плоскости даиы точки А, В, А\, Bi, для которых АВ—А\В\, то
существуют ровно два движения, удовлетворяющие условию
A—^Alr B—^Bi, (П
причем одно из них сохраняет, а другое меняет ориентацию.
Справедливость этого свойства легко пояснить. Пусть АВ —
=Д|В1. Мы можем теперь выполнить параллельный перенос плос-
кости иа вектор ДД| (при этом точка В перейдет в некоторую точ-
ку М, рис. 149), а затем осуществить поворот вокруг точки Дь при
котором точка М перейдет в Композиция этого параллельного
переноса и поворота представляет собой движение, сохраняющее
ориентацию и удовлетворяющее условию (1). Можно поступить и
иначе: сначала перевернуть плоскость в пространстве, наложив ее
на себя обратной стороной (изнанкой), а затем поступить, как
и прежде. Это даст движение, меняющее ориентацию и удовлетво-
ряющее условию (1). Других же движений, удовлетворяющих
условию (1), ие существует.
Рис. 149
225
Рнс. 150
Рис. 151
Задача 1. Выяснить, что представляет собой композиция
осевых симметрий Si, s% относительно пересекающихся прямых
Ль «2, образующих угол а.
Решение. Точка О пересечения этих прямых остается непод-
вижной при каждой из осевых симметрий, а потому и при их ком-
позиции. Пусть, далее, А — отличная от О точка прямой п(. При si
она остается неподвижной, а прн Sz переходит в точку В (рис. 150).
Таким образом при композиции sz о Si мы имеем:
О->О, Л—*-В. (2)
Поворот f вокруг точки О иа угол 2а также удовлетворяет ус-,
ловию (2). Но в силу свойства подвижности существует лишь
одно, сохраняющее ориентацию движение, удовлетворяющее усло-
вию (2). Значит, композиция S2°-Si совпадает с поворотом f.
Задача 2. Выяснить, что представляет собой композиция
осевых симметрий s? относительно параллельных прямых ng.
Решение. Возьмем две точки Д, В прямой «ь При s( они ос-
таются неподвижными, а прн $2 переходит в точки A i, Bi (рис. 151).
Таким образом, при композиции sg о Si мы имеем:
B—Bt (3)
При параллельном переносе на вектор AAt также выполняется
условие (3). Но существует лишь одно сохраняющее ориентацию
движение, удовлетворяющее условию (3). Следовательно, компо-
зиция за о si совпадает с этим параллельным переносом.
Задачи
92. На координатной плоскости взяты точки А (—2; 2),
В(1; 2), С(1; 0). Обозначим через f, g параллельные переносы иа
векторы АВ, ВС, а через h поворот иа —90° вокруг начала коорди-
226
иат. В какую точку переходит Д при отображении: а) Л © f;
б) h © g-, в) fog? Какая точка переходит в точку В при отобра-
жении: a) goh; б) gof?
93. Движение f есть композиция некоторых т осевых сим-
метрий. Это же движение f представлено также в виде композиции
некоторых п осевых симметрий. Докажите, что т—п четно.
94. Даны такие три точки А, В, С, что АВ=АС. Сколько су-
ществует движений, для которых А~~*А, В—+С? Назовите их.
95. Даны прямые а, Ь, точка А прямой а и точка В прямой Ь.
Сколько существует движений, переводящих прямую а в прямую Ь,
а точку А в точку В?
96. Что представляет собой композиция двух осевых симмет-
рий, оси которых перпендикулярны? Обладает ли эта композиция
свойством коммутативности?
97. Пусть Дь В\ — образы .4, В при сохраниющем ориентацию
движении f. Докажите, что это движение в том и только в том слу-
чае представляет собой параллельный перенос, если AB^AjB,.
98. Докажите, что композиция двух параллельных переносов
на векторы а и b представляет собой параллельный перенос иа
вектор a-f-b. Обладает ли композиция параллельных переносов
свойством коммутативности?
99. Движения f и g — повороты вокруг точек Р и Q на углы а
и ₽. Докажите, что если а4*₽ не кратно 2л, то g of представляет
собой поворот вокруг некоторой точки О иа угол а 4-0- Укажите,
как найти точку О. Если же ос4*0 кратно 2л, то g of— парал-
лельный перенос.
100. Докажите, что если ои 4-... 4- а* не кратно 2л, то компози-
ция поворотов вокруг некоторых точек Оь...»О* иа углы ои,..., а*
есть поворот иа угол ai4*...4-a* вокруг некоторой точки.
101. Шестиугольник ABCDEF переходит в себя при некотором
повороте на угол, не кратный л. Докажите, что треугольники АСЕ
н BDF равностороииие.
102. На плоскости указаны точки Ct, .., С*. являющиеся
последовательными серединами сторон некоторого многоугольни-
ка М, причем число k нечетно. Как построить многоугольник М
по этим точкам?
103. Докажите, что композиция центральных симметрий отно-
сительно точек Л и В представляет собой параллельный перенос
на вектор 2АВ.
104. Докажите, что если t — параллельный перенос, as —
центральная симметрия, то каждое из движений t о s, s © t являетси
центральной симметрией. Как найти их центры?
105. Докажите, что любое движение плоскости можно предста-
вить в виде композиции не более чем трех осевых симметрий.
106. В результате движения f прямая п переходят в параллель-
ную ей прямую. Докажите, что / есть либо параллельный перенос,
либо центральная симметрия.
227
107. На сторонах произвольного треугольника АВС построены
вне его равнобедренные треугольники МВС, NAC, РАВ с углами
120° при вершинах М, N, Р. Докажите, что треугольник MNP
равносторонний.
108. Докажите, что композиция поворота и параллельного пе-
реноса есть поворот на тот же угол. Вокруг какой точки осу-
ществляется этот поворот?
109. Шестиугольник ABCDEF вписан в окружность, причем
AB=CD=EF. Докажите, что середины отрезков ВС, DE, FA яв-
ляются вершинами равностороннего треугольника.
ТЕОРЕМА ШАЛЯ
Композиция / os, где s — симметрия относительно прямой п, а
£—параллельный перенос иа параллельный этой прямой вектор
ц=#=0 (рис. 152), называется скользящей симметрией; она является
движением, меняющим ориентацию.
В прошлом веке известный геометр и механик Шаль
(1793—1880) доказал следующую замечательную теорему о клас-
сификации движений плоскости:
Теорема. Всякое сохраняющее ориентацию движение плос-
кости представляет собой либо поворот (в частности, центральную
симметрию), либо параллельный перенос. Всякое меняющее ориен-
тацию движение плоскости является осевой или скользящей сим-
метрией.
Доказательство. Пусть f — движение, сохраняющее
ориентацию. Можно считать, что f ие является тождествен-
ным преобразованием е (поскольку е — частный случай парал-
лельного переноса), т. е. существует точка А, не совпадающая
со своим образом В. Пусть В—+С. Рассмотрим отдельно три воз-
можных случая:
а) Точка С совпадает с А (рис. 153). В этом случае
А-*В, В—А, (1)
Рис. 152
Рис. 153
228
Рис. 154
Рис. 155
Рис. 156
и потому середина О отрезка АВ остается неподвижной. Обозна-
чим через s симметрию относительно точки О, Каждое из движе-
ний f, s сохраняет ориентацию и удовлетворяет условию (1).
Но согласно свойству подвижности существует только одно такое
движение. Следовательно, f совпадает с s, т. е. f является централь-
ной симметрией.
б) Точки А, В, С различны и лежат на одной прямой (рис. 154).
В этом случае движение f удовлетворяет условию
А—В, В-+С.
(2)
Параллельный перенос t на вектор Л7? также удовлетворяет этому
условию (и сохраняет ориентацию). Из свойства подвижности вы-
текает, что f совпадает с t, т. е. в этом случае f является парал-
лельным переносом.
а) Точки Л, В, С не лежат на одной прямой (рис. 155). Дви-
жение f и в этом случае удовлетворяет условию (2). Проведя
перпендикуляры к отрезкам АВ, ВС через их середины, мы найдем
иа их пересечении такую точку М, что МА=МВ=МС и углы АМВ,
ВМС равны. Следовательно, существует поворот г вокруг точки М,
также удовлетворяющий условию (2). Согласно свойству подвиж-
ности f совпадает с г, т. е. f является поворотом.
Пусть теперь f — движение, меняющее ориентацию. Тогда
f не совпадает с е, и потому можно рассмотреть те же три случая.
В случае а) (рис. 153) движение f удовлетворяет условию (1) и
меняет ориентацию. Симметрия s0 относительно прямой, перпенди-
кулярной отрезку АВ и проходящей через его середину, также
удовлетворяет условию (1) и меняет ориентацию. Согласно свойст-
ву подвижности f совпадает с So, т. е. в этом случае f является
осевой симметрией.
В случае б) (рис. 154) обозначим через si симметрию отно-
сительно прямой АВ, через Ц параллельный перенос на век-
тор АВ. Каждое из движений f, /psi удовлетворяет условию (2) и
меняет ориентацию. Следовательно, f совпадает с h ° si. т. е. в этом
случае f является скользящей симметрией
Наконец, в случае в) (рис. 156) проведем в Д/1ВС среднюю
линию MN и обозначим через ss симметрию относительно пря-
мой MN, а чер^з Ь параллельный перенос иа вектор MN. Каждое
из движений f, П о S2 удовлетворяет условию (2) и меняет ориента-
цию. Следовательно, оии совпадают, т. е. и в этом случае f является
скользящей симметрией.
Задачи
ПО. Пусть s — симметрия плоскости относительно прямой п,
at — параллельный перенос на вектор, параллельный п. Докажи-
те, ЧТО t о S = S о t.
111. Какие из движений плоскости удовлетворяют условию
f <.f=e?
112. Докажите, что любое сохраняющее ориентацию движе-
ние представляется в виде композиции двух осевых симметрий.
113. Докажите, что при осевой симметрии неподвижными яв-
лиются точки, принадлежащие оси симметрии, и только оии
114. Докажите, что если движение имеет только одну непод-
вижную точку, то оно является поворотом.
115. Докажите, что если сохраняющее ориентацию движение
ие имеет неподвижных точек, то оно является параллельным пе-
реносом.
116. Докажите, что меняющее ориентацию движение, не имею-
щее неподвижных точек, является скользящей симметрией.
117. Докажите, что движение, ие являющееся тождественным
н имеющее более одной неподвижной точки, представляет собой
осевую симметрию.
118. Докажите, что если меняющее ориентацию движение
плоскости имеет хотя бы одну неподвижную точку, то оно пред-
ставляет собой осевую симметрию.
119. Дан многоугольник С\С2.. .Сь. Что представляет собой
композиция центральных симметрий относительно середин сто-
рон CiC-2, С2С3, .... СьС\, если k: а) нечетное; б) четное?
120. Какому условию должны удовлетворять точки Д, В, С, D,
чтобы композиция центральных симметрий относительно этих то-
чек была тождественным преобразованием?
121. Докажите, что если движение плоскости ие имеет ни
одной неподвижной прямой (т. е. прямой, совпадающей со своим
образом), то это движение является поворотом.
122. Докажите, что движение, имеющее единственную непод-
вижную прямую, является скользящей симметрией.
123. Докажите, что если при некотором движении каждая
прямая переходит в параллельную ей прямую, то это движение
является параллельным переносом или центральной симметрией.
124. Докажите, что если движение имеет бесконечно много
неподвижных прямых, причем все они параллельны, то это движе-
ние является параллельным переносом.
125. Докажите, что если движение имеет бесконечно много
неподвижных прямых, причем все оии проходят через одну точку,
то это движение является центральной симметрией.
230
ГРУППЫ ДВИЖЕНИЙ
Каждое движение f представляет собой взаимно однозначное
отображение плоскости на себя. Это означает, во-первых, что
/ есть отображение плоскости иа всю эту плоскость и, во-вторых,
что если точки А и В различны, то и их образы А и В различны.
Для каждого взаимно однозначного отображения плоскости на
себя существует обратное ему отображение, которое как бы
возвращает точки на свои прежние места. Именно если для ото-
бражения f мы имеем А -+В, то для обратного отображения
(обозначим его через g) справедливо соотношение В-+А. Если
g — обратное отображение для f, то и, наоборот, / является об-
ратным отображением для g. Часто обратное отображение для f
обозначают через f~*.
Если f — движение, то обратное ему отображение также явля-
ется движением. В самом деле, пусть М н N — две произвольные
точки плоскости. Так как f взаимно однозначно, то существуют
точки А, В, которые в результате движения / переходят в точки М,
N, т. е. А M-М, B-+N. Далее, так как f — движение, то AB—MN.
Прн обратном отображении (обозначим его через g) мы имеем
М -Л-Л, N-+B. Равенство AB^=MN означает теперь, что отображе-
ние g сохраняет расстояния, т. е. является движеинем.
Некоторое множество G движений называется группой движе-
ний, если оно обладает следующими двумя свойствами: а) если f —
некотороё движение, принадлежащее множеству G, то движение
f~l также принадлежит множеству G; б) если движения f, g при-
надлежат множеству G, то и движение g ° f принадлежит мно-
жеству G. Все движения плоскости образуют группу. Еще одним
примером группы движений является множество Т всех парал-
лельных переносов.
Движение, отображающее фигуру F на себя, называется само-
совмещением этой фигуры. Множество всех самосовмещеиий фи-
гуры F является группой движений; она называется группой само-
совмещений фигуры F.
Заметим, что параллельный перенос (не являющийся тож-
дественным преобразованием) не может совмещать ограниченную
фигуру с собой. То же относится к скользящей симметрии. Поэтому
самосовмещеннями ограниченной фигуры могут быть только пово-
роты или осевые симметрии.
Рассмотрим некоторый треугольник. Если его группа самосов-
мещений состоит только нз одного элемента (тождественного пре-
образования), то этот треугольник разносторонний.
Два элемента группа самосовмещеиий треугольника будет
иметь в том случае, если он, кроме тождественного преобразова-
ния, имеет еще одно самосовмещеине — осевую симметрию
(рис. 157). Из симметричности этого треугольника вытекает ряд
231
!z его свойств: а) две стороны треугольника
равны; б) два угла треугольника равны;
£ в) биссектриса одного нз углов является
также высотой; г) биссектриса одного нз
углов является также медианой; д) две вы-
j £ соты равны; е) две медианы равны; ж) две
I биссектрисы равны и т. д. Заметим, что
каждое нз этих свойств является необходи-
мым и достаточным условием для того, чтобы
Рис. 157 треугольник был равнобедренным, т. е. имел
ось симметрии.
Наконец, возможен случай, когда группа самосовмещеннй тре-
угольника содержит 6 элементов: трн осевые симметрии и три
поворота на углы 0°, 120°, 240°. Из этого вытекает ряд свойств:
все углы треугольника равны, все его стороны равны (т. е. тре-
угольник равносторонний), все медианы равны, вписанная и опи-
санная окружности концентричны и т. д. И опять каждое нз этих
свойств является необходимым и достаточным условием того,
чтобы треугольник обладал «поворотной симметрией», т. е. чтобы
существовал поворот (не являющийся тождественным отображе-
нием), который совмещает треугольник с самим собой.
Возьмем теперь параллелограмм общего вида (не являющийся
ии прямоугольником, ни ромбом). Он имеет два самосовмещения:
тождественное отображение е н симметрию г относительно точки
пересечения диагоналей. Из того, что в группе самосовмещеннй
параллелограмма имеется центральная симметрия, вытекает ряд
его свойств: противоположные стороны попарно равны и попарно
параллельны, противоположные углы попарно равны, диагонали
делятся в точке пересечения пополам, биссектрисы противополож-
ных углов попарно параллельны и т. д.
Группа самосовмещеннй ромба содержит, кроме в н г, еще
две осевые симметрии и Sa относительно прямых, на которых
расположены диагонали. Из наличия в группе самосовмещеннй
этих осевых симметрий вытекают дополнительные свойства (по
сравнению с параллелограммом): перпендикулярность диагона-
лей, совпадение диагоналей с бнссектрнсамн углов н т. д.
Вообще знание группы самосовмещеннй фигуры во многом
определяет ее геометрические свойства. Например, свойства пра-
вильных многоугольников, равнобочной трапеции, окружности н
многих других фигур легко выводятся нз рассмотрения их групп
самосовмещеннй.
Задачи
126. Какое движение является обратным для: а) симметрии s
относительно прямой АВ\ б) симметрии относительно центра О;
в) параллельного переноса t иа вектор ДВ; г) скользящей сим-
метрии t о s; д) поворота вокруг точки О на угол а?
232
127. Докажите, что множество всех параллельных переносов
представляет собой группу движений плоскости.
128. Будет ли группой движений множество всех поворотов
вокруг задаииой точки О? множество всех поворотов?
129. Является ли группой движений множество всех осевых
симметрий?
130. Докажите, что множество, состоящее из всех параллель-
ных переносов и всех центральных симметрий, является группой
движений.
131. Множество G содержит 4 элемента: тождественное ото-
бражение е и повороты вокруг заданной точки О на углы 90°, 180°,
270°. Докажите, что G — группа движений.
132. Постройте фигуру, группа самосовмещений которой со-
держит 6 элементов.
133. Сколько осей симметрии имеет полоса, прямоугольник,
ромб, квадрат? Сколько центров симметрии имеет каждая из
этих фигур?
134. Приведите примеры многоугольников, у которых в группе
самосовмещений имеется осевая симметрия: а) проходящая через
две вершины; б) проходящая через одну вершину; в) не проходя-
щая ни через одну его вершину
135. Дельтоидом называется четырехугольник, имеющий ось
симметрии, проходящую через две его вершины. Постройте дель-
тоид, не являющийся ромбом. Сколько элементов содержит его
группа самосовмещений? Какие свойства дельтоида вытекают нз
его симметричности?
136. Сколько элементов содержит группа самосовмещений рав-
нобочной трапеции? Какие свойства равнобочной трапеции вы-
текают из наличия у нее оси симметрии?
137. Докажите, что если группа самосовмещений четырех-
угольника содержит лишь два элемента е, f, причем f является
осевой симметрией, то этот четырехугольник является либо рав-
нобочной трапецией, либо дельтоидом (см. задачу 135).
138. Докажите, что если группа самосовмещений четырех-
угольника содержит 4 элемента, то этот четырехугольник яв-
ляется ромбом илн прямоугольником.
139. Сколько элементов содержит группа самосовмещений
квадрата?
140. Правильным называется п-угольннк, группа самосовме-
«, 360
щений которого содержит поворот на угол — градусов. Сколь-
ко элементов содержит группа самосовмещений правильного
п-угольннка? Сколько в этой группе осевых симметрий?
141. Верно ли, что если любая вершина многоугольника М
может быть переведена в любую другую некоторым самосовмеще-
нием этого многоугольника, то М — правильный многоугольник?
142. Докажите, что группа самосовмещений ограниченной фи-
гуры не может содержать двух центральных симметрий.
233
143. Докажите, что если многоугольник имеет четное число
осей симметрии, то он имеет центр симметрии.
144. Докажите, что если в группе самосовмещеннй фигуры F
имеется центральная симметрия относительно точки О, а также
некоторое движение g, то образ точки О прн движении g также
является центром симметрии фигуры.
РАССКАЗ О ГЕОМЕТРИЧЕСКИХ ИДЕЯХ Ф. КЛЕЙНА
Геометрическими свойствами фигур являются те, которые
одинаковы у всех равных между собой фигур. Например, прямая,
отрезок, треугольник, окружность являются геометрическими по-
нятиями, т. е. фигура, равная прямой, также представляет со-
бой прямую; фигура, равная отрезку, есть отрезок и т. д. Длина
отрезка, длина ломаной линии (например, периметр многоугольни-
ка) также являются геометрическими свойствами, поскольку они
одинаковы у равных фигур (т. е два равных отрезка имеют
одинаковую длину и т. д.).
Равными называются фигуры, которые можно перевести друг
в друга с помощью движения. Следовательно, геометрическими
свойствами являются те, которые сохраняются, не меняются в
результате движений или, как говорят, инвариантны прн движе-
ниях (от латинского слова invariant — неизменный). Иначе гово-
ря, геометрия изучает все те свойства фигур, которые инвариантны
при движениях. Выдающийся немецкий математик Феликс
Клейн (1849—1925) далеко развил эти первоначальные пред
ставления о связи изучаемых в геометрии свойств с движениями
На основе рассмотрения групп движений он показал глубокую ана-
логию различных геометрий (евклидовой геометрии, геометрии
Лобачевского и др.).
Кроме групп движений, в геометрии рассматриваются и другие
группы преобразований. Рассмотрим, например, аффинные пре-
образования, т. е. взаимно однозначные отображения плоскости на
себя, которые каждую прямую снова переводят в прямую
(рис. 158). В отличие от группы движений (которая определяет
евклидову геометрию) группа аффинных преобразований опреде-
ляет аффинную геометрию. В ней изучаются свойства фигур, ин-
Рнс. 158
234
вариантные относительно аффинных преобразований; например,
параллельность двух прямых — аффинное свойство (следователь-
но, свойство фигуры быть параллелограммом тоже аффинное),
тогда как перпендикулярность двух прямых аффинным свойством
не является. Согласно Клейну каждая группа преобразований за-
дает свою геометрию.
Если теперь вместо группы всех движений плоскости взять
какую-либо другую группу преобразований G некоторого мно-
жества М (необязательно плоскости), то можно следующим
образом построить «геометрию», которую задает эта группа иа
множестве М. Фигурой будем считать произвольное множество,
содержащееся в М. Две фигуры А, В будем называть «G-равны-
ми», если существует в группе G такое преобразование f, которое
переводит первую фигуру во вторую, т. е. Л—В рассматри-
ваемой геометрии (ее можио назвать «G-геометрией») изучаются
те н только те свойства фигур, которые являются инвариантны-
ми при «G-движениях», т. е. при всех преобразованиях, имеющихся
в группе G. Эта общая схема позволяет объединить большое
чнсло различных геометрий: евклидову и неевклидову, плоскую и
пространственную (пли даже многомерную), аффинную и многие
другие.
Групповая точка зрения иа геометрию находит очень важные
применения и в физике, хотя иа первый взгляд кажется далекой
от этой науки. Одним нз ярких примеров применения идей эрлан-
генской программы в физике является кристаллография. В 1908 г.
русский геометр и кристаллограф Е. Федоров доказал, что су-
ществует ровно 30 кристаллографических групп, т. е. таких j рупп,
с помощью которых можно из некоторого одного многогранника
получить заполнение всего пространства равными ему многогран-
никами — получить пространственную кристаллическую решетку.
С помощью полученного нм перечисления кристаллографических
групп Федоров вывел, что всего существует 230 возможных видов
пространственных многогранников, которыми, как кристаллами,
можио замостить пространство. А вскоре было обнаружено, что в
природе, действительно, существуют вещества (минералы), кото-
рые дают все эти 230 видов многогранников прн крнсталлнзации.
Неудивительно, что федоровские кристаллографические группы во
всем мире признаются научной основой кристаллографии.
Другим примером может служить специальная теория относи-
тельности, о которой вам предстоит узнать на уроках физики в
старших классах. И здесь все построено на клейновской груп-
повой точке зрения: можио сказать, что эта теория не столько
является физикой, сколько своеобразной геометрией четырехмер-
ного пространства-времени, построенной на основе специальной
группы преобразований, открытой немецким физиком Лоренцом
и осмысленной выдающимся французским математиком Пуанкаре,
что и дало возможность Эйнштейну заложить основы теории от-
носительности. Групповая точка зрения используется сейчас также
235
в физике атома и теории элементарных частиц. Таким образом,
понятие группы преобразований — это сегодня важнейший
инструмент не только математики, ио также физики и других раз-
делов естествознания.
ГОМОТЕТИЯ
Кроме движений, существует и ряд других геометрических
преобразований. Особенно важную роль играют преобразования
подобия, которые мы рассмотрим в этом и следующих пунктах.
Определение. Пусть О — некоторая точка плоскости и
k— отличное от нуля число. Геометрическое преобразование,
отображающее каждую точку А в такую точку Аь что OAi —kOA,
называется гомотетией с центром О и коэффициентом k.
На рисунке 159 показано построение фигур Flt F^, F3, полу-
чающихся нз F при помощи гомотетии с коэффициентами соответ-
ственно kt ==2, й2=-|-, й3= —1,5.
Теорема. Если Alt Bt — образы точек А, В при гомотетии с
центром О и коэффициентом k, то AiBt~kAB.
Доказательство.
А|В| = OB~i — ОА? = kOB—kOA =k(OB — ОЛ)=kAB.
Следствие 1. Отношение расстояний сохраняется при го-
мотетии.
Следствие 2. При гомотетии каждая прямая отображается
на параллельную ей прямую.
Приведем более подробную формулировку. Пусть I — произ-
вольная прямая, А — ее точка и А, — образ точки А при рассмат-
риваемой гомотетии. Обозначим через h прямую, параллельную I
и проходящую через точку Аь Тогда t\ и является образом пря-
мой / при рассматриваемой гомотетии.
Следствие 3. При гомотетии каждый угол отображается
на равный ему угол.
Следствие 4. При гомотетии окружность переходит в ок-
ружность.
Рис. 159
236
Рис. 161
Рис. 160
Более подробно: пусть р — окружность с центром Р н ра-
диусом г. При гомотетии с центром О и коэффициентом k окруж-
ность р переходит в окружность с центром Pi н радиусом kr, где
Pi — образ точки Р.
Задача 1. Доказать, что две секущие, проходящие через
точку касания двух касающихся окружностей, определяют в них
две параллельные хорды (рнс. 160).
Решение. Пусть О — точка касания окружностей т, п.
Центры окружностей обозначим через М, N, секущие — через р, q,
а точки пересечения секущих с окружностями — через Pi, Qi и Рг,
р2- Пусть h — гомотетия с центром О, переводящая точку М в N
(и, следовательно, переводящая окружность т в окружность п).
Так как т—*~'п, р—^р, то Pi -*-Ръ Аналогично Qi —*-р2- Сле-
довательно, PiQi —P2Q2, и поэтому эти прямые параллельны.
Задача 2. Построить квадрат, вписанный в данный тре-
угольник .(две вершины лежат на осиованни. а две другие — на
боковых сторонах)
Решение. Отбросим пока условие о том, что две вершины
лежат на боковых сторонах, н построим какой-нибудь квадрат
у которого две вершины лежат на основании и лишь одна — на
боковой стороне. Такой квадрат М НТ К легко построить (рнс. 161),
если из точки М стороны АВ провести перпендикуляр МН к осно-
ванию и отложить на основании отрезок НТ =МН. Любой квад-
рат, получающийся нз МНТК гомотетией с центром А, обладает
теми же двумя свойствами: две его вершины лежат на основа-
инн АС, а одна вершина лежит на прямой АВ. Следовательно,
задача будет решена, если мы подберем такой коэффициент гомо-
тетии, чтобы образ точки К принадлежал прямой ВС. Иначе гово-
ря, нужно провести луч АК и применить гомотетию с центром А
и коэффициентом где Ki —точка пересечения луча АК
со стороной ВС.
237
Задачи
145. Начертите пятиугольник ABCDE н возьмите вне его точ-
ку О. Постройте образ пятиугольника ABCDE прн гомотетии с
центром О н коэффициентом: а) Л=2; б) k=—\ в) fe= —1,5.
146. Что представляет собой гомотетия с центром О и коэф-
фициентом k= — 1? с коэффициентом fe=l? Является ли движе-
нием гомотетия с центром О и коэффициентом k при |fe|#=l?
147. Постройте окружность, гомотетичную данной окружности
с коэффициентом А=2, если центр гомотетии: а) совпадает с
центром окружности; б) лежит вне окружности; в) принадлежит
окружности.
148. Докажите, что прн гомотетии: а) окружность перехо-
дит в окружность; б) прямая переходит в прямую и отрезок —
в отрезок; в) середина отрезка переходит в середину отрезка;
г) касательная к окружности — в касательную к ее образу.
149. Диагонали четырехугольника ABCD пересекаются в точ-
ке О, причем ОА =3,6, ОВ=3, ОС=4,5, 00=2.4. Докажите,
что ABCD — трапеция.
150. Даны три параллельные прямые т, п, р. Прямая 1| пере-
секает их в точках Mi, М, Pi, а прямая fa — в точках Мг, Nz, Pz-
Докажите, что 7^=7^
151. В трапеции с основаниями Л В—6,2 и 00=9,3 н боко-
выми сторонами ВС=3,5 и ЛО=5 боковые стороны продолжены
до пересечения в точке М. Найдите длины отрезков АВ н ВМ.
152. Докажите, что если отрезки АВ и CD параллельны, но
ие лежат на одной прямой, то: а) существует такая точка О,
(внутренний центр гомотетии), что эти отрезки гомотетичны друг
другу с центром О н отрицательным коэффициентом гомотетии;
б) прн AB=f=CD существует такая точка О (внешний центр го-
мотетии), что эти отрезки гомотетичны друг другу с центром О
и положительным коэффициентом гомотетии.
153. Докажите, что для двух неконцеитричных окружностей
на отрезке, соединяющем их центры, существует такая точка О
(внутренний центр гомотетии окружностей), что этн окружности
гомотетичны друг другу с центром О н отрицательным коэффи-
циентом гомотетии.
154. Докажите, что для двух неконцентричных и неравных
окружностей существует такая точка О, лежащая на прямой,
проходящей через центры (вне отрезка, соединяющего центры),
что эти окружности гомотетичны друг другу с центром О н поло-
жительным коэффициентом гомотетии. Точка О называется внеш-
ним центром гомотетии окружностей.
155. Докажите, что если центр гомотетии двух окружнос-
тей (внешний или внутренний) лежит вне этих окружностей, то
238
он является точкой пересечения нх общих касательных (внешних
или внутренних).
156. Докажите, что каждый выпуклый многоугольник содер-
жит два многоугольника, которые гомотетичны ему с коэффициен-
том &=~ и друг с другом не имеют общих внутренних точек
157. Докажите, что композиция двух гомотетий с коэффициен-
тами ki н ki является прн гомотетией с коэффициентом
feifes, причем ее центр лежит на прямой, соединяющей центры этих
гомотетий. Исследуйте случай k\kz—\.
158. В окружность вписан четырехугольник ABCD. Докажите,
что точки пересечения медиан треугольников BCD. ACD. ABD.
АВС лежат на одной окружности.
159. Окружности Si, S%, S3 имеют различные радиусы, и нх
центры не лежат иа одной прямой. Внешние касательные к окруж-
ностям S/, Sj пересекаются в точке А1}. Докажите, что получен-
ные точки Л12, Л ,3, Л2з лежат на одной прямой.
160. Даны окружность п н точка Л вне ее. Проведите че-
рез А прямую, пересекающую окружность п в таких точках В, С,
что АВ=ЗВС.
161. На стороне ОМ угла МОР дана точка X. Найдите иа сто-
роне ОР такую точку У, что Z.OXY=3Z.OYX.
162. Постройте квадрат, две смежные вершины которого ле-
жат на дайной прямой, а две другие — на данной окружности.
163. Постройте прямую, параллельную данной и высекающую
из данного угла отрезок, середина которого принадлежит данной
окружности.
164. Постройте прямоугольный треугольник, зная длину ги-
потенузы и длниу медианы, проведенной к одному из катетов.
165. Постройте дАВС, зная а'.с, Z.B и радиус вписанной
окружности.
166. Впишите квадрат в данный сегмент (две вершины на
дуге сегмента и две на хорде).
167. Постройте окружность, касающуюся сторон данного
угла н касающуюся дайной окружности.
168. В окружности проведены два радиуса. Постройте хор-
ду, делящуюся этими радиусами на три равные части
ПОДОБИЕ
На рисунке 122 изображены два плана одной и той же мест-
ности в разных масштабах. Отношение расстояний между соответ-
ствующими точками этих планов равно отношению масштабов.
Таким образом, геометрическое преобразование, отображаю-
щее каждую точку первого плана в соответствующую точку второ-
го плана, не сохраняет расстояния между точками, но увеличи-
вает все расстояния в одинаковое число раз (в данном слу-
чае в 2,5 раза).
239
Определение. Геометрическое преобразование называет-
ся подобием с коэффициентом. Д>-0, если для любых двух точек
А и В расстояние между их образами А| и Bi равно kAB, т. е.
АВ К'
Из этого определения следует, что гомотетия с коэффниентом k
представляет собой подобие с коэффициентом |£|
Две фигуры F, Fi называются подобными, если существует
подобие, отображающее одну нз них иа другую. Подобие фигур
F н F1 принято обозначать записью FcoF\.
На рисунке 162 фигура Ft получена из Fi последовательным
применением двух геометрических преобразований: гомотетии h н
движения /. Ясно, что фигура Fz подобна Ft (поскольку отноше-
ние расстояний не изменяется ни при гомотетии, нн прн движе-
нии). Иначе говоря, результат последовательного выполнения
гомотетии и движения представляет собой подобие. Оказывается,
что справедливо и обратное утверждение.
Теорема 1. Всякое подобие с коэффициентом k можно пред-
ставить как композицию гомотетии с тем же коэффициентом k и
некоторого движения.
Доказательство. Пусть F\ со А, т. е. фигура Ft получа-
ется из Fi при помощи подобия g с коэффициентом k (рис. 162).
Возьмем две произвольные точки Af, В\, принадлежащие фигуре
Fi, и пусть Аг, Вг — нх образы прн преобразовании g. Тогда
A?Bt__.
AiBi '
Выберем теперь произвольную точку U и обозначим через h
гомотетию с центром О и тем же коэффициентом k. Пусть F —
образ фигуры Fi при этой гомотетии, а А, В — образы точек Аь
Bt. Тогда
Из написанных равенств следует, что А^Вг—АВ. Иначе гово-
ря, прн переходе от фигуры F к F% расстояния между соот-
ветствующими точками сохраняются, а это означает, что F% по-
240
лучается из F при пбмощи некоторого движения /. Таким об-
разом, последовательное применение гомотетии h и движения /
переводит фигуру F\ в Fz, т. е. f <> h=*g.
В задачах 187—190 содержится существенное обобщение до-
казанной выше теоремы 1: в этих задачах дается полная клас-
сификация всех подобий (т. е. результат, аналогичный тому,
который для случая движений содержится а теореме Шаля). Имен-
но оказывается, что любое преобразование подобия, имеющее
коэффициент k^l (т. е. не являющееся движением), представля-
ет собой либо гомотетию, либо поворотную гомотетию, т. е. ком-
позицию гомотетии с центром О н поворота вокруг О (рнс. 163),
либо зеркальную гомотетию, т. е. композицию гомотетии с цент-
ром О н симметрии относительно прямой, проходящей через О
(рис. 164).
Напомним две теоремы о подобии, известные нз школьного
курса геометрии.
Теорема 2 (признак подобия треугольников). Если два уг-
ла одного треугольника соответственно равны двум углам друго-
го, то эти тр угольника подобны.
Теорема 3. Если F — фигура, имеющая площадь S, и
F -Я- Ft, где g — подобие с коэффициентом k, то площадь фигу-
ры Ft равна k2S.
Задача 1. В прямоугольном треугольнике АВС нз верши-
ны С прямого угла проведена высота CD к гипотенузе. Доказать,
что h2=p-q, где h—CD — высота, а р, q—длины отрезков, иа
которые гипотенуза разбивается точкой D
Решение. На рисунке 165 треугольник AiCjD получается
из треугольника ACD поворотом иа —90° вокруг D. При этом
Z.2=Z.1 = Z.3/и потому А]С1||СВ. Следовательно, треуголь-
ники AjC|£> и CBD гомотетичны. Это позволяет без труда со-
Рис. 163
Рис. 164
241
Рис. 165 Рис. 166
ставить равенство отношений сторон; 7. е.
CD
~~DD ' чТ0 и дает Решенне 3аДачи
Схема этого решения такова: вместо применения признака
подобия треугольников мы находим такое движение (в данном
случае поворот), при котором первый треугольник переходит в
треугольник, гомотетичный второму (н тогда легко написать ра-
венство отношений сторон). На основании теоремы 1 этот прием
можно применить (вместо подобия) всегда.
Задача 2. На одной стороне угла с вершиной О взяты
точки А, В, а на другой — точки С, D, причем ОА=3, ОВ—4,
ОС=2 и jLOBD^^OCA. Найти OD.
Решение. При симметрии относительно биссектрисы угла О
треугольник АСО переходит в треугольник А^С^О (рнс. 166),
причем Z. 1 = Z.2, и потому согласно условию Z. 1 = Z 3. Следова-
тельно, прямые CiAi и BD параллельны, т. е. треугольники AiCiO и
DBO гомотетичны. Теперь имеем т- «•
OD=6.
Задача 3. Стороны треугольника АВС связаны соотношени-
ем а?—с(Ь + с). Доказать, что ZA=2ZC.
Решенне. Пусть D — такая точка прямой АВ, что AD =
—АС=Ь, причем А лежит между В и D (рнс. 167). Тогда треуголь-
ник ACD равнобедренный, и потому Z1 = Z2; кроме того,
BD=b-}-c. При симметрии относительно биссектрисы угла В точ-
ки А и С перейдут в такие точки А> н С|, что ВЛ|=ВА=с,
Рис. 167
Й42
BC\~BC=a', Z.3=Z.4. Заданное согласно условию задачи ра-
венство а?=с(Ь-\-с} можно переписать в виде т. е.
откуда следует, что при гомотетии с центром В и ко-
эффициентом fe=-|~ точки Ai, Ci переходят в С, D. Следователь-
но, прямые CD и AiCi параллельны, и потому £2-/14, т. е.
Z.1 = Z.2— Z.3— Z.4. Так как Z.BAC — внешний угол треуголь-
ника ACD, то ои равен сумме Z.1 и Z.2, т. е. равен удвоенному
углу С.
Задачи
169. Фигура F — круг радиуса г с центром О. Подобие g с
коэффициентом k переводит точку О в точку Оь В какую фигуру
перейдет F в результате подобия g?
170. Докажите: а) если отображение g представляет собой
подобие с коэффициентом k, то обратное преобразование g-1
является подобием с коэффициентом — ; б) композиция любых
двух преобразований подобия с коэффициентами k\ и k% является
подобием с коэффициентом kik?.
171. Подобны ли любые равносторонние треугольники? квад-
раты? прямоугольники? ромбы? окружности? Гомотетичны ли лю-
бые равносторонние треугольники? квадраты? окружности?
172. На стороне АС треугольника АВС взята такая точка D,
что Z.AJ3C=ZBDC. Найдите BD, если АВ= 12,1, ВС= 10,
АС=11.
173. Из вершины С прямого угла треугольника АВС проведен
перпендикуляр СИ к гипотенузе, а) Вычислите длину гипотенузы,
если АЯ=3, СН=8. б) Вычислите длину отрезка АН, если
ВС=6, АВ=9.
174. В треугольнике АВС даны а, с и ht,. Найдите радиус
описанной окружности треугольника.
175. В треугольнике АВС проведена биссектриса BD, а через
вершину С проведена прямая, параллельная BD. С помощью
этого построения докажите, что биссектриса угла треугольника
делит противоположную сторону на части, пропорциональные при-
лежащим сторонам, т. е.
176. На сторонах ВС н CD параллелограмма ABCD взяты та-
кие точки Р, Q, что Z.BAP— Z.DAQ. Найдите AQ, если АВ= 14,
АО=21, АР= 10.
177. В ромб ABCD вписана окружность н к ней проведена
касательная п, пересекающая стороны АВ и ВС в точках Р и Q.
Докажите, что произведение AP-CQ не зависит от положения
касательной.
243
178- В параллелограмме ABCD известно, что ДВ=6 и ВС=
= 10. Постройте прямую, параллельную АВ, которая отсекает
от параллелограмма ABCD подобный ему параллелограмм. Вы-
числите стороны построенного параллелограмма.
179. В правильном пятиугольнике ABCDE проведены диагона-
ли АС и BD, через О обозначена их точка пересечения. Докажи-
те что = вс_
’ ВС BD '
180. Даиы два правильных пятиугольника с одной общей вер-
шиной, которая отмечена цифрой 1. Вершины каждого пятиуголь-
ника нумеруются по часовой стрелке цифрами 1, 2, 3, 4, 5,
начиная от вершины 1. Докажите, что четыре прямые, соединяю-
щие вершины с одинаковыми номерами, пересекаются в одной
точке.
181. В прямоугольном треугольнике ЛВС из вершины прямо-
го угла С проведена высота CD. С помощью теоремы об отно-
шении площадей подобных фигур докажите соотношение
/ лс\2„ АР
\вс ) ~ во
182. Каждая сторона треугольника АВС разбита на п рав-
ных частей. Через точки деления проведены отрезки, параллель-
ные сторонам треугольника (рнс. 168). На сколько равных тре-
угольников разбивается этими прямыми треугольник АВС?
183. На стороне АВ треугольника АВС даиа точка Р. По-
стройте треугольник РЛ’У, вписанный в треугольник АВС и подоб-
ный данному треугольнику MNP.
184. Даны две окружности 5i, S2 и точка А. Постройте та-
кие секущие ABtCt и ЛВ2С2 к этим окружностям, что хорды В|С>
и В2С2 имеют данное отношеине k н образуют данный угол а.
185. Даиы две окружности и точка А. Постройте треуголь-
ник АВС, подобный данному треугольнику Л1В1С1, так, чтобы
точки В. С лежали на данных окружностях.
244
186. Даны отрезки ДВ и CD. Найдите такую точку О, что
треугольники АОВ и COD подобны и имеют при точке О равные
углы.
187. Докажите, что если подобие g имеет неподвижную точ-
ку О, то оно является либо гомотетией, либо поворотной гомо-
тетией, либо зеркальной гомотетией.
188. Докажите, что композиция гомотетии с коэффициентом
Лу=1 и параллельного переноса представляет собой гомотетию.
189. Дай угол с вершиной О, имеющий величину а, и пря-
мая п, перпендикулярная его биссектрисе и пересекающая его
стороны в точках А н В (рис. 169). Докажите при любом k=£\ су-
ществование такой точки М на прямой АВ, что композиция f oh,
где h — гомотетия с центром М и коэффициентом k, a f — пово-
рот вокруг точки О на угол а, переводит А в себя. Пользуясь
этим построением, докажите, что композиция любой гомотетии и
поворота имеет неподвижную точку.
190. Докажите, что если g=s о h, где h — гомотетия с коэф-
фициентом /г^= —1 с центром О, а $ — симметрия относительно
прямой п, то подобие g имеет неподвижную точку, лежащую
иа прямой, проходящей через О и перпендикулярной п
ГРУППА ПОДОБИЙ
Композиция двух подобий является подобием; преобразование,
обратное подобию, также является подобием. Иначе говоря, мно-
жество всех подобий представляет собой группу геометрических
преобразований плоскости. Поэтому согласно идеям эрлаигеи-
ской программы Клейна группа подобий определяет «свою» гео-
метрию. Легко понять, что инвариантами этой группы (т. е. те-
ми свойствами, которые сохраняются при всех преобразоваинях
подобия и потому изучаются в геометрии подобий) являются: угол,
отношение длин двух отрезков, параллельность двух прямых
н т. д. Однако длина отрезка уже не сохраняется при преобразова-
ниях подобия (с коэффициентом fe^=l), т. е. о длинах отрезков в
геометрии подобий говорить не приходится. Имеет ли смысл го-
ворить в этой геометрии, например, о равнобедренном треуголь-
нике? Если сказать, что равнобедренным называется треуголь-
ник, у которого длины двух сторон равны, то создается впе-
чатление, что это понятие ие относится к геометрии подобий
(ведь длин в ней не существует). Однако определение равно-
бедренного треугольника можно сформулировать и иначе: это
такой треугольник, у которого отношение двух сторон равно 1-
Теперь становится ясным, что понятие равнобедренного тре-
угольника сохраняется и в геометрии подобий. Имеет место в этой
геометрии н теорема о том, что в равнобедренном треугольнике
углы прн основании равны. Сохраняется и теорема Пифагора:
245
ее можио сформулировать в виде равенства +(7-) = 1.
где н — отношения длин катетов к длине гипотенузы.
Одиако не следует думать, что геометрия подобий ничем,
кроме формы изложения, не отличается от евклидовой геометрии.
Существуют факты, которые отличают эти две геометрии. Напри-
мер, условимся говорить, что линия $ может скользить по себе,
если для любых двух точек А, В этой линии найдется сохраняю-
щее ориентацию преобразование f (принадлежащее группе, зада-
ющей рассматриваемую геометрию), которое переводит лннню х
в себя, а точку А в точку В. В геометрии Евклида (т. е. в
геометрии, определяемой группой движений плоскости) существу-
ют только два типа связных линий (состоящих из одного куска),
которые могут скользить по себе: прямые и окружности. А в гео-
метрии подобий существуют связные линии, скользящие по себе
и отличные от прямых и окружностей. Такими линиями явля-
ются логарифмические спирали (рнс. 170). Они определяются в
полярных координатах уравнением г=го-а’, где ге и а — некото-
рые заданные числа
Еще один необычный факт геометрии подобий мы получим,
рассматривая поворотную гомотетию g с центром О, коэффициен-
том k и углом а. Пусть ..., А-г. А_ь Ао, Аь Л2, . — после-
довательность точек, переходящих друг в друга при преобразо-
вании g, т. е. А{ —> Аг+1 при любом целом i (рнс. 171). Эти точки
лежат на одной логарифмической спирали, причем для любого
целого i угол АОА,+1 имеет одну н ту же величину а. После-
довательно соединяя эти точки, мы получим бесконечную (не пе-
ресекающую себя) ломаную линию... А_2А_ 1А0А1А2 -. которая
переводится преобразованием g в себя, причем каждая вершина А/
Рис. 170
Рис. 171
246
переходит в соседнюю вершину A*+i. В евклидовой геометрии
таким свойством обладают лишь правильные многоугольники,
причем каждый из иих обязательно имеет лишь конечное число
сторон. Таким образом, описанные выше бесконечные ломаные
линии являются в геометрии подобий как бы «бесконечными
правильными многоугольниками» — факт, аналога которому в
евклидовой геометрии нет.
Литература
1. Болтянский В. Г. и др. Геометрия 6—8: Пробный учеб-
ник.— М.: Просвещение, 1979.
2. Болтянский В. Г. Элементарная геометрия.— М.: Про-
свещение, 1985.
3. Гн льде В. Зеркальный мир.— М.: Мир, 1982.
4. Коксетер Г. С., Грейтцер С. Л. Новые встречи с гео-
метрией.— М.: Наука, 1978.
5. Прасолов В. В. Задачи по планиметрии.— М.: Наука,
1986.
6. П о н а р и и Я. П., С к о п е ц 3. А. Перемещения и подобие
плоскости.— Киев: Радяиська школа, 1981.
7. Тарасов Л. В. Этот удивительно симметричный мнр.— М.:
Просвещение, 1982.
8. Ф е т и с о в А. И. Геометрия в задачах.— М.: Просвеще-
ние, 1977.
9. Шафраиовский И. И. Симметрия в природе.— Л.:
Недра, 1985.
10. III у б и и к о в А. В., К о п ц и к В. А. Симметрия в науке
н искусстве.—М.: Наука, 1972.
9 КЛАСС
ФУНКЦИИ И ГРАФИКИ
РОЖДЕНИЕ ФУНКЦИИ
Все течет, все изменяется в окружающем нас мире, как за-
метили еще древние. Вращается вокруг своей оси земной шар, и
день сменяет ночь. Земля вершит свой вечный бег вокруг Солнца.
Солнце вместе со всеми своими планетами вечно летит в косми-
ческие далн... Кажется, причем здесь математика, а тем более
функции и графики, которым посвящен этот раздел. Но, как образ-
но заметил великий Г. Галилей (1564—1642), книга природы
написана на математическом языке и ее буквы — математические
знаки н геометрические фигуры, без них невозможно понять ее
слова, без них тщетно блуждание в бесконечном лабиринте. А
именно функция является тем средством математического языка,
которое позволяет описывать процессы движения, изменения,
присущие природе.
Впервые функция вошла в математику под именем «переменная
величина» в знаменитом труде французского математика и фило-
софа Р. Декарта «Геометрия» (1637 г.), и ее появление по-
служило, по словам Энгельса, поворотным пунктом в математике,
благодаря чему в нее вошли движение н тем самым диалектика.
Без переменных величин Ньютон не смог бы выразить законы
динамики, описывающие процессы механического движения тел —
небесных и вполне земных, а современные ученые не могли бы
рассчитывать траектории движения космических кораблей и ре-
шать бесконечное множество технических проблем нашей эпохи.
С развитием науки понятие функции уточнялось и обобща-
лось. Сейчас оно стало настолько общим, что совпадает с поня-
тием соответствия. Например, каждый человек имеет имя (мы
имеем в виду только тех людей, которые уже получили имя).
Другими словами, каждому человеку соответствует определенное
имя. Поэтому можно говорить, что мы имеем функцию: областью
«значений» независимой переменной здесь служит множество всех
людей (имеющих имя), а множеством «значений» функции —
множество всевозможных имен. (Выпишите это множество для
вашего класса!)
Любопытно, что приведенная здесь функция является, вообще
говоря, неоднозначной, так как некоторые люди имеют по несколь-
ку имен. Рассмотрение неоднозначных функций неудобно, поэтому
248
стараются перейти к их однозначным ветвям, т. е. для каждого зна-
чения независимой переменной из всех значений функции выби-
рают какое-либо одно. Например, из всех имен человека, если их
несколько, одно объявляется первым именем. Если ограничиться
только первыми именами, то рассматриваемая функция является
однозначной. Обычно, если о функции ничего дополнительно не
сказано, она предполагается однозначной, а возможность много-
значности специально оговаривается. Так мы и будем впредь
делать.
Таким образом, функцией в общем понимании называется лю-
бой закон (правило), по которому каждому объекту из некото-
рого класса, области определения функции, поставлен в соответ-
ствие некоторый объект из другого (или того же) класса —
области возможных значений функции.
Однако мы ие будем далее рассматривать понятие функции в
столь общем понимании. Впредь мы будем считать, что как незави-
симая, так и зависимая переменные — это величины. Таким
образом, мы будем называть функцией зависимость, связываю-
щую с каждым значением одной переменной величины (аргу-
мента) из некоторой области ее изменения определенное значение
другой величины (функции). Если аргумент обозначить через х,
значение функции — через у, а саму зависимость-функцию — сим-
волом f, то связь между значениями функции и аргументом
запишется так: y—fix). Конечно, возможны и другие обозна-
чения, например: j/=g(x), y=h(f), x=<p(t/), 2=Ф(0> v=s(t),
5=7(2) н т. д. Если хотят только отметить, что величина у есть
функция величины х, то пишут просто: у=у(х). Во всех случаях
символ, стоящий «под знаком фуикции>, означает независимую
переменную (аргумент), а символ в левой части равенства —
зависимую переменную (функцию).
Как задаются функции? Более подробно мы поговорим об этом
позже. Сейчас отметим только самый простой способ: с помощью
формулы, например,
9=2х+5, у=±-,
и т. д., из которой по значению переменной (х, t и др.), входящей
в правую часть, однозначно вычисляется значение функции. При
этом область определения функции может быть дополнительно за-
дана: иапример, может быть сказано, что функция у=2x^-5
рассматривается при 1^х^3 и т. п. Если такого указания нет,
то областью определения функции, заданной формулой, считают
совокупность всех тех значений аргумента, при которых все вы-
числения по формуле могут быть выполнены н дают однозначно
определенный результат.
Но откуда появляются сами эти формулы? Некоторые нз иих
выводятся с помощью геометрических или физических рассужде-
ний. Так в геометрии выводится формула S —лг2, задающая пло-
249
щадь S круга как функцию его радиуса г. В физике выводится
„/2
формула S=—, задающая путь S, пройденный телом при дви-
жении с постоянным ускорением «, начиная нз положения покоя,
как функцию времени i движения. Комбинируя такие исходные
формулы, можно получать и другие, более сложные.
Порой формулы получаются в результате обработки экспери-
мента, такие формулы называют эмпирическими. Рассмотрим
пример.
Если через заданный проводник пропустить электрический
ток /, то проводник нагреется до определенной температуры 0.
(Так как разные точки проводника могут нагреться до различной
температуры, то будем иметь в виду какую-либо определенную
его точку; температуру окружающей среды примем за 0.) Ясно,
что 0 есть функция /. Но можио ли подобрать формулу, выра-
жающую эту зависимость с хорошей точностью?
Естественно искать эту формулу в виде многочлена:
0=a+W-f-c72+.. .+plm.
Но прежде чем определять коэффициенты а, Ь, ..обсудим си-
туацию теоретически. Ясно, что при /—0 получаем и 0=0.
Тем самым а=0. Далее, если мы заменим / на — I, то 0 ие изме-
нится, поэтому многочлен должен содержать только четные
степени /. Простейший многочлен, удовлетворяющий этим услови-
ям, имеет вид:
0=сЛ
Чтобы найти значение постоянной с, можно придать J не-
сколько значений н измерить соответствующие значения 0, а ре-
зультаты записать в таблицу:
/ h Ь Л
в в. ©2 05
Каждое нз измерений дает зиачеиия с. равные -у, , ....
которые, вообще говоря, различны, так как и формула (1),
н измерения были приближенными. Можно в качестве окончатель-
ного результата взять, например, среднее арифметическое полу-
ченных значений с, т. е. положить
250
И действительно, такой путь приводит к формуле (1), описываю-
щей зависимость 6(/) при сравнительно небольших значениях I
с хорошей точностью. Для больших значений / можно воспользо-
ваться формулой O=c/2-J-d/* и найти с помощью эксперимента
значения коэффициентов с и d и т. д. Подробнее о построениях
эмпирических формул можно прочитать в книге [3].
Если теоретические соображения о виде формулы отсутствуют,
то можно просто, нанеся данные эксперимента на координатную
плоскость, получить ряд точек и, глядя иа полученную картинку,
решить, какая из известных «хороших* кривых в большей мере со-
ответствует расположению этих точек. При этом надо мысленно пе-
ребирать наиболее простые кривые — прямую (думая о том, ие
группируются ли изображенные точки около некоторой прямой
и не является ли тем самым зависимость лииейиой), параболу
и т. д. Поскольку данные эксперимента никогда не бывают
абсолютно точными, то нет смысла искать «хорошую» кривую, в
точности проходящую через все полученные точки — важно лишь,
чтобы оиа проходила в достаточной близости от большинства
из них.
Остановившись иа некотором виде кривой (или прямой), надо
найти параметры соответствующей зависимости (линейной s—
~at-\-b, квадратичной s=a/24-6/4-c или иной), при которых
криваи «наименее отклоняется» от экспериментальных точек. Для
этого есть специальные приемы, например метод наименьших
квадратов при подборе коэффициентов лииейиой зависимости,
когда значения а и b находятся так, чтобы обеспечить наи-
меньшую величину суммы квадратов отклонений:
(so—ato~~ b)2 4-(Si—ай—6)2+. - -+(sn — atn—b)2.
(Подумайте иад геометрическим смыслом этой суммы.) При боль-
шом числе экспериментальных точек проводить вычисления
«вручную» оказывается затруднительным, и для подбора эмпири-
ческих коэффициентов применяют ЭВМ, используя стандартные
программы. Таким образом, эмпирическая формула может полу-
читься и в результате работы ЭВМ.
Получив подходящую формулу, надо оценить ее критически,
сделав выводы о приемлемости формулы и допустимых границах ее
применения. Последнее очень существенно: любая формула в фи-
зике, как и вообще любая формула, связывающая значения
реальных величии, справедлива лишь с некоторой точностью
и имеет определенную область применения. Понимание этого
стало особенно отчетливым в свете созданной А. Эйнштейном
(1879—1955) теории относительности, показавшей, в частности,
что классические, ньютоновские законы динамики ие выполняются
для больших скоростей, сравнимых со скоростью света. Так,
например, формулы равноускоренного движения »=a/,s=~-ne-
251
рестают соответствовать реальности при достаточно больших t
Сейчас это исио даже школьнику, который зиает, что скоростей,
больших, чем скорость света в вакууме, ие бывает. Ведь форму-
ла v=at дает сколь угодно большие значения скорости v прн
неограниченном увеличении t. Другой пример — формула, выра-
жающая закон всемирного тяготения, F—y^r~t где у — грави-
тационная постоянней, mi, ms — массы тел, аг — расстояние
между ними. Нетрудно понять, что эта формула теряет физи-
ческий смысл и ие описывает реальное взаимодействие тел, если
г обращается в нуль. Это создало трудности в теории элементар-
ных частиц, полностью ие преодоленные до сих пор.
В связи с обсуждавшимся вопросом о происхождении формул
интересно отметить, что и последняя формула была выведена
И. Ньютоном (1643—1727) с опорой на данные наблюдений
То, что сила тяготении пропорциональна каждой из рассматривае-
мых масс, можно вывести умозрительно. Но почему она обратно
пропорциональна именно второй, а ие какой-либо иной степени
расстоянии? Оказалось, что только при такой степени можио
вывести законы движения планет, полученные ранее И. Кепле-
ром (1571—1640) чисто эмпирически, на основе обработки дан-
ных многолетних наблюдений. Однако проверка этого была от-
нюдь ие проста и потребовала от Ньютона создания нового
математического аппарата, который сейчас лежит в основании
математического анализа. Таким образом, Ньютон проявил себя
здесь ие только как великий физик, выдвинув глубокую идею об
универсальном характере сил гравитации, ио и как великий
математик, создав математический аппарат для применения
этой идеи.
Задачи
1. Подберите подходящие формулы из числа известных вам для
описания каждой из эмпирических зависимостей, представленных
рядом точек на рисунке 172. Изобразите кривые, соответствую
шие подобранным вами формулам. Приведите примеры подобных
зависимостей между физическими или иными величинами, описы-
вающими реальные процессы.
2. По заданным с помощью таблиц результатам эксперимен-
тального исследовании зависимостей у=^у(х) подберите подхо
дящие формулы дли их описания. Найдите сумму квадратов
отклонений эмпирических точек от соответствующих точек выбран-
ной кривой.
JC 0 10 20 30 40
У 99,5 81 59,5 39 20,5
252
* 1 2 3 4 5
у 2,1 7,8 18,2 31,7 50,5
Указание. Постройте сначала эмпирические графики за-
висимостей, отвечающие данным таблицам. Дли случая зави-
симости, близкой к линейной, воспользуйтесь линейкой, приложив
ее так, чтобы ее край как можно меньше отклонялся от основной
массы эмпирических точек.
КАК ЗАДАЮТ ФУНКЦИИ
В описанном нами выше процессе рождения функции иа раз-
ных этапах присутствовали три основных способа выражения
зависимостей между двумя величинами: табличный, аналитичес-
кий («формульный») и графический. С этими классическими
способами представления функции часто приходится иметь дело
при установлении и изучении зависимостей как в естествознании,
так и в самой математике. Обсудим кратко преимущества и не-
достатки каждого из этих способов, о других широко применяемых
сейчас способах мы поговорим в этом пункте позже.
253
Табличный способ важен потому, что является основным при
обнаружении реальных зависимостей и может оказаться к тому
же единственным средством их задания (формулу ие всегда удает-
ся подобрать, а порой в ней и нет необходимости). К таблич-
ному заданию функции часто переходят при выполнении прак-
тических расчетов, с ней связанных: например, применение таблиц
квадратных корней удобно при проведении расчетов, в которых
участвуют такие корни. Появление современных ЭВМ с их без-
граничными возможностями хранения и переработки информации
неизмеримо расширило перспективы табличных представлений за-
висимостей, причем составление и преобразование многочислен-
ных таблиц часто образует промежуточные этапы сложного
вычисления.
С математической точки зрения табличное задание непрерыв-
ных зависимостей всегда неполно и дает лишь информацию о зна-
чениях функции в отдельных точках. В связи с этим возникают
задачи интерполяции и экстраполяции табличной зависимости,
т. е. «переноса» ее иа весь промежуток изменении аргумента,
соответствующий таблице, или за его пределы. Другим недостат-
ком табличного задания функции является его неудобство для
восприятия и теоретического анализа, его громоздкость.
Графический способ представлении зависимостей также явля-
ется одним из средств их фиксации при изучении реальных яв-
лений. Это позволяют делать различные «самопишущие» приборы,
такие, как сейсмограф, электрокардиограф, осциллограф и т. п.,
изображающие информацию об изменении измеряемых величии
в виде графиков. Но если есть график, то, значит, определена
и соответствующая ему функции. В таких случаях говорят о
графическом задании функции.
Графическое представление функции очень удобно для не-
посредственного восприятия ее особенностей, характерных
свойств. Такая возможность особенно благоприятна для изуче-
ния многих вопросов, связанных с функциями, в частности в
школьном курсе алгебры и начал анализа. Как говорится, лучше
один раз увидеть, чем сто раз услышать. Поэтому при исследо-
вании функции всегда желательно представить, хотя бы ориен-
тировочно, ее график.
Однако графический способ задания функций неудобен для
проведения расчетов; к тому же, подобно табличному, он является
приближенным и неполным. Так, скажем, рнсуя график функции
у=х2, мы изображаем его лишь иа некотором конечном про-
межутке изменения аргумента; линия, проведенная нами, имеет
определенную толщину, и значения функции не могут быть под-
считаны по ней с большой точностью и т. п. Это относится ко
всем реально изображаемым графикам, но именно о них и шла
речь.
«Математический» график ие обладает, конечно, неполнотой
илн приближенностью, ио вместе с тем он является, к сожалению,
254
«невидимкой» — его нельзя нм нарисовать, ии увидеть. Ведь ои
есть не что иное, как совокупность всех пар чисел (точек коор-
динатной плоскости) вида (х; f(x)). По сути, это бесконечная
таблица, включающая все значении функции, и в таком пони-
мании график и есть сама функция. То же, что мы рисуем, явля-
ется лишь эскизом, зримой моделью математического графика,
ио именно это и иужио при изучении функции.
Аналитическое (формульное) задание функции отличается сво-
ей компактностью, легко (хотя, откровенно говоря, и ие всегда)
запоминается и содержит в себе полную информацию о зависи-
мости. Этот способ удобен для проведения теоретических выкла-
док, применения классических методов анализа функций и запи-
си результатов.
Однако из формул ие всегда легко усмотреть свойства функции,
представить ее поведение. С этой целью функцию исследуют и
строят ее график, рисуя, так сказать, ее портрет.
Упомянутые три способа задания функции — табличный, гра-
фический и аналитический — применяются уже многие десятиле-
тия. В последнее время широко используются и другие способы,
о которых мы поговорим ниже.
Прежде всего заметим, что, как это ни парадоксально зву-
чит, чтобы задать функцию, достаточно иметь уверенность в том,
что она задана, даже если мы все еще не умеем вычислять ее зна-
чения. Вот простой пример. Пусть рассматривается пятиконечная
звезда, полученная в результате пересечения пяти отрезков дли-
ной а. Ясно, что площадь S этой звезды есть функции S=S (а).
Эта функция полностью задана своим геометрическим определе-
нием (описанием), хотя ответ на вопрос о том, как получить
значение S при заданном зиачеини а, требует размышления.
(Подумайте о том, как дать этот ответ хотя бы приближенно.)
Вот еще одни пример. Пусть функция у(х) задается уравне-
нием у3+у=х. График зависимости х от у показан на рисун-
ке 173,0. Так как значение измениется от — оо до +°°.
все времи возрастая, то наглядно ясно, что если задать зна-
чение х, то значение у однозначно определяется. Это можно
265
доказать и совершенно строго, чего мы здесь ие будем делать. Та-
ким образом, это уравнение задает вполне определенную функцию
у (х), хотя в виде формулы привычного вида ее представить затруд-
нительно (а если у3 заменить иа у5, то и совсем невозможно).
Правда, дли этой функции у(х) можио построить график, ои по-
казан иа рисунке 173, б. (Как свизаи этот график с кривой, изо-
браженной иа рисунке 173, а?) Но сейчас в математике и ее при-
ложениях приходится рассматривать функции, задаваемые урав-
нениями гораздо более сложной структуры (дифференциальными,
интегральными и др.), для которых графическое представление от-
сутствует. Это не мешает нам считать и такие функции заданны-
ми, изучать их свойства н вычислять их значения — обычно с по-
мощью ЭВМ. Возможности современных ЭВМ таковы, что, если
функция вполне четко определена независимо от того, каким имен-
но способом, ее значении, как правило, поддаются расчету с необ-
ходимой точностью.
Применяя ЭВМ, мы сталкиваемся еще с одним способом зада-
ния функции — с помощью программы, т. е. подробной инструк-
ции, в которой указана последовательность арифметических и ло-
гических действий, которые надо совершить иад значением неза-
висимой переменной, чтобы получить точное или приближенное
(с заданной точностью) значение функции. Такая программа, за-
писанная иа соответствующем алгоритмическом языке, вводится
в ЭВМ, чем и задается рассматриваемая функция; после работы
эта программа стирается. Программы для вычисления наиболее
распространенных функций постоянно хранятся в «долговремен-
ной» памяти ЭВМ, и составлять эти программы заново не тре-
буется.
Решение различных вопросов, связанных с функцией, требует
переходов к различным способам ее представления. Об одном из
них «таблица — график — формула» мы уже говорили как об ос-
новном пути получения эмпирических формул. Переход «форму-
ла — таблица — график» требуется при исследовании аналитичес-
ки заданной функции. Возможны и сокращенные варианты:
график — таблица, график — формула, формула — программа
и т. п.— все зависит от сути решаемых вопросов.
Задачи
3. Функция <₽(п), определенная иа множестве натуральных
чисел, называется также числовой последовательностью, посколь-
ку ее значения можио расположить в ряд щ, и%, .... ип, ...,
где щ=<р(1), ..ц„=<р(л), .... Одним из основных способов
задания таких функций является рекурсия, т. е. определение с по-
мощью выражения, позволяющего вычислять значение ф(я) по
значениям <р(х) дли х<я. Например, рекурсия 4>(п)=<₽(л—0+
2) с начальными условиями <р(1)—1, <р(2)=1 задает по-
266
следовательиость 1, 1, 2, 3, 5, 8, 13, ... (последовательность
Фибоначчи). Выпишите первые пять членов последовательностей,
заданных с помощью приведенных ниже рекурсий, и найдите
«обычные» формулы для вычисления <р(я) (последнее возможно
не для любых рекурсий):
а) ф(л) = ф(л—1)4-2, ф(1)=2;
б) Ф(л)=2ф(л-1), <₽(!)=!;
в) ф(л)=пф(л— I), ф(1)«=1;
г) ф(л)=ф(л—1) —ф(п—2), ф(1)=ф(2)= 1
ИЗ ЧЕГО И КАК КОНСТРУИРУЮТСЯ ФОРМУЛЫ
Вопрос о том, что понимать под формулой, задающей функцию,
не так прост и требует уточнения, которое мы и постараемся сей-
час дать. Речь будет идти не обо всех формулах и функциях, а о
так называемых элементарных функциях, к которым, в частности,
относятся практически все функции, встречающиеся в школьном
учебнике.
Прежде всего, имеется достаточно представительный набор
широко известных и хорошо изученных функций, которые назы-
вают основными элементарными функциями
Это функция у=С (рис. 174), называемая константой, степен-
ная функция (при а=1 получаем функцию у=х, назы-
ваемую тождественной, рнс. 175; графики степенной функции
при а—2; 3; —1; —2; у- изображены на рисунке 176). К основ-
ным элементарным относятся показательная у =ах, где а > 0, а ФI
(рис. 177), логарифмическая у—\о%а х, где в>0, 1, (рис. 178)
функции.
Особое место занимают основные тригонометрические функ-
ции ^=sinx (синус), y—cosx (косинус), y=tgx (тангенс),
y=ctgx (котангенс), а также обратные тригонометрические
функции r/=arcsinx (арксинус), y=arccosx (арккосинус), у=
=arctgx (арктангенс), у—arcctgх (арккотангенс), графики ко-
торых изображены на рисунках 179—180
Рве. 174
Рис. 175
257
С некоторыми из этих функций вы пока еще мало знакомы, ио
глубокого знания их вам сейчас и не требуется — достаточно
знакомства с их обозначениями и графиками.
Имея в распоряжении основные элементарные функции, можно
ввести ряд операций, позволяющих комбинировать их между собой
258
5)
Рис, 179
259
как детали для получения более сложных и разнообразных конст-
рукций. А именно допустим арифметические действия над функ-
циями — сложение (+), вычитание (—), умножение (•) и деле-
ние (:) функций —- и введем еще одну, специфическую для функ-
ций операцию — суперпозицию (о). Последняя операция позволиет
из двух функций fug строить новую, «сложную» функцию fog,
определенную формулой (f о g)(x)=f (g(x))- Таким образом, функ-
ция f°g получается подстановкой функции g вместо аргумента в f.
Заметьте, что f ° g и go f, вообще говоря, разные функции. Так,
например, если f (х)=лг, g (*)=*+1, то (f о g) 4-2xJ-1, тог-
да как
Отметим любопытный и практически полезный факт: любые
точки графиков функций, получающихся в результате применения
указанных операций к функциям f и g, можно легко строить
без всяких вычислений с помощью циркуля и линейки из данных
260
графиков исходных функций y=f(x). y=g(x) (см. зада-
чи 4—7).
Все те функции, которые можно получить из основных элемен-
тарных с помощью арифметических операций и образования
суперпозиций, и называются элементарными функциями (состав-
ляют, как говорят, класс элементарных функций). Именно эле-
ментарные функции, а также кусочно элементарные функции, о
которых мы поговорим позже, изучаются в школе и являются той
основой, на которой строится здание математического анализа —
одного нз важных разделов математики.
Конечно, не все функции являются элементарными. Так, в
ряде вопросов важную роль играет выражение
п! = 1-2-3*.. .-п
(читается: «эн-факториал») — произведение всех натуральных
чисел от 1 до заданного натурального п. Например:
11 = 1, 21=2, 31 = 1.2-3=6. 4! = 24, 51 = 120, 6! =720, ...
Принято также считать, что 01 = 1. Таким образом, функция
у=(х—1)! определена для нсех x£N. Оказывается, что ее можно
естественным образом распространить иа все зиачення (н да-
же вообще на все значения х, кроме х=0, —1, —2, . ..). Эта
«продолженная» функции (обозначается Г(х) гамма-функция)
оказывается не элементарной.
Хоти слова «элементарный» и «простой» почти синонимы,
тем не менее многие нз элементарных функций очень сложны н
разобраться в их поведении бывает непросто. С этой целью прово-
дят исследование функции и построение ее графика, о чем еще бу-
дет речь впереди. Сейчас же обратим внимание на то, что первым
шагом в исследовании функции является нахождение ее области
определения, т. е. установление совокупности всех тех значений ар-
гумента, прн которых все действия, предусмотренные формулой,
можно выполнить. Вне области определения рассматривать функ-
цию бессмысленно. Так, иапрнмер. формула у—-\/Т~хР задает эле-
ментарную функцию, определенную лишь иа промежутке [—1; 1J и
вие его говорить в данном случае не о чем (кстати, что является
графиком этой функции?). Формула у задает функцию, on -
ределенную лишь в одной точке х=0, а формула 1 ~х2 не
задает никакой функции, так как здесь область определения пуста.
Задачи
4. Обоснуйте методы построения точек графиков j/=x2, У=~,
y^yfx. показанные иа рисунке 181, и, применив их, постройте упо-
мянутые кривые.
261
5. Используя построенные кривые у=х2, у=—, путем графи-
ческого сложения и вычитания получите кривые y=xz-}-xt
y—x2—x, у=х—
6. На рисунке 182 показано, как, имея отрезки а, Ь и единичный
отрезок 1 (масштаб), построить отрезки, длины которых в данном
масштабе равны соответственно произведению и частному длин
исходных отрезков. Обоснуйте правильность этих построений и
предложите на их основе способы построения точек графиков
y=f (х) g(x) и по точкам исходных кривых y=f(x) и
y=g(x). Рассмотрите отдельно методы построения графиков
y=f(x) и по графику y=f(x).
7. Пусть f (х)=х2; g(x)=x-2. Получите формулы для функ-
ций: a) f (g(x)); б) g(f(x)); в) f(g(f(x))); г) g(f(g (*))). Постройте
графики «сложных» функций y=f (g (х)) и y=g (f (х)) двумя спосо-
бами: исходя из полученных формул и с помошью графического
метода, показанного на рнсуике 183.
8. Обоснуйте правила преобразований исходного графика
y=f (х), соответствующие данным изменениям формулы:
a) y=f(x)4~o — сдвиг по осн Оу на |а| единиц вверх, если
а>0, или вниз, если о<0;
б) y~f(x-l~a)—сдвиг по оси Ох на |о| единиц влево, если
о>0, или вправо, если а<0;
гх=оА ь а) Рис 182 262 1 Ий || ь S)
263
Рис. 186
в) y=kf (х), fe>0 — растяжение в k раз
(при fe>l) илн сжатие в ~ раз (при
fed) вдоль оси ординат;
г) У=1(^х), fe>0,—сжатие в fe раз
(при fe>l) или растяжение в • раз
(при fed) вдоль оси абсцисс;
264
д) j/=—f(x)-—симметричное отражение графика относитель-
но осн Ох;
е) y=f(—x)— симметричное отражение графика относитель-
но осн Оу;
ж) У= И (•*)! — замена частей графика, лежащих ниже оси Ох,
отражением относительно этой оси части, лежащей правее оси Оу
с сохранением праной части графика.
з) у —f (|xl) — замена части графика, лежащей левее оси Оу,
отражением относительно этой осн части, лежащей правее оси Оу,
с сохранением правой части графика.
Сверьте свое понимание указанных преобразований с показом
их иа рисунке 185, если исходный график y—f(x) дан иа рисунке
184.
9. По данному графику y=f(x) (рис. 185, е) постройте графики
функций:
a) »=f(x)+2; б) y=f(x)—2; в) у={ (х+2); г) y=f(x —2);
Д) y=2f(x);e) у=0,5)(х);ж) y=f (2х);з) y=f (0,5х); н) у-f(x),
k) л) </=f(|x|); м) y-lf(*)|.
10. Распознайте преобразование, переводящее исходную кри-
вую y=f (х) (рнс. 186) в новую (рис. 187), и укажите подходя-
щую формулу для полученной кривой среди приведенных ниже:
a) j/=f(2x); б) y=0,5f(x)'. в) у= If (х—1)1 +1; г) y=f(x—1);
Д) y=f(~х); е) №f(|x—11 + 1); ж) у= — f(x); з) !/=f(x)+l;
и) y—f(— |х|); к) y=f(x+l); л) j/=lf(x)|; м) y=f(|x|).
11. Найдите область определения функции:
a) W=Vx—2+V*—х: б) !+_; в) у=-^х’—4х—5:
г) у=-^2х—х2—2; д) а) у^Ы-\
КАК ОБРАЗУЮТСЯ КЛАССЫ ФУНКЦИЙ
Имея определенный набор базисных функций f h f?,..., fk и до-
пустимых операций Fi, F2, ..Fs (их разрешается применять
любое число раз) над ними, мы можем получать другие функции,
подобно тому как из деталей конструктора с помощью определен-
ных правил их соединения можно получать разные модели. Класс
нсех получаемых таким образом функций будем обозначать так:
(Ji, fe, • .. fk', Fi, Fz,..Fs). В частности, если принять за базис-
ные все основные элементарные функции н допустить лишь ариф-
метические операции и взитне суперпозиции, то получим класс
элементарных функций. Беря в качестве базисных часть основных
элементарных операций и допуская, возможно, лишь часть указан-
ных операций, получим некоторые подклассы класса элементарных
функций, некоторые семейства функций, порождаемые данным
базисом и данными операциями. Вот несколько примеров таких
265
семейств функций, где под (а) понимается операция умножения иа
любую константу:
{х; (•)> —семейство целых положительных степеней j/=x",
где n£N\
<х, 1; (а), (+)> — семейство линейных функций у—ах-\-Ь\
(х, 1; (а), ( + ), (•))—семейство многочленов j/=a0x"4~. .
+an-ix+an, где n£N
Если взять в качестве базисных лишь степенные функции с ра-
циональными показателями, а допустимыми считать все арифме-
тические операции и суперпозицию, то получаем класс так пазы
ваемых явных алгебраических функций, т. е. функций, получаемых
из тождественной у=х с помощью алгебраических операций, к
которым, помимо арифметических действий, относятся возведение
в рациональную степень и извлечение корни. Вот примеры таких
функций:
Неявные алгебраические функции у(х) определяются уравне-
ниями вида
ао + Ci (х)уп ' + .. .+ап(х)у=Ь(х),
где ао (X), .... ап (х), b (х) — многочлены относительно х, причем
Oo(x)^fe0.
Функции, не являющиеся алгебраическими, называются транс-
цендентными. Таковы, например, функции j/=2*, log2 х,
у—х2Л-2х, у—Xх и т. д.
Задачи
12. Опишите следующие семейства функций:
а) <^;(«)>;б) <х, 1; (+)>; в) <х, 1; ( + ),(•)); г) <х;(а),(+)>;
Д) <х, 1; (+),(:)>.
РАЗРЫВНЫЕ ФУНКЦИИ
Как мы уже говорили, одно из основных назначений функций —
описание реальных процессов, происходящих в природе. Но из-
давна ученые-философы и естествоиспытатели выделили два про-
тивоположных типа течения процессов: постепенное (непрерыв-
ное) и скачкообразное. Соответственно с этим рассматриваются и
два типа изменения величин. Так, при падении тела на землю сна-
чала происходит непрерывное нарастание скорости движения, а в
момент столкновения с поверхностью земли скорость изменяется
266
скачкообразно, становясь равной нулю или меняя направление
(знак) при «отскоке» тела от земли (например, если тело — мяч).
Возможные графики зависимости v~v(t) скорости от времени
приведены на рисунке 188. Разрывы на них отвечают моментам
столкновения. Другой пример — размыкание электрической цепи
илн же, наоборот, подключение ее к источнику напряжения и из-
менение силы тока в этой цепи.
Конечно, более тщательное рассмотрение указанных процессов,
взгляд на них сквозь «лупу времени», позволяет н в моменты раз-
рыва обнаружить непрерывное, ио очень быстро происходящее
изменение. Однако учет деталей этого изменения приводит к неоп-
равданным усложнениям, так что обычно разумнее применять раз-
рывные зависимости. (Впрочем, есть и такие процессы, для кото-
рых, как выяснилось лишь в начале XX в., внутренне присуще скач-
кообразное изменение,— это квантовые явления в «микромире».
Так, внутренняя энергия атома не может изменяться непрерывно
и меняется лишь «квантами», порциями вполне определенной
величины.)
Но раз есть разрывные процессы, то необходимы н средства
для нх описания. С этой целью вводятся в действие функции, имею-
щие разрывы, скачки. Одни из способов введения таких разрывов
следующий. Пусть функция y—f (л) при х<а определена форму-
лой y=g(x), а при х>о —другой формулой y=h(x), причем
будем считать, что каждая из функций я н ft определена при всех
к и разрывов не имеет. Тогда если
Я(й)#=Л(о), то функция / имеет при
х=а скачок (см. рис. 189, где пока-
зан график функции f). Кстати, в
прикладных вопросах значение функ-
ции f прн х=а чаще всего не играет
никакой роли и потому вообще не
определяется. Если же g(a)—h(a),
причем мы полагаем f(o)=g(a)—
~h (о), то «комбинированная» функ-
ция f разрывов не имеет.
Рис. 189
267
Если обе функции g и h элементарные, то функция f в описан-
ном выше случае называется кусочно-элементарной. Переход от
одной формулы к другой при описании реальных явлений обычно
связан с нарушениями, возмущениями течения процесса в отдель-
ные моменты, со скачкообразным изменением тех илн иных его ха-
рактеристик. Такой переход иногда может сохранять непрерыв
ность изменения величины, но вызывать излом ее графика, в
последнем случае скачком меняется не сама величина, а скорость
ее измеиеиия. Возможен й гладкий переход от одной формулы к
другой, ие вызывающий излома графика. Так, например, если
рассмотреть процесс падения камня в воду, то, пока падение
происходило в ноздухе, зависимости пути и скорости от времени
выражались формулами s=£~, v—gt (мы полагаем, что s(0)=0,
v(0)=0, и не учитываем сопротивление воздуха). При переходе
же в другую среду (воду) формулы станут иными, причем скачка
в изменении этих величии нет: непрерывность и даже гладкость
графика y—s (/) сохранится, график y=v(f) претерпит излом в
момент перехода. Разрыв имеет лишь график ускорения. Анало-
гичны особенности и процесса падения парашютиста — до мо-
мента раскрытия парашюта и после этого момента формулы для
пути и скорости различны.
Кусочно-элементарная функция может быть определена и более
чем двумя формулами, например:
х2 +1 при — оо<х^—1,
ffx\= х+3 при — 1<хС2,
• * * 20
— прн 2<Сх<оо
(проверьте, что эта функция не имеет скачков), и даже бесконеч-
ным множеством формул, например:
[х>л(лСх<п+1; п=0, ±1, ±2, .)
(эту функцию называют «целая часть числа» или, иначе, «антье»
от французского слова entiere, которое означает «целый»).
С этой функцией связана еще одна — «дробная часть числа»,
обозначаемая {х) и определяемая формулой {х}—к—[х) Графики
функций у=[х] н у—(х) изображены иа рисунке 190.
Можно доказать, что любая элементарная функция непрерывна
при всех значениях аргумента из области ее определения. Поэтому
если, например, кусочно-элементарная функция g(x) определена
при всех значениях х, то она может иметь разрыв только прн
значениях х, в которых происходит смена формул.
В приложениях математики значение х=а принято также
называть точкой разрыва функции ft если эта функция определена
иа некотором интервале, имеющем х=а левым или правым концом
268
(или на двух таких интервалах), ио прн х—а она не определена.
Мы тоже будем так говорить. Например, функции у—— определе-
на и прн х<0 и прн х>0, но не определена при х=0; значит,
точка х=0 служит для нее единственной точкой разрыва. Анало-
гично функция у— определена при — 1<х<1, но не
прн х=±1; значит, у нее две точки разрыва: х=1 н х= — 1.
Особо отметим понятие устранимого разрыва. В обозначениях,
связанных с рисунком 189, это означает, что g(a)=ft(a), но f (а)
не равно этому общему значению или даже не определено.
Например, функция
f«=^-
прн х=0 не определена. Но прн х<0 и при х>0 она равна х-)-2,
т. е. можно положить g(x)=h (x)=x-j~2. Так как g (0)=Л(0)=2,
то, если положить
.... /f(х) = х4-2 при х^О,
f (*)—( 2 при х=0.
мы получаем f* (х)=х-|-2 для всех х, т. е. продолжение функции
уже разрывов ие имеет, разрыв устранен.
Многие кусочно-элементарные функции можно выразить еди-
ной формулой с помощью так называемой «функции скачка», или
единичной функции Хевисайда Н (по имени английского физика
Хевисайда, впервые ее рассмотревшего) Согласно определе-
нию
° при х<0’
1 при х>0
269
(впрочем иногда полагают, что Н (0)=0, или или
7/(0) ие определено).
График этой функции изображен на рисунке 191. Единичной
она называется потому, что имеет один скачок величиной 1 при
л=0, а до н после скачка она постоянная, т. е., кроме этого скачка,
у нее нет никаких изменений. Функция а Н(х) имеет скачок вели-
чиной а при х=0, а функция аН(х — а) — такой же скачок при
х=а.
Функция у—Н (Ь — х) Н (х—а) носит название «прямоугольный
импульс». Она равна 1 на отрезке [а;6] и 0 вне его. С подобными
зависимостями часто приходится иметь дело в электротехнике.
Так, на рисунке 192 показано изменение тока в цепи, когда радист
передает букву «а» по азбуке Морзе. Соответствующую функ-
цию можно представить в виде суммы двух прямоугольных импуль-
сов (сделайте это).
Пусть А — некоторое множество точек на числовой примой. Ха-
рактеристической функцией этого множества называют функ-
цию %л, равную 1 при х£А и равную нулю при х$А. В частности,
единичная функция Хевисайда является характеристической для
промежутка (0; 4~ оо), а прямоугольный импульс J=H(b —
—х) Н (х—а) служит характеристической функцией отрезка [а; 6].
Легко понять, что если два промежутка Ji и /2 ие пересекаются,
то характеристическая функция их объединения равна сумме
характеристических функций этих промежутков: X/1U/teX/(+x, •
Подумайте сами, как получить характеристическую функцию пе-
ресечения двух промежутков из их характеристических функций.
С помощью одной лишь функции скачка, допустив умножение
на число, сложение и линейные преобразования аргумента, мы
можем получать только кусочно-постоянные, или, как их еще назы-
вают, ступенчатые, функции, графики которых состоят нз конечных
или бесконечных (по краим) горизонтальных участков — «сту-
пенек». Так, например, если числовая прямая разбита на три непе-
ресекающихся промежутка J2, h. то функцию, равную Ci при
x£Ji, С2 при х£/2 и равную С3 при xgj3, можно задать формулой
У=С1Х/1 + С2^,-|- СзХл к, значит, выразить через функцию скачка,
270
поскольку через нее выражается характеристическая функция лю-
бого промежутка.
Комбинируя функцию скачка с элементарными функциями,
можно получить любые кусочно-элементарные функции. Функцию,
равную х2 при х<2 и -у/х—2 при х^2, можно задать формулой
</=(1-H(x-Zj)x?+H(x-2) х/^2-
В заключение скажем несколько слов о функции #=|х|
Формально она является элементарной, так как |х| =-\/хт. Поэтому
если функция f (х) элементарная, то и функция If (х)| элементарная.
Однако чаще, основываясь на формулах
(х при х^О,
—х при лгСО,
причисляют функцию |х|, а с ней и If (х)1 к кусочно-элементарным
Функция </=|х| связана с функцией скачка Н (х) формулами
|x|=x(//w-« [-*))
Задачи
13. Определите зависимость q(h) расхода краски на окраску
стены здания, имеющей форму, показанную на рнсуике 193, до вы-
соты h, если на окраску 1м2 стены требуется а килограммов краски,
Постройте график этой зависимости. То же для зависимости h («?)
высоты окрашенной части от количества израсходованной краски
(окраска идет снизу).
14. Вода с по&тоянной скоростью v литров в минуту заполняет
сосуд, состоящий из цилиндрических частей, поперечное сече-
ние которого показано иа рисунке 194. Определите зависимость
h (t) уровня жидкости в сосуде от времени с начала заполнения со-
суда. Постройте график этой зависимости. То же сделайте для
зависимости V (h) объема заполненной части сосуда от уровня h
Рис. 193*
Рис. 194
Рис. 195
271
жидкости в нем. (Объем цилиндра радиуса г и высоты h находит-
ся по формуле V=nr2h.)
15. В цилиндрическом сосуде находятся в несмешанном состоя-
нии керосин н вода, причем объемы, занимаемые этими жидкостя-
ми, одинаковы, а граница раздела жидкостей находится на глуби-
не Н. Определите зависимость р (h) давлении жидкости иа глубине
h как функцию от h. Постройте график этой зависимости. Найдите
выталкивающую силу, действующую на куб с ребром а, помещен-
ный в данный сосуд так, что его нижняя грань находится на глу-
бине й, как функцию от h. Постройте график этой зависимости.
Определите, при какой плотности вещества куба он будет нахо-
диться в равновесии на глубине h.
16. Определите зависимость заштрихованной иа рисунке 195
площади S под графиком функции от значений к. Постройте
график этой зависимости.
17. Выразите через функцию скачка характеристические функ-
ции Промежутков (— оо; О); ( — оо; 0J, (О; -f- оо); (а; ft); (а; ft} [а; Ь).
18. Задайте одной формулой, используя функцию скачка, за-
висимости:
а) (хприх^О, б) рприх<—1,
У~~(х2 при t>0; 0 прн — 1<х<0.
в) f — 1 при х<0, ПРИ
*/=< О прн х=0,
} 1 при х>0.
(Последняя функция имеет специальное обозначение sgn и наз-
вание «сигнум» от латинского signum — знак.)
19. Через max<o, ft) (min {а, Ь}) обозначается большее
(меныпее) из чисел а, Ь, причем max (a, o)=min {а, а)=а.
Если функции f и g заданы на некотором интервале, то на том же
интервале определены следующие функции: max <f, g) (х)=
=max <f (х), g(x)> и min <f, g> (x)=min <f (x), g(x)>
Постройте графики функций:
a) //=max <x, x2>; 6) y=min <x, x2); в) y=min <1x1, 1);
r) t/ = max(-y6t, x2).
20. Пусть функции g н h заданы на некотором интервале.
Задайте формулами функции max (g, h) и min (g, ft) с по-
мощью знака модуля.
КУСОЧНО-ЛИНЕЙНЫЕ ФУНКЦИИ И МОДУЛИ
Пусть заданы Xi<X2<- • <хп — точки смены формул. Функ-
ция f, определенная при всех х, называется кусочно-линейной,
если она линейна на каждом интервале (— oo;xi), (xi;x2),
(х2; х3), ..(х„; 4- оо), т. е.
272
((xy^OiX+bi (Xi_t<x<zxi при i=l, 2, .... n+1), (1)
^де обозначено xo= — co. xrt+i =• 4- co. Если к тому же выполнены
условия согласования
aiXi-t-bj—Oi4-ix,-t-i>j+|s=Kf(xi) при i=l, 2, .... п, (2)
то рассматриваемая кусочно-линейная функция непрерывна. Не-
прерывная кусочно-лииейиая функция называется также линей-
ным сплайном. Ее график есть ломаная с двумя бесконечными
крайними звеньями — левым (отвечающим значениям x<xi) и
правым (отвечающим значениям х>хп). Подобный график изо*
бражен, например, иа рисунке 196.
Функцию с графиком, показанным на этом рисунке, можно за-
дать тремя формулами:
{—1 при х<0
2х— 1 при O^X^l,
1 при х> I
Однако нетрудно заметить, что эту же функцию можно задать и
одной формулой, используя модули: у— |х| — |х—1|. Оказывает-
ся, что и любую непрерывную кусочно-линейную функцию вида (1)
можно задать некоторой формулой вида
t/=ax-|-!>+c(|x—Х|Ц-с2|х—лг2| -Ь.. .4-ся|х—х„|, (3)
где числа a, b, Ci,..сп легко найти по графику данной функции.
Докажем это.
Заметим, что две ломаные с бесконечными крайними звеньями
н одинаковыми абсциссами вершин х>, х2, хп совпадают, если
у ннх равны угловые коэффициенты всех «одноименных» звеньев
н имеется общая точка. Иными словами, знание угловых коэффи-
циентов всех звеньев и координат одной точки такой ломаной пол-
ностью ее определяет. Это ясно из процесса построения ломаной
иа основе указанной информации, при котором данная точка М
берется за исходную (рис. 197)
Отмеченный факт мы и положим в основу получения формулы
для непрерывной кусочно-линейной функции, заданной своим гра-
фиком. Напомним, что |х—а| равняется —х-\-а, если х<а, и
х—а., если х^а. Поэтому на каждом из промежутков (— со; Xi),
(х>;хг)...(х«; Ч-оо), на которые числовая прямая разбивается
точками Xi, Х2,. •хп, функция, определяемая формулой (3), будет
линейная (как сумма линейных функций), и для нахождения угло-
вого коэффициента соответствующего звена ломаной достаточно
найти коэффициент при х в полученном выражении, приведя с этой
целью подобные члены.
Пусть kt — угловой коэффициент самого левого (бесконечного
крайнего) звена, kt — следующего за ним звена,..kn+i — само-
го правого (бесконечного крайнего) звена ломаной. Приравнивая
эти угловые коэффициенты коэффициентам, получающимся при х
после раскрытия всех модулей в выражении (3) иа соответствую-
щих этим звеньям промежутках, находим:
—О-~С\ . — cn,
Дг —Cz—'...—Cn,
ks “G-j-Ci , — Cn,
(4)
kn+l =G-|-Cl 4~C2“h. ♦
Вычитая из второго равенства первое, получаем kz— k)—2ct,
вычитая из третьего второе, получаем /?3—&2=2с2 и т. д. Мы при-
ходим в итоге к соотношениям
с—fcfl2 --при >•= 1, 2, , п.
(5)
* Складывая первое равенство с последним, получаем fei4-fen+i=
—2а, откуда
ga=fei+^r,iti <
(6)
Обратно, нетрудно проверить, что из равенств (5) и (6) вытека-
ют соотношения (4).
Итак, если коэффициенты a, Ci, сг, ..сп определяются фор-
мулами (5) и (6), то угловые коэффициенты всех звеньев гра-
фика функции (3) совпадают с соответствующими угловыми
коэффициентами заданного графика и, значит, остается обеспе-
чить всего одну общую точку этих ломаных для нх совпадения.
Этого всегда можно добиться выбором подходящего значения
оставшегося пока ие определенным коэффициента 6. С этой целью
достаточно подставить в формулу (3), коэффициенты которой уже
вычислены из соотношений (5) и (6), координаты какой-либо од-
ной точки данной ломаной н найти b из полученного равенства.
274
Пример 1. Найдем уравнение ломаной, изображенной на
рисунке 198 (треугольный импульс).
Угловые коэффициенты звеньев таковы: Я| =0, fe2== 1, £з= — 1»
Zu=O Поэтому Г1=-*^=Х,
с$——-2— ==4"’ а= kl^k* =0. Значит, уравнение данной лома-
ной имеет вид У=-|- |х4-1 | — |х|4-~|х—11 +Ь. Найдем значе-
ние b нз условия 0(О)=1, подставляя координаты вершины (О; 1)
нашей ломаной: у(0)=~—~|-6 = 1, откуда Ь=0, и уравнение
окончательно запишем в виде
у=|.|х + 1|-|х|+|-|х-1|
Как ясно из сказанного выше, график любой функции вида (3)
является ломаной с бесконечными крайними звеньями. Но чтобы
построить такую ломаную, достаточно знать все ее вершины и по
одной точке на левом и правом бесконечных звеньях. Эти сообра-
жения позволяют легко строить графики функций такого вида без
раскрытия модулей и перехода к их кусочному заданию. А именно
составляется таблица:
Хо Х\ *- *«+1
У . Уо У» У* У»+1
Здесь у,=^ у (х,) — значения данной функции при х=х, (t=0, 1 , . .
Значения xo<Xi н xn+i >хп здесь выбираются произвольно.
Определяемые этой таблицей точки Mi (хд yi) прн i= 1, 2,.п яв-
ляются вершинами строящейся ломаной, а точки М© (х©; у0) и M„+i
принадлежат ее крайним звеньям. Все эти точки наносят иа коор-
динатную плоскость. Остальное построение графика ясно.
Пример 2. Построим график функции у=3х4* 1 — 1х+11 4-
4-2|х|. Составляем таблицу:
X —2 — 1 0 1
У -2 0 0 4
Наносим точки Мо (—2; —2), Mj (—1; О), Мг (О; О), М3 (1; 4) на ко-
ординатную плоскость и соединяем соседние точки отрезками
(рис. 199).
275
Задачи
21. Найдите уравнение треугольного импульса на промежутке
[а; р] с амплитудой (высотой), равной h (рнс. 200). Решите задачу
двумя способами: получив непосредственно уравнение соответст-
вующей ломаной с помощью формул (5) и (6) и с помощью пре-
образований единичного треугольного импульса (рис. 198), урав-
нение которого было нами получено.
22. Найдите уравнения вида (1) ломаных, изображенных на
рисунках 201—202.
23. Постройте графики данных функций, пользуясь описанным
«методом вершин>:
а) у=х+|х—2| —|х|; б) у= |х+11 + |лг| — |х—2}; в) у=
= |х+2| + |х|-2|х-2|.
24. Изобразите график функции у=||х| —1|, построив для
этого сначала график t/=|x| — 1, и с его помощью представьте
эту функцию в виде (3). (Интересно, что аналогичным способом
можно представить в виде (3) любую функцию из класса <х, 1, (а),
(+), (||)>.)
25. Представьте в виде (1) функции, заданные следующими
формулами:
1) у=1|х—2| —1|; 2) у=х+\х- |х||; 3) у=|х-2|х| | -|ж|;
4) у=1||х|-2|-1|.
Указание. Воспользуйтесь методом, предложенным в зада-
че 24.
276
ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА
Если непрерывная зависимость представлена таблицей
X *1 Х2 ха
У «Л У* Уч
то возникает задача интерполяции, т. е. распространения, продол-
жения ее иа весь диапазон изменения аргумента (от x=xi до
х~хп) с помощью той или иной непрерывной функции. Графически
интерполяция сводится к нахождению непрерывной кривой, за-
данной достаточно простой формулой и проходящей через «таблич-
ные» точки М, {хе, у,).
На практике часто интерполирующую зависимость выбирают
кусочно-лииейной, т. е. линейной между двумя соседними таблич-
ными зиаченнями аргумента (узлами интерполяции). Однако ре-
альные зависимости бывают обычно гладкими — их графики ие
имеют изломов н потому интерполяция их кусочно-линейными
функциями не самая лучшая (хотя она и простейшая для вы-
числений и в связи с этим наиболее распространена). Гладкую
интерполяцию можно осуществить с помощью многочленов. Эту
задачу решает так называемый интерполяционный многочлен Ла-
гранжа, названный по имени известного французского матема-
тика Ж- Лагранжа (1736—1813):
р АЛ— (ж—ж,)(ж—J&). (ж—ж.) ,
' <А-ь)(х,-Л) . .(z,-x.)
, (*-»).. («-*.) , , (х-х,)(х-д)...(х-
' («г—Xi) (х2—xs) . .(х2—хя) У ' ' ' ' (хя—Xi) (*л~Xi). . (Хя—Хи_ () * "" ' '
Легко убедиться в том, что при х=я,- этот многочлен принимает
значение yt, т. е. график его проходит через все табличные точки
(проверьте это!). Заметим, что степень этого многочлена равна
п— 1 (т. е. на единицу меньше числа табличных точек) или меньше
(почему?). Можно доказать, что существует только один много-
член степени, меньшей или равной п—1. принимающий заданные
значения в п точках.
В частности, если заданы всего две точки Mt (xr, yi) и Мг (х?; у?),
то соответствующий многочлен Лагранжа
у=*=^ Уу^^-У2
у Х|—*2 V *2 —XI у
есть попросту линейная функция, а его график — прямая, проходя-
щая через эти точки. Одновременно мы получили уравнение пря-
мой, проходящей через две заданные точки с координатами
(xg yi) и (х2; у2).
277
Пример 1. Составим уравнение прямой, проходящей через
точки Afi(—1; —3) и М2(2;3). В данном случае многочлен Ла-
гранжа принимает вид 3)H-^J|- -3, откуда
у=2х— 1. Это и есть искомое уравнение.
Пример 2. Составим уравнение квадратичной зависимости,
график которой проходит через точки Mi (0; О), М2(1; 3), М3 (2; 4).
Записав многочлен Лагранжа
(х-1Дх-2) . _0 . _и-0)(х-2) .3 । (л-0)(х-1) >4
» (0-|)(0-2) О—0)(1—2) (2—О)(2—!) ’
после преобразований получаем у=4х—х2
На практике интерполяция с помощью многочлена Лагранжа
при большом п (реально при п>4) редко применяется. Дело в том,
что при большом п формулы усложняются и, самое главное, сум-
ма становится очень чувствительной к относительно малым изме-
нениям значений (х,} и (г/,}. Поэтому если этн значения известны
лишь с определенной точностью, то результат интерполяции стано-
вится недостоверным. Сейчас разработан ряд методов, позволяю-
щих преодолеть эту трудность
Задачи
26. В каких случаях многочлен Лагранжа для п точек (л^З)
имеет нулевую степень? первую степень? вторую степень?
27. Составьте уравнения прямых, проходящих через данные
точки:
a) Mt (2; 8), М2(3; 11); б) М, (О; -4), Л42(-2; -2).
28. Составьте уравнения графиков квадратичной зависимости,
проходящих через данные точки:
a) Mi (1; 5), М2 (2; 8), М3 (3; 9); б) Mi (— 1; О), М2 (0; 1), М3 (1; 4).
29. Какой вид имеет многочлен Лагранжа, если ординаты всех
табличных точек, кроме одной, равны нулю? Напишите многочлен
Лагранжа, если эти точки таковы: М| (— 1: О), М2 (0; 0), Мз (1; 1),
Mt (2; О).
О ПОСТРОЕНИИ ГРАФИКОВ ФУНКЦИЯ И О ТОМ,
ЧТО МОЖНО УВИДЕТЬ, ГЛЯДЯ НА ГРАФИК
Говоря о построении графика функции, мы будем иметь в виду
лишь его эскизное изображение, отражающее характерные осо-
бенности функции, передающее ее ход на всей области определе-
ния. Конечно, можно, ие размышляя, вычислить много значений
функции н построить ее график, соединяя полученные точки плав-
ной кривой. Сейчас с такой задачей легко справляется ЭВМ. Ваша
278
же цель — научиться передавать графически качественные особен-
ности функций, иными словами, рисовать ие столько графики-ко-
пии, сколько графики-портреты. Это сложнее простого копирова-
ния и требует размышления, продумывания того, иа что следует об-
ратить внимание и как передать те илн иные черты характера
функции на ее «портрете». То, насколько удачным окажется этот
«портрет», зависит от мастерства «художника». Набив руку, вы
научитесь быстро рисовать графики многих элементарных функ-
ций. Такое умение позволит вам как бы видеть функцию, переходя
мысленно от формулы к графику, рисуя его в уме, что очень важно
для правильного н быстрого решения многих вопросов, связанных
с функциями.
Глида на график, непосвященный увидит лишь некоторую кри-
вую, более сведущий свяжет ее с функцией н опишет некоторые
характерные черты последней (например, возрастание или убыва-
ние), наконец, искушенный в математике даст, насколько это воз-
можно, полную характеристику функции по данному графику, пе-
речислит все ее основные особенности, а быть может, и укажет
формулу, задающую функцию с таким или сходным по форме гра-
фиком.
Так, например, математик, взглянув на рисунок 211 (см. с. 290),
сказал бы примерно следующее: «Перед нами график некоторой
функции. Она всюду определена и непрерывна. Всюду положитель-
на, поскольку график расположен выше оси абсцисс. Четная, так
как график симметричен относительно осн ординат. Возрастает иа
промежутке от минус бесконечности до нуля и убывает на проме-
жутке от нуля до плюс бесконечности. Имеет единственный экстре-
мум — максимум прн х=0. Ось абсцисс является асимптотой,
поскольку график неограниченно к ней приближается при х—►+ оо
и при х—►—• оо, значит, функция стремится к нулю при стремле-
нии аргумента к плюс или минус бесконечности. График напоми-
нает знаменитую гауссову кривую у—е~х или, скажем, более прос-
то задаваемую кривую у= * »•
Чтобы правильно отражать на графике и считывать по нему
характерные свойства, особенности функции, следует хорошо
поинмать как сами этн свойства, так и способы нх графического
выражения. Приведем краткий перечень терминов и их графичес-
кое толкование.
Непрерывность — «сплошность», неразрывность кривой, изо-
бражающей график, возможность ее начертания без отрыва каран-
даша от бумаги.
Гпадкость — плавность кривой; график поворачивает посте-
пенно, не имеет изломов и заострений.
Возрастание — подъем точки, движущейся по графику слева
направо.
279
Убывание — спуск точки, движущейся по графику слева на-
право.
Постоянство функции — параллельность графика оси абсцисс.
Знакопостоянство функции — расположение графика выше
(ниже) осн абсцисс
Выпуклость вверх (вниз) — любая дуга графика лежит выше
(ниже) стягивающей ее хорды; касательная при движении точки
касания по графику слева направо поворачивается по часовой
стрелке (против иее).
Четность функции — симметричность графика относительно
оси ординат. (Аналитически выражается тождеством f(x)=f (—х).)
Нечетность функции — симметричность графика относительно
начала координат. (Аналитически выражается тождеством f (х)=
=—/(-*).)
Периодичность функции — график можно разбить иа одинако-
вые по форме участки, получаемые один нз другого сдвигом вдоль
оси абсцисс. (Аналитически выражается наличием такого числа
Г>0, что f(x-)-T)=f (х) для всех х.)
Ограниченность сверху (снизу) — расположение графика всю-
ду ниже (выше) некоторой прямой, параллельной оси абсцисс.
(Аналитически выражается наличием такого числа М, что
f (x)<M (f(x)>M) для всех х.)
Асимптота — прямая, к которой неограниченно приближается
точка, движущаяся по графику, неограниченно удаляясь от начала
координат.
Вертикальная асимптота — прямая х=с, где с — точка «беско-
нечного разрыва» графика, при стремлении аргумента к которой
слева или справа значения функции неограниченно возрастают
по абсолютной величине (при этом график уходит неограничен-
но вверх или вниз).
Горизонтальная асимптота — прямая у—а, к которой неогра-
ниченно приближается график при х—►+<» (правая асимптота)
или х—*~ со (левая асимптота). Запись х—► + оо (читается: «Икс
стремится к плюс бесконечности») выражает процесс неограничен-
ного увеличения х, безграничное удаление точки х вправо по оси
абсцисс; запись же х-*-— оо означает неограниченное удаление
точки х влево по оси абсцисс.
Наклонная асимптота— прямая y=kx-\-b, к которой график
неограниченно приближается при х—оо (правая асимптота)
или при х—>— оо (левая асимптота). Аналитически наличие
асимптоты у—kx-\-b обусловливается возможностью представле-
ния функции в виде y=kx4-^+0 (*). где 0(х) стремится к нулю
при х—►+ оо илн х—*— оо.
Характерные точки графиков:
Нули (корни) функции — точки, в которых график достигает
оси Ох. Аналитически — решения уравнения f(x)=O.
280
Точка максимума — абсцисса «вершины графика», точка, в ко-
торой функция определена и в которой возрастание функции
сменяется На ее убывание.
Точка минимума — абсцисса «дна впадины» и а графике,
точка, в которой функция определена и ее убывание сменяется
иа возрастание.
Точка экстремума — точка максимума или минимума функции.
Точка перегиба — точка графика, при переходе через которую
меняется направление его выпуклости.
Точка излома — точка графика, в которой резко, скачком
меняется направление движения по графику.
Точка разрыва — точка иа оси абсцисс, при прохождении
иад или под которой график терпит разрыв и для его продолжения
необходимо оторвать карандаш от бумаги. Как было сказано
ранее, мы к точкам разрыва причисляем также те концы области
определения функции, в которых она не определена.
При построении графика функции следует проводить ее анализ,
исследование, направленное иа выявление характерных особен-
ностей функции, и одновременно отражать схематически на рисун-
ке обнаруженные черты ее поведения. По изображенным элемен-
там строится затем общая картина — график функции. Исследо-
вание функции y—f(x) удобно выполнять по следующей схеме:
1. Найти область определения функции (символически D(f)).
2. Найти нули функции, т- е. решения уравнения f(x)=O.
3. Найти точки разрыва, если оии имеются (часто это нули
знаменателя в формуле, задающей функцию).
4. Определить знаки функции иа промежутках, иа которые
область определения разбивается ее нулями и точками разрыва.
Для этого нужно изобразить систему координат и пометить в ней
знаки функции, ставя « + » иад теми промежутками, где оиа поло-
жительна, и «—» под теми промежутками, где оиа отрицательна.
Этим определится то, в какой полуплоскости, верхней или иижней,
должен располагаться график при значениях аргумента, принад-
лежащих данному промежутку.
Замечание. Для определения знаков функции иа ука-
занных промежутках достаточно выяснить ее знак в одной (любой)
из точек исследуемого промежутка — во всех точках этого про-
межутка знак такой же.
5. Выяснить наличие вертикальных асимптот, т. е. значений
х=хо, при приближении х к которым график уходит неограничен-
но вверх илн вниз. Обычно такие значения являются нулями
знаменателя дробного выражения в формуле, задающей функцию
(как, например, хо==О У функции или «граничными»
точками области определения (как, например, Хо—0 у функции
z/=|og2 х). Изобразить асимптоты в системе координат и отметить
схематически характер приближения к ним графика слева и
справа.
281
6. Выисиить поведение функции при х—►+ со и при х—►—оо,
т. е. при больших по модулю положительных и отрицательных
значениях х. Установить наличие горизонтальных или наклонных
асимптот; если они есть, провести их в координатной плоскости
и изобразить схематически характер приближения к ним графика
функции.
7. Выяснить, будет ли функция четной, нечетной, периоди-
ческой. (Заметим, что эти вопросы полезно выяснить в начале
исследования, вслед за п. 1, так как наличие одного из названных
свойств упрощает дальнейшее. К сожалению, большинство функ-
ций подобными свойствами ие обладают.)
8. Учитывая проведенный анализ и уже полученные иа рисунке
элементы графика, доделать черновой набросок, эскиз графика.
Вычислить несколько контрольных точек графика, исходя из за-
данной формулы, и уточнить изображение.
Необходимость учета области определения и знаков функции
можно выразить следующими первыми «заповедями» тому, кто
строит график: «Не пытайся изображать график на тех промежут-
ках, где его быть не может» и «Не строй график в той полуплоскос-
ти, где его быть не может»
Задачи
30. Каковы основные особенности и характерные точки графи-
ков функции, изображенных на рисунке 203? Каковы черты «ха-
рактера», поведения соответствующих функций?
31. Какие из функций, графики которых изображены иа ри-
сунке 203, являются четными? нечетными? периодическими? не-
прерывными? ограниченными сверху (снизу)?
32. Какие из графиков, изображенных на рисунке 203, имеют
вертикальные асимптоты? горизонтальные асимптоты? наклонные
асимптоты?
33. Укажите все асимптоты графиков функций и изобразите
схематически приближение к ним:
а) 1/=^; 6) у=-^-- в) у=-~; г)(/=4т,
' х ' ' 9 х ' > * хф4 >/4-1
д) </=2': е) ж) з) !/=V*+ —V*-
34. Следуя приведенной выше схеме исследования функции,
изобразите графики функций:
а) б) у=х3—х;
в) *=;чт: г>
282
Рис. 203
ГРАФИКИ МНОГОЧЛЕНОВ
При построении графиков многочленов, т. е. функций вида
у=аол"+а1Лп *+.. где ас=/=0, n£N, (1)
следует учитывать, что любой многочлен всюду определен и его
график — непрерывная гладкая кривая. Характер поведения мно-
гочлена при больших по модулю значениях аргумента определяет-
283
ся только его старшим членом айх?. Это ясно из представления
многочлена в виде
«=°°41+£т+-
(2)
При больших значениях |х| все слагаемые в скобке, кроме
первого, становятся малыми, оии безгранично приближаются к
нулю, если х—*~ 4- сю или х—оо. Значение же у при этом неогра-
ниченно возрастает по абсолютной величине. Если п четно, то
обе уходящие в бесконечность ветви (правая и левая) графика
многочлена (1) направлены в одну сторону от оси Ох (направление
ветвей определяется знаком а0) Если же п нечетно, то эти ветви
направлены в разные стороны от оси Ох (как, например, у куби-
ческой параболы). В последнем случае, если оо>0, правая
ветвь направлена вверх, а левая — вниз; если же то на-
оборот.
Многочленами являются и функция-коистанта (многочлен ну-
левой степени у—ао), и линейная функция (многочлен первой сте-
пени у~aox+at). Графиками в этих случаях являются прямые,
и подробно говорить о иих мы ие будем
Многочлен второй степени, или квадратичная функция у=
=aox2+atx+a2, — это уже интересный и поучительный объект
для исследования, иа котором можно демонстрировать важные
особенности многочленов и методы анализа функций.
Важно понимать, что графики функций у—ах^Ьх+с и у=
—ах2 — это равные параболы, лишь по-разному расположенные
относительно осей координат. Действительно, поскольку
ахг + 6*+с=и(х!+^) +c=°[(*+^)!-S ] +с =
40’ + ^'
то параллельный перенос на вектор с началом в точке О (0; 0)
и концом в точке 4а^~* ) совмещает эти параболы.
Однако для многочленов выше второй степени аналогичное
утверждение уже неверно и формы графиков тем разнообразней,
чем выше степень многочлена.
Передать основные черты графика многочлена весьма просто
в случае, когда многочлен представлен в виде
у—а (х—xi)”’(x —Xs)”1... (х~хйл‘ Рт (х\ (3)
где Рт(х)— многочлен степени т ^2, ие имеющий корней, а все
числа Xi, Ха,..х* различны. Числа х», Xs,..., х* — это корни мно-
284
гочлеиа (I), а показатель степени щ называют кратностью корня
х,- Если и, — I, то корень х~х, называется простым; если же «,->• 1,
то кратным.
В рассматриваемом случае основным является определение
знаков многочлена иа всех промежутках, на которые числовая
ось разбивается его корнями. Делается это очень просто, если
воспользоваться правилом, которое сразу следует из формулы (3):
при переходе через корень х, иечетиой кратности знак (х—х,У\ а
потому и знак у меняется иа противоположный, тогда как при пе-
реходе через корень четной кратности знак у сохраняется. Имея
это в виду, достаточно определить знак многочлена (3) лишь иа од-
ном из промежутков. Удобно начать с самого правого промежутка
и продвигаться влево, меняя знаки в корнях иечетиой кратности
и не меняя в корнях четной кратности.
Для более точного изображения графика многочлена (3) сле-
дует учитывать, что в кратных корнях график всегда касается
оси Ох, приближаясь к ней тем плотнее вблизи корня, чем выше его
кратность, причем прн четной кратности касание происходит без
пересечения с осью Ох, а при нечетной — с пересечением.
Пример 1. Изобразим график многочлена у—х3—х.
Разлагая многочлен иа миожители, получаем у=(х +1) х (х—I).
Все корни здесь простые (кратности единица). Поэтому в каждой
из точек х= —1, х=0, к=1 происходит смеиа знака многочле-
на. Учитывая, что при х>1 многочлен положителен, рисуем
«змейку» смены знаков (рис. 204). Учитывая, что при больших по
модулю х форма ветвей графика такая же, как и у кубической
параболы у=х3, а также имея в виду нечетность функции, изобра-
жаем график в системе координат (рис. 205).
Пример 2.. Изобразим график многочлена у~х2— х4
Разлагая многочлен иа множители, получаем у— — jrfx— 1)Х
Х(*+ 1)- Здесь кореиь х=0 кратности два, а корни х— 1 и х = — 1
простые. Поэтому в точке х=0 знак многочлена ие меняется, а в
точках х= — 1 и х=1 знак изменяется иа противополож-
ный. В этом случае «змейка» смеиы знаков выглядит так, как по-
казано иа рисунке 206. Учитывая, что при больших по модулю
значениях х форма графика такая же, как и у функции у— —х4, а
Рис 204
Рнс. 205
285
ч о г
У|
Рис. 206
Рис 207
также имея в виду четность функции, изображаем график в систе-
ме координат (рис. 207).
Указанный метод удобен и в тех случаях, когда многочлен
удается представить в виде у=Р (x)+d, где многочлен Р(х)
представлен в виде (3). В этом случае сначала строится гра-
фик многочлена Р (х), а затем полученный график смещается на |d |
едиинц вверх, если d>0, или вниз, если d<Q, по оси ординат.
Так, для построения графика функции у=*х3—х+2 строим снача-
ла график многочлена у=х*—х (рис. 205), а затем поднимаем его
на 2 единицы вверх.
Подобным образом можно строить и график квадратного трех-
члена у=ах2-^Ьх~рс. Сначала строим параболу у=ах2+Ьх~
=ах^х4-—) . а затем смещаем иа с единиц по оси ординат. Заме-
тим, что абсцисса вершины вспомогательной параболы такая же,
что и у исходной, и равна хь— —“^точка — ~ лежит посереди-
не между корнями x=0t х=—--вспомогательной параболы).
Ордината вершины находится подстановкой значения к= —~ в
данный квадратный трехчлен.
Задачи
35. Изобразите графики следующих многочленов:
а) у=х2 — 4х; б) у=9х—X3; в) у=х4—х2-|-4:
г) у=х2—х3; д) у=х34-4хг-|-4х; е) t/=x2—4x-f~9.
36. Приведите пример многочлена, график которого сходен по
форме с изображенным на рисунке 208.
0
Рис. 208
288
ГРАФИКИ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Рациональной функцией называется функция, которую можио
представить в виде отношения двух многочленов:
_ длх',+ап-1/’~|+ 4-Д1Х+а0 ,. v
У b„x”+bm~vcm-'+. .. + Ь1Х+Ьо
К этому классу функций относятся и многочлены, которые иначе
называют целыми рациональными функциями. Мы же будем сей-
час вести речь о дробно-рациональных функциях (рациональ-
ных дробях), т. е. о таких, которые путем сокращений ие приводятся
к многочленам, подобно у—
Рациональиая дробь называется правильной, если степень
ее числителя меньше степени знаменателя, и неправильной в
противоположном случае. Любую неправильную дробь можно
представить в виде суммы некоторого многочлена (целой части) и
правильной дроби. Это можно сделать с помощью метода деле-
ния многочленов углом, который нетрудно понять, внимательно
рассмотрев приводимые ниже примеры:
По результатам деления получаем соответственно следующие ра-
венства:
Xs __..2 „it 1 . 2х!+х+1 _„2 11 х
7+Г—к -х+'~7+Т' —--------------------х
В справедливости полученных представлений легко убедиться,
приведя выражения в правых частях к общему знаменателю.
Вы, наверное, обратили внимание, что алгоритм деления и
запись результата аналогичны таковым для чисел. При этом и а
каждом шаге многочлены, подлежащие дальнейшему делению, за-
писываются в стандартном виде, т. е. по убыванию степеней, а
в качестве соответствующего слагаемого в частном записывают
результат деления старшего члена упомянутого многочлена иа
старший член делителя и деление выполняют до тех пор, пока сте-
пень этого многочлена ие станет меньше степени делителя.
При построении графиков рациональных дробей следует учи-
тывать ряд их специфических особенностей. Так, значение любой
правильной рациональной дроби безгранично приближается к ну-
лю при х—со, а значит, график ее неограниченно приближается
к оси абсцисс при неограниченном увеличении модуля аргумента,
287
и, таким образом, ось Ох является горизонтальной асимптотой
(подумайте, почему это происходит). Поведение неправильной
рациональной дроби при х—»-± со определяется поведением ее це-
лой части, к графику которой неограниченно приближается график
дайной дроби с ростом абсолютной величины аргумента. Так, для
=1 -ТТГ = =*"1 +4т ;
поведение при х—со такое же, как и у функций у= 1, у=х—Х,
у—х*—х-}-1 соответственно, и график первой из них приближает-
ся к прямой у = 1 (горизонтальная асимптота), второй — к прямой
у=*х— 1 (наклонная асимптота), а третьей к параболе у~х2-\~
4-хЦ-l- Поскольку целая часть дроби (Р„ и Sm — многочле-
Ли, (X)
ны соответственно степеней пит) имеет степень п—т, то при
п=т эта целая часть — константа, и, значит, график имеет гори-
зонтальную асимптоту, если п=ш4-1, то целая часть имеет вид
ахи, значит, график имеет наклонную асимптоту у=ах-^-Ь;
если же то график асимптотически приближается к
графику многочлена степени п—т, являющегося целой частью
дроби.
Еще одна характерная особенность графиков рациональных
дробей — наличие вертикальных асимптот в тех случаях, когда
знаменатель имеет корни. А именно если х=хо — корень знамена-
теля дроби, не являющийся в то же время корнем ее числителя, то
график такой дроби неограниченно приближается к прямой х—Хо,
уходя либо вверх, либо вниз при х, стремящемся к х0 слева (пи-
шут х—►хГ) или справа (пишут х—*-х^). Эта особенность вам
знакома из графика простейшей рациональной дроби у =-- (об-
ратной пропорциональности). В этом случае вертикальной асимп-
тотой служит ось ординат (прямая х=0) и ее не нужно было спе-
циально проводить. В других случаях асимптоту обязательно
изображают иа чертеже штриховой или тонкой сплошной линией.
Заметим, что график может приближаться к вертикальной
асимптоте с той или другой ее стороны (т. е. слева или справа)
лишь двумя способами: уходя иеограиичеиио вверх или же вниз.
То, какой из этих случаев имеет место, легко определяется по
знаку функции с соответствующей стороны вблизи асимптоты.
Если функция положительна, то ее график может уходить только
вверх, если же функция отрицательна — только вниз. Поэтому
вопрос о характере приближения рациональной дроби к верти-
кальным асимптотам легко решится после того, как будут опреде-
лены ее знаки (т. е. выполнен п. 4 схемы исследования функции).
Приведем несколько примеров построения графиков дробно-
рациональных функций с учетом сделанных замечаний.
288
Пример 1. Изобразим график
функции
Будем придерживаться пунктов приве- Рис. 209
денной ранее схемы.
1. Область определения функции*, х— любое действительное
число, кроме х— ±1
2. Нулей у данной функции нет.
3. Разложив знаменатель на множители, находим точки раз-
рыва: х= ±1.
4. Определяем с помощью «змейки» знаки функции (рис. 209).
Изображаем систему координат и наносим установленные знаки
функции (рис. 210, а}.
5. Корни знаменателя — 1 н 1. Значит, прямые х= — 1 и х== 1
являются вертикальными асимптотами графика данной дроби.
Проводим их на чертеже и, учитывая нанесенные знаки, изобра-
жаем «хвостиками» характер приближения графика к асимпто-
там (рис. 210, б).
6. Поскольку дробь правильная, то оиа стремится к нулю
прн х -> + оо и график ее имеет горизонтальную асимптоту —
ось абсцисс. Характер приближения к асимптоте изображаем пра-
вым и левым «хвостиками» графика (рис. 210, в).
289
7. Поскольку в формуле присутствует только четная степень х,
то функция четная и график ее симметричен относительно оси
ординат.
8. Соединяя изображенные «хвостики» плавными кривыми с
учетом знаков функции и ее четности, получаем эскиз графика,
отражающий характерные черты поведения данной функции
(рис. 210, г).
Пример 2. Изобразим график функции у= •
1- O(y)=R (функция определена при всех х, так как ии при
каких х знаменатель ие обращается в нуль).
2. Нулей у данной функции иет.
3. Точек разрыва иет.
4. Функция всюду положительна.
5. Вертикальных асимптот нет, так как функция всюду опреде-
лена.
6. Горизонтальная асимптота — ось Ох, поскольку дробь пра-
вильная.
7. Функция четная.
8. График функции изображен на рисунке 211.
Обратите внимание иа то, что рациональная дробь, у которой
знаменатель ие имеет корней, оказываетси всюду определенной и
график ее — непрерывная кривая. Вертикальных асимптот в этом
случае быть ие может.
А вот несколько примеров построения графиков дробной ра-
циональной функции, для случая, когда рациональная дробь не-
правильная
Пример 3. Изобразим график функции .
1. Область определения: х=#= —1.
2. Нуль функции: х = 0.
3. Точка разрыва: х~ — 1.
4. Определяем знаки функции (рис. 212).
-1 а 1 х Рис 211 -Xz-ZT * Рис. 212 290 у У — f -1 ^oi Л Рис. 213
5. Вертикальная асимптота — прямая х= — I.
6. Выделив целую часть, получим = 1 , и, зна-
чит. прямая является горизонтальной асимптотой. Поскольку
при х< — 1 дробная часть -^-у- , стремящаяся к нулю прн
х—*—оо, положительна, то график приближается к асимптоте
сверху, а прн х> — 1 дробная часть отрицательна н график при-
ближается к асимптоте j/=l снизу.
7. Функция не является ин четной, нн нечетной.
8. График функции у=—~ изображен иа рисунке 213.
хг
Пример 4. Изобразим график функции у—.
1. Область определения: x=#= —1.
2. Нуль функции: х=0.
3. Точка разрыва: х— — 1.
4. Определяем знаки функции (рис. 214).
5. Вертикальная асимптота х=— 1.
6. Выделив целую часть, получим у~х— 1 и» зна-
чит, прямая у—х—~ 1 является наклонной асимптотой. Учитывая
знак дробной части при больших по модулю положительных
и отрицательных значениях х. изображаем «хвостиками» прибли
жение к асимптоте.
7. Функция ие является нн четной, ни нечетной
8. График функции у= изображен на рисунке 215.
291
Рнс. 216
Пример 5. Изобразим график функции у=—i—
1. Область определения: х#=0.
2. Нуль функции: х== — 1.
3. Точка разрыва: х~0.
4. Определяем знаки функции (рисунок 216).
5. Вертикальная асимптота — прямая х=0 (ось ординат)
6. Из представления функции в виде у=х2+-ясно, что
при больших по модулю значениях х она ведет себя так же, как и
функция у—х2, т. е. график прн х—оо безгранично приближа-
ется к параболе у=х . Изображаем характер этого приближения,
учитывая знак дробной части-
7. Функция ие является ни четной, ни нечетной
8. График функции у= изображен на рисунке 217.
И в заключение пример обратной задачи иа конструирование
рациональной дроби с графиком, сходным с данным (рнс. 218).
292
Поскольку прямые x=s — 2, х=0, х=2 являются вертикальны-
ми асимптотами, то числа —2,0, 2 должны быть нулями знамена-
теля дроби. Будем искать знаменатель в виде (хЧ-2)" jf(x—2)’.
Поскольку в точке х=0 знак дроби не меняется, то р должно быть
четным. Изменение знака функции в точках х ——2 и х=2 обус-
ловливает нечетность чисел п и q. Положим и = I, р—2, д=1,т.е.
возьмем в качестве знаменателя многочлен (х-{-2)х2(х—2), тогда
приближение к асимптотам будет такое, как показано на рисунке
218, если положить числитель равным еднинЦе. Это можно сделать,
поскольку нулей у искомой функции ие должно быть и дробь долж-
на быть правильной, так как ось Ох является асимптотой ее графи-
ка. Итак, а качестве ответа можно положить _>, !—-г— .
Задачи
38. Изобразите графики дробно-рациональных функций:
а) 0=yAf- ; б) • а) 0=7535- : г) у=^~- :
и) ’ е) W=TT?" • ж> »=2'*=Г- з) у=-^^
39. Сконструируйте рациональные дроби, графики которых
сходны по форме с изображенными иа рисунке 219.
40. Для каждого из графиков, изображенных иа рисунке 203,
подберите соответствующую ему формулу из числа данных, зиая,
что каждой из этих формул отвечает один и только одни график иа
рисунке:
, а) У=^Т’ б) »=Т=?-; а) у=ТТ?-; г) у= ;
\ Д) У=х+2~я\ е) у = х + 2х; ж) 1/-2*2’1; з) У=^Г
Рис. 219
293
И) У= (-Ду-: к) л) »=1*1+?-;
«) у-^-.
Литература
1. Виленкин Н. Я. Функции в природе и технике.— М.: Про-
свещение, 1985.
2. Гельфанд И. М., Глаголева Е. Г., Ш н о л ь Э. 3.
Функции и графики.— М.: Наука, 1973.
3. Зельдович Я. В., М ы ш к и с А. Д. Элементы прикладной
математики.— М.: Физматгиз, 1965.
4. Зельдович Я. В., Я г л о м И. М. Высшая математика для
начинающих физиков и техников.— М.: Наука, 1982.
5. Колмогоров А. Н. Математика: наука и профессия.— М.:
Наука, 1988.
УРАВНЕНИЯ, НЕРАВЕНСТВА, ИХ СИСТЕМЫ
ДЕЛЕНИЕ МНОГОЧЛЕНОВ. КОРНИ МНОГОЧЛЕНОВ
1. Деление многочленов. Пусть А (х)=В (х) Q (х), где Д (х),
В (х\ Q (х) — многочлены от х. Тогда говорят, что многочлен
А (х) делится иа многочлен В(х), н пишут A(x)jfi(x). При этом
А (х) называют делимым, В (х) — делителем и Q (х) — частным от
деления А (х) на В(х). Свойства делимости многочленов похожи
на свойства делимости натуральных чисел. Например, если
Д(х)-В(х) и В(х):С(х), то Д(х)«С(х); если Д((х)-В(х) и
A2(x)iB(x)r то (Д] (x)XAs(x)):B(x); если А(х)1В(х), то н Д ЫХ
ХЛ4(х):В(х) н т. д.
В случае, когда А (х) не делится иа В (х), существует много-
член R (х), степень которого меньше степени В (х), такой, что
(Д (х)—Л(х));В(х). В самом деле, если степень А (х) меньше сте-
пени В(х), то полагаем R(x)—A (х). Тогда Д (х)—/?(х)=0 и по-
тому делится на В (х). Пусть теперь степень А (х) не меньше степе-
ни В (х), н пусть А (х)=аох" 4-... 4- «л, В (х)=/ох”+..•+/«,
ос#=0, /о#=О. Тогда у многочлена А (х)—^-х"_'пВ(х) ко-
эффициент при х" равен нулю, и потому его степень не превосхо-
дит п— 1. Продолжая описанный процесс далее, получим много-
член /?(х), такой, что степень /?(х)—Д (х)—В (х) меньше степени
В (х). Тогда имеем A (x)—R(x)—B (х) Q (х), и потому А (х)—R (х)
делится иа В(х).
Из равенства R{x)=A (х)— В (x)Q (х) следует, что Д(х)=
=B(x)Q (х)4-/?(х). Многочлен Q(x) называют неполным частным
от деления Д(х) на В (х), а многочлен R(x) — остатком от этого
деления. Покажем, что Q (х) н R (х) однозначно определяются
заданием А (х) н В (х). В самом деле, если
А (х)=В (x)Q1 (х)+Ri (х)=В (x)Q2 (x)+R2 (х),
где степень Ri (х) и R2(x} меньше степени В(х). то имеет
место равенство
В W (Qi (*)— Qz M)=R2 (х)—Ri (х). (1)
Но если Qi (x)=#Q2(x), то степень многочлена В (x)(Qi(x)~
— Qz(x)) не меньше, чем степень многочлена В (х), в то время как
295
степень многочлена /?2 (х)—Ri (х) меньше степени В (х). Поэтому
равенство (1) может иметь место лишь прн условии, что Qi (х) =
= Q2(x). Но тогда и Ri (х)=/?2(х).
Деление многочленов обычно выполняют по схеме деления
уголком. Приведем пример такого деления многочлена Зх* 6 + 2х4—
—2х3+х—6 на многочлен х4+2x4-2:
Зх6+2х4—2х3 + х— 6 |х4+2х+2
Зх6 +6х3+6х2 13х2 + 2
__2х4—8х3—6? + х— 6
2х4 4
/ —вх^—бх2—Зх—10
Неполное частное равно Зх2+2. а остаток равен —вх3—6х2—
—Зх—10.
Упражнения
1. Разделите с остатком следующие многочлены:
а) (х6-6х3 + 2х2-4):(хг-х+П: б) (х4+х2 + 1):(х+5);
в) (х7—1):(х3+х+1); г) (х6—64):(х—3).
2. При каком значении k выполняется без остатка деление
(х2+6х2+йх+ 12):(х+4)?
3. При каких значениях а и b выполняется без остатка деле-
ние (х4+Зх3-2х2+ах+6):(х2— З^+г)?
4. Упростите нижеследующие выражения и найдите области
определения исходных и получающихся после упрощения выра-
жений:
1____I 2х lx3 8х7
1—* 1+л 1+*г 14-** 14-л8 ’
а-^Ь____।___b+c___।_____с 4-о
(fe—-с) (с—а) ' (с—а)(а—b) ‘ (a~b)(b—-с) ’
(а-Ь?+(Ь-сУ+(с-аГ
( *-<* , - -2«\ л (1 _
\ as*+xa л3—вх’+л2*—оэ /\ а а*/
5. Докажите тождество:
а) (а2+Ь2+с2+d2) (х2 + у2+х2+/2)—(ах—by—cz—di)2+
+(fex 4- ay—dz+cf)2+(cx+dy + az—bt)2+(dx—cy + bz-j- at)2;
6) (a+b+c)4+(6+c—a)4+(c+a—Z?)*+(a+Z>—c)4=
—4 (a4 + b4 + c4)+24 (b2c2+a2b2+cza2).
6. Разложите многочлен на рациональные множители (коэф-
фициенты могут быть иррациональны):
а) х4+х2+1; б/ х4 + 1; в) х8 + х4 + 1; г) х,6-1.
а)
б)
в)
296
2. Теорема Безу. Корни многочлена. Пусть А (х) — многочлен
л-Й степени и & — некоторое число. Разделим А (х) на х—Ь.
Так как степень двучлена х—b равна 1, то остаток является неко-
торым числом г, поэтому имеем тождество А (х)=(х—b) Q(x)-f-r.
Чтобы вычислить г, подставим в обе части этого тождества зна-
чение х~Ь. Получаем А (Ь)=г. Итак, мы доказали следующую
теорему:
Теорема Безу. Остаток от деления многочлена А (х) на
двучлен х—Ь равен А (Ь), т. е. значению многочлена при х—Ъ.
Примеры.
1. Остаток от деления многочлена A (x)=x4-j- 15х8—ЗхЦ-6
на хД-3 равен А (—3)=(—3)*4-5(—З)3 —3(—3)4-6= — 39.
2. Многочлен А (х)=х”—отделится без остатка на х—а. В са-
мом деле, Д (а)=а"—а" = 0. Прямая проверка показывает, что
JC«_O"=(x_c)(je«-’+a/’-24-aV-34-.. .4-0"-’).
3. Многочлен A (x)=x2rt—а2" делится без остатка на хД-а.
В самом деле, А (—о)=(—а)2” —а2п=0.
Введем следующее определение:
Определение 1. Число а называют корнем многочлена
А (х), если А (а)—О.
Например, число 4 является корнем многочлена х8—6х24-6*4-
4-8, так как 43-6-424-6-44-8 = 0.
Из теоремы Безу вытекает следующее утверждение:
Если число а является корнем многочлена А (х), то А (х) де-
лится на х—а.
Очевидно, что справедливо обратное утверждение: если А (х)
делится на х—а, то а — корень А (х). Поэтому задача отыскания
корней многочлена равносильна задаче отыскания его линейных
делителей.
Покажем, что если а н ₽ — различные корни многочле-
на А (х), то А (х) делится иа (х—а)(х—р). В самом деле, так как
А (сс)=О, то Д (х) делится без остатка иа х—а, т. е. 4(х)=
=(х—cc)Q(x). Подставив в обе части этого равенства х=р,
получим А (р)=(Р—a) Q (Р)=0. Поскольку р#=а, то отсюда сле-
дует, что Q (Р)=0, и потому Q(x) делится на х—р, т. е. Q (х)=
=(х— р) Qi (х). Значит, А (х)—(х—а) (х—р) Qi (х), т. е. А (х) делит-
ся иа (х—сс)(х—р).
Предоставляем читателю возможность доказать, что если
ai, ..., а„— попарно различные корни многочлена А (х), то
А (х) делится иа (х—cci)... (х—сся). Из этого утверждения вытека-
ет следующая теорема:
Теорема 1. Если степень многочлена А (х) не превосходит н
и если А (х) обращается в нуль при п-[-1 различных значениях х,
то все коэффициенты А (х) равны нулю.
Доказательство. Пусть otj,_______ an+i — корни А (х). Тог-
да А (х)=(х—cci)... (х—a«+i) Q (х). Но степень (х—сы)...
297
(x—cc/i+t) равна п 4-1, а степень А(х) не превосходит п. Поэтому
равенство может иметь место лишь в случае, когда А (х) н Q (х) — ну-
левые многочлены.
Следствие. Если степени многочленов А (х) н В (х) не
превосходят п и если эти многочлены принимают одинаковые
значения при п 4-1 различных значениях х, то многочлены А (х)
и В (х) совпадают (т. е. они имеют одинаковые степени и одина-
ковые коэффициенты при соответствующих степенях х}.
Для доказательства достаточно применить теорему 1 к раз-
ности многочленов А (х)—В (х).
Пример. Докажем тождество
(х-ЪЦх-с) । (х-с)(х-а) . (х—а)(х—Ь) __ . , п
(а—Ь)(а—с) ’ (&—в) ' (с—а)(с—Ь) ‘ 1 1
Решение. Подставим в обе части тождества поочередно
значения х, равные a, bt с. При каждом нз этих значений обе части
принимают одинаковое значение, равное 1. Так как степени мно-
гочленов слева и справа не больше чем 2, то эти многочлены тож-
дественно равны.
Если а — корень многочлена Д (х), то А (х) делится на х—а.
Может случиться, что А (х) делится и на некоторую степень х—а.
Если А (х) делится на (х—а)‘, ио не делится на (х—cc)*+l, то гово-
рят, что а — корень кратности k для А (х).
Пример 5. Докажем, что 2 является корнем кратности 2 для
многочлена А (х)=х3—х2—8x4-12.
Решение. Имеем А (2)=23—22—8-2 4-12=0. Значит, 2 —
корень многочлена А (х). Разделив А (х) на х—2, получаем Q (х)=
—х24-х—6. Так как Q(2)=22-Ь2 —6=0, то Q(x) делится иа
х—2. Прн делении получаем х4-3. Для многочлена x-f-З число 2
не является корнем. Значит, А (х)=(х—2)2(х4^3), причем х-ЕЗ
не делится иа х—2. Поэтому х=2 — корень кратности 2 для А (х).
Упражнения
7. Найдите остаток от деления 6хе4-4х44-х3—2х2+5 иа х-|-3.
8. Докажите, что многочлен x2kj-a2k не делится иа x-j-o.
9. Докажите, что х2*+!4-а2*+* делится на х-^-а.
10. Докажите тождество:
а) а. (*-»)»-«) . . (х-д)(х-1>)
' (а-Ь)(а~с)^и (Ь-с)(Ь-а) (с-а)(с-Ь) ’
(x-fc)(x-c). , 2 (х-с)(х-д) . 2_ (x-c)(x-fc) 2
’ (а—Ь}(а~с)*° (Ь-сЦЬ-а) (с-а)(с-Ь)
11. Какую кратность имеет корень х=2 многочлена х''—5х*4-
-}-7х3—2х24-4х—8?
12. Какую кратность имеет корень х=5 многочлена х6—
- 15х< 4-76х2- 140х24-75х-125?
298
13. При каких а н b чнсло (—2) является корнем кратности 2
для многочлена хъ+ах?±Ьх-)-1?
14. Составьте алгоритм для отыскания кратности корня мно-
гочлена.
3. Формулы Виета. Пусть А (х) — многочлен степени п н
ai,..., вл корни этого многочлена (каждый корень выписывает-
ся столько раз, какова его кратность). Тогда А (х) делится на
(х—а0 ... (х—аи). причем частное является многочленом нулевой
степени, т. е. числом. Значит, А (х)=а(х—cq) ... (х—<xrt). Чтобы
найти а, раскроем справа скобки и найдем старший член многочле-
на. Он имеет вид сх". Значит, а равно коэффициенту при старшем
члене многочлена Л (х). Если А (х)=аохп+.. то а—ао- Итак,
А (х)—оо (х— со) . (х—аД (1)
Ряд тождеств, связывающих корни многочлена А (х) с его
коэффициентами, получается, если раскрыть скобки в тождестве
(1) и сравнить коэффициенты при одинаковых степенях х слева
и справа. Ради простоты сделаем это лишь в случаях, когда п—2
и п=3.
При л—2 равенство (1) имеет вид A (x)=ao(x—cti)(x—сс2),
откуда следует, что
Оох2+а1х 4- а2=а0х2—а0 (а» +а2) х+аьаде.
Поэтому
сС|-|-ссг—--, СС1СС2——
По Оо
Итак, сумма корней квадратного трехчлена равна отношению ко-
эффициентов при х н х , взятому с противоположным знаком,
а произведение этих корней равно отношению свободного члена
к коэффициенту при х2.
При п—3 аналогично выводим равенства:
-- , , ai
ai -|-а2-4аз— —>
a 1CI2 + СС1СС3-}-а2ССз=-^-.
aia2Ci3= —— .
во
Аналогичные тождества справедливы при любом п. Напри-
мер, при всех п имеем:
-разЧ-- - ,
(~!)явя
- ескхг.. .аи —5—<—.
во
Формулы, связывающие коэффициенты многочлена с его кор-
нями, называют формулами Виета по имени французского ученого
XVI в., впервые получившего их. Мы доказали эти формулы при
условии, что число корней уравнения (взятых столько раз, какова
их кратность) равно степени многочлена. Можно доказать, что
если брать и комплексные корни, то это условие всегда выполня-
ется.
Упражнения
15. Составьте кубический многочлен, имеющий корень 5 крат-
ности 1 и корень —4 кратности 2.
16. Найдите такое значение k, что корни квадратного много-
члена x24“2(fe—4) х 4-4-6^4-2 равны между собой.
17. Прн каком значении m корни квадратного уравнения
*равны по модулю н противоположны по знаку?
18. Напишите квадратный трехчлен, корни которого равны
квадратам корней трехчлена х2—7x4-13.
19. Напишите квадратный трехчлен, корни которого обратны
корням трехчлена х24- 11x4-3.
20. Напишите квадратный трехчлен, корни которого являются
кубами корней трехчлена хг4-13х—1.
21. Прн каких а, Ь, с оба корня квадратного трехчлена
ах2+Ьх-1-с положительны?
22. Докажите, что если корни трехчлена ох2 4-5x4-с Дей-
ствительны, то многочлен (2ах4-5)2—2а (ах2 4-Ьх 4-с) ие имеет
действительных корней.
4. Многочлены с целыми коэффициентами. В случае, когда все
коэффициенты многочлена — целые числа, а коэффициент при
старшем члене равен 1, целые корни этого многочлена можно
находить с помощью следующей теоремы:
Теорема 1. Пусть числа а1ж а2, • • •> ап — целые. Тогда
любой рациональный корень а. многочлена A (x)=xn4-aIxn~1 4-
4-а2х"~24-.. «Ч-а,! является целым числом, на которое делится
свободный член ап этого многочлена.
Доказательство. Сначала докажем, что а — целое чис-
ло. В самом деле, в противном случае а—где -------несокра-
тимая дробь и <7^2. Поскольку А (сс)=О, то имеем 4-
+• • -4-ал=0. Умножим обе части этого равенства
на qn^. Все члены, кроме первого, окажутся целыми числами, а
тогда и •£- должно быть целым числом. Но это не так: поскольку
р и q — взаимно простые числа, то рп и q тоже взаимно просты, а
300
тогда дробь несократима и •£- ие может быть целым числом.
Значит, многочлен А (х) не может иметь дробных корней.
Теперь докажем, что целое число k может быть корнем много-
члена А (х) лишь в случае, когда ar-k. В самом деле, если A (k)=0,
то имеем kn-j-alkn~i 4- .4-ая_1А+аЛ=0, и потому ап=— kn —
—a\kn~*—...—an-ik. Все слагаемые а правой части этого ра-
венства делятся на k, значит, и аа делится на k.
Из доказанной теоремы вытекает следующий метод отыскания
целых корней многочлена А (х) с целыми коэффициентами и тако-
го, что Оо=1: надо выписать все делители свободного члена
(как положительные, так и отрицательные) и по очереди под-
ставить их в многочлен. Те делители, подстановка которых обра-
тит многочлен в нуль, и являются его целыми корнями. Для каждо-
го из этих корней надо еще определить его кратность.
Замечание 1. Отбор корней можно ускорить с помощью
следующего утверждения, доказательство которого предоставляем
читателю:
Теорема 2. Пусть а — целый корень многочлена А (х)=хп4-
4-aix"“‘4-- - -+«л с целыми коэффициентами. Тогда для любого
целого k число A (k) делится на a — k. (При доказательстве
используйте тождество 0=А (а)—(а — k) Q (а)-|-А (fe).)
Замечание 2. Если ао, fli, ..ап — целые числа и а =-&-
Я
(где-^--несократимаи дробь) — корень многочлена аох" 4~ • • •+
4~Gn, то и Untp
Пр и м е р. Найдем целые корни многочлена
А (х)=х4 4-х3 —Их2—5x4-30.
Решение. Делителями свободного члена 30 являются числа
±1, ±2, ±3, ±5, ±6, ±10, ±15, ±30. Вычтем из каждого
делителя число 1 и выясним, какие из разностей являются дели-
телями числа А (1)= 16. Ими являются —2,1,2, —4,4, —16, соот-
ветствующие делителям — 1, 2,3, —3, 5, —15. Далее прибавляем
к этим делителям 1 и смотрим, какие из полученных сумм явля-
ются делителями числа А (— 1) = 24. Ими являются числа 3, 4, —2,
6, соответствующие делителям 2, 3, 3, 5. Подставляя эти числа
в А (х), находим, что целыми корнями А (х) являются числа 2 и —3.
Из теоремы Безу вытекает, что А (х)-(х—2)(х4-3). Выполняя
деление, получаем, что
X* 4-х3 -11х2—5х 4-30=(х—2) (х4-3) (х2 — 5).
Значит, данные корни ие являются кратными. Еще два корня дан-
ного многочлена можно иайти, решая уравнение х2—5=0. Ими
являются -^5 и —-^5 (не целые числа). Ответ: 2; —3.
301
Упражнения
23. Найдите целые корни многочлена:
а) х5 —2х3 —8х! + 13х-24;
б) х4+2х3 — 12х3—38% —24;
в) х5—2х4—4x3+4x®—5х+6;
г) х5+х4—бх3 —Нх3—Их—3.
24. Разложите на множители многочлен:
а) х3+9хг4-23х+15;
б) х3 — 10хг+23х—14;
в) х3—6хг4-11х—6;
г) х4-7х3+8хг+28х-48;
д) (х+ 1)(х + 2)(х+3)(х4-4)~24;
е) (x+l)(x+3j(x+5)(x+7)+15.
25. Сократите дробь
28. Докажите, что прн любом целом значении п число л5—
—5п34-4н делится на 120.
УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
1. Основные определения. Равенство айда А (х)=В (х), где
А (х) и В (х) — выражения, зависящие от х, называют уравнением
с неизвестным х. Если выражения А (х) и В (х) рациональны
(т. е. получаются из х и чисел с помощью операций сложения,
умножении и деления), то уравнение Л (х)=В (х) называют ра-
циональным. Примерами рациональных уравнений могут служить
х'-6х+5=0, x’ + l-O, |=£-1 и др.
Число а называют корнем уравнения А(х)=В(х), если прн
замене буквы х этим числом получается верное числовое равенст-
во, т. е. если выполняется равенство А (а)= В (а). Решить уравне-
ние — значит найти все его корни или доказать, что оио не имеет
корней. Если корнями уравнения являются числа ©ti.а», то от-
вет записывают либо в виде {ои, ..аЛ], либо в виде Xi =ai, ...»
х„=ая. В случае отсутствия корней пишут: «Уравнение ие имеет
корней».
Пример 1. Корнями уравнения (х—4)(хЧ~3)(х—л)=0 яв-
ляются числа 4, —3, п — при подстановке вместо х одного из этих
чисел один из множителей х—4, х-{-3, х—п обращается в нуль,
а остальные — в какие-то числа. Поэтому произведение равно
нулю. Иных корней это уравнение не имеет: если подставить
аместо х число, отличное от 4, —3, л, то все множители станут
отличными от нуля числами, а их произведение будет тоже от-
лично от нуля.
Пример 2. Уравнение ие имеет корней. В са-
мом деле, при любом значении х выражение положи-
302
тельно и потому отлично от нуля. Замечание. Позднее вы
познакомитесь с комплексными числами. Одним из этих чисел
является число I, такое, что /2-|-1=0. Ойо является корнем дан-
ного уравнения. Другим его корнем является число — i, и (—Г)2 +
+ 1=0. В дальнейшем мы будем говорить так: «Уравнение
ие имеет действительных корней».
Пример 3. Уравнение не имеет ни действи-
тельных, ни комплексных корней — при любом значении х раз-
ность х—х обращается в нуль и выражение * +х не имеет
числового значения.
Пример 4. Уравнение (х—2)2(х+3)4=0 имеет лишь два
корня: 2 и —3. Считают, что корень 2 имеет вторую кратность, а
корень — 3 — четвертую кратность.
Пример 5. Для уравнения (х+ 1)2=х2+2х+ 1 все числа яв-
ляются корнями — при любом значении х выполняется равенство
(*+ 1)2=х^ + 2х+ I. Решением этого уравнения является совокуп-
ность R всех действительных чисел. Это уравнение имеет беско-
нечно много корней.
Для уравнений более сложных, чем рациональные (иррацио-
нальных, тригонометрических и т. д.), может случиться, что реше-
нием является числовой отрезок, числовой луч, серия чисел, за-
даваемая выражением, зависящим от целого числа п, и т. д.
Прежде чем решать уравнение А (х)—В (х), полезно установить,
какие значения может принимать неизвестное х. Для этого надо
найти, при каких значениях х имеют числовое значение выраже-
ния А (х) и В (х). Совокупность таких значений называют областью
допустимых значений х для данного уравнения. Пишут кратко:
одз.
Пр и м е р 6. Найдем ОДЗ для уравнения
з 2
х— 2 *4-1
Решение. Левая часть уравнения тождественно равна
а З
—^7^**— Поэтому она имеет значение лишь при х, отличных
(х-2)(*+1)
от чисел 0, 1, —10, 2, —1. Значит, ОДЗ получается выбрасыва-
нием из числовой прямой указанных чисел. Пишут-
Я\(0; 1; —10; 2; -1}.
Заметим, что если заменить «четырехэтажиую» дробь обычной.
получаем уравнение
(х-3)(х-2) (*+!)_
х(х—1)(х+10) '
(2)
303
Его ОДЗ имеет вид R\{0; 1; —10} и потому отлична от ОДЗ урав-
нения (I). Дело а том, что равенство
х З
*(*-!) _у*—3)(х—2)(*4-l)
х+10 х(х— 1)(х+10)
(*—2)(*-J-l)
имеет место лишь прн условии, что х отлично от чисел 0; 1;
— 10; 2; 1.
Изменение ОДЗ может привести к изменению решения урав-
нения. Например, числа 2 и — 1 являются корнями уравнения (2),
ио ие удовлетворяют уравнению (1). Аналогично число 3 не явля-
ется, например, корнем уравнения 2х+*2.3'—но Удов‘
летворяет уравнению 2х=6, получаемому из данного приведением
подобных слагаемых и —•
2. Следствие уравнения. Равносильные уравнения. Введем сле-
дующие определения:
Определение 1. Уравнение
C(x)=D(x) (1)
называют следствием уравнения
Д(х)—(2)
если каждый корень уравнения (2) удовлетворяет уравнению (1).
Иными словами, если для некоторого числа а выполняется
равенство А (а)—В (а), то выполняется равенство C(a)—D (а).
Уравнение, получаемоеиз заданного путем приведения подоб-
ных членов, раскрытия скобок, сокращения дробей, является След-
ствием данного уравнения.
Пример 1. Уравнение х2+2х—8=0 является следствием
уравнения
Ц-—Ц-+ Р*-8И*±Д-=о, (3)
' X—2 X—2 *4-4
так как получается из него с помощью следующих операций: при-
ведение подобных членов Зх2 и —2х2, приведение к нулю разности
2—7—2 ’ сокРаш‘ение Дроби (2х~8Н*+.4) иа x-j-4.
Если решено уравнение (1), т. е. следствие данного уравне-
ния (2), то корни уравнения (2) содержатся среди найденных чи-
сел. Чтобы отобрать корни уравнении (2), надо проверить найден-
ные корни уравнения (1), подставив их в уравнение (2). В некото-
рых случаях задача отбора корней облегчается знанием ОДЗ дан-
ного уравнения — корни, ие принадлежащие ОДЗ, можно сразу
отбросить.
304
Например, решая уравнение х24-2х—8=0 из примера I,
находим корни Х|=2 и хг= —4. Но эти кории ие удовлетворяют
заданному уравнению, так как при х=2 ие имеет числового значе-
ния слагаемое , а при х= —4 обращается в нуль знаменатель
слагаемого • Значит, уравнение (3) ие имеет корней
При решении уравнений полезны следующие утверждения, по
зволяющие строить уравнения-следствия:
Теорема 1. Пусть выражение С (х) имеет числовое значе-
ние для всех х из ОДЗ уравнения
А(х)=В(х). (4)
Тогда уравнения
А(х) + С (х)=В (х) ±С (х), (5)
А (х) С. (х) В (х) С (х) (6)
являются следствиями уравнения (4).
Доказательство. Пусть а — корень уравнения (4). Тог-
да выполняется числовое равенство Д(а)=В(а). Поскольку при
х = а имеют числовые значения и А (а), и В (а), то а принадлежит
ОДЗ уравнения (4). Значит, при х=а имеет числовое значение
С (а) и выражение С(х). Прибавляя С (а) к обеим частям равенст-
ва А (а)=В (а), получаем верное равенство А (а)-|- С (а)=В (а)4
+ С (а). Оно показывает, что а является корнем и уравнения (5)
Значит, всякий корень уравнения (4) удовлетворяет уравне-
нию (5), т. е. (5) — следствие уравнения (4). Утверждение об
уравнении (6) доказывается аналогично.
Если нарушено условие существования значений С(х), то
при добавлении к обеим частям уравнения слагаемого С (х) может
получиться уравнение, не являющееся следствием заданного. На
пример, уравнение 2хЧ-^-у=8+-^-у ие является следствием
уравнения 2х=8. В самом деле, число 4 является корнем урав-
нения 2х=8, ио ие удовлетворяет уравнению 2х-Е *_4-=8-Е——
Серьезной ошибкой, которую часто делают при решении урав-
нений, является деление обеих частей уравиеиия на одно и то же
выражение. Получающееся при этом уравнение ие ивляется обыч-
но следствием заданного, т. е. при таком делении происходит по-
теря корней.
Пример 2. Одним из корней уравнения 6х(х—3)= 12 (х—3)
является число 3. Если разделить обе части уравнения на х—3
(как говорят, сократить уравнение иа х—3), то получится урав-
нение 6х= 12. Оно имеет лишь один корень 2. Корень 3 при сокра
щеийн потеряй.
305
Проверки корией можно избежать, если при переходе к ново-
му уравнению мы ие только не теряем корней, но и не приобретаем
новых.
Определение 2. Два уравнения называют равносильны-
ми, если каждый корень первого из них удовлетворяет второму
уравнению, а каждый корень второго уравнения удовлетворяет
первому.
Иными словами, два уравиения равносильны, если каждое из
них является следствием другого.
От уравнения (5) можио вернуться к уравнению (4), прибавиа
к обеим частям слагаемое — С (х) (которое тоже имеет числовое
значение для всех х из ОДЗ). Если, кроме того, С(х)=#О в ОДЗ
уравнения (4), то от уравнения (6) можио вернуться к уравнению
(4), разделив обе части уравнения на С(х) (из-за того, что
С(х)#=0, потери корией при этом ие произойдет). Поэтому спра-
ведлива еще одна теорема.
Теорема 2. Если С (х) имеет числовые значения для всех х
из ОДЗ уравнения (4), то это уравнение равносильно уравне-
нию (5). Если, кроме того, С (х) ие обращается в нуль в ОДЗ урав-
нения (4), то уравнение (4) равносильно уравнению (6).
Упражнения
27. Равносильны ли уравнения:
а) 4х2—2х—1— 2х и 4х2=1;
б) 4*—14-_|_=Зх+_Л_ и 4х—1=3х;
в) 4х— l+7^j-=3x+^j- и 4х—1 = 3х?
28. Решите уравнение и сделайте проверку
6) ^r-dr=2+S7^
ч Зх—1 2х—5 4 _।.
' л-1 х+3 * *®+2х—3
г) £+1— *+2 и- _. __—о
' х—1 л+З 3
3. Основные методы решения уравнении. Для решения урав-
нений чаще всего применяют следующие методы:
А) разложение на множители;
Б) введение нового неизвестного;
В) переход от уравнения А (х)— В(х) к уравнению вида
f(A(x))=f(8(x)).
306
Рассмотрим эти методы подробнее.
А) Любое уравнение А(х)—В(х) равносильно уравнению
(л)— Z?(x)=0. Поэтому будем рассматривать лишь уравнения,
^правая часть которых — нуль. Мы знаем, что произведение двух
|чисел равняется нулю лишь в случае, если хоть одно из инк
[равно нулю. Поэтому равенство А (а) В (а)=0 может выполняться
’лишь в случае, если хоть одно из чисел А (а), В (а) равно нулю.
Иными словами, любой корень а уравнения А (х) В (х)=0 являет-
ся корнем хотя бы одного из уравнений А(х)=0, В(х)=0
Итак, мы доказали следующее утверждение:
Теорема. Корнями уравнения А (х) В (х)=0 могут быть
лишь числа, являющиеся корнями хотя бы одного из уравнений
A<x)=0, Bfx)=0.
Заметим, что ие всякий корень уравнения А (х)=0 или урав-
нения 8(х)=0 удовлетворяет уравнению А(х)В(х)=О— может
случиться, что А (а)=0, ио В (х) ие ямеет значения при х—а. На-
пример, число 3 яе является корнем уравнения (х—в
=0, так как при х=3 выражение } х не имеет числового
значения. Поэтому, найдя корни уравнений А (х)=0 и В (x)s=0,
надо еще проверить их — выяснить, имеет ли при этом значении х
числовое значение другой миожитель.
Пример I. Решите уравнение 2х3—Зх2—8x4-12=0.
Решение. Так как 2х3—Зх2—8хЦ- 12=х2 (2х—3)—4 (2х —
—3)=(х2—4) (2х—3)= (х—2) (х 4-2) (2х—3), то для решения дан-
ного уравнения надо решить уравнения х—2=0, х4-2=0 и
2х—3=0. Корнем первого уравнения является число 2, второго —
число —2, а третьего — число -|-. Значит, решение уравнения
имеет вид ^2, —2, или иначе Х]=2. х2=—2, х3=-|-.
Б) Чтобы решить описываемым нами методом уравнение
А(х)=0, вводят новое неизвестное у=В{х) и выражают А (х)
через у, т. е. А{х)—С(у). После этого решают уравнение
С (у)=0. Приравнивая поочередно В (х) найденным корням yi.
уь уравнения С(у)=0, получаем k уравнений, из которых нахо-
дим корни заданного уравнения.
Пример 2. Решим уравнение ~ 12=0.
Решение. Положим Уравнение принимает вид
у2—8у4-12=0. Это квадратное уравнение имеет корни $л=2,
1/2=6. Теперь решаем уравнения —~—=2 и ~ГТ—6. Из пер-
307
вого находим х= — 2, а из второго х=—|-. Значит, решение
заданного уравнения имеет вид { —2;
Отметим два вида уравнений, решаемых указанным способом.
Уравнения вида 0 называют биквадратными.
Они сводятся к квадратным с помощью подстановки з^~у.
Пример 3. Решим уравнение х4—5х2—36=0.
Решение. Положим х2—у. Уравнение принимает вид у2—
—5у—36=0. Кориями этого квадратного уравнения являются
z/i=9, У2= —4. Уравнение х2= — 4 не имеет (действительных)
корней, а уравнение х2=9 имеет корни 3 и —3.
Теперь рассмотрим уравнения вида
ах4-|-6х34-сл^+6л+с=0 (1)
(т. е. уравнения четвертой степени), у которых равны коэффициен-
ты, одинаково удаленные от начала и от конца. Такне уравнения
называют возвратными. Для решения уравнения (1) разделим
обе части иа х2 и сгруппируем члены с одинаковыми коэф-
фициентами. Получим уравнение
+ь(х+*г)+с=0 <2>
Положим теперь х4”=У- Тогда имеем ==(*+”) =^2+
4-24—т» и потому х24-Л-=у2—2. Значит, уравнение (2) примет
вид а (у2—2)4-Ьу4'с=0- Решая это квадратное уравнение, на-
ходим корни yt и у%. Теперь осталось решить уравнения х4~
+4=»‘ и x-f-X-=g2.
Пример 4. Решим уравнение 6х44-35х34-62х24-35х4-6=0.
Решение. Полагая х 4-~= У, получим уравнение 6 (у2—2)4-
4-35^4-62=0. Его корнями являются yi = —y~> у?= —Ре-
шая уравнение х4~ -—•= — —, находим корни Х\ = — 3, х2= —
а из уравнения л 4-—- корни х3=— 2, х^~—Значит,
решение данного уравнения имеет вид{—-3; — —2; —
Предоставляем читателю проверить, что уравнения вида
ах4 4- bxs 4- сх2 4- ЬЛх 4- а.'к2=0
решаются подстановкой х-\-~-=у.
В) Применение этого метода будет изложено в п. 4
308
Упражнения
29. Решите уравнение:
а) х4- 13х2 + 36=0; б) х'+26х2 —360=9;
в) (2х— 1)2 + 3(2х-0—10=0; г) (х-2)6-19(х-2)3=216.
30. Решите уравнение:
а) х’ + 5х3 + 2х2 + 5х+ 1=0;
б) х4 — 10х3 + 26х2— 10x4-1=0.
4. Иррациональные уравнения. Выражение А (х), получаемое
из чисел и переменной х с помощью операций сложения, умно-
жения, деления и извлечения корня и содержащее переменную
под знаком корня, называют иррациональным. Примерами ирра-
циональных выражений от х могут служить
Vx+4—л/Зх+7, —бх+т/х+5, И т. д.
Уравнение вида А (х)=*В (х), где А (х) или В (х) — иррациональ-
ное выражение, называют иррациональным. Любое такое урав-
нение равносильно уравнению вида С(х)=0, где С(х)=А(х)—
—В (х) — иррациональное выражение. Напомним, что мы понима-
ем знак радикала следующим образом: 2!\/а, где а>0 — неотри-
цательное число, такое, что (2гх/а)2/г=а; 2я+\/а — число, такое, что
(2я+^а)2я+,=а. Имеет место равенство
Иррациональное уравнение -\/х4-7= —1 не имеет корией,
так как при любом значении х его левая часть неотрицательна,
а правая отрицательна. Не имеет корней и уравнение -\/х—6+
4—у^4—х=5. В самом деле, выражение -фс—6 определено при
Х>6, а выражение ^4~х — при х^4. Но лучи [6; 4-оо) и
(— оо; 4] не имеют общих точек. Поэтому ОДЗ данного уравнения
ие содержит нн одной точки (как говорят, она пуста). Не имеет
корией и уравнение х+^/х—3 = — 1 (легко проверить, что в его
ОДЗ левая часть положительна).
При решении иррациональных уравнений их стараются свести
к рациональным уравнениям. Для этого используют следующую
теорему:
Теорема. Уравнение Ап (х)=Вп (х) является следствием
уравнения А (х)=В (т).
В самом деле, если А(а)—В (а), то Ап (a)—Bn (а.).
Обратное утверждение, вообще говоря, неверно, т. е. уравне-
ния А(х)=В(х) и Ап (х)=Вп (х) могут быть не равносильными.
Например, уравнение А2(х)=В2(х) можно переписать в виде
А2(х)—В2(х)=0, т. е. (А(х)4-В(х))(А(х)—В(х))=0. Отсюда сле-
дует, что А (х)-ЬВ (х)=0 или А (х)—В (х)=0. Значит, кроме корией
уравнения А (х)=В (х), уравнению А2 (х)=В2 (х) удовлетворяют и
Э09
корни уравнения А(х)=—В(х). Эти корни являются, вообще го-
воря, посторонними для уравнения А(х)—В(х). Чтобы отделить
посторонние корни, надо подставить все найденные корни в за-
данное уравнение.
При решении иррациональных уравнений применяют способ
уединения радикалов — записывают уравнение в виде А (х)=
=Л]В (х) и возводят обе части в степень п, освобождаясь тем са-
мым от одного из радикалов. Иногда эту операцию приходится де-
лать несколько раз.
Пример 1. Решим уравнение:
а) Л/хг+х+1=х-4; б) V^+2x+10=2x—1,
в) дРф5+Т?+2Г=8; г) VhT+^4^x=5.
Р е ш е и и е. а) Возводя обе части в квадрат, получаем уравне-
ние х24-х4-1=х2—8x4-16. имеющее корень Этот корень
ие удовлетворяет заданному уравнению, так как при х=-|-правая
часть принимает отрицательное значение, в то время как левая
часть неотрицательна. Уравнение не имеет решений
б) Возводя обе части уравнения в квадрат, получаем квадрат-
ное уравнение х24-2х-|- 10=4х2—4x4- I, имеющее корни 3 и —I.
Проверка показывает, что из иих данному уравнению удовлетво-
ряет лишь х=3 (при х= —1 правая часть уравнения принимает
отрицательное значение).
в) Перенесем т/х*4-21 в правую часть уравнения и возведем
обе части уравнения в квадрат. Получаем:
х2 4- 5= 64 —16 + 21'4-х2 4-21.
Это уравнение равносильно уравнению ^х?4-2Г=5. Снова воз-
ведем обе части уравнения в квадрат: х2 4-21=25. Кориями
этого уравнения являются 2 и —2. Оба числа удовлетворяют
заданному уравнению. Значит, решение имеет вид {—2; 2}.
г) Возведем обе части уравнения в куб. Получаем х4-14~
4-3 V(^4-l)(34—х)4-3 V(x-H)(34-x)a4- 34 -х= 125, откуда
V(x4-1) (34—х) (^х 4-14-^34—х)=30, и так как V*+1 +
4-^34 — х=5, то выводим уравнение ^/(х 4-1) (34 — х)=6, являю-
щееся следствием данного уравнения. Возводя обе части полу-
ченного уравнения в куб, получаем квадратное уравнение
(х4-1)-(34—х)=216, имеющее корни 7 и 26. Проверка показывает,
что оба корня удовлетворяют заданному уравнению.
При решении иррациональных уравнении тоже иногда бывает
полезным введение новых неизвестных.
Пример 2. Решим иррациональное уравнение
х2 4- 2х 4- V?4-2x4-8— 12 =0.
ЗЮ
Решение. Положим Vх*+2*4-8—1Л Так как г/г=ха4-2х4-
4-8, то уравнение примет вид у^+у—20=0. Это квадратное урав-
нение имеет корни 4 и —5. Поскольку корень —5 отбра-
сываем, а из уравнения -\/х2 4-2*4-8=4 получаем ха4"2*__8 = 0,
откуда находим, что *i=—4, Хг=2
Упражнения
31. Докажите, что каждое из следующих иррациональных
уравнений не имеет действительных корней:
а) у/2х4-3-|-у/х—3=0; б) yfir+24-y/x—1 = —2;
в) V*-х—V*—8=2; г) Vx+Vx+9=2;
д) Vx—1+х2+х=0.
Решите уравнения (32—35):
б) у/х+9=2х-3;
32. а) у^2х—7х=—52;
в) 2х-|-у/4х—8=-|-,
г) y^x+7+y/3x-I8=y/Zx+t;
д) 2 у/х— 1 — 5= Д-; е)
ух—1
ж) у/2х— I —у/х —1 = 1; з)
у^=5+у/гГ7=2;
у/41—Зх—у/9—Зх=2 у/5+х.
б)
г)
Ух-з Vt-s .
Ух-4 Ух-8 '
т/5+х4-УЗ—х. , 5 .
y/S+x—75—* * ’
д)
34. а)
б) (а4-Ь}yfa24“624-x2— (а—Ь)-^а2+Ь2—я^ =а24-Ь2\
a) х 4-у/х 4“ "Vх 4-2 4-у/х2 4-2х=0;
. уг+г+ух‘-1 уг+т-ут^т
’ уРТ1-Ух’=тТуГх,'+14-У?^Т
д) у/х2 - Зах 4- as 4- у/х2 4- Зах 4- а2=V2 (с14- б2);
е)
ж) Vх—12=1.
311
35. а) x2+3—^хг—Зх+2=|-(х+1);
б) х (х+1)4-3 л/2х8+6х+5=25—2х;
в) хг-2уЗх2-2ах+4+4=^-(х+|-+1);
г) (а+х)’ 4-4(а—х)3 =5(о!—х2)'3.
СИСТЕМЫ УРАВНЕНИИ
1. Основные определения. Пусть А (х; у) и В (х; у) — выраже-
ния, зависящие от х и у. Равенство А (х; у)= В (х; у) называют
уравнением с двумя неизвестными хну. Любую пару чисел (а; ₽),
такую, что А (а; 0)=В (а; 0), называют решением этого уравнения.
Как правило, уравнение с двумя неизвестными имеет бесконечное
множество решений. Например, уравнению 2x4-$/—4=0 удовлет-
воряют пары чисел (0; 4), (2;0), (3; — 2) н т. д. Вообще
любая пара чисел (t 4—20, где 1 — любое число, удовлетворяет
этому уравнению.
Каждой паре чисел (а; 0) соответствует точка М (а; 0) коорди-
натной плоскости. Поэтому уравнение А (х; у)~В (х', у) задает,
вообще говоря, бесконечное множество точек на плоскости. Обыч-
но эти точки образуют некоторую кривую. Говорят, что А (х; у^=
=В(х; у) является уравнением этой кривой.
Пример 1. Найдем линии, изображаемые уравнениями:
а) Зх — 2^4-6=0; б) хг4-$/2—6x4-8$/=0.
Р е ш е и и е. а) Из заданного уравнения находим, что у—~-х-}-
4-3. Это -— уравнение прямой линии на плоскости, имеющей угло-
вой коэффициент ~н проходящей через точку М (0; 3) (рис. 220).
б) Выделяя полные квадраты, запишем данное уравнение в
виде (х—З)2 4-(У 4- 4)2=25, т. е. уравнение окружности радиуса 5 с
центром в точке Л(3; —4).
Рис. 220
Рис. 221
312
I
Пусть заданы два уравнения с двумя неизвестными:
[А(х;у)=В(х;у],
\C(x;y)=D(x-,y). (|)
Назовем (1) системой уравнений. Говорят, что пара чисел (а; 0)
удовлетворяет системе уравнений (1), если оиа удовлетворяет
каждому нз уравнений этой системы, т. е. если А (а; ₽)=В (а; ₽) и
С (а; р)=Р(а; р). Решением системы уравнений (1) называют со-
вокупность всех пар чисел, удовлетворяющих этой системе урав-
нений. Решить систему уравнений (1) — значит иайти ее решение
(в частности, доказать, что оно пусто, т. е. ие содержит ии одной
пары). Геометрический смысл решения системы уравнений заклю-
чается в отыскании всех точек пересечения линий, задаваемых
уравнениями этой системы.
Пример 2. Решим графически систему уравнений
( 4у—Зх=О,
=25.
Решение. Изобразим иа плоскости прямую 4#—Зх=0 и ок
ружность х24-#2=25. Оии пересекаются в точках А (—4; —3) и
В (4; 3) (рис. 221). Значит, данная система уравнений имеет реше-
ние {(-—4; —3), (4; 3)}. Пишут также xi = —4, yi~ — 3; х2=4,
#2=3. Проверка показывает правильность найденного решения:
4-(—3)—3-(—4)=0; ( —4)24-(—3)2=25; 4-3-4-3=0,42-j-32=
=25.
Определения понятий следствия системы уравнений, равно-
сильности двух систем уравнений и т. д. аналогичны соответствую-
щим определениям для одного уравнения с одним неизаестным.
Например, уравнение £ (х; y)~F(x-, у) является следствием систе-
мы уравнений (I), если для любой пары чисел (а; 0), удовлетво-
ряющей системе (1), выполняется равенство Е(a; p)=F (а; 0). Это
значит, что, линия, имеющая уравнение £ (х; y)=F (х; #), проходит
через точки пересечения лниий, задаваемых уравнениями систе-
мы (1)
При замене любого уравнения системы равносильным ему урав-
нением получаем систему уравнений, равносильную заданной. На-
пример, равносильная система получается, если прибавить к обеим
частям одного из уравнений выражение, имеющее числовые зна-
чения в ОДЗ этого уравнения, или умножить обе части уравнения
иа выражение, которое имеет значение и ие обращается в нуль в
ОДЗ этого урааиеиия (в частности, иа отличное от нуля число).
Проще всего решаются системы уравнений, в которых одно из
уравнений (например, первое) содержит лишь одно неизвестное
(например, х). Чтобы решить такую систему уравнений, надо
решить первое уравнение и подставить полученные значения х во
второе уравнение. Решая каждое из получившихся уравнений,
313
находим значения у, соответствующие найденным значениям х.
Если, например, первое уравнение имеет два корня Х| и х2,
причем корню Xi соответствуют значения yi, у2, уз для неизвест-
ного у, а корню х2 — значения у*, уь того же неизвестного, то
стает пишут в виде
((*i; »1). (*г, 0а), (ж»; 0з), (*2; 0»), to; 0s)).
Пример 3. Решим систему уравнений
г х2—5х 4-4=0,
( хуг=4.
Решение. Квадратное уравнение х2—5x4-4=0 имеет корни
Ki —1 и Х2=4. Подставляя во второе уравнение значение х» = 1,
получаем ураанение уг=4, имеющее корни yt =—2, 1/2=2. Под-
ставляя же х2 = 4, получаем уравнение у2=1, имеющее корни
№=-1 и £/4=1. Ответ: {(1; —2), (1;2), (4; —1), (4; 1)}.
В общем случае заданную систему уравнений стремятся свести
к системе уравнений описанного выше вида. Для этого надо исклю-
чить из заданных уравнений одно неизвестное. Чаще всего с этой
целью нз одного уравнения системы выражают одно неизвестное
через другое, например у через х. После этого заменяют во втором
уравнении системы у этим выражением и решают получившееся
уравнение относительно х. По найденным значениям х находят с
помощью имеющегося выражения соответствующие значения у.
Может случиться, что из первого уравнения получается несколько
выражений у через х. Тогда надо проделать описанную выше
процедуру с каждым из этих выражении.
Пример 4. Решим систему уравнений
г 2х—Зу—4,
(ух =10.
Решение. Из первого уравнения находим, что .
Подставляя это выражение во второе ураанение, получаем квад-
ратное уравнение—^-у----=10. Его корнями являются Xi = 5
и хг= —3. Подставляя значение Xj=5 в равенство у=2-^~*,
находим t/t=2. Аналогично находим у2=—у-. Значит, решение
системы имеет вид { (5; 2), ( — 3; -у-) }
Другим методом исключения неизвестных является сложение
соответствующих частей уравнений. При этом получается уравне-
ние, которое вместе с одним из уравнений заданной системы обра-
зует новую систему уравнений, равносильную дайной.
314
Пример 5. Решим систему уравнений
Г xs+.i/3=9,
I x2j/+xi/!=6.
Решение. Умножим второе уравнение системы иа 3 и при-
бавим к первому уравнению. Получаем систему уравнений, равно-
сильную заданной:
гх3+!/г+Зх2!/+Зх»2=27, / (х+803=27,
lx2y+xi/!=6; t*»(*+»)=6-
Из первого уравнения находим х+у=3. Подставляя значение
х+у во второе уравнение, получаем 3xi/==6, откуда ху=2. Полу-
„ ( х+у=3,
чаем систему уравнений | ^„2 имеющую решение
,Ц1;2),(2; I)}.
При решении систем уравнений применяют также введение ио-
•вых неизвестных. Пусть система уравнений имеет вид
<F(x,y)-O,
[ Ф(х, у}=0
и функции F (х, у), Ф jx, У} ие изменяются при замене х на у и у на х,
т. е. пусть F (у, x)—F (х, у), Ф (у, х)=Ф(х, у). Тогда полезно ввес-
ти новые неизвестные и—х-\-у, v~xy.
Пример 6. Решим систему уравнений
Г х+(/=5,
1 х*+</=97
Решение. При замене х на у, а у иа х функции х-J-t/ и х4+у4
не изменяются. Поэтому вводим новые неизвестные и—х+у, v=
—ху. Имеем иг=(х+у)2—хг+уг+2ху=х2^у2+2и, а потому
х2+у2=и2—2и. Аналогично имеем (и2—2о)2=(х2-Н/2)2=*4Ч-
-j-2xay2-Fy4=x4-Fy4-F2v2, а потому x4+y4~(u2-2v)2—2v2—
—u4—4u2v~j-2v2. Поэтому заданная система принимает вид:
{и—5,
и4 -4aW 2и*—97.
Подставляя значение и=5 во второе уравнение, получаем 2 г? —
— 100^4-528 = 0, т. е. v2—50v-}-264=0. Из этого квадратного
уравнения находим Р|=6, &2=44. Поскольку v=xyt задача све-
лась к решению двух систем уравнений
f*+»=5, гх+(/=5,
txi/=6 (х$/=44.
315
Их можно решать, например, подстановкой у=5—х во второе
уравнение. Вторая система ие имеет дейстаительяых решений, а
первая система имеет решения xi=2, jh~3; х2=3, t/2=2. Итак,
решение заданной системы таково: {(2; 3), (3; 2)}.
Упражнения
36. Равносильны ли системы уравнений
[ ху~а, txy=a,
1х2+у2=62 и Нх+^Ь’+га?
Решите систему уравнений (37—39):
37. а» г4х2 + 7у2=148,
(Зх2 — у2=П-
в) rxy=i,
( Зх—5у—2;
д) (х2+ху=15.
(ху—х!=2;
«) ( 1±£_ =12.
' ! «-а +*+в з ’
1х2+у2=45;
38. а) ( х+2у+^- = 16,
1зу4-х+^-=23;
в) г х2+ху+у2 = 13.
I х+у=4:
Д) гх+у—ху=1,
1 х2+ху2=30;
6) f x-i=i-=4.
I y-I±22 = f
Vй *+2
г) j х2-рху+2у2=74,
( 2х24-2ху+у2==73;
е) гх2—ху+у2=21,
(у2—2ху-)-15=0;
з) (х+у=х2.
(Зу—х=у2.
б>
U+f=4=
Г) ix+y+xy= — l,
lx2+y2—X—у=22;
е) (х+у=6,
\х3+р3~72;
а)
39.
б)
/ 2х-~У -1-В X _Л
V Чу—X ' V 2х—у
316
г) |a/x2+VxV+Vs2+V^V=o.
(x + y+3:‘Jbxy=b;
Д) ( х‘+у‘=^-ху, е) f х,+у,+^у+ху3=~- х3у\
lx2—1/2 = 7; (х-}-1/=4;
Ж) ( x'+y4=^-x2y3, 3) fx3+x2y+xys+y3=O,
V+y3=S; ix1+4y2=5.
НЕРАВЕНСТВА
» 1. Решение неравенств. Пусть А (х) и В (х) — выражения, за-
висящие от х. Решением неравенства А (х)< В (х) называют мно-
Йкество всех чисел, при подстановке которых вместо х получает-
ся верное числовое неравенство. Понятия следствия данного не-
равенства или данной системы неравенств, рааиосильиости нера-
венств определяются аналогично уравнениям. В частности, нера-
венство C{x)<D (х) называют следствием системы неравенств
Г A, (x)<Bi (х),
В \лл(х)<Вя(х),
fewiH для всех а, при которых выполняется каждое из неравенств
М*(а)<В*(а), 1 выполняется и неравенство C(a)<D(a).
Легко проверить, что неравенство А (хЦВ(х)<С(х)+О ДО
г А ДО < С ДО,
является следствием системы неравенств {ддо^рдо
а неравенство А ДО В ДО< С ДО D ДО — следствием системы нера-
венств 10<Л ДО<СДО,
10<В (x)<D (х).
Далее, если функция С ДО определена (определена и положи-
тельна) иа ОДЗ неравенства А (х)< В ДО, то это неравенство рав-
носильно Неравенству A (x)-j-C (х)<.В (x)-j-C (х)
(Л ДО С ДО <С В ДО С ДО). Отметим еще равносильность неравенств
ЛДО<ВДО и — А (х)>- — В(х), а также 0<Д(х)<В(х) и
О<'ВМ'<’Л«-
317
Из сказанного выше вытекает, что линейное неравенство
ax-J-&<0 при а>0 равносильно неравенству x<Z—~, а прн
а<0 — неравенству
Пример 1. Решим систему линейных неравенств
f 2х-8>-х-М,
< x-)-2< —Зх-4-26,
Цх+Кх-Нб.
Решение. Решением первого неравенства является луч
(3; + оо), второго — луч ( — оо; 6) и третьего — луч (— со; 5). По-
этому решением дайной системы неравенств является общая часть
(или, как говорят, пересечение) этих трех лучей. Из рисунка 222
видно, что этим решением является промежуток (3; 5).
К решению линейных неравенств сводится решение неравенства
вида
ао (х—eci)n'... (х—а*)"' >0.
(I)
Ясно, что левая часть этого неравенства может менять знак лишь
в случае, когда меняет знак хоть одни из множителей. Как мы ви-
дели выше, множитель х—а меняет знак в точке а. Поэтому иа
промежутке, не содержащем ни одной из точек at,..aA, каждый
множитель, а тем самым и все произведение сохраняют постоян-
ный знак. Отсюда вытекает следующий метод решения неравенст-
ва (1).
Отмечаем иа числовой прямой точки а,, ..а*. Эти точки
разбивают числовую прямую на промежутки зиакопостояиства
функции f (х)=а0 (х—at)"*... (x-a*)"'. Определяем знак функции
в «пробных точках>, взятых иа каждом из промежутков. Тот же
знак будет иметь функция и иа всем промежутке. Поэтому доста-
точно отобрать промежутки, иа которых эта функция положи
тельиа.
Замечание. Достаточно определить знак f (х) в одной проб-
ной точке, скажем, прн весьма больших значениях х (там ои
совпадает со знаком ао). После этого следует принять во внима-
ние, что при четном п-, знак (х—а/)"' неотрицателен для всех х,
а при нечетном п/ этот знак меняется при переходе через
точку CLj.
Рис, 222
Рис. 223
318
Пример 2. Решим неравенство х4 —34.x2 4-225 >0.
Решение. Решаем биквадратное уравнение х4 —34х24-
4-225=0. Его корнями являются —5, —3, 3, 5. Значит, х4—
—34а:24-225=(х4-5)(х4-3) (х—3) (х— 5). При весьма больших по-
ложительных значениях все множители положительны и потому
выполняется данное неравенство. Дальнейшее поведение функции
определяется чередованием знаков на рисунке 223. Значит, реше-
нием данного неравенства является объединение промежутков
(— оо; -5), (-3; 3), (5; 4- оо).
Аналогично решают неравенства вида
cofr-cti)"1.. • (х—а»)"* 0
(х-₽1)и‘...(х-р,Г
Здесь перемена знаков может быть как в точках, где обра-
щается в нуль числитель, так и в точках, где обращается в нуль
знаменатель.
Упражнения
40. Решите неравенства и системы неравенств (40—41):
В) б) (х+1)(х-2)(х+3)(х-4)>0;
. *’-9«+20 - . «‘+3*»+2«! „ п.
В> V-HM-ii >0, г) ?-х-30 >0-
д) х4— 10х’+35х’—50х+24>0; е) х3—6?+5х—12>0;
ж) Зх2 (х—4)2<32—5(х—2)2;
з) «’-«+1 + **-3*4-1 ->2.__!_
' х-1 + х-3 4«-8 •
41‘ а) ? + 7х+12 х*+3*+2 ’ х + (х+2? <8:
в) _______2_ . 3 4 .
' 1+2» 24-Зх т 3+4х 4+5х '
г> f f-f >Tx-f- А» Г <4х“5-
V+f>4-f.
2. Доказательство неравенств. Задание «Доказать неравен-
ство F (х)^Ф(х)» означает следующее: доказать, что при всех
значениях х данное неравенство выполняется. Обычно для этого
заменяют данное неравенство на F(x)—-Ф(х)^0 и стараются до-
казать, что это неравенство является следствием некоторых не-
равенств, имеющих место для всех х (в частности, неравенств
вида А2(х)^0).
319
Пример 1. Доказать неравенство х4—7л®>2х—20.
Решение. Это неравенство равносильно неравенству х4—
—7х2 —2х4-20>0. Перепишем левую часть в виде (х2—4)24-
4-(х — I)2 4-3. Так как при всех х имеем (х2—4)2^0, (х— I)2 5s О,'то
заданное неравенство доказано
Иногда доказывается лишь, что данное неравенство выполня-
ется для всех х, удовлетворяющих некоторому условию.
Пример 2. Докажем, что при х>0, а>0,6 >0 выполняется
неравенство
*4-Ь *
х+а-4-Ь х+а ’
Решение. Данное неравенство прн х>0, а>0, fe>0 равно-
сильно неравенству (х4- 6) (х 4-о)> х (х 4-а 4- Ь), т. е. х24-ах4-6х4-
4-оЬ>х24-ах4-6х. Но при с>0, 6>0 имеем ab>0, откуда и
следует наше утверждение.
Пример 3. Докажем, что для всех х^О и у^О выполняется
неравенство
Решение- Так как х_>0, то существует a=s=-^x, v—уу
Поэтому данное неравенство можно записать в виде k
—. Оно равносильно очевидному неравенству
0^ 1“--^- • Тем самым данное неравенство доказано.
Упражнения
42. Докажите, что при всех действительных значениях х спра-
ведливо неравенство:
а) (х—1)(х —3)(х—4) (х—6)4-10>0;
б) х4—6?4- 13х— 12x4-4>0.
43. Докажите, что при всех положительных значениях х спра-
ведливо неравенство X4 — 2х24-4х4-3>0.
44. Докажите, что 3 (1 4-х24-*4)^0 4"Х4-*2Л
45. Докажите, что (14-x)rt> 14-лх, если 14-х>0 и п — нату-
ральное число.
3. Графическое решение систем уравнений и неравенств. Мы
знаем, что решение системы двух уравнений с двумя неизвестными
интерпретируется геометрически как отыскание общих точек двух
линий. Этим можно воспользоваться для приближенного решения
такой системы уравнений.
320
Рнс. 224
Пример 1. Решим графически систему уравнений
[ »=x! + 4j< + 4
l2x+«+4=0.
Решение. Уравнение у=х2-\-4х-}-4 запишем в виде у—
=(x~^-2f. Это уравнение параболы, которая получается из пара-
болы у=х2 сдвигом иа 2 единицы влево вдоль оси абсцисс.
Уравнение 2х+у4-4=0 является уравнением прямой лиинн. На
рисунке 224 изображено графически решение дайной системы
уравнений. Видим, что прямая и парабола пересекаются в двух
। точках А (—4; 4) н В (—2; 0). О т в е т: {(—4; 4), (—2; 0)}.
Выясним теперь, как изображается графически решение нера-
венства F(x;y)>0. Проведем линию F(x;y)=0. Оиа разбивает
плоскость на области, в каждой нз которых функция F (х; у) сохра-
няет постоянный знак. Поэтому достаточно узнать знак этой функ-
ции в одной точке области, чтобы определить его во всех остальных
точках той же области.
Пример 2. Изобразим графически решение неравенства
x2-4x4-!/24-fy<12
Решение. Построим сначала линию х2—4*4-£/24-6у—12=0.
Для этого перепишем уравнение в виде (х~2)24-(^4-3)2=25. Это
уравнение окружности с центром А (2; —3) и радиусом 5 (рис. 225).
Она делит плоскость на две области. Так как в точке А (2; —3)
выполняется неравенство^—2)24-(^4-3)3<25, то оно выполняет-
ся н во всех точках, лежащих внутри окружности. Значит, ре-
шение изображается внутренней областью этой окружности
(рис. 225).
Во многих случаях области задают системами неравенств.
321
Пример 3. Изобразим графически решение системы нера-
венств
( _k + i/+1>0,
t x2 + i/2<25.
Решение. Неравенство x-J-y+13>0 перепишем в виде
у^ —х— 1. Ему удовлетворяют точки прямой —х— 1, а также
точки, лежащие над этой прямой, т. е. точки полуплоскости, за-
штрихованной горизонтальными линиями на рисунке 226, а. Нера-
венству х2-}-у2:С25 удовлетворяют точки окружности x24-f/2=25
и точки, лежащие внутри этой окружности. Решение системы изоб-
ражается фигурой, заштрихованвой дважды на рисунке 226, б.
Во многих случаях удобно задавать фигуры системами нера-
венств вида
1ф(х)<?<*(х)
либо изображать их как объединения фигур, задаваемых такими
системами неравенств.
Пример 4. Зададим указанным образом параллелограмм
ABCD с вершинами 4 (О; 0), В (4; 0), С (0; 2), D (2; 2).
Решение. Уравнение стороны АВ имеет вид у—0, сторо-
ны ВС — вид у=х—4, стороны CD — вид у = а и стороны AD —
вид у=х.
На отрезке [0; 2] точки параллелограмма лежат между сторо-
нами АВ н AD и поэтому задаются системой неравенств
|0<х<2,
322
Аналогично на отрезке [2; 4] они задаются системой неравенств
|2<х<4,
I 0<у<2,
а на отрезке [4; 6] — системой неравенств
х—4Су<2.
Литер атур а
1. Башмаков М. И. Уравнения и неравенства.— М.: Наука,
1976.
2. Беккенбах Э., Б ел л м а и Р. Введение в неравенства. —
М.: Мнр, 1965.
3. Болтянский В. Г., Сидоров Ю. В., Шабунни М. И.
Лекции и задачи по элементарной математике.— М.: Наука.
1977.
4. Коровкин П. Л. Неравенства.— М.: Наука, 1974
5. К у р о ш А. Г. Алгебраические уравнения произвольных сте-
пеней.— М.: Наука, 1983.
6. Солодовников А. С. Системы линейных неравенств.— М..
Наука, 1984.
7. Стройк Д. Я. Краткий очерк истории математики.— М.:
Наука, 1984.
ЗАМЕЧАТЕЛЬНЫЕ ТЕОРЕМЫ И ФАКТЫ ГЕОМЕТРИИ
ТЕОРЕМА ПИФАГОРА
Дноген Лаэртский сообщает, что Пифагор (ок. 570 — ок.
500 гг. до н. э.), доказав свою знаменитую теорему о прямоуголь-
ном треугольнике, принес богам гекатомбу (так называлось у древ-
них греков принесение в жертву ста быков). Эта легенда, одиако,
сильно противоречит сведениям о моральных н религиозных воз-
зрениях Пифагора. Тот же самый Диоген Лаэртский пишет, что
Пифагор «запрещал даже убивать животных, а тем более ими кор-
миться, ибо животные имеют душу, как и мы». Он сообщает также,
что Пифагор питался только медом, хлебом, овощами и изредка
рыбой. В связи со всем этим больше оснований поверить сообще-
нию Порфирия: «И даже когда он открыл, что в* прямоугольном
треугольнике гипотенуза имеет соответствие с катетами, он принес
в жертву быка, сделанного из пшеничного теста,— так говорят
надежнейшие писатели».
Неизвестно, каким именно способом доказывал Пифагор свою
теорему. Несомненно лишь то, что он открыл ее под сильным
влиянием египетской иауки. Частный случай теоремы Пифагора —
свойства треугольника со сторонами 3, 4 и 5 — был известен
строителям пирамид задолго до него, а Пифагор более 20 лет обу-
чался у египетских жрецов; многие древнегреческие источники
называют египтян создателями геометрии. Следует, впрочем, от-
метить, чтоегипетскаи математика имела чисто прикладной харак-
тер и сводилась к набору эмпирических закономерностей, при-
чем иногда ие точных, а приближенных. И именно у греков появи-
лись математические доказательства.
Популириость теоремы Пифагора столь велика, что ее доказа-
тельства встречаются даже в художественной литературе. На-
пример, одно нз доказательств приведено в рассказе известного
английского писателя Олдоса Хаксли «Юный Архимед» (см.:
Хаксли О. Новеллы.— М.: ИХЛ, 1985.—С. 131—132). Такое
же доказательство, но в частном случае — дли равнобедренного
прямоугольного треугольника, приводится в диалоге Платона
«Менон».
Мы тоже приведем именно это доказательство. Разре-
жем квадрат Со стороной а-}-Ь двумя способами, как показано иа ри-
сунке 227. В обоих случаях получится 4 прямоугольных треугольника
324
с катетами а и Ь, поэтому площадь квадрата I равна сумме площа-
дей квадратов 2 и 3. Но квадрат / построен на гипотенузе прямо-
угольного треугольника с катетами а и Ь, а квадраты 2 и 3 построе-
ны на его катетах.
О теореме Пифагора можно узнать много интересного нз кни-
ги [3].
АРХИМЕД
Как это ни странно, математикой Архимед (ок. 287—212 гг
до н. э.) начал заниматься уже в весьма немолодом возрасте —-
ему было около 50 лет. Толчком к раскрытию огромных математи-
ческих способностей Архимеда, сына математика и астронома Фи-
дия, послужила его поездка в Александрию и знакомство с Коно-
ном и Эратосфеном, которые были знамениты и как математики,
и как астрономы. Эратосфена, открывшего способ получения
простых чисел — решето Эратосфена — и первым измерившего
длину земного меридиана, за разносторонность его знаний и заня-
тий завистники прозвали «во всем второй». Коион известен в ос-
новном ловким использованием открытого им нового созвездия.
Когда египетский правитель Птолемей Ш Эвергет отправился в
поход на Антиохию, его жена Вереника, молясь за благополучное
окончание войны, принесла в жертву богам Свон волосы. По окон
чанин похода оказалось, что волосы из храма исчезли. Тогда
придворный астроном Конон заявил, что эти волосы помещены
богами на небе в качестве нового созвездия («Волосы Вереники»)
Легенды об Архимеде начали появляться уже при его жизни,
особенно много их породила оборона Сиракуз в 212 г. до и. э.
Римляне, обладая значительным хорошо вооруженным и опытным
войском, надеялись взять город с первого приступа. Историк
Полибий писал, что они «и сделали бы это, если бы кто-нибудь
изъял из среды сиракузян одного этого старика. Но ои был, и рим-
325
ляне не решались даже идти яа приступ». У них были причины для
страха: первые их атаки были неожиданно отбиты с помощью изго-
товленных под руководством Архимеда механизмов; меткие мета-
тельные орудия и железные лапы, топящие корабли, нанесли рим-
лянам большой урон. Плутарх пишет: «В конце концов римляне
стали так трусливы, что если замечали, как над стеной движется
обрывок каната или бревно, то кричали: «Вот, вот оно!», и, думая,
что Архимед хочет направить на ннх какую-либо машину, ударя-
лись в бегство. Видя это, предводитель войска Марнелл прекратил
всякого рода сражения и нападения»
Осада Сиракуз продолжалась 8 месяцев. Войско союзников,
идущее на помощь Сиракузам, погибло от эпидемии. Благодаря из-
мене сторонников Рима в Сиракузах Марцеллу удалось ворваться
в город. Римляне жестоко разграбили Сиракузы, убивая многих
жителей; был убит и 75-летннй Архимед.
Есть странная закономерность в рассказах об Архимеде: близ-
кие к нему по времени писатели характеризовали его как разно-
стороннего ученого; позднее его начинают изображать более од-
носторонним, интересующимся только математикой, и даже отчас-
ти человеком не от мира сего. Так складывается легенда об Ар-
химеде. Наиболее ярко она изложена Плутархом. В своих «Срав-
нительных жизнеописаниях» он создавал глубокий и разносторон-
ний нравственный идеал, идеал человеческой жизни. Не беда, что
в изображении Архимеда Плутарх, по-видимому, слегка отклоня-
ется от действительности,— «тьмы низких истин мне дороже нас
возвышающий обман».
Об Архимеде Плутарх пишет: «Архимед имел возвышенную ду-
шу и глубокий ум, я, обладая громадными богатствами геометри-
ческих теорий, он не хотел оставить ин одного сочинения относи-
тельно построения тех машин, которые доставили ему славу зна-
ния, не только доступного человеку, ио почти божественного...
Во всей геометрии нельзя найти более трудных и глубокомыслен-
ных задач, которые были бы решены так просто и ясно, как те, кото-
рыми занимался Архимед. Одни приписывают эту ясность его вы-
соким дарованиям, другие же — тому напряженному труду, при
помощи которого ему удавалось дать своим открытиям такое вы-
ражение, что они становятся доступными без труда. Если читатель
сам не находит доказательства, то при изучении архимедовых
сочинений у него создается впечатление, что ои и сам смог бы без
труда найтн решение, — таким легким и быстрым путем Архимед
приводит к тому, что он хотел доказать. Поэтому не кажется неве-
роятным, что он, как рассказывают, будучи околдован геометрией,
забывал о пище и пренебрегал заботами о своем теле. Часто его
насильно заставляли принимать ванну и натираться мазямн, а он
чертил на золе геометрические фигуры и на своем намазанном
маслом теле проводил пальцем линии,— настолько он был охвачен
этими занятиями и действительно одухотворен музами. И хотя у
него было много прекрасных открытий, он, говорят, просил своих
326
Рис, 228
Рис, 229
родственников и друзей начертить на его могиле только цилиндр
и содержащийся в ней шар н указать соотношение между объема-
ми этих тел. Таков был Архимед, который благодаря своим глубо-
ким познаниям в механике смог, насколько это от него зависело,
сохранять от поражений н самого себя и свой город».
В сочинениях Архимеда, большая часть из которых дошла до
нас в арабских переводах, встречается много интересных геомет-
рических задач. Одну из задач Архимеда редакция журнала
«Кваит» поместила под юбилейным тысячным номером в «Задач-
нике «Кванта». Мы разберем другую задачу Архимеда — задачу
об арбелосе (так у греков назывался скорняжный нож, предназ-
наченный для разделки н очистки кож; он имел форму, изображен-
ную на рисунке 228). Утверждение Архимеда заключается в том,
что радиусы окружностей, заштрихованных на рисунке 229, равны.
Докажем это, следуя в основном рассуждениям самого Архимеда.
Обратимся сначала к рисунку 230. Докажем, что С — середина
дуги АВ. В самом деле, равнобедренные треугольники MOXN н
МО2С (где Oj н Оз — центры окружностей) подобны, потому что
точка О| лежит на отрезке О2М. Следовательно, OsC||Oitf, а зна-
чит, ОгС Л АВ. Перейдем теперь непосредственно к доказательству
(рис. 231). Согласно доказанному выше точки Е, F и В лежат на
одной прямой, точки A, F н Н тоже лежат иа одной прямой; пусть
D — точка пересечения этой прямой с прямой СЕ. Точки Н, G и С
С
Рис. 230
Рас 231
327
D
лежат иа одной прямой; точки Е, G и А тоже лежат на одной пря-
мой, пересекающей окружность с диаметром АВ в некоторой точ-
ке /. В &ABD высоты DC и BF пересекаются в точке Е, поэтому
AI.LBD. А так как Z.A/B —90°, точки В, I и D лежат на одной
прямой. Поэтому BD \\СН, так как Z.AGC = Z- AIB =90°. Следова-
тельно, AC:HE=AD:DH=AB:BC, а значит, НЕ=АС^С Для
диаметра второй окружности получаем точно такое же выражение.
Следует отметить, что утверждение Архимеда легко доказать
аналитически. В самом деле, пусть Р, Q и R — середины отрезков
АС, АВ и НЕ\ АС=2а, АВ=2(с-}-Ь), иЯ£=2х. Тогда PR—a-\-x,
PQ=b н QR=QF— FR^a+b —х. Кроме того, проекция R' точ-
ки R на прямую АС удалена от точки С на расстояние к. Применяя
теорему Пифагора к ARR'P н &RR'Q, получаем нужное уравне-
ние.
Древние греки, однако, не пользовались подобного рода ме-
тодами, так как у них еще не было разработано в нужной степени
понятие о величинах и отождествление длин отрезков н площадей
с числами было для них чуждо.
ТЕОРЕМА ПТОЛЕМЕЯ
Мы сначала сформулируем н докажем теорему Птолемея, а за-
тем поговорим немного о ее истории.
Теорема. Если четырехугольник ABCD вписанный, то
АВ CD+BCAD =АС - BD.
Наше доказательство будет в основном следовать доказа-
тельству самого Птолемея, приведенному нм в книге «Альмагест».
Возьмем на диагонали АС такую точку £, что Z~ABE= Л.ОВС
(рис. 232). Тогда дАВЕсодОВС, так как ЛВАЕ=ЛВАС=
— /LBDC. Поэтому AB:DB~AE:DC, т. е. AB-DC—AE-DB.
32S
Ясно также, что Z_CBE= ЛОВА, а значит, дСВЕсю л DBA, так
как ЛВСЕ= ЛВИА. Поэтому CB:DB = CE:DA, т. е. CB-DA —
= CE-DB. Сложив полученные равенства, получим:
AB-CD+BC-AD=AE-BD-\-CE-BD^AC-BD.
Эта теорема понадобилась александрийскому астроному Клав-
дию Птолемею, жившему во II в. и. э„ для составления табли-
цы синусов, точнее, таблицы длин хорд. Если АС — диаметр
окружности, то теорема Птолемея перепишется в виде cos a sin р-}-
4-sin a cos p=sin(a+p) (рнс. 233); если же в качестве диа-
метра взять сторону АВ, то получим формулу для синуса раз-
ности двух углов. Именно эти частные случая использовал Птоле-
мей для составления своих таблиц, очень нужных для астрономи-
ческих расчетов; аналогичные таблицы составлялись н задолго до
Птолемея астрономами Гиппархом и Менелаем.
В эпоху средневековья книга Птолемея, в которой содержались
обширные сведения по астрономии, получила распространение в
странах арабского Востока; астрономы называли ее там «Аль
Маджистн» — «Величайшее», отсюда н происходит ее название
«Альмагест».
ТЕОРЕМЫ НЬЮТОНА
Одним из велнчайшях геинев научной мысли в истории челове-
чества является выдающийся английский физик, математик и фи-
лософ Исаак Ньютон (1643—1724). Сегодня его имя из-
вестно любому школьнику, начавшему изучать физику. И в наши
днн механика, изучаемая в школе, есть не что иное, как ньютонова
механика. Ее основы были изложены в знаменитых «Началах»
Ньютона, появившихся на свет в 1687 г. В этом труде впервые в
истории науки предлагалась в совершенстве разработанная мате-
матизированная аксиоматическая физическая теория — механика
тяготения.
Основным методом, при помощи которого Ньютон доказывал
н выводил свои утверждения, был геометрический метод. Более
того, всю свою механику он построил по образцу евклидовой гео-
метрии.
Разрабатывай свою механику, и прежде всего небесную ме-
ханику, Ньютон открыл целый ряд красивых геометрических фак-
тов. О двух теоремах элементарной геометрии, связанных с именем
Ньютона, мы и хотим рассказать в этом разделе.
Первая теорема
Теорема 1. Во всяком описанном четырехугольнике середи-
ны диагоналей и центр вписанной окружности расположены на
одной прямой.
ЗИ
A
Рнс. 234
Рис. 235
Дадим два доказательства этой теоремы. Первое, сходное с
рассуждениями самого Ньютона, основывается на следующей
лемме:
Лемма 1. Если на плоскости даны два отрезка АВ и CD (где
AB^CD), то геометрическим местом точек М, расположенных внут-
ри одного нз углов, образованных АВ и CD н таких, что сумма
площадей А АВМ и АСОМ постоянна, есть отрезок с концами
на прямых АВ н CD.
Докажем это утверждение. Пусть прямые АВ и CD пересекают-
ся в точке О (рис. 234). Отложим на сторонах этого угла отрезки
ОЕ и OF, равные соответственно АВ н CD. Площадь A OEM равна
площади дАВМ, (так как основания равны ОЕ=АВ, высота,
опущенная нз точки М — общая), площадь A OFM равна площа-
ди дСОМ. Таким образом, аналогично сумма площадей ДАВМ
н дСЛМ равна площади четырехуголь инка OEMF. В свою оче-
редь, этот четырехугольник можно составить из Л OEF и Л EMF.
Поскольку точка М перемещается так, что площадь четырех-
угольника остается постоянной, то постоянной будет и площадь
&EMF. Это означает, что точка М перемещается по прямой,
параллельной прямой EF.
Докажем теперь первую теорему Ньютона. Пусть ABCD — опи-
санный четырехугольник, О — центр вписанной окружности, М и
К — соответственно середины диагоналей АС н BD (рнс. 235).
Если мы докажем, что сумма площадей треугольников АВМ и CDM
равна сумме площадей треугольников АВ К и CDK н равна сумме
площадей треугольников АВО и CDO, то из предыдущего утверж-
дения будет следовать, что точки М, К и О лежат иа одной прямой.
Но площадь дАВМ равна половине площади дАВС, площадь
д СОМ равна половине площади дВСО, следовательно, сумма
площадей дАВМ н &CDM равна половине площади четырех-
угольника ABCD. Точно так же сумма площадей дАВК и &CDK
равна половине площади четырехугольника ABCD.
Пусть г — радиус окружности, вписанной в ABCD. Известно
(и нетрудно доказать), что где р — полупернметр
зэо
ABCD. С другой стороны, по свойству описанного четырехугольни-
ка AB+CD=BC+DA. Следовательно,
^ддво+^лсдо—~(AB-}-CD) r=~pr—~-SABCD.
Таким образом, в самом деле, суммы площадей ДЛВМ и
дСОЛГ, дЛВ/С и &CDf(, &АВО и &CDO равны между собой
(равны половине площади четырехугольника ABCD), т. е. точ-
ки М, К и О лежат иа одной прямой.
Второе доказательство также основывается иа вспомогатель-
ном (другом) утверждении:
Лемма 2. Рассмотрим равнобедренный треугольник PQL, в
котором PQ=QL. Построим окружность с центром на PL, касаю-
щуюся сторон PQ и QL. Пусть произвольная касательная к этой
окружности пересекает прямые PQ и QL в точках Е н F. Тогда
PE-LE=4-PZ.2.
4
Докажем это утверждение.
Пусть О —середина PL (рис. 236). ЕО и FO — биссектрисы
соответственно Z.PEF н Z-EFL. Обозначим Z_EPO— Z_FLO=
=ос, Z.P£7?=2₽, Z.£FL=2v. Поскольку 2а+2₽+2у=360°, то
а+Р+у—180°, и, значит, Z.£OP= 180° —а— Р=у, /LFOL —
—180°—а — Т = Р- Таким образом, &РЕОсо /±LOF, поэтому
, откуда PE‘LF=P0-0L=^-PL2. Наше утверждение
остается в силе, если точки Е и F (одна или обе) находятся иа
продолжении сторон PQ и QL (докажите это самостоятельно).
Докажем теперь еще раз первую теорему Ньютона. Пусть
ABCD — описанный четырехугольник, О — центр вписанной в не-
го окружности, М и К — соответственно середины АС н BD
(рис. 237). Обозначим через В\ и & точки, симметричные соответ-
ственно точкам В и С относительно точки О. Поскольку ACil\MO
(МО — средняя линия в ДЛСС1), a B\D\\OK, то, для того чтобы
точки М, О и К лежали на одной прямой, необходимо н достаточно,
чтобы Л С] и BtD были параллельны. Проводя касательную CiP
Рис. 236
831
а
(где Р лежит на АВ), параллельную CD, и касательную BtL,
параллельную АВ, и обозначив через Q н ф точки пересечения
РВ и CL, PCt и LBi соответственно, получим параллелограмм
PQLQi, описанный около окружности. Значит, PQLQ\ — ромб
Применяя к &PQL и /\PQiL доказанное выше утверждение, по
лучим:
AP-LD = ±PlJ, PC,-LB,=±-PL*.
4 4
т. е. AP’LD = PCl-LB], APzPCi—LBtzLD.
Учитывая, что Z_APCt = Z.BtLD, получим подобие дАРС| и
ABiLD. Из того, что две пары сторон этих треугольников парал-
лельны, будет следовать параллельность третьей пары, т. е
ACil|B»D, что н требовалось доказать.
Заметим, что утверждение теоремы Ньютона можно сформули
ровать и в более общем виде. А именно:
Пусть прямые АВ, ВС, CD и DA касаются окружности с цент
ром в точке О. Тогда точка О н середины отрезков АС и BD лежат
332
на одной прямой. На рисунке 238 показаны два возможных (отлич-
ных от рассмотренного нами) случая расположения точек А, В, С н
D и точки О, (Какие еще случаи возможны?)
Обозначим через Е и F точки пересечения АВ и CD, AD и ВС
соответственно. Легко сообразить, что середина EF лежит на той
же прямой, что н середины AC, BD и точка О. Для этого достаточно
в нашей теореме заменить А на Е, С иа F. Таким образом, середины
AC, BD н EF расположены на одной прямой. Оказывается, что
это свойство справедливо для произвольной четверки прямых, не-
обязательно касающихся одной окружности, т. е. имеет место сле-
дующая теорема:
Вторая теорема
Теорема 2. Пусть на плоскости даны четыре прямые в общем
положении, т. е. никакие две из этих прямых не параллельны, ни-
какие три из них не проходят через одну точку. Тогда середины
трех отрезков, концами которых являются точки попарного пере-
сечения этих прямых, не лежащих на этих прямых, расположены на
одной прямой (рис. 239).
В отечественной литературе эту прямую обычно называют пря-
мой Гаусса. В зарубежной — эту теорему иногда приписывают
Ньютону.
Известно много различных доказательств теоремы 2. Мы дока-
жем ее, основываясь на несколько модифицированной лемме 1.
Прежде чем переформулировать эту лемму, введем следующие
обозначения. Пусть на плоскости задана прямая АВ. Эта прямая
333
Рис. 239
Рис. 240
разбивает плоскость на две полуплоскости. Назовем одну из них
положительной (+), а другую отрицательной (—). Для произволь-
ной точки М плоскости обозначим через Q(ABM) площадь тре-
угольника АВМ, взятую со знаком «4-» илн «—> в зависимости
от того, в какой из двух полуплоскостей находится точка М. Точно
так же для прямой CD одну из двух полуплоскостей обозначим
через « », а другую — через « — » и введем обозначение Q (CDM).
Лемма 3. Геометрическим местом точек плоскости, для кото-
рых Q (ABM)-\-Q (СОМ) есть константа, является прямая линия.
Доказательство. Аналогично тому, как это делалось при
доказательстве леммы 1, отложим от О — точки пересечения АВ
н CD — отрезки ОЕ=АВ, OF —CD (рис. 240). Если М принадле-
жит углу между АВ и CD, являющемуся пересечением положитель-
ных (нлн отрицательных) плоскостей, то рассуждения те же, что и
прн доказательстве леммы 1, точка описывает отрезок прямой,
параллельной EF. Пусть М в другой части плоскости, например,
как на рисунке 240. Тогда Q(ABM)-\-Q(CDM)—Sabm—Scdm~
—Seom~Sfom=Seof~{Sefm' Поскольку &EOF постоянный, то
постоянной будет SEFM, т. е. М лежит на прямой, параллельной EF.
Легко видеть, что это та же прямая, что и внутри положительного
угла (эти прямые пересекают DC в одной и той же точке).
Вернемся к нашей теореме. На рисунке 239 точки М\, Мг, Л43 —
соответственно середины AC, BD, EF. В соответствии с леммой 3
достаточно доказать, что Q (ABMfi+Q (СDM,) одно н то же прн
»=1, 2, 3. Поскольку Q(ABMl)+Q(CDMi)*=Q(ABM2)+
^~Q (CDM'2)=-~Sabcd, то нам надо доказать, что Q(ABM3)4-
4~ Q (CDM^——SABCO. Так как SABM3—~SABF и Scdm3~~2~Scdf
(точка М — середниа FE), то имеем Q(ABM3)+Q (CDM3)=
—$авм3 Scdm3~~2~Sabf—г?"$cdf—-g'SabcD’ что и требовалось.
Значит, Mi, Ms, Мз лежат на одной прямой.
334
ТЕОРЕМА ШТЕЙНЕРА - ЛЕМУСА
Нетрудно построить треугольник по трем его медианам илн же
по трем высотам. (Попробуйте самостоятельно решить эти задачи)
Но, оказывается, по трем биссектрисам в общем случае треуголь-
ник построить нельзя. И вообще с биссектрисами все обстоит
гораздо «хуже», чем с медианами и высотами. Многие теоремы,
справедливые и легко доказываемые для медиан или высот,
становятся весьма труднодоказуемыми, а то и попросту невер-
ными для биссектрис. Как мы знаем, в равнобедренном треуголь-
нике равны соответствующие пары медиан, высот и биссектрис.
Верны н обратные теоремы: если в треугольнике равны две медиа-
ны (высоты, биссектрисы), то этот треугольник равнобедренный.
Для медиан и высот соответствующая теорема доказывается без
труда. Гораздо сложнее обстоит дело с биссектрисами. Впервые
доказательство того, что из равенства двух биссектрис следует
равнобедренность треугольника, дано в работах немецких геомет-
ров Штейнера и Лемуса. С тех пор это утверждение носит назва-
ние теоремы Штейнера — Лемуса.
До сих пор теорема Штейнера — Лемуса н различные вариа-
ции на ее тему вызывают живой интерес у математиков, как лю-
бителей, так и профессионалов, а различные математические жур-
налы время от времени возвращаются к этой старинной теме.
В 1963 г. журнал «American Mathematical Monthly» («Амери-
канский математический ежемесячник») объявил конкурс на луч-
шее доказательство теоремы Штейнера — Лемуса. Средн много-
численных откликов были обнаружены интересные и ранее неиз-
вестные доказательства. Одно из них, лучшее по мнению редакции
журнала, приводится в книге [1]. (Всем школьникам, интересую-
щимся геометрией, мы настоятельно советуем познакомиться с
этой прекрасной книгой.) Приведем его. Пусть в дЛВС равны
биссектрисы АА, и CCt. Предположим, что ДЛВС ие является
равнобедренным. Пусть для определенности Z.BCA > Z.BAC.
Возьмем на KAi точку Л2 так, что Z-CiCA2=-~Z.BAC= Z.C1AA2
(рнс. 241). Из равенства углов С|ЛЛ2 н CiCA2 следует, что точки Л,
С, Ci и Л2 лежат на одной окружности, 2.С1ЛС и Z_ACA2 острые.
(/2ЛСЛ2 острый, потому что ZAG42= ZACCi-f-Z-GCAa—
=-i-(ZBC^ + ZB^C)=90°—j-ЛАВС.) Значит, ДД2>СС,, по-
скольку хорде ЛЛ2 соответствует в построенной окружности боль-
ший острый угол (ЛАСА2), чем хорде CCi (это ZCiAC). Получи-
лось противоречие: СС| <ЛЛ2<ЛЛ । — СС|. Следовательно,
/.BAC=Z-BCA и ВА=ВС.
В советской литературе обычно встречается доказательство
теоремы Штейнера — Лемуса, основанное на следующем признаке
равенства треугольников: если сторона, противолежащий этой
стороне угол и биссектриса этого угла одного треугольника рав-
335
иы соответственно стороне, углу и биссектрисе другого треуголь-
ника, то такие треугольники равны. Докажем этот признак.
Данные треугольники можно расположить так, как располо-
жены ДАВ1С и дАВ2С иа рисунке 242: оии имеют общую сторону
АС, вершины Bt и В2 находятся по одну сторону от прямой АС и от
серединного перпендикуляра к АС (если В| и В2 по разные стороны
от серединного перпендикуляра, то можно вместо В2 взять точку,
симметричную В2 относительно этого перпендикуляра). По усло-
вию Z.ABiC= ЛАВ2С, следовательно, описанные окружности
ДЛВ|С и ДДВ2С совпадают. Проведем биссектрисы В1М1 и В2М2
(они равны) и продолжим их до пересечения с описанной окруж-
ностью. Обе биссектрисы при продолжении пересекут эту окруж-
ность в точке К — середине дуги АС. Если Bt н В2 ие совпадают
и расположены, как показано иа рисунке 242, то B2K>BiK, так
как хорда В2К ближе к центру окружности, чем хорда В\К, а
KM2<.KMi, так как проекция наклонной КМ2 иа прямую АС мень-
ше, чем проекция на ту же прямую наклонной KAfj.
Следовательно,
В?ЛЬ=ВгК- КМ2> BtK-KMi =BiM 1,
что противоречит условию B|Af| ==В2Л42. Значит, точки В2 и В|
должны совпасть.
Вернемся к рисунку 241 (в ДАВС биссектрисы AAi и CCi
равны). В дЛВЛ| и дСВС( имеем: угол В — общий, AAi=CCi,
биссектриса В К — общая, следовательно, по доказанному при-
знаку эти треугольники равны.
Заметим, что на самом деле мы доказали несколько более об-
щее утверждение: если в дАВС равны отрезки AAi н CCt (где At
иа ВС, Ci иа АВ), а нх точка пересечения находится на биссектрисе
угла В, то Л В—ВС.
336
После знакомства с теоремой Штейнера — Лемуса естествен-
ным образом возникает вопрос: верно лн аналогичное утверждение
для биссектрис внешних углов треугольников? Напомним, что бис-
сектрисой внешнего угла треугольника называется отрезок биссек
трисы угла, смежного с углом треугольника, от соответствующей
вершины до точки пересечения этой биссектрисы с продолжением
противоположной стороны треугольника. В упоминавшейся иамн
книге Коксетера приводится пример так называемого треугольника
Ботемы: в треугольнике АВС с углами Z-A — \2°, ZC=132°,
Z.B=36° биссектрисы внешних углов Л и С (рис. 243) равны
между собой (они равны стороне АС, докажите это самостоя-
тельно) .
Возможны и другие вариации на тему Штейнера — Лемуса
Так, например, легко видеть, что если расстояния от основания ме-
дианы (или высоты) треугольника до середины сторон, заключаю-
щих эту медиану (высоту), равны между собой, то треугольник
равнобедренный. Для биссектрисы аналогичное утверждение уже
неверно. Можно доказать, что в любом дЛВС, стороны которого
связаны соотношением АВ-\-ВС=АС^/2, основание биссектрисы
угла В обладает требуемым свойством. Проверить это можно, ис-
пользуя теорему о биссектрисе внутреннего угла треугольника
и формулу длины медианы треугольника. (Напомним эту формулу:
если стороны треугольника а, b и с, а та — медиана к стороне а, то
m?=-i-(262-Ь2с2—а2).) Обозначим для краткости стороны ДЛВС
стандартным образом: ВС=а, СА=Ь, АВ =с. По условию a -J- с—
~Ь^2. Пусть Проведем биссектрису ВВ\ угла В (рис. 244)
Нам надо проверить, что медианы в Д ABBi и Д CBBi, выходящие
из вершины Bi, равны между собой. Обозначим их соответственно
т н п. Поскольку ABi+BiC=b и по теореме о биссектрисе
ABr.BiC—АВ:ВС=с-.а, то АВ,----Имеем:
с+а
4m2=2(-^-^4-2BBf-c2, 4«2—2 2+2BBf-о2,
Рис. 243
Рис 244
337
откуда
W-W=2(-£-) —2(~—) +а’-с’=
-2 (с* - о2)+в8 - с* ° -??7+а °'' -(«-о) (<:+“)=
=7T7<2(’2-(fl+c)2)=0-
поскольку Ь-^2= а+с.
Еще неожиданнее ответ на следующий вопрос. Известно, что
треугольник с вершинами в основаниях биссектрис данного тре-
угольника является равнобедренным. Следует ли из этого, что и
данный треугольник является равнобедренным? (Для медиан и вы-
сот ответ на аналогичный вопрос будет утвердительным.) Ответ:
вообще говоря, ие следует. Пока, правда, ничего уж слишком не-
ожиданного в этом ответе для иас иет. Неожиданность кроется в
том, что стоит за этим оборотом «вообще говоря». Оказывается,
что если в ДАВС выполняется равенство A|Bi=BiCi, где Аь
Bi, С, — основания биссектрис этого треугольника, то возможны
треугольники, в которых АВ=£ВС, ио у всех таких треугольников
угол В будет заключен в интервале от (приблизительно) 102°40' до
104°28' (концы интервала соответствуют углам, косинусы которых
равны - и —|-). Во всех остальных случаях имеет место
равенство АВ—ВС. (Доказательство этого факта можно найти в
книге [5J, задача № 203, часть 2.)
ТЕОРЕМА МОРЛЕЯ
На рубеже XIX и XX столетий корона элементарной геометрии
обогатилась еще одной прекрасной жемчужиной — теоремой Мор-
лея о трисектрисах. Теорема эта представляется еще более неожи-
данной, если вспомнить, что сравнительно недавно математика на-
конец-то доказала неразрешимость задачи о делении произвольно-
го угла на три равные части с помощью циркуля и линейки (три-
секции угла) и ряда других классических задач (квадратуры круга,
удвоения куба и др.).
Формулировка теоремы Морлея о трисектрисах в классической
форме состоит в следующем.
Рассмотрим произвольный дАВС. Проведем лучи, делящие
каждый из его ннутренних углов иа три равные части (эти лучи
называютси трисектрисами). Обозначим через DEF треугольник,
вершинами которого являются точки пересечения трисектрис,
прилежащих к соответствующим сторонам треугольника (рис.
245). Тогда ДЭЕЕ является правильным.
Существует очень много различных доказательств теоремы
Морлея. Самое простое по своей идее, но далеко не самое кра-
338
сивое состоит в том, что стороны &DEF выражаются через углы
исходного ДАВС н радиус окружности, описанной около дАВС.
Вернее, выражается одна из сторон, и по виду полученной формулы
можно сделать заключение, что и другие стороны равны тому же
выражению. (Если углы дАВС равны За, 3₽, Зу, a R — радиус
описанной окружности, то каждая из сторон Д DEF равна
8Р sin a sin р sin у.)
Все известные иам геометрические доказательства теоремы
Мор лея являются косвенными, в отличие от прямого алгебраичес-
кого, о котором мы только что говорили. Правда, провести чет-
кое разграинчеиие между прямыми и косвенными доказательства-
ми не всегда возможно. Если ие вдаваться в детали, то суть этого
различия в следующем. В прямом доказательстве мы используем
лишь одну логическую фигуру — следствие. Исходя из условия за-
дачи, мы выстраиваем цепочку следствий, соединяющую это усло-
вие с тем, что иам нужно доказать. В косвенных доказательствах
участвуют и другие виды рассуждений, например рассуждение от
противного. Блюстители «чистоты» идут еще дальше. Они считают
доказательство прямым, если все используемые в его процессе тео-
ремы также имели прямое доказательство. Проверить это в кон-
кретных случаях возможно далеко не всегда.
Доказательство теоремы Морлея, которое мы хотим здесь
привести, основывается иа следующем простом многим известном
факте:
Пусть К—центр окружности, вписанной в &.PQR (точка
пересечения его биссектрис), тогда ZPKP =90° 4--—Z.PQP
(рис. 246).
Доказывается это утверждение очень просто: Z.PKp = 180°—
-(Z KPR + Z KRP)=180° - -i- (Z QPR 4- Z QRP) -180° —
—l-(180°- ^PQR)=90”+j-^FQR.
339
Нетрудно доказать и справедливость обратного ут-
верждения:
Если Ki — точка внутри &PQR, расположенная на биссектри-
се его внутреннего угла PQR и такая, что Z PKiR=$O° 4—~/LP(^R,
то Ki совпадает с К — центром вписанной в &.PQR окружности.
В самом деле, опишем около ДВА/? окружность. Для всех
точек дуги этой окружности, содержащей К, хорда PR видна
под одним и тем же углом 90° 4——/.PQR. Для всех других точек
этот угол будет иным. А поскольку эта дуга пересекается с бис-
сектрисой угла Q треугольника в единственной точке, то из условия
будет следовать, что Ki совпадает с К.
Вернемся теперь к теореме Морлея. Рассмотрим правильный
&.DEF (произвольный). Построим на его сторонах во внешнюю
сторону равнобедренные треугольники ESF, FTD и DRE, в кото-
рых ZESF=60°4-2a, ZFW=60°4-2₽ и ZD/?£=60°4-2y, где
через За, Зр и Зу обозначены углы исходного треугольника. Рас-
смотрим А АВС, вершинами которого являются точки пересечения
соответственно прямых TF и RE, SF и RD, TD и SE.
Если окажется, что дАВС подобен исходному треугольнику,
a &.DEF образован прн пересечении соответствующих трисектрис
дАВС, то мы тем самым докажем и теорему Морлея.
Рассмотрим дВВС. В этом треугольнике SD является бис-
сектрисой угла BSC. Это следует из того, что &FDE правильный,
a A FSE — равнобедренный. Найдем угол BDC. Для этого рас-
смотрим невыпуклый четырехугольник BSCD. Имеем: Z_BDC=
^ASBD 4- ZBSC4- ZDCS == 0+ (60°4-2a)4-v = 120° + a =
+±-Z_BSC.
Таким образом, из рассмотренного выше обратного утвержде-
ния следует, что D — точка пересечения биссектрис ABSC, а зна-
чит, Z.FBD— Z-DBC и /-BCD= Z_DCE. Рассматривая ДАГС
и ДАВ/? точно так же докажем, что точки EkF являются точками
пересечения биссектрис этих треугольников.
Таким образом, &DEF в самом деле образован прн пересече-
нии соответствующих трисектрис А АВС. Теорема Морлея дока-
зана. Прн этом мы доказали и некоторые свойства фнгур, полу-
ченных при пересечении трисектрис, в теореме эти свойства не
указаны (какие?).
Теорема Морлея допускает усиление. Можно наряду с трисект-
рисами внутренних углов дАВС рассматривать также н трисект-
рисы его внешних углов, а также углов, дополняющих углы тре-
угольника до 360°. Получившиеся 27 прямых образуют при пере-
сечении причудливую конфигурацию, в которой можно выделить
18 (!) морлеевских треугольников, причем все стороны этих 18 пра-
вильных треугольников параллельны сторонам основного тре-
угольника.
340
ТЕОРЕМА ВИКТОРА ТЕБО
Итак, мы добрались до нашего столетия. Как же развивалась
элементарная геометрия в. XX в? Появились ли новые красивые
геометрические теоремы? Возможны ли сегодня какие-то открытия
в элементарной геометрии? На оба последних вопроса мы смело
можем ответить: «Да, появились. Да, возможны».
Эта глава посвящена одной удивительной теореме; ее автор
Виктор Тебо, крупный французский геометр нашего столетия.
(Мы затрудняемся точно определить время, когда эта теорема
впервые увидела свет. Где-то между 1930 и 1940 гг.) Вот формули-
ровка теоремы Виктора Тебо:
Пусть АВС — произвольный треугольник, D — произвольная
точка на стороне АС, Ц — центр окружности, касающейся от-
резков AD, BD и описанной около А АВС окружности, /2 —
центр окружности, касающейся отрезков CD, BD и описанной около
дАВС окружности. Тогда отрезок hh проходит через точку I —
центр окружности, вписанной в А АВС, н при этом /1/://2=
=tg2-|-, где ср — ABDA.
Доказательство, которое мы сейчас приведем, найдено москов-
ским школьником (учившимся в то время в IX классе) Владими-
ром Протасовым. Оно основывается на вспомогательных утверж-
дениях (леммах).
Лемма 1. Пусть окружность касается дуги АВ некоторой
окружности и хорды АВ в точках М и N. Тогда прнмая MN прохо-
дит через середину дуги, дополняющей дугу АМВ до окружности.
Эта лемма была известна Архимеду и была нами доказана в разде-
ле, ему посвященном (рис. 230).
Лемма 2. Пусть / — центр окружности, вписанной в дАВС.
Продолжение биссектрисы угла В этого треугольника пересекает
описанную около аАВС окружность в точке Вь Тогда Bd=BtC.
Доказательство (рис. 247, а). Имеем АВ{1С= А1ВС-\-
Рнс. 247
341
= Д/СЛ + /-В). Таким образом, /_В^С—
Лемма 3. Пусть AC — хорда окружности; Bi — середина
дуги АС; прямая, проходящая через Вь пересекает АС в точке К
и окружность в точке ДО (рис. 247, б). Тогда BiK’B}N=BiC\
Доказательство. ДВ|ДОСоо /\BiCN, поскольку они
имеют общий угол (ZKBjC) и, кроме того,
г-CKBt—|-(ЛМ+вГс)—'-(AN+AB^-^-NAB^^NCBi.
Следовательно, B|/(:BiC=BiC:B|A/, В(К-В1ДО=В1С2. Учитывая
лемму 2, получим, что В|К-В|ДО = В1/2 (/— центр окружности,
вписанной в ДЛВС, где В — точка дуги, дополнительной к
лХс).
Лемма 4. Пусть 1 — центр окружности, вписанной в тре-
угольник ABC; Bi — середина дуги АС окружности, описанной
около ДЛВС; прямая, проходящая через Bi, пересекает АС в точ-
ке К и описанную окружность в точке ДО. Тогда Z_BIN = £JKN
(рис. 247, в).
Доказательство. Из леммы 3 следует, что B\K-B\N=
=BiI2, значит, А В/ДОоо Д В(ДО7 и Z_IKBi = Z-BJN, откуда
Z/KA/= ZB/ДО.
Лемма 5. Пусть D — точка иа стороне АС Л АВС. Рас-
смотрим окружность, касающуюся отрезков BD, DC н окружности,
описанной около дЛВС. Пусть М и К — точки касания этой
окружности с BD hDC соответственно. Тогда прямая /ИДО проходит
через точку I — центр окружности, вписанной в дЛВС.
Доказательство. Пойдем от обратного. Пусть окруж-
ность касается отрезка DC в точке К и дуги ВС, описанной около
дЛВС окружности в точке N.
Прямая К! пересекает эту окружность в точке М. Нам надо
доказать, что ВМ касается этой окружности. Пусть Bj — сере-
дина дуги АС. По доказанному Bt лежит на прямой ДОДО. Кроме
того, BI также проходит через Bi. Далее, угол NMK измеряется
половиной дуги KN маленькой окружности. Но ею же измеряется
и угол NKC (вписанный угол измеряется половиной дуги, иа кото-
рую он опирается; угол между касательной и хордой измеряется
половиной дуги, заключенной внутри этого угла). Следовательно,
£.NMK= £.NKC. Но угол NKC измеряется полусуммой дуг NC
и АВ большой окружности, т. е. ДДОДОС=-|-(ДОС-|-ЛВ1)=
—^(NC-\-BiC)—±-BiN =Z-.NBC Отсюда следует, что в четырех-
угольнике IBNM сумма противоположных углов равна 180°, а зна-
чит, вокруг этого четырехугольника можно описать окружность.
342
Рис- 248
Рис. 249
Следовательно, /_BMN=z Z_BIN, так как в этой новой окружности
эти углы опираются иа одну дугу BN.
Но по лемме 4 Z.BZJV = Z-/KN. Следовательно, £.BMN =
= Z. NKM, а это означает, что маленькая окружность касается
ВМ (£.BMN измеряется, как и ЛМКМ, половиной дуги MN.)
Из леммы следует, что прямая KI перпендикулярна биссектрисе
угла BDC. Докажем теперь теорему Тебо.
Пусть окружность с центром Л касается AD в точке L, а
окружность с центром касается DC в точке К (рис. 248)
По лемме 5 прямая IL перпендикулярна биссектрисе угла
ADB, IK перпендикулярна биссектрисе угла BDC-, это значит, что
hD параллельна /К, I^D параллельна IL. Продолжим К! и LI до
пересечения с Lfa н Kh в точках Р и Q соответственно (рис. 249).
Тогда ~ == ~, т. е. точки h н /2 делят основания LP и QK
трапеции LPQK (от вершин L и Q) в одинаковом отношении. А
это означает, что ltla проходит через I — точку пересечения диаго-
На этом доказательство теоремы Виктора Тебо завершается.
Задачи
1. В выпуклом четырехугольнике ABCD известны углы:
ZBAC=25°, ZBCA=40°, ZBDC = 50°, ABDA — 80°. Чему ра-
вен Z. АОВ, где О — точка пересечения диагоналей четырехуголь-
ника?
343
2. В выпуклом четырехугольнике ABCD известны углы:
АВАС=50°, АВСА = 80°, /L В DC—25°, /LBDA^40°. Чему ра-
вен Z.AOB, где О — точка пересечения диагоналей четырехуголь-
ника?
3. Докажите, что если угол В треугольника АВС равен 60°, то i
пять точек: центр описанной окружности, центр вписанной окруж-
ности, точка пересечения высот А АВС и вершины А и С — рас-
положены на одной окружности.
4. Докажите, что если стороны треугольника образуют арифме-
тическую прогрессию, то прямая, соединяющая точку пересечения
медиан и точку пересечения высот, параллельна средней стороне
треугольника.
5. Даны две точки Л и В. Докажите, что геометрическое место
точек М, таких, что AM2—МВ2 — величина постоянная, есть
прямая, перпендикулярная АВ.
6. Даны две точки А и В. Докажите, что геометрическое место
точек М, таких, что АМ2-|-МВ2— величина постоянная, есть
окружность.
7. Докажите, что если отрезки, соединяющие середины проти-
воположных сторон четырехугольника, равны, то диагонали четы-
рехугольника перпендикулярны.
8. Из произвольной точки А, расположенной вне окружности,
проведены к ней две касательные АВ и АС (где В й С — точки каса-
ния) и секущая, пересекающая окружность в точках М и N. Точ-
ка Ь — середина МЛ/. Докажите, что AD — биссектриса /_BDC.
9. Докажите, что площадь «арбелоса» равна -~л/2, где / —
длина наибольшего отрезка, расположенного внутри «арбелоса»,
перпендикулярного линии центров.
10. Докажите, что длина общей внешней касательной к двум
меньшим полукругам, образующим «арбелос», равна /.
11. В А Л ВС проведены биссектрисы внутренних углов АА{
н BBt, пересекающиеся в точке О. Докажите, что если OAi =ОВ\,
то или АС=ВС, или Z.ACB=60°.
12. Через точку М, расположенную внутри угла с вершиной А,
проведена прямая, пересекающая стороны утла в точках В и С
так, что площадь л АВС принимает наименьшее значение. Дока-
жите, что ВМ=МС.
13. Через точку М, расположенную внутри утла с вершиной А,
проведена прямая, пересекающая стороны угла в точках В и С так,
что периметр а АВС принимает наименьшее значение. Докажите,
что вневписанная окружность аАВС, касающаяся стороны ВС и
продолжений сторон АВ и АС, касается ВС в точке М.
14. На окружности, описанной около равностороннего тре-
угольника, взята точка М. Докажите, что из трех отрезков,
соединяющих М с вершинами треугольника, один равен сумме двух
других.
344
15. Докажите, что сумма расстояний от произвольной точки
внутри треугольника до его сторон есть величина постоянная.
16. Пусть AM, AN и AL — соответственно высота, биссектриса
и медиана А АВС, выходящие из вершины А. Докажите, что N при-
надлежит отрезку ML.
17. Даны окружность с диаметром АВ и точка М, не лежащая
ни иа окружности, ни на прямой АВ. При помощи одной лииейки
опустите нз М перпендикуляр на Л В.
18. Докажите, что точка пересечения высот остроугольного
треугольника является центром окружности, вписанной в треуголь-
ник с вершинами в основаниях высот.
19. В А АВС известно, что Z.A—36°, Z.C=42°. На сторо-
не АС взята точка М так, что AM ~R, где R — радиус окружности,
описанной около ДАВС. Найдите Z-MBA.
20. Пусть Я и г — радиусы окружностей, описанной около дан-
ного треугольника и вписанной в него, d — расстояние между
их центрами. Докажите формулу Эйлера d? = Rl-~2,Rr.
Литература
1. Коксетер Г. С., Грейтцер С. Л. Новые встречи с гео-
метрией. — М.: Наука, 1978.
2. Курант Р., Роббинс Г. Что такое математика?— М
Просвещение, 1967.
3. Литцмаи В. Теорема Пифагора.— М-: Физматгиз, I960.
4. Прасолов В. В. Задачи по планиметрии.— М.: Наука,
1986.—Ч. 1, 2.
5. Ш а р ы г и н И. Ф. Задачи по геометрии: Планиметрия.— Мл—
Наука, 1986.
ЛОГИЧЕСКОЕ СТРОЕНИЕ ГЕОМЕТРИИ
АРИСТОТЕЛЬ И МАТЕМАТИКА
Сама постановка вопроса о логическом строении научной тео-
рии принадлежит знаменитому древнегреческому мудрецу Ари-
стотелю (384—322 гг. до н. э.).
Великое творение Аристотеля было воздвигнуто иа заложен-
ном предшественниками фундаменте, а вовсе не иа пустом месте.
Сама идея «дедуктивного вывода», «логического доказательства»
возникла в Древней Греции примерно за два века до Аристотеля
в школах ионийцев (Древняя Иония охватывала греческие коло-
нии в Малой Азии и иа прибрежных островах Эгейского моря) и
пифагорейцев (пифагорейцы обосновались в так называемой Ве-
ликой Греции, т. е. в греческих колониях в Южной Италии и иа
острове Сицилия; столицей Ионии можно было считать город
Милет, а центром пифагорейского братства служил южнонтальян-
ский город Кротон); центральной фигурой ионийцев являлся
Фалес Милетский (ок. 625—547 гг. до и. э.), а учителем,
возможно даже пророком, пифагорейцев был прославленный
Пифагор Самосский, также иоииец по происхождению. Ника-
кие письменные труды ионийцев и ранних пифагорейцев до нас ие
дошли, однако сохранился фрагмент учебника геометрии Гиппо-
крата Хиосского (V в. до и. э.; не путайте с другим знаме-
нитым ноннйцем-врачом — Гиппократом Косским, преподававшим
в Афинах медицину примерно в те же годы, когда Гиппократ Хиос-
ский там же преподавал математику), логическая структура кото-
рого достаточно близка к прокламируемой Аристотелем.
Аристотель делил науки иа наблюдательные (индуктивные) и
выводные (дедуктивные). Эталонным образцом выводных наук
Аристотель считал математику; более того, само (введенное в
оборот как будто только учителем Аристотеля Платоном) гре-
ческое слово ростера (математика) служило у него синонимом
выводной науки.
По схеме Аристотеля выводные науки строятся следующим
образом. В основе каждой такой науки лежат основные (неопре-
деляемые) понятия. Аристотель требовал от этих понятий «наг-
лядной ясности», одна ко поскольку само это требование ника-
кой «наглядной ясностью» ие обладает и передать точно его смысл
довольно трудно, то сегодня мы предпочитаем о нем просто ие
346
упоминать. Далее, иа базе заданного списка неопределяемых
понятий вводятся новые, причем логическая процедура конструи-
рования новых понятий по уже известным была описана Аристо-
телем достаточно полно.
Но основу «выводной» теории составляют, разумеется, не сами
понятия, а их свойства, формируемые в виде определенных пред-
ложений. Эти предложения, по Аристотелю, также делятся на две
категории. Процесс доказательства того или иного предложения
(теоремы, греческое ¥Еырт)цата), по Аристотелю, заключается в
^сведении его к другим «более простым» предложениям, пока мы не
дойдем до предложения, истинность которого нам уже известна.
Поскольку рассматриваемое предложение выводится из этого
««ведомо истинного предложения (или нз заведомо истинных
г едложеиий, которых может быть и несколько), то и оно тоже
безусловно справедливо. Процедура вывода одних предложений
из других была изучена Аристотелем; однако здесь мы не имеем
.возможности иа этой процедуре задерживаться, ибо иначе изложе-
ние наше слишком бы разрослось. Но вот на одном тщательно
выделенном Аристотелем моменте остановиться необходимо. Ясно,
что цепочка: «Предложение А следует от предложения Б, ио
предложение Б является следствием предложения В, со своей же
стороны предложение В вытекает из предложения Г...» — должна
где-то оборваться, т. е. иа каком-то шагу мы должны прийти к
«предложению Щ», истинность которого сомнения у нас не вызы-
вает и которое мы заранее (apriori) готовы признать справедли-
вым, иначе «доказательство» предложения А окажется бесконеч-
ным, т. е. никакая конечная процедура установить справедливость
(или, напротив, ложность) А не позволит. Это обстоятельство
заставляет выделить какой-то набор «исходных» свойств анализи-
руемых объектов, исходных предложений, которые мы заранее счи-
таем истинными «по определению», без всякого доказательства;
такие предложения Аристотель предложил называть аксиомами
(греческое а^цющхта). При этом слова «по определению» в преды-
дущей фразе могут быть расшифрованы как «по определению
соответствующей теории», ибо сама дедуктивная теория (или арис-
тотелевская «выводная наука») задается, определяется перечисле
нием основных (неопределяемых) понятий и основных (недока
зываемых) предложений (аксиом).
На саму систему аксиом Аристотель также накладывал неко-
торые условия. Ясно, что эта система предложений должна быть
непротиворечивой, т. е. должно быть невозможно вывести из иее
два прямо друг другу противоречащих предложения: ведь если
система аксиом противоречива, то отвечающей ей теории просто
нет. Так, например, рассмотрим теорию, работающую с некото-
рым конечным множеством М==(а, 0, у, ...} неопределяемых объ-
ектов, которые мы назовем хотя бы эюяками (это слово мы только
что придумали!). Будем считать, что эюяки связаны единственным
отношением р, (X больше ц); это же отношение можно записать
347
также в форме р<Х, т. е. ц меньше X. Разумеется, поскольку мы
не фиксировали никакого реального (т. е. заимствованного не из
нашей головы, а из знакомого нам мира) смысла наших эюяков,
то совершенно беспредметно задумываться и о смысле отношений
< и >, для которого перечислим аксиомы нашей теории:
Эь Общее число эюяков нечетно,
Э2. Для каждого эюяка б ЕМ существует либо единственный
(отличный от б) больший 6 эюяк, либо единственный (отличный
от 6) меньший 6 эюяк.
Такая «теория» наверняка будет невозможной: ведь из ак-
сиомы Эг легко вывести, что все эюяки строго делятся иа пары
«сравнимых» (т. е. таких, что один из них больше другого), т. е.
что общее их число четно, что, однако, противоречит аксиоме Э(.
Менее категорический характер имеют два других требования,
предъявлявшиеся Аристотелем к системе аксиом. Аристотель счи-
тал, что аксиомы должны быть независимы, т. е. ии одна из них
ие должна выводиться из остальных аксиом: ведь если такой
вывод является возможным, то соответствующее предложение
уместно разжаловать нз разряда аксиом и присвоить ему
звание теоремы. В случае ограниченного списка аксиом вопрос
об их независимости зачастую удается легко решить —- и тогда его,
конечно, следует ставить и решать; одиако в более сложных слу-
чаях вопрос этот может оказаться очень непростым. В этих случаях
мы можем позволить себе и не углубляться в проблемы независи-
мости аксиом: опасаться мы здесь можем лишь того, что неоснова-
тельно назовем ту или иную теорему аксиомой, так что риск тут
иа самом деле достаточно невелик, ои связан лишь с точностью
употребления терминов «аксиома» и «теорема», ио никак не с
существом дела.
Совсем по-иному обстоит дело с последним выдвигавшимся
Аристотелем требованием — с требованием «самодостаточности»
(греческое «аподидактичиости») аксиом, которые должны исчер-
пывающим образом характеризовать всю развиваемую теорию.
Сегодня вместо этого принято говорить о полноте аксиоматики,
т. е. требовать, чтобы в рамках развиваемой теории каждое
сформулированное в используемых в ее построении терминах
предложение было бы истинно либо ложно (причем истинность
илн ложность предложения должно быть возможно вывести из сис-
темы аксиом). Древние греки не сомневались, что серьезного
внимания заслуживают лишь «самодостаточные» аксиоматики и
полные (в описанном выше смысле) математические теории, опи-
сывающие в определенном смысле единственную систему «вещей»
(основных объектов теории и основных отношений между ними).
Сегодня же мы, однако, не склонны считать неполноту аксиома-
тики ее серьезным дефектом, напротив, неполные аксиоматики,
охватывающие целый класс, набор, множество теорий, можно
в определенном смысле считать даже более богатыми (по откры-
ваемым ими возможностям), чем полные. На различии между пол-
348
иыми и неполными аксиоматиками мы еще остановимся позже. А
сейчас в качестве «рабочего примера» аксиоматической теории
рассмотрим имение неполную систему аксиом. Заметим тут
же, что, может быть, самый авторитетный математик современ-
! иости, знаменитый «многоголовый француз» Никола Б у р б а к и
(псевдоним группы французских математиков, образованной
!,в 1937 г.) склонен считать широкое использование неполных
; аксиоматик единственным принципиальным отличием современных
взглядов на математику от тех, которые сформировались в Древ-
ней Греции.
ИГРУШЕЧНАЯ ПЛОСКОСТЬ
В качестве примера построения аксиоматической теории
рассмотрим некоторое множество П={А, В, С, ...} объектов,
называемых точками, причем наряду с точками в нашей теории
будут фигурировать еще и прямые (а, Ь, с, ...), также сос-
тоящие из отдельных точек (запись А£а означает, что точка А
принадлежит прямой а или, что то же самое, прямая а прохо-
дит через точку А). Список аксиом, описывающих наши «плос-
кости», будет состоять всего из двух предложений:
А|. Существуют три точки, не принадлежащие одной прямой
Аг- Каждые две различные точки принадлежат единствен-
ной прямой.
Из аксиомы Аг вытекает важное следствие
Следствие. Пусть тип — две прямые нашей плоскости
В таком случае либо тип совпадают, либо тип имеют одну
общую точку (такие прямые m и п мы будем называть пересе-
кающимися), либо m и п не имеют ни одной общей точки (такие
две прямые мы будем называть иепересекающимися).
Доказательство. Если тип имеют две разные общие
точки А и В, то через Л и В проходят две прямые тип, поэтому
в силу аксиомы At, эти прямые могут только совпадать.
Прямые m и п мы будем называть параллельными
(это записывается так: т[|п), если оии либо совпадают, либо ие
пересекаются.
Аз (аксиома параллельных). Пусть М — точка, а
m — прямая; тогда существует единственная прямая п, такая,
что п£М (п проходит через М) и n||m.
Простейшее доказательство непротиворечивости аксиоматики
А,_3 доставляет изображенная иа рисунке 250 «плоскость» с че
тырьмя точками А, В, С и D и шестью прямыми АВ, AC, AD, ВС,
BD, CD (где прямые АС и BD ие пересекаются): эта «плоскость»
удовлетворяет всем нашим аксиомам (так, например, через точ-
ки А, В, С и D проходит прямые АВ, АВ, CD, CD, параллельные
АВ, и прямые AC-, BD, AC, BD, параллельные АС. Но этот же ри-
сунок устанавливает и неполноту нашей аксиоматики, которой
349
Рис. 250
Рис. 251
удовлетворяет как обычная (школьная, или евклидова) плоскость,
так и «игрушечная» плоскость (рис. 250), откуда следует, что
аксиомы А|_3 ие позволяют ответить, скажем, иа следующий ос-
новной вопрос: является лн общее число N точек нашей плос-
кости конечным или бесконечным (для «школьной» плоскости оно
бесконечно, а для изображенной иа рисунке 250 равно 4)?
Обратимся теперь к вопросу о независимости нашей системы
аксиом. Для того чтобы убедиться, что аксиома А( не может быть
выведена из аксиом А2_3, достаточно убедиться в непротиворе-
чивости аксиоматики А2_3 и А|, где аксиома Ai (отрицание ак-
сиомы А|) гласит: аксиома А| места не имеет. В самом деле, ес-
ли бы из А2-з можно было бы вывести А(, то аксиоматика
А$-з и Ai наверняка была бы противоречивой, так как из нее сле-
довали бы два взаимоисключающих друг друга предложения:
А| и А]. А непротиворечивость той или иной системы аксиом уста-
навливается построением модели этой аксиоматики, т. е. системы
условных объектов нашей аксиоматической теории, для которых
выполняются все аксиомы той системы, непротиворечивость ко-
торой нами исследуется. Так. например, непротиворечивость ак-
сиоматики Ai-з устанавливается моделью (рис. 250) с четырьмя
точками и шестью прямыми. Здесь слова об «условном» харак-
тере фигурирующих в модели основных объектов дедуктивной
(выводной) теории имеют следующий смысл: в самой теории
основные (неопределяемые) объекты и отношения никак не опи-
сываются, а только называются (сравните с эюяками противоре-
чивой теории Э»_2 в п. 1); в модели же мы исходим из ка-
ких-то ранее известных нам понятий, которые играют роль не-
определяемых объектов теории (т. е. называются этими
объектами).
Легко видеть, что независимость аксиомы А] от аксиом А2-з
устанавливается изображенной и а рисунке 251, а плоскостью
с двумя точками Л и В и единственной прямой АВ: ясно, что
для этой модели аксиомы А2 и А3 выполняются, а аксиома А]
места не имеет (верна аксиома Aj). Аналогично скажем: неза-
висимость вксномы А3 от аксиом А|_2 устанавливается «плос-
костью», изображенной иа рисунке 251, б, с тремя точками А, В, С
и тремя прямыми АВ, ВС, С А: здесь выполняются аксиомы А| _2, ио
не выполняется аксиома Аз-
яво
Вернемся теперь к изучению системы, задаваемой аксиомами
Al. А2, А3. При всей кажущейся бедности нашей аксиоматики оиа
позволяет сделать содержательные выводы об удовлетворяющих
этим аксиомам «плоскостях». Пусть некоторая прямая а нашей
«плоскости» содержит фиксированное число k точек. В таком
случае (как мы сейчас докажем):
а) каждая прямая «плоскости» содержит ровно k точек;
б) через каждую точку проходит ровно fe+l прямых;
в) вся «плоскость» содержит fe2 точек;
г) «плоскость» содержит k2-\-k прямых
Доказательство. Заметим прежде всего, что все прямые
плоскости разбиваются на пучки взаимно параллельных прямых —
каждый такой пучок мы называем направлением, поскольку и нв
«школьной» (евклидовой) плоскости то общее, что имеют все
параллельные между собой прямые,— это их направление. На ри-
сунке 250 мы имеем, очевидно, три направления: АВ и CD, AD и
ВС, АС и BD. Ясно, что если две прямые тип параллельны одной
и той же третьей прямой /, то они параллельны между собой: ведь
если бы т и п пересекались в точке Т, то через Т проходили бы две
параллельные I прямые (т и п), что, однако, противоречит ак-
сиоме А3. Понятие «направление» будет иам полезно для доказа-
тельства требуемого утверждения.
В силу А! плоскость содержит точку Р, не принадлежащую
прямой а (рис. 252). Согласно аксиомам А2 и Аз через Р про-
ходят ровно k прямых, пересекающих а в точках Ль Аз..... Ль этой
прямой, и кроме того, единственная прямая, параллельная а. Та-
ким образом, через Р проходит всего k 4- i прямых. Так как каждая
такая прямая отвечает своему
направлению иа плоскости (и в
силу Аз каждое направление со-
держит проходящую через Р
прямую), то всего иа плоскости
мы имеем направлений.
А отсюда, в свою очередь, выте-
кает, что через каждую точку
плоскости проходит ровно k 4-1
прямых — по одной прямой каж-
дого из имеющихся у иас k -J-1
направлений. Пусть теперь b —
произвольная прямая плоскости
н Q — не принадлежащая b
точка. Так как через Q прохо-
дят k +1 прямых, одна из кото-
рых параллельна Ь, а остальные
k прямых пересекают b в k раз-
ных точках: Ви В?, Вь, то b
содержит ровно k разных точек.
351
Нетрудно подсчитать и общее число прямых (и общее число
точек) плоскости. Ясно, что если направление а, т. е. пучок парал-
лельных прямых, не содержит прямую Ь, то каждая из пря-
мых нашего направления пересекает /, причем число прямых на-
правления а совпадает с числом точек прямой I (рис. 253). Таким
образом, каждое направление содержит k прямых. Поэтому
£4-1 направлений по k прямых в каждом дают нам всего {k 4- 1)Л=
=k3-\-k прямых. Каждая из этих прямых содержит по k точек; та-
ким образом мы как будто получим всего k—k3-{~k2 то-
чек плоскости. Одна ко этот подсчет, конечно, ошибочен: ведь через
каждую точку плоскости проходят k -|-1 прямых, поэтому, считая
точки «по прямым», мы каждую точку посчитаем k 4-1 раз. Тогда
истинное число точек плоскости будет в k-\-1 раз меньше найден-
Ь3_1_Ь2 9
кого нами — оно будет равно }—=k .
На рнсуике 254 изображена «плоскость», каждая прямая
которой содержит 3 точки, эта плоскость содержит 32=9 то-
чек А, В, Ct D, Е, F, G, Н, 1 и 94-3=12 прямых, распадающихся
иа 4 направления, по 3 прямые в каждом направлении.
Таким образом, весьма экономная система аксиом Af_g поз-
воляет сказать довольно много о структуре «конечных» плоскостей
с k точками на каждой прямой, но далеко ие все. Так, на-
пример, мы можем сказать, сколько всего точек содержит «плос-
кость» с k точками на прямой, если только она существует. Но
как узнать, существует нли нет такая «плоскость»? Другими
словами, как узнать, противоречива илн непротиворечива аксиома-
тика, состоящая из аксиом Ai-з н еще одной аксиомы?
А*. Существует прямая а нашей плоскости, содержащая ровно
k точек. Ведь ответа на этот вопрос наши конструкции ие дают.
Рисунки 250 и 254 доказывают непротиворечивость аксиом Ai_<
при k—2 н fe=3; но как обстоит дело при иных значениях £? Увы,
полного ответа иа этот вопрос мы до сих пор не имеем.
Еще в 1906 г. известный американский математик О. В е б л е и
(1880—1960) доказал, что если k=p\ где р — простое, a q — лю-
бое натуральное число, то плоскость с k точками иа прямой
Рис. 253
Рис. 254
352
безусловно существует; а в середине нашего века американские
специалисты по комбинаторике Р. Брук и Г. Рейзер гораз-
до более сложными методами установили, что если k имеет вид
4л 4-1 или 4л 4-2 (где л — натуральное число) и в разложение k
на простые множители хоть одни множитель вида 4т 4-3 входит
в нечетной степени, то плоскость с k точками на прямой ие
существует. Одиако этим пока ограничивается почти вся имеющая-
ся у нас по интересующему нас вопросу информация. Так,
например, мы знаем, что существуют плоскости с 2, 3, 4 =22, 5, 7,
8 = 23, 9 = 32, И, 13, 16=24, 17, 19, 23, 25=52, 27 = 33, 29, 31,
32=2s, ... точками на каждой прямой и что не существуют плос-
кости с 6 = 2-3, 14 = 2*7, 21=3-7, 22 = 2-11, ... точками на
прямой. Но вот существуют ли плоскости с 10 или с 12 точками
на прямой (со 100 илн со 144 точками)? На этот вопрос сегодня ие
может ответить ни один человек в мире, хотя за последнее время
к его решению активно подключены и мощные компьютеры (ЭВМ).
Наконец, мы знаем, например, что существует конечная
плоскость с 27=33 точками иа прямой (и значит, с 272=729
точками н с 272-|-27=756 прямыми на всей плоскости). Но
единственна ли такая плоскость? Другими словами, одинаковы
или необязательно одинаковы две плоскости с 729 точками каж-
дая, можно ли их точки н прямые обозначить одинаковыми сим-
волами: Ль Д2, - -Л729, соответственно Gi, аг, ..о?5б. так, что
если на одной плоскости прямая а-, проходит через точку Д> (где
1 ^«^729 и 1 ^/^756), то и иа другой плоскости прямая а, так-
же проходит через точку А? На вопросы такого рода мы тоже пока
полного ответа не имеем, правда, удалось, например, доказать,
что существует лишь по одной плоскости с 2 (рис. 250),
3 (рис. 254), 4, 5, 7 и 8 точками иа прямой и что имеется
не менее четырех существенно различных плоскостей с 9 точками
иа прямой и не менее семи разных плоскостей с 16 точками на пря-
мой, но до полной ясности в этом вопросе нам еще очень далеко.
Может показаться, что столь «эталонно игрушечные» объек-
ты, как плоскости из конечного числа точек, не заслуживают се-
рьезного внимания и углубляться в их теорию и пытаться решить
те вопросы, которые пока остаются открытыми, просто ие надо.
На самом деле, однако, ситуация здесь совсем ниая. Теория «ко-
нечных» плоскостей, о которых мы здесь рассказали, во второй
половине нашего века неожиданно приобрела большое прикладное
значение; крайне интересует оиа, например, инженеров-связис-
тов. С этим связан переживаемый этой теорией своеобразный
бум; ныне ей посвящено множество книг и статей и усиленно за-
нимаются математики и техники во многих странах мира. Некото-
рое представление об отношении теории связи к учению о «ко-
нечных» геометриях может дать, например, доступная н неопыт-
ным читателям (но притом вовсе ие такая уж простая) книга [13],
к которой когда-нибудь впоследствии вы, может быть, захотите
(и сможете) обратиться.
353
КОНЕЧНЫЕ НЕЕВКЛИДОВЫ ПЛОСКОСТИ
В намеченной выше теории конечных плоскостей существен-
ную роль играет аксиома параллельных Аз. Эту аксиому можно
также назвать аксиомой Евклида, поскольку оиа (в несколько иной
форме) была впервые высказана (причем именно как аксиома)
в прославленных «Началах» Евклида Алексаидрийско-
г о (конец IV в. до н. э.) и была существенна для всей развитой в
«Началах» (и проходимой ныие во всех школах мира?) геометри-
ческой системы. Одиако возможны и «конечные геометрии»
(т. е. конечные наборы объектов, именуемых точками, с выделе-
нием в этом множестве прямых как каких-то подмножеств всего
множества точек), для которых аксиома Евклида А3 места не
имеет: такие геометрии можно условно называть неевклидо-
выми.
Простейший пример неевклидовой конечной плоскости достав-
ляет нам рисунок 251, б, на котором имеются 3 точки и 3 прямые,
причем через каждые 2 точки проходит единственная прямая
н каждые 2 прямые пересекаются в единственной точке. По при-
чинам, которые мы еще объясним, такую конечную неевклидову
плоскость будем называть (неевклидовой!) плоскостью Римана.
Таким образом, конечная риманова плоскость характеризуется ак-
сиомами А| —2 и дополнительной аксиомой А'.
Аз. Каждые две прямые плоскости пересекаются в единствен-
ной точке. Еще одни пример конечной римановой плоскости
доставляет иам рисунок 255, на котором изображена «плоскость»
с 7 точками А, В, С, D, Е, F, G и 7 прямыми AFB — c, BDC=a,
CEA—b, AGD—d, BGE=l, CGF=f, EDF=g. При этом легко
проверяется, что н здесь через любые 2 точки проходит един-
ственная прямая (например, прямые, соединяющие точку А со
всеми остальными точками В, С, D, Е, F и G, таковы: с, b, d, b, с
и d) и любые 2 прямые пересекаются в единственной точке (точки
пересечения прямой а со всеми другими прямыми Ь, с, d, е, f, g та-
ковы: С, В, D, В, С и £>).
Теория конечных римаиовых плоскостей имеет много общего
с теорией евклидовых плоскостей. Пусть некоторая прямая а ко-
зы
иечной римановой плоскости содержит k точек, тогда либо плос-
кость содержит k +1 точек и k +1 прямых и «устроена» так, как
это изображено на рисунке 256, либо:
каждая прямая содержит k точек;
через каждую точку проходят k прямых:
плоскость содержит k?—k-\~1 точек;
плоскость содержит k2 —прямых.
Доказательство. В силу Ai наша плоскость содержит
точку Р£а. Так как каждая проходящая через Р прямая пере-
секает а в единственной точке и каждую точку прямой а можно
соединить прямой с точкой Р, то через Р проходит ровно k пря-
мых — в точности столько же, сколько точек содержит прямая а
(рис. 256).
Пусть, далее, а и b — две какие угодно прямые нашей плос-
кости. Ясно, что если иа плоскости есть точка Р, ие принад-
лежащая ни а, ни Ь, то число точек как прямой а, так и прямой b
совпадает с числом проходящих через Р прямцх, т. е. а и b содер-
жат одно и то же число точек. Если же все точки плоскости при
надлежат либо а, либо Ь, то обе эти прямые ие могут содержать
по две точки (соответственио At и Аг, Bi и В2), отличные от точ-
ки Р пересечения а и Ь: ведь в последнем случае как точка
пересечения AiBi и А2В2, так и точка пересечения AtB2 и A2Bi не
будут принадлежать ни а, ии b (рис. 257). Поэтому, скажем,
Ь должна содержать лишь две точки Р и В, откуда будет следовать
совпадение нашей «плоскости» с изображенной на рисунке 256. Во
всех остальных случаях все прямые плоскости содержат одно и то
же число точек, а именно А* точек, как и прямая а. А так как Р мож-
ио соединить с любой точкой плоскости и через Р проходит k пря-
мых, каждая из которых содержит по k— 1 отличных от Р точек,
то общее число точек плоскости равно (fe—1) k-}-l=k2—fe+1,
где -|-1 в выражении для числа точек отвечает точке Р
Далее, через каждую точку плоскости (неизбежно лежащую
вне хотя бы одиой прямой, содержащей k точек), как и через точ-
ку Р (рис. 256), проходят ровно k прямых. А теперь нам легко
подсчитать и общее число прямых. Через каждую нз k2—fe4-l
точек проходит по k прямых, что дает как будто (ks—fe-f-1) k пря-
Рис 257
Рис 258
мых. Одиако так как каждая прямая содержит k точек, то при
таком подсчете прямых по точкам мы каждую прямую засчитыва-
ем k раз, поэтому общее число прямых будет в k раз меньше
полученного — оно равно fe-|-1
Теория конечных римановых плоскостей тесно связана с тео-
рией конечных евклидовых плоскостей, и одна из них может быть
без труда выведена из другой. В самом деле, пусть мы имеем ко-
нечную римаиову плоскость R, такую, что вие каждой прямой
лежат по крайней мере 2 точки. Выберем одну прямую а нашей
плоскости и исключим ее из рассмотрения, т. е. будем считать
несуществующей; при этом каждые 2 сходящиеся в точке пря-
мой а прямые р и q придется считать не Пересе кающимися, па-
раллельными. Полученная таким путем (исключением прямой а и
всех ее точек) конечная плоскость е будет, очевидно, евкли-
довой. Обратно, пусть е — конечная евклидова плоскость.
Чтобы сконструировать конечную римаиову плоскость R, назовем
каждое направление е (пучок параллельных прямых) точкой и
включим в рассмотрение также еще одну новую прямую, которой
принадлежат все вновь введенные нами точки-напраалеиия. (Эта
конструкция переводит евклидову плоскость в римаиову плоскость
и наоборот.)
Более сложной является теория конечных неевклидовых пло-
скостей Лобачевского, характеризующаяся аксиомами А|_2 и до-
полнительной аксиомой Аз.
А"- Через каждую точку Р, не принадлежащую прямой а,
проходят по крайней мере две не пересекающие а прямые.
Не углубляясь в теорию таких плоскостей, мы ограничимся
рисунком 258, на котором прямые ai и аг, Ь\ и Ьг, Ci и Сг содер-
жат каждая лишь по одной точке. Легко видеть, что на этой плос-
кости, скажем, через точку С проходят две прямые Ci и Сг, ие
пересекающие прямую АВ, и три прямые С\, Сг и ВС, не пересе-
кающие прямую а.
ЕЩЕ О ЕВКЛИДОВОЙ ГЕОМЕТРИИ —
АКСИОМАТИКА ГИЛЬБЕРТА
Первая попытка строгого построения геометрии по принад-
лежащей Аристотелю схеме выводной науки была предпринята
в Древней Греции. Более того, хронологически эта попытка сов-
падала с осмыслением самой схемы дедуктивного вывода, так что
реально одновременно (и, разумеется, взаимозависимо) н созда-
валась аксиоматическая схема геометрии, и продумывался вопрос
об общем строении логических (выводных) наук. Просуммирова-
ны усилия многих греческих мыслителей были в <Началах> Ев-
клида. Эта книга тысячелетиями рассматривалась как эталонный
образец строго аксиоматического построения науки, хотя реально
Евклид в некоторых существенных пунктах от схемы Аристотеля и
356
отошел (например, в «Началах» отсутствовало понятие о неопре-
деляемых объектах и отношениях), а впоследствии в построениях
Евклида было обнаружено множество серьезных логических про-
белов
Характерное для науки 2-й половины XIX в. усиленное вни-
мание к математической строгости заставило заново поставить
задачу чисто логического построения всего здания «школьной»
(евклидовой) геометрии. Эта задача на рубеже XIX и XX вв. была
почти одновременно и независимо решена сразу несколькими
исследователями в разных странах.
Наиболее известное нз полных (логически безупречных) по-
строений аксиоматической схемы евклидовой геометрии принадле-
жало знаменитому немецкому математику Давиду Г ильберту
(1862—1943). Ойо было опубликовано в 1899 г. в праздничном
томе «Festsehrift», посвященном открытию в Геттингене памят-
ника математику Карлу Фридриху Гауссу (1777—1855) и его
другу физику Вильгельму Веберу (1804—1891). Ныне «Основа
иия геометрии» Гильберта издавались практически иа всех языках
мира (дважды издавалась эта книга и по-русски (см. 4]). Аксио-
матика Гильберта состояла из 15 планиметрических, т. е. от-
носящихся к геометрии на плоскости, аксиом. Три аксиомы имели
дело с двумя неопределяемыми понятиями точка н прямая и с
четырьмя неопределяемыми отношениями между точками и пря-
мыми: принадлежность точки прямой, расположение точки между
двумя другими, равенство (или конгруэнтность) двух отрезков
и равенство (конгруэнтность) двух углов, при этом понятия от-
резка и угла вводились с использованием других понятий и
«командующих» ими аксиом
Так, отрезком с концами А и В Гильберт называет множество
лежащих между А и В точек. При этом, скажем, аксиомы при-
надлежности распадаются на две группы: первая группа содер-
жит аксиомы, равносильные предложенным Aj_2 (с. 349); отдель-
ную группу составляет аксиома параллельных А3. Ниже мы еще
остановимся подробнее иа причинах, вынудивших Гильберта вы-
делить аксиому Аз в отдельную группу аксиом.
Успех, который имела разработанная Гильбертом система,
связан ие только с логической ее безупречностью, ио также с
тем, что аксиоматика Гильберта вполне могла рассматриваться
как естественное завершение аксиоматики Евклида, работавше-
го с теми же, по существу, основными понятиями и отношениями,
хотя, скажем, отношение «между» явно Евклидом ие вводилось
(но неявно оно присутствовало во многих его конструкциях). Для
иллюстрации мы перечислим здесь все гильбертовы аксиомы по-
рядка (аксиомы, описывающие отношение «между»); для краткос-
ти утверждение «С лежит между А и В» мы условимся записы-
вать как [АСВ]
357
Рис 259
Рис 260
Рис. 261
Мь Если [ДСВ} то А, В и С — три точки одной прямой и так-
же [ВСА] (в силу Мь если С лежит между А, В, то можно
никак не фиксировать порядок точек А, В);
М2- Для любых А и В существует хотя бы одна точка С,
такая, что [ЛВС] (М2 утверждает наличие на прямой АВ хотя бы
одной точки за точкой В);
Мз- Если А, В и С — три точки одной прямой, то не более од-
ной из них лежит между двумя другими (если точки А, В и С
ие принадлежат одной прямой, то, очевидно, ни одна из них между
двумя другими не лежит) ;
М4. Пусть А, В и С — три точки, не лежащие на одной прямой,
и прямая а не проходит ни через одну из этих точек (рис. 259).
Тогда если а ЭМ, где [АЛ4В], то либо аЭЫ, где [AiVC], либо а ЭР,
где [ВВС]. Другими словами, прямая а, пересекающая сторону АВ
треугольника АВС (т. е. отрезок АВ), пересекает также либо сторо-
ну АС, либо сторону ВС того же треугольника. Выражаясь нагляд-
но, М4 можио сформулировать так: если прямая входит внутрь
дАВС, то она из него где-то выйдет.
Отметим принципиальную разницу между аксиомами М5_3 и
аксиомой Л44: в то время как Mi-з суть «линейные» аксиомы, за-
трагивающие лишь точки одной (прямой) линии, М4 есть «плос-
костная» аксиома, существенно оперирующая с точками, ие при-
надлежащими одной прямой. Тот факт, что учение о порядке точек
на прямой нельзя строго обосновать чисто геометрически, ие
привлекая «плоскостных» аксиом, был доказан одним из пред-
шественников Гильберта немецким геометром М. Пашем
(1843—1930). Пашу же принадлежит и формулировка аксио-
мы Л14, которую обычно называют аксиомой Паша.
Аксиома М4 утверждает, что прямая а не может пересечь
лишь одну сторону дАВС: она должна пересечь минимум две его
стороны. Однако из иее нетрудно вывести также, что прямая I (не
проходящая ии через одну вершину треугольника) либо вовсе ие
пересекает его стороны, т. е. проходит вие треугольника (рис. 259),
либо (как прямая а) пересекает ровно две его стороны, т. е. иё
может пересечь всех трех сторон дАВС. В самом деле, пусть
прямая а пересекает сторону АВ треугольника АВС в точке М, сто-
рону ВС — в точке N и сторону С А — в точке Р, и пусть при этом
358
[MWPJ (На рисунке 260 прямая а неизбежно должна быть изобра-
жена искривленной, ибо «истинная» прямая требуемыми свойства-
ми обладать не может.) Рассмотрим теперь дАМР и пря-
мую 1~ВС. Так как I пересекает сторону нашего треугольника
(в точке N}, то по аксиоме Паша оиа должка пересекать либо
сторону ДМ, либо сторону АР. Однако точка В пересечения пря-
мых AM и I лежит вие отрезка AM (в силу аксиомы М$ — ведь М
лежит между Л и В). Поэтому / пересекает сторону АР треугольни-
ка, т. е. [АСР]. Но из последнего в силу той же аксиомы Мз вы-
текает, что (вопреки нашему предположению!) Р не лежит между
А и С.
С последним предложением связана следующая история. В
1945 г. иа VIII Московской математической олимпиаде учащимся
VII — VIII классов была предложена задача «На сторонах АВ,
ВС и СА треугольника АВС (ие в вершинах треугольника!) выбра-
ны три точки Ci, Ai и Вь Доказать, что середины отрезков AAi,
BBi, CCi ие могут принадлежать одной прямой».
Устроителям олимпиады эта задача ие казалась особенно
трудной. Они рассчитывали, что школьники легко заметят, что
середины Аг, Вг. Сг рассматриваемых отрезков принадлежат
средним лниням треугольника АВС (рис. 261). А так как инка
кая прямая не может пересекать все три стороны треугольника,
образованного средними линиями (если одна точка какой-то
стороны входит внутрь треугольника, то через точку одной из
двух других сторон она выйдет из него и пересечь третью сторону
уже ие сможет), то точки Аг, Вг я Сг наверняка не принадлежат
одной прямой.
Это решение нашли довольно много школьников. Одиако
восьмиклассник Юлик Добрушии (ныие известный советский мате
матик проф. Роланд Львович Добрушин) признался, что решить
эту задачу он не смог. «Я долго думал иад тем, как установить
что прямая ие может пересечь все три стороны треугольника,—
иаписал в своей работе Юлик,— ио убедился, что доказать это
не смогу, так как с ужасом понял, что я не зиаю, что такое пря-
мая». За это замечание (за нерешенную задачу!) жюри олимпиады
наградило Р. Л. Добру шина первой премией: ведь иаписаииая
школьником фраза была членам жюри гораздо более понятна,
чем, пожалуй, самому ее автору. Учебник геометрии А. П. Киселе-
ва, по которому учились тогда в наших школах, как и все до-
военные учебники геометрии во всех странах мира, представлял
собой, по существу, некоторую «школьную адаптацию» системы
Евклида; прямая в этой системе никак не определялась, а (кос-
венно) описывалась всей системой аксном, содержащей (в гиль-
бертовом ее варианте) аксиому Паша, родственную тому пред-
ложению, которое требовалось доказать.
Аксиоматику Гильберта школьник Добрушии, понятно, не
зиал, т. е. ои в самом деле не владел единственно возможным
в знакомой ему схеме изложения геометрии косвенным определе-
359
кием прямой, без которого невозможно было доказать и тре-
буемое ее свойство. Глубина мысли школьиика-восьмикл ассинка,
в процессе решения задачи понявшего эти достаточно тонкие
обстоятельства, привела в восторг зрелых математиков, читав-
ших работу школьника, которую они заслуженно высоко оценили.
Приведем теперь несколько примеров анализа свойств прямой
по перечисленным аксиомам.
Аксиома М2 утверждает, что иа прямой АВ за ее точкой В ле-
жит хотя бы одна точка. Докажем теперь, что справедлива также
следующая теорема:
Теорема I. Для каждых двух точек А и В найдется хоть од-
на точка С, такая, что [АСВ*. Другими словами, на прямой АВ
найдется точка не только за В (и за Л), ио и между А и В.
Доказательство. Согласно Mi вие прямой АВ найдется
точка D (рис. 262), а в силу М2 на прямой AD за точкой D най-
дется точка Е (такая, что [АО£]) и иа прямой ЕВ за точкой В
найдется точка F (такая, что [CBF]). Но тогда в силу аксиомы М4
прямая DF должна пересечь отрезок АВ во внутренней точке С
этого отрезка.
Верна и вторая теорема:
Теорема 2. Среди каждых трех точек А, В, С одной прямой
всегда найдется одна (ив силу М3 только одна) точка, ле-
жащая между двумя другими.
Доказательство. Пусть А не лежит между В и С и точ-
ка В ие лежит между А и С (т. е. отношения [ВАС]и [АВС] места не
имеют, рис. 263). Докажем, что С лежит между А и В (т. е. что
[АСВ]). Пусть D ие принадлежит прямой ЛВС (аксиома М[), и
пусть Е лежит на прямой CD за точкой D (аксиома Ms). При-
менив аксиому М4 сначала к А ВСЕ и прямой AD, а затем к A ACD
и прямой BD, мы заключим, что AD пересекает отрезок BE во
внутренней его точке F и BD пересекает отрезок АЕ во внутренней
его точке G. Применим теперь еще дважды ту же аксиому М4 —
сначала к A AFE и прямой BG, а затем к A ABF и прямой ЕС. Мы
увидим, что BG пересекает AF во внутренней точке D этого отрез-
ка (т. е. [АО/7]), а ЕС пересекает отрезок АВ во внутренней точ-
ке С этого отрезка, т. е. [АСВ], что н требовалось установить.
Этих примеров, пожалуй, достаточно, чтобы получить пред-
ставление о сложности логической системы Гильберта. Заметим,
Рис 262
Рис. 263
360
кстати, что в первом издании гильбертовых «Оснований геомет-
рии» предложение о том, что из трех точек, принадлежащих одной
прямой, одна обязательно лежит между двумя другими, включа-
лось в число аксиом; лишь позже ученик Гильберта А. Вальд
показал, что это утверждение является теоремой, т. е. что его
с помощью четырехкратного применения аксиомы М< можно вы-
вести из аксиом Мд и Мц.
Аксиомы М|_4 позволяют также установить, что между каж-
дыми двумя точками прямой расположено бесконечно много дру-
гих точек, что любые п точек прямой можио расположить «в ес-
тественном порядке», т. е. обозначить через А1г Ан, .... Ап так,
чтобы из любых трех точек А,, А/ и Аь (где 1 j, k^n) та, номер
которой заключен между номерами двух других точек, была рас-
положена между двумя другими и т. д. Но на одних лишь аксиомах
принадлежности и порядка полностью построить структуру пря-
мой нельзя: здесь приходится привлекать еще одну аксиому —
так называемую аксиому непрерывности, составляющую отдель-
ную группу в гильбертовой аксиоматике. Две другие группы
аксиом, «по Гильберту», составляют аксиома параллельных и ак-
сиомы равенства (конгруэнтности).
ИНЫЕ АКСИОМАТИЧЕСКИЕ ОБОСНОВАНИЯ
ЕВКЛИДОВОЙ ГЕОМЕТРИИ
Гильбертово обоснование евклидовой геометрии является
наиболее известным, однако чисто хронологически оио не было
первым: в том же 1899 г., ио за несколько месяцев до выхода
из печати геттингенского «юбилейного тома», посвященного
открытию памятника Гауссу и Веберу, в трудах итальянской
Туринской академии наук появилась обстоятельная статья мало-
известного в те годы математика М. Пиери (1860—1904)
«Элементарная геометрия как гипотетическая дедуктивная систе-
ма», содержащая безукоризненную аксиоматику геометрии, по-
строенную иа другой основе в отличие от аксиоматики Гильберта.
Наконец, независимо от Пиери и Гильберта еще одну систему
обоснования геометрии разработал примерно в те же годы приват-
доцеит Новороссийского (Одесского) университета Вениамин Фе
дорович К а га и (1869—1953); его аксиоматика была впервые
опубликована в 1902 г.
Установки Пиери, Гильберта и Кагана были таковы. Гиль-
бертовы аксиомы принадлежности, порядка, параллельных и не
прерывности полностью описывали знакомую нам из школы струк
туру плоскости как множества точек и прямых, однако они игнори-
ровали метрику, задаваемую расстояниями между точками и угла-
ми между прямыми. Соответственно этому в геометрии, базиру-
ющейся исключительно на этих четырех группах аксиом, ие могла
быть определена, скажем, окружность — множество точек, уда-
361
ленных от фиксированной точки Q (центра окружности) иа одно и
то же расстояние г (радиус окружности). Параллельное проекти-
рование плоскости л на другую плоскость п', переводящее точки
в точки, прямые в прямые (н прн этом сохраняющее отношение
принадлежности точки прямой, рис. 264), а окружность в эллипс,
не меняло никаких (выводимых из рассматриваемых аксиом)
свойств плоскости, подобие тому как евклидова структура плос-
кости полностью сохраняется при любых перемещениях (движе-
ниях) плоскости в пространстве. Лишенная метрики плоскость, для
которой выполняются все гильбертовы аксиомы, кроме аксиом
равенства, называется аффинной плоскостью (от латинского сло-
ва affinitas — родство по жене, свойство). Термин «аффинный»
ввел крупнейший математик XVIII в. швейцарец Леонард Эйлер
(1707—1783); большую часть своей жизни Эйлер жил и работал
в Петербурге. Полученные параллельным проектированием одна
из другой фигуры (вроде фигурирующих на рисунке 264 окруж-
ности и эллипса) Эйлер считал не идентичными, ио в каком-то
отношении родственными, «аффинными» друг другу.
Гильбертовы аксиомы равенства выявляли метрику плоскос-
ти и тем самым обращали аффинную плоскость в евклидову. Но
возможны были и иные способы фиксации существующей на
плоскости метрики.
Пожалуй, самым простым представляется нам сегодня прос-
то включить понятие расстояния между точками в число основных,
неопределяемых понятий геометрии, а основные свойства рас-
стояния (расстояние dAB от Л до В равно расстоянию dBA от В до Л;
расстояние dAB положительно прн Л#=В и равно нулю при совпа-
дающих А н В; dAns£dAC+dCB при любых Л, В и С и др.) включить
в число аксиом. Именно этим путем шел В. Ф. Каган; предложен-
ная нм система аксиом явилась первой аксиоматикой геометрии,
основанной иа понятии расстояния. Двумя годами позже
(в 1904 г.) родственную аксиоматику разработал видиый амери-
канский математик Освальд В е б л е и (1880—1960). По этой же
схеме строилась и аксиоматика знаменитого советского математи-
ка Андрея Николаевича Колмогорова, использовавшаяся в
созданном под его руководством школьном учебнике геометрии,
ряд лет служившем основным для нашей школы.
С другой стороны, в системе Евклида равными назывались
(являлись) фигуры, которые могут быть совмещены движением.
Последнее утверждение можно понимать двояко. Если, как посту-
пал Гильберт, включить понятие равенства (конгруэнтности) в
число неопределяемых понятий геометрии, то наше утверждение
можно принять за определение движения. Одиако можно, напро-
тив, считать неопределяемым понятием движение, тогда ска-,
заииое выше послужит определением равенства фигур. Идея вклю-
чить понятие движения в число неопределяемых понятий геомет-
рии принадлежала учителю Пиери, знаменитому итальянскому ма-
тематику Д. Пеано (1858—1932); Пеано же наметил н не-
362
Рнс. 264
Рис. 265
которые основные аксиомы движений вроде утверждения о степени
подвижности плоскости: если даны две точки А и А', два выходя-
щих из них луча а и а' и две ограниченные прямыми лучей а и а'
полуплоскости а и а', то существует единственное движение,
переводящее А в А', а в а' и а в а' (рис. 265). Пиери же раз-
работал полную систему аксиом геометрии, в которой движение
рассматривалось как неопределяемое понятие, а равенство фигур
определялось, как у Евклида.
Впоследствии были разработаны и многие иные системы обое
нования геометрии (см., например, [14]). Одна из педагогически
рациональных аксиоматик была предложена в 1932 г. ведущим
американским математиком Д, Биркгофом (1884—1947);
она базировалась на «аксиоме (измерительной) линейки», позво-
ляющей сопоставить точки прямой (вещественным) числам так,
что расстояние между двумя точками будет равно разности соот-
ветствующих этим точкам чисел, и иа «аксиоме транспортира»,
аналогичным образом сопоставляющей числа выходящим из од
ной точки лучам с тем, чтобы величина угла между двумя лучами
легко находилась по отвечающим этим лучам числам. В настоя-
щее время в большинстве американских школьных учебников
геометрии используется тот или иной вариант биркгофовской
аксиоматики.
Близка к этому и аксиоматика известного советского гео-
метра Алексея Васильевича Погорелова (род. в 1919 г.),
используемая в школьном учебнике геометрии.
Совсем иной является векторная система обоснования гео-
метрии, в которой основными (неопределяемыми) понятиями явля-
ются понятия точки и вектора. Этот путь обоснования геометрии
был впервые намечен одним из крупнейших математиков нашего
столетия немцем Г. Вейлем (1885—1955).
363
НЕЕВКЛИДОВА ГЕОМЕТРИЯ: НЕМНОГО ИСТОРИИ
Историю учения об основаниях геометрии естественно начи-
нать с «Начал» Евклида [7]; ии один более ранний учебник гео-
метрии до нас не дошел в первую очередь из-за того, что
высочайшая репутация сочинения Евклида буквально стерла па-
мять о всех его предшественниках. Книга Евклида начинается с
определений, затем следуют постулаты и аксиомы. Сейчас нам
трудно понять как причины, вынудившие Евклида разбить все мно-
жество недоказываемых предложений иа постулаты и аксиомы, так
и само различие между постулатами и аксиомами. С нашей сегод-
няшней точки зрения такое разбиение не нужно; это подчеркива-
ется, например, тем, что, скажем, существование прямой, соеди-
няющей две точки плоскости, Евклид отиес к постулатам (посту-
лат 1), а единственность подобной прямой — к аксиомам (к этому
сводится аксиома 9). Для нас, одиако, интересны в первую очередь
именно постулаты Евклида, на которых мы теперь н остановимся.
Первые три постулата Евклида, по существу, фиксируют опе-
рации, выполняемые циркулем и линейкой,— оии создают аксио-
матическую базу всего учения о таких построениях. Может удивить
4-й постулат «Все прямые углы равны-», ибо сформулированное
предложение безусловно является ие аксиомой, а теоремой: его
нетрудно доказать. Наконец, Евклид в своем изложении опустил
предложения о возможности нахождения точек пересечения двух
заданных примых, прямой и окружности или двух окружностей,
так что более точно аксиоматическую теорию построений цирку-
лем и линейкой сегодня базируют не на трех, а на шести посту-
латах.
Мы уже отмечали, что равными фигурами Евклид называет
совмещающиеся при движении. С учетом этого обстоятельства
можно считать, что смысл 4-го постулата Евклида состоит в фик-
сации степени подвижности плоскости (ср. рис. 266 с рис. 265).
5-й постулат Евклида звучит неожиданно сложно, в сов-
ременной терминологии он гласит: если две прямые образуют
с третьей прямой внутренние односторонние углы, в сумме меньшие
двух прямых, то эти прямые пересекаются, причем с той стороны от
третьей прямой, с какой названная сумма углов будет меньше
двух прямых углов (рис. 267).
Рис. 266
Рис. 267
364
Нетрудно установить равносильность 5-го постулата Евклида
аксиоме параллельных Аз (с. 349), более краткой и к тому же
и более наглядной; почему же Евклид включил в число основных
предложений теории столь сложное утверждение, как его 5-й пос-
тулат, не заменив его каким-либо эквивалентным, ио более про-
стым предложением? Нам кажется, что это, возможно, было сде-
лано не случайно: уже самой формулировкой Евклид выделил свой
5-й постулат из всего фундамента развиваемой им теории. Более
того, если все другие аксиомы н постулаты начинают «ра-
ботать» в его конструкциях с самого начала, то первая ссылка
на 5-й постулат возникает довольно поздно — лишь в 29-м пред-
ложении Евклида, в то время как первые 28 предложений доказы-
ваются без использования этого утверждения. Думается, что Ев-
клид включил 5-й постулат в число иедоказываемых предложений
«не от хорошей жизни»: ои сам пытался его, видимо, доказать,
ио не смог этого сделать и потому вынужден был постулиро-
вать соответствующий факт.
Несколько вызывающее положение 5-го постулата в ряду дру-
гих постулатов и аксиом, громоздкая его формулировка, позднее
использование этого предложения вызвали горячее желание у
последующих комментаторов и продолжателей Евклида доказать
5-й постулат: ведь Аристотель настаивал на наглядной очевид-
ности всех аксиом, а этому требованию сложный 5-й постулат
явно ие удовлетворял. Попытки доказательства продолжались
буквально тысячелетиями, но все онн неизбежно оканчивались
провалом: каждый раз, когда кому-либо казалось, что он нашел
истинное доказательство 5-го постулата, впоследствии выясня-
лось (иногда это обнаруживал сам автор «доказательства»), что в
рассуждении неявно используется какое-либо ие доказанное ра-
нее предложение, равносильное 5-му постулату Евклида.
Существенный прогресс в рассматриваемой области был дос-
тигнут лишь в XVIII столетии — более чем через 2000 лет после
Евклида! Естественным путем доказательства 5-го постулата
представляется путь «приведения к абсурду»: исследователь пред-
полагает, что 5-й постулат ие справедлив, н на этом пути приходят
к абсурдному предложению, невозможность которого и доказывает
ложность исходной предпосылки, отрицающей 5-й постулат. По
этому пути шли многие авторы, но дальше всего здесь продвину-
лись итальянский монах-иезуит Д. Саккери (1667—1733)
и видный немецкий математик И. Ламберт (1728—1777).
Они рассматривали «почти одинаковые» четырехугольники:
четырехугольник Саккери ABCD с двумя прямыми углами А
н D при основании и равными боковыми сторонами АВ и DC
(рис. 268, а) и четырехугольник Ламберта ABNM с тремя прямы-
ми углами А, М и N (рис. 268, б; нетрудно видеть, что четырех-
угольник Ламберта можно рассматривать как половину четырех-
угольника Саккери). Далее и Саккери, и Ламберт рассматривали
три возможные гипотезы: гипотезу примого угла, состоящую
365
Рис. 269
в том, что (равные между собой) углы В и С четырехугольника
Саккерн, соответственно угол В четырехугольника Ламберта пря-
мые; гипотезу тупого угла н гипотезу острого угла. Без большого
труда доказывается, что гипотеза прямого угла Саккерн и Ламбер-
та равносильна 5-му постулату Евклида; поэтому, чтобы доказать
этот постулат, достаточно убедиться, что гипотезы тупого угла
и острого угла места иметь не могут.
И Саккери. и незнакомый с его исследованиями Ламберт до-
вольно легко опровергли гипотезу тупого угла, доказав, что
она противоречит иным (явно сформулированном Евклидом или
неявно им предполагаемым) аксиомам, однако опровержение ги
потезы острого угла оказалось гораздо более трудным. Саккери
и Ламберт выводили из этой гипотезы предложение за предложе-
нием; эти предложения выглядели необычно, странно, но логичес-
ких противоречий оии не содержали. Увы, психологически ни Сак-
кери, ии Ламберт не были готовы признать возможной систему,
получаемую при принятии гипотезы острого угла, поэтому в кон-
це концов они все же признали н эту гипотезу ложной, хотя до-
статочно веских аргументов к тому они не имели. Ламберт раз-
вил даже тригонометрию в системе, базирующейся на гипотезе ост-
рого угта; эта «остроугольнаи тригонометрия» неожиданно оказа-
лась довольно близкой к сферической тригонометрии, т. е- к три-
гонометрии на поверхности сферы фиксированного радиуса г, о ко-
торой мы еще кратко скажем в п. 7. Формулы «остроугольной
тригонометрии» легко выводились из формул сферической триго-
нометрии — для этого достаточно было подставить всюду в сфери-
ческие формулы вместо фигурирующего в них радиуса г сферы
чисто мнимое число р=г-\[—Л. Заметив это, Ламберт с сожале-
нием констатировал, что в пространстве «мнимой сферы» (увы!)
существовать не может, а между тем если бы такая «сфера»
нашлась, писал Ламберт, то иа ней наверняка выполнялась бы
гипотеза острого угла.
Первым человеком, публично высказавшимся о невозможности
доказательства 5-го постулата, т. е. о возможности геометри
ческой системы, в которой этот постулат (а значит, и аксиома па-
раллельных) просто не выполняется, был ие математик, а про-
366
фессор-юрист Харьковского университета, немец Ф. Швей-
карт (1780—1857). Горячий поклонник математики, Швейкарт
сам попробовал идти тем же путем, что Саккери и Ламберт (ра-
боты которых ему известны не были), но он сделал нз своих рас-
суждений принципиально иной вывод, чем его предшественники.
Швейкарт предположил, что наряду с обычной, евклидовой геомет-
рией существует также необычная геометрия с другой теорией
параллельных. На Земле эта геометрия места не имеет, но, может
быть, она выполняется где-то в других мирах, на далеких звез-
дах? На этом основании Швейкарт назвал новую геометрию аст-
ральной (т. е. «звездной»); ои выписал довольно много теорем аст-
ральной геометрии, ие имеющих места в обычной (евклидовой)
геометрии; так, иапример, Швейкарт выяснил, что в астральной
геометрии существует «самый большой» (по площади и по линей-
ным размерам)’треугольник, больше которого ин один треуголь-
ник быть ие может (этот «треугольник» уместнее было бы назвать
«трехсторонииком», ибо углов-то у него как раз и нет: все его
стороны неограниченно приближаются одна к другой, ио общих
точек оин ие имеют; рнс. 269).
Через общего знакомого Швейкарт в 1818 г. довел свои по-
строения до сведения крупнейшего математика того времени Кар-
ла Фридриха Гаусса, имя которого нам уже встречалось выше.
Гаусс отозвался об исследоваииях Швейкарта с высокой похвалой,
но прибавил при этом, что ничего нового для него в трудах
Швейкарта не было, ибо как само существование астральной гео-
метрии, так и теоремы, найденные Швейкартом, были ему уже
знакомы.
Гораздо подробнее исследовал новую геометрию племянник
Швейкарта Ф. Тауринус (1794—1874), узнавший о ией от
диди. В 20-х годах XIX в. он опубликовал в Кельне за свой счет
две брошюры: «Теория параллельных линий» (1825, по-немецки)
н «Первые начала геометрии» (1826, по-латыни), в которых до-
вольно далеко продвинул астральную геометрию Швейкарта,
в частности, разработал до конца астральную тригонометрию.
Первую брошюру Тауринус послал Гауссу, который очень ее одоб-
рил, но и тут приписал, что все содержание брошюры было ему
известно раньше, о чем ои, впрочем, просил Таурниуса никогда
иикому ие рассказывать. Формально это запрещение Тауринус не
нарушил, одиако в предисловии ко 2-й брошюре ои высказал по-
желание, чтобы Гаусс публично высказался о ее содержании. Эта
фраза крайне рассердила Гаусса, вовсе не желавшего высказы-
ваться на эту тему; с этого момента он полностью прекратил пе-
реписку с Тауринусом, к которому первоначально отнесся столь
дружелюбно, своего мнения о 2-й брошюре он никак не высказал
и на последующие письма Тауринуса не отвечал. Это так огорчило
Тауринуса, что он постарался скупить все экземпляры обеих
брошюр и сжег их; в своей дальнейшей продолжительной жнзин
он больше никогда ие обращался к этой тематике.
367
Но Саккери, Ламберт, Тауринус были лишь предшественника-
ми неевклидовой геометрии, а ие ее создателями. Первое раз-
вернутое изложение воображаемой, как ее назвал автор, геомет-
рии, в которой ие выполняется 5-й постулат, было опубликовано
в 1829—1830 гг. Николаем Ивановичем Лобачевским в двух об-
ширных статьях. Гаусс, ценивший исследования Лобачевского
чрезвычайно высоко, критиковал термин «воображаемая геомет-
рия», поскольку новая геометрия в определенном смысле рав-
ноправна с евклидовой и название «воображаемая» создает о ией
превратное миеиие; сам он называл новую геометрию неевклидо-
вой — и именно его термин утвердилси в истории науки. Лоба-
чевский, видимо, сам понимал, что предложенный им термин не-
удачей, и поэтому впоследствии заменил его термином пангео-
метрия, для этого названия имелись серьезные основания, од-
нако ныие этот термин почти забыт.
Замечание. Неевклидова геометрия Лобачевского, подоб-
но сферической геометрии, зависит от некоторого фиксированного
числа р (в случае сферической геометрии роль такого числа играет
радиус г сферы, являющейся «полем действия» геометрии).
При р —*- со геометрия Лобачевского переходит в евклидову гео-
метрию, подобно тому как сферическая геометрия при г —► оо, ког-
да сфера обращается в плоскость, переходит в. евклидову пла-
ниметрию. Именно это обстоятельство и имел в виду Лобачевский,
введя термин «пангеометрия», т. е. «всеобщая геометрия»: ведь
и евклидову геометрию можно рассматривать как частный (или,
точнее, предельный) случай геометрии Лобачевского, отвечаю-
щий «значению» р=оо.
Выпускник, а позже профессор и ректор Казанского универ-
ситета Н. И. Лобачевский начал с того же, с чего и многочисленные
его предшественники, с попытки доказать 5-й постулат Евклида
методом «от противного» или «приведения к абсурду». Но чем
дальше исследовал он следствии из предположения о ложности
5-го постулата, тем больше убеждался, что никаких противоречий
здесь ие возникает и возникнуть ие может, что геометрическая
система, построенная на предположении о ложности этого посту-
лата, столь же логически совершенна, как евклидова геометрия.
Никак не позже 1826 г. его убеждения в этом полностью сфор-
мировались; в этом году он представил Совету Казанского уни-
верситета обстоятельное исследование «Сжатое изложение начал
геометрии со строгим доказательством теоремы о параллельных»,
доложенное на Совете и подготовленное к печати. К сожалению,
первоначальный текст этого исследования до иас не дошел:
Совет поручил высказать о нем мнение трем профессорам универ-
ситета, которые идей Лобачевского не поняли и из хорошего
отношения к коллеге предпочли попросту «потерять» его доклад.
Однако уже в 1829—1830 гг. Лобачевский напечатал в «Казанском
вестнике» статью в двух частях «О началах геометрии», и 1829 г.
справедливо считают годом создания неевклидовой геометрии.
368
Увы, судьба Лобачевского и его геометрии оказалась вовсе
не простой: до конца дней своих Лобачевский ин от кого ие
услышал слов поддержки и одобрения. Российская (Петербургс-
кая) академия наук устами одного из авторитетнейших своих чле-
нов, Михаила Васильевича Остроградского (1801—1862),
талантливого ученого, которому, однако, были глубоко чужды и
элементарная геометрия, н проблемы обоснования математики,
отозвалась о его творчестве уничижительно; это дало основание
безымянным журналистам развернуть настоящую травлю велико-
го ученого. Выпущенное Лобачевским за свой счет в Германии
(на немецком языке) замечательное сочинение «Геометрические
исследования по теории параллельных линий» получило в автори-
тетном немецком реферативном журнале столь же нелепый изде-
вательский отзыв, как и статьи о Лобачевском в русских жур-
налах. При этих условиях особенного уважения заслуживает стой-
кость Лобачевского, хорошо понимавшего ценность сделанного
нм открытия и вплоть до смерти продолжавшего заниматься соз-
данной им наукой, которой были посвящены его многочисленные
статьи и книги (на русском, немецком и французском языках)
Отрицательно отозвался о трудах Лобачевского ие понявший их
и другой выдающийся русский математик (впоследствии вице-
президент академии наук) Виктор Яковлевич Буняковский
(1804—1889), сам потративший много усилий на доказательство
5-го постулата; однако ои с уважением отзывался об эрудиции и
талантах Лобачевского.
Впрочем, были два читателя, которые полностью Лобачевского
поняли и весьма высоко ценили, жаль только, что Лобачев-
ский об этом так никогда и не узнал. Вышедшие в свет в 1840 г.
замечательные «Геометрические исследования» привлекли напря-
женное внимание Гаусса; поскольку в этой книге упоминались
предшествующие русские публикации Лобачевского, Гаусс даже
специально выучил русский язык, чтобы иметь возможность с ними
познакомиться. В переписке Гаусс неоднократно с глубоким ува-
жением упоминает труды Лобачевского; с презрением писал он
(но тоже, к сожалению, только в письме) о нелепом реферате
иа «Геометрические исследования», автор которого абсолютно не
понимал того, о чем взялся судить. По инициативе Гаусса Лоба-
чевский был выбран иностранным членом высокопрестижного Гет-
тингенского научного общества; однако, получив извещение об
этом, он не знал, что инициатором его избрания был Гаусс, и
ие подозревал, что это избрание выражает одобрение его науч-
ному творчеству. (Гаусс при рекомендации Лобачевского к избра-
нию ничего не сказал о его заслугах, что в силу высочайшего
авторитета рекомендателя было даже ие необходимо; Лобачев-
ский, как ректор одного из ведущих русских университетов, имел и
другие знаки призиаиия, относящиеся, однако, скорее к его ад-
министративной, чем к научной деятельности.) После смерти Гаус-
са его письма были изданы, и высокая оценка в этих письмах
369
никому тогда еще неизвестного русского математика послужила
трамплином для признания Лобачевского, одна ко произошло это,
к сожалению, уже после смерти казанского геометра.
Публикация писем и научных дневников Гаусса позволила
также установить, что и ои, как и Лобачевский, полностью осоз-
нал логическую непротиворечивость дедуктивной системы, назван-
ной им неевклидовой геометрией. Разумеется, продвинулся он в
рассматриваемой области гораздо меньше, чем Лобачевский, от-
давший всю жизнь разработке новой геометрии. Но причина, по-
чему неевклидову геометрию никто никогда не именует «геометри-
ей Гаусса», заключается не только (и не столько) в этом. Гаусс,
хорошо понимавший, насколько новые идеи обогнали свое время
и как трудно нм найти признание (две геометрии — откуда это?),
ничего ие напечатал по неевклидовой геометрии и категорически
запретил всем, знакомым с его взглядами, разглашать эти
взгляды.
Третьим первооткрывателем неевклидовой геометрии Лобачев-
ского можно считать замечательного венгерского математика
Я. Бой ан (1802—1860). Сын университетского друга Гаусса,
незаурядного математика и педагога Ф. Бой а и (1775—1856),
Янош сам, однако, полноценного математического образования
не получил: ои окончил военное училище, дающее лишь начальную
подготовку, и был армейским офицером, что ему никак ие под-
ходило; при первой возможности он уволился в отставку, полу-
чил крошечную пенсию, жить иа которую было трудно; ои даже
не смог жениться, не имея материальной возможности содержать
семью. К идее о неевклидовой геометрии Янош пришел в 20-х го-
дах, как и Лобачевский. Одна ко первая его и единственная
публикации на эту тему (латинская, ибо венгерский язык в те годы
никак не был языком научного общения) была выпущена в
1832 г.— тремя годами позже первой публикации Лобачевского.
Осуществленный в виде Приложения к толстой книге его отца этот
замечательный труд Я. Бойаи и сегодня называют латинским сло-
вом Appendix. Бойаи-старший, естественно, послал свою книгу
Гауссу, присовокупив при этом, что Янош очень ждет отзыва
Гаусса о своей работе. Однако отзыв этот пришел иескоро и Яноша
ои обескуражил, ибо и здесь Гаусс подчеркнул, что в публикации
Яноша для него ие было ничего нового (что на самом деле было
неверно: уже сам подход Яноша к неевклидовой геометрии заметно
отличался от подхода Гаусса, да и новые для Гаусса конкретные
результаты Appendix также содержал). Позже Гаусс обратил вни-
мание Яноша на «Геометрические исследования» Лобачевского,
из которых Янош узнал о первенстве русского геометра, ссылав-
шегося в своей книге и иа публикации 29—30-х годов. Бойан оста-
вил тщательные — и иногда не совсем справедливые — коммента
рии иа «Геометрические исследования», в которых он, впрочем,
отдает должное замечательному сочинению своего соперника и
признает его приоритет.
370
Яноша обижало также то, что в последующих своих беседах
с разными математиками (в том числе и со знакомыми Фаркаша
Бойаи) иа темы оснований геометрии Гаусс часто и охотно
упоминал Лобачевского, но, кажется, полностью игнорировал
Appendix Бойаи. Последнее обстоятельство связано, по-видимому,
не только с более продвинутым по сравнению с Гауссом и Бойан
исследованием феноменов неевклидовой геометрии Лобачевским,
но также и еще с одной причиной. Геометрия, как мы сегодня хоро-
шо понимаем, имеет два разных облика — «геометрни-физики» и
«геометрии-математики»: ее можно рассматривать как естествен-
нонаучную дисциплину, изучающую некоторую специфическую ка-
тегорию свойств (размеры, форма) реальных объектов, ио можно
смотреть иа нее так же как на чисто логическую («выводную», по
Аристотелю) дисциплину, развиваемую, исходя нз экономного
списка аксиом, и никак не связанную с наблюдением н экспери-
ментами. Весьма физически мыслящий Гаусс подходил к геометрии
лишь с первой точки зрения; в своих письмах он прямо писал, что
эту науку надо считать не «априорной», чисто логической, подобно
арифметике, а наблюдательной, экспериментальной, родственной,
скорее, механике. Точно так же воспринимал геометрию и Ло-
бачевский — недаром н для него, н для Гаусса коренным был
вопрос о геометрии реального мнра: является она евклидовой илн
неевклидовой? (Когда Гаусс специально изучал русский язык, что-
бы читать Лобачевского, то делал он это в первую очередь в на-
дежде найтн у Лобачевского ответ на этот волнующий обоих
вопрос.) В неевклидовой геометрии Лобачевского сумма углов
треугольника всегда меньше 180°, причем отлнчне этой суммы от
180° будет тем значительнее, чем больше площадь треугольника.
Это знали и Лобачевский, и Гаусс, н Бойаи, н первые двое пыта-
лись экспериментально определить сумму углоа очень большого
треугольника (образованного наблюдателем и двумя неподвиж-
ными звездами у Лобачевского, наблюдателем и двумя горными
вершинами у Гаусса): из значимого отличия этой суммы от 180°
следовала бы неевклидова природа физического пространства. Од-
нако в обоих случаях сумма углов треугольника в пределах точ-
ности измерений со 180° совпала; из этого же никакого вывода сде-
лать было нельзя, поскольку было возможно, что рассматриваемый
треугольник еще слишком мал для того, чтобы отлнчие суммы его
углов от 180° можно было экспериментально обнаружить.
Совсем по-другому подходил к неевклидовой геометрии Я. Бой-
аи, которому мысль об измерении суммы углов «реального тре-
угольника» и в голову ие могла прийти,— его подход Гауссу пол-
ностью чужд. Бойаи рассматривал геометрию как чисто логичес-
кую систему. Он даже специально выделил отдельно абсолютную
геометрию, вовсе не зависящую от 5-го постулата Евклида. К аб-
солютной геометрии (первой рассмотренной математиками непол-
ной аксиоматической системе!) относятся, в частности, первые
28 предложений евклидовских «Начал». Прн дальнейшем ее ана-
371
Лизе абсолютная геометрия распадается ла две разные схемы:
геометрию Евклида и геометрию Лобачевского. Именно отношение
к геометрии как к абстрактной логической схеме вызвало тре-
вогу Бойан по поводу отсутствия у него логически безупречного
доказательства непротиворечивости аксиоматики неевклидовой
геометрии — первое такое доказательство было даио итальянцем
Эужеиио Бельтрами (1835—1900) лишь в 1868 г., когда ин
Гаусса, нн Лобачевского, ни Бойаи уже давно ие было в живых.
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ:
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ,
ГЕОМЕТРИИ ЛОБАЧЕВСКОГО И РИМАНА
Простейшей неевклидовой (т. е. отличной от евклидовой)
геометрией можно считать сферическую геометрию, «полем дейст-
вия» которой служит сфера (радиуса 1, как мы будем далее счи-
тать); роль точек в этой геометрии играют точки сферы, а роль
прямых — так называемые большие окружности, получаемые в се-
чении сферы с проходящими через ее центр плоскостями. Ясно,
что геометрия на сфере во многом от школьной (евклидовой)
геометрии отлична: так, каждые две «прямые» здесь обязательно
пересекаются (причем в двух диаметрально противоположных точ-
ках), так что параллельных прямых в сферической геометрии
не существует.
Нетрудно проверить, что длина окружности радиуса г сфе-
рической геометрии (рнс. 270, а) равна 2л sin г, а площадь круга
того же радиуса 2л (1— cos г)=4л sin2-—-. (Мы оговорили равен-
ство R— 1, где R — радиус сферы; при произвольном же R обозна-
ченный иа рисунке 270, а как г угол будет иметь величину-^-. Соот-
ветственно этому длина окружности радиуса г и площадь огра-
ниченного этой окружностью круга будут равны 2л/? sin и
Рис 270
Рис 271
372
4л₽2 sin , что прн R —•- оо дает евклидовы значения 2пг и яг2.
Выписанные ниже формулы сферической тригонометрии перехо-
дят в евклидовы при R—*- оо.) Сумма углов треугольника в этой
геометрии всегда больше 180°; так, на рисунке 270,6 изображен
образованный экватором сферы и двумя меридианами треугольник
с тремя прямыми углами (и значит, с суммой углов, равной 270°).
Нетрудно доказать, что площадь треугольника сферической гео
метр ни полностью определяется его углами А, В и С — она рав-
на Л4-В4-С—-л. Заметьте, что площадь изображенного на рисуи
ке 270, б треугольника с суммой углов ~ равна —• (углы мы здесь
и далее измеряем в радианах). Основные тригонометрические соот-
ношения между сторонами а, Ь, с и углами А, В, С сферического
треугольника (рис. 270, а) будут таковы:
_si^_=_sinb синусов),
sin A sin В sin С J '
cos a=cos b cos c-f-sin b sin c cos А (1-я теорема косинусов),
cos A =cos В cos C+sin В sin C cos а (2-я теорема косинусов).
Наиболее резкое отличие сферической геометрии от евкли-
довой заключается в том, что «прямые» здесь пересекаются в двух
точках, в евклидовой геометрии это никогда места иметь не может.
Неевклидовой геометрией Римана часто называют геометрическую
систему, получаемую из сферической геометрии путем «склеива-
ния» диаметрально противоположных точек сферы, которые теперь
принимаются за одну точку новой, неевклидовой плоскости:
«полем действия» такой геометрии можио считать полусферу 2 со
«склеенными» (отождествленными) диаметрально противополож-
ными точками ограничивающего 2 «экватора» (рис. 271).
В своей диссертационной лекции 1854 г. (прочитанной в Гет-
тингенском университете для допуска его к работе в качестве
доцента) «О гипотезах, лежащих в основании геометрии» один
из двух крупнейших (наряду с Гауссом) математиков XIX в
Б. Р и м а н (1826—1866) определил целую систему «метрических»
(т. е. обладающих расстояниями между точками и углами между
пересекающимися линиями) геометрий, выделив из их числа три
(он их назвал евклидовой, гиперболической н эллиптической)
наиболее близкие к «школьной» геометрии. Впоследствии выясни-
лось, что гиперболическая геометрия — это давно уже открытая
(ио Риману ранее незнакомая) неевклидова геометрия Лобачевс-
кого, а эллиптическая — та, которую ныне часто называют не-
евклидовой геометрией Римана.
В неевклидовой геометрии Римана параллельных также не
существует, ио две прямые пересекаются здесь в единственной
точке. Прямые рассматриваемой нами геометрии замкнуты: каж-
373
Рис. 272
дая из них имеет длину л; вся плоскость Римана имеет площадь 2л
(площадь полусферы!). Легко понять, что все выпнсаиные выше
формулы — для длины окружности н площади круга, тригономет-
рические соотношения — сохраняют силу как для сферической
геометрии, так и для неевклидовой геометрии Римана, к сфери-
ческой очень близкой.
Близка к неевклидовой геометрии Римана и геометрия Ло
бачевского. Мы уже указывали, что в этой геометрической сис-
теме аксиома параллельных А3 места ие имеет: через точку А вне
прямой а здесь можно провести много как пересекающих а пря-
мых (как прямая AM илн AN на рисунке 272), так и не пересекаю-
щих а прямых (как PQ иа рисунке 272); отделяют эти прямые
друг от друга прямые AU и А V, неограниченно к а приближающие
ся, ио нигде с а ие встречающиеся,— именно эти две прямые
Лобачевский и назвал «параллельными а». Наличие двух разных
проходящих через А прямых, ие пересекающих а, обычно вклю-
чается в число аксиом неевклидовой геометрии Лобачевского.
Сумма углов дАВС геометрии Лобачевского всегда меньше эт
(т. е. 180°); более того, в удачно выбранных единицах площадь
ДАВС будет равна л—(А4-В + С), в силу чего наибольшую воз
можиую площадь будет иметь изображенный на рисунке 270,6
треугольник, все стороны которого попарно параллельны и все
«углы» которого можно считать нулевыми. Основные тригономет
рнческие формулы, связывающие стороны а, Ь, с и углы А, В, С про
нзвольного треугольника геометрии Лобачевского, имеют вид:
sh a sh b sh с , .
Рис. 274
ch a=ch b -ch c-f-sh fc-sh c-cos А (1-я теорема косинусов),
cos A ==cos B-cos C4-sin B.sin C«ch а (2-я теорема косинусов),
где sh а и ch а — так называемые гиперболический сииус и ги-
перболический косинус величины а, геометрический смысл кото-
рых проиллюстрирован на рисунке 273, б (для сравнения иа ри-
сунке 273, а изображены обычные, «круговые» сннус и косинус
угла а; прн этом иа обоих рисунках а равно удвоенной площади
заштрихованного сектора — соответственно кругового и гипербо-
лического) .
В 1868 г. Э. Бельтрамн показал, что неевклидова геометрия
Лобачевского выполняется на поверхности так напиваемой пгсв-
досферы (рис. 274), если расстояние между дну мн i очками »т<»Л
Поверхности измерять по кратчайшей соединяющей их линии
на поверхности (сами эти кратчайшие линии будут играть в
нашей «геометрии на псевдосфере» роль прямых), а углы между
пересекающимися линиями псевдосферы понимать как углы между
прямолинейными касательными к этим линиям. Соображения, иа
которых мы здесь, к сожалению, остановиться ие можем, позво-
ляют рассматривать псевдосферу Бельтрами как «сферу мнимого
радиуса».
Построенная Бельтрами модель геометрии Лобачевского иа
псевдосфере доставила первое доказательство непротиворечивости
геометрии Лобачевского (выводимой из непротиворечивости
обычной, евклидовой геометрии, которая сомнений никогда ие
вызывала): ведь псевдосферу можно описать» исходя из ее гео-
метрических свойств, т. е. в евклидовой геометрии в простран-
стве такая поверхность есть; существует и геометрия на ней —
откуда же здесь могут взяться какие-бы то ни было противоре-
чия? В той же работе 1868 г. Бельтрами наметил построение
еще одной, может быть, даже более простой «модели неевклидо-
вой геометрии Лобачевского», называемой сегодня чаще всего
моделью Бельтрамн — Клейна. (Знаменитый немецкий математик
Ф. Клейн (1849—1925) пришел к «модели Бельтрамн в круге»
неевклидовой геометрии Лобачевского двумя годами позже Бельт-
375
рами, но независимо от него.) В этой модели точками плоскости
Лобачевского называются точки круга К евклидовой плоскости
и прямыми — хорды круга К. Поскольку точки ограничивающей К
окружности н внешние по отношению к К точки мы просто от-
брасываем, то через точку А вне прямой (хорды круга К) а прохо
дят как пересекающие а прямые, так и множество не пересекаю-
щих а прямых (ср. рис. 275 с рис. 272; ясно, что прямые A U и А V
иа рисунке 272 «параллельны по Лобачевскому» прямой а).
Под расстоянием dMN между двумя точками М и N прямой а пони-
мается выражение » где и V — концы хор-
ды а круга, а выбор основания системы логарифмов может быть
любым (от него зависит лишь выбор единицы измерения длин)
Нетрудно проверить, что если L, М, N — три последовательные
точки прямой а, то ^ln (почему?) и «лучи» MU и MV
«неевклидовой прямой» имеют бесконечную (неевклидову) длину
Оба доказательства непротиворечивости геометрии Лобачев-
ского имеют, так сказать, условный характер: они устанавливают,
что геометрия Лобачевского не может содержать противоречий,
если их не содержит евклидова геометрия. Но непротиворечи-
вость евклидовой геометрии также можно доказать, построив так
называемую «арифметическую» модель евклидовой плоскости (илн
пространства): из существования этой модели следует, что если
учение о числах безошибочно, то н евклидова геометрия нн к ка
кому противоречию привести ие может. Для построения арифме-
тической модели отождествим геометрическую плоскость с коорди-
натной плоскостью, точками которой являются пары чнсел (х; у) —
координат точки, а прямые описываются уравнением y=kx-\-b или
х=а (рис. 276); точка М(х; у) принадлежит прямой y=kx-^-b
или прямой х—а, если ее координаты удовлетворяют уравнению
прямой. Далее, из трех принадлежащих одной прямой точек та ле-
жит между двумя другими, одна из координат которой (абсцис-
са х нлн ордината у) заключена между одноименнымн координа-
тами двух других точек. Наконец, растояние dAB=d между точ-
ками A (xi; yt) и В(х2; у2) определяется по формуле d2—
=(хг—Х|)2-|-(у2—£/i)2» после чего равные отрезки определяются как
такие, длины которых совпадают; аналогично же с помощью
Рис. 276
Рнс. 277
376
формулы для угла между прямыми (выпишите ее) определяются
равные углы. (Так как прямые y—kx+b и y=klx-]~bi образуют
с осью абсцисс такие углы а и ац что tga=fe н tgai=£|, то
угол <р=сс1 — а между этими прямыми определяется равенством
tg <f = 1g (“I — °0=(tg И| — tg и) (I +tg «I tg a)=(fc, — k) (1 + kk,);
еще проще определить угол между прямыми y=kx-l~b и х=а.)
Легко проверить, что в этой модели выполняются все аксиомы
евклидовой геометрии — гильбертовы или любые другие, поэтому
никаких противоречий аксиоматика евклидовой геометрии содер-
жать не может, ибо иначе эти противоречия не допустили бы
существования модели, в которой все аксиомы верны.
Задачи
Рассматривая историю возникновения аксиоматики евклидо-
вой геометрии, мы видели, что одной нз важнейших целей при
ее создании было упорядочение математических рассуждений
Приведенные ниже задачи 1—9 постарайтесь решить, возможно
более тщательно обращая внимание и а аккуратность ваших
выводов.
1. Пусть а, Ь, с. d — произвольные действительные числа
Докажите, что выполняется неравенство
дй’+Р'+т/сЧ у/(а+сУ+(Ь+<У.
Указание. Воспользуйтесь методом координат и сведите
доказываемое утверждение к хорошо вам известному свойству
расстояния.
2. Через точку D иа стороне АС треугольника АВС проведены
отрезки, параллельные медианам. Докажите, что отрезок XY раз-
бивается медианами иа три равные части (рис. 277).
Эта задача решается с использованием теоремы Фалеса — од-
ного из самых важных утверждений евклидовой геометрии. Инте-
ресно, что она была найдена Фалесом до выявления системы ак-
сиом геометрии. Как раз, наоборот, усилия геометров были сос-
редоточены иа том, чтобы подобрать возможно более простые, яс-
ные, наглядно очевидные утверждения и с их помощью доказывать
уже известные теоремы (и, конечно, открывать новые). По сущест-
ву, способ их рассуждений был похож на тот, прн помощи ко-
торого мы решаем задачи: утверждение есть, а требуется подо-
брать факты, которые мы считаем истинными, из которых чисто
логическими рассуждениями можно его вывести.
3. Имеется два равных правильных семиугольника. Вершины
одного из них занумерованы подряд числами 1, 2, ..., 7. Распо-
ложите в вершинах второго эти же числа так, чтобы при любом
наложении одного семиугольника на другой хотя бы при одной
(обшей) вершине стояли равные числа.
377
4. Пусть а, b, с, d — последовательные стороны четырех-
угольника, S — его площадь. Докажите, что ас -f- bd 2S.
Наверно, легче будет решить похожую задачу: доказать, что
ab^-cd~^2S, а потом свести первую задачу ко второй.
Аксиоматическое построение геометрии существует в матема-
тике со времен Древней Греции. Однако другие разделы ма-
тематики, например связанные с изучением числовой системы,
в то время ие были аксиоматизированы. Почему? Причина (глав-
ная, но ие единственная) состоит в том, что при проведении
числовых расчетов нужно было не доказывать, а вычислять. То,
что в области числовых соотношений можно проводить доказатель-
ства, было окончательно понято только в XIX в. Следующая
задача поможет вам почувствовать, в чем здесь дело.
5. Пусть Xt, х2—корни квадратного уравнения ах2+Ьх+
4-с—0. Найдите XiH-xl
Как можно было бы решить ее? Нам известна формула корней
квадратного уравнения, с помощью которой легко провести нуж-
ные вычисления. Усложним задачу: потребуем, чтобы значение
искомого выражения, т. е. х? -f-xl, было найдено без использования
этой формулы. Кажется, что это ограничение закрывает все пути
к нахождению ответа. Но это неверное впечатление: ведь известны
соотношения между корнями и коэффициентами квадратного урав-
нения (формулы Виета). Пользуясь имн как аксиомами, можно
вновь пытаться приступить к решению; вы увидите, что оно не так
уж сложно.
6. Множество целых чисел разбито иа два непересекающих-
ся подмножества. Можно ли утверждать, что хотя бы в одном нз
иих имеется бесконечная арифметическая прогрессия?
7. Число состоит нз 30 единиц и нескольких нулей. Докажите,
что это число не является квадратом натурального числа.
8. Из произвольной точки круглого биллиарда пущей шар.
Докажите, что внутри биллиарда найдется окружность, которую не
пересекает траектория шара.
На этой задаче стоит остановиться подробнее. Оиа резко отли-
чается от предыдущих. По постановке она не вполне математи
ческая, так что ее надо прежде всего перевести на язык математи-
ки, или, как говорят, составить ее математическую модель. Круг
лый биллиард — это, конечно, круг. Шар, который пущен,—
точка. Каков закон ее движения? По прямой, если она ие встречает
граничную окружность. Как изменяется направление движения
при встрече? Этот случай описывается специальной аксиомой
(которая, как и любая аксиома, имеет опытное происхождение)
прн встрече с окружностью траектория точки образует равные
углы с радиусом, проведенным в эту точку (рис. 278). Задача те-
перь превратилась в математическую задачу. Сформулируйте ее
н приступайте к решению.
378
9. а) Даны три точки, ие лежащие на одной прямой. Сколько-
существует параллелограммов, три вершины которых лежат в
данных точках? б) Дай выпуклый четырехугольник. Докажите, что
найдутся три его вершины 4, В, С, такие, что вершина D парал-
лелограмма ABCD лежит внутри илн на границе четырехуголь-
ника.
Задачи 10 и 11 вы должны решить, ссылаясь иа аксиомы из
учебника геометрии, т. е. привести предельно строгое математи-
ческое рассуждение.
10. Прямая АВ пересекает отрезок CD, прямая CD пересекает
отрезок АВ. Докажите, что отрезки АВ и CD пересекаются.
11. Точка В лежит между точками А н С, точка С лежит меж-
ду точками В и D. Докажите, что точка С лежит между точками
А н D.
12. а) Рассмотрите каждое из следующих трех множеств:
М| — множество всех точек на координатной плоскости с цело-
численными координатами; Мг — множество точек на координат-
ной плоскости, у которых обе координаты — рациональные числа,
по модулю меньшие единицы; Мз — множество точек трех задан-
ных параллельных прямых. Докажите, что в каждом из этих слу-
чаев выполняется такое свойство: любая прямая, проходящая
через две точки данного множества, проходит еще по крайней
мере через одну его точку, б) Приведенные множества все были
бесконечными. Может ли сформулированное свойство выполняться
для конечного множества точек? Оказывается, может, но только
если все точки лежат иа одной прямой. Докажите это.
13. Часто в математике некоторое понятие определяется при
помощи перечисления его свойств. В этом случае эти свойства
играют роль аксиом. Прн проведении рассуждений с таким по-
нятием, помимо известных математических фактов, постоянно при-
ходится учитывать и эти аксиомы. Вам известен пример такого
понятия — площадь фигуры. Напомним основные свойства (т. е.
аксиомы) площади: а) площадь фигуры — положительное число;
б) площади равных фигур равны; в) если у двух фигур нет общих
внутренних точек, то площадь третьей фигуры, составленной из
двух даияых, равна сумме площадей данных фигур; г) площадь
прямоугольника со сторонами а и Ь равна ab. Известно, что из
этих аксиом можно вывести формулы для площади многих фи-
гур — параллелограмма, треугольника, трапеции. Пользуясь при-
веденными аксиомами и известными вам формулами для площади
простых фигур, решите задачу: докажите, что площадь заштрихо-
ванной иа рисунке 279, а фигуры равна площади параллело-
грамма ABCD, а иа рисунке 279, б-----~ площади ABCD.
15. По кругу записано в произвольном порядке 4 нуля и
5 единиц. Над этими числами производится следующая операция:
если соседние числа одинаковы, то между ними записывается
379
О, а если различные, то 1; после этого исходные числа стираются.
При этом вновь получается набор чисел, записанных по кругу.
К этому набору вновь можно применить эту же операцию н т. д
Докажите, что, сколько бы раз ее ии применять подряд, нельзя
получить набор, состоящий из 9 нулей.
16. В некотором государстве для дипломатической переписки
используется алфавит нз трех букв а, Ь, с. Сообщение — это
любая последовательность букв, а расшифровка его ведется по
следующим правилам: 1) если рядом стоят две различные буквы,
то их разрешается менять местами; 2) если рядом стоят две
одинаковые буквы, то их разрешается стереть. При этом шиф-
ровальщик должен получить возможно более короткую строчку
н ее уже отдать министру иностранных дел. Спрашивается: сколь-
ко различных по смыслу сообщений можно передать, пользуясь
этим шифром?
Вам должно быть ясно, что условия 1 и 2 — это ие что иное,
как аксиомы, определяющие шифровку или дешифровку сообще-
ний. Заметим, что реальные шифры также часто используют
похожие приемы тайнописи (текст «портится» перестановкой
букв по определенным правилам, добавлеинем лишних букв
и т. п.).
Литература
1. Болтянский В. Г. и др. Геометрия 6—8: Пробный учеб-
ник.— М.: Просвещение, 1979.
2. Бурбаки Н. Очерки по историк математики.— М.: ИЛ,
1963.
3. Геометрия 6—8: Учебное пособие для 6—8 классов средней
школы/Под ред. А. Н. Колмогорова,— М.: Просвещение, 1982
4. Гильберт Д. Основания геометрии.— М.; Л.: ОГИЗ, 1948
5. Гильберт Д., К о н-Ф о с с е н С. С. Наглядная геомет-
рия.— М.: Наука, 1981.
6. Глейзер Г. И. История математики в школе: VII—
VIII классы.— М.: Просвещение, 1982.
380
7. Евклид Начала.— М.; Л.: Гостехиздат, 1948—1950.—
Т. I — III.
8. Курант Р., Роббинс Г. Что такое математика? Элемен-
тарный очерк идей и методов.— М.: Просвещение, 1967.
9. Розенфельд Б. А., Яглом ИМ. Неевклидовы гео-
метрии//ЭЭМ. Т. V (геометрия).— М.: Наука, 1966.
10. Смогоржевский А. С. О геометрии Лобачевского.—
М.: Наука, 1984.
11. Ст рой к Д- Я. Краткий очерк истории математики.— М.:
Наука, 1977.— (ПЛМ).
12. Ф е т и с о в А. И. Очерки по евклидовой и неевклидовой гео-
метрии.— М.: Просвещение, 1965.
13. Яглом А. М., Яглом И. М. Вероятность и информа-
ции.— М.: Наука, 1973.
14. Яглом И. М. Аксиоматические обоснования евклидовой
геометрим//Новое в школьной математике/Сост. И. М. Яг-
лом.— М.: Знание, 1972.
ПОСЛЕСЛОВИЕ ДЛЯ УЧИТЕЛЯ
Книга содержит учебные материалы для факультативных заня-
тий по математике в VII IX классах общеобразовательной
школы, представленные статьями по всем темам программы фа-
культатива «За страницами учебников математики» (см.: Мате-
матика в школе: Сб. иормат. документов.— М.: Просвещение,
1988.—С. 176—179).
Статьи написаны разными авторами, видными математиками и
педагогами, в присущем каждому из них стиле. Составитель счел
нецелесообразным унифицировать, «причесывая под одну гребен-
ку», стили изложения различных статей, так как это неизбежно
обеднило бы книгу, лишив ее многоцветия красок, отражающих
индивидуальности авторов.
Книга по своему характеру и назначению отличается от изда-
вавшихся ранее пособий такого рода, являясь своеобразной хре-
стоматией, в известной мере приобщающей школьника к чтению
научной литературы и работе с ней
Согласно объяснительной записке к программе темы данного
факультатива не зависят друг от друга и в принципе могут изу-
чаться в любом порядке. Соответственно каждая статья в пособии
представляет собой законченное самостоятельное целое и может
рассматриваться вие связи с остальными.
Количество тем, содержание соответствующих статей и число
задач к каждой статье несколько избыточны, что обеспечивает
учителю известную свободу выбора материала, подлежащего изу-
чению. Распределение тем по классам весьма условно и может быть
изменено по усмотрению учителя.
Каждая статья сопровождается списком литературы, в которой
учитель может почерпнуть необходимый дополнительный материал
для проведения занятий, организуя их по своему усмотрению.
С0ДЕРЖАНИ1
Обращение к юным читателям . 3
7 КЛАСС
Васильев И. Б. Системы счисления .... . . 4
Нестеренко Ю. В. Простые и составные числа ... . 23
Савин А. П. Геометрические построения........................ 66
Прасолов В. В., Шарыгин И. Ф. Замечательные точки в треугольнике . . 85
8 КЛАСС
Блох А. Я. Числовые множества ... - 104
Сатьянов П Г. Метод координат .... . ... 135
Виленкин Н. Я. Никольская И. Л. Элементы математической логики . 172
Болтянский В. Г. Геометрические преобразовапин плоскости , 2(Mi
9 КЛАСС
Мышкис А. Д., Сатьянов П. Г. Функции и графики . 248
Виленкин Н Я Уравнения, неравенства, их системы..............295
Прасолов В. В., Шарыгин И. Ф. Замечательные теоремы и факты гео-
метрии .................................................... - 324
Яглом И. М., Блох А. Я. Логическое строение геометрии........346
Послесловие для учителя. . -.................................382