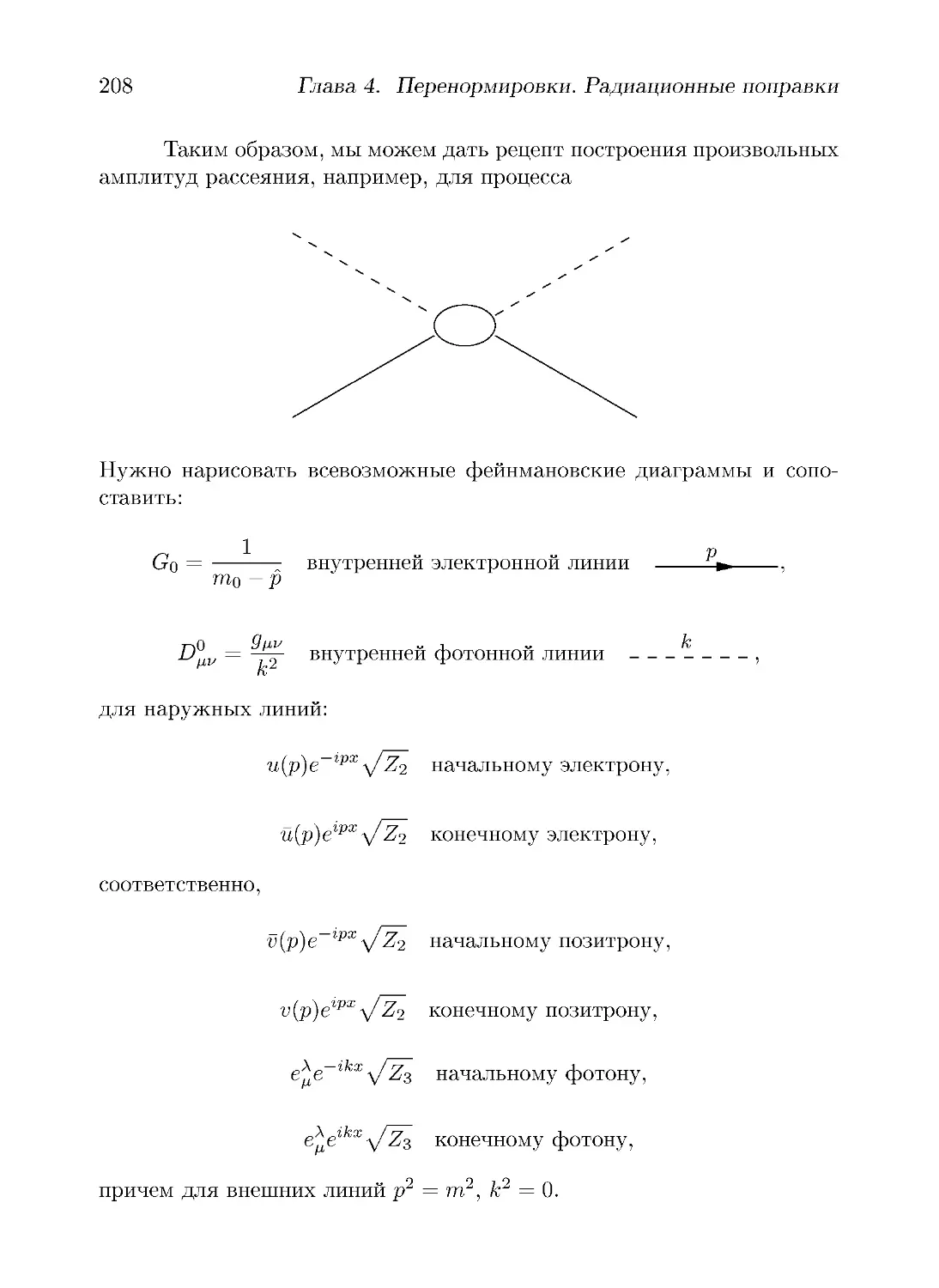
Автор: Грибов В.Н.
Теги: физика математика математическая физика электродинамика квантовая физика издательство москва
ISBN: 5-93972-089-7
Год: 2001
Текст
В. Н. Грибов
КВАНТОВАЯ
ЭЛЕКТРОДИНАМИКА
/?&с
Москва • Ижевск
2001
УДК 530.1 (075.8)
ББК 22.31
Интернет-магазин
http://shop.rcd.ru
• физика
• математика
• биология
• техника
Внимание!
Новые проекты издательства РХД
• Электронная библиотека на компакт-дисках
http://shop.rcd.ru/cdbooks
• Эксклюзивные книги — специально для Вас любая книга может быть
отпечатана в одном экземпляре
http://shop.rcd.ru/exclusive
Грибов В. Н.
Квантовая электродинамика. — Ижевск: НИЦ «Регулярная и хаотичес-
кая динамика», 2001, 288 стр.
Книга написана на основе лекций, прочитанных знаменитым российским
физиком в Ленинградском институте ядерной физики. Изложены основные
электродинамические явления, общие свойства рассеяния, метод перенорми-
ровок.
Для студентов и аспирантов, физиков-теоретиков, специалистов.
ISBN 5-93972-089-7 ББК 22.31
© НИЦ «Регулярная и хаотическая динамика», 2001
http: //rcd.ru
Оглавление
Предисловие............................................... 6
Глава 1. Частицы и их взаимодействие в релятивистской
квантовой механике ..................................... 8
1.1 Функция распространения............................ 8
1.2 Как вычислять наблюдаемые величины.................21
1.3 Электромагнитное поле .............................25
1.4 Фотоны во “внешнем поле”...........................34
1.5 Свободные релятивистские частицы с массой..........45
1.6 Взаимодействие бесспиновых частиц..................47
1.7 Взаимодействие бесспиновых частиц с электромагнитным
полем...................................................55
1.8 Примеры простейших электромагнитных процессов .... 59
1.9 Диаграммы и амплитуды в импульсном представлении . . 65
1.10 Амплитуды реально наблюдаемых процессов...........68
1.11 Мандельштамовская плоскость.......................86
1.12 Комптон-эффект (для л-мезона) ....................91
Глава 2. Частицы со спином 1/2. Основные электродинами-
ческие процессы........................................ 97
2.1 Свободная частица со спином J =1/2.................97
2.2 Функция Грина электрона...........................111
2.3 Матричные элементы амплитуд рассеяния для электронов 114
2.4 Взаимодействие электрона с фотоном................115
2.5 Рассеяние электронов. Связь спина со статистикой...119
2.6 Рассеяние фотона электроном (Комптон-эффект).......126
2.7 Аннигиляция электрон-позитронной пары в два фотона . .140
2.8 Рассеяние электронов во внешнем поле .............146
2.9 Тормозное излучение электрона во внешнем поле ....149
2.10 Формула Вайцзекера-Вильямса......................153
4
Оглавление
Глава 3. Общие свойства амплитуды рассеяния ........... 160
3.1 Симметрии в квантовой электродинамике............160
3.2 Причинность и унитарность........................171
Глава 4. Перенормировки. Радиационные поправки .... 190
4.1 Высшие приближения. Перенормировка массы электрона . 190
4.2 Перенормировка функции Грина фотона .............204
4.3 Перенормировка вершинной части...................210
4.4 Обобщенное тождество Уорда.......................216
4.5 Радиационные поправки к рассеянию электронов во внеш-
нем поле ............................................219
4.6 Уравнение Дирака во внешнем поле.................239
4.7 Радиационные поправки к уровням водородоподобных ато-
мов (Лэмб-сдвиг) ................................253
Глава 5. Трудности квантовой электродинамики........... 259
5.1 Перенормировки и расходимости....................259
5.2 Проблема нуля заряда в квантовой электродинамике . . . 279
В. Н.Грибов
Предисловие
На долю физиков моего поколения выпало большое счастье: мы бы-
ли современниками Владимира Наумовича Грибова, великого физика,
замечательного человека.
Грибов — целая эпоха в физике высоких энергий. Современные те-
оретические представления о процессах в этой области в огромной сте-
пени принадлежат ему. Не случайно в “героическую эпоху” этой науки
для теоретиков, занятых в ней, Ленинградский институт ядерной фи-
зики (ЛИЯФ) был поистине Меккой — в этом институте тогда работал
Грибов.
Впрочем, теоретический отдел института во времена Грибова был
Меккой не только для тех, кто исследовал процессы при больших энер-
гиях. Интересы Владимира Наумовича были несравненно шире, для
него физика была единым целым. Среди его работ есть исследования и
нейтринных осцилляций, и тонких вопросов квантования неабелевых
калибровочных полей. Но влияние Грибова определялось отнюдь не
только его опубликованными статьями. Насколько ценны были обсу-
ждения с ним! Грибов был готов обсуждать любую интересную задачу,
к какой бы области физики она ни относилась. Критика его была зача-
стую безжалостной, но всегда полезной. Если же Грибов убеждался в
правоте собеседника, он признавал ее въявь, амбиции для него роли не
играли.
Обсуждая, Грибов по-настоящему работал, нередко генерируя поис-
тине замечательные идеи. Так, в обсуждении Владимир Наумович дал
интерпретацию инстантона, классического решения нелинейных урав-
нений поля, как подбарьерной траектории, соединяющей вакуумы раз-
ной топологии. Сейчас эта интерпретация — фольклор.
Еще в 1971 или 1972 году, за 2-3 года до появления знаменитой рабо-
ты Хокинга, Грибов четко сформулировал в обсуждениях вывод о том,
что черные дыры излучают. В те относительно далекие времена его
утверждение вызвало резко отрицательную реакцию, по крайней ме-
ре части “гравитационной” общественности, настаивавшей на том, что
мысль об излучении черных дыр противоречит самим основам общей
теории относительности. Остается лишь сожалеть, что Владимир Нау-
Предисловие
7
мович не опубликовал этот результат, по-видимому, считая его самооче-
видным.
Грибов вообще спокойно относился к публикациям. Показательна в
этом отношении история настоящих лекций по квантовой электродина-
мике. Они были прочитаны Владимиром Наумовичем в Ленинградском
университете и опубликованы в трудах Зимней школы физики ЛИЯФ
1974 года. Лекции были подготовлены к печати В. В. Федоровым, ис-
пользовавшим записи Г. М. Амальского и К. Е. Кирьянова. Грибов не
только сам не писал этот текст, но, по-видимому, даже не читал его, во
всяком случае не читал его полностью. Впрочем, класс работы Федорова
таков, что при чтении книги порой возникает удивительное ощущение:
слышится живой голос Владимира Наумовича.
Труды Зимней школы физики ЛИЯФ с лекциями Грибова по кван-
товой электродинамике давно стали библиографической редкостью. Од-
нако сами лекции ничуть не устарели за четверть века. Одновременно с
настоящим изданием они выходят на английском языке в издательстве
Cambridge University Press.
Большая работа по подготовке книги к обоим изданиям была про-
делана Ю. Нири и М. И. Эйдесом.
***
Владимира Наумовича Грибова не стало 13 августа 1997 года. Тяжело
больной, он работал до последнего дня своей жизни. Уже после его смер-
ти были подготовлены к печати и опубликованы две работы Грибова,
посвященные проблеме удержания кварков. Осталась неоконченной его
последняя статья “Квантовая электродинамика на малых расстояниях”.
Свет погасшей звезды еще тысячу лет
К нам доходит. А что ей, звезде, до людей?
Ты добрей был ее, и теплей, и светлей...
Грибовский свет несет нам и эта книга.
И. Б. Хриплович
Глава 1
Частицы и их взаимодействие
в релятивистской квантовой механике
Квантовая электродинамика в настоящее время является достаточно
разработанной теорией. Существует несколько эквивалентных способов
ее изложения.
1. Подход, основанный на формализме вторичного квантования.
2. Метод функционального интегрирования.
3. Подход, основанный на диаграммах Фейнмана (метод функций
Грина). Последний подход является наиболее физически прозрач-
ным. Именно поэтому мы построим изложение квантовой электро-
динамики на языке функций Грина.
1.1 Функция распространения
В квантовой механике движение частицы описывается волновой функ-
цией Ф(гД), которая определяет амплитуды вероятностей всех физиче-
ских процессов и удовлетворяет уравнению Шредингера:
ЭФ
^К- = ЯФ. (1.1)
dt 1 7
Здесь и далее будем пользоваться системой единиц h = с = 1. Если
выбрать в качестве единицы длины (см), то этими двумя уравнениями
фиксируется единица времени (см) и единица массы (см-1) Действи-
тельно, комптоновская длина волны частицы с массой т есть А = К/тс,
А = 1/т(£ = 1см соответствует времени, за которое свет проходит
расстояние в 1 см; т = 1 см-1 соответствует массе частицы (гипотети-
ческой), комптоновская длина которой А = 1 см).
1.1. Функция распространения
9
Волновая функция неудобна в том смысле, что ее вид зависит от
начальных условий, т. е. одному и тому же процессу могут соответство-
вать различные волновые функции. Чем более универсальным можно
ее заменить?
Введем так называемую функцию распространения К(г2,Ч гх, Ч)-
Пусть в момент времени Ч частица находилась в точке гх, определим
ЛГ(г2, Ч; гх,Ч) как амплитуду вероятности того, что в момент време-
ни Ч > Ч эта частица будет находиться в точке гг- Графически этот
процесс можно изобразить линией
гх,Ч г2,Ч
Функция распространения является функцией уже не двух, а четырех
переменных, поскольку в нее мы фактически включили определенные
начальные условия. По своему смыслу К (г?, 12', ri, Ч) при Ч > Ч долж-
на удовлетворять уравнению Шредингера (1-1), т. е.
7Г(г2,Ч;г1,Н) = Ф(Г2,Ч) (1-2)
при начальном условии
7Г(Г2,Ч;Г1,Н) = Ф(г2,Ч)| =Я(Г2-Г1), (1.3)
I ^2 —£1
что является выражением того факта, что в момент времени Ч частица
находилась в точке гх- Зная функцию К, можно решить задачу Ко-
ши для уравнения (1.1), т. е. найти волновую функцию частицы при
произвольном начальном условии. А именно:
<^(г2,Ч) = У -К(Г2,Ч;Г1,£1)<А1(Г1)С?3Г1 . (1.4)
В самом деле, <^(г2,Ч) удовлетворяет уравнению (1-1), так как ему удо-
влетворяет К, и, кроме того, выполняется начальное условие
Лг2,чЖ=41 = аЖ)
в силу (1.3). Физически (1.4) выражает то, что амплитуда вероятности
нахождения частицы в точке Г2 в момент Ч есть произведение ампли-
туды перехода из (гх,Ч) в (гх>4) на амплитуду вероятности того, что
в момент Ч частица находилась в точке гх.
10
Глава 1. Частицы и их взаимодействие...
Если у нас имеется полная система решений стационарного урав-
нения Шредингера
ЯФ„(г, t) = Я„Ф„(г, t), (1.5)
то функцию К можно записать в виде
Я(г2, t2; Pi, й) = J2 ФДг2, £2)Фп(г1, ii). (1.6)
Очевидно, что эта функция удовлетворяет уравнению (1.1) (так как ему
удовлетворяет Фп(г2,^2)), а из условия полноты системы {Фп} следует
выполнение начального условия (1.3):
Я(г2,12;Г1,Н) = У2ф„(г2)Ф*(г1) = <5(ri - г2),
п
т. е. (1.6) действительно есть функция распространения.
Определим функцию распространения для свободной частицы:
Я = ; |^Ф„ = ЯПФП. (1.7)
2m 2m
Решением (1.7) является
Ф„(г,0 = e’pr-z(p2/2m)t , Еп = ^-. (1.8)
2m
Это решение принадлежит сплошному спектру, поскольку импульс, ко-
торый определяет данное состояние, может принимать любые значения.
Поэтому в (1.6) от суммирования нужно перейти к интегрированию по
всем состояниям. Известно, что в интервале от р до р + dp содержится
с?3р/(2тг)3 квантовых состояний, поэтому в (1.6) нужно сделать замену:
52 - / Л3р/(2тг)3 ,
П d
т. е. для свободной частицы получаем
d Р грг2-Др2/2m)t2 -ipri+Др2/2m)ti =
(2^)3
(2^)3 '
Яо(г2,£2;Г1,
1.1. Функция распространения
11
Легко видеть, что Кд удовлетворяет уравнению (1.1) и правильному
начальному условию
Из (1.9) также следует, что Кд в действительности является функцией
только двух переменных: Кд = Kg(y,t), где г = Гг — гд, 4 = 4г — И-
Это не удивительно, поскольку амплитуда перехода из гд, 41 в гг, t^ для
свободной частицы, если пространство и время однородны, не должны
зависеть от положения и момента времени.
Интеграл в (1.9) берется в явном виде:
Kn(r t) ~ f jLjP_e^pr-2(p2/2m')t _ (2m\ 2 lr2m/2t
0[ ’ ’j (2?г)3 "^714^
Очень естественно функции распространения сопоставить линию
Г1Л1
г2,42
Пусть теперь частица движется во внешнем поле, которое описы-
вается потенциалом V(г, 4). Рассмотрим амплитуду перехода частицы
из Pi,41 в Г2,42- При этом возможны следующие процессы.
1. Частица переходит из 1д,41 в Г2Л2, не взаимодействуя с внеш-
ним полем:
О, 41
г2,42
Я0(г2,42;Г1,41)
42 > 41
(1-Ю)
2. Частица свободно распространяется до некоторой точки г', 4', в
этой точке частица взаимодействует с внешним полем и далее свободно
распространяется до Г2,4г- Этот процесс изобразим графически так:
П,41
Г2,42
(1-U)
Чтобы найти амплитуду этого процесса, воспользуемся следующими со-
ображениями. Волновая функция частицы во внешнем поле удовлетво-
ряет уравнению
ЭФ
г— =Я0Ф + ИФ.
at
12
Глава 1. Частицы и их взаимодействие...
За время Д1 волновая функция изменяется на величину
ДФ = -гЯ0ФД1 - iV^At.
Первое слагаемое в правой части соответствует изменению волновой
функции при свободном движении, которое уже учтено в (1.10). Таким
образом, взаимодействие с внешним полем приводит к изменению вол-
новой функции
ДУФ = -гПФД1 .
То есть амплитуду процесса (1.11) можно записать в виде
Я1(г2, t2; Pi, И) = У Я0(г2,1г; (г', 4/)]Я0(г/, tr;r\,ti)d3r'dt'.
(1-12)
Интегрирование в (1.12) соответствует суммированию амплитуд
со всевозможными положениями точки (г', iz).
3. Следующим является процесс, когда частица дважды взаимо-
действует с полем в точках (г',!') и (г" ,t"\
ri,tl г',1' r",l" 1*2,12
Амплитуду этого процесса можно записать аналогично (1.12):
АГ2(г2,12;Г1,<1) = У А\|(г2.12:т'\1/')[-3/(г'/.С')]/<(|(г/'.1/':г/.1/) /
х [—iV(r', i/)]Jfo(r\ t', ri, ti)d3r"d3r'dt"dt', (1-13)
ii < t' < t" < i2 •
Аналогичные рассуждения можно провести для случая трех и
более взаимодействий. Полная амплитуда перехода Я(г2, i2; гх, ii) будет
равна сумме всех таких амплитуд:
AT(r2,i2;ri,ii) = Я„(г2,12; гх, П). (1.14)
п=0
Теперь покажем, что полученная таким образом К есть действи-
тельно функция распространения частицы во внешнем поле.
Работая с функциями Кп, мы связаны необходимостью заботить-
ся о правильной последовательности времен. Чтобы избавиться от этого
1.1. Функция распространения
13
неудобства, введем новую функцию
G„(r2,i2;ri,H) = 0(t2 -
= K(r2,t2\r1,t1),
(1-15)
где
= { 0
t > О,
t < 0.
Тем самым правильная последовательность времен будет соблюдать-
ся автоматически. Функция G называется функцией Грина. Выясним,
какому уравнению она удовлетворяет. Подействуем на G оператором
id/dt — Если функция К удовлетворяет уравнению Шрединге-
ра, то, учитывая, что
(1-16)
получим:
. д
1 dt2
H(r2,t2)
G(r2,i2;ri,ii) = K(r2, t2; rx, - И) =
= «5(г2 - Г1)<ф2 - й)-
Здесь мы учли, что оператор Н(г, t) не содержит дифференцирования
по времени, а также условие (1.3). Таким образом, функция Грина будет
удовлетворять уже неоднородному уравнению:
'. д
1 dt2
H(r2,t2)
G(r2, i2; n, П) = z^(r2 - ri)<5(f2 - H).
(1-17)
В дальнейшем каждой диаграмме будем сопоставлять соответствую-
щую функцию Грина. Например:
Г1,41 r2,t2 Go(r2,42;ri,4i),
----------------«------------------ Gi(r2,f2;ri,fi) = [ Go(r2,f2;r',f') х
Г1,Н г', Г Г2,^2 J
х [—iV(r', i/)]Go(r/, tr; r\,t\)dt’ d3r'
и т. д.
14
Глава 1. Частицы и их взаимодействие...
Теперь покажем, что полученная таким образом полная функция
Грина
G(r2, t2; ri, ti) = G„(r2, t2; гх, 1Х) (1-18)
п=0
удовлетворяет правильному уравнению. Если сопоставить полной функ-
ции Грина жирную линию, (1.18) можно записать графически так:
Go + G -iV Go
1*1,11 1*2,12 1*1,11 r',1' Г2,12
(1-19)
Поясним, как мы это получили. Все графики, начиная со второго, имеют
следующую структуру:
-IV Go
г' ,t'
-iV Go
—--------- + •••
r',1' r2,i2
Все они кончаются графиком
-iV________________Go
г' ,1' Г2,12
Если этот элемент “вынести за скобку”, то сумма в скобках даст снова
полную функцию Грина:
G
Этой “операции” и соответствует (1.19). Соотношение (1.19) есть не что
иное, как графическое уравнение для функции Грина. Ему соответству-
1.1. Функция распространения
15
ет интегральное уравнение:
G(r2,i2;ri,ii) = Go(r2,f2;ri,ii)+
+ [ Go(r2,t2;r/,4/)[—iV(r'. (1-20)
Покажем, что это уравнение эквивалентно (1.17). Подействуем на функ-
цию G (1-20) оператором Шредингера для свободного движения:
д
гту----Я0(г2, f2) G(r2, f2; П, <i) = i5(r2 - rx)J(f2 - fx)+
+ [ id(r2 — r')<5(f2 — t,')[—iV(r',t')]G(r', fz; rx, fx)<f3r/cff/ =
= г6(г2 - Г1)5(42 - И) + V(r2,t2)G(r2,t2;ri,ti).
Перенеся второе слагаемое в левую часть равенства, получим в точно-
сти (1.17). Функция G определяется однозначно как решение неодно-
родного дифференциального уравнения (1.17) с начальным условием
G(r2,t2;Pi,ti) = 0 при t2 < t±, или, что то же самое, как решение
интегрального уравнения (1.20). Отметим, что решение интегрально-
го уравнения, полученное итерациями по потенциалу, автоматически
удовлетворяет начальному условию — точная функция Грина G рав-
на нулю при f2 < fi, потому что свободная функция Gq обладает этим
свойством. Тем самым мы показали, что функция G, построенная по ре-
цепту (1.18), действительно является функцией Грина уравнения Шре-
дингера для частицы во внешнем поле, а это в силу (1-15) означает, что
функция К (1.14) есть функция распространения частицы во внешнем
поле.
Введенные нами графики фактически являются диаграммами
Фейнмана для рассеяния частицы во внешнем поле в нерелятивистском
случае. Отметим, в полученных нами выражениях время и простран-
ственные координаты входят абсолютно равноправно и в аргументах
функций Грина, и в последовательных интегралах, определяющих Gn.
Именно благодаря этому обстоятельству подход, основанный на функ-
циях Грина, становится особенно удобным, когда мы переходим к реля-
тивистской теории.
Аналогично можно построить функцию Грина для двух и боль-
шего числа частиц. Пусть, например, имеются две свободные частицы,
их движение опишем графиком
Г1’^ <4 (1.21)
f2,i2 r2,i2
16
Глава 1. Частицы и их взаимодействие...
Функция Грина в этом случае будет просто произведением одночастич-
ных функций Грина, поскольку частицы движутся независимо.
G0(r2,ri,t'2,t'1;r2,r1,t2,t1') = G0(r/1 —rx, —1х)С0(г2 — r2, i2 —i2)- (1-22)
Простейшим графиком, учитывающим взаимодействие между двумя
частицами, будет
Г1,11 Х1,Т1 г), ti
Г2,12
Х2,Т2
Г2,12
(1-23)
Пунктирная линия соответствует однократному взаимодействию меж-
ду частицами. По аналогии со случаем одной частицы сопоставим ей
выражение [—iV(x2 — Xi,r2 — ti)], где V — потенциал взаимодействия.
Для Gi получаем
Gi = УG0(ri,fi;xi,ri)[-jV(x2-xi;r2-Ti)]Go(xi,n;ri,fi) х
х Go(r'2, t2; x2, t2)Go(x2, t2; r2, (1-24)
В отличие от одной частицы во внешнем поле, в данном случае потен-
циал описывает взаимодействие двух частиц и поэтому в (1.24) учиты-
вается только один раз. Строгое доказательство (1.24) проведем позже.
В нерелятивистской теории взаимодействие распространяется мгновен-
но, т. е. потенциал зависит от времени как V(х2 — хх, т2 — т±) = 6(т2 — тх).
Вернемся к частице во внешнем поле. Обычно удобно работать
в импульсном представлении. Переход к импульсному представлению
проведем так, чтобы сохранить формальную симметрию между про-
странственными и временными переменными, в дальнейшем это приго-
дится при обобщении теории на релятивистский случай.
Функция Грина свободной частицы имеет вид (см. (1.15)):
G0(r,t)= /-^егрг-г(р2/2т)‘0(1) . (1.25)
J (2тг)3
1.1. Функция распространения
17
Здесь t и г входят не симметрично. Однако (1-25) можно переписать
Go(M) = / 7TTn6'o(p.Po)c'rJr ''Л1' , (1.26)
J (2я)4г
В выражении (1.26) как г и t, так и р, рд входят равноправно. Функция
Грина в импульсном представлении Go(p,po) имеет вид:
<2о(р,Ро) = ----------- • (1-27)
pJ/2m — pq — ге
где е — произвольное малое положительное число. Итак:
G0(r,i) = [ (1.28)
J (2тг)4г p2/2m — ро — zs
Теперь покажем, что (1-28) эквивалентно (1.25). Проинтегрируем по ро
в (1.28). Подынтегральное выражение имеет простой полюс в точке
т. е. в нижней полуплоскости. Если бы е = 0, то полюс находился бы на
вещественной оси и интеграл не имел бы смысла.
При t < 0 контур интегрирования можно замкнуть в верхней полу-
плоскости, тогда, поскольку внутри контура С\ не содержится полюсов,
18
Глава 1. Частицы и их взаимодействие...
интеграл по нему равен нулю, в то же время интеграл по верхней по-
луокружности при t < 0 равен нулю по лемме Жордана, это приводит
к обращению в нуль интеграла (1.28).
При t > 0 замкнем контур интегрирования в нижней полуплос-
кости (аналогично предыдущему интеграл по нижней полуокружности
равен нулю) и получим
d3PdP0 1 .ipr-ipot
W4i£-P0-iS
—2mRes\Pa.
Здесь Res\Po — вычет подынтегрального выражения в точке
Ро = р2/2т — is. Таким образом, при t > О
d3pdpo
(2тг)4г
V 7 9m
--------егрг-гро4 =
-Ро-ге
d3p eipr-i£Tt
(2тг)4г
т. е. в точности (1.25) при t > 0.
Итак, мы доказали, что выражение (1.25) совпадает с (1.28). Яв-
ный вид Go(p,po) (1-28) можно получить непосредственным решением
уравнения Шредингера для свободной функции Грина (в (1.27) мы его
просто угадали).
Имеем
/ d V2 \
('т + ) Go(r’ = • С1-29)
\ (Л/ Zt f 11 /
Ищем решение в виде (1.27):
G°CM) = / ^тСо(р,Ро)егрг-гро‘.
Подставив (1-27) в (1.29) и используя соотношение
(1.30)
(27Г)
получим
т. е.
Po-f- Go(P,Po)e2pMpot Р
2т /
Go(p,Po) =
(2тг)4г
1
_ ipr-ipot
,4 е
р2
о----Р0 —
2 т 7и
1.1. Функция распространения
19
малая добавка — ie введена для того, чтобы обеспечить выполнение усло-
вия: при t < 0, Go(i) = 0. Введем теперь импульсное представление для
потенциала внешнего поля:
V(r’t) = /(f^e”°V(,2)’ (L31)
V(g) = / d3rdte~icir+iqotV(r,t'), (1.32)
где q = (g0,q)-
Подставляя (1-27) и (1.31) в выражение для Gi(r2, ^2! ri, ti), будем
иметь для процесса:
Go —iV Go
-----------------•
ri,tl г',Г r2,t2
G^r2,t2-,ryG) = [ d3r'dt' [ 7^|тС0(р2)егр2(г2-г')-гг,2о(*2-*')х
J J (2тт)4г,
Go(r2,t2;r',t')
x(-o J / ^|тСо(Р1)егр1(г'-Г1Ь^(‘'-41) =
-iV(r',f) Go(r',t';ri,4i)
=
(27r)4<54(pi+g-p2)
xeZP2r2-tp2ot2e-Zpiri+lplotlGo(p2)[_y(9)]Go(pi)
(2тг)12г
Интегрирование no d3r', dt' привело к J-функции, что является
выражением закона сохранения энергии-импульса. Интегрируя по d^q,
получим окончательный результат:
Gi(r2,t2;ri,ii) = У rf4^yy2e~ipiri+ipiotleip2r2~2p2ot2 х
xGo(p2)[-V(p2-pi)]G0(pi). (1.33)
Таким образом, взаимодействие приводит к тому, что первая поправка к
свободной функции Грина уже не является функцией только разностей
20
Глава 1. Частицы и их взаимодействие...
Г2 — гх; t-2 — ti. Gq можно переписать в аналогичной форме
Go= /^^ф1-Р2)Со(Р1)егр2Г2-гр20<2е-гр1Г1+г₽10<1. (1.34)
Введя точную функцию Грина в импульсном представлении G(pi,p2)
по формуле
G(r2,i2;ri,fi) = [ , (1.35)
J (2л)вг
получим, учитывая (1.34), (1.33),
G(pi,p2) = (27r)4<5(pi-p2)Go(pi)+Go(P2)[-I/(P2-pi)]Go(pi)H- (1-36)
Графически (1.36) выглядит так:
G(p) (2тг)4д~(Р1 -p2)Go(p2) Gq(P1) -V Со(р2)
Pl Щ pi Р2 pi Р2
Если повторить аналогичные выкладки для следующей диаграммы
Pi р' Р2
ri,tl r',t' г" , t" F2,t2
получим для Сг(р1,Р2) следующее выражение:
G2(P1,P2) = Go(pi) [ ^V(p' -Pi)G0(pXp2 -p')G0(p2). (1.37)
J (2л)4
Выражение для Gi(pi,p2) (второе слагаемое в (1.36)) соответству-
ет первому борновскому приближению в обычной квантовой механике
(—V(p2~Pi) — амплитуда рассеяния в этом приближении). (1.37) соот-
ветствует второму борновскому приближению, причем интегрирование
по импульсам эквивалентно суммированию по промежуточным состоя-
ниям.
Аналогичным образом можно сформулировать общие правила
построения функций Грина Gn для любой диаграммы:
Р1________________Р________ р"___________________Р2________
-V(p'-pi) -V(p"-p') -V(p2-p")
Каждой линии сопоставляется свободная функция Грина Go(pi), каж-
дой вершине [—У] по всем импульсам промежуточных линий произво-
дится интегрирование с!4р/(2л)4.
1.2. Как вычислять наблюдаемые величины
21
1.2 Как вычислять наблюдаемые величины
1.2.1 Амплитуда рассеяния
Вычислим, к примеру, амплитуду рассеяния. Пусть нам задано началь-
ное состояние ФДг, t). В результате взаимодействия частица переходит
в состояние Ф(г, £). Волновая функция Ф(г, f) содержит информацию о
взаимодействии и “помнит” начальное состояние. Амплитуда вероятно-
сти того, что возникнет состояние Фу, есть
У Фу(г, £)Ф(г, £)с?3г.
Это выражение можно переписать при помощи функции распростране-
ния. Поскольку
Ф(г, £) = У K(r,t-,r' ,
то амплитуда перехода i -л f или матричный элемент матрицы рассея-
ния S запишется так:
Sfi = У Фу(г,£)Ф(г,£)й3г = У
Кроме того, в полученном выражении нужно времена устремить к бес-
конечности: / - эс. // - ос и окончательно, переходя от функции К
к G, получим
Sfi = У ^*f(r,t)G(r,f,r/,t/')^l(r,,t/)d3rd3r/. (1.38)
Вычислим (1.38) для реального процесса: пусть свободная частица с
импульсом pi, провзаимодействовав с полем, перешла в состояние с
импульсом р2, т. е.
= gipir-z(p)/2m)t _ егр2г-г(р2/2т)(.
Тогда
5р р =у 6/3r/(y3re-ip2r+z(p2/2m)teipir'-i(p)/2m)t'х
х / ^Х')?GGy.p'.y/P'21' г,'20'х (1.39)
22
Глава 1. Частицы и их взаимодействие...
Здесь мы использовали разложение (1.35) для функции Грина G(r, t; г', t').
Интегрирование в (1.39) по d3r, d3r' дает
(2тг)3<5(р2 - р'2)(2тг)3<5(р1 - р\).
В результате получим
Sp2;Pi = 7^7 [ d,pwdpwelt^^ (1.40)
(2tf)j« J
Теперь вспомним разложение G(pi,p2) в ряд (1-36):
G(pi,p2) = (2tt)4<5(pi ~P2)G0(pi) + G0(p2)[-V (р2 ~Pi)]G0(pi)+
+Gq(pi) [ ~ Pi)Gq(p')V(р2 — p'^Gq^pq') + • •
J (2л)4
Подставляя это выражение в (1.40), для первого члена разложения по-
лучим
С,Р1 = —г(2л)2<5(рх - р2) У dp1oG(t-f')(p2/2m-pi°)Go(p,Pio) =
= -г(2л)25(Р1 - р2) [ 2/9 dP0-----^е-(р2/2»-Ро) =
J p2/2m — pq — ге
= (2л)35(р1 - р2), (1.41)
т. е. рассеяния в этом приближении нет. При выводе (1.41) мы исполь-
зовали явный вид (1.28) для функции Грина Go(p,po) в силу того, что
г > 0, замкнули контур вниз, для интеграла в результате получили
значение 2-тгг.
Все остальные члены разложения G(pi,p2) содержат по краям
свободные функции Грина, так что можно написать
G(pi,p2) = (2тг)Ч(р1 -p2)G0(pi) + G0(pi)T(pi,p2)G0(p2), (1.42)
где T(pi,p2) содержит все внутренние линии и интегрирования по про-
межуточным импульсам.
Вычислим вклад в интеграл (1-40) от второго члена (1.42). При
t оо экспоненциальный множитель в подынтегральном выражении
быстро осциллирует и, если бы подынтегральная функция была глад-
кой, интеграл обратился бы в нуль. Однако она содержит полюсные
множители
Go(pi)Go(p2) = 2 ------------ 2 --------------— •
(Pl/2т - р10 - ге) (р2/2т - р20 - ге)
1.2. Как вычислять наблюдаемые величины
23
Функция T(pi,p2) является более гладкой, поскольку содержит инте-
грирования типа
d4p'
p,2/2m — р'о
Поэтому интеграл можно вычислить по вычетам. Окончательно для
SP2;Pi получаем
5Р2,Р1 = (2тг)35(Р2 - Pi) + (2тг)4гТ(р1,р2). (1.43)
Таким образом, T(pi,p2) является амплитудой рассеяния, и для ее вы-
числения нужно поступать следующим образом:
1. выписать интересующие нас графики
Pl Р' Р2
Pl Р2 Pl Р2 Pl р Р2
2. написать соответствующую функцию Грина по полученным нами
правилам:
G(P1,P2) = <5(pi -р2)Со(Р1)(2л)4 + --гТ(У22}9--------щ
(р2/2т - р2о) (Pi/2m - Рю)
3. выбросить полюсные множители;
4. положить рю = р2/2тп,р20 = Р2/2ш для всех частиц, относящихся
к внешним линиям.
1.2.2 Связанные состояния
Покажем, что полюса амплитуды рассеяния определяют энергии свя-
занных состояний. Согласно обычной квантовой механике амплитуда
рассеяния есть
2m Г i
f = ~JZ I е~гр г^(г)Фв(г)й3г, (1.44)
где р7 — импульс частицы в конечном состоянии, а Ф_е(г) — точная
волновая функция — решение стационарного уравнения Шредингера с
энергией Е = р/2/2т.
24
Глава 1. Частицы и их взаимодействие...
Для функции Грина мы написали выражение:
С(г2Д2;Г1Д1) = 6>(т) Фга(г2Д2)Ф*(г1Д1).
п
Рассмотрим функцию Грина с определенной энергией:
G'B(ri,r2)= У С(г2,Г1,т)ег'ЕтД-=
= £ф„(г2)ФДг1) Г е<Е-Е^ =
п
= 1 V Ф»(Г2)Ф»(Г1) (1 45)
Еп_Е ’
Эта функция удовлетворяет уравнению
(Я - E)GE(ri, г2) = |^(г1 - г2). (1-46)
Из (1.45) непосредственно видно, что Ge(ti, г2) имеет полюса в связан-
ных состояниях. При помощи С?£:(г1, г2) можно сконструировать точное
решение стационарного уравнения Шредингера, а именно:
ФДг) = eipr + (-г) У Gs(r, r')eiprV(r')dV.
Действительно,
(Я - Я)ФЕ = У(г)егрг - И(г)егрг = 0.
Тогда
/ = -? /7гчТДгД3г
4тг J
+ ^г У e-ip'rV(r')GE(.r,r/)eipr'V(r,)d3rd3r' =
= {в + ^ЕЬЧк (1.47)
т: /I 1 JTL 1 7
Здесь q = р—р', /в — амплитуда рассеяния в борновском приближении,
fnp = У е-гргР(г)Фп(г)Сг3г. (1.48)
Из (1.47) следует, что связанным состояниям действительно соответ-
ствуют полюса амплитуды рассеяния.
1.3. Электромагнитное поле
25
1.3 Электромагнитное поле
В этом параграфе мы рассмотрим квантовую механику фотона. Это
необходимо делать с учетом того, что фотон — объект релятивист-
ский. Напомним, что при классическом описании мы вводим 4-тензор
электромагнитного поля F^v{x) (здесь и далее х обозначает 4-вектор,
х = (х, f)), компонентами которого являются напряженности электри-
ческого и магнитного полей Е, Н.
Условимся всевозможные релятивистские инварианты писать в
виде
афУм = жоУо - - ^2У2 - ^зуз,
т. е. не будем различать верхние и нижние индексы, а будем помнить
такое правило суммирования по повторяющимся греческим значкам.
Иногда нам понадобится также метрический тензор <gw'.
Уоо = 1,511 = 522 = Узз =-1; 5^=0, если у v.
Будем пользоваться системой единиц Хэвисайда, в которой h =
= с = 1, а единица заряда определяется следующим образом:
е2/4тг/гс = а ~ 1/137 ; хэвисайдов заряд е2 = 4тга ~ 4тг/137.
При таком выборе системы единиц уравнения Максвелла для F^ix)
запишутся так:
ЭР
(1Л9)
фх, + Жа + = 0
ОХ\ ох^ oxv
Это релятивистски инвариантные классические уравнения, описываю-
щие электромагнитное поле. Обычно вводятся потенциалы Ам(ж):
дхц dxv
(1-51)
При этом уравнение (1.50) выполняется автоматически. Однако выбор
потенциалов неоднозначен и на них можно наложить одно дополнитель-
ное условие. Мы выберем его в виде
дА„
—А- = 0
дх„
(условие Лоренца).
(1-52)
26
Глава 1. Частицы и их взаимодействие...
Тогда из (1-49) получим следующее уравнение для потенциалов:
= Эр.(х). (1.53)
Рассмотрим волновое уравнение
□ /(;т) = 0 . (1.54)
Это уравнение описывает распространение волны (в частности, элек-
тромагнитной) в пустом пространстве.
Попытаемся описать свободное электромагнитное поле квантово-
механически. Хотя ничего нового для свободного поля мы не получим,
это нам понадобится при рассмотрении взаимодействия. Предположим,
что электромагнитное поле состоит из фотонов — квантовых частиц,
которые описываются некоторой волновой функцией. Свободные фото-
ны должны описываться одинаково хорошо и квантовомеханически, и
классически, поскольку квантовые эффекты начинают сказываться, ко-
гда обратное воздействие прибора на изучаемый объект становится не
малым, т. е. при наличии взаимодействия. Однако классическое поле
мы можем наблюдать непосредственно, поскольку изменение поля при
взаимодействии с прибором в этом случае несущественно. В квантовой
механике ситуация меняется. Частица описывается волновой функци-
ей Ф(ж), которая сама по себе непосредственно не измеряется. Квадрат
же Ф(ж) |2 (плотность вероятности) определяет физические величины и
потому измерим. Интеграл от плотности вероятности дает вероятность
найти квантовомеханическую частицу где-либо в пространстве и не за-
висит от времени
У Ф\2d3r = const. (1.55)
Сохранение вероятности является одним из основополагающих принци-
пов квантовой механики.
Попытаемся сконструировать для фотонов величину Ф, допуска-
ющую вероятностное толкование, т. е. обладающую свойством (1.55).
С другой стороны, она должна удовлетворять (1.54), которое описыва-
ет распространение фотонов в пустом пространстве со скоростью с.
Вспомним, как получается сохранение интеграла (1.55) в обычной
квантовой механике. Волновая функция Ф комплексна и удовлетворяет
1.3. Электромагнитное поле
27
уравнению Шредингера
ЭФ V2
i— = ЯФ, Н =------------. (1.56)
dt 2m 77
Комплексное сопряженное к (1.56) уравнение имеет вид
ЭФ*
-г—=Я*Ф*. (1.57)
Умножая (1.56) на Ф*, (1-57) на —Ф и складывая, получим
Э 1
i—ф*ф = (ф\72Ф* — Ф*\72Ф)
dt 2m7 7
или
^-Ф*Ф =-----^„^ф* - Ф*УФ). (1.58)
dt 2m
Уравнение непрерывности (1.58) и позволяет интерпретировать величи-
ну Ф*Ф как плотность вероятности, поскольку
Ф*Ф > 0 , У Ф*Фс!3г = const .
Но уравнение Шредингера явно приближенное, поскольку не являет-
ся релятивистски инвариантным. Уравнение же (1.54) релятивистски
инвариантно. Перепишем его в виде
S-V2/ = 0 (1.59)
Э/-
и попытаемся из / сконструировать нечто, удовлетворяющее уравнению
непрерывности типа (1.58). Будем считать f комплексным, хотя реаль-
ное электромагнитное поле вещественно. Поступим аналогично преды-
дущему:
®-v2r = o, (1.60)
otz
= d_ _ fdT\ =
J dt2 J dt2 dt V dt ' dt J
= div(/*V/ -/V/*). (1.61)
28
Глава 1. Частицы и их взаимодействие...
Мы видим, что, вообще говоря, есть величина, интеграл от которой
сохраняется, т. е. можно попытаться интерпретировать как плотность
вероятности
Из (1-62) непосредственно следует, что / должна быть комплексной,
иначе выражение обратится в нуль, т. е. отождествление f с полем
невозможно.
В отличие от обычной квантовой механики, в p(r, t) входят про-
изводные, это следствие того, что (1.59) — уравнение второго порядка
по времени, и для однозначного определения волновой функции нужно
в начальный момент задать и функцию, и ее производную. Ситуация
здесь такая же как с электромагнитным потенциалом в классической
механике: А удовлетворяет уравнению второго порядка, однако изме-
рение электрического Е и магнитного поля Н в один момент времени
позволяет фиксировать и А, и его производную А. В этом еще ничего
плохого нет.
Хуже обстоит дело с тем, что p(r,t), определенная в (1.62), мо-
жет принимать отрицательные значения. Чтобы обойти эту трудность,
попробуем выбрать из решений уравнения (1.59) такие, чтобы для них
p(r,i) была положительна. Для этой цели рассмотрим, какие вообще
решения имеет (1.59).
Будем искать решение в виде ряда Фурье:
/(х) = £е-^/(А:) , (1.63)
к
где кх = коХо — к±х± — — кдгд. ко, к±, к?, — четыре независимых
числа. Тогда
И = £(-^)e-fc/(^) = 0 , (1.64)
к
где к% = kfjtfj. = ку — к± — к% — fcj, как мы условились. Очевидно, что
решением (1.64) является
к0 = ±|к| . (1.65)
то есть имеется два решения. Общее решение можно написать так (ниже
под ко будем понимать положительный корень (1.65):
f(x) = f+(x) + f-(x),
(1.66)
1.3. Электромагнитное поле
29
где
/Дгг) = ]>>-^-кД(А:) (1.67)
к
— так называемое положительно-частотное решение,
/_(х) = ^2e-^-koX°-kr^ f(k) =
к
= ^2e^kox°-k'^f(k') (1.68)
к1
— отрицательно-частотное решение. Итак, в отличие от решения урав-
нения Шредингера, мы получили два комплексных решения с разными
частотами.
В качестве волновой функции выберем Ф = /+ (по аналогии с
нерелятивистским случаем, где мы выбирали е-гВ*). Тогда, если поло-
жить
'’ = Ч/+ДГ“/+ДГ) = /+'Й/+- (1ет)
легко показать, что интеграл от этой величины сохраняется и положи-
телен. Действительно,
J pd3r = J [eikx(-ik'0)e-ik'x - ik0e~ik'xeikx]d3r =
k,k'
= (2л)3 ДАДД Mo, (1.70)
k
t. e., если ко = |k|, это выражение положительно. Соответственно, для
отрицательно-частотного решения выражение (1-70) имело бы другой
знак.
Теперь возникает вопрос, можно ли функции р(х) придать смысл
локальной плотности вероятности. Для этого она сама должна быть
положительной: непосредственно этого сказать нельзя, так как р состо-
ит из экспонент, которые осциллируют, за исключением стационарного
случая, когда
/+ = е~гш‘Ф(г) , p(r,i) = 2ДФ(г)|2.
Значит, для стационарного состояния, р можно придать смысл
плотности вероятности, как и в нерелятивистской квантовой механике.
30
Глава 1. Частицы и их взаимодействие...
В общем случае этого сделать нельзя. Причина этого глубоко связана с
самой природой релятивистской квантовой теории. В нерелятивистской
теории в процессе измерения свойства частицы как таковой, не меня-
ются. В релятивистской же теории, как мы вскоре увидим, количество
частиц не сохраняется. Поэтому попытка измерения координаты фо-
тона за конечное время (что приводит к нестационарному состоянию)
приводит к рождению новых фотонов, и потому понятие одночастичной
волновой функции утрачивает смысл.
Итак, мы получили, что в качестве волновой функции фотона
можно выбрать, в частности, положительно-частотное решение урав-
нения Даламбера (1.59), тогда можно определить функцию р(ж) так,
что интеграл от нее по всему пространству сохраняется во времени, а в
случае стационарного состояния ей можно приписать смысл плотности
вероятности, как в обычной квантовой механике.
Как выглядит условие ортогональности для волновых функций
фотона, соответствующих различным к? В нерелятивистской квантовой
механике
У Ф£ФкД3г = (2тг)35(к' - к). (1.71)
В нашем случае соответствующее выражение имеет вид:
У = (2тг)35(к' - к). (1.72)
В этом смысле отрицательно- и положительно-частотные решения ор-
тогональны, т. е.
/ - °-
Свободное движение частицы описывается плоской волной:
/+(Л =е~гЬ7+(Ц
Подставляя в (1.72), получим
/+(O/X(fc/)2fc0(27r)3J(k - к') = (2тг)35(к - к'),
откуда
p — ikx
Мх)= (1.73)
V2fc0
1.3. Электромагнитное поле
31
Функция (1.73) описывает свободно распространяющийся фотон с за-
данной энергией и импульсом.
На самом деле мы описали пока не совсем фотоны, поскольку ре-
альные фотоны имеют векторный характер (описываются четырехмер-
ным потенциалом АД. Повторим теперь наши рассуждения для реаль-
ных фотонов. Также выделим положительно- и отрицательно-частотные
части из решений уравнения Даламбера для А;|:
□Л = о. (1.74)
Ищем решение в виде
Л(^) = / Шк)е-гкх + Д (fc)e^ ] . (1.75)
Это выражение записано в виде a + о* в силу вещественности А Дж).
Подставляя (1-75) в (1.74), получим, как и раньше,
к2 = к2 = 0 или ко = ±|к|.
Волновую функцию фотона можно записать:
Ш = / ^a^e~lkX- (176)
Нормированному состоянию с определенным импульсом соответствует
-Щ) = (gg , (1.77)
где ем — единичный вектор поляризации, (1.77) получается аналогич-
но (1.73).
Из условия Лоренца следует
Д = о
их it
или
ДД = . [ d3k к^ lkx =
Эжм J (2ДЗ 2к0
к^ = 0. (1.78)
32
Глава 1. Частицы и их взаимодействие...
Это условие четырехмерной поперечности фотона. Что оно озна-
чает? Вообще говоря, в четырехмерном пространстве можно ввести
4 независимых вектора е*, в силу (1-78) остается 3 независимых век-
тора, ортогональных но поскольку к'^ = 0, один из этих векторов
совпадет с к^, так как “он сам себе ортогонален”. Иначе говоря, в про-
странстве Минковского, в отличие от евклидового, нельзя построить
три вектора, ортогональных вектору, у которого к^ = 0.
Действительно, выберем систему координат так, что
к || z, т. е. /.р = (Ад,О,О, fcz) , ко = kz.
Два вектора, ортогональных данному, имеют вид:
= (ео, ех, еу, ez) = (0,1, 0,0),
= (0,0,1,0),
третий же вектор effl параллелен к^. Действительно,
fcae^ — kze^ = 0 ; = е^\ так как ко = kz.
Следовательно, оба вектора effl и к,, имеют структуру (а, 0,0, а), т. е.
отличаются численным множителем. Кроме того, при помощи калиб-
ровочного преобразования мы его всегда можем обратить в нуль, т. е.
на физических результатах наличие не должно сказываться. Дей-
ствительно, уравнения Максвелла инвариантны относительно замены
потенциалов
+ (i-79)
Разложив /(ж) в интеграл Фурье, получим
1г = / (1-80)
т. е. в импульсном пространстве калибровочному преобразованию соот-
ветствует замена волновой функции фотона:
aM(fc) aM(fc) - zfcM/(fc). (1.81)
А поскольку о'^\к') = е^\к) / у/Гко || то ясно, что выбором f(k) мы
всегда сможем обратить эту компоненту в нуль.
1.3. Электромагнитное поле
33
Таким образом, у фотона могут быть только две независимых
поляризации, роль которых играют пространственные компоненты век-
торного потенциала. Поэтому, хотя спин фотона равен 1, вклад в фи-
зически наблюдаемые величины могут дать только 2 поперечные про-
екции. Этот факт является следствием равенства нулю массы фотона
(fc2 = m2 = 0).
Итак, волновую функцию фотона мы можем записать в виде:
А — 1,2
Е (t1-82)
A=l,2J ’
Чтобы сконструировать плотность вероятности мы должны составить
величину, аналогичную (1.72), из и просуммировать по векторно-
му значку. В соответствии с нашим соглашением о метрике еу, еу, =
(2) (2) -1
= еД еД = —1 это подразумевает, что суммировать надо со знаком
минус, таким образом
Р — ( fv
Условие нормировки для фотона:
У /м2/£*(ж)г^/^1/г(а:)с?3г = -е/’е*1 (2тг)35(к - к') =
= 5А1А2(2тг)35(к — к'). (1.83)
Полученные нами волновые функции имеют простую классиче-
скую интерпретацию. Записав вектор-потенциал в форме (1-75) и вы-
числяя среднюю энергию электромагнитного поля
,3 Е2 + Н2
!3г--------------
2
мы видим, что нормировка нашей амплитуды <7;, отвечает ситуации,
когда имеется ровно один фотон в единичном объеме.
34
Глава 1. Частицы и их взаимодействие...
1.4 Фотоны во “внешнем поле”
Попытаемся найти функцию распространения релятивистской части-
цы, которая описывается волновой функцией /+(ж). (От индексов пока
снова отвлекаемся.)
В нерелятивистской теории мы получили функцию распростра-
нения в виде суммы
/С(ж2,Ж1) = ^2 Фп(^2)Ф:^1) , (1-84)
причем сконструировали ее таким образом, чтобы
Ф(л?2) = У К(%2, Ж1)Ф(Ж1)^3Г1. (1.85)
В релятивистской теории нужно учесть следующие моменты:
1. в начальный момент нам нужно задать и функцию, и ее произ-
водную по времени;
2. волновая функция у нас была определена как положительно-час-
тотное решение уравнения Даламбера, поэтому необходимо, чтобы
при действии функции распространения на начальное состояние
не появились отрицательные частоты.
Попытаемся угадать вид функции распространения. Напишем по ана-
логии с (1-84)
К(Ж2,Ж1) = (1.86)
п
и изменим формулу (1.85) следующим образом:
/+(^2)= [ ^(^2,Ж1)г-^-/+(ж1)с?3Г1. (1-87)
J
Теперь можно проверить, что выражения (1.86) и (1.86) правильно опи-
сывают изменение во времени волновой функции релятивистской части-
цы. Рассмотрим вначале волновую функцию, которая отвечает одному
стационарному состоянию, т. е. положим
/+(^1) = /+(Ж1),
1.4. Фотоны во “внешнем поле'
35
тогда
f+W = Е /П+Ы У /+*(Ж1)^= /+(Ж2). (1.88)
Мы учли условие ортогональности волновых функций в виде (1.72).
В нерелятивистском случае в соотношении, аналогичном (1.88), фигу-
рировало бы, соответственно, условие ортогональности в виде (1.71).
Таким образом, мы нашли правильный закон распространения
релятивистской частицы в стационарном состоянии fn, а поскольку лю-
бое состояние можно разложить по то этот закон справедлив для
любого состояния. Отметим, что вид (1-87) обусловлен тем, что урав-
нение Даламбера второго порядка по времени (1.87) как раз и дает его
решение при заданных начальных условиях (т. е. при заданном значе-
нии функции и ее производной в начальный момент времени).
Вычислим функцию распространения свободной безмассовой ча-
стицы. Мы уже знаем, что ее нормированная волновая функция
p — ikx
fn = ЛТТГ’
тогда мы получаем
/^Зд, e-ik(x2-x1)
W 2к0
к0 = |к|.
(1.89)
Наша функция распространения релятивистски инвариантна. Чтобы
увидеть это явно, используя соотношение
<№)) = Е
где Xi — корни уравнения f(%i) = 0, запишем ее в виде
—^k2)e-ik^-x^0(ko). (1.90)
Функция 0(fco) введена, чтобы отобрать только положительные часто-
ты. Выражение (1.90) имеет явно релятивистски инвариантный вид.
36
Глава 1. Частицы и их взаимодействие...
{Знак энергии также релятивистски инвариантен для частиц с А:2 О!)
Легко видеть, что К{х2,х±) удовлетворяет уравнению
□ 2-Д(яд,яд) = О
(1-91)
(где Пг обозначает оператор Даламбера). Действительно, подставляя
(1.90) в (1.91), получаем
fc25(fc2) = 0.
Теперь попробуем ввести взаимодействие V (х) в нашу реляти-
вистскую теорию. Мы введем его так, чтобы графику
Х1
Х2
как и раньше, соответствовала поправка к свободной функции распро-
странения:
У К(х2 — x)V(x)K(x — xi)dx. (1-92)
В нерелятивистском случае к аналогичному выражению мы требовали,
чтобы Д < t < Д. Это соответствует тому, что частица сначала возник-
ла, а потом взаимодействовала, мы учли это условие, введя функцию
Грина:
G{x2 - Яд) = 0{t2 - tl)K{x2 - ЯД).
Можно ли в релятивистской теории поставить такое условие? К сожа-
лению, вообще говоря, упорядочение по времени Д < t релятивистски
неинвариантно. Оно становится релятивистски инвариантным, только
если интервал {х — яд)2 > 0, т. е. времениподобен. Однако функция
К{х-^ — яд) отлична от нуля и для пространственно-подобных интер-
валов, и поэтому условие Д < t < Д привело бы к тому, что выраже-
ние (1-92) для амплитуды перехода стало бы релятивистски неинвари-
антным.
Наши рассуждения мы можем проверить непосредственно; вве-
дем
G = 0(Д - 1д)К(х2 - яд)
и посмотрим, какому уравнению удовлетворяет эта функция. Действуя
оператором Даламбера на G. мы получим
/я2 \ ГД2 К
00 дК д29 т.
+
1.4. Фотоны во “внешнем поле'
37
В этом выражении в правой части первый член равен нулю в силу (1.91),
оставшиеся же члены явно релятивистски не инвариантны, т. е. дей-
ствительно, условие 41 < 4 < 12 не имеет смысла. Таким образом, нам
не удалось совместить два требования:
1. чтобы функция распространения содержала только положитель-
ные частоты (мы ее строили именно так, поскольку только для
положительных частот можно ввести вероятностное толкование);
2. чтобы взаимодействие произошло в 4 между 41 и 42, т. е. требование
причинности.
Отказ от требования 1 равносилен отказу от вероятностной трак-
товки квантовой механики, так что посмотрим, нельзя ли пересмотреть
понятие причинности в форме 2. Может ли взаимодействие произой-
ти раньше момента времени 41, когда частица родилась? Иначе говоря,
возможен ли график
(считаем далее на графиках, что ось времени направлена слева напра-
во)?
В действительности этот график можно понимать и иначе: имен-
но, будем считать, что в момент 4 родились 2 частицы, а в момент 41
одна из них исчезла. При такой интерпретации причинность сохраня-
ется, и подобные графики имеют смысл. Рассмотрим еще один пример:
4
41
4' 42
Если t' < 4, то этот график можно интерпретировать иначе: в момент 4'
родилось 2 частицы, в момент 4 частицы, распространяющиеся из щ
и г', аннигилировали, и в момент 42 осталась одна частица.
38
Глава 1. Частицы и их взаимодействие...
Такая интерпретация возможна, если предположить, что функция рас-
пространения, в присутствии взаимодействия, описывает также и про-
цессы, в которых на некотором интервале времени может существовать
несколько частиц. Таким образом, в релятивистской теории, чтобы вве-
сти взаимодействие, нам приходится отказаться от сохранения числа
частиц. Это как раз и соответствует тому, что нам не удалось ввести
локальную плотность вероятности. Несохранение числа частиц, т. е. воз-
можность их рождения или уничтожения, ничему не противоречит, по-
скольку, в силу соотношения неопределенностей ~ 1, на короткий
промежуток времени может родиться сколько угодно частиц. Ясно, что
для того, чтобы описанная интерпретация распространения частицы от
ii до t при t < ii имела смысл, K(t,ti) ПРИ t < ti должно равняться
nPH t > ti, но при том же значении \t — ti\, если предполага-
ется, что в момент t < ti рождаются те же частицы. Для того, чтобы
это имело место, функция распространения должна быть разрывна при
t = Д. В результате так определенная функция распространения не мо-
жет удовлетворять однородному уравнению Даламбера. Она окажется
функцией Грина этого уравнения.
Рассмотрим теперь связь между функцией распространения (1.90)
и функциями Грина уравнения Даламбера:
□ Сф) = -гф). (1.93)
Разложим С(ж) в интеграл Фурье:
/,/М.
^-^e-^G(fc). (1.94)
1.4. Фотоны во “внешнем поле'
39
Аналогичное разложение для 6(х) имеет вид:
(1.95)
Подставляя (1.95), (1-94) в (1.93), получим
^-(-k2)e-^G(k) =
откуда
ад = (1-96)
к
тогда
Gw=-/(Se”fa^ (1-97)
Поскольку k2 = fcg — к2, подынтегральное выражение (1-97) имеет два
полюса по ко: ко = ±|к|. Чтобы интеграл (1.97) имел смысл, эти полюсы
нужно немного сдвинуть в комплексную область.
Рассмотрим комплексную плоскость ко.
+ х
ко = — |к|
о □
□ +
к0*= +|к|
х о
40
Глава 1. Частицы и их взаимодействие...
У нас имеется 4 возможности сдвига полюсов с вещественной оси, как
указано на рисунке.
1. Пусть оба полюса снизу (отмечены “°”), тогда если t < 0, то контур
нужно замкнуть наверх, и тогда
Сд=0, t<0. (1.98)
При t > 0 контур нужно замкнуть вниз, тогда
Г d3k е~4Ф+*кг d3k ei|fe|t+*kr
Gr = J (2^)3 2|к| J (2тг)3 2|к| ’ t>0' (L99)
Gr содержит отрицательные частоты и поэтому нас не устраивает.
2. Рассмотрим теперь случай расположения полюсов, отмеченный х
на рисунке, т. е.
при t > 0, замыкая контур вниз, получим:
/d3k
(2тг)3 2|k|
t > 0
(1.100)
1.4. Фотоны во “внешнем поле'
41
и, соответственно, при t < О
/,/3/. „i|fc|t+zkr
Сравнив (1.100) с (1.89), обнаруживаем замечательный факт: при
t > 0 наша функция Грина совпадает с функцией распространения
и устроена таким образом, что содержит отрицательные частоты
только при t < 0 (и только отрицательные). Более того, посколь-
ку фаза подынтегрального выражения (1.101) содержит \к\ > 0,
a t < 0, то
ад = с?(-ж). (1.Ю2)
Эту функцию G называют причинной или фейнмановской функ-
цией Грина. Как мы увидим ниже, именно эта функция описыва-
ет распространение релятивистских частиц таким образом, чтобы
причинность выполнялась. Положение полюсов в фейнмановской
функции Грина отвечает замене к2 —> к2 + is в знаменателе вы-
ражения (1.97).
Рассмотрим теперь, что будет, если принять во внимание спин
фотона, т. е. с учетом того, что волновая функция фотона имеет вид
/^(х). Функция распространения в этом случае будет зависеть от спи-
нов начального и конечного состояний, т. е. К = К^, причем
Мад) = £ /М%2)Л1)- (1-юз)
п,А=1,2
Аналогично и функция Грина фотона, ее обозначают D^, удовлетво-
ряет уже уравнению
DD^tx) = +igflvS(x'), (1.104)
/Д|/. р-гкх
(2^ik2+is- (1'105)
Малая мнимая добавка is сдвигает полюса как раз в нужную сторону;
действительно, к2 + is = 0 ко = ±\/k2 — is. При t > 0 (1.105) дает:
/,/3/. 1
эд, i>0’ fc° = |k|- (1'106)
42
Глава 1. Частицы и их взаимодействие...
Эта функция уже не совсем совпадает с функцией распространения
(1.103), поскольку
/дЗт, р-гкх __
(2^ТПА52^*е"’ (1'107)
В (1.107) суммирование происходит по двум физическим поляризациям
фотона, а в (1.106)
з
—е„,
А=о
т. е. выражение (1.106) не учитывает того факта, что независимых поля-
ризаций всего две. С другой стороны, это единственное решение урав-
нения (1.104), а в правой части (1.104) мы ничего изменить не можем
без потери релятивистской инвариантности.
Таким образом, вообще говоря, мы пришли в противоречие с ка-
либровочной инвариантностью, которая как раз и требует, чтобы фи-
зических поляризаций у фотона было всего две. Однако если взаимо-
действие так устроено, что фотоны с этими “лишними” поляризациями,
так называемые скалярные j и продольные (7y3i j фотоны, не рожда-
ются, то все будет согласовано. Иначе говоря, калибровочная инвари-
антность в релятивистской теории накладывает определенные условия
на вид взаимодействия, в чем, конечно, нет ничего удивительного. Мы
хорошо знаем это еще из классической теории. Действительно, рассмот-
рим уравнения Максвелла
_ .
dxv '>1‘'
Из антисимметричности ГцР немедленно следует, что
_ 0
дхидхц дхц
— ток должен сохраняться. Мы видим, что и в классической теории
описание электромагнитного поля возможно только при определенном
ограничении на взаимодействие, а именно: оно должно быть таким, что-
бы ток сохранялся,
|^=0. (1.108)
1.4. Фотоны во “внешнем поле'
43
Вернемся к сравнению функции распространения и функции Гри-
на. Функция распространения была построена для реальных фотонов,
для которых ко = ±|к|, а в функции Грина присутствует интегрирова-
ние по всем ко,к±, к?, кз и к2 0 т. е. виртуальный фотон не безмассов.
Условие Лоренца = 0 в этом случае определяет уже не два незави-
симых вектора, а три, т. е., казалось бы, суммирование должно произ-
водиться по трем поляризациям. Сумму по трем поляризациям мы уже
сможем записать в релятивистски инвариантном виде, а именно:
2 к к
А=0
Здесь мы вычли из суммы по всем поляризациям член, соответствую-
щий поляризации вдоль к^. Таким образом, единственное, как мы мо-
жем улучшить функцию Грина (1.105), это рассмотреть
/Л^к p — ikx Г t. в
(с) ,4.,2^. , (1-110)
(2тг)4г к2 + ге [ к2
а на взаимодействие наложить условие, чтобы член ~ kpkv/k2 не давал
вклада в физически наблюдаемые величины. Как мы убедимся ниже,
это условие полностью аналогично требованию сохранения тока, кото-
рое мы имели в классической теории. Фактически это не есть новое
требование, так как в любом случае для случая реальных фотонов с
к2 = 0 взаимодействие не должно приводить к появлению продольных
поляризаций.
Более того, условие, что взаимодействие при к2 0 не рождает
поляризаций, пропорциональных /.р для реальных фотонов, при к2 = 0
оставляет только две физические поляризации. Действительно, легко
видеть, что
к2
е*13)*е*?3)+е<°)*е<?0) = д^о^о^ + члены с
Поляризации, пропорциональные кц, к„, не рождаются благодаря свой-
ствам взаимодействия, а первый член обращается в ноль для безмассо-
вого фотона.
Подводя итоги, можно сказать, что сохранение тока приводит к
тому, что при к2 0, для виртуального фотона, из четырех поляриза-
ций в функции Грина остаются три, а для реального фотона — только
две физические поляризации.
44
Глава 1. Частицы и их взаимодействие...
Итак, если ток сохраняется, то можно использовать функцию
Грина (1.106) — сумму по всем четырем поляризациям. Легко также
видеть, что справедливо соотношение, аналогичное (1.102):
-^д^(^) — хр
(1-1П)
Этот факт говорит о том, что наряду с процессом
tz > tl
Xl
Х2
(возникновение фотона в и уничтожение в х%) описывает также
процесс, идущий как бы обратно во времени, т. е.
t2 < tl
Х2
Х1
и этот процесс можно в силу (1.111) интерпретировать как рождение
частицы в Ж2 и распространение в xi, причем эта частица тождественна
фотону. Примерами появления такой ситуации, в частности, являются
процессы, описываемые графиками на стр. 37.
Суммируем полученные результаты. Мы написали волновую функ-
цию фотона
х __ ____
и функцию Грина
f d4k е гкх
(2тг)4г к2 + ie ’
Кроме того, нам известны волновая функция нерелятивистской части-
цы
п2
Ф(Ж) = е-грх , Ро = ^~
2 m
и ее функция Грина
J (2тг)4г р2/2т— р0 — ie
1.5. Свободные релятивистские частицы с массой
45
Этого уже достаточно, чтобы построить квантовую электродинамику
нерелятивистских частиц, и она будет эквивалентна обычной квантовой
теории излучения. Но проще строить электродинамику релятивистских
частиц, из которой в пределе можно получить и нерелятивистские ре-
зультаты. Для этой цели займемся изучением релятивистских частиц с
массой.
1.5 Свободные релятивистские частицы с массой
Покоящаяся свободная частица характеризуется двумя аддитивными
интегралами движения: энергией, равной массе тп частицы, и внутрен-
ним моментом количества движения — спином J. Будем все частицы
классифицировать по массе и спину. Нам нужно построить теорию для
свободных частиц с любой массой и спином и движущихся с произволь-
ными скоростями, т. е. с любым импульсом р.
Чтобы понять, какие особенности теории связаны с релятивиз-
мом, а какие — со спином, начнем с частиц с J = 0; в природе таких
частиц много, например, -тг-мезоны: тг .7г°.тг с массой гп 140 МэВ.
Следствием классической релятивистской инвариантности явля-
ется соотношение между энергией Е и импульсом р:
Е2 = р2 + т2. (1-112)
Соответственно, квантовомеханическая частица имеет волновую функ-
цию
Ф(ж) ~ eipr~iEt, (1.113)
где Еир связаны (1.112).
Рассмотрим, какому уравнению удовлетворяет (1.113). Напишем
/я2 \
( Qpi _ V2 + т2 1 Ф(ж) = 0. (1-114)
Подставляя (1.113) в (1.114), получим (1.112), т. е. (1.112) эквивалент-
но квантовому уравнению (1.114). Если принять в качестве волновой
функции (1.113), а она удовлетворяет (1.114), то при попытке ввести
плотность вероятности р(х) мы встретимся точно с такими же трудно-
стями, как и в случае электромагнитного поля. Совершенно аналогично
р(х) Д |Ф(х)|2, поскольку / |Ф(ге)|2cZ3rr Д const.
46
Глава 1. Частицы и их взаимодействие...
Как и раньше, сохраняется величина Ф*гДф, удовлетворяющая урав-
нению непрерывности:
£
dt
Ф*(ж)г^Ф(ж)
= с!Кг[Ф*(ж)Х7Ф(я;) - Ф(х)Х7Ф*(х)].
(1.115)
И единственное, что мы можем принять за плотность вероятности, это
р(х) = ФДД^Ф+(ж), (1.116)
где Ф+ — положительно-частотное решение (1.114), соответствующее
Е = у/р2 Гт2. Отрицательно-частотное решение, соответствующее
Е = — \/р2 + пг2, будем обозначать Ф_.
В дальнейшем будем писать Ф+ = Ф. Как и для фотона, в случае
стационарного состояния Ф(ж) = Ф(г)е-г£^ функция р(г) имеет бук-
вальный смысл плотности вероятности:
р(г) = 2Б|Ф(г)|2.
Аналогичным образом можно ввести и волновую функцию для свобод-
ной частицы
e~ipx -------
Ф(ж) = —== , p0 = v/p2 + m2 (1-117)
V2po
и функцию Грина
г <i4r> e-ipx
G(x) = / ---5----5----• (1-118)
J (2тг)4г т2 — р2 — ге
(В D^ix) в знаменателе перед к2 тоже фактически знак минус, по-
скольку для фотона существенны пространственные компоненты <5M„,
а <5ц = <522 = —1-) Как и раньше,
С(х) = G(-x') (1.119)
и при t > 0 имеем из (1.118)
СМ — f 1* Дрг--ц/р2+т2 t
' ’ J (27г)32Б
т. е. вперед во времени распространяются положительные частоты.
1.6. Взаимодействие бесспиновых частиц
47
1.6 Взаимодействие бесспиновых частиц
Как можно описать взаимодействие в релятивистской квантовой тео-
рии? У нас нет потенциала, никаких сил, поскольку эти понятия су-
губо нерелятивистские, более того, поле тоже представлено частицами.
Итак, мы имеем всевозможные частицы, которые характеризуются сво-
ими массами и спинами, и более ничего. Рассмотрим две различные
частицы с массами mi и m2 без спина, их волновые функции Ф4, Ф2.
Сопоставим функции Грина первой частицы прямую линию, второй —
волнистую, т. е.
\
X. =С1(Х2-Х1),
=С2(ж4- хз).
хз Х4
Допустим, они провзаимодействовали (пока считаем, что больше ни-
каких частиц не существует). Что может случиться с двумя точечны-
ми объектами? Единственное: в точке х они столкнулись и разлетелись
каким-то образом, как показано на рис. 1.
Посмотрим, чему может быть равна амплитуда такого взаимодействия.
Амплитуду перехода двух частиц из точек xi, х-> в точки :/д. щ с учетом
того, что они встретились в точке х, можно записать так:
С12(Х2,ХЦХ1,ХЗ) =
G1(X2 — x)G2(x4 — x)V(x)Gl(x — Xi)G2(x — x3)d4x, (1.120)
48
Глава 1. Частицы и их взаимодействие...
где V(ж) есть некоторая амплитуда взаимодействия. Однако в силу од-
нородности пространства и времени, она не может зависеть от места и
времени встречи частиц, а следовательно, V(х) = const = А. Тем самым
мы получили конкретную формулу, содержащую единственную const, и
где все остальное известно.
Интегрирование в (1.120) производится по всем пространственно-
временным точкам х. В области
tl, t3 < t < t-2, ti
интерпретация данного процесса очевидна. Однако мы говорили, что
в силу релятивистской инвариантности так ограничивать область ин-
тегрирования нельзя, поскольку наверняка в интеграле есть и другая
область, например:
tl < t < t3, t-2,
В этом случае буквальная интерпретация теряет смысл, и картинку
естественно перерисовать так:
Этот график означает, что частица распространялась до точки х и в ней
в результате взаимодействия распалась на три частицы. Таким образом,
если мы хотим описать процесс, изображенный на рис. 1, то в силу ре-
лятивистской инвариантности нельзя избежать процессов, аналогичных
приведенному на рис. 2, поскольку в интеграле (1.120) обязательно су-
ществует такая область интегрирования, где процесс обязательно при-
водит к несохранению числа частиц. Это утверждение, вытекающее из
1.6. Взаимодействие бесспиновых частиц
49
релятивистской инвариантности теории, находит свое подтверждение в
эксперименте. Это есть то, что непосредственно наблюдается в природе.
Рассмотрим амплитуду процесса с рождением частиц, изображен-
ного на рис. 2, и напишем его амплитуду по сформулированным выше
правилам. Получаем
С(Ж2, Жз, ХЦ, ЖХ) =
= У СХ(ж2 — ж)Сг(жз — ж)Сг(ж4 — ж)П(ж)С1(ж — ЖХ)с?4Ж (1.121)
Мы можем сразу утверждать, что V(x) = А. С другой стороны, этот
процесс содержится и в (1.120), и при одинаковых временах форму-
ла (1.120) должна совпадать с (1.121). Сравнивая их, находим, что,
т. к. С*2(жз — х) = G-z(x — жз), значит А = А.
Таким образом, предположив существование процесса типа рас-
сеяния (рис. 1), мы с необходимостью пришли к существованию процес-
са, изображенного на рис. 2, и других, например, превращение частиц
типа 1 в частицы типа 2.
Рис. 3
Подведем итоги:
1. Все процессы типа распада и превращения частиц автоматически
получаются из процесса, изображенного на рис. 1, в силу симмет-
рии функции Грина.
2. Амплитуды этих процессов А равны между собой, т. е. реляти-
вистская инвариантность предсказывает не только существование
различных процессов, но и устанавливает связь между ними.
50
Глава 1. Частицы и их взаимодействие...
3. Для последовательной интерпретации таких процессов нужно при-
нять, что функция G(x — ад) описывает распространение частицы
из х\ в х, если 4i < t, и из х в яд, если 4д > t.
Частицы могут провзаимодействовать и не один раз, например:
Рис. 5
причем здесь тоже яд, я?з < х%, . Диаграмму на рис. 4 нельзя получить
из предыдущей в силу различной топологии диаграмм — эти две диа-
граммы отвечают существенно различным процессам. Полная ампли-
туда процесса в порядке А2 получается как сумма этих двух диаграмм.
Частицы, распространяющиеся из точек х% и хд., тождествен-
ны. Учитывает ли наша амплитуда рассеяния тождественность ча-
стиц? Выберем порядок времен в диаграммах рис. 3 и рис. 4 согласно
яд, яд < ^з, яд. Это эквивалентно тому, что мы рассматриваем эти диа-
граммы сверху (меняя соответственно ось времени). Мы приходим тогда
1.6. Взаимодействие бесспиновых частиц
51
к процессу рассеяния 1 + 1 —> 2 + 2 с двумя тождественными частицами
в конечном состоянии. Полная амплитуда этого процесса, полученная
как сумма амплитуд, соответствующих рис. 3 и рис. 4, автоматически
симметрична по отношению к перестановке координат тождественных
частиц: хз х±. Иначе говоря, наша амплитуда удовлетворяет обыч-
ному квантово-механическому требованию для рассеяния друг на друге
частиц со спином ноль.
Можно рассмотреть и процессы с рождением многих частиц, т. е.
возможно и такое:
А что если в нашем распоряжении частицы только одного сорта?
В качестве исходного процесса опять возьмем рассеяние
но имеется тогда и распад
52
Глава 1. Частицы и их взаимодействие...
Какой из этих процессов более фундаментальный и почему бы, скажем,
не быть такому процессу,
т. е. распаду частицы на две? Для реальных частиц этот процесс запре-
щен законом сохранения энергии-импульса, однако он возможен на ко-
нечных интервалах времени. Мы можем описать тогда амплитуду рас-
сеяния реальных частиц как обмен виртуальной частицей, как сумму
диаграмм вида
хл
а также
(Если ограничиться двукратным взаимодействием, то других диаграмм
1.6. Взаимодействие бесспиновых частиц
53
нет.) Для получения полной амплитуды рассеяния нужно сложить ам-
плитуды всех этих процессов.
Итак, мораль: в качестве исходного взаимодействия не обязатель-
но брать реальные процессы типа
, а все можно получить и
на . Это и есть простейшее возможное взаимодействие.
Займемся теорией, основанной на таком типе взаимодействия. На-
пишем для него амплитуду:
G(x2, х3; я?1) = У G(x2 — x)G(x3 — x)^G(x - x3)d4x.
Подставляя выражение для функций Грина (1.118), получим
С(ж2, х3-, ад) =
_ f d4p3d4p2d4p3 1
J [(2тг)4г]3 (m2 — р2)(т2 — — Рз)
х у d4xe^ip2^X2^* * * * * * x'l^i'P3^X3^x'l^ipi^x^X1'1 =
[ rf4pid4p2rf4p3(27r)4^(p2 + рз ~Р1) №^-гияХя+1^х, =
J [(2тг)4г]3(т2 — р2)(нг2 — Рз))777-2 — Рз)
_ Г d4pid4p2d4p3 4
J [(2тг)4г]3 (27r)d^2+^3 Pi) х
х С(,Р1,р2,р3)е-гр2Х2-1рзХз+гр1Х1. (1.122)
54
Глава 1. Частицы и их взаимодействие...
Здесь 5{р-2 + Рз — Pi) выражает закон сохранения энергии-импульса,
а функция Грина в импульсном пространстве выглядит очень просто:
С(Р1,Р2,Рз) = ^G{p1)G{p2)G{p3).
(1.123)
Из (1.123) следует, что частицы виртуальны, поскольку в G{p) входят
/г т2.
В импульсном представлении формуле (1.123) соответствует гра-
фик:
Можно показать, что
G(a?i,я?2;я?з) —> 0, если
41 -л —оо,
ЬЧз +оо.
(1.124)
Интегрируя в (1.122) по с14рз, получим
[' , ргр2(жз-Ж2)+гР1(а:1-а:з)
G{X2,X3-,X1) = 7 / (2тг)4—---------------------------------А2Г
J [(2тг)4г]-3 {тЛ — р^){т2 — Р2)[т2 — {рх — р2)2\
(1.125)
В области интегрирования (1.125) нет точки, где бы все три зна-
менателя обратились в нуль (все три частицы не могут быть реальны-
ми) , поэтому в силу частых осцилляций экспоненты в подынтегральном
выражении при больших временах интеграл (1.125) стремится к нулю.
Вопрос о возможности реального распада частицы на две решает-
ся законами сохранения энергии и импульса, для одинаковых частиц он
запрещен, но если бы массы у частиц были разные, то и такой процесс,
в принципе, мог бы быть реальным.
1.7. Взаимодействие бесспиновых частиц с электромагнитным...
55
1.7 Взаимодействие бесспиновых частиц
с электромагнитным полем
Какой процесс может соответствовать взаимодействию между заряжен-
ной частицей и фотоном?
- G(®2 - ®1)
Х2
- Х3)
Х% Х4
Нам известно, что заряды испускают электромагнитные волны, т.е. на-
ша частица могла бы испустить фотон. Таким образом, за основу можно
было бы принять процесс
Хз
Xi X Х2
Амплитуда испускания фотона с поляризацией ц есть
Сц(хз, Х2', ад) = У О^(хз — x)G(x2 — xyrv(x)G(x — xi)d.4x. (1.126)
Амплитуда взаимодействия Г,,. в принципе, может зависеть и от поля-
ризации, что мы и отметили индексом v. Как и раньше, не должна
зависеть от с другой стороны, это вектор, а единственный вектор,
который мы можем придумать, кроме есть д/дх^, т. е.
G(x2 — ж)ГгУ(а:)С(а: — ад) =
dG(x-xX) 9G{x2-x)
= aG(X2 — х)-------------Но---------G(x — ад), (1.127)
oxv oxv
где a и b — некоторые константы. Кроме того, на взаимодействие мы
должны наложить условие, чтобы избавиться от двух лишних поля-
ризаций, входящих в D/w ~ 8^. Поскольку полученное поле должно
56
Глава 1. Частицы и их взаимодействие...
(1.128)
удовлетворять условию Лоренца, то
dGfJ1(x3,x2;x1') _
дх3^
G,, зависит от х3 только через посредство D^, поэтому ее дифферен-
цирование в (1.128) сводится к дифференцированию D,w. Дифферен-
цирование Р!Ш дает следующий результат:
дР^з-х) _ г _d^ ik{X3_X) A A A f ,
дх3, J (2л)Че
Но fcMeA = 0 только для 3-х векторов еА (Л = 1, 2, 3), а Д 0. Чтобы
выполнялось условие Лоренца, этот член должен выпасть при интегри-
ровании в (1.126). Таким образом, сохранение тока требует такого усло-
вия на Гу, чтобы поляризация не давала вклада в интеграл (1.126).
Вычислим дСц/дх3ц и приравняем ее нулю (ЛМР = 5^D(x)\.
ЭСДж3,ж2;жх) Г дР(х3 - ж) 4
----J -------------------------0^G(x2 - ж)ГрО(ж - жх)й х =
= / Л(ж3 — ж)-^-(С(ж2 — ж)Г^С(ж — жх))с!4ж = 0. (1.130)
J иЯц
Здесь мы воспользовались тем, что dD(x3 — х)/дх3р1 = — dD(x3 — ж)/Эжм
и проинтегрировали по частям. (1.130) выполнится, если
-^-С?(ж2 - ж)ГмС(ж - жх) = 0. (1.131)
Мы получили условие на взаимодействие. Подставим (1.127) в (1.131):
(С(ж2 - ж)Гм(ж)С(ж - Ж1)) =
ЭС(ж2 - ж) dG(x - жх) ^<ЭС?(ж2 — ж) dG(x — жх)
5жм Эжм Ох,, д.г.,
d2G(x — x3~) d2G(x2-x) . .
+аС(ж2 - ж)---—------+Ь---------—----С(ж-Ж1). (1.132)
Oxi oxi
Н' (Л
Поскольку с*2С(ж)/Эж2 = — m2G — гд(х), если положить a = —Ь, члены
с массой в (1.132) взаимно уничтожаются, остается
д
——Gr^G = a[G(x2 — жх)(—г)5(жх — ж) — С(ж2 — жх)(—г)5(ж — ж2)],
1.7. Взаимодействие бесспиновых частиц с электромагнитным...
57
т. е. равенства нулю мы не получили. С другой стороны, член в правой
части отличен от нуля только при х3, х2 = х, т. е. в момент приготовле-
ния источника электрон, не успев никуда распространиться, испустил
фотон, нас же при реальной постановке эксперимента интересует, что
с электроном произошло потом, поэтому вклада в физические величи-
ны этот член не дает. В принципе, мы бы могли его скомпенсировать
введением взаимодействия типа
Х1
которое поддерживает точное сохранение тока в момент приготовления
частицы. Однако это дополнительное взаимодействие никогда не войдет
в амплитуды физических процессов. Заряженные частицы, которые мы
изучаем в природе, приготавливаются задолго до эксперимента — так,
что фотоны, испущенные в процессе приготовления, никогда не попадут
в детекторы.
Итак, за неимением лучшего мы получили
w = (1ЛЗЗ)
Соответственно,
Gll(x3,x2-x1') = 7 У D(x3 - x)G(x2 - x)-^-G(x - x-^d^x. (1.134)
Этой амплитуде соответствует график:
Х1 X Х2
Рис. 6
58
Глава 1. Частицы и их взаимодействие...
Посмотрим, является ли развитая нами теория удовлетворитель-
ной со следующей точки зрения. Рассмотрим область интегрирования
в (1.134), где ЧЧ? < Это соответствует диаграмме:
Рис. 7
описывающей превращение двух заряженных частиц в фотон, но нам
известно, что заряд-то вроде бы должен сохраняться. Есть и другое
формальное противоречие, не связанное с зарядом. Если есть две одина-
ковые частицы со спином нуль, как известно, амплитуда любого процес-
са с этими частицами должна быть симметрична относительно их пере-
становки. Мы же получили явно антисимметричную амплитуду
(см. (1.134)) (относительно перестановки х± х^)-
Выход из такой ситуации есть, и заключается он в гипотезе, что
для заряженных частиц имеет место вырождение по массе, т. е. для лю-
бой заряженной частицы существует античастица с той же массой, но
противоположного заряда. Такая гипотеза приводит к другой возмож-
ности интерпретации графика на рис. 7: из х% движется не частица,
а античастица. Можно считать, что G(x) при t > 0 имеет смысл функ-
ции распространения частицы, при t < 0 — античастицы. Для того,
чтобы спасти сохранение заряда, мы вынуждены приписать античасти-
це противоположный заряд. Этим самым мы сразу же решаем и про-
блему с симметрией амплитуды. Действительно, если Д < t < 42, при
замене х± х-> мы получим 4г < 4 < 41, т. е. мы получаем диаграмму с
распространением античастицы, а не частицы. Поскольку античастица
нетождественна частице, мы не должны требовать симметрии этой ам-
плитуды. Одновременно мы приходим к выводу, что амплитуда меняет
знак при замене частицы на античастицу. Как мы увидим ниже, у про-
порциональна электрическому заряду, так что это еще раз показывает,
что заряд античастицы противоположен по знаку заряду частицы.
1.8. Примеры простейших электромагнитных процессов
59
Существование античастиц в настоящее время является твердо
установленным экспериментальным фактом, а их предсказание, соб-
ственно, явилось следствием релятивистской инвариантности и сохра-
нения заряда. Вообще, существование античастиц есть всегда следствие
сохранения некоторого (не обязательно электрического) заряда, суще-
ствование антинейтрона, например, связано с сохранением барионного
заряда, анти-АГ-мезона — с сохранением гипер-заряда и т. д.
1.8 Примеры простейших
электромагнитных процессов
Наряду с рассмотренным нами процессом ---- , излучение мо-
жет произойти и более сложным образом, например:
х3
/
Х1 \ / Х2
Посмотрим, чем амплитуда этого процесса отличается от рассмотрен-
ной выше амплитуды простейшего процесса, которая описывается вы-
ражением (1.134). Для рассматриваемой теперь амплитуды имеем
А-'ц (х3 , Х-2', ад) =
G(x2 — x"')Vl,(x"')G(x" — а/)Гм(а/)С(а/ — а:)ГгУ(а:)С(а: — ад) х
xD(x" - x)D(x3 - x')d4xd4x'd4x". (1.135)
Здесь по сравнению с (1.134) две “лишние” функции Грина, две вер-
шины Гм, одна D и два интегрирования. Посмотрим размерность этой
“лишней части”:
GGDrrd4xd4x ~ -у —у—а;8 ~ у2.
Ж Л Ср Л гр Л гр гр
Лг КЛГ кЛГ кН
Поскольку обе амплитуды должны обладать одинаковой размерностью,
то постоянная у безразмерна. Если у2 < 1, то можно рассматривать
только простейшие амплитуды.
60
Глава 1. Частицы и их взаимодействие...
Как мы уже говорили, процесс ------- невозможен для ре-
альных частиц. Рассмотрим поэтому теперь для примера несколько про-
стейших диаграмм, описывающих реальные процессы.
1. Рассеяние заряженных частиц. При этом может произойти следу-
ющее:
a) Xi яд
х2 х'2
т. е. частицы не провзаимодействовали;
Это — так называемое контактное взаимодействие, но оно не име-
ет отношения к испусканию или поглощению фотонов, т.е. к элек-
тромагнитным взаимодействиям. Существует или нет такой про-
цесс — вопрос к эксперименту. Для некоторых частиц он есть, для
некоторых — нет. Для тг-мезонов, в частности, такое взаимодей-
ствие существует. Мы же будем изучать только электромагнитные
взаимодействия, т. е. полагать, что контактного взаимодействия
нет (это фактически упрощенная бесспиновая модель электронов
и д-мезонов).
1.8. Примеры простейших электромагнитных процессов
61
Рассеяние заряженных частиц с обменом фотонов:
Рис. 8
Оба таких процесса возможны, поскольку после испускания фо-
тона в х частица из яц может с одинаковым успехом попасть как
в х'}, так и в х2. Амплитуда запишется так:
G(x'2, х'р, х-2, яц) = У G(x'r — x)VpG(x' — х) х
х G(x2 — x')riyG(x' — X2)d4xd4x' + (1.136)
+ {%i 41-
Здесь X} -• x'2 означает такое же выражение, с заменой х^ на х2 и
наоборот. Удобно на диаграммах ввести стрелки, как мы делали
выше, тогда ясно, какую функцию G дифференцирует символ Г с
плюсом, а какую — с минусом (так как Г/; Кроме того, так
удобно различать частицы и античастицы:
здесь Г(, дифференцирует с плюсом,
/ здесь Г,, дифференцирует с минусом.
//
Рис. 9
62
Глава 1. Частицы и их взаимодействие...
Из первой диаграммы (рис. 9) следует существование такого гра-
а из второй —
Х1
Эти диаграммы отвечают уже рассеянию тг+-мезона на тг . Сле-
довательно, в амплитуде (1.136), т. е. в амплитуде рассеяния тг+-
мезона на тг+-мезоне (тг+7г+), автоматически содержится и ампли-
туда 7Г+7Г-.
Аналогично получается и рассеяние тг—тг—, в этом случае нужно
положить х'10,х'20 < хю,Х2о, т. е. график следует перерисовать
задом наперед: - -
1.8. Примеры простейших электромагнитных процессов
63
Таким образом, все возможные амплитуды рассеяния можно по-
лучить из (1.136), подбирая соответствующим образом времена.
Амплитуда рассеяния тг+7г+ тг+7г+ оказывается при этом рав-
ной амплитуде тт тг —> тг тт (эти амплитуды содержат два фак-
тора Г, каждый из которых меняет знак при замене частицы на
античастицу). Амплитуда же процесса с частицей и античастицей
в начальном состоянии тг+7г- тг+тг~ существенно отличается от
них. Это происходит потому, что в этом случае существует еще
один процесс — когда исходные тг-мезоны превращаются в проме-
жуточном состоянии в виртуальный фотон.
2. Комптон-эффект (рассеяние фотона на тг-мезоне). Пусть у нас
есть фотон и тг-мезон в начальном состоянии. Что с ними может
произойти? Как и в предыдущем случае, они могут не провзаимо-
действовать:
Х1
Х2 х'2
мезон может поглотить фотон в некоторой точке х, а в х! испу-
стить:
64
Глава 1. Частицы и их взаимодействие...
мезон в точке х может испустить фотон, а первоначальный погло-
тить в х':
А могут ли они провзаимодействовать в точке, как показано ниже?
Априори на этот вопрос ответить нельзя. С одной стороны, это
вопрос экспериментальный, но, с другой стороны, у нас имеется
требование к взаимодействию, чтобы скалярные и продольные фо-
тоны не давали вклада в физические величины (сохранение тока).
Оказывается, действительно, чтобы сохранялся ток в случае ска-
лярных частиц, должно существовать такое взаимодействие, и его
константа, как мы увидим далее, есть у2.
1.9. Диаграммы и амплитуды в импульсном представлении
65
1.9 Диаграммы и амплитуды в импульсном
представлении
Начнем, как обычно, с простейшего графика взаимодействия фотона с
электроном:
Д х3
/
/
/
/
/
/
/
Xi X / Х2
____________L____________
Найдем амплитуду в импульсном представлении, т. е. разложим
СДх3, ху Ж1) в интеграл Фурье:
СДхухух-у) =
= / fc Ж1 +гР2Ж2+tfa3 (Рь Р2, fc) (1-137)
Знак ” перед одним из слагаемых показателей экспоненты выбран
для удобства. Подставляя в выражение для (1.134) функции G и Diw в
виде разложений типа (1.137), получим
СДх3,хух3) =
f d4pid4p2d4k .
= 7у [(2л)Д D(fc№i№) х
х [ d4xe-ik(x3-x'> [ \ J38)
Выражение в круглых скобках равно
-^+р2Де-г^-хК-г^х-^.
Тогда, интегрируя по d4x, получим
ДДз^ят) = -7 [ d Z>(fc)G(pi)G(p2)^(piM + Р2М) х
J К27Г)гг
х (2л)4<5(р1 - р2 - к)егр1Х1-гр2Х2-гкхз. (1.139)
66
Глава 1. Частицы и их взаимодействие...
Сравнивая (1.137) с (1.138), получаем выражение для G^(pr,p2, к):
Gfl(pi,P2,k) = -(27r)4i5(pi-p2-A:)(piM+p2At)7G(pi)G(p2)£)(A:). (1.140)
Соответствующая диаграмма выглядит так:
Здесь линиям соответствуют функции Грина, а в вершине стоит
—+ P2ii) и закон сохранения (2tt)45(pi — Р2 — к).
Наша диаграмма соответствует процессу, когда мезон с импуль-
сом pi распадается на д-квант с импульсом к и мезон с импульсом
р2 = Pi — к. Поскольку здесь 4-импульсы лежат не на массовой поверх-
ности, т. е. Pq р2 + тп2 и /д / к2, говорят, что этот процесс виртуаль-
ный.
Правила сопоставления графикам амплитуд в импульсном пред-
ставлении проще, чем в пространственном, здесь каждой линии и вер-
шине сопоставляется соответствующий множитель: G(pi), Gfpgj.
П(А:), Гм.
Аналогично рассмотрим рассеяние мезонов друг на друге:
X X
! х'г ! х'<2 1 1 1 1 + ! । । । । । ।
х2 х' х2 х2 х' х'г
, ,. [ d4p1d4p2d4p,1d4p’2
G^x2,x1,x2,x1) J [(2тг)4г]4
x (1-141)
Диаграммы и амплитуды в импульсном...
67
Вычисление проводится точно так же. Первой диаграмме в коорди-
натном представлении можно сопоставить в импульсном представлении
следующую диаграмму:
Pi+Р1Д Pi
к
Р2 ДР2ц + рД) Р2
Действуем, как в предыдущем случае: пишем G(x'2, Д; %2, яд) в виде
(1.136) и раскладываем в интегралы Фурье входящие в нее свободные
функции Грина, получаем в результате выражение типа (1.138). Каж-
дой функции Грина будет соответствовать своя импульсная перемен-
ная от ее Фурье-разложения, в вершинах от дифференцирований, как и
раньше, появятся — г7(рщ +Рщ) и — гд(р2д1 + р2д)> а, соответственно, ин-
тегрирования по <Дх и d4x' дадут (2тг)4<5(р1 + к — р(), (2тг)45(р2 — к — р'2),
т. е. законы сохранения в каждой из вершин. Будет присутствовать одно
лишнее по сравнению с (1.140) интегрирование по d4k. Таким образом,
имеем
G(p'Y,p2,Pi,P2) =
х G'(Pi)G'(P2)G'(p/1)G(p/2)72(piAt+р'1м)(р2А1+Р2М) х
х (2тг)4г<5(р1 + А:-р/1)(2тг)4г<5(р2 - -Рг)- (1.142)
Выражение (1.142) содержит интегрирование по импульсу к промежу-
точного фотона.
Суммируя, мы можем сформулировать следующие правила сопо-
ставления амплитуды диаграммам в импульсном пространстве.
1. Каждой линии сопоставляется множитель — соответствующая функ
ция Грина: р
----------------------- G(P)
-------------D(k)
68
Глава 1. Частицы и их взаимодействие...
2. В каждой вершине — (2tt)4«5(pi — р2 — к)д(р^ + р2)м
/
/
к '
/
Pl Р2
3. Затем нужно проинтегрировать по импульсу промежуточных ча-
стиц, т. е. по импульсу, соответствующему каждой внутренней ли-
нии с весом й4/г/(2тг)4г.
Вернемся к выражению (1.142). Интеграл в правой части легко
вычисляется при помощи 5-функции. Учитывая наличие второй диа-
граммы, которой в импульсном пространстве соответствует график
Р1 Р2
к
Р2 Р'1
для суммарной амплитуды получим выражение
G(p/2,p/1;P2,Pi') = (2тг)4г<5(р1 +р2 - р{ - P^G^G^G^G^x
' 2(Р1 +Pi)M(P2 +Р2)М 2(Р1 +Р2)м(Р2 +pj)J П -.доч
7 (Р2-Р2)2 7 (P2-Pi)2 Г J
5-функция здесь выражает общий закон сохранения 4-импульса между
начальным и конечным состоянием системы.
1.10 Амплитуды реально наблюдаемых процессов
Пусть частица в некоторый момент времени t± описывалась волновой
функцией
р-грх
= -Л=, (1.144)
у
1.10. Амплитуды реально наблюдаемых процессов
69
тогда в некоторый другой момент она будет описываться функцией
Ф(У1) = I G(y! -x^i^— р(хз)(13хх,
J oxio
(1.145)
где
G(yi - Ж1) = -
Ж1
J/1
Однако она может и развалиться, например, на две, т. е.
= G(l/2,?/3;Xl) .
И волновая функция системы будет уже такой:
Ф(У2,Уз) = / G(y2,y3;a;i)i-^-^(2:i)d32:i
J C/Хю
(1.146)
и отвечать двухчастичному состоянию.
Вероятность обнаружения ровно одной частицы во всем объеме,
как мы уже говорили, есть
d 1
i——<pd3x = Pi.
ох0
Величина Р± < 1, поскольку при наличии взаимодействия имеется неко-
торая вероятность найти 2 и более частиц: Ру Рз и т. д. Например,
Р2 =
•г —— i —— р (ад) <р(х2) <13хз d3x-2.
ОТ10 ОГ20
Согласно нашему условию ортогональности (1.72) амплитуда вероят-
ности перехода частицы с импульсом pi в состояние с импульсом р> в
70
Глава 1. Частицы и их взаимодействие...
определенный момент времени есть
/ = / 9?;2(y)«^-G(y-x)z-|-^P1(2:)d32:d3y.
J Clyo J Cly0 OXq
(1.147)
Амплитуда вероятности распада этой частицы на две с импульсами Р2
и р3:
= / Фр2рз«Д—«д—С(уз,У2;я?1) х
J ду20 дузо
Q Q Q
X «д—<yJP1(a;i)d x3d y2d у3.
OXq
(1.148)
Здесь
e-iP2V2-ip3 Уз
ФР2РЗ . q тз
Таким образом, можно определить некоторую матрицу U, кото-
рая начальное одночастичное состояние в момент времени /у переводит
во всевозможные состояния в момент времени t2, т. е.
/ Ф(У1) \ Ф(У2,Уз) /ФР1\ п
Ф(У4,У5,Уб) \ j = и и 0 0 • /
(1.149)
Если устремить ti —оо, t2 +оо, то отличным от нуля останется
только матричный элемент [7ц, поскольку реальный развал частицы
запрещен законами сохранения.
Если в начальный момент было 2 частицы, тогда аналогично
(1.149) получаем
/ Ф(У1) \
ф(У2,Уз)
Ф(У4,У5,Уб)
(1.150)
/ ° \
ФР1 ,Р2
1.10. Амплитуды реально наблюдаемых процессов
71
Здесь уже при t± —> —сю, —> +сю, может быть много возможных про-
цессов, поскольку две частицы могут рассеяться друг на друге, а могут
родить и новые частицы. У нас есть единственное требование: полная
вероятность всех процессов должна быть равна единице. Отсюда сразу
следует, что оператор U должен быть унитарным, т. е.
E/+(WiF(Wi) =! (1.151)
Если константа взаимодействия мала, д <Д 1, то оператор U мало отли-
чается от единичного, т. е. его можно представить в виде
U = I + iV,
где величина V мала. Из (1.151) следует — iV+ +iV = 0, т. е.
V+ = V, (1.152)
что означает, что добавки за счет взаимодействия должны быть мнимы-
ми. (Мы и писали раньше — iV для нерелятивистской квантовой меха-
ники. Для взаимодействия же с фотоном мы также выделяли в вершине
множитель г, действительно, 1;, = — ?д(Р1 Н-рг)^- Из этого следует, кста-
ти, что можно ожидать, что константа д окажется вещественной.)
Устремив теперь Д -л —сю, t2 +оо, получим
U(<x>, — сю) = S, (1.153)
где S называется матрицей рассеяния или просто S-матрицей.
Амплитуды вероятностей различных процессов можно вычислять
аналогично (1.147), (1.148). Например, для рассеяния (2 частицы -л
2 частицы) имеем:
5(Ф,р) = f^*(y1,y2)i-^—i-^—G(y2,yi;x2,x1)x
J оу2о дую
д д
х i—---i—---X2)d3xid3X2d3yid3y2
ОХю 0X20
и т. д.
Мы для наглядности проделаем это вычисление чуть иначе. На-
рисуем диаграмму: до взаимодействия сколько-то частиц и сколько-то
частиц после взаимодействия, например:
12
Глава 1. Частицы и их взаимодействие...
Так можно изобразить любой процесс; кружочек обозначает всевоз-
можные промежуточные состояния. Все отличие здесь от прежних диа-
грамм для функций Грина заключается в следующем: мы должны вы-
числять эти диаграммы в пределе
xi0 -> -оо, т. е. x'i0 - xi0 > О,
yi0 -> +оо, т. е. yi0 - y'i0 > 0. (1.154)
В силу последних неравенств мы можем упростить функции Грина
внешних линий, поскольку (1.154) однозначно задает правила обхода
полюсов. Поэтому
Г d4P1 е-^У^ _ [d3pie-^^ . .
С(У1 J (2тг)4г m2 - pl - is J (2л)3 2Ei ' ( ' 55)
Здесь = у/р2 + т2, т. е. данная частица реальна. С другой стороны,
в силу (1.117) выражение (1.155) можно переписать так:
G(yi-yfi) = I (1-156)
Таким образом, произвольную функцию Грина х^ —сю, +сю
можно записать в виде
С(У1,У2, • , щ2, • ,Хт) =
J \^)
х [d^y',... (у()... ф;и (уОШ,...,у;;4,...,О х
1.10. Амплитуды реально наблюдаемых процессов
73
d3ki... d3km
(2тг)3т
х . Ф^ДДЛ^ ... d4x'm.
(1.157)
Это выражение можно переписать так:
G(yi,y2, ,Уп',ХцХ2, ,Хт) =
= [ d Р(^\зпРП^р^У^ ф?м(Уп)5(Рь • ’Рю kr,..., km) X
x Ф*ДЖ1)...ф*т(Жт)^--^, (1.158)
т. e. функция Грина есть суперпозиция плоских волн. Если начальные
и конечные импульсы частиц заданы, то амплитуда перехода между
этими состояниями есть по определению S(pi .. .рп; Ад ... /ст):
S(pi,... ,рп; к!,..., кт) =
= У d4y{... d4y'nV*pM • • • Ф;„(уО5(У;, ..., у'п, х[,... ,х'т) х
х ^kl(xi)...^km(x'm)d4xi...d4x'm. (1.159)
Таким образом, S-матрица может вычисляться с помощью тех же диа-
грамм, что и функция Грина, только внешним линиям следует сопо-
ставлять не свободные функции Грина, а волновые функции соответ-
ствующих частиц.
Вычислим теперь матричные элементы S для процессов рассея-
ния, которые мы рассматривали выше:
S = S(o) + S(1) + ...,
В этом случае все просто и мы получаем
s(o) = Ф1 - pi)<5(Р2 - Р2~) + - Рх/^РЪ - pi)-
74
Глава 1. Частицы и их взаимодействие...
В следующем порядке по у появляются процессы с обменом фотоном:
Р2
Pi
Pi
Pi
S(1)
Pi
Вычислим первую амплитуду по сформулированному нами правилу:
= 6(у[ - х'^б^ - x2)D(x2 -
xi хдА yi
Р2
Р2
Р2
Х2
Х2У2
У2
Тогда
Г Ргр1х1 С. p-ip-LX^
’ -/d
^Р2Х2 Q g —
х , ---, В(х2 — хГ) =
ф^’дх'^ у/2Ё2 v 2 17
= у2 J d^x^x^e^-P^l-i^ х
1 g —i/c(x2 —#1)
х[ г(р2+р2^]^^—2Е, . 2Е, к2 ^л)Ч~
= ?2/ + + х
х (2tt)45(pi - pi + /с)(2л)4<5(р2 -Р2 - fc) _
У2Е1 • 2Е2 2Е{ 2Е'2 ~
1.10. Амплитуды реально наблюдаемых процессов
75
' А Г(Р1 + Р1)ДР2 + Р2)М
= (2тг) г5(Р1 - pi + р2 -р2) -----_р^2--------
х __________7^________
У2Е1 • 2Е2 2Е[ 2Е2 '
Аналогичное выражение возникает и для второй диаграммы, т. е. окон-
чательно имеем
с(1) лАд ' / Л(Рщ+Рщ)(Р2М + р(Д
> = (2тг) гд(Р1 +Р2-Р1 - Р2) -(р2-р'2У- +
+ (W +рЦ(Р2М +Рщ)1 _____________________ и -
(Pi-Р2)2 . \/2Е\\/2 Е2х/2 Е\ \/2!d2
Сравнивая (1.160) с выражением для функции Грина (1.142), видим,
что все отличие в следующем: в (1.142) внешним линиям соответствуют
функции Грина (свободные), в (1.160) — множитель 1 /\/2Е. Поэтому
удобно в амплитудах S выделять множители, соответствующие внеш-
ним линиям.
Запишем S в виде
Др'п • ,P„;Pi,P2) = 1 + (2tt)4z5(^2p' -pi — р2)х
х ......(1.161)
Здесь Т — так называемая инвариантная амплитуда рассеяния. Ее смысл
аналогичен рассмотренной нами нерелятивистской амплитуде (1.43).
Мы для простоты ограничились в (1.161) переходом двух частиц с им-
пульсами pi, р2 в п с импульсами рф ...,р'п.
Вероятность такого перехода есть
dW = [(2тг)Ч(^2р' - pi -р2)]2х
2d3p'1...d3p,n 1__________1
(2тг)3п 2Е1 • 2Е2 2Е,1... 2Е’п
Воспользуемся тем, что |<5(х)|2 = 5(т:)5(0). Последнюю следует понимать
(1.162)
так:
(2тг)4 ДО) = / d4xeipx |р=0 = VT,
76
Глава 1. Частицы и их взаимодействие...
где V — объем пространства, а Т — время, в течение которого проис-
ходил процесс. Тогда для вероятности перехода в единице объема за
единицу времени получим
== Vf = +к -
Х|Г(Р1,...,Д:И,И)|» (1.163)
Обычно мы интересуемся сечением da данного процесса:
da = dT = 1,2 ^Д4,/
х\Т(р\,... ,р' ,pi,P2)\2d3p'1'"d3p'n----, (1.164)
। iPi, (27г)3п 2Д...2Б;’ 1 ;
где j — поток сталкивающихся частиц.
Величина
cPpi... d3p'n 1
(27г)3" 2Д ... 2Д,
носит название инвариантного фазового объема. Мы с подобной вели-
чиной уже сталкивались при вычислении функций Грина. Ее реляти-
вистская инвариантность непосредственно следует из сравнения соот-
ношений типа (1.105), (1.106)Л
Определим теперь поток для двух частиц, движущихся навстре-
чу друг другу. Используя выражение для тока одной частицы (правая
часть (1.115)), получим
. _ Pi Р2 _ Р1Е2 ~ Е1Р2
Е-2 Е1Е2
Здесь pi, р2 — проекции трехмерных импульсов на ось столкновения.
Числитель (1.165) инвариантен относительно преобразований Лоренца
вдоль оси движения, и эта величина называется инвариантным пото-
ком Д, т. е.
J = 4E1E2j = 4(E2pi - Е1Р2). (1.166)
хДля вычисления полных сечений столкновения в случае тождественных частиц
инвариантный фазовый объем следует делить на п! (если в конечном состоянии п
частиц), чтобы не учитывать тождественные конфигурации много раз.
1.10. Амплитуды реально наблюдаемых процессов
77
В лабораторной системе
J = 4mpL
(рь — импульс налетающей частицы, т — масса покоящейся частицы).
В системе центра масс
J = 1рсЕс.
Таким образом, сечение (1.164) полностью выражается через ре-
лятивистски инвариантные величины. Как мы уже отмечали, это есть
сечение для такого процесса:
Рассмотрим теперь подробнее случай рассеяния 2 2:
Для описания таких процессов удобно ввести инвариантные переменные
s, t, и:
s = (pi + Р2)2 = (.Pi + pi)2,
t = (pi - Pi)2 = (Р2 - pi)2,
и = (pi - pi)2 = (Р2 - pi)2-
(1.167)
78
Глава 1. Частицы и их взаимодействие...
Для выяснения физического смысла этих переменных рассмотрим их
значения в системе центра масс (с.ц.м.), тогда
s = (Рю +Р20)2 = Е2,
t = -(p'i - Pi)2 = -q2,
u=- (pi - Рг)2- (1.168)
То есть s есть квадрат полной энергии в с.ц.м., t — квадрат переданно-
го импульса частице V частицей 1, и — квадрат переданного импульса
частице 2' той же частицей 1. s, t, и называют мандельштамовскими
переменными. Они не являются независимыми, и можно показать, что
(для случая, когда все частицы, участвующие в процессе, имеют одина-
ковую массу тл)
s + t + u = 4m2. (1.169)
Действительно,
8 + t + U =
= pl + Р2 + Р1 + Рт + + 2pip2 - - 2р, Д =
= 4m2 + 2pi(pi Pi — Рг) = 4m2.
(Естественно, для частиц с различными массами было бы s + t + и =
= Ei ™2-)
Теперь при помощи (1.164) можно получить сечение. Переходим
в с.ц.м.:
Ei = Е2; |pi| = |р2 =р;
пЕ
3 = -рд-рц, гДе Е = Ei + Е2,
-С/1-С/2
И
a ГрЕ^ (р1+р2 4Б(Б'(27г)4(27г)22!’
Мы считаем здесь конечные частицы тождественными и поэтому делим
фазовый объем на 21, чтобы не учитывать одинаковые конфигурации,
возникающие в результате их перестановки. Интегрируя по d3p'2, полу-
чим
Перейдя к сферическим координатам, получим
d3p[ = p~dpdQ.
1.10. Амплитуды реально наблюдаемых процессов
79
^ = ^|ТД(Ж-2^)
4Б2(27г)22!'
Учитывая pdp = E±dE±, имеем
dO = ^Т^2Е1~2Е^
E\dE\dll
4Е2(2тг)22!
^-\Т\25(2Е1-2Е'1)
dE\dll
4Е1(2л)22!'
Интегрируя по энергиям, окончательно получаем
, _ 1 21
d<J 16Я2 (2л)2 |Т| 2'
(1.170)
Здесь мы учли, что 4^1 = 2Е', 5(2E'i — 2Ej) = l/25(Ei — Е[). Это выра-
жение можно записать в мандельштамовских переменных:
Т 2 dtt
8тгД 2
(1-171)
Вернемся теперь к процессу кулоновского рассеяния тг тг , кото-
рый в низшем порядке описывается диаграммой:
Pl Pl Pl P2
1 1 1 1 1 1 + 1 1 1 1 1
P2 pi P2 pi
Сравнивая (1.161) и (1.160), сразу можно написать инвариантную ам-
плитуду рассеяния:
Т(р,2,Р/1;Р2,Р1) = 72
(Pi + pj)M(P2 + pj)M , (Pi +Р2ЫР2 + pj)M
(pi-Pi)2 (Pi-Рг)2
(1.172)
80
Глава 1. Частицы и их взаимодействие...
Перепишем (1.172) в инвариантных переменных. Для этого раскроем
числители в квадратных скобках:
(Pi +Р1)д(Р2 + р2)м = (2Р1 + ^)м(2Р2 - А:)м =
= (из закона сохранения к = р) — рД = 4pip2 + 2fc(p2 — рД — к2 =
= 4pip2 + 2pip2 - 2pipi + 2pipi - 2pip2 + +2p2 - pf - p2 =
= 2pip2 + 2pip2 + p2 - pi2 + p2 - p2 = s - u,
аналогично для второго числителя получим s — t, тогда (1.172) запи-
шется:
8 — U 8 —
+
Т = у2
(1.173)
В выражение (1.173) вошла единственная неизвестная константа
9
7 , и ясно, что ее можно определить из эксперимента по рассеянию.
Но на самом деле эксперимента делать и не надо, поскольку в обла-
сти малых импульсов формула (1.173) должна переходить в известную
нерелятивистскую формулу для кулоновского рассеяния.
Для перехода к нерелятивистскому пределу вычислим s, t, и в
системе центра масс, где
Pi = -Рг; р'1 = -р'2,
Р10 — Р20 — p'w — Р20-
Тогда
8 = (Р10 +Р20)2 - (Р1 +Р2)2 = (Р10 +Р20)2 = Е2,
t = (р'ю -Рю)2 - (Р1 - р'1)2 = — |Р1|2 - |р'1|2 + 2|pi| Ip7! | COS 0 =
= —2р2(1 — cos#) .
и получается из t заменой р^ на рД т. е.
и = —2р2(1 + cos#); рю = Др2 + т2; -л s = 4(р2 + т2).
В нерелятивистском пределе s = Е2 ~ 4m2; t,u s. Тогда (1.173)
принимает вид:
Т = —д24т2
1 1
+ ф2
(1.174)
1.10. Амплитуды реально наблюдаемых процессов
81
С другой стороны, в нерелятивистской квантовой механике для ампли-
туды рассеяния f в борновском приближении имеем:
f = ~^/ e~^U^d3r + /обмен-
Здесь ц = т/2 — приведенная масса. В хэвисайдовых единицах куло-
новский потенциал имеет вид:
е2
4тгг ’
тогда
/ = -^2^+/обмен. (1.175)
При рассеянии на малые углы в <7 1 обменными членами в (1.174)
и (1.175) можно пренебречь.
Теперь мы можем найти связь между нерелятивистской ампли-
тудой f и Т. Сечение выражается через / как
da = |/|2dQ. (1.176)
Сравнивая с (1.171), получим
Т Т
f =------- - ---- (1.177)
8tt^/s 16тгт
Подставляя в (1.177) значение / (1.175) и Т (1.174), найдем наконец
значение нашей константы 7 :
m 91 9 4m2
----— = —'у2----------.
2тг q2 ц216тгт'
Отсюда следует, что
у2 = е2. (1.178)
Таким образом, 7 совпадает с зарядом частицы.
Отметим, что в наших единицах е2/4тг = 1/137 <7 1. Таким об-
разом, мы действительно с хорошей точностью можем ограничиться
простейшими процессами.
Подставляя теперь в (1.173) у2 = е2, получаем Т при произволь-
ных энергиях. В с.ц.м. (1.173) принимает вид:
Т 2 3 + cos0 + 2т2/р2 3 — cos# + 2т2/р2
1 — cos 0 1 + cos О
82
Глава 1. Частицы и их взаимодействие...
Результатом релятивизма здесь является появление зависимости ампли-
туды от величины импульса р налетающих частиц.
Приводим график зависимости Т от cos в:
\Т\
Суммируя, мы показали, что константа взаимодействия заряжен-
ных бесспиновых частиц с электромагнитным полем совпадает с заря-
дом этих частиц, т. е. у2 = е2, и получили формулу (1.179) для ин-
вариантной амплитуды рассеяния тг+ на тг+ (или тг- на тг-) в первом
9
порядке по е .
Рассмотрим теперь рассеяние тг- на тг+, т. е.
В координатном представлении простейшие диаграммы, описывающие
рассеяние заряженных частиц, имеют вид:
1.10. Амплитуды реально наблюдаемых процессов
83
Если устремить жццЯго —» —ею, x'w, я?20 +оо то, как мы говорили,
получим амплитуду рассеяния тг—тг—.
А что, если вычислить амплитуду при условии жццЖго —сю,
- ' X1-----------
Тогда процесс ----►—-=-С-- перейдет в и мы,
Х1 X Х2 Х2
чтобы сохранить заряд, интерпретировали этот процесс так: из х± в х'
распространяется частица, а из х'2 в х' —античастица с противополож-
ным зарядом, а также ввели стрелки, чтобы помнить, в какую сторону
дифференцировать со знаком “+”, а в какую — со знаком ”. Таким
образом, диаграммы можно переписать так:
т. е. получим рассеяние тг- на тг+. Второй график здесь уже не такой,
как при рассеянии тождественных частиц, и описывает аннигиляцию
двух мезонов, а потом превращение фотона опять в два мезона, т. е.
процесс через промежуточную частицу.
Вычислим амплитуду, соответствующую первому графику. Здесь
можно поступать как раньше, т. е. вычислить функции Грина для тг :
d4^ е грАх1 х~)
(2тг)4г т2 — р2
(1.180)
84
Глава 1. Частицы и их взаимодействие...
для тг+ аналогично:
G(x2-x') = I (1-181)
и т.д., но неудобно то, что необходимо помнить, в какую сторону опе-
ратор дифференцирования должен действовать со знаком “+”, а в ка-
кую — со знаком Гораздо удобнее написать сразу амплитуду для
рассеяния тг- на тг-, т. е. для “неразвернутых” стрелок, а в соответ-
ствующих функциях Грина замкнуть контур наоборот, в силу условия
гею,я?20 “* —сю, 2^20,23^0 —> +оо. Тогда, как и прежде, будет входить
функция Грина
G(x' -х2) = (1-182)
J (2тг)4г tn- — р^
Но контур здесь, в отличие от прежнего случая, надо замкнуть наверх,
т. е. на полюс //2П = — л/р2 + 777,2 • Тогда
G(x' - 2:2) =
_ f d р2 гЛ1/р^+т2(жп-ж2о~)+гР2(х'-х2') _
J (2тг)32Н0|
= (1.183)
поскольку замена +р на —р в интеграле ничего не изменит. Здесь
егрх ________
Ф-р = г-,—г, Ро = VP2 +т2.
V2 Ы
Сравнивая (1.181) и (1.183), видим, что распространение тг+-мезона
можно описать как в терминах Фр^, где р'+ обычный импульс, соот-
ветствующий положительной энергии, так и в терминах Ф-р(,, т. е. вол-
новой функции тг -мезона с отрицательной энергией. С этим связана
фейнмановская интерпретация античастицы как частицы с отрицатель-
ной энергией и распространяющейся обратно во времени.
1.10. Амплитуды реально наблюдаемых процессов
85
Таким образом, заменой р'+ = —р'2 мы получаем из функции
распространения тг--мезона из ад в х' функцию распространения тг+-
мезона из х' в яд, т. е. путем соответствующих замен импульсов мы
можем получить из амплитуды рассеяния тг- на тг- амплитуду тг+7г_.
На диаграмме
Pi
Pi
тг+-мезону будут соответствовать импульсы
Pi = ~Р21 Pi = -р^
(1.184)
аналогично для второго графика.
И если для рассеяния 7г-7г- мы имеем амплитуду
е
(Р1 +Р1)М(Р2 +Рг)м , (Pi + Р2ЫР2 +-Р1)м
(pi-pi)2 И-Р2)2
то заменой (1.184) получим амплитуду рассеяния тг тг+, т. е.
T(pi,pJ ;pi,pj) =
=е2
(Pl +Р1ЫР2 + pf )м , (Pl -pf )мИ -рЛм
(pi-pi)2 (р'1+р^)2
(1.185)
Выразим (1.185) через инвариантные переменные з, 4, и. Здесь
S = (р2 +Р1)2
t = (.Pl - Pl)2
и = (р%' ~Р1)2
86
Глава 1. Частицы и их взаимодействие...
Проводя вычисления, аналогичные выводу (1.173), получим
(1.186)
Вычисления можно было и не повторять, а просто посмотреть, во что
перейдут s, t, и, определенные в (1.167) при учете (1.184), и подставить
в (1.173). Действительно,
Проведя эту замену в (1.173), получим (1.186). Более подробное иссле-
дование амплитуд типа (1.186) проведем несколько позже для случая
электронов. А сейчас обсудим связь между амплитудами в более общем
плане.
1.11 Мандельштамовская плоскость
Рассмотрим рассеяние тг-тг- тг-7г_:
Мы говорили, что мандельштамовские переменные не являются неза-
висимыми и удовлетворяют соотношению
з + t + и = 4m2.
(1.187)
Чтобы помнить об этом, рисуется так называемая мандельштамовская
плоскость, на которой откладываются эти переменные в направлении
стрелок, как указано на рис. 10.
1.11. Мандельштамовская плоскость
87
Рис. 10
При этом используется свойство равностороннего треугольника, что сум-
ма высот, опущенных из некоторой точки на плоскости на стороны (или
продолжения сторон) треугольника, одинакова для всех точек плоско-
сти (с учетом знака высот; положительные направления указаны стрел-
ками). Таким образом, любой точке мандельштамовской плоскости со-
ответствуют значения s, t, и, связанные (1.187). Очевидно, на прямых,
проходящих через вершины треугольника параллельно соответствую-
щим основаниям, лежат точки s = 4m2, t = и = 0; t = 4m2, s = и = 0;
и = 4m2, s = t = 0.
Рассмотрим, что такое физическая область на этой плоскости (см.
рис. 11). В нашем случае рассеяния тг_ на тг_ в с.ц.м.
s = 4(р2 + т2),
т. е. s 4m2, t 0, и С 0. Это соответствует заштрихованной обла-
сти. Называется она областью s-канала, поскольку здесь з > 0, 1, и < 0.
Жирными линиями на рис. 11 выделены область малых 1, соответству-
ющая рассеянию вперед (нерелятивистская ситуация), и область малых
и, соответствующая рассеянию назад. Аналогично область и 4m2,
s, t 0 называется областью и-канала, t 4m2, и, з 0— 4-канала.
Рассмотрим, например, какому физическому процессу соответ-
ствует, например, область w-канала (рис. 12).
88
Глава 1. Частицы и их взаимодействие...
Рис. 11
Рис. 12
1.11. Мандельштамовская плоскость
89
Сделаем в амплитуде процесса подстановку р'г = pt; р\ = —р^
Здесь р^ > 0, т. е. мы аналитически продолжаем амплитуду в область
отрицательных частот. Диаграмму тогда можно перерисовать так:
Pi
Pi
Pi
Но, как мы уже говорили, такая диаграмма описывает уже тг+7г_-рас-
сеяние с импульсами pt = —р[, р+ = —pi , а переменные s, t, и в этом
случае станут теперь равны:
s =
t =
(Р2 -pf)2,
(Р2 -Й)2,
+Р2)2,
т. е. будет и 4m2; s,t < 0.
Таким образом, когда мы перешли от процесса тг~ +тг_ +тг_
к процессу 7г++7г_ 7г++7г-, наши переменные полностью изменились,
и мы перешли из области s-канала в область w-канала. Мы фактически
аналитически продолжили амплитуду Т из области s-канала в область
м-канала, и при этом она стала описывать другой процесс. Именно так
мы и получили (1.186) из (1.173).
Действительно, если исходная амплитуда была
Т = е2
s — и s — t
t
и была определена при s 4m2; t,u < 0, то, если теперь понимать под
и: и = 4(р2 + т2), т. е. называть и прежнюю s, а
t = — 2р2(1 — cos#), s = — 2р2(1 + cos#),
получим
= e2
и — s и — t
s
90
Глава 1. Частицы и их взаимодействие...
Именно это выражение мы и получали ранее для амплитуды тг+тг- -
рассеяния.
Таким образом, переход от частиц к античастицам можно делать
двумя способами: либо вычислять амплитуды, фиксируя знак энергии р,
а затем меняя его, либо фиксируя переменные s, t, и определенным
процессом, а затем аналитически продолжая амплитуду в другой канал.
Приведем еще один пример:
Если смотреть на диаграмму сверху, то в этом случае р± и р'2 являются
импульсами частиц, а р{ = pt' и р2 = — р2 — античастиц. С этой
точки зрения
S = (pi -р^)2,
U = (pi -р'2)2,
t = (pi +Р1')2,
т. е. теперь мы оказываемся в области 4-канала, который отвечает ре-
акции 7Г+ (р+>1 +7Г“(р1) -Л 7Г+(Р2 +ТГ_(Р2)
Итак, мы получили следующий важный результат: одна ампли-
туда описывает не один, а целый класс процессов:
в s-канале тг + л —> тг + тг ;
в м-канале тг+ + тг~ -л 7г+ + тг~;
в 4-канале тг+ + 7г~ -л + тг+.
В заключение этого параграфа заметим, что распад тг-мезона на
три запрещен законами сохранения, т. е. лежит в нефизической области.
Но если мы увеличим массу одной частицы, то наша амплитуда опишет
и этот процесс, а область распада на мандельштамовской плоскости
будет внутри треугольника.
1.12. Комптон-эффект (для л-мезона)
91
1.12 Комптон-эффект (для л-мезона)
Простейшие диаграммы, описывающие рассеяние фотона на я-мезоне,
следующие:
Волновая функция мезона имеет вид:
e~ipx
g — ikx
фотона —
2ko
Они у нас возникали в амплитудах при устремлении времен к бесконеч-
ности.
Для фотона
92
Глава 1. Частицы и их взаимодействие...
и мы отнесли к разным волновым функциям. Аналогично случаю
7Г7Г рассеяния можно сразу написать амплитуду, соответствующую двум
первым диаграммам, обозначая амплитуду, соответствующую третьей
диаграмме, через Мх2Х1, получим
Т — е2
-*• 7Г7 — С
(р2 +р2 + fc2)^2 + fc^2 (щ +Р1 + fci)Me^ +
+С?2 +Р2 ~ TO2_J2_fci)2(Pi +Pi - к2\е^
+ МХ2Х1- (1.188)
Вынесем из (1.188) множитель остаток обозначим Л/, т. е.
Т' — 1\/Г
-LTV^ — lv-LVfl‘
(1.189)
Как мы говорили, чтобы не возникло продольной поляризации, должно
выполняться условие
ki^M^ = 0, = 0.
(1.190)
При fc2 0 мы имеем три вектора, ортогональных к т. е. А = 1, 2, 3;
= Для А 0, А) ~ их вид такой (см. и.1.3):
Здесь принято обозначение:
/е°\
ci
е2
\е3/
(ось z направлена по трехмерному импульсу фотона). При выполнении
(1.190) из (1.189) выпадет член с е°, в силу его пропорциональности а
при к2 = 0, т. е. для реальных фотонов, обратится в нуль и член с е3, та-
ким образом, скалярные и продольные фотоны при выполнении (1.190)
не будут давать вклада в реальные физические процессы.
1.12. Комптон-эффект (для л-мезона)
93
Тензор имеет следующий вид:
— е
(2рг + к-2)и—~—щ(2рх + +
~2р2А:2
+
(2pi - к2)„
+ Мци
(1.191)
Вычислим
k2vMv[l = е2[-(2pi + fci)M + (2р2 - Ад)м] + к^М^.
Мы здесь учли, что 2р2к± = 2р^к2, так как щ + Ад = р2 + к2.
Учитывая также р2 — р± — к\ = —к2, окончательно получим
k2vM^ = -2e2k2fl + k2vM^, (1.192)
т. е. без введения контактной добавки условию (1.190) не удовлетворить,
а тем самым и не сохранить ток.
Исходя из соображений простоты, примем в качестве гипотезы,
что
= 2<2glw. (1.193)
В результате, мы действительно получим амплитуду, для которой со-
храняется ток и в которую не входят скалярные и продольные фотоны.
Теперь, пользуясь выражением (1.193) для контактного взаимо-
действия, вычислим Т^. Поскольку (1.188) релятивистски инвариант-
но, вычисления проведем в системе, где первоначально электрон поко-
ился, т. е.
Рю = m , pi = 0.
Так как вклад в (1.188) дадут только две компоненты еА, ортогональные
к кц, то члены, пропорциональные к,, в (1.188), обратятся в нуль. Кроме
того, эти еА содержат только пространственные компоненты, а р\, вхо-
дящий множителем в первые два члена, — только временную, поэтому
ненулевой вклад в амплитуду будет только от контактного члена.
Таким образом,
= е^*е^д^2е2,
(1.194)
т. е.
Ту = 2e2(eAyk2)-eA1(k1)).
94
Глава 1. Частицы и их взаимодействие...
Для случая рассеяния на малые углы kj/|ki | = ка/|кз | амплитуда рав-
на просто „
= -2е25А1Л2. (1.195)
Рассмотрим связь с обычной нерелятивистской амплитудой рас-
сеяния. Как мы говорили,
(1.196)
При — II в нерелятивистском пределе y/s —> т, т. е.
что совпадает с формулой для классического томсоновского рассеяния:
/ = —е/2/т, е' — обычный, не хэвисайдов заряд.
Рассмотрим теперь нашу амплитуду с точки зрения различных
каналов. Произведем замену:
Ад =
Ад = Ад.
т. е. перейдем в м-канал. Такой заменой мы переставили только гамма-
кванты, а поскольку они нейтральны, от этого ничего не изменилось, и
амплитуда в w-канале совпадает с амплитудой в s-канале. Замена
Р2 = “Р2 ,
Ад = Ад
приводит к новому процессу: двухфотонной аннигиляции двух тг-мезонов
и соответствует переходу в область А-капала.
-Ад
Р2 = -Р2
1.12. Комптон-эффект (для л-мезона)
95
Симметрия же амплитуды относительно пунктирной линии на мандель-
штамовской плоскости означает тождественность фотона и антифотона
в силу его нейтральности.
Итак, мы научились непосредственно по диаграммам вычислять
амплитуды различных процессов. Давайте посмотрим, нельзя ли с по-
мощью диаграмм сразу представить сечение. Мы уже писали сечение
для процесса
л 1 |2/о , \d3Ps г]3Р4 1
= ?|Т.Ь| (2») Ли +и -и
Заметим, что в смысле интегрирования справедливо такое соотношение:
= d'p3Kp( - тзМрзо) = d'p3dipz - тп2^, (1.198)
тогда выражение для сечения можно переписать так:
(to = ДЁТаЬ6+(р23 - m3)6+(p3 - ml)T*bd dC^Pi), (1.199)
т. e. по нашим обычным правилам нужно вычислить диаграмму
с учетом того, что в промежутке вместо функций Грина стоят 5-функции,
9 9 9 9
а это соответствует реальным частицам, для которых pg = mg, pg = mg.
96
Глава 1. Частицы и их взаимодействие...
Действительно, функцию Грина можно представить в виде
G = —z—----------- = Р—^—у + ixS(p2 - m2).
m — pz — ге m — p
(1.200)
Символ P означает интегрирование в смысле главного значения. Удоб-
ство записи сечения в виде (1.199) состоит в том, что сечения сразу
можно продолжать из канала в канал (при условии, что амплитуда Т
при этом не получит мнимой добавки). Этот вопрос мы обсудим позд-
нее.
Глава 2
Частицы со спином 1/2. Основные
электродинамические процессы
2.1 Свободная частица со спином J = 1/2
Состояние частицы с J = 1/2 можно описать при помощи двух величин
</д(А = 1,2), которые имеют смысл амплитуд вероятности обнаружения
частицы в состоянии с проекциями спина 1/2 и —1/2. Их мы можем
объединить в одну двухкомпонентную величину (Д). Тогда волновая
функция покоящейся частицы запишется как обычно:
Фо = Р1
\<^2/
(2.1)
Для движущейся частицы со спином J = 0 мы имели
р-грх
Ф =
V%Po
В нашем случае ситуация более сложная: чтобы получить волновую
функцию частицы с конечным импульсом, нужно сделать преобразо-
вание от покоящейся к движущейся системе отсчета. Для этого нужно
знать закон, по которому будут преобразовываться при преобразова-
ниях Лоренца. Другими словами, задача сводится к нахождению пред-
ставления группы Лоренца, по которому преобразуются наши двухком-
понентные величины.
Преобразования Лоренца имеют вид:
— ^ik^k -!
(2-2)
причем матрица преобразования зависит от шести параметров: трех уг-
лов Эйлера соответствующих пространственным поворотам, и трех
компонент скорости щ, соответствующих переходу из одной системы
отсчета в другую, движущуюся относительно первой.
98
Глава 2. Частицы со спином 1/2
Теперь обратимся к волновым функциям. Если в покоящейся си-
стеме мы имели некоторые величины ф, то при переходе к движу-
щейся системе они будут преобразовываться в общем случае так:
<Й = W11C1 +М12<2,
^2 = М21Ф + «21^2- (2.3)
Вообще говоря, как так и Щк комплексны. Поэтому матрица Uik со-
держит 8 параметров. Наложим на нее условие:
det(uik) = unu22 - u12u2i = 1. (2.4)
В (2.4) содержится два условия, на вещественную и мнимую части, так
что теперь матрица будет содержать 6 независимых параметров —
столько же, сколько в общем преобразовании Лоренца. Установим со-
ответствие между этими величинами и параметрами преобразований
Лоренца. Как известно, любую матрицу второго порядка можно пред-
ставить в виде суперпозиции четырех матриц: единичной и трех матриц
Паули:
т /1 о\ /oi\ (о -А /1 о \
о ) ’ (° -i ) '
Матрицы Паули обладают следующими свойствами:
= 2z6xfc/CT/c, <7х^у = C^y<7z = (Tz^x = (2-5)
т. e. ведут себя как генераторы поворота в трехмерном пространстве.
Поворотам в обычном трехмерном пространстве соответствует
следующее преобразование величины £ = (|^):
е' = < (2.6)
где
и = (2.7)
или
м = ез<т"'’”, (2.8)
где <тп — проекция “вектора” <т = {их, ay,az) на ось поворота, дп — угол
поворота относительно этой оси.
2.1. Свободная частица со спином J = 1/2
99
Сопряженная величина будет преобразовываться так:
транспонируя это соотношение, получим
2.9
или
в силу эрмитовости матриц Паули. Символом * мы обозначили ком-
плексное сопряжение, Т — транспонирование, “+” — эрмитово сопря-
жение, 1 1 означает здесь строчку , ££), вместо столбца (^). Величина
(</+^), согласно правилу обычного умножения матриц, есть
(е+е) = £1Ч1+ш (2.Ю)
что совпадает с обычным определением скалярного произведения в дву-
мерном пространстве. Рассмотрим, как она преобразуется при преоб-
разованиях (2.3), а соответственно, и при преобразованиях в обычном
пространстве. Видим, что в силу (2.8), (2.9)
(е/+е') = (е+а (2.11)
т. е. преобразование является унитарным.
Рассмотрим теперь закон преобразования для величины
л = eW-
После преобразования она переходит в
А'г = e'W-
Так, относительно вращения вокруг оси г, компонента Ах становится
равной
А'х = ^+e~iai,ezaxeiai,e^ =
= 1 1 (cos -az0z — i sin -o-z0z)(jx (cos -(Jz0z + i sin -<Jz0z)C
Поскольку разложение cos я; в ряд содержит только четные степени х,
а <т? = 1, получим
cos -<tz9z = I cos -0Z.
100
Глава 2. Частицы со спином 1/2
Аналогично
sin —uz9z = az sin -0Z,
2 2
поскольку разложение синуса содержит только нечетные степени, а нечет-
ная степень az равна az. Таким образом,
,, ,+(т 9Z . . 9 9Z . 9
Ax = t, (1 cos —— iaz sin — )(ax cos — + iaxaz sin —)£ =
/ 2^ 9Z 9Z 9Z 9Z A,,
= ? (^ COS — + Uy sin — COS — + ay sin — cos — - az sin —)£ =
Z Z Z Z Z
= £+(ax cos 9 + Uy sin0)</ = Ax cos# + Av sind. (2-12)
Величина Ax преобразуется при вращениях как ^-компонента трехмер-
ного вектора. Повторяя вычисления для других компонент, можно пока-
зать, что величина Af = ^+и^ преобразуется при поворотах, как обыч-
ный вектор в трехмерном пространстве. Единственное отличие в том,
что при отражениях он ведет себя как псевдовектор, т. е. не меняет
знак.
Мы фактически рассмотрели представление группы вращений
трехмерного пространства, являющейся трехпараметрической подгруп-
пой группы Лоренца. По аналогии с этим построим представление, со-
ответствующее преобразованиям Лоренца.
Пусть система отсчета движется вдоль оси z со скоростью г, тогда
в этой системе
, z + vt
z = = zchx + tshx,
Vl — w
или:
t “I- vz
t' = r----= = г sh у + Z chx, (2.13)
Vl — w
где thx = v. Эти преобразования очень похожи на поворот на комплекс-
ный угол, поэтому по аналогии для матрицы преобразования двухком-
понентных величин положим
uz = (возможно также йг = с ).
т. е.
= £'+ = (2.14)
Как и раньше, величина Az = S,+uzS, будет преобразовываться по зако-
ну (2.13), где роль временной компоненты играет Aq = и сама Aq
2.1. Свободная частица со спином J = 1/2
101
будет преобразовываться как время в (2.13). Действительно, из (2.14)
напишем
л'о = е'+е' = е+ехстч = е+( сьх + az shX)e =
($+оД) shy + (£+£) ch у = Az shy + Ao chy.
Аналогично и для Az, т. e. величина (Ao, A) = (С+СД+сгС) образует
4-вектор.
Итак, для движения вдоль произвольного направления п можно
написать
£' = (2.15)
Но, с другой стороны, представление группы Лоренца можно получить
преобразованиями
^ = е_^(СТп)ё. (2.16)
Точками мы обозначили величины, которые преобразуются по (2.16).
Это говорит о том, что в двумерном комплексном пространстве1 ре-
ализуются два представления группы Лоренца, или так называемое
двузначное представление. Закон преобразования (2.16) соответству-
ет движению в противоположном направлении (действительно, замена
X ~Х приводит в (2.13) к изменению знака скорости).
Итак, мы имеем два сорта величин £ и С которые преобразуют-
ся по различным представлениям группы Лоренца. Какие из них мы
выберем в качестве волновой функции частицы со спином 1/2?
Перейдем к системе отсчета, где частица движется со скоростью v:
Р 1 Ро ,
v = —; , = — = ch у.
Ро Д1 - v2 m
Из (2.15) следует
£' = [ch j +t6711)sh |] v>e~ipx =
I chy + 1 / chy - 1
у--------+ (^n)^---------- tpe p,
1 Векторы в таком пространстве называются спинорами, т. е. наши двухкомпо-
нентные величины — это спиноры.
102
Глава 2. Частицы со спином 1/2
т. е. если в качестве закона преобразования волновой функции взять (2.15),
то для движущейся частицы будем иметь
е' =
Ipo + m
V 2m
ре
— грх
(2.17)
Однако имеется и другая возможность: движение в противоположную
сторону. Используя (2.16), в этом случае получим
lp0 + m
V 2m
(2.18)
Которая из этих волновых функций верна — это вопрос эксперимента,
для нейтрино, например, имеются обе возможности.
Что произойдет при отражении z —z? Видно, что
Это означает, что если частица описывалась какой-то из этих функций
в правой системе координат, то при переходе в левую ее волновая функ-
ция изменится, т. е. в этом случае частица сама содержит в себе понятие
левого и правого. С нейтрино так и есть на самом деле.
Но если частица совершенно симметрична (т. е. “не знает”, где
право, где лево), то при отражении ничего не должно измениться. Опи-
сание частицы в правой и левой системе отсчета должны быть экви-
валентны (сохранение четности). Такие частицы должны описываться
некоторой суперпозицией £ и £. Но обычно поступают так: вводят четы-
рехкомпонентную величину (биспинор) и волновую функцию полагают
равной
Если все эти величины будут входить в различные выражения симмет-
рично, то четность будет сохраняться автоматически.
Описание частицы со спином 1/2 биспинором не диктуется зако-
нами природы, это просто удобная форма записи (она возникла из урав-
нения Дирака). Часто удобно вводить также двухкомпонентные волно-
2.1. Свободная частица со спином J = 1/2
103
вые функции с определенной четностью:
Ф1 = j(£ + G
Ф- = |(€ - €)-
(2.19)
Явный вид этих функций:
Ф1
(2.20)
Удобно в этом выражении исключить п:
тогда
Р
Ф2 = (^Р) Ро+^^е-грх
ро + ту 2т
(о~р)
Ро + т
Ф1.
(2-21)
Поскольку мы ввели две “лишние” величины (Фг) только для того, что-
бы поддержать симметрию волновой функции относительно простран-
ственного отражения, то, естественно, они выражаются через Ф1- Те-
перь попытаемся написать уравнение, связывающее все эти величины,
чтобы в нем поддерживалась симметрия между левым и правым и что-
бы покоящаяся частица имела определенную (например, положитель-
ную) четность (в системе покоя Ф2 = 0, как следует из (2.21)). Для этой
цели введем четырехмерные матрицы у (матрицы Дирака в стандарт-
ном представлении):
/ / 0 \ /О
70 = 0 -I) ’7г = -щ 0 J '
Тогда можно написать
где
(уоРо - 7Р - т)Ф = 0,
(2.22)
(2.23)
104
Глава 2. Частицы со спином 1/2
Уравнение (2.22) называется уравнением Дирака. Расписывая его в ком-
понентах, получим
(ро - т)Ф1 - (<тр)Ф2 = 0,
(2.24)
(—Ро - пг)Ф2 + (<тр)Ф1 = 0. (2.25)
Из (2.25) вытекает (2.21). А подставляя в (2.24) выражение для Ф2
из (2.21), получим связь между энергией и импульсом:
(ро - т) -
(о-р)2 '
Ро + тп_
Ф1 = 0,
или
9 9 9
Р°-т Р Ф1=0, т.е.р2-р2 = т2.
Ро+т
Уравнение (2.22) релятивистски инвариантно, поскольку 70Р0 ~ 7Р =
= умрм = р — релятивистский инвариант.
Таким образом, уравнение
(р — т)Ф = 0
(2.26)
выделяет состояния с положительной четностью, поскольку при v = 0
остается только Фр Соответственно, для состояний с отрицательной
четностью имеем
(р + т)Ф = 0. (2.27)
Чтобы наше описание годилось и для частиц с нулевой массой,
надо избавиться от масс в знаменателях волновых функций (2.20). Для
этой цели введем биспинор с другой нормировкой (умножая просто
выражения (2.20) на у/2т), т. е.
фЛ=/ Дро + трх =
\(о-п)Др0 - трх)
= VPoTm( = и\р)е-грх. (2.28)
\(^Р)/(Ро + m)pxj
Поскольку у имеет две компоненты, то имеется две линейно неза-
висимых функции рх- отвечающие двум проекциям спина; это обстоя-
тельство мы и отметили индексом А; (А = +1, — 1). В системе покоя А/2
есть просто проекция спина, т. е.
o'zpx — -^Ра-
(2.29)
2.1. Свободная частица со спином J = 1/2
105
Легко видеть, что
/0\ /Д\
= ^+1 = W’
и волновую функцию в состоянии покоя (^) можно записать в виде
(?Л _ /1\ /0\
I — 9Л п + +2 I 1 I •
\+2/ \0/ \1/
</?1 и </?2 как раз и имеют смысл амплитуд вероятности частице иметь,
соответственно, проекцию спина +1/2 и —1/2.
Запишем выражение (2.29) релятивистски инвариантным обра-
зом. Для этой цели введем единичный вектор ф £2 = 1 в неподвижной
системе, направленный вдоль спина, тогда (2.29) можно переписать:
(сг<Д</? = Хр. (2.30)
Можно ввести пространственноподобный 4-вектор СцСц = — 1, кото-
рый в системе покоя переходит в (0,£). Введя также четырехмерную
матрицу
/0 П
75 “ I 0 ) ’
можем записать релятивистски инвариантное выражение, соответству-
ющее (2.30):
ЬФПм - = 0. (2.31)
Действительно, в системе покоя мы имеем
-(75^7» + А)м = [(<т£) - 1]</? = 0.
Здесь мы использовали то, что
и то, что в системе покоя нижние компоненты и равны нулю. Таким
образом, чтобы однозначно определить спинор, необходимы два урав-
нения:
(р — т)и = 0,
(7зС - А)м = 0.
(2.32)
106
Глава 2. Частицы со спином 1/2
Решение этих уравнений будем обозначать либо и(р, £), либо их(р) (здесь
уже и А, и( фиксированы).
Обсудим вероятностную интерпретацию спинорных волновых
функций. Для этого, как и раньше, нам нужно составить сохраняю-
щуюся величину. Очевидно, релятивистским инвариантом будет произ-
ведение спиноров разных типов (т. е. преобразующихся по различным
представлениям группы Лоренца). Действительно,
+ = ^+е-2
Мы же пользуемся их линейными комбинациями:
Ф1 = |(€ + 4),
ф2 = |се - а
Тогда
(£+Д = (Ф?- - + Ф2) = - Ф^Ф2-
Введем биспинор (дираковски сопряженный к wA)
й\р) = Л(р)у0 = (Ф^ФП (о °/) =
Тогда величина
й\р)их' (р) = Ф+ф; - ф+ф'2 (2.33)
является релятивистским инвариантом.
Рассмотрим, какому уравнению удовлетворяет и\ Из первого урав-
нения (2.32) имеем
w+(p+ — m) = 0, (2.34)
где
Р+ = (уоРо - 7Р)+ = УоРо + Р7
в силу эрмитовости уо и антиэрмитовости у^. Домножая (2.34) на уо и
пользуясь перестановочными соотношениями для у-матриц
УмУ,, + У^Ум = 28^,
т. е.
7Уо = -Уо7,
2.1. Свободная частица со спином J = 1/2
107
получим
u{p-m)=0. (2.35)
А что произойдет со вторым уравнением (2.32)? Как и в предыдущем
случае, имеем
и+(С+75-А) =0.
Опять умножая справа на уо и пронося у-матрицы вправо, получим
й(у5С — А) = 0, (2.36)
т. е. Д является решением тех же уравнений, что и Д.
Поскольку, как мы показали, йи есть релятивистский инвариант,
а ум преобразуется как 4-вектор, величина = йумм будет преобра-
зовываться как 4-вектор, ее нулевую компоненту wyow = и+и можно
отождествить с плотностью вероятности, а йгци — с плотностью потока
вероятности.
Действительно, в координатном представлении уравнения (2.32)
и (2.35) запишутся:
Дд^Д "Д ВД = 0, (2-37)
ФД) ( 'Д—Д - ГП j = 0 (2.38)
\ Охр, J
(стрелками здесь обозначено направление дифференцирования). Умно-
жая (2.37) слева на Ф, а (2.38) справа на Ф и вычитая одно из другого,
получим
-^-ФумФ = 0. (2.39)
ОХц
Таким образом, д удовлетворяет уравнению непрерывности и j0, дей-
ствительно, можно приписать смысл плотности вероятности. Как и
прежде, частицы отвечают положительно-частотным решениям. Как
сконструировать такие решения уравнения Дирака?
Положительно- и отрицательно-частотные решения отличаются
заменой
Ро ~Ро, Р -> -Р- (2-40)
Выпишем наш спинор
>? Д vW+wa \ (241)
\(<тп)Дро - тр
108
Глава 2. Частицы со спином 1/2
После замены (2.40) получим
,?(-„) = ±!(/ у (242)
+ mpxj
Знаки ± возникают из квадратного корня. Какая связь между иА(р) и
иА(—р)? Для скалярной частицы она была тривиальной: р(— р) = р*(р).
Рассмотрим и здесь
ypTIlJ л/Ро — тГ\/
= Д «.-JWppyA \ (243)
у-о-Дстп^ро + mayp*xJ
Мы здесь умножили обе компоненты на ау = 1 и воспользовались тем,
что ст* = ах, a* = az, ахау = — ауах, azay = —<Jy<rz, а также <ту<гу =
= — О'уО'у = — 1.
Обозначим (ап)аурх = р'х, тогда Оурх = (<тп)р/, поскольку
(<тп)(сгп) = п2 = 1 и
мА*(-р) = ±f-^(°’n)Vp° - w/A =
\ i(Jyx/Po + тр'х )
= ±(° ,) . (2.44)
\гау 0 / \(<тп)Уро - тр//
Выясним, что такое р'. Покажем, что если р\ удовлетворяет
(<тп)<ра = А<ра, (2.45)
то для р'х имеем
(<тп)р/ = -Ар/, (2.46)
т. е. р/ описывает частицу с противоположной проекцией спина.
Из (2.45) имеем
(<7*п)р/ = Ар/.
Умножая слева на ау и используя
ауГх =
получим
о-у (сгп)*р/ = А(<тп)р/.
2.1. Свободная частица со спином J = 1/2
109
С другой стороны,
<Ту(<7*п)^ = (-<7П)<ТУ^ = -Д,
т. е.
~4>’х = А(о-п)<д/.
А поскольку Л может принимать лишь значения ±1, то
(о-ПуА = -АД,
т. е. действительно Д = <д_д. Используя этот факт, мы можем постро-
ить теперь спинор, дираковски сопряженный к wA(— р). Имеем
мА(-р) = ±(д/ро + W-a, (o-n)v'po - W-a)x
х (Тау И о % ) = \и-х(р)]тС, (2.47)
\ LO у U / \ U 1 !
где
С = г727о=Р (2.48)
\ LO у 'J J
— так называемая матрица зарядового сопряжения. Ее свойства:
С2 = -1, С+ = С-1 = -С,
= -Д. (2.49)
Итак, мы получили связь между дираковскими спинорами с положи-
тельными и отрицательными частотами
мА(— р) = [м~ А(р)]тС .
Часто вводят спинор Vх согласно
Д( — р) = Vх (р).
Найдем связь между v и и. Имеем
г?(-р)+ = [w-A(p)]TC'7o ,
тогда
г?(-р) = 7оС+ КЛ+]Т = C7oKa+]t = -[гРА(р)С]т,
по
Глава 2. Частицы со спином 1/2
т. е.
Л(р) = C'[)Fx(p)]T, (2.50)
vA(p) = [w~A(p)]TC*. (2-51)
А что если в выражении для йА(р) сделаем замену р -л —р? Получим
ли выражение (2.47)?
Из (2.28) имеем
йА(р) = y/po + rn .
\ po+m J
Делая замену, получим
йА(-р) = ±(VPo - тГх, -Д(о-п)+7р0 + т). (2.52)
Сравнивая это выражение с (2.43), видим, что
wA(-p) Д wA(-p).
Выражение йА(— р) означает, что мы сделали замену р —р в функции
uA(p), а иА(— р) — что мы взяли дираковское сопряжение от функции
иА(—р). Таким образом, функции йА(—р) и wA(— р) не совпадают и от-
личаются знаком. Поэтому, если у нас
Л(р) =Л(-р),
ТО
ц\р) = -йА(-р). (2.53)
Это означает, что решения wA(p) и йА(р) при переходе р —р перестают
быть дираковски сопряженными.
Приведем два полезных равенства.
1. Условие нормировки
йа(р)м« (р) = 2т<5ЛА/ (2.54)
(а нумеруют 4-компоненты спинора). Это равенство следует непо-
средственно из вида спиноров:
«а(р)«а (р) =
/ ,--.- + +/ \ /------Л Дро + трХ' \
= (А/ро + тД,-Д(а-п)Дро-т) ---- =
\(<тп)Др0 - mpx'J
= (ро + т - ро + т)6х\' = 2т§хх'
2.2. Функция Грина электрона
111
2. Правило суммирования по поляризациям:
52 = (Р + То)«/3- (2-55)
А=1,2
Его можно доказать следующим образом:
i 4
52 ДиД w = 52+то)«7м7и^
А=1,2 А=1
где введено суммирование по двум дополнительным состояниям с
другой четностью:
4
52 ДД = 2т57/з.
А=1
2.2 Функция Грина электрона
Мы получили уравнение Дирака для частицы со спином 1/2
huPn - mj'I’tp) = 0, (2.56)
или в координатном представлении
---= °' (2-57)
Функция Грина G(x) удовлетворяет уравнению
( Q \
(Ьма-----m I G(a?) =-ДД). (2.58)
\ UK/J, /
Переходя в импульсное пространство, получим
(р — m)G(p) = —1
G(p) =-----— = 2W+/ (2.59)
m — р — гг т/ — р2 — гг
Здесь мы использовали следующее соотношение:
РР = 'GPtGvPv = + y^lPvPv = Р2-
112
Глава 2. Частицы со спином 1/2
Тогда
Gap(x2-Xi) = [ (2W+f)a'3. (2.60)
J (2л)4? m2 — p2 — ге
Вычислим G(x2 — Ж1) при t2 > t\. Проверим, получится ли функ-
ция распространения электрона из х± в х2, т. е.
Р
Х2
Замыкая интеграл по ро на полюс ро = у/т2 + р2:
Gpa{x2 -Ж1) =
РО = у/т2 + Р2.
Мы здесь использовали (2.55).
Введя волновую функцию электрона:
тА/ \ Иа(Р) -ига
W = ~Ё=е грх,
\Др<>
получим
Gpa(x2 -Ж1) = V [ -^^ФУр,ж2)ФУр,а:1),
r~P9J (27Г)
Л — 1 , z
(2.61)
(2.62)
т. е. это, действительно, функция распространения электрона, причем
распространяются положительные частоты.
А что если t2 < И ? В этом случае контур надо замкнуть на
другой полюс ро = — \/т2 + р2. Тогда
С/За(ж2-Ж1) = [ d Р егр(-^-х^\т-р')/3а =
J (2тг)л2ро
= -V [ ——v^(v)vx(v}eip<'X2~X1') =
J (2л)32ро ’
= -^[ (2.63)
J (2лГ р
2.2. Функция Грина электрона
113
Здесь мы использовали
А
и то, что р) = 'i’a(p), а йр(—р) = —Vp(p), и ввели
Ф;Л(Ж,р) = (2.64)
v2Po
Из (2.63) следует, что отрицательно-частотное состояние распро-
страняется вспять по времени, и мы его можем интерпретировать как
распространение античастицы (позитрона), описываемой функцией
Ф (р. х), вперед во времени, т. е. из х-> в хц
Вспомним теперь следующее свойство матрицы зарядового сопря-
жения С:
' = -7J.
Тогда можно написать
(т - р)/за = [С(т + р)С-1]а/3
G. (x.-xG = f с-^-^^С(т+^С^
^/30:^2 ^1/ / /п АД- 9 9 >
J (2тг)4г т2 — р2
т. е.
./з) CG'(.7'i ./'2)6’ (2.65)
Как видим, при замене х? — х± -э х± — х? функция Грина электрона
не переходит сама в себя, как это было для случая скалярных или век-
торных частиц. Согласно (2.65) матрицы G(x) и G(—x) связаны между
собой унитарным преобразованием, которое осуществляется матрицей
зарядового сопряжения. Это означает фактически, что тот же процесс
описывается в другом представлении.
Таким образом, функции Грина электрона и позитрона различны,
и связь между ними осуществляется посредством матрицы зарядового
сопряжения. Это, однако, не вызывает проблем, так как в природе мы
не встретили частиц со спином 1/2, совпадающих со своими античасти-
цами. Поэтому в том, что их функции Грина разные, ничего плохого
нет, так что, как и раньше, мы можем приписать G(x2 — #i) при 42 < ti
смысл функции распространения позитрона из х% в х±. Если бы такая
114
Глава 2. Частицы со спином 1/2
(т.н. майорановская) частица существовала, то она могла бы описывать-
ся тем же способом, но ее взаимодействие не должно было бы меняться
при зарядовом сопряжении. Можно также было бы построить форма-
лизм, в котором асимметрия в описании не появлялась с самого начала.
2.3 Матричные элементы амплитуд
рассеяния для электронов
Рассмотрим процесс рассеяния электрона на электроне:
Для вычисления его амплитуды нужно устремить
2710,2720 ^-00, 2730,Ж40 +ОО.
Этим однозначно определяются правила обхода полюсов в функ-
циях Грина, соответствующих внешним линиям, и вместо них появятся
Ф^(жз)Ф^(жз) и т. д., которые, в отличие от случая скалярных частиц,
будут иметь матричный характер.
Посмотрим теперь на диаграмму сверху, т. е. устремим
Ж1О,Жзо —00, 2720, Ж40 +ОО.
Функции Грина, описывающие распространение из х± в ж/ и из ж/ в
Ж4, останутся прежними, а от оставшихся появятся (в силу изменения
направления обхода полюсов)
и т. д. (см. рис.).
2.4. Взаимодействие электрона с фотоном
115
Итак, при вычислении амплитуды рассеяния частиц со спином,
как и для бесспиновых частиц, вместо функций Грина внешним ли-
ниям надо сопоставлять волновые функции. Буквально повторяя вы-
кладки (1.157) - (1.159), получим, что наша амплитуда перехода будет
отличаться от (1.159) только спинорными множителями, причем будут
входить
от начального электрона и,
от конечного электрона й,
от начального позитрона —v,
от конечного позитрона — v.
Кроме того, из (2.63) следует, что каждой позитронной линии нужно
сопоставить множитель —1. (Это было несущественно в приведенном
выше примере, поскольку мы имели две античастицы, но существенно,
например, для процесса аннигиляции ее -э уд.)
Резюмируем: чтобы получить амплитуду перехода частиц со спи-
ном 1/2,
S(pi,P2; kr, fc2),
нужно вычислить внутреннюю часть диаграммы в импульсном пред-
ставлении и умножить ее на спиноры от внешних линий в соответствии
со сказанным выше (множители 1/^2ро будем, как и раньше, учиты-
вать при вычислении сечений в фазовых объемах).
2.4 Взаимодействие электрона с фотоном
Рассмотрим, как обычно, простейший процесс:
к
Pi
Р2
116
Глава 2. Частицы со спином 1/2
Попытаемся написать для него амплитуду
Ttk^pi).
Как мы показали, начальному состоянию электрона нужно сопоставить
uA(pi), конечному — йА (р2), фотону же, как обычно, Тогда можно
написать
Т(к,р2;Р1) = йд (р2)Г^(р1,р2,А:)мА(р1)е^ (2.66)
Г^а(р1,р2; к) соответствует вершине (т. е. внутренней части диаграм-
мы). Еще должна присутствовать 5-функция, выражающая закон со-
хранения 4-импульса, но ее, как и множители типа 1/у/2ро, будем учи-
тывать при вычислении сечений.
Выясним возможный вид матрицы Г^а. Из чего мы ее можем
сконструировать? Она имеет векторный характер (д — векторный ин-
декс), а в нашем распоряжении имеются четыре вектора, характеризу-
ющие процесс:
Р1ц,Р2ц,к^ И 7М.
Но, на самом деле, они связаны законом сохранения
Pi = Р2 + к.
Поэтому введем
Рц = (Pi +Р2)М, А:м,
и в самом общем виде напишем
Гм = а7м + Ьр^ + ск^ - (Г^рц + Фр27м- (2.67)
Однако надо помнить, что Г стоит в обкладках между двумя спинорами,
которые удовлетворяют уравнениям
(pi — m)w(pi) = О,
й(р2)(р2 - т) = О,
тогда в последних двух слагаемых (2.67) р\ и р2 дадут т, и оба они
сведутся к первому.
Можно добавить к (2.67) члены
dpi^n - <1'УцР2-
2.4. Взаимодействие электрона с фотоном
117
Однако
= ЛгЛгЛм = + 25ди/Р11/ = -7мР1 + 2Р1М’
т. е. такие члены сведутся к первому и второму слагаемым (2.67), так
что самый общий вид
Гм = + Ьр,, + скц. (2.68)
Перепишем (2.68) в несколько ином виде. Во-первых,
й(.Р2)ЪцР + Р7мМл) = 2рмй(р2)м(р1). (2.69)
С другой стороны,
Pi + Р2 = 2pi - к = 2р2 + к
и
й(р2)[^Р + РУ^Мрг) = 4mu(p2)y/1u(p1) + й(р2)(кум - у^^^рг), (2.70)
т. е. вместо можно написать кур — у^к и
Гм = ауц + 6(fcyM - 7м^) + скт.- (2-71)
(Естественно, а, Ь, с здесь уже другие, чем в (2.68) .)
Теперь определим коэффициенты а, Ь, с. У нас Г/1 должна удо-
влетворять условию поперечности
йкцГ^и = 0. (2.72)
Из (2.71) находим
= ак + ск2, (2.73)
тогда
w(p2)A:AtrAtw(pi) = а[й(р2)(р1 - p2)w(pi)] + cfc2w(p2)w(pi) = 0. (2.74)
Поскольку
Й(Р2)(Й - Р2>(Р1) = й(р2)(т - m)w(pi) = 0,
то из (2.74) следует, что с = 0.
118
Глава 2. Частицы со спином 1/2
О константе Ь ничего сказать из общих соображений нельзя, пока
известны две частицы, для которых с большой точностью 6 = 0 — это
электрон и д-мезон (хотя малая величина Ь генерируется даже для этих
частиц динамически при учете более сложных радиационных процес-
сов).
Обычно полагают
Ь = 0, а = const. (2-75)
Это так называемая гипотеза минимальности электромагнитного взаи-
модействия. Ее основания, с одной стороны, простота, с другой, то, что
при b Д 0 нельзя построить замкнутой теории. Далее мы покажем, что
b = const соответствует аномальному магнитному моменту частицы.
Таким образом,
Гм = едм (2.76)
(через некоторое время мы покажем, что коэффициент пропорциональ-
ности, как и раньше, равен заряду частицы). Инвариантную амплитуду
(2.66) испускания электроном фотона можно теперь переписать в виде
Те- = ейх (p2)eCTwA(pi), (2.77)
где
ест =
Чтобы описать излучение позитрона, как мы говорили, внешним лини-
ям надо сопоставить v и г, т. е.
те+ =егА(р+)ёстЛ'(р+). (2.78)
Здесь, хотя tA(pll) описывает начальный позитрон, мы его поставили
слева, поскольку он с чертой.
Рассмотрим связь этих амплитуд. Для этого вспомним, что
Л(р) = их(-р) = -[й-х(р)С]'т = С[й~А(р)]т,
их(р) = их(-р) = —йх(—р) = [и~х(р)]тС. (2.79)
Тогда, поскольку СёС = [ё]т, то
Те+ = ей х' (р^)ё°и А(Д),
(2.80)
2.5. Рассеяние электронов. Связь спина со статистикой
119
т. е. амплитуды Те- и Те+ одинаковы с точностью до спиновых перемен-
ных. Взглянем на их связь теперь с другой точки зрения. Перерисуем
для этого график, соответствующий излучению фотона электроном, в
виде
--------4------««----- Р10,Р20 < О
Р2 Р1
и сделаем замену
Р1 = ~Р2 , Р2 = ~pt-
Тогда получим аналитически продолженную амплитуду Тпрод
Гирод = eu(-pt )ё<ти(-р}) = -ev(pt )ё<тр(р}), (2.81)
которая с точностью до знака совпадает с амплитудой испускания фо-
тона позитроном. Это и следовало ожидать, поскольку замена знака
координат в ж-пространстве эквивалентна замене знака импульсов в р-
пространстве и, естественно, заменив р на — р, мы получим амплитуду
для античастицы, как и раньше. Но откуда взялся минус? Это связано
фактически с определением амплитуды
причем под интегралом стоят сопряженные функции. Однако, когда
мы имеем дело с частицами, описываемыми спинорами, это свойство
при продолжении в область отрицательных р не сохраняется, поскольку
й(—Pi") уже не является сопряженной для функции w(— pt) (см. (2.79) ).
Поэтому лучше ГПрод не называть амплитудой, а определить
Гирод = —Ге+7.
Этот знак не имеет значения при вычислении сечений.
2.5 Рассеяние электронов.
Связь спина со статистикой
При рассеянии электрона на электроне возможны следующие простей-
шие процессы:
120
Глава 2. Частицы со спином 1/2
Pi Рз Pi Pi
±
Р2 Pi Р2 РЗ
А как мы должны сложить эти амплитуды, с “+” или с ”? С точки
зрения принципа Паули, знака “+” быть не может, поскольку при замене
Рз Pi все перейдет в себя, а амплитуда для частиц со спином 1/2
должна быть антисимметричной, т. е. амплитуды нужно вычитать.
Но нельзя ли вопрос о знаке выяснить из более общих соображе-
ний? То есть не придем ли мы просто к противоречию, если положим
знак “+”? Оказывается, что достаточно следующих двух требований к
теории, чтобы однозначно решить вопрос о знаке:
1. условие унитарности
SS+ = 1
(это требование, чтобы сумма всех вероятностей равнялась едини-
це);
2. причинность.
Рассмотрим нерелятивистский случай:
У е-*к'г'У(г')Ф+(г')й3г'. (2.82)
Выражая Ф+(г/) через функцию Грина, получим
/ = fB + J e-ik'r'V(r')G(r', г) V(r)eikrrfWr',
где /в — амплитуда в борновском приближении. Поскольку
О(Г» = |£Ф"У)ФУГ,), (2.83)
гп Е" Е
то
/ = <2-84’
п п
2.5. Рассеяние электронов. Связь спина со статистикой
121
где
fnk = I е-гкгУ(г)Фп(г)й3г. (2.85)
Существенно здесь то, что в сумме (2.84) при к = к7 стоит положитель-
ная величина f^kfnk'- Как мы покажем ниже, этот факт есть прямое
следствие условия унитарности. Амплитуда, как функция энергии, име-
ет полюс при энергии связанного состояния, т. е. при Е = Еп. Вычет в
полюсе — всегда величина отрицательная (в знаменателе Еп — Е).
Покажем теперь, что условие унитарности фиксирует однозначно
знаки амплитуд, отвечающих различным диаграммам.
Рассмотрим сначала случай скалярных частиц. Имеем
Pl t рз Pl U Р4,
1 +
Р2 Р4 Р2 РЗ
s = (pi+p2)2, w = (pi-p4)2, 4 = (pi~p3)2.
В s-канале особенностей по з нет (т. е. фактически по энергии, а у нас
есть условие именно на вычет в полюсе по энергии).
Перейдем в 4-канал (для этого надо на первый процесс посмотреть
сверху). Это будет процесс
е+ + е~ е+ + е~
второго порядка, который идет через промежуточное состояние (гамма-
квант). Оно и соответствует сумме в (2.84), причем имеется полюс по
энергии (4 в этом канале отвечает энергии) в t = 0, это как раз соот-
ветствует энергии промежуточного состояния т7 = 0. Вычет же в по-
люсе должен быть определенного знака из условия унитарности. Этим
и определяется знак перед первой амплитудой. (Вторая же амплитуда
в 4-канале не имеет особенностей.) Поскольку в вершинах стоит
(pi-Рз )м(Р4-Д)м -4 s *Р1 (Р1~Р4)
в системе центра масс, так как Ед = Е^, Е% = Ед, то вычет в полюсе
отрицательный, следовательно, перед этой амплитудой должен стоять
знак плюс.
122
Глава 2. Частицы со спином 1/2
О знаке второй амплитуды мы пока ничего не можем сказать,
для его определения перейдем в w-канал. В u-канале эта амплитуда
уже имеет полюс по энергетической переменной (w играет роль квадра-
та энергии в с.ц.м.), и, буквально повторяя предыдущие рассуждения,
получим, что и перед второй амплитудой должет быть знак плюс. То
есть для бозонов (частиц со спином нуль) в нашем случае мы должны
складывать амплитуды.
Рассмотрим теперь фермионы (в нашем случае это частицы со
спином 1/2):
Pl t Рз
1 1 1 1 1
Р2 Р4
Pl U Р4
1 1 1 1 ~ й 1 1 1
Р2 РЗ
T(s) = ±е2(м(рз)7А1м(р1))-(м(р4)7мм(р2))±
±е2(й(р4)7мм(Р1))^(й(рз)7мм(р2)). (2.86)
Как и в предыдущем случае, для выяснения знака первой амплитуды
перейдем в 4-канал, для этого произведем замену
Рз = -pt,
Р2 = -pt
(2.87)
2.5. Рассеяние электронов. Связь спина со статистикой
123
(при этом помня, что поскольку u(—p) = —v(p), то Тпрод = —
тогда j
T(t) = ±e2(w(p+)7MM(pi))-(w(p4)7Mw(pJ))±
±е2(й(р4)7мм(Р1))^СФз h/XPit))- (2-88)
Если покажем, что скобки в первом слагаемом комплексно сопряжены,
то перед этим слагаемым должен стоять знак “+”, чтобы имела
отрицательный знак вычета, т. к. jo = 0 из сохранения тока.
Итак, рассмотрим
(w(P4)7mw(pJ))+ = (w+7o7mw)+ =«+(7о7д)+м =
= «+7m7^ u =
поскольку до эрмитова и коммутирует с 70, а 7г — антиэрмитовы и
антикоммутируют с 70. Таким образом, действительно, при р± /д
имеем отрицательный знак вычета и, следовательно, перед первой
амплитудой (2.86) должен быть знак “+”. Вторая диаграмма с точки
зрения i-канала имеет вид:
Pi Рз
а
а
Pt Р2
Ее знак мы можем выбрать, исходя из нерелятивистской аналогии. Ам-
плитуда рассеяния частицы на античастице должна быть противопо-
ложна по знаку амплитуде рассеяния частицы на частице (посколь-
ку знак потенциала противоположен). То есть i-канальная амплитуда
должна иметь знак, противоположный s-канальной, хотя бы при ма-
лых s. С другой стороны, мы получили, что амплитуды испускания
фотона частицей и античастицей одинаковы. Действительно, как мы
видели- w(-p^)7Mw(-pJ) =
124
Глава 2. Частицы со спином 1/2
но минус компенсируется тем, что = —Тпрод- Поэтому перед второй
амплитудой мы должны поставить знак “ —”.
Знак второй диаграммы можно установить и не обращаясь к нере-
лятивистскому пределу. Продолжим для этого амплитуду в с-канал.
Сделаем этот переход из Скапала, т. е. заменим
Pi = -Р4+ , Рз = ~Рз+-
Мы фактически два раза поменяли знак у рз, спинор при этом получит
знак ”, поскольку при каждой замене р —р он умножается на г.
То есть, чтобы получить отрицательный вычет у второй амплитуды в
i-канале, мы ее должны взять со знаком Можно сказать несколько
иначе. Если в Скапало аннигиляционная диаграмма написана со знаком
“+”, а диаграмма рассеяния — со знаком то при переходе в и-канал
диаграммы переходят друг в друга и меняют знаки, т. е. амплитуда
остается той же, что и требуется, потому что и- и Сканалы тождествен-
ные. Если бы мы обе диаграммы в Сканале написали со знаком плюс,
то в w-канале получили бы амплитуду противоположного знака, т. е. не
удовлетворяющую условию унитарности.
Мы приходим, таким образом, к тому, что аннигиляционная диа-
грамма и диаграмма рассеяния должны входить с разными знаками и,
следовательно, амплитуда рассеяния в s-канале должна быть антисим-
метрична по отношению к перестановке импульсов начальных или ко-
нечных частиц, т. е. электроны должны подчиняться статистике Ферми-
Дирака.
Общий знак амплитуд в s-канале при этом не определен, посколь-
ку если мы придем в s-канал, пройдя через t- и w-каналы, то получим ам-
плитуду противоположного знака. Однако в отличие от t- и и-каналов,
где взаимодействуют разные частицы, в s-канале это несущественно.
Причина состоит в том, что условие унитарности определяет только
знак амплитуды рассеяния вперед, но для тождественных частиц рас-
сеяние вперед и назад тождественно и, вообще, имеет смысл только рас-
сеяние в одну полусферу. Поэтому для амплитуды одного знака рассея-
нию вперед соответствует линия t = 0, а для другого знака линия и = 0.
То есть определенная запись амплитуды содержит в себе определения
понятия “вперед”. Эта ситуация имеет место уже в нерелятивистской
теории. Пусть
_ еФ1Г1егр2Г2 _ егр1Г2егр2Г1 _ егрзГ1еф4г2 _ ефзГ2еФ4П
fab - У (2’89)
2.5. Рассеяние электронов. Связь спина со статистикой
125
В (2.89) под интегралом будет стоять знакоопределенная величина при
знакоопределенном потенциале, только если Фа = Ф;,, т. е. /ц = рз,
Р2 = Р4- Обсудим, что произойдет, если, получив амплитуду противо-
положного знака, мы еще раз продолжим ее в t- и затем в и-каналы.
Очевидно, что мы получим в t- и w-каналах амплитуду тоже противо-
положного знака, т. е. в этом случае Т = Тпрод в отличие от того, что
мы писали раньше. Таким образом, соотношение между продолженной
амплитудой ее ее и амплитудой е '! е -л ее зависит от спосо-
ба продолжения, и это связано с неопределенностью знака амплитуды
ее е г .
Итак, мы получили связь спина со статистикой. При этом мы ис-
пользовали условие унитарности и то, что любую амплитуду можно по-
лучить аналитическим продолжением, т. е. фактически аналитичность
амплитуды, а это связано, как мы покажем вскоре, с причинностью.
Итак, действительно, двух условий — унитарности и причинности —
достаточно, чтобы установить знаки амплитуд. В нашей теории, таким
образом, принцип Паули, который согласуется с экспериментом, выпол-
няется автоматически.
В области малых углов рассеяния наша амплитуда перейдет в
обычную амплитуду кулоновского рассеяния. Исходя из этого, пока-
жем, что константа взаимодействия е является зарядом. Малые углы
рассеяния соответствуют
Р2~Р|.
т. е. t ~ 0, при этом второй (обменной) амплитудой можно пренебречь,
поскольку при t = 0 она не имеет сингулярности, а первая ~ 1/i, т. е.
при / - 0 стремится в сю.
Pi
Рз
1
t
Р4
Вычислим м(рз)7мм(р1). Поскольку pi + m = pi — m + 2m, (щ — m)u = 0
126
Глава 2. Частицы со спином 1/2
и рз pi, а также
7цР1 = -Р17д + 2рщ, (7МР1 +Р17М = Р1р(7м7^ + 7^7д) = 2рщ) ,
ТО 1
й(рз)7мм(Р1) = й(рз)7м(Р1 + m)w(pi)— =
_/ X/ . х u(pi} u(pi}u(pi)
= u Pl)(-pi + mYip-T—!- + 2piM——---------= 2piM. 2.90)
2m 2m
Аналогично,
й(Р4)7мм(Р2) = 2р2м. (2.91)
Тогда
р- Др2/?. 2
Т = — 2р1м • 2р2/, = (2.92)
в нерелятивистском пределе. Это обычная амплитуда кулоновского рас-
сеяния, совпадающая с (1.174) для бесспиновых частиц. Таким образом,
при малых переданных импульсах наличие спина электрона никак не
сказывается на рассеянии. Это следует уже из того, что вершинные ча-
сти превращаются в р1м + р3д = 2р1м, и р2/, + рщ = 2р2/, (см. (2.90),
(2.91)), т. е. в вершины для бесспиновых частиц. Из вида (2.92) следует,
что е, — действительно, электрический заряд электрона.
2.6 Рассеяние фотона электроном
(Комптон-эффект)
Как всегда, рассмотрим простейшие графики, описывающие рассеяние
фотона на электрона.
fclCTl
А-'2<72 felCl
fc2o-2
Рис. 13
2.6. Рассеяние фотона электроном (Комптон-эффект)
127
Второй график можно нарисовать и так:
Амплитуду рассеяния имеет вид:
Т = е^йхЦр2)М^ихЦР1)е°ф, (2.93)
где
= е2
1 1
7^------7----“7м + ---------- А 71;
m — pi — Ад m — pi + к2
7v(pi + fci + т)7м 7М (pi ~k2 + т)^
т2 — (pi + Ад)2 т2 — (pi — к2)2
Здесь (pi + кф)2 = s, (pi - к2)2 = и.
Покажем, что сохранение тока
(2.94)
= 0, k2vMVfJ, = 0 (2.95)
у нас выполняется автоматически. Действительно,
^212^1211 — е
Ад---;--j-Дм + 7м--;-г ^2
т-р2- к2 т-рг + к2
Поскольку Mvpi у нас входит только в обкладках между спинорами,
которые удовлетворяют уравнению Дирака, мы можем добавить в чис-
лителях слагаемые р2 — т и рф — т, т. е.
k2vMVil =
(к2 +р2-т)----+ дм---------т- (к2 + т — рф)
т — р2 — к2 т-рг + к-2
е
2
= е2(-дм + дм) = 0.
128
Глава 2. Частицы со спином 1/2
Трудность при вычислении амплитуды возникает из-за большого
числа спиновых переменных. Чтобы ее избежать, сразу напишем выра-
жение для сечения
7S I’ R (2.96)
и вычислим полное сечение рассеяния во все поляризации электронов и
фотонов для случая, когда падающие пучки не поляризованы (именно
такая ситуация часто реализуется на эксперименте). Для этого нужно
просуммировать по всем конечным поляризациям электрона и фотона
и усреднить по начальным, т. е. вычислить сумму У):
з Е 1гы,Т = зЕ7^х?х
°’2СТ1
X (йЛ2(р2)Л-ДммА1(р1))(йЛ2(р2)Л-Д/м/иЛ1(р1))+. (2.97)
У нас суммирование идет по двум значениям a = 1,2. Однако если
выполняются условия (2.95), то сумму по двум поляризациям можно
заменить суммой по четырем (поскольку остальные две поляризации в
силу (2.95) не дадут вклада в (2.97)). Тогда
Е 77 = - Е 77 =
171 = 1,2 (71=0
и (2.97) можно переписать так:
12 = | 12й'Л2Л/"-''<А|я«А2Л//-«Л|)+ =
Ai Аг
= | ^(й^ЛДДД^ПДлоЛ2) =
Ai А2
= J 52(йА2ММрИА1)(йА17оМ+,7оиА2) =
Ai А2
= | ^(йА2ММ!щА1)(йА1ММ!д?2). (2.98)
Ai Аг
Мы здесь использовали тождество До7о = 1 и ввели
= УоМ+^о. (2.99)
2.6. Рассеяние фотона электроном (Комптон-эффект)
129
Из явного вида (2.94) для непосредственно следует, что
(2.100)
(чтобы проверить это соотношение, необходимо использовать
{7o,?J = 0, = 7о, 7+ = - 7^).
Теперь просуммируем по А1А2. Для этого распишем (2.98) в мат-
ричном виде, т. е.
52 = | 52 ^4P2)(M^)a0U^\p1)u)/1(p1)(M^)-fsUg2(p2') =
Al А2
= “Ь ^)/37(А'Д^)-у(5(р2 Т =
а/Зуб
= |sp[MM!, (pi + т)М„^(р2 + т)]. (2.101)
Мы здесь воспользовались соотношением 5Д Д(р)Д(р) = (р + тп)ар.
В результате суммирование по поляризациям свелось к вычислению сле-
да некоторой матрицы.
Удобно записать фазовые объемы в виде
d3P2 ,4 г / 2 2 \
---- = d р28+(Р2 -т),
2Р20
= d4k28+(kl).
ХК20
Тогда выражение для сечения, с использованием (2.101), принимает вид
dcr = 2ySp[(pi + т)М^(р2 + т)Мрд] х
х <?+(Р2 ~ га2)<5+(^)(2тг)4ф1 + fci -Р2 - Ыd ^6Р2 • (2-102)
Процедуру вычисления сечения в виде (2.102) можно, как и в
случае скалярных частиц, изобразить графически. Рассмотрим первую
диаграмму. Для вычисления сечения амплитуду надо умножить на эр-
митово-сопряженную; это соответствует тому, что k±,pi и к2,Р2 поме-
няются местами, т. е.
130
Глава 2. Частицы со спином 1/2
Такая картинка удобна с чисто технической точки зрения. Она позволя-
ет сечение вычислять по тем же правилам, что и амплитуды; отличие в
том, что линиям, отмеченным крестиком, соответствуют, вместо знаме-
нателей 1/^2 и 1/(т—рг) = (m+p2)/(m2 — р^), <5-функции, т. е. части-
цы на массовой поверхности (мы их и отметили крестиком). Множитель
(р2 + т) = 53и(Р2)й(р2) возникает из суммирования по поляризациям
конечного электрона (а множитель (pi + m) = 52M(Pi)w(pi) появляется
из усреднения по поляризациям начального). Иначе говоря, диаграм-
мы для сечения получаются из диаграмм для амплитуды фактически
заменой 1/(тп2 — р2) —> (2тг)5_|_(р2) для линий конечных частиц.
Аналогично, возводя в квадрат вторую диаграмму:
кг Р2 кг
------------------*-------------------
Pi
- - X - -
к2
Pi
Кроме того, появятся интерференционные члены от смешанных произ-
2.6. Рассеяние фотона электроном (Комптон-эффект)
131
ведений первой диаграммы на вторую и второй на первую, т. е.
Вклады этих диаграмм можно получить непосредственно, расписывая
произведение в (2.102).
Таким образом, сечение представится в виде суммы диаграмм:
Перейдем к вычислению следа. Для первой диаграммы напишем
f(s,u) = |sp[(pi + ki + m)7p(p2 +
x (m +p2 + fe)7M(pi + Tn)^]—(2.103)
— s)z
Мы подставили в (2.101) первое слагаемое соответствующее первой
диаграмме, и, поскольку под знаком Sp можно менять местами множи-
тели, перенесли из начала в конец.
Приведем несколько полезных формул, которые нам пригодятся
при вычислениях:
jSp(7M7„) = д^, (2.104)
— Sp(7M17M27M37M4) = 5д1Д29мзМ4 + 9из из 9~ 9 ю из 9 из ил- (2.105)
След произведения нечетного числа 7-матриц равен нулю.
132
Глава 2. Частицы со спином 1/2
Покажем, для примера, как получается (2.104). С одной стороны,
|sp(7m^) =
с другой стороны,
1 12
^Sp(yMyp) = --Sp(7p7M) + -Splg^.
Вычитая из второго равенства первое, получим (2.104). Аналогично,
пользуясь перестановочными соотношениями для у-матриц, можно по-
лучить и остальные формулы.
Используя коммутационные соотношения для у-матриц, можно
получить также следующие соотношения (А, В, С — произвольные мат-
рицы) :
7мГум = C/y^ypy^ = -С/у^УдУд + 2C/5MI,yM =
= -4С.У, + 2С.У, = —2(7, (удуд = 4) ,
т. е.
УдСуц = —2(7 . (2.106)
Аналогично, легко видеть, что
УдАВСуд = -2СВА. (2.107)
Пользуясь (2.106), получим
_ . 11
Ж и) = —------------щ - X
(mJ — s)J 4
xSp[(pi + Ay + m)(4m - 2p2)(p2 + k2 + m)(4m - 2px)]. (2.108)
В (2.108) отличными от нуля будут члены, вообще не содержащие
у-матриц и содержащие произведения четного числа у-матриц. Вос-
пользовавшись (2.104), (2.105), в результате будем иметь
f(s,u) =
Д16т4 + 4m2(-2pi(pi + Ay)) + 4m2p1p2+
+ 4m2(-2p2(p2 + М) “ 4m2 • 2pi(pi + Ay) +
+16m2(pi + Ay)2 - 4m2 • 2p2(p2 + k2) + |sp[4(pi + Ay)p2(p2 + fc2)pi]}-
2.6. Рассеяние фотона электроном (Комптон-эффект)
133
Заметим, что
2pi(pi + fci) = 2m2 + 2pik± = s + m2,
2p2(p2 + fe) = 2m2 + 2p2k2 = s + m2,
|sp[4(pi + Ац)р2(Р2 + k2~)Pi] = ~4spip2 + 2(s + m2)2.
Тогда
f(s, u) = -— -— [16m4 — 4m2(s + m2) + 4m2pi»2 — 4m2(s + m2) —
(— q V L
—4m2(s + m2) + 16m2s — 4m2(s + m2) + 2(s + m2)2 — 4pip2s] =
2
(m2 — s)2
[(s + m2)2
2pip2(s - m2)].
Выразим 2pip2 через инвариантные переменные:
t = (pi - P2)2 = 2m2 - 2pip2,
откуда
2piP2 = 2m2 — t,
но s + t + u = 2m2, поэтому
2piP2 = s + u.
Окончательно, таким образом, имеем
2
/(s,w) = ——-----— [(s + m2)2 - (s + u)(s - m2)]. (2.109)
(m2 — s)2
Член, соответствующий второй диаграмме, получается из (2.109) просто
заменой з на и. Действительно, вторая диаграмма получается из первой
заменой Ад -л —к2, р заменятся на и, что при усреднении не имеет
значения, as- (щ — к2)2 = и, т. е. вклад от второй диаграммы есть
просто f(u, s).
Аналогично вычисляется след от интерференционных членов, их,
соответственно, мы обозначим д(з,и) и д(и, s), причем
2772-^
g(s, и) = -—------------[4m2 + s — m2 + и — m2l. (2.110)
(mJ — s)(mz — и)
134
Глава 2. Частицы со спином 1/2
Итак, мы нашли, что
|sp[(pi + m)Muli(p2 + m)M^\ =
= [/(s, u) + /(w, s) + g(u, s) + fl(s, w)]e4. (2-111)
Сечение (2.102) с учетом (2.111) запишется
e4
da = — [f(s, u) + f(u, s) + g(u, s) + g(s, u)] x
?4 л ,j4
x 5+(p^ -m2)5+(fc^)5(pi + fcx -p2 ~M (2'112)
Инвариантный поток, как и раньше, есть
J = fyoikoij. (2.113)
Для j также справедлива формула (1.165), хотя вычисляется несколько
по-иному:
|к|
j = |Ф(р1,х)7Ф(р1,х)| + =
ко
= |й(Р1)7«(Р1)1 + |ki| = pi + _Ад_
2рю kw рю fcio ’
т. е. с потоком все, как раньше.
Осталось вычислить фазовый объем. Сначала проинтегрируем
(2.112) по d4p2 при помощи 5-функции. Получим
е4
da = — [/(s, u) + /(w, s) + g(u, s') + g(s, u)] x
x ^((p-fc2)2-m2)5+(fc22)^, (2.114)
где p = pi + fci, (p — fc2)2 = p2 — 2pk2 + k2 = s — 2pk2. Переходя в систему
центра масс, получим
5+((р — к2)2 — m2) = 6(s — 2рок2о — т2) = 5(s — 2^sk2o — т2). (2.115)
Для инвариантного потока, соответственно,
J = 4(pifcio + fcipio) = 4A:i(fcio +рю) = 4fciy<s. (2.116)
2.6. Рассеяние фотона электроном (Комптон-эффект)
135
Введем величину dT:
dr = yS+((p k2)2 m2)5+(k2)^
(2.117)
С учетом (2.115), (2.116) можно написать
dr = 1 (2 Vs
r~
Js m
T~2VTs~kw
A 5^(k2 - k2 )
10+^20 K2 ^(27r)2
Интегрируя при помощи <5-функции по ко, получим
dr, J_J+([i^r_k2]^>
8fcxs + Ц 2^/s J 2J (2тг)2
Перейдем в (2.118) к сферическим координатам, т. е.
d3k2 = kldk2(Kl = ^-dkldtt.
Теперь можно проинтегрировать по dk2 :
1 к2 d<l 1 s — rn2 dkl
16s Ад (2тг)2 16sA?i 2y/s (2тг)2
Мы подставили из <5-функции
О
, s — m
к1 = ^лг-
но в с.ц.м. ki = к2 = к, поэтому
1 dQ
dr = --—щ-.
16s (2тг)2
Выразим теперь dPl через инвариантные переменные:
(2.118)
(2.119)
(2.120)
(2.121)
t = — 2fc2(l — cos#); dt = 2k2d(cosO).
С другой стороны, dCl = d(cosO)dip = 2tt<A(cos#), t. e.
2л
d^l = —xdt
2kz
136
Глава 2. Частицы со спином 1/2
и
dV =
1 dt 1
16s2fc2 2%’
Или окончательно, подставляя к2 из (2.120),
1 dt
16тг (ш2 — s)2
(2.122)
Такова стандартная схема вычисления фазовых объемов.
Теперь уже можно написать выражение для сечения, но для удоб-
ства сначала перепишем величину в квадратных скобках (2.109) в нес-
колько ином виде — раскрываем все выражения:
2 I О 2 I 4 2 2,2
s + 2m s + m —s — us + m s + m u =
= 2m2(s — m2) + 3m4 — su + sm2 + um2 =
= 2m2(s — m2) + 3m4 + um2 — s(u — m2) =
= 4m4 + 2m2(s — m2) — m2(m2 — w) — s(u — m2) =
= 4m4 — (u — m2)(s — m2) + 2m2(s — m2),
t. e.
2
s, u) = 7—5---?^[4m4 — (w — m2)(s — m2) + 2m2(s — m2)]. (2.
(m2 — s)2
Подставляя (2.123) и (2.110) в (2.114), получим окончательное выраже-
ние для сечения рассеяния фотона на электроне:
е4 dt
d<J = 2тг (m2 - s)2
(2.124)
1 к u — m2 s — m2
4 \ s — m2 u — m2
Это известная формула Клейна-Нишины для комптоновского сечения
рассеяния.
Рассмотрим область малых энергий. Здесь удобнее пользоваться
лабораторной системой координат (система, где начальный электрон
покоится). В этой системе имеем
s = (pi + fci)2 = (feio + rn)2 — k2 = m2 + 2ткю.
2.6. Рассеяние фотона электроном (Комптон-эффект)
137
Обозначим fcio = w, feo = ш', тогда
s = т2 + 2тгш. (2.125)
Аналогично,
u = (pi — А^)2 = т2 — 2пш', (2.126)
а для t имеем
t = (fci — fe)2 = —2АдА?2 = —2ол/ + 2wo/cos0 = — 2wo/(l — cos#).
С другой стороны,
t = (pi — P2)2 = 2m2 — 2mp2o = 2m(m — P20) = 2m(wz — u),
t. e.
2wo/(l — cos#) = 2m(w — cP),
откуда следует
= 1 — cos 0.
(2.127)
Мы получили формулу для комптоновского сдвига частоты.
Теперь посмотрим, как будут выглядеть отдельные члены (2.124)
в л.с.:
9 9
т т т т
s — т2 2и ’ и — т2 2л',
их сумма
т2 т2 т f 1 1 \ 1 .
------2 +------2 = -----7 = “й 1 - с08в •
s — т и — т2 2 \сл са'J 2
Аналогично,
9 г
и — т си
з — т2 ел
И
dt = 2иш'd(cos 0) — 2и(1 — cos 0)diK =
=-----(1 — cos 0)dt + 2lulPdices 0) ,
m
откуда
dt = 2(jj'2 d(cos 0).
138
Глава 2. Частицы со спином 1/2
Подставляя эти значения в (2.124), получим
1 ( W 1.9/,,/
------1-------snr(? d(cos$) ,
4 \ си ш' ) 4 v
или, вводя с1Г1Ш1 = 2ttc?(cos#), запишем окончательный результат в виде
где = 2тг c?(cos0).
При малых энергиях ш <?' m падающего фотона (томсоновский
предел) ш' -л щ и сечение стремится к постоянной величине (формула
Рэлея-Томсона):
/ е2 \ 1
du -л — -—Д2 - sin2 .
\ Л / Ь ) /W1 Л ' '
(2.129)
4тг / 2/п2
Заметим, что е2/4тгт = ге, ге = 2.8 • 10 13см — классический радиус
электрона, т. е. при малых энергиях сечение
du ~ 7ГГ2.
Теперь выясним, что происходит при высоких энергиях s т2.
Для этой цели удобнее воспользоваться формулой (2.124).
\ /в = 0
I = 0
8 ОО
и = 0
1. Рассмотрим область |t| s, — u ~ s (s m2). В этом случае
, е4 dt eidt d£l
4тг (m2 — s)2 4tts2 s
(2.130)
2.6. Рассеяние фотона электроном (Комптон-эффект)
139
т. е. сечение с малой передачей импульса с ростом s довольно быстро
падает.
2. В области малых и (т. е. больших переданных импульсов t)
сечение в единичный телесный угол больше:
е4 dt 1
8% s m2 — и m2 ’
(2.131)
и от s не зависит. Это означает, что, поскольку
и = (pi - k?)2 = -2pi(l + cos в),
т. О соответствуют углы в ~ тг, при больших энергиях фотоны
рассеиваются преимущественно назад. Хотя, казалось бы, из-из точеч-
ности взаимодействия вероятность его должна падать с ростом угла и,
кроме того, с ростом энергии, поскольку а ~ А2, а А ~ 1/к, т. е.
1 1
(T^k2^s'
Именно так и устроен вклад первой диаграммы.
Посмотрим теперь на вторую, которая как раз и ответственна за
указанное поведение сечения. Как объяснить, что фотоны в основном
рассеиваются на 180°? Процесс, который описывается этой диаграммой,
идет, в действительности, при малой передаче импульса \и\ ~ гл2, —
только в результате процесса электрон превращается в фотон. Однако
в релятивистской теории индивидуальность частицы не столь важна;
для величины сечения важнее, что данный процесс может идти с мень-
шей передачей импульса.
fci
к?
Также ясно, почему величина сечения в этом случае не падает с ро-
стом энергии, так как величина области, где может поглотиться фотон,
определяется уже не малой длиной волны фотона А, а тем, как далеко
успеют разойтись виртуальный электрон с исходным.
140
Глава 2. Частицы со спином 1/2
виртуальный
электрон
Ее можно оценить из соотношения неопределенностей. Виртуальный
электрон может просуществовать время Af ~ 1/ДЕ ~ 1/т и за это
время уйти на расстояние Аг ~ 1/т. Отсюда и следует, что при боль-
ших энергиях существенным является только обменный процесс и его
сечение а ~ в соответствии с (2.131). Однако полное сечение про-
цесса остается маленьким, поскольку пик рассеяния назад, где сечение
не мало:
da е4
dCl т2’
очень узок \d£l\ ~ т2/з.
2.7 Аннигиляция электрон-позитронной пары
в два фотона
Чтобы получить двухфотонную аннигиляцию электрон-позитронной па-
ры, достаточно рассмотреть рассеяние фотона на электроне с точки зре-
ния i-канала.
2.7. Аннигиляция электрон-позитронной пары в два фотона
141
Как всегда, сделаем замену
Р2 = ~Р^, k1=k[.
(2.132)
Диаграммы можно перерисовать так:
Внутренние части диаграмм те же самые, и им, как и раньше, соответ-
ствует М^. С учетом того, что
й(-р^) = -4pt), (2-133)
для сечения можно написать следующее выражение:
da = 152 i«A2(^)cAvePiMAi(pi)i2dr =
С71С72
Л1Л2
= -^Sp[(pi + т)МД-т +Д)М,мДГ. (2.134)
Мы учли здесь то, что вместо
А
142
Глава 2. Частицы со спином 1/2
в данном случае будет присутствовать
^ЖрЖдЖ) = -(m-p^al3.
А
Знак ” оттого, что и(— р) = г(р), а й(—р) = — г(р). Вычисление сле-
да даст тот же результат, что и в случае рассеяния, только с другим
знаком, а переменные s,i,w будут иметь другой смысл: t — квадрата
полной энергии в с.ц.м., s,u < 0 — переданных импульсов, так что се-
чение можно записать в виде
В этом случае dT — фазовый объем, деленный на поток — уже другой,
поскольку фазовый объем двух фотонов отличен от фазового объема
электрона с фотоном.
Вычислим ЧТ в с.ц.м. Инвариантный поток тогда будет иметь вид
У = 4рхЖ, (pi = |pi| = |р2|),
поскольку теперь роль энергетической переменной играет t. Тогда
= 1 ri4fc2<5+(fc^)<5+((fc2 -рх ~рЛ2) =
4рЖ (2л)2
_ 1 d4fc2<5+(fc2)<5((^2-р)2).
4рхд// (2л)2 ’
(fc2 — р)2 = t — 2к%р = t — у/ = 2а// ( 1 ЖМо “ М)<$+(др - feo) 4р1Ж (2 л)2 — 1 $+ ~ 1 k 1 dtt - 4P1Vt2Vt (27г)2 |к21 2 = _J |к2| 1 |к2| d<l 16pit (2л)2 16/ pi (2л)2 Здесь к2 = Ж/2. Ж , \ -у - Ж ); -dk2okldk2d£i = (2.136)
2.7. Аннигиляция электрон-позитронной пары в два фотона
143
Выразим теперь через инвариантные переменные (в данном
случае |pi| |кг| в с.ц.м., поскольку частицы обладают разными мас-
сами). Имеем
t = (Pi +Р2)2 =
= Pi +Р22 + 2РюР20 ~ 2Р1Р^ = ml + ml + 2pi0pJ0 - 2pipJ,
В с.ц.м.
(pi + Р2" )2 = 0 = pl + р^-2 + 2pipJ,
откуда
-2pip+ = р? + pj2 .
Следовательно,
t = ml + ml + pl + pj2 + 2д/(m2 + Р2))^ + pj2) , (2.137)
или
Д = yjml+pl + Ут|~+рУ. (2.138)
Учитывая, что
2 2
Р1 = Р2
О
, и решая квадратное уравнение относительно р^, получим
В нашем случае mi = m2 = т, поэтому
д/i — 4m2
В случае рассеяния (см. (2.120)) было бы mi — т, m2 = 0, и эта формула
дала бы с учетом .s - /
2
fci =
т. е. Ад действительно совпадает с к2, потому что Ад и к2 описывают
частицы с одинаковыми массами.
Итак, мы получили, что в с.ц.м.
m 1 dQ
<7Г = ----. = ----—.
16^/t(i — 4m2) (2тг)2
(2.140)
144
Глава 2. Частицы со спином 1/2
(Выразив d£l через инвариантные переменные, мы, в принципе, получи-
ли бы релятивистски инвариантное выражение, справедливое в любой
системе отсчета, хотя вычисления и проводились в с.ц.м. Это мы про-
делали в случае рассеяния.)
Теперь проанализируем полученное выражение для сечения ан-
нигиляции:
Физической областью этого процесса является t > 4m2.
1. При t ~ 4m2, (1Г оо, т. е. сечение очень велико (da оо).
Физически это понятно из следующих соображений: t ~ 4m2 — это со-
ответствует очень медленным частицам, т. е. поток налетающих частиц
очень мал, j ~ 0. а сечение — это отношение вероятности процесса к
потоку
1Я2
aa ------,
j
поэтому da оо. Но, с другой стороны, почему такая ситуация не
встретилась нам при рассеянии, при j -л 0? Дело здесь в том, что при
j —> 0 в упругом рассеянии число конечных состояний тоже мало, а при
этом 1У|2 —> 0, так что две малости сокращаются. В случае же анниги-
ляции, независимо от энергии начальных частиц, в конечном состоянии
2.7. Аннигиляция электрон-позитронной пары в два фотона
145
рождаются фотоны больших энергий, их фазовый объем конечен (не
стремится к нулю), поэтому сечение и растет.
2. t >> 4m2. В случае больших .s ~ с ~ 4 (т. е. рассеяние на угол
О ~ 90° )
е4 1 d£l
(2'142)
В области же больших переданных импульсов s ~ t, и ~ 0 имеем (рас-
сеяние на большие углы):
g4 1 Ш
8 т2 — и (2тг)2
(2.143)
Здесь ситуация аналогична случаю рассеяния: фотоны с большой
вероятностью летят назад, но вклад (2.143) обусловлен второй диаграм-
мой, и это есть фактически превращение электрона в фотон, как и рань-
ше, с малой передачей импульса.
Аналогично, при </, ~ Л .s ~ 0. вклад в сечение в основном от
первой диаграммы, и
е4 1 dti
~8 m2- s (2л-)2 ’
(2.144)
т. е. при больших энергиях налетающих частиц фотоны летят, в основ-
ном, назад и вперед.
146
Глава 2. Частицы со спином 1/2
Сравнивая (2.143) и (2.131), видим, что при больших энергиях и
одинаковых переданных импульсах сечения двух различных процессов
совпадают (эти области отмечены жирной линией на мандельштамов-
ской плоскости).
2.8 Рассеяние электронов во внешнем поле
Рассмотрим рассеяние электрона тяжелой частицей массы М (напри-
мер, протоном). Если тп <7 М, то эта частица почти не испытывает
отдачи, если импульс электрона не очень велик,
Q = Pi - Pi,
р'2 = P2 + q-
Pi pi
m -------------1-----------
i
▼ <z
. ..
P2 p'2
Если в начальный момент частица М покоилась, то
,2 2
р' ~ М + = М + —.
720 2М 2М
Энергия при ц2/2М 1 практически не изменяется. При этом можно
пренебречь движением частицы М и считать, что электрон рассеивается
внешним полем. Пусть частица М, как и электрон, обладает спином 1/2.
Вычислим нижнюю часть диаграммы. Обозначим
Рр. =Р2ц +p’2li-
Мы уже писали такую формулу:
2РМ = Р7М+7МР. (2.145)
Рассмотрим теперь
2w(p(,)PMu(p2) =
= й(р'2)[(Р2 +У2)7м + 7м (Р2 + Рг 2)Мр2) =
2.8. Рассеяние электронов во внешнем поле
147
(2.146)
(2.147)
= Л/иШТмЧл) + й(р2)р27мм(р2) +
+ Мйр2)^и(р2) + и(р2)^р'2и(р2) =
= 2М[й(р2)^и(р2)] + й(р2)[р27д + ^цР'2]и(.Р2) =
= 4M[w(j>2)7^u(p2)] + u(p2)[-^q - ^]и(р2)
(поскольку р2 = р2 + q, р2 = р2 — q). Отсюда получаем
-I ,ч / ч (Р2 +р2)м ,ч / ч
И(Р2ЛмИЫ = -------------и(р2)и{р2)-
Мы ввели матрицы
_ 7^ - 7Лд
а^~ 2
Вычислим й(р2)и(Р2), учитывая, что р2 ~ р2. Так как
и(р2) = уД20 I Л/ I
\(Тр2/(р20 + M)PJ
и в случае |р2| <7 М нижней компонентой спинора в произведении мож-
но пренебречь, то
й(р2)и(р2) = 2М (1 + 0
т. е.
й(£>2)и(Р2) = 2М (2.148)
с точностью до членов второго порядка по |р|/М.
Далее вычислим
й(р2)<т^и{р2).
Члены с <7oi = 7o7i дают малый вклад, т.к.
м+(Р2)7Л(р2) ~
- 2М (р+,р+^^
V 2М
нгар2/2Мр\ ~ \р\_м
-ам ) М
В первом порядке по |р|/М ими тоже можно пренебречь. Остались чле-
ны с
= 7i7j =
0
0
148
Глава 2. Частицы со спином 1/2
Из вида спинора видно, что вклад его нижних компонент в uaijU по-
рядка р2 /М2. Так что с точностью до линейных членов по р/М можно
записать из (2.146)
u(p'2hou(p2) = 2М,
u(p'2hiu(p2) = <p+(Jjqj(Tip.
Мы положили в (2.146)
Р2 = 0, р'2 = q.
Амплитуда рассеяния электрона на внешнем поле тогда запишется сле-
дующим образом:
Т = 2Ме [u(p'1)y0A0(q')u(p1') - й^р'^А^и^] , (2.149)
где
Л 1
А = е —,
q
Мы использовали то, что
=qi- ietjk&kqj = % + г [crq]^.
A)(q) представляет собой фурье-компоненту кулоновского поля, первый
член Аг — фурье-компоненту векторного потенциала, создаваемого то-
ком частицы, второй — ее магнитным моментом. Величина (еа/2М) со-
ответствует обычному магнетону Бора. Для электрона, действительно,
магнитный момент равен с хорошей точностью магнетону Бора. Для
протона же, например, нужно добавить так называемый аномальный
магнитный момент; соответственно, в (2.150) вместо [crq] нужно писать
(1 + Даном) [°-q]-
Рассеянию внешним полем соответствует предельный переход
М -л оо. В сечение при этом войдет (2Л/)2 от |Т|2 в числителе и (2М)2
в знаменателе от фазового объема и потока; члены, соответствующие
току и магнитному моменту, обратятся в нуль. Так что сечение в этом
случае будет определяться кулоновским потенциалом частицы
2.9. Тормозное излучение электрона во внешнем поле
149
2.9 Тормозное излучение электрона
во внешнем поле
В силу законов сохранения, свободный электрон излучить фотон не мо-
жет. Наличие внешнего поля делает этот процесс возможным.
Рассмотрим диаграммы:
7л - " ' 7л - " "
I I *
Р1 | Р2 Р1 | Р2
л ; ч + । q
Они описывают испускание электроном фотона, соответственно, до и
после рассеяния на внешнем поле. Амплитуда Гторм, отвечающая этим
графикам, запишется так:
ги -/ m+p2 +k J,., .
Рторм = eu(p2)em2 _ + А(д)ц(щ)+
+ eu(p2)A(q)^_+^ _^pew(pi). (2.151)
Ограничим наше рассмотрение двумя наиболее интересными случаями.
1- Рю — гп, к <?' т, т. е. испускание мягкого фотона электроном с
небольшой энергией. В этом случае из-за наличия функции Грина
электрона 1/(т — р± + к) амплитуда процесса очень велика. Это
связано с тем, что излучение мягких фотонов начинается далеко
от рассеивателя и происходит в большой области.
2. рю » т, к < Рю*
Итак, пусть рю ~ т, к <?' т. Вычислим величины, входящие в
числитель (2.151):
ё(т + р2) + ёк = (пг - р2)ё + 2(ер2) + ёк ~ 2{ер2), (2.152)
поскольку
ёр = е^руу^ = е^р^-у^у^ + 25М!7) = -рё + 2(ер).
150
Глава 2. Частицы со спином 1/2
Аналогично и для второго числителя в (2.151):
(m + pi)e — кё 2(epi).
Подставляя эти значения в (2.151), получаем
-^торм — е
2(ер2) + 2(epi)
пт-2 — (р2 + к)2 m2 — (pi
_ fc)2j w(P2)A(q)w(pi).
(2.153)
Величина
fs{q) = u(p2')A(q)u(p1')
есть не что иное, как амплитуда рассеяния электрона. Итак,
Т'торм — ejs(Q) —-------- .
\_Pik р2к
В нерелятивистском случае |pi| С m, р±к mko. При этом
Тгорм = /s(g)^-e(v2 - V1),
Ко
где vi,2 = Pi,2/™ — скорости электрона до и после рассеяния.
ла (2.155) совпадает с результатом классической электродинамики для
тормозного излучения.
Вычислим для этого случая сечение процесса:
(2.154)
(2.155)
Форму-
<fcrTOpM = |Тгорм|2Лр2^(р2 - т2)(2тг)45(р2 + к - рх - g)-^g 5(fc2).
<7 (27Г J
Величина
das = ^\fs\2^^d(.pl - т2)(2тг)4ф2 + к-P! - q)
J (27Г)л
— это сечение рассеяния электрона, так что
е2 d^k
(1<Ттюры = <1ае71е(у2 - vx)2 6(k2).
ко (27Г)
c?4fc 2 dk0kdk2 2 2 dk0 к0
(2.156)
т. е.
«Ьтори = tfos /- Л1'’-' -
(2.157)
2.9. Тормозное излучение электрона во внешнем поле
151
или, учитывая, что е2/4тг = a = 1/137,
си . . , .о ddl d,ko . .
do-торм = das — |e(v2 - vi)|2 — —. (2.158)
27Г 21Г fco
Мы видим, что с/сгТОрм —> сю при fco —* 0, и полное сечение расходится
логарифмически в области малых частот. Интегрируя сечение по энер-
гиям фотона от kOmin до kOmax, получим
dat = rfo-s^|e(v2 - vi)|2 2 In k°max . (2.159)
Верхние частоты испускаемых фотонов, очевидно, ограничены энергией
электрона, т. е. komax < р±о- Нижний же предел может быть выбран
произвольно малым, положив = 0, мы бы получили бесконечное
сечение (так называемая инфракрасная катастрофа). В данном случае
дело в том, что не работает первое приближение по константе связи а.
Выражение (2.159) фактически устанавливает критерий приме-
нимости первого порядка по а:
(2160)
Если это неравенство нарушается, процессы с испусканием од-
ного или более фотонов не подавлены. Это можно понять и с другой
точки зрения. При к —> 0 мы имеем классическое электромагнитное по-
ле, что отвечает большому числу фотонов, и, естественно, поэтому мы
не можем ограничиться однофотонным процессом.
При обсуждении высших поправок мы еще вернемся к этому воп-
росу, а теперь перейдем к другому случаю:
кр
Рю
(2.161)
Пренебрегая в числителях (2.151) членами ёк, как и раньше, получим
-Рторм — e/s(?)
epi
pifc
ер2
Рчк
Далее, для фотона, испущенного на угол 01, имеем
Pik= pwk0 - pik0 cos 0! = pifc0
1 - cos 01 +
2P1
(2.162)
152
Глава 2. Частицы со спином 1/2
поскольку рю можно разложить по т2/р2 в силу (2.161):
/ тп2
Рю = v/т2 +р1=Р1 + —,
V 2рх
или, введя 0q = т2/р2 и учитывая, что 1 — cos0i « 0^/2,
Р1к = ^(02 + 02). (2.163)
Если 0i 1 и т2/2р2 <g; 1, то знаменатель в амплитуде снова мал и
вероятность тормозного излучения велика. Таким образом, тормозные
фотоны, в основном, излучаются на малые углы.
Числитель в выражении для амплитуды равен
epi = —pi sin 01 ~ —pi0i
(2.164)
(фотоны поляризованы параллельно р2 — Pi). Аналогичные выражения
получаются и для второго слагаемого амплитуды, так что окончательно
имеем
,, а2 [01 02
торм - -е.^)- ~ ^2
(2.165)
Большие импульсы электрона здесь сокращаются.
2.10. Формула Вайцзекера-Вильямса
153
Из (2.165) видно, что если электрон рассеялся на очень малый
угол 0S ф ~ 02, то амплитуды излучения до и после рассеяния вычи-
таются и тормозного излучения практически нет. Однако, при рассея-
нии на достаточно большой угол, 0S 9 о одна из амплитуд может быть
много больше другой и сокращение более не имеет места. Это возможно
в двух случаях: 02 ~ 0 s 3> 01 или наоборот 0\ « 0S Д> 02-
Это означает, что в релятивистском случае тормозное излучение
сконцентрировано внутри двух узких конусов, 0^ «С 0S и 02 0S, кото-
рые направлены вдоль pi и рг - Эти конусы совершенно одинаковы.
Рассмотрим для примера сечение излучения в одном из этих ко-
нусов.
_ 4е2 6»2 d4k5(k2')
ЙСТторм d(TsJ^(0l + 02Y (2тг)3 ’
(2.166)
ri4fcj(fc2)
(2тг)3
kodko
(2тг)32
2tfc!cos0,
2е2 dko . 0?
1 ’(ef + Ф2
a dko 02d02
7Г k0 (0% + 0fi)2 ’
Интегрируя по углам в узком конусе Д0 и энергиям фотона, по-
лучим полное сечение тормозного излучения в виде (при Оо Д0):
, , a kOmax AG a Pi , Pi 1
dat = das— In ---In —= das— In -------In —5-, (2.167)
TT Щ)тт ^0 ^Omin ^7
поскольку kOmax =P1, 00 = m2/2pl .
Таким образом, сечение растет с ростом энергии налетающей час-
тицы как квадрат логарифма (это все при рассеянии на достаточно
большой угол). Следовательно, при очень больших энергиях наша тео-
рия (основанная на первом порядке по а) тоже неприменима.
2.10 Формула Вайцзекера-Вильямса
Рассмотрим следующую ситуацию. Пусть имеется тяжелая частица (на-
пример, ядро или протон), и на нее налетает легкая частица. При рас-
сеянии может произойти процесс с испусканием любых частиц (на пре-
дыдущей лекции, например, мы рассмотрели испускание фотонов), т. е.
154
Глава 2. Частицы со спином 1/2
Рис. 14
В амплитуду рассеяния частицы на кулоновском центре входит 1/q2
(<72 = (р —р')2), т. е. наибольший вклад в сечение дают малые q2. Нельзя
ли из того, что энергия налетающей частицы велика, a q мал, сделать
некоторые заключения о произвольном процессе, типа изображенного
на диаграммах?
Итак, пусть q2 m2, з т2. При малых q2 фотон почти реаль-
ный и задача фактически разбивается на две части: испускание ядром
фотона и рассеяние частицы на этом фотоне с испусканием чего угодно,
т. е.
Рис. 15
Рассмотрим весь процесс в системе покоя электрона (pi = (m, 0)), где
ядро налетает на него с большой скоростью.
m
Кулоновское поле быстрой частицы сжато в направлении движения.
Это поле, как мы покажем, можно представить в виде совокупности
2.10. Формула Вайцзекера-Вильямса
155
почти реальных фотонов. Сечение (рис. 14) тогда можно записать в
виде
= dac(yi)n(ci)d3q, (2.168)
где n(q)d3q — число фотонов с импульсами в интервале d3q, испуска-
емых ядром; dac — сечение процесса (рис. 15); n(q) можно вычислить
как вероятность найти фотон в кулоновском поле быстрой частицы из
разложения электрического и магнитного полей ядра в системе покоя
электрона по плоским волнам, как сделали это Вайцзекер и Вильямс.
А можно поступить и по-другому. Амплитуда (рис. 15) есть
Fc = M^q,P1,...)e^, (2.169)
здесь q2 = 0, поскольку фотон реальный. Для (рис. 14) же имеем
Fw = + (2.170)
Попытаемся найти связь между этими амплитудами. Если бы
можно было считать в (2.170) q2 = 0 везде, кроме полюсного множите-
ля, то множители в обеих формулах совпали бы. Это сделать мы
можем: поскольку q2/т2 1, то q2 мало по сравнению со всеми други-
ми импульсами, входящими в М^.
Далее, в силу сохранения тока, имеем
ЧцМц = 0 , емдм = 0. (2.171)
В системе покоя электрона импульс налетающего ядра имеет компонен-
ты
Р= (ро,рг,О,О). (2.172)
Имеем
p — q=p' , р2 = р2 = М2 , q2 <С М2,
отсюда
(р - q)2 =р2 = М2 ,
т. е.
—2pq + q2 = 0 ,
или в силу (2.172)
М2
-2(ро?о - PzQz) + q2 = -2рД<?о - qz)----qo + q2 = 0. (2.173)
Pz
156
Глава 2. Частицы со спином 1/2
Условие (2.173) может выполниться при
и
q pz _q Pz\
q° ~ м2 Pz\M2)^q° (2,174)
т. е. фотон возникает релятивистским, qo велико, хотя разница qo — qz
мала. Обозначим составляющую импульса фотона в плоскости, перпен-
дикулярной z, через </_L, тогда
q2 = ql - q2 - q± = 2io(io - qz) - ql, (2.175)
9 9
отсюда видно, что q ~ —q^_-
Теперь рассмотрим в (2.170) множитель
(p + p')nMl_l(q,p1,...') = (2p-q^M^.
Он равен
2рцМц — 2/Л)(Л/() - Mz)
в силу сохранения тока.
С другой стороны,
2//Л/,, = q0M0 - qzMz - q^Mr = q0(M0 - Mz) - q±Mo_ = 0,
t. e.
Mo - Mz = qyM1-
qo
(p+p')^ = —qiMi. (2.176)
qo
Покажем, что (2.176) выражается через (2.169). Рассмотрим емМм. Вы-
берем калибровку, где
eq = 0 (т. е. е0 = 0). (2.177)
Тогда
= B-zM-z
но из (2.177) следует
ezqz + e±qj_ = 0.
2.10. Формула Вайцзекера-Вильямса
157
Поскольку q±/qz С 1, то ez мало:
&Z
e±g±
Qz
Физический смысл этого в следующем: фотоны летят почти параллель-
но быстрой частице !q_ qz), естественно, что поляризация их лежит
в плоскости, перпендикулярной направлению движения этой частицы.
Таким образом,
емМм = -е±М±. (2.178)
Мы видим, что физика процесса полностью определяется поперечной
частью Mi амплитуды рассеяния фотона, как для виртуального фото-
на, так и для реального. Заметим далее, что при q± У' т амплитуда не
может зависеть от направления вектора q. При вычислении сечения
мы должны усреднить по двум поперечным поляризациям с (е^ = 1)
для случая реального фотона и проинтегрировать по всем поперечным
направлениям вектора q для случая виртуального фотона. Учитывая
это, мы можем просто использовать нормированные векторы q±/^/q±
в качестве векторов поляризации. Тогда
(р + р'^М^ = — |<?±|(е± • М±) = — |q±|F,
Qo Qo
т. е.
Для
daw
_ Ze 2р0
Pw — -у-----q± Рс-
q2 qo
сечения daw рассеяния электрона на ядре тогда получим
Z2e2 / 2р0 \2 2 1 А
= — q±~.— х
q \ qo J 4mp0
1 |2 d^k^Sik2 — т2).. .d^knSikn — m^) .4
(2.179)
(2.180)
4т</о С (2тг)3п
5(pi Pp-^ki-p' - pi)-|^<5(p'i2
(2тг)3
г/ '2
<ЧР
- М2).
Учтем
ф1 +р - fei - У - pi) = <5(pi + Q - fcj - pi),
так как р — р' = q.
158
Глава 2. Частицы со спином 1/2
Тогда выражение в квадратных скобках (2.180) — это просто се-
чение процесса (рис. 15) dac, т. е.
Z2e2 (2р0\ 2Q0 , f . d4q 2
daw = -- q±—dac(q)——z3(-2pq + q ),
q \ qo J Ро (2л)3
d‘q = dqodqzd2qo_-
Проинтегрируем no dqo при помощи 5-функций (в знаменателе появится
2р0), тогда
daw = n(q')dacdqzd2q±, (2.181)
z Л Z2e2 2q2 Z2a q2
П Q (2л)3 q0q4 л2 qoq4 ’
(2.182)
Мы получили таким образом плотность фотонов, испускаемых ядром,
на единицу импульса. Перепишем сечение в виде (поскольку qo q-: )
(2.183)
л2 q0 q4
Мы уже писали (2.173):
2
-2(роцо -Pzqz) + q2 = -2pz(.qo - qz)-----qo + q2 = 0,
Pz
T. e. q2 M2 M2
qo - qz = -----TT^qo ~ -д-^Qo,
2щ 2p2 2p2
если пренебречь q2 /pz. Тогда
1/2
q2 = -q2r + 2qo(qo ~ qz) ~ ~q± -q^ — -,
Pz
и если n n2A/T2
^«1.
Po Pz
то q4 очень малая величина и, если проинтегрировать по d2qo_, интеграл
логарифмически расходится:
Z2a dq0 p2z
d(Jw = d(yc----------In
тг qo Qo
(2.184)
при
M2q2
P20
<^q2±<§: M2.
2.10. Формула Вайцзекера-Вильямса
159
Мы рассматривали изменение переданного импульса, считая q2 малым;
аналогично интегрируя еще по dqo, получим (М < qq < Ро)
Z2a v2
daw = dac-----In2 (2.185)
do
Видим, что сечение велико. Следовательно, при рассеянии быстрой ча-
стицы с малой передачей импульса могут родиться много частиц. Ина-
че говоря, такой вайцзекеровский процесс может служить интенсивным
источником всяких частиц. А эффект велик потому, что рождается мно-
го фотонов, хотя сечение этого процесса на один фотон может быть и
небольшим.
Именно из такого процесса была получена в свое время нижняя
оценка массы ГУ-бозона. Пусть взаимодействие (слабое) имеет вид:
Как обнаружить существование ГК-бозона? Нейтрино практически не
взаимодействуют, однако при рассеянии на кулоновском поле ядра се-
чение велико за счет электромагнитного взаимодействия мюона с ядром
(рисунок ниже). Отсюда получили, что mw > 5 ГэВ.
Ze =
Глава 3
Общие свойства амплитуды рассеяния
3.1 Симметрии в квантовой
электродинамике
Во-первых, квантовая электродинамика релятивистски инвариантна.
Мы ее строили так с самого начала. Существуют еще дискретные пре-
образования, не сводящиеся к преобразованиям Лоренца, относительно
которых она инвариантна.
1. Р-инвариантность относительно инверсии пространственных ко-
ординат, т. е. замены х' = —х.
2. Т-инвариантность относительно инверсии времени, т. е. замены
t' = -t.
3. С-инвариантность относительно операции зарядового сопряжения,
т. е. замены всех частиц на античастицы.
Итак, начнем с пространственной инверсии.
3.1.1 Р-четность
При отражении координат Р импульс электрона р,, меняется следую-
щим образом:
(ро,р) (Ро,р') = Сро, — р),
поскольку р — вектор в трехмерном пространстве. Нулевая компонен-
та ро при преобразованиях координат не изменится, т. к. энергия ро
О
зависит от v .
Кроме импульса, электрон еще характеризуется спином рмСм=О,
£2 = —1. Как будет преобразовываться спин электрона при Р-инверсии?
В системе покоя имеет вид:
О = (о,С),
3.1. Симметрии в квантовой электродинамике
161
т. е. чисто пространственный вектор. В движущейся системе
д _ рС
" т’
= с+ Р(Р<) .
пг(ро + пг)
(3-1)
Исходя из аналогии £ с классическим моментом L = [гхр], можно
сказать, что при P-преобразовании С, знака не меняет (псевдовектор).
Из (3.1) видно, что (о изменит знак в силу изменении знака скорости,
т. е.
См = (Со,С)^С = (-Со,С).
Сравним амплитуды одного и того же процесса до и после про-
странственной инверсии. Рассмотрим для примера диаграмму:
б,Pi
£з,Рз
б,Р2
б,Р4
Рис. 16
При инверсии координат она перейдет в
£з,Рз
Й,Р2
б,Р4
Рис. 17
Симметрия относительно х -э — х означает равенство амплитуд этих
процессов. Выясним, так ли это?
б 5 Р1
162
Глава 3. Общие свойства амплитуды рассеяния
В диаграмме (рис. 16) имеется множитель (от верхней линии)
й(рз,Сз)7мм(р1,С1) ,
соответственно, в (рис. 17)
м(Рз,Сз)7дм(р'1Л)-
Выясним, чем они отличаются. Спиноры однозначно определя-
ются уравнениями
(р - m)u(p, С) = О,
(д5С-1>(р,С) = 0, (3.2)
а для u(p\ С) имеем:
(р' — m)u(p', С) = О,
(75С-1Мр',С) = о. (3.3)
Первые уравнения (3.2) и (3.3) отличаются знаком перед р:
в (3.2)
Ро7о - РТ,
в (3.3)
РоТо + РТ-
Умножая (3.3) слева на до, пользуясь тем, что доТ = 77о- получим
(р - т)дом(р', С) = 0. (3.4)
Теперь сравним вторые уравнения (3.2) и (3.3):
в (3.2)
7s(Co7o - С7),
в (3.3)
7s(-Со7о - Ст)-
При умножении на до получим уравнение, совпадающее с (3.2),
(7б(Со7о - Ст) - 1)7оЦр', С') = 0. (3.5)
Из сравнения (3.4), (3.5) с (3.2) видим, что
u(p',C) = 7?7ow(p,C), |7|=1-
(3-6)
3.1. Симметрии в квантовой электродинамике
163
Аналогично для дираковски сопряженных спиноров можно полу-
чить
й(р'Д') = 7*«(рД)7о- (3.7)
Таким образом,
й(.Рз, Сз)7ми(р'1 Л) = гм = й(Рз, Сз)7о7м7о«(Р1, С1), (3-8)
т. е.
Г' = Го, Г' = -Гг. (3.9)
Итак, вершина при пространственной инверсии меняется, но поскольку
в нашем случае две вершины, то амплитуда остается неизменной. Это
относится ко всем процессам с фотонами в промежуточном состоянии.
Если же мы рассматриваем процессы с испусканием или погло-
щением реальных фотонов, то вершина всегда умножается на вектор
поляризации е* фотона и тогда
Г' е'А - г ₽А
поскольку сА — пространственноподобный вектор и его пространствен-
ные компоненты меняют знак:
Ге е^ = (еА,_еА).
Таким образом, из приведенных рассуждений вытекает, что и вся
электродинамика Р-инвариантна, поскольку она строится из взаимодей-
ствия в виде -----.
Допустим, что взаимодействие у нас имело бы вид не а
Й7М(1 - 75)ц. (3.10)
Тогда, аналогично (3.8), мы бы получили
7о7м(1 -75)7о = 7о7м7о(1 + 7s), (3-11)
т. е. такое взаимодействие не сохраняет P-четность, и сразу выясняется,
в какой системе — правой или левой — мы работаем.
В сущности же, такое взаимодействие означало бы, что и сам объ-
ект, им описываемый, несимметричен относительно отражения. Слабое
взаимодействие, не сохраняющее P-четность, имеет как раз вид (3.10).
164
Глава 3. Общие свойства амплитуды рассеяния
3.1.2 Т-инвариантность
Процесс рассеяния в классической механике
при инверсии времени t' = —t переходит в
причем Vj = — vi, vJ> = — V2, V3 = — V3, V4 = — V4 (скорость частиц
меняет знак при обращении времени).
Одинаковы ли эти процессы?
Снова начнем с рассеяния электронов.
Pi Рз Рз Pi
Т
Р2 Р4, Р4 Pl
Очевидно, при обращении времени р' = (ро, — р). А что произойдет со
спином? Снова исходим из классической аналогии с L = [гхр]. По-
скольку импульс меняет знак, следовательно, и момент тоже, т. е.
С = (Со,-С).
3.1. Симметрии в квантовой электродинамике
165
Снова рассмотрим одну из вершин в каждой диаграмме:
^(.Рь С1)7ди(Рз> Сз)> (3-12)
й(рз,Сз)7дм(р1,С1). (3.13)
Вершины (3.12), (3.13) отличаются не только импульсами, но и поряд-
ком следования спиноров. Перепишем (3.12) в виде
м(Р1Л)7ми(РзЛ) = MT(P3,(3)7jwT(PbCi)- (3-14)
Видим, что устанавливать связь нужно между
иТ(Рз,(з) и й(Рз,Сз), й(Р1,С1) и
т. е. в эту связь должно войти комплексное сопряжение. Выпишем урав-
нения для транспонированных спиноров. Из уравнений
(р' — m)u(p', </) = О,
(7бС' - 1)м(У, С) = О
следует
uT(p',C)(p/T — т) =0,
иТ(р'ДЖ'Т75Т-1) = 0. (3.15)
Для дираковски сопряженных спиноров имеем
w(p, ()(р — т) =0,
йМЫ-1) = 0. (3.16)
Первые уравнения (3.16) и (3.15), соответственно, содержат
Ро7о - Р7,
Ро7о +Р7Т-
Поскольку до = 7о~> 7i~ = 'л- 7з~ = 7: и 72 = 7У т0 нужно изменить
знак перед 72 в (3.15). Это можно сделать, умножив данное уравнение
166
Глава 3. Общие свойства амплитуды рассеяния
справа на «707173 (г введено, чтобы («7о717з)2 = 1, поскольку двукрат-
ное отражение времени ничего не должно изменить). Действительно,
(Ро7о - Р171 + Р272 - Рз7з)?о717з =
= 7о(Ро7о +Р171 -Р272 +Рз7з)?17з =
= 7o7i(-Po7o +Р171 + Р272 -Рз7з)7з =
= 7о717з(Ро7о -Pi7i -Р272 -Рз7з)-
Аналогично и для спиновых уравнений, так что спинор и7«70717з
удовлетворяет уравнениям (3.16), т. е.
иТ(р', С')По717з = и{р, С) (3.17)
wT(p'X) = й(р,С)7з717о(-г); (3-18)
соответственно,
йТ(р', (') = «7о717з«(р, С) = -Пз717о«(р, О- (3.19)
Тогда, подставляя (3.18), (3.19) в (3.14), получим
гм(р'’ О = й(Р’ C)737i7o7j7o7i73w(p, () (3-20)
Отсюда видим, что
Г' = Го, Г' = -Гг. (3.21)
Мы видим, что отражение времени меняет вершину так же как и про-
странственное отражение. Опять диаграммы с виртуальными фотонами
не меняются, поскольку содержат четное число вершин. В диаграммах
с реальными фотонами имеем
ГХА = М, (3.22)
поскольку е меняет знак при отражении времени,
Следовательно, электродинамика Т-инвариантна.
3.1.3 С-инвариантность
Инвариантна ли электродинамика относительно зарядового сопряже-
ния, т. е. замены частиц на античастицы? Чтобы ответить на этот во-
прос, нужно сравнить наш процесс рассеяния с таким же для анти-
частиц с теми же импульсами, но противоположными поляризациями,
3.1. Симметрии в квантовой электродинамике
167
поскольку мы в свое время выяснили, что переходу от частицы к анти-
частице соответствует замена = —Q. Итак,
€i,pi 6,рз Ci,Pi &,р'з
и
— 1 + 1
е । б |
Ь,Р2 £а,Р± С2,Р2 Ci,Pi
(где р( = pi = —СО- Вершина рассеяния позитронов имеет вид:
«(Р1)7м«(рз)- (3.23)
Имеем
Гт(рз) = «(Рз)С'-1,
7T(pi) = СЦщ), (3.24)
тогда
ГД = v(pi)7Mw(p3) = ^Т(рз)7^т(щ) =
= й^С^^Си^) = -Гм ,
поскольку
С-^С = - 7М.
В итоге
ПД = -Гме^.
Следовательно, чтобы все было С-инвариантно, нужно положить
ф, = -ем , (3.25)
т. е. волновая функция фотона при зарядовом сопряжении должна ме-
нять знак. Это можно сделать, поскольку при зарядовом сопряжении
волновая функция нейтральной частицы переходит в себя, вообще го-
воря, с точностью до фазы. Условие С'-инвариантности и (3.25) накла-
дывает серьезные ограничения на возможные процессы. Например, два
фотона не могут превратиться в один. Такой процесс запрещен, посколь-
ку вначале (слева) два фотона, при зарядовом сопряжении знак не дол-
жен меняться, а справа он изменяется.
168
Глава 3. Общие свойства амплитуды рассеяния
Итак, мы получили законы преобразования волновых функций
при преобразованиях С,Р,Т:
Р : «(ДО = 7ом(р,Д (3.26)
Т : мт(У,ф) = -iu(p, С)7з717о, (3.27)
С : «Т(ДО = -й(р,С)П27о- (3.28)
Квантовая электродинамика инвариантна относительно всех этих
преобразований по отдельности.
Выше мы рассмотрели пример взаимодействия, которое наруша-
ет P-четность. Посмотрим, как оно себя ведет при обращении времени:
7о717з[7м(1 “ 7з)]Т7о717з = 7о717з(1 - 7з)Т7^7о717з =
= 7о717з7/Т(1 + 7б)7о717з = 7о717з7^7о717з(1 - 7s),
поскольку 7g = 7s и антикоммутирует со всеми 7М, т. е. слабое взаимо-
действие Т-четность сохраняет. Если же мы рассмотрим взаимодействие
вида
й(1 + 275)11,
то в этом случае
7о717з(1 + «7s)T7o7i73 = (1 - Пз),
т. е. такое взаимодействие нарушает Т-четность.
Вернемся к слабому взаимодействию. При зарядовом сопряжении
вершина преобразуется так:
С-1[7д(1-75)]ТС = С-1^ + ^75)С =
= -7м - 7м7s = —7м(х + 7s),
т. е. слабые взаимодействия также не инвариантны по отношению к
зарядовому сопряжению.
3.1. Симметрии в квантовой электродинамике
169
Рассмотрим теперь комбинацию СР (так называемая комбиниро-
ванная инверсия). Взаимодействие дм(1 — 75) является СТР-инвариант-
ным, поскольку оба преобразования приводят к изменению знака пе-
ред 75. А это означает, что хотя слабое взаимодействие нарушает Р-
четность, тем не менее мы не можем отличить правое от левого: мы
просто не знаем, с чем имеем дело — с частицей или античастицей. Нам
лишь известно, что если то, что мы назвали частицей, обладает правым
винтом, то античастица будет левовинтовой.
3.1.4 СРТ-теорема
Что произойдет, если мы последовательно проведем все три преобразо-
вания? Импульс преобразуется при этом следующим образом:
Р ' (Ро,~р) (ро,р) (ро,р), (3.29)
а спин преобразуется так:
С = (Со, С) (-Со, С) (-Со, -С) (Со, О- (3.30)
Для спиноров имеем
w(p,C) и(р',С) = йои(р,С) uv(p"C!"') =
= «7071734/, С') = «7о717з7о4р, С) v(p"'=
= -СТйТ{р",С") = “По72 • По717з7ом(р, С) =
= 71727з7оЦр, С) = «7sw(p, С)- (3.31)
На диаграммах эти преобразования будут выглядеть так:
Р1,Д , />3,6 р'1Д; । Рз,76 Pi,-Ci ~Рз,~6 , -Pi,-Ci
III I
: \ \ :
III I
III I
III I
III I
P2 ,^2 P4~, ll P2, £2 P4, 11 P4, —^4 P2, ~?2 — P4, —?4 —P2, ~?2
To есть преобразование CPT привело к тому, что по сравнению с ис-
ходной диаграммой все импульсы и поляризации поменяли знаки. Ин-
вариантность по отношению к СРТ означает, что амплитуда процесса
Pi,Ci;P2,C2 —>рз,Сз;р4,С4
170
Глава 3. Общие свойства амплитуды рассеяния
для частиц совпадает с амплитудой процесса
Рз, Сз;Р4, ► Pi, G;P2, (2
для античастиц.
Квантовая электродинамика, очевидно, инвариантна относитель-
но СРТ, поскольку есть инвариантность относительно каждого из этих
преобразований в отдельности. Можно убедиться в этом и непосред-
ственно, пользуясь полученным преобразованием спиноров.
гм = «(Р1)7мг(рз) = й(р1)757м75и(рз) = -w(pi)7Mu(p3),
но с другой стороны,
(70,е) > (е0, о) > (ео,е) > вд,
т. е.
ГрРц = Гмем.
А можем ли мы придумать такое взаимодействие, которое бы на-
рушало С-РТ-четность, но в то же время являлось бы релятивистски-
инвариантным? Очевидно нет, так как замену знаков у 4-импульсов и
поляризаций можно получить комплексным преобразованием Лоренца,
т. е. преобразование ОРТ является, при наличии аналитичности, эле-
ментом группы Лоренца.
Таким образом, СРТ является фундаментальным следствием на-
шей теории (следствием релятивистской инвариантности и причинно-
сти). Нарушение же Р, Т, СР, РТ и т. д. ничему не противоречит и
обусловлено свойствами взаимодействующих частиц. На самом деле, ни
одна из этих симметрий не выполняется строго. Смысл СРТ-теоремы
состоит в следующем. Частица может обладать винтом, часами, заря-
дом. Если мы припишем частице определенный винт, направление вре-
мени и заряд, то античастица будет обладать противоположными и вин-
том, и направлением времени, и зарядом, а в каком мире мы живем, мы
определить не можем.
Приведем в заключение некоторое полезное соотношение, кото-
рое справедливо в случае РТ-инвариантности. При преобразовании РТ
импульсы
(Ро,р) (Ро,р),
а спины изменяют знак:
(Со,С)^(-Со,-С).
3.2. Причинность и унитарность
171
Сохранение РТ означает равенство амплитуд:
^(Pl,CbP2,C2;P3,C3,P4,G) =
= -4(рз, - Сз,Р4, -G;P1, - Cl, Р2, ~Сг)-
(3.32)
На языке S-матрицы это означает:
Sab - $ba
(3.33)
(волной мы отметили то, что спины перевернуты). Однако если мы от
набора
Р1,Р2, ,Рп,
£1^2, • •, 6
перейдем к другим переменным, также полностью характеризующим
систему, в которой спины объединены в полный момент, т. е.
Е±, Е->,... Еп,... М,
то от М ничего не будет зависеть, поскольку это проекция полного
момента на произвольную ось, и в этом случае
Sab — S>ba-
(3.34)
3.2 Причинность и унитарность
Считается (гипотеза), что амплитуды любых реальных процессов долж-
ны с необходимостью удовлетворять условиям унитарности и причинно-
сти. Рассмотрим подробнее, что эти условия означают и к каким огра-
ничениям на амплитуды они приводят.
3.2.1 Причинность
Пусть имеется некоторый процесс (забудем пока про спины):
172
Глава 3. Общие свойства амплитуды рассеяния
С точки зрения причинности нас будут интересовать зависимость ам-
плитуды от точек Xi, х2, поэтому запишем ее в виде
F = у eik'X2^ikxi fppi (х±, x2)d4xid4x2, (3.35)
где
fPP'(.xi,x2) = у etp'y2~ipyif(x1,x2;y1,y2)d4y1d4y2. (3.36)
В силу трансляционной инвариантности (однородность пространства-
времени), амплитуда /(яд, х2; y-у у2) зависит только от разностей коор-
динат. Замена
Xi = х\ + а,
Уг = y'i+a (3.37)
приведет лишь к изменению показателей экспонент в (3.36), при этом
функция fpp> (xi,x2) преобразуется следующим образом:
fpp'^yx^ = e^p'-^afpp\x'yx'2). (3.38)
Поэтому функцию fppi можно представить в виде
/иИ^яд) = -Ж2). (3.39)
Действительно, при трансляции (3.37) функция (3.39) будет преобразо-
вываться по закону (3.38), поскольку
ЯД — х2 = — х'2,
яд + х2 = х'г + х'2 + 2a.
Тогда, перейдя в (3.35) к переменным х2 — х± = х±2 и х± + х2 для
амплитуды F, получим
р _ у gi(fc'-fc)(s:i+a:2)|+i(fe' + fe)xi2| х
х е*(р'-Р)(^+^)1/да,(Ж1 -Ж2)й4(Ж1 +Ж2)^Ж12.
Интегрируя по d4(xi +х2), получим
F = (2тг)45(р + к — р' — к1) х
х у etLJ^A,'X2~X1'>(x2 - x1)fpp>(x12')d4x12 =
= (27г)4ф + к - р' - k^^k'-p,^). (3.40)
3.2. Причинность и унитарность
173
Как всегда, следствием трансляционной инвариантности являет-
ся сохранение энергии-импульса. Итак, появление 5-функции в ампли-
туде — факт общий, который выражает однородность пространства-
времени.
Что означает причинность на языке амплитуды (3.40)? Причин-
ность означает, что область интегрирования Ж20 < яТо и < 0 не
должна давать вклада в амплитуду. Физический смысл этого утвер-
ждения следующий: если мы рассеиваем пучок частиц на некоторой
мишени, то рассеянные частицы не должны вылетать из мишени ранее,
чем прилетели падающие. Следовательно, /ррДщ) должна иметь вид:
/ррДД = #((Ж12)оМ2л2Мя42) + Д^ю), (3.41)
причем член (//(#12) при интегрировании должен давать нулевой вклад
в амплитуду.
В выражении (3.40) /с, kf, р, р' у нас не любые. Поскольку частицы
реальны, эти величины удовлетворяют соотношениям:
к0 = у/k2 + Л2 , к'о = у/к,2 Л2.
ро = у/р2 + т2 , р'о = \/р'2 + т2
и, кроме того, связаны законами сохранения:
к — к1 = р' — р.
Давайте предположим, что /рДжщ) имеет именно структуру (3.41),
т. е. причинность выполняется (в противном случае теория потеряла бы
всякий смысл). Пусть р = р', к = к’ (рассеяние вперед) и направим ось z
по вектору к. Тогда из (3.40) следует, что
f(k,k-p,p) = f(k,p) = I d4xeik°x°~ik’zfp(x) =
= У = (3.42)
Поскольку наша функция имеет вид (3.41), то вклад в интеграл дает
область
xq > 0 , Хд — z2 > 0 ,
откуда следует, что
я?о — z > 0.
174
Глава 3. Общие свойства амплитуды рассеяния
Из последнего неравенства и (3.42), в свою очередь, следует, что если
интеграл (3.42) сходится на вещественной оси fcg (т. е. если f(ko) име-
ет смысл), то в верхней полуплоскости он сходится еще лучше. Иначе
говоря, при выполнении условия причинности амплитуда аналитична в
верхней полуплоскости. Справедливо и обратное: если амплитуда ана-
литична, то она может быть записана в форме (3.42). Если же f(ko)
имеет в верхней полуплоскости особенность, то она не может быть при-
чинной.
Следуют ли из причинности какие-либо выводы о поведении ам-
плитуды f(ko) с ростом ко? Если ко велико, то при интегрировании в
(3.42) область xq — z ~ 0 дает максимальный вклад в интеграл. Ес-
ли /(я;2) имеет в нуле сингулярность, то /(fco) может расти с ко- Напри-
мер, если
/(ж2) ~ 5(ж0 - z),
ТО
f (&о) const,
но при
/(я:2) ~ 8\х0 - г)
имеем уже
Ж) ко,
т. е. если f(x2) имеет структуру
Ят2) = ]ГС>п)(;го-4 (3.43)
ТО
/(fco) = EC'"fco- (3-44)
п
В принципе, если (3.43) содержит бесконечное число производ-
ных <5-функций (т. е. f(ko) растет быстрее любой степени ко), мы не
гарантированы от того, что не нарушили причинность. Действительно,
явно антипричинная функция
О(-я?о + z) = C„5(n) (я?о - z)
п
как раз и содержит бесконечное число таких производных.
3.2. Причинность и унитарность
175
Таким образом, если потребуем, чтобы
Л&о) < кв при к0 -> оо,
(3.45)
что соответствует конечному набору 5(п)-функций в (3.43), то условие
причинности заведомо не нарушится. Функции /(&о), аналитичные в
верхней полуплоскости и растущие не быстрее некоторой степени ко,
мы будем называть причинными.
Хотя мы не доказали формально, что причинность требует, чтобы
амплитуда обладала этими свойствами, эта гипотеза, однако, довольно
хорошо аргументирована. Действительно, как мы проверяем причин-
ность на опыте? Пусть мы имеем пакет, описывающий налетающие ча-
стицы (фотоны в нашем случае):
Ф(ж) = / e-^^'-^C^dko.
(3.46)
Рассеянные вперед фотоны опишутся так:
Ф'(ж) = / e~ika^x°~z'> f(ko)C(ko)dko
(3.47)
Причинность для налетающих частиц здесь означает, что С (ко) должна
быть такой, чтобы
Ф(х) =0 если z — xq > а,
(3.48)
т. е. если источник фотонов помещен в а, то до того, как они были испу-
щены, их не было. Этого можно добиться выбором особенностей С(ко).
Именно, если С (ко) не имеет особенностей в верхней полуплоскости и
на большом круге ведет себя как е-г/с°а, то при z — хо > а в (3.46) мож-
но замкнуть контур в верхней полуплоскости и показать, что Ф(ж) = 0.
После рассеяния Ф'(ж) также должно равняться нулю при z — хо > а,
но если f(ko) ~ e-lk°c, (с > о) на большом круге, то Ф'(я;) будет равно
нулю только при z — хо > а + с, но не при z — хо > а.
Давайте теперь посмотрим, аналитичны ли наши борновские ам-
плитуды? Им соответствуют диаграммы:
176
Глава 3. Общие свойства амплитуды рассеяния
(А — малая масса фотона),
и = (р — к') = т2 + А2 — 2тк'о = т2 + А2 — 2гпк()
(fco = к'о при рассеянии вперед). Полюса амплитуды лежат в точках,
определяемых равенствами:
—А2 + 2тко = О,
А2 + 2тко = О,
т. е.
\2
/•’о = ±д—•
2т
Однако амплитуда определена в области ко А (жирная линия на
рис. 18), а полюса в точках ко| < А, т. е. не там, где определена амплиту-
да. Таким образом, борновская амплитуда имеет правильные аналити-
ческие свойства (не имеет полюсов в верхней полуплоскости и убывает
при |A:q| —» оо) и следовательно удовлетворяет причинности.
Как же это получилось? Ведь С(ж2 — ад), входящая в амплитуду,
отнюдь не равна нулю при адо — адо < 0. Первая диаграмма дает:
G(l2 -Ж1)хХ
Ж1
Х2
= F =
3.2. Причинность и унитарность
177
= у dix1dix2et(-k'+p'')X2-^k+p)xiG(x2 - жх) =
= (27г)4<5(р +к-рг -к') У d^XYie^+rt^GixYi-p (3.49)
(?Ы = / тУХе"^12 2 \ , (3-50)
J (2тг)4г пт/ — qz — ге
т. е.
/1 1
d^q5(p + к- q)—~-5---- = ----——------,
тп/ — qz — ie гпУ — (р + k)z — ie
а так как qo = ро + ко > 0, то левый полюс qo = \/m2 + q2 у функции
l/(m2 — <?2) заведомо не работает. Поэтому его можно считать распо-
ложенным не в верхней, а в нижней полуплоскости. Но, как мы знаем,
такое расположение полюсов отвечает запаздывающей функции Гри-
на, которая пропорциональна Сд(ж21) ~ 0(ж2о — жщ)- Значит область
ж2о < жю действительно не дает вклада в интеграл.
Во второй диаграмме знак е (положение полюса) несуществен,
поскольку знаменатель может обратиться в нуль, если только частица I
178
Глава 3. Общие свойства амплитуды рассеяния
нестабильна, т. е. может самопроизвольно распасться на две.
Поэтому при вычислении амплитуды для стабильной частицы функцию
Грина в этой диаграмме также можно заменить на запаздывающую.
Однако просто заменить всюду фейнмановские функции на запазды-
вающие нельзя, поскольку мы получили бы неправильный результат
для амплитуд рассеяния, в частности, если бы мы рассмотрели ту же
амплитуду в других каналах.
Рассмотрим соотношение между разными каналами на мандель-
штамовской плоскости с точки зрения причинности и аналитичности.
s + t + u = 2m2 + 2А2,
s = (m + A)2
— начало физической области.
Пользуясь аналитичностью амплитуды, мы в свое время продол-
жали ее в t- и м-каналы. Продолжение, указанное стрелкой на мандель-
штамовской плоскости, аналогично следующему продолжению в плос-
кости ко (см. рис. 19). Иначе говоря, в отличие от нерелятивистской
квантовой механики, область отрицательных ко тоже имеет смысл.
В этом как раз и состоит одна из основных особенностей реляти-
вистской теории: аналитичность амплитуды (т. е. причинность) обеспе-
чивает возможность ее продолжения в мандельштамовской плоскости
из канала в канал или в плоскости ко. Как мы покажем ниже из условия
унитарности, должна быть комплексна в физических областях разных
3.2. Причинность и унитарность
179
Рис. 19
каналов, отмеченных жирными линиями на рисунке. Мы увидим да-
лее, что амплитуда имеет точку ветвления в точках, которые отвечают
началу физических областей ко = ±Л, и жирные линии отвечают раз-
резам амплитуды в комплексной плоскости. Физическая амплитуда в
s-канале есть предельное значение на верхнем берегу правого разреза
(рис. 20).
Рис. 20
180
Глава 3. Общие свойства амплитуды рассеяния
Поскольку в верхней полуплоскости амплитуда аналитична, ее
можно продолжить, как указано на рис. 19 (т. е. в w-канал). Получим
ли мы при этом амплитуду нового процесса? Казалось бы, для этого
достаточно заменить ко на —ко. Однако, повторяя выкладку (3.42) в
с-канале, получим
Ju = / д4хегк°(хо-гу(х), x0-z<0,
т. е.
Л(-^о) = Ж).
Следовательно, в u-канале нужно к вещественной оси подходить снизу.
Это естественно, поскольку амплитуды отличаются знаком ко, то
ко + is —ко — is.
Этот переход изображен на рисунке:
А ко + is
— ко — is
и —А
Таким образом, физическая амплитуда в и-канале также есть предель-
ное значение на вещественной оси некоторой аналитической функции.
Поскольку в части комплексной плоскости (в области между разрезами)
эта функция есть аналитическое продолжение s-канальной амплитуды,
то данная функция — та же самая, чье предельное значение на правом
разрезе есть s-канальная амплитуда.
Рассмотрев требования причинности в w-канале, можно показать,
что амплитуду можно продолжать в нижнюю полуплоскость ко- Иначе
говоря, амплитуда должна быть аналитичной и в верхней, и в нижней
полуплоскостях (но с учетом разреза на вещественной оси). Верхняя и
нижняя полуплоскости ко есть, по существу, плоскости з-канальной и
(/-канальной амплитуд. Переход с одной из них в другую эквивалентен
аналитическому продолжению амплитуды из одного канала в другой.
3.2.2 Унитарность
Мы ввели S-матрицу, матричные элементы которой Sba определяют ам-
плитуды переходов из состояния |a)t=_oo в состояние &)t=+co, т. е. если
3.2. Причинность и унитарность
181
в t = — оо система находилась в состоянии
/фЛ
ф2
то в t = +оо
Ф' = 5Ф.
Волновые функции начального и конечного состояния имеют вид:
Ф = 52фаН (3.51)
a
= Е фэ> = Е ф«5и = Е
ba ab
фь = E<6i sia> ф« = Е ^«ф«- (3-52)
a a
Отсюда вытекает приведенный выше смысл Sba как амплитуды перехо-
да. Сохранение вероятности означает, что
Е |Фа|2 = Е 1фь12- (3.53)
a Ь
Принцип суперпозиции требует выполнения (3.53) для любых началь-
ных состояний. Это приводит к тому, что S-матрица должна быть уни-
тарной, т. е.
SS+ = 1 , (3.54)
или в матричном виде
Е SabS+ = 6ac. (3.55)
ь
Диагональная часть условия (3.55)
Е ^ab^ba = Е I $ab ।2 = 1
Ь Ь
означает сохранение вероятности, а недиагональная
Е SabSbc = 0 ’ с а
ъ
— ортогональность состояний.
182
Глава 3. Общие свойства амплитуды рассеяния
Представим S-матрицу в виде
S = 1 + iT. (3.56)
Тогда из условия унитарности (3.54) следует
l + iT-iT+ + ТТ+ = 1,
т. е.
-i[T-T+] =ТТ+. (3.57)
Обычно условием унитарности называется именно (3.57). В матричном
виде (3.57) запишется
-^[^a-Tbt] = ^TbcT+ ,
или, так как Т+ = Т*ь,
-г[Тьа-Кь]=^ТЬсТ:с. (3.58)
Предположим, что теория РТ-инвариантна, как, например, квантовая
электродинамика, тогда
Гоь = Т~ь~
(|&), |й) — состояния с противоположными спинами). Но, как мы обсу-
ждали выше, всегда можно выбрать базис так, что в нем
Tab = Тьа.
При этом (3.58) примет вид:
-i[Tab-T:b] = ^2TbcT^
ImTab = ^ТасТ*ь. (3.59)
А отсюда следует, что амплитуда не может быть вещественной, т. е.
сразу видно, что наши борновские амплитуды, наверняка, неточны, по-
скольку вещественны. Особенно ясна комплексность амплитуды при
рассеянии вперед, т. е. при а = Ь:
ImTaa = | ^2 |Тас|2. (3.60)
3.2. Причинность и унитарность
183
Соотношение (3.60) носит название оптической теоремы:
Taa~A(9 = 0), \Tac\2 ~ atot
— мнимая часть амплитуды рассеяния вперед пропорциональна полно-
му сечению рассеяния.
Таким образом, условие унитарности требует, чтобы амплитуды
рассеяния в физической области были комплексными.
Вернемся к нашему примеру Комптон-эффекта для фотона (с ма-
лой массой А). Физическая область на мандельштамовской плоскости —
это заштрихованная часть (см. рис. 21).
t
Рис. 21
Полюса амплитуды лежат на пунктирных линиях, отвечающих
s = пт2, u = т2. На комплексной плоскости ко картинка будет выгля-
деть так (рис. 22). Физические области отмечены жирными линиями.
Полюса борновской амплитуды отмечены крестиками.
Выясним теперь, имеют ли борновские амплитуды хотя бы какое-
нибудь отношение к условию унитарности. Для этой цели распишем его
подробнее. У нас было
Tab = (2тг)45 - У^Ръ} Fab П ~FFr=- (3.61)
4 7 а у & "V
Подставляя (3.61) в (3.59), получим
ImFab = | £ FacF^)4 §уа £рс) J] (3.62)
184
Глава 3. Общие свойства амплитуды рассеяния
Рис. 22
(помним, что в F выполняются законы сохранения), тогда
ImFab =
....MX
x F*(ky ...,kn-&)(2%)4<5(^ кг - Y^Pb)- (3.63)
Или, выражая d3fc/2fco через d4k8+(k2 — m2), окончательно получим
ImFab =
= ^“7 52 / 1 • • • rf4M+(fci - rn2)... 8+(k2 - m2) x
X FF (2^
(3.64)
Множитель 1/n! в (3.63), (3.64) учитывает тождественность частиц.
В случае рассеяния вперед (а с=: Ь) из (3.64) видно, что Ini Fo/, отли-
чается от полного сечения множителем
1 _ 1
4FiF2j 4л/зр
3.2. Причинность и унитарность
185
(а также общим множителем 1/2). Учитывая, что
= JP___Р_ =
Е-2 EiE-2
получим
ImF(s,0) = 2Vspat. (3.65)
Это и есть оптическая теорема. Выражение (3.64) будем писать в сим-
волическом виде:
ImF = ^FnF*.
п
Рассмотрим теперь борновскую амплитуду
т2 — s — is
В свое время мы писали соотношение
------ = Р—h т5(х),
х — is х
так что
е2
Im—---------- = e2?r5(s — m2). (3.66)
т2 — s — is
Точное же значение мнимой части дается (3.64), и мы можем ее изоб-
разить графически (аналогично изображению сечений) так:
-'X-
ImF ~ ---
все, что угодно
В промежуточных состояниях частицы реальные и поэтому, например,
одного электрона в промежуточном состоянии быть не может. Одна-
ко рассмотрим формально вклад в мнимую часть от одноэлектронного
промежуточного состояния, т. е.
186
Глава 3. Общие свойства амплитуды рассеяния
ImF22 = у У G?4q|F2i|25(q2 - m2)d(p + к - q),
ImF22 = tt|F2i |2J((p + к)2 - m2). (3.67)
Таким образом, борновское приближение в определенном смысле
удовлетворяет условию унитарности, а именно, в том смысле, что его
мнимая часть определяется вкладом одноэлектронного промежуточно-
го состояния.
В принципе, одноэлектронное промежуточное состояние может
давать вклад в мнимую часть амплитуды совершенно “честным” обра-
зом. Рассмотрим, например, процесс перехода трех частиц в три:
Электрон, отмеченный крестиком, может быть реальным (это не запре-
щено в данном случае законами сохранения), и за счет такого промежу-
точного состояния мы получим вклад в мнимую часть без противоречия
с законами сохранения. Но, с другой стороны, из всей суммы для мни-
мой части (3.66) отвечает только первому ее члену. Посмотрим, плохо
это или нет. Усложнение диаграммы на одну вершину приводит к мно-
жителю е, и если
то ImF = FnF7
Если рассмотреть вклад от промежуточного двухчастичного состояния
(п = 2), то порядок величины правой части е4, для п = 3 мы получили
3.2. Причинность и унитарность
187
бы е6 и т. д., а слева — Im А ~ е2, т. е. такие вклады и не должны
появляться. И единственный вклад — это
ImF = F2iFi2 ~ е2.
Таким образом, борновские амплитуды позволяют вычислять мни-
мые части амплитуд более высокого порядка в силу соотношения уни-
тарности. Например, в мнимой части амплитуды
ImF(2y е+е ) =
Если, допустим, хотим вычислить ее с точностью до е4, прене-
брегаем членами порядка е6 и выше, а все амплитуды, входящие в пер-
вую диаграмму, нам уже известны. Так можно найти мнимые части
амплитуд в высших приближениях во всех областях мандельштамов-
ской плоскости. Однако, чтобы знать всю амплитуду, нужно знать еще
и реальную часть, и здесь нам на помощь приходит аналитичность ам-
плитуды, которая позволяет вычислить вещественную часть по мнимой.
По теореме Коши, имеем
Ж) = I
dk'o f(fcp)
2тгг к'о — ко ’
(3.68)
контур интегрирования приведен на рис. 23.
С другой стороны, мы можем пренебречь интегралами по боль-
шим кругам и представить контур в виде, указанном на рис. 24.
При этом
dk'o f(k'o)
2тг/ к'о — ко
ri + г2
kw — ко к2о — ко
(3.69)
т+А
dk'o
-о - к0
dko т fll '\
ДТД1тЛ‘»>-
188
Глава 3. Общие свойства амплитуды рассеяния
Рис. 24
3.2. Причинность и унитарность
189
поскольку
- ге) - /(fcg + is)} = Im/(feo)-
Члены с Г1 и Г2 в(3.69) отвечают вкладу в интеграл от полюсов Ащ
и ко2 борновского приближения (высшие приближения в этих точках,
как увидим, особенностей не имеют). По этой амплитуде можно найти
мнимую часть в еще более высоком приближении и т. д. В частности,
используя борновские приближения для процесса, можно найти ампли-
туду рассеяния света на свете. Действительно,
ImF(27 2у) =
(3.70)
Амплитуды
и
нам известны, и, подставляя (3.70) в (3.69), найдем F(2y 27).
Таким образом, из амплитуды предыдущего приближения мы мо-
жем найти мнимую часть последующего, а по дисперсионному интегра-
лу (3.69) — и саму амплитуду. Повторяя последовательно эту процедуру,
можно найти амплитуду в любом порядке теории возмущений.
При выполнении этой программы мы можем, однако, столкнуть-
ся с проблемой сходимости дисперсионных интегралов. Сходимость же
определяется поведением амплитуд рассеяния при больших энергиях.
В действительности, эта проблема тесно связана с возможными ультра-
фиолетовыми расходимостями теории. Мы рассмотрим эту проблему в
главе 5.
Глава 4
Перенормировки. Радиационные поправки
В предыдущей главе мы показали, как при помощи дисперсионных со-
отношений можно получить амплитуды высших приближений из бор-
новских. Существует, однако, более простой метод непосредственного
построения амплитуд высших порядков — метод фейнмановских диа-
грамм.
4.1 Высшие приближения.
Перенормировка массы электрона
Начнем со свободной частицы. Что с ней может произойти? (Считаем,
что есть частицы только одного сорта и фотоны.)
1. Частица свободно распространяется из ад в х2:
ад ад.
2. В некоторой точке х^ частица может испустить фотон: ~
но поскольку реально этот процесс запрещен, то фотон может су-
ществовать лишь время, разрешенное соотношением неопределен-
ностей, а затем обязан поглотиться этой же частицей, т. е.
3. Возможны и более сложные процессы:
4.1. Высшие приближения. Перенормировка массы электрона
191
или
Точная функция Грина свободной частицы представляется сум-
мой функций Грина всех подобных процессов, причем, когда в диаграм-
ме присутствуют электрон-позитронные пары, на каждую надо вводить
множитель —1 (поскольку и(р) = —й(—р)). Метод Фейнмана как раз и
состоит в написании всех топологически разных диаграмм процессов во
всех порядках по константе взаимодействия и суммирования всех соот-
ветствующих функций Грина. Подчеркнем, что следует рисовать только
топологически различные диаграммы. Так, например, диаграмму
можно изобразить так
и так
Это, по существу, один и тот же процесс, поэтому его нужно учитывать
только один раз.
192
Глава 4. Перенормировки. Радиационные поправки
Сумма
/ х
---------------- + —L--------------*— +
описывает распространение свободной частицы и влияние на него все-
возможных виртуальных процессов. Видно, что процесс, например, та-
кой
есть просто повторение
так что ничего нового он в движение частицы фактически не вносит. По-
этому в дальнейшем нам будет удобно выделить те процессы, которые
не сводятся к простым повторениям. А пока сформулируем правила,
по которых мы будем сопоставлять диаграммам функции Грина. Как
обычно, для диаграммы
напишем
С2(ж2 - ад) =
= е2 У С(ж2 — — яд) х
х В^{х'2 — x'^d^d1^. (4-1)
Множитель е2 в (4.1) появился из-за наличия двух вершин, интеграл
берется по d4x,1 и </|я'/2 в силу того, что х^ и х'2 произвольны. В яхпрост-
ранстве вершине мы сопоставляем гдм (как и в импульсном), т. е.
4.1. Высшие приближения. Перенормировка массы электрона
193
В следующем порядке рассмотрим, к примеру, диаграмму
Для нее имеем
G'iG/x — яд) =
= е4 У 6(я?2 — x^iy^G^ — x2)GivG(x'2 — х'^ х
х - х"у1^С(х" - x^D^tx'z - х") х
х Dvvi (х'2 — x,1)d4x"d4x,1d4x'2d4x2 (4-2)
Здесь правило такое: под интегралом пишутся функции Грина, начиная
с конца диаграммы, по всем внутренним точкам х! производится инте-
грирование. (Нужно также следить за индексами д, д', ... фотонных
функций Грина, чтобы они соответствовали диаграмме.)
Перейдем в импульсное представление. Для этой цели напишем
функции Грина в виде
. _ f сГр е грх
Х J (2тг)4г m — р’
г. / х f d4k e~ikx
d^) - j (27r)4- fc2 (4-3)
При подстановке (4.3) в (4.1) или (4.2) мы видим, что вся зависи-
мость подынтегральной функции от координат ограничивается экспо-
ненциальными множителями. Поэтому интегралы по х\ легко возьмут-
ся.
Рассмотрим, например, (4.1):
2 Г d4p-Ld4p2d4p3d4k 1 1 1
62 я?2 ~ яд) = е / ------ 4 4--------------“Пм--------г^--------
J [(2тг)4г]4 m — m — р$ m — р±
х / е-гр2Х2е-гж2(-р2+рз + А:)-гх/1(-рз+Р1-/с)егр1Х1^4;Г/ ^4^,/
J с ,
/ e~lX2<'~P2+p3+k^~'lX1<'~P3+pi~k'>d4x,1d4x2 =
= (27г)4<5(дз + к - р2)(2л)4<5(д1 - к - р3).
(4-4)
194
Глава 4. Перенормировки. Радиационные поправки
То есть в каждой вершине диаграммы в импульсном представлении
(рис. 25) выполняется закон сохранения 4-импульса.
к
1 \
i ,
Р1________________________Рз_Р2
Рис. 25
После интегрирования при помощи 5-функции по d‘p2 и d]p2 оста-
нется
J (2тг)4г т-р! т _ - к) т - р± к2
По промежуточному состоянию осталось одно интегрирование (d4fc).
Переписывая (4.5) как
G2(x2 — х±) = J'
видим, что функция Грина G2(p) в импульсном представлении имеет
вид:
г ( \ е2 ( [ d4k 1 1 \ 1
G2{p) = ------- / Щ,-----------;--ГТ-77 ------’ 4-6)
m-p\J (2тг)4г т-р + к к2 J т - р
Итак, мы вычислили поправку к свободной функции Грина:
к
р р — к р
В (4.6) присутствует интегрирование по импульсу промежуточного фо-
тона, потому что, хотя в каждой вершине выполняется закон сохранения
4.1. Высшие приближения. Перенормировка массы электрона
195
4-импульса, сам испущенный квант может обладать любым импульсом.
Аналогично можно построить функцию Грина, соответствующую лю-
бой диаграмме. Например, в порядке е4:
fci
' к2 х ч
' '' \ \
___________i__I_____________________________ >
р р — fci р — fci — к2 р — fci р
ki к2
i l-'--------'-------- ,
р--------------------------------------------------р — fci р — fci — к2 р — к2 р
fci к2
z \ ' \
I I
р_____________________________________р — fci р_р — к2 р
Выпишем функцию Грина для средней диаграммы:
G4(p) = е4 z m — р / Г d4k1d4k2 V [(ММ2 1 х 7м , , г m — р + fci X 1 1 7м .;7^ , j- 1 m — р + к2 m — р+ к2 + fci ! 1 \ 1 fc2 fcg / m — р
Рассмотрим теперь, что может произойти со свободным фотоном.
Он может только распадаться на электрон и позитрон, больше никакого
196
Глава 4. Перенормировки. Радиационные поправки
взаимодействия у нас нет, так что могут быть следующие процессы:
и т.д.
Что мы сопоставим этим диаграммам? Свободному фотону, как
мы знаем, соответствует фотонная функция Грина pAH/-D(a;2 — яд), т. е.
можем, как обычно, написать выражение:
е2 / Г>МА1'(х2 - - a/Jx
х — x'^Dyiy^x^ — х^х'д^х'^. (4.9)
Однако электрон и позитрон могут рождаться с разными спинами, по-
этому надо просуммировать (4.9) по всем спиновым состояниям, т. е.
взять след от (4.9). Обсудим этот вопрос подробнее. Вспомним, что мы
сопоставляли
Р1
/X
= eu(pi)7Mt;(p2).
4.1. Высшие приближения. Перенормировка массы электрона
197
Если бы в диаграмме
в промежутке частицы были бы реальными, то для амплитуды мы на-
писали бы
А ~ 52 М>1 (Р2>Л2(Р1) =
Ai Аг
= - 52 йА1(Р1)7ммА2(-Р2)йА2(-Р2)7рМА1(Р1). (4.10)
Al Аг
Знак ” появился, так как v(p) = —й(—р). К следу выражение (4.10)
сводится при помощи равенства:
52 “«(^^(р) = (Р +
А
Таким образом, для того чтобы (4.9) для реальных частиц пе-
реходила в (4.10), мы должны след взять со знаком ”. Аналогично,
для произвольной диаграммы на каждую электрон-позитронную пару
должен входить множитель —1.
В импульсном представлении
(4.U)
Единственным усложнением по сравнению с правилами Фейнма-
на для петель, сделанных из скалярных частиц, является знак ” на
каждую электрон-позитронную пару и Sp по спинорным значкам.
198
Глава 4. Перенормировки. Радиационные поправки
Реально фотон не может распасться на две частицы, т. е. процесс
является виртуальным. Это отражается в том, что функция Грина (4.11)
содержит fc2 0, ро / \/р2 + ш2. На языке нерелятивистской кван-
товой механики можно сказать так: на короткое время (определяемое
соотношением неопределенностей) фотон распадается на электрон и по-
зитрон с нарушением закона сохранения энергии.
Поправки высокого порядка в фейнмановских диаграммах вклю-
чают в себя более сложные виртуальные процессы. Частицы в этих про-
цессах не находятся на массовой поверхности. Это следует сравнить с
обычной квантовомеханической теорией возмущений, в которой в про-
межуточных состояниях нарушается закон сохранения энергии. Метод
Фейнмана, в принципе, эквивалентен теории возмущений в квантовой
механике, однако, он гораздо удобнее, поскольку этот метод сохраняет
явную релятивистскую инвариантность в процессе вычислений.
Прежде чем перейти к обсуждению реальных процессов, рассмот-
рим более подробно функции Грина свободных частиц. (Будем в даль-
нейшем массу частицы обозначать то вместо т.)
Итак, функцию Грина свободной заряженной частицы с массой
то можно записать в виде суммы членов, отвечающих всевозможным
процессам с испусканием и поглощением всевозможного числа фотонов,
т. е.
G = ------- = -------- + -1------- + —+•••
Среди всех таких диаграмм есть в некотором смысле исключительные,
а именно, такие, которые соответствуют периодическому повторению
флуктуаций, происходящих с частицей, т. е. диаграммы типа
Такие флуктуации не связаны, так как могут быть разделены большими
промежутками времени, и фактически новой информации о движении
частицы не дают.
Флуктуации же типа
4.1. Высшие приближения. Перенормировка массы электрона
199
связаны и разделены очень малым промежутком времени. Поэтому,
чтобы выделить флуктуации, которые связаны и происходят в тече-
ние короткого промежутка времени, вводят понятие собственной энер-
гии частицы, которая является суммой всех диаграмм, не содержащих
повторений (т. е. которые не могут быть разделены на две части, соеди-
ненные одной линией).
В S(p) содержатся все флуктуации за короткий промежуток вре-
мени. Все остальные флуктуации получаются просто повторением, т. е.
полную функцию Грина можно записать так:
G(p) =
Выделив S(p) в блок, мы теперь легко можем просуммировать всю со-
вокупность диаграмм. Имеем
G(p) = ; [-ЭД ; +
то — р то — р то — р
+ ^—: [-ад] : [-ад] —; + • • •
то — р то — р то — р
1 ( 1 \2
1 + [_ад--------; + [-ад---------; +... . (4.12)
то — р \ то — р J
Таким образом, сумма свелась к геометрической прогрессии. Сум-
мируя ее, получим
т0-р 1 + S(p)^y^ m0-p + S(p)’
(4-13)
В нулевом приближении
Go(p) =
1
т0 -р
т0 +р
7Hq — р2
200
Глава 4. Перенормировки. Радиационные поправки
Здесь то имеет смысл массы частицы, поскольку Go(p) в точке р2 =
имеет полюс. Это вытекает из следующих рассуждений: функция рас-
пространения частицы из Xi в хр есть
Г(т [ d4P rWx^m0+P
т2-р2’
где ад2 = ад — ад. Взяв интеграл по вычетам, мы получим
где ро = у/mg + р2. А это и означает, что распространяется частица
с массой то; более того, при t-z оо вклад в интеграл дает только
полюсной член и, если бы не было полюса, из-за частых осцилляций
экспоненты он обратился бы в нуль, т. е. мы не наблюдали бы никакой
частицы. Именно наличие полюса делает интеграл отличным от нуля и
обеспечивает правильную связь между энергией и импульсом частицы.
Так что физически наблюдаемая масса определяется из условия
G(p)|p2=m2 = ОО.
(4-14)
Взглянув же на (4.13), видим, что точная функция Грина не обяза-
тельно имеет полюс при р2 = TOq, т. е. то не имеет непосредственного
отношения к массе. А реальная масса частицы определяется еще и ее
собственной энергией. И если мы хотим, чтобы свободная частица с
некоторой массой т существовала (т. е. мы могли бы ее наблюдать), то
мы должны наложить некоторые условия на У(р).
Поскольку S(p) зависит только от у матриц только через р, она
коммутирует ср. Пусть ит(р) — биспинор, описывающий свободную ча-
стицу с массой т ( pum(p) = тит(р) ). Уравнение 4.14 для определения
физической массы эквивалентно
G-1(p)wm(p) = (т0 -р + S(p)) ит(р) = 0,
которое эквивалентно
то — т + S(m) = 0.
(4-15)
Это уравнение должно иметь вещественные решения, которые и будут
иметь смысл реально наблюдаемой массы частицы. А поскольку то
4.1. Высшие приближения. Перенормировка массы электрона
201
ненаблюдаема, хорошо бы ее исключить из всех выражений, заменив
на некоторую комбинацию из т. Это сделать совсем просто: перепи-
шем (4.13) в виде
G-1(p) = m0 -р+ Е(р).
Выражая mo из (4.15), получим
G-1(p) = т — р + £(р) — S(m). (4-16)
Эта формула выражает функцию Грина электрона только через наблю-
даемые величины.
Рассмотрим теперь, как устроены поправки к волновой функции
заряженной частицы. Покажем, что они связаны с поправками к функ-
ции Грина.
Вспомним, как мы вычисляли амплитуды реальных процессов:
х'1
XI s'
J (2тг)4г т$—р2
Мы замыкали контур на полюс и интегрировали по dpQ: пользуясь ра-
венством
52«а(р)Мц = (р + ш0)а/3,
Л
получали
-Е/ 2М2ЛЗе~МЖ1~3:,1)йЛ(р)цЛ(р)’
А
где ро = у/р2 + mg. Далее выделили волновые функции свободных ча-
стиц:
—=иА(р)е-грХ1, —=егрх'^йх(р),
и оставшийся фактор назвали амплитудой рассеяния.
Теперь же у нас функция Грина имеет полюс в т. Посмотрим, что
произойдет с вычетом, который, как мы только что объяснили, входит
в амплитуду рассеяния. Для этой цели разложим S(p) в ряд вблизи т:
S(p) = Е(т) + (р — m)S'(m) + (р — т)2Ё(р). (4-17)
202
Глава 4. Перенормировки. Радиационные поправки
Последний член в этом выражении содержит степени р—т выше первой.
Перепишем его в виде
(р - т)2Ё(р) = [1 - S'("?-)] Sc(p),
вводя новую величину Ес(р)- Она выражается через собственную энер-
гию согласно
£(р) — S(m) — (р — т)Т'{р)
1 — S'(m)
Функция Грина может быть представлена через Sc(p) следующим об-
разом:
G-1(p) = I1 - -р- Sc(p)) = [1 - S'(m)]G;1(p), (4.18)
Мр) =
где
Gc(p) = -----/ v
m-p - Zc(p)
называется перенормированной функцией Грина. Поскольку вблизи по-
люса Sc(p) имеет лишь члены высокого порядка по р — т, видно, что
перенормированная функция Грина устроена вблизи полюса так же, как
функция Грина свободной частицы с массой т.
Вернемся к вычислению амплитуды. Величина Sc(p) не дает вкла-
да в полюс, поэтому при вычислении амплитуды (т. е. при х± —> оо) ею
можно пренебречь. В результате имеем
г d4p
J (2тг)4г (т — р)[1 — Z/(m)]
/|-ОС
А
Раньше у нас была нормировка йи = 2т, а сейчас появились спиноры
и' = Z^u , и' = Zpii. (4-19)
где
Zz = , (4.20)
1 — 2J(m)
4.1. Высшие приближения. Перенормировка массы электрона
203
То есть возникла перенормировка волновых функций электрона. Физи-
чески это отражает тот факт, что в настоящем случае система состоит
не из одного электрона, а содержит еще и фотоны, а также пары, т. е.
картинка такая:
И волновая функция всей системы имеет вид:
Ффиз = + Ф<7 + + Ф + • • • + Фе+е-е- + • • • •
Так что если общая нормировка функций выбрана единичной, то норма
Фе уже не равна единице, а представляет собой “долю” одноэлектрон-
ного состояния в возникающем многочастичном состоянии. Однако на
наблюдаемых величинах нормировка волновых функций сказываться
не должна. В нашем случае такой величиной является сечение, в него
входит поток начальных частиц и фазовый объем конечных. В них мы
обязаны включить возникающий нормировочный множитель.
В дальнейшем мы будем поступать так: один корень \fZ^, отнесем
к потоку или фазовому объему и будем их вычислять как обычно, дру-
гой корень \/~Z^ отнесем к амплитуде, а волновые функции нормируем
как прежде. То есть на каждый вход (или выход) свободной электрон-
ной линии припишем множитель \//ф:
Итак, в результате суммирования диаграмм возникла перенорми-
ровка массы электрона и амплитуды.
204
Глава 4. Перенормировки. Радиационные поправки
4.2 Перенормировка функции Грина
фотона
Посмотрим, что произойдет с фотонной функцией Грина в результа-
те всевозможных процессов. Обозначим точную функцию Грина фото-
на графически следующим образом: ====, тогда
Если в результате суммирования всех диаграмм возникнет пере-
нормировка массы фотона, то он перестанет быть фотоном, т. е. наша
теория приведет к неверному результату. Посмотрим, так ли это.
Аналогично собственной энергии электрона Е(р), введем для фо-
тона сумму всех диаграмм, которые не делятся однофотонной линией:
(4-21)
Эту сумму называют поляризационным оператором фотона. Тогда
= = = = = = ==-+ —о— т О “О— + • • •
(4.22)
или
D^(k) = D°„(k) + Р°м,(А:)Пмщ,Р° ДА:) +
Заметим, что
D^k) = D0^k)+D0^(k^liylD^k\ (4.23)
Подставляя = g^/k2, получим
= g^v +
ИЛИ
[к25^ - nilvl{k')\Dvlv = g^.
(4.24)
4.2. Перенормировка функции Грина фотона
205
II,,,, — тензор второго ранга, зависящий от к^, поэтому его можно пред-
ставить в виде
ПЩА:) = g^aitk2) + k^a^k2). (4.25)
Аналогично для D^y.
= g/J,vd1(k2') + kllkvd2(k2). (4.26)
Подставляя (4.25) в (4.24), получим
[к2 - a^k^D^h) - к^к»,Dv^a2(k2') = д^ (4.27)
и окончательно
[к2 - аУк2)ЦУк2)д^ + [к2 - a1(k2)]ktJ,kvd2(k2)-
- [k^kvdyk2)a2{k2)+ k2d2(k2')a2(k2')kllkv\= g^v. (4.28)
Приравнивая в (4.28) множители перед 5^ справа и слева, получим
[fc2 — ai(fc2)]di(fc2) = 1,
т. е.
dl(fc2) = А2-(ц(А2)' (4’29)
Аналогично,
, /,2\ _ ___________________________а2__________
21 ' (к2 - ai)(fc2 - «1 - к2а2ф
Благодаря сохранению тока член в D^,,. пропорциональный к^ки, вкла-
дов в реальные амплитуды не дает, и пока мы его оставим. Сосредото-
чимся поэтому на части DIIiy. пропорциональной д^:1
D
t
____________
к2 — ai(k2) ’
(4.30)
1 Обычно (4.26) переписывают в виде
/ к к \ ~
D^(k) = g^di(k2) + k^kud2(k2) = di(fe2) -----------+ d2(k2)k^ki
\ kz )
где
J2 = ±______1_______.
fc2 k2 — ai — k2a2
Поперечной частью функции Грина называют обычно d\ (_k2)(g^u — k^ku/к2). Она об-
ращается в нуль при умножении на к^, так как к^д/ли — kp,kv/к2} = 0. Обсуждаемая
нами функция d-\_(k2) как раз и входит в поперечную часть функции Грина.
206
Глава 4. Перенормировки. Радиационные поправки
Если предположим, что D* имеет полюс при к2 0, то получим
теорию, не имеющую отношения к электродинамике. Это означает, что
вид (4.30) для накладывает ограничения на вид ai(fc2), а следова-
тельно, и на поляризационный оператор ЩДА:). Попытаемся выяснить,
удовлетворяет ли ПМ1/(&) этим требованиям (т. е. не получится ли по-
люс при А:2 ф 0).
В силу сохранения тока, для амплитуды любого процесса име-
ем
= 0. (4.31)
Причем в (4.31) мы не предполагали к2 = 0, т. е. гипотеза сохранения
тока справедлива и для процессов с виртуальными фотонами. А тогда
для ПдгУ, поскольку он представляет амплитуду такого процесса
П,
можно написать
/щПМ!, = 0, (4.32)
или, подставляя (4.25),
к^д^а^к2) + к^к^к^сьцк2) = 0.
Отсюда следует, что
ai(fc2) = —fc2a2(A:2) , (4.33)
т. е. поляризационный оператор можно написать в виде
M) = (s^fc2 - fcMfc,)n(fc2), (4.34)
где
оДА:2) = fc2n(fc2).
Если при к2 —> 0 функция П(/г2) конечна, то ai(fc2) ~ к2, полюс f)/iv
остается в нуле и теория внутренне согласована. Проверим, что П(/г2)
в бесконечность при к2 —» 0 не обращается. Для этой цели достаточ-
но проверить, удовлетворяет ли П//;/ сохранению тока. Первый член в
разложении П;ш таков:
4.2. Перенормировка функции Грина фотона
207
т. е.
ттШ 2 f d4P с ( 1 1 А
6 J (2^4SpV^m-p^m-p + +kp
fcM>) = -e21 (^Sp G^7"m_p + +fc)- (4’35)
Представляя k = k + m — p — m + p, получим
поскольку заменой p — k = p' подынтегральное выражение сводится к
1
1
—z=0.
(Заметим, что каждый из интегралов расходится, как J (Гр/р2.) Анало-
гично все можно проделать и для высших порядков.
Таким образом, мы получили, что масса фотона не перенормиру-
ется, и это следствие сохранения тока.
Итак, функция Грина фотона имеет вид:
9цу
Г)"1' fc2[l-n(fc2)]’
(4.36)
Как и для электрона, можно ввести величину:
= П№Ц-Щ0)
v ’ 1-П(0)
которая обращается в нуль при к2 = 0, и записать функцию Грина в
форме:
— ____Zyp,,,___ = Г)С (к2\
к2[1 — Пс(к2)] ~ h
мы ввели перенормированную функцию Грина
где Z3 = 1/[1 - П(0)] и
фотона D(jp(fc2).
При вычислении
амплитуд, как и в случае электронов, возник-
нет перенормировка волновых функций фотона, т. е. множитель y/~Z/.
Как и раньше, один корень \[Z$ мы отнесем к потоку, а один — к ам-
плитуде, т. е. на каждую внешнюю фотонную линию будем добавлять
множитель а нормировку оставим прежнюю.
208
Глава 4. Перенормировки. Радиационные поправки
Таким образом, мы можем дать рецепт построения произвольных
амплитуд рассеяния, например, для процесса
Нужно нарисовать всевозможные фейнмановские диаграммы и сопо-
ставить:
Go = ------ внутренней электронной линии -----------,
то — р
D0^ = внутренней фотонной линии----------_----,
/с
для наружных линий:
и(р)е~грх y/Z^ начальному электрону,
и(р)е’рх конечному электрону,
соответственно,
в(р)е~грх -\/Z2 начальному позитрону,
у(р')егрх конечному позитрону,
е^е~гкхначальному фотону,
е^егкх конечному фотону,
причем для внешних линий р2 = m2, fc2 = 0.
4.2. Перенормировка функции Грина фотона
209
Все полученные выражения должны быть антисимметризованы
по внешним электронных линиям, т. е.
и симметризованы по внешним фотонным линиям. Внутри у нас пока
стоят “голые” электронные линии, т. е. Go и D0^/, ясно, что на самом
деле и внутри возможны процессы
и т. д.
Сумма всех таких диаграмм даст внутри точные функции Грина,
т. е. внутренним линиям нужно будет сопоставлять не “голые”, а точные
функции Грина. Мы уже знаем некоторые их свойства, а именно:
где
G(p) (4.37)
W m-p + Sc(p)’
(4.38)
fc2[l-nc(fc2)]’
Т(р) — T(m) — (р — (4.39)
1 - S'(m)
2 _ II(fc2) - П(0) с( к)~ 1-11(0) ’ (4.40)
т. е. точные функции Грина (4.37), (4.38) похожи на свободные.
210
Глава 4. Перенормировки. Радиационные поправки
4.3 Перенормировка вершинной части
В предыдущем разделе мы рассмотрели функции Грина электрона и
фотона с учетом высших приближений. Теперь рассмотрим, что про-
изойдет с амплитудой испускания фотона (т. е. с вершинной частью).
Итак, простейший процесс — это
Pi
Также возможны следующие:
Однако такие поправки мы уже рассмотрели при вычислении функ-
ций Грина. Введем поэтому величину l;,(pi, р?), которая не содержит
поправок к внешним линиям:
Из (4.41) видно, что величина амплитуды тоже изменяется за счет все-
возможных процессов высшего порядка. К чему это приведет в реаль-
ных физических процессах?
4.3. Перенормировка вершинной части
211
Мы рассматривали рассеяние электрона на электроне
е7^
q
При малых переданных импульсах q мы получили обычное кулоновское
рассеяние, поэтому величину е мы назвали зарядом. Однако реально в
вершине происходят всевозможные процессы, так что е не является на-
блюдаемым зарядом, а первым к нему приближением. Наблюдаемый
заряд проявляется на эксперименте при учете всех процессов, происхо-
дящих в вершине, и с ним, вообще говоря, тоже необходимо проделать
процедуру перенормировки, как и с массой.
Напишем Гм(р1,р2) в виде
ГМ(Р1,Р2) = 7д + ЛДр1,р2), (4.42)
где
Для покоящейся частицы при q = 0 можно написать
ГДгщт) = + ЛДгщт),
(4.43)
причем единственный вариант — это
ЛДт, т) = 7мЛ(пг, т),
(4.44)
поскольку никакого другого вектора нет. Тогда
ГДт, т) = 7М[1 + А(т,т)] = yflZ1 х.
(4.45)
212
Глава 4. Перенормировки. Радиационные поправки
(4.46)
(4.47)
(4.48)
Здесь Zt! — это множитель, на который изменяется амплитуда при
нулевом переданном импульсе в результате всевозможных процессов,
происходящих в вершине. Таким образом, можно написать
Гд(Р1,Р2) = 7м +7мЛ(т,т) + Лм(р1,р2) - ЛДтщт) =
7-1 Г Лм(р1,р2) - Лм(т,т)~
1 1+Л(т,7п) ’
или
Гд = ,
где мы обозначили
+ Л-С,
Ас _ Лм(р1,р2) ~ ЛДтщт)
м z-i
(при малых переданных импульсах имеем просто Г;, = Z~' ).
Вернемся теперь к рассеянию электронов. Простейшую диаграм-
му можно нарисовать так:
Здесь _ ----------. Дальнейшее усложнение будет
происходить следующим образом: войдут диаграммы
Рис. 26
4.3. Перенормировка вершинной части
213
Видно, что как бы мы ни усложняли диаграммы, в них нигде не войдут
ни затравочный (“голый”) заряд, ни “голые” функции Грина, а всюду
будут входить точные функции Грина и реальный заряд. Ясно также,
что нет смысла рисовать диаграммы типа
так как они уже учтены в функциях Грина. Диаграммы, подобные при-
веденным выше, называются скелетными.
Выделим из G(p) и соответственно, множители Z3 и Z3,
аналогично (4.46), т. е.
G(p) = Z2Gc(p), (4.49)
= Z3D^(k). (4.50)
Посмотрим, что произойдет при подстановке этих функций в диаграм-
му. Электронные линии всегда выходят из некоторой вершины и окан-
чиваются вершиной, аналогично и фотонные, поэтому удобно разбить
множители Z2, Z3 в (4.49), (4.50) на ДДз-ДД) и ДД)-л/Д? и каждый ко-
рень отнести к входу и выходу линии. Тогда в любой вершине появится
множитель
eZx 1Z2 фЖ).
поскольку в каждой вершине сходятся две электронные и одна фотон-
ная линия. (Прежде у нас в вершину входил заряд.) Если теперь назо-
вем зарядом величину
ес — eZx xZ2y/Z3,
(4.51)
то все Z исчезнут и все будет как раньше, только вместо “голого” заря-
да е в каждую вершину войдет перенормированный заряд ес.
Выясним смысл перенормированного заряда. Рассмотрим снова
рассеяние электронов на малые углы:
214
Глава 4. Перенормировки. Радиационные поправки
Как и раньше, от этой диаграммы возникнет полюс, так как
От остальных диаграмм полюсов не будет, поскольку в них войдет инте-
грирование по промежуточным импульсам, так что при малых передан-
ных импульсах основной вклад в амплитуду определится именно этой
диаграммой:
А = (eZf1 (4.52)
А это и есть амплитуда кулоновского рассеяния, причем ес и являет-
ся физическим зарядом, т. е. именно = 4тг/137. Таким образом, мы
получили, что за счет процессов высшего порядка возникает перенор-
мировка массы и заряда свободной частицы.
Рассмотрим формулу
ес = eZ1 1 Z-2\/~Z3
с несколько иной точки зрения. Введем несколько сортов частиц, на-
пример, е, д, р (электрон, мюон, протон), т. е.
G& е
Gp, д
GP р
Соответственно, вершины пусть будут Ге, Г/;, Гр. Эти величины, вообще
говоря, различны, поскольку совсем необязательно, что все интегралы,
4.3. Перенормировка вершинной части
215
куда входят функции Грина частиц с разными массами, дадут одина-
ковый результат. А как наличие существенно разных частиц скажется
на функции Грина фотона? Мы имели
--------=-----------+
Но если имеются и другие частицы, ничто не мешает произойти и таким
процессам
и т. д., т. е. в фотонную функцию Грина дадут вклад все заряженные
частицы, какие есть на свете. С этой точки зрения, она является ве-
личиной универсальной, тогда как функции Грина остальных частиц
зависят от рода частиц.
Обсудим теперь следующий вопрос. Предположим, что затравоч-
ные заряды электрона и протона одинаковы, тогда в результате взаи-
модействия получим
есе = Z1/Z2e\/Zse,
еср = Z1pZ2Py/~Z3e, (4.53)
т. е. перенормированные заряды электрона и протона, вообще говоря,
разные. Отсюда мы получили бы, например, что атом водорода (е~р) в
результате электромагнитного взаимодействия приобретает ненулевой
заряд. Это противоречит закону сохранения заряда — электромагнит-
ное взаимодействие не должно изменять заряд. Чтобы этого не проис-
ходило, должно выполняться универсальное соотношение, справедливое
для всех частиц —
Zi = Z2. (4.54)
Тогда Zi и зависящие от природы частиц, выпадают из соотноше-
ний (4.53). Докажем, что соотношение (4.54) действительно выполняет-
ся в электродинамике.
216
Глава 4. Перенормировки. Радиационные поправки
4.4 Обобщенное тождество Уорда
Мы видели, что для реальных частиц
кцГ^рцрз') = О,
(4.55)
где к1_1=р1-р2
к
В общем случае (включающем и виртуальные частицы) имеет место
тождество (обобщенное тождество Уорда)
fcMrM(pi,p2) = G '(щ j - G' '(р2). (4.56)
Покажем, что при выполнении (4.56) имеет место = Z2. а потом
докажем это тождество.
Рассмотрим (4.56) при нулевых переданных импульсах. При этом
слева останется а справа от каждой функции Грина —
G,G = т — р, т. е.
к^ = Z^[-p2 +pi] = Z2":k = Z2'I:.
откуда непосредственно следует, что Z\ = Z2.
А теперь докажем тождество Уорда (4.56). Для простейшей диа-
граммы
4.4. Обобщенное тождество Уорда
217
имеем
Go Х(р) = то ~Р,
так что, очевидно,
=Р1-Р2
и ясно, что для реальных частиц к^д^ = 0, так как pi = р2 = tn- Для
следующей диаграммы имеем
При вычислении вклада этой диаграммы в величину /.рГм в числителе
появится а это можно расписать в виде
к^Др. = k=pi-p2 = (т0 - р2 + к') - (т0 - pi + к'),
218
Глава 4. Перенормировки. Радиационные поправки
так что
В выражении для к^Л.^ сначала сократился пропагатор электрона с
импульсом р2 — к', а во втором слагаемом — с импульсом р\ — к'. Ре-
зультат есть не что иное, как
т. е.
к^ =£И(й)-£(1)(М (4.57)
Аналогичные выражения получаются и в высших приближениях, их
суммирование дает в точности (4.56).
При переходе к нулевым переданным импульсам обобщенное тож-
дество Уорда можно переписать в следующем виде:
fcMrM(pi,p2) =
яр-1 » дС-1
= G-1(p2) + G-1(P2 + к) =-—— к = - ,
Эр2 Эр2
т. е. при малых передачах импульса
г / \ Ж-1
ЬМ =--------
Но так как
др
дрц,
ТО
ГмДр) = (4-58)
4.5. Радиационные поправки к рассеянию...
219
Подведем итоги. Мы видим, что квантовую электродинамику нам
удается построить так, что в нее входят только наблюдаемые — пере-
нормированный заряд и функции Грина. Дальнейшие трудности свя-
заны с вычислением D, G, Гм. В низших приближениях, однако, все
вычисляется довольно просто. Мы рассмотрим простейшие радиацион-
ные поправки в следующих разделах.
4.5 Радиационные поправки к рассеянию
электронов во внешнем поле
Как мы уже отмечали, рассеяние электронов внешним полем есть рас-
сеяние на тяжелом объекте. Амплитуда такого процесса имеет вид:
Р1 Р2
-------1-----
।
। = ей(р2)7мм(Р1)Ам(д), (4.59)
где
р
(4-б°)
Д, — фурье-компонента макроскопического тока тяжелой частицы.
Что произойдет, если учтем процессы высших порядков? Во-пер-
вых, изменится вершина и на каждую электронную линию добавится
множитель т. е.
= ew(p2)r^(p2,Pi)w(pi)AM(q), (4.61)
где Г/; = хГс. Во-вторых, изменится внешнее поле, т. е. A^q). Дей-
ствительно, (4.60) имеет вид:
ЛДя) = е.О°Дф)Д,(ф),
а следовательно, с учетом высших приближений,
(4.62)
220
Глава 4. Перенормировки. Радиационные поправки
Поле изменяется за счет всевозможных процессов с образованием пар,
например,
О
I
I
' и т.д.
Окончательно амплитуда рассеяния принимает вид:
F = есм(р2)Д(р2,Р1)м(Р1)1 _nc(g2)A°(g) ’ (4-63)
здесь мы обозначили
W (4-64)
Таким образом, изменение амплитуды обусловлено двумя эффек-
тами: перенормировкой взаимодействия и изменением внешнего поля
в результате виртуального рождения электрон-позитронных пар. Знак
изменения поля легко определить из физических соображений. Пусть,
например, тяжелая частица обладает положительным зарядом. Тогда
при рождении в поле этой частицы электрон-позитронной пары пози-
трон отталкивается и уходит на большое расстояние, а частица оказы-
вается окруженной отрицательными зарядами, и наблюдаемый заряд
этой частицы должен уменьшиться.
• е+
е
О
Этот эффект называется поляризацией вакуума. Фактически он ана-
логичен поляризации диэлектрика, где роль электрон-позитронных пар
играют молекулярные диполи.
4.5. Радиационные поправки к рассеянию...
221
Физический и голый заряды связаны:
е2с = Z3e20
(напомним, что в соответствии с тождеством Уорда: Z\ = Z^). Поэтому
ясно, что Z3 < 1. Таким образом, заряд электрона как бы экранирован,
и именно этот экранированный заряд есть
е
2
4тг
137’
наблюдаемая величина на макроскопических расстояниях от электрона.
А если мы пойдем далеко вглубь, т. е. на очень малые расстояния к
электрону, то измерим затравочный заряд, который больше, чем 4тг/137.
Это означает, что
Пс(д2) > 0, Пс(0) = О,
т. е. взаимодействие растет при больших переданных импульсах, соот-
ветствующих малым расстояниям:
9 I |9
е0 ~ _ nc(g2) ПРИ М
Как мы видим, поправки к рассеянию электрона во внешнем поле
возникают благодаря двум эффектам — поляризации вакуума и поправ-
кам к вершине. Теперь вычислим вклад от обоих эффектов в амплитуду
рассеяния электрона внешним полем в первом порядке по е2. Начнем с
поляризации вакуума:
тт ПА 2 [ d4p с ( 1 1
Щр(А: =-е / .. Sp ;т
J (2тг)4г \ т—р m-p + k
(4.65)
222
Глава 4. Перенормировки. Радиационные поправки
Этому выражению соответствует диаграмма
Однако вклад в поляризационный оператор фотона дадут все частицы,
например, мюоны:
Эта диаграмма вычисляется аналогично (4.65). Однако для протонов
уже не ясно, как вычислять такой процесс:
поскольку протоны участвуют еще и в сильных взаимодействиях. Но мы
покажем, что вклад этих диаграмм ~ к2/т2, и поэтому при не слишком
больших энергиях даже мюоны дают малый вклад. При дальнейшем
увеличении энергии начинают сказываться сильные взаимодействия.
Тщательная проверка радиационных поправок при не очень высоких
энергиях гарантирует, что нет необнаруженных легких частиц.
Итак, перейдем к вычислению (4.65). Представим Пм„ в виде
ПМ!у = (рмД2 - к/1к„)П(к2)
И вычислим
SpnM„ = П;1;, = 3/с2П(А;2). (4.66)
4.5. Радиационные поправки к рассеянию...
223
С другой стороны,
П;,;, = 3/c2II(fc2) =-е2 f ^4.Sp(7i7(m+p)7i7(m+p-fc)) х
J (Z7T) I
(m2 — p2)(m2 — (р — А:)2)'
Пользуясь соотношениями
7^7^ = 4,
7^7^ = “2р,
получим
Sp(7iXm + Р)7^ (т + Р — fc)) = Sp[(4m — 2p)(m + р — k) =
= 16m2 — 8p(p — k). (4.68)
Здесь мы использовали то, что след произведения нечетного числа
7-матриц равен нулю, а
8р7м7^ = 4<V-
Интеграл (4.67) является расходящимся. Однако нас интересует не сама
величина П(А:2), а разность
nC(fc2) = n(fc22 - П(0) ~ n(fe2) _ п(0) (4 б9)
Она окажется сходящейся величиной.
Вычислим в (4.67) интеграл по dpo- От первого знаменателя в (4.67)
имеем полюса
Pi 2 = ±\/т2 + р2 — ie,
от второго —
Рз,4 = fco ± \/т2 + (р- k)2 - ie.
Рассмотрим область пространственноподобных к, т. е. к2 < О,
тогда можно найти систему отсчета, где ко = 0. Полюса при этом будут
расположены симметрично относительно мнимой оси ко, тогда контур
интегрирования можно развернуть и направить вдоль мнимой оси (так
как при таком повороте контур не пересечет особенностей), см. рис. 27.
А так как в этом случае
d‘p dpod3p idp'0d3p
(2тг)4г (2тг)4г (2тг)4г
224
Глава 4. Перенормировки. Радиационные поправки
Рис. 27
Рис. 28
4.5. Радиационные поправки к рассеянию...
225
— величина вещественная, то и весь интеграл (4.67) тоже веществен,
поскольку в подынтегральное выражение входят только квадраты pg.
Итак, если рассмотрим комплексную плоскость к2, то на веще-
ственной оси в области отрицательных к2 интеграл веществен (жирная
линия на рис. 28). И, кроме того, поскольку знаменатель (4.67) на повер-
нутом контуре нигде в нуль не обращается, он не имеет особенностей.
(Чтобы интеграл (4.67) не расходился при больших р2, можно ограни-
чить интегрирование сверху некоторым параметром обрезания Л, об
этом поговорим позднее.) Выясним, где интеграл (4.67) может стать
комплексным.
Рис. 29
Если в плоскости к2 пойти в область времениподобных к, т. е.
к2 > 0, то полюса р°, р° начнут двигаться в плоскости р0, и при р° = />!
либо при Рз = р§ полюса зажмут контур (рис. 29), так что его невозмож-
но будет деформировать, чтобы обойти полюс, не пересекая при этом
другого полюса. То есть при некотором ко подынтегральное выражение
на контуре интегрирования обращается в бесконечность, а это означа-
ет, что в этой точке интеграл (4.67) имеет особенность и может стать
комплексным. Определим ко из условия р° = р?:
ко — у/m2 + (р — к)2 = у/m2 + р2,
к0 = у/m2 + (р — к)2 + у/m2 + р2. (4.70)
226
Глава 4. Перенормировки. Радиационные поправки
То есть мнимость возникает при достаточно большом kg, когда реально
могут родиться две частицы с энергиями
\/ т2 + р2
и у/ т2 + (р — к)2,
соответственно
Есть и другая возможность:
fc0 = - у/™2 + Р2 ~ к)2;
(4.71)
этот случай неинтересен, так как соответствует отрицательным энерги-
ям фотона. Запись (4.70) релятивистски неинвариантна. Чтобы запи-
сать это выражение в инвариантном виде, перейдем сначала в систему
отсчета, где к = 0 (это можно сделать в силу к2 > 0 ), тогда
&о = к2 = 4(т2 + р2),
т. е. особенности возникают при
к2 > 4т2. (4.72)
На плоскости к2 проведем разрез от точки 4m2 вдоль вещественной оси
(рис. 30).
4m2
Рис. 30
4.5. Радиационные поправки к рассеянию...
227
Ясно, что больше никаких особенностей в комплексной плоскости инте-
грал не имеет. Пользуясь же аналитичностью интеграла (4.67), можем
сразу написать дисперсионный интеграл для Пс(/г2):
П'
dfc/2Imnc(fc/2)
к'2 - к2
(4.73)
Если он расходится, мы его можем улучшить, вычитая Пс(0) = 0, тогда
Пс(/г2) = | f Л/21шПс(А/2)
1 1
Д./2 _ Д.2 Д./2
(4.74)
А поскольку мнимость возникает при к2 > 4т2, то
п-дД = О I
4m2
dfc/2Imnc(fc/2)
к,2(к,2-к2) ’
(4-75)
Теперь вычислим мнимую часть 1тПс. Как мы видели, Im{3fc2n(fc2)}
возникает из-за пересечения контуром интегрирования С при его де-
формации полюса (рис. 31).
Рис. 31
228
Глава 4. Перенормировки. Радиационные поправки
Такой контур можно разбить на две части: С\ и С% (рис. 32):
причем интеграл по C*i — вещественный. Мнимая часть появится только
от интегрирования по С*2, а этот интеграл сводится к вычету в точке р%.
Итак, полюсной вклад в 3/с2П(А:2) равен
_е2 f _^Р__________________1_______________g
J (2тг)3 (т2 _ р2 _ ie^2(ko — ^/m2 + (р — к)2)
Но
—5---5----- = Р—5---л + iir8(m2 - р2),
ш- — — гг ггР — р-
т. е. вклад в мнимую часть дает только полюсной член (с 5-функцией).
Таким образом,
ЗЙ„,П«Д = -Л [ «г(). (4.76)
’ J (27г)3 2(£0-yW + tP-k)2) U
или, используя, как обычно, соотношение
—- = d4p0(po)<5(m2 — р2) = d4p6+(m2 — р2),
%Ро
4.5. Радиационные поправки к рассеянию...
229
окончательно получим
3/г21тП(/г2) =
= —е2тгУ -p2)5+(m2 - (р - fc)2)Sp(). (4.77)
Мы получили мнимую часть, совпадающую с той, которая выте-
кает из условия унитарности, т. е. дается диаграммой
где в промежутке реальные частицы. То есть снова подтвердили тот
факт, что фейнмановские диаграммы автоматически удовлетворяют
условию унитарности.
Раскрывая при помощи (4.68) выражение для SpQ, получим
из (4.77):
3/г21тП(/г2) = —е2 [ —^[16т2 — 8р2 + 8рк]5(т2 — р2')6+(т2 — (р — к)2),
J 8тг2
(4.78)
но из 5-функций следует, что
р2 = т2, т2 — (р — к)2 = 2рк — к2 = 0, 2рк = к2.
Отсюда
ImII(fc2) = - е2 8W ?~24fc [ ~ m2)5+((p - к)2 - т2). (4.79)
Огъ J о7Г
Для вычисления этого интеграла удобно перейти в систему, где к = О,
тогда (р — к)2 — т2 = —2роко + к2 и
У |^5(p2-m2)5+(A:2-2pofco) = У |^5(pg - р2 - т2)^- = - (4-80)
(здесь ро = к2/2кц = ко/2; переходя к сферической системе координат,
имеем cl3p = p2dp х 4тг = 2xpdp2. так что равенство можно продолжить
так)
1 1 О П 2
= —о——2'Kynf. — т2
8тг2 2к0 V
1 1 у/к$ — 4т2
8тг ко 2
1 /к2 — 4т2
16тг V к2
(4-81)
230
Глава 4. Перенормировки. Радиационные поправки
Таким образом,
1тП(А2) = -
е2 8т2 + 4А2
16тг ЗА:2
— 4т2
~к2
е2 2т2 + к2 I к2 — 4т2
4тг ЗА2 V к2
Окончательно,
т т-г/,9ч a А 2т2\ I 4т2
1тП(А2) = -Д1 + -^^/1--^.
(4.82)
Заметим, что в силу (4.69) 1тП(А2) = 1тПс(А2) с точностью до коэф-
фициента. Таким образом,
ак2 А00 <7/Ф -Д — 4т2/к2 к 2т2
Зтг Jim2 к2 (к2 — к2) \ + к2
(4.83)
Вычислим (4.83) в двух предельных случаях А2- 0 и А2- оо. В первом
случае (А2 0), проведя замену х = 4т/к2, получим
ПС(А2) = -
ак2
Зтг4т2
Ji + Д = - afc2
Уо V к 2> 15тг7п2 ’
(4.84)
т. е., как и следовало ожидать, ПС(А2) ~ к2 при к2 0.
Во втором случае (А2 оо) при к2 С А2 интеграл логарифмиче-
ски растет с А2, т. е. именно эта область и дает основной вклад, поэтому
можно написать
а Гк <4к2 а А2
Зтг Jim2 к2 Зя т2
(4.85)
(в (4.85) мы пренебрегли In 4 по сравнению с 1нА2/т2). Логарифм, во-
шедший в (4.85), фактически является главной проблемой квантовой
электродинамики. Например, в амплитуду рассеяния электрона внеш-
ним полем он входит следующим образом:
1 —ПС(А2) 1_^1пА1’
' Зтг пт/
т. е. амплитуда может иметь полюс, физический смысл которого неясен,
и это реальная трудность для нашей теории.
4.5. Радиационные поправки к рассеянию...
231
Пока мы оставим этот вопрос и посмотрим на вклад поляризации
вакуума в амплитуду (4.63) с несколько иной точки зрения, а именно:
амплитуда имеет вид:
F = есй(р2)Г))(р2,р1)ц(р1)1 _ дс^2^°(9),
9
но при малых q
1-Пс(д2) ~ 1 + ГГ^2);
учитывая, что
= + А-М’
получим
F « ecu^)^^ + nc(Q2)) + Лур2,Р1)МР1)А°(9). (4.86)
Все члены в квадратных скобках здесь пропорциональны и отличие
множителя перед в (4.86) связано со вкладом поляризации вакуума.
Ненулевой вклад вершинной части — выражает как бы неточечность
заряда; действительно, для неточечных частиц формфактор имеет вид:
9 9
F(9) = l + ^°,
где го — средний радиус распределения заряда.
Теперь займемся вычислением Лм в первом порядке:
।
।
9 f d4k 1 1 1 /л
М= Л = еЛ -----1—(4-87)
J (2тг)4г m_p2Jr jt т __|_ /j к
' к \
Pl Р2
У = Лм - Лм(т,т). (4.88)
Из соображений релятивистской инвариантности, как мы уже говорили,
можно написать
ЦР2)Лур2,р1)м(р1) = w(p2)[ayM + ba^q^utpi).
(4.89)
232
Глава 4. Перенормировки. Радиационные поправки
Мы также писали
Гм = + ba^qv,
где a = a(g2), b = b(q2), величину й(0) мы назвали зарядом.
Для величины же a(q2) имеем в силу (4.89)
ДО) д о,
но и 6(0 j может быть отличной от нуля. Мы показали, что в случае b = О,
электрон обладает магнитным моментом, равным магнетону Бора. Ес-
ли же b Д 0, то это означает наличие у электрона дополнительного мо-
мента, называемого аномальным магнитным моментом. Из вида (4.87)
ясно, что особых оснований полагать 6(0) = 0 нет, что подтверждается
и непосредственным вычислением интеграла.
Таким образом, хотя мы начали строить теорию, исходя из про-
стейшего взаимодействия a(q2) = const = е и 6(Д) = 0, при учете
высших приближений появляется и формфактор (зависимость й(Д))
и аномальный магнитный момент. Это легко понять из физических со-
ображений. Рассмотрим процесс
।
।
।
।
д
Он означает, что даже если электрон покоился в некоторый момент
времени, то, испустив фотон, он приобретает импульс, и внешнее поле
взаимодействует уже с током:
Естественно, из-за этого возникает магнитный момент. Кроме того, по-
явится некоторый формфактор, поскольку заряд эффективно распре-
4.5. Радиационные поправки к рассеянию...
233
делится по области го ~ 1/т:
Впервые вычисление магнитного момента провел Швингер в 1949 г. и
получил выражение
М = Мо (1 + —) • (4.90)
\ 2тг/
Приведем примерный путь вычисления фейнмановским методом.
В первом порядке по е1 2 для Л;, имеем
= Л = 2 [ 7^ (т+Р2~ (m + Pi - к'Уд
/ \ вс J (2тг)4г [т2 — (р2 — /г)2] [т2 — (pi — к)2]к2 '
/л\
Pl Р2
(4-91)
Для вычисления такого интеграла Фейнман пользуется тождеством
1
1 1 [ dct^dcczdotd(од -Н (Т2 аз — 1) 92)
abc 3! J acui + Ьод + сод)3
о
В нашем случае
1 _ 1
abc [т2 — (р2 — k)2][m2 — (pi — k)2]k2
1 f daxdot^da^d^yyoti — У
3! J {&зк2 + cn2[(p2 — к)2 — m2] + ai[(pi — к)2 — m2]}3 '
Из-за 5-функции од = 1 — ад — ад, тогда
1 If da\da2da2,5(^ai — X)
abc 3! j [к2 — 2fc(aipi + агРг)]3
234
Глава 4. Перенормировки. Радиационные поправки
Сделаем замену
k' = к — a-ppi - a2p2,
при этом
к[к - 2(адр1 + а2р2)] = (к' + аррз + a2p2')[k' - (одрз + a2p2)] ,
т. е.
1 If da±da2da35(^2ai — 1)
abc 3! J [к'2 - (oipi + a2p2)2]3 '
Таким образом, для Лм будем иметь
(4.93)
Лм = — / da^la2da35(y^ai
yv[m + (1 - a2)p2 - аррз - k'Y^m + (1 - ajpi - a2p2 - k']^
[к'2 — (ад + a2)2m2 + aia2q2]3
(4.94)
Здесь учтено, что q2 = (pi — p2)2 = 2m2 — 2ppp2. Числитель подынте-
грального выражения (с учетом того, что члены, линейные по к', вкла-
да в интеграл не дадут в силу их антисимметрии) можно представить
в виде:
/i(q2, од,а2)ум + /г(<?2, ад, ад.) + к 2ум. (4.95)
Теперь интегрирование по d4k' сводится к вычислению двух интегралов:
f d4kr 1
J (2л)4г (к'2 — А)3
и
Г d4k' к'2
J (2л)4г (fc'2 — А)3
(4.96)
(4.97)
В них всегда можно развернуть контур интегрирования по dk'o вдоль
4.5. Радиационные поправки к рассеянию...
235
мнимой оси, так как при этом он не пересечет особенностей:
При этом
k'o = ik'4 и к 2 = к02 — к/2 = — к2 — к/2,
т. е. получатся интегралы по евклидову пространству. Переходя к сфе-
рическим координатам и интегрируя по углам, получим
d4k' = тг2 к 2dk 2,
т. е. будем иметь
Г d4k' 1 _ Г K2k'2dk'2
1 ~ ~ J (2^)4 (fc'2 + Д)з - j (2тг)4(А/2 + Д)3 ’
аналогично,
Г 7T2k,4dk'2 f ?T2x2dx
2 У (2тг)4(А:/2 + А)3 У (2тг)4(х + Д)3
о
Первый интеграл равен
/Tv2xdx 1
(2тг)4(х + А)з
16тг2Д
о
236
Глава 4. Перенормировки. Радиационные поправки
Второй —
т. е. при больших к'2 он логарифмически расходится. Эта расходимость
убирается перенормировкой, т. е. вычитанием ЛДт, т), поскольку эта
величина содержит точно такой же логарифм 1н(у/Д(ц = 0)). Одна-
ко непосредственно из вида (4.91) вытекает логарифмическая расходи-
мость интеграла и при малых к , если = т и р% = т , т. е. для
реальных электронов.
Действительно, знаменатель (4.91) в этом случае имеет вид:
[т2 — (р2 — k')2][m2 — (pi — fc)2]fc2 ~ 2p2fc • 2pifcfc2,
и при малых к2 опять возникает J d^k/k^.
С такой ситуацией мы уже сталкивались при рассмотрении тор-
мозного излучения.
, 9 dw
da е —
На самом деле, эта расходимость связана с некорректной поста-
новкой задачи, поскольку при достаточно малых ш параметр разложе-
ния не мал и теория возмущений неприменима. С другой стороны, в
любом эксперименте, как только родилась частица, образовались и фо-
тоны. Реально создать частицу без фотонов нельзя, так как достаточно
сколь угодно малого воздействия на частицу, чтобы она испустила мяг-
кий фотон, и чем меньше частота фотонов, тем их больше. То есть труд-
ность связана также и с нефизичностью постановки задачи. Как можно
4.5. Радиационные поправки к рассеянию...
237
с ней справиться? Можно предположить, что начальное состояние —
это электрон и большое число фотонов, т. е.
Однако здесь тоже имеется некоторая неоднозначность, связанная с фи-
зикой рассматриваемого процесса.
Поскольку в природе нет заряженного вещества (все атомы ней-
тральны) , то число фотонов будет зависеть от способа “обдирки” атома
по существу (т. е. от конкретного способа, которым мы создали заря-
женные частицы). Таким образом, единственный физически последо-
вательный подход — исходить из нейтрального вещества и учитывать
способ образования заряженных частиц, например:
Из физических соображений ясно, что вероятность образования элек-
трона без фотонов равна нулю. Однако если вычислить по теории воз-
мущений сечение, например, такого процесса:
то получится бесконечность. Здесь, на самом деле, нужно учитывать
рождение многих фотонов. Пусть, например, две нерелятивистские ча-
238
Глава 4. Перенормировки. Радиационные поправки
стицы с противоположными зарядами е и — е и энергиями ~ е рождают-
ся с относительной скоростью v. Тогда сечение процесса с испусканием
п фотонов будет иметь такую структуру:
Отсюда сразу следует, что при - 0 вероятность испускания любого
заданного числа фотонов будет равна нулю. Однако
<тп = const.
Рассматриваемая теория применима только при фантастически малых
частотах, поскольку параметр а/тг ~ 1/500. Область частот, для кото-
рых произведение логарифма на этот параметр не мало, эксперимен-
тально недостижима. Поэтому обычно поступают иначе.
Пусть имеется процесс рассеяния. Приписывают фотону малую
массу А, при этом функция Грина фотона будет иметь вид:
1
/г2 - А2 ’
k
х х
/ \
_________I_____,____1_________
q
Для Лм тогда получим
л 1 т
Af, -7м1пу.
А поскольку реально измеряется всегда сечение, то запишем
da = das + da^,
где daa — сечение упругого рассеяния, drp — сечение неупругих про-
цессов с рождением фотонов, например:
4.6. Уравнение Дирака во внешнем поле
239
Так как всегда имеются нерегистрируемые фотоны с w < штгП, где
лт/п определяется условиями эксперимента, чувствительностью прибо-
ров И Т. Д-, то
d(J — da§ Т d(T^{<jJ ^min)
In — + In-----= In------
^min ^min
и результат оказывается не зависящим от А. Интеграл же для Лм, если
ввести А, оказывается вполне определенным и при q2/т2 1 равен
а Г т 3) q2 a
(4.98)
Первый член (4.98) был вычислен Фейнманом, второй — Швингером.
Второй член как раз соответствует аномальному магнитному моменту
электрона а/2тг.
4.6 Уравнение Дирака во внешнем поле
Мы вычислили поправки первого порядка к рассеянию электронов внеш-
ним полем.
240
Глава 4. Перенормировки. Радиационные поправки
Иногда приходится вычислять много поправок более высокого порядка,
например, в случае рассеяния на ядре с большим атомным номером Z,
так как параметром разложения здесь является Za. К счастью, ситу-
ация упрощается из-за того, что все частицы, обладающие большим
зарядом Z, имеют большую массу М Д' те. Пользуясь этим обстоя-
тельством, займемся изучением взаимодействия тяжелых заряженных
частиц с электроном и попытаемся найти все поправки по Za. Итак,
процесс взаимодействия описывается всевозможными диаграммами ви-
да:
Рассмотрим пока первые три графика:
Xl X Х2 Xi х’ х" Х2 Х1 х' х" ОД
; + ; ; + л
I I I \
2/1 У 2/2 2/1 У' У" 2/2 2/1 У' у" 2/2
4.6. Уравнение Дирака во внешнем поле
241
Для функции Грина тяжелой частицы имеем (предполагая, что она об-
ладает спином 1/2)
= (4-99'
Запишем р$ в виде (пользуясь тем, что р2 <?' М2)
Ро = М + £,
где с — кинетическая энергия, тогда
/о2 \
М2 -р2 = М2 - (М + е)2 + Р2 = —2Ме + р2 = 2М ( - е \
и
_ f ded3p e~dM+e)T[M(l + у0) + ед0 - Р7]егру _
У J (2тг)4г — 2Ме — i6 + р2
= / 7^е~г^ТегРУ М(1+7о) + ^7о-Р7 =
= 0(т)е-гМ-Цр^(у). (4.100)
Мы получили естественный результат — тяжелая частица покоится в
одной точке и распространяется вперед только по времени. (Мы везде
пренебрегли членами р2 по сравнению с массой покоя.) Нижней линии
диаграммы
Х1
Х2
У1
Vi
таким образом, будет отвечать выражение
Ze У G(y2 - у)ПмС(У yi)D(x - y)d4y =
242
Глава 4. Перенормировки. Радиационные поправки
. г? х/ х 1 + 7о 1 + 7о
= гЯе5(у2 - У1)—7мх
х у dre-^-^-^-^Dtx - у)О(т2 - т)0(т - л)
= <5(У2 - У1)дмое-гМ(т2-Т1)[-м(х - ух)]1 у7°,
где
Т2
u = —iZe j drD(t — т, х — yi)@(r2 — тх).
Т1
При выводе (4.101) мы использовали то, что
1 + 7о 1 + 7о 1 + 7о 1 ~ 7о „
”^7г^ = ^----------------^7г=°’
1 + 7о 1 + 7о 1 + 7о
2 70 2 ~ 2 ’
т. е.
1 + 7о 1 + 7о _ 1 + 7о
2 7м 2 — 2
Вычислим интеграл (4.102) при тх —сю, т2 +оо. Имеем
/d^k e-ifco(t-i‘)+»k(x-yi)
—•
тогда
/Г ^4^ e-z/c0(t-T)+zk(x-yi)
dTJ Wi—— =
/л4ь p-zfeot+ik(x-yi)
(й^ fc-pp <5(fco)27r =
. Г d3k егк<х-у1) _ Ze
J (2л)3г —к2 4тг|х —yi|’
(4.101)
(4.102)
(4.103)
т. е. получили выражение, совпадающее с обычным кулоновским потен-
циалом для заряда Ze:
Ze
4тг|х - у| ’
(4.104)
4.6. Уравнение Дирака во внешнем поле
243
Зависимость от координаты электрона в (4.101) вошла только в и, так
что график можно перерисовать так:
-иЗ^о
х
Нижней линии соответствует свободная функция Грина тяжелой части-
цы (4.100), а верхней, при т± —оо, т2 оо, — амплитуда рассеяния
электрона внешним (кулоновским) полем, создаваемым частицей Ze, а
именно:
d4xG(x2 — х)(Доеи(х, уУ)С(х — ад).
Рассмотрим следующую диаграмму:
х' х" Х2
У1 у' у" У2
Нижней ее части соответствует выражение
С(У2 - y'^i^ZeGty" - y')i^vZeG(y' - ух)х
х D(x' - y')D{x" - y")d4y'd4y" =
= Wo1 70 i9i>oZed(y2 - У1)е-гМ(т2-Т1) x
x I dr'd^'D^ - т’, Д - - t", k" - y"),
причем Ti < т’ < t" < T2-
244
Глава 4. Перенормировки. Радиационные поправки
Если бы не это неравенство, интеграл разбился бы на произведе-
ния. Однако диаграмме
У2
соответствует такое же выражение, но с другими ограничениями на пе-
ременные интегрирования: т± < т" < т' < Т2- Так что сложение этих
диаграмм означает просто переход к интегрированию по всем т', т", и
в результате для суммы будем иметь
Х1 х' х" Х2 Xi х' х" Х2
+ /\ ~ С(у2-У1)[-М(х/-У1)][-М(х"-У1)].
У1 У2 У1 У2
То есть результат опять разбился на две части: свободное движение
тяжелой частицы и рассеяние электрона на кулоновском поле этой ча-
стицы; это соответствует тому, что тяжелая частица не чувствует ни
отдачи, ни изменения времени. Сумме этих диаграмм можем сопоста-
вить, как и прежде, график
У1
У2
Аналогичная ситуация возникает и в следующих порядках, т. е. полную
4.6. Уравнение Дирака во внешнем поле
245
амплитуду рассеяния на тяжелой частице можно представить в виде
= G(y2 - yi)Ge(x2,x1-y1'), (4.105)
где Ge — функция Грина электрона во внешнем поле. Будем ее изобра-
жать жирной линией, т. е.
Х1
Х2
XI
+ —
Х2 XI
(4.106)
Это не что иное, как интегральное уравнение для функции Грина элек-
трона в графическом виде, его можно переписать так:
Ge(x2,xi;yi) = G(x2 - xi)+
+ У <1^хС(х2 — ж)[ге7ои(х, yi)]Ge(a:, ад; yi). (4.107)
От интегрального уравнения легко перейти к дифференциальному, если
вспомнить, что
/ д \
( Им а----т I G(x) = -гб(х).
Подействовав на (4.107) оператором Д^д/дх^ — т, получим
----!П^ Ge(x2,x1;y1) =
= -гд(х2 - Xi) + ey0u(x2,y1)Ge(x2,x1;y1),
246
Глава 4. Перенормировки. Радиационные поправки
т. е.
д
I ---------т - e7ou 1 Ge(a;2,a:i;yi) = -г6(х2 - яд).
Как обычно, функцию Грина можно представить в виде
(4.108)
Ge(a:2,a;i;yi) = <
- (яДФпДхх), t2 < ti
(4.109)
где Фп — волновые функции электрона, удовлетворяющие уравнению
Г- д Ze2 1 т / \ а
< -----т~ 7о -Г-,------1 f Фп(ж) = 0.
I дх2/1 4тг|х —yi| J
Это есть уравнение Дирака для электрона в кулоновском поле.
Мы пока рассмотрели все поправки по Za, связанные с обменом
фотонами, и получили
etc.
и т. д.
Однако есть поправки, например, такого вида:
Т2
G(V2 - У1)
(4.110)
Л
Т2
и т. д.
4.6. Уравнение Дирака во внешнем поле
247
Ясно, что суммирование таких диаграмм одинакового порядка,
как и раньше, эквивалентно переходу к интегрированию по всем про-
межуточным временам, а следовательно, интегралы разобьются на от-
дельные сомножители.
Для второго порядка будем иметь
т'<т". (4.111)
1/2! возникает из того, что число независимых диаграмм в 2! раз меньше
числа перестановок. Аналогично, для n-го порядка
Т2
С(У2 - У1)
т' < т". (4.112)
Т1
Если все сложить, получим
т2
— Z2e2 J4 dr!dr"— т")
G(y2 ~ yi)e T1 , т' < т" . (4.113)
Переходя к новым переменным в интеграле т = т" — т', х = т" + т',
имеем
— (т2 —ri)Z2e2 J ДгГ>оо(т)
G(y2-yi)e о , т'<т". (4.114)
При т2 оо, тх —оо легко убедиться, что интеграл в показателе
экспоненты чисто мнимый:
7 Г Дк e~ikaT _ 7 1'Дке-’ кт
J dT J ~ J dT J 2|Ат|(2тг)3 '
О о
Интеграл по dr равен
7 dre~iWT =
J г\к\
О
откуда
Z2e2 J drD00(T) = -iZ2e2 [ (4.115)
248
Глава 4. Перенормировки. Радиационные поправки
Следовательно, функция Грина тяжелой частицы
С(г/2 - У1) ~ е-^+бм^-т.)
(4.116)
т. е. возникла перенормировка массы. Видно, что в нашем приближении
интеграл (4.115) для Sm расходится линейно.
Есть еще такие поправки к движению тяжелой частицы:
а также
Учет этих поправок означает, что свободную функцию Грина фотона
нужно заменить на перенормированную
-Doo(T) —
На электрон же опять ничего не повлияло.
Таким образом, задача разбилась на две части: движение элек-
трона во внешнем поле и перенормировку массы тяжелой частицы.
Из уравнений Дирака (4.109) мы можем определить энергетиче-
ский спектр электрона во внешнем поле. Для этой цели сделаем под-
становку Фп = ехр(—_ЕД)Фп(г) в уравнении (4.109). Кроме того, умно-
жим (4.109) на до и- обозначив уоТ = &, получим стационарное уравне-
ние Дирака для частицы в поле:
Еп^п = —га\7 + тд0 - -— Фп.
\ 4тгг)
(4.117)
4.6. Уравнение Дирака во внешнем поле
249
При Е > т, Е < — т имеем сплошной спектр, при |Е < т — дискрет-
ный, соответствующий связанным состояниям:
Для энергии Е основного связанного состояния в поле ядра с зарядом Z
имеем Е г--------——
— = Д1 - (aZ)2. (4.118)
т
Если Е = т + е, где е — энергия связи, то
- = Д - (aZ)2 - 1.
т
Зависимость энергии основного состояния от Z имеет вид:
250
Глава 4. Перенормировки. Радиационные поправки
То есть при Z = 137 энергия обращается в нуль. Однако при Z 137
уравнение Дирака решений не имеет (энергия становится мнимой). Это
специальное свойство чисто кулоновского потенциала. Оно связано с
тем, что если уравнение Дирака переписать в виде уравнения Шре-
дингера с некоторым эффективным потенциалом, то эффективный по-
тенциал оказывается ~ 1/г2, т. е. приводит к падению на центр (при
Z > 137).
С другой стороны, реальное ядро имеет конечный размер, и ес-
ли это учесть, то можно увеличивать Z и дальше. Уровень при этом
опустится ниже нуля:
Это отвечает тому, что атом становится легче ядра. Действительно, мас-
са атома
Ma = Mz + + £ < Mz
Однако при Е > —т ядро еще не может распасться на атом и позитрон,
так как
Mz — (Ма + те) = — 2те — е < 0.
Будем дальше увеличивать Z: при некотором ZKp энергия связи
станет равной 2те (Е = — т) и ядро сможет распасться на атом и
позитрон (рис. 33).
4.6. Уравнение Дирака во внешнем поле
251
Рис. 33
Т. е. может произойти процесс
Z (Ze~)+e+.
При Z > ZKp ядро является нестабильной системой, атом же устойчив.
На языке функций Грина это выглядит следующим образом. Для
тяжелой частицы имеем
Gz(y2 - У1) - е-(^2е2ЛГ А>о(т)Щ)Ь-п).
При этом для свободной функции Грина фотона мы получали чисто
мнимый интеграл в показателе экспоненты. Однако если вместо Dqo(t)
подставить
и вычислить интеграл при Z > ZKp, то он окажется равным i(6M + гд),
т е. появится дополнительная мнимость, соответствующая реальному
рождению пары в поле ядра, а в функции Грина появится затухание
Gz ~
которое отвечает распаду ядра на атом и позитрон.
252
Глава 4. Перенормировки. Радиационные поправки
Атом же продолжает существовать стабильно, однако его описа-
ние становится, по существу, многочастичным. Действительно, решение
уравнения Дирака при Е < —т принадлежит сплошному спектру, сле-
довательно, не убывает на бесконечности. А атом тем не менее суще-
ствует. Дело в том, что, хотя состояние отдельного электрона не лока-
лизовано, при Z > ZKp возможны процессы, кроме
------X------------X------
такие:
когда в конце возник электрон в результате обмена, то есть электрон
непрерывно заменяется, хотя в целом заряд остается локализованным.
Ясно, что эта задача уже не одночастичная.
Реалистические расчеты (учитывающие размеры реальных ядер)
дают для ZKp величину
Дщ - 170.
Экспериментально реализовать такой заряд в принципе можно, стал-
кивая два тяжелых атома так, чтобы оба ядра оказались внутри элек-
тронного облака.
4.7. Лэмб-сдвиг
253
4.7 Радиационные поправки к уровням
водородоподобных атомов (Лэмб-сдвиг)
Рассмотренный в предыдущем разделе случай больших зарядов ядра Z
не единственный, когда надо рассматривать диаграммы высших поряд-
ков. Существует область энергий, когда и при малых Z теория возму-
щений неверна.
Действительно, мы уже рассматривали процессы рассеяния элек-
трона на тяжелой частице:
.2
Вторая диаграмма отвечает кулоновскому рассеянию и пропор-
циональна Ze2/д2 (д — переданный импульс), третья уже содержит ин-
теграл
(7 2x2 [ <ZAi Pi + qi+m 1
е J ql rn2 - (pi + gi)2 (g —gi)2'
Если электрон тоже нерелятивистский, т. е. рщ — т + рх/2т, тогда
т2 - (pi + дх)2 = т2 - (т + Е)2 + (рх + qx)2 = 2тЕ + (рх + qx)2 ,
где Е = р2/2пг, и если gx ~ pi, то с!3дх ~ /Д и интеграл по порядку
величины есть
(Ze2)2—д,
Рх
а сумма двух диаграмм есть
Ze2 A Ze2m\
—Т~ I 1 4-л--- ) •
Pi \ 4рх у
Второй член ~ Ze2 fv может быть большим при достаточно малой ско-
рости электрона v = px|/m, а следовательно, нужно суммировать все
порядки по Ze2, т. е. точно решать уравнение Дирака.
Мы уже просуммировали все поправки по Ze2 и получили инте-
гральное уравнение для электронной функции Грина в поле ядра (эк-
вивалентное уравнению Дирака):
254
Глава 4. Перенормировки. Радиационные поправки
Вычислим теперь поправки (Ze2)ne2 к движению электрона, для этого
нам нужно рассмотреть процессы типа:
Посмотрим, как при этом изменится уравнение для функции Грина.
Во-первых, из-за поляризации вакуума изменится потенциал, т. е.
u(q) —> w(q)[l +nc(Q2)].
Кроме того, в уравнении добавится еще один член, связанный с испус-
канием и поглощением фотона. В результате будем иметь
----------- =----------- + ------X--------
/' \ Псф2)и(ф
+ ------— +----X—
о
Рассмотрим поправку к собственной энергии электрона во внеш-
нем поле. Если электрон нерелятивистский, т. е. энергия связи мала:
Ро — т ~ q2/2т <?' т, то в промежуточном состоянии его можно счи-
тать свободным, когда испускаемые фотоны достаточно жесткие, так
как при этом энергия электрона ро — ко — т велика по сравнению с
энергией связи. Поскольку
q2 Z2a2m
2m 2
то для атома водорода (Z = 1) электрон, действительно, нерелятивист-
4.7. Лэмб-сдвиг
255
ский. Так что можем написать:
где в промежутках свободный электрон. (Вклад мягких фотонов обсу-
дим позднее.) Таким образом, наша поправка свелась к уже вычислен-
ным поправкам к собственной энергии свободного электрона и вершин-
ной части.
Аналогично, в процессе
~ Пс(дс)и(ф
I
о
тоже можно считать электрон свободным, поскольку основной вклад в
интеграл дают электроны с большой энергией. Оценим, какова величина
этих поправок по сравнению с u = Ze2/q2.
1.
П7=1Г = -^-А
и 15-тг т2
В атоме |р| ~ mZa, |р|2 ~ </2 -- m2(Za)2, так что
IT ~ (Za)2a.
2.
A^(q)u(q) .
Г-
a q т ~
5-----2 ln Т - о + W’1 - т)С1 + - т)С‘2
Зтг in- \ А 8 /
7м-
(4.119)
256
Глава 4. Перенормировки. Радиационные поправки
Первый член (4.119) отвечает электрону на массовой поверхно-
сти, т. е. р2 = т2, /д = т2. Он был найден ранее в (4.98). По-
следние слагаемые учитывают то, что электрон находится в свя-
занном состоянии, и представляют собой первые члены разложе-
ния Лм по степеням (щ — m) и (р2 — т). Эти величины порядка
Ро — т ~ q2/2m ~ Z2a2m/2.
-Ес .
При р ~ т имеем
Sc = с(р — т)2 q4.
Однако, поскольку в эту часть не входит множитель u(q), нужно
рассмотреть Sc/w, а эта величина
т. е. того же порядка, что поправки от последних членов Л;| : более
того, в силу тождества Уорда,
эти поправки сокращаются с поправкой от Ус.
Таким образом, остается вклад первого члена от Л ° и поправка от
поляризации вакуума. В результате получаем эффективный потенциал
вида
Видим, что радиационная поправка не зависит от переданного импуль-
са, поэтому в координатном пространстве ей будет соответствовать 5-об-
разный потенциал
1
5
(4.121)
4.7. Лэмб-сдвиг
257
Таким образом, для функции Грина получим уравнение:
9 / Ze2 \
т + 7о -Н и(г)
охц------------------\ 4тгг-/
Ge =
и, соответственно, для волновой функции:
f Za 4 Za2
ЕФ = < ар + тд0 Н-Н лг)-—
I г 3 ш-
, т 3
In---------
А 8
(4.122)
Поправку за счет высших приближений можем вычислить по тео-
рии возмущений, пользуясь нерелятивистскими волновыми функциями
водородоподобного атома. Тогда
д л 4 Za2 Г
&Епц =----—
J 3 т2
, т 3 1
In -------------
А 8 5
|Ф«уг(0)|2,
(4.123)
где п — главное квантовое число, j — полный момент, I — орбитальный
момент электрона.
В нерелятивистском случае Фпд(0) отлична от нуля только для
S-состояний (т. е. при I = 0). Для них имеем
/ \ 3
|ФпД0)|2 = -Г—) , (4.124)
7Г \ П J
т. е.
, 4a(Za)4m Г т 3 1 .
AEns = - v /------- In---------, (4.125
ns 3 n37T [ A 8 5 J ’ V 1
или, выражая эту величину через энергию первой боровской орбиты
Ев = а2т/2, получим
. _ 8 Z4o3 Г т 3 I „ ., . „ .
AEns = -------in Ев. 4.126
Зтг п3 [ А 8 5
Сдвиг 2S1/2 -уровня относительно 2Ру2 обусловлен как раз этой по-
правкой (впервые этот сдвиг обнаружили Лэмб и Резерфорд в 1947 г.).
Выясним теперь вопрос, почему в выражение для лэмбовского
сдвига (4.126) вошла величина А? При рассмотрении рассеяния элек-
тронов у нас возникла расходимость, связанная с малой энергией фо-
тона; чтобы от нее избавиться, мы и приписали фотону малую массу А.
Мы говорили, что при создании заряженной частицы возникает боль-
шое число мягких фотонов, и если их корректно учесть, то эта масса
258
Глава 4. Перенормировки. Радиационные поправки
исчезает из конечного результата. В последнем же случае мы имеем
нейтральную систему — атом, т. е. никаких фотонов нет, поэтому в вы-
ражение для радиационного сдвига уровней не должна входить никакая
масса. Почему же она возникла? Потому что мы заменили в диаграмме
функцию Грина связанного электрона на свободную функцию Грина.
Для мягких фотонов это явно несправедливо. При ко Zam такое
приближение работает, однако, когда ко меньше энергии связи, тогда
существенно то, что электрон связан.
ко С Zam
Однако при ко <?' т электрон нерелятивистский, и вклад от таких фо-
тонов можно вычислить при помощи нерелятивистской квантовой ме-
ханики. Поскольку в нашем случае aZ <?' 1, то области ко Zam
и ко т перекрываются; приравнивая интегралы по области пере-
крытия, вычисленные двумя способами, можно выразить величину Л
через параметры нерелятивистской теории. Из такого сравнения выте-
кает, что
, т , т 5
ш — = ш-----\—,
A 2s0 6
где Ео — средний потенциал ионизации атома. Здесь является суще-
ственным то обстоятельство, что Za <Д 1. При ~ 1 области пере-
крытия вообще нет, поскольку электрон в этом случае всегда реляти-
вистский, и поэтому расчеты возможны только численные.
Чтобы получить полное выражение для лэмбовского сдвига, сле-
дует еще добавить вклад аномального магнитного момента (4.98). Это
приводит к дополнительному слагаемому 3/8 в квадратных скобках в
уравнении (4.126). Окончательно получаем
AEns
4 a(Za)4m
Зтг п3
, т
In------
2eq
19
30
Глава 5
Трудности квантовой электродинамики
5.1 Перенормировки и расходимости
Выше мы рассмотрели следующие величины: функцию Грина электро-
на G, функцию Грина фотона f)/iv и вершинную часть Гм. Убедились,
что через них выражаются все наблюдаемые величины. Мы показали,
что точные функции Грина имеют вид:
с 1 D 1
то— р + У(р)’ /с2 [1 — П(/с2)]
Функция G, вообще говоря, не имеет полюса при р = то, т. е. эта “го-
лая” (или затравочная) масса не имеет физического смысла. Далее мы
явно выделили полюса этих функций, сопоставив им физические (или
перенормированные) массы т, и записали функции Грина в виде:
G(p) =-----2 ... = Z2Gc(p),
т— р + Zc{p)
где
У(р) — У(тп) — Т/(т)(р — т) , „
ад = ——\; w \ Л™2,
1 — 2у(т)
1 — S'(m) ’
Аналогично, функция Грина фотона
n(fc2) = fc2[i-nc(fc2)] = Z31?c(fc2)’
где
= щадщо) ~
с ' 1-11(0)
z3 =-------.
3 1 - П(0)
260
Глава 5. Трудности квантовой электродинамики
Перенормированная масса фотона остается равной нулю. Для вершин-
ной части мы получили
rAt = Zf1r^ , Г=(т,т)=7м.
Далее было показано, что все графики выражаются через перенорми-
рованные величины , Gc, Dc точно так же, как и через неперенорми-
рованные Гм, G, D, если ввести перенормированный заряд
е2с = Я3е2
и заменить “голые” массы на перенормированные (было показано, что
Zi = Z2).
Таким образом, все физические величины можно выразить через
наблюдаемые заряд и массу. Возникает вопрос, можно ли вычислить ес
и m через затравочные величины? Оказывается, нельзя, поскольку ин-
тегралы расходятся. С другой стороны, нам пришлось ввести перенор-
мированные Gc, Dc, Гс, а чтобы это имело смысл, мы должны показать,
что в эти величины не входят ни затравочная масса, ни затравочный
заряд. Для этого нам нужно найти уравнения для Гс, Sc, Пс и так их
сформулировать, чтобы в них вошли только перенормированные заряд
и масса, но не затравочные величины. Тогда вся процедура перенорми-
ровок будет иметь смысл.
Выясним сначала, какие бывают расходимости и отчего они про-
исходят. Укажем типы расходимостей:
1. ультрафиолетовая, возникает при к • оо;
2. инфракрасная, возникает при // - 0:
3. возможные полюса амплитуд.
Мы уже обсудили физический смысл инфракрасных расходимо-
стей и показали, что для разумно поставленных задач они отсутствуют.
Что касается последнего типа расходимостей, то при некоторых опреде-
ленных значениях внешних импульсов амплитуды, действительно, мо-
гут иметь особенности, например, если в каком-нибудь пропагаторе ока-
жется к2 — т2 = 0. Однако можно доказать, что если все наружные
импульсы пространственноподобны и удовлетворяют неравенству тре-
угольника, то эти сингулярности отсутствуют. Это ясно потому, что в
этом случае всегда можно все контуры интегрирования в фейнманов-
ских интегралах развернуть так, что все импульсы станут евклидовыми
(рис. 34).
5.1. Перенормировки и расходимости
261
Рис. 34
Физические амплитуды (которые имеют времениподобные внеш-
ние импульсы) получаются из амплитуд с евклидовскими импульсами с
помощью аналитического продолжения. Сингулярности в этих ампли-
тудах получаются именно в результате продолжения. Эти сингулярно-
сти имеют непосредственный физический смысл, связанный с условием
унитарности (см. главу 3), и мы не будем их здесь обсуждать.
Остаются лишь так называемые ультрафиолетовые расходимо-
сти, возникающие при к оо.
Рассмотрим произвольную скелетную диаграмму
262
Глава 5. Трудности квантовой электродинамики
Очевидно, что в силу сохранения тока число внешних электронных ли-
ний должно быть четным. Обозначим через Fe число внутренних элек-
тронных линий, F-y — внутренних фотонных линий, Ne — внешних элек-
тронных линий и Ny — внешних фотонных линий. Тогда амплитуда,
соответствующая такой диаграмме, будет описываться интегралом
_________________d^.-.d^___________________ (5
. k^Akp^ - m)(kF.i+2 - m)... (Адд+тд - m)
где I — число независимых внутренних линий, по которым ведется инте-
грирование. Его легко определить. Пусть в диаграмме п вершин, в каж-
дой вершине сходятся 3 линии, причем к{ + kj = kF
j
Так как имеется п законов сохранения (5-функций) по числу вершин,
а одна из этих 5-функций выражает общий закон сохранения и не со-
держит внутренних импульсов, то число независимых импульсов равно
I = Fe + F7 — п + 1.
Если в интеграле (5.1) суммарная степень дифференциалов больше или
равна степени знаменателя, то он расходится. То есть только при
41 - 2F7 - Fe = 3Fe + 2F7 - 4n + 4 < 0 (5.2)
интеграл сходится. Покажем теперь, что, в действительности, это вы-
ражение не зависит от процессов во внутренней части диаграммы, т. е.
ни от Fe, ни от F7. Она зависит только от числа внешних линий, т. е. от
5.1. Перенормировки и расходимости
263
вида самого процесса, описываемого диаграммой. Действительно, если
внутри имеем замкнутую электронную линию (см. рис. 35), то число
промежутков равно числу вершин, т. е.
п = Fe.
Рис. 35
Если электронную линию разомкнуть, то число внутренних линий умень-
шится на одну, а число внешних увеличивается на две, число вершин
не изменится, т. е.
п = Fe Ч---.
2
На каждую внутреннюю фотонную линию приходится две вершины,
так как она должна начаться на электронной линии и закончиться на
электронной линии, а на каждую внешнюю линию приходится одна вер-
шина, т. е.
п — 2F^ F Ny.
Таким образом, если задано число внешних линий и число вершин, то
этим определяется и число внутренних линий:
Тогда условие сходимости интеграла:
3
К, = 3Fe + 2F7 - 4n + 4 = --Ne - N.: + 4 < 0,
(5-3)
264
Глава 5. Трудности квантовой электродинамики
т. е. определяется числом внешних линий, как и говорилось выше. Вид-
но также, что когда число внешних линий велико, т. е. процесс достаточ-
но сложный, то, наверняка, никаких расходимостей нет и все в порядке.
Рассмотрим простейшие диаграммы.
1.
Ne = 2, Ny = О, К. = 1.
с I '
Как мы уже видели, собственная энергия электрона формально
расходится линейно (реально — логарифмически).
N = О, Му = 2, /С = 2.
с ' 1 '
Поляризационный оператор фотона расходится квадратично, на
самом же деле калибровочная инвариантность уменьшает расхо-
димость до логарифмической.
Ne = 2, М, = 1, К, = 0.
Вершинная часть расходится логарифмически.
4.
М = 0, М7 = 3, /С = 1.
с ' 1 '
Такая диаграмма расходится линейно, однако мы покажем, что
из инвариантности относительно зарядового сопряжения она об-
ращается в нуль.
5.1. Перенормировки и расходимости
265
Диаграмма сходится.
6.
Ne = 4, Ny = О, К. = —2.
с I ’
Тоже сходится.
Ne = О, JV7 = 4, К, = 0.
Расходится логарифмически (ниже будет показано, что реально
такая амплитуда сходится благодаря калибровочной инвариант-
ности) .
Сначала покажем, что
।
Точно так же обращается в нуль любая диаграмма без внешних заря-
женных частиц и с нечетным числом внешних фотонов. Это так назы-
ваемая теорема Фарри. Действительно, наша теория инвариантна от-
носительно зарядового сопряжения. Однако при зарядовом сопряжении
знак волновой функции фотона меняется: ем — ем, т. е. амплитуда для
266
Глава 5. Трудности квантовой электродинамики
нечетного числа фотонов должна изменить знак. Но с другой стороны,
откуда амплитуда “знает”, что внутри произошло изменение частиц на
античастицы? От этого ничего не изменится, поэтому она должна быть
тождественно равна нулю. Поясним это на простейшей диаграмме:
При зарядовом сопряжении эти две диаграммы меняются местами и,
кроме того, меняют знак, следовательно, их сумма равна нулю.
Рассмотрим теперь рассеяние света на свете:
М2МзМ4 (^17 , ?з, '
В силу сохранения тока должно быть
(5.4)
(5-5)
^М1М2МзМ4 — О
для импульса любого из внешних фотонов кг. Рассмотрим
5.1. Перенормировки и расходимости
267
Так как интеграл расходится при больших р, то ki в знаменателях мож-
но пренебречь и в амплитуде никакой зависимости от внешних импуль-
сов нет. Следовательно, расходящаяся часть амплитуды (5.4) не удовле-
творяет условию сохранения тока (5.5), поскольку величина, не завися-
щая от не может дать нуль при умножении на к. На самом деле,
нужно сложить все диаграммы
тогда оказывается, что (5.5) удовлетворяется автоматически, а сумма
интегралов конечна. Причем все величины, удовлетворяющие (5.5), схо-
дятся при любом способе регуляризации, не нарушающем закона сохра-
нения тока.
Таким образом, расходящимися оказываются только три величи-
ны: собственная энергия электрона, поляризационный оператор фотона
и вершинная часть:
Посмотрим, как перенормировки устраняют эти расходимости.
Сначала будем считать, что
G = G0, D = Do
и попробуем построить уравнение для вершинной части. По определе-
нию,
268
Глава 5. Трудности квантовой электродинамики
Это фактически и есть уравнение для Гм. Действительно, (5.6) можно
перерисовать и так:
Проинтегрировав (5.7), получим (5.6). Причем существенно, что в (5.7)
не входят диаграммы типа
5.1. Перенормировки и расходимости
269
поскольку такая диаграмма содержится уже в
Между тем диаграммы
। ।
расходятся по-разному. Выясним, как именно.
1.
।
Pl Р2
так как расходимость возникает при fci pi,P2, m-
270
Глава 5. Трудности квантовой электродинамики
2.
(а) При фиксированном расходимости нет, имеем при k± Д> к2
f сГк-у 1
/ М'
J л1 л2
fe
Интегрирование по (14к2 теперь дает
л" ~lnQ-
'2
(Ь) Если, наоборот, к2 к± (Ад фиксированно), то будем иметь
к2 , Л2
.4 111 Л.2 '
'2 Л1
При интегрировании по d^ki получим
f <Ркг А2 2 Л2
J fcf П fc2 ~ П р2'
р
То есть расходимость усилилась по сравнению с
. И это
5.1. Перенормировки и расходимости
271
естественно, поскольку в графике
।
содержится прежняя вершина ~ 1н Л2//;2 и фактически еще одна
диаграмма
।
।
тоже пропорциональная 1пЛ2/р2.
3. Вторая диаграмма
Интеграл сходится, если интегрировать по при фиксирован-
ном fci (fe 3> fci) или, наоборот, интегрировать по d]k\ при фик-
сированном к-2 (к± /сг)- Единственная ситуация, когда интеграл
может разойтись, — это к\ ~ /д. при этом получим
fd4k , Л2
J I4 ~ П
272
Глава 5. Трудности квантовой электродинамики
Это рассмотрение можно провести для более сложных диаграмм
и получить важное утверждение: сколько бы членов с точными вершин-
ными частями мы ни взяли в разложении (5.7) (скелетные диаграммы),
все они расходятся только логарифмически. Поэтому, как мы увидим,
процедура вычитаний (перенормировок) приводит к конечному резуль-
тату, и можно написать уравнение для вершинной части, которое вооб-
ще не будет содержать расходимостей.
Построим это, полностью конечное, уравнение для вершинной ча-
сти. Полная вершинная часть может быть записана в виде
Гм(Р1,Р2,<7) =7м + ЛА1(р1,Р2,<7)- (5.8)
На массовой поверхности имеем
Лм(т, т, 0) = 7мЛ(пг, т, 0). (5-9)
Представим уравнение (5.8) в виде
Гм(Р1,Р2,9) = 7М(1 +Л(т,т,0)) + Am(pi,p2,q) - AM(m,m,0). (5.10)
В терминах разложения по скелетным диаграммам уравнение (5.10)
имеет вид:
Гм(Р1,Р2,д) = 7д(1 + Л(т, т, 0))+
Уравнение (5.11) содержит Гм и в правой, и в левой части, т. е. это
интегральное уравнение для вершинной части. Подставим в (5.11) Г/;
в виде
Гм = Г^г1,
5.1. Перенормировки и расходимости
273
где
Тогда получим
1 = 1 + A(m, m, 0).
Z^1 в верхних вершинах сократились, а в остальных дали перенорми-
рованный заряд ес = Z, '!е (мы пока отвлекаемся от перенормировок
функций Грина). Расходимость же исчезла, поскольку в каждом по-
рядке под интегралы входят разности:
которые стремятся к нулю при /, -ос.н силу замечательного свойства:
Г(а, Ь, с) —> Г(&) при b а, с ,
т. е. Г зависит от наибольшего импульса. Это свойство легко подметить
из того же уравнения или прямо из диаграмм теории возмущений.
274
Глава 5. Трудности квантовой электродинамики
Перейдем теперь к реальной задаче, когда функции Грина элек-
трона и фотона точные. Вершинная часть будет иметь вид:
Как и в предыдущем случае, введем
•
Прибавляя Лм(т, т, 0) = 7мЛ(т,т, 0) и вычитая почленно, получим,
аналогично предыдущему,
Как и прежде, 1 в верхних вершинах сократятся, а в остальных по-
явится множитель Z^1; кроме того, так как G = ZzGc, D = Z^DC,
1.
в каждой вершине появятся множители Z2Z32. Вместе они дадут пере-
нормированный заряд
1
ес — (Z\ ,
5.1. Перенормировки и расходимости
275
а поскольку Z3 = Z2,
е2 = Z3e2.
Таким образом, действительно, мы получили интегральное урав-
нение для перенормированной вершины Г),, в которое входят только пе-
ренормированный заряд ес и перенормированные функции Грина элек-
трона и фотона Gc и Dc. Оно будет конечным, если нам удастся постро-
ить конечные уравнения для функций Грина.
Начнем с
-2(р)
Для собственной энергии имеем
(5.15)
-Др) =
Обратим внимание, что здесь в начале стоит а не точная вершинная
часть, поскольку все процессы начинаются с точки:
а далее может происходить все, что угодно. Таким образом,
-S(p) = e2 [ fc4 ЛмО(р - А:)Гм(р - k,p, fc)£>(fc2).
J (2тг)4г
(5.16)
Это уравнение Швингера-Дайсона. Аналогичное уравнение можно так-
же получить и для поляризационного оператора фотона:
276
Глава 5. Трудности квантовой электродинамики
к — р
т. е.
ЩДА:2) =
Пм„(&2) = —e2Sp I . {7^(руг^р, к - p)G{к - р)}. (5.17)
J (2тг)4г
Пользы, однако, от этих уравнений мало, поскольку интегралы для S(p)
и Пдг,(А;2) расходятся. Но нас интересуют не сами Е(р) и П(/г2), а раз-
ности вида
S(p) — S(m) — Г'(т)(р — m),
так как именно они входят в функции Грина. Такое двойное вычитание
и устраняет расходимость.
Посмотрим, как это происходит. Для этого рассмотрим производ-
ную дТ(р)/др^. Произвольный член разложения собственной энергии
электрона имеет вид:
р р — fci р — fcl — fc2
р- к3
Таким образом, имеется одна электронная линия, и внешний импульс р
входит в виде разностей р — ку р — Ад — к^ и т. д. Производная от каждого
электронного пропагатора будет иметь вид:
9 1 1 1
Эйр, m — р + к m — р + к М пт — р + к
5.1. Перенормировки и расходимости
277
Таким образом, производная содержит уже два пропагатора и т. е.
представляет собой не что иное, как вершинную часть с нулевым им-
пульсом фотона. Графически, дифференцируя почленно S(p), получаем
Итак, получено линейное уравнение относительно дУддр^. В частности,
из (5.18) следует тождество Уорда:
9S
В уравнении (5.18) можно проделать процедуру вычитания так
278
Глава 5. Трудности квантовой электродинамики
же, как и для вершинной части. Действительно,
Вводя перенормированную функцию Грина, согласно G-1 =
где Z2 1 = 1 — прибавляя и вычитая почленно 5У(т) (что экви-
валентно прибавлению и вычитанию Л(т, тп)), получим выражение:
dG-1
Эр^
I
I
I
р р
в которое входит только перенормированный заряд ес и которое не со-
держит расходимости.
Аналогично можно построить похожее по структуре линейное
уравнение для 9П(/с2)/<ЭА;м и убедиться, что его также можно перенор-
мировать.
Таким образом, все можно выразить через перенормированные
величины, заряд и массу, и нигде при этом расходимость не встретится.
Эти выводы мы получили, исходя из теории возмущений, и на самом
деле у нас нет уверенности, что они останутся верными при выходе за
ее рамки.
5.2. Проблема нуля заряда в квантовой электродинамике
279
5.2 Проблема нуля заряда в квантовой
электродинамике
Мы строили квантовую электродинамику следующим образом. Ввели
функции Грина электрона и фотона
--------------------- = G
=
рассмотрели простейшее взаимодействие
В случае тг-мезона нам понадобилось более сложное взаимодействие
Еще более сложные взаимодействия вводить нет смысла, так как теории
получаются неперенормируемыми.
Построенная таким образом теория оказалась в блестящем согла-
сии с экспериментом. Однако и она на очень малых расстояниях пере-
стает работать; с этим как раз и связана проблема нуля заряда, которую
мы собираемся обсуждать.
Мы видели, что диаграммы
280
Глава 5. Трудности квантовой электродинамики
расходятся в области больших виртуальных импульсов и при этом ока-
зываются практически не зависящими от внешних импульсов, напри-
мер,
Г d^k 1 11
/ 7о V47Тv ~ 7ТI1 ~ Г О'v ту
J (2тг)4г m—p1y]Q т—р2 + к к
(5.19)
от pi и р2 не зависит, так как pi,p-2 С к. В области больших к (т. е.
малых расстояний) интеграл расходится, т. е. теория неприменима, по-
этому мы ввели параметр обрезания Л, причем в области интегриро-
вания около Л при pi,P2 Л интеграл не зависит ни от щ, ни от р>-
Далее мы ввели Г(т,т,0) и вычли ее из ГДщргД), и все оказалось
сходящимся, а то, что мы ничего не знаем при больших к, вошло в кон-
станты перенормировок, т. е. фактически в перенормированный заряд
ес = Zx 1ДД.; е.
Однако все эти рассуждения справедливы при не очень больших
внешних импульсах, а именно: мы полагали pi,P2 Л. А что произой-
дет, если мы будем увеличивать внешние импульсы, т. е. при р2/т2 ^>1?
(Впервые эта задача была поставлена Гелл-Манном и Лоу, а решена
Ландау, Абрикосовым и Халатниковым.)
Рассмотрим поляризационный оператор фотона
= ПМР(А:) = (д1П,1;2 - АтХ)П(/г2).
5.2. Проблема нуля заряда в квантовой электродинамике
281
Мы вычислили
Зтг тб
Первые члены теории возмущений, таким образом, будут выглядеть
То есть при больших fc2 ряд может разойтись, и теория возмущений
перестает работать. Ясно, что член
содержит уже ln2fc2/m2, и, вообще говоря, более сложные диаграммы
будут расти еще сильнее с ростом к2. В вершинную часть же (5.19)
основной вклад дают фотоны с большим к ~ Л.
Однако посмотрим на интеграл (5.19), он содержит
1
----------- х
m — pi + к
С усложнением диаграмм растет число знаменателей, а вместе с ним
и степень р в знаменателе. То есть с увеличением р подынтегральные
выражения будут падать. Это происходит, однако, только при р ~ Л,
поскольку основной вклад в интеграл дают ~ Л.
Введем достаточно большое Л и рассмотрим область
р2 » т2 , Л2 /р2 » 1 .
Тогда (5.19) примет простой вид:
л(1) 2 f , л2
Ад ~ е J Д.4 ~ ° 0 11 р2 ’
282
Глава 5. Трудности квантовой электродинамики
так как легко убедиться, что основной вклад в интеграл (5.19) будет
давать область fc < Л. Выберем Л так, чтобы
Л2
or. In — ~ 1, «о С 1- (5.20)
Тогда вершина, например, будет иметь следующую структуру:
Г= £ In™ ^спт =
п^т
Л2 Л2 Л2
= 1о0 111 — I 1112 — I 111 — -------- (5-21)
//' //' //'
Ясно, что наибольший вклад дадут члены ~ ctg 1нп Л2/р2 ~ 1, а члены
~ ад+11пп Л2/р2 ~ ад будут уже малой поправкой, т. е. можно записать
/ Л2\ / Л2 \
Г = fi «о In + <W2 а:0 In — + cvq/з H------ (5.22)
\ P J \ P J
Можно ограничиться первым членом (главное логарифмическое при-
ближение), тогда задача упрощается. Определим Г, G, D в этом при-
ближении.
Нарисуем скелетные диаграммы
।
।
1 ।
' 7\ А
Первое упрощение связано с тождеством Уорда:
е2 = Z^2Z2Z3e2.
Так как Zi = Z2, то расходимости, связанные с вершинной частью и
функцией Грина электрона, в заряде сокращаются. А следовательно,
5.2. Проблема нуля заряда в квантовой электродинамике
283
можно переформулировать теорию так, чтобы они вообще не встрети-
лись. Это можно сделать подходящим выбором калибровки. В данном
случае, следуя Ландау, выберем поперечную часть фотонной функции
Грина в виде
(5.23)
и покажем, что при этом расходимости в Г действительно исчезают:
Первое слагаемое содержит kikj, в силу симметрии, при i j интеграл
от него равен нулю, т. е.
т. е. главные вклады в интеграл сократятся. Можно показать, что во
втором порядке главный член ~ су In2 А2///2 исчезнет и останется член
<Лд1пЛ2/р2, которым мы пренебрегаем в нашем приближении. Анало-
гичную работу можно проделать и для G; в результате, в главном ло-
гарифмическом приближении получим
Гд — 7м + °(ео)>
G(p) — -т + 0(cq).
(5-24)
Теперь вычислим П;ш в этом приближении. Очевидно,
Пм„(/г) =
G(p)
(5.25)
284
Глава 5. Трудности квантовой электродинамики
поскольку I), = 7М. В справедливости (5.25) можно убедиться и непо-
средственным вычислением диаграмм более высоких порядков:
+ • • •
В них логарифмические вклады сократятся. Таким образом, в логариф-
мическом приближении вычисление поляризационного оператора 1ф„
сводится к вычислению простейшей диаграммы.
Вычислим ПМ1?(А:) — Пдг,(0):
ЩД/с) - ПМДО) =
2 f d4P с J 1
е0 / /о м.8р4тм-------zTi,
J (2тг)4г ( т—р
(5.26)
Разложим в ряд по степеням к выражение (т — р + к) 1
1
т — р + к
1 1 ? 1 1-1-1 z
--------к--zH---к---к--- + • • (5.27)
т—р т—р т—р т—р т — р т—р
Первый член (5.27) сократится в подынтегральном выражении, второй
даст нуль из-за симметрии при вычислении интеграла. Действительно,
fd4p 11-1 Г <Гр д^рдрркр
/ о = / /о U-SP~^~6----- = °-
J (2тг)4г р р р J (2тг)4г рь
Третий член (5.27) как раз и дает логарифмическую расходимость, та-
ким образом, будем иметь
nM!/(fc) -ПМДО) = -el f ^.Зр'уЛ'уДк^к^. (5.28)
J (2тг)4г р р р р
Так как
Пдг, = - ДХ)П(/г2 *),
ТО
ПД = Зк2Пс(к2}.
рр 4 '
С другой стороны, из (5.28)
ЗА:2П(А:2) = 2е2 [ ^Spk-/k-^
J (2тг)4г pz р р
5.2. Проблема нуля заряда в квантовой электродинамике
285
поскольку
1„, 1 _ _ 2/л _ 2
Уц Л Уц Л л 4 о •
р р р4 р4 РЛ
После некоторых преобразований получим
П(/с2) = -~е20 [
V ’ 3 ° J (2л)4гр4
Введя ip'o = ро, т. е. разворачивая контур интегрирования, как обычно,
евклидовым образом, будем иметь
n(fc2) = - “6q [
4 Jk
d4p 1
(2л)4 p4~
(5.29)
Так как
л4 2 J 2 2 2 л 2
d p = p dp — = 7Г p dp ,
TO
Др2
II(fc2) =-----
V ’ 3 • 16л2
Л2 _ ад A2
11 k2 ~ Зл П k2 ’
(5.30)
Таким образом, в логарифмическом приближении
jj = Эру________1_____
k2 1 - П(/г2)
к2 1 +so In У
Зтг к2
(5.31)
1
Это неперенормированная функция Грина. Как ее перенормировать?
Обозначим
d =
1
1 + fa In У
Зтг к2
(5.32)
Это выражение можно переписать так:
1
d 1 + fa in у + «0 in Ai _ ao in Ai
Зтг к2 Зтг т2 Зтг т2
1 1 1
2~
fa In Ai _ so in
Зтг тпЛ Зтг тЛ
ap Л2
Зтг 1 m2 1 —
(5.33)
Обозначим
1
Хз —--------------п-,
1 + fa In Ai
Зтг тЛ
(5.34)
286
Глава 5. Трудности квантовой электродинамики
тогда
Z3
d Zz 1 - ln Al 1 _ ln ±1'
Зтг m2 Зтг m2
(5.35)
1
Таким образом, параметр обрезания вошел в постоянную перенорми-
ровки Из и в физический заряд ес, и то, что нам удалось вынести Z3 за
скобку, есть как раз свойство перенормируемости теории.
С другой стороны, мы получили
По
1 + in Ai '
Зтг m2
(5.36)
Казалось бы, все хорошо: ас < од, как и должно быть из-за поляризации
вакуума. Однако если устремим Л —> оо, то
Зтг
1Н<
т2
при Л -л оо,
(5.37)
о
т. е. при любом затравочном заряде (а мы считали «о 0) он полно-
стью экранируется в этом пределе, так что ас = 0. Это может означать,
что такой подход неверен на малых расстояниях, но если есть такое рас-
стояние, где электродинамика становится несправедливой, мы из этого
расстояния может вычислить ас и, наоборот, вычислить Л по значению
ас = 1/137. Из (5.37) вытекает
Л2
т2
откуда 1/Л ~ 1О-50 ст.
Ситуация несколько изменяется, если учесть вклад в поляриза-
цию вакуума от разных сортов частиц. Если имеется, допустим, и раз-
личных частиц со спином 1/2, то (5.36) изменится так:
ад
1 + In < ’
Зтг m2
(5.38)
Тогда, если принять, что квантовая электродинамика переста-
ет работать на расстояниях порядка планковской длины, т. е. 1р =
= у/G ~ 10 '!3 (G— ньютоновская гравитационная постоянная), то по-
лучим, что возможное число сортов частиц
v
12.
5.2. Проблема нуля заряда в квантовой электродинамике
287
Хуже обстоит дело с функцией Грина, так как выражение
1
1 - In Д-
Зтг тпЛ
при фиксированном ас имеет полюс в области k1 2 * * * * * В < 0, т. е. возникают
частицы с мнимой массой. Впрочем, в некотором смысле, это искус-
ственная трудность, поскольку в нашей теории Л = оо, т. е. ас = 0. И
полюса нет, но при этом нет и взаимодействия.
Эта проблема до сих пор не решена1. И если в квантовой элек-
тродинамике такая трудность возникает на безумно малых расстояниях
из-за малости ас, т. е. в реальных ситуациях она несущественна, то в
сильных взаимодействиях, где константа связи g ~ 1, мы сразу с ней
1 Остался черновик работы В.Н.Грибова “Квантовая электродинамика на малых
расстояниях”, которую он подготовил как дополнительный параграф этой главы.
Он планировал обсудить там возможное решение проблемы нуля заряда — полю-
са Ландау в квантовой электродинамике, или в более широком смысле, в единой
теории электрослабого взаимодействия. Это решение возникло в качестве “побочно-
го продукта” его многолетнего изучения проблемы удержания кварков в квантовой
хромодинамике (КХД) — теории “цветных” кварков и глюонов, которая описывает,
как полагают, микроскопическую структуру адронов и их взаимодействий. Грибов
показал, что когда константа связи превышает критическое значение, равное
7Г V 3
свойства теории принципиально меняются. В теории появляются связанные состоя-
ния фермионов с отрицательной энергией и обычный вакуум становится нестабиль-
ным. Происходит явление, напоминающее фазовый переход в физике твердого тела,
что приводит к кардинальному изменению свойств всех состояний.
В КХД константа связи между кварками и глюонами, в противоположность элек-
тродинамической а.е.т.-> растет с расстоянием и достигает критического значения
на расстояниях порядка 1 ферми (10—13 см). Грибов привел аргументы в пользу
точки зрения, что сверхкритическое связывание легких кварков приводит к неста-
бильности “цветных” состояний и, в конечном счете, к явлению невылетания цвета.
В квантовой электродинамике сверхкритические явления происходят на очень ма-
лых расстояниях, порядка планковского масштаба, 1р. Они, с одной стороны, могут
быть ответственны за появление хиггсовского бозона — скалярной частицы, которая
необходима в современной единой теории электрослабых взаимодействий — теории
Вейнберга-Салама. В.Н.Грибов предсказал, что масса составного хиггсовского бозо-
на должна быть немного больше, чем масса тяжелейшего из кварков (так называе-
мого top-кварка, zrz^op 200?TZproton )•
С другой стороны, сверхкритические явления приводят к решению проблемы по-
люса Ландау в КЭД — константа связи увеличивается на малых расстояниях, но
остается конечной.
Работа В.Н.Грибова “Квантовая электродинамика на малых расстояниях” будет
опубликована в сборнике его избранных работ, который подготавливается к печати.
288
Глава 5. Трудности квантовой электродинамики
сталкиваемся, так как вынуждены вводить параметр обрезания Л ~ тп.
Так что там эта трудность реальная.
Заметим, что при доказательстве нуля заряда мы пользовались
логарифмическим приближением:
Л2
6q 1П — ~ 1 , 6q < 1.
т. е. мы, формально говоря, не можем устремлять Л к сю. Однако (как
заметил Померанчук) выражение (5.36) получено для перенормирован-
ного заряда, который, как мы знаем, только и входит в высшие неучтен-
ные поправки. Поскольку о,, - 0 при Л -л сю, то и все поправки стре-
мятся к нулю при Л -л сю. Поэтому наше утверждение не зависит от
условия с/In Л2///2 ~ 1.
Единственная гипотеза, которая сделана, — это условие
Т « 1.
Если отказаться от него, то мы с самого начала не имеем теории воз-
мущений, и наша теория, по существу, не сформулирована.
Владимир Наумович Грибов
Квантовая электродинамика
Ответственный редактор И. Б. Хриплович
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Подписано в печать 29.10.01. Формат 60 х 84
Печать офсетная. Усл. печ. л. 16,74. Уч. изд. л. 16,83.
Гарнитура Computer Modern Roman. Бумага офсетная №1.
Тираж 500 экз. Заказ №14.
Научно-издательский центр «Регулярная и хаотическая динамика»
426057, г. Ижевск, ул. Пастухова, 13.
Лицензия на издательскую деятельность ЛУ №084 от 03.04.00.
http://rcd.ru E-mail: borisov@rcd.ru