Автор: Анго Андре
Теги: фундаментальные и общие проблемы математики электротехника справочник высшая математика
Год: 1965
Текст
COMPLEMENTS
DE MATHEMATIQUES
A L'USAGE DES
INGENIEURS DE L'ELEKTROTECHNIQUE
ET DES TELECOMMUNICATIONS
PAR
ANDRE ANGOT
PARIS, 1957
ФИЗИКО-МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА ИНЖЕНЕРА
АНДРЕ АНГО
МАТЕМАТИКА
для
ЭЛЕКТРО- И РАДИОИНЖЕНЕРО
С предисловием
ЛУИ ДЕ БРОЙЛЯ
Перевод с французского
под общей редакцией
К. С. ШИФРИНА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА -1965
517
A64
УДК 510:621.3
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию , 20
Предисловие Луи де Бройля 21
Введение 23
Глава I. Функции комплексной переменной 24
1.1. Комплексные величины 24
.1.1. Определения 24
.1.2. Сложение 25
.1.3. Умножение 25
.1.4, Замена обозначений 26
.5/. Сопряженные комплексные числа .27
.6. Степень комплексного числа 27
,7. Корин из комплексного числа 28
.8. Корин из единицы .28
.1.9: Ряды с комплексными членами 29
.10. Степенные ряды 29
.11. Экспоненциальная функция и логарифм 30
.12. Дифференцирование и интегрирование по аргументу ..... 31
.13. Суммирование тригонометрических функций, аргументы которых
составляют арифметическую прогрессию .' 31
1.2. Применение комплексных величин при расчете электрических цепей
в синусоидальном режиме 31
1.2.1. Введение '. . . 31
1.2.2. Графическое изображение синусоидальной функции 32
1.2.3. Представление с црмощью комплексных чисел ^.33
1.2.4. Ограничения метода .... 34
1.2.5. Понятие комплексного полного сопротивления 35
1.2.6. Комплексное полное сопротивление при последовательном и па-
параллельном соединении 36
1.2.7. Законы Кирхгофа 37
1.2.8. Обобщение понятия комплексного полного сопротивления ... 38
1.2.9. Комплексный вектор 41
1.3. Понятие о функции комплексной переменной 42
1.3.1. Непрерывность 42
1.3.2. Однозначные функции 42
1.3.3. Аналитическая функция . : . . 43
1.3.4. Голоморфная функция 44
1.3.5. Криволинейный интеграл от функции комплексной переменной. 44
1.3.6. Теорема Коши ' 45
1.3.7. Формула Коши 46
1.3.8. Ряд Тейлора 47
1.3.9. Особые точки .48
1.3.10. Разложение в ряд Лорана 48
Интегрирование по методу. вычетов 50
1.3.11. Теорема о вычетах : 50
1.3.12. Вычисление вычетов 50
ОГЛАВЛЕНИЕ
1.3.13. Вычисление вычетов относительно кратных полюсов с помощью
производных 52
1.3.14. Лемма Жордана 53
1.3.15. Применение леммы Жордана к единичной функции 54
1.3.16. Интегрирование при наличии точки разветвления 55
1.3.17. Контур Бромвича 56
1.3.18. Интеграл Бромвича — Вагнера 57
1.3.19. Эквивалентный контур 57
1.3.20. Теорема о числе полюсов и числе нулей 60
Применение теоремы о вычетах к вычислению некоторых определенных
интегралов 61
2тс
1.3.21. Интегралы вида Г /(cos 0, sin в) dO 61
о
+со
1.3.22. Интегралы вида I f (x) d.
-со
со
1.3.23. Интегралы вида I / (х) cos mx dx, I / (x) sin mx dx 63t
о
+со
х 62
-со
со со
о о
1.3.24. Интегралы вида I x"~f (x) dx
64
о
1.3.25. Применение теоремы о вычетах к суммированию некоторых
рядов 65
1.4. Конформные отображения 66
1.4.1. Определение 66
1.4.2. Несколько примеров конформных отображений 71
1.4.3. Последовательные отображения 76
1.4.4. Отображение Шварца 77
1.4.5. Различные применения конформных отображений 83
Литература к главе I 84
Глава И. Ряд Фурье. Интеграл Фурье 85
2.1. Ряд Фурье 85
2.1.0. Введение 85
2.1.1. Вычисление коэффициентов 85
2.1.2. Разложение в ряд по ортогональным функциям 86
2.1.3. Частные случаи 87
2.1.4. Интегрирование и дифференцирование 88
2.1.5. Случай, когда разложение в ряд Фурье ограничено первыми
п членами 90
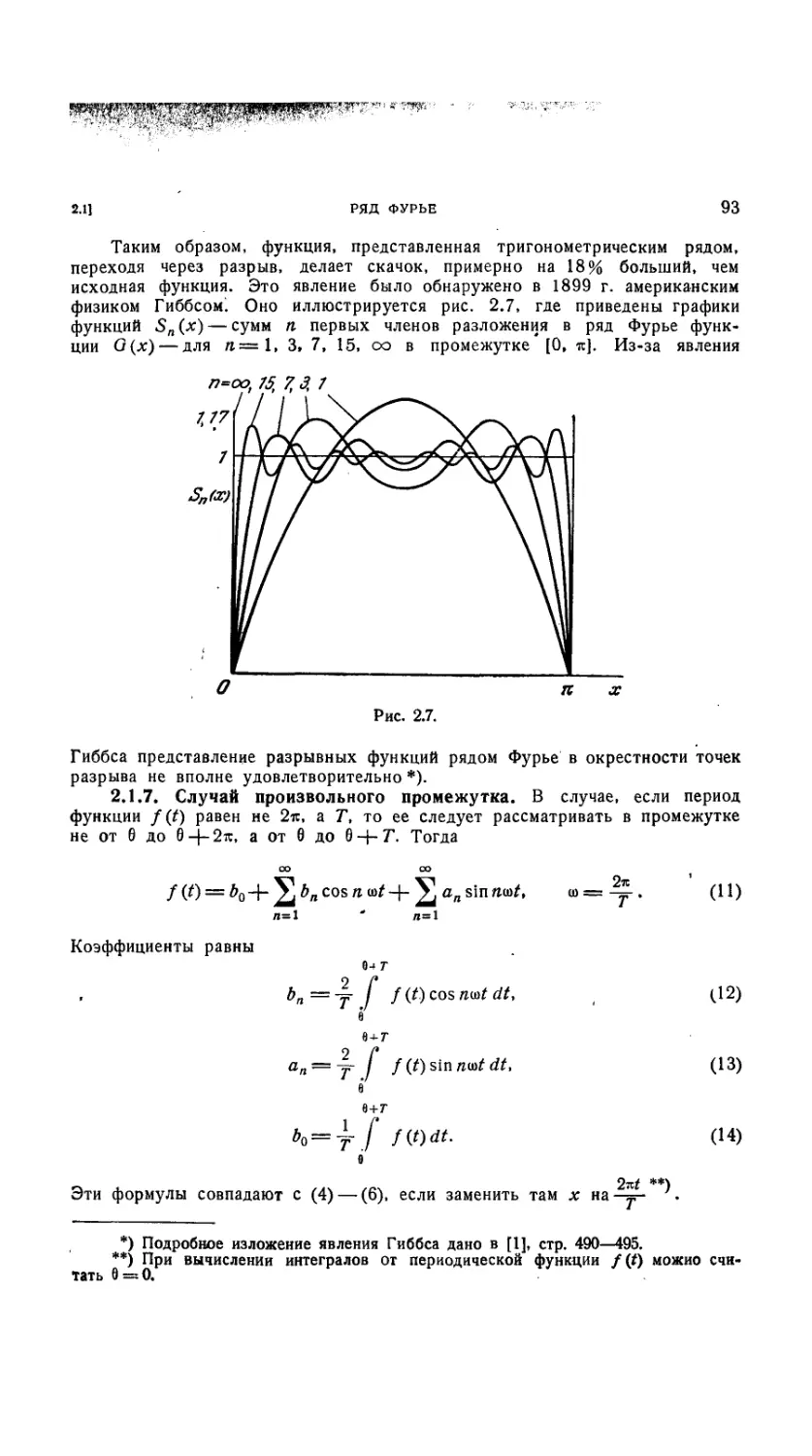
2.1.6. Изучение разложения в ряд Фурье вблизи точки разрыва.
Явление Гиббса 91
2.1.7. Случай произвольного промежутка 93
2.1.8. Ряды с комплексными членами 94
2.1.9. Графическое представление. Спектр 94
2.1.10. Среднее значение произведения двух функций одного периода,
разложимых в ряд Фурье 96
2.1.11. Распространение ряда Фурье на почти периодические функции 97
2.2. Интеграл Фурье 98
2.2.1. Вещественная форма интеграла Фурье 98
2.2.2. Комплексная форма интеграла Фурье 100
2.2.3. Применение к электрическим цепям 102
2.2.4. Случай незатухающей цепи 104
2.2.5. Спектр частот 105
2.2.6. Единичная функция Хевисайда 109
ОГЛАВЛЕНИЕ
2.2.7. Пары функций 109
2.2.8. Преобразование Фурье ПО
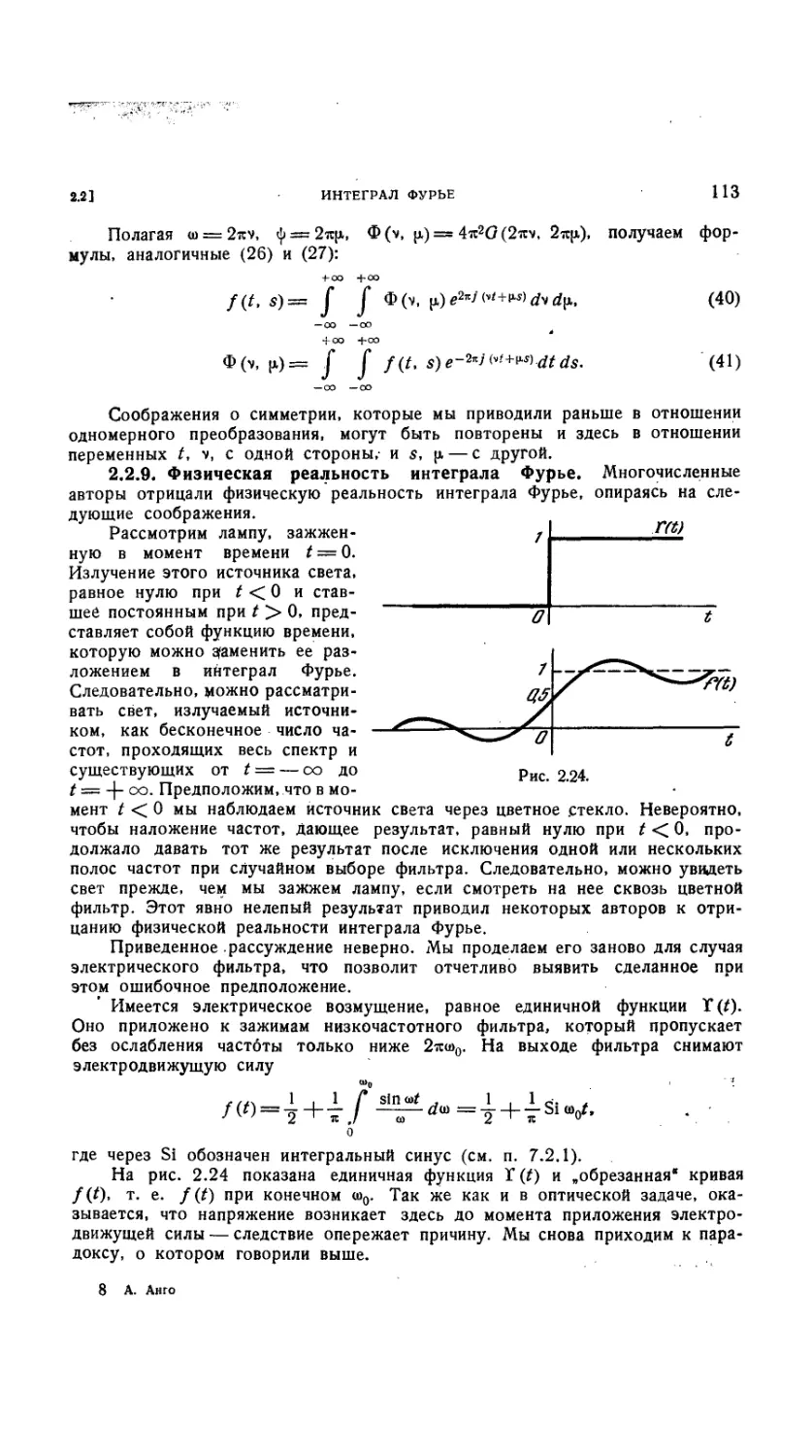
2.2.9. Физическая реальность интеграла Фурье 113
2.2.10. Изучение диаграмм направленности . 115
Литература к главе II • 116
Глава III. Векторное исчисление 117
3.1. Скалярные величины. Векторные величины. Определения 117
Скалярные величины 117
3.1.1. Чистые скаляры 117
3.1.2. Псевдоскаляры 117
Векторные величины 117
3.1.3. Ось 117
3.1.4. Направление вращения 118
3.1.5. Прямые и обратные трехгранники 118
3.1.6. Векторы 118
3.1.7. Положительное направление трех векторов а, Ь, с 120
3.1.8. Угол между двумя векторами а и b 120
Операции над векторами 120
3.1.9. Произведение вектора а иа скаляр / 120
3.1.10. Составляющие вектора 120
.11. Сложение векторов 120
.12. Скалярное произведение 121
.13. Векторное произведение . . . . ¦ 122
.14: Смешанное произведение трех векторов 123
.15. Двойное векторное произведение трех векторов 124
3.2. Дифференциальные операции с векторами 124
Дифференцирование 124
3.2.1. Производная вектора. Производная точки 124
3.2.2. Производная вектора по другому вектору 125
3.2.3. Основные формулы дифференцирования 125
3.2.4. Интеграл от вектора > . 126
Функции точек 126
3.2.5. Градиент ....*. 127
3.2.6. Нормальная производная 127
3.2.7. Поверхности уровня •. 128
3.2.8. Смысл вектора grad / 128
3.2.9. Силовые линии' 128
3.2.10. Градиент сложной скалярной функции 129
3.2.11. Дивергенция и вихрь 129
3.2.12. Оператор Лапласа ._ , . 130
3.2.13. Символический вектор набла (оператор Гамильтона) 130
3.2.14. Наиболее употребительные формулы 132
3.2.15. Смысл вектора rota ' 134
3.2.16. Скалярный потенциал 134
3.2.17. Частный случай: вектор проходит через фиксированную точку . 136
3.2.18. Векторный потенциал . . . 137
3.2.19. Общий случай векторного поля 139
3.3. Векторные интегралы 139
3.3.1. Циркуляция вектора 139
3.3.2. Поток вектора 140
Основные формулы 140
3.3.3. Теорема Остроградского 140
3.3.4. Смысл скаляра diva 142
ОГЛАВЛЕНИЕ
3.3.5. Формула для градиента 143
3.3.6. Формула для вихря 143
3.3.7. Инвариантность градиента, дивергенции, вихря . . .¦ 144
3.3.8. Формула Срина 144
3.3.9. Формула Стокса 145
Приложение векторного исчисления к теории электромагнитного поля 147
3.3.10. Электростатическое поле 147
3.3.11. Магнитное поле постоянных токов 149
3.3.12. Электромагнитное поле 150
3.3.13. Закон Фарадея 150
3.3.14. Закон Ампера 150
3.3.15. Уравнения Максвелла 151
3.3.16. Векторный потенциал магнитного поля, возбужденного током . 151
Системы ортогональных криволинейных координат 153
3.4.1. Определение 153
3.4.2. Дифференциальные операторы в ортогональных криволинейных
координатах 157
Важнейшие системы ортогональных криволинейных координат в про- •
странстве 158
3.4.3. Система цилиндрических координат 158
3.4.4. Система сферических координат , 159
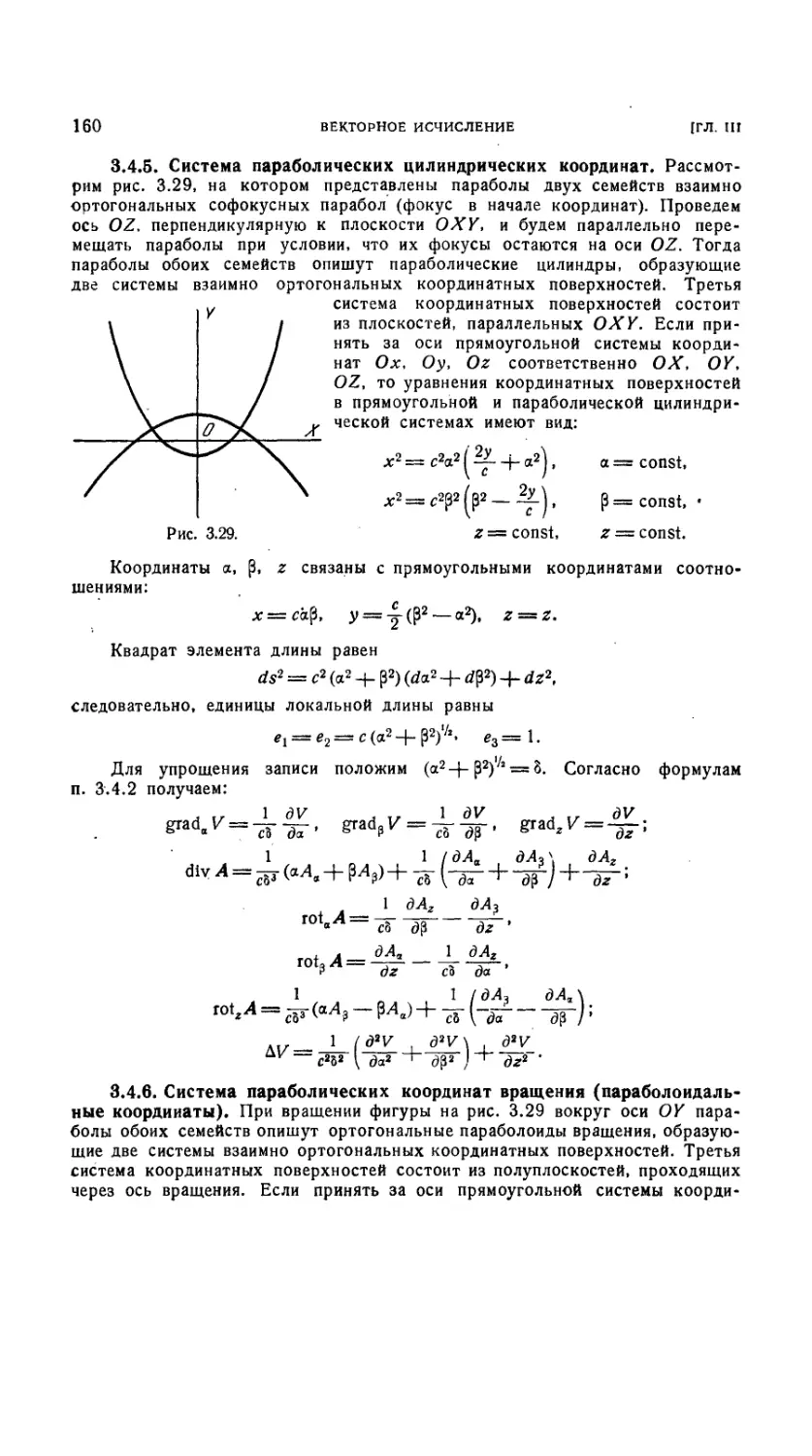
3.4.5. Система параболических цилиндрических координат 160
3.4.6. Система параболических координат вращения (параболоидальные
координаты) . 160
3.4.7. Система эллиптических цилиндрических координат 161
3.4.8. Система вытянутых эллипсоидальных координат (вращения) . . . 162
3.4.9. Система сплюснутых эллипсоидальных координат (вращения) . . 163
3.4.10. Система бицилиндрических координат 164
3.4.11. Системы тороидальных и бисферических координат 165
3.4.12. Система софокусных поверхностей второго порядка (система
общих эллипсоидальных координат) 167
3.4.13. Приложение к уравнениям Максвелла. .Уравнения Максвелла в
ортогональных криволинейных координатах 168
Литература к главе III 169
V. Матричное исчисление 170
Алгебра матриц .• 170
4.1.1. Плоское преобразование, понятие оператора 170
4.1.2. Сумма двух операторов 171
4.1.3. Произведение двух операторов 171
4.1.4. Представление плоских преобразований с помощью матриц . . . 171
4.1.5. Произведение двух матриц 172 V
4.1.6. Представление вектора посредством матрицы 173
4.1.7. Обобщение на «-мерное пространство 173
4.1.8. Равенство двух матриц 174
4.1.9. Сложение двух матриц 174
4.1.10. Умножение матрицы на число ¦ 174
4.1.11. Умножение матриц 174
4.1.12. Симметричные матрицы 176 *
4.1.13. Кососимметричные матрицы 176
4.1.14. Диагональные матрицы 177
4.1.15. Единичная матрица. Нулевая матрица 177 !¦
4.1.16. Порядок, ранг матрицы 177 *
4.1.17. Необходимые условия равенства нулю произведения двух мат-
матриц 178
4.1.18. Транспонированная матрица 179
4.1.19. Обратная матрица 180
4.1.20. Применение матричного исчисления к решению системы линей- %
ных уравнений 183
4.1.21. Преобразование системы координат . .* 185
ОГЛАВЛЕНИЕ 9
4.1.22. Ортогональное преобразование 186
4.1.23. Пример ортогональных преобразований. Поворот 187
Обобщение на комплексное пространство 187
4.1.24. Эрмитова матрица 187
4.1.25. ЭЬмитОво-Сопрйженная матрица . . . . « 187
4.1.26. Модуль н скалярное произведение в комплексном пространстве 188
4.1:27.' Ортогональное преобразование комплексного пространства (уни-
(унитарное преобразование) 189
' 4.1.28. Собственные значения, собственные векторы и характеристиче-
•¦ ское уравнение матрицы 189
4.1.29. Свойства характеристического уравнения 190
4.1.30. Матрица, отнесенная к собственным направлениям 191
4.1.31. Условия коммутативности двух матриц 192
4.1.32. Собственные значения и собственные направления эрмитовой
матрицы" . .' 192
Функции от матриц 193
4.1.33. Степень матрицы 193
4.1.34. Теорема Кели—Гамильтона 194
4.1.35. Функции от матриц. Теорема Сильвестра 194
4.1.36. Формула Бэкера 196
4.1.37. Высокие степени матрицы 198
4.1.38. Дробная степень матрицы 198
4.1.39. Приближенное вычисление собственных значений матрицы . . . 199
4Л.40. Приближенное вычисление корней уравнения га-й степени . . . 203
Дифференциальные операции иад матрицами. Применение к решению
дифференциальных уравнений .205
4.1.41. Дифференцирование и интегрирование матрицы 205
4.1.42. Решение айтемы линейных дифференциальных уравнений пер-
первого порядка 206
4.1.43. Система дифференциальных уравнений первого порядка с по-
постоянными коэффициентами 207
4.1.44. Случай линейного дифференциального уравнения «-го порядка 209
4.2. Применение матричного исчисления. Изучение четырехполюсников . . 210
4.2.1. Определение 210
4.2.2. Соединение четырехполюсников по цепной схеме ,. . 212
4.2.3. Параллельное соединение четырехполюсников 213
4.2.4. Последовательное соединение четырехполюсников .213
4.2.5. Последовательио-пар'аллельное и параллельно-последовательное
соединение четырехполюсников 214
4.2.6. Сопротивления холостого хода и короткого замыкания четырех-
четырехполюсника 216
4.2.7. Пассивные четырехполюсники 216
4.2.8. Симметричные четырехполюсники ¦ 217
Примеры простых четырехполюсников . 217
4.2.9. Четырехполюсник с одним последовательным сопротивлением . . 217
4.2.10. Четырехполюсник с одним параллельным сопротивлением .... 217
4.2.11. Г-образный четырехполюсник 218
4.2.12. Т-обраэный и П-образный четырехполюсники 218
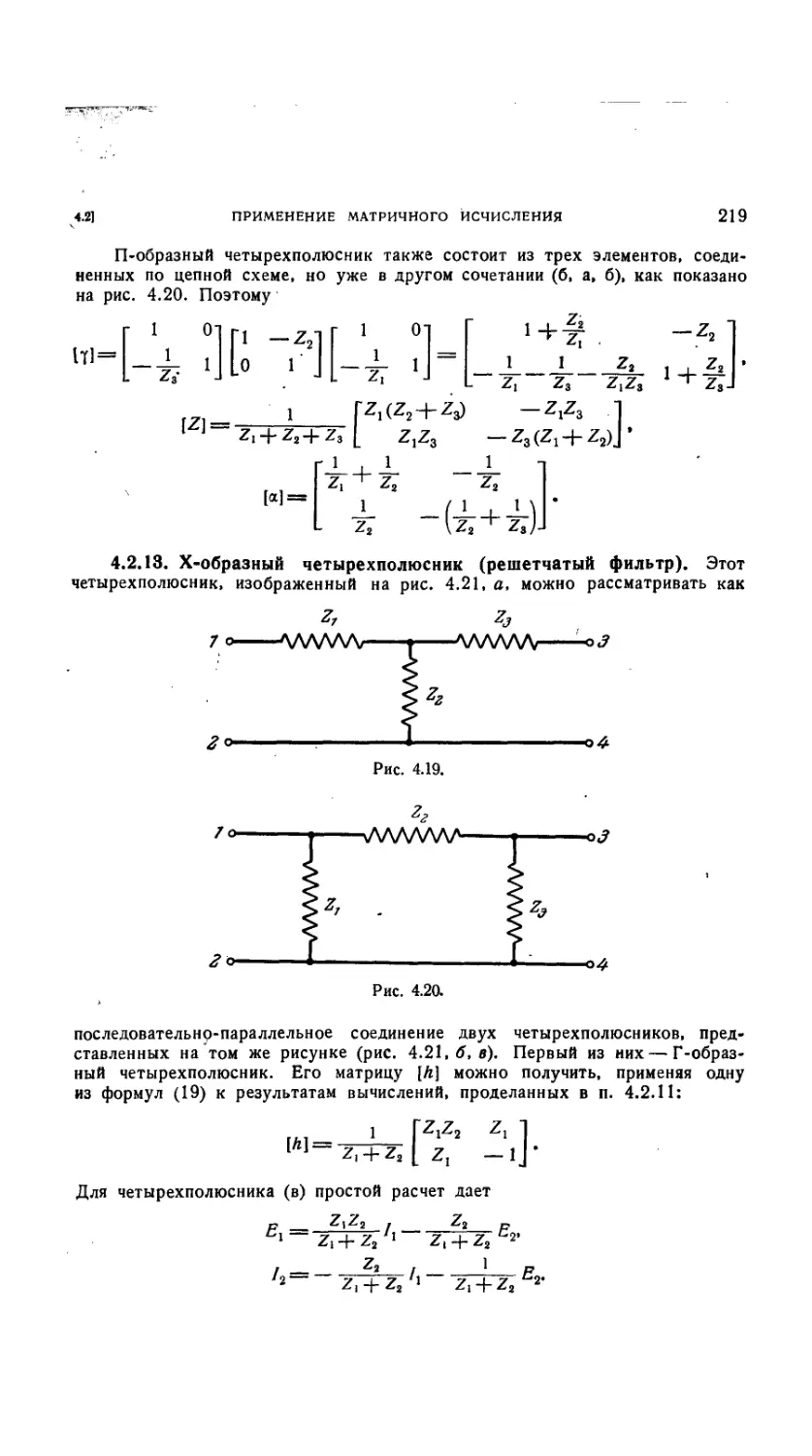
4.2.13. Х-образный четырехполюсник (решетчатый фильтр) 219
4.2.14. Трансформатор 220
4.2.15. Электронная лампа 221
4.2.16. Повторйое сопротивление четырехполюсника 224
4.2.17. Случай пассивного четырехполюсника 225
4.2.18. Цепные фильтры 226
4.2.19. Полоса пропускания четырехполюсника 228
4.2.20. Расчет свободных колебаний цепи • . 229
4.2.21. Контуры с периодически меняющимися параметрами 232
4.2.22. Матрицы в квантовой механике 235
Литература к главе IV 237
10 ОГЛАВЛЕНИЕ
Глава V. Тензорное исчисление. Приложения 238
5.1. Тензорная алгебра 238
Аффинное векторное пространство. Метрическое пространство .... 238
5.1.1. Определения 238
5.1.2. Преобразование координат 239
5.1.3. Ковариантные и контравариантные векторы 240
5.1.4. Определение тензора 241
5.1.5. Матричная форма формул преобразования координат 242
5.1.6. Немой индекс 245
5.1.7. Симметрия и антисимметрия 245
5.1.8. Псевдоскаляры. Скалярная плотность и скалярная емкость . . . 247
5.1.9. Тензорная плотность и тензорная емкость 248
5.1.10. Антисимметричный тензор второй валентности в трехмерном
пространстве 249
Операции над тензорами 250
5.1.11. Сложение двух тензоров * 250
5.1.12. Свертывание тензора ¦ 250
5.1.13. Умножение тензоров 251
5.1.14. Свертывание произведения 251
5.1.15. Установление типа тензора 251
5.2. Тензоры в криволинейной системе координат 252
5.2.1. Определение криволинейных координат. Криволинейные оси. Коор-
Координатная поверхность 252
5.2.2. Фундаментальный метрический тензор 254
5.2.3. Преобразование определителя g фундаментального метрического
тензора при преобразовании координат 255
5.2.4. Выражение для элемента объема, 255
5.2.5. Косоугольная система координат на плоскости 255
5.2.6. Ортогональные криволинейные координаты в трехмерном про-
пространстве 256
5.2.7. Случай произвольных криволинейных координат 257
5.2.8. Контравариантные или ковариантные составляющие компоненты
одного и того же вектора 257
5.2.9. Изменение вариантности тензора 258
5.2.10. Смешанный фундаментальный метрический тензор 258
5.2.11. Случай прямолинейной прямоугольной системы координат . . .258
Геометрическое представление контравариантных и ковариантных ком-
компонент вектора 258
5.2.12. Случай прямоугольной косоугольной системы координат . . . 258
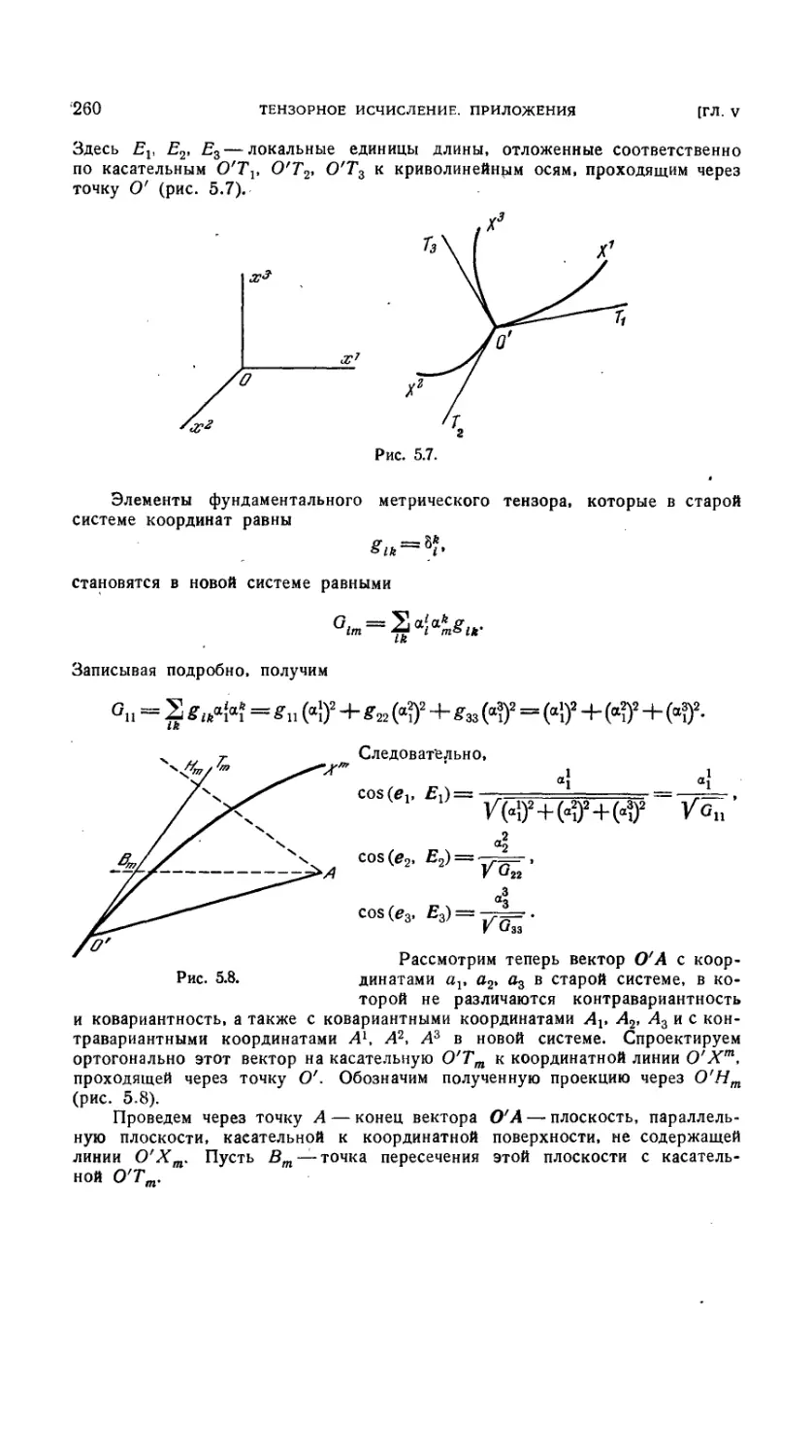
5.2.13. Случай криволинейных координат 259
5.2.14. Частный случай ортогональных криволинейных координат . . . 261
5.3. Дифференциальные операторы в криволинейных координатах .... 261
5.3.1. Градиент 261
5.3.2. Ротор (вихрь) 262
5.3.3. Дивергенция 262
5.3.4. Лапласиан (оператор Лапласа) 262
Частный случай ортогональных криволинейных координат 283
5.3.5. Градиент 263
5.3.6. Ротор 263
5.3.7. Дивергенция 263
5.3.8. Лапласиан 264
5.3.9. Тензорная форма уравнений Максвелла 264
5.4. Применение тензорного исчисления к исследованию электрических
цепей 265
5.4.1. Элементы ¦ электрических цепей с сосредоточенными постоянными 265
5.4.2. Метод составления уравнений для цепи наиболее общего вида . 268
5.4.3. Соединение цепей посредством проводников 277
ОГЛАВЛЕНИЕ 11
¦ 5.4.4. Соединение цепей посредством магнитопроводов 280
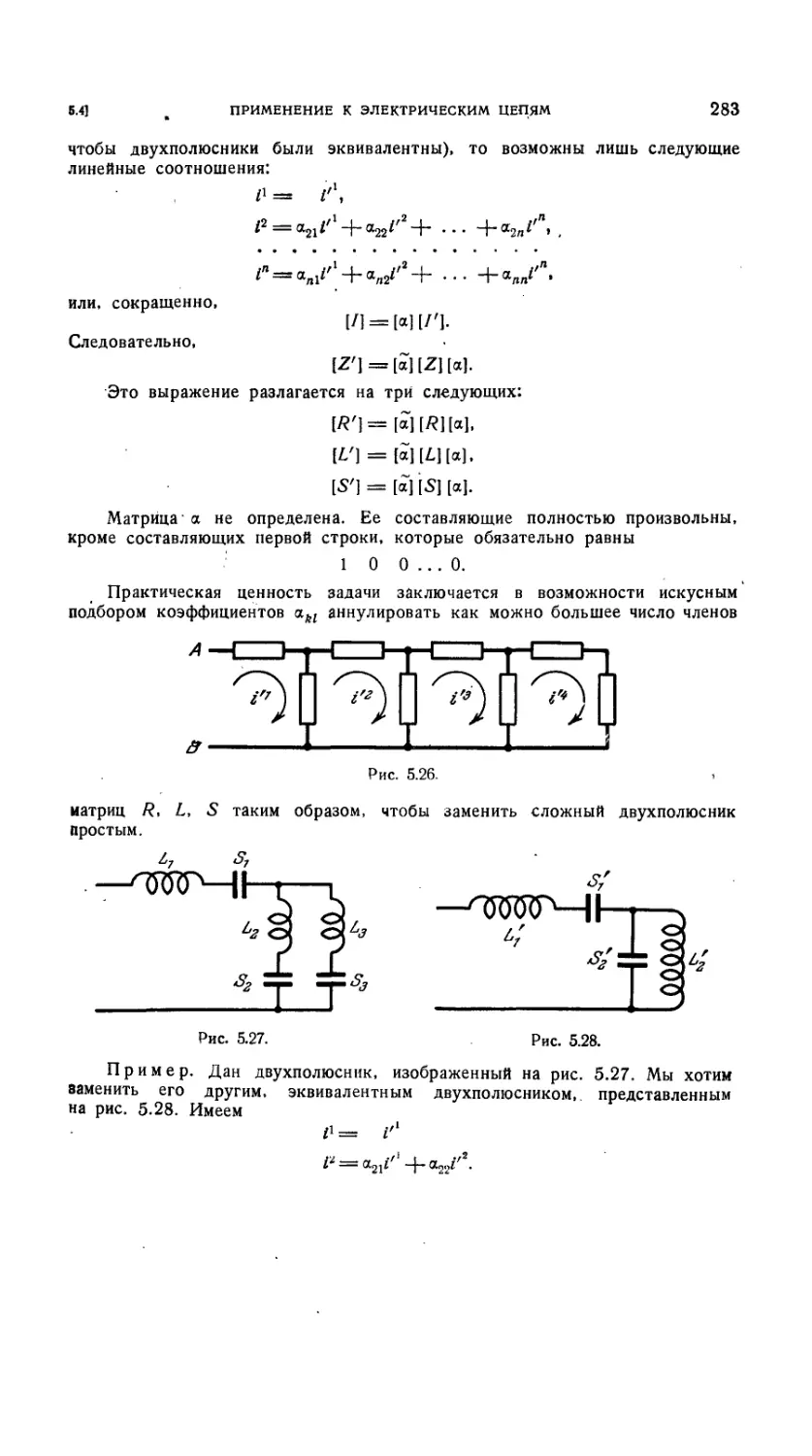
5.4.5. Анализ эквивалентных цепей 282
5.4.6. Цепи с внешним питанием 285
5.5. Применение тензорного исчисления к изучению анизотропных сред . . 288
5.5.1. Введение * 288
5.5.2. Диэлектрические свойства кристалла 288
5.5.3. Матрицы преобразования для некоторых часто встречающихся
систем координат 289
Механические свойства кристалла 291
5.5.4. Напряжение 291
5.5.5. Деформации 292
5.5.6. Тепловое расширение 293
5.5.7. Обобщенный закон Гука 293
5.5.8. Применение шестимерного пространства . 295
5.5.9. Модуль Юнга ........ 298
Пьезоэлектричество 298
5.5.10. Электрическая поляризация . 298
5.5.11. Закон Кюри 301
5.5.12. Пьезоэлектрические свойства кварца 301
5.5.13. Распространение упругих волн в кристаллах 303
5.5.14. Плоские волны . 304
Литература к главе V 305
Глава VI. Методы интегрировании дифференциальных уравнений еЗО6
6.1. Дифференциальные уравнения первого порядка 306
6.1.1. Ураннение вида fix, -|j)=0, / (у, -|~)=0 . 306
6.1.2. Уравнения с разделяющимися переменными 307
6.1.3. Однородные уравнения 308
6.1.4. Уравнение в полных дифференциалах 309
6.1.5. Линейное уравнение 310
6.1.6. Уравнение Бернулли 311
6.1.7. Уравнение Риккати 311
6.1.8. Уравнение Лагранжа ,. 311
6.1.9. Уравнение Клеро 311
6.1.10. Общий случай f(x,y, -|?)=0 • • . . . 312
6.2. Дифференциальные уравнения порядка выше .первого 313
Случаи понижения порядка уравнения 313
6.2.1. Уравнение ие содержит явно функцию у 313
6.2.2. Уравнение ие содержит явно независимой переменной х 313
6.2.3. Уравнение, однородное относительно у, у', ..., у(п) 313
6.2.4. Уравнение, однородное относительно х и dx 314
6.2.5. Уравнение, однородное относительно х, у, dx, dy, d2y, ..., dny . 314
6.2.6. Общий случай однородного уравнения 314
Линейное дифференциальное уравнение п-го порядка 315
6.2.7. Введение 315
6.2.8. Метод вариации произвольных постоянных (метод Лагранжа) . 315
6.2.9. Уравнение Эйлера 317
6.2.10. Интегрирование при помощи степенных рядов 317
6.2.11. Некоторые теоремы о свойствах решений линейного дифферен-
дифференциального уравнения второго порядка 322
Интегрирование линейных дифференциальных уравнений с постоянны-
постоянными коэффициентами 324
6.2.12. Интегрирование однородного дифференциального уравнения . . 325
lf
ОГЛАВЛЕНИЕ
6.2.13. Случай кратного корня 325
6.2.14. Частный интеграл неоднородного уравнения 326
6.2.15. Случай резонанса '. 328
6.2.16. Система линейных дифференциальных уравнений с постоянны-
постоянными коэффициентами 329
Уравнения с частными производными 330
6.3.1. Линейное уравненяе с постоянными коэффициентами, однородное
относительно частных производных 330
6.3.2. Уравнение с правой частью 331
6.3.3. Уравнение колебаний струны 331
6.3.4. Телеграфное уравнение 333
6.3.5. Уравнение Лапласа 333
6.3.6. Прямоугольная система координат 335
6.3.7. Система цилиндрических координат 335 у
6.3.8. Система сферических координат 337 |
6.3.9.# Система эллиптических и цилиндрических координат 338 |
6.3.10*. Система параболических цилиндрических координат 339 р
6.3.11. Другие системы координат 340 ?
6.3.12. Уравнение Пуассона ¦ 342 |
6.3.13. Решение уравнений Максвелла методом Бромвича .'343 |.
6.3.14. Пример. Электромагнитные колебания в прямоугольной полости 347 |
Литература к плаве VI 348 |
II. Наиболее употребительные специальные функции 349 '
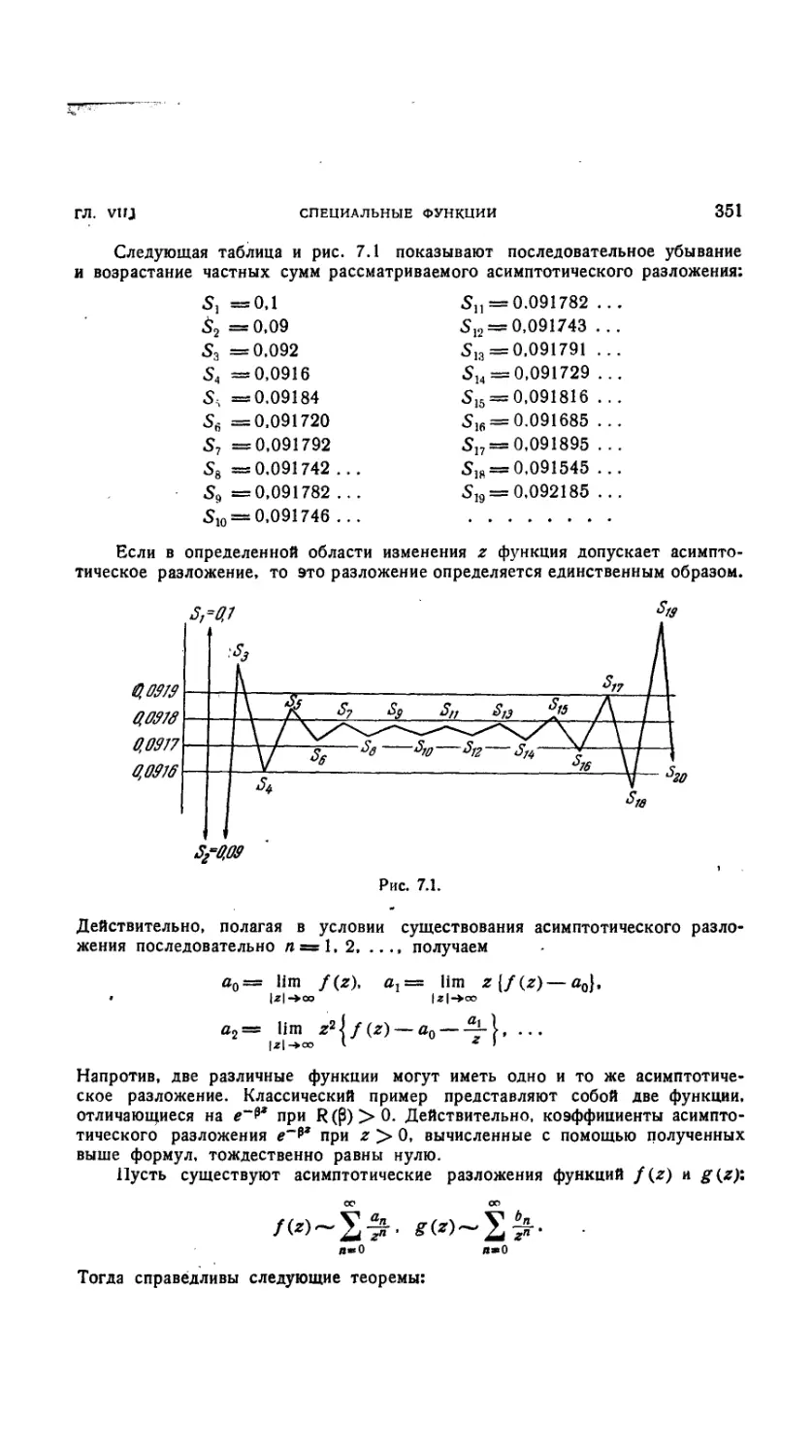
7.01. Асимптотическое разложение 349 [
Гиперболические функции 352 j
7.1.1. Определения 352
7.1.2. Обратные гиперболические функции 354
7.1.3. Приложение гиперболических функций к расчету длинных линий.
Метод Броуна. Абаки Блонделя — Кеннеди 354
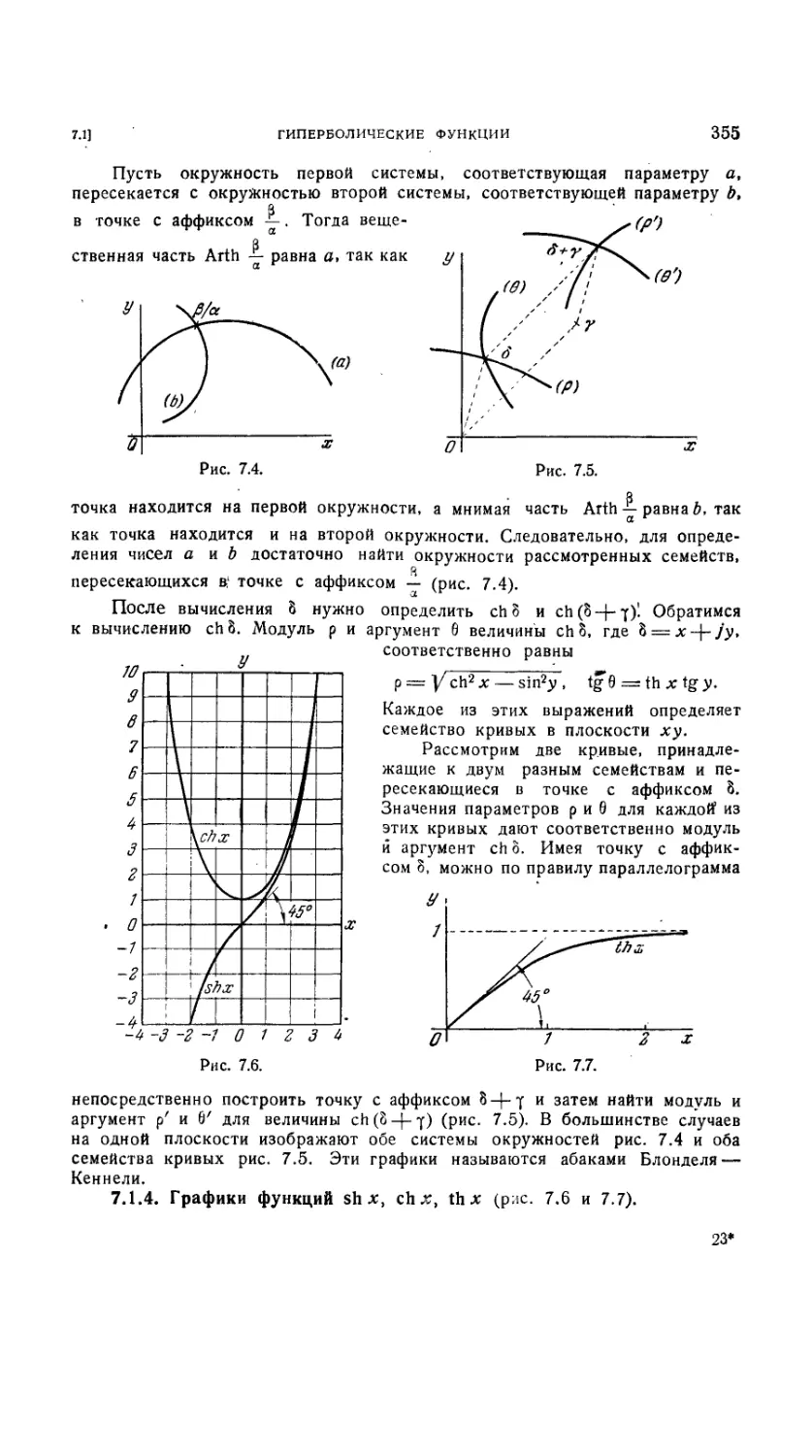
7.1.4. Графики функций sh x, ch х, th х 355
7.1.5. Таблицы показательной и гиперболической функций 356 Г-
Интегральный синус и косинус 356 (
7.2.1. Определение 356 tj
7.2.2. Разложение в степенной ряд 357
7.2.3. Разложение в асимптотический ряд 357
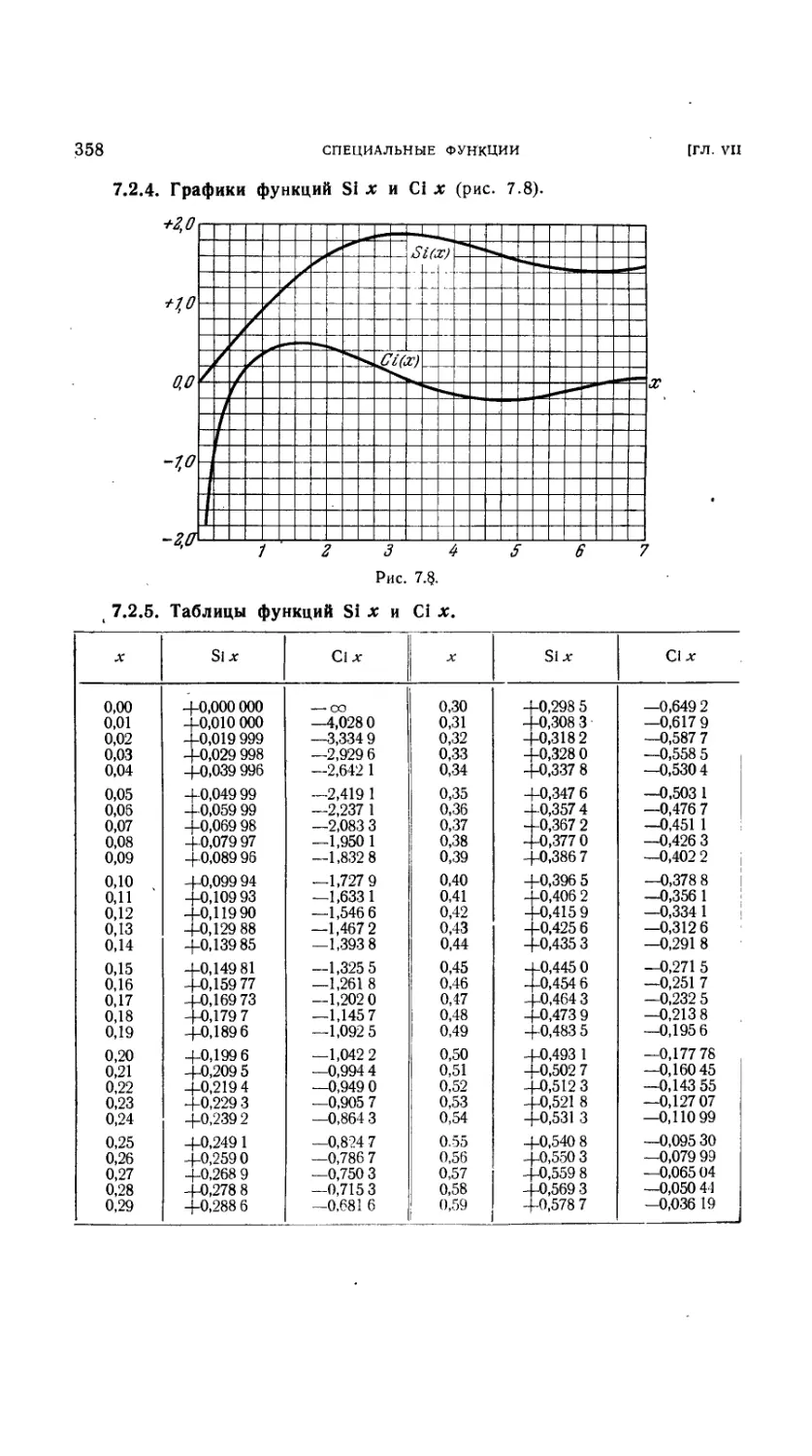
7.2.4. Графики функций Si x и Ci x 358
7.2.5. Таблицы функций Si x и Ci x 358
7.2.6. Положение экстремумов функций Ci х и Si х . . . 360
Функция вероятности ошибок 360
7.3.1. Определение 360
7.3.2. Разложение функции Ф(д;) в степенной ряд 361
7.3.3. Разложение в асимптотический ряд функции 1—Ф(д;) 361
7.3.4. Выражение функции 1 — *("о") через интеграл Коши 362
7.3.5. Таблица функции Ф(х) 363
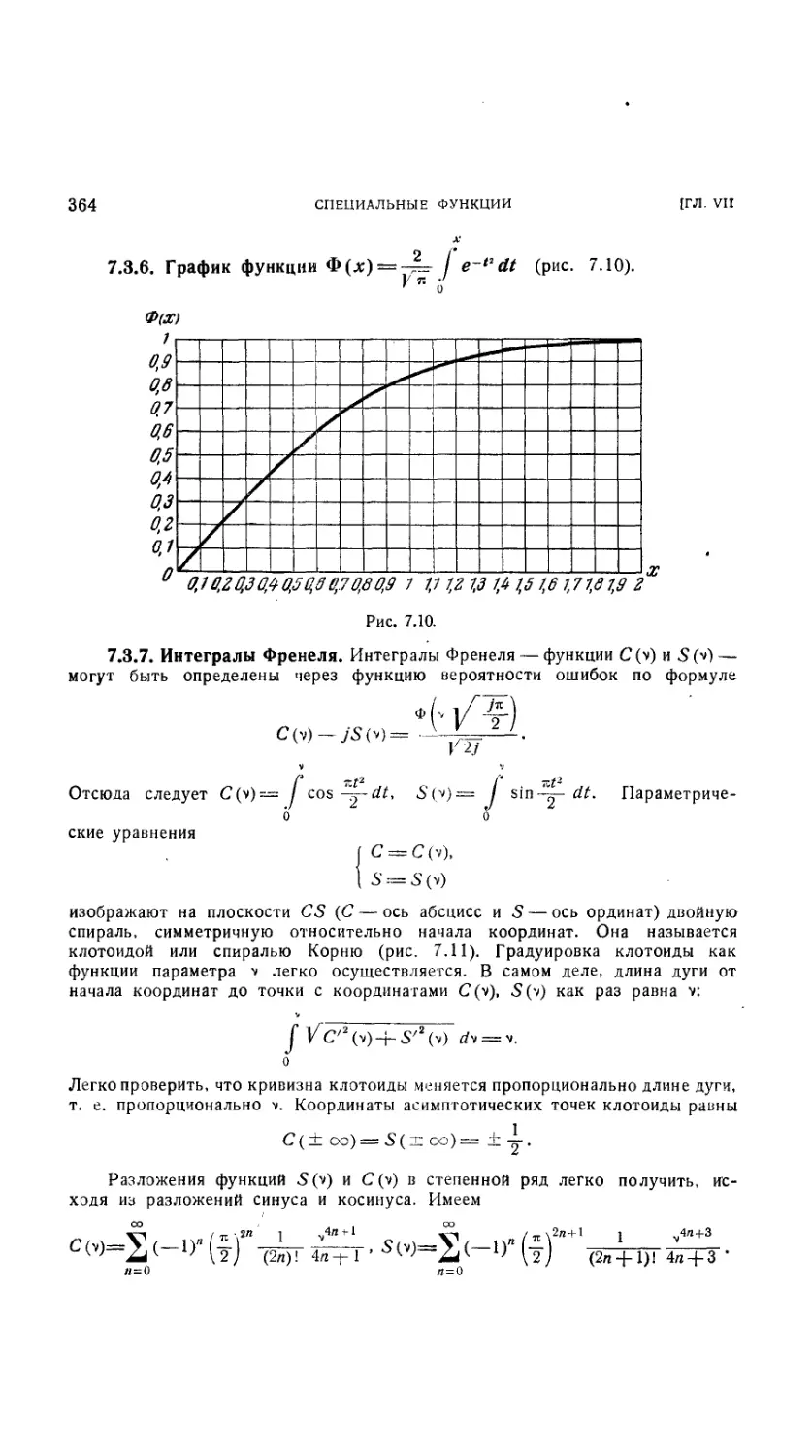
7.3.6. График функции Ф (х) 364
7.3.7. Интегралы Френеля 364 L
Гамма-функция 365 {
7.4.1. Определение 365 t
7.4.2. Свойства гамма-функции 367
7.4.3. Некоторые значения функции Г (г) 368
7.4.4. Логарифмическая производная гамма-функции 368
7.4.5. Представление гамма-функции через интеграл Коши 369
7.4.6. Связь между эйлеровыми интегралами первого и второго рода 370
ОГЛАВЛЕНИЕ 13
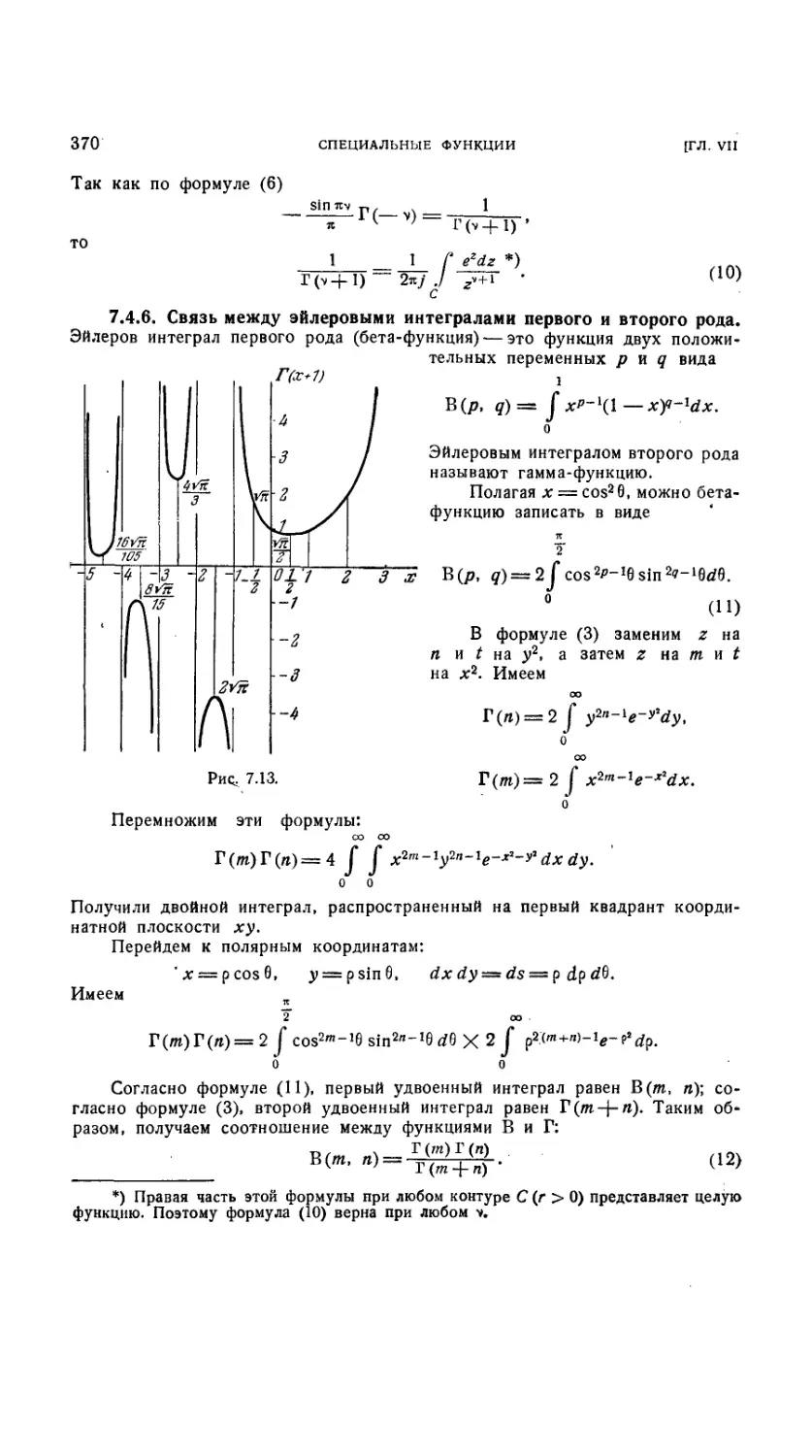
7.4.7. График функции у = Г(д; +1) 371
7.4.8. Таблица функции Г(х + 1) 371
7.5. Функции Бесселя 372
Функции Бесселя первого и второго рода 372
7.5.1. Определение функции первого рода 372
7.5.2. Соотношение между J4(z) и ./_*, (z) 373
7.5.3. Определение бесселевой функции второго рода 374
7.5.4. Рекуррентные соотношения 376
7.5.5. Применение рекуррентных соотношений к вычислению некоторых
интегралов 376
7.5.6. Интегралы Ломмеля 378
7.5.7. Соотношение между двумя функциями, индексы которых отли-
отличаются на целое число 379
7.5.8. Применение интегралов Ломмеля к разложению в ряд по бессе-
бесселевым функциям 380
7.5.9. Бесселевы функции первого и второго рода с полуцелым ин-
индексом ; 381
7.5.10. Применение бесселевых функций к вычислению интегралов
Френеля 382
7.5.11. Случай, когда индекс равен целому числу v — n . 383
7.5.12. Представление J4(z) через определенный интеграл 385
7.5.13. Представление J^(z) с помощью интеграла Коши 386
7.5.14. Теорема сложения 386
7.5.15. Бесселевы функции третьего рода или функции Ханкеля. Опре-
Определение 387
7.5.16. Асимптотические разложения ' : . . . .387
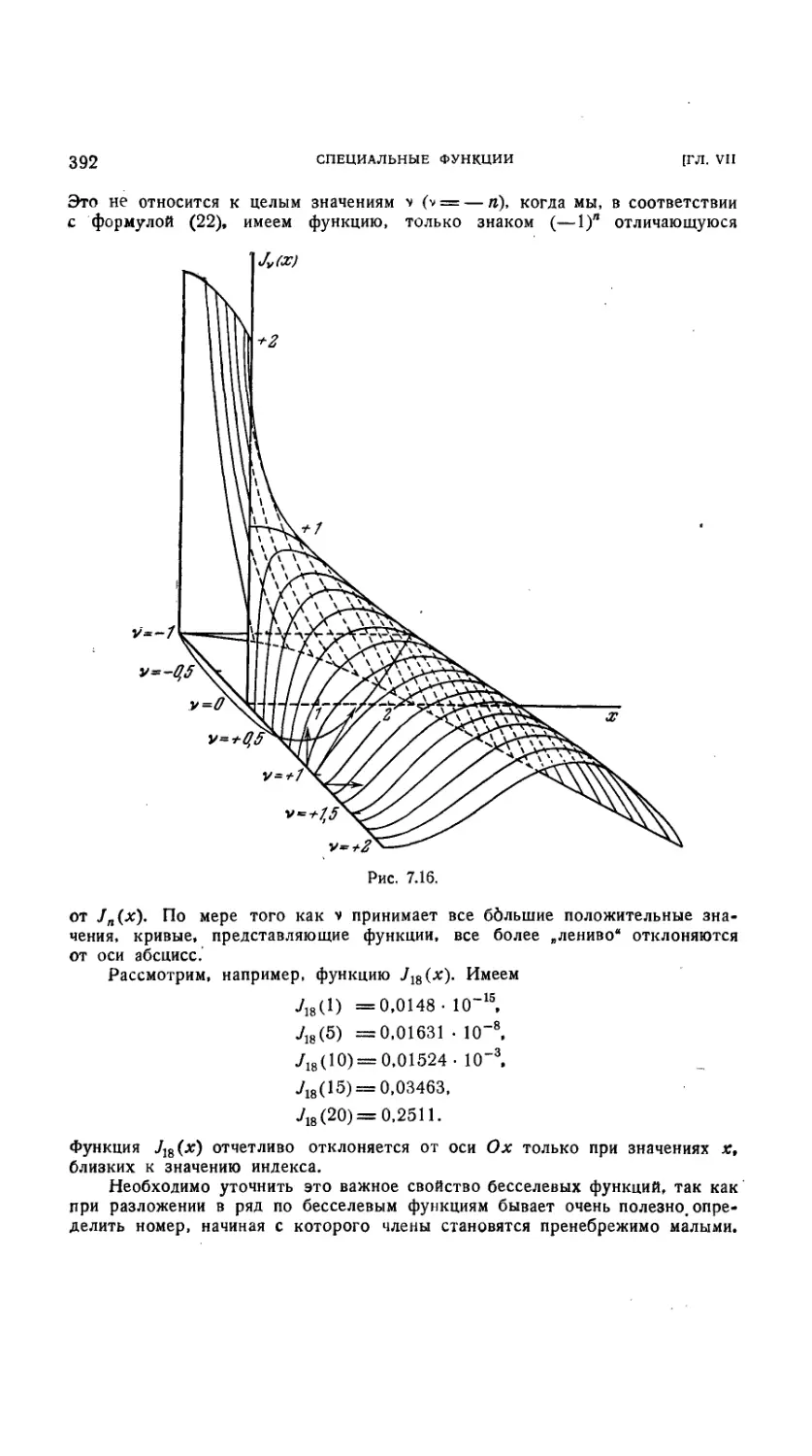
7.5.17. Нахождение численных значений бесселевых функций 388
7.5.18. Асимптотические выражения для бесселевых функций при
больших значениях аргумента 388
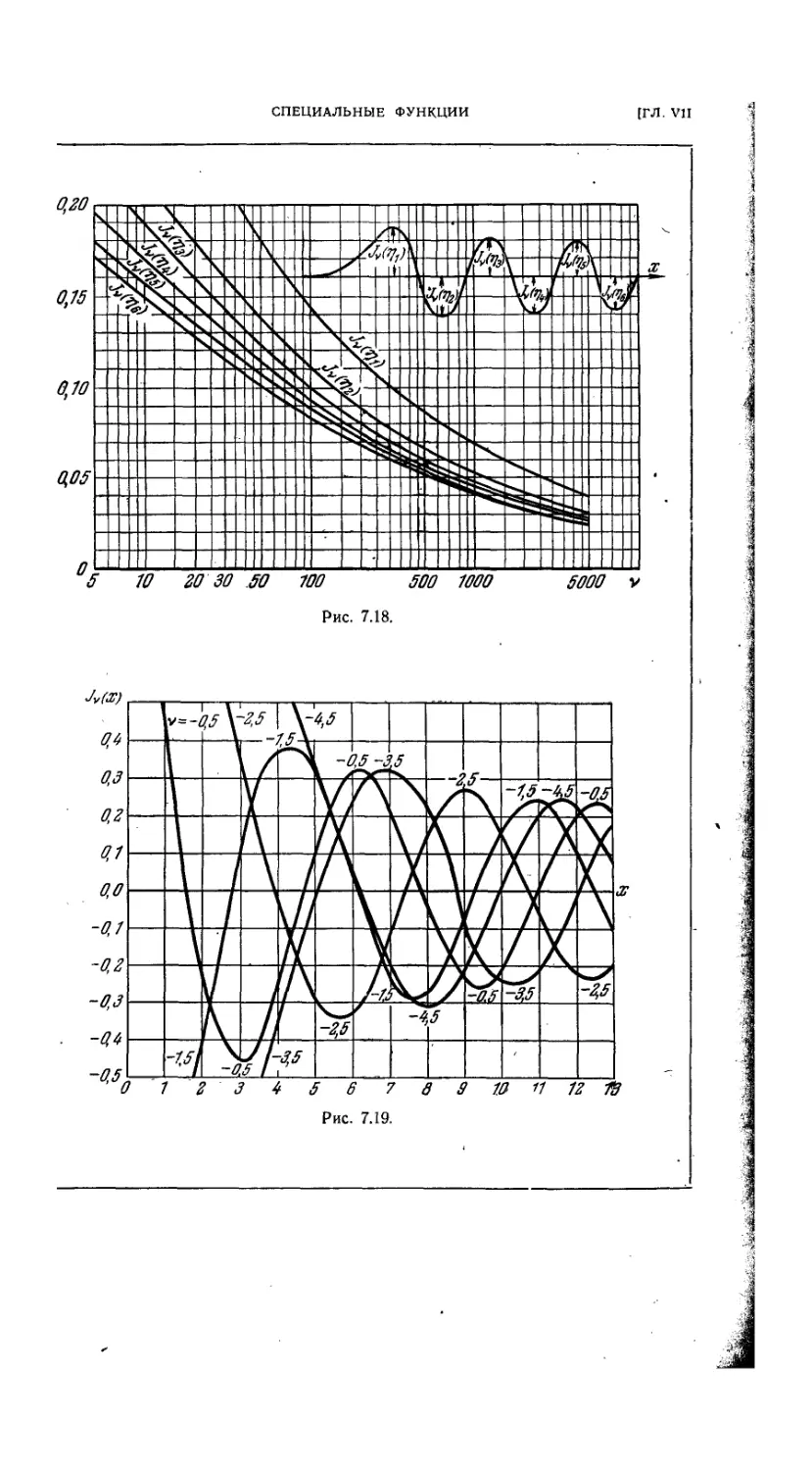
7.5.19. Корни бесселевых функций 389
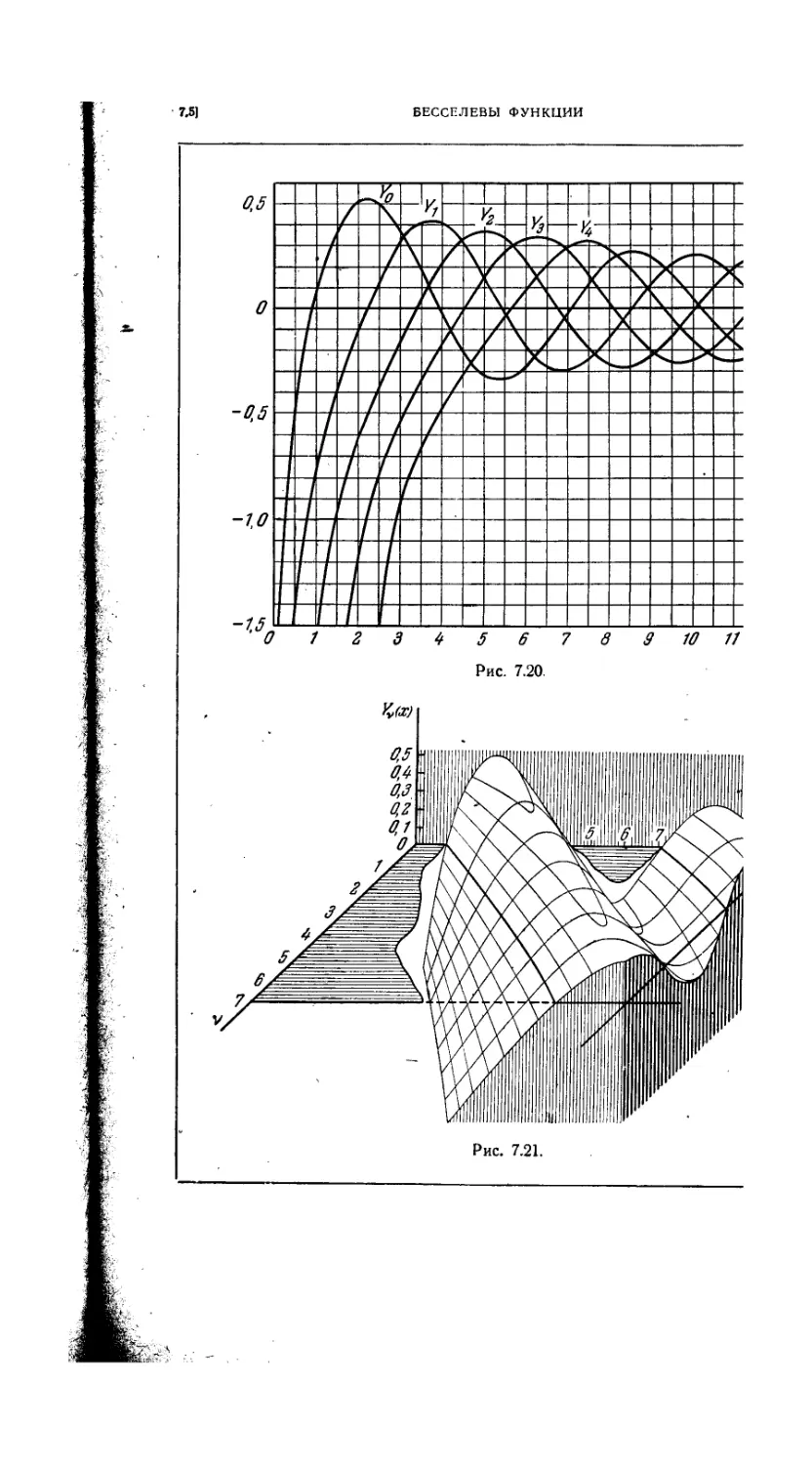
7.5.20. Криные J0(x), /,(*), J2(x) Js (х) 390
7.5.21. Поверхность z = / (х, ч) = У, (х) 390
7.5.22. Кривые J 1 (х), J 3 (*) J 9 (•*) ЗЭЗ
7.5.23. Кривые Ya (х), К, (х), Г2 {х), Г3 (х), Y<(x) 393
7.5.24. Понерхность г = / {х, м) = Yy (х) .393
Модифицированные бесселевы функции первого и второго рода . . . 393
7.5.25. Модифицированная бесселева функция первого рода ( . 393
у 7.5.26. Модифицированная бесселева функция второго рода 396
, 7.5.27. Асимптотические разложения 396
7.5.28 Рекуррентные формулы 397
7.5.29. Кривые 10(х), /,(*), . • •, Ai(X) • .... 398
7.5.30. Кривые Ко(х) и Kt(x) 398
Функции Кельвина 398
7.5.31. Функции Кельвина нулевого порядка 398
7.5.32. Функции Кельвина v-ro порядка 401
7.5.33. Представление функций Кельвина через модуль и аргумент . . 401
7.5.34. Производные функций Кельвина 401
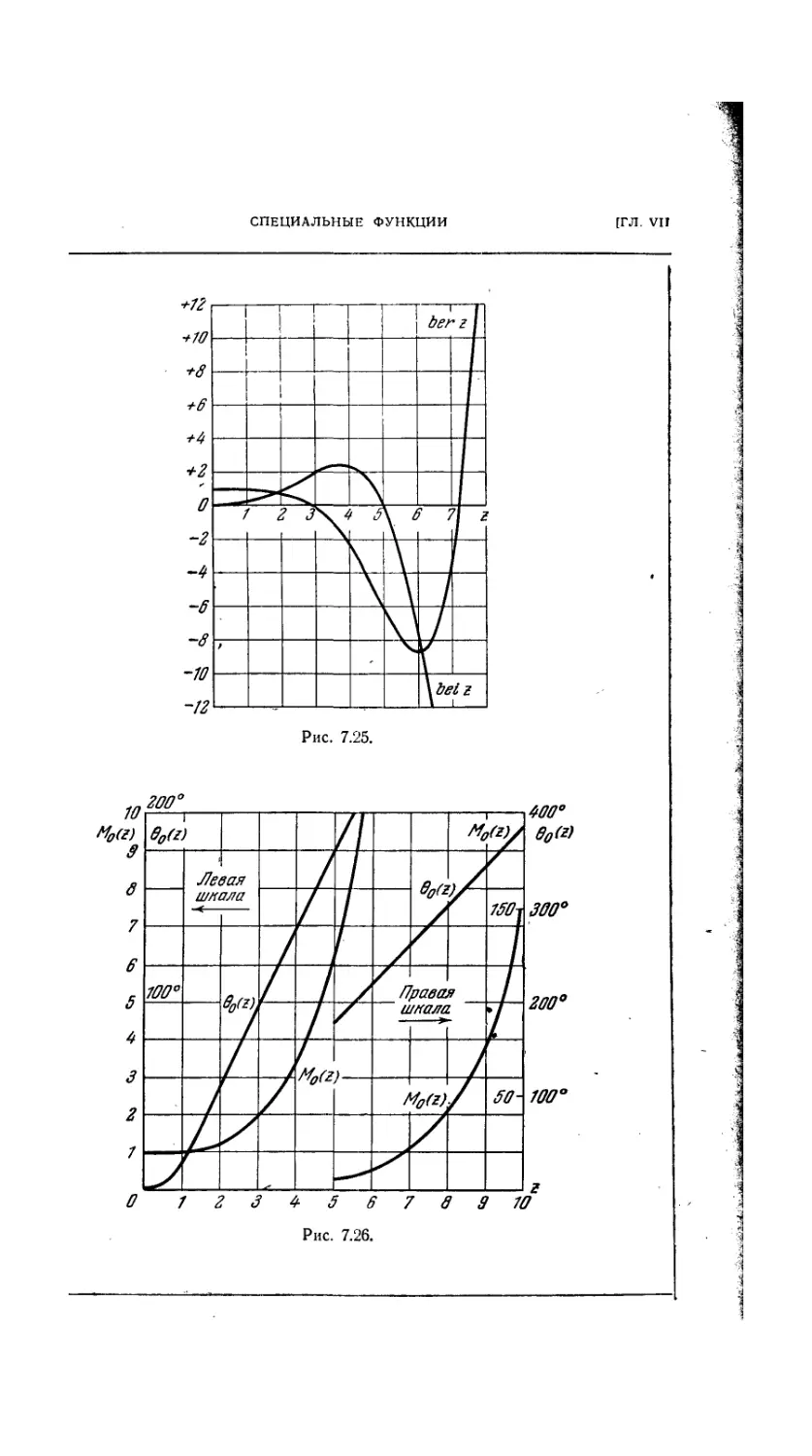
7.5.35. Графики функций ber(z), bei(z), M0(z), 90(z) . .403
Дифференциальные уравнения, решение которых может быть выра-
выражено через решение дифференциального уравнении Бесселя 403
7.5.36. Основные типы 403
Некоторые примеры применения бесселевых функций 405
7.5.37. Колебание однородной тяжелой нити, подвешенной за один
конец 405
7.5.38. Исследование решения волнового уравнения в цилиндрических
координатах 407
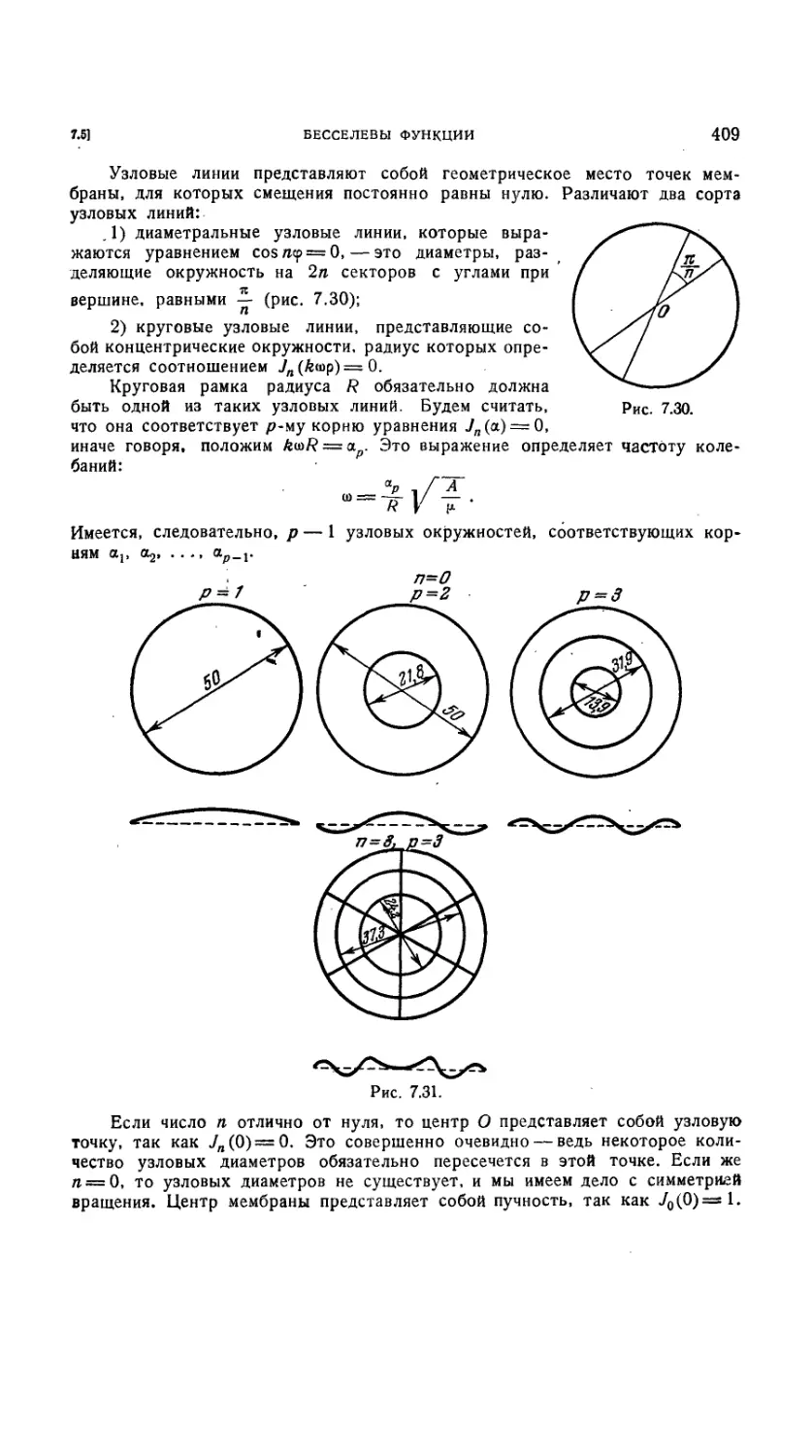
7.5.39. Колебания равномерно натянутой мембраны 408
7.5.40. Случай круглой мембраны 408
14 ОГЛАВЛЕНИЕ
7.5.41. Собственные электромагнитные колебания резонатора, имеюще-
имеющего форму кругового цилиндра 410
7.5.42. Распространение электромагнитной волны внутри бесконечного
кругового цилиндра 413
7.5.43. Случай коаксиального проводника 415
7.5.44. Скин-эффект переменных токов, проходящих по цилиндрическо-
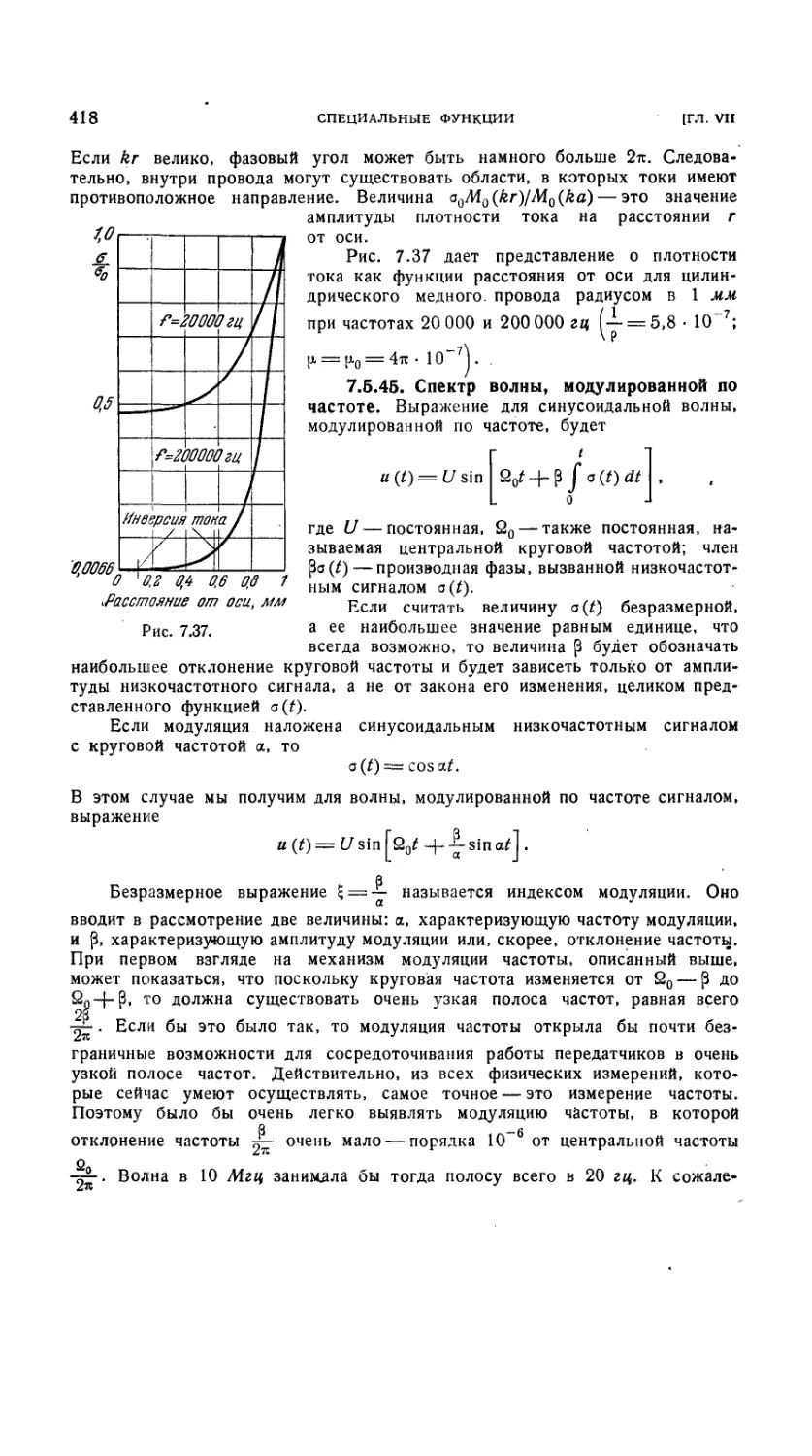
цилиндрическому проводнику круглого сечения 416
7.5.45. Спектр волны, модулированной по частоте 418
Таблицы бесселевых функций 422
7.5.46. Функции Jo, Л, Yo, У, 422
7.5.47. Бесселевы функции Jt, /3 h 425
7.5.48. Бесселевы функции Ао, 1\\, ¦ ¦ •> hi 425
7.5.49. Таблицы первых корней функций /n(z), Jn(z) 426
7.5.50. Бесселевы функции /р У3 J ш 4^7
Т Т
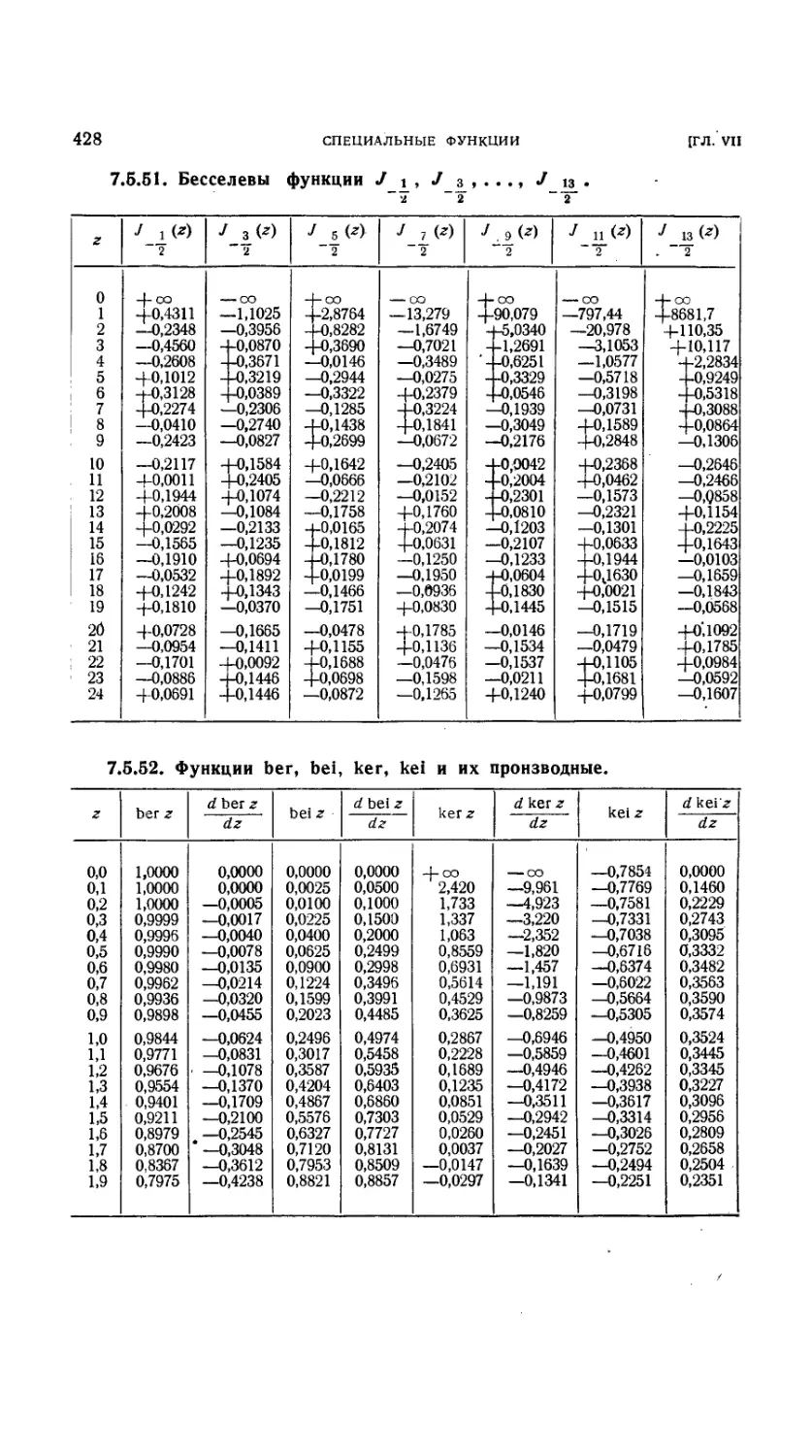
7.5.51. Бесселевы функции У lt J 3, ...,/ 13 428
~2 ~Т Г
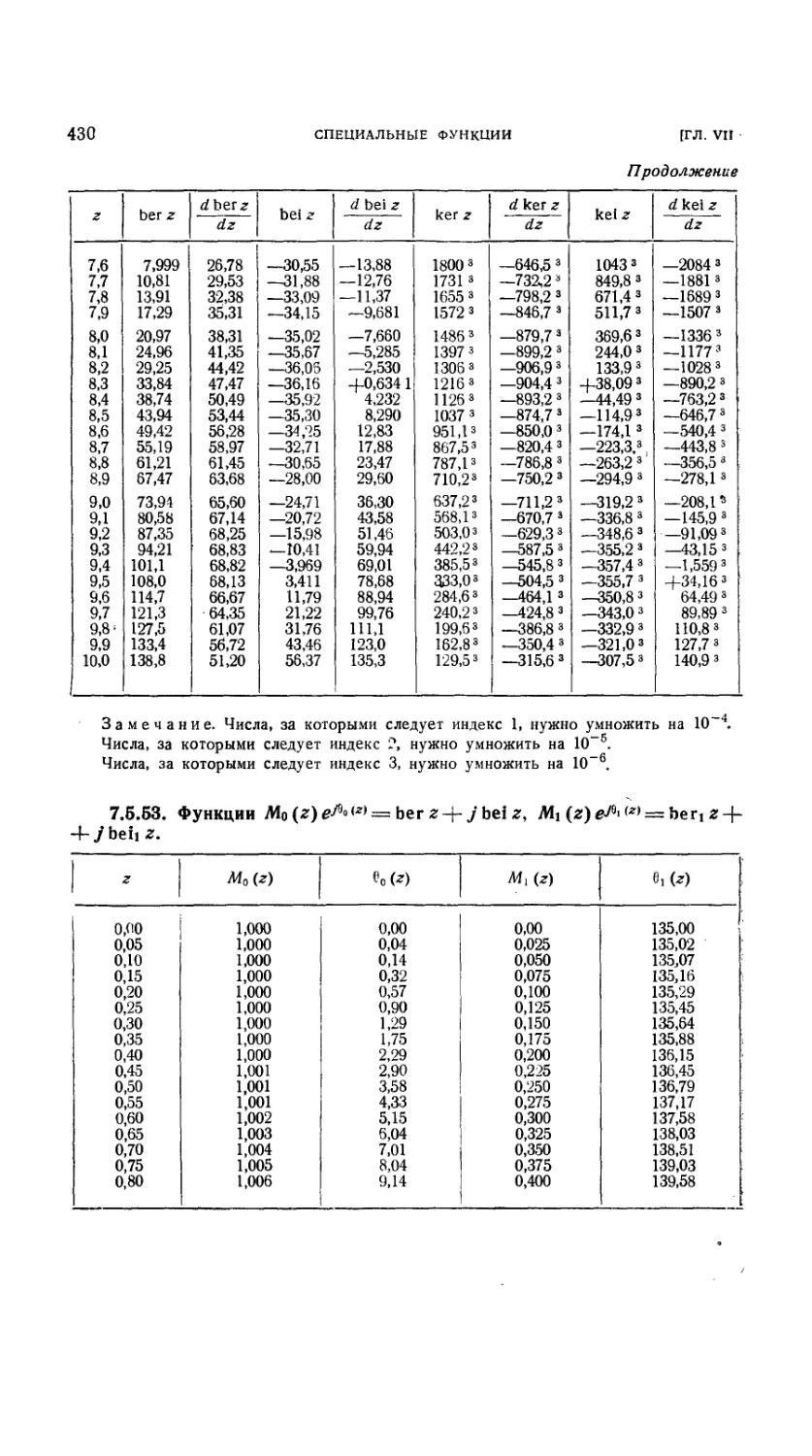
7.5.52. Функции ber, bei, ker, kei и их производные 428
7.5.53. Функции Af0> 8о, Ah, 61 430
7.6. Функции Лежандра 432
7.6.1. Введение 432
7.6.2. Разложения в степенные ряды 432
7.6.3. Полиномы Лежандра 434
7.6.4. Производящая функция полинамов Лежандра 434
7.6.5. Примеры полиномов Лежандра 436
7.6.6. Представление полиномов Лежандра через определенный инте-
1 грал. Формула Лапласа 436
7.6.7. Рекуррентные формулы 437
7.6.8. Формула Родрига 438
7.6.9. Ортогональность полиномов Лежандра 438
7.6.10. Некоторые значения полиномов Лежандра 440
7.6.11. Корни полиномов Лежандра 440
7.6.12. Интеграл Шлефли 440
7.6.13. Обобщение полиномов Лежандра. Полиномы Гегенбауера . . . 441
7.6.14. Функции Лежандра первого рода 441
7.6.15. Описание поверхности у «= Р „ (cos в) 443
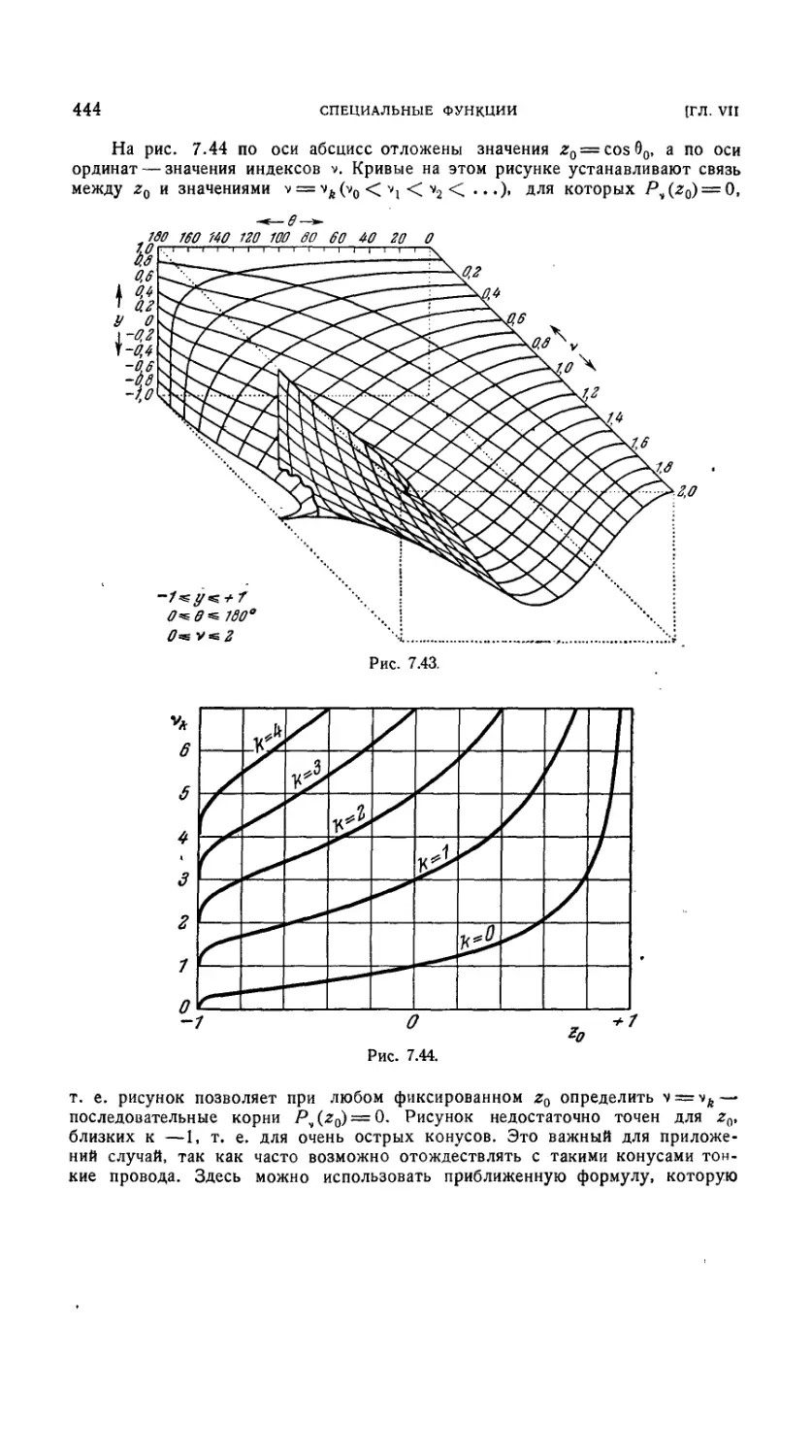
7.6.16. Корни функций Лежандра первого рода 443
7.6.17. Рекуррентные формулы 445
7.6.18. Определение функции Лежандра первого рода через интеграл
Коши 446
7.6.19. Функция Лежандра второго рода. Определения 447
7.6.20. Определение функции Лежандра второго рода через интеграл
Коши 449
7.6.21. Присоединенные функции Лежандра 450
7.6.22. Присоединенные функции Лежандра для целых положительных
индексов 451
7.6.23. Рекуррентные соотношения 454
7.6.24. Ортогональность присоединенных функций Лежандра ... . 455
7.6.25. Некоторые значения присоединенных функций Лежандра. Прило-
Приложение присоединенных функций 456
7.6.26. Сферические гармоники 457
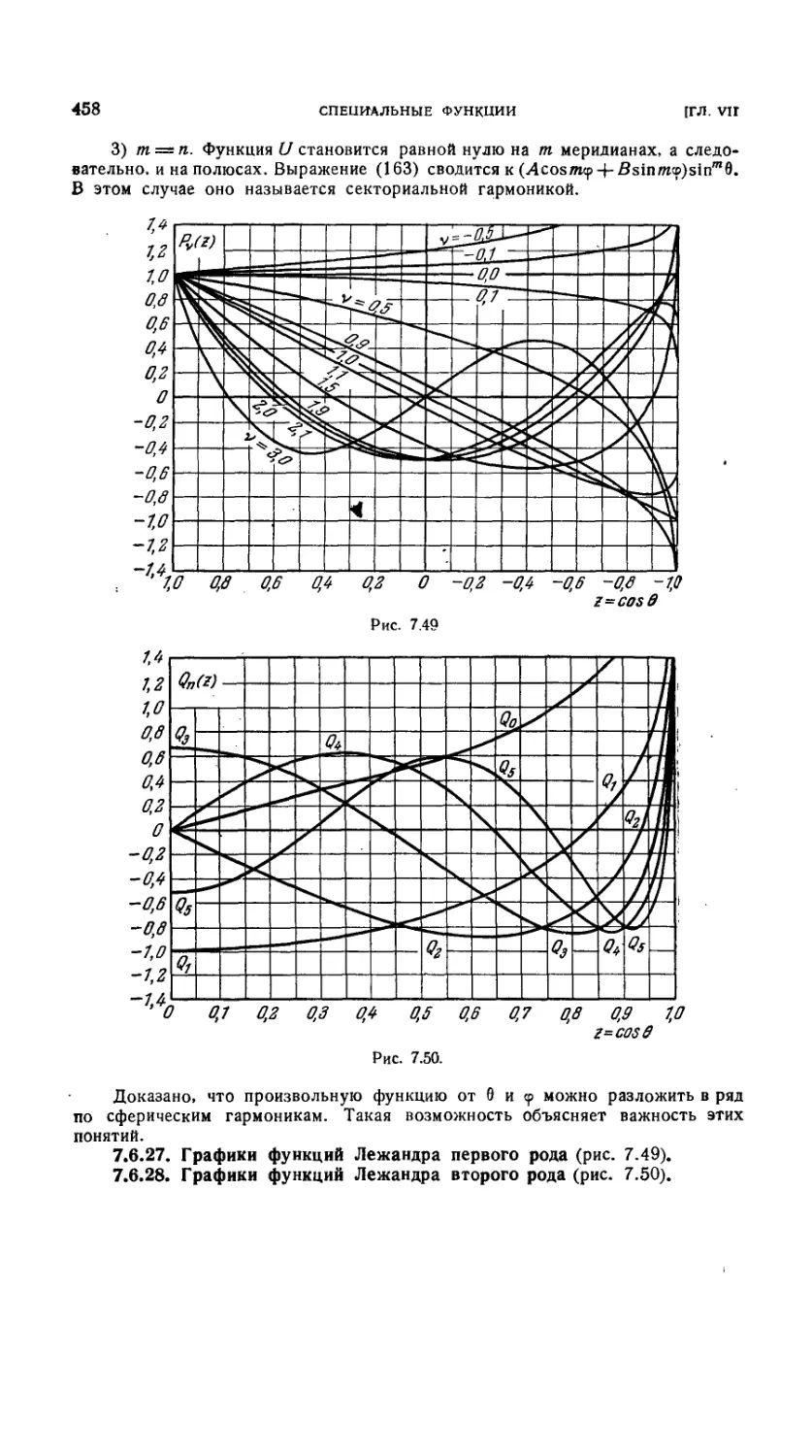
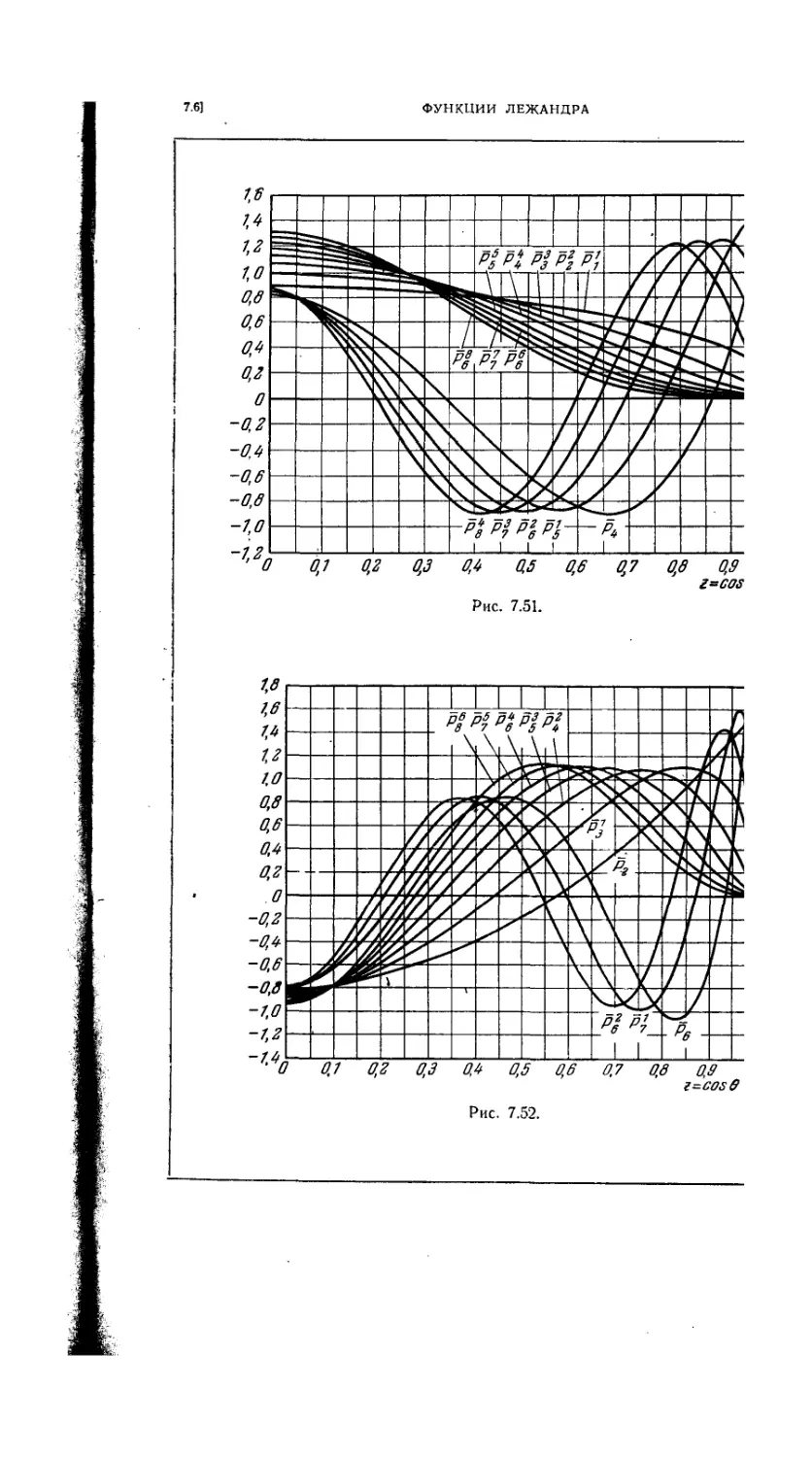
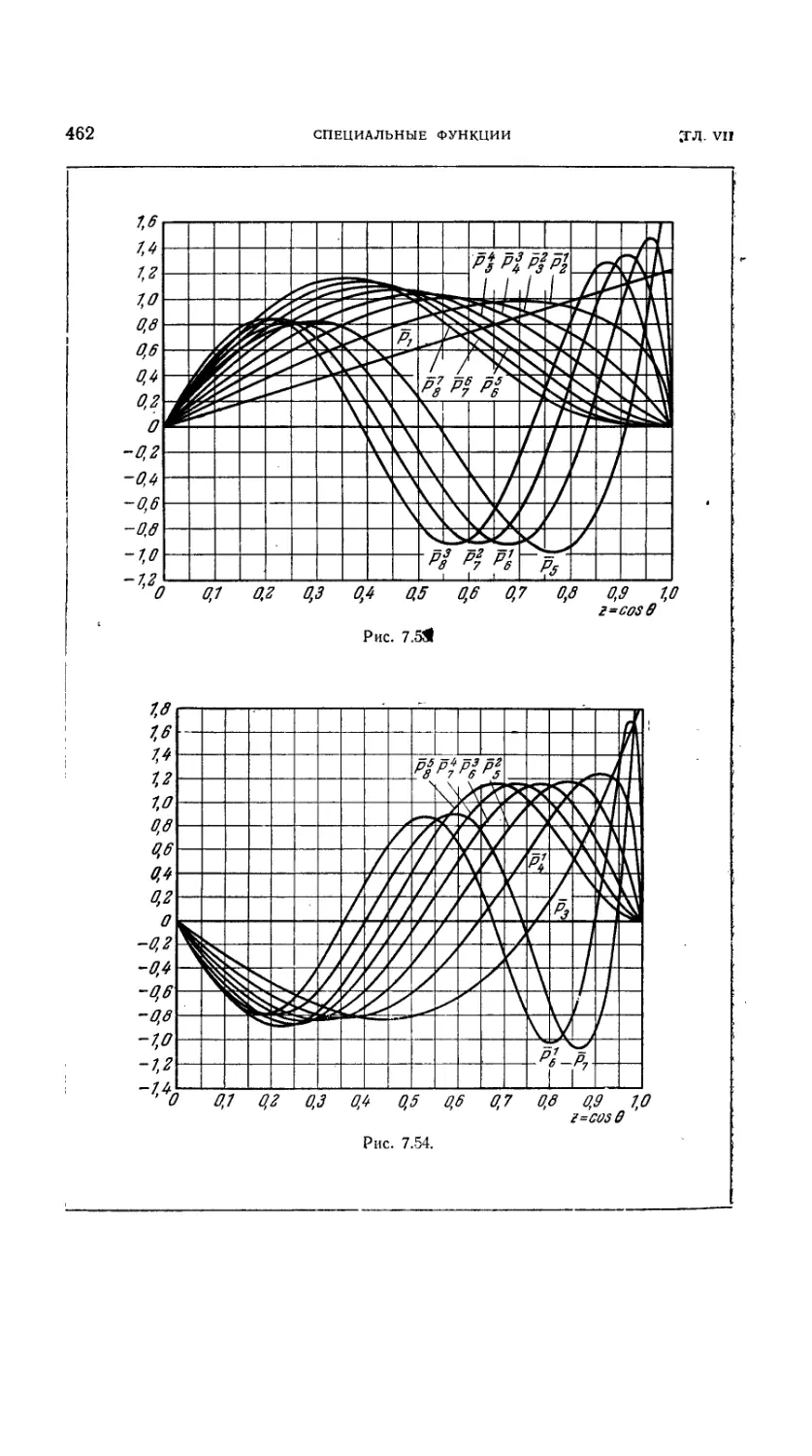
7.6.27. Графики функций Лежандра первого рода 458
7.6.28. Графики функций Лежандра второго рода 458
7.6.29. Таблица значений первых семи полиномов Лежандра 459
7.6.30. Графики нормированных присоединенных функций Лежандра
первого рода 460
7.6.31. Приложение функций Лежандра. Решение задачи об электро-
электромагнитных колебаниях сферического резонатора 460
7.7. Функции Матье 465
7.7.1. Функции' Матье первого рода 465
7.7.2. Ортогональность функции Матье первого рода 466
ОГЛАВЛЕНИЕ 15
7.7.3. Разложение в ряд Фурье 466
7.7.4. Характеристическое уравнение 468
7 J.5. Поведение функций сет (г, q), sem (г, q) 469
7.7.6. Присоединенные функции Матье первого рода 469
7.7.7. Функции Матье для произвольных аи</ 470
7.7.8. Разложение в ряды по бесселевым функциям 471
7.7.9. Функции Матье второго рода • 472
7.8. Функции Вебера — Эрмита. Полиномы Эрмита 473
7.8.1. Функции Вебера — Эрмита или функции параболического ци-
цилиндра 473
7.8.2. Полиномы Эрмита 475
7.8.3. Производящая функция и ортогональность полиномов Эрмита . 476
7.9. Полиномы Чебышева 478
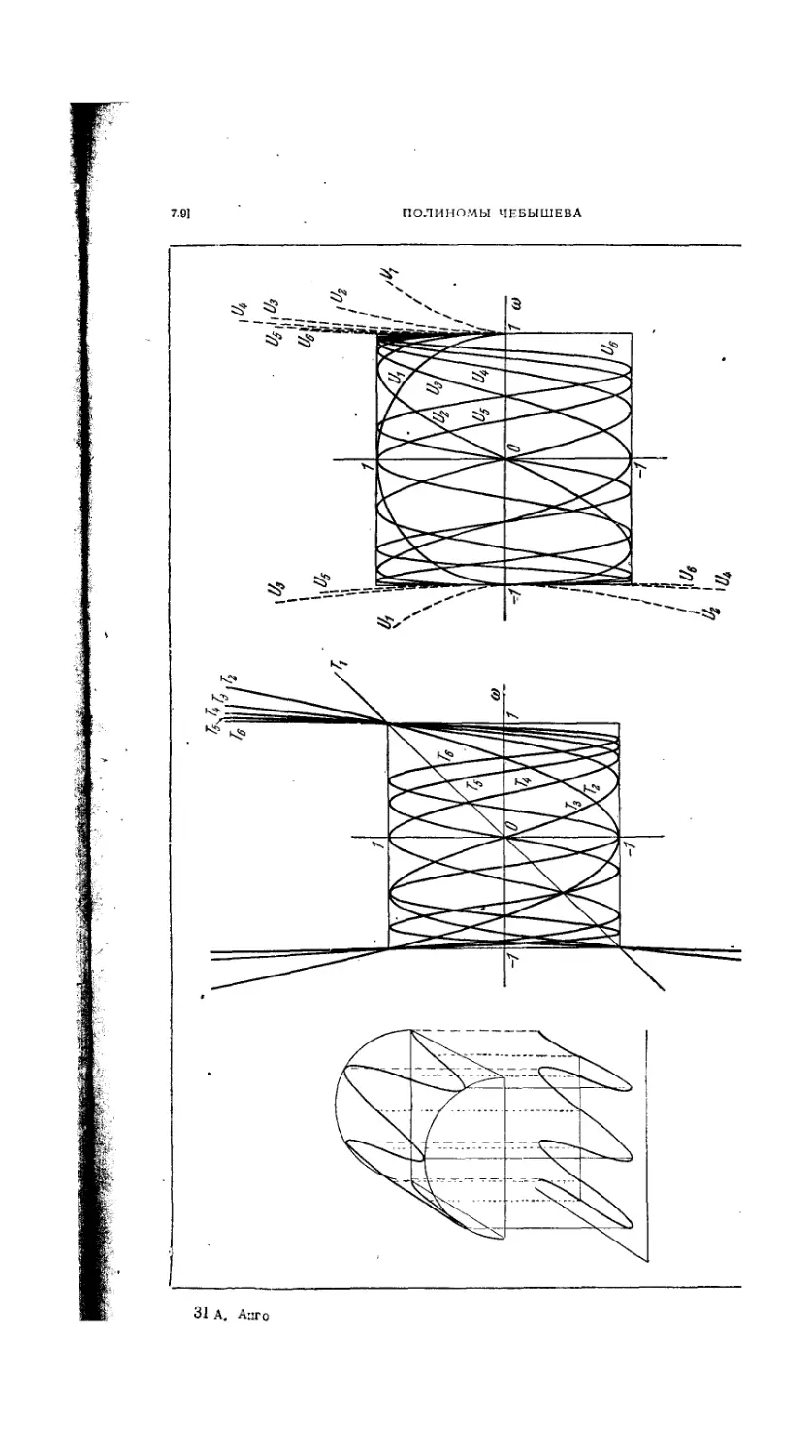
7.9.1. Определение 478
7.9.2. Графики Г„(ш) и 1/„(ш) 480
7.9.3. Основные свойства полиномов Чебышева 482
7.9.4. Фундаментальное свойство полиномов Чебышева 485
-7.9.5. Приложение • • • 486
Литература к главе VII 488
Глава VIII. Символическое, или операционное, исчисление 490
8.1. Введение 490
8.1.1. Ограничение области применения • • •' 490
8.1.2. Расчет установившихся режимов 490
8.1.3. Расчет переходных режимов . 491
8.1.4. Единичная ступень 493
8.2. Теория электрических цепей Хевисайда 493
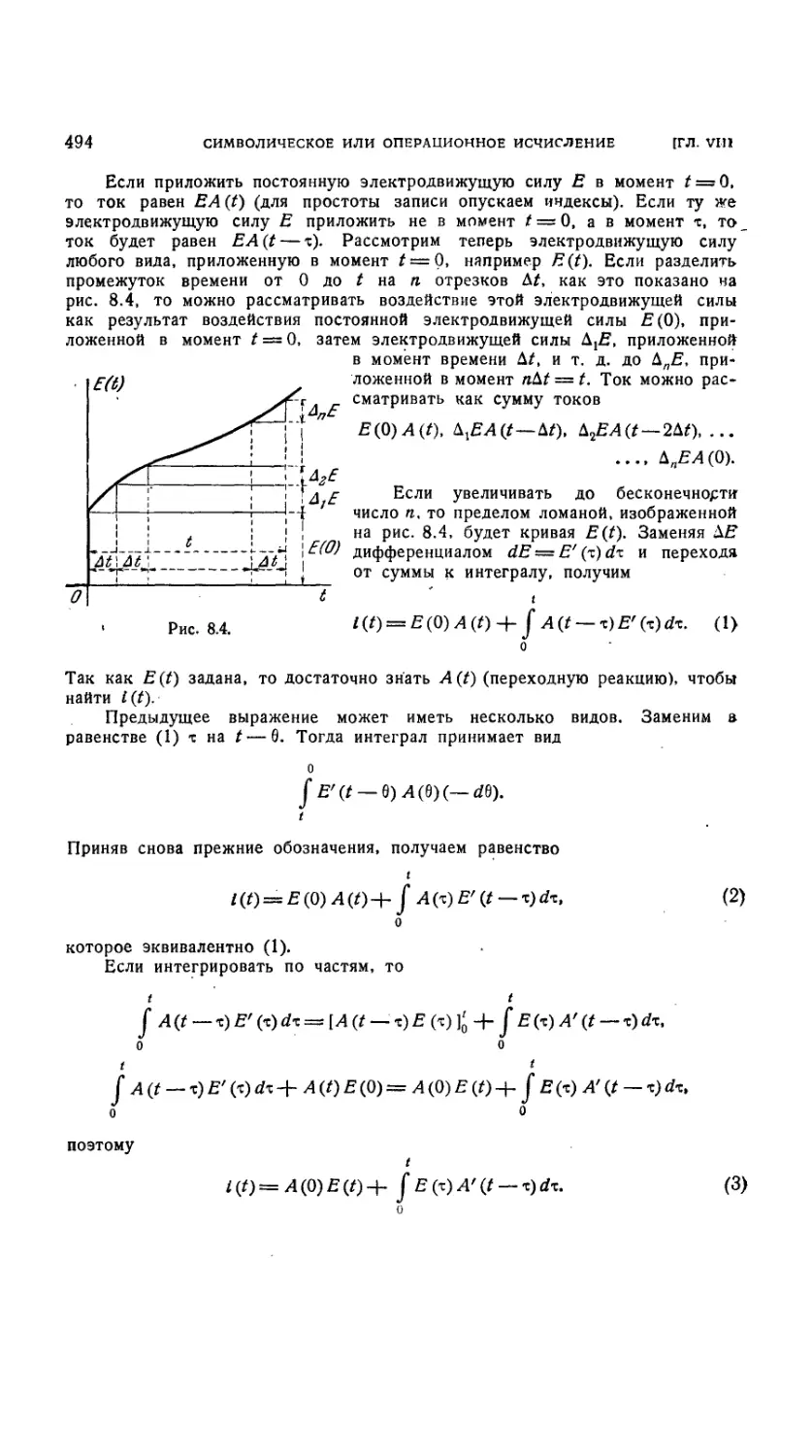
8.2.1. Определение переходной реакции 493
8.2.2. Вычисление переходной реакции 495
8.3. Операционное исчисление 498
8.3.1. Преобразование Лапласа. Преобразование Карсояа 498
Правила операционного исчисления . . . f . 500
8.3.2. Сложение 500
8.3.3. Изменение масштаба 502
8.3.4! Дифференцирование функции h(t) « 504
8.3.5. Интегрирование функции h(t) 504
1 8.3.6. Теорема смещения • 505
8.3.7. Теорема запаздывания 505
8.3.8. Дифференцирование функции F(p) 505
8.3.9. Интегрирование функции F(p) 506
8.3.10. Теорема свертывания, или теорема Бореля 506
8.3.11. Различные формулы 507
8.3.12. Теорема разложения Хевисайда 509
8.3.13. Приложение теоремы разложения к электрическим цепям. Слу-
. чай постоянного напряжения 510
8.3.14. Случай переменного напряжения 511
8.3.15. Случай кратных корней 512
Преобразование некоторых употребительных функций 513
8.3.16. Оригиналы некоторых рациональных функций 513
8.3.17. Изображения бесселевых функций целого порядка 515
8.3.18. Изображение In t 517
8.3.19. Изображение интегральных косинуса и синуса . 518
8.3.20. Изображение функции ошибок 518
8.3.21. Изображение единичного импульса 519
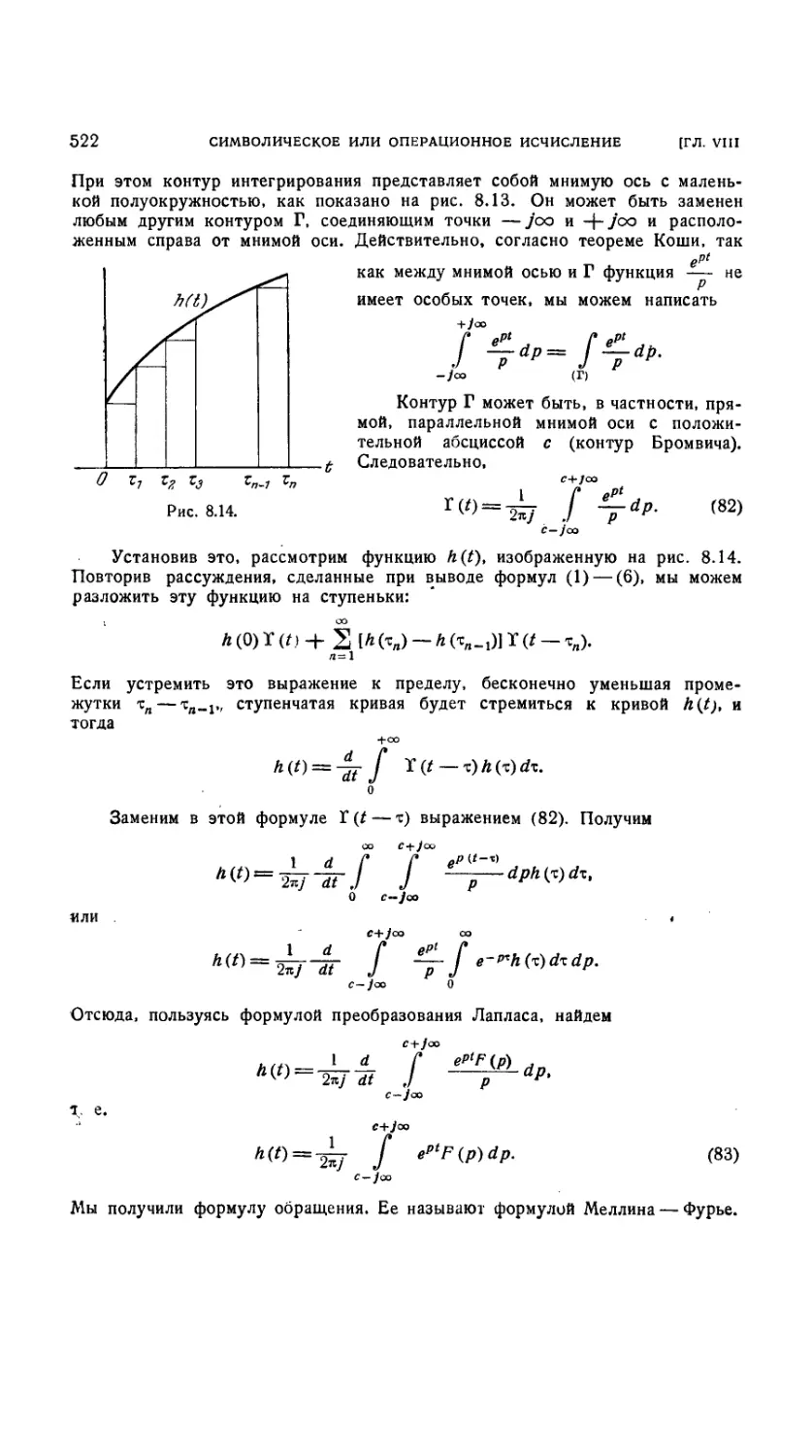
Применение формулы обращения 521
16 ОГЛАВЛЕНИЕ
8.3.22. Теорема Меллина — Фурье 521
8.3.23. Замечания о применении формулы обращения v . 523
8.3.24. Обобщение теоремы разложения Хевисайда 527
Изображения разрывных функций. Приложения 528
8.3.25. Введение • 528
8.3.26. Изображения непериодических разрывных функций 528
8.3.27. Изображение периодических разрывных функций 530
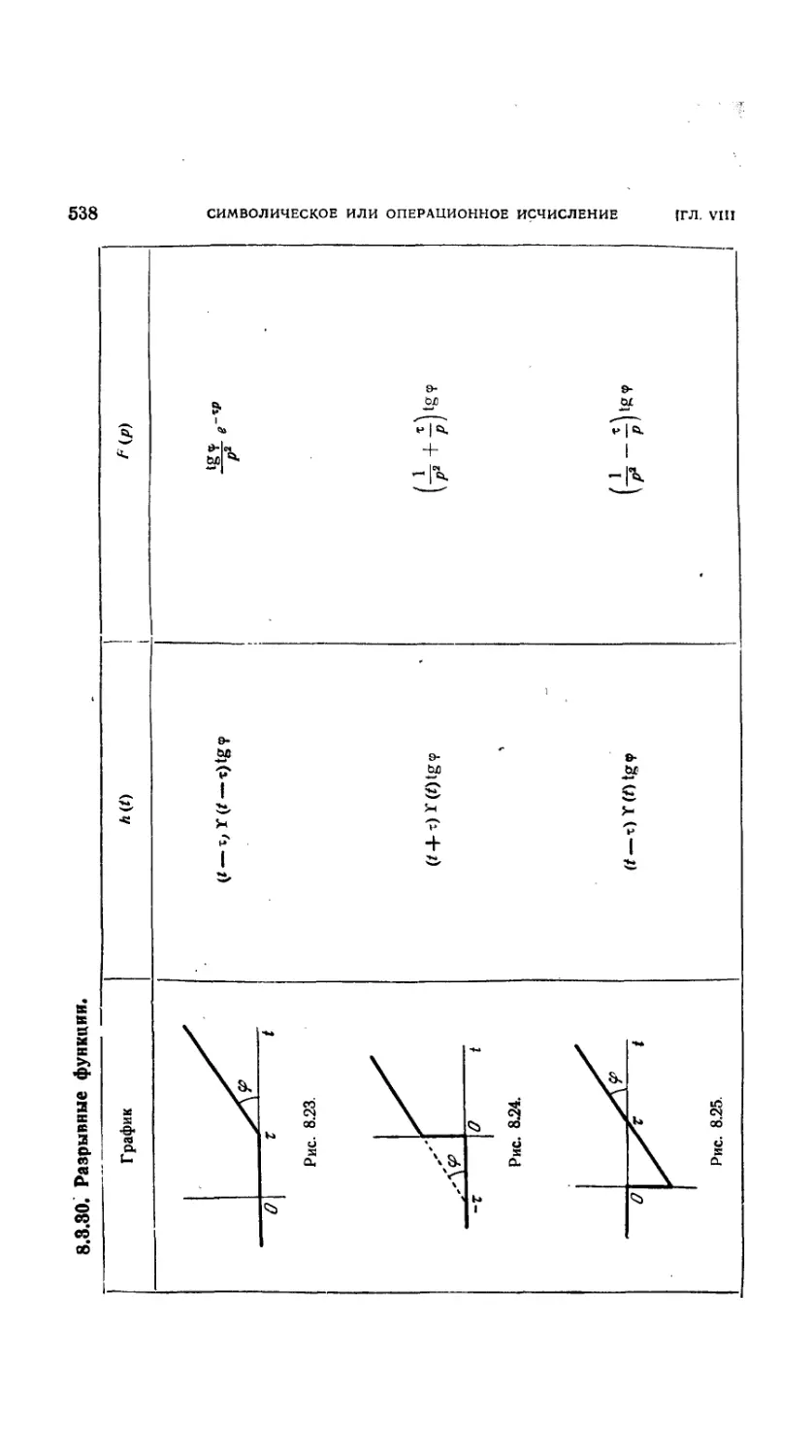
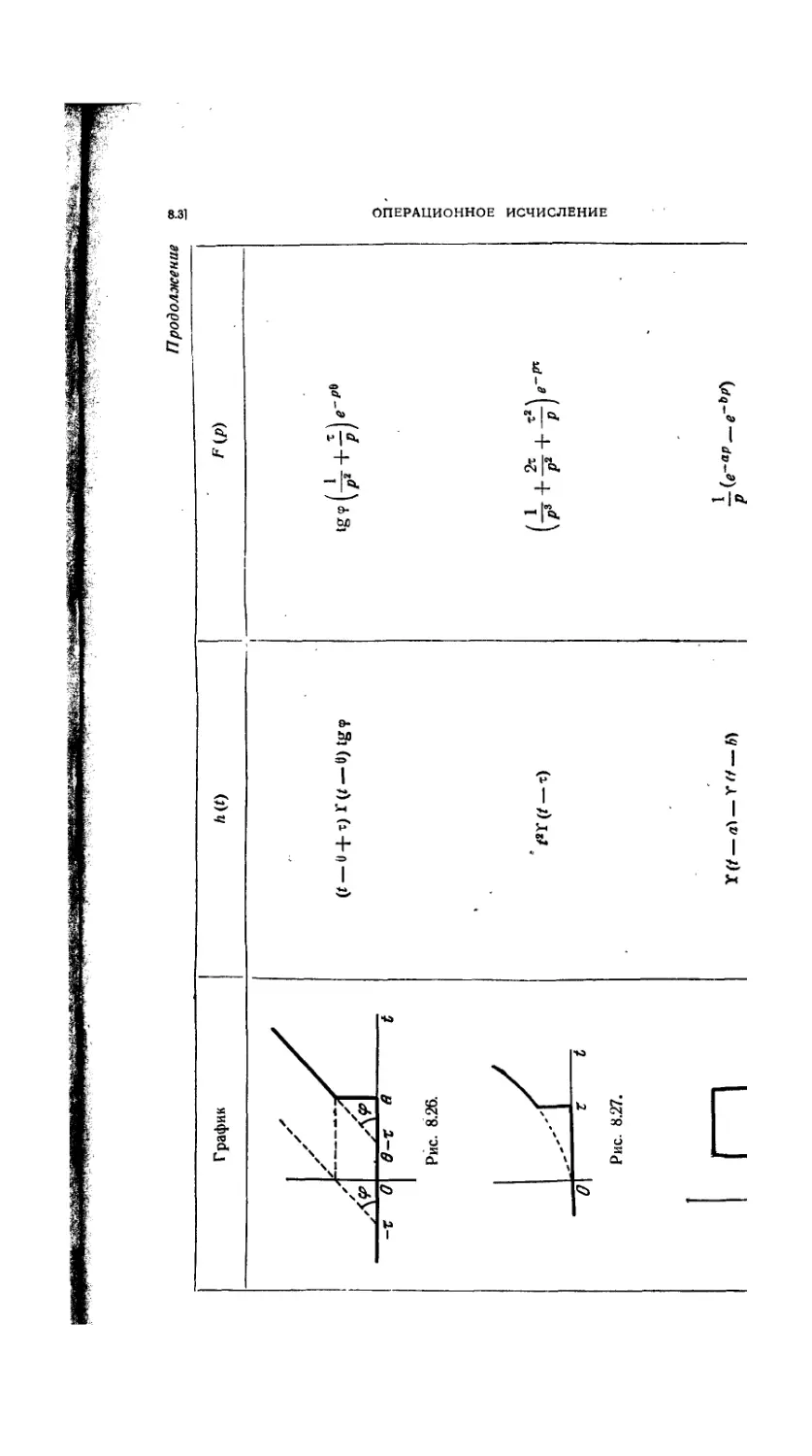
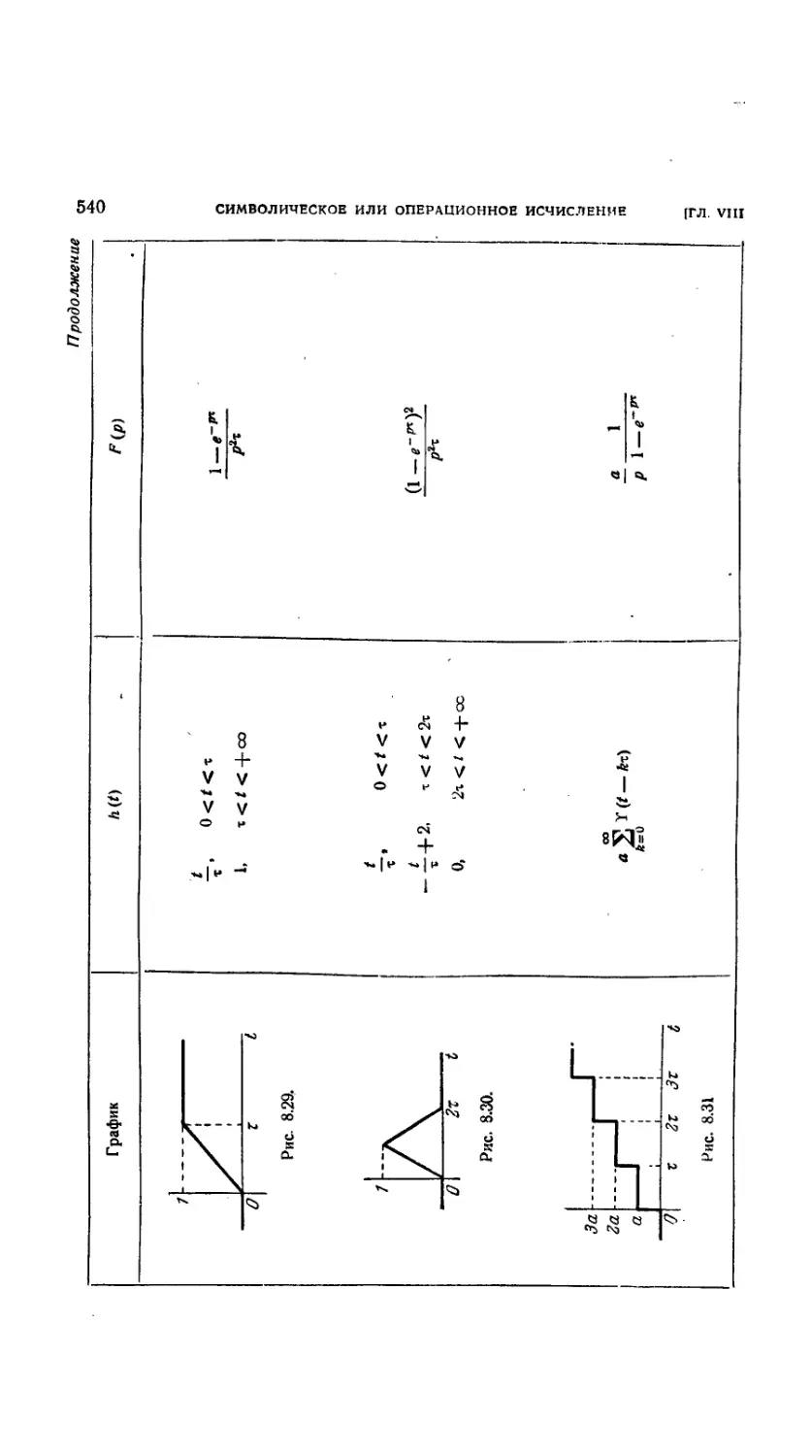
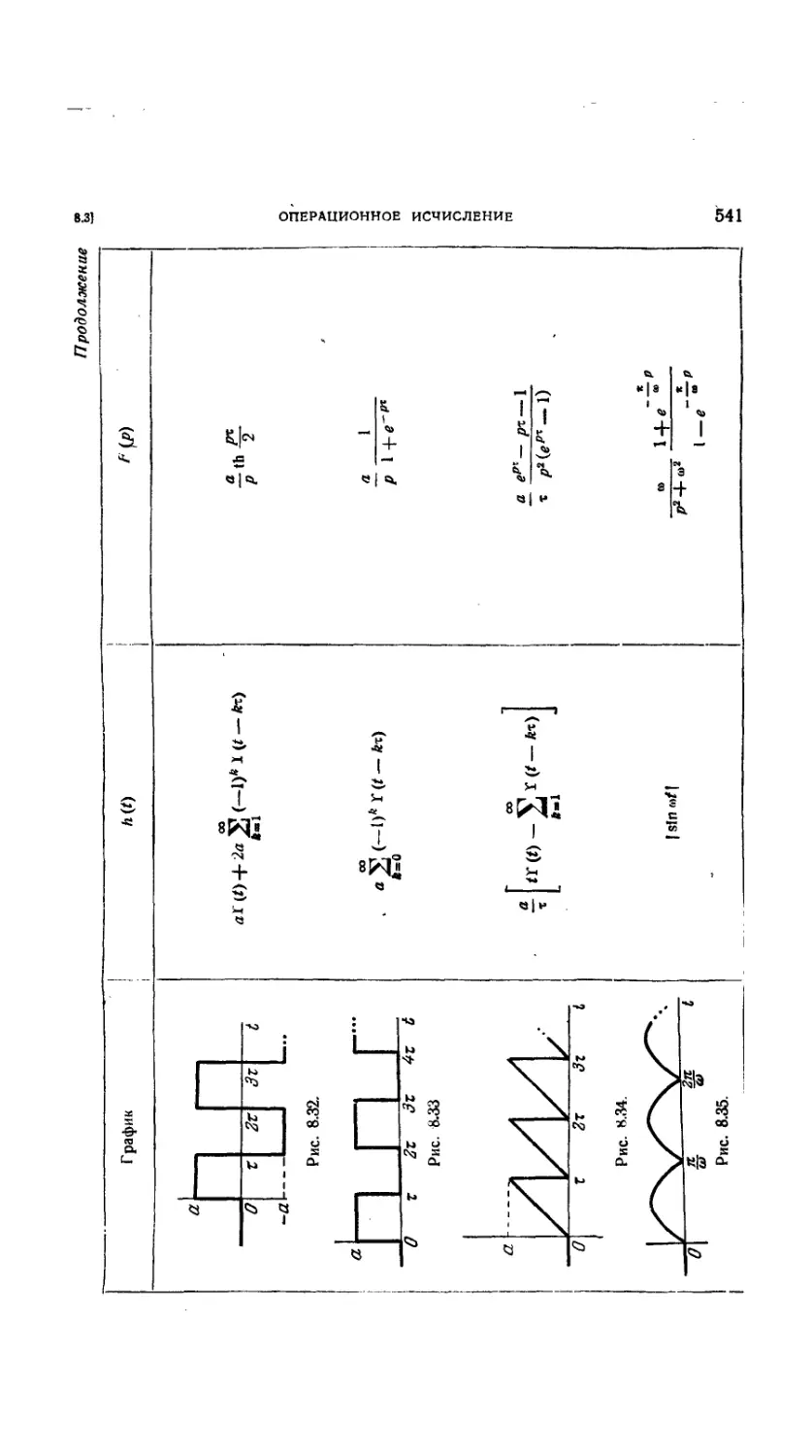
Таблица соответствия 532
8.3.28. Введение 532
8.3.29. Непрерывные функции 533
8.3.30. Разрывные функции. График 538
8.4. Приложения операционного исчисления к электрическим цепям . . . 543
8.4.1. Колебательные контуры 543
8.4.2. Пример применения к системе двух связанных контуров .... 544
8.4.3. Случай, когда цепь не находится в равновесии в начальный мо-
момент времени 547
8.4.4. Электрические фильтры 548
8.4.5. Фильтр нижних частот 549
8.4.6. Фильтр верхних частот 551
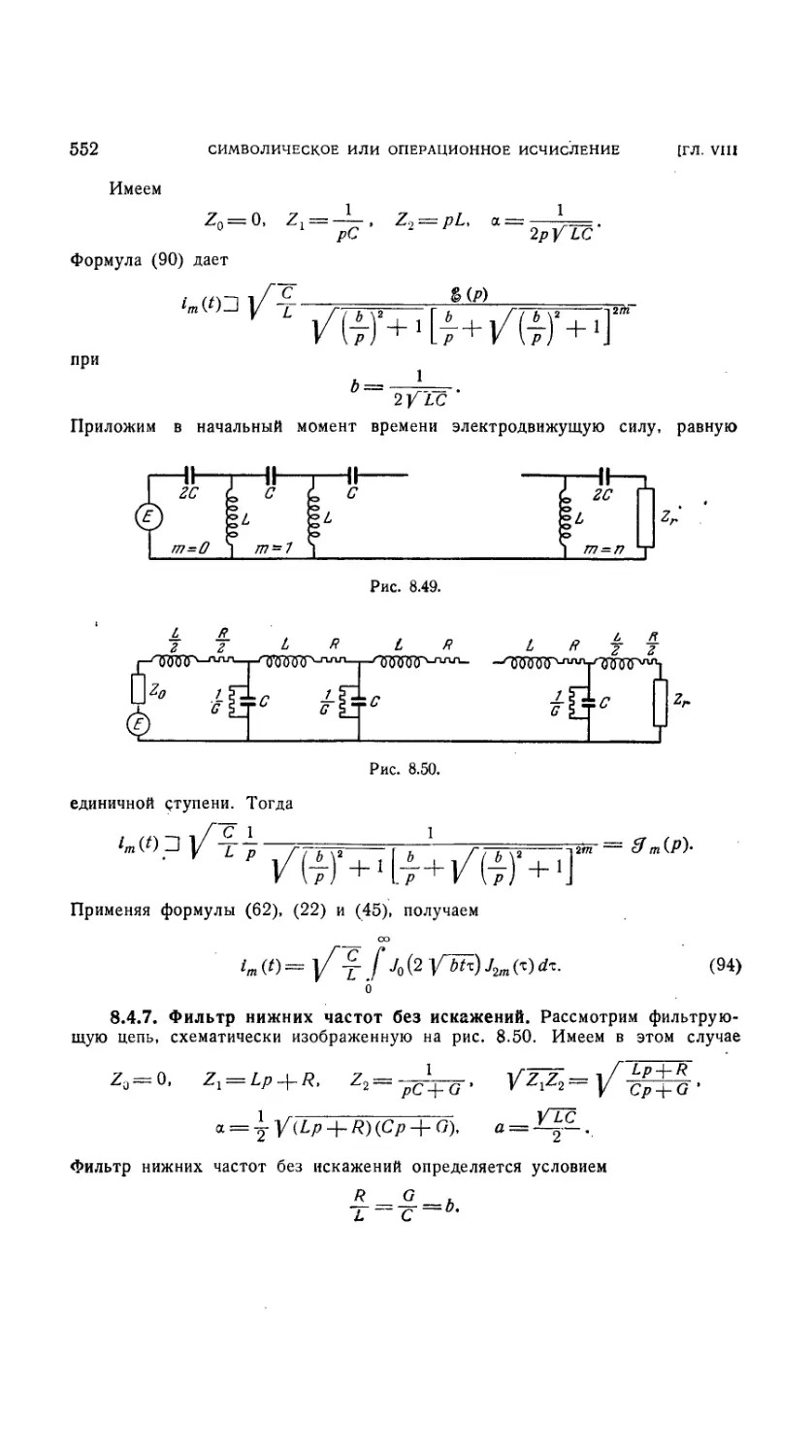
8.4.7. Фильтр нижних частот без искажений 552
8.4.8. Усилители. Отрицательная обратная связь. Критерий Найквиста 553
8.4.9. Расчет переходных явлений, вызванных размыканием или замы-
замыканием выключателя . . . . : 554
, Распространение электрических возмущений вдоль линий передач . . . 557
8.4.10. Общие соображения : . . . . 557
8.4.11. Бесконечная или замкнутая на волновое сопротивление линия . 560
8.4.12. Линия без потерь 560
8.4.13. Линия без искажений 561
8.4.14. Подземный кабель 561
8.4.15. Линия с идеальной изоляцией 562
8.4.16. Общий случай Произвольная линия 563
8.4.17. Линия передачи конечной длины 564
8.4.18. Закороченная с одного конца линия с пренебрежимо малыми
проводимостью изоляции и индуктивностью (подземный кабель) 564
8.4.19. Линия конечной длины без потерь, замкнутая на сопротивление 566
8.4.20. Сопротивление, сосредоточенное в начале линии 567
8.4.21. Повреждение на линии 568
8.5 Математические приложения операционного исчисления 568
8.5.1. Применение операционного исчисления к вычислению определен-
определенных интегралов 568
Применение операционного исчисления к решению линейных диффе-
дифференциальных уравнений 570
8.5.2. Линейные дифференциальные уравнения с постоянными коэффи-
коэффициентами 570
8.5.3. Линейное дифференциальное уравнение с переменными алге-
алгебраическими коэффициентами (метод ван дер Поля) 572
Применение операционного исчисления к решению некоторых инте-
интегральных уравнений 574
8.5.4. Линейные интегральные уравнения 574
8.5.5. Нелинейные интегральные уравнения 576
8.5.6. Интегродифференциальные уравнения 576
8.5.7. Применение операционного исчисления к исследованию функций 577
8.5.8. Применение операционного исчисления к разложению в асимп-
асимптотический ряд 581
ОГЛАВЛЕНИЕ 17
8,6/ Некоторые замечания 582
8.6.1. Замечания об операционном исчислении Хевисайда 582
8.6.2. Обозначения в операционном исчислении 584
Литература к главе VIII 584
Глава IX. Теория вероятностей. Приложения 585
9.1. Случайная величина '. 585
9.1.1. Определение вероятности 585
9.1.2. Независимые события. Теорема умножения вероятностей .... 586
9.1.3. Несовместные события. Теорема сложения вероятностей 586
9.1.4. Формула Стирлинга 587
Законы распределения случайных величин 589
9.1.5. Дискретные случайные величины 589
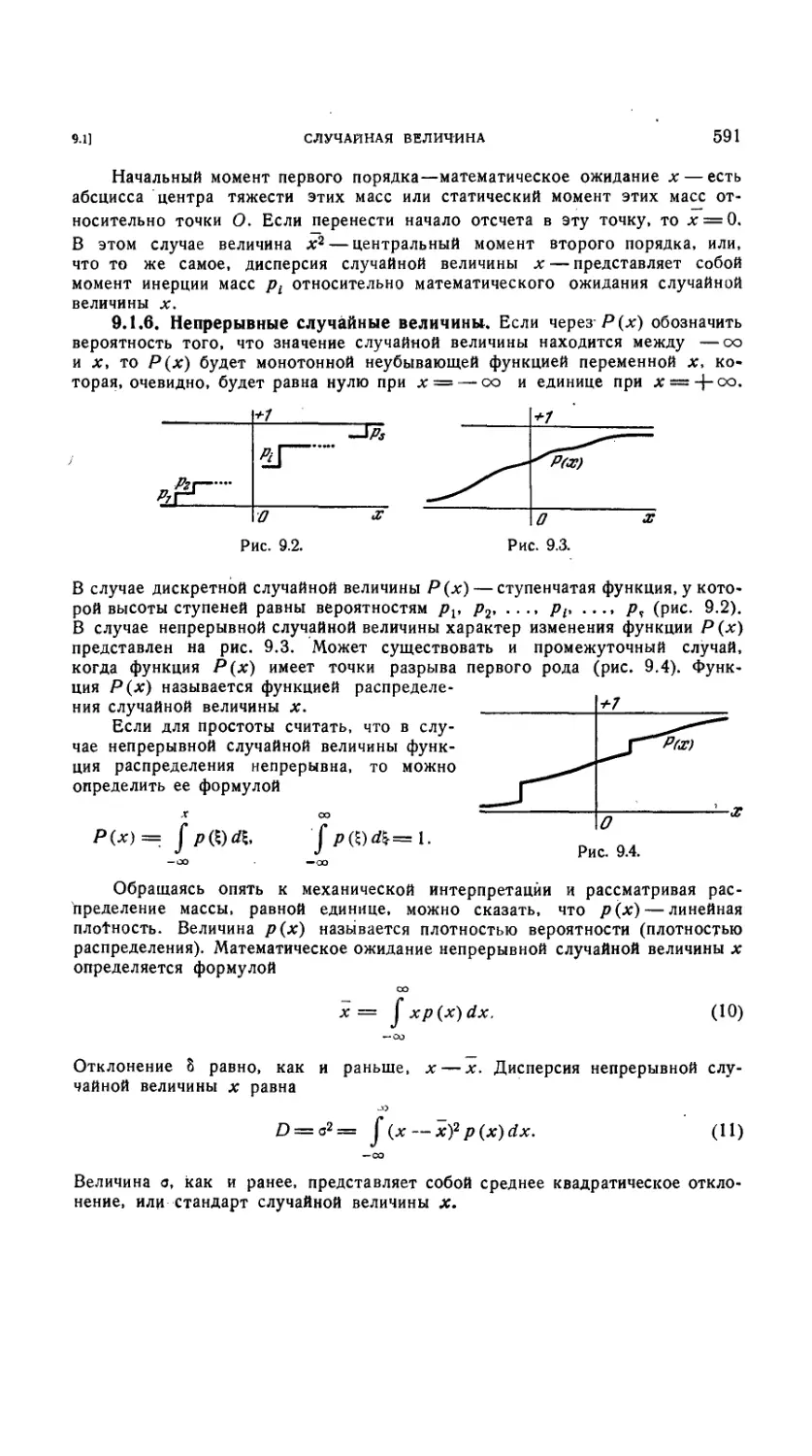
9.1.6. Непрерывные случайные величины 591
9.1.7. Характеристическая функция '. 592
9.1.8. Распределение системы двух случайных величин 594
9.1.9. Характеристическая функция суммы независимых случайных ве-
величин 595
Основные законы распределения случайных величии 596
9.1.10. Биномиальный закон распределения 596
9.1.11. Характеристическая функция биномиального закона 597
9.1.12. Формула Лапласа. Нормальный закон распределения (закон
, Лапласа — Гаусса) : 599
9.1.13. Характеристическая функция нормального закона распределе-
распределения : .602
9.1.14. Теорема Бериулли ; 602
9.1.15. Замечания о переходе от биномиального закона распределения
к нормальному 603
9.1.16. Закон распределения Пуассона 604
9.1.17. Характеристическая функция и моменты закона распределения
Пуассона . . 605
9.1.18. Приложение к задачам автоматической телефонии ..... .605
9.1.19. Согласование наблюденных данных с теоретическим законом
распределения. Разложение в ряд Грама — Шарлье 612
9.1.20. Частный случай нормального закона распределения '. 614
Ошибки измерений и спосб*б наименьших квадратов 615
9.1.21. Ошибки измерений и нормальный закон распределения .... 615
9.1.22. Способ наименьших квадратов . . . . • 617
9.1.23. Линейная комбинация ошибок . е . . . 617
9.1.24. Точность группы измерений 618
9.1.25. Наивероятнейшее значение меры точности 619
9.1.26. «Вес» наблюдения 620
9.1.27. Критерий ошибочного наблюдения 621
9.1.28. Срединная (вероятная) ошибка функции . .621
9.1.29. Эмпирические формулы 621
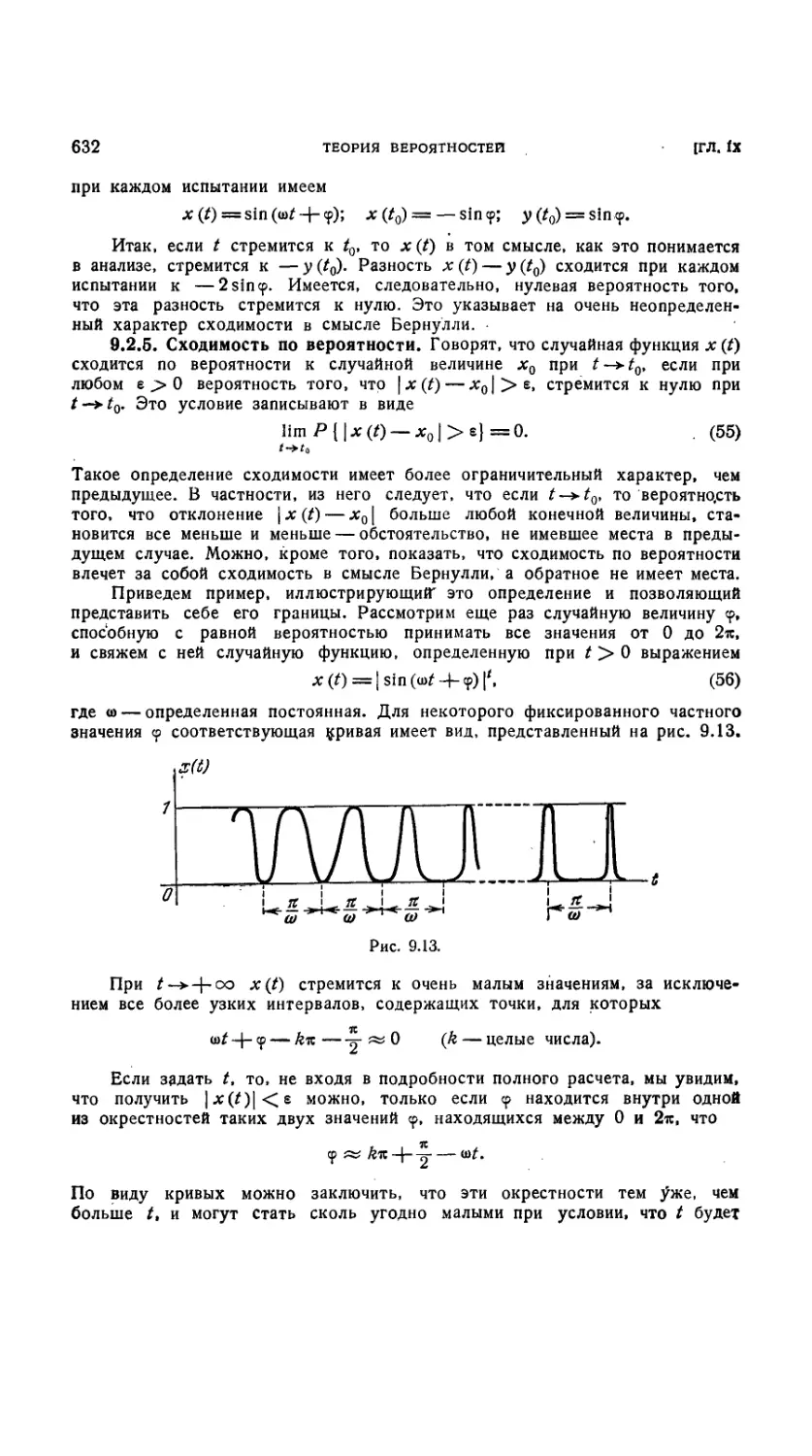
9.2. Понятие случайной функции 623
9.2.1. Введение понятия случайной функции на конкретном примере . . 623
9.2.2. Функции распределения 627
Проблема сходимости 631
9.2.3. Введение 631
9.2.4. Сходимость в смысле Бернулли 631
9.2л. Сходимость по вероятности 632
9.2.6. Сходимость в среднем квадратическом (сходимость с. к.) .... 633
9.2.7. Почти достоверная сходимость 635
2 А. Анго
18 ОГЛАВЛЕНИЕ
Стационарные случайные функции. Изучение постоянных режимов . . 636
9.2.8. Введение 636
9.2.9. Изучение моментов второго порядка. Определение 638
Общие свойства стационарных случайных функций второго порядка . 640
9.2.10. Корреляционные функции 640
9.2.11. Непрерывность. Дифференцируемость 641
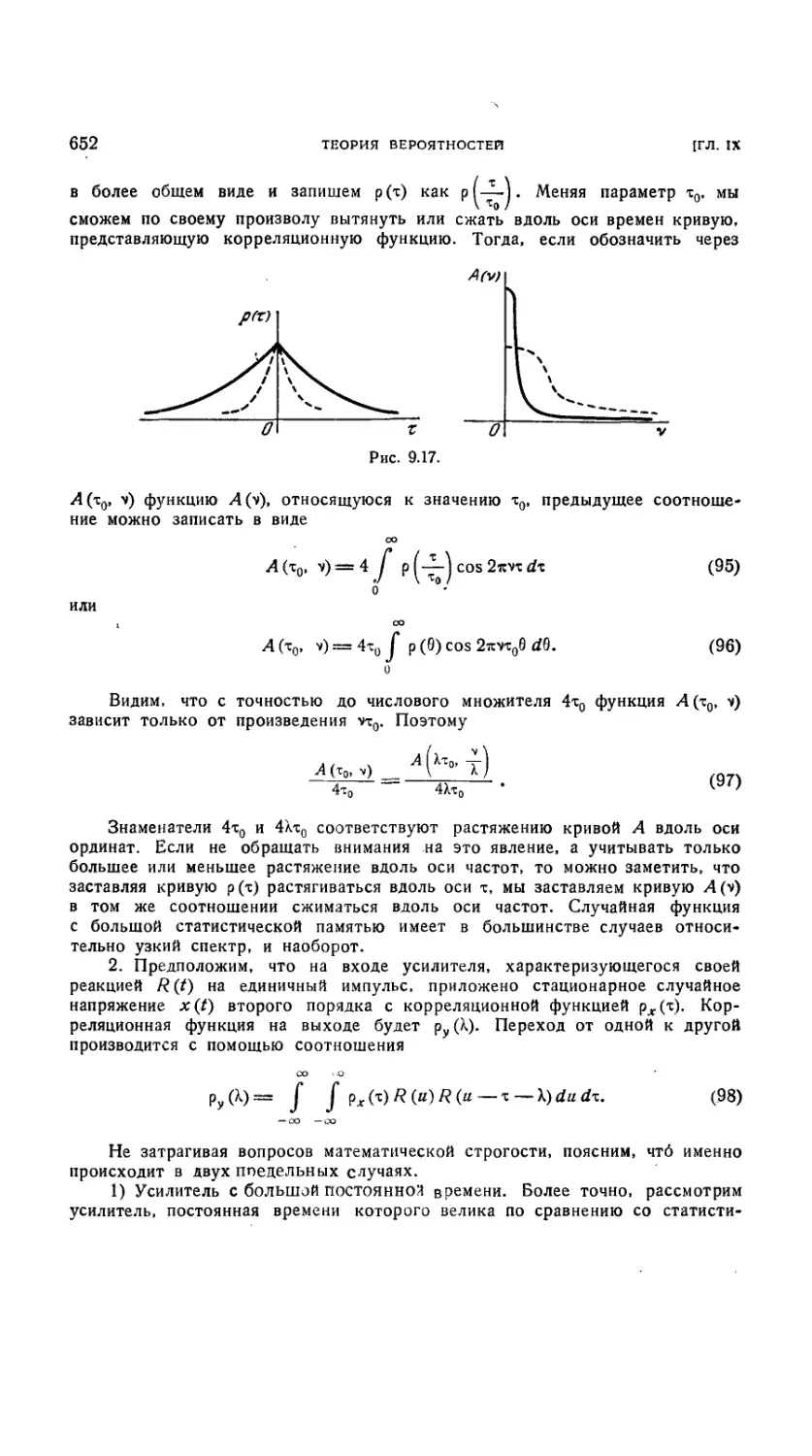
9.2.12. Энергетический спектр 644
9.2.13. Передача энергии стационарной линейной системой 650
9.2.14. Недостаточность рассмотрения моментов второго порядка и
корреляционной функции 654
Стационарные случайные функции Лапласа — Гаусса. Применение
к чисто дробовому эффекту 656
9.2.15. Общие замечания 656
9.2.16. Связь явлений во времени 660
9.2.17. #Флуктуации в нелинейных системах 661
9.2.18. Вычисление корреляциойной функции на выходе линейного
усилителя под действием дробового эффекта постоянного тока . 663
Литература к главе IX 665
Глава X. Приближенные и графические вычисления 666
10.1. Решение чясленных уравнений 666
10.1.1. Графическое решение 666
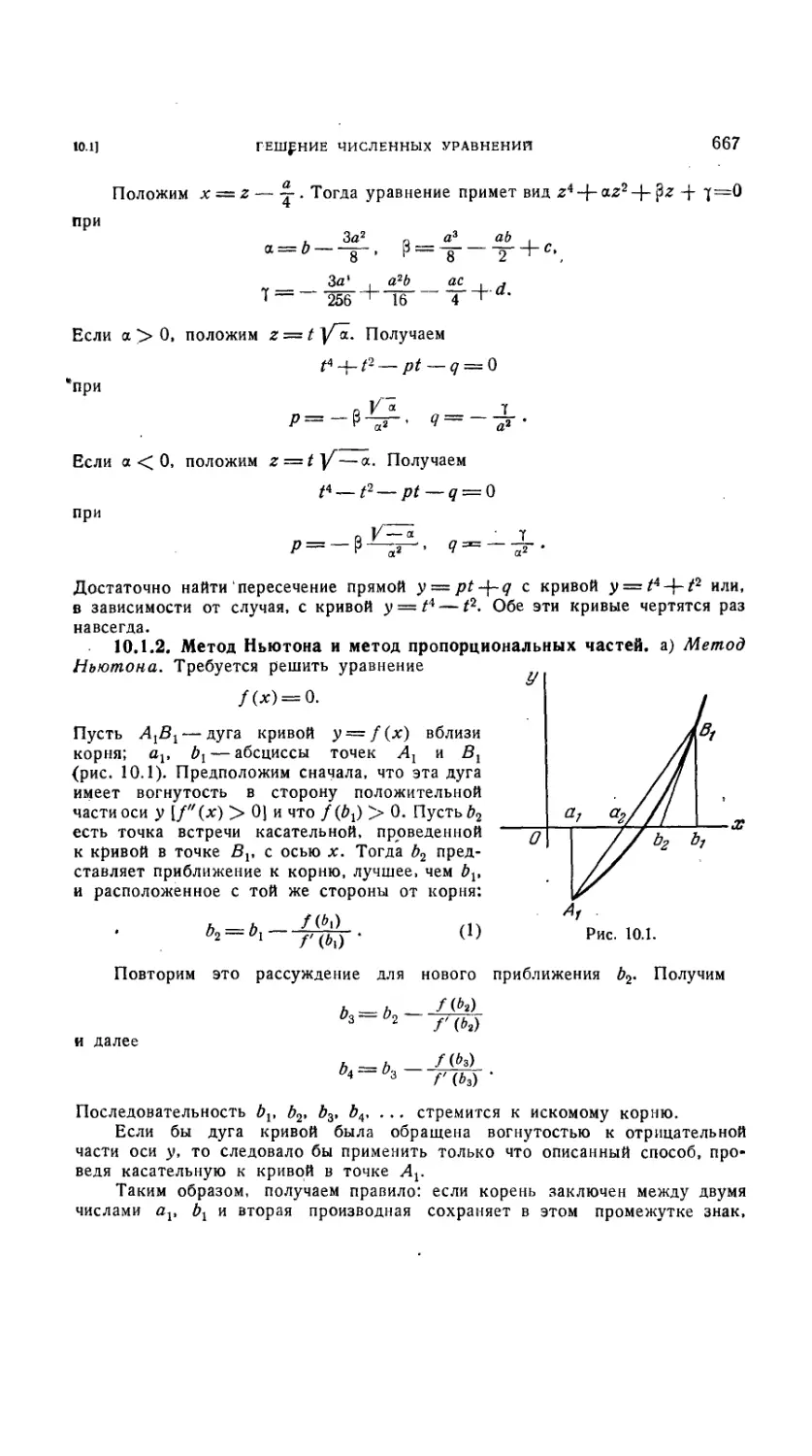
10.1.2. Метод Ньютона и метод пропорциональных частей 667
10.1.3. Метод итерации 669
10.1.4. Приближенное решение системы двух уравнений 671
10.2. Решение алгебраических уравнений 674
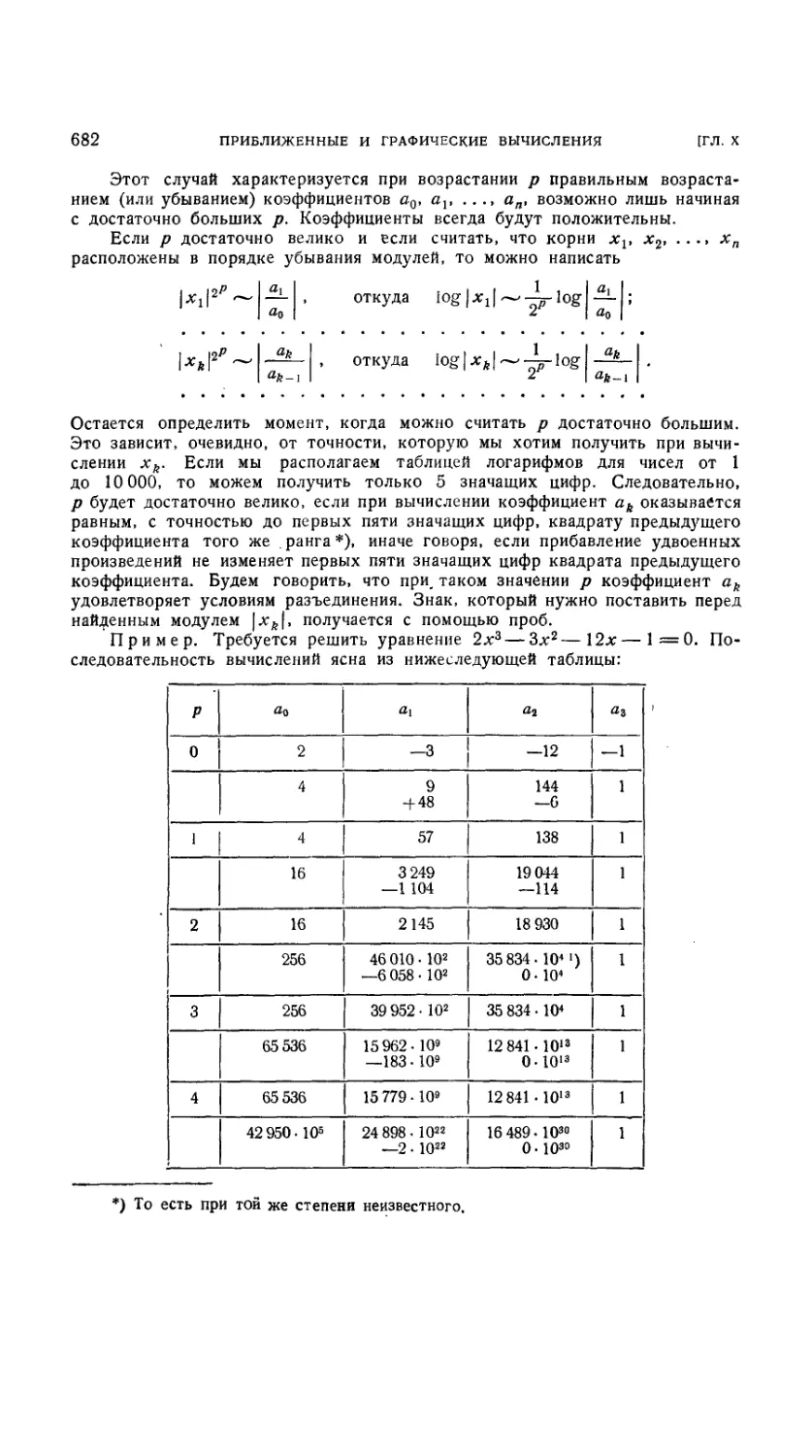
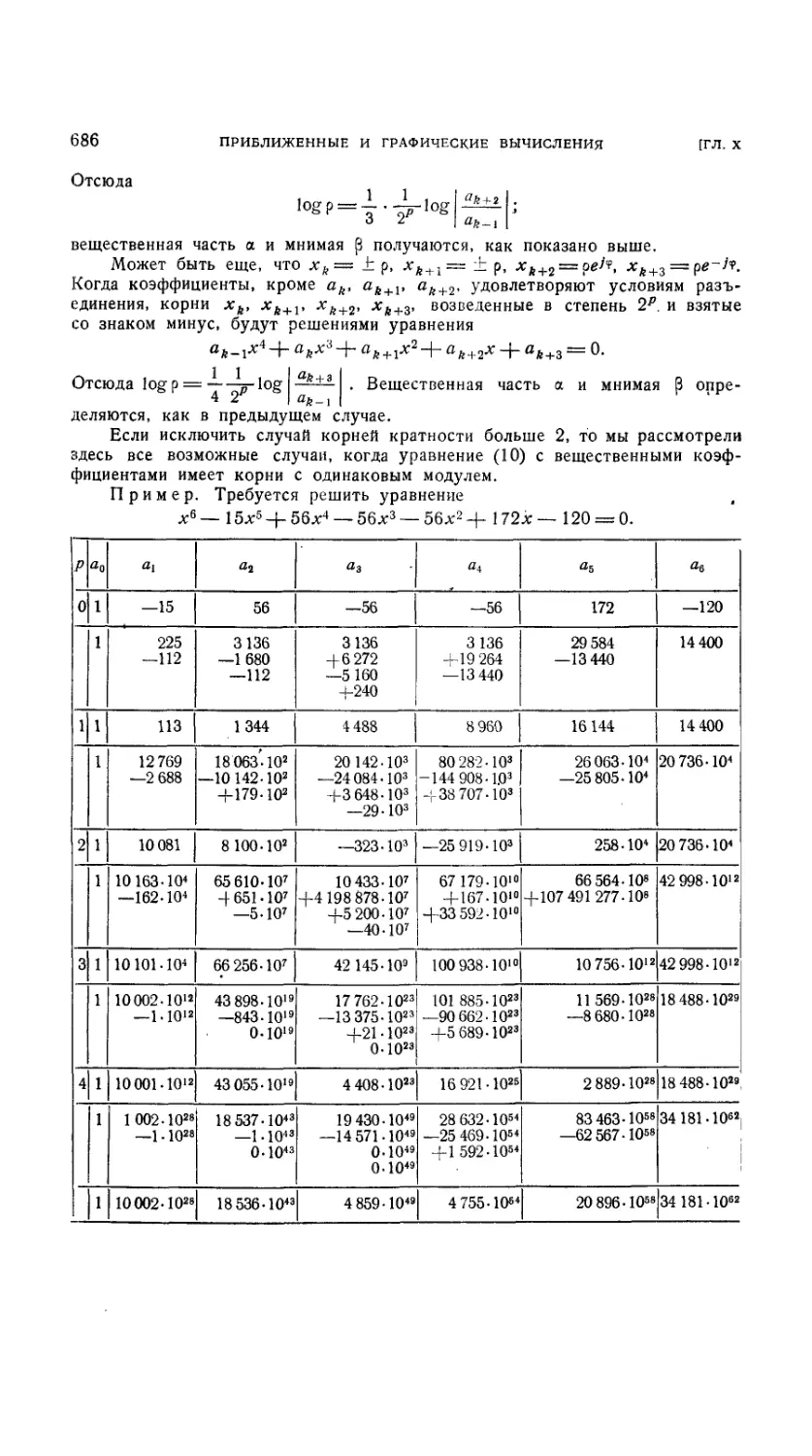
10.2.1. Численное решение уравнений третьей и четвертой степени . . 674
10.2.2. Схема Горнера 676
10.2.3. Построение Лилла 678
10.2.4. Способ Лагранжа 679
10.2.5. Метод Лобачевского—Греффе — Данделеиа 680
10.3 Приближение функции 688
Приближение функции полиномами 688
10.3.1. Введение 688
10.3.2. Значения аргумента распределены неравномерно. Интерполя-
Интерполяционный полином Лагсанжа ... 688
10.3.3. Значения переменной находятся в арифметической прогрессии.
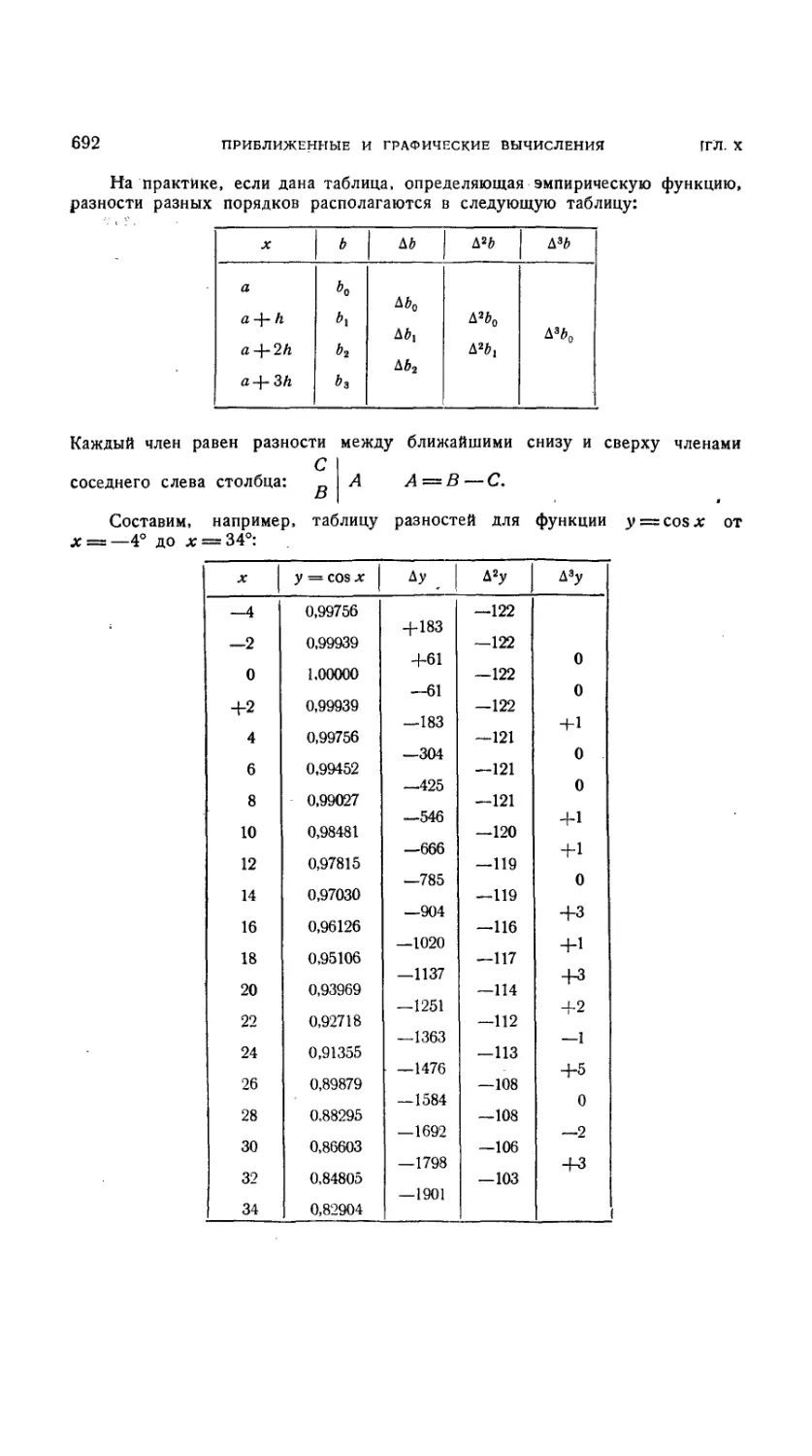
Таблица разностей 691
Интерполяционные полиномы 693
10.3.4. Интерполяционный полином Ньютона 693
10.3.5. Интерполяционный полином Стирлинга 696
10.3.6. Интерполяционный полином Бесселя 697
10.3.7. Области применения интерполяционных полиномов Ньютона,
Бесселя, Стирлинга 698
10.3.8. Верхний предел ошибки, совершаемой при применении интер-
интерполяционных формул Ньютона, Стирлинга, Бесселя 699
10.3.9 Приближение линейной комбинацией функций, определенной
с помощью критерия наименьших квадратов 700
10.3.10. Приближение полиномом, определенным с помощью критерия
наименьших квадратов 700
Приближение отрезком ряда Фурье. Задача гармонического анализа . 705
10.3.11. Функция задана аналитически 705
10.3.12. Эмпирическая функция 706
10.3.13. Практические способы вычисления 708
10.3.14. Приближение эмпирической функции линейной комбинацией
показательных функций 711
\
ОГЛАВЛЕНИЕ 19
10.3.15. Приближение функции по Чебышеву 714
10.3.16. Применение ряда Тейлора 716
10.4. Численное дифференцирование 717
10.5. Численное интегрирование 719
10.5.1. Числа Бернулли , 719
10.5.2. Полином Бернулли 720
10.5.3. Формула Эйлера 722
10.5.4. Формула трапеций 725
10.5.5. Формула Симпсона 726
10.5.6. Формула Уэддля : . . 727
10.5.7. Формула Грегори 728
10.5.8. Введение в методы Ньютона — Котеса, Чебышева, Гаусса . . . 730
10.5.9. Метод Ньютона — Котеса 730
10.5.10. Метод Чебышева 732
10.5.11. Метод Гаусса 733
10.5.12. Применение интерполяционных полиномов Ньютона 735
10.5.13. Исключительные случаи 737
10.6. Приближенное интегрирование дифференциальных уравнений .... 738
10.6.1. Введение . . ^ 738
10.6.2. Приближенное интегрирование дифференциального уравнения
первого порядка . 739
10.6.3. Решение с помощью ряда Тейлора 739
10.6.4. Способ Адамса 740
10.6.5. Сокращенный вариант 747
10.6.6. Приближенное интегрирование системы дифференциальных
уравнений первого порядка 748
10.6.71 Использование ряда Тейлора 748
10.6.8. Применение интерполяционного полинома Ньютона с нисходя-
нисходящими разностями 749
10.6.9. Способ Пикара 750
10.7. Графическое решение дифференциальных уравнений ... ..... 752
10.7.1. Дифференциальные уравнения первого порядка. Способ изоклин 752
10.7.2. Графическое решение дифференциальных уравнений второго
порядка способом радиусов кривизны 755
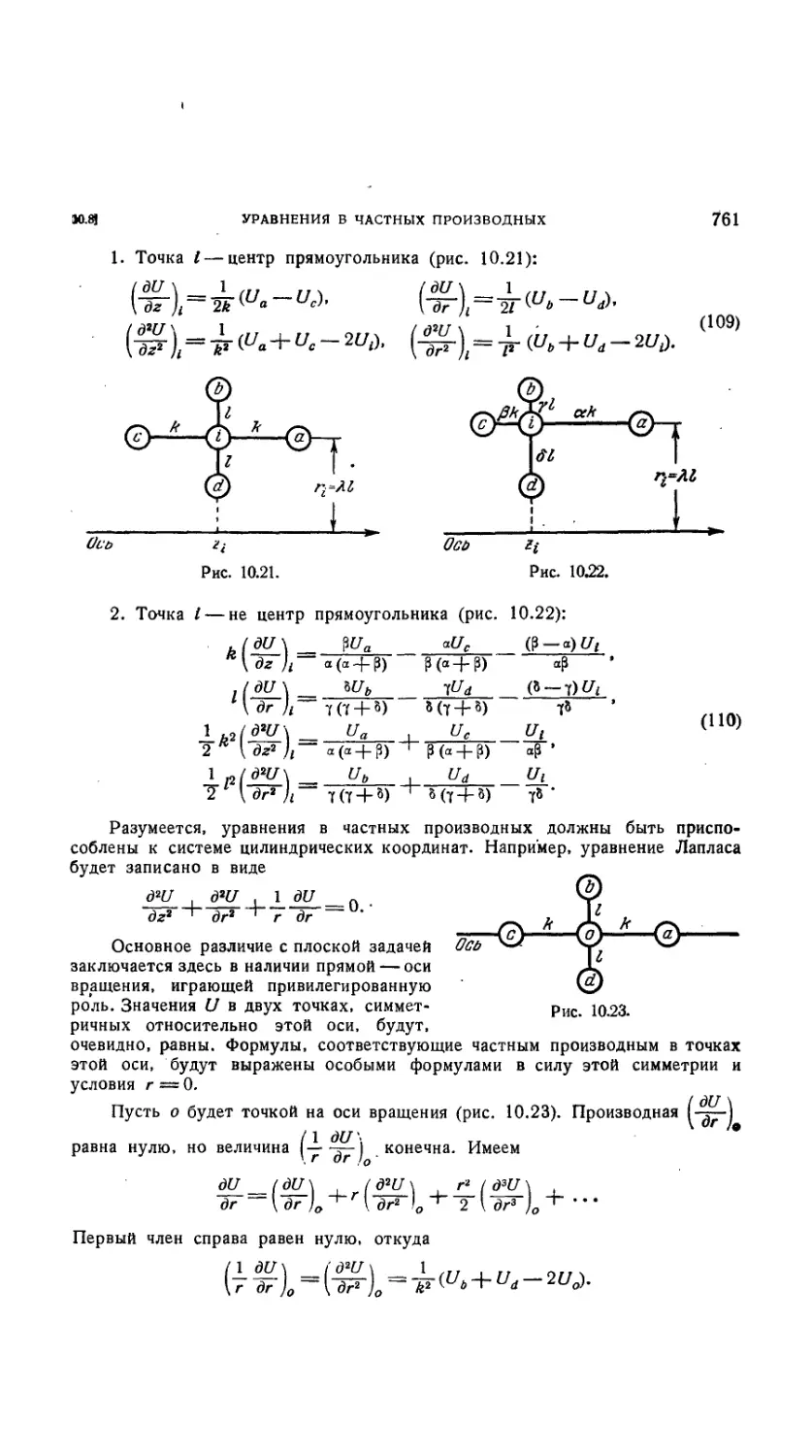
10.8. Численное решение уравнений в частных производных i . 757
10.8.1. Плоские задачи 757
10.8.2. Задачи вращения .* .- 760
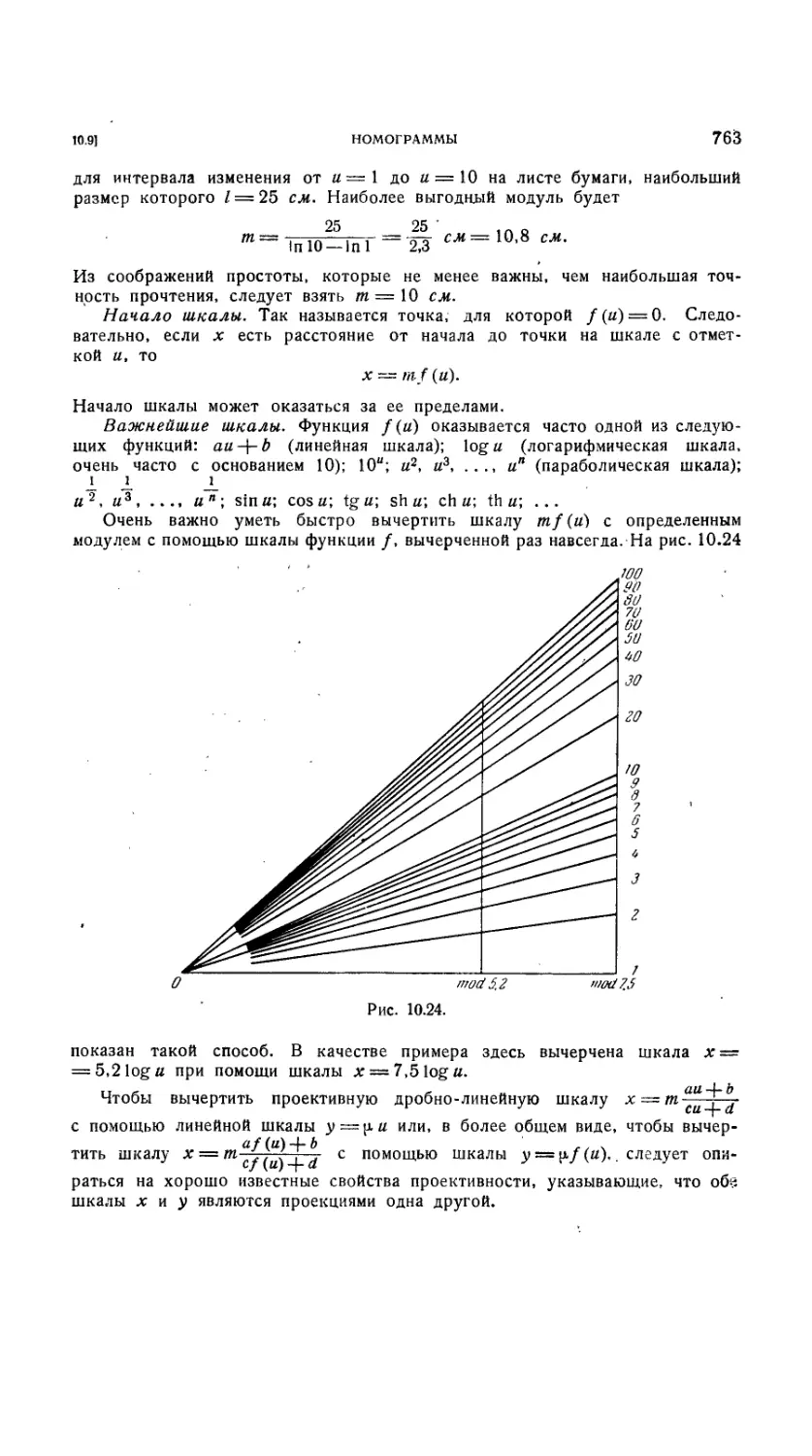
10.9. Номограммы 762
10.9.1. Введение 762
10.9.2. Определение. Графическая шкала 762
10.9.3. Номограммы «с выравненными точками 764
10.9.4. Номограммы с тремя параллельными прямолинейными шка-
шкалами . . . . е 765
10.9.5. Номограммы с двумя параллельными прямоугольными шкала-
шкалами и одной криволинейной 767
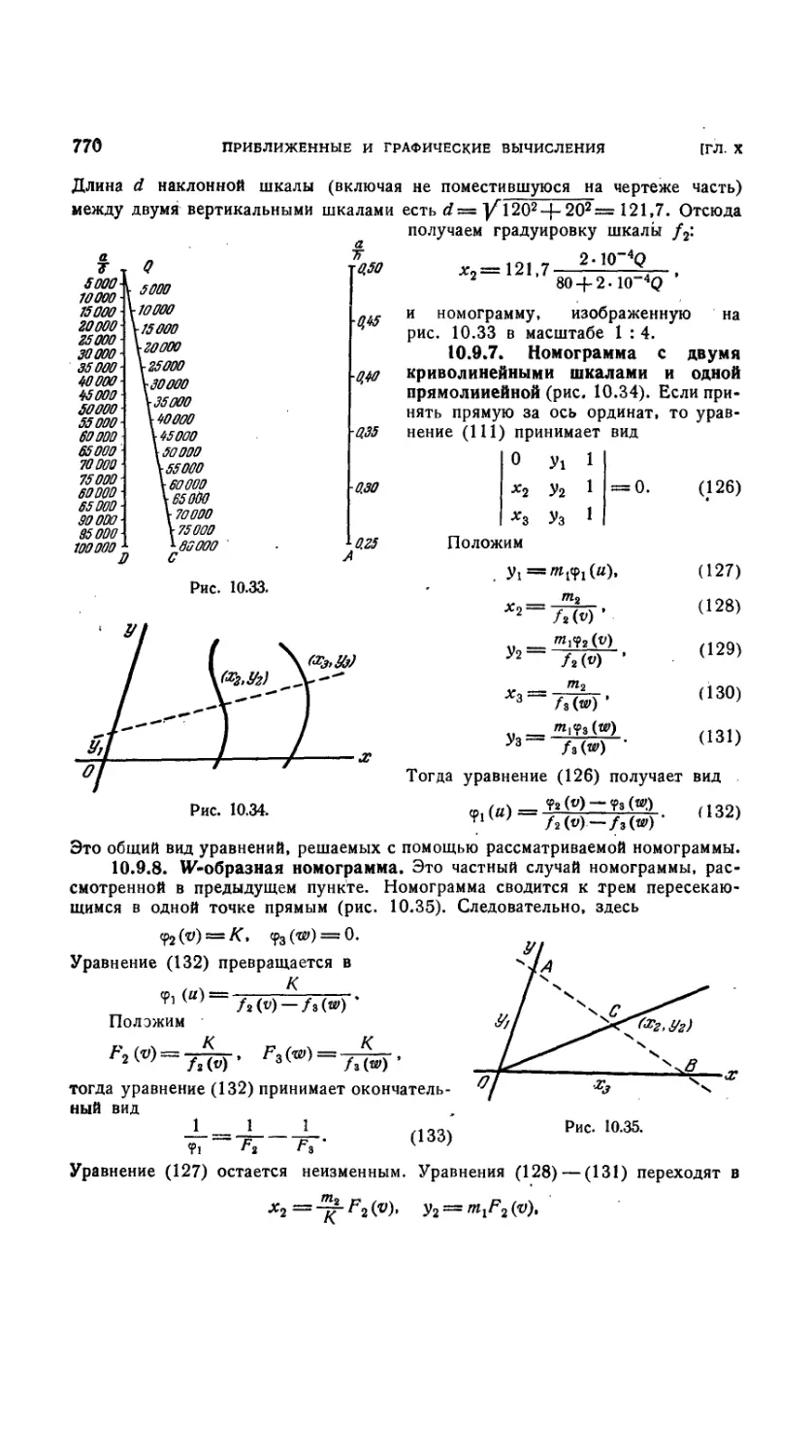
10.9.6. W-образиая номограмма 769
10.9.7. Номограмма с-двумя криволинейными шкалами и одной пря-
прямолинейной 770
10.9.8. U^-образная номограмма 770
10.9.9. Z-образная номограмма 771
10.9.10. Номограмма с тремя криволинейными шкалами -.771
10.9.11. Сложные номограммы 772
Литература к главе X 772
Предметный указатель 773
Указатель обозначений 779
2»
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Книга Андре Анго, перевод которой предлагается вниманию читателей,
содержит дополнительные гланы к общему втузовскому курсу высшей мате-
математики. Автору удалось в четкой и компактной форме изложить широкий
круг вопросон математики, знание которых в настоящее время необходимо
всякому образованному электро- и радиоинженеру.
Предисловие Луи де Бройля, введение автора и подробное оглавление
позволяют читателю получить полное представление о содержании книги.
Книга выдержала во Франции три издания A949, 1952, 1957 гг.). Она
написана живым языком,' причем центр тяжести изложения перенесен со
строгих доказательств на наглядность, физический смысл и практические
приложения.
Отдельные главы книги не очень тесно связаны между собой, так что их
можно читать независимо друг от друга. Большое количество формул, таб-
таблиц и графиков делает книгу ценным справочным пособием.
В книге рассматривается много интересных приложений, главным обра-
образом из области электро- и радиотехники. Все электротехнические формулы
написаны в рационализированной системе единиц МКСА (в международ-
международной системе СИ). В этой же системе единиц выполняются численные расчеты.
При изложении численных методов автор ограничился главным образом
приемами, которые могут быть выполнены с помощью ручной счетной ма-
машины и набора таблиц. Он не рассматривает специальных приемов, связан-
связанных с применением электронных вычислительных машин, полагая, что это
относится к компетенции специалистов-программистов.
При переводе испранлены все замеченные ошибки или описки оригинала,
сделаны некоторые сокращения и добавления. В тех случаях, где это пред-
представлялось удобным, редакторские вставки вынесены в подстрочные примеча-
примечания. Однако большая часть этих дополнений, органически слитых с автор-
авторским текстом, нигде специально не отмечена. Списки литературы, приводимые
в конце каждой главы, изменены. Опущены устаревшие, труднодоступные
работы и добавлены издания, легкодоступные советскому читателю.
Перевод книги с третьего французского издания выполнен Е. М. Шиф-
риной. Редактировали перевод: гл. I, II, III, VI, VII — А. Я. Перельман,
К. С. Шифрин; гл. IV —Ю. А. Седов, К. С. Шифрин; гл. V —Л. Б. Кома-
рон, К. С. Шифрин; гл. VIII — И. А. Назаров; гл. IX — Л. Б. Комаров;
гл. X — М. К. Гавурин. Общая редакция перевода выполнена К. С. Шифриным.
Мы надеемся, что содержательная книга А. Анго будет интересна не
только электро- и радиоинженерам, но и широкому кругу инженерно-техни-
инженерно-технических и научных работников, имеющих дело с математикой и ее многочис-
многочисленными приложениями, а также студентам и аспирантам втузов.
К. С. Шифрин
ПРЕДИСЛОВИЕ
По многим причинам во Франции преподавание математики физикам и ин-
инженерам в большинстве случаев не очень хорошо приспособлено к требова-
требованиям тех, для кого оно предназначено.
Всего лишь тридцать лет тому назад и физик и инженер могли превос-
превосходно обходиться знанием классических результатов дифференциального и ин-
интегрального исчисления. Но в наши дни, когда изучение новых теорий все
чаще требует владения весьма разнообразным математическим аппаратом, фи-
физик и инженер должны знать многочисленные и часто недавно развитые раз-
разделы математики, например тензорный анализ, матричный анализ, символи-
символическое исчисление Хевисайда, теорию собственных значений, подчас даже теорию
интегральных уравнений и теорию групп. Однако преподавание математики
в институтах и высших школах до сих пор недостаточно приспособлено к но-
новым потребностям в аналитических знаниях тех, кто интересуется приложе-
приложениями.
Более того, сама манера изложения лекций и книг по математическому
анализу, авторами которых в большинстве случаев бывают профессиональ-
профессиональные математики, не "совсем подходит физику или инженеру, для которых раз-
различные тонкости в доказательствах значат довольно мало, а решающее зна-
значение имеет знание различных математических методов, применяемых на прак-
практике. Имеются многочисленные труды по математическому анализу, в которых
многие страницы посвящены установлению существования решений дифферен-
дифференциальных уравнений и всего в нескольких строчках делается намек на поли-
полиномы Лежандра или бесселевы функции. Теория рядов Фурье излагается с боль-
большим обилием деталей, зачастую бесполезных для практика, а об интеграле
Фурье, значение которого столь велико в старых .и новых разделах матема-
математической физики, даже не упоминается. Можно было бы продолжить примеры
и, показать, что, несмотря на некоторые успехи, преподавание анализа лишь
в редких случаях отвечает требованиям тех, кто имеет практический уклон.
В других, в частности, в англо-саксонских странах, дело часто обстоит
иначе. Там имеются превосходные курсы по математике и ценные монографии
по вопросам, которые физику и инженеру необходимо хорошо знать. Авторы
этих работ, оставляя в стороне крайнюю математическую строгость и часто
заменяя безукоризненные доказательства простыми соображениями, стремятся
оттенитьгсмысл и практическую пользу математических методов расчета и по-
подробно ознакомить читателя с наиболее важными функциями, встречающимися
в приложениях. Цель таких трудов — на многочисленных примерах, взятых
из конкретных задач, помочь читателю овладеть математическим рабочим ин-
инструментом. Несомненно, это и есть правильный метод изучения приложений
математики к физике и технике.
Поэтому можно считать большой удачей, что профессор Высшего элек-
электротехнического училища А. Анго предлагает нам труд подобного рода (до
22 ПРЕДИСЛОВИЕ
настоящего времени такого редкого во Франции) под названием «Математика
для электро- и радиоинженеров». Это книга, чтение которой в высшей сте-
степени приятно и поучительно. Польза ее несомненна. Автор включил в нее
все определения, доказательства и способы расчетов, которые должен знать
современный инженер, если он хочет следить за развитием электро- и радио-
радиотехники и читать работы, в которых применяются математические методы.
Не добиваясь строгости доказательств, по поводу которых он отсылает чи-
читателя к трудам по анализу, автор в особенности настаивает на подробных
вычислениях и приводит многочисленные примеры практического применения
изложенных методов к конкретным задачам. Графики, кривые, таблицы до-
дополняют рассмотрение различных типов функций и придают этой книге, по-
помимо чисто познавательного интереса, характер ценного справочника. Список
библиографической литературы позволит читателю, желающему глубже изучить
какой-либо из рассматриваемых вопросов, обратиться к специальным моно-
монографиям.
Функции комплексной переменной, ряды и интегралы Фурье, векторное
и тензорное исчисление, матричная алгебра, дифференциальные уравнения
и уравнения в частных производных в прямоугольных или криволинейных
координатах, изучение важных функций, в частности, бесселевых и Лежандра,
операционный анализ — таковы вопросы, рассматриваемые в данной работе.
К этому следует также добавить изложение принципов теории вероятностей,
дополненное очерком о случайных функциях Блан-Лапьера, являющегося ма-
мастером этого вопроса. И все время, как лейтмотив, приводятся практические
задачи на расчеты электрических цепей, на примере которых читатель видит,
для чего служат излагаемые методы вычисления и как следует ими пользо-
пользоваться.
Эта книга специально предназначена для электро- и радиоинженеров, но
следует рекомендовать ее также и физикам, так как вся современная теоре-
теоретическая физика широко пользуется алгоритмами, рассматриваемыми здесь.
Для физика, как и для инженера, прекрасная книга А. Анго будет служить
неисчерпаемым источником необходимых сведений и ценных справок.
Луи де Бройль
Париж, 1949 г.
ВВЕДЕНИЕ
Предлагаемая работа не представляет собой курса математики в обычном
смысле слова. В ней не следует искать связи между отдельными главами,
кроме их общей направленности к применению в электро- и радиотехнике.
Главная задача книги — представить в удобной и доступной форме те основ-
основные математические сведения, которые должен иметь инженер со средней
подготовкой, чтобы с пользой для себя читать статьи и работы, в которых
рассматриваются достижения науки в области слабых и сильных токов.
Для этой цели автор кое-где намеренно поступился строгостью доказа-
доказательств в пользу краткости и ясности. Читатель, стремящийся к абсолютной
математической; строгости, должен будет обратиться к классическим трудам
по анализу или1 к работам, цитируемым в ссылках.
Для того чтобы быть в курсе развития своей области техники, инженер
должен следить за' специальной литературой. Однако легко заметить, что это
требует высокого уровня математических знаний. И если читатель будет вы-
вынужден, прежде чем приступить к чтению специальных работ, дополнительно
изучать некоторые разделы математики, необходимые для понимания текста,
то результат известен заранее: как бы ни была важна статья, она прочитана
не будет; мало того, что это требует скучного труда, но в большинстве слу-
случаев необходимые сведения разбросаны по отдельным книгам и статьям, часто
на иностранных языках, и собирать их долго и трудно.
Эту работу я и попытался проделать в данной книге. Особые старания
были приложены к тому, чтобы читатель мог найти формулы, таблицы to кри-
кривые, необходимые для численных расчетов, которыми обычно завершаются
инженерные исследования.
Эту книгу следует рассматривать, как некий рабочий инструмент.
Выражаю мою живейшую благодарность Луи Де Бройлю, оказавшему мне
честь представить эту работу читателю.
• Обращаюсь с признательностью к Блан-Лапьеру, который соблаговолил
взять на себя труд отредактировать часть IX главы, посвященной случайным
функциям.
Андре Анго
ГЛАВА I
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
х'
В
О
Рис. 1.1.
1.1. КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ
1.1.1.Определения. Вещественное число можно изобразить графически.
В самом деле, пусть х'х (рис. 1. 1) — бесконечная^прямая, на которой вы-
выбрано положительное направление. От точ-
—>. ки О, принятой за начало, отложим в опре-
——— деленном масштабе отрезок, длина которого
х пропорциональна рассматриваемому веще-
вещественному числу. На рис. 1.1 отрезок О А
представляет положительное число, а ОБ—
отрицательное. На прямой х'х размещаются все вещественные числа: целые,
дробные, алгебраические, трансцендентные, причем как положительные, так
и отрицательные.
Понятие вещественного числа можно обобщить, если ввести в рассмот-
рассмотрение число z, образованное парой вещественных чисел х и у, взятых в оп-
определенном порядке. Такое число назовем комплексным. Временно будем за-
записывать его bv виде „
z = [x, у].
Вещественные числа х я у со-
составляют соответственно вещественную
и мнимую части комплексного числа z.
Часто используются обозначения
x = R(z), y=\(z).
Комплексные числа также можно
изобразить графически. Это изображе-
изображение будет, двухмерным на плоско-
плоскости, образованной двумя взаимно пер-
перпендикулярными осями Ох и Оу.
Комплексное число на плоскости хОу (рис. 1.2) представляется точкой М
с координатами х, у; эту точку называют также изображением комплексного
числа. И обратно, пару чисел [х, у], образующих комплексное число z, на-
называют аффиксом точки ¦ М.
Два комплексных числа z — [x, у] и z' — [x', у'] считаются равными,
если совпадают изображающие их точки. Это означает, что равенство z и zr
имеет место в том, и'только в том случае, когда
О
z
рис. 1.2.
til
КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ
25
Если изображение комплексного числа совпадает с началом координат,
то его вещественная и мнимая части равны нулю. Такое комплексное число
называют нулем. Следовательно, равенства z = 0 ил' = 0, у = 0 равносильны.
Положительное число р = Ух2-\- у2, равное длине отрезка ОМ (рис. 1.2),
называется модулем комплексного числа z; модуль z вбычно обозначают | z \.
Угол ср. на который нужно повернуть ось Ох в положительном направлении
(против часовой стрелки) до совпадения с направлением ОМ, называется ар-
аргументом комплексного числа z. Этот угол определяется с точностью до це-
целого числа оборотов; углы ср-|-2&те также будут представлять собой аргу-
аргументы z (k может принимать все возможные целые значения:- положительные,
отрицательные и нуль).
Если заменить х на pcostp, а у на psincp, то комплексное число можно
написать в таком виде:
z — [pcostp. psincp].
Вместо того чтобы изображать комплексное число [х, у] точкой М, мы
можем представить его отрезком ОМ. И обратно, отрезок ОМ изображает
комплексное число [х, у].
1.1.2. Сложение. Суммой двух комплексных чисел z1 и z2 называется
комплексное число г, вещественная и мнимая части которого представляют
собой соответственно сумму вещественных и мнимых частей zx и z2:
Пусть точки Mv М2 а М — изображения чисел zv z2 и z. Из рис. 1.3
видно, что точка М может быть получена по точкам. Мх и М2 с помощью
М
Рис. 1.3.
правила параллелограмма. Следовательно, сложение комплексных чисел zx
и z2 графически представляется как геометрическое суммирование отрезков
ОМХ и ОМ2.
Если pj и р2 обозначают модули zx и z2, то из рис 1.3 непосредственно
следует справедливость двух неравенств:
l*i — *al>|pi — Pal-
1.1.8. Умножение. Пусть zx = \xv у,], z2 = [x2, y2]—два комплексных
числа, изображения которых суть точки Мх и М2. Произведением этих двух
¦26 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
чисел называют комплексное число, изображение которого М получается
следующим способом (рис. 1.4): выбирают точку F на оси Ох таким обра-
образом, чтобы OF=\, и строят подобные треугольники OFMl и ОМ2М. Этот
способ представляет собой распространение на плоскость обычного способа
умножения двух вещественных чисел,
изображенных на прямой двумя отрез-
отрезками О А и ОВ (рис. 1.5). Длина отрез-
отрезка ОС, который является произведением
этих чисел, такова, что
ОС _ ОА
~О~В~ 1 '
Легко получить
z = Zi-z2 = \ххх2—уху2,
! I I 1
О /IB C'
Рис. 1.4. . Рис. 1.5.
Из рис. 1.4 видно, что модуль произведения равен произведению моду-
модулей сомножителей:
ОМ = ОМХ ¦ ОМ2
и что аргумент произведения равен сумме аргументов сомножителей:
/ х ОМ — / х ОМ, + '/ М,ОМ — / х ОМХ + / х ОМ2.
Тот же прием, выполняемый в обратном порядке, позволяет осуществить
графически деление комплексных чисел. Очевидно, модуль частного равен
частному модулей числителя и знаменателя, а аргумент частного равен раз-
разности аргументов числителя и знаменателя.
1.1.4. Замена обозначений. Легко убедиться, что все вычисления с ком-
комплексными числами можно производить, применяя обычные правила алгебры,
если записывать эти числа в виде')
z — x-\-jy,
где х — вещественная, а. у — мнимая части комплексного числа, и условиться,
что в расчетах J2 заменяется —1. Покажем это на примере операции
умножения:
= xxx2 — yxy2 + j (xxy2 + x2yx).
Таким образом, для комплексных чисел нет нужды создавать специаль-
специальную алгебру.
В дальнейшем комплексное число будем записывать в виде z = x-\- jy
или гг == р (cos ср —|— у" sin cp).
') Математики обычно употребляют здесь букву / вместо буквы j. Мы же
пользуемся по традиции электриков буквой j, чтобы не создавать путаницу с
обозначением силы тока.
1,1]
КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ
27
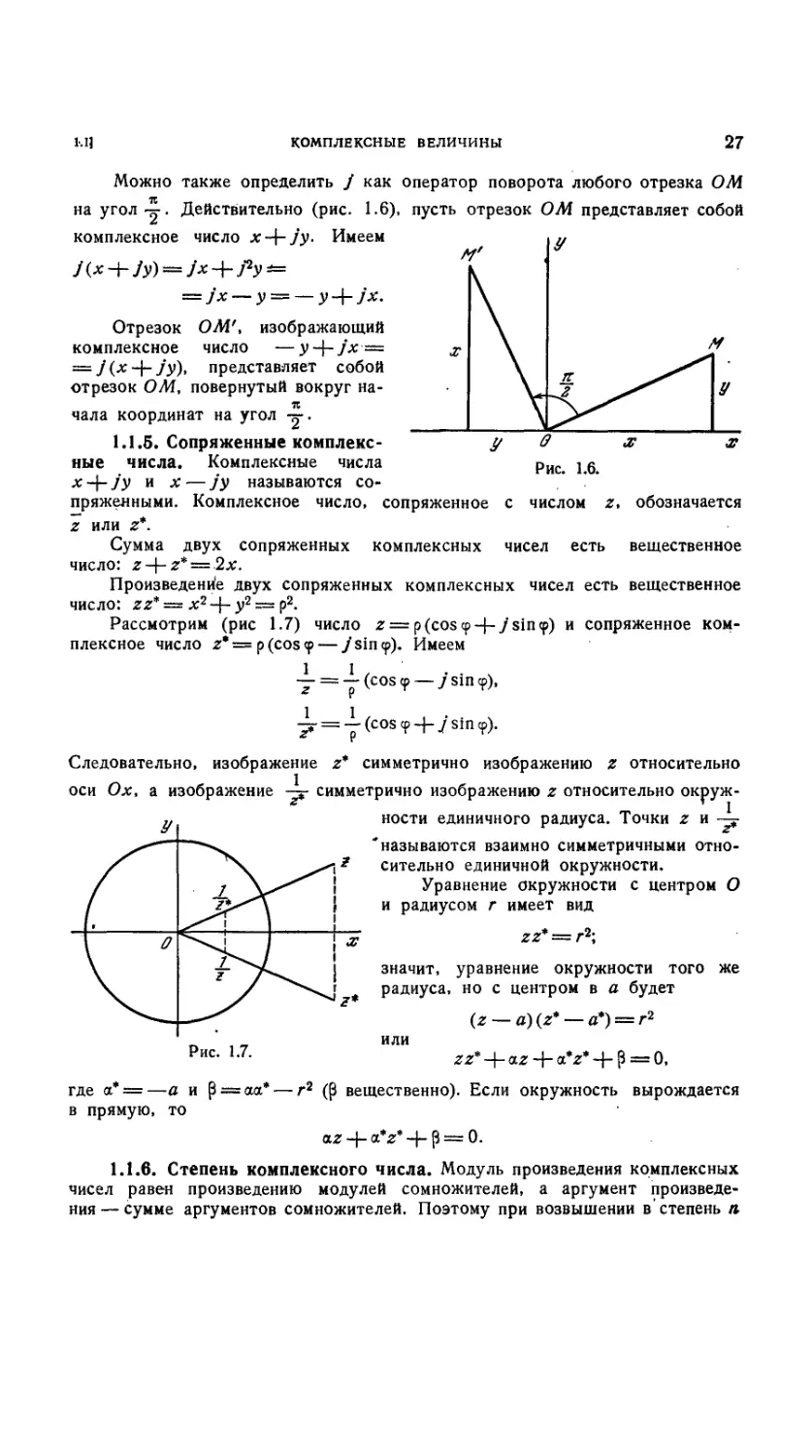
Можно также определить / как оператор поворота любого отрезка ОМ
на угол ~. Действительно (рис. 1.6), пусть отрезок ОМ представляет собой
комплексное число x-\-jy. Имеем у
= jx — у = — у -\- j'x.
Отрезок ОМ', изображающий
комплексное число —y-\-j'x —
= J(x~hJy)> представляет собой
отрезок ОМ, повернутый вокруг на-
начала координат на угол -j-
1.1.5. Сопряженные комплекс-
комплексные числа. Комплексные числа
x-\-jy и х — j'y называются со-
сопряженными. Комплексное число, сопряженное с числом z, обозначается
Z ИЛИ Z*.
Сумма двух сопряженных комплексных чисел есть вещественное
число: z-\-z* = 2x.
Произведение двух сопряженных комплексных чисел есть вещественное
число: zz* — х2 -f- У2 — р2-
Рассмотрим (рис 1.7) число .z = p(coscp4-/sin<p) и сопряженное ком-
комплексное число .z*=p(cos<p — /sincp). Имеем
1 1 , ' . . ч
— = — (cos tp — j sin cp),
Следовательно, изображение z* симметрично изображению г относительно
оси Ох, а изображение —^ симметрично изображению z относительно окруж-
„ ности единичного радиуса. Точки z и —w
'называются взаимно симметричными отно-
относительно единичной окружности.
Уравнение окружности с центром О
и радиусом г имеет вид
значит, уравнение окружности того же
радиуса, но с центром в а будет
(z — a) (z* — а*) = г2
или
zz* 4- a.z Ч- <**z* + Р = О,
где <х* = —а и р = <х<х* — г2 ф вещественно). Если окружность вырождается
в прямую, то
Рис. 1.7.
1.1.6. Степень комплексного числа. Модуль произведения комплексных
чисел равен произведению модулей сомножителей, а аргумент произведе-
произведения— сумме аргументов сомножителей. Поэтому при возвышении в степень а
28
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
комплексного числа р (cos ср —j— г sin cp) модуль степени будет равен р", а аргу-
аргумент— яср.
Строго говоря, поскольку ср определено с точностью до 2Air, аргумент
степени равен «cp-|-2«Air. Последнее слагаемое здесь не существенно, так
как лучи «ср и яср+2яйтг совпадают; поэтому оно опускается. Следовательно,
zn = р" (cos се -f- j sin 9)" = р" (cos яср + у sin яср)
и, в частности,
(cos ср -j- У sin ср)" = cos гаер -(- у sin лср-
Раскрывая левую часть по формуле бинома и приравнивая веществен-
вещественные и мнимые части, получаем следующие соотношения (формулы Муавра):
cos яср = cos" ср — С2, cos" cpsin2 cp+ С4, cos" ср sin4 ср — ....
где
sin яср = Cln cos" г cp sin cp — C3, cos" 3cpsin3cp + ....
гр n(n—-1) ... (n — p+l)
В частности,
cos 2ср = cos2 ср — sin2cp, •
cos Зср = cos3 ср — 3 cos ср sin2 cp,
cos 4<p = cos4 ср — 6 cos2 ср sin2 ср -f- sin4 cp;
sin 2cp = 2 sin cp cos cp,
sin Зср = 3 cos2 cp sin cp — sin3 cp,
sin 4cp = 4 cos3 cp sin cp — 4 cos cp sin3 cp.
1.1.7. Корни из комплексного числа. Если считать, что
2" = p(coscp-|-ysincp) и z = r (cos8 -|^ j sin б),
то, используя предыдущее рассуждение, находим
г" = р и «9 = ср -|- 2Й1г,
откуда получаем
г = о1 и Ч=—-—I
г п п
В отличие от п. 1.1.6 здесь слагаемым 2&тс пренебречь нельзя. В самом
деле, придавая k значения я последовательных целых чисел, получаем я
различных корней. Все эти корни имеют один
и тот же модуль р1'", но отличаются аргумен-
аргументами.
1.1.8. Корни из единицы. Единица может быть
записана в комплексной форме p(coscp-f-ysincp),
если положить р = 1 и ср = О.
Следовательно, корни я-й степени из единицы
определяются по формулам
cos2A — + У sin 2ft —
п ' J п
(ft = 0. I, 2 я —1).
Из рис. 1.8 видно, что изображения этих
корней совпадают с вершинами правильного много-
многоугольника с п сторонами, вписанного в окружность радиуса 1. Вершина,
соответствующая k = Q, находится в точке А A,0).
Если сравнить формулы
1.1] КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ 29
и
то увидим, что все корни я-и степени из р (cos cp -f- у sin ср) можно получить,
умножая любой такой корень zk последовательно на* п корней я-й степени
из единицы.
1.1.9. Ряды с комплексными членами. Рассмотрим ряд
2*
обший член которого zk = xk-\-jyk. Ряд будет называться сходящимся,
я
если его частичная сумма Sn = 2 (-^л + УУь) стремится к пределу X.-^-jY,
когда п -> оо. Для сходимости этого ряда необходимо и достаточно, чтобы
оо оо
СХОДИЛИСЬ. ПОрОЗНЬ РЯДЫ 2л:* И 2 Ук-
ft=0 ft=0
Рассмотрим ряд
оо
2 р*-
i ft=0
Общий член этого ряда рк = |/'х\ -\- у\ — модуль комплексного числа гк.
Так как
то сходимость ряда из модулей влечет сходимость обоих рядов 2 ¦*»•
оо оо
2 )V В этом случае про ряд 2 zk говорят, что он абсолютно сходящийся.
t=0 *=0
ио
1.1.10. Степенные ряды*). Рассмотрим ряд 2 в»г*, где et и z — ком-
*о
плексные числа.
Ряд
2/*Р М> = К|, Р=!г|).
составленный из модулей членов первого ряда, есть степенной ряд с веще-
вещественными членами. Для этих рядов доказывается существование числа R^-0
(оно может быть равно и бесконечности) такого, что ряд сходится при р < R
и расходится при р > R.
оо
Вернемся теперь к ряду 2 akz>t (степенному ряду с комплексными чле-
ft=0
нами) и рассмотрим в комплексной плоскости круг с центром О и радиусом R.
Этот ряд будет сходящимся или расходящимся в зависимости от того, где
будет находиться изображение z: .чнутри или вне круга.
Понятие равномерной сходимости, а также теоремы, относящиеся к сло-
сложению, умножению, дифференцированию и интегрированию вещественных сте-
степенных рядов, целиком применимы к комплексным степенным рядам.
*) Автор называет степенной ряд «целым рядом». Этот термин п?цш?< в неко-
некоторых французских руководствах. (Здесь и далее звездочкой отмечены подстрочные
примечания редакторов перевода.)
30 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
Пример. Рассмотрим разложение в степенной ряд (ряд Тейлора)
функции е*у:
е it- t ^ ^
'--^yU! 3! "Г" 5! 7! "*" * ' ' I"
е — i-t- Ц -t- 2! ^ 3!
6 ~ 2! "^ 4! 6!^
В вещественной и мнимой части этого разложения можно узнать ряды
для cosy и sin у. Таким образом, получаем формулу Эйлера:
е;у = cos у -\- j sin у.
Если заменить у на — у, то
e~ly — cosy — у sin у.
Складывая и вычитая полученные формулы, найдем:
ejy-\-e-jy _ e/y^e-jy
cosy =siny =
Отметим важные частные случаи формулы Эйлера:
' Формула Эйлера дает возможность комплексное число
z = х + jy = р (cos ср + у sin cp)
записать в виде *)
Последняя формула непосредственно иллюстрирует правило умножения
и деления двух комплексных чисел г = р1е('ч'', z2 = p2 в'452- В самом деле, имеем
.г^гзгр р еЛ<Р.+<р2>, lL^lL^ta-Ы.
1.1.11. Экспоненциальная функция и логарифм. Функцию w — ег, где
z = x-\- jy, с помощью формулы Эйлера можно написать в таком виде:
w — ех (cos у -f- у sin у).
Заменяя z на ^j = z + 2йтгу, где k — целое число, получаем
?*¦ == eze2k*J = ег.
Таким образом, экспоненциальная функция имеет период 2тгу.
Рассмотрим функцию w, определенную соотношением z = ew при z = х -\-
-j- jy =z pe'f. Имеем *)
w = 1 n z = -i In (x2 + у-) Ч- j arctg -J-,
') Иногда число г=| г| (cos tp + У sin cp) записывают в виде \z\\y при отрицатель-
отрицательном «р и |г||9 при полржительном tp. Например, г = 10 -f- 5у = 11,18 |26°34'.
*) Обычно различают главное значение логарифма In г и бесконечнозначную
функцию Ln г (см., например, [4], стр. 33—36).
1.2] ЦЕПИ В СИНУСОИДАЛЬНОМ РЕЖИМЕ 31
1.1.12. Дифференцирование и интегрирование по аргументу. Дана
комплексное число z = pei<?. Его производная по ср есть
-г- = уре7? = ре 2 eJV = ре v 2 '.
Таким образом, дифференцирование по аргументу приводит к повороту
отрезка ОМ на угол ~ (рис. 1.6). Очевидно, что интегрирование по ср при-
приводит к повороту отрезка ОМ на угол — -=¦.
1.1.13. Суммирование тригонометрических функций, аргументы
которых составляют арифметическую прогрессию. Требуется вычислить-
суммы
.$! = cos a + cos (a+ 8)+cos (а+ 28)_|- ... -|-cos [а + (/к — 1)8],
(а+28) + ••• +*sin [a + (/«—1)8]
т косинусов или синусов, аргументы которых составляют арифметическую-
прогрессию.
Рассмотрим сумму S = Sl-±-JS2:
Последовательно находим
т*Р _# [,+(„-1)8/2]
М ~ sin 5/2
-е)т*Р _# [,+(„-1)8/2] sinm8/2 _
—1)8/2]}
Разделяя вещественную и мнимую части, получаем
A)
-1)8/2] igj*^. B)-
1.2. ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ВЕЛИЧИН ПРИ РАСЧЕТЕ
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ В СИНУСОИДАЛЬНОМ РЕЖИМЕ
1.2.1. Введение. Рассмотрим периодическую функцию f (t) с периодом Т,
т. е. такую, что / (t) = f (t -\- nT) (я —целое). В гл. II мы увидим, что эта
функция может быть разложена в ряд Фурье. Иначе говоря, ее можно
написать в виде
bm cos mwt-{- 2^ amsmm<at, где ш==-уг.
m=1 m =1
ч «
Изучение поведения электрической цепи, в которой течет периодический
ток i = f(t), можно свести к рассмотрению той же цепи с синусоидальными
токами периода Т, Т/2, Т/3, ..., иначе говоря, к рассмотрению постоянных
синусоидальных режимов этой цепи.
Если функция / (t) непериодична, то, как мы увидим в гл. II, разложе-
разложением в интеграл Фурье ее можно представить в виде суммы синусоидальных.
32 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
функций, частоты которых сплошь заполняют числовую ось от нуля до
бесконечности:
со со
f
— x)dx.
Если, как в предыдущем случае, мы хотим изучить поведение электри-
электрической цепи с током i = f(t), то мы снова приходим к рассмотрению
постоянных синусоидальных режимов. Из этого видна важность синусоидаль-
синусоидальных функций времени и интерес, который может представить разработка
способов расчета, специально приспособленных для этих функций.
1.2.2. Графическое изображение синусоидальной функции. Рассмо-
Рассмотрим иектор постоянной длины /,, вращающийся в заданной плоскости вокруг
точки О с угловой скоростью ш. Введем в указанной плоскости систему
„ прямоугольных координат хОу (рис. 1.9).
-1* Пусть cpj—угол, образованный ОМХ с
осью Ох в начальный момент времени.
Тогда 1Х — ордината точки Мл в момент
времени t — выражается формулой
О
Вектор ОМ1 удобно использовать для
графического представления синусоидаль-
ных функций времени (синус получится
О
р 19 при проектировании на ось Оу, косинус -
на ось Ох).
Пусть нам нужно сложить две синусоидальные функции с одинаковым
периодом, но с разными начальными фазами
По известному правилу вектор ОМ, изображающий сумму обеих функций tx
и /2, можно получить как геометрическую сумму векторов ОМХ и ОМ2,
изображающих эти функции. Все три вектора вращаются одновременно
с угловой скоростью ш. Легко непосредственно проверить, что ордината
точки М представляет собой сумму функций /1sin((flf-f-cp)) и /2 sin (ш?-f-ср2).
Аналогично абсцисса точки М равна сумме функций /j cos (ш?-|-9i) и
2 p2
Вместо того чтобы вращать векторы с угловой скоростью ю, можно
предположить, что они неподвижны, а оси координат вращаются с угловой
скоростью — ш.
На рис. 1.9 изображено относительное расположение векторов и осей
(в момент t = 0).
Геометрическое построение, описанное выше, определяет амплитуду
ОМ = 1 и фазу ср и тем самым позволяет найти выражения
/sin (to/ —f— =р) = /х sin Соаг" —|— сра) —f— /2 sin (а>^ —(— ср2).
/ cos (ш? -f- ср) = /j cos (utf + cpi) H~ ^2cos (ш^ ~Ь %)¦
Часто нужно 'уметь вычислять производные или интегралы синусоидаль-
синусоидальных функций типа / = /sin(utf-|-ср)- Имеем
/
—- = ш/ cos (wt -f- ср) = <о/ sin I (at -f- cp -)- -^- J,
ldt = cos (ш?-|-ср) = — sin
1.2] ЦЕПИ В СИНУСОИДАЛЬНОМ РЕЖИМЕ 33
Производные и первообразные от функции / изображаются векторами, повер-
повернутыми по отношению к исходному вектору соответственно на угол -+--?
и —Y' Длины этих векторов будут ш/ и //ш. Такой прием позволяет гра-
графически получить синусоидальные решения дифференциальных или интегро-
дифференциальных уравнений с постоянными коэффициентами.
Рассмотренный нами способ векторного представления весьма употреби-
употребителен. Однако графические построения становятся неудобными и мало точ-
точными в случае длинных и сложных вычислений, особенно когда порядок
величин векторов ш/, /, //со весьма различен. Способ же, который мы сейчас
изложим, соединяет в себе простоту графического приема с точностью
алгебраических вычислений.
1.2.3. Представление с помощью комплексных чисел. Поскольку
речь идет о векторах, расположенных в одной плоскости, то можно пло-
плоскость на рис. 1.9 считать комплексной и трактовать вектор как комплекс-
комплексное число, вещественная и мнимая части которого представляют собой соот-
соответственно проекции вектора на оси Ох и Оу. Вектор ОМ определяется
комплексным числом 1)
I [cos (wt + <р) + J sin (at + <р)] = Iehe)mt.
Член д = 1е14 определяет собой неподвижный вектор ОМ, отнесенный
к неподвижным,осям (рис. 1.9). Величина 3 называется комплексной ампли-
амплитудой или просто комплексным током. Точно так же, рассматривая напряже-
напряжение и — f7 sin (ш/ —(— 6), мы можем ввести величину U — Ueib, которую будем
называть комплексным напряжением. i
Покажем теперь, что сложение двух синусоидальных функций, изобра-
изображенное на рис. 1.9, можно произвести и без графического построения.
Действительно, пусть даны две (или несколько) синусоидальных функций,
представляющих собой, например, ток
Положим, что
Так как сложение комплексных чисел подчиняется правилу векторного
сложения, то очевидно, что вектор ОМ на рис. 1.9 определяется комплекс-
комплексным числом 3' — 3'х-{- 3'2. Искомая синусоидальная функция будет пред-
представлять собой мнимую часть от 3е •
Производная по времени функции I = /sin(<fl? + cp) будет мнимой частью
производной по времени от функции &ei<at. В этом легко убедиться непо-
непосредственно, если сравнить оба выражения. Точно так же неопределенный
интеграл по времени от / совпадает с мнимой частью интеграла от geJa>t.
Отсюда можно вывести следующее правило: дано
/х = /j sin (to/ —I— cpj), t2 = /2 sin (otf -f- cp2), ...
несколько синусоидальных функций. Требуется определить синусоидальную
функцию, представляющую результат подстановки iv f2, ... в линейное и
') Иногда функцию Ае^ называют сиссоидальной и обозначают A els i>. Слог els
является сокращением от coslnus + / sinus. Здесь буква j заменена буквой i, как
это принято в математике.
3 А. Анго
34 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
однородное выражение первого порядка
t t
ffdt+... C)
Здесь коэффициенты а, р, f не зависят от времени. Положим
'i = 0 ieliot, l2 = g2eia" где g\ = //*, #2 = /2*'*. ...
Член е входит множителем во все слагаемые выражения C). Окончатель-
Окончательный результат, очевидно, может быть написан в виде
Мнимая часть этого выражения и есть искомая синусоидальная функция
/ = /sin (tot -J- 9)-
Вещественная часть дает результат подстановки в C) соответствующих
косинусоидальн ых функций.
1.2.4. Ограничения метода. Только что установленное правило приме-
применимо в тех случаях,, когда требуется произвести сложение, дифференцирова-
дифференцирование, интегрирование токов или синусоидальных напряжений либо линейные
комбинации этих операций. Правило это, однако, неприменимо, если нужно
подвергнуть токи или напряжения нелинейным алгебраическим операциям,
как, например, умножению или возведению в степень. Действительно, легко
видеть, что при таких операциях возникают круговые частоты, отличные от ш.
Это обрекает на неудачу векторное построение, изображенное на рис. 1.9,
а следовательно, и комплексное представление, которое является его ото-
отображением.
Рассмотрим это на примере умножения. Пусть
t г cr Jmt cr / Jfi a / J^1
• h c/2e • c/l —'1* • c/2 —'2* ¦
Правило умножения комплексных чисел, примененное к lxtv дает
/ / I Г J l'Pi
4*2 'V2e
Мнимая часть этого выражения равна
IXI2 sin (91 -f- cp
Если же непосредственно умножить ix =/j sin(o)^-(-cp1) на /2 = /2sin(W-f-cc2)I
то получим
hk = V2sin (wt + ?i) sin ((of -f- <p2) = j /,/2 [cos (9! — cp2) — cos Bш/ -j- <р: -f- y2)].
Результаты, как видим, получились совершенно различные.
Замечание. Комплексное исчисление может оказаться весьма полез-
полезным в тех случаях, когда требуется определить активную и реактивную
мощности в цепи переменного тока *).
*) Напомним, что в цепи переменного тока различают мгновенную мощность р,
активную мощность (среднее за период значение мгновенной мощности) Р и гак
называемую реактивную мощность Q.
Если мы обозначим соответственно мгновенные значения тока и напряжения
через i (t) и и (t), амплитуды этих величии через / и U, а сдвиг фаз между ними
через ?, то упомянутые выше мощности определяются формулами: p = ijif)u(t),
Р = р = 1С/ cos <f, Q = /U sin <j>.
tSS ЦЕПИ В СИНУСОИДАЛЬНОМ РЕЖИМЕ 35
Обозначим комплексный ток в цепи через 0 =1е , а напряжение —
2/±= Ue . Положим е — 8 = 9- Величина 0*, комплексно сопряженная току 0,
равна 0*=/е~^, а произведение U0 равно UIej(t~S) = U/ei<e. Активная
мощность в цепи будет ?//coscp, а реактивная — ?//sincp. Мы видим, таким
образом, что для отыскания активной и реактивной мощности, расходуемой
в цепи с комплексным током 0 и
комплексным напряжением U, доста-
точно взять вещественную и мнимую
части выражения U0*. r
1.2.6. Понятие комплексного
полного сопротивления. Рассмотрим Рис. 1.10.
цепь, составленную из омического
сопротивления R и самоиндукции L (рис. 1.10). Требуется найти разность
потенциалов a = ?/sin(<fl?-|-cp), возникающую на концах цепи, если в ней
течет ток / = / sin (со^ —}- а).
Имеем
u = L-§+Rt. D)
Положим
u = Uei<ot, i=0elwt, где U = Ue'\ 0==feJ".
Правая часть формулы D) представляет собой частный случай выражения C).
Мы можем найти 21, если подставим / в D) и опустим множитель e*wt,
содержащийся в обеих частях ра-
-Т_П_П_ПII
/7 п
Заметим, что в последнем ра-
Рис. 1.11. венстве время не фигурирует. Коэф-
Коэффициент пропорциональности Z ме-
между U к 0 является комплексным числом, не зависящим от времени. Он
имеет размерность сопротивления и называется комплексным полным сопро-
сопротивлением *).
Разность потенциалов определяется мнимой частью и. Сохраняя для
нее прежнее обозначение, имеем
где
u=f\z\—i
Рассмотрим теперь ту же задачу для цепи с емкостью С, соединенной
последовательно с сопротивлением R (рис. 1.11). Уравнение задачи следующее:
t
f
= Ri-\-^r f idt.
В тех же обозначениях имеем u = {R -\—^Л 0 =Z0.
В вещественной форме напряжение будет
» и = t/ sin (<u/ -(— ср),
*) Комплексное полное сопротивление цепи иногда называют импедансом цепи.
3*
36
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
(ГЛ. I
где
= /1 Z | =
tg" р = — l/RCio.
Замечание. Вычисления в обоих предыдущих примерах имели одно
несущественное осложнение — сдвиги фаз. Удобно, если это возможно, выби-
выбирать начало отсчета времени так, чтобы исходная величина имела нулевую
фазу. Например, если задан ток /, то следует выбрать начало так, чтобы
а = 0. Тогда
g=I и Р=9-
Заметим также, что совершенно не обязательно анализ задач, подобных
рассмотренным выше, производить в вещественной форме.
Комплексное полное сопротивление Z содержит все интересующие нас
данные, так как \Z\ есть коэффициент пропорциональности между ампли-
амплитудами тока и напряжения, a argZ равен разности фаз между ними.
Понятие комплексного полного сопротивления позволяет сохранить обыч-
обычный закон Ома для комплексных токов и разности потенциалов:
1.2.6. Комплексное полное соиротивление при последовательном и
параллельном соединении. Рассмотрим цепь, состоящую, из соединенных
последовательно самоиндукций, емкостей и сопротивлений (рис. 1.12).
Такую цепь всегда можно сгруппировать в виде отдельных участ-
участков, подобных рассмотренным в п. 1.2.5. Если по ней течет ком-
комплексный ток g, то разность комплексных потенциалов на концах
всей цепи представляет собой сумму разностей комплексных по-
потенциалов на концах каждого участка цепи:
Рис. 1.12.
Рис. 1.13.
Следовательно, комплексное полное сопро-
сопротивление всей цепи представляет собой сумму
комплексных полных сопротивлений отдель-
отдельных участков цепи. А комплексная разность
потенциалов равна произведению этого со-
сопротивления на комплексный ток.
В случае же если дано несколько цепей,
соединенных параллельно (рис. 1.13), то
Ц — ?. j с/ j — Z*2cJ 2 — • • * л с/ л"
Полный ток g представляет собой сумму парциальных токов gv g2<
Следовательно,
1,1,
-у -= \- у
у ¦
Значит, правила для комплексных токов здесь такие же, как и для постоян-
постоянных токов.
л-я
ЦЕПИ В СИНУСОИДАЛЬНОМ РЕЖИМЕ
37
1.2.7. Законы Кирхгофа. Рассмотрим некоторую цепь и узел О, в кото-
который стекаются р комплексных токов gv д2 др (рис. 1.14). Геоме-
Геометрическая сумма токов 1\-\-12-\- • • • -\-1р равна нулю, или, что то же самое,
р
сумма комплексных токов 2 <?п~®-
Если мы будем перемещаться по контуру (рис. 1.15), встречая по пути р
цепей с комплексными полными сопротивлениями Zv Z2 Zp, то будет
Рис. 1.14.
Рис. 1.15.
равна нулю геометрическая сумма встреченных разностей потенциалов
Ul-j-U2-\- ... -\-Up или, что то же самое, будет равна нулю сумма раз-
разностей комплексных потенциалов:
2
п=1
Замечание. Если наряду с комплексными полными сопротивле-
сопротивлениями Zj Zp в цепи содержатся также источники комплексной электродви-
электродвижущей силы $п той же частоты, что и питание основной сети, то сформу-
сформулированное выше правило получает такой вид:
л=1
Выведенные формулы позволяют свести вычисление комплексного пол-
полного сопротивления сложной цепи к вычислению комплексных полных сопро-
сопротивлений отдельных участков этой цепи.
В окончательном виде комплексное полное сопротивление Z(yio) можно
представить как
ZC/ш) =-/?(») +/А».
где R (со) — активное сопротивление, а X (ш) — реактивное сопротивление
цепи. Разность фаз между напряжением и током ср = arg Z (у'ш), а отношение
амплитуд напряжения и тока равно |Z(yo))|.
В конкретной физической задаче комплексное полное сопротивление
определяется через решение линейного дифференциального уравнения с веще-
вещественными коэффициентами. Следовательно, функция Z зависит только от
вещественных коэффициентов уравнения и от у'ш. Это означает, что мнимость
38 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
в Z входит только через уш. Поэтому при переходе к комплексному сопря-
сопряженному значению имеем
[Z (/и)]* = Z ([/«,]*) = ^ (— ».
Поэтому из формулы для Z(yV) получим
С другой стороны, если в выражении для Z(y<fl) заменить о> на —о>,
то
Z (— уш) = R (— ш) + /А" (— ш).
Откуда
/?(—о))=/?(ш) — четная функция со,
X (— ш) = — А" (ш) — нечетная функция со.
Величину, обратную Z(yo)), можно записать в таком виде:
Это — комплексная полная проводимость цепи, а О(ш) и 5 (со) — соответ-
соответственно активная и реактивная про-
A
" ^ ВОДИМОСТИ.
\г
Пример. Требуется рассчи-
рассчитать комплексное полное сопротив-
сопротивление цепи (рис. 1.16) между зажи-
зажимами А и В.
t ! Здесь налицо два связанных
"• между собой контура. Первый со-
Рис. 1.16. держит конденсатор с емкостью Г,
комплексное полное сопротивление
которого Zx равно —J—. Второй контур состоит из сопротивления R, само-
самоиндукции L и емкости С, подключенных последовательно. Комплексное пол-
полное сопротивление этого контура
Искомое комплексное полное сопротивление Z= 7 '. %- , т. е.
¦*-! "Т- ^2
i 1 '
т'
откуда
ср = arctg -j arctg^
/ (.\
С, l_j\U
О)
1.2.8. Обобщение понятия комплексного полного сопротивления.
Рассмотрим электрическую цепь самого общего вида, состоящую из п от-
отдельных контуров. Остановимся на контурах I и т.
1.2] „
ЦЕПИ В СИНУСОИДАЛЬНОМ РЕЖИМЕ
39
Пусть Llv Ru, Cn — самоиндукция, сопротивление и емкость, включен-
включенные последовательно в контур I; Lmm, Rmm и Стт — те же величины для
контура т.
Обозначим через Llm = LmV Rlm = Rml, Ctm = Cml самоиндукцию, сопро-
сопротивление и емкость связи между двумя контурами I и т. Для объяснения
смысла этих величин рассмотрим цепь на рис. 1.17„ состоящую из двух
Рис. 1.17.
(
связанных контуров I и т. В этом примере мы имеем при выбранном для
токов положительном направлении
JL
L
Cu
ml
lm
Вернемся к изучению цепи наиболее общего вида. Эта цепь описывается
следующей системой дифференциальных уравнений:
1
где ех, ev
еп обозначают электродвижущие силы, приложенные к рас-
рассматриваемым контурам. I-
Приложим к контуру / электродвижущую силу el = Ele'a". Электродви-
Электродвижущие силы, приложенные ко всем другим контурам цепи, будем считать
равными нулю.
Если положить
40 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
то система приобретает такой вид
[ГЛ. I
Обозначая через ?)(/ш) определитель системы, а через Mlm(jw) алгебраи-
алгебраическое дополнение элемента zlmUw)' получаем
а — М"п (-ft") F
" т D (уш) '*
Если положим
то окончательно получим El = ZlmfJm или Ete ' = Zlmgmeia>t. Величина
Zlm (у'ш) называется эквивалентным полным сопротивлением цепи / по отноше-
отношению к цепи т. Это — отношение комплексного напряжения, приложенного
к цепи /, к комплексному току, текущему по цепи т.
Величина, обратная эквивалентному полному сопротивлению, иногда на-
называется коэффициентом изоморфного отклика цепи т по отношению к цепи /.
Мы определили, таким образом, комплексное полное сопротивление, которое
позволяет связать синусоидальный ток, текущий по одному контуру, с сину-
синусоидальным возбуждением, возникающим в другом контуре, связанном с пер-
первым. На практике можно вычислить эквивалентное полное сопротивление,
выписав систему канонических интегро-дифференциальных уравнений рассмат-
рассматриваемой цепи и заменяя в этой
системе знак дифференцирова-
дифференцирования -тг на /ш, а знак интегри-
интегрирования на -rj-. После этого
остается решить систему по-
полученных таким способом алге-
алгебраических уравнений.
Пример. Рассмотрим два
связанных между собой кон-
контура, изображенных на рис. 1.18. Приложим к левому контуру электро-
электродвижущую силу Е= e'mt. Дифференциальные уравнения системы прини-
принимают вид:
Соответствующая алгебраическая система будет
/,-4-УшМ/2=1,
Определитель ее
D (у'.)
(>?2 + R2 -hjJc;) к + JvMli = 0.
о2М2.
1.2] ЦЕПИ В СИНУСОИДАЛЬНОМ РЕЖИМЕ 41
Алгебраические дополнения
Мп (/«о) = JwL2 +R, + j±-,
AI12 (y<n) = — JioM,
откуда
—ju>M
Zlt (» ~ D (» — D
1.2.9. Комплексный вектор. Рассмотрим вектор а, синусоидально за-
зависящий от времени. Его проекции на три оси прямоугольных координат
равны
ах = Ах cos (Ы + <р х), ау = Ау cos (W + сру), аг = Аг cos (Ы -f- срг).
Амплитуды Л^, Ау, Аг и фазы ср^> <ру> «рг не зависят от времени, а только
от координат х, у, z.
Проекции ах, ау, аг вектора а являются синусоидальными скалярными
величинами — вещественными частями комплексных чисел
i X у Z
Комплексные числа
можно рассматривать как координаты комплексного вектора Л. отнесенного
к комплексному пространству:).
Комплексный вектор Л*, сопряженный с вектором Л, имеет следующие
проекции на оси координат:
Для векторов, имеющих синусоидальную зависимость от времени, ком-
комплексный вектор играет роль, аналогичную той, которую играют комплекс-
комплексные токи и напряжения для токов и напряжений, синусоидально зависящих
от времени.
Вещественная часть вектора Ае1Ы — это вектор а, а мнимая его часть—
вектор а', отстоящий по фазе на -5- от а:
Если разделить вещественные и мнимые части комплексного вектора Л*
то его можно представить в виде
Очевидно,
а =
') Здесь идет речь о комплексном пространстве, существенно отличающемся
от комплексной плоскости, о которой говорилось в начале этой главы. В данном
случае комплексные числа откладываются по трем осям координат. Подробнее по-
понятие о комплексном пространстве развивается в п. 4.1.29 и последующих.
42 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
Вектор а вращается в плоскости, определенной двумя вещественными
векторами At и А2, с угловой скоростью со. Конец вектора а описывает
эллипс, причем А1 и А2 — два его сопряженных полудиаметра. Векторы Ах и А;
соответственно представляют собой положения, занимаемые вектором а
в начальный момент времени и в момент t = — Г/4 (Г — 2тг/ю).
Преимущество использования комплексных векторов при расчетах
с синусоидальными векторами заключается в том, что время t выпадает из
вычислений, так же как это имело место с комплексными токами и напря-
напряжениями. Точно так же комплексные векторы удобно использовать при
подстановке в линейные уравнения.
Возьмем для примера уравнение Максвелла:
Синусоидальным векторам Я и ? соответствуют комплексные векторы §? и
При этом уравнение Максвелла получит вид
Если ввести комплексную диэлектрическую постоянную
/о
71= ? — ,
' со
то
rot =к: = уи>т)8.
Следовательно, использование комплексных величин упрощает расчеты
с векторами, имеющими синусоидальную зависимость от времени, анало-
аналогично тому как оно упрощает расчеты с токами и напряжениями, синусои-
синусоидально зависящими от времени.
Основные определения и векторные операции (скалярное и векторное
умножение, операции grad, div, ...) легко обобщаются на комплексные
векторы.
13. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Если Р(х, у) и Q(x, у)— функции вещественных переменных х и у,
то комплексная величина
Р(х, y)-\-JQ(x. у)
получит одно или несколько строго определенных значений для каждой
пары величин х, у. Данное выражение рассматривается как функция ком-
комплексного переменного z== x-\-jy и записывается в виде f(z). Отметим,
что эта запись условна. В общем случае она не означает, что функция /
зависит от х и у только в комбинации x-\-Jy. Например, про выражение
x-\-2jy говорят, что оно является функцией переменной z.
1.3.1. Непрерывность. Функция f(z) непрерывна при z=a, если
всякому положительному сколь угодно малому числу е соответствует по-
положительное число •») такое, что неравенство \z — а \ < tj имеет следствием
1.3.2. Однозначные функции. Функция однозначна, если каждому зна-
значению независимой переменной соответствует единственное значение функции.
Например, функция u = zllm неоднозначна. Действительно, положим
z = re'f, и = ре^ . Тогда
1.3] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 43
Если принять k=0, 1, 2 т—1, то для одного значения z
получится т значений и.
1.3.3. Аналитическая функция. Производная однозначной функции
(или одного из ее значений, если функция многозначна) определяется как
предел
Если такой предел существует и не зависит от того, каким образом Дг
стремится к нулю, то говорят, что функция f (z) аналитическая.
Изучим подробнее условие независимости стремления Дг к нулю
(рис. 1.19). Пусть
f(z) — P(x, y)-\-jQ(x, у).
Дадим z приращение Дг; тогда функция /
получит приращение Д/. Можно написать
А/ __ AP + JAQ
Аг ~~ Ax + JAy '
Заменяя ДР и AQ их дифференциалами и пе-
переходя к пределу, получим
р„с11
dz ' dx + jdy
Для независимости этого предела от способа стремления Дг к нулю,
т. е. от ориентировки малого отрезка dz = dx-\-Jdy, нужно, чтобы это от-
отношение не зависело от ¦—-. Последнее обстоятельство имеет место, если
коэффициенты при dx и dy в числителе пропорциональны соответствующим
коэффициентам в знаменателе, т. е.
^._i_;^. дР | ; д<2
дх^-'дх __ ду "|"у ^у
Отсюда вытекают условия, которые называются условиями Коши — Римана:
дР^__^О_ дР _ dQ
дх ~ ду И ду ~ дх '
Эти условия необходимы для аналитичности функции. Они будут до-
достаточными, если дополнительно потребовать непрерывность частных про-
производных функций Р и Q *).
Дифференцируя полученные два уравнения и приравнивая смешанные
производные, имеем
дхг ^ ду" — и' дх2 ^ ду2 ~ и-
Следовательно, вещественная и мнимая части аналитической функции удо-
удовлетворяют уравнению Лапласа. Отметим, что последние условия недоста-
недостаточны для аналитичности функции, так как не всякая пара решений уравне-
уравнения Лапласа удовлетворяет условиям Коши — Римана.
*) Подробнее см. [1], стр. 72—75.
44 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
Существует удобный критерий для проверки аналитичности функции.
Функция комплексной переменной аналитична, если она, являясь по форме
функцией двух независимых переменных х и у, фактически зависит только
от их комбинации x-\-jy, т. е. является функцией одной независимой пе-
переменной z. Легко убедиться, что это требование эквивалентно выполни-
выполнимости условий Коши — Римана. В самом деле, если в выражении
. У)
заменим х на z — Jy и полученную функцию переменных z и у частным
образом продифференцируем по у, то находим
дх ду ду \дх ду ' ду}'
т. е.
ду '1~ дх '1~ J \ ду дх)'
Если функция аналитическая, то это выражение тождественно равно
нулю. Таким образом, полученная ранее функция переменных z и у не .за-
.зависит от у, т. е. является функцией одного z. Обратное очевидно.
Отсюда следует, что дифференцируемая функция <p(t) вещественной
переменной t, рассматриваемая как функция ср(л:-|-уу), —аналитическая.
Например, x-\-2jy — не аналитическая функция, х2—у2-\-2jxy = z2 —
аналитическая.
, 1.3.4. Голоморфная функция. Аналитическая функция может быть как
однозначной, так и многозначной. Однозначная аналитическая функция на-
называется голоморфной *).
1.3.5. Криволинейный интеграл от функции комплексной переменной.
Пусть f (z) — функция комплексной переменной z, С — непрерывная кривая,
a z0 и z — аффиксы концов этой кривой. Разделим кривую на произвольное
число частей с помощью промежуточных
у ^ - г 4 точек zv z2 zn_x, zn= z (рис. 1.20).
Пусть рт — точка, находящаяся ме-
между zm_1 и zm. Отрезок, началом кото-
которого является zm_v а концом zm, обо-
обозначим через &zm.
Рассмотрим сумму
5„= 2/(/»«)**«.
т=1
О х Устремим п к бесконечности при условии.
Рис. 1.20. что наибольшее | Дгт | стремится к нулю.
Если при этом сумма Sn имеет предел,
не зависящий от выбора промежуточных точек, то этот предел называется
криволинейным интегралом функции / (z) вдоль кривой С. Он обозначается так:
/¦
f(z)dz.
с
Величина этого интеграла зависит не только от f(z), но и от формы
кривой С. i
*) Часто голоморфную функцию определяют как функцию, разлагающуюся в
ряд Тейлора. Отметим, что оба эти определения эквивалентны (см., например, [1],
стр. 200—201).
1.3]
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
45
Предположим, что длина кривой С конечна и равна s и что на этой
кривой модуль / (г) не превосходит постоянной М. Тогда справедлива оценка
В самом деле,
но
ff(z)dz
ff(z)d
я
lim У |A*m|.
m=l
dz
что и доказывает оценку.
Если разложить f(z) и dz на их вещественную и мнимую части
/ B) = Р (х, у) Н- /Q (х. у). <** = d* -+¦ У dy.
то получим
ff(z)dz=
f(Pdy-\-Qdx).
E)
Как указано выше, интеграл! определенный таким образом, зависит не только
от положения концов кривой С, но и, вообще говоря, от формы этой кривой.
1.3.6. Теорема Коши. Пусть функция f (z) голоморфна внутри некото-
некоторой области. Тогда криволинейный интеграл от этой функции по любому
замкнутому контуру, расположенному внутри области, равен нулю
(рис. 1.21, аI).
Итак, требуется доказать, что Г / (z) dz = 0.
с
Применим формулу E) к замкнутому контуру С, ограничивающему
область S. Вещественные интегралы, стоящие в правой части этой фор-
формулы, преобразуем по формуле Грина *):
^y F)
Для голоморфной функции / (z) выполняются условия Коши — Римана,
т. е. оба выражения F) и G) равны нулю. Таким образом, теорема Коши
доказана **).
') Это условие достаточно, но не необходимо. Действительно, существуют
функции, не голоморфные во всех точках области и такие, что рассматриваемый
криволинейный интеграл равен нулю. Примером может служить функция (г — а)~а
при целых п > 1.
*) Эта формула является частным случаем теоремы Стокса (п. 3.3.9).
**) Отметим, что при использовании формулы Грина существенно предположе-
предположение о непрерывности частных производных функций Р и Q. Это предположение для
справедливости теоремы Коши является излишним (см. [1], стр. 148—155).'
46
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. Г
Замечание. Доказанная теорема справедлива не только для простых
контуров типа, изображенного на рис. 1.21, а. Она верна также в случае.
имеются дырки, окружен-
окруженВ этом случае под конту-
контуС
Рис. 1.21.
когда внутри области, ограниченной контуром Со
ные контурами С,, С2 и т. д. (см. рис. 1.21,6).
ром С в теореме Коши надо понимать сложный контур, состоящий из на-
наружной кривой Со, проходимой в положительном направлении (против часо-
часовой стрелки), и всех внутренних кривых Сх, С2 и т. д., проходимых
в отрицательном направлении (по часовой стрелке).
В случае голоморфности f(z) интеграл E) зависит только от положе-
положения начала и конца кривой С и не зависит от формы пути интегрирования.
Для доказательства достаточно применить теорему Коши к замкнутому кон-
контуру С~\-С, где С — любая кривая, соединяющая концы кривой С.
Замечание. Вещественный криволинейный интеграл не зависит от
формы пути, если он берется от функции, представляющей полный диффе-
дифференциал. Условия Коши — Римана совпадают с условиями полного диф-
дифференциала для E).
1.3.7. Формула Коши. Пусть f(z)—функция, голоморфная в замкнутой
области, ограниченной контуром С, a z0— внутренняя точка области
(рис. 1.22).
Коши
0р
Докажем, что имеет место формула
~ 2nj J г —
aZ'
(8)
С
где
контур С обходится в положительном на-
направлении. Действительно, функция голо-
Z —— 2q
морфна во всех точках внутри контура, кроме
точки z = z0. Исключим из рассматриваемой об-
области небольшой круг с центром z0 и радиусом р.
Окружность его обозначим через т (см. рис. 1.22).
голоморфна внутри кольцевой области, ограниченной С и f.
Если перемещаться по С и по j в положительном направлении, то по тео-
теореме Коши
Рис. 1.22.
Функция
Z Zn
Интеграл слева не зависит от р.
также не зависит от р.
Имеем
Следовательно, интеграл в правой части
f
J
z — z0
z — z0
1.3] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 47
Первый интеграл справа вычисляем непосредственно:
Г f(za)dz Г dz f JftJ'M
Так как f(z) непрерывна, то можно выбрать р настолько малым, что
в круге внутри f \f(z)— /(.zo)|<e, где г — сколь угодно малое положи-
положительное число. Для этого значения р
так как путь интегрирования равен 2тгр. Это и доказывает формулу Коши (8).
Продифференцировав (8) п раз, получаем
1.3.8. Ряд Тейлора. Пусть f(z)— функция, голоморфная внутри
круга С с центром в a; z0 — точка внутри этого круга. По формуле Коши
имеем
Запишем
z — z0 z — а — (za — a) z — а . z0 — а
z — а
Тогда
_/4g)___ /(г) 1 __ /(г) Г. zo — a . /zo — a\a T
г — г0 г — а , _ г0 — а г — а[ ~~*~ z — а ~*~ " ' '\ г — а ) . ' '" ' J '
z — а
так как \z0 — a\<.\z — а\. Умножим обе части этого выражения на -^у
и проинтегрируем вдоль контура С. Это возможно, так как рассматриваемый
ряд сходится равномерно относительно точек окружности. Имеем
го — а)" -т-..., A0)
с
где
с
Согласно формуле (9)
Таким образом, получаем разложение в ряд Тейлора, распространенное
на функции комплексной переменной:
=± /(«)+ ...+-^=
48 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
При а=0 (центр круга в начале координат) получим
Это ряд Маклорена.
1.3.9. Особые точки. Точка, в окрестности которой аналитическая
функция разложима в ряд Тейлора, называется обыкновенной точкой. Вся-
Всякая необыкновенная точка называется особой точкой.
Полюса — это изолированные особые точки, вблизи которых f(z)
остается однозначной и которые являются обыкновенными точками для ут-х-
Существенно особые точки — это изолированные особые точки, в окре-
окрестности которых / (z) остается рднозначной, но которые являются особыми
и для функции . ..
Критические точки или точки разветвления — это особые точки, вблизи
которых функция / (z) не остается однозначной.
Примеры особых точек. Функция —j- имеет полюс 2-го порядка
в начале координат.
Функция а , . имеет простые полюса z = -\-j и z = — /(ср. стр. 49).
Функция sin — имеет существенно особую точку в начале координат.
Функция gVz-e имеет в точке z=a существенно особую точку.
Функция z1/n имеет точку разветвления в начале координат.
1.3.10. Разложение в ряд Лорана. Дана функция / (z), имеющая полюс
или существенно особую точку z=a. Если выделить эту точку маленькой
окружностью f радиуса р, то функция / (z) стано-
становится голоморфной внутри круговой области, заклю-
заключенной между -у и окружностью Г с радиусом R,
также имеющей центром а (рис. 1.23). Применим
формулу Коши к контуру -f —)— Г. Обозначив через z0
точку внутри кругового кольца, получаем
Г
--±- f /{г) dz ' f Пг) dz
— 2nj J z~z0 dz -ЩЛ z-za dZ-
Рис. 1.23. ^ба криволинейных интеграла берутся в положи-
положительном направлении.
Согласно соотношению A0) предыдущего пункта первый интеграл
имеет вид
г
где в силу формулы A1)
л —L С /<г> dz
г
Равенство A2) в данном случае использовать нельзя, так как f (z) голо-
голоморфна не во всех точках внутри Г.
1Л] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 49
Второй интеграл вычисляем аналогично первому. Имеем
_J _J
г0 — г г,, — а — (г — а) г0 — а . г — д
Так как \z0— a|>|z — а\, то полученное выражение можно разло-
разложить в ряд и проинтегрировать:
где
A-» = ijJ' f^){z-af-ldz. A3)
г
Таким образом, получаем разложение в ряд Лорана
4- Zn H- + +
Коэффициенты Ап и Л_п определяются формулами A1) и A3).
Так как р можно выбрать сколь угодно малым, то точка z0 может
быть сколь угодно близка к точке а. Следовательно, разложение в ряд
Лорана представляет собой разложение в ряд функции f(z) вблизи полюса
или существенно особой точки. Использование разложения в ряд Лорана
позволяет более точно классифицировать полюсы и существенно особые точки.
Если в. ряде Лорана имеется только конечное число коэффициентов
типа А_п, то особая точка является полюсом для рассматриваемой функции.
Обозначим через п наивысшую степень ———, входящую в разложение Ло-
Лорана. Число п есть порядок полюса; если п= 1, то полюс называется простым.
Если разложение Лорана содержит бесконечное число членов с отрица-
отрицательными степенями z — а, то точка а является существенно особой точкой.
Примеры. Дана функция
1
Найдем ее разложение в ряд Лорана вблизи полюса г = 0. Имеем
1
2B-1) ~
Вблизи полюса z=l имеем
l 1 1
_1J_B_1K 4- ....]:
г(г— 1) ~ г—1 \ + (г —}
Рассмотрим, далее, функцию е11г. Найдем ее разложение в ряд Лорана вблизи
существенно особой тачки z = 0. Непосредственно получаем
11.11. ,11.
... ,.1
4 А. Анго
50 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
Интегрирование по методу вычетов
1.3.11. Теорема о вычетах. Пусть а—полюс функции f(z), а С—кон-
С—контур, окружающий точку а, на котором выбрано положительное направление:
функция / (z) голоморфна во всех точках внутри С, кроме, разумеется,
точки а. Покажем, что в принятых предположениях имеет место формула
J
где Л_1 — коэффициент при в разложении / (z) в ряд-Лорана. Вели-
Величина А_х называется вычетом функции /(z) относительно особой точки о*).
Действительно, если а — полюс порядка т, то
где ср (z) — голоморфная функция внутри контура С. Отсюда получаем
В силу голоморфности ср(г) по теореме Коши I y(z)dz = Q.
с
( Опишем из точки а как из центра окружность Г радиуса R, целиком
лежащую внутри контура С. Применяя теорему Коши к области, ограни-
ограниченной контурами Г и С (на С также выбрано положительное направление),
получим
f
с
с
Положим z—a=Reib, dz = jRe^J dG. Имеем
,/ (z — a)m Rm~l J
Г v 0
2*
-^гг f[cos(m — 1N — ysin(m— lN]rf9 = O (m > 1),
откуда
1.3.12. Вычисление вычетов. Рассмотрим сначала случай простого по-
полиса. Пусть f(z)/g(z) — отношение двух голоморфных функций. Тогда
= (z—a)t(z), Ь(а)Ф0. Имеем
*) Часто используется обозначение yl_, = Res(a) функции /(z).
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
51
Следовательно,
_ f(.a)
l~ 6(e)
Пример. Рассмотрим функцию 2. 2. Имеются два простых полюса:
= -f-/a и г = — ja. Применим предыдущую формулу:
= ^j-, Res (— ja) =
2Ja
Следовательно, сумма вычетов равна
sin a
a,dz = 2,j^±
Здесь С — произвольная кривая, окружающая оба полюса, как показано на
рис. 1.24, а.
Замечание 1. Можно последовательно изменять контур, окружающий
оба полюса до тех пор, пока не останутся маленькие круги с центрами
в полюсах, соединенные между собой беско-
бесконечно узким разрезом, берега которого про-
проходятся в противоположных направлениях.
При этой деформации интеграл сохранит свое
значение (теорема Коши). Значения интегра-
интегралов вдоль противоположных берегов разреза
в силу однозначности функции взаимно ком-
компенсируют друг друга. Поэтому в качестве
контура интегрирования можно брать сово-
совокупность отдельных замкнутых контуров,
каждый из которых содержит один полюс
функции (см. рис. 1.24,6, а также рис. 8.15).
Замечание 2. Указанный в начале
этого пункта способ вычисления вычета
в простом полюсе удобно нескблько видо-
видоизменить. Очевидно,
-Ja
Res(fl)=lim
Рис. 1.24.
0
Для раскрытия этой неопределенности типа -^ применим правило Лопиталж
Следовательно,
/(г)+ (г-а)/'(*) _ /(Д)
IlllI / - » — . «
Па)
Замечание 3. Пусть в,, а2 ап — простые полюса для +J^1. Тогда
VRes=
52 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. Г
Рассмотрим функцию вида f^V , g @) ф 0. Легко убедиться, что
в этом случае
/ («„)
' @) ^ JU amg' (em) •
т = \
Пример 1. Найти сумму вычетов — относительно полюсов, на-
находящихся на вещественнной оси между —со и 0.
Так как sinmz = 0 при z = ——, то имеем
т ,
СО ОО
у п„ - V Г е* 1 —IV г пТ"« —
л=о г=~7й" «=°
т
т
\\ + е т)
Приведем способ вычисления вычетов относительно кратных полюсов.
Пример 2. Вычислить /¦—; , где С — малая окружность вокруг
,i Z Sin TftZ
с
начала координат.
Разложим ег и sin mz. Для малых z имеем
m2z2 , m'z4 \ mz2
mz
Таким образом, в данном примере z = 0 — полюс второго порядка.
., . ' 1 1
Коэффициент при — равен —, следовательно,
/¦
г sin mz m
С
1.3.13. Вычисление вычетов относительно кратных полюсов с по-
поью производных. Пусть * i —функция,
порядка п. Разлагая ее в ряд Лорана, получаем
мощью производных. Пусть * i —функция, имеющая в точке а полюс
~^
Умножим обе части равенства на (z — а)п:
(z-af ?Щ = [Ло+ Л,(г-с)Ч- • • • ](z-a)" + А_,(г~а)"^ + • • • 4-Л_„.
Дифференцируем это тождество п — 1 раз и полагаем затем z = а. Имеем
Отсюда получаем искомый коэффициент Л_,
1.31 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 53
гег
гег
Пример. Найти вычет _ ,3 относительно z =
1-й способ.
т. е. '
2-й способ. Переместим начало координат в точку а, положив z = u-\-a:
Вычет равен коэффициенту при —, т. е. eall-|--^-)- Следовательно,
-н—т- / ге лъ dz = еа A -\- -§•) для любого контура С, окружающего точ-
с
ку 2 = а.
1.3.14. Лемма Жордана. Часто бывает полезно рассматривать открытые
контуры интегрирования, точнее, контуры, которые в действительности замы-
замыкаются бесконечной окружностью комплексной плоскости. В большинстве
случаев речь идет о прямолинейном контуре, замыкающемся полуокружностью
с центром в начале координат, радиус которой растет до бесконечности.
Если интеграл по этой полуокружности стремится к нулю, то контур инте-
интегрирования сводится к бесконечной прямой. Следующее положение, известное
как лемма Жордана, позволяет указать важный частный случай равенства
нулю интеграла по полуокружности бесконечного радиуса.
Пусть Ф(г) — функция, голоморфная в верхней полуплоскости
(О < arg z < it), за исключением конечного числа полюсов, и стремящаяся
к нулю при | z | —у оо равномерно относительно arg z. Тогда при t > О
lim f е*(гФ (z) dz = О,
I?-* CO Л
где контур С" представляет собой полуокружность с центром О и радиусом R,
замыкающую верхнюю полуплоскость.
Действительно, произведем замену переменной
Очевидно,
\gjtRcosb-t Я sin 6 I __ g-tRsIni^
В силу равномерного стремления Ф(г) к нулю, для достаточно больших R
имеет место неравенство | Ф (z) | < е, где е — положительное, произвольно
малое. Используя, далее, неравенство^-?-^-—, справедливое при 0<; argz<;
<у, получаем
I/'
it it/2
Г Г
< sR / e-'*slned8 ^ 2e/? / g-
6 о
что и доказывает лемму.
54
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
Если t отрицательно, то в условии леммы следует только заменить
верхнюю полуплоскость на нижнюю (— тс < arg z < 0) и соответственно
верхнюю полуокружность на нижнюю.
Рассмотрим теперь
lim -rrU f etz<b{z)dz.
Этот предел равен нулю при тех же условиях, что и предыдущий, если
для t положительного и отрицательного речь идет соответственно о левой
полуплоскости (-?- < arg2 < -^-j и о правой полуплоскости! — -^- < argz < ^j
относительно мнимой оси. Контур С обозначает соответственно полуокруж-
полуокружность с центром О и радиусом R справа или слева от мнимой оси.
Замечание. При вычислении интеграла по бесконечной оси с по-
помощью теоремы о вычетах следует помнить, что контур, образованный осью
и бесконечной полуокружностью, должен обходиться в положительном на-
направлении.
1.3.15. Применение леммы Жордана к единичной функции. Рассмотрим
функцию вещественной переменной t, определенную с помощью интеграла
в комплексной плоскости:
1 Г е1Ы
/Ю=-к7 /V*»- . (И)
Контур С представляет собой ось х с выемкой в форме полуокружности
со стороны отрицательных у (рис. 1.25).
Обозначим через f часть контура С, ограниченную двумя точками А
и В, равноотстоящими от начала координат, и через Г полуокружность
с центром О, проходящую через А а В н находящуюся под действительной
Г
В а:
Рис. 1.25.
Рис. 1.26.
осью.-Контур "Г +Г не содержит особых точек подынтегральной функции.
Следовательно, соответствующий криволинейный интеграл равен нулю.
Если предположить, что t отрицательно, то по лемме Жордана интеграл
по контуру Г стремится к нулю, когда радиус окружности бесконечно
возрастает. Следовательно, предел интеграла по контуру f (т. е. интеграл
по контуру С) равен нулю:
= 0 при
Положим теперь, что t положительно. Рассмотрим полуокружность Г',
проходящую через А и В к расположенную со стороны положительных у
(рис. 1.26). В этом случае
1 Г eJa>t __
1.3] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 55
так как вычет относительно точки 0 равен единице. По лемме Жордана
интеграл по контуру Г' стремится к нулю, если радиус окружности беско-
бесконечно растет. В пределе имеем
¦ъ—г / do)=l при t > 0.
С
Функция f (t), определенная равен-
равенством A4), равна нулю при /<0 и единице ————
при ?>0 (рис. 1.27). Она представляет " *
собой единичную функцию или единич- Рис. 1.27.
ный импульс и обозначается через -f)(t).
Приведем другое выражение для f)(t). Повторяя предыдущее рассужде-
рассуждение, получим
1_ Г
2nJ J
с 1 0 для t > 0.
Следовательно, мы можем написать
eJu" ... Г е-'* ^ 1 /*sln«rfJ.. f —Va *"•"
4-V2
1 1 Г Г eja>t . Г е-1ы . 1
2 2л/ U » ./ <о
Lc ; с J
Так как 3 "* является четной функцией, не имеющей особенности при
<0
<в = 0, то справедливо равенство
i. it j
/ sin u>t
О
1.3.16. Интегрирование при наличии точки разветвления. Рассмотрим
простой пример и проиллюстрируем на нем, какие следует принять предо-
предосторожности при интегрировании по контуру, внутри которого имеются точки
разветвления. А именно вычислим интеграл / Y^zdz. Контур С — окруж-
с
ность с центром А и радиусом R.
Если точка z перемещается по этой окружности, то можно положить
z — Re№. Рассмотрим точку zo=Re^«. В этой точке функция Yz имеет
два значения:
Возьмем первое значение этого корня, а саму точку z0 в качестве отправной.
Имеем
А Ё 3 ¦ 36a
__ / щге> 2 ^e = — 4 dT" 2
Величина интеграла зависит не только от значения, выбранного для z'l', но
также от отправной точки интегрирования и радиуса окружности.
Таким образом, при вычислении интеграла по контуру, внутри которого
¦Находятся точки разветвления функции, требуется предварительно фиксиро-
фиксировать определенную ветвь функции и отправную точку интегрирования.
56
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
Разрез
Рис. 1.28.
На практике вычисление производится следующим образом. Точку раз-
разветвления А соединяют с контуром С дугой, не имеющей двойных точек,
которую z при движении вдоль С не может пересечь. Таким образом осу-
осуществляется разрез. Точка z может перемещаться по замкнутому контуру Г,
состоящему из контура С, малой окруж-
окружности, заключающей точку разветвления, и
обоих берегов бесконечно узкого разреза
(эти берега обходятся в противоположных
направлениях). Отметим, что контур, со-
состоящий из обоих берегов разреза и ма-
малой окружности, иногда называют шнуром
(рис. 1.28).
Наличие разреза обязывает функцию
f (z) снова принимать прежнее значение,
когда z возвращается в исходную точку,
какой бы при этом ни был описан путь
внутри Г или на нем. Действительно, при
таком движении аргумент точки z может изменяться только на величину,
меньшую 2тс. Внутри контура Г функция / (z) становится голоморфной (кроме
как в конечном числе полюсов), и поэтому можно применить теорему о вы-
вычетах. Интеграл, взятый по контуру С, начиная от заданной начальной точки
(искомый интеграл), сложенный с интегралами по разрезу и по малой
окружности, будет равен сумме вычетов относительно полюсов, находящих-
находящихся'внутри Г.
Следует заметить, что существует глубокое различие между разрезом,
описанным в п. 1.3.12 (замечание 1) и рассмотренным в данном пункте.
В последнем случае интегралы по различным берегам разреза не компен-
компенсируют друг друга, так как значения, которые принимает функция f(z)
в двух бесконечно близких точках на разных берегах разреза, существенно
отличаются друг от друга. Рассмотрим, например, функцию zl*. Если бы
не было разреза, то любую точку R, 60 можно было бы
представить как точку/?, 60—|— 2тс,—для этого требуется У c+joo
лишь осуществить один поворот около точки разветвле-
разветвления (в положительном направлении). И тогда функция )/~г
вместо начального значения У Re2 приняла бы значе-
А_ О
ние У R e 2 eJ*. На верхнем и нижнем берегах разреза "~~~~
в точках окружности С функция г1!' принимает соответ-
соответственно значения jR'l* и —jR'h.
1.3.17. Контур Бромвича. Контур Бромвича пред-
представляет собой прямую, соединяющую точку с — у со
с точкой с-)-у со; оставляющую слева от себя все осо- c-Joo
бые точки рассматриваемой функции (рис. 1.29). Вели-
Величина с, равная расстоянию от контура до оси у, всегда Рис. 1.29.
положительна.
В задачах, относящихся к движению устойчивых механизмов или дисси-
пативным электрическим цепям, особенности функций в большинстве случаев
находятся либо слева от мнимой оси, либо на ней самой. В первом случае
мнимую ось можно считать контуром Бромвича. В задачах о распростране-
распространении электрических, или акустических волн некоторые из особых точек
являются точками разветвления, в других задачах — это, как правило, по-
полюса.
1.3]
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
57
1.3.18. Интеграл Бромвича — Вагнера. Бромвич и Вагнер определили
форму интеграла, встречающегося при решении технических задач с помощью
операционного исчисления (см. теорему Фурье — Меллина, п. 8.3.22). Этот
интеграл имеет следующий вид:
c+joo
2nj J
ег'Ф (z) dz,
c—joo
где Ф(г) — функция, все особенности которой лежат слева от контура
Бромвича.
1.3.19. Эквивалентный контур. Если функция Ф(г) удовлетворяет
условиям леммы Жордана, то интеграл по бесконечной полуокружности, рас-
расположенной слева от мнимой оси, равен нулю при t > 0.
Рассмотрим типичные эквивалентные контуры для особых точек разного
типа.
\. Все особенности являются полюсами. В этом случае контур,
эквивалентный контуру Бромвича, состоит из произвольной замкнутой кривой,
не имеющей двойных точек, внутри которой расположены все полюса. Зна-
Значение интеграла по контуру Бромвича равно сумме вычетов относительно
этих полюсов. ;
' 2. Функция имеет точки разветвления. В качестве контура, экви-
эквивалентного контуру Бромвича, можно взять малую окружность, заключаю-
заключающую точку разветвления, соединенную разрезом с бесконечной полуокруж-
полуокружностью, лежащей слева от мнимой оси.
gZt
Примерыэквивалентных контуров. Для функции -j- контур,
эквивалентный контуру Бромвича, — окружность с центром в начале коор-
координат (рис. 1.30).
е"
Для функции —у- контур, эквивалент-
эквивалентный контуру Бромвича, состоит из малой
окружности с центром в начале координат,
c+Jco •
a?
c-Jco
yc-ja>
Рис. 1.3G.
Рис. 1.31.
являющемся точкой разветвления, соединенной с бесконечным полукругом,
как это показано на рис. 1.31.
Для функции '¦¦ , имеющей две точки разветвления в z=±J,
можно начертить множество эквивалентных контуров. Несколько таких кон-
контуров показано на рис. 1,32.
58
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
Пример 1. Вычислить
?+/оо
г=— Г
2л/ ./
с -/со
гп+\
dz (га > 0, целое).
Особенность Ф(г) представляет собой кратный полюс в начале координат.
Так как условия Жордана выполняются, то интеграл будет равен вычету
функции относительно точки z = 0.
~1 C+Joo
I i=J+\x\e-J*
\
i. I c-joo
О
-j
c+Joo
с-/со
Рис. 1.32.
Разложим ezt в ряд. Вычет относительно особой точки 2 = 0 равен
коэффициенту при — в произведении
гЧ2
т. е.
I
11.
c + joo
Пример 2. Вычислить / = -g—г /
е2'dz
C-jco
г {I— e~hz)
Условия Жордана
выполнены. Особенностями функции являются, во-первых, двойной полюс
в начале координат, во-вторых, бесконечное число простых полюсов
z =—jt-п, когда п принимает все целые значения от —со до -(-со, кроме
значения z — О. Следовательно, интеграл / равен сумме вычетов относи-
относительно полюсов подынтегральной функции.
Вычислим вычет относительно точки z = 0. Для этого разложим в ряд
числитель и знаменатель подынтегральной функции:
2! "^ 3! •
При малых z это выражение можно записать в виде
hz2
_ , . 1 t , 1
Вычет равен коэффициенту при —, т. е. -т--\--п>
Z ft &t
1.3] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 59
Вычислим сумму вычетов относительно z = -—¦ п (п Ф 0). Имеем *)
-l-oo ¦ -t-oo
S' Г g 1 — J_ V
2*n/
: • « 2nn/<
Сгруппируем попарно в последней формуле члены, содержащие -^-т е h
с членами, содержащими -~j e h . Имеем
Если учесть вычет относительно начала координат, то находим
' 1 , ' " sin -
я=1
Пример 3. Вычислить интеграл
/== 1 г +***
,/ г2 + оJ '
—jfoo
Особенностями функции Ф(z) = 2_i_ г являются два полюса z== ~tj'm
я точка разветвления 2=0.
Рассмотрим разрез вдоль отрицательной части действительной оси и
обозначим соответствующий ему шнур через Г (см. рис. 1.31). Так как
¦функция Ф (z) удовлетворяет условиям леммы Жордана, то интеграл по
контуру Бромвича равен интегралу по шнуру Г (направление обхода указано
стрелками) плюс сумма вычетов относительно полюсов z= ±у"ш:
7i Ь Ь
где fi — окружность с центром О и бесконечно малым радиусом, f2 — путь,
проходимый по верхнему берегу разреза, ^з — путь, проходимый по нижнему
берегу разреза.
1. Вычислим вычеты относительно особых точек. Вычет относительно
«г = -|-./ш равен
Вычет относительно z = ^-Ju> равен
*) 2' означает, что суммирование идет для п Ф 0,
60 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. 1
Сумма вычетов дает
2. Для точек окружности радиуса р с центром О имеем z = ре'8.
Так как |.г|<С1ш> то
2*
3. На верхнем берегу разреза
z=\x\e".
f=~i Г
ъ
На нижнем берегу разреза
Следовательно,
со
Г Г ' Г p~xt г'/г
.1,1 г. j х2 + m
Т» Тз 0
и, наконец,
=—~r sin [ш^ ) / —^-—rdx.
Характерные примеры интегрирования на комплексной плоскости даны
в пп. 8.3.23 и 8.4.18.
1.3.20. Теорема о числе полюсов и числе нулей. Пусть функция / (z)
голоморфна внутри замкнутого контура С, за исключением конечного
числа полюсов, непрерывна и не обращается в нуль на С. Обозначим
через N и Р соответственно количество нулей и полюсов f(z) внутри кон-
контура С, причем каждый нуль и каждый полюс считается столько раз, какова
его кратность. Тогда произведение разности N — Я на 2тс/ равно интегралу
от логарифмической производной f(z) по контуру С при обходе его в положи-
положительном направлении.
Действительно, пусть а — нуль порядка а. В окрестности точки а имеем
f(z) = (z — а)Ц(г), ^(а)фО;
далее,
Г (?) = « | Ф'(*)
/(г) — z — a ^ ф(г) *
Если Сх — малый контур, окружающий точку а, то
J с.
t.3] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ §1
Точно так же, если b — полюс порядка р. то в окрестности точки b
имеем
•Функция ср (г) голоморфна в окрестности Ь. Поэтому вблизи b можно написать
_
Если С2 — малый контур, окружающий Ь, то
2*J J /(*) ~ Р<
с
Из доказанного следует, что для функции f (z), имеющей в области,
ограниченной контуром С, нули а1 ап порядков аа <х„ и полюса
bv .... 6Л порядков рр ...' р„, справедливо соотношение
т. е.
[?}§-dz==2icJ(N — P).
v J \z)
Теорема доказана.
Рассмотрим преобразование
Если точка z описывает контур С в плоскости г, то точка Z описывает
контур Г в плоскости Z. Имеем
11п
Этот интеграл равен числу Т оборотов, которые описывает кривая Г вокруг
начала координат. По доказанному,
Применение теоремы о вычетах
к вычислению некоторых определенных интегралов
2 ч
1.3.21. Интегралы вида J/(cos6, sin6)flf6 (/ — рациональная функ-
о
ция cos 9 и sin 9, конечная внутри промежутка интегрирования). Положим
eJb=z. Имеем
Интеграл получает вид Г tp (z) dz, где С — окружность единичного радиуса
с
с центром в начале координат. Этот интеграл равен 2тс/2, если через S
62
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
обозначить сумму вычетов относительно полюсов, заключенных внутри
окружности С.
Пример. Вычислить
'~J (a
-f 6cos6)J
(а > Ъ > 0).
Имеем
¦if
zdz
Единственный полюс, заключенный внутри круга радиуса 1, z = ¦
кратность его равна двум. Найдем вычет относительно этого полюса:
dz
Следовательно,
1.3.22. Интегралы вида jf(x)dx. Пусть f(x) — функция веществен-
— со
ной переменной х, удовлетворяющая следующим условиям:
а) /(z) голоморфна во всей полуплоскости, расположенной над веще-
вещественной осью, исключая конечное число полюсов;
б) f(z) не имеет полюсов на вещественной оси;
в) если \z\ стремится к бесконечности, то zf(z) стремится к нулю-
равномерно относительно аргумента г, изменяющегося от 0 до it.
оо 0
г) Г f(x)dx, С f(x)dx сходятся.
0 —сю
со
Легко показать, что Г f(x)dx pa-
—со
вен 2тс/?, где S представляет собой сумму-
вычетов относительно полюсов функции
f(z), расположенных над вещественной
осью.
Для доказательства достаточно рас-
рассмотреть (рис. 1.33) контур интегриро-
интегрирования, состоящий из части вещественной оси между — р и р и полуокруж-
полуокружности Г с центром О и радиусом р, причем р настолько велико, что все
полюса А, В, С, ... функции f(z) находятся внутри Г. Если устремлять р
к бесконечности, то часть интеграла, соответствующая Г, стремится к нулю
в силу допущения в). Следовательно,
Г
Рис. 1.33.
J
1.3] . ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 63-
При м.е р. Вычислить
+ ОО
/= J {X* +1K •
— oo
Положим '/(z)— ( 2_|_]\з • В z = j рассматриваемая функция имеет
единственный полюс над вещественной осью (его кратность равна трем)-
Вычет ? относительно этого полюса равен
у _ 1
41 — 2!
Следовательно,
г 3
/=-3-1С.
1.3.23. Интегралы вида //(•*) cos mxdx, С f(x) sin mxdx. Пусть-
¦ о • о
функция f (z) удовлетворяет условиям предыдущего параграфа, причем усло-
условие в) заменено менее обременительным: если \г\ стремится к бесконеч-
бесконечности, то -f(z) стремится к нулю равномерно относительно аргумента Z
(О <; arg z <; it).' Рассмотрим контур на рис. 1.33. Согласно лемме Жордана
имеем (т > 0)
+СО
J
—oo
где S обозначает сумму вычетов относительно полюсов функции f(z)e^mz,
находящихся в верхней полуплоскости. Отделяя вещественные и мнимые
части, можем написать
+оо _ +оо
J /(*)cosm*ur.* = — 2icI(S), J f(x)smmxdx=;2TzR(Z).
—oo' —oo
Из формулы
+ OO +00
j.f(x) emJx dx=j [f (x) emjx + / (— x) e-mix\ dx = 2%jS
— oo 0
вьГгекает, что если / (x) — четная функция, то
. +оо
Г / (х) cos mx dx = icy'S,
о
а если / (х) — нечетная функция, то
+ 00
Г / (х) sin mxdx s=i:S.
Пример. Вычислить
+ 00
у_ /' jcsinax ,.. „ ^ л t^ лч
о
64
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. Т
z sin аг
Функция г г- имеет над вещественной осью только один полюс
z = у/г. Вычет относительно этого полюса равен
Следовательно,
-аЬ
Замечание. Пусть /(г) имеет простые полюса на вещественной оси,
иначе говоря, условие б) п. 1.3.22 не выполняется. Пусть функция f(x)
такова, что ее интеграл в интервале, где f(x) получает бесконечные зна-
значения, сохраняет смысл. Тогда при вычислении интегралов, рассмотренных
в п. 1.3.22—23, следует к сумме вычетов S относительно полюсов над веще-
вещественной осью прибавить величину -=- о, где о означает сумму вычетов отно-
относительно полюсов на самой вещественной оси.
оо
1.3.24. Интегралы вида j xaf(x)dx. Полагаем, что f(x) — рациональ-
о
ная функция х, причем za+lf(z) стремится к нулю, когда \z\ стремится
к бесконечности и к нулю, и f(z) не
имеет полюсов на положительной части
вещественной оси. Если мы осуществим
разрез на этом отрезке вещественной оси,
то функция zaf(z) будет однозначной на
всем контуре, не пересекающем разрез
(в частности, на контуре рис. 1.34). Пусть
р — радиус малого круга, а /? — радиус
большого круга такие, что в полученном
кольце содержатся все полюса f(z). В силу
предположений относительно f(z) инте-
интеграл, взятый по большой окружности,
стремится к нулю, если R бесконечно воз-
возрастает, а интеграл, взятый по малой
окружности, стремится к нулю, вместе с р.
Следовательно, интеграл, взятый по АВ
и DC, равен сумме вычетов S относи-
относительно всех полюсов функции z"f(z), так как вычет относительно z = 0
равен нулю. В самом деле, za+1f(z) стремится к нулю вместе с \г\, и по-
поэтому коэффициент при \/z разложения функции zaf(z) должен быть рав-
равным нулю.
На АВ z = х, на CD z = xe2*K Таким образом,
Рис. 134.
lim Г [x*f (х) — x*e2*J'f (*)] dx = 2icy S.
p->0 J
Р
Наконец,
1.3] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Пример. Вычислить
оо
х" dx
65
/ ——¦
1
(— 1 < а < 3).
Функция / (z) == /1 г ;\г имеет два полюса второго порядка z =
= x J;
Следовательно.
4/
ж
2я/ те 1 — а
1.3.25. Применение теоремы о вычетах
рядов. Рассмотрим ряд
4 cos ая/2
к суммированию некоторых
2
/(«)•
Положим, что функция f(z) голоморфна на всей плоскости z за
исключением простых полюсов av .... ак, вычеты относительно которых
равны bv .... bk. Контур Сп заключает в себе все полюса f(z) и точки
О, ± 1, ..., ± п вещественной оси.
Числа аР .... аь, разумеется, не целые, так &
как иначе ряд не имел бы смысла.
Рассмотрим функцию ср (z) = « ctg «zf (z), ко- fK
торая внутри контура Сп имеет в качестве полюсов
полюса / (z) с вычетами izb^ ctg nav кЬ2 ctg ica2,...
.... Tzbk ctg иоЛ и точки 0, ± 1, ..., ± п с вы-
вычетами /@). /(±1), f(±n). Имеем
J cp (z) dz = 2icy {/ (—
— п + 1) -+- • • •
fa-
Если контур Сп при бесконечно возрастаю-
Рис. 1.35.
п
щем п отодвигается в бесконечность, причем кри-
воЛинейный интеграл функции tp(z) по С„ стремится к нулю, то можно
вычислить сумму рассматриваемого ряда. Эти условия соблюдаются, если,
например, в качестве контура Сп использовать квадрат, представленный на
рис. 1.35, и считать, что при бесконечном возрастании \z\ произведение zf(z)
равномерно стремится к нулю.
Выберем п достаточно большим, чтобы ге/(ге)<е; ctgitz ограничен
на Сп, пусть М — его верхняя граница. Тогда справедлива оценка
I
1/2
Следовательно, контур С„ отвечает поставленным условиям и
+ 0О
2 /(«) =
5 А. Анго
66
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. 1
со
Пример 1. Вычислить V —г , gr. Функция г * ^ стремится к нулю,
я=о
когда \z\ бесконечно возрастает. Функция 22,аг не имеет полюсов при
значениях г, равных целому числу, и голоморфна на всей плоскости, за
исключением z = ± ja. Следовательно,
Значит,
я=о
Замечание. Если вместо ctg-кг использовать
условиях можно суммировать ряды вида
2 (—1 )"/(»)¦
л= —оо
Пример 2.
2а2
+
2a sh па '
= | cth
то при тех же
п=о
1.4. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
1.4.1. Определение. Дана аналитическая функция Z = /(z). Если
точка т с аффиксом z = x -f-y'y описывает кривую т в плоскости г, то
точка Ж с аффиксом Z— X-\-JY описывает кривую Г в плоскости Z
Л О
Рис. 1.35.
(рис. 1.36). Кривая Г называется вбразом кривой у, точки Мит назы-
называются соответствующими. Основное свойство этого преобразования состоит
в том, что оно сохраняет углы и, следовательно, вид бесконечно малых
элементов. Поэтому, оно называется конформным (conforme — подобный).
Действительно, пусть т, т! — две соседние точки на кривой •{, а М
и М' — две соответствующие точки на кривой Г. Если обозначить через
1.4]
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
67
<р и Ф углы между mm' и Ох и между ММ' и ОХ, то
/ф AZ ЦФ-т ММ'
= mm'eJ
mm
В этих формулах mm' и ММ' означают длины соответствующих отрезков.
Если т' стремится к т, то М' будет стремиться к М. Можно показать*),
что при этом отношение длин
ММ'
mm'
стремится к \f'(z)\, а угбл поворота
(ф — <р)—к аргументу производной функции f(z). Таким образом,
dZ = eJiref4z)\f(z)\dz.
Это означает, что при конформном отображении элемент dz удлиняется
в \f'(z)\ раз и поворачивается на угол arg/'(z). Такое же преобразование
испытывает любой бесконечно малый элемент комплексной плоскости.
Если Yi и ^2 — Две кривые в плоскости z, проходящие через точку z
и образующие друг с другом некоторый угол, то такой же угол по величине
и по знаку образуют между собой образы этих кривых Г, и Г2.
Проведенные рассуждения перестают быть верными в точках, где про-
производная равна нулю или где ее модуль бесконечен. Действительно, рас-
рассмотрим, например, функции 2" = йг"(«> 1) и Z = — (см. случаи а) и г)
п. 1.4.2). Две/ прямые, проходящие через начало координат и образующие
между собой угол ср, преобразуются в плоскости Z в две прямые, образующие
между собой угол гаер (случай а) и — ср (случай д). В первом примере модуль
производной в начале координат равен нулю, во втором — бесконечности.
Отделяя в равенстве Z = f{z) вещественные и мнимые части, получим
Z=A- + /K = /(jc-b/y) = *(*. y) + JY(x, у).
Если точка z описывает кривые Х(х, у) = const или Y (х, у) = const
в плоскости z, то точка Z описывает прямые, параллельные осям OY, ОХ
(рис. 1.37). Следовательно, в силу сохранения углов кривые X (х, у) = const
4-
г 1
о
Рис. 1.37.
X
и Y(x, у) = const ортогональны. X (х, у) и Y(x, у) — вещественная и мнимая
части f(z) — называются сопряженными функциями.
Часто бывает проще рассматривать не Z = /(z), а обратное преобра-
преобразование z = F (Z). Приравнивая вещественную и мнимую части, получаем
х = х(Х,
У).
*) Подробнее см. [1], стр. 95—99.
5*
68 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
В этом случае кривые, которые преобразуются в прямые, параллельные
осям OX, OY, задаются в параметрической форме: Y фиксировано, X
меняется или X фиксировано, Y меняется.
Исключая из обоих равенств последовательно X и Y, получим соот-
соответственно
g(x, у, Y) = 0, h(x, у, Х) = 0
— уравнения семейств кривых, преобразующихся в параллели осям ОХ и OY,
причем Y л X играют здесь роль параметров, фиксирующих конкретную
кривую.
Из аналитичности f(z) следует (см. п. 1.3.3), что
дхг ~+~ дуг ~ °' дхг "+" дуг ~ U-
Таким образом, функции Х(х, у) и Y(x, у) — гармонические, причем
семейства X (х, у) = const и Y (х, у) — const ортогональны в плоскости г.
Эти семейства ортогональных гармонических функций преобразуются
в семейства прямых, параллельных осям координат плоскости Z.
Отметим, что задача отыскания функции Z — f(z), отображающей
кривую y=cp(jt) плоскости z в прямую, параллельную какой-нибудь оси
плоскости Z, в общем случае не решается. Поэтому обычно приходится
ограничиваться заранее известными конформными отображениями, используя
ортогональные семейства двухмерных гармонических функций (например,
отображения при помощи комбинаций элементарных функций). Эта задача
отыскания ортогональных семейств двухмерных гармонических функций
возникает при рассмотрении различных плоских полей.
Примеры: 1) отыскание силовых и эквипотенциальных*) линий элек-
электростатического или магнитного плоского полей; 2) отыскание линий тепло-
теплового потока и изотерм нагретого тела; 3) отыскание линий равного потен-
потенциала скорости и линий тока плоского установившегося движения жидкости;
4) отыскание линий электрического тока и эквипотенциальных линий в про-
проводнике и т. д.
Рассмотрим подробнее случай электростатики. Пусть даны два прово-
проводящих тела, помещенных в идеальный диэлектрик. Их потенциалы соответ-
соответственно Vi и V2. Основная задача в этом случае состоит в определении
конфигурации возникшего электростатического поля и величины заряда на
каждом из проводников. Известно, что эта задача сводится к отысканию
решения уравнения Лапласа, т. е. к отысканию гармонической функции,
которая принимает заданные величины Vj и V2 на поверхности проводников.
Если проводники представляют собой два цилиндра с параллельными осями,
продольные размеры которых велики по сравнению с поперечными, то,
изучая распределение поля в поперечном сечении средней части проводников,
можно пренебречь краевыми эффектами. Таким образом, мы приходим
к плоской задаче.
Если мы найдем конформное отображение, приводящее поперечные
сечения цилиндров, изображенные в плоскости г, в соответствие с парал-
параллелями X = VV X— V2, изображенными в плоскости Z, иначе говоря,
если нам удастся задать оба этих поперечных сечения в качестве предста-
представителей некоторого семейства гармонических функций, то прямые К = const
и X = const являются соответственно образами электростатических си-
силовых и эквипотенциальных линий, расположенных в плоскости г. В частности.
*) Линии равного потенциала или линии уровня.
1.4] КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 69
к эквипотенциальным линиям относятся и поперечные сечения данных
цилиндров, значения потенциалов на которых как раз равны Vl и V2-
И обратно: если задано какое-либо конформное отображение Z = f (г),
то с помощью функций Х(х, у), Y (х, у) можно решить соответствующую
электростатическую задачу. Мы уже отмечали, что 'вычисления в этом слу-
случае гораздо проще, чем в предыдущем. Выражения X (х, у) = const и
У(х, у) = const представляют собой уравнения эквипотенциальных и сило-
силовых линий.
Остается определить плотность заряда о и величину заряда q провод-
проводника 1). Пусть Е — вектор электрического поля; он является градиентом
скалярного потенциала. Если принять функцию Х(х, у) за потенциальною
функцию, то (п. 3.2.16)
Е- — grad Х(х, у).
Обозначим через е диэлектрическую проницаемость среды. Известно,
что поверхностная плотность электрического заряда о равна произведению е
на модуль вектора Е в рассматриваемой точке поверхности проводника.
Так как этот вектор нормален к поверхности, то
дХ
дп
или в силу ортогональности кривых X и Y будет
дУ
ds
Рассмотрим элемент нашей цилиндрической поверхности, имеющий
высоту единица и стягиваемый дугой длиной ds. Заряд, несомый этим
элементом, равен
Заряд участка поверхности единичной высоты, опирающегося на дугу АВ
поперечного сечения цилиндра, равен
в
Яав = *>$ dY = z(YB-YA).
А
Заряд единицы длины одного из цилиндров (единичный заряд), который
мы определим, если совершим полный поворот вокруг соответствующего
поперечного сечения, равен с точностью до коэффициента е приращению
функции Y. Если цилиндр заряжен, эта функция, очевидно, неоднозначна.
В нижеследующих примерах обе функции X и Y взаимно заменяемы
и одна из них, в зависимости от условий, играет роль функции потенциала.
Пример. Рассмотрим преобразование Z = arch-j, т. е. z = dchZ.
Имеем
х = dch X cos Y, y = ^s
Если считать X постоянным, то в плоскости z получаем кривую
„2
| У 1 Л
"I d* sh2 X ~~
|
d* ch2 X "I d* sh2 X
') Мы используем рационализированную систему единиц. В нерационализиро-
ваиной системе достаточно.заменить в нижестоящих формулах о на 4та и q на 4идг.
По поводу рациоиализироваиной системы см. сноску на стр. 147.
70
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
Если считать Y постоянным, то в плоскости z получаем кривую
d* cos2 Y d* sin2 Y
— 1=0.
Эти кривые образуют ортогональные семейства эллипсов и софокусных ги-
гипербол с фокусами F' и F, отстоящими друг от друга на расстоянии 2d.
Рассмотрим эллипсы и гиперболы соответственно как эквипотенциальные
и силовые линии некоторого плоского электростатического поля. В про-
пространстве эквипотенциальные поверхности представляют собой эллиптические
цилиндры. Поперечное сечение их изображено на рис. 1.38.
Ничего не меняя в распределении поля, можно материализовать одну из
этих поверхностей в виде проводника определенного потенциала. Таким
образом, мы определим силовые ли-
линии и поперечное сечение эквипотен-
эквипотенциальных поверхностей для наэлек-
наэлектризованного эллиптического цилиндра.
В частном случае X =0 наш цилиндр
вырождается в плоскую ленту шири-
шириной Id. Указанные выше формулы по-
позволяют и для этого проводника опре-
определить силовые линии и. эквипотен-
эквипотенциальные поверхности.
Определим емкость единицы длины
передающего кабеля, у которого вну-
внутренний и внешний проводники пред-
представляют собой соответственно ленту
и эллиптический цилиндр. Если через
а и b обозначить полуоси эллипса, то
а2 — Ь2 = й2. При обходе вокруг одного из проводников функция Y изме-
изменяется на 2тс. Следовательно, искомая единичная емкость С будет равна1)
Рис. 1.38.
— i у у i '
где Х^ и -Y2 — соответствующие потенциалы ленты и цилиндра. Поскольку
Л\ = 0, a chA'2 = -^-, для С получим
С = -
a In I
Рассмотрим теперь случай, когда гиперболы — эквипотенциальные линии,
а эллипсы — силовые линии. На рис. 1.38 изображены эти линии, вызванные
в данном случае электрическим полем, возникающим между двумя поверх-
поверхностями гиперболического цилиндра, наэлектризованными до определенного
потенциала. Рассмотрим, в частности, вырожденный гиперболический цилиндр,
соответствующий тем значениям Y, которые обращают в нуль sin К. Он сво-
сводится к двум полуплоскостям, разделенным разрезом шириной в 2d. Огра-
Ограничим эти полуплоскости прямыми, перпендикулярными F'F, с абсциссами х
и —х, и прямыми, параллельными оси F'F, на расстоянии / от нее
(рис. 1.39). Конечно,'чтобы не возмущать поле, остальная часть каждой по-
полуплоскости должна обладать тем же потенциалом, но по контурам ABCD
') В нерационализированной системе единиц следует правую часть формулы для
емкости С разделить на 4я.
1.41
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
71
и А'В'CD' отделяться от обоих прямоугольников очень узким промежутком
(охранным кольцом). Найдем емкость конденсатора, образованного указан-
указанными прямоугольниками.
Л' Л 'С
6' . А' А
Рис. 1.39.
Заряд одного прямоугольника равен
Q = 2/е [X]xxZxd = 2/s ("arch ^X,
Потенциал одной полуплоскости соответствует Н = 0, потенциал другой —
У = и. Следовательно, искомая емкость равна1)
Г— 2h In (Х Л-л/~Х*
Вернемся к рис. 1.38 и примем Y=-^. Гиперболический цилиндр све-
сведется в этом случае к плоскости, перпендикулярной прямой F'F. Следова-
Следовательно, рис. 1.38 представляет также силовые линии и линии уровня си-
системы, образованной плоскостью и перпендикулярной ей полуплоскостью,
разделенными разрезом шириной в d.
1.4.2. Несколько примеров конформных отображений. Конформные
отображения определяются функцией z = / (Z), где
z = х + /у = р (cos ср + j sin tp),
Z = X + JY = P (cos Ф + У sfn Ф).
Будем изображать кривые Х(х, у) = const и Y(x, у) = const в плоскости z.
Эти кривые соответствуют прямым X = const и К = const в плоскости Z.
а) Преобразование Z = kzn (кип вещественны). Имеем X-\-jY =
= Ре>ф = kpne"Jf, откуда
X = ftp" cos «cp,
при
tp = arctg -
Полная плоскость Z преобразуется в угол — плоскости z. Будем трак-
трактовать Y как потенциальную функцию. Нулевой потенциал получается при
двух значениях ср = О и <р = —. Рассмотрим наэлектризованный двугранный
') См. сноску на стр. 70.
72
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
(ГЛ. I
угол 6. В нем существует электрическое поле, силовые и эквипотенциальные
лииии которого задаются в полярных координатах равенствами:
тс
X = kp9 cos (у 9). X = const;
= йре sin(y
= const.
Плотность электрического заряда в точке на грани, отстоящей от вер-
вершины двугранного угла на расстоянии р, будет равна
б) Преобразование Z — kz2. Это частный случай примера а) при п = 2.
Полная плоскость Z преобразуется в верхнюю полуплоскость плоскости z.
Нетрудно найти силовые и эквипотенциальные линии наэлектризованного
прямого двугранного угла. Эти линии задаются в декартовых координатах
соотношениями
X == k (х2 — у2), Y == Ikxy
и представляют собой два семейства равносторонних ортогональных гипер-
гипербол. Они изображены на рис. 1.40 для X = —1, Н=1 (й = 1). Плотность
электрического заряда в данном случае равна
о = 2&ер.
^Преобразование Z — kz't>. Это тоже
частный случай примера а), здесь п = 72-
У
Рис. 1.41.
Верхняя полуплоскость плоскости Z преобразуется в полную плоскость г.
Кривые, конформные отображения которых параллельны осям ОХ и OY,
легко записываются в прямоугольных координатах плоскости z:
х ~~ ~w* w •
X2 k2v2
4Х* '
Это семейства софокусных парабол с фокусом О. Они изображены на
рис. 1.41 для X—.2, Н=1 (& = 1). Таким способом мы получаем силовые
и эквипотенциальные линии поля, вызванного наэлектризованным параболи-
параболическим цилиндром.
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
73
Рассмотрим параболу семейства, вырождающуюся в прямую Ох: Мы
получаем при этом такое же распределение электрического заряда, как
в случае заряженной полупло- ^
скости. Плотность заряда опре- Л=-— —*«^ У
деляется равенством
г) Преобразование Z = — .
Это отображение осуществляет
аналитическую инверсию, т. е.
сводится к выполнению двух по-
последовательных операций — гео-
геометрической инверсии _относи-
тельно круга радиуса ]f k и сим-
симметрии относительно веществен-
вещественной оси. Легко получить оба
ортогональных семейства, кон-
формные отображения которых
ОХ и OY Эт
рис-
формные отооражении китирыл
параллельны осям ОХ и OY. Это — окружности, касающиеся осей в начале
It
^(=0,7
V 0
-п/2
&
/wJy?^^~
Y=O
f Y=0
Y=O
-л
Рис. 1.43.
координат. На рис. 1.42 они изображены при
мейств имеют вид
, k \2 К*
А2
; = 1. Уравнения этих се-
д) Преобразование Z = ez. Имеем
74
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
(ГЛ. Г
Интересующие нас семейства кривых изображены на рис. 1.43. Любые кривые
каждого из семейств могут быть совмещены путем параллельного переноса:
х = \п X — lncosy,
x = \nY — lncosly—
e) Преобразование Z—k\nz. Имеем
Таким образом, получаем ортогональные семейства полупрямых и окруж-
окружностей с центром в начале координат (рис. 1.44 для k—\). Это отображе-
отображение дает силовые и эквипотенциальные поля, вызванные наэлектризованной
Рис. 1.44.
поверхностью прямого круглого цилиндра, в частности, вокруг наэлектризо-
наэлектризованной прямой, проходящей через точку О перпендикулярно плоскости
рис. 1.44. Та же картина силовых линий и линий уровня возникнет между
двумя концентрическими прямыми цилиндрами с круглыми основаниями, об-
обладающими разными потенциалами. Рассмотрим последний случай.
Пусть X— потенциальная функция, Хх и Х2 — соответствующие по-
потенциалы цилиндров с радиусами /?j и /?2 (R1 > R2). Имеем R1 = ex'>k,
a R2=ex^k. При полном повороте вокруг оси приращение функции Y
равно 2kn. Следовательно, единичный заряд будет равен 2к-кг. Отсюда
емкость С на единицу длины конденсатора, образованного двумя концентри-
концентрическими цилиндрами, равна !)
2b 2
венства
ж) Преобразование Z = k\n
z — d
z — d
. Приравнивая в обеих частях ра-
— ex/kejr/ii модули и аргументы, получаем
V- (а)
d1
~ . о У '
F)
') См. сноску на стр. 70.
1.41
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
75
Это — уравнения двух ортогональных семейств окружностей (рис. 1.45).
Окружности семейства (б) проходят через точки F и F' с абсциссами ±d.
к которым сводятся окружности семейства (а) при X = +оэ. Для одной
(а)
Рис. 1.45.
и той же окружности семейства (б) при переходе от верхней дуги F'MF
к нижней дуге F'M'F значения параметра -г- отличаются друг от друга на и.
Из этого следует, что если уравнение отрезка F'F будет K = tc, то уравне-
уравнение оси абсцисс, из которой вырезан этот отрезок, будет Н = 0. Точно
так же окружностям семейства (а), находящимся справа от оси Оу, соот-
соответствуют отрицательные значения X, находящимся слева—положительные.
Y
заметить, что -г- = ,/, FMF' для верхней дуги окружности (б).
'F' для нижней дуги окружности (б) и -г- = 1п
Легко
К
Пусть X — потенциальная функция. В этом случае предыдущие ра-
равенства дают силовые эквипотенциальные линии поля, вызванного двумя
наэлектризованными поверхностями прямых цилиндров с круглым основа-
основанием, оси которых параллельны друг другу и находятся на расстоянии 2а.
Положим, что радиусы цилиндров' равны R. Вычислим" емкость С на еди-
единицу длины конденсатора, образованного обеими поверхностями. Пусть X —
потенциал левого цилиндра, — X — потенциал правого, разность потенциалов
соответственно равна 2Х. Имеем
d cth -j- = а и у- = /<;
к . л.
значит, X = fearch
R '
При обходе вокруг цилиндра Y изменяется на величину 2)feic. Следова-
Следовательно, единичный заряд q = 2kvel) и
г _q
2Х —
Замечание. Если проводящий цилиндр сводится к прямолинейному
проводу пренебрежимо малого диаметра, то предыдущие равенства дают
') См. сноску на стр. 70.
76
ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
электрическое поле, вызванное двумя параллельными проводами, отстоящими
друг от друга на расстоянии 2d, или проводом, отстоящим на расстоянии d
от параллельной ему бесконечной проводящей плоскости (X = 0).
з) Преобразование z = Z-\-ez. Из этого равенства, придавая посто-
постоянное значение либо X, либо У, получаем семейства кривых х = A'-f-e^cos У,
у = У -\- e*sin У, записанных в па-
параметрической форме. Мы легко
можем определить эквипотен-
эквипотенциальные линии У(х, у) и сило-
силовые линии Х{х, у) электроста-
электростатического поля между двумя
бесконечными полуплоскостями
с потенциалами -\-к и —it
(рис. 1.46) и вблизи их границы.
Замечание. Все конформ-
конформные отображения представляют
кривые X (х, у) = const, и
У(х, у) = const как образы пря-
прямых X = const, У = const. В при-
примерах, рассмотренных выше,
отображения выбирались нами
априори. Затем мы находили соот-
соответствующую им картину сило-
силовых и эквипотенциальных линий.
Однако/как уже отмечалось выше,
Рис. 1.46. чаще приходится решать обратную
задачу: задана кривая у = <р (х);
найти функцию /(г), отображающую эту кривую на ось H = Q. К сожале-
сожалению, эта задача обычно бывает неразрешима, кроме следующих двух основ-
основных случаев.
1. Кривая у = <р(х) может быть выражена в параметрической форме:
x = u(t), y = v(t).
Тогда искомое преобразование имеет вид
где k — вещественная постоянная.
Действительно, приравняем Н = 0, тогда
x = u(kX), 'y-v(kX).
Эти равенства и являются параметрическими уравнениями данной кривой.
Найдем отображение, преобразующее, например,, ось Н = 0 в эллипс
х1 v2
—г + 4г—!• Имеем jc = acos?, y =
преобразование будет
y Как легко заметить, искомое
z = a cos Z + jb sin Z.
2. Кривая у = ср (х) задает замкнутый многоугольник. В этом случае
задача решается отображением Шварца (п. 1.4.4).
1.4.3. Последовательные отображения. Рассмотрим два отображения,
связывающие между собой три точки плоскостей комплексных переменных
Z, V, z:
1.4] : КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 77
Исключив переменную V из этих двух соотношений, получаем зависи-
зависимость
которая устанавливает непосредственное соответствие между точкой пло-
плоскости Z и точкой плоскости z. Следовательно, можно' сложные отображе-
отображения разложить на последовательно применяемые более простые отображения.
Пример 1. Дано отображение V = ф (г), устанавливающее соответствие
между точкой xo-\-jyo=zo и вещественной точкой d = ф(z0), а также между
кривой т и мнимой осью плоскости V. Известно (п. 1.4.2, ж)), что поле; соз-
созданное заряженным проводом, имеющим след в точке d, несущим линейный
заряд q и проходящим на расстоянии d параллельно бесконечной плоскости,
следом которой является мнимая ось плоскости V, описывается преобразо-
преобразованием
¦7 Л1 V — d
И если прямая со следом в точке z0 на плоскости z находится перед заря-
заряженной цилиндрической поверхностью, поперечное сечение которой пред-
представляет собой кривую 7- то линейный заряд q, несомый этой прямой, соз-
создает электростатическое поле, силовые и эквипотенциальные линии которого
могут быть найдены с помощью преобразования
Пример 2. Даны две цилиндрические поверхности, поперечные сече-
сечения которых в плоскости г' представляют собой кривые С и f. Пусть
V = ty(z) — отображение, переводящее кривые С и f соответственно в отри-
отрицательную и положительную части вещественной оси плоскости V. Рассмот-
Рассмотрим отображение Z—klnV.
Положив V = re^, имеем
X = klnr. Y — kB.
Положительная часть вещественной оси плоскости V соответствует значе-
значению Н = 0, т. е. полной вещественной оси плоскости Z. Отрицательная
часть вещественной оси плоскости V соответствует . значению У = kit, т. е.
прямой, параллельной вещественной оси плоскости Z и проходящей от нее
на расстоянии kit.
Следовательно, полное преобразование
отображает кривые С и f на две прямые Н = &тс и Н = 0. Значение К на С
равно feit, значение К на f равно нулю. Таким образом, с помощью найден-
найденного преобразования можно определить конфигурацию силовых и эквипотен-
эквипотенциальных линий электростатического поля, созданного двумя цилиндрами
(поперечные сечения их представляют собой кривые С и f), при разности
потенциалов между ними, равной /гтс.
1.4.4. Отображение Шварца. Рассмотрим функцию (Z — А)*'1, где А —
вещественное число, а а — число, меньшее единицы.
Введем функцию z, удовлетворяющую дифференциальному уравнению
dz Y7 А\а~х
78 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ . (ГЛ. I
Предположим, что точка Z пробегает ось У = 0 плоскости Z (рис. 1.47).
Найдем кривую, которую описывает соответствующая точка плоскости z.
Если точка X расположена левее точки А, то аргумент отрицательного
числа X—А равен тс. Если точка X
правее точки А, то аргумент положи- "^«^^
тельного числа X -¦— А равен нулю. Сле-
Следовательно, аргумент числа (X — А)"~
-QO д +СО
Рис. 1.47. Рис. 1.48.
будет скачкообразно изменяться на —тс(а—1), когда X пробегает прямую
К=0. Точка z при этом опишет две полупрямых, образующих между собой
такой же угол —тс(а—1) в плоскости z, ибо
dz dx + j dy . dy
соответственно внутренний угол между этими прямыми равен тса (рис. 1.48).
Ясно, что точке А в рассматриваемом отображении соответствует точка а.
Рассмотрим теперь замкнутый многоугольник с внутренними углами
icotji icotg. . •., тсад.
Из рассуждений, приведенных выше, вытекает, что с помощью пре-
преобразования
ij = (Z - Л,Г I'1 (Z - А,)"* ... (Z- АпГ'1
осуществляется отображение оси Н = 0 на многоугольник плоскости z
с углами при вершинах, равными тац, тса2, ....,тсая.
Величины Ах, .... Й.л C-^i < ••¦ <С Ап), соответствующие различным
вершинам многоугольника, подлежат определению. В силу замкнутости много-
многоугольника значения а, ап связаны между собой равенством
яа,4- ••• +к<хп — -к(п — 2)
или
Рассмотрим точку X(Y = Q), перемещающуюся по вещественной оси
плоскости Z от —со до Л]. Согласно A6) можно принять, что для этих
Z аргумент величины
(Х - А^-1 (X ~ А2р-' ... (Х-AS*'1
равен нулю. Тогда точка z будет перемещаться по вещественной оси пло-
плоскости z от точки а0, соответствующей Х = — со. Положение точки а0
зависит от постоянной интегрирования уравнения
^ = (Л" — -А,)"'"' (А" — Aj)-*-1 ... (А- — Л,)"».
Пусть точкам Ak(k= 1, . .., п) вещественной оси плоскости Z (рис. 1.49)
соответствуют точки ak плоскости z, являющиеся вершинами рассматри-
рассматриваемого многоугольника, а точка X продолжает перемещаться вдоль веще-
вещественной оси плоскости Z. При переходе точки X через Ах аргумент правой
части выписанного выше дифференциального уравнения изменяется на
1.4] КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 79
— it(aj — 1). Соответственно этому при переходе через ах аргумент z, рав-
равный до этого нулю, также получает приращение —it(aj — 1), т. е. в ах
точка переходит с вещественной оси плоскости z на прямую, образующую
с этой осью внутренний угол toxj (ср. рис. 1.48). Совершенно аналогично
-оо А, Аг Ап
Рис. 1.49.
при переходе точки X через А2 аргумент z получает приращение —тс(а2— 1)
и точка z переходит в а2 на новую прямую, образующую с прежней угол тах2
и т. д.
Следовательно, точка z описывает ломаную линию с углами при вер-
вершинах <Xj, a2, .... a.k, измеряемыми в полуокружностях. Эта ломаная линия
образует замкнутый многоугольник. Действительно, когда точка X пробегает
отрезок от точки Ап до со, точка z описывает прямую, образующую с по-
положительным направлением вещественной оси угол —тс2(ал—1)=2те, т. е.
крайние стороны ломаной линии параллельны вещественной оси. Отметим,
далее, что вершины аг и а„ расположены на вещественной оси плоскости z.
Остается определить числа Ах Ап так, чтобы они действительно
являлись образами вершин заданного многоугольника. Это обстоятельство
составляет главную трудность при практическом использовании отображения
Шварца. Доказывается, что можно произвольно выбрать образы трех вер-
вершин многоугольника (т. е. три числа из Аг, . .., Ап), а остальные числа Ак
определяются единственным образом. Рассмотрим способ их отыскания.
Пусть задан многоугольник с вершинами а,, .... а„. Через вершины а„ и ах
проводим вещественную ось плоскости z. Пусть углы при вершинах много-
многоугольника toxj, .... тсап. Тогда искомое преобразование имеет вид
z
Число ZQ и три числа из Ах Ап выбираются произвольно. Число k
ил — 3 числа из А^ А„ следует выбрать таким образом, чтобы сто-
стороны получаемого многоугольника были равны сторонам данного много-
многоугольника; п — 3 числа А определяются через интегралы! Трудность вычи-
вычислений быстро возрастает вместе с числом сторон. Однако в физике ото-
отображение Шварца очень редко применяется к многоугольникам с числом
сторон, большим 4.
Легко заметить, что преобразование Шварца отображает верхнюю по-
полуплоскость Z на внутренность многоугольника плоскости г, тогда как
нижняя полуплоскость Z соответствует внешности многоугольника плоскости z.
Пример 1. Найти отображение треугольника, расположенного в пло-
плоскости z, на вещественную ось плоскости Z. Если углы треугольника
равны тох, тер, щ, то функция, осуществляющая требуемое отображение,
имеет вид
Z Z
z= f(Z—A)'-1(Z — B)*-\Z—CI-1dZ=[f(Z)dZ. A7)
г, . z0
где
(а—1) + (Р—1) + (Т-1) = —2. A8)
80 S ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ (ГЛ. I
Если Z пробегает вещественную ось от —со до А, то точка z опи-
описывает вещественную ось от точки с абсциссой т, соответствующей X = —со,
до точки С абсциссой а, соответствующей Х=А (рис. 1.50), —это имеет
Плоскость г
-Жос-7)
—^
а
-к (у-7)
Плоскость Z
-со /iff С
Рис. 1.50.
место, если выбрать ту ветвь f (z), определяемую формулой A7), для-ко-
для-которой аргумент / (Z) при — со < X < А равен нулю. Возможность такого
выбора обеспечивается равенством A8).
Имеем
А
f) dX.
При переходе точки X через А соответствующая ей точка плоскости z
переходит с вещественной оси на прямую, составляющую с этой осью
угол —тс (а—1). По новой прямой точка z движется до точки д, которая
"соответствует точке Х = В вещественной оси плоскости Z, причем
b = а + «-./«<— « J f (X) dX.
При переходе точки X через В соответствующая ей точка плоскости z
снова переходит на другую прямую, составляющую с предыдущей угол
— тсф—1). По новой прямой точка z доходит до точки с, которая соот-
соответствует точке X —С вещественной оси плоскости Z, причем
с
Наконец, при переходе X через точку С соответствующая прямая в пло-
плоскости' z поворачивается на угол —тс (?—1), и при Л'->оо точка z стре-
стремится к начальной точке т, оставаясь на этой прямой. Имеем
+ со
я» = с-|-«-¦/«№-»> Г f(X)dX.
В силу соотношения A8) отрезки ст. и та являются продолжением
один другого.
Таким образом, каковы бы ни были числа А, В, С, функция A7) опре-
определяет отображение, которое преобразует треугольник, подобный данному, в ве-
вещественную ось Н = 0. Для перехода к заданному треугольнику достаточно
1.4] КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 81
в интеграле A7) ввести постоянный множитель, учитывающий отношение
сходственных сторон треугольника.
Многоугольник, рассматриваемый в отображении Шварца, всегда может
быть построен по заданным условиям; он может иметь вершины в бесконечности.
Пример 2. Рассмотрим две параллельные прямые, одна из которых
разорвана (рис. 1.51). Эту фигуру можно считать многоугольником. Вер-
Вершина а находится в бесконечности, сторона ab сливается со стороной be.
а Ъ
с К^У""
с +п
Рис. 1.51.
Вершины с и d находятся в бесконечности. Сторона de сливается со сто-
стороной ef, и многоугольник замыкается прямой на бесконечности. Величины
углов it(aj—1), it(a2—1), ... обозначены на рисунке.
Следовательно, функция, определяющая преобразование, имеет вид
z
г— С (Z-B)(Z-E) 7
.1 (Z-Q(Z-D) a '
Из четырех вещественных чисел В, С, D, Е три можно выбрать произвольно.
Учитывая, что В < С < D < ?, можно положить В = — 1,? = Ц-1. С= — d,
D = d(Q<d<l). Тогда
z
, , d2 — I , Z — d
Определим постоянную так, чтобы начало координат плоскости z отобра-
отображалось в начало координат плоскости Z. Имеем
const = J-к —25— •
т. е. искомое отображение принимает вид
Z-d \-d? .
. Отделяя вещественные и мнимые части, найдем соотношение
d*~ I 2dY , 1 — d* .
2d~ агс ё X2 -f Y" — d* "" 2d~yiC>
из него непосредственно получаются параметрические уравнения кривых,
отображениями которых служат прямые X = const и К = const, параллель-
параллельные осям координат плоскости Z. Покажем, что при перемещении точки Z
по оси К = 0 точка z описывает рассматриваемую фигуру в плоскости z.
Если X находится вне интервала (—d, d), то
_ v , d2 — 1 , X — d
6 А. Анго
82
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
[ГЛ. I
Если X находится внутри интервала (—d, d), то под знаком логарифма
стоит отрицательное число, аргумент которого равен -\- тс, и соответственно
находим
„ , d2 — I , d — X
1— d2
Id
Используя полученные формулы, заполним таблицу, описывающую изме-
изменения на плоскости z при пробегании X вдоль вещественной оси плоскости Z
(рис. 1.52):
X
dx
dX
X
У
Положение
— со
— со
а
—1 — d
+ 0 -
/ b \j— со
1— d2
¦ 2d *
— со
b с
ab be
Ч-
/ .
0
ы
+d
+ ОО
4-
d
со
de
+1
- 0
l—d2
2d
e
-boo
-f
-fco
Для полного совпадения полученной и заданной фигур достаточно,
чтобы отношение
расстояние _6е
расстояние между прямыми
для обеих фигур было бы равным. Из этого равенства определяется число d.
Только что описанное отображение позволяет решать задачи плоского
поля, в которых фигурируют две параллельные плоскости, причем одна из
в с
Л Е
-оо
-7
Рис. 1.52.
F
—I
+ао
них рассечена бесконечной трещиной. Найдем, например, силовые и экви-
эквипотенциальные линии электростатического поля, возбужденного бесконечной
плоскостью и двумя полуплоскостями, имеющими потенциал V.
Эквипотенциальные и силовые линии являются соответственно отобра-
отображениями прямых К = const и X = const. Отметим, что такие же линии воз-
возникают в электростатическом поле, созданном бесконечной плоскостью,
пересекающей плоскость Z по прямой К==0.
Рассмотрим ту же задачу для случая, когда на бесконечной плоскости
и на двух полуплоскостях созданы разные потенциалы. Эта задача сведется
к задаче для полосы шириной в Id в плоскости Z, окаймленной двумя
бесконечными полуплоскостями, причем полоса и полуплоскости обладают
разными потенциалами. Легко заметить, что решение задачи дается с помощью
отображения ж) п. 1.4.2. Действительно, при рассмотрении плоскости ком-
комплексной переменной С видно, что
" 1.4] КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ¦ 83
Повторяя предыдущие рассуждения, нетрудно убедиться в том, что при
перемещении точки вдоль вещественной оси от —оо до Х== — d, затем
от Х = — d до точки X=-\-d и отЛ'=-|-йдо-г-оо точка С переме-
перемещается в плоскости С по вещественной оси от 0 до -|-оо, затем по прямой,
параллельной вещественной оси, от —оо до -)-оо и „по вещественной оси
от — оо до 0. Следовательно, задача сводится к изучению электростати-
электростатического поля между двумя бесконечными плоскостями с разными потенциалами.
Нам известны силовые и эквипотенциальные линии этого поля, которые
являются прямыми, параллельными соответственно мнимой и вещественной
осям плоскости. Отображения этих линий представляют собой в плоскости Z
семейство ортогональных окружностей, показанных на рис. 1.45. Поэтому
задача, поставленная вначале, может быть решена применением отображения
Шварца к указанному семейству окружностей. Это 'отображение в конечном
счете даст эквипотенциальные и силовые линии в плоскости z. Таким об-
образом, задача решается с помощью двух последовательных отображений.
1.4.5. Различные применения конформных отображений. До сих пор
мы применяли конформные отображения только к задачам электростатики.
Рассмотрим применения конформных отображений для расчета других пло-
плоских полей, о которых упоминалось в п. 1.4.1.
а) Циркуляция токов в плоском однородном проводнике. Еслн
заряженные частицы, создающие электрический ток (электроны в твердых
телах, ионы в электролитах), испытывают значительное трение, пропорцио-
пропорциональное скорости, так что влияние инерции частиц пренебрежимо мало,
и если, кроме того, можно пренебречь явлениями, обязанными своим воз-
возникновением пространственному заряду, то, используя результаты предыдущих
параграфов, можно решать задачи о распределении тока в среде с сопротивле-
сопротивлением, в которой помещены электроды заданной формы с известными потен-
потенциалами. Эти электроды могут быть впаяны, если речь идет о твердом теле,
или погружены в электролитическую ванну, если речь идет о жидкой среде.
Итак, при переходе к рассматриваемой задаче достаточно заменить
в предыдущем тексте слова «силовые линии» на «линии тока» и «поверхност-
«поверхностная плотность заряда» на «плотность тока на электродах». В частности,
сопротивление R, препятствующее прохождению тока между двумя электро-
электродами, непосредственно связывается^ с емкостью С, образованной этими же
самыми электродами, погруженными в изолирующую среду.
Если р — удельное сопротивление проводящей среды, а е — диэлектри-
диэлектрическая проницаемость изолирующей среды, то')
CR = ер.
Мы, например, видели, что емкость на единицу длины конденсатора, образо-
образованного двумя одинаковыми цилиндрами с радиусом г, оси которых парал-
параллельны и находятся на расстоянии 2а, равна
С = —
Сопротивление на единицу длины между теми же двумя цилиндрам»
(предполагается, что они идеально проводящи), погруженными в среду
с удельным сопротивлением р, равно
') В нерационализироваиной системе единиц CR= ер/4я.
6*
84 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ [ГЛ. I
б) Распространение тепла. Все сказанное выше переносится и на
этот случай. Разности потенциалов здесь соответствует разность температур.
Линии одинаковой температуры, или изотермы, заменяют эквипотенциальные
линии, линии теплового тока — силовые линии, количество тепла в секунду —
силу тока или поток электростатической индукции, удельная теплопровод-
теплопроводность играет роль удельной проводимости или величины, обратной удельному
сопротивлению.
в) Движение вязкой жидкости. Легко показать, что перемещение
вязкой жидкости между двумя параллельными плоскостями, находящимися
друг от друга на расстоянии 2е, происходит параллельно плоскостям.
Если рассматривать перемещение плоского слоя, находящегося на рас-
расстоянии z от срединной плоскости, и обозначить через tj коэффициент вяз-
вязкости, а через р давление, отнесенное к единице длины, то скорость пере-
перемещения v равна
Таким образом, движение произвольного слоя определяется из движения сред-
среднего слоя B = 0). При этом имеет место полная аналогия предыдущим слу-
случаям: давление соответствует потенциалу, линии скорости — линиям тока, а ко-
количество жидкости, протекающей в единицу времени, — электрическому току.
г) Движение идеальной жидкости. В этом случае дело обстоит иначе,
даже если предположить, что движение безвихревое.
Действительно, вместо функции силовых линий можно составить функ-
функцию, представляющую линии тока жидкости. Точно так же можно определить
потенциал скоростей, частные производные которого представляют собой
проекции вектора скорости, играющего роль электрического потенциала.
Однако при этом может возникнуть явление, не имевшее места в предыдущих
случаях, а именно существование линий разрыва в течении. Если переходить
с одной стороны этих линий на другую, вектор скорости терпит разрыв.
Отсюда возникает новый тип задачи. Условия на границах задаются вдоль
одной из линий, форма которой входит в число неизвестных задачи.
д) Магнитные поля. Мы еще не говорили о применении конформного
отображения для определения силовых линий магнитных полей в присутствии
магнитных тел. Основные законы здесь те же, что и в электростатике,
однако между магнитным и электростатическим полем имеется глубокое раз-
различие. Магнитные заряды движутся всегда парами и на фиксированном рас-
расстоянии. Магнитное поле не равно нулю внутри магнитных тел, и силовые
линии не выходят из них нормально. Поэтому применение конформного
преобразования в том виде, как оно было выше изложено, может привести
в этом случае лишь к довольно неточным результатам.
ЛИТЕРАТУРА К ГЛАВЕ I
1. П р и в а л о в И. И., Введение в теорию функций комплексного переменного,
Физматгиз, 1960.
2. С м и р н о в В. И., Курс высшей математики, т. III, ч. 2, Гостехиздат, 1957.
3. Ф у к с Б. А., Ш а б а т Б. В., Функции комплексного переменного и некоторые
их приложения, Физматгиз, 1959.
4. Л а в р е н т ь е в М. А., Ш а б а т Б. В., Методы теории функций комплексного
переменного, Физматгиз, 1958.
5. М а р к у ш е в и ч А. И., Краткий курс теории аналитических функций. Физ-
Физматгиз, 1961.
6. Л у н ц Г. Л., Э л ь с г о л ь ц Л. Э., Функции комплексного переменного с эле-
элементами операционного исчисления, Физматгиз, 1958.
ГЛАВА II
РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
2.1. РЯД ФУРЬЕ
2.1.0. Введение. Рассмотрим функцию /(х) вещественной переменной х,
определенную в каждой точке промежутка [8, 6 —f— 2-re]. Предположим, что
в этом промежутке функция f(x) удовлетворяет следующим условиям (так
называемым условиям Дирихле):
1) всюду однрзначна, конечна и кусочно-непрерывна,
2) имеет ограниченное число максимумов и минимумов.
(Например, функции — и sin— не удовлетворяют соответственно условиям 1
\ х х
и 2 в промежутке, содержащем точку х = 0. ] В таком случае можно пред-
представить функцию f(x) в рассматриваемом промежутке в виде ряда
оо оэ
Ьот+- 2 onsinnx-f- 2 bncosnx.
п—\ п= 1
Здесь bQ, ап и Ьп — независимые от х коэффициенты. Этот ряд называется
рядом Фурье функции f(x). Он сходится к f (х) во всех точках непрерыв-
непрерывности функции и к значению <
в точках разрыва функции х=а. Это среднее арифметическое значение
двух предельных ординат, и его естественно принять за значение функции
в точке разрыва.
'2.1.1. Вычисление коэффициентов. Исходными здесь будут следующие
соотношения:
9
9+2*
9
Действительно,
sinnx sin mx dx =
cos nx cos mx dx -
Г sinnx cos
9
-{«
-\\
mx dx
для
для
для
для
= 0.
Пф
Пф
п =
/те,
/те;
/те,
т;
О)
B)
C)
sin их sin mx = -g-cos (я — m)x — -^-cos(n+ /re) дг.
86 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
Отсюда для первого интеграла при т Ф п найдем
\_ Г sin (п — т) х 16+2* 1_ г sin (п + т)х ]
2L п-т Je 2L п + т J
При п = т имеем
6+2it 9+2гс
/ sin2 nxdx== — / dx 2" / c
в в в
Подобными же элементарными расчетами легко убедиться в справедли-
справедливости соотношений B) и C).
Умножим обе части формулы для ряда Фурье на sinfftx и проинтегри-
проинтегрируем от 6 до 6 + 2ic. Тогда*)
6+2и 6+2и /со оо ч
Г /(x)sinmxdx= j sin тх \ b0 -\- 2_i an sm nx H~ 2j bn cos nx \dx.
в в \ n=i »=1 /
Согласно соотношениям A), B) и C) все интегралы справа равны нулю,
кроме
е+2*
I am sin/rex sin mx dx,
в
который равен атк. Поэтому
е+2«
ат=- I /(х)sinmxdx. D)
о
Аналогичный расчет дает
е+2ч
Ь"г — Т! f(x) cos mxdx, E)
0
2.1.2. Разложение в ряд по ортогональным функциям. Способ вы-
вычисления коэффициентов, описанный выше, может быть применен и в случае
разложения в более общие ряды — в ряды по произвольной системе орто-
ортогональных функций.
Рассмотрим совокупность функций вещественной переменной
их(х), и2(х) ип(х), ...
Если эти функции таковы, что
ь
fum(x)un(x)9(x)dx = 0 . G)
а
при тфп, то принято говорить, что функции ип(х) образуют в проме-
промежутке [а, Ь\ ортогональную систему с весовой1) функцией ср(х).
*) Нетрудно показать, что при выполнении условий Дирихле ряд можно инте-
интегрировать почленно.
') Она называется также базовой функцией.
2.1]
РЯД ФУРЬЕ
87
Пусть дана функция f(x), удовлетворяющая условиям Дирихле. Она
может быть представлена в виде бесконечной суммы ортогональных функ-
функций, т. е. ортогональным рядом вида
Чтобы вычислить коэффициент ст, умножим обе части последнего ра-
равенства на wm(x)cp(x) и проинтегрируем в промежутке [а, Ь\. Согласно
формуле G) все интегралы справа исчезают, кроме
ь
откуда
и
f am
dx
Ъ
J и2т (х) у (х) dx
(8)
Например, для полиномов Чебышева промежуток равен (—1, -\-1), а весовая
функция будет A—х2)^ (см. п. 7.9.3). В некоторых случаях весовая функ-
функция равна единице, например для
полиномов Лежандра (см. п. 7.6.9).
Если кроме равенства G) функ-
функции и„(х) удовлетворяют условию
2я
Рис. 2.1.
= l, (9)
то система называется ортонорми-
рованной.
Основная тригонометрическая
система функций
1, cosx, sinx, cos2x, sin2x. ...,
как следует из формул A)—C),
ортогональна с весовой функцией,
равной единице, но не ортонорми-
рована.
2.1.3. Частные случаи. Если
кривая, изображающая функцию,
имеет на оси Ох центр симметрии — точку О' (рис. 2.1), то, приняв эту точку
за начало координат, получим /(—х) = — /(*)• Функция/(х) — нечетная,
поэтому ее ряд Фурье должен содержать только синусы. Следовательно,
bo=bl = b2= ... =?„= ... =0.
Если кривая, изображающая функцию /(х), имеет ось симметрии, то,
приняв эту ось за ось ординат и выбрав начало координат в точке О',
в которой ось симметрии пересекает ось Ох (рис. 2.2), получим /(х) =
= /(—х). Функция /(х) — четная, поэтому ее ряд Фурье должен содер-
содержать только косинусы и постоянный член. Следовательно,
а, = а., = ... = а. — ... =0.
Рис. 2.2.
88 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
. > 2.1.4. Интегрирование и дифференцирование. Если функция удовле-
удовлетворяет условиям, поставленным в начале главы, то ряд Фурье для инте-
интеграла от /(х) получается почленным интегрированием ряда Фурье для функ-
ции /(х). Ряд для производной
f (х) может быть получен из ряда
для /(х) почленным дифференциро-
дифференцированием. Это верно, если только ряд
для /'(х) является сходящимся, что
бывает не всегда *).
Пример. Требуется разло-
разложить в ряд Фурье в промежутке
—и, -\- % (9=— тг) функцию y=f (x),
Рис. 2.3. равную — 1 при — к < х < 0 и
-f- 1 при 0 < х < -+- к. Из графика
функции (рис. 2.3) видно, что точка О является центром симметрии. Следо-
Следовательно,
Имеем
ч
1 ч
-л
Ч.
Ч\
\
Ч
\
ч
ч
уш
2
+1
ч
f
0
/ \
. 2 ., , 1чП,
т. е.
Отсюда получаем ряд
4
Производная заданной функции повсюду равна нулю, кроме точки х = 0,
где она обращается в бесконечность. Однако дифференцирование получен-
полученного ряда приводит к расходящемуся ряду.
Первообразная функция для функции у(х),' К = F(х), представляется
сходящимся рядом
График функции У (х) проходит (если константу справа считать равной нулю)
через точку 10, ^-1 )• На рис. 2.3 он показан пунктиром.
Положим в предыдущем разложении х = 0. Получим формулу
1 + + + + +
Замечание 1. Если у = f (x)— непериодическая функция, то ряд Фурье
совпадает с самой функцией только в промежутке от 9 до 9 + 2тс. Если /(х)
*) Последнее замечание очень важно. При дифференцировании cos пх и sin nx
члены ряда умножаются на п, что ухудшает сходимость. Подробнее см. [11, гл. 20,
стр. 577—578.
**) В этом легко убедиться, если, в соответствии с рис. 2.3, проинтегрировать
функцию у {х) от —н" до х.
2.1]
РЯД ФУРЬЕ
89
имеет период 2тс, то ряд Фурье равен этой функции для всех значений х
от — оо до -\- оо.
В рассмотренном примере разложения для у и К представляют собой
ступенчатую и пилообразную функции, графики которых указаны на рис. 2.4.
\
\
\
1 Л
/
ч
ч
ч
ч
У
/
ч
ч
ч
S
/
*
N
ч
ч
Рис. 2.4.
Замечание 2. В предыдущем примере функция /(л:) разрывна —
коэффициенты ее ряда Фурье имеют вид—. Функция F(x) непрерывна, но
ее первая производная разрывна — коэффициенты ряда для F(x) имеют
вид —. Нетрудно обобщить это правило и показать, что если дана перио-
периодическая функция, непрерывная вместе с ее первыми р — 1 производными,
и если ее р-я производная разрывна, то коэффициенты ее ряда Фурье бу-
будут порядка —^j-.
Пр и м е р. 'Разложим в ряд функции /(x)=cosax от —тс до +ir
(a — не целое число).
Функция f(x)— четная, поэтому все коэффициенты ап равны нулю.
Имеем
тс
. 1 С j I f Sin (a -J- я) те, sin (a — п\ я 1
Л = — I cos ах cos пх dx = — \—v Т ' * —^г =
п Я J JC I а-\-п ' а — п )
COS «я
___
. „ a sin arc
) ^
откуда
cos ax =
2a sin arc Г 1
•I2
cos 2x
"a2—22
cos 3x
Приложение. Положим в-предыдущей формуле х = % и обозначим a
через х. Разделив на sin теле, получим
или
Если х заключен в промежутке
внутри квадратных скобок меньше общего члена ряда
. то общий член ряда
Следовательно, ряд внутри квадратных скобок сходится равномерно, и можно
проинтегрировать обе части равенства от нуля до л:. Освобождаясь от мно-
множителя — и учитывая, что lim In s "" = In тс, имеем
к J 0 х
л=1
90 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ . ?ГЛ. II
ИЛИ
оо
Sin ъх _
КХ
Символ JJ означает бесконечное произведение. В данном случае это
2
зведение биномов вид
Отсюда получаем формулу
х2
произведение биномов вида 1 — —, п пробегает все целые значения
.. (Ю)
Если х придать значение у, получим формулу Валлиса:
¦к _ 2-2 4-4 2я ¦ 2л
2 ~ТТЗ ' ^5 •' " Bл—1)-Bл+1) ' ' *
2.1.6. Случай, когда разложение в ряд Фурье ограничено первыми
п членами. Дана функция /(х), определенная в интервале F, 6-|-2it), и
тригонометрический ряд, который оборван на первых п членах. Коэффици-
Коэффициенты ряда произвольны. Мы можем спросить себя, какими должны быть эти
коэффициенты, чтобы сумма первых п членов тригонометрического ряда
представляла наилучшим образом функцию /(х) в рассмотренном интервале.
Пусть сумма первых п членов тригонометрического ряда равна
Определим выражение для коэффициентов ряда ak, bk так, чтобы величина
Е=2^ [/(*) — Sn(x)]2dx — средняя квадратичная ошибка, которую мы
делаем, заменяя f(x) на 5„(х) в интервале от 6 до 6-f-2it, — была минималь-
минимальной. Для этого нужно коэффициенты ak и bk выбрать так, чтобы
IE- — JEJL— ~^Ё. — ^-—И.— =-^- = 0
да, да2 "' ' дап дЬй dbt " ' dbn
') При помощи символа JJ бесконечное произведение
(l + «o)(l + «
может быть кратко записано в виде
П
/1=0
Логарифм бесконечного произведения равен сумме ряда, общий член которого
1пA + и„). Так как ряды |1пA + "л)| и ]и„ | одновременно сходятся или расходятся,
то можно сформулировать следующее положение.
я
Произведение ТТ A -f- un) имеет при бесконечно возрастающем л предел, не
п=0 '
равный нулю и не зависящий от порядка сомножителей, если ряд, общий член ко-
которого равен ия, абсолютно сходящийся. Такое произведение называется абсолютно
сходящимся.
2.11
РЯД ФУРЬЕ
91
дЕ
Обратимся к коэффициенту ат. Он определяется из уравнения -^— = 0:
дЕ
дат
дЕ
= / / (х) — Ьо — V ak sin kx — \. 6ft cos йд: sin тел; of* = 0.
да„_ в
Это дает нам
откуда получаем
8+2* ¦
— / [/(•*)— amsmmx\sinmx dx = 0,
f (x)s'mmx dx.
Следовательно, разложение в ряд Фурье не только точно представляет
функцию f {х) при неограниченном числе членов*), но и обеспечивает наи-
наименьшую среднюю квадратичную ошибку по сравнению с любым тригоно-
тригонометрическим рядом по sin Ал: и cos/гд;, если эти ряды обрывать на произ-
произвольном конечном числе слагаемых. Замечательно, что при увеличении числа
членов в конечной тригонометрической сумме Sn(x) все прежние коэффи-
коэффициенты сохраняют свой вид.
Замечание. Рассуждения остаются точно такими же, если речь идет
о разложении в ряд по произвольной системе ортогональных функций и (г).
Это означает, что мы получим наилучшее представление функции f (х) в виде
ограниченного ряда по ортогональным функциям, если коэффициенты раз-
разложения определим по формуле (8). И здесь при увеличении числа членов
в конечной сумме прежние коэф-
коэффициенты сохраняют свой вид. '
2.1.6. Изучение разложения
в ряд Фурье вблизи точки раз-
разрыва. Явление Гиббса. Пусть
y = f(x) — функция, имеющая
разрыв в точке х=а (см.
рлс. 2.5):
lim/ (a —е) = А,
О
а
Рис. 2.5.
Введем в рассмотрение 0{х) — функцию, имеющую значение
¦ к < х < 0 и -j- 1 при 0 < х < it; Ряд Фурье для 0{х) будет
1 при
sin 3jc
-ь
sinBra — 1
2я—1
Функция / (х) может быть записана в виде
В —А
*) В том смысле, что при п -*¦ со lim ? = 0.
92 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
где fi(x) — функция, уже не имеющая разрыва при х = а f/j(a) =
Поэтому для изучения особенности разложения f(x) вблизи х = а доста-
достаточно рассмотреть поведение G(x) вблизи нуля.
При х = 0 G(x) имеет своим значением ±1 в зависимости от того,
как х стремится к нулю: принимая положительные или отрицательные зна-
значения. Сумма же ряда Фурье для G{x) при х —>0 стремится к единствен-
единственному значению — нулю. В этом нет ничего удивительного, так как ряд
справа — непрерывная функция х и не может иметь двух разных значений
при значении переменной х = 0.
Рассмотрим первые п членов разложения G(x):
с . . 4 р sin д: , sin Зх , , slnBra — \)x'
, sin Зх , , sin (In — 1) х "|
г- з -Г •••-!-¦ 2n~ZT\ J-
Начертим кривую, представленную этим рядом. Для этого изучим произ-
производную S'n(x):
Если в формуле A) п. 1.1.13 положим Ь—2х, а=х, то
...+cosBn-\)x=cosn*sinnx ±
sin x 2 sin x
Следовательно,
sin 2nt
at
2 f
о
Максимумы и минимумы 5„ (х) при изменении х от 0 до 4- определяются
равенством sin2rax = 0, откуда
2я
Кривая Sn(x) совершает ряд ко-
колебаний вокруг ординаты у = -f-1
(рис. 2.6). Нетрудно заметить,
что первый максимум (при k = 1)
наибольший. Его ордината равна
тс •
2л тс
_2_ Г sin 2nt _ 2_ f sin у dy
* J sint at — к J у '
о о 2nsin^-
где мы обозначили у = 2nt.
Рис. 2.6. При больших значениях п
(соответственно малых х) можно
заменить sin у- на ~-. Предел ординаты первого максимума при я—>оо
(х—>0) будет, следовательно,
тс
2 Г sin v . 2 „. , 1-тп
— / ¦——rfv = —Si it— 1,179...
О
вместо того, чтобы быть равным единице (символ Si обозначает интеграль-
интегральный синус — см. п. 7.2.1).
2.11
РЯД ФУРЬЕ
93
Таким образом, функция, представленная тригонометрическим рядом,
переходя через разрыв, делает скачок, примерно на 18% больший, чем
исходная функция. Это явление было обнаружено в 1899 г. американским
физиком Гиббсом^ Оно иллюстрируется рис. 2.7, где приведены графики
функций Sn(x) — сумм п первых членов разложения в ряд Фурье функ-
функции О(х) — для «= 1, 3, 7, 15, оэ в промежутке [0, тс]. Из-за явления
п=оо, 75,7,3,7
п
Рис. 2.7.
Гиббса представление разрывных функций рядом Фурье в окрестности точек
разрыва не вполне удовлетворительно *).
2.1.7. Случай произвольного промежутка. В случае, если период
функции f(t) равен не 2т:, а Т, то ее следует рассматривать в промежутке
не от 8 до в-\-2п, а от 6 до 8 + Т. Тогда
cos
л=1
Коэффициенты равны
64Г
=Y f
в
в+г
в+г
ansinnwt,
л=1
cos
dt>
(И)
A2)
A3)
A4)
Эти формулы совпадают с D) — F), если заменить там х на
*) Подробное изложение явления Гиббса дано в [1], стр. 490—495.
**) При вычислении интегралов от периодической функции f(t) можно счи-
считать 9 = 0.
94 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. И
2.1.8. Ряды с комплексными членами. Пусть
JO СО
/@=2 ап sin nwt + 2 bn cos nut -+- b0.
n=l n=I
Имеем
e 2 ¦&(e"""—«-
n=l
где на основании формул A2)—A4)
ч+т 0+г
f (t)(cosnut—jsinnut)dt=± f f(t)e-i"-»dt,
9
Й4-Г
I
Здесь отметим два обстоятельства:
1. Из формулы для "~Z " можно получить выражение для n~T~ja" t
изменив «на —п. Если первый коэффициент обозначить через сп, то вто-
второй должен быть обозначен как с_п.
ь+т
2. Постоянный член можно написать в таком виде: 60 = -=- / f(t)e°dt.
8
Он получится из общей формулы, дающей с±п, если положить в ней /г = 0.
Следовательно,
f ^cneJ^, A5)
Я= —оо
где
с„ = у f f{t)e-i"">ldt. A6)
Выражение A5) представляет собой разложение в ряд Фурье с комп-
комплексными членами, а A6) — формулу для коэффициентов, которые участвуют
в этом разложении. Мы получаем, таким образом, внешне более простой
ряд, чем разложение с вещественными членами. Он имеет то преимущество,
что коэффициенты разложения определяются одной общей формулой. В раз-
разложении с вещественными членами это не имеет места.
2.1.9. Графическое представление. Спектр. Если положить an = snsm^n
и ?л = $л cos ср„, то ряд A1) функции /(/) получает вид
СО
f(t) = bn-\- 2 sn cos (nut — cpj.
Функция f(t) разложена в сумму гармонических компонент; sn и ср„ пред-
представляют собой соответственно амплитуду и фазу отдельных гармоник.
Эти гармоники можно представить в векторной форме. Если располо-
расположить разные векторы, соответствующие каждой круговой частоте, вдоль
2.11
РЯД ФУРЬЕ
95
некоторой оси, то мы получим трехмерное представление гармоник разло-
разложения в ряд Фурье. На рис. 2.8 оно дано для момента t= 0. Такое пред-
представление, однако, не очень удобно. Поэтому его обычно заменяют двумя
a
0
t
bo \
/
/
/
f
b
/s».t
an-,
О G?-7)и> nw
о
bn+y
Рис. 2.8.
Г7СО
Рис. 2.9.
:. 2.9), которые являются проекциями совокупности предыдущих векто-
векторов соответственно на плоскости фаз ¦=- и нуля, иначе говоря, представ-
представлением величин ап и Ъп вдоль оси круговой частоты. Можно даже ограни-
ограничиться представлением одних только длин sn или их квадратов, опуская фа-
вовые соотношения отдельных компонент. Такое представление называют
спектром функции f (t) или, чаще, линейным спектром функции.
Что касается трехмерного представления на рис. 2.8, то здесь уместно
сделать следующее замечание: если принять за новое начало отсчета времени
момент tQ, то картина, изображенная на рис. 2.9, изменится, но длина -век-
-векторов на рис. 2.8 останется неизменной. Каждый вектор повернется только
на угол пЫ0, а вся совокупность векторов претерпит нечто вроде винто-
винтообразного скручивания. Поэтому представление, состоящее в том, чтобы
изображать только модули sn или их квадраты s^, удобнее, так как оно
инвариантно по отношению к изменению начала отсчета времени.
• Возьмем ряд функции /(О с комплексными членами A5). Совокупность
комплексных величин с„ может быть точно так же изображена в трехмер-
трехмерной векторной форме. Вещественная и мнимая части векторов сп играют
ту же роль, что и коэффициенты ап и Ьп, со следующим различием. Рис. 2.8
должен быть продолжен в сторону отрицательных круговых частот. Фор-
Формулы
дают
что приводит к очевидной симметрии картины. Аналогично представлениям
рис. 2.9 проекция на плоскости фаз -д- и нуля образуют удобные для
96
РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
[ГЛ. II
работы представления (рис. 2.10). Приведенные выше замечания относительно
влияния смещения начала отсчета времени действительны и в случае разло-
разложения с комплексными членами.
-(n+7)w -not -Сг7-7
О fr?-7)w пш (п+7)со
I I Г.
-(/7-1-7H) -то -Сп-7)О)
О {П-7)а> пси (т-7)ш
Рис. 2.10.
2.1.10. Среднее значение произведения двух функций одного периода,
разложимых в ряд Фурье. Даны
е]тЫ
m=l
m= —oo
+ OO
Исходя из формул A) — C), отнесенных к периоду 7* — , нетрудно
заметить, что
/в=1
Отсюда получаем
2 cmc_m. A8)
0 т = 1 пг= —оо
Так, например, если ср(?) — периодическая электродвижущая сила, при-
приложенная к цепи, а f (t) — текущий по этой цепи ток, то среднее значение
произведения—это средняя мощность, расходуемая в цепи. Она выражена
в формуле A7) с помощью коэффициентов обоих разложений в ряд Фурье.
Выражение A8), умноженное на /?, дает среднюю мощность Р, расходуемую
на сопротивлении R циркуляцией переменного тока /(?)• Эффективная сила
тока /Эф в этом случае определяется ив формулы
Заметим, что Ьо — это интенсивность постоянной составляющей тока,
/1/2 2 \
у \ат + Ьт) = 1т — интенсивность гармоники тока /га-го порядка. Фор-
Формула A8) при этом,дает
2i] : ряд фурье 97
2.1.11. Распространение ряда Фурье на почти периодические функ-
функции1). Рассмотрим функцию f(x), представляющую собой.сумму периоди-
периодических функций /](*), /2(х) fn(x) с периодами xlt х2, х3 х„
соответственно. Если периоды соизмеримы между собой или, иначе говоря,
они являются целыми кратными некоторого числа Т., то это Т и будет
периодом функции f(x). В противном случае функция f(x) не периодична.
Однако если разложить функции fi(x), f2(x), .... fn(x) в ряды Фурье
и просуммировать эти ряды, то мы получим разложение вида
со
f (*) = Ро + j? (Ря, cos *mx 4- am sin nmx).
Оно внешне походит на разложение в ряд Фурье, но это не ряд Фурье,
потому что множители сош — коэффициенты при х — не целые кратные
одного числа.
Попробуем вычислить коэффициенты р0> рда, am. Рассмотрим ряд Фурье
некоторой периодической функции ср(х):
со
у(х) = Ь0-\- 2 (bmcosтшх-\-amslnmu>x).
Согласно формуле A4) коэффициент Ьо равен среднему значению функ-
функции ср(ле) по периоду, но он равен также среднему значению функции (р(дг)
по бесконечному интервалу:
s
fto=lim4- I <?(x)dx.
Мы можем, следовательно, вычислить Ьо, не зная периода функции <р(дг).
Точно так же, заметив, что соотношения A2) и A3) являются не чем иным,
как средними значениями по периоду функций <?(x)slnma>x и у (х) cos ттх.
мы получим коэффициенты ат и Ьт из соотношений
•S
am=llm-s- / (
' s
bm = lim -^ / ю (jc) cos /racojc dx.
«-km J ./
Таким образом, коэффициенты разложения в ряд Фурье функции <?(х) можно
вычислить и не зная периода этой функции. Это наводит на мысль, что
коэффициенты C0, Cm, am получаются из соотношений
%= \im ^-J f(x)dx,
s
рот = lim -g- / f(x)cosa>mxdx,
s
=Iim^- / f(x)slnwmxdx.
') P. Levy, Cours d'Analyse, t. 1, p. 183, 1930.
7 А. Анго
98
РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
[ГЛ. II
Можно, впрочем, определить эти коэффициенты и не зная значений шт.
Действительно, коэффициенты определяются как те числа, для которых
интегралы
Urn
S-*oo
2 Г
~ё- / / (х) cos хх dx,
¦s i
s
2 Г
lim -я- / / (x) sin xx dx
отличны от нуля, когда т изменяется от нуля до бесконечности.
Если рассматривать сумму
как равномерно сходящийся ряд периодических функций, то функция / (х)
будет называться почти периодической. Она может быть разложена в р,яд,
очень похожий на. ряд Фурье.
Численный расчет коэффициентов ряда Фурье изложен в гл. X, посвя-
посвященной численным и графическим методам (п. 10.3.6).
2.2. ИНТЕГРАЛ ФУРЬЕ •
2.2.1. Вещественная форма интеграла Фурье. Пусть на всей веще-
вещественной оси задана некоторая функция /(/). Мы уже видели, что в проме-
промежутке [8, 6-\-Т] ее можно разложить в ряд Фурье. Если считать теперь,
, что t изменяется не от 8 до
-^^ ^**~ 0 -)- Т, а пробегает всю веществен-
вещественную ось от —оо до -(-оо, то
функция, представленная рядом
Фурье, уже не будет совпадать
с/(О вне промежутка [8, в-^-Т].
График этой функции получится
параллельным переносом (как на-
направо, так и налево) на участки
-7 длиной Т, 27\ ЪТ, ... графика
f (t) на основном промежутке.
Для целого ряда задач было
бы полезно вывести из ряда Фурье
разложение, могущее представить функцию f (t), заданную от —оо до -)-со.
Оно называется разложением f (t) в интеграл Фурье.
Возьмем функцию f(t) и рассмотрим, как уже было сказано, ее значе-
значения в промежутке [8, б-|-Г], иначе говоря, рассмотрим часть изображающей
ее кривой, заключенную между точками с абсциссами Л = 8 и B=Q-\-T
(рис. 2.11).
Переместим началб координат в среднюю точку С отрезка АВ.
Для значений t, заключенных между А и В, т. е. для таких t, что
Т Т
^ ^^h"o"» функция f (t) представляется разложением
U Г
Рис. 2.11.
/@= *о+ 2
2,2] ИНТЕГРАЛ ФУРЬЕ 99
где 2 = -^-, а коэффициенты ап, Ьп и Ьо даются формулами
4
2 /•
а„ = -~- /
2
г
2 /*
= -^г / / (т) cos «2т йт,
Y f
Рассмотрим, что произойдет с разложением, если Т устремить к беско-
бесконечности. Для этого запишем разложение в следующем виде:
оо
= h +-g- J 2 (Ь„ cos (о^ + апsinшО-
Мы обозначили я2 = ш; при суммировании учтем, что 2 — разность между
двумя последовательными значениями ш:
ев = («+1J и со = «2.
Можно, следовательно, рассматривать 2 как приращение Дш величины ш.
Заменяя ап, Ьп и Ьо их выражениями, найдем
-1.
2
Иначе говоря.
Г «1=9 Т_
Т
т т_
2
.Г Г
Т
Пусть Т стремится к бесконечности. В этом случае Д<о превращается
ОО 00
в rfio. а У в Г , Будем считать, что интеграл от /(т) по бесконечному
о>=2 , О
промежутку сходится. Тогда
п'
100 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. 1Г
и мы получим следующую формулу для функции f (t):
СО + <Х>
f(t)=~ Jdco У* /(x)cosu>(* — i)dt. A9)
0 -oo
Это разложение в интеграл Фурье функции f(t)*).
Если раскрыть cos со (t—х) и вывести из-под знака внутреннего инте-
интеграла члены, не зависящие от х, то можно написать
-Ьоо +-оо +оо \
/(/) = — / d<n cos со/ / /(x)cos coTofx-(-sincD^ / / (х) sin cox dx \.
О —oo —со )
Отсюда мы видим, что f(t) можно рассматривать как сумму бесконечного
числа синусоидальных колебаний с амплитудой
1 1 1/ / Г \ I Г I
— Л(со)=— у I / (х) cos сот их I + / /(x)sincoxdx I
* я Г V t/ I \ J I
\—со / \— с» /
и фазой
+ СО
I / (х) sfn шт dx
O(co)=arctg^s
I / (х) COS (ax dz
—oo
Формулу A9) можно теперь написать в следующем виде:
+ ОО
1 Г
f(t)=— / Л (со) cos [со^ — <P(co)]rfci>.
6
2.2.2. Комплексная форма интеграла Фурье. Применим формулы A5)
и A6) для ряда Фурье с комплексными членами к функции, изображенной
на рис. 2.11. Имеем
г
+Т
/(,)= ^ "*' - 1
я= —со _Г_
~ 2
Если обозначить, как это делалось в предыдущем пункте,
и, кроме того,
*) Интеграл по х с бесконечными пределами возник в результате предельного
перехода при Г-*оо. Его, следовательно, надо понимать в смысле главного значения
(Valeur principlale, см. [1], стр. 532—533). Знак главного значения (v. p.) будем для
краткости опускать.
21SJ ИНТЕГРАЛ ФУРЬЕ 101
та
т т
Оба эти выражения справедливы при тт- *С t *С-\--^.
Пусть Т бесконечно возрастает. Тогда в пределе
/@= / O((o)e/a"rf(o, B0)
А. j f^)edx. B1)
— ОО
Если подставить выражение B1) для G(o>) в формулу для /(*), то
Последнее выражение представляет собой комплексную форму интеграла
Фурье.
Отделим вещественную часть от мнимой:
0 +ОО -+-ОО +
dm J f (т) cos v(t-x)dx+j f dm f
Функция sina»(/ — т) — нечетная функция от ш. Отсюда вытекает, что мни-
мнимая часть полученной формулы равна нулю. Это, впрочем, очевидно, так как
f(t) — вещественная функция и мнимая часть справа должна отсутствовать.
Точно так же, поскольку cos ш (t — х) — четная функция от ш, мы можем,
введя коэффициент 2, свести область интегрирования по ш к интервалу [0, оо).
Следовательно, в конечном счете
+О
J
f(x)cosw(t —
Это в точности формула A9), найденная нами ранее.
Было бы интересно получить выражение интеграла Фурье в комплексной
форме, используя амплитудную функцию А (ш) и фазовую Ф (ш), определен-
определенные в п. 2.2.1.
Очевидно, что
откуда
+ОО
^ / Л(<о)*Лш'-ф@1I*о. B2)
-OO
-102 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
Замечание. Множитель -~- можно поместить в любую из формул B0)
или B1): в выражение для О(ш), как в данном пункте, либо в выражение
для / (t), как будет сделано в п. 2.2.8, в соответствии с принятым стандар-
стандартом для формул преобразования Фурье. Некоторые авторы из соображений
симметрии вводят множитель в обе формулы. Все это вопрос опреде-
V 2я
ления О(ш), иначе говоря, зависит от смысла вводимых в теорию обозначе-
обозначений. Здесь следует быть весьма внимательным, в частности, при пользовании
таблицами преобразований Фурье.
2.2.3. Применение к электрическим цепям. Положим, что функция / (t)
представляет собой электродвижущую силу, приложенную к контуру или
электрической цепи. Согласно формуле B0) можно рассматривать электро-
электродвижущую силу / (t) как сумму бесконечного числа синусоидальных соста-
составляющих, амплитуды которых даны выражением |О(ш)|, а частоты проходят
весь спектр от —оо до -|-со. Следует считать,- что эти элементарные
синусоидальные электродвижущие силы приложены бесконечно давно. Поэтрму
единственным электрическим током, который существует в цепи, будет ток
с постоянным синусоидальным режимом. Действительно, переходной ток,
вызванный внезапным приложением элементарной электродвижущей силы,
экспоненциально затухает и в стационарном режиме равняется нулю. Конечно,
для этого нужно, чтобы сопротивления цепи были положительны, иными
словами, чтобы это была рассеивающая цепь. Итак, нас будут интересовать
только синусоидальные токи.
Известно, что если представить через Z(/u>) полное сопротивление
контура или эквивалентное полное сопротивление цепи, а через ?ое —сину-
—синусоидальную электродвижущую силу, то стационарный синусоидальный ток
будет равен
Применим эту формулу к сумме синусоидальных электродвижущих сил,
представленных формулой B0). Электродвижущая сила, соответствующая
частотам, заключенным между ш и ш-\-йш, будет
Результирующий стационарный синусоидальный ток, вызванный такой электро-
электродвижущей силой, равен
G (<о) )ы
Z О
¦ da>.
Сумма этих токов даст реакцию контура или цепи на электродвижущую
силу /(/)• Суммарный ток выражается равенством
Если полное сопротивление контура или эквивалентное полное сопро-
сопротивление цепи выразить через модуль и фазовый угол
121
ИНТЕГРАЛ ФУРЬЕ
103
то формула B2) дает
== ~2л I В <а>) е " do*.
B3)
Пример. Электродвижущая сила /(*). разложение которой в интеграл
Фурье дано формулой B2), приложена к зажимам усилителя. Коэффициент
его комплексного усиления дается выражением
Пусть функции, характеризующие изменение амплитуды В(ш) и фазы Р(ш),
представляют собой соответственно четную и нечетную функции от вели-
величины ш (рис. 2.12). Величина С на рисунке имеет размерность времени.
— можно трактовать как полуширину
полосы пропускания.
Форма выходного сигнала усили-
усилителя может быть представлена форму-
формулой B4), аналогичной B3):
«(*) =
_!_
B4)
Если бы это был идеальный усилитель,
to четная функция В (о*) свелась бы
к постоянной Ьо (усиление, не зависи- Рис. 2.12.
мое от частоты), а нечетная функция
Р (ш) к линейной функции — аош (фазовый сдвиг пропорционален частоте).
Разложим в ряд Фурье разности между идеальными и реальными функ-
функциями. Имеем
оо
В (ш) = b0 -f- 2 bn cos new,
Тогда формула B4) принимает вид
+оо
л=1
Но известно (см. п. 7.5.11), что
2
ams\n теш.
S )am sin mco>
dot.
k=i
104
РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
(ГЛ. II
Если подставить это разложение в предыдущую формулу, то мы в соответ-
соответствии с B2) представим выходной сигнал е(() с помощью членов вида
— aQ-\-kmc)b0Jk(am),
—.ao — kmc)-(—\fboJk(am),
— ao±nc)^-Jk{am), ) от, я, /fe=l, 2, 3, ...
/ (t — a0 ± nc + kmc) -^ Jk (am),
f(t—a0 ± nc — kmc) ¦ (—Ifb-J^aj.
Таким образом, основной сигнал оказывается окруженным на расстояниях,
кратных с, рядом паразитных сигналов.
Рис. 2.13.
Картина будет более наглядной, если мы ограничимся в каждом из рядов
(для В(ш) и Р(ш)) только первыми членами. Тогда остается только
Vo(°i)/(* — ао)>
(т. е. входной сигнал, запаздывающий на а0 и умноженный на постоянный
коэффициент) и еще сигналы вида
Jo (*i) + Vi (<*i)] / it - a0 + с).
±- Jo (a,) — Vi (<
изображенные на схеме рис. 2.13.
2.2.4. Случай незатухающей цепи. Во всех предыдущих рассуждениях
предполагалось, что речь идет о рассеивающих электрических цепях, т. е.
что все корни характеристического дифференциального уравнения, опреде-
определяющего систему, имеют отрицательные вещественные части. Если же корни
чисто мнимые, то интеграл
= f
О (со)
не будет сходиться, так как Z(jw) становится равным нулю при веществен-
вещественных значениях ш, следовательно, внутри интервала интегрирования. Чтобы
найти, однако, решение в этом важном случае, обычно достаточно ввести
2.2]
ИНТЕГРАЛ ФУРЬЕ
105
малый коэффициент затухания, вычислить ответ, а затем устремить коэффи-
коэффициент затухания к нулю:
i(t)=\im
+ ОО
\im f
о И
2.2.5. Спектр частот. Имея функцию G(co), мы можем определить
спектр частот функции fit), аналогичный спектру ряда Фурье в комплекс-
комплексном виде, с той разницей, что здесь речь идет о непрерывном спектре.
При частном значении ш функция О(ш) может быть представлена вектором,
компоненты которого будут действительной и мнимой частью О(ш). Если
расположить начало этих векторов, соответствующее всем значениям со от
— оо до -j-oo, на оси Осо, перпендикулярной плоскости хОу, образованной
действительной и мнимой осями, то конец вектора О (со) опишет кривую
(в большинстве случаев пространственную), которая и будет графически
представлять непрерывный спектр частот
функции / (t) (рис. 2.14).
Это трехмерное довольно неудобное
изображение заменяют проекциями кривой
О (со) на плоскости хОч>, уОш, т. е. кривыми.
1@»
Рис 2.14.
Рис. 2.15.
представляющими отдельно вещественную R(co) и мнимую 1(со) части ком-
комплексной функции О (со) (рис. 2.15):
т) cos шт dx, 1
+ОО
(со) =—g— /
Эти две кривые полностью осведомляют нас об амплитуде и фазе каждой
составляющей. 1(ш) — нечетная функция, иначе говоря, начало координат
будет центром симметрии кривой I (ш). R(u>) — четная функция, иначе говоря,
ось ординат Оу будет осью симметрии кривой R(u>). Отсюда вытекает, что
если f(t) — четная функция, то спектр сводится только к действительной
части R(o>), совпадающей с модулем функции О(ш), или с амплитудой -4—.
Точно так же, если f(t) — нечетная функция, то спектр сводится к мнимой
части 1(ш), которая совпадает в этом случае с | О (со) | = —4—^- •
Можно пользоваться также и другим представлением, которое состоит
в том, что по оси ординат откладывают либо амплитуду
= | О (со) | =
12 (с
106 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
либо ее квадрат (рис. 2.16). Это представление неудобно тем, что не вы-
выявляет фаз отдельных составляющих, однако имеет то преимущество, что
остается неизменным при любом перемещении начала отсчета времени t0.
Действительно, легко заметить, что так же, как в случае спектра для ряда
Фурье, при смещении начала отсчета
времени кривая О(ш) претерпевает
винтообразное скручивание, пропор-
пропорциональное t0. Это изменяет составляю-
составляющие R (ш) и I (и>), но не амплитуду
Пример. Чтобы лучше понять
механизм перехода от разложения в ряд
*° Фурье к интегралу Фурье, рассмотрим
Рис. 2.16. следующий простой пример. Дана
функция времени, состоящая из прямо-
прямоугольных импульсов высотой h и шириной 2е, повторяющихся с частотой v.
Это функция с периодом
т=\=Ч (г>2?)-
Ее разложение в ряд Фурье будет
о Sin mQe jmGt
Спектр этой функции состоит из счетного числа отдельных линий (соответ-
(соответствующих последовательным целым числам), отстоящих друг от друга на 2nv.
График функции f(t) и ее спектр для нескольких значений отношения -=-
приведены на рис. 2.17, где введено обозначение отЙ = ш. Концы верти-
вертикальных линий, изображающих амплитуды, располагаются на кривых
h o sin we
*— Ufa
Ufa f
показанных на рисунке слева; самый большой максимум на этих кривых
равен 2/zve = 2h-^-.
Рассмотрим теперь кривые
h sin a>e
1Z
показанные на рис. 2.17 справа; самый большой максимум здесь равен —.
Ординаты правых кривых будут с точностью до коэффициента — равны
относительным амплитудам. Они отличаются от предыдущих множителем
2 = Дш, т. е. отнесены к Дсо=1. Если Q стремится к нулю, т. е. если
импульсы все дальше отстоят друг от друга по времени, сохраняя прежнюю
форму, то линии спектра все больше сближаются, левая кривая — вели-
величины их амплитуд — все больше сплющивается, но относительные амплитуды
на правой кривой остаются неизменными. В пределе, когда Q = 0, функция f(t)
сводится к одиночному импульсу в начале отсчета времени. Тогда в спектре
частот имеется несчетное число линий (т. е. столько, сколько точек на
прямой), кривая слева — бесконечно сплющенная — сливается с осью ш, но
2.2]
ИНТЕГРАЛ ФУРЬЕ
107
кривая справа — относительные амплитуды — остается невдме«ной, ее внут-
внутренняя область полностью заполняется бесконечно сближенными линиями.
Это спектр частот изолированного импульса. Его можно найти непосред-
непосредственно из формулы B1):
/ , h sin we
Это особенно простой пример, так как в силу симметрии подынтеграль-
подынтегральной функции мнимая часть 1(ш) равна нулю. Все составляющие находятся
в одинаковой фазе.
L-
лшшплшшяшшя
о t
А
гТУ
\ I /
о)
_л п.
t
со
i
/УЗУ
Y/Yt)
_m
со
Рис. 2.17.
П t
и
со
На рис. 2.17 изображен импульс высотой Л=1, шириной 2е=1 сек
для следующих случаев: один импульс за каждые две, восемь, двадцать
секунд и одиночный импульс.
Случай ударного импульса. Предположим, что h бесконечно возра-
возрастает, а е стремится к нулю так, что произведение h • 2е постоянно и равно
конечному числу Р. В этом случае
-,. . Р Sinus P
4 ' 2я ше 2л
108
РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
ГГЛ. И
Очень короиеий ударный импульс имеет спектр частот, не зависящий
от частоты (рис. 2.19).
rrt)
О
о
Рис. 2.18.
1(со)
Рис. 2.20.
1 Пример. Функция f(t) равна нулю при КО и равна «~w при t >O
(рис. 2.19). Имеем
= ~ J
откуда
P -f- У«
На рис. 2.20 воспроизведен спектр частот, т. е. кривые
R((°)==iFT^ и 1(и)) = -^"
Подставим О(ш) в формулу B0). Тогда
+ ОО
+ ОО
1 /*
1 /* со Sin «>t
-t-OO -f-OO
/ - 2 I Я2' rft0 /
(o COS
. B5)
Мнимая часть справа равна нулю. Интегралы, определяющие веществен-
вещественную часть, очень легко подсчитать по способу, указанному в п. 1.3.23.
Первый интеграл равен ^-е?' при /<0 и -^е-?' при *>0 (рис. 2.21).
2.2Ц.
ИНТЕГРАЛ ФУРЬЕ
109
1
1
Второй интеграл равен —-^е^ при t <0 и -^-е' ПРИ *>° (P^c- 2-22)-
Сумма, следовательно, равна нулю при t < 0 и e~w при ? > 0. Мы восста-
восстановили, таким образом, функцию /(О- Спектр частот, который можно по-
получить, возведя модуль О(ш)
в квадрат, будет jf
1 1
(см. рис. 2.23).
2.2.6. Единичная функция
Хевисайда. Дана функция Г(*),
равная нулю при КО и единице
при t > 0. Это единичная функция
Хевисайда или просто единичная
функция. Нетрудно получить ее
разложение в интеграл Фурье,
или, точнее, разложение функции
Г (Jt) s", среднее значение ко-
которой в промежутке от — оо до
-+- оо равно нулю.
Разложение функции, рассмо-
рассмотренной в предыдущем примере
(рис. 2.19), дается формулой B5).
Если fj стремится к нулю, то
первый интеграл в формуле B5),
представленный кривой на
рис. 2.21, стремится к '/г- Второй
интеграл стремится к
1
г
^^
О
1
~ г
^^-—
t
Рис. 2.22.
-»~оо ос
1 Г Since* . \ Г
¦к- / du> =a — /
2я «/ а> 1С ,/
Sin a>t
б Рис. 2.23.
и мы приходим к формуле, указанной нами ранее (Гл. I, формула A5)):
I , 1 f
=2- + irJ
Sin u>t
2.2.7. Пары функций. Можно заметить некоторую взаимосвязанность
формул B0) и B1). Уравнение B0) определяет f(t), если функция О(ш)
известна. Уравнение B1), наоборот, определяет О(ш), если известна f(t).
Эту симметрию можно сделать еще более явной, если круговую частоту и>
заменить частотой м = у-.
Положим 2гсО Btcv) = Ф (v). Имеем
f(t)= Г
B6)
+ О
= J
dt.
B7)
110 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
Если заменить t на —t, то
+ ОО
(—*) = J Ф (v) е-
— оо
+оо
Ф(у)= J f(—
Здесь функции /(—t) и Ф(у) поменялись местами. Спектр функции Ф(у)
стал спектром /(—(). Функции f(t) и Ф(?) принято называть парой; для
них построены специальные таблицы. Существует полная симметрия между
обеими переменными — временем и частотой. Формула B6) показывает, что
функцию f(t) можно рассматривать как сумму синусоидальных составляю-
составляющих времени. Точно так же формула B7) показывает, что функцию Ф (v)
можно рассматривать как сумму синусоидальных составляющих частоты.
Установление этого факта крайне важно и играет большую роль в совре-
современной теории информации.
2.2.8. Преобразование Фурье. Вместо симметричных формул B6)
и B7) для определения преобразования Фурье предпочтительнее пользоваться
соотношениями B0) и B1), но при этом следует ввести множитель -=—
в формулу взаимного преобразования.
Стандартная форма экспоненциальной трансформанты Фурье функ-
функции f (t) определяется соотношением
+ О
= J
-J^dt. B8)
Обратное преобразование определяется по формуле
e^da. B9)
Эти формулы не полностью симметричны. Экспоненциальная трансфор-
трансформанта Фурье для функции G(t) равна 2тс/(—ш).
Если функция fit) определена только при t > 0, если к тому же она,
как и функции, рассматриваемые в гл. VIII (преобразование Лапласа), равна
нулю при t < 0, то мы можем определить два других преобразования Фурье:
преобразование
оо
О,(о))=. J f{t) cos wtdt, t>0, C0)
о
называется косинус-преобразованием Фурье для fit); преобразование
оо
О2 (со) = J / it) sin at dt. t > 0. C1)
о
называется синус-преобразованием Фурье для fit).
2.2] ИНТЕГРАЛ ФУРЬЕ 111
Обратные преобразования будут
оо
= l f O^w) cos tat du>, *>0, C2)
6
2(w)smu>tdw, t>Q. C3)
6
Имеются очень полные таблицы трансформант Фурье для основных
функций г).
Можно вывести формулы преобразований Фурье из таблиц пп. 8.3.29,
8.3.30, в которых приводятся формулы преобразований Лапласа. Для этого,
однако, недостаточно заменить переменную р на /ш, следует еще убедиться,
что выполнены некоторые дополнительные условия. Действительно, замена
переменной приводит в соответствие мнимую и вещественную оси -=- пути
интегрирования. В преобразовании Лапласа путь интегрирования связывает
точки с — /оо и c-f-yoo. Замена р на /<о может быть произведена, если
функция F(p) не имеет полюсов вправо от мнимой оси или на ней самой.
Кроме того, функция времени h(t), рассматриваемая в преобразовании Лап-
Лапласа, равна нулю при t < 0. Это приводит к необходимости различать два
случая. '
1. Функция fit) равна нулю при t < 0. Достаточно заменить р на /ш
в F (р), если только эта функция не имеет полюсов справа от мнимой оси
или на ней самой.
Пример 1. /(О = 0 при *<0, f(t) — eat при t > 0. Функция
F{p)=—-j— удовлетворяет предыдущим условиям, если R(a)>0. Искомая
экспоненциальная трансформанта Фурье равна, следовательно, G(w)= , .
Так как f(t) — O при t < 0, то, взяв вещественные и мнимые части функ-
функции О(ш), мы непосредственно получаем косинус^ и синус-трансформанты
Фурье для f(t):
2. Функция не равна нулю при t < 0. Можно написать
+ СО ОО " ОО
О (о») = J / it) e-J»* dt = Jf it) «->' dt + ffi—t) e>< dt.
-co 0 0
Если fit) и '/(—t) соответственно имеют "в качестве трансформант
Лапласа функции Fx(p) и F2(p) и если обе эти функции не имеют полюсов
вправо от мнимой оси или на ней самой, то
Пример 2. Функции f(t) = sinyit соответствует трансформанта Лап-
Лапласа „^_ 2 , имеющая два полюса на мнимой оси.
Функции / it) = e~at sin 4t соответствует трансформанта Лапласа
, \ . 2 . Полюсы функции Fx (p) находятся слева от мнимой оси, полюсы
функции F2ip) находятся справа от нее.
') В частности, Tables of Integral Transforms, vol. I, Calif. Inst. of Technology, 1954.
112 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
Обе функции sinv? и e-a'sinv? не имеют экспоненциальной трансфор-
трансформанты Фурье, и это представляет большое затруднение при электротехниче-
электротехнических расчетах.
Пример 3. Трансформанта Лапласа от 1/ — е 2 равна
Функция F(p) не имеет особых точек на конечном расстоянии. Следова-
тельно, экспоненциальная трансформанта Фурье от е 2 будет у 2ir е 2 ,
так как функция Ф, будучи нечетной, исчезает в сумме Fl(jw)-^-F2(—./'<»).
ii
Поэтому трансформанта Фурье функции е 2 имеет такой же вид, как и она
сама, с точностью до коэффициента "у/тс.
Замечание. Иногда удобно использовать частоту v вместо круговой
частоты о). В этом случае нужно обратиться к формулам B6) и B7), кото-
которые определяют экспоненциальную трансформанту <b(v) для функции f(t)
и обратное преобразование.
Как и в предыдущем случае, если f(t) равна нулю при t < 0, преоб-
преобразования Фурье по косинусам и синусам будут соответственно:
х (v) = Г / (О cos 2wt dt, t > 0, C4)
о
оо
2О0 = J f(t)sm2wtdt, t>0; C5)
о
J
о
обратные преобразования:
оо
¦/(*) = 4 J <bl(v)cos2wtdv, t>0, C6)
о
оо
/@ = 4 Г Ф2 (v) sin 2Tzvt d-i, t > 0. C7)
о
Преобразование Фурье в случае двух переменных. Преобразование
Фурье легко обобщается на функции нескольких переменных. Приведем
формулы для случая двух переменных. Они представляют собой обобщение
формул B0) и B1):
+ ОО +ОО
fit, s) = ^ f f О(ш, ф)в"""-*'»*«*[.. C8)
— ОО —ОО
+oo
= J J f(t, s)e-J^'+^dtds. C9)
—ОО —ОО
*) Здесь Ф (л;) — функция вероятности ошибок. Она рассмотрена в п. 7.3.1.
2.2] ИНТЕГРАЛ ФУРЬЕ 113
Полагая w = 2itv, ty = 2ir|i, O(v, р) = 4ir2GBirv, 2it|x), получаем фор-
формулы, аналогичные B6) и B7):
+ 0О +0О
J J
— оо —оо
-boo +со
, |х)= J J f(t,s)e-2*iv+^dtds. D1)
— оо —оо
Соображения о симметрии, которые мы приводили раньше в отношении
одномерного преобразования, могут быть повторены и здесь в отношении
переменных (, ч, с одной стороны,- и s, |x — с другой.
2.2.9. Физическая реальность интеграла Фурье. Многочисленные
авторы отрицали физическую реальность интеграла Фурье, опираясь на сле-
следующие соображения.
Рассмотрим лампу, зажжен- » -ГЮ
ную в момент времени t = 0.
Излучение этого источника света,
равное нулю при t < 0 и став-
ставшее постоянным при t > 0, пред- """"
ставляет собой функцию времени,
которую можно заменить ее раз-
разложением в интеграл Фурье.
Следовательно, можно рассматри-
рассматривать свет, излучаемый источни-
ком, как бесконечное число ча- —^'~^?
стот, проходящих весь спектр и
существующих от t = — оо до рис 224.
t =-)- со. Предположим, что в мо-
момент t < 0 мы наблюдаем источник света через цветное стекло. Невероятно,
чтобы наложение частот, Дающее результат, равный нулю при t < 0, про-
продолжало давать тот же результат после исключения одной или нескольких
полос частот при случайном выборе фильтра. Следовательно, можно увидеть
свет прежде, чем мы зажжем лампу, если смотреть на нее сквозь цветной
фильтр. Этот явно нелепый результат приводил некоторых авторов к отри-
отрицанию физической реальности интеграла Фурье.
Приведенное рассуждение неверно. Мы проделаем его заново для случая
электрического фильтра, что позволит отчетливо выявить сделанное при
этом ошибочное предположение.
Имеется электрическое возмущение, равное единичной функции X(t).
Оно приложено к зажимам низкочастотного фильтра, который пропускает
без ослабления частбты только ниже 2itu>0. На выходе фильтра снимают
электродвижущую силу
"•о . > -^
1 , J_ Г Sinorf , 1 , 1 ,ч.
о
где через Si обозначен интегральный синус (см. п. 7.2.1).
На рис. 2.24 показана единичная функция Г (t) и „обрезанная" кривая
f(t), т. е. f(t) при конечном ш0. Так же как и в оптической задаче, ока-
оказывается, что напряжение возникает здесь до момента приложения электро-
электродвижущей силы — следствие опережает причину. Мы снова приходим к пара-
парадоксу, о котором говорили выше.
8 А. Анго
114
РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
(ГЛ. II
Но кроме гипотезы „интеграл Фурье имеет физический смысл" мы,
написав
ш0
1.1/*
sin Ы
1 . 1
+
или, что то же самое,
ш0
1 , 1 /*
сделали еще одно предположение: существуют фильтры с бесконечным
ослаблением вне полосы пропускания, такие, что изменение фазы либо
равно нулю, либо является линей-
О
Ослабление
Фаза
а>о ш О
Рис. 2.25.
СОп
ной функцией (о внутри полосы
пропускания (рис. 2.25). Однако
это предположение неверно.
Фильтр, характеристики ко-
которого даны на рис. 2.25, .назы-
.называется идеальным. В отличие от
идеального трансформатора, к ко-
которому можно заставить асимпто-
асимптотически приближаться реальную
физическую систему, идеальный
фильтр невозможен, это физи-
физический абсурд. Одна из лучших демонстраций этого абсурда — рассуждение,
приведенное в начале данного пункта.
Можно показать, что для реально осуществимого фильтра функция,
представляющая ослабление, и функция, представляющая изменение по фазе,
не независимы. В частности, обе функции, изображенные на рис. 2.25, не-
несовместны.
Итак, если приложить к фильтру, о котором уже говорилось, электро-
электродвижущую силу, представляемую единичной функцией, то мы обязательно
получим напряжение, начинающееся в момент времени t ^> О (рис. 2.26).
t7r
— ^-^ t'tg t
Рис. 2.26.
Иначе говоря, изменения фазы ср(ш) и амплитуды Л(ш), введенные прохо-
прохождением сигнала, имеющего характер единичной функции, через низкочас-
низкочастотный фильтр, таковы, что
при
Верхний предел интеграла — бесконечность, так как функция А (о>) не
может быть строго равна нулю, а может быть только близка к нулю при
значениях ш > ш0.
2.2]
ИНТЕГРАЛ ФУРЬЕ
115
Соображения, изложенные выше, приложимы и к оптическим примерам,
хотя конкретный анализ здесь часто весьма сложен *).
Добавим к сказанному, что, вообще говоря, можно осуществить фильтр
с характеристиками, указанными на рис. 2.25, если собрать его из беско-
бесконечного числа элементов. Распространение возмущения в нем будет длиться
бесконечно долго. В этом случае напряжение на выходе не сможет по-
появиться раньше приложения на входе электродвижущей силы.
2.2.10. Изучение диаграмм направленности. Кроме применения к изу-
изучению переходных режимов электрических цепей, преобразование Фурье
очень полезно при расчете диаграмм направленности излучателей радиоволн.
Рассмотрим излучающую рупорную антенну с плоским раструбом, по-
поверхность которого равна 5 (рис. 2.27). Положим, что вектор излучающего
электромагнитного поля в раструбе
имеет постоянное направление и
фазу. Тогда в плоскости рас-
раструба поле характеризуется ска-
скалярной функцией Е(х, у) коор-
координат точки по отношению к двум
прямоугольным осям Ох, Оу, рас-
расположенным в плоскости раструба.
Пусть Oz — нормаль, а Р —
весьма удаленная точка в направ-
направлении ОР, которое определяется
двумя углами а и р. Напряжен-
Напряженность результирующего электри-
электрического поля в точке Р обратно Рис. 2.27.
пропорциональна расстоянию ОР.
Произведение напряженности на это расстояние зависит только от направле-
направления, т. е. от углов аир. Можно получить диаграмму направленности
излучателя радиоволн, если отложить в направлении ОР отрезок, пропор-
пропорциональный этому произведению. Величина отрезка в тех направлениях,
где можно пренебречь членами порядка а3 и рз, равна функции р, опреде-
определяемой по формуле 1): '
х sin д+у sin Ь
sin a
dx dy.
Так как поле вне области S равно нулю, то можно распространить
двойное интегрирование на всю плоскость хОу. Тогда, считая, что
Sin a
= -т и
sin 3
мы видим, что диаграмма направленности описывается преобразованием Фурье
функции Е(х, у) (см. формулу D1)). И наоборот, если требуется получить
.*) В оптических задачах рассмотренный парадокс свидетельствует о том, что
имеется тесная связь между коэффициентом преломления, определяющим набег фазы,
и коэффициентом поглощения. Формулы связи были найдены в 1928 г. Р. Кронигом
и Г. Крамерсом в виде соотношений, связывающих вещественную и мнимую части
диэлектрической постоянной. Они называются дисперсионными соотношениями (см.
Л. Д. Ландау и Е. М. Лифшиц, Электродинамика сплошных сред, Гостехиздат,
1957).
В последние годы дисперсионные соотношения стали широко использоваться
при изучении взаимодействия элементарных частиц.
') О. О о u d e t, Les ondes electromagnetiques centlmetrlques, Paris, 1948, p. 154.
8*
116 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II
заданную диаграмму направленности, то распределение амплитуд в области S
можно получить с помощью обратного преобразования Фурье.
Пример. Положим, что поле у прямоугольного отверстия излучающей
рупорной антенны постоянно. Возьмем точку О в центре прямоугольника
и оси Ох и Оу, соответственно параллельные сторонам прямоугольника
с длиной а и Ь. Тогда непосредственно получаем
ли sin 3
sin a sin 8 \ Eab X
J
Ttasina 7i6sin
откуда диаграммы в плоскостях xOz и yOz будут соответственно описы-
описываться формулами
Eab sin и Eab sin v
где
7tasina tc6 sin 3
Направления нулевого излучения в этих плоскостях получаются из
формул
и — Къ, v = A/it (К, N — целые числа =^0),
иначе говоря,
в . sina = —К, sinC = -r-N
или же, поскольку синус приближенно равен дуге, <х = — К, $ — -rN.
Замечание. В большом количестве случаев раструбы излучающих
рупорных антенн прямоугольны, как в рассмотренном примере; кроме того,
Е не зависит от координаты у, а только от координаты х. Тогда диаграмма
излучения в плоскости хОу получается из формул B6) и B7) преобразова-
преобразования Фурье с одной переменной :).
ЛИТЕРАТУРА К ГЛАВЕ II
1. Ф и х т е н г о л ь ц Г. М., Курс дифференциального интегрального исчисления
т. Ill, Физматгиз, 1960.
2. Смирнов В. И., Курс высшей математики, т. П. Физматгиз, 1962.
3. Т о л с т о в Г. П., Ряды Фурье, Физматгиз, 1960.
') J. F. Ramsay, Fourier transforms in aerial theory, The Marconi Review,
№ 83—88.
ГЛАВА III
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
3.1. СКАЛЯРНЫЕ ВЕЛИЧИНЫ. ВЕКТОРНЫЕ ВЕЛИЧИНЫ. ОПРЕДЕЛЕНИЯ
Скалярные величины
Величины называются скалярными (скалярами), если они после выбора
единицы измерения полностью характеризуются одним числом. Примерами
скалярных величин являются угол, поверхность, объему масса, плотность,
электрический заряд, сопротивление, температура.
Следует различать два типа скалярных величин: чистые скаляры и псев-
псевдоскаляры.
3.1.1. Чистые скаляры. Чистые скаляры полностью определяются одним
числом, не зависящим от выбора осей отсчета. Примером чистых скаляров
могут служить температура и масса.
3.1.2. Псевдоскаляры. Как и чистые скаляры, пгевдоскаляры определяются
с помощью одного числа, абсолютная величина которого не зависит от выбора
осей отсчета. Однако знак этого числа зависит от выбора положительных
направлений на осях координат *).
Рассмотрим, например, прямоугольный параллелепипед, проекции ребер
которого на прямоугольные оси координат соответственно равны ах, ау, az,
bx, by, bz, cx, cy, сг. Объем этого параллелепипеда определяется с помощью
определителя
а'х ау
Ьх Ьу Ъг
сх су
абсолютная величина которого не зависит от выбора прямоугольных осей
координат. Однако, если переменить положительное направление на одной из
осей координат, то определитель изменит знак. Объем — это псевдоскаляр.
Псевдоскалярами являются также угол, площадь, поверхность. Ниже (п. 5.1.8)
мы увидим, что псевдоскаляр представляет собой в действительности тензор
особого рода.
Векторные величины
3.1.3. Ось. Ось — это бесконечная прямая, на которой выбрано поло-
положительное направление. Пусть хх'— такая прямая, а направление от х к х'
*) Иными словами, псевдоскаляры есть величины, которые изменяют знак при
переходе от правой системы координат к левой.
Иногда псевдоскалярами называют величины, полностью характеризующиеся од-
одним числом, которое зависит от выбора системы координат (проекция вектора, ста-
статический момент и др.), — см., например, [9], стр. 42.
118
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
[ГЛ. III
Рис. 3.1.
считается положительным. Рассмотрим отрезок АВ на этой прямой и поло-
положим, что число, измеряющее длину АВ, равно а (рис. 3.1). Тогда алгебраи-
алгебраическая длина отрезка АВ равна а.
алгебраическая длина отрезка ВА
равна — а.
Если взять несколько параллель-
параллельных прямых, то, определив положи-
положительное направление на одной из них,
мы тем самым определяем его на осталь-
остальных. Иначе обстоит дело, если пря-
прямые не параллельны; тогда нужно спе-
специально уславливаться относительно
выбора положительного направления для
каждой прямой.
3.1.4. Направление вращения.
Пусть хх'—ось. Вращение относи-
относительно оси хх' назовем положитель-
положительным или прямым, если оно осуще-
осуществляется для наблюдателя, стоящего вдоль положительного направления оси,
справа и налево (рис. 3:2). В противном случае оно называется отрицатель-
отрицательным или обратным.
3.1.5. Прямые и обратные трехгранники. Пусть Oxyz— некоторый
трехгранник (прямоугольный или непрямоугольный). Положительные направ-
направления выбраны на осях соответственно от О к х, от О к у и от О к z.
Рассмотрим вращение вокруг оси Oz полуплоскости xOz. приводящее ее
к совмещению с полуплоскостью yOz (угол поворота меньше it). Если при
этом направление вращения по-
положительно по отношению к
оси Oz, то говорят, что трехгран-
трехгранник Oxyz расположен положи-
положительно (рис. 3.3, а). В противном
случае трехгранник расположен
отрицательно (рис. 3.3, б).
При определении располо-
расположения трехгранника основное
значение имеет порядок следова-
следования букв х, у, z. Действительно,
трехгранники Oxyz, Oyzx,
Ozxy имеют одно расположе-
расположение, а трехгранники Oxzy, Oyxz, Ozyx — обратное. Одна перестановка
букв х, у, z меняет расположение трехгранника, две перестановки нэ
меняют.
3.1.6. Векторы. Векторная величина зависит от двух элементов разной
природы: алгебраического элемента — числа, измеряющего длину (модуль)
вектора, и геометрического элемента — направления вектора. Различают три
разных типа векторов. Каждый из них объединяет совокупность векторов
с одинаковыми свойствами.
Связанный вектор. Для определения связанного вектора АВ требуется
знать: его линию действия {хх'), направление на этой линии (от х к х'),
его начало (Л) и неотрицательное число, измеряющее длину а отрезка АВ
{рис. 3.4.). Это число а называется модулем вектора.
Если поместить вектор АВ на уже ориентированную ось, то алгебраи-
алгебраическая длина этого вектора равна его модулю, взятому со знаком плюс или
Рис. 3.3.
8-1)
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ
119
минус, в зависимости от того, имеют ли вектор и ось одинаковое направле-
направление или нет.
Скользящий вектор. Определение остается таким же, как и в преды-
предыдущем случае, если исключить требование о закреплении начала вектора.
Оно может находиться в любой точке оси хх' (рис. 3.5). Силы, рассматри-
рассматриваемые в статической механике, представляют собой скользящие векторы.
Рис. 3.4.
Рис. 3.5.
В самом деле, нельзя нарушить равновесие твердого тела, перемещая точку
приложения силы' вдоль линии действия этой силы.
Свободный вектор. Такой вектор определяется положительным направ-
направлением линии действия и модулем а (рис. 3.6). Два одинаково направленных
и равных по длине вектора называются эквиполентными. Свободные векторы
равны, если они эквиполентны. Обычно свободный вектор
обозначают через а.
В начале этой главы мы рассматриваем главным обра-
образом свободные векторы, но, когда речь пойдет о векторах
поля (п. 3.2.5. и следующие), будут иметься в виду свя-
связанные векторы.
Единичный вектор. Это вектор, модуль которого
равен единице. Обычно его называют ортом. Орт вектора
или оси имеет всегда то же направление, что и рассма-
рассматриваемый вектор или ось. Единичные векторы коорди-
координатных осей Ox, Oy, Oz обозначаются соответственно
через i, j, ft.
Полярный вектор. Осевой вектор. Некоторые век-
векторы не зависят от изменения направления, выбранного
на осях координат в качестве положительного (например, сила, скорость,
вектор электрического поля). Векторы, обладающие указанным свойством,
называются полярными.
Другие векторы, напротив, меняют знак, если изменить направление, вы-
выбранное на осях координат в качестве положительного. Такие векторы на-
называются осевыми.
Полярные и осевые векторы существенно отличаются друг от друга по
своей природе. Лишь полярные векторы являются векторами в чистом виде.
Ниже (п. 5.1.10) мы увидим, что осевой вектор представляет собой антисим-
антисимметричный тензор второго порядка. В случае трехмерного пространства (только
такое пространство и рассматривается нами) число составляющих этого тен-
тензора равно 3, поэтому его можно принять за вектор. В четырехмерном про-
пространстве этот особый тензор имел бы 6 составляющих, тогда как полярный
вектор только 4, т. е. там исключена возможность смешения.
Рис. 3.6.
120 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Отсюда следует, что векторное равенство может иметь место либо только
между полярными векторами, либо только между осевыми. Если, например,
вектор, являющийся первым членом векторного равенства,—осевой, той вто-
второй член этого равенства тоже должен быть осевым вектором. Такая одно-
однородность, присущая векторному исчислению, позволяет обнаруживать вычисли-
вычислительные ошибки.
3.1.7. Положительное расположение трех векторов а, Ь, с. Говорят,
что три вектора а, Ъ, с расположены положительно (отрицательно), если
расположен положительно (отрицательно) трехгранник, имеющий ребра,
параллельные этим векторам, таким же образом ориентированные и взятые
в том же порядке.
3.1.8. Угол между двумя векторами а и Ъ. Это угол, не превосхо-
превосходящий it, на который нужно повернуть вектор а, чтобы совместить его с век-
вектором, эквиполентным Ь, начало которого совпадает с началом вектора а.
Он обозначается (а, Ь).
Операции над векторами
3.1.9. Произведение вектора а на скаляр/. Результат умножения век-
вектора а на скаляр / — это вектор с модулем, равным fa, параллельный век-
вектору а, направленный в ту же сторону, что и а, при положительном /ив про-
противоположную при отрицательном /.
В частности, любой вектор а равен произведению его модуля |в| — ска-
скаляра — на орт и направления вектора а, т. е.
а = \а\а или а = аи. . A)
3.1.10. Составляющие вектора. Введем три оси прямоугольных коор-
координат и рассмотрим геометрические проекции (компоненты) вектора а на
эти оси:
ах, ау, аг.
Имеем
а = ах + ау-\-аг. B)
Используя i — орт оси Ох, можем написать ах = 1ах (ах — число, измеряю-
измеряющее алгебраическую длину ах по направлению оси Ох; следовательно, это
число положительно, если ах и i имеют одинаковое направление, и отрица-
отрицательно в противном случае). Аналогично
ay = jar аг = каг.
Таким образом,
a = iax-\-jay-\-kaz.
Числа ах, ау, аг называются составляющими вектора а относительно соот-
соответствующих осей координат *).
3.1.11. Сложение векторов. Сумма нескольких векторов а, Ь р
определяется следующим образом.
Из произвольной точки О проводим вектор ОА, эквиполентный вектору а,
затем из точки А проводим вектор АВ, эквиполентный вектору Ь, и т. д.
до получения точки Р — конца вектора, эквиполентного вектору р (рис. 3.7).
*) Числа ах, ау, аг называются также проекциями (алгебраическими проекциями)
и координатами вектора относительно соответствующих осей координат.
3,1]
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ
121
Вектор OP представляет собой сумму векторов а, Ь, ..., р. Эта сумма.
очевидно не зависит от выбора точки О. Следовательно, вектор суммы s так-
также представляет собой свободный вектор.
Векторное сложение записывается
в виде
C)
Из геометрического определения сум-
суммы векторов непосредственно следует,
что эта операция коммутативна, т. е.
и ассоциативна, т. е.
-*-
Составляющая по оси Ох вектора
суммы s векторов а, Ь, ..., р равна
сумме составляющих этих векторов отно-
относительно той же оси:
Рис. 3.7.
3.1.12. Скалярное произведение. Скалярное- произведение двух векто-
векторов а и Ъ — эт?о число, равное произведению трех величин а, Ь и cos (а, Ь);
оно обозначается через а • Ъ.
Легко заметить, что скалярное произведение коммутативно: а • Ь = Ь ¦ а
и дистрибутивно: (c-j-й) • с = а ¦ с~\-Ь • с.
Вопрос об ассоциативности скалярного произведения отпадает, тай как
формула (а • Ь) • с не имеет смысла; кроме того, очевидно, неверно равенство
(а • Ь) с = а (Ь ¦ с).
Замечание 1. Если скалярное произведение двух ненулевых векторов
равно нулю, то эти векторы ортогональны. Действительно, cos (а, й),= 0;
следовательно, (а, 6) = у.
Замечание 2. Пусть хх' — ориентиро-
ориентированная ось, аи — единичный вектор этой оси
(рис. 3.8). Тогда скалярное произведение лю-
любого вектора а на а равно проекции вектора а
на ось хх':
а ¦ и = а cos (а, а).
D)
Рис. 3.8.
Замечание 3. Скалярное произведение
вектора на самого себя равно квадрату модуля
этого вектора:
а-а — а2.
Замечание 4. Если через i, j, k обозначить единичные векторы осей
координат, то
Скалярное произведение в декартовых координатах. Пусть ах,
b Ьг — соответственно проекции на оси Ox, Oy, Oz векторов
х ау, by, аг
а и Ь. Имеем
а ¦ Ь = {aj -+- a
azk) ¦ {bxi + byj -+- bzk).
122 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Учитывая дистрибутивность скалярного произведения и замечание 4, по-
получим
а ¦ Ь = axbx + ауЬу + агЬг. E)
Замечание 5. Используя формулу E) и определение скалярного про-
произведения, получим выражение для косинуса угла между двумя векторами а,
Ь через проекции этих векторов:
cos (a, b) = —-=
3.1.13. Векторное произведение. Векторным произведением двух век-
векторов а, Ь называют вектор с, длина которого равна aft sin (а, Ь) и который
перпендикулярен обоим векторам а и Ь, причем векторы а, Ъ и с распо-
расположены положительно.
Векторное произведение обозначают так: oXi = t.
Замечание. Если ни один из векторов а и ft не равен нулю, то вы-
выражение аУ(Ь = 0 означает, что линии действия векторов параллельны, так
как sin (а, й) = 0. ¦ '
Модуль вектора с численно равен площади параллелограмма, построен-
построенного на векторах, эквиполентных а и Ъ, проведенных через любую точку О
пространства.
Это замечание позволяет дать более наглядное определение векторного
произведения. Пусть а и Ъ — два вектора. Проведем через точку О векторы
ОА и ОВ, эквиполентные а и Ь (рис. 3.9).
Тогда векторное произведение с векто-
векторов а и Ь будет определяться следующим
образом. •
Модуль вектора с равен числу, изме-
измеряющему площадь параллелограмма ОАРВ.
Линия действия этого вектора перпенди-
перпендикулярна плоскости ОАВ, а направление
его таково, что поворот на угол, не пре-
вышающий тс, совмещающий О А с ОВ,
происходит в положительном относи-
относительно с направлении.
Использование векторного произведе-
произведения двух векторов ОА и ОВ позволяет
легко определить алгебраическую площадь треугольника ОАВ. Ориентируем
плоскость ОАВ, иначе говоря, выберем в этой плоскости положительное
направление вращения. Алгебраическая площадь треугольника ОАВ равна
половине алгебраической длины векторного произведения ОА X ОВ, отсчи-
отсчитанной вдоль оси, перпендикулярной плоскости ОАВ и ориентированной таким
образом, чтобы выбранное направление вращения было для нее положитель-
положительным (см. п. 3.1.4).
Векторное произведение в декартовых координатах. Так как век-
вектор с = аУ(Ь перпендикулярен плоскости АОВ, а модуль его равен площади
параллелограмма ОАРВ, то проекция векторного произведения с на Ох равна
площади проекции параллелограмма на Oyz. Следовательно,
По аналогии находим
— «А'
3.11
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ
123
т. е.
aX b = i(ауЬг — агЬу) + j(azbx — axbz) + k(axbv — aybx).
Это выражение можно записать в более симметричной форме:
I j k
ахау
F)
G)
Эта формула равносильна соотношению
I j k i
Перечислим основные свойства векторного произведения.
Эта операция антикоммутативна, т. е. а X b = — Ь X о,. В самом деле,
обе тройки векторов а, Ь, с и Ь, а, с образуют противоположно располо-
расположенные трехгранники (см. п. 3.1.5).
Далее, векторное произведение не ассоциативно. Действительно, равенство
(а X Ь) X с — а X (Ь X с), вообще говоря, неверно, так как направления век-
векторов, записанных в левой и правой частях этого соотношения, отличаются
друг от друга. Однако векторное произведение — операция дистрибутивная,
т. е. справедлива формула
k
Замечание 1. Векторные произведения ортов координатных осей со-
соответственно равны: iXJ=k, JXk = i, kXi = j-
Замечание. 2. Момент вектора а относительно точки О равен вектор-
векторному произведению г X Л. Здесь г — вектор, имеющий начало в точке О, а
конец — в любой точке на линии действия вектора а.
3.1.14. Смешанное произведение трех векторов. Смешанным произве-
произведением трех векторов называется скаляр '
а* ФХ с).
Применяя формулы для скалярного и векторного произведений в декар-
декартовых координатах, получаем
т. е.
— фусг — Ьгсу) ах + фгсх — Ьхсг) ау + {Ьхсу — Ьусх) аг,
(8)
Мы видим, что смешанное произведение трех векторов численно равно
объему параллелепипеда, построенного на трех векторах ОА, ОВ, ОС
(с общим началом в точке О), эквиполентных векторам а, Ь, С. Объем
положителен или отрицателен в зависимости от того, положительно или
отрицательно расположены эти три вектора. Следовательно, роль векторов,
составляющих смешанное произведение, совершенно одинакова и
а ¦ ф X с) = Ь ¦ (с X а) = с ¦ (а X Ь),
124 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Первая строка показывает, что при круговой перестановке векторов
а, Ь, с их смешанное произведение не меняется, вторая — что можно менять
местами знаки скалярного и векторного произведений. Последнее обстоя-
обстоятельство служит обоснованием для упрощения обозначения смешанного
произведения: оно записывается в виде (abc) или аЬс.
3.1.15. Двойное векторное произведение трех векторов. Двойное
векторное произведение трех векторов выражается формулой
аХ(бХс) = (а-с)й — (а-Ь)с. (9)
В самом деле, например, проекции на ось Ох векторов левой и правой
части этой формулы соответственно равны
(ахСх + аусу-\- агсг)Ьх — (axbx + ayby-+¦ azbz) cx.
Легко проверить тождественность этих двух выражений.
Используя формулу (9) и правила перестановки векторов, составляющих
смешанное произведение, получим <
(а X Ь) ¦ (с X d) = (а ¦ с) (Ь ¦ О) — (а • О) (Ь ¦ с), A0)
A1)
3.2. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
Дифференцирование
3.2.1. Производная вектора. Производная точки. Допустим, что
каждому значению переменной t соответствует определенный вектор а.
В таком случае говорят, что этот вектор является функцией переменной t
и записывают его в виде a (t). Дадим переменной t приращение Д? и рас-
рассмотрим вектор &a = a{t-\-kt) — a(t). Если при Д?, стремящемся к нулю,
модуль вектора Да стремится к нулю, то a(t) есть непрерывная функция
от t. Предел вектора —тт- называется производной вектора a (t) no t.
Производная вектора a(t) обозначается через -тг или a' (t). Она равна
dax dav daz
i -^—h j —prr + k —vt- ¦ Аналогично определяется вторая производная
вектора и т. д.
Если вектор а зависит от нескольких переменных т, 6 то можно
также определить частные производные а различных порядков.
Если каждому значению переменной t соответствует точка простран-
пространства М, то говорят, что точка М есть функция от t. Для наглядности
запишем ее в виде M{t). Придадим переменной t приращение Д? и рас-
рассмотрим вектор
Ы\Л = М (t + ДО — М @ *).
Если при Д?, стремящемся к нулю, модуль этого вектора тоже стремится
к нулю, то M(t) есть непрерывная функция от t. Предел вектора -г^—
*) Здесь использована запись, введенная Грассманом: вектор АВ обозначается
с помощью выражения В — А.
3.2] ¦ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 125
называется производной точки M{t) no t:
dM .. AM
Iim
Используя определение производной первого порядка, можно определить
производные точки М высших порядков. Если точка М является функцией
нескольких независимых переменных, то для нее определяются также и
частные производные.
Замечание. Понятие производной точки сводится к понятию произ-
производной вектора. Для Этого достаточно зафиксировать любую точку О.
Производная точки M(t) представляет собой производную вектора ОМ.
3.2.2. Производная вектора по другому вектору. Даны два вектора
а и Ъ. Производной вектора а по вектору Ь называется вектор
да , . да . . да ,
\ дх х * ду у ' дг г
который обозначают через
da^
db *
Проекции этого вектора на оси Ox, Oy, Oz соответственно равны:
х
дх °х~т~ ,ду °у^ дг
дпу дпу дпу
ь+ь +
даг . даг . . даг
3.2.3. Основные формулы дифференцирования.
Производная суммы. Пусть
Очевидно,
s' =
Производная произведения вектора на число. Пусть
Ь = па.
Очевидно,
V = па'.
Следовательно, если п, т g — числа, то производная вектора
u = na-\-mb-\- ... + gp
равна
и' = па' + тЪ' + ... +gpf- A3)
Производная произведения векторной и скалярной функций.
Пусть f(t) и a(t) — скалярная и векторная функции от t и в = fa. Тогда
Аи _ (f + Af)(a+ba)—fa _ , Да . А/ , АаД/
"дг ~ : и ~I ~\t"+ а дг "г At, •
В пределе получим
«'=/« Л-fa. A4)
126 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Производная скалярного произведения. Пусть a(t) и b(t) — две
векторные функции и f = a-b — их скалярное произведение. Рассмотрим
Д/ _ (g+Afl)-(ft + Aft) — а-Ь _ Д& Да Да • ЛЬ
If— ; ~~Tt ~~а .ы~т~0' "дТ д7~-
Переходя к пределу, имеем
f' = ab' + af Ь. A5)
Производная векторного произведения. Аналогично предыдущему
получим, что производная векторного произведения с = а X Ь равна
xb. A6)
В этой формуле следует внимательно следить за порядком множителей, так
как by а' = — a' Xb.
Теорема 1. Пусть а — произвольный переменный вектор. Тогда
Для вывода этой формулы достаточно продифференцировать тождество
Теорема 2. Если переменный вектор а удовлетворяет равенству
а X а' = 0, то он параллелен одному и тому же направлению.
Дифференцируя отношение -~г, получаем \а\а ~]у а ; но
|а'|'= а'а , и, учитывая (9), имеем
/ а V [ а \2 а' — (а • а') а _ (а X а') X а
l|o|j \а\3 ~ \а\3
Согласно предположению правая часть равенства равна нулю и, значит,
-—-= const.
Следовательно, орт направления а постоянен, т. е. направление переменного
вектора а неизменно.
3.2.4. Интеграл от вектора. Дан переменный вектор a(t):
Обозначая через t0 и tx два значения t, имеем
<,' «, /i t,
j a(t)dt = i j axdt-\-j j aydt-\-k f azdt.
to h . t, t.
Функции точки
В математической физике часто рассматривается величина, которая
зависит не только от положения точки, т. е. от ее координат х, у, г, но
и еще от какой-либо другой переменной, в большинстве случаев от времени.
Если рассматриваемая величина является числом (вектором), то принято
говорить, что речь идет о скалярной (векторной) функции точки. В этих
случаях говорят также, что в рассматриваемой области пространства задано
скалярное или векторное поле.
Например, плотность заряда в различных точках изолированного на-
наэлектризованного тела представляет собой скалярную функцию точки;
3.2]
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
127
электрическое поле, которое создается этими зарядами в различных точках
тела, представляет собой векторную функцию точки. Электрические заряды
создают скалярное поле плотности и векторное поле электрических сил.
Если электрические заряды изменяются в зависимости от времени, то ска-
скалярное и векторное поля являются не только функциями координат рассма-
рассматриваемой точки, но также и функциями времени. •
Наиболее важные поля характеризуют следующие три функции:
1) градиент — векторная функция, аргументом которой является скалярная
функция точки;
2) дивергенция — скалярная функция, аргументом которой является
векторная функция точки;
3) вихрь — векторная функция, аргументом которой является векторная
функция точки.
3.2.5. Градиент. Дана скалярная функция f(x, у, г). Градиентом этой
функции называется вектор с координатами
df df df_
~дх"' ~ду' ~дг-
Он обозначается через grad /. Следовательно, согласно определению можно
написать
Пусть М(х, у, г) и M-\-dM — бесконечно близкие точки поверхности S
(рис. 3.10). Скалярное произведение grad/-c?Al равно df. Действительно
Отношение
df
\dM\
A8)
называется производной скалярной- функции / в точ-
точке М по направлению dM. Формула grad / • dM = df показывает, что эта
ffrad' Р
Рис. 3.10.
Рис. 3.11.
производная равна проекции вектора grad / на направление dM, так как
df _ dM
JdM\~~\dW\'graaf-
3.2.6. Нормальная производная. Рассмотрим нормаль в точке М
к некоторой поверхности Е, проходящей через эту точку (рис. 3.11). Про-
Производная от / в точке М по направлению нормали называется нормальной
производной от / для поверхности Е. Если п—единичный вектор нормали,
то эта производная равна grad / • п, т. е. проекции вектора grad / на
нормаль п.
128 ВЕКТОРНОЕ ИСЧИСЛЕЙИЕ [ГЛ. III
3.2.7. Поверхности уровня. Поверхности уровня определяются равен-
равенством f(x, у, 2) = const. Уравнение поверхности уровня, проходящей через
точку (х0, yQ, zQ), имеет вид
f(x, у, z) = f(x0, у0, z0).
Оно геометрически представляет одну поверхность, если функция f(x, у, z)
однозначна, что почти всегда и встречается в физике. Вектор grad / в каждой
точке нормален к рассматриваемой поверхности уровня, проходящей через
эту точку.
Действительно, формула A8) при любом перемещении dM точки М
дает grad / • dM = df. Так как на поверхности уровня / неизменно, то при
любом перемещении dM точки М по этой поверхности df = 0. Аналогичное
заключение можно сделать в случае, когда точка М перемещается по каса-
касательной плоскости, проведенной к поверхности уровня в этой точке.
Следовательно, dM и grad / перпендикулярны друг другу. Так как вектор
dM — произвольный вектор на касательной плоскости, проведенной в точке М
к поверхности уровня, то высказанное утверждение доказано.
3.2.8. Смысл вектора grad/. Вектор grad / полностью описывает
поведение функции / в окрестности рассматриваемой точки М. В частности,
самое быстрое изменение f происходит при перемещении по нормали
к поверхности уровня. Это максимальное изменение определяется пр величине
и направлению вектором grad /.
Для того чтобы представить поле вектора grad/, построим поверхности
уровня
f(x, у, z) = kc,
где k=l, 2 а с — достаточно малая постоянная.
Рассмотрим две поверхности уровня Sj и 52, соответствующие двум
значениям k: п и /t —J— 1. Пусть М — точка поверхности Sx и d — расстояние
от М до 52. Вектор grad / будет в точке М нормален к Sv направлен
в сторону возрастающих / и по модулю приближенно равен -г-. Следова-
Следовательно, |grad/| будет тем больше, чем ближе
друг к другу рассматриваемые поверхности.
Замечание. Как показывает формула
grad / • dM = df, вектор grad / не зависит от
выбора осей (см. также п. 3.3.7).
3.2.9. Силовые линии. Кривая, направле-
направление которой в каждой точке М совпадает с на-
направлением вектора grad /, соответствующего
этой точке, называется силовой линией. Вектор-
Векторное уравнение силовой линии: grad / X dM = 0.
Ее скалярные уравнения:
df df df
дх ду дг
Рис. o.lz. dx dy rfz
Следовательно, силовые линии представляют собой ортогональные траектории
к поверхностям уровня:
f(x, у, z) = const.
Силовая трубка — это поверхность, описанная силовой линией, переме-
перемещающейся вдоль замкнутого контура С (рис. 3.12).
3.21 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 129
3.2.10. Градиент сложной скалярной функции. Если скалярная функция
f(m, п, . . .) является функцией нескольких скаляров т., п которые
сами представляют собой функции координат х, у, г, то имеет место
формула:
Действительно,
но
dm = grad m • dM, dn = gradn ¦ dM.
Отсюда в силу произвольности вектора dM вытекает справедливость
формулы A9).
Сравнив эту формулу с формулой для полного дифференциала
d<? = ~- dx-\--j?- dy-\--^dz, убедимся, что знак grad ведет себя точно
так же, как знак дифференциала.
Применяя формулу A9) к функциям f {т, п) = т-\-п и f (т, n) — mnt
получим
grad (m + n) = grad m + grad n,
grad mn = т grad n-\~n grad т.
Далее, из соотношения grad / • dM = df следует, что уравнение
grad m = grad n
равносильно уравнению
m = «-|- const.
3.2.11. Дивергенция и вихрь. Дана векторная функция а точки
М (х, у, г). Пусть ах, ау, аг — проекции вектора а на соответствующие
оси координат.
Дивергенция. Дивергенция вектора а — это скалярная величина
да г dav да.
Вихрь. Вихрь вектора а — это векторная величина
да, da
Следовательно, проекции вектора rota1) равны:
даг дау
на ось Ox-.-jy- 5Г
/-> даг
на ось Оу : -—-
даг
дг дх
даг
на ось Oz : -~ —
дх ду
Замечание. Дивергенция представима в виде суммы следующих
скалярных произведений:
, да , . да . . да
') Иногда вместо rot а пишут curl a.
9 а. Анго
130 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ • [ГЛ. Ill
Вихрь представим в виде суммы следующих векторных произведений:
3.2.12. Оператор Лапласа. Оператором Лапласа (лапласианом) называют
Д ~ Ix2"^ Ну2 ^~ "Si2"'
Если применить его к скалярной функции, то
M-Vf I d2f I d2f
J ~ дх2 "^ ду2 ~г дг2 '
Название оператора происходит от уравнения Лапласа, которое записывается
в виде Д/ = 0.
Применим оператор Лапласа к вектору а. Имеем
дд_ д2а | д2а . д2а
~~ дх2 "г" ду2 ^^ дг2 '
Так как¦
а = iax -4- jay ¦+- kaz,
то для вектора Да получаем следующее выражение:
?Mi — i?bax-i-j?bay + kbaz.
3.2.13. Символический вектор набла (оператор Гамильтона). Опера-
Оператором Гамильтона называют векторный оператор
дх ^J ду
Применяя его к скаляру /, получаем *)
^ ^ ^ B3)
Скалярное произведение векторов V и а равно:
дах da,, да.
дах da,, да,
V- a = -r-^-4--^- + -x-L = diva. B4)
дх * ду * дг к '
Векторное произведение векторов V и а равно:
да, dav \ I да. да,
B5)
Поэтому для функций grad/, diva и rota часто используются следующие
обозначения:
7/, V • а, V X о-
Аналогично получаем
где скалярный оператор V2 = V • V обозначен через Д.
*) При выполнении действий по правилам, установленным ранее для обычных
д д д
скаляров и векторов, под „произведением" символов -^—, -^—, -^— на скаляр
. . . дч> дш dv
(х, у, г) будем понимать соответственно скаляры -^—, -~, -—-.
tH ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 131
Далее, выражение A2) для производной вектора а по вектору Ь можно
переписать в виде
т. е.
ф
При расчетах следует помнить, что символический вектор V обладает
не только свойствами вектора. В самом деле, рассмотрим произведение
V X (с X Ь).
Применяя к нему формулу (9), получим
V х (с X Ь) = (V • Ь) а — (V • с) Ь
или, возвращаясь к обычным обозначениям,
rot (с X b) = au\vb — Ь dive,
а это неверно.
Если применить ту же самую формулу (9) к произведению
V X (V X с),
то получим
V X (V х а) = V (V • а) — (V • V) а
или в обычных обозначениях
rot rot a = grad div с — До.
Эта формула верна (см. п. 3.2.14).
Неправильность первого результата объясняется тем, что вектор V, кроме
векторных свойств, обладает также дифференциальными свойствами, которые
не проявлялись, пока нужно было умножать на вектор V какое-либо число,
вектор или линейную комбинацию векторов, однако проявились при умно-
умножении на вектор V произведения Лекторов *).
Действительно, рассмотрим снова произведение V X (а X Ь). Согласно
формуле B2) имеем
или, ограничиваясь записью только первого члена,
Применим теперь формулу (9):
,, .. да
*) Встреченные затруднения можно обойти, если ввести дополнительное ограни-
ограничение при использовании символического вектора V (см., например, [4]). В этом
случае с помощью V можно получить все приведенные ниже формулы для векторных
и скалярных функций точки.
9»
132 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. Ш
Далее получаем последовательно:
(*' ' Ж") «+•••=« div 6 = с (V -ft),
откуда
VX(aXb) = a(V -b) — Ь(Ч ¦ a) + (b- V)c — (a
или в обычных обозначениях
rot(aX 6) = adivft —6diva + 4| —4^--
do da
Справедливость этого результата мы проверим в следующем пункте.
3.2.14. Наиболее употребительные формулы.
Градиент скалярного произведения.
grad(a-6) = aXrotft-f-6Xrota + -^- + —. B6)
Проекция левой части формулы B6) на ось Ох равна
дак дау даг dbx dby дЪг
Проекция правой части формулы B6) на ось Ох равна
/дЬу дЬЛ /dbx dbz\ I дау дах\
ay\~~dx~~~dy~I~aA~di Wl^byVdJc Wl
дах даг \ дах дах дах dbx dbx дЬх
)+Ь{Ь + Ь + + +
Нетрудно убедиться, что полученные выражения для проекций совпадают.
То же самое, очевидно, имеет место для проекций на оси Оу и Oz.
Дивергенция произведения скалярной функции на векторную.
B7)
Действительно,
d(fax) d(/ay) d(faz)
дах дау daz \ df df df
= / div a -+- a • grad /.
Дивергенция векторного произведения.
div(aXb) = b-rota — a-iotb. B8)
Действительно,
дЬ
дг
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 133
I"
|. Учитывая свойства смешанного произведения и формулу B2), получаем
div(cX6)=& • (i X -|f + • ..)'— с • (/ X 4| + • • .) = Ь • roto — с • rotft.
Дивергенция градиента.
div(grad/) = A/. B9)
Действительно,
<l Дивергенция вихря.
{ div(rota) = 0. C0)
! Действительно,
| д I daz day \ d I dax даг \ d I day dax \
" ~d~x\dy dTI+'bTVdi ~ЫГ) ~^ ~dT \dx ЬУ)~
) Дивергенция лапласиана.
; div(Aa) = A(diva). C1)
* Действительно,
t
Используя определение Лапласиана, придадим этому выражению следую-
щий вид:
дхг [ дх ~^~ ду ~*~ дг } ~T~ ду* { дх ^~ ду + дг
Вихрь градиента.
rot (grad /)=0. C2)
Действительно,
Вихрь произведения скалярной функции на векторную.
rot(/a) = grad/Xa + /rotc. C3)
Действительно,
= grad / X a -f- / rot с.
Вихрь векторного произведения.
^|- — -Ц-. C4)
134 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. Ill
Проекция, например, на ось Ох левой части равенства равна
-^ {axby — aybx) — -^ (агЬх — ахЬг).
Проекция на ось Ох правой части равенства равна
Ьх дЬу
дах
~дх~
bx
ьх
(да
+ ¦
дпу
Ьу +
-Г-ЗД +
и 2 1
ddv *
п
дг °*
дЪх
дх
ах~
дЪ
дЬх .
дг г'
Легко проверить, что обе эти проекции равны.
Вихрь вихря.
rot rot a = graddivc — До. C5)
Проекция на ось Ох вектора rot А равна
дАг дАу
ду дг
Если А = rot а, то
dav даг
Л*— дх ду '
. дах даг
У дг дх
Следовательно, проекция вектора rot rot с на ось Ох равна
дгау дгах дгах дгаг д 1дах дау даг\
дх ду ду2 дг2 ' дх дг дх \ дх * ду ' дг ) х~
Аналогично доказывается равенство проекций векторов обеих частей фор-
формулы C5) на оси Оу и Oz.
3.2.15. Смысл вектора rota. Рассмотрим вращательное движение ма-
материальной точки с угловой скоростью w вокруг некоторой оси. Из меха-
механики известно, что линейная скорость точки V связана с со и радиусом-век-
радиусом-вектором точки г соотношением
V=t»Xr.
Отсюда непосредственно получаем
rot V = 2 а.
Перейдем к более общему случаю. Рассмотрим поле скоростей текущей
жидкости V{x, у, z, t). Движение малого элемента жидкости складывается
из параллельного переноса, поворота как твердого тела и деформаций.
Можно показать, что и в этом случае вихрь скорости V равен удвоенной
угловой скорости вращения w элемента жидкости. •
3.2.16. Скалярный потенциал. Любая векторная функция точки М, вихрь
которой тождественно равен нулю, может рассматриваться как градиент не-
некоторой скалярной функции точки М.
Действительно, пусть вихрь вектора a = iax-\- jay-\-kaz равен нулю, т. е.
даг дйу дах даг дау дах
ду дг ' дг дх ' дх ду
C6)
3.2] ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
Введем функции / с помощью соотношения
~д~х~ ах'
Докажем, что тогда из равенств C6) следует
df__ dJL —
ду У дг г'
Согласно формуле C7)
X
п
. Z),
135
C7)
f— f a
где ср — произвольная функция. Продифференцируем C8) по у:
C8)
о
ду
Учитывая третье равенство из C6), находим
X
или
М- = а —а
~ду~'
' (У. г)
dy
? (У. г)
-Ту
Точно так же, дифференцируя равенство C8) по z и применяя второе
равенство C6), находим
df
(У. г)
= <) дг •
Далее, функцию ср(у, z) можно определить так, что
д<? (У. г)
Ту
х=0
d<f (у, г) __
дг ~~
дг
Действительно, положим
Отсюда
где ф(у)—произвольная функция. Дифференцируя по у, имеем
ду .1 ду
о
Применяя первое равенство C6), можем написать
д<? (У. г) С дау
дг
ду
136
откуда
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
[ГЛ. III
(У- г)
х=0
г=0
Для доказательства (*) достаточно положить
Используя (*), получим
7
Таким образом, если rot a = 0, то можно найти такую скалярную функ-
функцию /, что
д/ _
Обратно, если
дх ***' ду у> дг
df _
df
ТО
Это очевидно, так как в рассматриваемом случае а = grad/, а согласно
формуле C2) rot (grad /)=0.
Следовательно, для того чтобы данное векторное поле а являлось гра-
градиентом некоторой скалярной величины /, необходимо и достаточно обра-
обращение в нуль вихря а, т. е. выполнение равенства rota = 0.
Итак, если rot а = 0, то существует такая скалярная функция V = — /,
что а = — grad V. Если при этом функция V однозначна, то она называется
скалярным потенциалом, а про вектор а говорят, что
он равен производной от скалярного потенциала V.
Из равенства а — — grad V и формулы B9) следует:
diva = — bV.
Такое поле векторов а называется ¦ потенциальным,
ньютоновым, слоистым или безвихревым. Эти названия
напоминают, что поле всемирного тяготения относится
к рассматриваемому типу полей, что эти поля могут
быть разложены с помощью поверхностей уровня
V — const на слои и что rota = 0. Отметим, что ста-
стационарное электрическое поле равно производной от
скалярного потенциала.
3.2.17. Частный случай: вектор проходит через фиксированную
точку. Пусть О — фиксированная и М(х, у, z)—переменная точка
(рис. 3.13). Обозначим через/- расстояние ОМ, а через и орт вектора ОМ.
Таким образом,
ОМ —иг.
Рассмотрим вектор МА, линия действия которого проходит через
точку О. Если его модуль зависит только от расстояния ОМ = г, то мы
можем написать
MA = uf(r).
Имеем
Рис. 3.13.
grad
= ~f- grad r.
3.2] ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 137
Далее,
Следовательно,
grad/(/¦) = /'(г) а. . C9)
Вычислим дивергенцию вектора МА. Имеем
MA=af(r) = 2?-f(r).
Следовательно,
d i v МА = ^р. d i v ОМ + ОМ ¦ grad
но
дх , ду . дг о
Поэтому, учитывая C9), получаем
т. е.
div MA == у /(/¦) +/'(О- D0)
Пусть /=¦(/¦) такова, что /="(/¦) = /(/¦). Тогда, согласно C9),
МЛ = и/(г)== grad F (г), D1)
т. е. МЛ является производной от скалярного потенциала V= — F(r)- Поэтому
TotMA—0.
3.2.18. Векторный потенциал. Любая векторная функция точки М, для
которой дивергенция тождественно равна нулю, может рассматриваться как
вихрь некоторого вектора.
Действительно, пусть задан вектор a=iax-\-jay-\-fcaz, причем
да г dav да.
Отыскание вектора Ь = ib x,-\- jby-\- kbz, удовлетворяющего условию с = rot ft,
сводится к решению системы уравнений:
ду дг х v
дЬх дЬг
-дТ~Ш=аг D3>
дх ду z
Таких векторов Ь существует бесконечно много. Выберем один из них при
условии, что Ьг = 0. В этом случае равенства D2) и D3) переходят в
75? = «г <46>
138 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Из равенства D5) получаем
г
С, у).
сительно Ъх:
о
Дифференцируя равенство D6) по у, найдем
дЧх дау
В силу последнего соотношения равенство D4) переходит в уравнение отно-
отнодг ду ду
Используя это соотношение и равенство D7), продифференцированное по z,
имеем
да1 = _д\_
ду д2[ о
или
дау
ду дх дг
Эта формула справедлива в силу предположения, что divc = 0.
Таким образом, соотношение D4) является следствием формул D5), D6)
и уравнения diva = 0. Иначе говоря, равенства D5) и D6) при условии
diva = 0 определяют вектор Ь такой, что bz = 0 и rotb — a.
Пусть теперь вектор с удовлетворяет уравнению rot с = а. Тогда
rot с — rot b = О
или
rot (с — 6)= О,
т. е.
с — b = grad /.
Следовательно, вектор с определяется лишь с точностью до градиента
произвольной скалярной функции точки М. Это соотношение очевидно,
так как к полю векторов с, для которых rot с = а, можно добавить поле
любых других векторов с нулевым вихрем. Из бесконечного множества этих
векторов выберем вектор, дивергенция которого равна нулю. Обозначим его
через v. Вектор v можно представить в виде суммы определенного выше
вектора Ь и градиента произвольной скалярной функции /.
Имеем
| = 0,
v — 6 — grad /.
Из последнего равенства следует
— 6) = divgrad/= Д/,
— div 6 = Д/.
Так как div v = 0, то / определяется из уравнения Д/= — div b. Итак,
если div а = 0, то существует такой вектор V, что с = rot я ч div 47 = 0.
Вектор v называется векторным потенциалом с, а про вектор а говорят.
3.3] ВЕКТОРНЫЕ ИНТЕГРАЛЫ 139
что он равен производной от векторного потенциала v. Вектор а, для ко-
которого diva = 0, называется соленоидальным вектором. Поле векторов с ну-
нулевой дивергенцией называется соленоидальным или лапласовым (магнитное
поле системы токов, элементарные поля которых задаются законом Лапласа,
относится к рассмотренному типу полей).
Замечание. Векторный потенциал определяется'неоднозначно. В самом
деле, рассмотрим вектор
Имеем
rot vl = rot v -+- rot grad ср.
Так как rotgradcp = 0, то iotvl = a при любом ср. Условие
выполняется, если divgradcp = Дср= 0. Следовательно, векторный потенциал
определяется с точностью до градиента скалярной функции, удовлетворяю-
удовлетворяющей уравнению Лапласа.
3.2.19. Общий случай векторного поля. Любое векторное поле можно
рассматривать как наложение потенциального и соленоидального полей.
Действительно, пусть а — произвольное векторное поле. Рассмотрим
вектор Ь, вихрь которого равен нулю. Тогда b — grad/; вид скалярной
функции / указывается ниже.
Положим ( — а — Ь. Выберем вектор Ь так, чтобы divc;=0. Тогда
diva = div & = divgrad/ = Д/.
Отсюда следует, что dive =0, если A/ = diva. Так как а = Ь-\-с,
а rot Ь = 0, то теорема доказана.
Согласно п. 3.2.16 вектор Ь равен производной от скалярного потен-
потенциала V = — /. Вектор с равен производной от векторного потенциала v
(см. п. 3.2.18). Таким образом,
а = — grad V -\- rot v.
3.3. ВЕКТОРНЫЕ ИНТЕГРАЛЫ
3.3.1. Циркуляция вектора. Пусть М—: переменная точка дуги АВ
(рис. 3.14), а — векторная функция точки М.
Циркуляцией вектора а по дуге АВ называется
в
значение криволинейного интеграла I a • dAf*)(криво-
А
линейный интеграл берется от скалярного произвел
дения).
Если а — сила, то рассматриваемый интеграл пред-
представляет собой работу этой силы вдоль дуги АВ.
Замечание. Если вектор а равен производной
от скалярного потенциала V, то согласно формуле
в
grad V • dM = dV имеем I а • dM — VA — Vв. В этом случае циркуляция за-
А
висит только от начальной и конечной точек пути интегрирования.
*) Обычно циркуляцией называется криволинейный интеграл векторного поля,
взятый по замкнутому контуру. Если же контур не замкнут, то этот интеграл назы-
называют линейным.
140 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
3.3.2. Поток вектора. Пусть 5 — двухсторонняя поверхность, М —пере-
—переменная точка на S, а — векторная функция точки М, MN — нормаль к S,
на которой выбрано положительное направление, da — элемент поверхности,
окружающий точку М. Обозначим через da вектор, длина которого равна
площади da, а направление совпадает с положительным направлением нор-
нормали к этому элементу. Потоком вектора а через поверхность 5 называют
двойной интеграл .1 а ¦ da (двойной интеграл берется от скалярного произ-
s
ведения).
Основные формулы
Пусть 5 — замкнутая поверхность, ограничивающая объем т, М — пере-
переменная точка х (или на поверхности 5), dа — определенный выше вектор,
направленный по внешней нормали к поверхности 5. Пусть, далее, / —
скалярная и а — векторная функции точки М. Предполагается, что они не-
непрерывны вместе со своими первыми производными в любой точке объема т
и его границы 5.
Справедливы следующие три формулы, заменяющие тройной интеграл
двойным:
1) формула для градиента
Jgrad/dT= J fda;
¦ i s
2) формула для дивергенции (теорема Остроградского)
J divadx= j a- da; D9)
t S
3) формула для вихря *)
( rotadx— Г da X в.
3.3.3. Теорема Остроградского. Теорема Остроградского — это теорема,
выраженная формулой D9): интеграл от дивергенции а, распространенный
на объем т, равен потоку вектора а, направленному по внешней нормали
через замкнутую поверхность S, ограничивающую этот объем х **).
*) Используя символический вектор V, можно указать удобное для запоминания
операторное соотношение, из которого формулы D8) — E0) получаются в виде част-
частных случаев. Это соотношение имеет вид:
Г dx V = Г d.3, da = n da, (*)
* s
где и — внешняя нормаль к замкнутой поверхности S, ограничивающей объем т.
Формула D8) получается в результате умножения обеих частей (*) на скаляр /,
D9) — в результате скалярного умножения на вектор а н E0) — в результате век-
векторного умножения на вектор а.
**) Формула Остроградского, строго говоря, верна только для „пространственно"
односвязных областей (см. [2], стр. 336).
3.3] ВЕКТОРНЫЕ ИНТЕГРАЛЫ 141
Левая часть формулы D9) в декартовых координатах имеет вид
L
дх
ду
Лдах дач да,
т
fd^Ldxdydz.
•' дг
Рассмотрим интеграл / -~ dx dydz. В объеме т с помощью четырех
плоскостей у, y-\-dy, z, z~\~dz вырежем параллелепипед. На поверхности 5
указанные плоскости вырезают два криволинейных четырехугольника
A1B1C1D1 и A2B2C2D2, площади которых обозначим через da1 и do2 (рис. 3.15).
Пусть Мj и М2 — точки этих четырехугольников, МXNX и M2N2 — внешние
нормали к поверхности 5, орты которых соответственно пх и п2.
Нормаль MXNX образует с осью Ох тупой угол (i, n{); нормаль M2N2
образует с осью Ох острый угол (i, n2). Имеем
dydz = — cos (Л га,) da, = cos (г, n2)dc2.
Пусть (ах\ и (ахJ — значения ах в Мх и М2. Интеграл / -^ dx dy dz,
распространенный на элемент объема AXBXCXDXA2B2C2D2, равен
j^dx=dydzl(axJ—(axI]=(axJcos(i,
ио
cos (Л nl) =
cos(i, n2) = i-n2.
Векторы nldal и n^do2 совпадают с векторами й<зх и йч2, введенными
в предыдущем пункте, если считать, что направление внешней нормали
положительно.
Следовательно, имеем
м.
dy dz fj?dx =
откуда
f
Jj±dxdydz= j aj • da.
142 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Тройной интеграл распространяется на объем х, а двойной интеграл на по-
поверхность 5.
Л2. dx dy dz и / -?*- X
X dx dydz, покажем, что
jd\\adx= I (axi-\- ayj -f- azk) -da = a • da.
t . s ¦ s
3.3.4. Смысл скаляра diva. Из формулы Остроградского следует, что
полный поток вектора а через замкнутую поверхность, ограничивающую
бесконечно малый объем dx, равен divadx. Следовательно, дивергенция,
вычисленная в точке векторного поля, приближенно равна потоку, выходя-
выходящему из единицы объема, окружающего эту точку. Точное значение дивер-
дивергенции векторного поля а может быть определено следующим образом:
divo= lim —-—*).
Рассмотрим движение жидкости. Пусть ее плотность р и скорость дви-
движения а — соответственно скалярная и векторная функции точки пространства
и времени t. Предположим, что S — произвольная поверхность в пространстве,
заполненном жидкостью, и п — орт внешней нормали к этой поверхности.
Масса жидкости, проходящая в направлении п за единицу времени через
поверхность 5, равна
Г п ¦ pa do.
s
Если поверхность 5 замкнута и ограничивает объем х, то полученная
формула дает массу жидкости, вытекающую за единицу времени из х. С другой
стороны, увеличение массы жидкости внутри объема t за единицу времени
равно
Г до _,
I ~^г dx.
J От
z
Применяя теорему Остроградского, получим
Г п • pa do = Г div (pa) dx.
s t
Если предположить, что внутри т отсутствуют источники и стоки, то
Это равенство справедливо для любого объема т рассматриваемого поля.
В силу непрерывности функций и их производных (ср. п. 3.3.7)
| O. E1)
*) Этот предел представляет собой объемную производную векторного поля.
3.3] ВЕКТОРНЫЕ ИНТЕГРАЛЫ 143
Уравнение E1) называется уравнением неразрывности жидкости. Если жидкость
несжимаемая, то
div(pc) = 0.
Если, кроме того, скорость а равна производной от скалярного потенциала V,
а плотность р постоянна, то уравнение неразрывности принимает вид
Это уравнение можно непосредственно применить к электрическому полю,
если вместо плотности жидкости р взять плотность электрических зарядов,
движущихся со скоростью а.
Введем обозначения: 9 — температура, р — плотность, k — коэффициент
внутренней теплопроводности и с—удельная теплоемкость тела в рас-
рассматриваемой точке (скалярные функции). Количество тепла, вытекающего
через поверхность 5, равно
— Г kn ¦ grad 8 do.
s
С другой стороны, увеличение количества тепла внутри т равно
Отсюда по аналогии с предыдущим случаем получаем
ср-^ —div (A grad 9) = 0.
Это уравнение теплопроводности.
В случае однородной среды и при стационарном распределении темпе-
температуры ("лг=0) уравнение теплопроводности принимает вид
Д9 = 0.
3.3.5. Формула для градиента. Положим
a = fb,
где / — скалярная функция точки М, а Ъ — произвольный постоянный вектор.
Согласно формуле B7)
div а — div (fb) = f div b + b ¦ grad /.
Вектор b постоянен, поэтому
div a = b ¦ grad /.
Применим формулу D9) к вектору а:
Ъ- Jgrad/fih: = &. J fdv.
t S
В силу произвольности вектора b отсюда следует формула D8).
3.3.6. Формула для вихря. Пусть Ь — произвольный постоянный вектор.
Тогда по формуле B8)
div (а X Ь) = Ь ¦ rot а,
144 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
так как rot b = 0. Подставим в формулу D9) вместо вектора а вектор а X Ь:
Ь • J rot a dx = j (aXb) ¦ da.
t S
Смешанное произведение (а X Ь) ¦ da = b • (da X а) (см. п. 3.1.14),
следовательно,
b • I rot a dx = b • \ di X a.
В силу произвольности вектора Ь отсюда следует справедливость фор-
формулы E0).
3.3.7. Инвариантность*) градиента, дивергенции, вихря. Докажем
инвариантность дивергенции. Имеем (формула D9))
f divadt = Г а ¦ da.
т 5
Введем новые оси координат, и пусть divja — дивергенция, полученная
в новой системе координат. Так как скалярное произведение а • da не за-
зависит от выбора системы координат, то для любого объема т имеет место
равенство
Г div a dx = Г divj a dt
или
J (div1a — diva)dx = 0.
Если в какой-либо точке diVja отличается от diva, то эту точку можно
окружить объемом, внутри которого div, a — diva была бы не равна нулю
и сохраняла знак (вследствие непрерывности частных производных вектора а).
Следовательно, для этого объема интеграл
Г (divj a — diva)dT
<3ыл бы не равен нулю, что противоречит (*). Поэтому для любых осей
координат divja = diva, т. е. скаляр diva инвариантен относительно выбора
координатной системы.
Пользуясь формулами D8) и E0), можно провести аналогичное доказа-
доказательство инвариантности векторов grad/ и rota относительно выбора осей
координат.
3.3.8. Формула Грина. Пусть 5 — замкнутая поверхность, ограничиваю-
ограничивающая объем х, р и q — две скалярные функции точки М. Докажем, что имеет
место формула Грина:
Г (pAq — q Д/;) dx = J {p grad q — q grad p) ¦ da.
Используя формулу B7), получаем
div (/? grad q) = p div grad q-\-grad q • grad p = p Aq-f- grad q • grad p.
*) Независимость от выбора координатной системы.
3.3] ВЕКТОРНЫЕ ИНТЕГРАЛЫ 145
Подставим в формулу D9) вместо вектора а вектор pgt&dq. Имеем
Г (р kq + grad р • grad q) dx = Г p gtad q • da.
x S
Меняя роли функций р и q, находим *
Г (q Д/> -f- grad q • grad p)dx= j q grad p • da.
x S
Вычитая последнее выражение из предыдущего, получим формулу Грина.
3.3.9. Формула Стокса. Пусть двухсторонняя поверхность S ограни-
ограничена замкнутой кривой С, на которой указано определенное направление
обхода. Нормали к поверхности S ориентируем таким образом, чтобы
выбранное на С направление обхода оказалось
положительным *).
В каждой точке Р поверхности 5 отложим
вдоль отрицательного направления нормали отрезки
постоянной длины РР'. Точки Р', соответствую-
соответствующие точкам Р, образуют поверхность S', парал-
параллельную поверхности S и ограниченную замкну-
замкнутой кривой С. Обозначим через Е поверхность,
образованную нормалями, соединяющими точки
кривых С и С. Пусть т — объем тела, ограничен-
ограниченного поверхностями 5, 5', ? (рис. 3.16).
Будем считать, что отложенная вдоль направ-
направления нормали постоянная длина достаточно мала. Рис. 3.16.
Пусть М — точка внутри или на поверхности рас-
рассматриваемого тела х. Опустим из точки М перпендикуляр МР к поверх-
поверхности S\ I — длина МР. Тогда МР = 1п,гд,еп — единичный вектор нормали.
Рассмотрим точку M-\-dNl (см. п. 3.2.1). Ей соответствует точка
P+dP. Имеем
dP — dM = ldn-\-ndl**).
Это выражение умножим скалярно на га:
га • dP — га • dM = ln ¦ dn-\-n • ndl.
Но n-dP=0, т,ак как векторы п и dP перпендикулярны. Кроме того,
n-dn = 0, потому что вектор постоянной длины перпендикулярен своей_
производной (это следует из теоремы 1 п. 3.2.3). Учитывая также, что
П • га = 1, получаем
Далее, согласно (Д8) grad I • dM = dl. Следовательно, при любом dM
Имеет место —п • dM = gtad I • dM. Поэтому » = — grad I.
Возьмем вихрь от обеих частей этого равенства. Имеем
rot га = — rot grad / = 0.
*) Тем самым определяется рассматриваемая сторона поверхности. Очевидно
что выбор стороны поверхности и ее ориентация взаимно определяют друг друга.
**) В самом деле, пусть M4-dM соответствует точка М,, а Я + dP —точка Р..
Тогда dM^MM^dP^PPt. Имеем ДуИР= уИ.Р, —ЖР= МхМ + МР+РР, —МР =
= dP— dM. С другой стороны, &MPxdMP = d (In) = Idn + ndl, т. е. dP — dlA*
= idn+ndl.
10 A. Aaro
146 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Применим теорему Остроградского к вектору а X я:
iv(aXn)rft= J (а X »)•<*»•
Вектор da имеет длину da и отложен по нормали к поверхности. На
поверхности 5 вектор da = n da, а на поверхности Е вектор ds —/*! do
(через re, обозначается орт нормали к поверхности ?). Имеем
Jdiv(aX»)dT:= J (aX«)- «do-f- J(a X я) • nxda.
Смешанное произведение (а X я) • и, очевидно, равно нулю, так как
вгкторы аХя и п ортогональны. Поэтому предыдущая формула принимает вид
Г div (а X я) dx = | (а X я) ¦ пх do.
¦с S
Смешанное произведение (а X я) • п{ — (я X я;) • а. Но я X Я[ — это
орт t касательной к кривой С при условии, что точка Р находится на этой
кривой С (рис. 3.17). Следовательно,
Далее, согласно формуле B8) и доказанному
выше равенству rot п = 0, находим
div (а X п) = и • rot а — а • rot и = и • rot a.
Таким образом,
Г и • rot adi= Г а • tdc
Рис. 3.17. J J
т S
Если расстояние PP' = db мало, то dx = dod8, где do — элемент по-
поверхности 5. Если do — элемент поверхности Е, то do = d/d8, где dl —
элемент кривой С. Тогда
d§ Гя-rotado —d3 Ia-^d/ = d8 j a • dM,
s с с
откуда и получается формула Стокса
j n • rot a do= ja ¦ dM. E2)
s с
Итак, циркуляция вектора а по замкнутой кривой С равна потоку его
вихря через поверхность, ограниченную С *). В случае соленоидального
векторного поля а известно, что а является производной от вектор-
*) 1. Легко непосредственно убедиться в том, что в формуле E2) можно брать
любую поверхность S, стягиваемую замкнутой кривой С. Действительно, пусть S,
у р у у р у ,
н S2 — такие поверхности. Тогда поверхность S, + S2 ограничивает трехмерное тело
с объемом х. Учитывая, что только для одной поверхности S, или S2 направление
внешней нормали совпадает с положительным направлением нормали я, и применяя
формулу Остроградского, получим
Г я • rot a da — | я • rot a dn — Г я • rot a da = Г div rot a dz = 0,
5 S S
Si
так как div rot a = 0.
2. Формула Стокса может быть обобщена аналогично формуле Остроградского
(см. п. 3.3.2). Соответствующие формулы удобно получить из операторного соотно-
соотношения (ср. сноску на стр. 140):
fdaXV= Г dM, d3=nda, dM=tdl, (*)
3.3}
ВЕКТОРНЫЕ ИНТЕГРАЛЫ
147
ного потенциала v, т. е. а = rot v. По формуле Стокса потюк вектора
rot v через поверхность равен циркуляции v по контуру, ограничивающему
эту поверхность. Таким образом, поток соленоидального вектора через «по-
«поверхность равен циркуляции его векторного потенциала по контуру этой
поверхности.
Теорема Стокса позволяет дать новое определение вихря. Для этого
определим составляющую rot а в точке А по любому фиксированному напра-
направлению AW.
Опишем из точки А, как из центра, окруж-
окружность С малого радиуса г, лежащую в плоскости,
перпендикулярной рассматриваемому направлению
(рис. 3.18). Составляющая вихря по направлению AW
имеет следующий вид:
adl
кг'
E3)
Рис. 3.18.
Приложение векторного исчисления к теории электромагнитного поля :)
3.3.10. Электростатическое поле. Рассмотрим два точечных заряда Q1
и Q2, помещенных в пустоте в точках А и В на расстоянии г друг от
друга (рис. 3.19),' Тогда сила, действующая на заряд Qv равна
F==QiQi_ и (закон кулрна),
где и — орт вектора В А. Пусть в точ-
точке О помещен заряд Q. Электрическое
поле заряда Q в точке А равно силе;
действующей на единичный заряд, по-
помещенный в точке А (рис. 3.20):
Рис. 3.19.
Рис. 3.20.
Это электрическое поле представляет собой поле векторов, проходящих через
фиксированную точку О. Используем формулы D0) и D1) для /(/¦) =
*=-&7Г- Имеем
где поверхность S ограничена замкнутым контуром С, причем направления п и t —
ортов нормали к 5 и касательной к С — согласованы, как указано в начале настоя-
настоящего пункта. В частности, формула E2) получается в результате скалярного умно-
жевия обеих частей (*) на вектор а. Формула Стокса, строго говоря, верна только
для .поверхностно' односвязных областей (см. [2], стр. 305).
') Ниже все формулы даны в рационализированной системе единиц МКС, вклю-
яающей четыре основные единицы: метр, килограмм-массу, секунду и ампер или вольт.
В электротехнике для получения уравнений с наиболее простыми и симметричными*
размерностями часто берут за основные метр, секунду, вольт и ампер. Главные про-
производные единицы: кулон, ом, фарада, генрн и т. д. Единицы, входящие в формулы,
которыми мы пользуемся, это: единицы силы — ньютон A05 дин), единица напряжен-
напряженности электрического поля — вольт на метр, единица электростатической индукции —
Кулон на квадратный метр, единица электромагнитной индукции — вебер A04 гауссов)
на квадратный метр. Рационализация вводит множитель 7<л в оба основных закона
Кулона (в электростатике и магнитостатике), Поэтому значения для диэлектрической
и магнитной проницаемости в пустоте следующие:
е0 = 10~9 (Збя)-1 = 8,842 • 10~12 фарад на метр,
|х0 = 4я • 10 = 1,257 • 10~ 6 генри иа метр,
причем соРоС2 = 1> где скорость света с = 3 • 108 м/сек.
10»
148 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ 1ГЛ. Ill
л скалярный потенциал Е равен
V= Q !
Применяя формулу D9) к замкнутой поверхности, не содержащей внутри
•себя точки О (теорема Остроградского, вообще говоря, неверна, если в об-
области тройного интегрирования векторная функция имеет бесконечный раз-
разрыв), получим, что поток вектора Е через эту поверхность равен нулю.
С другой стороны, непосредственно очевидно, что поток вектора Е через
поверхность любого шара с центром в О равен Q/e0. Обозначим через 5
произвольную замкнутую поверхность, содержащую внутри себя точку О и
проведем сферу с центром О, целиком находящуюся внутри 5. Применяя
формулу D9) к области, ограниченной 5 и поверхностью этой сферы (учтем,
что внутренняя нормаль сферы является внешней для рассматриваемой об-
области), получим
Г
Е • dS = — (теорема Гаусса).
Если внутри поверхности 5 содержится несколько точечных зарядов
(=1
Предположим, что заряды распределены непрерывно внутри объема v и
плотность распределения зарядов дается скалярной функцией точки р. Тогда
соотношение div? = 0 нарушается. Распространяя на этот случай теорему
Гаусса, получим
а так как
f E-dS= f div Edv,
s
то при непрерывном распределении зарядов
Далее,
div?= — divgrad V = — ДУ.
и поэтому
AV-f- —= 0 (уравнение Пуассона).
?0
До сих пор мы рассматривали поле в пустоте. Обратимся теперь к полю
внутри диэлектрика. В этом случае молекулы тела ведут себя как электри-
электрические диполи — каждый элемент объема содержит большое число зарядов
противоположного знака, соединенных попарно.
При отсутствии внешнего поля моменты молекул ориентированы по-
разному, и их векторная сумма равна нулю. При наличии внешнего поля
диполи частично повернутся, и сумма моментов станет отличной от нуля.
Диэлектрик с ориентированными в той или иной степени дипольными мо-
моментами окажется поляризованным. Степень поляризации характеризуется
3.3] ВЕКТОРНЫЕ ИНТЕГРАЛЫ 149
вектором поляризации Р, который, по определению, равен суммарному мо-
моменту молекул, отнесенному к единице объема *). Учет поляризации можно
осуществить, если ввести фиктивную плотность электрических зарядов,
равную — div P. При этом условии теорема Гаусса записывается в следую-
следующей форме:
е0 СE-dS = Г pdv— J div Pdv.
S v v
Применяя формулу D9), получаем
f(SoE + P)-dS= fpdv.
S v
В данном случае векторное поле, удовлетворяющее теореме Гаусса, имеет вид
Вектор D называется вектором электростатической индукции. Он, оче-
очевидно, удовлетворяет уравнению
div ?> = р.
3.3.11. Магнитное поле постоянных токов. Все, что говорилось выше
относительно электрического поля Е, можно повторить для магнитного поля Н.
Однако следует учитывать, что свободные магнитные заряды не существуют,
т. е. вне магнитной среды
v div// = 0.
N.. 5
Внутри магнитной среды присутствуют элементарные магниты. Повторяя
предыдущие рассуждения, мы приходим к необходимости определить вектор
магнитной индукции /?, дивергенция которого равна нулю как внутри, так и
вне магнитной среды:
divfi = 0.
Рассмотрим контур С, окружающий ток /(рис. 3.21).
Циркуляция вектора магнитного поля по контуру С равна
Г Н • dl=/ (теорема Ампера),
с
Если внутри контура С тока нет, то
JH • dl= 0.
Из определения вихря по формуле E3) следует, что в точках, где тек от-
отсутствует,
fH-di
totwff= lim -—^ = 0 (W — любое), т. е. rot//=0.
o ^
*) Точнее, векторная функция точки Р определяется как производная от сум-
суммарного момеита молекул по трехмерной области ([2], стр. 311—312).
150 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
3.3.12. Электромагнитное поле. Выпишем формулы, используемые при
выводе уравнений Максвелла (см. 3.3.15):
divfi=0, E4)
div?> = p, E5)
fffdl = [. E6)
с
3.3.13. Закон Фарадея. Электродвижущая сила, индуктированная на
контуре С, помещенном в электрическом поле Е, выражается криволинейным
интегралом
с
Если обозначить через 5 какую-либо поверхность, опирающуюся на
контур С (рис. 3.22), то согласно теореме Стокса получим
J Edl= f rot E-dS.
с s
. По закону Фарадея индуктированная электродви-
жущая сила пропорциональна изменению потока В во
времени, т. е.
f rot E-dS = — J'^-dS.
s
В силу произвольности поверхности 5
3.3.14. Закон Ампера. Обозначим через J вектор плотности тока
в точке. Тогда закон Ампера можно записать в виде
J H dl= j J -dS. E7)
с s
так как поток вектора J через поверхность 5 равен интенсивности тока,
проходящего по контуру С. В силу теоремы Стокса
Г Н ¦ dl= J rot H ¦ dS.
С S
Сравнивая с формулой E7), получим
rot H = J. E8)
Ток J создается зарядами, движущимися со скоростью V. Обозначим
через р пространственную плотность этих зарядов. . Очевидно, что вектор
плотности тока
J = pV.
При этом формула E8) принимает вид
TotH = pV. E9)
Возьмем дивергенцию от обеих частей этого равенства. Учитывая формулу C0),
имеем
0. F0)
3.3) ВЕКТОРНЫЕ ИНТЕГРАЛЫ 151
Формула E1) дает
Дифференцируем по времени равенство E5):
,. dD __ до
Используя две последние формулы, получим
div(pV)= — div-^-. F1)
Формулы F0) и F1) противоречивы.
3.3.15. Уравнения Максвелла. Чтобы устранить полученное противоре-
противоречие, Максвелл видоизменил закон Ампера следующим образом: полный ток,
который мы рассматриваем, состоит не только из тока проводимости pV, но
и из тока смещения -тт-• Поэтому вектор J=pV следует заменить на
и тогда уравнение Ампера E9) примет вид
Таким образом, получаем систему уравнений Максвелла:
div D = p,
div B = 0,
rot ?=-4?-. F2)
rot H =.
Для пустоты система уравнений Максвелла F2) переписывается в виде
div H = 0,
rot? = — Ро-^г. ' F3)
rottf = s0^.
3.3.16. Векторный потенциал магнитного поля, возбужденного током.
Рассмотрим электрический заряд е, перемещающийся со скоростью V. Он
эквивалентен электрическому току силы /, текущему по элементу длины dl:
Idl=eV. F4)
Величина / положительна, если направление тока совпадает с направлением
вектора dl.
Магнитное поле, создаваемое рассматриваемым движущимся зарядом
на расстоянии г от этого заряда, равно (формула Био — Савара — Лапласа)
F5)
152
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
[ГЛ III
Так как divB=0, то для вектора В существует векторный потенциал А.
Определим его. Имеем
В = rot А.
В пустоте
поэтому
Преобразуем формулу F6):
101 А=Ы'У х'
C66)
x
i+'v х *¦?¦] =
Сравнивая полученную формулу с формулой B2), найдем, что
Применим полученную формулу для случая тока, текущего по проводу.
Это важный частный случай движения заряженных частиц. Пусть dS — эле-
элемент поверхности, через который проходит ток /, У—вектор плотности тока.
Имеем JdS = I. Используя формулы F4) и F5), полу-
получим выражение для векторного потенциала тока в про-
проводе А через интеграл, распространенный на объем V
(dv=dS dz) рассматриваемого провода:
Л *&
Применение этой формулы к электрической цепи,
по которой идет ток, может привести к некоторым за-
затруднениям. Рассмотрим, например, случай бесконеч-
бесконечного прямолинейного провода. Пусть его сечение dS,
а сила тока в нем /. Выделим мысленно отрезок АВ
Рис. 3.23. и найдем векторный потенциал, созданный tokqm, теку-,
щим по этому отрезку. Рассмотрим точку Р, отстоящую
от АВ на расстоянии d (рис. 3.23). Так как векторный потенциал обладает
осевой симметрией относительно АВ, то при определении точки Р достаточно
указать абсциссу точки Н и расстояние HP = d.
Пусть М — любая точка отрезка АВ, a zv z2, s и z — абсциссы точек
А, В, Н, М относительно фиксированной точки О. Обозначим через г рас-
расстояние МР. Имеем Jdv = JdSdz = Idz. Поэтому формула F7) дает сле-
следующее выражение для векторного потенциала А:
*1 <¦¦>
dz
=? /
а так как
(*,_«)•_(*,_*)
3.4]
ТО
ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
153
+ In
! — sJ - (*j —*)]}. F8)
Для перехода к бесконечному прямолинейному току нужно устремить гг
и 22 соответственно к —оо и +оо. При этом векторный потенциал также
стремится к бесконечности.
Следует заметить, однако, что магнитное поле В рассматриваемого
тока конечно. Поэтому должны быть конечны частные производные век-
векторного потенциала А, так как
В = tot А.
Положим в формуле F8) d = dx и s — sv и полученную постоянную
величину вычтем из правой части этой формулы. Имеем с точностью до по-
потенциала в фиксированной точке:
| In Л- —
\ d2
j [п
In-4 +
Fg>
Если теперь устремить гх и г2 соответственно к — оо и -t-оо, то-
4я \ d2 d\\
Так как векторный потенциал определяется
лишь с точностью до градиента скалярной
функции (см. п. 3.2.18), то можно на-
написать
4=g-/(— lnd2). -
Рис. 3.24.
Векторный потенциал тока в проводнике с любым поперечным сече-
сечением (рис. 3.24) выражается через поверхностный интеграл:
3.4. СИСТЕМЫ ОРТОГОНАЛЬНЫХ КРИВОЛИНЕЙНЫХ КООРДИНАТ
3.4.1. Определение. Рассмотрим трехмерное пространство, в котором
введена' система прямоугольных координат Ox, Oy, Oz. Мы можем связать
это пространство с системой криволинейных координат. Пусть между пря-
прямоугольными координатами х, у, z и криволинейными координатами и, v, w
устанавливается взаимно однозначное соответствие, описываемое формулами
х = р(и, v, w), y = q(u, v, w), z = r(u, v, w) G0)
и
u = P(x, у, г) v = Q(x, у, z), w = R(x, у, z). G1)
154
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
[ГЛ. III
Уравнения и = const, v = const, w = const представляют собой уравне-
уравнения координатных поверхностей криволинейной системы в прямоугольной
системе координат.
Каждая пара координатных поверхностей, проходящих через фиксиро-
фиксированную точку М, образует в пересечении координатную линию. Параметри-
Параметрические уравнения координатных
линий получаются из уравне-
уравнений G0), если в них поочередно
изменять только одну из пере-
переменных и, v, w, оставляя при
этом неизменными остальные две
(рис. 3.25).
В этой главе мы ограничимся
рассмотрением ортогональных
криволинейных координат, не-
неортогональные системы будут изу-
изучены в п. 5.2.1 и последующих.
По определению, криволинейные
координаты называются ортого-
ортогональными, если в любой точке М
касательные к координатным ли-
Рис. 3.25. ниям образуют прямоугольный
трехгранник.
Квадрат элемента длины ds в прямоугольных координатах дается фор-
формулой
2
В случае ортогональных криволинейных координат эта формула приобре-
приобретает следующий вид:
ds2 =
где е\, е2, е\ обозначают величины
е\ dv2
e\ dw2 *),
дх
dw
j)y_
dw
. I
dz\2
dv j '
dw
Если элемент ds параллелен касательной в точке М к оси Ми, то его
длина Судет равна ег du. Аналогично длины элементов, параллельных осям Mv
и Mw, равны e2dv и e3dw. Так как величины ev e2, ег являются функ-
функциями координат точки, их называют единицами локальной длины **).
Рассмотрим скалярную функцию точки V(х, у, z). Выражение этой
функции в криволинейной системе координат получается простой заменой
х, у, z их значениями G0). Пусть теперь А(х, у, z) — векторная функция
точки, Ах, Ау, Az — проекции вектора А на оси прямоугольной системы
*) Нетрудно показать, что необходимым и достаточным условием ортогональ-
ортогональности системы криволинейных координат является условие, состоящее в том, чтобы
выражение ds2 содержало только члены с квадратами дифференциалов (см., напри-
например, [3], стр. 340, 341).
**) Величины <?!, <?2. е3 называются также коэффициентами Ламе, метрическими
коэффициентами, масштабными множителями.
3.4]
ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
155
координат. Проведем в точке М (х, у, z) касательные к криволинейным
осям Ми, Mv, Mw и обозначим через Аа, Av, Aw проекции вектора А на
эти касательные. Используя формулы D) и E), получим
4И= A,, cos (л:, а)-\- Ау cos (у, и)-\- Azcos(z, и),
\v = Ах cos (л:, v)-\- Aycos(y, v) + Az cos (г, г»).
G2)
Лю = A,, cos (л:, w) -f- Ay cos (у, да) -f- Аг
В этих формулах *)
cos(;c,
1 = з—, cos (у, и)= —
cos (х, v) = з— ,
v e2 dv
cos (у, v) = —
cos(z,
COSB,
, w).
1
дг
cos(*.
> = T"?". CO8.(y.
\ дг
G3)
Пример. Рассмотрим систему координат %, ср, z, связанную с прямо-
прямоугольными .координатами х, у, z no
формулам:
х = a ch Ч, cos <р, у== a
Координатные
имеют вид:
поверхности
— 1=0
a2 ch2 5 '
(эллиптический цилиндр),
v-2 V2
¦* У j __ q
a2 cos2 <f a2 sin2 <p
(гиперболический цилиндр),
г = const (плоскость).
Рис. 3.26.
Эти три поверхности попарно орто-*
тональны, так как ортогональны
софокусные эллипсы и гиперболы, а плоскости Z = с перпендикулярны обра-
образующим полученных цилиндров (рис. 3.26).
, Координатные линии представляют собой гиперболу, эллипс (обе кривые
в плоскости, перпендикулярной оси Oz) и прямую, параллельную оси Oz
и проходящую через точку т (см. рисунок).
Квадрат элемента длины равен
ds2 = dx2 H- dy2 -f dz2 = a2 (ch2 $ — cos2 <p) d? -f- a2 (ch2 $ — cos2 cp) d<f -f- dz2.
*) Вектор
- дх i \ ду 1 \ дг к
длина которого равна ех, параллелен касательной к координатной линии и. Это сле-
следует из параметрических уравнений линии и (см. выше). Далее,
е\ • i — ех cos (jc, u),
откуда и вытекает первая из формул G3). Аналогично получаются и остальные фор-
формулы G3).
156 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. Ill
Следовательно, единицы локальной длины соответственно равны
Проекции векторной функции
относительно криволинейных осей координат находятся по формулам:
л ==д shScos? . . ch$sin?
(ch*5 — cos2<p)'/a ^ y (ch*5 — cos2?)'/» '
. . —ch?sin<p . . sh5cos<f
9~ x (ch25 — cos2 9)'/« """ y (ch25 —cos2<f)'/» '
Замечание. С криволинейными ортогональными координатами не так
легко обращаться, как с прямоугольными. Обычно уравнения G0) однозначно
определяют х, у, Z по криволинейным координатам, однако уравнения G1)
не являются однозначными функциями прямоугольных координат. Это нару-
нарушение взаимной однозначности приводит к существенным трудностям.
Рассмотрим эллиптические координаты на плоскости. Они определяются
по формулам рассмотренного выше примера, если ограничиться случаем по-
постоянного г.
Пусть 5 и ср принимают все возможные значения (т. е. все значения,
заключенные соответственно между —со и -(-от и между 0 и 2тс). Тогда
каждая точка плоскости хОу пробегается по два раза. Эти точки получатся
по одному разу, если принять одно из следующих двух ограничений:
1) 0 < ? <-|-оо. 0 < <р < 2те;
2) — <х>< $ < + от, 0 < ср < тс.
Однако и при этих ограничениях имеется неустранимое нарушение непре-
непрерывности. Изучим этот вопрос подробнее.
Точки, расположенные на отрезке F'F (см. рис. 3.26), находятся на
бесконечно сплюснутом эллипсе (? = 0) и в вершинах гипербол (ср== const).
Рассмотрим точки М1(^1, уг) и М2(^2, <р2), расположенные на гиперболе
вблизи отрезка F'F по разные стороны от него. Если ср меняется от 0 до 2тс
(случай 1), то 5^-0, и необходимо tp2=2u — ср,. Пусть точки М{ и М2
неограниченно приближаются друг к другу, оставаясь на одной и той же
гиперболе. Тогда 5i и ^ стремятся к нулю, а cpt и ср2 остаются постоянными.
Следовательно, в случае 1 бесконечно близкие к отрезку F'F точки имеют
существенно разные эллиптические координаты (по ср).
Далее, точки, расположенные на оси х'х вне отрезка F'F, находятся
на вырожденной гиперболе ср=О и в вершинах эллипсов (?== const). Рас-
Рассмотрим теперь точки на эллипсе N1(^i, ср,) и N2Q.2> <P2)> положение которых
показано на рис. 3.26. Если 5 меняется от —оо до -f-oo (случай 2), то
0 < ср < тс, и необходимо =2=—%v При неограниченном сближении N^ иЛ/2
по одному и тому же эллипсу ср, и ср2 стремятся к нулю, а %х и ;2 остаются
постоянными. Следовательно, в случае 2 бесконечно близкие к полупрямым
x'F' и Fx точки имеют существенно разные эллиптические координаты (по %).
Фактически в случаях 1 и 2 мы имеем две разные системы эллипти-
эллиптических координат.
3.41 ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 157
3.4.2. Дифференциальные операторы в ортогональных криволиней-
криволинейных координатах. Пусть V(x, у, г) и А(х, у, г) — скалярная и векторная
функции точки. Найдем выражения для gradV, div 4, AV, rot А в системе
ортогональных криволинейных координат, заданных уравнениями G0).
Рассмотрим малый криволинейный параллелепипед, построенный на осях
координат Ми, Mv, Mw, проходящих через точку М (рис. 8.25). Используя фор-
формулы G2) и G3), нетрудно показать, что проекция вектора grad V на направление
6V
касательной в точке М к дуге MB равна grad UV — —-т— ¦ Следовательно,
имеют место формулы:
в»**'-¦?"?¦• er4.v-.~S.. G4)
Чтобы вычислить выражение для дивергенции вектора А, мы восполь-
воспользуемся формулой D9), применяя ее к элементарному объему в криволиней-
криволинейной системе координат.
Разность между поверхностными интегралами по поверхности BCFE
и поверхности MAGD равна ¦ -
-^(е2е3Аа) dudvdw*).
Аналогичное/ выражение получится и для остальных пар противолежащих
граней. Таким образом **),
,. div А = ihr* [ж <'А*.> + ~ (*зМ*) 4- ?- (МИ.)] • G5)
Применяя формулу Стокса к поверхности MAGD, можно определить
проекцию вектора rot А на направление касательной к оси и. Линейные
интегралы вектора А вдоль MA, AG, GD, DM с точностью до бесконечно
малых высшего порядка соответственно равны
Ave2dv, Awezdw-\-~{eiAw)dvdw,
t
—Awe3dw,
причем значения проекций А и локальных длин ev е2, е3 вычислены в точке М
(рис. 3.25). Сумма этих интегралов равна произведению составляющей rota4
• *) Обозначим поверхности MA3D и BCFE соответственно (I) и (II), а орты
осей и, v, w — через е\, е% е\. Длины ребер рассматриваемого элементарного объема Дт
равны ех da, e2 dv, e3 dw. Учитывая ортогональность системы координат и направле-
направление внешней нормали на гранях At, имеем:
= — е1е2 dv e3 dw, dsu = e®e2 dv e3 dw,
J
(Гц
-j^(Aue2e3)dudvdw.
**) Очевидно, имеем
I div A di = I div Aex due2dve3dw x &\v Ae^^e^ dudvdw.
At At
158 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
на площадь поверхности MAGD, т. е.
[ГЛ. III
G6)
С помощью круговой перестановки цифр 1, 2, 3 и букв и, v, w, находим:
rot«А=Ь; [ш
dw
Отметим, что проекции
G2) и G3).
Положим в G5) A = gradV. Имеем
Av, Aw можно определить по формулам
L du \ ex du J
А
dv
Важнейшие системы ортогональных криволииейных координат
в пространстве
Рассмотрим несколько конкретных систем ортогональных координат.
Эти системы будут использованы в гл. VI при изучении уравнений распро-
распространения волн и Лапласа. С целью облегчения дальнейших вычислений мы
приведем выражения для дивергенции, лапласиана, проекций градиента и вихря
во всех рассмотренных ниже системах координат. Будем
считать, что V и А — соответственно скалярная и век-
векторная функции точки.
3.4.3. Система цилиндрических координат. Коор-
Координатные поверхности: круговые цилиндры с осью вра-
вращения Oz, плоскости, перпендикулярные оси Oz, и
полуплоскости, проходящие через Oz (рис. 3.27). Ци-
Цилиндрические координаты р, (р, z связаны с прямоуголь-
прямоугольными координатами х, у, z соотношениями
x = pcoscp, y = psintp, z = z.
Уравнения координатных поверхностей соответ-
соответственно в прямоугольной и цилиндрической системах
имеют вид:
д;24-у2 = р2, р= const,
Рис. 3.27. у/х — tg (р, ср = const,
z = const, z — const.
Квадрат элемента длины равен
следовательно, единицы локальной длины равны
*) Более детальный вывод формул этого пункта см., например, в [5].
3.4]
ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
159»
Согласно формулам п. 3.4.2 получаем:
dV „..„ y=\_dV_
Р
1
div4:= — An
дА,
^ + 7"
1 дАх
rot. А =
Р р
дА?
~дГ
дА,
дАг
dV
d*V
sлл. Система сферических координат. Координатные поверхности:
сферы с Центром О и радиусом р, круговые конусы с вершиной О, обра-
образующие которых составляют с осью вращения Oz угол 6, и полуплоскости,
проходящие через Oz под углом ср к плоско-
плоскости xOz (рис. 3.28).
Сферические координаты') р, 9, ср связаны
с координатами ^г, у, z соотношениями
х = р sin 6 cos <р, у = р sin 6 sin <p, z = pcos6.
- Уравнения координатных поверхностей со-
соответственно в прямоугольной и сферической
системах имеют вид:
x2-\-y2+z2~ p2=0, p = const,
х2-\-у2 — 22tg2e + 0, 6 = const,
^ cp = const.
Квадрат элемента длины равен
ds* = df + p2d62 + р2 sin2 6
следовательно, единицы локальной длины равны
ех=\, е2 = р, е3= psin 9.
Согласно формулам п. 3.4.2 получаем:
dV . ,, 1
2
-A
Р р
Рис. 3.28.
1
dp ~ ptg6 ' ' р d6 i^ psin 6 д<? '
pjg о v ' р оо р sin о- o(f
дАр
р sin в dtp
дА*
дА"
p2tg6
"р2 dO2 "i~ p2 sin2 в ду* *
') Координаты <f и в часто называются долготой и дополнением широты (зенит-
(зенитным расстоянием).
160
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
[ГЛ. III
3.4.5. Система параболических цилиндрических координат. Рассмот-
Рассмотрим рис. 3.29, на котором представлены параболы двух семейств взаимно
ортогональных софокусных парабол (фокус в начале координат). Проведем
ось OZ, перпендикулярную к плоскости OXY, и будем параллельно пере-
перемещать параболы при условии, что их фокусы остаются на оси OZ. Тогда
параболы обоих семейств опишут параболические цилиндры, образующие
две системы взаимно ортогональных координатных поверхностей. Третья
система координатных поверхностей состоит
из плоскостей, параллельных OXY. Если при-
принять за оси прямоугольной системы коорди-
координат Ox, Oy, Oz соответственно OX, OY,
OZ, то уравнения координатных поверхностей
в прямоугольной и параболической цилиндри-
ческой системах имеют вид:
Рис. 3.29.
z = const,
<х= const,
р= const,
z = const.
Координаты а, p, z связаны с прямоугольными координатами соотно-
соотношениями:
x=cb§, у = -|-ф2 —a2), z = z.
Квадрат элемента длины равен
ds2 = с1 (а2 -+- р2) (da2 + <*Р2) -f dz2,
следовательно, единицы локальной длины равны
Для упрощения записи положим (ос2-|-р2) — 8. Согласно формулам
п. 3.4.2 получаем:
1 dV
дА*\
dV
дАг
~~дг~'
, 1 дАг дА?
Г("И — Ж~д? дГ'
дА,
дА
3.4.6. Система параболических координат вращения (параболоидаль-
ные координаты). При вращении фигуры на рис. 3.29 вокруг оси OY пара-
параболы обоих семейств опишут ортогональные параболоиды вращения, образую-
образующие две системы взаимно ортогональных координатных поверхностей. Третья
система координатных поверхностей состоит из полуплоскостей, проходящих
через ось вращения. Если принять за оси прямоугольной системы коорди-
3.41 ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 161
натных поверхностей в прямоугольной системе и в системе „параболических
координат вращения имеют вид:
х2 + у2 = с2а2 №- + а?\, а = const,
2_2L\ p= const.
Координаты а, р, ф связаны с прямоугольными координатами соотно-
соотношениями
л: = cap cos ф, у = cap sin ф, z=y(P2 —a2).
Квадрат элемента длины и единицы локальной длины соответственно
равны
ds2 = с2(a2 + р2) (da2 -)- dp2) Ч- c2a2p2 df;
Положим (a2 + p2)''2 = 8. Согласно формулам п. 3.4.2 имеем:
, 1 dV ... 1 dV ... 1 dV
^ gradK gradK
сЧг \ даг * д$г I ~ c2tz2fi2 <?ф2 •
3.4.7. Система эллиптических цилиндрических координат. На рис. 3.30
изображены эллипс и гипербола —-представители двух взаимно ортогональных
семейств софокусных эллипсов и гипербол с осями О А и ОВ'). При парал-
параллельном переносе по перпендикуляру ОС к плоскости рисунка рассматриваемые
эллипсы и гиперболы опишут эллиптические и гиперболические цилиндры,
образующие две системы взаимно ортогональных координатных поверхностей.
Третья система координатных поверхностей состоит из плоскостей, парал-
параллельных плоскости ОАВ. Если ОА, ОВ, ОС принять за оси прямоуголь-
прямоугольной системы Ox, Oy. Oz, то уравнения координатных поверхностей в пря-
прямоугольной и эллиптической цилиндрической системах имеют вид:
— 1=0, % = const,
— 1=0, <p — const'
== COnst, Z = COnSt.
') Здесь полезно вспомнить замечание, сделанное в п. 3.4.1 по поводу плоских
эллиптических координат.
11 А. Аяго
162
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
[ГЛ. Ill
Координаты ?, ср, z связаны с прямоугольными координатами соотно-
соотношениями
х = a ch \ cos ср, у = a sh ? sin cp, z — z.
Квадрат элемента длины и локальные единицы равны
' ds2 = a2 (ch2 ? — cos2 ср) (d%2 + d<f2) 4- dz2,
gj = ^2 = a (ch2 $ — cos2cp)'/2, e3=l.
Положим (ch2$ — cos2cp)/2 = Д. Согласно формулам п. 3.4.2 имеем:
1 dV , ,, dV
дг '
дА„
дАг
~~дГ'
dAz
dA
1 dAz
ro\zA = -дз (sh \ ch ? А9 — sin cp cos ср Аг
1 (d2V , d2V\ , d2V
1
аК
, 3.4.8. Система вытянутых эллипсоидальных координат (вращения).
При вращении семейств софокусных эллипсов и гипербол (рис. 3.30) вокруг
оси ОА получаются соответственно взаимно ортогональные семейства вы-
вытянутых эллипсоидов вращения и двуполостных гиперболоидов вращения.
Они образуют две системы координатных поверхностей. Третья система
состоит из полуплоскостей, проходящих че-
через ось вращения. Если принять ОА, ОВ,
ОС (ОС—перпендикуляр в точке О к пло-
плоскости ОАВ) за оси Oz, Ox, Оу, то коор-
координатные поверхности в прямоугольной си-
системе и в системе вытянутых эллипсоидаль-
ных координат имеют вид:
a2 sin2 <f a2 cos2 <f
+1=0,
Рис. 3.30.
= const,
р = COnSt,
ф = const.
Если ограничить изменения координат следующими интервалами:
0<?<4-сх>. 0<срО, 0<ф<2тг,
то все точки пространства пробегаются по одному разу.
Уравнение ? = 0 соответствует вырожденному эллипсоиду — отрезку
прямой F'F. Уравнение ср = О соответствует вырожденному гиперболоиду —
прямой с вырезанным отрезком F'F.
Координаты \, ср. ф связаны с прямоугольными координатами х, у, z
соотношениями:
х = а sh S sin ср sin ф, у = а sh?sincpcost{i, z = ach?cos<p»
3.41 ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 163
Квадрат элемента длины и единицы локальной длины соответственно
равны
ds2 = a2 (ch2 ? — cos2 ср) (d\2 -f- rfcp2) + a2 sh2 ? sin2 с? а!ф2,
е, = е2 = a (ch2 ? — cos2 ср)'/г, е3 == а sh ; sin ср.
Положим для упрощения записи Д —(ch2? — cos2cpI/2. Согласно формулам
п. 3.4.2 имеем: . ¦ .
1 dV ... 1 dV. . ,, 1 <ЭК
a sh S sin <p
a sh ; sin
dA 1 / 1
1 1 / <?Л„ дА.
=Ж Cch Ssh Ы? - cos ? sin <p At) + ^- ^ jj
j
1 / 1 «?V .Л ^V^ i <^^ <^^\L ,' d2V
th 5 di + tg? d<p "•" di2 "•" d<p2 ) "^ a2sh2csin2f
3.4.9. Система сплюснутых эллипсоидальных координат (вращения).
При вращении семейств софокусных эллипсов и гипербол (рис. 3.30) вокруг
оси ОВ получаются взаимно ортогональные семейства сплюснутых эллипсоидов
вращения и однополостных гиперболоидов вращения. Они образуют две
системы координатных поверхностей. Третья система состоит из полупло-
полуплоскостей, проходящих через ось вращения. Если принять О А, ОВ, ОС (ОС —
перпендикуляр к ОА и ОВ) соответственно за оси Ox, Oz, Oy, то коор-
координатные поверхности в прямоугольной системе и в системе, сплюснутых
эллипсоидальных координат имеют вид: '
22
— 1=0, Е = const,
Координаты ?, ср, <|> связаны с координатами х, у, z соотношениями
х = achScoscpsinip. у = ach$coscpcos(p, z — ash?sin«p.
Квадрат элемента длины и единицы локальной длины равны
ds2 = a2 (ch2 Е — cos2 cp) (d$? -f df) + a2 ch2 ? cos2 cp df,
e1 = e2 = a(ch2? — cos2cp)'/j, ег = a ch ? cos cp.
Пусть длина интервала возможных значений ф равна 2те. Тогда все
точки пространства пробегаются по одному разу в следующих двух случаях:
1) 0<Е<-г-оо. — !"<<р<у;
2) . — oo<$<-f-po, ¦ 0 < <р < -J.
И*
164 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Уравнения поверхностей ?=0 и ср—0 описывают в прямоугольной
системе координат вырожденный эллипсоид (внутренность круга диаметра F'F,
лежащего в плоскости хОу) и вырожденный гиперболоид (плоскость хОу
с вырезанным кругом диаметра F'F). В первом случае для точек, находя-
находящихся над или под рассматриваемым кругом, имеет место ср > 0 или ср < 0.
Во втором случае для точек, находящихся над или под плоскостью с вы-
вырезанным кругом, имеет место ? > 0 или ? < 0.
Положим А = (ch2 ?— cos2cp) . Согласно формулам п. 3.4.2 имеем:
, .. \ dV , ., 1 dV . ., 1 dV
gradr V = —г- -зг- , grad V = —г- —г—, gradj. V — ;
6 fc аД <?? & ? аД ду ' s Ф
—г- -зг- , grad V = —г- —г—, gradj. V — —т—„
аД <?? & ? аД ду ' s Ф a ch s cos <p
div 4 == -^j- [th 6 B ch2 g — cos2 <p) ЛЕ + tg <p B cos2 cp — ch* g) л?] +
-+¦
a\ \ di df I a ch ? cos ?
\ 1 дА,„
rot A — —r-= -тЛ .- (-—¦ -i- th \A ) ,
f a ch 5 cos ср <?4* аА \ л ' ¦>]
1 ' 1 1дАа дАс
i = -дз (sh I ch \ A — sin cp cos cp
3.4.10. Система бицилиндрических координат. Рассмотрим два орто-
ортогональных семейства окружностей (рис. 3.31):
1) окружности, центры которых находятся на оси ОХ, вида
i^-+-a2 = 0; (а)
2) окружности, центры которых находятся на оси OY, вида
p —a2=0. (б)
Окружности (б) проходят через точки F' и F, в которые вырождаются
окружности (а) при ?— ±оо.
Пусть ось OZ перпендикулярна к плоскости XOY. Если рассматриваемые
окружности перемещать параллельно оси OZ, то получаются два взаимно
ортогональных семейства круговых цилиндров. Они образуют две системы
координатных плоскостей. Третья система состоит из плоскостей, параллель-
параллельных XOY. Если принять OX, OY, OZ соответственно за оси Ox, Oy, Oz,
то координатные поверхности в прямоугольной и бицилиндрической системах
координат имеют вид:
x2_|_y!__2a.*;cth?H-a2 = 0, ? = const,
Je2_|_y2_j_2ay ctgcp — a2 —0, cp = const,
z = const, z = const.
Следовательно, координаты ?, ср, 2 связаны с координатами jr, у, 2 соот-
соотношениями
sh ? __ sin <f
х — а rh е-)-cos? ' ' У — п ch'f.'+cosY ' г — г-
ЗЛ)
ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
165
Окружности семейства (а) целиком расположены справа или слева от
оси Оу соответственно при положительном или отрицательном значении ?.
При ?=±оо цилиндры (а) вырождаются в прямые, параллельные оси Oz
и проходящие через F и F'; пло-
плоскость yOz задается уравне- j у
нием (а) при ? = 0.
Значение параметра ср, соот-
соответствующее любой окружности
семейства (б), определяется лишь
с точностью до kit. Поэтому бу-
будем считать, что ср лежит в интер-
интервале 0 < tp <; тс. Отсюда следует,
что точки окружностей семей-
семейства (а), симметричные относи-
относительно оси ОХ, имеют коорди-
координаты ср и тс— ср I для точек ниж-
нижней полуплоскости ср ¦< -к-1 ¦ Если
полоса плоскости xOz, заключенная между двумя фокальными линиями,
выражается уравнением ср = 0, то часть этой же плоскости вне полосы имеет
уравнение ср — тс,'
Легко показать, что угол FmF' — тс — ср или ср в зависимости от по-
положения точки, пересечения окружностей т на верхней или нижней дуге и
Рис. 3.31.
Квадрат элемента длины и локальные единицы равны
ds= . . *' ^
(ch t-f-cos <pJ
ch S + cos
Положим ch ? -\- cos ср = I. Согласно формулам п. 3.4.2 имеем:
. ,, X dV '. ,г X dV
gradE V = —зе-» grad^, V = — -т- ,
1 X /<?Д
div Л = - (sin срЛ — sh 5/Ц) + - Kf
_ дУ .
дАг
~5Г
(?А X дАг
о, \ <?? dtp / а
a* [
3.4.11. Системы тороидальных и бисферических координат. 1. При
вращении фигуры на рис. 3.31 вокруг оси ОУ окружности (а) и (б) образуют
ортогональные семейства торов и сфер. Третья система координатных поверх-
поверхностей рассматриваемой тороидальной системы координат состоит из полу-
полуплоскостей, проходящих через ось вращения. Примем оси OX, OY, OZ
соответственно за оси Ox, Oz, Оу. Уравнения координатных поверхностей
166" 1 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
в прямоугольной и тороидальной системах имеют вид:
(х2-)-/-)-2г-|-а2J —4a2(x2 + y2)cth2S = 0, ? = const;
х2 -f- У2 -+¦ z2 — 2azctg<?— a2 = p, c? = const;
ф = const.
Координаты ?, <p. ф связаны с координатами х, у, г соотношениями *)
__ shSsIn^1 sh ;cosф sin?
x — a ch i + cos <? ' У — a "ыГ?4-' cos7 ' 2 a chS + coscp *
Все точки пространства пробегаются по одному разу, если изменение
координат ?, tp, ф ограничить интервалами
О < ? < + °°> — тс < ср < тс, 0 < ф < 2тс.
Уравнение ?=-|-оо соответствует вырожденному тору — кругу с диа-
диаметром F'F. Этот же круг получится, если мы примем «р=0. Внешность
этого круга (плоскость, из которой вырезан рассматриваемый круг) вы-
выражается уравнениями <р = ± тс.
Квадрат элемента Длины и локальные единицы равны
ash 5
Положим ch ?-]- cos «у = >ч. Согласно формулам п. 3.4.2 имеем:
* dV __л „ к dV __., „ к dV
1—sh2 5-f-ch 6 cos <f 2 sin 9 к I dA- dAv\ к е)А
divi4= * *
sin
1 dA: dЛф \ 1 + ch 5 cos
dA: dЛф \
X / (?.4Ф dA \ sin <f sh 5
f ОТф А—
¦ n~ a l й ~дУ1 а ^ а
f ch ?) dV к sin <p dV _. k2 I d2V d2
a2 she Ш"^ а1 ~ду~+ "о2" \"др~ "^ й?2" "^"ih2! "^jTJ '
AV_ X(l + cosych?) dV Xsiny dV I2 I d2V d*V 1 d2V\
V ~~ 2 5 "*" 2 + 2 d2 + ?2 + 2 5 )
2. При вращении фигуры на рис. 3.31 вокруг оси ОХ окружности (а)
и (б) образуют соответственно две сферы и ортогональные им тороидальные
поверхности. Эти тороидальные поверхности отличаются от торов, получен-
полученных выше при вращении рис. 3.31 вокруг оси OY, так как окружности
семейства (б) пересекают ось вращения. Третья система координатных поверх-
поверхностей бисферической системы координат состоит из полуплоскостей, про-
проходящих через ось вращения. Отметим, что при определенных условиях
сферы вырождаются в две точки F и F', играющие роль полюсов. Поэтому
*) Обычно в знаменателях формул связи между тороидальными и прямоуголь-
прямоугольными координатами стоит знак минус. Это соответствует замене у на те — у (см.,
например, [6]).
ЗА] ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 167
бисферическая система координат называется также биполярной системой
координат (в пространстве). Если OX, OY, OZ принять соответственно
за оси Oz, Ох, Оу, то уравнения координатных поверхностей в прямо-
прямоугольной и бисферической системах имеют вид:
x2-\-y2 + z2 — 2a2CthS+a2 = 0, Л = const,
(х2 4- у2 + г2 — а2J — 4а2 (х2 + у2) ctg2 Ф = 0, ср = const,
— = tg ф, ф = const.
Координаты ?, ср, ф и jr. у, г связаны соотношениями *)
sin tp sin ф sin ? cos ф sh ? '
•*: —fl ch?+cos? ' У~ flch? + .cos^' Z ~ fl ch S + cos <? '
Все точки пространства пробегаются по одному разу, если изменения коор-
координат \, ср, ф ограничить следующими интервалами:
— оо<?<+оо, 0<срО, 0<ф<2тс.
Квадрат элемента длины и локальные единицы длины равны
ds2 = (che+cosy)» №+<V+sin2
о ^ a sin t
2 ch5+costp ' 3
^
ch5+costp ' 3 chS + costp
Положим ch E + cos ср = \. Согласно формулам п. 3.4.2 имеем:
dV . ,. X dV ... \ dV
2sh5
X /<?Лф 1 дА9
дт/_ х /cosychS+1 dV htdv) Х2/а2Кd'K 1
t в2 I sin <р д<? S * di ) ~т~ а2 \, <??2 "+" <?ср2 "•" sin2 ? <?ф2 j"
3.4.12. Система софокусных поверхностей второго порядка (система
общих эллипсоидальных координат). Рассмотрим семейство софокусных
поверхностей второго порядка
-^Т + Т^ + ^Т- 1=0- 0<с2<*2<а2.
зависящих от одного параметра k. Через каждую точку пространства с коор-
координатами (х, у, z) проходят три поверхности указанного типа. В самом деле,
при любых фиксированных х, у, z относительно k получается уравнение
третьей степени. Все три корня этого уравнения к, р и v вещественны и под-
подчиняются неравенствам
\ < с2 < ц. < b2 < v < а2.
*) Относительно знака в знаменателях см. предыдущую сноску.
168 ВЕКТОРНОЕ ИСЧИСЛЕНИЕ [ГЛ. III
Отсюда следует, что через каждую точку пространства проходят эллипсоид,
однополостный и двуполостный гиперболоиды. Эти поверхности попарно
ортогональны, т. е. три величины X, [х, ч определяют ортогональную криво-
криволинейную систему координат.
Определим зависимость между координатами X, [х, м и х, у, г. С этой
целью рассмотрим тождество
х2 {Ь2 — k) (с2 — k) + у2 {а2 — k) (с2 — k) -+- z2 (а2 — k) ф2 — К) —
— (а2 — k){b2 — k)(c2 — k)^(k — \)(k — ji)(ft — v).
Приравнивая Л последовательно a2, b2, с2, получим выражения для х2,
у2, z2 вида
„2_ (а2 —Х)(аг —t^)(a2 —у)
•^ ~ (б» — а2) (с2 — а2)
y (a2 — b2) (c2 — b2)
?_ {c2 — X) (c2 — tx) (c2 — ч)
2 "" (a2 — e2) (u2 — e2)
Если координатам X, (x, v придать приращения d\, ф, dv, то, учитывая
взаимную ортогональность координатных поверхностей, найдем единицы
локальной длины:
ei = T (а2 — Х)(й2 — Х)(с2— X) '
I (ч-
_L
4 (а2 — (х) (й2 — м-) (с2 — (
ез 4 (а2 — ч) (Ь2 — ч) (с2 — ч) '
3.4.13. Приложение к уравнениям Максвелла. Уравнения Максвелла
в ортогональных криволинейных координатах. Формулы G5) и G6), при-
примененные к системе F2), позволяют написать уравнения Максвелла в системе
ортогональных, криволинейных координат н, v, w. Имеем
i^.P^_ д <» Р ^ __ „ „ дВи
Два других уравнения получаются круговой перестановкой индексов. По
аналогии
и, как выше, два других уравнения получаются круговой перестановкой
индексов.
Условия div/?=0 и div?>—p записываются в виде
А- (Вие2е3) + ~ {Bvezex) + A (fi^,,^) e о, G9)
(Dee)+ ^ (Лвв) + (De^) eee# (80)
Совокупность уравнений G7) — (80) может оказаться очень полезной,
например, при решении задачи о распространении электромагнитных волн,
направленных вдоль проводящей поверхности простой геометрической формы ').
') Использование уравнений Максвелла в ортогональных криволинейных коорди-
координатах при решении конкретных задач изложено п гл. VI.
ЛИТЕРАТУРА 169
ЛИТЕРАТУРА К ГЛАВЕ III
1. К о ч и и Н. Е., Векторное исчисление и начало тензорного исчисления, Изд. АН
СССР, 1951.
2. Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления,
т. III, Физматгиз, 1963.
3. Смирнов В. И., Курс высшей математики, т. II, Физматгиз, 1962.
4. Бронштейн И. Н., Семендяев К. А., Справочиик по математике, Физмат-
Физматгиз, 1959.
5. Романовский П. И., Ряды Фурье. Теория поля. Аналитические и специаль-
специальные функции. Преобразование Лапласа, Физматгиз, 1959.
6. Б е р м а н т А. Ф., Отображения. Криволинейные координаты. Преобразования.
Формулы Грина, Физматгиз, 1958.
7. М а д е л у н г Э., Математический аппарат физики, Физматгиз, 1960.
8. Г о л ь д ф а й н И. А., Векторный анализ и теория поля, Физматгиз, 1962.
9. М е р к и н Д. Р., Алгебра свободных и скользящих векторов, Физматгиз, 1962.
ГЛАВА IV
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
4.1. АЛГЕБРА МАТРИЦ
4.1.1. Плоское преобразование, понятие оператора. Обозначим через а
операцию, преобразующую вектор и в другой вектор v. Это преобразование
можно символически написать в виде
аи = v.
Если операция а преобразует каждый вектор в строго определенный
вектор, то рассматриваемое преобразование однозначно.
;Если операция а преобразует различные векторы в различные, т. е.
неравенство ифч) влечет за собой аи Ф а.4), то она называется неособенной.
Если
а (си) — с (аи),
а (й + г») — <хй + a.v,
где с — произвольная постоянная, а и и ч> — произвольные векторы, то пре-
преобразование называется линейным. Ниже мы ограничимся только линейными
операциями.
Принято называть а оператором преобразования.
Если вектор и, отличный от нуля, преобразуется в вектор <о, имеющий
то же направление, т. е. если преобразование а изменяет только длину или,
как принято говорить, модуль вектора и, то, обозначив через к коэффициент
растяжения или сжатия длины век-
вектора, получаем
аи = Хй.
(В этом равенстве а — оператор,
а А, — алгебраическое число.) При-
Принято говорить, что направление век-
. тора и — это собственное направле-
,4 ние оператора а, а А.— это соответ-
соответствующее собственное значение.
Пример 1. Даны две взаимно
перпендикулярные прямые ОА, ОВ
и вектор и. Пусть новый вектор v определяется следующим образом: его
проекция на ОА в 5 раз больше проекции и на ОА, а его проекция на ОВ
равна половине проекции и на О В (рис. 4.1).
Ясно, что если вектор и находится на прямой ОА, то
аи = 5и,
Рис. 4.1.
4.1]
АЛГЕБРА МАТРИЦ
171
а если он находится на ОВ, то'
аи = 0,5».
Следовательно, О А и ОВ— два собственных направления а, а числа 5
и 0,5 — два соответствующих им собственных значения.
4.1.2. Сумма двух операторов. Если две операции а и C по отдель-
отдельности приложены к вектору и, то сумма аи-\-$и обозначается через
Оператор о+р называется суммой операторов аир.
4.1.3. Произведение двух операторов. Пусть произведена операция а
над результатом операции р, проделанной над и. Если можно перейти
непосредственно от и к конечному результату действия обоих операторов
при помощи единственной операции -у, то опера-
оператор -у называется произведением операторов аир:
Рис. 4.2.
Символически это записывается в виде
Следует заметить, что в большинстве слу-
случаев оператор а[3 отличается от ра, поскольку по-
порядок, в котором производятся операции, не
безразличен. Это легко показать на следующем
примере.
Пример 2. Дана прямая хх', точка О на
этой прямой и некоторый вектор и (рис. 4.2).
Операцию а определим как зеркальное отображе-
отображение по отношению к прямой хх', а операцию р
как поворот на 90° в направлении часовой стрелки.
Операция а над и дает вектор vv а операция C над v1 — вектор wv Опера-
Операция -р над и дает вектор v2, а операция а над v2 — вектор да2, отличный
от Wj (концы векторов wx и чю2 симметричны по отношению к точке О).
Разность ар — [За назовем коммутатором операторов аир. Если комму-
коммутатор двух операторов равен нулю, то говорят, что операторы перестано-
перестановочны. В этом случае
ар = Ра.
4.1.4. Представление плоских преобразований с помощью матриц.
Даны две оси прямоугольных координат, вектор и с составляющими uv a2
и вектор V, полученный из и посредством преобразования а. Составляющие v1
и v2 нового вектора можно выразить как линейную функцию координат их
и и2 прежнего вектора. Получим два равенства, в которых коэффициенты
Рассматриваемое преобразование характеризуется таблицей коэффициен-
[<хп а12]
. Она называется матрицей преобразования..
а21 a22j
Пример 3. В примере 1 имеем t
v, = 5м, -f-'O • и2,
0,5и2.
172
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Матрица оператора а здесь равна
Г5 ° 1.
Lo 0.5J
Г1 01
Пример 4. В примере 2 операция а представлена матрицей п - I,
Г 0 II ~
а операция р — матрицей I I .
4.1.5. Произведение двух матриц. Даны два преобразования а и В,
характеризующиеся соответственно матрицами
Гап а12~] рн РшТ
[а21 a22j ' LP21 P22J'
Применив к вектору а преобразование 8, а к полученному таким обра-
образом вектору v преобразование а, найдем вектор w. Определим матрицу
преобразования f- позволяющего непосред-
ственно перейти от вектора и к вектору w.
Имеем
\
\
\
\
v2 = р21Й1 + р22и2.
К
\
\
Рис. 4.З.
Затем
или
Щ —
allPl2
?2l) "l H- (a2lPl2
Итак, матрица, определяющая преобразование ар, иначе говоря, матрица
произведения -у, имеет вид
Til Tia
T21 T22
Мы узнаем здесь обычное правило образования элементов произведения двух
определителей.
Пример 5. Рассмотрим обе матрицы из примера 4. Имеем
.о + О.(—1)
1-1-4-0-0
0-14-1-0 0-0
—1). 14-0-0 (—1)
ГО П
Ll OJ-
-(— 1)J = L-1
—
Преобразование aB является зеркальным отображением вектора и отно-
относительно биссектрисы координатного угла zz'', а преобразование pa — зер-
зеркальным отображением относительно биссектрисы tt'. Результаты преобразо-
преобразований, очевидно, симметричны по отношению к точке О (рис. 4.3).
Легко заметить правило образования элементов матрицы произведе-
произведения ав на приведенном примере произведения двух матриц, имеющих по две
4.1]
АЛГЕБРА МАТРИЦ
173
строки и два столбца. Каждый элемент строки матрицы а умножают на соот-
соответствующий элемент столбца матрицы C и полученные произведения склады-
складывают. Например, элемент f12 матрицы произведения, находящийся на пересече-
пересечении первой строки и второго столбца, является суммой произведений первого
элемента первой строки матрицы а на первый элемент, второго столбца C и
второго элемента той же строки а на второй элемент того же столбца C:
Гап М ГРп Ы = ГТп Tizl
U21 «22J LP21 P22J LT21 T22J '
4.1.6. Представление вектора посредством матрицы. Дан вектор и
с составляющими uv и2. Мы .можем представить его как матрицу
N.
L«2j
Преобразование вектора и с помощью операции, определяемой матри-
матрицей а, состоит теперь в умножении матриц
a22
Применяя предыдущее правило, получаем координаты вектора v:
4.1.7. Обобщение на n-мерное пространство. Все, что мы говорили
о двухмерном пространстве, легко обобщить на я-мерное пространство.
Пусть дан вектор а с координатами uv а2, .. ., ип. Группа линейных
преобразований
«1 = 21 °-ikuk
=1, 2 л)
позволяет перейти от вектора и к "вектору v с координатами vv v2 vn-
Матрица преобразования будет
Вектор и может быть представлен в виде матрицы, состоящей из одного
столбца
Матрицу с элементами a.lk будем обозначать через [л1к]. Для упрощения
записи и только в том случае, когда можно не опасаться путаницы, мы будем
обозначать ее просто через а. Точно так же будем обозначать через а одно-
одностолбцовую матрицу, образованную из координат вектора.
174
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
4.1.8. Равенство двух матриц. Две матрицы равны, если определяемое
ими преобразование, примененное к произвольному вектору, дает один
.и тот же результат.
Из
получаем
ik'
т. е. соответствующие элементы, составляющие две равные матрицы, должны
быть равны.
4.1.9. Сложение двух матриц. Даны векторы v и w, полученные
последовательным применением к одному и тому же вектору и преобразо-
преобразования, определяемого матрицами а и C:
•да,
•да = аи.
Сумму v-\-w можно получить, применяя к вектору и преобразование,
определяемое матрицей f> которая получена сложением соответствующих
элементов матриц а и [3:
Матрица f называется суммой двух матриц а и р. Сложение матриц
определено только в том случае, когда они имеют одинаковое число строк
и столбцов. Например,
I 1 2 31 П —2 О I Г2 0 31
. U 5 б] + [з —6 —iojr=[7 —1 —4J *
4.1.10. Умножение матрицы на число. Из предыдущего определения
следует, что если нужно сложить X одинаковых матриц а, т. е. умножить
матрицу а на число X, то результат этой операции можно получить, умно-
умножив каждый элемент матрицы а на X:
Например,
г 1 —1 о
2 0—3
4 —1 —2
7—7 0
14 0 —21
28 —7 —14
4.1.11. Умножение матриц. Вектор w может быть получен последо-
последовательным применением к вектору и преобразований, определяемых матри-.
цами р к а. Перейдем, как в п. 4.1.5, от « к да непосредственно, путем
преобразования, определяемого матрицей -j-
Имеем х
! = ZlP(*K*. W;. = 2j
я <
откуда
•да
7 =
4.1]
Сравнивая с
АЛГЕБРА МАТРИЦ
»; = .
175
получаем правило умножения матриц а
i
Ту* = 2
I
определяющее матрицу произведения
Следовательно, элемент на пересечении строки j и столбца k матрицы f
мы получим, умножая первый член строки j матрицы а на первый член
столбца k матрицы р и складывая с аналогичным произведением вторых
членов, потом третьих и т. д. по схеме рис. 4.4. Итак, правило умножения,
описанное в п. 4.1.5 для случая матриц в две строки и два столбца, имеет
общий характер.
Рассмотрим совокупность линейных преобразований, переводящих век-
вектор и в вектор v.
vi^= 2 au«*-
Эти преобразования можно получить, при-
применив правило умножения матриц:
Иначе говоря,
Строка J
Рис. 4.4.
Замечания. 1. Мы видели, что умножение матриц—некоммутативная
операция, но легко показать, что эта операция ассоциативная, т. е. что *
Из правила умножения матриц непосредственно видно, что определитель
произведения матриц равен произведению определителей. Поэтому если
то
где |а|, | р | и |-у | — определители соответствующих матриц. Понятно, что
9то замечание имеет смысл только в случке квадратных матриц.
2;"Очевидно, что понятие произведения двух матриц приложимо не только
к квадратным матрицам или матрицам в одну строку или один столбец,
но 'и к прямоугольным матрицам! Однако важно отметить, что произведение
матриц имеет смысл только в том случае, если число столбцов первой ма-
матрицы равно числу строк второй.
176
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Примеры. Применяя изложенные выше правила умножения, получаем
следующие результаты:
1 1
—3 —2
2 О
Oi
1
1
4i
2
1
П 4-У 1-У1Г О
L о у JL-4-У
1
—1
О 4п
3 О
О —1
[1 -1 4]
-3 2]
4
j
2
1-
2
3
1
3
— 1
6 71
О 1
Г 1 4 6i
3 —9 —15
5 2
—5 + Зу
1—4/
13т
— 7
.— 2
= — 6,
[7 —2 6].
9
-1+7/1
-2/ J'
О —4 1
'4.1.12. Симметричные матрицы. Рассмотрим квадратную матрицу а.
Общий элемент ее a.lk находится на пересечении строки i и столбца k:
4ft
_ал1ап2 •• • °-nk ¦¦¦ ап,
Элементы ап, а^ ли a.kk апп, расположенные по нисходящей
диагонали слева направо, образуют так называемую главную диагональ
матрицы.
• Симметричной называют матрицу, элементы которой, расположенные
симметрично по отношению к главной диагонали, равны между собой:
Например,
1 х — у
х 3 4
У 4 z
х 4—3
4 6 — z
— 3 —z 9
— симметричные матрицы.
4.1.13. Кососимметричные матрицы. Кососимметричной называют ма-
матрицу, элементы которой, расположенные симметрично по отношению
к главной диагонали, равны по величине и противоположны по знаку:
Из определения следует, что все элементы главной диагонали кососим-
кососимметричной матрицы равны нулю: aw = 0.
4.1]
АЛГЕБРА МАТРИЦ
177
Следующие матрицы кососимметричны:
• 0 х — 3 4
— х 0 — z 1
3 z О ху
_—4 —1 — ху О
4.1.14. Диагональные матрицы. Диагональной называется матрица, все
элементы которой равны нулю, кроме тех, что расположены на главной
диагонали:
= 0 для I Ф k,
Например, матрица
Ф 0 для
Г 1 О О
О у О
_0 0 z
диагональна.
Легко показать, что произведение двух диагональных матриц — тоже
диагональная матрица и что они перестановочны.
4.1. IS. Единичная матрица. Нулевая матрица. Единичная матрица —
это диагональная матрица, все элементы которой равны единице. Будем
обозначать ее через [1]. В матричном исчислении она играет такую же роль,
как число 1 в алгебре. Здесь удобно ввести символ Кронекера blk, который
понадобится нам в дальнейшем. Этот символ равен нулю при I Ф k и еди-
единице при l — k. Пользуясь этим обозначением, получаем для единичной
матрицы .
Единичная матрица, например, в 3 строки и 3 столбца может быть напи-
написана так:
-1
0
.0
0
1
0
о-
0
1.
=
*
г8п
§21
L»ai
8.2
822 8,
832 8:
J13
23
'33 J
Единичная матрица преобразует любой вектор в самого себя:
Действительно,
иь —
Соотношение [1]и = и соответствует формуле 1 •а = а для чисел.
Нулевая матрица — это матрица, все элементы которой равны нулю.
Мы обозначим ее через [0]. В матричном исчислении она играет ту же роль,
что число нуль в алгебре.
4.1.16. Порядок, ранг матрицы. Если квадратная матрица имеет п строк
и столбцов, то число п называется порядком матрицы.
Если определитель матрицы равен нулю, говорят, что она вырождена.
Минором матрицы называется определитель, полученный вычеркиванием
из матрицы одинакового числа столбцов и строк. Если все миноры порядка
выше г, которые можно составить из матрицы, равны нулю, а среди мино-
миноров порядка г хотя бы один отличен от нуля, то число г называется
12 А. Анго
178
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
|ГЛ IV
рангом этой матрицы. Иначе говоря, ранг матрицы равен наивысшему по-
порядку отличных от нуля миноров матрицы.
Пример. Матрица
3
9
—6
0
2
6
4
0
1
3
—2
0
— 1
—3
2
0
вырожденная. Порядок ее равен 4, а ранг 1.
4.1.17. Необходимые условия равенства нулю произведения двух
матриц. Рассмотрим произведение двух квадратных матриц порядка п, имею-
имеющих ранги гх и г2. Можно доказать, что ранг г матрицы произведения удо-
удовлетворяет неравенствам:
г<гх
(*)
(**)
Пусть даны две квадратные матрицы аир порядка д, такие, что
В отличие от алгебры, где равенство ai> = 0 влечет за собой одно из ра-
равенств а = 0 или ? = 0, произведение двух матриц может быть нулевой
матрицей и в случае, когда оба сомножителя отличны от нуля (точнее,
от нулевой матрицы).
Пусть матрицы аир — ненулевые. Если их произведение равно нулю,
значит, равен нулю ранг г матрицы этого произведения. Следовательно,
в этом случае неравенства (*) всегда удовлетворяются. Неравенство (**) дает
необходимое (но не достаточное) условие, которому должны удовлетворять
ранги матриц-сомножителей:
С п.
Отсюда следует, что обе матрицы обязательно вырождены. Представим себе
такой случай: матрица а вырождена, но один из ее миноров, составленный
из л—1 строк и столбцов, не равен нулю. Тогда ранг а равен п — 1. Так
как ранг матрицы р не равен нулю, то в силу предыдущего неравенства он
может быть равен только единице. Но, как легко заметить, квадратная
матрица может быть ранга 1 только в том случае, если все ее элементы
пропорциональны. Следовательно, матрица р обязательно имеет вид
Прим
0
0
_0
где [0]
е
0
1
0
0
л
ры.
0
0
0
0
0"
0
0
0 _
означает
~0
0
0
0
0
0
0
0
нулевую
"Рн
Ри
_Р-
0 0"
0 0
1 0
0 1_
«iPn ••• <
в1р21 ... <
«»P.i ¦ • • «
= [0]4.
матрицу порядка
3nVU
*nP21
гиРл1 _
-3 —2
4 1
2 ]
п.
— 1 -
—3
- 1
1
.1
2
2
2
3
3
3
= [0]3.
4.11
АЛГЕБРА МАТРИЦ
179
4.1.18. Транспонированная матрица. Транспонированной называют
матрицу, которую можно получить из матрицы а, заменив строки столбцами.
Обозначим ее через а. Тогда
Например, матрица ¦
Г2 3 7-
4 2 4
5 8 1.
является транспонированной по отношению к
г2 4 5-
2 8
^Матрица, транспонированная матрице произведения двух матриц, равна произ-
произведению транспонированных матриц, взятых в обратном порядке:
Действительно, матрица (ар) получена вначале умножением элементов-
строк а на элементы столбцов р, а затем заменой строк на столбцы. Тот же
результат можно получить, умножая элементы столбцов р, т. е. строк р.
на элементы строк о, т. е. столбцов а.
Указанное правило непосредственно распространяется на произведение
более чем двух матриц:
(о • {3 ... ш) = (о ... р а.
Замечания. 1. Рассмотрим скалярное произведение двух векторов а
и v, представленных соответственно матрицами
Оно может быть записано в системе прямоугольных координат:
Р =«!©, + U2V.2 -+- ... f- UnVn.
Чтобы получить это произведение по правилу матричного умножения, сле-
следует принять, что
~ V, ~
'=1В, И, ... и„
то есть
P—UV.
Квадрат модуля вектора а будет, следовательно, равен
2
1 —J—
2
-)-И„
ИИ.
12*
180
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ IV
2. Билинейная форма, иначе говоря, выражение, зависящее от двух
переменных
2
г=1
аг2*2 "Г • • ¦ + агтХт)'
может быть записана в матричном виде как уад: или хау, если через у, х, а
обозначить следующие матрицы:
У =
Уп
х =
х„
an ... aj
При х = у получаем квадратичную форму.
Примеры.
= У1 C*, -+- х2) 4- У22л:2 4- Уз (— *i
4.1.19. Обратная матрица. Рассмотрим матрицу а, преобразующую
вектор а в вектор V.
v = au.
Иначе говоря, речь идет о таблице коэффициентов, входящих в п линейных
соотношений
Рассмотрим матрицу C, определяющую обратное преобразование от но-
нового вектора v к прежнему вектору а
и = ^1),
иначе говоря, таблицу коэффициентов, входящих в следующие линейные
соотношения:
/=1. 2 «).
B)
Матрица р называется обратной по отношению к матрице а и обозна-
обозначается через а.
Коэффициенты Р/7 системы соотношений B) можно получить из си-
системы A), решив ее относительно uv u2 и} ип. Они могут быть
вычислены по известной формуле Крамера:
Здесь Д — определитель матрицы a, Atj — алгебраическое дополнение соот-
соответствующего элемента ai7-, т. е. определитель, который полунают, вычерки-
вычеркивая в Д строку и столбец, пересекающиеся на элементе аг,, снабженный
4.П
АЛГЕБРА МАТРИЦ
181
множителем (—l)t+*1). Следует обратить внимание на то, что элемент ^г,
находящийся на пересечении строки j и столбца / в {3, соответствует в <х
минору Ац, относящемуся к элементу atj, который находится на пересечении
строки / и столбца j. На практике вычисление матрицы, обратной а, осу-
осуществляется так:
. 1. Выписывают матрицу а. транспонированную по отношению к а.
2. Заменяют каждый элемент матрицы а определителем, полученным
в результате вычеркивания строки и столбца, на которых расположен дан-
данный элемент.
3. Этот определитель сопровождают знаком плюс, если сумма индексов
элемента четная, и знаком минус — в противном случае.
4. Делят полученную матрицу на Д — определитель матрицы а.
Пример. Требуется вычислить матрицу, обратную
1
4
2
1
2
3
2
5
8
4
5
6
3
6
9
T
8
9.
Матрица а будет
Заменим каждый элемент определителем, полученным при вычеркивании
соответствующей строки и столбца:
—3 —6 —3
24 3 —6
L 22 4 —3J
Переменим знаки у элементов с нечетной суммой индексов. Тогда
- _з -(-б —3-
—24 +3 f6 .
.4-22 —4 —3_
Разделим на Д =15. Таким образом, получаем
1
5
8
5
22
15"
2
5
1
~Е
4
15
1 -
~Т
2
5
1
—т
Матрица, обратная матрице произведения двух матриц, равна произве-
произведению обратных матриц, взятых в обратном порядке, т. е.
') Алгебраическое дополнение отличается от соотвгтствующего мвнора множи-
множителем (—1)'+*.
182
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Действительно, рассмотрим произведение <хрр а . В силу ассоциативности
операции умножения (п. 4.1.11), af
что f7~1:=[l]> находим
5-1 -1
a = [1]. Обозначая a{J = у и учитывая.
Это правило непосредственно распространяется и на произведение любого
числа матриц:
Замечания. 1. При вычислении обратной матрицы предполагается,
что определитель матрицы отличен от нуля, иначе говоря, что матрица невы-
невырождена. В противном случае определить обратную матрицу невозможно.
Сказанное относится и ко всем не квадратным матрицам. Их можно
всегда сделать квадратными, прибавив необходимое число нулей, но тогда
определитель матрицы будет равен нулю.
2. В случае диагональной матрицы обратная матрица также диагональна.
Элементы ее, не равные нулю, представляют собой обратные величины диа-
диагональных элементов заданной матрицы:
а О О О'
0*00
0 0 с 0
0 0 0 d
3. Мы видели, что правило умножения двух матриц то же, что и умно-
умножения двух определителей. Однако аналогия между матричным исчислением
и операциями с определителями на этом и заканчивается. В частности, пра-
правило умножения на число и правило сложения очень различны. Действи-
Действительно,
1
а
0
0
0
0
1
Ь
0
0
0
0
1
с
0
0
0
0
1
X
a
a,
_a2
Точно так
b
b\
b2
же
" a
a
a
с "
c2.
b
b\
г К
a
ai
a2
\
1
с
ci
C2
b
bx
b2
"Xa
u
Xa, X?>,
-Xa2 X*2
-
+
с
ci
C2
'a'
a[
t
4-
Xc-1
Xc,
XcJ
b
К
b2
a' b
a\ bx
a2 b2
, X
с
ci
C2_
С
C!
C2
a
a,
a5
=
a
ai
a2
a
a
a
b
b
b
l
2
С
1 С,
2 C2
+ a'
+«;
=
2*
2*,
2*2
*
*2
Xa
Xa,
Xa2
2c
2c,
2c2
с
ci
C2
*2
-
С
c2
Мы не останавливаемся, конечно, на глубоком различии сущности обоих
понятий. Предыдущее замечание было сделано только для того, чтобы
внешняя аналогия не привела к ошибкам из-за смешения правил вычисления.
4-П
АЛГЕБРА МАТРИЦ
183
4.1.20. Применение матричного исчисления к решению системы
линейных уравнений. Решение системы линейных уравнений может быть
выполнено по формулам Крамера. Матричные обозначения позволяют записать
систему в сжатой форме и, таким образом, делают более удобным обращение
с нею. В особенности матричные обозначения облегчают получение некото-
некоторых групп неизвестных, причем часто отпадает необходимость вычислять
остальные неизвестные.
Рассмотрим систему линейных уравнений
C)
а через а
Если обозначить через у матрицу
, через л: матрицу
матрицу коэффициентов, то система C) может быть записана в форме
у—ах.
Положим, что нам нужно решить эту систему относительно первых k
неизвестных *„•..., хк. Мы можем написать матрицу а в виде
а. "~
... а
k
ай1 ... а
ftft
aft+l,
... а
ft+l,ft
*i, ft + i • • •
*ft, ft + i
.. . а
ft/l
aft+i, ft + i • • • aft+i, л
n, ft + 1
Ее можно рассматривать как составленную из четырех матриц Av А2, A3, At.
Подобным же разложением получим
У —
У*
л:
л:
l
¦"^ft+i
л:
и _
Следовательно, систему, (З) можно представить как
[• т -| Г Л Я Т Г 1^ Т
у*\ Uz л,\[х2\-
Формулы умножения матриц показывают, что можно считать матрицы
Av А2, А3, АА, Xv X2, Yv У2 составными элементами и записать систему
в виде
184
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Исключим из этой системы Х2. Последовательным вычислением получим
= К2 —
yl = AlXl-trA2A7'(Y2 — .
и окончательно
Y\ — A2Alx Y2 = (А\ -
Это — группа из k линейных уравнений вида У = а.Х, она не содержит
больше дгй+1 хп.
Пример. Решить относительно xv x2 систему
дг,-г х.2А- хг-\- хх-\- хь = 3,
х,-!-2дг2н-2дг3-}-Зх4-)-4д:5= 9,
2a:j4- х2 — 2лг3 -I- 2х4 — Зд:5=—16,
Зд:,-^ 2лг2 -t- 3xt -t- 4л:4-Ь хъ— 2,
— дг, + дг2 — 4дг.,-|-4л-4-Ь 2дг, = —12.
Разложим матрицы х, у, а. следующим образом:
Л ==
1
1
2
3
— 1
1
2
1
2
1
1
2
—2
3
4
1
3
2
4
4
1
4
—3
1
2
, X =
хх
х2
х3
. *5_
. У =
3
9
— 16
2
.—12.
Имеем
л4-' =
последовательно:
4
— 10
. 28
— 16
— 16
0
14"
—7
—14.
Л2Л4 = — jy?:
112 [90
-32
—80
1 Г 3 32
32]
12J' К'-
Л2Л4 Аз
= 4-4-J
491
119J'
I, сод
[J]-
67
—49J *
1
63
105
Получаем систему уравнений, содержащих только хх и л:2:
67 63"
101 105
1 ГхЛ
jL^2J
которая может быть записана в виде
4= 67л;, + 63дг2,
-4= 101дг,+ Ю5л:2.
В заключение отметим, что теоретически систему C) можно полностью
решить очень быстро. В матричных обозначениях имеем
4.1]
АЛГЕБРА МАТРИЦ
185
откуда
:a-1y.
Практически расчет сводится к вычислению а. Это совпадает с вычисле-
вычислением по формулам Крамера.
4.1.21. Преобразование системы координат. Рассмотрим изменение
составляющих вектора и,, и2, .... ип при преобразовании системы координат.
Обозначим составляющие вектора в новой системе через Uv Uv .... Un.
Вектор, который в прежней системе был выражен матрицей
и„
будет в новой системе выражен матрицей
и=
и,
Имеет место однородное линейное соотношение между координа-
координатами и и U:
ui==
или и —
Матрица о и есть матрица преобразования координат.
Член alft — это составляющая по прежней оси I для единичного вектора,
расположенного вдоль новой оси k. Из этого вытекает, что матрица, обра-
образованная столбцом k матрицы о
представляет собой в прежней системе координат единичный вектор новой
оси k. И обратно, если известны составляющие единичных векторов, рас-
расположенных вдоль новых осей, матрица преобразования образуется последо-
последовательным сочетанием в надлежащем порядке я одностолбцовых матриц,
представляющих единичные векторы новых осей в старой системе.
Замечание. Если число независимых векторов (размерность) прежнего
и нового пространства различно, то матрица преобразования прямоугольна.
Вектор, представленный в прежнем пространстве матрицей
и =
186 МАТРИЧНОЕ ИСЧИСЛЕНИЕ [ГЛ. IV
¦будет представлен в новом пространстве матрицей
и2
-Um-
Всегда будет иметь место равенство u = ai/, но в матрице а будет я-строк
и т столбцов.
4.1.22. Ортогональное преобразование. Нам нужно определить матрицу
преобразования о, с помощью которого пространство, отнесенное к ортого-
ортогональным осям координат, преобразуется в новое пространство, также отне-
отнесенное к ортогональным осям *). Для этого достаточно, чтобы при таком
преобразовании сохранились длины векторов **).
Пусть задан вектор, представляемый в прежнем пространстве матрицей и;
¦квадрат его модуля равен ии. В новом пространстве, где тот же вектор
.выражен через матрицу U, этот квадрат будет равен UU. Следовательно,
ии = UU.
Но
и = aU, откуда и = Go;
.поэтому
т. е.
оо = [1] или о = о~1.
Итак, матрица а выражает ортогональное преобразование, если транспо-
транспонированная по отношению к ней матрица совпадает с обратной.
Рассмотрим два вектора, представленные в некоторой системе координат
матрицами и и г». Матрица а связывает проекции этих векторов на оси
координат.
Преобразуем систему координат с помощью матрицы о. Тогда коорди-
координаты обоих векторов образуют в новой системе матрицы U к V. Отыщем
матрицу fi, связывающую новые координаты этих векторов:
V" = р?/.
В матричных обозначениях имеем
aV = aaU.
Умножим обе части последнего равенства слева на о. Тогда
У = о
откуда
*) Система осей называется ортогональной, если скалярное произведение двух
любых ненулевых векторов, параллельных различным осям, равно нулю.
•*) Это равносильно сохранению скалярного произведения (см. [31, стр. 178).
4-U
АЛГЕБРА МАТРИЦ
187
Если преобразование а ортогонально, то о '—о. В этом случае
Р = оао. E)
4.1.23. Пример ортогональных преобразований. Поворот. Рассмотрим
трехмерную прямоугольную систему координат с осями Oxv Ox2, Ох3 и
новую систему, полученную из предыдущей поворотом на угол -|-ср вокруг
оси Одг3. Матрица преобразования координат будет
coscp —sincp 0
| sincp coscp 0
0 0 U
F)
Если бы были сделаны повороты на углы -f-i|> и -\-Ь вокруг осей Ох1
и Ох2, то мы получили бы матрицы
0 0
cos ф —sin ф
sin ф. cos ф-
cose
0
-sin6
0
1
0
sin
0
cosOJ
Они, очевидно, определяют ортогональные преобразования. Действительно,
легко убедиться, ' что обратные матрицы совпадают с* транспонированными.
Если последовательно осуществить повороты вокруг координатных осей
на углы ф, 6', ср, то матрица о полного преобразования будет равняться
О =
Обобщение на комплексное пространство
В я-мерном комплексном пространстве условно считают, что коорди-
координаты, отложенные на осях, являются комплексными числами. Это простран-
пространство существенно отличается от комплексной плоскости, используемой в тео-
теории комплексных чисел, где на осях откладывают вещественные числа,
являющиеся действительной и мнимой частью комплексных чисел.
Определим предварительно два'новых типа матриц.
4.1.24. Эрмитова матрица. Эрмитовой называется матрица, в которой
элементы, симметричные по отношению к главной диагонали, — комплексные
сопряженные числа:
Например, матрица
2
2 —ЗУ
- -У
эрмитова.
Элементы главной диагонали эрмитовой матрицы обязательно веще-
вещественны. Вещественная эрмитова матрица симметрична.
4.1.25. Эрмитово-сопряженная матрица. Эрмитово-сопряженная матрица
получается транспонированием исходной матрицы а и заменой полученных
элементов на комплексно-сопряженные. Обозначим ее через а+. Согласно
определению имеем
188
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Здесь дается пример а и ее эрмитово-сопряженной матрицы а+:
l+У 4 7
5 0 1—7
L3+27 —3 — /J
1—у о 3 — 2/
4 0—3
L—7 1 + 7 /
Можно заметить, что эрмитова матрица равна своей эрмитово-сопря-
эрмитово-сопряженной. Действительно, для эрмитовой матрицы а
Следовательно, a^ = a;s и а+ =а.
Пусть дано произведение двух матриц а и fi. Тогда
В самом деле,
В более общем влучае имеем
4.1.26. Модуль н скалярное произведение в комплексном простран-
пространстве. Рассмотрим в я-мерном комплексном пространстве вектор и, предста-
представленный я комплексными числами. Координаты вектора образуют матрицу
Чтобы модуль любого комплексного вектора был вещественной и поло-
положительной величиной, его определяют в ортогональных координатах фор-
формулой
|2>; ;
Мы видели, что квадрат модуля вектора равен произведению двух
матриц
~и,
«'¦]
а в сокращенной матричной записи
иг и.
Чтобы скалярное произведение вектора на самого себя было равно
квадрату длины этого вектора, мы определим здесь скалярное произведение
соотношением
4.1} ' АЛГЕБРА МАТРИЦ 189
или в сокращенной матричной записи
и ¦ V — u+v.
Определенное таким образом скалярное произведение уже не коммутативно.
Все правила, относящиеся к преобразованиям с помощью матриц,
к произведению матриц, к обратной матрице и т. д., 'легко обобщаются на
комплексное пространство.
4.1.27. Ортогональное преобразование комплексного пространства
(унитарное преобразование). Ортогональное комплексное пространство
называется унитарным. Определим характер матрицы о, преобразующей уни-
унитарное пространство в другое такое же. Для этого достаточно, чтобы со-
сохранялись длины векторов, т. е. модуль вектора, представленного двумя
матрицами и и U, был инвариантен. Поэтому
Рассуждение такое же, как в п. 4.1.22, приводит к следующему условию,
которому должна удовлетворять матрица о:
Следовательно, унитарная матрица такова, что ее эрмитово-сопряженная и
обратная матрицы совпадают. Если бы матрица была вещественной, то мы
имели бы о+=а'и пришли бы к уже известной формуле о = о~1.
Легко доказать, что формула D)
справедлива и в комплексном пространстве. Если о — унитарная матрица,
то D) принимает вид
4.1.28. Собственные значения, собственные векторы и характери-
характеристическое уравнение матрицы. Дана матрица з = [<х(>] и вектор, отличный
от нуля, представленный матрицей и. Если вектор и таков, что преобразо-
преобразования, которые выполняет над ним матрица а. сводятся к удлинению или
сжатию, то он называется собственным вектором, его направление — соб-
собственным направлением и коэффициент его удлинения или сжатия X— соб-
собственным значением матрицы а. Это имеет место, если
аи = ки (X—число)
или
2<%м( = ^й* (&=1, 2, :.., я).
Напишем это равенство в развернутом виде. Имеем я соотношений
(«„ — X) к, -+- а12иг 4- •¦¦ +з1ли„=0,
<*21«1 -f- (<*22 — X) й2 -(- ... -+- <Х2„ИП = О,
— Х)ы„ = О.
Так как по крайней мере одна из величин и, ип отлична от нуля,
то определитель системы я однородных линейных уравнений равен нулю:
— X
Д(Х) =
а12
= 0.
190
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Раскрыв определитель, получаем уравнение для вычисления собственных зна-
значений X. Оно называется характеристическим уравнением матрицы а.
Корень X,, подставленный в систему уравнений, позволяет вычислить
собственный вектор, иначе говоря, собственное направление, отвечающее
этому собственному значению X.
Пример. Дана матрица
" 11
— 6
2
— 6
10
— 4
2
—4
6
Ее характеристическое уравнение
11—X —6 2
_6 10 —X —4
2 —4 6 —X
= — Х3 + 27Х2— 180Х+324 =
Оно имеет корни
Л j 1 01 Л2 U , Ло =^ О.
Найдем собственное направление, соответствующее Xj. Подставляя
в систему, получим
8k, —6и2+2«3—0,
—6м, -f- 7и2 — 4и3 = 0,
2и,— 4и2
3«3 = 0.
Определитель этой системы равен нулю. Поэтому можно отбросить послед-
последнее уравнение и решать полученную систему по отношению к произвольной
переменной, например, м, = с3:
—6и24-2й3 = —8ср
7и2 —4и3 = 6с,.
Отсюда и получаем собственное направление для Х, = 3:
Таким же образом можно найти собственные направления для Х2 =
X, = 18:
2
1
—2
2'
2
1
4.1.29. Свойства характеристического уравнения. Расположим опре-
определитель Д(Х) по убывающим степеням X:
Коэффициент Л, не что иное, как сумма элементов главной' диагонали
2<*ftfc- Эту сумму называют следом матрицы. След матрицы по теореме-
к
Виета равен сумме ее собственных значений.
Коэффициент Ап равен определителю |сс| матрицы. Значит, по той же
теореме |а| равен произведению собственных значений а.
4.1]
АЛГЕБРА МАТРИЦ
19Г
Мы докажем важное свойство характеристического уравнения: оста-
оставаться инвариантным при всех преобразованиях системы координат. Действи-
Действительно, характеристический многочлен является определителем матрицы
[a] —Ml]. <7>
Преобразуем систему координат с помощью матрицы' о. Тогда матрица %
преобразуется по формуле D)
о~'<хо = р или ор = <хо.
Характеристический многочлен матрицы р равен определителю матрицы
[р] —Ml].
Очевидно,
Тогда из предыдущего ясно, что
[о] {IP1 — МП) = {[«! — МП) М-
Произведение определителей коммутативно. Поэтому после деления обеих,
частей равенства на |о| имеем
Это и показывает' инвариантность характеристического уравнения
4.1.30. Матрица, отнесенная к собственным направлениям. Предпо-
Предположим, что характеристическое уравнение Д(Х) = О имеет лишь простые,
корни. Тогда п собственных направлений различны. Их можно принять за оси
координат.
Пусть Xj, Xj, •.., Х„'—корни уравнения Д(Х) = О. Докажем, что в новой
системе координат матрица а получит вид
"X! О ... О
О Xj ... О
О О ...Х„
Это, очевидно, диагональная матрица; она сообщает вектору на 1-й ос»
лишь удлинение или сокращение в Х^ раз. Обозначим через икт проек-
проекцию на ось k собственного вектора, соответствующего собственному зна-
значению Хт. Тогда матрицей преобразования координат о станет матрица [икт\.
Произведение а~1ла представит в этом случае преобразование .матрицы а-
в системе координат, оси которой имеют направления собственных векто-
векторов а. Это будет, следовательно, матрица (8).
Пример. Обратимся к примеру п. 4.1.28. Матрица о и обратная ей
матрица о равны (с точностью до коэффициентов с,, с2, с3)
0 =
12 2
2 1 —2
2 —2 1
Произведение a-1ao будет
1
27
—3 —6 —6
—6 —3 6
—6 6 —3
11
— 6
2
- 6 2
10 —4
-4 6
_3 —6 —6
-6 —3 6
—6 6 —3
1
2
2
2
1
—2
2"
2
1
192
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ IV
4.1.31. Условия коммутативности двух матриц. Даны две матрицы
«ир. Предположим, что их характеристические уравнения содержат лишь
простые корни. Если матрицы коммутируют, то
<х8 = Ва.
Пусть и — собственный вектор
матрицей и. Тогда
аи = Хи
представленный одностолбцовой
(X— число).
Преобразуем вектор и с помощью матрицы аВ. Имеем
аВм = Ваи = ВХи = ХВи.
Соотношение аВи = ХВи показывает, что вектор, представленный матрицей Вм,
также является собственным вектором матрицы а с тем же собственным зна-
значением X. Он параллелен вектору а, так как корни характеристического
уравнения матрицы а простые. Можно поэтому написать
Ви = (ли ((л — число).
Последнее равенство показывает, что и — собственный вектор и матрицы В.
Итак, если две матрицы коммутируют, то у них одинаковые собствен-
собственные направления.
Докажем и обратное. Даны две матрицы аир, имеющие одинаковые
собственные направления. Если принять эти направления за оси координат,
то обе матрицы получают вид
0
0
0
0
0 ...
0 ...
0 ...
0
0
X
0
о
1*2
_0 0 0 ... ^
Так как обе они диагональны, то они, очевидно, коммутируют.
Нетрудно показать, что это свойство сохранится и в первоначальной
системе координат.
4.1.32. Собственные значения и собственные направления эрмито-
эрмитовой матрицы. Все собственные значения эрмитовой матрицы вещественны,
а собственные направления ортогональны. Докажем это.
Эрмитова матрица характеризуется равенством
а+=а. :
Пусть и — собственный вектор, а X — соответствующее собственное значе-
значение. Тогда
Умножим обе части уравнения на и + :
и+аи =:Хи + и.
Применим операцию „ +" к обеим частям равенства
Раскрывая скобки и замечая, что операция „ -\
к комплексно-сопряженному значению, имеем
для числа означает переход
41]
АЛГЕБРА МАТРИЦ
193
потому что и++ = и. Так как, кроме того, <х+ = <х, то
и+ли — к*и+и;
но <хи = Хи, поэтому
Следовательно, Х = Х*. Это доказывает, что X—вещественное число.
Покажем также, что собственные векторы ортогональны. Даны два раз-
различных собственных значения X и ji и два соответствующих им собственных
вектора и и v. Имеем
Х
Умножаем соответственно на v+ и и + :
(9)
A0)
A1)
Применим операцию „ -f-" к обеим частям равенства (9):
u+ol+v = X*u+v.
Так как at = <x+. a X = X*. то соотношение A1) принимает вид
u+av = Xu+v.
Сравнивая с A0),; получаем
((а —Х)и+г» = 0.
Так как (а Ф X то u+v = 0, а это доказывает, что оба вектора а и v орто-
ортогональны.
Замечание. Отсюда следует, что и для симметричной матрицы собствен-
собственные направления ортогональны, так как такая матрица представляет собой
частный случай эрмитовой.
Функции от матриц
4.1.33. Степень матрицы.1). Матрица ар равна произведению <х<х ... а.
р раз
Если матрица а отнесена к своим собственным направлениям, то она
имеет диагональную форму и, будучи возведена в степень р, дает
rXf 0 ... 0
0 X? ... 0
L0 0 ... XSJ
Действительно, лр должна преобразовать вектор v, расположенный по оси i,
в вектор, представленный матрицей
0
о
') Случай дробной степени изложен в п. 4.1.38.
13 А. Анго
194 МАТРИЧНОЕ ИСЧИСЛЕНИЕ [ГЛ. IV
Случай отрицательных р не представляет трудностей, если только
матрица а невырождена.
4.1.34. Теорема Кэли—Гамильтона. Покажем, что результат подста-
подстановки квадратной матрицы в ее характеристическое уравнение дает нулевую
матрицу
А (а) ==[01.
Пусть и — вектор, составляющие которого по собственным направлениям
матрицы а равны
«1, .... ип.
Матрица а преобразует составляющую иг B\ut, а матрица Д(а) преобразует
эту составляющую в Д(Х,)иг. Последнее выражение равно нулю, так как
Д(Хг)=:О. А следовательно, и все составляющие вектора Д(а)и равны нулю.
Поскольку вектор а произволен, то матрица А(а) должна быть нулевой*).
4.1.35. Функции от матриц. Теорема Сильвестра. Пусть Р(х) — мно-
многочлен степени я—1 и пусть av а2 ап — я различных произвольных
постоянных: Следующее тождество называется интерполяционной формулой
Лагранжа (см. п. 10.3.2):
U(x-as)
Символ JJ означает произведение одночленов для веет значений
s=\, 2 я, кроме s — r.
Определение степени матрицы дает возможность определить многочлен
от матрицы. Заменив в предыдущем тождестве х на- матрицу а, получаем
новое тождество
зфт
Теорема Кэли — Гамильтона позволяет показать, что матричный мно-
многочлен от а степени ^я может быть выражен при помощи матричного мно-
многочлена степени я—1. Действительно, пусть Д (X) = О— характеристическое
уравнение. Тогда, поскольку Д(а) = [0], имеем
Последовательные умножения на X и а этих соотношений показывают,
что степени кп+р и ап+р могут быть выражены соответственно как функ-
функции X X" и а а". Таким образом, если /(jc)—многочлен сте-
степени большей или равной я, то
*) Это доказательство справедливо при наличии п собственных направлений.
Общий случай рассмотрен, например, в [3], стр. 26, 27.
4.1] АЛГЕБРА МАТРИЦ 195
гдеР(д;)—некоторый многочлен степени п— 1. Применим к многочлену Р(<х)
тождество Лагранжа. Предположив, что все собственные значения различны,
мы можем, в Силу предыдущих соотношений, написать следующую формулу,
выражающую теорему Сильвестра:
при
2(г2г A2)
г=1
Д1
Пусть <р(х) — функция, разложимая в степенной ряд, сходящийся при
|д;| < р. Обозначим этот ряд через / (х). Тогда формула A2) показывает,
что ряд /(а) сходится в том случае, если все ряды /(Хг) сходятся. Это
позволяет применять теорему Сильвестра не только к многочлену, но также
и к функции, разложимой в степенной ряд.
Замечание. Легко показать, что матрица Zr имеет следующие свойства:
она вырождена и ранга 1;
О, если рфг,
Zr если р — г,
откуда
ZrZp —
По формуле A2) при /(Х)=1 имеем
1
Точно так же применение формулы A2) к /(<х) = а дает
п
/•=1
Пример. Применим формулу A2) к вычислению матричного много-
многочлена
где матрица <х равна
11—6 2
— 6 10—4
2—4 6
Собственные значения матрицы а. были вычислены ранее (см. п. 4.1.28):
Х,= 18, Х2 = 6, Х3 = 3.
Отсюда
55, <р(Хз)=19.
13*
196
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
Таким образом, ср (а) = ср (кх) Zx -\- ср (Х2) Z2 -+- ср (Xg) Z3,
11—6 2
— 6 10—4
2—4 6
6 О О
0 6 0
0 0 6
11—6 2
— 6 10—4
2 4' 6
C —6)C —18)
откуда
[ГЛ. IV
18 О О'
О 18 О
О 0 18
ет для Z2
" 4
2
4
1755
— 1368
576
и
2
1
2
Z, дает
—4 "
—2
4
-1368
1647
- 792
576 "
—792
675 _
=
1
- "о"
у
г
" 4
4
2
195
-152
64
1
~ 9
4
4
—2
— 152
183
— 88
" 1
2
_ 2
2 '
—2
1 _
2
4
4
64 ¦
—88
75
2
4
4
Прямое вычисление, гораздо более легкое в данном случае из-за про-
простоты функции ср, дает тот же результат:
?(<*) =
161
134
58
— 134
152
— 76
58"
—76
56.
+ 3
" 11
— 6
2
— 6
10
4
2"
—4
6
——
-
195
-152
64
0.
.0
0 0"
1 0
0 1.
-152
183
- 88
——
64
—88
75
4.1.36. Формула Бэкера. Формулу для ср(а) можно представить и в дру-
другом виде •):
A3)
В этой формуле D — определитель Вандермонда:
1
1
1
... л„
¦) Baker H. F., Proc. Lond. Math. Soc, 1902, pp. 347 — 360; 1905, pp. 293—296;
Phil. Trans. Roy. Soc. [A], 1916, pp. 129—186.
4-11
АЛГЕБРА МАТРИЦ
197
где Xlf ..., Х„— корни характеристического уравнения матрицы'a, aD,_,—
определитель, полученный из D заменой элементов г-й строки Hacp(Xj) 9(Х„):
1
*1
jr-2
1
... 1
... к
... к,-2
l) fO-2)---
l[
.Применим формулы A2) и A3) к простому случаю, в котором непо-
непосредственное вычисление также не представляет затруднений. Пусть требуется
МО!
матрицуеа, причем а = „ I. Так как эта матрица диаго-
вычислить
нальна, то прямое вычисление дает
но
р=0
1Р 0
Поэтому
е' =
р=0
р=0
2"
Р\
Применим теперь формулу A2):
Матрицы
и Z2 получаются следующим образом:
_«-2[Ц П 01 Г1 0-]_
>- 1-2 -2[о 1 J L 0 2 J —
1 01
О О]'
o I
Это дает
001 Ге
о 1 1 = 1 о
198
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
(ГЛ. IV
Воспользуемся формулой A3):
1 1
X, X2 I
1 1
1 1
1 2
1 1
е ё'
е е2
1 2
1
= е1 — е.
= 2е — в2.
По формуле Бэкера имеем
-pr a-
0
Г101
4.1.37. Высокие степени матрицы. Применим формулу A2) к
ции ар. Имеем
функ-
функОчевидно, Zr не зависит от р.
Предположим, что п корней характеристического многочлена Д(Х) рас-
расположены по убывающим модулям:
Если р очень велико, то можно пренебречь Xf X? по сравнению с Xf и
написать
Пример. Требуется вычислить приближенное значение
11—6 2
— 6 10—4
2—4 6
Корни характеристического многочлена равны
Х,= 18, Х2=6, Х3 = 3.
Zx уже было вычислено в п. 4.1.35:
Следовательно,
-
11
- 6
2
Z,
— 6
10
— 4
— _L
2 "
—4
6
¦ 4
—4
2
428
ягг 2
—4
2 "
4 —2
—2
• 18427
1 _
4 4
—4 4
Г
> —2
2
—2
1
4.1.38. Дробная степень матрицы. Рассмотрим для примера матрицу
степени !/г с двумя,строками и двумя столбцами. Формула Сильвестра A2),
примененная к функции ср(а) = а''|2, дает
4.1].
АЛГЕБРА МАТРИЦ
199
Это можно проверить и непосредственно. Действительно, возводя обе части
равенства в квадрат, получаем
= \XZ\ + к'№> (ZiZ2 + Z2ZO + hZl
В силу свойств матриц Zt (п. 4.1.35) правая часть сводится к
AjZ] И- X2Z2,
что по формуле A2) тождественно а.
Подобной же проверкой нетрудно убедиться, что в качестве квадратного
корня из матрицы а может быть взято любое из четырех выражений
±x'1/2z,±x2/sz2.
В более общем виде можно показать, что существует т" корней m-tt
степени из матрицы порядка п при условии, что все собственные значения
матрицы различны. Если это не так, то существует бесконечное множество
корней. Действительно, отыщем квадратный корень единичной матрицы вто-
второго порядка (ее собственные значения совпадают). Имеем
откуда искомый квадратный корень равен либо | Л , , I. либо
[а ЬЛ
при условии, что 1—а2 = Ьс. Иначе говоря, получаем беско-
I С ¦¦' От I
нечное множество решений.
4.1.39. Приближенное вычисление собственных значений матрицы.
Пусть Xj^to собственное значение, которое имеет наибольший модуль.
а) Собственное значение вещественно. В п. 4.1.37 мы видели, что ар
при бесконечно возрастающем р может быть представлена в виде XfZi. От-
Отсюда следует, что если р достаточно велико, то для матриц аР и ар+х спра-
справедливо приближенное равенство
занимающие одинаковые места соответ-
соответЕсли fu и gtj — два элемента,
ственно в матрицах о.р и аР+1, то
X, =lim
Пример. Найдем собственное значение с наибольшим модулем мат-
матрицы
Вычисление а8 дает
4 898 507 481 —4 897 385 550
—4 897 385 550 4 897 949 796
2 448135 090 —2 449 250 460
2 448135 090
-2 449 250 460
1225189 476
200
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Вычислим только элемент gn матрицы а9. Он равен 88164165771. Разде-
Разделив на элемент /п матрицы а8, получим Xj fa 17,9981... А нам известно, что
точное значение X, равно 18.
б) Собственное значение комплексно. Ограничимся матрицами с ве-
вещественными элементами. Пусть X, и Х2 — два комплексных сопряженных
собственных значения с наибольшим модулем. Напишем предельную форму
соотношения Сильвестра для функции хрР(х), где Р(х) — некоторый мно-
многочлен, не зависящий от р:
а"Р (а) « XfP (X,) Zi + XfP (X2) Z2.
Возьмем
Тогда
и
Отсюда
или
Р (*,) = Р (Х2) = 0.
_ лр+\
0.
Пусть hip gij, fij будут элементами, занимающими одинаковые места
соответственно в матрицах <х.р+2, <х0+1, а?. Если р достаточно велико, то
hi) — Si) (К + М + /</iX2 ~ °-
Для других соответствующих элементов имеем
hfci — Ski (xi + h) + fnfah ~ °-
Решая эти уравнения и полагая X, = a-j-у#, Х2 = а—jb, получаем
Si)
hu
fit
fkl
ftj
fkl
fll
fkl
Ski
hkl
Si)
Ski
*«
hki
Si)
Ski
Пример. Требуется найти собственные значения матрицы
0
0
10
1
1
—10
0
1
6
Найти их очень легко, так как характеристическое уравнение имеет про-
простой вид
Хз —7X2+16Х—10 = 0.
Его корни
Х2 = 3— /. Х3=1.
4.1]
АЛГЕБРА МАТРИЦ
20 Г
Воспользуемся предыдущим способом. Вычисляем последовательно
13 810 —13 809 3 837
[/у] = а8 = 38370 —38369 9213
38 640 —38 640 7 616
38 370 —38 369 9213
92 130 —92 129 16 909
76 960 —76 960 7 536
92 130 — 92 129 16 909
169 090 —169 089 9 225
75 3G0 — 75 360' —31 744
Взяв i = j=\, /г = / =
получим
gu
ft,,
g33
2с =
/п
/зз g
/и h
/зз h
gu
= 10,00035,
/и
/зз
gu
= 6,00040,
тогда как точные значения будут:
Замечание. Если собственное значение с наибольшим модулем ве-
вещественно, то элементы возрастающих степеней матрицы монотонно возра-
возрастают. Если это не так, то колебания, доходящие иногда до перемены
знака, указывают, что собственное значение с наибольшим модулем будет
комплексным числом.
Упрощение метода. Способ, состоящий в том, чтобы возводить мат-
матрицу а я-го порядка в возрастающие степени, требует каждый раз вычисле-
вычисления я3 произведений. Можно свести число произведений до я2, если, исполь-
используя ассоциативность, вместо матриц а, а2, .... аР, аР+1, аР+2 образовать
матрицы ad, a2d аР d, aP+1 d, aP+2 d, обозначив через d матрицу, пред-
представляющую собой произвольный вектор с координатами dx, d2, .... dn.
Пусть опять Xj — собственное значение, имеющее наибольший модуль.
Рассмотрим отдельно два случая.
а) Собственное значение \г вещественно. Как и в предыдущем слу-
случае, gtj и ftj—элементы матриц а.Р+1 и аР. Элементы ct и bt одностолб-
одностолбцовых матриц aP+ld, aPd соответственно равны
ci = %gl}dp bt =
i
tJ
Если р достаточно велико то отношение g к / близко к X,. Следо-
Следовательно, также дело обстоит и с элементами ct и Ь^ Поэтому мы можем
написать
•202 матричное исчисление [гл iv
б) Собственное значение Хг комплексно. Как и в предыдущем слу-
случае, пусть ftj, gtj, hy — элементы матриц о.р, o.p+1, о.р+2 a bt, ct, et — эле-
элементы одностолбцовых матриц о.р d, aP + 1d, a.P+2d. Если р достаточно ве-
велико, то мы имеем соотношение
и g,j Сг t 2)| /<М ~ 0.
Так как
то
«i-^^i +
Замечания. 1. Сказанное выше означает, что повторное умноже-
умножение матрицы на любой вектор стремится повернуть этот вектор вдоль соб-
собственного направления матрицы, соответствующего собственному значению
с наибольшим модулем. Следовательно, вектор, представленный матри-
матрицей аР d, стремится к собственному вектору, соответствующему собственному
значению Xlf и при достаточно большом р может слиться с этим собствен-
собственным вектором.
Докажем это положение. Числа, пропорциональные координатам uv
и2, .... ип собственного вектора, соответствующего собственному значению
-с наибольшим модулем Xt, получаются из однородного уравнения
Но по теореме Кэли — Гамильтона
Сравнив уравнения A4) и A5), мы видим, что элементы матриц и и Zxd
пропорциональны. С другой стороны, известно, что если р достаточно велико,
то apd я* \PZ\d, т. е. матрица Zxd является с точностью до постоянного
коэффициента пределом afd. Следовательно, этот предел определяет собствен-
собственное направление, соответствующее \v
2. Пусть после того, как найдено собственное значение \ с наибольшим
модулем, требуется определить собственное значение \2< модуль которого
является следующим по величине после модуля Xv В п. 4.1.35 получена
формула
r=l
В матрице
п
Р = a — XjZx = 2j \Zr
собственное значение \ заменено нулем, но сохраняются все остальные
собственные значения матрицы а. Поэтому, чтобы продолжить вычисление,
достаточно применить к матрице В тот или другой из рассмотренных методов.
Первый метод. Если р достаточно велико, то
a";
Отсюда
Способ вычисления ар и X, указан ранее.
U] • АЛГЕБРА МАТРИЦ 203
Второй метод. Если при вычислении \1 был использован вектор d, то
Способ вычисления одностолбцовых матриц ad и a.pd указан ранее.
Пример. Возьмем матрицу а. из первого примера п. 4.1.39. Получаем
11
—6
2
—6
10
—4
2"
4
6.
—
" 8
—8
. 4
—8
8
4
4"
—4
2.
=
" 3
2
2
2
2
0
2"
0
4_
Собственные значения матрицы C равны 0, 6, 3.
4.1.40.. Приближенное вычисление корней уравнения я-й степени.
Все предыдущие вычисления применимы без изменения к вычислению корня
с наибольшим модулем уравнения
при условии, что удастся составить матрицу, имеющую в качестве характе-
характеристического многочлена функцию / (z). Докажем, что это всегда возможно.
Сопоставим с многочленом / (z) матрицу
о
о
1
о
о
1
о
о
О 0 0 ... 1
_— ап —«n-i — а-п-г---— ai-
и докажем, что (•"—1)и/B) представляет собой характеристический много-
многочлен этой матрицы.
Действительно, характеристический многочлен матрицы а может быть
записан в виде
(*)
Допустим, что такой определитель из п— 1 строк и столбцов равен
(—1)"~1(г" + д1г"~2+ ... +а„_,)*). Тогда, разложив определитель (*)
по элементам первого столбца, получаем
2*
0
0
1
Z
0
— ап-г
0
1
0
ап-2
0
0
0
— ап-з ¦•¦
0
0
. у
— а2 —
0
0
1
с,—
-(-1)я+1 ап
или
т. е.
1)"
(—1 )»/(*)•
Так как правило очевидно при п= 1, то оно имеет место для
любого п.
*) Он отделен штриховой линией.
204
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Пример 1. Требуется решить уравнение
/(«) = z3— I6z2~\- 682 — 80 = 0.
Тогда
0 1 01
О О
1
L80 —68 16J
Возьмем вектор и—
О
Последовательным умножением получаем
L1J
20 811 520
<Аг=| 208 246 016
L2 082 983 936.1
208 246 016"
а1Ок = 2 082 983-936
.20 831 935 488 J
Отношение -у дает Xj = 10, 0010.. .,"¦ а решение уравнения второй сте-
степени, полученное после деления f(z) на z —10,0010, дает Х2 — 3,996....
\3= 2,003...
Точные значения корней 10, 4, 2.
Пример 2. Требуется решить уравнение
/ (z) = z3 — 7z2 + 1 lz + 25 = 0.
Тогда
О 1 О"
О
"П
Возьмем вектор и = I 1
О
L—25 —17
Последовательное умножение дает
-1J
918721
4 368 961
.11 983 645J
4 368 961"
11 983 6451
L—И 354 847-
Отсюда
2а =
11 983 645
— 13 354 847
__406 429 919j
= 25,0002...,
Ьх
= 7,99985...
Точные значения корней: Xj = 4-f-3y, Ъ2 = 4 — 3/ >.3 = — !•
Замечания. 1. В использованном методе ошибка при вычислениях
не имеет большого значения: она просто отодвигает момент получения иско-
4.Ц
АЛГЕБРА МАТРИЦ
205
мого корня. Действительно, ошибка в произведении ари приводит к изме-
изменению вектора и, а так как он произволен, то это не сказывается на
окончательном результате.
2. Приближенные методы, изложенные в п. 4.1.39 и 4.1.40, имеют своей
основой теорему Сильвестра, выраженную формулой A2). Эта формула не-
неверна, если имеется двойной корень характеристического уравнения. Однако,
устремив друг к другу два корня ~ks и ^+1, легко показать, что прибли-
приближенные методы не полностью изменяются при наличии двойного, а в более
общем случае — кратного корня, если только он не является также корнем
с наибольшим модулем >.,. В этом случае мы можем вывести новую формулу
для приближенного вычисления корней, но менее простую, чем предыдущие.
Если Xj — кратный корень, то порядок кратности всех корней удобно свести
к единице следующим способом.
У функций f(z) и f(z) кратные корни общие. Последовательным деле-
делением мы можем найти их общий наибольший делитель:
Получение нулевого остатка показывает, что R3 и есть общий наибольший
делитель. Уравнение <р—~5~ = 0 содержит все корни уравнения /==0, но
при этом кратность корней уже будет равна единице.
Дифференциальные операции над матрицами.
Применение к решению дифференциальных уравнений
4.1.41. Дифференцирование и интегрирований матрицы. Пусть дана
матрица [ос], элементы которой oci;- суть функции одной переменной t:
Производная матрицы [а] определяется соотношением
dt • •' /
d
dt
dt - - ' dt
dan
"Л1
L dt *'' dt Л
т. е., короче, если заменить -гг символом О, получим
О [а] = [Doc].
Аналогично
J[a\dt =
faudt... f а1я
dt
*nldt ... /аяя
dt
20б МАТРИЧНОЕ ИСЧИСЛЕНИЕ [ГЛ. IV
t
Если обозначить через Q операцию интегрирования I ( )dt, то
4.1.42. Решение системы линейных дифференциальных уравнений
первого порядка. Рассмотрим следующую систему, к которой всегда можно
привести любую линейную систему первого порядка:
dx2 iii
+ a22x2 "Г • • • "Г a2nxn'
Обозначив через D операцию дифференцирования, мы можем записать
систему при помощи матричных обозначений:
или
Рассмотрим сначала случай, когда п=\. Пусть дано уравнение
и поставлены начальные условия: у = у0 при t = t0. Тогда
t
¦ У ~ Уо + J a(t) у dt.
to
Это интегральное уравнение может быть решено последовательным
приближением (метод Пикара). Пусть Q — оператор, определяющий опера-
t
цию Г( )dt. Имеем
Подставляя это значение у в правую часть уравнения, последовательно
получаем:
У = Уо + Ф* (Уо + Qay).
У = Уо + Qa (Уо + Q« (Уо + Qay) )•
У == Уо + Уо^а + y0QaQa + Qa.Qa.Qay
и т. д. В результате имеем
Этот ряд быстро сходится. ¦
Аналогично поступим с матричным уравнением
Начальные условия: [х] = [х(^0)] в момент времени t = t0.
4.1] АЛГЕБРА МАТРИЦ 20Г
Интегральное уравнение задачи имеет вид
t
[x(t)] = \xito)\ -+- f [ос(*)] [jc(O] dt.
ft
Решая это уравнение последовательным приближение'м, получим
[х @1 = {[ 11H-Q [«] + Q [«] Q [*] 4- Q [a] Q [a] Q [а] Н- . . .} [Jf (*0)Ь
Обозначим через Q'0*' оператор, определенный следующим образом:
)dt
/<
ft
4-
)dt
t
f(
+
)dt
t
/<
)dt
t
Назовем его оператором интегрирования. Результат операции Q'""', произве-
произведенной над матрицей [а], равен
it t i i t t |
'°'' [a]= [
[a]= [1] -jr f [а]Л+ f [a] dt f [a]dt+ f [a] dt f [a] dt f [a] dt + .. Л.
I <« ft ft '.. ft ft '
Q
Мы можем достаточно долго продолжать вычисления, чтобы обеспечить любую
наперед заданную точность.
Итак, решение системы имеет вид
Заметим, что с помощью оператора интегрирования можно сразу же
написать
Q'»- to[a]==[l].
Если дифференцировать S'°'' [a] no t, то находим
Если элементы матрицы [а] — постоянные, то
Q'"'[a] = eIe|('"w.
так как в этом случае
л раз
4.1.43. Система дифференциальных уравнений первого порядка
с постоянными коэффициентами. В этом случае все элементы матрицы [а.]
не зависят от t и согласно предпоследней формуле решение
может быть записано в виде
Матрицу № С—'о) можно легко вычислить при помощи формулы Бэкера
(см. п. 4.1,36).
208 МАТРИЧНОЕ ИСЧИСЛЕНИЕ
Возьмем систему двух уравнений. Имеем
[о
[ГЛ. IV
м-Г М-
La21 a22j
Корни характеристического уравнения X2— (аи-|-а22)^Н-а11а22 — ^г^^1
будут
\ = а-\-Ь, \2 — а—Ь.
Применение формулы Бэкера дает
1 1
а -\-Ь а — Ъ
1
a-\-b
1
е(а-Ь) {t-ta)
a — b
== 2ea('-'»> {c sh b(t —10) — b ch b(t — *0)|,
ea(t-ta)
Отсюда
где
— to)-bchb(t-tQ)}[l].
Решение имеет вид
Г2П S121
L 1 M22J
Вернемся к общему случаю системы линейных дифференциальных урав-
уравнений первого порядка, где коэффициенты а являются функциями перемен-
переменной t, конечными для всех значений интервала (^0, t). Тогда вычисление
2'°''[а@] будет весьма затруднительным.
Мы получим приближенное решение, разделив промежуток (^0. t) на
отрезки, в которых коэффициенты а могут приблизительно рассматриваться
как постоянные. Пусть (ts, ts+{) — один из таких промежутков. Пользуясь
предыдущими результатами, получим выражение
которое легко может быть вычислено. Значение неизвестной функции x(t)
будет тем ближе к истинному, чем меньше будут промежутки (ts+v ts).
*Л]
АЛГЕБРА МАТРИЦ
209
4.1.44. Случай линейного дифференциального уравнения га-го по-
порядка. Пусть дано уравнение
-—ЫО-^Hr— •••— pi @ jc = о.
dt
dtn
Положив
dx
1 dt
dn-lx
мы приходим к системе
dx%
• — х2. .. — х3,
- +
Отсюда следует
где C — матрица вида
dxn _ о .
•••¦ ~dT~ PlJ
^-[^] = [р][х],
О 1 0 ... О
О 0 1 ... О
О 0 0 ... О
__ Pj P2 Р3 ... р,
Это — частный случай задачи, рассмотренной в п. 4.1.43.
Пример. Следуя Келлеру, применим этот метод к решению уравнения
dx
6
dt* 1^7J dt^l— *2
• при следующих начальных условиях: х@) = ^-, \~dj-) =0.
Положим
dxy
Имеем систему
или в матричных обозначениях
dxx
dx2
~dT
2t
ft X\ 7T~ I ft X2'
4гМ=\ -6
г 0
\ -6
Возьмем промежуток 0 <; t -^ 0,1. Будем в нем считать элементы а2,
и а22 постоянными и равными их среднему значению в этом промежутке:
0,1 0,1
— 6 Г dt 1С tdt
**=*-ЪГ j T^rF = -6,01o, a22=ojt/ JZTF^0'1-
о в
Тогда в этом промежутке матрица [а] заменится на
ГО 1 }
К]=[_6,015 O.i J"
14 А. Анго
210
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Решение уравнения -тт [х] = [ocj] [л:] будет
тт
Корни характеристического уравнения для [at] равны 0,05 ± 2,45/. Отсюда
Гл:,(ЛI »о,оо5 [
\ =-W"| B.45 cos 0,245 — 0,05 sin 0,245) [1] +
+ Sin0'245 [-6,015 0.1
'(Xl)t=M = — 0,48,
' 2
0 J
' dX\ \
Для промежутка 0,1 <. t < 0,2 таким же точно образом находим
и постепенно составляем следующую таблицу:
t
X
' dx
dt
0,0
—0,50
0,00
0,1
—0,48
0,30
0,2
—0,43
0,59
0,3
—0,34
0,86
0,4
—0,23
1,08
0,5
—0,11
1,21
Предложенное уравнение легко может быть решено непосредственно.
Находим
Естественно, что подобные уравнения не следует решать матричным
методом, который имеет смысл применять лишь в случае, когда прямое
интегрирование невозможно.
4.2. ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ.
ИЗУЧЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ
4.2.1. Определение. По определению четырехполюсник представляет
собой электрическую цепь, в которой различают два входных и два выход-
выходных зажима (рис. 4.5). Будем пред-
1' *2 полагать, что эта цепь содержит
§ только сопротивления, индуктивно-
^ сти, емкости, электродвигатели с оди-
^ наковой угловой частотой т или
усилители при непременном условии
работы в линейном режиме.
Пусть /j, ev i2, e2 — мгновенные токи и напряжения соответственно на
входе и на выходе цепи.
Мы будем рассматривать только установившиеся режимы четырех-
четырехполюсников при синусоидальных токах и напряжениях. Тогда
12 = 12е1и>*,
во = Eoeia>t.
Рис. 4.5.
/ / р
ti 1
4.21 ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ 211
/j, Ev Iv Е2 представляют собой комплексные амплитуды тока и напряжения
на входе и выходе четырехполюсника.
Эти четыре величины не являются независимыми. Между ними суще-
существуют два линейных соотношения:
l,=x,nEl-j-ix22E2.
/,, 12 и Е{, Е2 можно рассматривать как составляющие некоторого вектора
в двумерном комплексном пространстве. Сделаем предположение, что оно
отнесено к двум прямоугольным осям. Соотношения A6) в матричном обо-
обозначении запишутся в виде
Назовем [а] матрицей полной проводимости четырехполюсника. Будем
считать, что матрица [а] невырожденная. Тогда можно решить систему A6)
относительно Ех и Е2. При этом получаем новую систему
Матрицу [Z] = [a] назовем матрицей полного сопротивления или
импеданса четырехполюсника. Имеем
Можно решить систему A6) относительно других пар переменных,
например относительно Е2, 12 как функций Ev /,.
Будем считать, что (Ех, /,), (Е2, 12) — составляющие некоторого обоб-
обобщенного вектора: вектора входного тока — напряжения (обозначим его
через \UX]) и соответственно вектора выходного тока — напряжения (обозна-
(обозначим его [U2]). Векторы [#,] и \U2\ связаны соотношением ,
Матрицу [у] назовем характеристической матрицей четырехполюсника.
Она получается из коэффициентов системы A6), решенной относительно
Е2, /2. Предполагая, что а,2 Ф 0, имеем
/ —
'2—
A8)
Мы можем также с помощью системы A6) вычислить другую пару
переменных Ev l2 как функции /v E2- В связи с этим рассмотрим два
вектора [7°]] и [7°2]. составляющие которых соответственно равны ?,, /2
и Iv E2. Тогда
где [g] и [А] — две новые матрицы, обратные друг другу. Было бы удобно
иметь возможность представить каждую из матриц [я], [Z], (?J. [A], [g] как
14*
212
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
функцию элементов любой из оставшихся. Результат такого вычисления
собран здесь:
[-1 Г 7 7 ~\ Г f 1 П
аП а12 I 1 Л22 ^12 1 111 l
CLn 1 ^92 I * * L ~~~ 21 11 I ' ^ L I i I 122 I
kl §
|A|J'
pll Z«l _1_Г «22 — а12]=_1_Г— 722 1 1
1 ' LZ21 Z22J l"l L «21 «llj *' L ITl TllJ
1—Г7"
1 ЧТИ
LГ~a"
L
«22
A9)
ig\ =
Г II
-\g\
Л22 -|
|z|
...
11
ГА„ Au] Lp
~ LA21 vl «i. U21
72i ! ]=J_f Л22 —Аи]
ITI T12J 1*1 L— Aa, A,,]1
z" l-z2. 1 J
— Tl2 !
hi T21
1 J_f
J i^"i L—
4.2.2. Соединение четырехполюсников по цепной схеме*). Такое
соединение представлено схематически на рис. 4.6 для четырехполюсников
1
Рис. 4.6.
Q'. Q". Q'"- Так как выходной ток и напряжение каждого четырехполюс-
четырехполюсника равны входному току и напряжению последующего, то, учитывая связь
между входом и выходом,
получим
[*П=[Л[
Если ввести матрицу [f], определяемую формулой
то
B0)
*) Такое соединение иногда называют каскадным.
4.2]
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
213
Следует особо отметить, что матрицы здесь расположены в порядке,
обратном порядку последовательности четырехполюсников.
Таким образом, характеристическая матрица эквивалентного четырех-
четырехполюсника Q, состоящего из трех четырехполюсников Q', Q", Q'", соеди-
соединенных по цепной схекге, равна произведению характеристических матриц
каждого из составляющих четырехполюсников.
Можно заметить, что результирующий четырехполюсник будет в боль-
большинстве случаев меняться при перемене мест составляющих четырехполюс-
четырехполюсников, что согласуется с некоммутативностью исходных матриц. В случае
коммутирующих матриц, он не будет изменяться. Мы увидим далее, какой это
имеет физический смысл (см. п. 4. 2. 16). При п. одинаковых четырехпо-
четырехполюсниках имеем
4.2.3. Параллельное соединение четырехполюсников. Такое соединение
схематически изображено на рис. 4.7. Здесь
Так как при этом входные напряжения и, соответственно, выходные будут
у четырехполюсников одинаковы, то
Полные входные и выходные токи равны
сумме входных и выходных токов каждого
из четырехполюсников:
[/] = [
откуда
Следовательно,
B1)
Рис. 4.7.
Матрица полной проводимости эквивалентного четырехполюсника Q,
образованного параллельно соединенными четырехполюсниками, представляет
собой сумму матриц полной проводимости составляющих четырехполюсников.
4.2.4. Последовательное соединение четырехполюсников. Такое соеди-
соединение схематически представлено на рис. 4.8. Имеем
= [/'] = [/"].
Рис. 4.8.
откуда
B2)
Матрица полного сопротивления четырехполюсника, образованного
последовательным соединением четырехполюсников, равна сумме матриц
полных сопротивлений составляющих четырехполюсников *).
*) Будем в дальнейшем для краткости говорить просто «сопротивление четы-
четырёхполюсника», имея в виду его полное сопротивление.
214
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ IV
4.2.5. Последовательно-параллельное и параллельно-последователь-
параллельно-последовательное соединение четырехполюсников. Последовательно-параллельное соеди-
соединение двух четырехполюсников Q' и Q" представлено на рис. 4.9. Обе пары
входных зажимов соединены последовательно, а обе пары выходных зажимов
Q'
Рис. 4.9.
Рис. 4.10.
параллельно. При помощи вычисления, подобного предыдущим, легко полу-
получить, что в этом случае матрица [ft] эквивалентного четырехполюсника Q
равна сумме матриц [ft'] и [ft"] составляющих четырехполюсников Q' и Q":
.[ft] = [/*']-Н^-
Параллельно-последовательное соединение двух четырехполюсников Q'
и Q" представлено на рис. 4.10. Здесь обе пары входных зажимов соединены
параллельно, обе пары выходных зажимов — последовательно. В этом случае
Важное замечание. Условие равенства, которое должно существовать
между током, входящим через первый входной зажим и выходящим через
второй входной зажим, может не выполняться при параллельном или после-
последовательном соединении четырехполюсников. Действительно, один из соста-
составляющих четырехполюсников устанавливает внешнюю связь между двумя —
соответственво входным и выходным — зажимами одного из соседних четы-
четырехполюсников. Тогда формулы, найденные для последовательного или
параллельного соединения, могут оказаться неверными.
Рассмотрим сначала параллельное соединение двух четырехполюсников
Q и Q'. Соединим только входные зажимы. Можно также соединить выход-
выходные зажимы, если выходные напряжения каждого четырехполюсника окажутся
до этой операции равными между собой, или же, что одно и то же, если
напряжения U и U' между зажимами 2—4 и 2'—4' одинаковы. Эти напря-
напряжения выражаются для каждого четырехполюсника однородной линейной
функцией от входного и выходного напряжений:
U =siEi-j-s2E2>
где sv s2, s'v s'2—параметры обоих четырехполюсников.
Если два четырехполюсника таковы, что 5] = Sj, s2 = s'r то условие
U = U влечет за собой Е1 = Е\ и Е2 = Е2. Соединим параллельно входные
зажимы четырехполюсников и замкнем накоротко зажимы 3—4 и 3'—4'
(рис. 4.11, а). Тогда Е<2 — Е<2 = 0. Условие s\ = s\ равносильно U = U.
А условие U=U\ в свою очередь, равносильно i/ = 0, если обозначить
через v напряжение между выходными зажимами четырехполюсников. Если
возобновить этот опыт, заменив вход выходом и наоборот, то v = 0 будет
означать s'2 = s2.
4-.2]
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
215
Проверку обоих условий, которым удовлетворяют четырехполюсники,
можно в большинстве случаев осуществить непосредственным рассмотрением
их составляющих.
Рис. 4.11.
Что касается последовательного соединения, то мы можем рассуждать
аналогично. Оба условия представляют собой равенства Il = l\, /2 = /2-
Напряжения U и U' могут быть выражены как функции токов линейными
соотношениями:
U' = r'/i -+- r'2Ir
Соединим последовательно входные
зажимы и оставим выходные зажимы ра-
разомкнутыми (рис. 4.11, б). Условие v = 0
равносильно г1 = Гу Поменяем местами
входные и выходные зажимы. Теперь
условие v = 0 равносильно г2 = г'2.
Существуют два частных случая,
когда вышеописанные условия всегда
выполняются.
1. Один из четырехполюсников со-
содержит один или несколько трансформа-
трансформаторов, помещенных таким образом, что
между входными и выходными зажимами четырехполюсника нет непосред-
непосредственной электрической связи. При этом U и U' неопределенны. На рис. 4.12
изображены два примера таких четырехполюсников.-
2. Оба четырехполюсника таковы, что в каждом из них имеется безым-
педансная связь между входным и соответствующим выходным зажимами.
(Г
(Г
Рис. 4.13.
Последний пример отражает громадное большинство обычно применяемых
четырехполюсников. На рис. 4.13 показано последовательное и параллельное
соединение двух таких четырехполюсников. Соединены те зажимы, которые
связаны внутри каждого четырехполюсника безымпедансной связью.
216
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ.. IV
Формулы, найденные для последовательно-параллельного или парал-
параллельно-последовательного соединения, оказываются действительными только
при наличии некоторых условий, аналогичных условиям, указанным выше для по-
последовательного или параллельного соединения. При этом, так же как и для тех
соединений, имеются два случая отсутствия огра-
ограничений: когда трансформатор изолирует входные
и выходные зажимы одного из четырехполюсни-
четырехполюсников, и более существенный случай, когда имеет
место безымпедансная связь между входным и
выходным зажимом в каждом из двух четырех-
четырехполюсников Q' и Q". Такое соединение показано
на рис. 4.14.
4.2.6. Сопротивления холостого хода и ко-
Рис. 4.14. роткого замыкания четырехполюсника. Это со-
сопротивления, измеряемые на входе и выходе при
отключении входа или выхода или при замыкании накоротко. Обозначим
их через
(х. х — холостой ход, к. з — короткое замыкание). Указанные величины легко
измерить. Нетрудно также найти следующие соотношения между этими
величинами и элементами матриц [а], [2], [f], [A], [g]:
II
7.2 _
* I •- I П2 „ "II О^
__^22__2 — ТГ« _- г _ |А1
= __?и_==_2 = __ 111 = _ М = 1_
4.2.7. Пассивные четырехполюсники. Пассивным называется четырех-
четырехполюсник, не содержащий в себе источников энергии. В нем имеются лишь
емкости, индуктивности и активные сопротивления. Это ограничение несколько
упрощает матрицы [а], [2], [7], [h], [g].
Действительно, приложим напряжение Е ко входу пассивного четырех-
четырехполюсника, выход которого закорочен. При этом на выходе наблюдается
ток /. Если приложить то же напряжение к выходу, то на входе, если его
закоротить, должен наблюдаться тот же самый ток, что вытекает из весьма
общей теоремы обратимости. В этом случае система A6) сводится к следующей:
Знак минус во втором равенстве связан с условием о знаке тока. Ток /
считается положительным, если он течет в выбранном направлении по выход-
выходной цепи, и отрицательным, если он имеет то же направление во вход-
входной цепи.
Следовательно, ,а12 = — а21, и из A9) мы получаем
_?21_
г'21
^12
^2!
Z»
__ а21 II 1
B4)
$
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ 217
4.2.8. Симметричные четырехполюсники. Четырехполюсник называется
симметричным, если замена входа на выход не влечет за собой изменений
его свойств. Очевидно, что сопротивления холостого хода и короткого за-
замыкания такого четырехполюсника (п. 4.2.6) должны быть попарно равны:
Если, кроме того, такой четырехполюсник пассивен, то условия B3) вместе
с двумя последними равенствами дают
Это соотношение характеризует симметричный четырехполюсник.
Примеры простых четырехполюсников
Небезынтересно определить матрицы [а], [7], [Z] некоторых элементар-
элементарных четырехполюсников. Соединенные в различных комбинациях такие эле:
ментарные четырехполюсники образуют более сложные четырехполюсники,
матрицы которых можно получить путем применения изложенных выше пра-
правил вычисления.
:. ¦' г,
/о —JVWWV °3 /о ¦ 03
(а) < z, (б)
2о ; 04 2 о i 04
Рис. 4Л5. Рис. 4.16.
4.2.9. Четырехполюсник с одним последовательным сопротивлением.
Такой четырехполюсник изображен на рис. 4.15. Будем называть его четырех-
четырехполюсник (а). Имеем
Отсюда
4.2.10. Четырехполюсник с одним параллельным сопротивлением.
"" " Такой четырехполюсник изображен на рис. 4.16. Будем называть его четырех-
четырехполюсник (б). Имеем
/2 —
Отсюда
/2 — т~
fe Используя матрицы четырехполюсников (а) и (б), можно легко получить
¦ матрицы многих простых четырехполюсников.
218
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
4.2.11. Г-образный четырехполюсник. Четырехполюсник на рис. 4.17
состоит из четырехполюсника (б) и соединенного с ним по цепной схеме
четырехполюсника (а). Следовательно, имеем
-[
-
'
.%*
:ь
-z2
Отсюда
а =
11
z7+z;
l
Z2
1_
Z2J
[Z] =
_1_
i -Z,
Четырехполюсник на рис. 4.18 — также Г-образный, но составляющие
его элементарные четырехполюсники (а) и (б) соединены в другой последо-
/о
¦ллллл/w- °<з /° wwwv
Рис. 4.17.
Рис. 4.18.
вательности, чем на рис. 4.17. Характеризующие его матрицы можно полу-
получить из предыдущего выражения, переменив порядок умножения матриц:
при
rz, + z2 — z,i
r_l_
z,
J_
-z2
i_
z2
j i_
2 1
4.2.12. Т-образный и П-образный четырехполюсники. Т-образный
четырехполюсник состоит из трех элементов (а, б, а), соединенных по цеп-
цепной схеме (рис. 4.19). Поэтому мы имеем
"L
-,
rz,
-z2
Z2
Z,Z2+Z,Z3+Z2Z3
—Z2
Z2 —
4.2]
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
219
П-образный четырехполюсник также состоит из трех элементов, соеди-
соединенных по цепной схеме, но уже в другом сочетании (б, а, б), как показано
на рис. 4.20. Поэтому
[Z] = 1 FZ1 (Z2 + Z3> - Zl
^1 * ^2 ~r* ^3 I ^*3 ~™" 3 \ 1 *
Z,
J_
z2
4.2.13. Х-образный четырехполюсник (решетчатый фильтр). Этот
четырехполюсник, изображенный на рис. 4.21, о, можно рассматривать как
7о VWWV
¦ЛЛЛЛЛЛ ^>.
Рис. 4.19.
/о-
лЛЛЛЛАЛЛ
Рис. 4.20.
последовательнр-параллельное соединение двух четырехполюсников, пред-
представленных на том же рисунке (рис. 4.21, б, в). Первый из них — Г-образ-
ный четырехполюсник. Его матрицу [Л] можно получить, применяя одну
из формул A9) к результатам вычислений, проделанных в п. 4.2.11:
[*] = -
гад zx ]
U. -и*
Для четырехполюсника (в) простой расчет дает
220
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Следовательно, его матрица
г % ¦? ^
[А] = -у—пу- ' 7 1 2 '
Матрица [Л] Х-образного четырехполюсника равна сумме этих двух
матриц, или
1
T2Z,Z2 Zj-Zjl
Lz,-z2 -2 J-
Отсюда посредством формул A9) получаем характеристические матрицы про-
7° «ч. VWWWV ^ оЗ
7 о-
¦ЛЛЛЛЛЛЛЛг
в)
Рис. 4.21.
водимости и сопротивления:
W = -z^r.
—2
Z2J' lal 2
-z,
z2
J_
z,
J_
Zi
j_
z2
_1_
z,
1 ^-2 ^1 ^2j
4.2.14. Трансформатор (рис. 4.22). Даны две обмотки с сопротивлениями
Zj = /?j-}-yo)Z.i и Z2 = /?2"
и индуктивной связью
4.2] ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
Имеем два уравнения
221
= Z-J\ —
Отсюда
\ZX —оМЛ 1 Г—
— Z2 <Ж
4.2.15. Электронная лампа. Рассмотрим триод, работающий на линей-
линейном участке характеристики при нулевом сеточном токе. Если через (а, ig,
еа, eg, s, Rt обозначить соответственно анодный и сеточный ток, анэдное
и сеточное напряжение, крутизну ха-
характеристики и внутреннее сопротивле-
сопротивление, то, принимая во внимание условие
о знаке/ тока в четырехполюсниках,
имеем
/о-
Zr О
-од
•г
Ж
Рис. 4.22.
•О4
Различные способы соединения триода сводятся к трем схемам четырех-
четырехполюсников, изображенным на рис. 4.23. Если через г обозначить сопроти-
сопротивление утечки, то рассмотрение всех трех схем позволяет нам, приняв
Z
| )Ю
4
о-
—о
3
4
—О'
7
Z
3
а)
Рис. 4.23.
во внимание уравнения работы триода, написать матрицы [a], [Z],
четырехполюсников (или [~(]~1, если матрица [?1 не определена):
а) г
этих
¦ rRi
rJ
6)
\Z6\ =
1 +
r
srRi
L \+sRi
J— I
sRi s
1 J_
.sr J
222
в)
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
[7.1 =
Ri
1
После обзора простых четырехполюсников мы можем перейти к более
сложным, пользуясь правилами составления матриц элементарных четырех-
четырехполюсников, образующих элементы рассматриваемой схемы.
WWWWV з
Рис. 4.24.
Пример 1. Т-образная мостовая схема (рис. 4.24, а). Такую схему
можно разложить на две элементарные, соединенные параллельно (рис.
4.24, б, в). Имеем
1 —
— z
Z —
Отсюда
— 2Z(Z, + Z)
Z,(Z,+2Z)
[71= с
1
2Z(Z,+Z)
2Z(Z,
Zi-)-2ZiZ-|-2Z2 — ZiZ(Zi+2Z)'
— |S-(Z, -H2Z)
,]¦
Пример 2. Четырехполюсник состоит из двух трансформаторов
в каскадном соединении (рис. 4.25). Произведение матриц [^], характери-
4.2]
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
223
зующих каждый трансформатор, дает матрицу [~(] эквивалентного четырех-
четырехполюсника:
— Z\Z<i-\-o4l
\i
ада i
—1
»12
Отсюда непосредственно можно получить первичное и вторичное сопро-
о
о
о
о
о
1
о
о
о
о
ю
Z,
о
о
Z3G
о
о
о
g*
о
м.
72
М:
'3*
Рис. 4.25.
тивления и коэффициент связи фиктивного трансформатора, эквивалентного
двум данным трансформаторам
в каскадном соединении:
Пример З. Рассмотрим
усилительную схему на рис.
4.26. %тог четырехполюсник
можно разложить на три че-
тырехполюсника, соединенных
по цепной схеме, причем цен-
центральный состоит из двух че-
четырехполюсников, соединен-
соединенных параллельно (рис. 4.27).
Матрица [а'] центрального
четырехполюсника будет равна
сумме матриц [а], характери-
Рис. 4.26.
л VWWW—
Рис. 4.27.
зующих четырехполюсник вакуумной лампы и четырехполюсник вида (а).
Можно немного упростить расчеты, введя сопротивление утечки в сопро-
сопротивление Zy
[<*'] =
\
J
Z3
224
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Отсюда получаем матрицу
—1
— s —
к
Характеристическая матрица эквивалентного четырехполюсника будет равна
1т1=[_^_ ! -s-± 1+iJL^. l+ij-
Для изучения режима триода, работающего как усилитель с анодной
нагрузкой Z, следует принять во внимание емкости сетка — катод Ск ,
сетка — анод Cag, катод — анод Сак. Тогда
4.2.16. Повторное сопротивление четырехполюсника. Рассмотрим
четырехполюсник с характеристической матрицей
[71 =
Ti2
722
l
J '
Если замкнуть его на сопротивление Z, то на входе он покажет кажущееся
сопротивление ZBX (рис. 4.28). Имеем соотношения
( E2
Рис. 4.28.
= [7l[#i]. B7)
Выясним, каково" должно быть значение Z,
чтобы входное сопротивление ZBX было ему
равно, иначе говоря, чтобы
Если это равенство имеет место, то общее значение С представляет собой
повторное сопротивление четырехполюсника. Система B6) показывает, что
тогда
т. е. что
Чтобы можно было говорить о распространении гармонической волны,
необходимо отсутствие искажений. Это как раз наш случай, потому что
С п ¦- -
11) —'¦¦—
Так как составляющие векторов [U{\ и
пропорциональны, то
Выражение для
ство B7), дает
[#2] = 4#il- B8)
, полученное из уравнения B8) и подставленное в равен-
равен4.2] ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ ч 225
Следовательно, X представляет собой собственное значение матрицы [7]. т. е.
корень уравнения
71V" у Tl2 X = Х2 ~(?» + Т22) X + 171 = 0. B9)
721 722 л
Замечание. Если два четырехполюсника Q и Q' имеют одинаковые
повторные сопротивления, то порядок соединения их по цепной схеме без-
безразличен, т. е. соединение Q, Q' равносильно соединению Q', Q. Матрицы [~(]
и [7'1 должны при этом коммутировать, и это действительно имеет место,
так как у них одинаковы собственные направления.
4.2.17. Случай пассивного четырехполюсника. Здесь [f]=l. Следо-
Следовательно, произведение корней Х,Х2 равно единице. Если положить Xj = er,
то Х2= е~т.
Предположим, что корень X! соответствует распространению волн справа
налево. Тогда корень Х2 будет соответствовать распространению слева направо.
Попробуем вычислить отношение напряжения к току, т. е. повторное сопро-
сопротивление С. Имеем
ТяЛ
или
— = f" ^ —722 ? г
Л * —Ти Ь\
Вычислив X как функцию С и введя эту величину в характеристическое
уравнение для [7]. находим
7i2 = 0. C0)
Можно легко убедиться, что это — характеристическое уравнение матрицы
сопротивлений. Следовательно, повторные сопротивления представляют собой
собственные значения матрицы [Z]. ;
Пусть Ci и Сг — Два корня уравнения C0). С другой стороны, мы имеем
Найдем обе пары соответствующих друг другу значений. Иначе говоря,
если ет соответствует распространению справа налево, то найдем корень ^
или »С2- соответствующий этому направлению распространения. Так как мы
рассматриваем пассивный четырехполюсник, то усиление волны не может
иметь места. Поэтому вещественная часть Г должна быть положительной или
равна нулю. Корень, который этой волне соответствует, должен иметь наи-
наибольшую вещественную часть. Вычислив из уравнений B9) и C0) вели-
величины Хр Х2, С;. Сг и полагая
получаем следующие соотношения:
15 А.
Анго
^ 7м
С — т"
— 722 + Ь
— 722 — 5
272,
1 7П+722 + 8
1 2
} 711 +722 — 5
2
226
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Заметим, что Ct и С2 характеризуют собой наклон собственных напра-
направлений матрицы [f]. Таким образом, получаем следующие формулы:
-4|<x|) =
U-Z22J-4|Z|), C1)
fu — 722 ± /(Tn — 722>2 + 4712721) =
1 / , . , /-¦—
— 4 I « I) =
Z22 ±
Замечание. Если пассивный четырехполюсник к тому же и симме-
симметричен, то оба повторных сопротивления, естественно, совпадают. Так как
7п = 722, то эта °бщая величина равна
4.2.18. Цепные фильтры. Имеем п одинаковых четырехполюсников,
соединенных по цепной схеме (рис. 4.6). Если [^] — характеристическая мат-
матрица каждого четырехполюсника, то харак-
характеристическая матрица всей схемы будет [f ]".
Первый случай. Цепь замкнута на
повторное сопротивление. Если отнести
матрицу к ее собственным/направлениям, то
она получает такой вид
-Го' Ц
Поэтому характеристическая матрица схемы
будет
О
Рис. 4.29.
Вектор [26г] отложен по собственному на-
направлению, соответствующему \v поскольку
цепь замкнута на повторное сопротивление. После прохождения через п
четырехполюсников вектор [Ui] сохранит собственное направление с угловым
коэффициентом d, но уменьшится в —— раз.
xi
Второй случай. Цепь не замкнута на повторное сопротивление.
Мы приводим схему 4.29 только для наглядности рассуждений, так как
комплексные координаты не могут быть воспроизведены на двумерной
плоскости.
Итак, даны две прямоугольных оси / и Е. Пусть ^ и Д2 — собствен-
собственные направления матрицы [f], соответствующие Хх и Х2, a cpL и <р2 — углы,
образуемые Д[ и Д2 с /. Рассмотрим вектор [21{[, направление которого не
совпадает с собственным направлением, так как, по предположению, цепь
не замкнута на повторное сопротивление. Разложим вектор [U^\ по собст-
4.2] ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ 227^
венным направлениям Дх и Д2 на составляющие Охх и Ох2. Можно рас-
рассматривать Ох1 и Ох2 как некоторые гипотетические векторы тока — на-
напряжения. При прохождении по цепи четырехполюсников произойдет сокраще-
сокращение длин их модулей: первого в—, второго в — ==Х" раз. В результате
Х[ Х2
эти два сокращенных вектора будут представлять собой разложение полного
вектора [Un] после прохождения по цепи.
Все сказанное сводится к преобразованию координат, легко осущест-
осуществимому с помощью матриц.
Матрица, дающая возможность перейти от пространства /, Е к про-
пространству Дх, Д2, равна
р,?1 sin?2-|
?1 ?2|
COS?! cos?2j
Преобразование вектора [2i^\ в вектор \Un\ происходит в пространстве Aj, Д2
с помощью матрицы
1
Матрица, позволяющая вернуться к пространству /, Е, равна [2]:
mi = ___!___ Г C°S!p2 —sincp2n
sin (у, — <р2) [_ costp! sincpj"
Следовательно, матрица "полного преобразования будет
т. е.
1
sin (ч>, — <p2)
X"sincpjcoscp2 — X" sin cp2 cos cpj —sin cpx sin cp2 (X" — X2)
(X? — X?) cos (px cos cp2 — X? cos cp! sin cp2 4-X? cos cp2 sincp
Разделив числитель и знаменатель на coscp1coscp2 и заменив
на Сг. X" на епТ и X? = — на. е~пТ, получаем
2 sh яГ С^-" — С2е"г J '
что "представляет собой матрицу преобразования
р * \(Г anV г о-пГ\ р ОГ Г cti иТ1 / I
/1== {2s
Если четырехполюсники симметричны, что случается довольно часто,
то формулы существенно упрощаются:
При бесконечном возрастании числа элементов цепи, когда размеры их
становятся бесконечно малыми по сравнению с длиной волны, мы получаем
15*
228
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
линию передачи. Она определяется повторным (волновым) сопротивлением С
и коэффициентом распространения k (рис. 4.30). Если через L, R, С, G
к )
влод
Рис.
4.30.
У-
Зшод
обозначить соответственно индуктивность, активное сопротивление, емкость,
проводимость изоляции линии на единицу длины, а через I длину линии,
то (см. п. 8.4.10)
k =
Следовательно,
?Вх =
kl 4- С/вых Sh kl,
= ^f21-sh
/9ЫХ ch
Характеристическая матрица такого четырехполюсника равна
chkl —Csh/гГ
chkl
shkl
4.2.19. Полоса пропускания четырехполюсника. Предположим, что
четырехполюсник замкнут на повторное сопротивление. Мы знаем, что это
является необходимым условием распространения волны через фильтр без
искажения. Для передачи сигнала без затухания нужно, чтобы модуль X для
данной частоты был равен 1. При этом оба корня \ и Х2 являются ком-
комплексными и сопряженными. Следовательно, их сумма вещественна и заклю-
заключена между —2 и +2. Дей-
7 —-A/WWW—Т—-АЛЛЛЛЛЛг——<? ствительно, два сопряженных
Z* комплексных числа с модулем 1
могут быть написаны в виде
coscp-4-ysincp,
, coscp — у sin ср.
Рис. 4.31. Сумма их равна 2 coscp и за-
заключена между —2 и -р-2.
Сумма Хх —(— Х2 равна Тп + Ъг- Следовательно, частоты внутри полосы про-
пропускания определяются неравенством
Пример. Рассмотрим симметричный Т-образный фильтр (рис. 4.51).
Мы уже получили (п. 4.2.12)
Til" 722 = 1 Н~~Т7"
Поэтому
4
L
4:2]
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
229
Следовательно, неравенство, определяющее полосу пропускания, будет
— 1<1Н--ф-<1 или — 2 < ^- < 0.
Дана схема (рис. 4.32):
Z2 —
Отсюда
0<
Из этого мы делаем заключение, что полоса пропускания находится вне
интервала частот
1
V2LC '
LC
00051
Рис. 4.32.
Замечание. В предыдущем
расчете предполагается, что четырех-
четырехполюсник замкнут на свое повторное
сопротивление. Но чаще всего пов-
повторное сопротивление само изме-
изменяется вместе с частотой. Фильтры,
изготовляемые на практике, в боль-
большинстве случаев замкнуты на
сопротивление, которое можно отождествлять с повторным лишь в очень
узкой области изменений со.
4.2.20. Расчет свободных колебаний цепи.
Вычисление частот. Пусть дана цепь. Сопротивление контура / этой
цепи обозначим Zu. Сопротивление связи контуров обозначим через Zkl
(см. пп. 1.2.8 и 5.4.1).
Предположим, что электродвижущая сила отсутствует. Тогда
C2)
Положим, что
[Z\ =
... z
и
и [/] =
Л
Система C2) в матричной форме запишется так:
Сопротивление Zlk имеет вид
Предположим, что сопротивление Zlk — чисто реактивное, т. е. Rlk ¦¦
Пусть
- 1 1 -
и [с\ =
_Lnl ... Lnn
230
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ IV
Тогда матричное уравнение, дающее частоты собственных колебаний цепи ш,
будет иметь вид
{'Ш —[-!-]}[/] = [01
или после умножения на [L]
-1
Это матричное обобщение известной формулы
r2~zcj/ = o<
Положим
Тогда система C2) будет
Определитель первой матрицы должен быть равен нулю:.
= 0. C3)
Это означает, что величины р = ш2 представляют собой собственные зна-
значения матрицы \М\.
¦ Уравнение C3) может быть очень высокого порядка. В таком случае
естественно пользоваться методом решения, изложенным в п. 4.1.39. Этот
метод дает последовательные значения корней, начиная с наибольшего.
Отсюда следует, что вычисление самых низких частот, отягощенное всеми
ошибками, сделанными при вычислении предыдущих частот, может привести
к недостаточно точному результату. Во избежание этого достаточно умножить
исходное матричное уравнение не
О
о
'У
3
О
¦о
4?j
i-i
на [L] , а на
¦fir1
Тогда
Рис. 4.33.
Это показывает, что —~- = ч —
(й2
собственное вначение матрицы
\Ц.
Матричное решение характеристического уравнения для [N] начнется с наи-
наибольшего значения v, т. е. с самой низкой частоты.
Вычисление амплитуд. Амплитуды токов, соответствующих частоте
uJ = (j,1 в различных контурах, можно вычислить, решая однородную систему
{№ -МП} [/1=Ю]. ; C4)
Она дает величины, пропорциональные искомым амплитудам, иначе говоря,
координаты собственного направления, соответствующего jj,j. Применение
способа, изложенного в п. 4.1.39 при отыскании собственного значения
наибольшего модуля, приводит нас к вычислению приближенного значения
предела для [М]р [4]. Известно1), что такой предел представляет собой
') См. замечание на стр. 202.
4.2]
ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ
231
собственное направление, соответствующее собственному значению наиболь-
наибольшего модуля. Мы получим, таким образом, величины, пропорциональные
1Х, /2 /„.Приведем пример Л. Пайпса. Даны два колебательных кон-
контура, соединенные третьим (рис. 4.33) при следующих численных данных:
Си = С22 = С33= 10 ф,
_ 5 , _ 1
— -g- гн, z-22— 2
. _ 1
гн> 33 — 1Г гн'
1 == 3~ ^"' 23== 32== "g"
Имеем
- 5
6
1
~ 3
0 -
[?]т' =
1
' 3
1
2
1
' 6
2
.2
2
5
5
0
1
—
1
6
2'
5
11.
1
0
.0
2
2
2
2
5
5
0
1
0
0
0
1
2'
5
11.
Выберем вектор
\и\ =
LlJ
Отыщем собственные значения следующей матрицы:
2 2"
2 5 5
.2 5 11.
Достаточно умножить затем найденные значения на 106, чтобы получить
собственные значения [М].
Вычисляем последовательно:
[уМ'][и]=18
I 1 О 1С
= 1 о • 10*
15
1
Отсюда
10,256881 "I
0,584762 ,
1 J
Г0.255238-
[М']*[и]=18- 15- 14,533 • 14,4495- 0,584762
L 1 .
ц1=14,4-Ю6. (•>!== 3,8- 103.
232
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ IV
Амплитуды будут пропорциональны 0,25; 0,58 и 1.
Далее, легко определить (л2 и И'з- а п0 ним Ш2 и шз и соответствующие
им амплитуды.
4.2.21. Контуры с периодически меняющимися параметрами1)- Рас-
Рассмотрим свободные колебания контура, у которого активное сопротивление,
индуктивность и емкость периодически меняются во времени. Примерами
могут служить генератор переменного тока, индуктивность которого является
синусоидальной функцией времени, телефонные наушники, угольный микро-
микрофон, конденсаторный микрофон, периодически
изменяющие параметры контуров, в которые они
входят как составные элементы.
Рассмотрим контур, изображенный на рис. 4.34,
и положим
С
Нг
О
о
о
о
о
Рис. 4.34.
/? =
О = -рг = Oq -f- S (Г),
где r(t), l(t), s(t) — переменные члены, a Ro, Lo, So — постоянные. Кроме
того, положим, что постоянные члены больше соответствующих амплитуд
переменных членов, т. е.
\s\<S0. \1\<LO, \r\<R0.
Дифференциальное уравнение свободных колебаний цепи будет
d'Q
dt*
C5)
если принять за функцию заряд конденсатора Q.
Задача легко решается, если известны два предельных условия. Поло-
Положим, что
IL \ 1 . ,.; S
—я- Л (О Л
Тогда уравнение C5) принимает вид
d2y , (n I dA
2 dt
Положим
1 1А
2 ' dt
—-1 A2 = b2+ a (t).
Функции В а А периодичны. Следовательно, a(t) также периодична, и мы
получим дифференциальное уравнение
(t)] у = 0, C6)
которое называется уравнением Хилла.
•) См. [11].
4.2] ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ 233
Если gi(t) и g2(t) — два линейно независимых решения, то общее ре-
. шение представляет собой их линейную комбинацию и может быть написано
в таком виде:
у (О = C1ff,(O + C2ff2 (О. C7)
где Сг и С2 —две произвольные постоянные.
Найдем соотношение между двумя значениями функции у((), разделен-
разделенными периодом Т функции a (t). Положим
и будем искать соотношение между t\(t) и y(t). Положим
¦п (t)=>.(() у (t),
Воспользовавшись C6), получаем — = —, откуда
Х"у + 2Х'у' = 0.
Это равенство должно быть справедливо в любой момент времени t. Не-
Необходимо, следовательно, чтобы
Поэтому
Х = const.
Возьмем произвольный момент времени t0. Тогда получим последовательно
Отсюда
Величина модуля X позволит определить устойчивость решения. Положим
Им^ем
xx(t) = Cxg,{t) + C2g2(t),
х (f) — r d8i(jt) i Г dS2(t) - C8>
Если
[ft @ ft (О
10@1= d
\ХЩ ГГ1_ГС<
то система C8) может быть записана в виде
1х @1 = [0@1 [С].
Матрица. [С] из постоянных С, и С2 определяется начальными условиями:
234 . МАТРИЧНОЕ ИСЧИСЛЕНИЕ [ГЛ. IV
Отсюда получаем новую форму для системы C8):
Придавая величине t значение to~\-T, находим
I* ('„ + Т)] = X [лг (*„)] = [O(t0-\- Т)] [О(*0)Г'[* (t0)).
Это равенство показывает, что X — собственное значение матрицы
Производная определителя матрицы [О(^)] равна
Это выражение равно нулю в силу уравнения Хилла, которому удовлетво-
удовлетворяют gx(t) и g2(t)- Следовательно, определитель матрицы [О(?)] независим от t.
Определитель [G (to~\-T)\ равен величине, обратной определителю [G(to)]~l.
Поэтому определитель произведения, т. е. определитель [М\, равен единице.
Эта величина равна также произведению собственных значений матрицы [М].
Мы можем, следовательно, считать, что
Корни X, и Xj, произведение которых равно единице, могут быть написаны
в таком виде:
X=k± yW^T,
где k вещественно.
Если |&|> 1, то показатель степени рТ веществен и равен archk.
В этом случае решение неустойчиво, потому что один из корней X] или Xj
по абсолютному значению больше единицы. Если |&|<1, то показатель
степени \хТ — чисто мнимая величина, равная yarccosu. Если arccos k равен
рациональной дроби —, то решение будет периодичным с периодом sT, т. е.
устойчивым. Если arccos k не равен рациональной дроби, то решение непе-
непериодично, но продолжает оставаться конечным, а следовательно, устойчивым.
В общем если диагональные члены матрицы [М] будут Мп и Л122. то доста-
достаточно сравнить абсолютную величину j Л11а —j— ЛГ221 c 2.
Практическое вычисление устойчивости этих решений связано с очень
большими трудностями. Поэтому рассмотрим приближенный метод вычисле-
вычисления матрицы
1
Эта матрица определяется из уравнения
[x(to+T)] =
Будем исходить из уравнения Хилла
при начальных условиях, определенных для у и —^г ¦ Если ввести обозначе-
обозначения у = ;е1, ~df==xv T0 уравнение Хилла сводится к системе
d-
dt
-^ х2 = - {*2 + a (t)} х, = F (О xv
d-x —х
dt *! ~~ 2>
4:2} ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ 235
которая в матричной форме выглядит так:
Предположим, что a(t) примерно постоянна в промежутке времени
= ts — ts_v Тогда требуется решить дифференциальное уравнение
которое является уравнением с постоянными коэффициентами. Такая задача
ГО 11
уже решалась в п. 4.1.43. Характеристинеское уравнение матрицы \ Р ,. л п I
ГХ —11 .
будет . =0. Корни его равны ± у F(ts)= ±bs. Следовательно,
[x(ts)]=\
Lbssh(bsMs) chi
Итак, исходя из [#(^о)Ь мы постепенно приближаемся к [х(^-\~Т)], т.е.
к равенству вида
Теперь остается только сравнить с единицей корни характеристического
уравнения матрицы [М].
4.2.22. Матрицы в квантовой механике. Рассмотрим периодическое
движение электрона, положение которого зависит от одной только коорди-
координаты q. В классической теории электромагнитного поля мы разлагаем функ-
функцию времени q(J) в ряд Фурье:
р— —оо
«/""*• '<39>
Эта формула выявляет частоты электромагнитных волн /?v, которые может
излучать электрон. Чтобы учесть сдвиг фаз каждой волны, амплитуду ар
в формуле C9) нужно считать комплексным числом. Так как координата q
вещественна, то ар и а_р должны быть сопряженными комплексными вели-
величинами:
Интенсивность каждой гармоники дается квадратом амплитуды или про-
произведением
В квантовой механике механизм излучения электрона трактуется иначе.
Испускание частоты > происходит при переходе электрона с одной устойчи-
устойчивой траектории на другую, или, иначе, с одного энергетического уровня Wm
на другой энергетический уровень Wп. Частота излучения дается соотноше-
соотношением
^m-Wn = Av, D2)
где h — постоянная Планка.
236
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
[ГЛ. IV
Если Wm > Wn, происходит испускание; если Wm < Wn — поглощение.
Поэтому частоты > оказываются здесь зависящими от двух индексов тип.
Обозначим их в виде чтп. Это означает, что непрерывную функцию q(t), ко-
которую мы ранее писали в виде разложения в ряд Фурье, мы должны заме-
заменить прямоугольной таблицей членов вида
?»» = *»»«2i"W- D3)
Такая точка зрения, высказанная впервые Гейзенбергом, игнорирует всякие
представления о механизме атомных явлений и признает только величины, по-
полученные непосредственно из эксперимента, т. е. интенсивность спектральных
линий и их частоту. Эти величины, зависящие от двух индексов, можно раз-
разместить в виде прямоугольной таблицы
Яп Яп ¦ • ¦ ¦
\
Табличная форма записи в квантовой механике аналогична разложению в ряд
Фурье в максвелловской теории электромагнетизма.
Совершенно очевидно, что, исходя из формулы D2), мы получим
, D4)
•пп— 'mm — J-
Это означает, что при переходе из состояния т в состояние п испускается
та же частота, что и поглощается при обратном переходе, и что если атом
находится в устойчивом стационарном состоянии, он не излучает.
Величина атп — комплексная. Ее модуль является мерой вероятности
перехода из состояния т в состояние п. Квадрат модуля определяет интен-
интенсивность линии испускания. Так как возможен переход и в обратном направ-
направлении, то должно иметь место
\ат„ =
Это убеждает нас, что, так же как и в случае ряда Фурье, а„
комплексные сопряженные величины:
и а„т —
тп пт-
D5)
Из D5) и D4) мы получаем также
"тп "пт-
Для умножения двух таблиц [д] и {р} введено правило
совпадающее с правилом умножения матриц. Оно дано так, чтобы умножение
обеих таблиц не вводило в рассмотрение новых частот.
Действительно, рассмотрим общий член каждой таблицы:
4.2] ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ 237
Но
Следовательно,
vmft ~Т" v*n == vmn'
Таким образом, правило умножения не вводит частот, которые не со-
содержались бы -раньше в q и р.
Легко заметить, что рассмотренные таблицы подчиняются правилам мат-
матричного исчисления, а в силу соотношения Ятп — Я*пт, это эрмитовы матрицы.
Матрица, полученная из матрицы q дифференцированием каждого члена
по времени, — это новая матрица р. Гейзенберг принял за отправную точку
квантовой механики предположение, что выражение Bnaapq — qp — комму-
h
татор матриц р и q — равно -*—.
ЛИТЕРАТУРА К ГЛАВЕ IV
1. Смирнов В. И., Курс высшей математики, т. III, ч. 1, Физматгиз, 1962.
2. Фаддеев Д. К., Ф а д д е е в а В. Н., Вычислительные методы линейной алгебры,
Физматгиз, 1963.
3. Мальцев А. И., Основы линейной алгебры, Гостехиздат, 1956.
4. F а нт м а хер Ф. Р., Теория матриц, Гостехиздат, 1954.
5. Фрезер Р. А., Дункан В. И. и К о л л а р А. Р., Теория матриц и ее прило-
приложение, ИЛ, 1950.
6. Беккенбах Э. Ф. (ред.), Современная математика для инженеров, гл. 12, ИЛ, 1958.
7. Лайд а у Л. Д., Лившиц Е. М., Квантовая механика, ч. 1, Физматгиз, 1963.
8. D u n с a n W. J., С о 11 а г A. R., A method for the solution of oscillation problems
by matrices, Phil. Mag., № 5, 1934.
9. F e 1 d t k e 11 e r R., Einfiihrung in die Vierpoltheorie, Leipzig.
10. H о w i 11 N., Equivalent electrical networks Proc. IRE, № 6, 1932.
11. Pipes L. A., Matrices in engineering, Electrical Engineering, sept., 1937.
12. Pipes L. A., Matrix solution of polynomial equations., J. of Franklin Inst., № 4, 1938.
ГЛАВА V
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
5.1. ТЕНЗОРНАЯ АЛГЕБРА
Аффинное векторное пространство. Метрическое пространство
5.1.1. Определения. Рассмотрим л-мерное пространство. В этом случае
система координат состоит из г координатных осей. На каждой из них мы
определим свою единицу длины, которая будет служить для измерения коор-
координат вдоль этой оси. Единичные отрезки осей, имеющие положительное
направление, принято называть единичными векторами или ортами. Обозначим
их через ех, е2, . • •. ег.
Рассмотрим вектор V. Пусть V,, V2 Vr — его компоненты по осям
1, 2 г. Компоненту вектора по оси можно получить, проектируя вектор
на эту ось параллельно гиперплоскости, образованной другими осями. Век-
Вектор V будет, следовательно, представлять собой геометрическую сумму
k
Символ 2' означает, что сумма состоит из всех членов, которые можно
к
получить, если придавать k все возможные значения от 1 до л.
Если в рассматриваемом л-мерном пространстве не- предполагается воз-
возможным сравнение длин \ег\, \е2\, .... \ег\, мы будем называть его аффин-
аффинным векторным пространством. В противном случае, т. е. если возможно
найти эталон длины, сравнимый со всеми длинами | е, |, \е2\ \ег\, будем
называть пространство метрическим.
Аффинное векторное пространство позволяет изучать общие свойства
фигур, не изменяющиеся при произвольном преобразовании системы коорди-
координат. Однако оно ограничивает исследование лишь теми свойствами фигур, при
изучения которых не приходится прибегать к понятию расстояния, а следова-
следовательно, и к понятию угла. Пока эти понятия нам не потребуются, мы будем
рассматривать аффинное пространство, но, как только возникнет необходи-
необходимость ввести понятие расстояния, мы будем переходить к метрическому про-
пространству. При такой постановке мы сможем формулировать теоремы с на-
наибольшей общностью.
На первый взгляд рассмотрение пространств, в которых понятие рас-
расстояния между двумя точками не имеет смысла, может показаться странным.
Между тем ташиии пространствами часто пользуются. Классическим примером
может служияшштрехмерное пространство, в котором по координатным осям
откладывашсяшдавлеоие, удельный объем и температура. Очевидно, что не
существуедаабШвЛ единицы измерения для давлений, объемов и температур;
следователкиошняоиятие расе тояния между двумя точками в таком пространстве
5.1]
ТЕНЗОРНАЯ АЛГЕБРА
239
совершенно бессмысленно. Точно так же обстоит дело, например, с кривыми,,
которые чертит регистрирующий термометр или барометр.
5.1.2. Преобразование координат. Пусть ev е2
а Ег, Е2
-, ет — единичные
Ет— единичные век-
веквекторы старой системы координат,
торы новой системы. . . .
Если обозначить через a.km проекцию единичного вектора Ет на единич-
единичный вектор ек, полученную при проектировании параллельно гиперплоскости-
образованной всеми остальными осями старой системы, то получится г урав-
уравнений:
A)
Таблица коэффициентов
есть матрица а линейного преобразования.
По предположению, старые единичные векторы линейно независимы. Это-
значит, что нельзя построить такую их линейную комбинацию 2
к
в которой хотя бы один из коэффициентов рк был бы отличен от нуля.
Если определитель, составленный из величин ат
отличен от нуля, то новые векторы будут также линейно независимы. Это-
значит, что нельзя построить линейную комбинацию ^j РтЕт = 0, в которой
т
хотя бы один из коэффициентов рт был отличен от нуля. Другими словами,
если векторы ek не находятся в одной гиперплоскости и если определитель
Д отличен от нуля, то и векторы Ет также не находятся в одной гипер-
гиперплоскости.
Уравнения A), которые можно написать сокращенно в виде
Bm = ^iO.kmek (т—\, 2 г),
дают нам новые единичные векторы Ет как функции старых1 единичных
векторов ек.
Рассмотрим обратный случай, т. е. будем искать кмшрмеп единичные
векторы как функции новых. Эта задача сводится к рвшвшимшистемы A>
240 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ ГГЛ. V
относительно с,, ev .... ет- Найдя решение, получим систему г уравнений
вида
B)
er = № + frE2
или, в сокращенном виде,
eft = 2PX (k—l, 2 г).
Матрица fj этого линейного преобразования равна а. Общий элемент
матрицы р будет, следовательно, равен
где Акт — алгебраическое дополнение элемента акт определителя Д матрицы а.
Рассмотрим сумму произведений
s «ft»;
s
«ft»;.-
Эта сумма равна единице при k, равном у, и нулю при А, отличном от у.
Действительно, произведение двух матриц а и ^ = 7~' есть единичная ма-
матрица. Элементы 2атР™ этой матрицы находятся на главной диагонали —
т
они равны единице. Элементы 2amfC не находятся на главной диагонали —
га J
они равны нулю. Пользуясь символом Кронекера, будем обозначать
1, если т = п,
0, если те яЬ л.
Если требуется найти коэффициенты а как функции коэффициентов
то, учитывая, что a = jj~ , получим
где в™ — алгебраическое дополнение элемента р™ определителя Д' матрицы р.
5.1.3. Ковариантные и контравариантные векторы. Мы уже знаем
формулы преобразования векторов:
Всякий вектор, который при преобразовании системы координат пре-
преобразуется согласно правилам преобразования единичных векторов, назы-
называется ковариантным. Индекс, означающий номер координатной оси, у соот-
соответствующих проекций ковариантного вектора помещают внизу: av а2 аг.
Пусть дан вектор, составляющие которого в старой системе будут
av а2, .... аТ, а в новой системе — Av А2 Аг Если этот вектор
5.1] ТЕНЗОРНАЯ АЛГЕБРА 241
ковариантен, то формулы преобразования будут
Например, градиент скалярной функции будет ковариантным вектором.
Используемые на практике векторы обычно не следуют указанному
правилу преобразования. Такие векторы называются контравариантными.
Индекс у проекций вектора на оси координат в этом случае помещают
вверху: х1, х2, ..., хг.
Рассмотрим вектор, составляющие которого равны х1, х2 хг
и X1, X2 Хг в старой и новой системах соответственно. Пользуясь
формулами преобразования единичных векторов, получим
Следовательно,
и наоборот,
vft V
х —2j
nt
Получились формулы, обратные формулам преобразования единичных век-
векторов '). В случае метрического пространства и прямоугольной системы
координат нет надобности различать ковариантные и контравариантные
индексы, так как в этом случае <х*( = ф™ = ek • Ет.
5.1.4. Определение тензора. Скалярная величина является тензором
нулевой валентности и имеет только одну компоненту. Вектор является
тензором первой валентности и имеет г компонент. Этот тензор может быть
либо ковариантным — при этом его компоненты должны обозначаться через tk,
либо контравариантным — тогда его компоненты должны обозначаться через tk.
Тензор второй валентности имеет г2 компонент. Существует три типа
тензоров второй валентности:
дважды ковариантный тензор, общая компонента которого может быть
записана в виде tik;
дважды контравариантный тенЗор, общая компонента которого может
быть записана в виде tlk;
смешанный тензор — один раз ковариантный, один раз контравариант-
контравариантный,— общая компонента которого может быть записана в виде tf.
•Компоненты тензора второй валентности могут быть расположены
в виде квадратной таблицы. Ниже мы увидим, что между тензором и ма-
матрицей имеется существенная разница. Часто для указания того, что эле-
элементы, входящие в таблицу, являются тензорными, таблицу заключают
в круглые скобки:
t\ ... А ... t\\
1 .* ,r
i . . . t, . . . tj
•А .к А
tr . . . tr . . . tr
или сокращенно (tt).
') Эти соотношения показывают, что матрица § линейного преобразования равна
матрице о преобразования координат, определенной в п. 4.1.21.
16 А. Анго
242 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Тензор третьей валентности имеет г3 компонент, которые могут рас-
располагаться в виде кубической таблицы. Существует четыре типа тензоров
третьей валентности:
(.tkl\ (Jk\ j.i\
Произвольная 'компонента наиболее общего тензора запишется в виде
''iV-'-'n1"
с п ковариантными и т контравариантными индексами. Сумма tn~\-n = р—
валентность тензора, имеющего гр компонент. Это не означает, что „мате-
„математический объект", состоящий из гр элементов, является р-валентным
тензором в r-мерном пространстве. Определение тензора дается с помощью
формул преобразования координат.
Пусть **1*2'"*/в — произвольная компонента р-валентного тензора, п раз
11'" л
ковариантного и т раз контравариантного в некоторой системе координат,
a TV?" f —соответствующая компонента того же тензора в любой дру-
другой системе координат.
Если ^*1*2"'<Я| — компонента тензора, то преобразование компоненты t
в компоненту Т происходит по формуле
hh---'n i...k '\ 'пк\ *и 'Л-'п
Наличие п ковариантных и m контравариантных индексов влечет за собой
введение п множителей а и m множителей р.
Обратное преобразование имеет вид
,*,V--*m= ^ ^' ... Pf»a*i ... afm^i^-'y.
Если преобразование t в Т и обратно не подчиняется этим формулам, то t
не является тензором. Однако выяснение вопроса о том, является ли данная
совокупность элементов тензором, путем установления применимости или
неприменимости приведенных формул преобразования координат—длинная
и сложная операция. Ниже (п. 5.1.15) мы рассмотрим более быстрый спо-
способ выяснения этого вопроса.
5.1.5. Матричная форма формул преобразования координат. Исполь-
Используя матричную форму, можно конкретизировать и упростить формулы пре-
преобразования координат для наиболее важных тензоров — тензоров первой
и второй валентностей.
Пусть a — матрица преобразования координат:
__ г
Для контравариантного вектора имеем
«!
71
• • • Л1
...af
а*
...а;
• ••<*?
г
2
i
где суммирование происходит по нижнему индексу, означающему номер
строки. Изменяя этот индекс, мы перемещаемся в матрице а вдоль k-ro
5.1)
ТЕНЗОРНАЯ АЛГЕБРА
243
столбца. Рассматриваемая формула имеет обычный вид произведения двух
матриц (см. рис. 4.4), если ввести матрицу а, транспонированную по отно-
отношению к а; матричная формула преобразования контравариантного вектора
имеет вид
—<хГ или Г=а :t, где ? =
Рассмотрим формулу преобразования для ковариантного вектора:
tm
f
-71
jm
V
Так как индекс суммирования представляет собой номер столбца для ма-
матрицы а и номер строки для одностолбцовой матрицы t. то матрица Т
представляет собой произведение матрицы а на матрицу t. Формула пре-
преобразования ковариантного вектора в матричной форме принимает вид:
7\
— a.t или t = a~l
где t =
Jr _
Рассмотрим случай дважды ковариантного тензора. Имеем
В слагаемом
2
индекс суммы представляет собой номер столбца для матрицы а и номер
строки для матрицы t, т. е. суммирование идет вдоль строки с номером Z
матрицы а и вдоль столбца с номером k матрицы t. Следовательно, речь
идет об элементе произведения матриц А = at. В формуле
индекс суммы представляет собой номер столбца и для матрицы А, и для
матрицы а. Следовательно, речь идет о произведении матрицы А на матрицу,
транспонированную по отношению к а. Таким образом, матричная формула
преобразования для дважды ковариантного тензора имеет вид
T=Aa=ata.
Для дважды контравариантного тензора имеем
Тш =
2
ilt
16*
244
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Рассуждение, подобное предыдущему, позволяет получить для него следую-
следующую матричную формулу преобразования:
Т=Щ при р = а.
Наконец, для смешанного тензора имеем
ik
а в матричной форме
Замечание. Из приведенных формул не следует делать вывод, что
квадратная матрица является тензором, так же как нельзя заключить, что
совокупность двух чисел есть вектор на плоскости. Матрицы — это просто
таблицы чисел или символов, никак не зависящие от преобразования системы
координат. Тензором квадратная таблица чисел является только в том слу-
случае, если она состоит из компонент тензора *).
Можно сказать, что тензор второй валентности представляет собой
в некоторой системе координат матрицу, элементы которой подчиняются
законам преобразования, свойственным компонен-
компонентам тензора. .
Аналогично тому, как элементы матриц
~7\
представляют собой координаты вектора в двух
системах координат, причем свойства и существо-
существование этого вектора не зависят от системы коор-
координат, также и матрицы
содержат компоненты тензора второй валентности в двух системах коор-
координат. Свойства и существование этого тензора также не зависят от системы
координат.
Аналогичное рассуждение применимо и к тензорам более высоких
валентностей.
Тензор третьей валентности представляется в некоторой системе коор-
координат кубической матрицей (рис. 5.1). Она разлагается на г квадратных
матриц, которые можно получить, разрезав куб на слои в соответствии
с каким-нибудь из индексов.
Тензор четвертой валентности может быть представлен набором из
г кубических матриц или из г2 квадратных матриц и т. д.
Для тензора любой валентности можно получить общие формулы пре-
преобразования в матричной форме, используя матрицы а, а и обратные им,
В формулу преобразования для р-валентного тензора входят р матриц пре-
') Мы видели, что при преобразовании координат матрица, связывающая два
вектора, преобразовывалась по формуле D) гл. IV. Эта матрица является тензором.
Принимая во внимание сказанное в п. 5.1.3, заключаем, что указанная формула
характеризует смешанный тензор.
5.1) ТЕНЗОРНАЯ АЛГЕБРА 245
образования, которые должны быть соответствующим образом выбраны
из набора матриц:
а, а, р =
а
Описанные свойства тензоров по аналогии с химией позволяют называть
порядок тензора валентностью.
5.1.6. Немой индекс. Отметим, что суммирование в формулах преобра-
преобразования тензоров всегда' происходит по индексу, который применяется
дважды: один раз внизу и один раз вверху. Поэтому нет смысла ставить
знак 2 суммы и отмечать под ним, по каким индексам производится сум-
суммирование. Такие индексы называются немыми.
Это упрощение записи ввел в тензорный анализ Эйнштейн. Например,
для преобразования координат вектора мы используем формулы
<>* - 2 fkAv
Можно, упрощая запись и подразумевая суммирование, написать
Ат = a-kmak< где k — немой индекс;
где I—немой индекс.
Преобразование компонент тензора по формуле
,*,*,-W 2 а*. ... а?«р/| . . . tf «7}-';. .
'Г2"-'я /.../ I m 'i 'я '\ш''п
можно, подразумевая суммирование, записать в виде
,*,*,-*« = «*. ...«?»#. ...р^.'-1?.
'Г2 ••• 'я 1 'т Ч л ;1 "¦ ¦'я
Здесь lv —, lm, j\, .... Jn — это т-\- « = р немых индексов. Приведен-
Приведенный способ упрощения записи является классическим, и его можно встдетить
в большом количестве работ, но мы не будем им пользоваться.
5.1.7. Симметрия и антисимметрия. Рассмотрим случай тензоров вто-
второй валентности. Как мы видели, такие тензоры бывают трех видов: дважды
контравариантные tik, дважды ковариантные tlk и .смешанные it.
Остановимся сначала на тензорах первых двух видов. Они называются
симметричными, если
*'* = **• или *„=»*„.
и антисимметричными, если
*«=._*" ИЛИ *„ = -*„.
Симметричность или антисимметричность есть свойство тензора, которое
не изменяется при преобразовании координат. Обозначим через е вели-
величину ±1. Согласно определению, мы имеем в этом случае для дважды
контравариантного тензора
*'* = е*«.
Пусть Т1т — его компонента после любого преобразования координат.
Покажем, что будет также иметь место равенство
Т1т = гТт1.
246 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Действительно,
•plm V* р>'от/'* Vs ч'йт /'* fail
ik ' k ik ' *
Аналогичными выкладками можно показать, что если tkl = etik, то
'ml ' tin'
Смешанный тензор ti не может быть симметричным или антисимметрич-
антисимметричным, потому что если бы это свойство имело место при каком-то частном
выборе системы координат, то оно не сохранилось бы при преобразовании
координат. Действительно, положим, что в некоторой системе координат
После преобразования координат получим
Видим, что Г™ не равно sTlm.
Полученные результаты легко обобщить на случай тензоров более высоких
валентностей, симметричных или антисимметричных по двум индексам не-
непременно одинаковой вариантности (т. е. оба индекса должны быть нижними
или оба верхними). Их можно также легко обобщить на случай тензоров
любой валентности, в которых условия симметричности или антисимметрич-
антисимметричности рассматриваются более чем для двух индексов обязательно одинаковой
вариантности. Это обобщение очень просто по отношению к симметричности.
Пусть дан тензор t^n.".. "• в котором условия симметричности рассматри-
рассматриваются по отношению к четырем контравариантным индексам a, J3, ?• &•
Условие симметричности состоит в том, .что
Л (вРт5)*' ••¦ /' (р)«...
Lmn ... — lmn ... >
если через р обозначить любую перестановку индексов а, р, у, 8.
Что касается антисимметричности, то здесь обобщение сложнее, так как
при этом встает вопрос о знаках. Обозначим по-прежнему +1 через е. Усло-
Условие антисимметричности состоит в том, что
j.k (aW etk(p)l...
Lmn ... — "ил ... >
где р по-прежнему означает любую перестановку индексов a, f3, 7, 8.
Если перестановка р четная, т. е. если имеет место переход от aj^S
к р путем четного числа перестановок букв (например, P<x8f — четная пере-
перестановка), то е будет равно +1.
Если перестановка р нечетная, т. е. если имеет место переход от a^fS
к р путем нечетного числа перестановок букв (например, Saflf — нечетная
перестановка), то е будет равно —1.
Представляет интерес частный случай тензора порядка т, антисим-
антисимметричного по отношению ко всем своим индексам, которые либо ковариантны,
либо контравариантны. Простой расчет показывает, что число существенных
(не совпадающих по абсолютном величине) компонент, отличных от нуля,
г\
/и! (г — т)\
6.1)
ТЕНЗОРНАЯ АЛГЕБРА
247
5.1.8. Псевдоскаляры. Скалярная плотность и скалярная емкость.
Для примера рассмотрим в трехмерном пространстве антисимметричный по
всем индексам трижды контравариантный тензор. Пусть ti}k — его общая
компонента. Подставив в выражение —^7 гг г —3, т = 3, получим, что
число существенных, отличных от нуля компонент' будет равно 1. Если
через ] -с | обозначить общее абсолютное значение этих компонент, то они
будут равны либо —j— j -с ], либо —| -с | в зависимости от того, будут ли пере-
перестановки индексов четными или нечетными по отношению к начальной пере-
перестановке. Пусть, например, дана перестановка 123, т. е.
Как будет вести себя величина х после преобразования координат?
После преобразования тензор не перестает быть ни антисимметричным,
ни трижды контравариантным. Значит, он также будет иметь только одну
отличную от нуля существенную компоненту. Если обозначить буквами
с чертой сверху компоненты тензора после преобразования координат, то
Найдем соотношение между х и т. Применяем формулу преобразования
координат для случая тройной контравариантности:
2
Imn
Все элементы t и t, не равные нулю, имеют неодинаковые индексы, так как
Jlk
.ilk Jllk __ Tllk
Имеем tlmn = ex. Величина е будет равна либо +1. либо —1 в зависимости
от того, будет ли Imn четной или нечетной перестановкой чисел 123. Поэтому
2
Imn
представляет
Imn Imn
Учитывая смысл знака е, заключаем, что сумма
собой определитель
4 «2
Следовательно, т = Дт.
Таким образом, перед нами величина только с одной существенной
компонентой, но она тем не менее не является скаляром, так как после
преобразования координат претерпевает изменение. Эта величина называется
псевдоскаляром. В частном случае контравариантных индексов она называется
скалярной емкостью.
Возьмем теперь также в трехмерном пространстве трижды ковариант-
ный антисимметричный тензор третьей валентности
Повторяя предыдущие рассуждения и обозначив через Г величину ком-
компоненты сш. можно получить формулу преобразования координат
— С123 = * 2i еРф2 РЗ = Д 1 •
I
2i
Imn
248 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Определитель Д', который является определителем матрицы [3, равен -г-.
Поэтому
Г = i Г.
д
Найденный нами псевдоскаляр подчиняется правилу преобразования, которое
обратно правилу преобразования для псевдоскаляра типа емкости. Его на-
называют скалярной плотностью.
Полученные результаты легко обобщить на r-мерное пространство. Для
г раз ковариантного тензора Cijk...r можно прийти к понятию скалярной
плотности
Г=С.23.....
которая преобразуется по формуле
Для г раз контравариантного тензора t '" можно прийти к понятию ска-
скалярной емкости
которая преобразуется по формуле
х = Дт.
5.1.9. Тензорная плотность и тензорная емкость. Произведение ска-
скалярной емкости на тензор дает тензорную емкость. Если дан, например,
тензор t\k, то соответствующая тензорная емкость ш'* будет равна
ш\к =
Тензорная емкость при преобразовании координат преобразуется по формулам
тпр
ш
Аналогично произведение скалярной плотности на тензор дает тензор-
тензорную плотность. Если рассматривать тензор t\k, то произведение
2,'* = П'*
представляет собой тензорную плотность. Тензорная плотность преобразуется
по формулам
тпр
2~тп Л VI а
Ш
Замечание. Произведение тензорной емкости на тензорную плот-
плотность дает тензор, так как сомножители Д и -д- сокращаются.
5.1) ТЕНЗОРНАЯ АЛГЕБРА 249
5.1.10. Антисимметричный тензор второй валентности в трехмерном
пространстве. Такой тензор, если он дважды контравариантен, можно за-
записать в виде
0 t12. t™
— t12 0 t2
_ /13 _ /23 0
Примем какой-либо порядок индексов, например 123 для левой системы
координат и 132 для правой. Положим
где е = -)-1, если Ijk получается из 123 четной перестановкой, и е = —1
в противном случае. Тогда тензор примет вид
0 х3 -
0
х2 — хг 0
Формулы преобразования координат будут следующие:
lm lm
Записывая сумму подробно и располагая слагаемые по порядку, получим
n
Это псевдовектор типа емкости.
Точно так же, взяв тензор дважды ковариантный
о ta *18\ / о f -:
— tn 0 t0A = ( — Г3 О F
^13 123
получим
Это псевдовектор типа плотности.
, Рассмотрим прямоугольную систему координат, расположенную в метри-
метрическом трехмерном пространстве (покинем временно аффинное векторное про-
пространство). В этом случае
a'm = cos (х1, хт) = C™,-
следовательно,
Д = Д';
но
поэтому
Д2= 1. А=г ±1.
Рассмотрим теперь наш тензор. Он дважды ковариантен или контра-
контравариантен (что одно и то же в прямоугольной системе координат) и может
быть определен тремя существенными, отличными от нуля компонентами»
250 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Его можно рассматривать как вектор во всех случаях, за исключением того,
когда при преобразовании координат совершается переход от левой системы
координат к правой или наоборот. В этом случае вследствие того, что
Д= ±1, вектор меняет знак. Такой вектор в векторном исчислении называют
скользящим вектором. Это позволяет понять глубокое различие между сколь-
скользящим и свободным вектором.
Операции над тензорами
5.1.11. Сложение двух тензоров. Складывать можно только тензоры,
имеющие одинаковую валентность и одинаковую вариантность. Суммой двух
тензоров является тензор, компоненты которого представляют собой суммы
соответствующих компонент слагаемых:
tlk = г'" + sik.
т т >^ т
t
т
5.1.12. Свертывание тензора. Пусть дан тензор с ковариантными и
контравариантными индексами. Можно получить из него другой тензор с ва-
валентностью, на две единицы меньшей. Для этого нужно приравнять о\дин
из ковариантных индексов какому-нибудь контравариантному, иначе говоря,
поставить условие, чтобы эти два индекса имели всегда одинаковые значения,
и затем просуммировать компоненты тензора по совпадающему индексу. Эту
¦операцию называют свертыванием тензора.
Рассмотрим для примера тензор третьей валентности tm- Поставим
условие, чтобы было т = /, и просуммируем компоненты тензора по со-
совпадающему индексу I. Получим
где с* — элементы тензора первой валентности (в данном случае контра-
вариантног
имеет вид
вариантного вектора). Действительно, формула преобразования тензора tlm
2л Р
Ikm
Произведя операцию свертывания тензора Т{1; получим
С = 2i ' J — 2j 2л VI ?kbj tm •
j j ikm
Но известно, что
2 aj^i = К (символ Кронекера).
Следовательно,
Видим, что формулы преобразования с* представляют собой формулы пре-
преобразования тензора (в данном случае контравариантного вектора).
Это доказательство можно без труда обобщить на тензоры более высокой
валентности. В частном случае смешанного тензора второй валентности ti
свертывание тензора дает скаляр
Свертыванием получен тензор нулевой валентности. Отсюда следует, что
сумма компонент главной диагонали смешанного тензора второй валентности
5.1] ТЕНЗОРНАЯ АЛГЕБРА 251
инвариантна. При полном свертывании любого тензора по всем индексам по-
получается инвариант.
5.1.13. Умножение тензоров. Пусть rj* и s}n — общие компоненты двух
тензоров.
¦ Произведением тензора г'? (третьей валентности) на тензор s? (второй
валентности) является тензор р^ (пятой валентности), компоненты которого
определяются формулами
„Ik/ — riksj
rmn m n'
Произведение тензоров зависит от порядка сомножителей.
5.1.14. Свертывание произведения. Операция свертывания тензоров
была описана выше. Посмотрим, что дает ее применение к произведению
двух тензоров, например к приведенному выше тензору
. „ikj __ rtksj
rmn m n
В применении к двум индексам п и k операция свертывания дает
Cm Z± Pmk-
к
Второе свертывание, примененное к индексам J и /га, дает
Мы пришли к ксштравариантному вектору. Если бы количество ковариантных
и контравариантных индексов было одинаковым, мы получили бы в конечной
результате инвариант.
Возьмем, например, два вектора противоположной вариантности vt и и*
и образуем тензор tk='ukvr Производя свертывание, получим
с = 21\ = ulvl -Ь • • ¦ -f- urvr = 2 u*vk;
к к
величина с представляет собой инвариант — это скалярное произведение
двух векторов и", vt.
Изложенные выше результаты дают критерий, позволяющий более
быстрым способом, чем при использовании формул преобразования координат,
установить, является ли совокупность элементов тензором (см. п. 5.1.4).
5.1.15. Установление типа тензора. Предположим, что нам встретилась
величина, представленная совокупностью из г3 элементов, зависящих, на-
например, от трех индексов, которые меняются от 1 до г каждый. Мы не
знаем, является ли эта совокупность элементов тензором и если да, то какова
его вариантность, иначе говоря, положение его индексов. Обозначим рас-
рассматриваемую величину через t(i, k, /га), где /, k, m — индексы, которые мы
пока заключаем в скобки, так как еще не имеем возможности разместить
их должным образом.
Попробуем произвести свертывание произведения этой величины на три
вектора и, v, w (так как имеется только три индекса). Если мы найдем,
что в результате свертывания произведения
2 t(i, k, m)ulvkwm
ikm
получился инвариант по отношению к любому преобразованию координат,
то величина t(i, k, /га) представляет собой дважды ковариантный и один раз
контравариантный тензор tkim.
252 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Действительно, произведем произвольное преобразование координат.
Так как при свертывании произведения получается инвариант, то
Но
Следовательно,
2
ikm
и1-.
tit.
=1
t
k.
\ц
(t.
m)
k, ,
u'vkwm —
к
^_\ N^ т i
rrl) === J^ 1 \
jln
Jln
w»
, n)
=
/a*p
UiVtWa.
m
что указывает на тензорный характер величины t и дает его вариантность.
Пример. Перемещение точки представляет собой контравариантный
вектор Ьхк. Какова вариантность силы?
Известно, что величина ЬА = 2 fk^x" ~ это совершенная силой работа,
к
следовательно, скаляр. В правой части равенства стоит свернутое произве-
произведение силы на контравариантный вектор. Следовательно, сила представляет
собой ковариантный вектор.
5.2. ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ
5.2.1. Определение криволинейных координат. Криволинейные оси.
Координатная поверхность. Пусть дано трехмерное пространство, отнесен-
отнесенное к прямолинейным осям Охх, Ох2, Ох3, причем ev ev ег — соответствую-
соответствующие единичные векторы (рис. 5.2).
Отнесем то же пространство к криволинейной системе координат, т. е.
свяжем старые координаты х1, х2, х3 с новыми X1, X2, X3 соотношениями
X2, Хг). C)
При этом новые координаты связаны со старыми обратными соотношениями
Xm = Fm(x1; х2, х3). D)
Дадим Xх, X2, X3 частные значения, соответствующие произвольной
фиксированной точке О' пространства, координаты которой выражены в ста-
старой системе координат фор-
3 1 \ I мулами C). Начиная с этой
1х 3 \ I ,L точки О', меняем значения X1
и оставляем X2 и Xz фикси-
фиксированными.
Точка, определяемая коор-
координатами
X2, X3),
X2, X3), E)
л;3=/3(Лг1, X2, X3),
описывает кривую, для кото-
которой уравнения E) при условии.
что изменяется только величина Xх, являются параметрическими уравнениями.
Эта кривая есть криволинейная ось О'X1, проходящая через точку О'. Та-
Таким же образом можно определить криволинейные оси О'Х2 и О'Х3.
Если в уравнениях E) зафиксировать величину X3 и изменять только Xх
и X2, то точка опишет поверхность, которая определяется параметрическими
5.2] ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ 253
уравнениями E). Это координатная поверхность О'Х1Х2. Таким же образом
определяются координатные поверхности О'Х2Х3 и О'Х1Хг.
Приведенные определения легко обобщить на r-мерное пространство.
Криволинейные оси определяются с помощью г уравнений с одним перемен-
переменным параметром, а координатные поверхности становятся гиперповерхно-
гиперповерхностями, выраженными г уравнениями с двумя параметрами.
Знакомые нам формулы преобразования координат
ук "S1 „к Хт Y1
х = ^о.тл , л
применимы и в этом случае, но лишь к бесконечно малым перемещениям
относительно точки О'. В старой системе координат такие перемещения
равны dxl, в новой — dXm.
Перемещения в новой системе координат можно считать происходящими
по касательным О'Тт к криволинейным осям Хт.
Длины dXm и dxk выражаются с помощью локальных единиц длины,
определяемых для' каждой оси единичными векторами
Локальные единицы длины постоянны в бесконечно малом объеме вблизи
точки О' и меняются вместе с О'. Действительно, имеем
т дХт' Vk
Если к бесконечно малым перемещениям относительно точки О' при-
применить формулы преобразования координат, то эти формулы примут вид
Все эти формулы без всяких изменений применимы к случаю, когда старая
система координат х1, е1 является также криволинейной системой координат.
Начиная с этого момента, мы "будем вместо аффинного векторного про-
пространства рассматривать метрическое пространство, так как теперь нам
придется пользоваться понятием расстояния между двумя точками.
Пусть произошло перемещение dX1 по оси X1. Тогда соответствующие
перемещения в старой системе координат будут
Если предположить, что старая система координат прямолинейна и прямо-
прямоугольна, то будет справедливо равенство
ds2 = (dxlf + (dx2J + (dx3J = (Ej dX1J,
где
аналогично
Е2
-А
Л ( dfk \2
А\дХ*)
к
• Ег
dfk \2 .
дХ>) '
-у i(^)
254 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
5.2.2, Фундаментальный метрический тензор. Пусть дано простран-
пространство, в котором мы можем определить расстояние между двумя бесконечно
близкими точками. Если оси ортогональны, то, например, в трехмерном
пространстве имеем
ds2 = (их*J (е,J + (rfx2J (e2J -f- (rfx3J {e^
Если система координат косоугольная, то
ds2 = (rfx1) (rf*>) {e,f + (dx2) (<**2) (e2
-f- (dx2) (dx3) e2e3 cos (e2, e3)-j-(dx2)(dx1)e2e1cos(e2, е{)~\-
+ (dx3)(dx2)e3e2cos(e3, e2) + (dxz)(dxl)e3e1cos(e3, <?,).
В более общем виде I
ds2 = 2iglkdxldx\
Ik •
где
. Sik = Ski=:eiekC0Siei, ek).
Так как величина ds2 инвариантна при любом преобразовании координат,
то Sik — элементы дважды ковариантного тензора второй валентности.
Тензор (gik) называется фундаментальным метрическим тензором.
Обозначим через g определитель, составленный из элементов gik,
g=\gift\- Пусть Glk — алгебраическое дополнение элемента glk. Опре-
Определитель g можно записать в виде
Первое выражение — это разложение определителя по элементам /-й строки,
второе — его разложение по элементам У^го столбца.
Кроме того,
20;* =0. если i Ф j.
2
к
так как при I ф j получается определитель, имеющий две одинаковые строки, и
2 Sik^u = °> если k Ф1,
так как при k Ф I получается определитель, имеющий два одинаковых столбца.
Если положить
то glk — дважды контравариантный тензор, потому что
Определитель g' тензора glk равен обратной величине определителя g
тензора gik:
6.2] " ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ 255
5.2.3. Преобразование определителя g фундаментального метри-
метрического тензора при преобразовании координат. Имеем
где glk— компоненты тензора в старой, a glm— в новой системах коорди-
координат. Это выражение представляет собой не что иное, как общий элемент
произведения трех определителей g, Д и Д. Следовательно, определитель g
равен
или, иначе'),
Эта формула показывает, что ]/"|й1—скалярная плотность, а —ска-
V I о I
лярная емкость.
5.2.4. Выражение для элемента объема. Рассмотрим в /--мерном про-
пространстве г раз контравариантный антисимметричный тензор, общая компо-
компонента которого равна
*"*•¦ = dxldxJdx* ....
где dxl обозначает бесконечно малое перемещение по оси /, a ijk ... —
некоторая перестановка из чисел 1, 2, ..., г.
Известно, что все не равные нулю составляющие этого тензора имеют
общее значение ± dx:
dt= dxxdx2 ... dxr.
где dx — скалярная емкость. Поэтому произведение dt на величину
которая представляет собой скалярную плотность, будет независимо от выбора
системы координат. Чтобы выяснить, что собой представляет это произведение,
рассмотрим прямоугольную декартову
систему координат. Тогда dx пре-
преобразуется в dx по формуле
а V\s\ преобразуется в у \g\ = \
Так как произведение
V\g\
fa /Г J7T
...dx~r Рис. 5.3.
представляет собой в этой системе координат объем параллелепипеда с реб-
ребрами dx1 dxr, то величина Y\S\ dx представляет собой тот же объем
в произвольной системе координат.
5.2.5. Косоугольная система координат на плоскости. Пусть Ох1
я Ох2 — две неперпендикулярные оси (рис. 5.3), а е, и е2 — соответствующие
единицы длины.
Рассмотрим некоторую точку М на плоскости. Координаты этой точки
можно получить, измеряя отрезки ОК и КМ ломаной ОКМ, параллельные
') Величина g — это определитель; \g\ — абсолютная величина определителя.
Величина gik—это общий элемент матрицы [glk\ тензора (glk) в рассматриваемой
системе координат. Символом | glk | обозначается определитель этой матрицы.
256 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
осям координат Ох1 и Ох2. Их истинные длины равны
[ГЛ. V
где х1 и х2 — число соответствующих единиц длины в отрезках ОК и КМ.
Следовательно,
ОМ = (е1 dx1J + (е2 dx2f + 2ехе2ххх2 cos 612,
где 912— угол между осями Ох1 и Ох2.
Сравнивая с выражением
ds2 = g-n (^J + g-22 (dx2J + 2^12 rf*i Ac».
получаем
Следовательно, тензор gik имеет вид
Элементарный объем diY\g\ (в данном случае элемент площади) равен
da — dx1 dx2e1e2 \f\ — cos2 612 = exe2 sin 812 dx1 dx2.
5.2.6. Ортогональные криволинейные координаты в трехмерном про-
пространстве1). Пусть дана точка М; Мх1, Мх2, Mxz—криволинейные оси,
лроходящие через эту точку, a ev e2, ег — локальные единицы длины
Рис. 5.4.
Рис. 5.5.
-относительно точки М (рис. 5.4). Приращения координат dx1, dx2, dx3
соответствуют истинным перемещениям
e1dx1, e2dx2, e3dxz,
откуда получаем тензор gLk:
О О
Определитель g равен
Определитель g' равен
0 (ezf
g = (е1е2егJ.
g' = -
1
') Большое количество примеров ортогональных криволинейных координат при-
приведено в п. 3.4.1 и последующих.
5.2] ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ 257
5.2.7. Случай произвольных криволинейных координат. Имеем
(рис. 5.5)
/ к
Приращение dxk влечет за собой перемещение, истинная длина которого
равна
dl
Но ds'2 = gkk(dx'??. Следовательно, gkk = (ekJ.
Если одновременно изменять dxk и dxl, то эти изменения влекут за
собой в плоскости, касательной к координатной поверхности Мх1хк, пере-
перемещение, квадрат истинной длины которого равен
ds2 = gu (dxi? + gkk (dx"J + 2gik dx' dx"
и в то же время ,
ds2 = (et dx'J+-(ek dxkf -+- 2etek cos (et, ek) dx1 dx*.
Поэтому
Stk = ei4 cos («/• «*) = et. ek,
где et-ek — скалярное произведение векторов et и ек.
5.2.8. Контравариантные или ковариантные компоненты одного и
того же вектора. Вопрос о вариантности вектора является составной частью
аффинной векторной -геометрии. В метрическом пространстве вектор может
менять вариантность. Он может, например, быть контравариантным, если
рассматривать его компоненты как контравариантные, или ковариантным,
если рассматривать его компоненты как ковариантные.
Рассмотрим вектор с контравариантными составляющими и*. Его ко-
ковариантные составляющие равны, по определению,
«!=• 2 */*«*¦
И наоборот, для определения контравариантных составляющих, исходя
из ковариантных, справедлива формула
«* = 2**4
Действительно,
к} )
Точно так же, если контравариантные составляющие бесконечно малого
перемещения будут.dxk, а ковариантные составляющие будут dxt, то
dxi = 2igikdx*, dxJ==^i Sn dxt.
Следовательно,
ds2 = 2 gik dx'dxk = 2 dXi dx1 — 2 gu dx{ dx,.
ik i Ij
Скалярное произведение двух векторов, которое в аффинном векторном
пространстве можно было определить лишь для двух векторов противо-
противоположной вариантности, можно теперь записать в виде
a • <о = 2 ир' = 2 Sikukvi = 2 ukl°k — 2 gik4)ub-
i Ik - к jk .
17 А. Анго
258 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Заменяя v на а, получим
Учитывая, что
и • v=\u\ \v\ cos (в, v),
имеем
2.
cos (и, v) = ik
Si k ^
rft Ik
Если вектор в направлен по оси Ох1, а © по оси Ох2, то
cos @1, е9) = —р=
5.2.9. Изменение вариантности тензора. Пользуясь фундаментальным
метрическим тензором, можно внести изменения в вариантность одного и
того же данного тензора. Для этого достаточно произвести свертывание
произведения фундаментального метрического тензора lgik) на данный тензор,
например (titl). Действительно,
5.2.10. Смешанный фундаментальный метрический тензор. Формулы
п. 5.2.8 позволяют определить смешанный фундаментальный метрический
тензор:
Si —^iSihg —V
A
Следовательно,
5.2.11. Случай прямолинейной прямоугольной системы координат.
В этом случае тензоры (glk) и (gik) совпадают с тензором (екЛ:
10 0 ...'
Следовательно, в прямоугольной системе координат контравариантные и
ковариантные компоненты не отличаются друг от друга.
Геометрическое представление контравариаитных
и ковариантных компонент вектора
5.2.12. Случай, прямолинейной косоугольной системы координат.
Пусть дан вектор ОМ в трехмерном пространстве (рис. 5.6), ev e2, ea —
единичные векторы координатных осей.
6.2] ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ
Контравариантные составляющие вектора ОМ будут
х_ОА_ 2_АВ_ з_ ВМ
ei е2 е3
так как АВ- и ВМ соответственно параллельны Ох2 и Ох3.
259
или
Но
Рис. 5.6.
Обозначим через К ортогональную проекцию точки М на ось Ох1. Тогда
ОК — ОА-+- АВ cos {ех, е2)-+- ВМ cos (ev e^
OK = e1x1~\-e2x2 cos (ev e2) + e3x3 cos (ex, e3).
cosCe,, e2)=lll—-, cos(ep
У g\\g22
Следовательно, умножая на ev получим
ех0К = (
gngaa
Итак, ковариантная компонента вектора ОМ по оси / представляет
собой произведение ортогональной проекции этого вектора на ось I на еди-
единицу длины для этой оси.
5.2.13. Случай криволинейных координат. Пусть дана прямолинейная
и прямоугольная система координат в • трехмерном пространстве и пусть
х1—координаты произвольной точки в этой системе.
Расстояние между двумя бесконечно близкими точками определяется
формулой
ds2 =
2
при
=8*. так как е1 = е2 = г3==1.
Перейдем к наиболее общей системе криволинейных координат при
помощи формул
xl = fl{X\ X2, X3),
r=.f"(*i, x2, x3).
17*
•260
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Здесь Ev Е2, Еъ—локальные единицы длины, отложенные соответственно
по касательным O'TV O'T2, О'Тг к криволинейным осям, проходящим через
точку О' (рис. 5.7).
Рис. 5.7.
Элементы фундаментального метрического тензора, которые в старой
системе координат равны
становятся в новой системе равными
Записывая подробно, получим
о„ == 2 *„«{«?=su («О2+^22 («?J 4- ^зз (а?J=(aD2+КJ 4- КJ-
Следовательно,
Рассмотрим теперь вектор О'А с коор-
Рис. 5.8. динатами av o2, а3 в старой системе, в ко-
которой не различаются контравариантность
и ковариантность, а также с ковариантными координатами Л], Л2, Л3 и с кон-
травариантными координатами Л1, Л2, Л3 в новой системе. Спроектируем
ортогонально этот вектор на касательную О'Тт к координатной линии О'Хт,
проходящей через точку О'. Обозначим полученную проекцию через О'Нт
(рис. 5.8).
Проведем через точку Л — конец вектора О'А — плоскость, параллель-
параллельную плоскости, касательной к координатной поверхности, не содержащей
линии О'Хт. Пусть Вт — точка пересечения этой плоскости с касатель-
ной О'Тт.
5.3] ДИФФЕРЕНЦИРОВАНИЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Имеем
О'Нт = V at cos (En, et) = -^Z- =
, et),
уumm
261
В итоге получаем
O'Bm
VGmm ' .
lmVumm-
Это хорошо согласуется с результатом, полученным для более частного
случая прямолинейной косоугольной системы координат.
5.2.14. Частный случай ортогональных криволинейных координат.
В этом случае 0'Нт = О'Вт. Следовательно,
Ат
или
л
рас-
д
В векторном исчислении общее значение величин Ат \Qmm =
V @тт
сматривается как компонента ат вектора О'А (индекс в этом случае не
имеет ковариантного смысла).
Действительно, длина / вектора определяется выражением
Поскольку мы рассматриваем криволинейные ортогональные координаты, то
Отл==0. если тфп, а Отт = Е2т. Поэтому
> ( Ат\1 V (Дп)
Если пользоваться прямолинейной прямоугольной системой координат, то
откуда и следует, что А
= АтЕт =
т— е т'
'тт. '-¦т
5.3. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
5.3.1. Градиент. Рассмотрим скалярную функцию V. Компоненты гра-
градиента определяются формулой
dV
a
Вектор градиент ковариантен, так как полный дифференциал dV — это
262 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
инвариант, равный
5.3.2. Ротор (вихрь). Если а — ковариантный вектор, зависящий от
координат произвольной точки, то компоненты ротора от векторной функ-
функции а определяются формулами
откуда blk = — bki. Следовательно, ротор а — это дважды ковариантный
антисимметричный тензор (в трехмерном пространстве ротор можно уподо-
уподобить осевому вектору).
5.3.3. Дивергенция. Рассмотрим формулу (см. п. 3.3.4)
где через dm обозначена масса, вытекающая в единицу времени из беско-
бесконечно малого объема dx, р — плотность жидкости, а V—вектор скорости.
Необходимо уточнить природу величин, входящих в эту формулу, уста-
установленную для пространства, отнесенного к прямоугольной системе коор-
координат, чтобы затем можно было обобщить ее на пространство, отнесенное
к произвольным криволинейным координатам. Вектор V контравариантен.
Произведение элемента объема dx (скалярная емкость) на плотность р пред-
представляет собой массу (чистый скаляр). Следовательно, р — скалярная плот-
плотность. Поэтому произведение pV будет векторной плотностью. Произведение
дивергенции на элемент объема представляет собой массу. Следовательно,
дивергенция будет скалярной плотностью.
Таким образом, операция дивергенции приложима не к вектору,
л к векторной плотности о. Результат представляет собой скалярную плот-
плотность
5.3.4. Лапласиан (оператор Лапласа). Лапласиан — это скаляр, опре-
определяемый как дивергенция градиента скалярной функции V.
Градиент скалярной функции — это ковариантный вектор. Но, как мы
сейчас видели, дивергенция приложима к векторной плотности, т. е. к про-
произведению скалярной плотности на контравариантный вектор.
Фундаментальный метрический тензор нозволяет получить градиент
в контравариантной форме:
*dV
dxk
л
Соответствующая векторная плотность по оси / будет
Следовательно,
• V
5.3] ДИФФЕРЕНЦИРОВАНИЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ 263
Так как должен получиться чистый скаляр, то достаточно умножить полу-
полученное выражение на . Тогда
'4
Не следует забывать, что Ig^—это абсолютное значение определителя (,glle).
Мы получили выражение для лапласиана в наиболее общей системе
криволинейных координат.
Частный случай ортогональных криволинейных координат
Мы видели, что в случае ортогональных криволинейных координат
можно связать тензорное исчисление с векторным и что определения ком-
компонент вектора неодинаковы. Поэтому если мы хотим использовать в век-
векторных обозначениях различные дифференциальные операторы, то следует
изменить соответствующим образом полученные выше формулы.
Обозначим через а компоненты, используемые в векторном исчислении,
а через А — компоненты того же вектора, применяемые в тензорном исчи-
исчислении. Мы видели, что эти различные компоненты связаны соотношением
Покажем, как изменятся формулы для дифференциальных операторов
применительно к компонентам вектора, используемым в векторном исчи-
исчислении.
б.З.б. Градиент. Как уже было отмечено, составляющие вектора гра-
градиента равны
A
Следовательно, согласно формулам F),
I dV
G)
5.3.6. Ротор. Аналогичным образом получим для компонент ротора
. _ dAk dAi
5.3.7. Дивергенция. Дивергенция, которая представляет собой скаляр-
скалярную плотность, становится чистым скаляром, если умножить ее на
Общая формула этой скалярной дивергенции в произвольных криволинейных
координатах имеет вид
В трехмерных ортогональных криволинейных координатах получим
УТвТ= «1*2*8-
264
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Формула для скалярной дивергенции преобразуется к виду
Вводя обычные, для векторного исчисления компоненты, будем иметь
dlv а ^ [ (аее) Ь
5.3.8. Лапласиан. Так как лапласиан есть чистый скаляр, так же как
и функция V, то не требуется рассматривать вопрос о разнице в обозначе-
обозначениях, и мы можем вычислять лапласиан в ортогональных криволинейных
координатах для трехмерного пространства, исходя из общей формулы
Здесь
¦е-2 О О
О
VO О
е22 О
9-2 ,
Следовательно,
1 Г д (е2еа dV\, д /«,*, 6V
5.3.9. Тензорная форма уравнений Максвелла. Рассмотрим обычное
для теории относительности пространство. Величина ds2 в этом ортогональ-
ортогональном пространстве имеет форму
ds2 = dx\ -t- dx\ -+- dx2 — с2 dt2.
Следовательно, четыре координаты этого „пространства — времени" будут
Ль ^9* з j с* *
где через с обозначена скорость электромагнитных волн в пустоте. В таком
ортогональном пространстве обозначение вариантности несущественно. Поэтому
индексы расставляются произвольно в нижнем положении.
Рассмотрим вектор J с проекциями
Л- Л- J3- J'c?
и два антисимметричных тензора второго порядка:
О Я3 —Н2 — jcD{\
0
-и,
0
-в,
0
в!
0
J-E
— jcD2
-jcDs
0 /
— ^-Е2
с 2
с 3
0
B.fl ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 265
Уравнения Максвелла будут
-«—¦?.
Здесь Е, Н, D, В, J — это соответственно векторы напряженности электри-
электрического и магнитного поля, электрической и магнитной индукции и плотности
тока, а р — плотность электрических зарядов.
Мы получим первые два уравнения Максвелла, если в равенстве
J
придадим / значения 1, 2, 3, 4. Аналогично два последних уравнения Мак-
Максвелла получаются из равенства
дРИ _¦ dFki . dFjk _
dxk "•" дх) ~1~ dxi "
Замечание. Уравнения Максвелла написаны здесь в рационализиро-
рационализированной системе МКСА. Если бы их требовалось написать в системе Гаусса,
т. е. в виде
то достаточно было бы последнюю строку и последний столбец тензоре Q
разделить на с, а тензора F умножить на с и, кроме того, вектор J умно-
4
жить на
5.4. ПРИМЕНЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Этот оригинальный метод был разработан в США Габриэлем Кроном.
5.4.1. Элементы электрических цепей с сосредоточенными постоян-
постоянными. Электрическая цепь наиболее общего вида состоит из нескольких
ветвей, соединенных между собой определенным и не меняющимся во вре-
времени способом. Такая ветвь, схематически представленная на рис. 5.9, может
содержать катушки индуктивности, конденсаторы, активные сопротивления,
электронные усилители, электродвигатели и т. д. Между элементами цепи,
входящими в некоторые ветви, может иметь место электромагнитная или
электромеханическая J) связь. В некоторых ветвях, или даже в большинстве
из них, могут находиться источники э. д. с.
') Например, две механически связанные между собой катушки, находящиеся
в разных ветвях и помещённые в постоянное магнитное поле.
266
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Точка соединения нескольких ветвей называется узлом. Если два узла
соединены накоротко, они образуют один узел (рис. 5.10). Замкнутая цепь
называется контуром. Сложную цепь можно разложить на некоторое число
простейших цепей. Между двумя простейшими цепями нет непосредственного
электрического соединения, но существует электромагнитная или электро-
электромеханическая связь. Без этой связи обе простейшие цепи будут полностью
независимы друг от друга. Контуры и ветви представляют собой расчетные
единицы цепи. Пусть 5, N, М, В— соответственно
наименьшее число простейших цепей, узлов, кон-
контуров и ветвей, какое только можно различить
в данной цепи. Между ними существует соотно-
соотношение
М = В — N-\-S, A0)
позволяющее определить минимальное число кон-
контуров М, которое необходимо рассмотреть для
n/VW—
—VWV-1
Рис. 5.10.
расчета цепи. При непосредственном рассмотрении цепи это число не оче-
очевидно, но минимальное количество узлов N, ветвей В, простейших цепей 5
можно сразу увидеть из схемы цепи. Отсюда по формуле A0) определяем
число М.
Каждая ветвь содержит некоторое количество пассивных элементов,
совокупность которых образует собственное сопротивление ветви. Прохо-
Прохождение комплексного тока по этому сопротивлению вызывает появление
комплексного напряжения на его зажимах. Обозначим через Zaa отношение
комплексного напряжения на зажимах к комплексному току в ветви — соб-
собственное сопротивление ветви.
Если ветвь образована последовательным соединением индуктивности,
активного сопротивления и емкости, то
Если исследуется не стационарный синусоидальный, а переходный
режим, то величина Zaa становится функцией комплексной переменной р
и получает следующий вид:
Zaa = PLaa
Если две ветви а и b соединены друг с другом, это означает, что про-
прохождение комплексного тока в ветви а вызывает в ветви b появление ком-
комплексной электродвижущей силы, и наоборот. Сопротивление связи между а
и b измеряется соотношением между этим током и напряжением. Обозначим
его через Zab. Сопротивление связи между b и а обозначим через Zba
B.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
267
Принцип обратимости требует, чтобы
7 7 1\
**аЬ — t'ba )
При электромагнитной связи
а)
Рис. 5.11.
или
в зависимости от рассматриваемой задачи.
Набор некоторого количества Z и электродвижущих сил в ветвях может
оказаться недостаточным для полного расчета электрической цепи. Действи-
Действительно, необходимо еще иметь возможность легко различать по схеме на-
направление индуктивной связи между двумя ветвями.
Существуют два способа последовательного соеди-
соединения двух катушек индуктивности: потоки кату-
катушек могут быть либо противоположны друг другу,
либо иметь одинаковое направление (встречное
или согласное включение). Чтобы безошибочно
показать это на схеме (см. рис. 5.11), самое про-
простое — ввести нумерацию зажимов ветвей. Можно
начать с любой ветви, зажимы которой нуме-
нумеруются 1—2.
Рассмотрим какую-либо другую ветвь, индук-
индуктивно связанную с занумерованной. Если магнитный
поток взаимной индукции, обусловленный током
влияющей ветви, пронизывая рассматриваемую ветвь, будет иметь направление,
одинаковое с ее собственным потоком, обозначим ее зажимы 1—2 (соглас-
(согласное включение, рис. 5.11, а). В противном случае их следует обозначить
2—1 (встречное включение, рис. 5.11,G). При согласном включении смеж-
смежные индексы различны, при встречном одинаковы. При отсутствии индуктив-
индуктивной связи нумерация не имеет значения.
Условимся, далее, относительно связи между направлением токов в ветвях и
нумерацией зажимов. За положительное направление тока примем направле-
направление 1—2. То же правило будем
относить и к направлению элек-
электродвижущих сил.
Пример. Рассмотрим элек-
электрическую цепь на рис. 5.12. Она
содержит 3 узла, 5 ветвей и со-
состоит из одной простейшей цепи.
р
Следовательно, по формуле A0)
минимальное число контуров
равно 3. Предположим, что ветви
аи/ включены согласно, а а и b
встречно. Предположим также,
Рис. 5.12.
что электродвижущие силы, приложенные к ветвям d и /, имеют направле-
направления, указанные стрелками. Это обусловливает положительное направление
токов в ветвях а, / и электродвижущей силы в ветви /. За положитель-
положительные направления токов других ветвей могут быть приняты любые, однако
их следует считать до конца вычисления неизменными. Если направление
') Однако принцип обратимости может не иметь места, если, например, одна из
ветвей содержит электронный усилитель или вентиль и т. п. В этом случае 2ф2
268
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
тока в какой-либо ветви, принятое нами за положительное, не будет соот'
ветствовать действительному направлению тока, то это означает, что в ре-
результате решения мы получим для этой ветви отрицательную величину тока.
Если направления токов совпадают со стрелками на рисунке, то элек-
электродвижущая сила ветви d также будет положительна.
Ниже мы изложим метод быстрого составления уравнений, описывающих
режим цепи. Подчеркнем, что речь идет о методе составления уравнений,
а не об их решении.
5.4.2. Метод составления уравнений для цепи наиболее общего вида.
Рассмотрим цепь наиболее общего вида. Примем токи, текущие в некоторых
участках цепи, за вспомогательные неизвестные и с их помощью определим
остальные токи цепи. Вспомогательные токи определяются следующим пра-
правилом: они должны протекать по таким участкам цепи, разорвав которые
мы обесточим цепь. Это правило означает, что вспомогательные токи взаимно
независимы в смысле первого закона Кирхгофа. Максимальное число таких
токов равно минимальному числу контуров. Поэтому их называют контур-
иыми или независимыми токами в противоположность действительным токам,
текущим в ветвях. Отсюда следует, что токи ветвей могут рассматриваться
как результат наложения всех контурных токов, текущих по рассматривае-
рассматриваемой ветви. Существенно определить для контурных токов положительное
направление. Оно может быть совершенно произвольным, но, так же как
определенное выше положительное направление для токов ветвей, не должно
меняться до конца вычисления.
Обозначим контурные токи через ip, I4, .... а токи ветвей через
/", 1Ь', ... (поскольку ветви были обозначены буквами а, Ь, .... и т. д.).
Можно рассматривать контурные токи как координаты вектора /'
в М-мерном пространстве. Назовем его контурным пространством или,
проще, пространством o4t- Токи ветвей можно рассматривать как коорди-
координаты некоторого другого вектора / в В-мерном пространстве. Назовем его
пространством ветвей или, проще, пространством <%. Векторы / и /' выра-
выражены соответственно матрицами
/' =
1 =
Примем, что они контравариантны, что оправдывает расположение индек-
индексов вверху. Токи ветвей можно выразить с помощью первого закона
Кирхгофа или, что одно и то же, приравнять их сумме контурных токов,
протекающих в ветвях. Получаем следующие выражения:
ia = Capip + Caqi4-h ... A1)
Каждый коэффициент С равен 0, -+-1 или —1 в зависимости от нали-
наличия тока в рассматриваемой ветви и от совпадения его направления с напра-
направлением, принятым для данной ветви за положительное.
Таблица коэффициентов С может рассматриваться как матрица пре-
преобразования, позволяющая перейти от вектора, представленного матрицей /',
к вектору, представленному матрицей /. Назовем ее матрицей связи; при
этом совокупность уравнений A1) запишется в матричных обозначениях*) как
1=СГ.
') Матрица связи — это транспонированная матрица а. п. 5.1.5.
5.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
269
Обратимся к цепи, рассмотренной в предыдущем примере. Схема токов
в ней изображена на рис. 5.13. Ветви обозначены через а, Ь, с, d, f.
За положительные направления токов примем направления, указанные стрел-
стрелками. Для некоторых из токов эти направления обусловлены электромагнит-
электромагнитной связью. Если разъединить ветви с, d, /, цепь становится полностью
разомкнутой. Ее можно рассматривать, следовательно, как наложение трех
контуров, обозначенных пунктирными линиями. На каждом контуре стрел-
стрелками указано направление тока, произвольно принятое за положительное.
Матрицы / и /' будут равны
соответственно Ш)
/=
¦ ta-
if
I' =
i"
If J
Первый закон Кирхгофа дает
1» ==
Iе = +1Ч
Отсюда получаем матрицу С, уста-
устанавливающую связь между матри-
матрицами / и /':
С =
0
1
6
1
0
—1
1
1
0
0
1
—1
0
0
1
Рнс. 5.14.
Для описания той же цепи, которую можно обесточить, разъединив
другую тройку ветвей a, d, /, можно найти и другую систему контурных
токов, например, изображенную на рис. 5.14. При этом находим новую
матрицу связи Сг:
О 1 О'
1
0
1
0
1
—1
0
0
0
1
0
1
Вернемся к изучению цепи наиболее общего вида. Дана ветвь а (рис. 5.9)
с зажимами Ли В. Она содержит электродвижущую силу еа, и по ней
течет ток 1а, имеющий направление от А к В. Ветвь имеет собственное
сопротивление Zaa и связана с другими ветвями через сопротивления связи
270
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Zab, Zac, ... Пусть иа — разность потенциалов VА — Vв. Между всеми
указанными величинами имеется соотношение
A2)
Рассмотрим матрицы
U =
'а
«ft
'— 7 7
E =
ea
4
/=
Матрица / представляет собой, по предположению, контравариантный
вектор.
Мощность, получаемая от источников э. д. с, равна
w = 2 «/Л
1
Матрица Е представляет собой ковариантный вектор. Матрица с элемен-
элементами U* — контравариантный вектор, комплексно сопряженный с вектором /.
Произведение Е на Г* является скаляром.
Расходуемая мощность равна
2
тк
откуда следует, что матрица Z является дважды ковариантным тензором.
Он называется тензором полных сопротивлений.
Формула A2) показывает, что матрица U есть ковариантный вектор.
Соотношения типа A2), написанные для всех ветвей, могут быть в матрич-
матричном обозначении записаны в виде
U-\-ZI =
A3)
Это — соотношение между тензорными величинами.
Рассмотрим преобразование, позволяющее перейти от пространства J?
к пространству o/it. Оно определено матрицей связи С. Формулы преобра-
преобразования тензорных величин U, Z, I, E с учетом их вариантности следующие:
(определение матрицы связи),
(ковариантный вектор),
(ковариантный вектор),
(дважды ковариантный тензор)
ab
-ab
или, в матричном обозначении,
1=СГ,
Е' = СЕ,
W = CU.
Z' = CZC,
A4)
A5)
A6)
A7)
6.41
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
271
где /', Е', U', Z' — матрицы, представляющие соответствующие тензорные
величины в пространстве а4(-
Соотношение A3), связывающее тензорные величины, не зависит от вы-
выбора системы координат. В пространстве а4С оно получает вид
U' + Z'I' = E'. ' A8)
Элементы матрицы Е' представляют собой алгебраическую сумму элек-
электродвижущих сил, действующих в контурах. Элементы главной диагонали
матрицы Z' представляют собой собственные сопротивления контуров.
Остальные элементы этой матрицы являются сопротивлениями связи между
контурами. Каждый элемент матрицы U' — это сумма разностей потенциалов
между зажимами элементов ветвей, встречаемых при последовательном про-
прохождении по контуру. Известно, что эта геометрическая сумма равна нулю.
Отсюда
гоп
О
Таким образом, соотношение A8) значительно упрощается в простран-
пространстве а41 и становится системой из М уравнений с М искомыми неизвестными:
Е' = Z'V.
A9)
Замечание. Уравнение A9) — это соотношение между тензорными
величинами. Можно соблазниться свойством инвариантности тензорных
соотношений и возвратиться из пространства a/ft в пространство &, напи-
написав A3) в виде E = ZI. Это, однако, неверно. Дело в том, что матрица
связи С не допускает обращения, и перейти от пространства (Ж к про-
пространству <% невозможно, точно так же, как нельзя написать токи 1Р как
функцию токов 1а. '
Применим только что изложенное к примеру, рассмотренному на стр. 269.
Мы уже вычислили матрицу С. Поэтому получаем
О
-1
1
Тензор сопротивлений в пространстве jj
предположение, сделанное о строении цепи)
7-аа Zab О
7-ъ„ Zhh О
1
1
1
0
1
0
1
0
0
(Г
0
1.
-
0
0
ed
-ef-
=
' «d'
0
-ef-
равен (принимая во внимание
О
О
о
о
О
О
О
О
О
О
О
О
'-ft-
272 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
В пространстве а41 он будет равен
[ГЛ. V
Z
— Zab I Zbb
ab bb
~Zba +
Zaa~~
Z _|_
+ Zcc
~Zaa +
— Zfa +
~Zbb
Zbb
Zba
2-M +
Zba~
Zab —
Zba Zbb
Zaa i Zba ~i~
+ Zab Zbb
Zaa — Zba +
1 7 7 _i_
H~ zbb + ^o/ H~
Тензорное уравнение режима будет
E' — Z'I'.
Метод, изложенный в этом пункте, сводится к следующим простым
приемам:
а) Тщательно вычертить схему изучаемой цепи, обозначить ветви, про-
пронумеровав их зажимы в зависимости от связей, и обозначить имеющиеся
электродвижущие силы.
б) Сосчитать узлы, ветви и простейшие цепи. Определить по ним наи-
наименьшее число контуров. Ввести столько независимых токов, сколько имеется
контуров. Показать эти токи стрелками произвольных направлений.
в) С помощью независимых токов вычислить все токи в ветвях, поль-
пользуясь первым законом Кирхгофа и учитывая^ их направления. По полученной
системе написать матрицу связи С.
г) Вычислить матрицы ?' и Z' с помощью формул
Е' = СЕ, Z' = CZC.
Отсюда выводится соотношение ?'/ = Z7/, решающее задачу.
Для дальнейших вычислений нужно знать структуру ветвей и, кроме
того, более конкретно определить задачу. Если в задаче рассматривается
только стационарный синусоидальный режим, то, например, электродвижу-
электродвижущие силы и сопротивления будут иметь следующий вид:
При этом, решая систему A9), найдем комплексные токи /'.
Если требуется только составить систему дифференциальных уравнений,
описывающих работу цепи, то следует заменить комплексные токи и напря-
напряжения мгновенными токами и напряжениями и подставить вместо знаков
дифференцирования -?т и интегрирования / ( )dt соответственно /ш и -^-.
Если же требуется отыскать переходный режим, создаваемый несколь-
несколькими электродвижущими силами Aj(?), h2(t) приложенными в момент
времени ? = 0, то следует ввести в систему A9) изображения электродви-
электродвижущих сил /j (р) ф hx (t), f2 (p) =- h2 (t), ... *) и сопротивлений в виде
*) Употребляются еще следующие обозначения: /(р)-
/Wc/>@ (см. гл. 8).
¦* (9.
5.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
273
1
R-\ -гх--\- pL. Мы получим переходные токи как функцию времени, вычислив
оригиналы выражений
а1 (Р)
например, путем применения теоремы разложения Хевисайда (см. п. 8.3.12).
Очевидно, что в случае постоянного тока речь идет лишь о решении
системы, линейных уравнений E' = Z'f, где элементы Z' и Е'—вещественные
Рис. 5.15.
числа, выраженные соответственно в омах и в вольтах. При этом система
A9) дает токи в амперах.
Последнее замечание: очевидно, что отыскание тензорным способом
уравнений режима цепи, изображенной на рис. 5.13, невыгодно. Прямое
хЛЛЛЛЛ
вычисление было бы проще. Однако легко заметить, что по мере возраста-
возрастания сложности цепи тензорный способ получает преимущество над прямым
вычислением.
Другое важное достоинство вытекает из полного единообразия прие-
приемов описанного метода. Проиллюстрируем его на двух примерах цепей
довольно простой структуры, для которых, однако, уже составление урав-
уравнений режима прямым методом было бы весьма затруднительно.
18 А. Анго
274
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Пример 1. Приложим наш метод к цепи, изображенной на рис. 5.15.
а) Предположим, что ток, проходя по пути b, h, /, а, с, k, встречает
индуктивно связанные ветви. Причем конструкция такова, что одни ветви
будут иметь согласное включение (ас, af, bf, cf, fk, bk), другие — встреч-
встречное (ah, ch). Поэтому нужна нумерация ветвей, указанная на рис. 5.15.
б) Число ветвей равно 8, число узлов 5, число простейших цепей 1.
Число контуров, следовательно, равно 4.
В качестве независимых токов выберем 1Р, Iя, lT, is. Они указаны
на рис. 5.16 (буква i на данном и следующих рисунках опущена). •
в) Остается вычислить токи ветвей как функции выбранных нами не-
независимых токов. Результат такого вычисления показан на рис. 5.17.
Рис. 5.17.
Заметим, что независимый ток 1Р, проходящий по ветви а, имеет на-
направление 2—>1. Так как положительное направление тока 1а будет 1 —>2, то
То же относится к ветвям b, f и k. Сделав это замечание, мы можем напи-
написать выражения для токов ветвей как функции независимых токов. Запишем
их в виде соотношений между значками, опуская букву i *). Эти соотноше-
соотношения позволяют получить матрицу связи С:
а =
Ъ =
с =
й =
j
cr ——
h —
k =
— P
— P
+ Я
— Р-ГЧ
+ p
— Г + 5
-t-r — s
— r
-\-r
-Л-г
— s
Q
—1
J
0
0
— 1
0
1
0
0
0
0
1
1
0
0
0
0
—1
1
0
—1
1
1
0
0
1
—1
0
0
0
0
—1
*) Подобную запись будем применять и в дальнейшем.
6.4] ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
г) Вычислим матрицы Е' и Z':
275
Е'=С
еа
0
ес
ed
0
0
0
0 _
- «в-
ed
ес
- —ес-1
Zaa
0
Zca
0
Zfa
0
zha
0
Zbb
0
0
0
0
Zac
0
0
i Z)c
0
Zhc
0
0
0
0
0
0
0
Zaf
Zbf
Zcf
0
Zff
0
0
0
0
0
0
Zgg
0
Zah
0
zcft
0
Zfh
0
^Aft
0
Zftft
0 '
0
z/ft
0
0
_0 Zftft 0 0 Zft/ 0 0
— Zah-\- —Zaf — Zbf —
Zbb + Zbf — Zac -f- — Zbb — Zbf -)- Zac -f-
2 ^ + Z f Zu Z + Z
Zcft
— Zfh — Zah — Zffi -f-
— ZCf-\-Zch
Zaf —
— Zff -f-
— Zbf -\- ZCf —
7 7 7 . _J_ 7 1_7
*-ас ^af 'a«T *-bf ~T *-cf
¦zbf- -
-Z/h +
f
+ Zch — Zfh
' zac—zbb -\- zbtt
+ ZCf
Zcf -f
— Zcf +
— Zcf-
Zcc. — — Zift — Zbf — Zcc
— Zc
Zfk
zbf — Zcf — —
Zftft — Zcc —
— Z,,ft 4- Zcc —
Zkk
— Zbf + Zcf +Zfk
-ch
Искомая система уравнений — это Е' = Z'l'.
Пример 2. Рассмотрим цепь, изображенную на рис. 5.18.
а) По конструкции она содержит некоторое количество индуктивно
связанных ветвей (ab, cd, dg, gh, kf). Для тока, проходящего путь bagdch,
и для тока, проходящего путь kf, имеем встречное включение. Отсюда
проистекает нумерация ветвей, указанная на рис. 5.18.
б) Число ветвей равно 8, число узлов 4, число простейших цепей 1.
Следовательно, число контуров равно 5. Пять выбранных независимых токов
изображены на рис. 5.19.
в) Токи, протекающие по восьми ветвям, изображены на рис. 5.20.
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Рис. 5.18.
Рис. 5.19.
Рис. 6.20.
6.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
277
Выразим токи ветвей как функции пяти независимых токов. Имеем
систему уравнений, из которой получим матрицу связи С:
О
а =
Ь =
с *=
а =
/ =
g —
k —
— q
— P + q
P
— q
P — q
q —
+ s — t
— t
r —t
— s
t
C1 ——
Матрицы Е a Z равны
ea
—e" *-ab
—«, 0
0
0
0
0
0
г) Вычисление Е' и Z' дает
0
0
0
0
0
0
0
0
uC(t
0
0
0
0
1
0
1
0
0
0
0
0
zcd
—1
1
0
—1
—1
1
0
0
0
0
0
0
z
0
' 0
0
0
0
—1
0
0
0
0
0
//
0
1
0
0
0
0
0
J
0
0
0
0
0
0
0
0
6n ви & A ~~~ '
eh —
Zcc -f-
— 0
Zab
¦zff
Zab — ¦
0
'Zab
Zab+ '
Zdg —
7 7 i
%bb + Zdd — %dg + — Zgg
Zdg + Zgg
~~" ^ era ^
Z
Zab —
gh
gg
Zaa "T" Zab
4-
— z
^aa — Zab -f- Zab —
7-bh ¦+- Zdg — Zfk —
gg
Zgh
Zi 7, ,
aa t **hh
— Zaa — Zab -\-
"gg
— 1 )
—1
0
0
0
—1
0
1.
0
0
0
0
0
о
Zab + Zbb ¦+¦
-Z
• zdg — Zgg — zfk
bb
?g
?fln ~~ ^,
ab'
Zgg
Искомая система уравнений — это Е' = Z'V'.
5.4.3. Соединение цепей посредством проводников. Для анализа слож-
сложной цепи достаточно разложить ее на более простые, подобные тем, которые
278
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
рассматривались нами выше. Одно из основных преимуществ тензорного
метода и состоит в возможности постоянно использовать для расчета сложных
цепей расчеты простых цепей, произведенные ранее. *
Рассмотрим две цепи из примеров 1 и 2. Обозначим первую цепь
через R2, а вторую через Rv
Поместив их рядом без какой-либо связи, мы можем считать, что сово-
совокупность этих цепей образует цепь /?! + /?2 (рис. 5.21).
Рис. 5.21.
Если обозначить для цепей Rx и R2 соответственно через Ev Е2 Zx,
Z2, I\, l2 матрицы, которые в примерах 1 и 2 обозначались как ?", Z'. /',
то для цепи R\-\-R2 получим уравнения
Е2 =
Z2I2.
Обозначив через Е, Z, I матрицы
вЫ1 lo z2\ /==Ы'
мы можем написать уравнения B0) в виде
E=ZI.
Соединим совершенно произвольным образом цепи Rx и R2 и образуем
из них более сложную цепь R, например, как показано на рис. 5.22.
и
Рис. 5.22.
Выберем в цеди R независимые токи совершенно произвольно, однако
соблюдая правило о том, чтобы, разорвав ветви, по которым текут эти токи,
мы полиостью обесточивали цепь. Число независимых токов нетрудно опре-
5.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
279
делить. Одна только цепь Rt требует 5 таких токов, цепь R2—4 тока. Следова-
Следовательно, цепь /?! + R2 будет иметь их 9. При электрическом соединении обеих
цепей получим суммарное количество ветвей и узлов, но число простейших
цепей сократится до 1. Поэтому для объединенной цепи потребуется 9—1 =8
независимых токов. Пусть s, t, и, v, w, x, у, z — независимые токи, обра-
образующие элементы матрицы /'. Матрица / образована токами pv qv rv sv
' Pv 4v r2< S2- Вычисление последних токов как функций первых дает
С R С'
матрицу
/>i =
1i =
/-,== —s
s,=
л =
Рз =
Яг = '
f 2 =
S2 =
связи С для цепи
+ «
+ и
-\-и -\-w
—1-\- и — v-\-w-\- х
— w
-\-V —X
— X
-f- и — v-\~w
R, определяемую
—у
c =
— y — z
+ У+ г
0
0
—1
0
0
0
0
0
0
равенством
0
0
0
—1
0
0
0
0
0
1
1
1
1
0
0
0
0
1
0
0
0
—1
0
1
0
0
—1
/'—
0
0
1
1
1
0
0
0
1
СГ:
0
0
0
1
0
—1
—1
0
0
—1
0
0
0
0
—1
0
1
0
0
0
0
0
0
—1
0
1
0
Получаем E' = СЕ и Z' = CZC. Искомая система уравнений будет .
Е' = ггг.
Для вычисления удобно воспользоваться частной формой записи матриц:
и матрицы С в виде С =
г>
где Cj и С2 обозначают матрицы
—
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
—1
0
0
0
0
1
1
1
1-
1
0
1
0
0
1
0
0
0
—1
0
0
0
0
1
0
0
1
1
J
]
—1
0
0
0
0
0
1
0
—1
0
1
0
1
0
0
0
0
—1
0
1
0
0
0
0
0
0
-
Мы получим
' = 1С,С2]
Z2C2,
Используя результаты расчетов цепей Rl и R2, можно найти искомые урав-
уравнения задачи.
280
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
5.4.4. Соединение цепей посредством магнитопроводов. Мы уже видели,
что наложение дополнительных условий равенства нескольких токов умень-
уменьшает число составляющих вектора тока при соединении цепей. Это находит
свое отражение в структуре матрицы связи, характеризующей объединенную
цепь. Аналогично предыдущему дополнительные связи между токами могут быть
обусловлены введением в схему магнитопроводов с очень малым магнитным
сопротивлением. Действительно, пусть а, Ь, ... — несколько ветвей, состоя-
состоящих из катушек, надетых на магнитопровод (рис. 5.23).
Магнитодвижущая сила М равна
где через па, пь, ... обозначено число витков катушек а, Ь, .. . Если
магнитное сопротивление очень мало, то между токами ветвей I", ib, .. .
имеет место следующая дополни-
дополнительная связь: р
Заменим i", tb, ... их выра-
выражениями через независимые токи
lp, iq, .... текущие в данной
Рис. 5.23.
Рис. 5.24.
цепи, вначале без учета магнитной связи. С учетом (*) получим уравнение, по-
позволяющее исключить один из токов. Всего будет исключено столько токов,
сколько имеется независимых магнитных цепей. Т. е., как-и в п. 5.4.3,
произойдет уменьшение числа составляющих вектора тока. Это уменьшение
может быть учтено введением новой матрицы С, определяемой равенством
/' = С Г,
где через /' обозначен вектор тока с составляющими 1Р, Iя, .... а через
/" — вектор тока после уменьшения числа составляющих. В зависимости
от токов lp, lq которые требуется вычислить, отберем составляющие,
подлежащие исключению. Приводимый ниже пример поясняет эту мысль.
Рассмотрим трансформатор Скотта (рис. 5.24). Он служит для преобра-
преобразования трехфазных токов в двухфаз'ные, и наоборот.
а) Вначале не учитываем магнитные цепи:
а = р
b= q
с = г С =
d'= s
f — V — Я
1
0
0
0
1
0
1
0
0
— 1
0
0
1
0
0
0
0
0
1
0
S.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
281
б) Вводим магнитные цепи. Это приводит к следующим соотношениям:
па1а + «/ + «/ = О,
ndid + nfif = 0.
Заменяя la, tb, tc, td, tf их выражениями через lp, iq, 7r, is, получаем
nfip — nftq-\-ndis = 0. B1)
Если (р, Iя — составляющие, которые мы хотим оставить, то исклю-
исключим 1Т и Is. Получим систему
1Р= 1Р
iq = lq
/г ^^ П.д /р ^^ nb iq
fid nd
Запишем ее в виде /' = С'/", обозначив через /", С, Г матрицы
1 0
0 1
/" =
1Т
С =
Па,
nd nd -
Если Z и Е представляют собой соответственно матрицы тензора сопроти-
сопротивлений и вектора напряжений в пространстве <%, то искомое уравнение будет
Е" = Z"I"
при
Z" = (CC')Z{CC), E" = (CC')E.
Если бы нам требовалось узнать составляющие 1Т и Is, то уравнения B1),
решенные относительно (р и i9, дали бы систему ¦
1Р = -
iq= —
ir =
1Г —
¦Is
(па + nb) nf
nand _ f
f
и матрица С приняла бы вид
С =
nbnd
па + пь
ПС
па + пь
1
0
(«а
(Па
+ п
папс
+ п
0
1
i
b)tlf
282 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Уравнение, к которому мы приходим, на этот раз будет
yA=[Z"]-X[E"\
при
z" = (cc[)z(cc[), е"={сс\)е.
Замечание. При применении предыдущих формул необходимо помнить,
что транспонированная матрица произведения двух матриц равна произведе-
произведению транспонированных матриц, взятых в обратном порядке:
5.4.5. Анализ эквивалентных цепей. Дан двухполюсник, т. е. цепь,
в которой различают входной и выходной зажимы. Требуется найти другой
двухполюсник, имеющий при всех частотах приложенного к зажимам напря-
напряжения то же сопротивление, что и данный, т. е. характеристики обоих
двухполюсников должны быть одинаковы. Это представляет некоторый 'пра-
'практический интерес в, случае, когда желательно заменить одну схему другой
в целях упрощения или уменьшения стоимости производства.
Если при рассмотрении цепи принять за вспомогательные неизвестные
контурные токи, то уравнения режима будут
Составляющие тензора, представленные элементами матрицы [Z], будут
так как имеются в виду только стационарные режимы. Эти составляющие
будут либо собственными сопротивлениями, либо сопротивлениями связи
при обходе рассматриваемого контура.
Матрица [Z] может быть рассмотрена как сумма трех слагаемых:
\L} + ±[S\.
Матрицы [R], [L], [S] являются соответственно тензорами сопротивлений,
индуктивностей и величин, обратных емкостям (эластанцев).
Рис. 5.25.
Рассмотрим подробнее случай двухполюсника, образованного из п пас-
пассивных контуров, соединенных цепочкой (рис. 5.25). Выберем в качестве
вспомогательных неизвестных контурные токи, указанные на рисунке. Заме-
Заменим этот двухполюсник другим той же конструкции (рис. 5.26). Составляю-
Составляющие векторов тока обоих двухполюсников связаны линейными соотношениями.
Так как мы хотим, чтобы одному и тому же напряжению, приложенному
.между А и В, соответствовал один и тот же ток (условие необходимое.
Б.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
283
чтобы двухполюсники были эквивалентны), то возможны лишь следующие
линейные соотношения:
или, сокращенно,
Следовательно,
[/] = [а] [/'].
Это выражение разлагается на три следующих:
[Sf] = [a] IS] [а].
Матрица' а не определена. Ее составляющие полностью произвольны,
кроме составляющих первой строки, которые обязательно равны
1 0 0 ... 0.
Практическая ценность задачи заключается в возможности искусным
подбором коэффициентов akl аннулировать как можно большее число членов
Рис. 5.26.
матриц R, L, S таким образом, чтобы заменить сложный двухполюсник
простым.
тшгнн
о
о
Рис. 5.27.
Рис. 5.28.
Пример. Дан двухполюсник, изображенный на рис. 5.27. Мы хотим
ваменить его другим, эквивалентным двухполюсником, представленным
на рис. 5.28. Имеем
284 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ . [ГЛ. V
Матрица а в данном случае будет
Г 1 0
La21
Матрицы L, 5 первого двухполюсника и U, S1 второго равны
1 _ Г1 02,1
и [а]= "" .
2j L° a22 J
[/ n Г с j с с
, , [5'] =
О L2\ [ 52 52J
Мы должны определить коэффициенты а:2 и а^ таким образом, чтобы удо-
удовлетворялись равенства
[Z/] = [a][L][a], [5'] = [a] [5] [a],
т. е., подробнее, равенства
L.'\ О] fZ.i Ч- Z.2 -|- 2a2iZ,2 Ч- aij (Z.2 -4- Z,3) <*22Z2 4-a2i<*22 (Z? 4-^з) |
0 Z^J [ a^ -(- a21a22 (L2 -f- Lg)
5l -J- 52 5г] ji -+- 52 -h 2a2]52 + «21 E2 + 53) a2252-+- «21022 (S2 H- 53) I
52 52 J L a2252 + a21a22 (S2 + 5з) a22 E2-f-5з) J
Следовательно, a21 и a^ должны удовлетворять условиям:
= 0.
Отсюда получаем
a2252 + a21a22 E2 + Sg) = «4, E2 H- 53).
Подставляя эти значения в систему B2), легко вычислить L\, L2, S\, S2.
Для конкретности обратимся к следующим численным значениям
(L в мкгн, 5 в мкф~{):
Lx = 3, Ц=\, L3=C2, 5j=2, 52=1, 53=0,5.
Находим
1 1
«2! = — " • а22=з"-
Система B2) дает
Для проверки рассчитаем сопротивления обоих двухполюсников (рис. 5.27
и 5.28). Непосредственным вычислением находим одно и то же сопроти-
сопротивление
7 ' ~ Т
Б.4]
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
285
Замечание. В цепи, содержащей п контуров, можно уменьшить коли-
количество элементов (индуктивностей, емкостей или сопротивлений) на п(п— 1)
единиц. Это и было выполнено в предыдущем примере. Однако может слу-
случиться, что уравнения системы [аналогичной системе B2)], которым должны
удовлетворять akV окажутся несовместными. Кроме того, физически недо-
недопустимо рассматривать случай, когда они
приводят к отрицательным значениям 5, L
или R.
5.4.6. Цепи с внешним питанием.
Дана цепь, изображенная на рис. 5.29. Она
не является простейшей, поскольку питается
извне. К узлам этой цепи текут известные
токи
У, Г, / JN
(N обозначает количество узлов). Эти N то-
токов не незазисимы; в силу первого закона
Кирхгофа мы можем написать
Следовательно, число независимых внешних ИС- °-~^
токов равно Л/—1. Можно выразить В
токов ветвей /а, 1Ь, ... как функции М контурных токов 1Р, /*,... и
внешних токов J1 % Js, ...
Матрица связи С определяется соотношением
где векторы [/] и [/'] имеют составляющие
-IP-
С
(В).
JT
(Л/-1)
В силу соотношения В = М -\~М—1 матрица связи — квадратная.
ное уравнение режима в пространстве ветвей по-прежнему будет
*
[Z] [/] + [?/] = [?].
Матрич-
Матрицы Z, /, Ut E те же самые, которые мы определили в п. 5.4.2.
Матрица связи С позволяет перейти от пространства ветвей к другому
пространству, имеющему то же количество измерений. Формулы преобразо-
преобразования по-прежнему будут
Ввиду наличия N—1 неизвестных разностей потенциалов Ur, Us, ....
созданных прохождением внешних токов, вектор разности потенциалов
286
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
преобразуется не в нулевой вектор, а в вектор, равный
О
° (М)
V.
1)
Вид уравнения режима цепи не изменяется при преобразовании:
Данное уравнение представляет собой систему из В уравнений с В неиз-
неизвестными. Эти неизвестные суть М контурных токов ip, tq, ... к N — 1
разностей потенциалов Ur, Us, ... Для решения системы удобно предста-
представить ее в виде двух систем, используя специальную форму вектора [?/']:
М
N~\ .
М N~\
Отсюда получаем первую систему
"/I
которую легко решить относительно неизвестных [/J]:
и вторую систему
И = [fii]-[z5][/;]-[zg [ф
в правую часть которой надо ввести выражение для [/i].
Пример. Рассмотрим распределительную линию с тремя проводами I,
11, III (рис. 5.30). Между каждой парой этих проводов включен двигатель.
Л
Рис. 5.30.
Электродвижущие силы и собственные сопротивления обозначены соответ-
соответственно через еа, eb, ec, Zaa, Zbb, Zcc. Все сопротивления соединены между
5.41
ПРИМЕНЕНИЕ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
287
собой, и по конструкции поток аддитивен для тока, проходящего в напра-
направлении abc. Пусть Zab, Zac, Zbc — сопротивления связи. По проводам I,
II, III приходят известные нам токи: Js, J1, —(Js-\-Jl).
Имеем следующие численные значения:
2йй=1+2/, ZM=2 + /. ,
Zab= У. Zac= У- '
в.
.= J
/•=
Jt=\—J
, (в омах),
(в омах),
(в вольтах),
(в амперах).
Комплексное значение показывает, что, например, сопротивление Zaa
состоит из активного сопротивления в 1 ом и из индуктивного сопротивле-
сопротивления. u>L в 2 ома; кроме того* еь имеет амплитуду в ]А + 1 = |^2 вольта
и опережает еа по фазе на 45°. Аналогично ес имеет ту же амплитуду, что
и еь, но отстает от еа по фазе на 45°.
Возьмем, например, (а в качестве контурного тока и выразим i", Iй, f
как функции 1а и внешних токов Js, J':
Этим определяется матрица связи [С] и ее транспонированная
Имеем
1
.1
¦и
0
—1
¦ 1
С] =
[?'] =
0"
—1
0.
,
" 4 +
— 3 —
2
= [С] [?]
юу
5/
3/
=
¦'I==
г
(
¦ 2
— 2
.—1
1
0 —I
.0 —1
J-5/
-
—/-
Г
— 1
0.
— 2 —ЗУ
2 + 2/
2+ /-
Отсюда получаем уравнение
" 4+10/
— 3— 5/
-2— 3/
— 3 — 5у — 2 —
3+2/ 2 + 2/
2 + 2У 2+ j 1— У_
2 4- 2/
V,
" 3
— 2
Это уравнение можно представить в виде системы двух уравнений. Первое^
уравнение
D 4
Г2 + 2/1
-ЗУ]^_ yJ=3,
откуда определяем численное значение Iй, а затем I и ic:
la= 1,6+0,24/,
i"=— 1,4—О,76У,
f = — 0,4— 1,76/.
288 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Второе уравнение
J l-i
>+ГУ 2+2ЛГ2+2/|+Г'Ы
откуда находим численное значение Vs и Vt:
Vs = — 4,4 — 1,28у,
Vt = — 1,52 — 2,72 j.
Далее, легко проверить, что
zaja + zbbi»+zc/ + zj° + za/ + zrtCia + zaf+
+ Zte/» + Zb/ -ea-eb-ec = 0,
Vs = ea- Zaaia -Zablb - Zaf, ~Vt = eb - Zbbib - Zabi° - Zb/.
5.5. ПРИМЕНЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К ИЗУЧЕНИЮ
АНИЗОТРОПНЫХ СРЕД
5.5.1. Введение. Тензорное исчисление позволяет значительно упростить
изучение кристаллических сред (в большинстве своем анизотропных), опре-
определяя для кристаллов данного типа независимые постоянные, знания которых
достаточно для получения всех необходимых данных о свойствах изучаемого
явления. В частности, изучение пьезоэлектрических свойств кварца требует
использования громоздкого математического аппарата. Методы же тензорной
алгебры значительно упрощают исследование. Исторически тензорное исчи-
исчисление, которое получило сейчас широкое развитие и проникло во все от-
отрасли физики, было создано для изучения свойств анизотропных сред.
В дальнейшем мы будем рассматривать метрическое пространство, отне-
отнесенное к прямоугольной системе координат. Вследствие этого мы не будем
делать различия между ковариантностью и контравариантностью, однако
индексы будем по-прежнему размещать вверху и внизу, чтобы можно было
использовать правило суммирования, принятое в начале главы.
Разъясним смысл сказанного на примере.
5.5.2. Диэлектрические свойства кристалла. Сравним соотношения,
связывающие напряженность электрического поля А и электромагнитную
индукцию d в некоторой точке, для изотропного и анизотропного тел.
В первом случае оба вектора h и d имеют одинаковое направление,
и связывающая их диэлектрическая проницаемость е представляет собой
скаляр:
d=eh.
Для анизотропной среды связь между этими векторами гораздо сложнее.
Векторы d и h имеют уже различные направления, их составляющие связаны
линейными соотношениями, заменяющими пропорциональность, имевшую
место в первом случае. Здесь мы получим три равенства (трехмерное про-
пространство):
<*< = 2Wft, (/=1.2,3).
Эти формулы (свернутое произведение), определяющие вектор, показывают,
что Ш\ есть тензор второй валентности. Так как в декартовом пространстве
понятие вариантности не имеет смысла, то тензор Ш\ не является смешан-
смешанным. Этот симметричный тензор есть тензор диэлектрической проницаемости.
5.5] ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД 289
Qh имеет шесть существенных компонент, знание которых необходимо для
установления диэлектрических свойств кристалла. Действительно, если нам
требуется найти значение диэлектрической проницаемости в направлении,
определяемом углом 6, который оно составляет с осью 3, и углом ср, кото-
который его проекция на плоскость 1 — 2 образует с ось,ю 1 (сферические ко-
координаты), то достаточно осуществить два последовательных поворота на
углы ср и 6, приводящие к совпадению оси 1 с этим направлением.
Поворот против часовой стрелки на угол ср вокруг оси 3 и последую-
последующий поворот по часовой стрелке на угол -^ 8 вокруг нового положения
оси 2 определяется матрицей преобразования координат, которая является
произведением двух матриц, описывающих оба поворота, а именно:
sin 6 0 cos
. О 10
.— cos 6 0 sin 6 .
cos cp sincp 0'
— sincp cos cp 0
0 0 1.
cos cp sin 6 sincp sin 6 cos
— sincp cos cp 0
.— cos cpcos 6 —sin cpcos 9 sin 6.
В определенной таким образом новой системе координат тензор диэлектри-
диэлектрической проницаемости, представленный матрицей е, задается формулой *)
е = а'еа'.
Компонента ег этого тензора есть искомое значение диэлектрической прони-
проницаемости в требуемом направлении.
Вследствие имеющейся в кристалле симметрии число независимых ком-
компонент тензора (е^) уменьшается.
Действительно, рассмотрим, например, кристалл с осью симметрии
су—
re-го порядка. Если его повернуть на угол -— вокруг этой оси, то в новом
положении кристалл ничем не отличается от кристалла, находящегося
в прежнем положении. Если а — матрица, определяющая этот поворот, то
е = аеа.
. Равенство матриц е, входящих в обе части этого соотношения, накла-
накладывает на компоненты sj несколько условий, вследствие чего уменьшится
число независимых компонент. В частности, нередко встречающееся условие
е| = — ej приводит к результату:
5.5.3. Матрицы преобразования для некоторых часто встречающихся
систем координат. Рассмотрим матрицы преобразования прямоугольных
координат, используемые во всех тех случаях симметрии, которые могут
встретиться при изучении кристаллов.
') Здесь матрица а' определяет новую систему координат как функцию старой.
1 Следовательно, она является обратной по отношению к матрице преобразования коор-
координат а из п. 4.1.21: а' = о-'. Более того, она представляет собой ортогональную
матрицу, так как (а') = а.
19 А. Аыго
290
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
ГГЛ. V
а) Поворот на угол -f-<p (в направлении против часовой стрелки) вокруг
оси 1:
0 0
0 cos ср
_0 —since
вокруг оси 2:
вокруг оси 3:
sin 9
coscpJ
cos ср
0
_sin ср
0
1
0
cos ев
— sincp
О
—sin if
0
cos ср.
sin ср (
costp О
О U
Можно сразу же получить матрицы, соответствующие повооотам на
1Z 1Z TZ '
углы it, -jp "Т' "б" ВОКРУГ каждой из осей.
Рассмотрим поворот на угол ср вокруг оси 3 и последующий поворот
на угол -я- — 6 вокруг нового положения (после первого поворота) оси 2.
Такое преобразование приводит к совпадению новой оси 1 с направлением,
определяемым углами ср, 6 (сферические координаты). Матрица этого преоб-
преобразования обозначается а':
cos cp sin б sincp sin 0 cos б
— sincp coscp 0
.— cos cp cos б —sin со cos 6 sin 6.
б) Симметрия по отношению к плоскостям 1—2, 2—3, 1—3:
1
0
0
0
1
0
0"
0
—1.
г-1
; 0
L о
0
1
0
°1
0 ;
ll
0
-0
0
2
0
0"
0
1.
в) Симметрия по отношению к началу координат:
Г—1 0 01
0—1 0
О 0 —1.
Пример. Возьмем кристалл с осью симметрии четвертого порядка
(тетрагональный). При повороте на 90° вокруг оси 3 матрица преобразования
имеет вид
0 1 01
-10 0
0 0 1.
Примем ось симметрии за ось 3. Если повернуть кристалл вокруг этой
оси на 90°, то в физических свойствах кристалла не произойдет никаких
изменений, а следовательно, такой попорот не изменит тензора е, откуда
следует, что
е = аеа.
5.5]
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД
291
Представляя это равенство в развернутом виде, получим
-2 -3'
-1 -2
Ь2 2
Е3
S3j
0
1
0
1
0
0
0"
0
1
-.Л
Sl
1
2
1
e3~|
.3
S
0
1
0
—1
0
0
0
0
1
-—r
= — e?
.> -ез
«§ -?з
что, в силу симметрии матрицы, приводит к условиям:
S2 — el — ei — E3 __ S3 __ S2 __ A
61 2 3 1 2 a3 "'
Видим, что имеются только две не равные нулю независимые компо-
компоненты е{ и s|.
Кристаллы тетрагонального класса обладают и другими видами симме-
симметрии, которые в рассматриваемом случае не вносят никаких дополнительных
упрощений. Итак, если ось симметрии четвертого порядка тетрагонального,
кристалла принимается за ось 3, то тензор диэлектрической проницаемости
имеет вид
Л
О
•i
о
Диэлектрические свойства тетрагонального кристалла будут известны»
если будут определены экспериментально величины ej и е^, представляющие
собой значения диэлектрической проницаемости в направлениях, соответ-
соответственно перпендикулярном и параллельном оси симметрии кристалла.
Действительно, найдем для этого кристалла диэлектрическую проницае-
проницаемость в направлении, определяемом углами б, (р. Она будет равна ej, где
тензор s определяется равенством
Непосредственное вычисление дает -
Эта величина, как было очевидно и заранее, не зависит от угла <р> так как
ось. 1 является произвольной осью в плоскости, перпендикулярной оси 3,
и, Следовательно, угол 9 также является произвольным.
Механические свойства кристалла
Применим принципы, изложенные выше в связи с изучением диэлектри-
диэлектрических свойств кристаллов, к исследованию напряжений и деформаций среды,
а также их связи с электрической поляризацией (т. е. с пьезоэлектричеством).
5.5.4. Напряжение. Вырежем мысленно в твердом теле небольшой
тетраэдр, три грани которого параллельны координатным плоскостям. Уста-
Установим условия равновесия этого объема.
Обозначим через Тг, Т2, Т3 напряжения (т. е. силы, приложенные
к единице поверхности) на гранях тетраэдра, параллельных координатным
плоскостям, а через Т—напряжение на четвертой грани. Будем считать
напряжения положительными, если они направлены от плоскостей тетраэдра
19*
292 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
наружу. Если величины dsv ds2, ds3, ds представляют собой соответственно
площади граней тетраэдра, то одно из условий равновесия выражается век-
векторным равенством
Tds=T1 dSl + Т2 ds2 + Т3 ds3.
Если обозначить через п1, п2, п3 составляющие единичного вектора
внешней нормали к плоскости четвертой грани тетраэдра, то
ds1= n1 ds, ds2= n2ds, ds3= n3ds.
Если компоненты векторов Tv Т2, Т3, Т по осям 1, 2, 3 обозначить
соответственно через tn, t2V t31; t12, t22, t32; t13, t2S, t^; tv t2, t3, то ука-
указанное векторное условие равновесия получит следующую скалярную форму:
Эти соотношения определяют тензор t с общей компонентой tjt, который
называется тензором напряжений.
Второе условие равновесия тетраэдра состоит в равенстве нулю слав-
славного момента приложенных к нему внешних сил. Использование этого усло-
условия приводит к равенству тангенциальных составляющих напряжений:
Следовательно, тензор t симметричен и имеет шесть независимых компонент.
; б.б.б. Деформации. Рассмотрим в твердом теле малый отрезок ds,
проекции концов которого на координатную ось / обозначим через х1 и
xl~\-dxl. Деформируем каким-либо способом твердое тело. Тогда отрезок ds
перейдет в dS; начальная точка этого отрезка переместится на величину и1;
таким образом, после деформации координаты концов отрезка будут
х1~\-и1,
Величина и1 является непрерывной функцией координат х1. Поэтому
можно написать
откуда
dS2 — ds2 — 2 sik dxl dxk,
где обозначено:
дик \ VI duJ
В случае малых деформаций можно пренебречь членами второго порядка
малости; тогда
_ да1 1 I ди1 , ди" \
Величины slk образуют тензор 5 с общей компонентой slk, который
называется тензором деформации. Тензор деформации также симметричен,
так как sik—ski, и имеет шесть независимых существенных компонент.
Можно показать, что компоненты, расположенные по главной диаго-
диагонали su, представляют собой деформации, параллельные оси /. Иными сло-
словами, su — это растяжение вдоль оси / при положительных su или сжатие
при отрицательных su. Остальные компоненты sik представляют собой изме-
5.5] ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД 293
нение, которое претерпевает при деформации угол, стороны которого были
первоначально параллельны осям j и k.
Известно, что тензору можно придать диагональную форму, приняв за
оси координат собственные направления представляющей его матрицы. В слу-
случае симметричной матрицы собственные направления ортогональны. Если
указанным образом преобразовать тензор деформации, то он примет вид
О 0\
S2 0 .
О SJ
Это не означает, что тензор деформации зависит только от трех не равных
нулю компонент Sv 52, S3, так как остальные три компоненты первоначаль-
первоначального тензора были использованы для определения направлений собственных
осей при преобразовании тензора к диагональной форме.
Шаровидный элемент твердого тела, имеющий радиус р, становится
после деформации эллипсоидом с тремя неравными осями. Направления этих
осей совпадают с собственными направлениями матрицы, а их длины равны
2рA+51). 2РA+52), 2рA+53).
5.5.6. Тепловое расширение. Таким же образом можно рассматривать
деформацию, возникающую вследствие теплового расширения. Если темпера-
температура твердого тела изменяется от т0 до то-)-т, то вектор с началом в точке О
и с проекциями lt претерпит растяжение, в результате которого его проек-
проекции изменятся на величины Mt.
Если а — тензор теплового расширения, то
Этому симметричному тензору можно придать диагональную форму
м, о о
О А2 О
О 0
^
Шар радиуса р станет после' расширения эллипсоидом, оси которого
совпадают с собственными направлениями матрицы; длины осей равны
I- Л,) -с, 2рA+Л2)т, 2рA+Л3)-с.
Коэффициент расширения в направлении, задаваемом углами 9, ср, будет
представлять собой компоненту а\ тензора а, который определяется равен-
равенством
а = а.''аи!'.
5.5.7. Обобщенный закон Гука. В одномерной среде (нить) закон Гука
устанавливает зависимость между напряжением и деформацией:
t = ms.
Коэффициент пропорциональности т. называется модулем упругости.
Для трехмерной среды (изотропной или неизотропной) эта зависимость
в случае малых деформаций превращается в следующее тензорное соотно-
соотношение:
^i = S«JjSkl, B4)
294 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
где т — тензор четвертой валентности. Действительно, свертывание произ-
произведения этого тензора на тензор второй валентности stj приводит к тензору
второй валентности ttj. Тензор mf. называется тензором модулей упругости.
Так как тензоры t и s симметричны, то тензор т также симметричен
по отношению к обеим парам своих индексов /, j и k, l. Следовательно,
число его независимых компонент сократится с 81 до 36. Кроме того, по-
поскольку в данном случае не различаются ковариантность и контравариант-
ность (прямоугольные оси), то
что в самом общем случае сократит число независимых компонент до 21.
Систему B4) можно решить относительно величин ski, при этом получим
Тензор с, имеющий по тем же соображениям, что и тензор т, 21 ком-
компоненту, называется тензором коэффициентов упругости.
Наличие симметрии в кристалле значительно уменьшает число независи-
независимых компонент. При этом следует использовать метод, изложенный выше.
Примем одну из осей симметрии за ось координат, осуществим надлежащий
поворот, определяемый матрицей а, а затем приравняем элементы матрицы mf-,
отнесенной к старой системе координат (до поворота), элементам
матрицы т%Гр, отнесенной к новой системе координат (после поворота). Это
приведет нас к системе уравнений следующего вида:
ijkl
Так как речь идет о прямоугольной системе координат, то между
матрицами а и р существует соотношение
Пример. Рассмотрим кубический кристалл, имеющий три взаимно пер-
перпендикулярные оси симметрии четвертого порядка. Примем за ось 3 одну
из осей симметрии, а за оси 2 и 1—две другие.
Матрица, определяющая поворот на 90° вокруг оси 3, равна
0 1 01
— 10 0
0 0 1
Отличные от нуля члены:
Д1 ^ а2__ 1_ дЗ—^ 01 __^ R2 = 1, В3 1
Вследствие простоты матрицы а, которая содержит только по одному
не равному нулю члену в каждой строке и в каждом столбце, знак суммы,
имеющийся в общей формуле, исчезает.
Произведения, содержащие по одному разу а' или pj, приводят к равен-
равенству компонент, имеющих одинаковую абсолютную величину и противопо-
противоположные знаки; следовательно, эти компоненты равны нулю. Произведения,
совсем не содержащие или содержащие по два раза а' или (J', приводят
к равенству соответствующих компонент. Например,
5.5]
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД
295
Если произвести такой же расчет для поворотов на 90° вокруг двух
других осей, то окажется, что не равны нулю только следующие соста-
составляющие:
т
\\
ni
т\1 = тЦ = тЦ.
„,22 тЗЗ „,33
Отсюда следует, что для кристалла кубического типа тензор модулей упру-
упругости имеет только три независимые существенные компоненты.
5.5.8. Применение шестимерного пространства. Если речь идет о тен-
тензорах валентности выше второй, то формулы преобразования координат
довольно сложны. Вычисление компонент тензора в этом случае требует
большой затраты труда и времени. Что же касается тензоров второй валент-
валентности, то применение формулы
s = аеа
весьма упрощает вычисления. Естественно стремление найти аналогичную
формулу для тензоров четвертой валентности.
Тензоры ins симметричны и имеют по шесть составляющих в трех-
трехмерном пространстве (пространство d). В шестимерном пространстве (про-
(пространство D) мц можем рассматривать эти тензоры как векторы с компо-
компонентами
7"i ='п.
с ,,
О I ¦ Ом,
7"
1 5
о2 =
У3 = *33' М = B3' *5 = 'l3> J6 — 42'
с „ с - с с с „
о3 — ^33' 4 — 23' 5 —' 13* 6 — 12'
Тензор т станет в пространстве D симметричным тензором М второй
валентности, имеющим не более чем 21 компоненту. Равенство B4) превра-
превратится в пространстве D в равенство
Требуется решить задачу: какова должна быть матрица А преобразова-
преобразования координат в пространстве D, соответствующая матрице а. преобразова-
преобразования координат в пространстве d.
Если мы сможем образовать матрицу А с помощью элементов матрицы а,
то для преобразований в пространстве D получим формулу
М = АМА.
Для того чтобы найти матрицу А, достаточно сравнить формулы
Г= ati и Т — AT,
где t — тензор второй валентности, а Т — вектор с шестью составляющими
в пространстве D. Приравнивая соответствующие компоненты в левых и
правых частях этих равенств, получим
А —
"(.})
})»
КJ («з? («I?
1 f*l CL 17 ПУЛ
? О ? О
2а32а2
2-К
4»?
а
aa
296
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Видим, что матрицу А легко получить, исходя из элементов матрицы а.
Если разложить ее на четыре матрицы, имеющие по три строки и по три
столбца
Л21
]-
то:
1. Элемент матрицы Ах представляет собой квадрат элемента, занимаю-
занимающего в матрице а такое же место.
2. Элемент матрицы А2 является удвоенным произведением двух осталь-
остальных элементов, стоящих в той же строке, что и соответствующий элемент
матрицы а.
3. Элемент матрицы А3 является произведением двух остальных эле-
элементов, стоящих в том же столбце, что и соответствующий элемент
матрицы а.
4. Элемент матрицы А4 представляет собой сумму попарных произведе-
произведений взятых крест-накрест элементов, оставшихся после вычеркивания строки
и столбца, в которые входит соответствующий элемент матрицы а.
Если преобразование системы координат, определяемое матрицей а,
отвечает симметрии кристалла, то формула
М= AM A
B5)
позволяет уменьшить число независимых компонент.
Легко вернуться от обозначения Мчр в пространстве D к обозначению т.ц
в пространстве d. Действительно, соотношения между индексами tj и р,
kl и q дают возможность написать
11 — 1, 22~2, 33~3, 32~4. 31 —5, 21 —6.
Пример. Для пояснения этого метода рассмотрим кубический кристалл
и выберем те же оси, что и ранее (см. пример в п. 5.5.7).
Матрица а. (поворот на 90° вокруг оси 3) в соответствии с правилами,
перечисленными выше, дает для матрицы А:
м\ м\ м\ м\ м\ ж?1
м1 м\ м\ м\ м\ м\
Ml Ml Ml Ml Ml Ml
m\ m\ m\ m\ m\ m\
Ml Ml Ml Mi Ml Ml
M\ Ml M\ Ml Ml M%_
1
0
0
0
0
к
1
0
0
0
0
0
0 0
0 0
1 0
0 0
0 1
0 0
равенству
м\
M\
Ml
-Ml
Ml
-Ml
0
0
0
—1
0
0
Ml
M\
Ml
-Ml
M\
-Ml
0"
0
0
0
0
—1_
M\
M\
м\
-M\
m\
-m\
— Ml
— m\
-Ml
Ml
-Ml
Ml
Ml
M\
Ml
-Mt
Mt
-Ml
— mT
-Mt
— Ml
Ml
-Ml
5.5]
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД
29Г
Отсюда получаем первое упрощение тензора Ж:
ж;
ж?
..3
Mi
0
0
0
Mi
Ml
м\
0
0
0
Ml
м\
Ml
0
0
0
0
0
0
Mt
0
0
0
0
0
0
Mt
0
0
0
0
0
0
Ml
Заметим попутно, что этот тензор представляет собой в выбранной
системе координат тензор модулей упругости для четырехугольного кри-
кристалла. Для этого класса кристаллов, если вернуться в пространство d,
отличные от нуля компоненты тензора т равны
т
11 ^ т22
т,
22'
т
22
11'
т
зз
1Г
т
т.
¦ т
31
'31'
т,
Для кристаллов кубического типа мы должны воспользоваться свой-
свойством симметрии четвертого порядка относительно остальных двух осей.
Выберем за новую ось поворота ось 1. При повороте вокруг нее на 90°
матрица А равна
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
0
—1
0
0
0
0
0
0
0
1
0
0
0
0
—1
0
Применяя формулу B5) к тензору Ж, полученному после первого пре-
преобразования (поворота вокруг оси 3), будем иметь
ж!
Ml
ж?
0
0
0
Ml
Ml
м\
0
0
0
а получим
ж?
ж?
ж!
0
0
0
0
0
0
Mt
0
0
тензор Ж
Ml
Ml
Ml
0
0
0
0
0
0
0
м\
0
для
Ml
Ml
Ml
0
0
0
0"
0
0
0
0
Ж66_
ж!
ж?
м\
0
0
_ 0
ж?
Ml
м\
0
0
0
л
A
I
Ml
M\
Ml
0
0
0
кристалла кубического
Ml
Ml
Ml
0
0
• 0
0
0
0
Mt
0
0
0
0
0
0
Mt
0
0
0
0
0
0 Ml
¦
0
0
0
Mt
0
0
типа
0
0
0
0
Ml
0
0 '
0
0
0
0
Mt_
в виде
298 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ 1ГЛ. V
Остались только три независимые существенные компоненты: /Иь М\, М\.
Использование условия симметрии относительно третьей оси — оси 2 — не
дает дополнительных упрощений. Вернувшись к пространству d, находим
т
т
\\ т22 „.33 т22 ™33
Это уже известный нам результат.
5.5.9. Модуль Юнга. Рассмотрение модуля Юнга позволит нам проил-
проиллюстрировать нахождение некоторой характеристики, которая отвечает опре-
определенному направлению, заданному углами 9, ср. Для нити длины /, под-
подверженной напряжению Т, вызывающему приращение длины Д/, модуль
Юнга Y определяется соотношением
Д/_ 1
В трехмерном пространстве модуль Юнга Yx для оси 1 будет опреде-
определяться равенством
откуда
Yl=M\ = m\\.
Если требуется найти модуль Юнга для направления, заданного
углами 6, ср, достаточно проделать преобразование
М=А'МА'.
Матрица А' получается на основании матрицы а', с помощью которой
осуществляется преобразование при двух последовательных поворотах на
углы ср и -j 9. Модуль Юнга К?>е будет равен компоненте Mi матрицы М.
Если применить непосредственно тензорное преобразование, то для опреде-
определения модуля Юнга K?j g получим формулу
Пьезоэлектричество
5.5.10. Электрическая поляризация. Механическая деформация может
вызвать в кристалле электрическую поляризацию (пьезоэлектричество), кото-
которая в первом приближении пропорциональна этой деформации.
Если р — вектор поляризации, то три уравнения для его проекций на
оси координат 1, 2, 3 запишутся в виде
d — У, eiks
Эта формула вводит тензор е третьей валентности, симметричный относи-
относительно индексов j и к, в силу чего число его независимых компонент со-
сокращается с 27 до 18.
•Используя линейные соотношения, связывающие напряжения с деформа-
деформациями, можем написать
Это соотношение определяет новый тензор 8, который называется
¦пьезоэлектрическим тензором. Как и тензор е, это тензор третьей валент-
S.5] ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД 299
ности, симметричный относительно индексов у и А с 18 независимыми компо-
компонентами.
Если поместить кристалл в электрическое поле А, то деформации будут
в первом приближении пропорциональны составляющим напряжения электри-
электрического поля по осям координат hk; при этом получим шесть соотношений:
Тензор (8*у), определяемый последним выражением, тот же, что и пре-
предыдущий, поскольку положение индексов в случае прямоугольной системы
координат не имеет значения. Это можно показать, используя закон сохра-
сохранения энергии.
Формулы преобразования компонент тензоров для случая преобразова-
преобразования прямоугольной системы координат, определяемого матрицей а, будут
?, 2
причем
Можно также, вместо того чтобы пользоваться формулами тензорного
преобразования, использовать шестимерное пространство D. При этом тен-
тензор stj становится вектором 5 с шестью составляющими. Получим
Тензор е третьей валентности будет представлен в пространстве D
прямоугольной матрицей с 18 элементами. Так как последнее выражение
связывает вектор р трехмерного пространства d с вектором S шестимерного
пространства D, формула для преобразования компонент тензора Е, отве-
отвечающего преобразованию координат, определяемому матрицей а, будет иметь
вид
Если использовать преобразование, соответствующее характеру симмет-
симметрии кристалла, то матрицы Е и Е будут равны между собой. При этом
число независимых компонент уменьшится. Для того чтобы вернуться к обо-
обозначениям, отвечающим первоначальному пространству d, следует исполь-
использовать соответствие индексов, а именно
q ~ ij,
иначе говоря,
1 —11, 2~22, 3~33, 4~32, 5 — 31. 6~12.
Такое же вычисление можно проделать для тензора 8, который в про-
пространстве D представляется прямоугольной матрицей Д с 18 элементами.
Пример. Рассмотрим кристалл прямоугольно-ромбического типа, ха-
характеризуемого тремя взаимно перпендикулярными осями симметрии второго
300
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
порядка. Примем оси симметрии кристалла за оси координат. Поворот на
угол it вокруг оси 3 характеризуется матрицей
— 1 0 0
0—1 0
0 0 1 J
Применение формулы
приводит к равенству
откуда А
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
—1
0
0
0
0
0
0
J
0
0
0
0
0
0
1
"а!
д2
.Дз
А?
AS
Дз2
д?
Д3з
а1
А,4
Дз4
откуда получается
А?
дГ
.5 .6
.5 .6
Аз Аз_
=
"-а!
-Ai
. Дз
первое упрощение
"о
0
Дз
0
0
А
0
0
2 .3
i Дз
-А?
¦Да
д!
матрицы
д4
д4.
0
Д2
0
—
—
Д:
0
0
aS
А"
дг
1 А4
д4-
-А4
Af
д25
-Ai
-А?"
-AS "
дб
Поворот на угол те вокруг оси 2 осуществляется с помощью матриц
10 0 0 0 0
0 0 0
0 0 0
0 0
0
—1
0
0
0
1
0
0"
0
—1 „
, А =
О 1 О
О 0 1
0 0 0—1
0 0 0 0 1
0 0 0 0 0—1
Применение формулы
к упрощенной после поворота вокруг оси 3 матрице Д приводит к равенству
О О О А? А? О О О
ооод2д|о= о о
Дз Дз Дз 0 0 Дз _ _ — Дз — Дз
откуда получаем окончательный результат
0 0 At 0 0
0 0 0 0 Дг О
0 0 0 0 0 а?
О
О
-Дз3
д4
-д4.
-А?
д25
о
о
5.5] ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД 301
Единственные не равные нулю компоненты тензора 8 в рассматривае-
рассматриваемой системе координат в пространстве d — это
532 531 ,12
01 . 02 . 03 .
Следует учесть, что в матрице Д индекс строки отвечает пространству d,
а индекс столбца — пространству D.
Такое же вычисление приводит к выводу, что не равными нулю компо-
компонентами тензора е являются
-,32 „31 -,12
е1 • е2 ' еЗ •
Деформации, соответствующие компонентам s32, %, sl2. представляют
собой только деформации скольжения.
Итак, квадратная пластина сегнетовой соли (относящейся к кристаллам
рассматриваемого типа), вырезанная параллельно двум осям симметрии вто-
второго порядка, не обнаружит никакой электрической поляризации при сжатии,
за исключением случая сжатия вдоль направления диагонали квадрата. Если
поместить эту пластину в электрическое поле, направление напряжения кото-
которого перпендикулярно плоскости пластины, то она не будет испытывать ни
растяжения," ни сжатия, но примет форму ромба.
5.5.11. Закон Кюри. Кюри доказал, что кристалл, имеющий центр сим-
симметрии, не мож^ет быть пьезоэлектрическим. Такой кристалл по всем своим
физическим свойствам совпадает с кристаллом, который с ним симметричен
относительно центра. В частности, пьезоэлектрический тензор не должен
меняться при преобразовании координат, состоящем в том, что направления
всех трех осей меняются на противоположные. Такое преобразование коор-
координат определяется матрицей
-10 0
0—1 0
0 0 —1 J
Вследствие простоты этой матрицы из формул преобразования компонент тен-
тензоров исчезает символ суммы. Кроме того, так как а — диагональная матрица,
то получим
Видим, что все компоненты тензора 8 равны нулю, следовательно,
кристалл не пьезоэлектрический.
5.5.12. Пьезоэлектрические свойства кварца. В кристалле кварца
имеются следующие оси симметрии: ось третьего порядка — оптическая —
и три оси второго порядка — электрические, расположенные в плоскости,
пгрпендикулярной оптической оси, под углом в 120° друг к другу. Под ме-
механическими осями подразумевают три оси, каждая из которых перпенди-
перпендикулярна оптической и одной из электрических осей.
Примем оптическую ось за ось 3, а одну из электрических за ось 1.
Осью 2 будет соответствующая механическая ось. Воспользуемся для опре-
определения независимых компонент пьезоэлектрического тензора формулами
тензорного преобразования. Поворот на угол 180° векруг оси 1 опреде-
определяется матрицей
1 0 0
0—1 0
L0 0 —1 J
302
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
[ГЛ. V
Единственный положительный член этой диагональной матрицы а] = 8'=1.
Мы уже отмечали, что для матриц преобразования координат, имеющих по
одному члену в строке или столбце, символ суммы в формулах преобразо-
преобразования компонент тензоров исчезает. Поэтому
Члены, не содержащие индекса 1 или содержащие его дважды, уничтожаются.
Действительно, например,
откуда следует, что 8ц = 0. Следовательно, не равны нулю только члены
81 ¦> и 1 I n о о Ч
с\ S4 Э ^ S! S! X
1Г 22. °33> °32. ОЗЬ °ЗЬ °12> °12-
Осуществим поворот на угол 120° вокруг оси 3. Этот поворот опреде-
определяется матрицей
1
2
0
2
0
0
0
1
•а
1
2
2
0
о
о
о
1
Заметим, что в матрицах аир все элементы, содержащие индекс 3,
равны нулю, за исключением а3=р3):=1. Поэтому в формулах преобразова-
преобразования компонент тензора, если индекс 3 не содержится в преобразуемой ком-
компоненте, он не появится и в соответствующей компоненте после преобразо-
преобразования. Это соображение позволяет написать формулы преобразования коор-
координат сначала для b\u 8i2, 822:
Заменяя элементы матриц а и J3 их значениями и заметив, что 812 = 821,
получим
38ц -f- 2З12 -)- 822 = О,
8+28? 8 = 0
8},
откуда
Я1 ?2 S1
022 =^ й12 ==: ~~ ОЦ.
Рассмотрение формул преобразования компонент, содержащих индекс 3t
приводит к трем соотношениям:
2 зз' зз
8?,= 0,
si —
°зз —
83 04 Т 1йЧ ЙЧ
Ol ! ' о о 1 oi ^ ol
jjo f^'412i O^ 2 П Л S?3 5^3 Л
°12 == [РзаA I" Рз ia2J °12 == " 12* 12 == Ul
5.5]
ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД
303.
и к системе уравнений
откуда получаем
S32 = — 831.
Используя соответствие индексов для пространств d и D и заметив, что
аналогичный расчет приводит к таким же результатам для тензора е, можно
составить две следующие матрицы:
~ р1
Ei
А}
0
Ai
0
0
0
0
0
0
-Ai
-д!
0
0
0
0
0
0
0
0
0
0
Е\
Е\
0
0
0
0
0
0
_ о —е\
Если раскрыть соотношения между поляризацией, напряжением и дефор-
деформацией, мы получим для кварца в выбранной системе координат:
Эти системы позволяют сделать следующие выводы:
1. Любая деформация — сжатие или растяжение — вдоль оси 1 (su) или1
оси 2 (s22) приводит к появлению поляризаций вдоль оси 1 (р{) соответ-
соответственно противоположных направлений.
2. Кручение вокруг осей 1 (s32), 2 (s13). 3 (s12) создает поляризации со-
соответственно вдоль осей 1 (/>!>, 2 (р2), 2 (р2)-
3. Любая деформация — сжатие или растяжение — вдоль оси 3 не соз-
создает никакой поляризации (р3).
5.5.13. Распространение упругих волн в кристаллах. Рассмотрим,
в твердом теле плотности р элемент объема в виде параллелепипеда с,о сто-
сторонами dx1, dx2, dx3. Уравнение его движения вдоль оси 1 мы получим,,
приравнивая друг другу силу инерции
р dx^dx* dx3 ~
и совокупность сил, действующих на элемент объема в направлении оси 1, т. е.
dx* dx3
dx*
при этом получаем уравнение движения
dt2 дх* дх2 дх3 '
Поступая аналогичным образом для других осей, можем записать все
три уравнения движения в виде
Р
dt2
дх'
(г=1, 2, 3).
¦304 ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ [ГЛ. V
Известно, что тензор напряжений t связан с тензором деформаций s
•соотношением (обобщенный гакон Гука)
*ч = 5 m"SkV
где
1 / дик ди1 \ '
ski==~2\!hJ"~T~!hc*)'
¦откуда
«следствие симметрии по индексам I и k в рассматриваемой сумме.
Таким образом, получаем общее уравнение движения
5.5.14. Плоские волны. Рассмотрим простой случай распространения
плоских волн. Этот случай особенно важен практически. В самом деле,
кристаллы кварца, употребляемые для определения частот или как фильтры,
имеют почти всегда форму тонких пластин. А при такой форме упругие ко-
колебания сводятся главным образом к плоским волнам, параллельным пло-
-скостям пластины.
Плоскость определяется компонентами я1, я2, я3 единичного вектора п,
перпендикулярного к ней, и расстоянием р до плоскости от начала коорди-
координат (нормальное уравнение плоскости). Все точки любой плоскости, содер-
содержащей рассматриваемую плоскую волну, движутся в одинаковой фазе, иначе
говоря, их положение зависит только от переменной t (времени) и от пере-
переменной р (расстояния до плоскости от начала координат).
В этом случае
дик _ дик dp __ i дик
дх1 др дх1 др
Уравнение движения принимает вид
р "Ж = Zi пЧ ~Ъ1Р~'
где nij — общая компонента симметричного тензора я, который получится,
«ели обозначить
Если 1 — одно из собственных значений матрицы я (в силу симметрии
«е собственные значения вещественны, а собственные направления взаимно
перпендикулярны), то
иными словами»
При этом уравнение движения приобретает форму уравнения колебаний упру-
упругой нити
д"и1 д2и1
?
5.5) ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД 305
Если определить направление перемещения и с помощью единичного
вектора w этого направления (не зависящего от тензоров t и s и завися-
зависящего только от -[):
то получим
дЬс_ р_ д'х .
др2 ~~ 7 * дР '
при этом имеет место распространение плоской волны со скоростью
Так как характеристическое уравнение, определяющее собственные зна-
значения матрицы и, представляет собой уравнение третьей степени
«11 Т «12 «13
«12 «22 — Т «23
«13 «23 «33 Т
то в направлении вектора п с компонентами я1, я2, я3 распространяются
три плоские волны, соответствующие трем Корням этого уравнения fi» Тг> Тз>
со скоростями toi—Л/ —> ^2== ]/ ~< v3—\/~- Каждая из этих
волн создается движением частиц в направлении, определяемом вектором w.
Все три направления, отвечающие корням f i« Тг> Тз> взаимно, перпендику-
перпендикулярны. Движение любой частицы рассматриваемой плоскости является резуль-
результирующей трех движений, определенных указанным выше способом.
ЛИТЕРАТУРА К ГЛАВЕ V
1. К о ч и н Н. Е., Векторное нечисление и начала тензорного исчисления, Гостех-
нздат, 1951.
2. Зоммерфельд А., Механика, ИЛ, 1947. '
3. Д у б н о в Я. С, Основы векторного исчисления, ч. 2, Гостехиздат, 1952.
4. Ш и р о к о в П. А., Тензорный анализ, ч. 1, ГТТИ, 1934.
5. К и л ь ч е в с к и й Н. А., Элементы тензорного исчисления и его приложения к ме-
механике, Гостехиздат, 1954.
6. Фок В. А., Теория пространства, времени и тяготения; Физматгиз, 1961.
7. Крон Г., Применение тензорного анализа в электротехнике, ГЭИ, 1955.
20 А. Анго
Г Л А В А VI
МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ1)
6.1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Это дифференциальные уравнения вида
Точные способы интегрирования существуют лишь для небольшого числа
уравнений первого порядка. Ниже дается краткий обзор наиболее распро-
распространенных типов таких уравнений.
6.1.1. Уравнения вида fix, ^\ = Q, fiy, ^-j = 0. Это уравнения,
в которых у или х не входят в явной форме.
Рассмотрим два случая:
а) Уравнения разрешаются относительно —г-. Имеем
или -^- =
Решения уравнений получаются в квадратурах:
или x =
Различные интегральные кривые получаются одна из другой параллель-
параллельным переносом по направлениям осей Оу или Ох. Если интегралы нельзя
представить через известные функции, то их можно вычислить приближенно
с помощью методов, изложенных в гл. X.
dv
б) Уравнения разрешаются относительно х или у. Положим -jZ-= р.
Для первого вида уравнений получаем
х = h (p),
y=fph'(p)dp + C.
а для второго
У=ё(Р).
Эти выражения представляют собой уравнения интегральных кривых в пара-
параметрической форме.
') В этой главе излагаются точные методы решения дифференциальных уравне-
уравнений. Приближенные приемы указаны в гл. X, посвященной численным и графическим
методам.
6.1) УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 307
Замечание. Иногда удобнее параметр ввести другим способом. Для
уравнения fix, -^-\ = Q положим, например, x = v(^). Разрешая алгебраи-
dy
чески это уравнение относительно —-, найдем
& — СО.
Отсюда
Точно так же для уравнения /(у, •^-)==0 имеем
y=4t) = «@
Как и выше, мы получаем параметрические уравнения интегральных крив ых
Пример, у у1-\-у'г=1. Положим
у = cos t.
Решая уравнение относительно у', получим
Далее, ;
. dy —sin t dt . ..
dx = -Jr = = — cos t dt.
Ух №
т. е.
Таким "Образом, уравнения интегральных кривых в параметрической форме
имеют вид
(х = — sin t + С,
I у = cos t.
Очевидно, это окружности единичного радиуса, центры которых находятся
в точках (С, 0). .
6.1.2. Уравнения с разделяющимися переменными. Это уравнения
dy
вида "лТГ^/С*' У)» в которых функция f(x, у) может быть представлена
как
Отсюда следует
ty(y)dy ?(x)dx.
Общий интеграл этого уравнения Ф(х)—ЧГ (у) = const, где Ф(д;) и
ЧГ(у) — соответственно первообразные функций ср (лг) и 4"(У)>
Пример. Решим уравнение
В нем легко разделить переменные:
dx __ 1—у
-рг — -^г— «У-
20*
308 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ (ГЛ. VI
Интегрируя, получим общее решение:
Замечание 1. К рассматриваемому типу уравнений сводится уравне-
уравнение вида
Для этого достаточно ввести новую переменную
z = ax-\-by.
Тогда
dz
a
Замечание 2. Уравнения, рассмотренные в п. 6.1.1.
также относятся к типу уравнений с разделяющимися переменными.
6.1.3. Однородные уравнения. Это. уравнения вида -2- = f (х, у), в ко-
которых функция f{x, у) может быть представлена как
Имеем
Положим
у = их, dy = и dx-\- х du.
Подставляя в уравнение, получим
du
dx
du dx
9 (u) — и х '
1пСх= [—7^ .
,/ 9 (и) — и
Пример. Решим уравнение х2у dx—(д;3 — y3)dy = 0. Положим
у = их, dy = и dx -f- x du.
Подставляем в уравнение:
x4du(u3 — 1) = — и4х3 dx,
d
и*
Интегрируя, получаем
и, возвращаясь к функции у, находим
6.1] УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 309
Замечание. Рассмотрим уравнения вида
dx J \ a2x + b2y + c2)'
где av bv cv av b2, c2 — постоянные. Если прямые' ахх -\-^jy-j-Cj = 0 и
a2x -f- b2y + c2 = 0 пересекаются в точке (xv y{), то, полагая
приходим к однородному уравнению относительно Л" и К:
dY f((nX-\-b,Y\
dX~J \a2X+b2Y)'
Если прямые ахх -f- bxy -\- cx = 0 и а2х -\- Ь2у -\- с2 = 0 параллельны, то,
полагая z = ахх -\- Ьху. получаем уравнение с разделяющими переменными:
Пример. Решим уравнение 2(х — 2) dx -+- Bу — 5дг) dy = 0. Коорди-
Координаты точки пересечения прямых хх — 2, yj = 5; заменяя переменные х = Х-^2,
у=К-)-5, прихрдим к однородному уравнению 2ХdX-\-BY — 5X)dY = 0.
6.1.4. Уравнение в полных дифференциалах. Пусть общее уравнение
fix, у, "тМ^О написано в виде
Р{х, y)dx-\-Q(x, y)dy = Q.
Если функции Р и Q таковы, что
дР_ _ dQ_
ду ~~ дх '
то известно, что существует такая функция F(x, у), для которой
dF = P(x, y)dx~j-Q(x, y)dy.
Выражение F(x, у) = const и будет интегралом изучаемого уравнения.
Функцию F легко можно представить в виде
. y) — -~fp(x, y)dx\dy.
Пример. Решим уравнение — dx-\-(у3 + 1пд;)dy = 0. Вычислим —т—
дх
дР _ 1 _ dQ
ду ~х ~~ дх
Следовательно,
— общий интеграл уравнения.
310 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ (ГЛ. VI
6.1.6. Линейное уравнение. Это уравнение вида
л..
A)
Положим, что y=uv, где и и v — неизвестные функции х. Имеем
du . dv
~~dx~ V + U ~dx =
Выберем функцию v так, чтобы
Имеем
f
/= J
a
Тогда
J* - | fix)dx
е а '
а
X X
j tf(xidx * - J f{x)dx
a J e a i
Решение уравнения у представлено здесь как сумма двух функций.
Первая при х=а обращается в нуль, а вторая принимает значение С.
Применение интегрирующего множителя. Напишем линейное урав-
уравнение в виде
Попробуем определить такую функцию М (х), чтобы выражение
представляло собой производную произведения у на некоторую функцию от х.
Для этого нужно, чтобы
М<? (х) = — -??¦
или
X
1п М = — J tp (x) dx.
а
Выражение
X
М = е
6.1] УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 311
является интегрирующим множителем для линейного уравнения. Подставляя
в уравнение значение М, находим для у решение, полученное нами ранее.
6.1.6. Уравнение Бернулли. Это дифференциальное уравнение вида
| ¦ B)
Оно сводится к линейному, если сделать замену z = yi~a. Имеем
dz 1 — п dy
~dx у" ~dx '
Подставляя в уравнение, находим
/()+О*—
6.1.7. Уравнение Риккати. Это дифференциальное уравнение вида
где Pi(x), Р2(х), р3(х) — произвольные функции от х.
Если известен частный интеграл yv то разыскание общего интеграла
этого уравнения сводится к решению уравнения Бернулли. Действительно,
полагая z = y — yv имеем.
•g- + z [2ylPl (x) + р2 (х)] + z3Pl (x) = 0.
Если известны три частных интеграла уравнения Риккати Ух(х), у2(х), У$(х)
то легко показать, что общий интеграл этого уравнения у (дг) удовлетворяет
условию: ангармоническое отношение
= const.
У — У1 Уз — У\
Следовательно, у(х) определяется без интегрирования.
6.1.8. Уравнение Лагранжа. .Это уравнение вида
Продифференцируем по х и положим у' = р. Тогда
или
[«Р (Р) - Pi % + х? (р) + f (р) = 0.
Мы получили линейное уравнение для функции х(р). Пусть x = f(p, С) —
его общий интеграл. Заменяя в уравнении Лагранжа у' и х на р и /(/?, С),
найдем интегральные кривые этого уравнения в параметрической форме:
f x = f(p, С),
\.y=f(p.
6.1.9. Уравнение Клеро. Это частный случай уравнения Лагранжа
в котором гр(у') = у':
312 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ [ГЛ. VI
Повторяя предыдущие рассуждения, получим
g=0. C)
Здесь возможны два решения:
1. —?- = 0 или р = С. Подставляя это решение в уравнение Клеро, на-
ходим
Следовательно, общий интеграл представляет собой семейство прямых.
2. х-т-ф'(р) = 0. Это уравнение в сочетании с уравнением Клеро
у== xp-j-ty(p) дает параметрические уравнения огибающей к семейству най-
найденных выше прямых. Эта огибающая является особым решением уравнения
Клеро.
6.1.10. Общий случай fix, у, -^-)=0. Общего метода для решения
такого уравнения не существует. Отметим два искусственных приема, кото-
которые могут оказаться полезными в некоторых случаях.
Дифференцарованае. Рассмотрим уравнение у — у(х, у'). Положим
у' = р и продифференцируем по х. Тогда
Если мы сможем решить это дифференциальное уравнение, рассматривая
здесь х как функцию р, то получим искомые интегральные кривые в пара-
параметрической форме
x = h(p, с),
y=flh(p, с), р].
Отметим, что этим приемом решалось уравнение Лагранжа.
Преобразование Лежандра. Рассмотрим уравнение f(x, у, у') = 0.
Положим
z = — у + ху',
здесь z — новая функция, a s — новая независимая переменная. Это преобра-
преобразование называется преобразованием Лежандра. Получаем
dz =*= — у' dx~\-y' dx-\- х dy' = х dy' — х ds.
Отсюда
dz
, dz
Исходное уравнение переходит в уравнение
dz . dz
Ь z+s
которое часто оказывается проще заданного. Если его решение имеет вид
z = F(s, С).
6.2? УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 313
то переход к старый переменным осуществляется по формулам
dF
Не следует преувеличивать значения искусственных приемов. Они редко
удаются. В инженерной практике основным является метод численного реше-
решения дифференциального уравнения (см. гл. X).
6.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
Общий вид дифференциального уравнения порядка выше первого
Л у' dx ' dx2 dxn)~u- D'
Решить это уравнение в квадратурах можно лишь в исключительно редких
случаях. Иногда удается понизить порядок уравнения, что существенно облег-
облегчает решение.
Случаи понижения порядка уравнения
6.2.1. Уравнение не содержит явно функцию у. Достаточно ввести
dy
новую функцию ~- = z и порядок уравнения понижается на единицу. Бели,
кроме того, в уравнении D) отсутствуют производные —, ——, ..., ——2-,
dx dx2 dxe~1
dky
то, полагая —*- = z, мы снизим порядок уравнения на к единиц.
dx"
6.2.2. Уравнение не содержит явно независимой переменной х. В этом
dy
случае примем у за новую независимую переменную, a -j- = z — за новую-
функцию. Получим ч
аУ
-dx- = z'
d2y dz
dx2 dy '
dxa
Дифференциальное уравнение D) принимает вид
dz dn~lz
z
Порядок уравнения D) снизился на единицу.
6.2.3. Уравнение, однородное относительно у, у', ..., Ул). Положим
Отсюда
~dx=e Их'
ил l с*-*- у ил / j
%г , „ dz d2z , I dz
314 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Подставим эти выражения в уравнение D). Вследствие однородности
относительно у, у', ..., у(п) функция ег будет общим множителем членов
уравнения. После сокращения на ег новое дифференциальное уравнение уже
не будет содержать явно функцию z. Мы приходим, таким образом, к слу-
случаю, рассмотренному в п. 6.2.1.
6.2.4. Уравнение, однородное относительно X и dx. Положим
x — ez.
Отсюда
dx dz '
~dx* — e* Ylz* ~~ ~dz\ '
d3y _3z Г d3y „ d*y , o dy ~\
Их* ~e [ dz3 ~ д ~dz* "г" Z ~dz\ '
Подставим эти выражения в уравнение D). Вследствие однородности
относительно х и dx множители e~kz исчезают. Поэтому новое дифферен-
дифференциальное уравнение не содержит явно независимой переменной z, и мы при-
приходим к случаю, рассмотренному в п. 6.2.2.
6.2.5. Уравнение, однородное относительно х, у, dx, dy, d2y, ..., dny.
Положим у = ах, где и — и(х)—новая функция. После этой замены урав-
уравнение D) становится однородным относительно х и dx. Мы возвращаемся
к случаю, рассмотренному в предыдущем пункте.
6.2.6. Общий случай однородного уравнения. Будем считать х и dx
величинами первого измерения, а у, dy, d2y day — измерениями порядка А.
dv d v
Тогда ~- будет порядка А — 1, -т-4- — порядка А — 2 и т. д.
ах ах
Так же как и в предыдущем случае, мы приходим к дифференциальному
уравнению, рассмотренному в п. 6.2.4, лутем следующей замены функции:
у = их".
Пример. Решим уравнение
Оно, очевидно, принадлежит к рассмотренному типу при k = 2.
Положим
Отсюда
у = их2.
dy „ du , -
dx dx '
du .
Уравнение E) принимает вид
т. е. становится однородным относительно х и dx (см. п. 6.2.'4).
Полагаем
6.2| УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 315
отсюда
du _г du
dx dz '
d2u _2z / d2u du
~dx?~ \dzT~'dF
Подставляя в уравнение F), получаем
2 —— -4- а2 — 8и = 0. G)
Уравнение G) не содержит в явном виде переменной г. Положим
du _
dz '
Тогда
d2u dw
и уравнение G) принимает вид
dw о л
du '
Переменные разделяются, и z выражается с помощью эллиптического инте-
интеграла.
Линейное дифференциальное уравнение »-го порядка
6.2,7. Введение. Уравнение вида
называется линейным неоднородным уравнением «-го порядка. Не существует
никакого общего метода решения этого уравнения при » > 1. В большинстве
случаев' решения уравнения (8) не могут быть выражены с помощью конеч-
ногф*1исла элементарных функций.
Если правая часть (8) тождественно равна нулю, то уравнение 'назы-
'называется линейным однородным. Оно имеет вид
. , лП.. jfl — 1..
Пусть известны п частных интегралов yv y2> •••• Уп однородного ли-
линейного уравнения (&). Тогда общий интеграл этого уравнения
1- - . у = С1У1 + С2у2+ ... +Спуп.
Если a (z) — частный интеграл неоднородного линейного уравнения (8),
то общий интеграл этого уравнения
6.2.8. Метод вариации произвольных постоянных (метод Лагранжа).
Пусть известно п частных интегралов yv y2, .... уп однородного линейного
уравнения (9). Покажем, как в этом случае определяется частный интеграл
неоднородного линейного уравнения (8). Положим, что мы выбрали п таких
•функций
OiU), v2(z) vn(z),
НТО
+ ... -\-va(z)yn
316 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
представляет собой решение неоднородного уравнения (8). Вычислим
и предположим, что функции v удовлетворяют условию
v'1y1 + v'2y2+ ... -+-v'ayn = 0.
Найдем, далее.
и наложим на функции v второе условие:
Повторяя эти рассуждения еще п—3 раза, мы придем к следующей системе
п—1 линейных уравнений относительно v\, v'2 г/:
•Последовательные производные от у с учетом этих условий будут равны:
Подставим эти производные в уравнение (8). Так как yv ..., уп —
решения однородного уравнения (9), то имеем
vv
Это равенство — недостающее ге-е условие, необходимое для определения
>2 <¦
Полученная система из и уравнений будет совместна при условии, что
определитель')
У1 У2 ••¦ Уп
v' v' v'
не равен нулю. Это имеет место, если функции yv y2 уп представляют
собой линейно независимые частные решения однородного уравнения (9).
Тогда по правилу Крамера можно однозначно определить v'v v'2 v'n.
Сами же функции vv v2, ..., vn получатся с помощью интегрирования.
') Он называется определителем Вронского (вронскианом).
6.2] УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 317
Пример. Решим уравнение
dz'^l — z dz l—zy — lz-
Очевидно, что yt = ег и у2 = z — линейно независимые частные интегралы
однородного уравнения. Нужно найти такие две функции vl(z) и v2(z),
чтобы
v[ez^-v'2z = 0,
v[e^-\- v'2=\ — z,
откуда
vx = A -f- z) e~z, v2 — z.
Частный интеграл заданного неоднородного уравнения будет
1
Следовательно, общий интеграл
6.2.9. Уравнение Эйлера. Это уравнение вида
Z —т-
где коэффициенты Л — постоянные. Оно является частным случаем уравне-
уравнения, однородного относительно z и dz, рассмотренного в п. 6.2.4.
Уравнение Эйлера преобразуется в линейное уравнение с постоянными
коэффициентами путем замены независимой переменной
Пример.
Положим z = е". Имеем ,
dy__p-udy_ d*y _ 2ц / d*y dy \
dz da' Iz^ ~~e \ du* duj*
Уравнение приобретает вид
езае-зи (у'" _ з/' _|_ 2у') -+¦ еае~иу' — у = аеа
или
'"
у'" _ з/' + 3/ — у = аеа.
6.2.10. Интегрирование при помощи степенных рядов. Ограничимся
случаем линейных дифференциальных уравнений второго порядка
Весьма простая идея решения этого уравнения состоит в том, чтобы
попытаться написать его общий или частный интеграл в виде обобщенного
степенного ряда с неопределенными коэффициентами:
оо
у = х->'21аххК A0)
и
318 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Подставим этот ряд в дифференциальное уравнение, приведем подобные
члены и приравняем нулю коэффициенты при различных степенях х. При
этом мы получим бесконечную систему алгебраических уравнений, связываю-
связывающих показатель степени v и коэффициенты ах (А = 0, 1, 2, ...)• Первые
(одно или два) уравнения позволяют определить v. Уравнение, служащее для
вычисления ч, называется определяющим уравнением. Остальные уравнения
составляют систему рекуррентных соотношений, позволяющих последова-
последовательно вычислять коэффициенты разложения. Каждому корню определяющего
уравнения соответствует свое разложение в ряд вида A0), удовлетворяющее
исходному дифференциальному уравнению.
Рассмотрим, например, уравнение
Попробуем найти его решение в виде ряда A0). Подставим этот ряд.
в дифференциальное уравнение и приравняем нулю коэффициенты при л:
степени ч-±-\—2. Получим рекуррентное соотношение
ax(v4-X)(v + X—1)Н-ах+1 = 0 (Х = 0, 1, 2, ...)•
Уравнение, соответствующее коэффициенту при х с наименьшей сте-
степенью, равной v — 3, дает
а0 = 0.
Из рекуррентных соотношений, полученных выше, последовательно находим,
что'все коэффициенты av a2 ап, ... равны нулю. Это означает, что
рассмотренное дифференциальное уравнение не имеет решения в виде
обобщенного степенного ряда.
Возьмем другой пример:
Подстановка того же ряда дает (если приравнять нулю коэффициент
при х в степени ч-{-\—2) следующее рекуррентное соотношение:
Mv-bA0(v + X— 1) + аХ-И0'-МН-1) = 0 (\ = 0, 1,2....).
Коэффициент при х с наименьшей степенью, равной v — 3, приводит к опре-
определяющему уравнению
va0 = 0.
Единственное подходящее решение — это ч = 0; тогда а0 неопределенно-
Рекуррентное соотношение принимает вид
Остается проверить сходимость получающегося таким способом степенного
ряда. Имеем
с = hm кх ¦¦
J A.-V00
lim
:ОО,
т. е. полученный ряд расходится при любом х. Это означает, что рассма-
рассматриваемый способ снова оказывается несостоятельным или, точнее, что
дифференциальное уравнение не имеет решения в виде обобщенного степен-
степенного ряда. Совершенно очевидно, что эти неудачи связаны с особенностями,
функций fi(x) и /2(х) при х = 0. В приведенных примерах точка х = 0
представляет собой полюс функций /j(x) и /2(х). Однако наличие полюса
у функций fi(x) и /2(х) само по себе не исключает возможности успешного
6.2J УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 319*
применения рассматриваемого метода. Например, уравнение
может быть решено рассмотренным методом, т. е. оно имеет решение в виде
ряда A0). Действительно, подстановка ряда A0), если приравнять нулю-
коэффициент при х в степени v—(— X — 2, дает
• (X + vJax4-ax_2 = 0 (Х=0, 1, 2, ...; а_2 = а_1 = 0).
Это рекуррентное соотношение при Х = 0 и 1 приводит к двум опреде-
определяющим уравнениям:
Первое решение: v = 0, a0 неопределенно, аг = 0. В данном случае,
обозначая ^ = 2г, получим ряд, сходящийся при любом х:
S Г
т
С точностью, до постоянного множителя это ряд для бесселевой функции'
J0(x) (см. п. 7..5.1). .
Второе решение: ч = — 1, а0 = 0, а1 неопределенно. Обозначая X = 2г -\-1,
получим ряд того же типа, в котором роль постоянного множителя'
играет а1 *).
Класс уравнений, решаемых с помощью обобщенных степенных рядов,
определяется теоремой Фукса. Приведем ее без доказательства.
Если дифференциальное уравнение
таково, что fi(x) и /2(х) имеют полюсы при х = х0, то можно найти
решение в виде сходящегося обобщенного степенного ряда ,
оэ
у (х) = (х —х0? 2 «х(* — *о)х
х=о
при условии, что произведения
(х — х0) /1 (х), (х — х0J /2 (*)
остаются конечными при х = х0.
Ясно, что эти условия не выполняются для дифференциальных уравнений
но выполняются для уравнения
Отметим, что при помощи замены переменной можно всегда перенести
полюс в точку х = 0. Рассмотрим линейное дифференциальное уравнение A1)
.и предположим, что оно удовлетворяет условиям Фукса при х = 0. Тогда
*) Отметим, что и это решение, с точностью до постоянного множителя, равно
функции JOAX)- Второе, линейно независимое решение рассматриваемого уравнения
представляет сумму обобщенного степенного ряда и In лг (см. п. 7.5.3).
320 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
функции fx(x) и /2(х) можно представить в виде:
1
Коэффициенты р0, q0, qt не равны нулю одновременно. В противном случае
fi(x) и /20О не имели бы при д: = 0 особой точки, и определение общего
решения уравнения в виде степенного ряда не представляло бы никакого
затруднения.
Будем искать решение уравнения A1) в виде A0). Обозначим через D(y)
определяющее уравнение:
Приравнивая нулю коэффициенты при различных степенях х, получим:
х-. я2 D (v -f- 2) -+- ar [(v + 1) Pi -t- qd 4- a0 (vp2 + ^2) = 0,
Из определяющего уравнения находим для v два значения: ч1 и v2. Пред-
Предположим, что они отличны друг от друга и разность между ними — нецелое
число. В этом случае можно последовательно вычислить два ряда коэффи-
коэффициентов ах, соответствующих каждому корню определяющего уравнения.
Таким образом, мы получим два обобщенных степенных ряда типа A0). Эти
ряды представляют собой линейно независимые решения уравнения A1).
Коэффициент а0, входящий множителем во все члены рядов, остается
произвольным, т. е. каждое решение определено с точностью до постоянного
множителя. Общий интеграл уравнения получается в виде линейной комби-
комбинации этих двух решений.
Положим, что определяющее уравнение имеет двойной корень. В этом
случае имеется только одно решение типа A0). Второе, линейно незави-
независимое с первым решение придется искать с помощью других искусственных
приемов (см. п. 6.2.11). Определив его, мы сможем получить общий интеграл
уравнения A1).
Положим, что определяющее уравнение имеет два корня, отличающихся
друг от друга на целое число, т. е.
— целое положительное число).
Тогда нетрудно вычислить коэффициенты ряда, соответствующего корню v2,
так как D(v2-(- 1), D(v2-)-2), ... отличны от нуля. Для ряда, соответствую-
соответствующего корню Vj, дело обстоит значительно хуже. Здесь процесс вычисления
коэффициентов обрывается на (п—1)-м номере. Действительно, уравнение,
определяющее коэффициент ап как функцию а0, а1 an-v имеет вид
anD(b + n)+aa_1[p1(n+^— 1) + ^]+ ... -+-а0(рпчх + qn) = 0.
Коэффициент при ап равен нулю, так как Vj -f- n = ч2 — корень уравнения
D(v) = 0. Рассматриваемое уравнение сводится к равенству
«.21 УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 321
Если это линейное соотношение не удовлетворяется вычисленными ранее
коэффициентами ай, .... an_v что и бывает в большинстве случаев, то
найти разложение в ряд типа A0), соответствз'ющее корню Vj, невозможно,
т. е. рассматриваемый способ не позволяет получить общий интеграл. Если
же соотношение выполняется, то можно выразить все коэффициенты ап+1,
вя+2, ... через ап, который остается неопределенным. Это значит, что
решение, соответствующее Vj, содержит два произвольных параметра: коэф-
коэффициент а0, входящий общим множителем в решение, и коэффициент ап,
От которого зависят члены ряда ап+1, а„+2, ...
Пример. Гипергеометрический ряд. Рассмотрим уравнение
х (х — 1) у" + [A -4- а +• Р) х — 1 ] у Ч- *$у = 0.
где параметры a, f3, i— постоянные величины. Для особых точек коэффи-
коэффициентов этого уравнения х = 0 и х = 1 условия Фукса выполняются.
Построим, например, решение уравнения в окрестности особой точки
х = 0. Полагаем
со
у = *' jS чхК
Приравняем нулю коэффициенты при xv+x:
ах (v -+- A) (v -г- Л -^ 1) — ах+j (v + X -\- 1) (м -+-1) -|~
+• ах (v + X) A + а -+- р) — al+l (v -Ц X + 1) Т 4- «х*? = 0.
Члену с наименьшей степенью х, равной v—1, соответствует определяющее
уравнение
a0M(vl0
т. е.
Его корни: v = 0, v=l—f. Будем предполагать, что f — не нуль и не
целое число, т. е. рассматриваемое дифференциальное уравнение имеет два
линейно независимых решения в виде обобщенного степенного ряда A0).
1. Рассмотрим корень v = 0. Рекуррентное соотношение дает
Отсюда получаем частное решение
Этот ряд называется гипергеометрическим рядом Гаусса. Он сходится абсо-
абсолютно для любых а, р, f при \х\ < 1, а также при |лг| = 1, если
f—а — f > 0. Классическое обозначение такого ряда
y=aQF(a, p, f! х),
причем F(a, p, f; x) называется гипергеометрической функцией Гаусса.
2. Рассмотрим корень v= 1 — 7. Рекуррентное соотношение будет
21 А. Анго
322 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ [ГЛ. VI
Оно совпадает с предыдущим выражением, в котором параметры а, C, -j-
заменены соответственно на а. — -f —f— I, C— ^ —f— 1, 2 — f. Отсюда получаем
второе, линейно независимое с первым решение
y2=aox*-iF(cL — TH-1. p_T+i,2 — Т; х),
и общее решение имеет вид
У=Ау1 + Ву2.
Отметим некоторые частные случаи гипергеометрической функции:
A + х)п = F (—п, 1. 1; —х),
1пA+х) = х/7A, 1, 2; — х),
„A 13 ,\
arcsinx = x/7 |д, -g, -g-; x2),
arctgx = x/7 ^-g, 1, j; — x2).
В п. 7.6.14 мы увидим, что функции Лежандра также являются частным
случаем гипергеометрической функции. Нетрудно убедиться, что функция
F\n, —я, -н-5 ~ГХ) является решением дифференциального уравнения
Чебышева:
A — *2) / — ху' + п?у = 0.
При л целом это уравнение допускает в качестве решения обрывающийся
гцпергеомётрический ряд — полином /i-й степени. Он обозначается через
Тп (х) и называется полиномом Чебышева; с точностью до множителя,
зависящего от л *),
—^-х н ^ х
(л — четное),
«'-1 о ¦ (п°-1)(п*-9) д (Я»-1)(Я»-9)(я'-25) „7
д— X "Г" 5| 7J X +...
(л — нечетное).
6.2.11. Некоторые теоремы о свойствах решений линейного диффе-
дифференциального уравнения второго порядка. Рассмотрим уравнение
у"+//1(х)-(-у/2(х)=0. A1)
где fi(x) и /2(х)—произвольные функции.
Пусть Ух и у2 — два линейно независимых решения A1). Подставим их
в уравнение A1) и исключим /2(х) из обоих уравнений. Имеем
уГу2 - у\ у,+( у[ у2 - yjy,) A (*)=о.
Выражение в левой части представляет собой, с точностью до множителя
eJ /i (х) х ^ производную произведения
Отсюда получаем соотношение, связывающее yv y2, и их первые производные:
, . — Г/, (х) dx
*) Этот множитель определяется из условия Тп(\) = \, которое равносильно
требованию: коэффициент при х" полинома Тп (х) должен быть равен 2я "-1.
в.2] УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО ' 323
Разделив на у|, найдем
У1У2 — yjyi d У\ А -Г
У2 dx У2 Уг
откуда
/
М
1 г \h(x)dx
Эта формула позволяет по одному частному решению у2(-*0 найти второе,
линейно независимое с первым решение
/- Г f,(x)dx
е ¦> dx
3*
Относительно корней решений уравнения A1) мы можем сформулировать
следующие три теоремы:
1. Пусть функция ух(х), не равная тождественно нулю, —решение урав-
уравнения A1), и корни уг(х) не являются полюсами f^{x) и /%(х). Тогда корни
у, (х) — простые.
В самом деде, пусть а — двойной корень yj(x) = 0. Тогда yi(<*) =
= у'1(а.) = 0. В силу уравнения A1) и предположения теоремы обращается
в нуль также и у'^(а). Последовательно дифференцируя уравнение A1) и
подставляя затем значение х = а, получим, что
у1(а) = у'1(а)= ... =yW(a)= ... =0.
Разложим ^(х) в ряд Тейлора в окрестности точки х = а. Имеем
{; 4 •••по-
•••последовательно, у!(дО = О, что противоречит предположению.
2. Два линейно независимых решения уравнения A1) не могут икеть.
общих корней.
Положим в уравнении A1) у == u(x)v(x). Тогда
v {и" 4- a'/i + иД) Н- v' Bи' -+- «/0 -Ь- f"a = 0.
Выберем и таким образом, чтобы коэффициент при v' обратился в. нуль
Шеем
2аЧ-и/1=0,
откуда
-4- \ hWdx
Уравнение A1) примет вид
rf0. A2)
где *)
g (х) = /2 (х) - 4 jj А (*) — |
*) Функция ?¦(.*) называется инвариантом уравнения A1), так как все дифферен-
дифференциальные уравнения A1), решения которых отличаются множителем а{х), не рав-
равным нулю, приводятся к одному н тому же виду A2) (см. [3], стр. 243).
21*
324 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Корни функций v и у совпадают, так как
у
Пусть vx и vQ—два линейно независимых решения A2). Имеем
Отсюда находим
v\v2 — vvx = ~ (v[v2 — v'2v,) = О,
v\v2 — v'2vx = C.
Если vx (x) и v2(x) обращаются в нуль при одном и том же значении х = л,
то постоянная С должна быть равна нулю. Отсюда получаем
I/, t;9 dv, dv<, i/,
— — —-, т. е. —-==—- и — = const,
t;, v2 v, t»2 V2
что противоречит предположению о линейной независимости v1 и v2. Следо-
Следовательно, V\(x) и v2(x) не имеют общих корней, и это справедливо также
и для обоих линейно независимых решений A1).
3. Нули двух линейно независимых решений уравнения A1) взаимно
разделяют друг друга (теорема Штурма).
Из предыдущего вычисления имеем
v\ — v\ — ~dx
Отсюда
Положим, что а и р—два последовательных корня v1(x). Покажем,
что внутри интервала (а, р) лежит корень v2(x). Предположим противное.
Тогда функция ' \ ' будет непрерывна при а <1 х < р и равна нулю на
концах этого интервала, так как, согласно предыдущей теореме, числа аир
не будут корнями v2(x). Следовательно, -' . . =0. Но —zdv^O не
LV2\X)ix=.a J щ
Q
может быть равен нулю, так как —=- сохраняет в промежутке интегрирования
Щ
постоянный знак. Отсюда следует, что v2(x) должна обращаться в нуль
внутри интервала (а, р). При этом v2(x) имеет внутри (а, р) только один
корень. В противном случае, повторяя предыдущее рассуждение, но поменяв
местами vx и v2, мы могли бы показать, что vx (x) обращается между двумя
корнями v2(x) в нуль. А это противоречит предположению, что а и р—по-
р—последовательные корни v1 (х).
Интегрирование линейных дифференциальных уравнений
с постоянными коэффициентами
Линейное дифференциальное уравнение с постоянными коэффициентами
имеет вид
в.2] УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 325
где Ао, А1 Ап—коэффициенты, не зависящие от у и t. Можно полу
чить общее решение уравнения A3), отыскав общий интеграл соответствую-
соответствующего однородного уравнения
и прибавив к этому общему интегралу частный интеграл неоднородного
уравнения A3).
6.2.12. Интегрирование однородного дифференциального уравнения.
Положим
у = еР*.
Получим уравнение
(АоР" + А1р*-1+ ... +А„)еР' = 0.
Оно удовлетворяется, если р есть корень алгебраического уравнения
f(P) = Aop» + AlP»-1+ ... +Л„ = 0, A5)
которое называется характеристическим.
Пусть рх, р2, .... рп — корни уравнения A5). Предположим сначала,
то они все различные. Общий интеграл в этом случае будет
' у = С1*"'_|-С2*Л'+ ... +Сперп'.
Коэффициенты С — произвольные постоянные.
в. 2.13. Случай кратного корня. Положим, что уравнение A5)
ет^ один кратный корень р1 ?-го порядка. Тогда у нас только п — k -\-1
разлЙных корней, и
— уже'не общее решение, так как оно содержит только я— k-\-\ неопре-
неопределенных постоянных.
Положим
у~ие'.
Тогда
da ,
Введем следующие символические обозначения *):
du „ d2u „, dnu
di=Du' Ж*=°Ч
Имеем
dt *
dty. — aO.tidtu i о„ du
^¦=*">'(ОН-/>,)"«•
*) Ниже используется символический метод решения линейных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами. Более подробно этот метод описан,
например, в [1], стр. 114—122, или [4], стр. 117—124.
326 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Подставим в дифференциальное уравнение A4). Получим
или
[Ао(D +/>,)"+ Л,(D + Р/-Ч ... + Лп]а = 0. A6)
Заметим, что выражение в квадратных скобках равно f(D-\~p), где
задано формулой A5).
Так как рх — кратный корень f(p) порядка k, то можно написать
f(P) = ?(P)(.P — Pi)"' причем cpO^i)^0-
Подставляя вместо р выражение D+jPj и умножая результат на и, получим,
согласно A6),
ft * d и
Это символическое уравнение удовлетворяется, если D и = 0, т. е. = 0.
Мы нашли недостающие k — 1 произвольные постоянные. Таким образом,
общий интеграл уравнения A4) в рассматриваемом случае равен
Полученный результат, очевидно, обобщается на случай нескольких
кратных корней характеристического уравнения A5).
П р и м е р. Решим уравнение
Характеристическое уравнение р3 — Ър-\-2 = 0 имеет двойной корень р= 1:
рз _ 3jp _|_ 2 = (jp — IJ (p + 2).
Отсюда общее решение:
y = Ae-2'-\-(B-\-Ct)ef.
6.2.14. Частный интеграл неоднородного уравнения. Обратимся теперь
к неоднородному уравнению A3):
S|3: A3)
В соответствии со сказанным выше, для определения общего решения A3)
остается найти его частный интеграл. Во многих случаях вид частного инте-
интеграла продиктован видом функции g(t). Но в общем случае заранее опре-
определить этот вид нельзя — нужно решать уравнение A3) непосредственно.
Это удобно делать операционным методом, изложенным в п. 8.5.2.
Рассмотрим важный для электротехники частный случай, когда функ-
функция g (t) равна
g1(.t)=Se~at cos ^Ы
Частный интеграл естественно искать в виде
6.2] УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО 327
Коэффициенты А и В определяются путем подстановки. Удобно поступать
так. Функция gi(t) есть вещественная часть следующего комплексного
выражения:
Se-at е! <<¦><+?).
Рассмотрим дифференциальное уравнение
'+«. A7)
Пусть з>1 — частное решение A7). Выделяя вещественную и мнимую части,
мы запишем его в виде
Так как постоянные Ао Ап вещественны, то R(yj) — частное решение
уравнения A3) с правой частью, равной gi(t), a 1(У])— частное решение
вспомогательного уравнения
А+ +Ay = Se-
Попытаемся найти частное решение A7) в виде
Замена тригонометрической функции экспонентной очень упрощает вычисле-
вычисление, так как после подстановки у1 в A7) обе части уравнения можно со-
сократить на e<-«.+M«. Для $ получаем
Отсюда
т. е.
/<+у)- A8)
Следовательно, вещественная часть A8) R(yO есть решение уравнения A3)
с правой частью g1 (t), если у"ш — а не является корнем характеристического
уравнения A5). В частном случае, когда отсутствует затухание, имеем
• Общий интеграл однородного уравнения A4), соответствующего не-
неоднородному уравнению A3), представляет собой часть решения, описываю-
описывающего переходный режим. Только что определенный частный интеграл A9)
неоднородного уравнения A3) соответствует постоянному режиму (вынужден-
(вынужденные колебания).
Пример. Решим уравнение
1. Найдем общий интеграл однородного уравнения. Характеристическое
уравнение ръ -+- Ър2 -\- \р -f- 2 = 0 имеет корни
Следовательно, решение однородного уравнения будет
е-' (А -+- В cos t + С sin t).
328 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯ (ГЛ. VI
2. В соответствии с A9), частный интеграл уравнения вида A7)
e2jt е2*'
У1 = B/K + 3 Bу)* + 4 B/) + 2 — ~ "Ж"
in
10
и частное решение предложенного уравнения равно —s" . Отсюда общее
решение
Если предложенное уравнение относится к электрической или механи-
механической системе, подвергающейся воздействию периодической силы, пропор-
пропорциональной sin 2^, то переходный режим описывается выражением
cost-hCsint).
а режим вынужденных колебаний — выражением
-1 sin 2^.
6.2.15. Случай резонанса. Рассмотрим уравнение
¦ Предположим, что усо— а — кратный корень fc-ro порядка характеристи-
характеристического уравнения f(p) = 0. В этом случае формула A8) неприменима.
Будем искать частное решение в виде
AStkeiate-at.
Повторяя вычисления п. 6.2.13 для y = uePtt при usBtASt" и Р\
w — а, получим
Используя формулу Тейлора для многочленов, перепишем это равенство
в виде
'(ую-а)-?-+. ... 4-/*'(>-а)~+
Но
Dntk= . ..
и, по предположению (ju> — а — кратный корень k-rp порядка),
/ (Усе — а) = /' (> — а) = . . = Я*-1» (Усо — с) = 0. /<*> (Jw — а) ± 0.
Таким образом, в левой части рассматриваемой формулы только один
член не равен нулю. Учитывая, что Dktk = k\, находим
и частный интеграл уг будет
6.2] УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО S29
Если коэффициент затухания а мал, то ух может принимать большие
значения. Если нет затухания (а = 0), то з>1 будет беспредельно возрастать.
Речь идет о случае, когда частота вынужденных колебаний совпадает с соб-
собственной частотой электрической или механической системы. Это кончается
пробоем для электрической и разрывом для механической системы, если
только возрастающее затухание не изменит характера процесса. Соответ-
Соответствующим образом изменится тогда и дифференциальное уравнение задачи.
Пример. Решим уравнение у" -\- а2у = sin at. Частный интеграл пред-
представляет собой мнимую часть выражения
и равен
Следовательно, общий интеграл будет
у = A cos at -f- В sin at =- cos a^
6.2.16. Система линейных дифференциальных уравнений с постоян-
постоянными коэффициентами. Рассмотрим, например, систему
Положим
х = Aet', у = Bei*.
Коэффициенты А и В определяются из системы линейных алгебраических
уравнений
{ ill B1)
Для того чтобы она имела решения, отличные от нуля, нужно, чтобы опре-
определитель системы был равен нулю:
d~\2 4" е"\ 4~ /
,2 , ; = 0. (*)
Это уравнение имеет четыре корня: fv f2, f3- T* Рассмотрим корень f,.
Система B1) при fss-f], согласно (*), сводится к одному уравнению, что
дает для А и В значения, пропорцирнальные
Отсюда получаем частное решение системы:
Таким же образом найдем решения х2, у2; х3, у3 и хА, у4, соответствующие
корням 72, f3 и f4- Общее решение будет
v — С г -i- С v J- С v _1_ С у
Уз + С4У4-
330 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Очевидно, что рассмотренный метод распространяется на общий случай
решения р линейных дифференциальных уравнений га-го порядка с постоян-
постоянными коэффициентами. Все р неизвестных функций оказываются зависящими
от пр произвольных постоянных.
Если рассматривается неоднородная система, то следует, так же как
и в случае одного уравнения, сначала решить однородную систему, а затем
прибавить к общему решению этой системы частное решение неоднородной
системы.
6.3. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Если число независимых переменных больше единицы, то дифферен-
дифференциальные уравнения содержат частные производные. В случае, когда функ-
функция г зависит от двух переменных х и у, уравнение имеет вид
,/ дг_ дг д2г д2г d2z д3г \_-
•'Г" У> Z' дх ' ду ' дх2' дхду • W ~Ш' ¦¦¦) —и-
Аналитические методы решения уравнений в частных производных най-
найдены только для некоторых случаев. Важнейшие из них следующие: урав-
уравнение, однородное и линейное относительно частных производных, с постоян-
постоянными коэффициентами; уравнение колебаний струны; телеграфное уравнение;
уравнение Лапласа; уравнение ПуассонаГ уравнения Максвелла. Эти урав-
уравнения разбираются нами ниже.
6.3.1. Линейное уравнение с постоянными коэффициентами, одно-
однородное относительно частных производных. Рассмотрим сначала уравне-
уравнение без правой части. Для случая двух независимых переменных это урав-
уравнение имеет вид
. дпг , . дпг . . д"г . дпг .,
Л° дх" ~*~Л1 дхп~*ду ~т~ ••¦ ~т-Ап-\ дхдуп-^ -t-AnJyT—V:
Положим !) -т— = р, -г- = q. Тогда уравнение B3) принимает вид
")z = 0. B4)
Разложим однородный многочлен в левой части B4) на линейные множители:
(<*i/> + Pi?) (ЪР + Ы ¦ ¦ ¦ (*пР + Р«<7) * = 0. B5)
Уравнение B5) сводится к п уравнениям типа
•^+Р/# = °- B6>
Каждое уравнение B6) удовлетворяется выражением (см., например, [5])
г = <Ь}(°;У — $jx),
где Фу обозначает любую функцию. Следовательно, общее решение уравне-
уравнения B3) будет
г = Ф, (<х,у — р,*) + Ф2 («аУ — №) + ¦ • • + Ф„ КУ —'?„*)¦ B7)
') Частные производные обозначаются также следующим образом: гху вместо
д2г д2г
-5—г- . гхх вместо -т—=• и т. д.
дх ду х дх2
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 331
Мы предполагали, что однородный многочлен уравнения B4") имеет
только простые корни. Если он имеет корень ft-ro порядка, то общее реше-
решение уравнения типа
будет
2 = Ф1(а1у — $,х)+хФ,+1(а,у — р,*L- ¦•• 4- xk-^l+k_x(aty - p,je). B8)
Это решение займет место суммы
в общем решении B7).
6.3.2. Уравнение с правой частью. Если уравнение B3) имеет правую
часть, то оно легко решается для случая, когда эта правая часть — много-
многочлен, однородный относительно х и у:
р р1 ... -\-ару".
Частное решение ищется в виде
Коэффициенты b определяются путем подстановки.
Пример. Найдем общее решение уравнения
д*г
• 4 дх ду* ду* ~
_ _ _
дх* "*" дх3 ду Н~ дхг дуг • 4 дх ду* ду*
Разложим левую часть на множители:
Частное решение ищем в виде
z = Ьохв + blX5y -+- b2x V -+- М3У3 4-
Подсхавим это выражение в уравнение и приравняем коэффициенты при
л:2, ху, у2- Получим три уравнения с 7 неизвестными:
02~Г"^"з4~ "— ^"s О\)Рш^= U.
Так как нужно найти любое частное решение, примем *0 = *2 = *3 = *в = 0.
Тогда
*=—- Ь— —— * = ——
Следовательно, общее решение
z = Ф] (У 4- х) 4- Ф2 (У — *L- Ф3 (У — 2а:) +
+ л:Ф4 (у — 2х) — -^ Dл:5у + 10л:2у4 + Зл:у5).
6.3.3. Уравнение колебаний струны. Рассмотрим сначала уравнение
^ =0.
Получаем
дг
332 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
а затем
иначе говоря '),
Здесь ср и ф обозначают две произвольные функции.
Обратимся теперь к уравнению колебаний струны
d2z _ 2 д2г
~W~~a lx^-
Произведем замену переменных, положив if=x-\-at. v=x — at.
Тогда нетрудно показать, что это уравнение принимает вид
Отсюда
z = ф (и)—(— ср (v) •
и, возвращаясь к прежним переменным,
z = ф (х -\- at) -f- ср (х — at).
Рассмотрим частный случай, полагая
ф (х -+- at) = A sin k (x -+- at),
ср (х — at) = A sin k (x — at).
Соответствующее решение будет
z = 2A cos kat ¦ sin kx.
Покажем, как можно применить полученное решение к задачам из тео-
теории электричества.
Рассмотрим полностью изолированный линейный проводник, омическим
сопротивлением которого будем пренебрегать (рис. 6.1). Положение произ-
произвольной точки М этого проводника определяем
криволинейной абсциссой s. Пусть 5 — криволи-
^ ,'^г нейная абсцисса точки В.
Обозначим через I и v соответственно силу
тока и потенциал в точке М в момент времени t.
Если переместиться по проводнику на единицу
длины, то падение напряжения будет вызвано
самоиндукцией рассматриваемого участка. Отсюда
получаем
Рис. 6.1. ~1Ж=:Ж- B9)
Точно так же изменение силы тока на единицу длины будет вызвано тем,
что часть тока будет шунтирована емкостью рассматриваемого участка.
Отсюда
-С^- = 4. C0)
') Можно было бы получить этот результат, применяя соображения предыду-
предыдущего пункта, ио здесь проще прямое вычисление.
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 333
Дифференцируя уравнения B9) и C0) соответственно по t и s и исклю-
исключив функцию v, получим
дЧ _ 1 дЧ
dt2 ~ LC ds* "
Будем считать, что для любого момента времени '/ сила тока t = l(s, t)
равна нулю на концах проводника:
/@, t) = t(S, О = 0,
а при ? = 0
t(S. 0) = /(*).
где / (s) — известная функция, удовлетворяющая условиям
Легко видеть, что решение поставленной задачи может быть удовле-
удовлетворено суперпозицией полученных выше частных решений волнового урав-
уравнения, т. е.
., ,. VI пп t . s
Действительно, граничные условия удовлетворяются, так как /=0 при s =
и j,- = 5. При t =t= 0 получаем
Решение удовлетворяет начальному условию, если коэффициенты ап вычи-
вычисляются по формуле
s
ап = ~$ I
т. е. являются коэффициентами Фурье для функции f($).
6.3.4. Телеграфное уравнение. Это уравнение вида
Оно решается применением операционного исчисления (см. гл. VIII, п. 8.4.10
и последующие).
6.3.5. Уравнение Лапласа. Это уравнение кида
дЮ , d*U .
В задачах о распространении волн часто встречается уравнение вида
дЮ , d*U , d2U 1 дЮ д„ 1
+ +-? ~Ж или ш^-?
В этом случае, разлагая искомую функцию в ряд по синусоидальным функ-
функциям времени, члены которого имеют вид
?/(*, у, z, t) = ejkctU(x, у, г),
мы придем для функции U(x, у, z) к уравнению Гельмгольца
= O или ^ + ^i/=0. C2)
334 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Стояшая перед инженером задача заключается не в отыскании общего реше-
решения уравнения C1) или C2). Ему нужно найти такое конкретное решение,
которое удовлетворяет на некоторых поверхностях определенным граничным
условиям. В качестве граничных условий могут быть заданы значения функции
(задача Дирихле) или ее производной по некоторому направлению (задача
Неймана). Эти значения могут быть либо известными постоянными, либо,
чаще всего, известными функциями координат.
Решение задачи существенно упрощается, если рассматривать ее в системе
ортогональных криволинейных координат, для которой заданные поверхности
входят в семейство (или в несколько семейств) координатных поверх-
поверхностей.
Пусть р, <р. 9- — координаты выбранной системы. Естественно частный
интеграл уравнения C1) или C2) искать в виде
в котором каждая из функций /?, Ф, в зависит только от одной коорди-
координаты р, <р, Ь. Этот частный интеграл будем называть произведением Лапласа.
Функции R, Ф, в содержат произвольные постоянные. Линейный характер
уравнений C1) и C2) показывает, что эти уравнения удовлетворяются не-
некоторой конечной или бесконечной, дискретной или непрерывной суммой
произведений Лапласа, в которых произвольные постоянные принимают все
возможные значения. Кроме того, в этой сумме каждое произведение Лапласа
может сопровождаться произвольным коэффициентом. Искомым решением
будет такая сумма произведений Лапласа, в которой произвольные коэффи-
коэффициенты принимают значения, обеспечивающие выполнение граничных условий.
Таким образом, решение уравнений C1) и C2) сводится к следующей
задаче: найти произведения Лапласа в рассматриваемой ортогональной
системе криволинейных координат. Выражения для произведений Лапласа,
полученные в следующих пунктах, позволяют также найти решение некото-
некоторых часто встречающихся дифференциальных уравнений, например дифферен-
дифференциального уравнения для функции U Бромвича (формула (87) п. 6.3.13). j
Известно (п. 3.4.2), что в системе ортогональных криволинейных коор-
координат, где квадрат элемента длины равен
ds2 = e\ dx\ -+¦ e\ dx\ -+- е\ dx\.
лапласиан Ш имеет вид
Af/_ * Г д («*» ди) i д (e*ei dU\ t д (*i*2 д!1У\
ехе2е3 [_дхх \ ех дхх )'' дх2 \ е2 дх21 дх3 \ е3 дх3 /J '
Здесь ег, е2, е3 обозначают локальные единицы длины. В такой системе
уравнения C1) и C2) имеют вид:
д (е2е3 д(/\,д I e3ex dU \ , д 1ехе2 д[/\_п „„.
Тх^\~^"дх~х)'+~дх^\^Г'дГ2) ~j~~dx^[~es~'dxl}~ { '
В рассматриваемых ниже различных системах координат мы будем,
искать произведения Лапласа, удовлетворяющие уравнению C4). Из них,
полагая k = 0, мы получим произведения Лапласа, удовлетворяющие урав-
уравнению C3). Для некоторых менее употребительных .систем координат мы
ограничимся1 рассмотрением одного только уравнения C3).
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 335
6.3.6. Прямоугольная система координат. Положим
U(x, у, z)=X(x)Y(y)Z(z).
После подстановки в уравнение C2) и деления на XYZ получаем
Первые три члена уравнения C5) зависят соответственно только от х,
у, z. Следовательно, единственная возможность удовлетворить уравнению
C5) — положить
=0.
Постоянные т, р, q— это произвольные вещественные или комплексные
числа, подчиняющиеся единственному условию
dy2
Отсюда произведение Лапласа') имеет вид
,, sin sin sin
и= тх ¦ pv • qz.
cos cos ^ * cos ч
Граничные условия приводят к дополнительным соотношениям между
числами т, р, q. Искомое решение будет суммой всех произведений Лап-
Лапласа, каждое из которых удовлетворяет граничным условиям (см. п. 6.3.14).
6.3.7. Система цилиндрических координат. Если гр'аничные условия
для функции U заданы на цилиндре вращения с осью Oz, то нужно перейти
к системе цилиндрических координат, описанной в п. 3.4.3 и изображенной
на рйс. 3.27. В этой системе уравнение C4) будет ,
dU . 1 дЧ1 , d*U „.п
Будем искать решение в форме
U (p. <p. z) =
После подстановки и деления на /?<J>Z уравнение C6) приобретает вид
-I Г d*R _J_ I dR 1 ' l l ^!®. l_ l
R L dp2 "^ p ~df\ "^ Ф p2 d?2 Н"Т
Первые два члена C7) не зависят от z, поэтому и третий член не должен
зависеть от z.
Полагаем
1 d'z -2
cos
') Обозначение qz представляет собой сокращенную запись линейной ком-
комбинации A cos qz-\-B sin qz. В дальнейшем мы встретимся с подобными обозначениями:
R = ? (ар) вместо /? = Л/, (ар) + ?KV (ар); Z = в*?г вместо Z = Ае9* + Be~qz и т. д.
336 МЕТОПЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Знаку минус соответствует решение
2=cs°>. OS)
а знаку плюс —
Z = e±qz или z = c^qz. C9)
Тогда уравнение C7) может быть написано в виде
Рассуждение, подобное предыдущему, приводит к уравнению
1 <12Ф
— = ГС V2
Ф dv2 "+" *
Знаку минус отвечает решение
внаку плюс —
или Ф = с!'
sh
Для функции R (р) внак плюс приводит к бесселевым функциям с мнимым
индексом. Этот случай встречается на практике очень редко, и мы не будем
на нем останавливаться.
Если радиус-вектор может свободно вращаться в области существова-
существования функции U, то она должна принимать одинаковое значение при <р и
^-|~2ir, т. е. у должно быть целым числом п. При этом говорят, что имеет
место симметрия повторения порядка п. Особый случай представится, если,
например, область является полым цилиндром с радиальной перегородкой.
Подставляя *D1) в D0), получим
d2/? 1 dR . i, 2 _ 2
Это уравнение решается в бесселевых функциях (см. § 7,5). Рассмотрим
частные случаи:
1. Перед q2 знак плюс или знак минус, но при условии, что № — q2 > 0.
Обозначая для этого случая k2 :p q2 = а2', имеем
2. Перед q2 знак минус, причем k2 — q2 < 0. Полагая k2 — q2 = — а2 < 0,
найдем
R = J? (aP). D3)
Если ось Oz входит в область существования решения, то U должна
принимать конечные значения при р = 0. Это исключает решения Y и К.
Таким образом, произведение Лапласа будет
U = /?{?)<&(<?) Z(z),
где функции R, Ф, Z даются равенствами C8), C9), D1)—D3).
Замечание. Случаи, когда одна из постоянных q, v, а равна нулю,
следует рассматривать отдельно. Если 9 = 0, то решение C8) и C9) заме-
заменяется на
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 337
Точно так же, если v = 0, решение D1) заменяется на
Функции Бесселя имеют тогда нулевой порядок. По причинам, указанным
выше, при наличии симметрии вращения А' должно равняться нулю.
Если а = О, то решение D2) заменяется на
Если, кроме того, v равно нулю, то
R = A'"\nP-+B'".
Если ось Oz входит в область существования U, то В" = 0, А'" = 0.
6.3.8. Система сферических координат. Если граничные условия для
функции U заданы на шаре с центром О или на конусе вращения с верши-
вершиной О, то следует перейти к системе сферических координат, описанной
в п. 3.4.4 и изображенной на рис. 3.28. В этой системе уравнение C4)
имеет вид
p р 9 р р » ^ р2sin2a
Будем искать решение в форме
U (p. ft, <р) = Л(р)в(»)Ф(<р).
После подстановки и деления на /?6Ф получим
Рассуждение, аналогичное рассуждению предыдущего пункта, приводит к
Отсюда (см. п. 7.5.36)
D6)
Не будем останавливаться на случае, когда правая часть уравнения D5)
равна —р2. Это привело бы нас к бесселевым функциям с мнимым индексом.
'Если k = 0, т. е. если требуется найти произведение Лапласа как реше-
решение уравнения C3), то D5) принимает вид
1^-4« = 0. D7)'
' p dp p2
Это уравнение Эйлера (п. 6.2.9). Имеем
J4
р
Если точка О относится к области существования решения, то функ-
функции К. > j- и р ' +~* должны быть исключены из числа решений D6)
V '
22 А. Аиго
338 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ГГЛ. VI
и D8). Функция J / j- подходит, так как 1/ р2 -\- -j ^- -^, а значит,
У Р'+7
произведение р аЛ/ f конечно при р = 0.
Подставляя выражение для /?(р) в уравнение D4), получим
Так же как и в п. 6.3.7, заключаем, что
1
Отсюда
Если в области существования решения угол ср может принимать значе-
значения, превышающие 2ic, то р. должно быть целым числом т (ср. п. 6.3.7).
Исключение представляет собой задача для шара с полукруглой перегородкой.
Подставляя в D9) формулу E0) при \х = т, получим
, Если отрицательная полуось z (& = — и) входит в область существо-
существования решения, то единственным возможным решением будут функции (см.
п. 7.6.22)
"я
где п — целое число, связанное с р соотношением п(п-\- \) = р2. Это усло-
условие ограничивает произвол в выборе р. В частности, индекс бесселевых
функций из D6) становится полуцелым, равным ян
Если полная ось z входит в область существования решения, то сле-
следует исключить функции Q™ (см. п. 7.6.22).
Таким образом, произведение Лапласа будет
ср, »)=Я(р)Ф(<р)в(»),
где функции R, Ф, в даются равенствами D6), D8), E0), E2).
6.3.9. Система эллиптических цилиндрических координат. Если гра-
граничные условия заданы на поверхности эллиптического или гиперболического
цилиндра, то следует перейти к системе координат, описанной в (п. 3.4.7)
и показанной на рис. 3.30. В этой системе уравнение C4) записывается
в виде
a2 (ch2 ? — cos2 <р) \ д& 'с
Будем искать решение U в форме
U (?, ср, z) = S i
После подстановки и деления на U уравнение E3) приобретает вид
I Г 1 /У2С 1 ^2ф -I 1 //2 7
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 339
Полагаем
Z dz2 '
Отсюда
Z=CO8(i^ , Eб)
Если обозначить j32 = (ft2 — р.2) а2, то уравнение С54") примет вид
1 Й2* 0 2 П
U^~ —^ cos (Р = °-
Это уравнение распадается на два следующих:
¦fp- + (*•» - у />2 - у Р2 cos 2ср) Ф = О,
Полагая г2 ?- = ?, a p2 = 4q, получим
Й2Ф
E7)
E8)
Уравнение E7) называется дифференциальным уравнением Матье. Урав-
*?нение E8) сводится к предыдущему путем замены переменной 5 = У«р.
*¦ Для того чтобы функция U вернулась к первоначальному значению
после полного оборота по поверхности эллиптического цилиндра, она обя-
обязана иметь по ср период 2ir (ср. п. 6.3.7). Это должно иметь место, если
по условиям задачи отсутствует радиальная перегородка, препятствующая
изменению на угол, превосходящий 2ir. В этом важном случае мы оставляем
только те решения уравнения Матье E7), которые имеют период 2ic. Они
называются функциями Матье целого порядка*) и обозначаются (см. п. 7,.7.1)
cem(<p, q), sem(<p, q). E9)
Решения уравнения E8) в свою очередь представляют собой присоеди-
присоединенные функции Матье целого порядка (п. 7.7.4):
Cem(S, q). Sem(l q).
6.3.10. Система параболических цилиндрических координат. Если
граничные условия заданы на поверхности параболического цилиндра, то сле-
следует перейти к системе координат, описанной в п. 3.4.5 и изображенной
на рис. 3.29. В этой системе уравнение C4) записывается в виде
»-
Будем искать решение в форме
U {a, p, z)=A{*)B$)Z{z).
После подстановки и деления на U уравнение F0) принимает вид
1 Г 1 d2A , 1 d2B l , 1 d*Z
*) Или функциями Матье первого рода.
22*
340 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Полагаем
_L d2Z
Отсюда
Z==sinfftz """ sh
Если обозначить p2 = (± m2 — ft2)c2, то уравнение F1) примет вид
1 d*A , , , I d'B
или f.mz. F2)
F3)
Уравнение F3) распадается на два следующих:
d2A
da2
2 — рЧ2)А = 0, F4)
2_|_ p2^2)Bz=0. F5)
Эти уравнения переходят одно в другое путем замены переменной a = j$.
Они решаются с помощью функций Вебера — Эрмита (см. п. 7.8.1).
6.3.11. Другие системы координат. Ограничимся здесь определением
произведений Лапласа для уравнения Д?/ = 0.
Рассмотрим следующие системы координат:
'1. Система вытянутых эллипсоидальных координат вращения
(см. пп. 3.4.8 и 7.6.22):
х = a sh ? sin в sin ф, у= a sh ? sin 9 cos ф, 2 = ach;coscp>
i г d2U , d2U . I dU . \ dU\,
= a2(ch2« — cos2?) L д?2 ' д<?2 ~>~ЙП ~Ж~ ~^~tgf дч> } >
"+" a2 sh2 S sin2 <f дф2 ==
и=^ ^фз,
W = /4, cos р.ф -+- /42 sin р.ф,
Ф = В\ Р$ (cos 9) -I- 52Q^ (cos cp),
Е = Ci P? (ch s) 4- С2<Х (ch 5).
2. Система сплюснутых эллипсоидальных координат вращения
(см. п. 3.4.9):
х = a ch ? cos cp sin ф, у = a ch; cos 9 cos ф, ar = ash$sincp,
а-cu- cos- -¦==0'
W = >tj cos р.ф -("• Л2 sin р.ф,
Ф = BiPt (sin 9) +• #2<2Г (sin 9).
Е = С\Р* (у sh 5) ~j- C2Q? U sh ?)•
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 341
3. Система параболических координат вращения (параболой-
дальние координаты) (см. п. 3.4.6):
x = capcost|>, у = cap sin ф, z=j-c($2 — a2),
L"^" + ^F+ir"^r+|""drJ+ л^ "Щ^
=г ,4j cos р.ф -1- Л2 sin fjnp,
4 Система тороидальных координат (см. п. 3.4.11):
sh i s
"* Л chS+
_ (cht-fcos?)''
sh i sin ф sh 5 cos ф sin cp
"* Л chS+cos? ' У ° ch 54-cos <p ' Z ~ п ch'S + costp
. ch S + costp I"l + costpch5 dU . . dU Л
4 ?—I—si dr+sint?^fj=
U — /chT+coslp 2 ^Ф3'
У = /4t-cos [лф -+- A2 sin [лф,
Ф = flj cos vtp -+- 52 sin v<p,
E = CiP[l , (ch O + QQ11 , (chg).
5. Система бисферических координат (см. п. 3.4.1 IV
sin <p sin ф sin <p cos ф sh ;
a
chS+cos? '
&U . 1
sin2 <p йф2 J ^
chS-)-cos<p Г 1 4- cos <p ch 6 dU . . dUJ\ „
a* [ slnl d<f ~~sn ? <J5 J ~
Цг= /Ij cos |m[i -+- /42 sin (j.i[i,
Ф = fl,/ ± (cos <p) + S2Q11 i (cos <p). -
"a v 2
E = C, ch vE -f- C2 sh v$.
Замечание. Функции, входящие в приведенные выше произведения
Лапласа, написаны в наиболее общем виде. Совершенно ясно, что условие
существования функции U в определенной области приводит к ограничению
общего набора функций, составляющих произведение Лапласа. Это было
показано на примерах в предыдущих пунктах. В частности, нередко р и v
являются целыми числами, и тогда следует отбросить функции К, К. Q-
Следует также заметить, что определения функций Р^ и Q? различны
в зависимости от того, заключается ли их аргумент между —1 и -+-1.
342
МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ [ГЛ. VI
находится ли он вне этого интервала или, что бывает чаще всего, является
комплексным числом (см. приложение к п. 7.6.25).
6.3.12. Уравнение Пуассона. Это дифференциальное уравнение вида
Ш = /(х, у, z).
Оно совпадает с формулой Пуассона (см. п. 3.3.10)
у, z) = 0,
если предположить, что электрические заряды распределены с плотностью
— sf(x, у, г). Поэтому решение уравнения Пуассона естественно искать
в виде скалярного потенциала непрерывной системы электрических зарядов.
Докажем, что действительно выражение
U1~ —
поскольку
Д — =0.
лает частное решение уравнения Пуассона. Здесь х, у, z — текущие коор-
координаты точки, хг, yv zx — координаты точки наблюдения, a dx — элемент
объема области х.
Согласно формуле Грина (см. п. 3.3.8)
F6)
Поверхность о состоит из внутренней
стороны поверхности ах, ограничивающей
сферическую полость с центром (хх, yv zx),
и внешней стороны поверхности о2, ограни-
ограничивающей область х (рис. 6.2).
рис g2 Будем предполагать, что U вместе со
своими частными производными ограничена
внутри х и на о2. Устремим к нулю радиус г0 сферической полости.
Тогда / • dax тоже стремится к нулю, а пределом второго интеграла
по поверхности а,: / t/gradl — ] • й<зх будет 4%U(xv yx, zx)*). Пусть теперь
U — решение уравнения Пуассона, т. е. AU = f(x, у, г). В силу F6) получаем
Правая часть этого выражения представляет собой вклад в функцию U
интеграла по внешней поверхности области т. Отметим, что эта часть, с точ-
*) Напомним, что rfe4 направлена внутрь сферической полости.
6.3J УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 343
ностью до множителя -j—, дает решение уравнения Лапласа
Ш(Х„ Ух, 2,) = О,
которому соответствует / = 0.
Предположим, что в любой конечной области функция U и ее частные
производные ограничены и при стремлении г к бесконечности U имеет
порядок г, а ее производные — г~2. Будем называть такие функции U пра-
правильными. Для правильной функции выражение в квадратных скобках имеет
порядок г~3 (при больших г), и при г—>оо интеграл справа стремится
К нулю. Следовательно, выражение
где интеграл распространен на все пространство, представляет собой реше-
решение уравнения Пуассона.
Полагая в этой формуле / = 0 вне области т, убедимся *), что Ux из (•)
является частным решением уравнения Пуассона внутри х. Обозначим через U
общее решение уравнения Пуассона и положим U — Uy = W. Тогда ДШ7 = 0,
т. е. W — общее решение уравнения Лапласа.
Итак, общий интеграл уравнения Пуассона дается формулой
где Ux — частный интеграл уравнения Пуассона (¦*), a W — общий интеграл
уравнения Лапласа.
Отметим, что правильное решение уравнения Пуассона во всем про-
пространстве единственно, оно дается формулой (**). Это следует из теоремы
Лиувилля: гармоническая во всем пространстве функция, исчезающая на бес-
бесконечности, тождественно равна нулю **).
Замечание. Уравнение Пуассона играет основную роль не только
в электростатике. Оно. наряду с уравнениями динамики, описывает законы
электронной оптики.
6.3.13. Решение уравнений Максвелла методом Бромвича. Если выра-
выразить электрическое и магнитное поле в рационализированной системе МКСА.
то уравнения Максвелла для среды с диэлектрической постоянной е и маг-
магнитной проницаемостью jj. получают вид:
, „ дЕ
rot Н = s -^-,
div? = 0,
div// = 0.
Запишем эти уравнения в ортогональной системе координат, квадрат
элемента длины в которой равен
ds2 = е\ dx\ -Ь е2 dx\ + е3 dx\.
*) Строгий вывод см. в [8], стр. 171—175.
*) См. там же.
344 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ [ГЛ. VI
Получаем
дН,
дЕ2 <67>
дЕ3
^- (е2е3Яi) 4- -^ (*3«1^) 4- ^ («.«Л) = 0.
Можно доказать,- что общее решение системы F7) получается наложе-
наложением двух частных решений этой системы. Первое решение соответствует
предположению Н1 = 0. Это поперечная магнитная волна. Ее называют также
электрической волной или волной (?). Второе решение соответствует пред-
предположению Ех = 0. Это поперечная электрическая волна. Ее называют также-
магнитной волной или волной (Н).
Отметим, что излагаемый метод применим только к таким системам
ортогональных криволинейных координат, для которых локальная единица
длины ех является функцией только одной координаты xv а отношение
остальных локальных единиц длины не зависит от координаты xv
Не уменьшая общности, мы можем считать, что ех= I. В противном случае
можно ввести новую переменную х'^ с помощью соотношения dx'l = e1dxl.
Итак, предполагаем, что локальные единицы длины рассматриваемой системы
координат удовлетворяют соотношениям
ех = 1,
е2 F8)
— не зависит от х,.
е% 1
Поперечная магнитная волна, или волна (Е). Если приравнять Нх
нулю, то первое уравнение F7) принимает вид
^^ F9)
Отсюда следует, что
где Р — произвольная функция.
Так как локальные единицы длины не зависят от времени, то из пятого
и шестого уравнений F7), в силу G0) и G1), следует
=_d
дх{ к 3 3/ v >
ег dx2dt дх{
е3 dXidt дх
дх{ к 2 *' ч '
6.3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 345
Согласно допущениям F8) эти уравнения можно переписать в виде
= - Т -k (^) = - ^
Т3 k (^з) ^ №)• G4)
t
Положим Р—-л—• Отметим, что функцию U часто называют потен-
потенциалом электрических колебаний. С помощью U уравнения G4) и G5) можно
записать так:
г дЮ -еН (П\
Из уравнений G0), G1), G6), G7) получаем выражения для Е2, Е3, Я3, Н2
через потенциал U:
У2 dx2dxt '
tf3 = _eJ_jg_. (81)
Подставим выражения G9) и (80) во второе или выражения G8) и (81)
в третье уравнение F7). Тогда
А2ТГ Л2ГТ
(82)
Точно так же, если подставить выражения G9) и (81) в четвертое уравне-
уравнение F7). получаем
Е Lr_E_f?Li?L\_|_— f-^-— "ll ' (83)
1 e2?s L<?^2 V^2 <^^2/ ^з Ie% дхг)]' K
Приравняв правые части выражений (82) и (83), находим дифференциаль-
дифференциальное уравнение, которому должна удовлетворять функция U:
(^+~(~—М- (84)
дх \ е дх ) J
dt2 дх\ е^з I дх2 \ е2 дх2 J дх3 \ е3 дх-.
Если U — общее решение уравнения (84), то выражения составляющих
электромагнитного поля для магнитной поперечной волны [волны (Е)\ будут
F _ d*U d*U р _ 1 дЮ р _ 1 д*Ц
дх, dt e2 дххдх2 ег дххдх3
Поперечная электрическая волна, или волна (Я). Повторяя преды-
предыдущие рассуждения в предположении Ех = 0, получим следующие выражения
346 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ (ГЛ. VI
для составляющих электромагнитного поля волны (Н):
ь п г, 1 дЮ
1 2 г е3 дх3 dt ' 2 2
„ <W (86>
1 А*? г Л2 2 е2 дхудх2 3
где потенциал У определяется из того же самого уравнения (84).
Случай синусоидальной зависимости от времени. Будем считать
(а это почти всегда имеет место), что электромагнитное поле является сину-
синусоидальной функцией времени. Так как уравнения Максвелла F7) линейны.
то в этом случае следует заменить в них символ -^- на Jkv. Нетрудно убе-
убедиться, что тогда U также должна быть синусоидальной функцией вре-
времени вида
U(x, у, z, t)=U(x, у. z)eikvt,
где v обозначает скорость электромагнитной волны в среде, причем
vy.b =1 и & = — = -j-
Новая функция U, зависящая только от пространственных координат, опре-
определяется уравнением
, -г ¦ , . , i ¦ i л . i ¦ - - - <87)
°xl e^3 L "X2 \ e2 °X2 I dx3 \ e3 °X3
Согласно (85) и (86) в рассматриваемом случае имеем (множитель e*kvt при
записи опускаем):
1 d*U ' „ 1
г дх, '
^ Я2 = ±
дх2 е3 дхх дх3
Замечание. Сравним уравнение Бромвича (87) с уравнением C4).
в котором ej=sl. Легко заметить, что эти уравнения отличаются только
первым членом: в уравнении (87) он равен —2-, а в уравнении C4) —
оХу
-т—К2ез7?—)' Таким образом, все вычисления, проделанные при реше-
решении уравнения C4), могут быть перенесены на соответствующее уравнение
Бромвича. При этом выкладки будут мало отличаться друг от друга и в слу-
случае уравнения Бромвича (более простого по форме) приведут к менее сложным
функциям. Разумеется, эти соображения могут быть использованы только
для тех систем координат, в которых соблюдены условия F8). К числу таких
систем относятся: цилиндрические, параболические цилиндрические, эллипти-
эллиптические цилиндрические, бицилиндрические и сферические. Отметим, впрочем,
что уравнение (84) будет особо рассмотрено в случае цилиндрической
(п. 7.5.41) и сферической (п. 7.6.31) систем координат.
6.3]
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
347
6.3.14. Пример. Электромагнитные колебания в прямоугольной
полости. Предполагаем, что стенки сделаны из абсолютно проводящего мате-
материала (рис. 6.3).
Используем прямоугольные координаты, т. е. е1 = е2 = е3=?1. Если
ограничиться синусоидальными функциями времени, тр потенциал U Бром-
вича получается из уравнения (87), которое в этом случае совпадает с урав-
уравнением Гельмгольца (п. 6.3.6). Для этого уравнения произведение Лапласа будет
,, cos sin sin
u= , mx py qz
-¦- r J rn~ 4
sin
cos
при k2=
(Обозначение s п а, как и выше, заменяет бином A cos a -f- В sin a.)
\ COS /
Решение для поперечных магнитных
колебаний!):
,-, ,,о ,, cos sin sin
bx=(k2— m2) . mx py qz,
sin
с, —sin cos sin
Ev= mp mx , py qz,
У Г rr.e Sjn Г? CQS 4
COS
— sin
j
cos
sin
COS
COS
(90)
lj i-if* cos sin cos
^y = -J4]/1rslnmxcospy_sinqz,
О
H,=
™smx cos t
sin —sin'
sin
cos '
Рис. 6.З.
Решение для поперечных электрических колебаний!):
cos cos
sin «*_siii
sin
cos
sin
(91)
,_, —sin cos sin
//„ = mp mx , py qz,
У r cos — sin r* cos H
r, — sin sin cos
n, = mq mx py . qz.
z " ens rn4rJ —sin"
COS
COS
Граничные условия: тангенциальные составляющие электрического поля
на стенках параллелепипеда равны нулю. Таким образом, параметры т, р, q
(а, Ь, с — ребра параллелепипеда) таковы, что
Еу = Е2 = 0 при х = 0 и х = а,
Ег = Ех=0 при у = 0 и у — Ь,
Ех = Еу = 0 при z = 0 и z = c.
Отсюда следует, что в произведение Лапласа cos mx sin py sin qz, соответ-
соответствующее решению для поперечных магнитных колебаний, и в произведение
') Множитель eJkvt при записи опускается.
348 МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ [ГЛ. VI
Лапласа sin тх cos ру cos qz, соответствующее решению для поперечных элек-
электрических колебаний, могут входить только следующие величины т, р, q:
am [in га /пп
т = ~, /> = -%-' Я=-Т> (92)
где а, р, f — целые числа.
Теперь нетрудно написать окончательные выражения полей, зачеркнув
в формулах (90) или (91) неподходящие тригонометрические функции (стоя-
(стоящие вверху или внизу), учитывая, что значения m, n, p определяются фор-
формулами (92). Соответствующая длина волны будет
1 ^ 2
Заметим, что для поперечных магнитных колебаний сочетания следую-
следующих целых чисел a, fj, ? дают нулевое решение:
@, 0, 0), @. 0, 1), @, 1. 0), A, 0. 0), A. 0, 1), A, 1, 0).
Колебание с наибольшей длиной волны получается из сочетания @, 1, 1).
Если Ь = с, то эта максимальная длина волны равна диагонали квадрата.
Для поперечных электрических колебаний самые длинные волны даются
сочетанием A, 1, 0) или A, 0, 1):
A 1 \-'/» /1 1 \—V»
¦$+-jr) или 2^ + ^)
в зависимости от того, будет ли с меньше или больше Ь.
Замечание 1. Отметим, что к полученному выше решению нужно
добавить два других решения, которые находятся из предыдущего круговой
перестановкой х, у, г. В нашем решении ось Ох играет предпочтительную
роль. В действительности все три оси равноправны.
Замечание 2. Не следует забывать, что группы формул (90) и (91)
определялись, исходя из функции U, иначе говоря, через произведение Лапласа,
определенное с точностью до коэффициента. Этот коэффициент может ока-
оказаться различным для каждого вида колебаний, т. е. для каждой комбинации
чисел т, р, q. Он зависит от других граничных условий, описывающих воз-
возбуждение электромагнитных колебаний полости.
Замечание 3. Рассмотрение резонирующих объемов более сложной
формы, чем в примере этого пункта, будет сделано в пп. 7.5.41, 7.6.31.
Там будут существенно использованы свойства бесселевых и. сферических
функций.
ЛИТЕРАТУРА К ГЛАВЕ VI
1. Смирнов В. И., Курс высшей математики, т. II, Физматгиз, 1962.
2. Смирнов В. И., Курс высшей математики, т. III, ч. 2, Гостехиздат, 1957.
3. Степанов В. В., Курс дифференциальных уравнений, Физматгиз, 1959.
4. Э л ь с г о л ь ц Л. Э., Дифференциальные уравнения, Гостехиздат, 1957.
5. Матвеев Н. М., Методы интегрирования обыкновенных дифференциальных урав-
уравнений, Изд-во ЛГУ, 1955.
6. Петровский И. Г., Лекции об уравнениях с частными производными, Физмат-
Физматгиз, 1961.
7. Т р и к о м и Ф., Лекции по уравнениям в частных производных, ИЛ, 1957.
8. Соболев С. Л., Уравнения математической физики, Гостехиздат, 1954.
9. Айне Э. Л., Обыкновенные дифференциальные уравнения, Харьков, 1939.
ГЛАВА VII
НАИБОЛЕЕ УПОТРЕБИТЕЛЬНЫЕ СПЕЦИАЛЬНЫЕ ФУНКЦИИ
7.0.1. Асимптотическое разложение. Рассмотрим, вообще говоря,
расходящийся ряд
Сумму п-\-\ первых его членов обозначим Sn(z) (частная сумма). Согласно
Пуанкаре '), ряд представляет собой асимптотическое разложение функции )
в определенной области изменения argz, если при таких z выражение
удовлетворяет условию
lim Rn (z) = 0 (re — фиксированное),
|г|-*оо
даже если при этом
lim [f(z) — Sn(z)]=t=0 (z — фиксированное).
Запишем эту связь между рядом и функцией в виде
Согласно определению асимптотического разложения, отсюда следует, что
для любого положительного сколь угодно малого г при достаточно больших z
(при фиксированном ге) имеет место
\zn{f(z)-Sn(z))\ <e.
Покажем на -примере, как с помощью расходящегося асимптотического
разложения функции можно приближенно подсчитать ее численные значения.
Пусть функция /(дг) определена равенством
/(*)= J t-lex-' dt, x>0.
¦) Н. Polncare, Acta raatheraatica, 8 A886), p. 295.
350 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Повторным интегрированием по частям найдем
=Г_±е*-'"Г— С t-2e*-'dt = — — f r2ex-'dt =
x x
CO
= -L—ii+2! f t-*e*-'dt.
xx2] J
Рассмотрим ряд, частная сумма которого равна
* (Y\—X 1! ! 2! (-!)*-¦ (д-
В данном случае ао=О. Имеем
так как оба интеграла, входящие в эти соотношения, положительны. Значит,
\Rn(x)\=\x"{f{x)-Sn{x)}\ <4-
Если х бесконечно возрастает, то Rn(x) при фиксированном п стремится
к нулю. Следовательно, Sn(x) представляет собой частную сумму асимпто-
асимптотического разложения / (х). Соответствующий ряд расходится при любом х,
так как нарушается необходимый признак сходимости.
Используем этот расходящийся ряд для вычисления /A0). Тогда общий
( I)" п\
член разложения равен in/»+i— > он убывает по абсолютной величине от
ге=1 до ге=10, а затем растет до бесконечности. По доказанному выше,
\f(x)-Sa{x)\.<?
Поэтому за приближенное значение /A0) выгодно принять S10. Тогда соот-
соответствующая ошибка будет меньше
^щг = 0,0000362 ...
ГЛ. VIГJ
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
351
Следующая таблица и рис. 7.1 показывают последовательное убывание
и возрастание частных сумм рассматриваемого асимптотического разложения:
5, =0,1 5„ = 0.091782 ...
52=0,09 512 = 0,091743...
53 =0,092 51а = 0,091791 ...
54 =0,0916 514 = 0,091729 ...
5, =0.09184 515 = 0,091816 ...
5Й =0,091720 5,6 = 0.091685 ...
57 =0,091792 5]7 = 0,091895 ...
5„ =0,091742 ... 5,R = 0,091545 ...
59 =0,091782
5™ = 0,091746
5,0 = 0,092185
Если в определенной области изменения z функция допускает асимпто-
асимптотическое разложение, то это разложение определяется единственным образом.
SrO,1
QOS7S
0,0917
О,0№
Рис. 7.1.
Действительно, полагая в условии существования асимптотического разло-
разложения последовательно я = 1,2, ..., получаем
ао= lim f{z), а,= lim z[f(z) — a0].
lim
Напротив, две различные функции могут иметь одно и то же асимптотиче-
асимптотическое разложение. Классический пример представляют собой две функции,
отличающиеся на е~^ при R(p)>0. Действительно, коэффициенты асимпто-
асимптотического разложения е~$* при z > 0, вычисленные с помощью полученных
выше формул, тождественно равны нулю.
Пусть существуют асимптотические разложения функций /\z) и g(z)'.
Тогда справедливы следующие теоремы:
352 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
1. Общий член асимптотического разложения a/ (z) + $g (z) равен
2. Общий член асимптотического разложения произведения функций
f(z)g(z) равен
л
Замечание. Если 'р0 ф 0, то можно делить на асимптотическое раз-
разложение g(z).
3. Если функция ф(/) разложима в степенной ряд, сходящийся при
1/1 < Р> т0 асимптотическое разложение функции
получается непосредственной подстановкой в степенной ряд ф(/) асимпто-
асимптотического разложения f(z) (при условии |ао|<р).
4. Если f(z) и f (z) допускают асимптотические разложения, то асимп-
асимптотическое разложение /' (г) получается почленным дифференцированием
асимптотического разложения f(z).
оо
5. Если /C?)'~\]—j (т. е. ао = а\ = О), то асимптотическое разло-
k=2Z
1 оо
жение Г f(z)dz получается почленным интегрированием асимптотического
г
разложения f(z).
Замечание. Иногда функция f(z) не имеет асимптотического разло-
разложения, однако существует такая функция g(z), что отношение \ [ допу-
допускает асимптотическое разложение. Тогда можно написать
Произведение а^(г) называется главным членом асимптотического пред-
представления / (z).
7.1. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Гиперболические функции играют важную роль при расчете длин-
длинных линий.
7.1.1. Определения. Положим (ср. формулы, выражающие круговые
функции через e±ix, п. 1.1.10)
ch х = — (ех + е~х) (гиперболический косинус х),
s\\x — — (ex — е~х) (гиперболический синус х),
th х =в —г— = л. . _х (гиперболический тангенс х).
Полагая ?=cosa:, C = sinA:, имеем ;2-)-С2=1. Точно так же, полагая
? = chjc, C = shA;, имеем ? — С2= 1. Точка с координатами 5. С располо-
расположена на окружности в случае круговых функций и на равносторонней
гиперболе в случае гиперболических функций.
T.I]
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
353
Еще более глубокая аналогия существует между круговыми и гипербо-
гиперболическими линиями. Рассмотрим окружность ?2-|-С2=1 (рис. 7:2) и гипер-
гиперболу S-2— С2=1 (рис. 7.3). Пусть М— точки на этих кривых, Я — основания
ординат М, Т — точки пересечения ординаты А с лучом ОМ, М'—точки,
Рис. 7.2.
Рис. 7.3.
симметричные точкам М относительно оси абсцисс. Примем за независимую
переменную криволинейную площадь ОМАМ' и обозначим ее о. Вычислим
длины отрезков AT, OP и РМ как функции о.
Уравнение, гиперболы в полярных координатах: р2cos26=1. Отсюда
-1-D
1 Г
¦Т J
rf26
Используя эту зависимость между а и б и уравнение гиперболы p=(cos 28)~'/г.
получим (см. рис. 7.3)
А Т = tg 6 = ^—г^— = th о,
РМ = OP tg 0 = sh о.
Для окружности 0 = 8, и потому непосредственно получаем аналогичный
результат:
AT = tga, OP — cos о, РМ = sin о.
.Используя определения гиперболических функций, нетрудно вывести
следующие формулы:
cos х = ch/.v, ch л: = cos/a:;
jsinx=ihjx, jshx=,injx;
sh (a ± b) = sh a ch b ± ch a sh b,
ch(a ± b) = ch a ch b ± sh a sh b;
sh 2a = 2 sh a ch a,
ch 2a = ch2 a 4- sh2 a = 1 + 2 sh2 a = 2 ch2 a — 1;
Bл)!
23 А. Авго
354 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Гиперболические функции имеют период 2те/, совпадающий с периодом
функции ех:
sh (л: -+- 2k%j) = sh х, ch (х -+- 2?ir/) = ch x.
7.1.2. Обратные гиперболические функции. Пусть ;c = sh«, тогда
через Arsh x обозначают аргумент гиперболического синуса, т. е. функцию
и = Arsh х = In (x -+- Yx -f-1).
Таким же образом формуле х = ch и соответствует
и — Arch х = In (х ± Ух2— 1)
и формуле х = th и
и = Arth х = In
Функции Arsh х. Arch jc, Arth x читаются соответственно: ареасинус. ареако-
синус, ареатангенс.
7.1.3. Приложение гиперболических функций к расчету длинных
линий. Метод Броуна. Абаки Блонделя — Кеннели. Изучение распростра-
распространения электрических сигналов вдоль линий передач часто приводит к необ-
необходимости вычисления выражений вида
ach 7 + Э sh 7.
где комплексные числа а, {3, i зависят от характеристик линии.
' Разработан графический способ расчета этих выражений (метод Броуна).
о -
Положим — = th Й. Тогда
гг— , — - chB •
Очевидно, что
8 = Arth — = a -f- jb.
Выразим вещественную и мнимую части 8 (а и Ь) через х и v, пред-
а
ставляющие собой вещественную и мнимую часть z= —. Используй фор-
формулы пп. 7.1.2 и 1.1.11, получим
6 = Arth z = -j In . ~_г = y
Так как z = x -+- /у, то
1 + 2
1—2
и, значит,
1 /"
H+fE+Z ta , — У
1 Х2 _ V2 •
Рассмотрим кривую, определяемую уравнением
1 - Г A -4- х)г -\- у2
а = -j In у {1_хJ^_у2 (вещественная часть 8).
Легко заметить, что это — окружность с центром на оси Ох. Кривая, опре-
определяемая уравнением
b== — arctg . _ l__ 2 (мнимая часть S),
— тоже окружность,- но с центром на оси О у.
7.1]
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
355
Пусть окружность первой системы, соответствующая параметру а,
пересекается с окружностью второй системы, соответствующей параметру Ь,
(Рг)
в точке с аффиксом —. Тогда веще-
ственная часть Arth — равна а, так как
У
У
/
f
й
\
(bh
В/а
л—"
)
/
\
X
(а)
х
Рис. 7.4.
Рис. 7.5.
т
9
в
7
В
5
4
3
2
1
О
-1
-2
-3
-4
У
точка находится на первой окружности, а мнимая часть Arth — равна Ь, так
как точка находится и на второй окружности. Следовательно, для опреде-
определения чисел а и Ь достаточно найти окружности рассмотренных семейств,
пересекающихся в! точке с аффиксом — (рис. 7.4).
После вычисления 8 нужно определить ch 8 и ch(S-f-f)' Обратимся
к вычислению ch8. Модуль р и аргумент б величины ch 8, где b = x-+-jy,
соответственно равны
р — ]/"ch2 х — sin2y , tg 9 = th x tg y.
Каждое из этих выражений определяет
семейство кривых в плоскости ху.
Рассмотрим две кривые, принадле-
принадлежащие к двум разным семействам и пе-
пересекающиеся в точке с аффиксом 8.
Значения параметров р и 8 для каждой1 из
этих кривых дают соответственно модуль
и аргумент ch о. Имея точку с аффик-
аффиксом 8, можно по правилу параллелограмма
1
1
\
\
\
\
1
ч
/
fshx
1
|
/
/
/
/
/
Л\
\45°
1
X
У
1
-4 -3 -2 -1 0 1
Рис. 7.6.
2 3
О
1
Рис. 7.7.
непосредственно построить точку с аффиксом 8-\--\ и затем найти модуль и
аргумент р' и 6' для величины ch (8 -j-*f) (рис. 7.5). В большинстве случаев
на одной плоскости изображают обе системы окружностей рис. 7.4 и оба
семейства кривых рис. 7.5. Эти графики называются абаками Блонделя —
Кеннеди.
7.1.4. Графики функций sh jc, chx, th x (рис. 7.6 и 7.7).
23*
356 ' СПЕЦИАЛЬНЫЕ ФУНКЦИИ . [ГЛ. VII
7.1.5. Таблицы показательной и гиперболических функций.
X
0,0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4
4,2
4,4
4,6
4,8
5
5,2
5,4
5,6
5,8
6
ех
1,0000
1,221 4
1,491 8
1,822 1
2,225 5
2,718 3
3,320 1
4,055 2
4,953 0
6,049 6
7,389 1
9,025 0
11,023 2
13,4634
16,444 6
20,0855
24,532 5 .
29,964 1
36,598 3
44,701 2
54,598 1
66,686 3
81,450 9
99,484 3
121,510
148,413
181,274
221,406
270,426
331,061
403,429
е~х
1,0000
0,818 7
0,6703
0,548 8
0,449 3
0,367 9
0,301 2
0,246 6
0,201 9
0,1653
0,1353
0,110 8
0,0907
0,074 27
0,060 81
0,049 79
0,040 76
0,033 37
0,027 32
0,022 37
0,018 32
0,015 00
0,012 28
0,01005
0,008 23
0,006 74
0,005 52
0,004 52
0,003 70
0,003 03
0,002 48
сЪх
1,000 0
1,020 07
1,081 07
1,185 47
1,337 43
1,54308
1,81066
2,150 90
2,577 46
3,107 47
3,762 20
4,567 91
5,556 95
6,769 01
8,252 73
10,0677
12,286 6
14,998 7
18,312 8
22,361 8
27,308 2
33,350 7
40,731 6
49,747 2
60,759 3
74,209 9
90,6397
110,705
135,215
165,532
201,716
sh*
0,000 0
0,201 34
0,410 75
0,636 65
0,88811
1,175 20
1,509 46
1,904 30
2,37557
2,942 17
3,626 86
4,45711
5,466 25
6,694 73
8,19193 •
10,017 9
12,245 9
14,965 4
18,285 5
22,339 4
27,289 9
33,3357
40,719 3
49,737 1
60,751 1
74,203 2
90,634 2
110,701
135,211
165,529
201,713
7.2. ИНТЕГРАЛЬНЫЙ СИНУС И КОСИНУС
7.2.1. Определение. Формулы, определяющие интегральный синус и
косинус, имеют следующий вид:
х
Si х = / —-,— dt (интегральный сииус х);
о
со
Ci х — — / —-.— dt (интегральный косинус х)
X
Отметим, что данное определение Ci x пригодно только для положи-
положительных значений х *).
Часто интегральный синус определяют формулой
s\x = —
*) Если переменную х считать вещественной.
7.2] ИНТЕГРАЛЬНЫЙ СИНУС И КОСИНУС 357
Так как
со
/' sin t ,, те
J
t "- — 2 '
о
то оба определения интегрального синуса отличаются на величину -=¦:
Si х = ^ -f si x.
7.2.2. Разложение в степенной ряд. Интегрируя от нуля до х разло-
разложение в ряд функции S" -, легко получить разложение в степенной ряд
функции Si х. Находим
„ «3 v-5 ~2Я+|
С], •* •* I •* _!_/• 14"
al* 1 11 10 1 Т К . К ¦ • • • I \ ' >
Ы! 3-3!^5-5! •••-rv *; Bл+1)Bл4-1)!
Разложение в степенной ряд функции Ci x будет рассматриваться
в п. 8.3.19. Оно имеет вид
> 2л Bл)!
^обозначает постоянную Эйлера, см. п. 7.4.1). Заметив, что
X
х*
2-2! 4.
можно написать
х
1 — cos t
— f
dt.
На основе полученных разложений в степенной ряд легко изучить
поведение функций Si x и Ci x при малых значениях переменной х. Функ-
Функция Six для таких х практически совпадает с функцией х. а функция Cix —
с функцией т + In х.
7.2.3. Разложение в асимптотический ряд. Повторно интегрируя по
частям линейную комбинацию
Ci x--\-Jsix = — j ~ dt
X
и приравнивая вещественные и мнимые части, получаем
оо со
Six—™ C0SX Vr \\" Bл)! sinx
ых~т __^(—i) -
r2« + I
/1=0 " " л = 0
сю со
s'n х у , )И Bи)! cosjcV, ,чл Bя+1)!
Ci х
л = 0 " " л = 0
Эти соотношения позволяют изучить поведение функций Si x и Ci x при
больших значениях х.
358 СПЕЦИАЛЬНЫЕ ФУНКЦИИ
7.2.4. Графики функций Si х и Ci л; (рис. 7.8).
+2,0
Н,0
0,0
-1.0
W 12 3 4
Рис. 7.?.
7.2.5. Таблицы функций Si x и Ci x.
[ГЛ. VII
у
/
/
1
I
/
i
1
/
/
t
*
/»
¦Ьц,
С
,9
LJ
fC
¦МП
«**
--
¦**
Si A"
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
+0,000 000
- -0,010 000
- -0,019 999
--0,029 998
+0,039 996
--0,049 99
--0,059 99
--0,069 98
—0,079 97
--0,089 96
+0,099 94
+0,10993
+0,119 90
+0,129 88
+0,139 85
+0,149 81
+0,159 77
+0,169 73
+0,179 7
+0,189 6
+0,199 6
+0,209 5
+0,219 4
+0,229 3
+0,239 2
+0,249 1
--0,259 0
--0,268 9
—0,278 8
--0,288 6
— сю
—4,028 0
—3,334 9
—2,929 6
—2,642 1
—2,419 1
—2,237 1
—2,083 3
—1,950 1
—1,832 8
—1,727 9
—1,6331
—1,546 6
—1,467 2
—1,393 8
—1,325 5
—1,261 8
—1,202 0
—1,145 7
—1,092 5
—1,042 2
—0,994 4
—0,949 О
—0,905 7
—0,864 3
—0,824 7
—0,786 7
—0,750 3
—0,715 3
—0,681 6
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0.55
0,56
0,57
0,58
0,59
+0,298 5
- -0,308 3
--0,318 2
- -0,328 О
--0,337 8
+0,347 6
--0,357 4
--0,367 2
--0,377 0
--0,386 7
+0,396 5
--0,406 2
—0,415 9
--0,425 6
--0,435 3
—0,445 0
--0,454 6
--0,464 3
--0,473 9
+0,483 5
—0,493 1
--0,502 7
--0,512 3
--0,521 8
--0,531 3
—0,540 8
--0,550 3
--0,559 8
--0,569 3
--0,578 7
—0,649 2
—0,617 9
—0,587 7
—0,558 5
—0,530 4
—0,503 1
—0,476 7
—0,451 1
—0,426 3
—0,402 2
—0,378 8
—0,356 1
—0,334 1
—0,312 6
—0,291 8
—0,271 5
—0,251 7
—0,232 5
—0,213 8
—0,195 6
—0,177 78
—0,160 45
—0,143 55
—0,127 07
—0,110 99
—0,095 30
—0,079 99
—0,065 04
—0,050 45
—0,036 19
7.2]
ИНТЕГРАЛЬНЫЙ СИНУС И КОСИНУС
359
Продолжен ие
X
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67 .
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8.
1,9
2,0
Si*
+0,588 1
+0,597 5
+0,606 9
+0,616 3
+0,625 6
+0,634 9
(-0,644 2
^0,653 5
-0,662 8
-0,672 0
+0,681 2
+0,690 4
+0,699 6
+0,7087
+0,717 9
+0,727 0
+0,7360
+0,745 1
+0,7541
+0,763 1
+0,772 1
1-0,481 1
-0,790 0
4),7989
+0,807 8
+0,816 6
+0,825 4
+0,834 2
+0,8430
+0,851 8
+0,860 5
-
Ц),869 2
-0,877 8
-0,886 5
-0,895 1
+0,9036
+0,912 2
+0,920 7
+0,929 2
+0,937 7
+0,946 1
+1,028 7
+1,1080
+1,1840
+1,256 2
+1,324 7
+1,389 2
|-1,449 6
-1,505 8
-1,557 8
-1,605 4
Си
—0,022 27
—0,008 675
+0,004 606
+0,017 58
+0,030 26
+0,042 65
+0,054 76
+0,066 59
+0,078 16
+0,089 46
+0,100 51
+0,11132
+0,121 88
+0,132 20
+0,142 30
+0,152 16
+0,161 81
+0,171 24
+0,1805
+0,189 5
-
_
-
М),198 3
Ю.206 9
Ц),215 3
Ю.2235
+0,231 6
+0,239 4
+0,247 1
+0,254 6
+0,261 9
+0,269 1
+0,2761 -
+0,282 9
+0,289 6
+0,296 1
+0,302 4
+0,308 6
+0,314 7
+0,320 6
+0,326 3
-i-0,331 9
4-0,337 4
+0,384 9
+0,420 5
+0,445 7
+0,462 0
4-0,470 4
+0,471 7
+0,4670
+0,456 8
+0,441 9
4-0.423 0
X
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
6
7
8
9
10
11
12
13
14
15
20
25
30
35
40
45
50
55
60
65
Si*
+1,648 7
1-1,6876
-1,722 2
-1,7525
-1,778 5
+1,800 4
-1-1,818 2
+1,8321
+1,842 2
+1,848 7
И ,851 7
-1,851 4
-1,848 1
-1,841 9
-1,833 1
_
-
-
-
-
1,821 9
1,808 6
1,793 4
7-тс с;
1,758 2
+1,738 7
+1,7184
+1,697 3
+1,675 8
+1,654 1
1-1,632 5
-1,6110
_
_
-
-
-
-
-
,590 0
1,569 6
1,549 9
1,424 7
1,454 6
1,574 2
,6650
1,6583
+1,578 3
+1,5050
+1,499 4
+1,556 2
+1,618 2
_
_
_
_
-
И ,548 2
-1,531 5
-1,566 8
-1,596 9
Ц,587 0
-1,558 7
-1,551 6
-1,570 7
1-1,586 7
-1,579 2
С1*
+0,400 5
+0,375 1
+0,347 2
+0,317 3
+0,2859
+0,253 3
+0,220 1
+0,186 5
+0,1529
+0,1196
-1-0,086 99
4-0,05526
+0,024 68
—0,004 518
-0,032 13
—0,057 97
-0,081 90
—0,1038
-0,1235 -
—0,141 0
-0,1562
—0,169 0
—0,179 5
—0,187 7
—0,1935
—0,197 0
—0,1984
—0,197 6
—0,194 8
—0,1900 '
—0,068 06
+0,076 70
+0,1224
+0,05535
—0,04546
—0,089 56
—0,049 78
+0,026 76
+0,069 40
+0,046 28
+0,044 42
—0,006 85
—0,033 03
—0,01148
+0,019 02
+0,018 63
—0,005 63
—0,018 17
—0,004 81
+0,012 85
360
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Продолжение
X
70
75
80
85
90
95
100
ПО
120
130
140
150
160
170
180
Si*
+1,551 6
+1,558 6
+1,572 3
+1,582 4
+1,575 7
+1,5630
+1,552 2
+1,579 9
+1,564 0
+1,573 7
И ,572 2
-1,566 2
-1,576 9
-1,565 3
-1,574 1
С\х
+0,010 92
—0,005 33
—0,012 40
—0,001 935
+0,009 985
+0,007 110
—0,005 149
—0,000 320
+0,004 781
—0,007 132
+0,007 011
—0,004 800
+0,001 409
+0,002 010
—0,004 432
X
190
20Э
300
40,)
500
600
700
800
900
103
10*
105
106
10?
ОТ)
Si*
--1,570 4
-1,558 4
-1,570 9
1-1,572 1
-1,572 6
+1,572 5
+1,572 0
+1,5714
+1,570 7
+1,570 2
+1,570 9
+1,570 8
+1,570 8
+1,570 8
я/2
Cijc
+0,005 250
—0,004 378
—0,003 332
—0,002 124
—0,000 932 0
+0,000 076 4
+0,003 778 8
+0,001 118
+0,00.1 109
+0,000 826
—0,000 030 6
+0,000 000 4
—0,000 000 4
+0,0
0,0
7.2.6. Положение экстремумов функций Cix и
X
те
0,5
1,5
2,5
3,5
4,5
5,5
6,5
7,5
Мах
С\х
Min
+0,472 00
—0,198 41
+0,123 77
—0,089 554
+0,070 055
—0,057 501
+0,048 742
—0,042 292
X
—
*
8,5
9,5
10,5
11,5
12,5
13,5
14,5
15,5
Max „
Cix
Min
+0,037 345
—0,033 433
+0,030 260
—0,027 637
+0,025 432
—0,023 552
+0,021 931
—0,020 519
X
1
3
4
5
6
7
8
Max
SI x
Min
+1,85194
-1,418 16
-1,674 76
-1,492 161
+1,633 964
+1,518 034
+1,616 085
+1,531 131
X
—
r.
9
10
11
12
13
14
15
Max
S\x
Min
+1,605 076
+1,539 029
+ 1,599 685
+1,54-4 307
+1,595 252
+1,54a 083
+1,591 997
7.3. ФУНКЦИЯ ВЕРОЯТНОСТИ ОШИБОК
7.3.1. Определение. Функция вероятности ошибок Ф(х) >) определяется
интегралом
Рассмотрим функцию Гаусса
Она изображается кривой, представленной на рис. 7.9. Площадь, заключен-
заключенная между кривой ЧГ(лг) и осью абсцисс, равна единице. Действительно,
•) Ее часто называют интегралом вероятности ошибок или, просто, интегралом
вероятности. Функция Ф (х) обозначается также через erf x (error mnction).
7.3] ФУНКЦИЯ ВЕРОЯТНОСТИ ОШИБОК
полагая х2=2и, имеем
-ьоо со со
1 Г -— /"9~ Г - — 1 /" -i
—1=. / е 2 dx=y - е 2 dx = ~ / е-«и 2 da.
-со О О'
Согласно формуле C) из п. 7.4.1, получаем
со
361
что и требовалось доказать.
Площадь между кривой Ф(х) и осью абсцисс слева от абсциссы х обо-
обозначается через II (л;). Следовательно,
Обе функции Ф и П играют большую роль в теории вероятности. Пер-
Первая из них часто' используется при анализе возмущений, распространяющихся
по линиям передачи. Полезно установить зависимость между функциями ФиП,
так как функция П подробно затабулирована.
Если положить t \^2 = и, то
Так как
то
4г.Л
1
7.3.2. Разложение функции Ф(х) в степенной ряд. Достаточно про-
проинтегрировать разложение в ряд е*'1 от нуля до х, чтобы получить степен-
степенной ряд
)ЛГ
2 |;( л:-
„2л+ 1
2!5
сходящийся при любом х.
7.3.3. Разложение в асимптотический ряд функции 1—Ф(д;I).
Имеем
( со X
9
j
(
±^| / e-t'dt— / е-'2
тс I -/ ./
= 7Г./ •"""•
') Функция 1 — Ф(лО обозначается также через erfc x (complementary error
{unction).
362
Положим Р=г и:
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
СО j X' j
_<D(je) = .JL f e-au~~du = ~ f a"
C2 CO
Повторно интегрируя по частям, получаем
u"Id(e'a)'
Отсюда
1-
?-*'
1 , 1-3 1-3-5
2,х2 *2^х* 23xfi
•••+(-1)
4- ...
л-i 1-3-5,
— 3)
Отношение абсолютных величин двух последовательных членов равно
л?~7 - Оно близко к единице, если п близко к х2. Ясно, что член асим-
асимптотического разложения 1—Ф(л:)*), соответствующий этому и, имеет наи-
наименьшую абсолютную величину. Именно на нем и следует остановиться,
чтобы получить наименьшую ошибку при вычислении 1—Ф(х).
Замечание. В примере 3 п. 2.2.8 мы показали, что функция Гаусса W(x),
представленная на рис. 7.9, обладает свойством быть своей собственной
трансформантой Фурье. Поэтому понятна та важная роль, которую она иг-
играет при изучении спектра сигналов и диаграмм направленности источников
радиоволн.
7.3.4. Выражение функции 1 — Ф (—] через интеграл Коши. В раз-
разложении функции Ф(х) в степенной ряд заменим х на 4-. Получаем
„2л+ 1
n\2in+l B/г+1)
Согласно результатам п. 7.4.3, имеем (я > 0, целое)
1 при г = 0,
О при г = 2п,
(-1)" 1-3... Bл-1)
J
rii-4
2"
при г = zn~\- 1.
Это дает возможность написать
*) Нетрудно доказать, что полученное разложение _^ ' действительно
является асимптотическим (ср. п. 7.01, пример и замечание).
7.'3] ФУНКЦИЯ ВЕРОЯТНОСТИ ОШИБОК
Согласно формуле A0) п. 7.4.5. (см. также рис. 7.12),
363
1 _ 1 f егйг
г('-тГ с^
Отсюда
С Г=0
Функция —e~xVz (х > 0) удовлетворяет условиям леммы Жордана (п. 1.3.14).
Поэтому мы можем также написать
c+jco
-•(*)-? /
7.3.5. Таблица функции Ф(х)=—— j e-pdt*).
X
0,05
0,10
0,15
0,20
0,25
«,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
*(¦*)
0,056 37
0,112 46
0,167 99
0,222 70
0,276 32
0,328 62
0,379 38
0,428 39
0,475 48
0,520 50
0,563 32
0,60385
0,642 03
0,677 80
0,711 15
0,742 10
0,770 66
0,796 91
0,820 89
0,842 70
Д
0,056 37 '
0,056 09
0,05553
0,054 71
0,053 62
0,052 30
0,050 76
0,04901
0,047 09
0,045 02
0,042 82
0,040 53
0,038 18
0,03577
0,033 35
0,030 95
0,028 56
0,026 25
0,023 98
0,021 81
X
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
Ф(*)
0,862 44
0,880 20
0,895 12
0,910 31
0,922 90
0,934 01
0,943 76
0,952 28
0,959 69
0,966 10
0,971 62
0,976 35
0,980 37
0,983 79
0,986 67
0,989 09
0,991 11
0,992 79
0,994 18
0,99532
0,019 74
0,017 76
0,015 92
0,014 19
0,012 59
0,011 11
0,009 75
0,008 52
0,007 41
0,006 41
0,005 52
0,004 73
0,004 02
0,003 42
0,002 88
0,002 42
0,002 02
0,001 68
0,001 39
0,001 14
*) В таблице указаны также первые разности Д.
364
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
л.
7.3.6. График функции Ф{х) = ~ j e~t2 dt (рис. 7.10).
Ф(Х)
1
0,9
0,6
0.7
0,6
0,5
0,4
0,3
0,2
0,1
О
/
/
/
/
/
*>*
и**
ж—
OJ0,20,30,40,5Ц80,70,80,9 1 1,11,2 1,3 1,4 1,51,61,71,81,9 2
Рис. 7.10.
X
7.3.7. Интегралы Френеля. Интегралы Френеля — функции C(v) и S(V) —
могут быть определены через функцию вероятности ошибок по формуле
cos -iy-dt, SD)— J s'\n-y-dt. Параметриче-
0 0
ские уравнения
C
изображают на плоскости CS (С — ось абсцисс и 5 — ось ординат) двойную
спираль, симметричную относительно начала координат. Она называется
клотоидой или спиралью Корню (рис. 7.11). Градуировка клотоиды как
функции параметра ч легко осуществляется. В самом деле, длина дуги от
начала координат до точки с координатами C(v), 5(v) как раз равна v:
Легко проверить, что кривизна клотоиды меняется пропорционально длине дуги,
т. е. пропорционально v. Координаты асимптотических точек клотоиды равны
С(±оо)==5(хсо)= ±1.
Разложения функций S(ч) и С(v) в степенной ряд легко получить, ис-
исходя из разложений синуса и косинуса. Имеем
>"И'
=2 <-»" A
я=0
1
„4П+3
Bл+1)! 4/г + З ¦
7.41
ГАММА-ФУНКЦИЯ
Асимптотические разложения интегралов Френеля
07
0,6
0,5
0,4
0,3
0,2
OJ
-0,3-0,7-0,6-0,5-0,4 -0,3-0,2-0,7
til iiii
/
/ Ц
Г Т (Jf
0,5
г
*m
is
-*¦— ¦ о
-oj-
-0,2
-о,з
-0,4
\ -0.5
1 -0,6-
-0,7
t
S(v)
i
\
, ) у
0,1 0,2 0,3
365
получаются многократным
({
7
0,5
^*
3,5 t
C(v)
0,4 0,5 0.6 0,7 0,3
Рис. 7.11.
интегрированием по частям линейной комбинации
v)
-/;*«-№-/;*
dt
с последующим приравниванием вещественных и мнимых частей. Получаем
cos
sin-
• — В (v)
sin ¦
2
cos •¦
где асимптотические разложения функций .<4(v) и В(ч) имеют вид
n"+1 Ь5---Dя+1> вол
л=о
л=0
7.4. ГАММА-ФУНКЦИЯ
7.4.1. Определение. Гамму-функцию Г (z) можно определить для всех
вещественных или комплексных значений z с помощью бесконечного произ-
произведения
366 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII •'
В этой формуле 7 обозначает постоянную Эйлера. Она определяется фор-
формулой
1— Пт {1+2-+ ... -+• — — Intnl.
т -> со I л '" >
Очень возможно, что постоянная Эйлера — трансцендентное число, хотя это
еще не доказано строго. Первые цифры ее равны
т = 0,57721566490 . ..
Хорошее приближение к f дается простой формулой
Т«1(#70 — 0 = 0,5772173 ...
Другое определение гамма-функции можно дать с помощью соотношения
Нт , , ,? т* , ч ¦ B)
Действительно, формулу B) можно записать в виде
! lim
±±
откуда
г^т=г lim m-*.-TT(l-\-—\.
И m ->• оо ш = 1 ^ *" ^
' Умножим правую часть этой формулы на следующий множитель, равный
единице:
A 1 »
1 + -^+... + —)г -_-_-
...w с 1 т' • I I e m = 1.
т. -> uo J- J
т=1
Тогда
/, 1 1 \ оо ,
1 . П +тг + • • • -< In от I г тпг
Yjw— z lim e • X_i_
-*¦ l*i m -> со ^_^
Заметив, что величина l+^--f- ... Ч \пт стремится к -р мы прихо-
приходим к формуле A). Отсюда вытекает справедливость формулы B).
Можно также определить гамма-функцию через определенный интеграл:
со
Г0г)= / e-'t^dt, если RB)>0. C)
о
Для доказательства сначала вычислим
Положим — = т. Тогда
п
о
Интегрируя по частям, получаем
1
/A -
г .,
О и О
.7.41' ГАММА-ФУНКЦИЯ 367
Если R(?)>0, то внеинтегральный член равен нулю. Поэтому
1 к
/A -x)V-'dx = ^ Г
о . о
о
1
dx.
о
т. е.
-¦? 1 /' z-i-n-i
г-\- п — 1 ,/ (г + Д —
О
Следовательно,
(г 4-1)-.-(г 4-л) "
Переходя к пределу при п->оо, получим
со
/->ГB)= J g-'f-^dz.
о
7.4.2. Свойства гамма-функции. Согласно формуле B). имеем
Следовательно.
Отсюда получаем формулу
D)
Эта формула, повторно примененная в предположении, что г = я (я — целое
положительное), дает
Г(я-4-1) = я(я—1) ... 2- 1 •
Но
Игл "•"; =1,
поэтому
Г(я-+-1) = я! E)
Из-за этого свойства гамма-функцию иногда называют факториальной.
Докажем теперь следующую формулу:
368 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
¦Согласно формуле A), имеем
Г(г)Г(-г) ^ ~>~
По формуле D)
Следовательно,
1 °°
Г(г)ГA-г) =2II
m=\
В п. 2.1.4, была доказана формула
СО
sin z= z TT (l ^Л.
Сравнивая два последних выражения, получаем формулу F). Заменив в фор-
формуле F) z на z -f- -ту , найдем
7.4.3. Некоторые значения функции T(z). Если в формуле F) считать
z = y > т0
¦откуда
Из формулы A) видно, что при z целых неположительных гамма-функ-
гамма-функция бесконечна: Г( — «)=±оо.
Формула D), повторно примененная, дает
где п — целое число. Положив z = n-{-k, имеем
Т (п-\- k~{- \)--={п-\~ k)(n-\~ k — 1) ... (A-f-1) Г (Л 4-1)-
При k = — у получаем
Заменим в формуле G) 2 на п. Тогда формула (8) позволяет написать
Весь этот набор частных значений гамма-функции с учетом формулыГ(я-|-1)—и'
лозволяет построить график функции Г(г-\~1) для вещественных z (см.
рис. 7.13I).
7.4.4. Логарифмическая производная гамма-функции. Эта производная
равна, по определению *),
Г'(+1
') Асимптотическая формула для л! дается формулой Стирлинга (п. 9.1.4).
*) Часто полагают ф (г) — ^ (г) '
7.4] ГАММА-ФУНКЦИЯ
Используя формулы A) и D), найдем
369
Отсюда можно получить соотношения:
ф (—
— 1) Ч-
и частные значения
(9)
—i] = — T — 21n2 = —1,9635 ...
7.4.5. Представление гамма-функции через интеграл Коши. Рассмот-
Рассмотрим интеграл
, J_ Г
1= 2nj J
взятый по контуру С, изображенному на рис. 7.12. Контур С состоит из
малой окружности и двух берегов разреза у
вдоль отрицательной вещественной полуоси.
Интеграл по окружности (z = re^) равен .
'J— 2*\/
er(cose+/sine)-yver-v
Разрез
Рис. 7.12.
Если R(v)<0, то этот интеграл стремится к нулк» вместе с г. На нижнем
берегу разреза (z = xe~JK)
2 2kj ,]
На верхнем берегу разреза
Отсюда
оо
Ж±ГЛ
J J *"•
¦их.
*) Используем разложение ctg яг (п. 2.1.4.).
24 А. Анго
370
Так как по формуле F)
то
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
{ '
J J_ Г
v-fl) 2я/ ./
еЧг *)
A0)
7.4.6. Связь между эйлеровыми интегралами первого и второго рода.
Эйлеров интеграл первого рода (бета-функция) — это функция двух положи-
положительных переменных р и q вида
В(р, q) =
Эйлеровым интегралом второго рода
называют гамма-функцию.
Полагая х = cos26, можно бета-
функцию записать в виде
(И)
В формуле C) заменим z на
я и i на у2, а затем z на от и t
на х2. Имеем
со
Г (я) = 2 Г yin-le-^dy,
о
со
Рио, 7.13. Г(от)==2 Г х2т-1е-*Чх.
о
Перемножим эти формулы:
со со
Г(от)Г(я)=4 J J x^-^^e-x'-y'dxdy.
о о
Получили двойной интеграл, распространенный на первый квадрант коорди-
координатной плоскости ху.
Перейдем к полярным координатам:
-A;==pcos6, у = р sin 6, dx dy = ds = p dpdb.
Имеем ж
J со .
i-n^m-If) ein2n — If) /7f) V 9 I n2(in+n) — la— p1 /Vn
0 0
Согласно формуле A1), первый удвоенный интеграл равен В(от, я); со-
согласно формуле C), второй удвоенный интеграл равен Г(от-)-я). Таким об-
образом, получаем соотношение между функциями В и Г:
и.» -ч— rC»)r(«) A2)
*) Правая часть этой формулы при любом контуре С (г > 0) представляет целую
функцию. Поэтому формула A0) верна при любом v.
7-4]
ГАММА-ФУНКЦИЯ
371
7.4.7. График функции у = Г(х-\-1) (рис. 7.13). Координаты единст-
единственного минимума с положительной абсциссой равны
* = 0,46163 ....
7.4.8. Таблица функции
= 0,88560...
X
0,0
1
2
3
4
5
6
7
8
9
1,0
1
2
3
4
5
6
7
8
9
2,0
1
2
3
4
5
6
7
8
9
3,0
1
• 2
3
4
5
6
7
8
9
я
0,9
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,8
2
3
4
5
6
7
8
10
11
13
15
10X1
10X2
0
514
182
975
873
862
935
086
314
618
000
465
018
667
422
293
296
447
765
274
000
198
424
683
981
323
717
171
694
299
000
813
757
855
136
632
381
431
784
067
. 1
943
474
156
960
868
866
947
106
341
652
043
516
078
738
503
388
404
571
907
436
019
219
448
711
*013
360
760
220
751
365
076
901
859
975
275
795
572
655
810
098
2
888
436
131
946
864
870
959
126
368
688
086
568
140
809
586
483
514
696
*051
600
037
240
473
740
*046
398
803
269
808
431
153
990
963
*09б
417
960
766
882
837
129
3
835
399
108
934
860
876
972
147
397
724
131
621
202
882
670
580
625
824
*196
767
057
262
498
768
*079
436
846
320
867
499
231
*081
*069
*219
561
*128
962
*113
864
161
4
784
364
085
922
858
882
986
168
426
761
176
675
266
956
756
678
738
953
*344
936
076
284
524
798
*112
474
891
371
926
567
311
*173
*176
*344
707
*299
*162
*348
891
194
5
735
330
0S4
912
857
889
*001
191
45S
799
222
730
330
*031
842
777
852
*084
*494
*108
095
307
549
827
*146
513
936
423
986
637
391
*267
*285
*471
855
*472
*366
*586
920
227
6
687
298
044
902
•856
895
*017
214
487
837
269
786
395
*107
930
878
968
*216
*646
*281
115
330
575
857
*181- -
553
981
476
*047
707
473
*362
*396
*600
*005
*648
*572
*829
948
260
7
642
267
025
893
856
905
*033
238
518
877
316
842
462
*184
*019
981
*085
¦351
¦799
*457
136
353
602
888
' *216
593
*028
529
*108
779
556
*458
*508
*731
*158
*827
*782
**075
977
294
8
597
237
007
885
857
914
*050
262
551
917
365
900
529
*262
*109
*084
*204
*487
*955
*636
156
376
629
918
*251
634
*075
583
*171
851
640
*556
*622
*864
*314
**009
*995
**325
*005
329
9
555
209
*990
879
859
924
*068
288
584
958
415
959
598
*341
*201
*190
*325
*625
**из
*816
177
400
65S
950
*287
'675
*122
638
*235
925
726
*656
*73&
*999
*471
**194
**211
**579
*036
364
Столбец, помеченный буквой га, дает первую или две первые цифры
искомого числа. Так, например, Г A-f-1,23)= 1,1 | 202.
Значок * означает, что следует брать число га, увеличенное на единицу
(для х > 2) или на 0,1 (для х < 2). Аналогично значок ** означает, что сле-
следует брать число га, увеличенное на две единицы (для х > 2) или на 0,2
(для х<2).
24*
372 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Например, ГA + 3,72)== 15, | 882, ГA +3,73)= 16,1113 и ГA +3,77)=
= 17, | 075; ГA + 1,81)=1,6|907, ГA + 1,82)=1,7|051 и ГA + 1,89) =
= 1.8 1113.
В последних двух строках таблицы число п равно 1 или 2, а цифра 10
является множителем. Так, например, ГA+3,90)= 10 X 2, | 067 = 20,67.
Замечание. Повторное применение формулы D) позволяет произво-
производить вычисление ГA+х) для любого х.
7.5. ФУНКЦИИ БЕССЕЛЯ
Функции Бесселя первого и второго рода
Функции Бесселя первого и второго рода порядка ч представляют собой
частные решения следующего дифференциального уравнения:
Если /,(z) и Ys(z)— два независимых решения уравнения A3), то общий
интеграл уравнения запишется в виде
z). A4)
Здесь А к В означают две произвольные постоянные.
7.5.1. Определение функции первого рода. Функции Бесселя первого
рода, обозначаемые как У„(.г), определяются с помощью следующего ряда
(см. п. 6.2.10):
y 2x
х=о
Если мы подставим этот ряд в дифференциальное уравнение A3) и прирав-
приравняем нулю коэффициенты при z?+l, то получим, придавая X последовательные
значения 0, 1, 2, .... X—2,
(Р2 —v2)flo=O,
J-v2]fl1=:0, A6)
Если число v вещественное, то будем считать его положительным, если оно
комплексное, то предположим, что R(v)>0. Пусть а0ф0. Тогда из первого
уравнения A6) находим р= ±v.
Первый случай: p = v. Все нечетные коэффициенты равны нулю;
четные коэффициенты вычисляются через а0, который остается неопределен-
неопределенным. Обозначая \=2г, имеем
a-ir — ao
Для функции Бесселя первого рода /,B) порядка v произвольный коэффи-
коэффициент а0 принято выбирать в виде
1
а0 = — .
Так как
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 373
получим
_ , . / Z \ \1 (—1) ( Z \ /1Т\
/ (?\ \ ь i — I (lit
v ^ ' — I о I ^л r\ р /г. i f л_ 1\\2/x vxl/
Если v равно целому числу га, то имеем
г=0
В частном случае при га = 0
Второй случай: р = — ч. Четные коэффициенты а2г, а2г_2 свя-
связаны формулой
2г B/- — 2м) а2г + а2г-2 = 0>
а нечетные коэффициенты — формулой
Br+I)Br+l — 2v)a2r+1 + a2r_, = 0.
Если v не равно половине нечетного числа, то все нечетные коэффициенты
равны нулю. Аналогично предыдущему находим
г=0
Если v равно половине нечетного числа: ч = -^Bт~\- 1), то нечетные коэф-
коэффициенты, начиная с индекса г=т, не равны нулю. Этот случай будет особо
рассматриваться в п. 7.5.15.
Рассмотрим вариант ао = О. Тогда при at ф 0 второе уравнение A6) дает
р= ±v—1 и все четные коэффициенты в A6) равны нулю, а все нечетные
выражаются через аг. При соответствующем выборе а1 мы приходим к ре-
результатам, не отличающимся от формул A7) и B0).
7.5.2. Соотношение между J,(z) и /_„(?). Рассмотрим, в каких слу-
случаях решение Jv(z), представляемое формулой A7), и.У_,(г), представленное
соотношением B0), будут линейно независимы.
Предположим, что v не равно целому числу. Тогда функция F(r-f-l—v)
конечна при любых значениях г. Если стремить z к нулю, то функция 7V (z)
также будет стремиться к нулю. Напротив, функция У_у(г) будет при этом
2
/ z
бесконечно возрастать из-за наличия членов вида(-^-1 , показатель степени
у которых отрицателен по крайней мере у одного или нескольких первых
членов. В этом случае (v — не целое число!) оба решения 7V(z) и J_y(z),
очевидно, линейно независимы. Общий интеграл уравнения A3) может быть
написан в виде
z). B1)
Предположим теперь, что v равно целому числу га. Тогда формула B0)
принимает вид
(z\
) (\
r=0
374 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Первые члены этого ряда будут нули, пока г — п равно целому отрицатель-
отрицательному числу. Величина (г — и)! станет конечной при
/¦ = «, га-1-1 п-\-г'. ...
\
Если опустить первые нулевые члены, то предыдущая формула будет
выглядеть так:
, _(?_Y" V (-1)г'+л (?\2г'+2п
-n~\2) Li (n + r')\r'l \2)
r'=0
Отсюда
J_n(z) = (—l)"Jn(z). Г22)
Теперь обе функции Jn и J_n уже не будут линейно независимы, и общий
интеграл уравнения A3) нельзя написать в виде
Za(z) = AJa(z)+BJ_a{z).
Для целых значений индекса следует найти другой частный интеграл, кото-
который был бы линейно независим от Jn(z).
7.5.3. Определение бесселевой функции второго рода. Рассмотрим
функцию
B3)
Если v — не целое число, то это выражение представляет собой частный
интеграл дифференциального уравнения A3). Если устремить v к целому
числу и, то правая часть в B3) становится неопределенной. Раскроем эту
неопределенность по правилу Лопиталя. Получим
Пользуясь разложением в ряд A7), вычислим производную функцию
по индексу v;
оо
г_
г=0
(гУ+2г
V2)
Устремим v к целому числу. Тогда, в силу формул E) и (9), получим
г=0
B5)
Используя формулы B0) и F), выражение для функции 7_,(г) представим
в виде
л-1
^ V 2 ,1
где п — ближайшее целое число, большее ч.
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 375
Продифференцируем B6) по индексу v:
л-1
r=0
B7)
Устремим v к ге. Тогда формула B7) примет вид
л(г) . , М1| г , V, ш (л —г —1)! (z"~n+2r
r=0
r=0
Подставим выражения B5) и B8) в формулу B4). Учитывая соотноше-
соотношение B2), получим для Yn(z) следующее разложение в ряд, показывающее,
что эта функция (она называется функцией Вебера) линейно независима от
л —1 „
г=0
г=0
B9)
При /¦ = б^йта суммой в фигурных скобках надо понимать выражение
Можно было действовать и другим способом. Принимая во внимание из-
изложенное в п. 6.2.11, легко построить решение уг(г), линейно независимое
от y2 = J^(z), по формуле
При любом v модуль yt(z) бесконечно возрастает, если z стремится к нулю.
Отсюда следует, что у1 (z) и Уч (z) линейно независимы.
Нетрудно показать, что можно подобрать числа А и В таким образом,
чтобы уг(г) не отличалась от определенной выше функции К, (г).
Замечание. В качестве второго решения дифференциального уравне-
уравнения A3) используется также функция Неймана Yv, которая связана с функ-
функцией Вебера соотношением
lz). C0)
376 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
7.6.4. Рекуррентные соотношения. Продифференцируем формулу A7)
по z. Получим следующие выражения:
(—IV 1гУг+ч
оо _
Г=0
ОО
zj[ (z) = vyv (z) — z ^ -^^
Отсюда найдем первую рекуррентную формулу:
zJ-, (z) = vy, (г) — гУ,+1 (z). C1)
Точно таким же образом получим
zj[ (z) = — vyv (г) 4- 2/.-1 (г). ' C2)
Вычитая и складывая C1) и C2), найдем
2 — У,(г) = У,+1(г)+У,_1(гг), C3)
2У^ (г) = У,_1 (г) — У»+1 (z). C4)
Для v = 0 формула C1) примет вид
C5)
Нули функции Ji(z) совпадают с максимумами и минимумами JQ(z).
Применяя формулу B3), определяющую бесселеву функцию второго рода
К, (г), легко удостовериться, что эта функция удовлетворяет тем же рекур-
рекуррентным соотношениям, что и функция УД.г). Значит, так же будет обстоять
дело со всеми линейными комбинациями вида AJ^{z)-\-B\\(z), иначе говоря,
с общим решением дифференциального уравнения A3). В частности, рекур-
рекуррентным соотношениям C1)—C4) удовлетворяет функция Неймана Yv(z),
определенная формулой C0), и функции Ханкеля, определенные ниже соот-
соотношениями F2).
7.5.6. Применение рекуррентных соотношений к вычислению неко-
некоторых интегралов, а) Рассмотрим интеграл
Продифференцируем произведение 2vy, (z):
Сравнив с формулой C2), мы можем записать правую часть в виде
Отсюда, интегрируя от zQ до z, находим формулу
г
Г zV4_l{z)dz=[z^(z)]z. C6)
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 377
Таким же образом, но применяя на этот раз формулу C1), получаем
+ -[z-^(z)]2Zo. C7>
б) Рассмотрим интеграл
Интегрируя обе части формулы C4), в которой v заменено на v —|— 1,
получим
Аналогично
и т. д.
Складывая почленно всю эту цепочку равенств, найдем
г
J v 4+1 v+3
О
Ряд, фигурирующий в правой части, очень быстро сходится. Соображения,
излагаемые в конце п. 7.5.21, позволяют определить номер, начиная с кото-
которого члены этого ряда становятся пренебрежимо малыми,
в) Рассмотрим интеграл
г
I = j zmJn (z) dz (тип — целые положительные числа, т > п).
о
Этот интеграл можно записать в виде
г
/= j zm-n-1zn+lJn(z)dz.
о
Проинтегрируем по частям, пользуясь формулой C6):
г
J = [zm-n~l zn+1Jn+1(z)f0 ~(m — n — l)j zm~n-2zn+1Jn+1(z)dz,
0
иначе говоря,
г
J=zmJn+1 (z) — (m—n—l)f z'1 Jn+i(z) dz.
378 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Таким же образом получим
о о
г г
f zm~2Jn+2(z) dz = г«-аУя+3 (z) — (m — n — 5) J z"-*Jn+3 (z) dz.
Если можно найти такое целое число k, чтобы т — k = n-\-k-\-\, т. е.
«ели т — п — нечетное число, то мы снова приходим к интегралу, вычислен-
вычисленному в а). Но если т — га — четное число, то мы вынуждены продолжить
вычисление до такого номера k, чтобы т — k = 0. При этом мы приходим
к интегралу от Jm+n (z), способ вычисления которого был показан в б).
7.5.6. Интегралы Ломмеля. Рассмотрим два дифференциальных урав-
уравнения:
Умножим первое на —, а второе на —. После вычитания получим
d2x rf2y , dx dy .,,
иначе говоря,
Проинтегрируем обе стороны последнего равенства от нуля до z. Если в по-
полученной формуле заменить у на J^(kz), a x на J^ilz), то найдем при
(ЬЪ /2\ Г / (Ь?\ 1 Aг\ ? И? ? J 1 (Ь?\ " ( ' / (lz\ -
о
Но
dJ^ (Iz) ,
dz d(lz)
Отсюда
г
j Л (кг) У, (Iz) zdz= k2z_[2 [lJ,(kz) /-, (Iz) — kJ4 (Iz) У, (kz)).
Согласно соотношению C1), имеем
У, (kz) = ~^J~> (kz) — Л-ы (kz),
f, (Iz) = -^- У, (Iz) — У,+1 (Iz).
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 379
откуда
г
fj>(kz)J,(lz)zdz^=-I^=w{kJ^lz)^+1(kz)~ll(kz)J^:(lz)}. Г38)
о
Если бы мы выше подставили в полученную формулу' выражения, вытекаю-
вытекающие из соотношения C2):
X (kz) = — -^т У, (kz) + .A,-1 (kz),
то получили бы
г
f J,(kz)J,(lz) z dz = -gL—lu^lzWikz) — AJ,-i (A«U(te>]. C9)
f
о
Формулы C8) и C9) не годятся, если k — l. В этом случае непосред-
непосредственное вычисление дает
г кг
f z [У, {kz)? dz = ~f z[J4 (z)p dz. Я (v) > -1.
0 . 0
Интегрируя по частям, получим
кг кг
f z[Mz)fdz = ^f-[J,(kz)f — f z*Mz)/,(z)dz.
о о
Учтем, что У, (г) удовлетворяет дифференциальному уравнению A3). Это
дает
— /Л (z) = z2jl (z) + z/, (z) — v2yv (г).
Исследуемый интеграл можно теперь записать в виде
г кг kz ,
f z [Л (kz)f dz = ^ [Л {kz)f + JL J rf (/ [у: (г)]2) _ J!L J rf [у, (г)]2,
о "о о
иначе говоря,
J z [Л (**)]2 ^ = 1 ^ | [X (kz)Y + A - -j?r) [Л (*^)]2}. D0)
Это и есть искомая формула.
Формулы C8) — D0) называются интегралами Ломмеля.
7.5.7. Соотношение между двумя функциями, индексы которых от-
отличаются на целое число. Формула C7), которую можно написать в виде
поможет установить важное соотношение между двумя бесселевыми функ-
функциями, порядок которых отличается на целое число п.
Действительно, если в предыдущей формуле заменить v на v —|— 1, по.
лучим
380 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
или, в сокращенном виде,
и т. д. Постепенно найдем
z-'-»J4+n (*) = (-1)" -^уг {z-% (*)}. D1)
Это и есть искомое соотношение. Точно так же из формулы C6), которую
напишем в виде
получим
{z%(z)} D2)
7.6.8. Применение интегралов Ломмеля к разложению в ряд по бес-
бесселевым функциям. Последовательность функций
Ух Jn (А,х), \Гх Jn (Х2х), .. ., /х Jn (ktx)
в которых Xj, Х2 Хг, ...—корни уравнения У„(х) = 0, представляет
собой последовательность ортогональных функций в интервале @,1)
(см. п. 2.1.2).
Действительно, формула C8) дает
о
Если положить х=1, 1 = )н, k = ~kj, то
1
J Y~Z Jn (ktz) V~Z Jn (XjZ) dZ = 0,
0
Из формулы D0) находим
x
fz{Jn(kz)}*dz = ±x2 { [/„ (kxtf + (l —j^r) [Jn(kx)f}.
При x = 1 и k = \ получим
1
Рассмотрим теперь функцию /(х). Если нам нужно найти разложение
ее в ряд вида *)
2л(^)
то коэффициенты at будут даны выражением
1
2 j xf(x)Jn(klX)dx
*) Этот ряд называется рядом Фурье — Бесселя. Об условиях, которым должна
удовлетворять функция / (х), чтобы ее можно было разложить в ряд Фурье — Бес-
Бесселя, см. [19], гл. 18.
•7.5] БЕССЕЛЕВЫ ФУНКЦИИ 381
Пример. Требуется разложить в промежутке от 0 до 1 в ряд вида
оо
2 й/^о 0-1х) Функцию / {х) = 1. Предыдущая формула дает
1
2 Г xJ0 fax) dx
Исходя из соотношений C5) и C6), получим
h
2 Г lixJ0 fax) d fax) 2 Г xJ0 (x) dx
о о 2
Отсюда ряд будет
, _ 2/0 fax) . 2У0 fax) , 2J0fax) .
Г МОч) "*~ Х2/,(Х2) "Г ' • • "I" V, (X;) "Г •' •
7.5.9. Бесселевы функции первого и второго рода с полуцелым
индексом. Рассмотрим дифференциальное уравнение A3) для частного случая
v = г/2. Тогда это уравнение запишется в виде
Положим y = uz 2. Подстановка дает
Отсюда
и (z) = A cos z -f- В sin z,
у (z) = -у=- (A cos z + В sin z).
Попробуем определить коэффициенты А и В таким образом, чтобы у
совпало с функцией J\ или J \. Так как ,/i@)==0, то коэффициент А
1 ~Т
должен быть равен нулю. Сравнивая разложение в ряд J\ (г)иу(г), получим
Т
V 2
Отсюда
2
Точно такое же вычисление дает для J \:
= /Г-
= ]/^ sin г. D3)
D4)
382 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Если в формуле B3), определяющей К, (z), положим v = i/2. то
Yi_ (z) = — J__i_ (z) = — y~ cos z. D5)
Точно так же
K_i(z)=7i(z)= у ^ sin гг. D6)
Если в рекуррентной формуле C3) приравнять v= ±72> то найдем
Аналогично последовательным применением C3) получим:
.Mz)= j/i [(J;-l)sit
sitiz-f
J.L <z> = Zs [Dsln z + (I" - •)cos г]:
,/\( \ , /105 , 45
z)=|/-[(^r--)sinz + ( +
Пользуясь соотношениями D1) и D2), в которых v соответственно при-
придаются значения 1/2 и —1/2, найдем
/Т" л+- ^" (sin г)
/"о" n+i d" I cos z )
i* '(FrfH—Ь D8)
Если в формуле, B3), определяющей функцию К„(.г), придать v значение
' т0 получим
Кя+1(г) = (— l)"+1-/niB). D9)
7.5.10. Применение бесселевых функций к вычислению интегралов
Френеля. Интегралы Френеля, особенно часто встречающиеся в задачах по
дифракции, были определены в п. 7.3.7 следующими формулами:
ч 1
C(v)= I cos—dt, 5(v)= fsin^dt.
7,5] БЕССЕЛЕВЫ ФУНКЦИИ 383-
Положим ^-=2. После подстановки, учитывая формулы D3) и D4),.
получим
C(v) = -1
6
5(v) = 4/]/4 sin zdz==T
о 6 2
Принимая во внимание метод вычисления, указанный в п. 7.5.5, можно на-
написать
Оба ряда очень быстро сходятся и особенно удобны при вычислении C(v>
и S(y).
7.6.11. Случай, когда индекс равен целому числу v = «. Рассмотрим,
ряд для функции
Lit--\ - --
е2 V t)==e2e 2<_
Так как ряды
е 2<==1 ~2F+2tBF) "~ ¦•• +(~1)Л'7
сходятся абсолютно *), то ряд для произведения равен произведению рядов:
для сомножителей.
Соберем члены при одинаковой степени t. Легко заметить, что коэф-
коэффициент при t" представляет степенной ряд по z, который совпадает с рядом
для функции Jn(z), а коэффициент при t~" совпадает с рядом для J-n(z).
Мы можем, следовательно, написать
•/_„(*)+ ... E2)
или же, в силу соотношения B2),
z г 1 \
л=1
-С'-1)
Функция e2V tJ называется производящей функцией для бесселевых
функций первого рода целого порядка.
*) Ряды сходятся абсолютно для всех х и t, кроме t = 0, когда второй ряд рас-
расходится. Этот случай далее из рассмотрения исключается.
384 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ VTI
Ряд справа сходится при всех z и при всех t^O. Положим t — eW.
После подстановки получаем
2 n
л=1
Группируем в сумме отдельно четные («= 2р) и нечетные члены (п = 2р'—1):
J2p(z)cos2pQ-\-2j 2 V-i (z)s\nBpf — 1)Й.
p=i p'=i
Приравнивая вещественные и мнимые части, находим
ОО
cos(zsin9) = yo(z)+2 2 /2pB0cos2/>9. E3)
Р= 1
со
sin (г sin 8)= 2 2 •/2p'-iC2:)slnB/'' — !)9- E4)
p' = i
Заменяя 9 на -|- — 9, получаем
со
cos (z cos 9) = ./„(*)+ 2 2 (—О^УгрС^со^рЭ, E5)
с»
sin (г cos 9) = — 2 2 (— О"' J2o--i(z)C0SBP'~ l)Q- E6)
Эти формулы дают разложения в ряд Фурье функций, находящихся в левых
частях равенств. Пользуясь классическим способом вычисления коэффициен-
коэффициентов ряда Фурье, умножим обе части уравнения E3) на cos 2kb и проинте-
проинтегрируем от 0 до тс. Тогда, заметив, что все интегралы, содержащие произ-
произведение cos 2?9 cos 2/>9, равны нулю, если кфр, и равны -^-, если p = k,
лолучим
J2k (z) = ~ J cos (z sin 9) cos 2kb d8.
о
Применим этот же способ к формуле E4). Тогда
¦ J2k_1(z) = ^- /* sin (гг sin 9) sin Bfe — I)9d9.
о
Обе полученные формулы можно представить в виде одного соотношения
1С
Jn (z) = -^ / [cos (z sin 8) cos nb -f- sin (z sin 8) sin «0] db =
о
s(«9 — 2rsin8)rf9. E7)
Действительно, если га — четное число, то второе слагаемое в квадрат-
квадратных скобках равно нулю. Если же п — нечетное число, то равно нулю
первое слагаемое *).
*) Интеграл в E7) называется интегралом Бесселя.
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 386
7.5.12. Представление J4(z) через определенный интеграл. Сравнивая
формулы A1) и A2), получим
я
?
1 2 Г cos2"-1 9 sin2p—хв rf9
У C°S 0SU1 °fl0-
0
Положим a = r + -j, C = v -|- -^. Тогда предыдущее выражение можно за-
записать в виде
1С
Т
* ^гт- /" cos2'9 sin2'9 d9.
Если ввести выражение для Г (г -f- v -J- 1) в ряд для У, (г) (формулу A7))
и учесть выражение для rlr-f--j) по формуле (8), то
Сумма под знаком интеграла представляет собой разложение в степенной
ряд функции cos (z cos 9). Отсюда
т
/*sin2v е cos(-^cos 9)tf9'
IE
(гг) = у г-гDУ /"sin* 9 cos (г cos 9) d6. E8)
или
ИЛИ
1С
*(|у fd9. E9)
Считая и = cos 9, получим
Л (*)= —г-1 ГТ (тУ Л1 - ГТсо8 гг и da. F0)
Единственное ограничение относится к индексу v, который должен быть
таким, чтобы R (v-f--^-) >¦ 0.
25 А. Анго
386 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
7.5.13. Представление Jv(z) с помощью интеграла Коши. В фор-
формуле A7), дающей разложение в ряд функции /vB), заменим r(v-j-r-f-l)
его выражением через интеграл Коши, указанным в п. 7.4.5 [формула A0)].
Получим
(г2У
V (-1Г Г\п) e'dt
?i 1-к j J r\
r=0 С
иначе говоря,
Это и есть искомое выражение без какого-либо ограничения для иг. Кон-
Контур интегрирования здесь тот же, что и на рис. 7.12, или любой эквива-
эквивалентный ему. Это может быть контур Бромвича, если интегралы по дугам
окружности бесконечного радиуса, расположенным слева от него, будут
равны нулю, что справедливо при R(v)>—1. В этом случае имеем
— (?.V_L С
C-jco
' 7.6.14. Теорема сложения1). Положим, что в формуле E2) z = x -)- у.
Тогда
Л=—00
иначе говоря,
-Ьсо +со +со
2 tPJp(x) 2 t4Jq(y)= 2 '
р—~ со 5= — со л= —со ' -
Если произвести умножение рядов и ' приравнять коэффициенты при t", то
получим
р= —со
Пользуясь формулой B2), можно в этом ряду использовать только
функции с положительными индексами. Для и=0 имеем
(у) + •••;
для « = 1
¦Л (*+у)=Л (*) Л (у)+Л (*) Л» (у) — 1Л (*) Л (у)+Л (у) Л
• •• +(—0я 1^
Общая формула будет
л со
= 2 ^(*)^«-р(у)+ 2 (-
р=0 р=1
F1)
') Формула умножения аргументов дана в п. 8.5.7.
7,5] БЕССЕЛЕВЫ ФУНКЦИИ 387
7.5.15. Бесселевы функции третьего рода или функции Ханкеля.
Определение. Положим
. . F2)
Я<2> (z) = Л (*) - /Y. (г) = - J MZ)eZ~J~AZ) :
Функции Н^ и Hi' называются функциями Ханкеля соответственно
первой и второй, или функциями Бесселя третьего рода *). Мы покажем
целесообразность введения этих новых функций в последующих пунктах.
Непосредственно из определений функций Ханкеля — формул F2) —
следует, что
Н{1\ (г) = е}тН^ (z), НЧК (z) = е ~}тН® (z).
В частности, если v равно целому п, то
Н% (z) = (-1)" ^ B), Н% (z) = (~l)n Н(? (z).
Если v = -к, то прямо из F2) имеем
X ^н*\ (z)
| (Л - - j /X
Из этих выражений с помощью рекуррентных формул C3), которые здесь
также имеют место, можно вычислить функции Ханкеля для любого индекса v
вида п-\--^.
7.5.16. Асимптотические разложения. Можно показать, что для боль-
больших значений \z\ и для —к- < argz < -f- -к- имеют место формулы:
— Q,(*)sln<pl. F3)
У, (*) = ]/~г fpv («) sin <р -+¦ Q, (г) cos <p]. F4)
Hll) (z) = j/^ вЛ [Р, (г) + /Q, («)]. F5)
Я'2»(г) = |/^ в -Л [Р, (z) - /Qv (г)], F6)
где
( 4)f. F7)
Dn2 — З2) , Dv2 — I2) Dv2 — 32) Dv2 — 52) Dv2 — 72)
-* + -
*) При целых v правые части F2) становятся неопределенными. Эта неопре-
неопределенность может быть раскрыта так же, как это было сделано в п. 7.5.3 для бес-
бесселевых функций второго рода.
25*
388 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Выражения для P^(z) и Qv(z) представляют собой асимптотические ряды.
Можно показать, что если в них ограничиться k-u членом, таким, что
k>^^- Для Pv(z) G0)
и
к>^^- Для Q4(z). G1)
то погрешность будет меньше первого отброшенного члена. Вычисление
производится следующим образом: отыскивается член ряда F8) и F9), наи-
наименьший из всех возможных, номер которого удовлетворяет условиям G0)
и G1). Так как при этом погрешность меньше первого отбрасываемого
члена, то, остановившись на предыдущем члене, мы проведем вычисление
с максимальной точностью.
Замечание. Если ч = п-\--~, то ряды F8) и F9) обрываются и
приводятся к выражениям, совпадающим с указанными в п. 7.5.9. Формулы
F3) — F6) при этом оказываются точными.
7.5.17. Нахождение численных значений бесселевых функций.
Пример. Требуется вычислить Jx B) и Yt B). Имеем
= — 20°,4, sin tp=— 0,348, cos tp= 0,938,
PjB)= 1 +0,0293 — 0,0090 + 0,0156— ....
Q1 B)= 0,1875 — 0,0128 + 0,0086 — 0,0156+ ...
Здесь третий член наименьший. Так как условия G0) и G1) выполняются, то
Pj B) =1,0293 с погрешностью, меньшей 0,009,
Qj B) = 0,1747 с погрешностью, меньшей 0,0086.
Отсюда
У,B)= -Ц-A,0293 • 0,938 + 0,1747 • 0,348)= 0,580,
У it
YxB) = —L^(—1,0293 • 0,348 + 0,1747 • 0,938)= —0,109
у it
с погрешностью, меньшей 0,006.
Указанная оценка непосредственно подтверждается таблицами п. 7.5.46.
Это показывает, что асимптотические разложения F8) и F9) дают хороший
результат даже для не очень больших значений z.
7.5.18. Асимптотические выражения для бесселевых функций при
больших значениях аргумента. Асимптотические разложения F3)-—F6)
легко позволяют определить предельные выражения для бесселевых функций
при очень больших значениях аргумента z. Если z вещественно и беско-
бесконечно возрастает, то Л,B) стремится к единице, a Q4(z) — к нулю. Следо-
Следовательно, бесселевы функции получат следующие асимптотические выра-
выражения:
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ 389
где <в=г — -к- [v—^—я-) • Эти формулы показывают, что имеется аналогия
между бесселевыми и круговыми функциями, а также между функциями Хан-
Ханкеля и экспоненциальными функциями от чисто мнимого аргумента.
Из формул G2) видно, что бесселевы функции стремятся к нулю,
если Z вещественно и бесконечно возрастает. Если же z — комплексное
число и только его мнимая часть бесконечно возрастает, то дело обстоит
иначе. Действительно, пусть z = u-\- jv. Тогда
где
При очень большом v имеем
(
Это выражение бесконечно возрастает вместе с v. To же имеет место и
для |K,(z)|. Для функций Ханкеля оказывается, что когда одна из них стре-
стремится к нулю, модуль другой бесконечно возрастает. Это объясняет, почему
необходимо было дополнить бесселевы функции функциями Ханкеля. С по-
помощью последних легко сформулировать граничные условия для общего
интеграла уравнения A3), когда комплексная" переменная г обладает беско-
бесконечно возрастающей мнимой частью.
7.5.19. Корни бесселевых функций. В силу общих соображений, до-
доказанных в п. 6.2.11, решение уравнения Бесселя A3) может иметь лишь
простые корни (за исключением случая 2 = 0, v> 1). Два линейно незави-
независимых решения уравнения A3) не могут иметь общих корней, и корни эти
взаимно разделены.
Сейчас мы докажем несколько теорем, относящихся к корням бесселе-
бесселевых функций У, (х) для вещественных х и v > — 1.
Теорема. Все корни /„(.*) вещественны.
Действительно, пусть z0—комплексный корень. Он не может быть
чисто мнимым, так как при этом все члены ряда
г=0
были бы положительны н функция J4 (z0) не могла бы быть равна нулю.
Он не может быть и комплексным. Действительно, пусть z^—сопряженное
комплексное число, которое также является корнем, потому что У, (х) —
функция вещественная. Из формулы C8) имеем тогда
о
что дает для х = 1
390
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
ГГЛ. VII
Это равенство не может иметь места, так как величина под знаком инте-
интеграла существенно положительна.
Теорема. Корни /v и Jv+1 взаимно разделены.
Из формул C6) и C7) получаем посредством дифференцирования ^
dx
d
Первая формула показывает, что между двумя последовательными кор-
корнями x—'J^x) имеется по крайней мере один корень x~*J4+l (x).
Вторая формула показывает, что между двумя последовательными кор-
корнями xv+Vv+1(x) имеется по крайней мере один корень x*+1Js(x).
Формула C1) показывает, что у функций У, и ,/v+1 нет общих корней,
так как все корни функции ,/v простые. Повторное применение рекуррентных
формул и формул, из них вытекающих, позволяет показать, что корни J4
и Jw+m также взаимно разделены.
7.6.20. Кривые Jo(x), A(x), J2(x), .... Js(x) (рис. 7.14).
0,5
О
¦0,5
\
\
щ
/
/
/ j
ц
1
\
1
1
{о
V
\
1 A J
In/
/.
\Y0
j
|
V
л
\
г
V
Л
\ \
\
\
к
\
ч
А
V
л
¦
Г
\
\
у
д
\
Л/
_J
\
)
J
\
V
Д
V
-\
/
N
д
(с
*\
/
\
>
л
\
V
^>
Y
Ja
\
У/
X
у
</
Д
2
\
)
\^
у
%
X
10 15 20 25
Рис. 7.14.
7.6.21. Поверхность z=f(x, v) = J4(x) (рис. 7.15).
Поверхность z = J4(x) показывает, как изменяются функции /,(дг), если
непрерывно изменять переменные х и v. Для v = 0 функция J0(x) равна 1
при х = 0. Это единственная функция Бесселя, имеющая при ^ = 0 конеч-
конечное значение, не равное нулю. Для v>0 все функции J4(x) равны нулю
при х = 0.
Формулу C1) можно записать в виде
Разложим правую часть в ряд по х и рассмотрим член с низшей сте-
степенью х. Для малых значений х можно написать
/ v 1
v W~ г , , jj g.
.7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
391
Если v > 1, то 7,@) = 0, т. е. касательная горизонтальна в начале
координат.
Если v<l, то 7v@) = oo, т. е. касательная вертикальна в начале
координат.
Если v=l, то J, @) = . т. е. касательная наклонна в начале коор-
координат.
Это изменение наклона касательной ясно видно на рис. 7.16. Функ-
Функция Ji(x) и, конечно, функция J^l(x)— единственные бесселевы функции
первого рода, имеющие наклонную касательную в начале координат.
JV(X)
1 2 3 4 5 6 7 в 910111213П151В17Ю13г0
Рис. 7.15.
На рис. 7.16 подробно показана поверхность J4{x) для значений v, заклю-
заключенных между —1 и -f-2, и значений х, заключенных между 0 и -f-2.
Поверхность проведена до кривой, соответствующей первым корням функ-
функции 7V (jc) при различных значениях v.
Цели i отрицательно, то функции J4(x) при х — 0 равны ± оо в зави-
зависимости от внака (—1)" (где п — ближайшее целое число, меньшее —v).
392
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Это не относится к целым значениям v (v = — п), когда мы, в соответствии
с формулой B2), имеем функцию, только знаком (—1)" отличающуюся
Jv(x)
-15
-8
Рис. 7.16.
от Jn(x). По мере того как v принимает все ббльшие положительные зна-
значения, кривые, представляющие функции, все более „лениво" отклоняются
от оси абсцисс.
Рассмотрим, например, функцию J^(x). Имеем
У18A) =0,0148 • 10
У18E) =0,01631 - 10
/18A0)= 0,01524- 10,
У18A5) = 0,03463,
У18 B0) =0,2511.
Функция Jw(x) отчетливо отклоняется от оси Ох только при значениях х,
близких к значению индекса.
Необходимо уточнить это важное свойство бесселевых функций, так как
при разложении в ряд по бесселевым функциям бывает очень полезно, опре-
определить номер, начиная с которого члены становятся пренебрежимо малыми.
7.5J
БЕССЕЛЕВЫ ФУНКЦИИ
39S
Кривые на рис. 7.17 изображают наименьшие значения Xi и х2 вели-
величины х, для которых
/,(*,) = 0,005. /,(*2) = 0,001.
Для удобства графического изображения вместо xt и х2 отложены соответ-
соответственно 2 (v — jcj) и v — х2.
Найдем, например', для каких значений х, заключенных между 0 и х2,
J^{x) будет меньше 0,001. График рис. 7.17 дает v — х2—9, откуда лс2 = 36.
40
SO
20
70
***
in
1
/
•
f
t \
\
rj
1
,*
-
\
*
\
у
.1
s
s
*
/*
/
f
4
4 '
t
/
у
7
? ¦
10
50 100 500 1000
Рис. 7.17.
5000
По мере возрастания х бесселевы функции колеблются вокруг оси Ох
и их отклонения от оси убывают обратно пропорционально ~\fx. Кривые
рис. 7.18 дают абсолютные значения первых максимумов и минимумов
в зависимости от порядка v бесселевой функции.
, 7.6.22. Кривые J г_(х), J з^(х), ..., J »(х) (рис. 7.19).
7.6.23. Кривые У0(х), Yi(x), Y2(x), Y3(x), K4(jc) (рис. 7.20).
7.6.24. Поверхность z=f(x, v) = K,(jf) (рис. 7.21).
Модифицированные бесселевы функции первого и второго рода
Заменив z на jz в дифференциальном уравнении A3), получим
af2y . I dy
dz*
G3)
Решением этого дифференциального уравнения будет функция AJv(Jz).
7.6.25. Модифицированная бесселева функция первого рода. Поло-
Положим А = У~\ Модифицированной бесселевой функцией первого рода назы-
называют функцию
* G4)
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
0,20
0,15 -¦
0,70
0,05
ч
-?
\ Ч
Ш
ч
у
ч4;
\
\
ч]
S
ч
ч \
ч\
^ Ч
S
ч
s
S Ч,
s
V
ч
ч
\
s
s
ч
ч
ч
is
t
s
\
т
t
t
t
s
s
- iss
(
4.,
\
A
1
1
Г
ч>
1
ц
A .
!! —
X
5 10 20 30 50 100 500 WOO
Рис. 7.18.
5000 v
JV(X)
0 1 2 3
5 6 7 в 9 Ш 11 12
Рис. 7.19.
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
0,5
0
0,5
1.0
14
I/
\
|
1
/
/
/
/
/
I
f
i
/
/
Yo
1
f
1
1
1
I \
f\ /
7
/
/
/
\
7
у
_J
~J_
f
\
/
1
I
л
/
/ /
/ /
у
\
/
/
f
у
л
/
J
1
У,
*~
\
\
i
У
/
\
/
\
\
x
/
/
V
\
/
\
у
f
^^
j
\
К
\
/
\
\
s
/
\
\
s/
' \
v
\
/
Чаш
/
123456789 10 11
Рис. 7.20.
Рис. 7.21.
396 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Ряд для нее будет
($)•? ^tir- <75)
г=0
Если v — не целое число, то в качестве второго частного решения урав-
уравнения G3) можно взять функцию /_ч(^)- Нетрудно доказать, что /v(z)
и /_v(z) линейно независимы.
Если v равно целому числу п, то
/-„ (г) = П-п (jz) = Г (-1)" К Uz) = Г" К иг).
Отсюда
/_„(*) = /„(*)•
Следовательно, для целых значений индекса необходимо ввести другой
частный интеграл, который оказался бы линейно независимым от /,(z).
7.5.26. Модифицированная бесселева функция второго рода. Функция
представляет собой решение уравнения G3). Можно показать, что если
устремлять v к целому числу п, то функция К^ (z) будет стремиться к функ-
функции К„ (г), линейно независимой от /„ (z). Эта функция называется модифи-
модифицированной бесселевой функцией второго рода или функцией Макдональда.
Вычислением, подобным приведенному в п. 7.5.3, можно установить для Кп (z)
разложение в степенной ряд, очень похожий на разложение, полученное
для Yn(z).
Функцию /С, (z) можно легко выразить через функцию #iX) (z). Заме-
Заменив z на jz в первой формуле F2), получим
_ ,-v+i 1ЛгI-Лг)
Отсюда
1%ri1) G7)
7.5.27. Асимптотические разложения. Если | z \ велико, а аргумент г
заключен между 0 и и, то
<*>*-!*)<*.*-а»)
118*
¦ е __ [. . 4v»-l» . Dу»-1»)D^-Э) ¦ 1
К2я2 I 1!8г 2!(8гJ ' ' ' |'
Если R(z)>0, то вторым рядом можно пренебречь.
Если \z\ велико, а аргумент заключен между —и и 0, то
1 ,
... '' _ с-*{
1!8
2!(8гJ
Здесь также, если RB;)>0, вторым рядом можно пренебречь.
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 397
Если | z | велико, а аргумент заключен между — тс и -4- те, то
7.6.28. Рекурреитные формулы. Заменив z на jz в рекуррентной
формуле C1), получим, умножая обе части на у"~\
г gj У" V, (jz) = v- V, С/*) — Ду-'-Ч+х С/«)-
Отсюда, применяя определение G4), имеем
* ZF'.(*) = *Л СО+ *Л+1 СО- <78>
То же вычисление, примененное к формуле C2), дает
I(z) 4lAz)+zIv_1(z). G9)
Складывая и вычитая формулы G8) и G9), получаем
2-?-/,(*) = /, ^
Эти выражения аналогичны формулам C4) и C3), но не тождественны им.
Полагая в формуле G8) v —0, получим
l'o(z) = h(z). (80)
Функция K4(z) не удовлетворяет найденным выше рекуррентным соот-
соотношениям. Действительно, поскольку Н[1] (z) удовлетворяет соотношениям
C1) — C4), формула G7) приводит к выражениям
Отсюда
— 2K'Az) = K^
-jK4(z) = K.-i(z)-K,+1(z).
Поступая так, как это было сделано выше, можно, исходя из основных
формул для функций Jn (z), легко установить следующие соотношения для
модифицированных функций:
*•!,_! (г) dz = [z*/1(z)]lt.
/я (Z) = (~1)Я f е-'cos 8 cos пЧ db,
о
sh г, lt (г) - (/•§ ch z.
398
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
e~z V + 7]
/,(*)=
Ch (г cos 6) sin2*8 rf6 =
+1
./¦rW.. , i\ \2J «/ A
7.6.29. Кривые /0(Jc), /,(*), ..., /ц (*) (рис. 7.22 и 7.23).
7.6.30. Кривые Ко(х) и Кг (х) (рис. 7.24).
0,3
0,2
0,1
—
/
/
/
/
/
4
1
/
/
/
1
/
/
/
/
/
L
/
мй
-
J
f
<
/
f
/
/
/
/
/
Ф
71
/
у
/\
z
<.
i
/
/
1
/
I
/
/
4
7
/
/
/
r
—¦
У
_
i
/
J
1
/
/
/
/
I
s»-
У
/
/
V
***
—.
f
{
¦KM
=
/
^/
we
ч
I
/
/
/
7
>
r
**
r
У
»«^
i
/
/
r
и-
/
/
/
/
f
/
/
у
/
к:
-
*
/
/
/
I
:4
7
f
I
/
J
j
r
0**
i
J
у
A
\
=:
I
/1
/
/
1
/
/
/
/
-
t)
i
О
Рис. 7.22.
Функции Кельвина
7.5.31. Функции Кельвина нулевого порядка. В некоторых задачах
требуется найти общий интеграл дифференциального уравнения
d2y . 1 dy ..2 ___ ,gjv
dz2 'г dz ¦* *
Если принять k\= — jk2, мы снова придем к дифференциальному урав-
уравнению A3), в котором v = 0, a z заменено на kxz. Следовательно, общее
решение уравнения (81) будет
.7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
399
Параметр kl равен ± j'l'k. Возьмем положительный знак. Тогда общее
решение получит вид
Мсдули обеих функций J0(kzj'l') и Y0(kzf'*) бесконечно возрастают при
бесконечно возрастающем z. Это обстоятельство затрудняет нахождение
30
го
w
s
•ян
ШШ
IB
—
m*
m»
Ш
mt
Ш
г-
,—•
*?.
mm
IMi
mm
ss
«г
¦=
/
'.
ss
SS
\
zz
ь
/
*\
V
/
/7
a"
=
/
/
/
/
¦Ml
Г
1 1
If
N
/
I
I
1
'
в?
у
У
1
J
/
i
/
1
f
%
1
I
J
/
л
Й
_
г з
Рис. 7.23.
0,3
0,2
0,1
\\\\
\\\\
\\
\\
Кп'1-
\\
ш
V
>
\
\
s>
s
sS
ч
¦Hi
ни
9
Рис. 7.24.
частного решения конкретных задач, в которых решение должно быть конеч-
конечно на бесконечности. Чтобы избежать этого, мы возьмем в качестве вто-
второго решения функцию K0(kzfk). Покажем, что она является решением
400 СПЕЦИАЛЬНЫЕ ФУНКЦИИ • [ГЛ. VII
уравнения (81). Действительно, заменив в формуле G7) z на kzf/', получим
Функция Ho^kzf1*) представляет собой решение уравнения (81).
Очевидно, что решением будет и K0(kzfh). Общее решение (81) теперь
можно представить в виде
у = AJ0 (kzfl*) + ВК0 (kzfb). (82)
Если положить k = 1, то общее решение уравнения
¦будет
у = AJ0 (*//•) + ВК0 (zfl>). (83)
Разложение в ряд для функции J0(zf1') имеет вид
(?.\2 (±
•А)(^/'2)= 1 ~^~J~0Tp Bl
BlJ J C!)*
•Отделив вещественную и мнимую части, получим
!J \ 2 ) "'Г
C!J { 2 ) ^ E!)
Функции Ьег(г) (Bessel reelle — Бесселя вещественные) и bei(z) (Bessel
Imaginaire — Бесселя мнимые) представляют собой так называемые функции
Кельвина, связанные с функцией Jo. Легко показать, что
J0(zj-'h)=ber(z)— Jbei(z).
Аналогично определяются функции Кельвина ker(z) и kei(z), связанные
со вторым решением K0(zj4*):
{ 0( ). (85)
Имеют место следующие разложения в ряды этих функций:
ker(z). (ln|-+
Jcei
= - (in ± + 7J bei (z) — ~ ber (z) + -^ (jj —
7.5] БЕССЕЛЕВЫ ФУНКЦИИ . 401
7.5.32. Функция Кельвина v-ro порядка. Подобным же способом
можно определить функцию Кельвина v-ro порядка с помощью следующих
формул:
У, (zj~*) = bar,(z) — jbeiv(z),
( JL\ (88)
Х U/2 J = ker, (г) + у kei, (г).
7.5.33. Представление функций Кельвина через модуль и аргумент.
Кривые Ьег„(.г) и beivB) (см. рис. 7.25) колеблются вокруг оси абсцисс.
При интерполяции это представляет большое неудобство. Можно легко
определить другие функции, ведущие себя более регулярно. Напишем
р) = berv(z) + у beiv(z) =
положив
{z\
Mj(z) = /ber2B) + bei2B), 6v (z) - arctg
отсюда
Таким же образом можно написать
= kerv(z) + У keiv B) = Мч (z) eIv-> {z>.
положив
отсюда
kerv (z) = ^Vv B) cos cpv (z),
7.5.34. Производные функций Кельвина. Исходя из свойств
vC^). очень легко получить следующие формулы:
ber' z = Mt (z) cos (б, (я) —
B!)—J)
!_л(.г) = Мл(.г), 9_„(г) = б„B:L-я?: (л —целое число),
ker' г = /V, (г) cos (91 (г) — -j).'
26 А. Анго
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
+12
+10
+в
+6
+4
+2
О
-2
-4
-6
-8
-10
-12
f
7 3
**—
\
\
\
\ L
т
\
be г г \
1 71 г
1
vVl
11
\\шг
Рис. 7.25.
,200
123456789 10
О
. 7.SJ БЕССЕЛЕВЫ ФУНКЦИИ 403
sln("P'-i(г) ~ 1")} '
cos («P»+i (*> — т) ~^-!B)sln
N_ (z) = N (z), cp_ (г) = (р B)-)-ятс (я-1—целое число).
7.6.36. Графики функций Ьегг, bei2, M0(z), 60(г) (рис. 7.25 и 7.26)
Дифференциальные уравнения, решение которых может быть выражено
через решение дифференциального уравнения Бесселя
При решении различных задач уравнение Бесселя редко встречается
в каноническом виде A3).' Полезно уметь привести в тех случаях, когда
это возможно, решение рассматриваемого уравнения к решению уравнения A3).
Для упрощения записи полагаем
обозначив тем самым через Z^(z) общее решение уравнения A3).
7.6.36. Основные типы. Уравнение
d2y . I dy
сводится к уравнению A3) путем замены переменных
kx = z.
Отсюда получаем общий интеграл Z4(kx).
Рассмотрим в качестве примера дифференциальное уравнение
У" -h-^y' + by = 0. (90)
Мы приведем его к типу (89) при помощи замены функции
у = х*и.
Имеем
•., х*и"-+(аН- 2v) &-W -+- {[(а — 1) ч-\- ч2] х~-*-\-Ьх->) и = 0.
Если выбрать v таким образом, чтобы а -\- 2ч = 1, то предыдущее уравнение
преобразуется к виду (89):
Отсюда общее решение уравнения (90) будет
1-я
= х 2
Укажем несколько типов уравнений, общее решение которых строится
при помощи бесселевых функций. Заменой переменной и функции их легко
свести к каноническому виду A3). Для краткости мы ограничимся только
приведением окончательных результатов.
Уравнение
= 0 (91)
26*
404 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
имеет общее решение
(^^) 1Р—Г4С1* (92)
Уравнение (90) относится к типу (91) при т = 0, с = 0.
Положим в (91) параметр а равным нулю. Уравнение
имеет общее решение
у—У
Если, кроме того, мы приравняем т = 0 и напишем параметр с в виде
!)• то уравнение (91) принимает вид
Оно имеет общее решение
y = VxZp+1(
Если в уравнении (91) приравнять с=0, с = 0, то мы получим урав-
уравнение
у" ¦+- Ьхту = 0,
общее решение которого имеет вид
U^±E^-) (94)
т+2
Если, кроме того, т=\, то находим общий интеграл уравнения
у" + Ьху = 0,
который равен
з
Если в уравнении (91) параметр с положить равным нулю, то получим
у" 4- — УН- Ьхту = 0. (95)
Это уравнение имеет общее решение
/ „./-г т+2 \
(96)
га +
Часто встречающееся дифференциальное уравнение
не что иное, как уравнение (95), в котором /и = р — аиа = а.
Всюду в предыдущем предполагается, что т -f- 2 =t 0. В частности, общие'
решения -(92) — (94), (96) не годятся, если /и+ 2 = 0. Если предположить
т = — 2, то уравнение (91) получает вид
х2у" -г- аху' + Ау = 0.
.7.5] БЕССЕЛЕВЫ ФУНКЦИИ 405
Это уравнение Эйлера (п. 6.2.9). Оно сводится, если положить х = е",
к линейному дифференциальному уравнению с постоянными коэффициентами
Уравнение
при Ьфа2 имеет общее решение
у= e-aJCZ\(b — а2)* х\-
Если & = а2, то легко заметить, что
ух == х"е~ах, y2=zx~'e-ax
представляют собой при чфО два линейно независимых решения. Если ч»=О,
оба эти интеграла превращаются в один, но легко проверить, что тогда
выражение е~ах In x будет решением. В этом случае получаем общий инте-
интеграл в виде
у = е-ах (А -+- В In х).
Ниже указывается несколько видов дифференциальных уравнений, при-
приводящих к особенно простым решениям. Они не входят в типы уравнений,
приведенных выше.
Уравнение ,
допускает в качестве общего решения
Отметим также следующие два частных случая предыдущего уравнения:
Пример. Найдем общий интеграл
f+ ±/—16x^ = 0.
Сопоставление с уравнением (91) дает
а = 5, с = 0, Ь — — 16, т = 4.
Отсюда, подставляя эти значения в (92), получаем искомый общий интеграл
Некоторые примеры применения бесселевых функций
7.5.37. Колебание однородной тяжелой нити, подвешенной за один
конец. В качестве первого применения бесселевых функций естественно
привести именно этот пример, так как впервые бесселева функция 70 была
найдена Даниелем Бернулли в 1732 г. при изучении колебаний однородной
406
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
1ГЛ. VII
тяжелой нити. Разумеется, современное название и подробное описание
обширное семейство бесселевых функций получило лишь много времени
спустя, ибо только в 1824 г. Бессель, исследуя вопросы, связанные с воз-
возмущением движения планет, детально изучил свойства этих функций.
Итак, дана гибкая тяжелая нить длиной / единиц, подвешенная за конец А
(рис. 7.27). В состоянии покоя она свободно висит вдоль вертикали АО.
На практике модель совершенно гибкой нити можно осуществить, пользуясь
цепью с достаточно мелкими звеньями. Выведем нить из положения равно-
равновесия, сместив конец ее В налево и попробуем найти закон, описывающий
перемещения нити, ограничиваясь небольшими плоскими колебаниями. При-
Примем АО за ось Ох, а прямую, которую конец В
очертит при малом смещении, за ось Оу.
Пусть {1 — масса нити на единицу длины,
а М, М' — две бесконечно близкие точки. В каждой
точке нити действует натяжение Т, обусловленное
весом, горизонтальная составляющая которого будет
тду_
' дх ¦
(*)
Горизонтальная составляющая силы, действующей
на элемент длины нити ММ', будет равна прираще-
приращению величины (*) при переходе от Ж к М'. На
единицу длины нити эта сила будет равна
V 'f — A
Рис. 7.27.
~0~ На высоте х приближенно имеем T=\xgx, отсюда
д Г ..ду-\_о
d2v
Сила инерции на единицу длины равна jj. -~. Уравнение движения по гори-
горизонтали будет
jmt
1 д2у ду дгу
~g ~W~ ~Ыс ~т" Х ~дх* -
Ограничимся синусоидальными функциями времени вида у = у(х)е
Тогда
d^v I d® оJ ф п ¦
rfjc2 "^ л: rfx ^ л:
Чтобы вычислить общий интеграл этого уравнения, достаточно положить
2x = z2 или же, проще, сравнить его с уравнением (91). Решение (92)
получает в этом частном случае вид
= А/о Bсо |/-|) + BY
Так как решение должно иметь конечное значение для х = 0, то
При х = / (в точке подвеса) имеем у = 0. Следовательно, величина
2св 1/ корень функции J0(a). Пусть ар будет одним из корней уравне-
уравнения У0(а) = 0. Имеем
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
407
Так как корней бесчисленное множество, последнее равенство определяет
бесконечное количество видов возможных нормальных колебаний нити.
<-20
Рис. 7.28.
На рис. 7.28 изображены несколько первых видов этих колебаний.
Смещения нарисованы с большим увеличением для того, чтобы с большей
наглядностью показать формы, принимаемые нитью.
7.5.38. Исследование решения волнового уравнения в цилиндриче-
цилиндрических координатах. Рассмотрим произвольное поле, которое распростра-
распространяется вдоль некоторого направления. Примем это направление за ось z.
Поле характеризуется скалярной функцией времени и координат F(x, у, z, t).
Обычно при изучении явлений распространения функция F определяется как
решение волнового уравнения
с" dt" '
Здесь с обозначает скорость распространения. Если ограничиться рассмо-
рассмотрением синусоидальных функций времени, то, как мы видели в п. 6.3.7,
в цилиндрических координатах, которые часто, оказываются естественно
приспособленными к такого рода задачам, общий интеграл представляет
собой сумму всех частных произведений Лапласа вида
COS
sin
при
Мы уже видели, что если радиального ограничения не существует, иначе
говоря, если ср может свободно возрастать на углы, ббльшие чем 2тс, то v
является целым числом. При этом говорят, что для функции F имеет место
симметрия повторения порядка ч вокруг Oz. Если ось Oz является частью
области существования функции, то коэффициент В должен быть равен нулю,
так как из физических соображений функция F не может принимать беско-
бесконечные значения.
Если q— вещественное число, функция F представляет собой величину,
периодически изменяющуюся вдоль оси Oz. Если же q — комплексное число
408
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
a — y'p, функция F имеет псевдопериод — и экспоненциально затухает
вдоль Oz.
7.5.39. Колебания равномерно натянутой мембраны. Рассмотрим мем-
мембрану, т. е. упругую тонкую пластинку, равномерно натянутую на плоскую
раму. Исследуем свободные колебания этой мембраны, выведенной из поло-
положения равновесия, исходя из следующих упрощений:
1) затухание не происходит;
2) смещения достаточно малы, чтобы можно было считать натяжение
неизменным, а перемещения каждой точки совершающимися по малым пря-
прямым, перпендикулярным плоскости, которую представляет собой мембрана
в покое.
Теория поверхностного напряжения указывает, что каждая единица
поверхности мембраны подвергается воздействию нормальной силы, равной
(*)
где А — поверхностное натяжение, а /?, и /?2 — главные радиусы кривизны *).
За ось z примем ось, перпендикулярную к плоской поверхности мем-
мембраны в состоянии покоя и к двум прямоугольным осям Ох и Оу на этой
плоскости. Пусть [j. — поверхностная плотность мем-
мембраны. Уравнение движения будет
Если деформации малы, то, пренебрегая квадратами
малых величин, имеем
| | . Д ~
Колебание мембраны определяется волновым уравнением
^- —= Дг
A dt2
Рис. 7.29.
7.6.40. Случай круглой мембраны. Примем за ось z
нормаль к поверхности круга в центре О (рис. 7.29).
Если положить ¦— = k2, то уравнение движения в цилиндрических координа-
А
тах будет
д?
,df
На рис. 7.29 указаны мембрана, закрепляющая ее рамка (кольцо) и
координаты р и ср точки М мембраны. Если ограничиться только синусо-
синусоидальными функциями времени, то частное решение примет вид
Z (р. ср> 0 = е)ш'cos n9Jn (kwp),
так как смещение центра О конечно. Общим решением будет сумма всех
частных решений, в которых п принимает все возможные значения.
*) Формула (*) совпадает с известным выражением для силы поверхностного
натяжения жидкостей — выводится аналогичными рассуждениями. Разумеется, между А
и коэффициентом поверхностного натяжения вещества мембраны а нет ничего общего.
Величина А зависит от упругих констант, от толщины мембраны и т. д.
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
409
Узловые линии представляют собой геометрическое место точек мем-
мембраны, для которых смещения постоянно равны нулю. Различают два сорта
узловых линий:
.1) диаметральные узловые линии, которые выра-
выражаются уравнением cosn<p = Q, — это диаметры, раз-
разделяющие окружность на 2я секторов с углами при
вершине, равными — (рис. 7.30);
2) круговые узловые линии, представляющие со-
собой концентрические окружности, радиус которых опре-
определяется соотношением Jn(ktop)=0.
Круговая рамка радиуса R обязательно должна
быть одной из таких узловых линий. Будем считать,
что она соответствует р-му корню уравнения У„(а) =
R Э
Рис. 7.30.
иначе говоря,
баний:
положим ku>R = ap. Это выражение определяет частоту коле-
колеИмеется, следовательно, р — 1 узловых окружностей, соответствующих кор-
корням а,, а2 а.р_х.
; п=о
р=2
Рис. 7.31.
Если число п отлично от нуля, то центр О представляет собой узловую
точку, так как У„@)=0. Это совершенно очевидно — ведь некоторое коли-
количество узловых диаметров обязательно пересечется в этой точке. Если же
/1 = 0, то узловых диаметров не существует, и мы имеем дело с симметрией
вращения. Центр мембраны представляет собой пучность, так как Jq(O)— 1.
410 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
На рис. 7.31 даны примеры колебаний мембраны, равномерно натянутой
на круговую рамку.
7.5.41. Собственные электромагнитные колебания резонатора, имею-
имеющего форму кругового цилиндра. Будем предполагать, что вещество, обра-
образующее стенки, имеет бесконечно большую проводимость и что резонатор
замкнут двумя поперечными сечениями, отстоящими друг от друга на длину /.
-Ограничимся рассмотрением синусоидальных функций времени. В качестве
системы отсчета возьмем систему цилиндрических координат, причем за ось Oz
примем ось цилиндра. Положим xx = z, л:2 = р, л:3 = ср. При этом условия
Бромвича (см. п. 6.3.13, формула F8)) выполняются, так как е,—1, е2=1,
е3 == р. Функция U Бромвича (потенциал электрических колебаний) задается
уравнением
чсоторое совпадает с уравнением C6) п. 6.3.7, т. е. с уравнением &U-\-k2U — Q
в цилиндрических координатах. Соответствующее произведение Лапласа равно
,, COS COS У, . , >b,.f
и = vtp az Jl (ap) e'Rvt
sin T sin ^ Y4 '
лри
Если внутренность цилиндрического резонатора шуста и, в частности,
если малый коаксиальный проводящий цилиндр не изолирует ось Oz
от области существования U, то поле должно иметь конечные значения при
р = 0. Мы вынуждены тогда исключить функцию Y. Случай с коаксиальным
проводником разбирается в п. 7.5.43.
Предположим, что радиус-вектор может свободно поворачиваться на целое
число окружностей. (Случай радиальной перегородки рассматривается в конце
данного пункта.) При этом поле должно снова получить исходное значение;
следовательно, ч равно целому числу п. При таких условиях произведение
Лапласа будет
Электромагнитные поля типа поперечного электрического и поперечного
магнитного даны уравнениями (85) и (86) п. 6.3.13. Обозначив через Jn про-
производную Jn по аргументу ар, получим для поперечной магнитной волны
(волны Е): '
с Щ 1 / ч — sin —sin tkvt
Е — —L- J. (ар) пч? qze1 ,
» р п\ \TJ cos Y сад ч
иг = о,
,, . nk , / г
— Sin
cos
., • , -m / ? ш' , \ COS COS
H9 = - Jak у - Jn (op) sfn «cp
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 411
для поперечной электрической волны (волны Я):
, _
. kn , Г v. . , .s
= J Т V "Г У» (Ор) -
sin cos
cos Л? sin
COS COS
sin я* sin
COS COS
sin«9sin
cos — sin
81п»<Р Cos
~sin n9 ~sin
j COS Г COS
Обозначим через R радиус цилиндра. Тогда требование равенства нулю тан-
тангенциальных составляющих электрического поля на стенках цилиндра при-
приводит к граничным условиям
Е? = Е9 = 0 при 2 = 0 и z = l,
?2 = ?ф = 0 при р = Я.
Они вынуждают, определять параметры а и q для волны Е с помощью соот-
соотношений
Jn(aR) = 0, q = ^p- (m — целое число)
и за произведение Лапласа для этой волны принять выражение
- , . COS ikvt
Jn(ap)sln n<? cos qze}*vt.
Аналогично для волны Н параметры а и q следует определить из соот-
соотношений
Jn(oR) = 0, q = —p- (m — целое число)
и принять за произведение Лапласа
Обозначив через \t не равный нулю /-й корень уравнения Jn(x) = 0,
а через о,- — не равный нулю /-й корень Jn(x) = Q, получим следующие
выражения для полей.
Поперечная магнитная волна (волна Е):
— sin
cos
nk , / e , / h \ sin mitz >bVt
/ I ^ cos
412 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Если полость внутри пустая, частота этого колебания будет равна
2л ~ 2
Самая низкая частота соответствует /те —0 и первому корню /0(л:)=0. Она
равна, следовательно*
2,40483 • 3 • 10'° __ 72 145
2-izR 2kR
если R выражено в сантиметрах.
Поперечная электрическая волна (волна Н):
_
. in . /" A , / и; \ sin
COS
/6»/
cos
cos
sin
В пустой полости частота этого колебания равна
Самая низкая частота соответствует от=1. Первый неравный нулю корень
У0(л:)==0 равен 3,8317, а первый неравный нулю корень J1(x) = O
равен 1,8412 (ем. таблицу в п. 7.5.49). Следовательно, самая низкая частота
для волн Н соответствует не л = 0, а га—1.
Различные колебания, которые могут существовать , внутри цилиндри-
цилиндрического резонатора, определяются совокупностью допустимых значений
чисел га, т, I.
Число т определяет периодичность вдоль направления, параллельного Oz
(рис. 7.32). Число га определяет периодичность повторения, если радиус-
вектор вращается вокруг Oz
О
т=3
(рис. 7.33). Число / определяет
число узловых окружностей, на
которых некоторые составляющие
поля становятся равными нулю
(рис. 7.34). Самая низкая частота
Рис. 7.32. волн Е соответствует группе из
трех чисел @, 0, 1). Самая низкая
частота волн Н соответствует группе A, 1, 1). Например, при /=3 для
поперечной магнитной волны составляющие Ег, Е?, Hf становятся равными
нулю на утолщенных окружностях рис. 7.34, а, а составляющие Ер, Hf
становятся равными нулю на утолщенных окружностях рис. 7.34, б.
Ко всем указанным периодичностям прибавляется еще периодичность
ш
во времени, происходящая от множителя е
'ш.
.7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
413
Замечание. В группы формул, написанных для поперечных магнитных
и электрических волн, неявно входит постоянный коэффициент, зависящий
Рис. 7.33.
от выбора чисел от, п, i. Он зависит от других граничных требований, отно-
относящихся к условиям возбуждения колебаний в полости (см. замечание 2
к п. 6.3.14).
Рассмотрим случай наличия у цилиндра радиальных перегородок. Допу-
Допустим, что в цилиндре имеются две радиальные перегородки, образующие
между собой угол та*. К уже написанным выше условиям равенства нулю
тангенциальных • составляющих электрического поля на границе цилиндра
следует добавить аналогичные условия, касающиеся обеих перегородок:
Ё = Ег = О
и (р = 2тс —.таг.
при <? =
Нужно исключить cosvtp из формул, выражающих Ez и Ef, и добавить
к соотношениям, определяющим параметры, вместо условия v = « новое
соотношение
или
2 —а
ic — та*) =
(s — целое число).
2R
а)
б)
Рис. 7.34.
Число v, следовательно, теперь мо-
может отл'ичаться от целого числа.
В частности, в случае, когда а=0,
т. е. когда перегородки сливаются
в одну, v=2^- При четном s мы
снова приходим к уже полученным решениям, но при нечетном s имеет
Место ряд других решений, в которые входят J\, Уз> ^5. •••
7 1 ~2
7.5.42. Распространение электромагнитной волны внутри бесконеч-
бесконечного кругового цилиндра. Вычисление здесь подобно вычислению, прове-
проведенному в предыдущем пункте. Так как речь идет о распространении вдоль
оси Oz. то произведение Лапласа будет
Граничные условия сводятся к требованиям
Ег = Е9 = 0 при р = Я.
Параметр а определяется из уравнений Уп(ар) = 0 для поперечной магнитной
волны,-и У„(ар) = 0 для поперечной электрической волны. Отсюда получаем
следующие выражения для составляющих электромагнитного "поля.
414 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Поперечная магнитная волна (волна Е):
Н = 0,
Поперечная электрическая волна (волна Н):
Каждый тип волны определяется группой из двух целых чисел (I, п). Опре-
деленной частоте / = -^— соответствует ряд возможных значений q:
или <!2 =
Если дан волновод с определенным радиусом R, волна самой низкой
частоты, способная распространяться внутри цилиндра, будет соответство-
соответствовать <7 = 0. Для волн Е она, кроме того, соответствует наименьшему
не равному нулю корню Xt. Мы знаем, что эта наименьшая частота связана
с первым корнем JQ(x), равным 2,40483. Отсюда в пустоте для EOil имеем
* 72145 ..
Для волн Н наименьший не равный нулю корень at соответствует первому
корню j[(x) = Q, т. е. 1,8412. Отсюда в пустоте для Н1Л получим
_ 55 236
Естественно, что наименьшие частоты, соответствующие <7 = 0, имеют бес-
бесконечную длину волны и бесконечную скорость распространения фазы
в волноводе.
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 415-
Можно спросить, почему решение а = О не принимается за первый
корень Jn(x) (га ф 0) или Jn(x) (п > 1). Если а = 0, то мы вынуждады при-
принять за функцию /?(р) в произведении Лапласа выражение
Напишем Е , которая должна быть равна нулю при р = R и при р = 0<
(волна Е):
Е9 = - Jng Ир-
Отсюда А — —В и ге=0. Это решение не подходит, так как оно приводит,
с точностью до постоянного множителя, к выражению
Е ^Le-JqzeJkvt
р р
которое бесконечно на оси Oz. В действительности нельзя приравнять Е?
к нулю, так как случай ге = 0 был с самого начала исключен. Решение
не годится также для волн Н.
7.5.43. Случай коаксиального проводника. Этим названием обозначают
промежуток между двумя бесконечными цилиндрами, имеющими общую ось-
(рис. 7.35). Посмотрим, какие изменения следует
внести в предыдущие вычисления. Функцию Y п
больше исключать не нужно, поэтому произведе-
произведение Лапласа будет теперь иметь вид
Коэффициенты А и В определяются граничными
условиями, которые следует записать в виде
AJn(aR2)-hBYn(aR2) = 0. Рис
Эта однородная и линейная система будет иметь ненулевое решение, если:
определитель ее будет равен нулю:
= 0.
Если через \t обозначить один из корней этого уравнения, то мы получим
для поперечных магнитных волн
R (р) = Yn №i) ^ (h?) - Jn (V?i)
Это же относится и к поперечным электрическим волнам, но вдесь гранич-
граничные условия приводят к выражению
R (р) = К; faRJ Jn (у. .р) - J'n (y.iRl) Yn (y.lP).
где через \>.i обозначены корни уравнения
J'n (««О Y'n (««,) - J'n ИО К И,)=о.
Пользуясь формулами (88) и (89) п. 6.3.13, можно легко написать,
составляющие электромагнитного поля.
Если повторить рассуждения предыдущего пункта для наименьших
не равных нулю корней \ и о,, то может показаться, что здесь также
имеется наименьшая частота для заданного проводника (предельная частота).
416
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
На самом деле ничего подобного нет, так как решение г
Е =A-e-}qzeikvt
9 р
здесь годится, поскольку ось Oz находится вне области распространения.
Решение /?(р) = Ар" -\- Вр~" по-прежнему не годится для волн Н. Дей-
Действительно, невозможно найти значения для А, 5, п, которые приравняли бы
нулю составляющие Ег и Е? при р = Rx или R2.
Итак, мы имеем решение, не существовавшее в случае пустого
цилиндра:
0
Y (A 9 P p
Это решение может иметь произвольную частоту. Следовательно, для коак-
коаксиального проводника предельной частоты нет.
7.5.44. Скин-эффект переменных токов, проходящих по цилиндри-
цилиндрическому проводнику круглого сечения. Дан бесконечный проводящий
цилиндрический провод круглого сечения, по которому течет переменный
электрический ток (рис. 7.36).
q Пусть о будет плотность тока
В в точке, находящейся на рас-
расстоянии х от оси провода. Эта
плотность будет функцией х и
она одинакова для всех точек,
1 \dr
¦I-
находящихся на одинаковом рас-
Рис 7 3б' стоянии от оси. Рассмотрим ци-
цилиндрическую оболочку толщи-
толщиной dx и радиусом х. Сила тока, проходящего через оболочку, равна
dlx = 2тсах dx.
Магнитное поле, вызванное этим током, в точке Р, находящейся на рас-
расстоянии г от оси (г > х), равно
Магнитное поле, вызванное всеми линиями тока, расположенными в точ-
точках х < г, будет
г
Н=— ах dx.
о
Это выражение, продифференцированное по г, дает
dH 1 Г Н
— = o-^J oxdx = a- — ,
что можно записать в виде
Если через р обозначить удельное сопротивление вещества, из которого
состоит провод, то электродвижущая сила, приложенная к линии тока АВ,
будет
Е = pal,
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 417
где / — расстояние между точками А и В. Электродвижущая сила. вдоль
линии тока DC на расстоянии r-\-dr от оси будет
В плоском контуре ABCD электродвижущая сила равна dE. Она равна
электродвижущей силе, наведенной полем Н. Поэтому можно написать
dE=?ldo=\x~
иначе говоря,
dH p da
dt ~~T dr '
Продифференцируем по t уравнение
dr
Получаем
д2Н , 1 дН да _
drdt ¦ г dt dt
или
р д2а . 1 р да да .
Если предположить, что ток синусоидален, а частота его равна ш, то
-тт- == Ju>o и дифференциальное уравнение для о получит вид
d2a I rfa yu>,ua .
Положив
получим уравнение
drz * г dr
общее решение которого равно
Плотность о при р = 0 имеет конечное значение, поэтому постоянная
интегрирования В должна быть принята равной нулю. Отсюда
о = А/о (krp*) = АМ0 (kr) eJW'K
Пусть а — радиус провода, а о0 — плотность тока на его поверхности. Она
определяет значение коэффициента А. Можно написать
0
0
a
1
{ka)
Приняв фазовый угол на поверхности провода за начало отсчета фаз, получим
27 А. Анго
418
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Если kr велико, фазовый угол может быть намного больше 2it. Следова-
Следовательно, внутри провода могут существовать области, в которых токи имеют
противоположное направление. Величина a0M0(kr)/M0(ka) — это значение
амплитуды плотности тока на расстоянии г
от оси.
Рис. 7.37 дает представление о плотности
тока как функции расстояния от оси для цилин-
цилиндрического медного, провода радиусом в 1 мм
при частотах 20 000 и 200 000 гц (— = 5,8 • 10;
f
0,5
0.006б
~
f=2L
'0000 гц
у
/
10000гц
1
Инверсия тона 1
л Х^\\
\
1
1
1
I
)
7.5.45. Спектр волны, модулированной по
частоте. Выражение для синусоидальной волны,
модулированной по частоте, будет
J <s{t)
о
dt
К
О '0,2
0,6 О,в 1
Расстояние от оси, мм
Рис. 7.37,
где U — постоянная, 20 — также постоянная, на-
называемая центральной круговой частотой; член
Рв(О — производная фазы, вызванной низкочастот-
ЕыУ сигналом а (*).
Если считать величину о (О безразмерной,
а ее наибольшее значение равным единице, что
всегда возможно, то величина [3 будет обозначать
наибольшее отклонение круговой частоты и будет зависеть только от ампли-
амплитуды низкочастотного сигнала, а не от закона его изменения, целиком пред-
представленного функцией o(t).
Если модуляция наложена синусоидальным низкочастотным сигналом
с круговой частотой а, то
a(t) = cosotf.
В этом случае мы получим для волны, модулированной по частоте сигналом,
выражение
[t +1- sin otf]
Безразмерное выражение i- = — называется индексом модуляции. Оно
вводит в рассмотрение две величины: а, характеризующую частоту модуляции,
и р, характеризующую амплитуду модуляции или, скорее, отклонение частоты.
При первом взгляде на механизм модуляции частоты, описанный выше,
может показаться, что поскольку круговая частота изменяется от &0 — р до
Qo —[— р, то должна существовать очень узкая полоса частот, равная всего
¦н^-. Если бы это было так, то модуляция частоты открыла бы почти без-
безграничные возможности для сосредоточивания работы передатчиков в очень
узкой полосе частот. Действительно, из всех физических измерений, кото-
которые сейчас умеют осуществлять, самое точное — это измерение частоты.
Поэтому было бы очень легко выявлять модуляцию частоты, в которой
отклонение частоты ^- очень мало — порядка 10~6 от центральной частоты
-—¦. Волна в 10 Мгц занимала бы тогда полосу всего в 20 гц. К сожале-
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 419
нию, предыдущее рассуждение весьма неточно. Действительно, рассмотрим
выражение для волны, модулированной по частоте:
u{t) — U sin \Q.Qt +|- sin
Используя формулу для синуса суммы двух углов, находим
u(t)—U[sin Qot cos f|-sinat\-\-cos QQt sin(|-sinat\J.
Применяя формулы E3) и E4), дающие разложение в ряд cos (z sin 8) и
sin (z sin 6), получаем
u(t)=U [Jo (?) sin 2</ -f- ^ (?) 2 sin a? cos 20* + J2 (?) 2 cos 2a? sin Qot -f-
Эта формула показывает, что векторное представление комплексной волны
содержит векторы модуляции, соответствующие частотам а, 2а, За, ..., —
одни в фазе, другие сдвинутые по фазе на у по отношению к несущей волне.
Используя формулу B2), простым преобразованием произведения тригоно-
тригонометрических функций получаем
a{t)=U S Jn&sin(Q0-\-na)t.
п = — оо
Из последней формулы вытекает, что спектр амплитуд — это линейчатый
спектр, частоты, которого равны
20 — па 20— 2a, 20 —a, Q, 20 + a, Q0-f-2a 2 + rea, ...
а амплитуды пропорциональны
••-../„(О J2&, М\), Уо«). 4E). У2(?) Л«). ...
Следовательно, при чисто синусоидальной модуляции спектр амплитуд соста-
составляющих колебаний симметричен и теоретически не ограничен. Фактически
его можно считать ограниченным из-за свойства бесселевой' функции стано-
становиться пренебрежимо малой, когда ее индекс п становится значительно больше
аргумента z. '
Можно легко оценить практическую полуширину спектра, подсчитав пв
таблицам пп. 7.-6.47 и 7.5.48 для малых значений ? и по рис. 7.17 для больших
значений ? величину п, начиная с которой амплитуды будут меньше 0,001
или 0,005 и могут, таким образом, считаться пренебрежимо малыми. Если
это значение п обозначим через А\ то практическая ширина спектра будгт
2it
или, если обозначить через / частоту модуляции,
2/N.
Можно также задаться вопросом, каково значение индекса модуляции,
ниже которого спектр практически сводится к несущей частоте и двум пер-
первым боковым линиям. Для этого нужно | взять таким, чтобы J2{i) было
пренебрежимо мало, например меньше 0,005. Рассмотрев значения функции J2($),
мы видим, что это имеет место при ?< 0,2. Значит только при значениях
индекса модуляции, существенно меньших единицы, компактность по частоте
при частотной модуляции оказывается практически такой же, как при ампли-
амплитудной модуляции').
') Здесь речь идет только о волне, модулированной по частоте чисто синусоидаль-
синусоидальным сигналом. В случае телеграфной модуляции решение существенно усложняется
из-за переходных явлений.
27*
420 СПЕЦИАЛЬНЫЕ ФУНКЦИИ ,[ГЛ. VII
Следует заметить, что по своему строению такой сокращенный спектр,
несмотря на внешнее сходство, отличен от спектра при амплитудной моду-
модуляции, так как между частотой боковых линий и несущей частотой имеется
сдвиг по фазе в -J.
Индекс
модуляции
;
в
90
76
44
11
57 57
35 I 77 I 35
УI I f I I У
46 4в
31 I 33 ре 33 I 31
П I III I 1
Э6 Ы 36*?
Рис. 7.38.
*
Для некоторых значений индекса модуляции может иметь место исчезно-
исчезновение несущей частоты или линий, правильно расположенных относительно
этой частоты. Линии &0 — an и Q0-\-an исчезают, если i- является корнем
./„(?)= 0. Эти корни даны в таблице п. 7.5.49. В частности, несущая частота
исчезает при
5=2,40; 5,52; 8,65; 11,79; ...
— корнях функции Уо E) = 0. Это свойство очень ценно при некоторых
измерениях.
Рис. 7.38 показывает, как возрастает сложность спектра волны, моду-
модулированной по частоте, если увеличивать индекс модуляции. Цифры у верти-
вертикальных черточек характеризуют величину амплитуд различных гармоник.
7.5] БЕССЕЛЕВЫ ФУНКЦИИ 421
Модуляция по нескольким частотам. Мы уже видели, что спектр
амплитуд волны, модулированной по частоте чисто синусоидальным сигналом,
всегда симметричен по отношению к несущей частоте. Однако это не так,
если модуляция наложена суммой некоторого числа синусоидальных функций,
когда между соответствующими круговыми частотами существуют простые
линейные соотношения.
Рассмотрим сигнал модуляции
Члены -^-, -!-^- будут частными индексами модуляции $х, $2, Функция и (t)
в комплексном обозначении будет иметь вид
Формула ei*sln e = 2 Л (•г) einb позволяет записать и (f) в виде
Я ss —ОО
ТОО
л,, п„ ...= —оо
Это выражение делает очевидным присутствие в сигнале круговых частот
2o4-«l(Bl + «2uJ+ •••
с амплитудами, пропорциональными
Л, «О Л, (Ь) Л, «а)--.
Для противоположных по знаку значений п1, ге2, ... произведение под
знаком суммы будет, с точностью до знака, иметь одно и то же значение.
Амплитуды будут равны; следовательно, спектр симметричен.
Иначе обстоит дело в часто встречающемся случае, когда модулирующий
сигнал вместо того, чтобы содержать синусоидальные функции с несоизмери-
несоизмеримыми круговыми частотами, содержит две или несколько синусоидальных
функций, круговые частоты которых находятся в простом соотношении.
В частности, это будет в случае модуляции периодическим сигналом, раз-
разложенным в ряд Фурье.
Например, если между круговыми частотами шг и (в2 имеется соотношение
@2 = 2@,;
мьл получим одну и ту же частоту, иначе говоря, одну и ту же линию
ео-Н»1 («1 -Н2«2)-|- ••¦
для значений nl=\, «2 = 3 и для значений nl = 2>, «2 = 2. Результирующая
амплитуда будет иметь вид
Значения, противоположные по знаку предыдущим, т. е. ni = —1, Л2 = —3,
и Л[ = — 3, п2 = —2, приведут к частоте, симметричной ранее полученной
по отношению к несущей частоте. Но результирующая амплитуда в этом
случае будет
' Л &) Л (У — J» (Si) Л Fа)-
Это выражение не равно предыдущему, так как суммы индексов обоих
произведений разной четности (см. формулу B2)). Спектр в этом случае не
будет симметричен.
422 СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Таблицы бесселевых функций
7.5.46. Функции Jo, J\, Ко, Кь
[ГЛ. VII
г
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7 .
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
'1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
1,000 0
' 0,9975
0,9900
0,9776
0,960 4
0,938 5
0,912 0
0,881 2
0,846 3
0,807 5
0,7652
0,719 6
0,6711
0,620 1
0,566 9
0,5118
0,4554
0,398 0
0,340 0
0,281 8
0,223 9
0,166 6
0,110 4
0,055 5
0,002 5
—0,048 4
—0,096 8
—0,142 4
—0,185 0
—0,224 3
—0,2601
—0,292 1
—0,320 2
—0,344 3
—0,364 3
—0,380 1
—0,391 8
-0,3992
—0,402 6
—0,401 8
—0,397 1
—0,388 7
—0,376 6
—0,361 0
—0,342 3
—0,320 5
—0,296 1
—0,269 3
—0,240 4
—0,209 7
—0,177 6
—0,1443
—0,110 3
—0,075 8
У,'*.
0,000 0
0,049 9
0,0995
0,148 3
0,196 0
0,242 3
0,286 7
0,3290
0,368 8
0,405 9
0,4401
0,470 9
0,498 3
0,522 0
0,541 9
0,557 9
0,569 9
0,577 8 •
0,581 5
0,581 2
0,576 7
0,568 3
0,556 0
0,539 9
0,520 2
0,497 1
0,470 8
0,4416
0,409 7
0,375 4
0,339 1
0,300 9
0,261 3
0,220 7
0,179 2
0,137 4
0,095 5
0,053 8
0,012 8
—0,027 2
—0,066 0
—0,103 3
—0,138 6
—0,171 9
—0,202 8
—0,2311
—0,256 6
—0,279 1
—0,298 5
—0,314 7
—0,327 6
—0,337 1
—0,343 2
—0,346 0
У о (г)
— со
—1,534
—1,081
—0,807 3
—0,606 0
—0,444 5
—0,308 5
—0,190 7
—0,086 8
+0,005 6
0,088 3
0,162 2
0,228 1
0,286 5
0,337 9
0,382 4
0,420 4
0,452 0
0,477 4
0,496 8
0,510 4
0,518 3
0,520 8
0,518 1
0,510 4
0,498 1
0,481 3
0,4605
0,435 9
0,407 9
0,376 9
0,343 1
0,307 1
0,269 1
0,2296
0,1890
0,147 7
0,106 1
0,0345
0,0234
—0,016 9
—0,056 1
—0,093 8 .
—0,1296
—0,163 3
—0,194 7
—0,2235
—0,249 4
—0,272 3
—0,2921
—0,308 5
—0,321 6
—0,331 3
—0,3374
К, (г)
— оо
—6,459
—3,324
—2,293
—1,781
—1,471
—1,260
—1,103
—0,978 1
—0,8731
—0,7812
—0,698 1 .
—0,621 1
—0,548 5
—0,479 1
—0,412 3
—0,347 6
—0,284 7
—0,223 7
—0,164 4
—0,107 0
—0,051 7
+0,001 5
0,052 3
0,100 5
0,145 9
0,188 4
0,227 6
0,263 5
0,295 9
0,324 7
0,349 6
0,370 7
0,387 9
0,401 0
0,410 2
0,415 4
0,416 7
0,414 1
0,407 8
0,397 9
0,384 6
0,368 0
0,348 4
0,3260
0,301 0
0,2737
0,2445
0,213 6
0,181 2
0,147 9
0,1137
0,079 2
0,0445
7,5]
БЕССЕЛЕБЫ ФУНКЦИИ
423
Продолжение
г
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
¦7,9
8,0
8,1
•8,2
8,3
8,4
8,5
1 8,6
8,7
8,8
8,9
9,0
9,1
., 9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
10,1
10,2
10,3
10,4
10,5
10,6
10,7
10,8
10,9
Л>(*)
—0,041 2
—0,006 8
+0,027 0
0,059 9
0,0917
0,122 0
0,150 6
0,177 3
0,201 7
0,223 8
0,243 3
0,260 1
0,274 0
0,285 1
0,293 1
0,298 1
0,3001
0,299 1
0,295 1
0,288 2
0,2786 •
0,266 3
0,251 6
0,234 6
0,215 4
0,194 4
0,171 7
0,147 5
0,122 2
0,096 0
0,069 2
0,0419
0,014 6
—0,012 5
—0,039 2
—0,0653
—0,0903
—0,1142
—0,1367
—0,157 7
—0,176 8
—0,193 9
—0,209 0
—0,221 8
—0,232 3
—0,240 3
—0,245 9
—0,249 0
—0,2496
—0,247 7.
—0,243 4
—0,236 6
—0,227 6
—0,2164
—0,203 2
—0,188 1
У, (г)
—0,345 3
—0,341 4
—0,334 3
—0,324 1
—0,3110
—0,295 1
—0,276 7
—0,255 9
—0,232 9
—0,208 1
—0,181 6
—0,153 8
—0,125 0
—0,095 3
—0,065 2
—0,034 9
—0,0047
+0,025 2
0,054 3
0,082 6
0,1096
0,1352
0,1592
0,181 3
0,201 4
0,219 2
0,234 6
0,247 6
0,258 0
0,265 7
. 0,270 8
0,273 1
0,272 8
0,2^9 7
0,2641
0,255 9
0,245 3
0,232 4
0,217 4
0,200 4
0,1816
0,161 3
0,139 5
0,116 6
0,092 8
0,068 4
0,043 5
0,018 4
—0,006 6
—0,031 3
—0,055 5
—0,078 9
—0,101 2
—0,122 4
—0,142 2
—0,160 3
—0,340 2
—0,339 5
—0,335 4
—0,328 2
—0,317 7
—0,304 4
—0,288 2
—0,269 4
—0,2483
—0,225 1
—0,199 9
—0,173 2
—0,145 2
—0,116 2
—0,086 4
—0,0563
—0,025 9
+0,0042
0,0339
0,062 8
0,090 7
0,117 3
0,142 4
0,165 8
0,187 2
0,2065
0,2235
0,238 1
0,2501
0,2595
0,266 2
0,270 2
0,271 5
0,270 0
0,2659
0,2592
0,249 9
0,238 3
0,224 5
0,2086
0,190 7
0,171 2
0,150 2
0,127 9
0,104 5
0,080 4
0,055 7
0,0307
0,005 6
—0,019 3
—0,043 7
—0,067 5
—0,090 4
—0,112 2
—0,132 6
—0,151 6
К, (г)
0,010 1
—0,023 8
—0,056 8
—0,088 7
—0,119 2
—0,148 1
—0,175 0
—0,199 8
—0,222 3
—0,242 2
. —0,259 6
—0,274 1
—0,285 7
—0,2945
—0,300 2
—0,3029
—0,302 7
—0,2995
—0,293 4
—0,284 6
—0,2731
—0,2591
—0,242 8
—0,2243
—0,203 9
—0,181 7
—0,1581
—0,133 1
—0,1072
—0,080 6
—0,053 5
—0,026 2<
+0,0011
0,028 0
0,054 4
0,079 9
0,104 3
0,127 5
0,149 1
0,169 1
0,187 1
0,203 2
0,217 1
0,228 7
0,237 9
0,2447
0,249 0
0,250 8
0,250 2
0,247 1
0,241 6
0,2337
0,223 6
0,211 4
0,197 3
0,1813
424
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Продолжение
М*)
11,0
11,1
11,2
11,3
11,4
11,5
11,6
11,7
11,8
11,9
12,0
12,1
12,2
12,3
12,4
12,5
12,6
12,7
12,8
12,9
13,0
13,1
13,2
13,3
13,4
13,5
13,6
13,7
13,8
13,9
14,0
14,1
14,2
14,3
14,4
14,5
14,6
14,7
14,8
14,9
15,0
15,1
15,2
15,3
15,4
15,5
15,6
15,7
15,8
15,9
16,0
—0,171 2
—0,152 8
—0,133 О
—0,112 1
—0,090 2
—0,067 7
—0,0446
—0,021 3
+0,002 О
0,025 О
0,047 7
0,0697
0,0908
0,110 8
0,129 6
0,146 9
0,162 6
0,1766
0,1887
0,1988
0,206 9
0,212 9
0,216 7
0,218 3
0,217 7
0,215 О
0,210 1
0,203 2
0,194 3
0,1836
0,171 1
0,157 0
0,141 4
0,124 5
0,106 5
0,087 5
0,067 9
0,047 6
0,027 1
0,006 4
—0,014 2
—0,0346
—0,054 4
—0,073 6
—0,091 9
—0,109 2
—0,1253
—0,1401
—0,153 3
—0,165 О
—0,174 9
—0,176 8
—0,191 3
—0,203 9
—0,214 3
—0,222 5
—0,228 4
—0,232 О
—0,233 3
—0,232 3
—0,229 О
—0,223 4
—0,215 7
—0,206 О
—0,194 3
—0,180 7
—0,1655
—0,1487
—0,1307
—0,1114
—0,091 2
—0,070 3
—0,048 9
—0,027 1
—0,005 2
+0,016 6
0,038 О
0,059 О
0,079 1
0,098 4
0,116 5
0,1334
0,148 8
0,162 6
0,174 7
0,1850
0,193 4
0,199 9
0,204 3
0,206 6
0,206 9
0,2051
0,2013
0,195 5
0,187 9
0,178 4
0,167 2
0,1544
0,140 2
0,1247
0,108 О
0,090 4
—0,168 8
—0,184 3
—0,197 7
—0,209 1
—0,2183
—0,225 2
—0,229 9
—0,232 2
—0,232 2
—0,229 8
—0,225 2
—0,218 4
—0,2095
—0,198 6
—0,185 8
—0,171 2
—0,1551
—0,137 5
—0,1187
—0,098 9
—0,078 2
—0,0569
—0,035 2
—0,0134
+0,008 5
0,030 1
0,051 2
0,071 7
0,091 3
0,109 9
0,127 2
0,143 1
0,157 5
0,170 3
0,181 2
0,190 3
0,197 4
0,202 5
0,205 6
0,206 5
0,2055
0,202 3
0,197 2
0,1902
0,181 3
0,170 6
0,1584
0,1446
0,1295
0,113 2
0,1132
0,163 7
0,144 6
0,124 3
0,102 9
0,080 7
0,057 9
0,034 8
0,0114
—0,0118
—0,034 7
—0,057 1
—0,078 7
—0,099 4
—0,118 9
—0,137 1
—0,153 8
—0,168 9
—0,182 1
—0,1935
—0,202 8
—0,210 1
—0,215 2
—0,218 2
—0,219 О
—0,217 6
—0,214 0
—0,208 4
—0,200 7
—0,191 2
—0,179 8
—0,166 6
—0,152 0
—0,1359
—0,118 6
—0,100 3
—0,081 О
—0,0612
—0,040 8
—0,020 2
+0,000 5
0,021 1
0,041 3
0,060 9
0,079 9
0,097 9
0,114 8
0,130 5
0,1447
0,157 5
0,168 6
0,1686
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
425
Замечание. Эту таблицу можно легко распространить на бесселевы
функции с любым целым индексом, отличным от нуля и единицы. Для этого
достаточно применить рекуррентное соотношение C3):
Например, требуется вычислить У3 0>1). Имеем
J2 = ~ J1 -- Уо = 0,1366,
/, = 2 ~ J2 — Jl = 0,0258.
7.5.47. Бесселевы функции J%, Js, •¦-, Л.
JAz)
0
1
2
3
4
5
6
7
10
II
12
13.
14
15
16
17
18
19
20
21
22
23
24
0,000 0
+0,114 9
+0,352 8-
4-0,486 1
-j-0,3641
4-0,046 6
—0,242 9
—0,3014
—0,1130
4-0,144 8
4-0,2546
4-0,139 0
—0,084 9
—0,217 7
—0,152 0
4-0,041 6
4-0.186 2
4-0,158 4
—0,007 5
—0,157 8
—0,160 3
—0,020 3
4-0,131 3
4-0,159 0
4-0,043 4
0,000 0
4-0,0195
--0,128 9
^-0,309 1
4-0,430 2
--0,364 8
--0,1148
—0,167 6
—0,291 1
—0,180 9
4-0,058 4
--0,227 3
--0,1951
—0,003 3
—0,176 8
—0,194 0
—0,043 8
4-0,134 9
4-0.186 3
4-0,072 5
—0,098 9
—0,175 0
—0,093 3
4-0,067 2
4-0,161 3
0,000 0
4-0,002 5
4-0,034 0
4-0,132 0
4-0,281 1
4-0,391 2
4-0,357 6
4-0,157 8
—0,105 4
—0,265 5
—0,219 6
—0,0150
4-0,182 5
4-0,219 3
4-0,076 2
—0,119 2
—0,202 6
—0,110 7
4-0,069 6
4-0,180 6
4-0,130 7
—0,029 7
—0,156 8
—0,141 5
—0,0031
0,000 0
4-0,000 2
4-0,007 0
4-0,043 0
4-0,132 1
4-0,261 1
4-0,362 1
•4-0,347 9
4-0,185 8
—0,055 0
—0,234 1
—0,238 3
—0,073 5
4-0,131 6
4-0,220 4
4-0,130 5
—0,057 5
—0,187 0
—0,155 4
4-0,003 6
4-0,151 2
-4-0,163 7
4-0,036 3
—0,116 4
—0,162 3
0,000 0
0,000 0
4-0,001 2
4-0,0114
4-0,0491
--0,1310
--0,245 8
—0,339 2
—0,337 6
4-0,204 3
—0,014 5
—0,201 6
—0,243 7
—0,118 0
4-0,081 2
4-0,206 1
4-0,166 7
4-0,000 7
—0,156 0
—0,178 8
—0,055 1
4-0,107 6
--0,173 3
^-0,090 9
—0,064 5
0,000 0
0,000 0
4-0,000 2
--0,002 5
--0,0152
--0,053 4
--0,1296
--0,233 6
--0,320 6
--0,327 5
4-0,216 7
4-0,018 4
—0,170 3
—0,240 6
—0,150 8
4-0,034 5
--0,182 5
--0,187 5
--0,051 4
—0,116 5
—0,184 2
—0,102 2
4-0,058 2
4-0,163 8
4-0,130 0
0,000 0
0,000 0
0,000 0
4-0,000 5
--0,004 0
--0,018 4
—0,056 5
--0,128 0
4-0,2235
4-0,305 1
4-0,317 9
4-0,225 0
4-0,045 1
—0,141 0
—0,232 0
—0,174 0
—0,007 0
4-0,153 7
4-0,195 9
4-0,092 9
—0,073 9
—0,175 7
—0,136 2
4-0,008 8
4-0,140 4
0,0000
0,0000
0,0000
4-0,0001
- -0,000 9
- -0,005 5
--0,0212
- -0,058 9
--0,126 3
--0,214 9
--0,2919
--0,308 9
--0,230 4
--0,067 0
—0,114 3
—0,220 0
—0,1895
—0,042 9
4-0,122 8
4-0,194 7
4-0,125 1
—0,031 7
—0,157 3
—0,157 6
—0,0364
7.5.48. Бесселевы функции Jw, J\\, ¦•-, J\i.
A» (*)
J»
Л» (*)
4
5
6
7
4-0,000 2
- -0,001 5
- -0,007 0
- -0,023 5
--0,060 8
--0,124 7
0,000 0
4-0,000 3
- -0,002 0
- -0,008 3
- -0,025 6
- -0,062 2
0,000 0
4-0,0001
4-0,000 5
4-0,002 6
4-0,009 6
4-0,027 4
0,000 0
0,000 0
4-o,ooo i
—0,000 8
—0,003 3
—0,010 8
0,000 0
0,000 0
0,000 0
4-0,000 2
4-0,001 0
4-0,003 9
0,000 0
0,000 0
0,000 0
0,000 0
4-0,000 з
4-0,001 з
0,000 0
0,000 0
0,000 0
0,000 0
4-0,0001
4-0,000 4
0,000 0
0,0000
0,0000
0,000 0
0,000 0
4-0,0001
426
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Продолжение
-Ло (*)
At (*)
/„(*)
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
+0,207 5
--0,280 4
--0,300 5
--0,233 8
--0,0850
—0,090 О
—0,206 2
—0,1991
—0,073 2
+0,091 5
+0,186 5
+0,148 5
+0,007 5
—0,132 2
—0,167 7
—0,075 2
+0,071 2
+0,156 4
+0,115 2
—0,016 I
+0,123 1
--0,2010
--0,270 4
—0,292 7
--0,235 7
--0,099 9
—0,0682
—0,191 4
—0,2041
—0,098 4
+0,061 4
+0,173 2
+0,164 1
+0,042 7
—0,103 3
-^0,168 2
-Ю.106 3
+0,033 0
+0,141 8
+0,136 9
+0,063 4
+0,121 6
+0,1953
+0,261 5
+0,285 5
+0,236 7
+0,112 4
—0,048 6
—0,176 2
—0,205 5
—0,1190
+0,032 9
+0,156 6
+0,173 0
+0,073 0
—0,072 9
—0,161 1
—0,129 5
—0,003 8
+0,120 0
+0,029 0
+0,064 3
+0,120 1
+0,190 1
+0,253 6
--0,278 7
--0,236 8
--0,122 8
—0,030 9
—0,161 2
—0,204 1
—0,1356
+0,006 7
+0,137 9
--0,176 3
--0,098 3
—0,042 4
—0,148 1
—0,145 0
—0,037 6
+0,012 0
+0,030 4
+0,065 0
+0,118 8
+0,1855
+0,246 4
+0,272 4
+0,236 4
+0,131 6
—0,015 1
—0,146 4
—0,200 8
—0,1487
—0,017 2
+0,118 0
+0,175 1
+0,118 7
—0,013 1
—0,130 9
—0,1537
+0,004 5
+0,013 0
+0,031 6
--0,065 6
--0,117 4
--0,181 3
--0,2399
+0.266 6
+0,235 6
+0,138 9
—0,000 8
—0,132 1
—0,195 9
—0,158 8
—0,038 6
+0,097 8
+0,170 2
—0,134 5
--0,014 2
—0,110 8
+0,001 6
+0,005 1
+0,014 0
+0,032 7
+0,066 1
+0,116 2
+0,177 5
-^0,234 0
+0,261 1
+0,234 5
+0,145 2
+0,012 0
—0,1185
—0,189 9
—0,166 3
—0,057 7
+0,077 7
+0,162 5
+0,146 1
—0,039 1
+0,000 5
—0,001 8
—0,005 7
—0,014 9
—0,033 7
—0,066 5
—0,115 0
—0,173 9
—0,228 6
+0,255 9
+0,233 1
+0,150 5
+0,023 6
—0,105 5
—0,183 1
—0,171 7
—0,074 5
+0,058 2
+0,152 7
+0,153 9
7.5.49. Таблицы первых корней функций Jn (z), J'n {г) (рис. 7.39)
Рис. 7.39.
/л(г) = 0.
п
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Номер корня
1
0,0000
1,8412
3,0542
4,2012
5,3175
6,4156
7,5013
8,5778
9,6474
10,7114
11,7709
12,8265
13,8788
14,9284
15,9754
17,0203
18,0633
19,1045
20,1441
21,1823
22,2191
23,2548
24,2894
2
3,8317
5,3314
6,7061
8,0152
9,2824
10,5199
11,7349
12,9324
14,1156
15,2868
16,4479
17,6003
18,7451
19,8832
21,0154
22,1423
23,2644
24,3819
3
7,0156
8,5363
9,9695
11,3459
12,6819
13,9872
15,2682
16,5294
17,7740
19,0045
20,2230
21,4309
22,6293
23,8194
4
10,1735
11,7060
13,1704
14,5859
15,9641
17,3128
18,6374
19,9419
21,2291
22,3014
23,7608
5
13,3237
14,8636
16,3475
17,7888
19,1960
20,5755
21,9318
23,2681
24,5872
6
16,4706
18,0155
19,5129
20,9724
22,4010
23,8033
7
19,6159
21,1644
22,6721
24,1469
8
22,7601
24.3113
9
25,9037
7.5]
БЕССЕЛЕВЬТ ФУНКЦИИ
427
Продолжение
YI
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
m
1
2,40483
3,83171
5,13562
6,38016
7,58834
8,77142
9,93611
11,08637
12,22509
13,35430
14,47550
15,58985
16,6983
17,8014
18,9000
19,9944
21,0851
22,1725
23,2568
24,3383
2
5,52008
7,01559
8,41724
9,76102
11,06471
12,33860
13,58929
14,82127
16,0378
17,2412
18,4335
19,6160
20,7899
21,9562
23,1158
24,2692
3
8,65373
10,17347
11,61984
13,01520
14,37254
15,70017
17,0038
18,2876
19,5545
20,8070
22,0470
23,2759
24,4949
-/»(*) =
Номер
4
11,79153
13,32369
14,79595
16,22347
17,6160
18,9801
20,3208
21,6416
22,9452
24,2339
0.
корня
5
14,93092
16,47063
17,95982
19,40942
20,8269
22,2178
23,5861
24,9349
6
18,07106
19,61586
21,11700
22,58273
24,1990
7
21,21164
22,76008
24,27112
8
24,35247
7.5.50. Бесселевы функции J \ , J3 , .
z
0
l
2
3
4
5
6
7
••8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
У] (г)
Т
0,0000
+0,6714
+0,5130
4-0,0650
—0,3019
—0,3422
—0,0910
+0,1981
+0,2791
+0,1096
—0,1373
—0,2406
—0,1236
+0,0930
+0,2112
+0,1340
—0,0574
—0.V860
—0,1412
+0,0274
+0,1629
+0,1457
—0,0015
—0,1408
—0,1475
2
0,0000
+0,2403
+0,4913
+0,4777
+0,1853
—0,1697
—0,3279
—0,1991
+0,0759
+0,2545
+0,1980
—0,0229
—0,2047
—0,1937
—0,0141
+0,1654
+0,1874
+0,0423
—0,1320
—0,1795
—0,0646
+0,1023
+0,1700
+0,0825
—0,0752
2
0,0000
+0,0495
-
-
1-0,2239
-0,4127
-0,4409
-0,2404
—0,0729
—0,2834
—0,2506
—0,0248
+0,1967
+0,2343
+0,0724
—0,1377
—0,2143
—0,1009
+0,0926
+0,1935
+0.1192
—0,0558
—0,1726
—0,1311
+0,0247
+0,1516
+0,1381
2
0,0000
_
-
1-0,0072
-0,0685
-0,2101
-0,3658
+0,4100
+0,2671
—0,0034
—0,2326
—0,2683
—0,0996
+0,1294
+0,2348
+0,1407
—0,0524
—0,1991
—0,1585
+0,0146
+0,1651
+0,1649
+0,0215
—0,1335
—0,1644
—0,0496
+0,1040
J9(z)
1
0,0000
_
_
-0,0008
-0,0159
-0,0776
—0,1993
+0,3337
+0,3846
+0,2800
+0,0471
—0,1839
—0,2664
—0,1519
_
_
1-0,0646
-0,2134
-0,1830
-0,0080
—0,1619
—0,1875
—0,0550
+0,1165
+0,1801
+0,0866
—0,0770
—0,1666
— 0,1078
•?и С*)
т
0,0000
_
_
¦-
-
_
_
_
-
-0,0001
-0,0030
М),0226
-0,0826
-0,1906
-0,3098
(-0,3634
-0,2856
-0,0844
—0,1401
—0,2538
—0,1864
-
-0,0070
-0,1801
-0,2039
-0,0674
—0,1139
—0,1926
—0,1097
+0,0595
+0,1706
+0,1329
—0,0156
—0,1444
У]3 (г)
Т
0,0000
0,0000
-
_
-
_
_
-
1-0,0005
-0,0055
-0,0279
-0,0856
-0,1833
-0,2911
-0,3456
-0,2870
+0,1123
—0,1018
—0,2354
—0,2075
—0,0415
+0,1415
+0,2083
+0,1138
—0,0627
—0,1800
—0,1474
+0,0028
+0,1435
+0.1592
+0,0416
сооо-чспсл'^соТо'»-'© coooViojT'^
цишш
^ЪзЪэТоТон->—?-»о© "p'ooooobbpo
юо5ослн---асооооот i&coiohooooqo
COH'fit'QOSSCOW СЛ tO н* CO S fr <-> с -
OOtOOOCnOCOOOOt—* 4*> UlO^CnooOSC
5OP5
Ъо'-ч^аЪ^сл'^^.ЪоЪоТо Тон-^-ооооо^эо
00 CO i—« CO СЛ 00 tO Сл О 4^ О СЛ tO СО СП 4^ Ю н-О О
Ю СЛ Ю N3 -J СТ>© 00 >— СО (ОЩЮОЮОЮОЮО
н—СОО'ЧСП'Ч^'Ч'ЧСП С0С04^ОСлОСЛОСЛО
5ОО ©©©©©©©©,<
оооооо-^а^спспслЪ!^ ^ со со То То То и- н- © <
00 СЛ н--Ч СО 00 4^ СО 4^ СО 4^ СО 4^ СО 4^ © СЛ © СЛ <
сл©сою©сг>©соСл*^4 оососососо©оо©с
•"-асО"—'--асо©соо»оо4^ сл>—'О^оосооооос
U
,014
,029
»Г*Г-Г-^г
ОООООн-»— ЮЮ СО4^Сла:00©СО"Ч4^С
о+
420
733
337
063
8559
6931
5614
4529
3625
2867
2228
1689
1235
0851
0529
0260
0037
0147
0297
UiikUkU ik^kUli>
961
923
220
352
820
457
191
9873
8259
6946
5859
4946
4172
3511
2942
2451
2027
,1639
,1341
23
20
52
20
57
iUiUiikt 4UkUiikJ=
4262
3938
3617
3314
3026
,2752
2494
7854
7769
7581
7331
7038
6716
74
,3227
,3096
,2956
,2809
,2658
,2504
,2351
,14
,22
,27
,30
,33
,34
,35
,35
,35
,352
0000
460
2229
2743
3095
3332
3482
3563
3590
3574
524
ber
cr
2
2.
14
©1
bi
jo
V-
X
X
a*
n
a*
№
43
О
w
03
I
г
n
¦fc- CO Ю •—• O-
CO 00 --4 a> СЛ J^ CO Ю н- О CO OO --4 О) СЛ >?* CO tO и- О
4- I I I 4- 4-4- I I I 4-4-4-4- I I I 4-4-4- I I I 4-4-
pb.66.6 ppofcbtp.<b.<bp ЬЬЬЬЬЬЬЬЬ'
OO^-*QO м i- О м h>Q tO и1 О Ю Ю О КЗ CO >-' t Т^
O>00"^JCO-^ ООЮСЛСОСЛЮ О, фО"-" 4^4^Ю»—'О
СООООСЛЮ •—' 4^ СО '—'OICOOi^i—' •—' tO'—' -^ tO •—' О Cn 4^. i
•—' O> »—' 4^ 00 О tO Ю О СЛ tO 00 4> *—' *^4 CO О 4^ 00 Ю 00 О 00 •—•
LtttUJLttt
4C7) cocooocntO004сл ooacocotoaooo
*—' a> --j 4^ со со со со oo --j о оо ю 4> о oo •—• --a --j сл
•—• СЛ О CO tO 4^ СЛ CO 4^ 4^ СЛ 4^. О СП CO CO •—' О СП
oTo tO О COCO О Сон
сл oo-^acocotoa>ooco
оо ю 4> о oo •—• --a --j сл t
CO О СП С
itttjL
о о»—ч->о н»мЬ I-м о|-1"юо<-• То<—••—«coloocooooo
ooa>a>•—«4^ *^44^'—«--aoo»—'-^atocncT) сп^юсосо"—«cnto*^
•ч со оо сл -^а сл ф со оо»—• О5 сл •—' OJ 4^ to со oo to 4> 4> ср оо а>
ЮООООСЛОО •—'OiCOOtOaiOOtO
Щ
сэ.<Ь<Ь.<Ьб .<Ь.<ЬЬ
^-¦*н-он-н- о Ъ'н-^-otO'—© toto о н-со topco'^'c^To х
02CO--JCOOO СОСОСЛСЛСО--405СЛОС
СЛ СХ ОТ Oi СЛ О ОТ О О н-4* О Ю ГС <
¦*Юн-.©ЮЮО tO СО н- © СО С7) tO О ©
:>>—toooco©© >-t © со сл g5 to en со-s
3-«JCO©h-StO
tttu
- _)•—j^-а сл
СО 00 О "-4 •—• *^
СО»—' СЛ СО СО СЛ
.«—•>— Он- N3»—• О tO tO
ЛООСП"—' pi tO >—' 00 4^ О>
^ Сл о Ф*- (О Сл oi сл 4^>
со со со сл 4=^ оо ста ста
»Ъ СО СЛ Ъ tO н> СО S
OOOCOtOOO»—СЛ
> оо I—• 4^ со --J
ь оо оо со 4=>-
I
tcl со
to
00
91
СП
п
п
п
п
п
я
г
I
к
S
S
га
с
S
§¦
СГ
а
Е
га
р
<
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
429
Продолжение
Z
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
.5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
ber г
0,751 7
0,6987
0,637 7
0,568 0
0,489 0
0,400 0
0,3001
0,1887
0,0651
—0,071 4
—0,221 4
—0,3855
—0,564 4
—0,758 4
—0,968 0
—1,194
—1,435
—1,693
—1,967
—2,258-
—2,563
—2,884
—3,219
—3,568
—3,928
—4,299
—4,678
—5,064
—5,453
—5,843
—6,230
—6,611
—6,980
—7,334
—7,667
—7,974
—8,247
—8,479
—8,664
—8,794
—8,858
—8,849
—8,756
—8,569
—8,276
—7,867
—7,329
—6,649
^-5,816
—4,815
—3,633
—2,257
—0,673 7
+1.131
3,169
5,455
d Ьегг
dz
—0,493 1
—0,569 1
—0,6520
—0,742 0
—0,8392
—0,9436
—1,055
—1,174
—1,299
—1,431
—1,570
—1,714
—1,864
—2,018
—2,175
—2,336
—2,498
—2,661
—2,822
^-2,981
—3,135
—3,282
—3,420
—3,547
—3,659
—3,754
—3,828
—3,878
—3,901
—3,891
—3,845
—3,759
—3,627
—3,445
—3,206
—2,907
—2,541
—2,102
—1,586
—0,984 4
—0,293 1
+0,4943
1,384
2,380
3,490
4,717
6,067
7,544
9,151
10,89
12,76
14,77
16,92
19,19
21,60
24,13
Ье1г
0,972 3
1,065
1,161
1,259
1,357
1,457
1,557
1,656
1,753
1,847
1,938
2,023
2,102
2,172
2,203
2,283
2,320
2,341
2,345
2,330
2,293
2,231
2,142
2,024
1,873
1,686
1,461
1,195
0,883 7
0,525 1
0,116 0
—0,346 7
—0,865 8
—1,444
—2,085
—2,789
—3,560
—4,399
-^5,307
—6,285
—7,335
—8,454
—9,644
—10,90
—12,22
—13,61
—15,05
—16,34
—18,07
—19,64
—21,24
—22,85
—24,46
—26,05
—27,61
—29,12
dz
0,917 0
0,944 2
0,966 6
0,983 6
0,994 4
0,998 3
0,9943
0,981 5
0,959 0
0,925 7
0,880 5
0,822 3
0,749 9
0,662 1
0,557 7
0,435 3
0,293 7
0,131 5
—0,0525
—0,2597
—0,491 1
—0,748 1
—1,032
—1,343
—1,683
—2,053
—2,452
—2,882
—3,342
--3,833
—4,354
—4,903
—5,484
—6,089
--6,720
—7,373
—8,045
—8,734
—9,433
—10,14
—10,85
—11,55
—12,23
—12,90
—13,54
—14,13
—14,67
—15,15
—15,54
—15,85 .
—16,04
—16,11
—16,03
—15,79
—15,37
—14,74
кегг
—0,041 7
—0,051 1
—0,058 3
—0,063 7
—0,067 4
—0,069 7
—0,070 8
—0,071 0
—0,070 3
—0,068 9
—0,067 0
—0,064 7
—0,062 0
—0,059 0
—0,055 9
—0,052 6
—0,049 3
—0,046 0
—0,042 6
—0,039 4
—3618 2
—33082
—ЗОН 2
—27262
—24562
—22002
—19602
—1734 2
—15252
—13302
—11512
—986,52
—835,92
—698,92
—574,92
—463,22
—363,22
—274,02
—195,22
—125,82
—653,0»
—129,53
+319,13
699,13
1017 3
12783
1488 3
16533
1777 3
1866 s
19223
1951»
1956 3
19403
19073
1860 s
d leer г
dz
—1066 '
—828,2'
—623,4'
—447,5'
—297,1'
—169,3'
—61,36'
+29,04'
+104,0'
165,3'
214,8 '
253,7'
283,6'
305,6'
320,7'
329,9'
334,1'
334,0'
330,4'
323,8'
314,8'
303,8'
291,3'
277,7'
263,2'
248,1'
232,8'
217,3'
201,9'
186.8'
171,9'
157,9'
143,7'
130,4'
117,7 '
105,8 '
94,47'
¦ 83,88'
74,00'
64,81'
56,32'
48,50'
41,33'
34,79'
28,85'
23,49'
18,67 '
14,36'
10,54'
7,164'
420,53
163,33
—58,393
—247,43
—406,6 s
—538,8»
keiz
—0,202 4
—0,181 2
—0,161 4
—0,143 1
—0,126 2
—0,110 7
—0,096 4
—0,083 4
—0,071 6
—0,060 8
—51122
—42402
—34582
—2762 2
—21452
—16002
—11232
—707,72
—348,7 2
-41,082
+2198 й
4386 s
¦ 61943
76613
8826 3
9721а
10382
10832
1110 2
11212
11192
11052
10822
10512
10142
97163
92553
87663
82583
77393
72163
66963
61833
56813
51943
47243
42743
38463
34403
3058 3
27003
23663
2057 3
1770 3
1507 3
12673
dkeiz
dz
0,2198
0,204 8
0,1901
0,1759
0,162 1
0,1489
0,136 3
0,124 3
0,1129
0,102 1
92042
82592
73782
65582
57992
50982
4454 2
2664 2
33252
28352
23912
1991»
1631 2
1310 2
1024 2
771.52
549,2 2
355.02
186,5*
41.522
—820,03
—18613
—27263
—34333
—40003
—44403
—4769 й
—50003
—51463
—52173
-52243
-51763
—50823
—4951s
—47883
—46003
—4393 s
—4170s
—3939 s
—37013
—34603
—3218 s
—2979s
—27453
—2517 s
—2296 s
430
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Продолжение
Z
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8'
9,9
10,0
ber z
7,999
10,81
13,91
17,29
20,97
24,96
29,25
33,84
38,74
43,94
49,42
55,19
61,21
67,47
73,94
80,58
87,35
94,21
101,1
108,0
114,7
121,3
127,5
133,4
138,8
dberar
dz
26,78
29,53
32,38
35,31
38,31
41,35
44,42
47,47
50,49
53,44
56,28
58,97
61,45
63,68
65,60
67,14
68,25
68,83
68,82
68,13
66,67
64,35
61,07
56,72
51,20
bei г
—30,55
—31,88
—33,09
—34,15
—35,02
—35,67
—36,05
—36,16
—35,92
—35,30
—34/25
—32,71
—30,65
—28,00
—24,71
—20,72
—15,98
—10,41
—3,969
3,411
11,79
21,22
31,76
43,46
56,37
й bei z
dz
—13,88
—12,76
—11,37
—9,681
—7,660
—5,285
—2,530
+0,634 1
4,232
8,290
12,83
17,88
23,47
29,60
36,30
43,58
51,46
59,94
69,01
78,68
88,94
99,76
111,1
123,0
135,3
ker z
1800 3
173П
1655 3
1572 3
I4863
1397 3
1306 3
1216 3
1126 3
1037 3
951,13
867,53
787,13
710.23
637,23
568,13
503,03
442,23
385,53
333,03
284,63
240,23
199.63
162,83
129,53
d ker г
dz
—646,5 3
—732,2 3
—798,2 3
—846,7 3
—879,73
—899,2 3
—906,93
—904,4 3
—893,2 3
—874,73
—850,0 3
—820,4 3
—786,8 3
—750,2 3
—711,2 3
—670,7 3
—629,33
—587,5 3
—545,8 3
—504,5 3
—464,1 3
—424,8 3
—386,8 3
—350,4 3
—315,6 3
ке!г
1043 3
849,8 3
671,4 3
511,7 3
369,6 3
244,0 3
133,9 3
+38,093
—44,49 3
—114,9 3
—174,1 3
—223.3.3,
—263,2 3
—294,9 3
—319,23
—336,8 3
—348,6 3
—355,23
—357,43
—355,7 3
—350,8 3
—343,0 3
—332,9 3
—321.03
—307,53
dkeiz
dz
—2084 3
—18813
—1689 3
—1507 3
—1336 3
—11773
—10283
—890,2 3
—763,23
—646,73
—540,4 3
—443,8 3
—356,5 3
—278,13
—208,1 *
—145,9 3
—91,093
—43,15 3
—1,5593
+34,163
64,49 3
89,89 3
110,8 3
127,7 3
140,9 3
Замечание. Числа, за которыми следует индекс 1, нужно умножить на 10 4.
Числа, за которыми следует индекс ?, нужно умножить на 10~5.
Числа, за которыми следует индекс 3, нужно умножить на 10~6.
7.5.53. Функции Мо (г) <?А
4- j beli z.
> = ber z -\- j bei z, Mt (z) e^ <*> = bert z
z
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
M0(z)
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,001
1,001
1,001
1,002
1,003
1,004
1,005
1,006
eo(*)
0,00
0,04
0,14
0,32
0,57
0,90
1,29
1,75
2,29
2,90
3,58
4,33
5,15
6,04
7,01
8,04
9,14
M>(z)
0,00
0,025
0,050
0,075
0,100
0,125
0,150
0,175
0,200
0,225
0,250
0,275
0,300
0,325
0,350
0,375
0,400
8i(*)
135,00
135,02
135,07
135,16
135,29
135,45
135,64
135,88
136,15
136,45
136,79
137,17
137,58
138,03
138,51
139,03
139,58
7.5]
БЕССЕЛЕВЫ ФУНКЦИИ
431
Продолжение
i
г
0,85
0,90
0,95
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
,50
,55
,60
,65
,70
,80
,90
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
'3,00
3,20
3,40
3,60
3,80
4,00
4,50
5,00
5,50
6,00
. 7,00
' 8,00
9,00
10,00
11,00
12,00
14,00
16,00
18,00
20,00
25,00
30,00
35,00
40,00
45,00
М0(г)
1,008
1,010
1,013
1,016
1,019
1,023
1,027
1,032
1,038
1,044
1,051
1,059
1,067
1,077
1,087
1,098
1,111
1,124
1,154
' 1,189
1,229
1,274
1,325
1,381 .
1,443
1,511
1,586
1,666
1,754
1,849
1,950.
2,176
2,434
2,728
3,061
3,439
4,618
6,231
8,447
11,50
21,55
40,82
77,96
149,8
289,5
561,8
2137
8 217
31850
1,242-105
3,809-101
1,192-108
3,786 • 10 9
1,215- 10"
3,929 • 10 is
10,31
11,55
12,86
14,23
15,66
17,16
18,72
20,34
22,02
23,75
25,54
27,37
29,26
31,19
33,16
35,17
37,22
39,30
43,54
47,88
52,29
56,74
61,22
65,71
70,19
74,65
79,09
83,50
87,87
92,21
96,52
105,03
113,43
121,75
129,99
138,19
158,59
178,95
199,28
219,62
260,29
300,92
341,52
382,10
422,66
463,22
544,32
625,40
705,46
787,52
990,15
1 192,75
1 395,35
1 597,94
1 800,53
Mi {z)
0,425
0,450
0,476
0,501
0,526
0,552
0,577
0,603
0,629
0,654
0,680
0,707
0,733
0,759
0,786
0,813
0,840
0,868
0,924
0,981
1,041
1,102
1,166
1,232
1,301
1,374
1,450
1,530
1,615
1,705
1,800
2,009
2,246
2,515
2,823
3,173
4,278
5,809
7,925
10,85
20,50
39,07
74,97
144,7
280,4
545,6
2 084
8 038
31230
1,220 • 105
3,755 • 10 в
1,178-108
3,748 • 10s
1,204-10"
3,899 • 10 12
8, {г)
140,17
140,80
141,46
142,16
142,89
143,66
144,46
145,29
146,17
147,07
148,02
148,99
150,00
151,04
152,12
153,23
154,38
155,55
158,00
160,57
163,27
166,08
169,00
172,03
175,16
178,39
181,70
185,10
188,57
192,11
195,71
203,08
210,62
218,30 '
226,07
233,90
253,67
273,55
293,48
313,45
353,51
393,69
433,95
474,28
514,63
555,02
635,84
716,72
797,63
878,57
1 080,98
1 283,45
1 485,94
1 688,46
1 890,98
Замечание. й0 н В1 выражены з градусах.
432 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
7.6. ФУНКЦИИ ЛЕЖАНДРА
7.6.1. Введение. Мы уже встречали (пп. 6.3.8 и 6.3.11) следующие диффе-
дифференциальные уравнения:
Заменой переменных z = cosG, z = ch?, г —/sh?, z = sin<p эти урав-
уравнения сводятся к виду
A -г*)$-2г % Л- [п (п -t 1) - j^j2]f = 0 (97)
или, в более общей форме,
где постоянные v и («. могут быть отличны от целого числа.
При р. = 0 дифференциальное уравнение (98) сведется к
(l-*2)-g-2z-g + v(v+l)/ = 0.. (99)
Это дифференциальное уравнение Лежандра. Его решения называются функ-
функциями Лежандра (сферическими функциями Лежандра). Решения более общего
уравнения (98) называются присоединенными функциями Лежандра (присо-
(присоединенными сферическими функциями). Рассмотрим сначала сферические
функции Лежандра.
Замечание. Если/!*—решение уравнения (98), то функции /1X_V> /~*,
/3^_, также являются его решениями. Если Д — решение (99), то /_,_j —
также его решение. Это замечание позволяет уменьшить диапазон изменения
параметров.
7.6.2. Разложения в степенные ряды. Попробуем найти решение урав-
уравнения (99) в виде обобщенного степенного ряда по возрастающим степеням
переменной г:
f(z) = zk 2 агг\
Подставим этот ряд в (99) и приравняем нулю коэффициенты при различных
степенях z. Так как X неотрицательно, то наименьший показатель степени z
равен k — 2. Имеем
aok(k— l) = 0, axk{k+ l) = 0, A00)
Пусть k — 0. Тогда коэффициенты а0 и аг становятся произвольными и
7.6] ФУНКЦИИ ЛЕЖАНДРА 433
Отсюда
I ( 1vv(v-2)...(v-2A + 2)(v+l)(v + 3)...(v + 2*-l)
"П. U BХЯ ¦ г -r---j
A01)
Перепишем разложения A01) и A02), используя обозначения для гипергео-
гипергеометрических рядов (см. пример п. 6.2.10). Тогда общее решение уравнения
(99) примет вид
,.. -,( v v+1 1 л , с{ V —1 v + 2 3 2\
f(z) = a0F[— j, -f~, j; z^ + a^zF^ т~, —$—, -^\ z2].
Отношение двух последовательных членов каждого из рядов A01; и A02)
равно
Выражение, связывающее ах+2 с ах, показывает, что отношение ax+i при
бесконечно возрастающем X стремится к единице. Значит, ряды A01) и A02)
сходятся в интервале (—1, -{-!) и дают в нем решения уравнения (99). Этот
интервал особенно важен, так как часто переменная z представляет косинус
полюсного углового расстояния между точками в сферических координатах:
z = cos 6.
Вернемся к соотношениям A00). Они удовлетворяются также при k=l,
di=?0 (ао произвольно) и A=r—I, ao=O (я^ произвольно). Легко заме-
заметить, что эти условия приводят к разложениям, полученным выше.
Попробуем теперь представить решение дифференциального уравнения (99)
с помощью разложения в ряд по убывающим степеням переменной. Подста-
Подставим для этого в (99) ряд *,,
** I м-х
х=и
и приравняем нулю коэффициенты при различных степенях z. Учитывая, что
наивысший показатель степени z равен k, получаем
bo(k — v)(A+v+l) = O, b^k — v
bx(k — X — -t)(k — X + v-f-l) = 6x_2(A — X+
Возьмем k = t, 6, == 0 и произвольное Ьо. Получаем ряд
. A03)
Возьмем k = — v — 1, ?j = 0 и произвольное b0. Получаем ряд
^^ -,y A04)
28 А Анго
4 34
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VH
Ряды A03) и A04) определяют частные решения (99), сходящиеся
при |г|> 1.
7.6.3. Полиномы Лежандра. Если параметр v равен целому неотрица-
неотрицательному числу п, то все коэффициенты одного из рядов A01) или A02),
начиная с определенного номера,, будут равны нулю и, значит, этот ряд
сведется к полиному. Если п четное число, то ряд A01) оборвется на члене
n-й степени; если же п — нечетное число, то ряд A02) оборвется на члене
(и—1)-й степени. Если положить
1-3-5... п
2-4-6. ..п
«•,— v— ч 2-4-6... (n-1) '
то при z = 1 оба полинома будут принимать значения, равные единице.
Полученные таким образом полиномы называются полиномами Лежандра
Pn(z). Расположенные по возрастающим степеням z, они имеют вид (и —
любое):
р <~л- ЬЗ-5...Bгс-1) [ „ п(п-1)
п У }~ п\ \Z 2 Bп — 1) Z "*~
я(я-1)(я-2)(я-3) 4 _
~*~ 2-4'Bп—1)Bга —3) Z
7.6.4. Производящая функция полиномов Лежандра. Пусть А н М —
две точки, расположенные соответственно на расстоянии г и г' от начала
координат О (рис. 7.40). Расстояние AM равно
(г2 — 2rr' cos G —\- г'2) , т. е.
AM == г' (й2 — 2й cos 8 + 1)'/а
или
AM = r(h2 — 2h cos 0 + 1 f\
A05)
О
г
Рис. 7.40.
М
где через h обозначается отношение —г при г' > г
и отношение — при г'<г. Следовательно, величина h
в обоих случаях меньше единицы. Ньютоновский потенциал в точке Л, нахо-
находящейся на расстоянии f от начала координат, вызванный единичной массой,
помещенной в точку М на расстоянии г' от начала координат, выражается
формулой
1
1
AM
1
уA — 2/zcose-f /г2)
~A — 2/zcos 6 +/г2)"
h = — при г' < г.
ft =
при г' > г.
Разложим A—2й cos 6 -(- /г2) 2 в ряд по возрастающим степеням Л.
Тогда коэффициент при h" дается разложением A05), в котором z заменено
на cos 8, т. е.
A — 2/г cos Q~\-h2)~'k = P0(cos 6)-\-hPv(cos 6)+ ... +A"Pn(cos6)+...A06)
Это выражение оправдывает название коэффициентов Лежандра, данное по-
полиномам Pn(cos8).
Итак, коэффициенты Лежандра входят в распределение ньютоновских
потенциалов на шаре (п. 7.6.26). Они входят также в выражение для по-
потенциала электрического диполя. В самом деле, пусть даны два электриче-
7.6J
ФУНКЦИИ ЛЕЖАНДРА
435
ских заряда, равных по величине и противоположных по знаку; отстоящих
друг от друга на расстоянии 2г'. Потенциал в точке М (рис. 7.41) равен
V ~ q \АМ ~~ ~ВМ)'
Эта формула, согласно предыдущему расчету, может быть написана в виде
Г со °о "|
V = -f У h"pn (cos б) — У h"Pn (— cos 8) .
n=0
Предположим сначала, что г > г'; тогда h — -^-. Так как Рп(х) в со-
соответствии со своим индексом — функция четная или нечетная, то потен-
потенциал в окончательном виде равгн
я=>0
Для перехода к случаю г < г' доста-
достаточно в получе-нной формуле заменить г
на г', обозначив через h ' отношение -у. B(-q) О
Функция A—2hz-\-h2)~ называется Рис. 7.41.
производящей функцией полиномов Лежандра.
С помощью разложения в ряд Тейлора по г' при /•' = 0, учитывая, что
, 1
AM
дг'
г' = о
AM
дг
и полагая г = (х2-\-у2-\-z2I', находим
и, сравнив с выражением A06), получаем
Иногда может оказаться удобным разложить Pn(cos9) по косинусам
углов, кратных 6. Для этого запишем производящую функцию в виде
Биномиальные ряды для обоих двучленов абсолютно сходятся. Поэтому иско-
искомое разложение можно получить непосредственным перемножением бино-
биномиальных рядов. Вычисления дают
A07)
28*
436 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
7.6.5. Примеры полиномов Лежандра. Если в выражениях A05) и A07)
последовательно приравнять п = 0, 1, 2 7, то найдем:
Я0(г)=1.
P1(z) = z.
P2(z) = jCz*~l),
Р(г)
P5 (z) = -i F3г5 — 70z3 4-15z),
16
= 4r D29z7 — 693z5 4- 315z3 — 35z),
Id
Pn(cos8)=l,
Pi (cos 8) = cos 8,
P2 (cos 6) = -j C cos 26 4- 1),
P3 (cos 6) = -g- E cos 36 -I- 3 cos 6),
P4 (cos 6) = -i- C5 cos 40 4- 20 cos 26 4- 9),
P5 (cos 6) = -jig- F3 cos 56 4- 35 cos 36 4- 30 cos 8),
P6 (cos 6) =-^B31 cos 66 4-126 cos 46 4-105 cos 26 4-50),
P7(cos 8) = -7^-D29cos764-231 cos 564- 189cos364-175 cos 6),
7.6.6. Представление полиномов Лежандра через определенный инте-
интеграл. Формула Лапласа. Рассмотрим интеграл
a-\- b cos <p Ya2 — b1
о
В этой формуле положим
а=1—hz, ft= + Л ]/~z2.—i,
предполагая h таким, что | h \z ± 'Yz2 — 1 cos cp) | < 1. Разложим обе части
полученного тождества по возрастающим степеням h, используя разложе-
разложение A06) (считаем здесь, что \z\ < 1). Приравняв в обеих частях тождества
коэффициенты при hn, получим формулу Лапласа
ЯяB) = 1 f(z± УЖ^~\ cos<p)nd<p. A08)
7.6] ФУНКЦИИ ЛЕЖАНДРА 437
Введенное выше ограничение \z\ < 1 можно отбросить. В самом деле, фор-
формула A08) представляет равенство между полиномами, так как интегралы от
нечетных степеней costp равны нулю. Следовательн-о, A08) справедлива для
всех комплексных z.
Если h таково, что | h {z ± Уz2— 1 cos<p)| > 1, то обе части исходного
тождества можно разложить по возрастающим степеням -г. Приравнивая
в обеих частях тождества коэффициенты при -тд-, получим
A09)
[
* j' (г± Yz2 — 1 cos <p)
Знак перед интегралом совпадает со знаком
7.6.7. Рекуррентные формулы. Продифференцируем по h обе части
равенства
1
). (ПО)
Тогда
~' 21Pn(z) A11)
2ln
я=0
ИЛИ
1 °°
A— 2hz + h2)~2 (z — й) = A — 2hz+ h*) ^nh"'1 Pn(z).
я=о
Используем в левой части этого равенства формулу (ПО). Имеем
(z _ щ 2 hnPn (z)-= (l — 2hz + h?) 2 nhn~ lPn (z).
Приравнивая коэффициенты при hn, получаем рекуррентное соотношение,
связывающее три последовательных полинома Лежандра: t
1(z) = 0. A12)
Продифференцируем уравнение (ПО) по z. Тогда
з °°
h A _ 2hz + к*)"* = 2 А" -^ Рп (Z
я=0
Если учесть равенство A11), то
nhnPn (z) = i2-h)^ih"^IPn (z),
я»0 я=0
и, приравнивая коэффициенты при h", получаем рекуррентное соотношение
Продифференцируем формулу A12):
1> Р
438 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Исключая -т- Pn-\(z) из A13) и A14), получаем рекуррентную формулу
-fLpn+1(z)-z-^Pn(z) = (n+l)Pn(z). A15)
7.6.8. Формула Родрига. Функция
У = (^-1)я
удовлетворяет дифференциальному уравнению
(z2—l)y"-\-2z(l—n)y' — 2ny = 0. A16)
Продифференцируем это уравнение п раз по z:
Положим
dny
dzn
Тогда предыдущее соотношение принимает вид
(г2 — 1) w" + 2zw' — п (п + 1) w = О,
а это — дифференциальное уравнение Лежандра.
Но w(z) — полином л-й степени. Значит, он, с точностью до постоян-
постоянного множителя, равен полиному Лежандра Pn(z): ¦
В результате n-кратного дифференцирования получится 2nn\zn, а также сла-
слагаемые, содержащие множитель z2 — 1. Поэтому
Отсюда получаем формулу Родрига
7.6.9. Ортогональность полиномов Лежандра. Вычислим интеграл
/= Г Pn(z)zmdz (m — целое число < л).
Согласно формуле A17), имеем
+1
2"я!/= f zm~(z2—l)ndz.
-i
Интегрируя по частям:
+1
,, dn~X 2 nl+ t -I ^"~' 2 я
— 1
7.6] . ФУНКЦИИ ЛЕЖАНДРА 439
В'неинтегральный член равен нулю, так как производная (и—1)-го порядка
(г2—1)" содержит множитель z2—1. Продолжая интегрирование по частям,
получим выражение
С лп-т Г ип-т-\ Т + 1
/ _? (Z2 \\п dz— — (z2 '11й =0
Следовательно, 1=0. Отсюда вытекает, что интеграл
+i
f <?(z)Pn(z)dz
-1
равен нулю, если <f(z) — полином степени, меньшей п. Если, в частности,
ср (z) — полином Лежандра, то
+1
J Pm(z)Pn(z)dz = 0 (тфп), A18)
-1
что и доказывает ортогональность полиномов Лежандра.
Вычислим
У= / [Pn(z)?dz.
-1
Формула A17) позволяет написать
+i
,_ 1 f dn(z
~22n{n\Y J
dzn dzn
^
Интегрируем п раз по частям. Заметив, что все внеинтегральные члены
равны нулю, получим
+1
Но.
+1
-1
Отсюда
2^Г- 019)
-i
Функции, удовлетворяющие условиям Дирихле (п. 2.1.2), можно разло-
разложить в ряд по полиномам Лежандра:
Коэффициенты ak, очевидно, равны
+1
f f(z)Pk(z)dz. A20)
440 ' СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
7.6.10. Некоторые значения полиномов Лежандра. Как указано
в п. 7.6.3, полином A05) равен единице при z=l. Это легко проверяется
с помощью формулы (ПО). Положим в (ПО) z = 1. Учитывая, что
A—2й + й2) 2=A—й)-1= 2А".
л=0
получаем тождество
2/>„(!)*"= 2*".
я=0 я=0
из которого сразу следует РлA)=1.
Заменим в A10) г на —z. Это можно сделать двумя способами:
[1 — 2/г (— г) + /г2]' = [1 — 2 (— К) z H- /г2]~'/г.
Приравнивая соответствующие правые части разложений, получим
Pn(-z) = (~irPn(z). A-21)
Отсюда, в частности,
Положим в (ПО) z = 0, затем разложим левую часть в ряд и прирав-
приравняем коэффициенты при одинаковых степенях h. В результате получим
7.6.11. Корни полиномов Лежандра. В п. 6.2.11 мы показали, что
корни решений дифференциального линейного уравнения просты. Следова-
Следовательно, корни полиномов Лежандра просты. Функция g(z) = (z2—1)" имеет
я корней, равных -f-1. и п корней, равных —1. Функция g' (z), очевидно,
имеет п—1 корней, равных -)-1, п—1 корней, равных —1, и, как сле-
следует из теоремы Ролля, один корень между —1 и +1. Продолжая это рас-
рассуждение, получим, что полином л-й степени gin)(z) имеет я корней, заклю-
заключенных между —1 и -\-1, и, естественно, ни одного корня, равного —1
или 4-1- В силу формулы Родрига A17), это — корни Р„(г)=0. Следова-
Следовательно, все корни Pn(z) простые и находятся между
— 1 и +1.
7.6.12. Интеграл Шлефли. Пусть z — аффикс
точки комплексной плоскости переменной t. Рассмотрим
интеграл, взятый по контуру С (рис. 7.42):
* ¦ ^- „ +,<*<¦ A23)
Рис. 7.42. Если v = п — целое положительное число или нуль,
то этот интеграл представляет собой полином Лежан-
Лежандра Pn(z). Действительно, интеграл A23) равен вычету кратного полюса
порядка п-\-\ при t = z, т. е. (п. 1.3.13)
1 1 Г ап и* п
2я n! [df {t l) \t=/
который, в свою очередь, согласно формуле A17), равен Pn(z). Инте-
Интеграл A23) называется интегралом Шлефли.
7.6] ФУНКЦИИ ЛЕЖАНДРА 441
7.6.13. Обобщение полиномов Лежандра. Полиномы Гегенбауера.
Мы установили, что полиномы Лежандра могут рассматриваться как коэффи-
коэффициенты при различных степенях h в степенном ряде функции
A — 2hz-\-h2) 2 (Л < 1).
Полином Гегенбауера я-й степени с индексом р определяется как коэффи-
коэффициент при h" в степенном ряде функции
оо
A —2hz-\- h2)~p'= 2 ЛлС?(,г).
Случай /?=1/2, очевидно, соответствует полиномам Лежандра:
1
Способом, аналогичным способу установления рекуррентных формул для
полиномов Лежандра, получаем соотношения
) = -^±! С?+1 (z),
Полиномы Гегенбауера представляют собой решение дифференциального
уравнения
*/' 2 \)zy' —
и удовлетворяют соотношениям ортогональности
. +1 _i
f(z2— l/ 2Cp(z)Cpm(z)dz = 0 (тфп).
-i
Замечание. При р = 0 полиномы Гегенбауера Сп определяются'раз-
определяются'разложением в степенной ряд функции
* оо
In A — 2hz + h2) = 2 ftnC°n (z).
n = 0
7.6.14. Функции Лежандра первого рода. По определению, функция
Лежандра первого рода P,(z) представляет собой решение дифференциаль-
дифференциального уравнения (99), принимающее при z = 1 значение 1.
Если в уравнении (99) произвести замену переменной С = —<=>—• то
оно принимает вид
C(l-CLS? + (l-2CL? + v(v+l)/ = O. A24)
Это частный случай дифференциального уравнения, определяющего гипергео-
гипергеометрическую функцию Гаусса (см. пример из п. 6.2.10), при а=—v,
1
v+1. Т = 1, х=1==±.
Придадим постоянной а0 значение 1, тогда
442 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
или, в виде ряда,
я,(«)~1+2-(*-в+1)%^'"(*+вЧ^Г A25)
л=1
Если v равно целому положительному числу л или целому отрицательному
числу —п—1, то ряд обрывается на члене, содержащем A—z)n. Распола-
Располагая этот полином по степеням z, мы опять получаем полином Лежандра Pn(z),
определяемый формулой A05).
Если Pw(z) — решение (99), то Рч(—z) также будет его решением.
Предположим, что Pv(z) и Pv(—z) линейно независимы. В этом случае
общий интеграл (99) будет
f(z) = AP,(z)-hBP,(— г).
Рассмотрим вопрос о линейной независимости />„(—z) и P\{z). Для
этого изучим поведение Рч(г), когда z стремится к —1, или, при замене
переменной z = cos6, поведение Pv(cos6), когда 8 стремится к тс. При этой
замене переменной уравнение (99) приобретает вид
Если ограничиться рассмотрением значений 8, очень близких к нулю, то
общее решение уравнения A26) будет очень близким к общему решению
уравнения
I4
равному
CJ0(8 УТ^+Т)) + DYQF y\(v+-l)).
Это решение бесконечно возрастает, если 8 приближается к нулю. Так как
при 8—>-0 функция Pv(cos9) стремится к -\- 1, то Pv(z) и Pv(—z) линейно
независимы только в случае, если Рч(—z) бесконечно возрастает при z—>1.
Согласно A25), это имеет место при v нецелых, и, как нетрудно убедиться,
порядок возрастания Pv {z) при z —> — 1 тот же, что и у функции
±±^ ^. A27)
Так как обе функции Pv(cos8) и Уо(8 V"v(v-j- 1)) принимают одинаковое зна-
значение -\- 1 при 8 = 0, то У0(б У*(ч-\- 1)) можно рассматривать как апрок-
симацию Pv(cos8) при малых значениях 8.
Если у равно целому числу л, то дело обстоит иначе. Действительно,
в силу формулы A21),
Яв(—г) = (—1 )"/>„(*).
и общее решение уже не будет равно
APn(z)+BPn(— z),
так как Pn(z) не возрастает бесконечно, если z стремится к —1, а при-
принимает значение (—1)". Следует ввести другое решение Qn(z), линейно
независимое от Pa(z). При этом общее решение будет
Это решение Qn(z), называемое функцией Лежандра второго рода, опре-
определяется в конце п. 7.6.19.
7.6] ФУНКЦИИ ЛЕЖАНДРА 443
Ряд A25) достаточно быстро сходится только при z > 0. При z < 0
им неудобно пользоваться для вычисления P^(z), особенно при z, близких
к — 1. Гобсон нашел.разложение P4(z), быстро сходящееся при — 1 < z < 0,
для значений индекса v, не слишком больших по сравнению с единицей:
l±L\r\ П28)
Здесь ф (V) — логарифмическая производная функции F(l-(-v), a f — посто-
постоянная Эйлера (см. п. 7.4.1 и последующие).
Если индекс близок к нулю или единице, иначе говоря, равен е или
l-j-е (е мало), то можно написать
^ A30)
" A31)
с погрешностью, меньшей е2 при —1<2< + 1. Функции, соответствую-
соответствующие индексу v = « + e, можно получить из двух предыдущих, если несколько
раз применить рекуррентную формулу A34).
7.6.15. Описание поверхности у = Р„ (cos в). Поверхность y = Pv(cos6)
(рис. 7.43) проходит через прямую у=1, 6 = 0. Плоскость, касающаяся
поверхности по этой прямой, параллельна плоскости координат 6v. Кривые —
сечения поверхности y = Pv(cos6) плоскостями v = const — удаляются' от
касательной плоскости тем скорее, чем больше ч. Обозначим через п бли-
ближайшее целое число, меньшее v. "Если 6 стремится к тс, эти кривые стре-
стремятся после л колебаний к (—1)"+ оо, за исключением случая, когда v
равно целому числу л, —тогда они стремятся к (—1)л+ . Скорость беско-
бесконечного возрастания кривой тем больше, чем ближе ч к целому числу, и,
npif прочих равных условиях, чем v больше.
В заключение отметим, что рассматриваемую поверхность можно пред-
представить в виде полуполосы шириной тс, бесконечной в направлении возра-
возрастающих v.. Эта поверхность по мере удаления от оси 6 разделяется на
ленты шириной в единицу. Каждая из лент образует тем большее число
складок, чем больше v; ленты попеременно стремятся к -j-oo и —оо вдоль
плоскости 6 = тс.
7.6.16. Корни функций Лежандра первого рода. При решении в сфе-
сферических координатах задач теории потенциала обычно применяются функции
Лежандра Pv(cos8). В этих задачах часто приходится вводить следующее
граничное условие: потенциальная функция обращается в нуль на поверх-
поверхности конуса с вершиной в начале координат, образующая которого состав-
составляет с осью (прямой 6== тс) угол 80. Произведения Лапласа, образующие
потенциальную функцию, содержат Pv(cos6), где v принимает такие зна-
значения, что Рч (cos 90) = 0.
444
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
На рис. 7.44 по оси абсцисс отложены значения 20 = cos90, а по оси
ординат — значения индексов v. Кривые на этом рисунке устанавливают связь
между z0 и значениями v = vft(v0 < v; < v2 < ...), для которых PvB0) = 0,
760 760 740 ГZO
06
so 6o 40 го о
Рис. 7.43.
'л
6
5
4
3
г
1
п
У
—'
1 —
у
*^
У
-——
/
У
/
1/ & ^^
*--
/
У
/
у
1
и| -i
0
Рис. 7.44.
т. е. рисунок позволяет при любом фиксированном z0 определить v = vft—•
последовательные корни PvB0) = 0. Рисунок недостаточно точен для г0,
близких к —1, т. е. для очень острых конусов. Это важный для приложе-
приложений случай, так как часто возможно отождествлять с такими конусами тон-
тонкие провода. Здесь можно использовать приближенную формулу, которую
7.6] "ФУНКЦИИ ЛЕЖАНЯРА 445
мы получим из A28). В самом деле, при 20-|-1, близких к нулю, в A28)
можно пренебречь суммой и, пользуясь известными свойствами функции ф
(п. 7.4.4), для v и z0, удовлетворяющих уравнению Py{z0) = 0, находим
ln-^±i + 2-r + 2«l>(v) + itctgiw«^0. A32)
Это уравнение нетрудно решить графически.
Для очень малых zo-±-l (меньше 1/100) можно вывести приближенную
формулу, определяющую разность между значением индекса vn и его поряд-
порядковым номером я:
A33>
7.6.17. Рекуррентные формулы. Выражение
согласно ряду A25), равно
со
L (HiF (-г-) (Tirs
п=1
или
g;(
Отсюда получаем рекуррентную формулу
(vH-l)P,+1Br) —Bv+lJr/»,B;)+vP,_1Br) = a A34)
обобщающую формулу A12), которая была выведена для полиномов Ле-
жандра.
Составим выражение rr-P4+i(z) — -г- P4-\{z). Оно равно
я=1
Отсюда получаем следующую рекуррентную формулу:
• Продифференцировав по z тождество A34), определим выражение
-з— P^-i(z). Подставив его в A35), имеем
— рекуррентное соотношение, обобщающее A15).
Вычтем равенство A36) из A35). Получаем формулу, обобщающую A13):
zJ^p^z)—jLp^(z)=vP^z). A37)
Умножив уравнение A37) на z и вычтя из него уравнение A36), в ко-
котором предварительно v заменено на v — 1, получаем формулу
которая, конечно, справедлива и для полиномов Лежандра.
446
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ.-VH
7.6.18. Определение функции Лежандра первого рода через интег-
интеграл Коши. Рассмотрим интеграл Шлефли A23). Подставив его в диффе-
дифференциальное уравнение Лежандра, получим после несложных преобразо-
преобразований *)
d f C2-1)V + 1 }dt-Q
\ 2 )
y T J
dt \ (t-
Если v— целое положительное число, то полученное равенство удовлетво-
удовлетворяется. Это подтверждает то, что уже нам известно: интеграл Шлефли пред-
представляет собой решение дифференциального уравне-
ния Лежандра. Функция
A38)
если v — целое положительное, при полном обходе
1 контура С принимает первоначальное значение. В этом
случае интеграл Шлефли, как показано в п. 7.6.12,
совпадает с полиномом Лежандра Pn{z).
Пусть v — не целое число. Тогда интеграл Шлефли позволяет дать
другое определение функции Лежандра первого рода.
Рассмотрим функцию A38). Она имеет три особые точки (точки раз-
разветвления): t=\, t = — 1, t = z. Предположим, что контур С окружает
-оо -7
• г
А
Рис. 7.47.
только точку t=\. Если, исходя из точки А (рис. 7.45), обойти этот кон-
контур в положительном направлении, то новое значение функции w в точке А
равно первоначальному, умноженному на
Если же контур С окружает только точку t = z (рис. 7.46), то при об-
обходе этого контура в положительном направлении функция w приобретает
множитель
Значит, если контур С окружает две особые точки t=\ и t = z (рис. 7.47),
то при полном обходе контура функция w принимает первоначальное зна-
значение.
Следовательно, функция
*) Ср. [1], п 141.
7.6] ФУНКЦИИ ЛЕЖАНДРА 447
представляет собой решение дифференциального уравнения Лежандра, ко-
которое совпадает с полиномом Лежандра, если число v — целое положитель-
положительное. При произвольном v эта функция определяет функцию Лежандра пер-
первого рода PvB).
Чтобы добиться однозначности такого определенля сферической функ-
ици, принимают, что в исходной точке А (точке пересечения контура С
с осью абсцисс при t > 1) равны нулю аргументы t-\-\ и t—1, абсолют-
абсолютное значение аргумента t — z меньше тс и в плоскости t осуществлен раз-
разрез от точки t = —1 до точки t = — со (рис. 7.47).
7.6,19. Функция Лежандра второго рода. Определения. Используем
вычисления п. 6.2.11. Решением (99), линейно независимым от Pn(z), будет
Поэтому общее решение (99) для целых и положительных п имеет вид
n (z)f A_22)%я(г)}2 •
Полином Лежандра Pn(z) имеет только простые вещественные корни
ar(r—l я), лежащие внутри интервала (—1, 1). Поэтому Можно
написать
Ч г |' 1 | У а' | У "г
Ч | 1 | У
— 2 U-z ^ 1 + г\^А z~ar (гу
Коэффициенты аг вычисляются по формулам
_ d Г {г-*гУ 1 _. d Г 1 л .-.
пг — dz L A - г») {Р„ (г))« J,= ar ~ ^ L A - ^) (L (г)}' J,.^ '
где
Яя(г) = (г— ar)Z.(z). A39)
Отсюда
Подставим A39) в уравнение (99) и положим затем z — ar. Тогда
A—<ф?'(аг) —a,?(ar) = 0.
Следовательно,
и можно написать
U\±^^^\ A40)
r=l
Функция Лежандра второго рода, в соответствии с формулой A40),
определяется следующим образом: для вещественных z, заключенных внутри
интервала (—1, +1). по формуле
448 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
для комплексных z, а также для вещественных г, находящихся вне интер-
интервала (—1, +1), по формуле
При таком определении функция Лежандра второго рода Qn (z) вещественна
при вещественных значениях z.
Функция Лежандра второго рода имеет две точки разветвления z = — 1
и z = -\-\. Соединяя разрезом точки z = — 1 и z — -{-\, выделяем одно-
однозначную ветвь этой функции.
Если последовательно придавать п значения 0, 1, 2 то, согласно
формуле A41), находим
) = -?ln-I±
3
4 zjln 1— г JZ^3'
30 , , 3 \, 1 + ^ 35, .55
z2+rz3+
63 . 70 , . 15 \ . 1 + г 63 . , 49
Общая формула имеет вид
QAz) = ^Pn(z)lni±^-Wn_1(z), A43)
где
у.. 1-3...Bв-1) j „_, , „_3Г1 л(я-1)
— 12 \ ^ L3 2Bn —1)
-1) , л(я-1)(я-2)(я-3)
.5 . 3 2 Bл— 1) ^ 2
или
я-1)(я-2)(я-3I
-4Bп— 1)Bл — 3) J
г=1
Переход к формуле A42) при любом фиксированном п осуществляется
заменой в A43) 1п . _ на In -z~_ . .
Рассмотрим ряд A04), определяющий решение (99) для всех значений z,
удовлетворяющих условию |г|>1. Легко убедиться, что функция, заданная
рядом A04), при ч=п, где п — целое положительное число, совпадает
с функцией Qn (z) с точностью до постоянного коэффициента
д°~ 1-3-5... Bл—1) *
7.6] ФУНКЦИИ ЛЕЖАНДРА 449
Ряд A04) можно взять в качестве определения функции Q,(z) при про-
произвольном v, полагая множитель bQ равным
¦W1.V +
2V+1
В— эйлерова функция первого рода, определенная в п. 7.4.6.
Пусть v — целое положительное число и —1 <z<-j-l. Тогда можно
показать, что функция Лежандра второго рода A41) совпадает с функцией,
определенной тем рядом A01) или A02), который не вырождается в поли-
полином Лежандра, если положить
"+1 2.4 (п— П
ао=(—1) 2 .''о (л — нечетное число), ч
а, = (—1)г -г—о -. гг (л —четное число).
Аналогично тому, как это было сделано для бесселевых функций, можно
определить функцию Ле'жандра второго рода с помощью пределов:
Q (z) = \\mP^z)cos™-PA-2) ,
Sin 7CV
Q (z) = lim —J-i-J ^ь L .
Используя ряд A04) и повторяя рассуждения п. 7.6.17, можно пока-
показать,, что функция QvB) подчиняется тем же рекуррентным соотношениям,
что и P^(z). Следовательно, эти соотношения справедливы для любого ин-
интеграла (99). С помощью указанных выше формул определения нетрудно
установить, что функции Q принимают следующие значения:
О =
lim Qa(z)=0.
|г|->оо
• 7.6.20. Определение функции Лежандра второго рода через инте-
интеграл Коши. Мы видели в п. 7.6.18, что дифференциальное уравнение Ле-
Лежандра (99) допускает в качестве решения криволинейный интеграл от функции
1 (t2 — \у
21 (t — z)-+1 '
взятый по такому контуру (комплексной плоскости t), что при его обходе
функция A38) остается однозначной. Можно определить контур, отличный
от контура, приведенного на рис. 7.45, который обладал бы тем же свой-
свойством. Мы видели, что при полном обходе в положительном направлении
вокруг точки разветвления t=-\-\ функция A38) умножается на e2lz'^+l).
Ясно, что при обходе точки разветвления t — — 1 в отрицательном на-
направлении та же функция A38) умножается на е-2^^*1). Следовательно,
если в качестве контура Г взять любую кривую, имеющую форму восьмерки
29 А. Анго
460 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
и окружающую точки t = + 1 и t = — 1 (но не / = z), как показано на
рис. 7.48, то криволинейный интеграл
будет удовлетворять дифференциальному уравнению Лежандра. Это позволит
определить функцию Лежандра второго рода Qs{z) для любых значений ин-
индекса v и (за счет выбора допустимого кон-
контура) произвольных значений аргумента z вне
отрезка [—1, -f-1].
Замечание. Из рассуждений предыду-
предыдущих пунктов следует, что из всех уравнений
р _48 Лежандра (99) только уравнение с v, равным
целому числу я, допускает ограниченное реше-
решение в замкнутом интервале —1^гг«^1. Это решение единственное, оно
совпадает с полиномом Лежандра Pn(z).
Если значение z = —1 исключено, то при произвольном v сущесхвует
единственное конечное решение, совпадающее с Py(z).
Решение уравнения Лежандра, стремящееся к нулю при бесконечно
возрастающем \г\, дают только функции Лежандра второго рода.
7.6.21. Присоединенные функции Лежандра. Рассмотрим дифферен-
дифференциальное уравнение (98). Подставив в него
/(*) = (!—*2O У (*)•
получим
a-z2)^i-2(V-hl)z^ + ^-v,)(v + v,+ \)y = 0. A46)
Положим " С = —2— • тогда
Это гипергеометрическое уравнение Гаусса. Возьмем его второе решение
(пример п. 6.2.10) в качестве определения присоединенной функции Лежандра
первого рода. Имеем
при —1 < z < + 1 и
при z, лежащем вне отрезка [—1. -)-1].
Из вида уравнения (98) следует, что Р*(—z) также является его ре-
решением. Если v —|— р. — не целое число, то это решение линейно независимо
от Р* (z). Предположим, что это так. Тогда общий интеграл (98) будет
P^(—z). A47)
В приложениях переменная z обычно вещественна и заключена между
—1 и +1; тогда можно положить, что
z = cos 6.
7.6] < ФУНКЦИИ ЛЕЖАНДРА 451
Дифференциальное уравнение (98) относительно новой переменной 9 имеет вид
Если значения 9 близки к 0, то общий интеграл этого уравнения
АР* (cos 6) + ВР* (— cos 0)
будет близок к общему интегралу уравнения
равному C^ ^
Если v-|~jj,— целое число, то решения P^(cos8) и Я^(—cos 8) линейно
зависимы, так как эти функции связаны равенством
Я? (cos 6) = (— 1 )v+11 ЯГ (— cos 6),
и выражение A47) уже не дает общего интеграла уравнения (98).
Определим присоединенную функцию Лежандра второго рода Q^(z) как
предел выражения
я /* (cos 0) cos (-v -f (i) я — P? (— cos 6)
2 sin (v -f- p.) я
при v-)-{)., стремящемся к целому числу. Легко заметить, что введенная
функция Q*(z) бесконечна на обоих концах промежутка [—1, +1]. Следо-
Следовательно, не существует индексов, для которых уравнение (98) имеет ко-
нечноб решение в промежутке
Можно также определить присоединенную функцию Лежандра второго рода
при любых индексах с помощью разложения в ряд по убывающим степеням
переменной.
Положим в уравнении A46) С=22. Тогда оно принимает вид <
«О—С)§г-Н2 — ?
Это уравнение гипергеометрического типа, допускающее в качестве частного
решения следующее выражение, которое мы возьмем за определение при-
присоединенной функции Лежандра второго рода С?Г при | z \ > 1:
"•" 2 ' 22
2V+1 T( , 3\ г»+1Ч-1 ^ I 2 2 "•" 2
Обычно условия регулярности, которым должны удовлетворять решения
уравнения (98), автоматически выполняются при целых индексах v и [>..
Соответствующие функции имеют важное значение, и в дальнейшем мы будем
рассматривать только такие функции.
7.6.22. Присоединенные функции Лежандра для целых положитель-
положительных индексов. Предположим сначала, что z вещественное (—1^2.^-j-l)
или соответственно z = cos S @ -< 9 <; тс). Сделаем подстановку
29»
452
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
(ГЛ. VII
в дифференциальное уравнение (97). Функция у (z) должна удовлетворять
уравнению
Оно совпадает с дифференциальным уравнением Лежандра, продифферен-
продифференцированным т раз, в котором производная га-го порядка взята за новую
функцию. Отсюда
или yB)
Первая из этих функций — /ге-я производная полинома Лежандра Pn(z) —
это полином (и — да)-й степени, известный под названием функции Гельм-
гольца. Конечно, если /те > п. то функция Гельмгольца равна нулю. Таким
образом, получены частные решения *) дифференциального уравнения (97):
\{z), A48)
„B). A49)
Используя A05), находим
-.)— Г1 ~2<Ъ B">! ) zn-m ('
Z)—(l Z ) 2"п\(п — т)[ \Z
2 Bл —
¦ (я - т) (п - т — 1) (я — т — 2) (я — т — 3) ш _4 I
2-4.Bя-1)Bя-3) Z ""Г
Отсюда получаем таблицу присоединенных функций:
1
Р) (cos 0) = sin 8
PJ(«) = 3A —«8O
Р|(г)=3A— г2)
Р] (г)= 15A —г2) 2
Р|(г)=15A —г2J
_
з(г) =105A — г2J z
= 105A— г2J
)==-±A_ cos 28)
Р\ (cos 0) = j (sin 8 -f- 5 sin 36)
P2 (cos 6) = ~ (cos 8 — cos 38)
P3 (cos 6) = j- Csin 6 — sin 36)
pi (cos 6) = ^ B sin 29 + 7 sin 49)
рз (cos 6) = ^ C -+• 4 cos 26 — 7 cos 46)
рз (cos 0) = ^ B sin 20 — sin 49)
P\ (cos 0) = ^ C — 4 cos 26 + cos 46)
') Для сохранения непрерывности, при определении этих функций для комп-
комплексных и нецелых значений индексов, Гобсон ввел в формулы A48) и A49) мно-
множитель (—1)ш.
ФУНКЦИИ ЛЕЖАНДРА 453
Используя формулы A49), A43) и A44), получаем
Единственные конечные решения (97) в интервале —1 <; z <[ -\- 1 дают
функции Р„ (z).
Определим функции Pjj1 и Q™ (см. вычисления из п. 6.3.11) для комп-
комплексных z и для вещественных z, расположенных вне промежутка I—1, 4-1].
с помощью равенств:,
т
SJn(z), A51)
1 dm _
JQn(z) A52)
(ср. с A42)). Если т — нечетное число, то, чтобы сделать функцию Р™ одно-
однозначной, следует в плоскости z точки —1 и ~\-1 соединить разрезом. Что
касается функции Q", то этот разрез уже был сделан в силу ее определения.
При больших | z | имеем
Qn{Z)
Полезно заметить, что выражения ,
e-Jn^Pn С/У). Je'n^Qn С/У)
вещественны.
Свойства функций Р" (г) аналогичны свойствам полиномов Лежандра,
Равенство
соответствует формуле Родрига, к которой оно и сводится при т = 0. Про-
Продифференцировав от раз соотношение A06), мы убедимся, что коэффициент
1
— m — —
при hn-m в разложении A—1hz + Л2) 2 равен
A—z2) 2P%(z).
Отсюда получается производящая функция для P™(z).
Используя функцию
454 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
можно определить Р™ (z) через интеграл Коши, обобщающий интеграл
Шлефли A23). Точно так же можно определить Р™ (z) через определенный
интеграл, обобщающий интеграл Лапласа, из п. 7.6.6:
те
Z (z) = (± 1Г ^^ГГ^ Т f lz ± У~г*^
7Г
(л — /и)! л ./
cos cp]" cos
\z±Yz2 — 1 cos tf]
"
Рекуррентные формулы для присоединенных функций Лежандра вы-
выводятся в п. 7.6.23, а вопрос об ортогональности этих функций рассматри-
рассматривается в п. 7.6.24.
7.6.23. Рекуррентные соотношения. Функции Рп (z) и полином -т-шРп(г)
представляют собой соответственно частные решения дифференциального
уравнения (97) и уравнения
(i-22)g-2(m+l)^ + [«(«+l)-m(m+l)]/ = 0. A53)
т
Если умножить уравнение A53) на A — z2J, то, в силу A48), можно
написать равенство
1 ? = 0, A54)
представляющее собой рекуррентное соотношение между функциями
"п < "п < "п •
Рассмотрим рекуррентную формулу A35), написанную для ч = п. Это
соотношение, продифференцированное т — 1 раз, дает
z). A55)
Продифференцировав т раз формулу A12), получаем
(я Н- 1) P[nlx (z) — Bя + 1) zP'nm) (z) — Bя + 1) mPf~X) (z) + nP^\ {z) = 0.
Исключив Р*-™~1) из двух последних соотношений, находим
1Г) Г) TM A56)
Соотношение A56), умноженное на A —z2J, дает рекуррентную формулу
между
Рп. Р'п-Ъ />?+!
вида
Bя+1)гР"(г) = (я + т)Я"_1(г) + (я —m+O/^+iC*). A57)
Если в соотношении A55) заменить т на /и+1 и результат замены
т + \
умножить на A — z2) 2 , то получим
Bя + I) 1/1^^72 P?(z) = PnS {z) — P"_Y (z) A58)
— рекуррентное соотношение между Р„, Р™+\. Р„~1.
7.5] ¦ ФУНКЦИИ ЛЕЖАНДРА 455
Заменив в A54) т на т—1 и исключив zP%(z) с помощью соотноше-
соотношения A57), получим
(In -)- l)V 1 —z
)P?-\z) A59)
— рекуррентное соотношение между P™+1, P™-u Pn'+u P*n~l-
Заменив в A59) P™~ {z) его выражением, полученным из A58), где
от-)- 1 заменено на т, найдем
Bл-н 1) /Г=
Z1(z) A60)
— рекуррентное соотношение между Р™+х, Pt-ъ Pn+i-
7.6.24. Ортогональность присоединенных функций Лежандра. По-
Покажем, что функции Pn{z) ортогональны в промежутке [ — 1, -+-1]. если
пат — целые положительные числа. Помножим на Р„ (z) дифференциаль-
дифференциальное уравнение (97), где / заменено на Pf (z). Точно так же помножим
на P?(z) дифференциальное уравнение (97), где / заменена на P™(z). Раз-
Разность полученных выражений дает
Следовательно,
f?{z) = 0, если пфз. A61)
-1
На основании A48)
P^(z) = (l~zbJ~Pn~
отсюда, интегрируя по частям, находим
/ К (z)f dz = ~ f РГ1 (z) ? [A _ z2) _*_ pm-i wj dz _
-(m-l) f[Prl(z)fdz+ f ^I1^ \Pr1(z)fdz.
-i _i
Если учесть дифференциальное уравнение (97), которому удовлетворяет
функция P™(z), то получим последовательно
f[PT~1(z)fdzm
Pn (Z)\ dZ= K ^_'
g
-l -l
456 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
и, наконец,
J 1Г
J
Из формул A61) и A62) вытекает, что функции в'промежутке [—1, -\-\]
можно разлагать в ряд по присоединенным функциям Лежандра первого
рода.
Чтобы получить ортонормальную *) систему функций, мы должны ввести
нормированные присоединенные функции Лежандра первого рода (см.
рис. 7.51—7.54):
_ 1 /я+1 (я — т)\ рт .
— |/ —2— (Я+Я|), ^я («)•
Отметим, что при разложении в ряд по полиномам Лежандра часто
используются нормированные полиномы Лежандра
Г
7.6.25. Некоторые значения присоединенных функций Лежандра.
Приложение присоединенных функций-. Если пит — целые положитель-
положительные числа (я > /те), то можно написать
Г(п—т+1) рт, . г)"тСгч> Г(я —
Р (г) Q {Z) —
а также соответствующие формулы для
Я» и Q?.
При 2= ±1 имеем
Р™(±1) = 0. Q?(±l)=oo.
Если я — /те — нечетное число, то
п — m-J-1 с, . . . ..
/-„(U)_U, У„ (U) — (— 1) ЬЗ... (п+т)
Если я — m — четное число, то
Если т==л, то можно написать
j(«)=l -3-5 ... Bя—
j(O)=l -3-5 ... Bя—1).
В качестве примера на приложение функций Лежандра рассмотрим
электростатическое поле сплюснутого эллипсоида вращения с потенциалом Vo.
') См. п. 2.1.2.
7.6] ¦ ФУНКЦИИ ЛЕЖАНДРА 457
Этот простой пример может пояснить замечание, приведенное в конце
п. 6.3.11. Действительно, регулярность, которой должен обладать потенциал U,
ограничивает класс функций, входящих в произведения Лапласа. На данном
примере мы покажем, что выбор этих функций может быть сделан лишь
после достаточно глубокого изучения их свойств.
Координаты х, у, z, оператор Лапласа AU и множители *Р, Ф, Н, вхо-
входящие в произведение Лапласа, как функции сплюснутых эллипсоидальных
координат вращения даны в п. 6.3.11.
Совершенно очевидно, что потенциал обладает симметрией вращения,
следовательно, [а = 0. Потенциал должен быть конечным на оси Ох, т. е.
при ср= ±". Отсюда ч = п (целому числу), а ?^—0.
Если заменить С1 на C1e~-'t/2, а С2 на jC2einVP, то оба слагаемых функ-
функции S будут вещественны. Потенциал равен нулю на бесконечности, т. е.
при ? = -(-оо. Так как Cle-J!''2Pn (у sh %) и jC2e1n*l2Qn (у sh %) при беско-
бесконечном возрастании % стремятся соответственно к бесконечности и к нулю,
то С, = 0.
Таким образом, потенциал U сводится к выражению
U = /ОД S е1"х*Ря (sincp) Qn U sh !•).
я=0
Уравнение заданного эллипсоида 5 = $0; потенциал на нем постоянен.
Он не должен зависеть от ср, поэтому Рп(sincp) сводится к постоянной; зна-
значит, возможно только я=0. Если Vo— заданный потенциал, то в оконча-
окончательном виде имеем
U —у QoQshS) _y arcctg(shS) __y arctgg~?
0 QoO'shSo) ° arcctg(sh50) ° arctge- "
7.6.26. Сферические гармоники. Вернемся к концу п. 6.3.8, где мы
решали уравнение Ш -\- кЮ = 0 в системе сферических координат. Допустим,
что нужно найти функцию U на сфере заданного радиуса. Мы уже видели,
что эта функция зависит от множителя
\А cos пер Ч- В sin w] [CP* (cos 0) + DQ* (cos 8)],
который называется сферической гармоникой. Здесь р обязательно равно це-
целому числу т, так как функция после полного оборота должна остаться
неизменной. Кроме того, ?) = 0 и ч — п —целому, чтобы исключить функ-
функции, которые становятся бесконечными на полюсах сфэры. Итак, имеем
[j4cos/recp+?sin/recp]P™(cos9). A63)
Рассмотрим некоторые частные случаи A63):
1) т = 0. Функция U становится равной нулю одновременно с Pn(cos9),
иначе говоря, на п параллелях сферы, симметрично расположенных по обеим
сторонам экватора. Pn(cos6) называется зональной гармоникой.
2) 0 < т < п. Функция U становится равной нулю на меридианах, соот-
А
ветствующих корням tg /геср = ^-, иная — т параллелях, симметричных
относительно экватора. В этом случае выражение A63) называется тессе-
ральной гармоникой.
458
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VU
3) т = п. Функция U становится равной нулю на т меридианах, а следо-
следовательно, и на полюсах. Выражение A63) сводится к (Acosmy -\-Bsin/mp)sinm6.
В этом случае оно называется секториальной гармоникой.
' 1,0 0,8 0,6 0,4 0,2 О -0,2 -0,4 -0,6 -О.д -1,0
2=COS в
Рис. 7.49
1,2
1,0
0,8
0,6
0,4
0,2
О
-0,2
-0,4
-0,6
-0,8
-1,0
-1,2
~1>4о
0
W
1МЯ
<?.
ч
Яам
——
¦II —
<
——
<;
ч
>
ч
—'
Иг
<
s
——
^*
\
><
\
\
—¦
ч
у
ч
\
ч
у
\
п
*/
><
j
/
J
/1
/Л
/1
/1
'1
///
/1
У
<?^ ^
0,6 0,7
0,8 0,9 1,0
Z=COS0
Рис. 7.50.
Доказано, что произвольную функцию от б и tp можно разложить в ряд
по сферическим гармоникам. Такая возможность объясняет важность этих
понятий.
7.6.27. Графики функций Лежандра первого рода (рис. 7.49).
7.6.28. Графики функций Лежандра второго рода (рис. 7.50).
7.6] ФУНКЦИИ ЛЕЖАНДРА 459
7.6.29. Таблица значений первых семи полиномов Лежандра.
X
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
Я,(х)
0,0000
0,0100
0,020 0
0,030 0
0,040 0
0,050 0
0,0600
0,0700
0,080 0
0,0900
0,1000
0,110 0
0,1200
0,130 0
0,140 0
0,150 0
0,160 0
0,1700
0,180 0
0,190 0
0,200.0
0,2100
0,2200
0,2300
0,2400
0,250 0
0,260 0
0,270 0
0,280 0
0,290 0
0,300 0
0,310 0
0,320 0
0,330 0
0,340 0
0,350 0
0,3600
0,3700
0,380 0
0,390 0
0,400 0
0,4100
0,420 0
0,430 0
0,440 0
0,4500
0,4600
0,470 0
0,480 0
0,4900
0,500 0
0,510 0
0,5200
0,5300
0,5400
0,550 0
РЛ*)
—0,500 0
—0,499 8
—0,4994
—0,498 6
—0,497 6
—0,496 2
—0,494 6
—0,492 6
—0,4904
—0,487 8
—0,485 0
—0,481 8
—0,478 4
—0,474 6
—0,470 6
—0,466 2
—0,461 6
—0,456 6
—0,451 4
' —0,445 8
—0,440 0
—0,433 8
—0,427 4
—0,420 6
—0,413 6
—0,406 2
—0,398 6
—0,390 6
—0,382 4
—0,373 8
—0,365 0
—0,355 8
—0,346 4
—0,3366
—0,326 6
—0,316 2
—0,305 6
—0,294 6
—0,283 4
—0,271 8
—0,2600
—0,247 8
—0,235 4
—0,222 6
—0,209 3
—0,195 2
—0,182 6
—(Г, 168 6
—0,154 4
—0,1398
—0,125 0
—0,109 8
—0,094 4
—0,078 6
—0,062 6
—0,046 2
РА*)
0,000 0
—0,015 0
—0,030 0
—0,044 9
—0,059 8
—0,074 7
—0,089 5
—0,104 1
—0,118 7
—0,133 2
—0,147 2
—0,161 7
—0,175 7
—0,189 5
—0,203 1
—0,216 6
—0,229 8
—0,242 7
—0,255 4
—0,267 9
—0,280 0
—0,291 8
—0,303 4
—0,314 6
—0,325 4
—0,335 9
—0,346 1
—0,355 8
—0,365 1
—0,374 0
—0,382 5
—0,390 5
—0,398 1
—0,405 2
—0,411 1-
—0,417 8
—0,423 4
—0,428 4
—0,432 8
—0,436 7
—0,440 0
—0,442 7
—0,444 8
—0,446 2
—0,447 0
—0,447 2
—0,446 7
—0,445 4
—0,443 5
—0,440 9
—0,437 5
—0,433 4
—0,428 5
—0,422 8
—0,416 3
—0,409 1
Р4(х)
0,375 0
0,374 6
0,373 5
0,371 6
0,369 0
0,365 7
0,361 6
0,3567
0,3512
0,344 9
0,337 9
0,330 3
0,321 9
0,312 9
0,303 2
0,292 8
0,281 9
0,270 3
0,258 1
0,245 3
0,232 0
0,218 1
0,203 7
0,188 9
0,173 5
0,157 7
0,1415
0,124 9
0,107 9
0,090 6
0,072 9
0,055 0
0,036 9
0,018 5
0,000 0
—0,018 7
—0,037 5
—0,056 4
—0,075 3
—0,094 2
—0,1130
—0,131 7
—0,150 4
—0,168 8
—0,187 0
—0,205 0
—0,222 6
—0,239 9
—0,256 8
—0,273 2
—0,289 1
—0,304 4
—0,319 1
—0,333 2
—0,346 5
—0,359 0
Рв(х)
0,000 0
0,018 7
0,037 4
0,056 0
0,074 4
0,092 7
0,1106
0,128 3
0,145 5
0,162 4
0,178 8
0,194 7
0,210 1
0,224 8
0,238 9
0,252 3
0,265 0
0,276 9
0,288 0
0,298 2
0,307 5
0,315 9
0,323 4
0,3299
0,335 3
0,3397
0,343 1
0,345 3
0,346 5
0,346 5
0,345 4
0,343 1
0,339 7
0,3351
0,329 4
0,322 5
0,314 4
0,305 1
0,294 8
0,283 3
0,270 6
0,256 9
0,242 1
0,226 3
0,2095
0,191 7
0,1730
0,153 4
0,1330
0,1118
0,089 8
0,067 3
0,044 1
0,020 4
—0,003 7
—0,028 2
РА*)
—0,312 5
—0,311 8
—0,309 9
—0,306 6
—0,302 1
—0,293 2
—0,289 1
—0,280 8
—0,271 3
—0,260 6
—0,248 8
—0,236 0
—0,222 0
—0,207 1
—0,1-91 3
—0,174 6
—0,157 2
—0,138 9
—0,120 1
—0,100 6
—0,080 ]
—0,060 1
—0,039 4
—0,018 3
+0,002 9
0,024 3
0,045 6
0,066 9
0,087 9
0,108 7
0,1292
0,1492
0,168 6
0,187 3
0,205 3
0,222 5
0,238 8
0,254 0
0,268 1
0,281 0
0,292 6
0,302 9
0,3118
0,319 1
0,324 9
0,3290
0,3314
0,3321
0,3310
0,328 0
0,323 2
0,316 6
0,308 0
0,297 5
0,285 1
0,2708
Р7(х)
0,000 0
—0,021 9
—0,043 6
—0,065 1
—0,086 2
—0,106 9
—0,127 0
—0,1464
—0,165 1
—0,182 8
—0,1995
—0,215 1
—0,229 5
—0,242 7
—0,254 5
—0,264 9
—0,273 8
—0,281 2
—0,287 0
—0,291 1
—0,293 5
—0,294 3
—0,293 3
—0,290 6
—0,286 1
—0,279 9
—0,272 0
—0,262 5
—0,251 2
—0,238 4
—0,224 1
—0,208 2
—0,1^91 0
—0,172 4
—0,152 7
—0,131 8
—0,1098
—0,087 0
—0,0635
—0,039 3
—0,014 6
+0,010 4
0,035 6
0,060 8
0,085 9
0,1106
0,134 8
0,1584
0,181 1
0,2027
0,223 1
0,242 2
0,2596
0,275 3
0,289 1
0,300 7
460
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
Продолжение
X
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
0,5600
0,5700
0,5800
0,5900
0,600 0
0,6100
0,6200
0,630 0
0,640 0
0,650 0
0,6600
0,6700
0,6800
0,690 0
0,700 0
0,710 0
0,7200
0,7300
0,7400
0,7500
0,7600
0,770 0
0,7800
0,790 0
0,8000
0,8100
0,8200
0,8300
0,8400
0,8500
0,8600
0,870 0
0,880 0
0,8900
0,9000
0,9100
0,9200
0,9300
0,9400
0,9500
0,9600
0,9700
0,9800
0,9900
1,0000
—0,029 6
—0,012 6
+0,004 6
0,022 2
0,040 0
0,058 2
0,076 6
0,095 4
0,1144
0,133 8
0,1534
0,173 4
0,1936
0,214 2
0,235 0
0,256 2
0,277 6
0,2994
0,321 4
0,343 8
0,366 4
0,389 4
0,412 6
0,436 2
0,4600
0,484 2
0,508 6
0,5334
0,5584
0,583 8
0,609 4
0,635 4
0,661 6
0,688 2
0,715 0
0,742 2
0,769 6
0,797 4
0,825 4
0,853 8
0,882 4
0,911 4
0,9406
0,9702
1,000 0
РЛх)
—0,401 0
—0,392 0
—0,382 2
—0,371 6
—0,3600
—0,347 5
—0,334 2
—0,3199
—0,304 6
—0,288 4
—0,271 3
—0,253 1
—0,233 9
—0,213 7
—0,192 5
—0Л70 2
—0146 9
—0,122 5
—0,096 9
—0,0703
—0,042 6
—0,013 7
-f 0,016 4
0,047 6
0,080 0
0,1136
0,148 4
0,184 5
0,221 8
0,2603
03001
0,341 3
0,383 7
0,4274
0,472 5
0,518 9
0,566 7
0,615 9
0,666 5
0,718 4
0,771 8
0,826 7
0,883 0
0,9407
1,0000
Л(*)
—0,370 7
—0,381 5
—0,391 4
—0,400 2
—0,408 0
—0,414 6
—0,420 0
—0,424 2
—0,427 0
—0,428 4
—0,428 4
—0,426 8
—0,423 6
—0,418 7
—0,412 1
—0,403 6
—0,393 3
—0,381 0
—0,366 6
—6,350 1
—0,331 4
—0,310 4
—0,287 1
—0,261 3
—0,233 0
—0,202 1
—0,168 5
—0,132 1
—0,092 8
—0,050 6
—0,005 3
+0,043 1
0,094 7
0,149 6
0,207 9
0,269 8
0,335 2
0,404 4
0,477 3
0,554 1
0,634 9
0,719 8
0,808 9
0,902 2
1,0000
Ръ(х)
—0,052 9
—0,077 9
—0,102 8
—0,127 8
—0,152 6
—0,177 2
—0,201 4
—0,225 1
—0,248 2
—0,2705
—0,291 9
—0,312 2
—0,331 3
—0,3490
—0,365 2
—0,379 6
—0,392 2
—0,402 6
—0,410 7
—0,416 4
—0,419 3
—0,4193
—0,416 2
—0,409 7
—0,3995
—0,385 5
—0,367 4
—0,344 9
—0,3177
—0,285 7
—0,248 4
—0,205 6
—0,157 0
—0,102 3
—0,041 1
+0,026 8
0,101 7
0,184 2
0,274 4
0,372 7
0,479 6
0,595 4
0,720 4
0,855 2
1,0000
0,254 6
0,236 6
0,216 8
0,195 3
0,172 1
0,147 3
0,121 1
0,093 5
0,064 6
0,034 7
0,003 8
—0,027 8
—0,060 1
—0,0926
—0,125 3
—0,157 8
—0,189 9
—0,221 4
—0,251 8
—0,280 8
—0,308 1
—0,333 3
—0,355 9
—0,375 6
—0,391 8
—0,404 1
—0,4119
—0,414 7
—0,412 0
—0,403 0
—0,387 2
—0,363 8
—0,332 2
—0,291 6
--0,241 2
—0,180 2
—0,107 7
—0,022 9
+0,075 1
0,187 5
0,315 1
0,459 0
0,620 4
0,800 3
1,0000
Р7(х)
0,3102
0,317 2
0,321 7
0,323 5
0,322 6
0,318 8
0,312 1
0,302 3
0,289 5
0,273 7
0,254 8
0,232 9
0,208 1
0,1805
0,150 2
0,117 3
0,082 2
0,045 0
0,0061
—0,034 2
—0,075 4
—0,117 1
—0,158 8
—0,1999
—0,2397
—0,277 4
—0,312 4
—0,343 7
—0,3703
—0,391 3
—0,4055
—0,4116
—0,408 3
—0,394 2
—0,367 8
—0,327 4
—0,271 3
—0,197 5
—0,104 0
+0,0112
0,1506
0,316 5
0,5115
0,738 4
1,0000
7.6.30. Графики нормированных присоединенных функций Лежандра
первого рода (рис. 7.51—7.54).
7.6.31. Приложение функций Лежандра. Решение задачи об электро-
электромагнитных колебаниях сферического резонатора. Предположим, что стенки
сферы сделаны из абсолютно проводящего вещества. Введем сферическую
систему координат. В этой системе el=\, e2 = p, e3—psin9. Применим
к рассматриваемой задаче способ Бромвича (см. п. 6.3.13). Если ограничиться
синусоидальными функциями времени, т. е. функциями вида е*мО(р, 9, <р),
7.6]
ФУНКЦИИ ЛЕЖАНДРА
О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
Рис. 7.51.
1,6
1,4
Ю
0,8
0,6
0,4
o,z
О
-0,2
-0,4
-0,6
-0,8
-1,0
-1,2
-"б
It
It
у!
w
А
t
//
7/
Y,
I
р«р57 р* р>-р*
7
V,
/,
у
\
у
\
У
А
У,
\
л
у
\
\
У^
\
\
\
\
/
\
\
\_
\
з-с
}
\
s
/
/
pi pi
-i
щ
sfloflSJS
nr
п
1 1
h 1
/ /
-Pi
0,1 0,Z 0,3 0,4 0,5 0,6 0,7 0,8 0,9
Рис. 7.52.
462
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
УД. VI!
' О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
2 =COSв
Рис. 7.5Л
1.8
1,6
1,*
1.2
1,0
о,в
0,6
0,2
-0,2
-0,4
-0,6
-0,8
-1.0
-1.2
-1А
X
л
/
/
/
/
/
h
//
/у
/
f
/
/i
/
7
/
/
/
у
v
/
/
\р§р$р}р*3
V
л
К
2
у
/
/
у
у
у
/
ft
у
л
X
\
I
/
/
/
\
X
У
/
У
1
\
\
>
/
^'
/
7
\
\
у
\
\
V
/
/
Рз
V
к
\
Ш
ч\\
i / \l 11
Ш
/
/
j
*-/
Pn
/
/
I
' 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,6 0,9 1,0
S
Рис. 7.54.
».6] ФУНКЦИИ ЛЕЖАНДРА 463
то U будет решением уравнения
д ( . й dU\ , д ( 1 dU
(si6)+(
Положим
/^p, e,
Тогда предыдущее уравнение принимает вид
d*F , 1 dF I /=¦ 1 d'F 1 cos 6 ^ 1
ps "•" p dp 4 ps "+" ps ^
dps "•" p dp 4 ps "+" ps dB2 "T~ p2 sine дб "^ ps sins в dcp2
Будем искать частное решение в виде произведения Лапласа
Р> е, <р) =
Подставим его в уравнение и затем разделим на /?ЙФ. Имеем
_!_ Г diR _j_ i. -^.1 j_ J_ _L f d*Q a. costi rfel i _L I а?2Ф . 2
У? I df + p dp J + в p* L d& sin 6 rf6 J + Ф p2 sins 6 d<r2 + "
Отсюда вытекает
Решение этого' уравнения должно иметь период 2я. Следовательно, ja = т
(целое число) и
Далее,
1 ( сРв cos 0
cos т
Единственное решение этого уравнения, однозначное внутри сферы и конеч-
конечное на оси Ог, дают присоединенные функции Лежандра первого рода,,
индексы которых — целые положительные числа. Поэтому нужно считать
q2= я (я-|- 1) (я — целое число).
Отсюда
0 = />™ (cos 6).
*
Функция R определяется из уравнения
И I df р сЦ, J р2 ^
единственным решением которого, конечным в центре сферы, будет
R = /-,../, (Ар).
Если центр сферы исключен из области существования функции, то-
отбрасывать функцию К„+у, не следует.
Искомое частное решение — функция U (р, Ь, tp, /) — равно
U (р. 0. Т. О = ]/р ^ч ,/а (Ар) Рп (cos 8)cs
464 СПЕЦИАЛЬНЫЕ ФУНКЦИИ (ГЛ. VII
Формулы (88) и (89) п. 6.3.13 позволяют написать следующие выражения:
а) для поперечной магнитной волны (f-волна):
Е? = n{n+l) /ftp" Jn,./, (АР)Рп (cos Q)Zще*м.
m*(cos 9)*°" т
ll (cos 6)l°ssIn
=\4tf vY?J^ ^ -ж
-ж pm*(cos 9)*°"
f Sin 0 flip
: (cos бПп
H*=-Jj V i ^Jn^ (k?)^fp*(cos e)""
б) для поперечной электрической волны (/У-волна):
/
У Т V Ар Л+v, (ftp) ^« (cos 6П
= J j /f /АрЛ+.А (k?)-§fPn (cos
(ftp) Я™ (cos
= Т 4 [/АРЛ+V, (*Р)] 4
7 up
| [/ ] » (cos 6)?:in
Если обозначить радиус сферы через R, то граничные условия — равенство
нулю тангенциальных составляющих электрического поля — имеют вид
?^ = ?, = 0 при р = Д.
Отсюда получаем условия для поперечных магнитных волн:
т. е.
Но так как, согласно C2),
kRj'a+4, (ft«) = bRJa- v, (ft«) — (» + 1 /2) Л
то граничные условия принимают вид
Это уравнение дает для kR последовательность корней
kR — а,, а2, . . ., аг, . ..
Круговая частота возможных электрических колебаний внутри сферической
полости будет зависеть от я и номера I выбранного корня. Наиболее низкая
круговая частота будет соответствовать п = 1 и I = 1. Тогда предыдущее
уравнение примет вид
1 1 kR
^kR ИЛИ 1g(W)
7.7] . ФУНКЦИИ МАТЬЕ 465
Отсюда
а, = 2,744, а2==6,117, а3=9,317, а4=12.48. ...
Следовательно, в пустоте длина поперечной магнитной волны наиболее низ-
низкой частоты равна
Для электрических поперечных волн граничные условия дают
Из этого уравнения вытекает ряд допустимых значений kR:
Круговая частота электромагнитных колебаний зависит от я и номера / вы-
выбранного корня. Наиболее низкая частота будет при п=\ и 1=1. При
этом предыдущее уравнение принимает вид
kR = cos (fe/?) или
откуда
Р, =-4.4934. р2= 7,7253, Р3= 10,904, 04= 14,066, ...
Следовательно, в пустоте длина поперечной электрической волны наиболее
низкой частоты равна
7.7. ФУНКЦИИ МАТЬЕ
Будем искать решения дифференциального уравнения
4 0, A64)
ограничиваясь случаем; когда переменная г и параметры а и q вещественны.
7.7.1. Функции Матье первого рода. Соображения, изложенные в конце
п. 6.3.9, показывают особое значение периодических решений с периодом 2я
уравнения A64). Эти решения называются функциями Матье первого рода или
функциями Матье с целым индексом. Они существуют только при строго
определенных значениях параметров а и q, причем возможные значения пар а
и 'q связаны зависимостью весьма сложного вида (см. пп. 7.7.3 и 7.7.4).
Предположим, что функции Матье первого рода существуют для значе-
значений q, стремящихся к нулю. Разумеется, параметр а при этом соответствую-
соответствующим образом изменяется. Пусть q = 0. Тогда уравнение A64) сводится
к уравнению
которое имеет периодические решения с периодом 2я, если а @) равно
квадрату целого числа т. Эти решения суть
cos/rez, sin mz.
Функциями Матье целого порядка т называются 2я-периодические отно-
относительно переменной z решения A64), стремящиеся соответственно к cos mz
и sin mz при q, стремящемся к нулю. Ясно, что функции Матье целого по-
порядка зависят от двух переменных z и q и индекса т. определенного выше,
30 А. Анго
466 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Обычно эти функции обозначают с помощью символов cem(z, q), Stm(z, q)
или сокращенно cem, sem.
Формула, связывающая возможные значения параметров а и q при фикси-
фиксированном т., называется характеристическим уравнением, а соответствующий
график — характеристической кривой. Для сет характеристическое уравнение
можно записать в виде
Fm(a, q)=0, причем /^(/и2, 0) = 0; A65)
для sem
Фщ(а- Я)=°- причем Фт(т2, 0) = 0. A66)
Графики зависимостей A65) и A66) для различных т приведены на
рис. 7.55. Они дают сеть характеристических кривых функций Матье целого
порядка. Можно показать, что эти кривые не имеют общих точек (разу-
(разумеется, кроме точек (т2. 0) на оси а, через которые проходят кривые
Fm(a, q)=0 и Фт{а, q)-=0). Отсюда следует, что ни при каких значе-.
ниях а и q, кроме отмеченного выше тривиального случая, не существует
двух линейно независимых функций Матье первого рода. Поэтому для по-
получения общего решения уравнения A64) приходится вводить функции Матье
второго рода (см. п. 7.7.9). .
7.7.2. Ортогональность1 функций Матье первого рода. Для каждого q
имеется бесконечный, набор значений а таких, что им соответствуют функ^,
ции Матье первого рода. Другими словами, совокупность всех функций
Матье целого порядка при фиксированном q дает бесконечное мужество
функций Матье первого рода с различными а, соответствующими различ-
различным т (см. рис. 7.55). Пусть параметрам q, ay и q, а2 соответствуют у,
и у2— решения A64), являющиеся функциями Матье первого рода. Имеем
- 2? cos 2z) >>i = 0, -^Zf4-(a2 — 2qcos2z)y2 = U,.
отсюда
Интегрируем от 0 до 2я:
[чг л -
/
о
Так как функции yv y2 2гс-периодичны, то
2-я 2п
f cem cep dz = J sem sep dz = 0, тфр\
о
2ic
ctmstpdz=0.
7.7.3. Разложение в ряд Фурье. Функции Матье первого родя — 2« пе-
периодичные решения A64) — естественно искать с помощью разложения их
в ряд Фурье:
со
у = Вп-\- 2 [A, sin rz -f- В, cos rz\.
•' - ¦ ¦¦ /i '
7.71 ¦ ФУНКЦИИ МАТЬЕ 46?
Подставим это разложение в уравнение A64). Тогда получим два рекур-
рекуррентных соотношения одинакового вида: одно, связывающее три коэффи-
коэффициента А, другое — три коэффициента В, индексы которых отличаются на
две единицы. Например, для коэффициентов А имеем *)
(а-г*) A, — q(Ar+2+Ar_2) = 0. A67)
Отсюда находим четыре возможных разложения для функций сет и sem.
Коэффициенты этих разложений, очевидно, зависят от значений т, поэтому
они снабжены верхними индексами. Имеем
сю
ce2.(z, 0=2 5l?cos 2rz,
г=о
сю
Ce2/.+i (*• 0=2 Blt+lcos Bг Н- 1) z,
г=0
" 2л+1 A68)
2/1 + 1 ' г=0
со
Se2n+2(Z> 0= 2 ^2?+2SinBr-f-2)Z.
¦¦ r=0
Теперь решения се и se определены с точностью до постоянного мно-
множителя. Чтобы фиксировать этот множитель, положим, по определению,
2л 2л
,(z)]2dz= f [szm(z)]2dz=«.
С [cem
I
Эти условия аналогичны формулам, справедливым для круговых функций:
2* 2it
Г cos2x dx = Г sin2x dx = K.
0 0 '
Отсюда получаем дополнительные соотношения
оо
Г-0
оо
2л+2\2
\A2r+l) =
rsO r = 0
Замечание. Коэффициенты Л и В зависят от q. Если устремить q
к нулю, то из определений функций ctm(z) и sem<B) непосредственно сле-
следует
Л22" @) = A%% I @) = Bli @) = fi22?++} @) = Ьп„
где 8" — символ Кронекера.
*) Рекуррентные формулы относительно А и В приведены в [8] на стр. 383, 384
Отдельно для каждого из разложений A68). . •
30*
468
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
7.7.4. Характеристическое уравнение. Применение рекуррентной фор-
формулы A67) позволяет написать характеристические уравнения A65) и A66)
в виде сходящихся непрерывных дробей'). Мы приведем только окончатель-
окончательные результаты:
о- ч2 I
0 Т |4-л
I
4r3 — a
a=q+l—
0=4—0—!
д2 I
|9 — а
д3 I
16 —й
л2
а= -д+\--Л-±- ...-|
{F2n(a, q) = 0\, A69)
• •• {^2Л+1(а, 0=0}, A70)
0 = 0}, A71)
0=0}. A72)
Пример. Приведем пример использования предыдущих формул для
вычисления пары возможных значений а, д.
Рис. 7.55.
, Пусть требуется вычислить значение а, соответствующее ^=2. чтобы
уравнение A64) допускало в качестве решения се3B). Это значение а пред-
представляет собой ординату точки пересечения прямой q = 2 с кривой F3 (a, q) = 0.
Кривая F3(a, q) = 0 (рис. 7.55) пересекает ось а в точке а=9. Поэтому
искомое значение а близко к 9. Уточним его с помощью A70).
') По типографским соображениям непрерывная бесконечная дробь
записывается в виде
\
+ ¦•••
7.7]- ФУНКЦИИ МАТЬЕ 469
В правую часть равенства A70), оборванного при г = 2, подставим q=2.
ai=9,4 и q=2, a — 9,3. Тогда левая часть A70) соответственно равна
flj = 9,l и а2= 10,21 и линейная интерполяция приближенно дает а3=9,37.
Подставим теперь в правую часть A70), оборванного при г = 3, значе-
значения q=2, a = 9,37 и q=2, a =9,38. Тогда левая часть дает соответст-
соответственно aj = 9,373- и «2=9,272. С помощью линейной интерполяции полу-
получаем аз=9,3731. Значение 9,373 дает хорошее приближение величины а.
Рассмотренным выше способом можно по точкам построить кривую
Fa(a, g) = 0.
7.7.5. Поведение функций сет(г, q), sem(«, q). 1) Симметрия от-
относительно z. Функции cem(z, q), sem(z, q) имеют период и характер сим-
симметрии такие же, как функции cos z, sin z, если т—; нечетное число, и cos2z,-
sin 2z, если т — четное число.
2) Симметрия относительно q. Если в уравнении A64) заменить q на
— q, a z на -*¦ — z, то оно сохраняет первоначальный вид
В силу симметрии функций Fm и Фт относительно q имеем
се2л (г, — q) = (— 1)" се2л (у — Z, <?) ,
se2n+2(z, —q)=(—\f se2n+2 (j — *- я) •
-J — z, q} ,
j — Z, q}.
3) Корни. Функция sem обращается в нуль при z = 0, функции se2,
и се2л + 1 равны нулю при z = ^. Функции se2n + i, se2n+2> се2л, се2п+1 имеют,
кроме того, л корней в интервале @, =-). Эти корни приближаются к-к-
по мере роста qх). Наконец, функции sem (z) и cem (z) между 0 и я имеют
такое же количество корней, как sin mz и cos mz.
7.7.6. Присоединенные функции Матье первого рода. Если в A64) за-
заменить z на j'z, то это уравнение принимает вид
-0 — (a — 2qch2z)y = 0.
Для значений а, удовлетворяющих равенствам A69) — A72), существуют ре-
решения с периодом 2iry. Они называются присоединенными функциями Матье
первого рода и обозначаются Се,д и Sem. Эти функции, очевидно, связаны
с сет и sem соотношениями
Stm(z)=-jsem(jz). { }
') В [8] на стр. 386 и последующих приведены рельефы функций у=се0, св|,
se^ ce2, ses (x, q) в системе координат х, q, у. В книге [28] имеются графики первых
функций cem, sem для различных пар q n а.
470 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Изменение знака q у Сеш и Se,n сводится к замене z на z-\-j-^
(ср. п. 7. 7. 5). Нетрудно написать разложения в ряд, подобные A68),
используя гиперболические функции и соотношения A73).
7.7.7. Функции Матье для произвольных а и q. Уравнение Матье
представляет собой частный случай уравнения Хилла. Из вычислений 4.2.21
следует: если у {z)—частное решение уравнения Матье, то существует р.
такое, что
Рассмотрим функцию G(z) — e~*zy(z). Имеем
Следовательно, функция O(z) имеет период те и допускает разложение в ряд
Фурье вида
+ OO
2
r=—oo
Частное решение у (z) равно
Другое частное решение, линейно независимое от у (z) (при jx Ф 0), будет
у( — г) = е"|1гО( — z).
Следовательно, общее решение уравнения Матье имеет вид
-t-oo ~f~co
Ае 2^ С2ге -\-tie - 2а С2ге • A74)
/¦=—оо т—— оо
Решение называется устойчивым, если оно остается конечным при беско-
бесконечном возрастании г, и неустойчивым в противном случае. Характер устой-
устойчивости решения A74) определяется значением параметра (х.
Мы видели в п. 4.2.21, что число \х либо вещественное, либо чисто
мнимое. При вещественном [х решение неустойчиво. При чисто мнимом [л = у'Р
решение устойчиво. Если, кроме того, В—.рациональная дробь, В = т + —
(/те — целое число, р и s—взаимно простые, p<^s), то решение будет пе-
периодично с периодом 2ns. Эти решения называются функциями Матье с дроб-
дробным индексом. Если р = 0, мы снова приходим к функциям Матье первого
рода. В последнем случае частные решения из A74) линейно зависимы, т. е.
A74) не есть общий интеграл. Отсюда возникает необходимость наряду
с функциями Матье первого рода рассматривать функции Матье второго
рода (это уже отмечалось нами). Если [x = yf), а В — не рациональная дробь,
то решение устойчиво, но не периодично. Можно показать, что случай устой-
устойчивости соответствует таким значениям а и q, что изображающая их точка
на рис. 7.55 находится в одной из заштрихованных зон. Напомним, что ли-
линии на рис. 7.55 (кривые Fm{a, q) — 0, Фт(а, q) — 0) соответствуют функ-
функциям Матье первого рода. Эти кривые представляют собой границы, отде-
отделяющие зоны устойчивости от зон неустойчивости.
Рассмотрим более подробно решение с дробным индексом. Изменяя ин-
индекс суммирования, можно добиться выполнения условия 0<8<1. Тогда
общее решение A74) перепишется в виде
-t-oo . -f оо
-fflS c2ri
r~ — oo
7.7] ФУНКЦИИ МАТЬЕ 471
Мы можем рассматривать у (z) как линейную комбинацию двух частных ре-
решений:
+ 00
У\ — 2 Чт cos Br -f-
) z.
При помощи формул, аналогичных формулам A68), можно, с точностью
до постоянного множителя, определить функции Матье с дробным индексом:
too
= 2
r= —oo
COS(
Г= —OO (
+-OO
. q)= 2
ri —oo
Как и в п. 7.7.2, легко показать, что функции Матье с дробным ин-
.дексом. соответствующие однрму и тому же значению q (здесь функции se
и се могут одновременно существовать при одинаковых а и q), ортогональны.
Неопределенный постоянный множитель, содержащийся в формулах A75),
будем находить из условий:
о
из которых следует
+ор +оо
Г* —OO г а> —OO
Присоединенные функции Матье с дробным индексом определяются
выражениями
!, ±q) = cem+p(Jz, ±q),
iz, ± q).
Свойства этих функций выводятся из свойств сеш+э и sem+p (начиная с фор-
формул определения).
7.7.8. Разложение в ряды по бесселевым функциям. Предполагая
^ = й2>0, произведем в уравнении A64) замену переменной и —2&cos2.
Имеем
"-ж+( ~ ^2) ^ = °-
A76)
472 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Е>удем искать решение вида у(.г) = 2(—1 У с2^->т (и)- Подставим это выра-
жение в A76). Принимая во внимание известные соотношения
2r
4J-J -2J +У A77)
получаем
2 (
Г» О
Приравняем нулю коэффициенты при J2r. Тогда получаем рекуррентное
соотношение между коэффициентами с2г, с2г+2, с2г_2:
(а — 4г2) с2г — q (c2r_2 + с2г+2) = 0.
Это рекуррентная формула вида A67). Следовательно, коэффициенты с и 4
пропорциональны. Функция, определенная рядом
!(-l)M22;?y2rB*coSz). A78)
представляет собой решение A64). Это функция се2л с точностью до по-
постоянного множителя. Если придать z значение -к-> то все члены ряда A78),
кроме первого, становятся равными нулю. Это позволяет определить постоян-
постоянный множитель и написать
се2л (z, q) = ^—L ^ (-1У AnrJ2r BЛ cos z).
0 r=o
Можно выписать подобные разложения в ряд по бесселевым функциям
для
се2л+1' Se2n' se2n+i> Се2л+1, Се2л, Se2n+1, Se2n.:
7.7.9. Функции Матье второго рода. Мы видели, что функции Матье
с целым индексом (т. е. функции Матье первого рода) сет и sem, в отличие
от функций Матье с нецелым индексом, не могут одновременно существо-
существовать при одних и тех же q Ф 0 и а.
Чтобы получить общий интеграл дифференциального уравнения A64)
в случае, когда известна функция Матье первого рода, следует найти линейно
не зависящее от нее решение этого уравнения.
Функцией Матье второго рода (например, для сет) называют, в соот-
соответствии с общим результатом п. 6.2.11, решение A64) вида
dz
[ cem (z)f •
Решение, линейно независимое от функции Матье первого рода, можно также
определить, исходя из разложения A78). Действительно, бесселева функция
второго рода Yn{z) удовлетворяет соотношениям A77). Значит, разложение
со
2(— 1/Л2?К2г BA: cos z) A79)
7.8] ФУНКЦИИ ВЕБЕРА—ЭРМИТА 473
является линейно независимым от ce2n(z, q) решением A64). Можно принять
функцию, определенную рядом A79), за присоединенную функцию Матье
второго рода для се2л и действовать подобным же образом в случае анало-
аналогичных разложений в ряд по бесселевым функциям других решений уравне-
уравнения Матье.
7.8. ФУНКЦИИ ВЕБЕРА — ЭРМИТА. ПОЛИНОМЫ ЭРМИТА
7.8.1. Функции Вебера — Эрмита, или функции параболического ци-
цилиндра. Так называются частные решения дифференциального уравнения
$ К7т) = °- <180>
Положим
Тогда дифференциальное уравнение A80) приобретает вид
Найдем разложение У в степенной ряд
Имеем
«2в = (—I)" aO
Отсюда получаеж^иекомве разложение
где а0 и aj — два неопределенных коэффициента.
¦ По определению, функция Вебера — Эрмита Ц,B) получится из фор-
формулы A82), если принять
A83).
A84)
[2 2)
ГК
Если D^(z)—решение уравненияA80), тоDv(—z), D_^1 (jz), D_4_x{—Jz)—
также решения. Они, естественно, не все линейно независимы. С помощью-
474 СПЕЦИАЛЬНЫЕ ФУНКЦИИ ГГЛ. VII
формул A82) — A84) можно показать, что между ними существуют следую-
следующие соотношения:
A85)
D,(z) ш, «'"D, (- *) + т^ *> -1"t/2D_,_1 (- jz).
Если v отлично от целого числа, то общий интеграл уравнения A80)
¦будет
^~ z). A86)
Если v равно четному положительному числу 2р, то первое разложение
в формуле A82) обрывается на члене z2P, а коэффициент ах второго раз-
разложения равен нулю.
Если v равно нечетному положительному числу 2р-\-\, то второе раз-
разложение в формуле A82) обрывается на члене z2p+1, а коэффициент а0
равен нулю.
Следовательно, для v=/i (целое положительное нисло) можно написать
Dn(z)—e~*Ha(z). A87)
Hn(z)—полином /г-й степени, называемый полиномом Эрмита. Он является
четной функцией при четном п и нечетной функцией при п нечетном. Поэтому
выражение A86) уже не является общим интегралом A80). В качестве
¦общего интеграла при любом v можно принять выражение
y = AD^z)+BD_y_4(±Jz). A88)
Итак, решение уравнений F4) и F5) п. 6.3.10 описывается общими
интегралами A86), A88), в которых z = a V2р для первого случая и
z = j$Y%P Для второго. При этом v= ±-| =-. Величины А, В, v опре-
определяются граничными условиями.
Из формул A82) — A84) получаем при z = 0
^-, A89)
¦s-lsin-?-. A90)
\
Отсюда
D2p@) = (-l)M-3 ... Bр —1). D2p+1@) = 0, A91)
D2P@)=0, ?>2P+i@) = (— \)p\ -3 ... Bp-(-l). A92)
Если z лежит внутри угла
Зя ^ , Зл
— -4- < arg г < + -j-,
7.8) ФУНКЦИИ ВЕБЕРА-ЭРМИТА 475
то для функции Д,B) имеет место следующий асимптотический ряд
Если v равно целому положительному числу п, то этот ряд сводится к
Исходя из формул A82) — A84), можно проверить, что имеют место
следующие рекуррентные соотношения:
,(z) = 0. A94)
1(z)=:0. A95)
Точно так же нетрудно показать, что
_*
= v(v— I)... (v — m+\)e 4Dv_m(z) , (у > т),
m Г -- 1
7.8.2. Полиномы Эрмита. Функция yl = e 2 удовлетворяет дифферен-
дифференциальному уравнению
У! + 2^ = 0.
Продифференцируем это уравнение /г-)-1 раз. Тогда
rf» --
Следовательно, функция у2 = -т—пе 2 удовлетворяет уравнению
yJ+^ + (»+lK'2 = 0. A96)
г»
Положим у2==е 4 У- ПРИ этом уравнение A96) приобретает вид
иначе говоря, становится уравнением A80) при v=«. Известно, что решение
этого уравнения будет
Dn(z) = e-*Hn(z).
г- d" -г-
Полином Hn(z) и полином ё2--г-ц е 2 удовлетворяют одному и тому же
дифференциальному уравнению A81). Следовательно, они пропорциональны*).
Коэффициент пропорциональности равен (—1)". Отсюда получается очень
важная формула, которая может служить определением для полиномов Эрмита:
?_2 dn _*2
//„(«) = (— 1)пе21^е *. A97)
*) Из формулы A82) видно, что второе линейно-независимое частотное реше-
решение A81) не является полиномом.
476 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
Мы видели.выше, что у2 удовлетворяет дифференциальному уравнению A96).
Умножая все члены этого уравнения на е2, получаем в силу формулы A97):
+ z) = 0. A98)
Продифференцируем теперь формулу A97), написав ее для Hn+l(z). Тогда
H'n+i(z) = zHn+l(z)-~Hn+2(z). A99)
Сравнивая формулы A98) и A99), получаем
' B00)
Так как е4 равно единице при z = 0, то значения полиномов Эрмита и их
первых производных при z = 0 не отличаются от значений, найденных для
соответствующих функций Dn@) (формулы A91), A92)).
Первые двенадцать полиномов Эрмита следующие:
Hs = z5—\Oz3-\-\5z,
H6 = z6— 15z4 + 45z2— 15, B01)
H7 = z7 — 21z5 + 105z3 — 105г,
105,
945^,
Hl0 = zw— 45z8 + 630r6 — 3150^4 -+- 472522 — 945,
Hn = zn — 55z9 -{- 990z7 — 6930г54- 1732523— 10395z,
Ha = z12 — 66z10 + 148528 — 13860г6 H- 51975z4 - 62370г2 +10395-
Они отвечают общей формуле
Н —?п п(п-\) а Я(Я-1)(Я-2)(Я-3)
пп — z 2 ^ -I- 2.4 * -t- • • •
... +(_iy?(»-l)...(»-2f+I),.-H ^ B02)
7.8.3. Производящая функция и ортогональность полиномов Эрмита.
Рассмотрим функцию <р(г, () = ег'-B12 и разложим ее в ряд по возрастающим
степеням t:
ср(г, t) = hQ(z) + hx{z)t + h2(z)^-\- ... +Ая(г)-^-+. .. B03)
Можно сразу заметить, что hQ(z)=l, a hi(z) — z. Функция <?(z, t) удовле-
удовлетворяет уравнению
^- = («-0?. B04)
В B04) заменим ср на ряд B03). Приравняв нулю коэффициент при члене,
содержащем tn, получим
7.8) ФУНКЦИИ ВЕБЕРА—ЭРМИТА 477
Это рекуррентная формула, совпадающая с A98). Так как, кроме того,
A0(z) = H0(z), a h1(z) = Hi(z), то
hn(z) = Hn{z).
Отсюда получаем
fi СО
Zt~J%n(z)^. B05)
л=о
Функция, стоящая слева, называется производящей функцией для полиномов
Эрмита.
Если умножить обе части B05) на е 7, то, в силу формулы A87), най-
найдем производящую функцию для функций Вебера Э
Исследуем ортогональность функций Вебера — Эрмита. Вычислим ин-
интеграл
+со +оо
/- f Dn(z)Dm(z)dz= f e *Hn(z)Hm(z)dz.
—oo • —oo
Положим п > т и применим формулу A97). Имеем
/ = (-1)" f Hm(z)?ue-Tdz.
— GO
Интегрируя по частям, получим
?2
Внеинтегральный член является прризведением полинома на е 2. Он равен
нулю при z=±oo. Интегрирование по частям, повторенное т раз, дает
/ = (—1)т+л / H^Hz)— e~2dz. B06)
t —со
Но Hl?t\z)=tn\, следовательно,
Если п = т, формула B06) дает
+ ОО г2 +О0
/ = I /7Л (^) е dz = /i! I g 2 dz = я
—со —oo
Все это показывает, что если функция f(x) удовлетворяет условиям п. 2.1.0
(условиям Дирихле), то ее можно разложить в ряд по полиномам Эрмита:
= 2 слии (*)• B07>
478 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
где
— CO
Если предпочесть разложение в ряд вида
__. °°
= « 2 2 <**"*(*)• B08)
то коэффициенты определяются еще проще:
Вычисления упрощаются, если взять функции Вебера — Эрмитя сразу
в ортонормированной форме:
Д„(*)= ,f--^L' "B09)
То же относится и к полиномам Эрмита:
B10)
Замечание. Часто встречается определение полиномов Эрмита, отличаю-
отличающееся от только что рассмотренного, а именно
B11)
Между этими двумя видами полиномов существует простое соотношение
$ B12>
7.9. ПОЛИНОМЫ ЧЕБЫШЕВА
7.9.1. Определение. Рассмотрим дифференциальное уравнение
A — 0J)-^- — и-|?-f «2У = 0 (л — целое число). B13)
Положим _> = cos? или u> = ch?. Получаем
__.O или ^-пЬ = 0.
Эти уравнения допускают соответственно следующие два линейно независимых
решения:
у = cos nt, у = sin nt;
у _= ch /г?, у = sh nt.
Отсюда находим линейно независимые решения уравнения B13):
Тп (ш) = cos (n arccos ш) при |ш| < 1, B14)
Г. (ш) = ch(n arch ш) при |ш| > 1, B15)
_/. (ш) = sin(« arccos ш) при |ш| < 1, B16)
t/_(u>)_sh(/iarch_>) ПрИ |ш| > 1. B17)
7.9] ПОЛИНОМЫ ЧЕБЫШЕВА
Функции Тп и Un называются соответственно функциями Чебышева пер-
первого и второго рода я-го порядка.
Функция Тп(ш) представляет собой полином. Действительно, при |ш'| < t
имеем
Тп (ш) + Д/„ (ш) = (cos t + J sin tf = (ш ± /щя — \f,
Tn (ш) - JUn (ш) = (cos t — j sin tf = (ю + /"J - О"- ' >
Отсюда
7"» («) = T [(» ± /;ii?3ri)n + (» + f^3^)"] • B18a)
При |«)| > 1 имеем
„ (ш) -+- ия (») = ел/ = (ш ± /^=
что приводит для ^„(ш) к тому же соотношению B18а).
Полином Тп(и>) называется полиномом Чебышева первого рода.
Если при помощи формулы бинома разложить выражение B18а), то
найдем
Последний член в квадратных скобках равен
1
22* '
если п = 2А;
B*+1)<а, если «-2ft+l.
Функции Чебышева второго рода Un могут быть представлены следую-
следующими формулами: ,
ип(ш)= ± /1—шаря(ш). если |ш| < 1;
i/n(«o)= ± /4J— 1 рл(о)), если |ш| > 1,
где />„(<») — полином (п—1)-й степени от ш. Выражение для рп(ю) будет
2 л
О)
4-
Последний член в квадратных скобках равен
2k
^-j-ш, если n=2k;
1
—г, если я = 2?4-1.
22*
Полином Ря(.и>), равный Pn+i(u>). называется полиномом Чебышева вто-
второго рода.
Отметим, что эти же результаты можно легко получить, если приме-
применить к дифференциальному уравнению метод, указанный в п. 6.2.10 (искать
480 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII
решение в виде обобщенного степенного ряда). Первые одиннадцать полино-
полиномов Тп и рп следующие:
Го («0=1.
Тг (ш)=: Ш,
7\,(ш)=2ш2— 1,
Tz (ш) = 4ш3 — Зш,
Т5 (ш) = 16ш5 — 20ш3 + 5ш, B19)
Т6 (ш) = 32<о6 — 48ш4 -f-18ш2 — 1,
Г7(ш)=64ш7— 112uM 4-56uK— 7ш,
Г8(ш)= 128u)8 —256ш64-160ш4 —32ш24-1.
Т9 (ш) = 256ш9 — 57бш7 4- 432ш5 — 120ш3 + 9ш,
р1(ш)=1,
Р2 (Ш) = 2@,
=: 8(О3 -4@,
р5(ш)=16ш4—12ш24-1. ¦ B20)
) = 32ш5 — 32ш3 4- 6(о,
) = 64ш<5 _ 80ш- 24(о2 — 1,
))= 128ш7— 192(о54-80ш3 —8(о,
р9 (со) = 256и>8 — 448(о6 4- 240u)" — 40ш2 4-1.
р10(ш)=512ш9— Ю24ш74-672(о5— 160(о34- Юш.
7.9.2. Графики Тп(ы) и ?/„(»). Если мы вернемся к формуле B14),
то легко увидим, что график полинома Чебышева ^„(ш) в интервале (—1, 4-0
представляет собой проекцию синусоиды с периодом — и амплитудой еди-
единица, обвитой вокруг цилиндра вращения с радиусом единица, на плоскость,
параллельную оси цилиндра (см. рис. 7.56). Один из максимумов или мини-
минимумов синусоиды находится в плоскости, параллельной плоскости про-
проекции и проходящей через ось цилиндра. Изучаемая проекция предста-
представляет собой частный случай кривых Лиссажу. Каждая точка кривой является
проекцией двух точек, симметрично расположенных на цилиндре. Это соот-
соответствует тому, что согласно B18а) функцию Тп(ш) можно представить
как полусумму проекций двух комплексно сопряженных точек. На рис. 7.56
изображен полином Т6, представляющий собой проекцию шести периодов си-
синусоиды, обвитой вокруг цилиндра.
На рис. 7.57 приведены графики шести первых полиномов Чебышева.
Они выходят из (—1)"оо для отрицательных и очень больших ш, колеблются
п—1 раз между абсциссами и ординатами —1 и -{-I и быстро возрастают
-К 4" °° Для ш > 1.
7.9]
ПОЛИНОМЫ ЧЕБЫШЕВА
Э
V
i
31 А. Ааго
482 СПЕЦИАЛЬНЫЕ ФУНКЦИИ (ГЛ. VII
Если синусоида, обвитая вокруг цилиндра, помещена на нем таким обра-
вом, что одна из ее нулевых точек находится на плоскости, проходящей
через ось цилиндра параллельно плоскости проекции, то ее проекцией будет
кривая Un(io). В области внешней по отношению к интервалу |а>| < 1 функ-
функция будет вещественна, только если произвести здесь замену определения,
перейдя от ± УЧ — о>2 внутри к ± у\о2— 1 вне интервала (—1, -|-1). Пер-
Первые шесть функций Un представлены на рис. 7.58.
7.9.3. Основные свойства полиномов Чебышева. Корни. Все корнн Тп (о>)
вещественны н заключены между —1 и -j-1. Корень ш1 номера I дается
формулой
о>г = cosB1—1)-^ A=1, 2, 3 я).
Эти значения <о1 попарно симметричны, поэтому мы можем написать
Т2к ((О) == 22* @J — 0J) („,2 — 0J) ... (оJ _ оJ) ... (оJ — 0J),
Т2к+1 (о)) = 22*о) (uJ _ 0J) (о>2 — 0J) ... (о>2 — 0J) ... (о>2 — 0J).
Корни ?/„(«>) даются выражением
wi = cosiTz/n (f=l, 2, 3 я—1),
н здесь мы можем также написать
ри (ш) = 22*+1u) (to2 — оJ) ... (о>? — оJ) ... (оJ — оJ _j),
/>2* + 1 («) = 22* (оJ _ 0J) ... @J — 0J) ... (ОJ — 0Jft).
Корни Тл (о)) — это значения о>, при которых Un (o>) имеет максимум или
минимум, и наоборот.
Исходя из дифференциального уравнения B13), нетрудно проверить, что
имеют место соотношения, аналогичные формуле Родрига для полиномов
Лежандра *):
Если |о)| > 1, то во втором уравнении нужно УЧ —оJ заменить на у оJ — 1.
Ортогональность. Если в интеграле
[ 0 при тФ п,
cos nt cos mt dt = 1 ^ при т = пФ0,
о
^ it при т = я =
положить cos t = о), то получим
+1
du>
rri 5
VI—оJ
О при тФ я.
Y при т = п ФО,
тс при от = л = О.
*) Подобные соотношения верны для любой системы ортогональных многочле-
многочленов с произвольным весом ([4], стр. 570).
7.91 ПОЛИНОМЫ ЧЕБЫШЕВА 483
Та же подстановка в интеграле
У*
( 0 при т Ф п,
sin я/sin m/ dt — \ к
¦j при т==п
приводит к формуле
[0 при т Ф я,
/
Un (ш) Um (ш) d" ¦ = j n
j лч / т\ i Yx — ^ у при т = л.
Из этих формул видно, что функции ?/„(«>) и Г„((о) ортогональны в интер-
интервале (— 1, -|-1) с весовой функцией A —ш2) 2.
Связь с бесселевыми функциями. Функции Бесселя Jn(t) связаны
с полиномами н функциями Чебышева следующими формулами ¦):
J e-J
при
при
при |to
при |о>|
N
t со |
к
|>
<
>
1.
1.
1,
1;
I о
Эти формулы показывают, что при анализе спектра частот сигналов вида Jn(t)
и у ' мы должны вводить функции Чебышева и что в этом спектре отсут-
отсутствуют круговые частоты больше единицы.
Мы видели, что проекция кривых cos /ш, sin «to, обвитых вокруг круг-
круглого цилиндра с радиусом единица, на плоскость, параллельную оси ци-
цилиндра, — это кривые Тп (to) и Un (ш). Если обвить вокруг того же цилиндра
график периодической функции с периодом 2ic, представленной разложением
в ряд Фурье:
bQ -+- 2 (ап sin до) -J- bn cos лш),
п=1
то проекция его на ту же плоскость будет представлена разложением вида
л=1
При практическом применении полиномов Чебышева часто необходимо
решать уравнение я-й степени
Тп ((о) = с, (*)
где с — численная константа.
Если \с\ < 1, уравнение (*) имеет п вещественных корней. Положив
\2Ы
Ч-\-2Ы _, -у
cos a = to, cos т = с, имеем а = —— . Обозначив через <on = cos —, на-
1 п г и п
ходим следующую формулу для корней (*):
= UHCOS У1 —0J Sin (k=0, 1, 2 Л— 1).
я ' и п
') См. Van der Pol В., Wei jers Th., Tchebycheff polynomials and their rela-
relation to circular Bessel functions and Lissajous figures, Physica, 1, 1, pp. 78—94.
31*
484 СПЕЦИАЛЬНЫЕ ФУНКЦИИ [ГЛ. VII"
Если \с\ > 1, уравнение (*) имеет только один вещественный положи-
положительный корень:
Производящая функция. Из ряда
ао со
L = ? tV' = ^ '" cos «* + / S '" sin ЛХ>
л = 0 n=0 л=1
если положить cosx = (d, получим
л=0 п=1
Отсюда находим две производящие функции:
л=0
CO
1—0J у,
л=1
Если будем исходить из ряда
е'е =
и обозначим cos# = u), то найдем
etu> [cos {t у 1 — (o2j-f- j sinG ]/" 1 — (d2)] =
CO
= V [cos (« arccos u>) + у sin (я arccos u>)] —r-.
n = 0
Отсюда получим две другие производящие функции:
оо
etu> cos (t l/l — to2) = V -^- Т„ (ш),
etto sin (/ yi — to2) = У —f ^п(ш)-
Рекуррентные соотношения. Если исходить из формул для cosfa-f-&)
и sin(a-|-?>) и положить а = /их, b = nx, cos х = ы, то легко найдем
Точно так же, исходя из формул для cos (a—Ь) и sin (с—Ь), получим
Тт-п (ш) = Тп (Ш) Ги ((О) + Un ((О) t/m (О)),
7.9J . ПОЛИНОМЫ ЧЕБЫШЕВА 485
Это дает
Т„ И Тт ((о) = \ [Тт+п («,) + Тт_п (а))],
Un (ш) Um (ш) = I [Ги_„ ((о) - 7m+n («)],
Положив я=1 в первой и последней формуле, получим рекуррентные
соотношения:
_, ((о) = 0.
Формула умножения. Имеем
Тп \Тт («¦>)] = ^m [7-„ ((«)] = cos (га/и arccos ш) = Ттп (ш).
Если /и = 2, то
Г„ BоJ - 1) = 2Г2„ (ш) — 1 = Т2п ((о);
полагая здесь @2=х, получим
7.9.4. Фундаментальное свойство полиномов Чебышева. Для этих
полиномов имеет место следующая важная теорема.
Теорема. Пусть рп(х) — совокупность многочленов степени га с коэф-
коэффициентом при хп, равным единице, заданных на отрезке —1<^х<^1.
Рассмотрим
Мр = max \pn(x)\.
Наименьшее значение М„ доставляет
2я-1 ^« (•*)'
где Тп (х) — полином Чебышева *).
Полином Тп (х) называется наименее уклоняющимся от нуля.
Доказательство. На отрезке — 1-^x^1 полином Тп(х) имеет
экстремумы в га+1 точках
kit ., _ Л ч
xft = cos-— (k=0, 1, .... п),
причем
Все значения Тп (х) в экстремальных точках равны по модулю, а знаки по-
последовательно чередуются.
Для доказательства теоремы предположим противное. Пусть среди сово-
совокупности рп(х) есть некий многочлен р*п(х), который менее уклоняется от
нуля, чем - „_, Тп (х). Многочлен
¦) Напомним, что Тп (х) = 2п~1хп + ...
486
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
(ГЛ. VII
имеет степень я—1. По предположению, в л —|— 1 точках хк |p*(Jc)|<
"" '"" Поскольку знаки Тп{х) в этих точках чередуются, то
многочлен р*п j (jc) в этих я-|-1 точках последовательно меняет знаки (он
положителен там, где Tn{xk)<, 0, и отрицателен там, где Г„(хЛ)>0). Зна-
Значит, по теореме Коши многочлен p*n_l (x)
TgA,195х) x+f имеет не менее л корней, а это невоз-
невозможно.
Из теоремы вытекает, что полином
л-й степени
л0,в37
равный 1 при х=\, в промежутке
[—а, а] дает наименьшее отклонение, от
нуля, равное + -
Рис. 7.59.
Пример. Определим промежуток
" 1
изменения х, в котором QsW^fo
означает, что нужно найти а из уравнения Г5(—)=10. По формуле B21)
находим
= 1,195, а = 0,837.
Функция Q5(x) изображена на рис. 7.59.
Апроксимация, состоящая в том, чтобы заменять функцию другой, анали-
аналитически более простой (этот вопрос подробно разбирается в гл. X), опре-
определяемая из условия, чтобы максимальное отклонение было меньше некото-
некоторого предела, называется апроксимацией в смысле Чебышева.
7.9.5. Приложение. Если некоторая величина может быть представ-
представлена полиномом и если желательно, чтобы изменения ее были наименьшими
или, в крайнем случае, в заданном интервале не
превосходили определенный предел и, напротив, m Г^",
быстро росли вне этого интервала, то всегда удоб- Jo Jr \. /
но так скомбинировать физические переменные,
чтобы исследуемый полином оказался полиномом
Чебышева.
Пример1). Рассмотрим совокупность четного Рис. 7.60.
числа электромагнитных излучателей, расставленных
по прямой на расстоянии йдруг от друга. Они питаются токами 0й, 0\ 0„
(рис. 7.60). Предположим, что цепь симметрична {0р— 0п-р) и что Фаза то"
ков растет в арифметической прогрессии:
Обозначим Ф = -у- cos C — 8. Рассмотрим поле в направлении В в пло-
плоскости, нормальной к плоскости цепи. Оно равно полю, вызванному отдельным
') См. D о! р h С. L., Ргос. Inst. Rad. Eng., № 6, 1946, p. 335.
7.9) ПОЛИНОМЫ ЧЕБЫШЕВА 487
излучателем, умноженному на полином
при
во
Если нас интересует только амплитуда поля, то достаточно рассмотреть
модуль Pn_i(z), который для четного я равен
Pn_i(cos y)\~ 2 Г с0 cos (я—lJ-^H-C! cos (я—3)у+ •••+а?_, cos-f]|'
Можно легко раскрыть этот полином и расположить его по степеням
/Ф \ / Ф\
cos (-9-). поскольку каждое слагаемое вида coslm-j-l выражается через
/ Ф \
cos l-jj-l формулой
жением
Отождествим, Рл-1 (cos-и-) с полиномом Q степени я—1, т. е. с выра-
Тогда вторичные лепестки излучения будут все одинаковы и равны
1
в то время как главный лепесток будет равен единице. Если предел (*) будет
нам задан, то он определяет величину а, а следовательно, коэффициенты ап
и позволяет найти соотношение между питающими токами. Раствор главного
лепестка при этом будет равен
acos-|- (я— 1);
он наименьший из возможных.
Если же будет задан раствор главного лепестка, то последняя формула
определяет а и, следовательно, токи. При этом уровень вторичных лепе-
лепестков оказывается наиболее низким.
Рассмотрим численный пример. Дана цепь из шести диполей, питаемых
токами в одной фазе. Они находятся на расстоянии у друг от друга
|я=4, 8 = 0, d = -^-J Требуется определить соотношения токов -J- -у
Требуется определить соотношения токов -J-, -у
таким образом, чтобы отношение главного лепестка ко вторичным было
равно 10.
Имеем Т5(—1 = 10. Отсюда по формуле B21) находим
1=1.195
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
[ГЛ. VII
488
и, далее,
Р5 (cos -=-) = 2с0 cos 5 -к- + 2at cos 3 — -(- 2а2 cos -я- =
= 2а0Г5 (cos -|-) + 2а,Г3 (cos -|-j + 2а27\ (cos -|-) =
= 32a0cos5-|- — D0а0 — 8с,) cos3-|- +A0а0 —6с, + 2a2)cos —
Это выражение отождествляем с
'.(т~т)
Отсюда
= 2'907
7дО°-
,90°
4270
Т ~~ 2>95 cos3 Т + 0>597 cos Т-
ао = 0,0908,
с1 = 0,0857,
Следовательно,
Рис. 7.61.
9-= 0,944,
'о
4^= 1,113.
Диаграмма излучения здесь — это график функции Q5(x) (рис. 7.61), где
в качестве переменной взят угол {J, так что
Ф { ъЛ п\ (п п\
x = cos -у = cos 1-у- cos р = cos I-g- cos pi.
ЛИТЕРАТУРА К ГЛАВЕ VII
Общая, литература
1. Смирнов В. И., Курс высшей математики, т. III, ч. 2, Гостехиздат, 1957.
2. Лебедев Н. Н., Специальные функции и их приложения, Физматгиз, 1963.
3. Уиттекер Е. и Ватсон Г., Курс современного анализа, ч. II, Физматгиз, 1963.
4. Лаврентьев М. А. и Шабат Б. В., Методы теории функций комплексного
переменного, Физматгиз, 1958.
5. Айне Э. Л., Обыкновенные дифференциальные уравнения, Харьков, 1939.
6. Джексон Д., Ряды Фурье и ортогональные полиномы, ИЛ. 1948.
7. Курант Р., Гильберт Д., Методы математической физики, т. 1, Гостехиздат,
19,
IF.
8. Я н к е Е., Э м д е Ф., Таблицы функций с формулами и кривыми, Физматгиз, 1959.
9. Камке Э., Справочник по обыкновенным дифференциальным уравнениям, Физ-
Физматгиз, 1961.
10. Г рад штейн И. С, Рыжик И. М., Таблицы интегралов, сумм, рядов и произ-
произведений, Физматгиз, 1962.
ЛИТЕРАТУРА 489
П.Тихонов А. Н., Самарский А. А., Уравнения математической физики*
Гостехиздат, 1953.
12. К р а т ц е р А., Франц В., Трансцендентные функции, ИЛ, 1963.
• а) Асимптотические разложения
13. Эр д ей и А., Асимптотические разложения, Физматгиз, 1962.
14. Б р е й д Н. Г., Асимптотические методы в анализе, ИЛ, 1961.
15. Евграфов М. А., Асимптотические оценки и целые функции, Физматгиз, 1962.
б) Гиперболические функции
16. Я н п о л ь с к и й А. Р., Гиперболические функции, Физматгиз, 1960.
17. Ш е р в а т о в В. Г., Гиперболические функции, Гостехиздат, 1954.
в) Гамма-функция
18. Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления,,
т. II, Физматгиз, 1962.
г) Бесселевы функции
19. В а т с о н Г. Н., Теория бесселевых функций, ИЛ, 1949.
20. Грей Э. и Метьюз Г. В., Функции Бесселя и их приложение к физике и меха-
механике, ИЛ, 1949.
21. Кузьмин Р. О., Бесселевы функции, ОНТИ, 1935.
22. Фок В. А., Дифракция радиоволн вокруг земной поверхности, Изд-во АН СССР,.
1946.
23. М с L а с h I a n, Bessel functions for engineers, Clarendon Press, Oxford.
24. P e t i a n Q., La theorie des functions de Bessel, C. N. R. S., 1955.
д) Функции Лежандра
25. Г о б с о н Е. В., Теория сферических и эллипсоидальных функций, ИЛ, 1952.
26. Л е вин В. И. и Гросберг Ю. И., Дифференциальные уравнения математиче-
математической физики, Гостехиздат, 1951.
е) Функции Матье
27. М а к-Л а х л а н Н. В., Теория и приложения функций Матье, ИЛ, 1953.
28. Campbell R., Theorie generate de 1'equation de Mathieu, Masson ed., 1955. <
ж) Полиномы Чебышева
29. Ч е б ы ш е в П. Л., Теория механизмов, известных под названием параллелограм-
параллелограммов, Изд-во АН СССР, 1949.
30. Ч е б ы ш е в П. Л., Вопросы о наименьших величинах, связанных с приближен-
приближенным представлением функций, Изд-во АН СССР, 1947.
31.'Штагер В. В., Чебышевские приближения, применяемые в расчетах электриче-
электрических схем, Связьиздат, 1960. <
32. Никольский С. М., Квадратурные формулы, Физматгиз, 1958.
ГЛАВА VIII
СИМВОЛИЧЕСКОЕ, ИЛИ ОПЕРАЦИОННОЕ, ИСЧИСЛЕНИЕ
8.1. ВВЕДЕНИЕ
В настоящей главе рассматривается символическое, или операционное,
исчисление и его приложения к изучению переходных режимов электрических
цепей.
8.1.1. Ограничение, области применения. Необходимо оговорить усло-
условия, ограничивающие множество электрических цепей, к которым можно при-
применять операционный метод.
Следует исключить цепи, параметры и конфигурация которых меняются
во времени.
Следует также исключить нелинейные электрические цепи. Для линей-
линейных цепей справедлив принцип суперпозиции: если две электродвижущие
силы е1 и е2, поочередно включенные между двумя точками цепи, вызывают
во взятой наугад ветви соответственно токи /t и i2, то электродвижущая
сила el-\-e2, включенная между этими же двумя точками, вызовет в той
же ветви ток ii~j-ir
Это основное свойство линейных дифференциальных уравнений, кото-
которыми описываются линейные цепи: сумма двух частных интегралов пред-
представляет собой также частный интеграл.
Поэтому нельзя применять операционное исчисление к цепям, содер-
содержащим индукционные катушки с железными сердечниками (явление гисте-
гистерезиса) или вакуумные лампы, работающие за прямолинейной частью харак-
характеристик.
Короче говоря, оба предыдущих ограничения требуют от электрических
цепей, к которым применим аппарат операционного исчисления, режима,
описываемого линейными дифференциальными уравнениями (обыкновенными
или в частных производных) с постоянными коэффициентами.
Кроме того, будем считать, что рассматриваемые электрические цепи
диссипативны. Такие цепи стремятся к состоянию покоя, если устранена
причина, нарушившая равновесие. Иными словами, показатель степени у экс-
экспонент, фигурирующих в выражениях для переходных токов, должен иметь
отрицательную вещественную часть:
et'+Jftt, а < 0.
8.1.2. Расчет установившихся режимов. Мы уже рассмотрели в гл. I
(п. 1.2.1 и последующие), как рассчитать установившийся синусоидальный
режим электрической цепи.
Предположим, что синусоидальная электродвижущая сила u{t) = Ue^at
приложена в течение очень длительного времени. При этом возмущение,
внесенное внезапным приложением этой э. д. с, успело экспоненциально
S.I] . ВВЕДЕНИЕ 491
затухнуть и остался только ток, соответствующий установившемуся
режиму.
Рассмотрим сначала простую цепь (ветвь, звено, узел). Электродвижу-
Электродвижущая сила u(t) создает в этой цепи с комплексным сопротивлением Z(Jw),
или комплексной проводимостью A (Jw) = у-р~\ • установившийся ток
где
& = гТм или 3=uau^\
Если требуется найти установившийся ток, вызванный вещественной
электродвижущей силой
a (t) = U cos (wt -\- ср),
то достаточно взять вещественную часть i(t).
Положим, что мы имеем дело со сложной цепью и требуется найти ток,
соответствующий установившемуся режиму в контуре т при включении
электродвижущей силы a (t) в контур I. Все сказанное выше остается в силе
при условии замены Z(jm) на взаимное комплексное сопротивление конту-
контуров / и т, определенное в п. 1.2.8.
Если электродвижущая сила не синусоидальна, а только периодична,
то разложение в ряд Фурье легко приведет к предыдущему случаю. Действи-
Действительно, если Т — период, то, как мы видели в п. 2.1.8.
где
с -±f a(f)e-« dt
иfji —— rn I UU J C> Ut »
1 .1
9
Поэтому ток l(t) будет
"mZ(m»
m= —оо
ИЛИ
• +co
ш = — оо
Здесь через Z(mjw) и A(jnjm) обозначены комплексное сопротивление и
комплексная проводимость простой цепи на круговой частоте тш или же,
если речь идет о сложной цепи, комплексное взаимное сопротивление и
комплексная взаимная проводимость.
8.1.3. Расчет переходных режимов. Если электродвижущая сила не
периодична, то достаточно представить ее интегралом Фурье. Разложение на
сумму гармоник с одинаковыми интервалами по частоте можно заменить сум-
суммой гармоник, непрерывно пробегающих интервал частот от — оо до 4- со.
Тогда
= Г A (Jw) G (ш) etat dm
492
или
где
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
+ ОО
F
причем функции А (ja) и Z (у'ш) имеют смысл, указанный выше.
Таким образом, задача расчета переходных режимов полностью решена,
по крайней мере теоретически. На практике эта задача приводит к сложным
вычислениям. Действительно, требуется вычислить 0(<о) с помощью опре-
определенного интеграла. Этот интеграл в большинстве случаев легко найти, так
как соответствующий неопределенный интеграл
часто выражается с помощью элементарных функ-
функций. Но вычисление l(t) более затруднительно,
О (<">) 14
потому что неопределенный интеграл от у)-\eJ
большей частью нельзя выразить через элементар-
___ ные функции.
? Попробуем показать это на очень простом
примере. Приложим к цепи, состоящей из после-
последовательно включенных самоиндукции, сопротив-
сопротивления и емкости, электродвижущую силу, изображенную на рис. 8.1. Найдем
теперь ток как функцию времени. Имеем
-е О +i
Рис. 8.1.
Отсюда
~ . F sin сое
4 ' тс со
Sin
Найти l(t) весьма затруднительно.
Следует, однако, заметить, что применение теоремы вычетов и интегри-
интегрирования по контуру в комплексной плоскости при вычислении определенных
интегралов приводит к приемам, подобным приемам, вытекающим из приме-
применения формулы обращения Меллина—Фурье, рассмотренной дальше (п. 8.3.22).
Примечание. До сих пор мы находили токи, вызванные электро-
электродвижущей силой, заданной как функция времени. Это привело нас к опре-
определению комплексного сопротивления и комплексной проводимости. В более
общих случаях, когда нужно найти реакцию (до сих пор это был ток) на
воздействие (до сих пор это была электродвижущая сила) в установившемся
режиме, мы вынуждены ввести понятие обобщенного полного сопротивления
или полной проводимости. Тогда
реакция = воздействие X обобщенная полная проводимость =
воздействие
обобщенное полное сопротивление
В дальнейшем воздействия будут напряжениями, а реакции — токами, но они
могут быть заменены другими воздействиями, например силами, и реакциями,
которые могут быть тогда скоростями, или всякой другой парой „воздей-
„воздействие — реакциа"
8.2]
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ХЕВИСАЙДА
493
8.1.4. Единичная ступень. Так как разложение непериодической
электродвижущей силы на синусоидальные составляющие приводит к весьма
трудоемким расчетам, мы можем спросить себя, действительно ли это раз-
разложение так хорошо отвечает задаче нахождения реакции на внезапно при-
приложенное воздействие и не лучше ли подошло бы' разложение на сумму
других простейших функций. Простейшая выбранная нами функция — это
так называемая единичная функция Хевисайда Г (t), равная нулю при t < О
и единице при t > 0. Чтобы напомнить
о форме графика этой функции, на-
назовем ее единичной ступенью (рис. 8.2).
Электродвижущие силы, или, более
общо, воздействия, внезапно прило-
+1
О
№
6
А
о
Рис. 8.2.
Рис. 8.3.
женные в момент времени ^ = 0, представлены функциями, равными нулю
при t < 0 и равными непрерывной функции времени hit) при t > 0 (рис. 8.3).
Такие функции можно .записать в виде
А (О* (О-
Обычно мы будем вместо h (t) Г (t) писать h ((), но не следует никогда
забывать, что, за исключением специально оговоренных случаев, функция
h(t) равна нулю при t < 0.
Функция h(t)t(t) может быть разложена на ступени, как показано на
рис. 8.3. Это разложение приводит к гораздо более простым, а главное,
к более автоматическим расчетам при помощи операционного исчисления.
8.2. ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ХЕВИСАЙДА
Для цепи, находящейся в равновесии, основная задача — это отыскание
токов и потенциалов при приложении некоторой электродвижущей силы
в "момент времени ? = 0. Цепь должна находиться в равновесии до при-
приложения электродвижущей силы, иначе говоря, токи и заряды тождественно
равны нулю от t=—оо до ? = 0. Это основное предположение.
8.2.1. Определение переходной реакции. Дана цепь, находящаяся в
равновесии. Введем внезапно в контур I цепи воздействие (в данном случае
электродвижущую силу), равное единичной ступени Г (t).
Пусть Amil(t) — ток в контуре т этой цепи. Тогда принято говорить,
что Am<l(t) — переходная реакция контура т относительно контура /. Можно
показать с помощью обобщенной теоремы взаимности, что
Очевидно, что знание всех таких функций, как Лт> г (t), решает поставлен-
поставленную вначале задачу для электродвижущей силы 1'(t). Мы покажем, что
знание Amil(t) достаточно также для решения основной задачи при любой
электродвижущей силе, если только она приложена в момент времени * = 0.
494
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
Если приложить постоянную электродвижущую силу Е в момент ? = 0,
то ток равен ЕА (t) (для простоты записи опускаем индексы). Если ту же
электродвижущую силу Е приложить не в момент ? = 0, а в момент х, то
ток будет равен ЕА (t — х). Рассмотрим теперь электродвижущую силу
любого вида, приложенную в момент ? = 0, например E(t). Если разделить
промежуток времени от 0 до t на п отрезков АЛ как это показано на
рис. 8.4, то можно рассматривать воздействие этой электродвижущей силы
как результат воздействия постоянной электродвижущей силы Е@), при-
приложенной в момент ? = 0, затем электродвижущей силы АХЕ, приложенной
в момент времени ДЛ и т. д. до &„Е, при-
Eft) ложенной в момент пМ = t. Ток можно рас-
"pf. с сматривать как сумму токов
"* " E@)A(t),
. }д? Если увеличивать до бесконечнорта
¦j-4 число п., то пределом ломаной, изображенной
! [ на рис. 8.4, будет кривая E(t). Заменяя Д??
, .М \Е(О) дифференциалом dE = E'(x)dx и переходя
**-—! ] от суммы к интегралу, получим
Рис. 8.4.
A(t —
A)
Так как E(t) задана, то достаточно знать A{t) (переходную реакцию), чтобы
найти l{t).
Предыдущее выражение может иметь несколько видов. Заменим а
равенстве A) t на t — 9. Тогда интеграл принимает вид
f E'(t — 9) ЛF)(— dQ).
Приняв снова прежние обозначения, получаем равенство
которое эквивалентно A).
Если интегрировать по частям, то
t
f A(t
B)
t
A(t — x)E'{x)dx-\-A(t)E(Q)= Аф)Е{$)¦+- f E(x) A'(t — x)dx,
поэтому
JE(T)A'{t—t)d%.
C)
8.21 ' ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ХЕВИСАЙДА 495-
Сделав в этом выражении замену переменной х = t — 9, получим
I (*) =, А @) E(f)-\-$E(t — x) A' (x) dx. D>
о
Можно заметить, что формулы A) — D) являются результатом операции
t t
дифференцирования1) по t либо ГE(t—x)A(x)dx, либо ГE(x)A(t—x)dx.
о о
Поэтому имеем также
t
= ~J A(x)E(t—x)dx, E>
о
-^fA(t — x)E(x)dx. F>
6
Формулы A) — F) показывают, что знание переходной реакции достаточно
для вычисления l(t).
8.2.2. Вычисление переходной реакции. Рассмотрим в цепи два кон-
контура т и /. Мы видели (п. 1.2.8), что если приложить напряжение eJmt a
контуре I, то установившийся ток, идущий в контуре т, будет равен
') Припомним здесь формулу дифференцирования под знаком интеграла для слу-
случая, когда пределы интегрирования переменны. Требуется продифференцировать по t
bit)
¦/
ait)
f fit, x) dx.
г It)
Далии l приращение h. Мы легко получим
~h
** • am bit)
ait+k) ait)
Oit+Hl
I f
b
bip
Для вычисления первого и третьего интегралов воспользуемся теоремой о среднем,
значении:
г,
J /(t) aft = F— а)/((л), а<(л<*.
а
Если устремить А к нулю, то в пределе получим
С
a(t)
Это выражение, примененное к формулам E) и F), дает, как легко заметить, фор»
мулы A) —D).
496
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
Приложим напряжение ер1 в том же контуре (р — вещественное или комп-
комплексное число, причем R(p)>0). Тогда ток установившегося режима, те-
текущий в контуре т, будет равен
ept .
1т = ^АР)- G)
Выражение Zlm(p) представляет собой обобщенное взаимное сопротив-
сопротивление контуров I и т:
D
D(p) — симметричный определитель:
Z1\
Z1n
ni
Mlm(p) — алгебраическое дополнение элемента zlm.
Э
Элементы z
u,
znn — это собственные и взаимные обобщенные со-
сопротивления контуров. Имеем
Символы Llm, Rlm, Clm были определены в п. 1.2.8.
Рассмотрим формулу G). Если положить
получаем
Функция 1т имеет ту же форму, что и воздействие ept. Это очевидно,
поскольку речь идет об установившемся токе. В соответствии с выражением
„переходная реакция" назовем 1т „изоморфной реакцией". Коэффициент
У1т(Р)' который можно было бы назвать обобщенной переходной прово-
проводимостью, будет называться здесь коэффициентом изоморфной реакции.
Если требуется записать общий ток /т, идущий в контуре т при вне-
внезапном включении электродвижущей силы ept в контуре I, нужно прибавить
к установившемуся току 1т свободный ток хт (t):
Мы знаем также другое выражение для тока Im(t); оно дается формулой E),
где E(t) = ept. Тогда
oP*
I
I 0
t
(9)
Приравняем выражения (8) и (9):
t
f
А'т (х)
~ Х
*-P{
8.2] ' ' ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ХЕВИСАЙДА 497
Если устремить t к бесконечности, то
Мы видим, что переходная реакция, знать которую необходимо и до-
достаточно для определения тока, соответствующего приложенной электродви-
электродвижущей силе любого вида, связана с величиной, обратной обобщенному пол-
полному, сопротивлению, или с коэффициентом изоморфной реакции у (р), ин-
интегральным уравнением. Эта формула соответствия между функцией у(р)
и функцией A(t) называется „интегральным уравнением Карсона". Такое
функциональное соотношение позволяет, зная коэффициент изоморфной реак-
реакции (его можно получить простым вычислением), узнать переходную реак-
реакцию, а следовательно, и реакцию на совершенно произвольное воздействие.
Поэтому интегральное уравнение Карсона — это мостик, позволяющий пе-
перейти от установившихся токов к переходным.
Изучение пар функций /(р) и h(t), связанных соотношением
о
является целью операционного исчисления. Для того чтобы коротко вы-
выразить, что /(/») и h(t) связаны таким соотношением, принято пользоваться
особым значком, соединяющим эти функции. Так как функции, образую-
образующие пару, не равноправны, то значок не симметричен. Например,
/(/>) с А (О.
А (/) = /(/»)•
В интересующем нас случае мы видим, что, вычислив Угт(Р) = -т—г\ Уже
описанным способом, можно получить Alm(t) из соотношения
Atm(t)=3^AP)'
Дальнейшее рассуждение позволит осуществить это вычисление. Тогда легко
будет вычислить и ток.
Ток, идущий в контуре т при включении в контур I электродвижущей
силы E(t) в момент ?=0, равен
¦ t t
tmW^-Of f АшЮЕ«-V *¦* = ¦& f A*"{t-
0 0
Только теперь становится существенной форма электродвижущей силы.
Дальше (п. 8.3.10) мы увидим, что если
E(t)=>U(p),
т. е. если U(p) — функция, выраженная интегралом
Л, как мы уже имеем,
32 А. Анго
498 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIH
то соотношение
d (*
можно заменить на
Здесь мы снова встречаем закон Ома, но уже в операционной форме. Это
обобщение закона Ома для установившихся синусоидальных режимов:
которое само являлось обобщением классического закона постоянных токов
'-¦?¦
8.3. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
8.3.1. Преобразование Лапласа. Преобразование Карсона. Опера-
Операционное исчисление рассматривает либо функции, связанные интегральным
преобразованием Карсона
1
о
либо функции, связанные преобразованием Лапласа
Можно заметить, что между обеими функциями f(p) и F(p), связанными
с h(t) этими формулами, имеется соотношение
pF(p)=f(p).
Интегральное уравнение Карсона естественно входит в изучение элек-
электрических цепей. Мы, однако, будем пользоваться преобразованием Лап-
Лапласа, согласно, общему направлению, намечающемуся в международной тех-
технической литературе.
Мы записывали функциональное соотношение, определенное интеграль-
интегральным уравнением Карсона, в виде
/(/>) с А (О.
А (*) = /(/>).
В функциональном соотношении, определенном преобразованием Лапласа,
следует пользоваться другим значком:
Говорят, что F(p)—„изображение" h(t) и, наоборот, h(t) — это „оригинал"
F (р). Следует отметить, что р — комплексная, at — вещественная пере-
переменные.
8.3]
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
499
Если пользоваться преобразованием Лапласа, то соотношение A1) со-
сохранится. Оно будет иметь вид
lm{t)Z]^^ = ylm{p)U{p). A2)
Но здесь U(p)Z}E(t) (преобразование Лапласа).
Формула A2) показывает, что в случае преобразования Лапласа пере-
переходная реакция имеет вид
Теперь следует ответить на такой существенный вопрос: каким усло-
условиям должна удовлетворять функция h (t),
чтобы существовало изображение F(p).
Для сходимости интеграла
jh(t)e~ptdt
A3)
О
Рис. 8.5.
необходимо и достаточно, чтобы
А
1) интеграл Г Л (О dt существовал при любом
о
конечном А > 0;
2) существовало такое число о > 0, что
t
lim e~a> Г h(t)dt = Q. _шттт__
Ввиду того что проверка существования изо- Рис. 8.6.
бражения по необходимому и достаточному усло-
условию, как правило, оказывается затруднительной, приведем достаточное усло-
условие, более удобное практически:
Если h (t) кусочно-непрерывна- в любом конечном промежутке и суще-
существуют такие положительные числа Ж и о, что
\h(t)\<Me°<,
то A (t) имеет изображение.
¦ На протяжении гл. VIII мы все время будем предполагать, что все рас-
рассматриваемые функции вещественной переменной имеют изображения.
Рассмотрим несколько примеров.
Пусть h (t) == а. Найдем изображение функции (рис. 8.5)
Имеем
Отсюда
•/•-"*-*¦;
f
(О.
Найдем изображение функции А (О = —г (множитель — единичная сту-
ступень — подразумевается). Эта функция представлена на рис. 8.6. Изображение
32*
500 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
имеет вид
0
Этот интеграл легко вычисляется по частям:
Отсюда
/>-(»+I)cJ.' (Н)
Правила операционного исчисления
8.3.2. Сложение. Так как преобразование Лапласа — операция линейная,
то очевидно, что из
Fi (Р) С *» (О. F, (/>) С *2 @ Р„ (Р) С ha (Q
следует .
' Изображение суммы равно сумме изображений. Оригинал суммы равен
сумме оригиналов. Это верно при любом числе слагаемых. Отсюда вытекает
следствие. Рассмотрим разложение в степенной ряд функции h(t):
h(t)=ao + al 4у + а2+г+ ... +ап-^+ ...
Согласно правилу сложения и соотношению A4), получаем разложение функ-
функции F(p) в ряд по возрастающим степеням 1/р:
F(p)=f + ±L+ ...+-&-+...
Если же, зная функцию F(p), мы хотим определить функцию h(t),
то обратная операция позволит нам получить разложение h(t) в степенной
ряд из разложения F{p) по убывающим степеням 1/р. Может показаться,
что если сделать оговорку о существовании и сходимости рассмотренных
выше рядов, то этот прием можно считать общим, но, к сожалению, редко
оказывается возможным суммировать степенные ряды. Даже если не требуется
аналитическое выражение искомой функции, сходимость может оказаться
не достаточно быстрой для численных методов. Однако в некоторых слу-
случаях этот способ можно с успехом применять.
Пример 1. Найдем оригинал функции F(p) = —-j—. Разложим —-т—
в ряд по возрастающим степеням —:
Заменим в этом разложении -гд+г на ~т • Тогда
+ О0
¦ Не-.)
8.3] ' ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 501
Это разложение в степенной ряд е~а1. Следовательно,
¦Ее-"'. A5)
1 Ce~at
Приложение. Рассмотрим электрический контур R, L, С (рис. 8.7).
Включим в момент ? = 0 постоянную электродвижущую силу Е. Найдем
ток l(t). Формула A2) дает
J Z(p)m
Здесь
(p) Lp-\-R + -^. . Рис. 8.7.
Тогда
С*
где
„ R
LC
R ,,/ 1 R2
Оригиналы и соответственно равны ePit и ePit. Поэтому
P—Pi Р — Р2
r , sin
R2
4L2
Пример 2. Найдем изображение JQ(t). Известно, что
*оо
(-1)"
л=о
Заменим в этом разложении t2n на 2п1\ • Тогда
°° (-1)" 1 BяI _ .1 у. ,п ЬЗ...Bя-1) 1,
(л!J 22Я pin ~~ р LAK ' 2-4... 2л ^2Я
ч я=0 л=0
Можно узнать здесь разложение — A -\—Л 2. Следовательно,
Пример 3. Докажем следующее соответствие:
хп
рп+i
где х — параметр.
х" е р \Z(xtJ JttBYxt),
502 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Разлагая обе части в ряд, убедимся, что
ТшО
Сравнивая общие члены
S°° Г_П' хГ+П i
\ Ч pr+n+l г\
( 1 у _z L г~ с 1 у
У Ч pr+n+i г! И ч
_z L г с 1 у
pr+n+i г! И ч г!(г+я)! ¦
получаем
1 tr+n
что уже известно.
Если в общей формуле положить ге = 0, а затем л=1, то получаем
^ A8)
Таблица, помещенная в пп. 8.3.28—J3.3.30, — нечто вроде операционного
словаря—дает большое число преобразований. Приведем быстрый и удобный
способ вычислений с использованием этого словаря.
Решение физической или математической задачи ведет к отысканию
функции hit) — оригинала известной функции F(p). Просмотрев словарь,
мы найдем соответствие между некоторой функцией g(t) и Ф(/>), близкой
к функции F(p). Простыми преобразованиями можно добиться совпадения
ее с F(p). Применение правил соответствия, которые устанавливаются ниже,
даст коррективы, касающиеся одновременно и функции g(t). и задача
будет решена.
Во всем последующем мы будем предполагать, что функции F (р) и h (t)
связаны преобразованием Лапласа:
fi(t), B0)
иначе говоря,
F(p) = J e-pth{t)dt. B1)
о
8.3.3. Изменение масштаба. Если заменить в преобразовании Лап-
Лапласа B1) р на kp (k — положительное вещественное число), то '
со
F(kp)= J e-kp'h(t)dt.
о
Заменив t на -j-, получаем
Это равенство дает
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 503
Продифференцируем соотношение B2) по k. Это допустимо!), потому
что k —параметр, не зависящий ни от р, ни от t. Получаем
'Ш С ~ -У h'
Если положить k = 1, то
lpF(P)]C — tb'(t). B3)
Разделим выражение B2) на Л:
Проинтегрируем2) обе части по k от 0 до 1:
Положим s = kp, а х = -г- • Тогда
ff^ B4)
о /
Произведем предыдущее интегрирование от 1 до бесконечности. При
той же замене переменных находим
^p-dx. B5)
р о
Проинтегрируем по р от нуля до бесконечности обе части равен-
равенства B1), Так как
±-,
получаем равенство
') Дифференцирование по параметру * обеих частей
F (p, k)ch (t, k)
сводится, исходя из определяющей формулы B1), к дифференцированию под знаком
интеграла. Новый интеграл сходится, т. е. dh/dk имеет изображение, если только
условия, оговоренные в п. 8.3.1, выполняются.
!) Интегрирование по параметру k обеих частей равенства
F (р, k)ch (t, k)
сводится, исходя из формулы B1), к изменению порядка интегрирования
k7 ОО
J dk j e-P'h (t, k) dt,
*¦ о
CD ?2
что возможно, если интеграл \ е*?1 dt Г h(tfk)dk существует.
504 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
8.3.4. Дифференцирование функции h (t). Умножим на р обе части
преобразования Ланласа и проинтегрируем по частям. Получим
со со
РР (Р) = / Ре-"'/г @ dt = [— e~pth (/)]" + / «""*' {t) dt,
о о
pF(p) — h(O)Cfi'(t). B7)
Повторив п раз тот же прием, получаем последовательным интегриро-
интегрированием по частям
)- B8)
Если й@) = 0, то выражение B7) принимает вид
pF{p)U_h'{t). B9)
Если й@) = й'@)= ... =Л("-1)@)=:0, то выражение B8) преобразуется в
pnF(p)C^nHt). C0)
8.3.5. Интегрирование функции h(t). Найдем изображение функции
I h(t)dt. Согласно формуле преобразования Лапласа, это изображение равно
со Г / "I
f e-pt fh(t)dt\dt.
L I
о
L о
Интегрирование по частям дает
°° Г ' 1 Г '
fe-p'\ fh(t)dt dt= —-j-e-ptfh(t)dt
о L 6 J L о
+ 7 / e~"'h W dt*) = 7 / e~"tfl C> dt =
0 6
Следовательно,
о
Тот же прием, повторенный п раз, дает
t t *
t ... f h(t)dt. C2)
0 0 6
Формулы C0) и C2) показывают, что дифференцирование и интегриро-
интегрирование функции h{t) приводит соответственно к умножению и делению изо-
изображения F (р) на р.
*) Здесь следует учесть, что
lim e-P* f h(t)dt = Q.
8.3]
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
505
Аналитические операции над h (t) приводят к алгебраическим операциям
над F (р). Этим объясняется громадное упрощение, которое вносят в анализ
приемы операционного исчисления.
8.3.6. Теорема смещения. Дадим переменной р приращение X. Тогда
преобразование Лапласа примет вид
F {р +X) = J e-P'~uk (О dt,
о
GO
F (р И- X) = Г e-Ple-xth (t) dt.
о
Отсюда
C3)
О
8.3.7. Теорема запаздывания. »—-Л—-i
Вычтем из аргумента t положительное рис §8
число X. Функция h(t), или, точнее,
функция h(t)l'(t) (так как T(t) всегда подразумевается), преобразуется
в h(t — Х)Г(/— X) (рис. 8.8).
Заменим t на t — X в преобразовании Лапласа:
или, введя множитель
= J h(t — \)e-P'
— X) и разделив на ехР,
СО
Нижний предел интегрирования может быть взят равным нулю, так как
из-за присутствия Г(/ — X) вклад интервала @, X) равен нулю. Отсюда
оо
А
Рис. 8.9.
и, следовательно,"
__ e-xPF (р) С h (t — X) Г (t — X). C4)
* В случае, когда h(t) равна единичной
ступени, мы имеем (рис. 8.9)
1 ._,„_
—X).
C5)
8.3.8. Дифференцирование функции F(p). Продифференцируем по р
обе части формулы преобразования Лапласа. Получаем
= J —th(t)e-ptdt.
Отсюда
Продифференцировав п раз, получаем
(Р) С (— 1)" tnh {t) (n — целое положительное).
C6)
C7)
506 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
8.3.9. Интегрирование функции F(p). Проинтегрируем по р от р
до бесконечности обе части формулы преобразования Лапласа. Получаем
Отсюда
оо
ff(P)dpC1^1- C8)
р
Проинтегрировав п раз в тех же пределах, получаем
ОО ОО СО.
fdpfdp...fF(p)dpCJ$1- C9)
р р р
8.3.10. Теорема свертывания, или теорема Бореля. Даны две функ-
функции hx(t), h2(t), имеющие соответственно изображения Fl(p), F2(p). Найдем
оригинал для произведения Fl(p)F2(p). Рассмотрим формулу преобразования
Лапласа, относящуюся к функции /^(т):
о
Умножим обе части на F2(p)'-
оо
Fi (Р) Р2 (Р) = f e-^ (P) *i W
о
В силу формуЛы C4) получаем
e-i"F2(p)Cha(t — О Г (г — х).
Следовательно,
Ввиду наличия Г(^ — т) вклад интервала /<i<4~°° в интеграл равен
нулю, и можно написать
t
x)rfx=J*A1(x)A2(< —x)rfx.
Итак, теорема свертывания может быть сформулирована следующим образом:
Если
то
t t
! О») ^2 О») С / hl СО h (t — X) rfx = J At (* — X) A, (X) rfx. D0)
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 507
Примечание. Теория электрических цепей Хевисайда показала что
переходная реакция связана с обобщенным сопротивлением уравнением
о
Отсюда
Если приложить электродвижущую силу E{t), то получим выражения для
тока в виде
i i
о о
Пусть U{p)— такая функция, что
Теорема свертывания дает
t
f
о о
или
t t
. ¦ d
f **- D2)
6 6
Сравнив формулы D1) и D2), получаем
D3)
Это замечательное обобщение закона Ома для переходных режимов.
8.3.11. Различные формулы. Докажем формулу
"r' о
Она может быть полезной, если, зная оригинал F(p), мы хотим найти ори-
оригинал f(—\.
\р)
Заменим р на — в формуле преобразования Лапласа:
оо
... Г —
F(j)= I e~P A(t)fifx.
о
Разделим на pa+l:
j
Тогда, исходя из формулы A7), можно написать
оо п
*1 D5)
508 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Если ге = 0, то
^{jjf (t) А. D6)
о
Докажем формулу
F {V~p) С y=f J JL е~ » h (х) rfx. D7)
Для этого будем исходить из формулы
^Й~^ D8)
которая доказывается ниже (п. 8.9.20, формула G8)).
Продифференцируем обе части D8) по х:
-~*' D9)
Заменив р на Y~P B формуле преобразования Лапласа, получаем
со
F (У~р) = J e-^p'h (x) fifx.
. о
Пользуясь соотношением D9), найдем
Докажем формулу
1 г
При доказательстве формулы G7) мы придем к выводу, что
о
Заменим в этом равенстве и на $х. Тогда
Считая, что
получаем из предыдущего выражения
—
4*.
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 509
Установив это, обозначим через ср(/*) изображение h(t2). Имеем
оо
<р(/>) = fe-ptfi(t2)dt.
о
Если в этом выражении заменить t2 на t, то
Подставив (¦), получим
' о о
или
= ~ f e~** dx f e-tx2h(t)dt.
у те J J
' 0 0
Заменив р на х2 в формуле преобразования Лапласа, получаем
тогда
оо
Мы получили выражение, которое поможет вычислить изображение
если известно изображение h(t):
о
~ ,?/8.3.12. Теорема разложения Хевисайда. Теория разложения рациональ-
рациональных функций на простые дроби показывает, что если F (р) — полином т-й
степени, имеющий лишь простые корни ап, а /(р) — любой полином низшей
степени, то имеет место тождество
/(Р) _ /@) ¦ у /(*„) !_
pF(p) — PF@) ^Zi anF'(an) р — ая'
л=1
В силу соотношения A5)
Р—О-П "'
Обозначим через h(t) такую функцию, что
h rt\ —\ f(P) (ЪО\
Тогда
л= 1
Формулы E0) и "E1) представляют собой теорему разложения Хеви-
Хевисайда. ' • :
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 51 1
8.3.14. Случай переменного напряжения. Дано напряжение Еое'м.
Имеем
р —
I
(/> - У») Z О»)
Достаточно применить теорему разложения к дроби
Eapf(p)
чтобы получить
- Z(» c' ^ H (an-j»)F'(an) ' •
/1=1
Ток l{t) также можно рассматривать как сумму двух токов:
1) установившийся ток
р в
0 Z (ja>) '
что является уже известным результатом;
2) свободный ток
Конечно, если нужно узнать токи, соответствующие электродвижущей силе
EQ cos wt, то достаточно взять вещественную часть результата.
Пример. Рассмотрим ток, вызванный приложением электродвижущей
силы E0cos<ot к цепи, состоящей из дросселя с сопротивлением.
Обобщенное сопротивление равно
Применим формулу E3). Тогда
-S-t
е L
_^_ , \
Вещественная часть равна
Г -
Lcos((Ot~у)~cos9g
E Г --<
где
Примечание Рассмотрим рациональную дробь С, I • Пусть поли-
полином m-Vi степени F(p) имеет только простые корни ап. Тогда имеет место
тождество
f(p)
p V
F(p) — ZJL F'(an) р-а„ '
л=1
512 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Отсюда вытекает формула, несколько отличающаяся от теоремы разложения;
8.3.15. Случай кратных корней. Случай, когда полином F (р) имеет
кратные корни, приводит к более сложной формуле. Рассмотрим отноше-
отношение двух полиномов
f(p)
и предположим, что степень числителя меньше степени т знаменателя.
Если знаменатель имеет кратные корни, то его можно записать в виде
Р (Р) = (Р — «i) (Р — а2р • • • (Р — «*)"* ... (р — arfr,
где
= l^~a:^ "n.-i ~t~ ••• '1-j+i -r" ••• ~l—— 4-
Тогда
/(P)
или
r "ft
/(р) __
Вычислим коэффициенты ЛА1, Ак2 Akn . Умножим (*) на (р — ак) к.
Имеем
+ (р —ай)"*
где функция Ф(/>) сохраняет конечное значение при р = ак. Поэтому
Дифференцируя предыдущее выражение, получим тем же способом
/\ Ь9 **—
dp F (Р)
Осуществляя дифференцирование j—1 раз, находим
Аь1 = —
8.3J ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 513
С другой стороны, известно, что
Отсюда
где
А =
Примечание. На практике всегда полезно проделать непосредст-
непосредственно предыдущее вычисление, а не применять формулу E5), так как она
довольно сложна.
Пример. Требуется найти оригинал для
А В С , D
~ р—\ ^ (P-W ^ (я-1K ^
Умножим обе части на /> —(— 2 и подставим р = — 2. Тогда
D-±
U— 27 '
Умножим обе части на (р—IK. Тогда
Если положить в предыдущем равенстве и равенствах, полученных его
однократным и двукратным дифференцированием, р={, то найдем
Г-2 R— 1 А— -1
Отсюда искомый оригинал
^eL3^9 27J-
Преобразование некоторых употребительных функций
8.3.16. Оригиналы некоторых рациональных функций. Мы уже по-
получили формулу A4):
1^
Найдем оригинал функции ¦¦ v+1 для случая, когда v — любое комплекс-
комплексное число, но с вещественной частью, большей чем —1.
Известно, что одно из определений эйлеровой функции второго рода
(п. 7.4.1) — это
оо
rcv-f- 1) = je~*x-dx, R(v)>-1.
о
Положим х = pt. Тогда
со
T(v-j- 1) = p J e-P'p*t* dt.
и
33 А. Анго
514
Отсюда
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
dt
1 г ?_
pv + 1 ГСН- 1) '
Г56)
Формула E6) совпадает с формулой A4), если у равно целому числу п,
так как Г(/г+-1) = /г!
Придадим v значение 1/2. Тогда
Г" ^_ , так как Г[ — )=Yn.
Vp1
Применим формулу C3) к равенству E6). Получаем
E7)
/58)
Если положить в этом соотношении v=0, то мы получим уже известную
формулу A5):
1
Если придать X значение — у, то
или .
Р — У
-Qcos t-\~ jsint.
f ~Г x
Отделим вещественные части от мнимых:
Р .
1
E9)
sin
Придадим X значение X — /со. Тогда
1 _
т. е.
Отсюда, приравняв вещественные и мнимые части, получаем
-lt sin (ot.
F0)
Если в формулах E9) заменить t на jt, применив формулу изменения
масштаба B2), то
D
ch <ot
F1)
„,2 '
8.3) ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 515
8.3.17. Изображения бесселевых функций целого порядка. Будем
исходить из классического определения бесселевой функции первого рода
(га — целое число) (п. 7.5.11):
О
ИЛИ
Jn (t) = -i У cos (яб — t sin 6) db
—«
Изображение этой функции дается формулой преобразования Лапласа:
00 г * 1
F{p) = -~ f f eiina-'8|п e» db e-p' dt.
Проинтегрируем сначала по t:
п
I i* Г al («в-f sin b)-pt I00 i
= — / \^— db = —-
2я ^ L /7+/sine Jo 2я
0 2я ,/ p 4- / sin 6
db.
—«
1 rf г
Положим eib = г. откуда db = -г —— , sin 9 = —sj"" * Если обозначить
через С окружность единичного радиуса с центром в начале координат, то
интеграл принимает такой вид:
--L f *П*г
Интегрируемая функция имеет только один полюс, находящийся внутри
окружности С, а именно
г = —
Следовательно, интеграл равен удвоенному вычету относительно этого
полюса:
Отсюда
" F2)
Если в соотношении F2) заменить t на jt, пользуясь формулой B2)
изменения масштаба, и принять во внимание определение бесселевых функ-
функций мнимого аргумента (п. 7.5.25), то
у р2 — 1
Далее мы увидим (п. 8.5.3), что формулы F2) и F3) имеют общий ха-
характер и применяются в случае, когда индекс п — не целое число. Способом,
подобным предыдущему, можно легко вывести формулу
33*
516 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Сейчас мы установим некоторые соотношения, полезные при изучении
распространения электрических возмущений вдоль линии передач:
[(ft _
F5)
V Р — 1
Г?=Гг t>b< F6)
F7)
-1 т ( -\
Рассмотрим функцию f(x) = x 2 1т\х2). Дадим х приращение Л и
произведем разложение в ряд Тейлора: ,
Вычислим последовательные произведные / (х). Для этого положим
z='xJ. Тогда
Но, согласно свойствам бесселевых функций, мы имеем рекуррентное соот-
соотношение (п. 7.5.28)
Следовательно,
Возвращаясь к переменной х, находим
^ ^х 1т+\
Отсюда делается совершенно очевидной формула
„ г 1
Поэтому
1
1\1 , т+п I \\
t Li,——/ L?)
x /J — ^n x 'm+n\x }•
Если положить h = 2bt, x=t2, a m = 0, получим
B=U
8.31 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 517
Введя в это выражение изображение /„ (t), полученное из F3), находим
Отсюда вытекает и формула F5). Если к выражению (*) применить теорему
запаздывания (формула C4)). получим формулу F6).
Заменим в F6) Ь на 8, a t на at. Тогда
1/ 1 V"'"
/0 [a Vp —
01 V
Положим, что — = (а, и применим теорему смещения. Имеем
Положим
Р —а = 2а.
Отсюда
р = а-»-й. а=? — а,
и мы имеем
F8)
Разделим правую' часть F8) на р. Тогда
1 .,-11 V(p+2a) (p+2fti
/
Умножив формулу F9) на 2а и сложив ее почленно с F8). получим иско-
искомую формулу F7).
8.3.18. Изображение In t. Продифференцируем формулу E6) по v.
Тогда
1 dT(v + l) 1 1
т. е.
Г Д(у+1) I ¦
Ly?l[ r(v+D ^Jc^^ G0)
Но известно, что
Г(>-)-1)= lim
Поэтому
</v „ Г. . 1 1 11
—тГТ i—П—== "III III « i—5 r~n ••• i—Z~<—Г" •
Если придать v нулевое значение, то
*) Здесь 7 = 0,57721566490 ... —постоянная Эйлера.
518 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Подставив выражение G1) в равенство G0) и считая v=0, получаем
lnf=]_iILP±l. G2)
8.3.19. Изображение интегральных косинуса и синуса. По опреде-
определению, имеем
~T~~J
sin х ,
dx'
x
t
fi (t) = sin t 3-^-f=F(p), G3)
= ^(p). G4)
Поэтому, применяя последовательно к соотношениям G3) и G4) формулу B4),
получим
со р
f slnx , —, \ Г ds 1 , .,_.
=-y —dx^--J -sTTT = __arctgp, G5)
G6)
Можно воспользоваться изображением d(t), чтобы найти разложение
этой функции в ряд. Имеем
1п У р h ^(r tj ^D^)
1 / 1 11.11
Отсюда, так как
/2 it /6
U (f) = in t -+- f — 272Г-Г- 4T4T "~ "бТв
pn+1 л!
получаем разложение Ci (f):
- f — 272Г-Г- 4T4T
8.3.20. Изображение функции ошибок. Рассмотрим интеграл
1=\е ^~и> da.
о
Заменив а на —, получаем
8.31 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 51У
Складываем оба эти выражения. Считая, что v= а, получаем
2/= / 1+4-К du= / e-*dv=Yn
0 -co
и, следовательно,
CO -
G7)
о
Установив это, попробуем найти изображение функции
Формула преобразования Лапласа дает
Считая, что у= = и, получаем rf/ = —-—da. В силу соотноше-
соотношения G7), где приравниваем а = —тр^ • получаем
Поэтому .
^^tt^^- G8)
Проинтегрировав по л: обе части от 0 до х, имеем
—,— G9)
8.3.21. Изображение единичного импульса1). Рассмотрим единичную
ступень Г (О Z1— и функцию времени, изображенную на рис. 8.10, а. Она
представляет собой прямоугольный импульс длиной в б с амплитудой -*-.
Площадь прямоугольника равна единице. Изображение рассматриваемой
функции равно:
-e-P* _ pQ
J% —l 2
! 6 ••'
~ 6 -J J% —l 2—! 6
Если 0 стремится к нулю, то в пределе функция времени представляет
собой импульс (бесконечная амплитуда, действующая бесконечно малое время),
') Или единичного толчка.
520
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
но площадь прямоугольника остается все время равной единице. Предельная
функция !) называется единичным импульсом. Левая часть равенства (90)
стремится к производной Г (*), а правая часть—к единице. Поэтому можно
написать
Функцию T'(t) иногда называют функцией Дирака b(t). Она обладает
следующим важным свойством. Если f(t) — любая функция, то
а)
б)
3)
1/8
с
1/вг
. 0
1
в
9
20
J
6
t
• г/в3
в) 0
-2/в3
в
гв
п
зв t
3/8*
7/'в*
0
-г/в*
-з/е*
—
в
—
—
ze
Зв
49
U 6
Рис. 8.10.
(81)
На практике не существует явлений, сле-
следующих закону, описанному функцией Г'(^).
Имеются лишь явления, описываемые функ-
функциями, равными нулю всюду, кроме проме-
промежутка очень малой длины 6, а в этом
промежутке принимающими очень большие
значения -g- • Если пренебречь бесконечно
малыми первого порядка, то изображение
такой функции будет равно А.
Рассмотрим теперь два последователь-
последовательных прямоугольных импульса противополож-
противоположного направления с продолжительностью &
и амплитудой -р- (рис. 8.10, б"). Эта функ-
функция времени и ее изображение будут иметь
вид
рЦ ( _
Если 9 стремится к нулю, мы получим
в пределе два импульса 2), .следующих друг
за другом в течение бесконечно малого вре-
времени. Их можно рассматривать как вторую
производную Г (t):
Г" (О ИР-
Точно так же при 8 = 0 пределы функций, изображенных на рис. 8.10, в
и 8.10, г, будут соответственно
и т. д.
Примечание. Введем в контур / находящейся в равновесии цепи
электродвижущую силу, равную единичному импульсу Г'(/). Этот импульс
') Теория импульсной функции изложена в кн.: Б. ван дер Поль и
X. Б р е м м е р, Операционное исчисление на основе двустороннего преобразования
Лапласа, ИЛ, 1952 г. (гл. V).
¦ 2) Это не единичные импульсы, так как ограниченная ими площадь равна у,
а не 1.
8.3)
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
521
создаст в контуре т ток Rlm(t). По примеру п. 8.2.1 можно показать, что
достаточно знать функцию R, иначе говоря, импульсную реакцию контура т.
на контур /, чтобы определить ток im(t), текущий в /га в результате прило-
приложения к / любой электродвижущей силы,
равной нулю при t < 0.
Вместо того чтобы разлагать функцию Efn&t)
E{t) на ступеньки, как на рис. 8.4, разло-
разложим ее на вертикальные полосы (рис. 8.11). ?C&t)
Каждая часть E(t) будет при этом заклю- 'E(Zut)
чена между двумя импульсами шириной в Ы. E(At)
Обе определенные таким образом ступен- ?^
чатые функции будут стремиться к E(t)
при Л?, стремящемся к нулю, при условии,
если E(t) не имеет резких скачков.
Каждая элементарная реакция будет
равна
Еф) /?(/),
Рис 8.11.
Ток i{t) будет представлять собой сумму этих элементарных реакций.
Поэтому
Формула A2) показывает, что импульсная реакция контура m на кон-
контур / связана с обобщенным взаимным сопротивлением соотношением
Применение формулы обращения
8.3.22. Теорема Меллина — Фурье. Мы видели (п. 1.3.15), кто
единичная ступень может быть выражена
интегралом - *J°° . a+J°°
Контур интегрирования представляет собой
-оо
+оо
Рис. 8.12.
-joo c-joo
Рнс. 8.13
вещественную ось с маленькой полуокружностью (рис. 8.12). Положим
ja> = p. Тогда
-t-/oo
-jco
522
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
При этом контур интегрирования представляет собой мнимую ось с малень-
маленькой полуокружностью, как показано на рис. 8.13. Он может быть заменен
любым другим контуром Г, соединяющим точки —joo и -\-joo и располо-
расположенным справа от мнимой оси. Действительно, согласно теореме Коши, так
как между мнимой осью и Г функция — не
имеет особых точек, мы можем написать
+ JOO
-jco (Г)
Контур Г может быть, в частности, пря-
прямой, параллельной мнимой оси с положи-
положительной абсциссой с (контур Бромвича).
Следовательно,
C+JCO
/ ^
= -%р- I —dp. (82)
c—joo
Установив это, рассмотрим функцию h(t), изображенную на рис. 8.14.
Повторив рассуждения, сделанные при выводе формул A) — F), мы можем
разложить эту функцию на ступеньки:
оо
И @) Г (f) + 2 [* (х„) — h (*„_,)] Г (/ — х„).
/1=1
Если устремить это выражение к пределу, бесконечно уменьшая проме-
промежутки хп— х„_1,, ступенчатая кривая будет стремиться к кривой h(t), и
тогда
+оо
= 4t f r('-
«ли
Заменим в этой формуле X (t— х) выражением (82). Получим
оо C+joo
" . I Г е" т> dph (х) dx,
C+jca oo
c-joo 0
Отсюда, пользуясь формулой преобразования Лапласа, найдем
c+joo
=^ /
1. е.
А(О = -Дт
c—joo
c+joo
(83)
c—joo
Мы получили формулу обращения. Ее называют формулой Меллина — Фурье.
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 523
Рассмотрим функцию f(p). Это изображение h{t), определенное форму-
формулой преобразования Карсона. Имеем
c—joo
Таким образом, h(t), неявно выраженная интегральным уравнением
со
F(p)=fh(t)e-ptdt, (84)
о
дается в явном виде формулой (83) через интеграл по простому контуру
в плоскости комплексной переменной р. Если этот интеграл равен нулю
вдоль бесконечной полуокружности, находящейся слева от контура (п. 1.3.19),
то его вычисление сведется к простому вычислению вычетов при условии,
что особые точки являются полюсами или существенно особыми точками.
Если же особые точки являются точками разветвления, то это вычисление
сведется к интегрированию по эквивалентному контуру.
Формулы (83) и (84) эквивалентны. Можно применять любую из них.
Нужно, однако, заметить, что формула (83) более общая, чем формула (84),
и может дать результат, даже если формула Лапласа приводит к расходя-
расходящемуся интегралу.
В качестве примера найдем с помощью формулы (83) некоторые выра-
выражения, уже полученные раньше с помощью формулы Лапласа.
Пример 1. Найдем оригинал я+1 (п — целое положительное число).
Формула обращения (83) дает
C+jca
C—joo
Из первого примера п. 1.3.19 известно, что значение этого интеграла
tn '
—. Мы снова находим уже известное выражение
1' tn
* г— *
pn+i L. п[ •
Пример 2. Требуется найти оригинал —2 , 2 . Применим теорему
обращения. Искомый оригинал h{t) имеет вид
c+jca
1 Г еР'
= -j-j / —2 I г аР-
c-'jco
Вычисление (см. п. 1.3.12) дает h(t) = , а это приводит к уже
известному выражению —sina^^
sin at ^J—2 , 2 ¦.
8.3.23. Замечания о применении формулы обращения. Мы доказали
с помощью преобразования Лапласа формулу E6):
Эта формула, где v — вещественное число, была доказана для случая, когда
v > — 1. Если v < — 1, интеграл Лапласа не сходится. Докажем теперь
формулу E6), применяя теорему обращения.
524 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Рассмотрим сначала случай, когда —1 < v < 0. Функция —^т" много-
многозначна в плоскости р, и нетрудно заметить, что в интересующем нас слу-
случае контур Бромвича эквивалентен контуру С на рис. 7.12. При этом до-
достаточно заменить z на pt в формуле A0) п. 7.4.5, чтобы получить иско-
искомое выражение E6).
ept
Здесь следует сделать одно существенное замечание. Функция v+1
имеет в начале координат точку разветвления. Формулу E6) можно полу-
получить из теоремы обращения, если из всех ветвей функции ограничиться рас-
рассмотрением только первой ветви. Если выбрать вторую ветвь, то вместо
правой части формулы E6) мы получим выражение
К многозначным функциям, имеющим точку разветвления, теорему обра-
обращения следует применять, пользуясь только первой ветвью, т. е- такой,
для которой
— те < arg p -<С -f- к.
Это замечание будет учтено в дальнейшем.
Рассмотрим теперь случай, когда v > 0. Достаточно приравнять
v = ?-|-[a> обозначив через k целое число, а через (х такое число, чтобы
— 1 < (х < 0.
Интегрируя по частям, получаем
c+jao C+jca
1 Г eP'dp _ t 1 С ePl dp
и т. д., повторяя k раз это интегрирование по частям, имеем
c+jao
1 Г еРЫр **l f eP' a
Отсюда и получается искомая формула E6).
Итак, мы нашли формулу E6), применяя теорему обращения в случае,
когда v > — 1, т. е. при тех же условиях, что и применяя преобразование
Лапласа. Было бы желательно распространить формулу E6) на случай,
когда v < — 1. Действительно, если v—не целое отрицательное число, обе
части формулы имеют смысл. Однако интегралы Лапласа и Меллина — Фурье
не сходятся. Тем не менее можно применить интеграл, аналогичный инте-
интегралу Меллина — Фурье, пользуясь вместо контура Бромвича контуром,
изображенным на рис. 7.12, что приведет к сходящемуся интегралу. Фор-
Формула A0) п. 7.4.5 позволяет тогда написать, считая v = — (х.
р*~ Q ((х—не целое положительное число), (85)
но при соотношении
Итак, мы обобщили формулу E6) для всех значений v, пользуясь
то контуром Бромвича, то контуром С, так как оба они эквивалентны
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 525
в области — 1 < v < 0. Нужно заметить, что основное свойство операцион-
операционного равенства заключается в том, что некоторые преобразования одной
функции отражаются известным образом на другой функции, и наоборот.
Переход от функций t к функциям р и обратно не обязательно ограничи-
ограничивается формулами преобразования Лапласа — Карсона или Меллина — Фурье.
Поясним это примером, так как развитие теории вышло бы за рамки
настоящей книги. Контур, который можно свести к контуру С в случае,
когда имеется только одна особая точка в начале координат, был предло-
предложен Лоури'). Этот контур соединяет —со — /0, —oo-\~jQ и охватывает
особые точки функции.
Пример. Требуется найти функцию h (t) — оригинал для
Применяем теорему обращения.
Особые точки подынтегральной функции — это
1) точка разветвления при р = 0;
_з
2) полюсы при значениях р, обращающих в нуль р2~\~1.
Мы должны провести разрез от 0 до —со, чтобы сделать функцию
однозначной в плоскости р.
Если придать р значение рп, то мы будем
иметь два значения для р02. Одно соответствует
значению аргумента р0, заключенному между
— к и к, второе — значению аргумента р0, за-
заключенному между Ц-тс и -j-Зтс.
Полюсы определяются значениями р, являю- Разрез
!
щимися корнями уравнения р2 -+- 1 =0, т. е.
такими значениями р, аргументы которых соот-
соответственно равны
2 ,2 о Рис. 8.15.
— 3-й, +-д.*. 2*.
Для первой ветви следует рассматривать только два первых значения. В слу-
случае второй ветви следует оставить только третье значение.
Мы уже видели, что при нахождении оригинала с помощью теоремы
обращения следует оставлять только такое значение р, аргумент которого
заключен между —и и и. Поэтому нам нужно исследовать только два
полюса:
Контур, эквивалентный контуру Бромвича, будет, следовательно, таким, как
изображено на рис. 8.15, так как вклад бесконечной полуокружности, нахо-
находящейся слева, равен нулю.
1) Н. V. Lowry, Operational calculus, Phllos. Mag ^1932), 7 serie, t. 13.
526
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
ГГЛ. VIII
Легко заметить, что вклад малой окружности с центром в начале коор-
координат равен нулю. Действительно, положим, что р = ге^. Тогда интеграл
7t
if
grt (cos e+/ sin 6) g'
стремится к нулю вместе с г. Поэтому искомый интеграл будет состоять
из вычетов, относящихся к обоим полюсам, и интегралов вдоль верхнего
и нижнего края разреза.
1. Вычеты. В полюсе р = ^-(—1_|_у|/"з) вычет равен
ldp
Точно так же вычет в полюсе р = —R"
Отсюда сумма вычетов равна
2 --к
Равен з" е
2. Интеграл вдоль нижнего края разреза, если считать р = хе~1*. равен
о I
1 Г е-л'х2 dx
2я ./ i *
l + Jx2
Вдоль верхнего края разреза, если считать р = хе^п, интеграл равен
1 Г е~х1х2 dx
L Г
2п J 1
0 l-jx2
Отсюда в сумме получаем
и в результате
_1 f
я ,/
о
e~xtx2 dx
4 -T
я ./ 1
dx
В случае численного вычисления может оказаться интересным разложить
последний интеграл в асимптотический ряд. Напишем для этого
^ l + дгз
(*)
8.3] ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 527
Если обратиться к определению факториальной функции, данному
в формуле C) п. 7.4.1, и подставить (*) в искомый интеграл, то мы полу-
получим разложение в ряд, общий член которого равен
J
о
^(—l)»-1-! [ e-xt(xtfn~*d(xt)= (—I)"
Зл" о
Остается показать, что этот ряд асимптотичен, т. е. что Rn стремится,
к нулю, когда п постоянно, a t стремится к бесконечности. Имеем
. Зл+4
г(з«
-4)
Значит, ряд действительно асимптотичен.
8.3.24. Обобщение теоремы разложения Хевисайда. Дана функция h (Л.
изображение которой имеет вид Cf\ • Функции f(p) и F(p) могут быть
любыми, но частное должно иметь лишь простые полюсы (конечное алл
бесконечное число). Другие особые точки отсутствуют. Итак,
иначе говоря,
C+/OO
J
j
F(p) "*"
c—joo '
Рассмотрим ряд значений р, представляющих собой простые полюсыг
aV а2 «т- •••
Функция А (О равна сумме вычетов в этих полюсах* при условии, что вклад
бесконечной полуокружности, находящейся слева от прямой с абсциссой с, ра-
равен- нулю. Эта сумма вычетов записывается, согласно формуле п. 1.3.12, в виде
¦^ Р («ш)
Последнее выражение представляет собой обобщение формулы E4), которая
была справедлива только для отношения двух полиномов.
Если изображение функции h (t) имеет вид
то
m=l
Это обобщение формулы E1), называемой формулой разложения Хевисайда»
Она применялась только к отношению двух полиномов /(/?) и pF(p).
528
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Изображения разрывных функций. Приложения
8.3.25. Введение. Из формулы C4) следует
[ГЛ. VIII
g{t)
I h(t — X) при t> X,
0
при t < X.
Выражение e~KpF{p) представляет собой изображение функции времени,
график которой представлен на рис. 8.8 (пунктир). Эта функция получается
из к (t) T (t) сдвигом вдоль оси t на X.
Формула обращения (83) придает формуле C4) такой вид:
c+jaa
А
\7
где
Рис. 8.16.
c—J<x>
h(t—\) при t > X,
О при t < X.
Пример. Найдем изображение функции g{t), равной sinu)(? — к) при
?>Х и нулю при t <Х (рис. 8.16). Изображение sin at равно а , 2 . Зна-
Значит, искомое изображение равно
8.3.26. Изображения непериодических разрывных функций. Найдем,
для примера, изображение функции g (t), которая равна нулю при —со <
— X) при X<f<Xt
и снова равна нулю при X-j <
<t < Н-со (рис. 8.17).
Синусоида ABCDEFG .... начи-
начинающаяся в момент t=k. имеет, как
мы только что видели, своим изобра-
изображением
<ае-Кр
Поэтому синусоида EFG ..., начинающаяся в момент t = k-
своим изображение-м
имеет
Функция g(t), которая представляет собой разность между обеими
синусоидами, имеет изображение
8.3]
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
529
Пример 1. Найдем изображение функции, представленной на рис. 8.18
утолщенной линией.
Изображение функции, представленной полупрямой Ох, равно
АЛ.
X Рг "
Рассмотрим полупрямую Ах", проходящую через точку А с координатами
(О, —Е) и имеющую угловой коэффициент, равный по абсолютному значе-
значению угловому коэффициенту Ох, но противоположный ему по знаку. Изобра-
Изображение функции, представленной этой по-
полупрямой, равно
Р * Р2 '
Полупрямая Вх' параллельна Ах"
(рис. 8.18). Представленная ею функция
имеет изображение
-х'
Рис. 8.18.
?
О
г« Л »¦
F
В
х"
V
t
Искомую функцию g(t) можно
получить сложением обеих функций
представленных линиями — ооОх и
— ooOFBx'. Следовательно, изображение
функции g(t) будет
Ш)
Eft)
а
R
Пример 2. Импульс, имеющий вид
полупериода синусоиды fosinu)/, прила-
прилажен в момент ? = 0 к цепи, состоящей
из последовательно соединенных сопро-
сопротивления и емкости (рис. 8.19). Требуется
найти ток, текущий в момент времени
О
\?
Рис. 8.19.
Изображение синусоиды, начинающейся в момент, t =0, равно EQ . .—j
Изображение синусоиды, начинающейся в момент —, равно Ео 2 , - 2 е т .
Функция, представленная на рис. 8.19 утолщенной линией, будет иметь
своим изображением сумму этих двух изображений. Следовательно,
.-re
Обобщенное сопротивление цепи равно
Тогда
34 А. Анго
530 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ, VIH
Применяем формулу обращения
C + jca
Г
J
C—JQO
Вычеты, соответствующие полюсам р=±у'<в, равны нулк>1 так как
1 -г- е~ i7- = 0. Вычет, соответствующий полюсу р = — -^, дает искомый гок
-\~ eRC
Примечание. Если бы требовалось найти выражение i(t) при t < — ,
то функция Ь (р) была бы изображением бесконечной синусоиды Ео а . g ,
так как при t < — цепь „не знает", что эта синусоида будет прервана
в момент t = -^-.
8.3.27. Изображение периодических' разрывных функций. Пусть
А (О — однозначная функция с периодом X, начинающаяся в момент ? = 0,
не принимающая бесконечных значений и имеющая конечное число разры-
разрывов, максимумов и минимумов
в периоде (рис. 8.20),
Пусть F (р) — изображение
функши h(t), a Fn(p) — изобра-
t жение одного периода этой функ-
Рис. 8.20. ции> начинающегося в t = 0, т. е.
нулевого периода. Тогда изобра-
изображение первого периода равно F0(p)eKP, изображение второго периода равно
F0(p)e-2t-p изображение n-го периода равно F0(p)e~nkP. Отсюда
o(PJj
ИЛИ
р №=-?$,-• (86)
Примечание. Применяем теорему обращения:
Это выражение дает разложение в ряд Фурье функции h(t).
Пример 1. Требуется найти изображение и разложение в ряд Фурье
функции (рис. 8.21)
Найдем .изображение нулевого периода этой функции. Изображение сину-
синусоиды Y (t) sin t равно , . .. Изображение синусоиды Г (t — u)sin(?—ic) равно
е-рк
—2. .- . Следовательно, изображение нулевого периода функции ti(t) равно
8.31 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
По формуле (86) изображение функции h(t) равно
531
Разложение в ряд Фурье функции h{t) будет иметь вид
c+joo
f
J
ept х + е-кр
J
г—/со
c—joo
Вычеты, соответствующие полюсам р= ±/, равны нулю, так как \-\~e~]*=Q.
Имеется бесконечное число простых полюсов, удовлетворяющих уравнению
иначе говоря, полюсами будут точки р = 2nj, где п принимает целые
значения от — оо до -f- оо. Для полюса
р = 0 имеем
Рис. 8.21.
Для полюсов, соответствующих всем целым положительным и отрицательным
значениям п, кроме нуля, имеем
¦l-oo оо
2 vi е2/пг 4 у cos 2nt
Т 2л 1 — 4л2 ЧLA 4л2—1 "
п=— оо п=\
Отсюда получаем разложение в ряд Фурье:
Г оо
cos 2л/
'— 1 *
л=1
Пример 2. К катушке самоиндукции с сопротивлением прикладывают
напряжение, равное попеременно -\-Е или —? в течение промежутков вре-
времени, равных Т (рис. 8.22). При t 2> пТ это напряжение остается равным ir.E
ZT
пТ-
Рис. 8.22.
в зависимости от четности или нечетности п. Требуется вычислить ток, про-
проходящий по катушке в момент t, более поздний, чем пТ.
Изображение напряжения равно
т. е.
2? Г 1
Обобщенное сопротивление катушки с сопротивлением равно
34*
532 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Поэтому искомый ток будет
й(Г\ — -Ё- ?°° <>р! dn & 7 "«*«-*• [1 + (-1)"+1 e-"PT ] dp
K)—2*j J p(Lp+R)ap 2nJ J p(l +
Для второго интеграла должны быть рассмотрены полюсы
B*+iw „_ А „_о
а для первого интеграла — только два последних.
Так как
~Te~pT
Bft+i,n;
то следует принимать во внимание только полюсы р = j- и р = 0.
Ток i(t) может быть написан в виде
. / > лГ.
Примечание. Если число зубцов .кривой напряжения бесконечно, то
это выражение справедливо при
При л = 0 мы приходим, естественно, к примеру 1 п. 8.3.13.
Таблица соответствия
8.3.28. Введение. Решение физических или математических задач с по-
помощью операционного исчисления, как уже говорилось, содержит три фазы.
Первая состоит в переходе от реальных данных (переменная /) к опера-
операционной записи (переменная р) при помощи формулы преобразования Лапласа
h (О II F (/>)•
Вторая представляет собой ряд вычислений, приводящих к решению
поставленной задачи в операционной форме:
Третья состоит в переходе от операционной записи к реальной (пере-
(переменная t). Общая формула, применимая к такому переходу. — это, очевидно!
формула обращения
Ф О») С 1@-
Первая и третья фазы сильно облегчаются существованием таблицы,
содержащей преобразования наиболее часто встречающихся математических
выражений, и применением правил операционной алгебры, если искомые функ-
функции не находятся в таблице соответствия. Это помогает избежать вторичного
выполнения вычислений, которые были сделаны по крайней мере уже один раз.
Так как третья фаза вычислений (переход от переменной р к переменной t)
всегда наиболее затруднительна, то нам показалось разумным сгруппировать
непрерывные функции по семействам переменной р. Напротив, разрывные
функции *), которые входят чаще всего в первую фазу исчисления, были
сгруппированы по семействам функций переменной t.
*) Имеются в виду случаи, когда функция или ее производная терпят разрыв.
8.3) ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
8.3.29. Непрерывные функции.
533
*@')
/>+*
a> COS 4j T (p -f- A.) Sin cp
(/> -|- k) COS у у a> Sin у
to
_1_
Cfl
1
Ш
8
sin <o^
sh u><
0
COS a>t
1 ft*
— Vk2 4- <«a Sin [a>t + tf) , tg<p=?-g-
*~л' cos W
»"W Sin (Ы ± cp)
e"W COS (<»t ± <?)
ft — а
a»
—>)
a»
') Начиная с третьей строки, умножение на Г@ подразумевается/Умножение
на Г (^ — К) будет обозначено через г > к.
534
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Продолжение
f-(p)
h(t)
(/>-И)
p+fe
p+k
p+k
P'+fp+Ь
4о>3
(Р
—«)G —«) ! (« —Р)G-Р) '
—=- A — COS ш?)
Г)(Р —Т)
*-Р е-и , Г*-аг | Р-*
а(а —р)
а Л1 к
1
Р—а)
(fc
1 (в_
(Р_в)G_в) 1 (а_р)G
ч^+'
+
+ •
sin2*
cos2*
-L- (<ot — Sin mt)
•K—j- (Sin orf — W COS ш<)
-о— Sin a>t
2
-Д— (Sin a>t -f- <e* COS (D*)
* COS <ot
COS ш< — COS it
M2— U>S
sin <nt ch <л* — cos a>t sh
- Sin a>t Sh
-^3- (sh at — sin щ*)
-H^j- (Ch a>t — COS <B*)
8.3)
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
535
Продолжение
fip)
p
1
Pn
1
Y'p
l
V~p+*
Y'p
p — a*
1
Y~p (p-«2)
i
l
i
l
l
У pi 4. as
1 „>o
•g— Sin v< sin <ai
(„_!), (»«e«e>0)
n
e >. (—II5 7 .. . 3 fд (л целое > 0)
Г(/+1), R(v)>0
1
a
^»2' M ф (а 1<^7)]
С"*а'Ф (т/"й a l^T)
--^ 5— e-<a+P) '/„[(a — $)t], v>0
_^. .-'/,(«<), v>-l
536
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VHI
Продолжение
h(t)
Ур* —
-**+рУ
— е~"'р
Р
1 — а/л
V > О
ч > О
т
1
7Т'
,-«/р
, — e-"lp, v>0
1 -лУ~р
У~р
в>0
1 - v~
— е р, а>0
2а)
— е
\пр
¦\пр
-7=- COS B У at)
У Tit
1
= sh B У at)
v-1
v-l
CtX
, (a J/"F=
aX
Xs
— sin < Si t — cos * Ci t
8.3]
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Пр
h(t)
In
Р —
а>0
In-
In-
Р*
¦In
1 - p+Yp-a?
— a2
arctg —
S P
1 а
-arctg-
1 1
— cos —
р р
—
а>0
1
Т=р^
(cos p Ci p -4- sin p si p)
— (sinpClp — cos psi p)
21па — 2Ci4
— [at In a-(-Sin <rt — atCia^
2
-j- A — COS at)
(«0
— sin <л^
Si of
bei 2 V^l
j/lc
-i
arctg ?
538
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
•
s
к
HKI
¦&
a
в
в
о.
со
«в
О.
3.30.
00
s
<
м.
Гра
о,
1
э-
?
I
\
V
\
&
00
Рис.
э-
—^
IN
э-
!
\
\
\
\
V
и
а
9-
,—
в-
ър
С
1
ч
\
\
•
00
Рис.
8.31
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
I
s
•!•
Гра
a.
—
9-
]
И
7
\
V
\ '
V
>
4S ?
00
1 <j
4s a.
i
S.
i
+
1
Iю
\
\
\
\
1
to
30
Рис.
с
A
1
1
с
1
I
*
.
540
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
ft.
С:
i
I
8
V V
V V
О p
8
? +¦
V V
V 7
.*. *•
S
00
и
a
и
s
8.3]
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
541
a
1
дол
Про
s.
¦9-
га
О,
¦se
S.
8Wi
+
<a
-
1
1
32.
00
о
s
a.
—
t i.
~T" 1
^^ 1
«1
^> К 1Э t
*"¦' 1
1
\ ^
s -
i а
l
1
3
S 8^A 1
«If
S
l ^\
k> о ^^
^ a \^
^ I ^\.
: N.
^ q |
- С
\
s N
(
\
CO
00
s
K|3 a-
542
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
8.4) ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 543
8.4. ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
8.4.1. Колебательные контуры. Рассмотрим колебательный контур Rt
L С. В этот контур в момент ? = 0 включают некую электродвижущую
силу E(t). Пусть $(/>) — изображение E(t), а д (р) — изображение тока t(t),
идущего по контуру. Требуется найти напряжение на зажимах катушки. Это
напряжение v{t) имеет изображением У(р).
Имеем
Z(p)
Кроме того,
v(f) = L^ 3Lp g (/»=
Мы имеем право написать это соотношение, так как I @) = 0. Отсюда
где
Положим, что R достаточно мало, чтобы можно было пренебречь а2
по сравнению с ш2. Тогда можно написать знаменатель в виде (р -f- аJ -(- м2.
и корни его будут равны
— а — /<о, — а -+- У<о.
Найдем реакцию контура на некоторые внешние электродвижущие силы.
1. Электродвижущая сила Е (t) равна EQ sin vtY (t). В этом случае
Полученное соотношение можно записать в виде
^ ¦*-* (o>2 — n2J-j-4aV L/>2-j-v2 p2+v2
a) . о* (со» —
"
1
Г
Отсюда, пользуясь элементарными соответствиями, непосредственно получаем
- ^ ((о2 - v») sin
Положим, что (o = v, т. е. частота электродвижущей силы равна ча-
частоте собственных колебаний контура. Тогда
v (t) = ^-1 cos mt—e-al Tcos cof — -^- sin ort
Если, кроме того, мы можем пренебречь а по сравнению с ю, то преды-
предыдущее выражение может быть написано в виде
=^-C0SU)^(l —(?"<") Г (О-
544 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Если R=0, а (о Ф v, то
v (t) = J5^ [ю sin ш^ — v sin v^] Г (О-
2. Электродвижущая сила равна единичной ступени: Е (t) = ?0Г (?), тогда
Пренебрегая а2 по сравнению с ш2, получаем
«га ~1 рЕ° —
Отсюда непосредственно имеем
г; (О = ?0*-а< [cos ш^ ^ sin шЛ Г (^
и, пренебрегая а по сравнению с ш, получаем
?ое-<» cos (оПГ (О-
3. Электродвижущая сила EQ приложена в течение очень короткого вре-
времени 8?. В этом случае $(р) = Eabt. С тем же приближением, что и раньше,
получаем
или
Отсюда непосредственно имеем
(t)— e-at\2acosmt
и с теми же упрощающими предположениями
v {t) = EQ Ы [Г' (О + «Г (О sin ш(].
8.4.2. Пример применения к системе двух связанных контуров. При-
Применив к простому колебательному контуру методы операционного исчисле-
исчисления и получив таким образом известные резуль-
таты (которые, впрочем, легко найти и другим
способом), мы рассмотрим один пример. Пока-
Покажем, что применение к решению этого примера
классических методов приводит к гораздо более
сложным вычислениям, чем применение операцион-
операционного исчисления, где расчеты делаются почти
автоматически, так как различные граничные усло-
условия оказываются с самого начала включенными
в вычисления.
Рис. 8.40. Дана цепь, изображенная на рис. 8.40. Пусть
E(t) — электродвижущая сила источника, внутрен-
внутреннее сопротивление которого равно нулю, приложенная в момент ^ = 0. Мы
хотим найти ток i2 (t), текущий в ветви АВ этой цепи.
Дифференциальные уравнения системы имеют вид
8.4]
ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
545
Пусть д\(Р), дч(Р)> &(Р) — соответственно изображения ^(t), i2(t)
и E(t). Тогда система дифференциальных уравнений может быть записана
при помощи формулы C0) (так как /г @) = 0, г@) = 0) и формулы C1)
в виде
-?г + ^=0.
Отсюда
Рис. 8.41.
Вычислим I2(t) для случая, когда электродвижущая сила E(t) имеет форму
импульса, изображенного на рис. 8.41:
В этом случае
т).
Ток i2(t) представляет тогда собой сумму двух токов:
а
A 3zl
-со
Рис. 8.42.
Следовательно,
Так как
r LCp*+\ _
то получаем
i'2 ад = М
(о - f /g sin /^ ff @
Вычертим график
/2Т(Г я
-3- = -. Тогда
для случая, когда ширина х импульса равна
/2 @ = $f [Г @ - Г (/ - х)] - Щ-
sin \f-ftc t ГГ W + T С
Отсюда получаем график, изображенный на рис. 8.42, если считать
—о— = —?-• Тогда в формуле, даю*
щей 12 (/), синус исчезает при t > ¦;, так как выражение для /2 (t) принимает
35 А. Анго
546
вид
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
и мы получаем график, изображенный на рис. 8.43.
-оо
Рис. 8.43.
2т
Рис. 8.44.
г /1
Р С*
г /1 . Р С*
Величины —|— Г' (t) и —|— Г' (t — -с) представляют собой зарядный и
разрядный ток емкостей.
Возьмем теперь случай, немного более сложный, когда E(t) имеет гра-
график, изображенный на рис. 8.44. Вычислим изображение этой функции.
Имеем
Отсюда
где
Как и ранее,
СЕй Ьр-1)A.Ср?+П СЕ0 х 1
х \2 Зр
LC
3
2
СЕ0 х
- ?
•
Отсюда
_ -^ [Г (О cos
- Г (^ -
cos
2ЛС
-5-« — 2x)l .
2LCK '\
8.4]
ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
547
—д—
положив ш =
/ С*
и а ~ Aj 1/ "gr ¦
т0
l2{t) = ^[X'(t) — Г'(* —2х)] —?[Г@ — Г(* — 2х)] —
— ^-cosutf[Г (О— Г (/ — 2х)] — ?
— 2х)].
+ ОО
График тока /2@ изображен на рис. 8.45.
Примечание. Вычисления в пп. 8.4.1 и 8.4.2 были выполнены с по-
помощью разложения рациональных дробей на простейшие, а не с помощью
формулы обращения. Дело в том,
что рациональные дроби —.—. ,, ,—~-
(п. 8.4.1) и 2LCp'~+l3 (П> 8-4'2) не
удовлетворяют условиям Жордана (по-
(показатели степеней числителя и знаме-
знаменателя равны). Применение к этим дро-
дробям формулы обращения привело бы
к неверному результату, так как инте-
интеграл по бесконечной полуокружности,
расположенной слева от контура Бром-
вича, не равен в этом случае нулю.
8.4.3. Случай, когда цепь не
находится в равновесии в начальный
момент времени. Имеются случаи,
когда полезно было бы рассмотреть
электрическую цепь, не находящуюся
в равновесии при t < 0, и, в частности,
предположить, что заряды емкостей
не равны нулю в момент ? = 0. Приведем очень простой пример, который
покажет, каким образом поступать в этом случае.
Дана емкость с зарядом Q. Ее подключают в момент t-
катушки L. Дифференциальное уравнение системы имеет вид
-со
Рис. 8.45.
:0 к зажимам
Найдем изменение заряда q(t) на емкости во времени. Р1меем
Пусть б (р) — изображение q (t). Тогда предыдущее уравнение преобра-
преобразуется к виду
— pq(O)— ?'@)]4"?-6(/>) = 0.
Здесь вместо формулы C0) использована формула B8), потому что теперь
цепь не находится в равновесии в момент t = 0.
Имеем q(fi) = Q и q' @) = / @) = 0. Отсюда
PQ
q(t)=Qcos \/-^
35*
548 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Изображение 0 (/?) тока l(t) будет, если применить формулу B7), равно
g(j>) = pU{p) — 9@).
Отсюда
sin
Vlc
8.4.4. Электрические фильтры. Рассмотрим электрический фильтр,
схематически изображенный на рис. 8.46. Это цепной фильтр, состоящий
из п звеньев. В нулевое звено в момент t == О включают электродвижущую
7777777777777777777777777777. 7777777777777Л 777777777777/
Рис. 8.46.
i
силу E(t). Оба концевых звена отличаются от всех остальных. Нулевое
звено состоит из полных сопротивлений Zo и —J-. Последнее л-е звено со-
состоит из полных сопротивлений Zr и —ту-- Пусть lm~v tm> im+\ — соответ-
соответственно токи в полных сопротивлениях Z, (ш— 1)-, ш- и (ш-\- 1)-го звеньев.
Законы Кирхгофа дают
^ ^ 'mCZ, + 2Z2) = <m_,Z2 + /ra+1Z2. (87)
Предположим, что полное сопротивление Zr таково, что на конце
фильтра нет отражения возмущений, и положим
im = Ae-^, (88)
где Г и Л — величины, которые, мы сейчас определим. Заменим в (87) токи
на их выражение из (88). Тогда
1+-|^- = сИГ. (89)
В нулевом звене имеем
?(*) —/<>Zo= у'о?1 + ЗД —ПО-
—ПОБОЛИ заменить в этом выражении г0 на Ае", а /, на Ае~г, то
A— E(t)
Z2 sh Г -f- Zo
Ток im может быть написан в виде
(Z2 sh Г -f- Zo) (ch /яГ -f- sh /яГ) *
8.4] ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 549
Точно так же в последнем га-м звене имеем
откуда
Соотношение (89) позволяет написать
Выражение для Z/ дает условия отсутствия отражения. Это сопротивле-
сопротивление называют характеристическим сопротивлением фильтра.
Рассмотрим выражение для тока 1т. Полное взаимное сопротивление
нулевого и m-ro звеньев равно
(Z2 sh Г-+- Z0)(ch тГ+ sh mT).
Положив
получаем
.' спГ=1Ч-2аа, shr=2a
Если $(/>) представляет собой изображение E(t), то
Если Г — чисто мнимое число, то фильтр не внесет затухания, а лишь
вызовет изменение фазы. Положим
Формула (89) принимает вид
Отсюда получаем условия для полосы пропускания фильтра
cos v = 1 + -777- •
^ -г 222
ИЛИ
(91)
8.4.5. Фильтр нижних частот. Рассмотрим фильтрующую схему, изо-
изображенную на рис. 8.47. В этом случае
Отсюда, обозначив через ?>(р) изображение внешней электродвижущей
силы E(t), получим ток в /И--М звене:
где
550
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
Формула (91) дает условия для полосы пропускания, если р заменить
на уш, иначе говоря, если на мгновение перейти к расчету установившихся
режимов:
0<<
где
отсекающая частота.
Итак, наша фильтрующая схема передает без затухания круговые ча-
частоты ниже шс. Отсюда и ее название — фильтр нижних частот.
Рис. 8.47.
1. Внешняя электродвижущая сила равна единичной ступени:
1
Тогда
или, согласно формуле F2),
1 ( 4-\ —
Отсюда
(92)
Значения функции Бесселя J2m(t) очень малы при t < 2т. Поэтому ве-
величина тока im(t) становится заметно отличной от нуля лишь при wcf^.2m,
- и можно говорить о скорости распростра-
распространения фронта волны, равной -г-=-
Рис. 8.48.
„звеньев в секунду". Возмущение, которое
в нулевом звене имело форму единичной сту-
ступени, будет в /И--М звене выглядеть прибли-
приблизительно так, как изображено на рис. 8.48.
2. Случай электродвижущей силы произвольной формы. Положим
Тогда
/?
6 </>)
a? + 1 (У~р*а*+ 1 + ра)
2т
(93)
Теорема свертывания дает
8.4] ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 551
Эта формула неудобна для вычислений. Найдем другое выражение для
im (t). Положим в формуле (93) \/р2а2 +1 — ра = s, откуда
1 —s2
Р=-
2as '
Если сделать в $(р) подстановку, то получим функцию s. Пусть этой функ-
функцией будет U (s). Тогда формула (93) принимает вид
Предположим, что 21 (s) можно разложить по возрастающим степеням s:
Имеем
л=0
Отсюда
00
'm@ = y>>n.W
л=0
Этот способ имеет общий характер, и им можно пользоваться всегда при
разложении в ряд бесселевых функций, изображение которых—функция р —
имеет множителем
(a2p2-+-b2)~J.
Положим, что в нашем примере Е(t) = е>">1, тогда
1 ,., -. ias
Разложение в ряд по возрастающим степеням s будет иметь вид
U (s) = 2as [ 1 + 2jau>s + A — 4а2ш?) s2 + 2 jaw B — Аа2а>2) s3 ¦+
+ A — 12a2«J-f 16а4ш4M4 + 2уашC— 16а2и>2-\-
Отделив вещественную часть от мнимой, получим
4У /^ a. p2mr2 (-^) + B -
Вещественная и мнимая части представляют собой реакции, соответ-
соответствующие E(t)= cos tot и ?(?) = sin(oi.
8.4.6. Фильтр верхних частот. Рассмотрим электрический фильтр,
схематически изображенный на рис. 8.49. Легко заметить, что частоты выше
сос = — —¦ передаются без затухания.
552 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Имеем
Zn =0, Z, = , Z2 = pL, a = -=.
0 1 рС о_,А/^
Формула (90) дает
[ГЛ. VIII
1 /Ш"+'[у+ /(!)'+¦]'
при
Приложим в начальный момент времени электродвижущую силу, равную
-II-
гс
с с, с
/77 = 7
Рис. 8.49.
Рис. 8.50.
единичной ступени. Тогда
Применяя формулы F2), B2) и D5), получаем
оо
'«@=/"Т/./оB
(94)
8.4.7. Фильтр нижних частот без искажений. Рассмотрим фильтрую-
фильтрующую цепь, схематически изображенную на рис. 8.50. Имеем в этом случае
Фильтр нижних частот без искажений определяется условием
R _ О __.
Т~ С —°'
8.4] ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 553
Приложим в начальный момент времени электродвижущую силу, равную
единичной ступени. Ток в m-м звене определяется из формулы (90), в кото-
которой Zo, Zj, Z2 и а заменены приведенными выше значениями:
Имеем
h(t
n \i
Пользуясь
Отсюда
t
)-' l/
V
теоремой
th (f) ~] 1 /
1 e bth\i)ui _j у
6
Следовательно,
P \
смей
L 1
L
[^ения, найдем
1
P
Нр + ьу + i
\a(P-r
la(P +
r
' —(— 1 [tZ 1
6) + V «2 (/> +b.
l
l
6)+Va2(p+6:
i
iP + b) + Va4f
2 + 11
,_j_6J_)_l]^
или
Мы получили формулу, подобную полученной раньше для фильтра ниж-
нижних частот без потерь, но содержащую экспоненциальный множитель.
8.4.8. Усилители. Отрицательная обратная связь. Критерий Найк-
виста. Рассмотрим усилитель А (рис. 8.51). Пусть x{t) и y(t) — напряже-
напряжения на входе и выходе. При установившемся синусоидальном режиме цежду
этими напряжениями имеется соотношение
Л(у'о))—это комплексный коэффициент усиления, определяющий одновременно
изменение и амплитуды, и фазы. Если те-
теперь х (t) и у (t) означают любые функ-
х
ции времени, а не только синусоидаль-
синусоидальные, то
при
У
Рис. 8.51.
.?•(/») С* (О-
Соединим вход и выход усилителя посредством элемента f (часто это
бывает аттенюатор). Если f (/со) представляет собой коэффициент ослабле-
ослабления в синусоидальном режиме и если на входе усилителя выявить разность
между х и ~(у, то
У (/>) = Л (/7) [^Г (р) — 7 (/>) У (/»)]•
Отсюда
-up) A (pj
554
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIII
Мы определили таким образом, усилитель с отрицательной обратной
связью. Функцию у (t) можно получить, применяя теорему обращения, а в более
простых случаях — теорему разложения. Применение обеих этих теорем
•с очевидностью показывает, что система будет устойчива, если нули функ-
функции 1 4- у (р) А (р) будут все расположены слева от мнимой оси. Действи-
Действительно, если бы это было не так, то функция y{t) имела бы по крайней
мере один член вида «л' при R(Jt>1)>0. Следовательно, она бесконечно
возрастала бы во времени; в большинстве случаев
происходило бы возбуждение колебаний.
Преобразуем плоскость р в плоскость w при по-
помощи преобразования
w = T(/>)i4(p).
В результате такого преобразования все нули функции
1 -f- f (р) А (р) переходят в точку w= — 1. Мнимая
ось плоскости р становится в плоскости w кривой
и4(/ш).
иначе говоря, графиком полного усиления прямой и
обратной цепи как функции со. Полуплоскость вправо
от мнимой оси становится внутренней областью этой
кривой (рис. 8.52). Следовательно, для устойчивости системы нужно, чтобы
предыдущий график не окружал точку —1. Это условие называется критерием
Найквиста.
Рассматриваемая система (рис. 8.51) может быть электромеханической
или полностью механической. Все предыдущие соображения остаются в силе.
Величины х и у представляют тогда собой перемещения или угловые ско-
скорости. В этом случае название „усилитель с отрицательной обратной связью"
заменяется названием „следящая система", а название „отрицательная обрат-
обратная связь" — названием „автоматическое управление".
8.4.9. Расчет переходных явлений, вызванных размыканием или
замыканием выключателя. До сих пор мы рассматривали переходные явле-
лия в электрических цепях, в которых конфигурация схемы и свойства
r—vft)--\
В
а).
Рис. 8.53.
составляющих ее элементов не зависят от времени. Можно, однако, легко
представить себе достаточно важный для практики случай, когда внезапно
замыкают или размыкают выключатель, оставляя в цепи или вне цепи часть
обшей схемы.
Пусть R — линейная цепь, А и В — два зажима. В момент ЫО мы
соединяем оба зажима посредством проводника без сопротивления. Требуется
найти ток i(t), идущий по соединению АВ. Перед тем как мы замкнули
зажимы А и В, между ними имелась разность потенциалов v(t) (рис. 8.53, а).
8.4) ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ ¦ 555
^ Поместим между А и В генератор с полным внутренним сопротивлением,
равным нулю, и с электродвижущей силой, равной v{t) (рис. 8.53, б).
Совершенно очевидно, что работа системы остается без изменений. Сое-
Соединим последовательно с первым генератором точно такой же второй, но
с обратной полярностью (рис. 8.53, в). Все будет- происходить так же,
как если бы мы закоротили АВ. Между А и В больше не будет разности
потенциалов, и по АВ пойдет ток l(t), равный току короткого замыкания.
Сделаем цепь R пассивной, замыкая накоротко источники напряжения и раз-
размыкая источники тока. Уберем также первую электродвижущую силу, кото-
которая выражала собой активность цепи (рис. 8.53, г)—ничто не изменится,
по АВ будет идти тот же самый ток i(t).
Обозначим через Z(p) обобщенное сопротивление между зажима-
зажимами А и В цепи, ставшей пассивной. Тогда
и
где через 0 (р) и ТР (р) обозначены соответственно
изображения t{t) и v(t).
Пример. Для пояснения рассмотренного
способа приведем очень простой пример, реше- Рис. 8.54.
ние которого очевидно заранее. Дана катушка L,
соединенная последовательно с сопротивлением R. В момент t = О к вход-
входным зажимам подключают постоянное напряжение Е. В момент t — tx нако-
накоротко замыкают сопротивление R. Требуется найти ток, текущий в катушке
при t > tl (рис. 8.54).
Напряжение на важимах R равно
v(t) = E\\ —е~
Положим х = t — ty Имеем
(
Отсюда
Т(Р)-=Е\\— '
Обобщенная проводимость между зажимами R, когда цепь пассивна,
т. е. когда источник напряжения закорочен, равна
Z(p)
Отсюда
LP* '
Возвращаясь к переменной t, имеем при
(t-tl)^ + ±)
результат очевиден.
В случае, когда быстро размыкают соединения активной цепи, задача
решается совершенно таким же образом.
556
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
[ГЛ. VIIT
Пусть R — активная линейная цепь, а АВ — быстро разомкнутое в момент
t = 0 соединение. Такое размыкание создает между зажимами А и В напря-
напряжение v(t). Перед размыканием по соединению АВ идет ток i{t) (рис. 8.55, а).
Заменим соединение АВ источником тока, дающим тот же ток i(t) (рис. 8.55, б).
В работе системы ничего не изменится. Если параллельно первому источ-
источнику тока включить такой же, но обратной полярности, то от А к В ток
идти не будет (рис. 8.55, в). Мы осуществили условия, одинаковые с теми,
которые создаются при размыкании соединения АВ. Если убрать, как уже
говорилось, все реальные источники' тока и напряжения, а также первый
Рис. 8.55.
условный источник тока, показывавший активность цепи, мы получим пас-
пассивную цепь, создающую на зажимах А и В искомое напряжение v(t)
(рис. 8.55, г). Обозначив опять через Z(p) обобщенное сопротивление этой
пассивной цепи между зажимами А и В, получим так же, как раньше,
Пример. Для пояснения этого способа, возьмем предыдущий пример.
В момент t = 0 прилагается постоянное напряжение Е, в момент t — t^
убирается короткое замыкание сопротивления R.
При / < 11 ток i (t) равен
Положим
тогда
откуда
с v>— LP ~r Lp2 •
Если сделать цепь пассивной коротким замыканием Е, то
RLp
Отсюда
ZW=LP + R-
ERtx . ER
Tp+R "+¦ p(Lp+R)
ER
L
' L
8.4) ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 557
Распространение электрических возмущений вдоль линий передач
8.4.10. Общие соображения. Дана однородная электрическая линия
передач длиной I. На одном конце приложена электродвижущая сила E0(t).
Другой конец замкнут на обобщенное сопротивление Z(p). Обозначим
через L, С, R соответственнно коэффициент самоиндукции, емкость и сопро-
сопротивление единицы длины этой линии. Изоляция линии несовершенна, поэтому
через G обозначим величину,
обратную сопротивлению изоля
ции на единицу длины (проводи-
(проводимость изоляции).
Рассмотрим точку с абсцис-
абсциссой х (начало координат совме- Рис. 8.56.
щено с началом линии) и обозна-
обозначим через E(t) разность потенциалов между этой точкой и землей, а через
i(t) — ток, идущий в этой точке (рис. 8.56).
Изменение напряжения -^— при перемещении на единицу длины равно
сумме изменения напряжения — ^~кг> создаваемого самоиндукцией, и оми-
омического падения напряжения —Ri. Отсюда
¦#--*?-*¦ <*>
Изменение тока -т— при перемещении на единицу длины равно сумме
¦ч п1
тока утечки через емкость — С —^- и тока утечки через изоляцию —GE.
Отсюда
Функции Е и i следовало бы писать в виде E(t, x), i(t, x), а электро-
электродвижущую силу, приложенную к началу, в виде E(t, 0). Для упрощения
записи переменные х и t подразумеваются.
Если исключить функцию / из уравнений (96) и (97), получаем уравне-
уравнение в частных производных, определяющее функцию Е:
(98)
Оно называется телеграфным уравнением.
Пусть §>(р) и 0 (р)—такие функции, что
&(p)CE(t).
Эти две новые функции р и х определяются следующей системой уравне-
уравнений, полученной из уравнений (96) и (97) с помощью преобразования Лапласа:
^r-=—(Lp-\-R)ZJ, (99)
^- = — {Cp + G)&. A00)
ах
558 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Эта система уравнений приводит к
-g*-_tfC = O A01)
или
ig._^=0. A02>
если считать, что
>.2 = (Ср -+- О) {Lp -+/?). A03>
Решение уравнения A01) получается сразу. Имеем
S Q?) = А екх + Be 'Kx. A04)
Тогда уравнение (99) дает
Постоянные А и В определяются граничными условиями. Если считать,
то при х == 0 имеем
а при д; == /
Отсюда
Если считать
/"g±| A06)
то для определения А и В имеем два уравнения:
A-hB = $<)(.p), A07)
A(i-\-\)e"=B(i — \)e-u. A08)
Отсюда
или
В этой формуле
Функция ^7 (р) равна
Дальнейшее вычисление состоит в нахождении таких функций i(t) и E(t),
чтобы
8.4]
ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
55»
Эта задача представляет в общем случае незначительный интерес, так как
приводит к крайне сложным расчетам. Перед тем как рассмотреть несколько
простых частных случаев, сделаем замечание общего порядка.
Положим, что в наиболее общем случае мы нашли напряжение и ток
в любой точке линии передачи, приложив к началу ли,нии электродвижущую
силу, равную единичной ступени. Пусть
ад з*1 (/о.
— токи и напряжения при E0(t) = Г (t) Щ —. Положим теперь, что в начале
линии приложена любая электродвижущая сила
ад з*о о»)-
Мы можем написать формулы A09) и (ПО) в упрощенном виде
В случае электродвижущей силы, равной единичной ступени, имеем
^{р) = —М{р).
*.(/» = ?
Отсюда
Применяя теорему свертывания и формулу дифференцирования, получаем:
t
= -fj-t f >E0(t — x)E1(x)dx.
или! дифференцируя.
t
Е @ = Ео @) Ei (О Ч- / Е'о (х) Ei (t — х) Л.
о
t
Е @ = ?0 @) Ei (О + f Eo (t — х) Е, (х) dx,
о
I
? (О = ?, @) Eo (t) + J Яо (х) ?l (f — т) Л.
E(O = Ei @) Eo
(x) rft,
560
СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
t
i {t) = Ej @) h (/) + J Eo (x) h (t — x) dz,
0
t
I (t) = Eo @) /i @ + J E'tf — t) /i (x) dx.
[ГЛ. VIII
/ @ = ii @) ?0 @ + / Eo (t — x) /I (x) dx.
A11)
J
Как и следовало ожидать, мы снова находим формулы, полученные не-
непосредственно из соотношений A), F).
8.4.11. Бесконечная или замкнутая на волновое сопротивление линия.
Замкнем конец линии на обобщенное сопротивление, равное Zc(p) — воЛно-
вому сопротивлению линии
Ze(p) =
Lp + R
Тогда, согласно формуле A06),
Уравнение A08) дает в этом случае А = 0, а уравнение A07) дает
Функции S (р) и
(р) принимают вид
= g0 (p) e~xV 1LP
е~х v<Lp+RnCp+u>
A12)
A13)
Это как раз и есть случай бесконечной линии: на конце, замкнутом на обоб-
обобщенное сопротивление Zc, нет отражения. Действительно, выражение A04)
показывает, что если абсцисса х бесконечно возрастает, то для того, что-
чтобы $(р) сохраняла физический смысл, нужно, чтобы постоянная А была
равна нулю.
8.4.12. Линия без потерь. В этом случае # — 0=0. Тогда фор-
формула A12) принимает вид
Оригинал этого изображения представляет собой функцию E(t), разную нулю
при t < х YTC и равную E0(t — x УШ) при t > х У'СС.
Волна напряжения, приложенная в начале линии, перемещается без иска-
искажения со скоростью v — . Ток равен напряжению, умноженному
V LC '
на Л/ -г
-х
VLC-
A14)
8.4] ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 561
8.4.13. Линия без искажений. Такая линия определяется условием
R G
Уравнение A12) дает в этом случае
иначе говоря,
$ (р) = $0 (р) е-Р* Vic e-,x Vlca
Согласно вычислениям предыдущего пункта,
\ 0{t — х УТС) при t>xY~LC,
• A15)
1
?¦@ = 0 при t <x
Волна сохраняет форму, но распространяется с экспоненциальным ослабле-
ослаблением при скорости v——r=- .
Формула A13) дает
Отсюда
_ ' ' A16)
= 0 при t
8.4.14. Подземный кабель. В подземном кабеле емкость велика по от-
отношению к самоиндукции, а изоляция превосходна. Поэтому положим L := О — 0.
Приложим к началу линии электродвижущую силу, равную единичной сту-
ступени. Тогда формула A12) дает
Из G9) получаем непосредственно
'Формула A13) дает выражение для & (р):
а формула G8) — выражение для i(t):
Выражения для E{t) и l(t) показывают, что напряжение и ток в каждой
точке кабеля возникают в момент t = 0. В действительности же, если при
вычислении функций Е и t можно пренебречь L, то пренебречь этой вели-
величиной, рассматривая скорость распространения, нельзя.
Скорость распространения фронта волны конечна, так как самоиндук-
самоиндукция линии не равна точно нулю.
36 А. Анго
562 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VH1
8.4.15. Линия с идеальной изоляцией. Предположим, что электродви-
электродвижущая сила E0(t) приложена к началу и равна единичной ступени Г(^).
/? 1
Тогда, если G=0, -077 =а- a S0(j») = —, формула A13) дает
а формула F8)—
иначе говоря,
= (J при
Из соотношения A00) получаем
dx
или
" С'р
откуда
о
Для дифференцирования разрывной функции l(t) запишем ее в виде
*>7~ г I **
i @ = У^х Г1Г' 7° ("ЯГ ^2 —*2^С) Г (* - дс V"ZC),
т. е. объединяем в одной формуле два выражения для i(t). Выполняя диф-
фгренцирование, получаем
t
4. fe~TL' /0 (~ /^2 — д:2АС) Г' (/ — ж '(/Тс) Л.
о
Наличие Г(^ — д: y^LC) в первом интеграле позволяет исключить эту
функцию при условии замены нижнего предела интегрирования на х
Кроме того, согласно (81),
f f (t) Г (t — t,) dt = f (tx), tlt < *, < f8.
tn
и второй интеграл заменяется на
потому что /0 @) = 1.
•8.4) ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 563
Если к тому же заметить, что /0(у) = Л (у), то выражение для E(t)
принимает вид
xVlc ^ A26)
при t > х YLC,
Е (t) = 0 при t < х УТС.
Вид выражений для l(t) и E(t) показывает, что ток и напряжение
равны нулю при t < х YLC и внезапно принимают конечное значение при
t^-x yLC. Тем не менее нельзя говорить о распространении волны в точ-
точном смысле слова, так как форма единичной ступени сильно меняется при
перемещении. Можно говорить только о распространении фронта волны,
которое происходит со скоростью
v — •—.
8.4.16. Общий случай. Произвольная линия. Опять прилагаем к на-
началу напряжение ¦
Уравнение A13) дает в этом случае
ct (D\— l л/ CP+Q
с/ (Р)— р у LpJrR
R . G
~2L~ C~==a> V —
Положим
Тогда
Формула F7) дает возможность сразу написать
=?\ 4-
:2\dt при
i (t) = 0 при t < (x = .v
Из уравнения A12) получаем
Соотношение F8) дает
Продифференцируем обе части по [д.:
564 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. V1H
откуда
Как и в предыдущем случае, продифференцируем функцию / (t) Г (t — (i). По-
Получим
Принимая во внимание свойства функций Т (t— ji) и T'(t— ji), это выра-
выражение можно написать в виде
Так как /о —Л. а /о @) = 1. то
-ib+a)t Л [ (Ь — л) У t2 — X2LC\ м, . -(a+b) xVlq
> _ - : tZf ''' j' ¦ ?
1/^2 jc2L»C
xVLC
при * > л: /1С,
?• (t) = О при f < x y~LC. A22)
В этом случае фронт волны также распространяется со скоростью v= j^~-
8.4.17. Линия передачи конечной длины. Основные формулы, дающие
выражения для 8(р) и &(р), — это A09), (ПО), A06) и A03).
Рассмотрев формулы A09) и (ПО), видим, что несколько упростим их,
если примем за начало отсчета абсцисс правый конец линии передачи, схе-
схематически изображенной на рис. 8.57. При этом формулы принимают вид
' ch \х -)- sh \х ., „„.
I 5 где
////У///////////////УУУ/////////////, _^ \Л / Cp-\-G .. пс\
/?). A26)
Ограничимся нахождением функций ?'(OZ]^(/?)' l(fI2 if (Р) в не-
скольких частных случаях.
8.4.18. Закороченная с одного конца линия с пренебрежимо малыми
проводимостью изоляции и индуктивностью_ (подземный кабель). Имеем
G = L = Q, Z(p) = 0. Отсюда f == 0 и л = У~р YrC. Формула A23) прини-
принимает при этом вид
8.4] ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 565
Положим, что E0(t) = X(t). Тогда &0(р) = —. Следовательно,
p
Мы получим функцию E(t), применяя теорему обращения. Если считать,
что а = х Y~RC и р = / уТгС. то
C + JOD
— 1 /* р" Sh a V Z
E(t) = —— / rr- dz.
2nj J г sh p ]Лг
C-jca
Начало координат не является точкой разветвления для функции
—а , так как эта функция сохраняет одинаковое значение при обоих
определениях У~г. Следовательно, функция ?(О будет равна сумме вычетов
относительно полюсов, которые являются нулями функции g(z) = sh p }Лг.
При этом сумма вычетов дается формулой ^. , , где ат определяется
из уравнения
Отсюда
Член -к- появляется из-за вычета относительно полюса z = 0.
Р
Заметив, что ch j'tniz = cos tmz = (— 1 )m, получаем
mnx
°° Sin—-.— m V
v ' ^J v ' /Ял /
m=I
Уравнение (96) дает
откуда
"~ -гч^'+i. A28)
Проделаем те же вычисления, но будем предполагать, что к началу
линии приложена электродвижущая сила
E0(t) = cos is>t.
Если положить
a = —
то третье равенство A11) дает
i
a /
v
0
866 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
где
t
/„ i. ., , ft) Sin (O^ — OCOSft)^ , О „,
cos шгеа (t~x> dx = ^—= 5-j—5- eat.
ftJ + O2 ' ftJ -\- o2
0
Экспоненциальная часть последней формулы, подставленная в функцию
E(t), дает при замене а ее значением выражение переходной составляющей
Eb(t):
СО
/я3я3 , ,.т . тпх - l"* t
Точно так же составляющая, соответствующая установившемуся режиму,
будет
т = \
— 2U>PRCsinmt V (_iyn__^r__sin
При x = l мы опять находим ??„. (f) = cos (i>t, г. е. возбуждение, при-
приложенное ко входу линии.
' 8.4.19. Линия конечной длины без потерь, замкнутая на сопротив-
сопротивление. Пусть этим сопротивлением будет р. Основные формулы A23), A25),
A26) преобразуются в предположении G = R = O к виду
,р 7 ch Kx -\- sh kx
— ®oW T ch X/ + sh W •
Последнее равенство, если положить
можно написать в виде
Ш (р) = %>0 (р)
Если подставить сюда
\ = 1 + 8е-2 + ... + Ъ
то
L п = 0 п = 0
Но известно, что
&0(P)e-psCEn(t — s), t>s.
Принимая во внимание это соотношение, получаем решение
/V
я=0
/v
? @ *= 23 8"l?0 (' — [Bл + 1) I — х\ VIC) — ЬЕ0 (t
8.41 ПРИЛОЖЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ 567
Мы обозначили через N наибольшее из целых чисел п, при которых
величины
t-r- [Bл -f 1)/ — х] yic — t —
положительны. Если при n = N первое выражение положительно, а второе
отрицательно, то второе суммирование может быть сделано только до
N— 1.
Полная картина распределения напряжений на линии складывается из
суммы N элементарных волн. Каждая из них состоит из двух волн (с точ-
точностью до коэффициента 8я):
-bE0(t-G-xYLC).
Первая соответствует волне, перемещающейся слева направо (заставляя х
расти, мы пойдем ей навстречу) (см. рис. 8.57). Вторая соответствует волне,
перемещающейся справа налево (уменьшая х, мы пойдем ей навстречу) и от-
отразившейся на один раз больше, чем первая, от конца В.
Рассмотрим последнюю из этих пар волн (n — N). Если t — 6 — x^LC
отрицательно, то вторая волна не успела достигнуть точки с абсциссой х.
Коэффициент отражения конца линии В равен
8-1-Т
_ 1+7"
Если р = у -тт, то 7 равняется единице, а 8 — нулю. Тогда перед нами
случай бесконечной линии, и решение сводится к первому члену ряда
Если р < 1/ -тг, то 8 положительна, и отражение происходит с пере-
переменой знака. Это, например, случай закороченной линии.
Если р > 1/ -рг, то 8 отрицательна, и отражение происходит без пере-
перемены знака. Это, например, случай разомкнутой линии.
Примечание. Можно было бы легко увеличить количество примеров
распространения электрических возмущений вдоль линии передач. Небольшое
число рассмотренных задач дает основные приемы, которые операционное
исчисление предоставляет в распоряжение инже- _
неров. Самые сложные случаи могут быть легко л'ааал_.
сведены к случаю линии конечной (формулы |~"~WWV \ *
A09), (ПО), A23) и A24)) или бесконечной | !
(формулы A12) и A13)) длины. ?е<й>
П
мулы A12) и A13)) длины. ей o
Приведем два существенных примера. |
8.4.20. Сопротивление, сосредоточенное * « —
в начале линии. Пусть $е(р) — изображение Рис. 8.58.
входного напряжения и пусть Z0(p) — обобщен-
обобщенное сопротивление, находящееся между точкой приложения этого напряжения
и началом линии (рис. 8.58). Изображение начального напряжения равно
h (Р) = &е(Р) — д о 0») Zo (/>)•
Если считать, что
568 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII5
то уравнения для.определения постоянных А и В, выведенные в п. 8.4.10,
имеют вид
То) = *.(/»). A29)
—i)e-u = Q. A30)
Они приводят к формулам, подобным A09) и (ПО), но несколько более
сложным.
8.4.21. Повреждение иа линии. Предположим, что повреждение пред-
представлено обобщенным сопротивлением Z' (р), включенным параллельно на
расстоянии /j от начала линии / (рис. 8.59). Характеристики участка / —
это ?,,, Cv /?,, G,. Для большей общности положим также, что, начиная
с точки включения Z'(р), линия имеет другие характеристики L2, C2, R2, G2
и замкнута на обобщенное сопро-
сопротивление Z2(p) на расстоянии /2.
Тогда обобщенное входное сопро-
сопротивление линии 2 равно
2p-\-G2
При этом линия / замкнута на обобщенное сопротивление
7 (р\—
Формулы A23) и A24) дадут §, (р) и gx(p) в каждой точке с абс-
абсциссой xv находящейся между 1Х и 0. Напряжение §](/>) в точке с абсцис-
абсциссой 0 будет равно напряжению в начале линии 2. Формулы A09) и (ПО)
дадут тогда &2(Р) и &2(Р) в каждой точке с абсциссой х2, находящейся
между 0 и 12.
Если повреждение характеризуется обобщенным сопротивлением Z' (р),
подключенным последовательно, то в этом случае мы будем иметь
8.5. МАТЕМАТИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
8.5.1. Применение операционного исчисления к вычислению опре-
СО СО
/h (f\ ,'*
. dt, I fh(i)dt. Из формулы B6) непо-
о о
средственно имеем
со оо
f^p-dt=fF(p)dp. A31)
о о
По формуле C7)
(—l)n+1Fin+l)(p)Ctn+lh(t).
Поэтому формула B6) дает возможность написать
оо со
= (—\)n+l f Fin+1>(p)dp, A32)
8,5] ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 569
иначе говоря,
оо
/.**А@Л==(-1)"+1[-^г/г(Р)]°в. . A33)
о °
Пример 1. Требуется вычислить / s " " dt. По формуле A31)
о
оо
Пример 2. Требуется вычислить / ^ dt (интеграл Фруллани).
о
Известно, что
e-at р-Ы —1 !
a р+Ь'
Следовательно,
Пример 3. Треиуется вычислить
Известно, что
Отсюда
оо
Пример 4. Требуется вычислить J= * f . Положим # =
Тогда
/—_J__ Г ¦»'¦/, B/1)<ft
2
Но известно (формула D4)), что
О т 2
Если приравнять
570 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
ТО
v + l-f- J ' + 1—f
2 2
р 2 О Т 2
Следовательно, найдя оригинал левой части, получаем
г(т)
=
Если положить ? = 1, то
Применение операционного исчисления к решению линейных
дифференциальных уравнений
8.5.2. Линейные дифференциальные уравнения с постоянными коэф-
коэффициентами. Дано дифференциальное уравнение
Применим преобразование Лапласа к функциям Л (О и g(t) и обозначим
через ^(р) и Ф(^) их изображения. Тогда применение формулы B8) диф-
дифференцирования функции переменной t преобразует дифференциальное урав-
уравнение A34) в алгебраическое уравнение
]. A35)
Отсюда
где через Ф(р) обозначена функция, стоящая в правой части соотношения
A35), а через D(p) — характеристический полином
В весьма важном частном случае, когда функция h(t) и ее л—1 пер-
первых производных равны нулю при ?=0, имеем
F{p) =
D(P)
Применение формулы E4) к д . дает
Я1=1
8.5] ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 571
если считать, что полином D(p) степени я имеет только простые корни ат.
Применение теоремы свертывания (формула D0)) дает
j^A A36)
m=l
Такой способ решения линейных дифференциальных уравнений имеет
то громадное преимущество, что вводит начальные условия в начале вычи-
вычислений. Это помогает избежать отыскания общего решения, когда нужно
найти, а это почти всегда так и бывает, частное решение.
Найдем, для примера, решение уравнения -^- + 5 -Jf-\- 6у = 12 при
начальных условиях у@) = 2, у'@) = 0. Имеем
D(p) = p* + 5p + G; Ф(р) = ^-; У (р) = ~ + 2 (р + 5).
Отсюда
Следовательно,
y(t)=2.
Совершенно очевидно, что отыскание классическим способом общего реше-
решения и введение начальных условий в конце вычислений заняло бы гораздо
больше времени.
Пример 1. Требуется найти решение уравнения
dx . ' о/
4F + Zx = e '
равное нулю при ^ = 0. Имеем
4-3,
Следовательно,
р + 2
Пример 2. Требуется найти решение уравнения
dt3 ^ dt
равное нулю вместе с производной при t=0. Имеем
D (р) = р2 + Ар + 4 = {р + 2J.
Формула C7) дифференцирования функции переменной р дает
Следовательно,
572 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Из равенства
следует
8.5.3. Линейное дифференциальное уравнение с переменными алге-
алгебраическими коэффициентами (метод ван дер Поля). Такое уравнение
имеет члены вида
h (t). th (t), t4 (t)
h'(t), th'(t), t4'(t)
h"(t), th"(t), t2h"(t)
Найдем изображения этих членов. По формуле B8) имеем
b(tKF(p), h'(tKpF(P)-
h" @ 3 P2F (p) — ph @) - h' @),
Применяя к предыдущим выражениям формулу C7), составляем таблицу:
h(tKF(p),
th'(tK—pF'(p) — (p)
t4'(tKpF"(p)+2F'{p), A37)
h" (t) 3 — h' @) — ph @) + p*F (p),
th" (t) 3 h @) — 2pF{p) - p*F> (p),
Ph" (t) 3 2F (P) + *PF' (p) -+- p'F" (p),
Если в интересующем нас уравнении заменить каждый член левой части
его изображением и то же сделать для функции, фигурирующей в правой
части, то дифференциальное уравнение для h(t) оказывается замененным
дифференциальным уравнением для F (р). Если это последнее уравнение
решить легче, чем исходное, то можно определить h(t) по ег^ изображе-
изображению. Пойти дальше этого бывает трудно, так как функции h (t) часто не
могут быть выражены с помощью конечного числа элементарных функций.
Пример. Дано дифференциальное уравнение
ЗР+т4Н-('-¦?)»-¦>¦
Известно, что частное решение этого уравнения, имеющее конечное значе-
значение при / = 0, представляет собой бесселеву функцию первого рода.
Мы уже находили изображение бесселевой функции для целых значений
индекса (формула F2)). Поставим перед собой ту же задачу для любых
положительных значений индекса v.
6.5] ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 573
Умножаем дифференциальное уравнение на t2 и применяем формулы
преобразования A37). Получаем
(рй + Г) х"-\- Зрх' + A — v2) х = О,
где
без каких-либо предположений о начальных значениях y(t) и ее произ-
производных.
Для решения полученного уравнения положим
' p = sha,
_ Q
ch и '
что дает
d2x
dp2
dx
dp
du \dp)
dx
du
dp
du
dp
d2Q
du2
1
ch и
ch3u
г
L
1
du ch и
Q dQ sh
6 du
ch4
1
и
и
n sh и 1
~ ch2aj"
о ch2«
— 3 sh,2 и
ch6a
Уравнение приводится к виду
Отсюда получаем общий интеграл
2 = Ае-и ¦+- Ве~ш.
Так как
то
х(Р)= ,
Остается определить постоянные' А а В так, чтобы функция y(t) была
именно функцией J^(t).
Если приравнять v = 0, то
Так как известно (формула A6)), что
то получаем
А~\-В=1.
Положим у = 1. Известно, что ряд для У, (t) начинается с t, поэтому
ряд для х (р) должен начинаться с —т. Следовательно,
1-1-Л— 8 = 0,
откуда
Л —0, В—1.
574 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. V1H
Таким образом, имеем соотношение
Это показывает, что формула F2), установленная для целого индекса, дей-
действительна для любого положительного индекса.
Применение операционного исчисления к решению некоторых
интегральных уравнении
8.5.4. Линейные интегральные уравнения. Рассмотрим интегральное
уравнение вида
Неизвестная функция — это h (t). Функция g (t) известна, так же как и функ-
функция K(t), которую называют ядром. А, В, С — постоянные.
Рассматриваемый тип интегральных уравнений относится к группе так
называемого замкнутого цикла. Если А ф 0, уравнение называется уравне-
уравнением второго рода; если А = 0, оно называется уравнением первого рода.
Введем в рассмотрение изображения функций:
Теорема свертывания дает
t
f K(t — x)h
о
Отсюда получим соотношение
AF {р) + BF (р) W (р) = СФ (р)
и изображение неизвестной функции
Г(Р>—
Пример 1. Решим уравнение Абеля
о
Здесь мы имеем
откуда
' W— ГA—а) '
Напишем F(p~) в виде
F W = Т7Г—17 -т- ^ (°> + ^ф (Р) - S @)].
851 ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 575
Известно, что
Р Г (а)
— я)Г(а)=-?
Sin атс
Отсюда, пользуясь теоремой свертывания, получаем неизвестную функ-
функцию
Пример 2. Решим интегральное уравнение первого рода с логариф-
логарифмическим ядром:
t
о
Воспользуемся формулой G2). Тогда уравнение может быть написано в виде
Отсюда
Пользуясь способом, уже применявшимся в предыдущем примере, напи-
напишем F(p) в виде
pV-n
Если положить g-@)^0, то
Мы получим неизвестную функцию h(t), применяя теорему свертывания,
если будем знать оригинал для
1
Будем исходить из формулы E6). Проинтегрируем обе части этого выраже-
выражения' от 0 до бесконечности по параметру ч. Тогда
f __?Jy_ Г d-> __ г
Применяем формулу B2):
оо
1 1
"(v+1) -' р\п(ар) рAпр + \па) '
и
Если положить а = е1, то
576 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Отсюда получаем неизвестную функцию h {t)\
0 0 0
8.5.5. Нелинейные интегральные уравнения. Рассмотренный в преды-
предыдущем пункте способ можно применить к решению нелинейных интеграль-
интегральных уравнений, где ядро равно неизвестной функции:
t
Ah(t)-\-B f h(z)k(t — z)dz
о
При тех же обозначениях получаем
Отсюда ,_
-А±УЖ+АВСФ(р)
Пример. Требуется найти решение уравнения
t
2А (О — J* А (х) А (* — х) dt = sin *.
о
Имеем
Отсюда
F(p) =
Решением будет -
8.5.6. Интегродифференциальные уравнения. Тот же способ позволяет
решать некоторые интегральные уравнения, в которых неизвестная функ-
функция h(t) содержится также и под знаком производной. Это интегродиффе-
интегродифференциальные уравнения.
Выражения B8) и C7), дающие изображения h{n)(t) и tnh(t), позволяют
преобразовать интегродифференциальное уравнение в дифференциальное, где
F(p) — изображение A (t)— представляет собой неизвестную функцию. Началь-
Начальные условия даны значениями А@), А'@), А" @) фигурирующими в соот-
соотношениях B8).
Пример. При начальных условиях А@) = А'@) = А"@) = 0 требуется
найти решение h{t) уравнения
t
f \th (х) + А' (х) h" (t — x)] dx + ah @ + bh'" @ = g {t\
о
Имеем
t t
Так как
h'V) D pF (p).
8.5] ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 577
то теорема свертывания дает
t
Так как
h'"(tKP3F(P).
то, положив
определим изображение F(p) уравнением
+ р3 [F (/?)]2+ aF (р)+ЬрЬр Ц)=
иначе говоря, уравнением Риккати
F' (р) = Р< [F (р)? + [1 + ар + Ьр*] F (р) — рФ (р).
8.5.7. Применение операционного исчисления к исследованию функ-
функций.. Некоторые свойства трансцендентных функций можно наглядно пока-
показать с Помощью операционного исчисления.
Пример 1. Даны две функции
Теорема свертывания дает
Если положить -г =)~, то
Г (*) Г (у)
о
иначе говоря, мы получили определение эйлеровой функции первого рода
(п. 7.4.6):
В(х. у)=Л
(дг Ч- у)
' Можно заметить также, что некоторые трансцендентные функции имеют
простые и даже алгебраические изображения. Вспомним в качестве при-
примера Ci (t), 7, (t). Поэтому есть основание думать, что изучение свойств
функции переменной t значительно упростится, если исходить из изображе-
изображения этой функции.
Пример 2. Рассмотрим функцию Бесселя J4(t) и найдем несколько
уже установленных ранее формул, а также несколько новых. Имеем
Л (о и yJL— (Vp^TT - рУ = f, (p),
Одновременная запись обоих этих соотношений налагает условие
— 1 <v< 1.
37 А. Анго
578 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Имеем
Fl(p)F2(p)=-±-T.
Отсюда, применяя теорему свертывания, получаем
Положим
тогда
Сумма
4 (О —MO+Mt) — 77(o+ •••
имеет изображение
= 1—\
2
Отсюда
Л @ —
Имеем также
Но мы можем написать
pVp* + i Vp2 + i 1-х2 //>2 + i v '
Отсюда
О г=0
Известно, что У,(^) равна сумме ряда:
Заменив в этом выражении f на 2 |/~7, получим
г!
r=0
и, умножив обе части на t2 ,
r--o
8.5] ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 579
?г+* 1
Учитывая, что имеет изображением —^v~T~' п0ЛУчаем
Отсюда
A38)
Эта формула- легко позволяет установить большое количество свойств
бесселевой функции /,. Продифференцируем левую часть A38) и умножим
правую на р. Тогда
Следовательно, заменив в A38) v на ч—1, имеем
иначе говоря,
У, B \Л)+ X B V~t) = Л-, B
Если заменить 2 ]/""? на ?, то получим хорошо известную рекуррентную
формулу
у Л (ОН-/@ = ./.-i(O.
Рассмотрим тождество
^± , JL -2
Формула A38) преобразует это тождество по р в тождество по t:
Если заменить 2 У t на '• а У 1 Н- ° на t. то
г=0
Это формула умножения аргументов для функции Бесселя.
Формула A38) легко позволяет написать соотношение между двумя
функциями Бесселя с любыми индексами ./„(/) и J^(t) при v > р. > — 1. Имеем
37*
580 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Применив теорему свертывания, получаем
t
о
Отсюда
t
th, B 1/7) = TFir]ir f(t- x)-"-1 A, B
о
rfx.
Если заменить в этом выражении 2 \f t на t, a 2 У^т1 на х, получим
искомое выражение
t
t
tV(t) = =-? /V — хг)'--1 х^+
\ Г"/ Q
Пример 3. Полиномы, определенные равенством
называют полиномами Лагерра. Формуда A4) при применении формулы C3),
где X = 1, дает
Так как А(О) = /г'(О)= ... =/г(п 1)@) = 0, то по формуле C0)
" /уЯ. /ч 1
и применяя формулу C3), где Х = —1, получаем
т. е. получаем изображение полинома Лагерра Z.n(f)-
Если переменную обозначить через х, то, согласно последнему соотно-
соотношению, можно написать
?n(l) в! -J^J р \ Р) 1х
п=0 п=0 Р+ ;
Отсюда, применяя формулу A5), где а = ^-——> получим
«w п\ — 1-х
п=0
Следовательно, полиномы Лагерра являются коэффициентами при ~ в раз-
разложении в ряд функции
1-х
Эту функцию называют производящей функцией полиномов Лагерра.
8.5] ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 581
Можно написать
Согласно формуле C7), где и = 1,
,МО3_Я, * Г1A_±
nW-J dp[p\ р
Отсюда
Л+,@ —Bя + 1—
что представляет собой полезную рекуррентную формулу.
8.5.8. Применение операционного исчисления к разложению в асимп-
асимптотический ряд. Рассмотрим функцию h(t) и ее изображение F(p). Между
этими двумя функциями имеется соотношение
c+j со
* @ =2iJ / F(P)eptdp.
с~] со
Предположим, что функция F(p) голоморфна в полуплоскости р, нахо-
находящейся справа от вертикальной прямой с абсциссой х = Ь, за исключением
некоторого числа особых точек, находящихся на вертикали с абсциссой
х— а:
Ь<а<с.
Пусть рх — а-\- Jy1 Pi = a -\- jyt pk = a -\~ j'yk — эти особые
точки. Если они являются точками разветвления, то можно написать вблизи них
оо со
F(P) = 2 ani {p - Pif- X + (P- ptf* 2 bnl (p - Pi)"'1 A39)
n=0 n=0
при
0<p?< 1.
Если р обозначает радиус сходимости рядов, входящих в A39), то сле-
следует предполагать условие
\P — Pi\ <P-
Если F(p) стремится к нулю при у, стремящемся к бесконечности по
своим положительным или отрицательным значениям между двумя абсциссами
х = Ь и х = с, таким образом, что интеграл Г \F(p)\ dp сходится, то можно
показать *), что при t > О
hit) * ?•*' [а„ +«»&_21(-1Г1,ш11<Ш1) . A40)
\ n=0 t
Формула A40) дает искомый асимптотический ряд.
Примечания. Коэффициенты ani не входят в окончательную фор-
формулу A40), кроме первого аы. Если точка pt — простой полюс, а не точка
разветвления, в формуле A39) второй ряд исчезает, а коэффициент aOi равен
вычету, относящемуся к точке pt.
') W. О. L. S u 11 о n, The asymptotic expansion of a function whose operational
equivalent is known, J. London Math. Soc, 9, 1934, p. 131.
582 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Бели все точки разветвления F(р) сводятся к единственной точке, нахо-
находящейся в начале и вызванной наличием Ур, то
2я2
л=0 л=0
Отсюда получим асимптотический ряд
A41)
л=0 уа) г '"
Эта формула была предложена Хевисайдом и называется иногда „третьим
правилом Хевисайда".
Пример. Вернемся снова к примеру II. 8.3.23. Найдем асимптотиче-
асимптотический ряд функции t, изображением которой будет
В этом примере мы сначала находили, оригинал функции A42) и из него
выводили асимптотический ряд. Воспользуемся только что найденными резуль-
результатами, чтобы получить этот ряд непосредственно.
Можно написать
| 1-рЗ 1_р3
Отсюда
|]2
л=0 я=0
Получаем ряд
4 —- гЛз 1 \к^
Л@ —-те 2sinJ_,^ >.(—!)
3
8.6. НЕКОТОРЫЕ ЗАМЕЧАНИЯ
8.6.1. Замечания об операционном исчислении Хевисайда. В 1893 г.
английский физик О. Хевисайд в первый раз предложил способ вычисления,
который назвал операционным. Сейчас мы покажем, что операционное исчис-
исчисление, как его понимал Хевисайд, не отличается от только что изложенного
способа, основанного на преобразовании Лапласа — Карсона. Точка зрения
Хевисайда, который скорее руководствовался интуицией и физическим смыс-
смыслом явлений, чем математической строгостью, состояла в следующем.
Хевисайд рассматривал знак дифференцирования —& как оператор р.
Операция дифференцирования функции f(t) записывалась как pf(t); п-я произ-
i.6] НЕКОТОРЫЕ ЗАМЕЧАНИЯ 583
водная писалась как p"f(t) — оператор р прилагался п раз к функции /СО-
Оператор — или р~х представлял операцию интегрирования, так как опера-
оператор р, приложенный к p~lf(t), снова давал f(t):
Формула, содержащая интегралы или дифференциалы, сводилась при рас-
рассмотрении р в качестве алгебраической переменной к алгебраической форме.
Это Хевисайд называл „алгебраизацией" задачи.
Особенно подробно Хевисайд рассматривал функцию Г (/); функции h (t)
всегда были равны нулю при t < 0.
Можно заметить, что формулы B9) и C1) являются оправданием приема,
состоящего в том, чтобы рассматривать р и р~х соответственно как опера-
операторы дифференцирования и интегрирования. Можно показать, что, например,
отождествление р с оператором дифференцирования приводит к уже извест-
известным формулам.
Применив к h(t) оператор е~1Р, получим
но pnh{t) — то же самое, что h(n) (t), поэтому
= h(t — I).
Эту формулу можно сопоставить с полученной ранее формулой C4).
Для Хевисайда формула / (р) cz h(t) (преобразование Карсона) означала,
что оператор / (р), примененный к Г (t), дает в результате
/ О»М Г @} = *(*)• A43>
Мы увидим, что точки зрения Карсона и Хевисайда совпадают. Рассмотрим
формулу A43). Если допустить, что h (t) разлагается в целый ряд по /,
а /(/?) — в целый ряд по —:
А=0 й=0
то эти ряды совпадают, так как
/>-"{Г@} = -^ при *>0.
Покажем, что полученные таким образом функции h(t) и f(p) удовле-
удовлетворяют интегральному уравнению Карсона. Требуется установить, что
л=0 /
Рассмотрим общий член правой части
f HLe-ptdt.
,1 п\
584 СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ [ГЛ. VIII
Последовательное интегрирование по частям дает
Значит, равенство (*) подтверждается, и точка зрения Хевисайда, выражен-
выраженная равенством A43), совпадает с точкой зрения Карсона.
Нужно сознаться, что операционное исчисление до работ Карсона
и П. Леви, которые дали ему незыблемое математическое основание, таило
в себе множество ловушек. Небезопасно было обращаться с р как с алге-
алгебраическим числом, и только гениальная интуиция Хевисайда позволяла ему
обходиться без ошибок при вычислениях.
8.6.2. Обозначения в операционном исчислении. В работах, посвящен-
посвященных операционному исчислению, для обозначения функционального соотноше-
соотношения между функциями f (р) и h(t) применяются следующие обозначения.
Преобразование Лапласа:
1) F{p) = L{h{t)\, h(t) = L-l{F(p)}
(А. И. Лурье, Г. Дбч, Ян Микусинский, В. А. Диткин и А. П. Прудников,
Н. С. Пискунов).
2) F{p)-*-
(Н. С. Пискунов).
3) F(p)Ch(t
(А.'Анго).
Преобразование Карсона:
1) /(/») = А @. А @ =/(/»)
(Б. ван дер Поль).
. 2) F(p) = pL{h(t)}
(А. И. Лурье).
3) F(p)ch(t). h(t)-=>F(p)
(А. Анго).
ЛИТЕРАТУРА К ГЛАВЕ VIII
1. Конторович М. И., Операционное исчисление и нестационарные явления
в электрических цепях, Гостехиздат, 1953.
2. Лурье А. И., Операционное исчисление и его приложения к задачам механики,
Гостехиздат, 1950.
3. П и с к у н о в Н. С, Дифференциальное и интегральное исчисления для втузов,
Физматгиз, 1963.
4. Д е ч Г., Руководство к практическому применению преобразования Лапласа,
Физматгиз, 1960.
5. Диткин В. А. и Прудников А. П., Интегральные преобразования и опе-
операционное исчисление (СМБ), Физматгиз, 1961.
6. Д и т к и н В. А. и Кузнецов П. И., Справочник по операционному исчис-
исчислению, Гостехиздат, 1951.
7. Э ф р о с А. М., Данилевский А. М., Операционное исчисление и контур-
контурные интегралы, ДНТВУ, 1937.
8. Ван дер Поль Б. и Бреммер X., Операционное исчисление на основе
двустороннего преобразования Лапласа, ИЛ, 1952.
9. Микусинский Я-. Операторное исчисление, ИЛ, 1956.
10. Т е у м и н И. И., Справочник по переходным электрическим процессам, Связь-
издат, 1951.
Г Л А В А IX
ТЕОРИЯ ВЕРОЯТНОСТЕЙ. ПРИЛОЖЕНИЯ
9.1. СЛУЧАЙНАЯ ВЕЛИЧИНА
9.1.1. Определение вероятности. Рассмотрим некоторое событие А,
т. е. факт, который может произойти или не произойти в результате опыта.
Пусть из общего числа N равновозможных случаев имеется п благоприят-
благоприятствующих этому событию, т. е. таких случаев, когда событие происходит.
Тогда вероятность р совершения события А определяется формулой
D——*)
Р — N >¦
Если событие А не происходит, то имеет место событие не А, которое
мы назовем противоположным событием и обозначим через В. Число случаев,
благоприятствующих совершению события В, равно, очевидно, N — п. Вероят-
Вероятность В будет, следовательно, равна
_ N—n = 1 _
Если событие А достоверно, то n = N, а следовательно, и р=1.
Если событие А невозможно, то и ге = 0, и, следовательно, р = 0.
Пример. Какова вероятность извлечь наудачу 5 белых шаров из урны,
в которой лежит 12 белых шаров и 7 черных?
Общее число возможных случаев равно числу способов извлекать
5 шаров из 19, т. е. числу сочетаний из 19 предметов по 5. Следовательно,
ЛГ = С5 = 19!
Число благоприятных случаев равно числу способов извлекать 5 белых
шаров из 12, т. е.
_ 121
Л — 5! 7! "
Значит, искомая вероятность равна
_ п _ 22
р—77— 323 '
*) Вероятность события есть численная мера степени объективной возможности
этого события. Формула для непосредственного подсчета вероятностей, введенная
автором:
л
имеет место лишь для «схемы случаев". При этом, помимо равновозможности всех
случаев, необходимо, чтобы они составляли полную группу, т. е. чтобы в результате
опыта непременно произошел хотя бы один из случаев, а также чтобы они были
несовместными, т. е. чтобы никакие два из них не могли появиться одновременно
в данном опыте. i
586 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
9.1.2. Независимые события. Теорема умножения вероятностей. Го-
Говорят, что события независимы, если на осуществление одного из них не
влияет осуществление остальных.
Если обозначить вероятности независимых событий Ау А2, Л3 As
через Ру р2, />з Ps< T0 возможность совместного осуществления всех
событий Аг, ..., As будет равна произведению вероятностей pv р2 • ¦ ¦ ps-
В этом состоит теорема умножения вероятностей. Поясним для двух неза-
независимых событий Av А2. Пусть Nv N2 — соответственно числа равновоз-
можных случаев, пг, п2 — числа случаев, благоприятствующих осуществлению
событий Л[ и А2, а рг, р2 — их вероятности. Имеем
Общее число случаев, благоприятствующих совместному осуществлению обоих
событий Ау А2, равно пхп2, общее число возможных случаев равно NXN2,
поэтому
Р = P\Pv
где р обозначает вероятность совместного осуществления обоих событий
Аг и А2. Эту теорему легко обобщить на любое число событий.
Пусть р1 — вероятность осуществления событий Аг, а р2 — вероятность
осуществления события А2 после того, как событие Л1 произошло. Вероят-
Вероятность того, что события А1 и А2 осуществятся последовательно, будет равна
PiP2. Доказательство этой теоремы проводится подобно доказательству
предыдущей. Она легко обобщается на любое число событий *).
Пример. Рассмотрим снова предыдущий пример. Вероятность в первый
12
же раз извлечь белый шар равна -гд- . Как только мы произвели эту опе-
операцию, вероятность во второй раз извлечь белый шар равна уже
]о~1 = -то-: аналогично при третьем, четвертом и пятой извлечениях
вероятности извлечения белого шара будут соответственно равны
10 9 8
IT ' 16 • 15 "
Следовательно, вероятность извлечения пяти белых шаров при пяти после-
последовательных извлечениях равна
12-11-10-9-8 _ 22
19-18-17-16-15 ~- 323 '
9.1.3. Несовместные события. Теорема сложения вероятностей.
Говорят, что события Av A2,'..., As несовместны, если осуществление
одного из них исключает возможность осуществления остальных. При этом
условии вероятность того, что одно из группы событий Л,, ..., As осуще-
осуществится, равна сумме вероятностей осуществления каждого из этих событий
в отдельности.
Действительно, пусть вероятности событий Аг As равны соот-
соответственно р1 = ~- ps = ^.. Вероятность того, что какое-либо из
*) Теорема умножения вероятностей обычно формулируется так: вероятность
произведения двух событий равна произведению вероятности одного из них на услов-
условную вероятность другого, вычисленную при условии, что первое имело место. При
этом произведением нескольких событий называется событие, состоящее в совместном
появлении всех этих событий. В случае независимости событий условная вероят-
вероятность появления события равна его безусловной вероятности.
9.1]
СЛУЧАЙНАЯ ВЕЛИЧИНА
587
событий Av .... As осуществится, равна
,
... 4 Рг
В этом состоит теорема сложения вероятностей.
Пример. Вернемся к первому примеру с урной. Какова вероятность
при извлечении за один раз двух шаров получить один черный и один
белый шар?
Безразлично, извлечены ли оба шара из девятнадцати за один раз или
один шар из девятнадцати в первый раз и потом еще один из восемнадцати
во второй раз. При этом могут произойти два благоприятных несовместных
события:
1) в первый раз извлечен белый шар, во второй раз черный;
2) в первый раз извлечен черный шар, во второй раз белый.
Вероятность первого события на основании теоремы умножения вероят-
вероятностей равна
12 _7_
19 ' 18 '
Вероятность второго события по аналогии равна
19 ' 18 "
Искомая вероятность будет на основании теоремы сложения вероятностей равна
12 7 7 12 28
19 * 18
19 " 18 57
9.1.4. Формула Стирлинга. В полученные выше формулы часто входит
величина п\, прямое вычисление которой при больших значениях п требует
больших затрат труда и времени. Для упрощения этих вычислений часто
пользуются приближенной формулой Стирлинга, точность которой возрастает
с возрастанием числа п (асимптотическая формула).
Для вывода этой формулы рассмотрим площадь, заключенную между
осью х, кривой у = \пх и прямой, параллельной оси у в точке с абсциссой
х = п (рис. 9.1). Эта площадь выражается
интегралом
л
In xdx.
Интегрируя по частям, будем иметь
л
\ 1п х dx = n In п — п ¦+¦ 1.
Рис. 9.1.
С другой стороны, вычисляя этот интеграл приближенно по формуле тра-
трапеций, получим
lnxdx= 1п1+1пя
*) Теорема сложения вероятностей обычно формулируется так: вероятность
суммы несовместных событий равна сумме вероятностей этих событий. При этом
суммой, нескольких событий называется событие, состоящее в появлении хотя бы
оаного из этих событий (в случае несовместных событий суммой нескольких событий
называется событие, состоящее в появлении одного из этих событий).
588 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Учитывая выпуклость кривой у = !п х, заключаем, что формула трапе-
трапеций позволяет вычислить искомую площадь с недостатком, т. е
nln п — п-\- 1 > \пп\ — -д-!пге.
Приближенно можно принять
п\пп — п?а\пп\ — -jinn
или
\пп\ х in -\--Л\п п — п,
откуда для п ! получаем приближенное выражение
ппе~п У п.
Таким образом, можем написать
п\ = ппе~пУ~щ{п). A)
Покажем, что функция ср (/г.), компенсирующая ошибки приближенной фбр-
мулы, при п, стремящемся к бесконечное™, имеет предел и предел этот
равен yic.
Действительно, рассмотрим соотношение
Имеем
1п-
откуда следует, что ряд, общий член которого равен 1п —J _. , сходится.
Следовательно, сумма Sn первых п членов этого ряда имеет предел при
я—>оо. Эта сумма равна
Sn = !п ср (п) — 1псрA).
Поскольку последовательность In ср (п) имеет конечный предел, то и после-
последовательность ср(п) также имеет конечный предел.
Мы уже знакомы (п. 2.1.4) с формулой Валлиса, которая имеет вид
—- = игл
2 ~ „Too ЬЗ...Bп-1)-ЬЗ...Bл+1)
или
JL— у 2*п(п\у
1^
Если заменить в этом выражении величину п\ на основании формулы A),
то получим
о — "'"
откуда следует равенство
n[ = n"e-n
где е„ стремится к нулю при п, стремящемся к бесконечности. Можно
показать, что
В\ В2 В3 ^4 |
» ~ 1 ¦ 2л " 3 • in3 "г" 5 • 6л5 7 • 8л7 "т" " * "
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 589
где fip В2, В3, ...—числа Бернулли (п. 10.5.1):
В1 = -g-, В2 = -gQ-, fi3 = ^" • 54 = "зо"' ' •"
_... BяI V J_
На практике пользуются следующей приближенной асимптотической
формулой Стирлинга:
п\^ппе-п У^п B)
или, если требуется большая точность,
Последняя формула делает ошибку пренебрежимо малой даже при малых
значениях п.
Законы распределения случайных величин
9.1.5. Дискретные случайные величины. Пусть имеется некоторая
группа событий
Ах, А2 ..., As,
вероятности осуществления которых равны соответственно
Pv Pi' ¦¦¦' Ps-
Условия опыта таковы, что в каждом опыте осуществляется одно
и только одно событие (т. е. мы имеем полную группу несовместных
событий). Поэтому
Р\-\- Р2+ •¦• +Ps=1'
Рассмотрим переменную х, которая может принимать значения
JCj, Х2, ¦ . • , Х^, . . . , Xs
в зависимости от происходящего события. Такая величина называется
дискретной (прерывной) случайной величиной. Совокупность значений слу-
случайной величины вместе с их вероятностями определяет ее закон рас-
распределения.
• Выражение ' s
* = PiXi Н- Р2Х2 + •¦¦ + Psxs = Ё PlXi C)
называется математическим ожиданием случайной величины х *). Таким
образом, математическим ожиданием случайной величины называется сумма
произведений всех возможных значений случайной величины на вероятности
этих значений').
•) В советской литературе, помимо обозначения математического ожидания
чертой сверху (как это принято в настоящей книге) применяется обозначение М [х],
которое удобнее в случае, когда рассматривается математическое ожидание сложного
выражения. Мы будем использовать, как правило, обозначение математического
ожидания, принятое автором. Дисперсия случайной величины х обозначается D [х],
или просто D.
') Если х — выигрыш в азартной игре, то игра может считаться справедливой,
если математическое ожидание х равно ставке.
590 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Разность между значением случайной величины х и ее математическим
ожиданием х обозначается через В и называется отклонением (или центри-
центрированной случайной величиной):
Ь=х — х. D)
Математическое ожидание отклонения равно нулю:
1=0.
Средним арифметическим отклонением называется математическое ожида-
ожидание абсолютных значений случайной величины о:
8« = Ш- E)
Дисперсией случайной величины х называется величина D, определяемая
формулой
D=%(Xi-x?Pi = °2. F)
i
а величина о, представляющая собой квадратный корень из дисперсии, назы-
называется средним квадратическим отклонением или стандартом случайной
величины х. Дисперсия случайной величины характеризует рассеивание, раз-
разбросанность значений случайной величины около ее математического ожидания.
Легко заметить, что для величин Ьт и а справедливо следующее
неравенство:
Если f (х) — функция случайной величины х, определенная для всех
значений xt, то математическое ожидание этой функции относительно рас-
рассматриваемого закона распределения случайной величины х определится
формулой
s
7=21/(¦**) л- G)
Дисперсия функции f(x) будет равна \
D[f] = ^[f(xi)-J?pl. (8)
Величина хг, определяемая формулой
F = Jj*I/v ' (9)
называется начальным моментом порядка г случайной величины х. Если
математическое значение случайной величины х равно нулю, то величина
называется центральным моментом порядка г случайной величины х; при
этом х = х1 — 0.
Можно предложить следующую механическую интерпретацию закона
распределения, которая поясняет введение термина момент.
Рассмотрим ось х с началом в точке О и поместим в точках с абсцис-
абсциссами лг, Xj xs массы, равные рх Pj ps (распределение
общей массы, равной единице).
9.1]
СЛУЧАЙНАЯ ВЕЛИЧИНА
591
Начальный момент первого порядка—математическое ожидание х — есть
абсцисса центра тяжести этих масс или статический момент этих масс от-
относительно точки О. Если перенести начало отсчета в эту точку, то х = 0.
В этом случае величина х2 — центральный момент второго порядка, или,
что то же самое, дисперсия случайной величины х — представляет собой
момент инерции масс р1 относительно математического ожидания случайной
величины х.
9.1.6. Непрерывные случайные величины. Если через Р(х) обозначить
вероятность того, что значение случайной величины находится между —оо
и л:, то Р(х) будет монотонной неубывающей функцией переменной л:, ко-
которая, очевидно, будет равна нулю при лг = — оо и единице при л: = -|-оо.
\+1
О х
Рис. 9.2.
В случае дискретной случайной величины Р(х) — ступенчатая функция, у кото-
которой высоты ступеней равны вероятностям pv р2 Pi />, (рис. 9.2).
В случае непрерывной случайной величины характер изменения функции Р(х)
представлен на рис. 9.3. Может существовать и промежуточный случай,
когда функция Р(х) имеет точки разрыва первого рода (рис. 9.4). Функ-
Функция Р(х) называется функцией распределе-
распределения случайной величины л\
Если для простоты считать, что в слу-
случае непрерывной случайной величины функ-
функция распределения непрерывна, то можно
определить ее формулой
+7
X
= f
Обращаясь опять к механической интерпретации и рассматривая рас-
распределение массы, равной единице, можно сказать, что р(х) — линейная
плотность. Величина р(х) называется плотностью вероятности (плотностью
распределения). Математическое ожидание непрерывной случайной величины х
определяется формулой
х = Г хр (х) dx.
A0)
Отклонение 8 равно, как и раньше, х — х. Дисперсия непрерывной слу-
случайной величины х равна
D = a2= Г {х — хJ р (х) dx. A1)
Величина <з, как и ранее, представляет собой среднее квадратическое откло-
отклонение, или стандарт случайной величины х.
592 ¦ ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Обозначим через f(x) функцию> определенную для всех значений jc.
Математическое ожидание функции / и ее дисперсия определяются соответ-
соответственно формулами
со
7= / f(x)p(x)dx, A2)
— Jfp{x)dx. A3)
Можно считать, что функция Р(х) определяет на оси х распределение
общей массы, равной единице. Математическое ожидание х представляет
собой статический момент относительно точки О; одновременно это абсцисса
центра тяжести.
Математическое ожидание отклонения 8 равно нулю, так как это есть
статический момент относительно центра тяжести:
"8 = 0.
Начальный момент порядка г непрерывной случайной величины опре-
определяется выражением .
со
х7= jxrp(x)dx. A4)
t —СО !
Если выбрать за начало координат абсциссу математического ожида-
ожидания х, то центральный момент второго порядка, или дисперсия непрерывной
случайной величины х, будет представлять собой момент инерции рассмат-
рассматриваемой массы относительно центра тяжести. Если математическое ожида-
ожидание х не выбрано за начало координат, то можно выразить дисперсию D
через два первых начальных момента с помощью равенства
D = х^~2(хУ + (х? = х? — (xf. ¦ A5)
9.1.7. Характеристическая функция. Пусть дана непрерывная случай-
случайная величина х и соответствующая ей плотность вероятности р (х).
Для ряда задач удобно ввести функцию от переменной и, которая
представляет собой математическое ожидание величины е-*"*. Она называется
характеристической функцией случайной величины х *). По определению,
эта функция <р(и) равна
=е""= fejuxp(x)dx. A6)
Здесь J=Y — 1 — мнимая единица.
Из свойств интеграла Фурье (п. 2.2.2, формула B1)) следует обратная
формула
со
± f<?(u)edu. A7)
— со
Введение характеристической функции связано с тем, что ее последо-
последовательные производные, в которых положено и = 0, представляют собой,
*) Метод характеристических функций был создан А. М. Ляпуновым.
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 593
с точностью до коэффициента ±у, начальные моменты того же порядка.
Действительно,
со
<р@)= fp(x)dx = l.
-сх>
оо
?' @) = J j хр (х) dx = jx.
— ОО
<Р(Л @) = / / хгр (х) dx == /F.
-оо
Поэтому, если разложить функцию f(u) в ряд Маклорена
то
<р (и) = 1 -\- Jux -J- ... -+- . хт -)-... A8)
Если этот ряд сходится, то знание начальных моментов различных порядков
определяет при некоторых условиях характеристическую функцию, а следо-
следовательно, и функцию р(х).
Пример. Рассмотрим переменную х, для которой плотность вероят-
вероятности равна нулю вне интервала @, 1) и равна единице внутри этого ин-
интервала:
р(х) — 0 при лг < 0 и лг^-1,
р(х)=1 при 0<дг<1.
Функция распределения равна
х \ 0 для х < О,
Р(х)= J pifydt — l х для 0<дг<1,
~°° [ 1 для х >-1.
Математическое ожидание х равно
оо 1
х = j xp{x)dx — J xdx = -j,
-оо О
что было очевидно к priori.
Дисперсия равна
оо 1
о2= J(X—x)*p(x)dx = f(x — ±]j2dx = ±,
-оо 6
а характеристическая функция
38 А. Анго
594 ТЕОРИЯ ВЕРОЯТНОСТЕЙ {ГЛ. IX
1
Если перенести начало координат в точку х = х — -^ , иначе говоря,
если заменить х на х — -~-, то для ср (и) получим
() e
9.1.8. Распределение системы двух случайных величин. Рассмотрим
случай системы двух случайных величин х и у. Функция распределения си-
системы двух случайных величин Р(х, у) представляет собой вероятность
того, что обе случайные величины будут соответственно меньше х и у.
Функция распределения должна удовлетворять следующим условиям:
Р(—оо, — оо) = Я(—оо, у) = Р(х. — оо) = 0,
Р(+со, +со)=1.
Условие монотонности функции распределения, поведение которой для
одной случайной величины характеризовалось графиком, приведенным на
рис. 9.3, для системы двух случайных величин характеризуется неравенствами
P{x + h, y) — P{x, 3>)>0,
Р(х, y + k) — P{x, y)>0.
P(x + h, y + k) — P(x-\-h, у)>Р(х, y + k) — P(x. у),
где через ft и к обозначены положительные приращения величин х и у соот-
соответственно. Плотность вероятности системы двух случайных величин опре-
определяется формулой
, . д2Р (х, у)
откуда
х у
Р(х, у)= f f p(x, y)dxdy.
— i2O — ОО
Мы рассмотрели случай непрерывной функции распределения системы
двух непрерывных случайных величин. Легко представить себе функцию рас-
распределения для случая системы двух дискретных случайных величин, анало-
аналогичную функции распределения одной дискретной случайной величины, пред-
представленной на рис. 9.2, а также разрывную функцию распределения для
случая системы двух непрерывных случайных величин, аналогичную пред-
представленной на рис. 9.4 для одной непрерывной случайной величины.
Определим начальные моменты различных порядков для системы двух
случайных величин. Имеется п-\-\ момент га-го порядка:
хп— j J x"p(x, y)dxdy,
— СО —ОО
со оо
V= / j xn-kykp{x, y)dxdy.
— CO —OO
у" = j j y"p(x, y)dxdy.
— OO —OO
9.1J СЛУЧАЙНАЯ ВЕЛИЧИНА 595
Если рассматривать р(х, у) как величину, определяющую плотность
единичной массы, распределенной на плоскости Оху, в точке (х, у), то оба
момента первого порядка х и у определят абсциссу и ординату центра тя-
тяжести этой массы. Это будут моменты первого порядка системы случайных
величин (х, у), спроектированные соответственно на оси хну.
Если выбрать начало координат в точке (х, у), то получим централь-
центральные моменты второго порядка х2 и у2, которые примут вид
ОО
оо
— СО —ОО
оо оо
— оо —со
Характеристическая функция представляет собой математическое ожи-
ожидание функции
ej (ax+vy)t
т. е. _ „
оо со
¦<р(и, v)= J JeJ(ux+vy)p(x, y)dxdy.
Если разложить характеристическую функцию в ряд Маклорена по двум
переменным и и V, то получим
, 0)]+ ...
с, y)dxdy.
Приравнивая коэффициенты при одинаковых степенях переменных и и г»,
будем иметь
(р@, 0) = —у2,
A9)
Все рассмотренные выше понятия легко обобщить на системы любого
числа случайных величин.
9.1.9. Характеристическая функция суммы независимых случайных
величин. Пусть имеется случайная величина х, которая в процессе опыта
принимает значения дг,, х2, .... и другая случайная величина, независимая
от первой, которая в процессе опыта принимает значения yv y2, ... Опре-
Определим случайную величину х-\-у. В процессе опыта она .принимает зна-
значения
38*
596 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Для характеристической функции суммы х-\-у имеем
Учитывая, что случайные величины х и у независимы, заключаем, что
двойной интеграл от правой части сводится к двум простым интегралам.
Следовательно, правая часть равна произведению характеристических функ-
функций слагаемых, т. е.
<?х+у — 9х ' <Ру B0)
где через <ра обозначается характеристическая функция для случайной ве-
величины а. Итак, характеристическая функция суммы величин х-{-у равна
произведению характеристических функций величины х и величины у. Это
правило легко обобщается на любое число независимых случайных величин.
Основные законы распределения случайных величин
9.1.10. Биномиальный закон распределения. Пусть некоторое собы-
событие А может осуществиться в ходе испытаний. Если А не осуществится,
то осуществится противоположное событие В. Пусть р— вероятность осу-
осуществления события А. Очевидно, что вероятность осуществления противо-
противоположного события будет q=\—Р- Если проделать п последовательных
независимых опытов, то вероятность Р-п (k) того, что событие А осущест-
осуществится в точности k раз, событие В, следовательно, п — k раз, будет, если
не" учитывается порядок событий,
Яя(*) = С*р*?»-*.
р (k) />»о"-* B1)
yW Р Я
В связи с тем, что вероятности Pn(k) по форме представляют собой
члены разложения бинома (p-\-q)n, распределение вероятностей вида B1)
называется биномиальным законом распределения. Числа р и q определяются
условиями эксперимента, а число опытов п устанавливается заранее. Най-
Найдем при этих условиях значение k, при котором вероятность Рп (k) оказы-
оказывается наибольшей.
Сравнивая значения Pn(k) и Pn{k-\-\), имеем
Р,(*-И) _ Р п-к
Pn(k) q ' к + 1 -
Следовательно, Pn(k) возрастает вместе с k до тех пор, пока значение k
меньше или равно пр — q. Если пр — q — целое число, то наибольшее зна-
значение вероятности достигается при двух значениях k:
k — np — q и k = np-\- p.
Если пр — q — не целое число, то наибольшая вероятность достигается при
одном значении k, которое равно ближайшему целому числу, большему чем
пр — q, или, что то же самое, целой части числа пр-\-р. Так как в даль-
дальнейшем мы будем предполагать, что число п опытов велико, то можно без
заметной ошибки сказать, что наиболее вероятное число осуществлений со-
события А равно пр (оно отличается от точного значения меньше, чем на
k
единицу). Если через — обозначить частоту *) осуществления события А, то
*) Вместо термина частота иногда используют термины частость или статисти-
статистическая вероятность.
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 597
можно сказать, что наиболее вероятное значение частоты будет приближенно
равно вероятности р.
Найдем вероятность того, что событие А осуществится в п опытах по
крайней мере k раз. Эта вероятность будет равна сумме
т. е. сумме А-j-l первых членов разложения бинома (p-\~q)n.
Вычислим математическое ожидание и дисперсию переменной k бино-
биномиального закона. Для этого будем исходить из тождества
Продифференцируем обе части тождества по у. Тогда
пр (РУ + qf' ¦= S kPn (*) у"'1.
k— I
Полагая у=1 в обеих частях последнего равенства, получим
k=itkPa(k) = np. B2)
Продифференцируем еще раз обе' части тождества (*) и в полученном
выражении снова положим у = 1. При этом будем иметь
я(я— I)p2='tk(k— 1)ЯЯ(*)= 2*(*— 1)ЯЯ(*):=** -k. B3)
Согласно формуле A5), дисперсия равна
D = P — (k?
или _ _ _
D = k2~ k~\-{k — (кJ].
На основании формул B2) и B3) имеем
D = n(n—l)p2-±np — п2р2
или
D = npq,
откуда
о = У npq.
9.1.П. Характеристическая функция биномиального закона. Рассмот-
Рассмотрим случайную величину х, которая принимает значение 1 в случае осу-
осуществления события А и значение 0 в противоположном случае. Биномиаль-
Биномиальный закон распределения характеризует распределение массы, равной еди-
единице, при котором масса q находится в точке 0, а масса р — в точке 1.
Следовательно,
О при х < О,
Р(х) =
q при 0<;х < 1,
1 при х ;> 1.
Плотность вероятности р(х) равна нулю во всех точках, кроме точек
= 0, х = 1, где она принимает соответственно значения q и р.
598
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. IX
Характеристическая функция <р(и) в случае одного испытания будет,
следовательно, иметь вид
оо
<р(и)= Г eiuxdP(x) = q + peia.
— ОО
В случае п испытаний характеристическая функция ср(и) равна
25 30
Рис. 9.5.
Раскроем скобки в правой части:
•"". B4)
Переменная k в случае п испытаний
может принимать га-f-l возможных зна-
значений
О, 1, 2 п,
вероятности которых равны
Л,@). Л,О). Л,B). ••.-. рп(п).
Приравнивая друг другу оба выражения для
математического ожидания функции eiux,
будем иметь
оо
(«)= f
\ B5)
Сравнивая выражения B4) и B5) для <р(и), найдем
Таким образом, мы снова получили биномиальный закон распределения.
Пример. Рассмотрим событие, вероятность осуществления кото-
которого /> = -д-. Вычислим вероятности того, что событие осуществится 0, 1, 2,
3, .... 29, 30 раз при 30 повторных испытаниях.
Биномиальный закон позволяет составить такую таблицу:
Р D) =0,001.
Р E) =0,003.
Я F) =0,011.
Р G) =0,026.
Я(8)== 0,050.
Р (9) = 0,082.
= 0Л15.
= 0,139.
) = 0,147,
ЯA3)=0,136.
= 0,П0.
= 0,078.
ЯA6)=0,049...
ЯA7) = 0,027...
ЯA8)=0,013...
ЯA9) = 0,005. . .
Р B0) = 0,002...
ЯB1) = 0,000...
Если ь точках с абсциссами 0, 1, 2, ..., 29, 30 провести ординаты, длины
которых пропорциональны Я @), Я A), Я B), ...,ЯB9), ЯC0), то получим
схему, представленную на рис. 9.5. Когда число п становится очень большим,
схема деформируется: она сдвигается вправо и становится все более пологой.
Действительно, сумма ординат остается все время равной единице, так как
эти ординаты представляют собой сумму членов бинома (р ~\-q)" = 1.
Целесообразно рассмотреть такую схему в случае, когда за начало
отсчета на оси абсцисс принимается точка, соответствующая максимуму орди-
«.1] . СЛУЧАЙНАЯ ВЕЛИЧИНА 599
наты, т. е. значению k, при котором достигается наибольшая величина Рп (&).
Известно, что это значение k тем ближе к пр, чем больше п. Так как нас
интересуют главным образом большие значения п, то производим замену
переменной:.
Новая переменная х представляет собой отклонение
х = k — k.
При этом биномиальный закон распределения принимает вид
Вычисление Рп (k) по формуле B6) при больших х довольно неудобно.
Кроме того, вероятность Pn(k) дана здесь как функция трех параметров:
k, n, р. Покажем, как можно получить более простую формулу, прибли-
приближенно представляющую биномиальный закон распределения.
9.1.12. Формула Лапласа. Нормальный закон распределения (закон
Лапласа — Гаусса). Если использовать формулу Стирлинга для факториалов,
то выражение B6) запишется в виде
р /fo\
I, , X \пр + х i х \nq -x f I x \ I x\
1-J 1 1/ 2тс[р-4-.— \[q n
\ ^ npj \ nq) V V^nJV n)
Имеем
(nq-x)ln(l __) = _(Я?_Л)^_ + Т__Г + Т__._) J.
Отсюда
i_ x* I xl p-q
Y ~npq~ 6 n- pV
Pn(k)= A___ B7)
Формула B7) при сделанных допущениях позволяет приближенно найти ве-
вероятность того, что отклонение х имеет определенное значение (отличаю-
(отличающееся от k на целое число). Эта формула не симметрична относительно х,
что происходит из-за членов, содержащих х в нечетных степенях. Заметив,
что'все эти члены содержат множитель р — д, можно сделать вывод, что
если р не слишком отличается от q и если х не очень велико по сравне-
сравнению с npq, то эта формула приближенно симметрична.
При больших п, если учитывать только члены первого порядка малости
относительно — , формула B7) примет вид
Pnik)=-=L=re 2 »«• B8)
У 2-x.npq
Можно ввести в эту формулу математическое ожидание k = np или
среднее квадратическое отклонение о = Y^npq, в результате чего получаем
две эквивалентные формулы:
B9)
600 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
ИЛИ
_. „ X k — пр k— k
Величину ? = г = . = —j=- называют приведенным или
относительным отклонением (она безразмерна). Величина h = — ¦ =
V2npq
= —j=r называется мерой точности. Она по размерности обратна случайной
величине х *):
*-!
h '
Придадим k или х, что одно и то же, два близких значения, отличаю-
отличающиеся на несколько единиц. Пусть эти два значения будут kv k2, xv x2.
Разность между двумя соответствующими приведенными отклонениями ?, 'и \2
очень мала, если п велико. Ее можно без заметной ошибки принять за диф-
дифференциал:
d\ — h (kx — k2) = h (xr — х2).
Вероятность того, что случайное значение приведенного отклонения за-
заключается между 5 и 4,-\-d\, будет равна вероятности того, что значение k
заключается между kr и k2. Иначе говоря,
C1)
Мы получили один из основных законов распределения, закон Лап-
Лапласа— Гаусса, или нормальный закон, который представляет собой асимпто-
асимптотическую форму биномиального закона распределения для случая очень боль-
больших п, когда
Р k — пр
~ V2npq '
Примечательно, что нормальный закон распределения зависит только от
относительной переменной ?.
Вероятность того, что случайное значение k заключается между сильно
отличающимися друг от друга значениями kx и k2, будет
\2
1 С ._« ^ C2)
V*
где %l = h{kl — пр), %2 = h{k2 —
Биномиальный закон распределения, характеризуемый тремя параметрами,
при помощи некоторых упрощающих допущений, к исследованию которых
мы еще вернемся, заменен законом распределения с одной относительной
переменной.
*) В работах зарубежных авторов вместо меры точности используется величина
Т
величиной не пользуются.
и = —, которая называется единичным отклонением. В советской литературе этой
O.U
СЛУЧАЙНАЯ ВЕЛИЧИНА
601
Кривая у —
8"
называемая кривой Гаусса, изображена на рис. 9.6.
Вероятность того, что приведенное отклонение заключается между двумя
любыми значениями Х\ и ?2. равна площади криволинейной трапеции, заклю-
заключенной между этой кривой, осью ? и двумя прямыми, параллельными оси Оу,
пересекающими ось абсцисс в точках ^ и ?2. Если разность ?2 — ^1 по"
стоянна, то эта вероятность будет наибольшей в том случае, когда значе-
значения Xi и S2 равны по величине и противоположны по знаку. Наибольшую
вероятность имеет нулевое отклонение. Вероятность того, что приведенное
отклонение примет любое значение, очевидно, равна единице. Но эта ве-
вероятность равна
Р(Л)
Как известно (п. 7.3.1), данный
интеграл — интеграл Пуассона — равен
-^ У~к; это хорошо согласуется со всем
изложенным выше.
Функция Лапласа
вероятностей)
е
(или интеграл
_
*-?/'
-?dX
рассматривалась в п. 7.3.1 и последующих. К приведенной там числовой
таблице следует добавить следующие значения, играющие особую роль в тео-
теории вероятностей:
1,163
1,821
2,327
2,751
3,123
3,459
3,763
<
0,9
0,99
0,999
0,9999
0,99999
0,999999
0,9999999
= 1 — 10"'
= 1 — 10~2
= 1 _ ю"?
= 1 —10
= 1 —10~6
= 1 —10
= 1 —10
Если случайная величина представляет собой не приведенное отклоне-
отклонение \, а абсолютное отклонение х, то нормальный закон распределения при-
принимает вид
1 --?-
ay 2л
Так как нормальный закон распределения симметричен, то
C3>
Среднее квадратическое отклонение в этом случае совпадает с корнем квад-
квадратным из момента второго порядка. Вычислим в общем виде момент
€02 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
порядка 2г (все моменты нечетных порядков в силу симметрии равны нулю).
Интегрируя от нуля до бесконечности обе части тождества
получим
Отсюда при г = \ находим
1 = 2а2, a = -L
W— 1 • 3 ... Bг — 1)
Если бы мы взяли нормальный закон распределения в виде C3), то
получили бы
X = 1 'О ... \?l " 1 J О .
9.1.13. Характеристическая функция нормального закона распреде-
распределения. По определению, характеристическая функция <р(и) равна
1 С lux -?г ^
<р(и) =—-=г I eJ e la dx.
; —ОО
Вычисление ее легко сводится к вычислению интеграла
ОО
Г Vn
f/ l/ д
— CO
Отсюда, считая, что a = -^-j- и у = на2, получаем выражение
которое имеет ту же аналитическую форму, что и плотность вероятности.
Вычисление производных от функции <р(и) позволяет легко найти
л^ = (— 1УУ2О@)=1 -3 ... Bл—1)а2Г,
9.1.14. Теорема Бернулли. Пусть дано сколь угодно малое число ¦»).
Вероятность того, что разность между частотой появления события и ве-
вероятностью этого события окажется меньше т), стремится к единице, когда
число п опытов бесконечно возрастает. Иначе говоря, когда п бесконечно
возрастает, частоты осуществлений события А и противоположного события В
неограниченно приближаются к вероятностям р и q.
Высказанное выше предложение называется законом больших чисел.
Пусть т] — сколь угодно малое положительное число. Покажем, что
вероятность выполнения неравенства
— — р <¦») C4)
п
при бесконечно возрастающем п стремится к единице. Другими словами, ча-
частота появления события А стремится к вероятности р.
»Л1 СЛУЧАЙНАЯ ВЕЛИЧИНА ' . 603
Неравенство C4) можно написать в виде
Если положить
¦у) = ;
то вероятность того, что неравенство C4) будет удовлетворяться, стре-
стремится к Ф(Х) при условии, что п бесконечно возрастает, т. е. к
ф
При любом заданном т; можно всегда выбрать п достаточно большим,
чтобы эта величина была сколь угодно близка к единице. Следовательно.
вероятность того, что — стремится к р при бесконечно возрастающем п,
стремится к единице. Возьмем например, р =^ = 0,5. Из таблиц функции Ф(?)
находим, что если п > 7,6 • 10б, то вероятность того,, что — отличается от р
меньше, чем на 10 , больше, чем 1 — 10 .
9.1.15. Замечания о переходе от биномиального закона распределе-
распределения к нормальному. Вернемся к рассмотрению условий, позволяющих за-
заменить биномиальный закон распределения, представленный формулами B1)
или B6), нормальным законом, определяемым формулой C1).
При этом переходе мы допускаем несколько ошибок, а именно:
1) при замене истинного значения факториала его приближенным зна-
значением по формуле Стирлинга (при переходе от формулы B6) к формуле B7));
2) за счет пренебрежения бесконечно малыми высшего порядка при пере-
переходе от формулы B7) к формуле B8) или к формуле C1);
3) при замене дискретной случайной величины непрерывной.
Можно показать, что основная часть этих ошибок пропорциональна
, , если р отлично от о, и пропорционально , если р равно q.
у npq пРЧ '
Если п не слишком велико, а р близко к q, то кривая, представляющая
нормальный закон распределения.'пройдет очень близко от точек, изображаю-
изображающих биномиальный закон, кроме случаев очень больших значений отклонения.
Рассмотрим, например, случай п = 30, а р ='-=- (см. схему на рис. 9.5.
..^таблицу в примере п. 9.1.11). Ординаты при этом были вычислены по
биномиальному закону. Сравним их значения со значениями, полученными
по формуле B8).
При малом отклонении х =1 имеем
Р30A1) = 0,1396 (биномиальный закон),
Р30A1) = 0,1389 (нормальный закон);
ошибка составляет 0,5%.
При большом отклонении х = 7 имеем
Р30E) = 0,002634 (биномиальный закон),
Pw E) = 0,004970 (нормальный закон);
ошибка составляет 88%.
Если исследователь-статистик не располагает статистическими таблицами,
содержащими очень большое количество результатов измерений, ему следует
с большой осторожностью пользоваться нормальным законом распределения
604 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
и только для малых значений отклонений в случае, когда вероятности р и д не
слишком отличаются друг от друга. Следует также помнить, что „хвосты"
кривой Гаусса, соответствующие большим отклонениям, вовсе не представляют
собой в этом случае биномиальный закон. Напротив, физик, который иссле-
исследует столкновения молекул или электронные флюктуации, будет все время
иметь дело с очень большими числами п и сможет всегда отождествлять би-
биномиальный закон распределения с нормальным законом, за исключением,
однако, случая очень малой вероятности р.
Действительно, рассмотрим случай, когда р значительно отличается от д.
При этом точки, изображающие биномиальный закон распределения, не на-
находятся на кривой Гаусса на любом участке этой кривой. Отличие будет
тем больше, чем больше -р будет отличаться от q и чем меньше будет п.
Однако, если даже п — большое число, нельзя отождествить оба эти закона
в случае крайне малой вероятности, как это встречается в физике.
Если, например, р — \0~6, а <7 = 0,999999, то пренебречь величи-
величиной —==г можно, только если п будет порядка 1012.
У npq
Полезно было бы" найти промежуточный закон распределения для слу-
случая очень малых вероятностей р. Конечно, закон этот должен приближаться
к нормальному закону распределения, если п бесконечно возрастает.
9.1.16. Закон распределения Пуассона. Пусть р — вероятность осуще-
осуществления события А. Предполагаем, что эта вероятность очень мала. Наиве-
роятнейшее число осуществлений события А равно, как мы уже видели,
пр -\- р или, приближенно, пр.
Биномиальный закон распределения
может быть написан, если положить а. = пр, в виде
или
Так как р очень мало, то следует принимать во внимание только
числа k, малые по сравне! ию с п.
Произведение A )(l )...(l ) весьма близко к еди-
единице. Это же относится к величине A -) . Величина 11 -| очень
\ л/ V п]
близка к е~а. Отсюда получаем формулу
=-(' -4)(> -4) • •• («-^)(« -тП' -i№-
р-пр (пп\
Pn(k)= /Г ¦ C5)
Эта формула представляет собой закон распределения Пуассона.
В случае, если п бесконечно возрастает, формула C5) имеет своим пре-
пределом нормальный закон распределения. Введя математическое ожидание
чисел k, можно написать эту формулу в виде
PnW = -^^-. C6)
9.1] . СЛУЧАЙНАЯ ВЕЛИЧИНА 605
9.1.17. Характеристическая функция и моменты закона распределе-
распределения Пуассона. Характеристическая функция равна, по определению,
<р@)=1.
Имеем
откуда <р' @) = jx, что было очевидно;
ср" (И) == _ xefu<p (и) + ~xjeiu<?' (и),
откуда <р"@) =— х — (хJ, или x2 = (xJ-f-*-
Дисперсия вычисляется как функция двух первых начальных моментов
по формуле A5):
Следовательно, среднее квадратическое отклонение о равно квадратному
корню из математического ожидания х.
Этот весьма существенный вывод можно получить и прямым путем,
исходя из определения дисперсии (формула A1)):
Раскрывая скобки, можно написать
откуда
D = o2 = x.
9.1.18. Приложение к задачам автоматической телефонии. Когда
абонент автоматической телефонной сети снимает трубку, то через какое-то
время — обычно довольно короткое — гудок указывает ему момент, когда
он может набрать нужный номер: он оказался соединенным с коммутатором.
Очевидно, идеальным было бы снабдить каждого абонента коммутатором.
Но такое решение было бы весьма неэкономичным по причине высокой
стоимости коммутаторов, а также потому, что они бы очень плохо исполь-
использовались, простаивая без дела большую часть времени. Поэтому каждого
абонента снабжают (например, в системе Строуджера) искателем, назначение
которого — отыскивать свободный коммутатор, так как число коммутаторов
гораздо меньше, чем число абонентов в группе. В действительности имеет
место двойной поиск, но для упрощения мы ограничимся простым. Если все
коммутаторы, обслуживающие группу абонентов, заняты уже начатыми ранее
разговорами, искатель продолжает вращаться до тех пор, пока не заканчи-
заканчивается один из разговоров, после чего абонент соединяется с требуемым
номером. Здесь основным является следующий вопрос: если в распоряжение
группы, состоящей из а абонентов, предоставлены s коммутаторов (s<^_a),
то какова вероятность того, что один из абонентов найдет все коммутаторы
занятыми; если это произошло, то какова вероятность того, что время
606 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
ожидания освобождения какого-либо коммутатора будет не больше заданного
значения т. Пусть у — среднее число вызовов за единицу времени в группе
из а абонентов. Это означает, что есчи N— число вызовов за длительный
промежуток времени Т, то отношение -~- при бесконечно возрастающих N
и Т стремится к у. Пусть 6 — небольшой отрезок промежутка 7\ Примем
Тогда вероятность того, что любой вызов произойдет в промежуток времени 9,
1
равна —.
Найдем вероятность того, что определенные п вызовов, отобранных
из N, произойдут за время 0. Эта вероятность равна
Вероятность Рп того, что за время 9 произойдет п любых вызовов, отоб-
отобранных из N, больше в С% раз:
^п~ n\{N — n)l [a j \ a)
Заменим ЛП и (N — л)! их приближенными значениями по формуле
Стирлинга. Если N бесконечно возрастает вместе с Т так, что отношение
N N о о'
-у стремится к у, то отношение— стремится к у9, где уб — среднее число-
_ уу
вызовов за время 9, иначе говоря, п. Заменив — на у0 = п, получаем пре-
предыдущую формулу в окончательном виде
или
При бесконечно возрастающем iV имеем
n- n\N~"'¦
n n\
или
p
"~ n\
Видим, что вероятности Рп подчиняются закону распределения Пуассона.
Тот же закон распределеи-ия дает вероятность того, что состоится п одно-
одновременных разговоров одинаковой продолжительности 9. Действительно, эта
вероятность равна вероятиости того, что произойдет п вызовов за время 9.
Если продолжительность разговоров неодинакова, а именно имеется
в среднем уг разговоров продолжительности 9:, у2 — продолжительности 92
и т. д., то п одновременных разговоров могут состоять из щ разговоров
первого рода, п^ второго рода и т. д, причем
9.1J СЛУЧАЙНАЯ ВЕЛИЧИНА 607
Легко показать, что формула, представляющая вероятность Рп, останется
справедливой, если положить
Если взять за единицу времени среднюю продолжительность 0 разгово-
разговоров, то формула для вероятности Рп принимает вид
л -у
Р —Уе
В дальнейших расчетах мы примем эту среднюю продолжительность 0 за
единицу времени.
Необходимо принять гипотезу о законе распределения продолжитель-
продолжительностей разговоров. Это не нормальный закон. Действительно, на основании
нормального закона получилась бы вероятность, не равная нулю для отри-
отрицательных продолжительностей разговоров. Кроме того, статистическая про-
проверка показывает, что этот закон очень несимметричен, так как коротких
разговоров бывает гораздо больше, чем длинных.
Пусть Р (t)—вероятность того, что разговор продолжается меньше t.
Вероятность того, что разговор длится больше t, будет 1—Pit). Вероят-
Вероятность того, что разговор, длящийся уже время t, закончится между t и t-\~dt,
равна отношению числа благоприятных случаев к числу возможных, т. е-
Р' (t) dt
Логично сделать предположение, что эта вероятность не зависит от t.
Тогда
Следовательно, вероятность того, что разговор, длящийся уже время t, за-
закончится между t и dt, равна dt. Эти гипотезы о продолжительности раз-
разговоров и сделанное из них заключение используются в приводимом ниже
расчете.
Пусть имеется группа, состоящая из а абонентов, располагающих $•
коммутаторами. Найдем вероятность того, что в момент t имеется i заня-
занятых коммутаторов. Обозначим эту" вероятность через Pt. Это событие (за-
(занятость i коммутаторов в момент /) может произойти следующим образом.
Предположим, что в момент t — dt имеется t занятых коммутаторов
(вероятность Pj). В момент t их все еще будет' I, если только не произошло
вьщова (вероятность у dt) или если какой-нибудь коммутатор не освободился-
(вероятность i dt). При нашей гипотезе это единственно возможные случаи,
если пренебречь вероятностями, имеющими порядок малости выше первого:
(dff, (dtK, ... Действительно, вероятность того, что произойдет а вызовов,
равна (ydtf, а вероятность того, что освободятся р коммутаторов, равна
i(l—1) ... (/ — $-{-l)(dt). Следовательно, общая вероятность того, что
число занятых коммутаторов не меняется за время dt, равна
ЯД1 —ydt — idt).
Это же событие может произойти еще двумя способами:
1. Если число коммутаторов, занятых в момент t — dt, равно /—X
(вероятность Pt_{), то в момент t их будет i, если произойдет вызов за
время dt (вероятность ydt). Это единственный случай, если пренебречь,
величинами порядка выше dt. Следовательно, общая вероятность будет
608 ТЕОРИЯ ВЕРОЯТНОСТЕЙ (ГЛ. IX
2. Если число занятых коммутаторов в момент t — dt равно l~\~l (ве-
(вероятность Pi+i), то в момент t их будет I, если один коммутатор освобо-
освободится (вероятность (t-\-l)dt). Это также единственно возможный случай,
если пренебречь величинами порядка выше dt. Следовательно, общая веро-
вероятность будет
Pt+1(t-\-l)dt.
Все другие варианты, при которых происходит переход от числа j
коммутаторов, занятых в момент t — dt, к числу i коммутаторов, занятых
в момент t, причем i и j отличаются больше, чем на одну единицу, приводят
к вероятностям, которые имеют величины порядка более высокого, чем dt.
Ограничиваясь бесконечно малыми первого порядка, можем написать
или
Так как число занятых коммутаторов не может быть отрицательным,
то первое уравнение (i = 0) имеет вид
Таким образом, получаем систему уравнений
Если заменить /-е уравнение суммой первых i уравнений, то система упро-
упростится и примет вид
Решая эту систему, можем выразить все Pt через Ро:
р „р р У__ р р _У_ р р У__ р
*1 — УмI *2— 2! °* *'"' '— И ° s — ТГ °*
Предполагаем, что у нас нет ожидающего устройства, тогда единственно
возможные случаи это — занятость 0, 1, 2, ..., s коммутаторов. При этом
Если положить
1 , , У , Уг , , Vs '
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 609
ТО
Р = D^-
s si
Эти формулы называются формулами Эрланга. Так как Ps — вероятность
того, что абонент найдет все коммутаторы уже занятыми, то в среднем
имеется yPs напрасных вызовов.
Положим теперь, что имеется ожидающее устройство. При этом пусть
Pj — вероятность того, что накопилось j вызовов в ожидании. Вычисление,
аналогичное вычислению Pt, дает, если опять пренебречь бесконечно малыми
порядка выше первого:
Индекс J в действительности не может возрастать до бесконечности;
его наибольшее значение равно числу а абонентов. Вероятность Pq того,
что имеется нуль вызовов в ожидании, равна, очевидно, вероятности Ps того,
что все коммутаторы заняты. Сложив вероятности для всех возможных
случаев, имеем
' ' ... =1.
Если ввести в это равенство найденные выше значения Pt и Pj и восполь-
воспользоваться условием Po = />i, то получим
+*+ •¦¦+?)+'.?[*+¦¦• +(*)'+ ¦••]-'•
Сделаем предположение, что у < s, т. е. что среднее число вызовов
меньше числа коммутаторов. Тогда выражение в квадратных скобках во вто-
втором члене левой части представляет собой сумму членов бесконечно убы-
убывающей геометрической прогрессии, которая равна
s — у
Если положить
у'-1
д — ' -г-Ц -г-- • -г (s_iI-r s, s_y •
39 А. Анго
610 ' ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
то для Р2 и Pji получим
Я1 = АТГ'
\ У
s
Найдем вероятность того, что для некоторого абонента промежуток
времени ожидания освобождения коммутатора больше т. Примем гицотезу,
что вызовы в ожидании обслуживаются в порядке их поступления. Абонент
сможет набрать свой. номер, когда j разговоров будут закончены. Вероят-
Вероятность того, что за время х закончится ровно а разговоров, будет равна
Вероятность того, что закончилось любое число разговоров, меньшее или
равное j, будет
a! *
Следовательно, вероятность того, что время ожидания будет больше, чем х,
представится выражением
/=0 а=0
Подставляя выражение для Pj в написанную формулу, получаем
/=0 а=0
или, подробнее,
или, наконец,
1=0
Так как
i v \i
S (у\j— s (уV
в.IT СЛУЧАЙНАЯ ВЕЛИЧИНА 611
то формула приводится к виду
Итак, вероятность Р(х) равна
^х-> — s — y (s — 1)! a*
Поэтому средняя продолжительность ожидания (ее математическое ожидание)
равна
Числовой пример. Пусть имеется 5=10 коммутаторов в распо-
распоряжении группы абонентов, делающих в среднем 2 вызова в минуту. При
этом средняя продолжительность разговора равна 2 минутам.
Если принять 2 минуты за единицу времени, то мы получим в среднем
у = 4 вызова за единицу времени. Вероятность занятости i коммутаторов
будет
_. _у_, | у* | у' д
'"Г j, -Г ••¦ -Г (S_i)! f s! " s—y
Умножим числитель и знаменатель этого выражения на е~у и обозначим
через А(у; О величину
Л (у; 0==в-у^--
Выражение для Р{
р Л (у; 0
A(y;Q)+A(y;\)+ ...
можно легко вычислить с помощью таблицы для закона распределения
Пуассона. В выбранном нами примере получим
Л D; 0) = 0,0183; А (А; 4) = 0,1953; А (А; 8) = 0,0297;
• А (А; 1) = 0,0732; ЛD; 5) = 0.1562; А (А; 9) = 0.0132;
А (А; 2) = 0,1465; А (А; 6) = 0,1042; А (А; 10) = 0,0053.
Л D; 3) = 0,1953; А (А; 7) = 0,0595;
Отсюда
и, следовательно.
Р0 = 0,0183;
Р, = 0,0732;
Р2 = 0,1465;
Р3 = 0,1953;
Р =0,1953:
е-у
Д
р
Ря —
Р7 =
Ре =
Р9 =
0,1562;
0,1042;
0,0595;
0,0297;
0,0132;
в 1,
Р\
Р'2
1
= 0,0053;
= 0,0021;
= 0,0008;
= 0,0003;
39»
612 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Средняя продолжительность ожидания будет равна
^ = 0,0015.
Так как мы взяли единицу времени, равную 2 минутам, то
тт = 0,0015 • 2 • 60 = 0,18 сек.
9.1.19. Согласование наблюденных данных с теоретическим законом
распределения. Разложение в ряд Грама — Шарлье. Одним из основных
применений теории вероятностей для к®нтроля производственного процесса
является оценка расхождения между двумя законами распределения. Один
из них р(х) мы примем за теоретический, а другой закон q(x) будем ис-
исследовать. Обычно этот второй закон распределения является статисти-
статистическим. Нашей задачей является выяснение вопроса о том, согласуется ли
статистический закон распределения с данным теоретическим.
Закон р (х) всегда соответствует уже известному характеру совершения
событий. Если бы нам удалось найти степень общности между этими двумя
законами, мы смогли бы сделать заключения о скрытом еще от нас хар'ак-
тере явления, при котором возникновение событий подчиняется исследуемому
закону.
Если, например, q(x) представляет собой закон распределения измере-
измерений силы тока, возникающего при нагреве в водороде серии сопротивлений,
и если можно удовлетворительным образом связать закон q{x) с нормаль-
нормальным законом распределения, то от инженера, отвечающего за производство,
требуется только вести производство так, чтобы рассеивание и среднее зна-
значение х контролируемой величины оставались в пределах допусков.
Действительно, сродство с нормальным законом распределения укажет
ему, что величина х представляет собой случайную величину, и поэтому
рассеивание величины х вызывается не систематическим дефектом установки,
а лишь влиянием большого числа малых ошибок, действующих в любых
возможных направлениях.
Рассмотрим общий случай. Пусть q{x) — исследуемый закон, а р(х) —
теоретический. Положим
q(x)=p (х)-+-сс,р' (х)-j- . . . -+- а„р<"> (*). C7)
Если коэффициенты av ..., а„ малы, то закон р(х) хорошо представляет
закон q(x). Пусть ф(м) и ср(и) представляют собой соответственно характе-
характеристические функции законов q(x) и р{х). Положим
Тогда g @) = 1, так как коэффициент <х0 = 1.
Разложим g{u) по возрастающим степеням величины (— /и):
±^L = g{u)=l-aJu + ... +(-1)"а„G«/'+ ....
Тогда
eluxp(x)[\~ aju+ ... +(— 1)"а„ (-/«)"+ ¦ ¦ .\dx.
Интегрируя по частям общий член ряда, легко заметим, что
00 °О
J e'uxUu)np{x)dx = ~ f e>ux(Juf-xp'{.x)dx;
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 613
повторяя п раз интегрирование по частям, получим
со со
J «'«* Ju)" p (х)dx=(—l)" J е>их р(п)(х) dx,
— СО —СО '
отхуда
Так как, по определению,
со
ф С«)= / eiuxq{x)dx,
видим, что а.п = ап. Коэффициенты разложения в формуле C7) выражены,
таким образом, через коэффициенты разложения g(u) — отношения двух ха-
характеристических функций — по возрастающим степеням (—ju):
±^.= V-alju-\- ... -f(-l)» «„(/«)" + ...
Пусть хг и Хг — моменты порядка г соответственно для законов рас-
распределения q (х) и р (х). Тогда следует сначала выбрать закон р{х) таким
образом, чтобы математические ожидания х и X совпадали. Если отнести
оба закона к этому общему математическому ожиданию, то
Х = х=0.
Кроме того, нужно выбрать закон р(х) таким образом, чтобы для него
дисперсия совпадала с дисперсией для закона q(x):
Действительно, если это окажется невозможным, то сравнение q(x)
и р(х) будет бесполезным. Считая эти условия выполненными, можем на-
написать
д4 | .
=1 уц | д |
откуда получаем коэффициенты
а, = 0, а2 = 0,
<x5 = — ~ I*5 -Xs—\Ox2(л;3 — A'3)].
614 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
9.1.20. Частный случай нормального закона распределения. Очень
важным является частный случай, когда теоретическим законом р(х), с ко-
которым сравнивается экспериментальный закон q(x), является нормальный
закон распределения
Совмещаем математические ожидания обоих законов распределения:
Берем
Будем иметь последовательно <
откуда для коэффициентов at получим
Положим, с другой стороны, <зу = х. Нормальный закон приобретает
вид
1 «?
Вычислим последовательные производные:
(У) ==-^ (-!«№,
у /к
где Нп(у) означает полином Эрмита п-го порядка (см. п. 7.8.2).
Разложение q(x) принимает вид
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 615
где _ _ _
v-3 v-5 V*3
о ¦* о — „ 1 О —
Р-1 —— —г" | Ре; —— ~ i W —5^ »
Го -j3 ГО до -j3
Р4 = ^-3. р6 = ^-15^Н-30и т. д.
Это выражение называется рядом Грама— Шарлье.
Можно производить вычисленля и прямым способом, пользуясь свойством
ортогональности полиномов Эрмита.
Пусть
Мы видели, что если
1
р (у) — ,— е 2 ,
ТО
=(\)Hi(y)e.
Умножим обе части ряда на Ht(y) и проинтегрируем от —оо до оо.
Все интегралы в правой части будут равны нулю, за исключением интеграла,
имеющего сомножителем коэффициент at и равного (—l/г! (п. 7.8.3). По-
Поэтому
Отсюда получаем разложение в ряд Грама — Шарлье с прямым вычислением
коэффициентов ф(:
Мы снова получили уже известные результаты.
Ошибки измерений и способ наименьших квадратов
9.1.21. Ошибки измерений и нормальный закон распределения. Из-
Измерения всегда сопровождаются ошибками. Различают ошибки двух основных
видов: систематические и случайные. Систематические ошибки имеют опре-
определенные причины, которые искажают измерение всегда в одном направлении
и часто на постоянную величину. Они возникают за счет неисправности или
плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого
выполнения технологии и т. д. Во многих случаях можно найти причины
таких ошибок и устранить их.
616 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Случайные ошибки неопределенны, и причина их неизвестна. Свое не-
незнание причины ошибок мы обычно маскируем, говоря, что их порождает
случай. А это просто означает, что их можно приписать большому коли-
количеству причин, действующих в любом направлении и создающих каждая
свою погрешность. Такие случайные ошибки можно учитывать статисти-
статистическими методами.
Существует еще одна категория ошибок, о которой будет кратко ска-
сказано в п. 9.1.27; это категория отдельных промахов, происходящих по
однократной вине экспериментатора, например, если он по рассеянности один
раз неправильно считает показания со шкалы измерительного прибора. В этом
случае мы имеем дело с анормальным результатом измерения. Существует
простое правило, позволяющее исключить из таблицы результатов измерений
ошибки этой категории.
Мы займемся в основном категорией случайных ошибок. Допустим, что
имеется несколько в одинаковой степени надежных измерений физической*
величины, истинное значение которой равно X. Ошибки, соответствующие
измерениям Xv Х2 Xt Хп, будут равны
ATj = .A j — Xt х^ =z X2 — X, ¦ ¦ •, Х[ = Xi — X хп = Xп — X•
Это чисто случайные ошибки.
Мы не знаем точного значения величины ^ и не можем определить ее
на опыте, так как всякое измерение, сделанное для ее определения, иска-
искажается ошибкой. Обозначим через X наиболее вероятное значение вели-
величины X *).
Рассмотрим величины
Величины yv .... У; уп называются отклонениями. Так как речь здесь
идет только о случайных ошибках, то величины х и у могут быть и поло-
положительными, и отрицательными, а малые значения будут встречаться чаще,
чем большие. Примем допущение, что эти величины следуют нормальному
закону распределения
р(х) = — Xj^e~^.
а V 2-х
Положим
h2 L
" ~ 2а2 '
где А, как известно, называется мерой точности. При этом р(х) примет вид
где р(х) — относительное число ошибок, равных х.
Вычертим кривые Гаусса при двух различных значениях меры точ-
точности h. Легко заметить, что чем больше к, тем кривые острее, тем круче
их склоны. Это означает, что чем больше параметр /г, тем реже встречаются
большие ошибки. Поэтому величину h и называют мерой точности.
*) Приближенные значения параметров, характеризующих распределение случайных
величин, называются их оценками. Оценка называется несмещенной, если ее матема-
математическое ожидание равно математическому ожиданию исследуемой случайной ве-
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 617
Вероятность того, что ошибка будет заключаться между ±а, равна
а
1h
2^_ Г е_кгх, ах==ф (Aa)_
9.1.22. Способ наименьших квадратов. Пусть произведено п измере-
измерений величины X, величины xv х2, • ••> хп представляют собой соответ-
соответствующие ошибки.. Вероятность того, что ошибка х заключена между xt
и xl-\-dxi, равна
h -п2х2,
e '
'dxt.
Вероятность того, что при п измерениях допущено п ошибок, имеющих ве-
величины xv x2 хп соответственно, поскольку речь идет о независимых
событиях, равна
ТХ j / h \я -l?(x\+xt+ ... +х2„) , , ,пп
ПА |=:GГ) е n'dxx...dxn. C8)
Максимум произведения р1р2 • • - рп будет соответствовать минимуму
суммы
\ 2+ 2
Этот вывод известен под названием принципа наименьших квадратов. Он
означает, что наиболее вероятное значение величины X, полученное в ре-
результате я равноточных измерений, обращает в минимум сумму квадратов
ошибок.
Наиболее вероятное значение X, которое должно обеспечить минимум
суммы
2
равно
Х~ = xJ+x*+n-- +хп. C9)
Это наиболее вероятное значение X есть среднее арифметическое из всех
результатов измерений. Таким образом, оправдывается используемое для него
обозначение *).
Можно без труда подвергнуть критике рассуждения, связывающие прин-
принцип наименьших квадратов с нормальным законом Гаусса. Мы не станем
здесь останавливаться на этом довольно тонком вопросе и отошлем читателя
к специальной литературе ') **).
9.1.23. Линейная комбинация ошибок. Рассмотрим случайные перемен-
переменные xv x2, ..-, хп, подчиняющиеся нормальному закону распределения. Их
средние квадратические ошибки равны соответственно av ^ о„- Составим
*) Среднее арифметическое значение X представляет собой несмещенную оценку
математического ожидания случайной величины X.
') См. .Трактат по теории вероятностей" под ред. Э. Бореля, т. 1, раздел
.Ошибки и наименьшие квадраты" Р. Дельтейля, стр. 56, и др.
**) В советской литературе обоснование и сущность способа наименьших квад-
квадратов изложены в ряде работ, см., например, Ю. В. Л и н н и к, Метод наименьших
квадратов и основы теории обработки наблюдений, Физматгиз, 1962.
618 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
комбинацию XjXj. Эта переменная будет следовать нормальному закону рас-
распределения, средняя квадратическая ошиб.ка которого равна X]Olt а харак-
характеристическая функция выражается формулой
-\ А°\"\ D0)
Составим линейную комбинацию
* = *•!*!-Г •¦• -bV^-b ••• ~\-КХп'
Характеристическая функция закона, которому следует случайная величина х,
будет равна произведению функций, подобных D0), как это видно из фор-
формулы B0), иначе говоря,
и2 /,2 2 ,2 2\
Следовательно, х следует нормальному закону распределения со средней
квадратической ошибкой
Если перейти теперь к мере точности, то
1* *?'
9.1.24. Точность группы измерений. Если произведена группа п изме-
измерений Xt, то очень важно уметь определить величину, которая позволила бы
охарактеризовать ожидаемую точность результата или, что то же самое,
найти приближенное значение ошибки этого результата.
Итак, пусть
xt = Xt — X
есть ошибка /-го измерения. Если сложить все ошибки, то результат деле-
деления на п даст
Это уравнение с учетом формулы C9) принимает вид
Значит, выражения для отклонений у( могут быть написаны в виде
Поэтому п соотношений для у( запишутся следующим образом:
__ гс—1 1_ 1_ _ _1_
У\~ п xi n x<i n Хз ¦¦• п Хп<
п—\ 1
D2)
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 619
Итак, отклонения представляют собой линейные комбинации ошибок. Следо-
Следовательно, в силу формулы D1), отклонения подчиняются нормальному закону
распределения с мерой точности k, определяемой соотношением
1 1 Г/П_П2 1 , 1
откуда
? = л|/"-^ГТ- D3)
9.1.25. Наивероятнейшее значение меры точности. Если дана сово-
совокупность п измерений Xt, искаженных ошибками xt, то наиболее вероятное
значение величины h должно, в силу формулы C8), обратить в максимум
веЛичину
nXnh—tit^x].
Поэтому наиболее вероятное значение т; величины h должно обратить в нуль
производную этого выражения, откуда следует
Таким образом, нормальный закон распределения полностью определен.
Точность совокупности п измерений определяется одной из следующих трех
величин.
1. Средняя арифметическая ошибка:
Приближенное значение величины вт равно
2. Средняя квадратическая ошибка;
^ " *
I X I
D4.)
3. Срединная ошибка (вероятная ошибка, медианная ошибка). Это такая
ошибка, которая с одинаковой вероятностью может быть как превзойдена,
т,ак и не достигнута. Это определение выражается равенством
р, = 0.5.
откуда
р ^ = ±, где Р = 0,476936...
Все три величины ет, г„, е„ связаны между собой соотношениями:
ер = р УТ е, = 0,6745 ев. ер = р |ЛГ гт = 0.8453 ет,
ет= 1,1829^, = 0,7979 е0>
%= 1,4826 ер=1.2533 ет.
Геометрический смысл этих величин очень прост: ер — это абсцисса прямой,
параллельной оси Оу и разделяющей площадь А, заключенную между осями
координат и кривой Гаусса при х^-0, на две равные части; еш — абсцисса
620 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
центра тяжести этой площади; е, — радиус инерции площади А или абсцисса
точки перегиба кривой Гаусса.
Величины ер, ет, eJ изображены на рис. 9.6. Любая из них может слу-
служить для характеристики точности группы опытов. Удобно определять е3
и ер на основании величины гт, которую легко вычислять. Чаще других
пользуются величиной sp по той простой причине, что она меньше двух
других *).
Величины ет, е„, ер легко получить как функции отклонений yt. На осно-
основании системы уравнений D2) и формулы D3) получим
D7)
= 0,6745
Формулы D6) и D7) более удобны, чем формулы D4) и D5); они вы-
выражают ошибки е как функции отклонений у(, так как у1 — это известные
из опыта величины, чего нельзя сказать об истинных ошибках х(. Однако
практически даже при малых значениях п (порядка десяти) между этими
двумя группами формул большой разницы нет.
Наиболее вероятное или среднее арифметическое значение следует нор-
нормальному закону распределения с мерой точности, определяемой форму-
формулой D1), где \ ——. Следовательно, эта мера точности равна
она изменяется пропорционально квадратному корню из числа измерений.
Казалось бы, что, увеличивая число измерений, можно до бесконечности
увеличивать точность. Однако если теоретически можно получить еще одну
значащую цифру, перейдя от одного единственного измерения к 100 изме-
измерениям, или от группы в 10 измерений к 1000 измерениям, то практически
получение такого выигрыша весьма сомнительно. Действительно, следует
опасаться, что при тысячном измерении измеряемая физическая величина
будет уже не совсем та, что вначале. Другими словами, в условиях опыта
могут иметь место небольшие изменения, которые воздействуют на резуль-
результат неслучайным образом **). Это более чем вероятно, так как серия
в 1000 измерений должна продолжаться значительное время. Поэтому не
принято делать большие серии измерений и число п редко бывает больше 10.
Все сказанное хорошо согласуется с простым здравым смыслом. Лучше
усовершенствовать экспериментальный метод, чем увеличивать число измере-
измерений; 10 хороших измерений полезнее, чем 1000 посредственных.
9.1.26. „Вес" наблюдения. В некоторых случаях мы бываем вынуждены
пользоваться сериями наблюдений различного происхождения. Они могут быть
получены разными, не одинаково умелыми экспериментаторами, или методами,
имеющими различную точность, или в разное, не одинаково благоприятное
время. Для учета характера этих различных источников придают больший
*) Термин .срединная ошибка' имеет тот смысл, что при большом числе опы-
опытов в среднем половина значений случайной величины X будет отклоняться от X
меньше, чем ча гр, а половина больше.
**) Так называемое „сползание центра рассеивания".
9.1] СЛУЧАЙНАЯ ВЕЛИЧИНА 621
„вес" одним из них перед другими. Чтобы правильно оценить преимущество
более точных наблюдений, полученный из опыта результат умножают на коэф-
коэффициент, который должен быть тем больше, чем больше „вес" этого наблю-
наблюдения. Естественно, что знаменатель формулы для вычисления среднего зна-
значения будет суммой всех „весов".
Пусть ш1 — „вес" наблюдения Хг Тогда формула для среднего или
наиболее вероятного значения примет вид
Формулы D4) — D7) должны быть соответственно изменены.
Понятие „веса" фигурирует особенно часто в астрономии, где прихо-
приходится пользоваться измерениями, выполненными в различных пунктах и при
различных обстоятельствах. В электротехнике этим понятием пользуются
мало, и мы не будем здесь на нем останавливаться.
9.1.27. Критерий ошибочного наблюдения. Предположим, что во время
опытов наблюдатель совершает ошибку, обычно по рассеянности. Каким
образом в таблице измерений, где фигурирует п результатов наблюдений,
распознать неверный результат? Здесь можно применить следующее полезное
эмпирическое правило. Нужно вычислить отклонения от среднего значения,
соответствующие группе интересующих нас наблюдений. Если какое-либо из
отклонений превзойдет срединную ошибку более чем в 5 раз, то соответ-
соответствующее наблюдение следует отбросить. При этом срединная ошибка вы-
вычисляется без учета измерения, подвергнутого сомнению. Действительно,
пусть х — соответствующая ошибка. Отождествим ее с отклонением от сред-
среднего значения. Если она в 5 раз больше срединной ошибки, то
tjjc^ 2,327,
потому что
т;е„ = 0,4769.
Но
Ф B,327)= 0,999.
Следовательно, вероятность такой большой ошибки равна 0,001. Такой
сомнительный результат следует отбросить.
9.1.28. Срединная (вероятная) ошибка функции. Пусть даны X.Y, ... —
средние значения результатов измерений некоторых физических величин
X, Y, ... и ех, еу, ...—соответствующие срединные ошибки. Срединная
ошибка е функции
f(X, Y, ...)
будет, очевидно, равна
~dY ' " ' *
9.1.29. Эмпирические формулы. Пусть z — физическая величина, за-
зависящая от другой величины х. Изобразим в плоскости xOz точки, пред-
представляющие собой пары значений xt, zt, соответствующие некоторой таблице
измерений. Если эти точки расположены достаточно близко одна от другой,
то через них можно провести непрерывную кривую, представляющую экспе-
экспериментальную функцию
622 ТЕОРИЯ ВЕРОЯТНОСТЕЙ (ГЛ. IX
Часто задача состоит в том, чтобы придать функции f (х) аналитиче-
аналитическую форму. Во многих случаях для этой цели выбирают полином вида
A-\-Bx-\-Cx2~yDx3-\- ...
или показательную функцию
Выбор этот в большинстве случаев диктуется теоретическими соображениями
и тесно связан с измеряемым явлением. Мы не будем здесь рассматривать
вопрос о выборе вида функции.
Пусть, например, измеряется ток насыщения z диода как функция абсо-
абсолютной температуры х катода. Из теоретических соображений следует, что
этот ток, отнесенный к единице поверхности катода, связан с абсолютной
температурой зависимостью
в_
z = Ах2е~~.
После того как аналитическая форма функции выбрана, остается определить
наиболее подходящие значения параметров функции с помощью таблицы
результатов произведенных измерений.
Разберем сначала случай, когда выбранная функция представляет собой
полином. Эта задача решается очень просто элементарным методом, дающим
превосходные" практические результаты. Пусть п — количество измерений
xt, zt, а т — степень полинома. Таблица измерений позволяет получить п
линейных уравнений с т-\- 1 неизвестными, которыми являются коэффи-
коэффициенты А, В, ... Предположим, что т < п.
В большинстве случаев число п. гораздо больше, чем т-\-\, так что
количество уравнений больше количества неизвестных. Предположим, что
оно равно 7(/»-j-l). Тогда п измерений делят на /га-j-l группу по 7 изме-
измерений в каждой. Затем 7 уравнений каждой группы складывают и получают,
таким образом, тя-j-l линейных уравнений с /я—(-1 неизвестными, которые
можно решать обычным способом. Существенное возражение против этого
простейшего метода состоит в том, что существует С„ способов группиро-
группирования п уравнений в т-\- 1 группу по 7. Это возражение, теоретически
значительное, не имеет значения на практике, так как результаты, которые
можно получить при различном группировании уравнений, очень мало отли-
отличаются друг от друга.
Рассмотрим общий случай. Пусть выражение
z = f(x, А, В, С, ...)
представляет собой аналитическую форму выбранной эмпирической зависи-
зависимости. Число т неизвестных постоянных меньше числа п сделанных изме-
измерений. Предположим, что постоянные определены. Тогда должно существо-
существовать отклонение yt измеренной величины zt от величины z\ = f (xr А, В, С, .. А,
вычисленной при найденных значениях постоянных
причем принцип наименьших квадратов требует, чтобы выражение
11 У? D8)
было наименьшим.
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 623
Предположим, что методом эмпирического подбора или путем замеров
на экспериментальной кривой z = f(x) нам удалось найти более или менее
удовлетворительные значения Ао, Во, ... Мы можем воспользоваться спо-
способом наименьших квадратов для нахождения малых величин а, р, ...,
на которые отличаются наивероятнейшие значения постоянных А, В, ...
от их ориентировочных -значений Ао, Во, ... :
Если пренебречь частными производными высших порядков, то разность
/(*,. А, В, С, ...)=г, —3>i
f запишется в виде
(*. А0, Во, ...) + аД-+^+...Ц=г/-У, D9)
Если обозначить
zl — f(xl, Ао, Во. ...) = ?|.
то уравнение D9) принимает вид
Х,а + |*гР+ ••• — Фг-г-Уг = 0-
Для выражения D8) будем иметь
2((гц,рг- ••• — ?*J- E0)
Условие минимума этой суммы можно получить, приравняв нулю частные
производные выражения E0), взятые по а, р, ... При этом получим систему
уравнений
n
S
E1)
• Уравнения E1) называются нормальными. Число их равно числу неиз-
неизвестных a, p которые можно из этих уравнений определить.
9.2. ПОНЯТИЕ СЛУЧАЙНОЙ ФУНКЦИИ ') *)
9.2.1. Введение понятия случайной функции на конкретном при-
примере. Мы уже ознакомились с понятием случайной величины. Вернемся
к нему для того, чтобы лучше уяснить себе, что такое случайная функция.
') Раздел, посвященный случайным функциям, был отредактирован Андре Блан-
Лапьерром. Для более подробного ознакомления читатель может обратиться к книге
А. Блан-Лапьерра и Форте «Теория случайных функций. Приложения к различным
явлениям флуктуации", изданной в Собрании математических трудов для физиков"под
редакцией Г. Дармуа.
*) По теории случайных функций имеется ряд трудов советских авторов. Основ-
Основные из них приведены в конце главы в списке литературы.
624 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Будем исходить из классического примера игры в кости. Рассмотрим неко-
некоторую категорию испытаний С, которая представляет собой совокупность
следующих испытаний. В пакет кладут кость и после встряхивания выбра-
выбрасывают кость на стол. После этого отсчитывают цифру на верхней грани.
Результат каждого опыта — некоторое положение кости на столе. Это поло-
положение определяет численное значение X— цифру на верхней грани. X —
есть случайная величина, определенная по категории испытаний С. Случай-
Случайная величина, определенная по известной категории испытаний С,
представляет собой численную переменную X, значение которой
определяется результатом R каждого испытания. Определяя вероят-
вероятность по категории испытаний С, имеют в виду вероятность F (х0) того,
что результат индивидуального испытания приводит к численному значению
X < х0. Эта функция F представляет собой функцию распределения.случай-
распределения.случайной величины X по категории испытаний С.
В предыдущем примере мы поставили в соответствие с результатом R
испытания некоторое число. Но можно было бы поставить в соответствие
с ним математическую категорию любой природы, в частности некоторую
функцию. Например, условимся ставить в соответствие каждому значению Х:
случайной величины X, рассмотренной выше, функцию х времени t, опре-
определяемую выражением х(()=Хг(. Тогда результат каждого испытания опре-
определит некоторую функцию времени в интервале —со < t < -|- со. Обобщая
предыдущее определение, можно сказать, что x(t) — это случайная функ-
функция времени по категории испытаний С. Случайная функция по из-
известной категории испытаний С—это функция известного параметра t,
полностью определяемая результатом каждого испытания.
В нашем элементарном изложении будут рассматриваться только слу-
случайные функции с вещественными значениями. Конечно, вовсе не обязательно,
чтобы параметр t мог меняться от —со до -f-oo. Случайная функция вели-
величины t может быть определена только для некоторых значений t (например,
только в интервале a k^t ^.b или только для целых значений t). С другой
стороны, категории испытаний в большинстве случаев неизмеримо более
сложны, чем те, которые здесь рассматривались. В частности, число воз-
возможных результатов может быть бесконечным и даже следовать из беско-
бесконечного числа осуществленных результатов Rv R2, .... полученных для
бесконечного количества категорий испытаний Cv С2, ...
Приведенный пример случайной функции имеет то преимущество, что
он прост, но в то же время он слишком прост и не позволяет сделать
далеко идущих выводов. Рассмотренная выше схема допускает лишь очень
ограниченное вмешательство случайности, так как случайная природа функ-
функции проявляется лишь через величину Xv В частности, знание значения х
для какого-либо / ф О ведет за собой знание х для всех значений t. Оче-
Очевидно, что столь узкие рамки оставляют слишком мало возможностей для
проявления случайной природы таких резко изменчивых и непостоянных
явлений, как турбулентность жидкости или флуктуации электрических на-
напряжений, происходящие за счет шумового фона.
Возьмем другой пример. Рассмотрим частицу, способную перемещаться
по оси Ох и находящуюся в начале координат при t = Q. Предположим,
что скорость этой частицы может принимать значения только +1 или —1
и меняется только в моменты 0, 1, 2, 3 где она каждый раз с рав-
равными вероятностями может принять значение -\-\ или —1. Другими сло-
словами, в промежутке времени га < ? .< га-j-1 (п равно либо целому положи-
положительному числу, либо нулю) скорость представляет собой случайную
переменную va, которая с одинаковой вероятностью может принимать зна-
9.2]
СЛУЧАЙНАЯ ФУНКЦИЯ
625
чения +1 или —1. Кроме того, случайные переменные v0, vv .... vn, ...
независимы. Обозначим теперь через x{t) абсциссу частицы в момент t.
Можно составить себе представление о свойствах случайной функции х (t)
по рис. 9.7, где изображена частная реализация функции х (t). Здесь одно-
одновременно изображены и случайные значения членов последовательности
v0, vx vn и реализация функции х (t), полученная на основании
этой последовательности. Такой способ приводит к последовательному со-
составлению функции x(t) и допускает вмешательство случайности, не огра-
ограниченное во времени. Каждая реализа-
реализация х@ зависит от результатов беско- v"
нечного числа последовательных испы- +1
•танйй
Конечно,
+1
О
-1
-3
-и
\
\
' с
А
1 4
\
\
\
7 t
ь
Рис. 9.7.
ничто не мешает рассматривать эту _^
бесконечную совокупность испытаний
как одно суммарное испытание $ из
некоторой категории испытаний &*. xft)
Тогда результат испытания $ будет
определять частную последовательность
скоростей vn, т. е. некоторую после-
последовательность чисел -\-\ и —1, че-
чередующихся в известном порядке. Рас-
Рассмотренная схема случайного явления —2
представляет собой частный случай
схемы, использованной при изучении
явления турбулентности.
Рассмотрим теперь пример, взятый
из электротехники. Здесь речь идет
о флуктуациях, вызванных чистым дро-
дробовым эффектом в линейных усилителях. Если свести эту задачу к наиболее
упрощенной схеме, то она будет выглядеть следующим образом. Дан линей-
линейный усилитель А{, для простоты полагаем, что он не передает постоянной
составляющей. Воздействуем на него постоянным током /. Следует ожидать,
что на выходе ток усилителя будет равен нулю. В первом приближении это
и наблюдается. Однако при более тонком исследовании можно заметить на
выходе усилителя напряжение шума, более или менее беспорядочное. Если
записать это напряжение, то получим некоторую кривую x = x((t), где t
обозначает время.
Проделаем тот же опыт не с одним усилителем, а с большим числом ')
усилителей Av Аг .... Л„. находящихся в одинаковых макроскопических
условиях. Получим кривые xl(t), x2(t) xn(t). Они не тождественны,
но исследователь легко обнаружит их сходство. Разница между ними вызы-
вызывается случайным характером флуктуации, которые неизбежно требуют ста-
статистического подхода. Предположим для простоты, что эти флуктуации
вызывает только электронная природа входного тока / (иными словами,
пренебрежем собственными флуктуациями усилителя, чтобы не отвлекать
внимания от флуктуации, вызванных входным током /). Влияние тока / на
усилитель есть результирующая влияний отдельных электронов, образующих
') Мы говорим о большом числе усилителей, потому что эксперимент не может
быть проведен с бесконечно большим числом приборов. Но мысленно мы полагаем,
что число это достаточно велико, чтобы дать достаточно точное представление о том,
что произошло бы при рассмотрении .всех возможных макроскопически подобных
усилителей*. Как раз на такой бесконечной совокупности (генеральной совокупности)
и основана статистика.
40 А, Анго
626 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
ток /. Каждый электрон создает импульс, который вызывает некоторое
возмущение в усилителе, и электрические явления, которые в нем проис-
происходят, подобны в совокупности движению маятника, возбуждаемого последо-
последовательными толчками. Не уточняя пока, скажем только, что усилитель под-
подвергается ряду одинаковых очень коротких и беспорядочных ударов. Каждый
из них соответствует импульсу, создаваемому одним электронным зарядом е;
среднее число импульсов в секунду будет равно ро= — • Действие тока /
будет совершенно определено, если будет из-
известна бесконечная последовательность момен-
моментов времени
l(t)dt'1
в которые действуют отдельные электроны.
Мы можем охарактеризовать линейный усили-
усилитель реакцией R (t), которая соответствует очень
короткому единичному импульсу (т. е. очень
быстрому прохождению единичного заряда),
полученному в момент времени ^ = 0. Реак-
Реакция R(t) называется ударным ответом усили-
усилителя (рис. 9.8). Очевидно, что ответ R(t)
тождественно равен нулю при t < 0, так как
следствие не может предшествовать причине.
.s Ответ на импульс, полученный в момент tj,
очевидно, равен eR (t — tj) и в конечном счете
х (t) представляется как наложение в момент t
ответов усилителя на все удары, предшество-
Рис. 9.8. вавшие моменту t. Можно, впрочем, распро-
распространить суммирование на все удары как пред-
предшествующие, так и следующие за t, так как последующие удары все равно
исключаются сами собой как следствие условия R(t — tj) = O при t <.tj.
Поэтому
= 2
t, <+оо
2
= 2 eR(t-tj)= 2 eR(t — tj). E2)
t<t t>CO
2
tj<t j
В этом примере случайность входит через свойства последовательностей
.... tj, tj+1, tj+2, ...
Существует столько же возможных случайных реализаций функции x(t),
сколько имеется таких последовательностей.
Так же, как и ранее, можно считать, что влияние случайности про-
проявляется в бесконечной последовательности элементарных испытаний, в каждой
из которых случайным образом определяется момент tj+v если все моменты
tj, tj_v tj_2, ... известны1). Можно также назвать испытанием совокуп-
совокупность всех значений частного распределения tj от t = — оо до t = -\-oo.
В рассмотренных до сих пор примерах мы прежде всего выясняли
схему случайной природы явления, порождающей случайную функцию. Кате-
Категория испытаний могла при этом быть более или менее сложной, но она
была вполне определенной. При различных применениях теории вероятностей
') Эта точка зрения устанавливает четкое различие между прошедшими опытами,
результаты которых известны в момент t, и будущими опытами, сохраняющими еще
все случайные возможности.
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 627
довольно часто употребляется понятие случайной функции при менее ясных
на первый взгляд обстоятельствах. Возьмем пример: известно, что под влия-
влиянием перемещений масс на поверхности Земли, о которых еще нет доста-
достаточных сведений, полюс Земли претерпевает небольшие перемещения. Зна-
Значения координат хг и уг полюса, выраженные в большинстве случаев
в секундах дуги, определяются по отношению к системе прямоугольных
осей, за начало которых принимается среднее положение полюса, а ось Xj
проходит через Гринвичский меридиан. Рассмотрим, например, координату х,.
Ее изменения во времени за последние десятилетия представлены кривой,
ход которой дан на рис. 9.9. Ход этой кривой достаточно' незакономерен,
чтобы навести на мысль о случайном характере явления, однако на первый
Рис. 9.9.
взгляд всякий вопрос о вероятности из этой задачи исключен. Значения xx(t)
нам становятся известны лишь по мере того, как производятся с течением
времени наблюдения. Конечно, мы не знаем будущего функции X[(t), но эта
функция единственна, так как во Вселенной имеется всего одна Земля.
Однако если имеется некоторая теория о природе масс, случайные переме-
перемещения которых порождают изменения в положении полюса, или если нами
приняты достаточно точные гипотезы об этих массах и их перемещениях,
то нам ничто не мешает мысленно рассматривать бесконечное количество
систем, макроскопически тождественных Земле и отличающихся друг от друга
только случайным различием поверхностных масс, перемещения которых
мы подчиним некоторым случайным схемам. При этом мы должны будем
считать, что наблюдаемая функция Xj (t) представляет собой лишь возмож-
возможную реализацию случайной функции х (t), определенной по категории испы-
испытаний, имеющей, так сказать, только мысленное существование. Такой спо-
способ рассуждений законен лишь в том случае, если у нас есть причины
считать, что мы сможем, исходя из статистических свойств случайной функ-
функции x{t), определенной по воображаемой категории испытаний, вывести
результаты, справедливые для дальнейшего хода частной реализации функ-
цци х (t) и, в частности, для хх (t). Тогда мы сможем увидеть, приводят ли
принятые гипотезы к результатам, которые подтверждаются опытом, и в бла-
благоприятных случаях сможем предвидеть в известной мере будущее функ-
функции Xj (t). По аналогии с уже рассмотренными примерами можно сказать,
что скорость ветра или температура воздуха — случайные функции времени
в некоторой определенной точке Земного шара.
9.2.2. Функции распределения. Изучение случайной величины показало,
что не всегда нужно полностью знать схему случайности и что если известна
функция распределения случайной величины, то с вероятностной точки зре-
зрения поведение этой переменной, взятой изолированно, также будет опре-
определено. Что можно сделать при аналогии применительно к случайной функ-
функции x(t)}
Преж'де всего рассмотрим фиксированное значение tv При этом x{t{)
есть случайная величина и естественно будет ввести ее функцию распреде-
распределения. Обозначим эту функцию F (xx; t{), имея в виду, что F представляет
40*
628
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. IX
собой вероятность осуществления события х(^) < xv Очевидно, что момент tt
не имеет никаких преимуществ перед другими, и, следовательно, мы прихо-
приходим к постановке того же вопроса для всех моментов t, иными словами,
пытаемся найти функцию распределения F(x; t) для всех моментов t.
Зная F(x; t), мы будем знать в каждый момент времени распределение
наблюдаемых значений. Этого, однако, недостаточно, чтобы получить полное
представление о поведении функции х (t) и, в частно-
частности, чтобы определить ее развитие во времени, что
ясно видно на следующем примере. Пусть ср — случайная
величина, которая с равной вероятностью может при-
принимать все значения в интервале [0, 2тс]. Каждому зна-
значению ср соответствует функция x(O = sin(u)? -(-ср), где
со —известная постоянная. Таким образом, определена
случайная функция по категории испытаний, соответ-
соответствующей всем возможным значениям ср. Можно без
труда получить функцию F (x; t). Она не зависит от t
и отвечает плотности вероятности
dF l E3)
dx
— X*
представленной на рис. 9.10х).
Введем теперь еще одну случайную функцию y(t),
определенную по той же категории испытаний, что и
раньше, и рассмотрим для любого значения ср следующую функцию, постоян-
постоянную при всех t:
у (t) = sin ср.
Функция распределения F(y; t), соответствующая y(t), тождественна
функции F(x; t), соответствующей x(t), однако обе случайные функции
х (t) и у (t) имеют очень мало сходства.
В частности, каждая реализация х (t)
представляет собой синусоиду, тогда как
каждая реализация y(t) — прямая, парал- х q
лельная оси времен. На рис. 9.11 приве- ^
дены кривые, представляющие функции \ / y(t)
х (t) и y(t) для некоторого значения а
<р(Оа = sincp).
Этот простой пример показывает, Рис. 9.11.
что недостаточно знать F (x; t), чтобы
охарактеризовать цепь значений, которые последовательно принимает х
с течением времени. Другими словами, знание функции F(x, t) не дает
связи между различными случайными значениями, которые принимает x(t)
в различные моменты времени. Мы вынуждены поставить вопрос: если (г
и t2— два любых частных значения, то каковы дблжны быть статистические
свойства совокупности двух случайных величин х (t{) и х (t2)? (Речь идет
\ ,
') Вероятность AF того, что значение х (?,) заключается между лг, и лг, -f- Длг],
равна вероятности того, что значение ф заключается между arcsin лг, — Ы и
arcsin (лг, -f- &х) — <»t. Вследствие того, что случайная величина ф равномерно распре-
распределена между 0 и 2тс, вероятность &F равна
— [arcsin (л:, -{- Длг,)
dF
arcsin
AF dF
Отсюда находим -т—, а в пределе —г- при х = хг
HXi ИХ
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 629
в большинстве случаев о случайных величинах, связанных между собой
вследствие наличия некоторой непрерывности явлений во времени.) Мы узнаем
статистические свойства двух связанных между собой величин x{tx) и x(t2),
если нам станет известна функция распределения F(xv х2; tv t2), соответ-
соответствующая совокупности этих двух случайных величин.
Напоминаем, что функция F(xv x2; ty, t2) представляет собой вероят-
вероятность одновременного осуществления неравенств:
х (tt) < хх и х (t2) < х2.
* В. общем случае мы получим представление о статистических свойствах
случайной функции х (t), если сможем ответить на следующий вопрос.
Пусть tv t2 tn есть га значений t (га— любое, но конечное число),
выбранных любым способом. Какова функция распределения F (xv x2, .... хп;
tv t2 tn), соответствующая совокупности связанных между собой слу-
случайных переменных х (t^), x (t2) x (/„)? Вследствие изложенного мы
заключаем, что случайная функция определена, если известна функция рас-
распределения F, соответствующая наиболее общему случаю. Известную функ-
функцию распределения F(xlt х2 хп; tv t2 tn) можно заменить соот-
соответствующей характеристической функцией, определенной по совокупности
связанных между собой случайных величин x(tx), x(t2) x(tn). Напоми-
Напоминаем, что если xv x2, .... хп есть га случайных величин, определенных
по одной и той же категории испытаний, то характеристическая функция,
отвечающая этим п переменным, является математическим ожиданием вели-
величины еПи\х\+и2х2+ ••• +апхп], которое представляет собой функцию га перемен-
переменных их, и2 ип. В рассматриваемом случае характеристическая функция,
соответствующая функции распределения F, будет равна е1 [uix('i)+ "¦ +ипх('п)]
для заданных значений tlt t2 tn. Это функция п переменных их, и2 ип,
которая зависит от га параметров — п моментов времени tx, tv ..., tn. Сле-
Следовательно, характеристическая функция, соответствующая функции распре-
распределения F, — это функция Ф от 2га переменных их, и2 м„; tv t2, ...,, ta.
Она определяется формулой
Ф(«,. и2 ип; tv t2, ¦..., ^я) = ^[»1*('1)+•••+««*('»)]. E4)
Прежде чем покончить с вопросом о функции распределения, сделаем
еще три замечания.
. 1. Можно попытаться приближенно описать поведение функции x(t),
пользуясь ограниченным числом особенно типичных значений. Для этого
следует ввести моменты или средние значения 1). Это обстоятельство не
является новым при изучении случайных величин, но новым оказывается
весьма большое количество рассматриваемых моментов, что объясняется
введением переменного параметра t. Следует ввести:
а) момент первого порядка х (t), представляющий собой функцию одной
переменной t;
б) наиболее общий момент второго порядка — математическое ожидание
произведения х (t{) x (t2), представляющее собой функцию двух переменных
tx и t2. В частном случае, когда tx = t2=t, мы снова получаем начальный
момент второго порядка x2(t), зависящий только от одной переменной t;
') Термин .среднее значение" здесь употребляется в смысле математического
ожидания. Когда речь пойде* о средних по отношению к времени или к любому
другому параметру, это будет специально оговорено.
630
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. IX
в) наиболее общий момент порядка п — математическое ожидание про-
произведения x{t^x(t2) •-¦ x(tn), представляющее собой функцию п перемен-
переменных. Он включает все частные случаи, которые можно получить, связывая
между собой значения t, в частности момент x"(t), который получится при
условии, что все значения t одинаковы.
Совершенно очевидно, что все эти моменты можно получить, зная
F(xv х2 хп; tv t2, ..., tn)- Еще удобнее получить их, если известно
разложение в ряд в окрестности начала координат для характеристической
функции
ф(«х. «2 ««; *v к *»)•
Известно (п. 9.1.8), что знание характеристической функции позволяет
получить моменты любого порядка. Мы применяли это, в частности, для
случая совокупности двух связанных между собой случайных величин (фор-
(формулы A9)).
2. Чтобы уточнить связь явлений во времени, естественно поставить
вопрос, в какой мере знание значений хг, х2 xft, полученных для X'(t)
в моменты tv t2 tk, может определить значения х'у х'2, ..., х'г отве-
отвечающие моментам t'v t'2, ..., t'r Иными словами, речь идет о знании услов-
условной вероятности для / величин xtt'A, x(t'2\ x(t't)< B предположении,
что значения х (t{), x (t2), ..., х {tk) известны. Эта условная вероятность
описывается функцией распределения, которую мы обозначим F(x'v x'2, ...
..., x'Jxv х2-, ..., xk; t[, t'2 t'Jtv t2 tky Она представляет собой
вероятность одновременного выполнения неравенств
x(t$<x[; x(t'2)<x'2; ...; x(t't)<x't
в предположении, что справедливы k соотношений
t:, t2
Функции условного распределения, которые только что были введены,
получаются из априорных функций распределения (т. е. определенных при
отсутствии каких бы то ни было дополнительных условий) F (хх, х2 xk\
tk) путем применения теоремы умножения вероятностей. Пример
этого приводится ниже. В на-
настоящий момент ограничимся по-
показом на конкретном случае важ-
важности изучения условных вероят-
вероятностей.
Допустим, что мы наблюдаем
явление х (t), имеющее случай-
случайный характер, определенное по
известной категории &* испыта-
испытаний &. Рассмотрим определен-
Рис. 9.12. ный опыт, приводящий к явле-
явлению х, и отметим значения х
на графике (рис. 9.12) соответ-
Если явление х
в моменты 0, 1, 2, 3, .... k. Отложим
ствующие точки (t, х). Пусть это будут Ро, />! Pk.
развивается достаточно медленно, то мы можем соединить точки непрерыв-
непрерывной кривой, которая представит с хорошим приближением ход изменения х (t)
в интервале 0 ^ t ^ k. Положим теперь, что наша информация не превы-
превышает момента tk. Значения функции х (f) для моментов, будущих по отно-
отношению к моменту tk, являются случайными. Если бы мы все же захотели
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 631
произвести экстраполяцию, то, предполагая некоторую непрерывность явле-
явления, могли бы в течение некоторого, не слишком большого отрезка времени
продолжить кривую как ее касательную в точке Pk. Однако чем больше
мы станем продвигаться в будущее, тем меньше будет обоснована такая
экстраполяция. Строго говоря, начиная с момента tk, совокупность возмож-
возможных реализаций неограниченно расширяется, и становится возможным бес-
бесконечное количество кривых, как это показано на рис. 9.12. Некоторые
из этих возможных кривых имеют больше шансов быть наблюденными, чем
другие. Поэтому представляет интерес изучение случайных величин х (t'A,
х(('Л x(t'i)' К0ГДа хA), х B), ..., х (k) имеют значения, полученные
в предыдущем опыте (значения t\, t'2 t't все больше А).
3. Приведенные до сих пор примеры относились к случайным функ-
функциям времени. Это особое значение, придаваемое параметру t, дает возмож-
возможность сделать изложение более наглядным, но следует иметь в виду, что t
не обязательно должно представлять собой время и может быть любым
параметром. Можно, например, сказать, что в некоторый момент скорость
турбулентной жидкости является случайной функцией координат.
Проблема сходимости
9.2.3. Введение. Прежде чем покончить с вопросом об общих поня-
понятиях, мы должны сказать несколько слов о новом аспекте, который полу-
получает столь существенное в анализе понятие сходимости при замене опреде-
определенных величин случайными величинами. В анализе принято говорить, что
величина f (f) — функция параметра t — стремится к /0 при t, стремящемся
к t0, если по любому сколь угодно малому наперед заданному числу г > О
можно найти такое число -г\ > 0, что выполнение неравенства \t — to\<^fi
влечет за собой выполнение неравенства |/—./0|<е.
Рассмотрим теперь случайную переменную х (t), зависящую от пара-
параметра t (иначе говоря, случайную функцию), определенную по категории
испытаний §?. Когда можно сказать, что при t, стремящемся к tQ, x (t) стре-
стремится к некоторому пределу? Очевидно, что предел этот не может быть
ни чем иным, как только случайной величиной, которую мы назовем х0
(в частном случае случайная величина х0 может оказаться определенным
числом). Говоря, что случайная переменная х(t) стремится к случайной
величине х0, мы имеем в виду, что х (t) все меньше и меньше отличается
от х0. Но если в анализе это имеет тот однозначный смысл, что |/ — /0|
становится все меньше и меньше, то гораздо труднее определить, что именно
имеется в виду, когда говорят, что одна случайная величина мало отличается
от другой. Как мы увидим ниже, это выражение можно истолковывать раз-
различными способами, откуда следуют и различные определения понятия схо-
сходимости. Сделаем несколько замечаний.
9.2.4. Сходимость в смысле Бериулли. Говорят, что случайная функ-
функция х (t) стремится к х0 в смысле Бернулли, если функция распределения
F (х; t), относящаяся к х (t), стремится (равномерно в любом конечном
интервале) к функции распределения случайной величины х0. Такое опреде-
определение сходимости крайне неопределенно. Действительно, вернемся к обоим
примерам случайных функций, которые были рассмотрены в п. 9.2.2. Обо-
Обозначим через F (х; t) и F (у; t) соответствующие функции распределения.
Мы уже знаем, что они тождественны и не зависят от времени. Поэтому х (t)
сходится к y(tQ) в смысле Бернулли, если t стремится к t0. Что же проис-
происходит в действительности? Для большей наглядности положим t0 = —. Тогда
632
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. fX
при каждом испытании имеем
x(tQ) = — sincp; у (?0) = sin ср.
Итак, если t стремится к t0, то х (t) в том смысле, как это понимается
в анализе, стремится к — y(t0). Разность x(t) — y(t0) сходится при каждом
испытании к —2 sin ср. Имеется, следовательно, нулевая вероятность того,
что эта разность стремится к нулю. Это указывает на очень неопределен-
неопределенный характер сходимости в смысле Бернулли.
9.2.5. Сходимость по вероятности. Говорят, что случайная функция х (t)
сходится по вероятности к случайной величине х0 при t~*-t0, если при
любом е_>0 вероятность того, что |x(t) — xo\ > е, стремится к нулю при
t—>t0. Это условие записывают в виде
11 ¦* \*/ -*о I ^ 1 — ^* . E5)
Такое определение сходимости имеет более ограничительный характер, чем
предыдущее. В частности, из него следует, что если t-+t0, то вероятность
того, что отклонение \x(t) — дго| больше любой конечной величины, ста-
становится все меньше и меньше — обстоятельство, не имевшее места в преды-
предыдущем случае. Можно, кроме того, показать, что сходимость по вероятности
влечет за собой сходимость в смысле Бернулли, а обратное не имеет места.
Приведем пример, иллюстрирующий* это определение и позволяющий
представить себе его границы. Рассмотрим еще раз случайную величину ср.
способную с равной вероятностью принимать все значения от 0 до 2тс,
и свяжем с ней случайную функцию, определенную при t > 0 выражением
х if) = | si n (utf -|- ср) |', E6)
где <о — определенная постоянная. Для некоторого фиксированного частного
значения ср соответствующая кривая имеет вид, представленный на рис. 9.13.
Рис. 9.13.
При t-*-\-oo x(t) стремится к очень малым значениям, за исключе-
исключением все более узких интервалов, содержащих точки, для которых
at-\-<f — fin 2"
Ф— целые числа).
Если задать t, то, не входя в подробности полного расчета, мы увидим,
что получить |лг(?)|<е можно, только если ср находится внутри одной
из окрестностей таких двух значений ср, находящихся между 0 и 2п, что
По виду кривых можно заключить, что эти окрестности тем уже, чем
больше t, и могут стать сколь угодно малыми при условии, что t будет
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 633>
достаточно велико. Иначе говоря,
НтЯ{|*@|<«1=0. E7>
Итак, случайная величина x(t) сходится по вероятности при ^->оэ
к определенному числу 0. Рассмотренный пример представляет интерес,
так как показывает, что этот род сходимости вовсе не требует, чтобы при
каждом испытании имелась сходимость в том смысле, как это понимается
в анализе. В частности, из рис. 9.13 видно, что при любом ср имеется
бесконечное множество значений t, для которых х = \. Поэтому ни при
*каком испытании мы не имеем права сказать, что х (t) стремится к. нулю
в том смысле, как это понимается в анализе.
9.2.6. Сходимость в среднем квадратическом (сходимость с. к.).
Говорят, что x(t) сходится к дг0 в среднем квадратическом при t, стре-
стремящемся к t0, если
lim [*(*) — *о12 = °- E8>
t->ta
Сходимость в среднем квадратическом влечет за собой сходимость
по вероятности. Это следует из неравенства Бьенэмэ1), согласно которому
/>{|*(Q —*„|>»)< [*(f)t, *o]2*). E9>
Значит, если задано любое, сколь угодно малое е, то из соотношений E8).
и E9) следует
UmP{\x(t) — лго|>е}=О,
а это определяет сходимость по вероятности. Сходимость в среднем квадра-
квадратическом, так же как иг сходимость по вероятности, не предполагает для-
каждой реализации сходимости в том смысле, как ее понимают в анализе.
Можно пояснить этот пункт, заметив, что в примере, представленном
на рис. 9.13, x(t) при t, стремящемся к бесконечности, сходится к 0-
по вероятности и то же х (t) сходится к нулю в среднем квадратическом.
Мы, однако, уже выяснили, что вероятность сходимости функции x(t}
к нулю в том смысле, как это понимается в анализе, равна нулю.
') Пусть X — случайная величина, а Х2 = я2— ее дисперсия. Покажем, что можно
легко найти величциу, ограничивающую сверху вероятность того, что | X | > а, исходя-
из р2. Действительно, обозначим через dF (х) вероятность того, что х < X < х -f- dx.
Тогда, если а — любая положительная постоянная, то
оо +а —а 4-оо
о* = С х2 dF (х) = Г х2 dF (х) + Г х2 dF (х) + С х2 dF (x).
— со —а —оо 4-а
Все интегралы положительны; кроме того, в двух последних х2 > а2. Поэтому
[—а +со -|
Г dF(x) + Г dF (х) = а2Р {| Х\ > а}.
J J
-со +а А
Отсюда получаем неравенство Бьенэмэ
*) Неравенство E9) было впервые получено в 1846 г. известным русским мате-
математиком П. Л. Чебышевым и известно в советской научной литературе, а также и
в ряде зарубежных стран как неравенство Чебышева (лемма Чебышева).
€34 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Сходимость x(t) в среднем квадратическом следует из общего положе-
положения, согласно которому для случайной величины, модуль которой остается
ограниченным, сходимость к нулю по вероятности влечет за собой сходи-
сходимость к нулю в среднем квадратическом.
Действительно, предположим, что \x(t)\ <.А, где А — граница x(t),
не зависящая от t. Вернемся теперь к соотношению, которое помогло нам
установить неравенство Бьенэмэ (см. сноски на предыдущей странице).
Если а — любая положительная постоянная, то можно написать
в -а со
х~ЧЛ= f x2(t)dF(x; 0+ / x2(t)dF(x; t)-\- f x2(t)dF(x; t).
—а —oo а
Найдем для интегралов, стоящих в правой части, верхние границы:
х2 (О dF (x; t) < а2.
Г
j x2(t)dF(x; 0+ J x2(t)dF(x; t) < A2 ¦ P {\x | > a}.
—со а
Отсюда
xW) < a2 + Л2 ¦ P { | x @1 > a}.
Из этого неравенства следует, что x2(t) стремится к нулю при t, стремя-
стремящемся к бесконечности. Действительно, выберем сколь угодно малое поло-
положительное число е. Требуется доказать, что можно найти такое Т, что
при t >> Т будет лг2(^)^е. Для этого возьмем а2 — тт"! теперь достаточно
найти такое Т, чтобы при t > Т было
что возможно, так как из определения сходимости по вероятности имеем
lim P{\x(t)\>fi}=0
лри любом наперед заданном т;.
Замечание. Доказательство существенно основано на том, что функ-
функция x(t) ограничена при любом t и при любом испытаний. Если это усло-
условие не выполнено, то может иметь место сходимость по вероятности
без сходимости в среднем квадратическом. Подтвердим это примером. Будем
снова исходить из функции x(t), которую мы рассматривали ранее (рис. 9.13).
Если t стремится к бесконечности, x\t) стремится к нулю по вероятности,
т. е. равенство limP {| x(t) \ > е} =0 справедливо для всех е. Совершенно
очевидно, что достаточно соблюдения этого условия для малых значений е;
тогда оно будет иметь место и для больших, так как если е2 > slt то
^{|*@l>«2l<^{|*@l>«l}-
Отсюда следует, что мы можем произвольно изменять x(t) всюду, где х
больше некоторой величины tj и при этом ничего не изменится в сходимости х
к нулю по вероятности. Возьмем, например, tj=0,1 и заменим x(t) на функ-
функцию y(t), определенную следующим образом:
а) y(t) = x(t) при x(t)<7i;
б) y(t) = <?(t)x(t) при
9.2]. СЛУЧАЙНАЯ ФУНКЦИЯ 635
где cp(tf) — определенная (не случайная) функция t. Очевидно, что если cp(f)
достаточно быстро возрастает при возрастании t, то можно не допустить,
чтобы момент второго порядка x2(t) стремился к нулю, и даже заставить
его неограниченно возрастать при больших значениях, t. При этих условиях
функция y(t) будет сходиться к нулю по вероятности, но не в среднем
квадратическом.
Понятие сходимости в среднем квадратическом представляет интерес
по двум существенным причинам:
1) в большинстве случаев момент второго порядка легко вычисляется;
, 2) в большем числе практических приложений момент второго порядка
имеет простой физический смысл.
Уточним этот важный пункт.
Рассмотрим электрический ток флуктуации l{t), проходящий по катушке
самоиндукции L. Положим, что этот ток связан с некоторым параметром,
например с положением а указателя потенциометра. Сказать, что в опре-
определенный момент t1 при а, стремящемся к а0, этот ток флуктуации стре-
стремится к нулю в среднем квадратическом, значит сказать, что, взяв значе-
значение а достаточно близким к а0, можно среднюю энергию -?rLi2(t), накоплен-
накопленную в катушке самоиндукции в момент tv считать сколь угодно малой.
9.2.7. Почти достоверная сходимость. Те типы сходимости, о кото-
которых шла речь выше, могут иметь место и без наличия сходимости в том
смысле, как она понимается в анализе. Попробуем, однако, стать на точку
зрения физика, изучающего электрические флуктуации определенной цепи.
Допустим, что он регистрирует некоторое напряжение флуктуации и наблю-
наблюдает за ним достаточно долго. В конечном счете он получит единственную
кривую, зарегистрированную прибором, за которым велось наблюдение. Эта
кривая соответствует результату одного испытания. Сходимость, интересую-
интересующая исследователя, будет, прежде всего, сходимостью в том смысле, как ее
понимают в анализе, установленной по результатам этого испытания. Если
потребуется произвести упрощение, заменив исследуемую величину ее преде-
пределом, то необходимо, чтобы этот предел имел определенный смысл для1 по-
полученной исследователем кривой, а не для совокупности возможных кривых,
которых он никогда не видел. "Это соображение и приводит к понятию
почти достоверной сходимости.
Вернемся к случайной функции x(t) и случайной величине х0, опре-
определенным по одной и той же категории испытаний. По результатам одного
вполне определенного испытания может иметь или не иметь места сходи-
сходимость x(t) к х0 в том смысле, как она понимается в анализе. Следовательно,
такая сходимость — случайное событие, которое имеет или не имеет места
для каждого испытания. Можно сказать, что существует некоторая вероят-
вероятность такой сходимости.
Примем следующее определение: функция х (t) сходится почти досто-
достоверно к х0 при t, стремящемся к t0, если вероятность сходимости x(t)
к х0 равна единице. При этом условии, если пренебречь совокупностью реа-
реализаций, имеющих общую нулевую вероятность, можно считать, что при
каждом испытании х0 является пределом х (t) в том смысле, как это пони-
понимается в анализе. Однако быстрота сходимости х (t) к х0 может зависеть
от рассматриваемого испытания и, следовательно, сохраняет случайный
характер. Кроме того, можно показать, что почти достоверная сходимость
влечет за собой сходимость по вероятности.
После рассмотренных уточнений понятия сходимости можно обобщить
понятия анализа, основанные на понятии предела, в частности понятия
636 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
производных и интегралов. Рассмотрим, например, производную. Мы не бу-
будем заниматься сходимостью в смысле Бернулли, о которой уже известно,
что она очень неопределенна. С каждым из трех других видов сходимости
связано соответствующее определение производной:
1. Производная по вероятности. Случайная функция x(t) имеет в каче-
качестве производной по вероятности в точке t0 некоторую случайную вели-
L + ДО t)
0
... „ х (L + ДО — х (t0)
чину y(t0), если случайная величина —5-^—!—~ *-^ сходится по вероят-
вероятности к y(t0) при t, стремящемся к t0.
2. Производная в среднем квадратическом. Случайная функция х (t)
имеет в качестве производной в среднем квадратическом в точке t0 случай-
случайную величину y(t0), если
F0)
3. Почти достоверная производная. Случайная величина y(t0) пред-
представляет собой почти достоверную производную случайной функции x(t)
при t = t0, если с вероятностью, равной единице, справедливо равенство
причем предел здесь имеется в виду в том смысле, как это понимается
в анализе.
Аналогично, рассмотрение сходимости х(@-\-Ы) к x(t0) при Д^—>0
позволяет определить непрерывность по вероятности, непрерывность в сред-
среднем квадратическом и почти достоверную непрерывность в точке t = t0.
В дальнейшем мы будем еще много раз возвращаться -к понятию сходи-
сходимости одной случайной величины к другой. В частности, мы будем иметь
дело со случайной непрерывностью или со случайной производной. Однако
во многих приложениях теории вероятностей часто имеют место одновре-
одновременно все виды сходимости. Приводимые ниже теоремы относятся, строго
говоря, только к сходимости в среднем квадратическом, однако при доста-
достаточно общих условиях, которые мы здесь не будем уточнять, но которые
практически выполняются в большинстве приложений, они будут устанавли-
устанавливать и почти достоверную сходимость. Поэтому, когда речь пойдет, напри-
например, о производной случайной функции, это, строго говоря, будет означать
производную в среднем квадратическом, но практически это можно пони-
понимать также как почти достоверную производную и, следовательно, произ-
производную случайной функции почти достоверно можно отождествить с произ-
производной, которую можно вычислить по результатам „одного" определенного
испытания.
Стационарные случайные функции.
Изучение постоянных режимов
9.2.8. Введение. Рассмотрим особый класс случайных функций — ста-
стационарные случайные функции. Случайная функция x(t) называется стацио-
стационарной, если все ее статистические свойства не изменяются при любом
выборе начала отсчета времени. Точнее, будем называть в этом случае x(t)
стационарной случайной функцией в строгом смысле, в отличие от более
широкого определения характера стационарности, которое будет дано ниже.
Стационарные случайные функции нужны для изучения флуктуации при по-
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 637
стоянных режимах. С точки зрения математики, стационарный характер
функции влечет за собой следующие ее особенности.
1. Функция распределения F (х; t) не зависит от t; функция распреде-
распределения F(xv х2; tv t2) зависит только от разности t1 —12- В общем случае
по отношению ко всем переменным имеет место тождественное равенство:
F(xv х2 хк; tv t2; ..., tk) =
^F{xv x2 xk; t, + h, t2 + h tk + h). F2)
2. Такие же особенности встречаются при изучении моментов. Момент
^первого порядка x(t), т. е. математическое ожидание функции, представляет
собой постоянную т, не зависящую от t. В дальнейшем будем предполагать,
что /и = 0; очевидно, что это предположение не нарушает общности.
Момент второго порядка x(t1)x(t2) — математическое ожидание произведения
х (t{) х (t2) — есть функция только от разности tl —12 = т. Эта функция
будет играть важную роль в дальнейшем. Мы назовем ее корреляционной
функцией р(т) стационарной случайной функции x(t):
pW = x(t)x(t — T). F3)
По поводу определения понятия математического ожидания следует для
случая стационарных случайных функций сделать одно существенное замеча-
замечание. Для этой цели рассмотрим математическое ожидание х (t). Будем счи-
считать для простоты, что оно тождественно равно нулю. Предположим, что х (t)
представляет собой флуктуирующее электрическое напряжение, и поставим
вопрос, каким образом экспериментатор может определить его математи-
математическое ожидание. По определению, x(tx) есть математическое ожидание
случайной величины x(t{). Его экспериментальное определение сводится
к наблюдению в момент tx большого числа макроскопически тождественных
приборов, которые дадут показания хг^{), x2(t1), ..., и к нахождению
среднего значения этих показаний. На практике такой способ очень сложен
и неудобен, так как он требует одновременно большого числа приборов.
Если заменить такое одновременное наблюдение большого числа прибо-
приборов наблюдением в течение длительного времени напряжения x(t), записан-
записанного одним прибором, то это приведет к замене определения математи-
математического ожидания x(tx) в момент t1 средним значением по времени, взятым
за большой промежуток времени Т для одного определенного испытания.
Это временное среднее значение назовем р. (Г):
г
При довольно общих условиях, которые сводятся к требованию, чтобы кор-
корреляционная функция р(т) достаточно быстро стремилась к нулю при т—*-оо,
оо
и которые, в частности, выполняются, если существует интеграл J\p(x)\dx,
— оо
что имеет место в большинстве приложений, можно показать, что случайная
величина р. G") сходится в среднем квадратическом и почти достоверно
it x(t), если Г-*-оо.
Аналогичные результаты можно получить и для других моментов, на-
например для х (t) x(t — х). Поэтому в дальнейшем мы не будем проводить
различия между математическим ожиданием и пределом временнбго среднего
638 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
значения при Т—>оо. В частности, моменты первого и второго порядков
можно будет определять с помощью соотношений
т
m — ~x= lim ¦— I x(t)dt = O F4)
1
1 Г
p(x) = x(t)x(t — х)= lim -у / x(t)x(t — x)dt.
Г->оо -Q
9.2.9. Изучение моментов второго порядка. Определение. Флуктуа-
Флуктуации представляют собой весьма сложное явление, даже в какой-то мере
неуловимое, поскольку оно все время изменяется непредвиденным образом.
Поэтому экспериментатор должен ограничиться'несколькими характерными
величинами, которые могут дать качественное представление об изучаемом
явлении. В случае стационарных явлений часто довольствуются моментами
первого и второго порядков, т. е. математическим ожиданием x(t) = m
(предполагается, что оно равно нулю) и корреляционной функцией р(х) =
— x(t)x(t — х), физический смысл которой мы вскоре выясним. Это, оче-
очевидно, наиболее простые статистические характеристики. Кроме того, кор-
корреляционные функции удобны по следующей причине. Очень часто флуктуи-
флуктуирующая величина X (t) бывает суммой или наложением флуктуирующих
величин х1(?), x2(t) xn(t), независимых друг от друга; так, например,
флуктуирующее напряжение v(t) между двумя точками А к В электрической
схемы часто оказывается просто наложением флуктуирующих напряжений v5 (t),
\(t), .... создаваемых различными сопротивлениями Rv R2, ... Понятно,
что эти напряжения не зависят друг от друга. Корреляционную функцию
X(t)X(t — х) от суммы ЛГ = 2Х/ можно получить простым суммированием
корреляционных функций, относящихся к каждой составляющей. Это видно
из следующего преобразования:
(t—т) = 2*,(о*ус — -0=2 xt{t)xj(t — *)+ 2 *,(о*у('—*)•
t,i i=i 1Ф1
F5)
Вследствие независимости функций х, имеем 2 xi(t)xi(t — т) = 0 (пред-
4*1
полагается, что xl = Xj=0), откуда получаем требуемое соотношение
X (t) X(t — x) = 2 x,{t)xi(? — t). F6)
i
Легко заметить, что это свойство не распространяется на средние значения
типа
<j)(x, x', x") = x(?)x(?~x)xit — x') х (t — x"). F7)
Мы привели сейчас доводы в пользу применения моментов второго
порядка по соображениям простоты, однако имеются и гораздо более глу-
глубокие соображения. Моменты второго порядка всегда имеют физический
смысл. Это становится очевидным, если учесть, например, что средняя
мгновенная мощность, рассеянная флуктуирующим током i(t) на сопротивле-
сопротивлении R, равна Ri2(t), что средняя энергия, накопленная в момент t в катушке
с индуктивностью L, по которой течет ток i(t), равна -j^-''2. что средняя
мощность, переносимая в пустоте плоской электромагнитной волной через
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 6391
поверхность, перпендикулярную к направлению распространения, пропор-
пропорциональна моменту 2-го порядка ЕР- напряжения электрического поля.
Выясним теперь, с учетом сказанного, физический смысл корреляцион-
корреляционной функции. Рассмотрим световое излучение при постоянном режиме. Мы
представим его с помощью некоторой стационарной случайной функции x{t).
Рассмотрим интерференцию двух световых излучений. Это означает, что мы
каким-то способом получим сумму
где х — оптическое запаздывание, и изучим ее при различных значениях х.
^Вычислим среднюю энергию в точке, где оптическое запаздывание имеет
значение х. В этой точке имеем
X2 = x2(t)-{-x2(t — x)-\-2x(t)x(t — x),
или
(x)]. F8)
Мы видим, что средняя энергия X2 представляет собой сумму двух чле-
членов. Первый из них 2р@) = 2л:2 — это сумма собственных энергий, вызван-
вызванных каждым из излучений x(t) и x(t — х). Второй член 2р(х) — это член,
характеризующий взаимодействие двух световых излучений. Этот перемен-
переменный член 2р(х) регулирует изменение средней энергии X2 в зависимости
от оптического запаздывания. Следовательно, корреляционная функция дает
непосредственно форму интерференционных полос.
Имеется еще одно замечание по поводу изучения моментов второго
порядка. Рассмотрим пример из электротехники. Предположим, что ко входу
линейного усилителя приложено случайное напряжение x(t). Вследствие этого
в различных каскадах усилителя возникнут случайные напряжения yl(t).
Мы покажем, что моменты первого и второго порядков функций у, (t),
у2 (t), ... можно вывести из соответствующих моментов функции х (t). Сле-
Следовательно, можно рассмотреть моменты первых двух порядков в любой
линейной цепи приборов, переходя от одного к другому. При таком рас-
рассмотрении никогда не придется вводить моменты порядка выше второго.
Получается, таким образом, особое -исследование, и можно сказать, что изу-
изучение моментов второго порядка является в значительной мере изучением
передачи энергии в линейных системах.
Учитывая описанный выше характер свойств, связанных с моментами
второго порядка, видим, что целесообразно рассматривать случайные функ-
функции,' у которых стационарность относится только к моментам первого
и второго порядков. Они называются стационарными случайными функциями
второго порядка.
Случайная функция является стационарной случайной функцией второго
порядка, если она обладает следующими свойствами.
1. Математическое ожидание х (t) не зависит от t (всегда можно пред-
предположить, что x(t) — O).
2. Математическое ожидание произведения x(t1)x(t2) зависит только
от разности t1 — t2 = x. Это предположение обеспечивает существование
корреляционной, функции, определяемой равенством
p(z)=x(t)x(t—z).
Стационарность второго порядка отличается от стационарности в стро-
строгом смысле слова. Действительно, можно привести примеры случайной
«40
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. IX
функции второго порядка, у которой моменты высших порядков не остаются
неизменными при изменении начала отсчета времени. Следовательно, такие
•функции не стационарны в строгом смысле слова.
Можно легко убедиться, что так же обстоит дело и с функцией
х (t) = X cos (в t + Y sin (в t,
тле (в — определенная постоянная, а X и К две независимые случайные вели-
величины с одинаковым законом распределения и удовлетворяющие условию:
X = Y = 0. Сразу же можем написать
х У{) х (t2) = X cos (в (tx —12) = X2 cos шт.
В то же время легко заметить, что Xl(t) существенно зависит от t.
Общие свойства стационарных случайных функций
второго порядка
9.2.10. Корреляционные функции. Рассмотрим сначала несколько
простейших свойств корреляционных функций.
1. При х = 0 корреляционная функция равна дисперсии:
рп)
= х*. F9)
2. Корреляционная функция пред-
представляет собой четную функцию от х.
Действительно,
р (х) == х (t) х (t — т) = х (t — т) х (О-
Вследствие стационарности можно, заме-
заменить t на t.-\-z. Тогда имеем
р'П)
) = р(—х). G0)
Если корреляционная функция диф-
дифференцируема, то ее нечетные производ-
производные представляют собой нечетные функ-
функции, например, р'(х) = —р'(—х), а четные
производные представляют собой четные
функции. Характер соответствующих кри-
кривых представлен для частного случая на
рис. 9.14. Эти кривые соответствуют функ-
функции р(т) = е~1т1. Мы увидим в дальнейшем,
что это действительно корреляционная
функция. Если нечетные производные су-
существуют при х=0, иными словами, если имеются производная справа и про-
производная слева, равные между собой, то их значение может быть равным
только нулю. В нашем примере р'@) не существует. Но если бы функция
•р(х) не имела в начале координат угловой точки, а шла бы так, как это изо-
изображено пунктиром, то производная при х = 0, т. е. р'@), существовала бы,
но была бы обязательно равна нулю.
3. Корреляционная функция удовлетворяет важному соотношению
1рМ|<Р@) = лЛ G1)
Это соотношение вытекает из классического неравенства, называемого
Рис. 9.14.
9.2]
СЛУЧАЙНАЯ ФУНКЦИЯ
641
неравенством Буняковского — Шварца*). Пусть даны две случайные величины X
и К, независимые или зависимые. Кроме того, дано вещественное положи-
тельное или отрицательное число X. Тогда справедливо очевидное неравенство
(ХЛГ+КJ>0, откуда
Это должно иметь место при любом X, следовательно, квадратное уравне-
уравнение X2X2 -\- 2XY X -j- У2 = 0 не должно иметь различных вещественных кор-
корней. Поэтому
АГК <АГ2. К2.
G2)
Это и есть неравенство Буняковского — Шварца для рассматриваемого
случая. Применим его к двум случайным величинам x(t) и x(t — х), кото-
которые являются значениями случайной
функции х (/) в моменты t и t — т.
Имеем
I Y (+\ v(t тЛ <^ V-2 ( 4-\ у»2/V /г\
|л \лу X yl ~) | -^. X \1) ' X {I X).
Взяв квадратный корень, получаем
требуемое неравенство G1):
IpWKp(O).
Согласно соотношению G1), мо-
модуль корреляционной функции дости- рис. 9.15.
гает наибольшего значения при х= 0.
Если рассматривать корреляционную функцию применительно к явлению
интерференции, то неравенство G1) означает, что наибольшая интенсивность,
если речь идет о системе интерференции с блестящей средней полосой (или
наименьшая интенсивность, если речь идет о системе с темной средней по-
полосой), всегда бывает в средней полосе. В частности, таких полос, какие
изображены на рис. 9.15, наблюдать нельзя.
9.2.11. Непрерывность. Дифференцируемость. Выясним, при каких
условиях функция х (t) будет непрерывна по t в среднем квадратическом.
Непрерывность в среднем квадратическом существует, если x{t~\~U) схо-
сходится к x(t) в среднем квадратическом при At, стремящемся к нулю, иными
словами, если справедливо равенство
lira [x{t-\- Ы)~ x(t)}2=0. G3)
Необходимым и достаточным условием непрерывности случайной функции х (t)
в среднем квадратическом, является непрерывность корреляционной функции
в начале координат. В дальнейшем будем предполагать, что это условие
выполняется. При этом можно показать, что корреляционная функция будет
равномерно непрерывна при —oo<x<-f-°o.
Совершенно очевидно, что локальные свойства х (t) связаны с пове-
поведением р(т) при малых значениях х. Мы только что видели, что непрерыв-
непрерывность x(t) в среднем квадратическом зависит от непрерывности р(х) в на-
начале координат. Исходя из этого, можно теперь сформулировать следующую
*) Неравенство Буияковского — Шварца имеет вид
г * 12 ь ь
\ j f (х) g (х) dx\ ^Jf*(x)dx- fg'(x)dx.
41 А. Анго
642 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
теорему: Для того чтобы стационарная случайная функция второго порядка x(t)
имела я-ю производную в среднем квадратическом, необходимо и достаточно,
чтобы при х = 0 существовали все производные корреляционной функции р(т)
до 2я-го порядка включительно.
Если обратиться к рис. 9.14, то ясно, что корреляционная функция, изо-
изображенная сплошной линией, соответствует случайной функции, не имеющей
производной в среднем квадратическом. Действительно, производная р'@)
не определена. Напротив, корреляционная функция, которая вблизи точки
т = 0 идет по пунктирной кривой, соответствует случайной функции, имею-
имеющей производную в среднем квадратическом. Предположим, например, что
do (Pa d2no „ ,
производные -j- , . 2 , .. ., 2П существуют при т = О (тогда можно по-
показать, что они существуют при любом х). Из этого следует, что случайные
dx d2x d"x
производные —тг , ~ттг • • • • • ~ш~ существуют. Для простоты записи обо-
обозначим их через д:A) (t), xB) (t) д;(я) (t). Напоминаем, что они опреде-
определяются соотношениями
к.
к.
дг->о
= Нтс. к.
G4)
Прежде чем идти дальше, необходимо указать на одно свойство схо-
сходимости в среднем квадратическом.
Если две случайные величины X (а) и К (а), зависящие от параметра а,
сходятся в среднем квадратическом соответственно к Хо и Ко при а, стре-
стремящемся к <х0, то X (а) У (а.) стремится к XqYq1).
Если в частном случае X не изменяется вместе с а, то
lim XY (а) = XYQ.
Применим этот результат к случайным величинам
Имеем
¦^-[р(т + М) — р(т)]. G5)
Имеем
') Действительно, положим
Х(я) = Х(а) — Х0; у(а) = Г(а) — Y,
lim х2 (а) = (У, lim у2 (а) = 0.
С другой стороны,
X (а) Y (а) = [Хо + X (а)] [К„ + У (")] = Х0У0 + X (а) Ко + У (а) Х0 + х (а) у (а).
Из неравенства Шварца следует, что
откуда
_^
lim Z (а) К (a) = ЛГ0К0.
••2]
СЛУЧАЙНАЯ ФУНКЦИЯ
643
Устремим Д/ к нулю: x(t — -с) не изменяется, а величина л v" т " . —
стремится в среднем квадратическом к xXl) (t). Следовательно, левая часть
равенства G5) стремится к х^^ (t) x (t — ¦:); взяв предел правой части,
получаем
*-A) ( + \ v it тЛ ^ /ЛЛ
Л It) Л It 1^ , . I / О I
Таким же образом можно найти
Y (f\ *-A) (f -Л г (Т7\
Мы свели в табл. I выражения типа G7). Они выражают то, что можно
назвать „смешанными корреляционными связями" между х (t) и ее производ-
производными. В верхней строке и в левом столбце этой таблицы помещены вели-
величины, служащие сомножителями:
v ({Л v(l) С/"> rB) (f\
Л I ?_ t -^- ^ /' \ /' • • • »
V It аЛ v(D it т4» vB) (t -\
Л It */* ^ \ /¦ *^ \ /' ...
Из табл. I можно определить значения математического ожидания произве-
произведения двух величин, помещенных в заголовках соответствующих строки и
x(t-x)
xW(t — x)
XW (t — x)
,»(,-„
д:(<) (t — x)
x(t)
P(^)
dp
dx
lx*
d3p
d4p
rfP
dx
d2?
d*?
dx*
XM (t)
lx*
~~"сГг*
dT*
-8
Та
Jf(8) (t)
dT*
~~dx*
d5p
блица I
rf'p
dx^
d6p
"lx7
столбца. Если приравнять - = 0, то, принимая во внимание, что производ-
производные нечетного порядка равны нулю при т —0, получим результаты, приве-
приведенные в табл. II.
Полезно напомнить, что значения, принимаемые в определенный момент
случайной функцией и ее производной в среднем квадратическом, не кор-
коррелируют:
x(t)x'(t) == 0. G8)
Мы приводим здесь снова замечание, которое было уже сделано, когда
речь шла о различных видах сходимости последовательностей случайных
величин. Производные, которые мы сейчас рассматривали, — это производные
41*
644
ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Таблица II
x(t)
xW (t)
xW (t)
xW (t)
;c<4> @
x(t)
P@)
0
d2p
!z~i
T=0
0
dz*
t=0
дг(') (t)
0
rf2p
~dx*
i=0
0
d*f
dz*
t=0
0
jt<2> @
dx2
x=0
0
т = 0
0
d°9
dz6
1 = 0
x^i @
0
d«p
dx4
t=0
0
d*f
dxe
t = 0
0
дг<4> @
rf4p
dz*
x = 0
0
d"p
dx6
x=0
0
d»p
dT*
1=0
в среднем квадратическом. Но если случайные функции ведут себя доста-
достаточно правильно, то эти производные являются в то же время и почти досто-
достоверными производными. Поэтому с вероятностью, равной единице, их можно
отождествить с производными в том смысле, как они понимаются в анализе,
которые экспериментатор может вычислить при каждом отдельном испытании.
9.2.12. Энергетический спектр. Рассмотрим вначале, каковы исходные
положения при физическом подходе к вопросу об энергетических спектрах.
Наиболее наглядны в данном случае оптические явления, при которых частота
колебаний непосредственно доступна восприятию наших органов чувств,
поскольку она отождествляется с цветом. Чтобы получить понятие о спектраль-
спектральном распределении энергии, достаточно представить себе прохождение свето-
светового излучения через цветной экран или, лучше, разложение светового луча
с помощью призмы. Этот опыт непосредственно приводит нас к понятию
спектрального распределения средней энергии. Можно выделить полосу
спектра, заключенную, например, между частотами iij и ~v2, и измерить
термопарой мощность W, соответствующую этому диапазону частот. Можно
сделать то же самое с другой полосой частот ч[, ч'2, не имеющей общей
части с Vj, v2 (одна, например, в красной части спектра, другая — в синей);
ей соответствует мощность W. Если наложить друг на друга излучения,
относящиеся к обеим полосам частот, и снова измерить среднюю мощность,
то получим мощность W-\-W. Таким образом, средние мощности, относя-
относящиеся к разным частотам, складываются, или, иначе, средняя энергия взаимо-
взаимодействия между отдельными частотами отсутствует.
Эти чисто экспериментальные заключения приводят к тому, что оказы-
оказывается возможным приписать некоторую среднюю энергию каждому интервалу
частот. Естественно ввести функцию %(ч), которую назовем функцией спек-
спектрального распределения энергии, со следующими свойствами:
a) g(v) равна средней энергии (или средней мощности), соответствующей
интервалу.частот [0, vj;
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 645
б) g@) = 0, и можно положить, что g(v) = O при v < 0;
в) §(v) может только возрастать вместе с v, так как любой полосе
частот соответствует энергия либо положительная, либо нулевая;
г) %(сю) = Ж
Функция §(v) вводилась различными способами. В чисто математических
исследованиях, таких, как работы Бохнера и Хинчина, строго доказан»
существование функции %(v), имеющей перечисленные свойства, но доказа-
доказательства эти абстрактны и не имеют наглядного физического смысла. С другой
стороны, имеются работы, в которых существование функции §(v) обоснован»
Г1утем соображений, очень наглядных с точки зрения физика, но недоста-
недостаточно строгих математически. Авторы этих работ предполагают, что случай-
случайная функция х (t) разложима в ряд Фурье, или по крайней мере представляют
функцию х (t) в виде ряда Фурье на очень большом интервале [— Т; Т].
Такое введение ряда Фурье в явление, которое, вообще говоря, не
является периодическим, довольно произвольно и приводит к рассуждениям,
спорным с математической точки зрения. Способ, который мы предлагаем»
представляется нам способным примирить стремление к математической?
строгости с желанием сохранить физический смысл изучаемого явления.
Сейчас мы покажем, каким образом можно точно определить функцию
по корреляционной функции.
Переведем для этого на язык математики представления, очевидные
с точки зрения физики. Что бы мы сделали прежде всего, если бы захотел»
произвести в лаборатории энергетический анализ тока флуктуации x(t)?
Мы бы его „профильтровали" через избирательный усилитель, пропускающий
только заранее выбранную полосу частот, энергетическое содержание которой
нам нужно измерить. Усилитель преобразовал бы x(t) Ъ y(t), и энергия на
выходе фильтра была бы равна у2. Основное свойство фильтров с точки-
зрения математики состоит в том, что они являются стационарными линей-
линейными системами, характер работы которых остается неизменным с течение»
времени.
Введем ответ R(t) фильтра на единичный импульс, приходящий в момент
t = 0. Известно, что функцию на выходе у (t) можно получить по сигналу
х (t) с помощью уравнения
00
f x(O)R(t — в) rfe = 3t [*.(*)]• G9>
— оо
Напомним, что собой представляет преобразование SR, с помощью кото-
которого линейный фильтр переводит случайную функцию x(t) в случайную
функцию у((). Конечно, в реальном фильтре, т. е. в фильтре, который можно-
экспериментально осуществить в лаборатории, функция R(t) не произвольна.
В частности, функция R(t) должна быть тождественно равна нулю при>
t ¦< 0, так как следствие не может опережать причину (п. 9.2.1). Кроме
того, свойства электрических цепей требуют, чтобы функция R(t) при t >0
была равна линейной комбинации экспонент. Очевидно, что при этом пре-
преобразование 9t[x(t)] представляет собой линейное дифференциальное урав-
уравнение с постоянными коэффициентами. Здесь мы обобщим понятие фильтра:
пренебрежем перечисленными условиями, налагаемыми на R(t), и постараемся
выяснить математический смысл преобразования G9). В частности, не будем
требовать, чтобы функция R(t) была равна нулю при t < 0. Мы лишь
наложим на нее условия, имеющие целью обеспечить существование несоб-
несобственного интеграла с бесконечными пределами, входящего в выражение G9)т
646
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. IX
а именно предположим, что функция R(t) абсолютно интегрируема в беско-
бесконечных пределах. При этом интеграл, входящий в выражение G9), сходится
с вероятностью, равной единице.
Так же, как в теории линейных усилителей, удобно использовать пре-
преобразование Фурье для функции R(t):
G(v)— Г
(80)
где G(v) — комплексный сомножитель, называемый частотной характеристикой
стационарной линейной системы. Через g-(v) мы обозначим его модуль, а через
cp(v) — его аргумент. Предположение об абсолютной интегрируемости функ-
функции R требует, чтобы функция g"(v) была гладкой, в частности, нельзя
пользоваться кривой усиления, изображенной на рис. 9.16, а, но можно
a? О
П
а)
6)
Рис. 9.16.
пользоваться сколь угодно близкими к ней кривыми усиления типа кривой,
изображенной на рис. 9.16, б. Функция O(v) в случае фильтра, представлен-
представленного функцией g (v) на рис. 9.16, б, тождественно равна нулю вне интервала
Vj — s, v2~|-e, где е сколь угодно мало.
Впрочем, более широкое толкование, на подробностях которого мы не
будем останавливаться, позволяет рассматривать математические фильтры
гораздо более общего типа, в частности с функцией g (v), представленной
на рис. 9.16, а.
Физический смысл функции g"(v) ясно виден на примере преобразования
синусоидальной функции
[sin
= g (v) sin [2icv/ + cp (v)].
(81)
Можно заметить, что при синусоидальном сигнале его эффективная вели-
величина при прохождении через фильтр умножается на g"(v). Для частоты v
передаваемая энергия равна приходящей, умноженной на коэффициент энерге-
энергетической передачи, а именно на g(v). Это замечание проливает свет на
весь механизм избирательности: меняя g (у), можно отдавать предпочтение
одним частотам и заглушать другие.
После сделанных замечаний мы сможем ввести функцию спектрального
распределения энергии g (v). Для простоты будем предполагать, что корре-
корреляционная функция р (х) имеет в качестве коэффициента преобразования
Фурье А(ч) — непрерывную функцию от v, абсолютно интегрируемую1).
') Эти предположения делаются здесь лишь для простоты. Они несущественны
для возможности определения функции спектрального распределения g (v). Кроме
того, можно сказать, что с точки зрения практики эти ограничения несущественны.
В частности, они законны, если корреляционная функция р (т) и две ее первые
производные существуют и являются абсолютно интегрируемыми. Пользуясь языком
9.2) СЛУЧАЙНАЯ ФУНКЦИЯ 647
Так как р(х) функция четная, то преобразование Фурье приведется к виду
р(х)= Г A (v) cos 2icvx rfv.
(82)
Вычислим среднюю энергию на выходе фильтра. Возводя в квадрат обе
части выражения G9) и определяя их средние значения, получим
но
откуда
[
J
—сю
[сю
J f
— СЮ —СЮ
оо оо
у2= J J Af [ж F) * (в')] Я (* — 8)/? (( — 6')
— СЮ —ОО
сю
M[x(Q)x F')] = р F — б') = J A (v) cos 2uv(8 — 6') dv,
—сю
сю оо
(83)
оо со Г оо
у2= Г Г Г A (v) cos 2irvt d-i \R (и) R (и — x)dudx.
(84)
(85)
—сю —оо L0
оо оо оо
=Re Г (
- —оо —оо О
Так как функции fin Л абсолютно интегрируемы, то можно переменить
порядок интегрирования, и тогда мы получим следующую окончательйую
формулу:
y2 =
R(
1
u)e2n'"udu I
f R(U — x)e-2
(u— t) rfv.
Отсюда, вспоминая определение для функции O(v) — формулу (80) — и учи-
учитывая, что квадрат ее модуля g(v) равен произведению функции G(v) на
сопряженную с ней комплексную величину, стоящую в первых квадратных
скобках, получим
оо
(86)
Соотношение (86) является фундаментальным, так как показывает, что
коэффициент .d(v) обязательно положителен или равен нулю. Действительно*
оптика, можно сказать, что изучение непрерывных спектров возвращает нас в рамки
этих предположений. Но спектр, содержащий линии в математическом смысле слова
т. е. бесконечно тонкие, не удовлетворяет им. Напомним также, что рассуждения
которые будут дальше сделаны в рамках этих предположений, без труда распро-
распространяются на самые общие случаи.
648 ТЕОРИЯ ВЕРОЯТНОСТЕЙ {ГЛ. IX
если функция А(ч) отрицательна вблизи какой-то частоты v0, то, выбрав
для 9t фильтр, пропускающий только частоты, соседние с v0, мы сделали бы
правую часть выражения (86) отрицательной, что невозможно, поскольку речь
идет о дисперсии. Следовательно, коэффициент ^(v) положителен или равен
нулю. Поэтому можно толковать величину tf g (v) = ^ (v) ^v как элементар-
элементарную энергию. Если учесть, что коэффициент передачи энергии равен g(v),
и вспомнить о понятиях, изложенных в начале п. 9.2.12, то приходим к сле-
следующему истолкованию соотношения (86), законность которого вытекает из
приведенных выше рассуждений. Для случайной функции x(t) полосе частот
(у, v-j-tfv) соответствует средняя энергия tfg(v) — ^4(v)rfv. После преобразо-
преобразования эта энергия умножается на коэффициент передачи g(v) при частоте v
и становится равной g(v) tfg(v); полная переданная энергия получится, если
произвести суммирование по всем элементарным полосам частот. Это и есть
интерпретация основного соотношения (86), в котором выражено содержание
весьма важной теоремы Бохнера и Хинчина.
Итак, если корреляционная функция р(х) имеет непрерывный и абсолютно
интегрируемый коэффициент преобразования Фурье А(ч), то функция 4(v)
обязательно положительна или равна нулю1). Функцию А(ч) можно толковать
как спектральную плотность энергии, а функция спектрального распределе-
распределения энергии §(v) есть интеграл А(ч):
J(v)rfv. (87)
Очевидно, что g@) = 0; функция g(v) может только возрастать; при v=oo
снова получим полную энергию. Действительно,
o). (88)
На основании принятых гипотез о корреляционной функции р(х) удалось
решить задачу определения функции спектрального распределения энергии.
Эти гипотезы соответствуют тому, что в оптике называется непрерывным
спектром. Случаем непрерывного спектра мы и ограничимся. Полученные
в этом пункте результаты могут быть распространены на самый общий случай,
и всегда можно поставить в соответствие корреляционной функции р(х)
некоторый спектр частот; но этот спектр может быть более или менее
сложным и, в частности, может содержать линии, т. е. такие частоты, которым
соответствует конечная энергия.
Напомним основные соотношения, которые для случая непрерывного
спектра связывают между собой величины р, А и §(v):
оо
р (т) = Г А (у) cos 2icvc dt, (89a)
') Величина A (v) существенно подчинена условию быть неотрицательной и давать
ОО
конечную полную энергию Г A (v) йч. Всякая функция, для которой преобразование
о
Фурье удовлетворяет этим условиям, очевидно, является корреляционной функцией.
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 549*
откуда, обращая формулы Фурье, получаем
оо
A (v) = 4 Г р (х) cos 2im tfx,
V
g(v) = J
(896)
Соответствие между р (т) и Л (v) — это соответствие преобразования Фурье.
Свойства его являются классическими. Свойства моментов второго порядка
определяются в одинаковой степени как корреляционной функцией р(х), так
и спектральной плотностью A (v).
оо
Примечания. 1. Предположим, что интеграл I vM(v)dv сходится.
о
Исходим из соотношения
оо
р (х) = Г A (v) cos 2im rfv.
о
Здесь можно дважды произвести дифференцирование под знаком интеграла.
Это позволяет вывести два следствия:
а) р"(х) существует при всех х и, в частности, при х = 0. Существует,
следовательно, производная в среднем квадратическом от функции x{t)»
о которой известно, что ее корреляционная функция равна — р"(х)-
б) Имеем
оо
«. — р" (х) = Г 4ic2vM О) cos 2icvx йч, (90>
о
откуда следует, что спектральная плотность для производной х' (t) равна
4к'гч2А (v). При каждом значении v вычисления производных выполняются так,
как если бы речь шла о чистой синусоиде. Известно, что при дифференциро-
дифференцировании функции sin2itv? появляется сомножитель 2itv.
2. Из предыдущих расчетов мы узнали величину у2 средней энергии на
выходе фильтра. Аналогичные расчеты могут нам дать корреляционную
функцию на выходе. Укажем на главные промежуточные этапы этого важного-
вычисления:
оо
= f
— СЮ —ОО
ОО СО
9', (91)
M[y(t)y(t — \)]= j J р (т) Я (и) Я (и — х — \)dudx, (92>
— 00 —ОО
ОО
М [у (О у (t — X)] = J A (v) g2 (v) cos 2uvX rfv. (93)
о
Соотношения (92) и (93) позволяют вычислить корреляционную функцию-
преобразования sJt[x(f)] либо как функцию от /l(v) и g(v), либо как функ-
функцию от р(х) и R(t). Сравнив соотношения (93) и (89), видим, что спек-
спектральная плотность на выходе равна произведению i4(v)^2(v). Этот вывод
можно сразу объяснить, заметив, что коэффициент передачи энергии при
•650 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
частоте v равен ?f2(v) и что A(v)dv— это энергия, соответствующая для
функции х (t) полосе частот (м, v-j-dV). С точки зрения энергетики разные
частоты взаимно независимы в линейных системах, представленных преобразо-
преобразованием *Л. Получаем простое и важное правило: при преобразовании стацио-
стационарной случайной функции стационарной линейной системой ее спектральная
плотность умножается на квадрат модуля частотной характеристики.
9.2.13. Передача энергии стационарной линейной снстемой. Для уточ-
уточнения задачи рассмотрим конкретный пример. Прилагаем флуктуирующее
напряжение х(t) на входе линейного усилителя. Тогда на выходе первого
усиливающего каскада мы получим флуктуирующее напряжение Х[ (t), на
выходе второго каскада — флуктуирующее напряжение х2 (t) и т. д. Энерге-
Энергетические свойства x(t) вьфажаются заданной корреляционной функцией р^(х)
или заданной спектральной плотностью Ах(ч). Энергетические свойства x^lt)
определяются заданием рх (х) или Ах (v); энергетические свойства x2(t)—зада-
x2(t)—заданием р^ (х) или Ах (v) и т. д. Задача состоит в том, чтобы подробно про-
проследить изменения энергетических свойств, т. е. в том, чтобы перейти рт
р^Дт) [или Ах{у)\ к p^(x) [или А^ОО], а затем к px>(t) [или ^.„(v)j и т. д.
При этом собственными флуктуациями усилителя мы пренебрегаем. Доста-
Достаточно, очевидно, решить этот вопрос для одного каскада. Формулируя задачу
в. более общих терминах, можно сказать, что мы рассматриваем стационар-
стационарную случайную функцию x{t) и заставляем ее претерпеть линейное преобразо-
преобразование y(t) = SRlx(t)]. Требуется перейти от энергетических свойств функ-
функции x(t) (т. е. от рх и Ах) к энергетическим свойствам функции y(t) (т. е.
к ру и Ау). Ранее мы указали все соотношения, которые при этом необхо-
необходимо использовать. Однако представляется полезным придать последователь-
последовательности соотношений более систематический вид и для этого расположить
наиболее важные соотношения в виде схемы. Линейное преобразование можно
определить через его частотную характеристику О (у) или через его ответ
R(t) на единичный импульс. Полезно отметить, что в подобного рода энерге-
энергетических задачах частотная характеристика O(v) входит только через ее
модуль g (v). Нужные соотношения сведены в схему (на стр. 651).
Замечания. Для упрощения описанных выше расчетов полезно сделать
несколько практических замечаний.
1. Корреляционные функции, вводимые в приложениях, стремятся всегда
к нулю при больших значениях х, потому что x(t) и x(t — х) стремятся
стать взаимно независимыми. Можно сказать, что случайная функция x(t)
обладает „статистической памятью", тем меньшей, чем быстрее р(х) стре-
стремится к нулю. Из соответствия, определяемого формулами (89), легко заме-
заметить, что при прочих равных условиях чем больше „статистическая память"
явления, тем более ограничен его спектр частот. Возьмем для примера,
энергетическое распределение, определяемое спектральной плотностью
Находим
— I
р(т)=<; •*<> I. (94)
На рис. 9.17 представлены кривые р(т) и /l(v) для больших значений х0
[сплошные линии) и для малых значений х0 (пунктир).
Вернемся к уравнению
GO
A (v) = 4 Г р (х) cos 2im dx
9.2]
Pv
СЛУЧАЙНАЯ ФУНКЦИЯ
Данные, относящиеся
к сигналу х (t)
?х (*) = j Ах ('') COS 2jivt
О
со
Л^(т) = 4 I p^(t) cos 2icv
о
oo
^ = ?x @) = J Лг (v)
d4
di
Данные, относящиеся
к линейному преоб-
преобразованию di
g (v) =
Методы расчета
651
G (v) I
\
Расчет корреляций
Расчет спектральных
плотностей
\
Результаты, относящиеся
к функции на выходе у (t)
= J
Ау (v) = Ах (v) g* (v)
— OO —OO
OO
РУ(Х)= J Ay
0
CO
^y(v)=4jpy
0
(v) cos 2jc
(>.) cos 2jc
.hd* = f Axb
0
g-2 (v) cos 2я-<Х Л
,= Г Г
-/
(v)
— QO —CO
652
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
(ГЛ. IX
в более общем виде и запишем р(х) как р( — I. Меняя параметр х0, мы
сможем по своему произволу Е1ытянуть или сжать вдоль оси времен кривую,
представляющую корреляционную функцию. Тогда, если обозначить через
am
и
V
А(х0, v) функцию А(ч), относящуюся к значению х0, предыдущее соотноше-
соотношение можно записать в виде
Л(х0, v)=4 / р(—
6
или
оо
А (т0, v) = 4t0 Г р (9) cos 2wno6 db.
(95)
(96)
Видим, что с точностью до числового множителя 4х0 функция Л(х0, ч)
зависит только от произведения vx0. Поэтому
A (t0, v) _
4t0 "'
А (\i0, у
(97)
Знаменатели 4х0 и 4Хх0 соответствуют растяжению кривой А вдоль оси
ординат. Е:сли не обращать внимания на это явление, а учитывать только
большее или меньшее растяжение вдоль оси частот, то можно заметить, что
заставляя кривую р(х) растягиваться вдоль оси х, мы заставляем кривую Л(у)
в том же соотношении сжиматься вдоль оси частот. Случайная функция
с большой статистической памятью имеет в большинстве случаев относи-
относительно узкий спектр, и наоборот.
2. Предположим, что на входе усилителя, характеризующегося своей
реакцией R(t) на единичный импульс, приложено стационарное случайное
напряжение x(f) второго порядка с корреляционной функцией р^(х). Кор-
Корреляционная функция на выходе будет ру(^). Переход от одной к другой
производится с помощью соотношения
Ру(Х)= f f Px(T)R(u)R(u—x—\)dudx.
(98)
— со —со
Не затрагивая вопросов математической строгости, поясним, чтб именно
происходит в двух ппедельных случаях.
1) Усилитель с большой постоянной времени. Более точно, рассмотрим
усилитель, постоянная времени которого велика по сравнению со статисти-
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 653
ческой памятью функции x(t). Это означает, что существуют значения а
а . оо
такие, что С px(x)dx весьма мало отличаются от Г px(x)dx, хотя /?(а)
—а —оо
практически не отличается от R@) или, лучше сказать, хотя R(u-^-a) мало
отличается от /?(и). При этом соотношение (98) дает (если не останавли-
останавливаться на вопросе о сходимости)
оо
/ R(u)R(u — X)du. (99)
Первый множитель — число, не зависящее от X. Только второй множи-
множитель определяет вид функции ру(Х). Итак, вид корреляционной функции на
выходе определяется усилителем, так как от величины сигнала зависит только
числовой коэффициент.
2) Усилитель с малой постоянной времени. Рассуждая так же, как и
раньше, получим
Г оо 2
A00)
В этом случае усилитель определяет только числовой множитель, а кор-
корреляционная функция на выходе имеет тот же вид, что и на входе. В обоих
случаях то явление, в котором изменение происходит более медленно, опре-
определяет вид корреляционной функции.
В частности, если мы наблюдаем явление электронных флуктуации, при
которых корреляции становятся практически равными нулю за короткое
время или, во всяком случае, за время, гораздо меньшее, чем постоянные
времени наших приборов, то корреляционная функция флуктуации зависит
только от наблюдающих приборов, а не от характера начальных флук-
флуктуации.
3. Можно повторить предыдущие рассуждения, переведя их на язык
спектральной плотности. Тогда
видим, что ход кривой Ау(v) зависит от того, насколько избирательно явле-
явление, т. е. от того, насколько тесно оно связано с частотой. Если, в част-
частности, случайная функция x(t) представляет какое-либо молекулярное или
электронное явление, не имеющее преимущественных частот, то функцию A(v)
можно заменить постоянной. Впрочем, согласно замечанию 1, можно сказать,
что спектральная плотность А(ч) постоянна вплоть до очень больших частот
или что корреляционная функция р(х) практически становится равной нулю,
как только х становится больше некоторого малого значения xv Когда это
случается, мы говорим, что имеет место микроскопическая корреляция.
4. Мы видели, что в случае молекулярных или электронных явлений
корреляция зависит только от приборов наблюдения. Это означает, иными
словами»- что спектральная плотность, соответствующая явлению в чистом
виде, не зависит от v. Можно сказать, что спектры этих явлений имеют
одинаковое, по отношению к частоте, энергетическое распределение плот-
плотности. В частности, так же обстоит дело и с флуктуациями электродвижу-
электродвижущей силы e(t) на концах некоторого сопротивления R.
654
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. IX
Рассмотрим теперь контур, состоящий из сопротивления и шунтирован-
шунтированного конденсатора (рис. 9.18). Будем считать, что электродвижущая сила
с флуктуацией e(t) последовательно подключена к сопротивлению R.
Определим разность потенциалов V {t) на зажимах А и В конденсатора.
При этом преобразование e(t) в V {t) происходит с помощью частотной
характеристики
J
V(t)
G(v) = .
2mCR
откуда
Следовательно,
S (У)'— 1
¦dt.
Рис. 9.18.
Но из предыдущего видно, что Ае(ч) — постоянная, не зависящая от ч.
Можно поэтому вынести ее из-под знака интеграла:
~2
Принцип равномерного распределения энергии приводит к соотношению
где k — постоянная Больцмана, а Т — абсолютная температура. Сравнив два
предыдущих выражения, находим
Ае (v) = AkRT;
это соотношение представляет собой формулу Найквис.
9.2.14. Недостаточность рассмотрения моментов второго порядка
и корреляционной функции. Все, о чем говорилось в пп. 9.2.8—9.2.13;
ограничивалось рассмотрением моментов второго порядка, иначе говоря,
энергетических свойств стационарных случайных функций. Мы видели, что
это рассмотрение можно вести двумя параллельными путями, пользуясь либо
корреляционной функцией, либо спектральной плотностью. Обе эти функции
представлялись нам до сих пор весьма сильными инструментами для изуче-
изучения энергетических свойств во всех звеньях стационарной линейной системы.
Но в большинстве случаев дей-
действенность их исчезает, как f(t)
только потребуется вычислить ^^
что-нибудь помимо моментов вто-
второго порядка или рассмотреть
нелинейные системы. Приведем
пример. Рассмотрим установку,
изображенную на рис. 9.19. Она может служить для усиления фотоэлектри-
фотоэлектрических токов. В ней имеется линейный усилитель (/), квадратичный выпрями-
выпрямитель у = х2 B) и гальванометр C). Гальванометр представляет собой линейную
систему. Чтобы вычислить дисперсию г2 флуктуации „зайчика" гальванометра,
требуется знать корреляционную функцию y(t)y(t — 6) •выпрямленного
1
X(t)
2
t/ft)
3
Рис. 9.19.
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 655-
напряжения. Если предположить, что выпрямитель квадратичен, то нужно
знать момент x2(t)x2(t— 6). По отношению к функции x(t) — это момент
четвертого порядка. Если бы характеристика выпрямителя была у = хр,
потребовалось бы для функции x(t) знать момент порядка 2р. Изложенные
ранее формулы не позволяют вычислять моменты пор'ядка выше второго.
До сих пор корреляционная функция служила инструментом для вычи-
вычислений, но в строгом смысле слова не оправдывала своего названия, пред-
предполагающего непрерывность явлений во времени. Оценивая качественно,
можно сказать, что часто, если т достаточно велико, то x(t) и x{t — х)
становятся практически независимыми, так что
x(t)x(t — x)-+x(t)-x(t — т) = 0. A01)
Поэтому часто стремление х к бесконечности влечет за собой одновременно
и стремление x(t)x(t — х) к нулю и стремление x(t) и x(t — т) к незави-
независимости. Мы можем также сказать, что если спектр богат низкими частотами,
то он соответствует режиму медленных флуктуации, т. е. представляет собой
режим с большой статистической памятью.
Однако все эти замечания весьма нечетки, и легко привести большое
число примеров, которые позволяют выявить их неубедительность. В част-
частности, не следует забывать, что две случайные величины могут быть очень
тесно связаны и в то же время иметь нулевую корреляцию. Рассмотрим
в качестве примера стационарную случайную функцию
x(t) —cos (Ы ¦+-<?), A02)
где ср — случайная величина, принимающая с одинаковой вероятностью любое
значение от 0 до 2тс. При этом
р (%) = х (t) х (t — х) = -i- cos an, A03)
-i
где р(У) обращается в нуль, в частности, при сот = -у. Было бы совершенно-
неправильно заключать из этого, что x{t^) и дг!^-)—я—) взаимно независимы.
Действительно,
х (*,) = cos Ы\ -Ь ф) и -^ (^i -h -^7) = — sin (co^t -f- 9).
Между x{t{) и x (fj H—2пГ) сУществУет соотношение, не зависящее от ср:
Знание величины x(t{) определяет абсолютную величину х If, -(- —) •
Следовательно, между этими случайными величинами имеется строгая (неслу-
(неслучайная) связь, и, однако, они не коррелируют. Не нужно упускать из виду,
что сама по себе корреляционная функция имеет только энергетический смысл
(т. е. определяет только моменты второго порядка). Две случайные функции
не коррелируют между собой, если у них нет энергии взаимодействия.
Но это не означает, что они взаимно независимы, как видно из предыду-
предыдущего примера. Как мы увидим ниже, в некоторых случаях, которые с точки
зрения математики следует рассматривать как частные случаи, но которые
тем не менее включают в себя многочисленные задачи о флуктуациях, поста-
поставленные физикой, корреляционная функция полностью характеризует все
статистические свойства х (t) и тогда вполне оправдывает свое название.
656 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
Это происходит в тех случаях, когда х (t) представляет собой стационарную
случайную функцию Лапласа — Гаусса. Мы поясним свойства этих функций
на конкретном примере флуктуации, возникающих на выходе линейного
усилителя под действием дробового эффекта постоянного тока, приложенного
на входе.
Стационарные случайные функции Лапласа — Гаусса.
Применение к чисто дробовому эффекту
Все последующие рассуждения относятся к флуктуациям, возникающим
под влиянием чисто дробового эффекта. Об этом же шла речь в п. 9.2.1.
Сущность задачи будет изложена на примере, предназначенном сделать изло-
изложение более конкретным. Но выводы будут иметь весьма общее значение,
что не ускользнет от внимания читателя.
9.2.15. Общие замечания. В начале этой главы приводился пример,
связанный с извлечением шаров из урны с неограниченным числом белых
и черных шаров. Если произвести очень большое число N извлечений на-
наудачу и если р и 9—1—Р— соответственно вероятности появления белого
и черного шаров при каждом независимом извлечении, то случайная вели-
величина n(N), равная числу белых шаров, появившихся при N извлечениях,
приближенно подчиняется закону нормального распределения, причем погреш-
погрешность этого приближения можно сделать сколь угодно малой при достаточно
большом ЛЛ Указанное нормальное распределение группируется вокруг мате-
математического ожидания n(N) = Np, а его среднее квадратическое отклонение
равно y^Npq. Этот пример представляет собой частный случай гораздо
более общего результата (центральная предельная теорема).
Пусть N—число независимых случайных величин, а 5—их сумма.
Предположим, кроме того, что относительный вклад в сумму 5 каждой
из этих величин весьма мал или, по крайней мере, весьма мал во всех слу-
случаях, за исключением очень маловероятных. При таких условиях для доста-
достаточно большого ./V сумма 5 подчиняется нормальному закону распределения
с соответственно выбранным центром. Например, если случайное явление х (t)
является результирующим для очень большого числа независимых элементар-
элементарных явлений, то в большинстве случаев можно сказать, что в любой
момент tx величина х (t{) будет подчиняться нормальному закону распре-
распределения. Тогда, предполагая х(?г) — 0, для вероятности того, что выпол-
выполняется неравенство
X\^.x(t1)^.x1-{-dx1,
будем иметь
йР=*г^.У-е"&йх. A05)
причем
Выяснив эти предварительные обстоятельства, займемся изучением слу-
случайной функции, приведенной в конкретном примере п. 9.2.1. Речь идет
о флуктуациях напряжения на выходе линейного усилителя под действием
.дробового эффекта сигнала, который мы назовем, с макроскопической точки
зрения, постоянным током. В конечном счете, нам нужно рассмотреть слу-
случайную функцию
tj <+ОО
B.2] СЛУЧАЙНАЯ ФУНКЦИЯ 657
Последовательность значений tj представляет собой последовательность
случайно распределенных моментов времени. Что понимается под выражением
случайно распределенные моменты? Сейчас мы это уточним, не входя в тон-
тонкости математических рассуждений. Очевидно, речь идет о распределении,
статистические свойства которого стационарны, поскольку рассматриваемые
нами электроны составляют макроскопически постоянный ток, определенный
от t= — оэ до t = -j~oo. Рассмотрим очень большой промежуток времени Т
и пусть N — число происходящих за это время электронных ударов. Утвер-
Утверждая, что существует плотность р0, мы тем самым говорим, что при доста-
ДГ
точно больших Т частное -=- будет мало отличаться от величины р0. Если Т
достаточно велико, то приближенно будем иметь N = pQT электронных
ударов.
Выберем очень большое значение Т и возьмем р0Т точек, которые пред-
предположим распределенными случайным образом в промежутке Т. Для этого
рассмотрим последовательность из N независимых испытаний. Каждое из них
состоит в выборе точки отрезка Т, причем вероятность поместить эту точку
Ах
на любой отрезок Дх (внутри отрезка Т) равна -у-. После осуществления Л/
таких испытаний можно вычислить вероятность того, что я любых точек
находятся в отрезке Дх внутри отрезка Т. Эта вероятность равна
Ах
Естественно, мы не хотим вводить каких-либо преимущественных значений Т,
и распределение значений tj должно быть сделано для бесконечного интер-
интервала от t = — оо до t~-j~oo. Поэтому за характеристические свойства
распределения мы примем такие свойства, которые можно получить, переходя
к пределу при Т—>оо.
Предельные свойства заключаются в следующем:
1. Вероятность Р того, что за любой промежуток времени At произой-
произойдет я электронных ударов, подчиняется закону Пуассона (п. 9.1.18). Иначе
говоря,
Р(п; М) = — П'*{ "¦¦ , где п~РоДЛ A06)
2. Имеет место взаимная независимость между промежутками времени,
у которых нет никакой общей части (разъединенные промежутки времени).
В частности, если Д^ и At2— два разъединенных промежутка, то вероят-
вероятность того, что за Д^! произошло я,, а за Д?2 — я2 электронных ударов,
равна
2; At2). A07)
Распределения, свойства которых мы сейчас уточнили, называются рас-
распределениями Пуассона. Установив таким образом свойства последователь-
последовательности моментов tj, можно полностью изучить случайную функцию x(t) и,
в частности, вычислить функцию распределения F (х:, х2 xw; tv t2 tN).
Мы ограничимся указаниями, справедливыми в частном случае, который крайне
важен в приложениях.
Усилитель обладает некоторой инерцией, и можно связать с ним по-
постоянную времени х0. Нас интересует только порядок ее величины. Среднее
число электронных ударов за время т0 равно рот0. Ясно, что характер явле-
явления будет очень различным в зависимости от того, мала величина poto или
велика по сравнению с единицей. Большое рото означает, что колебание,
42 А. Анго
658
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
[ГЛ. I*
вызванное электронным ударом, практически еще не начало затухать, когда
произошел новый удар, иначе говоря, значение x(t), наблюдаемое в момент t.
зависит от очень большого числа ударов, происшедших в близком прошедшем
по отношению к t. Малое р0т0 означает, напротив, что колебание, вызванное
столкновением, практически уже затухло, когда последовал новый удар. Зна-
Значение x(t) зависит главным образом от момента удара, непосредственно
предшествующего t. Заметим для ясности, что если мы имеем дело с уси-
усилителем, обладающим достаточно большой избирательностью, то в зависи-
зависимости от величин рото мы получим промежуточный случай между крайними
случаями, представленными на рис. 9.20.
Уточним порядки величин. Рассмотрим для примера усилитель с неболь-
небольшой постоянной времени то=1О~6. С другой стороны, возьмем ток с силой
в 10~8Л, который может считаться слабым в большинстве приложений.
potg большое
О
О
р0 т0 малое
Рис. 9.20.
Соответствующее значение рото равно 60 000. Этого примера достаточно,
чтобы показать, что в повседневных случаях произведение рохо будет очень
велико. Значение x(t) в момент t1 зависит теоретически от всех электрон-
электронных ударов, предшествующих tv На практике оно зависит только от столк-
столкновений в промежутке (tv tl—8), где о — величина порядка, большего чем х0.
Так как рохо очень велико, то в этом промежутке имеется много столкно-
столкновений, соответственные положения которых взаимно независимы. Слагаемые
eR(t — tj), отвечающие этим ударам, представляют собой независимые слу-
случайные величины, и можно предвидеть, что x{t{) будет подчиняться нор-
нормальному закону распределения. Это подтверждается^ и строгим рассужде-
рассуждением. Случайная величина х (tt) (предполагается, что х == 0; если х Ф 0, то
те же рассуждения следует применить к величине х—х) имеет плотность
вероятности, определяемую формулой f
P(x)dx=
¦ — e
3
dx.
A08)
где
и характеристическую функцию
-—
ф(и)=е 2
A09)
Кроме того, если, вместо того чтобы рассматривать один момент tv иссле-
исследовать к моментов tv t2, .... tk, выбранных любым образом, то k случай-
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 659
ных величин x(t{), x(t2) x(tk) подчиняются нормальному закону рас-
распределения для к случайных величин. Такие законы представляют собой
обобщения нормального закона распределения, относящегося к одной слу-
случайной величине. Проще всего определить их, обобщая соотношение A09).
Можно сказать, что характеристическая функция нормального закона рас-
распределения для k случайных величин — это функция Ф(и1, м2 ик),
определяемая соотношением типа
Ф(В1. «а И,):=Л<3("""'--1Ч (ПО)
где Q — неотрицательная квадратичная форма:
Q(«i. и2 «*)== 2 Auuiui- (НО
Коэффициенты Ац имеют очень простой смысл. Мы уже видели, что коэф-
коэффициенты разложения функции Ф в ряд вблизи точки и1 — и2— ... =«^
непосредственно связаны с моментами. Следовательно, можем написать
=Ati = x (tt) x (tj) = р (tt — tj).
4 «*) = , S
Если нам нужно снова перейти к закону распределения, то достаточно
вспомнить, что плотность вероятности P(xv x2. .... xk) представляет собой
коэффициент преобразования Фурье для характеристической функции
Ф(И], и2 ик), как это следует из определяющего соотношения
ф — е> Ки\х\+ ••¦ +ukxk) =
В общем случае, если через |Q| обозначить главный определитель квадра-
квадратичной формы Q, а через Q' — обратную квадратичную форму, то
Х2 хк)~ Г * лгп^-:'е ' (П5)
Напомним, что если коэффициенты квадратичной формы Q образуют
квадратную матрицу \Alt], то коэффициенты обратной квадратичной
формы Q' образуют квадратную матрицу \a\j\, где A'ij~T77T' a aij — алге-
алгебраическое дополнение элемента Ai} в определителе \Q\.
Основное следствие предыдущих соотношений заключается в том, что
закон распределения, которому подчиняются к случайных величин х\, х2, ..., хк,
всегда можно полностью определить, если известна корреляционная функция.
Корреляционная функция, которая в общем случае имеет только энер-
энергетическое значение, определяет теперь все статистические свойства случай-
случайной функции x{f). Именно потому, что многие случайные процессы, изучаемые
в приложениях, описываются стационарными случайными функциями Лапласа—
Гаусса, корреляционные функции играют такую важную роль. В частности.
42*
660 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
шумовой фон в линейных усилителях приводит во всех случаях к режимам,
описываемым стационарными случайными функциями Лапласа—Гаусса.
Уточним предыдущие выводы, рассмотрев два частных случая k = 1
и k = 2.
a) k — 1.
Мы уже получили выражения для характеристической функции и плот-
плотности вероятности. Разложение характеристической функции в ряд дает
сразу же значение всех моментов. Как известно из п. 9.1.13,
д-27+i—O; x2" = a2l4 • 3 ... Bq~ 1), A16)
где q — целое положительное число.
b) k = 2.
Рассматриваются две случайные функции x(t{) и x(t2). Положим, что
6 = /, —t2. Тогда
причем очевидно, что
Соответствующая плотность вероятности равна
Сделаем несколько выводов из соотношений A17) и A18).
9.2.16. Связь явлений во времени. Возьмем фиксированное значение хх
и найдем условную плотность вероятности Р(х2/хг) значения х2, если
известно jct. Вероятность P(xv x2)dx^dx2 получения в моменты ?j и t2
значений хх и х2 (с точностью до dxl и dx2) равна, согласно правилу умно-
умножения вероятностей, произведению вероятности P(x1)dx1 иметь в момент tl
значение хх (с точностью до dx{) на вероятность P(x2lx^)dx2 иметь в мо-
момент t2 значение х2 (с точностью до dx2), если известно, что в момент tl
получено значение хх (с точностью до dx{). Поэтому
P{x2lx{)dx2
Отсюда, используя предыдущие результаты, получаем
И»)
A20)
P(O)
Это снова закон нормального распределения. Математическое ожидание
дается формулой
2— р@) 1 —" v *• '
а среднее квадратическое отклонение равно
"" A22)
Если 6 меняется от 0 до оо, то fS меняется от 1 до 0.
9.2)
СЛУЧАЙНАЯ ФУНКЦИЯ
661
_ На рис. 9.21 представлено изменение математического ожидания
,х2 = $х1 A) и значений, отстоящих от него на одно среднее квадратическое
отклонение в каждую сторону B).
Рис. 9.21 дает очень точное представление о том, что можно назвать
непрерывностью явления во времени или еще статистической памятью функ-
функции x(t), так как он показывает, каким образом знание значения хх влияет
на возможность получения значения х2.
Можно заметить, что эта непрерывность
явления во времени находится в прямой и
исключительной зависимости от корреляцион-
корреляционной функции, чем и оправдывается ее назва-
название; при этом не следует упускать из виду,
что все сказанное справедливо только для
стационарной случайной функции Лапласа—
Гаусса.
9.2.17. Флуктуации в нелинейных
системах. Обратимся снова к схеме на
рис. 9.19. Мы уже видели, что изучение
флуктуации после выпрямления требует зна- р .
ния корреляционной функции y(t)y(t — -с).
Если речь идет о стационарной случайной функции Лапласа — Гаусса, то
вычисление этой корреляционной функции несложно во многих случаях, т. е.
для довольно многочисленных вариантов характеристик выпрямителей. При-
Приведем несколько примеров.
/) Квадратичный выпрямитель (характеристика у = х2). Матема-
Математическое ожидание для выпрямленного тока равно
у = ^=р(О). A23)
Вычислим корреляционную функцию, относящуюся к отклонению Y(t)~
= y(t) — y(t). Имеем
О
/3
— х2} =
х2} = х2 (t) x2 (t — x) — (x2J.
Момент четвертого порядка получается из разложения в ряд характеристи-
характеристической функции Ф(к!, и2) для функций x(t{) и x(t2) при t1 = t и t2 = t — т.
Применяя уже указанный метод, находим
Отсюда
х2 (t) х2 {t — т) = 2р2 (т) -4- р2 @).
A24)
Y(t)Y{t — т)=2р2(х). A25)
Таким образом, корреляционная функция на выходе квадратичного вы-
выпрямителя равна удвоенному квадрату корреляционной функции на входе.
Аналогичные расчеты позволяют рассматривать случаи характеристик
более сложного вида, в частности, характеристики у = хр (р — целое) или
У ~ «и + в\Х -1- а2х2 + ...
Вычисление моментов второго порядка Y(t) Y(t~x)=(y(t)~^)(y{t—z)—~y)
сводится к вычислению моментов, которые получаются на основании разло-
разложения в ряд характеристической функции <!>(«!, и2).
2) Линейный выпрямитель. Если характеристика у = у(х) имеет более
сложный вид, то вычисление моментов функции у уже нельзя свести к вы-
вычислению моментов функции х. Но тогда можно непосредственно вычислить
момент '
У (t) у (t — x).
662 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [ГЛ. IX
исходя из плотности вероятности, относящейся к двум случайным величинам
xl = x(t) и x2 = x(t—т).
Положим
У1 = У(*1) и У2=У(*2);
тогда
оо оо
—x) = y~~y~2 = / f yix^yix^Pix,, x2)dx,dx2. A26)
— оо —оо
Этот способ можно применять, например, к случаю линейного выпря-
выпрямителя. Возьмем для пояснения линейный выпрямитель, выпрямляющий два
полупериода переменного тока. Уравнение характеристики будет у=|л;|.
Если х^х2 > 0, то У1У2 = л-*' а если ххх2 < 0, то уху2=—ххх2. Отсюда
легко выводим
оо оо сх> О
У^У2=2/ j x1x2P(xv x2)dxxdx2— 2 J J x^/»^, x^d^ dx2. A27)
0 0 0 -co
Заменяя вероятность Р(Ху х2) ее выражением, полученным из выражения
A18), имеем
х\+х\ I" 23*^2 2Рл-,лг2 Л
/"ИГв^р~ + в""^~И*1''*а. О28)
' о о
где
р = р(т), а = р@). Л=/о^Гр2.
Можно разложить выражение для уху2 в ряд по степеням отношения
— = р 1. ¦ При этом получаем результат в следующем виде:
4а h ^ Р2 1-1 .Р4 1 1 , Р6 ьз 1
[1+ + + +
Прямое вычисление математического ожидания у дает
Используя это соотношение, получаем
YXY2 = (у, — у) (у2 — у) = У1у2 - (уJ.
В конечном счете имеем для линейного выпрямителя, выпрямляющего два
полупериода переменного тока:
/^; A30)
'^Т + ^- 2ТТ--3+ •
Мы в некотором смысле разложили спектр линейного выпрямителя
на более простые спектры. В ряде случаев можно довольствоваться первым
членом в квадратных скобках, т. е. членом, содержащим (З2. Это равно-
равносильно замене спектра данного выпрямителя спектром квадратичного выпря-
выпрямителя.
*.2] СЛУЧАЙНАЯ ФУНКЦИЯ 663
Примечание. В случае выпрямителя, выпрямляющего только один
полупериод переменного тока, мы нашли бы
* 3" +"?" 2-4-6 + "Ч+Т- A33)
9.2.18. Вычисление корреляционной функции иа выходе линейного
усилителя под действием дробового эффекта постоянного тока. Мы по-
показали, что все свойства стационарной случайной функции Лапласа — Гаусса
x(t) содержатся в корреляционной функции. Остается вычислить корреля-
корреляционную функцию x(t)x(t — т) для случая флуктуации, вызванных дробовым
эффектом в линейном усилителе. Для этого мы будем предполагать, что
ось времен разделена на очень малые последовательно расположенные равные
отрезки длиной в Д?. Пусть rij — число импульсов е, расположенных в про-
промежутке (tj, tj+l). Так как промежуток At очень мал по отношению к по-
постоянным времени усилителя, то реакция на совокупность электронных уда-
ударов, происшедших за время между tj и ?;Ч1 (их число равно nj) будет равна
UjeR(t — tj).
Уравнение,
x{t)=^eR{t — tj) ' E2)
— ОО
мы заменяем уравнением
4- ОО
Y tl). A34)
Если нас интересует отклонение X(t) = x(t) — х, то можно заменить я,
на rij—п или, что то же самое, исключить нефлуктуирующую постоянную
составляющую входного тока. Тогда
-*-оо
X(t)=yi{ni — n)eR(t — tj). A35)
— ОО
Вычислим
— оо<у <со
-оо</<оо
Мы знаем, что переменные tij и nt взаимно независимы, если / и j — разъеди-
разъединенные промежутки. Отсюда следует, что
• (nJ — n)(ni — n) = 0 при 1ф). A37)
Поэтому
Р (*) = 2 (»/ — пJ e*R (t — tj)R(t — z — tj).
— ОО
Центральный момент второго порядка («у — пJ вычисляется, исходя
из закона Пуассона, которому подчиняются tit (см. соотношение A06)).
Находим
(л, — «J = « = РоДЛ A38)
664 ТЕОРИЯ ВЕРОЯТНОСТЕЙ j [ГЛ. IX
где р0—средняя плотность, т. е. среднее число электронов в секунду:
/
Поэтому
+ 0О
Р W = 2 Ро*2Я (t — tj)R(t — x — tj)
-оо
Устремляя Д? к нулю, получаем в конечном счете
оо сю
Р (?) = / P0e2R @ R{t — z)dt = el j R (t) R(t — -:) dt. A39)
Это уравнение следует сопоставить с уравнением (99). Явление флуктуации
в чистом виде, т. е. до того, как ее исказила инерция усилителя, предста-
представляет собой явление с микроскопической корреляцией. Говоря точнее, при
сколь угодно малом At корреляция между двумя переменными (щ— п) и
{tij—п), соответствующими двум последовательным промежуткам времени
(tt, tj — ti-\-kt) и (tj, tj-\-At), равна нулю, как в выражении A37). Но мы
знаем, согласно выражению (99), что р(т) принимает вид произведения по-
постоянного числа, зависящего от начальной флуктуации, на функцию от г,
зависящую от фильтра. Это мы и получаем на основании соотношения A39).
Вычислим теперь спектральную плотность. Для этого достаточно при-
применить теорему Парсеваля, которая заключается в следующем. Пусть F1 (t)
и F2(t) абсолютно интегрируемые функции, ограниченные в промежутке
от —оо до -f-oo, a G, (v) и G2Cv)— их коэффициенты преобразования Фурье:
4-ОО
Gj(v)= J /=¦, (f) е-2"'1" dt.
— со
+оо
G2(v)= J F2(t) e-W dt.
— oo
Теорема Парсеваля выражается соотношением
оо со
J Gi (v) Gs(v)dv = J Fi @ F\(t) dt, A40)
— oo —oo
где звездочкой помечена сопряженная комплексная величина.
Если за Fl и F2 принять вещественные функции R(t) и R(t—г), то
вводя частотную характеристику G(v), получим
Gj (v) == G (ч) и G2 (v) = G (v) e -2жЫ.
Отсюда
J R(t)R(t — t)dt= J
— oo —oo
Тогда соотношение A39) запишется в виде
оо оо
р (т) = Г elg2 (v) e2**" dv = J 2elg2 (v) cos 2icvt dv.
9.2] СЛУЧАЙНАЯ ФУНКЦИЯ 665
Сравним теперь результат с соотношением (93), дающим корреляцион-
корреляционную функцию на выходе линейного усилителя. Мы видим, что значение 2е/
представляет собой спектральную плотность, соответствующую сигналу, иначе
говоря, дробовому эффекту тока.
Чтобы рассчитать действие дробового эффекта на усилитель, достаточна
приписать этому явлению равномерный спектр со спектральной плотностью,
равной 2еГ. Это согласуется с тем, что здесь речь идет о явлении с микро-
микроскопической корреляцией. Понятно, что говорить о равномерном спектре
бессмысленно, так как в этом случае при интегрировании по всем частотам
получим бесконечность. В действительности, наблюдать за дробовым эффек-
* том можно только с помощью прибора; при этом главное, чтобы существовал
со
интеграл I 2elg2(y)dv, что зависит только от величины g(v) иными словами
о '
от прибора наблюдения.
Примечание. В заключение следует отметить, что все сказанное
о дробовом эффекте применимо также к эффекту Джонсона (эффект мер-
мерцания), т. е. к флуктуациям электродвижущей силы шумов в сопротивлении.
Действительно, здесь также речь идет о явлении микроскопической корре-
корреляции, которое с помощью некоторой стационарной линейной системы при-
приводит к появлению стационарной случайной функции Лапласа — Гаусса.
ЛИТЕРАТУРА К ГЛАВЕ IX
1. П у г а ч е в В. С, Теория случайных функций и ее применение к задачам авто-
автоматического управления, Физматгиз, 1962.
2. Л е в и н Б. Р., Теория случайных процессов и ее применение в радиотехнике,
.Советское радио", 1960.
3. Миддлтон Д., Введение в статистическую теорию связи, .Советское радио",
1961.
4. С т ратоно в и ч Р. Л., Избранные вопросы теории флуктуации в радиотехнике,
.Советское радио", 1961.
5. Свешников А. А., Прикладные методы теории случайных функций, СудпрЪм-
гиз, 1961.
6. В I a nc-Lapierre A., Stir certaines.fonctions aleatoires stationnaires. Application»
d l'etude des fluctuations dues a la structure electronique de l'electricite, Publications
des Laboratoires de l'Ecole Normale Superieure, Paris, 1945.
7. В1 a n c-L apierre A. et Fortet R., Analyse spectrale de l'energie dans les-
phenomenes de fluctuations, Annales de Telecommunications, 2, № 7, 1947.
8. Borel E., Traite de calcul des probabilites et ses applications, Paris, 1924—1932.
9. P г у Т. С, Probability and its engineering uses. New York, 1928.
10. L о e v e M., Fonctions aleatoires de second ordre, La Revue Scientifique, 84, 1946,
p. 195.
11. Vauiot A., Calcul des probabilites applique a la thelephonie, Cours de l'Ecolfr
Superieure des Telecommunications.
ГЛА ВА X
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
10.1. РЕШЕНИЕ ЧИСЛЕННЫХ УРАВНЕНИЙ
10.1.1. Графическое решение. Очень простой способ вычисления кор-
коржей уравнения /(х) = 0 состоит в том, чтобы тщательно вычертить на'мил-
на'миллиметровке кривую y = f(x). Абсциссы пересечения этой кривой с осью
-абсцисс будут равны искомым корням с приближением, часто достаточным
лля инженера. Они могут служить также отправной точкой для методов
алгебраической апроксимации, описанных ниже. Построение кривой у = /(.*)
полезно для применения этих методов, так как сведения, которые оно ласт
¦о коде кривой, позволят выбрать приближение или метод, наиболее подхо-
.дящий для быстрого вычисления.
Часто можно написать уравнение /(л;) = 0 в виде
При этом решения будут даны абсциссами точек пересечения двух кривых:
у=ср(лг) и y =
Т2сли представление / = '? — Ф выбрано удачно, то начертить эти кривые
будет гораздо легче, чем кривую y = f(x). Например, решение уравнения
•sin л; сп х= 1 легче получить, найдя пересечение кривых y,= sinx, У^^ъТ*'
•чем вычерчивая кривую
у = sin х ch х — 1.
Такое графическое решение может дать очень точные результаты. В п. 10.1.4
этот способ рассматривается более полно и в большей общности.
Если в уравнении /(х) = 0 фигурируют параметры, то иногда оказы-
оказывается возможным собрать их в одну из функций <о(х) или $(х), а другая
оказывается от них независящей. При этом удается получить схему, пригод-
пригодную для графического решения, всех уравнений некоторого типа.
Пример. Графическое решение уравнений третьей и четвертой степени.
а) Требуется решить уравнение xz-\-ax2-^bx-\- с = 0. Положим
х = г—-j . Тогда уравнение принимает вид г3— pz—q = Q при
а2 , ab_ 2aL
о 3 2,{
Достаточно найти пересечение прямой y = pz-\-q с кривой y = z3, которая
¦будет начерчена раз навсегда.
б) Требуется решить уравнение х4 -\~ ах3 -\- bx2 -J- сх -(- d = 0.
10.1] ГЕШрНИЕ ЧИСЛЕННЫХ УРАВНЕНИЙ 667
Положим х = z — — . Тогда уравнение примет вид zi -f- az -\- $z -J- f =0
За2 н a3 ei ,
За1 , a2b ac . .
при
Если а > 0, положим z = t \/~a. Получаем
f-И2 — pt — q = \
•при
Если а < 0, положим z = tY—<*• Получаем
при
Достаточно найти пересечение прямой у = р?-(-<7 с кривой y = t*-\-t2 или,
в зависимости от случая, с кривой y = f* — t2. Обе эти кривые чертятся раз
навсегда.
10.1.2. Метод Ньютона и метод пропорциональных частей, а) Метод
Ньютона. Требуется решить уравнение
/(лс) = О.
Пусть А1В1 — дуга кривой y = f{x) вблизи
корня; flj, bi — абсциссы точек А1 и Б,
(рис. 10.1). Предположим сначала, что эта дуга
имеет вогнутость в сторону положительной
части оси у [f"{x) > 0] и что f(bY) > 0. Пусть Ь2
есть точка встречи касательной, проведенной
к кривой в точке Bv с осью х. Тогда Ь2 пред-
представляет приближение к корню, лучшее, чем blt
и расположенное с той же стороны от корня:
У
о
I
в,
/' (ftl)
A)
Рис. 10.1.
Повторим это рассуждение для нового приближения ?2. Получим
и далее
— h /<6з)
Г (Аз) '
Последовательность bv b2, by ft4, ... стремится к искомому корню.
Если бы дуга кривой была обращена вогнутостью к отрицательной
части оси у, то следовало бы применить только что описанный способ, про-
проведя касательную к кривой в точке Ау
Таким образом, получаем правило: если корень заключен между двумя
числами av bl и вторая производная сохраняет в этом промежутке знак,
668
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
П"Л X
то за первое приближение следует принять то из чисел ах или bv для кото-
которого знак f(x) совпадает со знаком f" (х), иначе говоря, нужно, чтобы
в выбранной точке было f(x)f"(x) > 0.
Замечание 1. Если f"(x) меняет знак в промежутке (а1, ?,), то
может случиться, что вторые приближения окажутся хуже, чем первые
(рис. 10.2). Поэтому полезно перед началом вычисления приближенно вычер-
вычертить кривую y = f(x). Однако иногда применяют метод Ньютона и тогда,
когда f'(x) меняет знак, или даже вообще без всякого исследования.
В таком случае получаемая последовательность приближений может сходиться
к корню или расходиться в зависимости от
обстоятельств.
Замечание 2. Можно легко полу-
получить формулу A), применив формулу Тей-
Тейлора. Если л:0 — точный корень, то
О
х
/ (*о) =
Рис. 10.2.
Считая х0 — Ьх малой величиной и пренебрегая ее степенями выше первой,
находим для л:0 приближенную формулу. Это и есть формула Ньютона.
б) Способ пропорциональных частей. Удобно сочетать только что
изложенный способ Ньютона со способом пропорциональных частей. Имея
отрезок (flj, ?>,), в котором f(x) меняет знак, обозначим через а2 абсциссу
точки пересечения прямой Афх с осью х (рис. 10.1):
_
2~
а через b2— абсциссу, полученную способом Ньютона. Найдя отрезок (а2, Ь2),
поступаем с ним так же, как с (а,, #,), что дает нам а3 и Ья. Продолжая
этот процесс, получаем две последовательности:
_
2~
b, = b<
/F|)
— /, /(h)
f(b2)
которые все ближе и ближе охватывают с двух сторон искомый корень
(если только f"{x) не меняет знака в промежутке (av b{)).
Замечание 1. Для того чтобы уже первые приближения по способу
пропорциональных частей были достаточно близки к искомому корню, необ-
необходимо, чтобы f (,х) не обращалась в интервале в нуль.
Замечание 2. Если иметь возможность все время точно вычислять
/(х), то приведенные выше способы позволяют находить сколь угодно дале-
далекие приближения и, следовательно, получать корень с любой точностью.
Но если f(x) находится из таблиц, которые неизбежно имеют лишь огра-
ограниченную точность, то и корень можно получить также только с ограни-
ограниченной точностью.
Пусть 8/ (х) — совершенная при вычислении f(x) ошибка. Она снижает
точность вычисления х на такую величину Ьх, что
ЮЛ]
РЕШЕНИЕ ЧИСЛЕННЫХ УРАВНЕНИЙ
669
Пример. Требуется решить уравнение хех = 2. Очень упрощенный
чертеж показывает, что искомый корень заключен между 0 и 1 и вогнутость
такова, что можно взять
Имеем последовательности
а2 = 0,735,
а3 = 0,8516.
Ь2 = 0,867,
А, = 0.8531,
а4 = 0,852625. ?4 = 0,852627.
Если ех находить из пятизначных таблиц десятичных логарифмов с по-
погрешностью, не превышающей 10~5, то погрешность в определении f(x)
будет того же порядка, а так как при х = 0,85 ... /' (х) = A -4- х) ех =» 3,3,
то Ьх « -S-S- • 10~5=3- 10~6. Следовательно, нет смысла строить дальней-
дальнейшие приближения.
10.1.3. Метод итерации. Напишем уравнение f(x) = Q в виде
9 (х) = ¦>(*).
Грубое графическое изображение кривых
у = <р (х), у = ф (х)
дает значение л:0 абсциссы точки пересечения. Оно будет грубым приближе-
приближением искомого значения корня. В действительности прямая х = х0 встретит
рассматриваемые кривые в двух разных точках.
Возьмем ту из этих двух точек, для которой наклон касательной имеет
меньшую по абсолютному значению величину. Положим, например, что
и возьмем точку л:0, у0 = у(х0). Проведем из нее прямую, параллельную оси
абсцисс, которая пересечет кривую у=фО) в точке с координатами хл,
( Из точки xv у0 проведем параллель к оси ординат, кот'орая
встречается с кривой у = у(х) в точке с координатами х^, у1 = '
рируем с точкой xv yl так же, как с точкой х0, у0, и т. д.
). Опе-
ОпеО
Xq
Рис. 10.3.
О
Сип Ж7 vuj
Рис. 10.4.
Если наклоны обеих кривых имеют вблизи точки пересечения одинако-
одинаковый знак, то абсциссы хх, х2, • ¦ ¦ стремятся к корню с одной стороны
(рис. 10.3).
Если наклоны кривых имеют противоположные знаки, то абсциссы xv
х2, ¦ ¦ ¦ принимают попеременно значения, то ббльшие, то меньшие корня
(рис. 10.4).
670 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Легко заметить, что скорость сходимости тем больше, чем больше отли-
отличаются наклоны кривых ср и ф.
Пример. Требуется вычислить вещественный корень уравнения
cosx = х — 4.
Построение кривых у = cos х, у — х — 4 показывает, что абсцисса точки
встречи приближенно равна 3. Берем
cos х, ty(x) = x — 4.
Неравенство B) соблюдено. Имеем последовательно
y0 = cosjc0 =cos3 = — 0,93999,
jc, = .yo-f 4 = 3,01001,
yt = cos x, = cos 3,01001 = — 0,99135,
jc2 = у, 4-4 = 3,00865,
y2 = cosx2 = cos 3,00865 = — 0,99013,
jc3 = y2 + 4 = 3,00987.
y3 = cosx3 = cos 3,00987 == — 0,990135,
jc4=ry3 4-4 = 3,009865.
Поэтому искомый корень равен 3,00986 -со всеми верными значащими циф-
цифрами.
•Замечание. Остановимся, в частности, на применении метода итерации
для решения алгебраических уравнений.
Пусть требуется вычислить корень полинома
близкий к г0. Положим
х = г гй.
Мы должны найти близкий к нулю корень полинома
Если коэффициент bn_1 = g'(z0) не мал по сравнению с другими коэффици-
коэффициентами полинома f(x), можно принять
= — Ьохп— ... —Ьп_2х* — Ьп.
При этом
Y@) = ba.v cp'(O) = O
и эти величины сильно разнятся. Можно надеяться, что в точке пересечения
кривых ср и ф, лежащей вблизи от точки х = 0, наклоны кривых будут все
еще сильно отличаться.
Пример. Вычислить близкий к 2 корень уравнения
г3 — 22 — 5 = 0.
Положим
х = г — 2.
Получаем
/ (х) = х3 + 6х2 + 10х — 1 = 0.
Иначе говоря, требуется решить уравнение
10!) РЕШЕНИЕ ЧИСЛЕННЫХ УРАВНЕНИЙ
Имеем последовательно:
671
у, = <р @,1) = 0,939.
с? = у, = 0,939.
, = ср(л:2) = 0.946. ..,
j = y2 = 0,946...,
y3 = <p(jc3) = 0.94546..
10x4 = y3 = 0.94546. ...
y4 = ?(jc4) = 0.94552.,
= у. =0,94552...,
х2 = 0.0939.
х3 = 0,0946...,
хА = 0,094546...,
х5 = 0,094552...
Ня этой степени приближения 0 = 2,094552... (точный корень равен-
0 = 2,09455148...)
10.1.4. Приближенное решение системы двух уравнений. Решение
системы двух уравнений
/2(х, у) = 0
может встретиться, в частности, при нахождении комплексных корней урав-
уравнения
Действительно, положим г = х -\-jy. Тогда, если отделить веществен-
вещественную часть от мнимой, уравнение D) может быть написано в виде
и мы приходим к системе C).
Может показаться соблазнительным решить систему C), исключив, на-
например, переменную у и решив полученное таким образом уравнение отно-
относительно х. В большинстве случаев это оказывается невыгодным. Напротив,
как мы видели в п. 10.1.1, часто бывает проще представить уравнение /(л:) = 0-
в виде равенства двух функций у == /г (х) и у = /2 (х), так как при этом
легче нарисовать соответствующие кривые.
а) Графический способ. Вычерчиваются графики двух уравнений си-
системы C). Координаты точек пересечения дают пары вещественных значений.
xv у,; х2, у2; удовле-
удовлетворяющих данной системе. ^^
Пример 1. Требуется
решить систему
х2 — 2х — у+2 = 0.
Эта задача сводится к тому,
чтобы найти точки пересе-
пересечения кривой третьего по-
порядка и параболы. Грубо Рис. 10.5. Рис. 10.6.
нарисовав обе кривые, мы
видим, что кроме очевидного корня л; = у=1 имеется еще только один1
корень, с абсциссой, близкой к л: = 0,7 (рис. 10.5).
Более подробный чертеж интересующей нас части кривых в большем
масштабе показывает, что этот вещественный корень заключен между
672
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ X'
= 0,70 и jc = 0,71 (рис. 10.6). Последний чертеж сделан на основании
следующей таблицы:
х — 0
х = 0
х = 0
х=1
,6
,7
,8
,0
Кривая третьего
порядка
у = 0,979
у= 1,0836
у== 1,158
у= 1,0
Парабола
у = 1,16
у= 1,09
у =1,04
у = 1,0
Представим интервал между лг = 0,7 и * = 0,71 в еще большем мас-
масштабе. При этом можно заменить кривые отрезками прямых, соединяющих
точки (рис. 10.7)
л; = 0,7
л; = 0,7
л; = 0,71 у =1,084
у= 1,0836
у =1,092
у =1,09
кривая третьего порядка.
парабола.
Точка пересечения имеет абсциссу, заключенную между 0,704 и 0,705.
1,05737
1.092 '
/,03762
1007,5
7,0д5
'W36
7,Ов7О7
Рис. 10.7.
@,7044)
Рис. 10.8.
1,08703
Действуем также в интервале 0,704; 0,705. На этот раз отрезки пря-
прямой соединяют точки (рис. 10.8)
х = 0,704
л; = 0,705
л: = 0,704
* = 0,705
у =1,08701
у =1,087912
у= 1,087616
у=. 1,087025
кривая третьего порядка,
парабола.
Можно продолжать построение до бесконечности, но если рстановиться
на этом этапе вычисления, то пересечение кривых дает в качестве решения
системы
дг = 0,70440,
у =1,08738.
(Точные значения равны х = 0,704402...; у = 1,087378.;.)
10.1]
РЕШЕНИЕ ЧИСЛЕННЫХ УРАВНЕНИЯ
673
Замечание. Умножив второе уравнение на х и вычтя его из пер-
первого, можно заменить данную систему на систему
2дг2 _|_ у2 — ху — 2лг = О,
х2 — 2х — y-f^ = O-
Но вычерчивание по точкам эллипса не проще, чем вычерчивание кривой
третьего порядка.
Пример 2. Найти сопряженные комплексные корни уравнения
4z3 — Ъг2 — 6z — 3 = 0.
Положим z = x-\- jy. Получаем два уравнения:
4л:3—12лгу2 —Зл:2-(-Зу2—блг —3 = 0, E)
у (блг2 — 2у2 — Злт — 3) = 0.
Решение у = 0 соответствует вещественному корню. В плоскости пере-
переменных х, у кривая
блт2 — 2у2 — Злт — 3 = 0
является гиперболой. Она изображена пунк-
пунктиром на рис. 10.9 и пересекает кривую
третьего порядка E) в двух симметричных
точках, координаты которых приближенно
равны х = —0,5, у = ±0,37. Применение -1,0 jQ5 О 1,0
ранее описанного способа быстро привело бы
к значениям, которые мы найдем в п. 10.2.5,
пользуясь способом Лобачевского—Греффе—
Данделена.
Замечание. Если кривые, представ-
представляющие систему C), пересекаются под очень Рис. 10.9.
острым углом, точность может оказаться
не слишком хорошей. Такой опасности нет при нахождении комплексных
корней, когда коэффициенты уравнения вещественны, так как обе кривые
при этом ортогональны.
б) Способ Ньютона. Пусть xs=a0, у~Ьа — первое приближение реше-
решения системы C) и пусть а и Р — точные значения этого решения.
Имеем
Можно написать
во.
)
'До,
Пренебрежем членами Q и R второго порядка по h и k. Тогда можем
найти приближения лучшие, чем а0, Ьо:
где hl и kx определяются системой
43 А. Анго
674 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Теперь, отправляясь от аг и bv можно вычислить следующее приближение
и т. д.
Пример. Вернемся к примеру 1 и будем исходить из приближения
а = 0,7, *=1,1.
Имеем
±.
9 0
дх ду
Отсюда получаем систему
— 0,73/?!+ 0,8^! = — 0,013,
— 0,6 hx— йг = -(-0,01,
а из нее
Л1 = 0,0041, ^! = — 0,0125,
а1 = 0,7+0,0041 =0,7041,
^ = 1,1 —0,0125= 1,0875.
Если действовать таким же образом, отправляясь от значений av bx,
то получим
h2, k2 определяются из системы
— 0,68773/224- О,7668Й2 = — 0,00030112,
0,5918 /г24- *2= 0,00005681,
откуда
Й2 = О, 00030195, /г2==—0,00012188
и
а2 = 0,70440195, Ь2 = 1,08737812.
10.2. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1)
10.2.1. Численное решение уравнений третьей и четвертой степени.
1. Требуется решить уравнение х3-\- ах2-\-Ьх-\-с = 0. Припомним вкратце
классический способ решения. Осуществим замену переменной х = z—-f-.
о
Тогда уравнение примет вид
z3 — pz — q = 0.
Могут встретиться следующие случаи:
1) р < 0. Положим
Корни равны
3 tg2? ~J У
') См. в п. 4.1.10 матричный способ приближенного решения уравнений
попялка.
)
я-го порядка
10.2] РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 675
2) р > 0, (-?¦) < |-|-| . Положим
sin9=-f/?• **=/*!¦
Корни равны
К ~3" " sin2<p ' К Т sin 2? — Jr P ' tg2f '
3) j0 > 0, (-f-T > (-f-| . Положим
Корни равны
4) ^>0, (^K = (-|J. Корни равны
Замена дг = г:—-~- дает корни исходного уравнения.
Пример. Требуется решить уравнение лг3 — Зд;2—8лг-(-4 = 0. Поло-
Положим х = z-\-\. Уравнение принимает вид
z3— 112 — 6 = 0.
Здесь имеет место третий случай:
cos <р = -^! /^- = 0,42728, ср=64э42'17",
cos 21° 34'5"= 2 /-у- -0,92998 = 3,5615,
22 = — 2 |/ ^- cos 38° 25' 55" = — 2 /-у- ¦ 0,78334 = — 2,9999.
•zz = — 2/-J- cos 81° 34'5" = — 2 /-у- -0,14664 = —0,56158.
Отсюда
*!= 4,5615, лг2= — 1,9999, х3 = 0,43841.
Произведение (лг — Xj) (х — лг2) (дг — дг3) дает
л-3 —3,00001х2—7,9995x4-3,9994.
2. Требуется решить уравнение х44" ах34-^х24-с^4"^ = 0- Клас-
Классический способ решения таков: рассматриваем уравнение третьей степени
z3-\-rz2-\-sz-\-t = 0, F)
коэффициенты которого определяются формулами
r = — b, s = ac — 4d, t = d Db — a2) — с2.
43*
676 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Пусть Z — наибольший вещественный корень уравнения F). Этот корень
может быть найден предыдущим способом. Вычисляем величины:
/ Z , ft Z \2 Т
в которых
б == -{— 1, если —- — с>0,
е = — 1, если ~2 с < 0.
Искомые корни суть корни двух уравнений
+ с/ =0,
Пример. Требуется решить уравнение
х4 + 2дг3 + Зл:2 — 2х + 1 = 0.
Получаем
/• = — 3, s = — 8. f = 4.
Вспомогательное уравнение
было только что решено. Поэтому Z== 4,5615.
Имеем е = -j- 1 и
р=1 -|-]Л—3 + 4,5615 = 2,6005, ^'= 1 —]/l— 3 + 4,5615 = — 0,6005
4,5615 , / , ,lUUlu \- _l== 0>23092.
4 ~ 2
Отсюда получаем два уравнения
х2 + 2,6005* + 4,33058 = 0,
х2 — 0,6005* + 0,23092 = 0,
корни которых
— 1,3002 ±1,6248/ 0,3002 ±0.37519/.
Вычислив произведение левых частей обоих уравнений второй степени,
находим
*4+2,0000*3+2,9999*2 —2,000005*+1,00001=0,
что является превосходной проверкой вычислений.
10.2.2. Схема Горнера. Эта схема позволяет удобно расположить вычис-
вычисления при подстановке числа в полином.
Даны полином
и некоторое значение х = а. Напишем очевидное равенство
, (8)
10.2] РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 677
где /, (лт) — некоторый полином степени л — 1 (частное от деления / (л:)
на х — а):
/W 4M-4
Отсюда
/W = V + (*,-»*o)^1 + (*2-«*1)^2+ ¦•• +(/(«) —айя_,). (9)
Отождествление G) и (9) дает
b2 = a2-\-ab1 f{a) = an-\-abn_v
Если нужно вычислить при лг = а значения не только /, но и ее пос-
последовательных производных, построим по образцу f\(x) полиномы
/2 (лт) /„ (лг), определяемые тождествами
f, (a).
/ft_! (лг) = {x — a) fk (x) -f- /ft_! (a),
Последовательное дифференцирование дает
/ъ-\(х)==(х— a)/ft (х)~\~Р/ц (x)> fk-\ (a) = Pftt (a)
(p = 1 л — ft).
Следовательно,
/(p) (a) = ^/(р-*> (a) = /7 (/, - 1) /2P~2) (a) =...=/,! /p (a).
Все свелось к нахождению величин fp(p-) = —r/(p)(a). которое выпол-
выполняется по тому же образцу, что и нахождение /(а). Последовательно нахо-
находятся величины
ft (a) = bn_l-\-acn_2>
Вычисление производится механически, если расположить эти величины
по приведенной здесь схеме Горнера:
а0 а, а2 а3 • • • ал-2 ап-\ ап
аЬп чЬл abn . . . аЬ„ о &Ь„ о аЬ„_,
со = <
Ао=<
ас0
h с,
ас,
с*
А2
ас 2
сз
... а"с~\
¦•• ^-2
gn—p—1
*hn-p-1
. «« /<а)
/»
g п—р
-i- /(p) (a)
678
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Пример. Дан многочлен f(x)=x5-\-20x'i—1 Олг3 —|- 2лг2 — Ъх—15.
Для а =— 1 схема осуществляется так:
1
20
—1
— 10
— 19
2
29
— 3
—31
— 15
34
1
1
1
19
— 1
18
j
17
—1
16
1
15 =
24/
—29
— 18
—47
— 17
—64
— 16
—80
v(—1
)
31
47
78
64
142=1/
(-1)
—34 19 = /(—1)
—78
—112 = /'(—1)
¦"(-о
; 10.2.3. Построение Лилла. Это построение осуществляет графически
операции, дающие коэффициенты Ьо, Ьх bn = f(a) из схемы Горнера.
Иначе говоря, оно графически дает результат подстановки числа а в полином
aoJf-r-ajjf"-^ ... -\-an_lX-\-an.
Дан квадрат MNPQ, стороны которого ориентированы в направлении, ука-
указанном стрелками (рис. 10.10). Выберем единицу длины и отложим от точки О
параллельно стороне MN отрезок длиной а0.
Если число а0 положительно, то отрезок откла-
откладывается в направлении MN, если оно отри-
отрицательно, то в обратном направлении.Получаем
точку Ао. От этой точки параллельно сто-
стороне NP откладываем отрезок длиной аг при
той же договоренности о знаках. Получаем
точку Av Продолжаем таким же образом по-
построение, проводя параллели к последователь-
последовательным сторонам квадрата. Получаем точки
А2, Л3 An_v An. После этого из точки О
проводим луч, образующий с лучом ОА0 такой
угол 0, что tg0=a. Он будет, следовательно,
справа от ОА0 при отрицательном а и слева —
при положительном. Этот луч пересекает А0А^
в точке Во. Восставим в Во перпендикуляр
к ОВ0, пересекающий AtA2 в точке Bv и т. д.
Последний перпендикуляр, восставленный
из точки Вп_2, пересекает прямую Ап_1Ап в такой точке Bn_v что
^л-iAj —/(а)- Действительно, имеем
ВоАо—аоа, В0Л1
Рис. 10.10.
10.2] РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИИ 679
Таким образом, операции первой строки схемы Горнера осуществлены
графически. Если точка Вп_х совпадает с Ап, то a = tg0 таково, что /(а) = 0.
Следовательно, а есть корень. Отсюда получаем способ нахождения „на ощупь"
вещественных корней полинома.
Рис. 10.10 составлен для полинома
2дг5-4-2х4 — лг3 + Злг2 — 5х-4-2;
тонкие линии показывают подстановку a=l=tg-^-. Находим В4А5 = 3.
10.2.4. Способ Лагранжа. Пусть fi(x{) — алгебраическое уравнение,
которое нужно решить. Предположим, что требуется найти корень а, заклю-
заключенный между двумя последовательными целыми числами
ах и al-\- 1.
Производим замену переменных
*i = *i + h
Получаем при этом алгебраическое уравнение /2{х2), один корень которого
заключен между -f-1 и бесконечностью. Пусть а2 и а2-\~\—два целых
числа, между которыми лежит этот корень. Производим замену переменной
х2 = а2-\ и т. д. Искомый корень равен
1
Если он рационален, то эта непрерывная дробь конечна.
Пример. Требуется определить заключенный между -j-З и -f-4 корень
уравнения
f1 (Xj) = 2лг3 — Зх\ — 12х1 — 1 = 0,
Положим х1 = 3-\ . Получаем уравнение
/2 (*2) = 1 О*3 - 24*2 _ 15х2 - 2 = 0,
корень которого, больший чем -f-1, заключен между 2 и 3. На это указы-
указывает то обстоятельство, что в ряду чисел /2A). /2B), /2C), ... впервые
перемена знака наблюдается при переходе от /2B) к /2C). Положим
Получаем уравнение
о \ о/ о о о
корень которого, больший чем -4-1, заключен между 1 и 2. Положим
Получаем уравнение
f (у \ 7jr3 ЧОлг2 1 3Rjc 48 — О
680 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
корень которого, больший чем +1, заключен между 14 и 15. Положим
Получаем уравнение
/8(*6)= 370*3-1461*§-204*5-7 = 0.
корень которого, больший чем —|— 1, заключен между 4 и 5.
Если здесь остановить приближение, то искомый корень будет заключен
между
3 + - г =3,34078
3 + - г- =3,34080.
о i J
1+J
14 + 1
10.2.5. Метод Лобачевского — Греффе — Данделена. Дано алгебраи-
алгебраическое уравнение
= 0. A0)
Коэффициенты Ло, Л, Ап вещественны. Обозначим корни уравнения
через Xj, x2 хп. Излагаемый способ решения опирается на следующие
положения:
а) Если уравнение A0) имеет k корней хг, х2, ..., хк, модули которых
имеют порядок величины, значительно больший, чем модули п—k других
корней xk+1 хп, то уравнение можно разъединить на два уравнения:
Лох^+Л^*-1-^ ... +Ак = 0, A1)
КОрНЯМИ КОТОРОГО Приближенно будут Jfj Xk, И
1х''-*-1+ ... +Л„ = 0, A2)
корнями которого приближенно будут х1г + 1 хп.
Действительно, пусть для определенности & = 2. Тогда из представления
f(x)— А0(х — хг)(х — х2)(х — х3) ... (х — хп)
находим
Л, = — Л0(лг1Н-дг2+х3+ ... ~\-хп)^ — А0(х1-\-х2),
Л2= Л0(лг1дг2-(-дг1дГз+х2дГз+ ... +х1хл+ ... +лг„_1л:л)« Лох,л:2.
Уравнение
Л0х2+Л,х + Л2=0 A3)
имеет коэффициенты, близкие к коэффициентам уравнения
А0х2 — Ло (х{ ~-\- х2) х + Л0лг,х2 = 0.
Следовательно, и корни уравнения A3) близки к корням хх и х2 этого
последнего уравнения.
10.2] РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 681
Аналогично проводится рассуждение для любого k.
Уравнение A2) найдем, если произведем замену переменной дг = —
и повторим предыдущее рассуждение.
Пример. Уравнение
л:4 — 15 ООЗлт3 -+- 50 045 002л:2 — 150 030 000л: -+-100 000 000 = 0
имеет корни 10 000, 5000, 2 и 1. Уравнение х2 — 15 003л: + 50 045 002 = 0
имеет корни 9997 и 5006; уравнение 50 045 002л:2—150 030 ОООлг+
+ 100 000 000 = 0 имеет корни 1,0008 и 1,9964.
б) Если два числа а и b таковы, что \а\ < \Ь\, и если е — сколь угодно
малое положительное число, то можно всегда найти число р, настолько
большое, что
Р
<8
в) Поставим перед собой задачу построить уравнение, имеющее в ка-
качестве корней величины, противоположные квадратам корней уравнения A0),
т. е. —х\ —л:2. Для этого достаточно найти произведение f(x)f(—х)
и заменить — лг2 на х. Тогда получим
а\ |
— 2А,А3 |л-»-2+ ... =0. A4)
4-24И4 |
Закон образования коэффициентов прост. Коэффициент ранга k равен ква-
квадрату коэффициента ранга k уравнения A0), к которому прибавляют удвоен-
удвоенные произведения симметрично расположенных коэффициентов, попеременно
сопровождаемые знаками —, -)-, —, -)-, ...
Метод Лобачевского — Греффе — Данделена заключается в следующем.
Способом, описанным в в), из уравнения A0) получают уравнение A4). Затем
из уравнения A4) таким же способом получают уравнение, имеющее в ка-
качестве корней —л:4, .... —л:4, и т. д., вплоть до уравнения
имеющего корни —х\ , .... —л:2 .
Если р достаточно велико, то уравнение A5) может быть разъединено
на некоторое число частичных уравнений, имеющих в качестве корней, с точ-
точностью до знака, корни уравнения A0), возведенные в степень 2Р.
Действительно, если разбить корни на группы, отнеся к одной группе
все корни, имеющие общий модуль, а затем расположить эти группы в порядке
убывания модулей, то после возведения в степень 2р модули корней одной
группы становятся пренебрежимо малыми по сравнению с модулями корней
предыдущей группы.
Пользуясь методом Лобачевского — Греффе — Данделена, мы можем
встретиться с несколькими различными случаями.
Первый случай. Все корни уравнения A0) простые, а их модули
различны. Следовательно, все корни вещественны, так как коэффициенты
уравнения A0) вещественны по предположению. Разъединение даст частич-
частичные уравнения первого порядка.
682
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Этот случай характеризуется при возрастании р правильным возраста-
возрастанием (или убыванием) коэффициентов а0, ах а„, возможно лишь начиная
с достаточно больших р. Коэффициенты всегда будут положительны.
Если р достаточно велико и если считать, что корни xv x2 хп
расположены в порядке убывания модулей, то можно написать
\x,
откуда
_1_
2P
log
l**l2
откуда
Остается определить момент, когда можно считать р достаточно большим.
Это зависит, очевидно, от точности, которую мы хотим получить при вычи-
вычислении xk. Если мы располагаем таблицей логарифмов для чисел от 1
до 10 000, то можем получить только 5 значащих цифр. Следовательно,
р будет достаточно велико, если при вычислении коэффициент ak оказывается
равным, с точностью до первых пяти значащих цифр, квадрату предыдущего
коэффициента того же ранга*), иначе говоря, если прибавление удвоенных
произведений не изменяет первых пяти значащих цифр квадрата предыдущего
коэффициента. Будем говорить, что при, таком значении р коэффициент ак
удовлетворяет условиям разъединения. Знак, который нужно поставить перед
найденным модулем \хк\, получается с помощью проб.
Пример. Требуется решить уравнение 2х3 — Зх2—12л:—1=0. По-
Последовательность вычислений ясна из нижеследующей таблицы:
р
0
1
2
3
4
2
4
4
16
16
256
256
65 536
65 536
42950-105
а.
О
9
+48
57
3 249
—1104
2145
46010-Ю2
—6 058-102
39 952 • 102
15 962-109
—183 • 109
15 779 • 109
24 898-1022
—2 • 1022
аг
—12
144
—G
138
19 044
—114
18 930
35834-1041)
0-10»
35 834 - W
12 84Ы013
0-Ю13
12 841-1013
16 489 • 103°
0-103°
—1
1
1
1
1
1
1
1
1
1
*) То есть при той же степени неизвестного.
10.2]
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
683
Продолжение
р
5
6
42 950 • 105
18 447-Ю15
18 447-Ю15
а,
24 896 • 1022
61 981 -10<81)
0-Ю48
61 981 • 10<8
1648?-103°
27 189 • Ю64
0 • 10"
27 189 • Ю64
а3
1
1
1
') Коэффициент а2 удовлетворяет условиям разъединения
при ^ = 3; коэффициент ах — при р = 6. Большое различие
между этими двумя значениями р показывает, что два боль-
больших по модулю корня имеют одинаковый порядок величины,
а меньший по модулю корень отличается весьма значительно.
lOg I X; I
J0g |*2 I
• 1016) = Ж
= -?4-log C,3600- 1033), [je-il — 3,3407;
@,43867 • 1016), |л:21 — 1,7555;
= ¦& log @,36780- 108), |лг3|—0,085254.
Находим, что левая часть уравнения имеет попеременно противополож-
противоположные знаки в точках —2, —1, 0, -f-oo, откуда
= + 3,3407,
= — 1,7555,
—— 0,085254.
Второй случай. Несколько корней имеют один и тот же модуль.
Важнейшим является случай, когда имеется несколько пар сопряженных ком-
комплексных корней. Он характеризуется колебаниями одного или нескольких
коэффициентов при возрастании р.
Пусть, например, этим коэффициентом будет ak. Сумма удвоенных
произведений —2aft_]aft+1-j-2ай_2ай+2— ... никогда не будет'прене-
будет'пренебрежимо мала по сравнению с первыми значащими цифрами а|, как бы ни
было велико р. Положим, что Имеется только пара сопряженных комплекс-
комплексных корней. Если р достаточно велико, чтобы все остальные коэффици-
коэффициенты, кроме ak, удовлетворяли условиям разъединения, то можно разъединить
уравнение на несколько уравнений первого порядка и одно-уравнение второго
порядка
Оно, с точностью до знака, будет иметь в качестве корней искомые ком-
комплексные корни, возведенные в степень 2Р. Модуль этих комплексных кор-
корней р находится из соотношения
откуда
A6)
Вычислив вещественные корни уравнения A0) и обозначив через
два искомых комплексных корня, получим
~:7
Отсюда находим а, а следовательно, и C = У"р2 — <*2-
684
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Пример. Требуется решить уравнение 4х3— Зх2 — 6л: — 3 = 0. Вычи-
Вычисления приведены в следующей таблице:
р
0
1
2
3
4
4
16
16
526
256
65536
6553&
42950-105
42 950-105
а,
—3
9
+48
57
3249
+576
2 673
71 449 • Ю2
+3 594 - Ю2
75 043 • 102
56 314-Ю9
—7 - 10»
56 307 -109
в!1)
—6
36
—18
18
324
—1026
—702
49 280-10
—43 302-10
5 978-10
- 3 573-10в
—98 471 - 10е
—94 898 • 106
а3
—3
9
9
81
81
6561
6561
43 047-1О3
43047-Ю3
') Флуктуация коэффициента а2 делает очевидным суще-
существование пары сопряженных комплексных корней, модуль
которых меньше абсолютного значения вещественного корня.
,! = 1,8086;
1= 1,80864-2а, а = — 0,5293, р = /р2 — а? = 0,36667,
xl= -т 1.8086, х2 = — 0,5293 + 0,3666/, хг = — 0,5293 — 0,3666/.
Случай, когда имеются две пары сопряженных комплексных корней,
характеризуется колебаниями двух не соседних коэффициентов. Когда для
других коэффициентов будут получены условия разъединения, оба квадрат-
квадратных уравнения дадут, как и в предыдущем случае, модули р и р' комплекс-
комплексных корней.
Пусть xv х2 л^ (s = п — 4) — вещественные корни. Получим
Отсюда находим
а, а', р =
= V р'2 —а'
Третий случай. Пары комплексных сопряженных корней — не един-
единственный случай, когда два корня имеют одинаковый модуль. Это будет
также, если имеется двойной корень или если два корня имеют противо-
10.2]
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
685
положные значения, что сводится к двойному корню уравнения, полученного в
результате первого преобразования уравнения A0) (р== 1). Модуль этих корней
может быть вычислен по формуле A6). Прикидка в уравнении A0) покажет, что
будет иметь место: хк = р, xk+1 —— р или xk = xk + l=t ± р. Коэффи-
Коэффициент ak во время возрастания р будет изменяться иначе, чем в предыдущем
случае, он не колеблется, а все время остается положительным и стремится
стать равным не квадрату коэффициента ak, соответствующего р— 1, а поло-
половине этого квадрата.
Пример. Требуется решить уравнение 2хг-\-Ъх2—12х-)-7 = 0. Вы-
Вычисления приведены в таблице:
р
0
1
2
3
4
2
4
4
16
16
256
256
65536
65536
а,
3
9
+48
57
3249
—816
2 433
59 193 • 102
—1 542 ¦ 102
57 653- 102
33 238 • 10е
—6 • 109
33 232-109
а„
—12
144
—42
102
10 404
—5586
4 818
23 213-Ю3
—11683-Ю3
11530-Ю3
132 936-109
—66 472 • Ю9
66 464 • Ю9
7
49
49
2 401
2401
57 648 • 10!
57 648-Ю2
33 232 • 109
33 232 • Ю9
Условия разъединения выполняются для ах, но не для а2. Удвоенное произ-
произведение 2а1а3 становится равным -д- а\, что доказывает наличие двойного корня.
Имеем
1 - /33232 откуда
65 536
1 1 . 33 232
logp = -g-grlog-
\хх\ =3,500, х1 — — 3,500;
откуда р = 1.
Прикидка показывает, что лг2 = х3=1.
Четвертый случай. В этом довольно редком случае имеется веще-
вещественный корень хк = + р и два сопряженных комплексных корня хк+1 = peJf,
xk+2 — pe~i<f. При возрастании р коэффициенты ак и ак+1 не удовлетво-
удовлетворяют условиям разъединения. Так как они расположены последовательно, то
это характеризует случай одного вещественного и двух комплексных корней
с одинаковым модулем. '
Когда все остальные коэффициенты удовлетворяют условиям разъедине-
разъединения, корни хк, xk+v xk+2, возведенные в степень 2Р и взятые со знаком
минус, будут представлять собой решения уравнения
л v-З _1_ n v!j_ я v _1_ л — (\
Uh— 1* —Г" «Ь-* ~Г" «Ь-И-* ~Г~ иЪл.О — "•
C86
Отсюда
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
вещественная часть а и мнимая C получаются, как показано выше.
Может быть еще, что хк — ± р, xft + 1 — ± р, xk+2 = peJf, xk+3 — pe-}v.
Когда коэффициенты, кроме ak, ak+v ak+2, удовлетворяют условиям разъ-
разъединения, корни xk, xk+v xk+i, xk+z, возведенные в степень 2Р. и взятые
со знаком минус, будут решениями уравнения
Отсюда log р = —
4
log
. Вещественная часть а и мнимая [3 опре-
определяются, как в предыдущем случае.
Если исключить случай корней кратности больше 2, то мы рассмотрели
здесь все возможные случаи, когда уравнение A0) с вещественными коэф-
коэффициентами имеет корни с одинаковым модулем.
Пример. Требуется решить уравнение
— 56х3 — 56x2+- 172х — 120 = 0.
р
0
1
2
3
4
а0
1
1
1
1
1
1
1
1
1
1
1
а.
—15
225
—112
113
12769
—2 688
10 081
10163-10*
—162-10*
10101-Ю4
10002-Ю'2
— Ы0'2
10 001-Ю'2
1002-Ю28
—1 • Ю2"
10 002-1028
56
3136
—1680
—112
1344
18 063-Ю2
—10 142-102
+179-102
8100-Ю2
65 610-10'
¦4 651 • 10'
—5-10'
66 256-10'
43 898-Ю'9
—843-Ю'9
0-Ю'9
43 055-Ю19
18 537-10*3
—1-Ю43
0-Ю*3
18 536-10*3
а3
—56
3136
+6272
—5160
+240
4 488
20 142-Ю3
—24 084-103
+3 648-Ю3
—29-Ю3
—323-Ю3
10 433-10'
+4198 878-10'
+5 200-10'
—40-10'
42145-Юэ
17 762-1023
—13 375-Ю23
+21-Ю23
0-Ю23
4 408-Ю23
19 430-Ю*9
—14 571-10*9
0-Ю49
0-10*9
4 859-Ю*9
—56
3 136
+19 264
—13 440
8 960
80 282-Ю3
-144 908-Ю3
+ 38 707-103
—25 919-Ю3
67179-10'°
+167-10'°
+33 592-10'°
100 938-10'°
101 885-Ю23
—90 662-Ю23
+5 689-1023
16 921-Ю2^
28 632-Ю5*
—25 469-Ю5*
+1 592-Ю54
4 755-105*
172
29 584
—13 440
16144
26 063-10*
—25805-10*
258-10*
66 564-Ю8
+107 491 277- Ю8
10 756-10'2
11 569-Ю28
—8 680-Ю28
2 889-Ю28
83 463-Ю58
—62 567-Ю58
20 896-Ю58
—120
14 400
14 400
20 736-10*
20 736-10*
42 998-10'2
42 998-Ю12
18 488-1029
18 488-1029
3418Ы062
34181-Ю62
10.2]
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
687
Как показывает таблица (стр. 686), коэффициенты ах и а2 удовлетворяют
условиям разъединения. Следовательно, имеется два вещественных корня.
Но три последовательных коэффициента а3, а4> а5 не удовлетворяют этим
условиям. Следовательно, имеются 4 корня с одинаковым модулем, связан-
связанные в одном уравнении четвертого порядка.
Имеем
log 1*!!=-^-log A,0002- 1032), 1^1 = 10,0005,
log|JC2| = 25-log (
18 536
10 002
34181
1015) ,
• Ю19),
I x2| =3,00002,
18 536
15 = 10,0005 + 3,00002 -+- 2a,
p= 1.4142,
a = 0,9996,
P=yp2_a2, p= 1,0004.
Точные значения корней равны 10, 3, ± \f2, I ± ].
Пятый случай. Если уравнение A0) имеет два вещественных
корня xk, xk+v абсолютные значения которых очень близки, то коэффи-
коэффициент ak стремится к условиям разъединения очень медленно. Если условия
разъединения уже получены для других коэффициентов, то можно в этот
момент разъединить уравнение на некоторое число уравнений первой степени
и одно уравнение второй степени, имеющее в качестве корней взятые со зна-
знаком минус степени 2Р величин xk, xk+1. Вычисления при этом аналогичны
вычислениям для случая двойного корня, но коэффициент ak не будет равен
половине квадрата предыдущего коэффициента того же ранга.
Пример. Требуется решить уравнение хъ—65х2-{- 1087х— 1023 = 0.
Вычисления приведены в таблице:
р
0
1
9
3
4
1
1
1
1
1
1
1
1
1
а.
—65
4 225
—2174
2 051
42 066- 102
—20 972 • 102
21 094 - 102
44 496- Ш8
—21 906 • Ю8
22590-108
51 031 • 1020
23 994 ¦ Ю20
27 037 • 1020
1087
11816-102
—1 330 • 10!
10 486-Ю2
10 996 • 108
—43 • Ю8
10 953 ¦ 10s
11997- 1020
0 • 1020
11997-1020
14 393-1044
0 ¦ 1044
14 393 • 1044
—1023
10465-102
" 10 465 • 10!
10 952-108
10 952 • 10s
11 995-Ю2о
11995-Ю20
14 388 • 104'
14 388-10"
Коэффициент ах лишь очень медленно стремится к условиям разъединения.
Дл*я коэффициента а2 они выполняются уже при р = 3.
688 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Имеем
= ¦&¦ log "ЦЦ. |*3| =1.00002.
log Ixil =-^-log u "*" о r """° 1020, |*,| =32,996,
(л:2| =31,003.
Точные значения корней равны 1, 31 и 33.
10.3. ПРИБЛИЖЕНИЕ ФУНКЦИИ
Приближение функции полиномами
10.3.1. Введение. Если дана функция /(*) вещественной переменной х,
может оказаться полезным заменить ее в данном промежутке изменения х
другой функцией более простого вида. В большинстве случаев функция f(x)
известна лишь эмпирически, т. е. известна лишь таблица значений b0, bv .... bn,
которые она принимает при значениях а0, av ..., ап аргумента. Самая про-
простая мысль состоит в том, чтобы заменить f(x) полиномом я-й степени,
принимающим те же значения, что и f (х). Иначе говоря, заменить кривую f(x),
проходящую через я-f-1 точку а0, Ьо; ...; ап, Ьп параболой я-й степени, про-
проходящей через те же точки. При этом могут представиться два случая:
1) абсциссы а0, ах ап распределены неравномерно; 2) абсциссы а0, av ..., ап
составляют арифметическую прогрессию. Это наиболее частый случай, и мы
на нетя остановимся подробнее.
Можно поступить и иначе: вместо того чтобы искать параболу я-й сте-
степени, проходящую точно через я-f-1 точку, можно найти параболу низшей
степени р, проходящую возможно ближе к этим я-f-1 точкам. Если при этом
абсциссы находятся в арифметической прогрессии, вычисления упростятся, но
лишь в небольшой степени.
Функция f (х) может быть задана также аналитически. Замена ее поли-
полиномом имеет целью получить вместо сложного аналитического выражения,
плохо поддающегося расчету, гораздо более простое. Если при этом воз-
возможно вычисление последовательных производных, мы можем применить кроме
способов, изложенных для эмпирических функций, еще и другие способы.
Замена / (л:) более простой функцией должна облегчить не только вычисле-
вычисление значения функции для значения аргумента, отсутствующего в отправной
таблице, но также 'и вычисление значения производной для любой точки
интервала и в особенности приближенное вычисление интеграла, которое при-
применяется, в частности, для приближенного решения дифференциальных урав-
уравнений.
10.3.2. Значения аргумента распределены неравномерно. Интерполя-
Интерполяционный полином Лагранжа. Пусть а0, ах ап — значения аргумента
и Ьо, Ьх Ьп — значения функции f (х). Пусть Р(х) — искомый полином
я-й степени, принимающий те же значения при тех же значениях аргумента.
Р (х)
Разложим на простые дроби отношение д v обозначив через D(x) поли-
полином степени я-f-1:
(х — ао)(х — ах)(х — а2) ... (х — ап).
10.3] ПРИБЛИЖЕНИЕ ФУНКЦИИ 689
Получим
Ak
D(x) ?йх~аь '
иначе говоря,
"\х)— 7t ль ii (л — ал.
Дадим х значение at. P(x) принимает значение bit и все члены суммы
равны нулю, кроме произведения, для которого &=/. Отсюда
п
Искомый полином Р(х) может быть записан в виде
(х — as)
Это интерполяционная формула Лагранжа. Важно отметить, что она
мало удобна для быстрых вычислений, но имеет большое теоретическое
значение.
Полином Р(х) лучше найти следующим образом. Запишем Р(х)
в виде
... + Вп (х — а0) (х — aj) ... (х — ап_{).
Имеем
Рассмотрим полином
Q(a)
Затем рассмотрим полином
х —
44 А. Анго
690
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
и т. д. Шаг за шагом определяем все коэффициенты В, что и дает искомый
полином Р(х). Практически вычисления располагают в виде следующей
таблицы:
X
a0
a,
a2
a3
an
P(x)
b3
bn
a, — a0
a2 — a0
Ьз — *o
a3-a0 *
an — a0 q"
R(x)
Яг — Я\ f B
&2 "~" ^1 *" '*"
Яъ — Я\ r
a3 —-a,
Яп — Я\ f
an~at
S(x)
a3 — a2
Найдем предел ошибки, совершенной при замене f(x) на Р(х). Рас-
Рассмотрим функцию
F(в) = /(в)-Р(в)- [/(х)-Р(х)) (»-*)(»-«.) -<"-"»)
v у ^ v ' у v (jc — а0) (х — а^ ... (х — ап)
и предположим, что функция /(и) дифференцируется л —(— 1 раз. Имеем
k»,-j W iyW ' ^»{x-aa)(x-ai)...(x-an)-
Функция F (и) обращается в нуль при значениях
и = а0, av
., ап и и=х.
Повторное применение теоремы Ролля позволяет показать, что производ-
производная Fl'n+ \u) обратится в нуль при значении т\, заключенном между самым
большим и самым малым из предыдущих чисел. Следовательно,
Если Мп+1 — верхний предел |/ (jc)| в интервале, содержащем все
точки а0, ах
Теперь понятно, что ошибка будет тем меньше, чем ближе х будет к одной
из точек at, и что интерполяция будет точнее, чем экстраполяция.
Пример. Экспериментально была получена таблица, определяющая
некую эмпирическую функцию:
ао = 23,30, а2 = 25,25, Ьй =
04 = 24,25, а3 = 26,10, Ьх =
Речь идет о действительном сопротивлении антенны как функции от-
отношения ее длины к длине волны a=100-Y-.
10.31
ПРИБЛИЖЕНИЕ ФУНКЦИИ
691
Найдем параболу третьей степени, проходящую через четыре данные
точки.
1. Способ Лагранжа состоит в замене букв их значениями в выражении
(х — ах)(х — аг)(х — а3) . . (х — а0) (х — а2) (х — а3)
К > ~ ° (а0 — вО («о — а„) (а0 — а3) "^ 1 (а, — а0) (а, — d2) (а, — а3) "^
~\~ Ьп -.—
(х — аа)(х — сц)(х — а2)
з (аз_
После подстановки и довольно долгих вычислений находим
р (х) = — 1,7992л;3 + 138,40л;2 — 3497,8л; + 29 444.
2. Второй способ дает таблицу
X
23,30
24,25
25,25
26,10
299
328
373
415
Ь
= Ьй = Вй
=*,
= ь%
= 6з
Я
30,5263 = q, =
37,9487 = q%
41,4286 = 4-3
Bi
г
7,4224 = r2 = Вг
5,8931 = r3
s
1 7009 с, R
Отсюда находим полином
Р{х) = 299-f 30,5263 (л; — 23,30) + 7,4224 (л; — 23,30)(л; — 24,25) —
— 1,7992 (х — 23,30) (х — 24,25) (х — 25,25) =
= — 1,7992х3 -|- 138,40л;2 — 3499х ¦+- 29450,
который совпадает с точностью до погрешностей вычисления с уже найден-
найденным полиномом.
10.3.3. Значения переменной находятся в арифметической прогрессии.
Таблица разностей. Дана функция f(x), принимающая значения b0, bv .,.., ba
при значениях a, a-\-h, a-\-2h, ..., a-\-nh переменной л;.
Выражение
Abo = b\ — bo = f(a + h) — /(a)
называют первой разностью для значения а аргумента. Первая разность для
значения а-\- ph будет
Вторую разность, третью разность fe-ro порядка определяют, применяя
предыдущее вычисление к первой разности, второй, .... разности порядка
к —I:
Легко заметить, что в частном случае, когда f (х) представляет собой
полином &-й степени, разности ft-ro порядка равны между собой, а разности
выше &-го порядка равны нулю. Действительно, первые разности для зна-
значения х переменной — это полиномы степени k— 1 и т. д. до разностей k-то
порядка, которые сводятся к постоянному члену.
44*
692
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
ГГЛ. X
На практике, если дана таблица, определяющая эмпирическую функцию,
разности разных порядков располагаются в следующую таблицу:
X
a
a-\-h
a + 2h
a+3h
ft
ft,
ft2
ft3
Aft
Aft0
Aft,
A2ft
A2ft0
A2ft,
A3ft
A3ft0
Каждый член равен разности между ближайшими снизу и сверху членами
С
соседнего слева столбца:
В
= В—С.
Составим, например, таблицу разностей для функции
х==— 4° до х = Ъ4°:
X
—4
—2
0
+2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
у = cos х
0,99756
0,99939
1,00000
0,99939
0,99756
0,99452
0,99027
0,98481
0,97815
0,97030
0,96126
0,95106
0,93969
0,92718
0,91355
0,89879
0,88295
0,86603
0,84805
0,82904
Ду _
+183
+61
—61
—183
—304
—425
—546
—666
—785
—904
—1020
—1137
—1251
—1363
—1476
—1584
—1692
—1798
—1901
Д2у
—122
—122
—122
—122
—121
—121
—121
—120
—119
—119
—116
—117
—114
—112
—ИЗ
—108
—108
—106
—103
ДЗу
0
0
+1
0
0
4-1
+1
0
+з
+1
+3
42
—1
4-5
0
—2
+3
= cosx от
ГО.З]
ПРИБЛИЖЕНИЕ ФУНКЦИИ
693
Пример. Дана функция /(х)—arctgx. Таблицы дают значения /(х)
для значений х, меняющихся через 0,001 между 0,515 и 0,520. Получаем
следующую таблицу разностей:
X
0,515
0,516
0,517
0,518
0,519
0,520
Ь
0,475575472717
0,476365524222
0,477154932097
0,477943696145
0,478731816173
0,479519291993
Д6
790051505
789407875
788764048
788120028
787475820
Д2Ь
—643630
—643827
—644020
—644208
Д36
—197
—193
—188
Д*6
4
5
Д5?
1
Замечание. Значение а не обязательно должно быть начальным.
Если известны значения функции для х = а — h, а — 2й, а — ЗА, .... то
можно, пользуясь отрицательными индексами, продолжить вверх таблицу
для b и Д?, Д2#, ...:
X
a —Ah
a — Zh
a — 2h
a — h
a
a+h
a + 2h
a + Zh
a + \h
b
ft-
6-2
»-1
V
b\
b2
b3
hb
A...
~2
д*_,
. °
Д2*
Д2*-з
Д26_2
Д2*_,
Д26о
Д3*
Д3Ь_4
-3
~г
~1
А3*,
Д4*
Д4*_4
Д46_з
Д46_2
Д46_,
Д'бо
Интерполяционные полиномы
Найдем полином Р(х) п-го порядка, принимающий точно ге-{-1 значе-
значение Ьо, Ьх Ъп для значений
а, а-\~ h, .... a -\~nh
аргумента. Напишем его в -нескольких видах, которые дадут нам основные
классические интерполяционные полиномы.
10.3.4. Интерполяционный полином Ньютона. Напишем полином Р(х)
в виде
Р (х) = Ао -Н A j (х — а) + А2 (х — а) (х — а — h) -+- • • •
... + Л„(х — а)(х — а — А) ... [х — a — {n — \)h\. B2)
694 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ 1ГЛ. X
Дадим последовательно величине х значения с, a-j-Л, .... a-j-яя. Тогда
Ьо = Ао.
Отсюда
2hA1-\-2\h2A2,
АЧ- ••
... +n\hnAn.
bx — ftp A ftp
~ h ~ h '
b2 — bj — (ft, — b0)
21ft2 ~ 2!Л2 '
_дЧ_
k\hk
A,,=
11 ~ n\hn *
x — <
Положим и= ^"Д . Тогда полином B2) принимает вид
... + J-B(B_l) ... [и — (»— 1)]Д"*0. B3)
Напишем полином Р(х) в виде
... -\-В„(х — а)(х—а-\-Н) ... [* —а+(я—1) А]. B4)
Определим коэффициенты В условием, что Р(х) принимает значения
b0, b_l Ь_„ для значений а, а — h а — яд переменной. Вычисле-
Вычисление, подобное предыдущему, последовательно дает
Отсюда
bo = Bo
b-2 = Bo
b-n = Bti
Вг
вп
"tfZD i
bo
I
I
+ 2!
+ •
"_b_
ft
\kb_k
k\bk
n\hn
h2B2,
.. +(—l)nn
A6_,
ft '
•
10.31
ПРИБЛИЖЕНИЕ ФУНКЦИИ
695
Положим и =—т—• Тогда полином B4) пишется в форме
-L
B5)
В связи с тем, что разности Ьа, Дб0, Д2?0 Д0 расположены
в таблице разностей на нисходящей косой строке, а разности b0, ^b_u
Д2?>_2. • • •. Д"*-л — на восходящей косой строке, полином B3) называется
интерполяционным полиномом Ньютона по нисходящим разностям, а поли-
полином B5) — интерполяционным полиномом Ньютона по восходящим раз-
разностям.
Пример. Пример уточнит условия применения обоих интерполяцион-
интерполяционных полиномов Ньютона.
Рассмотрим таблицу, взятую из п. 7.5.46. Она дает значения
для !<;*<; 2 при А = 0,1:
X
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
Ъ
4401
4709
4983
5220
5419
5579
5699
5778
5815
5812
5767
АЬ
308
274
237
199
160
120
79
- 37
—3
—45
—34
—37
—38
—39
—40
—41
—42
—40
—42 '
—3
—1
—1
—1
—1
—1
2
—2
Естественно, мы будем предполагать, что таблица представляет единствен-
единственные данные, находящиеся в нашем распоряжении.
Попробуем вычислить JxA,049), заменив функцию J\(x) параболой
третьей степени, проходящей через 4 последовательно расположенные точки.
Так как аргумент близок к началу таблицы, то выгодно взять интерполя-
интерполяционный полином Ньютона по нисходящим разностям B3) при а=\, ибо
он вводит только Ьо = 4401, Д?о= 308, Д2й0 = — 34, Д360 = — 3. Вводимые
значения функции равны b0, bv b2, b3 с преобладающим влиянием Ьо. Это
логично, так как 1,049 находится очень близко от а = 1. И было бы очень
невыгодно взять полином B5) при а = 1,3. Действительно, пришлось бы
вводить ?0 = 5220, Д?_1 = 237, Д26_2 = —37, Д36_3 = —3 при преобладаю-
преобладающем влиянии Ьо, которое соответствует аргументу 1,3, находящемуся далеко
от 1,049.
696 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Полином Ньютона B3) для а = 1 пишется в виде
у = 4401+ 308м — 17и (и — 1) — -1 в (и — 1) (и — 2),
1 пдп 1
что при в= ' pj = 0,49 дает ^ A,049) = 0,4556.
Посмотрев более подробные таблицы, находим-значение УхA,049)=0,45558.
Следовательно, мы получили по формуле B3) превосходное приближение,
несмотря на грубость исходной таблицы, в которой погрешность задания
чисел Ь может достигать 5 • 10~ .
Если же пользоваться формулой полинома Ньютона по восходящим
разностям B5) для а =1,3, то
у = 5220 + 237м— 18,5м (м + 1) —1в(в+1)(в + 2).
| Q4Q 1 3
Прии = —'-—^—— = — 2,51 это дает Ух A,049) = 0,4557, т. е. приближе-
ние хуже.
Вычислим теперь ../j A,941). Так как аргумент находится в конце
таблицы, следует пользоваться как раз формой B5) полинома Ньютона.
Она при а=2 имеет вид
у = 5767 — 45и — 21 и (м + 1) — 4- м (и + 1) (и + 2).
о
1 Q41 9
При м= ' ^ = — 0,59 получаем Jx A,941) = 0,5799. Более подроб-
ная таблица дает 0,57982. Форма B3) полинома Ньютона, использующая
а =1,7, по причинам, изложенным выше, не дала бы хорошего приближения.
10.3.5. Интерполяционный полином Стирлинга. Напишем полином Р(х)
в виде
х — а)-\-С2(х — a
+ С3(д:— а-|-/г)(х — а)(х — а — А)+ ... +C2ft(x — a + feA) ...
[х — a — (k — l)A] + C2ft+1(x — a-t-kh) ... (л: — a — kh)-\- . . . B6)
Придавая х значения а, а — h, a-\-h, a — 2А, а + 2А, ..., можно по-
постепенно вывести
Отсюда вычислением, подобным вычислению предыдущего пункта, получаем
Со = Ьо,
ft2*
1
1)! й2*+1
10.3] ПРИБЛИЖЕНИЕ ФУНКЦИИ 697
Положим и = —т— . Тогда полином B6) принимает вид
у = Ьй + иЬ.Ь_, + ~и(и + \)\Ч_^~и(^
+ 1-и(Ц2_ 1)(ц + 2)Д»?_2 + ±«(«2_ 1)(Ц2_4)Д5*_3+ ... B7)
Напишем интерполяционный полином Р(х) в виде
a) + D2{x — a)(x — a — А) +
— а)(лг — а— А)+ ... -\-D2k[x—a-A-(k— \)h\ ...
... (х — a — kh)-\-D2k + l(x — a + kh) ... (x — a—kh)--\- ... B8)
Ha этот раз коэффициенты будут равны
1
Bft 4-Ч)!
Полином B8) пишут с той же заменой переменных в форме
60+иД?0 + -1«(«— 1)Д2й_,+^-И(
+ •.. B9)
Сложив равенства B7) и B9) и разделив на 2, получим
z
Этот полином называется интерполяционным полиномом Стирлинга. Приме-
Применение его дает особую точность для точек х, близких к а.
Замечание. Вычисление полинома Стирлинга следует оборвать на
члене Д2*6_й, а не на предыдущем члене-j {Д2*~1?_й+1+ Д2*^^}, так как
знание двух последних разностей дает разность Д2*6-й без вычисления функ-
функции в новых точках. Следовательно, полином Стирлинга — четной степени
Bk), и, чтобы построить его, требуется знать функцию в нечетном коли-
количестве точек B*+'!)'.
10.3.6. Интерполяционный полином Бесселя. Напишем для точки
a~\-h, Ъх формулу B7), полученную для точки а0. Ьо. Это сводится к за-
замене в формуле B7) и на и—1 и b0, b_lt b_v ... на bv b0, b_v ...
Находим
698 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Сложив C1) и B9) и разделив на 2, получаем
У—г Ь(« —-2]Д*оЧ 2! 2
"(" 1}(" 2)
Этот полином называется интерполяционным полиномом Бесселя. Примене-
Применение его дает особую точность для точек х, близких к середине интер-
интервала а -\- -у .
Замечание. Легко можно заметить, что, так же как и для поли-
полинома Стирлинга, следует прервать вычисление полинома Бесселя на члене
Степень полинома Бесселя должна быть нечетной Bfe-|-l), а для по-
построения его требуется знать функцию в четном числе точек Bfe-|-2).
Пример. Вернемся к таблице п. 10.3.4 и вычислим Jx A,511). Поль-
Пользуемся полиномом Стирлинга, ограниченным членом второй степени, иначе
говоря, требующим знания трех точек. Имеем
а =1,5, 60 = 5579, Д&0=120, Д*_1 = 160, #*_, = — 40.
Полином равен у = 5579 -f- 140м — 20м2, откуда при
1,511 -1,5 - -
И— дд =0,11
находим Jx A,511) = 0,5594.
Более точные таблицы дают J1 A,511) = 0,55945 ...
Вычислим Jj A,541). Пользуемся полиномом Бесселя, ограниченным чле-
членом третьей степени, иначе говоря, требующим знания четырех точек. Имеем
а = 1,5, ?0 = 5579, ^ = 5699,
Д60=120, Д2?0 = —41, A2*_! = — 40, Д3&_! = —1.
Отсюда находим полином
R1 1
у = 5639 4- 120 (и — 0,5) —-^-м(м—1) — -i-M(a—1)(ц — 0,5),
что при в = 0,41 дает Jx A,541) = 0,5633.
Более точные таблицы дают JxA,541) = 0,56333 ...
10.3.7. Области применения интерполяционных полиномов Ньютона,
Стирлинга, Бесселя. Значение а должно быть выбрано в непосредственной
близости к значению, для которого мы хотим вычислить приближение функ-
функции. Можно пользоваться любой из интерполяционных формул B3), B5),
C0), C2) при единственном условии, чтобы разности, необходимые для вы-
вычисления, находились в таблице. Поэтому при не очень подробных таблицах
формулы Ньютона должны применяться для значений аргумента, лежащих
у краев таблицы, а формулы Стирлинга и Бесселя — для значений аргумента,
лежащих в середине таблицы.
10.3]
ПРИБЛИЖЕНИЕ ФУНКЦИИ
699
Приводимая схема показывает положение в таблицах разностей, необхо-
необходимых для вычисления, в зависимости от применяемых формул:
а ->
|
h
t
а ->
а ->
а ->
а
X
X
х
X
X
X
X
X
X
X
X
X
X
ь
X
N
V
• \
X
X
S
X
X
В
в
X
X
X
N
Д6
X
N
X
у
s
с
о
X
X
В
X
X
X
N
Д26
X
N
W
X
X
S
X
X
В
В
X
X
N
X
N
X
s
с
о
X
X
в
X
X
N
х
\т
IN
X
S
X
X
В
в
X
N
Применяемые формулы
^_ Ньютона по нисходя-
нисходящим разностям
<- Стирлинга
<- Бесселя
Ньютона по восходя-
*~ щим разностям
10.3.8. Верхний предел ошибки, совершаемой при применении интер-
интерполяционных формул Ньютона, Стирлинга, Бесселя. Если можно вычислить
последовательные производные функции /(х), то применение формул, даю-
дающих верхний предел ошибки, допущенной при использовании полинома Ла-
гранжа, позволяет легко получить следующие результаты.
1) Формула Ньютона по нисходящим разностям. Если Мп+1 —
верхний предел |/(в+1)(д:)| в интервале a, a~\-nh, то мы имеем (при п-\-1
точках)
2) Формула Ньютона по восходящим разностям. Если Мп+1 —
тот же предел, но в интервале а, а — nh, то мы имеем (при л+1 точках)
hn+1
, ... v-т-'-л (п+1)! "*«+»•
3) Формула Стирлинга. Если М2п+Х — верхний предел | fBn+1)(x) I
в интервале а — nh,. a-\- (n-\- I)h, то мы имеем (при 2л+1 точках)
(,2л
М
2/1 + 1*
700 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
4) Формула Бесселя. Если ЛГ2«+2 — верхний предел I /<2л+2>(х)| в ин-
интервале а — nh, а-\-{п-\- l)h, то мы имеем (при 2я + 2 точках)
|Я2л+21<1«(«2— О ••• (~ "?) [и— {п +1)Ц (
10.3.9. Приближение линейной комбинацией функций, определенной
с помощью критерия наименьших квадратов.
а) Эмпирическая функция. Пусть /(х)— данная функция, принимающая
для абсцисс а0, ах ап значения b0, bv .... Ъп. Пусть сро- "Pi ?/> — Р
выбранных заранее функций и р < п. Попробуем определить коэффициенты А
в выражении
так, чтобы сумма Е квадратов ошибок, совершенных при замене /(х) на
Ф(х) в рассматриваемых точках, была наименьшей.
Имеем
E=s2oe? при el = bl — A0<?0(at) —
Мы получим требуемый минимум, если положим
л п
_ =Ao2ll9it(ai)'?o(at)-+ •¦•+A
(k = 0, 1, 2 jp),
откуда определяем коэффициенты Ak. Тогда средняя величина квадрата
ошибки будет равна
L г=о \ ыо i-o /J
б) Функция, определенная аналитически. При тех же обозначениях
требуется определить коэффициенты А таким образом, чтобы интеграл
квадрата ошибки при замене / (х) на Ф (х) в интервале a, b был наимень-
наименьшим. Этот интеграл равен
с — I е \Xj их при е \х) — j \Х) — -^от \~) — • * ¦ — ртр \ )т
а
Коэффициенты Ak определяются системой, полученной из условия минимума:
ь ь ъ
= Ао Jcpft (х) ср0 (х) dx + ... + Ар Jcpft (х) <рр (х) dx — Jcpft (x)/(xyx=0.
10.3.10. Приближение полиномом, определенным с помощью кри-
критерия наименьших квадратов.
а) Эмпирическая функция. Здесь выбранные функции
10.3J ПРИБЛИЖЕНИЕ ФУНКЦИИ 701
и приближающая функция — полином
Следовательно, вместо того чтобы заменить график эмпирической функции,
заданной га+1 точками, параболой я-й степени, проходящей как раз через
эти п + 1 точки, можно выбрать параболу степени р <; и. Такая парабола,
естественно, не сможет пройти через эти п~\-\ точки и в действительности,
как правило, не пройдет ни через одну из них, но будет определена требо-
требованием пройти возможно ближе к ним. Математически мы определим это
условие требованием сделать наименьшей сумму квадратов ошибок 1). В точ-
точках а0, b0; av b{, .. -; ап, Ь„ получаем ошибки
Сумма квадратов ошибок равна
Условия для минимума Е даны уравнениями
дАа дАх
Отсюда получается следующая система для определения А*,. Л, Ар
А^а^ + А^Г^ ... +Ар2аГ=ЪЬ1аГ- C8)
Если данные абсциссы являются равноотстоящими или, более общо,
симметрично расположены вокруг центра тяжести, то полезно принять этот
центр тяжести за новое начало координат. Это обратит в нуль суммы
Средняя величина квадрата ошибки М равна
1=0
В п. 10.3.17 приводится другая математическая версия этого условия.
702 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Пример. За эмпирическую функцию примем функцию, определенную
четырьмя первыми строками таблицы п. 10.3.4 для функции 10% (х). По-
Попробуем представить эту функцию параболой второй степени.
Помещаем начало координат в точку л: =1,15. Эмпирическая функция
определяется следующими данными:
а1==~0Л5, а2— — 0,05, аз = 0'05- а4 = °-15-
Й1=44О1, *2 = 4709, *з=4983> *4=5220.
Коэффициенты Ло, Av Л2 определяются системой
иначе говоря,
4
1
4
0 I '
1
4
А У а2
л\ Zu ai
)
i
4
2 1 '
4
2 I
4
1 ' ''
4
= yjaibt,
4
I /f
0,001025Л0+ 0,05Л2 = 240,70,
0,05 Л! =136,55,
0,05Л0+4Л2 =19313.
Отсюда
Ло = — 1781,2, Л1 = 2731, Л2 = 4850,5.
Парабола, которая представляет в среднем данную функцию в промежутке
между 1 и 1,3, есть
у = — 1781,2 (* — 1Л5J+2731 (х — 1,15)+ 4850,5.
Средняя величина квадрата ошибки равна
М — -i [@,2J+ @,5J + @,4J + @,1J] = 0,11.
б) Функция определена аналитически. Если функция f (х) опре-
определена аналитически и, кроме того, легко вычислить интегралы
ь
I xkf(x)dx (k — целое положительное число или нуль),
а
то для определения полинома Айхр-{- ... +Лр, который может заменить
в интервале а, Ъ функцию / (х) с наименьшим интегралом от квадрата
ошибки, нужно действовать следующим образом.
Ошибка в точке х будет
е (х) = / (*) — [AqXp + ... + Ар\. ' C4)
Интеграл от квадрата ошибки равен
ь
. Е= fs2(x)dx. C5)
а
Коэффициенты Ло, Аг Ар определяются условиями минимума Е, т. е.
р
ь
... +Ap-f(x)]dx =
10.3] ПРИБЛИЖЕНИЕ ФУНКЦИИ 703
Отсюда получается система
ь ь
А,
о
a
О U
... -{-Ар fxP dx=* fxP f (x)dx,
b b b b
AQ I xpdx + Ax Jxp-1 dx + ... -\-Ap j dx = j f(x)dx.
C6)
Вычисления значительно упростятся, если промежуток интегрирования
равен —1, -\-1. Перейдем к этому случаю с помощью замены переменной
а-\-Ь 1 6 — о, у
Итак, нам нужно найти полином ВОХР-\- ... -\-Вр, который наилуч-
наилучшим образом приближается в среднем к функции ср(ЛГ) = /( —t—| -,— Х\
в промежутке между —1 и —|— 1.
Положим
Так как
i i
fx2kdx=^ и [x2k+1dx = o,
то система C6) принимает вид
1 1
1 „
э-1
... =/,.
... =/3.
... =/4,
Средняя величина квадрата ошибки равна М = ~, -.—ry = -pj-. Учитывая
формулы C4) и C5) и систему C6), можем написать
i
-I / = 0
р
Результат вычисления коэффициентов В и величин ар = Д] В lIl как
704
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
ГГЛ. X
функции интегралов / для различных значений р приведен в следующей
таблице:
p
1
2
3
4
5
В
«:=/„'¦
в =ii[_/0+3/2]
Й2=|-[3/0-5/2]
fia=|-[3/0-5/2]
В*=Ж[~ 5/° + 42/* ~ 45Л1
B4=i|[15/0-70/2 + 63/4]
fi4 = J^2. [35/, — 126/3 + 99/5]
а
7
а4 = /2 -(- З/2 + -7- [3/2 — /0]2 +
9
1 г ос / Ог\ г I or m о
—г~ „ . 1 OtJj д ' Ol/in ¦¦¦>- *Jtf\ |^
+ Z.[5/3_3/l]2 +
9
^_ il [63/s — 70/3 + 15/j]2
Ю31 ; ПРИБЛИЖЕНИЕ ФУНКЦИИ 705
Пример. Попробуем определить полином третьей степени, который
в промежутке от 1 до 2 наиболее близок к функции In x. Это можно свести
к определению полинома
наиболее близкому к функции
1:1A,5 + 0,5*)
в промежутке от —1 до 1.
Имеем
2
= f\nxdx==2\n2 — l,
i
-i i
1 2
lx—\ f XlaA.5 + 0,5X)dX = f Bх — 3) In xdx = — 2 In 2 + |-.
-i i
i - i
/2 = 1 f
-i ' . -I
l l
i3 = — f X3ln(l,5 + 0,5X)dX= f Bx —
-i -i
Отсюда, пользуясь формулами предыдущей таблицы и значением. In 2 =
= 0,6931472, ошибка которого не превосходит 2- 10~8, получаем
Я0 = 0,0133, 5, = —0,0583, Я2 = 0,3331, В3~0А057.
Имеем
2
(lnxJd;t = 2(ln2J —41п2 + 2 = 0,18831736, а = 0,18831731.
1
Следовательно, средняя квадратичная ошибка (т. е. корень из средней вели-
величины квадрата ошибки) есть ]/Ж = 2 ¦ 10~ . Итак, можно приближенно за-
заменить функцию 1п х между 1 и 2 полиномом
' 0,0133B*—ЗK —0,0583 Bл: — 3J + 0,3331 Bх — 3) + 0,4057.
Замечание. Рассмотренный способ вычисления в равной степени под-
подходит и к случаю, когда функция — эмпирическая, заданная графиком. При
этом интегралы /0, Iv ... вычисляются тоже графически.
Приближение отрезком ряда Фурье. Задача гармонического анализа
Как и для приближения полиномом, мы будем различать случаи, когда
функция задана аналитически, графически или таблицей ординат, соответ-
соответствующих равноотстоящим абсциссам.
10.3.11. Функция задана аналитически. Предположим, что функ-
функция <р(Х) известна в промежутке 0,2ic. В п. 2.1.5 мы видели, что коэффи-
коэффициенты выражения
л л
Sn(X)=bQ-+- 2 в* sin ЛАГ + 2 bkcoskX C7)
k=i k=i
45 А. Анго
706 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
такого, что средняя величина квадрата ошибки
2%
М *) = —
о
минимальна, даны выражениями
2% 2%
aft = i- f <f(X)sinkXdX. bk = \ f <?(X)coskX dX,
6 о
C8)
о
2*
0
При этом средняя величина квадрата ошибки равна
М = ^-
Если функция / (л;) определена в промежутке б, 6 -|- Т, то мы придеч
к предыдущему случаю при помощи замены переменной
x==(i+T_X. C9)
Тогда задача будет заключаться в приближении к функции
при помощи тригонометрической суммы C7).
Этим приемом можно также пользоваться в силу примечания, сделан-
сделанного по поводу приближения полиномами, если функция известна из графика.
При этом нужно графически же производить интегрирование, которого
требует применение формул C8).
10.3.12. Эмпирическая функция. Функция известна из таблицы, даю-
дающей я-4-1 значение у0, уг уп для п~\-\ значений л;0, xv .... х„
аргумента, делящих промежуток 0, 2те на п равных частей.
Если бы промежуток простирался от 0 до б-(-Г, то достаточно было бы
произвести замену переменной по формуле C9).
Пусть
р р
Sp(x) = bQ-{- У, bkcoskx-{- 2 aksinkx D0)
— р-я частная сумма ряда Фурье. Задача будет иметь смысл, лишь если
число 2/> —|— 1 коэффициентов, которые нужно определить, меньше или равно
числу уравнений
* р р
У{ =*о~Ь 2 bkcoskX[-\- 2 aks\nkxr D1)
s=i *=i
Если 2р > n, то 2p -p-1 коэффициентов могут быть определены беско-
бесконечным количеством способов.
*) В п. 2.1.5. эта величина обозначалась буквой ?.
10.3] ПРИБЛИЖЕНИЕ ФУНКЦИИ 707
Если 2р=п, то система D1) допускает единственное решение. Все
ошибки Sp(xt) — yt равны нулю. Сумма квадратов ошибок, очевидно, также
равна нулю.
Если 2р < п, коэффициенты определяются условием сделать сумму
квадратов ошибок наименьшей. При этом система D1) не удовлетворяется.
Два последних случая можно рассматривать совместно. Вместо того
чтобы решать систему D1), коэффициенты находят таким образом, чтобы
сделать сумму квадратов ошибок наименьшей. Если 2р — п, этот минимум
равен нулю.
Сумма квадратов ошибок равна
«Г / Р Р . \Т2
=2 \У1— *о+ 2 bkcoskxt+ 2 в* sin ft*,) .
Коэффициент bk определяется из уравнения
я
р
*' cos *'xi
D2)
= 0. D3)
Если й+1 чисел xt делят интервал 0, 2ir на равные части, т. е.
хо = О, *i=-7f хп_1 = 2(п— 1)-J,
и если ft и k' — различные целые числа, заключенные между 0 и /?
то можно написать
л л
2 sin Axj = 2 cos &xi — О-
л
cos kxi cos ft'*/ = 2 cos kxi sin */jci = 0»
л
л
sinftx.
sin
л
i =
л
i=0 i=0
Следовательно, формула D3) дает ..
л
2
Точно так же
л
О ж-»
*,, D5)
1 = 0
л
У/. D6)
i = 0
Средняя величина квадрата ошибки равна
45*
708
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Замечание 1. Мы предполагали до сих пор, чтоу0 = у„, иначе говоря,
что функция у = f (х) не имеет точек разрыва первого рода в начале. Если
УоФуп, то, чтобы уничтожить разрывность, достаточно из данной функции
вычесть подобранную должным образом пилообразную функцию й (х)
{рис. 10.11). Разложение этой последней функции в ряд равно
d(X):
¦+Уа 2yn[sinx->r±sin2x-{- ...-\-jSinnx-t- ...].
Замечание 2. Если бы мы захотели пользоваться способом, изложен-
изложенным в предыдущем пункте, то, вычисляя методом трапеций интегралы, вхо-
входящие в формулы C8), мы получили бы
формулы D4) — D6).
10.3.13. Практические способы
вычисления. Если таблица чисел, опре-
определяющих эмпирическую функцию, дана
заранее, то дело сводится к вычисле-
вычислениям по формулам D4) — D6). Если же
эмпирическая функция дана графически,
то число ra-j-l, которое служит для
составления таблицы, находится в на-
щем распоряжении.
При «=12 вычисления значительно упрощаются, так как фигурирую-
фигурирующие в расчетах 24 значения синуса и косинуса с точностью до знака прини-
принимают лишь три значения, отличные от нуля:
Уо
ч
Уп ,,
•
о
Рис. 10.11.
0,5, -^- = 0,866. 1.
Вычисление ведется при этом следующим образом:
1. Записываем 12 значений функции:
/i /2 /з /4 /5 /б
/12 /и /ю /э /б /7
Суммы ... So
Разности ...
*^3
2. Записываем суммы и разности:
Og Oj О2 О3
с С С
°6 °5 °4
Суммы ... о0 0[ о2 о3
Разности ... 80 8j 82
3. Составляем таблицы:
а) Вычисление коэффициентов при синусах
dx d2
0,500
0,866
1,000
Суммы произведе-
произведений
1 + 11
¦ 1 — 11
в,
вз
I
е2
11
бв!
6а5
1
II
6а2
6а4
в!
I
вз
II
6а3
10.3] ПРИБЛИЖЕНИЕ ФУНКЦИИ
б) Вычисление коэффициентов при косинусах
709
0,500
0,866
1,000
Суммы произ-
произведений
I + II
I —II
I
II
12*о
12*,
h
So
I
И
6Й!
6Й5
— а2
Оо
I
°i
_о3
II
бй2
бй4
Ьо
I
Ь2
II
6ЙЗ
В этих таблицах числа 0,500, 0,866, 1,000 умножаются на соответствующие
(стоящие в той же строке) значения 0, г\ или 8. Произведения в каждом
столбце складываются. Сложение и вы-
вычитание полученных сумм A +II и I—II)
дает искомые коэффициенты ак и bk.
Графический метод. Можно поль-
пользоваться графическим методом для вы-
n-fl . л-fl
числения величин —^— bk, —^—ak,
определенных формулами D4), D5).
Рассмотрим векторы с модулями
yv y2, .-. и аргументами kxv kx2, ...
¦ 1 л+1 i. л
ak. —^—bk будут со-
соВеличины
ответственно проекциями на оси Оу
и Ох геометрической суммы этих век-
векторов.
Пример. Дана функция, изобра-
изображенная на рис. 10.12, а. Вычисления
коэффициентов ак и bk приведены на
стр. 710.
Графический способ, применяемый
на рис. 10.12, б, дает результаты, пре-
прекрасно согласующиеся с предыдущим
вычислением. Чтобы не загромождать
чертеж, ломаная линия, соответствую-
а5 и Ь5
не изо-
Рис. 10.12.
щая определению
бражена.
, Если требуется найти более короткое тригонометрическое выражение
S(x) = bo-\-bl cos x~\- b2 cos 1x~\- b3 cos 3x -|- аг sin x -(- a2 s'n ^x H~ аз s'n ^x,
возможно лучше приближающееся к графически заданной функции, вычис-
вычисление коэффициентов можно осуществить только сложением и вычитанием:
1
— Ую.
h = ¦§¦ (У4 — У2 + У& —
= j (Уо ~ Уз + Уе ~
710
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
1Л
со
«л
«СО
3,5
с*
II
п
COi-h
о I
оо чз •«•«
I I
oo чГ
N N , W
оооо
оооо
О ОСО
II II II
О О (С
СО 0000
COCO
о
СО I
СО
О
ОО'
СО
о.
3
О1
ОО
СО
1
II
i
со с>
= -2,5
и
—35
II
о
«о
|> 1
II II
II II
—• т
О О
1
¦-" л
1 со"
II II
f'
= -5,3
«Г
7 1
II II
3,7
II
ю
О*
II
II
еч
О
о
в
,500
,866
,000
оо —
= —2,5
и
1Л
II
т
1
II
II
= —4,5898
II
•—4
I = —4,75
13л
JI
и
II
т
II
II
«о
СО
11
II II
0O(N
О) ^Р
со со
СО 1—
ft
II1
U2U2
(М —
IMI
счсч
10,3] • ПРИБЛИЖЕНИЕ ФУНКЦИИ 711
Для вычисления а2 нужно ввести ординаты, соответствующие —, -j ir,
-г- it, -jir, иначе говоря уз, уя, yis. угь Тогда
Т 7 2 Т
°2 = X (Уз — У.9 4" Ук> — У 21).
2 2 2 2 '
Пример. Применим этот способ к предыдущему примеру. Тогда
Ш0 = 28,7, 6*з = —1. 6а3= —3,7, 6^ = 8,3.
6*!==—10,5, 4*2 =—2,5, 4а2=1,7.
Это хорошо согласуется с полученными ранее результатами. Кривая
^ = 2,391 — 1,584 cos x-\- 1,384 sin x — 0,625 cos 2x -f
+ 0,425 sin 2л; — 0,166 cos Ъх — 0,616 sin Зх
изображена пунктиром на рис. 10.12.
10.3.14. Приближение эмпирической функции линейной комбинацией
показательных функций. Пусть / (х) — функция, данная значениями Ьо,
bi bn, взятыми на равноотстоящих абсциссах
а0, ao-\-h, ao
Пусть Ф (х) = A -j- Be?* + Ceix -)- Debx — линейная комбинация, ограниченная
тремя показательными функциями (легко провести вычисление и для боль-
большего их числа). Определим 7 параметров А, В, С, D, [3, •(•> 8 при помощи
критерия наименьших квадратов (и+1 > 7).
Имеем
ф (ао-\- th) = A
(/ = 0, 1, 2 n).
Положим
ePA=Hj, eth = u2, ebh
Если бы функция Ф (л;) совпадала с /(х) в л —|— 1 рассматриваемых точках,
мы имели бы
bt
*/+i = А
Первая разность таблицы для Ъ{ дает
Д*=А(«1 —1) +9: (и2—П +^(Из—1).
Д(+1 = Pi («i — 1) «1Н- Qi (и2 — 1) и2 + /"((и3 — 1) и3-
Исключаем pt, qt, ri из этих уравнений. Тогда
2(— И1 — И2 — и
712 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ • [ГЛ.-'Х
Положим
— uxu2uz = s3,
ихи2~\- й,й3 + и2и3 = s2.
— И, —«2 —Й3 = «1-
Предыдущее уравнение принимает вид
з = 0.
Имеем систему из я — 3 уравнений с тремя неизвестными. Мы получаем
ее, придавая / значения 0, 1, ..., п — 4. Так как я больше 6, то эта
система несовместна. Если в нее подставить какую-нибудь систему значений
sv s2, s3, то я — 3 результата подстановки равны не нулю, а соответ-
соответственно е0, ер ,.., еп_4. Определим систему значений sv s2, s3 таким обра-
образом, чтобы сумма квадратов ошибок
П-4
2^ Д(Д/+:
1 = 0
¦ n-4
n-4
1 = 0
^¦Д/ +
л-4
3 = 0.
была минимальной. Тогда
п-4 п-4
1 дЕ
1=0 1=0
п-4 п-4
1 дЕ _
2 ds2 '
/=0 i = 0 / = 0 1 = 0
п—4 п —4 п-4 п —4
1 дЕ VI А . VI . . VI Д2 V1 л а п
""^- = s3 ^ '*i+2^(H- *2^ ^i+2^i + i + si^ Д/4 2 + ^j Д;+гД/+з = U.
Пусть Sj, s2, s3 — значения, полученные из трех предыдущих уравнений.
Тогда uv u2, и3 — корни уравнения
И3 + SjM2 + S2U + 53 = 0.
Отсюда
1 1 1
Сумма квадратов ошибок будет
п—4 п — 4 п—4 п-4
*2
«=0 j=0 (=0 1=0
Если уравнение по и имеет сопряженные комплексные корни, предста-
представление через комбинацию экспонент не подойдет. Тут следует испробовать
комбинацию из экспоненты и экспоненты, умноженной на тригонометриче-
тригонометрическую функцию.
Так как величины [3, f, 8 известны, то при обозначениях p'lz=e9ia+ili),
q'[ = e'i 'ао+'А), r't — еь (аО4Ш) получаем для определения А, В, С, D следую-
следующую систему из я-f-l несовместных уравнений:
A-f-Bp\ + Cq't-\-Dr't — b(= 0 (/ = 0, 1, 2, ..., я).
Тогда сумма квадратов ошибок равна
п
i=i>^
10.3J ПРИБЛИЖЕНИЕ ФУНКЦИИ
Отсюда получается система
1=0
713-
»=о
1 = 0
i = 0
i = 0
i = 0
1 = 0
1 = 0
i = 0
1 = 0
1 = 0
1 = 0 1 = 0 1 = 0 i = 0 1 = 0
определяющая А, В, С, D с суммой квадратов ошибок, равной
E^A^bi + B^P'tbi + C JZq'ibi+D 2 #>< — S ft?-
Пример. Эмпирическая функция задана таблицей
X
h
0
—12,2
0,6
1
—11,6
0,8
2
—10,8
1,37
3
—9,43
2,11
4
—7,32
3,32
5
—4,00
5,00
6
+1,00
8,00
. 7
+9,00
12,40
8
+21,4
19,40
9
+40,8
Из природы рассматриваемого явления следует, что для приближения рас-
рассматриваемой функции следует взять формулу типа
Так как имеется только одна экспонента, то суммирование в уравнении,
служащим для определения {J, должно простираться от 0 до я — 2. Имеем
л-2 я-2
Д/Д*+1 = 261,11s, 4-407.83 = 0.
о
откуда И] = — «1 = 1,562 и р = In u1 = 0,446 при сумме квадратов ошибок.
л-2 л-2
? = si 2 Д/Д/+1Н- 2 Д?+1 = 407,83s, + 637,11 = 0,08.
i=0 l=o
Применение способа наименьших квадратов к 10 уравнениям
bi = A+Bel$ или bi = A-\-Bu[ (/ = 0, 1 9)
дает систему
2 « = 2h
(=0
1=0
2
/=0
714 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ ?ГЛ. X
иначе говоря,
10Л+1525= 16,8,
152Л + 5191Я = 3091.
Отсюда
Л = —13,12 и Я = 0,974
при сумме квадратов ошибок
Е=А 2 ft/+ Я 23 u[bi = — 2,14.
1=0 (=0
Следовательно, приближенная формула есть
у = 0,974е°-446-г— 13,12.
10.3.15. Приближение функции по Чебышеву. Дана функция f(x),
непрерывная вместе со своими производными, в интервале а, Ь. Как мы уже
видели, общая задача приближения заключается в том, чтобы найти функ-
функцию g(x), которая наилучшим образом приближает f (х) в этом интервале.
Выражение „наилучшим образом" может быть определено критерием наи-
наименьших квадратов, что приведет к способам приближения, описанным
в п. 10.3.9 и последующих. Выражение это может быть также определено
условием сделать как можно меньшим наибольшее отклонение между f(x)
и g(x). Это называется приближением по Чебышеву.
Функция g(x) должна быть удобнее в обращении, чем функция /(*)•
Мы ограничимся случаем, когда g(x) представляет собой полином Р(х).
Нахождение полинома, который делает максимум отклонения от f (х)
на промежутке а, Ъ наименьшим по сравнению с любым другим полиномом
той же степени, есть очень трудная задача. Мы будем поэтому решать не-
несколько более легкую задачу и искать полином, который делает этот макси-
максимум „по возможност"и" малым.
Не уменьшая общности, всегда можно предположить, что интервал опре-
определения равен —1, -f-.l, так как перенос начала на -^(а-\-Ь) и изменение
масштаба в отношении -туф—а) немедленно приведут к этому случаю.
Мы видели в п. 10.3.2, что полином Р (х) я-й степени, совпадающий
с данной функцией f(x) в я+1 точках интервала с абсциссами at, пред-
представляет собой интерполяционный полином Лагранжа и что ошибка, совер-
совершенная в точке х при замене f (х) полиномом Р(х), равна
Rn(x) = f(x) — Р(х) = (х — ао)(х — ах)... (х — ап)
Абсцисса 7j здесь такова, что | т\ | < 1.
Определим последовательность абсцисс а таким образом, чтобы абсо-
абсолютное значение максимума Rn (x) было возможно меньшим, когда х про-
пробегает интервал —1, -(-1.
Возьмем (х — ао)(х — аг) ... (х — ап) — 2~п Тп+1 (х). Здесь Тп+1(х) —
полином Чебышева (я+1)-й степени, и поэтому а будут нулями этого
полинома.
Известно, что, в силу свойств полинома Чебышева (п. 7.9.4), полином
2~"Тп + 1(х) принимает попеременно п-\-2 раза значения ±2~", когда х
возрастает от —1 до —j— 1, и что это единственный полином вида xn+l + ...,
лаибольшие абсолютные значения амплитуд которого (все равные 2~") —
10.3) ПРИБЛИЖЕНИЕ ФУНКЦИИ 715
самые малые из всех возможных. Последовательность значений а1 будет
поэтому
($) с--0- 1-2
Теперь искомый полином Р(х) может быть написан в виде формулы,
дающей интерполяционный полином Лагранжа для абсцисс at, определенных
предыдущим выражением. Однако предпочтительнее поступить иначе. Всякая
степень хг может быть разложена в линейную комбинацию полиномов Чебы-
шева степеней <; г. Например,
Поэтому искомый полином Р(х) может быть записан в виде
Достаточно определить коэффициенты Ь.
Функцию f (х) можно написать в виде
(n+1>
л
Положим at = cos6. Имеем
л
/(cos6)==(pF) = 2*ftcosA9 + /?B(x).
Для значений а; = cos (—?V --я-1 мы имеем
V я+1 ^ /
Следовательно, для значений 9, = —4-т-• тг мы имеем
Значит, коэффициенты b представляют собой коэффициенты разложения в ряд
Фурье, ограниченный я-м членом, четной функции /(cos8) (п. 7.9.3). Отсюда
п л
Пример. Найдем полином третьей степени, приближающийся, по Чебы-
шеву, к функции /(л;) = In A,5 + 0,5*) между —1 и +1. Полином, прибли-
приближающий эту функцию, был уже определен критерием наименьших квадратов
(п. 10.3.10).
716 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Мы имеем л —3, ai = cos(—3—•-у) • Поэтому
O0 = cos-|- = 0,923879, 90 = -|-,
ei = cos-^ = 0,382683, ^ = ^-.
a2 = cos^=-0,382683, 62 = ^,
a3 = cos ^- = — 0,923879, 83=^,
' /(ao) = ln 1,96194 = 0,673941,
f(a1) = ln 1,69134 = 0,525519,
/(c2) = ln 1,30866 = 0,269011,
/ (a3) = In 1,03806 = 0,037357,
з
Ьо = ^^/ К) = 0,376457.
¦ 1 = 0
з
b} = ^ ^ / (a,) cos 9,-= 0.343144.
( = 0
з
^) cos 20, = — 0.029427.
;= 0,003313.
Отсюда полином будет
P {x) = ba + Ь1Т1 (x) + b2T2 (x) + Й3Г3 (л;),
иначе говоря,
P (л;) = 0,40588 +0,33320л; — 0,05885л;2+ 0,01325л;3.
Ошибка будет порядка
1 6 0,54 ^ 4
23 ' 4! 1,54 ^ 10000'
если заменить tj числом 0, которое является серединой рассматриваемого
интервала.
10.3.16. Применение ряда Тейлора. Если функция f (х) задана ана-
аналитически, то вычислить значение, которое она принимает для значения х
переменной, можно кроме уже описанных еще и другими способами. Наи-
Наиболее употребительно разложение в ряд Тейлора.
Если можно определить функцию и ее последовательные производные
для значения с, близкого к х, то ряд Тейлора вблизи а может быть напи-
написан в виде
- а) /'{а)+...+±-(х-а)п />
при
10.4) ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ 717
М здесь обозначает наибольшее значение, которое может принимать
между х к а.
Пример. Вычислить е~0>9. Разложение в ряд Тейлора е~х вблизи х = 1
будет
[ 1 IJ — ^-
Ошибка разложения в скобках равна, если ограничиться четырьмя первыми
планами, (л;—1L-щ-=10 -щ.
Обозначим через Де ошибку, которая получается, если писать не все
цифры е~1. Предположим, что имеющаяся в нашем распоряжении таблица
дает только первые 6 значащих цифр. Общая ошибка по недостатку будет
тогда
Если принять е~1 = 0,367879 с ошибкой, меньшей 10~6, то мы получим
общую ошибку по недостатку, меньшую 2,6 ¦ 10~ . Можно поэтому на-
на,1-+ ^21 + -^^-^--0,3.67.87.9 = 0,406,56.76. .
писать
с точностью до 2,6 - 10 -по недостатку.
Истинное значение е"°>9 равно 0.406569659.
10.4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
Пусть функция задана таблично. Заменим ее интерполяционным поли-
полиномом. Дифференцирование этого полинома даст нам приближения для
последовательных производных функции.
Будем всегда обозначать шаг интерполяции через h, начальное значе-
значение л; через а и через и — переменную и= х~~а. Дифференцирование ин-
интерполяционного полинома Ньютона по нисходящим разностям (формула B3))
дает
4и3 — 18и2 + 22ц —6 д4.
4! --0-Г---. D7)
12
Если в этих выражениях и = 0, то
718 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
В последней строчке запись дана в операционной форме. Она не должна
вызывать трудностей.
Если в выражении D7) придавать и последовательно значения 1, 2,
3 то легко получить y'{a-\-h), y"(a-\-h), ...; /(a-f-2A), у"(а-\-
+ 2Л), ...; /(с + ЗА). У(а + ЗЛ). ...
В формулах D7) и D8) используются разности на нисходящей диаго-
диагонали, проходящей через f(a) = b0. Полезно привести соответствующие фор-
формулы, полученные из интерполяционного полинома Ньютона по восходящим
разностям и интерполяционного полинома Стирлинга, где используются раз-
разности, расположенные соответственно на восходящей диагонали и по обеим
сторонам горизонтали, проходящей через Ьо.
Интерполяционный полином Ньютона по восходящим разностям дает
где индекс а равен показателю при Д.
Точно так же применение интерполяционного полинома Стирлинга дает
У W— h [ 2 6 2 ^30
i 7
!~Т2"
E0)
Пример. Вычислим производную y = arctgx для лг == 0,515, польт
зуясь таблицей разностей этой функции, приведенной в п. 10.3.3 (А = 0,001).
Здесь следует применить первую формулу D8), где используются разности,
находящиеся на нисходящей диагонали, начиная с 0,515. Тогда
1 I 0,000 790 051005
/@,515)«w)+ з21815
1 = 0,790 373 256.
¦-I- 1
Точное значение у' @,515) равно
-=0,790 373 254...
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
С помощью той же таблицы вычислим у' @,518). При этом следует-
применить первую формулу, полученную из полинома Стирлинга, где ис-
используются разности, находящиеся в непосредственной близости с гори-
горизонталью, проходящей через 0,518. Тогда
Точное значение у' @,518) равно
1
: 0,788 442 070.
0,5182+1
Замечание. В случае эмпирической кривой, где ординаты получаются-
с погрешностями, рассмотренные способы вычисления производных приводят
часто к обескураживающим результатам. Можно сравнить численное разыс-
разыскание производной функции, известной приближенно, с графическим про--
ведением касательной к грубо начерченной кривой. Легко сообразить, что
небольшое изменение формы кривой вблизи рассматриваемой точки значи-
значительно влияет на ход касательной, тогда как область, ограниченная кривой.,
меняется при этом очень мало.
10.5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
10.5.1. Числа Бернулли. По определению, я-е число Бернулли — эта
коэффициент при ТГ^ в Разложении в РЯД по возрастающим степеням t
функции y ctg ~:
t t t2 t* t2n
ctglBBB
Левую часть можно написать в виде j— е., . Заменив jt на t в обеих
2 е'1 — 1
частях формулы E1), получим
Уменьшив на -^ обе части уравнения E2), можем написать
— = l f- a, o, \- ... -+-(—1) an r- .. •
e' — l 2 J 2! 24! "Bл)!
Умножим обе части уравнения E2) на е' —1 и разложим е' в ряд. Тогда,
отождествление коэффициентов при одинаковых степенях t в обеих частях,
уравнения дает для первых чисел Бернулли:
R — l R — * R — l R — ! fi — 5 Я — 691 Я —I-
о 3617 43867 R 174611 R 854513
—-798 ^1° ~ 330 ' "и — 138
236 364 091 _ 8 553 103
й]2~~ 2730 ' Й13— 6
В п. 2.1.4 была установлена формула
1 2х г 1
720 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Заменив izx на -я-, получим
Ч'2Т~'
р=1
:ИЛИ
t t _ . 1 V <2n V *
Сравнив E1) и E4), получаем
r — l Bra>! V !
n 2 BtcJ« ^J /Jn '
Начиная с я = 5, числа Бернулли возрастают очень быстро вместе с п.
10.5.2. Полином Бернулли. Обозначим через Фп (z) полином Бернулли
71-й степени. Мы определим его с помощью производящей функции
п=1
Имеем
в' —1 И 2! /I 2^2! 4! ^ j
¦Сравнив эту формулу с E5), получим
Ф„ (z) -=z" — ~ nz"-1 н- C^fi^"-2 —
Если я — четное число, большее 2, то последний член равен
Если га — нечетное число, большее 1, то последний член равен
я + 1
(-1) 2 nBnj±z.
2
Полиномы Бернулли обладают следующим свойством: если, используя
определяющую формулу E5), написать
л=1
то, разложив левую часть в степенной ряд и приравняв коэффициенты при
tn
—г в обеих частях, мы получим
Ф„(.г+1) — Фв(г)=яг»-». E7)
Заменив последовательно z целыми числами р — 1, /) — 2, ... и сложив
долученные таким образом выражения, находим для га> 1, считая Ф0(.г) = 0:
iaids» l"-1 -рг'-'-НЗ"-1-}- ... +(/, — I)"-1.
10.5) ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ '721
Разложив в ряд обе части тождества
, е"-1 , e-«('-«>-i
1~7^Л i~~t е~'-\
и приравняв коэффициенты при —г- в обеих частях, имеем
Ф„B) = (— 1)ЛФ„A— z). E8)
Из формул E6) — E8) получаем
Ф„@) = ФпA) = 0 (я>1), E9)
= 0 (т> 1). F0)
Чтобы найти значение Ф2т l-g- j, достаточно отыскать коэффициент при
t2m 1
-,„ ч, в разложении производящей функции E5), где 2 = -^-. Имеем
t
е2 — 1 _ t 2t__
Из разложения в ряд E3) находим искомый коэффициент
F1)
Производная ФпB) полинома Бернулли я-го порядка такова, что
SI 4FI t26 t^ (в 1^ t^
I " rel" ~~ e< — 1 ~~ e' — l *~ e*— 1 '
n=l
Если ra = 2/rc (m > 1), то, так как разложение второго члейа правой части
F2) не содержит, согласно E3), членов нечетного порядка, большего 2,
можно написать Ф'2т (г) = 2тФ2т_1 (z). Следовательно,
Подобным же вычислением можно показать, что
f2+i
Если я = 2/и-|-1. то, приравняв коэффициенты при -^—, ...- в обеих
частях F2), получим, учитывая E3) и E5),
F3)
Теперь можно сделать следующие выводы о корнях Ф„ (г). Полином
Ф2я1+1(г), равный нулю при 2 = 0, 2 = 1, не обращается в нуль в интер-
интервале @, 1) за исключением точки z = -~. Действительно, если бы полином
Ф2т+1 обращался в этом интервале в нуль, два раза, то его производная
Ф2т+1 обращалась бы в нуль по крайней мере три раза, а его вторая про-
производная— по крайней мере два раза. Иначе говоря, полином Ф2т_1
обращался бы в нуль по крайней мере два раза. Продолжая рассуждение до Ф3,
мы можем показать, что этот полином третьей степени два раза обращался
46 А. Анго
722
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
бы в нуль внутри промежутка @, 1), а с учетом точек 0 и 1 —четыре раза,
что невозможно.
Полином Ф2т. равный нулю при z = 0, г = \, не обращается в нуль
в интервале @, 1). Действительно, если бы это было не так, то его первая
производная обращалась бы в нуль в промежутке @, 1) по крайней мере два
раза. Но это невозможно в силу предыдущего рассуждения, так как Фгт =
=*2даФ2т_1. Полином Ф2т проходит через максимум при z=l/2.
Первые полиномы Бернулли таковы:
= г2 — z = z{z— 1),
Ф4 = Z4 — 22? +¦ Z2 = Z2 (Z — 1 J,
10.5.3.-Формула Эйлера. Рассмотрим тождество
X+h А
F(xJf-h) — F(x)==j F'(t)dt = j F'(x-\-h
. x о
Проинтегрируем последовательно по частям. Получаем
А
dt.
F4)
Применим формулу F4) к последовательным производным F'(x), F"(х), ...
.... Fl2p~1)(д;), ограничив разложения членами, содержащими производную
(х). Умножив соответственно на А, Л2 h2p~\ получаем
I/7' (* +. А) - /=" (*)] = h2F"
F5)
= /i2pFl2p) (x) + Л2"-'
* 4-А -0
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 723
Умножим равенство F4) на единицу, первое равенство F5) на —^, второе
равенство F5) на -щ- , третье равенство F5) на нуль, четвертое на jf •
..., B/7 — 2)-е на —^ г^т" и результаты сложим.. В лравой части полу-
ченной таким образом суммы коэффициент при F" будет равен нулю, коэф-
1 11 В
фициент при /?'", равный -тг\ Г Т "^ ТГ ' бУдет также нулем. Легко
показать, что коэффициент при F^k), равный
r__J 1 1 . В, 1 В2 1 . В3 1
С~*! 2 (*— 1)! ~1~ 2! (k — 2)! "t~
есть нуль. Действительно, вынося множитель -гг, получаем
т. е. в силу формулы E6), где взято z=\,
Это выражение равно нулю, как показывает формула E9). Поэтому результат
сложения равен
F{x + h)-F(x) = \ h IF' (x + h) - F' (x)] — |
F6)
По формуле E6) полином в квадратных скобках под знаком интеграла
может быть написан в виде
л2р d (L)
Положим F' (х) = f (x). Тогда равенство F6) можно записать в виде
JC+ft
/
-/"-"(*)]+«.. F7)
где
46*
724 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Выведем для R две формулы, удобные для использования.
1. Известно, что Ф2/,(.г) сохраняет знак между 0 и 1. Поэтому можно
применить теорему о среднем и, обозначив через 9j число, заключенное между О
и 1, написать
к
Но согласно формуле F3) можно заменить Ф2р на 2 4-1 ^
Так как Ф2/,+1@) = Ф2р+1A) = 0, R сводится к
F8)
2. Ф2рG2)—наибольшее по абсолютной величине значение Ф2р(.г) между О
и 1. Если ) , сохраняет между х и x-\-h постоянный знак, то теорема
о среднем дает возможность написать
h2p Л ,п
\-tjdt
при
Ф2р(91)=92Ф2рA).
1*де Ьх и 92 обозначают два числа между 0 и 1.
Вводим значение Ф^С/гI данное уравнением F1). Тогда
F9)
Применяем формулу F7) последовательно к интервалам a, a
a~\-h, a-\-2h; ...;'а-\-(п—1)А, a-\-ah = b. Положим
Складывая п полученных выражений, получаем формулу Эйлера:
ь
J f(x)dx =А(уу0Ч-у1-|-у2н- ... +у„-1+уУ„)-
а
§ ' (а)] +-|^ А4 [/'" (*) - /'" (а)] + ...
3)] 1 G0)
при
^2+1li2)f) B)(^)]- GD
Это последнее выражение получаем из формулы F8), обозначив через
ATj хп абсциссы точек, заключенных в интервалах a, a-\-h; ...
...; a-j-(n—1)А, Ь. Если функция /2р) (х) сохраняет постоянный знак
в интервале а, Ь, то в силу формулы F9) можно написать
^ G2)
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ' 725
Существенное замечание. Так как числа Бернулли очень быстро
возрастают вместе с р, то весьма важно заметить, что остаточный член R,
вообще говоря, бесконечно возрастает вместе с р, если h фиксировано.
Но если h стремится к нулю, а р фиксировано, то R быстро стремится
к нулю. Формула Эйлера G0) представляет собой асимптотический ряд.
1,6
Пример. Требуется найти / —?-. Результат известен заранее:
f/ Л
1
In 1,6 =0,4700036292 ...
Делим промежуток интегрирования на шесть частичных интервалов (А = 0, 1)
и применяем формулу Эйлера при р, равном 3.
Вычислим сначала верхнюю границу совершенной ошибки. Так как
последовательные производные — сохраняют постоянный знак между 1 и 1,6,
то R следует взять в виде G2):
D = 9r—2) — @ П6 — Г— - —1 8-10~99.
Применение формулы Эйлера дает
— ^тг I -тг — тгйчг- 1Н- 4п • °-000114" — ТГНГ \ = +0,0500000000
и ( 1 A'Ь) ' /2U l l A>Ь) ' 0,0909090909
0,0833333333
0,0769230769
0,0714285714
0,0666666666
0,0312500000
—0,0005078125
-f-0,0000007061
0,4700036327,
откуда 0,470003624 < In 1,6 < 0,470003632.
Замечание. Из предыдущего примера видно, ' что применение фор-
формулы Эйлера позволяет получить очень большую точность при приближенном
вычислении определенного интеграла. Это, однако, верно при условии, что
имеется возможность вычислить последовательные значения' производных
интегрируемой функции на концах промежутка интегрирования и, сверх того,
для вычисления совершенной ошибки найти оценку производной высокого
порядка внутри этого промежутка. Это, конечно, невозможно, если функция
дана в эмпирической форме, и часто бывает затруднительно, если аналити-
аналитическая форма интегрируемой функции сложна. Отсюда возникает необхо-
необходимость установить некоторое количество формул достаточной точности,
вводящих производные интегрируемой функции только в необязательный пер-
первый поправочный член.
10.5.4. Формула трапеций. Если в формуле Эйлера положить р=\, то
получим формулу трапеций:
726 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Если функция эмпирическая, то вычислить ошибку Rt невозможно. Если
можно вычислить вторую производную и обозначить через М" верхний предел
абсолютного значения этой производной в интервале а, Ь, то
G4)
Применим формулу трапеций к предыдущему примеру. Имеем
In 1,6 = 0,1 { 0,5 4-tV + Т2 + ТЗ + ТТ + Т5 + Т Тб } = 0-050000
{ 1,1 1,2 1,4 1,4 1,5 2 l,b J 0,090909
0,083333
0,076923
0,071428
0,066666
0,031250
0,470509
при ошибке /?j < j2"@,lK • 2 = 0,001. Точность здесь довольно посредствен-
посредственная. Если вычисление первых производных доступно, то можно вычислить
поправочный член, положив р = 2 в формуле Эйлера:
ь
G5)
с ошибкой
^5^. G6)
где Mlw обозначает верхний предел абсолютного значения производной /iv(jc).
В рассмотренном примере этот поправочный член равен —0,000507, откуда
In 1,6 = 0,470002 при ошибке, меньшей 0,000002 по абсолютному значению.
10.5.5. Формула Симпсона. Предположим, что число частичных интер-
интервалов четное. Пишем формулу Эйлера для р = 2, иначе говоря, равенство G5)
с остаточным членом, получающимся из G1), если положить р = 2:
Применяем формулу G5) к га/2 интервалов, полученных слиянием каждых
двух смежных интервалов. Тогда
ь
f
f (x) dx =2А[1о2 4 „|„]^
G7)
при
где х[—точка интервала а, а —|— 2/г, х'2—точка интервала a-\~2h, a-\-Ah, ...
Исключаем поправочный член из выражений G5) и G7). Для этого
достаточно вычесть второе из первого, умноженного на 4. Получаем фор-
формулу Симпсона:
V
/.
10.5] ' ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 727
Если можно вычислить верхний предел M1V абсолютного значения чет-
четвертой производной в интервале а, Ь, то мы совершаем погрешность
4Д,—Я,
G9)
Применяем формулу Симпсона к предыдущему примеру:
In 1.6 = -^-1 +ттН-тЬ- + -ггН-тт-4-тт + -гг =°.°3333333
3 V 1,1 U W 1.4 1,5 l,t>; 0,12121212
0.05555555
0,10256410
0,04761904
0,08888888
0,02083333
0,47000636
с погрешностью
|/?3| < -j^g- @,1M- 24 = 1.3. 10~5.
Если в формуле Эйлера положить р = 3, предыдущие вычисления дают
возможность написать формулу Симпсона с поправочным членом:
/
(80)
Это улучшение дает в качестве верхнего предела абсолютного значения
погрешности
W*7^1' (81>
где MW1 — верхний предел абсолютного значения /VI (x) в интервале а, Ь.
Применим формулу (80) к предыдущему примеру. Поправочный член равен
—0,00000282... Отсюда 1п 1,6 =^0,47000356... с ошибкой, меньшей по
абсолютному значению
^ (О,1O6! = 0,00000032.
' 10.5.6. Формула Уэддля. Предположим, что интервал интегрирования
разделен на п интервалов, где п кратно 6. Тогда с помощью вычисления,
совершенно подобного предыдущему, можно написать формулу Эйлера при
р = 3 сначала для п интервалов, затем для /г/2 интервалов, полученных
соединением смежных интервалов по два, а потом для /г/3 интервалов, полу-
полученных соединением смежных интервалов по три. Все три написанных таким
образом выражения позволяют исключить оба члена, содержащие первые и
третьи производные. Достаточно для этого первое выражение, умноженное
на 15, сложить с третьим и вычесть второе, умноженное на 6. Так получаем
формулу Уэддля:
v
о и
f (x) dx = -jg-[y0 + 5yj + у2 + 6у3 + УА 4- 5ys -+• 2у6 -+- 5у7 ¦+¦
(82)
728 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
с оценкой ошибки
*7Л1У1. (83)
где Мщ — верхний предел абсолютного значения /VI (x) в интервале а, Ь.
Вернемся к предыдущему примеру:
1п 1,6 = 0,03 \\ + -^- +*+ в _,_ 1 + 5 + 1 1 = 0,030000000
l Li и м 1.4 1,5 1,0 j 0,136363636
0,025000000
0,138461538
0,021428571
0,100000000
0,018750000
0,470003745
47 «
с ошибкой, меньшей по абсолютному значению -т^гж 6@,1O6! = 0,0000016.
Если бы мы производили выкладки, исходя из формул Эйлера для
то получили бы формулу Уэддля с поправочным членом:
^ (84)
при
где УИ —верхний предел абсолютного значения / (х) в интервале а, Ь.
Для предыдущего примера поправочный член в формуле (84) будет
равен —0,000000134. Отсюда In 1,6 = 0,470003612 при ошибке, меньшей
по абсолютному значению
у5^0 6@,1)981 = 0,00000016.
10.5.7. Формула Грегори. Когда функция известна эмпирически, можно
составить таблицу разностей. Если в формулу Эйлера ввести значения про-
производных, выраженных по формулам D8) через разности, то мы получим
после некоторых вычислений формулу Грегори:
А [4-уо + У1 + Уа+
^ + Д4У1
ШШ ^Уп-е + **%] - ^^ [Д7Уя-7 ~ Д7Уо1 ~ ••• (86)
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 729
0,520
Пример. Вычислить/ = Г ardgxdx. Таблица разностей /(je) = arctgA;,.
0,515
составленная в п. 10.3.3, дает
0,001
0,001
0,001
0,001
0,001
0,001
Уо
2
У\
У2
У4
Ув
2
Уз+^
Уг
.0,001
., .0,001
Уо) 24
кз.. л 19 0,001
Уъ) 720
= 0,000237787736358
= 0,000476365524222
= 0,000477154932097
= 0,000477943696145
= 0,000478731816173
= 0,000239759645996
— 214640
= 53660
0,002387743619291
Замечание. Нетрудно вычислить первообразную для функции y=arctg;c:
/
arctg x dx = х arctg x — у In A -+- x2),
но, несмотря на это, вычисление интеграла посредством нахождения перво-
первообразной
/ = 0,520 arctg 0,520 —0,515 arctg 0,515 — у In 1,2704-(--i-In 1,265225
гораздо более громоздко и (если пользоваться таблицами арктангенсов
и логарифмов с невысокой точностью) дает менее точные результаты, чем
прямой подсчет по таблице разностей и формуле Грегори.
Формула Грегори использует разности, помещенные на нисходящей
и восходящей диагоналях таблицы разностей, имеющих начало ваий.
Пользуясь при вычислении, подобном предыдущему, выражениями для после-
последовательных производных, данными формулами E0), и произведя подстановку
в формуле Эйлера, получаем формулу интегрирования. Она образуется
с помощью разностей, находящихся по обе стороны от горизонтальных строк
таблицы разностей, имеющих начало ваий:
ь •
Н
2
"+" 720 1 2 2 ' J ~~
f
1
720
191А f А'Уя_2+А«у,,-з
60480
Пример. Требуется вычислить I = f cosxdx = 0,5. Берем таблицу
о
косинусов, приведенную в п. 10.3.3. Интервал 2°, выраженный в радианах,
730 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
равен 0,0349066. Формула трапеций дает
7=0,49994942.
Ограничимся вычислением первого поправочного члена из-за неправиль-
неправильного поведения третьих разностей. Этот поправочный член равен 0,00005076,
откуда
7 = 0,50000018.
Обращаем внимание на превосходное приближение, полученное несмотря
на краткость таблицы.
10.5.8. Введение в методы Ньютона — Котеса, Чебышева, Гаусса41).
Требуется вычислить приближенное значение интеграла
ь
I=ff(x)dx
а
Положим
Имеем
+ 1. +
1_ b — а Г /a+b b — a\d b — a f
-I " -1
Мы,пришли к приближенному вычислению интеграла
+1
р(и)йи. (88)
+1
= J
Попробуем представить J в виде суммы
W,ff(«o) + Wi<p(«i) + ... +/У„ср(и„). (89)
Неизвестные, входящие в формулу (89), определяются следующим критерием:
значения .выражений (88) и (89) должны совпадать, если tp(a) есть полином,
степень которого не превосходит некоторого заданного числа.
Правило это допускает три способа применения. По методу Ньютона —
Котеса следует заранее выбрать числа «,-, разделяющие интервал —1, -f-1
на равные части, и определять числа //,- (не зависящие от вида <р(и))
из требования точного равенства между (88) и (89) при замене ср(и) поли-
полиномом степени до и-j-l. По методу Чебышева следует взять равные между
собой числа Ht и определить из того же требования числа ut. Если же мы
определяем одновременно Ht и а1 таким образом, чтобы значения выраже-
выражений (88) и (89) совпадали при замене ср(«) полиномом степени до 2й+1,—
это будет метод Гаусса, более точный, чем предыдущие.
10.5.9. Метод Ньютона — Котеса. Рассмотрим полином степени д —J— 1,
принимающий те же значения, что и tp (и) при значениях ut аргумента. Это,
очевидно, интерполяционный полином Лагранжа. Интегрируя его, получаем
(90)
*) Более подробно этот вопрос изложен в кн. В. И. Крылов а, Приближенное
вычисление интегралов, Физматгиз, 1959.
10.5]
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
731
2/
Точки ut делят на равные части интервал —1, 4-1 • т- е- ui = —1 -|
Положим
п '
Тогда
-i-\) ... (t-n)dt. (91)
Вернемся к переменной х. Считая Ь—a = nh, имеем
Коэффициент Ht всегда определяется выражением (91). Можно составить
таблицу чисел Ht для нескольких первых значений п. Более подробное
изучение способа Ньютона — Котеса позволяет вычислить главную часть ошиб-
ошибки е„, приведенную в последнем столбце таблицы. Из рассмотрения этого
столбца видно, что выгоднее брать п четное. Прибавив е„ к результату вычис-
вычисления /, мы получим лучшее приближенное значение.
Нг
i
1/3
1/4
7/45
19/144
41/420
751
8640
1
4/3
3/4
32/45
75/144
216/420
3 577
8 640
5 888
1/3
3/4
12/45
50/144
27/420
1323
8 640
-928
1/4
32/45
50/144
272/420
2 989
8640
10496
2 880
1
6 480
7/45
75/144
27/420
2 989
8 640
-4 540
19/144
216/420
1323
8 640
10 496
4Г/420
3 577
8 64U
-928
751
8 640
5 888
989
1 567 641 600l ' ' \ 2 )
426 924 691 200 { ' ' \ 2 )
37
14175
14 175
14175
14175
14175
14175
14175
14175
14175
62 782 739 712 000
11.x
2 )
1,6
Пример. Требуется вычислить 1= \ —^- при я = 6. Имеем
840/У0/A)
840 ^/A,1)
840 Я2/A,2)
840 H3f A,3)
840 /У4/ A,4)
840 #5/ A,5)
840 HJ A,6)
41
216/1
27/1
272/1
27/1
216/1
41/1
: 41,000000
=196,363636
: 22,500000
:209,230769
: 19,285714
:144,000000
: 25,625000
¦^/ = 658,005119
(Ли
732
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Отсюда / = 0,470003656. Прибавив поправочный член е6 = — 0,000000023,
получим / = 0,470003633.
Замечание. Если разделить интервал a, b на некоторое количество
интервалов длиной h и применить формулу Ньютона — Котеса для я=1 в каж-
каждом интервале, мы снова придем к формуле трапеций. Применив эту же формулу
при л = 2 в каждом интервале длиной 2/г, опять находим формулу Симпсона.
10.5.10. Метод Чебышева. В этом методе принимается, что все Ht
имеют общее значение Н. Такой выбор коэффициентов обосновывается
следующим образом. Предположим, что ординаты <р(иг) измерены с одина-
одинаковой точностью. Тогда обусловленная ошибками измерения ошибка в инте-
интеграле будет наименьшей, если коэффициенты равны между собой.
Приравняем выражения (88) и (89) при <р(й), равном полиному сте-
степени п -\~ 1. Тогда
+ i
_/
Приравняв коэффициенты в обеих частях равенства, получаем га + 2-урав-
2
нения. Одно из них дает нам Н = <_i • Остается п-\- 1 уравнение, чтобы
определить ге-f-l число яг. Эти уравнения суть
я+1 ' +1
/=o
/=о
Заметим, что следует ограничиться значениями га=1, 2, 3, 4, 5, 6, 8,
так как только они приводят к вещественным ut. Вычисление дает следую-
следующую таблицу (последний столбец отведен для основной части совершенной
погрешности):
Н
2/з
'/2
2/7
ч
±0,57735026
±0,70710678
0
±0,79465448
±0,18759248
±0,83248748
±0,37454144
0
±0,86624682
±0,42251866
±0,26663540
±0,88386170
±0,52965678
±0,32391182
0
±0,91158930
±0,60101866
±0,52876178
±0,16790618
0
1 1
180 4TV" **' J \2)
-4>-«M/"(ф)
>->7'VI(^
480
1 1
3780
1
7444
1 1 ,. v
50 400 8! К '
1 1
88 552 8!
1
1
822180 10!
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 733
Вернувшись снова к переменной х, получаем xl = —^ 1 g—at.
... +f(xn)].
1,6
Пример. Требуется вычислить / способом Чебышева. При га =6
таблица дает
xo = 1,034841490, — = 0,96633156;
Xq
x, = l, 141102966, — = 0,87634510;
x\
x2 —1,202826454, — = 0,83137513;
x3—1,300000000, — = 0,76923077;
x, —1,397173546, — = 0,71573070;
xt
x s = l,458897034, — = 0,68544933;
хъ
xR—1,565158510, — = 0,63891292
6
/ = 0,3-y-5,48337551
/== 0,470003615
efi= 0,000000011
0,470003626
10.5.11. Метод Гаусса. При этом способе Н( и ut определяются, как
мы уже отметили, равенством формул (88) и (89) при условии, что ср{й)
есть полином степени 2га+1. Примем за такой полином произведение любого
полинома степени п на полином Лежандра степени га+1:
Из элементарных свойств полинома Лежандра известно, что
Г ф (и) Рп+Х {и) du = 0.
-i
Следовательно, выражение (89) для полинома ф(й)Ял+1(«) также равно нулю:
Это верно для любого полинома ф (и) степени га, следовательно,
Все а1 представляют собой корни полинома Лежандра степени га+1,
Н1 (не зависящие от вида <р(«)) всегда определяются выражением (90).
734
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[гл. х
Узлы ut и коэффициенты Ht для различных значений п даны в следующей
таблице:
щ
±0,577350269188
±0,774596669240
0
±0,861136311594
±0,339981043784
±0,906179845938
±0,538469310104
±0,932469514202
±0,661209386466
±0,238619186082
±0,949107912342
±0,741531185598
±0,405845151376
О
±0,960289856496
±0,796666477412
±0,525532409916
±0,183434642494
±0,968160239506
±0,836031107326
±0,613371432700
±0,324253423402
О
__
9
_8_
9
0,347854845136
0,652145154862
0,236926885056
0,478628670498
512
0,171324492378
0,360761573048
0,467913934572
0,129484966168
0,279705391488
0,381830050504
0,417959183672
0,101228536290
0,222381034452
0,313706645876
0,362683783378
0,081274388361
0,180648160694
0,260610696402
0,312347077040
0,330239355001
.11099088
1 1
•176 679 360 14!
— a)
а)
13
m{ a+b
[
L
_L
2815827300 16!
44 914183600 18 !(
/XVI
/a+b\
2 j
Вернувшись к переменной х, получаем
= -^t 1 g—ai'
Пример. Требуется вычислить / — способом Гаусса для п = 3.
= 0,34785484,
i
Из таблицы получаем
*0= 1,04165910, Н0 3
*! = 1,19800569,
х2= 1,40199431, Я1 = Я2 = 0,65214516;
хъ— 1,55834089,
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 735
Ik
A.
Ik
x3
I
0,3
e3
= 0,33394307
= 0,54435898
= 0,46515535
= 0,22322127
= 1,56667867
= 0,470003601
= 0,000000022
0,470003623
Точность вычисления близка к точности, полученной при использовании
формул Ньютона — Котеса и Чебышева для вдвое большего числа интервалов.
10.5.12. Применение интерполяционных полиномов Ньютона. Тре-
Требуется вычислить
b
Положим
Имеем
b—a=nfi, и= х~а-, у (и) = f (a + hu).
л
/ = h I
Если подставить вместо ср (и) интерполяционный полином Ньютона по нисхо-
нисходящим разностям (формула B3)), проходящий через «-(-1 точку a, f(a);
a-\-h, f(a-\-h); ...; a-\-nh, f(a-\-nh), то, возвращаясь к переменной х,
мы получим
= h [nf (a) +1 «2 д/
(92)
Действуя точно так же, но пользуясь полиномом Ньютона по восходящим
разностям (формула B5)), получаем
(93)
736 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Замечание. Если в формуле (92) считать га = 1 и после применения
этой формулы к каждому элементарному интервалу
a, a-\-k; a-\-k, a-\-2h; ...; а-\-(р—1)га, a-\-ph
произвести сложение, то
a+ph
f
Мы снова приходим к формуле трапеций.
Действуя точно так же при четном числе р и га = 2 с каждым из эле-
элементарных интервалов a, а + 2га; a-f-2/г, а + 4га; ... длины 2га, получаем
коэффициент при Д3/(а), равный нулю. Погрешность здесь порядка Д4/(я)-
Получаем
f f(x)dx=-j[f(a)+ 4/(а + га) + 2/(аЧ-2га)-(-4/(а + ЗгаL- •••
Зто' формула Симпсона.
Точно так же при р, делящемся на 6, возьмем га = 6 и применим фор-
формулу для каждого из интервалов a, a-\-6h; a-f-6ra, a-j- 12га; ... длины 6га,
причем коэффициент при величине Д7/(а) равен нулю.
Для первого интервала получаем
Г 41 216 97
л[^/(а) + -/(вН*) +
/
Прибавим к этому выражению пренебрежимо малую величину
-А- Д«/ (в) = -А- [/ (а) - 6/ (а + га) + 15/ (а + 2га) - 20/ (а -+¦ Зга) +
Поступив таким же образом для каждого из -— интервалов и сложив резуль-
результаты, мы получим с погрешностью порядка 0,007гаД8/(а)
Это формула Уэддля. Вследствие своей простоты она является одной из луч-
лучших формул интегрирования.
10.5] ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 737
10.5.13. Исключительные случаи. Изложенные способы интегрирования
функций, заданных аналитически, не дают хороших результатов в следующих
случаях:
а) подынтегральная функция обращается в бесконечность в промежутке
интегрирования 1);
б) производная подынтегральной функции бесконечна в промежутке
интегрирования;
в) один из пределов интегрирования бесконечен *).
В этих случаях приходится прибегать к замене переменной под знаком
интеграла.
а) Требуется, например, вычислить интеграл
/== С dx
Разложим его на три интеграла:
dx
I
dX
где 0 < *j < *2 < 1. Вычисление интеграла /2 не представляет затруднений.
Для вычисления /j производим замену переменной х=у2:
Возьмем х1 = 0,36, откуда )»! = Yxi = 0,6. Способ Уэддля при й = 0,1
дает 1Х= 1,2165.
Для вычисления /3 производим замену переменной 1—х==у2:
У 1-х,
-У2) B-W
Возьмем x2—0,Q4, откуда у2 = V^1—х2 = 0,6. Тот же способ при сохра-
сохранении шага й = 0,1 дает /3 = 0,9416.
' Способ трапеций, примененный к вычислению /2 при 7 интервалах,
равных 0,04, дает /2 = 0,4642. Отсюда / = 2,6223. Точное значение
равно 2,622056...
. б) Приведем очень простой пример для второго случая, когда интеграл
легко вычислить и непосредственно. Требуется найти
1
/ = f VT^
о
I
Положим 1-х —у2. Тогда / = 2 Г у2 У2 — у2 dy.
о
Способ Симпсона при 10 интервалах, равных 0,1, дает /=0,78537.
') Предполагается, конечно, что интеграл сохраняет смысл.
47 А, Анго
738 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Точное значение равно-j- = 0,78539...
в) Когда один из пределов бесконечен, самая естественная замена пере-
переменной — это х = —. Такая замена плоха, если второй предел равен нулю.
Тогда можно произвести более сложную замену переменной х = е~У. Лучше,
однако, расчленить интегрирование на две части, как это показано в сле-
следующем примере (в котором интеграл также вычисляется непосредственно).
Требуется найти
¦/
dx
1+х2
и
Имеем
1 + JC*— J I+Xt^j \+y*—ZJ
dx
0 10 0
Способ Симпсона при 10 интервалах, равных 0,1, дает У = 1,57079. Точный
результат есть -^- = 1,570769 ...
10.6. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
10.6.1. Введение. Рассмотрим дифференциальное уравнение порядка р.
Решенное относительно у(р> оно записывается в виде
dt d(< ¦¦-¦ dt^ I (94)
Если положить
4Н«. ?=« ¦?=*. ^>
иначе говоря.
dt dt2 ' dtp~l
то р — 1 уравнений (95) вместе с
_ = /(у, и, v z, t)
образуют систему из р дифференциальных уравнений первого порядка.
Таким образом, численные методы решения системы из р дифферен-
дифференциальных уравнений первого порядка
¦|f =g(y> и, v, .... z, t).
i
=r/(y, U, V Z, t)
включают в себя методы численного решения уравнения (94) как частный
случай.
Настоящий параграф делится на две части. Первая часть касается числен-
численного решения одного дифференциального уравнения первого порядка 1). Вто-
') См. в пп. 4.1.43 и 4.1.44 матричный способ решения системы дифференциаль-
дифференциальных уравнений первого порядка и решение дифференциального уравнения л-го порядка.
10.6] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 739
рая часть обобщает полученные выводы на случай системы р дифференциаль-
дифференциальных уравнений первого порядка, включающий в себя, как мы только что
видели, случай численного решения дифференциального уравнения р-го
порядка, а также случай системы из s уравнений порядка г (sr = р).
10.6.2. Приближенное интегрирование дифференциального уравнения
первого порядка. Дано дифференциальное уравнение
-?=/(*• у)- (96)
Решить его численно — это значит найти возможно точные значения yv y2
принимаемые для значений хх, х2, ... независимой переменной функцией у,
которая является решением уравнения (96), принимающим значение у0
при х = х0.
Существуют многочисленные способы для успешного проведения этой
операции. Мы приведем два из них из числа наиболее простых и удобных.
В одном способе используется ряд Тейлора, и применение его ограничивается
случаем, когда частные производные /(х, у) вычисляются легко. Второй,
абсолютно общий способ — способ Адамса — требует меньшего объема вычи-
вычислений, чем другие общие классические способы, как, например, способ
Рунге — Кутта и его варианты. Мы дадим также изложение способа Пикара,
или способа итерации, так как применение его часто бывает удобно, а теоре-
теоретическое значение велико.
10.6.3. Решение с помощью ряда Тейлора. Предположим, что значе-
значения переменной х возрастают, в арифметической прогрессии с разностью h:
х0, х, = х0Н-й xk = x0 + kh.
Разложение в ряд Тейлора искомой функции у дает значение yk+l для значе-
значения xk+l независимой переменной как функции значения у и ее последова-
последовательных производных в точке xk\
Но дифференциальное уравнение, которое требуется решить, дает
Отсюда последовательным дифференцированием получаем
Формулу (97) применяют для k — 0, 1, 2, ...
Если остановить разложение на члене га —/>, то это сводится к замене
решения у между абсциссами xk и хк^_х полиномом, имеющим в точке xk, ул
соприкосновение р-го порядка с решением, проходящим через эту точку1).
Пример. Требуется вычислить для абсцисс 0,1; 0,2; 0,3; 0,4 решение
дифференциального уравнения
подчиняющегося начальным условиям хо = уо —0.
') Это значит, что указанный полином и решение дифференциального уравнения
(принимающее при х = хк значение у ) совпадают при х = хк вместе с производными
до порядка р.
47*
740
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Так как интеграл вычисляется точно, то можно будет проверить расчеты.
Действительно, если положить х-\- у = z, то
— =1 i dy
dx ~ dx '
и предложенное дифференциальное уравнение принимает вид
Отсюда
Следовательно, вычисляемый интеграл равен
Установив это, вычислим у", у'", ... последовательным дифференцированием
рассматриваемого уравнения. Тогда
У' =
у" = 2
..in о
у — I
yiv =6;
yv = 8у'" A 4- У 0 + 6 (у"J Н- 2 (х 4- У) У1У<
уvii = 12yV A 4- у') 4 20 (у'"J 4 30y"yiv 4- 2 (* + У) Уп
Вначале у=гу/ = у"=0, у'" =2, yiv = 0, yV==16, yVI = 0, у
При Л = 0,1 восьмой член разложения в ряд Тейлора равен 10~7 • 272/7!
Он порядка 5 • 10" . В разложении мы пренебрегаем этим членом.
По формуле (97) вычисляется последовательно yft+i- а по только что
полученным формулам — У'ц+у У"к+\ • • • Результаты приведены в таблице:
X
у
У'
У"
у"' -
yIV
«V
Л'
У
Уточное
Уточное — У
0
0
0
0
2
0
16
0
0
0
0,1
0,00033467
0,01006704
0,2026895
2,081144
1,64600
17,3936
28,55
0,00033467
0
0,2
0,00271002
0,04109135
0,4220793
2,338856
3,58476
22,0020
65,98
0,00271004
2
0,3
0,00933623
0,09568890
0,6778725
2,820449
6,20136
31,3164
125,56
0,00933625
2
0,4
0,02279317
0,02279322
5
10.6.4. Способ Адамса. Предположим, как и раньше, что значения
независимой переменной х находятся в арифметической прогрессии с раз-
разностью h, и пусть у0 — значение, принимаемое решением при х = х0.
Интегрируем (96) от xt до xl+v Тогда
10.6] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ 741,
Заменяем f(x,y) интерполяционным полиномом Ньютона по восходящим
разностям:
f(x, у) = /(*,. ^
при
Получаем
й^-5. У,-5
19087
Если в выражении (98) остановиться на k-ft разности, пренебрегая
(k-\-l)-H. разностью, то это сводится к тому, что f(x, у) заменяется пара-
параболой k-й степени, проходящей через k-{-l точек: xt, у2; xi_l, y^x', ...
... ; xt_k, yt_k.
Способ Адамса состоит из двух этапов: прежде всего установление
исходной базы, которая состоит из k значений ух, у2 yk, соответствую-
соответствующих хх, х2, ..., xk и определенных возможно точнее (у0 известно). Далее
экстраполяция, которая заключается в том, чтобы применять формулу (98),
ограниченную k-й разностью, последовательно для / = ?, что дает yft+i.
для i =s k + 1, что дает yft+2. .. • Для простоты мы покажем сейчас по-
подробно применение этого способа при k=4. Это очень распространенная
степень приближения.
а) Установление исходной базы. Речь идет об определении ух, у2, у3, уЛ.
Очень удобно пользоваться ранее изложенным решением с помощью ряда
Тейлора, но можно также применять способ, при котором функция f(x, у)
заменена полиномом Ньютона по нисходящим разностям: ,
/(*. У)=/(*о. Уо) + «д/(*о. Уо)+-5F « («
+ «(й 1)(« 2)Д3/(л У)+й(и
Интегрируя уравнение (96), в котором f(x, у) заменена предыдущим
полиномом, ограниченным четвертой разностью, получаем
У)+^д/(^ У)
i
- ~ h ДЗ/ (x0, y0) — -A. h Д4/ (x0, y0),
90
— Уо + 4Й/ (*о- Уо) + 8Й д/ (*о- Уо) -Ь X Л д2/ (*о.
- -3- ^ Д3/ (^o> Уо) + т|-й Д4/ (^о. Уо)>
742 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Далее мы обозначим первые, вторые, третьи, четвертые и пятые при-
приближения величины К через
(/С)', (К)", {К)'", (/C)IV, (/C)v.
Вычисление производится последовательными приближениями:
1)
(УгУ = Уо + hf (х0' Уо)'
что позволяет вычислить
/[*,. (у,)'] и [Д/(х0, у0)]';
2)
(yi)" = Уо + А/(х0, уо) + у/г[Д/(^0, у0)]',
о- Уо)]'.
откуда находятся
fix. (УгУ'Ь flx2(y2)"], [A/(*o. Уо)Г« [Д7(*о- Уо)Г;
3)
: (У i)'" = Уо + А/ (*0. У0) 4- у А IV (*о- УоI" — -^ А [Д2/ С*о- Уо)Г.
(У2)'" = Уо + 2А/ (х0, у„) + 2А [Д/ (х0, у0)]" +1 А [Д2/ (*0. у0)]",
(Уз)'" = Уо + ЗА/ (х0. Уо) +|- А [Д/ (х0, у0)]" + -у А [Д2/ (*0. у0}]".
откуда вычисляются
Я*1. (У:)'"]. Я*2. (У2П. Я*з. (УзЛ.
[д/(*о- Уо)Г". [Д2/(^о. Уо)]'". [дз
4)
А[Д/(*о. уо)Г—jj
(У2IУ = Уо + 2А/ (х0. у0) 4- 2А [Д/ (х0, у0)]"' + у А [Д«/ (*0,- у0)]'" + 0.
(УзIУ = Уо 4- ЗА/ (*0. уо) 4- y А [д/ (*0. Уо)]'" 4
0. уо)Г.
(У4IУ = Уо + 4А/ (*0. уо) + 8А [Д/ (*0. уо)Т" 4
90 ft
+ -f- А [ Д2/ (х0, у0)]'" +1А [ДЗ/ (*„, у0)]'",
откуда находятся
/1*1. (У01У]. /1*2. (У2IУ]. /[*з. №)IV3- /1*4
[д2/(^о. Уо)Р.
Ш.6] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ 743
5)
*[Д/(*. y)]n
1
10
% , yo)]iv —^L h [Д«/ (х0, yo)]>v,
[Д/(хо, yo)]iv+^.A [Д»/(*о. yo)F +
1, уо)р.
(Уз)у = Уо + ЗА/ (х0. у0) + -| А [Д/ (х0, yo)]>v + -g- /г [Д2/ (х0, yo)IIV +
+ ¦§¦ A tД3/ (*„• УоI1у - -^ А [Д4/ (х0, yo)]>v,
90
-у-А [/(о Уо)Р4
+ |а[Дз/(х0, yo)]>v + iiA[A4/(xo. yo)]>v.
Можно улучшить значения у, вычислив /[(х, (y)v], затем разности и приме-
применяя предыдущие формулы по второму разу и т. д. до тех пор, пока резуль-
результаты не станут повторяться.
б) Экстраполяция. Мы получим приближенное значение у5, применяя
формулу (98), ограниченную членом с Д4 для г = 4;
+ 4 ДЗ/ (*,. у,) + ^i Д4/ (х0, у0) | . (99)
Значения Д/3, Д2/г' Д3/1- Д4/о Даны восходящими разностями таблицы для /.
Нужно уточнить полученное значение у5. Для этого с помощью / [дг5, (у5)']
вычисляют таблицу разностей. Пусть [Д/(лг4, у4)]', [Д2/^- УзI'- •••,—
улучшенные разности этой таблицы. Имеем
J
где .функция f (X, у) выражена через интерполяционный полином Ньютона
по восходящим разностям.
Интегрирование дает для / = 5
(Уз)" = У4 -+- h / / [лг5, (у5)'] — -1 [Д/ (х4, у4)]' } — -^- [Д2/ (*а. Уз)]' —
При помощи этого улучшенного значения вычисляют новую таблицу разно-
разностей и т. д. до тех пор, пока не получатся два равных последовательных
приближения.
Пример. Требуется численно решить дифференциальное уравнение
при начальных условиях хо = уо = 2 с шагом А = 0.05.
744
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Имеем:
1) 0>i)' = 2 + 0,05 A-1) = 2,
f[xv (yi)'] = l -4= 0,0244,
X
2
2,05
/
0
0,0244
л/
0,0244
2) (>>,)" = 2+ 0,05 • 0 + y0,05 ¦ 0,0244 = 2,00061,
(y2)" = 2 + 0,10- 0 + 2 • 0,05 • 0,0244 = 2,00244,
= 0,0241,
/ [х2, (у2)"] = 1 - Щ~ = 0,0465
X
2
2,05
2,10
/
0
0,0241
0,0465
д/
0,0241
0,0224
д2/
—0,0017
3) (yx)'" == 2 + 0 + y 0,05 • 0,0241 + ~ 0,05 • 0,0017 = 2,0006095,
0,05- 0,0241 —4-0,05-0,0017 = 2,0023817,
О
•I 0,05- 0,0241 —-f- 0,05 -0,0017 = 2,0052312,
= 0,02409293,
= 0,04648491,
(у3)'"=
2,05
2,0023817
2,10
= 0,06733433,
X
2
2,05
2,10
2,15
/
0
0,02409293
0,04648491
0,06733433
д/
0,02409293
0,02239198
0,02084942
д2/
—0,00170095
—0,00154256
0,00015839
10.6]
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
745
4)
= 2,0006099,
' = 2,0023809,
= 2,0052343,
(y4)iv = 2,0091046,
/[*i>(y,)IV]=i--
= 0,02409273,
/ lx2, (У2)Щ = 1 - 2'°°2130809 = 0,04648529,
10
= 0,06733288,
= 0,08677064,
2
2,05
2,10
2,15
2,20
/
0
0,02409273
0,04648529
0,06733288
0,08677064
л/
0,02409273
0,02239256
0,02084759
0,01943776
л2/
—0,00170017
—0,00154497
—0,00140983
ДЗ/
0,00015520
0,00013514
—0,00002006
5) (y!)V = 2,00060975,
(y2)V= 2,00238095,
(y3)v = 2,00523256,
(y4)V = 2,00909080.
Эти значения можно считать окончательными, только если последовательные
улучшения дают тот же результат. Поэтому вычислим новую таблицу раз-
разностей функции f(x, у):
/l*i. (yi)v] = 0,02409280,
/1*2- 0>2)vl = 0,04648526,
/[лг3, (y3)vl = 0,06733369,
flx4. Cy4)v] = 0,08677691,
X
2
2,05
2,10
2,15
2,20
/
0
0,02409280
0,04648526
0,06733369
0,08677691
д/
0,02409280
0,02239246
0,02084843
0,01944322
ду
—0,00170034
—0,00154403
—0,00140521
Д»/
0,00015631
0,00013882
Д«/
—0,00001749
746
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
что дает улучшенные значения
(yi)vi = 2,00060975,
(y2)Vi = 2,00238095.
(y3)VI = 2,00523255,
(y4)Vi = 2,00909091.
Новое вычисление таблицы разностей функции f{x; у) приводит к прибли-
приближению, в точности повторяющему предыдущие значения, которые могут
быть, следовательно, приняты за окончательную исходную базу.
Переходим к экстраполяции. Из формулы (99) имеем
(у5)' = 2,01388846,
Я*.. (*Л = 1 -^^ = 0,10493846. •
Отсюда получаем новую таблицу разностей, ограниченную пятой разностью.
Так как нам нужны лишь восходящие разности, то приведена только нижняя
часть таблицы:
X
2,20
2,25
/
0,08677691
0,10493846
д/
0,01944322
0,01816155
д2/
—0,00140521
—0,00128167
. Д»/
0,00013882
0,00012354
Д4/
—0,00001749
—0,00001528
А»/
0,00000221
Формула A00) дает в качестве первого улучшения у5
(у5)" = 2,01388889.
Новое вычисление таблицы разностей, основанное на этом значении у5.
в точности повторяет тот же результат. Значит, можно перейти теперь
к вычислению у6 и т. д.
Заметив, что данное дифференциальное уравнение является линейным,
мы можем точно вычислить решение, проходящее через точку х0 = у0 = 2.
Данное уравнение может быть записано в виде
(ху)' = х,
откуда получаем искомое частное решение:
У = ± + -.
у 2 ^ х
Точное вычисление у для различных значений х показывает, что апрок-
апроксимации у верны до восьмого десятичного знака.
Замечание. В большинстве случаев не требуется вычислять такие
далекие приближения, как в предыдущем примере. Либо значение h бывает
задано, и тогда можно позволить себе применять формулу апроксимации лишь
при значении k, меньшем чем 4. При этом формулы будут соответствующим
образом урезаны; этапы установления исходной базы сократятся, так же как
и все вычисления, касающиеся разностей менее высокого порядка. Либо А
10.6] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ 747
не задается и можно выбрать его достаточно большим, чтобы сократить
сумму вычислений, нужных для заполнения полного промежутка, в котором
желательно знать у с заданным приближением. Можно также соединить оба
способа действий удачным выбором h и k. Здесь трудно предписать твердые
правила. Нужно самому заметить по мере вычислений момент, когда следует
изменить значение h либо путем удвоения, либо путем уменьшения вдвое,
таким образом, чтобы получить при наименьшем количестве вычислений и
с нужной точностью повторение последовательных приближений у.
10.6.5. Сокращенный вариант. Если можно довольствоваться исходной
базой, состоящей из значений у0 (точно известного), ylt y2, у3, то бывает
удобно пользоваться следующим способом.
Пренебрегая четвертой разностью, можно установить исключительно
простую формулу. Интегрируем (96) от xt до xi+i:
Уг+4 — У/= / fix. У)
dx.
Заменяем f(x, у) интерполяционным полиномом Ньютона по нисходящим
разностям, ограниченным третьей разностью. После интегрирования получаем
A01)
Заменив Д, Д2, Д3 их выражениями, находим
Ah
У^
28
Первый отброшенный член равен -^ h Д4/-
Как только у1+4 вычислено, нетрудно вычислить fl+i и снова полу-
получить значение yi+4 с помощью следующей формулы, выведенной из фор-
формулы Симпсона:
\ ). (ЮЗ)
Мы пренебрегаем при этом членом порядка -щ-
Необходимо, очевидно, прежде чем начать вычисление шаг за шагом,
иметь исходную базу, образованную значениями у0 (точно известными), ylt
у2', Уз (вычисленными). Ее легко найти с помощью ряда Тейлора.
Разность значений yi+4, полученных из формул A02) и A03), равна
примерно
Она приблизительно в 30 раз больше, чем поправка, которую требуется
внести в результат, полученный в формуле A03). Таким образом, если одна
тридцатая этой разности меньше искомой точности в вычислениях, мы можем
пренебречь погрешностью формулы A03).
Если эта разность очень велика, то выгодно уменьшить вдвое интер-
интервал h. Если же она пренебрежимо мала, то мы удвоим интервал, что зна-
значительно сократит вычисления.
Пример. Требуется для х=0,4 получить численное решение
уравнения
/ + *
748 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
при начальных условиях уо=1, хо = 1. Результат требуется найти с точ-
точностью до пятой значащей цифры.
Исходную базу легко получаем с помощью ряда Тейлора:
У! = 1,1055, у2 — 1,2242, у3=1-3595.
Для Л =0,1 имеем
/, = ?, + *?=!.1155.
U = )'2 + *2= 1.2642.
Отсюда
у4= 1,5154.
Формула Симпсона дает
(/+4
откуда
у4 = 1,5154.
Уточнять значение у4 больше не нужно.
Вычисление у на следующем интервале следует производить при А = 0,2.
10.6.6. Приближенное интегрирование системы дифференциальных
уравнений первого порядка. Ограничимся изложением способа Адамса для
системы из двух дифференциальных уравнений первого порядка. Способ этот
может быть легко распространен на любое число уравнений. Дана система
? = /(*. У. *)•
dz .
-^ = g(x, у. г).
и пусть у0, z0— значения, принимаемые двумя неизвестными функциями для
одного и того же значения х0 независимой переменной (начальные условия).
Так же как и при решении дифференциального уравнения первого
порядка, отыскание значений ylt у2, ...', zx, z2, .... принимаемых функ-
функциями у п z для значений независимой переменной х, составляющих ариф-
арифметическую прогрессию с разностью h, следует разделить на два этапа:
установление исходной базы и экстраполяция.
Установить исходную базу можно, либо пользуясь способом Тейлора,
либо способом, подобным только что изложенному, при помощи Интерполя-
Интерполяционного полинома Ньютона по нисходящим рмзностям Ньютона.
10.6.7. Использование ряда Тейлора. Этот способ, который излагается
здесь для установления исходной базы, является также способом полного
решения системы дифференциальных уравнений. Чтобы убедиться в этом,
достаточно продолжить описанное ниже вычисление таким образом, чтобы
покрыть весь рассматриваемый интервал.
Пусть у0 и z0 — значения функций у и г для значения х = х0 незави-
независимой переменной. Значения yj и zx для xl=x0-\-h даны выражениями
+ -тУь+ ¦¦¦ +ТГУоп + ••••
Л2 ,, fi"
10.6] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ 749
при
У5 = /(*о- Уо- гоУ
*'0 = g(x0. у0, г0),
16.6.8. Применение интерполяционного полинома Ньютона с нисхо-
нисходящими разностями. Находим величины
o. у0, z0).
откуда мы можем вычислить
и
д/(*0. Уо> z0), bg(x0, у0, z0),
откуда
(*,)" = *„ + **<> +y
и т. д.
С помощью формул, совершенно тождественных тем, что применяются
в случае решения одного уравнения, мы получаем шаг за шагом таблицу
f(x0, у0, z0)
Д/(х0, у0, z0)
f(xv у„ zx) Д2/о
д/(*1. У1. *i) дз/о
У2. «а) • д2/, д4/о
Д/(х2, у2. z2) 3
у3. 23) Д2/2 •
и такую же таблицу для g.
Как только сделаны улучшения и получены окончательные значения
У1. У2- Уз- У4-
Zj, г2, г3, 24,
переходим к экстраполяции, производимой по формулам:
у4, 24) + уД/(х3, Уз- 23) + 4-Д2/(^2. У2.
Уо-
У4- ^4) + уД^(^3. Уз
3 251
b Д^С* У «0+
251 1
. Ур «0+ 720 Д4^(хо. Уо. «o)J-
750 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Так же, как и ранее, необходимо улучшить эти значения по формулам:
(Ув)" = Уа + * { f [*8. (Ув)'. (*б)'] — Y
-12
у4, г4)Г -
10.6.9. Способ Пнкара. Дано дифференциальное уравнение, решенное
относительло —р- :
с начальным условием у = у0 для х = х0.
Проинтегрировав от х0 до х, получаем
у х
fdy=ff(x,y)dx
Уо х„
ИЛИ
= Уо+ ff(x, y)dx, A04)
где у — неизвестная функция от х, находящаяся также под знаком инте-
интеграла. Будем решать это интегральное уравнение последовательными при-
приближениями.
За первое приближенное значение неизвестной функции примем
X
f(x, yo)dx.
Хо
Подставив это значение ух !в правую часть интегрального уравнения A04),.
получим
= у0+ J f(x, yx(x))dx
Ул-1<
Все функции Уг(х), .... уп(х) принимают значение у0 при х = х0 и могут
рассматриваться как все более точные приближения к у(х):
lim yn (х) — у (х).
Сходимость получается в предположении, что f(x, у) и * у'у' непре-
непрерывны вблизи точки х0, у0. Рассмотренный способ, легкий в изложении,
10.6] ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ 751
оказывается часто трудным для применения. Последовательные интегриро-
интегрирования могут быть очень сложными, а главное, сходимость в большинстве
случаев очень медленная, что крайне неудобно при численных расчетах.
Можно значительно улучшить этот способ, усовершенствовав исходную базу,
иначе говоря, первое приближение. Действительно, принять у0 за первое
приближение — то же самое, что принять --^- = 0, а это является очень
грубым приближением. Чтобы иметь более точное первое приближение, раз-
разложим /(х, у) (как функцию аргумента у) в ряд Тейлора вблизи у0:
Подставим это выражение в дифференциальное уравнение, пренебрегая
остатком R {х, у). Тогда
Это — линейное уравнение, рассмотренное в п. 6.1.5. В нем
Если ввести решение, принимающее значение у0 для х = х0, в правую
часть уравнения A04), получаем приближение, часто оказывающееся доста-
достаточным для большинства случаев.
Пример. Требуется решить дифференциальное уравнение
—
dx
=у3
при начальных условиях хо = О, уо=1. В этом уравнении переменные 'раз-
'разделяются, что позволяет найти точное решение у = A—2х)~'1г. Оно будет
служить для проверки.
Применяем способ Пикара. Первое приближение равно уо=1. Вто~
рое равно
X
ух = 1 + J dx = 1 + х, .
о
захем
у,= 1 -I--L / [3-И1 -(-хL]3dx = 1 4-х4-
Заметим, что первые 4 члена совпадают с началом разложения в ряд_
Тейлора точного решения.
752 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Применяем измененный способ Пикара. Имеем
<p(jc) = 3. <]>(*) = —2.
откуда первое приближение получается из уравнения
иначе говоря,
У о — з у 3
Второе приближение будет
X
Сравниваем четвертое приближение у3< второе приближение у1 и точное
решение у для х=0,2. Имеем
у @,2) = 1,29099, уг @,2) = 1,28776, у3 @.2) = 1,28676.
Из этого примера видно, что при использовании способа Пикара хорошее
начальное приближение приносит значительную -выгоду.
10.7. ГРАФИЧЕСКОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
10.7.1. Дифференциальные уравнения первого порядка. Способ изо-
изоклин. Дано дифференциальное уравнение cp(je, у, у') = 0. Решив его отно-
относительно у', получаем у' —/(х, у).
Будем предполагать, что f(x, у) — однозначная функция л; и у, имеющая
конечные первые производные по х и у. Геометрическое место точек пло-
р скости, в которых интегральные кривые имеют
<3? ч^ крутизну (т. е. тангенс угла наклона касатель-
касательной), равную р,—это, очевидно, кривая
p = f(x, у).
Ее называют изоклиной. Если построить изо-
изоклины легко (в противном случае способ не
представляет интереса), можно начертить на
плоскости несколько изоклин 1Рх, 1Рг соот-
соответствующих крутизнам pv p2, '...
Пусть Жо — точка с координатами х0, у0
-х (начальные условия) и пусть
О
Рис. 10.13. Ро = /(*о. Уо)
— крутизна интегральной кривой, проходящей через эту точку; IPl—бли-
IPl—ближайшая изоклина (рис. 10.13). Требуется найти точку Мх пересечения инте-
интегральной кривой с изоклиной IPi. Известно, что крутизна интегральной кривой
в точке Мг есть pt. Поэтому мы заменим участок Ж0Ж, интегральной кривой
на прямолинейный отрезок с крутизной, имеющей среднее значение Po~^Pi .
Проведя через Мо прямую с такой крутизной, найдем точку Мх как пере-
пересечение этой прямой с изоклиной IPl. Потом проведем через Мх прямую
с крутизной Рх1Рг и в пересечении ее с изоклиной 1Рг найдем точку М2 и т. д.
10.7] ГРАФИЧЕСКОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 753
Гладкая кривая /, проведенная через точки Мо, М1 будет прибли-
приближать искомую интегральную кривую. При этом ломаная М0МгМ2 . • ¦ вписана
в I. Описанную ломаную М0Т0Т{Г2 . ¦ ¦ получим, проведя через точки Мо,
Mv М2, ... прямые с крутизнами р0, pv p2, .... касательные к I.
Полезно получить некоторые сведения о форме иучка интегральных
кривых, облегчающие его построение.
Место точек перегиба. На каждой изоклине может находиться точка,
dy
в которой интегральная кривая касательна к ней. В такой точке крутизна -—¦
интегральной кривой, равная /(х, у), удовлетворяет уравнению -——\- . У =0.
справедливому для крутизны изоклины. Поэтому в такой точке
d2y df dy df
Так. как на интегральной кривой —г^ — -~тг~ + ~j~ ~^г • т0 в рассматриваемой
d2v I
точке 2 = 0, т. е. интегральная кривая имеет перегиб 1при . условии, что
d3v , \
-j~ отлично от нуля, чтобы имела место перемена знака кривизны .
Таким образом, / -J- -f--^-= 0 есть уравнение места точек перегиба
интегральных кривых.
В случае, если дифференциальное уравнение не разрешено относительно
производной <?(х, у, у') = 0, место точек перегиба получается исключением р
из уравнений <?(х. у, р) — 0 и ^l-+|i-p = 0.
Место точек возврата. Положим, что пучок изоклин имеет огибаю-
огибающую. Тогда уравнение этой огибающей можно получить, исключив р из урав-
уравнения изоклин у(х, у, р) = 0 и -^- = 0. Изоклины, касательные к огибаю-
огибающей, находятся вблизи нее с одной ее стороны. Интегральные кривые,
проходящие вблизи огибающей, не могут ее пересечь, и в большинстве слу-
случаев точка, общая с огибающей, является для них точкой возврата.
Если изоклины имеют двойную точку, то в этой точке интегральная
кривая возвращается с той же крутизной. Следовательно, это точки, где
интегральные кривые касательны сами к себе. Если это Имеет место, то
уравнения
?=о. ¦*=<>. ,(*.у.р)=.о
совместимы, и исключение р дает искомое место.
Асимптоты. Если пучок интегральных кривых имеет общую асимптоту,
то при бесконечном возрастании х предел —2- и — будет один и тот же.
Заменим в дифференциальном уравнении у' на р и у на рх. Тогда
tp (х, рх, />) = 0.
Если при бесконечно возрастающем х величина р, полученная из этого
уравнения, имеет пределом pv то прямая у = рхх ¦+• ql — асимптота, если
значение q, полученное из
1/448 Д. Анго
754
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
при бесконечно возрастающем х имеет конечный предел qv Если же преды-
предыдущее уравнение не зависит от х, то прямая у = p1x-\-q1 входит в пучок
интегральных кривых. Это особое решение, которое обычно входит в оги-
огибающую пучка.
Пример. Дано у'г = х2 — у2.
В той части плоскости, где х2 — у2 < 0, интегральных кривых нет. Че-
Через точку, где х2 — у2 > 0, проходят две. интегральные кривые, крутизны
Рис. 10.14.
которых, противоположны. Пучок интегральных кривых симметричен по от-
отношению к осям Ох и Оу.
1. Изоклины. Это гиперболы х2 — у2 = р2.
2. Место точек перегиба. Из х2—у2 = р2 и 2х — 2ру = 0 исклю-
исключают р. Тогда х2 = у2(х2— у2).
Дважды продифференцировав дифференциальное уравнение, получаем
2/у'" + 2/'2 = 2 — 2/2 — 2уу". .
Условие у"=д не влечет за собой у'" — 0. Следовательно, кривая х2=
— yi(x2 — у2) и есть место точек перегиба.
3. Для изоклин нет огибающих.
4. Место точек возврата. Исключим р из р2=х2 — у2 и 2р = 0.
Тогда получим х2 — у2 = 0, иначе говоря, биссектрисы осей координат. Здесь
изоклины не имеют двойных точек. Значит, кривая х2 — у2 = 0 "есть место
точек возврата.
5. Уравнение горизонтальной касательной к интегральной кривой — это
х2*— у2 = 0. Следовательно, в точках возврата касательная горизонтальна.
10.7]
ГРАФИЧЕСКОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
755
6. Асимптоты. Имеем <р(х, рх, р) = р2—х2{\ —р2) — 0. Иначе говоря,
•^-=1—р2. Если х стремится к бесконечности, то р стремится к ± 1.
Подставляем у = ±x-\-q и р= + \ в х2— у2 = р. Тогда
= ±2qx— ф.
Когда х стремится к бесконечности, q стремится к 0. Следовательно, у = х
и у = — х — асимптоты, общие для пучка интегральных кривых, так как
у'= ±1, у= ±х не удовлетворяют тождественно данному дифференциаль-
дифференциальному уравнению.
На рис. 10.14 пунктиром изображены изоклины, точечным пунктиром —
место точек перегиба и сплошными линиями — несколько интегральных кривых.
Замечание. Если функция у не фигурирует в дифференциальном
уравнении, то его можно записать в виде
dx—J W-
При этом изоклины представляют собой параллели к оси Оу. Способ изо-
изоклин дает возможность графически осуществить квадратуру, т. е. начертить
одну из кривых
= ff(x)dx,
где а — произвольная постоянная, каждому значению которой соответствует
отдельная интегральная кривая. Эти кривые получаются одна из другой простым
перемещением вдоль оси Оу.
10.7.2. Графическое решение дифференциальных уравнений второго
порядка способом радиусов кривизны. Рассмотрим дифференциальное урав-
уравнение, решенное относительно у":
Делим обе части на (l
У" /
2.
у'2) 2. Тогда получаем
1
_ / (У. /¦ х) _
i i 9 (У- У'<
2J A + у'2J
. 0
Мы определили радиус кривизны интегральных
кривых. Он равен
У • X). -щ х
Отсюда вытекает следующий способ графи- рис. ю.15.
ческого решения уравнений. Пусть при х = х0
функция у и ее производная у' принимают соответственно значения у&
и уо- Это означает, что из всего пучка интегральных кривых мы хо-
хотим начертить такую, которая проходит через точку xQ, yQ и имеет в
этой точке крутизну у'о. Пусть будет дана точка Р0(х0, у0) и касатель-
касательная Р0Т0 (рис. 10.15). Радиус кривизны интегральной кривой равен в
этой точке /?о = ср(уо, уо, Xq). Начертим этим радиусом дугу окружности,
соприкасающейся с искомой кривой, и примем, что в промежутке х0, хх эта
48*
756
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
дуга совпадает с интегральной кривой. На дуге возьмем точку Рх с абсцис-
абсциссой xv Ордината ее равна yv а крутизна касательной Р{Г1 в этой точке
равна
¦>оа.„
Рис. 10.16.
Радиусом, равным Ri = ср(уь yi. *i). начертим дугу окружности, прохо-
проходящей через точку Рх и касательной к P{TV и т. д. Мы последовательно
вычерчиваем таким образом дуги окружностей, практически сливающиеся
с искомой интегральной кривой, если последовательные интервалы (х0, Xj),
(xv дг2) достаточно малы.
10.8]
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
757
Имеем
Пример. Попробуем начертить одну из интегральных кривых уравнения
у" — A — У2)У'-Ь у = 0.
Начертим проходящую через точку х = О, у = 0 кривую, имеющую
в этой точке касательную, наклон которой к оси х равен 45°, т. е. у'0=\.
Получаем кривую, изображенную на рис. 10.16.
10.8. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ В. ЧАСТНЫХ
ПРОИЗВОДНЫХ
10.8.1. Плоские задачи. Мы ограничимся здесь уравнениями в частных
производных второго порядка вида
dU дги
~ду~' ~дх?'
.[ .. dU
f[x, у, U, -^-,
= U.
A05)
Задача состоит в том, чтобы отыскать функцию, удовлетворяющую уравне-
уравнению A05) и совпадающую на данном контуре с данной функцией U = <р(х, у).
Искомую функцию мы определим ее значениями
в узлах прямоугольной сетки. Предварительно мы
решим две простые задачи.'
1. Рассматриваются четыре точки а, Ь, с, d —
середины сторон прямоугольника и точка / —
центр прямоугольника (рис. 10.17). Попро-
буем найти приближенные формулы, дающие пер- t_ _ /*>. J
ые и орые чаые роизодные фуки U ---.-'-
вые и вторые частные производные функции U
в точке / как функции значений U в точках
а, Ь, с, d, I.
Разлагаем функцию U в ряд Тейлора вблизи
точки i:
Рис. 10.17.
A06)
агА
Рис. 10.18.
Пишем этот ряд, ограничиваясь членами второго порядка, в точках а, Ь,
с, d. Нетрудно получить
A07)
2. Поставим ту же задачу, но при этом пусть точка / не будет больше
в центре прямоугольника. Положение ее определяется отношениями -i-, -J-
расстояний до сторон прямоугольника (рис. 10.18). Предыдущее разложение,
48 А. Анго
758 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
примененное к точкам а, Ь, с, d, дает
[ГЛ. X
dU
ьи„
5 G + 5)
A08)
(« + Р)
Уг)Г
После того как обе эти задачи решены, можно взяться за основную за-
задачу. Разложим область внутри заданного контура на некоторое число пря-
прямоугольников. В уравнении A05) следует заменить частные производные
приближенными формулами A08) или A07). Мы получим таким образом урав-
уравнения, которые дают возможность вычислить значения U в точках внутри
контура как функцию значений U на контуре, данных из условий задачи.
Формула A07) применяется главным образом в центральной части зоны,
ограниченной контуром, там, где узлы прямоугольной сетки являются равно-
равноотстоящими. Формула A08) применяется в основном в периферической части
этой зоны, если близость границы вносит неправильность в положение узло-
узловых точек прямоугольной сетки (рис. 10.19).
25 26jy28 29 30
Рис. 10.20.
Пример. Рассмотрим очень простой пример. Требуется найти функ-
функцию U, принимающую соответственно значения -\-\ и —1 на двух прямых
углах, определяемых точками 19, 1'3," 7, 1, 2, 3, 4, 5 и 12, 18, 24, 30. 29,
28, 27, 26, и удовлетворяющую уравнению Лапласа внутри прямоугольника
(рис. 10.20). Сетка образована квадратами (k = l). Если перенести в урав-
нение Лапласа значения
из формулы A07), то получим
Применим это выражение к 12 точкам внутри прямоугольника. Тогда
10.8] УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 759
Но
f/2==f/a=f/4=f/5==t/7==t/l3=t/1Q=-l-l.
t/l2 = Uls = U24 — U24 ™ ^28 == ^27 == ^26 == * •
Предыдущая система принимает вид
4l/ao=l/21
4t/a = t/ffi + t/17 —2*).
Можно попытаться прямо решить эту систему из 12 уравнений с 12 не-
неизвестными. Однако для более сложных систем, где внутренние точки насчи-
насчитываются сотнями, надо решительно отказаться от этого способа и приме-
применять следующий способ последовательных приближений1).
Мы будем обозначать первое, второе, ... приближение U в точке а
через Ua, Ua, ... Значения, взятые в качестве начальных для внутренних
точек, могут быть любыми, но удобнее выбирать значения, не слишком от-
отличающиеся от результатов вычислений. Простое рассмотрение рисунка под-
подсказывает нам выбор в качестве начальных значений:
U21 = U я = t/23 = Un = — °-5-
ип = и20 = и15 = t/16 = о.
Перенеся эти значения в предыдущие уравнения, получим первые прибли-
приближения:
=0,5 +0,5 -+-2 =3 , U's = 0,75,
=0,75 4-0,5 4-1 =2,25, l/'9 = 0,562,
4U'w=Ug 4-[/1I4-i/164-l =0,5624-1 =1,562, f/{0= 0,390.
4t/n=t/lo+f/i7 =0,390 — 0,5 =— 0,110, Un = ~0,027,
i =0.75+1 = 1,75, t/i4=0,437,
,562 — 0,5 = 0,499, f/{s =
*) Если учесть симметрию задачи, число уравнений и неизвестных можно умень-
уменьшить вдвое.
') То, что в английских и американских работах называется .методом ре-
релаксации'.
48*
760
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
?/22 = 0.125 — 0.5 + 0.390 — 0,5 = — 0,485.
Uw = — 0,121.
n = U'16-\-Uu-t~U23— 1 = — 0.121—0,027 — 0,5—1 =—1,648,
U'17 = — 0,412.
= ?/2i + ?/м = — 0,5 + 0,437 = —0.063. l4 = —0,016.
—1 = — 0,016 —0,5 + 0.125—1=—1.391,
{/21= —0,348,
— 1 = — 0,348 —0,5 —0.121 —1 = —1.969.
t/22 = — 0,492,
—2 " = — 0.492 —0.412 —2 = — 2,904,
?/» = — 0,726.
Затем получаем вторые приближения:
4?/в =?/9 + ?/м+2 =0,562 + 0,437 + 2 = 2,999, ?/8=0,750.
4?/s =?/8' + ?/io + ?/i5+ 1=0,750+0^390+0,125+ 1 = 2,265,
?/9 = 0,566.
4?/и= ?/9 + ?/11 + ?/16 + 1 = 0,566 — 0,027 — 0,121 + 1 = 1,418,
и т. д. Продолжив вычисления до пятого приближения, получим таблицу:
Точки
8
9
10
11
14
15
16
17
20
21
22
23
Приближения U
исход-
исходное
0,5
0,5
0,5
0,0
0,5
0,0
0,0
—0,5
0,0
—0,5
—0,5
—0,5
первое
0,750
0,562
0,390
—0,027
0,437
0,125
—0,121
—0,412
—0,016
—0,348
—0,492
—0,726
второе
0,750
0,566
0,354
—0,014
0,465
0,140
—0,102
—0,460
0,029
—0,331
—0,540
—0,750
третье
0,758
0,563
0,362
—0,024
0,482
0,153
—0,121
—0,474
0,038
—0,337
—0,552
—0,754
четвер-
четвертое
0,761
0,569
0,356
—0,029
0,488
0,150
—0,130
—0,478
0,038
—0,341
—0,556
—0,758
пятое
0,764
0,567
0,352
—0,031
0,488
0,146
—0,134
—0,481
0,037
—0,343
—0,559
—0,760
10.8.2. Задачи вращения. В предыдущем пункте речь шла об оты-
отыскании U как функции декартовых координат х, у. Здесь стоит та же задача*
для цилиндрических координат г и z. Однако имеются некоторые отличия,
которые будут изложены ниже.
Рассмотрим разложение в ряд A06), ограниченное членами второго
порядка, и заменим х на z, а у на г. Мы получим следующие группы фор-
формул, тождественные по виду с уравнениями A07) и (Д08).
».8! УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
1. Точка I — центр прямоугольника (рис. 10.21):
761
A09)
Ось
Ось
Рис. 10.21. Рис. 10.22.
2. Точка / — не центр прямоугольника (рис. 10.22):
и ( dU \ _ Wa aUc Ф~
\ OZ 11 a [a —j— pj p (a -J- p^ )
4*
l
"'
дг ) — 7G + 5)
л5г" I = !
"с
(ПО)
-fi
Разумеется, уравнения в частных производных должны быть приспо-
приспособлены к системе цилиндрических координат. Например, уравнение Лапласа
будет записано в виде
1 №
Основное различие с плоской задачей Ось
заключается здесь в наличии прямой — оси
вращения, играющей привилегированную
роль. Значения U в двух точках, симмет- Рис
ричных относительно этой оси, будут,
очевидно, равны. Формулы, соответствующие частным производным в точках
этой оси, будут выражены особыми формулами в силу этой симметрии и
условия г=0.
Пусть о будет точкой на оси вращения (рис. 10.23). Производная (-г—\
равна нулю, но величина (—з—j конечна. Имеем
\ *" or !o ¦
dU
dU
г*
Первый член справа равен нулю, откуда
762 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ [ГЛ. X
Так как Ud = Ub в силу симметрии, то
г дг }0 -^ \ dr2 )о — /г*
Вторая производная по г в точке на оси всегда выражается третьим
равенством A10). Например, для точки, находящейся от оси на расстоянии ak,
и для квадратной сетки уравнение Лапласа будет
а для точки на оси
10.9. НОМОГРАММЫ
10.9.1. Введение. Подробное изучение номографии должно включать в себя
знакомство с большим количеством типов номограмм. Выбор наилучшего ва-
варианта номограммы может быть сделан только специалистом. Здесь же мы за-
задаемся лишь целью дать возможность инженеру вычертить основные номо-
номограммы, полезные в его работе. Поэтому ограничим изложение наиболее
употребительными номограммами. Мы займемся лишь номограммами с вырав-
выравненными точками. Они просты и читаются легко и точно. Из них мы рас-
рассмотрим только номограммы с тремя параллельными прямыми шкалами,
TV-образными, W-образными, с двумя параллельными прямолинейными шка-
шкалами и криволинейной шкалой, с прямолинейной и двумя криволинейными
шкалами, с тремя- криволинейными шкалами. Для изучения номограмм кру-
круговых, прямоугольных и с огибающей мы отсылаем читателя к специальным
трудам. Так как номограммы с перекрещением могут почти всегда быть заме-
заменены номограммами с выравненными точками, более простыми по своему
строению и более удобочитаемыми, нам показалось ненужным рассматривать
их здесь.
10.9.2. Определения. Графическая шкала. Графическая шкала состоит
из основания (прямая или кривая), на котором нанесены отметки, соответ-
соответствующие последовательности возрастающих чисел. Если функция /(и) непре-
непрерывна и строго возрастает (или убывает) в заданном интервале, то можно
эту функцию изобразить графической шкалой.
Модуль. Графические шкалы, которые мы ниже будем строить, должны
вычерчиваться на бумаге обычного формата. Если требуется рассмотреть
два крайних значения функции /(и) для двух крайних значений переменной и,
то следует выбрать на основании такую единицу длины, чтобы формат
бумаги использовался для графической шкалы наилучшим образом. Эта еди-
единица длины называется модулем графической шкалы.
Например, для прямолинейной шкалы, если нельзя по соображениям
удобства превысить длину в / сантиметров и если их и и2 — крайние значе-
значения полезного изменения переменной и, то самый выгодный модуль, т. е.
дающий самое точное прочтение, будет
т
Пример. Требуется построить графическую шкалу функции
10.9]
НОМОГРАММЫ
763
для интервала изменения от и=1 до и = 10 на листе бумаги, наибольший
размер которого / = 25 см. Наиболее выгодный модуль будет
т.—
25
25 '
= 23 ™=10-8 см.
Из соображений простоты, которые не менее важны, чем наибольшая точ-
точность прочтения, следует взять т = 10 см.
Начало шкалы. Так называется точка, для которой /(и) = 0. Следо-
Следовательно, если х есть расстояние от начала до точки на шкале с отмет-
отметкой и, то
х = mf (и).
Начало шкалы может оказаться за ее пределами.
Важнейшие шкалы. Функция /(и) оказывается часто одной из следую-
следующих функций: аи-\-Ь (линейная шкала); log и (логарифмическая шкала,
очень часто с основанием 10); 10"; и2, и3, ..., и" (параболическая шкала);
111.
и2, и3 а " ; sin a; cos и; tga; sh и; chu; th и; ...
Очень важно уметь быстро вычертить шкалу mf (и) с определенным
модулем с помощью шкалы функции /, вычерченной раз навсегда. На рис. 10.24
mod'5.2
mod 7.5
Рис. 10.24.
показан такой способ. В качестве примера здесь вычерчена шкала х =
= 5,2 log и при помощи шкалы х = 7,5 log a.
Чтобы вычертить проективную дробно-линейную шкалу х =
с помощью линейной шкалы у=[хи или, в более общем виде, чтобы вычер-
af(u)-\-b ' , .
тить шкалу х = т . i\d с помощью шкалы у = ja/ (и).. следует опи-
опираться на хорошо известные свойства проективности, указывающие, что обз
шкалы х и у являются проекциями одна другой.
764
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
На рис. 10.25 показано построение шкалы (логарифмы десятичные)
х= 15 liLTi с помощью y—7,5lgu. Центр перспективы S дается пере-
пересечением двух прямых, соединяющих точки, соответствующие и = 10 и и =
= 100. Обе точки и=1 совпа-
Г00(у=Т5) дают. Имеем а=1, у = 0,
л:=15; я=10, у = 7,5, л: = 22,5;
й=100, у = 15, # = 25.
Весьма важный частный слу-
случай состоит в том, чтобы построить
шкалу х = —, обратную линей-
линейной шкале y = {t(e). Как и в пре-
предыдущем случае, заставляем сов-
совпасть две соответственные точки
(например, и =2). Точка с абс-
абсциссой х = оо соответствует
Рис. 10.25. точке с абсциссой у = 0, и' на-
наоборот. Это дает возможность
легко определить центр перспек-
перспективы 5 (рис. 10.26). Графическое
построение х= с по-
помощью у = р./(й) не представляет
затруднений.
10.9.3. Номограммы с вырав-
выравненными точками. Известно, что,
для того чтобы три точки, отне-
отнесенные к любым прямолинейным
осям координат (прямоугольным
или косоугольным), находились на одной прямой», необходимо и достаточно.
Рис. 10.26.
чтобы их координаты xv yt; x2, y2; х3
1
1
удовлетворяли уравнению
Уз
1
= 0.
(Ш).
Рассмотрим три кривые Cv C2, С3
(рис. 10.27), параметрические уравнения ко-
которых будут
С, хх— fi(u), з>1=ср1(м),
Рис. 10.27.
Если принять эти кривые за основание трех шкал, градуированных по зна-
значениям и, v, w, и если задаться двумя определенными значениями и и v.
например их и vv то прямая, проходящая через точки с отметками я, и vv
пересекает кривую С3 в точке с отметкой wv Это позволяет решить отно-
относительно w уравнение
¦0.
10.91
НОМОГРАММЫ
765
Это уравнение просто выражает общий принцип номограмм с выровненными
точками. Обязательное по изложенным выше причинам введение модулей
и необходимость описать практические детали требуют более подробного
изложения. Поэтому мы сделаем обзор наиболее употребительных номограмм
с выровненными точками.
10.9.4. Номограммы с тремя параллельными прямолинейными шка-
шкалами. При обозначениях рис. 10.28 имеем
0
Ух 1
у2 1
Уз 1
= 0.
Иначе говоря, при
0
а
а-\-Ь
Рис. 10.28.
= 0.
Положим
Ьтх = атъ,
(а -\-Ь)т2 — атг.
Уравнение A12) принимает вид
(П2)
(ИЗ)
Это общий вид уравнения, которое можно решать с помощью рассматри-
рассматриваемой номограммы.
Уравнения A13) позволяют вычислить отношение -г и один модуль как
функцию двух других модулей. Например,
Ь ТК$ ТП\ -р /Из
'Пример. Отношение модулей напряжений на входе и выходе s—^?-
четырехполюсника, образованного емкостью С и сопротивлением /?(рис. 10.29),
выражается' формулой
V
Эта формула может быть написана в виде (логарифмы десятичные)
Положим
9 а. Анго
766
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Мы располагаем листом бумаги в 26 X 20 см, / меняется от 1 до 20 000 гц,
RC меняется от 0,0002 до 0,2. Имеем
y1 = «jcpj (RC), откуда
y3 = /»3cp3 Bкf), откуда
0,2 ¦
26
|lg- 2-10~4 — lff 0,2
26
lg20000 —lgl
6 см—т3
a off
doe
0,07
O.O6
0,05
O.O4
0,03
0,02
O.O1
' 0,009
0,008
O.OO7
0,006
0,005
O.OO4
0,003
0,002
O.0O7
0,0003
6,0008
O.OOO7
0,0008
0J0005
0,0004
0,0003
0,0002
RC
Отсюда
С
-И-
г- 0,999933
- 0,99999
¦ 0,9993
- 0,93в
- 0,99
-0,9
¦0.0
iff
'0,2
-0,1
--д.оа
-^0,06
-0,05
• &О4
" 0,03
¦ 0,02
-0,07
S
Рис. 10.29.
a 8
7 = "РИ
20 см;
20000
т
4ООО
ЗООО
гооЬ
- 1000
8ш
400
300
200
70
60
50
to
30
20
_ 19
4
3
!- 1
берем а = 10 см, Ь—7,5 см.
Взаимное расположение шкал по вертикали определяется из условия,
что отметки для любой тройки значений RC, /, s, удовлетворяющих дан-
10.9] НОМОГРАММЫ ' 767
ному уравнению s = — ~ , должны лежать на одной прямой.
V l +
(/)
Из этих трех значений два (например, RC и /) произвольны, а третье вы-
вычисляется. Номограмма изображена (в масштабе 1 :2), на рис. 10.29.
Для RC= 1/1000 (например, С=\ мкф и #=1000 ом) и для / = 90 гц
находим s = 0,5. Вычисление дает s = 0,49.
Замечание. Номограмма с тремя параллельными прямолинейными
шкалами является наиболее простой. Очень важно просмотреть все соотно-
соотношения, которые могут быть представлены таким образом, т. е. могут быть
сведены к канонической форме A14). Соотношение
сводится к форме A14), если взять логарифмы обеих частей. Это же отно-
относится и к соотношению
если дважды взять логарифм правой и левой части.
Совершенно очевидно, что оба соотношения
fx (и) ~г~ /з (ш) /2 (f)
легко свести: первое к форме A16), считая -т- = <р2. второе к канонической
Г
форме A14), считая -у =<р^.
Уравнение
да) 'A18)
можно также свести к форме A14) путем менее явной замены переменной.
Соотношение A18) может быть написано в виде
1) А > 0. Положим <р/ = arctg ['y~A_ft]. Тогда cpi (и) -+- % (f) = kit — cpj (w).
2)Л<0. Положим cpf = arth [|^Л /J. Тогда cpt (a) ~f cpj (v) = — cp3 (w).
Замечание. Путем введения коэффициентов следует сделать область
изменения- функций fv /2, /3 для используемой области изменения перемен-
переменных и, v, w меньшей —т=-.
У А
10.9.5. Номограммы с двумя параллельными прямолинейными шка-
шкалами н одной криволинейной. Имеем (см. рис. 10.30;
0 у, 1
х2 у2 1 =0. - (,П9>
d у3 1
49*
768 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
Положим
ГГЛ. X
A20)
A21)
Хп =: п ; . . . .
Тогда уравнение A19) принимает вид
A24)
Это общий вид уравнений, которые можно решать с помощью номограмм
рассматриваемой формы. Обе прямолинейные шкалы выражаются формулами
A20) и A21). Кривая и ее градуировка вы-
выражены двумя параметрическими уравне-
уравнениями A22) и A23).
Пример. Требуется вычертить номо-
номограмму для соотношения
/"п 1 _
В этом выражении п — общее число импуль-
импульсов за время эксперимента t, выраженное
в минутах. Оно измеряется счётчиком на
радиоактивном образце. Величина р — число
импульсов, производимых шумами; а — совершенная стандартная ошибка,
принятая за 5%. Эту формулу можно написать в виде
VT ^ Уп
а это и есть формула A24) при
<?i(t) = y^' <Р2 С») == «/я
У нас имеется лист бумаги в 25 X 20 см. Поэтому делаем следующее
вычисление модулей с обозначением практической области изменения пере-
переменных:
, = —^, 2 < t < оо, откуда т, = ¦
35 см;
25
150
i = m3p, 0</7<150, откуда т.3= -j^= 0,166 ...
ad_
35
35
х—
0,15 + 35
-В
0.15/п+1,75
°'15'35а ^~" —
0,15 + 35 -±г ~
Уп
0,15 см;
при а=5% и d = 20 см,
0,2625л
1,75
10.9]
НОМОГРАММЫ
г.5
з
3,5
4
5
6
8
10
15
20
100
Мы по-прежнему имеем оба урав-
уравнения A20) и A21), но параметри-
параметрические уравнения A22) и A23^ суть
у2 = 0, откуда ср2 (v) = 0,
Кривая х2, у2 легко строится по точкам для различных значений п. Одно-
Одновременно получается и ее градуировка. Рис. 10.31 изображает номограмму
в масштабе 1 : 4.
10.9.6. ЛГ-образная номограмма. Это частный случай номограммы, рас-
рассмотренной в предыдущем пункте. Кривая сводится к прямой, не параллель-
параллельной двум другим прямым. Такая номограмма часто называется ЛЛобразной
или Z-образной. В этом случае третья прямая может быть принята за ось Ох
(рис. 10.32).
р
ISO
150
140
130
120
110
100
90
80
70
ВО
50
U0
30
го
10
а
Рис 10.31.
Общий вид уравнений, решаемых с помощью ЛЛобразной номо-
номограммы, — это
cp1(M)-j-/2(o)cp3(te') = 0. ;A25_)
Пример. Требуется вычерхить номограмму для формулы
а 1
2 /Из + Wi/2 («)
Последнее уравнение дает
ческую шкалу оси х.
У
Рис. 10.32.
графи-
^ х
дающей коэффициенты перенапряжения цилиндрического резонатора как функ-
функцию отношения радиуса а к глубине проникновения S и высоты h.
Берем
В нашем распоряжении поверхность в 20 X 20 см, область изменения у
от 0 до 105, область изменения -.- от 0,25 до 0,50. Отсюда получаем модули
20
= 7Й5"= 80 см-
mi = ^°_^2.10-4 см.
Нуль функции срз находится на 1 метр под точкой А (рис. 10.33). Следо-
Следовательно, точка С наклонной шкалы делит DA = 20 см в отношении iU.
770
ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
[ГЛ. X
Длина d наклонной шкалы
между двумя вертикальными
а
7
5000-
70000-
75000
го ооо
25000
30000-
35000-
40000
45000
SOO00
55000-
60000
65000
70000
75000
60000
65000
90000
35000
100000
Q
5000
V юооо
\ 75 ООО
\ 25000
\30OO0
\35OO0
\ 40000
\ 45000
\ 50000
V 55000
\ бо ооо
\В50в0
V 70000
V 75000
^ as ооо
с
(включая не поместившуюся на чертеже часть)
шкалами есть d = ]/"l202 + 202— 121,7. Отсюда
получаем градуировку шкалы /2:
2-10~4Q
а
0,50
— 121,7
80 + 2 • 10~4Q
045
040
О35
0.30
0.25
на
и номограмму, изображенную
рис. 10.33 в масштабе 1 : 4.
10.9.7. Номограмма с двумя
криволинейными шкалами и одной
прямолинейной (рис. 10.34). Если при-
принять прямую за ось ординат, то урав-
уравнение A11) принимает вид
Рис. 10.33.
0
х2
*з
Положим
. Уг =
У\
Уг
Уз
= mfl
- * 1.
1
1
1
= 0.
(и).
A26)
A27)
A28)
Ttt-2
==7
X
A29)
A30)
A31)
Тогда уравнение A26) получает вид
Рис. 10.34.
/а(»)-— /з(м») "
Это общий вид уравнений, решаемых с помощью рассматриваемой номограммы.
10.9.8. W-образная номограмма. Это частный случай номограммы, рас-
рассмотренной в предыдущем пункте. Номограмма сводится к трем пересекаю-
пересекающимся в одной точке прямым (рис. 10.35). Следовательно, здесь
ср2(О) = /С, Cp3(W)=:0.
Уравнение A32) превращается в
Положим
К
тогда уравнение A32) принимает окончатель- ^
ный вид
J___ J 1_ 133 Рис. 10.35.
Уравнение A27) остается неизменным. Уравнения A28) — A31) переходят в
10.91
откуда
НОМОГРАММЫ
К
771
Пример. Требуется построить номограмму для формулы
X
которая выражает связь длины волны в волноводе Xg с длиной критической
волны Хс и длиной волны в свободном пространстве X. Эту формулу можно
представить в виде
_1_ 1 1_
х2, ~ х2 ху
откуда
Берем прямоугольные оси. Пусть имеется
лист размером 20 X Ю см. Следовательно,
наибольшая длина шкал ОА и ОВ будет
равна 14 см (рис. 10.36). Длины волн \g
и X меняются в пределах от 3 до 15 см,
14
Отсюда 1с2 _ у ~ 0-06 см = /rtj.
•Возьмем тх=т2 и /С=1. Следова-
Следовательно, шкала ОС будет биссектрисой пря-
прямого угла и может быть получена проектиро-
проектированием параллельно ОА шкалы, начерченной
на ОВ.
Замечание. Номограмма из трех пе-
пересекающихся в одной точке прямых позво-
позволяет решать все формулы, которые могут быть
решены с помощью номограмм с тремя парал-
параллельными прямыми. Это" не удивительно,
так как оба типа номограмм преобразуются Рис. 10.36.
друг в друга с помощью перспективного
преобразования, переносящего точку пересечения прямых в бесконечность.
10.9.9. Z-образная номограмма. Эта номограмма может служить для
решения уравнения с четырьмя переменными:
Л С)
то уравнения решаются
ПОЛОЖИМ J»j = /»jCpj (И), у2 = /К2Ср2 (t),
Если модули отвечают соотношению—- =
nit mt
графическим построением, изображенным на рис. 10.37, т. к. при этом —= —.
10.9.10. Номограмма с тремя криволинейными шкалами. Опреде-
Определитель
1
У1
У2
Уз
= 0.
772 ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
если принять
ГГЛ. X
•> х, =
т2
(и) '
У2-
X,
преобразуется в
Уз (w) — У] (и) _ /з («О — fi (и)
Это наиболее общий вид уравнения, которое может быть представлено номо-
номограммой с тремя криволинейными шкалами.
10.9.11. Сложные номограммы. При помощи комбинации из двух номо-
номограмм мы легко можем представить формулу, содержащую четыре перемен-
переменных и, v, w, t, если эта формула может
быть представлена в виде
[Г
4 V-
Фг(и, v) = f
и если оба уравнения
Ф1(и, v) =a, <Э
у. t)
Рис. 10.37.
Рис. 10.38.
могут быть по отдельности представлены двумя номограммами с выравнен-
выравненными точками.
Для облегчения графического вычисления принято обе номограммы
помещать рядом и соединять соответственные точки обеих шкал вспомога-
вспомогательной переменной отрезком прямой (рис. 10.38).
Если основания а прямолинейны в обеих номограммах и можно взять
одни и те же модули, то обе шкалы можно совместить, если только площадь
бумаги не слишком плохо использована для номограммы O2(w, t) = a., мо-
модули которой при этом заданы. В этом случае не нужно градуировать
прямолинейную шкалу а, которая тогда называется немой шкалой сложной
номограммы (рис. 10.39).
1962.
ЛИТЕРАТУРА К ГЛАВЕ X
1. Б е р е з и н И. С. и Жидков Н. П., Методы вычислений, т. I и II, Физматгиз,
2. Д е м и до в и ч Б. П., Марон И. А., Основы вычислительной математики,
Физматгиз, 1960.
3. Д е м и до в и ч Б. П., М а р о н' И. А., Шувалова Э. 3., Численные методы
анализа, Физматгиз, 1952.
4. Крылов В. И., Приближенное вычисление интегралов, Физматгиз, 1959.
5. МысовскихИ. П., Лекции по методам вычислений, Физматгиз, 1962.
6. П а н о в Д. Ю., Справочник по численному решению дифференциальных
уравнений в частных производных, Гостехиздат, 1951.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адамса способ 740—748
Алгебраические уравнения, численное
решение 674—688
Алгебраическое дополнение 180
Аналитическая функция 43
Антисимметричный тензор 245, 249
Аргумент комплексного числа 25
Ареакосинус 354
Ареасинус 354
Ареатангенс 354
Асимптотическая ¦ формула Стирлинга
589
Асимптотическое разложение 349—352
Ьикс 24
векторное пространство
Безвихревое поле 136
Бернулли полиномы 720—722
— теорема 602
— уравнение 311
— числа 719
Бесконечное произведение 90
Бесселя интеграл 384
— интерполяционный полином 697—
699
— уравнение 372, 403
— функции 372—405
— — второго рода 372
— — — — модифицированные 396
— —, изображение 515
—'— первого рода 374
— — — — модифицированные 393
— —, приложения к изучению колеба-
колебательных процессов 405—421
— — третьего рода 387
Бета-функция 370
Билинейная форма 180
Биномиальное распределение 596
Бисферические координаты 166, 167,
341
Бицилиндрические координаты 164,
165
Бореля теорема 506
Бохнера — Хинчина теорема 648
Бромвича контур 56
— метод 343
Бромвича — Вагнера интеграл 57
Бьенэмэ неравенство 633
Бэкера формула 196—198
Валлиса формула 90
Вариации произвольных постоянных
метод 315—317
Вебера функция 375
Вебера — Эрмита функции 473, 477
Вектор 118—124
—, дифференцирование 124—126
— единичный 119, 238
—, интегрирование 126
—, ковариантные и контравариаитные
компоненты 240, 257—261
—, матричное представление 173 ¦
— осевой 119
— полярный 119
— свободный 119
— связанный 119
— скользящий 119
Векторная величина 117
Векторное исчисление 117—169
— —, приложение к теории электро-
электромагнитного поля 147—153
—, поле 126, 139
— произведение 122
— —, вихрь 133
— — двойное 124
— —, дивергенция 132
— пространство 238
Векторный интеграл 139—147
— потенциал 137—139
Вероятная ошибка 619, 621
Вероятности ошибок функция 360
— — —, график 364
— — —, таблица значений 363
Вероятность 585
— статистическая 596
Вес наблюдения 620
Весовая функция 86
Вещественная часть комплексного чис-
числа 24
Вихрь 129, 133, 134, 140, 143, 144, 147,
158—167, 262, 263
Волновое уравнение 331, 407—410 '
Вронскиан 316
Вронского определитель 316
Вычеты 50—53
—, применение к вычислению опреде-
определенных интегралов 61—66
Гамильтона оператор 130
Гамма-функция 365—370
774
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Гамма-функция, график 370
— —, таблица значений 371
Гармоники сферические 457
Гармоническая функция 68
Гармонический анализ 705
Гаусса птергеометрическая функция
321
— гипергеометрический ряд 321
— кривая 601
— метод 733—735
— функция 360
— —, график 361
Гегеибауера полиномы 441
Гельмгольца уравнение 333
— функция 452
Гиббса явление 93
Гиперболические функции 352—356
обратные 354
— —, применение к расчету длинных
линий 354, 355
Гипергеометрическая функция 321
Гипергеометрический ряд 321
Главная диагональ матрицы 176
Голоморфная функция 44
Горнера схема 676—678
Градиент 127—129, 132, 133, 140, 143,
144, 157, 159—167, 241, 261, 263
Грама — Шарлье ряд 612, 615
Графическая шкала 762
Графическое решение дифференциаль-
дифференциальных уравнений 752—757
уравнений 666, 671
Грегори формула 728—730
Греффе метод 680—688
Грина формула 144
Данделена метод 680—688
Двойное векторное произведение 124
Диагональная матрица 177
Диаграмма направленности 115, 116
Дивергенция 129, 132, 133, 140, 142, 144,
157, 159—167, 262, 263
Дирака функция 520
Дирихле задача 334
— условия 85
Дискретная случайная величина 589
Дисперсия 590, 591, 592
Дифференциальное уравнение 306—
348
— — Бернулли 311
Бесселя 372, 403
в полных дифференциалах 309
— —, графическое решение 752—757
Клеро 311
— — Лагранжа 311
— — Лапласа 333
— — Лежандра 432
линейное 310, 315—324
— — — с постоянными коэффициен-
коэффициентами 324—330
— — Максвелла 343
Матье 339
однородное 308
¦ порядка выше первого 313—315
Пуассона 341
Дифференциальное уравнение, разре-
разрешающееся относительно аргумента306
— —, неизвестной функции 306
— —, — — производной 306
— — Риккати 311
— — с разделяющимися переменными
307
— — — частными производными 330—
348
— —, численное решение 738—752,
757—762
Эйлера 317
Дифференцирование численное 717—
719
Долгота 159
Единицы локальной длины 154
Единичная матрица 177
— функция 493
— — Хевисайда 109
Единичное отклонение 600
Единичные векторы 119, 238
Емкость скалярная 247
— тензорная 248
Жордана лемма 53—55
Запаздывания теорема 505
Зенитное расстояние 159
Зональная гармоника 457
Изменение масштаба 502
Изображение 498
—¦, дифференцирование 505
—, интегрирование 506
—, сложение 500
Интеграл вероятности 360, 601
— —, график 364
— —, таблица значений 363
— криволинейный 44
— линейный 139
— Ломмеля 379
— от вектора 126
— Френеля 364, 382
— Фурье 98—116
— Шлефли 440
Интегральное преобразование Карсона
498
— — Лапласа 498
Интегральный косинус 356
, график 358
— —, изображение 518
— —, таблица значений 358—360
— синус 356
— —, график 358
— —, изображение 518
— —, таблица значений 358—360
Интегрирование численное 719—738
— — дифференциальных уравнений
738—752, 757—762
Интерполяционная формула Лагранжа
689
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
775
Интерполяционный полином Бесселя
697—699
Ньютона 693—696, 698, 699, 735,
736, 749
Стирлинга 696—699
Итерации метод 669
Карсона преобразование 498
Квадратичная форма 180
Кельвина функции 398—403
Клеро уравнение 311
Клотоида 364
Ковариантные и контравариантные
компоненты вектора 257—261
Ковариантный вектор 240
Колебаний мембраны уравнение 408
— струны уравнение 331
Комплексного переменного функции 42
Комплексные числа 24
— —, деление 30
— —, извлечение корня 28
— —, показательная форма 30
— —, применение к расчету электриче-
электрических цепей в синусоидальном режиме
31—42
— —, сложение 25
— — сопряженные 27
— —, степень 27
— —, тригонометрическая форма 26
— —, умножение 25
Комплексный вектор 41
Компоненты вектора 120
Контравариантный вектор 240
Контур Бромвича 56
— интегрирования 45
— эквивалентный 57
Конформное отображение 66
, применения 68—71, 83, 84
Координатные линии 154
— поверхности 154, 252
Координаты криволинейные 154
— — ортогональные 154
— — —, важнейшие системы 158—168
Корни из единицы 28
Корню спираль 364, 365
Корреляционная функция 638—641
Корреляционные связи 643
Косинус гиперболический 352
— —, график 355
— —, таблица значений 356
— интегральный 356
— —, график 358
— —, таблица значевий 358—360
Косинус-преобразование Фурье ПО
Кососимметричная матрица 176
Котеса метод 730—732
Коши теорема 45
— формула 46
Коши — Римана условия 43
Криволинейные координаты 153, 252,
256, 257
— — ортогональные 154
— оси 252
Криволинейный интеграл 44
Критическая точка 48
Кронекера символ 240
Кэли — Гамильтона теорема 194
Лагранжа интерполяционная формула
689
— метод 315—317, 679—680
— уравнение 311
Ламе коэффициенты 154
Лапласа оператор 130, 133, 158—167,
262, 264
— преобразование 498
— произведение 334—336, 338—340
— уравнение 333
— формула 436
— функция 601
Лапласа — Гаусса закон 599
— — стационарная случайная функция
656—661
Лапласиан 130, 334
Лапласово поле 139
Лежаидра полиномы 434
— преобразование 313
— уравнение 432
— функции 322, 432—464
— — второго рода 447
— — — — присоединенные 451
— — первого рода 441
— — — — присоединенные 450
— —, приложение к теории электромаг-
электромагнитного поля 456, 457, 460—465
Лилла построение 678
Линейная шкала 763
Линейное дифференциальное уравнение
310, 315—330
— второго порядка 322—324
— — —, интегрирование при помощи
рядов 317—322
— — —, метод вариации произвольных
постоянных 315—317
— — —, применение матричного исчис-
исчисления 209
— — — с постоянными коэффициен-
коэффициентами 324—330
— — — неоднородное 326—
328
— однородное 325
— уравнение 310
Линейный интеграл 139
— спектр функции 95
Лобачевского — Греффе — Данделена
метод 680—688
Логарифм 30
—, изображение 517
Логарифмическая шкала 763
Ломмеля интегралы 379
Лорана ряд 48
Максвелла уравнения 151, 168, 264, 343
Масштабные коэффициенты 154
Математическое ожидание 589, 591, 592
Матрица 171
— диагональная 177
—, дифференцирование и интегрирова-
интегрирование 205
776
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Матрица единичная 177
— кососимметрическая 176
— нулевая 177
— обратная. 180
— симметричная 176
— транспонированная 179
— эрмитова 187, 192
Матричное исчисление 170—235
— —, применение к изучению четырех-
четырехполюсников 210—237
— —, — — решению дифференциаль-
дифференциальных уравнений 206—210
— —, — — — систем линейных алге-
алгебраических уравнений 183—185
Матье уравнение 339
— функции 339, 465—478
— — второго рода 472
— — первого рода 465
— — присоединенные 339, 469
Медианная ошибка 619
Меллина — Фурье теорема 521
Мера точности 600
Метрические коэффициенты 154
Метрический тензор 254, 255, 258
Метрическое пространство 238
Минор 177
Мнимая .часть комплексного числа 24
Модифицированные функции Бесселя
393^-398
Модуль вектора 118
— — в комплексном пространстве 188
— графической шкалы 762
— комплексного числа 25
Момент 629, 630
— вектора 123
— начальный 592, 594
Муавра формула 28
Набла 130
Наименьших квадратов способ 617
Независимые события 586
Неймана задача 334
— функция 375
Немой индекс 245
Непрерывная случайная величина 591
Непрерывный спектр 648
Несмещенная оценка 616
Несовместные события 586
Номограммы 762—772
Нормальная производная 127
Нормальное распределение 599, 614
Нормальные уравнения 623
Нулевая матрица 177
Нуль функции 60
Ньютона интерполяционный полином
693—696, 698, 699, 735, 736, 749
— метод 667, 673
Ньютона — Котеса метод 730—732
Ньютоново поле 136
Обратная матрица 180
Обратные гиперболические функции 354
Обращения формула 522
Однозначная функция 42
Однородное уравнение 308
Ожидание математическое 589, 591, 592
Оператор Гамильтона 130
— Лапласа 130, 133, 158—167, 262, 264
— преобразования 170, 171
Операционное исчисление 498—532
— —, правила 500—509
— —, применение к вычислению опре-
определенных интегралов 568—570
— —, — — изучению электрических
цепей 490—498, 510—512, 543—568
, исследованию функций
577—582
— —, — — решению интегральных
уравнений 574—577
, — линейных дифференци-
дифференциальных уравнений 570—574
— —, список обозначений 584
-, таблицы 533—542
Оригинал 498
—, дифференцирование 504
—, интегрирование 504
—, сложение 500
Орт 119, 238
Ортогональное преобразование ]86
— — комплексного пространства 189
Ортогональные криволинейные коорди-
координаты 154
— системы функций 86
Ортонормированные системы функций 87
Осевой вектор 119
Особые точки 48
Остроградского теорема 140
Отклонение 590, 591
— единичное 600
— относительное 600
— среднее квадратическое 590, 591
Оценка 616
— несмещенная 616
Ошибка срединная 619, 621
— средняя арифметическая 619
— — квадрэтическая 619
Ошибки измерений 615—617
Параболическая шкала 763
Параболические координаты вращения
160, 161
— цилиндрические координаты 160, 339
Параболического цилиндра функции 473
Параболоидальные координаты 160, 161,
341
Парсеваля теорема 664
Пикара способ 750—752
Плотность вероятности 591, 594
— скалярная 248
— тензорная 248
Шоверхности уровня 128
Поворот 187, 290
Поле векторное 126, 139
— лапласово 139
— ньютоново 136
— потенциальное 136
— скалярное 126
— соленоидальное 139
Полюс 48, 60
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
777
Полярный вектор 119
Потенциал векторный 137—139
— скалярный 134—136
Потенциальное поле 136
Поток вектора 140
Почти периодическая функция 98
Преобразование Карсона 498
— координат в матричной форме 242—
245
— Лапласа 488
— Лежандра 313
— ортогональное 186, 189
— унитарное 189
— Фурье ПО, 112
Приближение по Чебышеву 714—716
Присоединенные сферические функции
432, 450
— функции Лежандра 432, 450
Производная вектора 124
— нормальная 127
Производящая функция 383, 434, 453,
476, 484
Пропорциональных частей метод 668
Противоположное событие 585
Псевдоскаляр 117, 247
Пуассона распределение 604
— —, приложение к задачам автомати-
автоматической телефонии 605—612
— уравнение 341
Равномерное распределение 593
Разветвления точка 48
Разложения теорема Хевисайда 509
Разность порядка k 691
Ранг матрицы 177
Распределение 591
— биномиальное 596
— нормальное 599, 614
— Пуассона 604
— равномерное 593
— системы случайных величин 594
Распределения функция 591, 594
— — случайной функции 628, 629
— — условная 630
Резонанс 328
Риккати уравнение 311
Родрига формула 438, 453, 482
Ротор 129, 133, 134, 140, 143, 144, 147,
158—167, 262, 263
Свертывание тензора 250, 251
Свертывания теорема 506
Свободный вектор 119
Связанный вектор 118
Секториальная гармоника 458
Силовая трубка 128
Силовые линии 128
Сильвестра теорема 194
Симметричная матрица 176
Симметричный теизор 245
Симметрия 290
Симпсона формула 726
Синус гиперболический 352
— —, график 355
Синус гиперболический, таблица зна-
значений 356
— интегральный 356
— —, график 358
— —, таблица значений 358—360
Синусоидальная функция 32
Синус-преобразование Фурье 110
Скалярная величина 117
— емкость 247
— плотность 248
Скалярное поле 126
— произведение 121
— — в комплексном пространстве 189
— —, градиент 132
— —, матричное представление 179
Скалярный потенциал 134—136
Скользящий вектор 119
След матрицы 190
Сложения вероятностей теорема 586
Слоистое поле 136
Случайная величина 589, 591
— функция 624
, моменты 629, 630
— —, применение к исследованию ли-
линейных и нелинейных систем 644—665
— — стационарная 636
— — —, применение к исследованию
флуктуации при постоянных режимах
636—638
, сходимость 631—636 .
— —, функция распределения 628, 629
— —, — — условная 630
— —, характеристическая функция 629
Случайное событие 585
Смешанное произведение 123
Смещения теорема 505
Собственные векторы 189, 192
— значения 189, 192
— —, приближенное вычисление 199—
203
Соленоидальное поле 139
Сопряженные комплексные числа 27
Составляющие вектора 120
Спектр непрерывный 648
— функции-95
— частот 105
— энергетический 644—650
Спектрального распределения энергии
функция 644, 646
Срединная ошибка 619, 621
Среднее квадрат и чес кое отклонение 590.
591
Средняя арифметическая ошибка 619
— квадратическая ошибка 619
Стандарт (случайной величины) 590, 591
Стационарная случайная функция 636
— — —, дифференцируемость 642
Лапласа — Гаусса 656—661
— — —, непрерывность 641
Степенной ряд 29
Степень матрицы 193, 198, 199
Стирлинга интерполяционный полином
696, 697, 698, 699
Стирлинга формула 589
Стокса формула 145
Струны уравнение 331
778
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Существенно особая точка 48
Сферические гармоники 457
— координаты 159, 337
— функции 432
— — присоединенные 432
Сходимость в смысле Бернулли 631
— — среднем квадрэтическом 633
— по вероятности 632
— почти достоверная 635
Тангенс гиперболический 352
— —, график 355
Тейлора ряд 47
Телеграфное уравнение 333
Тензор 241, 242, 250—252
— антисимметричный 245, 249
— в криволинейных координатах 252—
265
— деформации 292
— коэффициентов упругости 294
— метрический 254, 255, 258
— модулей упругости 294
— напряжений 292
— пьезоэлектрический 298'
— симметричный 245
— теплового расширения 293
Тензорная емкость 248
— плотность 248
Тензорное исчисление 238—305
— —, применение к изучению анизо-
анизотропных сред 288—305
— —, — — исследованию электриче-
электрических цепей 265—288
Тессеральная гармоника 457
Тороидальные координаты 165, 166, 341
Транспонированная матрица 179
Трапеций формула 725, 726
Трехграник 118
Умножения вероятностей теорема 586
Унитарное преобразование 189
Уравнения с частными производными
330—348
— — — —, численное решение 757—
762
Уровня поверхности 128
Условная функция распределения 630
Уэддля формула 727
Факториальная функция 367
Френеля интегралы 364, 382
Фукса теорема 319
Фундаментальный метрический тензор
254, 255, 258
Функция от матриц 193—205
— точки 126
Фурье интеграл 98—116
, комплексная форма 100
— —, применение к электрическим
цепям 102—105
— —, физическая реальность 113
— косииус-преобразование 110
— коэффициенты 86
— преобразование 110, 112
Фурье ряд 85—98
— синус-преобразование ПО
Фурье — Бесселя ряд 380
Ханкеля функции 387—389
Характеристическая функция 592, 629
— — системы случайных величин 595
— — суммы независимых случайных
величин 595
Характеристическое уравнение 189—
191, 325
Хевисайда единичная функция 109, 493
— — —, изображение 499
— теорема разложения 509, 527
Цилиндрические координаты 158, 159,
Циркуляция вектора 139
Частость 596
Частота 596
Частотная характеристика стационар-
стационарной линейной системы 646
Чебышева метод 732, 733
-г неравенство 633
— полиномы 322, 478—488
— — второго рода 479
— — первого рода 479
— —, приложение к исследованию эле-
электромагнитных излучателей 486—488
— функция 479
Численное дифференцирование 717—719
— интегрирование 719—738
— решение уравнений 667—688
Шварца отображение 77
Шкалы 763
Шлефли интеграл 440 »
Штурма теорема 324
Эйлера постоянная 366
— уравнение 317
— формула 30, 722—725
Эйлеровы интегралы 370
Эквивалентный контур 57
Эквиполентные векторы 119
Экспоненциальная функция 30
Элемент длины 154
— объема 255
Эллипсоидальные вытянутые координа-
координаты 162,. 163, 340
— общие координаты 167, 168
— сплюснутые координаты 163, 340
Эллиптические координаты 156
— цилиндрические координаты 161, 162,
338
Эмпирическая функция 700, 701, 706,
711
Эмпирические формулы 621
Эрланга формулы 609
Эрмита полиномы 475
Эрмитова матрица 187, 192
Эрмитово-сопряженная матрица 187, 188
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
а—вектор 119
АВ—вектор 118 .
Arch*—ареакосинус 354
Arsh х — ареасннус 354
Arth*—ареатангенс 354
к V) \ г Функции Кельвина 400
С (v)—интеграл Френеля 364
)—полиномы Гегенбауера 441
^ — присоединенные функции
Матье 339, 469
сет(ф, Я) — функции Матье первого рода
339, 466
ch*—гиперболический косинус 352
Ci х—интегральный косинус 356
COS
. qz = A cos qz-\-В sinqz 339
curio—вихрь вектора 129
Dv(z) — функции Вебера — Эрмита 473
dive—дивергенция вектора 129
erf х — функция вероятности ошибок,
интеграл вероятности 360
grad/ — градиент функции 127
Нп(г)—полиномы Эрмита 475
ffv'(z)
функции Ханкеля 387
I (z)—мнимая часть комплексного чис-
числа 24
/v(z)—модифицированная функция Бес-
Бесселя первого рода порядка v 393
/, j, k—орты 119
•fv(z)—функция Бесселя первого рода
порядка v 372
/—мнимая единица 26
Kv(z)—модифицированная функция Бес-
Бесселя второго рода порядка v 396
v , | функции Кельвина 400
kerv (z) j
Рп (х) — полиномы Лежандра 434
Рп (<¦>) — полиномы Чебышева второго
рода 479
Pv(z)—функции Лежандра первого рода
441
v vz) I присоединенные функции Ле-
рМ' /г\ | жандра первого рода 450
Qv (г) функции Лежандра второго ро-
Qv (z) J Да 449
(г)
449
присоединенные функции Ле-
Лежандра второго рода 451
R (г)—вещественная часть комплексного
числа 24
Res (а)—вычет функции относительно
особой точки а 50
rote — вихрь вектора 129
S (v)—интеграл Френеля 364
Sem(?, Q) — присоединенные функции
Матье 339, 469
sem(<P. <7)—функции Матье первого
рода 339, 466
sh х — гиперболический синус 352
Si х 1
J- интегральный синус 356
Тп (<¦>) — полиномы Чебышева первого
рода 479
th х—гиперболический тангенс 352
U п (<¦>) — функции Чебышева второго
рода 479
yv(z)—функция Бесселя второго рода
(функция Вебера) порядка v
374
Yv(z)—функция Неймана 375
Г (г)—гамма-функция 365
Y—постоянная Эйлера 366
Д—лапласиан, оператор Лапласа 130
6@—дельта-функция Дирака 520
Г (t)—единичная функция Хевисайда
493
Ф(*)—функция вероятности ошибок,
интеграл вероятности 360
W (х)—функция Гаусса 360
V — набла, оператор Гамильтона 130
Андре Анго
Математика для электро- й радиоинженеров
М., 1965 г., 780 стр. с илл.
Редактор Н. М. Розенгауз
Техн. редактор С. Я- Шкляр
Корректор Г. Г. Желтова
Печать с матриц. Подп, к печати 10/VI 1965 г.
Бумага 70xl08/ie. Фнз. печ. л. 48,75.
Условн. печ. л, 68,25. Уч.-изд. л. 53,62
Допечатка тиража 40 000 экз.
Цена книги 2 р. 88 к. Заказ № 999.
Издательство «Наука»
Главная редакция
физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
Московская типография № 16 Главполиграфпрома
Государственного комитета Совета
Министров СССР по печати.
Москва, Трехпрудный пер., д, 9.