Ижевск	V 20
2001
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
А.А. Коновалов
УДАРЫ В ОРУЖИИ
И 3 Д А Т Е Л Ь С К И Й
"Удмуртский университет"
Ижевск 2001
УДК 623.44
ББК 68.512.1
К 647
К 647 Коновалов А.А. Удары в оружии. Ижевск; Издательский дом
“Удмуртский университет”, 2001.90 с.
ISBN 5-7029-0231-9
В книге излагается важнейший в проектировании стрелкового оружия раздел
о соударениях деталей, являющихся основным процессом при обмене энергией
в механизмах перезаряжания. Разобраны наиболее часто встречающиеся в прак-
тике случаи, некоторые задачи решены впервые
Книга предназначена для конструкторов-оружейников и студентов соответ-
ствующих специальностей.
ISBN 5-7029-0231-9
ББК 68.512.1
© А.А. Коновалов, 2001
© Издательский дом “Удмуртский
университет”, 2001
ПРЕДИСЛОВИЕ
Ударные механизмы применяются в автоматическом оружии. Име-
ется хорошо разработанная теория удара. Однако при решении конкрет-
ных задач, особенно в многомассовых системах, анализ сталкивается с
существенными трудностями.
В представленной книге впервые в оружейной литературе показана
возможность исследования удара на основании уравнений Лагранжа вто-
рого рода, что существенно облегчает анализ. Решен ряд практических
задач, таких, как задача о противоотскоке, о начале открывания затвора,
что представляет собой многомассовую систему.
Интерес представляют и исследования поведения системы соударя-
ющихся тел при отклонении их параметров от теоретически оптималь-
ных, поскольку при реальном проектировании к такому отклонению при-
ходится прибегать постоянно.
Академик РАРАН,
доктор техн, наук, профессор	В.П. Грязев
1. ВВЕДЕНИЕ
1.1. Термины и определения
Под ударом понимается непосредственное взаимодействие упругих
или упругопластических тел массамит, и т„ движущихся первоначально
со скоростями Vl0 и К,и по перекрещивающимся траекториям так, что в
некоторый момент времени они приходят в соприкосновение. В резуль-
тате упругого или упругопластического взаимодействия тела опреде-
ленным образом обмениваются энергиями, а их векторы скоростей из-
меняют величину и направление. Этот обмен энергиями и изменения
векторов скоростей являются предметом исследования удара с кинема-
тических позиций. В более общем случае в ударе могут участвовать
одновременно несколько масс. При исследовании удара предполагает-
ся, что реакции взаимодействия тел направлены перпендикулярно плос-
кости, проходящей по касательной к поверхностям обоих тел в точке их
первоначального касания. При этом игнорируются особенности конфи-
гурации тел вблизи точки первоначального касания. Линия, на которой
лежат векторы контактных реакций, называется линией удара. В общем
случае линия удара располагается достаточно произвольно относитель-
но центров масс соударяющихся тел, но на расстояниях от центров масс,
не превышающих их размеры. А векторы скоростей до и после удара
располагаются достаточно произвольно относительно линии удара.
В частном случае линия удара и векторы скоростей лежат в одной
плоскости, проходящей через центры масс соударяющихся тел. Такой
удар называется плоским. Плоский удар, при котором линия удара про-
ходит через центры масс соударяющихся тел, называется центральным.
Центральный удар, при котором векторы скоростей проходят через
центры масс соударяющихся тел, называется прямым. В противном
случае говорят о косом ударе.
4
1.2. О некоторых количественных соотношениях
в процессе удара
Удар протекает во времени и пространстве, сопровождается развити-
ем значительных контактных усилий и деформацией соударяющихся тел.
В общем случае исследование этих процессов не поддается ни теорети-
ческому, ни численному анализу. Затруднены и экспериментальные ис-
следования, поскольку контактные напряжения в своем регистрируемом
с достаточной точностью значении замкнуты в малых объемах. Поэтому
количественные соотношения в них проследим на наиболее простом при-
Рис 1. Прямой центральный удар
мере, а именно на соударении двух шаров (рис. I). Исследования соударе-
ния шаров велись в начале века многими авторами на основе теории кон-
тактных напряжений Герца и дали следующие результаты.
Для контактного усилия:
3
2 = иа2;
для величины сближения центров масс:
а
5 ппх
2
5
для времени соударения:
/ = 2,94^ ,
при
где Е - модуль Юнга,
Y - модуль Пуассона,
R - радиусы шаров,
т - массы шаров,
V- скорость соударения.
В частном случае соударения двух одинаковых шаров (7?, =Т?2 ,т=т^
имеем:
6
п =
2
ni=~
т
и далее
Наконец, если выберем в качестве материала шаров сталь
(Е = 200 ГРа, у = 1/3, р = 0,008 кг/м2) и примем радиусы шаров R = 0,05 м,
а скорость соударения 5 м/с, то получим:
а= 0,443 * 10-Зм, Q = 1,93 * 106Н, t = 0,00026 с.
Прокомментируем полученный результат. Прежде всего обратим
внимание на большие значения сил и деформаций. Ясно, что произой-
дет сминание поверхности соударения. И действительно, поскольку
V = 5 м/с не является предельной для деталей автоматики оружия, в
местах соударения их мы замечаем площадки смятия. То есть пер-
воначальный контакт из точечного стремится переродиться в плос-
кий. С другой стороны, перемещения и время соударения малы на-
столько, что работой и импульсами сил внешнего трения или внешних
упругих сил в периоде соударения можно пренебречь. Заметим так-
же, что уменьшение первоначальной кривизны контактной площадки
приводит к увеличению жесткости удара, еще большему возраста-
нию контактных сил и сокращению времени контакта. Итак, при ки-
нематическом исследовании удара его можно считать мгновенным,
из приложенных к соударяющимся телам сил учитывать только им-
пульс контактных сил, вызывающий мгновенное изменение скорос-
тей соударяющихся тел.
7
2.	ЦЕНТРАЛЬНЫЙ УДАР
2.1.	Прямой удар
Пусть два тела массами т/ и т2 движутся до удара со скоростями
Vni и так, что векторы скоростей их лежат на линии, соединяющей их
центры масс. При этом должно быть К/о > К , иначе соударение не
произойдет (рис.1). Пусть линия удара также проходит через центры
масс соударяющихся тел. То есть можно говорить о прямом ударе. За-
пишем уравнение сохранения количества движения, которое, как извес-
тно, справедливо при всех обстоятельствах:
",iri0+m2r20=mTl|-'n2r2l-
(2.1.1)
В отдельных случаях последнее уравнение удобнее использовать в
виде
WjAK, =m2^V2,	(2.1.1а)
где ДГ] = К)0-Г],,АК2 = К21 -Иго-
Решим сначала задачу при условии, что потерь механической энер-
гии при ударе не происходит. В этом случае можем записать уравнение
сохранения механической энергии:
Разделив почленно последнее уравнение на уравнение (2.1.1а) и со-
кратив двойки, получим:
(^о + ^ОЧ^+^о).	<2.1.3)
Решим уравнения (2.1.1) и (2.1.3) относительно скоростей после удара:
8
V _2m2720+(m-m2)710_y	2m:
' 1 1 “	1 1
m} +m2
_2/и1Г10+(/и1-/и2)Г20
K2| -	—V->n +
ml+m2
/72] +m2
2/И]
20 ”l”	'
m}+m2
(2-1.4)
Из этих зависимостей можно получить некоторую интересную ин-
формацию. Например, если m; = т,, то Vn = К,й и K,z = V10, то есть тела
просто обменялись скоростями. Этот результат можно проверить на
бильярдном столе, поскольку потеря энергии при соударении шаров из
слоновой кости и при малых скоростях минимальны. Если по неподвиж-
ному шару ударить другим шаром “в лоб”, то ударяющий шар остано-
вится, а ударяемый будет двигаться с той же, что и ударяющий до уда-
ра, скоростью и в том же направлении. Эксперимент удается и при
соударении монеток на полированном столе. Изменение скоростей зави-
сит только от относительной скорости тел до удара, что делает возмож-
ным изучать некоторые закономерности удара при = 0.
В общем случае при соударении имеют место потери энергии, иногда
значительные. Попробуем решить задачу традиционным для механики
способом - через коэффициент полезного действия. При этом для про-
стоты примем V2n = 0.
Имеем систему уравнений:
«>1(п
где Т| - коэффициент полезного действия.
Система уже не поддается линеаризации путем деления второго урав-
нения на первое. Приходится решать нелинейную систему. Однако в
данном случае это несложно. Получим:
9
При вполне реальных соотношениях ri^ и может получиться
невещественное решение, что противоречит физике процесса. Можно
полагать, что именно эта, по-видимому, неустранимая, сугубо матема-
тическая трудность вынудила Исаака Ньютона искать другой путь ре-
шения задачи, а именно - через введение понятия о коэффициенте вос-
становления скорости.
2.2.	Понятие о коэффициенте восстановления скорости
Разобьем удар на два периода. Первый период от момента первона-
чального касания до момента, когда скорости центров масс соударяю-
щихся тел становятся равными скорости К центра масс системы до
удара и которая остается неизменной во время и после удара. Посколь-
ку в этот период происходит сближение центров масс, сжатие тел, дис-
сипативные силы и силы инерции препятствуют этому сближению, уве-
личивая контактные силы по сравнению с их значением в абсолютно
упругом теле и без учета сил инерции.
Во втором периоде, когда центры масс начинают расходиться, до
момента потери контакта между телами эти же силы вычитаются из
упругих, снижая общую величину контактных реакций.
Поскольку уравнение (2.1.1) справедливо для любого момента вре-
мени, можем записать для периода сближения центров масс:
Л
и для периода расхождения центров масс:
«>, fc-Г, I > т2(г, 1 -Ке> 'f Qdt=Pt,
10
где t - время сближения центров масс:
время контакта тел.
Согласно сказанному, Р> Рк
Отношение импульса сил во время расхождения центров масс к им-
пульсу сил во время их сближения называется коэффициентом восста-
новления скорости:
В -Рк ^Ус-Уп _У2Х-УС
Рс Ую-Ус Ус-У2о
Итак, имеем два линейных уравнения:
<-г20)=г2|-/.
Исключая из них V, получим:
Ую ~У2о
Также можно записать равенство
ДГ| + Д/2 = (1+Р)(И1о-И20).
(2.2.1)
(2.2.1а)
Ньютон определял коэффициент восстановления скорости, бросая
стержни из различных металлов на тяжелую мраморную плиту, и сделал
заключение, что указанный коэффициент зависит от материала соударя-
ющихся тел. Более поздние исследования показали, что коэффициент
восстановления скорости зависит от многих факторов, большинство из
которых не удается описать в аналитической форме. Так что этот коэф-
фициент в реальных расчетах приходится считать коэффициентом со-
гласования с опытом. Имеющиеся экспериментальные данные дают
значение коэффициента восстановления скорости 0,3 < [3 < 0,7. Наблюда-
11
ются и большие отклонения от среднего значения. В предварительных
расчетах будем принимав•!$ = 0,5.
2.3.	Прямой удар (продолжение)
Итак, после введения понятия о коэффициенте восстановления скоро-
сти имеем следующую систему уравнений:
-m2AV2 = 0;
ЛК1+ЛК2=(1 + Р)(К1О-К2О),
откуда
ди,
ди2
-т2
(^10 ^20 ) ’
^+^2
(2.3.1.а)
или
У =У	)л/ _у \ .
"	10 т{+т2 (-1° 2°-’’
^+^2
(2.3.1)
При р = 1 уравнения (2.3.1) обращаются в уравнения (2.1.4)
ДляИ20=0 имеем:
12
_W1-P т2
*11	,	*10’
т{+т2
у _ V+P/ml у
21 m m 10*
т{+т2
(2.3.2)
Замечаем, что в случаер Ф 0 скорость также может обратиться
т\ о Г-
в нуль, но уже при отношении —L = р • Скорость второго тела при этом
т2
будет = р И10, то есть тела уже обмениваются скоростями не в пол-
ной мере. Этим обстоятельством можно воспользоваться при опреде-
лении коэффициента восстановления в специально поставленных экспе-
риментах.
2.4.	Потери энергии при прямом ударе
Потери энергии определяются соотношением
_ ^1 (^10 ^11) | т2 ^21	^20 )
2	2
С учетом уравнений (2.1.1 а), (2.2.1 а) и (2.3.1 а) это выражение можно
переписать в виде
2Дэ=ти Д^ (2Г10+ДГ1)-ди2ДГ2(2Г20+ДГ2)=
= ^рМ-\/10-^2о)[2^0-^2оМ+₽)^0-^20^
2Qn1+w2j L	J
13
Окончательно имеем:
Лэ=
тхт2 1-р
2(тх +т2 )
(2.4.1)
Это выражение еще раз подчеркивает, что процесс удара зависит
только от относительной скорости соударяющихся тел. Поэтому рас-
смотрим некоторые частные случаи при V20 = 0. Выражение для общей
потери энергии в этом случае запишется как
Лэ=
2 А
(2.42)
\+к
тЛ2	, т2
гдеЭп= 1 -	- начальная энергия удара, fc = —-.
2	/И]
Заметим, что потери энергии непрерывно увеличиваются с возраста-
нием к.
Но чаще всего нас интересуют не общие потери энергии, а “коэффи-
циент полезного действия” ударного механизма, то есть отношение энер-
гии, получаемой вторым телом, к начальной энергии первого. Имеем с
учетом уравнения (2.3.2):
э2 = ди2Г22 2 = ДИ]ДИ2(1-Р У = к (1+Р )2	(24з)
э0 2 ДП]ИО2 (дИ]+ди2)2	(1+&)2
, т2	_
Определим, при каком значении л=—КПД удара наибольший. Для
этого функцию
14
(1+Aj
продифференцируем по & и результат приравняем к нулю:
f * L1+£-2£ =
dk (1+&)2 ? (1+&)3
откуда Л=1.
Этот результат следует учитывать, например, при проектировании
ударного воспламенительного механизма при поступательном движе-
нии курка (рис.2). Для уменьшения потерь энергии массы курка и удар-
ника должны быть равны. Но и в этом случае КПД оказывается доста-
точно малым. Прир = 0,5 КПД = 0,5625.
Рис 2. Курковый воспламенительный механизм
В реальном проекте почти всегда приходится отступать от идеаль-
ных рекомендаций. Поэтому полезно проследить, как меняется иссле-
дуемая функция вблизи точки экстремума. Для нашего случая соста-
вим таблицу:
к	0,5	0,75	1	1,5	2
к (НУ	0,222	0245	0250	0240	0222
Как видим, без особого ухудшения энергетического баланса ударно-
го механизма можно отступать от идеального соотношения масс в до-
вольно широких пределах.
15
2.5.	Косой центральный удар
Пусть два тела соударяются так, что удар остается центральным,
то есть контактные реакции лежат на линии, соединяющей центры
масс тел, а векторы начальных скоростей не лежат на этой линии
(рис.З). В этом случае задача решается так. Разложим векторы ско-
Рис 3. Косой центральный удар
ростей на составляющие и w„ лежащие на линии взаимодействия
(линии, соединяющие центры масс соударяющихся тел) и перпенди-
кулярные ей w/ и w 7. При отсутствии сил трения векторы и и>2 не
изменят своего значения, а векторы и w, изменятся в соответствии
с формулами прямого удара:
Остается определить модули векторов после удара:
16
^11 _VWH+W10’
^21 =VW21+W1O
и их направление по отношению к линии взаимодействия:


11
=ж
г/ц
21
^20
W21
2.6.	Повторный удар. Первый случай
Пусть два тела находятся в жесткой двусторонней связи, осуществ-
ляемой с некоторым зазором (рис. 4). После первого удара, согласно
формуле (2.2.1), имеем:
После второго удара:
Г|2-Г22=₽ (^21-^11>₽2^10-^о) •
Рис 4. Повторный удар
17
Продолжая таким образом, получим:
= "во-Гго)-
Поскольку при р < 1
ются до равенства. То
когда р — 0. Имеем:
Р” ^ = 0, то скорости в конце концов сближа-
есть результат должен совпадать со случаем,
т2	r \
m!+m2	w1+z?Z2
что можно было бы получить непосредственно из уравнения (2.3.1), по-
лагая р = 0.
Определим потери энергии. В п-м ударе потеря энергии:
V =V =V
loo 2оо 10
дэ
f	\ \ я*
2 \тп\+т2)
Суммарная потеря энергии:
тхт2 (1-р
2 (т^+т^
Дэ=еДэ„=™=^(Г10
о 2 [гщ +т2 )
Но, согласно разложению в ряд Тейлора,
2 .
То есть
л т,т2
2 \т1+т2 )
что также совпадает с уравнением (2.4.1) при0 = 0.
18
2.7.	Повторные удары. Второй случай
Пусть соударяются два таких тела, что »т^, но на второе тело
действует сила сопротивления, быстро замедляющая его движение. В
этом случае первое тело снова догонит второе и произойдет еще одно
соударение, а затем все повторится сначала. Такая ситуация возника-
ет, например, при ударе тяжелого курка по легкому ударнику, который
сминает капсюль. Поскольку сила сопротивления движения второго
тела в общем случае трудно поддается аналитическому описанию, то
сделаем относительно ее предположение, что перед каждым последу-
ющим ударом она полностью останавливает второе тело. Естественно
при этом считать, что и перед первым ударом второе тело неподвиж-
но. После первого удара ударяющее тело будет иметь скорость
(согласно2.3.2):
1 , (
т1+т2
После второго удара:
Продолжая таким образом, получим после и-го удара:
(2.7.1)
Поскольку при любых сочетаниях параметров удара множитель
19
Wj-p m2
mx+m2
—>0. To есть тела в конце концов останавливаются.
Необходимо проследить еще потери энергии в повторных (для рас-
сматриваемого случая) ударах. В п-м ударе будем иметь (формула 2.7.1):
Дэ
Суммируя эти потери и обозначая z = x2, имеем:
Дз = mlm2 6~Р2) К,2
п=о
Но, согласно формулам рядов Тейлора,
Окончательно получим:
Дэ=_)
(ml+tn2)^.tnl+tn2 (1-р j) 0
Пусть
m2 = 0,1/??!, р = 0,5,
тогда
20
А 0,952*0,5
Аз =--------—
1,1*2,05
эо О,2ООэо
Значение потерь на последовательное соударение получилось суще-
ственным. Оценим, однако, погрешность формулы (2.7.2). При р = 0 со-
ударения тел должны закончиться на первом ударе, и далее тела будут
двигаться как одно целое, расходуя энергию только на преодоление внеш-
него сопротивления. Потери энергии при единичном ударе в этом случае
определятся по формуле (2.4.1):
0
Аз=’ °=0,045эп.
2*1,1	0
Разница, как видим, существенная. Это говорит о том, что гипотеза о
последовательных ударах первого тела по уже остановившемуся второ-
му в общем случае неудовлетворительна. Однако для оценки верхнего
возможного предела потерь на удары и соответственно с этим назначе-
ния запаса энергии для совершения работы вторым телом формула (2.7.2)
может применяться. Тем более, что с возрастанием |3 ее ошибка, как
можно полагать, уменьшается. Следует также иметь в виду, что энер-
гия курка назначается с запасом и ход его ограничен, поэтому количе-
ство соударений его с ударником не будет бесконечным.
3.	СОУДАРЕНИЯ МНОГОМАССОВЫХ СИСТЕМ
В предыдущих примерах в каждом отдельном соударении участво-
вали два тела. Однако могут быть случаи, когда нельзя разбить соуда-
рение многомассовой системы (или системы с многими степенями сво-
боды) на отдельные единичные удары. Рассмотрим несколько примеров.
21
3.1.	Последовательное соударение трех тел
Представим себе ситуацию, когда тело массой т|, движущееся со
скоростью V/g ударяет по телу массой /«„ движущемуся со скоростью
и находящемуся в момент удара в соприкосновении с телом т3 ,
Рис 5. Последовательное соударение трех тел
движущимся со скоростью V30. Совершенно очевидно, что добиться
повторяемости опыта с тем, чтобы в момент удара все тела находились
в соприкосновении, можно лишь в том случае, если К = V3I) (рис. 5).
Наблюдение за шарами на бильярдном столе (монетами на полиро-
ванном столе) показывает, что если тела /и, и т3 неподвижны и нахо-
дятся в соприкосновении, то при прямом ударе тела/иД/и^ /и,= т3) по
телу т, первые два тела останавливаются, а третье тело получает
скорость V(l Это позволяет рассматривать процесс соударения трех
тел, последовательно расположенных, как последовательный удар сна-
чала первого по второму, а затем второго по первому. Понятно, что
если щ1 <р/и7, а т2 <рщ,, то процесс заканчивается после двух
первых соударений. В противном случае может последовать вторая,
третья и т.д. серия соударений.
22
После удара первого тела о второе скорости их распределятся со-
гласно формулам (2.3.1):
V =V
11	10
у ' = v
21	20
тх+т2
Затем совершается удар второго тела по третьему:
V "
21
V =v
*31	20
Продолжая подобным образом, получим для ( и+1 )-й серии соуда-
рений:
^+/«2
г;(„+1)=г2л-+^1^Й(г1„-г2„) ;
^+/«2
Г2'(л+1)= Г2’(л+1)-^^Й(г2(„+1)-Г3„) ;
т2+т3
У (п+1}=¥ + у, J-y
F3V+1/ *Зл .	Г2(л+1) У3п •
/п2+т3 <	J
23
Например. Пусть mt = 1/2 т2, т} = 2 т2, Vl0 = Vg,0 = 0 , V = О.
В первой серии соударений:
1—Q 5*0 5
Г/ _ 1	т/ _ л ст/
И 15 О ’ О’
V ' = JZ = у
21 1,5 0 °’
У „ _	у __Q2jz
zi 5 го и’ ro’
V = ^7 = 037
31 о о*
Во второй серии соударений:
Т|2 =О,5То	(0,5+0,2)= 0,15Г0,
1,Э
¥г' =-0,2Го+Ь| (О,5+О,2>О,5Го,
^'=О^о-^(О^-ОЗ>ОД6Ко,
из2 =ОЗГо + °^*J’5(0,5-0,3)= О,36Ио.
Скорости тел распределились так, что они больше не встретятся.
При уменьшении массы т2 по отношению к двум крайним количество
серий соударений быстро растет. Поэтому попробуем решить задачу
24
приближенно, а именно при допущении, что скорость промежуточного
тела после серии соударений равна среднему арифметическому скорос-
тей крайних тел.
Имеем систему уравнений:
'/2о=°;
т, (^0-^11)= т2(И21-^оХтз(К31“К2о);
2Г2|=Г||+И3|;
Решив эти уравнения, получим:
^-(3 (т3+0,5тс)
*11	,	,	ко’
т{ +т2 +т3
_^(1+Р )t-O,5|3 т2
Г31	*0’
т{ +т2 +т3
и2|=о^(г11+г31).
(3.1.2)
Прорешаем ранее решенный по формулам (2.7.1) пример еще и по
формулам (3.1.2):
у _1 0,5(2+0,25) р, =_QQ267
11	25	°	’ с
У _ 1,5+0,125
31	3,5
Г21 =0,214 Го.
Ио=О,464Го;
25
Расхождения значительные. Однако обращает на себя внимание боль-
шая, чем при расчетах по формулам (3.1.2), разница К31-Ки= 0,5 Ко
вместоК3]-F] ] =0,21 Ко по формулам (3.1.1) То есть для того, чтобы
получить близкий к формулам (3.1.1) результат, мы должны принять в
формулах (3.1.2) коэффициент восстановления скорости р = 0,21.
Снова считаем:
Hl
1-0 21*2 25
=	А23- = О,15О7Го,
1,21+0,21*0,25=03607
Г21=О,256Го.
Результаты практически совпадают. При расчетах по формулам
(3.1.1) мы имеем четыре соударения тел, и в каждом соударении теря-
ется кинетическая энергия. Эти потери складываются, что и приводит
к необходимости формального уменьшения коэффициента в формулах
(3.1.2), представляющего процесс как единичный удар. Вспомним, что
при повторных соударениях жестко, через зазор, связанных тел полу-
чается р = 0.
Поскольку коэффициент восстановления скорости трактуется как
коэффициент согласования с опытом, который должен уточняться в
любом случае, то формулы (3.1.1) и (3.1.2) можно считать идентич-
ными по точности.
Но при этом следует иметь в виду, что в формулах (3.1.1) коэффи-
циент р более стабилен; его некоторое изменение возможно только в
связи с уменьшением относительной скорости соударения при каждом
последовательном ударе.
В формулах (3.1.2) коэффициент восстановления зависит еще и от
количества состоявшихся соударений, которое заранее определить нельзя.
26
С другой стороны, с уменьшением т2 должен наступить момент,
когда промежуточное тело будет просто зажато между двумя крайни-
ми и будет работать как упругое тело. В этом случае возможно даже
увеличение 0 по сравнению с непосредственным единичным ударом
двух тел. Этот вопрос заслуживает специального исследования, что
выходит за пределы принятой здесь методики.
3.2.	Параллельное соударение трех тел
Тело массой mt ударяет со скоростью Vg по рычагу, с которым сопри-
касаются в момент удара массы т, и /и?, первоначально неподвижные
(рис.6). Требуется определить скорости всех трех масс после удара.
Прежде всего запишем уравнения количества движения и момента
количества движения относительно точки А:
т^о-^Ут2У2-тзУз]
аГП2 ^2 = (° +Ь)т3 ^3 ’
где Vi - скорости тел после удара,
а и b - соответствующие плечи рычага.
Использование в качестве третьего уравнения для коэффициента вос-
становления скорости затруднено следующими обстоятельствами:
1)	удар происходит сразу в трех точках рычага, и коэффициенты вос-
становления должны быть в каждой точке свои;
2)	неясно, как распределятся начальные скорости рычага перед
ударом.
Первое затруднение может быть преодолено за счет допущения,
что коэффициенты восстановления во всех трех точках одинаковы.
Это допущение тем более правомерно, что коэффициент восстанов-
ления есть коэффициент согласования с опытом, окончательное зна-
чение которого, в данном случае среднего для всех трех точек, опре-
делится в результате соответствующего эксперимента.
27
Рис 6. Параллельное соударение трех тел
Найти логическое разрешение второго препятствия не удалось, по-
этому решим задачу только для случая упругого удара. Тогда можем
записать уравнение сохранения механической энергии:
(б)
Из второго уравнения (а) находим:
а+b ГП-,
г2=----------1V	(в)
а т2
Подставив это выражение в первое уравнение (а) и в (б), получим
систему уравнений:
m^+V\)=-m3Vy
а
(г,2 Тг2\ Г, a+b
)= 1+— — ™у32-
'	7 а т7
к 2 7
(г)
28
Разделив почленно второе уравнение на первое, получим:
(А)
Исключив из первого уравнения (г) и уравнения (д) скорость, а также
присоединяя выражения для К, и V2 из выражений (в) и (г) соответствен-
но, получим окончательно:
У  а+b тъ
а т2
(3-2.1)
г = у -—тз у
1 о L 3
о т{
По аналогии с уравнениями (2.3.1) можно подставить в (3.2.1) вмес-
то двойки р . Но более подробное исследование показывает, что в этом
случае коэффициент восстановления существенным образом зависит от
соотношения масс.
Эти выражения позволяют получить первое представление о распре-
делении скоростей после удара, которое затем должно быть уточнено в
процессе эксперимента.
29
Например. Пусть т2 = 4т f, т3 = 1 /4т t, а = b .
Тогда
3.3.	Уравнения Лагранжа второго рода для случая удара
Если тела во время удара находятся в жесткой ненарушаемой связи,
то к ним применимы уравнения Лагранжа второго рода с некоторыми
упрощениями. Заметим, что к этому случаю относится пространствен-
ное соударение двух тел, где роль масс, наряду с действительной мас-
сой тела, выполняют моменты их инерции относительно трех осей пово-
рота для каждого.
Поскольку мы условились не рассматривать работу внешних сил,
приложенных к системе соударяющихся тел во время удара, то можно
воспользоваться уравнениями Лагранжа второго рода для системы с
голономными (не зависящими от обобщенных координат) связями:
д Т _
dt^d q( J д qt
где Т - кинетическая энергия системы;
qt - обобщенные координаты;
Qj - обобщенные скорости;
Qi - обобщенные силы.
30
Проинтегрируем последнее уравнение по/:
td(dT}J tdT
j-----dt-\---
odt^dq, J odqi
dt=\Qjdt.
о
В силу кратности удара второй член в левой части равен нулю. Пер-
вый член получает конечное приращение за счет конечного изменения
скоростей при ударе. Выражение в правой части представляет собой
импульс контактных сил. Таким образом, имеем систему уравнений дви-
жения при ударе
(33.1)
где Р - импульс контактных сил.
Если две соударяющиеся системы после удара не вступают в жест-
кую двустороннюю связь, то снова приходится прибегать к понятию ко-
эффициента восстановления скоростей, который будет относиться к про-
екциям скоростей соударяющихся масс на линию удара и к приведенным
к линии удара массам.
3.4.	Косой удар. Общий случай
В части пункта 2.5 мы рассмотрели центральный косой удар, то есть
когда линия удара проходит через центры масс соударяющихся тел. В
общем случае линия удара не проходит через центры масс (рис. 7). Ог-
раничимся в данном пункте плоским ударом. Кроме того, учтем силы
трения по площади контакта, импульс которых Р связан с импульсом
контактных сил соотношением
Pf=fP (а, *0).	(3.4.1)
где f -динамический коэффициенттрения.
31
Разложим, как и в пункте 2.5, скорость /-го тела К (/=1,2 ) на две
составляющих: проекцию скорости на линию удара и.=Kcos а, и проек-
цию на площадку контакта w. =К sin а, , где а, - угол между линией
удара и вектором скорости. Тогда выражение для кинетической энергии
/-го тела примет вид
2Т. =m.\ui2+wi2+pi2(j)i),
где со. - угловая скорость /-го тела,
р - собственный радиус инерции данного тела.
В качестве обобщенных координат назначим перемещение точки
первоначального контакта Л вдоль линии ударах/(;, вдоль площадки кон-
такта yAi и угол поворота ср,. тел относительно точки А так, что
х=и.., yA.=w.., ф.
Ai Аг Ai Аг ' Ai Аг
обобщенные скорости связаны с составляющими скоростей центра масс
зависимостями:
U. =U ~(d.a.,W. = W ~(£).Ь., (D =(D.;	<3.4.2)
i Ai i г i Ai -i г Ai г
где a. - расстояние от центра масс /-го тела до линии удара,
Ь- расстояние от центра масс до линии, проходящей через пло-
щадку контакта.
32
С учетом последних равенств выражение для кинетической энергии
(б) перепишется:
При этом уравнения движения запишутся следующим образом:
Л—L=тА \uAl-^la\=m.An
_	I \ Al I J II
duAi
Л—=mA
~	I \ Л1 I
SwAi
Д—L
дсо,
=тЛ -^(иА^«^р>(кя/-^>р?а>(|=0.
Присоединив к уравнениям движения выражение для коэффициента
восстановления скорости
АиЯ1+А^2 =(1+3)(^1О“МЛ2о) >
где
U Л1Л=М1Л+й[1Ю j МЯЭЛ=МЭЛ+<3ЭЮ 5
/410	10	1 ю	Л20	20	2 20
Ан =и ,1Л-иAw =и -и
А1	/410	/411’	/42	А21	А20
33
Получим замкнутую систему уравнений, которую, исключая из нее
импульс р и с учетом уравнения (3.4.1), запишем:
W1A	)=т2^ \^А2~а2^2) J
Aw^+Aw^ =(1+Р)(^Ю-^2о) ; •
Aw,. = f Au.;
Ai J r
Д(0 = ai+bif^uAi
i 2r2
a, +bj +p i
(3.4.3)
Система легко решается, но достаточно громоздка для дальнейших
аналитических преобразований, поэтому исследуем ее поведение на не-
скольких частных случаях.
3.5.	Соударение шаров с учетом трения по площадке
контакта
Удар шаров всегда центральный, поэтому а = О, Ь, = г,
где г - радиусы шаров.
В этом случае иА. = и. и система легко решается:
34
=UIO -Un = ^2(ч+^(м10-м20) ;
m{+m2
\u2 =w20-u21 = ~^^(w10-w20)
т^т2
Ди'1=и’1о-И'11=^д“1;
ДИ'2=И'20“И’21=/Д"2;
(3.5.1)
Д®1=®ю-®11
Д®2=®20-®21
_ 2t\Au{
2 2’
р i+r2
 2г2Ам2
2
Р 2+Г2
Пусть VIn = Vo, V2n = 0, со(О = О. Пусть также шары одинаковы, то
есть г = г, т = т..
I ’ I 2
С учетом того, что для шара р2 = 0,4г2 , получим:
M11=M1O"O’5(1+3)M1O’
W21 (l+P)uiQ,
wH =°’5/(1+з)м1О;
w2i = °’5/(l+P)w10;
rco(1 =0,714 (l+p)w10.
Угол между линией удара и направлением скорости второго тела пос-
ле удара:
35
, W,,	± г г
а21 = arctg 21=arctg / « /
М21
Даже если предположить, что при ударе бильярдных шаров коэффи-
циент трения на порядок меньше, чем принимаются в машиностроении
для пары сталь по стали, то есть равен/= 0,01, то отклонение от линии
удара с расстояния в 0,5 м составит 5 мм, что вполне достаточно, что-
бы шар не вошел в лузу. Очевидно, что опытные игроки в состоянии
учитывать столь тонкий эффект. Формулы (3.5.1) позволяют сделать
еще одно интересное наблюдение. Замечаем прежде всего, что угловые
скорости шаров прямо пропорциональны коэффициенту трения. А тан-
генс угла между направлением скорости первого тела после удара и ли-
нией удара определится отношением

 Wn  у" 1+Р
Иц 1-р
Направление линии удара проще всего определить по направлению
движения второго тела, сделав поправку на угол трения. Заменим шары
на шайбы одинакового диаметра. Массы их выровняем за счет толщи-
ны. Учтем также, что для шайбы р2 - 0,5г2. Сверху на шайбу нанесем
крестообразные диски. Осуществляя соударение шайб из разных мате-
риалов на скользкой поверхности, фиксируя углы векторов скоростей и
угловые скорости шайб после удара, например, с помощью скоростной
кинокамеры, получим данные для вычислений f и 0 .
3.6.	Внецентренный удар двух кубов
Пусть два куба со сторонами 1}=2а и / = 4а движутся со скорос-
тями V и 7,0 (Vlo > К,о) по параллельным направляющим. И пусть
линия центров масс также параллельна направляющим. Один из кубов
36
имеет ребро, смещающее линию удара на расстояние b от линии цент-
ров масс (рис.8). Кинетическая энергия куба запишется как
И+pW
где m - масса куба;
V - скорость его центра масс;
<й - угловая скорость;
р - радиус инерции куба.
Скорость центра масс связана со скоростью в точке удара А соотно-
шением
V = V -bay .
а
Следовательно, можем записать:
7’ = ^((И„-*<о)2+р2<в2).
Принимая в качестве обобщенных координат величины и со, по-
лучим уравнения движения:
37
m\ tya-b^)=P,
-b\fya-b<£) jl-p2(D = 0.
Исключив из этих уравнений угловую скорость, приведем их к виду
т W=P,
пр А ’
где
2
Р
т	=т—-—
пр	2
Угловая скорость при этом определится как
ЬЛУА
(D = -——'
Z.2 ,	2
Для куба со стороной С квадрат радиуса инерции равен
Тогда, с учетом соотношения заданных размеров, будем иметь для
каждого куба:
1	= т-----------
прХ {?>Ь2+2а2
2	64а
'	— >27 ------= И7 ----------
23ft+8a2	ЗЛ2+8а2
Уравнения сохранения количества движения для приведенных масс
запишется как
38
---!---ду =—32—
3/>2+2л2 Al 3b2+8a2 A2
Присовокупим к этому уравнению выражение для коэффициента вос-
становления скорости
д^2-д^1=('+₽Жо-М>
получим окончательно:
Д^1
Д^2
99/>2+72а2
(3.6.1)
99/>2+72я2
Пусть b=a, 0 = 0,5 , K,fl =0 , со1О = со2о = 0 тогда
1 5*32*5я2
VAX = V0 ~	2 V0 =
0	171а2	0	0
1 5*1 1а2
^2=haLUf-^0=0’096r0’
А2 171а2 °	°
ав> =-Д7„ =--1,4047 =-0,8427 
1 5 А1	5	0	0
ав) =-Л7,=—0,0967 = 0,0267п.
11 А2 11 0 0
Скорости центров масс определятся как
39
и21=дил2-ао>2=о,о7оио.
Поскольку Vu > V, , то после того, как угловые скорости затухнут
при ударах по направляющим, произойдет новое соударение. И так да-
лее до тех пор, пока скорости кубов сравняются. На этом эффекте пост-
роен самый действенный и простой механизм противоотскока. Так, рама
затвора автомата Калашникова ударяет в муфту ствола левой, если
смотреть по направлению стрельбы, щекой.
Представляет интерес еще и предельное значение плеча Ь, при кото-
ром механизм противоотскока еще действует. С этой целью выразим
скорости центров масс в более общем виде:

-I-Ej___д|/	64 О+Р)Д
362+р2 Л1 0 99Ь2+72а2 0
-Ь(й =
21 А2 2
8(1+р)а2
99Ь2+72а2

Приравнивая эти скорости, при 0 = 0,5 получим 62=0,364а2 или
b = 0,60 За,
v =v =--------------------V =-V
11	21 (99*0,364+72>2 0 9 0
При меньших b отскок, пусть сильно ослабленный, будет проис-
ходить.
Определим еще скорости вращательного движения кубов:
40
aw
i
abt^VA\
______/11
62+p?
aw
2
ab^VA2
b2+p2{
О,6ОЗа2*32(1+р)*ЗГо^
(99*0,364+72)a2	’	(
0,603a2 *3*(l+{3 X
(99*0,364+72)a2	’	(
Сравним энергии поступательного и вращательного движения для
второго тела:
2
Т = ^j± = ^h_r2 =000617/и»К2;
пост 2	162 0	2 0’
2	2
Т =^2Р	1 =0000417/и9И2.
вр 2	2 о
То есть в данном случае энергия вращения не превосходит 7% от
энергии поступательного движения. Этим обстоятельством мы будем
пользоваться, когда плечо импульса мало по сравнению с размером тела.
3.7.	Ударный механизм с вращающимся курком
Пусть курок массой mt и собственным радиусом инерции р вращает-
ся вокруг оси О (рис.9), причем угловая скорость его перед соударением с
ударником равна coQ. Если расстояние от линии удара до центра масс кур-
ка обозначим через а, а расстояние от центра масс до оси вращения -
через Ь, то начальная обобщенная скорость VAU на линии удара
И =(a+/>)w .
Если точка А расположена достаточно близко от основания перпен-
дикуляра а, то составляющей w можно пренебречь. Опираясь на резуль-
41
Рис 9. Ударный механизм
тэты параграфа “Последовательное соударение трех тел”, можем зак-
лючить, что при ударе по ударнику курок будет вести себя как свобод-
ное тело, и лишь затем удар при определенных обстоятельствах может
передаться на ось. Таким образом, обобщенная скорость VA выразится
через скорость центра масс К и угловую скорость следующим образом:
V=V +aw .
Al С	J
Решение уравнений (4.2.2) в этом случае:
АГ = у -V
Al АО А1
= m2(l+ft)K
тПр+т2
(3.7.1)
V2
тПр+т2
Aojj =®0-®1
= <Щ1
а2+р2
42
Представляют интерес следующие случаи. Определим, при каких
обстоятельствах удар не будет передаваться на ось курка, что прежде
всего имеет смысл с точки зрения экономии энергии. Скорость Vo на
оси выразится через скорость на линии удара и угловую скорость равен-
ством
= ГЛ1 -(a+i> ,
Совершенно очевидно, что = Л V = 0, если
-(a+Z^AcOj =0.
Подставляя в последнюю формулу значения из уравнений (3.7.1), по-
лучим:
ДГ<1
отсюда
Р2
а = ~Г •	(3-7.2)
Ь
Представляет также интерес значение к, при котором КПД удара
был бы наибольший. Энергия ударника запишется как
т,?,2 _
Раскроем зависимость типр от а по формуле (3.7.2), а также выражая
начальную кинетическую энергию из уравнений (3.7.1), получим:
43
, _ Л (1+р)(а+£>)2
(р2+£(р2+а2
7 TWn	>7 О'.
где	к = —(3.7.3)
тх
Таким образом, наивыгоднейшее с энергетической точки зрения зна-
чение к определится из условия максимума функции
Приравнивая производную от f(kta) к нулю, получим после сокра-
щений:
Р2
2 , 2 •	(3-7.4)
+а
Желательно, чтобы уравнения (3.7.2) и (3.7.4) выполнялись одновре-
менно. При этом замечаем, что достаточно легко оперировать пара-
метром к за счет массы ударника при заданных (из конструктивных со-
ображений) параметрах курка mt, р и Ь. Подставляя в (3.7.4) выражение
для а из (3.7.2), получим:
к=-^-
р2 2'
(3.7.5)
Чувствительность к отклонению параметров ударного механизма от
найденных оптимальных зависит от конкретного его исполнения и долж-
на исследоваться в каждом частном случае самостоятельно. Тем не
44
менее попробуем получить некоторые сведения о чувствительности к
нарушению оптимумов на упрощенном примере.
Пусть курок представляет собой квадратную призму, поперечными
размерами которой можно пренебречь при определении собственного
радиуса инерции. Тогда, если длина курка равна /,квадрат его радиуса
/2
инерции р2 = —Примем еще b = 0,4/ .
12
Для оптимального положения линии удара будем иметь:
2	,
а = Р = —-— = 0,208 /
b 12*0,4
Для оптимального соотношения масс:
wi2
р 2 +Ь2 1+0,16*12
Проиллюстрируем чувствительность КПД ударного механизма к
отклонению его параметров от оптимальных. С этой целью сведем зна-
чение функции
в следующую таблицу: f(k,aJ
	0,5	0,658	0,08
0,1	5,47	7,85	8,01
ода	8,60	8,77	8,68
03	8,48	8,28	7,95
45
Заключаем, что чувствительность КПД к отступлению от оптималь-
ных параметров для параметра а выше, чем для параметра к.
3.8.	Расчет механизма отражения гильзы
Одним из наиболее сложных при “точном” решении задачи может
быть механизм отражения стреляной гильзы. Действительно, сначала
гильза краем фланца ударяется в отражатель. Затем противоположным
краем фланца - в выбрасыватель. Выбрасыватель через свою ось уда-
ряется в затвор, затвор - в раму затвора. Эта последовательность уда-
ров может многократно повторяться.
Если имеется специальная программа для расчета удара многомассо-
вых систем, описанная выше, многократно повторяемая последователь-
ность ударов не представляет серьезного вычислительного труда. Но и
большого смысла в этом “точном” решении нет в силу крайней неопреде-
ленности коэффициента восстановления скорости при каждом последую-
щем ударе. Поэтому следует упрощать постановку задачи в каждом кон-
кретном случае расчета, то есть дополнять возможности вычислительной
техники здравым человеческим смыслом. При этом следует иметь в виду,
что “здравый человеческий смысл” может иногда, при недостаточной ком-
петенции исполнителя, привести к ошибочным результатам.
В рассматриваемом случае имеет смысл считать систему рама зат-
вора- затвор - выбрасыватель единым телом (рис. 10).
Итак, энергия системы затвора и гильзы запишется соответственно
(скорость гильзы до удара равна скорости затвора 73):
2T = m^+mV^+m^ p^+Z^
(3.8.1)
где ти3- суммарная масса затвора с выбрасывателем и рамы затвора;
И3 - их линейная скорость;
т2- масса гильзы;
р - радиус инерции гильзы;
СО - угловая скорость гильзы после удара;
I - расстояние от кромки фланца до центра масс гильзы:
46
где / - расстояние от торца гильзы до центра масс;
R - радиус гильзы перед фланцем.
Здесь мы пренебрегли угловой скоростью затвора, на что нам дают
право результаты пункта 3.6 о соударении двух кубов. Следовательно,
скорость затвора во всех точках равна, и тогда = V} а скорость зат-
вора связана со скоростью гильзы в точке А на фланце и выразится:
V = K-2Ra;
А 3
АИ =АК-2ЯА®.
А 3
(3.8.2)
Подставив выражения (3.8.2) в формулу (3.8.1) и продифференциро-
вав уравнение энергии по обобщенным координатам VA и со, получим
уравнения движения:
2Т = (т2+т3^(ИА+2Ра>У+т2(р2+/2^а>2;
= (т2 +т3)к(УА +27?ю)= Р;
А
= 2R(m2 +т3 )д(РА +2Я(о)е т2 (о2 +/2 V = 0;
д(£>	х /
Att)=tt);
ю = __ 27?fe+/n3>r4 Г АГл Л
4R2m3+^R2+p2+l2)m2 ’ 2Я ,
Если предположить массу автомата достаточно большой по сравне-
нию с массой гильзы, то можно считать, что гильза ударяется в непод-
вижный отражатель, и тогда для скорости точки А имеем жесткий удар:
47
ДРл = -(1+₽К
где Vu - скорость гильзы перед ударом в отражатель.
Далее получим:
2R (1+р)(т2+т3)И0
47?2 т3+(д/?2+р2 +/2 )/и2 >
(3.8.3)
V3=Va+2Rg) = (2Rg)-$Vq).
Скорость центра масс гильзы определится как векторная сумма ско-
рости Кли®7:
=	(3.8.4)
На рис. 10 показана траектория гильзы автомата Калашникова при
отражении.
Рис 10. Отражение гильзы
3.9.	Замечания к общему случаю соударения двух тел
Если имеется некоторая ортогональная система координат О , точ-
ка О которой находится в центре масс тела и в которой определены мо-
менты инерции какого-либо из соударяющихся тел J , J , Jz и центро-
бежные моменты J , Jxz, то выражение для кинетической энергии
записывается:
48
2T = mV2 + J w2+J2tt)2 +J g)2+J w w +
C XX У У z z xy X у
(3.9.1)
где co , co , co - составляющие угловой скорости по осям координат,
х у Z
Сделаем еще существенное замечание относительно выбора исход-
ной системы координат О , при котором имеет смысл учитывать неко-
торую особенность реальных конструкций.
Дело в том, что конструктор стремится любую деталь спроектиро-
вать из простых объемов: параллелепипедов, пирамид, цилиндров, кону-
сов, торов и т.д.
Этим в дальнейшем обеспечивается максимальная технологичность
изготовления детали. Упрощается и процесс конструирования, поскольку
оказывается возможным пользоваться только линейкой и циркулем или
соответствующими элементами на экране дисплея. Привлекаемые к кон-
струированию простейшие объемы имеют плоскости, а часто и оси сим-
метрии. Эти плоскости и оси симметрии конструктор располагает на чер-
тежи вдоль плоскостей проекций, что также упрощает вычерчивание
детали. Таким образом, задается некоторая связанная система ортого-
нальных координат, оси которой совпадают по направлению с линиями пе-
ресечения плоскостей проекций. Будем помещать начало координат этой
системы в центр масс детали, саму эту систему называть естественной.
В естественной системе координат достаточно просто определяют-
ся моменты инерции. Элементарные объемы (в том числе вычитаемые)
имеют табличные значения главных моментов и радиусов инерции. По-
этому общие моменты инерции могут быть подсчитаны по формулам:
Jlj=^mkatbk,
1 J 1
где тк - масса элементарного объема,
рк - его радиус инерции относительно центра масс,
ак - расстояние от центра масс до /-ой оси,
Ьк - расстояние от центра масс до j-ой оси.
49
Пусть в пространстве координат О тем или иным образом задана
линия удара. Построим плоскость, проходящую через линию удара и центр
масс тела. Это будет плоскость удара. В плоскости удара проведем ось
, параллельную линии удара, и ось , перпендикулярную ей. Из точ-
ки О построим ось Оп, перпендикулярную плоскости удара. Косинусы
углов между ортогональными системами координат Охг иОйп удобно
выразить через так называемые углы Эйлера, которые определяются
следующим образом (рис. 11).
50
Проведем линию ON пересечения плоскости удара Oriri с плоскостью
О^.. Повернем систему координат вокруг осиОп на угол <р до совпаде-
ния оси с линией ON. Далее повернем эту же систему относительно
линии ON на угол 6 до совпадения плоскости О с плоскостью удара.
Ось О, совпадает с осью Оп. Повернем систему координат относитель-
но оси Оц на угол кр до совпадения оси Ох с осью О^. Система уг-
лов ср, 0,\|/ и является углами Эйлера.
Косинусы углов между системами координат 0^. и выражают-
ся через углы Эйлера следующим образом:
COS (х,^)= О-! = СО8ф cos ср — sin sin ф cos 0,
cos а 2 = cos ф sin ф - sin ф cos ф cos О,
cos (х,г|)=а3 = sin ф sin 6,
cos	)= 0 j = sin ф cos ф+cos ф sin ф cos 0,
COS (>,,£;)= 02 = -8Шф 8Шф+СО8ф COSфcos0,
cos (кп)= P3 = -cos ф sin 0,
COS	=8Шф8Ш0,
COS Y2 =СО8ф8Ш0,
cos(z,t|)=y3 =cos0.
(3.9.2)
51
Выпишем кинематические уравнения Эйлера:
(дх = 0cos\|/+(psinOsin \|/,
cd^ =Ocos(p+y sinOsincp,
=0 cosy-ф sin 0 cosy,
cd^ = —0siny+ysin0cos<p,
(Dz =ф + фсО80,
= ф + ф COS 0.
(3.9.3)
Направляющие, по которым движутся тела, как правило, параллель-
ны плоскостям системы координат Oxvz, что определяет направление их
начальных скоростей. В оружии наиболее распространен случай, когда
векторы линейной и угловой скоростей тела до удара направлены вдоль
оси О , так что V =V, V =V =0, con = con,co n =co n = o. Именно такой
X7	X(> (r yt)	’ U.r U V U	ZU
случай мы будем рассматривать в дальнейшем, что не нарушает общ-
ности результатов исследования.
Разложим вектор Vn по осям связанной системы координат 0^ :
(3.9.4)
Если не учитывать трение при ударе, то изменению в процессе удара
подлежит только составляющая скорости = VcO-\ •
Сама же скорость
связана со скоростью VA по линии удара соот-
ношением
52
V=V,-G) a,
A t, r| ’
(3.9.5)
где a - расстояние между линией удара и осью О ?
С учетом равенств (3.9.2), (3.9.3), (3.9.4), (3.9.5) выражение для ки-
нетической энергии тела, опуская неизменяющиеся слагаемые (3.9.1),
перепишется:
27=ти(ил+(ф+\)/со80)аУ +Jx^0cos\|/+\j/sin0sin\|/j
(3.9.6)
+Jxzfecos\|/+\j/sin0sin\|/j(\j/+(pcos0)+
+Jyz (0 sin	sin 0 cos \|/ ](\j/+<p cos0).
Принимая за обобщенные скорости величины Ил,ф, 0, ф , подстав-
ляя выражения (3.9.6) в (3.9.1), получим четыре уравнения с пятью не-
известными (пятое - импульс Р) для каждого тела, присовокупляя сюда
выражение для коэффициента восстановления скорости (2.2.1), получим
замкнутую систему уравнений для применения обобщенных скоростей
в процессе удара. Система не представляет собой вычислительных труд-
ностей для современной вычислительной техники, но даже при сделан-
ных упрощениях достаточно пригодна для аналитических выкладок. По-
этому исследуем ее в некоторых частных случаях.
Пусть плоскость удара совпадает с плоскостью , то есть 0 = 0.
В этом случае угол у становится неопределенным и его можно принять
любым значением, в том числе равным нулю вместе с его производной.
Пусть также линия удара параллельна оси Ох, то есть ф = 0. Уравнение
для кинетической энергии при этих условиях перепишется в виде
53
2Т = т (УА +actf + / О2 + Jz<p2 + J^Оф .
Уравнения движения b запишутся:
Д	= т Д (И. +лф )- Р,
8V.
/1
А	= mal\ (VA+аф)+ У^ф++ф = О,
A^I = JO + J ф = 0.
ао х
Поскольку ф Ф 0, то из последнего уравнения следует, что 0 = Столь-
ко в том случае, если J v = 0 . То есть для того, чтобы удар действитель-
но был плоским, недостаточно, чтобы плоскость удара совпадала с плос-
костью О (или любой другой из координатных плоскостей неподвижной
системы), необходимо еще, чтобы плоскость удара была плоскостью
симметрии тела.
Однако в реальных деталях это далеко не так. Если взять раму затво-
ра автомата Калашникова, можно убедиться, что она не имеет ни осей, ни
плоскостей симметрии. Поэтому все предыдущее исследование плоского
удара носит скорее иллюстративный характер, демонстрирующий некото-
рые закономерности удара, чем реальное руководство к расчетам.
Рассмотрим упрощенный вариант удара в начале открывания зат-
вора типа винтовки Ml6. Упрощения будут касаться того, что мы бу-
дем считать затвор цилиндром радиуса/? и длиной 12 = 24/? и не учиты-
вать влияние на массу и моменты инерции боевых упоров и ведущих
стержня и ролика. Раму затвора также будем считать полым цилинд-
ром с радиусами/? и 2R и длиной l=20R, пренебрегая при этом различ-
ными вырезами, в том числе фигурным пазом для ведущих ролика.
Впрочем, все эти допущения нетрудно устранить при желании иметь
более точный расчет.
54
Обозначим массу рамы затвора через т, тогда, если все детали сде-
ланы из одного материала, масса затвора при назначенных соотношени-
ях размеров будет равна т2 = 0,4т г Массу короба примем т3 = 6т г
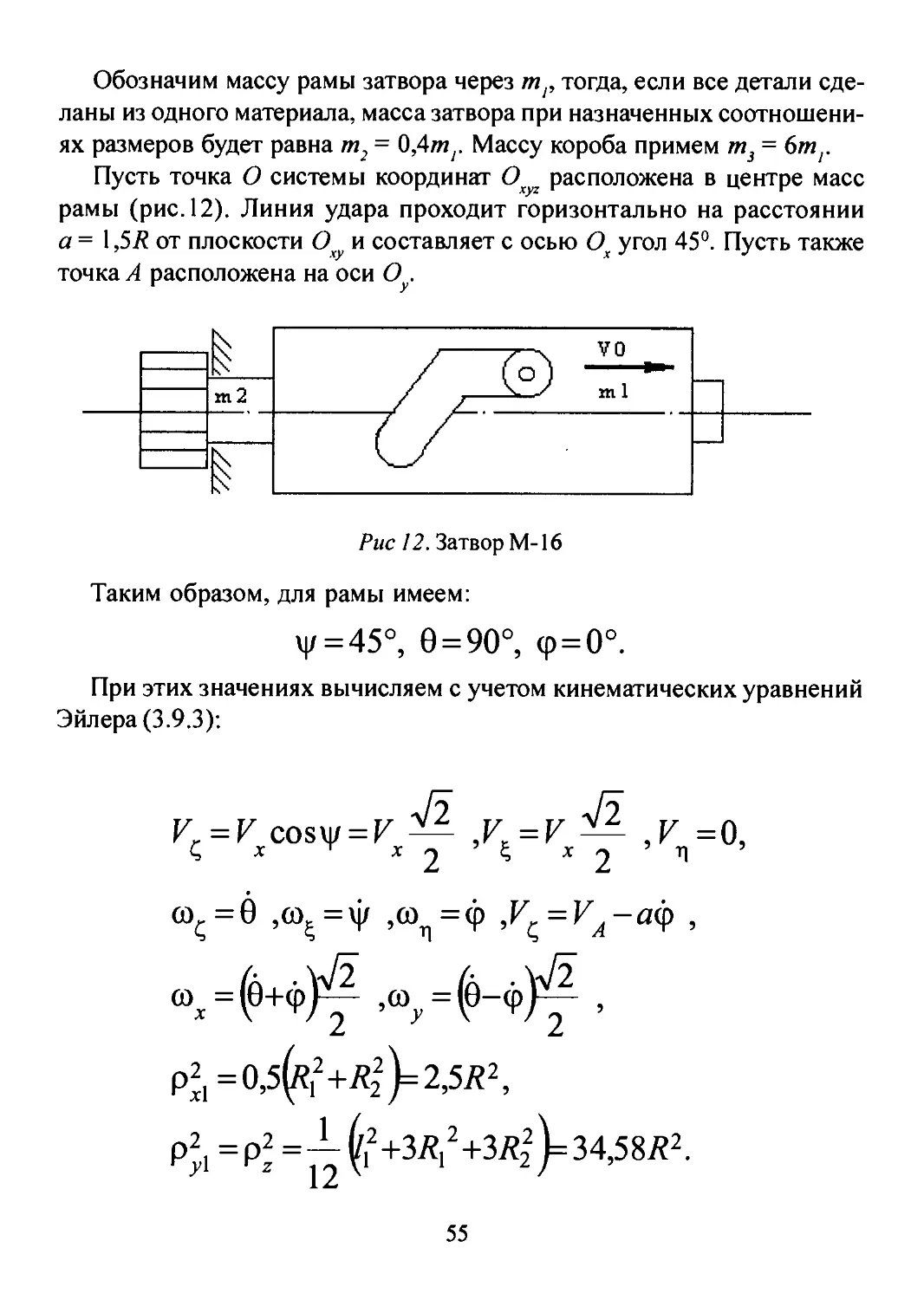
Пусть точка О системы координат О расположена в центре масс
рамы (рис. 12). Линия удара проходит горизонтально на расстоянии
а = 1,5R от плоскости О и составляет с осью Ох угол 45°. Пусть также
точка А расположена на оси О .
Рис 12. Затвор М-16
Таким образом, для рамы имеем:
\|/ = 45°, 0 = 90°, (р=0°.
При этих значениях вычисляем с учетом кинематических уравнений
Эйлера (3.9.3):
V =V cosy = И — ,V=V ,V =0,
С х т х 2	$ Х2 П
«>с=0 ,с^=ф ,а>п=ф ,V^ = VA-a^ ,
55
Уравнение энергии запишется как
Запишем уравнение движения:
2т1Д(Ия/-аф1)=/>,рд = 0 ,
Р^1-лФ1Хр^1-Ф1)=0 ,
0.
Из второго уравнения следует: ф =0.
Из третьего:
2	2
OrT.T'i'rOR
Но тогда
2 2
р^ё.+ф.^р^(ё -ф )=^1Р^-ф =93бЯ2ф,.
Pxl+Pyl
Из четвертого уравнения:
<р =—аАГЯ!	=0,327—^.
а2+2,3317?2 R
И, наконец, из первого уравнения:
т AV=P,
пр\ А1
56
где
т .
пр l
= 2 1-0,327- ти. =l,019zn..
D 1	1
R
Рассмотрим систему короб - затвор.
Речь идет именно о системе, поскольку затвор в момент удара плот-
но зажат между донцем гильзы и упорами ствольной коробки. Следова-
тельно, в момент удара короб и затвор перемещаются в линейных на-
правлениях как одно целое. В то же время, если не учитывать трение, в
повороте относительно оси Ох участвует только затвор.
Таким образом, уравнение для кинетической энергии относительно
системы короб - затвор запишется как
2Т = (т2+тЛУ\ + J A£>\+J AsP\+J ло2
X 2	’/ с2 х2 х2 у2 у2 z2 z2’
где J - момент инерции затвора относительно оси Ох,
Jv2 ,J„, - моменты инерции короба с затвором относительно соот-
ветствующих осей.
Заметим, что формально оно не отличается от уравнения энергии для
затвора. Если еще принять, что центр масс системы совпадает с цент-
ром масс рамы затвора, то решение формально также не будет отли-
чаться от решения для последнего.
То есть имеем, если учесть, что J » J:
у=о,
(/Л(ё+ф)-/у(ё-ф))=^^ф « 4/лф.
J х^ у
Таким образом, задача сводится к решению уравнений
1{т2 +т3 ) А(Ил2 -аф)= Р,
-а(т2 +т3) А(ИЛ2 -аф)+ р2ти2ф = 0.
57
Откуда
ф2 = a(m2+m^VA2 =0,65753
a уп2+т3р-рх2т2	fi-
rn ЛУ=Р,
пр2 А2 7
где т - 2	-0175,,,
ГДе	пр2 2/	, Y 2 и,1/ЖГ
а [пг2+т3)+-рх2т2
Запишем уравнения сохранения количества движения:
т ЛУл,=т -ЛУ
пр\ Al пр2 А2
Присовокупим к нему формулу для коэффициента восстановления
скорости
Д^1+Д^2=<1 + ₽)^0-
Поскольку паз рамы затвора накладывает двустороннюю связь на
ролик затвора, нужно принять р = 0. Тогда
ДИ. +ДК , =——И =0,853И,„,
al А2	,	АО 7 АО7
/П,:!,1+т„р2
Д^=0>147^-
Окончательно вычислим:
58
Г, =	=л/2(д ГЛ| -аф, > 0,140 ио,
cosy
Г, = -Л2-=VI (ДГ,2-а<р2)=0,0147Г,
cosy
<р. =0,068 ^,<р =0,793^-,
1	R 2 R
0, = 0,058^,0 =ф„
1	R 2	2
со =0,126 ^,а> =1,793^.
х!	R’ х2	R
Величина cot2 служит начальным условием для расчета открывания
затвора. Остальные составляющие угловых скоростей гасятся при уда-
рах о направляющие. Заметим, что скорость рамы затвора падает на
14 %, следовательно, ее энергия теряется на 28 %.
4.	ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ ВЕЛИЧИНУ
КОЭФФИЦИЕНТА ВОССТАНОВЛЕНИЯ
Мы указывали, что на коэффициент восстановления влияет множе-
ство факторов, проследить которые в общем виде не удается. Однако
понятие о некоторых из них можно получить, исследуя деформации стер-
жней при их продольном соударении. Информация, полученная при этом,
может оказаться полезной при конструировании конкретных деталей.
59
4.1.	Уравнение для продольных колебаний стержня
Рассмотрим движение элемента стержня длиной dx (рис. 13) под дей-
ствием сил упругости:
N + dN
U + dU
Рис. 13. Элемент стержня под действием сил упругости
о2
(N+dN)-N = p Sy^dx,
где N- продольная сила;
S - площадь сечения;
р - плотность материала стержня;
и - смещение сечения.
После сокращения формула приводится к виду
dN с д2и
dx д г
60
*7 0	„5 и
Но N = ост, где а - напряжение в сечении, и далее ст = Е-, сле-
д х
довательно, окончательно можем записать:
7 д2и д2и
д х2 dt2
(4.1.1)
где а = - - скорость распространения звука в материале.
VP
Уравнение (4.1.1) описывает продольные колебания в стержне посто-
янного сечения. В общем виде решение его может быть записано как
u=f(at-xjl-ф (at+X^	(4.1.2)
где /(z)hcp(z) - произвольные функции, значения которых должны быть
определены из начальных и граничных условий.
Функция f(z^сохраняет постоянное значение вдоль характеристики
at - х = const. Функция <p(z) - вдоль характеристики at + х = const. Это
значит, что процесс колебаний стержня можно рассматривать как нало-
жение двух волн постоянной конфигурации, движущихся в противополож-
ном направлении со скоростью а.
4.2.	Удар стержня о жесткую плиту
Пусть стержень длиной I ударяется со скоростью Vn о жесткую пли-
ту (рис. 14). Нужно заметить, что абсолютно жестких плит не бывает, и
их податливость может оказать существенное влияние на измеряемое
значение коэффициента восстановления. Чтобы убедиться в этом, бросьте
теннисный шарик на табурет, покрытый трехмиллиметровой фанерой.
Шарик практически не отскочит. Хотя жесткость и масса фанеры во
61
X
/77777777
Рис. 14. Схема распространения волн сжатия и отражения при ударе
стержня о плиту
много раз больше, чем жесткость и масса шарика. Чтобы шарик долж-
ным образом отскакивал, нужна прессованная фанера толщиной
10... 15 мм или дюймовая доска.
Впрочем, если направить два одинаковых стержня навстречу друг
другу с одинаковой скоростью, это будет имитировать жесткую стенку.
Начальные условия для этого случая запишем:
д и	д и п
при/ = 0,	=-Г0,	=0.	(4.2.1)
О t	ох
Граничные условия запишутся:
д и п
при х = 0	и = 0(при - <0),	(4.2.2)
д х
д и п
при х = 1	=0.	(4.2.3)
д х
По поводу условия (4.2.2) заметим, что при неудерживающей связи,
которая имеет место в данном случае, не может быть
62
ди	ди
>0 при х = 0 и - =0 при х = 0 означает конец удара.
д х	д х
Условие (4.2.2) приводит к соотношению
f(at)=-(p (at\
При этом время t может принимать любые значения. Обозначив at = z,
можем переписать предыдущее равенство:
(4
где z - соответствующий каждой функции аргумент.
Следовательно, можем записать:
и = f(at-xy~ f(at+x^.
Используя условие (4.2.2), получим:
-f'(at-l)-f(at+l)=O,	(4.2.4)
где штрих означает дифференцирование по аргументу. На этом же осно-
вании, что z может принимать любые значения,
f’(z)=-f’(z-2l)
Откуда заключаем, что функция f'(z^ является периодической с пе-
риодом 4/.
Начальные условия (4.2.1) приводят к системе уравнений:
а[/'(-х)-/'(х)]=-Г0;
Г(-х>-/’(х).	|
(42.5)
Поскольку х также может принимать любые значения от 0 до Дто
последнее равенство означает, что функция должна быть симметрич-
ной относительно точки z = 0.
Решая систему (4.2.5) и обозначив в данном случае z = х, получим:
63
(4.2.6)
Используя обнаруженные ранее свойства симметричности и перио-
дичности, можем приступить к построению функции:
-2/<z<0,/'(z>-^-;
v 7 la
0<z<2/,/'(z>^.
(4.2.7)
При необходимости построение может быть продолжено за выписан-
ные пределы. Используя (4.2.6), получим решение для всего периода
удара. В результате удара в стержне возникает волна сжатия, которая
движется со скоростью а в сторону положительных х .
В момент времени t. < - она достигнет сечения xt = atf (рис. 14).
а
При х <xf имеем:
z1=a/-x>0, /'(z)=--^;
la
z2=at+x-ll<0, Г(?У~
2а
и тогда
д и Л д и
----= 0, ------
д t д х
При х > xf имеем:
К)	17д и
<з = Е----
а д х
О'
64
z{=at{-x>$,
la
z2=ati+x-H<0, f'(z)=--^-,
2a
и тогда =—
дх ° дх
Сечения выше еще “не знают”, что произошел удар и продолжают
двигаться с прежней скоростью.
При достижении волной сжатия свободного торца она отразится от
него, и обратная волна будет двигаться со скоростью а в сторону умень-
шения х. В момент Г,, такой, что at2 > 0, волна достигнет сечения
х, = 2l-atr Параметры волны в сечениях х > х, определяются из соот-
ношений:
zx=at2-x>$, f(z)-
2а
z2=at2+x-ll<0,
2а
д и гг д и Л
откуда =И,	=0.
д х ° дх
21
При t= эта волна достигнет сечения х = 0, и при неудерживаю-
а
щей связи стержень отскочит от плиты со скоростью Vn, что согласует-
ся с расчетом по формулам (2.3.2) при 0 = 1.
Интересно вычислить время соударения стержня с плитой. В общем
. 2/
виде оно выразится формулой т = .
а
65
Скорость распространения волны в стальном стержне
= 5000 м/с.
Таким образом, для стержня длиной 2 см, что соответствует радиу-
су шара R = 1 см из (1.1), получим:
_ 2*2*10~2
Т” 5000
0,8*10’4
то есть время соударения шара в четыре раза больше, чем время соуда-
рения стержня с плоским торцем. Заключаем, что время соударения в
существенной степени зависит от жесткости в области контакта.
4.3.	Учет демпфирования при ударе по стержню
Предположим далее, что при деформации стержня в нем возникают
силы, препятствующие этой деформации. Рассмотрим частный случай
таких сил, а именно предположим, что в материале стержня действуют
силы кулонова трения: при изменении скорости деформации от нуля до
некоторого значения возникают силы трения, характеризуемые напря-
жением трения а так, что сжимающая сила выразится как
д и
N=ES—±5q ,
дх тр
причем знак в этой формуле совпадает со знаком скорости деформации.
Поскольку предполагается, что <Утр-const, то процесс будет описы-
ваться тем же уравнением (4.1.2), но с той лишь разницей, что при из-
менении деформации из состояния первоначального покоя до некото-
66
рой величины сила N делает скачок на величину , при изменении
мр
знака скорости деформации - на величину 25ст
тр
Согласно начальных условий (4.2.1), в области левее характеристики
at-x = 0,
2а
2а
При пересечении характеристики at-x = Q функция должна
скачком меняться на величину • р.
Е
В области правее характеристики at-x=l должно быть:
ди=	°тр
д х а Е
При пересечении характеристики at+x = l функция f'\z) в силу того,
что на ней скорость деформации меняет знак на обратный, должна ме-
няться на —2 и, следовательно:
Е
67
Коэффициент восстановления е
Рис 15. Диаграмма,
а - жесткая бронза; b - мрамор; с - алюминий; d - латунь; е - свинец
ди= Jimp
д х Е ’
^=Г-2^а.
dt 0 Е
Коэффициент восстановления для этого случая
В = 1-2^—
Е Го
68
что показывает зависимость его также от скорости. Зависимость коэф-
фициента восстановления от скорости подтверждается и опытами при
соударении шаров из разного материала [4 ]. На рис. 15 представлены
результаты измерения коэффициента восстановления при соударении
шаров, заимствованные из различных источников (отсюда различные
обозначения для опытов из одного и того же материала).
4.4.	Соударение стержней различной длины
Пусть два стержня одинакового сечения, но различной длины дви-
жутся навстречу друг другу с одинаковыми скоростями Vo (рис. 16). В
момент времени tn они сталкиваются. В силу симметрии их граница ос-
танавливается и в обоих стержнях начинается процесс, аналогичный опи-
санному в предыдущем параграфе. Пусть lf < 12, тогда процесс в пер-
вом стержне закончится раньше, в момент времени tf = 217/ а Если
I = 21J а, то к этому времени во втором стержне отраженная волна до-
стигнет сечения х = 2 /2 - аЛх = 2 (/2 -). При х > х2 скорость сечений
будет равна Vn. При х < х2 скорость равна нулю, но зато напряжение
равно yjpEV0 . Количество движения второго стержня:
/2
где т2 = ps 12 - масса второго стержня.
Рис 16. Схема соударения двух стержней одинакового сечения и
различной длины
69
Средняя скорость, а следовательно, и скорость центра масс второго
стержня после затухания колебаний:
г _^2 Х2 У -^1 у
2 /2 ° /2 °'
Если lt = 12, то V2 = Vn, что соответствует расчетам по формуле (2.3.2).
Если же Zz=2Z2 (т2 - 2т,), то стержни разминутся со скоростями центров
масс V.	= V- V, = 0,	вместо V	= -^К	иК=-К	по формулам (2.3.2).
/	**	*	1 з и 2 з 0
И потеря энергии будет равна 2 (при начальной энергии стержней
2^1 ^д2) вместо нулевой потери по формуле (2.4.1). Эта потерянная ки-
нетическая энергия перешла в потенциальную энергию сжатия второго
стержня, которая, в свою очередь, вызовет собственные колебания стер-
жня. Последние будут рассеяны под влиянием демпфирующих факто-
ров. Таким образом, коэффициент восстановления зависит не только от
материала соударяющихся тел, как полагал Ньютон при выводе формул
(2.3.1) и (2.4.1), но, в данном случае, и от соотношения размеров тел в
направлении линии удара.
4.5.	Удар ступенчатого стержня о жесткую стенку
Рассмотрим более сложный случай. Пусть ступенчатый стержень
ударяется о жесткую стенку (рис. 17). Для упрощения анализа примем
длины ступеней равными. Площади поперечных сечений ступеней отно-
S2
сятся как а = - .
Поскольку уравнение (4.1.2) справедливо только для цилиндрических
стержней, то необходимо записать решение для каждой ступени отдельно:
70
5
8
Рис 17. Диаграмма
М1 =
М2 =
Имеем серию граничных условий:
при	х=0	wz = 0
		д ii\ д и2
		dt~dt’
при	х = /	д м. ,д и2 = а ; д х д х
при	х = 2/	а“2=о. д х
(4.5.2)
Начальное условие запишется как
д щ_д и2_
dt dt °’
при t = О
5 м! =5 м2=0
д х д х
(4.5.3)
Из граничных условий имеем:
71
(4.5.4)
Если известны /Дз—2/j и <р^ (z+2/J при некотором значении z на гра-
нице ступеней, то формулы (4.4.4) позволяют последовательно постро-
ить решение для аргумента z + 21.
Для получения исходных данных для расчета воспользуемся началь-
ными условиями (4.4.3), получим:
а М]=-^о’
а [/2(-*Хф2(*)]=-^0’
- /J-x)+)=О,
-/'f-x)+(p' fxl=O.
2l )	2\ )
(4.5.5)
Последние два равенства в сочетании с (4.5.1) показывают, что фун-
кции^ (z) (/ = 1,2) симметричны относительно точки z = 0.
Из условия (4.5.2) имеем:
72
2a
<p;(z)=-^, 0 < Z < 2Z;
2a
(p;(z)=-^-, 27<z<47.
2V 7 2a
(4.5.6)
Интервал изменения z определяется интервалом на оси at, в котором
пересекаются с этой осью характеристики at - х = const и at + х =const,
проведенные из точки, в которой ищется решение. Так, для треугольни-
ка 2 на рис. 17 характеристика at - х = const проходит через интервал
О < z < 2/, а характеристика at + х = const - через интервал 21 < z < 4/.
Имея условия (4.4.4) для пересечения границы между треугольниками
2 и 3, можем записать на основании (4.5.6):
/;(z)=^,o<z<2/.
2а
Далее, на основании условий (4.5.6):
2fl(0<z<2l)=^^+^^ =—\
а+12а а+12а 1+а 2а
2(p'2(27<z<47)=-—
а+12а а+12а 1+а 2а
И на основании (4.5.6)
ф (47 <z<6l )= —
2V 7 1+а
73
Значения функций, характеризующие продольные
колебания в стержне
<z<	Z(Z)	4>',(Z)	/2(Z)	4>’2(Z)
-21 0	- 1	-1	- 1	- 1
0	2/	1	- 1	3-а 1 + а	- 1
2/	4/	За-1 1 + а	1-За 1 + а	3-а 1 + а	- 1
4/ 6/	5а2 -10а+ 1	-5а2 +10а-1	-а2 +10а-5	3-а \+а
	(1 + а)2	(1 + а)2	(1 + а)2	
6/ 8/		- 7а’ +35а2 -21а + 1	-а’ +21а2 -25а-3	-а2 +10а-5
		(1 + а)’	(1 + а)’	(1 + а)2
8/	10/				-а’ +21а2 -25а-3
				(1+а)’
Продолжая подобным образом, заполним таблицу.
Имея таким образом построенные функциии ф' (z), можем при-
ступить к определению скоростей и деформаций в различных зонах ди-
аграммы х - at.
Для треугольника Г.
/1/(0<z<2/J - как и в таблице выписываем только коэффициенты
при , ф'(0<г<2/)=-/,и, следовательно, получим:
2а
£±1 = 0 а Ц1 = Ко
д t д х а
Для треугольника 5:
74
f;(2l<z<4l)=	<p; (2/<z<4/>
и, следовательно, имеем:
gUi =l-3ay0
дх 1+a a
1 д u,	i
При a< , и, следовательно, в момент времени t = удар за-
3 д %!	а
кончится. Скорость стержня, одинаковая по всей его длине, определится
ее значением в треугольниках 2 и 3. Например, в треугольнике 2 имеем:
О
V =	= [/2'(o<z<27>(p'2(27<z<47)]=
д t
Ио 3-а
2 1+а
1 а у
1+а 0
Поскольку при ударе о жесткую стенку коэффициент восстановле-
, V,	, 1-af.	1^1
ния Ь = — * , то имеем: b= U<a<
Го	1+4	3 J
Продолжая подобным образом, построим график коэффициента вос-
становления (рис. 18).
Из графика видно, что коэффициент восстановления во многом зави-
сит от соотношения площадей сечения, то есть в конечном счете от фор-
мы стержня. Например, при a = Ь = 0,5; при а = 3,0 = 1 .То есть, если
в данном случае бросать один и тот же упругий стержень разными конца-
ми на жесткую стенку, то коэффициент восстановления меняется вдвое.
75
I
Рис. 18. Зависимость коэффициента восстановления от отношения площадей
поперечных сечений отдельных ступеней
4.6. Учет местных деформаций при ударе стержней
Ударяющий конец стержня может быть не плоским, и тогда первона-
чальный контакт будет осуществляться по линии или в точке. Усилие на
конце будет в общем случае выражаться формулой
р = кип,	(4.6.1)
где и - перемещение некоторой точки, достаточно удаленной от пло-
щади контакта;
к,п ~ постоянные, которые могут быть определены теоретически
(для тел простейших форм) или экспериментально.
Вблизи ударяющего конца деформация в данном случае будет трех-
мерной или, в простейшем случае, двухмерная осесимметричная. Но в
том и другом случае уравнение (4.5.2) уже не описывает процесс. Одна-
ко и уточненное описание оказывается достаточно сложным, не только
не поддающимся аналитическому решению, но, при сегодняшнем со-
стоянии вычислительной техники, и численному. Поэтому задачу прихо-
дится решать при дополнительных упрощениях.
Будем считать деформацию цилиндрической части стержня плоской,
а местную деформацию, описываемую формулой (4.6.1), замыкающей-
76
ся в криволинейном торце. Другими словами, заменим криволинейный
торец плоской прокладкой, имеющей нелинейную жесткость:
При такой постановке задачи формула (4.6.1) обращается в гранич-
ное условие при х = 0. Следовательно, при граничном условии (4.5.2)
можем записать:
ES [-	к [/(а(+(р («0)}’»
^'(at^=-f'(at-2l^.	<4,6,3)
Эти соотношения связывают между собой значения функций (р и f
с интервалом отставания 21. Начальные значения должны определяться
из условий (4.2.1). Уравнения (4.6.3) образуют нелинейную систему и
могут быть решены численно. Однако для качественного анализа зада-
чи достаточно рассмотреть случай, когда п =1. Тогда, продифференци-
ровав (4.6.3) по аргументу, можем записать:
Решение этого уравнения запишем как
f'(z)=Ce~^z -е~к^ \f"(z-2l)-klf'(z-2l)]e!ciZdz =
'	о
= Cek'z +f'(z-2iy2kle^z]eklZf'(z-2l)lz, (4М)
о
k
где к, = ,С - произвольная постоянная.
1 ES
На основании начальных условий (4.2.1) имеем для 1=0:
77
Подставляя это значение в (4.5.4), получим для 0 < z < 21:
Г(г)=Се-^+^ .
' 2а
Откуда имеем:
д и _к. ди „ , к
—- = аСе 1 , —- = -Ce~kz~-
д t	д х	а
П	7 А	.	5 U А г Ко
1 юскольку при Z=0 должно быть	= U, то С = — v, и окончатель-
д х	а
но имеем для 0 < Z < 2/,	*,z-0,5).
и
Далее, согласно формуле (4.6.4), можем вычислить для 2/ < Z < 4:
/'(z>-^[e’‘iz+(/+2z>’tl(z’2')-0,5 итд.
a	J
Для скоростей и деформаций имеем:
для 0 < Z < 2/
д и
д t
e-kz
д и
д х
Щ 1-е~6‘
а '
для 0 < Z < 2/
78
-=-V e’ilZ+2(/-z>’il<z’2z)],
d t
^=JiL-iiz-2ze~i|(z'2') .
d x a
Замечаем, что при наличии контактной жесткости (так же, как и про-
кладки из любого материала) удар не заканчивается, как это было при
ударе стержня с плоским торцем, в периоде Т=2/ / а, а напряжение не
достигает своей предельной величины VJa. Другое дело, что снижение
напряжения может быть незначительным.
При 2 < z < 4 удар может закончиться, если оказывается, что
2l<at = 0,5e2k^ <47.
Но в этом случае напряжение в стержне в целом отлично от нуля, то
есть часть энергии будет сосредоточена в виде его потенциальной энер-
гии, которая затем перейдет в его собственные колебания. Это значит,
что криволинейная поверхность контакта смягчает удар, одновременно
уменьшая коэффициент восстановления.
4.7. Удар жестким грузом по стержню
Пусть жесткое тело массой И ударяет по упругому стержню
(рис. 19). В стержне при этом возникает колебательные процессы, опи-
сываемые решением уравнения (4.1.1). Задача состоит в соответству-
ющем данному случаю определении вида функции f(x) и q(z) из на-
чальных и граничных условий.
Будем считать, что груз, соприкоснувшись со стержнем, движется
совместно без отрыва с его верхним концом. Тогда сила инерции груза
79
Рис. 19. Удар по упругому стержню
„d 2U
М ---7-
dt2
гасится силой сопротивления стержня EF-------. Здесь
х=0
принято, что начало координат для описания динамических процессов в
стержне находится в точке первоначального соприкосновения груза со
стержнем.
Таким образом, уравнение движения груза имеет вид
2 Е
Или, учитывая что а - —
Р
d2U	a2 dU
—— = а-----
dt	е dx х=0
(4.7.1)
где через а обозначено отношение массы стержня к массе груза
pF/
а = -—
М
С учетом граничного условия, что при х=1, где / -длина стер-
жня, должно быть £7=0, получим
80
f (at - /) + <p(at + /) = 0.
Так как t при этом может принимать любые значения, то
<p(z) = -/(z-2/)
при произвольном значении z=at± I.
Подставляя последнее выражение в (4.2.4) получим
f"(z) + -f'(z) = f\z - 21) -±f\z - 21).	(4.7.2)
Формула связывает значения функции f(z) с ее значением, отстоя-
щим по аргументу на расстояние 21, что и подтверждает колебательный
характер процесса.
При z < 0 стержень находится в спокойном состоянии. То есть правая
часть в первом периоде колебаний равна нулю. В результате для перво-
го полупериода колебаний имеем уравнение
€1
nz) + yf'(z) = 0,
откуда
f'(z) = Ce~a>-
При z=0 (t=0, х=0) должно быть f\z) = Vo, где Vo - скорость груза
у
до удара. И тогда С = — • Таким образом, при 0<z<2l функция
а
/'(2)0ПРеДеляется выражением

(4.7.3)
Для следующего периода колебаний будем иметь уравнение
81
Cl
f(z) + —f'(z) = -2
a I
Постоянная в решении этого уравнения определяется из условия, что
при х=0 скорость груза не может меняться скачками, и тогда
Продолжая таким образом, можно проследить процесс до момента
когда и=0, то есть стержень приобретет свою первоначальную длину и
силовой контакт между грузом и стержнем нарушается.
Поскольку перемещения в стержне выражаются в нашем случае
u=f(z)-f(z-2l),
а напряжение
S = E^- = f(z) + f'(z-2l),
ах
можем построить их графики (рис. 19).
Следует сказать, что в оружии в качестве основных деталей автома-
тики используется исключительно сталь. И ударяющий груз имеет со-
измеримую со стержнем жесткость. Это в значительной мере сглажи-
вает картину распределения напряжений. Но к удару жестким грузом по
стержню можно свести задачу расчета удара грузом по пружине, если
рассматривать пружину как стержень с соответствующей жесткостью,
много меньшей, чем жесткость ударяющей по ней детали.
К расчету буферных пружин
Итак, будем рассматривать пружину как стержень, имеющий жест-
кость, отнесенную к единице длины
4С1
82
где / - длина пружины в свободном состоянии;
Д- средний диаметр навивки;
С — жесткость поперечного сечения витка;
/ - число витков.
Например, для круглого сечения
32
Для квадратного сечения
С = 0,141 cfG,
где G - модуль сдвига;
d - диаметр проволоки;
а - сторона квадрата.
Масса единицы длины пружины
z т oF-InDi
(PF7,=7=—j—.
где т - общая масса пружины;
F- площадь поперечного сечения витка.
Таким образом, для скорости распространения ударной волны в пру-
жине - эквивалентном стержне будем иметь
к^
У (PF\cn
Далее задачу можем решить тем же методом, что и в предыдущем
параграфе. Но, как правило, отношение массы пружины к массе ударя-
ющего груза мало, и приходится учитывать достаточно много периодов
колебаний, при этом вычислительные сложности с каждым периодом
нарастают. Поэтому мы прибегнем к другому способу решения уравне-
ния, а именно разложению его в тригонометрический ряд
. .	. х
и = Л sin pt • Sing J.
83
Подставляя это выражение в уравнение, находим, что оно удовлетво-
ряется, если
т
р = —а
I
Подставляя в граничное условие, получим, что должно быть
Это уравнение дает для ц бесконечное число решений ц. , так что
превращается в бесконечный тригонометрический ряд. Суммировать
бесконечные ряды также сложно, поэтому будем искать приближенное
решение для этого ряда. При этом учтем, что, как правило, масса пру-
жины мала по сравнению с массой ударяющего груза, то есть а « I.
Тогда можно записать для первого корня
/	1 зч
ц(ц + -ц ) = «.
Окончательно получим
а
„ =ТС(«-1)+—----
7С(« -1)
Заметим, что второй член в цп угле при п=2 отличается от единицы
на порядок больше, чем ц;. Поэтому для дальнейших примем
=я(л-1), п*\.
Окончательно запишем
ТТ V Л Упа1 х
и = у А„ sin ——smii —.
Z—I п	Г~п }
При х=1 и Z=0 должно быть = Уо тогда Уо =	sinpn .
Формула для Ап находится с помощью предельного перехода, кото-
рый дает (при малости отличия jtot ли)
84
^=^cosp A
a |i2 ’
W
qi2
n Ф 1
Таким образом, ряд распадается на два слагаемых
тт Vol (	at . х 1	2	•
и= — ~ cos^sm^—smM1- + —2,--------^sinp^-sinp -
«Hi	I i л=2(л-1)	I )
Бесконечный ряд представляет собой пилообразную функцию, гра-
фик которой представлен на рис. 20.
Первый член в скобках представляет собой обычное энергетическое
решение, которое после преобразования может быть заменено
du	V 1+ % а
р = Z---= Z— ———sinp\t, х = 0;
dx	а а
у 1-2/ а	(4.7.3)
p = Z—------——sinp}t, x = l.
а а
Накладывая на это решение пилообразную функцию, получим реше-
ние в динамике. На рис. 21 представлено такое решение в сравнении с
осциллограммой.
85
Рис. 21. Удар по пружине
Здесь следует иметь в виду два обстоятельства. Первое: если полу-
ченный график усилия с учетом собственных колебаний превзойдет ста-
тическое усилие при сжатии пружины до соприкосновения витков, то это
свидетельствует о том, что витки будут соударяться. Соударение вит-
ков вызовет развитие контактных напряжений на поверхности соударе-
ния, образуя хорошо видимые плоские полосы. Кроме того, на границе
перегиба фронта волны соударения возникают значительные изгибные
напряжения. Все это отрицательно сказывается на прочности пружины.
Но расчетных методов для этого случая не существует. И избежать
соударений в большинстве случаев в оружии не удается.
d
Второе: при увеличении жесткости пружины, то есть отношение —,
динамические составляющие существенно сглаживаются, вплоть до
того, что их можно не учитывать.
Посчитаем потери энергии при ударе. При этом будем иметь в виду,
что во многих случаях, особенно при конструировании буферов, имеется
86
промежуточное тело массой тг Тогда при ударе массы М по m.t их об-
щая скорость будет равна (считаем удар неупругим)
V MV°
01 М + т,-
именно эту скорость и нужно учитывать при ударе.
Потери энергии при этом будут
----
1	2(ЛГ + ли,) 0 •
Далее нужно учесть потери на создание собственных колебаний пру-
жины, выраженных пилообразной функцией. Учитывая ее периодичность,
достаточно учесть энергию колебаний в первом полупериоде, когда
7t
pt = —, и I < z <0. С учетом (4.7.3) имеем
z
A32=^L~4fe=^(l-^“)
2	2/ J	4а
Или, в предложении, что а< 1
mV2
ДЭ2=-^-(1-а +...).
Эта энергия рассеивается в результате затухания колебаний.
Литература
1.	Лойцянский Л.Г., Лурье А.Н. Курс теоретической механики. Ч. 1,2.
М., 1957.
2.	Вернер Гольдсмит. Удар. М.,1965.
3.	Александров Е.В., Соколинский В.Б. Прикладная теория и расче-
ты ударных систем. М.: Наука, 1969. 199 с.
4.	Батуев С.Г. и др. Инженерные методы исследования ударных про-
цессов. М.: Машиностроение, 1973. 247 с.
Содержание
ПРЕДИСЛОВИЕ...................................................3
1.	ВВЕДЕНИЕ...................................................4
1.1	. Термины и определения...................................4
1.2	.0 некоторых количественных соотношениях в процессе удара.5
2.	ЦЕНТРАЛЬНЫЙ УДАР...........................................8
2.1.	Прямой удар..............................................8
2.2.	Понятие о коэффициенте восстановления скорости......... 10
2.3.	Прямой удар (продолжение).............................. 12
2.4.	Потери энергии при прямом ударе........................ 13
2.5.	Косой центральный удар................................. 16
2.6.	Повторный удар. Первый случай.......................... 17
2.7.	Повторные удары. Второй случай......................... 19
3.	СОУДАРЕНИЯ МНОГОМАССОВЫХ СИСТЕМ............................21
3.1.	Последовательное соударение трех тел....................22
3.2.	Параллельное соударение трех тел........................27
3.3.	Уравнения Лагранжа второго рода для случая удара........30
3.4.	Косой удар. Общий случай.................................31
3.5.	Соударение шаров с учетом трения по площадке контакта...34
3.6.	Внецентренный удар двух кубов...........................36
3.7.	Ударный механизм с вращающимся курком.................  41
3.8.	Расчет механизма отражения гильзы........................46
3.9.	Замечания к общему случаю соударения двух тел...........48
4.	ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ ВЕЛИЧИНУ КОЭФФИЦИЕНТА
ВОССТАНОВЛЕНИЯ...............................................59
4.1.	Уравнение для продольных колебаний стержня..............60
4.2.	Удар стержня о жесткую плиту............................61
4.3.	Учет демпфирования при ударе по стержню.................66
4.4.	Соударение стержней различной длины.....................69
4.5.	Удар ступенчатого стержня о жесткую стенку..............70
4.6.	Учет местных деформаций при ударе стержней..............76
4.7.	Удар жестким грузом по стержню..........................79
Литература...................................................88
Алексей Афанасьевич Коновалов
УДАРЫ В ОРУЖИИ
В авторской редакции
Корректор Н.Н. Пирогова
Технический редактор С.И. Зянкина
Компьютерная верстка: А.Л. Кожевников
ЛицензияЛР№020411 от 16.02.97.
Сдано в производство 10.11.2000. Формат 60x80 '/|6. Печать офсетная.
Гарнитура Таймс. Уч. изд. л. 4,8.Усл. печ. л. 5,34. Заказ №5007.
Тираж 1000 экз.
Издательский дом “Удмуртский университет”,
426034, г. Ижевск, ул. Университетская, 1, корп. 2.
Республиканская типография,
426057, г. Ижевск, ул. Пастухова, 13.
Издательский дом “Удмуртский университет”
приглашает к сотрудничеству:
переводчиков, литераторов, авторов индивидуальных
и коллективных проектов, гуманитариев всех
профилей; ждем ваших рукописей,
издательских идей,
предложений
и т.д., и т.п.
С вашей помощью мы рассчитываем осуществить
поиск и дальнейшее издание новых занимательных
и познавательных книг различных направлений,
в том числе биографической, научно-популярной,
учебной литературы, беллетристики,
справочников, изданий но искусст ву
и т.д., представляющих
интерес для современного
читателя.
ПИШИТЕ, ЗВОНИТЕ, ЗАХОДИТЕ!
Наш адрес: 426034, Удмуртская Республика, г. Ижевск,
ул. Университетская, 1.
Тел / факс: (3412) 75-21-55