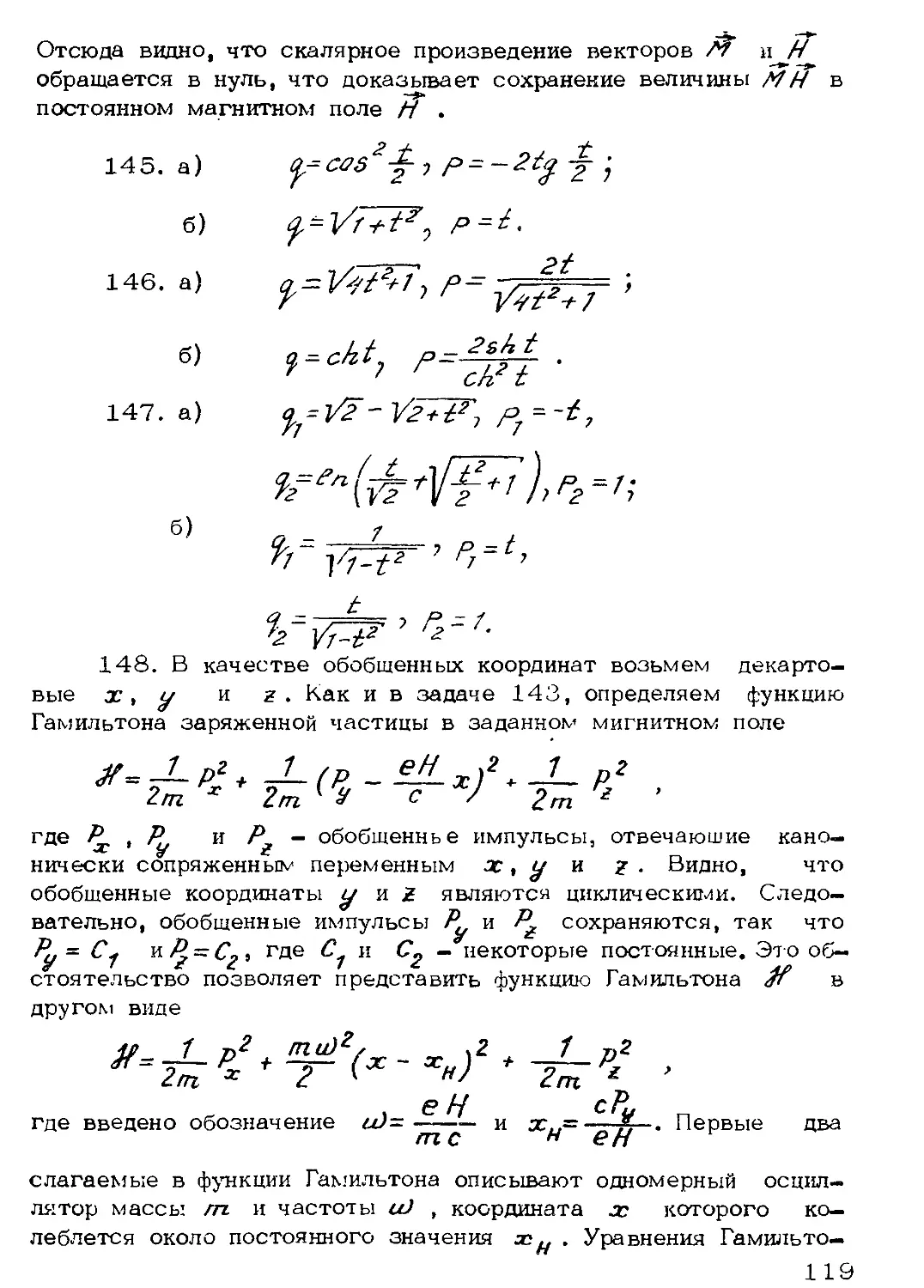Si
л 41
МОСКОВСКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ
А. И. Алексеев
ТЕХНИИА ВЫЧИСЛЕНИЙ
КЛАССИЧЕСКОЙ МЕХАНИКЕ

ЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ СССР
БСКИЙ ОРДБНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ
А.И.Алексеев
ТЕХНИКА ВЫЧИСЛЕНИЙ
Е КЛАССИЧЕСКОЙ МЕХАНИКЕ
Утверждено
репсоветом институте
в качестве учебного аосо1.
№ гг. два 1984

УДК 531.11
А.И.Алексеев. Хе2ШДШ.„^ь^^£ний в классической^
механике. Учебное пособие. - М,: Изд. МИФИ, 1984,- 148 с.
Данное пособие представляет собой сборник задач,
которые предназначены для студентов всех факультетов, где изуче-
етия курс: теоретической физики.. Оно содержит около 300
задач по классической механике и специальной теории
относительности. Задачи снабжены ответами, а некоторые -
подробными решениями или указаниями. Содержание и объем учебного
пособия достаточны, чтобы обеспечить семинарские занятия по
курсу •'Механика и теория относительности''' с учетом специфики
преподавания теоретической физики в МИФИ
Рецензенты;
В.И.Коган, В.П.Силин
(Cj Московский инженерно-физический институт, 19S4 г.
Редактор С.А.Са фронова
Технический редактор Н.М.Воронцова
Корректор Т.В.Стаферова
Л-83365 Подписано в печать 25/1Х-1984 г.
Формат. 60x84 1/16 Объем 3,25п.л. Уч.-изд.л. 9
Тираж 950 экз. Заказ 501 Пена 60 коп.
Изд. № 038-1
Типография МИФИ, Каширское шоссе, 31

Содержание
Задачи Ответы и
решения
П редис л овие .,.„... .., Ч
ГЛАВА I. Лагранжева_^1е_ханик_а...., S 52
§ 1. Написание функции Лагранжа.. 5 52
§ 2, Составление уравнений Лагранжа 7 56
§ 3. Особенности движения,
вытекающие иа законов сохранения 3 58
§ 4. Интегрирование уравнений
движения.. 71 63
§ 5. Движение в центральном поле.. 15 74
§ 6. Столкновение и рассеяние
частиц.... .... 19 85
§ 7. Малые одномерные колебания... 23 94
§ 8. Малые колебания системы со
многими степенями свободы..,. 27 700
§ 9. Нелинейные колебания 32 70S
ГЛАВА П. Гамильтоьова механика 33 715
§ 10. Уравнение Гамильтона...., 33 115
§ 11. Скобки Пуассона 35 1?д
§ 12. Канонические преобразования 37 722
§ 13. Метод Гамильтона-Якоби 40 727
§ 14. Адиабатические инварианты... 43 757
ГЛАВА 11'. Специальная i теория
относительности 46 740
§ 15. Релятивистская кинематика.. % fto
§ 16. Релятивистская динамика ^д 74 Ъ
Приложение. Табличные интегралы 147
Список литературы 748

ПРЕДИСЛОВИЕ
В предлагаемом учебном пособии собраны задачи по
классической механике, которые автор многие годы использовал на
практических занятиях в МИФИ. При составлении учебного по—
собия прежде всего ставилась цель подобрать задачи не
сложные, но разнообразные по своей тематике настолько, что
решение их потребует предварительной проработки всего курса
классической механики, включая ее релятивистскую часть. В сьязи с
этим большинство задач являются достаточно простыми и
предназначены для работы в аудитории. Ьолее трудные задачи
полезны для составления домашних заданий и самоконтроля,
дающего возможность проверить, насколько глубоко усвоен
материал изучаемой дисциплины, Подавляющая часть типовых
задач имеет решение или содержит краткое указание„ а для одно-»
типных приводится лишь ответ. Причем однотипных задач, как
правило, несколько. Такое построение учебного пособия
рассчитано как на самостоятельную работу с книгоГг, так и на
использование его на семинарских занятиях и при проведении
контрольных работ. Подбор задач и перечень рассматриваемых
вопросов соответствуют программе теоретической физики для
студентов МИФИ. Заданный объем книги не позволил включить
вопросы, выходящие за рамки указанной программы, а также
задачи сложные, которые необходимо сопровождать подробным
решением или указанием. По этой же причине опущень решения
многих однотипных примеров и оставлены только ответы.
Теоретический материал, необходимый для решения предложенных
задач, можно найти в книгах £l - 3 j , а также в
дополнительной литературе /-127

ЗАДАЧИ
Глава I
ЛАГРАНЖЕВА МЕХАНИКА
§ 1. НАПИСАНИЕ ФУНКЦИИ ЛАГРАНЖА
1. Написать функцию Лагранжа материальной точки
массы гть , движущейся: ^%_
а) в потенциальном поле с/- — +—f, где а ~& ь
-постоянные величины, а г- расстояние до начала координат
(использовать сферические координаты);
б) в аксиально-симметричном потенциальном поле l/=l/(f)i
где /"— расстояние до его оси симметрии (использовать
цилиндрические координаты);
в) по кривой линии, описываемой уравнениями:
где параметр S принимает произвольные значения, а ось Z
декартовой системы координат антипараллельна силе тяжести;
г) по спирали /~ - F( V) в потенциальном поле U - l/(t~} <р),
где А*" и 9^ - полярные координаты, выбранные в плоскости
X У ) 2 2
д) по поверхности врашения Z =■ F (х. * У ) , если ось Z
декартовой системы координат антипараллельна силе тяжести.
2. Сферический маятник представляет собой материальную
точку массы т. , движущуюся по поверхности сферы радиуса
^ в поле тяжести. Найти его функцию Лагранжа.
3. Функция Лагранжа I. — /. D?t) ъ безразмерном
обозначении задана. Перейти к новой функции Лагранжа L'- L (Ъ^)
путем исключения из выражения /. (о, £) полной производной
по времени от некоторой функции обобщенной координаты о, и
времени t в следующих случаях:
5

в) I = i -t(tsin 2^ -tcy J j, -cos a \
где /7(<2J и £„(■£) - произвольные функции своего аргументе.
4. Написать функцию Лагранжа плоского маятника, у
которого масса т постоянна, а длина f меняется по задан»»
ному закону С ~ Р (i) .
5. Найти функцию Лагранжа плоского маятника массы пъ
и длины / , точка подвеса которого с координатами ^с0 и Уа
движется в вертикальной плоскости Л У по кривой, описывав-»
мой уравнениями jc0~jcc (i) и у0 = у £{:} , где заданные функции
•x<,i£i и У<>№) зависят от времени I произвольно, a ось
X параллельна силе тяжести.
6. Электрон с массой /-п и зарядом е движется
вокруг покоящегося ядра с зарядом & . Определить функцию
Лагранжа электрона з сферических координатах, предполагая.чтс
система находится в постоянном однородном внешнем
электрическом поле с напряженностью Т .
7. Функция Лагранжа 1< механической системы, состоя-
шей из д/ материальных точек, в дек£фТСБЫХ координатах
записывается так'^ = Г-£/" , где Т - кинетическая энергия, «
V — энергия взаимодействия материальных точек между ео~
бои и с внешнем полем. На материальные точки нало» ены го.-
леномные связи, которые описываются уравнениями:
/. (Р}?...,~rN)i) = o, j=/, ... ,п,
где г. - радиус-вектор / -й материальной точки {I = 1,...,Л").
Доказать, что после перехода к обобщенным координатам а ,
• ••f AК функция Лагранжа принимает вид:
i = 27 -?а.а «. <г + 2Z ё а - W.
Здесь К =3N~n- число степеней свободы, а величины яг. , В иУ»'
являются определенными функциями обобщенных координат и
времени. При каком условии величины £ -L a, i Q и Y/ имеют
физический смысл соответственно кинетической и
потенциальной энергий данной механической системы?
6

8. Маленькое кольцо массы т подвешено на
невесомой пружине с коэффициентом жесткости к и может пере..»
мешаться только вдоль вертикального стержня, на который на«»
низаны эти кольцо и пружина. Длина недогруженной пружинь1 f .
К этому кольцу прикреплен плоский маятник длины f и мае-»
сы т2 . Определить функцию Лагранжа данной механической си™
стемы, совершающей движение в поле тяжести.
9. Вдоль невесомого стержня длины f плоского маят™.
HHica с массой тп перемещается без трения маленькое кольцо
с массой т0 , которое прикреплено к точке подвеса маятника
невесомой пружиной жесткости к » Длина ненагруженной
пружины ?„ , причем fc < f . Найти функцию Лагранжа этой ме™
ханической системы.
10. Система состоит из двух плоских маятников
одинаковой длины ? , но с разными массами т и -тг .
Маятники связань между собой невесомой пружиной с коэффициентом
жесткости к , которая при сжатии и растяжении остается
прямолинейной. Концы пружины прикреплены к маятникам в сред»-
них точках. В ненатянутом состоянии пружина имеет длину Ра ,
совпадающую с расстоянием между точками подвеса. Найти
функцию Лагранжа механической системы, если маятники
совершают движение в одной плоскости в поле тяжести.
§ 2. СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА
11. Выразить ускорение через обобщенные координаты и
скорости в тех случаях, когда функция Лагранжа в
безразмерном обозначении имеет вид*.
а) I = j,2сМ + $* ; б) £- = ($?+<}+*)$*;
в) L=f^2fy ; г) *>=$?+frfyfaffa.
12. Движение частицы массы пг в декартовых коерди-»
натах описывается функцией Лагранжа
L - 2~ т ■& ~ t~ t JT--g-oC <Х ?
где /^ и ос - постоянные. Определить силу F ,
приложенную к частице.
13. Непосредственным вычислением доказать, что
уравнения Лагранжа механической системы с К степенями свободы
7

не меняют вида при замене функции Лагранжа I, =L (у, у.,., ^И,И
на новую функцию Лагранжа L-L (fy 7...., Qk £} по формуле
где / - / [ф ,7 a £} - произвольная функция обобщенных
координат а , ..., а и времени / .
14. Материальная точка массы т, движется в поле
тяжести по поверхности конуса с углом 29а при вершине.
Конус расположен вертикально вершиной вниз по направлению
силы тяжести. Составить уравнения Лагранжа, описывающие
движение материальной точки в сферических координатах.
15. Материальная точка массы rrv движется по
поверхности параболоида вращения О.В. =.Х + уг . Ось Z декартовой
системы координат антипараллельна силе тяжести. Найти
уравнения Лагранжа в цилиндрических координатах.
16. Протон с массой т и зарядом е движется в
потенциальном поле U=2еа Рп ■— равномерно заряженной нити,
которая параллельна силе тяжести. Здесь а - линейная
плотность заряда нити, /~ - расстояние от нее до протона, а /? -
некоторая постоянная с размерностью длины. Определить
уравнения Лагранжа в цилиндрических координатах.
АШ> 17. Написать урс-внения Лагранжа
i\£ для: а) сферического маятника из
задачи 2; б) двойного плоского маятника
,/*. (рис. 1); в) плоского маятника длины t и
и\ч массы т , точка подвеса которого
|^ >v вращается с постоянной угловой скоро-
1 тг стью С? по окружности радиуса /? в
р вертикальной плоскости, причем в
момент времени Г=0 точка подвеса
занимала крайнее нижнее положение.
18. Пружина свернута в виде тонкого кольца, одна точка
которого неподвижна. К пружине последовательно прикреплены
материальные точки с массами т7 , ...t mn t которые делят
пружину на п +1 звеньев с коэффициентами жесткости
соответственно К , ..., кгг + 1 • ^Ри движении материальных
точек плоскость кольца неподвижна, а его радиус не меняется.
Написать уравнения Лагранжа, взяв в качестве обобщенных
координат О , ..., у смещения материальных точек с
массами пъ. , ..., тп относительно их равновесного положения.
1У. Функция Лагранжа частицы с массой т и зарядом е,
движущейся со скоростью гА в электромагнитном поле, имеет
8

вид т -*.«? е т"-*-
где <? - электродинамическая постоянная, равная скорости
света в вакууме, а /7 - А (^ t) и (f~(f(j^f) - электромагнитные
потенциалы, которые связаны с напряженностями злектрическо— ^
го /f* и_магнитного FT полей соотношениями Е — ~ <2,глс1 f-^-^4г
пЛТ-ГЯ^Я • Написать уравнения Лагранжа и показать, что
после некоторых преобразований они переходят в уравнение
Ньютона, в правой части которого стоит сила Лоренца F-eCE + i-tF*./Г).
8 3. ОСОБЕННОСТИ ДВИЖЕНИЯ,
ВЫТЕКАЮЩИЕ ИЗ ЗАКОНОВ СОХРАНЕНИЯ
20. Найти точки остановки механической системы, если
ее функция Лагранжа /_, и начальные условия при t-О
заданы:
2 „J..2.
■2 2
Г) L=-Vf-fz~<}y ?(O) = 0, j,@) = -f
3
2.1l. Частица с массой гп и энергией & движется в
одномерной потенциальной яме Zf(x) . Найти период т
движения, если
а) Щх)=и0 -^ при эс^О и V(x) = U0 —^ при^с.^о \
~ £ J<L
б) U(x)=Uoe а при^<G и U(x)-Uoe § npvijc^D;
JC2 2
в) tf(x) = U7 -^ при х<;0 и U(jc/=U,£o -f при ж^О ♦
22. Определить условия, при которых движение финитно,
и найти период Т этого движения в зависимости от энергии <§ ,
9

в
если функция Лагранжа в безразмерном обозначении имеет
вид: ? р
a) L=f*- tk $ \ б) £ = f - fr<j~<p ;
23. Частица массы т приближается к точке ее-6 , в
которой потенциальная энергия I/(х) имеет максимум. Фук—
кция U- U(jc) и ее производные непрерывны в этой точке.
Определить закон одномерного движения в малой окрестности
точки jc = £ слева х < 6 я справа. ? ^ х от
нее, если энергия <£ частицы совпадает с высотой потекци—
альнсго барьера <£ =1/F) , а в момент времени t—C она на—
ходилась в точке x~jc0.
24. Механическая система с К степенями свободы
описывается функцией Лагранжа
Л" К
Здесь величины Ct^ a , S^ w W являются функциями
обобщенных координат Л , ..., ^ и времени t » где пг-^К . Сп«»
ределить энергию 8 и обобщенный импульс /=^ „ Сохраняют-»
ся ли эти величины при движении механической системы?
25. Доказать, что в кулоновском поле if -- —~— вектор
~*~ ->■- -г- /»"
1 = гг*М*<*-р сохраняет постоянное значение, Здесь л^ — радг-гус-.
вектор, тг — скорость и М - момент материальной точки.
26. Частица массы т движется в
сферически-симметричном потенциальном поле U-y-ar"< Доказать, что тензор
J^a=^x^^a^a'xU*z'jb является интегралом движения, где
величины jc^ при ^ = 1, 2 и 3 обозначают компоненты ее , у
и g радиус—вектора г~ частицы,
27. Доказать, что при движении заряженной частицы в
постоянном однородном электрическом поле с напряженностью г
величины ТГ=£М и XГ?-с"(г?*Mi]*■-§-(***Ё~) являются интегралами
движения. Здесь Я" , гг , М и е3 - соответственно ради~
ус—вектор, скорость, момент и заряд частицы.
10

28. Частица с массой т и зарядом е движется
в постоянном однородном магнитном поле с напряженностью /Г.
Показать, что величины Z^lmir-t -£-м~*р-J ъ/^=/п(/?к v'lff'+j-ir'nfff
являются интегралами движения. Здесь /^ и ■vr— радиус—*
вектор и скорость частицы, а с - электродинамическая
постоянная, равная скорости света в вакууме.
29. Какие из физических величин S , F~ и М сохра»
няют постоянное значение при движении заряженной частицы е
постоянном электрическом поле: а) равномерно заряженного
шара; б) равномерно заряженного бесконечного цилиндра; в)
равномерно заряженной плоскости* г) двух параллельньх
равномерно заряженных нитей; д) двух точечных зарядов?
30. Перечислить все независимые интегралы движения, не
содержащие время явно, для следующих механических систем:
а) свободной материальной точки массы т. ; б) частицы мас™
сы rn в кулоновском поле U- ■—■ \ в) частицы с зарядом
е в постоянном однородном электрическом поле с напряжен-,
ностью £
§ 4, ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ .ДВИЖЕНИЯ
31. Материальная точка движется в поле тяжести по пря~<
мой, которая вращается с постоянной угло.есй скоростью со ь
вертикальной плоскости. Найти закон движения материальной
точки, если в начальный момент времени t-O она покоилась
в неподвижном центре вращения, а прямая занимала
горизонтальное положение, перпендикулярное силе тяжести,
32. Прямая прецессирует с постоянной угловой скоростью
со , составляя угол 9 с направлением силы тяжести. В
начальный момент времени t-О на этой прямой покоилась
материальная точка на расстоянии Р от неподвижного
центра. В последующее время она движется вдоль прецессирующей
прямой. Определить характер этого движения, если в начальный
момент времени материальная точка находилась: а) выше
неподвижного центра; б) ниже него.
33. Определить закон движения материальной точки на
вертикальной плоскости, которая вращается около оси Z
декартовой системы координат с постоянной угловой скоростью сО .
^сь Z антипараллельна силе тяжести. В начальный момент
времени t~0 материальная точка имела скорость & и
находилась на оси Л на расстоянии f= V /си от начала
координат. ■" '
11

34. Определить закон движения материальной точки на
расширяющейся цилиндрической поверхности радиуса R=R0chat ,
ось которой параллельна силе тяжести и служит осью Z
декартовой системы координат, В начальный момент времени /-#
материальная точка имела скорость jF и находилась на оси Л"
на расстоянии R от начала координат.
35. Электрон с массой т и зарядом е влетает в
полупространство, в котором напряженность £ электрического
поля однородна, постоянна и перпендикулярна граничной
плоскости. Начальная скорость гр составляет острый угол ы. с
вектором с . Определить время t- движения электрона во
внешнем электрическом поле, а также глубину Р
проникновения в это поле.
36. Скорость 2£ протона в начальнь й момент времени
составляла острый угол &с с напряженностью М внешнего
постоянного однородного магнитного поля. Найти число
оборотов /V , которые совершит протон, пролетев большое расстояние
/ вдоль магнитного поля. Масса и заряд протона равны
соответственно гп и е
37. По заданной функции Лагранжа 1^ и начальным
условиям при £=■(? определить характер движения механической
системы двумя способами: решением уравнения Лагранжа и при
помощи закона сохранения энергии. Рассмотреть следующие
случаи:
в) L = jr*+<f + f*, f@) = Of f@)=T.
38. Функция Лагранжа L и начальные условия при t = 0
заданы. Пользуясь законом сохранения энергии, определить
обобщенную координату^- Q/(t} и убедиться непосредственной
подстановкой, что найденная функция Cj,{t) удовлетворяет
уравнению Лагранжа в следующих случаях:
а) l-K---^F о $(*/=', <}@)=а;
б) L=<f2-e2t, ftoj^ ф(о)=0.
12

39. Найти обобщенную координату £ = o/i), если дана
функция Лагранжа Z и начальные условия при i = Q , а
именно: . 2 -Q,
б)
* «?
в
) L=^2'7^1 9(°l=°, i(°) = f,
г) L--Y'-?2-k? ; f@)^0} ytOj^O,
40. Частица с массой /гг и энергией <f движется по
оси X в одномерном потенциальном поле У(ж). Определить
характер движения^ -jc(&) , если:
а) lf(x)^-U0^2\ М0)=УЦ&\ *@)=0(ио>0);
б) и(х)=иеа, jo(o)=<x0> xio) = 0.
где Uo>0 и <&;># , а «Я^- корень уравнения 6 =U(x0)\
с X2
в) U(xh
г
{ и2 "^2 ПРИ ^»0,
гл -^з
где ио> О , а -З^,- наименьший корень уравнения cf- W(х0),
41. Найти закон движения механической системы, которая
в обобщенных координатах описывается следующей функцией
Лагранжа и начальными условиями при t = 0 :
13

б)
в)
г)
/ / ■ 2 -. i.i
L - - VP-f^i- j t,
2 ; с г у
4- Q * 4 SA/,
4-2. Найти обобщенные координаты <?, itj и fys(l) > ecu
дана функция Лагранжа 1, и начальные условия при / -.- о , <'■
именно:
а;
z.2
f'r У! УI
43, В начальный момент времени t-Q частица с
.массой ni и положительным зарядом t? находилась ъ точке с
радиус—вектором га и имела скорость if . В дзпьпейшем он.
движется ь однородных постояннь'х электрическом и магнитном
полях с напряженностями £ и И , которые удовлетворяю!
условиям ВН= О и £-^Н. Определить характер движения
заряженной частицы в этих скрещенных полях. Исследовать
полученное решение при /~Г = т?~0 = О .
44, Векторы и Н электрического и магнитного полег
образуют уг?ол в . Указанные поля однородны и постоянны^ при»,
чем £ «■// . Определить закон движения частицы с массой пт.
и зарядом е>0 , если в момент времени t = О она покоилась
в начале декартовой системы координат, у которой ось £
выбрана вдоль п , а ось / параллельна вектору ft * Е
45, Напряженность Н постоянного однородного
магнитного поля параллельна поверхности Земли. Определить закон
14

движения протона с массой т и зарядом е над плоским
участком земной поверхности, если в момент времени & ~ с он
находился в начале декартовой системы координат с осью Л .
параллельной силе тяжести. и осью Z , выбранной вдоль
вектора Н . Начальна*.; скорость lr (гыпи перпендикулярна силе
тяжести и вектору Н .
46. Определить характер движения электрона с массой РЪ
и зарядом-" в постоянном однородном магнитном поле с на™»
пряженностью Н и перпендикулярном к нему электрическом пс«
ле которое в декартовой системе координат^с осыс Z -. па™
раллельной вектору Н г имеет вид c--a,jr.£x , где # ~
положительная постоянная и ? - орт оси Л „ В момент
времени t- О частица находилась в начале координат и имела
скорость гР , направленную вдоль осч У' .
47. Решить предыдущую задачу, считая постоянную а
отрицательной и удовлетворяющей условию / ct j > -^^V , где £*-
скорость света в вакууме. Рассмотреть предельный случай
-^ тс*
48. Напряженность И постоянного однородного магнит*»
ного поля перпендикулярна напряженности электрического ir^ctt,
где <jf— постоянный вектор. Определить закон движения
частицы с массой т. и положительным зарядом е в этих
скрещенных полях, если в момент времени i - О она покоилась з
начале декартовой системы координат с осями X и Z ,
направленными вдоль векторов £ и // соответственно.
Влиянием переменного во времени электрического поля на
магнитное пренебречь.
49. Напряженности С и Н электрического и магнитного
полей взаимно ортогональны, а сами поля однородны. С
момента времени t ^ О напряженность электрического поля
убывает по закону £*—/f с» , а магнитное поле остается
приблизительно постоянным. Определить закон движения протона с
массой т и зарядом е , если в момент времени t— О он
покоился в начале декартовой системы координат с осями X и
У} параллельными векторам /• и /Т .
§ 5. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ
50. Определить наименьшее и наибольшее расстояние до
начала координат в случае движения материальной точки массы

гП в сферически-симметричном потенциальном поле:
51. Частица массы /гг движется в сферически-симмет-»
ричном потенциальном поле притяжения Z/~ U(r) . В начальный
момент времени t~Q она покоилась на расстоянии R от
центра поля. Определить время £п падения частицы в центр
поля, если:
&)V=--p-; б) 71= аг2; в) U=~a
ния, если:
а)
в)
Vf->- U°
а-
и
V Г) - °
5k2'^ ?
б)
г)
52. Определить закон падения t~=f~(£) частицы массы
пг в центр сферически-симметричного потенциального поля
притяжения U(г). В начальный момент времени t-D частица
имела энергию £ и покоилась. Найти также время £ паде—
а ■>
JZ
а
53. Частица с массой т , энергией £ и моментом М
движется в сферически-симметричном потенциальном поле
притяжения Z/- сгл . Определить закон изменения радиальной
координаты t-= f(t) частицы, если в начальный момент времени
t~G она находилась в экстремальной точке траектории.
54. Найти период Т радиальных колебаний
материальной точки массы, z-тг , движущейся с энергией 6 и моментом
А/ в сферически-симметричном потенциальном поле (и >0,
ё>0 ):
a) u=^ + gS; б) U = f2~*L.
55. При каких абсолютных значениях момента М
радиальное движение материальной точки массы ггг периодично в
сферически-симметричном потенциальном поле
U=-Uoe \> Uo>0?
16

56. При каких абсолютных значениях момента /у
возможно финитное движение частицы массы т. в
сферически-симметричном потенциальном поле:
a) U=-Tf^, а>о, &>0; б) V=-Vo'n(r+jb)tUo>0?
57. Частица массы /п движется в
сферически-симметричном потенциальном поле U=U(h)t имея энергию £ и
момент № . Определить скорость -& б экстремальной точке
траектории с радиус-вектором f0 , выразив ее через заданные
величины.
58. Материальная точка со скоростью тг и моментом И
движется в кулоновском поле U~-^ . Доказать, что:
а) уравнение траектории в полярных координатах можно
получить скалярным умножением сохраняющегося вектора J =
= jF*M^+c<r на радиус-вектор /*" материальной точки;
б) вектор /= 7Г*М-*-с< -рг направлен по большой полуоси
эллипса при эллиптическом движении материальной точки и пс
оси симметрии траектории в случае движения по гиперболе или
параболе.
59. В полярных координатах найти траекторию
материальной точки массы т , движущейся в сферически— симметричном
потенциальном поле (л> О , в>0 )\
в) v =*.£.* г) и=-&ъ + ёгг.
!~г г ">
А"
60. Найти уравнение траектории частицы массы т ,
которая движется в сферически-симметричном потенциальном
поле притяжения U= —%-• Энергия частицы равна нулю, а ее
момент М произволен.
61. Найти уравнение траектории частицы массы /■**
движущейся с энергией 6 и моментом М в
сферически-симметричном потенциальном поле ?,
~ 7*"
/-»* о
если заданные параметры удовлетворяют соотношениям:
и=- а +ие
М2=2та ; о<с S^U0; ё>0.

62. В начальный момент времени частица находилась в
экстремальной точке траектории. Определить число оборотов п. ,
которые совершит частица около силового центра при удалении
от него на бесконечно большое расстояние. Параметры задан™
ного потенциального поля 7J- ~--> + --связаны с энергией 6- . мо-
ментом № и массой т частицы соотношениями /V - ^гтса к
63. Материальная точка массы <•?•? движется по
конической поверхности с углом 2 6'0 при вершине. Потенциальное
поле убывает обратно пропорционально квадрату расстояния от
вершины U =■ -75 ? где &>в > Найти уравнение траектории,
64. Определить эксцентриситет £,, а также большую а
и малую / полуоси эллиптической траектории частицы массы
/т2 , которая движется с энергией £ и моментом /V в
потенциальном поле притяжения V' ~ -Jr /~J .
65. Материальная точка массы т движется в
сферически—симметричном потенциальном поде U (г) , совершая
радиальные колебания между точками ^^ и /^.^^ . Определить
угол a W поворота оси симметрии траектории за период
радиальных колебаний, если:
a) U(r)=-~r+-~2> '<•><>■> f>>0'>
5) U(i-) =-^2+ $f2^ U>0, S > О .
66. Частица массы т совершает движение по квази—
эллиптической орбите в потенциальном поле Ц~.~ —^- у- -£- , где
/" /~Г
второе слагаемое является малым возмущением. Найти угол А Ч'
поворота большой полуоси эллипса за период радиального
движения .
67. Потенциальная энергия if(rj = U0 (/-'J*3~lf{p) частицы
массы rn состоит из двух слагаемых, из которьх l/(t~)
основное, a 6~U(г) малое возмущение. Найти вклад лТ в период
радиальных колебаний частицы в данном
сферически-симметричном потенциальном поле, обусловленный влиянием малого
возмущения tFlT(f-~) . Основное слагаемое if (t~) и малое
возмущение tf[f(r} имеют следующий вид:
а) 1/0 (г/ ■-= - с*/ а- , &u(f~) = a/r *;
18

6) U0(r)-:-cclr -, (Tl'(r)'-U0 {СГ0= const);
о
§ 6. СТОЛКНОВЕНИЕ И РАССЕЯНИЕ ЧЛСТИН
68. Частица движется с прицельным расстоянием /-> в
потенциальном поле отталкивания if- -~j . Ее энергия £ . Опре-
делить угол 0 отклонения частицы от начального направления
движения после пролета через силовое поле. Исследовать по—
лученный результат в предельном случае малых углов с? -«•< / .
69. Найти связь между углом рассеяния О и
прицельным расстоянием у3 для частицы с массой /^ «
рассеивающейся в сферически-симметричном потенциальном поле
п< I и <?6
</• ~ 4~- / - ■-.- -г-
.-' I /"■ /•
где 1&1-£(ftr^)''. Скорость d/^ частииь на бс-оконечностн
Задана. Исследовать полученной результат в предельном слу-ас
малых углов О « /
70. Определить связь между угчом рассеяния О и прл~
цельным расстоянием /> для частнць1, движущейся г. no'iu-
жительной энергией /, по траектории
Здесь /- и <jJ - полярные координаты частицы, гп и /V - • -
масса и модуль момента, С'— I/ / —~^ / -. постоянна,: ь;.п:-
чина, а параметры а > О и § >0 характеризуют ыи-ч-щ'.-. v.;.~
рически-симметричное потенциальное поле, которое моноточл-
стремится к нулю на больших расстояниях от центра <л:\^" т-
рии. Исследовать полученную формулу в предельном г .уин
малых углов # « / .
71. Частицы рассеиваются на абсолютно твердом
неподвижном шаре радиуса R .<-. Найти дифференциальное и полно* •
сечения рассеяния.
72. Абсолютно твердая поверхность оСраюпана зрпнчш-
ем кривой i/-f(jc/ около оси X . Найти дифференциально.'

сечение рассеяния частиц, падающих ыа эту поверхность
параллельно оси X , если:
а) у — clBSjc ~jc2) 7 О^х^гё-,
в) У - Р tkcur^ О а£ JC .
J о у
73. Однородный поток частиц падает на выпуклую
сторону абсолютно твердого параболоида вращения аз- эс/+уг
параллельно его оси симметрии. Найти дифференциальное сечение
рассеяния.
74. Частица сталкивается с абсолютно твердой
поверхностью вращения г=Р(?сг-+ уг) , где F - монотонная функция
своего аргумента и 0£ £ ^ «=> . До столкновения скорость
частицы была параллельна оси симметрии поверхности. Найти
связь между углом рассеяния О и прицельным расстоянием/*,
75. Ось симметрии абсолютно твердого эллипсоида враще-
НИЯ 2 и2 *г
а,' а. с*
расположена параллельно однородному потоку частиц.
Определить дифференциальное и полное сечения рассеяния.
76. Определить дифференциальное сечение рассеяния
частиц, движущихся с энергией <5 в потенциальном поле
отталкивания If- —_ .
г*
77. Траектория частицы в сферически-симметричном по—
тенци&льном поле V = U(h) в полярных координатах/- и (р
имеет вид
где <5 , М и /гг - энергия, абсолютная величина момента и
масса частицы, а ос - произвольная постоянная,
характеризующая функцию U= U [г) ; которая обращается в нуль на
бесконечности. Используя данное выражение для траектории в
случае 6 >0 , определить дифференциальное сечение рассеяния.
78. Определить связь между углом рассеяния (? и гри—
цельным расстоянием /> для частишь., движущейся с
энергией £ в сферически-симметричном потенциальном поле
U=Uе , где UQ и зе - некоторые постоянные, а рассеяние
происходит на малые углы О «■ / .

79. Частицы с энергией g рассеиваются в сферически-
симметричном потенциальном поле XJ- f—r » гДе ^ и <зе -
постоянные, причем UQ«&. Определить связь между углом
рассеяния 9 и прицельным расстоянием f в области
малых углов в<-<1 .
80. Найти дифференциальное сечение рассеяния на малые
углы в сферически-симметричном потенциальном поле
отталкивания V- ——J- i если частицы движутся с энергией 6
81. Электроны с массой т и зарядом е пролетают на
большом расстоянии от нейтрального атома „поляризуемость
которого р . Последнее означает, что во внешнем
электрическом поле с напряженностью iT у атома появляется
электрический дипольный момент ^~ft>5 . Определить
дифференциальное сечение рассеяния на малые углы, считая скорость ?Гж>
электронов на бесконечности заданной.
82. Частицы с энергией 6 рассеиваются на
сферической потенциальной яме 1/-а(^- -^ j при г < /? и U-0 для
Г > R • Определить дифференциальное сечение рассеяния на
малые углы, если энергия & налетающей частицы удов-"
летворяет условию la\«R£>. Убедиться, что в пределе /?-s~°~
полученное дифференциальное сечение совпадает с формулой Fe«-
зерфорда для рассеяния на малые углы.
83. Определить дифференциальное сечение рассеяния на
малые углы в случае, когда частицы с энергией 6 движутся
в сферическИ'-скмметричном потенциальном поле у~ -— у- -&- ,
у, г f~
где <х> О и ё > О .
84. Частицы с одинаковой энергией £ движутся в
сферически-симметричном потенциальном поле притяжения U~Cf(r)
с произвольными прицельными расстояниями. Определить эф—
фективное сечение
ного поля, если:
а) сг = --Щг;
в) U- а •
r2S ?
6~
б)
г)
падения частиц в центр потенциалы
u = ~~f^^-> **£>S2;
U=fz--**v 4SZ>*2.
85. Пучок электронов плотности j-0 входит в газовую
среду, состоящую из одинаковых атомов, число которых в
единице объема равно Д/. Полное сечение рассеяния электронов на
отдельном атоме равно & . Определить закон убывания плот—
21

ности J(x) электронного пучка в зависимости от глубины jc
проникновения электронов в газовую среду. Найти среднюю
длину / свободного пробега электрона.
86. Разреженный сгусток заряженных частиц вращается
по окружности радиуса Я в магнитном поле и рассеивается
на атомах газа, число которых в единице объема N .
Поперечные размеры сгустка малы по сравнению с Л* . Полное
сечение рассеяния заряженной частицы на отдельном атоме
равно 6" . Определить, во сколько раз уменьшится число заряжен»
ных частиц в рассматриваемом сгустке после гг оборотов.
87. Однородный поток нейтронов плотности }0 падает не
толстую мишень, число ядер в единице объема которой равно N „
Ядра мишени бесконечно тяжелые и распределены хаотично. Рас-,
сматривая нейтроны и ядра мишени как абсолютно твердые
шарики радиусов соответственно /?; и Rz * определить закон
убывания плотности J (x) потока нейтронов в мишени в зависимо»*
сти от пройденного ими расстояния х .
88. Частица массы т.? сталкивается с покоившейся
частицей массы т2 . После столкновения в лабораторной
системе координат угол рассеяния налетающей частиць вТ = 30°, а
в системе координат центра инерции эта частица отклонилась от
направления первоначального движения на угол в = 150°=
Найти отношение масс -—}■ сталкивающихся частиц.
т2
89. Тяжелая частица массы т>7 рассеивается на
покоившейся легкой частице массы 'пь2 . Потенциальная энергия
взаимодействия этих частиц монотонно убывает с расстоянием по
произвольному закону. Найти максимальный угол &7ггг£их
рассеяния налетающей частицы в лабораторной системе координат.
90. Частицы в виде маленьких абсолютно твердых
шариков радиуса R рассеиваются на покоившихся частицах
радиуса Я2 • Массы всех частиц одинаковы. Найти
дифференциальные сечения рассеяния d 6" и d &2 налетающих и
первоначально покоившихся частиц в лабораторной системе координат.
91. Ядра с энергией 6f и зарядом Qf рассеиваются на
ядрах с зарядом Q„ , которые до столкновения
покоились.Массы налетаюших и покоившихся ядер одинаковы. Определить
дифференциальные сечения рассеяния ds и ds? налетающих и
покоившихся ядер в лабораторной системе координат.
92. Тяжелые ядра с массой Ат(А»1)к зарядом Ze
рассеиваются на покоившихся протонах с массой т и
зарядом <? . Определить дифференциальные сечения рассеяния d6
22 я

d6 соответственно ядра и протона в лабораторной системе
координат, считая скорость ir^ налетающих ядер заданной.
93. Протоны с массой т , зарядом е и энергией £
рассеиваются на ядрах с массой А т к зарядом Ze .
Определить дифференциальное сечение рассеяния ядра,которое до
столкновения с протоном покоилось.
94. Одинаковые абсолютно твердые шарики радиуса /?
рассеиваются друг на друге. Определить дифференциальное и
полное сечения рассеяния в лабораторной системе координат
с учетом тождественности сталкивающихся шариков.
95. Однородный пучок нейтронов рассеивается на
свободных нейтронах мишени, которые распределены в ней с
плотностью /V • Рассматривая нейтроны как абсолютно твердые
шарики радиуса /? , определить число нейтронов d f^^ac >
рассеянных в единицу времени в телесный угол d&f=2jrsln j( d jf
Длина мишени / . Плотность падающего на мишень потока J0 .
Поперечные сечения пучка и мишени одинаковы и равны 0
Полное число нейтронов, рассеянных за время эксперимента,
мало по сравнению с их числом в мишени.
96. Вычислить дифференциальное сечение рассеяния
одинаковых частиц друг на друге, если энергия налетающей
частицы в лабораторной системе координат равна 6 , а
потенциальная энергия взаимодействия налетающей и покоившейся
частиц имеет вид U — -^-~ , где а, >0 .
Г*
§ 7. МАЛЫЕ ОДНОМЕРНЫЕ КОЛЕБАНИЯ
97. Найти частоту малых колебаний частицы массы пь в
одномерном потенциальном поле U~ У'Сх) , которое задано как
функция декартовой координаты дг в следующем виде:
a) U=—?t3xe) б) £/--%-— 5
х ' ' х> х >
в) U=U0(cha.x-Sjc)] г) U-U0 (вах-6ссг)) S>a.
Здесь постоянные О- , б и U0 положительны.
98. Определить возможные частоты малых колебаний
механической системы, описываемой следующей функцией Лаг-
ранжа:
23

в) 1*=?**А?г<,{е**-е*),
г) L-=cfi<p(j*-4c/if) -7 Д) t^f2f~ 2cesJ.
99. Определить возможные частоты малых колебаний
частицы, движущейся по кривой у~ У(&) в вертикальной плоско-
сти X Y . Ось Y декартовой системы координат антиларал ,
лельна силе тяжести, а заданная кривая описывается уравнен и-»
еы(л>0, 6>0):
а) у = а.(в%с3~3 вх+з) '-, б) у = лок (Вгэьг-4&х *3" ■
в) у = & 3vtz v<x,
100. Частица массы т. и заряда <? движется по npt ч
moiIj наклоненной к силе тяжести под углом £■ . В некотор-..;;
точке указанной прямой закреплен одноименный заряд £0 , к<" -
торый препятствует неограниченному падению частицы. Опреде ,
лить частоту малых колебаний частицы вблизи ее равновесног ,
положения.
101. Взаимодействие двух частиц с массами т.7 и гпг ■,
свободном пространстве описывается потенциальной энергии'
U-Bf , где о >0 , а /~~ расстояние между частицами.
Считая момент М частиц отличным от нуля, найти частоту маль,•
радиальных колебаний.
102. Невесомые пружины с коэффициентом жесткости /■•
и кг расположены на вертикальной прямой» параллельной сил:
тяжести. Одним концом пружины прикреплены к материальна •
точке с массой w , а их противоположные концы закреплень ,
В начальный момент времени t~0 материальная точка
покоилась, а пружины были не натянуты. Найти малые колебал*.,
системы.
103. Упругая струна длины Р натянута силой F0 ''
расположена перпендикулярно силе тяжести. На середине струн-.
прикреплена материальная точка с массой гп , которая в
начальный момент времени £~Q была отклонена от положение
равновесия на расстояние р^ и покоилась. Найти малые
гармонические колебания материальной точки, пренебрегая массой
струны и изменением ее начального натяжения.
24

104. Нижний конец маятника длины С и массы т.
прикреплен к середине тонкой пружины с коэффициентом
жесткости к 12 i которая имеет форму полуокружности радиуса /е-/
с центром в точке подвеса маятника и лежит в плоскости
колебания. В положении равновесия пружина не натянута.
Определить малые колебания маятника в поле тяжести, если в
начальный момент времени t•=■ О он был отклонен от вертикального
положения равновесия на угол <pD и покоился.
105. К свободному концу плоского маятника длины Л и
массы
конец
т прикреплена невесомая пружина длины е.
р.
Рис.
жении
лой Р^
времени
Другой
этой пружины закреплен в точке, лежащей на
вертикальной равновесной прямой ниже маятника
(рис. 2). Когда маятник занимает
вертикальное положение, пружина натянута силой F
Определить гармонические колебания маятника
в поле тяжести, если в начальный момент
времени £-0 он был отклонен на малый угол <р
и покоился. Изменением натяжения пружины
при колебании пренебречь.
106. Один конец невесомой пружины
закреплен, а другой прикреплен к материальной
точке с массой -*rz , которая может
перемещаться по прямой, перпендикулярной равно-
2 весному положению пружины (рис, 3}„ В поло-
равновесия пружина имеет длину £' и натянута си—
. Найти малые колебания, если в начальный момент
£ = 0
материальная течка находилась в
положении равновесия и имела скорость V0 .
Изменением натяжения пружины при
колебании пренебречь.
107. К свободному концу невесомой
пружины с коэффициентом жесткости к
прикреплена материальная точка массы т ,
которая может перемещаться по прямой,
перпендикулярной равновесному положению
пружины (см. рис. 3). В положение
равновесия пружина имеет длину f и не
натянута. Найти малые колебания
материальной точки, если в начальный момент
времени t - О она была отклонена от
положения равновесия на расстояние jc0 и покоилась. Ответ
представить в виде интеграла.
25
Рис. 3

108. В начальный момент времени t=0 частица массы
гп находилась в положении равновесия и имела скорость гг ,
направленную вдоль оси Я . Найти малью колебания, если
внешнее потенциальное поле имеет вид
U(xh*
U0 агхг
при
U о л> при
109. Плоский маятник длины С и массы ггг-
совершает колебания в вертикальной плоскости XY . Причем его
точка подвеса с координатами jc0 и у0 колеблется вдоль
горизонтальной прямой Х0= const no заданному закону и = acosSlt.
Найти малые колебания плоского маятника, если в начальный
момент времени t = О он был отклонен от вертикали на угол
Ро и покоился.
110. Одномерный осциллятор с массой г™ и частотой сО
до начального момента времени
t=0
покоился в равновесном
положении. Найти его закон движения, если в начальный
момент времени включается сила F~fF
единичный вектор, a F имеет вид:
t
где е -
постоянный
а)
б)
в)
г)
F = Fo (Г+т)'>
F=F0 ch cot;
F = Foe
at
$£П UL>t 7
F COS uH1 при
F>
Г F
Д) F~<
О
Ж
при
< t
При О *= t ^ ^J" 9
cO.
e)
F =
о
F„ при О £= / ^ T,
ipn
при
О —о
О при
T^t.
26

111. Первоначально покоившийся в равновесном
положении одномерный осциллятор с^массой т _^и частотой со0
подвергся действию силы F- £F , где в - постоянный
единичный вектор. Определить энергию <5 , приобретенную
осциллятором за все время -<=*>^t£ ««» действия силы, если:
-4 z2F
а) F=F0e ** у б) F=-jj^p •
112. Сдин конец пружины с коэффициентом жесткости £
совершает продольные колебания по закону ?с0= <х co&(a>t+oc)9
а к другому концу с координатой Х- прикреплена
материальная точка массы т , которая может перемешаться только
вдоль оси X i совпадающей с осью пружины. Определить
установившиеся колебания материальной точки при наличии силы
трения / =-£*? ^ У^ • ^ _^
113. Под действием внешней силы F~= ^F03£rt((Vt +<?с)
осциллятор совершает установившиеся колебания вдоль оси Л
при^галичии силы трения j^-ty.rnfx t где их - орт оси X ,
а £сх — его скорость. Масса и частота осциллятора равны
соответственно т и с00 . Длина ненатянутой пружины равна £0 .
Определить потерю энергии на трение в единицу времени в
среднем за период колебаний.
114^_ В области /•*><? на осциллятор действует внешняя
сила Р^е^^е sin- cot . Определить вынужденные колебания
осциллятора массы т и частоты €00 при наличии силы
трения Т^-^^Г^ , где^ Т-С- орт оси X , вдоль которой
колеблется осциллятор, а l^x, - его скорость.
§ 8. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ
СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
115. Определить частоты малых колебаний частицы
массы rrvf движущейся в поле тяжести по поверхности j?~z?(jc?y) .
Ось Z декартовой системы координат антипараллельна силе
тяжести, а поверхность описывается уравнением:
б) г=-^|/7-^f-^ \ 0<zo>\x\<a,\y\<b-)

116. Определить частоты колебаний механической
системы, которая в обобщенных координатах описывается следующей
функцией Лагранжа:
а> ^HhH,V€*9>11-г if,*Ь %+&%%* fi);
б» *=Hi> ihhffril)~i(fr<&■> i%wV,;
D t.°i(ti+g+je%* Ц) - Ktf+f ь v ф £).
117. Представить обобщенные координаты в виде суммы
нормальных колебаний, если механическая система описывается
следующей функцией Лагранжа:
в) i-if-*i,4*-§■ $*-fфз9г%уг9f;
D i-" i (iff* Ц, аг +3tf)- J Gф ЮЬ %t г,*,).
118. Механическая система совершает малы*.- колебания
около положения устойчивого равновесия. Представить это
движение в виде суммы нормальных колебаний. Функция Лагранжа
данной механической системы имеет вид;
а) л -- fdfif < 9f jfj- i(jy> -^ + гь h) ■>
B) >- = i%ff+H,%* -t f&+ iif-H+ ifi&
119. Найти колебания механической системы, если
функция Лагранжа и начальные условия при f = О имеют вид:
28

б) t-Ч(&№**№' г ЬНъ^гУН/Н/0^ 'ti°№;
r) l=tf+2Jff/f*'*f?-2& f,W^(ohfa(oh07 f2(oj= | -
120. Противоположные концы пружины прикреплены к не.»
подвижным стенкам. С пружиной скреплены две материальные
точки с массами /тг/-/тг и /п2~2т , которые делят пружину
в положении равновесия на три части с одинаковыми
коэффициентами жесткости}{рис. 4). Под действием упругих сил
материальные точки могут перемещаться только вдоль прямой,
проходящей через закрепленные концы пружины. Представить
движение материальных точек в виде суммы нормальных коле»
баний.
Рис. 4
121. Невесомая пружина с коэффициентом жесткости A/j
расположена вертикально е поле тяжести. Ее концы закреплены.
На пружине находятся две одинаковые материальные точки с
массами т , которые делят пружину в ненатянутом состоянии
на три равные части. Представить движение материальных
точек в виде суммы нормальных колебаний.
122. Две пружины одинаковой длины f , но с разными
коэффициентами жесткости kj и кг , расположены на одной пря«.
мой. Одним концом они прикреплены к общей материальной
точке с массой тг % а их противоположные концы — к
материальным точкам с массами ту и пг^ (рис. 5). Под действием
пружин материальные точки могут двигаться только вдоль
ш. т*
л "Ч ' g
Рис. 5
29

прямой, на которой расположены пружины. Полагая /77,— ггъ
т3-~ 2т » и к _у - 2 К^ 2/71 СО'представить движение
материальных точек в*"внде суммы нормальных колебаний.
123. Пружина свернута з ви-
'*/ дэ тонкого кольпа. точка О которого
^■^Ц^^-Ч* неподвижна (рис. 6). К этой пружи*---
* %. не прикреплены две материальные
X точки одинаковой .классы /-п.^~ т -n~,f
\ которые вместе с неподвижной точ-
Ж if?
г "'У коч кольца делят пружину в равно»
ffb л ■$ веснсм состоянии на три части с
jt оди"чакоаыми коэффициентами жест-
: 1ри движении материальные
точки, могут перемещаться только пс
Рис, 8 контуру кольца. Плоскость кольиа
неподвижна, а его радиус не
меняется, Определить .-закон- движения материальных точек, если v
начальный момент времени t~ О они находились в
равновесном положении и имели линейные скопости VI - "'/L и ~j/i -~ О
—*. * / о з
где вектор 1/ направлен по касательной к кольцу в
противоположную сторону от его неподвижной точки.
124. Невесомая пружина имеет коэффициент
жесткости к/2 . Один конец пружинь. закреплен,
а с ее середине и да противоположном конце
находятся материальные точки одинаковой массы т.
Пружина все время занимает вертикальное
положение в поле тяжести (рис. 7). Определить закон
движения механической системы, если в начальны*,
момент времени t-О пружина была не натянута,
а материальные точки покоились.
125. Двойной плоский маятник совершаем
малые колебания в поле тяжести (см. рис. 1 ).
Длины его звеньев одинаковы Р — Р? = Р , а массы
материальных точек различаются в два раза.'/гг^— т. и тп^=: 2пг .
В начальный момент времени t ~ О оба звена маятника
были отклонены от положения равновесия на один и тот же угол
W « / , а сам двойной маятник покоился. Найти закон
движения двойного маятника.
126. Длинная пружина имеет форму окружности большого
радиуса (см. рис. 6). Точка О пружины под действием внеш-
30

° силы совершает малые колебания вдоль окружности по
заданному закону yo~CLCCSrtt% где ^ - отклонение от положения
авновесия. К пружине прикреплены две материальные точки,
массы которых различаются между собой в два раза:/?"г;-/тг
-^ -2гтг, Коэффициенты жесткости всех трех звеньев
пружинь? одинаковы и равны к . Под действием упругих сил ма~.
еоиальные точки могут перемещаться только вдоль окружности,
сложение которой в пространстве остается неизменньм,
Определить вынужденные колебания материальных точек, если
частота ей не является собственной частотой механической
системы.
127. К нижней материальной точке системы из^ двух
пружин, изображенных на рис. 7, приложена сила F~Fe С OS cot „
где вектор FD направлен вдоль вертикальной прямой
параллельно силе тяжести. Коэффициент жесткости каждой пружины
равен к . Определить вынужденные колебания материальных
точек под действием силы W б отсутствии резонанса.
128. Левая 5С0* и правая зсог точки закрепления
пружин, изображенных на рис. 4, совершают продольные колебания
по закону соответственно а:ог - Яу с&$ &7 £ и ооог =d2 cosQa t .
Коэффициент жесткости каждой пружины равен к . Найти
вынужденные колебания материальных точек в отсутствии
резонанса, считая их массы одинаковыми т, = т^, => т .
129. Две материальные точки с массами т.*и
/"тг^скреплены пружиной с коэффициентом жесткости к ,
расположенной параллельно оси X декартовой системы координат.
Определить вынужденные колебания под действием гармонических
сил ^^exFOJco5{^7t +JS7 ) и % = Гх F0£ соэ(pzttfg,
приложенных к материальным точкам соответственно т^ и тг ■
Частоты Q и <^L не совпадают с собственными частотами
колебаний данной механической системы} a tx -орг осп X.
130. Две материальные точки с одинаковыми массами т-
-т^^гп прикреплены к длинной пружине, свернутой в виде
окружности большого радиуса (см. рис. 6). Точка О пружины
совершает малые колебания вдоль окружности по закону A^'ЛС05(цЬ
где fyo "* Уклонение от положения равновесия. Коэффициенты
жесткости всех трех звеньев пружины одинаковы и равны к .
j материальные точки могут перемещаться лишь вдоль
окружности, положение которой в пространстве остается неизменным.
К материальным точкам приложены силы трения
соответственно j-j гпу£ и J. - -/-к у A t которые направлены по
касательной к окружности и пропорциональны скоростям су и Q, дви-
31

жения. Здесь а, и ^ - отклонение материальных точек оа
положения равновесия. Определить установившиеся колебанш
мате риал ьных точек в отсутствии резонанса.
§ 9. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
131. Частица массы т движется по кривой </'(&} в
вертикальнГой плоскости ХУ • Ось У декартовой системы ко.*
ординат антипараллельна силе тяжести. Найти малые нелиней»^
ные колебания с учетом первой отличной от нуля поправки,
обусловленной нелинейностью уравнения движения, если в началь»
ный момент времени t - О частица находилась в положений
равновесия к имела скорость г^ , направленную вдоль оси X -
Рассмотреть случаи:
а) у- -&г t ёх7 а>о1 &>о-у б) у ~cb£nj^+c3Cj a>o-7
в) у = а,(-£?--£-), а£>о.
132. Функция Лагранжа осциллятора с учетом малых
подправок имеет вид
L = ~2~ ( х - &J0X J + ~з~^л + ~YftJC .
В начальный момент времени t-О осциллятор покоился, а
отклонение от положения равновесия было M&n.o:x,(Gj=a. Найтг
ангармонические колебания с учетом первой и второй лоправо;:
к амплитуде и соответствующей поправки к частоте,
133. Найти малые ангармонические колебания плоского
маятника длины £ и массы т с учетом первой отличной o-i
нуля поправки к амплитуде и соответствующей поправки к час»
тоте„ В начальный момент времени i = О маятник был от»
клонен от положения равновесия на малый угол ^ и покоился..
134. Механическая система с одной степенью свободы
описывается функцией Лагранжа
где аЭ0 , сС и р — постоянные. Определить малые нелинейные
колебания с учетом первой и второй поправок к амплитуде и
соответствующей поправки к частоте, если начальные условия
при /.= *? имеют вид: f (G)= О и ф(а/=2Г.
32

Глава II
ГАМИЛЬТОНОВА МЕХАНИКА
§ 10. УРАВНЕНИЯ ГАМИЛЬТОНА
135. По заданной функции Лагранжа L найти функцию
Гамильтона «# в следующих случаях:
a) * = 7/fc~i?/*5
в)
L=-Vf-irff+$1u-
136. Найти функцию Лагранжа L , если функция
Гамильтона 3€ имеет вид:
б) ^_с у^г^^ г , где т и С -
постоянные;
в) *=p?+rfra-
137. Протон с массой т, и зарядом <? движется в
кулоновском поле неподвижного ядра с зарядом Ze •
Определить функцию Гамильтона данной механической снстемы в
сферических координатах.
138. Частица массы т движется по поверхности
параболоида вращения X +<Г= & z , Ось Z антипараллельна силе
тяжести. Определить функцию Гамильтона, используя
цилиндрические координаты.
13 9. Частица с массой т и зарядом £ движется в
произвольном электромагнитном поле, кот-орое описывается
векторным А и скалярным ^ потенциалами. Используя функ«*
цию Лагранжа заряженной частицы
L - ^ гР? -§■ X"ir- e f 7
найти ее функцию Гамильтона: а) в цилиндрических координа—
3-501
33

тах; б) в сферических координатах. Здесь с —
электродинамическая постоянная, равная скорости света в вакууме,
140. Написать уравнения Гамильтона для частицы с
массой tn. t движущейся в поле тяжести по поверхности конуса с
углом 290 при вершине. Вершина конуса направлена
вертикально вниз по направлению силы тяжести. Использовать
сферические координаты,
141. Написать уравнения Гамильтона для материальной
точки с массой т. , движущейся в поле тяжести по
поверхности сферы» радиус R которой как функция времени меняется
по заданному закону»
142. Обобщенный импульс /=> механической системы с
одной степенью свободы связан с энергией S соотношением
p = tkb . Представить обобщенную скорость q, как функцию
энергии.
143. Используя функцию Лагранжа
L = i^ ^^ -jr*'^- е v
для частицы с массой пг и зарядом & , которая движется в
электромагнитном поле, определить гамильтониан ^€ этой
частицы и написать уравнения Гамильтона в декартовых
координатах. Здесь с — скорость света, а векторный // и
скалярный У потенциалы электромагнитного поля произвольно
зависят от декартовых координат и времени. Показать, что из
полученных уравнений Гамильтона вытекает уравнение Ньютона,
в правой части которого стоит сила Лоренца г—д^/Г+^гР^Н ) «
где напряженности электрического £ и магнитного /7" полей
связаны с электромагнитными потенциалами следующим
образом: Й'=-^гас/ч,~-^- f^ , fT=t-otT
144. При помощи уравнений Гамильтона, написанных для
радиус—вектора /~~ и обобщенного импульса }=> заряженной
частицы в постоянном магнитном поле /г , показать, что
проекция момента М —Г~*Р на направление вектора /7"
сохраняется.
145. Проинтегрировать канонические уравнения
механической системы с одной степенью свободы, если функция
Гамильтона $ в безразмерном обозначении и начальные условия
при t - О имеют вид:
а) Я = -$-P*W> $(Oj=r, p@l = 0-
34 б) %-V}+F* -$, $(oj*r, p(o)=o.

146. Используя уравнения Гамильтона и закон сохранения
ергии, найти канонически сопряженные переменные q и/э.ес-
функция Гамильтона Л в безразмерном обозначении и
начальные условия при t=0 заданы:
б) *~^У^ ' ?'"■'-'' ^"'-^
147, Проинтегрировать канонические уравнения
механической системы с двумя степенями свободы, если функция Га~
мильтона <% в безразмерном обозначении и начальные
условия при t=# имеют вид:
б) %=-—=£=—-*, <цо)*р2(о)*?7%(о1 = р(о)=о.
148. Проинтегрировать уравнения Гамильтона для частицы
с массой т и зарядом е , движущейся в постоянном
однородном магнитном поле с напряженностью И . Векторный
потенциал А магнитного поля выбрать в виде А^/ЬО'и А а-Их. ,
где ось Z декартовой системы координат направлена вдоль
вектора И . Начальные условия произвольны.
§ 11. СКОБКИ ПУАССОНА
149. Проекции Мх и My момента М ~ Р~ *р~ сохраняют
постоянное -значение при движении частицы в
сферически-симметричном потенциальном поле U= If (r) . Используя
сохраняющиеся величины Мх и /Vy , найти еще один интеграл
движения при помощи теоремы Пуассона.
150. Вычислить скобки Пуассона f М^ л~} , (М^fyfи £м/ЧЛ
составленные из декартовых компонент радиус-вектора /*" ,
импульса f> и момента М~ Г •*• р материальной точки.
151. Дано, что } = ЦсЕР) и y^f/cC^-. произвольные
функции своих аргументов, а Я^ , р~ и М'-г~*]^ - соответственно
радиус-вектор, импульс и момент частицы. Считая <2
постоянным вектором, определить скобки Пуассона:
35

152. Пусть Ж и 8 — постоянные векторы, a f=f(r^ /S~J и
P=F(f^ /3 - произвольные дифференцируемые функции радиус-
вектора /*"" и импульса р~ материальной точки. Вычислить
скобки Пуассонаг ^ _ . . г^.-*л
«о {is-»),я>~;, {(-<?>*;, (Гр-)/}, {(*п (ffit}.
153. Путем вычисления соответствующих скобок Пуассона
доказать, что момент АГ= Р~* W сохраняется при движении
частицы в централ ьно«симметричном потенциальном поле U=U(r}°
154. Убедиться в том, что для частицы массы ni , дви-
жущейся в сферически-симметричном потенциальном поле U(r) -
~ ~р~гг , скобки Пуассона, составленные из величин f»f-f?~*'p~ s
Т*р= ю?и?&Фа~:Ъ1-:^ъ ^^p~^j + 'р'?'" » удовлетворяют
соотношениям:
где индексы сС и f> принимают значения от 1 до 3, отме«-
чая проекции векторов F~ и ,р" на декартовые оси
соответственно X , Y и Z , a S., , /f, и f7 - орты этих декартовых
ч. 7 2 о
осей.
155. Специфический интеграл движения в иулоновском по-»
ле Z/= ^L имеет вид: J*^ -£- (/&"* /£f) + <*Hl , где jf , ]$~ п // -» ра-=
диус-вектор, импульс и момент частицы с массой m .
Определить скобки Пуассона, составленные из декартовых
компонент указанных векторов:
{&ъ}> {*-<Ы' 1****), {*«/,}•
156. Представить уравнения Гамильтона £^= ~^~ и/^.---^^
{ ос = 1, 2, ..., Д- ) механической системы с А степенями
свободы в следующем виде:
157. Функция Гамильтона Ж равномерно заряженного вра~
шающегося шара в однородном магнитном поле с напряженностью/-/
36

записывается как 2
I - момент инерции шара, И - момент шара относи-
ГЯльНО его центра, а у - гиромагнитное отношение. При по-
•оши формулы для производной по времени, написанной через
обки Пуассона, составить уравнение движения для вектора
158. Гамильтониан Ж частицы с массой т и зарядом
<° которая движется в произвольном электромагнитном иоле,
имеет вид ^
Здесь Д"- обобщенный импульс частицы, а /? и <f -
электромагнитные потенциалы, являющиеся функциями декартовых
координат и времени. Вычислением скобок Пуассона найти
явный вид уравнений Гамильтона
159. Частица массы т и заряда е движется со
скоростью ZA" в произвольном магнитном поле //- f'Ot А ,
которое описывается векторным потенциалом А . Взяв в
качестве канонических переменных компоненты обобщенного им—
пульса Р-Р , Р= Р и/5~^ »а также декартовые
координаты jCr = jc , zCg~ г/ к эс,=£ , вычислить скобки Пуассона
§ 12. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
160. Написать формулы канонических преобразований от
старых переменных £ и р к новым Q и Р в тех
случаях, когда производящая функция зависит от указанных
переменных следующим образом: a) F~F(a,; Q,t) ; б) Gr-Cr (*},%£} \
B)V=<P(p,Q9t J ; г) Ф = ф(р,Ру t) • Здесь 0 и /> , а
также Q ж р обозначают совокупности канонически сопря—
женных переменных, описывающих механическую систему с
некоторым конечным числом степеней свободы.
161. Используя формулы канонических преобразований с
некоторой производящей функцией, доказать, что якобиан
перехода от канонически сопряженных переменных f и р к
другим канонически сопряженным переменным B и Р равен
единице.
3 7

162. Доказать, что скобки Пуассона {л в } , составлен»,
ные для произвольных функций /1 ~A{p;f>?fJii B-Btf'fifJtmiB&pMai;*
тны относительно канонических преобразований от одних канс
нически сопряженных переменных а, и р к другим <£ г.
Р , а именно:
{а в I - Ыз }
L JPf - PGL '
163. Доказать, что преобразование
от канонически сопряженных переменных f и /= к други ».
переменным Q и Р является каноническим.
184. Найти каноническое преобразование от переменных ?
и р к новым переменным i< и Р , которое характерна;;.^
ется производящей функцией
165. Каноническое преобразование от переменных $ и /
к новым переменным 1< и Р определено при помои;и прсиз-
всдяшей функции Cr(f7P)=P е~* - Найти производящую фунь-
цию вида F-p(ftA) , которая приводит к такому же
каноническому преобразованию.
166. А'еханическая система состоит из материальной тс- -
ки массы m , движущейся в произвольном внешнем потевщ.-
альном поле U'-U(&~/. Определить производящую функцию Сг
бесконечно малого канонического преобразования от перемени! х
Й~ и /?" к новым переменным Я и Р , которое
представляет собой:
а) параллельный сдвиг механической системы как целен :
на величину fret ;
б) поворот механической системы как целого на угол о"^ •
в) сдвиг во времени на величину $Т ;
г) переход от одной инерциальной системы кооодикат i.
другой, движущейся со скоростью frV •
167. Преобразование подобия представляет собой перех-. J
к системе отсчета8 в которой масштаб декартовых осей
увеличен в А/ раз, а маси>аб времени увеличен в /V раз. В
случае частицы, движущейся во внешнем поле, указаннокгу лреоО
разованию подобия отвечает переход от канонически
сопряженных переменных pup к новым переменным /?~ и р
Убедиться в том, что данное преобразование к переменным R
и Р является каноническим и найти его производящую функ-
38

О- которая зависит от переменных ли/3.
^ 1 6*8 Функция Гамильтона гармонического осциллятора
имеет вид ^ ^г ^^г
•a <-lJ - масса и частота колеблющейся частицы. Напи—
рде /т2 и t*/ .
функцию Гамильтона Я? и уравнения 1амильтона в ноеых
°анонически сопряженных переменных в> и Р , взяь в
качестве производящей функции следующие выражения:
a) r(t,a) = imc01'ifc4b\
6) *(f,n~^', в) ^(Л^^~
169. Показать., что преобразование от канонически
сопряженных переменных <p(t) и p(t) к новым переменным
в случае гармонического осциллятора является
преобразованием вращения в фазовой плоскости. Здесь Т- произвольный
фиксированный промежуток времени. Убедиться в том. что это
преобразование является каноническим я найти его
производящую функцию Ф , зависящую от переменных р и F* .
170. Частица движется вдоль оси X в одномерном
потенциальном поле. Изменению масштаба X-fi&y t) на оси X
соответствует в фазовом пространство переход от старых
канонически сопряженных переменных х. и р к новым
переменным X и .Р . Определить связь между старыми и новыми
переменными. Доказать, что переход к переменным X и р
представляет собой каноническое преобразование. Найти
производящую функцию Сг этого канонического преобразования, за-»
висящую от переменных jc и Р .
171. Известно, что переход от одной функции Лагранжа
L($,j>,t) к другой
не изменяет уравнение движения для переменной ср . Здесь/^£/-
нроизвольная функции обобщенной координаты и времени. С
другой стороны, замене функции Лагранжа L(f, ft t) на новую
L (fifi?/ в фазовом пространстве соответствует переход ст пе~-

ременных f к /> к новым переменным & yl Р . Опреч
делить связь между этими переменными. Доказать, что переход
к переменным Q и Р представляет собой каноническое пре„
образование. Найти производящую функцию Q- этого каноничес»,
кого преобразования, которая зависит от переменных #. и Р
§ 13. МЕТОД ГАМИЛЬТОНА - ЯКОБИ
172. Найти действие 0 как функцию координат и вре.
мени для частицы массы п-г , движущейся: а) в поле тяжест-,
по сферической поверхности радиуса А \ б) по поверхности
конуса с углом 29 при вершине, ось симметрии которого па рал.
лельна силе тяжести, а вершина направлена вниз; в) в потен«.
циальном поле С/--^~у- , где а- постоянный вектор.
173. В переменных а та. о гамильтониан осциллятора
имеет вид:
г 2
р т и) 2
Найти производящую функцию Cr ~-Q(f7P>^} каноническог ■
преобразования от переменных f и /> к таким канонически
сопряженным переменным B и Р % для которь х
гамильтониан осциллятора обращается в нуль тождественно.
174. Частица с массой m и зарядом <? движется
постоянном однородном _магнитном поле с напряженностью Н
Векторный потенциал А магнитного поля имеет следующи
компоненты: А^~/47 =0 и Аи~^х- Определить действие $ ка
функцию декартовых координат и времени.
175. Постоянные однородные электрическое В и магнит»
ное Н поля взаимно ортогональны. Выбирая электромагнит*
ные потенциалы А и У данных скрещенных полей а вид.
A^-Ag-О , Лу-tf-c и f--^^* , найти полный интеграл урав»
нения Гамильтона — Якоби для частшш с массой m и заря.*
дом (?
17 6; Векторный потенциал А постоянного однородного
магнитного поля в цилиндрических координатах имеет
следующие компоненты: А^~А = о> и Ау~ ~j>Hr. Найти полный интеграл
уравнения Гамильтона - Якоби для частицы с массой пг. и
зарядом <? ? которая движется в заданном магнитном поле.

177. Используя соотношения
Рп > ri = f,...,k,
at "•> <9f.n
также уравнения Гамильтона, доказать, что производные от
действия 0=$(£,?1У->$м}с*п.<., сск) по произвольным постоян-
ым ^ являются интегралами движения
-£-£_ = свл $t, /яг /, ,.. к .
178. Методом Гамильтона - Якоби определить ьакон^
движения частицы массы т, в однородном силовом поле/\ Ось
Z параллельна вектору F , а начальные условия при t~o
имеют вид: jc(o)*x0 % у(а)= Уд • £(Q)^Z0 *x/0)*(rf, yf°)=V:
и ilo)*Vb , гдеср<7.
179. Механическая система характеризуется функцией
Гамильтона
x-H&ff+rfkutyb.b)-
Методом Гамильтон - Якоби найти закон движения
механической системы, если функция U-lf(aJ,Qm начальные условия
при t=0 имеют вид: '
а) V=ff-t*+-£r,
б) TJ- ~ * ? ?
Ь'Ъ
у
Ц°Нг(°)=ъ t°^G> W^bW^U0!'-- ?;
В) i/=-—^—+ik2a ,
CQS'Q d Ь '
41

180. Частица массы гп движется в
сферически-симметричном потенциальном поле притяжения и = -kcif~ - В начальный
момент времени t0~ О она имела координаты jo@) ~JC0 и У@)~
= Е@)-0 и проекции скорости V^.((?)-?/} %Уу@)*Уг и V^@}-G.
Используя метод Гамильтона - Якоби, найти закон движения
частицы в декартовых координатах,
181. Материальная точка массы т движется по
окружности радиуса R f которая расположена в вертикальной
плоскости в поле тяжести (математический маятник). При по»
моши метода Гамильтона - Якоби найти закон движения
математического маятника в квадратурах. Начальные условия
произвольны.
182. Электрон с массой гп и зарядом е движется в
поле электромагнитной волны, которая описывается векторным
потенциалом A ^A0cos (oof. - *Гt~), Используя метод
Гамильтона - Якоби, найти закон движения электрона, если в начальный
момент времени t= О электрон находился в начале декар«
товой системы координат и имел нулевую скорость. Исследовав
ние провести в течение промежутка времени, пока поперечные
размеры области движения малы по сравнению с длиной волны
183. Частица массы ггг движется в плоскости XZ в
потенциальном поле V-ct(f-)t -^Щг, raectfrj и В (в) - произ-
вольнье функции сферических координат г и & . Используя
метод Гамильтона — Якоби, выразить траекторию частицы
через квадратуры. _^
184. Диполь с моментом d создает в пространстве
электрическое поле с потенциалом f =Л~^. „ в электрическом
поле диполя рассеивается протон с массой гп и зарядом с •
До рассеяния протон двигался с прицельным расстоянием р к
имел скорость IP , антипараллельную вектору а . Выразите
траекторию протона через квадратуры. В случае далеких про**,
летов протона с большой энергией 6 определить траекторию
в аналитическом виде путем разложения полученного выражения
в ряд по малому параметру ed/s р* « 7
185. Рассеяние частиц г.роисходит в потенциальном поло
& ~ ~^г f 161 » где г и 9 - сферические координаты., 5-
постоянная, а ■?■(&} — некоторая безразмерная функция. На бес-~
конечно большем расстоянии от силового центра скорости
частиц актипараллельнь; полярной осп Z сферической системы
42

координат. Прицельное рассеяние f и энергия 6 каждой
частицы удовлетворяют неравенству Sp2»S ■ Определить
дифференциальное сечение cL(T(у.) ' рассеяния на малые
углы %<*1 t если функция f(pj имеет вид:
a) f(9)sSine; б) f(e) = scn?e- ъ) fF)=case.*-'
§ 14.АДИАБАТИЧЕСКИЕ ИНВАРИАНТЫ
186. В качестве одномерного осциллятора служит
частица массы ггь , которая движется в потенциальном поле 11= 9^~.
Энергия осциллятора 6 - Определить адиабатический инвариант
I осциллятора двумя способами: 1) путем вычисления
площади, ограниченной замкнутой траекторией в фазовой плоскости;
2) при помощи вычисления интеграла, который входит в
выражение для адиабатического инварианта.
187. Упругий шарик подскакивает на высоту ,4 над
жесткой плитой, совершая периодическое движение в поле тяжести.
Определить адиабатический инвариант X этого шарика.
188. Частица массы т совершает периодическое
движение в одномерном потенциальном поле XJ~ Uix) . Представив
период Т движения как Функцию энергии <S , определить
адиабатический инвариант I частицы при помощи соотношения
2Я - с ~ Т D следующих случаях:
a)i/^_J^__ б) z/^l/j/ax- в) 1/--{/р(еа-/}*
COS2OJC 1 ° I
189. Частица движется в одномерной прямоугольной
потенциальной яме:
о при а*\х\ + е,
U(x)= <
[
Uc при
С момента времени i —О протяженность ямы
адиабатически уменьшается по закону С - £ - ]/t • До изменения
потенциальной ямь' энергия £0 частииы ~не превышала выесгы потен-
циального барьера g *с 1/0 . Найти момент времени t , koi an
энергия частицы достигает высоты потенциального барье;*1.

190. Частица движется в одномерной потенциальной
с бесконечно высокими стенками:
при 0<&\х\<е,
лме
Щ{'~
-<Г
€
\х I \
е I
При ?■<. \#\ ,
Внутри ямы имеется потенциальный барьер высоты Ц& , кото~
рый разделяет между собой неглубокие потенциальные ямки
меньшей протяженности (рис. 8). С момента t~0 высота бары»
ера медленно увеличивается по
закону IL-U (l + -^iF-) « До изменения по=-
тенциального поля энергия £ части—
цы была выше высоты потенциального
барьера 60 >UQ. Найти момент
времени / , когда частица захва—
тывается одной из двух потенциаль—
.,. AJX ных ямок.
X 191. Маятник совершает малые
колебания в наклонной плоскости,
которая составляет угол оС с направо
лением силы тяжести. Амплитуда ко—
. Определить амплитуду Тр колебания
маятника после того» как угол наклона плоскости колебаний
адиабатически медленно изменится до значения р .
192. Под действием пружины шарик совершает
гармонические колебания с амплитудой (X . С течением времени
коэффициент к жесткости пружины медленно уменьшается.
Определить закон изменения амплитудь: колебания шарика в
зависимости от к
193. Маятник совершает малые колебания в поле
тяжести. Максимальный угол отклонения маятника иг вергикали
составляет величину уу , Длина € маятника адиабатически
меняется со временем. По какому закону изменяется угол ^
при изменении длины в маятника '
194. Частица массы т движется внутри бесконечного
цилиндра с упругими стенками. Определить закон изменения
энергии £ частицы, если радиус R цилиндра изменяется
адиабатически медленно.
195. Частица движется внутри сферически
потенциальной ямы: г
0
Рис 8
лебания маятника Ф
U (г)
О
при
при
- симметричной
44

С момента времени t-О радиус потенциальной ямы медленно
меньшается по закону/?- К0- Vt . До изменения радиуса R
еогия частицы составляла величину £о . Найти момент време-
/ когда частица покинет потенциальную яму.
° 196. Механическая система совершает колебания вблизи
оложения устойчивого равновесия. Найти адиабатические
инварианты механической системы, если она описывается
следующей функцией Лагранжа:
191. Заряженная частица движется в постоянном
однородном магнитном поле. Доказать, что поток магнитного поля
сквозь поверхность, натянутую на замкнутую траекторию
поперечного движения, остается постоянным при адиабатическом
изменении магнитного поля.
198. Гамильтониан частицы с массой т и зарядом е
в постоянном однородном магнитном поле с напряженностью Й~
имеет вид ■?
где /Г- векторный потенциал магнитного пояя, а с - скорость
света в вакууме. Выбрав векторный потенциал X в виде Ajc-
= Ag=0 и Ay = Их , вычислить адиабатический инвариант/
заряженной частицы в магнитном поле. Пользуясь полученными
формулами, убедиться в том, что центр круговой траектории
частицы в поперечной плоскости смещается при адиабатическом
изменении модуля напряженности магнитного поля.
199. Магнитный момент ас создает в пространстве
магнитное поле, векторный потенциал которого имеет вид А ~
- р.з • В экваториальной плоскости /гср~=- о движется
частица с массой пг и зарядом е . Исследуя
адиабатические инварианты заряженной частицы, определить закон
изменения ее энергии <f при медленном изменении модуля вектора^ .
200. Напряженность постоянного магнитного поля в
цилиндрических координатах имеет вид: JT-Й~0 +ff'(г г) , где
первое слагаемое не зависит от координат и велико по
сравнению со вторым И0»\Н~'[г?2)\ . Малое слагаемое /Г(r9Z)
выражается через произвольную функцию f(£) следующим
образом:
45

где 7Z и ^г -■ °PTbi цилиндрической системы координат (£.||,-
В данном магнитном иоле движется частица с массой т , з< ,
рядом 6 и энергией £ . Движение заря жен ной частицы мож* ,
рассматривать как сложнее, состоящее из движения ь лонере: .,
к>">й плоскости и перемещения вдоль ос>- Z вместе с поперек ,
ной плоскостью. Пусть первое движс-^ле быстрое, а второе
медленное. При помощи адиабатического ил варианта, отвечав -
щего погеречному движению, v-a.k:.-- :?£кок '^о^енения энергии ^
поперечного движения б оазис^иосп: :r? й- Иогользуя полу .
ченный результат, определить лзриок 7' движения частиц
вдоль оси Z ., если :,-£ )=/*/_ . £""/ <;.' "' : гае «••• некото,
рая постоянная.
Г л .? ъ -. ><!
СПЕ11ИАЛЬН/^Ц;1^
5 15. РЕЛЯТИВИСТСКАЯ КИНЕМАТИКА
20 JL Н'ейтрон массы т. , летящий со скоростью г? , за
хватывается покоящимся ядром массы л/0 Определить масс
М ядра отдачи.
2C2. Ядро массы M и нейтрон массы f?.. движутся с
скоростями соответственно Щ и zF . При столкновении ядр<.
поглощает нейтрон. Найти скорость "z£ образовавшегося ядра
203. Покоившееся ядро с массой М в некоторой
момент времени испустило ос -частицу массы т. ) превратившие?:
в новое ядро с массой М . Найти энергии 6 и <5~ соответст.
венно d. -частицы ь образовавшегося ядра.
204. Из эксперимента известно, что покоящийся л +
—мезон с массой "Зг-- 273/тг распадается на нейтральную части»,
цу и ум''-мезон с массой /г? =■■ 207 ю , который имеет киле-»
тхгческую энергию приблизительно 7,85п?с . Здесь массы
обоих мезонов выражены через массу т. электрона.
Определить массу тг^ нейтральной частицы, с той же точностью, с
какой представлены заданные величины,
205. Покоившийся атом находился в возбужденном
состоянии с энергией £ . В результате излучения фотона атом пе—
46

низшее энергетическое состояние с энергией 6? , Be-
^еШ с и f включают энергию покоя и описывают энерге-
ЛИЧИНЫ Of "■ Ч?
о оогтояние в системе координат, связанной с атомом,
тическое с«л-
о еделить частоту а) испущенного фотона в системе отсчета,
гпГатом первоначально покоился.
906 Некоторый источник испускает поток нейтронов плст-
7" которые движутся прямолинейно со скоростью гг .
НОСТИ fn »
К- ждый нейтрон распадается по радиоактивному закону, порож-
протон и электрон. Вероятность JW распада покоящегося
Jтрона в интервале dt( по истечении промежутка времени i!
имеет вятс/УГ^тге*'^'* г«е X/- среднее время жизни по-
кояшегося нейтрона. Определить характер убывания плотности
j(jc) потока нейтронов в зависимости от пройденного расстояния
х в лабораторной системе координат,, где они движутся со
скоростью гР .
207. Написать преобразование Лоренца
в векторной форме так, чтобы оно было применимо для
произвольного направления вектора у относительной скорости
штрихованной инерциальной системы координат относительно не~
штрихованной.
208. Используя векторное обозначение для трехмерных
векторов, представить формулы преобразованш;
четырехмерного вектора Л,={А^1 А0) в таком виде, чтобы они
были применимы для произвольного направления вектора у ,
представляющего собой скорость штрихованной инерциальной
системы координат относительно нештрихованной.
209. Если штрихованная инерциальная система координат
движется относительно нештрихованной со скоростыс у' вдоль
°си Д , а одноименные декартовы оси параллельны., тс
формулы преобразования скорости if материальной точки имеют вид
ре дета вить эти формулы преобразование в виде одного вектор—
°го равенства так^ чтобы оно было применимо для произволь~
НОГо направления вектора V . ' * 47

210. Движущаяся электронейтральная частица с массой ПЬ
и энергией 6 распадается на два у —кванта одинаковой
энергии. Определить угол 9 разлета ^-"квант°ь.
211. Доказать, что свободный электрон не может
излучить или поглотить ^-квант.
212. Определить минимальную энергию & налетающего
электрона массы т , необходимую для образования
электронно—позитронной пары при столкновении с покоящимся электроном.
213. Определить минимальную энергию £ налетающего
У-кванта, необходимую для образования электронно-позитрон-
ной пары при столкновении с покоящимся электроном массы т .
214. Определить минимальную кинетическую энергию Т
налетающего протона массы пг , необходимую для
образования J/- мезона массы ^^ в следующей реакции перезарядки:
ptn-*~ntn t ЭС^ , где буквы р и гъ до реакции обозначают
соответственно налетающий протон и покоящийся нейтрон, а п
и ^-образовавшиеся частицы после реакции. Принять, что
массы нейтрона и протона одинаковы.
215. Определить минимальную кинетическую энергию 7*
налетающего протона массы пг , необходимую для образования
протон-антипротонной пары при столкновении с покоящимся
ядром. Считать, что ядро имеет массу М и не возбуждается
при столкновении.
216. Определить минимальную энергию ё^ налетающего
у -кванта необходимую для образования .Я^-мезона массы т^
при столкновении с покоящимся протоном массы т в
следующей реакции: $ tp -*>• п. +jrf, где индексами р и п обозначены
покоившийся протон и образовавшийся нейтрон, массы которых
приближенно одинаковы.
217. Два /-кванта с энергиями 6? и б2 превращаются
в электронно- позитронную пару. Найти минимальный угол в
между импульсами у -квантов, для которого данная реакция
еще возможна.
218. Частица массы т , движущаяся с энергией <£ ,
распадается на две частицы с массами т^ и та и энергиями <f и
£, . Найти связь между углами вылета в и вг и энергиями £
и 8- вторичных частиц.
219. Фотон частоты и> рассеивается на первоначально
покоившемся электроне с массой гп. . Представить частоту со'
рассеянного фотона как функцию угла рассеяния в в
лабораторной системе координат (эффект Комптона).
48

220. Доказать, что одноквантовая аннигиляция электрон-
но-позитронной пары невозможна.
221. Позитрон с массой т, и энергией 6+ сталкивается
с покоящимся электроном, после чего они аннигилируют в два
У -кванта. Определить связь между углом вылета каждого из
г—квантов и его энергией в лабораторной системе координат,
222. Движущийся нейтрон с массой т и энергией 6
захватывается покоящимся ядром массы М0 • В результате
образуется новое ядро массы М и J* -квант. Найти связь между
углом 8 вылета у -кванта и его энергией £„ в лабораторной
системе координат.
223. Протон с энергией £j рассеивается на покоившемся
протоне, масса которого т . Представить энергии <f и <5
протонов после упругого рассеяния как функции их углов рассеяния
0'и во в лабораторной системе координат.
§ 16. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
224. Быстрая частица массы т движется в
произвольном силовом поле F . Выразить ускорение zF частицы через ее
скорость 2р и силу у .
22 5. В некоторой фиксированной инерциальной системе
координат частица движется с переменной скоростью V - V Lt)
\41lL£l_\
Определить модуль ускорения — \t J | частицы в той
инерциальной системе отсчета, в которой она в данный момент
покоится в двух случаях: а) скорость 'V меняется только по
направлению; б) скорость & меняется только по абсолютной
величине.
226. Представить квадрат сОа четырехмерного ускорения
релятивистской частицы как функцию ее скорости tF и
ускорения ~?р .
227. Скорость у- и ускорение ?р частицы в покоящейся
системе координат известны. Найти компоненты -у*' , 2^ц и if*
ускорения в штрихованной системе координат, которая движется
со скоростью %f относительно покоящейся. Одноименные
декартовые оси координатных систем параллельны, а вектор V на-
правлен вдоль оси X . Написать полученный результат в виде
векторного равенства, снразедливого для произвольного
направления у .
1-501
■Ю

228. Определить скорость 2У релятивистской частицы с
массой /гг. и зарядом е после прохождения ускоряющей разнос*»
ти потенциалов у> в линейно!,; ускорителе. До ускорения она
имела скорость гл .
о
229. Заряженная частица движется с произвольной
скоростью j£" в однородном постоянном электрическом поле с
напряженностью £ . Доказать^ что величина
является интегралом движения,
230. Релятивистская частица движется со скоростью 2?'
параллельно или антипараллельно однородному постоянному
силовому полю F~ , Доказать, что величию
-W
V
J= (j-v*/PrJr
является интегралом движения,
231. Доказать£ что функция Лагранжа релятивистской
частицы определена с точностью до слагаемого, равного полной
производной по времени от произвольной функции/-/ ('Т^
координат и времени, которая является четырехмерным скаляром.
232. Под действием силы F частица движется с
переменной скоростью г?" в покоящейся системе координат.
Определить силу F' , которая приложена к частице в сопутствующей
инерциальной системе координат, где частица в данный момент
неподвижна. Найти также формулы обратного преобразования
указанных векторов.
233. Шар радиуса Д" был разогнан до очень большой
скорости 2У . После этого он стал двигаться прямолинейно б
разреженном нерелятивистском газе. Aiacca отдельной молекулы
газа т , а их число в единице объема И „ А'юлекулы газа
упруго отражаются от гладкой поверхности движущегося шара. В
системе координатs связанной с шаром, найти силу Г , с кото—
рой газ действует на данный шар. Определить эту же
силу F в лабораторной системе координат, где газ как целое
покоится, а шар движется со скоростью 1£ .
234. Релятивистская частица с положительным зарядом <?
и массой т влетает в большой конденсатор пол тупым углом
к направлению напряженности £ постоянного однородного
электрического поля. Начальный импульс частицы р~> Найти глу—
50

бину проникновения f-c частицы внутрь конденсатора, время tn
пребывания в нем, а таюке расстояние £ между точками
входа и выхода из конденсатора,
23 5= Частица с массой т- и зарядом е влетает с
большой скоростью & в полупространство, в котором
напряженность И постоянного однородного магнитного поля парал—
дельна граничной плоскости. Найти глубину к проникновения
частицы а это полупространство, время t:J пребывания в нем.
а также расстояние >? между точками входа и выхода из
магнитного поля
23Ь, Движение релятивистской частицы с массой т, и
зарядом е происходит в плоскости, проходящей через центр
сферически-симметричного электрического поля с потенциалом
У = У (г), Написать уравнения Лагранжа в полярных координатах,
выбранных в указанной плоскости.
237. Написать уравнения Лагранжа в сферических
координатах Г - О и Y для заряженной частицы массы ю. } кото—
рая движе^я с произвольной скоростью V и электрическом
потенциальном поле t/~ U(гг> Q, V) ,
238. Ре;тятивиетская .заряженная частица с массой ггь и
энергией & движется в электрическом потенциальном поле при—
тяжения и'-" " г - '^омент П частицы удовлетворяет
неравенству /Ус >с/ , где с — скорость света в вакууме. Используя
уравнения л!агранжа в полярных координатах /" и ^' , а также
законы сохранения энергии и момента, определить траекторию
частицы.
23'.,1. Опрецелить траекторию релятивистской частицы с
массой т и зарядом е , которая движется с потенциальном
поле покоящегося заряда а . Энергии! £ частицы
произвольна, а момент М удовлетворяет устоьшо Мс-0,е . где с -
скорость света в вакууме.

ОТВЕТЫ И РЕШЕНИЯ
ГЛАВА I
§ 1
1. а) В декартовых координатах функция Лагранжа L
материальной точки массы т равна разности кинетической 7~ -
= jp Л и потен^^^льной U= ■# -^ 3 энергии {L-T^TJ ).
При переходе от декартовых jc , у и я к сферическим /~ , ^
и У координатам направим полярную ось сферической
системы координат вдоль физически выделенного направления вектора
g . Тогда потенциальная энергия частицы в сферических
координатах запишется наиболее просто: lf= -Q- + осо$ О . Чтобы
h f 2
выразить кинетическую энергию Т в сферических
координатах, воспользуемся тем, что за время dt радиус—вектор р~
частицы получает приращение dF* , которое можно представить
как d^^dr-f-i^rde'-t^rSin-O' d<P , где Jp , Т0 и Т^- орты
сферической системы координат. Поделив это выражение на dt ,
находим скорость р~— С l~+cei~6+t'SlnQij>% что позволяет
определить искомое выражение для Т в сферических координатах.
Окончательно функция Лагранжа записывается так
)
д) согласно общему правилу напишем функцию /1агранжа
L в виде разности кинетической и потенциальной энергий
L- ~2~ *~ ~ ту £ t где декартовые координать: jc t у \\ Е
материальной точки подчиняются уравнению связи z~F(x^ + У2) •

Следовательно, независимых координат здесь только две, т.е.
данная механическая система имеет две степени свободы.
Чтобы функция Лагранжа имела простой вид, выразим ее в
цилиндрических координатах г , Ч* и z , взяв в качестве
независимых переменных г и Ц> . Входящая в функцию Лагранжа
координата z выражается через независимую переменную Г* при
помощи уравнения связи z = F (г2) . Скорость р~ в
цилиндрических коо]£динатах определим делением приращения радиус-
вектора <У>Г= er dr+t^rdV * (£dz на приращение времени dt,
где с^. , Чр и <^. - орты цилиндрической системы координат, а
величины dt~ , с/у и d& обусловлены приращением времени.
Поэтому квадрат скорости в цилиндрических координатах
запишется так: г" = /~ +r (ft + Z . Величина я легко
выражается через А* и Л дифференцированием обеих частей
уравнения связи, что дает £ — -°^v-УД В результате функция Лагран—
жа в цилиндрических координатах принимает вид
L- 2
{[*<jU%FLf\*M-'4*<'*>-
2. 1> — ^2~R (9 + Sin*в Ф )-/7?а Rcos в i где полярная
ось сферической системы координат антипараллельна силе
тяжести.
3. Функция Лагранжа l> = £ (<Lf с/ определена с точностью
до слагаемого, представляющего собой полную производную по
времени от произвольной функции / - / ( о,, i) , зависящей от
обобщенной координаты а и времени / • Такая
неоднозначность в определении функции Лагранжа позволяет упростить ее
вид путем прибавления или вычитания величины dfLt/it}. , Пе—
at , ,
реход от одной функции Лагранжа L—L(att/ к другой L — Li&t)
при помощи формулы преобразования
не изменяет уравнение движения для обобщенной координаты а .
а) В рассматриваемом случае имеем Z-=0 +2q,tlx,t+-&j-.
Легко догадаться, что величина входит в правую часть
равенства ~
Это обстоятельство позволяет записать данную фора/улу Ла«-
53

гранжа в виде:
<■-*'-эк* ж(г91к*>-
Опуская последнее слагаемое, приходим к более простому
выражению для функции Ла гранжа
L ? ch2t >
/ • 2 ? в ' • 2 t • 2
б) £-=<p+-g-f ', в) L~f ; г) L=f.
4. L = tnett}{^-e(t}<i>*+$coe>-y ) , где у/- угол
отклонения маятника от положения равновесия.
5. При движении материальной точки массы пи в
вертикальной плоскости X Y кинетическая и потенциальная энергии
имеют вид соответственно 7~—-4р(jc ■/■ у )и U— - ГПОХ, поэтому
функция Лагранжа записывается как L - —- (jc*Vy } + mоX .
Координаты jc и У материальной точки связаны между собой
при помощи уравнения связи (jc-jcQ)'-t (У-уа)-£ ♦ Таким
образом, данная механическая система в виде перемещающегося
маятника имеет одну степень свободы. В качестве обобщенной
координаты.,полностью описывающей положение этого
маятника, возьмем угол Ц> отклонения его от оси X . Тогда
координаты х и у будут функциями независимой переменной ys
согласно уравнениям
jc=jc0(t) + ta?s4>j y=yo(t) + £sin4>.
Дифференцированием по времени находим Jc ну, что
дает возможность выразить i, через у/ и if' сл-едуюшим
образом :
L^-pf ф2+т?Ф(У0соэ </> -Jbosin*p)+mQ fcosф+Щ- (<хг+У*+ ^jTi(f ?x0).
Последнее слагаемое является заданной функцией времени и
поэтому его можно опустить в силу неоднозначности определения
функции Лагранжа. Кроме того, при помощи равенств
^(хо<™9) = £0 cos у-хб ф serifs
jf(y0 sin f) =jf0 Sin (/Jtyo ф cos <P
54

следует исключить из L полные производные по времени от
определенных функций, зависящих от ^ и / . После этого
функция Лагранжа данного плоского маятника принимает
упрошенный вид
L = m6[-f- ф*- Уо sln.y>i-(f-X0 j COS у] ,
Ъ.^^{г2+г2'в*+Г%сг1*е^)-~£ + е£оЪ05в. здесь по-
лярная ось сферической системы координат параллельна векто—
РУ В •
7. Поскольку обобщенные координаты р^ при^- 1,...,/(
полностью описывают положение механической системы,
декартовые координаты материальных точек являются определенными
функциями переменных G. и / , которые можно найти из
уравнений связи. Это обстоятельство дает право написать /~- =
= /*1 ' ^7 ' "" у &?^/пРи £=■ h • ' ") М • Дифференцируя обе части
последнего равенства по времени, находим скорость /•*: как
функцию переменных а , d. и t • Подставляя найденные
функции г; - /"• (а о fl и г*~= У^ _j£_ p^fq ,.„.,a i)q в кинетичес-
кую энергию Т=£ J-m. Я"^ и энергию взаимодействия U-
-U(F~T..,f%-,t) i'1, выражаем функцию У'агранжа jL^T'U
в обобщенньл координатах
к к
Z - £ i- a, qy,q +2l! 8. о -W
где принять' обозначения
/V
N
а
ЭП ЭГ/ Р = Г' „-> ЭГ; ЭГ;
.-jrm.iU^i, §=Епг
UP i*i l э^ afy * /-; 'dfx at
Если голономные связи постоянны, то функции Л — ^-{Я >>;0, )
при /—/,-. .; /V не зависят от времени t явно. В этом
случае 6 . = 0 при<зС=/, ,..,/< и величина J7 -£- а 4-/ 4^ приобре-
<* ? > ы,р=1* ^fi ycC КР
тает физический смысл кинетической энергии системы
материальных точек. Наряду с этим имеем W= U , так что величина у/
служит потенциальной энергией данной механической системы,
когда функция U не зависит от времени явно.
55

8. L = —Jy-^ л +гегУ™2ег*Ф5*пЧ'~2 1х-ег1 +
-4
■^(mj+m^acc-ttTi^Q.^ 005^ t где х- координата
кольца, а у— угол отклонения маятника от вертикали (оси X ).
где Г— расстояние от точки подвеса маятника до кольца, а
угол у - угол отклонения маятника от направления силы
тяжести.
10. ^^^^■^^^^i7f^Cff3^*m^fcffSf2-
где ^ и *#,- углы отклонения первого к второго маятников
от направления силы тяжести.
§ 2
1г.Р = (Р0-ы.х)^<. .где ^-ортоси*.
14. r-rY*si.n?eo+&cos9j=o-, ~^г(ггф)-о-
15. (г + £)£-фг*^у*+у,о, -&UV)=0.
16. r-ryif=-££&, ^-(ry^o, mZ=.eE-mqz,
где ось iT антипараллельна силе тяжести.
56

17. a) e-(j^iy2eos9)stn9 = Qy-^D>s,Ltv2d}=Q-y
+(^ + ^2H. sin. fy^Q,
18. Кинетическая энергия материальных точек равна
Т-Д' ~2^rrbCj/L • Первое и последнее звенья пружины,
примыкающие к неподвижной точке, имеют потенциальные энергии
соответственно -^- /с л,^ и ~к~ к 1 Я/ • Суммарная
потенциальная энергия промежуточных звеньев зависит от разности
обобщенных координат следующим образом: У" —д- /0 ^0 \% .
Поэтому функция Лагранжа L механической системы запишется
как п-1
Каждая обобщенная координата удовлетворяет уравнению
Лагранжа .
eft *9c. р9/ >
Вычисляя производные, находим окончательно
19. Уравнения Лагранжа
запишем как одно векторное уравнение
Здесь векторный потенциал Т~ А/Т3", t) берется в точке с
57

радиус—вектором /*"= Л" (£) , в которой находится заряженная
частица. Поэтому полная производная по времени в правой
части написанного векторного уравнения имеет вид: <^п — .€/f. Ф
+(tf(lh'au/Aj\ipvi. вычислении частной производной от функции Ла-
гранжа по координате скорость ^ частиць.
рассматривается как постоянная, так что grac/ 1^^[(^агсУс{)Л+2Гм fOtA^l'CGrad
Принимая по внимание полученные производные по времени и
координатам, а также используя связь между
электромагнитными потенциалами^ и напряженностями полей, приходим к
уравнению Ньютона ^г^~= О(£Г+ 1~~"к ") •
§ 3
20. а) При движении рассматриваемой механической
системы энергия S — <Z ~+3ty <j, сохраняется. Численное
значение энергии определяется из начальных условий, так что
закон сохранения энергии принимает вид а у 3 to, fy- 7 .В
точках остановки скорость обращается в нуль. Поэтому из закона
сохранения энергии вытекает алгебраическое уравнение Stofy-l^
корни которого представляют собой возможные точки остановки
механической системы. Из бесчисленного множества корней
отбираем только соседние два # — - -^г- на- -~- , между ко-
rj ь 'во
торыми расположено начальное значение обобщенной координаты
<l(o)~0 , так как при движении механическая система не выходит
из области а ^ £ ;= ^ , заключенной между двумя
соседними точками остановки;
г) b'lh--*-
21. В случае механической системы с одной степенью
свободы закон сохранения энергии дает возможность найти
зависимость координаты от времени без использования уравнения Ла-
гранжа (или Ньютона). Например, при движении частицы массы
т в потенциальном поле U(x) закон сохранения энергии
С - ~р~х ~+1/(эс/ позволяет выразить скорость как функцию
координаты /

Полученное соотношение будем рассматривать как
дифференциальное уравнение относительно координаты ос . Оно
решается методом разделения переменных, согласно которому имеем
Возьмем интеграл слева равенства по времени t от t-. до ир
(t^-io} ' а спРава по координате <х от одной точки
остановки <x,(t7) до другой д: (^ У . Неравенству Jc(£)<cc(tz)
отвечает знак плюс, а неравенствузс(^^) >зс (&2.) - минус.
Промежуток времени /„ - £- движения от ж(Ь?) до ^с(^) равен
времени обратного движения, в результате которого частица
проходит те же состояния, но в обратном порядке, возвращаясь
в исходное состояние. Значит движение периодично, а период Т
равен удвоенному промежутку времени /- £ . Полагая x(tA - х7У
7 «• ос-
по л уч а ем
г
Эта общая формула применима для произвольной функции U=UtX).
а) В рассматриваемом конкретном случае область
интегрирования разбиваем на две: от JC^ до О и от Q до jc9. При ,=.
интегрировании по первому отрезку [jc.. , О] используем U(dc)-U^~г
и делаем замену переменной интегрирования согласно формуле
{ —р-° I --г—.- £' , которая сводит искомый интеграл к таблич—
HON1y dx _ а f с/%
Л а
VU
*i'~ v а* ' ~с: ч ". " ..." . ° ^
I jlrr______ _ и- I w г ла.
Интегрирование по отрезку \ п ,х. ] , где I/(сг)-'(/■£- «проводим
аналогично. В итоге имеем Т-л(а-^ё)[ -jrr \ )
в)
р р
22. а) Из закона сохранения энергии 5=0, + tn Q, следует,
что точки остановки механической системы являются корнями
алгебраического уравнения S = ik О, . Тогда а =О отвечает
59

состоянию покоя с энергией 8 — 0 . Для положительной
энергии О -<■ <S •< 7 существуют две точки остановки а, и <1г
.которые ограничивают область движения а, . ^ а ^ <&2 . Таким
образом, условием финитности движения является неравенство
0^. 6 <t .
Время движения от одной точки остановки ff, до другой
а, равно времени обратного движения, причем механическая
система возращается в первоначальное состояние.
Следовательно, движение периодично с периодом
где использовано У =/ty^-^.^^ '. Для вычисления интеграла
умножим числитель и знаменатель на положительную величину
thq, . После внесения множителя cha под знак корня
воспользуемся формулой ch <fi -7+ Sп fy и сделаем замену
переменной интегрирования ^ ls& ) shq= *r • тогДа придем к
табличному интегралу f
Т=
где принято во внимание, что в точках остановки выполняются
равенства
Shi
2JT
(*?-г>**'->> (ФГ'Ъ'г,
при /, £ >о;
(£гЬг
\L/ У1+6
в) Т= 23с ■ при - / -с £ < о:
г) -г- 2х при -/ -с £ < О;
д) r= **f/2 пр* -а^б^Оу
е) Т=2Л ПРИ 6 > \cl\ .
23. Сначала предположим, что частица приближается к
потенциальному барьеру слева зс ^ эс *£. С , имея
положительную проекцию скорости. Вблизи точки jc = С максимума
разлагаем функцию U — £/(jc) в ряд Тейлора и сохраняем только
6G

два члена этого ряде U = VF)*4-£r-£f'' ^=-/^ , а другие ела-
<£х*-
гаемые опускаем как пренебрежимо малые. Из закона
сохранения энергии в - ^p-^i- Ufa) получаем ,£_= _£=, (e~jc) , где
использовано обозначение ,К'--и иd>0 . Решение
дифференциального уравнения ^/zf — -1ЙГ—<^£. имеет вид^--~~р £п(С-х)+С
где постоянная С находится из начальных условий, причем
) . Таким образом, частица приближается к
потенциальному барьеру по закону
из которого видно, что для достижения точки сс=Е потребуется
бесконечно большой промежуток времени. Если частица
приближается к потенциальному барьеру с противоположной стороны
£^ сс^. ^с0 , имея отрицательную проекцию скорости, то
рассуждения аналогичны, а найденный закон движения сохраняет
силу и в этом случае.
к 1
'& ^=1 г \ ^<5г ты &Ы Ты I е-
Энергия £ не сохраняется. Обобщенные импульсы р с
индексами т+/^ & «* к сохраняются, а с индексами 1^.б"£.т
нет.
25. Поскольку моментM-nv(hx ir/ сохраняется при
движении в кулоновском поле, производная по времени от вектора
X имеет вид
Ускорение ту исключаем при помощи уравнения Ньютона пг2Г=:
= з— . Величину r находим дифференцированием по времени
обеих частей тождества /- —^Р~ , что дает г — . После
указанных преобразований подобные члены взаимно сокращают-
Ся и правая часть исходного равенства обращается в нуль ?Ц— =»#.
Таким образом, вектор / сохраняет постоянное значение,
61

26. Выпишем производную по времени от заданного тен.
зора
Воспользуемся уравнением Ньютона гтьг = — а^г~ и исключи?
ускорения при помощи проекций этого уравнения на декартовы
оси mjc — ~G-Z'cL к rrijc,= - CL-X-jz, . Тогда в правой части ис
ходного равенства подобные члены взаимно сокращаются, та
i
что ji Т^= О . Следовательно, тензор Т сохраняет пост;.
d v oys> о& g
янное значение при движении частицы.
27. Указание. При доказательстве соотношений -^гт^~.~о
и ^А^~= q необходимо принять во внимание уравнение
Ньютона/гг'^-/1" } а также/V — /"" * F , где р~-~ сила, приложенная
заряженной частице.
28. Указание. Для вычисления полных производных ik
времени от заданных величин J7 и X, следует использоват?
уравнение движения mi?--£-~iy*~Н
20. а) Энергия g и момент м относительно центра
шара; б) энергия <f , а также проекции импульса р и мо.
мента М на ось цилиндра; в) энергия <5 , проекция
импульса {>' на заряженную плоскость и составляющая .моменте
М~ , перпендикулярная этой плоскости; г) энергия £ и
составляющая импульса jp~ , параллельная нитях.; д) энергия £
и проекция момента Д/ на ось симметрии, проходящую чере;.
оба заряда.
30. а) Три компоненты импульса jo* и две компоненты
момента М . Третья компонента момента и энергия d являют-'
ся функциями пдти указанных интегралов движения, так как б г
-р Bm \\p~/i=0 ; б) в качестве независимых интегралом
движения можно взять три компоненты момента /У
относительно центра потенциального поля и две компоненты
сохраняющегося вектора Г-ТГ*Л//**./3/г . Третья компонента вектора _Г
является функцией ука.занных пяти интегралов движения, так как
М1 = 0 . Энергия S и модуль I сохраняющегося вектора
связаны с расстоянием г до экстремальной точки траектории
соотношениями:
fi - Я* *. <* г Й* ^
62

\\з последнего соотношения получаем/£-/V А^м-Г-^/ . Подстав»»
ляя эту величину в выражение для энергии £ , находим , что
она полностью определяется заданием отобранных пяти
интегралов движения* в) пятью независимыми интегралами движе^.
вця являются 6 , р г р i М^ и величина I— В (?f *М)t j?(r*£Tfy
где ось Z декартовой системы координат выбрана вдоль ?Г .
3 1. В декартовых координатах jz м у функция Лагранжа
материальной точки, движущейся в вертикальной плоскости,
известна Z. - -4р (jc^f- if J - 7'гъои • Здесь начало координат
выбрано в центре вращения, а ось у направлена антипарал—
лельно силе тяжести. Переменные х и У удовлетворяют
уравнению связи, которое проще Есего записывается в полярных
координатах f и <f> . Для правого вращения прямой от оси X
к Y уравнение связи имеет вид p-Tt-f- oJt f в то время как
для левого вращения оно записывается как </■'■= —6JГ , где
использовано, что в начальный момент времени f= о
материальная точка покоилась в начале координат, а прямая занимала
горизонтальное положение, совпадающее с полярной осью. В
последующие моменты времени О -^ t материальная точка будет
находиться ниже полярной осп из-за действия силы тяжести,
что также отражено в уравнениях связи. Независимо от
направления вращения прямой функция Лагранжа в полярных
координатах с учетом уравнения связи имеет вид
L = jr(i'-2+ СО*/-2) + tn^r Sen COL
Сравнение Лагранжа —rjr ~;r =■ — Q записывается так.*
Г - со2г = а зС/ъ oat.
Его решение р — р -f- /~° равно сумме общего решения
cpcjh час ^ J F
/^ - С в*** ■+ C„(?~oJ соответствующего однородного уравне-
пая Р'- сО /^-0 и частного решения Г~час-~f2$Ltl&*исходного
неоднородного уравнения„ где С и С'р - произвольные
постоянные, которые определяются из начальных условий t"(o) ~ О и
h@}~0 • Окончательно получаем
Г = ^-r fshcot -smcot).

32. Начало координат расположим в неподвижной точке,
являющейся центром прецессии, а ось Z выберем антипарал-
лельно силе тяжести. В цилиндрических координатах г , У и 2
функция Лагранжа имеет вид
^■^(^^2фМ2)-гг^г.
Переменные /■* , <р и Z подчиняются уравнениям связи
I
Г- \z I ty в, у = cut^
которые выражают гот факт, что материальная точка находится
на прецессирующей прямой. Здесь ось X выбрана так, чтобы
в момент времени t^O прецессирующая прямая находилась в
плоскости XZ . В качестве независимой переменной возьмем
координату g 9 тогда функция Лагренжа примет вид
Вытекающее отсюда уравнение движения
£-(оо $1гъ&) 2 -- <% OGSrQ
тлеет общее решение
в котором постоянные интегрирования С^ и С~ определяются
из начальных условий.
а) Если в начальный момент времени it ~ Q материальная
точка находилась выше центра прецессии, то начальные
условия запишутся как g@}= вСОвЦ^О^в&ркг £@}-и .
Отвечающее им решение уравнения движения выглядит так .'
В1ЩН0, что при выполнении неравенства С СО SChs6^Cf.Gi%Q
материальная точка удаляется от центра прецессии, б то время
как для неравенства противоположного смысла £ой Sltbe<Qctqy6
она приближается к центру прецессии, достигает его и затем
продолжает движение вниз по прецессирующей прямой.
Равенство С°СО 6Сгъв=Qct<3 @ отвечает неустойчивому равновесию;
б) Для начального усяоъ1ая£(в)=-£с0*9(О£в£-%£)и.г(о)=О%
отвечающего исходному положению материальной точки ниже
центра прецессии, решение записывается иначе ;
64

где Л*
точки.
f-0^?
, f и г ~
QHo описывает движение материальной точки вниз по прецес-
сирующей прямой.
33- Г'ыЫх^сои^сЬсоЦ,
цилиндрические координаты материальной
34. а- * eAaJ, Ч>= -f*- thai, Z'Sf+vt,
где ось Z выбрана параллельно силе тяжести.
35, В отсутствие связей, ограничивающих движение
частицы, уравнения Лагрэнжа в декартовых координатах
совпадают с проекциями уравнения Ньютона пгг^^еЕ на декартовые
оси координат. Для удобства начало координат поместим
в точке влета электрона в электрическое поле. Направим ось Л
вдоль вектора £ , а ось У выберем в плоскости векторов £
и 7F • Тогда движение будет происходить е плоскости XК .Оно
описывается уравнениями jc. - —■-£ и У ~- О , решение которых с
учетом начальных условий запишется как
При вьлоде электрона из полупространства, где действует
электрическое поле, его координата jc обращается в нуль.
Отсюда находим время t пребывания электрона зо внешнем
электрическом ноле ^ t =:—£n—za-cos ос • Из полученных вы-
2 /е/с
ражений для координат дс и у видно, что в электрическом
поле электрон описывает параболу rg - —^-^^- ц2+—&& и , верши-
на которой расположена в точке ц ■л — 7Гах]^и. Следовательно, глу-
оина проникновения электрона в электрическое поле
определяется ее -й коорд!шатой вершины этой параболы и равна f ~
2leiTCDSci ■
S-S01 в5

30. Уравнение движения
т& =£-(&*&)
целесообразно решать в системе координат с осью Z . направ—
ленной вдоль вектора Н . Тогда его проекции на декартовые
оси примут вид
« £=-тЧ; "Ч - - ¥- *с i mii = ° ■
Из первых двух дифференциалы-:Ь'х равнении получаем
г^-^ а $£гь(си Ь+ос ) у Vy-fr сои (ajl + oc)^
еИ
где aJ — - ;„- » а постояпнъ'е <я, и о£ определяются из на»»
чальных условий. Интегрируя по времени f: обе части
равенств
~fj-^ &-> SL/ъ (aft * aij > -Л- = С/. со$(сО£+оС))
находим координаты X и у протона, по которым видно, что в
плоскости X У он вращается по окружности с частотой &->
Между тем вдоль оси Z согласно уравнению z£ ~ О протон
движется с постоянной скоростыс VI - 4J1 0?Э °L . Значит его
траектория в пространство представляет собой винтовую линию.
ГЗремя, затраченное протоном ца преодоление пути С вдоль
магнитного поля, равно i - 6J'г/' cosd . За это время он со~
вершит число оборотов Д/ = o.)t J*^или
N S**- •
2Ж тс t^Cff$ oC
37. а) Используя выражение L = Q, ~4fy-4'fy , составляем
уравнение лагранжа <fi"9q — — 2 . Иго решение <л = ~СОЗ Гу
отвечающее заданным начальным условиям, находится
стандартным способом.
Реи'им поставленную задачу при помощи закона сохранение
энергии. По заданной функции Лагранжа определяем энергию
6~<р- -*"?&+ -У<fr , численное значение которой £ =& берем из
начальных условий. Пользуясь законом сохранения энергии
^ -f^a^^^'-^ , находим скорость £ -± V~~y/^ ~ ^ff2 .
Согласно начальным услоьиям механическая система из
исходной точки &(<?/--/ может двигаться только б область ~f £-. $
с положительной скоростью 0< ^ . Движение в область a*z-J
отсутствует, так как там скорость £, принимает комтекс««
GO " '

ные значения. Следовательно, перед корнем знак минус следует
опустить. Для определения закона движения воспользуемся
формулой dt -■ ~-f , в которой скорость £ как функция координаты о
определена вьлне. В результате приходим к дифферекциальному
уравненшо
dt =
2'
с начальным условием Q,@}~~1 • Подкоренное вь'ражение
запишем в удобном виде ?—Bа, +7)г, тогда при интегрировании
можно воспользоваться табличным интегралом. После
интегрирования получаем /■=.- -^-fcu^C SinB<Э, + 1'/'^~jf] или 4--С05 t'}
б) <f^ch2£; в) (£=-*-(е*+skt -7) .
38. а) По обшему правилу определяем энергию б= -^ ^~т-
f $
Сна сохраняет постоянное значение 6 = / , которое вытекает из
начальных условий. Используя закон сохранения энергии J --#*>
t-1 — 0 г находим скорость $~Vq,2- / - Перед корж м г.: .-.■-: ;
положительный знак, так как из исходном точки 'J@J-1 ,\ч-\.нчг^-
ческам система может двигаться только в о", и.стл, /■< q < :ii..'i-
жительной скоростью 0<fy . Область /^/</ подсн тупил
при двих-енни, так как в этой области скорость а ирилпм, . i
комплекснь:е значения. Полученное дифференциальное \ райи' -чп»
j t =■-■*£%--
Vf~7 '
с начальным условием fy(())= / интегрируется э [емоч'ырло
приводит к закону движения а ~с/ъ t . lienorp.i-.jc i ;s.-4<;: i>- Ui. ..
ференцированием убеждаемся, что найденная обобщенна • wao. v-
пата удовлетворяет у равней то - !агранжа а а- ил-■ / ?
б) Q - - tn, Crbi . Эта обобщенная координата \ угл ь ы-ор-.~.
от уравнении) „'.'агранжа A -t- C?*~'~ О
30. а) Задачу следует решать без непосредственного
интегрирования уравнений лагранжа, Более короткий hvj.j t«. ict
в использовании закона сохранения энергии» По . >лллпноц фии-
ции Лагранжа находим энергию £.-- с7 > б»"^- , численное зн.с!'-
ние которой <f - / определяется начальными условиями. При
помощи закона сохранения энергии а"^ С -~ / получаем
скорость^' -Vf~C~f - Перед корнем взят положительны'! -пак, гак

как из начальной точки с^@} = 0 механическая система движет-
ся в сторону возрастания обобщенной координаты q . Область
a,<Q не доступна для движения с энергией £~/ , так как там
скорость а принимает комплексные значения. Из формулы dt-
da .
- - S с учетом выражения для скорости о.- вытекает
дифференциальное уравнение
в правой части которого числитель и знаменатель следует
умножить на множитель е^ • Если внести его под знак корня,
то подкоренное выражение легко преобразовать к виду (е ~ -к)--
Следовательно, при. взятии интеграла справа от знака равенства
полезна замена переменной интегрирования^ ~ ~? — £ »
которая сводит его к табличному. В результате интегрирования
находим
t~At~ch[2el'+ г)+С9
где постоянная интегрирования С согласно начальнь м
условиям равна нулю. Окончательно fy = 2 бп> oh -|- :
б) n=r7iLS£n,t'r) в) a,~at"cs>tfv
sc/ъ y£t
40. а) Проще всего воспользоваться законом сохранения
энергии £ = -jr~ х'ч-1/(Х)% где потенциальная энергия задана
л/
2Jfe/ = -l^—-р-, а сохраняющаяся энергия б согласно
начальным условиям отрицательна <f- -\& \ . Из точки я@)-(-6а>/ио)
частица с заданной энергией S -^ О движется только в область
ЭС(,0) ^ ЭС С положительной скоростью ^■-[^(^о'а/ *& U »
так как при ос <х(о)скорость с£ комплексна. Полученное
дифференциальное уравнение
легко интегрируется, а окончательный ответ приводится к виду
в&
а окончательный ответ г

б) ^еп^Ц^Щ^)}.
в) л=-а]Щсов(][Ж-±) при 0*t*te,
*-*^«(|^'irIi6j при г-^ЫГ,
гае (£г ~\{Ш1 , а Т=ЗГ^л][^*е^)- период движения;
7 I z
41. а) Поскольку обобщенная координата О, не входит
явно в функцию Лагранжа L — -£- а 2e^-t $> е , уравнение Ла-
d 3L
"Л* -.А 2*
обобщенный импульс /=>- 2-h~- А<? у-<р сохраняется при дви—
гранжа принимает вид -^ —=0 > из которого следует, что
жении. Его численное значение /° = 2 находим из начальных
условий. Полученный интеграл движения а—^ё^—е^ и на~
чальное условие <?(&/= О дают возможность найти закон
движения механической системы: 0,-3~С ~2е $
б) р=£-сМ+г-, в) t^-Vr+t2';
г) ь=£(е-т), %=^Ct„etj.
связи
42. а) Интегрирование уравнений Лагранжа в случае I,-
,г 1 -2 7
•fyЛ2^y9j>~ ~A— является сложной задачей. В этой
представляет интерес отыскание ^ = tyf(t) и %=%э$Другим путем
с использованием интегралов движения, которые" легко
определить по виду функции Лагранжа. Поскольку время не входит
явно в If , энергия <?-£?■/• Jlл ф^^-ZL. сохраняется. Кроме
G9

того, в функцию Лагранжа не входит явно обобщенная
координата & . Поэтому соответствующий ей обобщенньй импульс
Д~Т" = <р h, также сохраняется. Численное значение
указанных интегралов движения находится из начальньх условий,
так что 6=7 и f> — -£- . Таким Образом, вместо уравнений Ла=»
гранжа рассмотрим независимые интегралы движения
где для упрощения выражения для энергии использовано
соотношение Q, 4,Р~-р~ * Учтем далее, что из начальной точки а@)~/
механическая система движется в область /"^ <г, с положи—
о г 7
тельной скоростью 0< ty« , а движение в области а. ^ /
невозможно, так как скорость 3,^ принимает комплексные значения.
После этого для определения обобщенных координат приходим к
необходимости решать совместно два дифференциальных уравне
ния первого порядка .
с начальными условиями а■ (о) - / ъ$р@)~0 ■ Первое из них
интегрируется сравнительно легко и приводит к результату
который определяет функцию fyf-Qj.tJ
в неявном виде. Для отыскания другой обобщенной координаты
приравняем между собой правые части указанных
дифференциальных уравнений, тогда получим полезное
соотношение
dh=i
<&
Вычислим неопределенные интегралы слева и справа. Замена
переменной интегрирования У~а — fy сводит интеграл справа
к табличному и позволяет найти связь между обобщенными
координатами в видеЛ-С/г fy , где использовано, что при
ff{Of = f другая переменная принимает значение Ф[О}-0. После
этого второе из написанных выше дифференциальных уравнений
принимает простую форму dt-2ch fy~d<f, с решением t-^t
^^hfy г г * котоРое определяет искомую координату а =
-tf (t) в неявном виде;
б) f=*(t-Cost + rO fg = ftsint;
70

в) a-chi, q,2=2a,rcta th -jr^cwcta sht = 2 ocrctqe-2L .
r) b^jh'yh^'en('-7~t}:>
43. Уравнение Ньютона запишем как дифференциальное
уравнение первого порядка относительно скорости ?/- заряжен»
ной частицы .'
rn zr= еЕ + -—- (v7* /ГJ
и примем во внимание начальное условие V(OJ = V0 . Ради
удобства направим_оси X и Z декартовой системы координат
вдоль Е и п соответственно. Тогда проекции исходного
векторного дифференциального уравнения на декартовые оси
после сокращения на множитель т примут вид
где GO—■rffh - циклотронная частота. Дифференцируя первое
уравнение и используя второе, приходим к простому
дифференциальному уравнению втооого порядка г*- + <л) ~tfL=Q с решением
VL^CL&otiicdt'f-oCJ . После этого из первого уравнения нетрудно
найти (/ -ю проекцию скорости 2t- -~^r-fac0S(a)t +оС) • Здесь
постоянные а и (X определяются из начальных условий так
Уа
a=[l/i-(v+-£f-) J ; oC=ayrclq —-%=
oy + jf-c
Из оставшегося третьего уравнения вытекает 3£ - 7К ,
т.е. движение вдоль оси J7" прямолинейное и равномерное^
Интегрируя дифференциальные уравнения
£=a, S£fz(<vt+c>c)} у - - ~~j- -i- a CO$(a)t+cc)
с заданными начальными условиями jc@/=ZCo кУСО)~у0?
определяем координаты заряженной частицы в плоскости XY в виде
71

В частности, при £0~V^= О движение происходит б
поперечной плоскости по отношеншо к направлению магнитного поля,,
а средние по времени за период ■£& проекции скорости
заряби
женнои частицы
Таким образом, заряженная частица дрейфует поперек
скрещенным полям £. и Н . Если в начальный момент
времени t - О заряженная частица покоилась в начале координат
f@)=ty(O)=Qf то ее траектория представляет собой циклоиду
*-lkzp(t-c°*<vtO У^-^777^ (c*>t-stn,cot).
44. jc= J£. srrl # /7 . co5 ^j
И со l
У= Ш- *'«*&« cot-a}*), z~ —cosB; o> = -gL
45- x= ■£(%»+ £)(r-cos*>t),
"Jf CO rn, С
46. CC = j^p(CffsS2t-r),
Sd - у со -t ? со — .
11

COV-,
47. я:~ЩЬ.(г-сАе*),
Q2 \ /у
т,
, I то/
После перехода к пределу \0-\~*~ ~z— координаты электрона
принимают следующие значения:
48. ос = -£-^4l (cot-Sin, cv/)^
^ £& ('-"* "tyf *>'*'!, *=°:
rrzC
4S, Поскольку протон в начальный момент времени
покоился в начале декартовой системы координат, а сила Лоренца
F ~&(£ + ^~2^лг7 / ортоххжальна оси Z » движение будет
происходить в плоскости ХУ . Уравнение Ньютона запишем ток,'
rro ir = <?Е~+ £— гР* /у\
Его проекш!И на оси X и \ после сокращения на множитель т
принимают вид
где введено обозначение CjJ — ~~ . От этих двух уравнении
перейдем к одному дифференциальному уравненшо второго
порядка /
Его решение &'='&+ ?Х содержит два слагаемых, из кото-
Ъъ^у:=-e^Q^e'^/m'( &?г+ СЪа) представляет собой
частное решение, a Z£ = £$m(a)£-f/3j~ обшее решение соответ-
73

ствующего однородного уравнения тУ^0^ %а = ^ - Здесь & и в -
произвольные постоянные. При помощи первого уравнения
£?£ -Ct-i i
^~~ 7па£>^ ^ аУ ас определяем у ню проекцию скорости.
После этого используем начальные условия, чтобы определить
постоянные интегрирования
6 = е*£е _=-7 р -сьгсsin --7=Д= .
Координаты £& и и протона найдем интегрированием уравнений
M*8,cn(at+fi) —fff*£ г, *~**,
at i ГI го (аз ^ + со*} >
с начальными условиями je@)~ y(o)-Q . Окончательно
*-"^Ь) (f^cos cot+£ sen cot) ,
§ 5
50. а) При М~>~<?гпа движение инфинитно, а
наименьшее расстояние до начала координат равно /-" — \ ±J-^JL?I£CL
Если М -< -2/rww В^О , то движение финитно, причем
наибольшее расстояние до начала координат дается тем же
выражением. В случае М ^~2f*?a и <5-><? траектория не содержит
экстремальных точек;
б) в случае 8^0 движение инфинитно, а наименьшее
расстояние до начала координат
^-гг'^-'-т^х*- пщ'-£>0
Г — —LL у- -^ при /г - п
' О о JP Р ОС'.

Если €•<■ О , то движение финитно, причем наименьшее Onia.
и наибольшее f ^^ расстояния до начала координат
г™* ге + У fs^^—j^s- ,
в) при 8<0 и любом значении 8 движение инфииитно,
а наименьшее расстояние до начала координат
Если &>о « то движение финитно, причем £ > у ^-^(М^+2та)* а
наименьшее /^^ и наибольшее ^^^ расстояния до начала
координат
х1/г
г) при о > О энергия & положительна и движение
инфииитно, а наименьшее расстояние до начала координат
Если &<0 и €0<6 t где £Q = JTTT (~^~ * а) » то
'траектория не содержит экстремальных точек. В случае $"< О и
0<£< б движение может быть инфинитным с минимальным
расстоянием до начала координат
+2"?* , \/7мЪ2/па К _£' У2
<юё> *\\ ^гпб J 6 J •
Для &< О и <?<<?<* 60 возможно также финитное движение
максимальным расстояние\< до начала координат
75

.2
При В< О и -о°<&** 0 движение финитно с
максимальным расстоянием до начала координат
Го-[ *„& +Ц 7^~) + X J при-~<Ъ<0*
*4
2гп\б\_ ПрИ
51. а) Поскольку в начальный момент времени t' = О
частица покоилась, в последующие моменты времени о < t она
будет двигаться по радиусу в центр потенциального поля при-»
тяжения. Ее энергия g=z-£2jZ —^сохраняется. Из начальных
условий имеем б=--~. При помощи закона сохранения
энергии JQf.?-cL(-L-^L\ -q находим радиальную скорость как функцию
* \f К I \ 1 1/
f в виде /~~—[^;(-р r)\ у » которую
подставляем в правую часть соотношения olt—4^~ . После интегрирования
полученного дифференциального уравнения время падения
частицы в центр поля представится в виде интеграла
*»s«lffl
г
В числителе подьштегрального выражения положим 7 — -h~ (?*?'-f)-\
-f-p- , тогда интеграл разобьется на два. Из них первый равен
нулю, а второй сводится к табличному. Окончательно / =2£К\1П2К. •
52. а) При движении частицы в сферически-симметричном
потенциальном поле£/~ -If Sin ~£ сохраняется энергия & и
момент М~т(р* ЕР). Так как при t- О частица покоилась, ее
энергия отрицательна &~~\6[ , а момент равен нулю. Закон
сохранения энергии запишется как (j--^/" —u$itv -~
<- О CL
Под действием центрального поля притяжения частица при 0<t
движется по радиусу с радиальной скоростью >>»-%./-d. (у <. :ff^j:
76 -\*>Ч}' -

Если подставить это выражение в формулу то
получим дифференциальное уравнение, описывающее искомый
закон движения.. Проинтегрируем обе части этого уравнения с
учетом начальных условий, тогда
Sin £ dr
где /z. - расстояние от частицы до центра_при £-0 , кото-
Замена пе -
/ V?Ifa-ltls*"* о»
/~ - расстояние
рое определяется из соотношения j £ \ sen-
ременной интегрирования vl&\sin,
интеграла и приводит к ответу
а
-1
СЬ о
облегчает
COS
JZ.
<х
i^F^iiW'^).
Полагая г~ 0 % находим время падения частицы в
потенциального поля притяжения
взятие
центр
^ш*"^
ил
б)
в)
СО 5
Л.
■^^i^rij^a^^f
Л*
гЩ-уЛлгссо^1^.
53. В сферически-симметричном потенциальном поле lf=a.r,i
энергия £ и момент М сохраняются, а радиальное движение
частицы можно рассматривать как одномерное в эффективном
потенциальном поле У?<тГ ? g i-CLf - Поэтому координату
проше всего найти при помощи закона сохранения
энергии б = -Я^-/^ у- --W -f ol/ » из которого получаем
,1 _ .л[TnJ ГdГ
2/THZ
Возьмем интегралы слева по времени от О до t , а справа по
радиальной координате от/^ до /*/V).где /^ - экстремальная
точка траектории, в которой радиальная скорость обращается в
нуль и выполняется соотношение /~ *- -£—h v- -Z£__ _ n . Спра—
о а Го Prnn - о ^
2ma

2
ва заменим переменную интегрирования по закону /» ~ *? , а
подкоренное выражение запишем как <$ М / g I *?
В результате получим с
i^fYg-ances ;£*=£?■
Т ?
где использовано, что в экстремальной точке траектории
выполняется равенство гр~——-/—£—,- ^ ) /г - Не-
сложные преобразования приводят к следующему закону дБиже»
ния частицы .'
'А
Г-
1Н£-& msBW*)}
54. a) T-xYfi; б, г~*1Щ^.
55. Чтобы радиальное движение было периодичным ,
координата Г должна изменяться в ограниченной области А*^ Г£ 1\ ,
где А* и г - две точки остановки, в которых радиальная
скорость г обращается в нуль. Согласно закону сохранения
энергии эти точки остановки"определяются по уравнения
2
Найдем условия, при которых имеются два корня этого
уравнения,т.е. две точки остановки. Для stoi о эффективная
потенциальная энергия I/ (r}~———rr-Upirnf-aer'2} должна
Эф 2?Г) f* <? г { °~ /
иметь минимум при конечных значениях р , а ее значение ь
точке минимума должно быть меньше & т. Введем удобное
обозначение зс.~ (зе Л ) и U -~М J3Gr. , тогда V =Ml-i/ext
I 2*г> 5>ф X о
Видно, что при ос—**-О зеличина Оэ(ь стремится к
положительной бесконечности, а при <х—*-о» обращается в нуль. Значит
в точке минимума величина U&Cb отрицательна. Кроме того, в
точке минимума выполняются два соотношения -_ ,?<P— n к
$Ф >0 • Первое приводит к уравнению СС2£~Х— -=-*-
относительно переменной JC . Корень JC этого уравнения дол-
78

жен лежать в области О < JCQ ^ 1 , чтобы при jc, - JC0 одно-
временно выполнялись неравенства г/-,^-,^ О и ~—%Р > О . По-»
скольку функция Z(zc<l-«C G монотонно возрастает в
области 0-ё: 2С <z 2 , указанный корень <зе0 сушествует, если
/р I/. _
Xi -1 ■£- J , где £> - основание натурального логарифма.
Таким образом, радиальное движение периодично, если модуль
момента М удовлетворяет условию
56. а) М<с У 2т ее ' • б) M^R V2mZT.
57.
о
59. а) Траектория частицы в потенциальном поле U~br
расположена в плоскости, проходящей через его центр, и имеет
экстремальные точки, в которых радиальная скорость
обращается в нуль. Они определяются как корни алгебраического
уравнения 2т 5 /-* -2т в?* -М -О , где £ - энергия, а А/-
абсолютная величина момента М . Последние сохраняются при
двюкении частицы в заданном центральном поле. Полярную ось
в плоскости движения частицы выберем так, чтобы она
проходила через одну из экстремальных точек траектории с
радиальной координатой Р~Г0 . Воспользуемся обшей формулой для
траектории частицы в центральном поле и запишем ответ в
интегральной форме
где /* и ty - полярные координаты частицы.
Интеграл легко можно преобразовать к табличному, если
вынести множитель t~ ? из-под ксрня, а подкоренное
выражение представить как -~# -2m^~(-^L. _ Л*3)г. Замена пе-
ременной интегрирования -^ —^—= & с учетом особенности
/~а Л/ с
экстремальной точки JL..IH1- (ЛШ£ ptr?8) '"'приводит к сле-
/*/ М КМ* I
79

дуюшему результату: /♦/ _ пъ&
* г2 М
Окончательно траектория частицы принимает вид
,2
Когда угловая координата <р изменяется от У до Ут ^jt
частица возвращается в исходную точку траектории с
координатами г и <// , т.е. траектория представляет собой замкнутую
кривую;
6> V^S&'^'ilfcWr);
61.
62. П -
ЯГ 6
63.
l/ M2 _, а' 1 ( . п\1 2гг?а.5тг9' )
64. Траектория частицы в потенциальном поле
притяжения U- ~2~ t~ представляет собой замкнутую кривую,
которая в полярных координатах Л и ф описывается формулой
80

где начало координат выбрано в центре поля, а полярная ось
Проходит через экстремальную точку траектории (см. задачу
59 а). Воспользуемся тождеством соз2Ч/~2с0& У*-7 и
перепишем приведенную формулу иначе.'
' -1* 7/ тГг ™гЧ>.
V^W* >-Vf-
m62 V ^£?
Видно, что данная замкнутая кривая представляет собой
эллипс, малая полуось которого совпадает с полярной осью
(осью X )i а фокусы лежат на ортогональной оси Y .
Действительно, положим X = Г COS ft и ys /-* $ln (ft и воспользуемся
известными формулами <% -&2=i £ 2 (X2 и В =CL A-&2)
.которые связывают между собой эксцентриситет £ , а также
большую CL и малую g полуоси эллипса, тогда каноническое
уравнение эллипса
в полярных координатах запишется следующим образом:
Кз сравнения находим
* = Ь?+
2
]^
гг?
S2
7 +
VT-
2
65. а) Подставим потенциальную энергию Zf(h)- - — -t- -*-p
в общую формулу для траектории частицы в центральном поле,
выраженную в полярньх координатах f и <ft с полярной осью,
^проходящей через экстремальную точку. Тогда получим
• ~$01 о1

*ч
Melt
t~
^%2т6- 2r"'P ttt.9+ 2"L2L.y/g '
где t* — расстояние от центра пол^. до экстремальной точки
Гс к г* г*
ние от центра пол^. до экстрем
траектории. Подкоренное выражение запишем как
Замена переменной интегрирования -^—\//4z-f2rrzB-t? позволяет
вычислить интеграл, так что окончательно находим
Умг+2г*/>[ т. ос I ^^г
Г
-/Щ=^гт6. jrpf- С05 Ы„-Щ?)
За период радиальных колебаний координата /~ частицы
меняется от значения t"=t~= ^rnln до *" ~ 1~п?алс* а 3aTeN- в°3—
вращается к исходному значению/-1--Z^*. За это же время
угловая координата (// частицы получит приращение А У. Чтобы
радиальная координата f по истечении периода движения
приняла исходное значение /~=?}*„•* , аргумент у косинуса должен
измениться от нуля aoi^Jf. Следовательно, угловая координата
луча, идущего в соседнюю экстремальную точку траектории с
координатой Г- Г . , определяется из соотношения
f i-RtZUQ. лф-2УГ . Этот ЛУЧ» проведенный под углом
' Ртг М
ду- -г- рявляртся осью симметрии ветвей траектории, бе~
Ум*+2тй
руших начало из этой экстремальной точки Г"= Ггп1п и
простирающихся по обе стороны от оси симметрии до соответствующих
экстремальных точек с координатой t~=? Г . Рассуждения о
луче, проведенном под углом Дф — -JL2LLL—_ , аналогичны;
б) л^-±
2ЖМ
У*
бб. По условию задачи траектория частит, в кулоноьском
поле U (r J--—в отсутствие возмущения представляет собой
эллипс, лежащий в плоскости, проходящей через центр поля. Б
случае небольшого отклонения от кулоноьского поля имеем
82

l/(f)-U0(t") -t&Ufr) и траектория становится незамкнутой.
Приближенно она имеет вид эллипса, большая полуось которого
медленно вращается по мере движения частицы. За период
радиальных колебаний частицы в потенциальном none[/(r)=(/0(}*) + dU(r)
координата г увеличивается от ^=^1п до t"=tyr7CUX:, а затем
вновь уменьшается до Г=Г . - За это время угловая
координата ср частицы изменится от нуля до <р-2я;+д р, где / А<р/<< 7 ,
так как отклонение от кулоновского поля мало. Если
воспользоваться общей формулой для траектории частицы в полярных
координатах, то можно написать
**>
' /г)сП
г**
таьх
В подьштегральном выражении подставим U(t~}= U0[!~) + &&(f~) и
сделаем разложение по малому возмущению JС/(г) i тогда
получим f„ajc
г
rr>tn
где другие слагаемые опущень" как малые. Первый интеграл
равен J?jl , так как при (FU(r) = 0 имеем Л^-0 ♦ Чтобы
вычислить второй интеграл, сделаем замену переменной
интегрирования, воспользовавшись законом сохранения момента Af~/nr* ft9
из которого следует 4^ = "lT*dy , где г - ^[2m(&-Ujr)}-£\
После перехода к новой переменной интегрирования Ц/ получим
\ п
Здесь f и (f* связаны между собой согласно уравнению
траектории частицы в кулоновском поле JJ (t~ 1= --££ , которое име-
ет вид
—■=//£ COS у,
S3

где /э- фокальный параметр, а £ ~ эксцентриситет эллипса.
Проведенные рассуждения справедливы для любого возму-
щения 6V(f) . В частности, подставляя fill(f~) ~ —^U и выражау
Гу
г* через полярный угол у> , приходим к простому интегралу.
который вычисляется элементарно
67. Движение частицы в сферически-симметричном потен~
циальном поле W(/~) можно рассматривать как одномерное t
мг
эффективном поле t/ = '' tU(f)sv^ M - абсолютная вели-.
чина момента, Закон сохранения энергии S — -g- /* ■+Z/^ф
позволяет найти радиальную скорость Л как функцию F
Подставляя полученное выражение для скорости /"* в
формулу dt = -у- ,
, найдем дифференциальное уравнение, описывающее
особенности радиального движения частицы. Например, период J
радиальных колебаний выражается через интеграл
где Г и Г — точки остановки, в которых радиальная скорость
частицы обращается в нуль.
Пусть потенциальная энергия разбивается на два
слагаемых U(r)~ 1/0(г} + &и(г) , из которых первое основное, а
второе малое возмущение. Эффективное поле также разобьется на
два слагаемых U=U°, + &U(r) . где lf° =-МЛ- ,тт /г)
Подставим U9(p- и&ф ■/■ fflf(r) в подынтегральное выражение
и разложим подынтегральную функцию в ряд по малому
возмущению iTU(f). Тогда интеграл также представится в виде
ряда, первый член которого представляет собой период
радиальных колебаний в потенциальном поле U0 {h) в отсутствие
возмущения, а второй - поправка Д Т к периоду радиальных
колебаний, обусловленная возмущением d'Vit) . Другие члены
опустим как малые, поскольку поправку А Т будем вьнислять
в первом отличном от нуля приближении. Таким образом,
изменение периода под действием малого возмущения имеет вид
,г~^£/ *Ш=*,
84
п Уё^э<р

а) Если основное потенциальное поле является кулонов—
ским JJ (t*) = — jz-(ct>0), а возмущение имеет вид &U(r)= -—- »
то целесообразно сделать замену переменной интегрирования и
перейти к интегрированию по угловой переменной у , которая
связана с /~ соотношением
-£-=7* 6 COS Фч
где р — -—- - фокальный параметр, а £ ^/// - ^ / - зкс-
центриситет эллиптической траектории частицы в указанном ку-
лоновском поле. При помощи закона сохранения момента rf -
-тг^Ф и соотношения c/t~ ^Р- , в котором /~ =f-^ (%-1/° )] &
получаем связь между дифференциалами с!Г и а<р в виде
Vs^U,
о
м
df.
Э<£>
В результате изменение а Т периода радиального движения,
обусловленное влиянием возмущения ^l/(fj= -— , запишется так:
р^Л/ <?ё J l ' Мл }
б) лТ - - 3ЛЫ U"
в) лТ=- _*L*J2?.
/73
У2\&\ *
§ 6
68. Связь между углом рассеяния д и прицельным
расстоянием Р дается общей формулой
2
« г" I/ /_ -
р 6 Г<
в которой А" - экстремальная точка траектории, обращаю»
Щая подкоренное выражение в нуль. В соответствии с условием
Задачи положим U(f) ~ — . Замена переменной интегрирования
(—-f р J 'г — ~ h дает возможность вычислить интеграл
85

и записать ответ в компактной форме
V?
а
Видно, что малым углам рассеяния в ■с<-1 отвечают большт
прицельные расстоянияу?,»/-^- /' . Поэтому разложим выраже
ние справа равенства в ряд по малому параметру —^-- « /
ограничимся первым отличным от нуля слагаемым, а другие
отбросим как малые более высокого порядка, В результате
находим связь между Q и Р в случае малых углов рассеяния;
q __ Ж a
2
69. в=эс- . ^ &rccos
J при О <<с /.
70. Полярная ось служит осью симметрии траектории,.
Максимальный угол ifL?ajC отклонения частицы от указанной ос!'
симметрии найдем, полагая (р— </s и г-°° в уравнени;:
траектории, что дает
f - -у- arc со о
Угол рассеяния 9 связан с углом ср соотношением
2^ +Q=Jt , а прицельное расстояние р входит в абсолют—
ную величину момента п^гпр 2/^ , где 1К^- модуль скоростл
частицы в бесконечно удаленной точке траектории с
координатами /-= то и У/~~<Рат?ох' Поскольку при г=с^>
потенциальная энергия частицы обращается в нуль, имеем <5 = -^ ^ v
М = Ртгб/> . Полученные соотношения позволяют записатг
связь между Q и j° в следующем виде:
в -Ж- 2 CU-CCQ$ I - _- .
Если частица движется в центрально-симметричном
потенциальном поле, которое по модулю монотонно обращается е нуль н-
бесконечности, то малым углам рассеяния @«. 7 отвечают
86

большие прицельные расстояния. Разлагая правую часть
равенства в ряд по малым параметрам ~^-=«7 и (-—— ) ^* 4 » по~
аем
луч
71. d&=-lrR2dQ, б?=ЯК*.
72. Обозначим через сх. угол наклона касательной в точке
падения частицы на данную поверхность. Так как угол падения
равен углу отражения, то из симметрии траектории
относительно нормали, проведенной к поверхности в указанной точке,
можно написать 2оС = в , где Q - угол рассеяния. После этого
воспользуемся соотношениями ieoC= sLtiJ^. чМхЬ Р , где р — при—
цельное расстояние падающей частицы. Эти формулы позволяют
найти связь между углом рассеяния 9 и прицельным
расстоянием Р в неявном виде fn -S~ = SJj^l t поскольку переменная
d <~ dx
SC выражается через j при помощи равенства f(cc) - Р .
а) Полагая f-(oc)= а[28а: -3^} , находим ^ ^-=^а (g-cc)
и Ci[S~ (F'-X) J— P • Откуда следует искомая связь Р -а[£ -
4<&г 7 2 J ЪС/jc max J1 '
максимальный угол рассеяния. При помощи известной формулы
и& — Р \ -те \ —.—~п ползаем дифференциальное сечение
рассеяли
ния
dff=*?Ll-Z2--L- do при о^9^9,
32аГсо5*-&-
тазс 1
d& - О при Q < О ^ л х
majc '
*<* SCn f-COS> -f "пгаис >
d^=0 пои 9mQJ<e± Jt , где emaj = 2arctf(af>0)i
в) d&= 4*~ р~^г-б~ при Q^Q ^ вт„^ .
б a sin -#- соъ $ _£_ ^ max 1
d<> = 0 пРн 0та^в^ Ж , где 0maJr2anotf(aj>}&1

о/Я
73. def = (%f-
1 ' Bin'1
7 cff
76. Как и в задаче 68, находим связь между углом
рассеяния д и прицельным расстоянием f в следующем виде:
^ <* Г E BЛ-&H
Для вычисления дифференциального сечения рассеяния
воспользуемся формулой d& = 2&р с/ Р , тогда получим
б (гл-врд* sen в '
где принято во внимание, что величина д^ должна быть
положительной.
77. Проводя рассуждения,аналогичные задаче 70,
определяем связь между углом рассеяния & и прицельным
расстоянием р 2 ,
Далее при помощи формулы (J6~2Лрс(р находим
дифференциальное сечение рассеяния
d* =
W<5 / c£i
* J&
$гп«-§-
8. Целесообразно использовать общую формулу рассеяния
на малые углы в сферически-симметричном потенциальном поле
U (р) , которую представим в следующем виде:
оо
Полагая U(t)-Uoex.f> (~ ЗС t~2) , приходим к
известному интегралу Пуассона, так что окончательно получаем
88
Л У я эеиор / г*\

2 6 (f+as*^)*^'
80. Здесь полезна общая формула рассеяния на малый
угол со
>-н
где U(f~)- внешнее сферически-симметричное потенциальное поле,
в котором рассеивается частица . В рассматриваемом случае
имеем со
Ь
_ 3cLf i ^^
^-"^ ' "'fprrp4'
£ J r«]/P ~a
Замена переменной интегрирования -•* ~ ъ упрощает
взятие интеграла
в - 3a f ? d? га.
" 2ер* J j/jzj- 6f>*
Окончательно °
81,
82,
~W*
2гтгг£ в &
83. df?~
(ЯлK 6 J&
V*'
(ур+2ЯабО'-е)ЪЧ'б2+2Лабв'
в
84. Радиальное движение частицы с энергией S и массой
m в центрально-симметричном потенциальном поле U(*~)
будем рассматривать как одномерное в элективном nonet? (г)-
А/
= р „2 ■+ U(f) . Здесь величина W(r) обращается в нуль при
г->-оо , а модуль момента М -VF^fp за висит от прицельного
расстояния f> , которое имеет различные значения у падающих
частиц. Чтобы падение частиц в центр потенциального поля
притяжения было возможным, функция U-U(r)по модулю должна
обращаться в бесконечность при f -*-0 быстрее центробежной
мг
энергии ■ " 2 . Предположим также, что при /"—?-<=>=. функция
m *" 89

U ~ U'(h) стремится к нулю быстрее, чем ~--^—^~ . В этом слу~
чае эффективное поле £/ Ah) - -— +U(г)ъ некоторой точке
достигает максимума, который называется высотой
потенциального барьера для частиц, совершающих одномерное радиальное
движение. Видно, что для каждой частицы с фиксированной
энергией & высота потенциального барьера зависит от ее
прицельного расстояния. Обозначим через /^ пороговое значен
ние прицельного расстояния, при котором высота
потенциального барьера совпадает с <§ . Тогда для частицы, движущейся
с прицельным расстоянием р* > f>n , высота потенциального
барьера больше <g t а при f-cf* меньше <$ . Это означает,
что частицы, налетающие на силовое поле с прицельными
расстояниями/? > J3- , отразятся от потенциального барьера и
будут двигаться в обратном направлении, удаляясь от центра
потенциального поля притяжения. Напротив, частицы с
прицельными расстояниями f* <■ рп пролетят над потенциальным
барьером и упадут в центр. Число частиц, упавших в центр в
единицу времени» вычисляется по формуле N- Л/> / , где
} — плотность потока налетаюших частиц. Следовательно, эф«
с ~ /-v. 2
фективное сечение падения частиц в центр равно о - ^f3^ -
а) В конкретном случае с/(г)-—%. эффективное поле
2 h
7/ />*1= Ас _ достигает максимума в точке/- -_^L_ . Вы-
сота потенциального барьера £/ (fn) зависит от прицельного
расстояния как (/ (г) — -О-( ^ \~ р*° • Если эту величину
положить равной энергии <$ , то получим алгебраическое
уравнение для вычисления порогового значения прицельного
расстояния с решением f> — V3 (~%~} • ^ итоге эффективное
сечение падения частиц в центр потенциального поля притяжения
принимает следующее значениег^-Д^"/-^- )/Ч
V 2 с I 1
7-5 7/
б) €r=:J^r(^a,&-i2); в) e=jrs(s-r) s (fj .
) в'^'J'B Vis -a,)
85. Движение атомов в газе хаотично, поэтому электрон
с некоторой вероятностью проходит путь sc перед столкнове—
90

нием с агомом, приводящим к рассеянию. Обозначим черезJ(x)
интенсивность пучка электронов на глубине Х- от границы
газовой среды, Убыль интенсивности на отрезке doe описывается
формулой ~<jj(x-)=jlx)&A/c/3:.GTKyiia. получаем закон изменения
интенсивности в зависимости от расстояния ос от границы
среды в BnaeJ(~*h/0£'-xp(-&'/\tJJ4HCiio электронов, прошедших
путь sr перед рассеянием на отрезке cIjc , равно G'N(joexp^&Nx(d.
Если эту величину поделить на плотность падающего потока I ,
то получим вероятность с/W (?с ' того, что электрон пройдет
путь ос перед рассеянием на отрезке dzc , а именно: d И/'(XJ~
~ ti^j'^C TU&f(jc}-6'N€Xp(-6'Nx}- плотность вероятности или
функция распределения электронов по переменной х . По
определению средняя длина свободного пробега электрона
вычисляется по формуле
86. Число частиц уменьшается в & раз.
87. <?(*)=Л<? 7 г.
88. g*=V¥.
89. Sine, =~^ •
1т сие ^у
90. В лабораторной системе отсчета (л-системе) первая
частица с радиус-вектором /«* налетает, а вторая с радиус-
вектором р покоится. _Их потенциальную энергию
взаимодействия обозначим как l/( (fZ - Р2 //. Задача о движении двух
сталкивающихся частиц сводится к задаче о движении одной ча-
стицы с приведенной массой/V- /—^— в потенциальном поле
U(r/ ~[/(/f^-/^/j, где t~jp~ pji a frLj и т^- массы
соответственно налетающей и покоившейся частиц, Обозначим через Q
и Q углы рассеяния первой и второй частиц в л-системе, а
Q - угол рассеяния частицы с приведенной массой. Поскольку
движение последней описывается радиус-вектором р — р. - Р- ,
угол рассеяния^? определяется поворотом относительной
скорости 'if ^р*'.—7*1 . Следовательно, угол рассеяния частицы с
приведенной массой — один и тот же во всех инерциальных
системах, в том числе и в системе координат центра инерции
91

сталкивающихся частиц (ц-системе). Связь между углами
рассеяния следующая:
гггР sin & п -<7r r>n
Частица с приведенной массой /^ рассеивается во
внешнем ноле U(г) , которое представляет собой потенциальную
энергию взаимодействия сталкивающихся частиц. Значит
дифференциальное сечение рассеяния этой частицы определяется
обшей формулой , . /
в которой связь между углом рассеяния Q и прицельным
расстоянием р находится в результате взятия интеграла
ж в _ Г rdr
г E А*
где Г - точка, обращающая подкоренное выражение в нуль; £ =
= 2^сх> *~ энеРгия частицы с приведенной массой, a V^-
модуль ее скорости до рассеяния.
Каждой частице с приведенной массой JV отвечает одна
частица с массой mf , причем их скорости до рассеяния при
£--<?& совпадают:2£_~ AV~ (~ ^ • Поэтому совпадают также
и плотности потока этих частиц. Кроме того, каждому акту
рассеяния частицы с приведенной массой отвечает один акт
рассеяния исходных частиц с массами Ю f и т^ .
Следовательно, число частиц с приведенной массой [У , рассеянных на
угол 6 , равно числу частиц с массой /г? , рассеянных на угол
&f , а также числу частиц с массой тг , рассеянных на угол
у . Из этих фактов и определения дифференциального сечения
рассеяния вытекает, что дифференциальные сечения рассеяния
первой u&j (О,)и второйс!& (Q' J частиц в л-системе численно
совпадают с дифференциальным сечением рассеяния d6"(Q)
частицы с приведенной массой
d6-f(a7)^c(er(e)^ с/€гг(ог1=а/е-(е),
если только углы рассеяния 0 , ff и О связаны между собой
формулами, указанными выше.
Ради общности рассуждения проведены для частиц с
любыми массами mf и //?*, при произвольной потенциальной
энергии взаимодействия If'IF^-'j*'*)- В случае твердых шариков с
92

91.
92.
одинаковыми массами тп - ггьг= пг имеем Uflp"- p~/) = <^> при
lfy^l^R^R2 *С/Щ-Г21)=0 w!P;-?$l>kt+R* • а
связь между углами рассеяния принимает наиболее простой вид
# = <?6* и &=Ж~20^. Для частицы с приведенной массой /v = J?2
п г г
находим f = (,Rf -/ Ft2)cos -f и с!^(в) = jf (/?;+/%) Sin Q ol& .
Используя представленные выше формулы, получаем искомые
дифференциальные сечения рассеяния первой и второй частиц в
л-системе: _,
/^ _(AZe2 \2 dQj_
Je-^ (iLLAlzei) г„ е/Яг .
К 2/16 J co5B92
94. Дифференциальные сечения рассеяния С1б'.(в'}и ^f^C^J
для налетающих и первоначально покоившихся частиц (шариков)
в л-системе находим так же, как в задаче 90. Поймав в
ловушку рассеянную частицу, нельзя определить,покоилась она до
рассеяния или налетала, так как частицы тождественны.
Поэтому общее число частиц, рассеянных в единицу времени в
телесный угол aSl% -2^5сп\Aх равно сумме вкладов от налетавших и
первоначально покоившихся частиц:
где / - плотность потока налетающих частиц.
По известному правилу введем понятие дифференциального
сечения рассеяния тождественных частиц следующим образом:
d<rl*\= "^7^ = d*r I *) * d*g (?).
Используя полученные ранее выражения пня с/б". @ ) к d& (&\
при Q = &э~ % » находим окончательно
93,
с(бг(?) = 3R2cq5 X d£j при 0*X^-jf j
93

с/б-(XI ^О при Л< % £ jt%
Полное сечение рассеяния тождественных частиц &= 4KR2.
95. dNFa* ■% s}q A-е j cos x c(qx при о*?$*
drfpac^0 "РИ -jf<X^Jt-
(*'Х)г + ЫЧЯ*[2} sin?'
§ 7
97. Частица совершает малые колебания около точки х.= JC^
в которой потенциальная энергия U'- U (лс) имеет минимум и
выполняются соотношения <Ш(*°1~ п -л Я-Ш^М-уп. Указанная
с/я с(осг
точка представляет собой положение устойчивого равновесия.
Отклонение от него обозначим как^^дг-л^, . Разложим
функцию 1Т~и(^) в ряд по малому отклонению ^ и сохраним
первые два слагаемых, а другие опустим как малые:
Уравнение движения, описывающее малые колебания частицы
массы m вблизи положения устойчивого равновесия, имеет
вид .г , .
,* * Г с/ 7Jfscc)
iff СЛ) <^ = 0, U) =— -J^2?
где <х) - частота малых колебаний.
а) Для конкретного случая G"-' —
ку JZ -^с устойчивого положения равновесия из уравнения
<Ш(х0)^ 0 при уСЛоВИИ ^ U(Xol 0 t что ц&етхп= *(■£■)/у. Вы-
числяя далее вторую производную от заданной функции V(х.) в
точке jc-X- , получаем частоту малых колебаний ей ~ 2 у -— •
а) Для конкретного случая Z/-'—%-i- бос определяем точ-
\ m cl I •
94

98. а)сй^2'7 б> "Jj'ly <*2^2 \ ъ) оО--§-7
г) ей = <?; a)ai_-7 / >^ пр* п-/,2,..,
7 Л Bгъ-1OГ ' >
99. *)о0=в}/б^Г-} б) at^CVZy) в) i*?-SV2a.<j.
100. со
I V£J22jl )
?A
/
101. со-уб
^1^2
102. Декартовую ось Х совместим с осью обеих
пружин и направим параллельно силе тяжести, а начало отсчета
выберем в точке, где частица покоилась в начальный момент
времени t-О . Кинетическая энергия частицы Г~ -£гдь , а ее
потенциальная энергия U~U1^02 состоит из двух слагаемых.
Первое представля-ет собой потенциальную энергию пружин
Uf~2~(Kf * ^у)^ » а втоРое - потенциальную энергию данной
частицы в поле тяжести W - -гтгох. Поэтому функция У!агранжа
данной механической системы запишется как /,- -^rje-^-fxлКр)х.2+
•+ ггьйос . Отсюда получаем уравнение Лагранжа зс+сигх= О. п
где ooQ=(kjf?<?)/m . Его общее решение йг~ a cesfat+c/.)*
+ -f~2 . Постоянные интегрирования cl и ос определяются из
начальных условий &(о) - О и dc(o) — 0 . Окончательно
малые колебания описываются выражением
о
х^(хо--£ )со5 ajj0 оз0 =?
ЮЗ. ^__/^ __& ,_ ^4 л, .9-\fbt
mi
104. V =W cosV' -2^+JJl /
105. y>,f>cmy±^(,^Ji ^
106. X=Y& Vsinv—% t » где декартовая ось X на-
правлена вдоль вектора т? , а начало отсчета совпадает с
точкой равновесия.
95

t=ze\"" ' d*
Y¥f
.V
при jc^o,
при «x*^#.
a
109. Функцию Лагранжа находим тем же способом9 как ?
в задаче J , что дает
где f/ - угол отклонения от направления силы тяжести.
Вытекающее отсюда уравнение Лагранжа для малых колебаний
ф + оо2^ - —^ cos S?t
имеет общее решение
<? = С $1/г out* C2 C05 cot + У¥ас ,
в котором c*J — */$■/? ~ собственная частота колебаний маят-
пика, С1 и С2 - постоянные интегрирования, определяемые и:
начальных условий УСО/-^ и ^(О)~0 % ^%ас" частное
решение, имеющее разный вид в случаях й/^' и SZ- О .
В отсутствие резонанса Q '-f= Сл> частное решение
ищется в виде ФJ?^c°3&t • Подставляя его га уравнение Лагранжа
находим постоянную С= ~тг,—5 5Т~ ■■ Для заданные
начальных условий получаем
2
<р-~ % соз alt* ^ф^~~ (cos &t-cos cot).
В случае резонанса £?-бО частное решение
записывается иначе:<^> --^—^ 5б/г cot , а закон колебания с учеток
начальных условий принимает вид
у, „. •,/ a cot / cbcot
<р-<Роа>5 cOti- —дГ£-Sin, cot, ~^J^<:< /*
110. tei/^^^i.i^j.
той* ^ ° Г conT h
96

б) эь =—-, , * -уТ (сЛ oJt'■-cos ей t J ■
в) x= — __*_— zA(a2-t cof-co*)*
^(e^ifbajt-^-scn oJ0t)+2a.co(e cob<x>t-cosaHt-t
о
т) jc = Ck£__sln0)t при 0^t^-^T7
2 St i
jz/K-> . , /- при -< г;
Д} ^ = _5l- /^ ^-5*W *A £) при ^ 4< ^ ^ — ?
^-=:~q-F<^^ ПрИ 4§'^t
о
e)
^ = -Jlo--G~COS uJ i) при Oikt^ Ty
о
x = ^Ц 5сгь ^in со (t- f)n?»T±t.
о
111. а) Энергию осциллятора в произвольный момент
времени t г. />едставим так ;
где комплексная переменная %=z sc t iaHX удовлетворяет диф~
деренциальному уравнению первого порядка
которое получается из уравнения движения осциллятора oc+oQ jc-
1-501 °91

=r -J—p % если в его левой части прибавить и вьнесть величину
сод СС и положить сО(^С=-с^0(Ш0Х-) . Здесь ось <£: выбрана
вдоль вектора -с . Общее решение £ = %о<ш * %vac указанного
дифференциального уравнения первого порядка включает два
слагаемых. Первое ^0аМ^^ ехр(с00о £) является общим
решением соответствующего однородного уравнения %-i><jJo%~0
а второе А,^— частным решением исходного неоднородного
уравнения. Последнее находится методом вариации постоянных,
согласно которому величина £^ ищется в виде %„ajr£'ftJ&'Xpfa i)
где функция C(t) подлежит определению. Подставляя %„ос в
неоднородное уравнение, получаем
l£ltL=jLFexp(-la,eti
Проинтегрируем обе части этого соотношения по времени от t0
до t , где t0 - начальный момент времени. Е результате
имеем t
?va= e(t„ I **р(Ш. tj+ £j F(t ')exp[we (t-fjj dt'
где F = F (t/ - заданная внешняя сила. В полученной сумме
^~ Урйн* &ча<- постоянную C?(t0j объединим с произвольное
постоянной /I , написав A-* C?(t0)~ & GJcp(ccC) , где а и оС -
новые вещественные постоянные, определяемые из начальных
условий. После этого общее решение запишется так ;
Согласно условию задачи до начального момента времени
осциллятор покоился в равновесном состоянии, так что *1~£'
при t^Ь0 • Откуда OL - О , а полученная функция £ ^ % (г)
описывает вынужденные колебания осциллятора под действиек
силы F-F(t) . Если последняя имела вид F~ f eXf> /- — \ ъ
действовала в промежутке Бремени - «о ^ zf"^0^, то, полагав
£ 5Г-СЮ и /=<=>о в выражении для /£/'2, получаем
В показателе экспоненты положим
г } 4
(£)-ш.*'~(*'г
98

> /■' СО *Г
и проведем замену переменной интегрирования £ — -£- +1 в t
тогда придем к известному интегралу Пуассона, а искомая
энергия осциллятора примет вид
6 =
6) &=л!з±Е2-еяр(-га>0'г)
ъ
112. Изменение длины пружины в произвольный момент
времени t равно рс - эс^^,где функция jc0= a- C05(u>t+pt)
задана. По закону Гука сила, приложенная к материальной точке
со стороны пружины, имеет вид: ^/п/а= -к (ее- cc0~Q.Rnn
определения закона движения материальной точки массы ггг, __
воспользуемся уравнением Ньютона rriSc =~#(х-^р^^)-тп^Х}
которое после замены х-Х0~£0 -^ принимает вид:
Установившиеся колебания материальной точки
описываются частным решением последнего уравнения. Ради удобства
сначала найдем частное решение более простого вспомогательного
уравнения
X + fX + oooX=aa)*ex$.(cot+ acj ]?
тогда fi^sRe X . Решение вспомогательного уравнения ии.ем в
виде X = Сeocfffaot + рс)\ , так как при подстановке этой
функции в данное уравнение экспонента после дифференцирования
сокращается в обеих частях равенства, а для коэффициента С
получаем
г со0- со - i со у
С = CLOU,
° (со*-оо2J+ео*Г
Вычисг. ^ние реальной части от X с учетом
соотношения Х-Со +1 + хо приводит к следующему результату:
*•-/*, ^ (<Vq-cQ2) cos (cot + <*.) + со у sin (alt + d) >
113. г- Ъ2 ">£Г
2m {o0?0-oo2J-+CO2frZ
114. _ ^eqt (a2* ajj~ £*>2-<Lf)sin u)t+coBa-r)cos<jJt
>ъ {л<со*- ou2-afft-cJBa-fJ
99

§ 8
115. а) Функция Лагранжа описывается выражение?..
L=-%г (х + у + 2г)- m.az , где координаты X , у и з
частицы удовлетворяют уравнению связи з~£(я^уу) с заданно
функцией Я(х,у)-achS-XchBy. В качестве независимых коорди
нат выберем х и у . Найдем точку устойчивого положена
равновесия с координатами ас0 и yQ , около которой частиц.
совершает малые колебания. Поскольку в этой точке потенци-
альная энергия XJ = ma g (jcfy) имеет минимум, для опреде.
ления кооринат х0 и yQ служат уравнения ^J^&zlsL. — q j
~ аУ ~° или sh£x0=0 и sh6y0-0 с решением Х0
= yo ~ О . Разложим функцию Лагранжа в ряд по малым
отклонениям эс и у от положения равновесия и сохраним
слагаемые не выше второго порядка малости по отношению к а
и у . В результате получим
L = -f- [ро^у2-^Ссё2(^с2^у2)]-ггь^ .
Вытекающие отсюда уравнения Лагранжа
х+а<х£ jc =0, y-t-алб у = О
представляют собой независимые уравнения движения дву*.
одномерных осцилляторов с одинаковыми частотами cO=cO = SYo 7
°>г=Ъ*о{а+с-У(*-сJч. б2')I*.
116. а) Заданная функция Лагранжа
является квадратичной функцией обобщенных координат, что
характерно для механических систем, совершающих малые колеба
ния. Чтобы исследовать особенности движения, воспользуемся
уравнениями Лагранжа:
юс % + Т% + Ъ+-Т% = °}

J-n
J-
L„ _
t?S%+f%+%+f%=o,
f/ib + % = °-
Для определения частот малых колебаний будем искать
решение этих уравнений в комплексной форме 0^ = С,е1 %
где величины Q, при оС = 1, 2, 3 связаны с обобщенными
координатами так:a, ^ReQ.^ . После подстановки величин Q^Cfjs
с <*= 1, 2, 3 в исходные уравнения и сокращения на множительега)^
получаем алгебраическую систему однородных уравнения
относительно Cr % CL ml С. . Сна имеет нетривиальное решение
только в том случае, если определитель
/- аJ
и>-<*>)
о
fO-oo2)
1 - со2
1
2
0
2
/-со
этой системы равен нулю. Приравнивая его нулю, приходим к
характеристическому уравнению(г-а}г}{зоо'-6а?+2)-О i корни
которого oOj=:f , a?.f-/> т4=~ к ей2-/ 4=- определяют частоты
6&г = 7 %^=(^ ЧТт)'2 и сО, = (/ 1=)/2 малых колебаний ме—
ханическои системы;
7"'? -4
б) Ojrr/„ CO<,~-£=,COA
г) (^=10 сог
2 7
в) сд1 = оо2~аK=\/Гб
117. а) На основе функции Лагранжа
составляем уравнения движения, описывающие малые
ния механической системы:
колеоа—
101

В силу линейности полученной системы дифференциальных
уравнений будем искать ее общее решение в комплексной форме
t*j~ u?& и 66,-С,<? , где величина CO и комплексные посте-
янные С1 и £^, подлежат определению. Реальные или мнимы*;
части велич*ш $7 и $ совпадают с обобщенными координата-
N4i ty и <£ . Подставляв искомье функции бЛ-^б'' и Q2-£?£?'
з уравнения движения и сокращай ;;а обший множитель/? ,
приходим к системе однородных алгебраических уравнений относи
тельно С w Ср -,
C-2 СО Р) Crf * (сО2-J J С?г -■=<?,
C -с^2)С'.,тEс-0^~3) С?-й ,
Приравниваем нулю определитесь этой системь и получаек*
характеристическое уравнение сх!> * " 3 СО*'/- <? = О s при помощи
которого находим соСственные частоты ее?--/ и (/)? = Y2 ма-
"ых колебаний. Далее подставляем первую частоту а% в одя<.
из алгебраических уравнений (второе является следствие:,
первого) и определяем свяоь Ci ~2Cj- между коэффициента~
ми С J и Су . Верхний индекс ~/ отмечает их
принадлежность первой частоте с*^-, . Целесообразно ввести обозна-
/-//77 . г■><-*? п (fj ->' iff
чение С J -■= с>f6 '/ и 6Р =. J-nQ ' с вещественными величина-
/•; / --; - 2 7
мн о-, и 'f , птооы представить комплексное решение,
отвечавшее частоте OlZ , в удобном виде
^"-а, exp[i(t* r7/j 9 Ql^-i-a,rcxp[i{ti if;)\ ,
Комплексное решение, отвечающее второй частоте иЗ ;;о~
лучаем аналопшно
, Общее решение равно сумме вкладов от обеих частот: с2.
-aj'^a1/1 л Q2^Qf>+ аB2) .. Чтобы получить ^ (I fe. ^ь-
мем реальную часть от п-i Пленных величин Ui и 6?у , что
дает
?/ ~i^/ coblt+f^^cos^i + %),
где произвольные постоянные <# , £оэ , <f и V определяют—
ся из начальных условий-
102

Видно, что каждая обобщенная координата « и /^
совершает движение, которое является суперпозицией_ простых
гармонических колебаний ctf cv$ (t+Уу) и &z COS (V~2t'^ v^ J
Последние называются нормальными колебаниями;
б) (f, ^ci1(X5(Wti-(fJ)+a,x<os(V3't + fs),
в) £,-- агсю$(Уг^^)*о.га?5 (^ +%),
г) ^ =a7cvs(t+%)+а*,сс>зA/з£* %) ,
f = -a7 со 5 (t + fr) + л2 соэ (l^l -t<f2).
118. а) Слагаемые в функции .Чагранжа L - pity Q, + <1 4,Р)"
.-£(~3 * 2"*£fyj\«квадратичные относительно обобщенных скоростей,
описывают кинетическую энергию данной механической системы,
в то время как другие слагаемые, не содержащие обобщенных
скоростей, представляют потенциальную энергию Ц= -£■ (-Цу- —'— /
+Z fa <fr2_j , которая входит в L со знаком минус. Б точке
устойчивого положения равновесия с координатами Qaf и Ф 2
потенциальная энергия имеет минимум и выполняются соотно—
^ьшя^Щ0г,^о2)/ц^О и Э U(%n%2)fo([f0 . Раскрывая
производные, приходим к результату <2 ^ о г~ / . Отклонение от
положения равновесия обозначим T&K:jc, = a-& ил^-б*-tf „, где
(xfl«f и/д^/«/, так. как колебания малые. Разлол.им
кинетическую и потенциальную энергии в ряд по матым отклонениях"
от положения равновесия и сохраним слагаемые не выше
второго порядка малости относительно X, и J£^> . В результате
функция Лагранжа^ описывающая малые колебания, примет вид:
L*£(**+£*)- -fCx*+ 3X22t 2*1С£г} -2 .
Тем же способом, как и в предыдущей задаче,
определяем собственные частоты 6J„~ г? и Ц- Y]> , а также величины
X. и Х0 в виде суперпозиции нормальных колебаний. В итоге
обобщенные координаты запишутся так:
£ =/> CljCGS [2t-r f^tCLjCOS^Vit + fz),
103

t^f+Clf С-0* B* + %)~^2 C°3 №1 *%))
где си , CL % <f и <f - произвольные постоянные;
в) ^-/^^^^^^/^(^^A
r) ^r^OLf ca${V2t t <ff)-ta.2co3(YZ'-t+ tf2 O
^!~2cirt0s(V2t+yi)+a2eos(}/rf~ti-4>2).
119. a) ^= sln2t-Vz SlnVZ't, ^ *din2i + -^slnV2t;
б) i=33ln^:+$in V*l, %^3Siti^-^ln -fit;
в) £ =2(a>s4=+cos I/JO, %^COd'ft-Cg5 ^t°->
r) $=CObt~CO$V/6 ty n=CO3t+-jC0S)/6t.
120, Обозначим ,#-, и <Я?г- отклонения материальных
точек от их положения равновесия, тогда потенциальные энергии
трех пружин запишутся как кх>5/2 % ki'^-^y J /2 и кХ£/2 >
Функция Лагранжа механической системы равна разности
кинетической к потенциальной энергий:
Решение уравнений Лагранжа
£f + coZBxrx2j=09 2^ со B*>2~xi)=0
ищем в комплексной форме Х^х^^6 , где со и С^ при оС~
= 1,2 - искомые постоянные. После подстановки указанных
функций в уравнения движения получаем
[2со*- оог) £~оого С ^ Q

^20Cr2(cOZo-oJ2)C2=0.
Приравнивание нулю определителя полученной
алгебраической системы уравнений дает характеристическое уравнение:
Cfi*-5a)*0GOZ+-~ СО*-О , из которого определяем собствен*,
ные частоты ^ %. / 3+уз_у/2 ^ и (/) -[IzvAaA^ .Согласно
исходным алгебраическим уравнениям коэффициенты С. и С2 ,
отвечающие первой частоте бЛ » связаны между собой как <?z =
= —^—- С , В случае второй частоты <24, связь другая ;
<с /. <=
£" - JLt-kAgW . Для комплексных коэффициентов введем
обозначение С'У-Г(х el¥s , где <2-5 и <£ - произвольные
вещественные постоянные (s= 13?) . После этого общее решение в
комплексной форме, содержащее вклады от обеих собственных
частот, запишется так*.
 2 П^ ^ 
Чтобы найти закон движения в виде суперпозиции
нормальных колебаний, вычислим реальные части величин Xj и ХР ,
которые совпадают с координатами материальных точек, тогда
получим
&7 =ccf cos (co? t+ <pf ) +&2 cos (co2£+ f2O
121. <ъ = -&+аfco5 (V3aiJ + <f }+azC<?s(ciJ0t+%),
jc2=Jb -a.jCes(yZco0t+ fr) +&zc0s(ooot + <f2),
где сй0 ~Л//79 , а <х7 и jc2 - смещения верхней и нижней
материальных точек относительно тех положений, которые они
занимают, когда пружина не натянута. Величины Яу , Си2 , f и
^ являются произвольными постоянными.
122. Задачу будем решать в системе координат центра
инерции (ц-системе), чтобы исключить прямолинейное и
равномерное движение последнего. В и-системе координаты *С* , <Х2
и «Яу материальнь.х точек с массами гтг1 , тг и т^ связаны
между собой соотношением пг пс tm. х +лг*х -О • Следова-
7 Т 2 г д * .105

тельно, данная механическая система имеет две степени
свободы. В качестве независимых обобщенных координат выберет
величины у,- а>г~ х1- <f и ty = jc3- jc2-8 , которые пред.
ставляют собой растяжение первой к второй пружин . Тогд.
функция Лагранжа L , равная разности кинетической 7~- •£-(m]Xj~.,
+mg &2 + гп, jc/ ) я потенциальной У - -^(х£- ^ -е) г+ -g2 ( jc -
—Du?— Р.}2 энергий, в новых переменных с учетом соотно»
шений rrtj-rrb -tn , /tzj~ 2пг и kz-2k~2rr?cO^ примет
вид „ , ,2. „
Как обычно, решение уравнений Лагранжа
ищем в комплексной форме GL^- C^ <?1С° (°^^ 1, 2). Для
определения комплексньх постоянных £1 и Ср получаем систему
однородных алгебраических уравнений
из которой вытекает характеристическое уравнение С0-5о00@ +
i-^CO^=0 для собственных частот Ой7 =2СО0 и (л) -сР0.
Подставляя первую из них в алгебраические уравнения, находим
связь (У ~-Ci между комплексными коэффициентами,
отвечающими этой частоте COj . Аналогично получаем С^ — 2 С?^
для второй частоты оЛ . Вводя обозначениям, ~af6 к QW-cue '
можно написать общее решение уравнений Лагранжа в
комплексной форме: ,/Л . , Л ,
которая удобна для последующих вычислений. При помоши
соотношений <f-iRe(lf и ^ =/?<?^? определяем £ и ^ , что
дает возможность представить координаты jc , jc и эс^ в
виде суперпозиции нормальных колебаний
хг~ ~¥~[СС/ c0S>(<?CL>ct + ¥7h faz жз (oj0 £+<ег) +5e] ?
106

л3 - -ф- [д Р- ctj co5Bojc £ + У7 )?2 &2 cos (tuv£+ %JJ t
Ь ~_ ih0 Cln ^- Yf5ln ^ a)<> *J>
где Ca) ~k /m , а о, и <?„ — смещения материальных точек отно—
сительно положения равновесия.
, ,2- A±Vl ' JL cqz - з~ Уб _к_
Величины^ и ~С„ представляют собой смещения материельньл.
точек относительно тех положений, которь;е они занимали в
начальный момент времени.
% = #£ [(w - £1а?3 ^ * * dk " i)С05 ч {h
.2S
/ ^ o/ 2 2 о / с m
Здесь <}■ и ty7 ~ смещения материальных точек относительно
положения равновесия.
127. .-«.
^. Fa аЗг0 cos cot
Tool ^-oJ?)(v2-oO*) '
М- !=оB<Лго-сюг)с05шЬ .
107
2 <»i m(.i>'?-C0*) (uf~ (jj*) ?

хг~ /77
2 3 + V5 ,z ,,2 3-V3 2 г к
Здесь ^; и -*^- смещения материальных точек относительно
тех положений, которые они занимали, когда пружины были не
натянуты.
128. ^'(я^1Н^гзс4) (**-*41(фЗ*£)>
2 к 2 — к
130. = aoQo[(o)£-co2)coscoUrMsincA)t] 2_j^
§ 9
131. Из двух координат х и у частицы, движущейся в
плоскости XY по кривой У =У(ж), только одна является
независимой. В качестве последней выберем «2 . Функцию Ла~
гранжа напишем как разность кинетической Т- -^-(jc /у / к
потенциальной U— т$У (&) энергии, приняв во внимание
уравнение связи у- у (ее) :
i*?H^ }*]*'-»>/*(*>■
Разложим эту функцию Лагранжа в ряд по малому откло«>
нению cl~x~oc0 от точки <г=х0 устойчивого положения
равновесия, где потенциальная энергия имеет минимум и
выполняются соотношения —~V-°^= О и -&--&. -° ?>#.В этом разле-
4 х dxr-
жении сохраним слагаемые не выше трети его порядка малости
относительно О , тогда получим
1.08

После этого имеется возможность написать уравнение
движения с учетом нелинейного слагаемого, являюигегося малым
возмущением:
..2 .2
j + oJ0f = Uf ,
где обозначено лЛ а " У[ХН и оС=- £- ^Ы. Начальные
° f сЫ2 a doc*
условия а,(о) = О и f@)=lt.
Если пренебречь малым возмущением оС<1 , то решение,
удовлетворяющее начальным условиям, представляет собой
гармоническое колебание <£=-—■ &in cOnt
7 со0 о
При наличии в уравнении движения нелинейного члена & #-
будем искать решение в виде о - 4,(/' у- <р> ' , где о; '-
основное слагаемое, а Ф '- первая поправка, обусловленная
указанной нелинейностью. Подставляя искомое решение в уравнение
и начальные условия и приравнивая члень одного порядка
малости слева и справа равенства, 1И\-еем
'jft)+ <°l f(f)=°> f}(°h 07 j, {/J ( О) - V)
p'>+a>lf<*> = ocf>\ fl2)(o) = Q, ^(o)--o.
Из первого уравнения и начальных условий получаем # =
-~ si/г oO„~t | а второе уравнение запишем в удобном виде
ос гг*
2 со*
Его решение й'г4а^/^ г' содержит два слагаемых,
из которых %фГ ьг&ыъса0ги C2co$c*j0t - общее решение
соответствующего однородного уравнения, a of2' — частное реше—
rl/Ct-C
ние, имеющее вид:
% =~-х 7Г+ г? COS 2 C00t.
гуле, 2oj* 6a>? °
о о
Произвольные постоянные С, и С? определяются из на— 0
чальных условий и имеют следующие значения: С~0 и сР-~~-~т
В7 -3 СО '
итоге о
г
7У оС 7/~
f -£Г sin <Ч ^ * TT7v C-4C05 cv0tt cos2qj0 t).
109

а) Для конкретного случая у(х)= —~ySx определяем точку
Х = Х0 устойчивого положения равновесия из уравнения d-y[Xo)_ ^
или $- -~jr=0 при <г {/J °г>0 что дает jon=V^- После этого находим
о? и «xi при помощи найденных выше формул: с^>0= Bа§ у ^) »
. Окончательно
а
2
Х" ~B05in ^оЬ+ o&fc-'fabGOj+cosZ&oiK
б)
о £ i ®
132. Напишем уравнение движения х+й00ос=<?С<х> +J5X. и
начальные условия <x@j=cz ъх(о)-0 . Поскольку нелинейные
члены малы, будем искать решение уравнения методом последо~
ва тельных приближений, который состоит в том, что координата
jc и частота сО колебаний ищутся в виде рядов:
О B) (Г) B)
о (Щ П. ,
Здесь ~С - слагаемое, пропорциональное &- (/г= 1, 2, ...), а
0>,п'— поправка п -го порядка к собственной частоте со ,
пропорциональная а!/г) {п- = 1, 2, ,..).
Чтобы применить метод последовательньх приближений,
перепишем исходное уравнение движения в другом виде
Левая часть этого уравнения содержит искомую частоту
колебаний сО , а правая является величиной более высокого
порядка малости по сравнению с X и служит определенным
возмущением. ,
Решение уравнения движения в первом, приближении X -X
получим, если пренебрежем нелинейными членами и положим (л>~
= с0о . В результате преходим к гармоническому колебанию X -
= ac0£O)ot с частотой со = со0 .
Решение уравнения движения во втором приближении
запишем как х. ~дс(;'+ссB'У1 СО -О00+ co(fJ. Подставим искомое
решение в уравнение движения и начальные условия и приравняем
110

между собой члены одного порядка малости:
Левая часть уравнений для эо и <х, ' содержит искомую
частоту erf ~oJp ■/• СО**} с учетом малой поправки, чтобы избежать
нежелательного разложения в ряд гармонических функций вида
сод cot- соэ сОа t- co(,U $in,aHt- 4f (co(t)i) cos CJ0t+ ... .
Все слагаемые этого ряда, кроме первого, растут со временем
и поэтому теряют физический смысл в области ой 6у> 1. Такое
разложение в ряд не возникает, если в левой части указанных
уравнений стоит частота сО , включаюшая соответствующую
поправку.
Из первого уравнения с учетом начальных условий
находим х -a,COS oot , где сО-СОс-& СО ', Поправка со*-7'к.
частоте сО~о определяется вместе с поправкой iC^ при помоши
второго уравнения. Для этого выпишем в явном виде правую
часть указанного уравнения:
£ *г)+а)г-х(г1=с<.<ь cos oot-t-2cAJ0 а?(Г/}а cos cut\
Преобразуем правую часть так, чтобы она содержала
гармонические функции в первой степени:
„(г) г (г) оса2 о^сгг ~ ,/^^ (О ±
Резонансное слагаемое <?оэ0СО ctCOScot в правой части
уравнения должно отсутствовать, так как оно привносит в об-
шее решение такие слагаемые, которые растут линейно со
временем. Эти слагаемые с некоторого момента времени
перестают быть малыми. Между тем поправкам по определению
должна быть малой (пропорциональной со ). Заметим также, что
в замкнутой механической системе из—за отсутствия внешнего
источника энергии амплитуда колебаний не может возрастать
неограниченно. Отсюда следует со - О и СО~<ХРп , так что
последнее уравнение упрощается:
~(гК,,г^B) ^а2 ocaf о 4.
СС +0О0 ЭС --J- + ~2~~ cos ^^о t -
111

Решение этого уравнения находим по общему правилу
где £>с'и - обшее решение соответствующего однородного урав~
•9" (г)
нения, a ^cv^c - частное решение, которое ишем в виде
Здесь А2 и &2 — произвольные постоянные, а коэффициенты С. и
С*2 подлежат определению. После подстановки зс^^ в исход-*
ное уравнение и приравнивания между собой однотипных
слагаемых слева и справа равенства получим С=-—^-и С = - ^ °%~ .
' <== Ь00 «? 6 СО3
и о
Таким образом, поправка второго порядка принимает вид
Из начальных условий находим Л = — -з—-& и 3^=0 . В ито-
2 3cog *
ге получаем следующую поправку к первому приближению:
jct2L jfL^_ C-2cos co0 t-co5 2cO0t)„
Характерно, что поправка иторого порядка содержит
постоянное слагаемое, а также колебания с одинарной и
удвоенной частотой. Окончательно решение уравнения движения во
втором приближении запишется как
? о о
<?с си
где -з—яг — поправка к амплитуде, а поправка к частоте
колебаний отсутствует.
Найдем решение уравнения движения в третьем
приближении, полагая
Подставляем искомое решение в уравнение движения и
начальные условия и приравниваем между собой члены одного
порядка малости;
JC
112

Если учесть предыдущие результаты, то решение первых
двух уравнений с учетом начальных условий можно написать
сразу 2
jZ^La cos cut jc B)= *" a'P ( 3-2 c^s cot-^eo52oot),
где cO = cJ0 + co( 'и os> - О ,ав множителе, входящем в х, ,
квадрат частоты со2 заменен на oj^ , чтобы не превышать
принятую точность вычисления.
Поправка со к частоте определяется вместе с поправкой
эе. при помощи последнего уравнения, правую часть которого
выпишем в явном виде
ХШ^00^13)=^4(Зсоь cot -2co&*cot-cos cotcosZalt) +
3co0
+f,cb3cos 3 out + 2иЭ0 a)Ba. cos cot.
Преобразуем правую часть этого уравнения так, чтобы
она содержала гармонические функции в первой степени. Для
этого воспользуемся формулами:
cos2Qjt= -£-(j+cos 2cotO cos cot соз 2u?t= -£-(c<?53ait+co$o)t)
cos 3cot= -2- cos 3oot+ -%■ cas cut%
После приведения подобных членов получим
* faia,**"L - Щ- ^4 cos 2*>t+ (^- ^)cos3*>t +
о
/Art *r,3
Согласно сказанному выше резонансное слагаемое в
правой части данного уравнения должно отсутствовать, что
выполняется при условии
■?с0о \3с0§ 2 I '
Решение оставшегося уравнения ищем в виде:
(з) (*) (з) а) , ,
ж -=«£• -toe • jcn„u=A,coscot+BsincOt,
о$н час ? одн д 3 >
^цас^^Г* ^2 COS ^^ f ^3 С°5 3 °>£ .
Z'JOI ИЗ

Произвольные постоянные A3 и ЕЦ определяются из
начальных условий, а коэффициенты C-t , Со и Сд находим
подстановкой Х\?' в исследуемое уравнение, что дает
Г'~ *«/ ' г~ Scot ' с»-кс*;\**>1 г)>
2 г
где вместо <%? подставлено о00 , чтобы не превышать
принятую точность вьнисления. В итоге поправка третьего порядка
запишется как
2 з
& = A COS a)t+ B3 Sin coti- *** ^- (со5 2ajt-д) +
о
а? / *,*
+ -г т 1 -Г~г
16оо* \3с#0
-^— I cos 3 <*>£ .
Из начальных условий вытекает
Окончательная поправка третьего порядка принимает вид
J&i а3 / 29*ог . ^
Поправка третьего порядка наравне с постоянным членом
содержит колебания с одинарной, удвоенной и утроенной
частотами. Итак, решение уравнения движения в третьем приближении
найдено
об CZ л & { 29оС2_ J3
„(г °* а ■ <* (
9 С* о
2 2
■f-"— I СО 5 Оо£ +
*7^г(тг^-4) cosiest; „^JZI &?.*£. ).
13 3. Используя функцию Лагранжа L~-j>-/-n,£ Ф2+ тй fcobfy
плоского маятника, составляем уравнение движения <p+OQ0 slaty~С
г 9-
где Ой — -р~ , a (f — отклонение маятника от направления силы
114

тяжести. Начальные условия #(о}=у и ф(о)-0 . Разложим
функцию sin Ф в ряд и сохраним первь е два слагаемых, а другие
опустим как малые в силу неравенства \ty\^l . После этого
уравнение движения принимает вид
f + oo2y= -%> <р3+ (а)г- со20) ^
Оно совпадает с исследованным в предыдущей задаче, как и
начальные условия. Это обстоятельство позволяет
воспользоваться полученными там общими формулами, положив в ниХсД?- f> ,
CL-*/^ лоС=0 и fL-gCx>0 • В результате находим амплитуду
и частоту со колебаний маятника с учетом первой отличной
от нуля поправки:
2
* ITco* C ~^ сов ^^ °°5 2 coi) ф
134.
9а?0
IS la 3 cot \
oj^-^L. fJA + 4*1 )„=jr
ГЛАВА Л
б 10
135. а) Функция Гамильтона £g представляет собой
энергию S - £ ^ 4 -L механической системы, выраженную
через обобщенные координаты а и обобщенные импульсы р =
= -^т~ , где L - функция Лагранжа, а к - число степеней
свободы. Из данного определения функции Гамильтона вытекает
способ ее вычисления по заданной функции Лагранжа. Если
функция Лагранжа механической системы с двумя степенями
свободы имеет вид £,- о, а - -£- 6 / , то по общим
формулам находим энергию £= 0.0,-оЯ, t ,a также обоб-
У172 2 7? 115

щенные импульсы р. -<?,, и р ■- 4-^/ . Последние два
соотношения позволяют выразить обобщенные скорости через обобщен^
ные импульсы: ф7=р?+р?^ , с\, ~ р1 . Это обстоятельство дает
возможность исключить обобщенные скорости из выражения дл^
энергии <э f после чего она приобретает физический смысл
функции Гамильтона £?-р}р2+- -£-p?t %
136. а) Функции Лагранжа L и Гамильтона 2£ связаны
соотношением L = £ р q, - сН! , в котором ау - обобщен-
оЬ-Г 'ос "оЬ '<*-
ная скорость, р^ - обобщенный импульс, а к - число степеней
свободы механической системы. Поскольку функция Лагракж^
зависит от обобщенных координат О , обобщенных скоростей а
и времени / , в правой части написанного равенства
необходимо выразить обобщенные импульсы р через # и # при
помощи уравнений Гамильтона — -ф3(^ ~;? •■•?/1с/ • Применяя
изложенную методику к механической системе с тремя степе,
нями свободы, которая описывается функцией Гамильтона а¥ -■
б) i,--mc
УЧГ;
.; г
2^2 ^2
138. # = -J-(±£^,+ *%)+=&,.*.
2т \аг+4гг гг I л
р
13 9. а) Чтобы в функции Лагранжа L-^- lP +-£-А тг-еч
перейти от декартовых к цилиндрическим координатам,
воспользуемся разложением векторов V и А по ортам cr , TL,
и ся цилиндрической системы координат:
116

rr^r + fyry+e^Z) /T^FrA^TpAp+iTg Аг>
где компоненты А(~ , А<р и Аг вектора А*~ выражены через
цилиндрические координаты Г , У и Z , которые выбраны в
качестве обобщенных. После этого функция Лагранжа запишется
так,'
где скалярный потенциал <f выражен через переменные А- , (f
и £ . Зная функцию Лагранжа, нетрудно найти энергию <f =
гу2 / • 2 2*9 * 2 \
- -g~ (t"+h </s -+g j + Ctp и обобщенные импульсы
р^ПГ+^-Аг, %="* **& + •§-*<?'', P£ = m* + -§-Ag.
Последние соотношения позволяют выразить обобщенные
скорости /- , У и 2 через ft , ft и /^ . После этого энергию
& можно представить как функцию обобщенньос координат и
обобщенных импульсов, чтобы она приняла физический смысл
функции Гамильтона J£ . Окончательно получаем
140.
р2 р
р J^—— -ma cos P , /-- —£■ ,
А=0, <f= —^ ■ г А- ■
141 -Put C(?S 9 „ /О
142. По условию задачи энергия £ ~ Arth р является
функшюй обобщенного импульса Р . Следовательно, она служит
функцией Гамильтона Ж~ At~£hp . При помощи уравнения
Гамильтона ^~- -fy находим искомую обобщенную скорость. Произ*»
водную JktiL ' вь.числяем дифференцированием по переменной р
обеих частей равенства tkdC= P 5 а после дифференцирования
полагаем Ж = <%> , Окончательно получаем q-thz'S .
143с По заданной Функции Лагранжа заряженной^ частицы в
электромагнитном доле определяем эн-эргию 5 ~-~-?р 5^*/- г? f
''" ' 117

и обобщенный импульс р = n-iir-f--§-А . Используя эти величины,
находим функцию Гамильтона в декартовых координатах
Уравнения Гамильтона запишем в векторной форме
p=-ft-ac/X, ^ЖСР-ё-Л-
При вычислении градиента воспользуемся формулой векторного
ан&пкз&gj-ad&—2(&£f~cid)&+2(V*f~otct к учтем, что при
взятии частной производной по координате обобщенный импульс
рассматривается как постоянная. В итоге первое из написанных
уравнений Гамильтона принимает вид
Чтобы получить уравнение Ньютона, левую часть этого
уравнения запишем как miP-^ — f^4-f-(^raj'CLc/)AJ , а в правой
положим Р-^А - miF и f-otA*~=-H . В результате указанных
преобразований приходим к искомому уравнению Ньютона тг" -
144. Если величина M~fT сохраняется, то ее полная
производная по времени обращается в нуль ~T7-/rf'/f=rf~tf=Q.
Наоборот, выполнение равенства М Н~0 означает сохранение
величины М Н в постоянномтмагнитном поле п .Представим
правую часть соотношения /У = /*% Р + h K Р в другом виде при
помощи уравнений Гамильтона
р=& [((р- £ Т)^)г* (р- -§г). rot г],
которые в общем виде приведены в предыдущей задаче. Здесь е-
и т - заряд и масса частицы, с - скорость света в вакууме,
а А — векторный потенциал магнитного поля. . Исследование
значительно упрощается, если величины р и Р выразить
через радиус-вектор г- и скорость 2^ частицы, а в качестве
векторного потенциала взять'A-pH*t~ . Для этого
воспользуемся соотношениями Р~=т ~гГ+^д*х Р~ и Р= -§-[(lF(lh<ZG/)A*+V'*rt\i
вытекающими из уравнений Гамильтона, а также формулой
векторного анализа (Waro^dr JA^S^cn/fz^Tj-z^^o^ % тогда получим
118 М=^[v:(F'Hl-r(vH)}.

Отсюда видно, что скалярное произведение векторов /V и И
обращается в нуль, что доказывает сохранение величины Л/И в
постоянном магнитном поле Н .
145. a) (j^COS24г >> P=~2t$Y 1
б) f-Vf + t^j Р=£,
146. a) ^=l<ffiy р= ^-0— •,
в) ,.М, ^ .
147. a) <j,^V2-V2+t2i p7 = -£,
148. В качестве обобщенных координат возьмем
декартовые х, у и z. Как и в задаче 143, определяем функцию
Гамильтона заряженной частицы в заданном мигнитном поле
где Р , Р и Р - обобщеннье импульсы, отвечающие
канонически сопряженным переменным х, у и ? . Видно, что
обобщенные координаты у и г являются циклическими.
Следовательно, обобщенные импульсы Ру и Р сохраняются, так что
Ру = С* иР=:Ср, где С и С2 - некоторые постоянные. Это
обстоятельство позволяет представить функцию Гамильтона Ж в
другом виде
е И
где введено обозначение и)= — и х,.=—-К—. Первые два
mc H еН
слагаемые в функции Гамильтона описывают одномерный
осциллятор массы т и частоты и) , координата jc которого
колеблется около постоянного значения осн . Уравнения Гамильто-
119
/
2т
X = •
Р2
сРу
еН

на этого осциллятора после дифференцирования величины ${ по
переменным зс и Р принимают вид:
<*">*(*-*„)—Ря , -~P* = i ■
Последние приводят к уравнению движения
с решением
х = cl cos (u)i *■ оС) + эсн ?
где а. и оС - постоянные интегрирования.
Обобщенный импульс Р^ определяем из соотношения Рх =
--=/пх , что дает Р^-лг аи) sin. (u)t +<L) .
Обобщенные координаты у и г находим из уравнений Га-
мильтош: _ ^
dPi, ~* ' ^Г=Д •
Первое из них преобразуем так:
Откуда получаем закон изменения обобщенной координаты у-
= -a,$in(u)t. +оС) + Сj , где С3- произвольная постоянная.
Оставшееся уравнение Гамильтона _£_/> =•£ с учетом Р * £* лри-
л /77- £ £ с
водит к выражению ^ — —^—'i + С , содержащему произвольные
постоянные £_ и С, .
Вьшцшем найденные выше решения уравнений Гамильтона:
Px^-mau)sln(a>t^yP^=C1 y Pg = С2 ,
с С С
х ~ a cos(u)i +aL) + —j3~ , у =: - a sist (и)£ +^)+ С3 у^=~2.£ + г
где произвольные постоянные С^ , С~ , С~ t С, t Q. и <^
определяются из начальных условий.
§ 11
149. Если величины tf и Ма - интегралы движения, то
скобки Пуассона для этих величин jM^My} также являются
интегралом движения, т.е.{г!хМу}~Со/г5>т (теорема Пуассона). Та»»
ким образом, чтобы получить новый интеграл движения,
необходимо вычислить скобки Пуассона {/i Mu\-Z! (—->£ ^JliL. „
120 1 ' *Ч\эГы. эл^

~ TZT -, п I , где приняты обозначения схт- х , <аг, = у,
JCra, = 2 и аналогично для проекций импульса. Вычисляя про«*
изводные по координатам и проекциям импульса от величин
Мз?х2ра-эс3Рг и /^ух-х3Р7''Х1Р3)находим [МхМу}~Мг.
Следовательно, новый интеграл движения имеет вид M£-ca5t .
Заметим, что для механической системы с конечным числом
степеней свободы количество независимых интегралов движения
ограничено. Поэтому интеграл движения, полученный при помощи
скобок Пуассона, является или новым интегралом движения, или
функцией исходных, или числовой константой.
150. Для удобства запишем сС-$с проекцию векторного
произведения векторов /*" и р в виде (^'r^lr^Uffr^s Р* » где
<5> — совершенно антисимметричный единичный псевдотензор
третьего ранга. По дважды повторяющимся векторным и
тензорным индексам предполагается суммирование от 1 до 3, а
знак суммы опускается. В принятых обозначениях имеем
Скобки Пуассона {М. /=> } вычисляются аналогично//^,/" jz
="^oiBYlPy ' ^Ри БЬ1числении оставшейся скобки Пуассона//у. /уС/
следует использовать полученные выше результаты и свойства
тензора &, , а именно:
te MJ- Vr {*?РГ > "J* %<f (•> (/> "A +pt {y м,}) -
151. {?fHr.ar)da£E{, {ИГчЫр.щ d£KEl,
{,%гс(г-Ю}= (FF) (F*F)-r*(F« F).
152. *){?;{$rr\-n(ccn""<z, (F, F^j'SnF^-'ip^
{f$\=cji-adf, {p~F\^dlvF;
Ъ){К1С?р)п1^-п{С1р) ct,{r?Jo \=-?.np p,
121

far), (*?Щ~(<я\нЩ<ь&р£ % %%,■>**&).
fab }=Мр«ъ-?%.)+ £ ^-/=%,;,
Щ } - -bfy, ft. /,/ -tf£/* ^i e Mr .
157. fr=t(j?.jf).
§ 12
160. а) Преобразование от старых переменных а и р к
новым #, и /^ вида
наэьшается каноническим, если новые переменные также
удовлетворяют уравнениям Гамильтона, независимо от строения
гамильтониана. Здесь К - число степеней свободы. Чтобы найти
условие, при котором преобразование к новым переменив м
является каноническим, воспользуемся тем, что уравнения
Гамильтона можно получить из принципа наименьшего действия. Из
всех кинематически возможных движений, совершаемых
механической системой за один и тот же промежуток времени между
фиксированными положениями, реальное движение отличается
тем, что для него вариация действия равна нулю:
4, к
122 *7
*j 1&,ы*-*(ьк*№=0> A)

где M(fcp7t) - гамильтониан механической системы, а сь и р -
вся совокупность переменных л, и р при сС=17...,/С , причем
fy/x.(^I}~^9оС (^2^~^ ' °тсюДа вытекают уравнения
Гамильтона для независимых переменных й, и р .
Чтобы новые переменные Q, и р также удовлетворяли
уравнениям Гамильтона, необходимо выполнение аналогичного
равенства, записанного в этих переменных. По виду оно может
отличаться от предыдущего A) только произвольным
постоянным множителем С , а именно:
<rf с[Е я, a*- aft*, р, tftdt • о,
где о% fa jpy t) - функция Гамильтона той же механической
системы в новых переменных, а $ и Р обозначают
совокупность переменных Ct^ и Р^ при <рс =/?..., /С , причем PQUftj) ~
~ (fGL(£z)- 0 . Наличие произвольного множителя С является
следствием неоднозначности определения функции Лагранжа,
которая входит в выражение для действия, когда оно
рассматривается как функционал относительно обобщенных координат и
скоростей. В дальнейшем для простоты положим С-7 , сузив
тем самым класс рассматриваемых канонических
преобразований. В этом случае для новых переменных имеем соотношение
^гф, Ъ&х'(*,р, НУ*=о, <2»
Вытекающие из принципа наименьшего действия уравнения
Гамильтона в переменных (f, и р не меняются, если к
подынтегральному выражению в A) прибавить полную производную по
времени f \f7 от произвольной функции Fj^Fjifyt)
координат а и времени / . Аналогично уравнения Гамильтона в
переменных Q. и Р не изменятся, если к подынтегральному
выражению в B) прибавить А&(Я;£/ _ , где Fz=F2((lft) -
произвольная функция. Поэтому можно заключить, что разность
подынтегральных выражений в A) и B) равна полной
производной по времени от некоторой функции F- V (<Lj Oi, t) :
Умножим обе части этого равенства на dt , чтобы
получить связь между дифференциалами:
123

Переменные ли ^ возьмем в качестве независимых,
так как величины р и /^ можно выразить через «^и GL^
при помощи исходных формул преобразования рассматриваемых
переменных. Поскольку равенство C) выполняется
тождественно при любых значениях f и независимых переменных
Л и # , , отсюда находим
Полученные соотношения называются формулами
канонического преобразования, a F~TЫ^О.-)Ь) - производящая
функция этого преобразования\
б) чтобы найти производящую функцию Cf=Cf(^0P?t) ,
прибавим к обеим частям равенства C ) следующее тождество:
тате получим
где введено обозначение
Будем рассматривать переменные а> и Ри как независим
мне, так как другие величины Р. к о?_ можно выразить через
&, и /-v при помощи формул преобразования рассматриваемых
переменных. Тогда величина
представляет собой полный дифференциал функции G~ — G(<l}P1i) .
зависящей от переменных £ , Р и t - Приравнивая между
собой однотипные члены слева и справа тождества D), получав-
ем формулы канонического преобразования с производящей
функцией G-~Cr(^) P, t) :
Формулы канонических преобразований с производящей футь
кцией, зависящей от/о f Q и t или р , Р> и / ,
находятся аналогично;
124

r) JL--
ЭР<^
9<р
ЭФ
161. Предположим, что данное каноническое
преобразование характеризуется производящей функцией F—F(^y
^^удовлетворяющей формулам канонического преобразования р- J£±— и
Р=-
ЭР
ределяется так
Якобиан
(9^7 Г)
J J Э&,Р) rlllJp ЭЬ?Р{ -
перехода к новым переменным оп—
за эр
эа
эр
эР
Поскольку с якобианами можно обращаться как с дробями,
представим исследуемую величину в виде
£i±2p)
*(9>р) = э(^,р) э(<?7 а) ?&,&)
э(аур) э(а?Р) э(%а) э
Вычислим отдельно числитель и зна*/ен'а?ель полученной
сложной дроби при помощи формул канонического преобразования:
&(9->Р) =
I
О
эр
эа 1
Э-fy
Отсюда видно, что якобиан
eF>
9гР
^f- эуэ-й
канонически сопряженным переменным' равен единице.
uki.Pl..
новьш
162. Скобку Пуассона [A3 } представим как якобиан
fj g \ - эА_ э 3 _ ЭА Эв _\ЭР &<}
Pf
*Р
Э<$ Эр
г>8 эв
эр &f
Примем во внимание, что с якобианами можно обращаться
как с дробями, и сделаем следующее тождественное
преобразование: - _ ) У _ ^ .
э(а,в)= *(*iB) э(р,а)
~э{р9су) д(Р, а) Э(Ртф)
125

Множитель .^ С ? ./,_ представляет собой якобиан перехо—
dJpTfT
да от одних канонически сопряженных переменных к другим, ко~,
торый равен единице. Оставшийся якобиан можно записать как
скобку Пуассона для величин А и 3 , рассматриваемых как
функции переменных Р и $ ,
д(А,в) __ ЭА д& _ Э/) £&_ -IАв\
э(р0а)~ эр еа эа <?р I IFa-
Если учесть предыдущие формулы, то приходим к выводу
163. Скобки Пуассона [А 3} для любых величин A-A (<faF7 ■-.
и Bz3(<7 оу t) инвариантны относительно канонического преобра-
зования р<р —*-РЦ ({/13}- -- (А6}„Л а новые канонически
сопряженные переменные удовлетворяют соотношениям:
[pql}=i, {ppj-o, (aa}-=o-
Эти требования являются необходимым и достаточным условием
канонического преобразования.
Проверим выполнимость этих требований ь отношении
данного преобразования 61= £'гь ( f-р) и Р--&Р&ъ<1> Положим А ~Р
и 3=^B и вычислим скобки Пуассона, составленные из величин
/-* и 6? , пользуясь инвариантностью скобок Пуассона
относительно указанного преобразования,
/ эР s>F>
I эр эq I
(pa}PQ= iP&yo, laa}p& = (aa}p^o.
Полученные результаты доказывают, что данное
преобразование является каноническим.
164. d-2(pe*)biPHre'*)'/2.
165. F=-^r%2e?.
166. а) Сг^+РЯ)?; б) Q-=r~P+C£*p)$-fh
в) Q=?p+C?i + V)frb
126

167. O-^Nf^P.
168. а) Ж'=С0Р^ P = Q, Q = CO',
б) ж'^соа(ир2}} р=-соG+ргIа=2боар)
169- *=id^l*^-№p')t»*€*rl-
170. X=f(x7t}9 p=£-i $=Pf(*,t).
эх
171. Q = f7 P=p-f§f', Cr=f,P-H<t,t)
'9
§ 13
172. a) f^-et+Pyf±j^KRP6~~^-2rr>22X5CO30cle4
где Sup- постоянные интегрирования, а полярная ось
сферической системы координат антипараллельна силе тяжести;
где е> и р - постоянные интегрирования;
в) S=-tt+P4,Y±f)l<*-jl%b-2~>a.cose с/01
где & , Рф и оС- постоянные интегрирования, а полярная ось
сферической системы координат выбрана вдоль вектора Ж .
173. *_- ffzf-(*f*ji &«ran(]/g<o9)-Pt;
f 1 +
['rryCOqf 127

2 *2
174-'- -* ЫЩ*(*-х°) f^f^ZJ,
t a-rc
*n (Щс°(х-*°%+ргу+р^-(*,+-£ M
<sH CjP
rae cO=j^£ и 2C0= eW , а величины £ , P и P являются
независимыми постоянными интегрирования.
*»/'
175. t = * ^[]/щ оХ*-*.)^- ffi* -
raeCt?=7^c и :хо~'ёН ^mZS2'>a величины £г » % и^ являют-
ся независимыми постоянными интегрирования.
176. S**jYf„ef_*2°>5f(pl-£.fJr +
где СО— и 1~0— ЕР » а величины <5- , о и /=> - произ-
вольные постоянные.
= ЭХ t *# .^
17 8. Составляем функцию Гамильтона
и уравнение Гамильтона - Якоби
aS ^ 1
at 2m
128
ШЧП-п+£№-™-

Поскольку энергия £ , а также проекции /^ •=* Р; и р ~р
импульса р~ частицы на оси Л и К сохраняются, полный
интеграл уравнения Гамильтона - Якоби ищем в виде
где f(z) - неизвестная функция. Чтобы найти f(e-J, подставим
искомое решение A) в уравнение Гамильтона - Якоби. Тогда
получим f/г 2\ / t Л \2
Видно, что сумма двух последних слагаемых левой части
полученного уравнения есть величина постоянная
_^ld£)iF^c. B)
2т \ с/г I
Причем из четырех постоянных р , Р , £ и С независимы
только три, так как все они связаны между собой
соотношением: 1 / г 2\
Из предыдущего уравнения B) находим
Функцию £(г) можно оставить в виде неопределенного
интеграла особенно в тех случаях, когда последний
вычисляется сложно. Таким образом, имеем
9=~et+pfx+pay±jy2„(e+F3) 'dz.
Правильный знак перед радикалом легко установить,
исследуя iT -4о проекцию импульса j£~ частицы
%=а ^ - v^^tftf .
Чтобы выполнялось начальное условие, необходимо перед
радикалом взять знак плюс, тогда
mt5 ^V^te+FZe) >0*
В итоге полньй интеграл уравнения Гамильтона - Якоби
запишется как
SSOt i2v

В качестве независимых произвольных постоянных
интегрирования уравнения Гамильтона - Якоби возьмем р , f> и С .
После этого дифференцируем $ по произвольным постоянным% а
результат дифференцирования приравниваем новым постоянными
Со и С^ , а именно:
Э 3 __. л1 & S _ /■* Э5 __ .
ЭРГ 1 У эРг ~ 21 ~2?~~ 3 '
Раскрываем полученные соотношения:
Последний интеграл легко вычисляется:
Постоянные интегрирования С; , С2 и ^ находим из начальных
условий с учетом соотношения С = -^г V* ~Fz » которое
вытекает из выражения для Z -и проекции импульса р ^T/ZsrtfCfFg-J7.
взятой в начальный момент времени. В результате имеем
L7~Xo-> L2~?о> Сз~ F '
После этого определяем зависимость координаты 2 от
времени
2^F*~F42-hZFrntrit *mzxr^-ZmS.
Окончательно получаем
179. а) Выпишем уравнение Гамильтона — Якоби
Поскольку энергия g сохраняется, искомая велич1ша 5
содержит слагаемое -&t . Кроме того, гамильтониан JC
разбивается на сумму ела гаем ых$ каждое из которых зависит
только от одной обобщенной координаты и соответствующего
обобщенного импульса. Это позволяет искать полный интеграл
уравнения Гамильтона — Якоби в виде суммы:
**+*,(Ь*+5*(?г) + 3з(*б)
Подставим искомое решение в уравнение Гамильтона
Якоби
130

Левая часть равенства содержит три группы слагаемых,
каждое из которых зависит лишь от одной обобщенной
координаты соответственно О , fy и # . Поскольку это равенство
должно выполняться для произвольных значений а , ар и сг ,
отсюда вытекает '
где S. , &г и ё' — произвольные постоянные, которые
связаны с энергией g соотношением:
Интегрируя полученные дифференциальные уравнения, находим
Чтобы установить правильный знак перед радикалом,
воспользуемся равенствами:
*=5J£'?£-*-• *"W A>
в начальный момент времени. Тогда придем к заключению, что
перед радикалами следует взять знак плюс. Таким образом,
действие принимает вид:
В качестве независимых постоянных интегрирования
уравнения Гамильтона - Якоби возьмем Sf , &2 и &3 .
Продифференцируем действие 5 по произвольным постоянным d; , 62 и
S, , а результат дифференцирования приравняем новым
постоянным соответственно CL , <£> и С3 , а именно:
Выпишем эти соотношения в явном виде:
При взятии интегралов иногда полезно использовать чис—
леннье значения постоянных £, , dL и 6\ , которые находят
1 3 131

из соотношений A) и начальных условий. После вычисления
указанных интегралов получим
f^vT,senile,), ^VE^skit+cj,
v*iti-i'= %(* + *»)■
Из начальных условий определяем постоянные
интегрирования. Окончательно
г) <p=encAt, (p2=a>rcstn(^3iny54)
%3~ Я-&ГСС05 SinVet щ
П К?
181 f "*<*? =+(t-t)
t0 °
где энергия 6 и угол y/Q определяются из начальных условий
при /= tD • Знаки плюс и минус отвечают соответственно
положительному и отрицательному значениям обобщенного импуль-
са/^/77/ГУ . _
182. F^^Ao^fajt-scn cot),
183. При помощи функции Лагранжа
2
определяем обобщенные импульсы/э =гпг и р ~т^ & , а
затем выписываем функцию Гамильтона °
■or- -L. ,'2^ 1 ? L „ / / Ж0!
13 2

Поскольку энергия 6 сохраняется, полный интеграл
уравнения Гамильтона - Якоби
имеет вид:
где ^оС^в) - функция, подлежащая определению. После
подстановки искомого решения B) в уравнение A) и умножения
обеих частей равенства на 2гг> /-^ получим
Уравнения такого вида решают разделением переменных,
полагая
S0(r,e)'$,(r)+s2(e). D)
Подстановка функции D) в уравнение C) дает
*■'{(Ф)г+н^-4+{Шгт f(*i-°- <5)
Первые три слагаемых зависят лишь от переменной /- , а
последние два - только от в . Причем равенство E) должно
выполняться при любых значениях г и в . Это возможно при
условии
где с( - произвольная постоянная. Решая последние
дифференциальные уравнения, находим «5- и 5^. В результате полный
интеграл уравнения Гамильтона - Якоби принимает вид:
s=-6t*fV2^[£-a.M]-£ 'dftj^Z-2mB(e)d&1 F)
где £ и о<Г — независимые постоянные, которые определяются
из начальных условий. Правильный знак перед интегралом
легко установить, приравнивая между собой значения обобщенных
импульсов, которые вычислены двумя способами:
р =. —— * р = &s
133

Производная от функции 5 по произвольной постоянной
равна новой постоянной в > а именно:
ЭоС Г'
Это соотношение не содержит время / явно и связывает
между собой переменные г и & , т.е. является уравнением
траектории. Выполняя дифференцирование по аС » находим иско».
мый результат
У<*-2тё(в)' f>*
■i.
r2V2m[e-a(r)]-f2
>h
184. Начало координат выберем в центре потенциального
поля, а полярную ось J? сферической системы координат на—
правим вдоль вектора . Протон движется в плоскости XZ .
Положение протона в этой плоскости будем отмечать
сферическими координатами /- и Q (рис. 9).
Рис. 9
Используя функцию Лагранжа
L
Г-+ Гг9г)
&*"*,
определяем обобщенные импульсы/»-/^/5, и р=тг в . Это
позволяет написать гамильтониан протона, а затем уравнение
Гамильтона - Якоби:
Как и в предыдущей задаче, последнее уравнение решаем
разделением переменных. В результате искомое действие S
принимает вид /- Q /
S
=~ei±jV^e-f2
clrtj^oL-Znoec/cosQ 'с/в э (Г)
где £ и оС- независимые постоянные, а в качестве нижних
пределов интегрирования в полученных интегралах взяты коор-
134

динаты бесконечно удаленной начальной точки траектории.
Постоянная S является энергией протона.
Чтобы установить правильный знак перед радикалами,
приравняем между собой значения обобщенных импульсов, вычис—
ленных двумя способами: р =—— и р = -^-$- , а также р ^ J2J*-
3 '/-* эг '/* эг ' гв dQ
up- JL§- . Это дает
в дв
т.г = ±у2т&--^ > т.г?в- ±\'ы, - 2medcos 0. Сг)
Когда протон приближается к началу координат, имеем А<о
ъв>0 в области О^ Q <&0 , где 9Q - угловая координата точ-
ки траектории, в которой радиальная скорость обращается в
нуль Г = 0 . В другой области 9 ■<. 9 протон удаляется от
начала координат, и обе производные положительны Г > q и в >0 .
Эти особенности движения позволяют установить правильные
знаки перед радикалами в B) и A), так что полный интеграл
уравнения Гамильтона — Якоби запишется как
>~ , в .
S=-&t-\y2m6--jrz df~+ \]flc-2rr>edcosв cjd при O^Q^BQ
00 о
г ^ О
S=-gt + f]/&Ze--pr!> ^^+[]/<*-Zme a/cos & с/в при 90*в,
где /-» и 0О- координаты точки, в которой }~ = 0
^Производную от 5 по произвольной постоянной ос
приравняем новой постоянной в , тогда получим уравнение
траектории
Выпишем последнее соотношение для области О£ 9 ■<■ в0 в
явном виде •'
Г dr + Г с/в ^гр ^
со г"* о
Бесконечно удаленная точка с координатами г = <=>о и 0 = 0
принадлежит траектории, поэтому^ =0 .
После вычисления интегралов по переменной /- получим

с
Видно, что величина 90 определяется выражением
а другая коорданата экстремальной точки траектории /£ ~~)/£thm6'
Таким образом, обе координаты /• и 90 зависят от ос .
Чтобы найти постоянную ^ , воспользуемся
соотношением _^ ^,
При /--#-<» и 9-^0 имеем
Откуда находим ы. - 2т F о2 + ed) .
Окончательно уравнение траектории протона принимает вид
/
в
ed cos О
О У7' £0*+ed
arc sin -&, 0<9<ео1
Я -arc&n, --?, в<в.
t 5p-
где Г0=]/р2+ес//£ , а угол в0 определен выше.
В случае далеких пролетов ed « 6f> подынтегральную
функцию в левой части полученного равенства разложим в
быстро сходящийся ряд по малому параметру ?d # Ограничимся
первыми двумя членами этого ряда, тогда интеграл
вычисляется легко. Взяв синус от обеих частей полученного равенства,
приходим к соотношению
V £0р ' I
Второе слагаемое в аргументе синуса мало. Разлагая
синус в ряд по переменной 9 g4> ScriO и отбрасывая
слагаемые более высокого порядкаЛмалости, находим уравнение
траектории протона в случае далеких пролетов:
г sin 9 ^J> (V + f^ *1 п2 -§- ).
185. Воспользуемся результатом предыдущей задачи и
выпишем соотношение, которое определяет максимальный угол вм
отклонения протона от оси Z (см, рис. 9):
136

л
r>-
Je , = л.
вне)
Подынтегральную функцию разложим в ряд по малому па-
р
раметру > °2 и оставим лишь два члена этого ряда.
Тогда получим./ ^
Ь+гЬ!"*»"*'
Gf
J о
где отброшены слагаемые, которые содержат малый параметр
-^5- во второй и более высокой степени. Угол 8 связан с
углом рассеяния рС равенством
Поэтому искомая связь угла рассеяния с прицельным
параметром выражается формулой
72- I f fa )*№=*>
из которой видно, что угол рассеяния мал ; Z << ^
Окончательно дифференциальное сечение с/ff рассеяния в
телесный угол dd -2ЖХ<^Хв тРех заданных случаях имеет вид
в) ds= -УЩ-. с/Я .
166 Х5^
§ 14
186. Т-- -4- , где со = Voc/ni'.
181 ■ ^1ТУ~г?Г.
137

188. a) f = )/^(v7-Yb)i
189. /e«^,-J^j.
191. ^(^V,,
где значение угла у9 ограничено условием f« / ,
характеризующим малые колебания.
192. ci2V^~co/bst.
193. e3/ay* = a?n.st„
194. Совместим ось Z' с осью цилиндра и выпишем
функцию Лагранжа в цилиндрических координатах
Видно, что обобщенные импульсы Я^—mry* vif> -mg
сохраняются, а энергия £ зависит от переменной /-• и
обобщенного импульса р =/-nf~ следующим образом:
F — -l-*1- -t * - -4- £
г^ 2*7 2mr2 + *Zi
где //у- Р и &J= f* fern являются интегралами движения.
Согласно общей формуле адиабатический инвариант имеет
Г*
где г - то значение переменной /- , для которой радиальная
скорость обращается в нуль, а именно:
И.
'Л.
« V2mF-6J'
Сделаем замену переменной интегрирования /~-кд , тогда
получим
138

i £г
Видно, что адиабатический инвариант X. является
функцией двух независимых величин F - 6 )Кгк Мк'• Чтобы
адиабатический инвариант оставался неизменным при медленном
изменении радиуса цилиндра, необходимо, чтобы величины F - б-)^2
и М£ были бы также постоянными. Поскольку & и Mg.
являются интегралами движения, получаем следующий закон
изменения энергии £ при адиабатическом расширении цилиндра:
(&-6z)#z= canst.
196- J^v^7' ^vPtF'
где £ ■+ 62= £ - энергия механической системы.
198.1~ 6^/ со , где <Х>г=еИ(тс , а £- энергия
поперечного движения, которая вместе с энергией £, продольного
движения составляют полную энергию частицы 6~ё,+ ёц .
199. & а/, - canst,
200. &j. = Jh~c№0+ £Ы)\ , где /-инвариант
заряженной частицы в магнитном поле. Искомый период Т дается
выражением: fz
Т=У^1.У^Ж0Ш!
£7 г° гтгс<
где точки остановки j? и Zg являются корнями уравнения
В частном случае ^{г) =И0^г/ СЬг имеем Т— j , где
V @) - модуль скорости поперечного движения в экваториальной
плоскости Z~ О .
139

ГЛАВА Ш
§ 15
202. 2Г~Ъ" УТ-Уг/с2'+ Ът Vf-у?/сг'
2
vVr-^/c2'* *п Vt-vf/c*'
204. Wv ^/«^(/-^/C^-/^ ]Й -- ^л.
205- ^2&Л •
206. J(^hf0^/>(-^V7^W),
207 Г- r'+JSi' . ( I ) (/** ]Г>у
У1-Уг/сг '
210. C069~7-2(^f
2.X2.. Минимальную энергию налетающей частицы, при
которой процесс образования новых частиц еще возможен, легко
140

определить в ц-системе. Действительно, в ц-системе энергия
рассматриваемой механической системы минимальна, когда
после столкновения и образования новых частиц все они покоятся.
Поэтому целесообразно установить связь между 4-импульсом
частиц в л-системе до столкновения и полным 4-импульсом
частиц в ц-системе после столкновения. Будем помечать
штрихом величины после столкновения и образования новых частиц.
Полные 4-импульсы частиц до и после столкновения в
л-системе обозначим как 1% (л) и j£ (ji) . Аналогичные величины в
ц-системе сутъР(ц) иР'^д]. Поскольку квадрат любого 4-
вектора инвариантен относительно преобразования Лоренца,
имеем Pifinj-FL (Ц) » гДе по повторяющимся векторным индексам
предполагается суммирование от 1 до 4. Далее воспользуемся
законом сохранения энергии и импульса в четырехмерном
обозначении Р(Ц)=Н (Ч) . Указанные два равенства позволяют
установить искомую связь Р2(л) = Р/. ( Ц) • Полученное
соотношение дает возможность определить минимальную
энергию налетающей частицы, необходимую для образования новых
частиц.
Применительно к задаче о столкновении двух электронов
имеем пг, . / .2 2 2
ЪМ={Р„ + Ргк) =Ъ+2Р,*Р2к+Ргк-
= -2m2c2-2&jtrL}
где Рг/=(Лу i -jf-) и P2ki- (Oji/тьс) - 4-импульсы
налетающего и покоящегося электронов в л-системе. После
столкновения и образования новых частиц в ц-системе все они
покоятся, поэтому ,Р г (ц)--16т С . Приравнивая полученные
выражения, приходим к алгебраическому уравнению относительно <£
с решением &7~ 7пг с2
213. 6г = 4пьсг.
214. Т=B+^)тжС2.
215. r=2(r+-&zk }mc
216' £?=('+%£)"**
2\2
217. cos9 = 7- 2(r°J- .
67 6г
141

218. Энергия и импульс механической системы
сохраняются при распаде частицы на две, поэтому р.-р..+ р2. , где
Р ~ { р~ -,1 4$- \ - 4-импульс исходной частицы перед
распадом, ар -(fi~j i-&-) и р ~(р~у L ~7^-) " 4-импульсы обра-
зовавшихся частиц. Чтобы найти 9* , возведем обе части
равенства р - /э — р в квадрат и воспользуемся инвариантами
р*~-(гпсJ . р^ ~{тгсJ и р/к= ~(гъгС)г•
Скалярное произведение/^, /3=r/3^o*l^-^<tf содержит косинус искомого
угла &j . Решая полученное алгебраическое уравнение
относительно COS 9j и выражая модули импульсов частиц через их
энергии при помощи соотношений С2/р~( — 6 3~Z72 Cv и
С2/pJj2= 6*-т*СV . находим
COS в, -
26f6 + ('-rrlZr/7z2)c'/f
Аналогично определяем COS @2 путем возведения обеих
р = р в квадрат, что
Г2к гГк
2б?6г(югг-'ъг2- ггг2)с1/
частей равенства р~ р = р в квадрат, что дает
COS в9 - —л2*
219. /_ со
СО —
со
1+я^(г^~соГё)
тс*l '
«»*,=(>-^)Щ
221. /7Л< а -//- ЛЩ1 I Vb+'mpr
тс
си 0, = (,-&£?) у.
&2 '*£■+— ГПО2
где 0, и 62- углы вылета, a 6j и 62 - энергии ^
-квантов в лабораторной системе координат.
222. ^e.M^Ajl^^fK.
223 /'- Sf^^C2-fCf-mc^Jco5 6>r 2
' 61+гггсг-(бггггс2)с<?ь?вг "** '
/•' = ^ +гп,сг+ FТ -m.c2)c0S2Q2 2
2 61+т-Сг-(£7-тс2)соьг вг
142

§ 16
224. V.bit-V-'lc'fiP-^iP),
225. a) [ 4l!\ _ / \^2/\ .
Icft'r i-v2/c2 \Ш~\>
б) \$]=-(F^7PT&\lffl •
226. fcig- &*-(&* £)*/с;
c4(t-<vz/o2K '
/../iK^Pi^
* .3
227 • ^={тъ&?)ъ>
228. тГ=.сУг- (■ ^^ J
229. Направим ось J^ параллельно вектору £~ , тогда
rj-I~ 6 - —ft = (me2) +с'(Ру + P£ I,
£2 л ~" с
где использовано £ =(ггъсгJ-(-с2р~ и р^~6'гг/С2'. Здесь
fn. и р" — масса и импульс движущейся частицы. Из уравнения
движения . -*.
dt C
имеем rx=e£(t-t0]tpojc ,f>y=f>oy " /J =/-Qz . где /Г - импульс
в некоторый фиксированный момент времени £ . Поскольку
143

f> + f^ ~ f>0„ & f>0~-const , величина I также не меняется со
временем.
230. Подставим в уравнение движения ^=. f величину
p-S^F/c2 и воспользуемся соотношением £ = трр* , тогда по—
с* с2
Поскольку скорость тР параллельна или антипараллельна
вектору Р , последнее равенство можно записать в виде
с. с*
Решая это уравнение относительно величины F , находим
= corvst.
jr* &2
<~ (j-tS/c2K
232. Л _£_ ,//-.-_!« )££j!?
234. k e£ , rQ е£ ? е£ оа &^ ,
где ось X антипараллельна вектору В , а ось У лежит
плоскости движения. Кроме того, введено обозначение
235- ^Яъ+у&ЪЬ *°=^> ЧШ<&
где использовано обозначение
а * й Vi-vg/c*' ' * I Vox h
Здесь принято, что ось Z лежит в граничной плоскости и
расположена параллельно вектору ff~ , а ось Л направлена в
сторону магнитного поля перпендикулярно граничной плоскости.
^ ^^ - mrV2 e с/У(г)
144 236" ЛУ^? V^W dr '

d гпггф
dt Vl-V2/C*' г \
где У-Л**/* ^ • а величина r—--// представляет со-
Yuv^/c2
бой момент частицы.
oo7 J /ггл _ гтгг(д%$£п?вф2)_ &У_
^ mr2& /nr2strz0CQ39ф _ &1Г
</ m,r2stn20f> _ <?U
где ^.^ fi*+r20Z+ rZ$ i/b ?0ф2.
238. Поскольку момент//- A* */*" сохраняется,
движение частицы происходит в плоскости РМ = О , проходящей через
центр потенциального поля. Выберем в этой плоскости
полярные координаты г и <f/ и выпишем уравнение движения:
rnr mrp2 ot
<Н Yr-if/c* VF^Jc2 r
т >
d т**ф
df Vl-v2/c2'~
Сохраняющимися величинами являются энергия
_ &~У7-^2/с2' г
и момент /У , который по абсолютной величине запишется как
Vl-vz/c2
Используя закон сохранения момента, проведем замену
переменной дифференцирования в первом уравнении движения
согласно формуле / ■=-—-,
d ^ МУг-У^/с2 d
В результате получим
J* f . Л <*? \ f ОСЕ
-L-t-if- <* \J--.*±
dy2 г 'Г н*с* I r №сг
Общее решение этого уравнения:
10-501 145

-£- = -£- +г}с»[у&Г(*-ег/];
.2 2 Р
i оСЖ 1 мс >
где £у и Л> - постоянные интегрирования.
Полярную ось выберем так, чтобы Сг-0 . Кроме того,
введем удобное обозначение ^ - б/р , где £- новая постоян«-
ная интегрирования. После этого искомое решение примет кано«.
нический вид
Полученное выражение является уравнением траектории, в
котором параметр £ определяется из условия задачи. Выра-
зим его через сохраняющиеся величинь. о и М . Для этого
продифференцируем по времени обе части уравнения траектории
-tjr = l Уг^^'Ф Sen, (J/г- ёг'У ).
Видно, что в точке пересечения траектории с полярной
осью радиальная скорость обращается в нуль, а скорость 7^
перпендикулярна радиус-вектору. Поэтому в этой точке с
координатами Г-Г0 VL~<£f~0 имеют место равенства:
г - гпсг £L M=,JZLVb . ^f__ fM с
Vf-VS/c2 Го Vl'V^/c2 Го
Первые два соотношения дают возможность выразить га
через % и М , а третье позволяет представить искомый
параметр £ как функцию сохраняющихся величин
Вид траектории существенно зависит от £ и М . В
данной задаче движение финитно при £<стс2 и инфинитно в
случае § ^ 7~гъС
239. Повторяя рассуждения, которые были приведены при
оешении предыдущей задачи, приходим к уравнению
d* / = S
dfB r Qe
с общим решением
146

где ^и С0 - постоянные интегрирования. Для определения
последних продифференцируем по времени обе части полученного
соотношения:
Т?~ Qe
Видно, что существует точка траектории с координатами
f~f и y^-yjQ , в которой радиальная скорость обращается в
нуль, а скорость 7р перпендикулярна радиус-вектору. В этой
точке выполняются соотношения:
которые позволяют найти одну из постоянных интегрирования
о ZQe&
Другая постоянная интегрирования у/0 зависит от
выбора полярной оси. Направим полярную ось в точку траектории,
где радиальная скорость обращается в нуль. Тогда у ~ о и
уравнение траектории примет вид
2QeS
ТАБЛИЧНЫЕ ИНТЕГРАЛЫ
ПРИЛОЖЕНИЕ
1. IX Jx-^ , /гФ-Г.
J п+1 7
2. j&.= епх.
3' iVa?^x^ = arcain f-=7T-<»-<:c°s f •
5- fyzfa1 '""* *'*(**V&?).
147

8. \ud?r=uv--(>vclu>
СПИСОК ЛИТЕРАТУРЫ
1. Ландау ЛЛ.. Лифшиц Е.М. Механика. - М.: Наука, 1973.
2. Ландау Л.ДП ЛиФшиц Е.М. Теория поля. -М.: Наука,
1973.
3. Гольдстейн Г. Классическая механика. - М.: Наука,
1975.
4. Компанеец А.С. Курс теоретической физики. Т. 1.-М.
Просвещение, 1972.
5. Савельев И.В. Основы теоретической физики. Т. 1.-М.
Наука, 1975.
6. Медведев Б.В. Начала теоретической физики. - М.:
Наука, 1977.
7. Ольховский И.И. Курс теоретической механики для
физиков. - М.: Изд. МГУ, 1978.
8. Хаар Д. Тер. Основы гамильтововой механики. - М.:
Наука, 1974.
9. Лич Дж. У. Классическая механика. - М.: Изд-во
иностр. лит., 1961.
10. Ланцош К. Вариационные принципы механики. - М.:
Мир, 1965.
11. Арнольд В.И. Математические методы классической
механики. - М.: Наука, 1974.
12. Коткин Г. Л.. Сербо В .Г. Сборник задач по
классической механике. - М.: Наука, 1977.