ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО КУРСУ
«ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ»
2014-2015 УЧ. Г.
1. СИГНАЛЫ. ОСОБЕННОСТИ И ОТЛИЧИЯ.

-Сигналом

называют

физический

носитель

сообщения,

т.е.

информации, предназначенной для передачи. Сигналами могут быть
напряжение, ток, напряженность поля. В большинстве случаев носителями
радиотехнических сигналов являются электромагнитные колебания.
Сигналы могут быть детерминированными или случайными. Для
детерминированных сигналов на основании математической модели можно
узнать мгновенное значение сигнала в любой момент времени. Примером
детерминированного

сигнала

является

синусоидальное

напряжение,

u(t )  Um *cos(t  0 )

Для случайного сигнала рассчитать значение согласно математической
модели невозможно. Примером случайного сигнала является белый шум.
Осциллограмма белого шума показана на рисунке 1.

Сигналы могут быть импульсными и аналоговыми. Импульсные
сигналы существуют только в пределах конечного отрезка времени. Примеры
импульсных сигналов: видеоимпульс (рис. 2а) и радиоимпульс (рис.2б).

Среди

аналоговых

сигналов

выделяют

периодические

и

апериодические.
Периодический сигнал S(t), период Т обладает следующим свойством:
S(t)=S(t±nT) n=1,2,.. Пример периодического сигнала показан на рисунке 4.

Период сигнала связан с частотой f и круговой частотой w следующим
соотношением: f=1/T=w/2π. Другие примеры периодических сигналов
показаны на рисунке 5.

2. АНАЛОГО-ЦИФРОВОЕ И ЦИФРО-АНАЛОГОВОЕ
ПРЕОБРАЗОВАНИЕ.
Сигнал от аналогового источника информации поступает на аналогово
– цифровой преобразователь (АЦП). С функциональной точки зрения АЦП
переводит сигнал в цифровой вид в два этапа, осуществляя дискретизацию по
времени и квантование по уровню. Дискретизация сигнала сводится к тому,
чтобы из аналогово напряжения, поданного на вход АЦП брать точки и брать
эти точки через равные промежутки времени.
Рис. Аналоговый сигнал

Рис. Дискретный сигнал

Сигнал, который представляет собой точки, взятые через определённый
промежуток времени, называется дискретным. Сигнал дискретный по оси
времени по напряжению сигнал остаётся непрерывным. АЦП срабатывает
одни раз за промежуток времени называемым периодом дискретизации.
Период дискретизации — это величина постоянная.
Чем больший временной интервал дискретизации, тем больше будет
дискретных значений при условии, что частота дискретизации остаётся
неизменной. Последовательность отчётов представляет собой конечную
последовательность – она имеет конечную длину. Аналоговый сигнал
считается бесконечным.
Чтобы восстановление сигнала произошло полностью должны быть
выполнены условия. Эти условия определяются теоремой Котельникова,
которая говорит о том, как связать период дискретизации с параметрами

сигнала.
Полученные дискретные значения в дальнейшем должны быть
квантованы по уровню. Определяется шаг квантования

по которому

определяются уровни квантования, в соответствии с которыми изменяемый
сигнал может быть квантован. Каждое значения напряжения сигнала
округляется до уровня квантования.

Округление происходи в сторону ближайшего уровня квантования.
Уровни

квантования

сформированы

внутри

АЦП.

Число

уровней

квантования определяется разрядностью АЦП.
Число уровней квантования:

, где – разрядность АЦП.

Число разрядов кода:
N – число уровней квантования, n – разрядность кода, int –
определение наименьшего целого числа, не менее заданного.
Каждому из уровней квантования присваивается определённый код
(порядковый номер).
Обычно уровни квантования кодируются целыми беззнаковыми
числами. АЦП с повышенной разрядностью стоят дороже и работают
медленнее.
ЦАП производит операции, обратные АЦП.
3. ТЕОРЕМА КОТЕЛЬНИКОВА.
-Согласно этой теореме любой непрерывный сигнал с конечным
спектром (имеющим максимальное значение
виде дискретных отсчетов

) можно представить в

, частота дискретизации которых

должна быть выбрана не менее чем в два раза выше максимального значения

спектра сигнала:

, передать его по линии связи, а затем

восстановить исходный аналоговый сигнал.
Теорема

Котельникова

является

основой

для

дискретизации

непрерывных сигналов по времени, так как, во – первых, доказывает, что
непрерывный сигнал можно заменить его дискретными значениями, во –
вторых, дает правило вычисления шага дискретизации –

. При

таком шаге дискретизации ряд Котельникова дает точное временное
представление сложного сигнала.
Смысл теоремы Котельникова иллюстрирует (рис. 29).

Как видно из рисунка, если частота дискретизации равна удвоенной
частоте синусоидального сигнала, что по полученным отсчетам можно
восстановить исходный сигнал. Если частоту дискретизации выбрать
меньшей, что частота сигнала, восстановленного по отсчетам будет меньше,
чем у исходного сигнала и восстановленный сигнал можно будет принять за
более низкочастотный. Данное явление называется наложением.
Для уменьшения искажений необходимо либо увеличивать частоту
дискретизации, либо использовать перед АЦП дополнительный фильтр
нижних частот, ограничивающий спектр исходного сигнала перед его
аналого-цифровым преобразованием.

4. ПРИНЦИПЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ (ЦОС).
ОПЕРАЦИИ НАД ДИСКРЕТНЫМИ СИГНАЛАМИ. ОСНОВНЫЕ
ХАРАКТЕРНЫЕ ДИСКРЕТНЫЕ СИГНАЛЫ И ИХ СВОЙСТВА.

-

5. ДИСКРЕТНЫЕ СИСТЕМЫ. СИСТЕМЫ С ПАМЯТЬЮ, БЕЗ
ПАМЯТИ, ЛИНЕЙНЫЕ СИСТЕМЫ.
-С

математической

временем определяется

как

точки

зрения, система

преобразование,

с

дискретным

переводящее

входную

последовательность (сигнал) {x[n]} в выходную последовательность {y[n]}
последняя называется откликом или реакцией системы. С физической же
точки зрения, систему с дискретным временем можно представлять как

«черный ящик» ,

на вход которого подаются

разные дискретные сигналы.
Системой с памятью называется идеальная система задержки.

Системой без памяти называется система с задержкой nd = 0 Такой

системой будет, например,
Система

называется линейной

6. ДИСКРЕТНЫЕ СИСТЕМЫ. СТАЦИОНАРНЫЕ СИСТЕМЫ,
ПРИЧИННЫЕ СИСТЕМЫ. УСТОЙЧИВОСТЬ СИСТЕМ.

-

Система

называется устойчивой,

если

ее

отклик

на

любой ограниченный входной сигнал будет также ограниченным.
Пример. Система y[n]=x[n]^2 устойчива, т.к. при любой ограниченной
входной последовательности {x[n]}: |x[n]|≤B при n ∈ Z. для выходной
последовательности будет выполнено |y[n]| ≤ B2. Система y[n]=lg|x[n]|,
напротив, неустойчива поскольку y[n]=−∞ для любого x[n] равного нулю
даже при условии ограниченности всей входной последовательности.
7. ДИСКРЕТНЫЕ СИСТЕМЫ. ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ
СИСТЕМЫ.
ЛСС - это система, которая удовлетворяет условиям линейности и
стационарности. Линейные стационарные системы бывают непрерывными и
дискретными
Систему называют линейной, если она обладает свойствами:
- аддитивности: реакция на сумму воздействий равна сумме реакций на
каждое из воздействий (принцип суперпозиции);
- однородности: умножению воздействия на весовой коэффициент
соответствует реакция, умноженная на тот же коэффициент. Соотношение
вход/выход линейной системы описывается линейным уравнением.
Систему называют стационарной, если она выдает один и тот же отклик
на одинаковое входное воздействие вне зависимости от времени. То есть мы
не можем получить разные сигналы на выходе, если подали один и тот же
импульс вчера и сегодня. Результат будет одинаковым.
Первый способ описания – это разностное уравнение. Этот способ
оперирует непосредственно отсчётами сигнала во временной области. По

сути, разностное уравнение показывает, как из задержанных и текущих
отсчётов входа, а также задержанных отсчётов выхода посчитать текущее
значение на выходе системы.

Текущее значение выхода системы – это y(n). Текущее значение входа
– x(n). У нас также присутствуют предыдущие значения входа и
выхода. Решим это уравнение относительно текущего значения выхода. Оно
получается из суммы входа, входа, задержанного на один такт, и выхода,
задержанного на один и два такта. Соответствующие коэффициенты при
Динамику системы мы можем описать импульсной характеристикой. У
дискретной системы импульсная характеристика получается в результате
реакции её на единичный дискретный импульс.

Ещё один способ описания ЛДСС - z-преобразование. Также, как
преобразование Фурье является основой анализа сигналов, z-преобразование
– это основа анализа систем. Оно ставит в соответствие значениям сигнала во
временной области отсчёты в комплексной частотной области. Задержка
сигнала на k-отсчётов становится умножением на z в степени k. Умножение
на коэффициент отправляется в знаменатель, и самое главное – операция
свёртки заменяется простым умножением.

Выход системы, который мы рассчитывали при помощи свёркти входа
с импульсной характеристикой в z-области высчитывается как перемножение
с z-формой импульсной характеристики. Отношение входа и выхода в zоблатси

называется передаточной

функцией

системы. Это

дробная

функция с полиномами в числителе и знаменателе.
Ещё одно описание линейных стационарных систем - нуль полюсное
описание. Переменная z – это некоторая комплексная величина, которую
можно отобразить на комплексной плоскости. А передаточная функция
определена для всех значений z, то есть может быть представлена
трёхмерной поверхностью на комплексной плоскости. Мы можем решить
уравнения числителя и знаменателя, определить корни. Корни числителя –
это так называемые нули функции, а корни знаменателя – полюса.

8. СВОЙСТВА ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ.

-

9. РЯДЫ ФУРЬЕ. СИНУСНО-КОСИНУСНАЯ ФОРМА.

10. РЯДЫ ФУРЬЕ. ВЕЩЕСТВЕННАЯ ФОРМА.

11. РЯДЫ ФУРЬЕ КОМПЛЕКСНАЯ ФОРМА.

12. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ПРЯМОЕ ПРЕОБРАЗОВАНИЕ
ФУРЬЕ.
- Разложение в ряд Фурье позволяет получить спектр только для
периодических

сигналов.

Преобразование

Фурье

расширяет

область

применения спектрального анализа на непериодические сигналы.
Пусть s(t) – одиночный импульсный сигнал конечной длительности.
Дополним его таким же, периодически следующим сигналом, с периодом Т.
Получим последовательность импульсов (рис.15).

Чтобы перейти к преобразованию Фурье и найти спектр одиночного
импульса необходимо найти предельный вид ряда Фурье в комплексной
форме при Т  
Расчет спектра:
S ( )  F [ s(t )] 



 s(t )* e

 jt

dt



Физический смыл спектральной плотности состоит в том, что она
является

коэффициентом

пропорциональности

между длиной

малого

интервала частот Δf в близи частоты f0 и амплитуды гармонического сигнала
с частотой f0. Сигнал s(t) как бы складывается из множества разных
синусоидальных сигналов малой амплитуды. Спектр плотности показывает
вклад в сигнал элементарных синусоидальных сигналов каждой частоты.
Спектр плотности вероятности S ( ) является комплексным числом и
отображается кривой на комплексной плоскости.
| S ( ) | - действительное число – амплитудный спектр

| S ( ) |2 - спектр мощности
arg( S ( )) - фазовый спектр

Свойства преобразования Фурье
1.

Линейность – спектр суммы нескольких сигналов умножить на

постоянные коэффициенты равен сумме этих сигналов. Если амплитуда
сигнала меняется в А раз, то его спектральная плотность тоже меняется в А
раз.


F   Ai Si  t     Ai Si  



2.

Свойство вещественной и мнимой частей спектра. Вещественная

часть спектра, то есть амплитудный спектр – четный функция частоты.
Амплитудный спектр симметричен относительно нулевой частоты. Мнимая
часть

спектра

–

нечетная

функция

частоты.

Фазовый

спектр

антисимметричен относительно нулевой частоты.
Re  S     Re  S    
Im  S     Im  S    

3.

Смещение сигнала во времени. При смещении сигнала во

времени амплитудный спектр не меняется, а фазовый спектр смещается по
фазе.
F  s  t  t0    S   e  j0t

4.

Изменение масштаба сигнала по времени. Пусть сигнал s(t) сжат
1
k



по времени в k-раз. Сжатый сигнал записывается, как s(kt). F [ s(kt )]  S ( )
5.

k

Свертка и произведение двух сигналов.

Спектр произведения сигналов равен свертке спектров и наоборот.
F [h(t )  u (t )]  U ( ) *V ( )

Свойство применяется для отыскания сигнала на выходе, если известна
АЧХ.
Y ( )  X ( )  K ( j )
| Y ( ) || X ( ) |  | K ( j ) |

Комплексная амплитуда Ck к-ой гармоники ряда Фурье связана со

1 2 k 

T  T 


спектральной плотностью так: Ck  s 

Зная преобразование для одного периода периодического сигнала
можно вычислить его разложение в ряд Фурье.
13. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОБРАТНОЕ
ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
- Служит для нахождения сигнала по спектру.
1
s(t )  F [ S ( )] 
2
1



 S ( )* e

jt

dt



14. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ.
СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ.
- Спектр дискретного сигнала представляет собой сумму бесконечного
числа копий спектра исходного сигнала. Каждая копия спектра аналогового
сигнала сдвинута по оси частот на расстояние, равное частоте дискретизации.
s t  

n 

 S  f  nF 

n 

x

s

S x  f   F  x  t  

Sx  f  - спектр цифрового сигнала
x  t  - исходный сигнал

Характер спектра дискредитизированного сигнала демонстрирует
частотно – временную дуальность преобразования Фурье:
1)

Периодический сигнал имеет дискретный спектр;

2)

Дискретный сигнал имеет периодический спектр

Спектры аналогового и цифрового сигналов показаны на (рис. 30).

Видно, что:
1.

Спектр

идентичен

спектру

исходного

сигнала,

только

повторяется в точках кратных частоте дискретизации.
2.

Если частота дискретизации недостаточно высока, то частоты

будут накладываться. В этом случае полезную информацию, содержащуюся
в сигнале невозможно восстановить с достаточной достоверностью.
3.

1
2

Частота Fn равная половине частоты дискретизации - Fn  Fs

называется частотой Найквиста. В данной точке (на данной частоте)
происходит наложение. Так же данную частоту называют максимальной
частотой сигнала.
Для борьбы с наложением можно либо ограничивать полосу частот

сигнала, пропуская его через ФНЧ, либо повышать частоту дискретизации,
чтобы отодвинуть по оси частот спектр сигнала и зеркальный спектр дальше
друг от друга.
15. СВОЙСТВА ДИСКРЕТНЫХ СИГНАЛОВ И СПЕКТРОВ.
-основные свойства спектров дискретных сигналов, вытекающие из
формул Фурье-преобразования
Линейность

2. Задержка на время τ эквивалентна умножению его спектра на
экспоненту

3. Изменение масштаба сигнала по оси времени

4. Дифференцирование сигнала
.
5.

Интегрирование сигнала (без постоянной составляющей)
.

5.

Cпектр свертки сигналов

.
5.

Cвязь между энергией (дискретного) сигнала во временной и

частотной области (теорема Парсеваля)

.
В последнем выражении Т-период дискретизации аналогового сигнала.
16. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
- Преобразование Фурье нельзя применить к дискретному сигналу. Для
спектрального анализа дискретного и в том числе цифрового сигнала служит
ДПФ.
ДПФ это алгоритм, который позволяет получать амплитудный спектр
сигнала из временной формы сигнала. ДПФ позволяет из временной формы
сигнала получить частотную форму. Обратное преобразование Фурье
позволяет получить из частотной формы сигнала временную.
ДПФ есть ничто иное как разложение дискретного сигнала на
гармонические составляющие. Произвольный сигнал представляется в виде
суммы гармоник (синусоид, косинусоид). В ряд Фурье можно раскладывать
любые сигналы, периодические и непериодические. Гармонический сигнал
раскладывается сам в себя. Дискретное преобразование Фурье:
N 1

X  k   FD  x  n    x  n  e

 jk

2 n
N

n 0

ДПФ есть ничто иное как разложение дискретного сигнала на
гармонические составляющие. Произвольный сигнал представляется в виде
суммы гармоник (синусоид, косинусоид). В ряд Фурье можно раскладывать
любые сигналы, периодические и непериодические. Гармонический сигнал
раскладывается сам в себя.
Результат ДПФ обычно содержит отрицательные частоты. Если
имеются 100 отсчётов сигнала, то получится 100 отсчётов амплитудного
спектра и обязательно 50 из этих будет отдано на представление
отрицательных частот. После преобразования Фурье, по сути, получается 200

чисел (мнимая и действительная части). На каждый отчёт сигнала
приходится одно комплексное число. У этих комплексных чисел берётся
модуль и аргумент. Модуль откладывается по оси ординат и получается
амплитудный спектр. Если по оси ординат отложить аргумент, то получится
фазовый спектр.
17. СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ И
ОБРАТНОЕ ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
- ДПФ линейно. Преобразование Фурье линейной комбинации
функций будет такой же линейной комбинацией результатов преобразования
Фурье этих функций по отдельности. Данное свойство позволяет сводить
сложные функции и их спектры к более простым.
Задержка. Амплитудный спектр не зависит от сдвига сигнала по
времени. Если сдвинуть функцию влево или вправо по оси t, то поменяется
лишь её фазовый спектр.
Растяжение сжатие. Возможность растяжения сжатия исходной
функции по оси времени. Растяжение исходной функции по оси t
пропорционально сжимает её амплитудный спектр по оси частот f. И
наоборот сжатие исходной функции по оси t пропорционально растягивает её
амплитудный спектр по оси частот f. В частности, спектр сигнала конечной
длительности всегда бесконечно широк и наоборот, спектр конечной ширины
всегда соответствует сигналу неограниченной длительности. Чем более
длительным является импульс, тем уже у него спектр. Чем более узкий
импульс, тем более широкий у него спектр. Чем меньшую длительность
имеет импульс, тем из синусоид с большими частотами будет этот импульс
состоять.
Свёртка

функций.

Возможность

свести

свёртку

функций

к

поточечному перемножению их Фурье-образов. Данное свойство служит
основой для алгоритмов линейной цифровой фильтрации.

Поточечное

перемножение.

Возможность

свести

поточечное

перемножение функций к свёртке из Фурье-образов. Данное свойство
используется для проектирования цифровых фильтров.
Симметрия.

Симметрия

амплитудного

спектра

вещественного

сигнала. На практике большинство сигналов описываются действительными
функциями. Амплитудный спектр действительнозначной функции является
чётной функцией, а фазовый спектр (если его перевести к диапазону от

до

) – нечётный. По этой причине на графиках спектров часто не изображают
отрицательную часть спектра. Тоесть изображают только в виде физического
спектра.

Для

действительнозначимых

соответствующая

отрицательным

частотам,

сигналов
не

даёт

часть
никакой

спектра,
новой

информации.
Применение для сигналов, имеющих конечную энергию. Применение
ПФ к сигналам, имеющим конечную энергию. Преобразование Фурье
осмысленно только для сигналов конечной продолжительности. Спектр
таких сигналов должен быть отличным от нуля только на некотором
конечном временном отрезке.

18. ТЕОРЕМЫ О ПРЕОБРАЗОВАНИИ ФУРЬЕ.
-

19. ПРЕДСТАВЛЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ С
ПОМОЩЬЮ Z-ПРЕОБРАЗОВАНИЯ.
- Также, как преобразование Лапласа является основой анализа
непрерывных систем, z-преобразование – это основа анализа дискретных и
цифровых систем. Оно ставит в соответствие значениям сигнала во
временной области отсчёты в комплексной частотной области. Задержка
сигнала на k-отсчётов становится умножением на z в степени k. Умножение
на коэффициент отправляется в знаменатель, и самое главное – операция
свёртки заменяется простым умножением.

Отношение входа и выхода в z-области называется передаточной
функцией системы. Это дробная функция с полиномами в числителе и
знаменателе.

20. СВЯЗЬ Z-ПРЕОБРАЗОВАНИЯ И ПРЕОБРАЗОВАНИЯ
ФУРЬЕ.

21. ПРИНЦИПЫ ЦИФРОВОЙ ФИЛЬТРАЦИИ.

-

Рис. 6.15. К фильтрации сигналов:
а — исходный сигнал с шумом; б — сигнал на выходе аналогового
фильтра; в — дискретизированный исходный сигнал с шумом; г — сигнал на
выходе цифрового фильтра
Рассмотрим упрощенную структурную схему цифровой обработки
сигналов (рис. 6.16). Непрерывный сигнал uBX(t) = ивх поступает на вход
АЦП,

на

выходе

код {u(k№)} = {щ) = ит

которого
с

создастся

фиксированным

соответствующий

дискретным

Последовательность

отсчетов

{м 7},

отсчетам

двоичный

цифровой

количеством

разрядов,

входного

сигнала.

закодированных

определенными

цифрами, поступает в цифровой фильтр (ЦФ. В цифровом фильтре
проводится цифровая обработка сигнала в соответствии с определенным
алгоритмом, в результате чего на его выходе появляются новые цифровые
коды {un(kAC)} = {мц} = иц, соответствующие профильтрованному входному

сигналу.

Рис. 6.16. Упрощенная структурная схема цифровой обработки
сигналов
Обрабатываемый сигнал с цифрового фильтра поступает на ЦАП, в
котором цифровая форма сигнала преобразуется в аналоговую. При
включении ЦАП в схему обработки сигнала на ее выходе необходим
синтезирующий

фильтр

(СФ)

низкой

частоты,

который

будет

производить сглаживание аналогового сигнала. В результате сглаживания
низкочастотным фильтром форма кривой выходного сигнала становится
плавной.
Цифровой

фильтр

должен

обеспечить

максимально

возможное

подавление спектральных составляющих помех при минимально допустимых
искажениях полезного сигнала.
Цифровые

фильтры

имеют

ряд

принципиальных

отличий

от

аналоговых. Основное отличие заключается в том, что в аналоговых
фильтрах входной и выходной сигналы u(t) и y(t) являются непрерывными
функциями времени, а в цифровых — дискретными последовательностями
22. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦИФРОВОГО ФИЛЬТРА.

23. ЛИНЕЙНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ. ТРАНСВЕРСАЛЬНЫЕ
ЦИФРОВЫЕ ФИЛЬТРЫ.
-Трансверсальными принято называть фильтры, которые работают в
соответствии
где

с

алгоритмом
– последовательность коэффициентов, число m является

порядком трансверсального цифрового фильтра.
Трансверсальный

фильтр

проводит

взвешенное

суммирование

предшествующих отсчетов входного сигнала и не используют прошлые
отсчеты выходного сигнала. Применив z-преобразование к обеим частям
выражения (15.1), убеждаемся, что
Отсюда следует, что системная функция

является
полюс

при z =

дробно-рациональной
0

и m нулей,

функцией z,

координаты

имеющей m-кратный

которых

определяются

коэффициентами фильтра.
Алгоритм

функционирования

трансверсального

структурной схемой, приведенной на рисунке.

ЦФ

поясняется

Вид
24. ЛИНЕЙНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ. РЕКУРСИВНЫЕ
ЦИФРОВЫЕ ФИЛЬТРЫ.
- Отличатся тем, что текущий отсчет отклика y(n) определяется не
только

текущим

и

предшествующими

значениями

входной

последовательности, но и предшествующими значениями отклика.
y(i)  a0 x(i)  a1 x(i  1)  a2 x(i  2)  ...  am x(i  m)  b1 y(i  1)  b2 y(i  2)  ...  bn y(i  n)

bn – коэффициенты рекурсивной части, bn  0 одновременно.
Задержка на один такт означает, что берётся предыдущий отчёт
сигнала. Задержка на один шаг является элементом памяти. Это такой
элемент, который получает на вход значение и возвращает значение, которое
находится до него. Он хранит отчёты сигнала и при необходимости их
выдаёт.
Применим Z – преобразование и рассчитаем системную функцию:
H (Z ) 

a0  a1Z 1  a2 Z 2  ...  am Z  m a0 Z n  a1Z n1  a2 Z n2  ...  am Z

1  b1Z 1  ...  bn Z  n
Z n  b1Z n1  ...  bn

У рекурсивного фильтра две линии задержки. Коэффициенты,
расположенные в числителе это коэффициенты не рекурсивной части.
Коэффициенты в знаменателе — это коэффициенты рекурсивной части.
Прямая форма реализации рекурсивного ЦФ показана на рисунке 46.

Верхняя часть схемы соответствует не рекурсивной части алгоритма
фильтрации. Нижняя часть схемы реализует рекурсивную часть алгоритма.
Так как в алгоритме имеются обратные связи, то фильтр имеет БИХ.
Недостатком реализации рекурсивного ЦФ по прямой форме принято
считать большое число элементов задержки (большой объем памяти).
25. ЛИНЕЙНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ. КАНОНИЧЕСКИЕ
СХЕМЫ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ.
-Предназначен для оптимизации использования памяти рекурсивным
алгоритмом фильтрации. Использует минимальное возможное число ячеек
памяти (максимальное из чисел m и n). Структурная схема фильтра показана
на рис. 47.

На рисунке изображен фильтр 2-ого порядка, системная функция
a0  a1Z 1  a2 Z 2
которого равна: H ( Z ) 
1  b1Z 1  b2 Z 2

26. ЛИНЕЙНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ. ЧАСТОТНЫЕ
ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ФИЛЬТРОВ.
- Частотные характеристики — это характеристики у которых какая-то
из

осей

(обычно

характеристикой,

ось

абсцисс)

связанной

с

является

частотой

частотой

или

(нормированной

какой-то
частотой,

соотношение частот).
Информативной характеристикой является АЧХ. АЧХ зависит как от
коэффициентов фильтра, так и от его порядка. Порядок фильтра равен числу
элементов

задержки.

Коэффициенты

фильтра

и

АЧХ

связаны

преобразованием Фурье.
Рекурсивный и трансверсальный линейные фильтры позволяют
реализовать фильтры с следующими типами избирательности: фильтр
нижних частот, фильтр верхних частот, полосовой фильтр, режекторный
фильтр, многополосный фильтр.

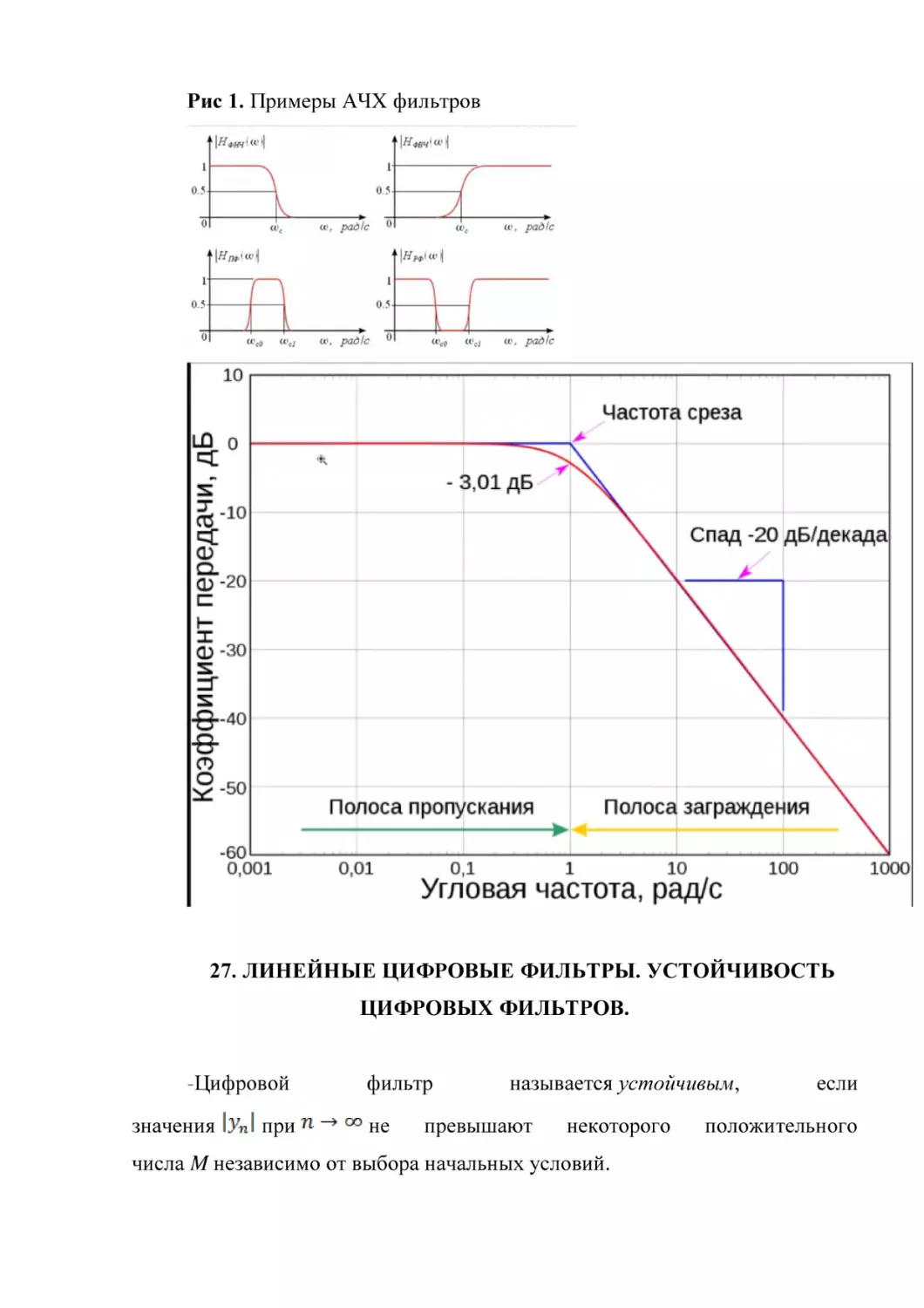
Рис 1. Примеры АЧХ фильтров

27. ЛИНЕЙНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ. УСТОЙЧИВОСТЬ
ЦИФРОВЫХ ФИЛЬТРОВ.

-Цифровой
значения

при

фильтр
не

называется устойчивым,

превышают

некоторого

числа M независимо от выбора начальных условий.

если

положительного

Если
числа

все

полюсы

системной

функции

,

т.е.

по модулю не превосходят единицы,

располагаясь внутри единичного круга с центром в точке

то на

основании (15.15) любой свободный процесс в ЦФ будет описываться
членами убывающих геометрических прогрессий и фильтр будет устойчив.
Ясно, что практически применяться могут только устойчивые цифровые
фильтры.