Великаны и карлики в мире чисел - Литцман В.

Автор: Литцман В.

Теги: математика

Год: 1959

Похожие

Фантастические задачки на нестандартное мышление

Войсковая разведка

Энтропия и информация

Самовнушение и его влияние на организм человека

Текст

В.ЛИТЦМАН
В. ЛИТЦМАН
ВЕЛИКАНЫ И КАРЛИКИ
В МИРЕ ЧИСЕЛ
ПЕРЕВОД С ПЯТОГО
НЕМЕЦКОГО ИЗДАНИЯ
Л. С. ТОВАЛЕВОЙ
Под редакцией И. М. ЯГЛОМ А
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1959
MATHEMATISCH-PHYSIKALISCHE BIBLIOTHEK.
R E l H E I
Hera i« sgegeben von Prof.Dr. W L i e t z m a n n
2$
RIESEN UND ZWERGE
IM ZAHLENREICH
vqq Dr.W. Lietzmann
Professor an dcr Univctsitat Gottingen
РйпПе Auflage
Mit 9 Abbildungcn
s
B. G. TEUBNER
VERLAGSGESELLSCHAFTLEIPZIG
• 9 J >
ОГЛАВЛЕНИЕ
От редактора перевода..................................... 4
1. О счете................................................ 5
2. Числовая система....................................... 10
3. Наглядное представление больших чисел с помощью мер длины
и времени, площадей и объемов........................... 14
4. Кое-что о вычислениях с большими числами............... 21
5. Наибольшее число, которое можно записать тремя цифрами . 26
6. О числах простых и совершенных......................... 33
7. Еще несколько примеров числовых великанов.............. 45
8. Числовые карлики....................................... 53
9. В мире великанов и карликов также считают обыкновенными
числами..................................................... 65
!♦
ОТ РЕДАКТОРА ПЕРЕВОДА
Эта маленькая книжка принадлежит перу известного
немецкого популяризатора математики Вальтера Литцма-
на. Она рассчитана на широкий круг читателей и вполне
может быть рекомендована школьникам средних клас-
сов, так как для ее понимания требуется знакомство в ос-
новном лишь с элементами арифметики. Однако в конце
книги автор переходит к более сложным вопросам, с кото-
рыми интересно будет познакомиться и более подготовлен-
ному читателю. Книга может быть полезной также и пе-
дагогам, которые найдут здесь обширный материал как
для классных занятий, так и для работы школьного мате-
матического кружка.
Настоящий перевод выполнен с.пятого немецкого изда-
ния 1953 года, заметно отличающегося от предыдущих.
Несмотря на то, что со времени выхода этого издания про-
шло не так много времени, возможно, что некоторые из
приведенных в книге сведений могут уже сейчас считаться
устаревшими. Редакция не ставила целью привести все
имеющиеся здесь данйые в полное соответствие с самыми пос-
ледними достижениями науки, поскольку задача книжки
состоит лишь в том, чтобы проиллюстрировать некоторые
из тех разделов математики и естествознания, в которых
встречаются очень большие и очень маленькие числа.
Книжка снабжена небольшим числом примечаний редак-
тора (обозначенных звездочками в отличие от нумерованных
подстрочных сносок автора), в которых, в частности, даны
ссылки на другую доступную читателю книги литературу
и отмечены некоторые последние результаты, полученные
с использованием современных вычислительных машин.
И. М. Яглом
1. О СЧЕТЕ
Нарисуй на листке бумаги несколько маленьких кру-
жочков примерно так, как изображено на рис. 1. Затем
предложи своему приятелю закрыть глаза и положи перед
ним этот листок; пусть он быстро откроет глаза и тотчас
опять закроет их. А теперь спроси у него, сколько кружоч-
ков было нарисовано на бумаге. Он почти наверняка оши-
бется — если, конечно, не схитрил, но в этом мы его подоз-
ревать не станем. «Значит приятель даже
не умеет быстро сосчитать до девяти»,—
подумаешь ты, если нарисовано было имен-
но девять кружков.
Теперь повтори этот опыт. Нарисуй толь-
ко четыре кружка примерно так, как пока-
зано на рис. 2. В этом случае твой прия-
тель определенно правильно укажет число
кружков. Следовательно, мы можем одно-
временно охватить глазом лишь сравнительно небольшое
число предметов. Возможно, ты теперь попробуешь уста-
новить, где проходит граница между числом предметов,
которые ты сам сможешь или не сможешь
сразу воспринять.
В этой связи можно вспомнить о следу-
ющей игре. Один из играющих отворачи-
вается, а остальные кладут на стол в один
ряд несколько оказавшихся под рукой
различных предметов: перочинный нож,
ножницы, карандаш, листок бумаги, пугови-
цу, почтовую марку и т. д. Теперь водящему
разрешается повернуться и недолго,— скажем, минуты
две,— рассматривать лежащие на столе предметы. Затем
он должен снова отвернуться и назвать предметы, которые
запомнил. Удивительно, как мало их окажется. И здесь
О О
О
О
О
О
° О
О
Рис. 1.
о
о
о
о
Рис. 2.
5
О О О
ООО
ООО
Рис. 3.
встает благодарная задача — определить степень восприим-
чивости каждого участника игры.
Однако совсем нетрудно при помощи специального
приема увеличить число запоминаемых предметов. Если
расположить изображенные на рис. 1 девять кружков так,
как это показано на рис. 3, то твой приятель с одного взгля-
да сумеет правильно определить их число. И в приведенной
выше игре можно увеличить свои шансы запомнить не толь-
ко число и вид отдельных предметов, но, возможно, даже
и порядок, в котором они лежат. За то
время, пока ты осматриваешь предметы,
быстро придумай какую-нибудь историю,
и чем более нелепую, тем лучше. Напри-
мер: одноногий ножи двуногие иожн и-
ц ы, прогуливаясь, встретили карандаш.
Ножницы говорят ножу: «Очини каран-
даш, а я тем временем отрежу кусочек
бумаги, и карандаш нам напишет
письмо. За неимением другого, мы запечатаем его п у-
говицей и наклеим марку» и т. д. «История»,
правда, довольно глупая, но тем легче ее запомнить. Фокус
заключается лишь в том, чтобы придумать ее за две минуты.
Если твой приятель, которому ты показал нарисован-
ные на рис. 1 кружки, захочет все же узнать, сколько их
нарисовано, то он их попросту сосчитает. Можно сосчи-
тать предметы и по памяти; один окажется при этом более
искусным, другой — менее. Если тебя спросят, сколько
окон твоего дома или твоей школы смотрят на улицу, то ты,
наверно, не сумеешь быстро ответить, хотя и видишь эти
дома постоянно. Но ты сможешь мысленно представить се-
бе эти дома и попробовать сосчитать их окна. Или же ты
вспомнишь, сколько классов школы выходят на улицу и
сколько окон в каждом из них. В сущности, это — тот же
самый прием, что и в опыте с девятью кружками, располо-
женными на рис. 3, где тоже достаточно представить себе
кружки — и ты определишь их число: ведь расположе-
ние этих кружков тебе знакомо так же хорошо, как, ска-
жем, расположение кружков на костяшке домино. В опи-
санной выше игре тебе на помощь пришло воображение
точно так же, как и при подсчете окон дома.
Посмотрим, какие еще условия необходимы, чтобы мож-
но было сосчитать какие-то предметы. Для этого, прежде
всего, нужно, чтобы число предметов во время счета оста-
6
валось неизменным. Ты скажешь, что это само собой разу-
меется. Не совсем! Вспомни сказку о пастушонке, кото-
рый должен был ответить царю на три вопроса. Один из
них гласил: сколько капель в море? Мальчик не расте-
рялся; он воспользовался тем, что число это все время
меняется, и уклонился от прямого ответа: «Останови все
реки и ручьи, которые вливаются в море, и тогда я отвечу
на твой вопрос!».
Следующее условие: считающий должен уметь считать.
И это тоже не само собой разумеется! Маленькие дети не
умеют считать; для того чтобы научиться счету, они должны
несколько подрасти. Не умеют считать и некоторые перво-
бытные народы. Есть такие народы, которые обозначают
числа свыше четырех просто словом «много». У племени
янкосов на Амазонке число 3 называется «поэттаррарорин-
коароак». «К счастью, на этом их арифметика кончается»,—
сказал тот, от кого я это узнал.
Но и взрослые культурные люди тоже не всегда имеют
навыки к счету. Мы ведь хотим считать быстро и не заду-
мываясь. Если мы после каждого числа будем думать, как
называется следующее, то, значит, мы плохо считаем.
Однако, если мы будем считать быстро и машинально, то
нам легко ошибиться. Заставь кого-нибудь считать: 1090,
1091, 1092 и т. д.; часто после 1099 назовут 2000. В немец-
ком языке источником многих ошибок при быстром счете
является неудобная перестановка порядка единиц и десят-
ков в названиях чисел: здесь говорят, например, «шесть
и пятьдесят» (sechsundfiinfzig) вместо «пятьдесят шесть».
Изменение этого порядка приветствовали бы вое, кто в силу
своей профессии связан со счетом.
С другим затруднением мы встречаемся в том случае,
когда, наоборот, счет приходится вести слишком медленно.
Как считает угольщик мешки, которые он один за другим
вносит в подвал? Как считает ученик дни, остающиеся до
начала школьных каникул? То, что в последнем случае счет
ведется назад, а не вперед, существенного значения не имеет.
В обоих случаях трудно все время держать в памяти нужное
число. Поэтому приходится прибегать к значкам или от-
меткам. Угольщик одну за другой ставит черточки каждый
раз, когда вносит в подвал мешок; мальчик же, наоборот,
зачеркивает каждый раз черточку, когда проходит еще один
день. Таким образом, здесь пересчитываются не сами пред-
меты, а черточки.
7
Мы достаточно много говорили о счете и о том, как сле-
дует поступать в различных случаях; пора уже заняться
этим делом на практике.
Сосчитай спички в спичечной коробке! Наполни стакан
горошинами и определи их число! Сосчитай буквы на одной
странице этой книги! Эти три примера покажут тебе, что не
так уж легко подсчитать точно число предметов, если оно
достаточно велико. Считать придется внимательно и для
проверки пересчитывать несколько раз.
Впрочем, в счете можно совершенствоваться — если
только достаточно практиковаться в нем. Кассир в банке,
постоянно считающий денежные знаки, или почтовый слу-
жащий, отсчитывающий открытки, более искусны в счете
этих предметов, чем все другие люди.
Не думай, однако, что всегда можно сосчитать все пред-
меты, число которых нам хочется узнать. Можно потра-
тить лучшие годы своей жизни на подобные подсчеты и все
же не сосчитать многого. Ведь если считать со скоростью
одного числа в секунду, то за минуту мы сможем насчитать
60 чисел, за час — 3600, а за десятичасовой «рабочий день»—
36 000. И если посвятить такой работе 50 лет, проводя
за этим остроумным занятием 300 рабочих дней в году, то
мы досчитали бы до 540 000 000, т. е. примерно до полумил-
лиарда. Все, что превосходит это число,— а такого в нашей
жизни имеется немало,— не может быть сосчитано никаким
сколь угодно добросовестным счетчиком.
Тут нам на помощь приходят считающие машины. Мы
все знакомы, например, с газовым и электрическим счет-
чиками. Что бы мы стали делать, если бы нам самим при-
ходилось подсчитывать расход газа и электричества? Но
даже, и там, где мы могли бы сами справиться, мы часто
привлекаем на помощь приборы, например секундомер или
шагомер. В тех же случаях, когда требуемая быстрота сче-
та превосходит возможности человека, единственным на-
шим спасением является машина. Отсчитывающее устрой-
ство ротационной машины, например, отсчитывает в час
20 000 газет пачками по 50 штук в каждой.
Так как не все можно подсчитать (а иногда нам просто
не хочется тратить на это силы), то даже в тех случаях,
когда было бы интересно знать точное количество предме-
тов, часто довольствуются приблизительной оценкой их
числа. Организм человека состоит из 18 000 000 000 000 000
клеток; у слона их даже 700 000 000 000 000 000. Говорят,
8
что самка термита (белого муравья) в течение 10 лет откла-
дывает каждые две секунды по яйцу, что составляет
15 552 000 яиц в год. Никто, однако, не вообразит, что
эти числа точны —ясно, что они представляют собой лишь
примерные оценки действительных чисел. Подобные оценки
для практики необычайно важны. Однако и здесь сноровка
не приходит сама!
Попробуй-ка оценить какое-либо большое количество
предметов. Например, пусть в праздник на площади собра-
лась большая толпа людей; сколько их: 200, 1000 или 5000?
Или еще: покажи компании банку с горошинами; кто
точнее всех оценит их число, тот получит приз. Трудно
себе представить, насколько велик бывает разрыв между
оценками, которые дают различные люди (а также меж-
ду всеми этими оценками и действительным числом).
Однако часто беспомощность в оценках является не-
допустимой.
Как можно упражняться в оценках? Прежде всего, нуж-
но заняться точным счетом и измерением величин. При этом
мы научимся представлять себе, скажем, толпу в 100,
500, 1000 человек или расстояние в 100, 200, 300, 400, 500
метров. Если же случается иметь дело с предметами, не
поддающимися непосредственному подсчету, то приходится
призывать на помощь оценки. Приведем простой пример.
В одном немецком городе пришлось всем семьям, имеющим
детей, выдать карточки на получение молока. Город насчи-
тывал 50 000 жителей. Для выдачи карточек были назна-
чены 2 дня, по 5 часов в день. Требовалось отдельно за-
полнить карточки на каждую семью; при этом нужно было
предъявлять метрические свидетельства детей, для того
чтобы можно было занести их имена в специальные списки.
Однако, когда наступили дни выдачи карточек, то, ко всеоб-
щему неудовольствию, оказалось, что выдававшие карточки
лица никак не могут справиться с этим делом. Долгое и
для многих бесплодное ожидание! А ведь предварительный
расчет и примерная оценка могли бы помочь делу. Если на
каждого человека тратить только по 2 минуты, то за час
можно отпустить 30 человек, а за 10 часов — 300. Ясно
поэтому, что если посадить за эту работу только 5 человек,
то они никак не смогут справиться с нею.
Но здесь мы уже вышли за рамки, намеченные для этой
главы. Мы вычисляли, а не считали. Прежде чем вернуться
к этой теме, следует решить один вопрос, от которого
9
мы отклонились выше. Как овладеть большими числами,
как справиться с числовыми великанами, до которых мы
никак не можем дойти при фактическом счете?
2. ЧИСЛОВАЯ СИСТЕМА
Если требуется Сосчитать большое число предметов, то
не мешает повторить счет несколько раз. Почтальон прино-
сит вам 832 рубля; пока он их вам отсчитывает, вы следите
за счетом; затем он их еще раз пересчитывает, а вы, прежде
чем взять деньги, вероятно, еще раз проверите их. Но
даже и после всего этого вы не были бы уверены в правиль-
ности счета, если бы он не производился особым образом.
Предположим, что почтальон принес вам эту сумму руб-
лями (на самом деле этого, конечно, не бывает). При этом
он не положит все рубли на стол беспорядочной кучей, а
сгруппирует их определенным образом, например, отсчи-
тает по 10 штук и положит отдельные десятки рублей малень-
кими кучками, причем еще позаботится, чтобы в одном ряду
лежало по 10 таких кучек. Таким образом, получится 8 ря-
дов, 3 пачки и еще 2 отдельные бумажки.
Прием, которым мы пользовались здесь, применяют
всегда, когда нужно сосчитать очень много предметов. То-
вары, поступающие в продажу в большом количестве, на-
пример булавки, пуговицы, перья и т. д., считают дюжи-
нами и гроссами*). Угольщик, о котором мы говорили выше
(стр. 7), не просто ставит черточку за черточкой; каждой
пятой он перечеркивает предыдущие четыре. Поэтому,
например, число 1 Зу него имеет следующий вид: -Ц11 1111IJI.
Также и при приближенной оценке больших чисел прибе-
гают к подобной группировке. Из всех способов группи-
ровки важнейшим является тот, который связан с нашими
правилами образования чисел, с их написанием и наимено-
ваниями. Мы, как и почтальон, о котором рассказывалось
выше, объединяем десять предметов в десяток, десять де-
сятков — в сотню и т. д. Такое объединение удобно для
наглядной иллюстрации больших чисел. Так, учитель сче-
та Буссе, живший около 1800 года, представлял число
2326 так, как это изображено на рис. 4: шесть точек в кон-
це — это единицы, следующие за ними два бумажных куль-
) Гросс — двенадцать дюжин.
10
ка — десятки, три мешочка — сотни, а два ящика, изобра-
женных прямоугольниками,— тысячи.
Насколько десятичная система облегчает овладение
большими числами, видно по системам записи чисел, цели-
ком игнорирующим связанное с этим преимущество или
не использующим его полностью. Числа, написанные рим-
скими цифрами, как MDCCLIX или MMDCCCLXXIV
не прочтешь так быстро, как, например, 1888 или 1797.
Рис. 4.
Если же иметь дело с очень большими числами, то даже
и наша простая система их изображения не слишком прак-
тична, ни в смысле чтения, нив смысле записи. Вот пример
из книги «Математические развлечения», вышедшей в 1636 го-
ду: «Астрономы вычислили, что длина окружности не-
бесного свода равна 508781250 милям..., поверхность же
его — 82364023748224431 yj квадратным милям... Из этого
следует, что объем шара такого же радиуса равен примерно
3596299963139791266979190761957504 кубическим милям».
Сможешь ли ты без затруднения прочесть эти числа, в осо-
бенности последнее из них?
Как сделать запись таких больших чисел более нагляд-
ной? Для этого группируют цифры по три, начиная справа.
Другими словами, в нашу десятичную систему дополни-
тельно вводят еще группировку по тысячам. Числа
508 781 250 миль
82364 023748224 431 кв. миля
3596299963 139 791 266979 190761 957504 куб. мили
уже гораздо более наглядны. Правда, для того чтобы чи-
тать такие числа, нужно хорошо знать их названия. Для
чисел до тысячи их знает каждый школьник, даже младших
классов. До миллиона дело тоже еще идет легко. Следова-
тельно, мы владеем уже всеми названиями чисел до чи-
сла 999 999 999 999 включительно; словами «девятьсот девя-
носто девять тысяч девятьсот девяносто девять миллионов
девятьсот девяносто девять тысяч девятьсот девяносто
девять». Число наверху в первом ряду — 508 миллионов
781 тысяча 250.
При этом мы обошли число, которое употребляется
весьма часто: миллиард. Это широко распространенное сей-
час слово, означающее тысячу миллионов, в Германии вош-
ло в употребление лишь с XIX река.
Однако продолжим наш разговор о числовой системе!
Миллион миллионов называют биллионом*). Второе из
выписанных выше чисел читается так: 82 тысячи 364 бил-
лиона 23 тысячи 748 миллионов 224 тысячи 431. Далее,
миллион биллионов называется триллионом, миллион трил-
лионов — квадриллионом и т. д. Третье из наших чисел
начинается с 3 тысяч 596 квинтиллионов. Дальше прочти
его сам.
Если мы продолжим ряд названий: биллион, триллион,
квадриллион и т. д. достаточно далеко, то мы сможем не
только написать, но и прочесть любое число, как бы велико
оно ни было. Тебе кажется, что это само собой разумеется.
Однако не всегда это было так. Греческий ученый Архимед,
замечательнейший математик древнего мира, написал по
этому вопросу очень поучительное сочинение под названием
«Исчисление песчинок», которое сохранилось до нашего вре-
мени **). Он ставит целью определить количество песчинок,
вмещающихся в шар величиной во всю вселенную. Что Архи-
мед понимает под вселенной, мы уточнять не станем, как бы
важно это ни было для истории астрономии. Да Архимед,
в сущности, и не стремился указать точное число песчинок,'
помещающихся в его вселенной. Ему важно было показать,
что можно образовать числа большие, чем невероятно боль-
*) Автор описывает принятую в Германии систему наименова-
ний чисел, отличную от общепринятой в СССР, да и в ряде других
стран (США, Франция). У нас обычно биллионом называют то
число, которое автор называет миллиардом (тысяча миллионов, а
не миллион миллионов), соответственно этому триллионом называ-
ется тысяча биллионов (немецкий биллион), квадриллионом — ты-
сяча триллионов и т. д.
Мы не стали менять здесь текст автора, тем более, что вопрос о наи-
менованиях чисел не имеет большого значения: названия чисел свыше
биллиона употребляются крайне редко; вместо этого обычно исполь-
зуют записи больших чисел в виде произведений некоторых множителей
на степени числа 10 (см. ниже, стр. 28). Также и далее все названия
чисел понимаются в том смысле, который объяснен в тексте.
**) См. Архимед, Исчисление песчинок (Псаммит), М.— Л.,
ГТТИ, 1932.
12
шое число — число песчинок во вселенной. Стоящая
перед ним задача относилась не к астрономии, а к ариф-
метике!
Архимед предположил, что в объеме одного макового
зернышка могут поместиться около 10 000 песчинок (что
с лихвой покрывает истинное значение!) и что сорок мако-
вых зерен, положенных рядом, достигают ширины пальца х).
Если знать радиус вселенной, то легко можно вычислить,
какое число песчинок может в ней поместиться. Для подоб-
ных вычислений существуют формулы, которые Архимед
хорошо знал. Задача была бы сравнительно проста, если
бы существовала такая система счисления, какую мы имеем
теперь. Однако тогда ее нужно было еще создать. Это и бы-
ло истинной целью работы Архимеда.
Проследим немного за этой работой. Наибольшим чис-
лом, для которого греки имели специальное наименование,
было 10 000. Это число они называли мириадой. Чи-
сла до мириады мириад (т. е. до 10 000 х 10 000 = 100 000 000)
Архимед назвал числами первого порядка; числа от ми-
риады мириад до 100 000 000 х 100 000 000 — числами вто-
рого порядка; от этого числа и до 100 000 000 х 100 000 000 х
X 100 000 000 — числами третьего порядка и т. д. до числа
100 000 000-го или мириад-мириадного порядка. Послед-
нее число — единицу с 800 000 000 нулями — обозначим
через Р. Числа от 1 до Р Архимед назвал числами первого
периода. Числа от Р до 100 000 000 Р образуют первый по-
рядок второго периода; затем Архимед переходит ко вто-
рому порядку второго периода, к третьему порядку и т. д.
до 100 000 000-го порядка второго периода, после которого
начинается третий период. Таким же образом можно обра-
зовать четвертый, пятый период и т. д. Архимед доводит эту
систему до 100000000-го, т. е. мириад-мириадного периода,
и находит, наконец, ее последнее число: мириада мириад
единиц мириад-мириадного порядка мириад-мириадного
периода.
Изображается это число единицей с 80 000 биллионов
нулей. Это поистине числовой исполин, превосходящий вся-
кое воображение!
0 Мне сообщили, что несколько школьников действительно терпе-
ливо сосчитали число песчинок в 1 см3 песка, чтобы проверить предпо-
ложение Архимеда. Они получили совершенно другой результат. Сочи-
нение Архимеда следовало бы назвать «Исчисление пылинок»,— на-
столько малы его песчинки.
13
Если бы Архимеда не привлекало само создание число-
вой системы, ему бы вовсе не нужен был такой огромный
числовой аппарат. Для решения его задачи достаточно срав-
нительно небольшого числа. Ему не нужно забираться даже
во второй период, не говоря уже о высших. Число песчи-
нок меньше 10 000 000 единиц восьмого порядка первого
периода.
Эти соображения Архимеда больше,чем что-либо другое,
показывают важность приемов, которые позволяют сде-
лать числовые исполины более наглядными.
3. НАГЛЯДНОЕ ПРЕДСТАВЛЕНИЕ
БОЛЬШИХ ЧИСЕЛ С ПОМОЩЬЮ МЕР ДЛИНЫ
И ВРЕМЕНИ, ПЛОЩАДЕЙ И ОБЪЕМОВ
Ты, вероятно, уже встречался с числовыми исполинами,
о которых говорил себе: «Я не могу их себе представить!».
Ты знаешь, что в газетах, книгах и таблицах иногда при-
бегают к различного рода сравнениям, позволяющим сде-
лать большие числа более доступными пониманию. В по-
пулярных книгах по астрономии, например, где все время
приходится иметь дело с величинами, превосходящими
наши представления, часто прибегают к подобному нагляд-
ному изображению больших чисел.
1--1----1-1----1--1---1—
0 12 3 4 6 6
Рис. 5.
Чтобы лучше представить себе числа, их последователь-
ность, величину и действия над ними, их изображают точ-
ками луча, расположенными на одинаковом расстоянии
друг от друга (рис. 5). Этот луч называется числовым
лучом. Понятно, что на рисунке мы можем показать
лишь часть числового луча. Представим себе этот луч с на-
несенными на нем на одинаковом расстоянии друг от друга
числовыми отметками, неограниченно продолженным в на-
правлении стрелки. На нашем рисунке начальная точка лу-
ча, обозначенная числом 0, расположена слева. При таком
способе изображения чисел, прежде всегд, надо установить
длину отрезка, служащего единицей измерения, т. е. рас-
14
стояние между точками 0 и 1 числового луча. Если мы при-
мем за единицу измерения 1 см, то расстояние между на-
чальной точкой и точкой, обозначенной числом 7, соста-
вит 7 см; расстояние от 0 до числа 817 составит 8 м 17 см,
до числа 233 588—2 км 335 м 88 см. О числах порядка мил-
лиона таким способом еще можно получить довольно чет-
кое представление. (Как велико расстояние между началь-
ной точкой и числом 1 000 000 при единице измерения
в 1 см? в 1 мм?) Числа же, доходящие до биллионов, уже
трудно вообразить себе с помощью числового луча, так как
отрезки получаются слишком длинные. Если принять за еди-
ницу 1 мм, то для изображения 1 миллиарда уже потре-
буется отрезок в 1000 км. Если составить 1 миллиард
рублей 20-копеечными монетами, положенными друг на
друга, то, принимая толщину монеты за 1 мм, мы получим
«столбик» высотой 5000 км.
Другой пример. В Германии перед последней войной
выкуривали примерно 80 миллиардов папирос в год. Если
их положить цепочкой, то при длине одной папиросы в 6,5 см
они составят «отрезок» в 5 200 000 км. Километр — это
(примерно) одна сорокатысячная часть земного экватора.
Следовательно, цепочка из папирос обовьет экватор 130 раз!
Вот еще пример изображения чисел с помощью длин.
Кто-то вычислил, что объем знаменитой пирамиды Хеопса
в Египте равен 2 678 257 л<3; отсюда можно вывести, что ее
вес составляет 7 231 294 т. Последние цифры этого числа
сомнительны, первые же, по-видимому, точны. Чтобы пред-
ставить себе наглядно этот громадный вес, заметим, что
грузоподъемность обычного товарного вагона равна 16 т
(грузоподъемность написана на каждом вагоне!). Значит,
поезд, состоящий из 50 вагонов, может перевезти 800 т.
Следовательно, чтобы доставить материал для постройки
пирамиды Хеопса, потребовалось бы около 9000 товарных
составов. Это поистине грандиозное количество. Сколько же
несчастных людей должны были отдать свои силы этой
стройке!
Для наглядного изображения больших чисел часто ис-
пользуется и время. Мы все хорошо знаем, что такое
секунда, минута, сутки, год. Старые люди могут предста-
вить себе несколько десятилетий. Но о столетиях и тысяче-
летиях тоже можно составить себе представление, если
только связать их с определенными историческими собы-
тиями. В вопросе о продолжительности геологических фор-
15
маций (известной в настоящее время довольно достоверно)
мы попадаем в область миллионов лет. Из приведенной здесь
таблицы, составленной палеонтологом Марбле (J. В. Marble),
Геологическая формация Продол- житель- ность Возраст
(в милли онах лет)
Четвертичный период. . . 0,6 0,6
Третичный » ... 60 60
Меловой » ... 80 140
Юрский » ... 35 175
Триазойский » ... 25 200
Пермский » ... 40 240
Каменноугольный » ... 70 310
Девонский » ... 40 350
Силурийский » ... 100 450
Кембрийский » ... 90 540
Прекембрийский » ... 1360 1900
видно, что от начала Третичного периода нас отделяют при-
мерно 60 миллионов лет, от Кембрийского — около 540
миллионов, от начала Прекембрийского — 1900 миллионов
лет. Согласно современной теории возникновения Земли
ее возраст исчисляют примерно в 5 миллиардов лет.
Чтобы дать представление об объеме земного шара, при-
нято указывать время, необходимое для кругосветного пу-
тешествия. В восьмидесятые годы прошлого столетия в Гер-
мании большой известностью пользовалась пьеса «Путе-
шествие вокруг света в 80 дней», поставленная по одноимен-
ному роману Жюля Верна. Сейчас на такое путешествие
самолетом потребуется около 80 часов. Наше представле-
ние об охвате земного шара будет более точным, если исхо-
дить из какого-либо определенного вида транспорта, на-
пример курьерского поезда, делающего 75 км в час. Сколько
времени потребуется для кругосветного путешествия по эк-
ватору в курьерском поезде? Такие же путешествия можно
совершить и по вселенной. Сколько времени длилось бы пу-
тешествие в курьерском поезде на Луну, на Солнце? Здесь
получатся уже довольно значительные числа. Луна, даже
когда она находится на самом близком расстоянии от Зем-
ли, удалена от нас на 357 000 км; поездка курьерским поез-
дом на Луну, следовательно, потребует около 200 дней. Пу-
16
тешествие до Солнца, удаленного от нас на 150 000 000 км,
продлится 2 000 000 часов, а так как год содержит мень-
ше 10 000 часов, то эта поездка займет свыше 200 лет, т. е;
она значительно превосходит продолжительность челове-
ческой жизни.
Поэт Гебель в своей «Сокровищнице» воспользовался
другим наглядным образом: артиллерист, находясь на
Солнце, направляет орудийный снаряд как раз на тебя. Ты
в испуге убегаешь. Но поэт успокаивает тебя: нечего спе-
шить; ты имеешь еще много времени, чтобы избежать сна-
ряда. Посмотрим, почему это так. Скорость современного
снаряда составляет около 5000 км в час. Путь, который
он должен пройти, равен 150 000 000 км. Следовательно,
снаряду потребуется около трех с половиной лет. Однако
расстояния, подобные указанным выше, в астрономии счи-
таются совсем небольшими. Так, например, планета Неп-
тун удалена от Солнца на расстояние, в 30 раз большее,
чем Земля, а последняя открытая планета Плутон — еще
дальше. Эти тридцать единиц — можно ведь принять рас-
стояние от Солнца до Земли за единицу длины для измере-
ния межпланетных расстояний — читаются очень легко,
но лишь потому, что сама единица длины столь велика.
Если же мы захотим добраться до ближайшей неподвиж-
ной звезды, то нам предстоит пройти путь, равный примерно
206 000 радиусов земной орбиты. Это расстояние доходит
уже до биллионов километров. Чтобы не оперировать с по-
добными числовыми величинами, мы вынуждены ввести
новую единицу длины. За такую единицу принимают све-
товой год. В одну секунду луч света проходит расстояние
в 300 000 км. От Солнца до нас он доходит примерно за
8 минут (проверь это!). Какой путь проходит луч света за
час, за день, за год, ты тоже сможешь подсчитать; труднее
тебе будет составить правильное представление об этих
колоссальных расстояниях. Во всяком случае, мы прихо-
дим таким образом к новой единице длины, использование
которой приводит к вполне приемлемым числам для рас-
стояний до неподвижных звезд; так, ближайшая неподвиж-
ная звезда удалена от нас (всего!) на 4 световых года.
Мы подошли уже к числовым великанам, и лишь при по-
мощи искусного приема нам удалось создать видимость наг-
лядного их представления: выбирая большой масштаб, мы
как бы остались в мире небольших чисел. Существуют,
однако, такие числовые гиганты, по отношению к которым
2 В. Литцман
17
оказывается бессильным и подобный прием. Так, мы не смо-
жем сладить с упомянутым во второй главе числом Р Архи-
меда и, тем более, с его самым большим числом, изображае-
мым единицей с 80 000 биллионов нулей. Чтобы сделать
это колоссальное число хотя бы немного более доступным
нашему пониманию, попытаемся изобразить наглядно не его
значение, а лишь место, которое оно заняло бы, если его
записать в нашей числовой системе'. Положим, что две ря-
дом написанные цифры занимают 1 см. Какой длины будет
все число? Ты подсчитаешь, что оно составит 40 000 биллио-
нов сантиметров или 400 миллиардов километров — рас-
стояние, равное примерно 3000 радиусов земной орбиты.
Теперь ты видишь, что написание этого числа на самом деле
натолкнется на непреодолимые трудности. Предположим,
что кто-либо смог бы написать за минуту 100 нулей (здесь
учитываются и перерывы, во время которых пишущий отды-
хает). С начала .нашего летоисчисления прошло немногим
более. 1 миллиарда минут; за это время можно было бы
написать одну десятую часть биллиона нулей. Следователь-
но, 800 000 человек должны были бы от начала нашего
летоисчисления непрерывно писать нули! Только таким
путем удалось бы действительно написать придуманное
Архимедом число.
Возьмем отрезок длиной 10 см, квадрат со стороной
в 10 см, куб с ребром в 10 см и удвоим все эти длины; при
этом мы получим отрезок, в 2 раза больший исходного, квад-
рат — в 4 и куб в 8 раз большие исходного. Это различие
является источником многочисленных ошибок в оценке
площадей и объемов.
Сколько человек могут поместиться на льду Боденского
озера? Ты, вероятно, ответишь, что очень много, возможно—
целый миллион. Поместим на площади в один квадратный
метр трех человек; они смогут разместиться довольно удоб-
но (в толпе люди стоят гораздо теснее). Площадь Боден-
ского озера равна 539 км2. А 1 км2— 1 000 000 м2, сле-
довательно, на поле площадью 1 км2 можно поместить 3 мил-
лиона человек. На льду Боденского озера, значит, хватит
места больше чем для полутора миллиардов человек, т. е.
более чем для половины населения земного шара.
Еще чаще встречаются ошибки при оценке объемов.
Как правило, не представляют себе, что, например, увели-
чив длину, ширину и высоту обыкновенной сигары в 2 раза,
18
мы получим сигару, в 8 раз (по объему) большую, курить
которую можно будет в 8 раз дольше. По договору Гулли-
вера с лилипутами он должен был получать столько же еды
и питья, сколько получают 1728 лилипутов. Маленькие лю-
ди определили, что ростом Гулливер больше их в 12 раз,—
а теперь сообрази-ка сам, откуда в этом договоре появилось
число 1728?
Если тебя спросят, сколько кирпичей или спичечных
коробков можно уместить в кубическом километре, то ты,
наверное, назовешь числа, гораздо меньшие действительных.
Вычисли-ка их; для этого достаточно измерить ребра этих'
тел, перемножить длины трех ребер и подсчитать, сколько
раз полученный таким образом объем содержится в 1 км3.
Диаметр Солнца в 109 раз больше диаметра Земли. Отсюда
следует, что поверхность Солнца в 11 900 раз, а объем —
даже в 1 300 000 раз больше соответственно поверхности
и объема Земли.
Мне вспоминается интересное вычисление Леберехта
Хюнхена (герой рассказов Генриха Зайделя). Лежа на
своем земельном участке, Хюнхен размышлял над вопро-
сом, являются ли земля под ним и воздух и эфир над ним
его собственностью. Пользуясь теоремой, согласно которой
площадь поперечного разреза пирамиды увеличивается про-
порционально квадрату его расстояния от вершины, Хюнхен
прикидывает, что его участок на Земле, равный 1300 м2,
на Солнце (удаленном от центра Земли на расстояние, близ-
кое к 24 000 радиусов Земли) окажется больше всей терри-
тории Германии. Эти размышления о величине своего уча-
стка он затем распространил и на расстояния от Земли до
неподвижных звезд; что при этом получается, можно про-
честь у Зайделя,— ты же вычисли это сам.
Вес тела получается, если умножить его объем на спе-
циальный множитель, называемый удельным весом. Удель-
ный вес показывает, во сколько раз больше весит тело (или
часть его), чем вода, занимающая тот же объем. Следова-
тельно, вес теснейшим образом связан с объемом. И здесь
очень часты грубые ошибки в оценке величин. Сколько ве-
сит пробковый шар радиусом в 1 jw? Ты вряд ли предполо-
жишь, что он весит больше чем 5—10 кг — пробка ведь очень
легка. Удельный вес пробки — 0,24, т. е. она в 4 раза лег-
че воды того же объема. Для определения объема шара име-
4
ется простая формула: у пг’, где г. — радиус, а п— число,
2*
19
которым мы еще займемся подробнее в дальнейшем. Здесь
мы только скажем, что оно примерно равно 3,14. Литр
воды весит 1 кг. Литр — это то же самое, что кубический
дециметр. Один кубический метр содержит 1000 литров.
Следовательно, вес кубического метра воды составляет
1000 кг или 1 т. Отсюда следует, что пробковый шар весит
А-тг-0,24 т, т. е. примерно тонну, так как п лишь очень
О
немногим больше 3. Значит, пробковый шар весит не 10 кг,
а в 100 раз больше.
Я предложу тебе еще несколько задач с тем, чтобы ты
их сам разобрал и увидел разницу между поверхностной
оценкой и результатом более или менее точного подсчета.
Можешь затем предложить эти задачи твоим товарищам,—
они, наверное, тоже оконфузятся.
Как велико ребро золотого куба, который весит столько
же, сколько все население земного шара? Средний вес каж-
дого из 2,5 миллиардов людей можно принять равным од-
ному центнеру; удельный вес золота немногим более 19.
Сколько весит воздух в зале шириной 12 м, длиной 30 м и
высотой 8 м> Удельный вес воздуха — 0,001293.
Увеличение площадей и объемов можно использовать
для наглядного изображения больших чисел. Мы уже ви-
дели, что затруднительно использовать отрезки для нагляд-
ного представления чисел порядка миллиарда. Иначе об-
стоит дело, если привлечь для этой цели объемы. Пусть
число 1 изображается кубиком с ребром, в 1 мм\ в таком
случае столбик в 1 см высотой, состоящий из 10 таких куби-
ков, представит число 10; слой в 1 см длины и 1 см шири-
ны — число 100; 10 таких слоев, образующих куб с ребром
в 1 см, будут изображать уже число 1000. Из кубических
сантиметров можно построить кубический дециметр; он
будет изображать число 1 000 000. Кубический метр будет
представлять миллиард, а кубический километр (чтобы
представить себе такую величину, нужно уже вспомнить
о горах) — триллион. Пользуясь пространственными об-
разами, можно с легкостью перейти в область еще больших
чисел, особенно, если привлечь к рассмотрению не только
обычные на Земле величины, но и астрономические. Объ-
емы Земли (сколько это будет кубических километров?),
Солнца (а это сколько?), пространства, занимаемого нашей
планетной системой, и т. д. могут служить для наглядного
изображения несравненно больших чисел, чем триллион.
20
Но все же и здесь пока имеется предел; его намечает тот
факт, что самые отдаленные объекты звездного неба, обо-
зримые с помощью современных средств наблюдения, уда-
лены от нас на несколько миллионов световых лет.
4. КОЕ-ЧТО О ВЫЧИСЛЕНИЯХ С БОЛЬШИМИ ЧИСЛАМИ
В школе учат, что сложение есть сокращенное продолже-
ние счета. 7 -|-3 означает, что, начиная от 7, нужно продол-
жить счет еще на 3 шага, т. е. считать: 8, 9, 10. Сложение
небольших чисел нередко фактически выполняют таким
образом. Многие, например, будут складывать десятые
доли, указанные в задаче 1, так:
Задача 1 Задача
0,10 руб. 0,15 руб.
0,20 » 0,25 >
0,25 » 0,95 »
0,15 » 0,20 »
0,30 » 0,35 »
0,20 » 0,85 »
0,10 » 1,20 »
0,05 » 0,75 »
0,20 » 1,05 »
1,55 руб. 5,75 руб.
1 (эта единица образована тремя пятерками на втором ме-
сте после запятой), 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.
Цифры, напечатанные жирным шрифтом, при счете произ-
носятся несколько громче и указывают промежуточные
результаты.
Как сложение является сокращенной записью процесса
продолжения счета, так и вычитание указывает на продол-
жение обратного счета, т. е. счета от больших чисел к мень-
шим. Умножение же представляет собой сокращенную за-
пись сложения одинаковых слагаемых; так, например,
в задаче 2 можно просто подсчитать количество пятерок
в самом правом столбце и заключить, что этот столбец
даст 7-5 = 35. Наконец, деление является сокращенной
записью многократного вычитания. Четырем арифме-
тическим действиям можно дать и другие определения
(ведь наши определения относятся только к целымчислам),—
но я не собираюсь писать учебник арифметики.
21
Необходимо, прежде всего, объяснить слово «сокращен*
ное». Каждому, конечно, понятно, что если бы я действи-
тельно стал вычислять сумму 7388 5149, продолжая счет
от 7388 еще на 5149 шагов, то это было бы довольно скучным
занятием; кроме того, я легко мог бы просчитаться. Я дол-
жен был бы быть очень внимательным, ибо, как нетрудно за-
метить, здесь мне пришлось бы одновременно производить
два счета. Если же имеешь дело с еще большими числами,
например, с миллионами или биллионами, то, как мы ви-
дели выше, при подобном порядке счета понадобились бы
годы, а может быть, и такой срок был бы мал. По этому по-
воду существует очаровательная история. Карлуше задали
в школе задачу: сколько раз можно вычесть из миллиона
число 3? Он в обычное время садится за работу, однако
дело идет очень медленно. Тогда на помощь приходит мать,
а когда возвращается с работы отец, то начинает считать и он.
Сестры, братья, тети и дяди тоже были мобилизованы на по-
мощь и работали, пока у них от усталости не стали смыкать-
ся глаза, а на завтра все они ругали неразумного учителя,
задающего маленьким детям такие задачи!
Гамбургский математик Г. Шуберт вычислил, что 29 ап-
реля 1902 года в 10 часов 40 минут истек ровно один мил-
лиард минут с начала нашего летоисчисления. Это может
служить хорошим примером (уже использованным нами
однажды) наглядного представления числа 1 000 000 000.
Один юмористический журнал сострил по этому поводу:
«Сколько же тысяч минут затратил почтенный ученый на
это вычисление?». Журнал, видимо, считал, что этот ре-
зультат является плодом длительных и трудных подсчетов.
Однако здесь он так же заблуждался, как и упомянутое
выше милое семейство: для того чтобы получить результат,
достаточно разделить один миллиард на число минут в го-
ду и перевести остаток в месяцы и часы1). То, что Шуберт
дал наглядное представление о величине миллиарда,— это-
го насмешник из журнала не понял.
Не станем вдаваться в дальнейшие подробности отно-
сительно четырех арифметических действий над большими
числами. Хотя они и требуют много времени и большого
внимания, но ты не встретишь серьезных затруднений при
9 Конечно, Шуберт должен был учесть также и високосные годы.
Впрочем, как я узнал впоследствии от В. Аренса, Шуберт написал
в журнал письмо, в котором сообщил, что потратил на вычисление
всего 15 минут.
22
их выполнении. На практике часто прибегают к различным
средствам вычислений, из которых наиболее важными яв-
ляются вычислительные машины, начиная от счетных па-
лочек, кассовых аппаратов (применяемых в магазинах)*)
и «малых вычислительных машин», выполняющих умноже-
ние, до больших современных электронных счетных машин,
таких, как ЭНИАК и другие **).
Нередко удается сравнительно сложные вычисления,
приводящие к большим числам, значительно упростить
при помощи удачной догадки. Я хочу привести .здесь хотя
бы два примера; далее нам встретятся еще и другие. Рас-
скажем одну историю из детства великого математика Кар-
ла. Фридриха Гаусса. В юности он посещал Екатеринин-
скую школу в Брауншвейге. Чтобы занять часть своих уче-
ников,— а их было 100, и притом различного возраста,—
учитель предложил однажды сложить все числа от 1 до 100.
Едва он успел дать это задание, как маленький Гаусс вы-
шел вперед и положил свою грифельную доску на стол учи-
теля: «Готово!». Учитель не знал, что и подумать — шалость
ли это или лень. Однако результат был верен: маленький
математик сообразил, что 1 и 100, 2 и 99, 3 и 98 и т. д. со-
ставляют в каждом случае в сумме 101; так как таких пар
будет 50, то результат равен 50-101 = 5050.
Легко убедиться, что так можно суммировать не только
ряд чисел, начинающийся с единицы, но и ряд, начинаю-
щийся любым другим числом. Да и числа ряда не обяза-
тельно должны непосредственно следовать одно за другим.
*) Кассовые аппараты, имеющиеся во всех магазинах, автоматиче-
ски складывают суммы, выбиваемые на чеках.
**) ЭНИАК (ENIAC)— сокращенное наименование универсальной
вычислительной машины Пенсильванского университета в Филадель-
фии (США) — одной из первых больших электронных счетных машин.
В то время, когда подобных машин было еще не много, их названия и
индивидуальные особенности (и возможности) каждой машины были хо-
рошо известны всем работающим в этой области. Ниже нам еще встре-
тится электронная вычислительная машина СВАК (SWAC), принад-
лежащая Калифорнийскому университету (США); первая советская
машина такого рода сокращенно называется БЭСМ (Большая электрон-
ная счетная машина Академии наук СССР); позже появились у нас
меньшие машины типа «Стрела», «Урал» и др.
Первоначальные сведения о современных электронных вычисли-
тельных машинах можно найти, например, в последнем издании «Зани-
мательной алгебры» Я- И. Перельмана, М., 1959. Более серьез-
ной является книжка Н. А. А р х а н г е л ь с к о г о и Б. И. Зай-
цева «Автоматические цифровые машины», М., 1958 (серия «Популяр-
ные лекции по математике», вып. 28).
23
Например, я ставлю задачу: сложить все нечетные числа
от 1001 до 1999. Здесь имеется 250 пар чисел, сумма которых
равна 3000, поэтому искомый результат будет равен 750 000.
Этот прием всегда приводит к цели, если числа образуют
так называемый арифметический ряд, т. е. та-
кой ряд, в котором каждое число больше предшествующего
на одну и ту же величину. (Определи, например, сумму
всех четных чисел от 1200 до 1500!)
Вот еще один пример. Одному человеку предложили
определить сумму цифр всех чисел от единицы до миллиар-
да. Он рассуждал таким образом: сумма цифр числа
999 999 999 равна 81. Числа 1 и 999 999 998 в сумме также
дают 81, сумма цифр чисел 2 и 999 999 997 — тоже равна
81 и т. д. Всего мы будем иметь 500 000 000 подобных пар
чисел. Следовательно, сумма цифр чисел от 1 до 999 999 999
плюс сумма цифр числа миллиард равна
500 000 000-81 +1 —40 500 000 001.
До сих пор мы говорили о точном выполнении дей-
ствий с большими числами. Однако в практической жизни
гораздо чаще встречаются вычисления приближен-
н ы е. Обыкновенно довольствуются приближенным ре-
зультатом, имеющим верными лишь первые три, четыре
или пять цифр. Иногда при приближенных вычисле-
ниях ограничиваются нахождением только первой верной
цифры числа или лишь определяют место, занимаемое этой
цифрой,— в таких случаях говорят об определении п о-
рядка величины. Приведу пример: представь себе, что
Земля по экватору опоясана веревкой. Если эту веревку
туго натянуть, то останется свободный конец в 10 м; те-
перь ослабим веревку настолько, чтобы концы ее сошлись.
Спрашивается: сможет ли между Землей и слабо натянутой
веревкой пролезть муха? Исходя из здравого смысла, ты бу-
дешь, конечно, решительно отрицать это,— ведь по сравне-
нию с длиной экватора (составляющей, как мы уже отме-
чали на стр. 15, 40000000 м), излишек в Ю.и будет столь
незначительным, что им, по-видимому, свободнр можно
пренебречь.
Исследуем внимательнее этот вопрос. Пусть расстояние
между экватором и слабо натянутой веревкой будет- х.
Длина окружности экватора равна 2п-/?, где R — радиус
Земли,ап — уже знакомое нам число, выражающее отно-
24
шение длины окружности к диаметру; оно равно прибли-
зительно 3,14. Радиус большего круга, образованного ве-
ревкой, равен -|- х, следовательно, длина его окружно-
сти равна 2п-(Р + х). Отсюда следует, что разность между
длинами этих окружностей равна 2тг•(/?-{-х)—2тг-7?,
то есть 2тг-х. С другой стороны, эта разность и состав-
ляет наши 10 м. Так как 2п лишь немногим более 6, отсюда
получаем, что х приблизительно равно 1,5 м. Видишь,
как обманула тебя способность представлять себе порядок
чисел.
Дадим эту задачу и в несколько иной форме; теперь ты,
конечно, легче с ней справишься. Человек идет по экватору
вокруг Земли (практически это, конечно, также невыпол-
нимо, как и задача — обтянуть земной шар веревкой).
Насколько путь, пройденный головой человека, больше
пути, пройденного его ногами? По существу, эта задача
совпадает с предыдущей, с той лишь разницей, что
искомая в первой задаче величина х здесь дана, а задан-
ная там величина 10 м здесь является искомой. Ясно,
что голова человека не может описать путь, на несколько
тысяч метров больший, чем пройденное его ногами рас-
стояние.
В предыдущих примерах мы все же вычисляли, хотя и
приближенно. Рассмотрим теперь пример, в котором при-
дется не вычислять, а соображать. Рассказывают, что ког-
да философ Кант был еще мальчиком, то однажды, вовремя
прогулки по лесу, ему был задан вопрос — найдутся ли
в этом большом лесу два дерева с одинаковым числом ли-
стьев? Аналогично можно спросить, существуют ли на све-
те два человека, имеющие одинаковое число волос на го-
лове? Чтобы ответить на эти вопросы, вовсе не нужно счи-
тать листья на каждом дереве или волосы на голове у каж-
дого человека. Достаточно знать наибольшее число листьев
на дереве или наибольшее число волос на голове человека;
при этом и в том, и в другом случае нам достаточно знать
лишь порядок величины этих чисел. Так как число волрс
на голове человека не превосходит 200 000, то можно быть
уверенным, что из 200 001 человека по меньшей мере двое
имеют одинаковое число волос. Уже этого приблизитель-
ного подсчета достаточно, чтобы ответить на поставленный
вопрос. Попытайся теперь сам ответить на вопрос, относя-
щийся к деревьям. Конечно, для этого ты должен знать при-
мерное число листьев на деревьях и деревьев в большом лесу.
25
5. НАИБОЛЬШЕЕ ЧИСЛО, КОТОРОЕ МОЖНО
ЗАПИСАТЬ ТРЕМЯ ЦИФРАМИ
Ты, вероятно, слышал рассказ о том, как изобретатель
шахматной игры потребовал себе в награду столько пше-
ничных зерен, сколько их получится, если на первую клет-
ку шахматной доски положить 1 зерно, на вторую клетку—
2 зерна, на третью — 4, на четвертую — 8 и т. д., т. е. на
каждую клетку доски класть зерен вдвое больше, чем на
предыдущую. Это число кажется довольно скромным,
и король, к которому была обращена просьба, не подозре-
вал, о каком громадном количестве пшеницы идет речь. На
последней клетке должно лежать число зерен, равное произ-
ведению 63 множителей, каждый из которых равен 2.
Однако записывать это число таким образом очень скучно;
вместо этого пишут сокращенно 263 (что читается: 2 в 63-й
степени). Сомножитель — в данном случае 2 — называют
основанием степени, а число сомножителей — здесь 63 —
показателем степени. Все выражение 2вз называется степе-
нью. Таким способом можно довольно легко записывать
весьма большие числа. Для примера я привожу здесь таб-
лицу, содержащую первые сорок степеней числа 2. Хотя
таблица и не доведена до 63-й степени, ты теперь легко смо-
жешь ответить на вопрос о том, сколько зерен должно бы-
ло лежать на последней клетке; для этого достаточно соро-
ковую степень двух (1 099 511 627 776) умножить на двад-
цать третью (8 388 608). К какому огромному количеству
пшеницы мы при этом придем, ты увидишь, если подсчи-
таешь, сколько примерно пшеничных зерен помещается
в одном мешке, в железнодорожном вагоне и т. д.
Возьмем достаточно большой лист бумаги толщиной,
скажем, в */,*мм. Сложим его пополам, затем снова попо-
лам, затем еще раз пополам и т. д.— всего сорок раз. Какой
толщины будет теперь слой бумаги? Как видно из таблицы,
его толщина составит 109 951 162 777,6 мм, т. е. более
100 000 км.
Степени числа 2 до 2400 включительно вычислил Моль-
терер 4). Приведу здесь число 2‘00; оно лучше всяких слов
убедит тебя, с какими числовыми великанами приходится
иметь дело, когда возводишь в степень число, кажущееся
*) I. Molterer, Tabellen zur Zahlentheorie, Weis, Welsermflhi,
1937.
26
Таблица степеней числа 2
Показатель Степень Показатель Степень
1 2 21 2 097 152
2 4 22 4 194 304
3 8 23 8388608
4 16 24 16 777 216
5 32 25 33 554 432
6 64 26 67 108 864
7 128 27 134 217 728
8 256 28 268435 456
9 512 29 536870912
10 1 024 30 1 073 741 824
И 2 048 31 2 147 483 648
12 4 096 32 4 294 967 296
13 8192 33 8 589 934 592
14 16384 34 17 179 869 184
15 32 768 35 34 359 738 368
16 65536 36 68 719 476 736
17 131 072 37 137 438 953 472
18 262 144 38 274 877 906 944
19 524288 39 549 755 813 888
20 1048576 40 1 099 511 627 776
вполне безобидным. Представь себе занимающее здесь не-
сколько строчек число написанным в одну строку:
2 582 249 878 086 908 589 655 919 172 003 011 874 329 705
792 829 223 512 830 659 356 540 647 622 016 841 194 629
645 353 280 137 831 435 903 171 972 747 493 376.
Быстрое возрастание степени с увеличением показателя
было Использовано уже в древности для составления забав-
ных задач. В самом древнем из известных нам математиче-
ских руководств (которое составил Ахмес около 1700 года
до нашей эры *)) находим следующую задачу: 7 человек
имеют по 7 кошек, каждая кошка'съедает по 7 мышей, каж-
дая мышь съедает 7 колосьев ячменя, из каждого колоса
вырастает 7 мер зерна. Сколько всех мер зерна? Ответ
можно написать в форме степени: 75; вычислить это число
нетрудно.
*) Речь идет о так называемом «папирусе Ринда», хранящемся
в Британском музее в Лондоне и являющемся замечательным памятни-
ком египетской математики. [Писец Ахмес (переписавший этот папирус
около 1700 года до нашей эры), по-видимому, не был его составителем;
оригинал, с которого переписывал Ахмес, восходит, надо думать, к еще
большей древности.]
27
Чтобы указать порядок величины, чаще всего исполь-
зуют степени числа 10. Так, например, масса Земли равна
приблизительно 6-Ю2’ г, а масса Солнца — 2-1033 г.
Массу нашей Галактики (Млечного Пути) принимают рав-
ной примерно 1010 масс Солнца. Предполагают, что подоб-
ных галактик имеется около 1012. Повторяю: все эти числа
приближенные. Если принять число протонов (т. е. самых
маленьких материальных частиц) в одном грамме массы
равным 6-Ю23, то общее число протонов во вселенной
составит:
6-10“-2-10”. 1010-1012.
Если вспомнить определение понятия «степень», то мы
поймем, что общее число сомножителей 10 здесь равно
23+33+10+12 = 78, а если вместо 6-2 = 12 написать
еще десятку,— в этом весьма проблематичном приближен-
ном вычислении мы не будем мелочны,— то мы придем
к числу протонов, равному 1079.
Удивительно, что Архимед в своих вычислениях (стр. 12
и след.) пришел к такому же числу песчинок, а именно:
10 000 000 • 1 000 000 0008 = 107 • (109)8=10’ • 1072 = 10”.
Как мы подсчитывали степени в последней строчке, ты, ве-
роятно, сумеешь объяснить сам.
Приведу еще интересную историю, которая покажет,
сколь осторожным нужно быть в своих выводах, а кроме
того, продемонстрирует значение понятия степени в' при-
менении к живым существам. Каждый человек имеет 2 ро-
дителей, 4 прародителей, 8 прапрародителей и т. д. Если
вернуться на 40 поколений назад, т. е. примерно на 1200 лет,
то окажется, что у каждого человека было 240 или, соглас-
но нашей таблице, 1 099 511 627 776 предков. Следователь-
но, не верно, что в то время, т. е. примерно в эпоху Карла
Великого, жило меньше людей, чем сейчас; напротив того,
выходит, что на каждого современного человека приходится
свыше биллиона живших в те времена людей. Значит, тог-
да было в биллион раз больше людей, чем теперь. Так ли это?
Ты, конечно, сразу догадаешься, в чем тут дело.
Можно также заменить предков потомками. Существуют
грибки, бактерии, которые при благоприятных условиях
подрастают так быстро, что уже через два часа делятся на
две части. Каждая из этих частей размножается таким же
28
образом. Следовательно, из одного грибка в течение 24 ча-
сов образуется уже 21а грибка, а через двое суток — 224.
Число грибков растет с колоссальной быстротой. Имея под
рукой приведенную на стр. 27 таблицу, совсем нетрудно
вычислить, сколько потребуется времени для того, чтобы
число бактерий оказалось настолько большим, что, несмот-
ря на их микроскопические размеры, они могли бы по-
крыть равномерным слоем всю Землю.
Растение курослеп трижды в год дает по 15 000 семян;
следовательно, от одного растения могло бы в год произой-
ти более 15 0003 — 3375 миллиардов растений. Сельдь от-
кладывает 30 000 икринок, карп — свыше миллиона, тре-
ска от 4 до 6 миллионов, солитер — около 42 миллионов,
аскарида — приблизительно 64 миллиона. Какие же по
сравнению с ними ленивые существа зайцы!
Даже при медленном размножении какого-либо вида
животных определенная территория могла бы быть в срав-
нительно короткое время буквально наводнена им, если
бы борьба за существование между видами не ставила пре-
дела этому распространению. Если бы это препятствие на
какое-то время исчезло, мы наблюдали бы неслыханное
размножение животных. Ты, конечно, слыхал об опусто-
шениях, которые производят тучи саранчи, затемняющие
при полете солнце, и массы гусениц, сплошным ковром
покрывающие огромные пространства. Гибельное распро-
странение эпидемии также объясняется колоссальным раз-
множением определенных видов бактерий.
Возможно, ты уже встречался с задачей, которая на
первый взгляд не имеет ничего общего с понятием степени:
в какую сумму обратилась бы одна копейка, отданная на
проценты в начале нашей эры? Если бы эта копейка была
внесена в одну из современных сберегательных касс, то на
нее бы не начисляли процентов — они начисляются только
на рубли. Но предположим, что за копейку платят процен-
ты, скажем, 5% в год. Тогда положенная сумма ежегодно
5
возрастала бы на коп., и, значит, за 1950 лет она увели-
5
чится на Удо коп. х 1950 или на 97,50 коп. На большую
сумму вкладчик (или, вернее, его наследники) не может
притязать, если речь идет о так называемых простых про-
центах. Другое дело, когда проценты сложные, т. е. когда
процентные деньги за каждый год присоединяются к основ-
29
ному капиталу; тогда уже на следующий год и на них на-
числяются проценты. Так делают, например, в сберега-
тельных кассах. Ты, наверное, возразишь: «Ну что ж, если
даже и так, то сложные проценты вряд ли дадут намного
больше денег, чем простые». Посмотрим! В конце первого
года мы будем иметь 1 коп. 4- 0,05 коп.= 1,05 коп. Проценты
за второй год составят 1,05 коп. х 0,05, так что к концу вто-
рого года наша копейка превратится в 1,05 коп. 4-1,05 коп. х
х0,05, или 1,05 (14-0,05)коп., или 1,052 коп. Следователь-
но, к началу третьего года наш капитал будет составлять
1,052 коп. К концу же этого года капитал вместе с про-
центными деньгами превратится в 1,053 коп., к концу
четвертого года — в 1,054коп., а к концу 1950 года — в
1,051950 коп.
Теперь ты видишь, что мы здесь имеем дело с задачей
на возведение в степень. При решении таких задач обычно
употребляют логарифмы. Но здесь мы не_ будем пользовать-
ся этим удобным методом, так как в нескольких словах
изложить его сущность невозможно. Поэтому прибегнем
К другому способу, который даст нам возможность прибли-
женно вычислить результат. Нетрудно убедиться, что
1,0514 уже больше 2. Следовательно, отданная на проценты
копейка удваивается Менее, чем за 14 лет. Для определен-
ности предположим, что она удвоится ровно через 14 лет.
Значит, через 28 лет копейка превратится уже в 4 копейки,
через 3 х 14, или 42 года,— в 8 коп. Но частное от деления
1950 на 14 равно 139 (а остаток равен 4). Следовательно,
одна копейка за 1950 лет превратится в более чем в
2139 копеек. Эта сумма неимоверно превосходит ту, в которую
превращается копейка, отданная на простые проценты. Де-
сять миллиардов рублей, т. е. 1 биллион копеек, Состав-
ляют, как видно из таблицы на стр. 27, приблизительно
240 копеек. Наша сумма, однако, в 2" раз больше; точнее,
она выражается числом, состоящим из 47 цифр. Значит,
речь идет о сумме, которая намного превосходит все денеж-
ные запасы земного шара. Попытайся-ка представить эту
сумму в более наглядной форме.
Наши вычисления, конечно, беспочвенны. В нулевом
году не существовало копеек! Не было и сберегательных
касс; кроме того, в более близкое к нам время были инфля-
ции и денежные реформы. Но это не играет для нас роли.
Нам важно было показать, что даже в том случае, когда ос-
нование степени лишь немногим более единицы, степень
30
с возрастанием ее показателя увеличивается до колоссаль-
ных размеров.
После всего сказанного ты вряд ли станешь утверж-
дать, что наибольшее число, которое можно написать тремя
цифрами, есть 999 (как может показаться на первый взгляд).
По всей вероятности, ты теперь ответишь, что число равно
9". Тремя девятками можно записать и число 999, но ты,
конечно, понимаешь, что 9" гораздо больше, чем 999.
Однако и этим ответом нельзя удовлетвориться. Число
99 безусловно больше 99 и может быть точно вычислено;
это число равно 387 420 489. Отсюда ясно, что если возвы-
сить 9 в 99-ю степень, то получится число, написанное также
тремя цифрами, но значительно большее 9". Это число при-
нято записывать так: 99’. Точнее была бы запись 9(9’’,
чтобы не смешивать его с числом (99)9. Последнее означает
произведение 9 множителей, каждый из которых в свою
очередь состоит из 9 множителей, равных девяти. Следо-
вательно, это число есть произведение, содержащее толь-
ко 9x9 или 81 множитель, каждый из которых равен 9.
Но такое число, конечно, меньше даже, чем 9"; оно содер-
жит «только» 78 цифр.
Я приведу здесь еще некоторые сведения о числе 99’ *).
Это число имеет 369 693 100 цифр, т. е. около одной трети
миллиарда цифр; начинается оно следующими цифрами:
428 124 773 175 747 048 036 987 115 930 563 521 339 055
482 241 443 514 174 753; последние его цифры 24 178 799
359 681 422 627 177 289. Какие цифры стоят в промежутке
между выписанными — неизвестно. Если бы это число напе-
чатать более или менее четко на полоске бумаги, то эта по-
лоска оказалась бы длиной 1200—1800 км. Если же напе-
чатать это число в книге так, чтобы на каждой странице
имелось 14000 цифр, то из такой книги можно было бы со-
ставить 33 тома по 800 страниц в каждом.
В одной изданной в 1874 году книге под названием «Бы-
тие бога» (автор книги — Крёниг) рассматривается ряд
чисел: 21 2, Зз3,4*41.0 последнем из этих чисел автор говорит:
«Представьте себе отрезок такой длины, что световому лу-
чу понадобился бы квинтиллион лет, чтобы пройти этот путь.
1)Сами результаты и объяснение, как они были получены приве-
дены в статье X. Вейсс (Chr. Weiss), «Ни», Tallet 9(99)og Endecifrene i
Potenser of 9, Matematisk Tidsskrift, cep. A, 1941 г., стр. 63 и след.
31
Затем представьте себе шар с диаметром, равным этому
отрезку, наполненный типографской краской. Всей этой
краски не хватило бы, чтобы четко напечатать это число
даже самыми мелкими цифрами, какие только существуют».
X. Маурер исследовал эти числа с точки зрения теории
чисел. Обозначив для простоты число Xх* через Зх и введя
затем общее обозначение nx=x{n"ix} (где х и п — целые по-
ложительные числа), он показал, как можно найти послед-
ние цифры этих числовых великанов^ Так, например, 29
(т. е. 9е) оканчивается на 89, 39 — на 289, 49 — на 5289, 59 —
на 45 289 и т. д., наконец, 109 — на 9 392 745 289. Таким
образом, последние п цифр числа "9 повторяются во всех
последующих числах "+19, п+29, ..., и т. д. Аналогичными
свойствами обладает и любой другой ряд Ъс=х, 2х, Зх..
и т. д., где х— целое.
После этого короткого путешествия в мир гигантов пх
вернемся к нашему исходному пункту — к степеням числа 2.
Изобретатель'шахматной игры просил у царя не столько зе-
рен, сколько их будет лежать на последней клетке шахматной
доски, а все зерна, лежащие на всех 64 клетках. Следова-
тельно, для определения числа зерен нельзя довольство-
ваться только лишь вычислением 2е3; необходимо найти
все степени числа 2, до 2вз включительно, и подсчитать сум-
му этих чисел. Это очень длительная работа. Посмотрим,
не может ли нам здесь помочь какой-либо удачный прием,
вроде того, который применил маленький Гаусс, когда он
имел дело с арифметическим рядом чисел? Оказывается, мо-
жет. Нетрудно подметить, что 1 -|-2=22—1, 1 -|-2-|-4=23—1,
1Н-2 + 4-|-8=24—1. Исходя из этого, мы полагаем, что
1+2+:4+...+2”=26‘—1.
Для доказательства допустим, что наше предположение
выполняется для суммы степеней двойки, кончающейся
2"-1, т. е. что
l+2+3+...+2n"1=2rt —1.
В таком случае оно будет справедливо и для суммы, следую-
щей за этой суммой степеней. Действительно, для того чтобы
образовать такую сумму, надо к левой части последнего ра-
венства только прибавить 2"; тогда справа получим(2"—1) -|-
-|-2" , т. е. 2-2"—1 или 2”+*—1.Этим наше предполо-
жение доказано для любого значения м; так как оно вер-
32
йо при п=4, то отсюда следует справедливость его и при
п=5, а поэтому и при п=6 и т. д., какое бы значение п
мы ни взяли. Такой метод доказательства математики назы-
вают методом полной (или математиче-
ской) индукции*).
6. О ЧИСЛАХ ПРОСТЫХ И СОВЕРШЕННЫХ
Одни числа, как, например, 6=2-3 или 18=2-32,
можно разложить на множйтели, другие, как 5 или 11,
не разлагаются (при этом мы, конечно, не принимаем во
внимание, что всякое число может быть представлено в виде
произведения 1 на самого себя). Такие числа, как 2, 3, 5, 7,
11, 13 и т. д., которые нельзя разложить на множители, на-
зывают простыми числами, остальные — составными.
Выписывая одно за другим все простые числа, мы заме-
тим, что в ряду натуральных чисел они встречаются все реже
и реже; другими словами, в промежутке от 1 до 100 про-
стых чисел больше,чем в промежутке от 101 до 200, и т. д.
Приведенная ниже (стр. 37) таблица подтверждает это.
Естественно возникает вопрос: существует ли граница, да-
лее которой простые числа более не встречаются, т. е. су-
ществует ли последнее, самое большое простое число? Еще
греческий математик Евклид доказал, что последнего про-
стого числа нет. Действительно, предположим, что самое
последнее простое число существует, и обозначим его че-
рез р. Образуем произведение Рр всех простых чисел 2, 3,
5 и т. д. до р включительно. Так как р, по-видимому, уже
довольно большое число, то тем более это относится к чи-
слу Рр, однако нам, к счастью, нет необходимости подсчи-
тывать его. Прибавим теперь к полученному произведению
Рр еще 1. Мы утверждаем, что число не делится ни
на одно из существующих простых чисел от 2 до р включи-
тельно. В самом деле, легко убедиться, что при делении
числа Рр+1 на каждое из этих простых чисел получится
остаток 1. Если, например, разделить это число на 2, то,
так как произведение Рр всех простых чисел нацело де-
лится на 2, а прибавленная к этому произведению единица
не делится на 2, то в остатке получится 1. Тот же результат
получается и при делении Р^-|-1 на 3, на 5 и т. д., наконец,
*) Про этот метод можно прочитать в книжке: И. С. С о м и н с к и <1,
Метод математической индукции, М., 1959 (серия «Популярныелекции
по математике», вып. 3),
3 в. Литцман
83
на р. Итак, нам приходится признать, что это вновь обра-
зованное число либо само является простым (и, конечно,
большим, чем р), либо разлагается на множители, каждый
из которых является простым числом, большим, чем р.
И в том, и в другом случае мы приходим к простым числам,
превосходящим р. Таким образом, наше предположение
о том, что р есть наибольшее простое число, оказывается
ложным: наибольшего простого числа вообще не сущест-
вует, т. е. число простых чисел «бесконечно велико».
Не все вопросы, возникающие в связи с простыми чис-
лами, разрешаются так легко. Напротив, существует немало
вопросов, ответ на которые до сих пор еще не получен. Нам
известны пары простых чисел, отличающиеся друг от друга
на 2: 11 и 13, 17 и 19, 29 и 31 и т. д. Английский математик
Глэшер (Glaisher) непосредственным подсчетом установил,
что между 1 и 100 000 имеется 1125 таких пар; между
1 000 000 и 1 100 000 — только 725, а между 8 000 000 и
8 100 000 — всего лишь 518. Словом, таких пар становится
все меньше и меньше *). Перестают ли когда-либо они встре-
чаться вовсе, другими словами, есть ли последняя, наиболь-
шая из таких пар, или число их бесконечно? Ответ на этот
вопрос до сих пор неизвестен.
Один из читавших эти строки в предыдущем издании
книги написал мне, что, по его мнению, ответить на послед-
ний вопрос очень легко. Все сказанное выше о числе
можно с небольшими изменениями перенести и на
число Рр—1. Таким образом, оба эти числа не делятся
на меньшие простые числа 2, 3, 5 и т. д. до р, т. е. являются
простыми. Вот мы и получили пару простых чисел искомого
вида! А так как ряд простых чисел р бесконечен, то беско-
нечен и ряд таких чисел, как Р -j-1 и Р—1; поэтому и
число таких пар простых чисел бесконечно велико. Чита-
тель сможет самостоятельно обнаружить ошибку в этом
рассуждении.
Пары простых чисел, отличающихся на 2, называют
близнецами. Определение близнецов можно еще обоб-
щить; при этом мы придем к числам, о которых известно
еще меньше, чем о близнецах. Назовем 2q-4 и с л а м и
такие два простых числа, разность между которыми равна
2g; если q= 1, мы приходим к случаю близнецов. Неизвест-
9 Таблицу пар близнецов, не превосходящих 300 000, опубликовал
Тице (Н. Tietze) в Sitzungsberichten der Bayerischen Akademie der Wis-
senschaften, Math.-naturw. Klasse, 1947, стр. 57 и далее.
34
но, для каждого ли q имеется хотя бы одна такая пара;
неизвестно также, будет ли количество 2<?-чисел бесконеч-
ным хоть при каком-нибудь q.
Можно ли найти два последовательных простых числа,
промежуток между которыми превосходит любое число,
например 100, 1000 и т. д.? Чтобы убедиться в этом, обра-
зуем, скажем, произведение простых чисел.
Р101=2-3-5-7-. . . -101.
Тогда из 100 следующих друг за другом чисел Р1014-2,
Р1014-3, Р101+4,..., Р101 -[-101 ни одно не является простым.
Если заменить в этом рассуждении первое превосходя-
щее 100 простое число 101 числом 1009 — первым простым
числом, большим 1000,— то мы придем к ряду из 1000
чисел
Р.00.+ 2, Р.,0,+3,..., Лоо.+ 1001
(где Р1009 = 2 - 3 - 5 - 7-...• 1009), каждое из которых на-
верное можно разложить на множители. Читателю, конеч-
но, понятно, что так же можно доказать существование
в ряду простых чисел промежутков любой длины.
Раньше полагали, что для того, чтобы раскрыть тайны
простых чисел, надо отыскать их как можно больше. Так
появились таблицы, содержащие все известные простые
числа, а также разложения больших чисел на простые мно-
жители. Естественно, что при составлении подобных таб-
лиц стремились сделать их не слишком объемистыми, по-
этому в них не включали числа, которые имеют легко рас-
познаваемые делители, вроде 2, 3, 5 и т. д. Кроме того,
в этих таблицах выписывались только наименьшие дели-
тели больших составных чисел. Разделив составное число
на этот наименьший делитель, мы получим новое число,
отыскав которое в таблице, мы можем удостовериться,
является ли оно простым или разлагается на множители
дальше *).
Уже к началу XIX столетия существовали такие табли-
цы, простирающиеся до 3 000 000 (таблицы Буркхарта).
*) Подобные таблицы, позволяющие разложить на простые мно-
жители любое число, не превосходящее 108 000, приложены, например,
к старой книге: Д. Г р а в е, Элементарный курс теории чисел, Киев,
1913; предполагается, что они будут воспроизведены в новой книге;
А. А. Б у х ш т а б, Курс теории чисел, подготовляемой к печати Уч-
педгизом.
35
По инициативе Гаусса гамбургский вычислитель Захария
Дазе составил таблицы для чисел от 6 000 000 до 8 000 000;
впоследствии они были доведены Розенбергом до 9 000 000
и опубликованы им. Уже упоминавшийся выше англичанин
Глэшер заполнил промежуток Между 3 000 000 и 6 000 000.
В 1909 году появилась таблица, доходящая до 10 миллио-
нов; в 1914 году вышла продолженная еще немного далее
таблица простых чисел Лемера, в которой, в частности, бы-
ли исправлены ошибки всех ранее опубликованных таб-
лиц. В архивах Венской Академии наук хранится рукопись
Кулика, 4212 страниц которой составляют 8 томов; содер-
жащаяся в рукописи таблица простых чисел и разложений
на множители доведена до 100 000 000 (впрочем, второй том
этого сочинения, кажется, утерян). Правда, Лемер, кото-
рый сличил результаты Кулика, относящиеся к 10-му мил-
лиону, со своей таблицей, нашел здесь у Кулика 226 ошибок;
он считал поэтому, что работа Кулика может иметь значе-
ние для дальнейших вычислений лишь как первый опыт.
А
Э ••••
• •
7 ....
5 • • • •
• •
3
Zj*
/ 3 5 7 9 11 13 15 17 19 31 33 п
Рис. 6.
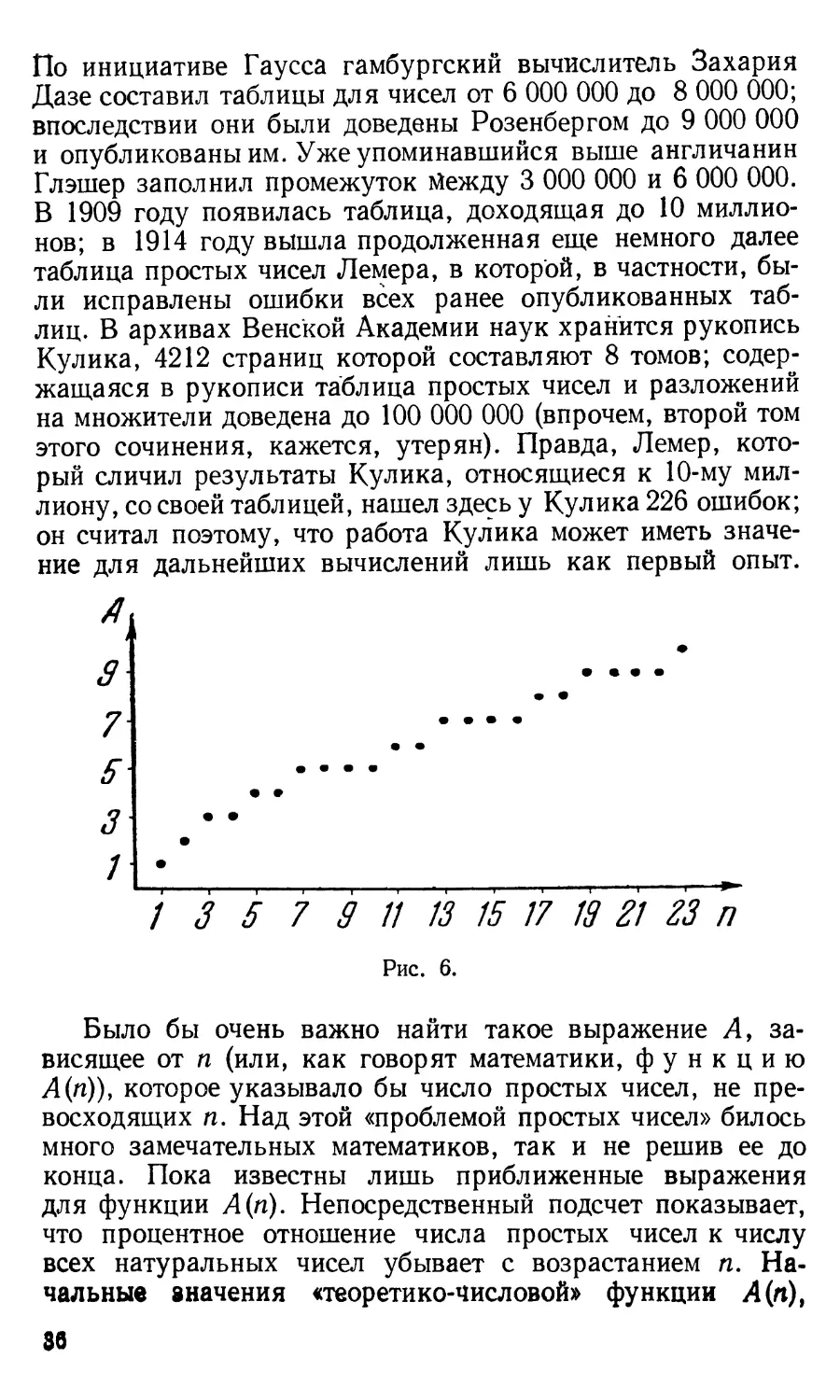
Было бы очень важно найти такое выражение А, за-
висящее от п (или, как говорят математики, функцию
А(п)), которое указывало бы число простых чисел, не пре-
восходящих п. Над этой «проблемой простых чисел» билось
много замечательных математиков, так и не решив ее до
конца. Пока известны лишь приближенные выражения
для функции А(п). Непосредственный подсчет показывает,
что процентное отношение числа простых чисел к числу
всех натуральных чисел убывает с возрастанием п. На-
чальные аначения «теоретико-числовой» функции Л (л),
Зв
имеющей смысл лишь для целых значений п, показаны на
рис. 6. Убывание отношения числа простых чисел к числу
всех целых можно, согласно Лешмайеру, непосредственно
усмотреть из следующей таблицы, левый столбец которой
растет гораздо быстрее правого. При этом в таблице, как
и на рис. 6, 1 принимается за простое число.
А (п)
10
100
1 000
10 000
100 000
1 000 000
10000 000
100 000 000
1 000 000000
5
26
169
1 230
9593
78 499
664 580
5 761 456
50 847 479
В некоторых случаях приходится иметь дело с числа-
ми, которые далеко превосходят пределы упомянутых выше
таблиц и о которых важно знать, являются ли они про-
стыми или составными. В геометрии большую роль играют
числа вида 22” -|-1. Если п здесь равно нулю, то мы получим
3 (ибо считают,что 2°= 1); если вместо п подставить 1, то
получим 5; при п—2 имеем 17; при п=3— уже 257, а при
п=4 — даже 65 537, как следует из таблицы, приведенной
на стр. 27. Гаусс доказал, что правильный многоугольник,
число сторон которого выражается простым числом вида
22 -|-1, может быть построен с помощью циркуля и линей-
ки. Он был первым, кто доказал возможность построения
с помощью циркуля и линейки правильного 17-угольника.
Построением 257-угольника занимался математик Ришело
(1832 год); позднее Майвальдом было указано более простое
построение правильного 514-угольника. Ставший впоследст-
вии директором реальной гимназии Гермес, ученик Ри-
шело, занимался даже задачей построения 65 537-угольни-
ка. Свои рассуждения относительно построения 17-уголь-
ника Гаусс сумел уместить на грифельной доске, которую
подарил своему товарищу по университету Фаркашу Больяи;
тот сохранил ее до старости, как самое дорогое воспомина-
37
ние. Сочинение Ришело занимает уже 80 страниц. Вычис-
ления же Гермеса, над которыми он работалЮ лет, запол-
няют довольно вместительный чемодан, который хранится
в Математическом институте Геттингенского университета.
Впрочем, эти работы не имеют большого значения, посколь-
ку еще Гаусс исследовал вопрос о построении правильных
многоугольников в самом общем виде.. Результаты, к кото-
рым он пришел, таковы: правильный zn-угольник может
быть в том и только втом случае построен цир-
кулем и линейкой, если т представляет собой произведе-
ние числа 2 в любой степени и (различных) простых чисел
Fn вида 22"-)-1. Это заключение справедливо и тогда,
когда число т нечетно, т. е. показатель степени числа
2 равен 0.
Теперь возникает новый, очень интересный вопрос:
все ли числа вида Fn являются простыми или нет? Заме-
чательный французский математик, юрист Ферма, ответил
на этот вопрос утвердительно. Однако Лендри, который
в 1867 году исследовал, как разлагаются на множители все
числа вида 2" -ф1 и 2”—1, где п не превосходит 64 (при этом
он перешел далеко за пределы упомянутых выше таблиц),
показал на примерах, что Ферма ошибся. Так, например,
число F6=232-|-l делится на 641 *). Наибольшее простое
число, найденное Лендри, есть
2’1 — 1 =2 305 843 009 213 693 951.
Заметим, между прочим, что самым трудным числом, с ко-
торым Лендри пришлось иметь дело было 268 4-1. Это число
содержало множитель 57 646 075 230 342 349, который нуж-
но было исследовать дальше. Вначале Лендри предполагал,
что это число — простое, но затем выяснилось, что оно
является ироизведением двух девятизначных чисел. Этот
пример дает нам некоторое представление о том, с какими
трудностями приходится сталкиваться при разложении
больших чисел на простые множители * х).
*) Впервые это показал еще в 1732 году знаменитый математик Лео-
нард Эйлер, швейцарец по национальности, большую часть своей жи-
зни живший и работавший в Петербурге.
х) К. Френцель (Franzel) обратил мое внимание на следующие
формулы:
2’+1=(Р-[-2г).(21+Зг),
2ч>4-1=(.Зг-|-4!).(4г+5!)
38
Вернемся, однако, обратно к числам вида 22"+1. После
того как предположение Ферма было опровергнуто, воз-
ник вопрос: имеется ли в ряду таких чисел бесконечное
множество простых или их число конечно? Если верно пос-
леднее предположение, то какое же из простых чисел, вы-
ражаемых формулой 2%п 4-1, является наибольшим? Отве-
ты на эти вопросы не получены до сих пор. Прихо-
дится довольствоваться исследованием каждого числа
в отдельности.
При п = 5 получается, как уже было сказано выше, сос-
тавное число:
4 294967297=641-6700417.
Число, получающееся при п = 6, также является составным;
его наименьший делитель равен 274 177:
F,=274 177-67 280421 310721,
где второй сомножитель также является простым числом.
F, и Fg— тоже не простые числа; F, содержит множитель
37-216-|-1, Fn—не простое число, FiS содержит множите-
ли 7- 2144-1 > 397-21в4-1 и 7-139-216-|-1. FIg имеет множи-
тель 13-2204-1, F23 делится на 5-2254-1, F,g—на 5- 249-|-1,
Fss—на 3-241-[-1, F75—на 5-275-|-1. Это, вероятно, наи-
большее число, которое когда-либо разлагали на множи-
тели. Если его, как заметил Кармихаэль, напечатать
в ряде томов по 400 страниц в каждом, то общее число
томов оказалось бы столь большим, что на каждого жи-
теля земного шара пришлось по библиотеке в 2 мил-
лиона томов. Само собой разумеется, что этот число-
вой великан, да и его довольно большие делители были опре-
делены не обычным путем — возведением двойки в нужную
и вообще
[(2й — 1)!4-22И]. [22'’+(2и4-1)!]=
=(22" — 2”+*4-14- 2гп) • (22"4-2гп4-2п+'4-1)==
=(22И+Х — 2л+14-1).(22"+14-2"+,4-1)=
-=(2г'>+1-|_ 1)2 22”+2=
= 24П + 2_|_22« + 2_|_1 22п + 2=
=24«+2+1.
Пользуясь этим, Лендри мог бы разложить число 2584-.1 на множители
совсем легко.
39
степень 273 и последующим делением числа F7S=22’3-|-1
на последовательные простые числа, начиная с 2 *).
Одно исполинское число исследовал несколько лет тому
назад с помощью непосредственных вычислений ученик
одной из берлинских гимназий. На основании чисто теоре-
тических рассуждений можно доказать, что число 2364—1
делится на 10932 (это обстоятельство, находится в тесной
связи с одной весьма важной проблемой теории чисел). Упо-
мянутый ученик произвел все вычисления до конца — речь
здесь шла о делении 110-значного числа, причем в частном
получалось 104-значное число,— и убедился, что этот ре-
зультат действительно имеет место. Если бы этот ученик
воспользовался таблицей Мольтерера, о которой говорится
на стр. 26, он мог бы ограничиться в своих вычислениях
лишь этим сложным делением.
Число 6 обладает замечательным свойством: сумма всех
его делителей равна самому числу. Действительно,
6= 1+2+3.
Говоря здесь о всех делителях какого-либо числа, мы
включаем в их число и 1, но исключаем само число, иначе
указанное свойство никак не могло бы иметь места. Ближай-
шее к 6 число, обладающее тем же свойством, есть 28:
28=1+2+4+7+14.
Подобные числа называют совершенными числами.
В древности были известны еще два совершенных числа,
следующих за 28,— 496 и 8128. (Проверь, так ли это!).
Следующее совершенное число 33 550 336 впервые было вы-
числено в одной мюнхенской рукописи, относящейся к
1461 году. Затем, в XVI столетии были найдены три даль-
нейших совершенных числа: 8 589 869 056, 137, 438 691 328
и 2 305 843 008 139 952 128. Лишь в конце XIX столетия два
*) Все указанные здесь результаты были получены довольно дав-
но — еще в то время, когда отсутствовали столь совершенные средства
вычислений, как современные электронные счетные машины. В 1956 году
американский математик Сельфридж (J. L. Selfridge) применил для
решения вопроса о природе чисел FN электронную вычислительную ма-
шину Калифорнийского университета СВАК. С помощью этой машины
он обнаружил, что числа Fs„ Fss, Fe„ Fu7, FiM, Fw, F150, F20„ F226,
Fiia, F2e8. FS84, И Ftst— составные. Таким образом наибольшим из
известных на сегодняшний день составных чисел такого вида является
число F452= 22 +1, которое состоит не менее чем из 1015S цифр. Один
из его делителей равен 27-2И5+1 и состоит из 139 цифр.
40
математика (Зеельгоф и Первушин) присоединили к най-
денным ранее девятое совершенное число. Вот этот число-
вой великан:
2658455991 569831 744654 692615953842 176.
Совершенные числа, как доказал еще Евклид (около 300
лет до нашей эры), получаются от перемножения чисел
2"-1и 2”—1, если только 2"—1 —п ростов. Да-
вайте убедимся в этом. Прежде всего, следует установить,
какие делители имеет число jV=2”_’(2" — 1). Простое
число 2" —1 для сокращения обозначим через р. Тогда
мы имеем две группы делителей:
1, 2, 22,..., 2"-* (1)
и
р, 2р, 22р..2п~гр (2)
(напоминаем, что число2”"’р мы условились не учитывать!);
все эти делители следует сложить. Но согласно формуле,
выведенной на стр. 32,
l+2+22+...+2n-1=2n —1
и
р+2р+2гр+... +2”-2р=р(1+2+22+...+2"-2)=
=р(2”-1 —1).
Отсюда видно, что сумма двух рядов делителей дает:
2"— 1 +р (2"-1 — 1)=2” — 1 + (2п — 1) (2П-1 — 1)=
=2Ч-*(2П —1)=А^,
что и доказывает утверждение Евклида.
Теперь все зависит от того, какие из чисел вида 2"—1,
т. е. так называемых чисел Мерсенна*), являются
простыми. При исследовании этого вопроса можно ограни-
читься теми случаями, когда п — число простое. Ведь
если п, к примеру, равно произведению p-q, где р — простое
число, a q — множитель, больший единицы, то 2Р ч— 1 =
=(2/’)9—I9 делится на 2Р —1 и, значит, не является прос-
тым числом. С другой стороны, одного требования о том,
чтобы п было простым числом, оказывается недостаточно.
Так, например, 211—1=23-89. Лукас составил список чи-
*) Мерсенн (Mersenne) — французский математик XVII века,
занимавшийся вопросом о совершенных числах,
41
сел Мерсенна 2Р—1 (где р — простое), простирающийся
от р = 11 до р=251, и указал для каждого из этих чисел его
наименьшие делители d. Следующая таблица воспроизво-
дит этот список:
р= d= 11 23 23 47 29 233 37 223 41 13 367 43 431 47 2351 53 6361
Р= 59 73 79 83 97 113 131 151
d= 179951 439 2 687 167 11 447 3391 263 18121
р= 179 191 211 223 233 239 251
d= 359 383 15193 18287 1 399 479 503
Не вошедшие в эту таблицу простые числа р, большие 11,
приведены во второй таблице, где буква «с» под простым чис-
лом означает, что число Мерсенна 2Р—1 является составным,
буква «п» — что оно является простым, а буква «н»—что ре-
зультат неизвестен:
р= 13 17 19 31 61 67 71 89 ЮГ 103
п пппнссп с с
р=107 109 127 137 139 149 157 163 173 181
п спннннссс
р==193 197 199 227 229 241 257
Н С Н Н Н Н II
Самым большим простым числом вида 2Р—1, фигурирующим
в этой таблице, является число 2127—1. (Хочу еще раз под-
черкнуть, что общее число простых чисел бесконечно ве-
лико.) Поэтому совершенные числа получаются по нашей
формуле при
р=1, 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 и 127.
Укажу здесь еще одну любопытную деталь. Долгое вре-
мя предполагали, что число 267—1—простое. Однако ока-
залось, что
2е7 — 1 = 193 707 721 -761 838 257 287,
где оба множителя, стоящие справа,— простые числа. При
р=71 число вида 2Р—1 имеет множитель 228 479, при р=
= 163 — множитель 150287, при р= 173—множитель 730 753,
при р = 181 —множитель 43 441, при р=197— множитель
7487. Известны также множители чисел 2Р—1, где р=317,
337 и даже 5011.
42
Так как 289—1, 2107—1 и 2127—1 — простые числа, то мы
можем получить три следующих совершенных числа. Вот
эти числа, которые вычислил Мольтерер *):
191 651942 608 236 107 294 793 378 084 303 638 130 997 331 548
169216,
131 164 036 458 569 648 337 239 753 460 458 722 910 223 472 318
386943117 783 728128
и
14 474 011 154 664 524 427 946 373 126 085 988 481 573 677 491
474 853 889 066 354 349 131 199 152 128.
Все перечисленные совершенные числа — четные; они
оканчиваются либо на 6, либо на 28. Конечно ли или беско-
нечно число таких совершенных чисел — неизвестно. Эй-
лер доказал, что не существует иных законов образования
четных совершенных чисел, кроме того, который был ука-
зан Евклидом.
Любое четное совершенное число, за исключением 6,
можно, как доказал Хэт (R. V. Heath), представить в виде
п-1
суммы 2 * 2 полных кубов (причем кубов нечетных чисел);
так, например,
28—1’4-3’, 496= 1’4-3’ +5’4-7*,
8128 = 1’4-3’4-5’4-7’4-9’4-11’4-13’+15’.
*) Данные Литцмана (и Приведенная на предыдущей странице таб-
личка) относятся к «доэлектронному» периоду развития теории чисел,
когда математики не обладали еще таким мощным средством вычисле-
ний, как современные электронные вычислительные машины (ср. со
сноской на стр. 40). Незадолго до появления немецкого оригинала
этой книги летом 1952 года, американский математик Робинсон с по-
мощью упоминавшейся выше электронной машины СВАК, показал, что
следующими за 2127—1 простыми числами Мерсенна являются числа
2Ш—1 и 2е0’—1; все числа между 2127—1 и 2s21—1 — составные,
Затем с помощью той же машины было обнаружено, что число
2й”—1 является простым; отвечающее этому числу Мерсенна совер-
шенное число записывается 770 цифрами. Следующие простые числа
Мерсенна, найденные с помощью машины СВАК, таковы: 22203—1 и
222*1—1. Наконец, в 1957 года шведский математик Ризель с помощью эле-
ктронной счетной машины BECK (BESK, Стокгольм) установил простоту
числа 2’21’—1. Это число состоит из 969 цифр и является, по-видимому,
самым большим из известных в настоящее время простых чисел; соот-
ветствующее совершенное число 23216(2’217—1) содержит около 2000 цифр.
43
Чтобы доказать это в общем виде, воспользуемся форму-
лами *)
S,= 1’4-2’4-3’+... +fe’=fe2 (|t-1)8,
S2=l2+224-3’+... +fe’= fe(fe+1^(2fe+1)-,
S1=l+2+3+...+^=-^t21.
Отсюда получаем:
S = l’+3’+5’+... +(2k — 1)’= 2 (2r — 1)’=
r=l
k
= 2 (8r‘ — 12r2+6r — 1)=8S, — 12Sj+ 6S. — k.
r=l
Следовательно,
S=2fe2(fe + 1)2 —2fe-(fe+l)(2fe+l)+3fe(fe+l) —
=2^+4fe’-J-2fe2 —4fe’ —6fe2 —2fe+3fe2+3fe -6 =
=2/г4 —Ajs=F(262 —1).
И-1
Если здесь положить &=2 2 , то получим
S=2B-* 1(2n —1).
Но такой вид имеет любое четное совершенное число.
Более сложен вопрос о том, не существуют ли еще и не-
четные совершенные числа. До сих пор не известно ни одного
такого числа; однако у нас нет уверенности в том, что
таких чисел не существует. Этот вопрос исследовал, напри-
мер, Канольд (Н. J. Kanold) т). Во всяком случае, твердо
установлено, что если нечетные совершенные числа и
имеются, то они чрезвычайно велики; ни одно из них не
может быть, например, меньше 10зв.
Противоположностью простым числам, «бедным делите-
лями» (они делятся только на 1 и самого себя), являются
«богатые делителями» числа. Ими часто пользуются как
единицами измерения. Такое применение находят, напри-
*) Их можно доказать, например, с помощью метода математической
индукции (ср. выше, стр. 33).
1) Ср. Bericht uber die Mathematiker — Tagung in Tubingen vom
23. bis 27. September 1946. Laupp, Tiibingen, стр. 84 и след. (Один из
первых результатов в этом направлении принадлежит советскому ма-
тематику И. С. Градштейну, в то время студенту Одесского универси-
тета. См. И. С. Гр ад штейн, О нечетных совершенных числах,
Математический сборник 32, 1925, стр. 476—510. Прим, ред.]
44
мер, 12—дюжина, 144 — гросс; можно вспомнить также
день с его 24 часами, 1440 минутами и 86 400 секундами;
полный угол, содержащий 360 градусов, 21 600 минут,
1 896 000 секунд.
Существует формула, позволяющая определить число
делителей любого числа:
N=pm-qn-r\..
(где р, q, г, ...— простые числа).
Эта формула такова:
ТЛ-=(т+1)(п+1)(о+1)...-1
(здесь, как и выше, 1 влючается в число делителей числа М,
но зато исключается из допустимых значений самого
числа N). Таким образом, мы, например, получаем:
для 12=2’-3 7\s =(2+1)(Ц-1)-1=5;
для 24=2’-3 Т24 =(3+1)(1 + 1)- 1=7;
для 60=22-3-5Т60 =(2+1)(1 + 1)(1 + 1) - 1 = 11;
для 144=2*-32 Т1М=(4+1)(2+1) —1 = 14.
Приведенное выше число 86 400=2’-33-52 имеет 95
делителей, число 1 896 000 = 27-34-53 имеет 159 делите-
лей. Таблицу таких чисел TNсоставил Маурер. Так, напри-
мер, число 21 621 600 имеет 575 делителей. Мерсенн уста-
новил х), что наименьшее число, имеющее миллион дели-
телей, есть
А=(1 267 650600228229 401 496703205376)”-
• (847 288609 443)4.
Это число записывается 2028 цифрами.
Первое из стоящих в скобках чисел имеет 100 делителей.
С увеличением числа одновременно увеличивается и число
его делителей, однако простые числа, встречающиеся сколь
угодно далеко, не позволяют числам TN расти очень
быстро.
7. ЕЩЕ НЕСКОЛЬКО ПРИМЕРОВ
ЧИСЛОВЫХ ВЕЛИКАНОВ
Прежде всего, возьмем какие-либо два предмета, или
понятия, например точку (•) и тире (—). Сколькими спо-
собами можно их расположить в последовательность друг
г) Согласно математическому бюллетеню Буэнос-Айреса в Cogi-
taeta physico-matematica, Париж, 1644. На вопрос в Bolletino di Ма-
tematica (4-я серия, т. II, стр. 28), было ли доказано это утверждение,
до сих пор, насколько мне известно, ответ не получен,
45
за другом? Вы, конечно, сразу ответите, что таких способов
два, а именно: — или —. Возможных расположений трех
предметов будет уже больше. Если взять нож, вилку и
ложку, то их можно расположить в последовательность
шестью различными способами:
нож — вилка — ложка,
вилка — нож — ложка,
ложка — нож — вилка,
нож — ложка — вилка,
вилка — ложка — нож,
ложка — вилка — нож;
других вариантов здесь, очевидно, не существует. Присое-
динив сюда еще и четвертый предмет, например карандаш,
мы в каждом из этих шести расположений трех предметов
сможем поместить карандаш на четырех различных местах:
перед ножом, перед вилкой, перед ложкой и позади всех
трех предметов. Следовательно, каждое из шести располо-
жений приводит к четырем новым, т. е. четыре предмета
можно расположить уже 6-4 различными способами. Число
6, показывающее число возможных расположений трех
предметов, также можно изобразить в виде произведения
двух множителей 2-3; при этом число расположений четы-
рех предметов запишется как 2-3-4. Если к четырем пред-
метам присоединить пятый, то число возможных расположе-
ний выразится уже произведением 2-3-4-5 и т. д. Для
произведения ряда последовательных .целых чисел, начи-
нающихся с 1, введен сокращен-
ный знак ! (читается: факто-
риал). Например, 3!=6, 4! =24,
51 = 120, 61=720, 71=5040 и т.д.
Вы видите, как быстро возрастает
число п! (эн факториал) с рос-
том п.
Существует игра (ее часто
Рис. 7.
называют «игра в пятнадцать»),
которая была изобретена одним американцем в 1878 году
и одно время пользовалась очень большой популярностью.
Для этой игры нужно иметь квадрат, разделенный на 16
равных квадратиков, и 15 пронумерованных шашек, имею-
щих одинаковый размер с маленькими квадратиками. Шаш-
ки расположены произвольным образом, однако так, что
крайняя справа клетка нижнего ряда остается свободной.
Задача состоит в том, чтобы, передвигая шашки по доске,
перевести их из любого другого в «основное» расположение,
изображенное на рис. 7. При этом изменять расположение
46
шашек можно только, передвигая одну из соседних с пус-
тым местом шашку на это пустое место. Сколько в этой игре
может быть разных исходных положений? На этот вопрос
нетрудно ответить, если воспользоваться нашим новым сим-
волом: 15! Это составляет 1 307 674 368 000 различных слу-
чаев, т. е. заметно больше биллиона случаев. Если же еще
отбросить требование, согласно которому свободной долж-
на оставаться именно нижняя клетка справа, то исходных
расположений костей будет 16! Это число в шестнадцать
раз больше выписанного выше и равно 20 922 789.888 000.
Один из читателей этой книжечки предложил исполь-
зовать факториал для получения еще большего числа, ко-
торое можно записать тремя цифрами, чем то, о котором
говорилось в главе 5. Здесь мы можем выбирать между
[99’]! 9!91’’ или даже [9!9|9|]1 Однако это значило бы зайти
слишком далеко в нашей игре с колоссальными числами!
Чтобы продемонстрировать на конкретном примере
быстроту роста числа п! при возрастании и, приведу здесь
значение 100!, вычисленное Мольтерером *):
93 326 215 443944 152 681 699 238 856 266 700 490 715 968 264
381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156
518 286 253 697 920827 223 758 251 185 210916 864 000 000 000
000000000 000000.
Может быть, ты сообразишь, почему у этого числа в кон-
це стоит ровно 24 нуля?
Следующий пример снова приведет нас к уже знакомым
вычислениям. Тебе, наверное, знакома игра в кегли. Девять
кеглей расставляются на площадке так, как показано на
рис. 8. Расставленные как-то на площадке кегли образуют
«фигуру», задача состоит в том, чтобы шарами, которые иг-
рающий катит по направлению к кеглям, сбить все входя-
щие в «фигуру» кегли, не задев при этом остальные. «Фигу-
ры» могут быть разными; так,, например, на рис. 9, пока-
зана «фигура», которая называется «веревочкой» (черные
*) Можно доказать, что для каждого п число п! больше (-у ) ,
\ о 1
f fl\n
т. е. п! растет быстрее, чем -х- ) • При этом такая оценка роста п! ян-
\ J
ляется довольно точной, ибо (по крайней мере при n>6) n!< I-g- 1 .
См., например, Д. О. Шклярский и др., Избранные задачи и
теоремы элементарной математики, ч. 1, М., 1959, задача 148.
47
кружки означают входящие в «фигуру» кегли). Названия
отдельных «фигур», если таковые вообще существуют, ме-
няются. Когда требуется сбить все кегли, то говорят о «де-
вятке»; если же надо оставить кеглю в центре, сбив все
остальные, то мы имеем другую «фигуру», выбить которую
гораздо труднее, чем «девятку». Очевидно, что всего имеется
девять групп «фигур». К первой группе относятся «фигуры»,
содержащие только одну кеглю, ко второй группе — две
кегли и т. д. Ясно, что в первую группу входят девять
различных «фигур»; сколько же их насчитывает вторая
О
О О
ООО
О О
О
О О
О • О
о о
Рис. 8.
Рис. 9.
группа? Возьмем одну кеглю и поставим ее на любое место.
Тогда для второй кегли остается 8 свободных мест, что дает
нам 8 «фигур». А так как для первой кегли можно выбирать
любое из девяти мест, то можно решить, что общее число
«фигур» второй группы равно 8-9. Однако этот вывод слиш-
ком поспешен. Дело в том, что в образованных таким обра-
зом 8-9 «фигурах» каждая повторяется дважды. «Фигуру»,
показанную на рис. 10, можно получить, поставив сперва
правую, а затем левую кеглю; но можно сделать и наоборот:
О
О О
• О •
О О
О
Рис. 10.
поставить сначала левую, а потом правую
кеглю; точно так же дело обстоит в каждом
из 72 случаев. Следовательно, имеется всего
лишь 72 : 2 = 36 различных «фигур», относя-
щихся ко второй группе.
Рассмотрим теперь «фигуры», образован-
ные тремя кеглями. Будем образовывать их
из «фигур», содержащих по две кегли. Рас-
смотрим какую-либо из таких «фигур», при
этом останется 7 свободных мест, и на каждое из них мож-
но поставить третью кеглю. Следовательно, всех «фигур»
третьей группы будет 36-7. Но и здесь нужно проследить,
не встречаются ли среди этих 36-7 «фигур» одинаковые.
И действительно, так оно и есть. Рассмотрим, например,
«веревочку» на рис. 9. Ее можно образовать присоедине-
нием третьей кегли из трех различных «фигур» второй
48
группы. Именно, две первые кегли могли занимать либо
оба передние места, либо оба задние, либо, наконец, одна —
переднее, а другая — заднее. Поэтому полученное выше
число 36*7 нужно еще разделить на 3. Так же придется
рассуждать и дальше, когда мы перейдем от «фигур» тре-
тьей группы к «фигурам» четвертой группы. Снова сначала
мы получим в 6 раз большее число «фигур», так как четвер-
тую кеглю можно поставить на любое из шести свободных
мест. Однако каждая образованная таким образом «фигура»
четвертой группы может получиться из четырех различных
«фигур» третьей группы; поэтому результат нужно разде-
лить на 4. Переходя к «фигурам» пятой группы, следует
умножить число «фигур» четвертой группы на 5, но одновре-
менно и разделить на 5 и т. д. В следующей таблице при-
водятся подсчеты числа различных «фигур»:
Число фигур первой группы 9 =9
» » второй » 1 2 =36
» » третьей » 9-8-7 1-2-3 =84
» » четвертой » 9-8-7 6 1 2-3-4 = 126
» » пятой » Э-8-7-6 5 1-2 3-4-5 = 126
» » шестой » 9-8 7-6-5-4 1-2-3-4 5-6 =84
» » седьмой » 9-8-7-6-5-4-3 1-2-3-4-5-6-7 = 36
987-65 4-3- 2 п
» » восьмой » 1-2-3 4 5 6-7- 8-В 9
В итоге это составит 510 «фигур». Прибавив сюда еще «фи-
гуру», образованную всеми девятью кеглями, и «пустую фи-
гуру» (когда сбиты все кегли), получим 512 «фигур». Это
число равно как раз 29. Случайное ли это совпадение?
Из нашей таблички можно сделать еще некоторые заме-
чательные выводы. Во всяком случае, число «фигур» оказа-
лось намного больше, чем можно было предположить зара-
нее. Если бы в той же игре участвовали 10 кеглей и наши
рассуждения были верны, то число возможных «фигур» бы-
ло бы равно 1024 (т. е. 210 *), при 12 кеглях — 4096 (т. е.
212), и т. д.
Можно было бы привести еще целый ряд подобных за-
дач. Многие из них связаны с различного рода играми, на-
пример, задача об определении возможного числа различных
49
партий в какой-либо карточной игре, хотя бы в игре в «пья-
ницу», К подобного рода задачам относится и задача из
совсем уже другой области, а именно, определение числа ме-
лодий, какие можно образовать из семи звуков октавы.
Во всех этих задачах получаются огромные числа. Особен-
но велики они в последней задаче, где следует еще учесть
возможность использования не одной, а ряда последователь-
ных октав.
Курт Лассвитц много лет тому назад рассказал историю,
которая связана с очень поучительным подсчетом. Приведем
здесь лишь задачу, о которой идет речь в этой истории, и
окончательный результат, опуская вычисления, которые ты
сможешь восстановить самостоятельно. Курт Лассвитц го-
ворил о замечательном книгохранилище — универсальной
библиотеке, в которой имелись бы все книги вообще, не
только написанные, но и те, которым еще только предстоит
быть написанными. В каждой книге должно быть 500 стра-
ниц, на каждой странице 40 строчек, в каждой строчке 50
букв. Понятно, что для того, чтобы напечатать все книгй,
достаточно иметь обычный шрифт с особыми литерами для
знаков препинания: , ; : и т. д., и еще некоторыми другими
специальными литерами, например для цифр или матема-
тических символов. Более ста литер наборщику во всяком
случае не понадобится. Теперь достаточно перепробовать
только все возможные расположения всех этих различных
литер, и тогда наряду со всякого рода чушью и бессмысли-
цей будет напечатано в этих книгах и все разумное *).
Число томов такой «универсальной библиотеки» оказы-
вается равным «только» 10а 000 °00. Представим себе, что эти
книги, каждая толщиной в 2 см, поставлены рядом друг
с другом в этом огромном книгохранилище и что мимо
них скользит луч света со скоростью 300 000 км в секунду.
Сколько «световых лет» понадобится лучу на это путешест-
вие? Лассвитц произвел этот подсчет. Число лет изобра-
жается 1 с 1 999 982 нулями,— его почти также трудно
себе представить, как и количество томов.
*) Разумеется, эта «универсальная библиотека» в силу ограничен-
ного объема томов, никак не может вместить всю совокупность доступ-
ных человеку знаний (этого не сможет достигнуть никакая библиотека,
ибо как бы колоссален ни был ее объем, он все-таки всегда остается ко-
нечным). Так, например, никакая библиотека не сможет исчерпать на-
ших знаний о числе я, разложение которого в десятичную дробь может
быть продолжено неограниченно далеко (ср. ниже, стр. 62
и след.).
50
Вернемся, однако, к математике. В предыдущем разделе
мы говорили о разложимости чисел на множители. Но их
можно разлагать и на слагаемые. Число 4 равно 3+1, или
2+2 или 2+1+1, или 1+1+1+1. Следовательно, это
число можно представить четырьмя различными способами
в виде суммы целых чисел. Обозначим число, которое мы хо-
тим представить в виде суммы нескольких слагаемых, через
п; а число способов, которыми можно представить это число
в виде суммы целых слагаемых (включая сюда и представле-
ние п=п), через р (п)1). Тогда р (1) = 1, р (2)=2, р (3)=3,
р (4)=5, р (5)=7 и т. д. Далее, например, р(22)=1002,
р (33)= 10143, р(46) = 105 558, р(61)=1 121 505 и т. д. Со-
гласно таблице, составленной Мак Магоном, имеем:
р (100) = 190 569 292,
р (200) = 3972 999 029 388.
Для приближенного вычисления р (п) можно воспользова-
ться формулой, которая, правда, передает значение р(п)
не совсем точно, но с очень хорошей степенью точности; для
небольших же п она дает даже истинные значения р (п).
Пользуясь этой формулой, Лемер установил, что прибли-
зительно
р (599)=435 350 207 840 317 348 270 000,
р (721) = 161 061 755750279477 635534762.
А вот еще несколько числовых великанов, которые появ-
ляются в таких задачах, где никакой математик не ожидает
с ними встретиться. Под диофантовыми уравне-
ниями понимаются такие уравнения, в которых число
неизвестных больше общего числа уравнений (уравнение
может быть и только одно); при этом ищутся лишь такие
решения уравнений, которые выражаются целыми чис-
лами. Самым известным примером подобного уравнения
является «уравнение Пифагора»: x2+t/2=z2, имеющее бес-
конечное множество целочисленных решений, например:
х=3, р=4, 2=5 или х=5, z/=12, z=13. Ферма поставил за-
дачу о нахождении решений «уравнений Пифагора», удовлет-
воряющих еще двум дополнительным условиям,— сумма
х+у и число z должны быть квадратами целых чисел; дру-
гими словами, требуется отыскать такие прямоугольные
х) Я следую здесь статье Н. D. Kloosterman, Partities, Euclides 21,
1945/46 г,, стр. 67 и след.
51
треугольники, все стороны которых выражаются целыми
числами, причем гипотенуза и сумма катетов являются
даже квадратами целых чисел *). Наименьшими числами,
удовлетворяющими этому уравнению, будут, как он ука-
зывает,
х=1 061652 293 520,
«/=4 565486 027761,
2=4 687 298610289.
Ближайшее по величине решение,— а решений у этой
задачи бесконечно много,— содержит уже значительно боль-
ше цифр.
Наименьшие целые числа, являющиеся решением до-
вольно безобидного с виду диофантова уравнения х2—109t/=
= 1, суть * * * * * х)
х= 158 070 671 986249 и у= 15140 424 455 100.
Эйлер поставил задачу о решении в целых числах системы
уравнений
х+«/+г=м, xy+xz+zy—v2, ху, z=w3,
т. едиными словами, об отыскании кубических уравнений
х3— ux2+v2x — w3—0
(где и, v, w — целые числа), имеющих целые корни. Наи-
меньшее решение этой системы имеет вид
х= 1633780814400,
«/=252782 198 228,
2=3474 741 085 973.
Архимед составил следующую «задачу о коровах»:
обозначим через Б число белых быков, через Ч — черных,
через П — пестрых и через Р — рыжих; через б число бе-
лых коров, ч— черных, п — пестрых и р— рыжих, и пусть
Б = ~Ч~Р, Ч=^П+Р, П=^Б + Р,
б=^(Ч+ч), ч=^П+п), п=^(Р+р), р=£(Б+б).
*) В этой задаче требуется найти решения системы диофантовых
уравнений: х2+у2=г2, г=Р, x-f-y—u2. Относительно ее решения см.
В. Серпинский, Пифагоровы треугольники, § 12, Учпедгиз,
1959; в этой интересной книге читатель может найти и другие примеры
числовых великанов.
х) Ср. Н. D о г г i е, Quadratische Gleichungen, Oldenbourg, Мйпс-
hen, 1943, стр. 358.
52
Кроме того, пусть Б -\-Ч является квадратом(т. е. Б -\-Ч=п2),
а П -}-Р — так называемым «треугольным числом», т. е.
имеет вид . Если не учитывать этих дополнитель-
ных условий, то нетрудно получить, что (% — произволь-
ный целочисленный множитель)
Б=2-3-7-53-4657-х =10366482%,
V=2-32-89-4657-x =7460514%,
/7=22-5-79-4657-х =7 358 060%,
Р=34-11-4657-х =4 149 387%,
б=2’-3-5-7-23-373-% =7206 360%,
ч=2 -З2 -17 -15991-% =4 893246%,
п=22-3-5-7-11-761-х =3 515 820х,
р=32-13-46489-х =5439213%.
Наименьшее решение, учитывающее дополнительные усло-
вия, приводит к очень большим числам. Так, например, Б
представляется числом, имеющим 206 545 цифр; это число
начинается цифрами 1598..Л).
8. ЧИСЛОВЫЕ КАРЛИКИ
До сих пор мы оставались в пределах ряда натуральных
чисел 1, 2, 3, ..., из которых наименьшее — единица. Если
считать числом также и нуль, то он еще меньше единицы.
Нуль — это самое меньшее число, потому что ведь не мо-
жет же существовать что-то меньщее, чем «ничего»,— так
думают люди, незнакомые с математикой. Математик же го-
ворит этим людям: можно, однако, иметь долги, а термо-
метр может показывать температуру и ниже нуля. Но мы
не будем здесь касаться отрицательных чисел, которые
имеет в виду математик; к ним мы обратимся позже в дру-
гих целях.
К числовым карликам мы сможем прийти лишь тогда,
когда введем в круг нашего рассмотрения, кроме натураль-
ных чисел, еще и дроби. Вопрос о числовых карликах, в сущ-
ности, уже был исчерпан нашим разбором числовых вели-
канов. Ведь если число п — числовой великан, то -—
*) По этому поводу см. A. A m t h о г, Das Problema bovinum
des Archimedes, Zeitschr. f. Math. u. Phys. №25(1880), Hist.-lit Abt.,
стр. 153 и дальше; Euclides, № 20 (1943), стр. 58, H. D о г г i е, Triumph
der Mathematik, 3. Aufl., Breslau, 1940, стр. 1 и дальше.
53
Числовой карлик; так, большому числу 1 000 000 соответ-
ствует «обратное» ему малое число t OOQ . В самом
деле, при неизменном числителе чем больше будет знаме-
натель дроби, тем меньше ее значение и тем больше приб-
лижается она к нулю.
Давайте поищем вокруг нас подобные числовые кар-
лики. В свое время для наглядного изображения больших,
хотя и не чрезмерно больших, чисел мы пользовались вре-
менем и расстоянием. Теперь познакомимся с малыми про-
межутками времени и малыми расстояниями; попытаемся
создать себе о них наглядное представление.
Секунда — достаточно малая единица времени. В кино
отдельные кадры быстро сменяются один другим. Первый
кадр, изображающий определенную картину, проектирует-
ся на экран; затем он сразу заменяется вторым кадром и т. д.
В обычных фильмах в секунду сменяется от 16 до 24 таких
кадров. Почему же, несмотря на это, глядя на экран, мы
видим непрерывно происходящее движение? Причина кроет-
ся в том, что впечатление, которое производит какая-либо
картина на наш глаз, не является мгновенным — оно сохра-
1
няется на определенное время, примерно на секунды.
Доказательством этого может служить тот факт, что при
быстром вращении перед нашими глазами раскаленного
тела, скажем уголька, мы видим не движущуюся точку, а
огненный круг. Если закрепить один конец вязальной спи-
цы, а другой отвести в сторону и затем отпустить, то мы ви-
дим не отдельные положения свободного конца спицы, а од-
ну блестящую полосу.
Эти опыты показывают, что наш глаз не в состоянии раз-
дельно воспринимать явления, длящиеся менее се-
кунды *). Вот еще один поучительный пример. До появле-
ния моментальной фотографии все представляли себе поло-
жение на скачущей лошади неправильно. На всех карти-
нах старых художников ноги лошадей изображены в таком
положении, в каком они в действительности никогда не бы-
вают, а именно: передние ноги вынесены вперед, а задние
отведены назад. Лишь с тех пор, как фотография раскрыла
нам глаза, художники тоже стали правильно видеть. Мно-
*) Существуют животные, глаза которых способны воспринимать
явления, длящиеся значительно менее 0,1 секунды.
54
гие фокусы, в том числе и карточные, основываются исклю-
чительно на быстроте движений. Поэтому понятно, что
при наблюдении явлений, происходящих в малые отрезки
времени, глаз приходится заменять фотографической пла-
стинкой.
Во всех тех случаях, когда мы имеем дело с движением,
измерение времени связано с измерением расстояний. Для
измерения малых величин наименьшую из общеупотре-
бительных единиц длины — 1 мм — делят на 1000 частей
и называют одну такую часть 1 ц (читается: один микрон).
Микрон в свою очередь делится на 1000 тр. (миллимикро-
нов). Миллимикрон, разумеется, уже чрезвычайно малая
единица длины. В миллиметре содержится столько же мил-
лимикронов, сколько в километре содержится миллимет-
ров. Миллиметр составляет миллионную часть километра,
а, значит, миллимикрон составляет такую же долю мил-
лиметра. За метр первоначально была принята одна соро-
камиллионная часть земного меридиана. Теперь же метром
называют расстояние между двумя штрихами на плати-
но-иридиевом стержне (эталоне метра), хранящемся в Меж-
дународном бюро мер и весов в Севре, близ Парижа. Это
расстояние оказалось не совсем точно равным 40 р00
длины меридиана. Считается, что точность, с которой мож-
но измерить длину эталона метра, достигает 200 тц.
Недавно было решено определить метр, исходя из длины
волны определенных световых лучей; точность здесь дости-
гает 20 /при Если обозначить через длину волны красной
линии спектра кадмия, а через длину волны желто-зе-
леной линии спектра криптона, то
1 = 1 555 164,131е
и
1 л«= 1 769 557,93 Хд.
Каковы же величины и ).*?
Возникает вопрос: имеют ли какое-либо практическое
значение столь малые единицы длины? В самый сильный
микроскоп невозможно обнаружить объект размером в 1 мил-
лимикрон — в микроскоп можно увидеть лишь предметы,
поперечник которых не менее 200 тц. Появление ультра-
микроскопа, изобретенного на рубеже прошлого и нынеш-
него столетий, означало значительный шаг вперед в этом
отношении. Еще лучшие результаты дает применение элект-
55
ронного микроскопа и, особенно, появившегося совсем
недавно электронного микроскопа — проектора.
При цветных съемках по методу, предложенному фир-
мой Агфа (Agfa), кинопленку покрывают тремя различными
светочувствительными слоями толщиной от 4 до 5 р.
Здесь требуется точность в 1 р.
В настоящее время механическим молотом удается рас-
плющить кусок золота в чрезвычайно тонкую пластинку.
Так, один кубический миллиметр (1 ммя) расплющивается
в пластинку, поверхность которой равна примерно одному
квадратному дециметру (1 дм2). Обозначим толщину та-
кого листочка через х; тогда если х выразится в миллимет-
рах, то 1 • 10 000 мм2, так как 1 дм2= 10 000 мм2.
„ 1
Отсюда получаем, что толщина пластинки равна 10 QQ0 мм
или 100 /пр.
Еще тоньше бывают некоторые масляные пленки, кото-
рые получаются, если капнуть жидким маслом на воду.
Масло тотчас же расплывается по поверхности воды, и слой
его становится все более тонким. Если известно количество
масла на поверхности воды и площадь масляного пятна,
то легко вычислить толщину слоя. При этом наблюдается
следующее явление: по мере того как масляный слой стано-
вится все тоньше и тоньше, он начинает разрываться на от-
дельные части; это происходит тогда,- когда толщина плен-
ки достигает примерно 100 /пр. Но среди отдельных, раз-
личимых глазом пленок имеются значительно более тон-
кие, толщина которых доходит до 20 /пр и меньше. При
последующем уменьшении толщины масляной пленки су-
щественно меняются и ее физические свойства, особенно,
когда толщина пленки доходит до 1 /пр. Эти изменения
лучше всего объяснить, исходя из предположения о зер-
нистой структуре масла. При этом тонкий слой уже не
имеет свойств однородной жидкости; скорее он имеет свой-
ства вещества, состоящего из отдельных, не связанных друг
с другом зерен.
Уже давно ученые интересовались вопросом о том, можно
ли материю бесконечно делить на все меньшие и меньшие
доли. Различные факты привели к мысли, что это не так,
что материя, как твердая, так и жидкая и газообразная,
состоит из мельчайших «неделимых» частичек — молекул
и атомов. Величину этих частичек можно определить раз-
личными способами; при этом получаются значения
56
порядка /пр. Опыты с масляными пленками, описанные
выше, подтверждают это заключение. В 1912 году Лауэ
проложил путь в мир этих мельчайших частиц; с помощью
рентгеновских лучей удалось получить картину расположе-
ния атомов в кристаллах, которой можно воспользоваться
для измерений и вычислений. Открытие Лауэ, а также и
дальнейшие исследования, привели к созданию нового боль-
шого раздела физики, изучающего строение атомов, в тайны
которых современная наука далеко проникла.
Замечу еще, что с помощью электронного микроскопа
удалось сфотографировать отдельные молекулы, напри-
мер вирус «табачной мозаики», и тем самым получить о них
наглядное представление. Электронный микроскоп— проек-
тор позволяет различить четыре бензольных кольца в моле-
куле галоцианина меди, напоминающей по форме четырех-
листный клевер.
Чтобы получить представление о величине подобных
мельчайших частиц микромира, нам надо будет позна-
комиться с самыми малыми единицами веса. Единицы веса
тесно связаны с единицами объема, а именно: вес одного
кубического дециметра (одного литра) воды при определен-
ных, тщательно оговоренных условиях и есть 1 кг. В свою
очередь 1 кг=1000г, а 1 г равен 1000 миллиграммам (мг).
Более мелкие весовые единицы физики обычно изобра-
жают степенями с отрицательными показателями. Напри-
мер, =10~”, в частности, = 10-3.
Потребность человеческого организма в витаминах в ве-
совом выражении определяется следующими числами: че-
ловеку требуется в день от 2 до 3 мг витамина А, от 1 до 2 мг
витаминов В, и В2, от 50 до 60 мг витамина С и около 10-3 мг
витамина D. Однако существуют вещества, потребность
организма в которых выражается еще меньшими числами.
Так, биотин, играющий существенную роль в процессе де-
ления клеток, обнаружен в некоторых микроорганизмах
в количестве, составляющем одну четырехсотбиллионную
от общего веса клетки. 2,5 т сухого желтка утиных яиц
содержат 1,1 мг этого вещества — здесь отношение количе-
ства биотина ко всему весу равно 1 : 2,3 миллиарда. Аук-
син, вещество, обнаруженное в ростках овса и стимулирую-
щее его рост, обнаружен в растворе, в котором 1 г вещества
приходится на миллион литров воды. Существует одно
57
вещество—краситель Safranfarbstoff, необходимый морским
водорослям для процесса размножения; потребность в этом
красителе настолько мала, что одной капли раствора,
в котором на 250 миллиардов литров воды (т. е. на массу
воды, которая может образовать большое озеро) приходится
10 г вещества, может хватить на тысячи клеток водорослей х).
Встречаясь со столь малыми, однако эффективными коли-
чествами вещества, мы приближаемся к величинам, близ-
ким к молекулярным.
Число Лошмидта 6,022-1023 указывает количество мо-
лекул в одном моле (т. е. в 18 г* *)) воды. Если бы удалось по-
метить все молекулы двух столовых ложек воды, вылить
эту воду в мировой океан и хорошенько перемешать все
1370 кубических километров воды, чтобы молекулы распре-
делились равномерно, то, зачерпнув затем из какого то
места мирового океана один литр воды, мы обнаружили бы
в нем примерно 440 меченых молекул.
Диаметр молекулы водорода равен приблизительно
0,4 /пр. Если собрать воедино все молекулы, содержащиеся
водном кубическом сантиметре этого газа, то их объем ока-
жется гораздо меньше одного кубического сантиметра, так
как расстояния между отдельными молекулами весьма значи-
тельны. А что получится, если расположить все эти молеку-
лы в одну линию, скажем, нанизать их, как бусы, на одну
нитку? Длина этой нитки была бы близка к 11 миллионам
километров. Такой цепочкой молекул можно было бы поч-
ти триста раз обхватить земной шар. Попробуем теперь
расположить все эти молекулы на плоскости. Возьмем до-
ску шириной в 0,5 л; какой длины она должна быть, чтобы
на ней уместились все молекулы? Выложим столько рядов,
сколько раз по 0,5 м содержится в 11 миллионах километ-
ров. Получим 22 миллиарда. Каждый из этих 22 миллиардов
рядов имеет ширину в 0,4 тр,— ведь такова ширина од-
ной молекулы. Следовательно, длина доски будет равна
0,4 mji-22 000 000 000, что составит 8,8 м. Значит, моле-
кулы можно уместить на доске, по размерам подобной той,
из каких состоит пол довольно обширной залы. Впрочем,
для этого было бы достаточно и большого стола.
*) Все эти данные заимствованы из книги О. Westphal, Th.
Wieland und H. Huebsch-mann, 1 ebensregler, Sozietatsver-
lag, Frankfurt a. M.
*) 1 моль вещества, молекулярный вес которого равен т, содержит
т г вещества.
58
Урок, который можно извлечь из этого мысленного эк-
сперимента, учитывается в несколько измененном виде
природой. Вот пример этого: решающее значение для дыха-
ния и кровообращения имеет поверхность легочных пу-
зырьков, красных кровяных телец и кровеносных сосудов,
в особенности капилляров. При дыхании человек исполь-
зует почти 100 м2 поверхности легких, приблизительно
130 ;и2 поверхности красных кровяных телец и около 80 л2
поверхности капилляров.
Атом не является однородной частицей; это скорее си-
стема, образованная атомным ядром, вокруг которого вра-
щаются электроны. Если радиус атома водорода имеет
величину порядка 10"8 см, то радиус атомного ядра
равен лишь 10"13 см, а радиус электрона приблизительно
3-10"13 см. Денк дал этому следующее «наглядное»
пояснение: радиус видимой вселенной равен приблизи-
тельно 3-1028 см. Сколько электронов можно уместить ря-
дом друг с другом в одну линию поперек всей вселенной?
Простой подсчет дает число 104*. Если расположить эти
электроны в виде квадрата, то сторона квадрата будет
близка к 100 км, длина же ребра куба, сплошь заполнен-
ного этими электронами, составит всего лишь около 30 см.
В то время как колесо довольно быстро едущего авто-
мобиля делает в секунду приблизительно 10 оборотов, про-
пеллер самолета — 25, гирокомпас — около 300, а под-
шипники в таком компасе примерно 1000 оборотов, элект-
рон совершает вокруг атома водорода за одну секунду около
7-Ю15 оборотов.
Вот еще одно следствие этого своеобразного строения
атома: кубический метр свинца весит 11,34 т. Однако
если бы отсутствовали межатомные пустоты, то данный сви-
нец занимал бы весьма небольшой объем — всего лишь
около одного кубического миллиметра. И в этом кубиче-
ском миллиметре вещества был бы сконцентрирован вес
в 11,34 т. Какие перспективы открылись бы технике,
если бы люди нашли возможность получать атомы в чистом
виде *)!
*) Современная техника не имеет возможностей получать тела,
«сплошь» заполненные атомами; однако возможно, что вне нашей пла-
неты они и существуют. Известно, что плотность вещества, из которого
состоят звезды определенного типа (так называемые «белые карлики»),
колоссальная она может в сотни тысяч раз превосходить плотность
воды (спичечный коробок этого вещества уравновесит полный вагон
вместимостью в 50 tn). В самое последнее время появились сообщения об
59
При измерении углов градус подразделяют на 60 минут,
минуту — на 60 секунд. Так, например, в полнолуние по-
перечник луны виден с Земли под углом примерно в 30 ми-
нут. У астрономов существует специальная «астрономиче-
ская» единица длины — 1 парсек. Так называют расстояние,
с которого диаметр земной орбиты виден под углом в 1 се-
кунду; это расстояние составляет 3,26 светового года
(ср. стр. 17). Известны звездные скопления, удаленные от
нас на 70 000 парсек и на еще большие расстояния. Из этих
скоплений земная орбита видна под углом зрения в
секунды или даже менее того. Приведу еще пример прак-
тического измерения углов. При определении силы земного
притяжения Этвеш пользовался такими точными приборами,
которые позволяли учитывать столь незначительное измене-
356
ние направления силы тяжести, как отклонение на ППА ААА
ZUU иии иии
секунды. Это — угол, под которым мы увидели бы на по-
верхности Луны маленькую монетку диаметром у см.
Мы убедились, как далеко заводят нас в мир крошечных
промежутков времени, ничтожных расстояний, углов и масс
современные научные теории и эксперименты. Вернемся,
однако, в мир «чистых» чисел, не связанных ни с какими
измерениями.
В математике малые числа играют особую роль там, где
приходится иметь дело с величинами, которые в нашей
десятичной системе счисления невозможно выразить точно,
и потому приходится заменять их приближенными значе-
ниями. Простой пример пояснит, что мы имеем в виду. При
обращении обыкновенной дроби -i- в десятичную получает-
ся так называемая бесконечная десятичная дробь 0,3333...,
которую невозможно записать до конца. На каком бы знаке
мы ни оборвали данную дробь, всегда допустим некоторую
ошибку. Однако эту ошибку можно сделать меньше любого
наперед заданного числа, как бы мало оно ни было. Можно
оборвать дробь на таком знаке, чтобы ошибка была меньше
0,0001, меньше 0,0000001 и т. д. Для этого лишь нужно
открытии звезд (так называемые «нейтронные звезды»), плотность которых
в миллионы и большее число раз превосходит плотность «белых кар-
ликов» (1). Если эти сообщения подтвердятся, то из них будет следовать
существование во вселенной материи, в которой межатомные пустоты
почти полностью отсутствуют.
60
нашу бесконечную десятичную дробь продолжить доста-
точно далеко: в первом случае до 0,3333, а во втором —
до 0,3333333.
В нашем примере, где в десятичную дробь обращалось
1 ,
число у, мы получили периодическую дробь с очень корот-
ким периодом. Этот период состоит всего из одного знака.
Нетрудно понять, что период дроби 1/р, где р — простое
число, не равное 2 и 5, не может иметь более р—1 знаков.
Действительно, ведь если реально выполнять деление,
то в качестве остатков у нас могут встретиться лишь р—1
различных чисел (от 1 до р—1); поэтому не позже, чем на
р-м шаге, мы придем к остатку, который уже встречался
раньше. С появлением такого остатка все дальнейшее бу-
дет повторяться в той же последовательности. Однако, как
видно на примере у=0,3333 или ^=0,090909..., на-
личие точно р—1 знаков в периоде дроби 1/р совершенно не
обязательно, их может быть и значительно меньше. При
обращении в десятичную дробь числа у мы получаем в пе-
риоде всего лишь один знак вместо двух; при обращении
числа -у — лишь два знака вместо 10.
Периоды «полной длины» (т. е. периоды из р—1 цифр)
х 1 1 1 1 1 1 1 1 1 1 „ m
имеют дроби 7 , 17 > 1э > 23 ’ 29 ’ 47 ’ 59 ’ 61 ’ 97 ’ 109 и Т' Д‘
При этом справа от запятой получится значительное число
цифр, прежде чем они повторятся в той же последователь-
ности. Возьмем, к примеру, дробь у^. Ее вид
0,009 174 311 926 605 504 587 155 963 302 752 293 577 981 651
376 146 788 990 825 688 073 394 495 412 844 036 697 247 706 422
018 348623853211...
Здесь второй период начинается лишь со 109-го знака.
Теория чисел раскрывает нам удивительные закономер-
ности в строении таких периодов. Если, например, обра-
, «23 108
тить обыкновенные дроби yog , yog , ... , в десятичные,
то в каждом случае мы получим те же цифры и в той же
последовательности, что и раньше, но с той лишь разницей,
что теперь период будет начинаться с другой цифры.
2
Так, например, дробь имеет период, начинающийся с
61
018 348 623 853 211, это — последние 15 цифр периода
дроби . Обычно эту закономерность демонстрируют
на примере обращения у в десятичную дробь; получает-
ся 0,142 857... Задача ставится следующим образом:
число 142 857 требуется умножить на 2, на 3 и т. д.
Любитель числовых великанов может применить эту
- 1
процедуру и к периоду дроби .
Обратимся теперь к уже знакомому нам числу, с которым
мы встречались в этой книжечке, когда объясняли, как
вычисляется длина окружности (стр. 19). Буква тс есть сок-
ращенное обозначение числа, на которое надо умножить
диаметр круга, чтобы получить длину окружности. Это
число имеет очень интересную историю *). Если взять но-
вый пятак и определить тс опытным путем,. то мы получим
значение, немного большее 3. На практике часто пользуют-
ся значением Зу или, переходя к десятичной дроби, 3,14.
Но и это значение не вполне точно. Архимед, заслуги кото-
рого в вычислении числа тс очень велики, показал, что тс
заключено между 3^ и Зу. С течением времени научились
вычислять это число с большей точностью. Первые
цифры числа тс таковы: 3,141 592 653... Для запоминания
их придумано много стишков — немецких, французских,
английских и других, довольно далеких от всякой поэзии,
но зато таких, что число букв каждого слова дает соответ-
ствующую цифру числа тс**).
Число тс раньше часто называли лудольфовым числом, по
имени жившего на рубеже XV и XVI столетий математи-
ка Лудольфа ван Койлена, который первым вычислил боль-
шое число первых знаков тс: сначала 20, затем 32 и, наконец,
35. Вега, таблицы логарифмов которого широко известны,
вычислил 140 знаков числа тс; замечательный вычислитель
Захария Дазе — 200 десятичных знаков, Резерфорд (1833)—
440, профессор Рихтер из Эльбинга (1853) — 500 и, нако-
*) См. Ф. Руди о, О квадратуре круга, М.— Л., ОНТИ, 1936.
**) В русской дореволюционной литературе имелся «стих»;
Кто и шутя и скоро пожелает(ъ)
3 14 15 9
Пи узнать, число уж(ъ) знает(ъ).
2 6 5 3 6
62
нец, англичанин Шенке (1873) — 707 знаков. Но его по-
стигла неудача. Долгое время никто не проверял получен-
ного им результата, упоминание о котором, в силу его ре-
кордного характера, проникло даже в школьные учебники.
Лишь в 1948году Фергюсон и Уренч1),пользуясь различными
формулами2), вновь принялись, независимо друг от друга,
за вычисление числа тг и получили 808 знаков. При этом они
установили, что у Шенкса при вычислении 528-го знака
допущена ошибка и все дальнейшие полученные им цифры
не верны. Вот найденное ими значение числа п:
п%3, 14159 26535 89793 23846 26433 83279 50288 41971
69399 37510 58209 74944 59230 78164 06286 20899
86280 34825 34211 70679 82148 08651 32823 06647
09384 46095 50582 23172 53594 08128 48111 74502
84102 70193 85211 05559 64462 29489 54930 38196
44288 10975 66593 34461 28475 64823 37867 83165
27120 19091 45648 56692 34603 48610 45432 66482
13393 60726 02491 41273 72458 70066 06315 58817
48815 20920 96282 92540 91715 36436 78925 90360
01133 05305 48820 46652 13841 46951 94151 16094
33057 27036 57595 91953 09218 61173 81932 61179
31051 18548 07446 23799 62749 56735 18857 52724
89122 79381 83011 94912 98336 73362 44065 66430
86021 '39494 63952 24737 19070 21798 60943 70277
05392 17176 29317 67523 84674 81846 76694 05132
00056 81271 45263 56082 77857 71342 75778 96091
73637 17872 14684 40901 22495 34301 46549 58537
10507 92279 68925 89235 42019 95611 21290 21960
86403 44181 59813 62977 47713 09960 51870 72113
49999 99837 29780 49951 05973 17328 16096 31859
50244 594(55)
*) Ср. Intermediate des Recherches Mathematiques 4, № 15, (июль
1948).
2) Для математиков замечу, что Фергюсон использовал известную
формулу
^=4.arclgl—aretgi,
в то время как Уренч исходил из того, что
л 1 1 1
T=3.arctgl- + arctg + arctg .
63
Это число дает повод к различного рода исследованиям.
Так, например, можно установить ч а с т о т ы, с которыми
повторяются в полученном значении числа я отдельные
цифры. Если ни одна цифра не имеет преимущества перед
другой, то среди 800 знаков каждая из них должна встре-
чаться около 80 раз. Когда было проверено, так ли обстоит
дело для числа, полученного Шенксом, то оказалось, что
цифра 7 нарушает эту закономерность: как указывалось
в сообщении Гофмана о числе Шенкса, среди 707 знаков эта
цифра встречается всего 53 раза вместо 70. Было много
споров о том, является ли причиной этого строение числа тс
или же мы обязаны этим «случаю» и при вычислении тс с
большей точностью подобное явление уже не будет иметь
места. Однако выяснилось, что отклонение от общей зако-
номерности произошло благодаря сделанной ошибке; если
рассмотреть полученное в наши дни значение числа тс,
то можно убедиться, что цифра 7 повторяется в нем приб-
лизительно столько же раз, как и всякая иная х). Дру-
гие «вероятностные» (или «частотные») проблемы, связан-
ные с числом тс, читатель легко сможет указать самостоя-
тельно.
Воспользуемся числом тс, чтобы выяснить величину оши-
бок, допускаемых при замене какого-либо числа его приб-
лиженным значением. Если мы возьмем для тс приближенное
значение с четырьмя знаками после запятой, т. е. примем
тс——3,1416, то допущенная при этом ошибка не будет пре-
восходить 0,001. Значит, если бы можно было точно измерить
диаметр D круга, то, приняв за приближенное значение тс
число 3,1416, а длину окружности соответственно равной
3,1416 D, мы сделали бы ошибку, меньшую 10 Одо- длины
диаметра. Например, если диаметр равен 100 м, то длина
окружности будет вычислена с точностью до у0 от 100 м,
т. е. до 1 см. Ясно, что это уже довольно большая точность,
которая далеко превосходит достигаемую, например, в сов-
ременной архитектуре.
Однако, продолжим. Возьмем тс с 26 цифрами после за-
пятой. В этом случае ошибка не будет превосходить одной
стоквадриллионной. Представим себе круг с радиусом в 50
’) Это подтверждается и первыми 2040 знаками (!) числа вычис-
ленными недавно на электронной счетной машине ЭНИАК за 96 часов.
64
биллионов километров: это есть расстояние, равное пяти
световым годам; оно несколько больше расстояния до бли-
жайшей неподвижной звезды. Точность, с которой мы можем
вычислить длину этой гигантской окружности, взяв Tt
с 26 знаками, составляет одну стоквадриллионную часть
диаметра, равного ста биллионам километров. Это зна-
чит, что ошибка не превзойдет одной биллионной части
километра или, что то же самое, одного миллимикрона.
Сравните эту исполинскую окружность, простирающую-
ся до неподвижных звезд, с маленькой ошибкой, имею-
щей порядок величины молекулы! А ведь мы взяли тг
только с 26 десятичными знаками, а не с 808, выписан-
ными выше!
Наряду с числом тг математиков очень занимает число е—
основание системы натуральных логарифмов. Эйлер полу-
чил для е значение е=2,718 281 828 459 04... В конце XIX
века было вычислено 346 десятичных знаков числа е\ счет-
ная машина ЭНИАК за 36 часов вычислила 2016 знаков этого
числа * **)).
Заслуживает внимания также число i‘ (где i — мнимая
------------------------------------------------— * * \
единица). Оно — действительно (!) и имеет значениее 2 >'
В 1921 году это число было вычислено с 55 знаками. Пер-
вые цифры его таковы: /'=0,207 879 57 ...
9. В МИРЕ ВЕЛИКАНОВ И КАРЛИКОВ
ТАКЖЕ СЧИТАЮТ ОБЫКНОВЕННЫМИ ЧИСЛАМИ
Вообрази себе страну великанов. Средний рост жителей
этой страны достигает, скажем, 10 м (дети, конечно, будут
ниже). Ты думаешь, эти люди в своей стране чувствуют себя
великанами? Или вообрази страну карликов, рост которых
не превосходит 10 см. Ты полагаешь, что подобный «маль-
чик с пальчик» считает себя в своей стране карликом? Это,
безусловно, не так. Но если бы ты, как некогда Гулливерс
приехал к ним! Великаны, завидев тебя, воскликнули бы:
«Какой карлик!» А посети ты карликов, они сказали бы:
«Какой великан!»
*) 2500 первых цифр (!) десятичного разложения числа е приведены,
например, в 3-м издании «Задачника по алгебре» В. А. Кречмара
(Физматгиз, 1959). Первые 16 знаков е очень легко запомнить:
е= 2, 7 18 28 18 28 45 90 45 ...
**) См., например, Р. О. Кузьмин и Д. К. Фаддее в. «Ариф-
метика и алгебра комплексных чисел», Л., 1939.
65
Понятно, конечно, что всё зависит от выбора единицы
измерения. Ты исходишь из своего роста, великаны—из
своих 10 м, а карлики — из своих 10 см. Однако продол-
жим наши фантастические мысли. Вообрази, что электроны,
вращающиеся вокруг атомного ядра, обитаемы: на них,
как мы на Земле, живут маленькие человечки, которые так
же, как и мы, занимаются математикой. Расстояния и про-
межутки времени, с нашей точки зрения, выражающиеся
числовыми карликами, им будут казаться огромными чис-
ловыми великанами. Вот обратный пример. Представь себе,
что Земля, планеты, Солнце и звезды — это электроны и ато-
мы, из которых построены некие исполинские существа.
Что для этих сверхлюдей наши числовые великаны, часто
недоступные даже воображению?
Все, что здесь сказано, относится к числам, выражающим
длины, площади, объемы, промежутки времени, а также и
веса, скорости и все остальное, связанное с перечисленными
величинами. Система единиц человека, размером с молеку-
лу, отлична от нашей; совсем другая система единиц
будет у «сверхчеловека». Но все вычисления этих
«людей» будут сходны с нашими. У них не будет какой-то
особой «карликовой» или «великаньей» таблицы умноже-
ния — она будет иметь в точности тот же вид, что и
у нас. Их повседневные расчеты будут совершенно такими
же, как и наши.
Расстояния сами по себе не отвечают никаким опреде-
ленным числам. Их «величины», т. е. числовые значения,
всецело зависят от выбранной единицы измерения. Понят-
но, конечно, что так же обстоит дело с интервалами време-
ни, весами, скоростями и т. п.
Мы пришли к концу нашего странствования по обширной
стране чисел, простирающейся от нуля (0) до бесконечности
(ею). В отличие от школьной математики и повседневных рас-
четов мы стремились держаться поближе к пограничным об-
ластям этой страны — и все же границ ее не достигли. Мы
часто думали о «бесконечности», говоря о числах, по сравне-
нию с которыми «конечные» числа, например те, к которым
пришел в свое время Архимед, являются числовыми кар-
ликами. Бесконечное великолепие красок, бесконечное мно-
гообразие событий, бесконечная глубина чувств и мыслей
окружают человека повсюду. Так мы часто говорим. И все
же! Число всех мыслей, приходивших когда-либо кому-
нибудь в голову, конечно. Ибо на каждую мысль требуется
66
определенное время, и, следовательно, каждый человек за
свою жизнь может продумать лишь конечное число мыслей.
А так как число людей, живших когда-либо на Земле, ко-
нечно, то конечно и число всех возникавших у них мыслей.
Так же обстоит дело с глубиной чувств, впечатлениями,
красками, звуками.
Одним из величайших достижений математики является
то, что она преодолела «конечность» окружения человека и
перенесла понятие «бесконечного» из области туманных
представлений в мир точной науки.
Вальтер Латцман
Великаны и карлики
в мире чисел
Редактор И. В. Морозова
Техн, редактор Е. А. Ермакова
Корректор С. А. Мозгалевская.
Сдано в набор 9/IX 1959 г. Подписано к пе-
чати 19/XI 1959 г. Бумага 84Х108/за. Физ. печ.
л. 2,125. Условн. печ. л. 3,47. Уч.-изд. л. 3,68.
Тираж 50 000 экз, Т-11052. Цена книги 1 р. 10 к.
Заказ 3544.
Государственное издательство
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Первая Образцовая типография
имени А. А. Жданова
Московского городского Совнархоза.
Москва, Ж-54, Валовая, 28.
Jena 1 p. 10 к.
ФИЗМАТГИЗ • 1959