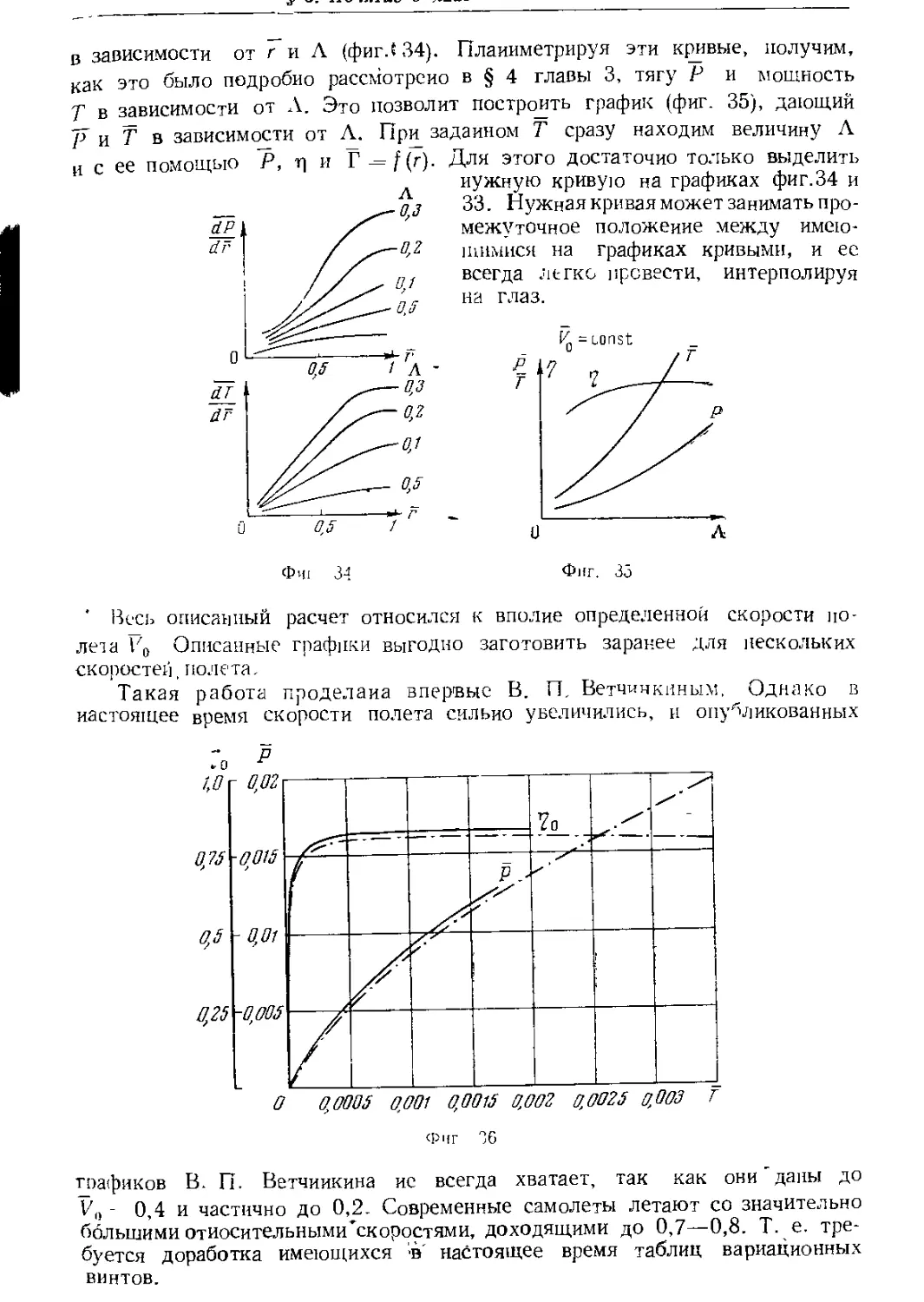
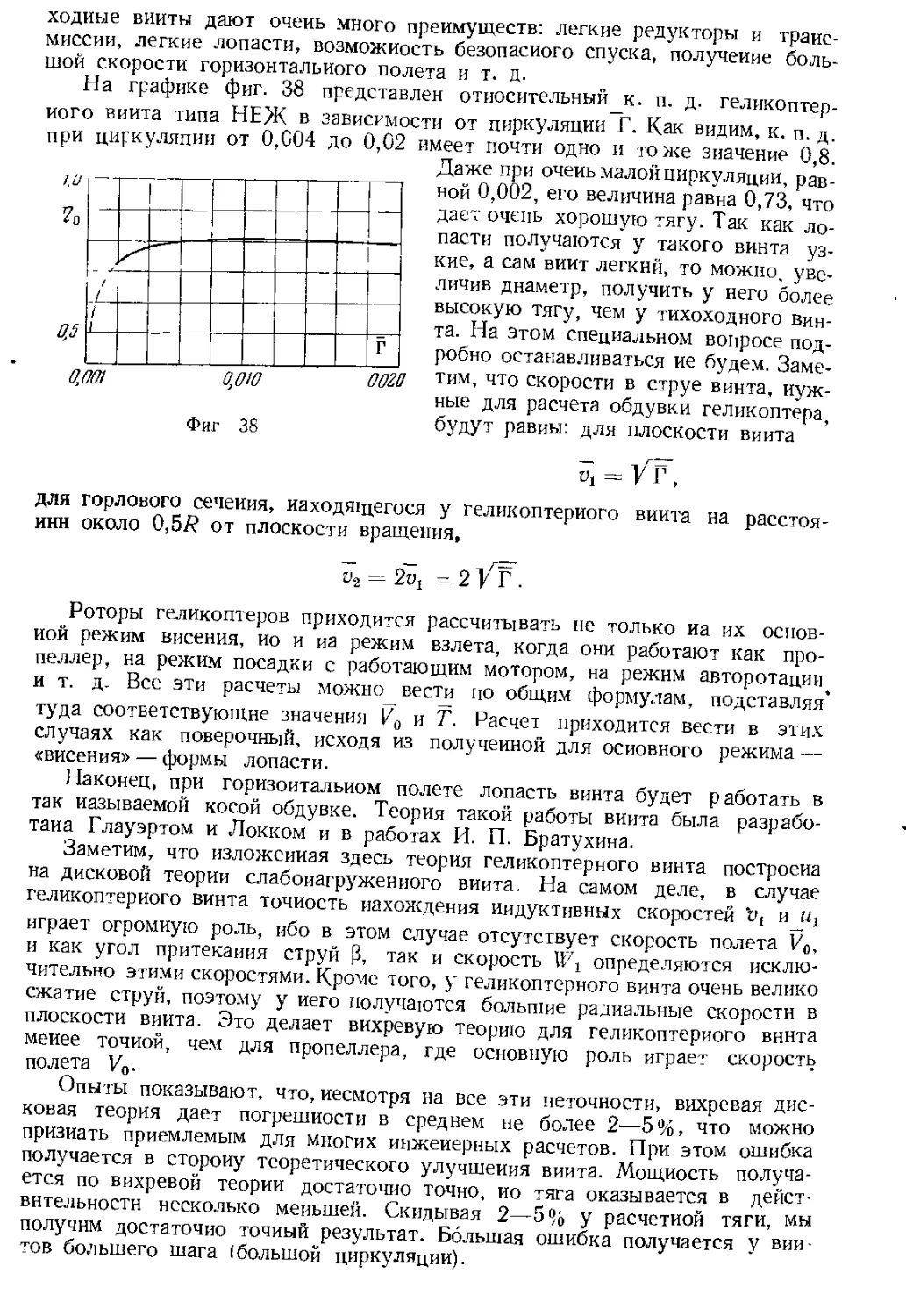
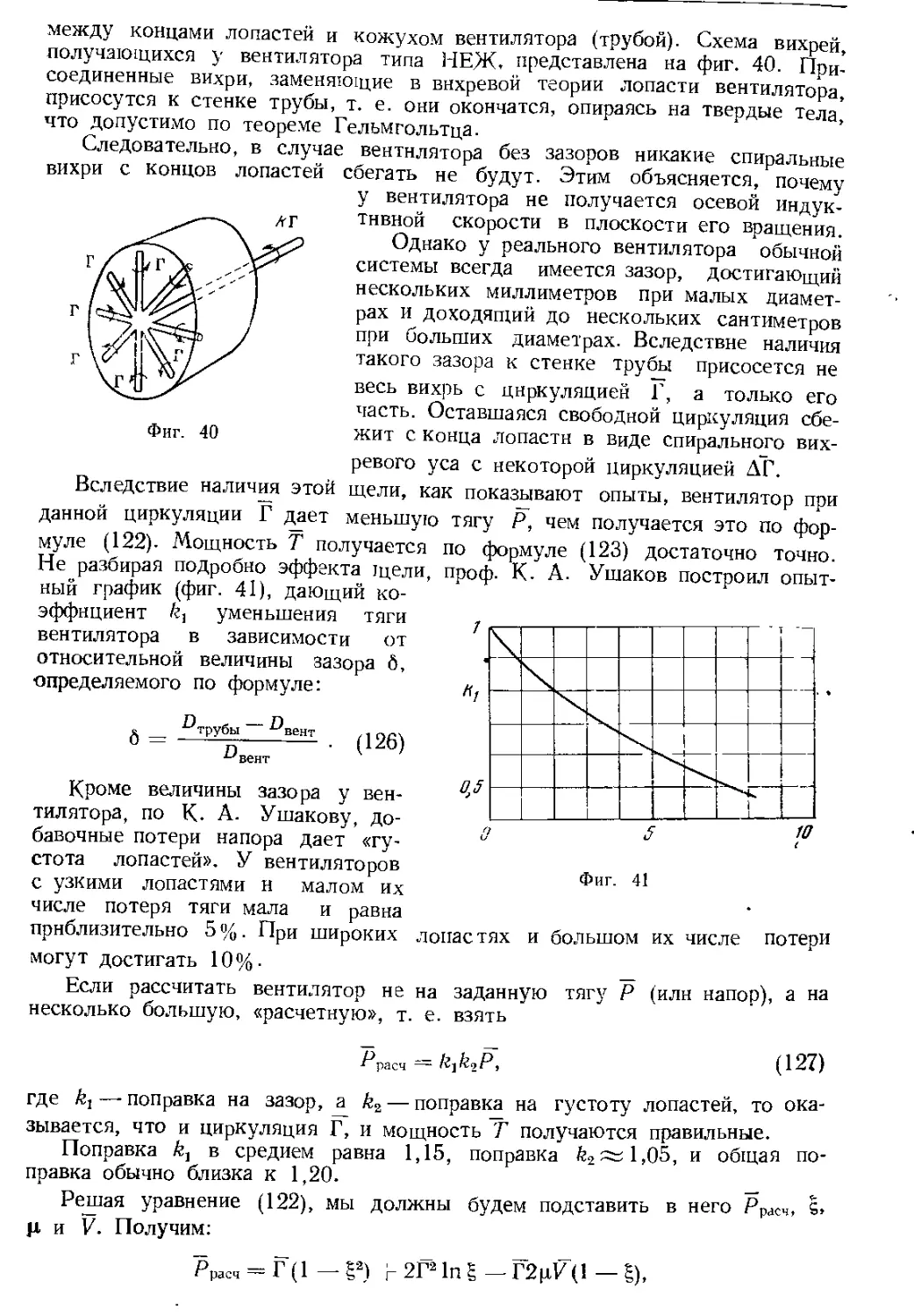
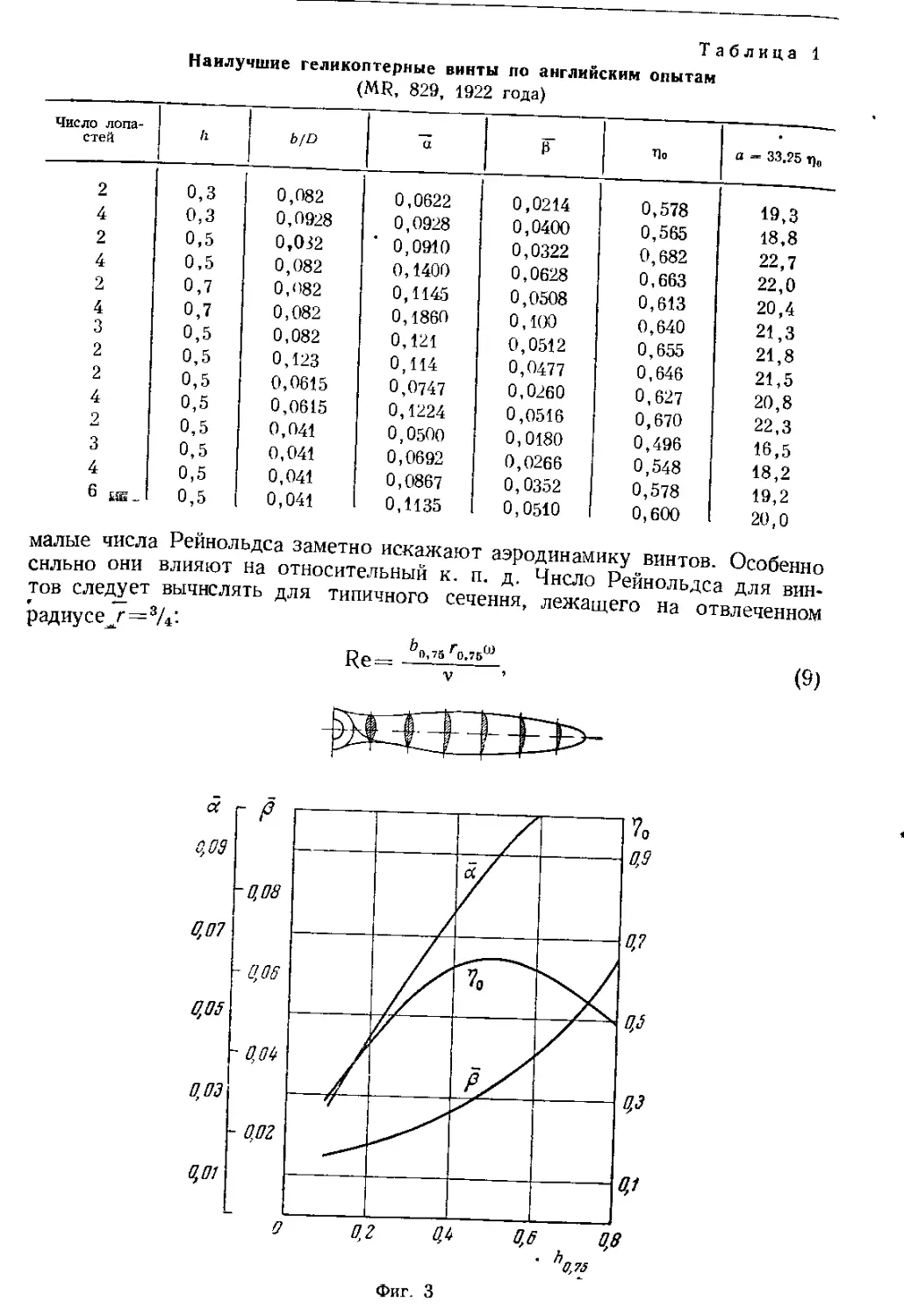
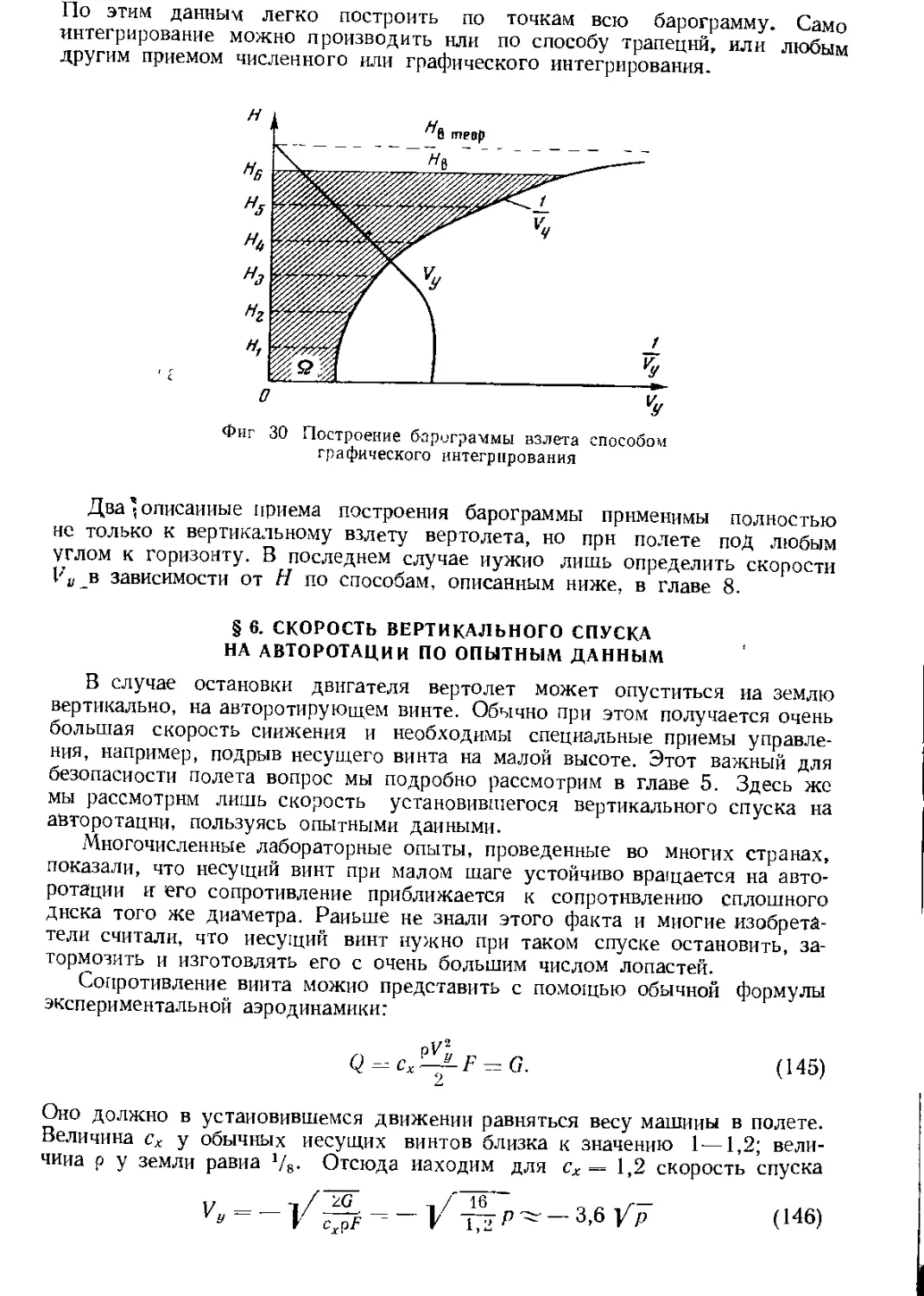
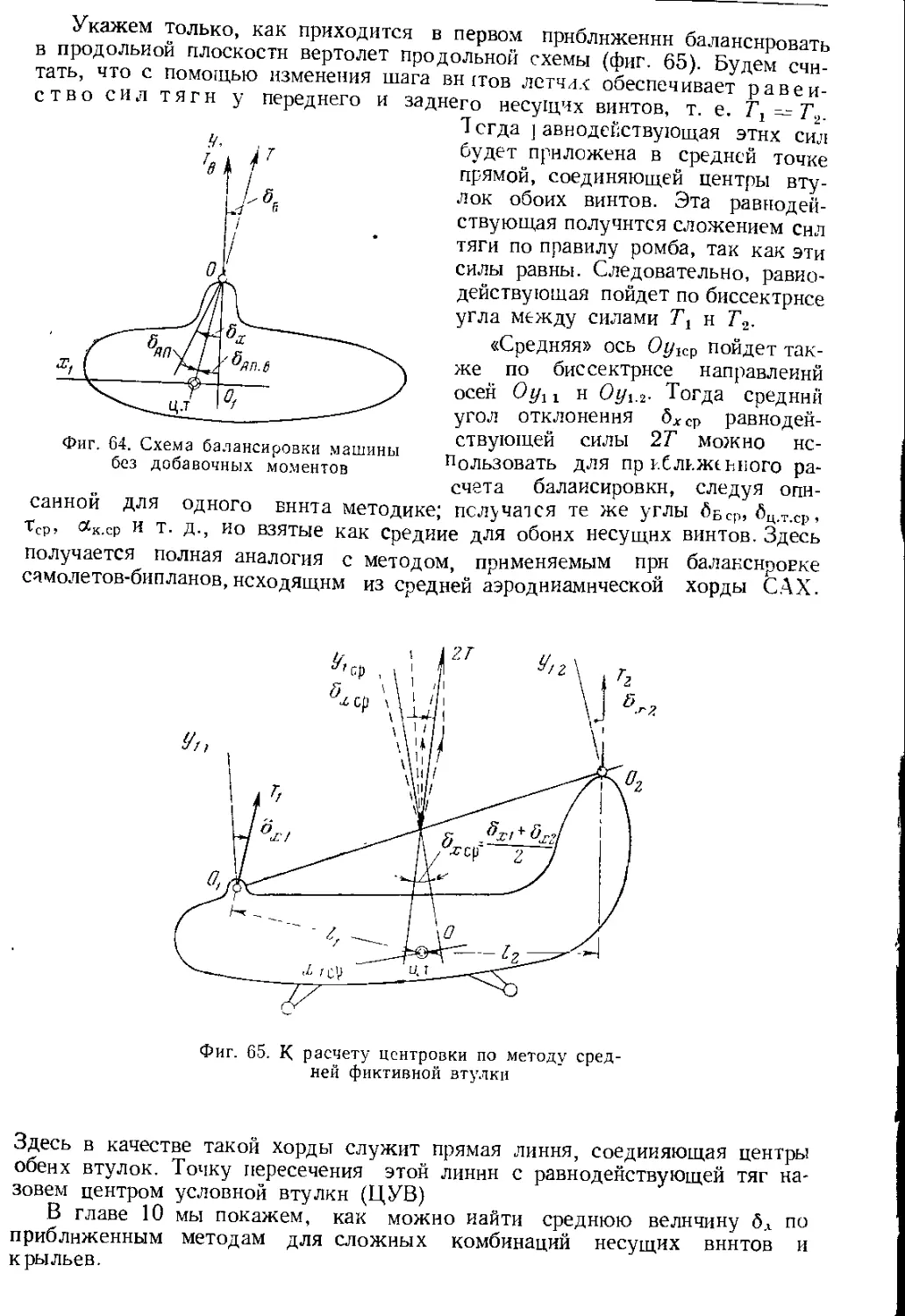
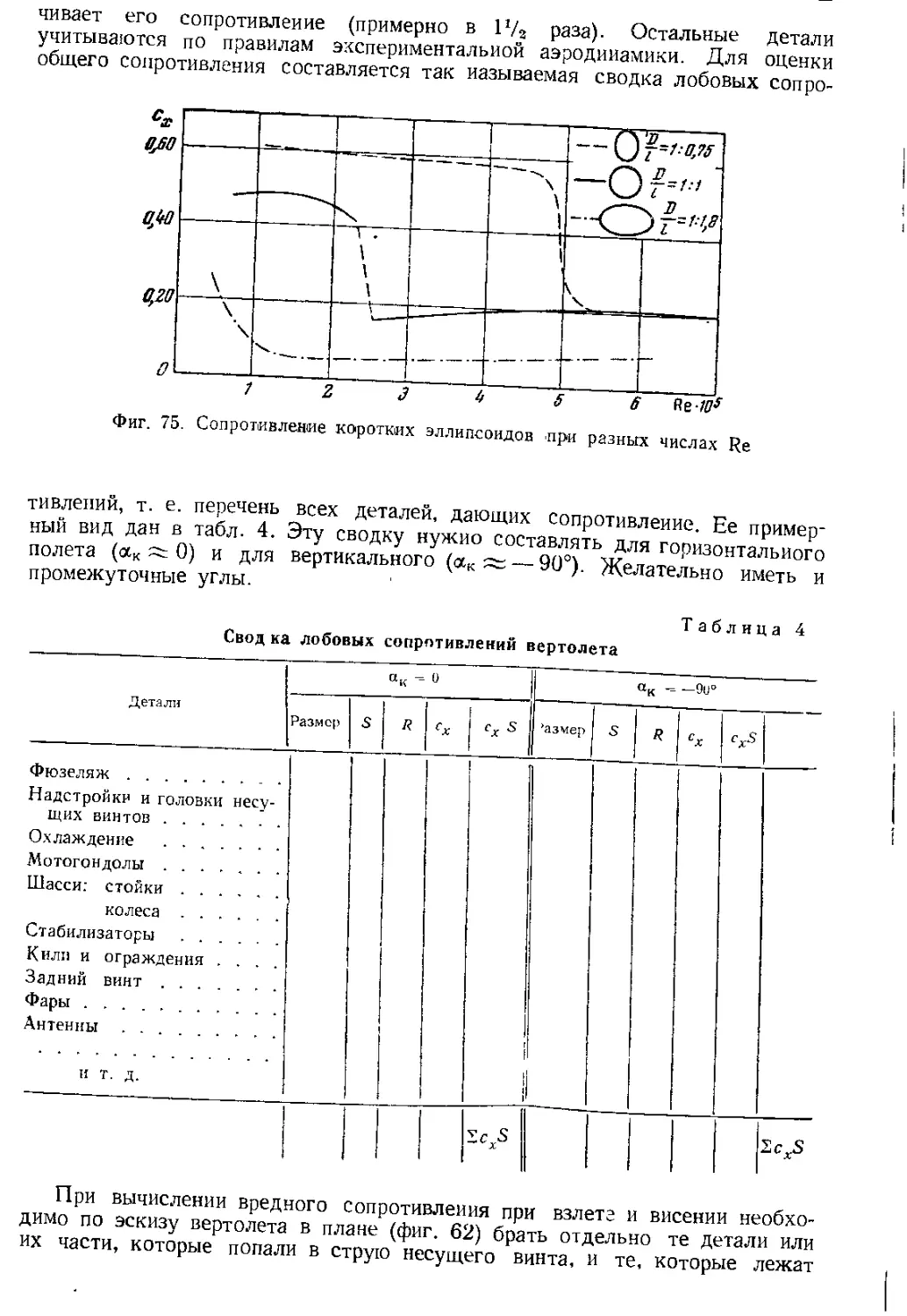
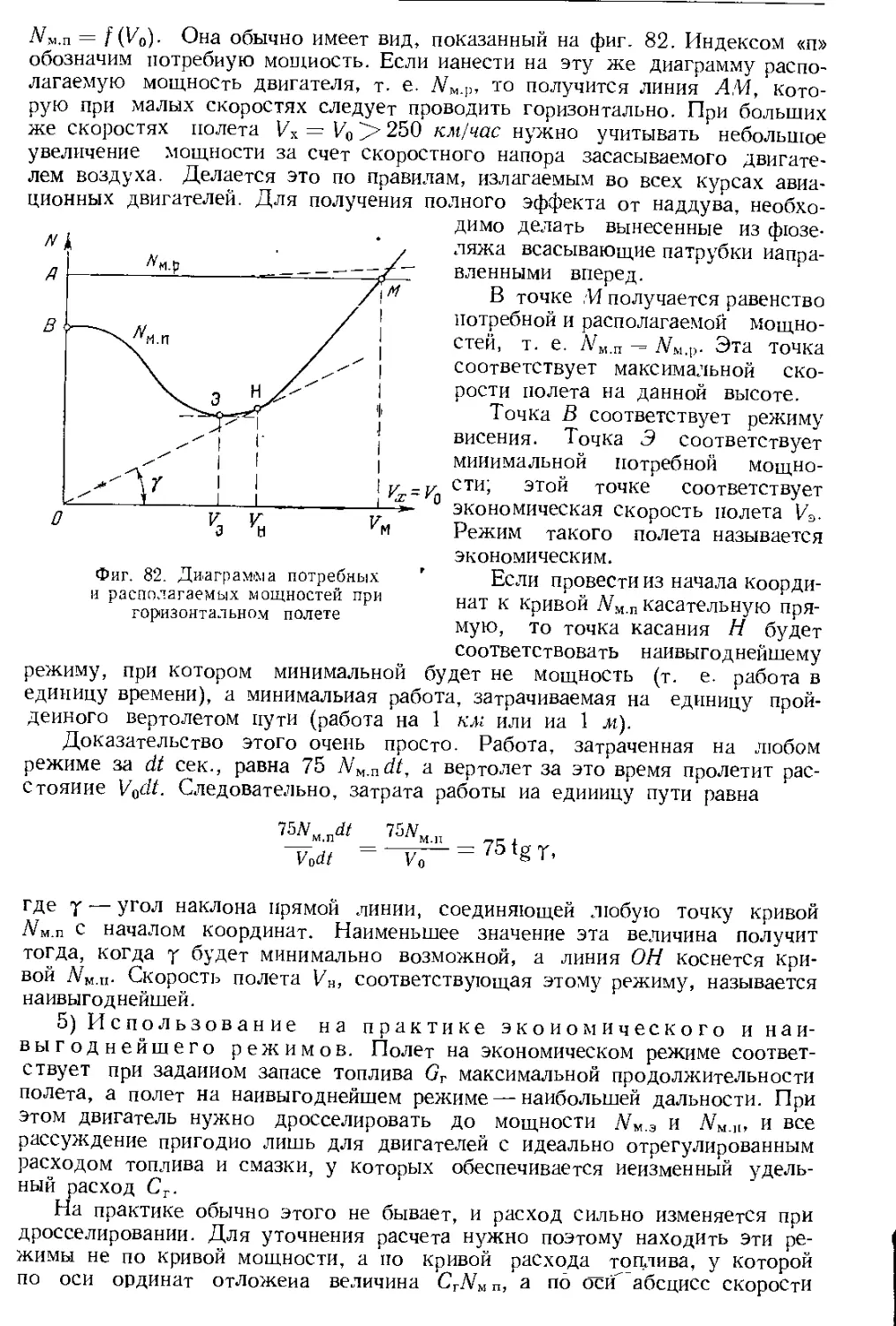
Автор: Юрьев Б.Н.
Теги: вертолеты авиастроение избранные труды академия наук ссср воздушные
Год: 1961
Текст
АКАДЕМИЯ НАУК СССР
l-o g Я
Б. И. ЮРЬЕВ
ИЗБРАННЫЕ ТРУДЫ
том
I
ВОЗДУШНЫЕ ВИНТЫ
ВЕРТОЛЕТЫ
ИЗДАТЕЛЬСТВО АКАДЕМИИ НАУ К СССР
МО С КВА -1961
Научное наследие академика Б. Н. Юрьева весьма много-
образно. Оно охватывает область воздушных винтов, верто-
летов, самолетов, экспериментальной и теоретической аэро-
динамики, механики, баллистики и истории техники.
В настоящее двухтомное издание включены рабо'ты ака-
демика Б. Н. Юрьева лишь по тем разделам, по которым его
вклад был особенно значительным.
Первый том состоит из разделов: I. Воздушные винты,
II. Вертолеты.
Второй • том состоит из разделов: I Аэродинамика.
II. История авиационной техники.
Издание подготовлено комиссией по изданию трудов
академика Б Н ЮРЬЕВА.
состав комиссии
академик И. И. АРТОБОЛЕВСКИЙ (председатель),
проф. И. П. БРАТУХИН (зам. председателя), проф. С. Г. КОЗЛОВ,
проф. А. К МАРТЫНОВ, проф А. К. ФЕДЯЕВСКИИ,
канд. техн наук В. А. КОНСТАНТИНОВ,
канд. техн, наук Н П ЛЕСНИКОВА (ученый секретарь)
ответственный редактор
академик И И АРТОБОЛЕВСКИЙ
ЗАМ. ОТВ. РЕДАКТОРА
проф. И. П. БРАТУХИН
ПРЕДИСЛОВИЕ
В научных трудах академика Бориса Николаевича Юрьева особое
место занимают работы по теории воздушных винтов. Область воздуш
иых винтов он понимал весьма широко, включая сюда пропеллеры,
предназначенные для создания тяги самолета, контрпропеллеры, несу-
щие винты вертолетов, ветряки, осевые компрессоры, лопастные турбины
и т. п.
Вопросами теории воздушных винтов — пропеллеров и вертолетных
несущих винтов Б. Н. Юрьев начал заниматься еще в студенческие
годы и не переставал работать в этом направлении в течение всём жизни
Эти работы были подытожены в книге «Импульсная теория воздушных
винтов», изданной в 1948 г.
В рукописи «Уточнение импульсной теории винтов», датированной
6 июля 1955 г., Юрьев, учел неравномерность давлений в горлышке
струи, а при вычислений окружных индуктивных скоростей —поджатйё;
струи за винтом. К. сожалению, эта работа не доведена до конца, поэтому
публикуется только та ее часть, в которой дается вывод формул, опре-
деляющих соотношение индуктивных скоростей в струе винтд.
Много внимания Юрьев уделял и вихревой теории винтй. Будучи'
опытным педагогом, он видел, что выводы вихревой теории в том виде,
в каком они даны ее автором Н. Е. Жуковским, трудны для инженеров
и тем более для студентов технических вузов. Поэтому на протяжении
многих лет Юрьев стремился упростить эти выводы, не снижая их
строгости и точности. В результате появилась книга «Вихревая тёория
винтов», которая до настоящего времени служит прекрасным учебным
пособием; она включена в данный том без сокращений.
В своих научных исследованиях по теории воздушных винтов Юрьев
всегда был впереди своего времени. В 1923 г. в статье «О современном
положении теории гребного виита», опубликованной в «Вестнике воз-
душного флота», заложены основы современной наиболее точной теории
винтов, названной им «относительной», которая теперь известна под
названием «лопастной»
В оставшихся после смерти Юрьева рукописях изложены,соображе
ния и имеются отдельные разработки единой теории виитов, включаю-
щей все многообразие их типов. Найденные материалы показывают,
какое большое значение придавал Юрьев созданию этой универсаль-
ной теории.
Все перечисленные работы помещены в первом разделе настоящего
тома.
Б. Н. Юрьев является основоположником пауки о вертолетах. Будучи
горячим сторонником и пропагандистом идеи вертолета, он системати-
чески выступал с докладами и статьями по этому интересному ц в тси
Предисловие
время еще спорному вопросу. В 1939 г. вышел в свег его труд «Исследо-
вание летных свойств геликоптеров», являющийся результатом его
долголетней работы, связанной с решением этой сложной проблемы
Эта книга была прекрасным и единственным в jo время руководством
для инженеров и конструкторов, занимающихся разработкой и проекти-
рованием вертолетов различных схем.
Итогом исследований Юрьева в области вертолетов явилась моно-
графия, написанная в форме учебника «Аэродинамический расчет вер-
толетов», включающая сведения по воздушным винтам и дающая в ясном
изложении методы расчета летных характеристик вертолета. Книга была
написана в 1954 г. и вышла из печати за год до смерти ее автора.
Эги две работы с некоторыми сокращениями вошли во второй раз-
дел настоящего тома.
Изобретенный Юрьевым еще в 1911 г вертолет является прообра-
зом современных вертолетов одновинтовой схемы. Так как это имеет
большое историческое значение, в приложении к данному тому мы поме-
щаем описание вертолета системы Б. Н. Юрьева, которое представляет
собой текст литографированной листовки, раздававшейся всем желаю-
щим на Международной выставке автомобилизма и воздухоплавания в
Москве (1912 г.), где экспонировался этот вертолет.
Из-за ограничения объема в настоящий (первый) том вошли только
наиболее интересные работы Юрьева по теории винтов и вертолетов
которые не потеряли практической ценности и с успехом могут быть
использованы на современном этапе развития авиационной техники.
Вопросам теории несущего винта вертолета Борис Николаевич уде-
лял весьма существенное внимание. Во всех его работах по винтам, как
правило, рассматривается частный случай — геликоптерный несущий
винт. Кроме того, большая часть публикуемых работ написана в форме
учебных пособий, в которых исследуемый вопрос изложен наиболее
полно. Все это ведет к неизбежным повторениям, поэтому помещаемые
здесь работы даются с сокращениями.
Так, например, из «Импульсной теории воздушных винтов» выпущена
глава VI *, посвященная расчету теликоптерных винтов, и § 6, где рас-
сматривается критический режим вихревого кольца, поскольку более
подробно этот материал представлен в работе «Аэродинамический рас-
чет вертолетов». Исключен также § 23, в котором излагается ход упро-
щенного расчета винта-пропеллера, так как метод, описанный в § 10,
значительно точнее.
В работе «Исследование летных свойств геликоптера» сокращения
коснулись в основном той части, где на основе весовых формул прове-
дены исследования оптимальных параметров вертолетов различных
схем (§ 6—8). Вследствие того, что весовые формулы построены иа
устаревшем статистическом материале, полученные выводы к настоя-
щему времени утратили свой практический интерес. Изъяты также
§ 13—16, в которых рассматриваются режимы вертикального сниже-
ния вертолета (вихревое кольцо и авторотация), подрыв вертолета при
посадке и шасси.
Наиболее подробно и современно эти вопросы изложены в послед-
ней работе «Аэродинамический расчет вертолетов», которая дается со
значительными сокращениями. Глава 1, посвященная истории развития
вертолетов, будет помещена во втором томе. Главы 3—6 исключены,
поскольку они носят общий характер, и вопросы, изложенные в них,
* Нумерация глав и параграфов дана по оригиналам публикуемых работ
АКАДЕМИК
Б. Н ЮРЬЕВ
развивали, кроме Б. Н. Юрьева, многие другие авторы. В этих главах
даны общие сведения по винтам, рассмотрены аэродинамические схемы
вертолетов, законы подобия для винтов и их использование, изложена
теория идеального винта с ее приложениями. В главе 8 выпущен § 8
(аэродинамические характеристики винтовых профилей), поскольку в
нем дается материал чисто прикладного характера. Из § 11 выпущен
материал по «воздушной подушке», так как он заимствован из работ дру-
гих авторов.
Сокращения коснулись также некоторых материалов иллюстратив-
ного характера.
Вследствие указанных сокращений возникла необходимость привести
в единую систему нумерацию глав, параграфов, формул и фигур. Терми-
нология и система обозначений оставлены в том виде, в каком они приме-
нялись автором.
Следует отметить большую работу, проделанную секретарем комис-
сии Н. П. Лесниковой по обработке рукописей академика Б. Н. Юрьева,
и составителя тома, подготовившего его к печати, каид. техн, наук
В. И. Шайдакова. ,
Проф. И. П. Братухин
Проф. С. Г. Козлов
БОРИС НИКОЛАЕВИЧ ЮРЬЕВ
(Очерк жизни и деятельности)
ДЕТСТВО, ШКОЛЬНЫЕ ГОДЫ, СТУДЕНЧЕСТВО
Борис Николаевич Юрьев родился 29 октября (по старому стилю)
1889 г. в городе Смоленске в семье артиллерийского офицера Николая
Александровича Юрьева.
С малых лет он пристрастился к чтению, а пример отца, имевшего в
своем кабинете верстак, приохотил его к ручному труду. Впоследствии,
будучи уже известным ученым,' академик Борис Николаевич находил
время поработать и за верстаком.
Отец его отличался вдумчивым, серьезным характером. Он много
читал, имел обширную библиотеку, занимался изобретательством. Ему
принадлежит ряд патентов, не утративших значения и в настоящее
время. Недавно имя Н. А. Юрьева упоминалось в газете «Красная
Звезда» *, где отмечались его работы в области совершенствования артил-
лерии. Будучи передовым и прогрессивным человеком, Н. А. Юрьев
одним из первых перешел на сторону советской власти..Это не могло
не отразиться на характере и деятельности Бориса Николаевича.
Лето Юрьевы проводили недалеко от Смоленска, в Темниках, у
деда Бориса Николаевича, Александра Семеновича Юрьева, безвыездно
жившего у себя на родине после тяжелого ранения, полученного во
время Севастопольской кампании. На воображение мальчика влияли
рассказы несколько сурового деда. Он слышал и про боевые схватки на
Кавказе, где его дед служил в знаменитом Тенгинском пехотном полку,
и о героических подвигах наших русских солдат и офицеров во время
Севастопольской кампании.
В 1898 г., после переезда в Коломну, Борис Николаевич начал учиться
в гимназии. Однако через два года отца перевели, и на семейном совете
было решено поместить мальчика во Второй Московский кадетский
корпус, где дети офицеров обучались бесплатно, что имело немаловаж-
ное значение для бюджета семьи.
Во время обучения в корпусе (1900—1907 гг.) Борис Николаевич
увлекался естественными науками и математикой. В своих воспомина-
ниях об этом периоде он рассказывает следующее:
«Склонность к изобретательству проявилась у меня весьма рано.
Еще кадетом 4-го класса я пытался изобретать. Нечего н говорить, что
я зачитывался романами Жюль Верна, Уэльса и Робида. Книги по
физике и популярные книжки по технике были любимым чтением.
• 20 августа 1949 г.
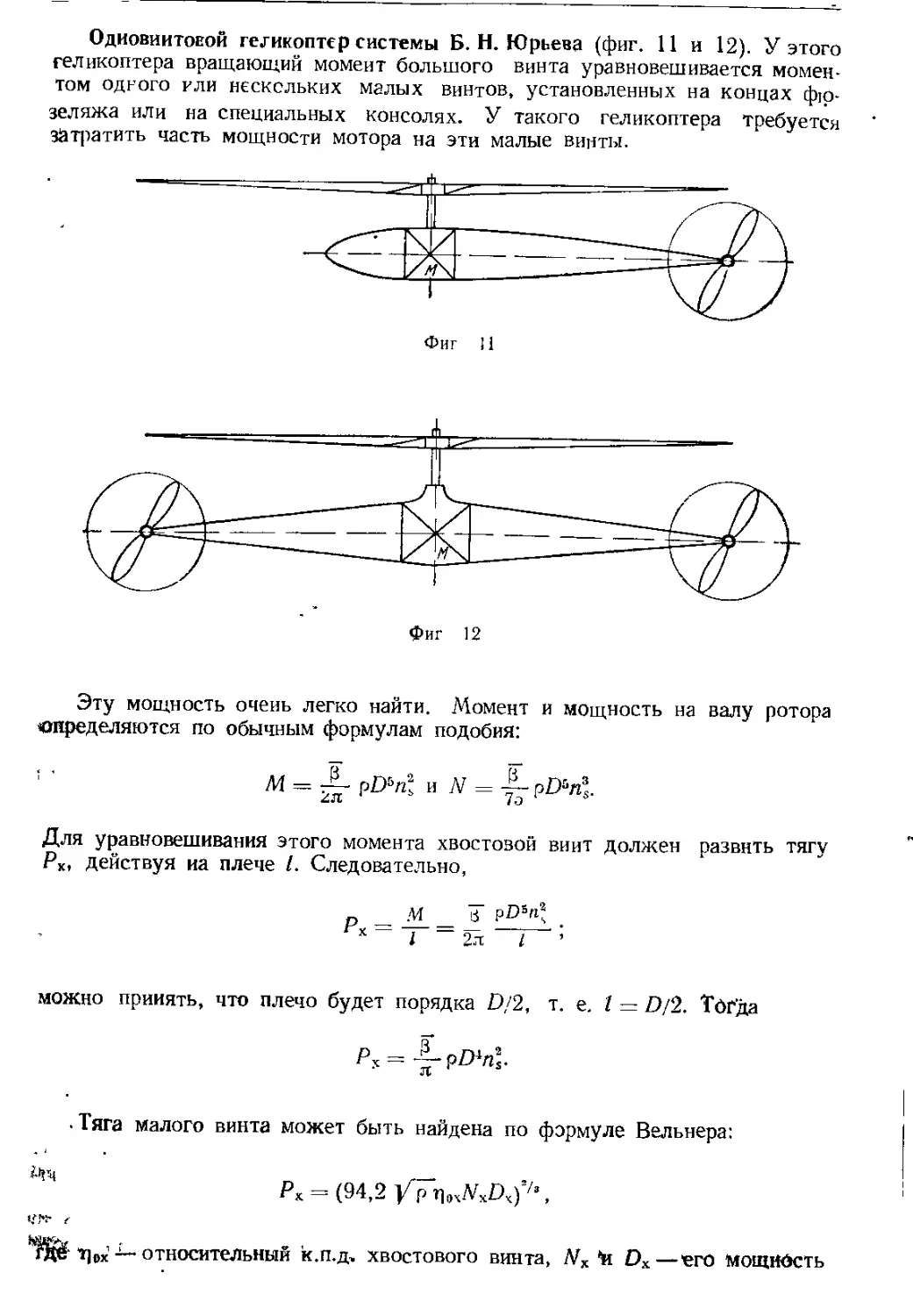
♦иг 1 Одновинтовой вертолет поперечной схемы с двумя рулевыми винтами
Чертеж патентной заипкп Б, Н. Юрьева (1910 ( ) за № 45212
Научился я читать очень рано и читал без разбора все, что попадалось
Отец мой интересовался философией и естествознанием, поэтому у нас
были в русском-переводе Кант, Спенсер, Бэкон, Дарвин, Уоллес и др
Отец мой летом бывал в лагерях, куда брал свою семью. При тогдаш-
ней простоте иравов я все время вертелся около пушек, бывал на стрель-
бах, а после стрельб ездил со знакомыми офицерами к мишеням и
участвовал в подрывании иеразорвавшнхся снарядов. Я хорошо зиал
Рис, 2. Автомат-перекос, изобретенный студентом Б. Н. Юрьевым (Мемориальный
музей Н. Е. Жуковского, фонд академика Б. Н. Юрьева, № 3490/1;
собственный чертеж)
правила стрельбы, был знаком с элементами теории вероятностей и
отличио изучил материальную часть артиллерии. Одно время я увле-
кался пиротехникой, делал ракеты, римские свечи, китайские колеса и
бенгальские огни. На именинах отца бывали всегда гости, офицеры его
батареи и просто знакомые. Пока отец и гости спорили на философские
темы — тогда это было модой у интеллигентов (1901 —1905 гг.),—-я
готовил фейерверк, который и сжигал после ужина.
Игры у меня с немногими товарищами были серьезные. Мы строили
чудодейственные плоты с парусами, рыли в земле крепости и делали
самодельные пушки из всяких трубок, какие только могли получить
или где-либо стащить Здесь годились и старые водопроводные трубы,
футляры от термометров, старые патроны, центральные трубки от
шрапнелей. Пороха было вдоволь. Солдаты артиллерийской лаборато-
рии снабжали нас им в неограниченном количестве к ужасу наших
родителей. Мы проводили из наших самопалов стрельбы, вводя в них
всяческие тонкости, какие видели на действительных стрельбах.
Все это было, понятно, прекрасной технической школой для всех
нас».
Под влиянием романов Жюль Верна, как писал Борис Николаевич,
он заинтересовался проблемой полета и особенно геликоптером. По-
этому, окончив в 1907 г. кадетский корпус с похвальным листом и
наградой, он не пошел в военное училище, а в том же юду поступил
в Московское Высшее техническое училище (МВТУ), где преподавал
проф Н Е Жуковский.
Борис Николаевич прнимал деятельное участие в воздухоплаватель-
ном кружке МВТУ и в период с 1908 по 1910 г. построил с товарищами
три планера, иа которых было осуществлено несколько полетов Им был
Фиг. S Студент Б Н Юрьев — изобретатель геликоптера, экспонируемого
на 2-й Международной выставке воздухоплавания
прочитан ряд докладов по теории и расчету летательных машин. Доклад
о наибольшем полезном грузе, поднимаемом аэропланами и геликоп-
терами при дайной силе моторов, был напечатан в журнале «Автомо-
биль и воздухоплавание» в 1911 г. и явился его первой печатной
работой.
Очень много сил и времени пришлось потратить Борису Николаевичу
и другим членам воздухоплавательного кружка на создание аэродина-
мической лаборатории МВТУ, которая строилась в общественном по-
рядке силами кружковцев. В этой лаборатории Борис Николаевич
спроектировал ряд различных приборов для исследования винтов и
моделей геликоптеров В ней он провел многочисленные опыты с
Фиг 4 Диплом к малой золотой медали, присужденной студенту Б Н Юрьев\ га Межл\народной выставке возлухоплаяания
и автомобилизма в Москве
винтами и летающими моделями. Интерес к геликоптеру, естественно,
заставил его ознакомиться с теорией и расчетом гребного винта.
В то время не существовало теорий, позволяющих конструктору
рассчитывать несущий винт. И вот два молодых энтузиаста, студенты
МВТУ Б. Н. Юрьев и Г. X. Сабинин, взялись за ее разработку. В резуль-
тате была создана теория пропеллера, намного опередившая загра-
ничные работы в этой области, что дало возможность рассчитывать
любые винты, в том числе и геликоптерные. Эта теория была впервые
доложена на Первом Воздухоплавательном съезде (в Петербурге) в
1911 г., где студентом Юрьевым был прочитан доклад о его проекте гели-
коптера и подробно изложен расчет поддерживающего винта.
Впервые теория была проверена на маленьком винте диаметром 0,5 м,
собственноручно изготовленном Борисом Николаевичем из березового
полена. Виит был испытан на только что построенной В. А. Слесаревым
ротативной машине. Замеры показали хорошую сходимость теории с
эксперимейтом. Выводы этой теории были включены Н. Е. Жуковским
в его курс лекций по теоретическим основам воздухоплавания (1911 —
1912 гг.)(под названием «Теория Сабинина — Юрьева». Эта теория
не потеряла своего значения и в наше время, несмотря на то, что сей-
час мы имеем классическую вихревую теорию винтов Н. Е. Жуков-
ского.
Совпадение теории с опытом позволило Борису Николаевичу более
обоснованно приступить к давно задуманной им постройке геликоптера,
о котором он делал доклад на Первом Воздухоплавательном съезде.
Кружок и Леденцовское общество дали ему средства на постройку
геликоптера, и ко Второму Воздухоплавательному съезду (в Москве)
геликоптер был готов и выставлен иа Всероссийской Воздухоплава-
тельной выставке в помещении манежа (ныне выставочный зал). Там
студент Борис Юрьев получил малую золотую медаль за «прекрасную
теоретическую разработку проекта геликоптера». Опыты с этим аппа-
ратом не были доведены до конца, так как выполнение неизбежных для
новых машин переделок и улучшений было не по‘силам студенческой
организации. В то же время Борис Николаевич был вынужден отбывать
воинскую повинность и мог работать в лаборатории лишь в свободное
от занятий время. Мировая империалистическая война 1914 г. заста-
вила прекратить всякие опыты. Борис Николаевич был мобилизован на
фронт.
ПЕРВАЯ МИРОВАЯ ВОЙНА. ГОДЫ ПОСЛЕ РЕВОЛЮЦИИ.
СТРОИТЕЛЬСТВО АЭРОДИНАМИЧЕСКИХ ЛАБОРАТОРИЙ
Блестящее вступление на путь научно-исследовательской деятельно-
сти было прервано наступившей войной, принесшей неисчислимые бед-
ствия всем народам. Борис Николаевич был направлен в крепость Ново-
георгиевск, откуда вскоре его перевели в экскадру воздушных кораблей
типа «Илья .Муромец». Пребывание в эскадре единственных в то время
в-мире воздушных кораблей явилось для него ппекрасным дополнением
к практике московского аэродрома. В июле 1915 г. ои был вызван в
Москву в комиссию Н. Е. Жуковского по разработке зажигательных
бомб. Возвращаясь с партией бомб иа фронт, он при Варшавском отступ-
лении остался в крепости Новогеоргиевск, где принял активное участие в
обороие южного форта крепости. При штурме крепости в августе 1915 г.
после взрыва окруженного неприятельскими войсками форта Борис
Очерк, жизни и деятельности
13
Николаевич с остатками уцелевшего гарнизона был взят в плен (7 авгу-
ста 1915 г.) н более трех лет пробыл в плену.
Несмотря на тяжелые условия жизни в концентрационных лагерях,
молодой ученый старался максимально использовать все возможности
для научной деятельности. При отъезде на фронт он взял с собой разные
книги, но когда его брали в плен, они были уничтожены вместе с дру-
гим имуществом офицеров. Воспользовавшись тем, чго немцы разрешили
пленным выписывать книги, Юрьев собрал для себя небольшую тех-
ническую библиотеку н усердно занялся изучением интересующих его
вопросов. Emv удалось провести там и некоторые самостоятельные
работы по аэромеханике. До настоящего времени сохранился состав-
ленный им в плену конспект по винтам, где он сделал обзор существую-
щих теорий н изложил свои мысли *.
После заключения мира (в конце декабря 1918 г.) Борис Николаевич
вернулся в Россию, вновь был зачислен студентом МВТУ и 5 мая 1919 г.
окончил его, защитив дипломный проект на тему: «Четырехмоторный
тяжелый самолет», сделанный под руководством проф. Н. Е. Жуков-
ского. •
После окончания МВТУ Борис Николаевич активно начал свою тру-
довую деятельность.
Революция коренным образом изменила жизнь страны. Перед науч-
ными работниками открылись невиданные горизонты, открылись такие
возможности, о которых в царское время нельзя было и мечтать, но это
было время полной разрухи в нашей стране. В такой обстановке могли
работать и что-то создавать только подлинные энтузиасты науки и
патриоты, которых было много; к ним принадлежал и Борис Николаевич.
1 октября 1919 г. по представлению проф. Н. Е. Жуковского он был
единогласно избран преподавателем МВТУ и начальником аэродина-
мической лаборатории. С этого момента началась кипучая деятель-
ность Бориса Николаевича сразу в нескольких направлениях, главным
образом по строительству Центрального аэро-гидродинамического ин-
ститута (ЦАГИ).
В 1920 г. он был избран членом коллегии ЦАГИ и одновременно,
кроме МВТУ, начал преподавать в Институте инженеров красного воз-
душного флота, вскоре реорганизованного в Воздушную инженерную
академию имени Н. Е. Жуковского, где он был назначен на должность
начальника кафедры аэродинамики. В это же время он — заместитель
проф. Н. Е. Жуковского в комиссии по тяжелой авиации (КОМТА) и
начальник Конструкторского бюро этой комиссии.
После смерти Н. Е. Жуковского (1921 г.) Борис Николавич во?гла-
вил всю авиационную специализацию (1921 —1930 гг.). Одновременно
ои был заместителем председателя Строительной комиссии ЦАГИ, где
непосредственно руководил проектированием и постройкой аэродина-
мической лаборатории, пущенной в эксплуатацию в 1926 г. и бывшей до
1930 г. самой мощной лабораторией мира.
Еще в 1923 г. Борисом Николаевичем в МВТУ была построена новая
аэродинамическая труба по предложенной им оригинальной схеме.
В 1930 г. начала работать созданная под его руководством аэродина-
мическая лаборатория ВВИА.
В дальнейшем Борне Николаевич участвовал в^работах по постройке
аэродинамических труб ЦАГИ н налаживал в них научно-исследователь-
скую работу.
Этот конспект находится в музее Н Е Жуковского.
Во время второй мировой войны под его руководством в Свердловске
была построена аэродинамическая лаборатория, состоящая из четырех
труб и другого оборудования.
Руководя много лет основными аэродинамическими лабораториями.
Борис Николаевич много занимался разработкой методики аэродина-
мических исследований и стандартизацией применявшихся в этих иссле-
дованиях обозначений. В 1928 г. он предложил новую систему безраз-
мерных обозначений. В 1940 г. он выступил против попытки заменить
отечественные стандарты англо-американскими. Создание при его уча-
стии улучшенного стандарта осей координат и обозначений позволи-
ло упорядочить многочисленные экспериментальные и расчетные ра-
боты. Борис Николаевич был одним из редакторов первого тома
первого издания «Руководства для авиационных конструкторов». За
участие в разработке этого руководства Борису Николаевичу и группе
сотрудников ЦАГИ в 1943 г. была присуждена Государственная премия
второй степени.
Необходимо отмстить работы Бориса Николаевича, связанные с раз-
работкой методики экспериментирования в аэродинамических трубах:
«Аэродинамические исследования» (совместно с Н. П. Лесниковой;
Труды ЦАГИ, № 33, 1928) и «Картина давления» (Труды ВВИА, 1942).
ИССЛЕДОВАНИЯ ПО ВОЗДУШНЫМ ВИНТАМ
Воздушными винтами, как указывалось, Борис Николаевич начал
заниматься с первых лет студенчества, когда им совместно со студентом'
Г. X. Сабининым была разработана новая теория винтов. Толчком к
этому послужил интерес Бориса Николаевича к геликоптерам.
В то время существовали две теории винтов: теория идеального винта
и теория С. К- Джевецкого.
Основы первой были намечены Ранкиным еще в 1865 г. и продол-
жены Фрудсм в 1889 г. Окончательное сфлг.мленне эта теория пол"чила
почти одновременно у Финстервальдера (1909 г.), Рябушинского (1909 г.).
Беидсмаиа (1910 г.), Кюммеля (1910 г.)'и Жуковского (1911 г.). Это
была так называемая обшая теория, по которой нельзя было рассчитать
конкретный винт.
При помощи второй теории, созданной в 1892 г. С. К- Джевецким, уже
можно было решать задачу о проверочном расчете винта заданной
формы.
Расчеты геликоптера по этой теории сильно расходились с данными,
полученными в результате опыта. Наблюдениями было обнаружено, что
у висящего в воздухе геликоптера возникает сильная струя, пересекаю-
щая плоскость вращения несущего винта, однако по теории Джевец-
кого осевая скорость в этом случае равнялась нулю.
Для определения этой обнаруженной скорости было решено объеди-
нить теорию Джевецкого с теорией идеального винта. В результате
было выведено уравнение, названное Б. Н. Юрьевым уравнением связи.
Оно является основой всей теории и содержит группу сомножителей,
которая, как известно, представляет собой циркуляцию скорости. Это
сближает данную теорию с вихревой теорией, возникшей у нас на два
года позднее.
Г. X. Сабинин распространил эту теорию на' случай пропеллера.
Таким образом, уже в 1910 г. мы имели вполне законченную теорию,
охватывающую случаи и геликоптера и пропеллера. За границей подоб-
ные теории появились значительно позже.
Очерк жизни и деятельности
15
В 1922 г. на основе этой теории Борис Николаевич разработал графо-
аналитический метод расчета воздушных винтов, который учитывает
влияние вращения струи н лобовое сопротивление. В дальнейшем, ана-
лизируя вихревую теорию, он задался вопросом: насколько законно при-
менение формул, выведенных для бесконечного числа лопастей, к винтам
с двумя-тремя лопастями? Задача, решенная Жуковским, представляет^
в сущности,' частный случай; в своей первой статье он указывает, что
все вычисления можно было бы вести, опираясь на истинные скорости
'относительного движения жидкости (т. е. не пользуясь средними ско-
ростями), но тогда анализ вышел бы очень сложным.
В работе, напечатанной в «Вестнике воздушного флота» (1923, № 5),
Борис Николаевич ясно показал, что можно преодолеть эту сложность.
Он дал дифференциальные выражения для вызванных скоростей, пред-
ложил графический метод их вычисления и начал эти вычисления.
Но такая работа оказалась для того времени слишком трудоемкой. Пере-
груженный другими работами и никем в то время не поддержанный он не
довел эту работу до конца.
У нас, к сожалению, этим вопросом занялись только после того,
когда японский профессор Томизиро Морийя в 1933 г., т. е. на десять
лет позже, проделал все высчисления по методу, указанному Бописом
Николаевичем, и дал графики функций, необходимые для аэродинами-
ческого расчета винта.
Го, что сделано Борисом Николаевичем для вихревой теории, на-
столько существенно, что получилась как бы новая теория. Поэтому в
отличие от теории, разработанной Жуковским, он назвал ее «относи-
тельной».
В 1925 г. вышла работа Бориса Николаевича «Воздушные гребные
винты (пропеллеры)»*, в которой изложены: теория идеального про-
пеллера, закон подобия для винтов, расчет винтов в присутствии само-
лета, расчет винтомоторной группы, винта тандем и т. д. В 1927 г. эта
книга была переведена на итальянский язык.
В 1934 г. вышел в свет учебник Бориса Николаевича «Воздушные
винты», который был принят во всех авиационных втузах. В нем впер-
вые теории винта рассматривались в их взаимной связи, например,,
теория идеального винта излагалась на базе безразмерных коэффициен-.
тов, принятых в теории подобия. Это позволило более глубоко и с
единой точки зрения рассматривать работу винта и дало возможность
строить более удобные диаграммы для расчета. Примененные в его
книгах обозначения вошли в наш действующий в авиации стандарт
СР-49.
В связи с преподавательской деятельностью Борис Николаевич много
занимался методическими вопросами, в частности уточнением и упроще-
нием классической вихревой теории, которая для начинающих была
несколько тяжела. В результате в 1947 г. появилась его работа «Вихре-
вая теория винтов» — краткое руководство по аэродинамике вннтов для
студентов и инженеров, дающая все необходимое для начала практиче-
ской работы.
Вихревая теория, несомненно, более совершенна, чем теория Саби-
нина— Юрьева. Однако последняя обладает большим преимуществом —
простотой, не уступая по точности классической вихревой теории. Учи-
тывая это, Борис Николаевич переработал и значительно дополнил ее.
Данная работа вышла в свет в 1948 г. под названием «Импульсная
теория воздушных вннтов».
* Изд. ЦАГИ, вып. № 10.
РАБОТЫ ПО СОЗДАНИЮ ВЕРТОЛЕТОВ
Борис Николаевич был ученым-инженером с широким научным круго-
зором; он успешно работал в различных областях науки. Поражает
разносторонность его научных интересов. Наряду с теоретической и при-
кладкой аэрогидродинамикой, Бориса Николаевича увлекали теоретиче-
ская механика, термодинамика, баллистика, ракетная техника, радио-
техника, космогония, история техники. Из многогранной деятельности
особенно ярко выделяется его творческий труд в области геликоптеров
или, как теперь принято называть, вертолетов.
Борис Николаевич, как было упомянуто, является изобретателем
одновинтовой схемы вертолета. Это поистине крупное изобретение, полу-
чившее мировую известность, было сделано им еще в 1910—1911’гг.
К этому же периоду относится изобретение оригинальною меха-
низма для управления геликоптерами — автомата-перекоса. До настоя-
щего времени, т. е. спустя полвека, вертолеты во всем мире, за немно-
гими исключениями, строятся с автоматом перекоса Б. Н. Юрьева.
В условиях самодержавия трудно было чего-либо добиться. Царские
чиновники не могли по достоинству оценить эти замечательные изобре-
тения, а наступившая империалистическая война прервала работы
Бориса Николаевича в области гелико'птеростроения. Однако он никогда
не расставался с мечтой о решении проблемы вертолета.
Только при Советской власти были созданы все условия для реали-
зации задуманных им проектов. В первые же годы после революции
Борис Николаевич начал увлекаться конструкторской инженерной дея-
тельностью. В 1925—1926 гг. он руководил специально созданным
отделом ЦАГИ, занимавшимся проектированием вертолетов. Именно в
этот период ои проанализировал все основные схемы вертолетов: одно-
винтовую, соосную, продольную, поперечную. Несколько позднее вместе
со своими учениками он произвел глубокий анализ летных свойств всех
этих схем и показал перспективы их развития.
В 1930 г. по одновинтовой схеме Юрьева был создан первый совет-
ский вертолет ЦАГИ 1-ЭА, спроектированный под руководством Бориса
Николаевича группой его сотрудников и учеников. Это был первый в
мире успешно летавший вертолет, на котором в 1932 г. инженер, а впо-
следствии профессор А. М. Черемухин поставил неслыханный по тому
времени мировой рекорд высоты 600 м.
Много времени и сил тратил Борис Николаевич на обдумывание раз-
личных схем вертолетов. Ему принадлежит большое количество патентов,
ярко свидетельствующих о приоритете нашей страны в области всрто-
летостроения. Так, в 1922 г. он получил патент на многовннговой вер-
толет со специальной системой управления (патент № 1526), описание
которого дано им в ряде работ по истории вертолетов.
В 1924 г. Борис Николаевич сделал заявку о выдаче ему авторского
свидетельства на реактивный турбопропеллер и устройство для его
использования (патент № 761, авторское свидетельство № 77996). Идея
реактивного винта в то время была >же известна: воздух, подаю-
щийся внутрь полых лопастей при помощи компрессора, приводимо-
го в действие мотором, выходил из их концов, вызывая реактивную
тягу.
Борис Николаевич разработал новую схему реактивного винта.
Ои предложил сжигать горючее внутри полых лопастей винта, исполь-
зуя подводимый к ним воздух, а продукты горения выводить через сопла
на концах лопастей. Пон этом благодаря реакции струн подогретого
К ПАТЕНТУ Б. Н. ЮРЬЕВА № 761
Фиг. 5 Реактивный турбо-пропеллер и устройство для его использования
(чертеж к патенту Б. Н. Юрьева за № 761. 1924 г)
воздуха пропеллер получает энергию вращения. Идея сжигания горю
чего внутри лопастей в настоящее время претворена,в жизнь на ряде
вертолетов заграничных конструкций.
В дальнейшем Борис Николаевич неоднократно возвращался к реак-
тивным винтам. В 1948 г. его привлекла идея привязного реактивного
вертолета. В отлнчне от вертолетов подобного типа, имеющих воздушные
винты, питаемые током с земли, ротор предложенного им вертолета был
выполнен в виде реактивного винт?, внутри лопастей которого установ-
лены электрические элементы для подогрева воздуха, используемого
в качестве рабочего тела и подсасываемого самим винтом у втулки
(авторское свидетельство № 378843 от 17 м^я 1948 г.).
В 1951 г. Б. Н. Юрьеву был выдан патент на новый тип реактивного
винта (авторское свидетельство № 13475).
В 1940 г. Юрьев организовал и возглавил специализированное верто-
летное конструкторское бюро при Московском авиационном институте,
где под руководством И. П. Братухина был спроектирован и построен
вертолет поперечной схемы.
21 января 1946 г. за создание нового типа самолета-геликоптера
(совместно с И. П. Братухиным) Б. Н. Юрьеву второй раз была присуж
дена Государственная премия.
В последние годы жизни Борис Николаевич много занимается кры
латыми -вертолетами, вертикально взлетающими самолетами; в этой
области ои имеет запатентованные схемы.
Борис Николаевич является основоположником науки о вертолетах.
В его Трудах: «О наибольшем полезном грузе, поднимаемом самолетом
и геликоптером» (1911 г.), «Исследование летных свойств геликоптеров»
(1939 г.), «Импульсная теория воздушных винтов» (1948 г.) и «Аэро
динамический расчет вертолетов» (1956 г.) изложены основы теории
несущего виита, динамика и аэродинамический расчет вертолетов, изы
екания рациональных размеров, опенка схем, заложены научные основы
весового анализа вертолетов, обобщены и проанализированы экспери-
ментальные данные, полученные в аэродинамических трубах с моделями
несущих винтов. Этими работами пользуются в конструкторских бюро,
они являются прекрасными учебными пособиями для подготовки кадров..
По инициативе Б. Н. Юрьева в 1953 г. в МАИ была организована
кафедра «конструкции и проектирования вертолетов», которой он руко
водил в течение пяти последних лет своей жизни. В лице Бориса Нико
лаевича вертолетостроение находило пламенного защитника. Ои сплотил
вокруг себя коллектив инженеров-конструкторов, направлял их на
решение задач вертолетостроения. Его боевая горячая пропаганда идеи
вертолета много содействовала тому, что мы сейчас имеем многочислен-
ные высококвалифицированные кадры, создающие и внедряющие в-
жизнь советские вертолеты.
РАБОТЫ ПО АЭРОДИНАМИКЕ САМОЛЕТА
Эти работы большей частью возникали в связи с запросами практики
Еще будучи студентом, Борис Николаевич прочитал в Воздухоплава
тельиом кружке несколько докладов по теории аэроплана.
В советское время он впервые на русском языке систематически
изложил теорию индуктивного сопротивления крыльев. Эта теория в
1918 г. была разработана проф. Прандтлем и его учениками. Одиако
значительно раньше, в 1910—1913 гг., основные положения теории ин
луктнвного сопротивления были изложены в неизданных работах
С. А. Чаплыгина и применены Н. Е. Жуковским в вихревой теории винтов
(1912 г.). Для практического же применения к крылу самолета эти основы
разработаны не были.
Борис Николаевич ие только систематически изложил теорию инд>к
тивного сопротивления с присущей ему ясностью, но и детально разра-
ботал ряд весьма важных для практики вопросов. Ои выпустил по этому
вопросу три работы. Первой вышла литографированная брошюра, издан
ная в 1922 г. Институтом инженеров красного воздушного флота *
(ныне Академия имени Н. Е. Жуковского). Затем в ЦАГИ была напеча-
тана его книга «Индуктивное сопротивление крыльев аэроплана». Ряд
предложенных там методов применяется и в настоящее время.
Вышедшая в 1938 г. вторая часть курса «Экспериментальной аэро-
динамики» была в основном посвящена вопросам индуктивного сопро
тивлення н имела объем 19 печатных листов — настолько развилась к
этому времени эта теория. В нее Борне Николаевич включил ряд своих
исследований и исследований других, преимущественно отечественных
авторов. Изложенные в ней методы расчетов применяются у нас в
самолетных конструкторских бюро и во втузах.
В 1923 г. Б. Н. Юрьевым была напечатана статья «Определение
аэродинамических свойств крыльев произвольного очертания в плане»*,
в которой изложен простой и наглядный способ расчета.
В работе «Пересчет монопланов на биплан» ** Борисом Николаеви-
чем предложен инженерный прием расчета бипланной коробки крыльев
на основе теории индхкции. Впоследствии его развил проф. С. Г. Коз-
юв.
Борис Николаевич принимал участие и в усовершенствовании аэро
динамического расчета самолета; главное внимание он уделял более
точному, чем это делалось ранее, учету характеристик винтомоторной
группы. У нас до 1925 г. тягу винта рассчитывали, принимая постоян-
ный коэффициент полезного действия, или исходили из теории идеаль-
ного пропеллера. Кроме того, мощность мотора бралась, по Жуковскому,
прямо пропорциональной плотности воздуха. Вследствие этого потолки
некоторых наших опытных самолетов в период с 1923 по 1930 г. во
время летных испытаний равнялись всего 3000—5000 я вместо «расчет-
ных» 5000—8000 м Скороподъемность самолетов также оказывалась в
несколько раз меньшей. Изложенный Борисом Николаевичем метод
расчета, применяемый и в настоящее время, и приведенный материал
по зарубежному опыту позволили нашим конструкторам получить
хорошее совпадение расчетов с результатами летных испытаний. В этот
метод внесено теперь много усовершенствований, в основном советскими
учеными.
В 1922 г. Юрьев предложил графический способ аэродинамического
расчета самолета, основанный на положенной на бок поляре***. Этот
способ нашел отражение в ряде учебников и в исследовательских рабо-
тах наших авторов (В. С. Пышнова, В. Л. Моисеенко, И. В. Остослав-
ского и др), под названием способа Юрьева.
До второй мировой войны Борис Николаевич был председателем
Экспертной комиссии по новым самолетам в Народном комиссариате
авиационной промышленности, что весьма способствовало его научной
работе.
ПЕДАГОГИЧЕСКАЯ И ОБЩЕСТВЕННАЯ ДЕЯТЕЛЬНОСТЬ
Вся научно-экспериментальная база для развития авиации в нашей
стране — основные аэродинамические лаборатории, без которых не-
мыслимо успешное развитие авиации,—создана при непосредственном
* «Вестник воздушного флота», № 2, 1923
** Тоуды ВВИА, № 5, 1933
*** Б. Н. Юрьев Новый прием аэродинамического расчета, М. изд. Высшего во
енного редакц Совета *
участии и под руководством Бориса Николаевича. -Его трудам мы обя-
заны развитию основ теории воздушного винта, прежде стоявшей
на неправильных представлениях; его трудами заложен и фундамент
так называемой «относительной» или «лопастной» теории винтов, наи-
более точной и совершенной в настоящее время. Мы с гордостью мо-
жем сказать, что благодаря трудам Б. Н. Юрьева наша страна яв-
ляется родиной вертолетостроения; весь мир использует его изобре-
тение.
Почти сорок лет своей жизни (1920—1957 гг.) Борис Николаевич
посвятил преподавательской работе, внося в нее тот же живой огонь,
что и в научную н инженерную деятельность.
Огромные познания, исключительная память, знание нескольких
языков, личное участие во многих проводимых по авиации мероприятиях
давали ему возможность строить лекции иа высоком уровне. Его заме-
чательные лекторские данные неоднократно отмечались приказами и
наградами. Успеху лекций Бориса Николаевича способствовало также
то, что ои, будучи пламенным энтузиастом авиации, сумел передать
этот энтузиазм и молодежи. За годы педагогической деятельности он
читал курсы аэродинамики, воздушных винтов, винтокрылых машин,
занимался проектированием самолетов, вертолетов, аэродинамических
труб, временами возглавлял кафедры аэродинамики одновременно в
нескольких учебных заведениях. Так, ои руководил кафедрой аэроди-
намики в ВВИА (1920—1949 гг.) и в Московском авиационном инсти-
туте (1929—1940 гг.), который был выделен из МВТУ по его инициа-
тиве.
В 1925 г. Борис Николаевич был утвержден в звании профессора.
В 1935 г. ему была присвоена ученая степень доктора технических
наук. В 1940 г. за работу в Московском авиационном институте ои по-
лучил звание заслуженного деятеля науки и техники РСФСР; 27 сен-
тября 1943 г. был избран в действительные члены Академии наук
СССР.
Борис Николаевич имел и воинские звания: в -1939 г. ему было при-
своено звание бригадного инженера, в 1942 г.— звание генерал-майора,
в 1944 г.— звание генерал-лейтенанта. В Военно-воздушной академии
имени Н. Е. Жуковского Борис Николаевич проработал с 1920 по 1949 г.,
когда по приказу Министра Вооруженных сил был откомандирован в
распоряжение Академии наук СССР.
Занимая ответственные должности (заместитель начальника Военно-
воздушной академии по научной работе, заместитель академика-секре-
таря Технического отделения Академии наук СССР, заместитель пред-
седателя Совета филиалов Академии наук, руководитель группы при-
кладной аэродинамики Института механики АН СССР и др.), Борне
Николаевич всегда был прост, доступен каждому; особенно сердечно он
относился к молодежи. Ему абсолютно чужды были самомнение и за-
знайство. Им подготовлено большое число научных работников; многие
из них имеют теперь ученые степени кандидатов и докторов наук, мно-
гие стали лауреатами.
Борис Николаевич является автором многочисленных научных тру-
дов. Им опубликовано более 100 работ. Его учебники по эксперимен-
тальной аэродинамике и воздушным винтам широко используются в
конструкторских бюро и втузах, многочисленные статьи в журналах и
газетах по широкому кругу научно-технических вопоосов способство-
вали популяризации многих проблем советской техники, помогли уста-
новить приоритет советских ученых и изооретателей. В этом отношении
Очеок жизни и деятельности
Фиг. б Факсимиле одной из страниц рукописи книги Б Н. Юрьева
«Аэродинамический расчет вертолетов» (Оборонгиз. 1956)
особенно интересны его работы по истории авиации, о его учителе
Н. Е. Жуковском, о С. А. Чаплыгине и другие.
Борис Николаевич всегда проявлял большую активность при реше-
нии различных общественных вопросов. Он был активным членом раз-
ного рода добровольных обществ и организаций по авиации, депутатом
Московского совета (1928 — 1930 гг.), председателем месткома Москов-
ского авиационного института, председателем секции научных работ-
Очерк жизни и деятельности
ников (там же), активно работал в Обществе по распространению по-
литических и научных знаний, где состоял членом Правления (с 1947 г..),
руководил научной деятельностью Политехнического музея (был пред
ссдателем Ученого совета).
Правительство высоко оценило заслуги Бориса Николаевича Юрь
ева и наградило его двумя орденами Ленина, орденом Красной Звезды,
орденом Отечественной войны 1-й степени и несколькими медалями
Академик, генерал-лейтенант инженерно-авиационной службы, дваж-
ды лауреат Государственных премий, заслуженный деятель науки и тех-
Борис Николаевич Юрьев скончался в Москве на 68-м году жизни
14 марта 1957 года.
Старший научный сотрудник Института механики АН СССР
В Л. Константинов
Раздел I
ВОЗДУШНЫЕ ВИНТЫ
ИМПУЛЬСНАЯ ТЕОРИЯ ВОЗДУШНЫХ винтов
Глава 1
ОСНОВНЫЕ ФОРМУЛЫ
ИМПУЛЬСНОЙ ТЕОРИИ ВИНТА
§ 1. СКОРОСТИ В СТРУЕ, СОЗДАВАЕМОЙ ВИНТОМ
Струя винта. Винт в этой теории рассматривается, как и в других
теориях, в обращенном движении: он вращается с числом оборотов
ns в секунду, но не летит вперед, а обдувается потоком воздуха, име-
ющим скорость, равную, но противоположную скорости полета. На чер-
тежах скорость полета и окружную скорость вращения г<о будем
обозначать оперенными стрелками, скорости воздуха относительно вин-
та, т. е. обратные скорости, будем
буквы же будем применять од-
ни и те же.
Для изучения работы лопа-
стей винта на радиусе г будем
вырезать элементы лопасти с
помощью двух бесконечно
близких цилиндрических сече-
ний: одного с радиусом г, а
Другого с радиусом r + rfr. При
^-лопастном винте получится k
изображать простыми стрелками,
Фиг 1 Фиг 2
таких элементов (на фиг. 1 залиты черной краской). Эти k элементов
бУдут развивать общую тягу dP и требовать на вращение общее окруж-
ное усилие tlQ.
При работе эти сечения будут ометать заштрихованную кольцевую
площадку (фиг. 1) и заставят окружающий воздух протекать через это
.кольцо. В результате возникает элементарная кольцевая струя воздуха,
имеющая, как показывают опыты, воронкообразную форму (фиг. 2).
Пересекая эту струю плоскостями, нормальными к осн винта, будем
получать кольцевые сечения; в пределах каждого такого сечения можно
считать скорость текущего воздуха величиной постоянной.
Первой и основной задачей излагаемой теории является нахожде-
ние скоростей течения воздуха в кольцевой струйке. Проведем трн нор-
мальных к оси винта сечения 0, 1 и 2. Сечейне 0 выберем так далеко
от винта, что там не будет сказываться его влияние. Скорость набега-
ющего потока будет там равна скорости полета /о, но направлена в
противоположную сторону.
Сечение 1 проведем через плоскость вращения вннта. В этом сече-
нии благодаря подсасывающему эффекту винта скорость потока будет
больше скорости потока в сечении 0. Обозначим осевую составляющую
этой скорости через VY Тогда можно написать
(1)
Скорость Vi называется скоростью подходящего воздуха, а добавоч-
ная скор.ость Vf—скоростью подсасывания.
Кроме подсасывания, винт будет закручивать струю в сторону сво-
его вращения. Обозначим скорость вращения струн в сечении /, т. е.
скорость, "перпендикулярную к оси винта и осн лопасти через Uj. Заме-
тим, что перед сечением 1 струя не будет вращаться, так как никаких
вращательных импульсов к ней приложено не было. После прохождения
через сеченне 1 струя будет вращаться со скоростью и', так как к ней
приложен окружной импульс от силы dQ. Далее покажем, что
Сеченне 2 проведем далеко за винтом, где струя перестает сжимать-
ся н делается цилиндрической. Осевая скорость в этом сечении будет
больше, чем в сечении 1. Обозначив ее через V2, можем написать
У%=У0+^2- (2)
Скорость V2 называется скоростью уходящего-воздуха, а Уг — ско-
ростью отбрасывания. Струя в этом сечении будет вращаться со скоро-
стью «2- Эта скорость в обычных условиях работы винтов, как увидим
далее, близка к скорости id.
Давление воздуха в сечении 0 равно атмосферному, так как до него
не доходит влияние вннта. Давление воздуха в сечении 2 также можно
принять равным атмосферному, так как струйка 1ам имеет цилиндриче-
скую форму, и разность давлений на разных радиусах может получить-
ся лишь за счет центробежных сил вращающейся струн. Так как ско-
рость закручивания в обычных условиях работы вннта очень мала, то,
как показывает опыт н подтверждает вихревая теория, изменением дав-
ления воздуха в ссченнн 2 можно во многих случаях пренебречь.
Применение теорем импульса и живой силы к струе
Приняв этн условия, мы приходим к выводу, что на воздух, заклю-
ченный в воронкообразную кольцевую струйку, будут действовать по
закону действия н противодействия элементарная сила тяги dP и ок-
ружное усилие JQ, взятые в обратную сторону. Воздух действует на
лопастн, вызывая силы dP и dQ, а лопастн с равными, но обратно1 на-
правленными силами действуют на воздух.
Напишем равенство импульса силы, действующей на воздух и обрат-
ной тяге, приросту осевой составляющей количества движения воздуха,
проходящего через нашу струйку. Пусть масса воздуха, протекающего
§ 1. Скорости в струе, создаваемой винтом.
через кольцевые сечения вннта в секунду, будет равна dm; эта масса,
или, точнее, массовый расход струи, будет в силу неразрывности потока
одинаковым в сечеинях 0, 1 н 2. Количество движения проходящего че-
рез сечение 0 воздуха будет равно dm-Vo, а количество движения, ухо-
дящего через сечеиие 2 воздуха, будет равно dm - V2. Интервал времени
возьмем в одну секунду. Тогда импульс силы dP будет равен самой
силе.
В этих условиях уравнение импульсов напишется в виде:
dP = dm V2-dm 14 = dm (V2—Vo)>
но
, 14 = Ko + 02
и, следовательно,
dP—dmv2. (3)
Тяга винта равна секундному количеству движения, соответствующего
скорости отбрасывания v2. ,
Силу окружного сопротивления dQ вычислим по теореме о равен-
стве момента импульса силы приросту момента количества движения в
струе. Так как до винта струя не вращается, то секундный прирост мо-
нета количества движения будет равен dm и', где и' — скорость вра-
щения струн непосредственно за сечением 1. Беря для импульса интер-
вал времени в одну секунду, получим:
г dQ = г dm и’
или
dQ~dmu'. (4)
Скорость и1, соответствующая радиусу г, при переходе к сечению 2
изменится, так как вследствие воронкообразной формы струи радиус струй-
ки изменится и будет равен уже г2. Обозначив эгу скорость через и2 и
применяя теорему о постоянстве секториальной скорости, можем напи-
сать
и'г = «2г2.
У обычных винтов сжатие струи мало. Кроме того, в центре струи
обычно находится фюзеляж или мотогондола, расширяющие струю. Поэто-
му в обычных случаях можно с достаточной точностью считать, что
тогда из предыдущего выражения получим
и' ^и2,
и формула (4) примет внд:
dQ — dm и2. (5)
Напишем уравнение живых сил, применительно к нашей кольцевой
струйке. Работа, полученная струей в сеченин / от лопастей вннта, вызовет
прирост в струйке кинетической энергии.
Полученная струей в секунду энергия будет равна
dP + dQ их.
Пользуясь выражениями для dP и dQ, можно записать:
dm VtVj + dm (6)
Для подсчета живых сил возьмем два поперечных сечения струи:
нулевое — далеко перед виитом и второе—-далеко за виитом, там, где
давление воздуха можно принять равным атмосферному. В нулевом сечении
секундная живая сила будет равна:
— dm V®.
2
Во втором сечении струя будет иметь скорость IF2, полученную вектор-
ным сложением скоростей V2 и и2; радиальной скорости вследствие цилин-
дричиостн струи во втором сечении не будет. Тогда мы сможем написать:
IT’s -~-dru 1/1-у -L dm и2.
(7)
енл:
Пользуясь выражениями (6) и (7), можно написать уравнение живых
dmv2ViJrdm u2U! — ~-dm(V2 + ul) ——dmVo,
Сокращая на dm и вводя обозначения •= Va -f- vz и — Vz0-~- получим
(Vo + yi) + — — ((Vo 4* vj)2 4- u® Vl}.
Раскроем скобки н перегруппируем члены:
+ utu2 = (и2 + и22)
или
(8)
Полученное уравнение должно всегда соблюдаться для рассматриваемой
кольцевой струйки воздуха. Однако скорости v3 и и2 ничем друг с другом
не связаны, и для соблюдения условия (8) для любых значений v2 и и2
необходимо, чтобы выражения в скобках равнялись нулю, т. е.
или
«2=2«i.
(9)
Этот вывод чрезвычайно важен для теории винтов. Его можно сфор-
мулировать кратко так: у винта скорость отбрасывания в два раза боль-
ше скорости подсасывания, и скорость вращения струи за виитом в два
раза больше скорости вращения в плоскости винта.
Вывод этой зависимости был основан на предположении, что давле-
ние в сечении 2 равнялось атмосферному. На самом деле отходящая от
винта струя медленно вращается, и от действия центробежных сил дав-
ление воздуха в сечении 2 несколько изменяется по радиусу Одиако эта
разность давлений обычно очень мала и, как показывают многочислен-
ные лабораторные исследования винтов, ею можно пренебрегать. Вихре-
вая теория Жуковского позволяет учитывать эти давления, но так как
они очень малы, то при обычных расчетах по теории Жуковского ими
обычно пренебрегают.
Соотношения (9) можно считать доказанными прямыми опытами по
изучению струи винта. В настоящее время этими соотношениями пользу-
ются во всех новейших теориях винтов.
Скоростной многоугольник сечення винта
Развернем на плоскости цилиндрическое сечение винта для какого-
нибудь радиуса г (фиг. 3). Тогда получим разрез лопасти в виде крылооб-
разного профиля и сможем нанести на чертеж скоростной и силовой мно-
гоугольники. Этот профиль будет вращаться с окружной скоростью г<о н
двигаться поступательно с осевой скоростью Vz0, как указано оперенными
-стрелками. Для рассмотрения явления в относительном движения обратим
на чертеже эти скорости, как показано простыми стрелками. К этим ско-
ростям мы должны еще прибавить вызванные самим винтом скорости vt
и щ. Результирующая скорость, с какой воздух будет набегать на наш
Профиль, представится вектором WIt причем
- TW Vo + + ttp
Скорости ц-j и можно заменить вектором w,. Тогда
J Wi | = Н- «г
или
•w, = а-! н W] гы -- Ко -г (10)
Угол р называется углом притекания потока к профилю лопасти. Раз-
ность между ф и 3 будет углом атаки профиля, т. е.
<х = ф — 3-* (и)
Вектор Wo = гы -г Ко называется кажущейся скоростью относительного
движения, а угол 30 — кажущимся углом притекания потока. Соответствен-
но угол атаки ak ~ ф —- Зо будем называть кажущимся углом атаки про-
По аналогии с крыльями, угол е между векторами Wj и Wo будем
называть углом скоса потока, а скорость — индуктивной скоростью.
В сечении 2 мы получим скорости г>2 = 2^ и n2 = 2uj. Складывая их
геометрически, получим:
|Wj| V* -I- U2.
(12}
Очевидно, что
w2 = 2w,.
(13)
Теория С. К- Джевецкого, разработанная в 1892 г., не учитывала совер-
шенно индуктивных скоростей. В излагаемой теории эти скорости играют
основную роль.
л ’§ 2. УРАВНЕНИЕ СВЯЗИ
Рассмотрим теперь силы, действующие на один элемент лопасти: осевую
dPt и окружную (/Qj. Для fe-лопастного виита получим:
dP, = - dP,
k
dQt = - dQ.
k
(14)
Складывая силы dPx и dQlt получим полную аэродинамическую силу dR^,
действующую иа этот элемент:
dRv = V dP* + dQj =
±Vdp-‘+ dQ*.
R
(15}
Подставляя найденные ранее выражения для dP и dQ [формулы (3) и (5)],
получим:
dRi = (dm и2)2 -j- (dm u2)2 = — У u2 -j- u2 = — w2, (16}
k k k
где — индуктивная скорость далеко за винтом.
Следовательно, равнодействующая аэродинамических сил, действующих
4
на элементы лопасти, равна --й полного секундного прироста количества
Движения в элементарной струйке. Замечая, что по формуле (13) &y2 = 2^j,
получим:
Так как сила dRt направлена в сторону, обратную приросту количества
движения, то скорость до, будет параллельна силе dRi.
dR.Ww,. (18)
Формулы (16) и (17) выражают равенство импульса обратно направленной
силы dRt изменению количества движения в струйке.
у V риопепис соло-
Напишем формулу (17) в развернутом виде Массовый расход струйки
можно записать в таком виде:
dm = р2лг dr |V\|. (19)
Здесь p — массовая плотность воздуха, а 2лг dr — площадь кольцевого
сечення струйки .в плоскости 1. Скорость должна подставляться в эту
формулу по абсолютному значению, так как масса является скаляром и от
направления скорости Vy не зависит. В дальнейшем будут рассматриваться
случаи, когда знаки скоростей будут меняться, и без соблюдения этого
правила могут получаться ошибки.
Там, где это не вызовет недоразумений, будем писать вместо | |
просто
Подставляя это выражение в формулу (17), получим:
(//?] = у р | /Д w^rdr. (20)
Эта формула дает элементарную силу dRt, вычисленную по струе. Однако
эту же силу можно вычислить по обычной формуле экспериментальной
аэродинамики:
г,
(21)
где cR— коэффициент полной аэродинамической силы, — относительная
скорость воздуха, a S— площадь крыла. В нашем случае ширина крыла Ь,
длина dr, площадь его dS — bdr. Коэффициент следует брать не прямо из
опытов, а после пересчета крыла на бесконечное удлинение по правилам
теории индуктивного сопротивления, так как индуктивная скорость уже
учтена *.
Для нашего случая можно написать:
d$L — cR - bdr. (22)
Очевидно, что сила dR{, вычисленная по струе [формула (20)], должна
равняться силе, вычисленной по крылу [формула (22)]. Следовательно,
----Р /1 w-.rdr = с,У----bdr.
k 1 1 1 1 н 2
Сокращая и перенося скорости в левую часть равенства, получим:
Это соотношение является основной формулой излагаемой теории. Бу-
дем называть его уравнением связи, так как оно связывает скорости в струе
(левая часть формулы), с сечением винта (правая часть формулы).
* Б. Н. Юрьев. Экспериментальная аэродинамика, ч. I М., Оборонгиз, 1939,
стр. 158; Экспериментальная аэродинамика, ч. 1! Оборонгиз, 1938, стр. 3.
Введем для краткости обозначение
Величину К будем называть коэффициентом ширины профиля, и урав-
нение связи напишем окончательно в виде:
= (25)
С помощью этой формулы находятся скорости в струе виита.
Заметим, что сила dRr с направлением скорости составит угол, рав-
ный 90J 4- ц. Если бы не было трения, то сила dRr была бы перпендикулярна
к скорости сила трения отклоняет полную аэродинамическую силу на
угол ц назад. Величину этого угла можно найти, как известно из курса
экспериментальной аэродинамики, из соотношения:
ц = arctg , (26)
где схр и Су — обычные коэффициенты сопротивления и подъемной силы
крыла для бесконечного размаха.
С осью винта сила dRi составляет угол 3 4- ц, как это легко усмотреть
из фиг. 3, для чего достаточно провести иормаль ON к скорости угол
OyON = 3 вследствие того, что j_ ON и rco _l OOi. Если это так, то и
вектор индуктивной скорости Wj будет в силу условия (18) стоять под
углом 3 4- р, к оси винта, т. е.
Z (®il ООГ) = / (dRf, Wt) = PZp. (27)
Заметим, что обычно элементы лопасти винта работают на углах атаки,
лежащих в пределах 0—15°, и с достаточной точностью можно принять
что
CR-C!t (27')
и
М-1 (в радианах) (28)
1
или
р. —57,3—(в градусах) (28')
S
Уравнение связи (23) является основным уравнением излагаемой теории
с его помощью и с помощью соотношений (18), (24) — (27) можно решать
все аэродинамические задачи о работе винта.
Заметим, что величина Wi является вектором, всегда противоположным
вектору dRi- Вычисляя величину wL по формуле (25), можно получить как
положительное, так и отрицательное значение. Условимся брать всегда
по абсолютному значению, направляя ее в обратную сторону по отноше-
нию dRv
§ 3 Силы, действующие на элемент лопасти, и мощность
33
§ 3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЭЛЕМЕНТ ЛОПАСТИ,
И МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ЕГО ВРАЩЕНИЯ
Вычислим силы, действующие на кольцевой элемент виита. В кольце бу-
дет работать k элементов лопастей шириной b и длиной dr.
Из фиг. 4 видно, что, разлагая силу dRi на осевую и окружную со-
ставляющие, мы получим элементарную силу тяги dPi и элементарное ок-
ружное усилие dQi, действующие на одну лопасть.
Тяга и усилие, развиваемые всем кольцевым эле-
ментом, будут в k раз больше:
dP = k dP, ^k^dRi cos (p 4- g), ) 9q,
dQ = k dQi=\k dRi sin (Р]+p,). / ' '
Мощность, затрачиваемая иа кольцевой ^элемент
виита, получится в виде:
dT = dQr<i).
Подставляя в найденные формулы величину dRj по формуле (22), получим:
dP = cRk —cos (Р4* р.) bdr\ (31)
dQ = cRk sin (Р 4- И) bdr;
dT = cRk sin (Р + р.) bra dr.
(32)
(33)
Полная сила тяги Р кг и потребляемая винтом мощность Т кгм/сек полу-
чаются путем интегрирования найденных выражений по всей длине лопа-
стей.
На практике ввиду сложности этих выражений задачу решают обычно
графически, для чего удобно строить диаграммы (фиг. 5), на которых по
оси абсцисс отложено значение радиусов винта, а по ординатам вычислен-
ные по формулам (31) и (33) производные и -у— . Эти производные
являются, очевидно, погонной нагрузкой лопастей тягой и мощностью-
dP 1.1. р1Г1 /о , ,
— = cRkb — cos(3 + ц).
ИТ
----= cDkb--------га) sin (р 4- р.).
dr R 2 v
(34)
(35)
v_j , _ dp dT
па фиг. 5 приведены типовые кривые —— и —
34
Г лава 1. Основные формулы импульсной теории винта
Полная тяга и мощность винта могут быть представлены формулами:
мня-
я
dT \
dr )
dr,
(36)
(37)
где г0 — радиус, на котором начинается нерабочая часть винта (колпак-об-
текатель втулки), и 7?— полный радиус винта. На фиг. 5 интегралы (36)
и (37) представятся заштрихованными площадками Fp и FT. При графиче-
ском решении задачи приходится эти площадки на-
’ ходить с помощью планиметра или вычислять раз
личными численными методами по ординатам. Най-
денные таким образом площадки будут получены
в квадратных сантиметрах. Окончательные величи-
ны Р и Т получатся по формулам:
Р Fpmn, Т = F?de, (38)
где tn, п, d и с — цена одного сантиметра соот-
ветственно для величин, входящих в формулы (36)
/О-7Х dP dT
и (37), т. е. для г,- и ----.
dr dr
Если бы мы интегрировали не по всей лопасти,
а на интервале R и г, где г — произвольный ра-
диус, то получили бы тягу, развиваемую участком
лопасти от ее конца до данного сечения. Это
ая сила для лопасти на радиусе г. Совершенно ана-
логично, если бы мы построили диаграмму для по г, то интеграл или-
dr
соответствующая площадка позволили бы найти секущее окружное уси-
лие для лопасти на любом радиусе г. При этом следует помнить, что
величины dP, dQ и dT относятся к кольцевому элементу, а для рас-
чета лопасти на прочность мы должны брать усилия, действующие на од-
ну лопасть, т. е. dP! =г= и dQj — .
Заметим, что нахождение погонных нагрузок по формулам (34) и (35)
связано с решением уравнения связи, что мы подробно рассмотрим в сле-
дующих параграфах.
Примечание 1. Мы вычисляли силу и мощность, исходя из крыла, т е поль-
зовались формулой экспериментальной аэродинамики с коэффициентом ср. Двойствен-
ный характер излагаемой теории позволяет находить эти же силы и мощность, исходя
из струи После неизбежного решения уравнения связи будем знать не только угол
атаки а и скорость набегающего потока Wlt но и все остальные скорости, т е
иг и w1. Вследствие этого можно вычислить силы dQ и dP по осевому и окружному
импульсам и количеству движения, помня, что секундная масса воздуха, проходящего
через кольцевое сечение, равна
dm = p2nr Vidr.
(39>
Тогда сразу получим'
, dP — dm v» — dm 2yx = 4npV1y1r dr, ]
dQ = dm u2 — dm 2ut — inpV^r dr, (40)
dT = dQ ra> — 4npV1u1r2 w dr. J
Окончательно можем написать эти выражения для погонных нагрузок в таком виде
dP
—— 4лрУ1т'1<. (41)
Эти формулы значительно проще формул (34) и (35). Однако в практических pacnefax
нередко малые величины и их определяются сравнительно грубо: точность определе-
ния скорости и угла атаки ct обычно больше, поэтому npij пользовании формулами
(34), (35) и (32) результат получаемся более точный, почему мы и рекомендовали поль-
зование этими формулами. Но при внимательном и точном нахождении величин су и и,
формулы ('ll) — (43) имеют явное преимущество перед предыдущими из-за сокращения
вычислений.
, dP dQ dT
Примечание 2. При вычислении погонных нагрузок, т. е ----, ---- и --- ,
dr dr dr
на практике удобнее определять сперва „погонную нагрузку полной аэродинамической
силой , так как ее выражение (22) входит во все эти формулы Следовательно.
нужно сначала находить
Глава 2
ПОВЕРОЧНЫЙ РАСЧЕТ ВИНТА
§ 1 ГРАФО АНАЛИТИЧЕСКИЙ МЕТОД
ПОВЕРОЧНОГО РАСЧЕТА ВИНТА
В НАТУРАЛЬНЫХ ВЕЛИЧИНАХ НА ОДНОМ РЕЖИМЕ
Изложенная простая теория позволяет очень легко проводить повероч-
ный расчет винта заданной формы для любых условий его работы. Этот
вопрос весьма существенен для современных скоростных винтов, у которых
при малых скоростях наблюдается иногда весьма сильное падение тяги,
что значительно увеличивает длину разбега самолета. Сечения лопастей
винта при этом нередко работают на закритическом угле атаки. Следова-
тельно, аналитические формулы, основанные обычно на линейной зависимости
су от угла атаки а, оказываются в этом случае неверными. Описываемый
метод позволяет вести расчет при любом характере изменения cR от а, и,
кроме того, он учатызает влияние больших сил сопротивления на вра-
щение потока в струе винта, чего не делает современная вихревая
теория.
Основной задачей в этом расчете язляется иахэкцение углов атаки
сечений винта, т. е. построение правильных скоростных многоугольников
для ряда сечений винта. При решении этого вопроса используются уравне-
ние связи (25) и соотношения (24), (26) и (27).
Решать задачу можно двояко: или искать решение для одного заданного
режима полета, т. е. при заданном числе оборотов для одной скорости по-
лета, или же находить сразу решения для всех режимов полета, т. е. для
разных скоростей.
Расчет работы винта для одной скорости полета
Рассмотрим сначала первую задачу. Пусть дан чертеж винта. Следова-
тельно, на любом радиусе г будет известна ширина лопасти Ь, наклон се-
чения ф, тип профиля и, по его продувке в аэродинамической лаборатории,
кривая зависимости cR и ц от а.
Требуется при заданной скорости полета Уо, числе оборотов п5 и плот-
ности воздуха р (иа заданной высоте) найти развиваемую винтом тягу Р и
Т
потребляемую мощность N = — . Попутно для учета обдувки самолета
струей винта желательно найти скорость отброшенного винтом воздуха.
Для расчета выберем у винта ряд сечений иа подходящих радиусах.
Обычно положение сечений задают отвлеченными или относительными ра-
диусами г - —.
Для грубых расчетов берут: г — 0,9, 0,75, 0,55, 0,35; при обычных рас-
четах г = 0,95, 0,85, 0,75, 0,6, 0,45, 0,3 и при особо точных г = 0,95,
0,85, 0,75, 0,65, 0,55, 0,45, 0,35, 0,25. Центральная часть лопасти иа ра-
диусе г = 0,2—0,3 (в среднем на г = 0,25) обычно закрыта коком и из
расчета исключается.
На фиг. 6 Изображено одно из сечений виита. Найдем угол атаки а, с
которым будет работать это сеченне винта при заданном режиме полета,
т. е. при заданных ns и Vo. Находить его для общего случая приходится
или методом последователи ых приближений, или, что проще, графическим
методом засечек. Для этого задаемся подходящим углом атаки а' и нахо-
дим по диаграмме фиг. 7, пересчитанной на бесконечное удлинение и даю-
щей результат продувки профиля виита в трубе, величину коэффициента
со и обратного качества ц = —~.
Далее проще всего построить графически скоростной многоугольник
(фиг. 6). Для этого откладываем в подходящем масштабе окружную ско-
рость сечеиия, т. е. гео, и скорость полета 10; берем, как обычно, обрат-
ные им величины, т. е. соответствующие скорости воздуха. Нам будет из-
вестно направление сксцссти VV'i, так как дан наклон хорды сечения ф, а
образует с ней угол а'; следовательно,
Р' — а'. (48)
Известно также направление скорссти wlt так как мы знаем, что
+ (49)
Проводя из точки О направление а из точки В направление wlt мы в
точке С получим засечку этих направлений и, следовательно, величину
скоростей и Попутно, проектируя точку С на линию АЕ, получим
скорость как отрезок ЕА.
Если бы мы случайно задались правильным углом атаки а', то эти ско-
рости были бы найдены верно. Для поверки их правильности пользуемся
уравнением связи, для чего сначала вычисляем
., аь
Л =- ----
8лг
и из уравнения связи (25) находим величину сЛ, т. с. пишем:
" 1 v' “'i
Cr~ ~К ‘
Найденное значение с'ц откладываем, как показано иа фиг. 7. Задаемся
другим значением угла атаки а", находим по продувке с Д и ц"', повторяем
весь указанный расчет и снова находим с#. Через точки, соответствую-
• щие cR и с ft, проводим прямую, которая пересечет кривую cR = f(a) в
точке М. Соответствующие ей значения a, cR и р можно принять за истинные.
При самом небольшом навыке точки и с'р сразу ложатся очень близко
к истинному значению cR (к точке М). Если же эти точки имеют разбег,
то следует взять еще несколько промежуточных углов атаки и сделать за-
сечку не прямой Ср>Ср> , а провести через ряд полученных точек плавную
кривую.
После получения истинных значений a, cR и р скоростной треугольник
будет увязан и найденные окончательные значения скоростей Wlt и
угол 3 будут верными.
Фиг 6
Фиг. 7
Проделав такую увязку для всех выбранных сечений, можно приступить ,
к вычислению силы тяги и мощности. Для этого вычисляем погоиные на-
грузки по формулам (44) — (47), т. е.
dr я 2
dP dR ,п , ,
— = - cos [4+ |1;
dr dr
dQ
dr
ак . /O . .
sin P+ ц).
dr
dT _ dQ
dr dr
и, далее, методом графического интегрирования определяем (фиг. 5) вели-
чины Р и Т.
d R
Заметим, что, отложив на фиг. 6 вместо вектора величину мы,
dr
проектируя ее графически на ось винта 001 и на плоскость вращения О А,
получим сразу ~~~ и . Если построение делать в крупном масштабе,
то точность получается вполне достаточная.
Имея тягу и затраченную мощность, легко найти коэффициент полезного
действия винта, равный отношению полезной работы РУ, к затраченной Т, т. е.
PV0
и ~------
1 1’
(50)
§ 2. РАСЧЕТ ВИНТА НА ВСЕХ РЕЖИМАХ
В НАТУРАЛЬНЫХ ВЕЛИЧИНАХ
Разобранный нами поверочный расчет вннта делался для одного режима
работы, т. е. для заданных 1'0 и п5. На практике нередко нужно знать ра-
боту винта на различных скоростях Например, для расчета разбега са-
молета перед взлетом пришлось бы задаться рядом скоростей Vo и для
каждой полностью повторить разобранный расчет. Это требует большой вы-
числительной работы, которую можно значительно сократить излагаемым
здесь методом, впервые предложенным Г. X. Сабининым.
Опять задаются углом атаки сечения, но увязывают скоростной много-
угольник подбором скорости полета 1/0. Это позволяет для каждого угла
dP dT г,
атаки наити скорость полета и ----- и ---. Построив для каждого про-
dr dr
dP dT
филя кривые изменения —— н в зависимости от скорости полета, можно
брать для любой скорости полета значения этих производных. Далее задача
решается так же, как это уже было описано.
Разберем подробнее этот метод расчета винта.
Задаемся углом атаки а и находим по продувке cR и и. Тогда нам бу-
дет известно направление скорости Wlt так как Р = Ф — а.
Вместо построения истинного скоростного многоугольника, построим
сначала произвольный многоугольник, но подобный истинному (фиг. 8). Для
этого отложим на известном нам направлении ее произвольную услов-
ную величину (W\), например, отрезок 0(\ длиной 100—200 мм. Тогда
мы сможем вычертить весь условный многоугольник. Для этого находим
по чертежу условную скорость (VT) •= и вычисляем по уравнению связи
условную индуктивную скорость
(да‘)= (51)
Отложив из точки С{ -под углом к вертикали 3 4- н эту скорость (Wi),
мы получим точку Многоугольник OCiBiAtO будет подобен истинному
многоугольнику ОСВАО, и для получения последнего нам достаточно про-
вести через точку Bi луч ОВг до пересечения с линией АЕ в точке В.
Справедливость этого построения видна из того,-что скорости в уравне-
s Viau
ние связи входят в виде безразмерного отношения ——- , которое не за-
висит от абсолютных величин скоростей; все скорости можно умножить иа
постоянный множитель, а величина этого отношения не изменится.
Поэтому нет надобности проводить луч 0Вь как это изображено иа
фиг. 8, а проще, построив наш скоростной многоугольник ОС&А^, найти
переходный множитель с, на который следует умножить стороны нашего
многоугольника для получения сторон истинного'. Для этого воспользуемся
(и)
Фиг. 9
тем, что длина (£7) = ОД соответствует у истинного ^многоугольника ско-
рости Г(о. Следовательно,
Далее находим все скорости;
U7, = (W^c, )
(52)
(53)
Таким образом мы найдем скорость полета VQ, соответствующую углу атаки
а иа радиусе г. Эта величина получится не в круглых цифрах, а так, как
это даст построение.
Зная скорость и угол атаки, сможем по предыдущему [формулы ,
(44) — (47)) вычислить погонную нагрузку полной силой, т. е. производную
dR P^i . , n
— cRko ——, и затем, отложив ее в подходящем масштабе нафиг. 9
под углом р + и к оси вращения винта,
ось винта 00i и
dP с
изводные----, -
dr ।
dQ
dr
можем спроектировать ее на
на направление вращения лопасти и получить про-
dT dQ
- и ----— —— гы.
dr dr
В целом получается очень простое построение, изображенное на фиг. 9.
Такой расчет нужно проделать для нескольких углов атаки у каждого се-
чения винта. Нет надобности проводить на чертеже все линии: вместо от-
кладывания вектора (lFy) можно начертить окружность, на которой отметить
углы 3, соответствующие выбранным углам атаки а (фиг. 10). Проекции
(IFi) иа оси очень легко брать прямо линейкой без прочерчивания линий,
для чего надо внимательно (на глаз) класть линейку параллельно осям (ЭО1
и OAl. Особенно удобно пользоваться клетчатой бумагой или миллимет-
ровкой.
После нахождения для всех избранных сечений и для всех углов атаки
dP dT
величии Vo,--- и ---- следует построить интерполяционные диаграммы
df dr
(фиг. 11). По этим диаграммам нужно иайти величины и , соот-
dr dr
ветствующие одним н тем же скоростям полета, имеющие одни и те же
абсциссы, например находящиеся на линиях, проведенных на фиг. 11 пунк-
тиром .
о д, dp dT . —
Зная эти величины, можем построить графики---- и --- в функции г;
dr dr
получим знакомую нам диаграмму (см. фиг. 5), ио с несколькими кривыми,
соответствующими избранным скоростям полета (фиг. 12). После графиче-
ского или численного интегрирования получим величины Р и Т для выбран-
ных нами скоростей полета Va.
Аэродинамическая характеристика виита
Проделав указанные вычисления для нескольких скоростей полета, мы
сможем составить таблицу соответствующих значений тяг и мощностей:
К, V"o, V"'o, 1/Г;
Р', Р", Р"', Р""-
N’, N", N"', N"" и т. д.
По этим данным можно построить полную аэродинамическую характе-
ристику винта для всех интересующих нас режимов полета. Для обычных
винтов она имеет вид, изображенный на фнг. 13. На эту диаграмму можно
нанести и соответствующие значения к. п. д. винта, вычислив его по фор-
муле (50)
1 'Г
РУд
75 N
Заметим, что такой расчет, проводимый в натуральных величинах, хотя
очень прост и нагляден, но обладает тем недостатком, что связан с кон-
кретным винтом. Поэтому при расчете винтов принято пользоваться безмер-
ными величинами. В дальнейшем подробно рассмотрим расчет винта в таких
обозначениях. Теперь же заметим, что полученную нами характеристику
винта, изображенную на фиг. 13, можно перечертить в безразмерную диа-
грамму, если ввести обычные винтовые безразмерные коэффициенты: а —
коэффициент тяги, — коэффициент мощности и X— коэффициент ско-
рости. На основании^закона подобия* их можно получить по формулам:
Р
т
pD6n’’
Vo
О"»
(54)
(55)
(56)
В написанных фурмулах над а и [1 поставлены черточки во избежание смеше-
ния их с углами атаки и притекания потока. В тех случаях, когда такого
опасения нет, эти черточки не ставят.
Диаграмма винта в безразмерных величинах имеет вид, изображенный
на фиг. 14.
IC il д. винта можно представить с помощью винтовых коэффициен-
тов а, 3 и X:
П = П° = =
г
Замечая, что — К, получим
D*s
а л
= у- <57>
У винта имеется на’диаграмме ряд интересных точек, положение которых
можно указывать с помощью величины X.
При I = 0 мы имеем работу вннта на месте или геликоптепную рабо-
ту. При этом 0 и т) = 0.
* Б. Н. Юрьев. Экспериментальная аэродинамика
винты, ч I. М., ОНТИ, 1934.
ч. I; его же. Воздушные
При некотором наивыгоднейшем значении Хнаив к. п.д. достигает своей ма-
ксимальной величины. У хороших винтов к. п. д. достигает значения 0,85—0,9.
В некоторой точке а ~-= 0, следовательно, и тяга Р — 0, такой режим
называется режимом нулевой тяги.
Далее имеется точка, где р = 0, следовательно, и Т = 0. Винт не тре-
бует при таком X работы мотора и вращается сам собою. Это — режим
авторотации.
Коэффициент полезного действия -q при режиме авторотации претерпе-
вает разрыв, так как при р—» + 0 величина •q-* + co-
Исследование всех этих режимов представляет большой теоретический
и практический интерес, и мы в следующих параграфах подробно разберем
работу винта на всех режимах.
§ 3. РАБОТА ВИНТА НА 20 РЕЖИМАХ
Рассмотрим работу винта иа всех^ режимах. Для простоты мы ограни-
чимся рассмотрением работы характерного сечения винта иа г _ R. Его
аэродинамические характеристики, как известно, близ-
ки к характеристикам всего винта.
Нам придется проделать ряд поверочных расче-
тов этого сечения для разных скоростей по из-
ложенному методу. В результате подсчетов можно
построить сводную диаграмму (фиг. 15), на кото-
рой даны все получающиеся при этом характерные
скоростные многоугольники.
Скоростной многоугольник ОСГАО изображает
режим работы винта иа месте, или гелнкоптерный
режим. Скоростной многоугольник ОСВ 40 дает план
скоростей для нормальной работы винта иа режиме
пропеллера пои скорости набегающего потока к0.
Увеличивая скорость полета ^0, мы придем
к режиму нулевой тяги, когда скорость распо-
ложится горизонтально и скорость vt будет равна
нулю. При этом в струе не будет прироста количе-
ства движения в осевом направлеиин и dP будет
равно нулю, так как
dP = v2dm 2vtdni — 0. (58)
Скоростной многоугольник примет вид OCiB{AO
Хотя при этом тяга н равна нулю, мощность не
будет равна нулю, так как окружное усилие dQ
будет иметь вполне определенное значение:
dQ = dm и2 = dm 2uv.
Если еще более увеличить скорость полета, то
можно достигнуть такой скорости, что индук-
тивная скорость сделается параллельной оси
винта. Тогда, как показывает скоростной много-
угольник ОС2В2АО, иг = 0 и vj <Г 0. Следовательно, Фиг.
на этом режиме винт не требует для своего враще-
ния подвода мощности двигателя, ои будет вращаться автоматически. Та-
• кои режим называется авторотацией винта. Сила тяги при этом меняет на-
правление и .обращается в силу торможения, так как при »j<0h dP<^0.
При дальнейшем увеличении скорости полета мы получим многоуголь-
ник ОС3В8АО, соответствующий режиму ветряной мельницы нлн турбины.
Скорость dz/j даст проекции f] < 0 н ux<Q0. Следовательно, окружное уси-
лие dQ = hiidtn переменит знак, и вннт начнет не получать, а отдавать
мощность валу, на который он посажен. Сила тяги dP 2v1r/m будет при
этом отрицательна.
При дальнейшем увеличении скорости полета вектор скорости набега-
ния потока Wzi будет все более и более приближаться к направлению, па-
раллельному оси винта. Предельный случай, соответствующий при задан-
ной окружной скорости бесконечной скорости Уй, можно рассматривать
как случай, когда гео—*0 при конечном Уо. Это будет обдувка неподвиж-
ного (не вращающегося) виита потоком, набегающим вдоль оси винта со
скоростью Уо. При этом возникнет определенное окружное усилие и от-
рицательная тяга. Такой случай назовем режимом передней обдувки или
остановки винта. Скоростной многоугольник обратится в треугольник
0С4Вх0.
Рассмотрим, что произойдет, когда скорость Уо станет отрицательной.
Соответствующий скоростной многоугольник примет форму ОС5В5АО. Та-
кой режим работы назовем вторым режимом торможения. При дальнейшем
увеличении скорости мы можем получить вихревые кольца, чему будет
соответствовать скоростной треугольник ОВ6АО', точка Со совпадает при
этом с точкой О. На нашей фигуре мы отметили пунктирной линией все
положения точек CCjC2C3.
На всех рассмотренных режимах работы виита угол атаки а был мень-
ше угла установки элемента лопасти <р. Соответственно этому и угол
притекания потока [3 был все время положительным. На режиме вихревого
кольца он был равен нулю: (3=ф— а =-0. Если нам удастся перейти за
этот режим, то мы получим а^>ср и 0. Скоростные многоугольники’
в этом случае будут иметь форму ОС7В-АО. Это третий режим торможения.
Если мы будем продолжать увеличивать отрицательную скорость V’o,
то опять придем к режиму остановки, но при услбвии обдувки невращаю-
щегося винта сзади. Скоростной треугольник будет иметь вид, изображен-
ный буквами ОВ^СьО.
Мы рассмотрели все режимы, получающиеся у винта, вращающегося
с постоянной скоростью гео, при изменении скорости полета от + со до
Составим таблицу характерных режимов работы винта н соответствую-
щих им точек С на фиг. 15.
Режим передней обдувки (остановки) при со — 0, С4.
Режим ветряной мельницы 0, их < 0, С3.
Режим авторотации р, 0, их = 0, С2.
Первый режим торможения ^<^0, их 0, Сг.
Режим нулевой тяги vx — 0, их 0, Сх.
Режим пропеллера и, > 0, nx'^>Q, С.
Режим геликоптера Уо = 0, их'^-0, Сг.
Второй режим торможения V0<^0, vx~^>0, Cb.
Режим вихревого кольца Vk = гео etg dP = 0, dQ — 0, С6 совпала с О.
Третий режим торможения vf <С 0, wf>-0, С?.
Режим задней обдувки (остановки) г<о = 0, С8.
В соответствии с этими точками у винта имеются участки работы:
1) от геликоптерного режима до режима нулевой тяги — участок про-
пеллерной работы;
2) от режима нулевой тяги до режима авторотации — участок первого
торможения; . •
N6
прямое
Ветряная
мелЬницо
(турбина)
N9
Нулевая тяга
Вихревое Нолбцо
1-е торможение
rh.>. IА
При ;
ник 0С3£
Скорость
лие dQ =
мошиость
этом отри
При д
НИЯ ПОТО1
раллельнс
ной окру
как случ;
ного (не
скоростьк
ринате лън
остановки
ОС4ВХО.
Рассмо
Соответст
кой режиь
увеличени
соответств
этом с то1
положения
На все
ше угла
притекания
кольца он
этот режи
в этом слу
Если м
то опять п
щегося виь
иый буквам
Мь] рас
с постояни
Состави’
щИХ ИМ ТО1 <
Режим перс
Режим вет[
Режим автс
Первый рел
Режим нуле
Режим прог
Режим гелт
Второй реж
Режим вихр
Третий реж
Режим задн
В соотв<
1) от ге;
пеллериой р
2) от режима нулевой тяги до режима авторотации — участок первого
торможения;
у
3) от режима авторотации до режима передней обдувки — участок ветря-
ного двигателя; .
4) от геликоптериого режима до режима вихревого кольца — участок
второго торможения;
5) от режима вихревого кольца до режима задней обдувки — участок
третьего торможения.
На фиг. 16 представлены все характерные режимы работы винта. До-
бавлены режимы обратного вращения винта, что может иметь место у
реверсивных двигателей. При обратном вращении получаем те же режимы,
как и при прямом вращении, но силы будут направлены в другую сто-
рону. На некоторых режимах при этом элемент лопасти обдувается с вы-
пуклой стороны и, следовательно, работает плохо.
§ 4. ФОРМА'СТРУИ ВИНТА
НА РАЗНЫХ РЕЖИМАХ
Рассмотрим теперь форму воздушной струи, получающейся у винта
на всех этих режимах. При выводе формул мы исходили из струи, полу-
чающейся на режиме пропеллера. Струя имеет воронкообразную форму
(фиг. 16, № 2), так как скоростй Vi^>V0 и и, следовательно,
сечения струи, из условия ее неразрывности, должны по длине уменьшать-
ся. Теоретически1 скорость V2 должна получиться далеко за винтом, и
струя должна там иметь цилиндрическую форму. В действительности же
сжатое сечение у струи получается на расстоянии около одного радиуса
за виитом; далее, вследствие вязкости воздуха, струя начинает медленно
размываться.
После прохождения плоскости, ометаемой винтом, струя получает вра-
щательное движение. Режим пропеллера показан на фиг. 16, № 2; там же
нарисована струя для этого режима, на поверхности которой нанесены
траектории частиц воздуха. Такие же схематические рисунки даны на
фиг. 16 для всех остальных режимов винта.
Так, на фиг. 16, № 1 изображена работа винта на режиме геликоп-
тера. Воздух подсасывается в этом случае широким веером со всех сто-
рон и отбрасывается в виде очень сильно сжимающейся струи. Сжатие
в этом случае очень велико, так как площади струи Ft и F2, взятые в
сечениях 1 и 2, относятся друг к другу, в силу неразрывности струи, как
Fj : F» -- v.2:
но v2 — 2»i и, следовательно,
F1:F2 = 2.
Таким образом, на геликоптерном режиме площадь уходящей вдаль
струи в два раза меньше ометаемой площади винта. Опыты очень хорошо
подтверждают это соотношение.
На режиме нулевой тяги струя делается цилиндрической, так как
— 0 и V2 = Vi, следовательно, сжатие отсутствует, закручивание же в
струе имеется, так как их = =/= 0. Этот режим изображен нафиг. 16, № 3.
На режиме первого торможения (фиг. 16, № 4) струя за винтом уже
ие сжимается, а расширяется, так как f l 0 и, следовательно, Va <1 Vi и
Винт продолжает закручивать струю.
Фиг. 17
На режиме авторотации расширение струи становится еще большим,
но вращение пропадает, так как на этом режиме их = 0 (фиг. 16, № 5)-
На режиме ветряного двигателя струя имеет расширяющуюся форму
(фиг. 16, № 6). Закручивание получается обратного по сравнению с про-
пеллером знака; Mt<0. Отходящая струя вращается против вращения
винта. Заметим, что сечения винта у нас обдуваются иа этом режиме с
выпуклой стороны; это очень невыгодно с аэродинамической точки зре-
ния, так как профиль при отрицательных углах атаки имеет плохое ка-
чество и р. очень велико. Получилось это потому, что исходное положение
профиля'у нас взято таким, какое имеется у пропеллера (фиг. 16, № 2);
мы изучаем работу именно пропеллера на всех ре-
жимах. В действительности у ветряных двигателей
сечение располагают обратной стороной, как это по-
казано на фнг. 17. Тогда профиль работает правиль-
но, и к. п. д. соответственно повышается.
Наконец, на режиме остановки о струе прихо-
дится говорить условно: мы имеем здесь случай об-
текания лопастей как отдельных крыльев.
При многолопастном винте, однако, струя будет
все же существовать, и скорость W\ будет иметь
прежний смысл. Вообще изложенная теория, так
же как обычная вихревая, применима с достаточной строгостью лишь
к винтам многолопастным. Однако опыт показывает, что выводы, полу-
ченные в этих теориях, оказываются достаточно точными и для трех- и
даже двухлопастных винтов.
Рассмотрим теперь струю, возникающую при отрицательных скоро-
стях Vo- Представим сперва геликоптериую работу винта (фиг. 18, а).
В точке А влит вызовет скорость подсасывания Va- Если заставим снизу
набегать поток воздуха, то получим, грубо говоря, наложение скоростей
подсасывания иа скорости поступательного потока. В точке 'А произой-
дет сложение обратно направленных скоростей ?а и Vq. Так как Va изме
няется от 0 (вдали от винта) до значения щ (в плоскости винта), то мож-
но найти такое положение точки Л, что Vo = Va и результирующая ско-
рость обратится в нуль. Геометрическое место таких точек образует
перед винтом поверхность раздела АА[. Течение воздуха на втором ре-
жиме торможения будет иметь примерно вид, изображенный иа фиг. 18, а
и фиг. 16 (№ 20).
Если скорость Уо будет стремиться сравниться со скоростью vlt то
поверхность раздела ААг будет стремиться совпасть с плоскостью винта,
и У, обратится в нуль.
Если величина скорости Уо будет заключаться между величинами vt
11 2t\, то поверхность раздела возникнет за винтом в такой точке В, где
vb — Ео (фиг. 18, Ь). Это будет начало третьего режима торможения. При
приближении скорости Vo к скорости и здесь поверхность раздела будет
стремиться к совпадению с плоскостью вращения.
Этот предельный для обоих случаев режим и есть режим вихревого
кольца. Поверхности раздела ААг и ВВк сближаются, и воздух между
ними приходит во вращательное движение, напоминающее известное дви-
жение воздуха около вихревого кольца. Сил при этом не получается, так
как никакие импульсы на струю в этом случае не передаются. Лопасти
работают как «мешалка» в воздухе, вращающемся с той же скоростью,
как лопасть.
Если скорость набегающего сзади воздуха будет большой и
то точки А а В (фиг. 18) уйдут в бесконечность, и мы получим струю,
$ 5. Характеристики профиля, приспособленные к расчету винтов
47
изображенную иа сводной фиг. 16, № 18.' Там же изображены все разо-
бранные здесь режимы (№ 20 н 19).
При очень больших отрицательных скоростях мы получим заднюю
обдувку стоящего неподвижно винта (фиг. 16, № 17). К этому режиму
применимо все сказанное о режиме передней обдувки.
При изменении направления вращения винта картины обтекания винта
останутся, по существу, прежними.
► Вообще все скоростные многоугольники и
схемы обтекания можно получить для обратно
вращающегося винта путем симметричного от-
носительно точки О перестроения чертежей для
прямо вращающегося винта. Так и были полу-
чены на фиг. 16 режимы для обратного враще-
ния винта.
Примечание Вектор полной элементарной
силы, действующей на элемент лопасти, т. е
занимает при разных режимах работы винта различ-
ные положения по отношению к хорде сечения Если
от какой-нибудь точки профиля сечения, например О
(фигг 19), отложим по величине и направлению эти
векторы, то получим полярную диаграмму силы, дей-
ствующей на лопасть. Если вместо самих сил отло-
жить совпадающие с ними по направлению векторы
коэффициентов потных аэродинамических сил сR, то
получится аэродинамическая поляра 2-го рода, т. е.г полярная диаграмма вектора cR, от
несенная к хорде крыла, как к полярной оси* *. На кривой, которую описывает вектор
cR, делают разметку соответствующих углов атаки а.
Имея поляру 2-го рода и выбрав какой-нибудь угол атаки а, мы можем сразу най-
ти величину и направление вектора cR и направление скорости Wlt образующей с хор^
дой сечения угол а. Кроме этого, вектор индуктивной скорости всегда имеет прямо
противоположное направление вектору aRi и, следовательно,» вектору cR на флг 19
Векторы Cr и W] будут всегда лежать на одной прямой.
§ 5. ХАРАКТЕРИСТИКИ ПРОФИЛЯ,
ПРИСПОСОБЛЕННЫЕ К РАСЧЕТУ ВИНТОВ
Опубликовано, много испытаний серий винтовых, профилей. Но все оии
обычно дают характеристики в виде пересчитанных иа бесконечное удлине-
ние кривых Су, схр, качества k = — или обратного качества щ =
схр С'
* См. Б. Н. Юрьев. Экспериментальная аэродинамика, ч ], стр. 184
в функции угла атаки а. Для быстрого расчета винтов по предлагаемому спо-
собу желательно иметь кривые cR и р (26), т.е. коэффициент полной аэро-
динамической силы и угол р, иа который он отклонится от нормали к ис-
тинной скорости потока Wj. При обычных углах атаки cR~cy, так как
cR = Vc* + 1 н- (59)
и при малых р выражение под корнем очень близко по величине к едини-
це. Величину р. можно при малых углах атаки подсчитывать по дуге, а
не по тангенсу дуги (28).
Следовательно, при малых углах атаки, что соответствует нормальным
режимам работы винта, можно пользоваться обычными графиками серий
винтовых профилей.
Однако при изучении работы винта на малых скоростях полета или на
режимах торможения нужно иметь продувки профилей лопасти на очень
больших углах атаки, превосходящих наклон сечения винта Для расчета
винта иа всех режимах нужна, строго говоря, круговая обдувка. Если не
разбирать обратного направления вращения виита, то можно ограничиться
продувками в пределах изменения а от 90 до —90°.
К сожалению, до сих пор опубликовано мало круговых продувок
крыльев и отсутствуют круговые продувки серий винтовых профилей. Это
объясняется увлечением конструкторов максимальными скоростями полета,
на которых нужны для расчета винтов углы атаки лишь в пределах от
— 5 до — 15°.
Нам пришлось поэтому сделать условный, осредиеииый, составной гра-
фик (фиг. 20), на котором для нормального диапазона угла атаки взят
обычный профиль СВ-2 с относительной толщиной с = 0,09; далее кривые
продолжены иа основании имеющихся круговых продувок других профилей.
Следовательно, иаш график дает лишь примерное протекание кривых cR и р.
Характер кривых cR и су общеизвестен. Кривая и имеет разрыв при
угле атаки, при котором си — 0. Так как при этом pj изменяется от оо
до —со, то p — arctgpt изменяется от -г 90 до —90°. В точке, где р,
делается минимальным, и р, достигает минимального значения. При углах
атаки + 90° величина р близка к + 90°.
$ 5 Характеристики профиля, приспособленные к расчету винтов
4H
График фиг. 20 нами построен, как мы отмечали, условно по ряду раз
личных продувок. Прн получении новых экспериментальных материалов сле-
дует постронть^болеелнадежные графики.
Нахождение характерных ежимов
по кривой {! = /(«)
Ряд разобранных режимов работы сечеиня вннта можно просто и на-
глядно получить с помощью кривой р = f (а), изображенной на фиг. 21 и 20.
। Если взять на фиг. 2i на осн абсцисс точку С, в которой р = ср, а на
осн^ординат — точку В, в которой р ——ср, и соединить их прямой ВС,
то* ординаты* этой линии будут, очевидно, равиы а — ср, ио у виита 3 =
— ф — а последовательно,
— 3 — а — ср.
Если масштабы р и а выбраны одинаковые, то лнння ВС будет обра-
зовывать с осями координат угол в 45°.
Сразу видно, что абсцисса точки С, где а — ср н 3 --= 0, соответствует
режиму вихревого кольца. По имеющимся на диаграмме кривым мы можем
найти соответствующие значения ср и р (фиг. 20).
Если вспомогательную линию ВС продолжить до пересечения с кривой
p = f(a), то в точках пересечения Л2 н А3 мы будем иметь режимы
авторотации, при которых вектор dR должен быть параллелен оси вннта н,
следовательно, З-гР-'-О нлн —3 = р- Последнее соотношение как раз
и имеет место в точках А,, А2 и А3. Режим, изображенный точкой
соответствует авторотации вннта при очень больших Л; это тот режим авто-
ротации (3 — 0), который фигурирует во всех нормальных диаграммах внн-
та пропеллера.
Режимы А2 и А3 получаются прн обратном осевом движении винта,
т. е. прн что на практике соответствует безмоторному спуску гели-
коптера нлн автожира. Этн режимы возможны лишь прн малых наклонах
элемента винта, т. е. при малых углах ср. При больших величинах <р пря-
мая ВС может совсем не пересечься с правой ветвью кривой р, и точки
А и А3 тогда ие получатся. Это будет значить, что виит авторотировать
не будет. Предельным случаем будет такой, когда прямая ВС коснется
кривой и в точке Д'. Точка С тогда определит тот предельный наклон ср
элемента винта, прн котором еще возможна авторотация. Для обычных
профилей этот угол равен 5—6°, поэтому прн безмоторном спуске геликоп-
теров и автожиров приходится устанавливать лопасти под углом ср 4°.
С помощью этой же диаграммы легко найти режим нулевой тяги сече-
ния винта. Для этого заметим, что на этом режиме вектор dR должен ле-
жать в плоскости вращения винта, т. е. Р Д- ц = 90°. Если провести пря-
мую линию 8^1 параллельно лииин ВС, причем ВВГ — 90°, то, как видно
по чертежу, в точке пересечения этой линии с кривой и в точке Р мы и
получим это соотношение: 3 + ц — 90°. Точка Д4 получится при большом
отрицательном угле атаки, соответствующем обратному вращению винта (ре-
жим 13 иа фиг. 16).
С помощью двух вспомогательных прямых ВС и В^, проведенных на
диаграмме продувки профиля, мы можем получить углы атаки а, коэффи-
циент Сд и величину р для режимов вихревого кольца, авторотации и нуле-
вой тяги. Это облегчает выбор углов атаки при поверочном расчете вннта.
§ 6. УПРОЩЕННОЕ УРАВНЕНИЕ СВЯЗИ
И ЕГО АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
Главную трудность при расчете винтов представляет решение уравне-
ния связи. Его можно значительно упростить, если ограничиться нормаль-
ными режимами работы винта, т е. от скорости взлета до скорости нуле-
вой тяги. В этих условиях угол атаки у профилей сравнительно мал, и
можно считать Cr су.
Если уравнение связи написать в форме
JS-LKiJ _ кс
— Х У'
то первый член достаточно точно дает величину малого угла скоса е — £ —
— Ро е радианах, отношение будет в точности равно sin 0. Если под-
ставить скос е в градусах, то уравнение запишется в форме:
4,3 si" |Р| К.с„
или
Кс
8 = 57,3-----. (60)
’ sin 13 I ' >
Подробный разбор этого выражения, который сделан в § 3 главы 3,
показывает, что при изменении а в пределах от —5 до 4-10° и для е не
свыше 10° ошибка получается меньше 1%. Если искусственно подставить
вместо коэффициента 57,3 просто 57, то уравнением можно будет пользо-
ваться до углов атаки 14—15°. Однако у обычных винтовых профилей уже
при 10—12° начинается срыв потока, и расчет делается мало надежным.
Следовательно, упрощенное уравнение связи можно писать окончательно
в виде:
е = 57 - , (61)
Sin 13 I ' ’
С помощью этого уравнения очень легко решать скоростной многоуголь-
ник, делая поверочный расчет винта по второму способу, т. е. сразу для
ряда режимов. Действительно, задавшись а, находим 0 = ср—а и по про-
дувке Су и p,j. Далее по уравнению связи (61) вычисляем скос потока е и
находим 30 = р— е. После этого сразу получаем скорость полета, при
которой находится у рассчитываемого элемента заданный угол атаки а, так
как из фиг. 3 непосредственно видно, что
= Г10 tg 3G.
Дальнейший расчет можно вести уже описанным в § 2 главы 2 способом.
Заметим, что при малых углах скоса вполне возможно вычислять скорость
IV] по упрощенной формуле, основанной на допущении, что щ перпендику-
лярна к (фИ1. 3), что очень близко к истине при малых величинах ц.
Тогда IV, lV0cose,
скорость W'o = (62) - и cos р0 v '
н, следовательно, ,,,, cos e = rw . 1 cos p0
Точность н пределы применимости этой формулы мы разберем в § 3
главы 3. В табл. 1 приведен формуляр этого упрощенного метода повероч-
ного расчета винта.
Таблица 1
Формуляр упрощенного расчета вннта на обычных режимах
(при которых ц < 15° и е < 10J)
X» no nop. Величины r= o,e; r = ...<p Г—0.75 Г=0.6 Г=0.45
1 3 a cy Hi —5° O3 5° 10° 20° 30°
4 5 6 7 8 9 10 11 12 13 3 - <p — a в = 57 Sin IP, 3o = 3 — 8 Vo =rco tg po ш — cos e 1 cos p0 dR dr sc Cfjib 2 P +h dP = (9) cos (3 + ц) dQ -^=^(9)sin((3 + ц) dT
Примечание Здесь и во всех аналогичных таблицах цифры в скобках показы-
вают, что в данное выражение следует подставить значение из соответствующей
строки таблицы.
4
Далее следует построение интерполяционной сетки по фиг. 11 н инте-
грирование по схеме фиг. 12. Такой расчет может быть помещен на одном
листе бумаги. Точность для обычных режимов пропеллера получается впол-
не удовлетворительная. Достаточная точность получается и для геликоп-
тера на режиме моторного полета, когда угол наклона лопастей <р, как
правило, лежит в пределах от 10 до 15°.
Расчет этот совершенно непригоден для режи-
мов прн больших углах а, когда р. очень велико.
Сюда относится в первую очередь задняя обдувка
винтов большого шага, т. е. тормозные режимы.
Режим нормального спуска геликоптера этим
приемом можно рассчитывать с достаточной точно-
стью, так как углы атаки сечении лопастей при
этом равны 3—6°.
Если будет задан лишь одни режим винта, то
проще всего не изменять расчета н поступить так,
Фиг 22 как это только что было описано, но взять более
узкий интервал углов атаки н, построив диаграмму
Vo по а, сделать засечку заданной скоростью Умл
(фиг. 22); тогда в точке Л11 мы получим правильную величину угла ата-
ки а для данного сечения.
„ dS dP dT
Величины -г-, —, т- можно вычислить лишь для одного этого угла
dr dr dr J
атаки. Формуляр расчета остается прежним.
Аналитическое решение уравнения связи
Пользуясь упрощенным уравнением связи, можно найти решение скоро-
стного многоугольника, непосредственно решая это уравнение. Обычно в зада-
чах техники аналитические решения основаны на различных упрощениях,
чаще всего на замене сложных функции линейными.
Такое упрощение можно сделать, подставив в наш; уравнение выраже-
ние для Су через аэродинамический угол аа, отсчитываемый от аэродинами-
ческой хорды*:
с„ = ааа -- а (<р„ — р),
(63)
где —наклон аэродинамической хорды к плоскости вращения винта. То-
гда формула (61) примет вид:
= <64>
но
е = Н — Зо -
и мы получим окончательно:
₽“Р» = 57й7ТГ<<*’“~^ <64')
Б. Н. Юрьев. Экспериментальная аэродинамика, ч. II, стр. 38.
$ 6. Упрощенное уравнение связи и его аналитическое решение
53
Решать это уравнение приходится или подбором, или все же графически,
например строя завнснмости величин левой и правой частей этого уравне-
ния в функции 3 и находя точку пересечения (фиг. 23). Это уравнение не-
удобно тем, что в нем содержится не только 0, но и sin 0. Обойти эту
трудность аналитически очень трудно, так как, если разложить sin 0 в ряд
Тейлора и удержать лишь два члена разложения,
т. е. принять, что
• о . 331 .
Sin 0 = 0!---------3~
то и тогда прн решении'уравнения (64’) относитель-
но 0 мы получим уравнение четвертой степени, весь-
ма неудобное для решения. Следовательно, прн сколь-
ко-нибудь больших значениях 0 нужно решать задачу
Фиг. 23
графически или следовать формуляру табл. 1.
Однако для винтов типа геликоптерных роторов такое решение вполне
возможно и дает достаточную точность. Будем считать угол ср малым (8—
15°), угол 0
— 10°. Тогда
МНИМ, ЧТО 0!
случае наше
также малым, изменяющимся, например, в пределах от -}-5 до
вполне законной будет замена sin 0 дугой 0] = (иапо-
у нас обозначает угол в радианах, а 0 — в градусах). В этом
уравнение перепишется в виде:
3 — 3» = 57р/5713
3270. № (<ра - 3)
— Й =
0
Решая его относительно 0, получим
квадратное уравнение
02 > (3270- К а — 0О) 0 - 3270 Косра =- 0.
Корни этого уравнения будут такими:
3 - 3270f ~ ± /( - fa )а+ 3270 /<афа . (65)
По смыслу задачи берем под корнем знак плюс, так как при минусе полу-
чается несоблюдение противоположности направлений и dRv Величина а
практически не зависит ни от толщины профиля, ни от его формы и равна
приблизительно 0,1 (если углы даны в градусах).
В этом случае ответ получается в таком простом виде:
р = ,.^^^+ 327.^. (66)
Для режима «висения» геликоптера 0 и 0О = 0 (вообще же 0q—arctg
и формула примет вид:
0= — 163,5. К + УТТбЗ.бТХ)2 + 327 - К<?а. (67)
Величина 0 здесь может быть как положительной, так и отрицательной.
•и расчет винта
Пример геликоптера
В качестве примера применения аналитических формул (64) и (66) рас-
смотрим случай геликоптерного ротора. Вместо рассмотрения всего винта
в целом можно для упрощения рассматривать одно сечение, лежащее на
отвлеченном радиусе г = 3/4. Как известно,
характеристики такого сечения близки к ха-
рактеристикам всего винта.
1) Работа иа режиме висеиия (фнг. 24,/).
Пусть характерное сечение имеет следую-
щие параметры: К = 0,01 н ф = 10w.
Нужно построить ’его скоростной много-
угольник. Из формулы (67) сразу получаем:
Фиг. 24
?= — 163,5 • К + /(163,5 • K)s + 327 •
= —1,635 + /2,70+ 32,7 = 4,31°.
Далее находим:
aQ = <pa= 10° — 4,31 = ^5,69°;
е ^£ = 4,31°.
Коэффициент подъемной силы сечения
будет
Су - ау.а = 0,1 -5,69^0,57.
Коэффициент профильного сопротивления
обычно берут порядка с = 0,01, хотя у
хороших ламинарных профилей ок может
доходить до значения 0,005 и даже меньше-
го. Этим учитываются шероховатость и
вибрации лопастей, создающие большую турбулентность в пограничном слое
профиля. Следовательно,
щ-, = 4// = 0,0175
1 Су 0,5”
р —57,3р. = 1,0°.
Далее расчет можно вести для ряда сечений, с последующим графиче-
ским интегрированием или по средним значениям су и схр, как описано в § 2
главы 4. На фиг. 24, / изображен соответствующий скоростной много-
угольник.
2) Работа иа режиме взлета (фнг. 24, 2). По заданной скорости взлета
Ко находим: tgP0 = — и угол Этот угол у современных геликоптеров
невелик и его можно вычислять по формуле Ро = 57,3 . Мы примем,
ЧТО Ро = 6°. Угол установки лопастей пусть будет на взлете равен <рд = 12°;
К = 0,01. Тогда из формулы (66) получим:
р = — 327-0^01 = 6 + у^-327^01-бу 327.0,01. |2 = 7,770.
Далее находим:
аа = фд — ?= 12° — 7,77° = 4,23°;
е = р — Зо = 7,77° — 6° = 1,77°.
Как видим, и здесь получается угол атаки, близкий к наивыгоднейшему
для винтовых профилей. Схема скоростного многоугольника для этого слу-
чая изображена на фиг. 24, 2.
3) Работа профиля на режиме вертикального спуска (фиг. 24, <?). При
спуске примем угол наклона характерного сечения <ра = 4°. Зададимся ско-
ростью вертикального снижения Уо н из формулы tgpo = “- найдем для
этого элемента угол В приводимом расчете мы взяли Зо — 6°. Тогда по
формуле (66) получим: z
3 -= — + К (3,27.+-1-3,27-4 =3-1,25°.
Далее находим
<ха = (ра — р = 4° — 1,25° = 2,75°; су = ааа = 0,1 2,75 = 0,275;
*=v=Ж °’03G2-
ц = 57,3 ц, = 2,08.
Равнодействующая аэродинамических сил dRt будет отклонена назад на угол
3+ 1,25 + 2,08 — 3,33°.
Это дает исходные величины для приближенного расчета винта по мето-
дам, изложенным в § 1 главы 4. При точном расчете нужно проделать
такое вычисление для ряда сечений винта и далее следовать формуляру
табл. 1. На фиг. 24, 3 дана схема скоростного многоугольника для этого
случая.
4) Авторотация ротора при вертикальном спуске с остановленным мото-
ром (фиг. 24, 4). Рассмотрим опять одно сечение. Для авторотации необхо-
димо, чтобы вектор полной аэродинамической силы dR был перпендикуля-
рен к плоскости вращения винта, т. е. 3+ц~0. Угол атаки профиля
должен быть выбран небольшим, близким к наивыгоднейшему, т. е. около 5°,
что необходимо для получения малой скорости снижения. Считаем аа = 5°;
тогда су = ааа == 0,1 -5 = 0,5 и, следовательно,
.. — Схр — °’01 — о по
ц = 57,3 щ == 1,15°.
При авторотации 3 4- |х — 0 или, в нашем случае, р — = — 1,15°.
Необходимый угол наклона сечения получим из соотношения % = Р +
которое для нашего случая можно написать в виде:
% = 3 ~г «а = — р, - аа = — 1,15° + 5° = 3,854
Скос потока е получим из формулы (60), в которую нужно теперь под-
ставить sin|£j — sin] — — Mil. т, e.
нли, более точно,
‘8е-^ = 0’248
И
£ = 13°57' 144
Следовательно,
Р0 = В—е = — и — е = —1,15°—14,0° = —15,15°.
Отсюда находим скорость снижения
V'o -= гы tg {i0 rco tg (— 15°25') = —гш0,277.
Схема скоростного многоугольника дана на фиг. 25, 4.
Этот расчет был сделан для одного сечения (г = 0,75), и для винта в
целом это будет лишь приближенным результатом. Для получения характе*
ристик всего ротора нужно проделать поверочный расчет по формуляру
табл. 1, исходя из полученного угла <рв = 3,85° и для нескольких скоро-
стей снижения, близких к полученной для сечения г = 0,75. После Этого
можно построить график изменения мощности в зависимости от скорости
снижения. Скорость, при которой мощность окажется равной нулю, и бу-
дет скоростью авторотации для автожира. У геликоптера нужно взять точ-
ку, где получается отрицательная мощность, равная мощности, потребной
на вращение трансмиссий геликоптера и его рулевых винтов. Эту мощность
нужно предварительно подсчитать хотя бы приблизительно.
Глава 3
РАСЧЕТ ВИНТА В ОТВЛЕЧЕННЫХ ОБОЗНАЧЕНИЯХ
§ 1. ОТВЛЕЧЕННЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ВИНТА
При расчете винтов выгодно пользоваться не именованными величинами,
а отвлеченными. Это упрощает формулы и, главное, придает выводам боль-
шую общность. Установились следующие отвлеченные обозначения. Для
всех длин берут в качестве единицы радиус винта R. Таким образом по-
лучаются отвлеченные радиус винта и ширина лопасти:
7 = 7Т и b 7Г • (68)
За единицу скоростей принимают окружную скорость конца лопасти,
т. е. R(a. Тогда получаются отвлеченные скорости:
Vn гу Vi — W,
= и т-д- <69>
Все отвлеченные величины обозначаются у нас, как предложил В. П. Вет-
чинкин в 1913 г., теми же буквами, как именованные, но над ними ста-
вится черта.
Отвлеченная скорость 1/0 связана очень простым соотношением с обыч-
ным коэффициентом скорости Л. Действительно, мы можем написать:
? _-= = лГ» - л^ =
Dns R-2nns R(s) " °’
следовательно,
Vo = * . (70)
Вместо тяги н мощностн’пншут **:
Р -a,oD4ns2,}
(70
Т = £ pD5ns3.)
* У нас иногда по примеру американцев и англичан во время обработки опытов
—
пользуются величиной д4-=-р-. Такую величину мы предлагаем отмечать снизу бук-
вой А (английская).
** Б. Н. Юрьев. Воздушные винты. М.— Л., ОНТИ, 1934.
Во избежание смешения с углом атаки а и углом притекания струй 3, бу-
дем ставить над коэффициентом тяги и мощности черту.
Для элементарной силы тяги и мощности можно писать:
dP = pD4ns2da = pl6/?4ns2da; (72)
dT = pD5nsdp = p32/?6rtsd£. (73)
При расчете винтов в отвлеченных обозначениях удобно вместо dP и
dT пользоваться этими безразмерными величинами da и
Преобразуем основные формулы (31) и (33), дающие элементарную тягу
и мощность, так, чтобы в них входили лишь безразмерные величины. Для
этого перепишем их, подставив соответствующие безразмерные величины с
их именованными множителями:
pl6/?a/isda = c#kbRR ^-/?2(2jtns)2cos(3-!-'n)rfr;
p32R5ns d^ — cRRbRR Rz(2jtns)2 rR-2jrzzsSin (3 -j- [i)dr.
Сокращая в этих уравнениях именованные множители, найдем оконча-
тельно:
da ~ сд/гЬЖ2! cos (3 у.) dr; (74)
d3 = сцШ/^г sin (р 4~ [i)dr. (75)
При расчете винта удобнее сперва, как мы видели, вычислять не тягу
и мощность, а их производные. Для этого полученные выражения следует
писать в таком виде:
= у cRkbW2r cos (Р + и); (76)
^L = ^cRfebir?7sin(P^-ц). (77)
Последние две формулы и будут у нас основными для вычисления тяги
и мощности винта. Ввиду того, что эти величины будут при обычных ме-
тодах расчета получаться в числовом виде, для получения полной тяги и
момента придется их интегрировать или численно, или, что обычно и де-
лается, графически.
Для этого нужно построить графики (фиг. 25), на которых по оси абс-
цисс отложено значение г, а по оси ординат значения -^= Полу-
чится полная аналогия с фиг. 5.
Сами величины а и 3 получатся из очевидных формул:
$> 1. итвлеченные величины в ширии виши
где верхний предел соответствует концу лопасти (r= 1), а нижний дает
величину нерабочей части винта = г0 .
Интегралы эти будут представлены иа фиг. 25 площадями и Qp и,
следовательно,
а = Qamn,
3 = Qpafr,
где m, п, a nk— соответственные цены одного сантиметра для откладывае-
— da dB*
мых по осям координат величии г, —~ и —— .
dr dr
Пользуясь отвлеченными обозначениями,
мы получаем как величины аир, так и кри-
da d$
вне —=- и , относящиеся не к одному кон-
dr dr
кретному винту, а ко всем виитам, подобны.м
данному. Это дает значительно большую об-
щность всем расчетам. z
da dR
Кривые -^=- и —£= , представленные на
dr" dr
фиг. 25, мы будем называть диаграммами
распределения коэффициента тяги и мощности
вдоль лопасти винта. В практических расче-
тах приходится строить такие диаграммы для
ряда значений отвлеченной скорости полета
1/р или коэффициента скорости к = л]/0 и на-
ходить ряд соответствующих значений аир.
Окончательный результат изображается в виде
диаграммы, дающей зависимости от X вели-
77 аХ
чин а, р и п -= — .
3
(78')
dr
Фиг. 25
Примечание. При расчете вннта на прочность нужно еще иметь выражения для
отвлеченной силы сопротивления Q, Для этого случая можно написать формулу подобия
в таком виде:
dQ = pD4rijdaQ,
где a.q—коэффициент силы окружного усилия винта
Проделав описанные в этом параграфе преобразования, мы получим фор-
мулу, аналогичную (76).'
dan л2--------„
=- — CrAW? sin (3 + |Х).
dr 8
(76-)
Ею можно пользоваться для графического вычисления секущего усилия в
плоскости вращения винта.
* Иногда пользуются обратными величинами— масштабами, дающими длину
(в см) единицы той или иной величины, откладываемой на- осях координат. В таком
случае найденные площади следует делить на масштабы, ,
Совершенно аналогично формуле (44), дающей значение , можно,
введя в расчеты коэффициент полной силы по формуле
dR ?D4id,,dax,
получить выражение для производной
= —cKkbWlv (79)
dr 8
С помощью этой величины, удобной прн расчетах, можно полученные нами
формулы (76) и (77) переписать н виде:
da dap = -^cos(3-r p); dr (76")
da.Q dr da a = —-- -sill(3 p); dr (76'")
cip da® — dr dr (77')
§ 2. ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ
ДЛЯ СКОРОСТЕЙ В СТРУЕ ВИНТА
Очень полезны при расчете винтов тригонометрические формулы, связы-
вающие скорости потока в струе винта. Удобнее их выразить через окруж-
ную скорость конца лопасти что позволит ввести в формулы безраз-
мерные скорости.
Из скоростного многоугольника, изображенного на фиг. 26, сразу же
можно получить:
V„ = rutg(3„;
(80)
(81)
(82)
Далее из косоугольного треугольника ОВС получим:
откуда
________№)
sin (3 — Ро) sin (90° + ц) ’
U>, =
sin (3 — 3„)
COS ц
Пользуясь формулой (81), получим:
Wt = Г(0
sin (3 — ftp)
COS COS 30
_ no
0 ~ cos 30 ’
V, = Wl sin з.
Из того же косоугольного треугольника находим:
Wi
sin (90° — 3 — ц 4- — <жф — Зо + н) — sin (90° — |л)
или
7 cos (В — Во + ц)
0 sin (9UJ — ц)
Подставляя сюда WQ по формуле (81), получим:
U2-, = +
COS Ц COS Во
Наконец,
(83)
V, = IT,sin₽ = rm g°s(3 -3« +rising
* 11 COS Ц COS Bo
Заметим, что во многие формулы входит разность |3— Во; ее, но аналогии
с крылом, назовем углом скоса потока и будем обозначать в дальнейшем
через е.
Разделив все полученные выражения для скоростей на /?<о, получим
слева отвлеченные скорости, а справа их тригонометрические выражения:
v„ = rtg3„ = ^'; ' (84) = <85> — — sine ,OP, -r cos ц cos ₽„ ; <8G> p jn.sfe.jq • (87) 1 COS Ц COS Bo p = pin 3 cos (в 4- Ц) j 3 (88) 1 COS JI COS Bo Ui - telcos (3 4-ц); (89)
sin (3 4- р).
(90)
Этими формулами удобно пользоваться при расчете винтов в отвлеченных
обозначениях.
Из формулы (80) можно получить весьма полезное соотношение:
Зо = arctg-4 = arctg^-. (91)
§ 3. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА УРАВНЕНИЯ СВЯЗИ
При расчете винтов в безразмерных величинах (в отвлеченных обозначе-
ниях) удобно пользоваться тригонометрическим выражением для уравнения
связи.
В натуральных обозначениях это уравнение имело вид:
!-'УЛ1= '
где
„ kb kb
l\ = — =- —=
8яг 8лг
В левой части мы можем и числитель и знаменатель разделить на
тогда получим отвлеченные скорости:
1 I W1 1г Г.
Подставляя в эту формулу найденные нами тригонометрические выражения
дляУх, и W'n получим окончательно:
sin I В I sm е
“ Кск
(92)
Вместо абсолютной величины | sin£| мы написали sin|3|, что одно и тоже.
В это основное уравнение теперь не входят совершенно скорости, а
входят лишь характерные углы скоростного многоугольника.
В случае работы винта на месте, формула напишется еще проще, так
как в этом случае
= 0 и 8 -• [к Следовательно,
sin2 3
COS (3^1*) -^с«-
(93)
Упрощение уравнения связи
В § 6 главы 2 мы рекомендовали пользоваться для расчета работы вин-
та на нормальных режимах полета упрощенным уравнением связи (61). По-
смотрим теперь, какую погрешность вызвало такое уярощение.
Возьмем уравнение связи (92). Развернем выражения в знаменателе по
формуле cos (е + ц) cos е cos р — sin е sin ц и вместо подставим равное
ему —Тогда получим:
sin | р ] sin е __ су
cose cos ц — sin е sin ц-" ^созц
Углы е и р, обычно малы и лишь на некоторых режимах достигают
10—15°. При этом один угол обычно имеет меньшую величииу, чем дру-
гой. Вследствие этого можно считать произведение cos&cosp. близким к
единице, а произведение sin ц sin 8 очень малой величиной, которую можно
отбросить. Оценим величину получающейся при этом ошибки. При 8 = ц = 5°
получаем sin е sin ja = sin2 ja — 0,0076; отбрасывая это произведение и счи-
тая cose cos 1, получаем относительную ошибку всего лишь в 3/4 %.
При е = ц = 10° подсчитанная так ошибка равна уже 3%. При одном угле,
равном 5°, а другом, равном 15°, ошибка равна 2%.
Следовательно, для обычных условий работы винтов можно с достаточ-
ной точностью пользоваться упрощенным выражением:
sin | В ’sin е _д.
cos е !/
или
sin | р| tg е = Ксу.
(94)
Его можно еще более упростить, если заменить tg е дугой . Тогда
получим:
КСу
sin | 3 j '
е — 57,3
(95)
Такая замена дает погрешность* при 8 = 5° около ’/4% и при е= 10° —
около 1% в сторону преувеличения 8.
Если в формулу (95) вместо 57,3 подставить 57, то ошибка «сполови-
нится» и формула будет давать погрешность менее ’/•>% Для углов р. и е.
меньших 5°, н около 1% для углов 10°.
Эту формулу мы и привели в§ 6 главы 2 [формула (61)]. Помимо прос-
тоты, она еще удобна потому, что в нее входит не с%, а су. Для с„ имеют-
ся многочисленные таблицы и графики, а величину сц обычно приходится
вычислять.
Ошибка от такого упрощения получается в конечном результате очень
небольшая, так как здесь погрешности компенсируются. До значений е <_ 10°
точность получается очень хорошая, и в этих случаях нужно прямо реко-
мендовать пользоваться формулой (95) вместо значительно более сложной
формулы (92).
В эту формулу, для использования ее при малых углах атаки, можно
ввести линейный закон изменения, т. е. принять, что су = яад, и восполь-
зоваться соотношением 3 = фа — аа- Тогда получим:
с„ ЛДз
= 57 —= 57—г—-----------i
sin | [3 | sin | cpa —
(96)
где
5,4,
sin ]cpe — aa )
57_________«______
sin <pa — aa |
= f (<₽a, ao)-
Величину 8 легко вычислить для разных значений <ра и аа и построить
график, дающий зависимость 8 от угла ла и наклона сечения <рв (фнг. 27).
Величину 8 будем называть отвлеченным скосом потока.
Этот график облегчает вычисления. Так, при прверочном расчете вин-
та с его помощью можно очень быстро найти угол атаки сечения. Для
этого нужно задаться подходящим углом а' и найти, зная <ра, величину 8
по графику и вычислить г = /(е. Далее, по заданной величине Зо вайти
idoo
Фиг 27
3 = Po + & и снова вычислить ад -= q,u — ?. Если теперь возьмем среднее
а " 4- а'
значение угла атаки, т. е. ац =--------, то получим уже очень близкую
неистинному значению величину «а. Проделав с нею описанную операцию,
мы получим практически точный ответ. Быстрая сходимость этого процес-
са объясняется тем, что если мы задаемся преувеличенной величиной угла ай,
то после указанного расчета получим преуменьшенное значение: среднее
будет близко к истинному.
Если угол е велик, то его следует находить по более точной формуле
(94)
tgs = tgK’s. ' (96')
При вычисления скорости вместо точной формулы
U/'l = ГСО
COS (Е + ц)
cos ц cos Зо
прн очень малых углах е можно пользоваться более простой формулой
117. == = 117.
1 cos >0
(97)
Прн этом получается погрешность вследствие отбрасывания дроби
cos (е — ц) cos е cos ц — sin е sin ц
COS |А COS |А
Если пренебрежем произведением синусов малых углов £ и р., то получим
погрешность, оцениваемую множителем cos 8. Следовательно, можно писать
более точно:
UZi^-q-coss. (97')
1 COS 30 ' ‘ '
Геометрически это соотношение обозначает, что мы считаем вектор
©J J. Wi- Такое же допущение сделано н в вихревой теории воздушного
вннта у Н. Е. Жуковского. За границей многие авторы считают w, I Wnt
как это делается в теории индуктивного сопротивления, где скорость скоса
считается перпендикулярной к скорости невозмущенного потока. По нашей
теории, учитывающей влияние лобового сопротивления на струю, вектор Wj
отклонен от перпендикуляра к на угол р. назад. Малость угла р. на
основных режимах полета позволяет с хорошей точностью пользоваться
формулой (97), но, конечно, для расчета режимов торможения, остановки,
вихревого кольца приближенное уравнение не пригодно, так как р. иа не-
которых из этих режимов достигает значения 4~ 90°.
§ 4. ПОВЕРОЧНЫЙ РАСЧЕТ ВИНТА
В ОТВЛЕЧЕННЫХ ОБОЗНАЧЕНИЯХ
Винт в отвлеченных обозначениях рассчитывается в том же порядке,
как и прн графо-аналитическом методе (§ 1 и 2 главы 2). Как и там, рас-
чет можно вести илн для одного режима, илн для всех режимов сразу.
Благодаря удобному аналитическому выражению для скоростей весь
расчет можно вести аналитически, используя графики продувки профиля
лишь для определения с % и ц.
Расчет винта иа одном режиме
_ Имея чертеж вннта, мы знаем на любом выбранном радиусе г величину
b и тнп профиля лопасти. Следовательно, легко вычислить для ряда ра-
диусов г величину
L'
/\ = ---=— .
8лг
Далее задаемся режимом работы вннта, т. е. нли коэффициентом ско-
рости X = , или отвлеченной скоростью V’o = ~~ . После этого на-
£)7is г ли)
ходим для выбранных радиусов угол притекания потока Ро по формуле (91).
По способу последовательных приближений находим истинный угол ата-
ки сечений. Для этого задаемся для каждого сечения несколькими подхо-
дящими углами атаки а н находим по продувке профиля соответствующие
Таблица 2
Формуляр поверочного расчета вннта для одного режима
Л — ; k ~ ; тип сечении . . . ; чертеж . . . ; D ;
лп п
п = '• " = 30 “ ns = "60“ =
1 г 0,9 0,75 0.6 0.4S 0.3
2 <р
3 Ь
Ч . с
5 Тип профиля
6 b R
7 С = ~
. 8 г kb 8яг
9 Л яг
10 А, Зо arc tg —~ лг
И а
12
.13 Нх^-т1- У
14 |Л =1 arc tg ц.
is : 3 = <р — а
те ' -sin
17 е — (3 — Зп
18 sine
19 ® + о ; '
20 cos(е +- р)
21 1 sin 3 sin е
~ К cos(e + ц)
22 т _ c°s <е +1*) 1 COS Ц COS Зо
23
24 sin(P + (i)
25 cos (3 + и)
26 Л2 - — „ -g— cR kbV^‘
' 27 da -=- = (26) cos (g + и> ar
ouniu о v'lUUKtcnnou ииизначениЯХ
Примечание. В пунктах 32—34—графическое интегрирование в интервале
от г = 1 до г = $.
величины Cr и р, находим углы 3 = <р — а, е — р — ^ие + цн снова
вычисляем по уравнению связи (92) величину
1 sin | | sin е
Cr — К cos (е + р)
(98)
Несколько полученных парных значений исходного а н вычисленных
значений cr наносим на продувку профиля в виде кривой потребных Cr и
ищем пересечение этой кривой с кривой располагаемых cr (т. е. продувоч-
ных, пересчитанных на бесконечный размах). В точке пересечения мы най-
дем истинный угол профиля н соответствующие значения Cr н р.
Далее находим отвлеченную скорость набегающего на профиль потока
— 7 cos (е + Н) е
1 _ COS Р COS Зо cos р0
и производные
-S- = ^^to^cos([3+ |*)
dr 8
н
^- = ^cRkbWlr sin(B+ й)-
dr о
После этого с помощью графического интегрирования находим величин^»
а н [1, согласно фнг. 25; к. п. д. вннта найдется подформуле
При расчете винта на прочность нужно найтн окружное сопротивление
элемента. Для этого необходимо графически проинтегрировать выражение
(76') для ряда сечений винта, согласно изложенному в § 1 главы 3. Тогда
получим аСекуш.ее и а q секущее, необходимые для расчета прочности.
Подобный расчет нужно сделать для ряда режимов винта, охватываю-
щих его нормальную работу. Для обычных винтов потребуется взять ре-
жимы около нулевой тяги, максимального к. п.д., половинной скорости по-
лета, что соответствует взлету самолета, и рассчитать тягу на месте. Если
желательно более точно проследить характер изменения характеристик
винта, то необходимо взять еще несколько промежуточных точек. Всего
получается около шести-восьми режимов. Это представляет хотя и прос-
тую, но довольно большую расчетную работу.
Можно несколько сократить вычисления, производя расчет всей харак-
теристики винта сразу, как это мы делали в натуральных величинах в §. 2
главы 2. Для безразмерных величии мы такой расчет изложим в следую-
щем § 5.
В заключение мы прилагаем подробный формуляр точного расчета винта
для одного режима (табл. 2).
§ 5. РАСЧЕТ ВИНТА ДЛЯ ВСЕХ РЕЖИМОВ ОДНОВРЕМЕННО
В ОТВЛЕЧЕННЫХ ОБОЗНАЧЕНИЯХ
С помощью отвлеченных величин расчет винта для всех режимов может
вестись полностью аналитически. Можно получить формулу, прямо дающую
величину К, соответствующую выбранному углу атаки сечеиия.
Вывод этой формулы проще всего сделать так. Берем угол атаки а, по
продувке находим cR и ц. Кроме того, получаем £ = — а.
Будем считать пока скорость избегающего потока известной. Тогда
по предыдущему (см. фиг. 26)
Вводя эту величину в уравнение связи, получим:
wi sin з
Отсюда
Далее по фиг. 26 получаем;
U = гео = cos 3 + ©1 sin (3 + p.) = ir^cos p + KcR s—j ;
V, = У,-о,= IF, sin 0-to, cos (3 + H) = IF, |sin'i-KcR
Вычислим теперь с помощью найденных формул коэффициент скорости X,
при котором будет работать иаш элемент:
Ур
— лг
Уо
и
= лг
sin 3 — KcR
cos(3 + n)
Sin 3
cos 3 4- KcR
sin(3+ Ц)
sin 3
Делая приведение, получим окончательно:
. __ - sin23 —Ксц cos ф + И)
sin 3 cos 3 -I- Кск sin (3 + ц) ' '
В эту интересную формулу не входят скорость и угол 30, поэтому,
задавшись углом атаки а, зная по продувке с# и ц и помня, что 3 = <р — а,
мы сможем сразу вычислить ^коэффициент скорости винта Л, при котором
сечение, лежащее на радиусе г, будет иметь именно этот угол атаки.
Найдя величину X, легко получить кажущийся угол притекания потока
Зо = arc tg -L-
лг
и скорость набегающего потока’
w = 7 cos(e + h) .
1 COS U cos 30 ’
где
В = ₽— й>.
Далее расчет идет просто по уже известному нам методу. Нужно вы-
числить производные -^=т- и по формулам (74) и (75), затем, если
предполагается произвести расчет прочности винта, следует вычислить н
da0
производную —=? . Такой расчет необходимо проделать для нескольких уг-
dr
лов атаки а, и, найдя соответствующее X, нужно построить график изме-
нения этих производных в зависимости от X. Получится для каждого вы-
бранного нами значения г своя характеристика элемента лопасти (фиг. 28).
После этого следует найти значения производных, соответствующие одному
и тому же значению X, для чего нужно взять нх значения, лежащие на
одной абсциссе.
г-г da d3 .
По этим значениям —= и —приведенным к одному X, нужно no-
dr dr
строить график (фиг. 29), с помощью которого можно сделать графическое
интегрирование по способу § 1.
После интегрирования получим ряд значений а и [3, соответствующих
ряду значений X, и можно построить полную аэродинамическую характери-
стику вннта, т. е. кривые а, р и т] в функции Л (фиг. 14).
При некотором навыке описанные расчеты производятся достаточно
быстро. Кроме того, случайные ошибки сразу же обнаруживаются, так как
ошибочные величины дают на диаграммах точки, не ложащиеся на кривую.
Примечание. Найденное выражение для А. позволяет сразу находить ряд инте-
ресных режимов для выбранного сечения винта. Так, режим вихревого кольца получится,
когда a — ср и 3 = ср — a = 0. Наша формула даст для этого случая критическое зна-
чение коэффициента скорости А.:
_ Кск cos (3 + И)
= - яг K^'sin (3+ ц) = - яг ctS <Иф). (10°)
Таблица 3
Формуляр поверочного расчета винта для ряда режимов
Сечение г профиль . . .
8лг
R
1 а -5° 0° +5° 10° 20° 25° 30a 40*
2 3 4 ск сч. и'-“ ц - arc tg Ht
5 6 7 з = ф -- а sin 3 COS 3
8 9 10 s + l* rin (g + Ц) cos(P + ir)
11 12 13 14 15 ' sin2 3 sin 3 cos 3 (13) sin (3 -4- fl) (13) cos (g + u)
16 (11)— (15) <12>-b(14>
17 18 19 20 X nr X =arctg — e = 3 — 3o e + H
21 22 23 24 25 26 27 COS Ц COS 3o cos (e 4- ц) лМ(«сд) Г costf+H) у dr < * L cos Ц cos go J da _ (25) cos (g + n) —=- = (25) sin ф + ц) ar
Таблица 3 (окончание)
(101)
sin2|3 — KcR
— лг sin 3 cos р
Когда p-j- р. — 90э, то векторы dR и wx лежат в плоскости вращения винта, т. е. по-
лучаются режимы нулевой тяги. При этом
sin2 3
sin 3 cos 3
(102)
Для применения этих формул нужно знать получающиеся на этих режимах величи-
ны и ц, что легко может быть сделано по способу, изложенному в § 5 (гл. 2), с помощью
проведения двух вспомогательных прямых ВС и на продувочной диаграмме про-
филя (фиг. 21). Следует помнить, что все эти рассуждения относятся не к винту в це-
лом, а лишь к выбранному сечению, лежащему на радиусе г.
Фиг. 28
Обычно приходится делать расчет винта лишь для основных режи-
мов полета, и тогда вполне законно воспользоваться упрощенным урав-
нением связи. Расчет удобно вести для ряда режимов сразу, по типу
расчета, описанного в § 2 главы 2. Мы не будем, повторять сделанный
там вывод, а лишь даем готовый формуляр расчета в отвлеченных обоз-
начениях, которым рекомендуем пользоваться при расчете общих режи-
мов работы винтов.
Таблица 4
Формуляр для упрощенного расчета винта на основных режимах полета
Г=0.9
Величины
Профиль
Ф=...-, Z>=...;
8 ПЛ
Профиль
Профиль
Профиль
* Или Vo = Г 51П Pq.
§ 6. О ТОЧНОСТИ И ПРЕДЕЛАХ ПРИМЕНЕНИЯ
ИЗЛОЖЕННОЙ ТЕОРИИ
Изложенная теория дает достаточно хорошее совпадение расчетов с ре-
зультатами опытов. Практически результаты расчетов по этой теории со-
впадают с расчетами, произведенными по вихревой теории Жуковского.
В теории Жуковского также пользуются средними скоростями в струе вин-
та, которые крайне мало отличаются от получающихся у нас. Следователь-
но, импульсная теория имеет практически ту же точность, как н вихревая.
Расхождение этих теорий получается лишь при необычных режимах.
Основными различиями теорий являются учет в импульсной теории влия-
ния сил трения на струю виита и пренебрежение давлениями в далеком за
винтом сечении. Индуктивная скорость w, в вихревой теории перпенди-
кулярна к скорости U7], в импульсной же теории она отклонена от перпен-
дикуляра к Wt на угол и, назад по потоку из-за наличия сил трения.
В уравнение связи в вихревой теории входит лишь аэродинамический коэффи-
циент су, а у нас cR =JVc’p 4- Су .
$ 6. (J точности и пределах применения изложенной теории
73-
Преимуществом излагаемой теории являются ее простота и наглядность,
а также учет действия на струю винта сил лобового сопротивления профи-
ля. Она очень удобна для поверочного расчета винтов, но не учитывает
давления в сечеиин 2, что дает небольшую погрешность. Наконец, в этой
теории трудно получить удобные для ряда расчетов аналитические форму-
лы. Вихревая теория дает удобные окончательные формулы, облегчающие
проектирование и расчет нового винта. Расчет вентиляторов, у которых по-
лучается иногда очень большое закручивание струи, также надежнее вести
по вихревой теории. Но в общем, как мы
уже указывали, обе теории дают одина-
ковый результат и одинаковые погреш-
ности. Их общий недостаток заключает-
ся в том, что расчет ведется по средним
скоростям. Теории эти, строго .говоря,
соответствуют винту с бесконечно боль-
шим числом лопастей. Такой винт у нас
часто называют «дисковым» винтом.
Уточнение этих теорий может быть
достигнуто лишь учетом числа лопастей
и переходом к истинным скоростям по-
тока. Такие вихревые теории появились
/ср
Фиг. 30
лишь в самое последнее время; их называют у нас, по предложению ав-
тора, «относительными», так как в иих рассматриваются истинные относи-
тельные скорости воздуха и лопастей. Этн теории крайне сложны и гро-
моздки. Чаще всего предлагают вести расчет по дисковой вихревой теории
или по импульсной и вводить в них затем поправки, вычисленные по
относительной теории. Таковы известные поправки Праидтля и Гольд-
штейна.
В излагаемую теорию очень легко вводить такие поправки, беря их нли
ез относительной теории, илн прямо из опытов с винтами.
Заметим, что мы еще в 1910 г. пользовались при расчете геликоптеров
поправкой на несовершенство сжатия струн (термин, заимствованный из
гидравлики) и считали скорость у сечения = vlt что равносильно замене
средней скорости vcp истинной скоростью Vi — £i»cp, где величина £ бралась
из опытов.
Такого типа поправки применяют некоторые авторы за границей. Оии
не играют сколько-нибудь заметной роли при работе винта иа режиме
пропеллера и становятся ощутительными у геликоптерных винтов и вет-
ряков.
Если рассмотрим развертку цилиндрического сечения винта, то получим
в плоскости винта ряд сечений лопасти. Индуктивная скорость vx будет
иметь наибольшее значение в том месте, где находится лопасть. Пункти-
ром мы изобразили среднюю скорость i»lcp (фиг. 30, /).
В далеком сечении (фиг. 30,2) можно считать, что скорости выравнива-
ются и будут равны скорости v2, находимой по теории идеального пропел-
лера, т. е. по Средним величинам. Эти же рассуждения можно провести
и относительно окружной составляющей индуктивных скоростей. Можно
принять, что
»1 = £»1СР = ? .
U = ?Ulcp = S у-,
(103)
следовательно,
= fet^icp = Ь — •
По нашим данным, у винтов с весьма узкими лопастями, какие встре-
чаются лишь у геликоптеров, величина £ = 1,25, т. е. скорости у профиля
на 25% больше средних скоростей потока.
Ширина лопастей в этих случаях была Ь0.п = — 0,06 — 0,1. При
Фиг 31
более широких лопастях эта поправка получа-
ется меньшей; при 60ЛБ == ——°- =0,15—0,25 она
примерно в два раза меньше. К сожалению, точ-
ных исследований по этому вопросу пока еще
не имеется.
Поправка эта, в случае современного пропел-
лера, когда сама скорость очень мала по
сравнению со скоростью полета Уо, не имеет
большого значения. Но у геликоптера и ветряка
она существенна.
Было бы полезным выяснить изменение этого коэффициента вдоль по
радиусу винта: этим излагаемая теория была бы приближена к относи-
тельной.
Учет неравномерного распределения скоростей мы рекомендуем делать,
вводя в скоростной многоугольник винта вместо получающейся по уравне-
нию связи средней скорости истинную скорость как это показано
на фиг. 31. Для отличия полученных при таком предположении величйн
мы будем ставить у них индекс t, например: У^, и т. д.
Отметим еще одно преимущество импульсной теории перед вихревой.
Когда мы рассматривали 20 режимов работы винта, то при построении
струи винта не получали никаких противоречий. Если бы мы стали делать
расчет по вихревой теории в ее чистом виде, то получили бы ряд противо-
речий вследствие неучета влияния сил трения на струю. Так, например,
при Р = 0 у нас струя не была бы цилиндрической, так как циркуляция не
была бы равна нулю; это, однако, означает, что в струе создается количе-
ство движения без соответствующего импульса. Точно так же при Т = 0-
струя в вихревой теории имеет вращение, чего, конечно, быть не может.
В. П. Ветчинкин предлагал исправлять этот недостаток вихревой теории,
вводя особые множители, но это вызывает сильное ее осложнение. Прием
этот распространения не получил.
В импульсной теории пренебрегают разностью давлений в сжатом
сечении струи, получающемся вследствие наличия центробежных сил.
Однако давления эти малы и пренебрежение ими менее отзывается иа
конечном результате и методически более логично, чем нарушение
теоремы об импульсе в вихревой теории.
Заметим, что все эти неувязки появляются лишь на необычных ре-
жимах полета. На основных же режимах обе теории дают практически
совпадающие результаты.
Глава 4
НОРМАЛЬНЫЙ ВИНТ
§ 1. СКОРОСТЬ ПОТОКА У НОРМАЛЬНОГО ВИНТА
В предыдущих главах мы рассмотрели способы поверочного расчета
винтов по импульсной теории. Однако на практике очень часто приходит-
ся решать задачу о подборе виита иа заданные условия работы. В та-
ком случае нужно иметь или готовые графики, илн простые формулы,
дающие полную тягу Р и мощность Т винта, или их аэродинамические
коэффициенты. Такие формулы можно получить, проинтегрировав диф-
ференциальные выражения для тяги и мощности. Как вы видели в § 3
главы 1, эти выражения сложны и на практике их приходится интегри-
ровать в общем случае графически.
В частном случае, при особой форме винта, так называемой нор-
мальной, можно произвести интегрирование и получить достаточно
удобные расчетные формулы. Такой «нормальный винт» был предложен
нами в 1910 г. Он имеет постоянную скорость подсасывания по всей
ометаемой площади, и все его сечения работают с наивыгоднейшими
углами атаки.
Проф. Н. Е. Жуковский, разрабатывая в 1912 г. вихревую теорию,
также остановился на таком типе винта, как на простейшем. Рассчи-
танный по вихревой теории такой винт у нас называется по имени Ни-
колая Егоровича Жуковского винтом НЕЖ. По форме винты НЕЖ и
нормальный практически совпадают. Небольшая разница получается в
ширине сечений лишь у самой втулки за счет учета давлений в вихре-
вой теории.
Основанием для выбора такого винта послужили следующие рассужде-
ния. Если мы сравним винт с постоянной скоростью по ометаемой площади
с таким же винтом, но с переменной скоростью, то у последнего потеря
энергии будет больше, так как уносимая кинетическая энергия пропорци-
ональна квадрату скорости, а тяга пропорциональна количеству движения,
т. е. скорости. Потери на трение получаются минимальные, когда каждое
схр
сечение будет иметь наивыгодиейший угол атаки, т. е. когда Цх = ——
у
будет минимальным.
Хотя оба эти положения порознь верны, их совместное утверждение
не совсем правильно. Как показал впервые В. П. Ветчинкин, задачу о на-
ивыгоднейшем винте нужио решать по правилам вариационного исчисления,
и тогда получается несколько другая форма винта. Такие винты называ-
ются у нас вариационными. Их рассчитывать удобнее по вихоевой теории.
Сравиеиие вариационных винтов с нормальными или НЕЖ показало,
что оии дают выигрыш в коэффициенте полезного действия винта очеиь
небольшой, обычно это доли процента н иногда -1—2%. Следовательно,
нормальный винт очень близок к наивыгоднейшему по к. п. д., и в то же
время его можно рассчитывать по очень простым формулам. Он является
как бы эталоном винтов, с которым можно сравнивать другие винты и по
формулам которого можно во многих случаях делать все предварительные
расчеты и подбор винта.
Скорость подсасывания у нормального винта
В § 1 главы 1 мы получили формулу (3), связывающую элементарную
тягу со скоростью на данном радиусе винта: dP = и^т, у нормального
винта V] = const, и теорему об импульсе можем написать в виде:
Р = mv2 — 2mvi. (104)
Массу воздуха, протекающего через винт, найдем по ометаемой площади
и скорости потока; она равна pF^Vi.
□метаемая площадь F*, с учетом центральной нерабочей части, полу-
чится по формуле:
А; ---я/?2 - р — = л«2(1 —У), (105)
где £—отвлеченный радиус нерабочей части. Скорость протекающего воз-
духа Vi = l-'o + 14. Следовательно,
Р = 2pft I (Vo+ «J | и, = 2лрй21 (Ц, + | И1(1 — У).
Введем величину
_______Р_______
oV2
(1-г-)
2
Она называется коэффициентом нагрузки на ометаемую площадь
С ее помощью Выражение (106) может быть переписано в виде:
(Ю6)
(107)
винта*
или
Отсюда, решая полученное квадратное уравнение и выбирая по смыслу
задачи знак плюс, получим:
I'o 2
или
-1+/ 1+B6
(108)
1Ю9)
2
Так как 1+ = V,, + оъ то
(109')
Формулы эти хорошо известны в настоящее время как основные формулы
теории идеального пропеллера. У нас в нее введена действительная омета-
емая площадь, а не площадь диска винта, как это делается обычно при
грубых подсчетах. Вследствие этого мы и ввели обозначение вместо
общепринятого В.
Величину Bt удобно выразить через безразмерные коэффициенты, для
чего достаточно заменить Р и lz0 через их выражения по закону подобия
(54) и (56). Тогда получим:
р ар£>4п®
PJT’l1
(110)
8
Х3тг(1_^)
После этого .выражение для скорости подсасывания может быть написано
в виде: __________
-1+1/1+-------—
Ol = l/0-V ^*(1-?). (Ш)
Очень близкая величина для скорости Vi получается и по вихревой те-
ории. Однако, по нашему мнению, при вычислении скоростного многоуголь-
ника у элемента винта нужно брать не эту среднюю скорость vlt а несколько
большую Viz = ±vlt где £ учитывает неравномерное распределение истинных
скоростей в плоскости вращения (см. § 6 главы 3). Тогда наша формула
может быть переписана в виде:
-1+1/1+“------—
. “1/ Г л (1 —С®) /но.
«и = = Л-------------1--— (112)
Скорость подходящего воздуха Vj выразится без учета £ формулой
^ + ^^+^/1 + -^^) (ИЗ)
и с учетом £ формулой
^^+^=4^+2/1 + 444]. du.
Напишем теперь эту формулу в безразмерных величинах, для чего
введем еще одну отвлеченную величину — коэффициент скорости винта
по потоку, определив ее формулой
Dn:
(115)
В тех случаях, когда берется скорость подходящего воздуха с учетом
неравномерности струи, мы будем писать
С помощью этих величин предыдущая формула перепишется в таком
виде:
= + т/14----------§--— L (117)
X 2 2 V Я (1 - £2) V / '
Вводя сюда £ = 1,25 и £ = */4, получим рабочие формулы
Vlt = Vo(o,375 4-O,625j/ 1 + 2,72-^-) (118)
Mj = Ц 0,375 + 0,625 т/ 14-2,72 —
(119)
Большинство авторов, разрабатывавших импульсную теорию, считает
£ — 1, что вносит заметную ошибку лишь в расчет геликоптерных вннтов.
Заметим, что выведенные формулы можно писать в различном виде,
пользуясь теми или ииымн величинами. Например, формулу (118) можно
написать для безразмерных скоростей в таком виде:
V,( о,375 4-0,625 l/l+24 “ V (118')
\ V лг v0 ;
§ 2. ФОРМУЛЫ силы тяги и мощности
НОРМАЛЬНОГО ВИНТА
Элементарная тяга вннта выражается формулой
dP = 4jtp|Vilvirdr. (40)
В случае нормального винта = const и Vi = Vo 4~ = const, и тогда
предыдущее выражение очень легко проинтегрировать:
я
P = 4^p|V1|v1J rdr = 2np]VI|o1(fl2 — ^) = 2npll/!pi>?2(l — И-
(Ю6)
Получилась очень простая формула для тяги, уже найденная нами ранее
непосредственно. Найдем теперь мощность вннта. Сопротивление элемента
винта dQ можно получить нз силового треугольника в виде:
dQ = dPtgGk + n).
(120).
Тогда элементарная мощность получится по формуле
dT ~ dQ гм — dP г a tg (pj р). (121)
Мы здесь пишем учитывая неравномерность скоростей в струе винта.
Последнее выражение неудобно для интегрирования. Мы заменим его
приближенным, достаточно точным. Для этого заметим, что
tg(P н- И) = ; , , , -
1—tg tg p.
Ввиду малости второго члена в знаменателе по сравнению с единицей,
заменим делитель миожителем по известному правилу приближенных вы
числений (-----= 1 + k при малых k] . Тогда получим:
\ 1 — k ~ 1
tg + Н) = (tg 3s + tg g) (1 + tg tg g) = tg p- + tg g + tg2 pt tg g -g
+ tg3jtg2g.
Угол p у нормального винта мал, и вполне законно заменить tg р через
ДУГУ М-р Величина pi очень мала, и ее можно отбросить. Тогда останется
tg (₽: 4- м) = tg 3; + м-1 + м-1 tg2?:
Vp
Величина tgpg ~ —2- (если пренебречь за малостью величиной Ui). Вводя
ее, получим окончательно
tg(3; + g) =-= + gl -t- gi ( . (122)
F(O V Г<£> ’
Точность этой формулы высока, и тем больше, чем меньше величина 3;
Так, при pj = 43° и р = 2° ошибка меньше 0,1 %.
Теперь формулу мощности мы можем переписать в таком виде:
dT — dPrw Г-^ + рг- р., i 1 . (123)
L rt0 \ r<jj J J
Подставляя сюда известное выражение (40) для элементарной тяги,
раскрывая скобки и интегрируя, получим для нормального виита:
Т от/ I Л т/ ? 2 л ,
Т = PV^ Ч- p,i® 4лр ViVj, \ г2 dr 4--------l dr.
о»
Выделяя в этом выражении полную силу тяги по формуле (106), т. е.
Р~ 2лрУ1к1/?2(1 — В2), для чего вводим в подынтегральные выражения
отвлеченный радиус, получим:
Т = рул + Qd7 + ^PRla l^-\Qd7
1— 52 •) 1 - 52 к Яо J J
Произведя^ вычисление интегралов в пределах рабочей части виита, т. е.
от г = В до г = 1, найдем:
(124)'
Обычно £ = >/4; тогда
Т = PVK + ^PRa 0,7 + 1,6 ( -±
L \ к<»
(125)
Подставляя сюда V,; = V„ + получим:
Г = + + |^0,7 + 1,6 (126)
Получились, как видим, очень простые и наглядные формулы для мощ-
ности. Первый член в формуле (125) дает мощность, затраченную на про-
качивание воздуха через скачок давления Гр =--------------"I, какой име-
L л/?2(1-12) J
ется в плоскости его вращения. Эту мощность называют мощностью иде-
ального пропеллера, йли вентиляционной мощностью. Второй член дает
потери, связанные с ц, т. е. с треинем лопастей о воздух; если бы щ = 0,
то их бы не было.
Формула (126) расчленяет мощность винта на три слагаемых. Первое
дает полезную мощность винта, которая идет на продвижение самолета
(PV0). Второе дает потери, связанные с уносимой струей кинетической
энергией, — их часто называют индуктивными потерями винта. Третье дает
потери на трение воздуха о лопасть.
При пользовании этими формулами следует помнить, что они относятся
не к одному винту заданной, постоянной, нормальной формы, а для винтов,
каждый раз, для каждого режима заново рассчитываемых. Следовательно,
форма винта у нас будет все время изменяться с изменением X.
Переход к отвлеченным величинам
Для получения большей общности формул выгодно перейти к отвле-
ченным величинам. Для этого подставляем в выведенные формулы (106)
и (124) известные нам соотношения:
Р =
Т = Хк = ; Хг = Ль-;
Dns Dn3
® = 2nns и Vi — Vo — Dns (X, — X)
и получим:
apD1^ = 2^,pXiDns (X! — X) Dns — (1 — £2);
4
BpD^: apD^Vit + Ц|ар/7‘п';2.'тп, -5- Г —
2 (_ 3
1 — s3
l-v
+2-—______
\ 2
Сокращая именованные множители и делая приведение, получим:
(127)
. (128)
В случае ^=*V4 получим:
st = 1,471 Л} (Л। — X), (129)
(5- a>M!g Jr рга (2,20 4-0,51Х[»). (130)
Наконец, мы можем найти к. п. д. нормального винта по формуле (57)
aZ_____________X_____________
~3 (2,20-0,51?^)'
(131)
§ 3. РАСЧЕТ НОРМАЛЬНОГО ВИНТА
С помощью выведенных формул очень быстро и просто ведется расчет
нормального винта. Особенно прост расчет, когда задана тяга винта Р,
диаметр D, плотность ноздуха р ю число оборотов ns = — . Тогда мы
60
сразу можем найти
— Р
а =------
рО4п*
Затем вычисляем
Далее, по формуле (119), учитывающей неравномерность скоростей, находим
Mg. После этого вычисляем потребный коэффициент мощности |5 по формуле
(130) и находим к. п. д. винта:
аХ
После этого получаем мощность в лошадиных силах по тяге Р или
по 3:
/V = *^2- = ~ &D5n3s.
л 751] 75
На этом расчет винта заканчивается и можно переходить к компоновке
и вычерчиванию винта.
6 Б Н Юрьев, т. I
На практике задача ставится обычно в обратном виде: заданы бывают
мощность мотора N, число оборотов винта ns = — , плотность воздуха
60
и диаметр винта D и требуется найти развиваемую винтом тягу Р. Решать
эту задачу аналитически мало целесообразно, так как при подстановке
в формулу (130) величины по формуле (119) получается полное отно-
сительно а уравнение пятой степени, неразрешимое алгебраически. Следо-
вательно, нужно прибегать к сложным обходным решениям. Проще всего
на практике решать эту задачу графически. Для этого нужно задаться
рядом подходящих значений Р2, Ps, вычислить по описанному методу
коэффициенты мощности р2, Зз и построить в коорди-
натах а и р кривую а = /(р) (фиг. 32). По заданию мо-
тор требует величину коэффициента мощности
> 7г 75N
.
pD6n3
Фиг. 32
Если теперь провести на этой диаграмме вертикаль-
ную линию с абсциссой, равной то она пересечет на-
шу кривую в точке М, дающей требуемое решение за-
дачи, т. е. величину а при заданной мощности . Для
экономии вычислительной работы нужно вычисление де-
лать не сразу для всех Рг, Р2, Р3, а последовательно, нанося каждый раз
полученные точки на диаграмму (фиг. 32) и соображая, какую величину
следует выбрать для следующих точек, чтобы быстрее получить пересече-
ние кривой с линией заданного рЯ1.
После этого можно вычислить к. п. д. винта
П = —
3
н найти тягу
Р = л Z5X = apDJn";.
Весьма удобно при таких расчетах пользоваться заранее составленным
графиком-сеткой, дающим связь между аир для разных значений Л. Тогда
можно решать любые задачи по подбору нормальных винтов. При аккурат-
ной интерполяции между кривыми, можно получить вполне достаточную
для практики точность расчета.
На фиг. 33 представлен график, вычисленный для винтов, имеющих
J/4 и ц = 0,03. При Л - 0 получаем работу винтов иа месте (геликоп-
терную). Следует помнить, что форма винта на этой диаграмме не по-
стоянна, а изменяется от точки к точке. Для получения характеристик
подобранного винта для других, не расчетных режимов, необходимо
проделать поверочный расчет по способам, описанным в предыдущих пара-
графах.
На потери, связанные со втулкой, можно сбрасывать примерно 1 %
мощности.
Случай геликоптерного ротора
Этот режим является частным случаем работы винта и иа него распро-
страняются все выведенные нами формулы. В этом случае X = 0. Из фор-
мулы (117), раскрыв скобки и приняв X -= 0, получим:
- т - ‘’03 <132>
При этом
Х1 - ]/ = 0,826 /а . (132')
Формулу (128) для мощности можно упростить, отбросив в скобках
второй член, обычно очень малый, так как в него входит квадрат малой
величины Xie- Тогда получим:
. _ _ _ 2 1___Е3
[3 = ах1С + щал •— • -—~
о 1 — s
(133)
В эту формулу удобно ввести значение по формуле (132). Тогда полу-
чим весьма полезную формулу:
“,/г£ (134)
Беря в ней $ == V4, находим:
{* = 1,03а3/'2 + 2,20цга. (134)
Величину р.,, учитывая шероховатость лопастей и их колебания, берем
несколько повышенную, равную 0,05. Тогда получим:
1,03а3/'3 4- 0,11а. (134')
Округляя, можно 'писать р = - а3/'3 4- -а— , что хорошо сходится с опы-
тами.
На практике обычно задают мощность мотора и, следовательно, £ и
вычислить а можно, решая уравнение (134). Гораздо удобнее иметь зара-
нее составленный график зависимости а и как на фиг. 34. На этот
график нанесены также величина относительного к. п. д. геликоптериого
ротора, вычисленная по обычной формуле *
В нашем случае получим:
По = 0,8 44 = (135)
g 1,29-^-2,751^0, 11
Этой величиной пользуются для оценки совершенства роторов.
• Б. Н. Юрьев. Воздушные винты, стр. 174.
Расчет геликоптера*. Обычно заданы мощность мотора Nm, диаметр
ротора D, его число оборотов ns и плотность воздуха р. Сначала нужно
найти мощность М, которая дойдет до ротора. В геликоптере часть мощ-
ности расходуется на вентилятор охлаждения, рулевые вииты и трение
в трансмиссиях. В среднем до ротора доходит лишь 80% мощности мотора
Таким образом, N ^0,8Nm, и мы получим заданную величину
pD°n$
По графику фиг. 34 находим ос и вычисляем
Р = apL^nf.
Скорость потока в плоскости ротора найдем по формуле (132'):
% =4 0,826 |/ а и Vf -= /^Dris.
В сжатом сечеиии скорость будет в два раза больше:
v2 = 2иР
Эти скорости нужны для расчета обдувки фюзеляжа геликоптера.
. § 4. ФОРМА ЛОПАСТИ У НОРМАЛЬНОГО ВИНТА
Найдем теперь форму лопасти у нормального винта. После расчета
винта на. данном режиме мы будем знать коэффициенты а, 3» Хи Ар Кроме
того, нам будут известны скорости 1% и vL, постоянные иа всех радиусах
винта. Расчет будем вести, учитывая изменяемость Ц, vt и о.1! по окруж-
ности сечения с помощью величины
Тогда мы получаем непосредственно из скоростного многоугольника
(фиг. 35):
= (136)
ГСО — U1Z
скорость
= Цк tg (Зс 4-|г). (137)
Следовательно,
It Pt =--------------. I I’-'UI
гсо-сМёФс+Ю
С помощью этой формулы мы можем для любого ..радиуса винта г найти
угол рс, так как угол р нам известен: он соответствует наивыгодиейшему
Углу атаки для выбранного нами профиля. Решать уравнение (138) отно-
сительно Зс проще всего последовательными приближениями, пользуясь тем,
что р мало. Сначала нужно вычислить tgfr — —, найти вычислить р
ГО)
и по формуле (138) снова вычислить рс. Обычно после второго приближе-
ния величина перестает изменяться, и это значение будет истинным.
Подробнее см. Б. Н. Юрьев. Летные свойства геликоптеров. ВВИА, 1939.
Найдя для данного сечения величину угла ft, определяем по скорост-
ному многоугольнику (фиг. 35) величину полной индуктивной, скорости:
cos (3 -j- jx) cos (ft + ц)
Скорость набегающего потока
W'i: «tc)a-r (140)
Фиг. 36
После этого по уравнению связи (25) находим ширину лопасти на лю-
бом радиусе г, учитывая, что скорости и явлнются’ средними скоро-
стями (по ним вычислялся импульс), а Издает истинную местную скорость
для сечения:
(141)
У2. kcR
В правой части этого выражения нам все уже известно, и мы получим
вполне определенную величину для Ь. Легко найти и угол ф, под которым
надо поставить на радиусе г наше сечение, так как
Ф = ft + а.
Таким образом, мы получили чертеж нормального винта для данного
режима полета.
Если строго придерживаться правила, что cr берется все время для
наивыгоднейшего угла атаки, то формула (141) дает очень сильно расши-
ряющуюся ко втулке форму лопасти. Действительно, wt --const, грубо
близко к гео, c# = const; тогда формулу (141) можно написать в виде:
Получается, как видим, почти гиперболический закон изменения ширины
по радиусу, изображенный на фиг. 36 пунктиром. Осуществить такую
форму удается лишь на участке лопасти, лежащем от г = 1 до г — 0,5,
иногда до 0,4. На меньших радиусах приходится давать сечениям несколько
большие углы атаки, т. е. увеличивать Сд; благодаря этому ширина лопасти
значительно уменьшается. Величина р.х при этом меняется сравнительно
слабо, так как при углах атаки, близких к наивыгоднейшему, fij почти
постоянно. Следовательно, интегральные величины Р и Т изменяются при
этом очень мало, тем более, что центральная часть лопасти работает слабо
(мала скорость Wr). На общем результате такая «компенсация ширины
винта» отражается слабо, и расчет обычно не приходится переделывать.
При сильных отступлениях нужно проделать по уже описанным мето-
дам поверочный расчет виита. Изложенная теория нормального винта пока-
зывает, что помимо простоты его расчетных форм и высокого к. п. д. ои
легко вычерчивается.
Проще делать эту компоновку графически, строя скоростной много-
угольник по скоростям г<о, Vv vlf Кс> и по углу ц. Потребуется лишь
вычисление ширины лопасти по формуле (141). В практических расчетах
следует рекомендовать пользоваться именно графическим приемом компо-
новки.
Заметим еще раз, что большинство авторов, разрабатывавших импульс-
ную теорию, не вводит в расчет поправку что в случае пропеллера дает
небольшую погрешность. При нежелании учитывать эту поправку, нужно
во всех формулах с (136) по (141) просто отбросить значок В тех же
случах, когда почему-либо желательно вести компоновку аналитически,
нужно рекомендовать применять отвлеченные обозначения и вести расчет
по формуляру табл. 5. •
Таблица 5
Формуляр компоновки нормального винта
(l/jj и известны)
1 г 0,9 0,75 0,60 0,45 0,30
3 Vo •tg ₽„ = Но
5 6 (X су р. = 57,3p-i
7 8 9 10 tgl^ ~r~tg (?£ + М-) х К tg в = —=—= Р Г.- t'l tg (3 + Ц) It
11 12 13 14 ф = 3g 4- a e — — 8л r e sin 3 b-_ kcy57,3 b= ~bR
Глава 5
ПРИБЛИЖЕННЫЙ РАСЧЕТ ВИНТА-ПРОПЕЛЛЕРА
ПРОИЗВОЛЬНОЙ ФОРМЫ
§ 1. ОСРЕДНЕНИЕ СКОРОСТЕЙ И УПРОЩЕННЫЕ ФОРМУЛЫ
ТЯГИ И МОЩНОСТИ
В предыдущих главах мы познакомились с методами поверочного
расчета винта любой формы. Часто на практике требуется лишь при-
близительный ответ, и тогда нет смысла делать полный, трудоемкий по-
верочный расчет. В этих случаях желательно иметь простые формулы
для быстрого вычисления тяги и мощности винта.
Такие формулы предлагали многие авторы: Ботезат, Тейлор, Рябу-
шинский, Жуковский, Ветчинкин, а в последнее время в Америке Кол-
дуэлл и другие (см. библиографию). Все эти формулы получены с по-
мощью вынесения за знак интеграла ряда величин, принимаемых авто-
рами за малоизменяющиеся.
Очень часто (а до 1920 г.— как правило) при этом пренебрегал^
скоростью подсасывания. Как показал В. П. Ветчинкин, уже это одно
делало все такие формулы слишком грубыми. Мы будем учитывать
скорость подсасывания.
Изложим свой подход к вопросу и дадим простой метод ускоренно-
го расчета винта, как нам кажется, более точный, чем у других авторов.
Будем рассчитывать винт на режимах с малыми углами атаки сече-
ний. Это соответствует режимам, начиная от максимальной скорости
полета до режима минимальной скорости полета. Скорость подходяще-
го воздуха И; будем считать постоянной для всех радиусов винта.
Скоростью вращения в струе винта будем пренебрегать. Если принять
динамический шаг винта близким к постоянному, то активные сечения
винта, лежащие между г=1 и г = 0,5, будут иметь почти одинаковые
углы атаки. Мы будем считать, что у них угол атаки равен углу атаки
характерного сечения, лежащего на №0,75. Все величины, относящиеся
к этому среднему сечению, мы будем отмечать индексом «с» (напри-
мер ас).
Угол атаки этого сечения и ряд других величин мы сможем легко
найти, если будем считать заданной не скорость полета Vo, а скорость
подходящего воздуха Vj. Мы покажем, как можно в конце расчета пе-
рейти к скорости Vo.
В соответствии со скоростью Vi, выгодно ввести в расчет коэффи-
циент скорости по потоку М (см. § 1 главы 4), определив его формулой
(115).
Задавшись величиной Хх, мы, пренебрегая малой скоростью Uj, легко
найдем угол притекания потока на любом радиусе винта, так как
tg =±L = __Z1—„Ь. (143)
' rt,J rR 2лпь лг
Здесь не будем учитывать коэффициент неравномерности струн £. Сле-
довательно,
p^arctg-^ , (144)
Лг
Для характерного сечения
fr^arctg—--------— arc tg 0,425 (145)
л-0,75
Зная рс, находим угол атаки характерного сечения
ас = <Рс — Рс,
где фс —наклон сечения на г — 0,75.
На малых углах атаки величину с_;/ ^. можно вычислить по обычной
формуле аэродинамики;
— а<^а-
Здесь я!2 — аэродинамический угол атаки, равный
яа — я — я0,
(146)
а угол а0— угол нулевой подъемной силы профиля.
Теперь можем перейти к вычислению элементарной силы тяги и мощ-
ности. Повторяя полностью рассуждения § 3 главы 1, напишем:
pW?
dP = ааа —-- kb cos (р +
P^i
dT = ала-^-kb sin (P -J- |i) r^dr.
В эти формулы входит величина полной относительной скорости Й7Х.
Пренебрегая скоростью вращения струи, напишем:
tt'-’Г rV- 4-И =rW^l 4- .А.) = г2Д1 + -А-). (147)
Вводя это выражение в наши формулы и подставляя в них вместо ш вели-
чину 2jt/zs, получим: 4
dP = - 2л2кааа?п\ \ 1 ---^=- |cos (р + ц) br2dr;
\ Л2Г2 /
(X2 \
1 -- ) sin (Р + ц) brzdr.
Для определения тяги Р и мощности Т интегрируем эти выражения, причем
считаем постоянными для всех активных сечений яа, 1 +
X2 \
, cos(p-f- ц>
и sin $4- р), которые берем по средним значениям, соответствующим ра-
диусу г = 0,75. Тогда получим:
Р = 2л2/гааас ря21 1 -j- ) cos (3 + н)с j" br2dr\
I 1 \ ’ ?
Т = 4л2kacf.acpns 11 ------------1 sin (3 + ц)с\br3dr.
\ л20,752 / J
'с г0
§ 2. факторы СКОРОСТИ, тяги и мощности
Для обобщения результатов переходим к безразмерным величинам, для
чего переписываем э^и формулы в развернутом виде:
/ ?.2 \ х__ _
Р = = 2л2^ааЙСр^ ( 1 4------1— I cos (3 + ji)c R* I b r2dr,
\ л2-0,752 J J
T = ^D^n3s = 4n3kaac?n3f, (1 4---J*'1-' 'j sin (3 + n)c R5 { b r3 dr.
\ лг0,7ог / J
Сократив именованные множители, получим:
a = — kaaac (1 + 0,180 - Xi)cos (3 + ц)с ^ЬгЧг; (148)
3 = ~ &aaac(l -h 0,180 л.£) sin (p p)c '\b7'dr. (149)
Введем обозначения: Фу = 1 < 0,180 Xt (150)
ФР = ^br2dr, i. (151)
Фр = (b r3d r (152)
и назовем нх так: Фу — фактор скорости, Фр — фактор формы для тяги и
Фг — фактор формы для мощности.
Вычислить эти интегралы нужно один раз для типичных форм винтов,
и затем можно пользоваться готовыми значениями.
Так, для вннта постоянной шириной лопасти b получим:
Фр = <\Ьr2dr = b ^dr = b 1 -p- ,
Зная b и сразу можем вычислить Фр и Ф?- по этим простым форму-
лам. Беря в среднем для таких винтов £ = Vi и b = 0,2, получим средние
значения: Фр ~ 0,066 и Ф-^0,05.
Ьр
В случае нормального винта гдеЬр— ширина лопасти на радиусе
т. е. иа конце лопасти. Тогда находим:
Ьц rdr = 6р
фр -= J b rsdr = bR (j r2dr = bn 1
S - £
для пропеллеров Ь% = 0,15 и £ = l/it полу-
Беря в этом случае в среднем
чим Фр ~ 0,07 и Фг — 0,049.
У геликоптеров лопасти в среднем в 2,5 ра-
за уже, чем у пропеллеров. Тогда Фр^0,03 и
Фг ^0,02.
Обычно форма лопастей задана чертежом, и
тогда эти интегралы приходится вычислять гра-
фически. Для этого нужно построить диа-
грамму (фиг, 37), где по оси абсцисс отложе-
на величина г, а по ординатам Ьг2 и Ьг3.
Заштрихованные площади дадут ,величину иско-
мых интегралов.
С их помощью наши формулы перепишутся
в простом виде:
( 154)
а = — &паасФуФр cos (3 + н)с
Р = #ааасФуФр sin (р + ц)с.
(155)
(156)
Величина а для обычных профилей равна 0,10, если брать углы атаки
в градусах. Вводя это ее значение в наши формулы и вычисляя числовые
коэффициенты, получим окончательно:
а = 0,1234 • ЫасФуФр cos (р •+- ц)с:
р = 0,387 • Ьсас-ФуФт sin (р ;л)с.
(157)
(158)
Фактор скорости нужно вычислять для каждого режима полета, зада-
ваемого величиной %,» по формуле (150). Факторы же формы Фр и Фг для
данного типа винтов постоянны. Излагаемый способ расчета можно еще
более усовершенствовать, если ввести в расчет покрытие или перекрытие
винта, выражаемое обычно формулой
fe&c kbc
б = ----- - -------.
лК л
(159)
Для этого достаточно умножить и разделить наши формулы (155) и
/'Ч &С 31
(156) на — и отнести миожитель — к факторам тяги и мощности, написав
л Ьс
их в таком виде:
Ф’Р= ~ (йгМг, | '
° \______I (160)
Ф'г = r-f br'dr. |
|
С помощью этих величин нашим основным формулам можно придать
вид:
а = 0,1234-ааасФиФ> cos (р + ц)(, 1
— /• (lol)
р — 0,387• ааагФ1/Ф'7 sin (р -- р)с. j
В таком виде формулы позволяют «пересчитывать» винты на любое
перекрытие а. Не следует думать, что формулы (161) дают вообще про-
порциональность тяги и мощности величине перекрытия винта, — это спра-
ведливо лишь при неизменной скорости потока Vt и соответствующего ей
коэффициента скорости по потоку
При разных покрытиях скорость полета будет получаться разная при
неизменных Уг или i,.
Полученные формулы выведены в предположении, что величины
т. е. Ух, известны. Для окончания расчета необходимо найти истиннуюскорость
полета У() и соответствующую величину Л = • Воспользуемся основным
уравнеиием тяги теории идеального пропеллера
Отсюда находим скорость подсасывания t>| и затем истинную скорость по-
лета Vo — Vi — vlt которая в отвлеченных обозначениях напишется так:
Эта формула и решает нашу задачу: задавшись и найдя а, можем по-
лучить величину Л- Сделав расчет для нескольких значений получим ряд
значений Л, а и Р, по которым строим всю характеристику винта. В силу
введенных в расчет допущений, следует брать лишь те режимы, где
аас< 12°.
Глава 6
ОБЩИЙ АНАЛИЗ ИМПУЛЬСНОЙ ТЕОРИИ ВИНТОВ
§1. ОСНОВНЫЕ ФОРМУЛЫ УРАВНЕНИЕ СВЯЗИ—ОСНОВА ТЕОРИИ
Мы неоднократно указывали, что импульсная теория дает результаты,
очень близкие к вихревой теории К ее достоинствам следует отнести тот
факт, что она учитывает профильные потери, чего вихревая ^теория не де-
лает, но зато она пренебрегает неболь-
шой неравномерностью давлений, в ухо-
дящей струе винта.
Излагая импульсную теорию, мы поль-
зовались обычно индуктивной скоростью
Wj. Это позволило разработать быстрые
•и эффективные методы поверочного рас-
чета вннтов, предложенные еще в 1922 г.
Одиако в вихревой теории и в поздней-
шем развитии импульсной теории поль-
зуются в вычислениях разложением ин-
дуктивной скорости на две компоненты:
осевую щ и окружную uv При таком
написании формул они становятся весьма
близкими к формулам вихревой теории.
Изложим импульсную теорию при-
емом, неоднократно применявшимся многими авторами Коэффициент нерав-
номерности скоростей в струе винта £ для простоты не вводим.
На фиг. 38 изображен скоростной многоугольник некоторого сечения
винта, лежащего на радиусе г. Можно сразу написать выражения для ско-
ростей в зависимости от углов:
tg3
sin
Vi Уо -г
ГЫ — U1 ГЫ — Щ
ГЫ — иг
W7! = ]/~(/’Cl) — Ml)2 — (У0 -г t^)2 И -г и2.
(162)
Аэродинамические силы, действующие на элемент профиля с хордой b и
Длиной dr, сводятся к подъемной силе dYi и силе профильного сопротив-
ления dXt. Элементарная сила тяги dPj получится проектированием этих
сил на ось винта, а окружное элементарное усилие dQt найдется проекти-
рованием этих же сил на плоскость вращения:
dPt = dYx cosp — dXt sin p = dYi (cos 3 — pj sin 3), (163)
dQz = d^sinp-i-dXiCosB d}\ (sin p — щ cos £). (164)
Вводя сюда силу dYlt написанную по правилам экспериментальной аэро-
динамики, т. е. dYi ~Cy~bdr и подставляя значения sin 6 и cos3 по
формуле (162), получим:
dpi = c!/36ll7’(cosij^iiis'nW dr (165)
d<?, - су-~-Ж(5Ш 3 + и, cos р) dr dr. (166)
У винта с /г-лопастями получим силы в k раз большие. Раскрывая скобки,
получим окончательно:
dP — су kbVi\ (/то — их — MaVj) dr, (167)
dQ — c,f Т-(Vj 4- (i/iD— pp/i)dr. (168)
Потребляемая этим сечением мощность будет, очевидно, такова:
dT — rwlQ — Су ^-kbW\ (Vi -f- — p^i)rwdr. (169)
Последние трн формулы кладутся в основу всех теорий винтов. Вся
разница сводится к вычислению скоростей с\ и wt и к тем допущениям н
упрощениям, которые прн этом делаются.
Импульсная теория исходит из равенства создаваемого в струе импульса
действующим иа лопасть силам. Поэтому оиа допускает двоякое написание
сил и мощностей: их можно вычислять или по профилю, беря а основу
формулы экспериментальной аэродинамики, илн по струе, по секундному
количеству движения и по моменту количества движения.
Так, для силы тяги мы можем написать, как это мы делали уже неод-
нократно,
dP = 2v! dm = 4лрг [ V, [ vtdr,
и для сопротивления и мощности.
dQ - - 2utdm = 4льг | Vt } f^br,
dT = dQrw = 2uLrtadm = 4лрг2<о1/1и1б/г.
Заметим, что при разборе различных режимов, когда знаки vlf Vo н
меняются, иужио в предыдущие формулы подставлять скорость | V-i | по
абсолютному значению, так как она представляет здесь массу, т. е. скаляр.
Из этих формул следует, что ; но по чертежу фиг. 3 8
dPi ui
- tg (Р м).
dPi
Отсюда видим, что
- = tg(P + н).
(170)
ТЯГИ
Возможность писать двумя способами формулу тяги и мощности поз-
воляет составить два выражения для уравнения связи. С помощью
dP —- Gy — kbWl (cos 3 — Hi sln 3) = 4 лр IJ vtrdr,
откуда
IVil^i =
VT:
kbc
(cos p — Hi sin 3).
(171)
Можно
написать уравнение
связи и по окружному усилию:
dQ — Су kbW‘{ (sin Р -г Hi cos Р) dr = 4лрг 1 | uxdr.
• Отсюда
kbc„
(sin 3 + Hicos 3)-
(172)
Эти два уравнения иа практике оказываются менее удобными, чем одно
уравнение (23), положенное нами в основу расчетов, в котором главную
роль играла полная индуктивная скорость = ]'v! -И
Если теперь возвести оба полученных уравнения связи в квадрат и сло-
жить, то после тригонометрических упрощений получим:
W*
'4 1
Заметим, что ц. •= tgu и, следовательно, 1 4- Hi = ——. Извлекая ко-
cos2H
реиь квадратный, получим:
I Vil /
6Ь %
8лг cos р.
Заменяя V у2 4- и2 через w г и —-— через с%, получим:
* 1 cos ц
I V11 ^1 = kb .CRr
ц?2 8лг
т. е. то уравнение связи, которое мы вывели в. § 2 главы I н широко
применяли в нашей работе. Ойо оказалось очеиь удобным для поверочных
расчетов винтов, и мы привели здесь ряд приемов расчета, основанных на
этом уравнении. Однако при проектировании винта, когда приходится зада-
ваться или скоростью ух = /(г), или каким-либо другим законом, определя-
ющим форму виита, это уравнение неудобно, и решать его приходится,
делая ряд упрощающих допущений.
Самым простым упрощением является допущение, что вектора IFj.
На самом деле wx образует с угол £-!- р. Для перпендикулярности необ-
ходимо, как видно из фиг. 38, положить ц - 0. Но тогда ие будет учтено
действие сил профильного сопротивления на струю: скорости vt, и гл,
ие будут зависеть от сил, связанных с ц.
Такое допущение положено в основу вихревой теории Жуковского и
часто делается в импульсной теории. Оно не вызывает больших ошибок
при нормальных режимах работы виита, ибо замена tg([3-r р) на tg(3 при
малых величинах р. очеиь мало изменяет конфигурацию скоростного много-
угольника. Однако иа некоторых режимах, как мы это видели в § 5 главы
2, р достигает зиачеиий 90° и ~ -Т ос. Следовательно, для них такое
упрощение недопустимо, почему нам и пришлось в ряде мест пользоваться
точной формой уравнения связи с
При подсчете сил, действующих на элемент лопасти, пренебрегать си-
лами треиия (профильным сопротивлением) совершенно недопустимо. Их
приходится обязательно учитывать. Но тогда, при J-lFi, эти силы
«висят в воздухе», т. е. ие отражаются иа струе, и силовая схема виита
оказывается незамкнутой. Тем не менее для нормальных режимов виита
это допустимо, так как ошибка получается малая.
Некоторые авторы, стремясь еще более упростить теорию, допускают,
что Мы считаем, что такое упрощение является для пропеллеров
слишком большой натяжкой. В этом случае, при работе иа месте, когда
= гш, мы получим J. гю и Wj 0. Такое допущение, как мы видели,
делается при расчете геликоптеров. Там, ввиду малости угла [1, это не
вызывает больших ошибок.
Можно пойти еще дальше в упрощениях и считать, что на всех режимах
щ = 0. При расчете винтов для больших относительных скоростей Vo и
для роторов геликоптеров это допущение все еще ие вызывает больших
ошибок. Такое допущение было сделано в старом варианте (1910 г.) теории
Сабинина — Юрьева.
Мы сейчас остановимся иа наиболее невинном допущении, какое де-
лается и в вихревой теории, т. е. что __ W\.
Тогда из условия tg? — — и имея из скоростного многоугольника
У,
фиг. 38, что tgp= ———, получим:
ГСО — «]
Щ _ V1 Vo + vt
Vt ГО) — Uy Ге) — Uy
Отсюда
(Vo ux) ид - z/j (rw — (173)
Это уравнение связывает окружную индуктивную скорость Ut с осевой
скоростью fj. Благодаря этому иам придется теперь решать ие оба урав-
нения связи, а лишь одно, так как, найдя одну индуктивную скорость,
обычно мы получим tit или по уравнению (173), или прямо по формуле
U1 — Щ tg 3.
§ 2. УРАВНЕНИЕ СВЯЗИ ПО ОСЕВОМУ ИМПУЛЬСУ
Вводя в полученное нами уравнение (171) взамен тригонометрических
величии их выражения через скорости но формулам (162), получим:
, | Vi' vL kbc/ гш — ly
Г2 ” 8лг
Замечая, что IFj --- V (гш — uj2 -г V2, находим:
I г 8кг Vit'j
ct/kb ---------------------1 1— .
(rw — щ — HiV])|A(ru> — их)г 4- V2
(174)
Получается выражение, усложиеииое величиной ut. Если при решении
уравнения связи пренебрежем этой, обычно весьма малой, величиной, то
получим уравнение связи, впервые предложенное в 1910 г. в теории Саби-
нин? — Юрьева:
с _ 8
“ (га - у(гаГ -.-V*
В старой теории, изложенной Н. Е. Жуковским в «Теоретических осно-
вах воздухоплавания» в 1911 г., в нее вместо скоростей в знаменателе
входили числа модулей по потоку. Числом модулей по потоку называется
FW *
величина = —
Vi
Вводя эту величину в наше уравнение, получим:
c„kb ----------— 1 --------. (176)
й/4 + 1
Такую формулу в этой работе мы не применяли из-за нежелания вводить
еще одни безразмерный параметр 24 =- В настоящее время чис-
лом модулей при расчете винтов не пользуются; их применяют лишь
изредка в теории вентиляторов и ветряков.
В дальнейшем будем пользоваться безразмерными величинами вихревой
теории, т. е. vlt г, Р,Т и так далее за исключением ширины лопа-
сти, которую из практических соображений будем относить к радиусу винта
R, т. е. Ь = — .
R
_Эти величины уже встречались в нашей работе за исключением Р, Q
и Т. Последние определяются из формул:
Р = Р 2 'i
Q ~ Q 2 jrpAjW, ? (177)
Т Т 2 Лр/^w3. J
Оии были предложены в 1913 г. профессорами Н. Е. Жуковским и
В. П. Ветчинкииым.
* Н. Е. Жуковский. Полное собрание сочинений, т. VI.
7 Б Н. Юрьев, т. I
Переход к отвлеченным величинам
Переводя наши основные формулы в безразмерные, получим:
d'P -с, (178)
4Л
dP = 2 V, v.rdr, ' (179)
= + fiir—!i,ut)rdr. (180)
4л
Уравнение связи (175) напишется теперь так:
.т~ 8 Jti>i Vl г
, Ct/kb — 1---------.
('-Hl V1)
В вихревой теории уравнение связи пишется с помощью циркуляции в
таком виде:
cykb=&i^ . (182)
Если в уравнения (178) н (180) подставим cykb, взятые по уравнению
связи через циркуляцию скорости, то получим в точности уравнения вих-
ревой теории:
dP = 2Г (г — иг — pi Vr) dr.
d T --- 2 Г (У,. + — pi«7) rdr? | (183)
Однако здесь совпадение не будет полным, так как у нас на скоро
стях Vy и Ui отражается и профильное сопротивление, а в вихревой теории
оно не отражено. Следовательно, эти скорости в обеих теориях хотя очень
близки и практически совпадают, однако принципиально различны. Так. по
вихревой теории
—Г(1—Г),
а по импульсной (181)
----kbc.. — —
V^i= —fWi (r-^ УД
т. е. в импульсной теории профильное сопротивление, представленное в этой
формуле величиной влияет на скорости, чего нет в вихревой теории.
§ 3. РЕШЕНИЕ УРАВНЕНИЯ СВЯЗИ
Рассмотрим теперь решение практических задач с помощью этих фор-
мул. В вихревой теории тип винта задается законом изменения циркуляции,
т. е. зависимостью Г = f(r). В импульсной вместо этого нужно задаваться
* Б. Н. Юрьев. Вихревая теория винтов. Изд-во ВВИА, 1947, стр. 4в.
законом изменения vx = f (г). Если будем пользоваться при этом упрощени
ем, что wt 1 Wy, то сразу же по формуле (173) найдем и закон и1=ф(г).
Зная этот закон, мы по уравнению связи находим ширину лопасти b и
далее, найдя 3 по уравнению tg 3 — rtu~~ ц1 и выбрав угол атаки а,
находим наклон сечения виита на любом радиусе, так как ф = 34-а.
Следовательно, форма виита полностью определяется имеющимся законом
ъ = н~).
Самым простым случаем является тот, когда = const, т. е. Vj не за-
висит от радиуса винта. Это — нормальный винт, подробно рассмотренный
нами в главе 4. Он весьма близок по конфигурации к винту НЕЖ вихре-
вой теории.
Значительно труднее, как мы видели, решается обратная задача, т. е.
поверочный расчет винта. То же имеет место и в вихревой теории. Труд-
ность заключается в том, что уравнение связи как в вихревой, так и в
импульсной теории требует включения явной зависимости су от угла атаки,
а это при аналитическом решении неизбежно приводит к тому, что угол 3,
который необходимо найти (или, что то же, 1/\), входит в формулу один
раз как угол, а другой раз как sin 3. Г1ри малых углах 3, что бывает лишь
в случае геликоптерных роторов, вполне законна замена синуса другой, и
тогда задача легко решается и приводится к простому квадратному урав-
нению.
Но при больших ^глах притекания 3 решать задачу приходится графи-
чески. Для этого нужно прибегать при точном учете сил трения к урав-
нению с индуктивной скоростью и применять один из описанных у нас
методов. Если допустить, чтоШ] I то задачу проще решать с помощью
уравнения (174) или (175).
Ход решения таков Задавшись величиной найти по формуле (173)
«1, Vi = Vo Vi и 3 = arctg . Далее по известному наклону сече-
r — ut
иия ф находим а — ф —• 3- По продувке профиля или аналитически по
формуле су = ау. находим величины а и
После этого по уравнению связи (181) снова находим:
-^-^(г —Vi).
8лг Vx 1 1 '
Получится, вообще говоря, другая величина. Если мы задались пре-
увеличенным значением v1} то получится преуменьшенным угол атаки су, и
Уравнение (181) даст преуменьшенное значение tij.
- V + v”
Среднее значение Uj —---:--будет очень близко к истинному значению
2
»i. Повторив все это вычисление, получим второе приближение, которое
обычно можно принять за окончательное.
Легко найти истинное значение графическим методом. Надо вычислить
ряд значений v1} задаваясь vlt и построить их зависимость в координатах
vlt ^1 (фиг. 39). Если провести из начала координат прямую ОЕ под углом
45° к оси абсцисс, то точка пересечения этих линий М и даст правильную
величину vt.
Приемы таких вычислений могут быть самыми различными, но все они
сводятся к решению уравнения связи непрямыми методами.
Следующее упрощение, которое делается в этой теории многими авто-
рами, сводится к отбрасыванию скорости вращения и\. Если отбрасывать
при решении скоростного многоугольника по уравнению связи, то это
упрощает расчетную работу, и если при вычислении сил и мощности ско-
рость вращения ввести по упрощенной формуле tg£, то получа-
ющиеся окончательно dP и dT практически на основных режимах виита
совпадают с тем, что дает точное решение, гораздо более сложное.
Наконец, в случае роторов геликоптеров, когда
величина мала, ее можно отбросить в уравнении
связи в правой части, и тогда получится:
_ kbc„r
V= —у~ Kr2cit.
8л
Решение приводится к квадратному уравнению
относительно vt, ибо н, следовательно,
Фиг. 39
— Ксу=-0.
Мы с этим уравнением в различных модификациях встречались в ряде
мест нашего изложения. В случае работы ротора иа месте Vo — 0 и оно
сводится к еще более простому уравнению:
v; = КЛ,,.
Дальнейший расчет ие представляет никаких затруднений и ведется
путем аналитического или графического интегрирования. Наиболее простое
решение получается в предположении Uj — const. Такой винт, названный
нормальным, был предложен автором этой работы и Г. X. Сабининым еще
в 1910 г. В 1912 г. появилась вихревая теория Н. Е. Жуковского, в ко-
торой также отдавалось предпочтение винту с гл -= const. Это — винт НЕЖ-
Он очень близок по форме к нормальному винту. В 1916 г. В. П. Вет-
чинкин поставил и решил вариационную задачу о винте с наивыгод нейшнм
законом циркуляции Г (г). Здесь щ получилось уже переменным по
радиусу. С помощью импульсной теории можно точно так же решить ва-
риационную задачу, отыскивая наивыгоднейший закон Однако в этом
нет надобности, ибо полученный результат будет практически совпадать с
результатом, найденным по вихревой теории.
ВЫВОДЫ
Как мы видим, современная дисковая теория (а ею мы только и за-
нимались в этой работе) получила у нас очень большое развитие. Ее
разрабатывал ряд авторов, и полученные результаты на много лет опе-
режали успехи иностранных ученых. Теория эта развивалась в дву!
направлениях — в виде импульсной теории и вихревой. Все различие
этих теорий, как мы видим, сводится к различному написанию уравне-
ния связи. Импульсная теория учитывает действие профильного сопро-
тивления иа скорости, вихревая теория этого не делает. Поэтому по-
следняя более приспособлена к расчету нормальных режимов, а пер-
вая— к расчету критических и срывных режимов, когда pi велико.
Не представляет никакого труда ввести и в импульсную теорию из-
меняемость давления по радиусу в уходящей струе, как это делает внх-
Выводы
ревая теория. В работе автора «Вихревая теория винтов» сделан вывод
формулы для давлений в уходящей струе, без применения понятия цир-
куляции скорости.
Мы, однако, этого здесь не делали, не желая осложнять эту простую
теорию. Таким образом, мы видим, чго в сущности имеем единую тео-
рию винтов.
Дальнейшее уточнение теории винтов должно Достигаться переходом
к относительной теории винта. Некоторый, простейший учет истинных
относительных скоростей мы делали, вводя коэффициент неравномер-
ности струи £. Его можно вводить и в вихревхю теорию. Различные
авторы по-разному вводят такие поправки, называя их чаще всего кон-
цевыми потерями винта. Самой грубой из них является обрезание кон-
ца винта на некоторую величину v: тогда при вычислении интеграла
тяги берут пределы интегрирования от £ до 1 —v. Мы предпочитали бо-
лее простой прием введения Эта поправка не существенна для про-
пеллеров и имеет очень большое значение для роторов геликоптера.
В заключение приходим к выводу, что импульсная и вихревая тео-
рии должны существовать и развиваться одновременно, так как они яв-
ляются дополняющими друг друга вариантами общей теории винтов,
созданной н развитой в нашей стране проф. Н. Е. Жуковским и его мно-
гочисленными учениками, задолго до создания таких теорий за границей.
УТОЧНЕНИЕ ИМПУЛЬСНОЙ ТЕОРИИ ВИНТОВ
§ 1. СКОРОСТЬ ВРАЩЕНИЯ В СТРУЕ ВИНТА* **
Импульсная теория является гидравлической теорией, и расчеты в
ней ведутся по средним скоростям, как бы для винта с бесконечным
числом лопастей.
Рассмотрим
иа фиг.
соотношение для кольцевой струи, изображенной
1. Булем применять наши обычные обозначения. Пусть
площадь сечения кольцевой струи равна dF.
Секундная масса воздуха, протекающего че-
рез сечения этой струн, равна pV\dF, а объ-
ем воздуха, считая последний несжимае-
мым, равен V]dF.
Напишем уравнение Бернулли для сече-
ний 1.1 и 1-2, очень близких к плоскости
вращения винта, т. е. к сечению 1. Виит
считается здесь узким, сечения 1.1 и 1-2
очень близки, и осевая скорость в этих се-
чениях равна
Скорость вращения до винта, в сечении
1.1, равна нулю, так как до этого сечения к
к струе не было приложено никаких импуль-
сов. В сечении 1 струя вращается со ско-
ростью W], а в сечении 1.2 со скоростью «1.2.
струя получит от виита в секунду энергию
Кроме того, в сечении
(мощность) dL.
Следовательно,
pV’i oVj рм? 2 dL
+ Pl.I = - ~ +Pl^-77-^-
I 2 VidF
Энергия в уравнении Бернулли отнесена к единице объема, и ^формулу
введена ие dL, а
VrfF
Энергия dL будет состоять из двух частей: из работы, затраченной ок-
ружным усилием dQ и равной u^dQ, и работы «вентиляторной», рав-
ной VjdT. Окружную силу легко найти по приросту момента количества
* Публикуется впервые.
** В этой статье Б. Н. Юрьев употребляет обозначения, принятые нм в его послед-
них работах, т. е. обозначает силу тяги через Т, мощность — через L и коэффициент
силы тяги — через Ст.
S i- скорость вращения в струе винта
1U6
движения в плоскости вращения, так как, очевидно,
rdQ = rdmu.j'2,
dQ — dm U/.2 = pViUj^dF.
Теперь
u,dQ
Вентиляторную работу можно вычислять по перепаду давления рЛ2—
— pi.i = р', я тогда
V,dT (Pi.2 — Pn>VidF
W =------------------= Р= БР-PU-
VidF
После этого уравнение Бернулли примет вид:
pvj pvj р42
—----Pl 1 — ----1-------К Р1.2 — Р1.2 + Р1.1 — РЩи1.2-
Сокращая,, получим
ui.2 2ыг (184)
Эта формула очень важна. Она показывает, что окружная скорость
& плоскости виита в 2 раза меньше скорости вращения струн, выходящей
из-под лопастей.
Струя воздуха за виитом сильно сжимается. Если допустить, что сжа-
тие равномерно, то отношение средних скоростей У.г и (обычно их берут
в теории ротора иа г = 0,7) определит отношение сечений струи, т. е.
А = А
Fi V/
Это — условие неразрывности струн. Но Fx ~ л7?2 и F2 = л#®; следова-
тельно,
Будем считать, что все радиусы находятся в таком же соотношении,
т. е.
г2 = гУе или — = |/"е. (185)
По теореме площадей можем сразу написать
ГЩ.2 = rzu2 (185')
Отсюда
Г и1.2
lit — ---И/ 2 = -?=-•
га Уе
Величину е в классической вихревой теории и в импульсной обычно
не учитывают, внося в результаты некоторую погрешность. Введением вели-
чины 8 — f (г) хотя бы со средним значением 8 ~ ~ мы заметно уточняем
результаты вычислений.
Итак,
и. 2 2их -
и2 = -~= —
(186)
§ 2. ВЫЧИСЛЕНИЕ СКОРОСТИ ВРАЩЕНИЯ «у
Для ВЫЧНС нулли, вводя dQ их + dT Ух VxdF ления скорости можно воспользоваться уравнением Бер- в него подведенную энергию, относящуюся к 1 ж3 не в виде как мы1 делаем в § 1, а в виде rw dQ pVy dF и[ 2r<j) VrdF " V.dF - ₽“'-2ГЮ - 2Puira>-
Тогда, взяв с гчения 1.1 и 1.2, получим: pV? , рЧ , P“h — + Pl.l = — + + Pl.i — PUl.2r<S>
или, замечая, ЧТО Uj.2 =- 2 , P1.2~ Pl.l n Ux — U,r(i) - =; 0. 2p
Обозначая pi.2 — Pn через p —f(r), получим: Uy —«</-(>) <- -p - - = 0. -p
Решая най денное квадратное уравнение, найдем: о87
Перед корне! должна т Н. Е. Жуков и берем знак минус, так как с уменьшением р скорость акже уменьшаться. Переходим к безразмерным величинам icKoro г ~ , г/, — — ир — —£—. Получаем-. R /?о) р (jRw)2 2 М' = Т-]/ ’
или . (188)
Эта форм; ула связывает давление в струе, т. е. величину р~ со dF
скоростью вр< в ней обязате зщения щ. Оиа показывает, что если струйка дает тягу, то :льио получается вращение.
§ 3. Давления в уходящей струе воздуха
105
Формула (188) теряет смысл, когда подкоренное выражение делается
мнимым, т. е.‘ границей применения этой формулы будет равенство
? = р.
В этом случае
или
7 =--2t7A = 7^.
Это значит, что иа таком радиусе скорость вращения элемента стано-
вится равной скорости уходящего из-под винта воздуха.
Скорость щ определяет тип винта. Ола изменяется по радиусу по не-
которому закону
=f(r}
и играет такую же роль, как циркуляция скорости в вихревой теории.
В частности, она может равняться
7 _ "I
где и0 — соответствует поверхности струн.
В этом случае получается то же самое, что у вннта НЕЖ» с тем
только отличием, что профильное сопротивление войдет в скрытом виде
в выражение для щ.
§ 3. ДАВЛЕНИЯ В УХОДЯЩЕЙ СТРУЕ ВОЗДУХА
Возьмем горловое сеченне струн. Давление на ее внешнюю поверхность
равно атмосферному давлению р0. По мере приближения к центру оно
должно уменьшаться из-за эффекта центробежных сил.
Проведя данное сечение 2, мы получим картину, представленную на
фиг. 2. Выделим небольшой элемент струйки, на чертеже залитый черным,
с площадью сечения /, лежащий иа радиусе г н имеющий длину по
радиусу dr. Напишем для него равенство сил радиального давления f dp2
и*
н Центробежной силы dm——.
Г2
Масса его равна р/ dr, и условие равновесия примет вид:
f dp2 = pf dr —,
или
, U2 J
dp2 — p —— dr.
Замечая, что
получим:
Интегрируя это выражение в пределах от Rs,
когда р2 = pQy до текущего сечения г2, где дав-
ление равно рз, получим:
(189)
ковского без поправочного
яым путем.
Этот интеграл входит в формулы Н. Е. Жу-
коэффициента 8, н получен он более слож-
§ 4. ВЫЧИСЛЕНИЕ ОСЕВОЙ ИНДУКТИВНОЙ СКОРОСТИ
Напишем уравнение Бернулли для сечений 0 и 2. По пути струя полу;
ннт энергию от двигателя, которую мы представили уже встречавшимся
иам методом в форме:
dQ г(а рИ1 dF iij 2r<s>
’ V^dF ~
Это уравнение напишется теперь в таком виде:
pv; , р (V'o + ^)2 , р<4 t
~ + Ро ------------2-------~ Р«~
. R- Z/2
4р р ui
— “3 — Яра/со.
Сократим это выражение н заменим и2 на
V &
2pVoo2 ро® 2р«*
—------Н — + —--------2pivm —
z < . О2
/ V» \ 1 Ui \ 4с ut
щ (/<>+-£•) = 2«! (™~т) + “Г J ~7dr-
у t. uoituc.icnuc ut eouu иниуктионои скорости
Переходя к безразмерным величинам, получим:
Это основное уравнение теории винта было получено В. П. Ветчинкн-
ным в 1913 г. с помощью вихревой теории. Мы здесь получили его с по-
мощью импульсной теории.
Граничные условия. Если предыдущее выражение написать для границы
струи в горловом ее сечении, то \ = 0 и = «0, и оно примет вид:
t I
о
И
V2.0 = - Г, + у
Формула (188) запишется так:
~ _ 1 — — Ро
!1о — 2
Вообще же
Тяга и коэффициент тяги. Очень часто принимают, что v2 = 2wt, как
это имеет место у идеального винта. Однако у реальных винтов отходя-
щая струя вращается и центробежные силы создают в горловом сечении,
как мы видим, некоторое разрежение. Взяв, как обычно, контрольные се-
чения 0 и 2 (фиг. 3), можно написать, что импульс тяги минус подсасы-
вающий эффект донышка за 1 сек. равен притоку количества движения:
. R V е 2
4р Г “7
dT = v2dtn 4- “ dF \ — dr.
6 г /Г г
Подставляя сюда dm = p2nrl/xdr и dF = 2^rdr, получаем:
dT = 2pJtrVxf2dr 4- ^p2jlrrfr — dr-,
E Xf— Г
/ 4 ?rs “i \
dr 2pXrV,v2dr (1 + — 4 — dr).
Переходим к безразмерным величинам, разделив полученное выражение
на ~-р/?4<оа:
—___- / ч
dCr WtV^dr I 1 +
У обычных винтов выражение в скобках для радиусов, больших г=0,25,
близко к единице. Находим выражение, получаемое в теории идеального
винта:
dCr -- 4У1Р2<ла.
Соотношение между и v2. Для при-
менения всех этих формул весьма важно
найти соотношение между осевыми скоро-
стями Uj н и2. Для этого пишем выраже-
ние мощности в двух видах, а именно:
„ u? -dm и? 4dm
dL = V.dT 4- s V'dT 4- —1—
1 2 ^2
и
e u~ \ 4ufdm
\ — dr I -J-----i— =
Vj (dT + dF^-
dL^^-(yl^+^^V1±dFX i-dr.
2 2 e .%- r
г V e
Приравнивая их друг к другу, получим:
RVT .
Г/Г f 7
, \ 4u2,dm
= dm ^Vo + ] a2 -I- ——.
Замечая, что
2
dT -\-dF~ — dr = v2drn,
e r
получим, сокращая предыдущее выражение на dm-.
(Ki + у2 + 2и® -—) — ^Vo 4—у2
или
Окончательно находим искомую зависимость:
у2
2
У обычных несущих винтов на средних радиусах— 0,075 и е прн работе
на месте равно 1/2- Тогда
1 — 4(0,075)2 (~~^1 = -у 1,022,
т. е. при работе на месте погрешность достигает всего 2%. Этим и объяс-
няется, почему очень многие теоретики принимают v2 = 2Vi.
ВИХРЕВАЯ ТЕОРИЯ ВИНТОВ
Вихревая теория винта была разработана, как известно, в нашей
стране еще задолго до того, как аналогичные теории появились за гра-
ницей. ,
Наиболее законченной теорией является и в настоящее время вихре-
вая теория, разработанная проф. Н. Е. Жуковским в его четырех клас-
сических работах (первая нз ннх была опубликована в 1912 г.). Эта
теория была усовершенствована н приведена к удобному для инженер-
ных расчетов виду проф. В. П. Ветчинкиным. В последние годы эта тео-
рия подверглась дальнейшим усовершенствованиям, нашла всеобщее
признание и является в настоящее время основой проектирования вин-
тов.
Теория Жуковского обладает исключительной общностью. Она
охватывает едиными формулами все случаи работы винтов, т. е. пропел-
лера, гелнкоптерного винта, осевого вентилятора и ветряного двигателя,
Однако несмотря на то, что у нас имеется большая и фундаменталь-
ная литература по воздушным винтам, у нас нет книг, дающих краткое
и достаточно строгое изложение этой теории. При прохождении курса
воздушных вннтов в наших авиационных втузах на вихревую теорию
отводится лишь около 10 час. лекций, н отсылать слушателя к перво-
источникам или монографиям совершенно невозможно. Многие инже-
неры, встретившись на практике с расчетом воздушных винтов или
вентиляторов, оказываются в затруднении, так как изучение имеющих-
ся книг требует большого времени и значительных математических знаний.
Кроме того, книги содержат много материалов, представляющих
лишь чисто исследовательский или исторический интерес или же посвя-
щенных вопросами, не связанным непосредственно с проектированием
вннтов н их эксплуатацией.
Настоящая работа должна дать студентам и инженерам краткое
руководство по аэродинамике винтов, не содержащее, по возможности,
ничего лишнего и дающее все нужное для начала практической работы.
Нужно помнить, что по любому разделу винтостроения теперь
имеется много литературы, позволяющей уточнить тот или иной расчет.
Мы не преследовали цель дать в этой книге исчерпывающее изложение
всех обширных материалов, а стремились охватить все случаи расчета
винтов едиными простыми формулами, основанными на картине вих-
рей, изученной Жуковским. Уточнение этих формул проще всего делать
с помощью поправок, взятых нз опыта.
В изложении материала мы придерживались стиля четвертой ста-
тьи Ы. Е. Жуковского, в которой ои делает выводы, исходя из основных
теорем механики и теорем гидромеханики о вихрях, а не нз общих
уравнений гидродинамики. Этот прием, основанный на геометрических
соображениях, оказался очень удачным. Мы в этой работе несколько'
его углубили и дополнили, что позволило весьма быстро, не снижая ни
точности, ни строгости выводов, получить все нужные для расчета вин-
тов формулы.
От читателя требуется знание гидромеханики в объеме современных
курсов гидравлики и знакомство с основными положениями экспери-
ментальной аэродинамики.
В настоящей работе, помимо изложения самой вихревой теории, мы
добавили три главы, в которых распространяем ее на случай винтов с
контрпропеллером и соосных винтов. Мы изложили также вихревую
теорию осевых вентиляторов и ветряных двигателей.
В последние годы многие исследователи работают над дальнейшим
уточнением вихревой теории, над так называемой «относительной тео-
рией винтов». В настоящей работе мы ее затрагивать не будем, а лишь
отметим, что у многих авторов эта новая теория приводится к поправ-
кам, вводимым в классическую вихревую теорию.
Такими же поправками, но взятыми прямо из опытов, пользуются
многие конструкторы винтов, вентиляторов и ветряных двигателей. По-
следний путь мы считаем в настоящее время наиболее простым и пра-
вильным и придерживались его в этой работе.
Общие сведения о винтах в этой работе не излагаются, и мы отсы-
лаем по этому вопросу читателей к нашим учебникам по винтам.
Глава 1
СКОРОСТИ В СТРУЕ ВИНТА
Ф'ИГ. I
§ 1. СКОРОСТЬ ПОТОКА, НАБЕГАЮЩЕГО НА ЛОПАСТЬ ВИНТА
Основным в теории винта является вопрос о величине и направле-
нии скорости потока, набегающего иа лопасть в разных ее точках.
Если сделать сечение винта цилиндром радиуса г и с осью, совпа-
дающей с осью вращения винта, то на развертке такого цилиндра мы
получим профиль лопасти, соответствующий этому сечению (фиг. 1).
Он будет иметь некоторую ширину b и угол наклона ср к плоскости
вращения ОО\.
Этот профиль будет вращаться с окружной скоростью t/ = rco, где
го — угловая скорость вращения вннта, и двигаться поступательно со
скоростью Vo- Если сложить геометри-
чески эти скорости, то получится ско-
рость Wo1, дающая величину и иаправ-.
ление равнодействующей скорости дви-
жений данного сечения лопасти.
С. К- Джевецкин, разработавший свою
классическую теорию винтов еще в
1892 г., предполагал, что воздушный
поток будет притекать к лопасти под
углом ро и иметь скорость Wo, равную,
но противоположную скорости движения сечения, т. е. Wo'. Разработан-
ная им теория является простейшей из возможных теорий винта; одна-
ко точность се получается удовлетворительной лишь для пропеллеров,
летящих со значительной поступательной скоростью, и для вентилято-
ров. В случае расчета винта, работающего на месте (геликоптера)
или в случае ветряного двигателя теория эта допускает грубые
ошибки.
При вычерчивании скоростного многоугольника можно изображать
как скорость воздуха, так и скорость движения сечения винта. Во из-
бежание путаницы, условимся скорость воздуха изображать на черте,-
жах простыми стрелками, а скорость сечения — оперенными. Этого пра-
вила будем придерживаться во всей нашей работе.
Более точной является теория, разработанная в 1910 г. студентами,
учениками проф Н. Е. Жуковского, Г. X. Сабининым и Б. Н. Юрь-
евым. В этой теории учитывается скорость подсасывания щ, полу-
чающаяся в плоскости врашеиия винта, и скоростной многоуголь-
ник сечения для скорости воздуха, набегающего на сечение, имеет
вид, изображенный на фиг. 2. В случае геликоптера скорость Vo = O, но
скорость I»! будет существовать. Вследствие этого теория Сабииииа —
Юрьева могла применяться к расчету винтов, работающих иа месте, и
ветряков. Кроме того, оиа ддвала более точные результаты и для про-
пеллеров. В 1912 г. Сабииин сделал попытку учесть вращение струи,
отходящей от винта. Для этого в скоростной многоугольник была вве-
дена окружная скорость вращения струи и\ (фиг. 3).
Значительно более полное решение задачи о скоростях, возникаю-
щих около работающего винта, было дано проф. Н. Е. Жуковским в
1912 г. Ои применил к вычислению скоростей потока и сил, действую-
щих на винт, гидродинамическое понятие о циркуляции скорости и
создал изящную «вихревую теорию винта». В этой теории, кроме ско-
рости подсасывания t>i, учитывается и скорость закручивания струи щ.
Скоростной многоугольник изображен иа фиг. 3.
Фиг. 2
Фиг. 3
Его можно изобразить еще так, как это даио на фиг. 3, пункти-
ром; вектор 27, полученный сложением скоростей и\ и «ь называется
полной индуктивной скоростью на данном радиусе г. Скорости vi и щ ча-
сто называют осевой н окружной, или тангенциальной, индуктивными
скоростями.
Основанная на рассмотрении вписанного скоростного многоугольни-
ка «вихревая теория» и была разработана Н. Е. Жуковским в упомя-
нутых его четырех классических работах.
Теория Н. Е. Жуковского является приближенной, так как поль-
зуется осредненными скоростями i и Uj и делает упрощения при учете
трения лопастей. Способ осреднения будет изложен в следующем па-
раграфе. Заметим, что в последние годы делаются попытки уточнить
величину скоростей t>j и щ, сводящиеся к замене средиих скоростей
истинными.
Такая уточненная теория получила у нас название относительной
или лопастной теории винта.
В этой книге будем излагать дисковую теорию винта, осиоваиную
иа средиих скоростях.
§ 2. СХЕМА ВИХРЕЙ, СБЕГАЮЩИХ С ВИНТА.
СТРУЯ ВИНТА
Вычисление индуктивных скоростей vj и получающихся в плоско-
сти винта, является важиейшей задачей теории винта. Их можно вы-
числить или исходя из общих теорем механики, как это сделано в тео-
рии Сабинина — Юрьева, или найти, как указал Н. Е. Жуковский, с
помощью теории вихрей. Некоторые опыты прямо указывают на нали-
чие позади работающего виита спиральных вихрей. Такие вихри неред-
ко наблюдаются у пароходных винтов. Жуковский приводит в своей
первой статье по вихревой теории виитов фотографии моделей морских
винтов, работавших в бассейне со стеклянными стенками, из опытов,
проведенных в Германии инж. Фламмом (фиг. 4). На стейках видны
пузырьки воздуха, выделившиеся на осях вихрен, т. е. там, где давле-
ние в потоке минимальное.
В настоящее время, когда полностью разработана теория крыла ко-
нечного размаха, картина вихрей, получающаяся у вннта, совершенно
Фиг. 4
Фиг. 5
ясна (фиг. 5). По любому контуру, охватывающему лопасть, будет
иметься циркуляция скорости Г. Лопасти или крылья, как указал
Н. Е. Жуковский в 1906 г., можно заменить присоединенными вихря-»
мн; этн вихри, по теореме Гельмгольтца, не могут окончиться внутри
потока и, следовательно, у втулки винта, и на концах лопастей должны
появиться вихревые усы, являющиеся про-
должением присоединенных вихрей.
Вследствие вращения винта эти усы бу-
дут иметь форму спиралей. В простей-
шем случае циркуляция скорости во-
круг лопасти будет на всех радиусах ве-
личиной постоянной и равной Г. В цент-
ре при ^-лопастном винте от слияния при-
соединенных вихрей полечится так назы-
ваемый центральный вихреной шиур, с
циркуляцией, равной £Г. С концов лопа-
стей сбегут вихри с циркуляцией Г. Та-
кая простейшая схема вихрей вполне
соответствует П-образным вихрям, рас-
сматриваемым в теории индуктивного со.-
противлення крыльев.
Более точная теория должна рассмат-
Фиг. 6
ривать переменную по длине лопасти
циркуляцию, т. е. считать, что Г=/(г), тогда, как мы знаем из теории
индуктивного сопротивления, с лопасти сбежит вихревая пелена, и них-
ревая система винта будет иметь вид, приведенный на фиг. 6. Впервые
это было отмечено В. П. Ветчинкнным.
Прямой путь вычисления индуктивных скоростей t>j и «1 был бы та-
ким. Нужно разбить все вихревые шиуры по их длине на бесконечно
малые элементы и вычислить вызванные ими индуктивные скорости в
у z. к^хема вихреи, сиегающих с винта. Струя винта
115
любой точке А, находящейся на лопастн и вращающейся вместе с нею.
Для этого придется пользоваться известной из гидродинамики теоремой
Бно-Савара о действии элементов вихрей и вычислять полную скорость
как интеграл скоростей, получающихся ог элементарных вихрей. Найден-
ные так относительные скорости позволили бы в дальнейшем вычислить
силы, действующие на лопасть.
Однако получающиеся при этом формулы оказываются в высшей
степени громоздкими и неудобными. На возможность такого решения
задачи о винте указывал сам Н. Е. Жуковский в конце своей первой
Фиг 7
Фиг. 8 1 Фиг. 9
статьи по вихревой теории винта; он назвал найденные так скорости
«истиными скоростями относительного движения». Отсюда у нас и воз-
никло название — относительная теория винта, для тех случаев,, когда
рассматривается вращающаяся вместе с лопастью точка А.
Вместо вычисления относительных скоростей проф. Н. Е. Жуковский
предложил, как мы уже упоминали, находить средние иа данном ра-
диусе винта индуктивные скорости (фиг. 7). Точка А считается не вра-
щающейся и лежащей в плоскости вращеиия винта. Лопасти вращаю-
щегося винта занимают тогда всевозможные положения относительно
точки А. Эффект действия винта в этом случае будет таким, как будто
число лопастей k возросло до бесконечности, а циркуляция стала беско-
нечно малой. Величина произведения kT должна при этом оставаться
постоянной. Винт в этом случае заменяется диском, состоящим из
радиальных, бесконечно слабых вихрей. Этот диск Н. Е. Жуковский
назвал вихревым донышком винта. Такой фиктивный вннт, по предложе-
нию проф. В. П. Ветчинкина, теперь часто называют дисковым, проти-
вопоставляя его лопастному винту, с конечным числом лопастей. Под-
счеты показывают, что найденные у дискового винта скорости сравни-
тельно мало отличаются в обычных условиях работы от истинных
скоростей лопастного виита. Формулы же значительно упрощаются. Сле-
довательно, теория дискового вннта, строго говоря, применяемая лишь
к винту с бесконечным числом лопастей, оказывается во многих слу-
чаях достаточно точной даже для двухлопастного винта.
Н. Е. Жуковский произвел исчерпывающий анализ работы дисково-
го винта, у которого k = со. В первых трех статьях он считал, что вихри,
сбежавшие с коицов лопастей, располагаются по спиралям, навернутым
на цилиндры. Особо подробно был изучен Жуковским винт с постоян-
ной по лопасти циркуляцией — такой винт называется в научиой лите-
ратуре по его имени винтом НЕЖ (NEJ). Схема вихрей винта НЕЖ
приведена на фиг. 7.
В случае переменной по радиусу циркуляции, т. е. когда Г=/(г),
получается бесчисленное количество вихревых цилиндров, нанизанных
один на другой и покрытых вихрями (фиг. 8).
Наконец, в четвертой статье по вихревой теории винта Жуковский
показал, что у винта вихри должны располагаться по поверхностям
тока, а так как у струи винта получается за винтом сжатие, то эти fio-
верхности имеют не цилиндрическую, а более сложную форму, изобра-
женную на фиг. 9. Учет этого весьма сильно усложняет теорию винта.
Сильное сжатие струи получается лишь у сильно нагруженных виитов,
а у слабо нагруженных оно мало. В настоящее время принято называть
схему вихрей, изображенную на фиг. 9. схемой вихрей сильнонагружен-
ного винта, а на фиг. 7 и 8—। слабонагруженного. Следовательно, у
винта слабонагруженного вихри лежат на цилиндрических поверхно-
стях.
Поток, текущий около винта, можно рассматривать с двух точек
зрения. Можно рассматривать абсолютное течение, т. е. такое, какое
представляется летчику, сидящему в самолете (фиг. 10). Тогда воздух
будет набегать на винт издалека со скоростью Со, подсасываться к нему
и, пройдя через винт, закручиваться. Можно также рассматривать дви-
жение воздуха по отношению к сечениям самого винта. Тогда получит-
ся относительное течение (фиг. 11). Для получения такого движения
мы должны остановить вращение винта и придать всему воздушному
пространству скорость вращения со в сторону, обратную скорости вра-
щения винта. Тогда винт будет неподвижен, а воздух будет набегать на
винт со скоростью Т’о и вращаться с угловой скоростью со.
Этими двумя точками зрения приходится постоянно пользоваться
в теории винта.
В этой книге мы разберем главным образом слабонагруженные
вииты, хотя многие выводы пригодны и для случая сильионагружениых
винтов.
Условимся теперь относительно обозначений. При иследоваиии вии-
тов нам придется неоднократно проводить три перпендикулярных к оси
виита сечения (фнг. 10 и И). Нулевое сечение берется далеко перед
винтом, сечение 1 берется ё плоскости вращения самого винта и сече-
ние 2, нлн горловое сечение, проводится далеко за винтом, там, где
струя получила полное сжатие и стала цилиндрической.
Все величины, относящиеся к тому нлн иному сечению, будут отме-
чаться соответствующей цифрой снизу, например: а2, щ, и2 и т. д.
Исключения будут допускаться лишь в тех случаях, когда это не может
вызвать недоразумений (например, для скорости полета в окончатель-
ных формулах).
Кроме этих трех основных сечений, нам придется иногда пользоваться
еще двумя сечениями Г и Г, проводимыми непосредственно перед и за
виитом, причем размеры винта вдоль по оси будут считаться очень малыми
и сечения 1, Г н Г бесконечно близкими. Относящиеся к этим сечениям
величины мы будем отмечать штрихами, например: и', v", и', и" н т. д.
§ 3. СКАЧОК ОКРУЖНОЙ скорости
направленную по радиусу.
Фиг, 12
Скорость воздуха, текущего около винта, можно разложить в любой
точке А пространства на три слагающих: осевую скорость Ел, окружную
иА, направленную параллельно Плоскости вращения и перпендикулярную
к радиусу гА точки А, и радиальную w
Вихревая теория позволяет
очень легко вычислить окруж-
ную составляющую скорости по-
тока, так называемую индуктив-
ную окружную скорость ил для
любого радиуса гА. Для этого
проведем через точку А плос-
кость, перпендикулярную к оси
вннта, и очертим на ней окруж-
ность радиуса ГА = ОАЛ (фиг.
12). Через этот круговой кон-
тур пройдут внхри, сбежавшие
с лопастей винта; назовем их
общую циркуляцию Гвнхр- По
теореме Стокса циркуляция ско-
рости по этому контуру должна
равняться алгебраической сумме
циркуляций прошедших через
него вихрей. Следовательно,
2 Л Г =
где иА — средняя окружная скорость на радиусе гА. Если мы проведем
через эту окружность воронкообразную круговую поверхность тока, то
последняя пересечет лопасть винта. Из чертежа видно, что если обозначить
циркуляцию скорости по контуру abc, лежащему на круговой поверхности
тока н охватывающему лопасть, через Г, то прн ^-лопастном винте с общей
циркуляцией kV все вихри пройдут через эту круговую поверхность тока
и, следовательно, через окружность, проходящую через точку А. Кроме того,
через этот контур могут пройти еще внхри, наброшенные в виде петель
на лопасть; однако такие внхри пересекут наш контур два раза, вращаясь
в противоположных направлениях, их циркуляции будут иметь противопо-
ложные знаки и в общую циркуляцию по контуру не войдут.
Следовательно, Гвихр ~ kV и
2лгАид = кГ.
Отсюда находим:
ЛГ
2лг/
по этой формуле, надо брать
винта не на радиусе гд, а иа
тогда г = гА и формула при-
Следует помнить, что, вычисляя скорость
циркуляцию у лопасти сильнонагружеиного
радиусе г лопасти (фиг. 12).
Обычно считают винт слабонагружеиным;
мет более простой вид:
2лг
Для скорости вращения в сечеини 2, т. е. в горле, получим
лг
и для слабонагруженного винта
2лг2
ЛГ
2лг
(2)
(3)
«2
Если будет задан закон изменения циркуляции по лопасти, т. * е.
Г то по формуле (2) можно вычислить скорость вращения струи иа
любом радиусе горлового сечения и получить зависимость
U2 - f(r2).
(4)
Для сильнонагружеиного винта, как мы уже указывали, придется учесть
то, что, вычисляя скорости на радиусе г3, мы должны брать циркуляцию
у лопасти на радиусе г. Это сильно усложняет расчеты. Приходятся обычно
вычислять эту скорость методом последовательных приближений. В прак-
тических расчетах чаще всего считают вннт слабонагружеиным, т. е. по-
лагают, что г = г2. Для обычных винтов это упрощение не дает заметной
ошибки. В случае вннтов геликоптериых или ветряных двигателей ошибка
эта может быть заметной.
Рассмотрим, какой будет скорость вращения струи, если возьмем точку
А перед винтом. Тогда, очевидно, через контур окружности, лежащей
в плоскости О и описанной радиусом ОоЛ0 (фиг. 12), никакие вихри про-
ходить не будут. Следовательно, Гвихр = 0 н по формуле
U ф™ = О,
ло 2ЛГЛ<(
т. е. перед винтом струя не вращается Если возьмем точку А, лежащую
непосредственно за винтом, то получим по формуле (1) вполне определен-
ную скорость вращения:
Следовательно, при переходе через ометаемую винтом поверхность (се-
чение /) струя мгновенно закручивается. До винта вращения не было, но
при переходе точки А через винт скорость вращения возрастает скачком.
Чуковский назвал формулу (5) выражением для окружного скачка
скорости струн. Для слабонагруженного винта, как видно из формул (3)
и (4) получим:
kT
(6)
§ 4. ДАВЛЕНИЯ В ГОРЛОВОМ СЕЧЕНИИ СТРУИ ВИНТА
Для дальнейших выводов нам нужно знать, как изменяется давление
на разных радиусах горлового сечения
В этом сечении струя полностью
сжалась, и поверхности тока имеют
форму цилиндров. Давление на внеш-
нюю поверхность струи в этом месте
равно атмосферному; обозначим его
через р0. Но внутри струи давление
будет меньше, так как на вращающие-
ся частицы воздуха будут действо-
вать центробежные силы, направлеи-
ные от центра к периферии.
Пусть скорость абсолютного враще-
ния струи на внешнем радиусе R2
будет равна а на радиусе г2 —
соответственно и2. Давление на произ-
вольном радиусе г2 обозначим через р2.
Выделим в струе винта, в горловом
сечении, колонку воздуха, с осно-
ванием f, направленную по радиусу
(фиг. 13). Тогда на элемент этой ко-
лонки, лежащий на радиусе г2 и имею-
винта, т. е. в сечении 2 (фиг. 13).
щий длину dr2, будет действовать центробежная
масса элемента, равная pfdr2. Следовательио,
ствующая иа этот элемент, будет равна
сила dm —, где dm —
Г2
центробежная сила, дей-
dm—- = pf — dr2.
Эта сила должна уравновеситься разностью давлений, действующих на
торцы выделенного элемента: давление иа радиусе г3 будет равно р2, а на
радиусе r2 -f- dr2 оно будет уже равно р2 4- dp2. Следовательно, на этот
элемент будет действовать сила f dp2. Она должна равняться центробежной
силе, т. е.
fdp2 pf~dr2 .
Г»
Сокращая полученное выражение на f и интегрируя его в пределах от г2
до получим:
Ла о
С л
Ро Р-2 — Р \ dr2.
Г2 Г*
В случае сильнонагруженного винта величина и2 связана с циркуляцией
соотношением (2). Подставляя это выражение в найденный интеграл, полу-
чим окончательно:
(7}
В случае слабоиагружсиного винта г2 г, и полученная формула пере-
пишется в обычно применяющемся в расчетах виитов виде.
С \2л I , ...
Р2-Р0—(8)
где R будет радиусом винта, а г —• радиусом сечения лопасти.
§ 5. ОСЕВАЯ СКОРОСТЬ ПОТОКА
Найдем осевую скорость потока в горловом сечеиин винта. Для этого
напишем уравнение Бернулли для элементарной кольцевой струйки винта,
изображенной на фиг. 14 пунктиром. Нулевое сечение возьмем далеко
Фиг. 14
перед винтом и рассмотрим абсолютное
течение воздуха: скорость потока в этом
сечении на любом радиусе г будет равна
Ео, а давление равно атмосферному, т. е.
р0. Второе сечение возьмем в горле струи.
Радиус струи в этом месте обозначим
через г2, давление через р., и скорость
через W2. Эту скорость можно разложить
на три составляющих: V2 — осевую, и2 —
окружную и w2— радиальную. Если сечение 2
взять в горле, т- е. в том месте, где струя
сделалась цилиндрической, то радиальная
скорость w2 ~ 0. Очевидно, что тогда V7-, --=
Уравнение Бернулли для этих сечёиий
напишется в виде:
PV° О Р^ ' . К
—- +• Ро - - —~ }Ъ — К,
где К дает величину потерь в струе. В
данном случае эти потери отрицательны,
так как наша струйка в сечении 1 не отдала, а получила энергию от
лопастей винта.
Для удобства дальнейших расчетов разделим обе части написанного
уравнения иа р и тогда получим
ZL + al = 4 ;
2 ' р 2 р
(9)
В таком виде уравнение Бернулли будет отнесено к единице массы
-кидкости.
Вычислим величину £ отрицательных потерь струйки. Для этого нужно
иайти, какую мощность получила наша кольцевая струйка от вннта. Нахо-
дим сперва момент вращения dM, приложенный к струйке между радиу-
сами г и г 4- dr, пользуясь теоремой о равенстве приложенного к системе
момента, секундному изменению момента количества движения. Обозначив
секундную массу воздуха, проходящего через сечення кольцевой струйки,
через dm и помня, что подходящий к винту воздух не закручен (м0 — 0),
а и сечении 2 он имеет окружную скорость и2, можем написать:
dM = dm u>r2.
Мощность, полученная этой струйкой, будет равна
dT = со dM = u2r2(£> dm.
В формулу Бернулли входит мощность, отнесенная к единице массы.
<_ dT u2r2(a dm
= -Ч------ - и2г.2а, (10)
dm dm
Возвращаемся к уравнению Бернулли. Вводим в него’найденное значе-
ние £ по формуле (10), значение р2 по формуле (7), заменяем — через
ul
——4 — и получаем:
л. w _ _4 _i_ г». _ ( fa _иг ш
.-- । — „ I . I \ о 2 '2<J->
2 Р 2 2 Р X г*
Сокращая в этом выражении члены и делая перегруппировку осталь-
р
ных членов, получим:
^2~ ^0 f и-г\ , С 1 2л i , .4
—-— = м2 (ог2—+\—~dr2. (И)
2 V 2 ! Гг г2
Левую часть этого уравнения удобно преобразовать, написав, как это при-
нято в теории идеального пропеллера, = 1/0 4- v2, где v2— скорость
отбрасывания воздуха на радиусе г2. Тогда получим:
(То-г^а)й — Vo V^ 4-2Voti3 4-— Vg /. v2 \
- 2------ ’-------2 = 2 4° “ T )
В правую часть вводим вместо и2 его значение, равное --------, и
2лг2
чаем тогда основное уравнение вихревой теории:
полу-
(12)
В случае слабонагруженного винта это уравнение примет более простой
для расчетов вид:
(13)
Жуковский назвал это выражение уравнением осевого скачка скорости.
Скорость вне струи винта, например в точке ’В, лежащей у горлового се-
чения (фиг), 14, равна скорости набегающего невозмущенного потока Ео.
Но если мы пройдем через боковую поверхность струи, то скорость сразу
же в точке Ло возрастет скачком до значения V2 = V’o 4-
В общем случае Г ~ f (г) и по найденному уравнению можно найти ве-
личину скорости отбрасывания для любого радиуса струи, т. е. получить
зависимость и2 = <р(г). Если винт считать сильнонагруженным, то расчеты
затрудняются тем, что в формулы войдут радиусы г2 и г. Для винта слабо-
нагруженного г2—-г/ и вычисление v2 по формуле (13) при заданном за-
коне изменения циркуляции Г = f (г) не представляет трудностей.
§ 6. ПОВЕРХНОСТНОЕ УСЛОВИЕ И СКОРОСТЬ ОТБРАСЫВАНИЯ
У ВИНТА ТИПА НЕЖ
Полученное нами уравнение осевого скачка скорости принимает простой
вид, если у винта берется крайняя, внешняя струйка, лежащая на поверх-
ности струи вннта.
Обозначив радиус такой струйки через R2, циркуляцию иа этом радиусе
через Гд и скорость через v2r, из формулы (12) получим
Входящий в уравнение (12) интеграл в этом случае обращается в нуль,
так как у него пределы сливаются; г2==/?2. Уравнение (14) Жуковский
назвал поверхностным условием струи винта.
В дальнейшем мы будем подробно разбирать простейший тип винта,
предложенный Н. Е. Жуковским,— винт НЕЖ с постоянной на всех рд-
диусах циркуляцией скорости Г = Г«. В этом случае уравнение скачка
упрощается и обращается, как увидим, в поверхностное условие.
Для доказательства этого достаточно вычислить интеграл, входящий
в уравнение (12), исходя из условия Г = const. Тогда получаем:
__ /Агу _i_/лгу t
2г| Ьл ! 27?' '
Подставляя найденное значение интеграла в основное уравнение (12),
получим:
И2 (V, + = <„ _ I 1 + m24(try± =
( 2л) 2л 2лг2 /2 (2л > 2г® \ 2л / 2/?|
АГ /ArV 1 kV ( о АГ \
2я \2п! 2R® 2n£s\,
т. е. у вннта НЕЖ поверхностное условие совпадает с условием скачка.
Из этого вытекает важный вывод, а именно* у вннта НЕЖ скорость от-
брасывания и2 постоянна по всему горловому сечению струн. Действитель-
но, при Г = const правая часть уравнения будет величиной постоянной
(от радиуса г2 не зависящей). Обозначив ее через /, мы сможем написать
поверхностное условие в таком виде:
(15)
Отсюда, решая квадратное уравнение, получаем ве-
личину и2:
+ (16)
Берем у корня знак так как ПРН нормальной
работе винта скорость v2 должна быть положитель-
ной. Из последней формулы видно, что v2 будет
при заданных условиях работы ' вннта величиной
постоянной. Постоянной будет и скорость уходя-
щего воздуха:
V-! = V„ + о2.
Заметим, что этот важный вывод можно очень
Фиг. 15
легко получить непосредственно нз геометрических
соображений. Выделим для этого в горле струн прямоугольный малый кон-
тур 12341, лежащий в меридиональной плоскости винта (фиг). 15). Пусть
осевая скорость на его грани 12 будет V2, а на грани 34 — будет У'.
Пусть длина сторон 12 и 34 равна а.
Циркуляция скорости по этому контуру будет равна
Г12341 — Е2й — lz2a.
Такое простое выражение получается потому, что на участках 23 н 14
нет радиальных скоростей, ибо мы рассматриваем струю в горловом се-
чении, а окружные скорости перпендикулярны к контуру и на циркуляции
не отражаются.
В случае винта НЕЖ вихри сбегают лишь на боковой поверхности
струи и в ее центре. Внутри струи вихрей нет. Следовательно, ни один
внхрь не пройдет через контур 12341. Тогда по теореме Стокса циркуля-
ция скорости по этому контуру должна быть равна нулю:
Г123Л = V2O — V2a — О
или
что и доказывает постоянство скорости V2 иа всех радиусах горлового
сечения винта НЕЖ-
§ 7. ТЕОРЕМА ФРУДА-ФИНСТЕРВАЛЬДЕРА —ЖУКОВСКОГО
В теории идеального пропеллера доказывается теорема Фруда —- Фнн-
стервальдера, согласно которой скорость отбрасывания и2 в два раза боль-
ше скорости подсасывания V\*. Под скоростью подсасывания понимается
осевая индуктивная скорость в плоскости вннта, т. е. в сечении 1 (фиг.
16), а под скоростью отбрасывания — осевая индуктивная скорость в гор-
ле, т. е. в сечении 2.
Н. Е. Жуковский доказал, что аналогичная теорема может быть полу-
чена с помощью вихревой теории и что помимо соотношении
v2 2Vj,
имеется еще соотношение
w2 — 2ии
де iii—скорость вращения струи в самой
плоскости вихревого донышка (сечение У),
а «2 — скорость в горловом сечении. При
этом как скорости и и2, так и и
могут быть переменными по радиусу винта.
Эта теорема может быть доказана не
только для дискового винта (k = ос), но
и для /г-лопастного. Единственное ограни-
чение доказательства — это допущение, что
сбегающие с лопастей спиральные вихри
расположены на цилиндрических поверх-
ностях. Это, как мы знаем, случай слабо-
нагруженного винта.
Для доказательства этой важной теоре-
мы очертим вокруг вннта цилиндр радиуса
г. На этот цилиндр наложатся вихревые
нити, сбежавшие с /г-лопастей. Они будут
иметь форму спиралей. Индуктивная ско-
рость в любой точке Ль лежащей на лопа-
сти (сечение /),может быть вычислена, как
Фиг. 16
известно из курса гидромеханики, по формуле Бно-Савара. Для этого-нуж-
но разбить каждую вихревую нить на элементы Е (фиг. 16) длиной dL и,
написав выражение для элементарной индуктивной скорости, вызванной в
точке Aj таким элементом, просуммировать действие всех элементов.
Легко видеть, что если мы возьмем аналогичную точку А2 в горловом,
т. е. очень далеком от винта сеченин 2, то там вихревые нити будут тя-
нуться и за плоскостью 2 и перед нею. При вычислении индуктивных
скоростей в точке А2 придется учесть и задние, и передние части спиралей.
Для такого подсчета нам придется опять применить формулу Био-
Савара и разбивать вихревые нити на элементы. Если мы разобьем заднн е
части спиралей на такие же элементы, на какие мы разбивали нить возле
сечении 1, то, очевидно, получим после суммирования эффекта всех эле-
ментов тот же самый результат, какой получился в сеченин I от эле-
ментов Е.
* Б Н. Юрьев Воздушные винты, стр 177.
Но на точки, лежащие в сечении 2, будет действовать ие только зад-
ние спиральные вихри, но и. передние. Если мы разобьем теперь передние
спирали на элементы £2, симметрично расположенные относительно ра-
диуса 02А2, то, как это непосредственно видно из фиг. 16, элемент £2
даст точно такой же эффект, как и элемент EL, элемент Ег— такой же
эффект, как £3 и элемент Ё[ — как Е2.
Этот вывод вытекает непосредственно из формулы Био-Савара:
dw = i sin (р dL,
ini
где I — расстояние между точкой At и элементом вихря Е, dL — длина
этих элементов и ср — угол между вектором вращения вихря и направле-
нием /.
У нас по построению, в силу симметричности, /в, — 1е2, Ге, = Ге2>
dLE = dLEi н sin ср£ = sincp£n, так как ср^ = 180° — ср£ . Следовательно,
накрест лежащие элементы дадут одинаковые как по величине, так и по
направлению индуктивные скорости.
Таким образом, какой, бы элемент мы ни взяли на задних спиралях,
всегда можно найти в передних спиралях аналогичный элемент (накрест
лежащий), дающий по теореме Био-Савара такой же эффект, как задний.
Это рассуждение справедливо для спиральных вихрей, лежащих на любом
радиусе винта.
Следовательно, индуктивные скорости в сечении 2 будут в два раза
большими, чем в сечении /. Это позволяет сразу написать формулы:
v2 = 2vt (17)
и
«2 — 2»!. (18)
§ 8. СКОРОСТНОЕ ПОЛЕ ВИНТА
Для получения расчетных формул нам нужно найти скорость потока
воздуха, набегающего на лопасть винта. Для этого нужно найти сначала
индуктивные скорости v2 и uv в плоскости вннта. Мы уже получили фор-
мулы для вычисления скоростей v2 н и2 для горлового сечения струн (2)
и (12). Последняя формула для винта НЕЖ или для поверхностной струй-
ки любого вннта получает более простой вид (14).
Будем считать вннт слабонагруженным. Тогда г2 — г, н будет справед-
ливой теорема Фруда — Фннстервальдера — Жуковского о том, что
V., — 2vi и и2 - 2иР
Используя эти значения, получим окончательные формулы:
«(-у
«1 (Vo + И1) = уг С иг __ 2L1 + А ( XAg. dr, (20)
inr \ 4лг I 2 *
а для вннта НЕЖ или поверхности струн любого винта
<2')
С помощью этих формул вычисляют по заданным условиям скорости н
ult получающиеся в плоскости винта.
Зная эти скорости, легко найти относительную скорость потока, набе-
гающего на винт. Для этого нам придется построить скоростной много-
угольник для сечения винта, лежащего иа радиусе г (фиг. 17). К индук-
тивным скоростям нужно прибавить взятые в обратном направлении окруж-
ную скорость элемента w и скорость полета Vo. _
v< Замыкающая сторона скоростного р, многоугольника и дает результирующую ско- рость потока. Будем называть скорость Vi осевой ско- ростью потока в плоскости винта + (22)
Фиг. 17 , а скорость U — окружной скоростью
,, ,, kV
и i (jq — иг = cor--------------.
4лг
(23)
Результирующая этих скоростей найдется, если пренебречь радиальной
скоростью, по формуле
\Vt == /РГТЪ} (24)
или, более развернуто
И7! = У (К, 3- »!)2 + у. (25)
Угол наклона этой скорости к плоскости вращения виита (обозначим его
через 3) найдется, как видно из фиг. 17, по формуле
Если сечение наклонено на этом радиусе г к плоскости вращения под
углом ср, То угол атаки профиля будет равен
а = ф — 3. (27)
Глава 2
ТЯГА, МОЩНОСТЬ И К. П. Д. ВИНТА
§ 1. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЭЛЕМЕНТ ВИНТА
Вырежем из винта бесконечно узкий элемент лопасти, для чего очертим
на оси винта два цилиндра: один радиусом г, другой радиусом г 4- dr.
На развертке (фиг. 18) мы получим сечение лопасти шириной b и с углом
наклона к плоскости вращения <р. Заключенный между этими цилиндриче-
скими сечениями элемент лопасти будет иметь
длину dr. Площадь этого элемента, как кры-
лышка, будет
dS bdr.
Воздух набегает на этот элемент со скоро-
стью IF,. Вокруг элемента имеется циркуля-
ция скорости Т.
По теореме Н, Е. Жуковского на этот
элемент должна действовать подъемная си-
ла dYlt которую можио вычислить по фор-
муле
АГг
О,
V,
Фиг. 18
dYA - pl'U/j dr. (28)
Эта сила перпендикулярна к направлению
) скорости HZ,. Кроме подъемной
силы, возникнет еще профильное сопротивление dXu которое проще всего
подсчитать по формуле
dXv = и (/Гь
где ц -------обратное качество профиля. Его нужно брать, считая крыло
. су
(профиль) имеющим бесконечный размах, так как в вихревой теории винта
скос потока уже входит в индуктивную скорость струи. Пользуясь выра-
жением для d\\, переписываем предыдущую формулу в таком виде:
dXx - - pprU/j dr. (29)
Для расчета винтов нам нужно найти элементарную тягу dP^, направ-
ленную по оси винта, и элементарное окружное усилие dQlt направленное
против скорости вращения но. Для этого нужно спроектировать силы dYt
и dX-L на ось н на плоскость вращения вннта. Угол между силой dYt и
осью винта 00± равен углу притекания потока, т. е. 3, в силу перпенди-
кулярности направлений dYy и 00х к соответствующим скоростям W\ и
Угол между силой dXt и скоростью TQ равен также 3, так как сила dXx
направлена по скорости
Из скоростного треугольника имеем:
sin 3 = и cos 3 = . (30)
Проектируя силы d\\ и dX, на ось винта- и на плоскость вращения,
получим:
dPy = dYt cos p — dX\ sin 3,
dQy = dYt sin 3 + dXr cos 3-
Подставляя сюда найденные значения sin 3 и cos3, а также выражения
для dY\ и dXn полупим:
dP, = рГГ, —-dr — ИрГГ, yfrdr,
dQ, = рПГ, -^-dr + «ПТ, -^-dr,
или окончательно
</Рг^РГ(£Л — pK)dr, (31)
dQi = рГ (К -г Ц^А) dr. 32)
Мощность, затрачиваемая на вращение такого элемента, будет равна *
dTt = dQ rw = рГ (V\ + ц6\) rw dr. (33)
В вихревой теории принято вычислять тягу и мощность не для отдель-
ного элемента лопасти, а для всего кольцевого элемента, заключающего
k лопастей. В таком случае мы получим:
dP = АрГ (t/j — цУ1) dr, (34)
dQ^kpT^-Y pdJJdr, ' (35)
dT = fepr (Vr 4~ r& dr. (36)
Эти формулы мы в дальнейшем будем называть формулами элементарной
тяги, сопротивления и мощности винта. Они являются основными форму-
лами теории винта.
Элементарный коэффициент полезного действия. Выведенные формулы
для элементарных силы тяги и мощности позволяют вычислить элементар-
ный к. п. д_, показывающий, насколько совершенно работает сечение вии-
та, лежащее иа том или другом радиусе.
Элементарный к. п. д. равен отношению полезной мощности элемента
к мощности, затраченной на его вращение:
(38)
(39)
Пользуясь формулами (34) и (36), пишем это выражение в более раз-
вернутом виде:
_ ((A — pVi)drV0 __ Vo Ui — НУ»
(Vi -г Иб\) Г'О dr " гш Vi +
Это выражение может быть переписано еще в виде:
1 n-VT
Vo (Ух U1
“ Их гш U, '
1 -г И -у/
Первый множитель в этом выражении дает идеальный или аксиальный
к.п.д. на данном радиусе, хорошо известный из теории идеального вннта.
Его обозначим через т]9а.
„ „ U, по — и.
Второй множитель °йенивает потери, зависящие от на-
личия закручивания струи, т. е. связанные со скоростью щ. Его называют
элементарным окружным к. п. д. Обозначим его через т]9И.
Третий множитель оценивает потери, связанные с величиной р =
- которую можно рассматривать как своего рода коэффициент трения
су
воздуха о крыло. Если ц == 0, то весь третий множитель обращается в
единицу. Третий множитель является элементарным коэффициентом механи-
ческих потерь (потерь на трение). Обозначим его через Лги-
• Таким образом мы разложили элементарный к.п.д. винта для данного
сечения на три к. п. д., каждый из которых оценивает характерные потери
винта. Мы получим, следовательно, что
Лэ = (40)
Рассмотрим эти к.п.д,винта более подробно.
Элементарный к. и. д. Лэ сильно изменяется вдоль лопасти винта.
У винта с постоянной циркуляцией (НЕЖ) скорость V, постоянна на всех
радиусах и, следовательно, постоянен н к.п.д. Лэа- Коэффициент окруж-
ных потерь
Величина и1г согласно формуле (19), связана с радиусом и циркуляцией
соотношением «. = —~; следовательно,
4Jtr
1 kV
1ЭЫ ~ ’
т. е. и величина т)9„ сильно изменяется по радиусу винта.
Механический к.п.д.также сильно изменяется по радиусу винта. Вхо-
дящее в выражение этого к.п.д. отношение есть, как мы знаем
из формулы (26), tg 3- Следовательно, можно написать:
ЛэЦ-------.' < ~ ( }
1 tg(5
9 Б. Н. Юрьев, т I
Эта величина имеет максимум при tg3~ 1, в чем легко убедиться, про-
дифференцировав по tg t3 полученное выражение и приравняв результат
нулю. Мы тогда получим
_^_=0
dtg(3
и, проделав вычисления, придем к квадратному уравнению
tg23 + 2ц tg 3- 1 =0,
решая которое, найдем ответ:
tg₽ = V1 + и2 — и-
Перед радикалом стоит знак плюс, так как по смыслу задачи tg 3 > 0.
При малых величинах ц, что всегда имеет место, формула дает tg3^ 1
и 3^45°. Следовательно, г|Эр. тем больше, чем больше наклон сечения
винта; таким образом, г|Э1Л достигает больших величин у винтов большого
шага, а у винтов малого шага он увеличивается по мере приближения
сечений к втулке.
Можно поставить задачу о наибольшем элементарном к. п. д. винта.
Действительно, формулу (37) можно привести к виду:
Пэ = f (Vo, И, г. Г), (42}
для чего нужно в нее подставить скорости и с/ъ выраженные через
циркуляцию. Для данного элемента 1’0 н г будут заданы, а величина ц
практически постоянна. Следовательно, в выражении (42) переменной вели-,
чиной будет лишь циркуляция скорости Г. Наибольшую величину для ч»
мы получим, решив уравнение
dtk
--^ = 0. (43)
Получается неудобное, весьма громоздкое выражение, которое, однако,
можно так или иначе решить и найти наивыгоднейшую для данного эле-
мента величину Г.
Очень часто полагают, что вннт, у которого на всех радиусах цирку-
ляция выбрана по уравнению (43), будет цаивыгоднейшнм. Это неверно.
У нанвыгодненшего винта нужно получить максимум к. п. д. всего винта,
а не его элементов, и он определяется из соотношения
PVo
ч = —•
где Р и Т относятся ко всему винту. В § 5 главы 3 мы разберем, как
должен проектироваться наивыгоднейший винт.
§ 2. ОТВЛЕЧЕННЫЕ ОБОЗНАЧЕНИЯ
Для получения общности всех формул и удобства расчетов по предло-
жению В. П. Ветчинкнна, сделанному в 1913 г., в теории} винта были
введены отвлеченные обозначения.
Эти обозначения оказались чрезвычайно удобными и нашли всеобщее
признание. Советские ученые составили ряд таблиц, облегчающих и уско-
ряющих расчеты винтов по вихревой теории.
Построены эти обозначения таким образом, что всякая переменная
величина представляется как произведение постоянной величины, имеющей
ту же самую размерность, как перемениая, на переменное отвлеченное
число- Это число показывает, какую долю составляет переменная величина
от постоянной- Эта постоянная является как бы новой единицей. Отвлечен-
ные величины изображаются у нас теми же буквами, как размерные, но
с чертой сверху. _ _
Для длин пишут: r — rR, b = bR* и т. д.
За единицу длины берется, как видим, радиус винта R. Для скоростей
пишут:
Vo/?(o с. = ViRa щ = UiRio и т. д.
За единицу скорости берут, как видим, окружную скорость конца лопасти
Rv) = U.
Для циркуляции берут выражение
Г = Г^^Ш. (44)
Для сил, действующих иа винт, напродер силы тяги,
Р = ?2np/?4w2 (45)
или
Р = P2x?R2U2- (46)
Для моментов, например момента вращения,
М = Л42лр/?5ы2 = Л42лр/№. (47)
Для мощности пользуются формулой: /
Т = 72лр/?5®3 = T2xPR2U3. (48)
Так как Т — Мео, то из сравнения формул (47) и (48) следует
/Й = Г. (49)
Заметим, что отвлеченные тяга Р и мощность Т связаны очень простым
соотношением с обычными коэффициентами тяги и мощности винта ос и [5,
применяющимися при лабораторных исследованиях винтов. Чтобы не сме-
шать эти коэффициенты с углом атаки а и углом притекания потока ₽,
МЫ будем над первыми ставить сверху черту. Сравним обычные формулы
подобия для винтов, т. е.
Р = apfHzis (50)
и
(51)
* У В. П Ветчинкина отвлеченная ширина лопасти определялась из соотношения
b = Мы здесь для однообразия приняли ЬЯ
9*
с формулами вихревой теории (45) и (48). Подставим- в формулы вихревой
теории вместо 7? равную ей величину D/2 и вместо <о — величину 2«*tns.
Тогда получим:
Р = Р2лр-^-(2лп,)г = ^-PpD'n*
И
Т = '72лр-^- (2л/15)3 = -£.7рО»л>
Сравнивая эти формулы с формулами подобия, заключаем, что
а = 2^7= 15,502-7, <52)
^=^-7 = 48,700.7. (53)
Следовательно, Р и Т представляют собой обычные коэффициенты а и "5
и отличаются от них лишь постоянными множителями.
Совершенно аналогично, если мы сравним формулу отвлечённой скоро-
сти полета, т. е. Уо = V0/7?<o, с формулой коэффициента скорости А ~
— VG/Dns, то, подставив в первую 7? ~ D/2 и 6) = - 2txns, получим:
р Уп _ Уо _
° Нш ~ ЛОП^ л '
ИЛИ
X = лУ0, (54)
т. е. коэффициент скорости винта X равен безразмерной скорости вихревой
теории Уо, помноженной на л.
§ 3. ПЕРЕХОД К ОТВЛЕЧЕННЫМ ОБОЗНАЧЕНИЯМ
Полученные выше формулы при практическом их использовании пишут
почти всегда в безразмерном виде. Для перехода к безразмерным величи-
нам нужно в обычные формулы подставить значения всех величин, выра-
женные по формулам предыдущего параграфа. Тогда именованный множи-
тель, получающийся в обеих частях формул, сократится и останутся лишь
отвлеченные величины.
Например, формула (19) напишется в виде:
— 4л
ЛГ—Я2со
щЯм ----------------
4r. г R
или, после сокращения, величина получится в таком простом виде:
(55)
Из формулы (20) получим:
_ 4п _ 4л
- \ ki——R4» / _ йг—я2ы \
vtR(i) (V0Rtn + yt7?(o) = ----=------I (or??--------—------) +
4пгк ' 4лг/? 7
или, после сокращения,
«1 (Vo + = Г (1 --=г) + 2^Х- dr. (56)
В последней формуле пределы интеграла изменились, так как мы пере-
шли от прежнего переменного г к новому г, и границы интегрирования
сделались дэугими: верхняя г=-1, нижняя г — текущее значение отвле-
ченного радиуса.
Поверхностное условие (14) в отвлеченных обозначениях примет вид:
У|« (Уо -Т rR (1 — Г’/,). (56')
Для относительной окружной скорости, выражаемой формулой (23),
получим теперь
и\ =-.7—17 = 7-----Т- . (57)
При пользовании выведенными формулами для скоростей следует по-
мнить, что в общем случае i' = f(r).
Вихревая теория позволяет, как видим, находить все скорости в плос-
кости виита в зависимости от г, Ио и Г. На любом радиусе г два пара-
метра, Уо и Г, определяют u, U, vlt V, и т. д.
Формула (56) дает величину в неявном виде. Одиако ее легко ре-
шить относительно так как это уравнение приводится к квадратному:
Ui + Ка — Гр— j — 2 \ -Ц- dr -- 0.
Решая это уравнение и беря по смыслу задачи для нормального случая
положительный корень, получим:
В этой формуле приходится сначала вычислять входящий в нее интеграл.
В случае вннта типа НЕЖ это выражение упрощается (§ 6) и получает вид,
«1 = --у- + |/^+г(1-о
или
\60)
Как видим, у винта НЕЖ получается значительно более простое выра-
жение для ut, чем в случае винта с переменной циркуляцией. Однако под-
робное исследование этого вопроса, сделанное В. П. Ветчинкиным, пока-
зывает, что формулой (59), справедливой, строго говоря, только для винта
НЕЖ, можио пользоваться как приближенной и для винтов с произволь-
ным законом изменения циркуляции по радиусу. Заметная разница полу-
чается лишь у втулки винта, при малых г. Однако у современных винтов
рабочая часть лопасти Лёжит обычно между г ~ 1 и г — 0,3, а централь-
ная ее часть бывает или прикрыта винтовым коком, или сделана в виде
неработающих спиц, служащих лишь для соединения рабочей части лопас-
ти со втулкой. Следовательно, у винта, как правило, можно считать ло-
пасть на участке г от 0,25 до 0 неработающей- Кроме того, следует по-
мнить, что наиболее активно работает лопасть на внешней части, где по-
лучаются большие окружные скорости; возле центра лопасть дает малую
силу тяги. Не вполне точное вычисление силы тяги и мощности возле
втулки нз-за ошибки в определении скорости не по формуле (58), а по
формуле (60) дает в окончательной величине силы тяги и мощности незна-
чительную ошибку. По этой причине обычно при расчете любых винтов
пользуются формулой (60) и лишь в случаях, требующих особой точности,
применяют формулу (58).
Заметим, что у современных винтов величина отвлеченной циркуляции
очень мала по сравнению с единицей; обычно она имеет порядок Г =
= 0,005-г-0,003. Следовательно, можно предыдущую формулу без особой
погрешности писать еще в таком виде:
(61) .
Найдя скорость получаем отвлеченную скорость потока в плоско-
сти винта = V'o + и отвлеченную результирующую скорость набегаю-
щего потока:
(62)
Угол притекания' потока к профилю лопасти на радиусе г найдется по-
формуле (26), которая примет в безразмерном написании следующий вид:
(63)
Часто скоростной многоугольник для сечения винта вычерчивают в от-
влеченных скоростях. Если возьмем скоростной многоугольник фиг. 17 и
разделим все его стороны на /?<о, то получим многоугольник фнг. 19.
Точно таким же приемом преобразуем полученные в § I главы 2 выра-
жения (34)—(36) для аэродинамических сил и мощности. Вводя в иих от-
влеченные обозначения и произведя сокращение именованных множителей,
получим основные расчетные формулы
теории:
dP = 2Г (IP — p/j) dr,
ЛЦ = 2Г (К -Т ИЦ) dr,
dT= 2T(V'i + VlA)rdr. (66)
Эти формулы дают элементарные отвлеченные силы и мощность, приходя-
щиеся иа кольцевой элемент виитаГ заключающий k элементов лопасти.
Ими приходится постоянно пользоваться при аэродинамическом расчете
винта и при расчете виита иа прочность.
Для расчета винта как пропеллера нам нужно знать полную тягу и
мощность всего виита, для чего необходимо проинтегрировать только что
полученные выражения. Это мы сделаем в следующем параграфе.
§ 4. СИЛА ТЯГИ, МОЩНОСТЬ И К.П.Д. ВИНТА ТИПА НЕЖ
Для получения силы тяги и мощности виита нужно проинтегрировать
найденные в предыдущем параграфе дифференциальные выражения сил и
мощности. Интегрировать придется от конца лопасти, где г — I, до нача-
ла нерабочей части, где г= ё. Для доведения формул до окончательного
вида нам нужно знать величину циркуляции на любом радиусе г, т. е.
иметь зависимость Г = f (г). Тогда, подставив эту функцию в наши урав-
нения и выразив через нее же величины V, и (7|я мы сможем довести, во-
обще говоря, интегрирование до конца. Формулы при этом получаются
чрезвычайно громоздкими.
В этом отношении винт типа НЕЖ является исключением: у него фор-
мулы получаются простые. Так как винт НЕЖ близок к иаивыгоднейше-
му вннту, то очеиь часто в различных расчетах и пользуются виитом НЕЖ,
как своего рода эталоном. Кооме того, многие конструкторы применяют и
До сих пор иа практике такие винты. Поэтому мы рассмотрим сперва винт
именно этого типа.
Виит типа НЕЖ. У такого винта Г — const и — const. Кроме того,
будем считать, что мы выбрали иаивыгоднейший профиль и поставили его
иа всех радиусах под иаивыгоднейшим углом атаки; тогда р = const. За-
метим, что при углах атаки, близких к наивыгодиейшему, величина ц из-
меняется мало и можно с достаточной точностью и при изменяющемся уг-
ле атаки брать среднюю величину ц —const. Это значительно облегчит
интегрирование формулы (64). Вводим в нее (Д по формуле (57) и вычис-
ляем интеграл:
Р = 2Г $ ( 7 — £ - цУ1) dr =- 2Г 4 — Г 1п7 — цР,7 =
.-=Г[1 — S2 : 2Г ins — 2цЙ, (1—5)1. (67)
Таким же путем из формулы (66) получим:
1 = 5 + й/г = 2Г [?i Y + g ——цГг"^ =
= r[v1(l-^) 4- |ц(1 _^-2цГ(1 -э] . (68)
Вихревая теория позволяет найти для винта НЕЖ отвлеченные тягу и
мощность, выраженные через параметры Г, Кь I н g. Как мы знаем, от-
влеченные силы и мощность связаны с коэффициентами силы и мощности
винта соотношениями (52) и (53). Следовательно, можно окончательно на-
писать:
Д = Л? = Г [I — ё3 2Г !пё- 2g?. (1 - (69)
и
Т = = Г [(1 - 6*) У, + 4 и (1 — (1 — 6)] • (70)
Напомним еще раз, что, согласно формуле (49), коэффициент момента М = Т-
Коэффициент полезного действия винта НЕЖ- Вычислим теперь
к. п. д. вннта типа НЕЖ- По определению к. п. д. винта можем напи-
сать:
т
(71’)
Подставляя в это выражение отвлеченные величины, получим:
T2xpR\,P Т
(72)
Этой формулой обычно и пользуются при расчете винтов по вихревой
теории. В случае винта НЕЖ можно детально проанализировать, рт чего
зависит к.п.д. винта. Для этого подставим в формулу 71 найденные, зна-
чения Р н Тогда получим аналитическое выражение для к.п.д. винта
типа НЕЖ:
в В - I3 + 2Г 1п £ — 2ц71 (1 - Я)1 Й______ . (73>
1(1 - F) Vt +4 ц (1 - V) - 2^Г (1 - 6)1
Формула показывает, что к.п.д. вннта зависит от Г, ? и g. К.п.д.
винта можно разбить на отдельные к.п.д., оценивающие влияние разных
факторов. Так, если умножим и разделим найденное выражение на Ух, то
получим:
И — V -к 2Г in — 2цУ. fl — Е)1 Vi
V* |(1-S2) P1 + 4l‘(l-|a)-2f.T-(l-|)j
(74)
Первый множитель в этсм гыргжении есть не что иное, как известный
из теории идеалы его пропеллера идеальный или аксиальный к.п.д. вин-
та, обозначаемый через т]а. Он учитывает потери, связанные с созданием
осевой скорости у винта*. Второй миожитель (дробь) представляет собой
относительный к. п. д. т]0, оцениваю ций все остальные потери винта. Та-
ким образом, с помощью вихревой теории мы получили формулу, извест-
ную из теории идеального пропеллера:
П = ПЛ0, (75)
но теперь величину т|0 мы сможем брать не из опытов, а по формуле
[1 — V + 2Г In q — 2uVt (1 — 1Л
~ 7 __
fd ~ £2) V1 4- 7 р. (1 - £;i) ~ 2|1Г (1 - £)
(76)
Вихревая теория позволяет еще больше углубить аиализ к.п.д. винта.
Мы можем заранее сказать, что потери, входящие в выражение для q0,
можно разбить на два типа. Во-первых, мы будем затрачивать энергию иа
закручивание струи виита и, во-вторых, будем терять энергию на трение
воздуха о лопасти винта. Разделить эти потери можно таеим образом. По-
тери иа треиие связаны с величиной ц— обратным качеством сечеиий вии-
та. Если бы треиие отсутствовало, ~то д. = 0. Очевидно, в этом случае
останутся лишь пртери на закручивание струи, так называемые окружные
потери. Обозначив к. п. д., оценивающий эти потери, через г]й, получим,
полагая р,— 0, из формулы (76) следующее выражение для окружного к. п .д.
винта:
. — (Ло^11=о
(1 — ^4- 2Г In £) V, _ 1 —2Г Ing
(1 - S-) Р, ~ 1 — Е'
ИЛИ
(77)
Остальные потери, входящие в выражение (76), следует считать
потерями иа трение. Обозначим соответствующий к.п.д. через и бу-
дем его называть механическим к.п.д. виита. Тогда мы можем написать,
что
По = Ч«П«- (78)
Величину г|ц можно легко найти, зная т|0 и Для этого достаточно
вычислить отношение Y|0/tjw, т. е.
„ По (l-g24-2ring-2HVI(l-l)lVi(l-^) ,7Qx
n u — —.----------2-------------------i • P '
u [(1 - 5.2) Vi 4- у н (1 - g3) - 2ИГ (1 - I) J (1 - g2+ 2Г in g)
Вихревая теория позволяет разложить к.п.д. виита на три коэффици-
ента, характеризующих каждый специфические потери энергии у винга.
Можно записать полученный результат в таком виде:
(80)
* См. Б. Н. Юрьев. Воздушные винты, § 41,
Иногда вводят еще одно обозначение:
= Т|аПи ’ (81)
и называют т|г индуктивным к. п. д. винта. Пользуясь им, можно преды-
дущее выражение формулы (80) написать еще в таком виде:
П = ПЛи- (82)
Скажем несколько слов об этих коэффициентах. Осевой коэффициент
г|0 оценивает совершенно неизбежные при работе винта потери иа отбрасы-
вание воздуха. Эти потери связаны с самим принципом работы винта: тяга
получается за счзт количества движения в уходящей струе, и эта струя
неизбежно уносит кинетическую энергию. Коэффициент окружных потерь
т],г может быть сделан , равным единице; он связан с закручиванием струи
винта. Если за виитом поставить спрямляющий аппарат или применять ком-
бинацию соосиых винтов (фиг. 51 и 56), вращающихся в противополож-
ные стороны, то т|ы будет равняться единице, так как никакого закручи-
вания в струе ие будет и потери энергии на закручивание струи будут
отсутствовать. Такие винты будут рассмотрены в главах 4—6.
Коэффициент механических потерь (трение) всегда меньше единицы,
гак как при обтекании реальных лопастей всегда возникают потери на
трение.
Глава 3
РАСЧЕТ И КОМПОНОВКА ВИНТОВ
§ 1. ПОДБОР ЦИРКУЛЯЦИИ ВИНТА НЕЖ
ДЛЯ ЗАДАННЫХ УСЛОВИИ РАБОТЫ
При расчете винтов или их проектировании основным вопросом яв-
ляется определение величины циркуляции и закона ее изменения по радиусу
винта. Для вннта НЕЖ задача упрощается, так как циркуляция не зави-
сит от радиуса винта. Ее приходится определять, исходя из условий рабо-
ты винта. Обычно бывает задана мощность мотора л. с., число оборо-
тов виита п, об/мин, скорость полета V, м/сек и плотность воздуха р,
кг-секР/м* на высоте полета //. Сначала нужно выбрать радиус винта 7?—
= 0/2. Сделать это можно проще всего, воспользовавшись логарифмическим
графиком какого-либо подходящего вннта, испытанного в лаборатории, или
логарифмическим графиком винта НЕЖ, данным в приложении Ц. Наивы-
годнейший диаметр виита мало зависит от формы вннта, и выбор его по
вииту, близкому по форме, даст хороший результат и для винта НЕЖ.
Если надо сделать выбор диаметра более точно, то задаются несколькими
подходящими диаметрами винтов и делают для каждого варианта полный
расчет.
Прн расчете винта предполагается, что высотная мощность У исправ-
лена иа эффект скоростного иаддува и уменьшена на потери, связанные с
числом Маха.
Найдем отвлеченные величины, характеризующие задание на винт. Уг-
ловая скорость вращения виита
со = 1/се/с, (83)
заданная отвлеченная скорость
Правильно подобранный винт должен поглощать всю мощность мотора.
Следовательно, по формуле (48) получим:
Т = 75N
(85)
По этим данным мы должны иайти циркуляцию Г, рассчитать и спроекти-
ровать винт. Однако аналитическое вычисление Г затруднительно. Дейст-
вительно, зная Уо и Г, можно вычислить по формуле (59) отвлеченную
скорость подсасывания v. Обычно величина отвлеченной циркуляции очен^
мала (0,003—0,007) и величину 1 — 1' можно считать равной единице.
Тогда вместо формулы (59) можно пользоваться более простой формулой
(61), и скорость потока в плоскости виита будет
14 = v„ + ^ = !^ + |/21 + r(i_fj (g6)
или
v> = i7»+^~'r + j/v+r: <87)
Если подставим это, выражение в формулу мощности виита (70) и при-
равняем полученное выражение 7’м, то получим:
Т = Г [(!-?) +|/=Г )--4н(1-У)-2цГ(1-^-7„. (88)
При выбранных или заданных значениях ц, £, Тм и можно решить это
уравнение относительно Г. Однако уравнение это неудобно для решения:
оно четвертой степени. Если в него подставить
/ более точную величину для ut по формуле (59),
-------—гм то оно будет уже пятой степени, т. е. не разрс-
/ шимым в радикалах.
Вследствие этого циркуляцию ищут графиче-
ским способом, для чего задаются предварительно
| _ вероятной величиной циркуляции Г и вычисляют
гок1<11Г г по формуле (86) или (87) скорость После этого
фиг 20 вычисляют? по формуле (70) и строят график (Фиг.
20), где по оси абсцисс отложена циркуляция Г, а
по оси ординат мощность Г. Проделав такой подсчет для нескольких зна-
чений Г, строят на графике кривую 7' — /(Г). Если теперь провести горизон-
тально линию с ординатой, равной Тм, то, очевидно, в точке А пересече-
ния этих линий мы получим правильную величину циркуляции, при которой
будет соблюдено условие
Найдя окончательно циркуляцию, вычисляют сиова скорость Vi и, поль-
зуясь формулами (69) и (70), определяют отвлеченную тягу и мощность.
В большинстве случаев можно считать, что £=0,25. Тогда наши рабо-
чие формулы примут простой вид:
= ^ = 40,9375-2,771= 1,5(0/,). (89)
7 = = ^ = f (0,9375V, + 0,656(1 - 1,5(iT). (90)
Подставляя в них V, и Г и беря в среднем ц — 0,03, получим Р и 7’
После этого можно найти к. п. д. rj винта, рассчитанного иа заданные
условия, по формуле
РИ0
Т) = -----5^-
н если требуется, можно проанализировать потери этого винта, т. е. раз-
бить его к- п. д. на множители, согласно формуле (80). Если винт оказы-
вается удовлетворительным, переходят к компоновке его.
§ 2. РАСЧЕТ И КОМПОНОВКА ВИНТА НЕЖ
И ВИНТА С ПЕРЕМЕННОЙ ПО РАДИУСУ ЦИРКУЛЯЦИЕЙ
Виит НЕЖ. После подбора циркуляции приступают к расчету винта.
Для этого вычисляют для нескольких радиусов г значения скоростей их,
Ui, ЙД и находят угол притекания’потока 0. В качестве стандартных ра-
диусов берут или г= 1,0, 0,9, 0,8, 0,7, 0,6, 0,5. 0,4, 0,3, илн, в менее
ответственных случаях, г = 0,9, 0,75, 0,6, 0,45, 0,3. Вычисление ведут в
виде табл. 1, заполняя ее графы последовательно сверху вниз.
Таблица 1
Расчет винта НЕЖ
(Циркуляция Г и скорость считаются найденными)
1 Величины 1 о э 0,8 0.7 0.0 0,5 0.4 0,3
2 3 4 6 |iV '-Г '| II 1= /
7 8 const Лс„ — — у WYm № профиля или с
9 to 11 а (по графику) И
12 12 14 ф — 3 т а — const b = — b = bR
15 b' = b cos ф h = л г tg ф
Во второй строке находят величину абсолютной • безразмерной скорости
вращения струи гг,, затем вычисляют относительную скорость вращения
иг — г — щ и в четвертой строке находят результирующую скорость
i₽, = Ур, -тб/, (У винта НЕЖ Vzi постоянна). Затем находят tg (3 и {3.
В случае, когда прочность винта внушает подозрения, учитывают изгиб
винта, вычисляя строки 7 и 8; относящаяся к ним теория будет изложена
в параграфе 3 главы 3. Если прочность виита не внушает сомнений, то по
продувке сечений винта выбирают угол атаки а и находят соответствую-
щую величину Су и р.
Зная угол атаки, получают угол наклона элемента <р на данном радиу-
се г по формуле
ф - 3 + а.
Ширину лопасти bJHa данном радиусе г находим, пользуясь уравнени-
ем связи, которое получаем следующим способом. Пишем величину
подъемной силы d\\, действующей на элемент лопасти два раза: один
раз по правилам экспериментальной аэродинамики, другой — по правилам
теоретической аэродинамики:
dYx — су --6 dr
dYt = pflFj dr.
Приравнивая эти выражения, получим:
Г = уСв&Ц7,. (91)
Отсюда , 2Г -
Переходя к отвлеченным обозначениям, находим: г ±1/?>«,=
или Г = (92)
Отсюда Ь — Д= 193>
Для виита НЕЖ Г — const и формула имеет более простой вид:
ft-=_£SL. , 1 (94)
По этой формуле заполняется 13-я строка. Далее находим ширину лопа-
сти по формуле - __
b = bR. (95)
По этим данным можно начать вычерчивание винта, так как мы будем
знать на каждом радиусе
чивании винта 15 строчка,
где вычислена длина про-
екции хорды сечения на
плоскость вращения винта,
т. е. b' = 6cos<p. Часто
еще заполняют, хотя это
и не обязательно, послед-
нюю строчку, дающую ме-
стный относительный шаг
лопасти на радиусе г.
Как известно*, относи-
тельный шаг
где Н — шаг данного сече-
ния в м. Но Н — 2nrtg(p,
следовательно,
г величину <р и Ь. Приносит пользу при вычер-
Фиг. 21
h = лг tg ф. (96)
При вычерчивании вин-
та нужно придерживаться
какого-либо правила для рас-
становки сечений виита. По-
ступают при этом наши кон-
структоры по-разному: они
или устанавливают на одну
прямую линию, перпендику-
лярную к оси вращения вин-
та (ось лопасти), центры хорд сечений (фиг. 21, а), илн же устанавливают
все центры тяжести площадей сечений на прямую линию (фиг. 21, Ь), или,
наконец, помещают эти центры тяжести на некоторую изогнутую линию.
Учитывая разгрузку винта центробежными силами (фиг. 21, с). Об этом см.
В упомянутой книге Б. Н. Юрьева, § 8 «Вычерчивание винтов» и § 34
«Изгиб лопасти в работе». Очень часто применяют второй прием, как это
изображено на фиг. 21, Ь.
Легко видеть, что если проектировать винт НЕЖ с постоянным углом
атаки а на всех радиусах, то ширина лопастей очень сильно возрастает по
мере приближения ко втулке. Действительно, полагая а — const, мы полу-
чим и Су — const и, следовательно, по формуле (93) найдем:
__________________________________const
Б. Н. К)рьев Воздушные винты, § 7, стр. 39.
Входящая в нее величина
и/, = Г/j -i- ui = у (K> + ai)! + — у)
приблизительно равна г; следовательно, закон изменения ширины лопасти
по радиусу будет близок к гиперболическому, и лопасть будет чрезмерно
расширяться ко втулке, как это показано на фиг. 22 пунктиром. Такую
форму удается осуществлять лишь
Фиг. 22
у винтов с большой нерабочей ча-
стью, £ 0,35, что иа практике
встречается лишь у вентиляторов. У
большинства винтов такая форма
лопасти непригодна, так как винт по-
лучается очеиь тяжелый и неудоб-
ный в производстве.
Вследствие этого обычно отсту
пают от условия а — const для се
чений, близких ко втулке, и беру»
по мере приближения ко втулке
большие углы атаки, а следователь-
но, и большие су. Тогда ширина
лопасти у втулки уменьшается, и ее
форма делается более удобной; та-
кая форма лопасти изображена на
фиг. 22 сплошной линией.
Изменяя угол атаки, нужно каждый раз подсчитывать угол наклона
•сечения <р и ширину лопасти Ь. После ряда проб удастся получить хоро-
шую форму лопасти с плавным изменением ширины b и угла наклона ее
сечений <;
Если величина ц сильно изменяется вдоль
лопасти, то приходится делать проверочный
расчет винта с учетом изменяемости ц по
радиусу. Он будет описан в §4 главы 3.
Винты с переменной циркуляцией. Винт
НЕЖ, как видим, рассчитывается и вычерчи-
вается весьма просто. Его недостатком явля-
ется большая ширина лопасти у втулки и
Фиг. 23
конечное значение циркуляции на конце лопа-
сти. На самом деле, как учит теория индуктивного сопротивления крыльев,
циркуляция должна иа конце крыла, в данном случае — лопасти, плавно
сходить иа иет. Если сделать лопасть так, как получается по приведенному
расчету, то иа конце получится вполне определенная величина хорды
(фиг. 23). В действительности такая лопасть будет обтекаться иа конце
ие плоским потоком, а пространственным и работа концевых сечений будет
очеиь плохой из-за перетекания воздуха из-под лопасти через ее край в перед-
нюю часть.
Поэтому многие авторы считают, что при прямоугольном или трапе-
циевидном конце лопасти концевой участок ее, длиной до 5 % радиуса, во-
обще ие работает. Таким образом, они предлагают в расчет вводить ие
радиус виита 2?, а несколько меньшую величину, а именно /?расч = 0,95/?-
Так поступают Ботезат, Локк, Глауэрт и многие другие.
У нас принято считать виит по его истинному радиусу, ио коиец лопа-
сти округляется на глаз примерно так, как это изображена на фиг. 23
В § 5 главы 3 мы покажем, как можно найти наивыгоднейший закон
изменения циркуляции по радиусу для заданных условий работы вннта. Такая
задача впервые была поставлена и решена В. П. Ветчннкиным в 1916 г.
Так как ее решать приходится с помощью вариационного исчисления, то
такие винты получили у нас название «вариационных винтов». Они оказыва-
ются на 1—3% выше по к.п.д. винтов типа НЕЖ. Однако расчеты эти
очень сложны и требуют больших предварительных вычислений по состав-
лению специальных таблиц и графиков.
Вариационные винты менее широки у втукли, чем винты НЕЖ. н это
является нх несомненным преимуществом. Однако и у вариационного винта
в дисковой теории конец лопасти полу-
чается конечной ширины, и остается откры-
тым вопрос об округлении конца лопасти
или введении в расчет искусственно умень-
шенного радиуса винта.
Все это побуждает многих конструкто-
ров еще более упростить расчеты и при
проектировании винтов применять следую-
щий прием. Циркуляцию скорости подбира-
ют как для винта НЕЖ. по правилам
§ 1 главы 3. Затем задаются каким-либо
законом изменения циркуляции, но выбира-
ют при этомордимазы кривой Г — f (г) так,
что площадь, охваченная этой кривой, бу-
дет равна площади прямоугольника Гщ_ж(Д — £)• Такие кривые, охваты-
вающие равные площади, будем называть равновеликими (фиг. 24).
Ряд проделанных расчетов в наших конструкторских бюро и во втузах
показывает, что при равновеликих кривых Г -f(r) мощности у винтов
получаются практически одинаковые.
Гягу же приходится находить, производя поверочный расчет, исходя из
чамечеиного закона изменения циркуляции. Для этого нужно воспользовать-
ся формулой
dP = 2Г цР,) dr
и вычислить по ней полную тягу, как это будет подробно указано в § 4
главы 3, посвященному поверочному расчету винтов.
Найденная таким способом тяга может оказаться на несколько процен-
тов отличающейся от той, что получалась у винта НЕЖ- Если закон цирку-
ляции более близок к наивыгоднейшему, то получится увеличение тяги,
в противном случае — уменьшение.
При вычерчивании виита при изображенном на рис. 24 законе измеиения
циркуляции у нас получится округленный конец лопасти и малая ширина
ее у втулки. Многие наши конструкторы применяют при этом эллиптиче-
ский закон изменения циркуляции, что дает очень хорошие формы лопастей.
§ 3. УЧЕТ ПРОЧНОСТИ ВИНТА ПРИ ЕГО КОМПОНОВКЕ
Мы не будем здесь разбирать вопросы прочности винта во всем их объеме
и лишь остановимся на вопросе учета прочности винта при компоновке
его формы.
Основным напряжением у винта обычной формы является напряжение
от изгиба воздушными силами. Это напряжение складывается с напряже-
10 В. Н Юрьев, г I
нием от изгиба центробежными силами и с напряжением от растяжения ло-
пасти центробежными же силами. Можно, однако, вести расчет только на
изгиб воздушными силами, учтя другие напряжения простым изменением,
допускаемого напряжения.
Такой прием и предложил В. П. Ветчиикин для подбора сечеиий винта
при его компоновке, что позволило построить удобные диаграммы для одно-
временного аэродинамического расчета виита и расчета иа прочность.
Напряжение в лопасти от изгиба воздушными силами. Если мы возьмем
какое-либо сечение лопасти, лежащее иа радиусе г. то от действия отрезан-
ной части лопасти возникнет изгиб в двух плоскостях — в меридиональной н
в плоскости вращения виита (фиг. 25). Изгибающий момеит М-р, действую-
щий в меридиональной плоскости, возникнет от элементарных сил тяги dPy
Фиг. 25
Фиг. 26
а действующий в плоскости вращения момеит Му получится от элементар-
ных сил сопротивления dQx. Если иа сечеиие винта нанести векторы этих
моментов Мр и MQ. то, сложив их геометрически, получим вектор изгибаю-
щего виит момента Мх. Он будет несколько больше момента Мр.
При расчете сечения иа изгиб в плоскости наименьшего сопротивления
иам нужно найти нейтральную линию сечения ппх и спроектировать вектор1
/Wj на иее. При этом расчетный момент Л1 получится меньше момеита
В. П. Ветчинкин показал, что у обычных виитов Мр^М. Для получе-
ния запаса прочности можно принять, что
М - 1,05 И,
Следовательно, при вычислении изгибающего момента от воздушных сил
достаточно подсчитать величину момента Мр. возникающего от элементар-
ных сил тяги. Возьмем сечеиие виита, лежащее на радиусе г. и рассмотрим.
)Г1 ‘ dP
какой момеит вызовет в этом сечеиии элементарная сила тяги d/-'I = -у от
элемента лопасти, лежащего иа радиусе гх и имеющего ширину drx (фиг. 26С
Получим, очевидно,
Сила ^Р = ^рГ(С'1 — pV’jdrj, следовательно.
ЛЬ = —Г) = (рГ (Ь, - —г)*-,.
Это выражение можно упростить. Во-первых, величииа (Д — г/е.
Во-вторых, у большинства применяющихся винтов циркуляция изменяется
мало и ее можно принять за величину постоянную. Если проектируется винт
НЕЖ, то циркуляция будет’ точно величиной постоянной. Тогда наше
предыдущее выражение можно переписать более просто
R
Мр ~ рГ(о (г( — г) drx.
Вводим в подынтегральное выражение отвлеченные радиусы г и rt и полу-
чаем окончательно:
Мр = рГсо/?3 \ (г, — г) drl = рГй)/?®/п3,
где
(97)
Величину т можно вычислить заранее; ее мы даем ниже для винта НЕЖ
а
г ;п‘ '11 Г ms in
1,0 0 о 0,5 0,1011 0,465
0.95 0,0012 0,1063 0,4 0,1440 0,524
0,9 о,0050 0.1710 0,3 0,1878 0,573
0,8 0,0180 0,265 0,2 0,2347 0,616
. 0,75 0,0286 0,304 0,1 0,2835 0,656
0,7 0,0404 0,343 0.0 0,333 0,693
0,0 0,0693 0,410
С помощью величины т легко найти по формуле (97) момент Мр и да-
лее вычислить /И--- 1,05Мр.
При подборе сечения винта мы должны соблюдать условие прочности.
Модуль прочности сечеиия лопасти на изгиб (обозначим его через IFM) дол-
жен быть равен или больше /VI.’g, где з— допускаемое напряжение материа-
ла лопасти, взятое с учетом остальных нагрузок.
Сам модуль прочности может быть вычислен по формуле:
где b — ширина сечения, а А — коэффициент пропорциональности, зависящий
от формы н толщины профиля. Его можно вычислить заранее для всех,
профилей, применяющихся в виитостроении. Он зависит от формы сечеиия
и от относительной толщины профиля с = с/Ь, где с—толщина профиля
(см. приложение J). Теперь условие прочности для сечения, лежащего иа
радиусе г. напишется в таком виде:
Связь аэродинамики с прочностью. В. П. Ветчиикин предложил ввести
в полученное условие прочности аэродинамически^ характеристики винта
для чего достаточно подставить вместо ширины b ее значение, взятое из
уравнения связи (91):
Тогда получим:
, 2Г \з м
Это выражение можно переписать в виде:
Ас ! f—
Пользуясь выражением момента М= 1,05 И/> = 1,О5<рГ<о/?3/п\ получим:
Ас аг Л с _ 2 /
У 1,05-pno/W У 1,05-^3 •
У винта типа НЕЖ для заданного режима полета радикал будет иметь
определенную величину; обозначим ее const. Тогда
. const
(100)
Последняя формула и позволяет вести подбор сечения с одновременным
учетом аэродинамики и прочности. Для этого нужно иметь (для применяе-
мых семейств винтовых профилей) специальные графики (фиг. 27), па кото-
рых по оси абсцисс отложена величина Асу, а по оси ординат величина су.
Тогда для каждого профиля, характеризующегося в семействе относительной
толщиной профиля с —~ , зависимость су от Асу представится прямой ли-
нией. Для разных относительных толщин получатся свои прямые. На этих
прямых можно отметить по соответствующему су точки с определенными
значениями угла атаки а. Для этого нужно иметь «продувку» этих профи-
лен, пересчитанную на бесконечное удлинение. Соединяя точки с одинако-
выми а, получим кривые угла атаки.
На ннжней части диаграммы следует отложить величину ц -- или,
что удобнее, величину качества k -= , тоже пересчитанные на бесконеч-
ное удлинение. Величина k конечная, а величина при >0, послед-
нее неудобно для графического изображения ц f(Acy).
Подбор сечения по этой диаграмме ведется таким способом.
В табл. 1 приведен расчет винта НЕЖ- Вычисляем в^этой таблице
строку 7, т. е. Ас по формуле (100). В правой части этой "формулы иам
все известно- Неравенство (100) указывает, что на фиг. 27 мы можем брать
лишь те значения приведенных на ней величин, у которых абсциссы мень-
ше найденного значения Асу. Можно положить на диаграмму лист бумаги
или линейку, как показано на фиг. 27 пунктиром, и тогда останется види-
мой лишь та часть диаграммы, где условие прочности соблюдается. Из
имеющихся кривых нужно выбрать ту, где величина k максимальна (ц —
минимально), так как это уменьшит
потери на трение. Однако выбирая с, мы
должны взять такое cf/, при котором по-
лучается плавная форма лопасти. Если
же всегда брать те профили, где цт}п, то
может получиться волнистая форма лопа-
сти в плане. Приходится поэтому, выбрав
профиль, т- е. с и угол атаки а, вычис-
лять по уравнению связи несколько раз
ширину хорды
и наклон сечения
ср = р а,
Фиг. 27
винта обеспечивается лишь для
пока не получится плавное очертание ло-
пасти. Это желательно из соображений
технологических. На практике такая ком-
поновка делается очень быстро с помо-
щью описанной диаграммы.
При таком способе расчета прочность
данного режима. Если винт, например пропеллер самолета, работает на раз-
личных режимах, то необходимо сделать поверочный расчет уже вычерчен-
ного винта для всех опасных режимов. Вихревая теория дает для этого
исходные данные, т- е. нагрузки dP\ и dQv
В этой работе не будем рассматривать расчет прочности винта*, а лишь
отметим, что такой расчет можно вести по обычным правилам сопротивле-
ния материалов, но с учетом изгиба винта в поле центробежных сил-
§ 4. ПОВЕРОЧНЫЙ расчет винта
Вихревая теория позволяет по чертежу винта сделать его поверочный
аэродинамический расчет, т- е. определить при заданной скорости полета Р’о
тягу и мощность. Расчет выгодно вести в отвлеченных обозначениях. Дан
чертеж винта с R = 1. Найти, какая у него будет тяга Р и мощность Т
при скорости полета Ио- Сделав расчет для нескольких скоростей полета,
можно получить полную характеристику винта, т. е. закон изменения Р, Т
* См. Д. Ю. Панов. Расчет воздушного винта на прочность. Труды ЦАГИ,
вып. 288, 1937; В. П. Ветчинкини Н. Н. По ляхов Теория и расчет воздушного
гребного винта. Оборонгиз, 1940.
и и с изменением Vn. Получится диаграмма, аналогичная обычной экспери-
ментальной характеристике винта, дающей а. 0 и т) как функцию л.
Циркуляция скорости будет в этом случае величиной переменной: Г--- [(г).
Если даже возьмем винт НЕЖ, то у него циркуляция будет постоянной
лишь на расчетном режиме (при заданной скорости Уо); при других скоро-
стях она будет функцией г.
Основной задачей поверочного расчета и является нахождение величины
Г на разных г для любой заданной скорости полета Vo. На каждом радиу.
се нам будет известна ширина лопасти b и наклон сечення винта к пло-
скости вращения <р и тип профиля (номер дужки).
Определение циркуляции удобнее всего вести так. Задаемся величиной
Г на выбранном радиусе г и находим
И = - |/ г I'd—Г).
Далее находим последовательно:
Г
'i-arctg-^,
а = <р — 0.
Получив угол атаки и зная тип профиля, находим по продувкам, пере-
считанным на бесконечное удлинение, величины с„ и ц.
Пользуясь уравнением связи (92), вычисляем снова величину циркуляции.
Как правило, найденное значение циркуляции Г'будет отличаться от пред-
положенного Г.
Для быстрого подбора циркуляции полезно строить вспомогательный
график, на котором по оси абсцисс отложено значение Г, а по оси орди-
нат значение Г' (фнг. 28). Проделав такой расчет, мы получим на диаграм-
ме точку А. Если мы задались сразу верной циркуляцией, то полученная
точка попала бы на прямую линии ОВ, наклоненную под углом 45г* к осям
координат и проходящую через начало. Сделав несколько попыток, мы
получим ряд точек: Д1, Д, Д3 и т. д. Проведя через них плавную линию,
мы, очевидно, в точке пересечения этой кривой с прямой ОВ получим пра-
вильную величину циркуляции (отрезок ОС или ОС’).
Проделав такой расчет для ряда значений г, мы сможем построить
кривую Г = /(г). Заметим, что в случаях, требующих особо большой точ-
ности и прн большой величине Г, можно пользоваться вместо уравнения (59)
более точным уравнением (58). В этом случае нужно расчет начинать с
конца лопасти (г —- 1) и, переходя последовательно к меньшим радиусам,
подсчитывать графически или численно величину входящего в формулу инте-
$ 4. Поверочный расчет винта
151
града. Для этого нужно построить кривую -£-'(фиг. 29) и планиметрировать
указанную на чертеже площадь для всех радиусов, где ищутся величины Г.
Обычно пользуются приближенным выражением (86', так как уточне-
ние от описанного метода получается небольшое, а расчетная работа зна-
чительно увеличивается.
Фиг. 28
Фиг. 29
После нахождения истинной циркуляции находят снова И,, Щ и ц,
после чего переходят к вычислению “Силы тяги и мощности виита. Удобнее
всего воспользоваться формулами (64) и (66), написав их в таком виде:
- 2Г ((Д — мН)
dr
(101)
или
-£ = 2Г(Н -Н
dr
(Ю2)
Величины этих производных легко вычислить, так как на каждом ра-
диусе г мы будем уже знать Г, Ц. и М- Далее строим диаграммы фиг.
30, а и Ь, изображающие изменение этих производных в зависимости от г-
Легко видеть, что площади, лежащие между этими кривыми и осью
абсцисс, дают соответственно тягу и мощность винта. Действительно, мы
можем написать тождества:
с г
Выражения в скобках будут ординатами наших кривых и, следователь-
но, заштрихованные иа фиг. 30, и и b площади и Qr дадут, с учетом
масштабов, величину Р и Г.
Масштабы учтутся так. Пусть на д а\эп п: единица радиуса пред-
ставлена гп сантиметрами, а единицы величии ~ и соответственно р см
и t см. Тогда
dr dr
Зная Р и Т, находим
PVn
71 -=г- .
Т _
Если проделать ряд^таких расчетов для разных Уо, то можно постро-
ить график изменения р, Т и т) (фиг. 31). На этом графике можно на-
нести и масштабы для обычных винтовых экспериментальных коэффициен-
тов а, р и для чего нужно воспользоваться выражениями
г = ^Р, 3 = ^-Т, Z -=- лУ„. ' Таблица 2 Поверочный расчет вннта Уо = . ..
1 у 0.9 0 75 0,6 0 45 0 30
3 4 F По чертелх винта тип и № проф
5 6 8 Задаться Г
5 и- 4 .1 С 1, 11 1 1 ilT lb
9 10 11 12 Pi р = arctg-==^- а - ф — 3 су и
13 14 Истинная величина Г по графику
15 16 17 18 Кх (по строке 6) аг ат __ _ = 2Г (Vxц'ЛИ dr
На основании полученного графика можно построить характеристику
винто-моторной группы *.
Зесь описанный рас чет удобно вести ио табл 2
§ 5. ПОНЯТИЕ О НАИВЫГОДНЕЙШЕМ ВИНТЕ
По вихревой теории можно рассчитать винт с любым законом
ния циркуляции по длине лопасти Если задана зависимость
измене-
r = f(r),
то, применяя выведенные в главе 2 формулы, мы сможем рассчитать и
спроектировать соответствующий винт. Наиболее простые формулы полу-
чаются для винта НЕЖ, У которого Г — const на всех радиусах.
Какой же закон изменения циркуляции по радиусу будет наивыгодией-
шим^ Пусть задана мощность мотора скорость полета V, радиус винта
R и высота полета Н (т. е. р). Мы должны получить в этих условиях
максимум тяги- Вихревая теория дает для мощности и тяги следующие
формулы
•Г = j 2Г (Г; + Ц(А) г ЛГ= = const,
? = j 2Г (й. - рЩ* = = max.
Б Н Юрьев Воздушные винты, глава XIJ
Следовательно, первый интеграл задан по величине, а второй должен
дать максимум- При этом максимум зависит не от какой-либо величины,
а от формы кривой Г =f(r). Такие задачи решаются с помощью вариаци-
онного исчисления*. Наш случай называется там задачей об изоперимет-
рах, так как впервые с этими математическими вопросами встретились
при рассмотрении задачи о максимальной площади, охваченной нерастяжи-
мой иитью иа какой-нибудь поверхности. Длина нити (периметр), выража-
емая интегралом, будет постоянной, а охваченная ею площадь, также вы-
ражаемая некоторым интегралом, должна дать максимум. Задачи этого
типа были решены Эйлером, Бернулли и Лагранжем, создавшими на основе
их вариационное исчисление.
В общем виде, задача формулируется так. Даны два интеграла:
первый должен быть постоянным, а второй должен дать максимум:
\ F(y, х) dx = const, (ЮЗ)
G (у, х) dx -- max. (104)
При этом величина интегралов зависит от вида функции г/ = /(х), в них
входящей. Какой должна быть эта функция, дающая максимум второго
интеграла?
Ответ получается из особого дифференциального уравнения Эйлера—
Лагранжа, которое в иашем случае имеет следующий простой вид?
ал
ду *
36 ’ ’
d//
где А — постоянный множитель Лагранжа, величина которого находится
по условиям задачи. Решение этого дифференциального
ответ, т, е. зависимость между х и у. У нас х это /•, а у
Следовательно, в нашем случае
F- dL --2F(V, -HiiTO,
dr
a .. 2m- nV,),
dr
и уравнение Эйлера — Лагранжа запишется в таком виде:
21 (Г, - Г
V- '
Т=2Г(171 -Ц1',)
уравнения и дает
— это Г.
(105)
(106)
(107)
* Д. ф. Егоров. Основания вариационного исчисления. Госиздат, 1923;
В И. Смирнов, В. И. Крилов, Л. В. Канторович. Вариационное исчисление.
М„ КУБУЧ, 1933.
5 з. понятие о наивыгоонеишем винте
При вычислении этого выражения следует помнить, что и являются
функциями Г.
Кроме того, величина ц может изменяться но длине лопасти по неко-
торому закону,.например:
I* = 4: (г).
Вследствие сложности получающихся выражений приходится вводить в
них различные упрощения. Прежде всего вместо точной формулы (86)
можно пользоваться приближенной формулой (87), так как величииа I’
обычно очень мала и можно считать I — Г-=^1. Величина р, на наиболее
активных, концевых сечеииях винта близка к постоянству, н во многих
случаях можно принять рconst. Впрочем, В. П. Ветчинкин и другие
авторы иногда вводят в расчет и изменение р, что особо больших труд-
ностей не представляет. _ _
Вводя такие упрощения и производя подстановку й'| и V, в уравнение
(107), получим:
Гг|г|,(7-Т'Ч: + Г) + "Т[’~"Г,| _ .
Произведя дифференцирование, находим1
1/ + Г (iv-r 2и?-41хТ) + г 7 г ( Т + г)
- V -_4 ------------------------------Ц-------- = Л. (108)
/ V'z — , - Г _ \ — / У2 _ \
]/ + -2(Ц^ ?Г)
При работе виита на месте, на так называемом геликоптерном режиме,
уравнение это упростится, так как Уо -- 0, и примет вид:
V?’/2+ —2цТ
~----------3 = л- (109)
г - 2---—• |лГ,/г
г 1
Полученное нами уравнение (108) имеет вид.
Ч'(Г, 7) = Л. (НО)
Если бы мы знали для нашего вннта постоянную величину А, то фор-
мула (НО) и давала бы нам искомую зависимость Г от г. Решая получен-
ное уравнение относительно Г, мы получили бы
г - /(Г, Л).
Пользуясь формулами (105) и (106), подставив в них найденную вели-
чину Г и произведя интегрирование, мы получили бы
Р —<р(Л), Т = Я) GV
Зная величину Т, которую найдем по мощности, ‘числу оборотов,мото-
ра и плотности воздуха, мы получим по последнему^ уравнению с 'одной
неизвестной необходимое значение Л; затем находим Р и получаем из (НО)
окончательную зависимость
г
После этого расчет винта можно считать оконченным. Далее идет ком-
поновка его по правилам, изложенным в § 2 главы 3.
Однако описанный метод ие может быть примеиеи в чистом виде к
решению этой задачи. Уже основное уравнение (НО) имеет относительно
Г третью или четвертую степень (в зависимости от сделанных упрощений).
Таким образом, получение явной зависимости r~f(r, Л) уже дает гро-
моздкие выражения. Подстановка найденного выражения Г в формулы эле-
ментарной тяги и мощности и последующее интегрирование этих выраже-
ний еще более усложняют даиные формулы.
Вследствие этого приходится прибегать к различным упрощениям ос-
новных формул и отбрасывать малые члены. Гораздо удобиее решать эту
задачу графически с помощью зараиее составленных сеток кривых.
Такие расчеты, как и сама идея построения вариационных винтов, были
разработаны впервые В. П. Ветчиикииым в 1916 г.
Проще всего поступить так. Для заданной величины 14 построить
график, связывающий г, Г и Л. Для этого нужно подставить в уравнение
(108) ряд значений г п Г и вычислить дробь, дающую значение Л. Такой
график изображен иа фиг. 32. По оси абсцисс отложена величина Г, по
оси ординат Л; радиусы г даиы параметрически. Перестраивая этот гра-
фик, получаем зависимость Г от г в виде кривых с параметром Л (фиг. 33).
С помощью этого графика легко построить графики производных
F - ~ 2Г (Ui — иИа
dr
Gл7 =-2Г (V;
dr
в зависимости от г и Л (фиг.С34). Плаииметрируя эти кривые, получим,
как это было подробно рассмотрено в § 4 главы 3, тягу Р и мощность
Т в зависимости от Л. Это позволит построить график (фиг. 35), дающий
-р и т в зависимости от Л. При заданном Т сразу находим величину Л
Для этого достаточно только выделить
нужную кривую на графиках фиг.34 и
33. Нужная кривая может занимать про-
межуточное положение между имею-
щимися на графиках кривыми, и ее
всегда легко провести, интерполируя
на глаз.
Фч1 34
Фиг. 35
Весь описанный расчет относился к вполне определенной скорости по-
лета lz0 Описанные графики выгодно заготовить заранее для нескольких
скоростей, полета.
Такая работа проделана впервые В. П. Ветчичкнным. Однако в
настоящее время скорости полета сильно увеличились, ц опубликованных
трафиков В. П. Ветчиикина не всегда хватает, так как они'даны до
1Д - 0,4 и частично до 0,2. Современные самолеты летают со значительно
большими отиоснтельнымиДкоростями, доходящими до 0,7—0,8. Т. е. тре-
буется доработка имеющихся -в настоящее время таблиц вариационных
винтов.
Случай геликоптерного вариационного виита является частным случаем
винта-пропеллера с Уо -.= 0. Для геликоптера удобно на заключительный
график нанести величину относительно к. п. д. л о (фиг- 36), пунктир — виит
НЕЖ, сплошная линия — вариационный виит. Это позволяет очень нагляд-
но выбирать винт и быстро вычислять тягу по формуле Велльнера
Р (94,2 у р f|0A'D)3 =- (aND)J.
Приведенный на фиг. 36 график был вычислен в работе инженера В. Е. Ка-
сторского.
Примечание. При решении вариационной задачи очень часто для компактности
окончательных формул делают различные упрощения. Так, вместо сложного полного
уравнения скачка осевой скорости (56), пользуются поверхностным условием (56’), под-
ставляя в это выражение текущие значения Г и i\, т. е. пишут
^(Ho-^i) = f(l — Г).
Это не вызывает больших ошибок, и прием этот часто применяется при расчете
винтов. Кроме того, для обычных винтов ввиду малости величины Г, можно принять,
что 1—Г — 1 и писать
-iKo т fl) ~ Г.
Однако иногда делают еще более смелые упрощения, а именно: принимают, что
Ио — Ki. Тогда получают рхЁ0 — Г и
Последнее упрощение нам кажется неправильным по следующим соображениям.
Во-первых, мы отказываемся от рассмотрения геликоптерных винтов, где ко==О, и тогда
по приближенной формуле получаем pf = oe. Следовательно, теория оказывается непри-
менимой к расчету винтов для геликоптеров, аэросаней и ветряных двигателей, где
индуктивные скорости играют главную роль. Во-вторых, расчет винта для современного
самолета, если исходить из его максимальной скорости, как показывает летная практика,
сам по себе неправилен. При современных огромных нагрузках на крылья длина разбега
современных самолетов стала большой, доходящей до 1 — 1,5 км. Виной этого в значи-
тельной мере являются неправильно рассчитанные вцнты, дающие очень .высокий
к.п.д. на максимальной скорости и плохо, со срывом потока, работающие на малых
скоростях разбега самолета.
Правильным методом является расчет винта иа малые скорости полета и повероч-
ный расчет на максимальной скорости. И опыт и теория показывают, что всякий вичт
большого шага на больших скоростях дает очень высокий к.п.д.. доходящий до 85%.
если, конечно, нет волновых потерь. Следовательно, заботиться о большом к.п.д. на
максимальной скорости полета практически не приходится.
На малых же скоростях можно улучшить к. п. д., при правильном подборе циркуля-
ции, на десятки процентов, устранив срыв потока. При этом потеря к. п. д. на максималь-
ной скорости нередко получается порядка 2—3%. что практически почти незаметно
снижает скорость горизонтального полета. Общие же летные данные у самолета с таким
винтом будут значительно улучшены.
Следовательно, для современного винта главное внимание нужно уделять обеспе-
чению его хорошей работы при малых скоростях полета; математические упрощения
расчетных формул не должны делать теорию неприменимой для этих режимов работ
винта.
Б. Н. Юрьев. Воздушные винты, глава XVI, § 40.
Из этого, однако, не следует, что для получения хорошей работы винта нужно
строго придерживаться закона циркуляции, получаемого из решения вариационной
задачи. Можно делать большие отступления от вариационного закона изменения цирку-
ляции по радиусу винта, не изменяя заметно его к.п.д. Происходит это потому, что около
своего максимума функция, в подавляющем числе случаев, изменяется слабо. В дан-
ном случае сравнение даже вннта НЕЖ с вариационным впитом показывает, что
выигрыш получается в среднем лишь 1—3%. Кроме того, следует помнить, что совре-
менные теории винта довольно грубы и .в них имеется много скрытых и явных допуще-
ний и неточностей. Например, в классической теории, которую мы развиваем в этой
книге, сделаны следующие допущения: малая нагружснность, отсутствие влияния трения
чопастей на струю, пренебрежение концевыми потерями лопастей, пренебрежение
радиальными скоростями потока и многие другие упрощения.
С другой стороны, огромное значение имеет правильный выбор основных парамет-
ров винта, в особенности диаметра и передаточного числа редуктора. Правильный или
неправильный выбор этих величин, как показывает наша практика, может изменить
к.п.д. на 15—20%.
Вследствие этого нужно признать, что вариационная задача играет в проектиро-
вании винтов подчиненную роль. Многие конструкторы вместо постройки винтов с ва-
риационным законом циркуляции берут более простой закон; близкий к вариационному
и дающий, кроме того, удобную в конструктивном отношении форму лопасти. Недо-
статком винта НЕЖ и вариационного является конечная величина циркуляции при
г Конец лопасти вообще работает в очень сложных условиях; там имеются большие
радиальные скорости; циркуляция скорости, согласно теории индукции, должна на
самом деле у конца крыла или лопасти сходить постепенно на нет. Все это делает
расчет концевых сечений винта неточным. Некоторые авторы, как мы уже указывали,
предлагали просто считать к^нец.лопасти на участке длиной 5% от радиуса винта
неработающим (проф, Ботезат). Поэтому лучше и в дисковой теории кривую цирку-
ляции выбрать так, чтобы Г на копне лопасти плавно падала до нуля.
Винт НЕЖ неудобен в том отношении, что у него в центре получается чрезмер-
ная ширина лопастей. Вариационный винт в этом отношении значительно лучше. Лишь
иногда, при моторах воздушного охлаждения, приходится заботиться о развитии
центральной части винта для обеспечения обдувки при гонке мотора на месте.
Очень хорошая форма получается у винта с эллиптическим законом изменена
циркуляции. Она дает весьма высокий к.п.д.. отличающийся от вариационного обычно
га доли процента, и его форма весьма удобна в конструктивном отношении. Расчет
такого винта, как мы показали в § 2 главы 3, очень прост, поэтому многие наши кюн-
стрмктхры пользуются таким шкивом изменения циркуляции у проектируемых Винтов
Глава 4
ОСОБЫЕ СЛУЧАИ РАБОТЫ ВИНТОВ
§ I. РАСЧЕТ ГЕЛИКОПТЕРНЫХ ВИНТОВ
В настоящее время во всех странах возрос интерес к геликоптерам.
Подъемная сила у них получается с помощью виита с вертикальной осью.
Преимущество геликоптеров — вертикальный взлет, возможность неподвиж-
ного висеиия иа одном месте в воздухе и отсюда—возможность обойтись
без аэродромов. Имеется еще ряд других преимуществ, о которых мы
здесь говорить не будем. Гелико рный винт подробно изучался как про-
фессором Жуковским, так и его учениками. Наша страна добилась в по-
стройке таких аппаратов больших успехов и, одио время, далеко обогна-
ла заграницу *.
Под геликоптерпым винтом в теории понимается виит, работающий
при нулевой осевой скорости = 0. Следовательно, все выведенные в
предыдущих параграфах формулы будут пригодны и для частного случая.
Формулы для скоростей примут более простой вид:
Vt (1Н)
или приближенно, а для винта НЕЖ — точно:
о, -= КгД—7)~ CF - (Ц2)
Щ-77- 4; • (НЗ)
Г
= у7 (114)
<i!5?
Г
Скоростной многоугольник в случае геликоптерного винта упрощается
(фиг. 37). Интегральные формулы тяги и мощности получают также более
простой ВИД'
-- 2НЖ5Г-(i -51) (116)
* Б. Н. Юрьев. Летные свойства геликоптеров. Труды ВВА, 1939 № 49 его же.
Проблема геликоптера Труды конференции ВВА. 1915 (доклад на пленуме)’
•леча геликоптерных винтов
161
И
Величина циркуляции у новейших геликоптерных винтов очень мала,
порядка 0,005, и можно поэтому с достаточной точностью пользоваться
формулой Uj = Уг. Нерабочая часть у геликоптерных винтов обычно
близка к £ = 0,25. Это приводит к таким окончательным формулам для
геликоптерного винта типа НЕЖ:
Р = Г(0,9375 —2,77Г—1,5(1 Кг). (118)
Т = Г (0,9375 УТ -ь 0,656/1 - 1,5(1 Г). (119)
По этим формулам и ведется расчет геликоптерного виита. При задан-
ной мощности мотора сперва вычисляют Тп и затем, считая обычно Ц =
= 0,03, находят графически циркуляцию и,
Г по способу, описанному в § 1 главы 3.
Зная циркуляцию Г, переходят к компо-
новке винта, пользуясь уравнением связи.
Находят для ряда радиусов угол |3"По фор-
муле (115) И ширину лопасти ПО формуле Фиг. 37
(93)- После этого вычерчивают винт. Ком-
поновка получается такой же, как и для пропеллера (§ 2 главы 3).
У современных геликоптеров циркуляция мала и лопасть получается
узкая. Для прочности лопасть делается не жесткой, а на шарнирном
креплении ко втулке, благодаря чему она устанавливается так, что изги-
бающий эффект силы тяги компенсируется моментом центробежных сил.
Благодаря специфической форме таких винтов их часто называют рото-
рами геликоптера.
При оценке совершенства геликоптерных винтов принято пользоваться
относительным к. п. д. т)я. Полный к.п.д, геликоптерного винта равен
нулю, так как при Уо = 0 винт никакой полезной работы не производит
и PV0 = 0. Однако мы можем разложить, как мы видели, в § 4 главы 2
полный к. п. д. г) на составляющие (75). Аксиальный или идеальный ко-
эффициент в нашем случае
Vi
но относительный не равен нулю (76).
Подставив в формулу (76) значения Р, Т и — "Кг", найдем величину
Ло- Так же можно разложить т]0 на т]м и (см. § 4 главы 2).
В современных геликоптерах стараются получить достаточно большую
величину г]0, но очень большие ее значения получаются лишь у тихоход-
ных винтов, с широкими лопастями. Для геликоптера в целом такое ре-
шение невыгодно, так как это утяжеляет как сам винт, так и особенно
трансмиссии и редукторы, и без того отнимающие очень большую часть
подъемной силы геликоптеров. Оказывается возможным получить вполне
приемлемые значения т]0 у быстроходных винтов. Для геликоптера быстро-
11 Б Н, Юрьев, т. I
ходиые вииты дают очень много преимуществ: легкие редукторы и транс-
миссии, легкие лопасти, возможность безопасного спуска, получение боль-
шой скорости горизонтального полета и т. д.
На графике фиг. 38 представлен отиосительный_к. п. д. геликоптер-
иого виита типа НЕЖ в зависимости от циркуляции Г. Как видим, к.п.д.
чеет почти одно и тоже значение 0,8.
Даже при очень малой циркуляции, рав-
ной 0,002, его величина равна 0,73, что
дает очень хорошую тягу. Так как ло-
пасти получаются у такого винта уз-
кие, а сам виит легкий, то можно, уве-
личив диаметр, получить у него более
высокую тягу, чем у тихоходного вин-
та. На этом специальном вопросе под-
робно останавливаться не будем. Заме-
тим, что скорости в струе винта, нуж-
ные для расчета обдувки геликоптера,
будут равны: для плоскости виита
о, = /г,
для горлового сечения, находящегося у геликоптериого виита на расстоя-
нии около 0,5/? от плоскости вращения,
F. = 2Й, =2/Г.
Роторы геликоптеров приходится рассчитывать не только иа их основ-
ной режим висения, ио и на режим взлета, когда они работают как про-
пеллер, на режим посадки с работающим мотором, на режим авторотации
и т. д- Все эти расчеты можно вести по общим формулам, подставляя’
туда соответствующие значения Уо и Т. Расчет приходится вести в этих
случаях как поверочный, исходя из полученной для основного режима —
«висения» — формы лопасти.
Наконец, при горизонтальном полете лопасть винта будет работать в
так называемой косой обдувке. Теория такой работы виита была разрабо-
тана Глауэртом и Локком и в работах И. П. Братухина.
Заметим, что изложенная здесь теория геликоптериого винта построена
на дисковой теории слабоиагружениого виита. На самом деле, в случае
геликоптериого винта точность нахождения индуктивных скоростей и и3
играет огромную роль, ибо в этом случае отсутствует скорость полета Уо,
и как угол притекания струй 3, так и скорость определяются исклю-
чительно этими скоростями. Кроме того, у геликоптериого винта очень велико
сжатие струй, поэтому у него получаются большие радиальные скорости в
плоскости виита. Это делает вихревую теорию для геликоптериого вннта
менее точной, чем для пропеллера, где основную роль играет скорость
полета Vo.
Опыты показывают, что, несмотря на все эти неточности, вихревая дис-
ковая теория дает погрешности в среднем не более 2—5%, что можно
признать приемлемым для многих инженерных расчетов. При этом ошибка
получается в сторону теоретического улучшения виита. Мощность получа-
ется по вихревой теории достаточно точно, ио тяга оказывается в дейст-
вительности несколько меиьшей. Скидывая 2—5% у расчетной тяги, мы
получим достаточно точный результат. Большая ошибка получается у вин-
тов большего шага (большой циркуляции).
Когда желательна большая точность, нужно более точно учитывать
сжатие струи или переходить к расчету на основе опытов или более точ-
ной, относительной теории.
Здесь не будем разбирать этот специальный вопрос.
§ 2- РАСЧЕТ OCEBbU ВЕНТИЛЯТОРОВ
Общие формулы вихревой теории очень легко применить к расчету
осевых вентиляторов. Вентилятор работает в трубе или в кожухе (фиг. 39)
и должен дать заданный напор р кг/м2 при заданном расходе воздуха Q м3.
Если его нерабочая часть будет начинаться на отвлеченном радиусе
то площадь струи, проходящей через вентилятор, будет равна F ~
= TtR2 (1 — £2) и скорость потока будет равняться
(120)
Тяга этого вентилятора будет равна -
P = pF =ряР2(1—ег). (121) '
Особенностью вентилятора по сравнению с пропел- Ь""
лером является то, что скорость в плоскости вентиля- Фиг. 39
тора V будет величиной заданной. В этом случае ut О
и = V. В этом параграфе мы не будем ставить значок 0 у ско-
рости V.
Особо выгодными оказались вентиляторы типа НЕЖ с постоянной цир*
куляцией, так как они дают постоянную по радиусу скорость V. Их сей->
час выпускает большими сериями наша промышленность. Для такого вен-
тилятора полностью применимы формулы (69) и (70), которые напишутся
теперь, когда = V, в таком безразмерном виде:
= Г11-‘62 + 2Г1пВ-2|й/(1-‘6)], , (122)
(123)
У вентилятора при его расчете бывает задан напор р, им создаваемый,
и, следовательно, выбрав R, <о, | и ц по конструктивным соображениям/
мы сможем вычислить Р ~ pnR* (1 — g2) и далее получить:
Р = р = рл*а(1-Н = Р 1 -12 (J24)
27tpR4to2 2jtr»R4w2 рК3<о2 2 ' ’
Величину -р/^а- = называют иногда приведенным напором венти-
лятора. Мы будем обозначать ее через р. Следовательно,
Р = р- Д . (125)
Зная^ величину Р, можно по формуле (122) вычислить величину цирку-
ляции Г. Однако на этом этапе расчета необходимо учесть наличие зазора
между концами лопастей и кожухом вентилятора (трубой). Схема вихрей,
получающихся у вентилятора типа МЕЖ. представлена на фиг. 40. При-
соединенные вихри, заменяющие в внхревой теории лопасти вентилятора,
присосутся к стенке трубы, т. е. они окончатся, опираясь на твердые тела,
что допустимо по теореме Гельмгольтца.
Следовательно, в случае вентилятора без зазоров никакие спиральные
вихри с концов лопастей сбегать не будут. Этим объясняется, почему
у вентилятора не получается осевой индук-
тивной скорости в плоскости его вращения.
Однако у реального вентилятора обычной
системы всегда имеется зазор, достигающий
нескольких миллиметров при малых диамет-
рах и доходящий до нескольких сантиметров
при больших диаметрах. Вследствие наличия
такого зазора к стенке трубы присосется не
весь вихрь с циркуляцией Г, а только его
часть. Оставшаяся свободной циркуляция сбе-
жит с конца лопастн в виде спирального вих-
ревого уса с некоторой циркуляцией АГ.
щели, как показывают опыты, вентилятор при
_ меньшую тягу Р, чем получается это по фор-
муле (122). Мощность Т получается
Не разбирая подробно эффекта щели,
ный график (фиг. 41), дающий ко-
эффициент k] уменьшения тяги
вентилятора в зависимости от
относительной величины зазора 6,
определяемого по формуле:
б = . (126)
Т^вент
Кроме величины зазора у вен-
тилятора, по К. А. Ушакову, до-
бавочные потери напора дает «гу-
стота лопастей». У вентиляторов
с узкими лопастями н малом их
числе потеря тяги мала и равна
приблизительно 5%. При широких лопастях и большом
могут достигать 10%. _
Если рассчитать вентилятор не на заданную тягу Р
несколько большую, «расчетную», т. е. взять
Фиг. 40
Вследствие наличия этой
данной циркуляции Г дает
по формуле (123) достаточно точно,
проф. К. А. Ушаков построил опыт-
их числе потери
(или напор), а на
Ррасч ~— k-\k<>P,
(127)
где kj —- поправка на зазор, a k2 — поправка на густоту лопастей, то ока-
зывается, что и циркуляция Г, и мощность Г получаются правильные.
Поправка в среднем равна 1,15, поправка k2 1,05, и общая по-
правка обычно близка к 1,20. _
Решая уравнение (122), мы должны будем подставить в него Ррасч, S>
ц и V. Получим:
Ррасч - г (1 - g2) г 2Га In £ - Г2р1/(1 - g),
что дает квадратное уравнение:
Г2-2 in s -ь Г [ 1 — е2 — 2g7(i -^)] — Рр,сч = 0.
Решая это уравнение, получим два значения Г — большое и малое.
Останавливаемся на малом корне, -так как большая циркуляция дает очень
низкий к. п. д. и вызывает сильное закручивание отходящей струи.
Зная циркуляцию, вычисляем мощность Т по формуле (123) и перехо-
дим к вычерчиванию вентилятора по правилам § 2 главы 3.
У вентилятора, особенно при больших напорах, получается большая цирку-
ляция Г. Это создает в струе вентилятора большие скорости вращения струи
их = -1г- Иногда у втулки вентилятора, особенно если взята малая вели-
чина относительного радиуса втулки скорость uxzzr, и, следовательно,
лопасть не может догнать вращающийся воздух. В таких случаях нужно
увеличивать У осевых вентиляторов, рассчитанных на большой иапор,
нередко £ = 0,5—0,8 и лопатки очень короткие, как у турбин.
Воздух нередко бывает закручен так, что струйки образуют угол с
осью вентилятора больше 45°. В таких случаях полезно) применять спрям-
ляющий аппарат, уничтожающий это вращение.
Спрямляющий аппарат увеличит тягу иа величину Pk, которую можно
вычислить по формуле (154), приведенной в § 5 главы 4. Это увеличит
А
напор на величину —р- .
Коэффициент полезного
винтовой формуле
действия вентилятора получится по обычной
PV PV
Y] =
т т
по формуле
а в случае контрпропеллера
(P + Ph)V (P + Pk)V
т т
Поверочный расчет вентилятора. Некоторые вентиляторы работают с
переменной нагрузкой. Чаще всего у нйх число оборотов остается посто-
янным, а изменяется скорость потока V илн, что то же» расход Q м3/сек.
В таком случае у них изменяются напор р и, следовательно, тяга Р.
Проведенные в ЦАГИ опыты показали, что поток, набегающий на
вентилятор, определяется не только самим вентилятором, но и в значи-
тельной мере трубопроводом. Вследствие этого даже при изменяющейся
по радиусу винта циркуляции [Г = f (г)] скорость подходящего к вентиля-
тору воздуха близка к постоянному значению. Это упрощает поверочный
расчет первого приближения, так как позволяет считать величину V одной
и той же на всех радиусах.
Поверочный расчет вентилятора в этих условиях может быть сделан
прямо по правилам, изложенным в § 4 главы 3, т. е., подобрав циркуля-
цию Г, находим Р и Т по формулам (101) и (102). Интегрируя эти выра-
жения графически, получим РраСч и Т. Полученная таким образом расчет-
ная тяга Ррасч будет больше действительной тяги Р, так как по формуле
(127) мы в действительности будем иметь потери на зазор и густоту ло-
пастей. Истинная тяга получится по формуле:
(129)
Заметим, что при таком расчете напор р будет различным на разных ра-
диусах. Однако, как показывает опыт, давления за вентилятором очень
быстро выравниваются, и мы можем принять, что вентилятор создает
средний напор р, определяемый формулой:
PcV ~ ~ (130)
Сделав поверочный расчет для ряда скоростей V (т. е. расходов Q), мы
получим соответствующие значения напора р (или тяги Р).
По этим данным можно построить отвлеченную или безразмерную ха-
рактеристику вентилятора (фиг. 42), дающую изменение Г и Р (или р) в
зависимости от V. Имея эту характеристику, относящуюся к изучаемому
типу вентиляторов, можно построить индивидуальную характеристику дан-
ного вентилятора этого типа, имею цего заданные диаметр D, число обо-
ротов п и работающего с жидкостью плотности р. Удобнее всего отло-
жить по оси абсцисс величину расхода жидкости, проходящей через
вентилятор, т. е. Q л^/сек, а по оси ординат — величину среднего напора
р кг/м2 и потребную на вращение вентилятора мощность N л. с. (фиг. 43)-
Иногда иа эти диаграммы наносят еще к.п.д. вентилятора, определя-
емый чаще всего по обычной винтовой формуле
С помощью таких характеристик легко делать расчет вентиляторов
для разных трубопроводов. Для этого достаточно рассчитать и построить
по правилам, излагаемым в курсах гидродинамики, характеристику трубо-
провода, т. е. зависимость потребного перепада давления или напора р
от скорости потока V или расхода О лР/сек. Начертив эту характеристику
на характеристике вентилятора, мы получим ответ в точке пересечения
характеристик вентилятора и трубопровода и найдем получающиеся в этом
случае расход Q и напор р\ кроме того, мы находим потребную на вра-
щение вентилятора мощность N л. с.
Заметим еще, что при турбулентном потоке и при больших числах
Рейнольдса сопротивление трубопровода изменяется пропорционально квад-
рату скорости, т. е. можно тогда написать
р — constt V2 или p = const2Q2. (131)
Следовательно, в этом случае потребный напор изобразится на нашей
диаграмме квадратной параболой
Описанный расчет велся при постоянном числе оборотов вентилятора.
Такая задача чаще всего и встречается при расчете промышленных венти-
ляторов.
Существуют, однако, вентиляторы, работающие с переменной скоростью
вращения. Сюда прежде всего следует отнести вентиляторы аэродинами-
ческих труб, в которых скорость потока изменяется в широких пределах
при изменении числа оборотов вентилятора. В обычных трубах их соб-
ственная характеристика может быть представлена формулой (131). Но тяга
вентилятора, при соблюдении подобия, точно так же представляется зави-
симостью типа Р = const /г2 и, если п и V будут пропорциональны, то и
режим вентилятора будет неизменным. Действительно, в этих условиях
угол притекания струй 3 = arctg будет тот же на соответствующих
радиусах, циркуляция будет пропорциональна числу оборотов и скорости
и полное подобие будет обеспечено*.
Следовательно, в таком случае, сделав расчет вентилятора на один
режим, мы получим все режимы, так как V будет пропорционально п,
р пропорционален V2, а потребная мощность пропорциональна V'; или п3.
В скоростных трубах иногда бывает очень сильно заметно влияние числа
Рейнольдса и Маха. Такие трубы надо рассчитывать детально для всех
режимов работы, учитывая наличие в них различных испытуемых моделей,
вызывающих различное сопротивление.
В заключение заметим, что изложенная теория применима лишь для
вентиляторов с малым перепадом давления, когда можно пренебрегать
сжимаемостью воздуха.
§ 3. ВЕТРЯНЫЕ ДВИГАТЕЛИ
Ветряные двигатели применяются для получения энергии в сельском
хозяйстве и в авиации В авиации их используют для привода электрогене-
раторов, дающих ток для радио, освещения и обогрева; применяют их для
привода масляных и бензиновых помп, для обслуживания фотокамер марш-
рутной съемки и т. д. Во всех случаях такой двигатель является винтом,
получающим энергию от набегающего на него потока воздуха и передающим
ее на вращаемый им вал.
Теория Н. Е. Жуковского полностью охватывает и этот случай. Общие
Уравнения остаются в силе, но только в случае ветряного двигателя нужно
подставить в уравнения отрицательную циркуляцию Гв. Вихревая картина
и форма струи изображена для этого случая на фиг. 44. В теории ветряка
выгодно пользоваться теми же безразмерными обозначениями, какие приме-
няются для винтов.
Струя у ветряка ие сжимается, как у пропеллера, а расширяется.
Перед ветряком скорость потока равна V'o в плоскости ветряка V] — Vo 4-
* Б. Н Юрьев. Экспериментальная аэродинамика, ч. I.
+ и за ним V2 = Vo -J- 2иг. При этом скорость будет отрицательной,
как это видно из уравнения (61), если в него подставить Г = —Гв в
явном виде:
__ (7 / _
“ = -> + }/ --Т1 (132)
Следовательно,
Vi = К. —Ы- (133)
Фиг 44
фиг. 45
Точно так же изменится и знак скорости закручивания, так как при от-
рицательной циркуляции
= - -Ь-
и
- - - - Гв
и\ = г — щ - г . (134)
Скоростной многоугольник в случае ветряка изображен иа фиг. 45.
Из него получаем
3 = arctg (135)
и
<р = р — а.
Для ветряков выгодной оказалась форма лопастей, соответствующая
постоянной циркуляции Г- Такие ветряки у нас называются ветряками НЕЖ-
Выведенные для винтов типа НЕЖ формулы полностью применимы и для
ветряков-
Сила тяги и мощность получаются, как видно из формул (69) и (70),
отрицательными, что и должно быть по смыслу задачи, так как здесь мы
не отдаем работу винту, а получаем ее от него. Винт теперь не тянет,
а дает силу сопротивления.
Новых формул для тяги и мощности выводить не требуется, достаточно
в них подставить лишь отрицательную циркуляцию, чтобы получить мощ-
ность и сопротивление ветряка. Компоновка лопасти ветряка ведется по
правилам § 2 главы 3.
Обычный к. п. д. виита в данном случае мало удобен. Действительно,
величина
будет давать отношение секундной работы набегающего потока PV0 к се-
кундной работе, полученной на валу двигателя. Из-за неизбежных потерь
мощность Т будет меньше мощности РУ0 и, следовательно, для ветряка,
обычный к. п. д. винта будет больше единицы; это, конечно, неудобно.
Гораздо удобнее пользоваться специальным к. п. д. ветряного двигателя £
и определять его по формуле
Отношение мощности Т, полученной по валу двигателя, к мощности
PV0, затраченной потоком, будет теперь меньше единицы н будет более
соответствовать привычному определению к. п. д.
В случае установки ветряка на самолете мощность PV0 будет той
мощностью, какую мы затратим на проталкивание ветряка, дающего сопро-
тивление Р и движущегося со скоростью вперед. Эта мощность будет
получаться от винто-моторной Группы самолета. Очевидно, наилучшим
будет ветряк с более высоким к. п. д.
Так н выбирают ветряки для самолетов*.
Заметим, что в настоящее . время на быстроходных самолетах нетряков
не ставят, а предпочитают приводить во вращение электрогенераторы
непосредственно от мотора, так как при установке ветряка энергия пере-
дается через винт и общий к. п. д.
Пуст “ Пвинтаъветряка
получается малым.
В среднем Пвинта = 0,75; ветряка = 0,7 и общий Пуст ~ 0,5. При механи-
ческом приводе (шестеренками) к. п. д. равен 0,97—0,95.
Для промышленных ветряков, использующих энергию ветра, к. п. д.
роли не играет, так как энергия ветра «бесплатная». Здесь выгоднее
ввести понятие коэффициент использования энергии ветра,
понимая под этим термином отношение полученной на валу энергии t
к кинетической энергии подходящего к ветряку воздуха в колонне, имею-
щей диаметр, равный диаметру ветряка. Последняя энергия в единицу вре-
мени будет равна
oFVn л ,
—Л. — .1____L____лО21/3
где F — сметаемая ветряком
использования энергии ветра
площадь, равная л/?2. Обозначив коэффициент
через £, получим:
Т
S = —г-------•
-^-PRW30
Подставляя сюда значение Т — Т-2лр7?5(о3 и получим:
g = _ 4 Т
~ P&VIR4)3
Б Н. Юрьев. Воздушные винты, глава XXV
Замечая, что Г = ^PVq, найдем окончательно связь между s и £:
s-4;4r- (138)
vo
Следовательно, коэффициент использования энергии ветра может сильно
отличаться от к. п. д. £ ветряка. Смысл величины £ заключается в том
что мы сравниваем ветряки по использованию их диаметра; при равных
диаметрах и, следовательно, при равной приблизительно стоимости, тот
ветряк лучше, у которого мощность больше. С этой точки зрения оказы-
ваются выгодными весьма быстроходные ветряки, с большой окружной
скоростью, т. е. с малой величиной Уо = • Такие ветряки одно вре-
мя строила наша промышленность по проектам ЦАГИ. Они, несомненно,
очень выгодны для промышленных электроустановок.
Однако у быстроходных ветряков есть один неприятный недостаток —
малый момент вращения во время начала их движения. Поэтому в тех
случаях, когда нагрузка почти постоянна и не зависит от скорости враще-
ния, выгоднее делать тихоходные ветряки с большим числом широких
лопастей. Иначе они будут плохо «брать с места», у них будет малой
«приемистость».
На самолете пользоваться ветряками с большим £ невыгодно, так как
у них мал к. п. д. £, а на самолете энергия получается не бесплатно,
а от мотора.
Опытная поверка вихревой теории ветряных двигателей показала, что
хотя она и дает в общем очень хорошее приближение к действительности,
все же для более точных расчетов приходится вводить в теорию различ-
ные небольшие поправки.
На этом специальном вопросе здесь останавливаться не будем.
§ 4. ТЕОРИЯ РЕШЕТОК
При расчете любого винта приходится вычислять циркуляцию скорости
вокруг сечений лопасти, расположенных на различных радиусах. Для этого
нужно знать величину скорости набегающего на данное сечение потока
воздуха и угол 3> образуемый ею с плоскостью вращения. Сразу же воз-
никает вопрос, что принимать за скорость вращения? Воздух перед обычным
винтом не вращается, а непосредственно за ним он вращается со скоростью
и2. Осевая скорость V, может считаться при узких лопастях одинаковой как
непосредственно перед винтом, так и за ним.
Мы уже вывели в § 7 главы 1 теорему о том, что скорость вращения
струи в плоскости вихревого донышка (сечение 1) равна и} Однако
во многих случаях (например у винтов-спарок, винтов-тандем, в спрямляю-
щем поток аппарате) воздух вращается непосредствевно перед винтом
с окружной скоростью и', а за винтом — со скоростью и". Неясно, что
принимать в таких случаях за скорость вращения струи при расчете про-
филя винта.
Как показал проф. Н. Е. Жуковский, здесь следует пользоваться раз-
работанной им и проф. С. А. Чаплыгиным теорией бесконечных решеток.
Решетка состоит из бесконечного ряда крыльев, простирающихся н вправо,
и влево (фиг. 46). Работа решетки аналогична работе сечений винта; каж-
дому сечению предшествуют и за каждым сечением следуют другие сече-
fHHfl и, в силу круглости струи винта, мы можем двигаться и вперед, и
назад, делая сколько угодно оборотов и встречая все время как бы новые
сечения винта.
Теория решеток, разработанная как строгим методом, так и элементар-
ным, показала, что в качестве скорости потока, набегающего на сечение,
следует брать геометрическую (векторную) полусумму скоростей потока
до решетки н за нею. Так, если перед решеткой, в сечении вектор
скорости относительного потока был равен W', а за решеткой, в сечении Г
Фиг. 46
— W", то вектор скорости Wx набегающего потока получится по фор-
муле
_ W' + W"
- 2
(139)
Эту формулу мы применим для расчета винтов-тандем и контрпропелле-
ров. В этих случаях осевая составляющая скорости обычно легко нахо-
дится из общих соображений, на основе условия неразрывности струи.
Окружная же составляющая будет равна: перед винтом г<о — и', а за
винтом г(о — и". Вычисляя полусумму, для окружной скорости получим:
= ,(140)
Следовательно, при расчете скорости вращения нужно брать среднюю
арифметическую скоростей вращения струи до н после винта.
Мы сейчас приступим к выводу этой формулы, причем будем исходить
не из теории решеток, а из общих теорем механики.
Пусть у нас имеется некоторый винт, находящийся в сложных условиях
работы. Выделим радиусами г и г — dr кольцевой элемент струи, изобра-
женный пунктиром иа фиг. 47. Проведем два перпендикулярных к оси
винта сечения: Г — непосредственно перед лопастями н Г — непосред-
ственно за лопастями. Будем считать осевую скорость потока в силу
неразрывности течения, одинаковой в обоих сечениях. Скорость будет
вообще различной в различных точках окружности радиуса г. Однако если
будем считать число лопастей стремящимся к бесконечности, то можно
принять, что скорость VL будет постоянной по всей окружности. Такое же
допущение можно сделать и относительно давлений р' и р” перед винтом
и за ним.
Сделав такие допущения, пишем уравнение Бернулли для сечений Г и
не забывая прибавить энергию, полученную кольцевой струйкой от
винта.
Рассуждая совершенно так же, как при выводе формулы (10), можем
написать, что момент, действующий на выделенный элемент вннта, равен
изменению в струйке ее момента количества движения за секунду, т. е.
dM = dm (и" — и') г.
Мощность, затраченная на вращение элемента, равна
dT = со dM = {и" — и') гы dm.
Отсюда отрицательные потери винта £, отнесен-
ные к единице массы, будут
га- (|41)
Уравнение Бернулли напишется теперь в таком
виде:
Фиг 47 2
. „ . и"“
— (U — U ) По ----.
Здесь «штрих» отмечает сечение, лежащее перед винтом, а «двойной
штрих» — за виитом. Отсюда
= р («" — и') гы-------(и" — и') (и" + и')
или
Тяга всего кольца, имеющего площадь 2лг4г, будет равна
dP = (//' — р') 2лг dr = р (и"2лг — г/'2лг) (гсо — и dr. .
Выражения м"2лг н и’2лг —• не что иное, как циркуляции скорости по кру-
говым контурам за виитом и перед ним. Обозначим их через кГ' и kF".
Теперь выражение для элементарной тяги напишется в виде:
dP = р (feT" — fef') (гю — dr. (142)
Окружное усилие найдем по приросту количества движения в струйке,
т. е. по формуле:
dQ = dm (и" — и') = р 2лг drVi (и" — и') = р(и"2лг — и'2лг) V^dr.
Замечая, что и"2лг = kF" и и'2лг — кГ\ получим:
dQ = P(kr — dr.
(143)
Результирующая аэродинамических сил, действующих на один элемент
лопасти, определится по формуле:
dRr-^V(dP)2+W -
= 4- У Р2 (£Г" — *Г')2 [(га--у-"' У + Vi] dr,
или
dR, = р (Г" —- Г') J//'(ra-и" + и' у + К dr. (144)
Последняя формула является обобщением теории Жуковского о подъ-
емной силе для случая закрученной перед винтом струи. Действительно,
разность циркуляций Г" — Г', очевидно, равна циркуляции, добавленной
данным сечением лопасти. Обозначим ее через Гсеч = Г"— Г'. Тогда выра-
жение под радикалом будет скоростью набегающего в сечении 1 потока
на элемент лопасти, т. е.
W. = jZ(ra - у + V?
(145)
формула (144) может быть написана в обычном виде
dR} = рГссч^7! dr.
(Кб)
Угол р, образуемый скоростью с плоскостью вращения (фиг. 48),
может быть найден из формулы (145). Видно, что скорость получается
путем геометрического сложения осевой скорости с окружной ско-
ростью, равной
где Г(о — скорость вращения винта, а скорость и 11---------средняя ско-
рость вращения струи. Отсюда
—fe- • <147)
ПО —----П---
Легко показать, что сила dRt будет перпендикулярна к скорости
Действительно, иайдем угол у, образуемый силой dR с осью винта. Для
этого вычислим
. dQ
~dP
Пользуясь формулами (142) и (143), получим:
tgr= Л
ё ‘ dP
?{kr -kV) Vt dr
,fcr" ЬГ'\ ( U" + \ A U" + u'
P («I —£Г)(г<о—---------J dr гш —-----2----
т. е. у = 3. Следовательно, в вихревой теории сила dRx, в которую мы
сейчас не вводили потерь на профильное сопротивление, должна быть
перпендикулярной к скорости
Мы имеем полное право пользоваться и в нашем случае теоремой Жу-
ковского о подъемной силе крыла, если будем исходить из скорости Ц7Ь
в которую введена скорость вращения струи, равная средней скорости вра-
и" + и'
щен ия —.
Сила dRi, которую мы сейчас нашли, совпадает с подъемной силой
крыла dYx. Другими словами, лобовое сопротивление лопасти на струе винта
Фиг 48
в вихревой теории ие отражается. На самом деле, сила dRlf вследствие
профильного сопротивления несколько отклонится назад от перпендикуляра
к направлению скорости Профильное сопротивление (обозначим его
через dXJ можно вычислить по обратному качеству р. =• —~ ло формуле
dXY - ndYr
Величина ц для винтовых сечений должна браться по крылу бесконеч-
ного удлинения; обычно она очень мала. У хороших профилей эта величина
имеет порядок 0,02—0,015; тогда угол отклонения силы dRr от нормали
к скорости не превосходит 1—3/4°. Такое отклонение очень мало
скажется на потоке вннта.
Исходя из этих соображений, Н. Е. Жуковский предложил считать,
что Профильное сопротивление у обычных виитов ие влияет заметно иа
струю виита; это значительно упростило все формулы вихревой теории.
При вычислении же сил. действующих на винт, эту силу учитывают (см.
§ 1 главы 2), благодаря чему все окончательные формулы получают до-
статочную для расчетов точность.
Этот же прием следует применить и для рассматриваемых в § 5 и 6
главы 4 более сложных случаев. Все отличие новых формул от прежних
сводится лишь к тому, что в них входит средняя скорость вращения струи,
£Z"+ U'
равная —~ .
В случае простого вннта вращения перед ним ие будет и, следовательно,
= 0. Тогда мы получим скорость в плоскости винта, равную -рт.е.
в точности ту, какую мы н ввели в расчет в § 7 главы 1.
Искривление сечений широких лопастей. Все приведенные рассуждения
относились к узким лопастям. На практике нередко лопасти контрпропелле-
ров бывают довольно широкими, и при их проектирования приходится
вводить в изложенную теорию поправки, простейшей из которых является
искусственное искривление лопастей.
Пусть относительная скорость перед лопастями равна W', а за ними
(фиг. 48); складывая по-предыдущему эти скорости геометрически и беря
их полусумму, получим скорость 1Г1т образующую с плоскостью вращения
угол Р- Найдя угол атаки а по уравнению связи, мы должны поставить
хорДУ нашего сечения под углом ср = р -j- а к плоскости вращения 1.
Однако это было бы вполне справедливым лишь для поступательного
потока, имеющего скорость Тогда мы могли бы сравнивать работу
нашего профиля с обычной продувкой в трубе и брать величину су, соот-
ветствующую углу а. У нас же струя будет изогнута. Если провести из
точки Е линию, параллельную W7',
до пересечения с плоскостью / в л____________ / __________
точке G и из точки G провести -
линию, параллельную W’", то струйка жУ Жг/
воздуха, идущая между лопастями,' —
будет иметь форму ЕСгЕ, т. е. она Ж/v
будет искривленной. Эта кривизна Ж Ш/
обычно мала и можно принять, что „ у й/
струйка будет иметь форму окружно- / /
сти или параболы.
В последнем случае очень легко г
построить эту параболу чю ‘хорошо
известному графическому правилу: нужно разбить отрезки EG и FG на
равное число частей и соединить полученные точки деления прямыми ли-
ниями так, как указано у нас на фиг. 48, справа. Огибающая этих линий
и будет параболой.
Далее исходят из гипотезы, что если первоначальное сечение изогнуть
так, как изогнута найденная нами струйка, то аэродинамические свойства
профиля будут такими же, как первоначально, прн поступательном потоке.
Само искривление легко сделать графически, используя хорду сечения (или
среднюю линию профиля), которая теперь будет не прямолинейной,
а примет криволинейную форму струйки; , толщины профиля при этом со-
храняются неизменными (фиг. 49). Короче говоря, к стрелке кривизны
профиля нужно прибавить стрелку f изгиба струйки.
Примечание Изложенная здесь упрощенная теория решегок справедлива при
очень большой густоте решетки, т. е. при большом отношении b/t, где b— ширина
лопастей решетки и t—шаг решетки при бесконечно тонких сечениях лопастей.
При малой густоте скорость между лопат-
ками будет переменной и получится эффект
«числа лопастей». Это влияние обычно мало и
им можно пренебрегать. Этого нельзя сказать
о влиянии толщины лопаток При большой
густоте уменьшается за счет толщины лопаток
сечение струи, текущей между ними, и скорость
между лопатками несколько повышается. Точ-
ные методы }чета этого еще не разработаны
Еще сложнее обстоит дело с учетом сжи-
маемости воздуха при больших изменениях
давления воздуха перед и за решеткой. Слож-
фиг JQ ность и неразработанность имеющихся теорий
заставляет конструктора прибегать к упрощен-
ным приемам. Чаще всего расчет ведут по
давлению и по средней плотности воздуха, текущего между лопатками
лопаток учитывают, просто увеличивая скорость воздуха, набегающего на
в отношении -----где — толщина лопасти, взятая по ган1 енциальномх
среднему
Толщину
лопатки,
направлению. Делитель 2 введен для получения средней скорости.
Несовершенство этих приемов заставило заводы, изготовляющие лопаточные ма-
шины, рассчитанные на большие перепады давления, прибегнуть к опытному исследо-
ванию таких решеток Опыты очень просты по идее (фиг. 50). Струя воздуха или пара
через направляющий аппарат А натекает на решетку В, укрепленную на весах С,
измеряющих две компоненты — тягу по оси Р и тангенциальное усилие Q Однако
Н эти опыты не дали еще хороших результатов.
В конце концов, большинство конструкторов ведет расчет по элементарной теории
и вносит в окончательный результат поправки, взятые прямо из опытов с построен
ними ранее машинами.
§ 5. КОНТРПРОПЕЛЛЕР
Как мы знаем, струя воздуха, отходящая от обычного пропеллера,
вращается, что вызывает у винта потери, так как для получения тяги
это вращение, уносящее кинетическую энергию, совершенно не нужно.
Возникает же оно потому, что обычиый пропеллер передает иа жид-
кость свой момент вращения; тогда секундное приращение момента
количества движения ,в струе должно равняться этому моменту. Унич-
тожить этот момент можно лишь приложив
'Ч. к струе обратный момент.
д*--- ш Достигнуть этого можно двумя способа-
/ \ ми: применением двух соосных винтов, вра-
I I шающихся в противоположные стороны (та-
1 / \КГ/ кие вИИтЬ1 рассмотрим, в § 6 главы 4) или
11 устроив перед винтом или за ним так назы-
—XgMl— ваемый контрпропеллер с неподвижными ло-
JT пастями (фиг. 51).
\ В этом параграфе рассмотрим два типа
4-S контрпропеллеров: установленный за работа-
\ I . ющим винтом и перед ним.
——"—— Укажем смысл контрпропеллера у винтов
разного назначения.
Для пропеллеров такое устройство полез-
фиг- 51 но с двух точек зрения. Во-первых, улучшает-
ся к.п.д. винта, так как контрпропеллер, как
увидим далее, дает некоторую добавочную тягу. Затем контрпропеллер
уничтожает реактивный момент, действующий на самолет. Этот момент
у современных моторов очень велик; ои стремится повалить самолет
на крыло, т. е. повернуть его вокруг продольной оси в сторону, проти-
воположную вращению винта. Однако у обычного самолета вращение
струи все же невелико, =0,99 и выигрыш в к. п, д, обычно получается
небольшой. Кроме того, на самолетах нормальной схемы крыло пере-
секает струю винта и фактически само является спрямляющим аппа
ратом. Опыты показывают, что крыло принимает на себя до 2/з реактив-
ного момента винта. Правда, при этом весьма возрастает лобовое
сопротивление крыла, особенно при разбеге самолета
Вследствие всего указанного на самолетах нормальной схемы
контрпропеллеры не устанавливают. У самолетов с толкающим винтом
при хстановие очень мощных моторов придется, по-видимому, делать
обязательно или контрпропеллер, или винт-спарку. На буксирных паро-
ходах контрпропеллеры оказались полезными и их там уже широко при-
меняют. На самолетах до сих пор делались лишь отдельные опыты.
Большую пользу приносят контрпропеллеры или спрямляющие ло-
патки у вентиляторов. Струя вентилятора иногда бывает очень сильно
закручена, и ее спрямление сильно повышает к.п.д. установки. Кроме
того, иногда (например, в аэродинамических трубах) вращение струи
недопустимо из-за условий точности экспериментов.
У некоторых типов одновинтовых геликоптеров спрямляющий ап-
парат является основным элементом их конструкции, так как без него
вращалась бы гондола аппарата, а винт был бы почти непод-
вижным. Поэтому в таких системах н^жно к гондоле приложить момент
обратного знака, равный по величине реактивному моменту винта,
тогда гондола будет неподвижной, а
Контрпропеллер, стоящий за йин-
том. Рассмотрим теорию коятрпропел-
лера, расположенного за винтом.
Пусть винт будет типа НЕЖ- Тогда
в центре винта сбежит вихревой шнур
с циркуляцией kT. Если сразу же
за этим винтом поставить спрямляю-
щий поток, неподвижный контрпропел-.
лер, то для уничтожения вращения
в струе винта нужно уничтожить этот
центральный вихрь. Сделать это мож-
но, лишь разбив этот вихрь по лопас-
Фиг. 52
будет вращаться винт (фиг. 52).
тям контрпропеллера на присоединенные вихри, как это изображено схе-
матически на верхней части фиг. 53. Тогда, если у контрпропеллера будет
kK лопастей, а циркуляция вокруг каждой из них будет равна Гл, то усло-
вие спрямления потока выразится формулой:
йГ-= feKrK. (148)
Если сложить вихревые схемы пропеллера и контрпропеллера, то полу-
чим эквивалентную вихревую схему, изображенную на фиг. 53.
Введем в теорию контрпропеллера отвлеченные обозначения, аналогич-
ные принятым в теории винта:
1'к = Гк — -; dMK =-----------------—— ; г = — и т. д.
2лрЛ4о)2 2лрЯ&<о* R
Тогда условие незакрученности струи (148) напишется в таком виде:
№ — R2a = /гкГ„ —
*
или
Д-.М -к- -1\Д
г - Гк. (149)
12 Б. Н Юрьев, т. I
щеиия перед винтом равна нулю, в
Фиг 54
Рассмотрим скорости, получающиеся в плоскости контрпропеллера.
Пусть В— лопасть винта, Вк — лопасть контрпропеллера (фиг. 54). Будем
считать их расположенными в очень близких плоскостях. Тогда осевая
скорость ]/г = V’o -I* будет у них практически одинаковой. Скорость вра-
плоскости пропеллера она равна щ
ьг
=------и сразу за пропеллером, т. е.
4лг
перед коитрпропеллером, она равна 2и{.
За коитрпропеллером скорость враще-
ния равна нулю. На фиг. 54, справа,
изображен закон изменения скорости .
Следовательно, в плоскости коитрпро-
пеллера мы, согласно §4 главы 4, дол-
+ и'
ЖНЫ принять скорость «к — —-— ut.
Из скоростного многоугольника видно,
что скорость воздуха, набегающего на
лопасть, коитрпропеллера, будет рав-
на вектору W- к, она образует с плоско-
стью вращения винта угол Зк (берем угол меньший 90°).
Из чертежа видно, что
V (Г„ + О,)2 + / Й -^ui, 1 150)
tg3K (151)
U1 ul
и, кроме того,
Vl ft «I
sin Зк —— и cos iK = —- .
Вычислим силы, действующие на элемент лопасти коитрпропеллера. тем
же приемом, как вычислялись силы, действующие на винт в § 1 главы 2
Находим силы
dY г — рГк U"Kdr и dXt [idY^ = црГк117к dr.
По этим силам находим силу тяги dPK1 и окружное усилие dQK„ дей-
ствующие на одну лопасть коитрпропеллера. Положительные направления
этих сил считаем совпадающими с положительными направлениями анало-
гичных сил у пропеллера:
dPKl ’ к dr cos Зк — црГкН’ к dr sin Зк-
Подставляя сюда найденные значения sin Зк и cos Зк, получим:
dPK1—рГк«1^г— цр ГКУ1 dr - о[\ (ит — ^V,)dr.
Совершенно аналогично находим
dQKl =- — рГк1^к dr sin Зк — црГД' к dr cos Зк =
- — рГкУг dr — црГк«! dr — — рГк (Vj -J- gu,) dr
и для элементарного момеита
dMKt - dQKl г = — рГк (Vj 4- nut) г dr.
Относя эти силы и момент к кольцевому элементу струи, где работают
Лк лопастей, получим:
dPK -= рЛкГк (и, — gV,) dr,
dQK = — рКГк (V, + .ни,) dr,
dMK - — р^кГк (V] -- $iUi)rdr.
(152)
Переходя к отвлеченным обозначениям, приводим эти формулы к виду
<//', =- 2Г (и, — pV,)dr = 2Г —l»Vi) dr,
dM,, — — 2Г (V; + puj) г dr = — 2Г ( Vt 4- p -T- "j r dr.
(153)
Интегрируя эти выражения по всей рабочей части коитрпропеллера, т. е.
в пределах от г _ % до г =- L и считая Г — const, получим:
Р„ = рй'рТ- 2Г |^Г1пу — pV,(l -б)р (154)
К- -2rj(V!-- p-C|f А7, pT(l — g)J . (155)
Из формулы (154) видно, что контриропеллер дает положительную тягу
в тех Случаях, когда
Г In ^>pV,(l-y.
(156)
Эю условие практически всегда имеет место, и, следовательно, уста-
новка контрпропеллера всегда увеличивает тягу, правда, иногда иа очень
небольшую величину.
Не внесет ли установка коитрпропеллера заметных изменении в осевую
скорость винта Vj? Для этого вычислим величину осевой скорости потока
тем же приемом, как это мы сделали в § 6 главы 1. Дли этого выделим
кольцевую струйку и возьмем два сечеиия: О — далеко перед винтом и 2—
в сжатом сеченни (в горле) струи. Давление в горле в нашем случае
всюду равно атмосферному, так как у Hat отсутствует вращение струн
и нет центробежных сил. Работа, сообщенная струе виитом, по-прежнему
будет равна <ог«2, где и2 — скорость непосредственно за винтом и перед
контрпропеллером, т. е. в зазоре между ними.
Уравнение Бернулли для этого случая напишется в таком виде:
и2 „ Vs
~+^ = ~ + — — «>ги2.
2 р 2 р
Замечая, что V2 = Vo И- у2 и «2 = , получим:
л г
— юг----.
2лг
Переходя к отвлеченным обозначениям и считая винт слабо нагружен-
ным, т. е. принимая v2 = 2ох и «2 = 2«i, находим окончательно:
(Vo + 01) = Г или и, =---у + + (157)
т. е. получаем уже известное нам по § 3 главы 2 уравнение (61); там оно
было приближенным по отношению к более точному уравнению (60), а те-
перь оно стало точным. Мы уже указывали, что как уравнение (60), так н
уравнение (61) дают практически совпадающие результаты. Следовательно,
установка спрямляющего аппарата отражается очень слабо на осевой ско-
рости винта Vj. Здесь мы не учитываем влияние на скорость сил лобо-
вого сопротивления (ввиду их малости), как это и принято делать в вихре-
вой теории.
Компоновка и вычерчивание лопастей контрпропеллера не представляют
затруднений. Зная угол Зк на всех радиусах г и задавшись углом атаки
ак, получаем по фиг. 54 наклон сечения лопасти контрпропеллера срк на
любом радиусе
<рк ~ Зк “ &к.
Ширина лопасти контрпропеллера найдется по уравнению связи:
Гк = ~ ^к^кбк,
или, в безразмерном написании,
- - -----------------------------------------
1 = 1 к — " СукЬк№к. (^56)
«Л
По этой формуле, помня, что Г = Гк, можно найти ширину лопасти
контрпропеллера Ьк на любом радиусе г. По этим, данным, т. е. по фк
и Ьк, и компонуется контрпропеллер.
Сравнивая полученное выражение для Гк (158) с ранее найденным для
пропеллера (92), найдем что
Скорость пропеллера значительно больше скорости WK у контрпро-
пеллера. Величина сук может быть взята в 2—3 раза большей, чем у про-
пеллера. Следовательно, в большинстве случаев суммарная ширина лопа*
стей контрпропеллера будет больше суммарной ширины лопастей kb
у вннта.
Коитрпропеллер, стоящий перед винтом. Нетрудно вывести формулы
для расчета контрпропеллера, стоящего перед винтом. Скоростные много-
угольники для этого случая приведены на фнг. 55. Контрпропеллер должен
закрутить воздух перед пропеллером так, чтобы после пропеллера он шел
ие вращаясь.
Изменение скорости в разных плоскостях изображено на фиг. 55, справа.
Скорость ик, с какой контрпропелер с постоянной циркуляцией Гк бу-
§ 5. Контрпропеллер
181
дет закручивать воздух в своей плоскости, найдется по обычной винтовой
формуле:
За контрпропеллером эта скорость удвоится.
Из скоростного треугольника контрпропеллера находим:
Vl ик
sin X = —i и cos Зк •- —- •
Подъемная сила и сопротивление про-
филя определяются по формулам:
dYK = РГКГК dr и dQa = и dYK =
= pprKVtX dr.
Отсюда элементарная тяга * 'при k лопа-
стях будет равна
(/Рк k (— рГк1Ук dr cos [Зк — Иргк№к dr sin Зк) =
= — feprK (zzK]-j- \iVJdr. (160)
Совеошенно аналогично
dQK = k(— рГк1Ук dr sin -г ррГк1Ук dr cos Зк) =
= — feprK(Vi— iLUK)dr (161)
и момент
zLWK — fePrK(V, — [iuK)rdr. (162)
Интегрируя эти выражения, считая Гк — const и VJ = const, получим:
Рк = ^рГк^|-----— -у- цУ]4) dr feprK Г— 1пг + 1 , (163)
.* \ 4лг / L 4л
Мс = — &рГк С Z у г — ц —Xr\ dr = —/?р]’к Г у _С------ц^-JL Я (164)
J 4лг ) L 2 4л Jr
илн, переходя к отвлеченным обозначениям, находим:
Рк = 2ГК [-Гк In s + рК (1 - £)},
Як = - 2Г„ - ИГК (1 - £) ] .
Перейдем теперь к винту. До винта струя будет вращаться со скоро-
стью 2«к. за ним при правильном устройстве коитрпропеллера и = 0. По
теореме о средней скорости, рассмотренной в § 4 главы 4, заключаем, что
82
Глава 4. Особые случаи работы винтов
у нашего винта скорость вращения будет равна ик, но направлена в про-
тивоположную обычному винту сторону. Следовательно, обычные винтовые
формулы (34) и (36) примут теперь вид:
dP = fepr (Ui — цУ]) dr --- fepr I rto 4- —-цУ, I dr,
\ 4ЛГ I
dT — fepr (I/j 4- iiU^ra dr /грГ ( 14 pro + p. r(i) dr,
\ 4лг I
или, в безразмерном написании,
dP = 2Г (U, - цК) dr - 2Г ( г 4- I--цУх) dr,
dT = 2Г (Vi + pit7i) r dr = 2Г / 14 + 4- ц —'j r dr.
После интегрирования получим:
Р = Г [1 — £3— 2Г In £ — 2ц14 (1 -£)]; (165)
Т = Г р 1 - V, + 4 ц (1 - £’) -I- 2цГ( 1 - g) ] . (166)
Коэффициент подсчитывать по полезного формуле: действия винта с контрпропеллером нужно
П = Р — р — т Р + Рк = KV0. т (167)
Примечание. Мы выводили условие незакрученности струи, исходя из потока,
текущего около винта, и пришли к выводу, что в этом случае &КГК = &Г. Однако ес-
ли мы подсчитаем по формулам (70) и (155) момент у винта М = Т и момент у контр-
пропеллера Мк, то полного равенства их не получим. Если же исходить из условия
Мк = М, то условие &КГК = &Г не будет соблюдено, но тогда за винтом и контрпро-
пеллером получится центральный вихрь с циркуляцией kV — &КГК, т. е. струя будет
вращаться. Происходит это от неувязки в вихревой теории. Лобовые сопротивления в
теории Жуковского на струе не отражаются.
Мы исходили из физической картины спрямления и пользовались условием ЛКГ —
~ kV Это дало и более простые формулы и, кроме того, ик = и1.
Неточность этой теории в несколько процентов не опасна, так как у всех винтов
на практике режимы работы несколько изменяются и спрямляющий аппарат не может
дать во всех случаях полного спрямления. У геликоптера (фиг. 52) требуется полное
равенство моментов и лопасти контрпропеллера устраивают поворотными вдоль их
оси. Правильный наклон лопастей подбирают во время полета.
Заметим еще, что на самом деле струя после винта сжимается (особенно у гели-
коптера), и обычно трудно сделать контрпропеллер с лопастями малой ширины. Сле-
довательно, допущение, сделанное при выводе основных формул, о том. что винт и
контрпропеллер очень близки и осевая скорость 14 у них одинакова, на самом деле
будет соблюдаться лишь приближенно Поэтому контрпропеллер, помещенный за вин-
том, делают меньшего диаметра, а спереди большего, чем диаметр самого винта.
Теория эта дает хороший результат для спрямляющих аппаратов у вентиляторов,
так как там отсутствует сжатие струи. Если контрпропеллер имеет много лопастей,
то в расчет трубы, в которой работает вентилятор, вводят гидравлические потери,
вызванные трением воздуха о лопатки
S> t) соосные винты
§ 6. СООСНЫЕ ВИНТЫ
Под соосными винтами будем понимать пару винтов, оси вращения
которых совпадают. Будем’различать винты-спарки (фиг. 56), у которых
расстояние между втулками очень мало, и вииты-тандем, у которых это
расстояние велико (фиг. 57).
^Такие винты приходится в настоящее время ставить иа высотные само-
леты при очеиь большой мощности мотора. У одиночного винта получилась
бы слишком большая ширина и большое число лопастей и, кроме того,
получился бы весьма большой реактивный момент. У винтов-спарок и вин-
тов-таидем, как правило, заставляют вращаться винты в противоположные
стороны. Этим достигается спрямление отброшеииой струи и повышение
к. п. д. всей установки.
Аэродинамический расчет таких винтов легко сделать при помощи вих-
ревой теории. Для этого нужно рассмотреть сбегающие с винта вихри и
вычислить скорости, получающиеся у таких виитов. Будем отмечать вели-
чины, относящиеся к переднему винту, индексом «п» и к заднему—индексом «з».
Рассмотрим сперва спарку. Можно принять, что осевая скорость
у обоих виитов будет одинаковой. Скорость вращения и циркуляция
у центрального вихревого шнура равна разности циркуляции осевых шиуров,
т. е. /гпГп — /г3Г3 и будет очень малой. Поэтому вычислить общую осевую
скорость можно, исходя из суммарной циркуляции скорости обоих вин-
тов, равной /?ПГП Ч- &3Г3. и воспользоваться формулой
+ Гп + Г3.
(168)
Эту формулу легко получить непосредственно из уравнения Бернулли
для кольцевой струйки (см. фиг. 47). Берем одно сечение далеко впереди перед
спаркой и другое — за спаркой, там, где получилось полное сжатие струи.
При написании уравнения Бернулли нужно учесть работу, полученную
струйкой от винтов. Скорость вращения в плоскости переднего виита равна
нп. а за ним 2«ц. Аналогично имеем щ и 2ч3. Пользуясь рассуждениями,
приведенными в § 5 главы 1, заключаем, что энергия, полученная от двух
винтов и отнесенная к единице массы, будет равна г<»2«п -г гы 2п3. В обыч-
ной снарке вращения в горловом сечеиии практически нет, и нам ие при-
дется учитывать центробежные силы и скорости вращения. Следовательно,
уравиение Бериулли примет в этом случае вид:
Д-- Ро = + — 2гошл — 2г(о«3
2 р 2 р
или
(Vo ч- -у) = гш (и„ + и3).
Подставляя в найденное выражение значения скоростей, получим:
-у- ( V, + (6„Г„ 4- *3Г3). (170)
Вводим обычные безразмерные обозначения, а именно:
Г„ = Г„ ~ R2ui; Г3 = Г3 ~ R*a; и, = v,Ra и V„ = V„ Rm
яп "з
н получаем:
f (Го + ^ -Г„ + Г3. (171)
Считая систему слабо нагруженной, можем принять, что = 2ох. Получим
окончательно:
(Vo “Ь yi) ~ Гп 13. (172)
Отсюда находим:
г; = -^- + |/4+г"+Тз (173)
и
7. =7. + ^ =4’ + )/ -J + ^+n. (174)
Для обычных соотношений можно в среднем принять, что при равных
мощностях обоих моторов
Гз^0,97Гп. (175)
Передний винт можно рассчитать по обычным формулам, но беря V\,
как описано. Будем считать, что наш винт имеет постоянную циркуляцию
(НЕЖ). Тогда величину циркуляции у переднего винта можно найти опи-
санным в § 1 главы 3 приемом, т. е. по формуле (70).
Но скорость нужно вычислять теперь по формуле (174), т. е. по
циркуляции Гп + Г3 ~ 1,97 Гя. Само нахождение циркуляции следует вести
графически, как это было изложено в § 1 главы 3.
Найдя _циркуляцию у переднего виита Гп и взяв в качестве первого при-
ближения Г3 = 0,97 Гп , мы сможем вычислить мощность заднего винта по
формуле, аналогичной (70), но подставив в иее скорость вращения, вычис-
§ б. Соосные винты
185
лениую по теории решеток. Так как у спарки за задним винтом практи-
чески вращение равно нулю (w31 = 0), то можно принять, что и3 = — и„.
Задний винт в спарке вращается навстречу направлению вращения струи
(фиг. 58), следовательно, относительная скорость элемента будет равна
или, в безразмерных величинах
Вводя это значение в основные
формулы виита и произведя интег-
рирование, приняв Г3 = const, по-
лучим:
Рз = 2Г, ^г +Т- nl/J dr = Г3(1 -s2 + 2Г„1п-|-- 2цУ,(1
Т3 = 2Г3 (7, + -U) /dr - Г,| (1 - 7, , i II (i-S3) ;
5 r
+ 2цГ„(1 — s)|.
При полном спрямлении потока Гп — Г3.
Если мощность заднего винта Т3 окажется близкой к мощности перед-
него Гп, то расчет можно считать законченным. Если разница велика, то
придется, уточнив величину циркуляций Г3 и Гп , снова повторить расчет.
При этом небольшая разность мощностей (несколько процентов) является
несущественной, так как современные спарки имеют поворотные лопасти и
автоматическое регулирование. Лопасти виита во время работы сами вста-
нут под нужным углом наклона.
Имея циркуляции обоих винтов, находим их тягу:
рп ... Гп [1 - ¥ -г гйп £ - (1 - б)], (17b)
Р3 = г3п -5)]. (177}
Полная тяга спарки
Р = Рп г Р3-
(178)
Отсюда к. п. д. всей спарки в целом будет равен
(179)
Далее остается компоновка винтя Из фиг. 58 получаем:
Г„^аГ, (при вычислении индуктивных скоростей)
(180)
Далее, по уравнению связи находят ширину лопасш и поступают, как
было описано в § 2 главы 3.
Вииты-таидем. В случае виитов-тандем задний винт удален от перед-
него так далеко (обычно на длину двух моторов), что влиянием заднего
винта на передний можно пренебречь. Тог-
да расчет переднего винта можно вести
обычным методом по § 1 и 2 главы 3
Для заднего вннта придется учесть,
что осевая скорость подходящего возду-
ха увеличится н будет равиа не Vj. а
У„ У04-2у|1. Кроме того, струя будет
вращаться со скоростью wni -= 2«н перед
задним винтом. Следовательно, за осе-
вую скорость набегающего на задний винт
воздуха нужно считать скорость |/2. Осе-
вая скорость в плоскости второго винта
будет равняться
Ки = Уо + + v3. (181)
Скорость вращения струи непосред-
ственно перед плоскостью второго
виита будет равна 2wn, за плоскостью практически вращения не будет, так
как Гп ~ Г3 и, следовательно, за скорость в плоскости винта следует принять
скорость и3 ~ н = wn. Эта скорость будет направлена навстречу вра-
щения заднего винта. Следовательно,
,, - - - , !'п
С , = г ип — г ——- .
г
Скоростной многоугольник будет в этом случае иметь вид, показанный
на фиг. 59.
Передний винт можно рассчитывать как одиночный, изолированный винт.
У заднего же вннта рабочие формулы примут вид:
р3 -v-2rn 1п&-2цУ31 (1 —5)1;
§ б Соосные винты
187
'Л = Г3 [(! - s2) Vir - 4 И (1 - е3) - 2М.Щ1 - ?)]
В заключение заметим, что расчет соосных винтов по вихревой теории
дает лишь исходные их формы. Работа заднего вннта происходит в значи-
тельно более сложных условиях, чем это учитывает вихревая теория. Преж-
де всего поток за передним винтом получается пульсирующий; кроме того,
струя сначала несколько сжимается, затем начинает расширяться от сил
вязкости и может случиться, что концы лопастей заднего винта выйдут из
струи переднего. Для устранения последнего явления нередко в винтах-
таидем делают задний винт с несколько меньшим диаметром.
Окончательные характеристики таких винтов следует получать экспери-
ментальным путем, изучая их в аэродинамических трубах.
Геликоптерные соосные винты. Особо сложные явления проис-
ходят при работе соосных геликоптерных винтов. Струя воздуха
имеет в этим случае форму, изображенную на фиг. 60. Передний винт
создает обычную воздушную струю в виде воронки. Задний винт рабо-
тает частично в струе переднего,
как бы на режиме пропеллера
прн осевой скорости Рг или 2fi
в зависимости от расстояния
между винтами; кроме того, он
подсасывает концами своих ло-
пастей добавочный воздух. Полу-
чается внешняя струя (фиг. 60).
Концы лопастей заднего (ниж-
него) винта работают на гели-
коптерном режиме.
Расчет в этом случае удобнее
вести, не переходя к безразмер-
ным величинам. На нижнем вин-
те нужно наметить, хотя бы на глаз, какая его часть будет работать как
пропеллер и какая как геликоптер. После этого нетрудно получить рас-
четные формулы. Мы здесь этот вопрос разбирать подробно не будем.
Вихревая теория для такой сложной работы виитов может дать лишь
приближенный результат.
Приложение I
ХАРАКТЕРИСТИКИ ВИНТОВЫХ ПРОФИЛЕЙ
Для расчета винтов нужны характеристики винтовых профилей.
Опубликовано довольно мало материалов о таких профилях. До самого
последнего времени употребительными у нас являются профили вин-
товой серии ЦАГИ ВС-2. Приводим здесь нх характеристики в об-
работке профессоров Г. И. Кузьмина и Д. В. Халезова. В последнее
Фиг. 61
время всюду ведутся исследования по новым профилям, менее чувстви-
тельным к большим окружным скоростям. Профили ВС-2 в этом от-
ношении мало уступают таким улучшенным профилям.
На фнг. 61 дан чертеж типового профиля. Все профили различной
толшины получаются в этом семействе простым пропорциональным из-
менением ординат. В табл. 3 даны их ординаты (как обычно — в про-
центах от максимальной толщины профиля с).
Таблица 3
Ординаты профилей серии ВС-2
Расстояние от носика, в % хорды г 100 2,5 । 5 !0 20 30 40 60 70 80 90 95 Радих’сы носики К ХВОСТИК.!
Ордина- ты, в % макси- мальной толщи- ны у, 18,9 30,4 46,2 65,2 72,6 73,7 70,6 63,3 52,8 40,0 24,2 15,4 ги = 0,08(7
Ун 12,1 18,7 21,9 25,9 25,9 23,5 20,8 18,1 15,4 12,7 10,0 8,6 гх -0.О8С
При расчете профиля пользуются часто относительной толщиной с,
определяя ее из соотношения с = -г-.
о
С помощью величин Ь, с и с можно выразить все геометрические
характеристики сечения, которыми приходится пользоваться в расче-
тах. Все эти формулы построены по одному липу: числовой, постоян-
ный для всех профилей коэффициент множится на соответствующий
именованный множитель.
Таким образом получаются:
1. Площадь сечения профиля...................................S = О,7О5сЬ
2 Расстояние центра тяжести от хорды ........................Уо — 0,195с
3. Расстояние центра тяжести от носика.......................х0 = 0,448b
4. Момент инерции относительно оси, проходящей через центр тяже-
сти параллельно хорде.........................................7 = 0,0423^5
5. Момеит инерции относительно оси, проходящей через центр тяже-
сти перпендикулярно к хорде.................................../ = 0,0410cb-i
6. Центробежный момент инерции относительно осей х и у.......Ку = 0>00^39с2Ь2
7. Угол оси наименьшей жесткости с хордой:
is радианах .......................”. . ....................<р = О,О35с
в градусах................................................<р° — 2 с
8. Моменты инерции относительно осей эллипса инерции ё и гр
наименьший момент ........................................
наибольший момент . . '...............................
9. Модули сопротивления на изгиб относительно главной оси
инерции:
для верхних, сжатых волокон...............................
для нижних, растянутых волокон........................
10. Коэффициенты модуля сопротивления изгибу относительно
главной оси инерции:
b 2,34
для верхних, сжатых волокон ............................. А ~ —---= —------
с3Ь
-~0,0423с3Ь -
cb3
/„ •= 0,0410сЬ3 = 777-7
ч ’ 24,4
W = G,onic-b
W = 0.0930с2Ь
Аэродинамические характеристики профилей получены продувкой
моделей при малых числах Маха, порядка 0,1—0,2. После обработки
протоколов эти крылья были пересчитаны обычными способами на
бесконечный размах *.
На фиг. 62 изображена в большом масштабе диаграмма, описан-
ная в § 3 главы 3. Ею и следует пользоваться при расчете винтов и
их компоновке. Кривые для с = 0,07 и 0,08 даны пунктиром, так как
получены экстраполяцией опытных кривых.
Влияние больших окружных скоростей следует учитывать обычным
способом, рекомендуемым ЦАГИ, в котором винт сначала рассчиты-
вается на уменьшенную мощность, а затем его интегральные характе-
ристики исправляются на влияние числа Маха с помощью специаль-
ных графиков.
Более точным был бы способ исправления самих характеристик
профилей при расчете и компоновке винта. Однако при современном
состоянии аэродинамики мы не умеем рассчитывать профили при
* Б. Н. Юрьев. Экспериментальная аэродинамика, ч. II.
Фиг 62
числах Маха, близких к единице, которые наблюдаются \ сечений совр^
менных винтов
Фиг 63
У вентиляторов и ветряных двшателей нередко применяют .топасги,-
изготозлениые из листа железа Они обычно имеют параболическую
форму, н максимальная стрелка / расположена \ них на 'Д Ь, считая
от носика. На фиг. 63 дана пересчитанная на бесконечное удлинение
продувка такого профиля с относительной вогнутостью /76 = 0.1.
Приложение II
ПОДБОР циркуляции
С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКОЙ ДИАГРАММЫ
При подборе винтов на основе их испытаний часто пользуются логариф-
мической диаграммой. Подробное описание таких диаграмм дано в курсе
винтов.
Аналогичная диаграмма может быть построена и на основе вихревой тео-
рии. Если выбрать тип винта (мы остановились на винте НЕ/К). то для
каждой скорости полета Ио мы можем вычислить значения Р и Т. По этим
величинам мы находим:
А - л/;
-- 0,64507;
1 = 4-7 = 0,020547.
Пользуясь ими, мы можем нанести на логарифмическую диаграмму пар-
ные точки А и р, и тогда получим для какого-либо выбранного значения Г
кпивук*' линию. На ней можем сделать отметку величин тр Нанеся на диа.
грамму ряд таких кривых для разных Г, мы сможем, соединяя точки с оди
наковым значением гр получить кривые постоянных к. п. д. Все это изо-
бражено на прилагаемой диаграмме (фиг. 64).
Все отличне этой диаграммы от обычной заключается в том, что на ли-
нии Г const лежат разные по форме винты, так как форма винта в вих-
ревой теории определяется не только величиной Г, но и Го, которая в на-
шем случае будет различной, в различных местах кривой Г — const. В обыч-
ной же логарифмической диаграмме каждая кривая соответствовала неиз-
менному ио форме винту.
Пользоваться этой логарифмической диаграммой при подборе винта сле-
дует, руководствуясь общими правилами. По фиктивной мощности Мф, ско-
рости полета км/час, по числу оборотов п об/мин и намеченному диа-
метру винта получается графически циркуляция Г и к. п. д. гр По этим
данным можно найти тягу винта, и скомпоновать винт по заданным Г и.V'.
Этой диаграммой нельзя пользоваться для построения характеристики
винто-моторной группы, так как все кривые не соответствуют винту по-
стоянной формы, а представляют изменяющиеся от точки к точке винты
различных форм.
Можно построить аналогичную диаграмму для винтов, рассчитанных по
вихревой теории и по параметру cs — ~~ , т. е. по коэффицйену быстро-
го
ходности, что. однако, особых преимуществ не дает.
ь
Фиг 64 Теоретическая логарифмическая диаграмма винта типа НЕЖ для ц -- 0,02
•кая диаграмма винта типа НЕЖ для ц - 0,02 и | = 0,25 (бе? учета сжимаемости воздуха)
Приведенная диаграмма вычислена при р. = 0,02, Поэтому она дает
несколько завышенные значения к. п. д. На фиг. 65 приведены теоретиче-
ские значения полного к. п. д. винта НЕЖ для р = 0,02 и £ - 0,25 (без
учета числа Маха). На самом деле от 0,5 до I % мощности будет затрачено
на вращение втулки и в среднем около 5% на потери, связанные с волной
Маха, Кроме того, будет затрачено 2—3% на потери от взаимного влия-
ния винта и самолета. Поэтому при пользовании этой диаграммой нужно
соответственно уменьшать расчетную мощность.
13 Б Я Юрьев
О СОВРЕМЕННОМ ПОЛОЖЕНИИ
ТЕОРИИ ГРЕБНОГО ВИНТА
Разработкою теории гребного виита занималось множество инже
неров и ученых. Пи этому вопросу написано много научных работ. Та-
кое внимание к винту объясняется важной ролью его в общем балансе
энергии у приводимых им в движение аппаратов. Для оценки роли
винта достаточно вспомнить, что через него проходит вся энергия мо-
торов, доходящая у современных больших аэропланов до 2 тыс. л. с.,
а у морских трансатлантических судов — до 70 тыс. л. с. Несколько
выигранных процентов в отдаче пропеллера дают уже огромную
выгоду. Более или менее удовлетворительные теории были разработа-
ны за последние 10—15 лет.
В статье В. Маргулиса, помещенной в журнале «L'eronauuque»
(август 1920 г.) * и посвященной памяти Н. Е. Жуковского, сделан
обзор теорий, разработанных в России. Автор делает лестное для нас
признание, что модные сейчас за границей теории винтов были разра-
ботаны у нас школой проф. Н. Е. Жуковского еще в 1910 — 1912 гг
За границей они были вновь созданы лишь в 1916—1920 гг.
В капитальных английских руководствах но винтам, например, в
«Watts-Screw-Propellers» нли в «Park-Air-Scrcws», почти точно изла-
гаются методы расчета, уже известные в России под названием теории
Сабинина — Юрьева. Иногда в этих руководствах используется и более
поздний вариант данной теории, предложенный в 1917 г. петроград
ским профессором Г. А. Ботезатом.
Завершением русских теорий гребного винта является вихревая тео-
рия, разработанная проф. Н. Е. Жуковским и В. П. Встчинкиным в
1912—1913 гг. По окончательным числовым результатам эта теория
очень мало отличается от теории Сабинина — Юрьева и почти точно
совпадает с теорией проф. Ботезата, однако выводы ее значительно
точнее и строже.
Первые же опыты с винтами, построенными как по теории Саби-
нина — Юрьева, так и по вихревой теории, показали, что обе эти теории
дают хорошее приближение к действительности и ими, следовательно,
можно пользоваться для практических расчетов винтов.
Теории эти подвергались дальнейшим усовершенствованиям, кото-
рые заключались в том, что их уточняли введением поправок в рас-
четные коэффициенты; затем начали искать рациональные формы вин-
тов. В. П. Ветчинкин решил при помощи вихревой теории задачу о
наивыгоднейшем винте и предложил «вариационный винт».
* Эта статья была перепечатана в журнале «Вестник воздушного флота» (1923,
№ 2).
реипи’о винта
195
Большое исправление теории было сделано после гражданской вой-
ны, когда к нам начала приходить иностранная литература, в первую-
очередь германская. Нам пришлось учесть работы школы проф. Прандтля
по изучению влияния размаха крыльев иа их аэродинамические
свойства и использовать данные для уточнения наших теорий винтов.
Теория профессора Прандтля является простым перенесением вихре-
вой теории виита иа крылья, но дает новую исходную точку зрения на
учет вихрей, сбегающих с виитов. Интересно отметить, что Н. Е. Жу-
ковским эта точка зрения была предвидена еще в 1912 г., однако труд-
ность .математической обработки ее была столь велика, что Н. Е. Жу-
ковский предпочел приближенный метод расчета. В первой статье по
вихревой теории гребного винта Н. Е. Жуковский пишет: «Основная
"идея присоединенных вихрей, положенная в основание этой статьи, по-
зволила бы вести все вычисления, опираясь иа истинные скорости от-
носительного движения жидкости, ио анализ этот вышел бы очень
СЛОЖНЫМ').
В настоящее время развитие теории крыльев Прандтля настоятель-
но требует согласования ее с теорией виитов.
В 1922 г. автор настоящей статьи начал разрабатывать теорию но-
вых приближенных методов инженерного расчета винтов. Так как эта
теория рассматривает поток винта в относительном движении, то и
всю эту теорию в Центральном аэро-гидродинамическом ипештуте на-
звали «относительной теорией гребного винта».
Прн разработке вопросов этой теории возникало много различных
споров, но постепенно она была признана наиболее правильной и точ-
ной. Трудности математической обработки «относительной теории»
были так велики, что было решено для окончательной разработки ее
провести ряд опытов с винтами и выяснить основные явления их
работы.
Из-за недостатка средств изготовление необходимых приборов за-
держалось. и приступить к опытам удалось лишь в самое последнее
время. К моменту написания этой статьи было выполнено лишь около
половины намеченной программы.
Из иностранной литературы стало известно, что параллельно с нам'*
по теории винтов работали и англичане.
В «Журнале Королевского аэронавтического обшества» * имеется
отчет о заседании общества, посвященном теории виитов. На этом за-
седании майор Лоу (Low) сделал доклад о своих работах по теории
винтов. Оказывается, что он в точности повторил выводы «относитель-
ной теории». Более того, один из руководителей Английской Националь-
ной лаборатории Фэдж (Fage) указал, что ои проводил опыты по
изучению основных вопросов работы винта; его опыты совершенно
совпадают с нашими.
Всего же интереснее то, что английский ученый Глоерт (Glauert)1
разработал в 1922 г. вихревую теорию виита, являющуюся точным по-
вторением вихревой теории проф. Н. Е. Жуковского.
Как видим, в Англии 10 лет ничего не знали о работах Н. Е. Жу-
ковского по теории виитов. За границей более или менее было известно
лишь то, что в кратком виде излагалось иа иностранных языках.
Странно, что статья В. Маргулиса, напечатанная в 1920 г. в таком
известном журнале, как «L’Aeronautique», была неизвестна, по-види-
мому, в Англии даже в 1922 г.
* «The journal of the Royal Aeronautical Society».
Все это очень печально, но хуже всего то, что таких примеров можно
привести множество. Мы многое начинаем очень удачно, ио почти ни-
когда не доводим до конца. За границей снова проделывают нашу ра-
боту, доводят се до успешного конца, и мы получаем оттуда резуль-
таты под видом последнего слова науки и техники.
Объясняется это главным образом скептическим отношением к на-
шим научным работам. Из-за этого у нас ие удалось до сйх пор пол-
ностью провести ни одного научного опыта, так как всегда ие хватало
отпускаемых на такие работы средств.
Естественно задать вопрос: как поставлено это дело за границей?
Для получения исчерпывающего ответа достаточно просмотреть тол-
стые тома американских годичных отчетов («Annual Reports»), бесчис-
ленные тетради английских отчетов (R. а. М.) и многотомную коллек-
цию немецких Технических Известий («Technische Berichte»). Там не
жалеют средств иа научные нсследоваиия и опыты, и успехи их авиации
становятся понятными.
Если мы хотим «сдвинуть с места» нашу авиацию, то необходимо
немедленно и резко изменить отношение к исследовательской работе.
Не следует забывать, что, экономя средства на опытах и исследова-
ниях, мы будем расходовать во много раз большие средства при экс-
плуатации воздушного флота из-за несовершенства отечественных ма-
шин и дороговизны за1раничных.
§ 1. ОБЗОР ХАРАКТЕРНЫХ ТЕОРИЙ ВИНТА
Сделаем краткий обзор наиболее характерных теорий работы винта.
Самой простой теорией винтов является теория С. К. Джевецкого,
разработанная нм еше в 1897 г. и рассматривающая лопасть виита, как
изогнутое крыло. Для изучения
работы такого крыла Джевец-
кий разрезает винт цилиндри-
ческими сечениями иа элемен-
ты и строит для каждого эле-
мента скоростной треугольник.
Этот прием позднее был широ-
ко использован. Скоростной
треугольник по теории Дже-
вецкого изображен на фиг. 1.
Относительная скорость по-
тока U7 у элемента лопасти
получается как результат гео-
метрического сложения скоро-
Фиг. 1. Нормальный винт С. К. Джевецкого
и скоростной треугольник по теории
Джевецкого
сти вращения элемента го и
поступательной основной скорости виита V. Угол атаки а очень легко
находится по наклону хорды сечения <р. Обозначив угол притекания че-
рез р, получаем его величину из соотношения:
и- далее
V
3-arctS,V
а = <р—Э.
Зная угол атаки а и скорость воздуха, набегающего на элемент ло-
насти, легко вычислить по обычным формулам аэродинамики полное
давление воздуха R иа данный элемент и затем найти тягу элемента Р
I
и его сопротивление Q. Далее задача сводится к суммированию дей-
ствия всех элементов лопастн.
Теория Джевецкою очень удобна для инженерных расчетов. Зная
форму винта, по йен можно вычислить его тягу и мощность прн задан-
ных условиях работы, т. е. при данной скорости полета и данном числе
оборотов мотора.
Джевецкий решил и обратную задачу: ои
указал наиболее удобный винт для практи-
ческих целей — нормальный винт. Таким нор-
мальным винтом Джевенкий считает винт с
.постоянным углом атаки и постоянной шири-
ной лопасти (фиг. 1).
Недостатком этой теории является прене-
брежение скоростью подсасывания воздуха.
Опыт показывает, что работающий виит со-
здает струю воздуха, изображенную на фиг. 2,
теория же Джевецкого совершенно не учиты-
вает этой струи.
Поток, создаваемый работающим виитом,
изучался довольно подробно рядом ученых.
Всюду признанная теперь теория потока вин-
та принадлежит Фруду н Фннстервальдеру.
По этой теории основной теоремой для пото-
ка является равенство скорости отбрасывания
воздуха щ двойной скорости подсасывания v
(см. фиг. 2). Эта теория наметила предел со-
вершенства вннтов и позволила развить так
Фиг. 2. Схема струи
пропеллера
называемую теорию идеального пропеллера.
Опыты очень хорошо подтвердили формулы, выведенные на основании
этой теории.
С точки зрения инженера, эта теория являлась мало полезной, так
как она совершенно не затрагивала вопроса о том, каким должен быть
винт, создающий тог или иной поток воздуха. Иными словами, по этой
теории нельзя спроектировать винт.
Фиг. 3. Скоросгчой т?еугаг«.«ич rto теории
Са^и.-.нзй — Ю;ьеаа
Так как поток воздуха вызывается винтом, то возникает предполо-
жение, что поток и винт связаны какой-то зависимостью.
Первой теорией, связавшей поток с лопаегыо, является, по-видимо-
му, теория Сабинина — Юрьева, разработанная у нас в России в 1910 г.
Она состоит в применении точки зрения Джевецкого, т. е. в расчете*
винта по элементам лопастн, но с учетом скорости подсасывания. Эта
теория является как бы объединением теорий Джсвецкого и Фруда —
Фннстервальдера.
Скоростнои треугольник по этой теории изображен иа фиг. 3. Ско
рость подсасывания v берегся здесь не произвольно, а определяется из
уравнения связи — основного уравнения атой теории. Уравнение связи
ФИг. 4 Схема работы винта
по теории Сабинина — Юрьева
ростью подсасывания иа всех, радиусах лопасти*.
Дальнейшим шагом в развитии теории винта является применение
к ним теории вихрей. Ее возникновение связано с фотографиями Флям-
мд, установившими существо-
вание спиральных вихгсй за
водяными винтами. Основы-
вается эта теория на известных
теоремах гидродинамики.
В 1907 г. английский уче-
ный Ланчестер первый предло-
жил схему работы вннта с вих-
рями. В 1912 г. в трудах Ку-
чинского института появилась
статья Д. П. Рябушинского,
изучавшего вихревую картину
работы вннта. В том же году
Н. Е. Жуковскому удалось по-
дойти более глубоко к реше-
нию этой задачи.
Схема работы винта была
взята несколько упрощенной
(фиг. 5). Вихрь, существую-
щий как бы внутпк крыла, развивающего подъемную силу, был открыт
Н. Е. Жуковским еще в 1906 г. и был назван .им «присоединенным
вихрем». С точки зрения гидродинамики эти присоединенные вихри
получается из следующих сообра-
жений. Силу тяги винта мы можем
вычислить двумя способами. Во-пер
вых, мы ее можем найти, рассмат-
ривая действие потока воздуха иа
элемент лопасти, подобно тому, как
это делается в теории Джевепкого,
беря только вместо скорости V сю-
рость Vi = V + v, во-вторых, мы ее
можем вычислить на основании тео-
рии Фруда — Фннстервальдера, т. е.
рассматривая кольцевую струйку
воздуха, омывающую тот же эле-
мент лопасти (фиг. 4). Использова-
ние обеих точек зрения и дает урав-
нение, связывающее поток с ло
пастью. Мы уже указывали, что ре-
зультаты опытной проверки этой
теории близки к действительности
За нормальный винт по этой тео
рнн принимается винт с постоян-
ным углом атаки и постоянной ско-
Фиг 5. Схема работы винта по вих-
ревой теории, i — циркуляция вихря
* В Англии эти теории разрабатывались с 1916 г. (Fage, Collins, Riech и ДР^)
? 7 иозор характерных теорий винта
499
должны простираться концами в бесконечность и не могут где-нибудь
исчезнуть, просто оборвавшись Вихри эти должны сбегать с концов ло-
пастей и со втулки, вследствие чего при работе винта образуются не-
сколько спиральных вихрей и одни центральный вихревой шнур.
Для упрощения было принято, что концевые вихри образуют вихре-
вые винтовые линии постоянного шага и радиуса. Далее по теоремам
гидродинамики Н. Е. Жуковский определяет скорости, вызванные систе-
мой вихрей в жидкости, и исследует условия стационарности такой
Фиг 6. Вихревая модель винта по теории
Н. Е. Жуковского
Фиг 7. Вихревая модель винта по теории •
В. П. Ветчиякина
системы. Так как виит очень быстро вращается, то Н. Е. Жуковский опре-
деляет средний эфсЬекг действия вихрей на точку в абсолютном движе-
нии винта, т. е относительно плоскости вращения виита *. В этом слу-
чае действие вихревых спиралей сводится к действию на поток завих-
ренного цилиндра (фиг. 6). Поверхность этого цилиндра получается
как бы покрытой большим количеством спиральных вихрей бесконечно
малого напряжения. Строго говоря, эта схема соответствует винту с
очень большим количеством лопастей. В такой форме задача и была
решена Н. Е Жуковским.
' Уравнением связи служило условие постоянства циркуляции вдоль
лопасти и вокруг сбежавших вихревых шнуров.
В. П. Ветчиикии расширил эту теорию на винты с переменной цирку-
ляцией вдоль лопасти **. Схема вихрей получается в этом случае сле-
дующая: вместо одного вихревого слоя, как иа фиг. 6, у Ветчннкииа
как бы нанизывался бесчисленное множество охватывающих друг дру-
га вихревых цилиндров (фиг. 7). Таким приемом Ветчиикии мог произ-
вести расчет виита произвольной, наперед заданной формы.
*Н F Жуковский Статьи по вихревои теории гребных винтов (I, 2, 3 и 4).
Собр соч т VI. 1937, Собр соч, т IV. 1949
*“ В П. Ветчинки н. Расчет гребного винта «Бюллетени Политехнич. об ва», М,
1913, № 5. - - 1
Винт с постоянной циркуляцией был назван по имени Н. Е. Жуков-
ского винтом НЕЖ..
Исследования Н. Е. Жуковского показали, что лишь винт типа НЕЖ
обладает постоянной величиной скорости подсасывания v на всех радиу-
сах лопасти. Если спроектировать винт НЕЖ с постоянным углом ата-
ки и сравнить его с винтом, построенным по теории Сабинина — Юрье-
ва, то окажется, что обе теории дают практически совпадающие резуль-
таты. Разница получается лишь вследствие учета в вихревой теорйи
скорости вращения воздуха от действия лопастей. На фиг. 8 дан'ско-
ростной многоугольник, построенный на основании вихревой теории:
к окружной скорости вращения элемента гик скорости V прибав-
ляются соответственно небольшие величины — и и v.
Фиг. 8. Скоростной многоугольник по вихревой теории
I
В. П. Ветчинкин детально разработал расчет винтов по вихревой
теории *. Он ввел в нее отвлеченные обозначения, весьма упростившие
расчеты, и разработал метод расчета винта на прочность. Завершением
его работ по винтам явилось решение вариационной задачи о наивы-
годнейшей форме винта. Подобные вариационные винты им строи-
лись весьма успешно для многих аппаратов нашего воздушного
флота.
Скорость вращения и можно без труда ввести и в теорию Сабини-
на— Юрьева и тем самым увеличить ее точность. Это и было сделано
в 1917 г. проф. Г. А. Ботезатом, который ввел в теорию Сабинина —
Юрьева вращение и исследовал, исходя из уравнения связи, работу
винта с очень общей точки зрения. Получился весьма изящный анализ
работы гребного винта как пропеллера, вентилятора, ветряной мель-
ницы и т. д.
В этом же направлении работал и автор настоящей статьи, разра-
ботавший в 1920—1921 гг. графо-аналитический метод расчета гребных
пиитов **.
После введения малой поправки на вращение все изложенные выше
теории практически стали давать один и тот же результат. Казалось,
что все вопросы теории винтов разрешены и оставалось лишь учесть
различные второстепенные явления, влияющие на работу винта, как-то:
влияние фюзеляжа, крыльев и т. д.
Несмотря иа достаточную в общем точность расчетов по этим теори-
ям, в действительности постоянно наблюдались отклонения расчетных
данных, правда не превосходящие обычно нескольких процентов. Чаше
всего винт оказывался несколько тяжелым, т. е. он не развивал пол-
* В П. Ветчинкин Расчет гребного винта, «Бюллетени Политехнич. об-ва», М..
1913. № 5.
** Б. Н. Юрьев. Графо-аналитический метод расчету гребных винтов. Изд. Выс-
шего военного редакц. совета, 1922.
ного числа оборотов на моторе. Это явление раньше приписывали влияг
нию больших скоростей, на которых приходится работать сечениям
винта, значительно превосходящих скорости, при которых проводились
испытания тех же сечений в аэродинамических трубах и по данным
которых велись все расчеты.
На основании таких наблюдений В. П. Ветчинкиным были введены в
продувки крыльев некоторые поправки; так, при расчетах винта вместо
опытного «качества» профиля тт- он брал ц = 0,6 ~ , т. е. около
% %
двух Третей опытного, и увеличивал
для винтов на 10% по сравне- г
иию с опытным. г
Объяснить эти, хотя и иезиачи-
тельные, расхождения теории с
практикой удалось лищь в самое
последнее время, когда у иас стала t
известна теория «Индуктивного со-
противления» проф. Праидтля, раз-
работанная им в 1918—1920 гг. для
крыльев аэроплана. ссГаТ—-—-^
Общеизвестная теперь схема |
этого явления такова: подъемная ^222^
сила у крыла возникает по теореме
Н. Е. Жуковского вследствие воз- Фиг. g Схема вихревых усов v крыла
иикновения вокруг него циркуля-
ции скорости. Эта циркуляция сбе-
гает с конпов крыльев в виде вихревых усов (фиг. 9), указанных еще
в 1907 г. Ланчестером и в 1910 г. проф. С. А. Чаплыгиным. Эти вихри
вызывают в набегающем на крыло воздухе вертикальную скорость и,
которая у крыла конечного размаха сильно уменьшает истинный угол
атаки at. Величина Act = ct—а< носит название скоса потока перед
крылом.
Если при расчете винтов брать опытные данные по крылу конечного
размаха, то их следует пересчитать на бесконечный размах, иначе в
расчет два раза введем скос потока. Раньше подобных пересчетов
не делали, чем и объисняегси то, что старые винты получались несколь-
ко тяжелыми.
Влияние вихревых усов у крыла аналогично действию спиральных
и центрального вихрей у винта.
Попытки пользоваться вихревой теорией Н. Е. Жуковского с введе-
нием в нее пересчета на бесконечный размах крыльев показали, что
теория стала точнее, но винты, рассчитанные таким приемом, оказались
слишком легкими на моторе, т. е. давали несколько повышенное число
оборотов. Как ни малы все эти поправки, но с принципиальной стороны
было очень важно выяснить их истинную причину. В конце концов при-
шлось пересмотреть основы вихревой теории.
В формулировке Н. Е. Жуковского влияние вихрей определялось
не у самой лопасти винта, а на окружности, описываемой лопастями,
другими словами — изучалось абсолютное движение жидкости. Вслед-
ствие пульсации потока в абсолютном движении, как было указано
выше, при расчете бралась средняя скорость течения жидкости через
плоскость виита, получаемая иа основании схем фиг. 6 и 7.
Схема на фиг. 6 не безупречна в теоретическом отношении. Приве-
денный в статье Н Е Жуковского * чертеж течения жидкости пбйазы-
вает, что эта схема не соответствует установившемуся движению жид-
кости, так как линия тока в этой схеме пересекает вихревую поверх
ность.
В позднейших работах Н Е Жуковского ** прежняя вихревая
картина заменена другой (фиг. 10) Математическая обработка за-
дачи в такой постановке очень трудна, так как форма вихревой по-
верхности зависит от формы линий тока воздуха, а последняя опреде-
ляется формой вихревого слоя
Однако и в том, и в другом случае
с современной точки зрения не ясно,
почему в теории крыльев мы рассмат-
риваем относительное движение воз-
духа, а при изучении винтов берем
абсолютное движение Естественно
правильным подходом было бы и в
случае винтов рассматривать движе-
ние воздуха в относительном движе-
нии, благодаря чему Совершенно от-
Фиг 10 Схема более
точной формы вихревой
поверхности
Фиг. 11 Схема действия вихревых усов
ла крыло
дал бы вопрос, какого размаха следует брать крылья при расчете
ринтов
Неточность старой вихревой теории следует хотя бы из того, что
скорость подсасывания v считается постоянной и одинаковой как у кон-
ца лопасти, так и v ее середины Между тем у концов лопастей сбегают
вихри, и, на основании теорем гидродинамики, они неизбежно вызывают
очень большие вертикальные скорости потока, аналогичные скоростям
у концов крыльев по теории проф Прапдтля (фиг 11) Влияние этих
скоростей на винт значительно, так как сказывается главным образом
на самой его активной части — на конце лопасти.
Как известно, схема вихрей фиг. 9 в действительности не может су-
ществовать, так как не существует бесконечных скоростей. Физически
это сводится к тому, что у концов крыльев получается такой большой
перекос, что угол атаки сильно уменьшается, циркуляция к концу крыла
постепенно обращается в нуль, и за коылом образуется вихревая полоса
(фиг. 12) ***.
У лопасти винта должна получиться аналогичная картина.
* н Е Жуковский Вихревая теория гребного винта, статья 1 Собр. соч.,
г. VI 1937. Себр соч, т IV, 1949
**Н Е Жуковский Вихревая теория гребного винта статья 4 Собр. соч
г.-Л 1, 1937, Себр соч, т IV. 1949
*** Такая полоса далеко за крылом скатывается, по Прандтлю, в два вихревы^уса
Теперь задача исследования потока около винта стала вполне ясной
1 Необходимо, во-первых, изучить влияние спиральных вихрей на точки,
лежащие по оси лопастей, и затем попытаться перейти к более общему
Фиг 12 Схема вихревой поверхности
у овальных крыльев \
Фиг 13 Схема вихревой поверхности,
образующейся за винтом
случаю, наблюдающемуся в действительности, т. е. к исследованию дей-
ствия ие отдельного вихревого шнура, а всей вихревой винтовой поверх-
ности по схеме фиг. 13.
§ 2. ОСНОВНЫЕ ПОЛОЖЕНИЯ НОВОЙ ТЕОРИИ ВИНТОВ
Для упрощения задачи считаем, что вихревой шиур, сбегающий с кон-
ца. лоласти, образует спираль постоянного радиуса R и постоянного угла
наклона ф к плоскости пропеллера
Возьмем начало правой системы координат в точке О и направим ось
OZ вниз (фиг. 14). Условия стационарности такой системы вихоей по от-
ношению к вращающемуся винту были подэобио разработаны Н Е. Жу-
ковским в его первой статье по вихревой теории гребного винта, н на этом
вопросе мы останавливаться ие будем
Действие какого-нибудь бесконечно малого завихренного элемента А,
объема dr, с координатами х', у' и / на точку B(.v, г/, z} выражается, как
известно*, так:
dvz = Щ dr;
dv - --
aVy ~ I* ax'
dvx = A^~zl^~'.Odr.
ХЛ 4s
В этих формулах dvx, dvy и dvz — компоненты вызванной элементом^
скорости, £, т] и £ — компоненты по осям координат его угловой скорости
вращения со, /—расстояние между точками А и В;
I =. У(.г—г/ + H-iz — z')2.
* А А Саткевич Теоретические основы гидроаэродинамики, т 1, 1933; т. 2, 1934
Л . ОНТИ
о в
Фиг. 14. Схема действия вихря на лстпасть
Полное действие всего вихревого шнура будет выражаться интегралами:
иг
Uy
vx
Д dt.
(1)
Очень легко найти компоненты угловой скорости для случая винта, так
как там будет известна циркуляция скорости вокруг вихревого шнура. Как
известно, угловая скорость вращения шнура выражается через циркуляцию
i следующим образом:
где а площадь поперечного сечения шиура.
Обозначив угол, образованный лучем ОА с осью ОХ через ф и наклон
винтовой линии через ф (фнг. 14), получим;
£ = — 4т cos q> sin ф;
Кроме того.
х' — R cos ср,
у' — R sin ф;
z! = 2n/?tgip-^- = Нф tg ip.
Длину dL бесконечно малого элемента объема dr легко выразить через
угол ф, для чего достаточно воспользоваться тем, что при возрастании уг-
ла ф на dtp проекция длины элемента шнура на плоскость Хг будет рав-
на Rdq> и длина dL получится как гипотенуза бесконечно малого треуголь-
ника со стороной Rdq> и прилежащим углом ip, т. е.
Объем элемента выразится теперь так:
Так как мы интересуемся в первую очередь лишь точками В, лежащи-
ми на оси лопастн, т. е. на линии ОС, то можем положить, что у = 0, и
z = 0.
Принимая, что размеры сечений вихревых шнуров очень малы по срав-
нению с радиусом винта, мы должны считать постоянными в каждом сече-
иии велич 1ны л» £ и х', у', г'.
Тогда, поставив найденные выражения для х', у', г' и л и С в фор-
мулы (1), получим:
iR ? R — г cos ср
= 0 d<f-
о
iR х — R cos ф — Rq> sin <р
Ш tg Ч> J Р d4>’
о
iR f’t? sin гр -г (f>R cos <р ,
= 4л" tg Ф J--------Р «Ф
о
И
I -= У (х — R cos ф)2 4- R2 sin2 ф 4- /?2ф2 tg2 ip
Вводим отвлеченные обозначения
Теперь выведенные форлулы примут вид
I г 1 — Г COS ф Г
Ог —=—^Лр,
4л/< J / з
о
„„ <еФ С ФД'П се d<p.
UR J
I , , ЫП CD — ч COS Ч .
Dv = —— tgty J ---z------d(p,
4 xR J /3
отвлечениное расстояние
/ У-------CQS ^2 sjn2 ф2/£2ф.
Следовательно, задача сводится к интегр фэванию трех полученных урав-
нений. Легко убедиться в невозможности решпъ их простыми квадратурами.
Приходится решать их приближенными методами Примеиим графический
метод, как наиболее простой.
Обозначив расстояния АВ в плоскости виита через р и расстояние точ-
ки А от плоскости вращения XY через h (фиг. 14), найдем величину / из
прямоугольного треугольника со сторонами р и h, т. е.
/ == У р1 тг Л2.
Эту величину удобно находить графически по развертке цилиндра радиуса
R, на который как бы намотана вихревая линия. Величииу sin (р и coscp
точно так же легко получить граф тески, начертив окружность радиуса 1
и построив сбычным спосгбом синусоиды. Весь расчет ведется в виде гра-
ф 1ка (фиг. 15). Для контроля все величины наносятся на нем в влде кри-
вых линий.
Hai более важной величиной является vz. Для ее определения на фиг. 15
приведены вспомогатель’ые кривые для частиого случая, когда =0,267
или, следовательно, H/D — 0,84 (где Н — шаг винтовой линии и D — ее
диаметр)*.
Подсчеты показывают, что выведенные интегралы очеиь быстро сходят-
ся, и после двух витков винтовой вихрь почти перестает действовать на
точки, лежащие на оси лопасти.
Для дальнейшего развития теории необходимо составить таблицы для
выражений:
ь .^-ZJ^'P- d(p
.1 /3
d(p
J i3
* Подсчеты и построение графиков для этого частного случая были проделаны в
ЦАГИ инж. К. А. Бункиным.
i-Q,8 cos </>
И-
IB-
я.
1Й
ч-
13
а
Р
1
Теперь вые
отвлечении
Слегов<
нений. Лег
Приходите!
метод, как
Обозна1
ки А от п.
прямоуголь
Эту величг
7?, на коте
точно так
и построив
фика (фиг.
вых линий.
Нагболе
приведены
или, следо!
диаметр)*.
Подсчет
ся, и после
точки, леж
Для да,
выражений:
* Подсче
ЦАГИ и нж.
для разных значений гиф. Эта работа ведется в настоящее- время в
ЦАГИ, и уже получены интересные результаты.
Оказывается, что осевая скорость vz у винта с постоянной циркуляцией.’
сильно изменяется вдоль по лопасти, согласно же старой теории она счи-
талась постоянной по всему сечению струи винта (фиг. 16}.
Фиг. 16. Сравнение крыла и лопасти винта. Коэффициент а
дает скорость потока по формуле: и, = а----------.
4л/?
По старой теории эта скорость будет *
Г 2
vz =-----------
4л/? tg ф
Найдем величину коэффициента перед множителем —— для частного-
4л/?
случая (фиг. 15), т. е. для tgi|? = 0,267:
— •7,5.
4л/?
Это величина нанесена на фиг. 16.
Видим, что эта скорость является средней величиной; дейстЕНтельные-
скоростй у элементов получаются другими.
' •* Н ЕЖуко&ский. Вихревая теория гребного винта, статья I.
Если лопасть винта сравнить с крылом размаха, равным радиусу винта
R, и постоянной циркуляцией i (по схеме Прандтля), то по известным
формулам легко пслучить вертикальные скорости потока*:
2 4лх ‘ 4л (R — х) 4rtR V г 1—г
В центре крыла мы получим
Соедияя же скорость по всему размаху, по которой обычно и рассчиты-
ваются крылья, будет в два раза больше, чем скорость в центре крыла**,
т. е.
Получаем интересный результат: скорость подсасывания у виита, вычис-
ленная по старой вихревой теории (или, что то же самое, по теории иде-
ального пропеллера), почти в точности равна средней вертикальной ско-
рости потока перед крьлсм размаха R.
Отсюда получается любопытный вывод, что теория Джевецкого должна
давать довольно точные результаты, если только брать при расчете коэф-
фициенты Ку и Кх!Ку по продувке крыла с таким же размахом, что и
у лопасти винта. В случае же применения вихревой теории следует брать
крыло бесконечного размаха. Следовательно, приблизительно с одинаковой
степенью точности можно пользоваться и той, и другой теорией.
Конечно, расчеты по средним скоростям являются лишь грубым прибли-
жением к действительности, н крайне желательно более точно изучить ис-
тинну.о картину распределения скоростей по лопастн винта.
Прежде всего необходимо отметить, что винт с постоянной по всей
лопасти циркуляцией скорости не может на самом деле су дествовать, так
как бескоиечтые скорости на самом деле не могут получаться. Так же
как и у крыла, у конца лопасти вследствие больших скоростей vz углы
атаки уменьшатся, и часть циркуляции начзет сходить с лопасти в виде
завихренного слоя. Надо думать, что циркуляция скорости по лопасти
винта типа НЕЖ в действительности будет иметь вид, близкий к изобра-
женному на фиг. 17. Тогда и вертикальные скорости будут более по-
стоянны.
Как доказал Мунк, иаивыгоднейшим крылом является крыло с циркуля-
цией, распределенной по его размаху по закону эллипса. У такого крыла
вертикальная скорость будет постоянной по всему размаху. Если и у винта
сделать лопасть такой формы, то циркуляция будет изменяться по закону
эллипса, и вертикальная скорость будет приблизительно постоянна на
всех радиусах. Можно попытаться решить совершенно точно задачу о
винте с постоянной скоростью vz, одчако нам сделать это пока не удалось.
Имея же закон распрэделения циркуляции, необходимый для получения
такого винта, можно очень упростить все расчеты. Пока же мы pi комзи-
Дуем брать для простоты эллиптическое распределение циркуляции. Тогда
* См. Б. И. Ю р ь е в. Индуктивное сопротивление крыльев аэроплана.Труды ЦАГИ.
№ 20. 1926. (Прим, ред )
•* При выводе этой зависимости делается дополнительное допущение о положе-
нии вихрей по отношению к крылу.
расчет винта можно вести по такой схеме: по теории идеального пропел-
лера найти скорость подсасывания; исправив ее при помощи некоторого
коэффициента, оценивающего неравномерность распределения скоростей
в плоскости винта, получим вертикальную скорость потока перед лопастью.
Скоэость врадения потока обычно мала на больших радиусах и ее
приходится принимать во рннмание лишь у втулки; ее можно вычислять
по циркуляции центрального шнура, т. е. писать
Здесь k — число лопастей и г — радиус, на котором определяется эта
скорость.
Далее строятся скоростные много-
угольники для ряда сечений винта,
подбираются угол атаки и ширина
профиля при условии получения
заданной циркуляции и достаточной
прочности сечения. Эта часть расчета
ничем не отличается от обычно прак-
тикующегося приема расчета винта
по вихревой теории. При таком рас-
чете надо брать для профилей коэф-
фициенты, соответствующие бесконеч-
ному размаху крыла.
Следовательно, расчет ведется как
бы по теории Сабинина—Юрьева, но
уравнение связи пишется не для от-
дельных элементов, а для всего вин-
Фиг. 17. Схема циркуляции ,и скорости vz
у винта НЕЖ в относительном потоке
та.
Точность этого способа для случая поопеллера хорошая, так как ско-
рость vz является лишь незначительной прибавкой к скорости полета.
Более точным приемом будет определение скоростей vz, vy, vx при по-
мощи таблиц величии а, b и с. В случае переменной циркуляции придется
расчет вести подобно тому, как это делается у крыла произвольной формы
в плане*.
Окончательно относительные скорости потока получатся путем сло-
жения скоростей, вызванных спиральными вихрями, осевым вихрем, враще-
нием винта и скоростью полета.
Осевая скорость получится в виде:
Vz = V+^vz.
Скорость относительного вращения будет
vu — ГСО — LVy-----------.
4лг
Здесь ki / 4nr — влияние осевого шнура, k— число лопастей вннта.
Радиальная скорость в плоскости винта
* Б. Н. Юрьев. Определение аэродинамических свойств крыльев произвольного
очертания в плане. «Вестник воздушного флота», 1923, № 2.
14 Б. Н. Юрьев, т. I
Самой важной величиной является скорость скорость играет уже
малую роль, а скоростью Vx обычно пренебрегают во всех теориях винтов.
Из изложенного следует, что новая теория весьма трудна для точных
расчетов, но приближенные расчеты по ией могут быть сделаны цроще,
чем по старой теории.
Для окончательного суждения о точности той или другой теории не-
обходимо проделать ряд опытов с винтами и определить углы атаки у их
профилей. В ближайшем будущем мы предполагаем подробно остановиться
на этом вопросе и изложить результаты опытных исследований по винтам,
ведущихся в настоящее время в ЦАГИ.
Раздел II
ВЕРТОЛЕТЫ
ИССЛЕДОВАНИЕ ЛЕТНЫХ СВОЙСТВ
ГЕЛИКОПТЕРОВ
Проблема геликоптера весьма стара. Идея полета с помощью под-
держивающего виита зародилась значительно раньше идеи аэроплана.
Однако постройка геликоптера требовала весьма развитой техники и,
кроме того, теоретического и экспериментального обоснования работы
винта на различных режимах. Без этих данных нельзя было сделать
расчет геликоптера и осуществить те сложные механизмы, без которых
он не может летать. По этой причине внимание всех работников авиа-
ции и сосредоточилось на более легкой проблеме — на разработке ле-
тательных аппаратов типа аэроплана.
Развитие аэропланов в течение каких-нибудь тридцати лет Достигло
поразительных результатов, свидетелями которых мы и являемся. Аэро-
планы дают громадные скорости полета и обладают исключительной
грузоподъемностью; дальность их полета далеко превосходит обычные
потребности. Самолет навсегда вошел в жизнь человечества, как сред-
ство самого дальнего и сверхбыстрого транспорта.
Однако у аэроплана имеется один весьма существенный недостаток,
связанный с принципом его работы: необходимость все время двигаться
с достаточно большой скоростью.
Если перевозка грузов по воздуху л есть та цель, для которой стро-
ятся летательные аппараты, то большая горизонтальная скорость во
время взлета и посадки вредна и опасна. Многие аварии происходят с
самолетами именно при взлете и посадке. Из-за этого современная
авиация оказывается связанной в своих возможностях, так как для
безопасной эксплуатации самолетов требуются аэродромы.
Идеалом была бы машина, имеющая возможность совершать взлет
и посадку по вертикали; тогда совершенно отпала бы нужда в аэро-
дромах. Иногда в мирных или военных целях требуется остановить лета-
тельный аппарат в воздухе, т. е. «висеть» в воздухе. Аэроплан по прин-
ципу своего действия делать этого не может.
Только летательные аппараты типа геликоптеров могут решать эти
заманчивые проблемы. Однако лишь в самое последнее время гели-
коптеры начали летать; до этого они совершали лишь прыжки. Такие
Достижения стали возможными благодаря накопленному огромному
опыту в области самолето- и моторостроения и развитию точной меха-
ники. Имеется огромный, правда еще довольно бессистемный материал
по аэродинамическим испытаниям винтов и роторов разных типов. Ин-
женером Сиерва был с успехом создан промежуточный между самоле-
том и геликоптером тип летательного аппарата — автожир.
Все это позволило конструкторам геликоптеров более сознательно
проектировать эти сложные аппараты. Этим и объясняются порази-
тельные успехи, достигнутые за последние два года. Приведем в каче-
стве характеристики данные двух новых геликоптеров—французского
Бреге-Доран и германского Фоке-Вульф:
Достигнутая высота полета
Достигнутая скорость . . .
Достигнутое время полета .
Расстояние по кругу . . .
Дальность по прямой . . .
Бреге-Доран
158 м
99 км/час
1 ч 2 мин. 50 сек.
44 км
Фоке-Вульф
2439 м
122,6 км/час
1ч .20 мин. 50 сек.
80,6 км
230,2 км
Мы видим, что геликоптер выходит из стадии первых опытов. Это
уже летательные машины, правда еще плохие, несовершенные, но все-
таки они уже не прыгают, а летают.
(Отсюда понятен интерес к подобным аппаратам в последние годы.
Заграничная литература уделяет много внимания этому вопросу, что
можно видеть, по- выпущенному ЦАГИ указателю литературы по ле-
тательным аппаратам особого типа. Все ведущие заграничные журналы
постоянно помещают статьи по этому вопросу.
У нас в этой области имеется также немало работ; по многим про-
блемам мы были пионерами *. Однако все эти материалы разбросаны по
различным журналам, трудам конференций, трудам институтов и не си-
стематизированы.
Настоящая работа подводит итоги полученных экспериментальных
материалов и анализирует проблему полета геликоптера в целом. Она
построена в виде общего изыскйния летных свойств геликоптеров и
близка к нашей работе «Пределы современной авиации и способы их
преодоления».
Здесь мы не будем разбирать теорию несущих винтов и роторов и
рассматривать конструктивные формы геликоптеров. По этим вопросам
у нас уже имеется достаточно большая литература.
Результаты проделанной нами работы приводят к заключению, что
геликоптер как летательный аппарат значительно хуже аэроплана. Его
преимущество — возможность висения в воздухе, а отсюда — возмож-
ность посадки и взлета с любого места.
Полученные нами данные могут показаться несколько пессимисти-
ческими. Имеются как пламенные сторонники геликоптера, так и не
менее яростные противники этих аппаратов. Мы полагаем, что истина
лежит посредине. Геликоптер хуже летит, чем самолет, зато его спе-
цифические свойства крайне ценны. Не конкурировать призваны эти
два типа летательных аппаратов, а дополнять друг друга. Кроме того,
геликоптер как летательный аппарат еще молод, и что сулит ближай-
шее будущее, иам еще неизвестно.
В основу нашей работы положен курс лекций автора по винтокры-
лым аппаратам. Ряд расчетов и чертежей сделан инженером Ф. П. Ку-
рочкиным, которому автор выражает свою благодарность.
* См. работы московской школы аэродинамиков — Н. Е. Жуковского, В. П. Вет-
чинкина, Б. Н. Юрьева, работы Кучинского аэродинамического института, работы
Глава I
ВИСЕНИЕ В ВОЗДУХЕ
§ 1. АЭРОДИНАМИЧЕСКИЕ СВОЙСТВА ВИНТОВ,
РАБОТАЮЩИХ НА МЕСТЕ
Для изучения вопросов висения геликоптера в воздухе необходимо
знать, какую мощность потребляет несущий винт-ротор. Ответ на это
можно получить путем теории или путем экспериментов. Наиболее
разработанная в настоящее время вихревая теория проф. Н. Е. Жуков-
ского не дает ответ с нужной для конструктора точностью (ее точность
для этого случая работы винта ие выше 10—15%). Эта теория дает
хороший ответ лишь для режима пропеллера. Поэтому приходится ба-
зироваться на экспериментальном изучении винтов, которое ведется
уже давно, но все же далеко не закончено. У геликоптеров шаг виита
берется малым, а большинство испытаний винтов было проведено с
винтами большого шага. Кроме того, большая часть опытов велась
иа малых моделях винтов, и вследствие малых чисел Рейнольдса по-
лученные опытом характеристики винтов искажены из-за влияния
вязкости воздуха.
Наиболее широкие опыты с винтами разной формы и разного ша-
га были проведены в Германии Бенденмаиом (1911 г.), в Англии в
NPL (1922 г.) Фейджем, Локком, Батеманом и Вилляамсом (RM-830,
1922), в Америке Дюрэнцом в Стэнфордском университете и И. В. Осто-
сл.авским и Д. В. Халсзовымв ЦАГИ (1936 г.).
Большое количество опытов было проведено недавно в ЦАГИ с одним
виитом чисто геликоптериого типа* **.
Обработка опытов производится обычно по формулам подобия, которые,
в нашей стандартной форме написания*** имеют такой вид:
P = rtPD42 (1)
и
N = Д 0р£М (2)
Здесь 7V— мощность, потребляемая одним винтом, Р —тяга виита, р—
массовая плотность воздуха, D — диаметр винта, ns —число оборотов
виита в секунду, <х и — безразмерные коэффициенты тяги и мощности
* Груды ЦАГИ, № 300.
** «Техника воздушного флота», 1934, № 8; 1936, № 4.
*** Б. Н. Юрьев. Воздушные винты. ОНТИ, 1934.
К ним надо добавить относительный к. п. д. винта
(3)
Часто при расчете работающих на месте винтов пользуются формулой
проф. Г. Вельнера
формула (4) примет вид:
Р = (33,25т]0ТО)3/а. (5)
Величину коэффициента, стоящего в скобках, часто обозначают через
а (коэффициент Вельнера) и пишут
Р = (aND)!\ (6)
где а = 33,25т]0.
Число оборотов винта находят по формуле (2):
Форма лопастей у построенных в последние годы аппаратов обычно
близка к форме, даваемой вихревой теорией (расширяющиеся в плане
к втулке). Такие лопасти называют иногда ланцетовидными (фиг. 1,а).
Очень часто встречаются лопасти с постоянной шириной (фиг. 1,с) н фор-
мой, близкой к эллиптической (фиг. 1, Ь}.
Профиль лопастей у построенных винтов в общемоднообразен. Это или
RAF-6, или Clark-Y, или при симметричных профилях Gottingen-429.
$> 1 Аэродинамические свойства винтов, раишиклцих ни меые
На аэродинамике винта профиль отражается несильно; сравнительно
слабо влияет и форма в плане: типы а и b дают близкие результаты.
Всего сильнее иа аэродинамике ротора отражается величина относитель-
ного шага
А = - (8)
D 1 '
или, что то же, характерный угол наклона лопасти <р°, берущийся, как
правило, на отвлеченном радиусе г = 0,75.
Поэтому чаще всего диаграммы для изучения винтов строятся так, что
по оси абсцисс откладывается относительный шаг h (или <р°), а по оси
ординат — остальные аэродинамические характеристики винта.
Приводим две такие диаграммы: фиг. 2—геликоптериый винт
ЦАГИ и фиг. 3 — английские винты. Наверху даны чертежи этих виитов.
Наибольший относительный к. п. д. у моделей виитов равен 0,68 при
относительном шаге винта 0,5 — 0,3 и при двух или трех лопастях.
В табл. 1 поиведены данные английских опытов с наилучпшми винтами.
Данные для узких лопастей, имевших Ь/£> = 0,041, получились, по-вид и-
мому, сильно заниженными из-за малых чисел Рейнольдса. Их следует уве-
личить на 5—15%. Одиако точных опытных данных о таких винтах еще
не имеется. Желательно в ближайшее время провести эксперименты с вин-
тами геликоптера в натуру.
Испрнленне опытов на влиянче числа Рейнольдса. Исследования
В. С. Маргулиса и других показывают, что получающиеся в лабораториях
Та блица 1
Наилучшие геликоптерные винты по английским опытам (MR, 829, 1922 года)
, —
стей b/D и 6 По а - 33.25
2 0,3 0,082 0,0622 0,0214 0,578 19,3
4 0,3 0,0928 0,0928 0,0400 0,565 18,8
2 0,5 0,032 ’ 0,0910 0,0322 0,682 22,7
4 0,5 0,082 0,1400 0,0628 0,663 22,0
2 0,7 0,082 0,1145 0,0508 0,613 20,4
4 0,7 0,082 0,1860 0,100 0,640 21,3
3 0,5 0,082 0,121 0,0512 0,655 21,8
2 0,5 0,123 0,114 0,0477 0,646 21,5
2 0,5 0,0615 0,0747 0,0260 0,627 20,8
4 0,5 0,0615 0,1224 0,0516 0,670 22.3
0,5 0,041 0,0500 0,0180 0,496 16,5
3 0,5 0,041 0,0692 0,0266 0,548 18,2
4 0,5 0,041 0,0867 0,0352 0,578 19,2
6 и. 0,5 0,041 0,1135 0,0510 0,600 20,0
малые числа Рейнольдса заметно искажают аэродинамику винтов. Особенно
сильно они влияют на относительный к. п. д. Число Рейнольдса для вин-
тов следует вычислять для типичного сечения, лежащего на отвлеченном
радиусеу=3/4-
Re= 2-5^, (9)
Фиг. 3
где v — кинематическая вязкость воздуха, равная 1,45-10~5, и со —окруж-
ная скорость винта.
Скорость потока мы считаем здесь приближенно равной окружной
скорости элемента. Замечая, что
_ 3 г-. „ лп
Л1.76 =-—£>, со = 2лл5 = —
8 30
и вводя отвлеченную ширину лопасти Ь0.75 = Ь0,1Ъ D, получим:
Re = = 27306,., .О2 п.
4-60-V
(10
В. С. Маргулис построил гоафик, дающий р„ в функции числа Re для
изученных им шести винтов. Винты 11 и 55 были парными, таидемы (фиг
4). Эта диаграмма показывает,
что т]о сильно изменяется при ма-
л*-’х числах Рейнольдса, однако
очень быстро достигает максиму-
ма и перестает изменяться (у ;Чар-
г} лиса при Re = 400 000—500 00 ,).
Следовательно, для получен, я
правильных результатов винты
нужно испытывать при числах
Рейнольдса не меньших 500 000,
К сожалению, большинство
лабораторных исследований про-
ведено при малых числах Рейноль-
дса (100 000—200 000). Это дает
по графику Маргулиса огромную
ошибку, так как при испытании
модели можно получить т]о = О,40,
тогда как ппи испытании винта
в натуру должно получиться
По=О,72. Исправлять эту ошибку можно или с помощью графика Маргулиса,
или с помощью более точного приема, который мы сейчас изложим.
Можно принять, что у винтового профиля, работающего иа малом угле
атаки, коэффициент су не зависит от Re, а сх сильно зависит от него.
Тяга винта малого шага зависит практически только от су. Следовательно,
коэффициент тяги винта не должен зависеть от Re. Это довольно точно
подтверждается опытами. Мощность же винта зависит и от су и от сх.
У винта в натуру и у модели будут получаться для профилей разные сх. Это
позволит делать пересчет, если будет известен закон изменения с( от Re.
В настоящее время имеются результаты достаточно надежных исследо-
ваний, произведенных в Америке в трубе переменной плотности *. Ввиду
малости углов атаки у винтовых профилей, вместо сх можно брать просто
коэффициент профильного сопротивления, т. е. скр.
На фиг. 5 приведены такие графики для крыльев NACA-4412 и NACA-
4415, очень близких к обычным «английским» профилям, и для крыльев
NACA-0012, 0015, симметричных, близких к употребляющимся у автожи-
ров. В американской системе обозначений профилей первая цифра дает по-
ложение наибольшей стрелки в 1/10 хорды, вторая — величину стрелки
• КЛСЛ-587, 1937.
средней линнн в процентах хорды; последние две цифры дают наибольшую
толщину профиля, тоже в процентах хорды.
Вычислим теперь работу, какую приходится затрачивать на преодоление
профильного сопротивления винта. Выделим у винта’ элементы лопастн на
радиусе г с хордой b и шириной dr. Тогда работа профильного сопротив-
ления dTp получится, если считать схр лежащим в плоскости вращения
винта, по обычной формуле экспериментальной аэродинамики:
dTp = cxp^-kb dr (гы)3 = ~CtpkbRr3 dr ?D5n3s-
Здесь г = , bR = и — 2itns.
Относительную скорость потока мы приняли для элемента равной
окружной его скорости, что для геликоптерных винтов малого шага иа обыч-
ных режимах их работы дает ничтожную погрешность.
Полная работа профильного сопротивления получится как интеграл
предыдущего выражения:
Тр ~ kpD^ cxpbRr3 dr.
8 о
Находим теперь коэффициент мощности, затраченной иа профильное
сопротивление:
о»
Число Рейнольдса изменяется у рабочих элементов винта вдоль ло-
пасти не сильно, примерно в три раза. Следовательно, схр можно считать
практически постоянным и написать формулу (11) окончательно в таком
виде:
= ~kcxp bRr3dr.
8 о
(12)
При переходе от винта модели к винту геликоптера в натуру, число
Рейнольдса непедко изменяется в 15—30 раз. Прн этом схр у модели
с несимметричнjm профилем при Re— 150 000 имеет величину порядка
0,027 и соответственно 0,02 — у модели с симметричным профилем. У ро-
тора геликоптера в натуру в тех же случаях будем иметь прн Re — 2 000 000
величины 0,009 и 0,008.
Следовательно, полученные в опытах с моделью величины нужно
исправлять на разность работ профильного сопротивления, т. е. на вели-
чину
= = (13)
8 а
Величину входящего в эту формулу интеграла
(14)
легко найти для обычных форм винтов путем графического интегрирования,
Его значения следующие: для винта с лопастью, близкой к эллипсу,
0,020, для виитас ланцетовидной лопастью 0,0195, для прямоугольной лопасти
с округленным концом 0,212. В среднем можно принять величину I — 0,02
при ^о.75 = 0,1. Отсюда поправка для лопасти любой ширины Ь0.75 полу-
чится по формуле:
ДЗ „ £LS W (с;р __ Слр) I „ O,775too.,s (КР - Cvp). (15)
8 0,1
Таблица 2
Поправки для винтов
Опыты Ь 0-Т5 Re к • схр схр схр ~~ схр •М
Английские (RM-829) 0,082 167 000 4 0,024 0,009 0,015 0,0038
NPL D—0,915 м «.-=1800 об/мин 0,123 0,164 260 000 335 000 4 4 0,019 0,015 0,009 0,009 0,010 0,006 0,0038 0,0030
ЦАГИ D-0,734 м л=1200 об/мин 0,13 120 000 4 0,27 0,009 0,018 0,0064
ВВА D=0,8x я —1200 об/мин 0,10 105 000 3 0 02 0,008 0,012 0,0028
Подставляя в эту формулу найденную ранее
чим окончательное выражение для поправок:
Вииты с несимметричными профилями
величину схр — схр, полу-
Вииты с симметричными профилями
Лр = 0,0094 feF0,r.
Напомним, что здесь отвлеченная ширина лопасти i>0,7S отиесеиа к D, как
это обычно делается при испытаниях винтов.
В табл. 2 мы приводим поправки для наиболее интересных испытаний
виитов. Как видно из таблицы, поправка для винтов малого шага очень
велика, так как сама величина# имеет иногда порядок 0,01—0,005. Отно-
сительная поправка может достигать десятков процентов. Ее нужно обя-
зательно вводить в опыты, иначе получится неправильный переход к винту
геликоптера в натуральную величину.
Заметим, что некоторые опыты дают основание думать, что эта поправка
может в действительности оказаться еще большей. При расчетах автожи-
ров обычно профильное сопротивление увеличивают в полтора раза. Если
делать это при исправлении продувок винтов, то и поправку придется уве-
личить в полтора раза.
Формула тяги для виита малого шага. Для расчета геликоптера очень
важно иметь надежную и простую формулу для вычисления силы тяги
винтов малого шага. Работу, затрачиваемую на врацение виита малого
шага, обычно разбивают на две части: на работу поддержания* и на ра-
боту треиия. С потерями на вращение струи в этом случае можно не счи-
таться ввиду их малости.
Работа поддержания может быть проще всего получена из обычной
формулы теории идеального пропеллера **, дающей относительный к.п.д
виита:
Полагая в этой формуле Т]о = 1, получим коэффициент мощности ft, за-
траченной иа работу поддержания
й = Уа3 ‘ 0,8а3/2. (16)
К такой же формуле приводит и вихревая теория Жуковского.
Однако, как показывают английские опыты по исследованию струи винта,
скорость отбрасываемого винтом воздуха по всей ометаемой винтом пло-
щади далека от постоянства, как это ппедполагается согласно теории
идеального пропеллера. Эта скорость оказывается наибольшей в том месте,
где находится в данное мгновение лопасть. Таким образом, осевая скорость
потока возле лопастей будет равняться ие v, как предполагает теория
идеального пропеллера, a %v, где £ —коэффициент неравномерности. Эта
поправка очень мала для обычных пропеллеров, так как у них осевая
скорость близка к скорости полета, а скорость подсасывания является лишь
небольшим добавком к ней. У геликоптерного винта эта поправка велика,
и ее нужно учитывать. Тогда формула (16) примет вид:
Й = 5 • 0,8а3/2. (1Т>
* Индуктивные потери. [Прим, ред.)
** Б. Н. Юрьев. Воздушные винты.
По-видимому, для обычных винтов геликоптера можно принять, что
g = 1,25. Тогда получим весьма простую формулу:
К т *3/2-
(18)
к этим потерям нужно прибавить потери на трение, т. е. на профильное
сопротивление, которое можно вычислить по формуле (12). Окончательно
получим:
[1 = ft, + азд.
(19)
Фиг. 6
оси ординат значение а. На этом графике нанесены результаты испытаний
различных винтов. Огибающая наил\чших винтов может быть представлена
кривой, нанесенной пунктиром, уравнение которой напишется следующим
образом:
3 = 0,002 + а3/г. (20)
Величина 0,002 очень близка к величине, даваемой формулой (12) для
винтов в натуру. Легко объяснить, почему у некоторых виитов характе-
ристики (фиг. 6) сильно отклоняются вправо. Это происходит потому, что
лишь иа расчетном шаге профили винтов обтекаются без срыва потока; при
изменении же шага путем поворота лопасти, как это обычно делается в ла-
бораторных опытах, профили начинают работать со срывом, и потери винта
сильно возрастают.
Следовательно, формулу (20) можно рассматривать как достаточно на-
дежную. Найдем с ее помощью относительный к.п.д. геликоптерных вин-
тов:
По = О,8^Д =0,8 0,8 fl---М (21)
Ниже приведены результаты такого вычисления. В последней графе дан
коэффициент Вельнера а = 33,25 т|0.
а 0.01 0,02 0,03 0,05 0,07 0,10
0,0030 0,0028 0,0072 0,0132 0.0206 0,0336
По 0,267 0,470 0,578 0,680 0,722 0,752
а 8,85 15,6 19,2 22,6 24,0 25,0
На фиг. 7 изображена полученная зависимость графически.
7о
#7 -
0,6 -
0,6 -
оь -
0,6 -
%2-
0,1 -
Как видим, относительный к.п.д. очень быстро возрастает с увеличе-
нием р. В новейших геликоптерах желательно брать наиболее быстроход-
ные винты, т. е. винты с малым Р; это облегчает трансмиссию геликоптера
и ротор получается более легким. Однако для получения достаточной
подъемной силы относительный к.п.д. вннта не должен быть низким.
Диаграмма на фиг. 7 показывает, что для получения большой тяги нет
смысла брать р больше 0,025, чему соответствует а = 24,3. Во многих
случаях можно брать и более быстроходные винты, с р = 0,01. Тогда
«~21, что дает довольно большую тягу. Учитывая обдувку фюзеляжа н
потерн, связанные с наличием у геликоптеров различных выступов иа ло-
пастях, можно принять в качестве достаточно надежных величин следую-
щие значения основных аэродинамических коэффициентов ротора: при
Р 0,025 значение а = 22,3, при р = 0,01 значение а — 20.
Интересной проблемой является вопрос о работе парных винтов.
Сюда входит изучение винтов, работающих рядом, винтов, пересекаю-
щихся в одной плоскости, винтов, взаимно перекрывающихся, и внн-
тов-тандем (фиг. 8 и 9). Сюда же можно отнести вопрос о работе
больших групп вннтов.
К сожалению, имеется очень мало экспериментальных данных о
работе таких сочетаний винтов, применяющихся в разных системах
геликоптеров.
Основываясь на очень ограниченном числе опытов и на общих сооб-
ражениях, можно считать, что комбинации а и е (фиг. 8) обеспечивают
е
Фиг. 8
практически независимую работу во время висения. В комбинации d
мы имеем наибольшее взаимное влияние, комбинации Ь и с — промежу-
точные случаи.
Какой же эффект дают винты-тандем, показавшие ряд хороших
результатов (Асканиа, Пескара, Бреге)?
Теоретически разбор этого вопроса с помощью вихревой теории
Н. Е. Жуковского был сделан В. С. Маргулисом и позднее Б. Н. Его-
ровым и В. А. Кузнецовым (см. библиографию). Маргулис провел ряд
опытов с такими винтами.
Здесь нужно различать два случая. Первый — когда плоскости вра-
щения винтов очень близки. Тогда имеется, в сущности, один виит
(фиг. 9, а), у которого получится двойное перекрытие и будет уничто-
жено вращение в отходящей струе. Это дает увеличение г|0 на 1—2%.
По-другому обстоит дело, когда винты достаточно удалены друг от
друга (примерно иа расстояние не менее D/8), тогда нижний виит под-
сасывает свежий воздух с боков, и масса отброшенного воздуха делает-
ся большей, чем в случае одного винта (фиг. 9,6).
Фиг. 9
Из опытов Маргулиса и других можно принять увеличение гювиита-
таидем по сравнению с одиночным винтом в среднем на 13%. При-
мерно такую же вепш’ину можно получить из иедавио опубликован-
ных опытов Бреге, учтя имевшееся в иих влияние близости земли.
В этой работе мы ие будем, делать расчета такого виита, а просто
примем указанную величину улучшения, как достаточно точную.
В настоящее время можно с достаточной надежностью вычислить
тягу геликоптериого винта, например, по формуле Вельнера, беря а
по фиг. 7. Бели пользоваться формулой Вельнера, то коэффициент а.
входящий в нее, не будет намного превышать значение 22—24. Следо-
вательно, подъемная сила геликоптера весьма сильно лимитирована.
Проф, Карман сравнил геликоптер с аэропланом, причем размах
аэроплана ои брал равным диаметру винта геликоптера, а мощность
моторов’ принимал одинаковой. Оказалось, что геликоптер дает в
1!/г—2 раза меньшую подъемную силу, чем аэроплан.
§ 2. ТРАНСМИССИЯ ГЕЛИКОПТЕРА
Баланс мощностей. .Мощность мотора передается к винтам у ге-
ликоптеров. с помощью более или менее длинных трансмиссий. Кроме
того, современные бензиновые моторы быстроходны и делают обычно1
ст 1300 до 2200 об/.чин, а роторы имеют от 100 до 300 об/мин. Сле-
довательно, приходится делать редукторы с передаточным числом по-
рядка Это дает весьма большого объема н тяжелые валы,
зубчатки, картеры.
Бес трансмиссий — главная беда современных геликоптеров. Облег-
чение трансмиссий путем понижения запаса прочности нерационально
и ведет к частым поломкам этих механизмов у опытных аппаратов.
Необходима весьма серьезная изобретательская и исследовательская
работа по разработке новых типов легких трансмиссий. Не следует
Фиг. 10
заранее отвергать ни гидравлических, ни электрических, ни ременных
Vi других передач.
Эти передачи, помимо увеличения веса геликоптера, еще снижают
подъемную силу, так как они имеют некоторый механический к. п. д.
и часть работы мотора до винта не доходит. Охлаждение моторов тре-
бует у геликоптеров установки вентилятора; на это идет 5% мощности
мотора.
У большинства геликоптеров мощность (до 5% от мощности мо-
тора) тратится еще на органы управления-—на вращение рулевых
винтов, на лишнее сопротивление ротора при автомате-перекосе
и I. п.
Рассмотрим баланс мощности у характерных типов геликоптеров.
Обычный геликоптер с двумя роторами. Пара лобовых зубчатых колее
имеет при хорошем выполнении и шаровых опорах к.п.д. т]^Д^0,98; у ко-
нических колес Пт ~ 0,95.
В пеоедаче геликоптера имеется обычно пара последовательных зацеп*
леиий. Это дает для случая лобовых передач Н™ = 0,932 •= 0,95 (фиг. 10,а),
для случая конических передач т]м = 0,952 = 0,90 (фиг. 10,£). Иногда- при-
меняются планетарные передачи; у них к.п.д. может быть принят равным
0,92—0,9. Чаще всего в геликоптерах встречается одна лобовая передача
и одна коническая (фиг. 10,с). Тогда к.п.д. равен 0,92.
В общем трудно обеспечить к.п.д. больший 0,92. Учитызая потерю на
охлаждение мотора в5%, находим, что лишь 0,85-»--,,880всей мощности
в лучшем случае дойдет до ротора1 •
Одиовиитоеой геликоптер системы Б. Н. Юрьева (фиг. 11 и 12). У этого
геликоптера вращающий момеит большого винта уравновешивается момен-
том одного или нескольких малых винтов, установленных на концах фю-
зеляжа или на специальных консолях. У такого геликоптера требуется
затратить часть мощности мотора на эти малые винты.
фиг 12
Эту мощность очень легко найти. Момент и мощность на валу ротора
определяются по обычным формулам подобия:
М = A pD5«: и N =
* 7а 1 6
Для уравновешивания этого момента хвостовой виит должен развить тягу
Рх, действуя иа плече /. Следовательно,
М _ a pD5»s
I ~ 2л Z '
можно принять, что плечо будет порядка D/2, т. е. t = D/2. Тогда
р,=1р^.
• Тяга малого винта может быть найдена по формуле Вельнера:
= (94,2 Ур^УД)7’,
7|»х относительный к.п.д, хвостового винта, Мх to Dx—его мощность
$21 рансмиссия геликоптера
229
и диаметр. Решая это выражение относительно N* и пользуясь найденной
ранее формулой для Рх, получаем:
94,2 |/нп„Л
( УЛ
~94,2VptioxDx
Отсюда
94,2 )
75
5,6.94,2
Г)
Приняв т]Ох — 0.64, получаем окончательно:
> = О'221^Й7-
Если возьмем современный быстроходный ротор с 0 = 0,025, то полу*
чим:
N„.
N
D
= 0,035—.
По конструктивным соображениям трудно брать £)х больше х/4 —
Беря = 5, получаем: —* — 0,175. При наличии двух хвостовых винтов
мощность, затрачиваемая на малые винты, уменьшится иа 25%. Если по-
жертвовать подъемной силой ротора и взять у него — 0,01, то это даст:
VVj. Z'
— = 0,11. Следовательно, эти потери достигают величины 11 —17,5%.
Детальные подсчеты различных вариантов такого геликоптера с учетом
потерь в трансмиссиях показывают, что от 15 до 20% всей мощности
у него неизбежно уходит на эти вннты. Распределение потерь (в процен-
тах) следующее:
редуктор ротора r)nj=0.95............. 5
малые винты........................... 15—20
охлаждение мотора..................... 5
Все потери . . . 25—30%*
Одновинтовой геликоптер Г. Вельнера. У такого геликоптера мощность
подается на маленькие винты, установленные на лопастях ротора. Они при-
водятся во вращение или отдельными моторами (фиг. 13,а), установлен-
ными на лопастях, или вращаются с помощью трансмиссий от мотора
(фиг. 13,5), стоящего в гондоле. К.п.д. таких винтов, работающих в ие-
* Согласно последним статистическим данным, величина мощностных потерь на хво-
стовой винт одновинтового вертолета равна 7—8%. При особо тщательном проектирова-
нии и изготовлении ебшие потери могут составить всего 20% (Б. Н. Юрьев. Аэроди-
намический расчет вертолета. Оборонгиз, 1956, стр. 116). {Прим, ред.)
равномерном потоке, не выше 0,75. При наличии трансмиссий он упадет
до 0,70.
Управлять таким геликоптером придется, по-видимому, с помощью р.у
левых виитов, на что будет затрачиваться ие меиее 5% мощности.
Баланс мощности геликоптера (потери в процентах) следую ций:
кпд пропеллеров ротора
0,75—0,7 потери . . .25—30
рулевые винты » ... 5
охлаждение » ... 5
Все потери . . . 35—40%*
Многовинтовой геликоптер (включая двухвинтовой). Потеэи у миого-
Винтового геликоптера намечаются следующего порядка (в процентах):
к п. д редуктора т)от=0,95, потери.............5
рулевые bi нты » ............5
охлаждение » ............5
Все потери . . . 15%
Реактивный геликоптер. Реактивный геликоптер имеет полые лопасти,
в которые вдувается центробежным насосом воздух. Этот воздух выходит
из концов лопастей и вращает своим реактивным действием несущий винт,
получается схема Сегнерова колеса** (фш. 14).
* В авторском экземпляре книги рукой Б Н Юрьева сделана следующая пометка
<НЬ может быть при пра&иаьном расчете
- кпд пропеллеров ротора 0,9—0,85. потери . .10—15%
рулевые винты » . -2%
охлаждение » . .5%
Все потери 17—22%
** М Ру а О полезном действии и услотиях применения ракетных аппаратов
ОНТИ. 1936, стр 140
2 Трансмиссия геликоптера
231
Теория такого колеса весьма проста, если считать воздух несжимаемым.
Тяга Q сопла равна секундному количеству движения, создаваемому струей.
Обозначая относительную скорость истечения через v н окружную скорость
на радиусе сопла через U, получаем:
Q = trtv — tnU = m(v — U)~ ?Fcv (v — U).
Здесь tn—-секундная масса, fc — сечение сопла на выходе:
гп = ?Fqv.
Затраченная работа равна разности уходящей и приходящей живой силы
струи, т. е.
У — mv‘ ___07 (у2_________
Полезная работа Т = QrJ. Следовательно, механический кл.д. такой
турбины
Г 2(u — U)U 2U
Л"! — - ~ ,, ~ । •
Т V — и- v + U
Из первого уравнения получаем тягу на единицу площади сопла:
Окружная скорость геликоптерных винтов берется малой нз-за необхо-
димости снять возможно большую тягу с затраченной мощности. Обычно
U — 100 м'сек*. Если заставить воздух вытекать из сопла со скоростью
V— 150 At/сек, то получится довольно хороший к.п.д 71,71 = 0,8. Однако
трудно будет подвести воздух внутрь лопасти, так как в этом случае
Q/Fc = 940 кг/лг. Следовательно, канал для подведения воздуха должен
* Окружные скорости концов лопастей современных несущих винтов достигают
180—200 м/сек. (Прим ред )
иметь сечение в несколько квадратных дециметров, и его трудно вписать
в профиль лопасти.
В этой системе мощность мотора затрачивается сначала на нагнетание
воздуха. К.п.д. нагнетателя можно взять равным 0,75; сам реактивный
аппарат даст, как мы видели, к.п.д. около 0,8. В этих условиях получится
примерно такой баланс мощностей (потери в процентах):
вентилятор т} = 0,75.....................
реактивн. аппарат т|т = 0,8..............
рулевые винты ...........................
охлаждение...............................
25
20
5
Все потери около 50%
Следовательно, в реактивном геликоптере лишь половина мощности
дойдет до несущего вннта н создаст подъемную силу. Это — весьма небла-
гоприятный результат, свидетельствующий против такой системы геликоп-
тера. Эту систему можно несколько улучшить, подогревая воздух внутри
лопастей или сжигая в них горючее (см. труды ВВА № 11, 1934 г.).
Следовательно, в порядке экономичного доставления мощности к ро-
тору, геликоптеры располагаются в такой ряд (|от—коэффициент исполь-
зования мощности):
многовинтоесй без рулевых пиитов, потери 10%............... 0,90
двух- и МНСГСРИН1СГОЙ, потери 15%....................... 0,85
односин1се<й сгсюы Б. Н. Юрьева, потери 25—30% . . 0,75—0,70
одновиитоеой системы Г. Вельнера, потери 35—40% .... 0,65—0,60
1еактиы.ый, потери 50%.................................. 0,50
Здесь коэффициент дает величину используемой для получения тяги
мощности. Он показывает, какая деля всей мощности дойдет до ротора.
Таким образом, в обычные аэ} одинамическне формулы следует подстав-
лять не мощность мотора N, а величину Формулу Вельнера поэтому
надо писать в виде:
Р =
(22)
В тех случаях, когда будет задана значительная высота полета, при-
дется вводить еще запас мощности на взлет до потолка. Кроме того, при-
дется брать коэффициент избытка мощности и писать формулу Вель-
нера в виде:
Р = (23)
Здесь величина
£ = ЫЯ (24)
может быть названа коэффициентом полного избытка мощности.
§ 3. ВЕС РЕДУКТОРОВ И ТРАНСМИССИИ
Для нашего исследования нужно иметь хотя бы грубую, но удобную
для анализа формулу для вычисления веса трансмиссий геликоптера. Ее
необходимо составить так, чтобы вес трансмиссий явно зависел от основ-
ных параметров геликоптера, т. е. от D и N. Сделать это нетрудно. Пока-
жем это на примере общеизвестной формулы Лера и на примере простей-
шего редуктора. Формулы этн зависят от типа передачи.
Затем мы еще более упростим формулы н эудем в дальнейших расче-
тах пользоваться совсем простой формулой (39), которая дает для нашей
цели вполне достаточную- точность.
Формула, предложенная Лером*, имеет вид:
Gr= 16 + 0,05 (1 ф- + (25)
Здесь т = РИНТ'* н Мт = 716,2- - .
лл.отора пт
Анализ этой формулы, сделанный инженером В. А. Доллежалем **, пока-
зал, что в ней нужно коэффициенты для конструкций 1936 г. уменьшить в 1,5—
3 раза. Он исправляет формулу Лера так:
aR = 14 + 0,04 (П- У) м„. + /М2т (26)
и для особо легких планетарных конструкций
GK = 14 + 0,02 (1 + У) М„ + М2„. (27)
Преобразуем эту формулу, введя в иее мощность мотора и диаметр
винта. Для этого находим число оборотов винта по формуле (7) и вычис-
ляем момент на валу мотора по обычной формуле
716’2Т+Ь’
где А/ — мощность мотора и nsm — число оборотов его вала в секунду.
Передаточное число т примет теперь вид:
Теперь формула (27) перепишется в виде:
3 __
= 14 + 0,02-716,2~ -и °-02^16’2 р/ув‘/-;У'л +
0,6.10-4.716,22 /рЗ
г 00- ' 7о - ’
т. е. при заданных р и р формула имеет вид:
Gfi = а + b — + cD'W1 +
nsm
(28)
* «Bulletin Trimstrielle de Service de I'Aeronautique». 1921.
•• В. А. Доллежаль. Редукторы числа оборотов авиационных двигателей. Маш-
издат, 1&36. , '• : ;
Этен фээмулэй можно пользоваться с достаточной точностью, подстав-
ляя в нээ подходя цие значения коэффициентов а, Ь, с н d. Однако для
общего аяалва проблемы полета геликоптера она излишне сложна. Ее
структура такоза, что третий н четвертый члены ее близки к выражению
KD'N, второй член обычно мал, а первый можно отнести или к фюзе-
ляжу иля прямо прибавлять к весу геликоптера в виде постоянной^ при-
бавки.
Можно попытаться’"'наметить весовую формулу для трансмиссий гели-
коптера, рассчитав простейший тнп та сих передач (фиг. 15). Мы интересу-
емся в этой работе не точ4ыми величинами, а лишь тенденциями изменения
веса, поэтому будем искать только струсгуэу формул, а не величину вхо-
дящих в н 1х коэффициентов. Эти коэффициенты должны браться по ста-
тистике передач, построенных или детально спроектированных, вес которых
точзо вычислен.
Пусть мощность от мотора передается на малую шестерню редуктора
(фиг. 15). Для заданного мотора вес этой шестерни не зависит от пере-
даточного числа, так как шаг ее t найдется по обычной формуле деталей
машин’
3 ___ 3 ____
г = 1/Д* = 101/ip!-. . (29)
Г СфХ F сфгп 1
Здесь с — допускаемое на изгиб напряжение, ф—отношение ширины зуба
b к его толщине, z — число зубьев шестерни*. Выбирая минимально до-
* Дли нашей дели достаточно пользоваться этой простейшей формулой
цустнмое число зубьев, получим для данного материала и конфигурации
колеса:
= (30)
Здесь чэрез ku k2, k3 обозначены постоянные коэффициенты. Мы видим
что для данного мотора, т. е. при заданных Л/ и nsl, получаем размеры
первого колеса (например, а{\ вполне определенные.
Вес колеса находим по формуле:
G, = гМ- (31)
Здесь у — условная плотность колеса. Подставляя в это выражение най-
денные значения для b и dlt получаем:
Gi = 7*21/-^1/ V = • (32)
V nsl V Я51 Л51
Здесь с\ — коэффициент.
Ищем теперь вес второго колеса (роторного). Число оборотов ротора
определяем по формуле (7).
Отношение диаметров колес будет
d2 _ -i/Точ
аг - ~ ”я " "тблг
или
3 ____
/рВ£)5
- --Г .
75N
Вес второго колеса получится по формуле (31), которая для данного
случая после преобразований примет внд:
G. = kkji (j/ A. j п\ = ctD"'-N'''nsl. (32')
Вес картера и остальных частей может быть принят пропорциональным
весу шестерен, так как последним определяются все размеры редуктора.
Число оборотов мотооа в настоящее время близко к 1800 об/мин. и может
быть введено в числовой коэффициент, как и вес картера.
У простейшего редуктоэа, построенного по принципу лобовой зубчатой
передачи, вес может вычисляться по формуле:
Вес трансмиссионных валов, передающих мощность от мотора к ротору,
можно подсчитывать следующим образом. Пусть промежуточный вал имеет
число оборотов, равное числу оборотов мотора. Тогда, рассчитывая его на
кручение, находим диаметр:
3 ___
d = (33)
Здесь, как н в дальнейшем, через k будем обозначать различные постоян-
ные коэффициенты.
Вес вала, длину которого можно считать пропорциональной диаметру
роторов (или ротора), найдется по формуле:
3
G„„a = k^D = D = с , (34)
т. е. его нес гочтн пропорционален мощности мотора и диаметру роторов.
Это же произведение входит в формулу Вельнера (6), н для заданного
рнпа винта оно пропорционально тяге ротора, т. е. весу всего ггллхопте-
та G. Следовательно, вес валов может быть вычислен по формуле:
(35)
Считая число оборотов мотора (промежуточного вала) постоянным и от-
нося вес опор вала к коэффициенту, получаем формулу:
G3 = c;,VI/-Z>«c
(36)
Полный вес такой передачи получается по следующей формуле:
G,, = c.N + + csG.
(37)
Для каждого типа трансмиссий мокко получить общие зависимости
веса от мспп:сстн геликоптера, диаметра его винтов н веса всей системы
в полете. Это очень удобно для исследования рациональных размеров ге-
ликоптера какого-либо заданного типа.
Однако для обшего исследования желательно иметь более общую н
простую формулу, не связанную с выбранным типом трансмиссии.
Рассмотрение формулы Лера (28), нашей формулы (37) н ряда просче-
тов имеющихся редукторов позволяет приближенно вычислять вес по такой
упрощенной н осредненной формуле:
(38)
Точность этой формулы не велнка, но она достаточна для общих ис-
следований, которыми мы н занимаемся в этой работе.
Величину cG будем относить к весу фюзеляжа аппарата. Тогда вес
редукторов н трансмиссий в основном получится по формуле:
+ <39’
§ 4. ВЕС ВИНТОВ И РОТОРОВ
Вес самолетных вннтов-пропеллеров 6В можно находить по простой
формуле
GB = kD\ (40)
форма таких вннтов обычно сохраняется одна н та же при различных
диаметрах; изменяется лишь их шаг. Другими словами, такие винты геоме-
В результате обработки статистических данных* получены следующие
средние величины коэффициента веса вннтов k:
деревянные винты без втулки . . . .. ..................0,63
дюралевые винты со втулкой.................................1,63
винты регулируемого шага со втулкой . ................ . . 3,5
легкие полые клепанные дюралевые винты.....................0,0
винты предыдущего типа с передачей и редактором.............3,4
Применительно к роторам гел коптеэоз или автожиров эта формула
будет недостаточно точна, так как эти роторы всегда внимательно рассчиты-
вают на точность, и вес их зависит от нагрузки. Для простых же внитов-
Пропеллеоов довольствуются обцчно пооверочтым расчетом прочности, по-
этому слабэнагруженные винты-пропеллеры бывают излишне прочными н,
следовательно, тяжелыми.
Но и у роторов геликоптера внешняя форма обычно сохраняется при
изменениях диаметра, т. е., выоэав иаивыгоднейшую форму винта, от нее
ие отступают, а стараются силовую конструкцию вписать в имеющийся
объем лопасти. Так как лопасти автожиоа или геликоптера делаются из
тонкостенных профилей, различная прочность их получается за счет различ-
ной толщины стенок профиля.
Основным элементом, определяющим конструкцию лопасти, является ее
лонжерон.
* Б. Н. Юрьев, Воздушные винты. ОНТИ, 1934.
Рассмотрим вес лонжерона. Для получения формул будем считать сече-
ние лонжерона кольцевым (труба) диаметром d и тол циной тонкой стенкн
Ъ (фиг. 16). Тогда в опасном сеченин на этот лонжерон будет действовать
изгибающий момент М, находить который можно по формуле-
М -- kxDP -= fejDG,
где Р — тяга, равная при висении весу геликоптера G, приходящемуся на
один винт, и D — диаметр вннта, a — коэффициент*.
Для воспринятия этого момента потребуется модуль сечеиия лонжерона-
(41)
в
где ов — допускаемое на изгиб напряжение.
Для кольцевого тонкостенного сечения, как известно,
= (42)
и формула (41) перепишется в виде:
0,16^ = ^
° в
Отсюда
Для винта заданной формы и числа лопастей d~kdD, где kd—коэф-
фициент пропорциональности. Отсюда
й — k*DG — G
Вес лонжерона найдется по его объему и по удельному весу т, т. е
Для лонжеронов, сделанных из одного материала, у и бв будут неиз
менными, и мы получаем формулу:
= kGD, (43)
Не следует думать, что указанный вывод относится лишь к винтам с
жесткими лопастями. В случае взмахивающих лопастей изгибающий момент
хотя и получится значительно меньшим, но все же он будет существовать
и будет пропорционален величине GD. Следовательно, машущие винты бу
дут иметь меньший коэффициент k.
Полный вес ротора можно принять в основном пропорциональным весу
лонжеронов Тогде вес всего ротора можно вычислять по формуле1
GpoT = feGD (44)
Б Н Юрьев Воздушные винты, стр 136.
Величина k должна браться из статистики. По нашим подсчетам можно
принимать ориентировочно следующие величины fe:
жесткий ротор с автоматом перокоса и валом, ротор с
тандемными винтами типа Бреге ..........
жесткий ротор и ват ....................
двойной ротор с автсматом перекоса .....
ротор со взмахгвающими лопастями и валом
ротор автожира . ...............
1
ЬО
ьо ’
1
70 ’
1
80’
1
100
В более точную формулу веса этих роторов войдет и постоянная величина
и величина, пропорциональная общему весу вс_го аппарата. Но основная
зависимость веса ротора от его размеров и мощности выражается, по-види-
мому, этой простой формулой достаточно хорошо. В тех случаях, когда
это нужно, вес ротора может быть рассчитан точно по его чертежу.
Кроме указанных винтов-пропеллеров и роторов, на геликоптерах мно-
гих систем встречаются еще рулевые винты Они имеют обычно малый диа-
метр DK = 1 —2 м, делаются из листового дюраля и имеют поворотные
лопасти. Такие винты (Омишеи, Аскаиия, Берлинер и др) обычно очень
легки Их вес приближенно можно вычислить по формуле:
G = 0,6Z)x-
(45)
Вес рулевых вннтов вместе с редуктором н валом, передающим к ним
мощность, можно грубо оценить формулой
6^3,5Ох3.
(46)
Диаметр рулевого виита зависит от мощности н диаметра ротора. В общем
можно предполагать, что их вес будет пропорционален общему весу фюзе-
ляжа и трансмиссий. Вводить в расчет вес этих органов управления гели-
коптером можно просто, несколько увеличивая числовые коэффициенты,
входящие в формулу веса фоззляжа и трансмиссий. Изложенных данных
Достаточно для вычисления общего веса геликоптера с той грубой точно-
стью, какая нужна для наших общих исследований
§ 5. ПОЛНЫЙ ВЕС ГЕЛИКОПТЕРОВ
Пользуясь приведенными формулами, можно вычислить приближенно вес
геликоптера. В него нужно включить еще вес самого корпуса (фюзеляжа)
и вес моторной группы
Вес фюзеляжа с рулевыми поверхностями можно считать равным (как
и у самолета) 0,15—0,2 полного веса. Вес моторной группы можно считать
пропорциональным мощности мотора, т е.
- GM = kMN. 1 ™ г (47)
В этот вес мы будем включать вес всей моторной установки с охлаж-
дающей системой, органами управления и контроля и вес основных баков.
Вес горючего и смазочного материала можно вычислить при /-часовом
полете по формуле:
5Г = CeNt, (48)
где Се—-удельный расход горючего и смазочного материала, равный в сред-
нем 0,25 кг/л. с. ч для моторов водяного охлаждения и 0,285 кг/л. с. ч —
для моторов воздушного охлаждения.
Путем сравнения получающихся весов с весами самолета и автожира
н обработки Статистики геликоптеров можно наметить следующие прибли-
женные формулы для вычисления веса конструкции всего аппарата GK.
Самолеты *:
С» = С(°-3 + ^<г)- (49)
Здесь G— полетный нес, / — раамах крыльев. В среднем получается:
GK Q,3bG. (50)
Автожиры крылатые:
Ск = б(о,35 + ^). (5!)
В среднем
GK = 0,453.
Автожиры бескрылые:
6К = 6(0,25 + ^). (52)
В среднем
6к = 0,355.
Геликоптер одновинтовой с жестким винтом н автоматом перекоса:
= + + (53)
В среднем
5К = 0,505.
Геликоптеры одновинтовые со взмахивающими лопастями и автоматом
перекоса:
С»“С(0.2+4) + Л'(0,1 + 1^г). (54)
В среднем
GK = 0,455.
* Б. Н. Юрьев Пределы современной авиации и способы их преодоления. Изд
НАГИ, 1936
Геликоптеры одновинтовые со взмахивающими лопастями и рулевыми
винтами:
Gk = G(0.25 + HL) + 5/(0,1 + -^7-). (55)
В среднем
GK = 0,48G.
Геликоптеры многовинтовые со взмахивающими лопастями и рулевыми
винтами:
= 0(0,25 +HL) .^(0,1 + ^L-). (56)
В среднем
GK = 0135 — 0,403.
В этих формулах первый член 0,25 G — в основном вес фюзеляжа с
GD
рулевыми винтами и рулевыми поверхностями, член ---вес ротора и вала
/ D3 \
и член — в основном вес трансмиссий геликоптера. Эти
коэффициенты подобраны иа основании ряда описанных в литературе типов
геликоптеров и дают довольно хорошее совпадение с действительными
результатами. В общем эти формулы, несмотря на их простоту, дают впол-
не достаточную для нашего общего исследования точность.
Имея точные данные весов для того или иного типа геликоптера, мож-
но всегда уточнить весовую формулу. Так, например, по опубликованным
данным о геликоптере системы Бреге*, мы получили следующую уточнен-
ную для этого типа геликоптера формулу:
Ск = с(о,175+^-) + ^(О,1 + ^г). (57)'
§ 6. СТАТИЧЕСКИЙ ПОТОЛОК ГЕЛИКОПТЕРА
Статическим потолком геликоптера назовем ту предельную высоту,
иа которую он сможет подняться при отсутствии горизонтальной скорости
полета. При наличии последней, как увидим, потолок значительно повышается.
Разберем сперва потолок геликоптера с невысотным мотором. Тогда мощ-
ность мотора будет изменяться с высотой по общеизвестной формуле
Ny = A’oA, (58)
где величину А можно брать по американской формуле, дающей следую-
щую зависимость:
1591
«Chronique des avioys>, 1935, № 4: 1936. № 8
здесь у — высота полета (в метрах). Плотность воздуха иа этой высоте
получится по формуле Бьеркеиса:
, и \4,25й
Р = Р» (1 - -44МГ) <60>.
Тяга виита на высоте может быть вычислена по формуле Вельиера (4) *.
Подставляя в иее указанное значение р и Ny, получим:
- [0 - 4ЙЮГ’3^Г - О - -^Г"' •
Величина (aNeD) —наибольшая тяга, какую разовьет геликоптер у земли-
Назовем ее через Ро. На потолке (у—Н) подъемная сила равна весу, т. е*
Р^ = С.Следовательио, предыдущая формула будет иметь вид:
Отсюда
<б1>
Если задаться рядом значении высот потолка, то можно вычислить вели
чину G/Pq или, что удобнее, P^/G. Последняя величина дает избыток тяги
у земли, необходимый для заданного потолка. Ниже даиы полученные по
формуле (61) значения:
И, м . ,. 1000 2000 2215
G
-гг . . . 0,90 0,797 0,777
“ о
-ТгЧ . . 1,11 1,25 1,29
О 1 ’
3000 4000 4430 5000
0,708 0,627 0,592 0,552
1,41 1,59 1,70 1,81
На фнг. 17 эта зависимость представлена графически. Из графика видно,
что для получения больших высот полета требуется весьма большой избы-
ток тяги. Так, для получения потолка 2215 м требуется почти 30%, а для
потолка 4430 м— уже 70% избытка тяги.
По формуле Вельнера получим следующий необходимый избыток мощ-
ности мотора:
Ро = (aNQD)2/i = const N^3
или
Az0 = const Pq/2.
Для отрыва от земли потребуется мощность
W = const G>fi
Отсюда избыток мощности будет
,б2)
Б. Н. Юльев Воздушные винты. ОНТИ, 1934. стр. 173.
Л ля избытка тяги, равного 1,3, потребуется, следовательно, увеличе-
ние мощности по формуле
1н = 1,3,Л = 1,48,
т. е. избыток мощности в 48%.
Фиг. 17
Ниже приведены значения коэффициентов избытка мощности необходй-
мые для достижения соответствующего потолка Н:
м . 1000 2000 2215 3000 4000 4430 5000
. 1,17 1,40 1,48 1,68 2,00 2,22 2,44
Видно, что потолок у геликоптера получается низкий. Отсюда вырс; ,
что на геликоптеры, как и на самолеты, желательно ставить высотные
моторы. В таком случае величина А будет задаваться эмпирически, ее при-
дется брать по высотной внешней характеристике мотора.
Формулу Вельнера придется в этом случае иаписать в таком виде1
Р, = (/7.94^.п,ВД’л =
= _ (Л /Л)’-'' Р„ = G
Отсюда „ ,‘и
Л ’ -т-Л ' - ^ = (ЛУХ)’-. " ' . :Д63,
1Ь*
Удобнее знать не избыточную тягу, а избыточную мощность, потребную
для достижения заданного потолка. Ее очень легко вычислить по форму-
ле (62), подставив в нее величину б/Р0 формулы (63).
Проделав это, получим окончательно
Величина Л]/Д встречается в аэродинамическом расчете самолета, и
имеются готовые графики и таблицы ее значений.
Мы приводим график (фиг. 18) и табл. для условного высотного МО-
тора с пределом высотности 5000 м. Его высотная характеристика даиа
на фиг. 19.
У Л А А /Г Ън
0 1 1 1 1
1000 ’0,9073 1,04 0,99 1,01
2000 0,8215 1,08 0,978 1,02
3000 0,7410 1,12 0,965 1,03
01' 4000 0-6685 1,16 0,950 1,05
S3 5000 0,60и7 1.20 0,931 1,07
6000 0.5383 1,03 0,757 1.32
7000 0,4810 0,92 0,637 1,56
8000 0,4284 0,77 0,504 1,98
9000 0,3804 0,67 0,413 2,42
10000 0,3366 0,60 0,348 2,88
С высотным мотором потолки значительно возрастают, но при этом
несколько возрастает вес мотора из-за нагнетателя. Кроме того, воз-
растает вес охлаждающей системы.
..Из данных видно, что у выротных моторов потребный избыток мощ-
ности значительно меньше, чем V невысотных. Для достижения высо-
ты 1000 At требуется избыток мощности лишь 5°/о> а ранее требовалось
100%.
Однако после 5000 .и (высотность взятого мотора) потребная мощ-
ность начинает катастрофически расти. Следовательно, геликоптеры в
Фиг. 19
том виде, как они мыслятся в настоящее время, ие смогут поднимать-
ся иа большие высоты.
Напомним снова, что оечь здесь шла о статическом потолке гели*
коптеров, получающемся при вертикальном взлете. При наличии го*
ризонтальной скорости получается значительно более высокий пото-
лок (см. §>5 главы 3).
Глава 2
ВЕРТИКАЛЬНОЕ ДВИЖЕНИЕ ГЕЛИКОПТЕРА
§ 1. ВЗЛЕТ ГЕЛИКОПТЕРА. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ
У вертикально взлетающего геликоптера роторы работают на режиме
пропеллеров. Они преодолевают вес геликоптера, сопротивление воздуха и
возникающие при ускоренном движении силы инерции.
Уравнение вертикального движения геликоптера пишется так:
г dV
P = G + 0,64.oPV: + -~^. (65)
Здесь о—эквивалентная вредная пластинка геликоптера при вертикальном
взлете, Уу — вертикальная скорость; остальные обозначения обычные, такие
же, какие приняты в самолетостроении. Влияние обдувки невелико; его мож-
но не учитывать или относить, как это делается в самолетостроении, к тяге Р,
уменьшая ее иа оодувку. Для этого берем пониженную величину коэффи-
циента а в формуле Г. Вельнера (§ 1).
Для решения этой задачи нужно злать зависимость Р от Vy. Другими словами,
нужно построить обычную характеристику винтомоторной группы для ротора,
рассматривая его как пропеллер.
К сожалению, имеется весьма немного исследований винтов малого шага
на режиме пропеллера. До сих пор наиболее подробными исследованиями
являются английские опыты* и опыты ЦАГИ**.
Для роторов следует брать винты с шагом /1 = 0,3—0,5. Такие шаги
обычно и были у построенных геликоптеров.
Фиг. 21
Геликоптерные винты работают при взлете на малых Л, так как на боль-
ших X тяга их сильно падает. Избыток тяги вряд ли будет превосходить
вес геликоптера более чем иа 30—50%, и роторы при взлете будут обычно
работать на начальном участке характеристки винта а — В этом слу-
чае характеристику можно считать прямой линией. Проводя касательные
иа диаграммах фиг. 20, грубо ориентировочно можно найти, что а = 0 при
kn^2/i (кривая 1 — винт № 1, /1 = 0,3, i = 4, b/D =0,082; кривая 2—виит
№ 2, /1 = 0,5, г = 3, b/D = 0,082).
Винты у геликоптера, как правило, имеют изменяемый в полете шаг
Следовательно, расчет винтомоторной группы можно вести, исходя из ус-
ловия п = const.
Решение задачи взлета чисто аналитически ведет к сложным и не на-
глядным формулам. Проще вести расчеты графически, ио в несколько
обобщенном виде.
, Графический расчет взлета геликоптера. Обозначим тягу винтов-роторов
через Р = £6, где £— функция скорости и высоты полета. Если пренебречь
• RM-829, 1922.
** «Техника воздушного флота», 1936, № 4.
малой величиной вредного сопротивления и ускорением при взлете, то из
уравнения (65) получим
P = G. (66)
Назовем такой взлет медленным (безынерционным). Тогда, имея харак-
теристику винтомоторной группы (фиг. 21), мы решим задачу простым на-
несением на нее линии постоянного веса GGt. В точках пересечения /, 2, 3...
получим скорость Vy установившегося на каждой высоте режима подъема
геликоптера.
Фиг. 22
Не представляет никакого труда нанести на эту диаграмму и лобовое
рр2
сопротивление, равное 1,28—£-з, которое дает иа фиг. 21 параболу GA.
Точки Г, 2', 3'... определяют скорость взлета с учетом лобового со-
противления. Удобно внизу на диаграмме разбить ось ординат по высотам.
Тогда внизу можно построить кривую Vy ~ f (у). Эта кривая дает в точке
пересечения с осью абсцисс величину потолка самолета.
Пользуясь этой кривой, можно тем же приемом, как и для самолета,
вычислить барограмму взлета. Для этого замечаем, что
Отсюда
dt = ——dy
V у
или
(67)
о Vy
Построим вспомогательную кривую —1— и, планиметрируя ааштрихован-
vu
$ 2. Графический расчет взлета геликоптера
249
ные на фиг. 21 площади F, получим для любой высоты у величину потреб-
ного иа взлет времени t. Другими словами, мы получим данные для по-
строения барограммы взлета фиг. 22.
После этого можно учесть силы инерции и исправить полученную баро-
грамму. Для этого ищем, по фиг. 22 ускорение, нанося иа кривую, дающую
скорость \'у как функцию времени. Из формулы
dV„
а = (68)
видно, что ускорение получится на диаграмме, как тангенс наклона кривой
у =f(t). Найдя величину ускорения, мы можем вычислить силу инерции
G dv
-----— и отложить ее на верхней части диаграммы (фиг. 21) в виде добавка
S dt
к ординатам кривой GA. Получится новая кривая GB, которая пересечется
с кривыми тяг и точках 2", 3" и т. д.
Теперь будут учтены и силы сопротивления 1,28
рЦ
2
б, и силы инерции
G dV _
-----—. При этом скорости взлета несколько изменятся, придется снова
Я, dt
повторить все построения и иайти новую, исправленную барограмму. Такую-
работу иужио вести до тех пор, пока ие перестанут заметно изменяться
получающиеся каждый раз барограммы. Следовательно, таким приближен-
ным методом мы можем решить полное уравнение (65), учитывая, что
p = f(V„,y).
Заметим, что вследствие малой мощности всех построенных гели-
коптеров силы инерции и сопротивление фюзеляжа играют при взлете
весьма подчиненную роль и во многих случаях могут не учитываться.
Отметим также, что при обычном расчете скороподъемности само-
летов силами инерции, как правило, пренебрегают, хотя у самолета
вертикальные ускорении иногда бывают в несколько раз большими,
чем у геликоптеров.
Описанное построение удобно тем, что можно воспользоваться лю-
бым законом характеристики винтомоторной группы (например, по-
строить ее для высотного мотора).
§ 2. ГРАФИЧЕСКИЙ РАСЧЕТ ВЗЛЕТА ГЕЛИКОПТЕРА
С ИНТЕГРИРОВАНИЕМ ПО СПОСОБУ МАДЕЛУНГА
К расчету взлетных свойств геликоптера легко применить хорошо из-
вестный нашим самолетчикам спосоо интегрирования, предложенный Л1а-
делуигом. Ои заключается в том, что на полосе, заключенной между кривой
тяги и кривой сопротивления, строится зигзагообразная линия («змейка»),
дающая ответ о затраченном иа ускорение машины времени. Обычно этот
метод применяется для расчета разбега самолета. Мы приспособим его для
асчета взлета геликоптера. Пусть у нас на тяговой диаграмме (фиг. 23)
аиесены кривые тяги Р, веса G и воздушного сопротивления В. Избыток
рУ*
тяги Р' ~ Р — G — 1,28—тр-з пойдет иа сообщение геликоптеру ускорения а.
При этом
а
“У*
dt
Если взять малый интервал времени, равный А£ сек., то скорость в те-
чение его изменится на величину ДУ^. Следовательно, предыдущую формулу
можно заменить приближенной:
-сможем легко построить формулу (69)
Д1/ g
_____Ч, _ 6 р>
Ы____G
или
= -*-Р'Ы. (69)
G
Если взять малый интервал
времени, например 2 сек., то
скорость увеличится на величи-
ну АУу, пропорциональную Р',
Разбив весь процесс взлета на
равные интервалы времени Аг,
графически. Она примет вид:
ДК, = cP'.
(70)
.Величина с будет постоянной. Проведем теперь змейку на фиг. 23, прини-
.мая тангенсы наклона ее отрезков по отношению к оси ординат равными с.
Тогда разность абсцисс двух полученных соседних точек будет определять
изменение скорости за интервал времени Af (например, 2 сек.), а абсциссы
дадут получившуюся скорость. Время получится простым подсчетом числа
интервалов. Далее можно по-
строить кривую Vy =- f (/) и вы-
числить обычным путем баро-
грамму взлета. Пользуясь этим
графиком, можно быстро полу-
чить характеристику взлета
геликоптера у земли. Расчет
на больших высотах вести
указанным приемом более труд-
но, так как вместо одной
кривой тяги = мы
должны будем найти ряд
кривых для разных высот
[Р =f(Vy, у)]. Придется вычис-
лить сначала барограмму при-
ближенно, затем, зная высоты,
Фиг. 24
делать пересечения змейки с
кривыми тяги для соответствующих высот и последовательными приближе-
ниями получить точный результат. Для ускорения работы желательно оп-
ределить, хотя бы грубо, высоту при получении засечек змейки. В способе
Маделунга сделать это нетрудно. Для этого нужно для каждого звена змей-
ки подсчитать высоту подъема.
Беря среднюю скорость в каждом интервале и умножая ее на Af, полу-
чим величину пути Аг/, пройденного за интервал времени АЛ Сумма
этих величин дасг высоту полета, и по ней можно будет выбрать нужную
кривую нз характеристики винтомоторной группы (фиг. 24). Получится
змейка, вершины которой будут лежать на различных кривых тяги ротора.
§\3. Аналитическое решение задачи о взлете геликоптера
251
При этом придется иногда проводить недостающие интерполяционные кри-
вые на глаз.
В общем и этим способом можно:получить точную увязку всех вели-
чин и решить задачу с любой точностью.
6 3. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ О ВЗЛЕТЕ ГЕЛИКОПТЕРА
Силы инерции играют заметную роль лишь в самом начале взлета. Да-
лее можно считать движение псевдоустаиовившимся (безынерционным) и
вести расчет по формуле:
рК3 --
P^G^r\,^ — c
2
или даже по формуле
Р =TG.
' Вследствие этого можно, ' построив точную.' барограмму для высоты
50—100 м, продолжить ее (§ 1 главы 2) простым^построением, без учета
Фиг. 25
инерции геликоптера. Для высоты же до 100 м можно пренебрегать из-
менением плотности (конечно, все эти рассуждения справедливы для гели-
коптеров с потолком не менее 2000—3000 .и). Тогда тягу можно предста-
вить линейным законом (фиг. 25):
P = P0-pV„ . (71)
где р, как видно из фиг. 25, найдется так:
Vo
Здесь Уо — скорость, при которой тяга равна нулю. Уравнение валета на-
пишется теперь в виде:
Pa-pV„ = G+ 1,2841 □ 4--- (72)
2 е df ' '
или
dV„ pg в а
4-—V„ + 1,28-^ а- + —(G-Po) = O,
Л ' G " ‘ ' 2 Q О ' '
т. е. получилось дифференциальное уравнение типа
~ + yb + y'‘hi + с = 0.
dx
Его решение дает крайне сложное выражение. Можно уравнение движения
PV2
упростить, пренебрегая малыми силами сопротивления воздуха 1,28—— с.
Тогда он? примет вид:
dV„ рт g
<73>
Получилось линейное уравнение первого порядка ст- свободным членом
типа
—- -}- ау 4- с = 0,
dx
Его решение, как известно, таково:
у = И “dx (с - 5 С J “ ixdx) = С------с- е" )..
В нашем случае оно напишется в виде:
\ р J р
Постоянная С найдется из граничных условий:
Vy = 0 при / 0.
Это дает
с = ^.
р
Теперь уравнение перепишется в окончательном виде:
= (74)
р
Это уравнение дает возможность вычислить скорость в функции времени.
Для нахождения уравнения барограммы вычисляем величину у как
функцию t. Заметим, что
Отсюда
dy ~ Vy dt.
Подставляя в последнюю формулу
я интегрируя, получим окончательно:
найденную величину скорости (74)
(75)
Полученные выражения для V у и у удобнее сделать боАее общими. Для
этого вводим в формулы (74) и (75) величину коэффициента избытка тяги
£ = —. Вводим в расчеты еще скорость Vo. Последнюю легко найти для
G
каждого частного случая; кроме того, она довольно постоянна у обычных
геликоптеров. Ее будем брать по фиг. 20, проводя Касательную. В § 1
главы 2 мы видели, что
2й.
Отсюда
Vo = A.0Drts^.2/tDns.
Обычно у геликоптеров
h0,4—0,5 и Dn&^'30—40.
В среднем получим!
Ув — 30 м/сек; р = .
Vo Vo
Введя эти величины в расчет, получим из формул (74) и (75) следующие
более удобные выражения:
^ = ^^(1-^'). (76)
г/ = А—[/„ (t Н-— е~^~ — . (77)
I I 5S U J
Подставляя сюда средние значения £ = 1,2, = 30 м.[сек и считая
g^ 10 м/сек? t получим:
^ = 5(1~Дг'Ь <78>
(79>
Заметим, что избытку тяги £ = 1,2 соответствует, по графику (фиг, 17)
потолок порядка 1700 м. У земли, в конце разгона геликоптера (£—> оо).
скорость по формуле (76) будет равна
v’y = « 5 м!сек.
Каким бы способом ни вычислять скороподъемность геликоптера,
рыгоднее сперва вычислить вертикальную скорость без учета сил
инерции (фиг. 26,/). Получится крив'ая которая определит
потолок геликоптера совершенно правильно, так как сила инерции и
скорость у потолка равны нулю.
-Эта кривая для невысотного мотора очень близка к прямой линии»
и ее можно приближенно’построить, соединив прямой две точки: точку
Н, определяемую высотой потолка, и точку В, соответствующую
безынерционной скорости у земли, р-авножв нашем случае приблизатель-
но 5 1л!сек, .и. .ч Л.
После этого следует рассчитать по формулам (76) и (77) взлет у
земли с учетом сил инерции. Получится кривая ODC, имеющая ассимп-
тотой ординату в точке В (фиг. 26,-2).
В точке D кривые пересекутся. Если теперь считать, что у самой
земли разгон геликоптера идет по кривой ODC, а на высоте — по кри-
вой ВН, то, соединив Главной линией обе кривые около точки D, мы
получим достаточно точную кривую скорости по высоте с учетом раз-
гонного участка взлета
В нашем среднем случае получились следующие данные: потолок
1700 м, скорость безынерционного взлета у земли У/==5 1л(сек.
Кривые разгона могут быть построены по следующим данным-
t, сек . . . 0 2,2 5,0 10,0
Vy, м/сек . О 3,14 4,32 4,9
у, м . . . . 0 4,62 14,1 38,0
На основании этих данных построена фиг. 26, а по ней (§ 6 главы 1),
вычислена барограмма взлета (фиг. 27). Видим, что геликоптер с
невысотным мотором при вертикальном взлете уступает самолету. Гели-
коптер с указанными параметрами достигает высоты 500 м за 2 мин.,
высоты 1000 м— за 5,1 мин. и высоты 1500 м— за 11,8 мни. Через
10 сек. движение можно считать уже безынерционным, так как скорость
взлета равна 4,9 м)сек, а скорость установившегося движения в нашем
случае равна 5 м/сек.
В случае высотного мотора результаты получаются значительно»
лучше.
Глава 3
ДВИЖЕНИЕ ГЕЛИКОПТЕРА С ГОРИЗОНТАЛЬНОЙ СКОРОСТЬЮ
§ I. ПЛАНИРОВАНИЕ ГЕЛИКОПТЕРА
Под планированием геликоптера мы понимаем спуск без мотора под
углом к горизонту. В этом случае винт авторотирует свободно и [1 — 0.
Поляра для этого случая приведена на фиг. 28. Ее принято изображать
не с помощью винтовых коэффициентов, а с помощью обычных коэффици-
ентов аэродинамики н су. Тогда
2
Y = c„-^-F,
У 2
*~^F,
(80)
(81)
(8z)
где F— отметаемая ротором площадь.
Фиг. 28 относится к винту, испытанному в ЦАГИ*. Особый интерес
представляет поляра на малых углах атаки. Наиболее совершенным иссле-
дованием являются амернкаискне опыты, проделанные в самолетной трубе в
«Langley Field» с ротором автожира РСА-2 в натуру**
* Труды ЦАГИ. № 47. 1930
• NACA-515. 1935
В дополнение к этим кривым приходится пользоваться еще кривой
приведенной на фиг. 29; здесь i — угол атаки плоскости вращения.
Для полного изучения вопросов планирования нужно иметь кривую не
только для данного угла установки лопастей qr, а для ряда углов. Этих
материалов опубликовано довольно много; к сожалению, большинство их ие
систематизировано. Желательно в ближайшее время проделать исследова-
ния, подводящие итоги всем этим работам.
Если имеется поляра описанного типа (фиг. 28), то аэродинамический
расчет планирования геликоптера, по существу, ие отличается от аэроди-
намического расчета планирования самолета.
Нужно/, как известно, для каждого угла атаки ротора i найти коэффи-
циент полной аэродинамической силы
cR=V^T^, (83)
который можно брать прямо по поляре, если она построена с одинаковыми
масштабами для сх и ctl. Затем, приравнивая полную аэродинамическую
силу весу аппарата, получаем скорость полета по траектории
г. V2
R = G-cr^-F.
Отсюда
Угол планирования у получится как угол между вектором cR и осью ор-
динат иа поляре. Аналитически это значит, что
tg Г J V” •
су
По этим данным можно построить кривую — указательницу глиссад для
геликоптера, совершенно аналогичную такой же кривой, построенной для
самолета.
Удобно при этом кривую Лилиенталя вычерчивать так, как показано
на фиг. 30. Тогда, взяв какой-нибудь угол атаки i, мы можем, проведя
луч 01, иайти по масштабу коэффициентов величину cR = Oi. Далее нахо-
дим скорость V по формуле (84).
Угол плакирования у определится при этом как угол между осью
скоростей и Oi (фнг. 30). Отложив вектор в масштабе скоростей, най-
дем точку V указательницы глиссад. Проделав такое построение для
ряда углов атаки, найдем, соединяя копны векторов V, указательницу
глиссад геликоптера. В точке А получится иаивыгоднейший угол пла-
нирования геликоптера, дающий наибольшую дальность планирования
с заданной высоты, в точке В— угол атаки, соответствующий мини-
мальной скорости снижения геликоптера. Точно так же, как и у само-
лета, получаются здесь два режима планирования, разделяющихся иа
наивыгоднейшем угле планирования, в точке В.
Интерес представляет наивыгоднейший режим (точка А), так как
с ним связана дальность планирования и экономический режим (точ-
ка В); при полете на этом режиме можно получить наименьшую ско-
рость снижения геликоптера. Точка С соответствует максимальной ско-
рости горизонтального полета.
Оказывается, что геликоптеры и автожиры планируют значительно
хуже самолетов. Наибольшее качество у ротора весьма невелико,—
порядка 7—8 при малых углах установки лопасти. Сам геликоптер
до настоящего времени имеет громоздкую конструкцию, дающую боль-
шое лобовое сопротивление. В результате общее качество геликоптера
или автожира равняется 4—6, что дает довольно крутой предельный
угол планирования.
Наименьшая скорость снижения оказывается меньше скорости
вертикального парашютирования.
Для обычных роторов — Это показывает, что при спуске
геликоптера под углом к горизонту вертикальная скорость получится
значительно меньшей, чем при вертикальном спуске. Так как при этом
скорость по траектории будет заметно больше, чем при вертикальном
снижении, то путем увеличения у земли угла атаки I всего геликопте-
ра можно значительно снизить и даже сделать нулевой вертикальную
скорость. Таким образом, посадку можно произвести совершенно так
же, как иа самолетах, или, говоря точнее, как на автожирах. Это спо-
собствует безопасности спуска. При расчете планирования приходится
учитывать и число оборотов ротора. Его легко находить по продувоч-
ной диаграмме (фиг. 29), дающей Л=/(/). Зная Л и V, находим число
оборотов ротора диаметром D я по формуле:
Отсюда
"s = DZ <85)
Возникает вопрос, при каком угле установки лопастей ротора ф
следует планировать^* Многочисленные исследования показывают, что
выгодными являются углы порядка 2—4°. При этом выгодно иметь
лопасти плоские, т. е. шаг винтовой поверхности должен быть нуле-
вым при ф = 0°. Хорошие несущие винты-роторы имеют шаг поверхно-
сти лопасти порядка 0,2—0,5 и несимметричные профили, следователь-
но, они планируют несколько хуже специальных роторов, рассчитан-
ных на планирование. Угол установки ф (или Л) получается у них при
планировании отрицательным. У нас диаграммы (фиг. 28 и 30) по-
строены для геликоптерного винта, плохо планирующего.
Однако степень ухудшения не столь велика, чтобы из-за этого при-'
ходилось значительно ухудшать аэродинамические характеристики не-
сущего винта на его основном _ геликоптериом режиме. Приходится
выбирать некоторый компромисс и у поворотной лопасти делать шаг
порядка 0,15—0,25, доводя его до величины 0,4—0,5 путем поворота.
Тогда такой впит, потеряв очень немного на основной своей работе,
работает неплохо и как планирующий. Заметим, однако, что многие
конструкторы применяли у геликоптеров и плоские винты (Бреге, Иза-
ко), которые планируют при положительных ф. В нашу задачу не вхо-
дят вопросы расчета самого ротора, и мы ограничимся здесь приведен-
ными материалами.
Укажем также, что в случае остановки мотора летчику нужно сраз\
же уменьшить угол установки лопастей ф н дать геликоптеру угол
наклона вперед.
Неоднократно строились геликоптеры с поворотными лопастями,
снабженными, подобно самолету, стабилизаторами (Асканиа, Изако,
Бликкер и др). Такие лопасти должны сами, автоматически перево-
дить ротор геликоптера иа планирование. Однако имеющиеся опыты,
главным образом американские, показывают, что такие вииты плохо
работают на режиме поддерживания.
Во всяком случае, этот режим геликоптера — режим планирования
хороню изучен в настоящее время на автожирах, и применение его
на геликоптерах не представляет ничего загадочного или неизвестного.
§ 2. ПОЛЯРЫ РОТОРОВ
Для изучения полета геликоптеров с горизонтальной скоростью
необходимо знать действие их роторов При обдувке под различными
углами атаки. Эти исследования начались давно, ио далеко не закон-
чены. Первая теория винта, обдуваемого потоком сбоку, была разви-
та Н. Е. Жуковским в 1908—1909 гг. В 1909 г. были проведены в Ку-
чинском аэродинамическом институте первые опыты с такими вин-
тами. В более поздние годы эти опыты ставились Маргулисом во
Франции (1922 г.), Flahsbart.H Krober в Германии (1929 г.). В 1930 г.
такие опыты уже велись в ряде стран. Обширные опыты были прове-
У
дены в ЦАГИ * в период с
1927 по 1936 г. Обширные ис-
следования ведутся в аэроди-
намической лаборатории Воен-
но-воздушной академии.
Общая картина работы вин-
та в этих условиях изучена до-
статочно хорошо; однако мно-
гие стороны данного явления
освещены еще недостаточно.
Рассмотрим полученные ре-
зультаты. Введем следующие
обозначения (фиг. 31). Ротор
связан с системой осей коорди-
нат Ал, У\, Z[. Поточные оси
обозначим, как обычно, х, у, z.
Тягу винта по иормали к плос-
(ииогда будем применять и винто-
хости вращения обозначим через V]
вое обозначение Р).
Остальные компоненты будем обозначать по обычным правилам экспе-
риментальной аэродинамики. В поточной системе осей получаются три си-
ловых компонента X, Y, Z и три момента Мх, Му и Mz.
Компонент в связанной системе дает момеит, вращающий винт.
Для приведения результатов к безразмерным величинам вводят абсолют-
ные коэффициенты:
pD4n^
pDbi*
- - Z
pD<n* ’
R .
(86)
где
R = У № + Уг + Z2;
«Техника воздушного флота», 1934, № 8; 1936, № 4.
pDsn*
pD’n*
pD5n*
(87)
и в поточных, и в связанных осях
коэффициент момента относительно
Эти коэффициенты можно вычислять
координат.
Особенно большое значение имеет
оси г/j — это момент вращения винта:
X = Х^
pZJ’Hj • '
По этому моменту находится мощность, потребляемая винтом. Обычно
для вычисления мощности пользуются безразмерным коэффициентом мощ-
ности винта |i, применяя формулу подобия
W = (89)
Из соотношения
N = Му2яп5
следует формула*, связывающая коэффициент х с коэффициентом
Угол атаки ротора обозначим через i. Его будем отсчитывать
скости вращения. Кроме этих коэффициентов, вводим еще два:
— обычный коэффициент скорости винта (число Струхаля) и
(90)
от пло-
(9В
(92)
е. нахо-
— к. п. д. виита-ротора как пропеллера.
В результате опытов обычно строят поляру винта-ротора, т.
дят ах, cLy и 3 в зависимости от i и К. Этих данных вполне достаточно
для аэродинамического расчета геликоптера. Остальные величины изуча-
лись пока мало; онн необходимы для расчета геликоптера на устойчивость
и управляемость. Мало изучены винты с шарнирными лопастями. Большин-
ство исследований проведено по винтам с жесткими лопастями.
* Б. Н. Юрьев. Воздушные винты, стр. 88.
В результате таких исследований даются кривые ах, ау и р по i и X
Фиг. 32
Л’=/0,4, лаборатория ВВА). Кривая X = 0 представляет собой окружность;
при возрастании X кривые смещаются вправо, и прн Л = 1—1,5 ах стано-
вится положительной, т. е. ротор дает сопротивление.
Компонент &у по мере увеличения X обычно растет. Кроме этих кри-
вых, строится сетка коэффициента мощности £ (фиг. 33) (винт № 14,
h = 0,4, лаборатория ВВА). Для полного анализа проблемы геликоптера
нужно иметь подобные кривые для разных относительных шагов h (илн ср),
так как у геликоптеров винты делаются обычно с поворотными лопастями.
Для изучения всех режимов необходимо иметь углы атаки от -ф 90 до
—90°.
До настоящего времени полных исследований еще не имеется,
в одних взяты более широко одни параметры, в других — другие. Для
нашего общего исследования приходится получать поляру комбини-
рованием ряда исследований. Следовательно, она носит условный ха-
рактер.
В настоящее время на многих геликоптерах делаются шарнирные,
взмахивающие лопасти (Аскання, Бреге, Флорин и др.). К сожале-
нию, систематических данных о таких винтах пока не имеется.
§ 3. ГОРИЗОНТАЛЬНЫЙ ПОЛЕТ ГЕЛИКОПТЕРА БЕЗ ПРОПЕЛЛЕРА
Для сообщения геликоптеру поступательной скорости пользуются дву-
мя способами. Прн первом, наиболее простом, наклоняют ось ротора впе-
ред под некоторым углом (фиг. 34). Тогда горизонтальная составляющая
полной аэродинамической силы, действующей на ротор, является тягой и
преодолевает вредное лобовое сопротивление геликоптера. ~ Такой метод
иногда называют методом пропульсивного ро-
тора. Другой способ состоит в том, что на
геликоптере устанавливают специальный пропел-
лер, который и сообщает аппарату горизонталь-
ную скорость.
Рассмотрим сперва горизонтальный полет бес-
пропеллерного геликоптера.
Прн таком полете подъемная сила должна
равняться весу геликоптера, а горизонтальная
слагающая полной аэродинамической силы,
действующей на ротор, должна уравновеши-
ваться вредным лобовым сопротивлением. Поль-
зуясь винтовыми коэффициентами, мы из пер-
вого условия получаем для z винтов:
G = Y — za-y^D^rTs
или
G
= aG.
(93)
Если расчет вести для ns = const и р = const, то ад = const. Лобовое
сопротивление корпуса и других частей геликоптера даст вредное сопро-
тивление Хвр. Его можно вычислить с помощью эквивалентной вредной
пластинки <5, как это делается у самолетов. Тогда
□у2
ХВ|, = 1,28
(94)
Здесь принято, что сх пластинки равен 1,28 (старый коэффициент
сх = 0,64).
Удобно это сопротивление выразить через винтовой коэффициент, на-
писав
pV2
х 1,28Va
— __ лвр _____ 2
Bp zpD<n* zpD4rtg
= 0,64^V.
(95)
Для данного геликоптера отношение ~ можно считать постоянным.
Тогда авр будет зависеть лишь от X. В нашем случае он должен равнять-
ся, по второму условию, ах ротора. Так как авр и_ах зависят от X, то
строим вспомогательный график (фиг. 35) величин яср и oc.v в зависимости
от X; av берем для •= const. Точка А пересечения кривых даст
величину X, при которой такой полет возможен. По кривой Лилиенталя
найдем угол атаки ротора г, затем по опытной кривой [3 = f (X, z) (см.
фиг. 33) найдем величину коэффициента мощности и вычислим мощность
Лг1, затрачиваемую на одии винт:
Л'1 - рО5лф (96)
Полная мощность, потребная для полета, получится по формуле:
(97)
где £ — коэффициент использования мощности.
Скорость полета вычнслится по величине X, так как V = XDns. Если
мощность мотора задана, то может случиться, что вычисленная мощность
окажется больше располагаемой. Для точного определения скорости при
заданном моторе нужно сделать такой расчет для нескольких углов уста-
новки лопасти ф (шага h) н построить график (фиг. 36) N и V в функции
Ф (или h). По этому графику в точке А получаем ту скорость, какую мо-
жет развить геликоптер при располагаемой мощности А/р. Точио таким же
способом рассчитывается скорость на высоте; в расчете изменяются лишь
? и N в зависимости от высоты полета и типа мотора.
Посмотрим, какую скорость можно получить этим способом у гели-
коптера.
Мы проделали ряд расчетов геликоптеров по описанному методу.
Получилась скорость полета не слишком большая. Если взять за осно-
ву расчета жесткие роторы, описанные в работе ЦАГИ*, то скорость
оказывается очень малой — рорядка 50—80 км/час — в зависимости
от типа геликоптера.
* «Техника воздушного флота», 1934, № 4.
Современные быстроходные роторы малого шага, применяющиеся
у новейших геликоптеров, дают, как показали испытания их моделей,
проведенные в ВВА, значительно лучший результат: нх скорость до-
ходит до 120—140 км/час, что и получалось на геликоптерах Бреге-
Доран и Фоке-Вульф.
Надо думать, что можно найти еще более совершенные с этой точ-
ки зрения роторы и еще более увеличить скорость полета. Однако в
настоящее время приходится считать, что известные в настоящее вре-
мя роторы не позволят получить у беспропеллерного геликоптера боль-
ших скоростей, н для увеличения последних придется, по-виднмому,
все же прибегнуть к постановке отдельного винта-пропеллера.
§ 4. АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ БЕСПРОПЕЛЛЕРНОГО ГЕЛИКОПТЕРА,
ЛЕТЯЩЕГО ПОД УГЛОМ К ГОРИЗОНТУ
Аэродинамический расчет геликоптера значительно сложнее, чем аэро-
плана. У аэроплана и автожира аэродинамика крыльев и ротора опреде-
ляется одним параметром — углом атаки. У геликоптера она зависит еще от
коэффициента скорости винта Л. Вследствие этого, у геликоптера прихо-
дится пользоваться не одной полярой, как у аэроплана, а нх семейством,
построенным по параметру Л. Кроме того, прн разных режимах полета у
геликоптера приходится меиять и шаг ротора.
Рассмотрим действующие на геликоптер силы. На ротор будет действо-
вать сила R
R =
с компонентами
X = 1
У = apPDM- /
(98)
Вредное лобовое сопротивление, по предыдущему, может быть представ-
лено в виде коэффициента явр (95).
Наконец, на геликоптер будет действовать сила веса G. Ее мы также
представим с помощью винтового коэффициента ац, определяемого из фор-
мулы
G
ас =
(99)
Прн установившемся движении силы R, Хкр и G находятся в равнове-
сии. Следовательно, и коэффициенты ад, ав?, ац должны образовывать
замкнутый треугольник ОАВ (фиг. 37). Так как коэффициент дается в
виде семейства кривых Лилиенталя, то выгодно увязку коэффициентного
треугольника производить на этой диаграмме.
Коэффициент нлн его компоненты ах н а„ даны самой кривой; ко-
эффициент авр откладывается по скорости потока V, т. е. по осн ах, но
с_ обратным знаком, а коэффициент веса должен иметь заданную величину
aG н замыкать этот треугольник. Угол, образуемый вектором aG с перпен-
дикуляром к скорости (или авр), дает угол взлета геликоптера -у.
Расчет следует вести так. Задаться сперва постоянным числом оборо-
тов ротора ns, подсчитать вредную пластинку геликоптера з н затем, зная
D, вычислить для изучаемой высоты полета коэффициент eta (99).
После этого нужно, задавшись величиной X, найти авр (95), отложить
его величину влево (фиг. 37) и получить точку В. Из точки В отрезком
ас надо сделать засечку на кривой
Лилиенталя с тем же значением Л,
какое было взято при вычислении
отложенного авр . Получится точка
А, которая и даст ответ. Далее
находим угол атаки ротора i по
семейству кривых угла атаки. Угол
взлета у находим как угол между
вектором а<, н осью ординат ау.
Скорость по траектории находим,
зная X, по формуле:
Этих данных достаточно для
построения указательницы глнссад.
Нужно взять несколько значений
А и для них определить V ну.
Получится график фиг. 38. От са-
молетного графика он отличается
тем, что на нем имеется вертикаль-
ная скорость взлета. В точке А
получится скорость горизонталь-
ного полета.
Пользуясь графиком [3 = /(«,%), находим еще величину коэффициента
мощности £ и вычисляем потребную для вращения одного ротора мощ-
ность по обычной винтовой формуле:
Мощность мотора вычисляется по формуле
АГ М
Ум = Z ~
где z— число роторов, £— коэффициент использования мощности. В таком
расчете при п = const может оказаться, что имеющейся мощности на по-
лет не хватит. Тогда расчет следует сделать для уменьшенных чисел обо-
ротов. Следовательно, расчет придется повторить несколько раз для раз-
ных чисел оборотов, и указательницы глиссад получатся в виде, приведен-
ном на фиг. 39 (ф = const — 8°). На этих кривых мы можем отметить
числа оборотов мотора н нанести сверху потребную для полета мощность.
Если теперь провести линию действительно имеющейся мощности мотора
Уд, то эта горизонтальная лнння пересечет кривые Ум в ряде точек. Все,
что лежит выше линии Уд, будет областью, невозможной для полета.
Снося эти точки вниз (пунктир), мы отметим на указательницах глнссад
соответствующих величин п те области, которые не могут быть реалнзо-
ваны с наличным мотором. Следовательно, указательннцы глиссад (на фиг.
39) могут быть использованы лишь в части, лежащей ниже СВ. Все, что
лежит выше ее, требует мощности,, большей имеющейся.
При полете по глиссадам, лежащим ниже линии СВ, придется для со-
блюдения условия п = const дросселировать мотор. Понятно, что благода-
ря этому геликоптер не разовьет полной скорости. Для полного исполь-
зования мотора придется изменять шаг несущего винта-ротора.
Таким образом, придется весь расчет повторить еще для нескольких
углов установки лопастей ротора. То же самое приходится сказать н о
работе геликоптера на высоте.
Результаты полного расчета геликоптера могут быть представлены
лишь несколькими диаграммами типа, данного на фиг. 39. Все это пока-
зывает, насколько работа геликоптера сложнее работы аэроплана. Отсюда
же вндиа н трудность управления геликоптером, так как у летчика полу-
чается очень много параметров, связанных друг с другом сложной зависи-
мостью (п, ф, i н V).
Из диаграмм типа, приведенного на фнг. 39, н построенных для раз-
ных высот, видно, что прн наличии горизонтальной скорости полета пото-
лок геликоптера значительно повышается.
для разных углов установки
В геликоптерах будущего,
несомненно, будут ставиться,
как это теперь уже делается на
самолетах, центробежные регу-
ляторы шага. Тогда всегда будет
соблюдено условие п = const н
/V = const. Это значит, что для
данной высоты полета
р-------г - const
oD'n\
Такое устройство должно зна-
чительно облегчить работу лет-
чика. Однако расчет прн этом
мало упрощается. Для такого
расчета надо иметь ряд псляр
а ф. Нужно на каждой поляре
найти точки, где 0 равно заданной величине, сделать это легко по кри-
вой (фнг. 33), где дано 0 •= f(i, X). Проводя горизонтальную линию 0
--const, мы найдем по кривым величины i и X. Найдя соответственные точ-
ки иа диаграмме фиг. 32, мы получим <ху н ал. Сделав это на ряде диаг-
рамм с разными ф (илн ft), мы сможем построить новую диаграмму
(фнг. 40), на которой получится сетка значений ф и X.
Повторяя описанное ранее нестроение треугольника ао, освр ак (фнг. 37),
мы получим величины X, ф и угол взлета у Далее иаходнм скорость
полета н строим указательннцу глиссад.
Мы будем знать для каждого режима угол установки лопастей при ус-
ловии п = const и N = const. Однако для изучения работы геликоптера
на высоте придется повторить описанный расчет еще для нескольких зна-
чений р. Следовательно, аэродинамический расчет геликоптера сам по себе
не сложнее такого же расчета аэроплана, но его приходится повторять
несколько раз из-за множества параметров, от которых зависит полет гели-
коптера.
§ 5. ГОРИЗОНТАЛЬНЫЙ ПОЛЕТ ГЕЛИКОПТЕРА С ПРОПЕЛЛЕРОМ
У такого геликоптера поступательное движение получается от спе;
циального вннта-пропеллера. Из рассмотрения поляр н кривых 0
(фнг. 32 н 33) сразу видно, что лететь с вертикальной осью вннта не-
рационально. Коэффициент ау несколько возрастает с увеличением X,
а коэффициент мощности почти постоянен н лишь слегка возрастает.
Следовательно, винт-ротор будет требовать на вращение почти той же
мощности, как прн неподвижном внеенип, однако он дает большое со-
противление, н вннт-пропеллер потребует дополнительной мощности.
Выгодно поэтому дать ротору некоторый положительный угол атаки
и еще уменьшить шаг. Тогда мощность, потребляемая ротором, резко
снижается н может быть сделана равной нулю. В последнем случае мы
переходим к автожиру. Большинство конструкторов геликоптеров счи-
тает в настоящее время целесообразным для горизонтального полета
переводить геликоптер на режим автожира.
Расчет геликоптера на этом режиме совпадает с расчетом автожира
илв самолета. Для его проведения нужно иметь поляру ротора на режи-
ме авторотации. В настоящее время имеется довольно много опублико-
ванных материалов. Мы уже приводили данные о такой продувке в § 1
главы 3. Главный недостаток всех многочисленных продувок гелнкоп-
терных роторов заключается в их разрозненности. Тяга изучена на
одних винтах, косая обдувка — на других, а поляры при авторотации —
на третьих. Получается своего рода некомплектность продувок.
Рассмотрим, как найти горизонтальную скорость полета геликоптера на
автожирном режиме. Проще всего сделать расчет по методу мощностей
(как для самолета), дающему достаточную точность. Исправив поляру на
вредное сопротивление, т. е. на величину
с„р = 1,28-4 (100)
гг
строим затем кривую Пено по обычным формулам, т. е, для скорости
V - 1 /--------= 1/-^- (101)
и для потребной мощности
Nпотр -
Здесь ц — обратное качество
в этом случае такие же, как
сетку потребных мощностей (АСотр) сетку полезных мощностей (А/пол) винта-
пропеллера, получим в точках пересечения скорости полета на разных вы-
сотах. Кроме того, по кривым непосредственно находится высота потолка.
Оказывается, что таким путем можно получить значительно боль-
шие скорости полета, чем у беспропеллерного геликоптера.
Следовательно, перевод геликоптера прн горизонтальном полете с
чисто геликоптерного режима полета на автожирный вполне целесо-
образен. Это может быть сделано сравнительно просто, так как ротор
геликоптера для безопасности вынужденного спуска все равно должен
иметь изменяемый шаг, а малый вннт-пропеллер весит очень немного.
В некоторых типах геликоптеров уже имеются включенные в их схему
винты, которые могут служить пропеллерами 4
Весьма благоприятные данные получатся у обычного двухвинто-
вого геликоптера. Такие геликоптеры предлагались многими конструк-
торами и часть нх была построена. Некоторые конструкторы (Сантос-
Дюмон, Сорокин, Корню, Флорин и др.) предлагали сообщить гелн-
XV 11GV сх GV
75 ““ ~^5~ “ лГ'
геликоптера как самолета. Кривые Пено
н для самолета (фиг. 41). Накладывая на
* Геликоптер системы Юрьева описан в «Трудах ВВА» (№ II, 1935) и в патентной
заявке Б. Н. Юрьева (1910 г.); см также немецкий патент № 410678/77Н 6 на имя
W Koschd (1926 г.), голландский геликоптер Baumhamer и др
коптеру продольное движение (фиг. 42,а). Другие считали более
целесообразным заставлять геликоптер двигаться в поперечном направ-
лении (фиг. 42, Ь) (Корню, Деказ, Лакоэн, Дамбланка, Берлинер и др.).
Какой геликоптер лучше? Окон-
чу» нательный ответ дать трудно, так
как в этом вопросе много нсизвест-
| ___ . ного. Все же можно ожидать, что в
I J ^отр отношении скорости большой разни-
\\ z' иы ЭтИ типы, по-видимому, не дадут.
\\ / y’yf'/x Первый тип имеет явно меньшее
у\/ \ вредное лобовое сопротивление, так
\ I как ег0 Фюзеляж движется вдоль
\ \ потока. Однако использование вин-
\ \ I тов тандем невыгодно, так как это
' \ \ \ И ВЫЗЬ1вает увеличение индуктивного
q----------------——*- сопротивления роторов. Во втором
^пол типе, несомненно, получится зиачи-
Ф,)г. 41 тельно большее вредное сопротивле-
ние от различных консолей, валов.
редукторов и т. п. Зато винты будут
в таком аппарате работать один независимо от другого. Иногда в такой
системе стараются придать консолям возможно обтекаемую форму н
делают их в виде крыла (например, в геликоптере Фокке-Вульф). Такое
крыло помогает геликоптеру в
горизонтальном полете. Мы
считаем последний прием мало
полезным, так как при взлете
по вертикали подобные крылья
уменьшают и без того малую
подъемную силу роторов.
Покажем, как подсчитать
а
возрастание сопротивления ро-
торов при переходе от одиноч-
ного вннта к винтам, стоящим
друг за другом.
Индуктивное сопротивление
любой иссушен системы может
быть написано в виде:
(103)
Ъ
где F— несущая Тплощадь, к
которой отнесены коэффициен-
ты, и / — размах этой площади,
в данном случае равный днамет- ФИГ 49
ру роторов D.
При использования для двух систем комбинации тандем мы по теореме
Мунка получим как бы одну систему, но с двойной площадью. Следова-
тельно, увеличение коэффициента сопротивления прн двух роторах полу-
чится по формуле (103), которую мы перепишем в виде:
nD
1 F 2 _ 2
— D* С’ ~ “ 4
(104)
Если поляра одного ротора автожира имела вид, приведенный на
фиг. 43, то, чтобы получить поляру для двух винтов, придется, построив
по правилам индуктивного сопротивления вспомогательную параболу ОР,
исправить по формуле (104), как показано на фигуре, кривую Лилиенталя
одиночного ротора. Получится изо-
браженная пунктиром-исправленная
кривая, которую и нужно использо-
вать в аэродинамическом расчете.
При малых cv, на которых проис-
ходит автожирный полет, добавоч-
ное невелико. Добавление вред-
ного лобового сопротивления при
поперечном движении получается
приблизительно такого же порядка.
Для ускорения аэродинамических
расчетов геликоптеров, летящих
на режиме автожира, целесообразно
применять логарифмическую поляру.
Мы построили такую поляру для
одиночного и двойного ротора*.
Для этого по осн абсцисс
(фиг. 44) отложена величина
/Vr|
т - —
zFAj
(Ю5)
а по оси ординат — величина
_б_
zF\
(Ю6)
Обозначения стандартные: F - -~
иг — число роторов.
С помощью этого графика скорости полета определяют в несколько
минут. При построении графика было принято, что схвр - - 0,004. Поляра
ротора построена по последним американским продувкам**.
Коэффициент полезного действия винта-пропеллера был принят при
построении графика равным 0,75.
Скооость геликоптера по сравнению со скоростью самолетов неве-
лика. Для описанных систем геликоптеров это неизбежно, так как вес
их конструкции значительно больше, чем вес самолета, а размах не-
сущей системы весьма мал. Наибольшее количество роторов авто-
жира не превосходит обычно 7, тогда как у крыла оно доходит до
18-22
За вертикальный взлет приходится платить, как видим, дорогой
пеной.
Б. Н. Юрьев. Пределы современной авиации и способы их преодоления. Изд.
ЦАГИ. 1936.
NACA-515, 1935.
Обычно предлагают два способа включения винта-пропеллера:
устройство сцепной муфты или устройство у него регулируемого шага.
Первый способ приходится сочетать со вторым, так как если сразу
включить винт фиксированного шага, то он возьмет всю мощность мо-
тора, и ротор потеряет подъемную силу. Поступательная же скорость
получится не сразу, и переход на режим автожира потребует времени.
Следовательно, при таком устройстве геликоптер сперва провалится, а
затем, набрав скорость, перейдет иа режим автожира. При плавном
изменении шага этого не случится, так как можно будет, одновременно из-
меняя шаги несущего винта и пропеллера, получить плавный переход от
одного режима к другому Можно вообще не делать сцепления, если У
пропеллера можно доводить шаг до нулевого, так как мощность, потреб-
ляемая винтом при Л=0, сравнительно мала.
Мы здесь не будем разбирать наклонных полетов геликоптера с про-
пеллером, так как получается весьма много возможных вариантов по-
лета. Общую мощность мотора можно самым разнообразным способом
распределять между ротором и пропеллером. Исследование нужно вести
тем же путем, как указано в § 4 главы 3, но с добавлением в коэффи-
циентный треугольник еще вектора коэффициента тяги пропеллера, от-
несенного к pD4ns2 ротора.
§ 6. ГЕЛИКОПТЕРЫ, ПРЕВРАЩАЮЩИЕСЯ В АЭРОПЛАНЫ
Фиг. 45
Имеется огромное количество иностранных патентов, в которых
предлагается превращать геликоптер для горизонтального полета в
аэроплан. Чаще всего предлагают поворачивать ось роторов из вер-
тикального положенная при взлете в горизонтальное (фиг. 45). Иногда
предлагают ставить роторы под некото-
рым углом к горизонту. Такие системы
ведут ц весьма большому утяжелению
всего аппарата, так как фактически в иих
имеется и аэроплан и геликоптер При
этом во время висения в воздухе вся
аэропланная часть бесполезна и лишь
хтяжеляет систему, а при горизонтальном
полете геликоптерная часть является
лишней. Кроме того, почти во всех таких?
аппаратах требуются две системы управ-
ления — геликоптерная и самолетная.
При висении в воздухе с пулевой ско-
ростью самолетные органы управления
не будут работать. Нечего и говорить, что
поворотные механизмы для несущих вин-
тов получаются тяжелыми.
Все это делает оиисаиные типы аппа-
ратов неспособными оторваться от земли.
Более законченными являются системы,
у которых поворачиваются не роторы, а
весь аппарат (Фиат и Др.). Здесь воз-
можны следующие решения (фиг. 46): обычный самолет, но устанавли-
ваемый вертикально перед взлетом* (а), особо изогнутый самолет (Ь)
или первый вариант, но бесхвостый, дающий меньшую высоту си-
стемы (с).
Такие аппараты, по мысли авторов, могут взлетать с помощью тяги
винтов, которые здесь должны браться достаточно большими; затем,
набрав высоту, они должны наклоняться и постепенно переходить на
режим самолета., (Такие аппараты могут быть более компактными, чем
аппараты с поворачивающимися роторами. Однако у них получается
большой вес. Если сделать большие роторы для получения хорошей
подъемной силы, то такие роторы потребуют тяжелых редукторов и бу-
дут плохо работать на режиме пропеллера.
По-видимому, такие системы взлета смогут применяться лишь у
весьма легких самолетов типа истребителей-перехватчиков.
Следует заметить, что взлет на таких машинах чрезвычайно опах
сен, так как в случае остановки мотора получается скольжение маши-
ны на хвост. Винты на иих должны быть сравнительно малого диамет-
ра, и их тормозящее дейстние ничтожно. Кроме того, авторы таких
проектов проявляют обычно беззаботность к вопросам управления ап-
паратом во время висения и взлета, а также к вопросам уравновешива-
ния момента вращения винта.
Без геликоптериого управления такая машина не может летать, так
как любой порыв ветра сможет ее опрокинуть на взлете. Уничтожить
, , * «Aircraft Engineering», February 1938, стр. 48.
18 Б. Н. Юрьев, т. I
момент можно применением или парных виитов или каких-либо других
средств. Вес это опять усложняет первоначально простую по идее си-‘
стему и делает ее менее заманчивой, чем это кажется с первого взгляда
Для получения общего суждения о таких аппаратах возьмем нстрс
битель с мотором в 1000 л. с. Просматривая описанные в литературы-
истребители с такой мощностью, приходим к выводу, что их вер в сред
нем нс ниже 1800 кг и доходит до 2200 кг и более (Девуатин с «Йена-
но» 12 Yers, М = 925 л. с.}. Не рискуя впасть в излишний оптимизм, мы
можем принять вес такого самолета в 1800 кг, а его утяжеление за счет
редукторов и увеличения винтов — в 200 кг. Следовательно, полетный
вес получится порядка 2000 кг. Прн наличии двух винтов геликоптер
кого типа получится тяга Р, которую мы найдем по формуле Вельиера
Р = 2( 22U^-O)!/3.
Беря = 0,9, получаем тягу для диаметров D — 3—4 м, Р — 1920 -
2320 кг.
Учитывая необходимость иметь хотя бы небольшой избыток тяги, при
ходим к выводу, что винты должны иметь диаметр 4 м.
Посмотрим теперь, как будет работать такой винт иа режиме пропел-
лера. Для решения воспользуемся работой И. В. Осгославского и Д. В. Ха-
лезова «Характеристики трехлопастиых металлических виитов ЦАГИ,
З-СМВ-1 и З-СМВ-2»*, содержащей богатый материал по работе виитов
различного шага.
Сперва зададимся числом оборотов виита; мы выбрали его равным
900 об/мин или ns = 15 об /сек. Такое число оборотов не требует тяжелых
редукторов. Тогда мы должны требовать от винта
= = 0,0783.
1/8-46-153
При работе иа месте для трехлопастиого виита типа ЗСМВ-2 получаем
а = 0,146 н находим тягу одного винта по обычной формуле:
Л = ар£4п*= 0,146 —256-225 = 1040 кг.
1 8
Полная тяга Р = 2Р\ = 2080 кг, т. е. несколько меньше, чем мы рассчи-
тывали раньше, так как винт ЦАГИ ие специально геликоптерный, а про-
пеллерный и имеет меньший относительный к.п.д.
Посмотрим теперь, какой получится к.п.д. винта на режиме пропеллера
при разных X и при том же р. Пользуясь графиком из работы ЦАГИ
№ 300 (фиг. 24,а), получаем ответ:
X........... 1 1,5 2.0
П........... 0,76 0,74 0,66
При этом обдувка крыла уже учтена самим экспериментом. Следовательно,
к.п.д. виита получается хотя и ниже возможных для самолетного пропел-
лера, но все же довольно высокий. Взятые величины X соответствуют ско-
ростям полета.
V = XDns = Х-4-15 = Х-60,
что дает:
X........... 1 1,5 2,о
V, м/сек . . 60 90 120
Аэродинамика такого самолета будет хуже, чем у нормальных само-
летов, так как придется сделать обтекатели иа редукторы н установить
геликоптериое управление. Горизонтальную скорость иа режиме самолета
можно вычислить по обычной формуле
У = 1/2-р-75.Л> (107)
Г
Для полета у земли р = 1/г у нас — = = 0,5.
G 2000
“ Вып ЦАГИ. № 500. 1936
18*
Нагрузку иа единицу площади крыла можно взять равной р == 200 кг/.и2,
а коэффициент лобового сопротивления сх можно оценить для таких машин
величиной не ниже 0,04. К-п.д. винта, как мы виделн, р ^-0,66. Это дает:*
' 8 ____________ 3 __________
V = 1/ = у J 98Q 000 = 126 м/сек, ~ 450 км/час.
Г 1 г '1/8-0,04-2
Для истребителя скорость получилась довольно умеренная. Следова-
тельно, такие машины работают плохо и как геликоптеры (нет избытка
тяги) и как самолеты (тяжелы, и плохой к.п.д. виита). Правда, при уста-
новке иа такой самолет высотного мотора скорость иа высоте значительно
увеличится.
Однако в этой области возможны всякие усовершенствования.
выводы
Полученные данные позволяют рассмотреть всю проблему геликоп-
тера довольно широко. Мы изучили вопрос о наибольшем грузе и о ско-
рости полета. Если взять три типичных геликоптера: одновинтовой, тан-
демный н обычный двухвинтовой, то, вычислив статический потолок
(§ 6 главы 1) и иайдя для инх горизонтальную скорость (§ 5 и 6 гла-
вы 3), мы получим весьма наглядное сопоставление летных свойств этих
аппаратов.
В юбщем наиболее благоприятные результаты дает обычный двух-
винтовой геликоптер.
Конструируя геликоптер, приходится выбирать некоторые компро
миссные решения между грузоподъемностью, скоростью полета и ско-
ростью посадки. Такое же решение приходится выбирать и при проек-
тировании самолета.
Полученные графики показывают, что летные свойства трех типич-
ных геликоптеров значительно хуже, чем могут быть у самолета. Од-
нако способность геликоптера взлетать р любого места без разбега,
висеть неподвижно в воздухе и садиться без пробега столь заманчива
и представляет такой контраст с работой самолета, что это одно уже
полностью оправдывает геликоптер как летное средство.
Отвергать эти системы, как абсолютно нерациональные, в настоя-
щее время нельзя. Они все же дают заманчивое решение проблемы'
летать быстро, ио взлетать и садиться с нулевой скоростью. Здесь же-
лательна большая исследовательская работа. г
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВЕРТОЛЕТОВ
Часть 1
ТЕОРИЯ ВИНТОВ И ВЕРТИКАЛЬНЫЙ ПОЛЕТ
ВЕРТОЛЕТА
Глава I
ОСНОВНЫЕ ТЕРМИНЫ И ОБОЗНАЧЕНИЯ,
ПРИНЯТЫЕ В КНИГЕ
§ 1. ОБЩИЕ УКАЗАНИЯ И ПОЯСНЕНИЯ
Прн изучении сложных явлений, происходящих при работе вертоле-
та, важно иметь хорошо разработанную систему терминов и математи-
ческих обозначений. Это могло бы значительно облегчить изучение
теории вертолета.
К сожалению, у пас нет вполне установившейся терминологии в
вингостроенни и вертолетостроеиии. Наряду с совершенной системой
обозначений, применявшейся еще проф. Н. Е. Жуковским, у нас поль-
зуются французскими и немецкими обозначениями, греческими н латин-
скими терминами, а в последнее время стали применяться еще н англо-
американские.
Несмотря на то, что но теории воздушных винтов и вертолетов мы
имеем большую научную литературу, в математических обозначениях
основных величии у нас нет единой системы. Достаточно сказать, что
у нас встречается четыре типа основных аэродинамических коэффици-
ентов, отличающихся, в сущности, лишь постоянными множителями.
Точно так же наряду с удобными «относительными скоростями», вве-
денными в науку проф. Н. Е. Жуковским и В. П. Ветчинкииым еще в
1912 г., встречаются англо-американские обозначения этих скоростей,
например ц и г, причем х имеет обратный знак относительной скорости
потока в плоскости винта. Такой произвол в выборе знаков величин
вызывает большую путаницу и ведет к различным ошибкам.
Создание новой, рациональной, терминологии в области авиации,
как показала работа Комитета по технической терминологии Акаде-
мии паук СССР,— дело весьма трудоемкое и Академия наук смогла
рекомендовать только основные термины и их определения, воздер-
жавшись пока от рекомендации математических символов и обозна!-
чений ‘.
* Терминология воздушных вт,чтов п вертолетов Комитет технической терминоло-
гии Изд-во АН СССР, вып. 20, 1954.
Автор всюду придерживался этих новых терминов, применяя старые
лишь в исторических справках. Некоторые греко-латинские термины имев
шие широкое применение в иашей обширной классической литературе по
винтам и вертолетам, приводятся в соответствующих местах текста в скоб-
Здесь мы будем строго придерживаться следующих общих правил*
а) Оси координат выбираются такие же (фиг. 1), как это принято в тео
рии самолета (стандарт СР-49). Подробнее см. § 3, п. 4.
б) Силовые коэффициенты у винтов обозначаются прописными буквами С
а моменты буквами т с соответствующими индексами. В теории крыла
силовые кээф|)1циенты, как
у известно, обозначаются с по-
мощью строчных букв с. Все
новейшие работы по теории са-
молета используют у нас коэф-
фициент момента, обозначаемый
через т.
в) Тягу винта мы будем
обозначать, как правило, буквой
Т, а буквой Р будем пользовать-
ся для обозначения тяги до-
полнительных винтов и т. и.
Работу и мощность, потребляе-
мую винтами, мы будем обозна-
чать буквами Ькем/секи N л.с..
Фиг. L Оси координат v вертолета 0-хуг— ско- как ЭТо принято теперь во
ростные, связанные всех наших курсах термодинами-
ки и теории тепловых двигателей.
г) Знаки у компонентов сил и моментов всегда берутся в соответствии
с осями координат.
д) Знаки скоростей тел (вертолета, его лопастей и т. д.) берутся в соот-
ветствии с осями координат. На чертежах мы будем их обозначать оперен-
ными стрелками. Компоненты относительной скорости воздуха всегда
берутся положительными, когда они направлены против положительно
направленных осей координат. На чертежах мы будем их обозначать про-
стыми стрелками.
е) Знаки углов всегда берутся в соответствии со стандартными осями
координат.
ж) Все безразмерные скорости получаются делением именованных ско-
ростей на скорость вращения внешнего конца лопасти U = /?со л‘!сек и
обозначаются теми же буквами, как и именованные, но с чертой сверху,
например: К = —; № = — и т. д. Этот прием был введен в теорию
/^<0
винтов Н. Е. Жуковским и В. П. Ветчинкиным.
з) Скорости потока, отнесенные к характеристической скоро-
d f С. т*
Сти несущего винта а1в ——J/ —-U, обозначаются теми же буквами.
Что и именованные, но с волнистой чертой сверху.
и) Некоторые устаревшие обозначения мы будем приводить в тех слу-
чаях, когда имеется справочная литература, написанная в этих обозначе-
ниях.
§ 2. ПОЯСНЕНИЯ К НЕКОТОРЫМ ТЕРМИНАМ
Вертолет — летательный алпаоат, поднимающи<ся в воздух с помощью
тянущих его вверх одного или нескольких ' винтов, приводимых во враще-
ние двигателем.
Международное греческое название—геликоптер (винтокоьп).
Автожир — летательный аптарат, несущий винт ил i взяты у которого
вращаются в начете от набегающего на них потока встречного воздуха и
движение которого обеспечивается гребным винтом (пропеллером), работаю-
щим от двигателя.
Винт — общее название винтов любого назначения.
Несущий винт — винт, счециалыо поиспосэбленный для получения
подъемной силы у вертолетов и автожшюв. Устаревший термин — ротор.
Гребной винт — винт, специально п редназиачеяный для приведения
в горизонтальное движение летательных аппаратов. Устарезший термин —
пропеллер.
Рулевой винт — винт изменяемого шага, устаназл гааемый на неко-
ivpoM плече (хвостовой балке?\Коясол 1) и служащий для урав юзешивания
реактивного момента несущего винта и для создания момента, поворачи-
вающего вертолет в желаемом для летчика направлении.
Крылатый вертолет — аппазатсмешанного типа, имеющий крылья
и несущие винты и могу ций взлетать вертикально.
Конвертоплан — аппазат, взлета о ций по принципу вертолета и
превращающийся в воздухе в самолет путем ссладызаяил иля перестановки
лопастей.
Главный редуктор — редуктор, передающий мощность двигателя
непосзедстзэнно к несущему винту.
Ко опус вертолета — состоит из фозеляжа или кабины, мотогондол
(если очи имеются), хвостовой балки, консолей и шасси, оперения, верх-
него кабана и т. д.
Горизонтальный полет — полет, когда вертикальная скорость
вертолета оавна нулю.
Полет с горизонтальной скоростью —полет, когда имеется
горизонтальная скорссчь; при этом вертикальная скорость не равна нулю.
Висение вертолета в воздухе — режим, когда вертолет
не имеет ни вертикальной, ни гозизоя.тальчой скорости относительно воз-
духа. Иногда пользуются тгрмиом «падение» вертолета, что неправильно,
так как парящая птица всегда быстро движется обычно по кругам.
Висение вертолета над землей — режим полета, когда
вертолет не имеет ни вертикальиол, ни горизонтальной скорости относи-
тельно земли. При этом он движется относительно воздуха со скоростью
ветра.
Парашютирование вертолета — вертикалы>u ciycc иа авторо-
тации несущего винта при выключенном двигателе.
Планирование вертолета—нактызьн к горизокту спуск вер-
толета на азторотации при всклоченном двигателе.
Конструктивная плоскость вращения несущего виита
перпендикулярна к оси втулки.
Угол атаки несущего вннта берется по ко щтруктивнри плоско-
сти вращения, т. е. по втулке.
Конус — поверхность, гп гсываемая шарниэно лэдзелеччымг лэизстями.
Маховое движение лопастей — колебагельнэе дви келие ло-
пастей около горизонтального шарнира.
Качание лопастей происходит около вертикалыэго шарнира.
§ 3. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
1. Общие обозначения
D — диаметр вннта;
R— радиус вннта;
b — хорда сечения лопасти;
с — толщина сечения лопасти;
' ~ •— окружная скорость конца лопасти;
п — число оборотов в минуту;
п -
п$ ~ — — число оборотов в секунду;
лп
ю = — — 2лп$ — угловая скорость вращения;
г — раднус сечення лопасти;
— г
г — —----относительный раднус сечення винта;
с =- — относительная толщина профиля;
г Ь
о = —----относительная ширина профиля;
а = — = — — местный коэффициент заполнения на любом радиусе,
itR я
а-/(г);
Ь-— относительная ширина на характерном радиусе г =0,7.
б7 — —-—коэффициент заполнения вннта;
л А!
k — число лопастей;
z — число несущих вннтов, приходящихся на одни двигатель;
de
А ~ — наклон кривой су = f(oQ для профиля прн бесконечном
detg
удлинении;
N— мощность винта, в л. с.;
NM — мощность двигателя, в л. с.;
L — мощность винта, в кем/сек;
г jiD2 ,,2
г=-----~:iR—площадь, ометаемая винтом;
4
gj — относительный радиус неработающей части лопасти
у втулки; ,
g2 — относительный радиус неработающей части лопасти у ее
внешнего конца.
2. Правило знаков для углов
(фиг, 2)
Все без исключения углы берутся в соответствии со стандартными
осями координат.
ф — азимут лопасти, отсчитываемый от заднего (флюгерного)
положения лопасти в сторону правого вращения;
3 — угол взмаха лопасти, отсчитываемый от конструктивной
плоскости вращения;
а — угол атаки крыла у крылатых вертолетов;
§ 3. Основные обозначения
.281
ле — угол атаки элемента лопасти <хе ~ f(r);
а7 — угол атаки характерного элемента лопасти, лежащего на
Г= 0,7;
ак — угол атаки несущего винта, взятый по конструктивной'
плоскости вращения, т. е. по плоскости, перпендикулярной-
к оси втулки; ,
Д. —угол притекания потока к элементу лопасти;
Фиг 2. Углы азимута и ьзмаха лопасти 0 при маховом дви-
жении
Ось Oyi совмещена с осью втулки Конструктивный угол атаки а к
отрицателен (это соответствует вертолетному режиму)
—угол притекания потока на характерном радиусе;
фе — угол установки аэродинамической хорды сечения (элемента)
лопасти по отношению к конструктивной плоскости враще-
ния;
«0 — угол конусности лопастей несущего винта;
Qi — угол завала назад осн конуса, описываемого лопастями;
8 — скос потока;
8{ — средний индуктивный скос потока у несущего винта;
— отклонение полной силы тягн Т назад от добавления про-
фильного сопротивления;
— е{ 4- — полное отклонение тяги Т от оси вращения 0ух-,
бдп— отклонение силы тяги Т, вызванное действием автомат-пе-
рекоса;
$б — угол балансировочный, образуемый полной силой тяги с кон-
структивной осью вращения Оуъ
т — угол, образуемый полной силой тяги со скоростной осью Оу
(т. е. с перпендикуляром к скорости полета в плоскости
симметрии);
q — угол взлета, т. е. угол траектории с горизонтом;
О— угол тангажа, т. е. угол, образуемый конструктивной пло-
скостью вращения с горизонтом;
' —угол тангажа фюзеляжа;
° — значок, указывающий, что угол взят в градусах.
3. Правило знаков для скоростей
Знаки для компонентов скоростей тел всегда берутся в соответствии
с осями координат и изображаются на чертежах оперенными стрелками.
Знаки для скоростей потока воздуха всегда считаются положитель-
ными, когда они направлены пэотив положительного направления осей ко-
ординат и изображаются на чертежах простыми стрелками.
Безразмерные скорости пэлуча отся делением именованных скоростей
на U = /?« и обозначаются теми же буквами, как именованные, но с чер-
той сверху.
Отвлеченными скоростями называются скорости, разделенные на харак-
теристическую скорость винта, равную и1в = — U (см. далее), и
обозначаются теми же буквами, как именованные, ио с волнистой чер
той сверху.
V’o— скорость полета и ссорость невозмущенного потока;
Vx — горизонтальная скорость;
Vy—вертикальная скорость;
VA—скорость протекания — компонент скорости набегающего на
несущий винт потока в направлении, обратном силе тягн Т;
VT — скорость ссольжеяия — комюяент скорости набегаю него иа
несущий випт потока в направлении, перпендикулярном к
с 1ле тяги Т, лежзций в плоскости симметрии;
Va — аксиальная скорость —компонент скорости наозгаоцего на
несу ций винт потока в направлении, обратном направлению
конструктивной оси воа цения 0у{',
Vt — тангенциальная скоюсть — компонент скорости набегаю цего
на несущий винт потока в наюавлепни, обратном оси Ох^,
U = — окружная скорость конца лопасти;
V,—индуктивная средняя скорость в плоскости диска (скорость
подсасывания);
v2 — индуктивная средняя скорость в сжатом сечении струи вин-
та (скорость отбрасывания);
vL — соедняп индуктивная скорость для нескольких несущих вин-
тов;
Vi= Vo + Vi — средняя скорость воздуха в плоскости диска при осевом
движении несу.цего винта;
^2= + v2 — средний скорость воздуха в плоскости сжатого сечення
струи прн осевом движении несущего винта;
Vi — полпая средняя скорость воздуха в плоскости диска при
косой обдувке несущего винта;
V?, v7 и т. д. — скорости в плоскости диска винта на радиусе г -= 0,7;
v1B — характеристическая скорость винта, т. е. средняя индук-
тивная скорость в плоскости винта на режиме висения
(индекс «в»);
— индуктивная скорость потока в плоскости несущего вннта
на режиме висения на г = 0,7;
— осружюл компонент скорости потока относительно элемен-
та лопасти;
Wy — осевой компонент скорости потока относительно элемента
лопастн;
W— полная скорость потока, набегающего на элемент лопасти.
а — скорость звука
Индексы
в —обозначает «висение»; втулка;
i — индуктивный или идеальный;
р — профильный;
е —элемента;
э— экономический;
е — иаивыгоднейший;
р — располагаемый;
п — потребный;
Ср — средний.
В тех случаях, когда в тексте сделана соответствую пая оговорка или
когда путаница невозможна, мы эти индексы ставить не будем.
4. Оси координат
(фиг. 1)
Связанная с вертолетом. Поавая прямоугольная система, в ко-
торой ось 0yt направлена по оси втул<и, т. е. по конструктивной оси не-
сущего виита, ось Oi-j направлена bi а о ед и лежит в плоскости симметрии
и ось Ozx идет вправо от летчика.
Скоростная система. Правая прямоугольная система, в которой
ось Оу лежит в плоскости симметрии и образует с осью 0У\ угол атаки ак.
ось Ох направлена по скорости полета вертолета V’o и ось Oz идет вправо,
образуя правую систему с осями Ох и Оу.
Общее правило знаков
Все компоненты векторных величии и углы всегда берутся у нас в со-
ответствии с указанными осями координат. Скорости потока воздуха бе-
рутся всегда в обратную сторону. Для запоминания правила знаков можно
Фиг. 3. Правило левой руки для получения
осей правой системы координат
пользоваться «правилом левой руки» (фиг. 3). Если направить указатель-
ный палец по скорости полета^ (ось Ох), то большой покажет направление
осн Оу, а средний укажет положение оси Oz.
t лава i исновные термины и обозначения, принятые в-работе
5. Силы, моменты и их аэродинамические
коэффициенты
Т — сила тяги несущего винта,
Р — запасное обозначение для тяги (например, тяга гребного
винта у вертолета);
Qp — профильное сопротивление несущего винта в целом,
QBP — вредное сопротивление несущих частей вертолета;
свр — эквивалентная вредная пластинка;
X, Y, Z — компоненты полной силы тяги в скоростных осях координат.
Xlt Ylt Zi — компоненты полной силы тяги в связанных осях координат;
Мя, Му, Мг — компоненты полного аэродинамического момента, действую-
щего на несущий винт, в скоростных осях;
МХ1 — момент крена, т. е. компонент по оси 0хг полного аэроди-
намического момента,
—= — момент рысканья, он же крутящий момеит с обратным зна
ком; это — компонент полного момента около оси Oyi,
Мг1 — момент тангажа, т. е компонент полного аэродинамичес
кого момента около оси 0zt.
Аэродинамические коэффициенты
Силовые в связанных осях
X, = С,, -5- Р«4О>2,
У, = Сп " р/?*со2 или Т = Ст ~ p/?W;
Z, = С, 4 pF1'.)2
Моментные в связанных осях:
Мх, = tnX1 -у р№*<л2.
= тУ1 р/?Есо2 или Мк - rnK -у р/?5©2;
Мг, = р/?5ы2.
Мощность несущего винта
L = /Ик© = тк р/?5©3.
Часто пишут U — /?© и тогда получают:
Т = ст F ;
MK = mK^-RF-r ' ' '
, pLJ’ . 1 LVJ
Формулы в скоростных осях пишутся так же, ио без индекса «1».
Коэффициенты полезного действия
^=-£•2 — винтовой к.п.д.;
q0 — относительный к.п.д.
qa— аксиальный к.п.д.;
— идеальный к.п.д.;
Яй — окружной к.п.д.
11м — механический к.п.д.
£— коэффициент использования мощности.
6, Крыловые, самолетные и аэродинамические
коэффициенты и др.
(пишутся, как обычно, с помощью строчных букв по правилам эксперимен-
тальной аэродинамики).
Q — — X =-- Сх — S —лобовое сопротивление;
Y = cv — S — подъемная сила;
<7 pV2o
Z ~ cz ~-S — боковая сила;
Cxi — коэффициент индуктивного сопротивления;
сХр — коэффициент профильного сопротивления;
К — ------качество крыла бесконечного удлинения,
сх
ц =------обратное качество крыла бесконечного удлинения;
сг/
с
е = —^ — обратное экономическое качество профиля для крыла
сТ
v
бесконечного удлинения,
Т
р = -р- — нагрузка на ометаемую площадь,
Т
q — — нагрузка на 1 л. с. мощности, подводимой к валу винта;
Т
Рм = -г;-нагрузка на 1 л. с. мощности двигателя;
£ “ 4 У'^'д—энергетическое качество несущего вннта;
fu = <7м — энергетическое качество вертолета;
О — полетный вес вертолета;
GK— вес конструкции вертолета;
Он —вес нагрузки вертолета (с горючим);
(7 л— вес лопастей вертолета;
(?э — эксплуатационная (коммерческая нагрузка);
Г — циркуляция скорости;
Г = — относительная циркуляция скорости;
S— площадь крыла;
Sr о — площадь горизонтального оперения;
S'b.o—площадь вертикального оперения;
Lr о — плечо от ц.т. аппарата до центра горизонтального оперения;
LB.O — плечо от ц.т. аппарата до центра вертикального оперения.
Сокращения
ГШ — горизонтальный шарнир;
ВШ — вертикальный шарнир;
А1 — автомат-перекос;
РВ —регулятор взмаха;
ц.т. — центр тяжести;
ц.к. — центр качания.
7. Устаревшие обозначения, ссылки иа которые
встречаются в настоящей книге
Французские
X = —---коэффициент скорости винта (X. = лУ0);
- Т * ,, / - л3 „ \
а-——--—— коэффициент тяги (,;J.
{5 = - ---коэффициент мощности ( р — — mK V
к 8 /
Англо-американские
Vt -
ц = —— характеристика режима (ц = Vt— безразмерная тангенциаль-
ная скорость воздуха в плоскости диска);
V _
к — — -j~ — «коэффициент протекания» (к = — Va — аксиальная скорость
воздуха с обратным знаком).
Глава 2
ИМПУЛЬСНАЯ ТЕОРИЯ НЕСУЩЕГО ВИНТА ПРИ ОСЕВОМ
ДВИЖЕНИИ
(общая теория несущего виита)
§ I. ИСТОРИЯ РАЗРАБОТКИ ИМПУЛЬСНОЙ ТЕОРИИ ВИНТОВ
Для получения расчетных формул для вертолета, движущегося по
вертикали или висящего в воздухе неподвижно, проще всего восполь-
зоваться импульсной теорией воздушных винтов, впервые развитой в
1910 г. студентами .МВТУ, учениками проф. Ы. Е. Жуковского. Г. X. Са-
бининым и Б. Н. Юрьевым. Эта теория в более позднем развитии часто
называется у нас импульсной теорией. Она очень проста и на-
глядна и потому ею охотно пользуются в теории несущего винта вер-
толета, где она особенно удобна.
Как известно, эта теория развилась у нас в связи с работами сту-
денческого «Воздухоплавательного кружка» при Московском Высшем
Техническом Училище, почетным председателем которого был Н.Е. Жу-
ковский. Кружок занимался тогда, в частности, разработкой проблемы
вертолета и даже приступил к постройке первого одновинтового аппа-
рата по системе Б. Н. Юрьева. Теория Г. X. Сабинина — Б. Н. Юрьева
была разработана в связи с необходимостью иметь теорию, пригодную
для расчета несущих винтов вертолетов. В ней делались с самого нача-
ла допущения, чго давления, возникающие в струе, создаваемой самим
несущим винтом, невелики, и скорость вращения в струе уходящего от
несущего винта воздуха мала. Для вертолета эти допущения очень
близки к действительности Однако для сильно нагруженных гребных
винтов, особенно для осевых вентиляторов, эти допущения не вполне
точны, и Н. Е. Жуковский с помощью студента В. П. Ветчинкина в
1912 г. создал свою классическую вихревую теорию воздушных
винтов, охватившую единым анализом и едиными формулами все типы
винтов: гребные винты, несущие винты вертолетов, вентиляторы и вет-
ряные двигатели. Она более точно учитывает давления и скорость вра-
щения в струе винта и является огромным научным достижением
в аэродинамике.
Однако ь применении к вертолетам вихревая теория дает те же са-
мые формулы, как и импульсная теория, если отбросить в формулах
очень м-алые для несущих винтов члены, зависящие от давлений и ско-
ростей вращения струи. Выводы же по импульсной теории во много
раз проще, чем в вихревой теории. Поэтому при изложении при-
ближенных методов расчета вертолета мы будем пользоваться в
основном импульсной теорией, делая лишь ссылки, где это требуется.
на результаты, получаемые с помощью более совершенной вихревой
теории.
За границей аналогичные теории появились на 10—15 лет позже. Им-
пульсная и вихревая теории подробно излагались у нас во множестве
статей, в десятках книг и в ряде учебников, начиная с 1911 г., однако
иностранные авторы обычно ссылок на наши работы не делают и в луч-
шем случае отмечают в сноске, что аналогичные теории несколько ранее
были разработаны в России.
§ 2. СТРУЯ ВОЗДУХА,'СОЗДАВАЕМАЯ РЕАЛЬНЫМ ВИНТОМ
В ОБЩЕМ СЛУЧАЕ
Если исходить из теории так называемого идеального виита, то ско-
рости потока в пределах каждого сечения струи (0, 1 и 2) были бы
постоянными. Для применения ее в случае винтов, у которых это усло-
Фиг. 4. Схема струм, создаваемой винтом
вне не соблюдается, пользуются
средними скоростями, беря их
обычно на г=0,7. Импульсная
теория не делает этого грубого
приближения и считает скорости
V[ и V2 переменными по радиусу
виита. Поэтому в импульсной тео-
рии рассматривают не всю струю
сразу, а ее разбивают на отдель-
ные кольцевые струйки, как по-
казано на фиг. 4. Для этого в се-
чении / радиусами г и r + dr очер-
чиваем из центра втулки две ок-
ружности и проводим через них
линии тока. Получается элемен-
тарная кольцевая струйка; ее рас-
сматривают так же, как в теории
идеального виита. Винт и здесь
рассматривается в обращенном
движении; проводится три сече-
иия: 0,1 и 2. Скорость потока в
нулевом сечении равна Ио, а в
сечении 1 она возрастает до ве-
личины
/1 = У0 + Уь (И
где 01 — скорость подсасывания или индуктивная скорость. В сечении 2
получится скорость воздуха
V2 = V„ + »a. (2)
гдр v2— скорость отбрасывания.
Скорость называется скоростью воздуха в плоскости винта,
a V2 — скоростью уходящего воздуха.
Все эти скорости будут в общем случае переменными и по радиу-
сам и по окружности. Изменением скоростей по окружности в этой тео
рии обычно пренебрегают и считают, что скорости О] и v2 берутся .по
средним значениям. Изменение же скоростей по радиусу в этой теории
учитывается. Внутри выделенной кольцевой струйки у ^-лопастного
виита будет находиться k элементов лопасти (фиг. 5). У каждого из
них ширина лопасти будет b (длина хорды сечения) и длина по радиу-
су dr. Площадь каждого элемента будет равна
dS = bdr.
Импульсная теория, как увидим далее, исходит при выводе своих фор-
мул или из рассмотрения элементарной струнки нли нз рассмотрения
работы элемента лопасти как крыла с площадью dS. Такой двоякий
подход позволяет сделать много цен-
ных выводов, в частности, получить
основное выражение этой теории, так
называемое уравнение связи.
Теорема о скоростях в струе
несущего вннта
Во время работы несущего винта
элементы лопастей, набегая на воздух,
создают общую тягу dT. Реакция этой
силы приложена к воздуху, равна силе
тяги, но противоположна ей. Давления,
действующие иа боковую поверхность
кольцевой струйки, практически не
дают осевой проекции, так как они
близки к атмосферному давлению и
направлены навстречу. Давления в се-
чениях 0 и 2 также близки к атмосфер-
ному.
Применим теперь к кольцевой
струйке два основных закона механи-
Фиг. 5. Кольцевая струйка и находя-
щиеся в ней k элементов лопастей
ки, а именно — равенство импульса
действующей силы приросту количества движения в системе и закон
сохранения энергии.
Будем брать импульс за 1 сек. Тогда импульс действующей на воз-
дух вдоль оси Ох силы dT будет равен секундному приросту количества
движения в кольцевой струе. Черьез сечение 0 приносится секундное
количество движения dmVQ, где dm — секундная масса воздуха, про'
ходящая через сечения винта; уходит же через сечение 2 количество дви-
жения, равное dmV2- Следовательно, соблюдая указанное в главе 1
правило знаков, мы можем написать:
dT ~ dm V» — dm = dm (V2 — Vo) •
Замечая, что V2 — Vo -r v2. можно предыдущее выражение написать так-
dT = dm v2. (3)
На вращение элементов лопасти, находящихся'в рассматриваемой коль-
цевой струйке, придется затрачивать мощность dL кгм/сек. Эта мощность
будет расходоваться на увеличение кинетической энергии в струйке и на
преодоление трения лопастей о воздух. Так как давления в сечениях 0 и
2 мы считаем равными атмосферному, то никакой энергии на преодоление
разности давлений в сечениях 0 и 2 мы ие должны затрачивать.
Кинетическая энергия, приносимая в секунду через сечеиие 0, равна
19 Б. Н Юрьев, т. I
ШИ к 0 ШП v„
——, а энергия, уходящая через сечеиие 2, равна —~ Следовательно,
баланс мощности будет таким:
где dLp — мощность, затрачиваемая на трение (профильиое сопротивление)
элементов лопасти» находящихся в изучаемой кольцевой струйке. Эту фор-
мулу можно переписать в таком виде:
dL = (V‘ - 4- dL„ = (V2 ]- V„) (V2 - V„) + dL„.
Замечая, что v2 = V2 — Vo, получаем:
dL = ^P(2V0 4- Vz)v2 -b dLp = dm (yo ~h (4)
Ho dmv2 dT, следовательно,
dL dLp. (5)
Это выражение для мощности мы получили, исходя из изменения кинети-
ческой энергии струи. Можно вычислить эту же мощность по-дпугому.
Сила реакции dT приложена в сечении / к движущемуся со скоростью
V4 воздуху и, следовательно, производит в секунду работу dTV}. Мы
здесь рассматриваем винт как вентилятор, преодолевающий перепад давле-
ния, создающий силу d7\, приходящуюся на кольцеиую струйку. Этот пе-
репад давления прогоняет воздух со скоростью 1^.
Баланс энергии в этом случае напишется так:
dL =dTV1^-dLp^dT(V0 + v1) + dLp. (6)
Выражения (5) и (6) должны быть равными, так как в них идет речь об
одной и той же мощности, следовательно,
dL = dT (V„ + о,) + dL„ = dT (Ч + у) + dL„.
Отсюда следует, что
или
v2 = 2vlt
(7>
т. е. скорость отбрасывания в элемеитарной струе вии-
та в 2 раза больше скорости подсасывания. Это очеиь важ-
ная теорема, лежащая в основе всей импульсиой теории.
§ 3. ЭЛЕМЕНТАРНЫЕ СИЛА ТЯГИ И МОЩНОСТЬ,
ВЫЧИСЛЕННЫЕ ПО СТРУЕ. БЕЗРАЗМЕРНЫЕ ВЕЛИЧИНЫ
Пользуясь найденной теоремой, мы можем переписать формулы (3) и
(4) в таком виде:
dT — dm v2 — 2dm v^, (8)
dL = dm (Vo + y-J + dLp = 2dm + dLp. (9)
Секундную массу воздуха dm, проходящего через сечения кольцевой
струйки, заключенной между радиусами г и г -г dr, найдем, умножив пло-
щадь кольца, т. е. 2nrdr, на скорость Vlt что даст объем проходящего
в секунду воздуха. Умножив этот объем на массовую плотность воздуха
р кг сек?/м*, получим:
dm = 2л rdr Ухр. ЦО)
Подставляя эту величину dm в формулы для dT и dL, получим:
dT -= 4npV1t!1rrfr; (11)
dL = 4лр^У|Г^г dl,p = dT + dLp. (12)
Эти формулы находят очень широкое применение в импульсной теории
Последнюю формулу можно написать еще так:
dL = t/T(V0 -г + dLp = dT + dT + dLp. (13)
Следовательно, получаемая кольцевой струйкой мощность расходуется по
трем путям: первый член в формуле (13) дает полезную работу элемента
винта, как гребного винта, второй дает так называемые индуктивные по-
тери, связанные с наличием индуктивной скорости а последний член
дает потери на трение элементов лопастей о воздух (в основном — это
профильные потери).
У сильно нагруженных винтов прибавляются еще потери на закручива-
ние отходящей струи. У обычных гребных и несущих винтов они малы.
У несущих винтов они меньше 1%, но у вентиляторов могут быть зна-
чительными и тогда их необходимо учитывать.
Переход к безразмерным величинам
Формулы (И) и (12) выведены в именованных величинах. Для расче-
тов удобно писать их в безразмерной форме, что делает их более общими
Мы будем пользоваться следующими величинами:
коэффициентом тяги
- л ? л
-у рЯ4о>2 —
коэффициентом крутящего момента (он же коэффициент мощности)
L . dL
mK —---------- и dmK =-- -------,
— pT^6CD3 -ур/?5Ш3
4 Q*
отвлеченным радиусом г, т. е. будем писать
1 и относительными скоростями
I v, = v,Rr, = v,U; Vo = V„A’o> = Vj.’;
o2 = -j27)w = vJJ; Vi = ViRra = V,U.
Разделив формулу (11) иа р7?4юа и формулу (12) на pR5<o3, получим:
dCT = SV'j r>j г dr; (14)
dmK = 8V‘v,r dr + dmKJ> = dCT J- dmKp. (15)
В случае работы винта иа маете Vo = 0 и V, = v, = vu, следовательно,
dCT= Sv^rdr; (16)
dm„ = 8v,Br dr 4- dmr„ = dCT + dmKp. (17)
Формулы (11), (12), (15) и (16) будем называть формулами тяги и мощ-
иости, вычисленными «по струе».
§ 4. ЭЛЕМЕНТАРНЫЕ СИЛА ТЯГИ И МОЩНОСТЬ,
ВЫЧИСЛЕННЫЕ ПО ПРОФИЛЮ ЛОПАСТИ
Если развернуть иа плоскости цилиндрическое сечение виита, то полу-
чится картина, изображенная на фиг. 6. Сечение лопасти представится в
виде крылового профиля, с хордой Ь, установленной под углом к пло-
Фиг. 6. Схема действия сил, и скоро-
сти у элемента лопасти, лежащего на
радиусе г
скости вращения. Этот профиль
во время работы виита вращается
с окэужяой скоростью го» и дви-
жется вдоль оси ОЭХ со скоро-
стью Уо. Обрацая движение и
прибавив индуктивную скорость ft,
мы получкм стоящи неподвижно
пэофщь, на который воздух набе-
гает (сеченне 1) со скоростью \V\,
компоненты которой равны г<о и
V\ = Vo
Скорость набегаю цего на про-
филь потока очевидно, будет
равна
If, V (ги)2 + Vf (18)
У несущих винтов вертолетов (гео)2 велико, а VI мало, и с очень малой
погрешностью можно для иих считать, что
1^ = ™. (19)
I
Эта скорость образует с плоскостью вращения угол притекания потока
к элементу, равный
ре = arctg — . (20)
Значком «?» мы будем отмечать величины, относящиеся к элементу, когда
возможна путаница.
Ввиду малости этого угла у несущих винтов вертолетои, для которых
ои равен 3—8°, можно считать, что в радианах
= (21)
г ш г
и в градусах
Й = 57,3 Д1-= 57,3 " (22)
г ‘
Угол атаки элемента ас, т. е. угол между хордой профиля и скоростью
V/i, как видно из фиг. 6, будет равен
«г = 4>г — ft = 4>е — -Ц (23)
Г
Угол атаки элемента лопасти ае будет отсчитываться у нас от аэродина-
мической хорды сечений, т. е. такой хорды, при отсчете от которой полу-
чается, что если а£ = 0, то су — 0.
Видим, что каждый элемент лопасти, имеющий плошадь dS~bdr,
обдувается воздушным потоком со скоростью образующим с аэроди-
намической хордой профиля угол атаки ае. В таких условиях на этот эле-
мент будут действовать подъемная сила dYe и лобовое сопротивление dQp
и, по правилам экспериментальной аэродинамики, можно написать:
_ L J рГ2(О2 , ,
dQP = сХр bdr = схр —b dr,
JV А Л pf8'.)3 , .
dYe — Cy—^-b dr = Cyt—^—bdr.
Значком «е» мы будем отмечать, что силы dQe, dY е и другие взяты для
одного элемента. Коэффициенты слр и су берутся из продувок крыльев,
пересчитанных на бесконечное удлинение по правилам экспериментальной
аэродинамики, т. е. отнесенных к профилю, а ие к крылу в целом.
Делается это потому, что у винтов индуктивная скс^сстьучгль гается особо
— это скорость Ор Если бы мы взяли продувку крыла, то в ней уже была
бы учтена эта скорость, и мы, вводя в теорию винта скорость vlf сделали
бы ошибку: скорость индукции вошла бы 2 раза.
Сила dYе является подъемной силой профиля и направлена перпендику-
лярно к скорости UZ,, образующей с плоскостью вращения угол р* следо-
вательно, и сила dYe образует с осью 00 угол $е. Сила лобового про-
фильного сопротивления dQp направлена по скорости Ищем теперь
силу тяги одного элемента dTe и его сопротивление dQe, для чего проек-
тируем силы dYe и dQp на ось винта 00х и на плоскость вращения
(см. фиг. 6), что дает:
dTe = dYe cos -dQ/: sin (24)
dQe = dYe sin Зй +dQp cos [V (25)
У иесущнх виитов угол 3* мал и можно принять, что sin Зе == 3« и
cos Зе = 1. Тогда, подставив в формулы (24) и (25) величины dYe и
dQp, получим:
dTe = си b dr - dQp [V,
pr2(02 , . о , РГ2<02 , ,
dQe = Cy b dr Зй + Cxp b dr
Произведение dQp$e мало, так как оба множителя малы по сравнению с
dYe, и его можно отбросить в первой формуле. Подставляя во вторую
Vi
формулу вместо 3« равную ему величину получим
гш
dTe = cyp-^-bdr; (26)
dQ, = Су V,b dr + cxp^b dr. (27)
Для всех k лопастей получим:
dT = k dT„ = Су kb dr; (28)
dQ—k dQe =cy9~ V,kb dr + cv dr. (29)
Сила dQ является окружным усилием, приложенным ко всем k элементам.
Умножив его иа окружную скорость вращения элементов на рассматривае-
мом радиусе г, т. е. на вэлмдяу л», мы получим элементарную мощность
dL кем/сек, потребляемую этими элементами, т. е.
dL — dQ r<o = Cy^-^-Vikb dr + схр ^~kb dr. (30)
Переход к безразмерным обозначениям
Приводим полученные формулы к безразмерным обозначениям, пользуясь
уже известными формулами, добавив к ним коэффициент заполнения
° = = # = <31)
Поступая так, как было объяснено при выводе формул (16) и (17), мы
теперь получим:
dCT = cyar2 dr-, (32)
dmK = CyOVir'2 dr + cXPcr3dr. (33)
Для расчета прочности несущего винта полезно ввести коэффициент окруж-
ной силы dCQ = —— и тогда, помня, что dL ~ dQ ret, мы можем Ha-
Д. pWtf
2
писать
dm„
dGQ = — . (34)
Г
Полученные формулы дают величины dCr, dmK и dCQ, вычисленные по
профилю. Интегрируя их выражения по всей лопасти, мы получим основные
величины, необходимые для аэродинамического расчета вертолета, т. е. Ст
и /пк, но для этого нам нужно знать величину скорости У у и угол ае-
Для этого служит уравнение связи, к рассмотрению которого мы и пере-
ходим.
§ 5. УРАВНЕНИЕ СВЯЗИ
До 1910 г. в теорию винтов не вводили скорости подсасывания и
считали осевую скорость в плоскости диска равной Vo. При работе на
месте -= 0; и тогда ае = <ре. Так излагалась теория винта в 1890 г.
Н. Е. Жуковским н в 1892 г. С. К- Джевецким. Это давало очень боль-
шую погрешность при расчете работы винта на месте. В 1910 г., как мы
указывали, была разработана импульсная теория и было впервые составлено
уравнение связи, связывающее профиль лопасти, т. е. величины су, о и
с создаваемыми в струе скоростями t>i и В 1912 г. Н. Е. Жуковским
была разработана классическая вихревая теория воздушных винтов, в кото-
рой было применено уравнение связи. В него вошла циркуляция скорости
вокруг контура, охватывающего профиль лопасти.
В импульсной теории уравнение связи получается очень просто. Мы
уже видели, что выражение для элементаоного коэффициента силы тяги
(14) можно получить, исходя из струи. Его можно получить также из
рассмотрения работы сечения лопасти (32).
Эти выражения должны быть равными, так как оба они относятся к
силе тяги (или ее коэффициенту), и как бы мы не вычисляли тягу, оиа
должна быть одной и той же. Следовательно, приравняв друг к Другу
выражения (14) и (32), получим:
= Субг,
нли, вводя в него V, = vlf
(+ й) "1=7
Раскрывая скобки, получаем квадратное уравнение:
+ Ц,», — -i- Суог = 0.
Решая его относительно vlf находим:
= + | (35)
Знак перед корнем берем положительный, так как прн положительной тяге .
н, следовательно, коэффициенте су, скорость должна быть положитель-
ной в применяемой нами системе обозначений.
Теперь легко находим скорость V,, так как
+ = + (36)
В общем случае величины су и с различны иа разных радиусах винта
г, и скорости vj и Vi будут функциями г.
Зная Vlt можно найтн угол притекания потока & иа данном радиусе
г по формуле (21), н угол атаки элемента по формуле (23).
Зная же ае, мы можем найти для данного г по продувке профиля су и
схр. Однако решая уравнение (36), нужно помнить, что входящий в него
Су сам зависит от У,. Поэтому решать это уравнение приходится или ме-
тодом последовательных приближений, или аналитически, пользуясь линей-
ным законом изменения су в зависимости от ае.
Мы рассмотрим сначала аналитическое решение уравнения связи. Зависи-
мость су от обычно представляют в аэродинамике в виде
Су — Аае, (37)
где А имеет у хороших профилей почти постоянное значение и равно при-
мерно 5,6, если углы ае брать в радианах. Если же углы ае брать в
градусах, то
су = А°а°е (38)
и А°^0,1.
Более развернуто можно написать
су = Аае = А (<ре — &) = А ^(ре — . (39)
Подставляя это выражение су в уравнение связи (36), получим:
Освободив полученное выражение от радикала и сделав приведение, полу-
чим квадратное уравнение относительно Ур
Решая его, находим:
= + (41)
2 1С, |/ V 2 16 / 8 '
Знак перед корнем берем + иа основании соображений, приведенных при
выводе формулы (35). Прн работе винта иа месте = 0, и уравнение свя-
зи (41) сильно упростится:
Из —
-фег.
(42)
Введя в полученные уравнения А = 5,6 и <p°e = 57,3 получим оконча-
тельный внд этих основных выражений импульсной теории винтов, а именно:
VZ, =^>-0,35=+ р/ ^-0,35оУ+^7, (43)
а при работе на месте
fie = V'i = — 0,35 з + (0,35 з)2 4- г. (44)
Последнюю формулу для удобства вычислений можно написать также в
следующем виде:
71в = Р1 = 0,353[-1+]/1 + 4У-[ (45)
Очень часто приходится находить эту скорость на относительном радиусе
винта г — 0,7. Тогда получим весьма полезную формулу:
v,. = 4- О.Збо, ^-1-41/1+ 0,07 J. (46)
С помощью этих формул, имея чертеж несущего винта, находим для
— kb — —
заданного г величины б = — и <pt и затем находим скорости или
Заметим еще, что эти формулы свя-
заны с линейным законом изменения
су, что справедливо до критического
угла атаки, равного примерно 12—14°.
Далее начинается срыв потока с профи-
лей лопасти, что обычно сопровож-
дается сильной тряской всего верто-
лета. Поэтому при проектировании
вертолетов стараются, чтобы на лопа-
стях углы атаки не достигали крити-
ческой величины. В тех редких и ненор-
мальных случаях, когда кривая су
по ае сильно отличается от прямой,
Удобно применить графический способ
засечки, заключающийся в том, что
Фиг 7, Определение скорости Vi
и угла ае° способом засечки
сначала задаются углом атаки ав1 иа
глаз, по продувке ппофиля (фиг. 7) находят су1 и вычисляют по уравнению
связи (35) скорость Vj. После этого находят снова угол атаки
= ф’ — -Kl 57Д
который может лишь случайно совпасть с тем углом ап, которым мы
первоначально задались; нанеся иа диаграмму испытания профиля точку
с координатами су1 и аег, мы увидим, насколько предполагаемое значение
сУ1 отличается от возможного Суг- Сделав несколько таких расчетов, полу-
чим ряд точек Вг, В», В3 . .. , через которые проведем плавную кривую
Пересечение этой кривой с кривой су = f (ав) даст правильное значение с
и ае. Этот способ называют способом «засечки». У
Так или иначе, уравнение_ связи легко решается, и мы можем найти для
любого радиуса г величины ав и Су, если нам известна форма лопастн
и задана скорость осевого движения Уо.
Заметим, что выведенное нами уравнение связи (36) пригодно лишь для
режимов взлета и режима 'висения. При спуске оно теряет силу и дает
совершенно неправильные результаты. Этот вопрос мы подробно рассмот-
рим в главе 5.
Фиг. 8. Неработающая концевая
часть лопасти
§ 6. КОНЦЕВЫЕ ПОТЕРИ У ВИНТОВ
Выведенные формулы для элементарных тяги и мощности и уравне-
ине связи предполагают отсутствие срыва потока у профилей. Это
атаки ас, меньших критического угла.
Однако на концах лопастей и у втул-
ки происходит перетекание воздуха
снизу вверх, что вызывает там беспо-
рядочные завихрения, резко изменяю-
щие обтекание профилей. На конце
лопастей при работе на месте наблю-
дается радиальное течение воздуха н
даже прнтеканне струй воздуха сни-
зу. Как известно, такие же явления
наблюдаются н на концах обычных
крыльев, где теория индуктивного сс-
противления оказывается непримени-
мой. Имеются еще другие причины,
изменяющие скорость потока в струе,
рассматриваемые в так называемой «относительной» теории винтов,
учитывающей число лопастей винта. Все эти теории, несмотря на слож-
ность получающихся формул, не учитывают срывных явлений, являю-
щихся источником больших потерь. Поэтому в настоящее время боль-
шинство авторов применяет упрощенный прием расчета, сводящийся к
отбрасыванию концов лопастей при вычислении тягн винтов. Предло-
жено много различных формул для такого учета. Мы будем применять
здесь простейший метод.
Рассмотрим конец лопасти (фиг. 8). Он обычно несколько округлен.
Если провести плавное продолжение передней и задней кромок лопасти,
тона чертеже легко найти длину хорды условного концевого сечения
Ьц. Эффект конца сводится к тому, что на участке длиной Дг лопасть не
развивает тяги. На основании различных опытов с распределением давле-
ния по крыльям н винтам и на основании общих соображений можно счи-
тать, что длина этого участка приблизительно равна
Лг —
(47)
т. е. пропорциональна коицевой хорде Ьд и коэффициенту подъемной силы
концевого профиля су#. Чем шире лопасть на конце и чем больше у
нее угол атаки сечения, тем больше длина Дг. Это — простейшее, доста-
точно логичное и хорошо совпадающее с опытами предположение. Коэф-
фициент 72 получается у лопастей с округленным концом. При прямо-
угольном конце лопасти он возрастает примерно до единицы, а при очень
остром конце лопасти падает примерно до величины 73-
Поправка на влияние концов невелика, поэтому при вычислении ее
можно делать различные упрощения.
При расчете несущих винтов обычно пользуются не шириной лопасти
на конце, а ее шириной на характерном радиусе г — 0,7. Кроме того, в
основную формулу теории винта входит, как мы видели, не ширина лопа-
сти, а пропорциональная ей величина — коэффициент заполнения
• kb,
,
л
берущийся в окончательных формулах на радиусе г = 0,7. Поэтому удобно
ввести в формулу (47), дающую Дг, величину б7 и с^, взятые на г 0,7.
У современных винтов стараются иметь су постоянным или почти по-
стоянным на всей лопасти, и можно принять, что Cyn^zc^. Лопасть у
большинства современных несущих винтов несколько суживается к концу и
в среднем можно принять
bR = 0,867.
Следовательно, можно написать, что
0,8т-
Дг = —ЬцСуЛ =
0,8 &&7 те
------- — Сут
2 Л k
Замечая, что = б7, получаем
л
Дг = л-0,4-~. (48)
В дальнейшем (см. главу 3) мы увидим, что коэффициент тяги у обычных
несущих винтов можно вычислять по формуле
Вводя его в последнюю формулу, получаем
- Ст
Аг = л-0,4-3,2-г ,
’ я ’
или, вычислив чжуювой коэффициент, находим
Д7= 4,0 . (49)
Таким образом, концевые потери тем больше, чем больше величина Ст, и
тем меньше, чем больше число лопастей k.
Получается так, что на относительном радиусе, большем чем г = л от-
пасть не дает тяги. Величина S2 будет, очевидно, такой:
Ц =- 1 - Дг = 1 - 4,0 .
k
(50)
Во многие формулы она входит в квадрате, и тогда мы получим:
й=(1-4,0^Р1-8^+(4,0^)г.
Величина в скобках мала (в среднем равна 0,01) н ее квадратом по срав-
нению с единицей следует пренебречь. Тогда можно написать:
(51)
В центре, возле втулки, лопастн нет: там находится нли 'обтекатель
(кок), или просто идет оголенный лонжерон лбпасти (фиг. 9). .Следова-
тельно, на круге с относительным радиусом также нет тяги.
Фиг 9. Неработающая центральная часть
несущего винта
У работающего вннта заштрихованные на фиг. 10 части ометаемой
лопастями площади силы тяги не дают. Тягу развивает не вся ометаемая
винтом площадь F = nR2, а меньшая, «эффективная», площадь струи
F1 == л (W - я (1.Я)2 - xR2 ® — Й-
(52)
С такой формулой мы уже встречались в теории идеального вннта. Вели-
чина £2— очень часто встречается в винтовых формулах, мы будем на-
зывать ее коэффициентом концевых потерь лопасти и обозначать через
х, т. е.
-
(53)
Пользуясь формулой (51), можно написать очень удобную формулу для
вычисления х:
- %-
х == 1 — 8
(54)
При расчете вертолетов величина Ст
обычно известна, известно также число ло-
пастей k и по выбранной форме лопасти по
чертежу легко определить 5Ь поэтому вы-
числение по указанной формуле величины
% не представляет никаких затруднений.
Вычислять ее достаточно с точностью до
двух цифр.
Обычно у несущих винтов в среднем
Ст^ 0,008, fe = 3 и £1 = 0,25. Тогда
х^0,92.
В случае иезакругленных лопастей, с
Фиг 10. Определение конце-
вых потерь у лопастей вин-
тов
прямоугольным концом нужно уменьшить
х примерно на 0,01—0,03; в случае лопа-
стей с сильно заостренными концами ее
можно увеличить на 0,01. В среднем
хд=.0,90. В случае необычных форм лопастей надежнее будет прибегнуть
к опытам с моделями несущих винтов.
§ 7. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ ДЛЯ ТЯГИ И МОЩНОСТИ
НЕСУЩЕГО ВИНТА ПРИ ОСЕВОМ ДВИЖЕНИИ
В § 4 мы вывели выражения для элементарной тяги и мощности эле
мента лопасти несущего винта. Для получения ,полной тяги и мэцнэсти
всего винта нам нужно проинтегрировать найденные ранее выражения (14),
(15), (32) и (33).
Выражения для тягн надо интегрировать не по всей длине лопасти, а
лишь на участке между £2 и (ввиду наличия концевых потерь). При
определении же мощности нужно учесть, что хотя конец лопасти и не
дает силы тяги, но требует затраты мощности иа преодоление трения и
вихреобразовання, причем эта мощность близка к затрачиваемой прн отсут-
ствии срыва. В центральной части винта лопасти нет, но там находится
оголенный лонжерон, механизмы головки, автомат-перекос с его тягами
ит. д. Все это требует затраты мощности на вращение, приблизительно равной
той, которая затрачивалась бы, если бы лопасть доходила до центра втулки.
Это подтверждают прикидочные расчеты вертолетов. Поэтому при интег-
рировании формулы элементарного крутящего момента (он же коэффициент
мощности в нашей системе обозначений) нужно брать пределы интегриро-
вания г = I и 7=0.
Следовательно, рассматривая струю несущего вннта, мы получаем сле-
дующие основные формулы:
______
Ст =8 dr; (55)
mK - 8\ Vi Vi rdr -г f cX(pr3dr.
(56)
Пользуясь выражениями (32) и (33), написанными при рассмотрении
профиля, получим:
Ст
ъ - -
суаг2 dr.
(57)
\CytsVi г* dr + ^cX!/sr3dr.
G . О
(58)
Эти интегралы можно вычислить, задавшись теми или иными величинами.
Прн этом приходится пользоваться еще уравнением связи. В зависимости
от выбранных условий мы получим различные типы несущих винтов. Этим
вопросом мы займемся в следующей главе.
Формулы для Ст н пгк могут, как видим, писаться в двух видах в
зависимости от того, исходим ли мы при их выводе из рассмотрения струи
или из рассмотрения профиля. На практике чаще пользуются формулами.
(57) и (58).
§8. ЗАМЕЧАНИЕ ОБ ИНДУКТИВНОЙ СКОРОСТИ
У ВИНТОВ
В излагаемой здесь теории принимается, что индуктивная скорость
хотя изменяется по радиусу лопасти г, но постоянна по окружности, опи-
санной этим радиусом г. На самом деле она изменяется и по окружности.
Под лопастью эта скорость достигает наибольшей величины, а между
•> г_г 1 /
лопастями — наименьшей. Находимая по импульсу скорость с1ср — у —
дает на самом деле лишь среднюю индуктивную скорость внутри элемен-
тарной кольцевой струйки, а скорость у профиля будет несколько большей.
В работе «Импульсная теория воздушных винтов» (изд. ВВИА, 1948) мы
указали, как учесть такую неравномерность струн.
Глава 3
РАБОЧИЕ ФОРМУЛЫ ИМПУЛЬСНОЙ ТЕОРИИ
§ 1. НЕСУЩИЙ ВИНТ ТИПА НЕЖ
На практике встречается несколько типичных форм лопастей у несущих
винтов вертолетов. Наиболее характерными являются несущий винт с силь-
но расширяющейся ко втулке лопастью, несущий винт с лопастью, посто-
янной ширины и винт с лопастью, слегка расширяющейся ко втулке.
В импульсной теории форма лопасти задается законом изменения индук-
тивной скорости по лопасти, т. е. величиной y1 = f(r). В вихревой теории
она задается законом изменения циркуляции скорости Г вокруг профилей
лопасти, т. е. функцией Г Как мы уже указывали в главе 8,
импульсная и вихревая теории для несущего винта дают совпадающие
результаты; при этом на режиме висения щ = У"1’.
Теоретически наиболее простым является винт, у которого = const
по всей ометаемой площади; в этом случае и Г = const. Такие вииты, как
мы уже указывали, у нас принято называть по имени Николая Егоровича
Жуковского винтами типа НЕЖ- Эти вииты дают очень хорошие резуль-
таты и близки по качеству к наивыгоднейшему винту. Расчетные формулы
у таких винтов наиболее просты. Далее мы покажем, что и доугие формы
винтов, встречающиеся на практике, дают результаты, близкие к несуще-
му вииту типа НЕЖ; рабочие формулы для них имеют ту же самую фор-
му и отличаются от формул, выведенных для виита НЕЖ, лишь коэффици-
ентами. Поэтому несущий винт НЕЖ можно рассматривать как своего рода
эталон винтов.
Рассмотрим сначала общий случай, когда несущий винт движется по
направлению оси вращения со скоростью Уо. Это соответствует подъему
вертолета со скоростью Vu = Vo.
Скорость Ух у винта НЕЖ постоянна по всей лопасти и ее можно вы-
числить по уравнению связи (36). Для режима, заданного скоростью Уо,
постоянство получится, очевидно, если
СуйГ = — const.
Если брать на всех радиусах одинаковый угол атаки ле, то су = с у = const
и схр = схт = const. Тогда предыдущую формулу можно переписать в та-
ком виде:
зг = з70,7,
или
Зт0,7 __ const
(59)
Т «О «о? .
1ак как б = —и з7 = —, то последнюю формулу можно написать так:
нлн
(60)
Последняя" формула’показывает,₽что ширина лопасти у несущего винта
типа НЕЖ очень сильно (по гиперболическому закону) возрастает ко
втулке, если строго соблюдать условие су =€const (фиг. 11).
Фиг. 11. Форма лопасти винта НЕЖ
Пунктирная кривая — компенсированный винт
(с
Ф const)
Для'коэффициента тяги несущего винта мы получили формулу (57).
Подставляя в нее
Сузг = с^(3-»0,7 = const,
вынося за зиак интеграла постоянные величины н интегрируя, получим:
Ст = г,,7з7 0,7 $ г dr (й — Й) св,а-
Величина Й — Si = х—это коэффициент концевых потерь несущего винта.
Вводя его, получаем окончательно основную формулу импульсной теории
для винтов НЕЖ-
(61)
Величину Ср всегда можно вычислить по заданным параметрам вертолета,
так как
и, следовательно, с помощью формулы (61) легко получить необходимую
величину коэффициента заполнения <з7, т. е.
Скорость легко выразить для винта НЕЖ через Ст, преобразовав фор-
мулу (36) так:
ИЛИ
Эта формула весьма удобна для различных вычислений. Она является урав-
нением связи, написанным через Ст- Найдем теперь коэффициент крутящего
момента (ои же коэффициент мощности) для несущего винта НЕЖ, поль-
зуясь интегральной формулой (58). Получаем: ,
mK = CyCVir2dr н- § схрзг*(1г =
о о
= cs7s7 0,7V! jj г dr + Cw,3, -0,7 \ r2 dr =
0 0
Замечая, что = Ст, получим окончательно:
mK = ~ CtV. + . (64)
Это основное уравнение для вычисления коэффициента тк для винта НЕЖ
Легко найти угол притекания струй к элементу лопасти, так как,
согласно формуле (22),
£ = 57,3-=?- — 57,3 К|1± °* . (65)
20 Б. Н. Юпы*п т Т
Угол установки сечений лопасти будет равен
фе = Ре + = 57,3 -р ае- (66)
На фиг. 12 представлено изменение Ь, {£, Фе и ае в зависимости от от-
носительного радиуса г для винта НЕЖ- Лопасть получается сильно рас-
ширяющейся ко втулке и угол фе сильно растет по мере уменьшения
г — получается сильно закрученная лопасть.
Фиг. 12. Изменение в, и а°е у несущего
винта НЕЖ в зависимости от г
Г Рассмотрим’теперь работу несущего винта иа режиме висения. Втэтом
случае во всех выведенных формулах нужно положить = и1в и. тогда
получится из формулы (63) уравнение связи для* работы на. месте:
°'» = Т1/С7- <67)
Формулы (65) и (66) напишутся так:
[£ = 57,3 4^, (68)
Г
ф; = 57,3 415-+ «;. (69)
г
Выражение для коэффициента крутящего [момеита для ’этого случая при-
мет вид:
'Пк в = 4 Ст Ри + С74~ • (7°>
х 4,3
В последнюю формулу можно ввести скорость »1В, выраженную через
С-р
—. Тогда мы получим:
п ~~ 1
Ст, т. е. v1B = —
Последние две формулы находят очень широкое применение при рас-
чете вертолетов. Заметим, что если мы построим несущий винт с и1Р = const
для работы на висении, то при движении с некоторой осевой скоростью-
величина Vi у него будет изменяться вдоль по радиусу лопасти и несущий
вннт не будет уже винтом НЦЖ- Однако поверочные расчеты винтов типа
НЕЖ показывают, что формула (71) дает очень хороший результат, если в
нее подставлять среднюю по лопасти скорость взятую на радиусе
Фиг. 13. Изменение углов атаки лопастей несущего винта НЕЖ
на разных режимах вертикального полета
г = 0,7. Такую скорость мы будем отмечать значком «7» (номер профиля),
а указатель сечеиия 1 отбрасывать, т. е. мы будем в дальнейшем писать
,(72)
(73)
,ns = ±CTV7-,-C^--.
х 4,3
/«К В ' CtV?b , -
у. 4,3
1 ст2 ,
2 х3/2 Г 4,3
(74)
(75)
Формула (61) для Ст пригодна и для работы на режиме висения и для
подъема, если пользоваться величиной су1, взятой по а7, т. е. на радиусе
г = 0,7.
Несущий вннт типа НЕЖ дает очень хорошие результаты для висеиня
и подъема и неплохо работает при полете с горизонтальной скоростью.
Однако при спуске на авторотации у него в центре получаются большие
углы атаки, вызывающие срыв потока, уменьшение Ст и тряску вертолета.
20*
Фиг 14. Изменение углов атаки лопа
стей несущего винта при о—const
и слабой закрученности лопастей
стояниой ширины (верхняя диаграмма
ция). Он на авторотации работает J.
На фиг. 13 несущий винт подоб-
ран для Ст =0,006 и ае = 6°. На верх-
ней левой диаграмме даны углы
(ре, и <%е на разных г для несущего
винта, рассчитанного для режима ви-
сения; на правой диаграмме те же ве-
личины даны для подъема со скоростью
Vo = — р7в и на нижней фигуре по-
казано, что получается при авторота-
ции, когда скорость снижения равна
VyA - 2v7b н V- _1 и7В . В последнем
случае уже на относительном ра-
диусе г = 0,4 получаются недопусти-
мо большие углы атаки, значительно
больше критического угла ае = 12°.
Это обстоятельство, а также
слишком большая ширина лопастей
в центре, заставляют многих конст-
рукторов отказываться от винта типа
НЕЖ и брать винты, несколько от-
ступающие от такой формы, с мень-
шей степенью расширения лопасти ко
втулке и менее закрученными сечени-
ями. На фиг. 14 даны эти же углы
для несущего винта с лопастью по-
— режим висения, нижняя—авторота-
§ 2. НЕСУЩИЙ ВИНТ С o^const И су =const
Удовлетворительные результаты дает несущий винт с постоянной ши-
риной лопастей s = б7 = const н со слегка закрученными лопастями.
У такого несущего винта
у । I f । 1 с "
ь
Й1 = — у + у4
и при Су — const скорости Vi и с»! сильно изменяются по радиусу.
Вычисляя Ст у такого виита, учитывая, что су -= ctJ1 = const н 5 =
<з7 = const, получим:
Ст = \ Су<зг2 dr = Суб \ г2 dr = ———.
Si 6i 3
Величина —S? оказывается близкой к х = в чем можно убе-
диться, проделав ряд сравнительных подсчетов. В дальнейшем будем
писать: — М — х, и тогда
г v су1^1
Ст = X --------.
3
(76)
Как видим,
НЕЖ (61).
Вычисляя
получается формула,
очеиь близкая к найденной для винта
мощность по формуле (58), получим:
CySV^dr + cxpar3dr =
о о
= С(,737 5 Vi^dr + с1р7з7 § г3dr.
V о
Для точного интегрирования этого выражения нужно в него подставить
значение 171 = + ^-Сувг и провести подробное вычисление по
правилам интегрирования корней (подстановка Эйлера). Одиако при этом по-
лучается очень неудобная и длинная формула. Проще подставить в первый
интеграл среднее значение V’7 и вынести его за знак интеграла. Тогда
получим:
§r2dr + cxp7G7 ^r3dr
о о
X CXD1^
и, окончательно вводя в формулу Ст, получим
m 1 С V ; C*P7S?
шк = —C7-V7 ~|--------
х 4
(77)
т. е. формула при использовании V- почти ничем не отличается от фор-
мулы (74), выведенной для несущего винта НЕЖ, и лишь во втором члене
вместо делителя 4,3 стоит ровно 4.
Скорость у такого винта изменяется вдоль радиуса по некоторому
закону. Самое сильное изменение будет при работе на режиме висения.
Тогда
V1 = »1В = |/ ~с„а,г = 0,я Vr -- у (78)
где скорость иа конце лопасти, г == 1 и г = R. Этот закон измене-
ния изображен на фиг. 14.
Точное выражение для ткъ, пользуясь формулой (78), вычислить очень
легко, так как
=
_ Зх ^ДтР,в _ 3 СТУп _ 1,025 _
хЗ 3,5 УОД ~3,5Уо/7 -z - и TVn'
•и, следовательно,
тк. = ^Ст«7„ + С-^-. (79)
Если бы мы прямо подставили с7в в формулу (77), то получили бы
m.. = - CTv„ + (80)
х 4 ' '
« полная ошибка была бы при работе иа месте равна примерно 2%. При
Vo =/= 0 она зиачительно меньше.
Угол установки сечений лопастей найдется так:
“,»]/ — /-----------------
£ = ^57,3 =-----L—— 57,3 = ряТ/ j-^-57,3 (81)
На фиг. 14 сверху изображено примерное протекание кривых Фе на
режиме висения, внизу — на режиме вертикального спуска на авторотации.
Фиг 15 Эпюры С К Джевецкого для висения (а)
и авторотации (б). Винт НЕЖ
Закрутка такого винта получается небольшой, поэтому на режиме авторо-
тации срывов потока с профилей не получается.
На фиг. 15 даны эпюры С. К. Джевецкого для висения н для авторо-
тации несущего винта типа НЕЖ-
§ 3. НЕСУЩИЙ ВИНТ СРЕДНЕЙ ФОРМЫ
Мы получили формулы для определения Ст и тк для двух несущих винтов
различной формы. Несущий винт НЕЖ имеет сильно расшиэя оцуюся ко
втулке лопасть и большую крутку сечений. Второй винт имеет постоян-
ную ширину лопастей и малую крутку. Тем ие меиее, полученные фор-
мулы оказались очень близкими. Эта близость оказывается еще большей,
если учесть, что коэффициент концевых потерь в первом случае выражает-
ся формулой
н равен в среднем примерно 0,92, а во втором случае он выражается фор-
мулой
и равен в среднем 0,93 — 0,95. Учитывая это, мы можем написать для
Ст такие выражения:
для НЕЖ Ст = Z —
2,9 2,9 3,16
, „ cu7S7 ________,0,95 С1л'3'1
ДЛЯ (5 = const Ст = X —-----~ -1— с^(57 — .
3 3 3,18
Аналогично для коэффициента крутящего момента получим для НЕЖ
прн работе на месте
m к = — CTv7B + - 1,09Сг?„ + !
х 4,3 4,3
для б — const при работе на месте
1,025,-, —’ , ^хр7^7 ^,1,025- — . ^хр7^7 -J гхог' I
тк =------Сго7В Ч-----— ——— Сго7В Ч------— 1,08Стп,в Ч-------— .
х 4 0,95 4 4
Это позволяет написать для всех несущих винтов любой промежуточной
формы единые формулы, дающие погрешность порядка 1 —2,5%, а именно:
Сг = х^-; (82)
х 4
(83)
(84)
Формула для коэффициента крутящего момеита разбивается у винтов
иа два слагаемых. Первое слагаемое дает работу, зависящую от тяги
винта; мы будем обозначать его через тлТ- - — СгУ7, причем среднюю ско-
рость V’7 мы часто будем брать на г = 0,7. Второй член дает работу тре-
ния, точнее,* профильных потерь, лопастей. Его мы будем обозначать через
Следовательно,
где
и
= ткГ 4- ткр,
тлТ = —
(85)
Концевые потери нужно оценивать по формуле (54), где Ст можно брать
средней для высоты, равной половине потолка висеиия; она мало влияет
на и. В среднем х ^ 0,92 н тогда
Сг =
3,2
(86)
(87)
При работе на режиме висения формулы эти упрощаются и принимают вид:
или
(88)
2 у х (89)
'«< в = —- X 4 ’ (90)
1 тк в ~ ~ И ' 2 х /г СХР1^ 4 (91)
В среднем у хороших несущих винтов х ^ 0,92. а схр~ 0,01. Подставляя
в полученные формулы эти величины, получим очеиь простые и.удобные
формулы для расчета вертолетов:
о7в = 0,52 у'Ст;
= !,08 Сто„ + ;
400
= 0,56 & ^4;-
(92)
(93)
(94)
(95)
Формулой (92) приходится очеиь часто пользоваться прн расчете вер-
толетов, поэтому мы даем график (фиг. 16), позволяющий находить по
Фиг 16. Номограмма
Ст ~~ f(cyi' 3?)
су1 и <з7 величину Ст или, зиая Ст и задавшись величиной су1, находить б,.
Заметим еще, что в формулу для Ст можно подставить при отсутствии
срыва потока су7 = Д°а7 = O.loif, тогда получим
= (96)
На практике чаще всего встречается промежуточная форма лопасти, уме-
ренно расширяющаяся ко втулке и умеренно закрученная. Хсрошая форма
получается тогда, когда берется
Тогда лопасть имеет форму, изображенную иа фиг. 17, а-, у корня хорда
сечеиня лопасти возрастает примерно в 2 раза, а ие в 4, как у винта НЕЖ.
Закрутку можно дать по закону <р° ~ ср? . Тогда по уравнению
связи для висеиия (44) получим:
«и = — 0,35s + У (0,35s)2 + 0,7s<pr =
0,35s, 1/ ^+у/ (0,35s,)2 + 0,7s,,f,0,7 .
Фиг. 17. Несущий винт средней формы
,/0?7 t
а —лопасть с ff—сг? I/ . о—лопасть трапецевидной
формы
На фиг. 18 (кривая а) дано изменение угла <р® по радиусу несущего
винта. Угол атаки изменяется мало. Такой несущий винт наряду с винтом
з = const наиболее часто встречается _на вертолетах. Чистый винт НЕЖ
встречается реже.
Фиг. 18. Зависимости fie и <ре от г для несущих
винтов средней формы
1 /"OJ
а —лопасть ((T—CTzl/ b — винт с трапецевидной ло-
пастью и с линейной закруткой
Часто применяют еще более простые формы лопастей, имеющие трапе-
цевидную форму в плане и линейную закрутку (фиг. 17, б). Их аэродина-
мические коэффициенты достаточно точно получаются по изложенным
здесь формулам. Более точно их можно определять или путем интегриро-
вания основных выражений или путем поверочного расчета, что изложено
ниже, в § 7.
Историческая справка
Формулу типа
а737
32
за границей и у нас часто называют формулой Сисинга (Sissingh), что ис-
торически совершенно неправильно.
В работе Н. Е. Жуковского «К теории летания», напечатанной в 1890 г.,
уже имеется аналогичная одночленная формула, дающая тягу элементар-
ного несущего винта; эта тяга пропорциональна углу а. Там же имеется
двучленная формула мощности несущего вннта, выведенная для элемен-
тарного винта. В эту теорию тогда не вводилась индуктивная скорость.
В 1910 г. у нас в России была разработана импульсная теория и в 1911 г.
начали применяться двучленные формулы при проектировании вертолетов.
Их вывод приводился автором в докладах о вертолете на Всероссийских
воздухоплавательных съездах в 1911 и 1912 гг. Подробный вывод этих
формул и их исследование были сделаны в двух напечатанных в 1935 и
1939 гг. работах автора*.
§ 4. ОДНОЧЛЕННЫЕ ФОРМУЛЫ С ИСПОЛЬЗОВАНИЕМ
ОТНОСИТЕЛЬНОГО К.П.Д.
При расчете несущих винтов широко применяются одночленные фор-
мулы:
(97)
и
-Г f’/z
__ 75
4 /пк
на валу виита. Если обозначить через
(98)
мощности в данной схеме вертолетов
и z — число несущих винтов, приходящихся иа один двигатель.
При пользовании этими формулами необходимо брать величины Ст и
тк нз опытов над геометрически подобными винтами. Теория струн винта
1 Ст*
показала, что входящее в эти формулы выражение т
стой физический смысл: это относительный к.п.д.
месте, так как
п г А
Здесь У и (/ взяты по мощности
мощность иа валу двигателя, то
N =
где £ — коэффициент использования
—-------имеет про-
2 /пк 1
винта при работе на
(99)
затрачивается на иде-
потери. Вводя его в
Он показывает, какая часть подведенной мощности
альиый процесс и какая часть идет на различные
предыдущие формулы и используя формулу (98), получим:
Tz = z ^33,25ЛоУ^
(100)
* Б. Н. Юрьев. Некоторые вопросы теории геликоптера. Изд-во ЦАГИ, 1935 (Тру-
ды Конференции по аэродинамике, 1933); его же. Исследование летных свойств ге-
ликоптеров. Труды ВВЙА. № 49. 1939
q" yr
(101)
Импульсная теория позволяет вычислить величину г)0 в зависимости от
параметров несущего винта и сделать ряд ценных выводов для вертолето-
строения.
Величина по импульсной теории
Подставив в основную формулу (99) выражение тк (91) для несущего
винта средней формы, получим:
Формула эта показывает, что г)0 тем больше, чем больше Ст и чем меньше
величины схр7 и <з7. Эти величины не независимы, а связаны друг с другом
основной формулой теории винтов (76). Пользуясь этой связью, предыду-
щее выражение для г)0 можно переписать в таком виде:
1 W? 3 1 ’ 1 3 1 .
и7г + 2 хс^б7 с72 х’/* + 2х су- c'f
Величина = ц7, т. е. равна обратному качеству профиля на харак-
су? —
терном сечении (г—0,7). Эту величину легко получить по продувкам
профилей.
Вводя величину ц7, переписываем выведенную формулу окончательно
в виде:
1»=т---------<103>
-// +11’ х су. '
Из этой формулы получается важный вывод о том, что при заданной
величине Ст относительный к.п.д. г)0 достигает максимума, когда про-
фили винта работают на наивыгоднейшем угле атаки осн, при котором
Ц имеет минимальную величину. Этот угол для обычных профилен близок
к 6° и с,,н 0,6. В формулу (ЮЗ) входит средняя величина ц7, получаю-
щаяся на г = 0,7. Коэффициент заполнения такого винта найдем из фор-
мулы Ст = —£— х и тогда
Ширину лопасти иа г = 0,7 получим нз формулы з7 =
На фнг. 19 приведен график значений i]0 для ц7 = 0,02 (кривая /), что
соответствует хорошей поверхности лопастей, и для и? ~ 0,04 (кривая 2),
что соответствует шероховатой поверхности. Величина к была принята
равной 0,93.
Выражению для i]0 можно придать еще такой вид, что в него не вой-
дет в явном виде величина Ст, но появится величина <з7. Для этого пере-
писываем формулу (102) в виде:
По =
(Ю4)
Замечая, что ----- еэ — об-
ратное экономическое каче-
ство профиля иа г = 0,7,
переписываем это выражение
окончательно
---—— (105)
1 4- 2,6еэ —гт-
а '*
Эта формула показывает, что
при заданном коэффициенте
заполнения, т. е. при задаи-
Фиг. 19. Зависимость относительного к.п.д.
р0 от Ст п ц,
ной ширине лопасти иа г = 0,7, величина т)о достигает максимума, когда
профили работают иа экономическом угле атаки аэ. Для обычных про-
филей это получается примерно при
аэ^-8°; с^э^ОЗ и еэ % 0,03.
Если рассчитать наивыгоднейший винт на заданную величину Ст и выбрать
в соответствии с этим величину о-, то при увеличении угла атаки до аэ,
что может быть достигнуто поворотом лопастей на больший угол уста-
новки <р7, мы получим увеличение т)0. Одиако при этом коэффициент тяги
Ст возрастет в отношении —. Такое увеличение Ст получается при ви-
Сг/7Н
сении вертолета на некоторой высоте или при полете у земли с перегруз-
кой. Следовательно, нужно всегда помнить об изменении По при различных
условиях полета. Приводимые далее двучленные формулы более удобны,
так как в них яснее видно влияние различных параметров (см. ниже, § 5).
Заметим еще, что вертолет при висеиии у земли должен иметь а7,
значительно меиьший, чем ап или аэ. Дело в том, что при полете с гори-
зонтальной скоростью у идущей назад лопасти получаются значительно
большие углы атаки, чем во время висеиия. Если ие учесть этого, то при
полете с горизонтальной скоростью у профилей идущей назад лопасти
Может получиться срыв потока (ае^>акр, или су-, тпах). При этом
несущий винт и весь вертолет начинают сильно вибрировать и получается
так называемая тряска вертолета, вызывающая добавочное динамиче-
ское напряжение и усталостные явления в ряде деталей вертолета. Поэто-
ik
му угол атаки а7 и су7 приходится выбирать с некоторым запасом, завися-
щим в основном от скорости полета Уо = . О таких расчетах мы
подробно расскажем в части III настоящей книги, посвящеииой изложению
так называемой классической теории несущего винта, разработанной в
1927—1928 гг. в Англии Глауэртом и Локком. Эта теория позволяет
находить истинные углы атаки профилей лопастей при разных условиях
работы винта.
Ниже приведены примерные данные для выбора значений а7 и су7 для
режима висения.
о 0,i
1,2 0,96
12 9,6
0,2 0,25
0,84 0,57
8,4 5,7
0,3 0,4 0,5
0,46 0,3 0,19
4,6 3 1,9
Эти данные составил Л. С. Вильдгрубе, исходя из профилей NACA-230
и предполагая плоскую лопасть и малые числа М и Re у лопастей. У ло-
пастей, имеющих большие окружные скорости, эти величины могут сильно
изменяться. Поэтому нужно с помощью классической теории каждый раз
проверять несущий винт и убеждаться в том, что углы атаки нигде не
превысят критического значения.
У современных вертолетов обычных схем величина V0~0,25 и тогда
нужно брать cv7^0,5—0,57.
У крылатых вертолетов часть подъемной силы создается крыльями,
и тогда угол атаки профилей на идущей назад лопасти до скоростей по-
рядка Vo = 0,4—0,5 удается получить меньше критического, что устраняет
опасную тряску машины.
Величина схр получается в среднем равной 0,007—0,01. Учитывая виб-
рации лопастей, их шероховатость н малую точность имеющихся теорий
виита, обычно в расчетах берут сх/?<^0,01. Тогда величина обратного ка-
чества ц7 будет сильно зависеть от допущенного значения су7, так как
__ _0.01
и? — ~~— •
r/7 V7
При Vo = 0,25—0,3 величина р7^г0,02, при Vo^O,4—0,5 величина Ц;
^0,04. Следовательно, устранение тряски заставляет несколько снижать
и тем уменьшать тягу несущих виитов на режиме висения. Большое вли-
яние на г)0 оказывает степень гладкости поверхности лопастей.
Опыты, проведенные с двумя несущими винтами одинаковой геометри-
ческой формы, но сделанными из разного материала, показали, что в слу-
чае обшнвки лопастей материей по нервюрам величина г)0 на меньше
той, которая получается при обшивке лопастей фанерой. Поэтому иа чис-
тоту и точность изготовления лопастей нужно обращать особое внимание.
Лучше всего пользоваться металлическим покрытием по жестким металли-
ческим нервюрам. В случае необходимости окраски несущих винтов нужно
применять иешероховатые краски и уменьшать в расчетах таких лопастей
величину г]0 примерно иа 3—5%.
§ 5. ДВУЧЛЕННЫЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА
НЕСУЩИХ ВИНТОВ НА РЕЖИМЕ ВИСЕНИЯ
Одночленные формулы имеют относительный к. п. д. т]0, зависящий от
ц7, Ст и др. Если брать его по статистике, то не будут учтены многие
условия работы винта во вновь проектируемом вертолете. Опираясь на
практику, статистика, как известно, дает лишь осредненные данные.
Но при проектировании новых машин конструктор должен стремиться к
созданию лучших образцов, чем построенные ранее. Следовательно, не
вскрывая имеющихся возможностей, статистика в какой-то мере удерживает
конструктора от смелых шагов вперед н этим невольно тянет его назад.
Теория же позволяет более смело идти вперед, опираясь на науку, а не
только иа старую, хотя и хорошо проверенную практику.
Импульсная и вихревая теории и дают конструктору такие возможности.
Величину По можно, как было установлено в § 4, находить теоретически
и пользоваться одночленными формулами, подставляя в них уточненное
значение По- Еще удобнее прямо ввести в рабочие формулы величину
в развернутом виде. Тогда потучатся весьма наглядные двучленные форму-
лы, в которых будет совершенно ясной зависимость всех главных величин,
определяющих работу несущего вннта вертолета при висении.
Мы начали пользоваться такими формулами еще в 1911 г. и приводили
их в докладах на I н II Воздухоплавательных съездах, происходивших в
1911 и 1912 гг. За границей они появились значительно позже и теперь
применяются при расчете вертолстов во всех странах.
Мы приведем здесь две таких формулы. Первая дает связь между q,
р, ц, U и Д при висении и является удобной универсальной формулой для
расчета вертолета в стадии увязки его проекта и выбора основных пара-
метров. Вторая формула дает зависимость мощности N от D, р7, со и Т,
т. е. она пишется в натуральных величинах. Ею удобно пользоваться при
поверочном расчете вертолетов.
Универсальная формула
Эту формулу проще всего получить из известного выражения (101).
Подставив в него значение т]0 по формуле (103), получим;
Входящую сюда величину Ст2 можно заменить выражением
после чего предыдущая формула примет вид:
’"/1 =------------------------ U06)
1 +--7-----7=-
VI
Разделив обе части полученного выражения на "|/ и вычислив коэф-
фициенты, получим окончательно
37,sk'-: ,1п,.
<?>.= —--------------•• (Ю7)
у 4- 0,375и l^-iU
Это и есть универсальная формула для расчета вертолетов на режиме ви-
сения. Величина коэффициента концевых потерь к обычно близка к 0,9 и,
подставив в выведенную формулу эту величину, мы получим очень удобную
для различных расчетов формулу:
(108)
Этой формулой удобно пользоваться при отработке эскизного проекта вер-
толета. В этом случае величины, входящие в правую часть формулы, или
заданы или легко могут быть выбраны из условий эксплуатации машины.
Так, величина £ получается для выбранной схемы вертолета по его энерге-
тическому балансу. Величину р можно выбрать из условий экономичной
работы вертолета или условий безопасности спуска на авторотации. Вели-
чина относительной плотности Д берется из таблицы международной стан-
дартной атмосферы для заданной высоты полета. Окружную скорость
U = /?со можно выбрать из условий экономичной работы вертолета и из
условий горизонтального полета, о чем мы скажем в части II.
Когда все эти величины выбраны, формула (108) сразу дает величину
ды кг/л. с., отнесенную к мощности двигателя на высоте. Зная полетный
вес машины G или найдя его по весовой отдаче k, исходя из полной на-
грузки машины 6Н, т. е.
мы можем вычислить необходимую мощность двигателя иа заданной высоте
полета
л/м = дмб (109)
и найти полную ометаемую площадь всех несущих винтов
-7-
Ометаемая площадь одного несущего винта будет равна
с Fz G
г =----= — .
2 Zp
По площади находим диаметр винта D = и, исходя из равенства
Z7 = со, получаем угловую скорость вращения
2U
откуда число оборотов винта в минуту будет равно
Таким образом получаются все основные параметры проектируемого
аппарата.
Фиг 20, Зависимость удельной тяги несущего винта 7М
от£и (7=R<0 (gz-0,02 и С=0,8)
*На фиг. 20 приведен график, дающий величину q* в зависимости от
и U\ величина р.7 была взята равной 0,02. Из него видно, что при
обычной теперь нагрузке /’^20 кг/м1 вертолеты поднимают иа 1 л. с.
всего лишь 4—5 кг.
Двучленные формулы мощности
в натуральных величинах
В некоторых случаях очеиь удобно пользоваться формулами для мощ-
ности, выраженными через натуральные величины. Эти формулы были нами
предложены также в 19Н г. и подробно разобраны*. Они охватывают
случаи висения и вертикального взлета.
Проще всего этн формулы получаются из двух основных формул им-
пульсной теории (84) и (91). Умножая обе части этих формул на
1 рЦя г 77 V,
-jg- г, замечая, что и вводя дополнительные множители в
скобках, равные единице, получим соответственно:
,^7
F=с^и F + ‘г//-
75 2 х/э 2 4-75 2
1 pl/3 с 1 С*/1 1 Fpt/’/pFy/» ( схгГ!^ pUi С11/ cyi \
75 2 Г ‘2 ./Л 75 2 \ pF ) 4-70 2 ГU { Иг. ) \ J
Перегруппировывая множители, подучим, замечая, что Ст — х у‘.^ . сле-
дующие выражения в именованных величинах:
Б. Н. Юрьев. Некоторые вопросы теории геликоптера. Труды ЦАГИ, 1935-
21 Б. н Юрьев, т. I
Подставляя сюда р = и Л и вычисляя коэффициенты, получим
окончательно:
'V ~75х"TV1 ТооТ (40)
и
Л” = '33,25-//* I'T/J + W !‘;77;' (111 >
В среднем у хороших несущих винтов z ^r 0,9; подставив эту величину,
получим очень удобные для прикидочных расчетов формулы
Л ту-ь А-И,(112)
1 Т А J_ т
28 I/Л п 9» L
(113)
Первый член в этой формуле дает так называемые вентиляторные
потери, связанные с тягой Т; мы будем обозначать их через Nt; второй
член дает потери на профильное сопротивление (на трение) и их можно
обозначить через Nf). Следовательно,
где
Nt‘ = "75У 7’И1”-
Np = Лоо7 И;ТО-
(114)
Средняя скорость, входящая в нашу формулу, будет:
16 =
Эти формулы наглядны и удобны, так как в них входят все основные па-
раметры, определяющие работу вертолета. Следует помнить, что эти фор-
мулы относятся к одному несущему винту; у многовинтовых вертолетов
при z винтах на двигатель и при коэффициенте использования схемы - мы
получим прн полетном весе машины G:
1) тягу на одни винт у машины с г несущими винтами Т =
__ -1—1 Трбд^ , где тобД — коэффициент обдувки;
2) мощность двигателя будет равна Л% = N.
С помощью всех этих формул можно решить много различных задач.
Например, подставив в формулу (111) U ~~NM' можно Реши'1Ъ задачу о
иаивыгоднейшем диаметре винта при заданных на валу W н w, т. е. таком
диаметре, при котором при заданной тяге получится минимальная мощность.
Для этого нужно лишь по общему правилу продифференцировать полу-
ченное выражение по D и приравнять результат нулю. Оказывается, что
это получится при очень больших диаметрах винтов, при которых скорость
конца лопасти U делается близкой и даже больше скорости звука, что
вызовет очень большие потери на сжимаемость воздуха, и сильно
уменьшится. Кроме того, у таких винтов получается очень малая ширина
лопастей, и трудно обеспечить надлежащую прочность.
Мощность у таких винтов при отсутствии потерь на сжимаемость воз-
духа оказывается распределенной так, что вентиляторные потери равны
потерям иа трение и Nt = Np.
§ 6. ФОРМУЛЫ ДЛЯ РАСЧЕТА МНОГОВИНТОВЫХ ВЕРТОЛЕТОВ
Мы уже получили формулы (100) и (108), позволяющие находить
тягу или у многовинтовых вертолетов.
Если несущие винты размещены так, что при висении вертолета они
не оказывают взаимного влияния, то указанными формулами можно поль-
зоваться непосредственно. Нужно лишь помнить, что коэффициент исполь-
зования мощности X у одновинтовых машин близок к 0,8, а у многовин-
товых он достигает значения 0,9. Вследствие этого при одинаковом
значении всех прочих величин в формуле (108) увеличатся у миоговинто-
0,9 , 1О
вого вертолета, по сравнению с одновинтовым в отношении ^^1,13,
т. е. получится заметный выигрыш в тяге.
В случае соосной схемы или схемы с пересекающимися винтами полу-
чается еще аэродинамический выигрыш Его можно включить в £ или
вводить условно в т|0. В последнем случае величина Г|о может достигнуть
и превзойти значение единицы. В среднем соосная схема дает увеличение
тяги от 13 до 15%, что является очень существенным добавком, так как
эксплуатационная нагрузка вертолетов обычно близка к 15—20% при
независимых винтах.
Прн решении вопроса о выгодности той нли иной схемы вертолетов
нужно оценивать и вес их конструкций, и заданный потолок, и другие
условия их работы.
Впервые такое исследование вертолетов сделал Н. Е. Жуковский в
работе «О наибольшем полезном грузе, поднимаемом геликоптерами»,
в 1904 г. Он показал, что многовннтовая машина дает значительно боль-
ший полезный груз, чем двухвинтовая. Одновинтовая машина тогда еще
не была изобретена.
Выведенные формулы позволяют оценить безопасность полета на много-
виитовых вертолетах с отдельными двигателями на каждом вннте. Условия
безопасности и управляемости заставляют соединять все вннты кинемати-
чески в одно целое, например, с помощью синхронных валов. Тогда в слу-
чае аварийной остановки одного двигателя остальные продолжают вращать
все вннты, и управляемость машины не нарушается. Кроме того, при этом
сила тягн падает менее резко, чем это было бы при отсутствии синхрон-
ных валов.
Действительно, у двухвинтовой схемы с двумя двигателями мы по фор-
муле (100) получим прн остановке одного двигателя:
27' = 2(33,2511о/Д 0,63-27,
т. е. тяга упадет не в 2 раза, а иа 37%. В случае чэтырехвинтового веп
толета с четырьмя двигателями мы будем иметь при остановке одного
двигателя
47' = 4 ( 33,25п0 /Д D- nJL} = 0,83 47,
т. е. тяга упадет на !7%, а не на 25%. Здесь NM — суммарная мощность
двигателей.
Хотя эти преимущества миоговинтовых вертолетов давно известны и
делалось миого попыток их практической разработки, ио до сих пор такие
машины не вышли нз экспериментальной фазы развития.
Нет никакого сомнения, чго когда жизнь поставит перед авиационной
наукой задачу создания тяжелых вертолетов, то многовиитовая схема будет
взята за основу прн конструировании таких машин.
§ 7. ПОВЕРОЧНЫЙ РАСЧЕТ НЕСУЩЕГО ВИНТА
ЛЮБОЙ ФОРМЫ
Задача поверочного расчета
Импульсная теория позволяет найти для несущего винта любой формы
величину его аэродинамических коэффициентов Су н тк в зависимости от
Ф7 и 1% = . Для этого нужно иметь чертеж винта. По чертежу можно
найти для любого значения г величину b и, следовательно, б = вели
чину и тнп профиля на этом радиусе.
Радиусы для более точных расчетов выбирают через 0,1. т. е. берут-
г =1,0, 0,9, 0,8, 0,7, 0,6, 0,5, 0,4, 0,3. Обычно ограничиваются ра-
диусами, выбранными через 0,15, т. е. берут г = 1,0, 0,85, 0,7, 0,55,
0,4, 0,25.
Режим работы винта при осевом движении задается величинами Vo и
Ф7. При висеннн 1/0 =з0.
Поверочный расчет
Первым шагом в расчете несущего виита является нахождение угла
атаки сечений, что делается с помощью уравнения связи, о чем мы по-
дробно говорили в § 8, Для этого пользуемся или уравнением связи в
форме (36) и решаем его способом засечки, или исходим из второго вида
этого уравнения (41) и находим сразу, подставив в него для любого
значения соответствующие величины <з, <ре и А. Для обычных профилей
Д~5,6.
Найдя величину Уг, находим далее ае по формуле (23) и получаем из
соотношения су = Аае, или по продувке, величину су и величину схр.
При несущих винтах, имеющих большие окружные скорости, нужно
учитывать числа М и Re.
После этого нужно провести графическое интегрирование выражений
для Ст и тк. Пользуясь дифференциальными формулами, дающими элемен-
тарные значения dCT и dmK, т. е. формулами (32) и (33), пишем их в
таком виде:
dCT -
= (115)
dmy
dr
(116)
dCT dmK
Выражения —=r- и —=----погонные нагрузки винта тягой и мощностью.
dr dr
dCT
dr
Фиг. 21- Погонная нагрузка
лопасти тягой
Фиг. 22. Погонная нагрузка
лопасти мощностью
Если начертить диаграммы, приведенные на фиг. 21 и фиг. 22, где по
оси абсцисс отложен относительный радиус г, а по оси ординат величи-
ны -и —, то заштрихованные площади йс и Дадут в некотором
масштабе величины Ст и пгк, так как очевидно, что
(117)
5, V '
И
(118)
Пределы интегрирования, т. е. концевые радиусы 51 н £г, берем в соот-
ветствии с указаниями, сделанными в § 6. Величину площадей и
можно найти с помощью планиметра или любым приемом численных или
графических измерений площадей диаграмм. Эти площади получатся в см .
Для перехода к Ст и тк нужно учесть масштаб диаграммы. Пусть 1 см
длины по осн абсцисс соответствует значению г, равному kx. а 1 см дли-
dCT
ны по оси ординат — значению равному ky; на второй диаграмме зна-
dr
dm
чению -=- соответствует величина ky.
dr
Тогда можно написать, что
Ст = (Йс см2) k,ky (119)
и
mK = CM2) kxky. (120)
Этот расчет нужно повторить для ряда значений 1/0 и <р7. Его удобно ве-
сти в виде таблицы (см. табл. 1).
Таблица 1
Заметим еще, что мы исходили здесь из формул, полученных «по кры-
лу», однако можно вести расчет, пользуясь формулами (14) и 45), полу-
ченными «по струе», и писать:
^££=8^ Vlr
dr
dm,, ------ —
—^ = 8V1u1r +схрагг.
dr
(121)
(122)
Принципиально можно пользоваться как этими, так и первыми формулами,
ио практически удобнее пользоваться первыми, так как в них в явной фор-
ме входят характеристики профилей су и схр, что позволяет следить за
наступлением срыва потока у сечений винта и облегчает введение поправок
в величину схр и т. п.
Мы описали здесь простейший прием поверочного расчета несущего вии-
та, имеющего малый относительный шаг, т. е. величину <р7. При ф7^>15°
он делается не вполне точным и необходимо пользоваться более сложными
формулами *.
В некоторых случаях удобно перейти к расчету виитов по вихревой
теории.
Аэродинамическая нагрузка несущего винта
при осевом движении
Производя поверочный расчет лопасти вертолета мы получаем одиовре-'
dCT
менно и материалы для расчета лопасти на прочность. Величина —— яв-
dr
ляется погонной нагрузкой лопасти тягой (в меридиональной плоскости).
Эта нагрузка дана в безразмерной форме. Для получения ее величины в
dCr л
кг/м величину —= нужно умножить наименованный множитель р/?3о>2;
dr
тогда получим:
Окружное усилие для элемента в безразмерной форме мы уже получили
в § 7 [формула (34)]. Следовательно, безразмерная погонная нагрузка в пло-
скости вращения будет
dCQ dmK 1
dr dr г
(124)
•а погонная нагрузка в кг/м получится в виде
dQ
dr
1
d7 7
(125)
Б. Н Юрьев. Импульсная теооия воздушных винтов. Труды ВВИА, 1948.
Кроме этих нагрузок, у сечений несущего винта возникает еще аэродина-
мический момент закручивания. Он, как видно из фиг. 23, равен относи-
тельно оси О для элемента лопасти длиной dr следующей величине:
dM = dCT -i-+ dCQ -%- + ст й2 dr,
Фиг. 23. Схема действия аэро-
динамических сил, скручиваю-
щих лопасть
где ст — коэффициент момента профиля как
крыла, отнесенный к передней кромке
(Сп,^0). У несущего винта W7^rco, и мож-
но написать предыдущее выражение в таком
виде:
dM
dr
dCT л „ dC/э л .
-2“ Р«4Л1 + -57-9- РЯ “ !/1 +
+ cmv-^b^dr. (126)
о dM
Здесь —— погонная скручивающая аэроди-
намическая нагрузка. Кроме аэродинамической
нагрузки, на лопасть действует еще нагрузка
от центробежных сил. Рассмотрение этих на-
грузок относится к курсу расчета несущего
винта на прочность.
В некоторых расчетах пользуются величиной г г — радиусом точки прило-
жения силы тяги Т. Ее легко найти по эпюре нагружения вннта (фиг. 21),
/dCr\ п
так как эта точка является центром тяжести грузовой площадки Рас-
четы показывают, что для винтов, близких к НЕЖ, величина гт блнзка
к 0,7, а у винтов с постоянной шириной лопасти она близка к 0,8. Для
несущего винта средней формы можно принять, что гг^0,75.
Глава. 4
ВЕРТИКАЛЬНЫЙ ПОЛЕТ ВЕРТОЛЕТА
§ 1. ЗНАЧЕНИЕ ВЕРТИКАЛЬНОГО ПОЛЕТА ВЕРТОЛЕТА
Специфической особенностью вертолетов является возможность вер-
тикального полета, что и дает им большие преимущества перед самоле-
том. Однако достигается это ценой уменьшения горизонтальной скоро-
сти полета, снижением полезной нагрузки и т. д. по сравнению с само-
летом.
Вследствие этого конструктор всегда стремится ограничиться допу-
стимо малой скоростью вертикального взлета и минимальным потолком
машины, для того чтобы уменьшить вес моторной установки и увеличить
грузоподъемность машины. Здесь приходится быть очень осторожным
и внимательно анализировать поставленную задачу. Во всяком случае,
вертолет должен иметь высоту потолка висения не меньшую, чем воз-
можная наибольшая высота местности, где ему придется делать посад-
ку, плюс некоторый запас на неблагоприятные метеорологические
условия, т. е. пониженное барометрическое давление и повышенную
температуру воздуха. В зависимости от местности метеорологические
условия могут снижать потолок вертолета на 300—500 я и более.
Обычно потолок висения у вертолетов лежит в пределах от 1000
до 2500 ж. В специальных случаях он может быть задан более вы-
соким (вертолеты, предназначенные для метеорологических целей, ма-
шины, специально предназначенные для работы в горной местности,
И Т. д.).
При расчете взлета нужно использовать у земли взлетную мощность
двигателя (продолжительность работы иа этом режиме допускается
обычно в течение 5 мин.).
Вертолеты могут эксплуатироваться в самых различных условиях.
На равнине они могут набирать высоту с горизонтальной скоростью,
что дает значительно большую вертикальную скорость взлета, при
взлете с лесной поляны они должны подниматься с большой вертикаль-
ной скоростью, чтобы их не бросило порывом ветра на деревья, при
взлете со дна горного ущелья им приходится подниматься по вертикали
на большую высоту.
Целесообразно поэтому намечать при расчете вертикального взлета
вертолета три варианта нагрузки: нормальную, перегрузку и облегчен-
ную и давать указания о получающихся при этом летных свойствах ма-
шины. Тогда летчик сможет иайти правильную нагрузку для выполнения
того или иного конкретного задания.
Следует всегда помнить о возможности отказа двигателя в полете и
необходимости обеспечить безопасный спуск машины на авторотации.
Этот важный вопрос мы рассмотрим в § 3 и снова вернемся к нему в гл. 5.
§2. ОПРЕДЕЛЕНИЕ ВЫСОТЫ ПОТОЛКА ВИСЕНИЯ
И СКОРОПОДЪЕМНОСТИ ВЕРТОЛЕТА
ПО ИЗБЫТКУ МОЩНОСТЕЙ
Потолок висения
Прежде чем начать аэродинамический расчет вертикального взлета верто-
лета, полезно проверить, получается ли при выбранных параметрах верто-
лета заданный потолок висения. Если он не получится, то нужно изменить
параметры вертолета.
Ранее мы имели формулу (101). В этой формуле — качество вертоле-
та— берется или по статистике вертолетов или вычисляется по формуле
г- 75 г, Т G ,
Еы - £т]и- Величина , входящая в эту формулу, вычисле-
на по действительной мощности двигателя. Мощность двигателя изменяет-
ся с высотой полета по формуле
— AN мо.
(127)
Здесь — мощность двигателя у земли, обычно номинальная и А — коэф
фициент падения мощности с высотой. Тогда
<7 = =
“м ДК1 Д ’
(128)
где qK0 — вес данного вертолета (в кг), приходящийся на 1 л. с. у земли,
т. е. номинальная нагрузка на силу.
Подставляя выражение для q^ по формуле (128) в формулу (101), полу-
чим:
^мо-|/' Р р
Л И А ^м-
Отсюда найдем
См
(129)
Величина Лу^Д характеризует высотные свойства двигателей и жляется
функцией высоты полета Н, т. е.
Ау/Д = {(Н).
Задавшись величинами р — -Др и q = и выбрав по статистике Бели-
ла Чмо 7VM0
чииу Ем, находим по формуле (129) величину А^Л; по графику фиг. 24
находим для данного типа двигателя величину И, соответствующую этому
значению А^Ад. Эта высота и будет потолком висения вертолета, так как
мощность, развиваемая двигателем, будет равна мощности, потребляемой
вертолетом (т. е. несущим винтом, хвостовым винтом, трансмнссней, гене-
ратором и т. д.1.
Из этой диаграммы ясно видно, какое большое значение имеет для
вертолетов высотность двигателя. При невысотных двигателях потолки
получаются низкие, а при высотных они могут быть на 1000—1500 м вы-
ше расчетной высоты двигателя. У двигателей, имеющих двухскоростные
нагнетатели и на характеристике которых, как на флг. 24, имеются два
зубца, получается иногда недостижимый возле второго зубца потолок, так
Фиг. 24. Величина Л]/А для типичных двигателей,
отнесенная к номинальной земной мощности
/—невысотныЛ двигатель, ^ном “120 л- с.; 2— двигатель с высотно-
стью 2000 м N =750 л. с ; 3 — двигатель с высотностью 4000 м, N —
' НОМ I ом
=8i>0 л. с ; 4 — высотный двигатель с двухскоростным нагнетателем
Уноч = !500 л с
как между этими зубцами у двигателя нет избытка мощности для подъема
вертолета вверх. Достигнуть его можно, лишь сообщив вертолету горизон-
тальную скорость, тогда он требует меньшей мощности и может подняться
«до зубца мощности», там остановиться и повиснуть неподвижно.
Скороподъемность вертолета
(приближенные формулы)
Легко найти н вертикальную скорость вертолета, использовав постоян-
но применяющийся при расчете самолетов прием, основанный на определении
избытка располагаемой мощности над потребной (фиг. 25). Обозна-
чив мощность, потребную для висения, через Л^в, получим
Л^кзб = N Na.
Однако эти мощности у вертолетов относятся к валу двигателя и в полез-
ную работу обратится лишь часть этой мощности. Величина е оценивает в
схеме вертолета, а х дает потери на концах лопастей. Поэтому при-
нимают, что мощность, которую возможно использовать, будет равна в
к,гм!сек. следующей величине:
(А —Л/в)75 = 75£хЛ/изб.
Приравнивая эту мощность мощности, потребной для подъема веса G со
скоростью Vv, получаем уравнение
Хх(М—VB)75 - GV{„
Фиг. 25. Нахождение избыточной
мощности при взлете вертолета
откуда и находим скорость взлета
N — N
Vy = &—~75. (130)
Эта формула и аналогичные ей очень часто
приводятся в работах по вертолетам, одна-
ко она дает сильно заниженные скорости
взлета. Дело в том, что в ней ие учиты-
ваются индуктивные потери винта, сильно
уменьшающиеся со скоростью взлета
Поэтому авторы, пользующиеся такими фор-
мулами, вводят в них различные поправ-
ки. Так, в книге Р. А. Янга * эта формула
дается в виде
Для более современных машин (на основании опытов) в книге А. Гессоу
и Г- Мейерса** дается в 2 раза большая величина Vy, чем в формуле (130):
N — NB
^ = 2-75-^-=.
(132)
Недостатком этих формул является то, что в них неточно учитывается
изменение режима работы винта при наличии осевой скорости Vo = Vy. Эта
скорость улучшает работу винта, что в указанной приближенной теории
не учитывается.
Более точная теория
Более точные результаты могут быть получены с помощью импульсной
теории. Так, прн висении мы имеем по формуле (114) следующее выраже-
ние для мощности:
75Ж = A Ga“"; 75Л/>"
При осевой скорости Vo = Vy мы получим по формуле (114)
75^ = GV, + 75 .V,, = 4" ° (Уо + °i) + 75Л'«-
* Р А. Я н г. Теория и расчет геликоптера. Оборонгиз, 1951.
** Л feccov и Г. Мейерс. Аэродинамика вертолета. Оборонгиз, 1954
Вычитая почленно из второй формулы первую, получим:
75UV - ЛГВ) +^G«1---ЩИ1в.
Отсюда находим скорость взлета:
Vy = q 75 + Щв — £Д-
(133)
Эта формула и объясняет получающееся по приближенным формулам
расхождение с опытами: скорость v1B значительно больше, чем v(* и это
дает значительное добавление к скорости VtJ. Последней формулой можно
пользоваться для точного определения скорости Уи. Дая этого находим
сначала величину характерной скорости
и находим скорость щ из формулы, написанной в натуральных выражениях.
Тогда получим:
‘г’ |/ ~Т + '
Если в формулу (133) подставить величину из последней формулы и ре- •
шить полученное уравнение относительно Уу, то получится следующая
формула:
Ч-----75 4-
(134)
Эта формула дает точное значение скорости Уу с учетом индуктивных ско-
ростей. Мощность V берется здесь прямо по высотной характеристике дви-
гателя, а потребную для висения мощность приходится вычислять по уже
известным нравтам, например, по формуте (114).
Вместо указанного .способа вычисления скороподъемности гораздо удоб-
нее пользоваться аналогичным способом, приведенным в § 4. При его приме-
нении значительно сокращается вычислительная работа-
§ 3. РАСЧЕТ СКОРОПОДЪЕМНОСТИ И ПОТОЛКА ВИСЕНИЯ
НА ОСНОВЕ ОПЫТНЫХ ДАННЫХ
Для такого расчета необходимо иметь испытание несущего винта (обыч-
но его модели) в аэродинамической трубе. Результаты испытаний можно
представить в виде двух диаграмм (фиг. 26), дающих величину Ст и тк в
зависимости от Vo и угла установки лопастей ср°. Число оборотов считаем
постоянным.
На любой высоте нам будут известны величины
2
т,
ГЛ^М75
я
z -г£-рКъы3
Проведя для какой-либо высоты полета иа верхней диаграмме линию
АВ (СМ — Ст), мы получим в точках пересечения этой прямой с кривыми
Фнг 26 Определение скороподъемности
вертолета при помощи продувок несуще-
го вннта
ряд величин и ср°, при ко-
торых получается заданное
значение Ст. Отметив на ниж-
них кривых точки с такими
же величинами Уу и ср? , мы
сможем провести по иим
вспомогательную кривую CD.
Сделав засечку этой линии
прямой EF (ОЕ = тк, мы по-
лучим в точке К такие зна-
чения Vy и <р’, при которых
получаются заданные вели-
чины Ст и тк. Другими сло-
вами, мы получим необходи-
мый угол усзанозки ср° и по-
лучающуюся при этом ско-
рость взлета
Vy = VQR(D. (135)
Потолок получится там. где
Vy - Vo =-- 0.
Описанный способ расчета
в принципе является самым
точным (так как мощность
двигателя и несущего винта
берется по опытным данным),
но он требует надежных ха-
рактеристик винта, т. е. харак-
теристик, полученных для
возможно осуществить По-
еальных чисел Re н М, что не всегда
тому характеристики приходится исправлять на эти числа, что вносит неко-
орую неточность. Наконец, в литературе опубликовано мало подобных
арактеристик, полученных при опытах с большими винтами.
Гораздо более приемлемыми являются теоретические методы, наиболее
ростой из которых и будет описан в следующем параграфе.
Примечание При расчете скороподъемности как самолетоз, так и вертолетов
в учитывают обычно инерционных сил, так как изменение вертикальной скорости
dV„
ало, особенно у вертолетов, и величина т_— очень мала и ею вполне можно прене-
речь по сравнению с весом машины G
§ 4. РАСЧЕТ СКОРОПОДЪЕМНОСТИ
НА ОСНОВЕ ТЕОРЕТИЧЕСКИХ ФОРМУЛ
Существует много приемов такого расчета. Мы здесь изложим наиболее
простой и наглядный, основанный на импульсной теории (§ 2 и 3 главы 3).
Потребный коэффициент мощности несущего виита при вертикальном
полете, когда Vy = Vo, выражается формулой (84). Величину безразмерной
скорости воздуха в плоскости диска можно получить по уравнению свя-
зи (83), т. е. Vi^VT.
Подставляя V7 в выражение тк, получаем:
Введем сюда обозначение
т тк — п1кр = тк
СХС7°1
4
(136)
и, изолировав корень, получим из предыдущего выражения, после замены
Уо через Vy,
2-. Lq .
Возведя это уравнение в квадрат, получим:
/п2х2 4тх г; 1 ~
~vCt-
Решая последнее уравнение относительно Vy, находим окончательно:
‘ - zm Сг
<137>
Расчет по этой формуле очень прост. Для ряда высот нужно найти по
характеристике двигателя величину
/Пк
75Лм £
л
~р/?5<03
(138)
и вычислить
СТ
1 G
z л
-Л-рК*йГ
(139)
В итоге по формуле (137) определяется Vy и вычисляется Vy = VyR(o. Рас-
чет удобно вести в виде табл. 2. В таблицу введена величина СГо для
упрощения расчета, так как
„ 1 °сто
— z л “Д’
— р/?43)2
(НО)
где Сто—коэффициент тяги несущего винта при висении у земли. В по-
следней строке дана средняя величина су1 профиля для проверки винта на
срыв потока.
Таблица 2
Полученная таким образом величина потолка висения называется теоре-
тической. Практический потолок висения берется более низким. Обычно
практический потолок принимают равным Н3 пр = 0,9//в, или берут в каче-
стве НЪп? ту высоту, где Vy = 0,3—0,5 м/сек.
Графическое определение скороподъемности
Простым и наглядным способом определения скороподъемности является
графический метод (фиг. 27). На характеристику двигателя, т. е. на диа-
грамму располагаемых мощностей, наносят сетку потребных мощностей
для разных скоростей взлета Vy и высот полета Н. Такую сетку легко
построить по импульсной теории, исходя из формулы (114)
lb'N = ~ GV, + Ы„,
в которую нужно подставить
Высота полета войдет в величину ViB,
так как
где У1во — характерная скорость у
земли. Выбрав несколько высот и ско-
ростей Vy, легко построить пучок
кривых, дающих потребную мощность.
В точках пересечения нх с характери-
стикой двигателя получатся нужные
нам парные значения Vy и Н. Способ
очень нагляден, и по сеткам очень
легко проследить, например, влияние
форсажа двигателя и т- д. Сразу получается искомая величина Нв.
Сетку Мп можно строить и по опытным данным, т. е. по кривым Ст
и пгк. Последнее настолько просто, что не требует объяснения. Недостат-
ком этого способа является необходимость определять скорость Vy по сет-
ке, оценивая дроби на глаз.
§ 5. КРИВАЯ СКОРОПОДЪЕМНОСТИ И ПОСТРОЕНИЕ
барограммы вертикального взлета
На основании описанных способов определения скорости Vy можно по-
строить кривую скороподъемности вертолета Vy - /(//) (фиг. 28).
Эта кривая в точке пересечения с осью ординат дает более точную вели-
чину потолка висения, чем та, которую можно
__л0геор______________ определить по таблице отдельных величин Vy и
поакт ' интерполируя на глаз. '
Кривая скороподъемности позволяет
просто построить барограмму взлета, т. е. кри-
вую, дающую время набора вертолетом опре-
. деленных высот.
Применяется два способа нахождения ба-
рограммы: способ «змейки» и способ графиче-
ского интегрирования.
очень
Способ «змейки»
Этот способ основан на построении на ди-
аграмме скороподъемности особой «змейки» с
помощью масштабного треугольника. По суще-
ству он является способом интегрирования с по-
мощью трапеций.
Сначала выбираем относительно малый ин-
тервал времени Ы. За это время вертолет, име-
ющий на этом интервале среднюю скорость Уу, поднимется на высоту \Н,
равную
0й
Фиг. 28. Диаграмма скоро-
подъем пости вертолета
= Уум.
(141
22 Б. н. Юрьев, т. I
Величину Д// можно получить графически для любого значения Vy,
построив вспомогательный масштабный равнобедренный треугольник АВС
(фиг. 29), имеющий базу (Л//), соответствующую некоторой произвольно
выбранной скорости взлета (Vr/) н выбранному интервалу времени, т. е
(Л//)- (У.)ДЛ
Величину (Vу) нужно брать равной 3—6 м/сек (в среднем 4 м сек)', интер-
вал времени удобно брать в 1—2 мин. т. е. в 60—120 сек. Откладывать
величины (Д/f) и (Уг/) нужно-в масштабах диаграммы скорости взлета.
Фиг. 29. Построение барограммы взлета опособом «змейки»
Если теперь построим змейку, как показано на фиг. 29, проводя ее
стороны параллельно бедрам равнобедренного треугольника АВС, то полу-
чим ряд треугольников, которые разобьют кривую Vy~f(H) на участки,
соответствующие одному и тому же интервалу времени ДЛ Это следует
из того, что каждый элементарный треугольник автоматически дает вели-
чину Д/f = Vy\t, т. е. умножает переменную, среднюю на участке, вели-
чину Vv иа Дл То, что треугольники получаются хотя и близкие к равно-
бедренному, но все же с несколько скошенной базой, очень мало
сказывается на точности результата, так как в этом случае берется авто-
матически средняя скорость V у.
Время подъема на любую высоту, например Н', получится простым
подсчетом числа полученных отрезков иа кривой Vy — f(H) и оценкой доли
последнего участка; если это число равно п, то время подъема будет равно
t = n\t.
Например, на нашем чертеже для высоты Н' получилось п -= 4,6; а так как
Д/ = 120 сек., то получится t — 4,6-120 = 552 сек. = 9 мии. 12 сек.
Для построения барограммы взлета нужно построить рядом с диаграм-
мой Vy = f(H) еще и оси координат для барограммы и разбить ось абсцисс
на одинаковые интервалы времени, равные At Построение барограммы
сводится в этом случае к простым горизонтальным перенесениям точек
кривой а, Ь, с и так далее на соответствующие ординаты барограммы.
Получается простое построение, ясно видное на фиг. 29.
Время подъема на высоту потолка висения бесконечно велико и змейка
никогда не достигнет точки /7В и будет иметь сверху бесчисленное число
звеньев. Поэтому нужно лишь получить время подъема на высоту практи-
ческого потолка висения, что всегда легко сделать.
Если вертолет имеет очень малую скороподъемность и змейка вяло
поднимается вверх, то можно уменьшить высоту CD, т. е. (Vy) масштаб-
ного треугольника в 2 раза, что будет соответствовать увеличению интер-
вала времени в 2 раза. Такую замену можно сделать на любом звене
змейки.
Для получения хорошей точности желательно иметь у змейки от 10 до
20 звеньев. Большее число звеньев дает меньшую точность из-за накопле-
ния ошибок графического построения.
Способ графического интегрирования
Дифференциальное уравнение, связывающее dH, Vy и dt, имеет вид:
dH = Vudt.
(142)
Скорость Vy является функцией Н и потому в этом уравнении можно раз-
делить переменные
' U
Отсюда, интегрируя, получим:
Этот интеграл легко вычислить графически, построив кривую для величины
-L = f(H), как показано на фиг. 30. Заштрихованная площадь Q см2 дает
при учете масштабов величину нашего интеграла, т. е.
" 1
t = -гг- dH = (Q см2) kxky, (144>
? *
где ky — масштаб Н, т. е. число метров в 1 см диаграммы и 1гх — масштаб*
—, т. е. число единиц р— в 1 см диаграммы по оси абсцисс.
•у * У
1
Если разбить площадь над кривой р—на несколько кусков горизонталь-
vy
нымн линиями, то после вычисления мы получим таблицу, связывающую
Hi, Н2, Н3 и так далее с затраченным на подъем временем t, и т- Д-
22*-
По этим данным легко построить по точкам всю барограмму. Само
интегрирование можно производить нли по способу трапеций, или любым
другим приемом численного или графического интегрирования.
Фиг 30 Построение барограммы взлета способом
графического интегрирования
Два’описанные приема построения барограммы применимы полностью
не только к вертикальному взлету вертолета, но прн полете под любым
углом к горизонту. В последнем случае нужно лишь определить скорости
Ев__в зависимости от Н по способам, описанным ниже, в главе 8.
§ 6. СКОРОСТЬ ВЕРТИКАЛЬНОГО СПУСКА
НА АВТОРОТАЦИИ ПО ОПЫТНЫМ ДАННЫМ
В случае остановки двигателя вертолет может опуститься иа землю
вертикально, на авторотирующем винте. Обычно при этом получается очень
большая скорость снижения и необходимы специальные приемы управле-
ния, например, подрыв несущего винта на малой высоте. Этот важный для
безопасности полета вопрос мы подробно рассмотрим в главе 5. Здесь же
мы рассмотрим лишь скорость установившегося вертикального спуска на
авторотации, пользуясь опытными данными.
Многочисленные лабораторные опыты, проведенные во многих странах,
показали, что несущий винт при малом шаге устойчиво вращается на авто-
ротации и его сопротивление приближается к сопротивлению сплошного
диска того же диаметра. Раньше не знали этого факта и многие изобрета-
тели считали, что несущий винт нужно при таком спуске остановить, за-
тормозить и изготовлять его с очень большим числом лопастей.
Сопротивление виита можно представить с помощью обычной формулы
экспериментальной аэродинамики:
oV2
Q^cJIdLF^G. (145)
Оно должно в установившемся движении равняться весу машины в полете.
Величина сх у обычных несущих винтов близка к значению 1 —1,2; вели-
чина р у земли равна Vs- Отсюда находим для сх = 1,2 скорость спуска
Г, /5 ~ С ТГГ Г -3’6 Vp <146’
341
и для cx^el,0
V,, = - 4/р.
Так, например, для средней у современных машин величины р = 16 кг/м2,
получим скорость снижения от 14,5 до 16 м}сек,, т, е. скорость снижения
оказывается довольно большой и представляет большую опасность. Поэтому
мы выделяем все вопросы, связанные с вертикальным спуском, в особую
главу, а здесь лишь укажем, что величина сх = 1,0 получается у лопастей
с большой круткой, дающих большую тягу на моторном полете. У плоских
лопастей величина сх достигает значения 1,2 и даже несколько превосходит
его.
Обычно иа вертолетах безмоторный спуск производят ие вертикально,
а под углом к горизонту, т. е. на планировании. Тогда скорость снижения
Vy уменьшается примерно в 2,5—3,0 раза.
§ 7. ПРЕДЕЛЬНАЯ НАГРУЗКА ВЕРТОЛЕТА
Допустимая нагрузка вертолета зависит от высоты, на которой он дол-
жен производить вертикальный взлет и посадку. Если нагрузить его так,
что максимальная тяга у земли будет равна весу машины, то такой верто-
лет не сможет подняться по вертикали, а сможет лишь подниматься по
наклонной линии, т- е. с наличием горизонтальной составляющей скорости
полета. При этом при неблагоприятных метеорологических условиях верто-
лет может оказаться неспособным вовсе отделиться от земли. Очевидно,
что такая нагрузка недопустима при эксплуатации вертолетов, за исключе-
нием каких-либо специальных случаев.
Очевидно, что, совершая полеты в горах, где зачастую отсутствуют
подходящие для взлета и посадки площадки, вертолет должен иметь во"*
можность садиться и взлетать вертикально.
Следовательно, нагрузка вертолета определяется высотой тех площадок,
иа которые он должен садиться, и тем запасом высоты, какой необходим
для преодоления неблагоприятных метеорологических условий.
Поэтому для эксплуатации является ценным график или таблица, да-
ющие высоту потолка висения для разных эксплуатационных нагрузок
машины и для различной продолжительности полета.
Задача эта сводится к нахождению максимальной тяги вертолета на
разных высотах при полном использовании мощности двигателя. Решить
эту задачу можно, пользуясь продувками несущих виитов, или аналити-
чески, Рассмотрим оба эти приема.
Определение наибольшей тяги
на различных высотах на основе продувок
Для таких расчетов необходимо иметь внешнюю характеристику дви-
гателя. Зная мощность на высоте, находим коэффициент крутящего момеита
при висеиии для несущих винтов:
Шк. в
7&V
~ №.F '
2
(147)
где
М = /V,
Пользуясь графиком испытания несущего винта (фиг. 31), по величине
тк в находим необходимую установку лопастей ср7 н коэффициент тяги Ст.
Далее находим тягу
Фиг. 31. График испытания несущего винта
при работе на месте; Vp=0
T = CT^F (148)
и вычисляем допустимый вес ма-
шины G по формуле
G = Tz(l — тобд),
где тОбд — коэффициент обдувки
частей вертолета струей винтов.
Поправка тОбд у многих схем вер-
толетов мала, и часто принимают,
что G = Т2. Вес машины разбиваем
на три части; вес пустого верто-
лета Gn, вес топлива и масла Gr и
эксплуатационную нагрузку G3K.
Тогда
Сэк -= G — Gn — GT.
Если задаться несколькими высотами полета и разной продолжитель-
ностью полета (на номинальной мощности), то можно построить очень по-
лезный график (фиг. 32), дающий допустимую нагрузку на различных вы-
сотах. Влияние неблагоприятных метеорологических условий можно оценить
сдвигом шкалы высот Нъ на некоторую величину. В среднем этот сдвиг
Фиг. 32. Грузоподъемность вертолета па разных высотах
I — Сг =0; 2 —запас топлива на I час полета; 3 — запас топлива на
2 часа полета. Нижняя масштабная ось—для случая неблагоприятных
метеорологических условий
можно оценить в 500 м. По этой диаграмме очень легко найти допустимую
нагрузку машины для заданной высоты посадочной площадки и заданного
времени полета.
Иностранные фирмы нередко в рекламных целях дают завышенные зна-
чения нагрузок у своих машни, при реальной эксплуатации приходится
сильно снижать допустимую нагрузку.
На диаграмму фиг. 32 полезно нанести на малых высотах избыточную
тягу, получающуюся у пустой машины (кривая 1). Такой случай встреча-
ется на практике при испытаниях вертолетов на привязи. Тросы, привя-
зывающие вертолет к земле, и шасси вертолета должны быть рассчитаны
иа это условие, так как обрыв тросов может повести к аварии.
Аналитический расчет предельной нагрузки
Величину G3K очень просто найти по формулам импульсной теории.
Зная гпк.в, можно по обычной формуле
вычислить Ст и получить:
2
Ст = z2T-'
Зная Ст, находим тягу
Т = Ст F;
2
вычисляем, как и в первом случае, поддерживаемый на высоте вес машины
G —Тобд)
и находим:
бэк = G — G„ — Gr.
Потолок на подушке
Трудность получения высоких потолков висения заставила в последнее
время ряд иностранных фирм ввести новое понятие: «потолок иа подушке».
Если допустить, что вертолет в горах всегда взлетает и садится, поль-
зуясь горизонтальными площадками, то сила тяги заметно увеличивается
от эффекта близости земли.
Величина
— = р—
где То, — тяга вдали от земли, a h •— высота втулки над землей.
h Т
При —^0,5 величина 1,5.
R
Для учета этого влияния нужно Ст умножить иа -I-.
* со
Поднявшись иа высоту 2—5 м, вертолет может полететь горизонтально
н набрать большую высоту. Однако висеть в горах он не сможет вдали
от площадки.
Глава 5
РЕЖИМ ВЕРТИКАЛЬНОГО СПУСКА ВЕРТОЛЕТА
С РАБОТАЮЩИМ ДВИГАТЕЛЕМ И НА АВТОРОТАЦИИ
§ I. БЕЗОПАСНОСТЬ СПУСКА ВЕРТОЛЕТА
Безопасность спуска важна для любого летательного аппарата.
О самолете говорят, что взлет на нем труден, полет легок, а посадка
опасна. У вертолета же взлет легок, полет труден, а посадка опасна
Посадка опасна потому, что скорость соприкосновения этих довольно
хрупких машин с землей получается большой из-за целого ряда эксплу-
атационных условий, которым должен удовлетворять летательный ап-
парат.
Первые самолеты имели посадочную скорость порядка 30—40 км/час
и полет на ннх был сравнительно безопасным. Но теперь они имеют
посадочную скорость, доходящую до 150—200 км/час. Как правило, по
садка самолета производится с выключенным двигателем или с двига-
телем, работающим на малом газе. Опытный летчик может при посадке
обеспечить вертикальную скорость самолета, равную нулю, но горизон-
тальную посадочную скорость он уничтожить нс может, и если ему на
пути встретится какое-либо препятствие — неровность на поверхности
земли, кочка, столб, провода, кусты и т. д.,— неминуема тяжелая
авария.
Вертолет при моторном полете может садиться с нулевыми (верти-
кальной и горизонтальной) скоростями, т. е без какого-либо толчка в
момент приземления. Поэтому на некоторых вертолетах делают весьма
упрощенное шасси, с малым ходом, с маленькими колесами, а иногда
и вовсе без колес, на резиновых баллонах-мячах.
Однако всегда возможна аварийная остановка двигателя в полете,
и тогда вертолету необходимо спуститься на землю и коснуться ее с
малой скоростью. При наличии достаточно большой высоты или прн
остановке двигателя прн полете с большой горизонтальной скоростью
вертолет может перейти на режим планирования и, подобно самолету,
спуститься по наклонной траектории и сесть после «выравнивания», как
это делается на обычном самолете. При этом посадочная скорость
у вертолетов значительно меньше, чем \ самолетов.
В этих условиях вертолет садится с большей безопасностью, чем
самолет. Пробег его по земле при торможении полхчается около
20—30 м.
Однако при остановке двигателя иа малой высоте, во время «висе-
ния» вертолета или когда он работает над неудобной Для посадки мест-
ностью, например, над городом, ему приходится садиться по вертикати,
с авторотирующим несущим виитом. При этом получаются большие
вертикальные скорости спуска, опасные для приземления. В настоящей
главе мы рассмотрим различные способы, которые предлагались для
увеличения безопасности спуска в этих условиях
Вопрос этот для вертолета весьма существен, так как ему в соот-
ветствии с его назначением приходится летать иа малых высотах и там,
где местность загромождена зданиями или труднопроходима: скалы,
леса, болота и т. п. По своим свойствам вертолет способен сесть «на пя-
тачок» по вертикали, но обеспечение малой скорости снижения — зада-
ча нелегкая для конструктора. К этим трудностям прибавляется еще
трудность точного расчета работы несущего винта иа спуске: для этого
случая до сих пор еще ие создано хорошо разработанной теории, не-
смотря на то, что во многих странах были произведены обширные тео-
ретические и экспериментальные исследования по этому вопрос’--.
Мы здесь излагаем простейшую теорию, так как оиа, не слишком усту
пая в точности более сложным теориям, обладает большой нагляд-
ностью
Работа виитов на авторотации и иа режиме ветряного двигателя
изучалась советскими учеными на много лет ранее, чем за границей.
Мы имеем исследования проф. Н. Е. Жуковского и его учеников— про-
фессоров В. П. Ветчиикина, Г. X. Сабинина и др. В трудах Кучинского
аэродинамического института в 1909 г. были опубликованы обширные
исследования по этому вопросу. Русские ученые впервые указали в
1917 г. иа возникновение при спуске вертолетов особого режима— «вих-
ревого кольца». Экспериментальное изучение простейших несущих вин-
юв провели еще в 1910 г. ученик Н. Е. Жуковского студент Г. А. Соро-
коумовский и ииж. В. А. Слесарев. Много опытов с различными несу-
щими винтами произвел в наше время ииж. А. М. Изаксои; В. А. Кожгв-
ииков провел экспериментально-теоретическое исследование влияния
близости земли на работу виита. Много работ на эту тему было прове-
дено и за границей. В этой области работали Глауэрт, Бенист, Стюард,
Ботезат и др. В библиографическом списке указаны некоторые из та-
ких работ и мы отсылаем к иим читателей, интересующихся более глу-
боко этой проблемой.
§ 2. СТРУЯ У НЕСУЩЕГО ВИНТА НА РАЗНЫХ РЕЖИМАХ
вертикального полета, режим вихревого кольца
В главах 2 и 4 был подробно рассмотрен вопрос о работе несущего
виита на режиме висения и при вертикальном взлете. Осевая скорость
изменялась от V'p=Vo = 0 до больших положительных значений.
Одиако при спуске вертолета, когда Vv=Vo<'O, возникает много
особенностей в работе несущего виита, а также в форме создаваемой
им струи; это ие позволяет непосредственно пользоваться формулами,
уже выведенными нами в главе 2.
Рассмотрим основную формулу импульсной теории, а именно фор-
мулу тяги
Т =-- xSoEVjUv (149)
В рассмотренных ранее случаях все величины были положительными
и формула давала правильный результат. При спуске величина Vi
может быть отрицательной; вошла она в формулу потому, что секунд-
ная масса воздуха т, проходящая через диск виита, связана с ней
очевидным соотношением m--xpFVi.
Обычно для определенности среднюю скорость Vj берут на радиусе
г = 0.7 и мы будем считать, что Vi~V7; тогда
т ~ хрГУ7.
Масса по физическому смыслу — величина скалярная, всегда положи-
тельная, и она не должна изменять знака в зависимости от знака Vr Сле-
довательно, мы должны были бы писать эту формулу в таком виде:
яг = рГ|У, (х, (150)
т. е. брать абсолютное значение скорости | У71 или писать эту формулу
для случая, когда У7<^0 в таком виде:
m^ — KpFV7. (151)
Знак силы тяги Т, направленной всегда вверх, будем считать положитель-
ным; знак нидуктнвной скорости v- также будет всегда положительным,
так как оиа направлена вниз, в сторону, противоположную Т, а по пра-
вилу знаков (глава 1) и7 в этом случае больше нуля. Осевую скорость Vo
мы в этой главе будем обозначать через Vy, так как она направлена по
оси Оу. Скорость потока в плоскости диска всегда равна алгебраической
сумме скоростей v7 и Vu, т. е.
= Уо -у + v7.
Подставив значение V7 в формулы (150) и (151), получим:
m = xpf |(Vy4- и7)^
и прн У7 <С 0
m - — KpF(Vу + Vi}-
Следовательно, выражение для тяги Т должно писаться
1) Для случая, когда V, > 0, получим:
в двух видах.
Т = x2pf (V? -т i»7) v7,
что приводится к квадратному уравнению относительно у7:
и* + VyV7------ — 0.
x2pF
Отсюда находим:
2
4 x2pF ’
при Т > 0 мы
здесь у корня нужно брать знак «плюс», так как иначе
получим прн минусе перед корнем v7 0, что противоречит указанному
правилу знаков. Следовательно,
К
(152)
<.<уул у пеиущеси suniu пи pujhwx рем,имих нимии
^^"4-/4+^- <15з>
Мы получаем в этом случае уже известные нам формулы.
2) Для случая, когда У7 0, получим:
Т - x2?F + v7) v7,
что приводится к квадратному уравнению относительно 7><
Щ + —— = О,
x2pF
тогда
V7 = K№7 = 4-±l/ 4—Г7- ' (155)
2 г 4 x2pF
Упрощая формулы, заметим, что
где v7B — характеристическая скорость несущего винта на заданной высоте.
Введя ее в формулы (152) — (155), получим соответственно:
1) для полета при V7^>0
= + + ; (157)
V; = 4 + v4r + a?B <158)
V2, = Vs + 2a7 = 2|/-^ + a;„ = / Vj + 4v‘„, (159)
здесь V2.7 — скорость в сжатом сечении;
2) для спуска при У7 < О
Vy ( 1 ~
v- = — ~ ± |/ ~ ; (160)
<161)
V,., = Vs + 2u7 = +2|/ -----u?. = ±
(162)
У вертолета тяга T во все время полета приблизительно равна Весу
машины, и, следовательно, она постоянна и положительна, так как направ-
~ 1/ ------ Для данной высоты полета
г 7.2pf
лена вверх. Поэтому скорость
Фиг. 33. Связь между скоростьями Vy и V?
на iBcex режимах осевого движения
также постоянна и положитель-
на. Изменяться будут прн из-
менении Vy скорости и?, V7, V2.7-
Летчик прн этом все время из-
меняет угол установки лопастей
в зависимости от режима
полета.
Полученные зависимости (158)
и (161) представлены графически
на фиг. 33. Получаются две гипер-
болы: верхняя гипербола DB имеет
асимптотами ось абсцисс 0Vy и
прямую, заданную уравнением
V-, = V,,.
Ннжияя гипербола GPC имеет
асимптотами те же самые пря-
мые. Отрезок OF = и7в. Вершина
Р нижней гиперболы имеет
координаты: Vy = —2у7в и V7 =
= — и7и. Для величии V—2ит
у нижней гиперболы получаются
мнимые значения для V7. Заме-
от оси абсцисс, а от
как следует из формулы
тим, что если отсчитывать ординаты кривых не
асимптоты V7=Vy, то, очевидно, получим,
у. Vy и7, величину
т. е. среднюю индуктивную скорость.
Однако иа полученных кривых ие все точки соответствуют физической
картине, положенной в основу всей теории, т. е. наличию четкой струн
воздуха.
Такая струя действительно получается на участке BF— режим греб-
ного винта. В точке F, соответствующей работе иа месте, струя в области
подсасывания имеет размытый характер и воздух подходит к несущему
винту со всех сторон (фиг. 34). Следовательно, здесь нет плоского «нуле-
вого» сечення и его нужно заменить сферой большого радиуса, описанной
около несущего винта. Но так как на этой сфере влияние виита пропадает,
то давления иа ее поверхности будут равны атмосферному н взаимно урав-
новесятся. Давления в цилиндрической струе за винтом будут также равны
атмосферному (если пренебречь малым вращением струи), так как если бы
давление в ней было больше атмосферного, то она расширялась бы,
а если меньше, то она сжималась бы. Скорости потока на сфере будут
стремиться к нулю, а так как они направлены по разным направлениям,
то приносимое ими секундное количество движения будет равным нулю.
Следовательно, секундный импульс силы тяги Т должен быть равен се-
кундному приросту количества движения, т- е,
Т = = Zv^m,
а секундная кинетическая энергия плюс потери на треиие будут равны
потребляемой мощности, т. е.
L - + Лтр = 2ту*в 4- Ц
2
Следовательно, общие формулы теории
ннмы и в том случае, когда Vy = О-
струи (155) и (149) будут приме-
Фиг. 34. Вычисление импульса силы и эпюра
давлений по струе иа режиме висения вер-
толуа
Фиг. 35. Схема потоков воздуха при
списке малой скоростью Vу
Вышедшая из указанной сферы струя воздуха вследствие вязкости мед-
ленно размывается, ее сечение увеличивается, а скорость в ней уменьша-
ется, стремясь к нулю. Справа па фиг. 34 дана эпюра скоростей и дав-
лений.
Если вертолет начнет медленно спускаться, что равносильно обдувке его
снизу со скоростью Vy, то для приблизительного получения картины обтекания
можно применить (не совсем законно для вязкой жидкости и турбулент-
ного движения) принцип наложения скоростей, столь широко применяемый
в аэрогидродинамике идеальной жидкости. Тогда в точках, отмеченных на
фиг. 35 крестиками, получится равенство противоположно направленных
скоростей н Vy, воздух там остановится, н возникнут две поверхности
раздела: / — сверху и II—снизу. Между этими поверхностями возникнут
кольцевые потоки н вихри, указанные штриховкой. При малой скорости
Уу эти вихри мало влияют иа работу несущего винта. При увеличении
скорости спуска V,. поверхности раздела / и // сближаются и тогда неко-
торые струйки отброшенного воздуха искривляются у нижней поверхности
раздела, идут кверху и снова подсасываются несущим винтом. Получаются
кольцевые струйки, легко наблюдаемые прн опытах в аэродинамических,
трубах и в натуру. На фиг. 36 приведена фотография дымового следа, полу-
ченная в опытах с вертолетом в натуру. На ней видна внизу штанга
прикрепленная к шасси вертолета; на штанге, на г = 0,7, был укреплен
дымарь. Наверху виден след лопасти в косой проекции.
На этом снимке относительная скорость снижения была равна — = 0,3
Т' ^7В
и получилась четкая кольцевая струйка. J акой поток сильно отличается. от
принятого в импульсной теории, и опыты в этой области ей сильно протн-
воречат. Получающиеся поверхности раздела I и И неустойчивы и сильно
Фиг. 36. Фотография нижнего вихревого кольца,
сделанная в полете
колеблются. Вихревые области, возникшие под вертолетом, частично раз-
рушаются потоком, «осколки» вихрей (в вязкой жидкости существуют
азомкнутые вихри) уносятся вверх и, подсасываясь несущим винтом,
попадают иа лопасти. Все это вызывает колебания вертолета и толчки в не-
сущем вннте. Получается беспорядочная тряска машины. Управление де-
лается менее эффективным. Все же на этих режимах опытный летчик вполне
уверенно управляет машиной при вертикальном спуске.
При больших скоростях снижения поверхности раздела сближаются
и плавно переходят одна в другую, — получается хорошо известная в те-
оретической аэродинамике картина обтекания потоком вихревого кольца
(фиг. 37). Вертолет на этом режиме сильно бросает из стороны в сторону,
и управляемость машины очень сильно ухудшается. Этот режим полета
вертолета называется режимом вихревого кольца.
Полученные выражения для, У7 и У2Л позволяют разобраться в этих
явлениях, хотя формулы импульсной теории здесь применимы лишь условно,
так как возникает форма потока, отличная от той, которая предполагалась
при выводе этих формул.
Легко видеть, что входящий в формулы (160)—(162) радикал
/ V2
/ ___Ч___у“в обращается в нуль, когда
V2. 2
~ V7B = 0,
4
т. е. тогда, когда
V„ = ±/4& = -2£i7b. (163)
Берем здесь перед всегда положительной
у нас величиной у7в знак минус, так как
мы интересуемся режимом снижения верто-
лета, когда Vy < 0. При этом указанные
формулы сСрашаются в следующие;
Фиг. 37. Схема обтекания винта
иа режиме вихревого кольца
Щ = —
v,=
2
V2.7 — Vy 2у7 — 0.
Подставляя сюда Vy = — 2и7Б, получим:
^7 — ^7В»
Vy = — 2^;
V7 = ---- ^7В И V2.7 == 0.
(164)
Этому режиму полета соответствует иа фиг. 33 точка Р.
В сечении 2, бывшем для режима гребного винта «сжатым сечением»,
теперь получится скорость потока V27 = 0, и, следовательно, в силу
Фиг. 39. Схема обтекания
винта при переходе на ре-
жим ветряной мельницы
Фиг. 38 Обтекание несу-
щего винта как диска
неразрывности струи площадь сечения должна становиться бесконечно
большой.
Другим характерным режимом является такой, когда V7 = 0, т. е.
поток воздуха не пересекает ометаемую винтом площадь (фиг. 38). Поток
при этом соответствует обтеканию сплошного диска. При этом несущий
винт затрачивает работу лишь иатрение . Если для опреде-
ления точки, где У7 ~ 0, воспользуемся импульсной теорией, т. е. фиг. 33,
то получим ответ, что это произойдет при Уу = —ос, где ветви гипербол
BD и PG асимптотически приближаются к оси абсцисс. Однако опыты
показывают, что такая точка находится ие при Уи = — оо, а лежит при-
близительно на абсциссе Уу = — 1 ,6утв; это точка L. Происходит это
потому, что все явление получается другим и формулы иа участке кривых
FE дают малую точность, а иа ветви ED дают совершенно неправильный
результат.
Ветвь нижней гиперболы PG изображает неустойчивые, невозможные
в природе потоки.
Действительные явления, происходящие на скоростях —v1K~>Vy^—2ц7ь.
очень сложны, и их теоретическое изучение трудно. Поэтому было проде-
лано много опытов по изучению явлений, происходящих в этой области.
Эти опыты показали, что в интервале РЕ можно провести эксперименталь-
ную кривую, изображенную у нас пунктиром. В этой области наблюдаются
сильные пульсации потока и возникают вихревые кольца.
При еще большем увеличении скорости (Уь. 3> — 2утв) поток снова успо-
каивается (фиг. 39), вихревые кольца уносятся вверх и винт начинает ра-
ботать на режиме ветря-ной мельницы, отдавая мощность валу.
В некоторой точке А (фиг.-33) получается авторотация, и винт вращается,
не требуя подвода мощности. Следовательно, правильными оказываются на
диаграмме (фиг. 33) ветви BF и СР; ветвь FEP приходится строить на
основе опытов.
Таковы скорости в струе, получающиеся у несущего винта при спуске
вертолета. Много делалось опытов и по непосредственному измерению силы
тяги и мощности у несущего винта в этих условиях. Первые такие опыты
были проведены в России в 1909 г. в Кучинском аэродинамическом инсти-
туте под руководством проф. Н. Е. Жуковского, т. е. за 30 лет до начала
таких работ за границей (см. библиографию).
На фиг. 40 приведены результаты опытов, проведенных в 1937 г.
в Академии имени Н. Е. Жуковского. Они типичны для всех таких иссле-
дований. В верхней части фиг. 40 приведена величина Ст в зависимости
от Vo = Vy для разных углов установки лопастей, а внизу даны аналогич-
ные кривые для коэффициента крутящего момента тк. Эти кривые соответ-
ствуют режиму спуска с работающим двигателем. Важно отметить (как
обнаружилось еще в опытах Н. Е. Жуковского), что кривые Ст при Уу Ж 0
сильно сближаются и угол установки лопастей мало сказывается на вели-
чине коэффициента тяги Ст. Это показывает, что управляемость вертолета
иа этом режиме сильно уменьшается, так как тяга винтов будет мало
зависеть от шага у многовинтовых схем и малоэффективной будет работа
автомата-перекоса у одновинтовых и двухвинтовых схем. Моменты управле-
ния машиной будут малыми, что хорошо подтверждается практикой. Это
явление впервые было обнаружено в Кучинском аэродинамическом инсти-
туте в 1909 г.
Не всегда струю винтов на этом режиме изучают с помощью наблюдения
самого потока. Очень часто идут обратным путем и, имея полученные из
опытов кривые Ст и тк, находят среднюю скорость У7, исходя из основ-
ной формулы импульсной теории
/Пк
— crv, + ^.
х 4
Фиг. 40. Результаты опытов с моделями винтов
на режиме торможения и вихревого кольца
Решая ее относительно У-, получаем:
(165)
\ 4 / сг
Проведенная на фиг. 23 пунктирная кривая и была получена на основании
опытов, проведенных в разных странах.
§ 3. ИСГСЛЬсСЕАНИЕ КРИВОЙ Г7=/(У tQ
Кривую зависимости V- от* вертикальной скорости l/v и величины на-
гружения несущего винта, измеряемой скоростью v-„, можно очоиь широко
использовать для различных прикидочных расчетов первого приближения.
По этой кривой легко находится мощность несущего винта' на любом ре-
жиме, так как, согласно формулам (110) и (114),
V = -l-7-l/, + .V0.
23 В. Н. Юрьев, т. I
Величина тяги Т всегда очень близка к полетному весу вертолета G. Ве-
личину Np легко найти по формуле (114) Здесь нуж-
но при расчете авторотации прибавлять еще потери на трение в под-
шипниках главного вала и мощность, затрачиваемую на рулевой винт.
Фиг. 41. Скорости V7 и ’Л ? в зависимости от п V7B
FB — pe/MiM гребного вини, точк i Г —режим висения ГГ —
тормозной режим, ЛГ—режим вихревого кольца и турбулент-
ный режим, точка Л — авторотация, PH — режим ветряного дви-
гателя
радио, освещение и т. д. Обычно можно принять, что на авторотации все
потери на трение равны А/тр = \,‘2Nr; множитель 1,2 дает 20%
иа указанные добавочные потери*. При моторном полете такой
делать не нужно: она входит в £.
Для удобства нанесения на диаграмму величины /VTp можно
что она может быть представлена так:
А7 = 7?7
где fTp — фиктивная «скорость трения».
Пользуясь найденным выражением для А/тр, находим.:
х75Л/гр 1,2 9ChoV0
°тр - т т ~ т '
С помощью этой величины мощность, затрачиваемая на вращение несущего
винта, может быть выражена так
JV = -j-rv, + -l-rBIP = -T-(v7-i-M- <168>
прибавки
прибавки
принять,
(166)
(167)
* Строго говоря, спуск вертолета с остановленным двигателем происходит на ре-
жиме ветряного двигателя.
Откладывая на фиг. 41, где дана кривая - f(V'v), отрезок игр для мо-
торной работы и l,2-vip для авторотации и проводя горизонтальные пунк-
тирные линии, получим в некотором масштабе кривую потребных для по-
лета мощностей, если будем отсчитывать ординаты от этой пунктирной
линии как от оси абсцисс. Авторотация произойдет в точке А, где получае-
мая винтом мощность (отрицательная потребная мощность) равна мощности
трения; скорость снижения при этом будет равна
Указанные расчеты можно уточнить, учтя обдувку фюзеляжа и других
частей струей несущего винта. Это вредное сопротивление равно приблизи-
тельно 2—3°о от веса вертолета и мало изменяется со скоростью 1/у.
Следовательно, при вычислении скорости ц7в нужно брать увеличенный на
2—3% вес вертолета, т. е. считать Т — (1,02—1,03)0.
Нанесенная нами на фиг. 41 кривая соответствовала определенной ско-
рости v-R. Поэтому для расчета любых вертолетов нужно на диаграмму
У? = f (Vw) нанести ряд кривых, задаваясь определенной величиной v:a. Тогда
получится сетка кргвых (фиг. 42), дающих зависимость = f (Vyt v7B)- Вели-
чина и в у современных веотолэтоз ле-ки в уз сих пзздзлк от 10 до-
30 м/сек, и ее всегда можно вычислять по нззестяым формулам, т. е.
/ Т >
0;- v
= 2
Еще удобнее перейти к безразмерным скооостям, отнесенным к характе-
ристической скорости вертолета v в. Мы будем обозначать их, как уже
указывалось, буквами с волнистей чертой сверху, т. е.
V 17 1’ ~ VI
У у =----; ; v? =----; и7В=1.
°;в v,B v7B
23*
Введя эти обозначения, мы сможем все формулы с (157) Шо (162) перепи-
сать в таком виде:
ветвь BE (фиг. 41) V, > О
V7 = V„+57 = 4 + ]/ 4 + 1;
г~у1----- г---------
Vt.7 = v„ + 2o7 = 2]/ -^- + 1 = Vv', т-4;
ветвь PH V7 О
V2., = -2 = - |'Щ- -4.
По этим формулам построен график фиг. 43. Промежуточную ветвь РЕ
наносим по имеющимся экспериментальным исследованиям. Тогда получаем
универсальный график V-=f(Py), пригодный для веек значений и7в. По-
лученные с его помощью безразмерные скорости нужно лишь умножить на v7B.
«чтобы получить реальные скорости V7, 14-, v, и т. д.
Пользуясь этой кривой, легко сделать аэродинамический |а:чет верти-
кального движения вертолета. Как увидим далее, кривая V~ = f^y) пред-
ставляет собой сразу кривую осевой скорости, мощности и угла прите-
кания потока [3? на разлтчзых режимах.
Приближенный расчет вертикального движения вертолета с помощью
этой конвой сводится к следующим операциям.
1) Характеристическая скорость. Сначала находим характер-
ную скорость для разных высот по формуле
/~Т /~р~ 1 / ~С~~
тр -ти-
Таким образом, единичный отрезок 0—1 на диаграмме (фиг. 43) будет ра-
вен ц-.в м/сек* и на основании этого легко вычертить масштаб скоростей
или разбить оси координат по скоростям в м/сек.
Скорость и7в изменяется при изменении высоты полета; обозначив ее
величину у земли через иц, можем написать:
f7B = .
/л
Следовательно, масштаб скоростей получится для разных высот различный
То же нужно сказать о масштабах мощности и углов 37.
2) Потребная мощность н скороподъемность. Для опре-
деления мощности нужно сначала найти мощность профильных потерь не-
сущего винта по формулам (85), т. е.» найдя /?гКр = ———L > вычислить
, mun я л
(169)
(О Z 1ZUU
илн прямо воспользоваться формулой (114). У современных вертолетов о
в полете почти не меняется н jVp зависит практически лишь от р. На
Фиг. 43 Обобщенные зависимости
V? = f(Vy) И V..7- /(?,,)
авторотации вннту необходимо преодолевать трение главного вала, вращать
рулевой винт, масляные насосы динамомашины для освещения кабины н т. д
Этот добавок мощности можно оценить в 20 % от мощности Np.
Мощность, потребляемую вертолетом при наличии осевой скорости, можно,
согласно формуле (112), представить в таком виде:
zn„^~tv7 + np
75х
Отсюда
(170)
(171)
Разделив V7 на ц7В , получим «располагаемую» величину
Г/ __ Ут (^,-Л^)и75
У 7Р-----— ------------- •
V-B Tv.3
Эту величину легко вычислить, зная NM, L Np и ц7в. Если сделать на
фиг. 44 «засечку» кривой l/7 = f(Va) горизонтальной линией, соответствующей
1/7р — const, то в точке пересечения /И получится скорость Vy — 170. Умно-
жив ее на v-B, найдем получающуюся на этом режиме вертикальную ско
рость взлета в м/сек, т. е.
^ = U>7B. (172)
Задаваясь несколькими высотами полета и беря по характеристике дви-
гателя высотную мощность Л/м, получим на фиг. 44 ряд горизонтальных
прямых и соответствующих им скоростей подъема вертолета Vy м/сек
(точкауИ' и_т. д.). По этим данным можно построить, как это было под-
Фиг. 44..^\эродина‘лический расчет верти-
кальяогд движения вертолета с помощью
КрИВОЙ V7~[{Vb)
робно описано в § 5 главы 4,
диаграмму скороподъемности,
т. е. Vy = найти потолок
висения вертолета и построить
барограмму вертикального азле-
та. Короче говоря, с помощью
фиг. 44 можно сделать полный
приближенный расчет вертикаль-
ного взлета вертолета и спуска
3) Авторотация. Режим
авторотации получатся тогда,
когда АС = 0; тогда NTpA =
= 1,2 Np. Из общей формулы (171)
находим скорость Via на авто
ротации:
г- е. V?a в этом случае отрицательно. Делая ззеечху, находим VyA и за-
тем
VyA = Vy4 О7в-
Эбычио величина Vva~—2 и, следовательно,
VyA^~ 2с-в.
Получается это потому, что кривая y7 = f(l/y) круто опускается вниз, и
>азиым значениям Р7л соответствует почти одно и то же значение VyA-
4) Углы установки лопасти. В этой приближенной теории рас-
чет ведется по средней скорости V-, близкой, как мы видели в § 3 главы 3,
с истинной скорости на радиусе / = 0,7. Поэтому угол установки лопастей
>удем определять для этого радиуса. Считая осевую скорость У7 малой по
Этиошению к окружной скорости гео, можно написать:
- v7 57,3 VV7B 57.3o_ —
=57,3-------= —---------'-^=-----------Bl/71
rw 0,7 Ru> 0,/Ru)
(174)
e. угол притекания струй пропорционален V-, и, следовательно, кривая
\ — f(Vy) дает в некотором масштабе для всех режимов полета. При-
0авив к Зе7 угол атаки ае1, избранный нами согласно § 4 главы 3, т. е.
обеспечивающий отсутствие срыва потока у профилей, получим:
о о о / ,Л17_ .— о
Ф? “ Ре? + З-ei ~ ~ V7 + ае7.
0,7/? J)
(175)
Эта величина зависит от высоты полета. Удобнее не разбивать новый мас-
штаб на фиг. 44. а построить отдельную диаграмму угла
тей несущего винта (ф^г. 45). Так как мы считаем гео = const,
формуле для коэффициента тяги
(88), для даяной высоты полета с^,
а следовательно и а?, не зависит
установки, лопас-
то, согласно
от скорости 1/у. Угол <р, иа ре-
жиме висения лежи обычзо в
границах 8—12°; пои подъеме и
на потолке он достигает вшчжы
12—15°, а при авторотации нахо-
дится обычно в пределах 3—5Э.
5) Полет на неполной
мощности. Эга диаграмма по-
зволяет решить, например, вопэос
о том, с ка<ой сюоостью будет
снижаться двухмоторный вертолет
в случае останов<и одного дви-
гателя. Тогда располагаемая мэ ц-
ность упадет в 2 раза, и, делая
Фиг. 45 Углы остановки лопастей ср?
на разных высотах и режимах верти-
кального полета ,
засечку, как показано на фиг. 44,
двумя горизонтальными линиями, соответствующими: сплошная — полету
на двух двигателях и пунктирная К7р — на одном двигателе, мы получим в
точках пересечения этих линий с кривой l/7 = f (^у) в первом случае ско-
рость подъема V у, а во втоэом — скорость снижения У таких машин
скорость снижения при вертикальном спуске получается примерно в 1,5—2
раза меньшая, чем на авторотации. При очень большом избытке мощности
можно получить еще меньшую скорость снижения.
Точно таким же путем можно решить аналогичную задачу и для мно-
говинтовых и многомоторных вертолетов.
6) Обдувка на разных режимах. Мы уже указывали, что ско-
рость обдувки вертолета при взлете остается все время почти постоянной.
Обычно фюзеляж вертолета, шасси, оперение и прочие части находятся в
зоне, где скорость потока равна
Кг 7 = 4‘ 2у7.
Переходя к безразмерным величинам, получим:
I/2.7 = Vy -Ь2у7.
Такую линию легко построить циркулем на диаграмме, приведенной на
фиг. 43. Получается новая пунктирная кривая l/2,7 = f (У у). Как виднм,
Уг ? действительно на протяжении от Уу = 1 до V? =-----идет почти па-
раллельно оси абсцисс. При приближении к режиму авторотации скорость
обдувки быстро падает. На авторотации мэжзо считать, что обдувка фю-
зеляжа и прочих частей совершается со скоростью, близкой к = —2п7в.
Из этого следует, что вредное сопротивление частей вертолета при мотор-
ном полете изменяется мало, и его можно считать постоянным и равным
сопротивлению при висеини, когда
V2_7 = 2и7Е.
Имея сводку лобовых сопротивлений для вертикального полета, т. е.
величину это сопротивление можно вычислить по формуле:
Как известно, оно близко к 1—2% от полетного веса машины у одно-
винтовых вертолетов: у вертолетов продольной схемы QBP Достигает зна-
чений 1—5% и у двухвинтовых вертолетов поперечной схемы с крыльями
может достигать 5—7% и более.
Постоянство этой величины позволяет вводить в расчеты обдувку фю-
зеляжа и крыльев простым увеличением веса G иа несколько процентов, т. е.
писать, например, при z винтах
т = —--------= осбд
Щ-Чвд)
и вести далее весь расчет вертикального полета, исходя из этой величины Т.
§ 4. ШАССИ ВЕРТОЛЕТА
Скорость снижения, как мы видели, можно найти по кривой V? — f (Vy):
оиа получится равной приблизительно 2у7В, т. е. 1/^4 ~ — 2г»;в.
Пользуясь полученными ранее зависимостями, можем теперь написать:
(176)
Эту же скорость можно вычислить, исходя из многочисленных опытов,
проведенных с моделями винтов в аэродинамических трубах. Эти опыты
дают для хороших несущих виитов сх=1,0—1,2. Приравняв лобовое
сопротивление несущего винта весу вертолета G, получим уже найденную
в § 6 главы 4 формулу
Следовательно, скорость установившегося вертикального спуска вертолета
на авторотации достаточно надежно может быть найдена по формуле (176).
Ниже приведены значения VyA в зависимости от р кг/м2:
р, кг/м2 . . 4
VyA, м/сек 8
6 8 10 12 16
9,9 11,3 12,8 14 16
20 23 25
17,9 19,1 20 28
Получаются, как видим, очень большие скорости, требующие для обес-
печения безопасности вертикального спуска вертолета в первую очередь
большого хода шасси и применения других средств для уменьшения этой
скорости.
В настоящее врэмя замечается тенденция к узеличечио нагрузки р до-
20—25 кг/м'1 и более. Это неизбежно вызывает очень большие скорости
спуска вертолета. Их, как увидим далее, можно
с помощью подрыва несущего виита у земли.
Тогда удар о землю произойдет со скоростью
на которую и должно быть рассчитано
шасси.
значительно уменьшить
Необходимая длина хода шасси
Будем считать, что во время удава, о землю
тяга несущего винта уравновешивает вес маш шы
(фиг. 46). Тогда шасси должно будет поглотить
всю кинетическую энергию поступательного движе-
ния вертолета, т. е.
2 tg
Фиг. 46. Схема работы
шасси на вертолете
где Р— общее среднее усилие всех йог шасси, которое мы считаем посто-
янным; h, — длина хода шасси в м и Уш — вертикальная скорость вертолета
в момент начала работы шасси. Отсюда
(177)
Торможение силой Р вызовет у вертолета перегрузку п, равную в наших
условиях отношению
п =
P + G = ,P ,
G G -I"
1.
(178)
Следовательно, при ударе о землю к обычному весу летчика прибавится
р
еще сила инерции, равная его весу, умноженному на -g-, т. е. его вес
возрастает в п раз.
Авиационная медицина установила, что человек в течение копоткого
времени может выдержать перегрузку п= 10 — 11 без вредных для себя
последствий. Исходя из этой величины и подставляя в формулу (177} вели-
Р
чину -Q-, взятую из формулы (178), получим:
Г v ’И
n-2g(n-l)‘
Принимая 10 и n = И, получим окончательно:
(179>
(180)
L/2
v Ш
ийо
h
Скорость снижения вертолета в момент удара о землю у некоторых машин
может быть доведена до нуля с помощью подрыва. Ниже приведены вели-
тииы безэтсчого хода шасси (в мэтрах) при перегрузке п — 11 в зависи-
мости от 1/ш:
Уш, м!сек. .
h, м . . . О 0,125 0,320 0,500 0,720 1,13 2,00 3,13
:сли не применять подрыва, то 1/ш = и требуется очень большой ход
ласси. Подставив в формулу (179) 1/ш = 1/м = — 4 ]/р, получим-
= OfiSp.
1иже приведен потребный в этом случае ход шасси:
р, кг/м”* . . 10 12 16 20 23 25
h, м ... 0,80 0,96 1,28 1,60 1,84 2,00
,ак видим, результат получается малоутешительный, так как коиструк-
•ивио осуществить шасси со столь большим ходом весьма затрудн мтельно.
Такой ход шасси встречается лишь на тяжелых вертолетах типа «летающего
рана» или на машинах с очень большой грузоподъемностью (типа «летаю-
тая лошадь»), у которых для увеличения грузоподъемности берется малая
агрузса р> На многих же вертолетах делается шасси очень малого хода,
ригодчое л гшь для посадки с работаю цим двигателем или для посадки
горизонтальной скоростью, т. е. по наклонной траектории планирования,
огда вертолет садится «ао-самэлетному» и везти сальная скорость может
ыть после выравнивания машины доведена до нуля. Однако специфика
абэты вертолета (малые высоты и пересеченная местность) может выну-
ить его садиться вертикально, и тогда, если не применить подрыв несу-
щего винта, неминуема авария.
§ 5. ВЕРТИКАЛЬНАЯ ПОСАДКА ВЕРТОЛЕТА
С «ПОДРЫВОМ» НЕСУЩЕГО ВИНТА
Для уменьшения вертикальной скорости при спуске иа авторотации дав-
• предлагался очень простой прием: перед самым ударом о землю летчик
зхо увеличивает шаг винта и тормозит спуск машины.
Дело в том, что кинетическая энергия вращающегося с большой ско-
стыо несущего винта иногда в несколько раз превосходит кинетическую
ергию поступательного движения всего вертолета. Несущий виит являет-
как бы аккумулятором энергии, и эту энергию можно израсходовать
1Я торможения спуска. Винт при этом работает как бы на моторном ре-
1ме спуска и быстро теряет свои обороты. Этот вопрос был подообно
и рассмотрен в книге «Исследование летных свойств гэл жэлтеров»
1939 г. Рассматривался он и другими авторами. Здесь мы дадим упро-
иный ачал 13.
Летчик может увеличить угол установки лопастей лишь до такой
личины, при которой угол атаки, а следовательно, су1 достигнут крнти-
<ого з1ачэчия. При переходе за этот угол тяга начнет падать и начнет-
опасная тряска машины. Следовательно, коэффициент тяги несущего виита
ограничен значением с^пих» тал как, согласно формуле (88),
(88)
Тяга принтом будет равна
Т = Ст max -у- Р^4«2 = Const (О2.
В начальный момеит подрыва ы==ад и Т имеет мдсечмальчэз значение.
До подрыва
TA^G-=CT^-pR*tfA.
Величина cJB найдется так же легко, так как, зная Т, находим:
т. е. Ста пропорционально со. Мощность, потребляемая несущим винтом,
получится по общей формуле (114), которую пишем в кгм/сек'.
L = ±TVi + LTII,
где
Д1Р= 1,2^р-^-р«5<03= ( 1,2 ^p-^-p«5)<03 = const <о3. (182)
Во воемя подрыва угловая скорость воащения несущего вчнта ы умень-
шается, Выведенные формулы позволяет легко пэстооить кривые изменения
Т, и7в и Lrp в функции со: они нанесены иа фпг. 47 жирными линиями.
Дальнейшая задача сводится к совместному интегрированию дифферен-
циальных уэав пений вращательного движения виита и поступательного дви-
жения всего веэтолета. Эго интегрирование можно вести самыми разлпчны*
Ми, хорошо известными способами численных и графических вычислений.
Прэстейш /и из них язляется расчет по малым элементам, по средним зна-
чениям ве мч пи, в данном случае V\,cp, Гср, и7ВСр и 1/7ср.Дпя этого иа ф in. 47 на-
носим в подходящем масштабе исходные данные для ординаты в точке сод: это
будут для условий установившегося спуска иа авторотации величины УуА
и у7в- Расчет ведем, задаваясь уменьшением угловой скорости вращения
несущего виита иа некоторую величину Дю. По гоафлку мы сразу же полу-
чим о)ср, и«ер, Лр и Атр.ер иа этом интервале. Для удобства расчета про-
водим иа диаграмме, приведенной иа фиг. 47, сплошные и пунктирные
ординаты, причем интервал между сплошными берем равным выбранному
значению До (примерно 1—2 'Лек); пунктирные ординаты проводим посре-
дине. Тогда значения всех величин, взятых по пуиктиэиым ординатам, и
будут средними значениями. Момент инерции J несущего виита можно
вычислить по приведенной далее формуле (187).
Интервал Дю должен быть таким, чтобы все кривые на диаграмме
были близки в пределах интервала к прямым линиям. Пользуясь этой диа-
граммой, иедем расчет в такой последовательности.
Сначала пользуемся уравнениями кинетической энергии при вращении.
Пусть в начале интервала угловая скорость вэащения была (о0, а в конце
интервала юг Тогда изменение кинетической энергии за время Д£, соответ-
ствующее падению <о иа величину Дю, будет таким:
— (ю® — со") = J (ю0 — G)j) = ЛосрЛю.
Это изменение получится от торможения несущего винта, причем потерянная
кинетическая энергия виита должна равняться работе
ТсрД/ = ТсрУ7l р + ттр ср^ ДЛ
Отсюда получаем:
ЛосрД(о = Tcpl/jcp “Р Ттр_Ср^ ДЛ
Решая это уравнение относительно Д/, получим:
Jio_nAci> 7а)„Да)
д/=—----------<183)
(--TV A- L 1 х'ср
\ X СР ?СР 1 тр.ср/
В этой формуле нам все известно, кроме |/7Ср. Для определения 1/7ср (счи-
тая поток установившимся) нам нужно знать Иуср.
Для решения задачи считаем ведущей величиной и задаемся
сначала иа глаз скоростью Vy(.p (точка Л), как показано стрелкой, идущей
из ординаты VtiA на фиг. 47. Зная |/у<р и ц7вг1_, находим по графику, приве-
денному иа фиг. 33, среднюю величину |/7ср = f (УУ сР, t>7BC1)) и вычисляем:
Др ~ ГсрИ7ср 4- Др.ср,
затем находим:
Ло,_Дсо
Д^-f^-
ьср
После этого обращаемся к уравнению поступательного движения, для
чего приравниваем изменение количества движения машины,
G
равное —
ДУ,
импульсу избытка силы тяги Тср иад весом G за найденный нами интервал
времени АЛ т. е.
-у AV = (Гер — G) At.
Отсюда
А?
(Т„ — С) А/
(j
После этого снона находим величину Куср
V -У 4-^.
v у ср — V уо л •
Нужно помнить, что УуСр и Уу0 — величины отрицательные. Наносим
полученную величину Уу ср иа фиг. 47 в виде крестика. Полученная точка К'
в общем случае не совпадает с точ<ой К, соответствую цей предположен-
ному значению 1/уср. Беря среднюю величину, повторяем расчет, пока предпо-
ложенное значение не совпадает со значением, полученным указанным
путем, что получается обычно с двух попыток. Когда это будет достиг-
нуто, продолжим линию Уу, далее, экстраполируя ее на соседний участок
до пунктирной линии, где находим снова Ууср, и расчет повторяется пол-
ностью до этого интервала и т. д., пока не получится вся кривая в интере-
сующем нас диапазоне,
В точке, где Уу = 0, получится полная остановка вертолета, причем
скорость вращения несущего винта будет равна некоторой величине сот|П
Г
Подрыв в значительной степени зависит от отношения •
Для азторэтацтн мы имел! определенные значения су1 и Ст = и тя-
га несущего винта Та тогда равнялась весу машины, т. е.
Обозначив Су-, при подрыве через сУттлк, мы можем написать:
Л. Lyi mix '7
Ьу т.1х — '---—--
И
СУ7 max3’ П г>, >
I max = ---------о
Следовательно.
Т С (,)2
* mix _ ‘•у? тпхш
При подрыве <> падает, и при ш^,п= ~ 1 или <omit, = <0.1 \/
У су max
тяга Т сравняется с весом машины G. Обычно вертолет летает при су1
^0.5 — 0,6, a ~ 1,2. Следовательно, отношение —-—~~ и тогда
cyt шах *
<omin = «л = (184}
Переходить этот предел ие следует, иначе начнется падение машины с уско-
рением под действием силы тяжести, и скорость иашет возрастать. Таким
образом, интервал для величины со лежит в пределах сод и со^п, причем
comm -ту сод.
Кинетическая энергия несущего виита пропорциональна со2; следователь
но, в обычных условиях можно использовать лишь половину всей кинети-
ческой энергии несущего винта.
После окончательной увязки основных кривых нужно нанести на диа-
грамму время i = SA?, прошедшее от начала подрыва, и нанести потерю
высоты, равную для каждого интервала Aw величине
ДН = ^срД^:
тогда
Н= ГЛН.
Кроме того, иа диаграмму следует нанести величину среднего угла уста
новки лопастей ср", равного для каждого интервала величине
V
с=*;+ (185>
Таблица 3
Результаты расчетов подрыва вертолета при вертикальном спуске
на авторотации ((JA = 200 м[сек)
Расчетные случаи р. дг/л1* ^/Д, м/сек % Vin. м/сек /1.
1-й случай Легкая лопасть 21,6 19,4 6 11,2 0,63 2,62
2й случай Тяжелая лопасть 15,6 16,4 7 4,7 0,11 4,6
3-й случай Тяжелая лопасть и добавоч- ные грузы 15,2 16,2 9 0 0 7,24
Получается полная характеристика всего процесса подрыва.
Недостатком этого расчета является приближенный характер положен-
ных в его основу предположений; в частности, допущено, что поток у не-
сущего винта установившийся, но при быстром изменении Vy это предполо-
жение недостаточно точно. Сама кривая 1/7 = f(l/y, и7в) в исследуемой обла-
сти является, как мы указывали, мало надежной. Но для ориентировочных
расчетов изложенный прием допустим и дает достаточную точность. На
сводной диаграмме (фиг. 48) и в табл. 3 приведены результаты трех таких
расчетов.
Фиг, 48 Сводная диаграмма расчета под-
рыва вертолета для трех теоретических
случаев
В первом случае р 21,6 кг/At2 и лопасти были легкими 100 = 6% j.
Кривые для этого случая отмечены индексом 1. Окружная скорость во всех
трех случаях была равна 200 м/сек.
Оказалось, что у машины с таки-
ми параметрами скорость снижения
может быть уменьшена подрывом
лишь до величины 1/щ = Ущ =
= 11,2 м/сек. По формуле полу-
чаем в этом случае безопасный
ход шасси, равный 0,63 м, что
очень трудно осуществить на прак-
тике.
Во втором случае нагрузка на
ометаемую площадь была взята
малая и р = 15,6 к-/м2, а лопасти
I \
более тяжелые —100 = 7% .
\ о )
В этом случае подрыв мог умень-
шить скорость снижения очень эф-
фективно и — Учч = 4,7 м/сек;
тогда безопасный ход шасси умень-
шается до значения 0,11 м, что
уже легко осуществимо.
Наконец, третья кривая 1/рз по-
казывает, что получится при еще
меньшей величине р -— 15,2 к'/м2, и
искусственно утяжеленных лопастях:
их относительный вес был увели-
чен с помощью грузов, располо-
женных на концах лопастей и имев-
ших общий вес 100 ке. Оказалось,
что в этом случае после подрыва
несущего винта получается ну-
левая скорость снижения и
|/ш ~ |/^3 = 0. При такой пссадке
чески шасси не испытывает добавочной наг; узки. Высота Н, иа которой
надо начинать подрыв, лежит во всех случаях, как это видно из кривых,
нанесенных в верхней части фиг. 48, в пределах 20—25 м, а весь процесс под-
рыва занимает 2—3 сек. ' «Ч
Общий вывод получается следующий: для обеспечения полной безопас-
ности посадки нужно обеспечивать скорость 17ш порядка 8—10 м/сек, тог-
да будет достаточен ход шасси порядка 0,5 м, что легко осуществимо.
получается спуск без удара, и теорети-
Критерий возможности полного подрыва вертолета
Как мы ендсли, еозмсжио использовать не всю кинетическую энергию
вра ниicil<гсся ia гвтсротацги несущего винта, а лииь rpi блисиклы.о
половину ее. Кроме того, и эта располагаемая энергия обратится в энергию
торможения скорости спуска с некоторым к. и. д.» так как у нас имеются
потеря иа трение, концевые потери и индуктивные. В конечном счете, как
показывают приведенные расчеты, обращается в энергию торможения лишь
около '/5—'Л всей кинетической энергии вращения несу цего винта. Следо-
вательно. если последняя энергия в 7 раз больше кинетической энергии
поступательного движения вертолета, то возможна полная остановка верто-
лета в воздухе, т. е. получение |/щ = 1/у 0 в момент касания земли.
Рассмотрим это более подробно.
Кинетическая энергия вра цеиля несущего виита в начале подрыва бу-
дет равна
(186)
Величина момента инерции несущего виита может быть представлена в виде
J = тг-
(187)
где г t — относительный
вес всех лопастей (без
тов. Следовательно,
радиус инерции лопасти виита, а Сл— суммарный
1
втулки). Величина г] —— у обычных несущих вин-
GnR2 а „и-.
Кинетическая энергия вертикального движения вертолета равна
GV*.
(188)
(189)
и так как скорость снижения ]/уа~—2у7В, то можно написать:
Kv = уИ-’,-
Отношение этих энергий будет выражаться теперь так
_ о^, g , ол км,
&V G V1B
На основе приведенных расчетов, длт пзлиэгэ пэдрызз это отношение
должно быть больше 7. Отсюда получаем критерий
G,
U7B
(190)
или
О,
^->84.
(191)
4^-’
а
Эта формула показывает, что полный подрыв тем легче получить,
чем тяжелее лэ!зсти, чем больше диаметр несущего винта, чем больше
окружная скорость в начале подрыва, и тем труднее, чем больше характерн-
стическая скорость вертолета. Этот критерий можно выразить и через дру-
гие параметры, пользуясь тем, что
Тогда получим, считая Д= 1,
£i_J_ = Zi21
G а сТв
Сл 'Л^А
G 4р
>84.
(192)
°
Все величины в этом выражении взяты для висения у земли. Эта формула
показывает, как влияют иа возможность подрыва основные параметры не-
сущего виита. Интересно по своей простоте выражение с Срв, которое
можно переписать в таком виде;
8±
G Срв 4х ’
или
Сл х
Ств <~G21 ’
У хороших несущих виитов х = 0,92, и тогда
G„ 1
(193)
У большинства современных вертолетов 0,065, и тогда
G„
CT.<G^ :S°’0028L
Такая малая величина СТв ие встречается у современных машин и вер-
толеты с Сг> 0,00284 не могут садиться с полным подрывом, т. е.
с нулевой вертикальной скоростью. Однако и у таких вертолетов подрыв
может принести пользу, так как он может уменьшить кинетическую энер-
гию спуска довольно значительно.
Из приведенных расчетов видно, что
У>УЛ 1 — 0,15А>/А>
и для Уш/Ул « 0,5 требуется як 3,1. В этом случае мы получим крите-
рий частичного подрыва, равный
G„
— -Л > 37
G
(194)
и формула (193) получит следующий вид:
1
СГВ < 7Г10-
24 Б- Н. Юрьев, т. Т
Если ввести в эту формулу относительный вес лопастей в процентах,
— Сл
6Л % = -^-100, то она перепишется в таком виде:
СТп<1обо' С95)
Следовательно, для того чтобы обеспечить уменьшение скорости снижения
путем подрыва до Кш = 0,5VА> нужно иметь при -^100 = 6,5% коэффи-
циент тяги у земли СГв <. 0,0065. Более точные результаты можно полу-
чить, проделав описанный расчет для данной машины.
§ 6. СПЕЦИАЛЬНЫЕ МЕРОПРИЯТИЯ ПО УЛУЧШЕНИЮ
ВЕРТИКАЛЬНОГО СПУСКА ВЕРТОЛЕТА.
ВОЗДУШНАЯ ПОДУШКА
Кроме указанных основных приемов уменьшения Ст (т. е. р кг/м2}
и увеличения хода шасси, в авиационной литературе предлагалось мно-
жество различных способов для улучшения вертикального спуска вер-
толета.
Простейшим из иих является прикрепление в концах лопастей гру-
зов, увеличивающих момент инерции лопастей. Того же эффекта мож-
но добиться просто увеличением прочности лопастей, что во многих
случаях вполне рационально. Лопасти весят обычно от 4 до 6,5% от
полетного веса машины и увеличение их веса до 7—9%, особенно при
небольшом увеличении диаметра виита, практически мало скажется на
полезном грузе машины.
Другим, более эффективным, методом является установка на концах
лопастей не мертвых грузов, а небольших жидкостных или пороховых
ракет. Для обеспечения безопасности спуска достаточна продолжитель-
ность горения этих ракет порядка нескольких десятков секунд, что по-
зволяет сделать их очень малых размеров и полностью утопить в ло-
пасти для уменьшения аэродинамических потерь.
Более примитивными предложениями являются те, которые основа-
ны на применении парашютов. Очеиь трудно сделать парашют для ма-
шины в целом, так как он получается очень тяжелым, а применение
малого парашюта, способного обеспечить спуск лишь кабины с людьми,
встречает большие затруднения из-за необходимости вывести парашют
из-под диска несущего винта.
Предлагали устраивать специальные крылья для спуска, на которых
вся машина могла бы спуститься как планер. Это связано уже с ком-
поновкой машины в целом, и мы рассмотрим такие схемы в главе 10.
Наконец, с целью обеспечения большей безопасности вертикального
спуска на авторотации, когда у некоторых машин наблюдается тенден-
ция к сильному раскачиванию, следует применять специальные виды
пилотирования. Большей частью сильное раскачивание происходит
тогда, когда летчик хочет уменьшить кажущуюся ему слишком большой
скорость снижения вертолета и начинает увеличивать шаг несущего
винта. Тогда начинается частичный срыв потока, и это вызывает тряску
машины; «осколки» вихревого кольца при больших углах атаки лопасти
также могут вызвать срывы потока в разных местах диска иесушего
виита, что может привести к раскачиванию машины. Кроме того, при
большом шаге управляемость вертолета всегда уменьшается (мал
запас су7), и машина может перестать слушаться летчика. Следует
всегда помнить, что скорость вертикального снижения на авторотации
велика и у современных вертолетов достигает значения 15—20 м)сек,
поэтому ее бояться не следует, а нужно стремиться возможно быстрее
поставить винт на режим установившейся авторотации, ио для этого
иужио уменьшатьшагнесущего винта, а не увеличивать его.
Когда машина встанет иа правильную авторотацию, то вернется и уп-
равляемость.
Еще более радикальным способом явился бы отказ от спуска на
авторотации и переход к спуску иа режиме ветряной мельницы, где
пропадают вихревые кольца и начинается опять плавное течение возду-
ха с образованием четкой струи (фиг. 39).
Фиг. 49. Взлет вертолета с ограниченной площадки
При переходе на такой режим скорость снижения возрастает по
сравнению с чистой авторотацией лишь иа 10—15%, ио получается
полная управляемость машины. Трудностью является здесь то, что не-
сущий виит на режиме ветряной мельницы дает очень большую отри-
цательную мощность. Для поглощения этой мощности нужны очень
мощные тормоза. В настоящее время иа многих вертолетах устаиавли
ваются подобные тормоза, но обычно очень малой мощности. Они при
годны лишь для торможения вращающегося на земле несущего винта
что применяется для обеспечения безопасности обслуживания машины,
высадки пассажиров и т. д.
Для торможения спуска иа режиме ветряного двигателя нужны мощ-
ные тормоза; их проще всего осуществить в виде столь распространен-
ных в настоящее время на самолетах закрылков, предкрылков и интер-
септоров. Все такие приемы требуют уменьшения р, что уменьшает ско-
рость горизонтального полета. Поэтому они и ие нашли до сих пор
применения.
Наконец, наиболее хорошим средством повышения безопасности
полета является установка двух и более двигателей. При поломке од-
ного двигателя вертолет может медленно опускаться, правда в усло-
виях вихревого кольца, т. е. при наличии неожиданных колебаний,
«бросков» машины, чго при достаточной управляемости не представ-
ляет опасности.
Во всех случаях, когда это ие является необходимым, следует спу-
скаться по наклонным траекториям, так как даже небольшая горизои-
тальная скорость будет «сдувать» вихревое кольцо и его «осколки» на-
зад, и они не будут попадать в несущий вннт. Спуск же под углом в 45°
практически мало отличается от вертикального, но происходит гораздо
спокойнее последнего. При наличии ветра такой спуск может быть от-
носительно земли вертикальным. При таком спуске при приторможен-
ных колесах пробега по земле не получается, н машина останавливает-
ся после проскальзывания 2—3 м. Взлет с очень малой площадки, на-
пример с крыши здания, рекомендуется производить обязательно
против ветра и затем набирать высоту, пятясь назад (фиг. 49). Тогда
в случае падения мощности двигателя в полете («скисания двигателя»)
можно будет спуститься не строго по вертикали, а по несколько наклон-
ной траектории, что делает спуск гораздо более спокойным.
Часть II
ПОЛЕТ С ГОРИЗОНТАЛЬНОЙ СКОРОСТЬЮ
Глава 6
ХАРАКТЕРИСТИЧЕСКИЕ УГЛЫ И СКОРОСТИ
У НЕСУЩЕГО ВИНТА ПРИ ПОЛЕТЕ
С ГОРИЗОНТАЛЬНОЙ СКОРОСТЬЮ
§ 1. УГЛЫ, ОБРАЗОВАННЫЕ ПОЛНОЙ СИЛОЙ ТЯГИ Т
с осями КООРДИНАТ
Чтобы понять работу несущего винта при полете с горизонтальной
скоростью, важно изучить углы, образуемые силой тяги несущего виита
с осями коордииат, и получить необходимые для расчета зависимости меж-
ду этими углами.
В этом параграфе мы будем рассматривать лишь углы, лежащие в пло-
скости полета вертолета. Существуют еще небольшие отклонения силы тя-
ги вбок, но мы будем считать в этой главе, что они уничтожаются летчи-
ком с помощью автомата-перекоса.
На фиг. 50 изображен несущий винт в условиях так называемой «косой
обдувки». Ось его втулки дает положение связаииой с ним оси координат
Ot/i. Перпендикулярная к ней плоскость называется конструктивной
плоскостью вращения. Связанная ось Oxt идет согласно нашему
стандарту вперед, как показано на чертеже. Если бы скорость набегаю-
щего потока была равна нулю, то тяга несущего винта Тв была бы на-
правлена по связанной или конструктивной оси Oyi-
Если теперь вертолет начнет двигаться по направлению оперенной
стрелки Vo, то сила тяги изменит свою величину и займет новое положе-
ние Т. Летчик с помощью изменения угла ф7 опять сделает тягу практи-
чески равной весу машины. Пусть скорость Уо образует с конструктивной
плоскостью вращения так называемый конструктивный угол ата-
ки ак. Проведем скоростные оси координат Ох, Оу, как по-
казано на чертеже. Угол между осями Оу и Оуг будет равен ак; знак
этого угла на вертолетном режиме будет отрицательным, так как отсчет
от оси Оу к оси Оу! будет на фнг. 50 против часовой стрелки.
Этот знак мы поставим на чертеже в явном виде. Напомним, что, как
указано в главе 1, все знаки углов у нас берутся в строгом соответствии
с осями координат. Отклонение силы тяги назад, т. е. переход ее из по-
ложения Тв в положение Т произойдет в общем случае от двух причин.
Во-первых, от косой обдувки сила тяги отклонится назад на угол 8Л.; во
вторых, летчик с помощью автомата-перекоса может отклонить полную
силу тяги на некоторый угол 8АП. Полный поворот силы тяги будет ра-
вен ох + одп. Этот угол играет большую роль при аэродинамическом рас.
чете н балансировке вертолетов, и мы будем его называть углом ба-
лансировки и писать
+ »ЛП-
(196)
Для аэродинамического расчета важен угол т, образуемый полной аэро-
динамической ^силой несущего винта с перпендикуляром к скорости полета,
Фиг 50 Характерные -углы и скорости при косой
обдувке несущего виита
ак <0
т. е. с осью Оу. Ппи вертолетном режиме (фнг. 50) он отрицателен, и
его величина при соблюдении знаков будет
— «к = д* 4- 6ДП —т,
ИЛИ
X ак н- 6^ -Г 6ЛИ - -н 6Б.
(197)
Угол т можно назвать углом качества несущего винта, так
как, разложив силу Т на две составляющих X и Y по скоростным осям,
мы получим
tgx--.
На удобство применения этого угла в аэродинамическом расчете впервые
было указано в работе М. Л. Миля и В. И. Ярошенко*. Здесь имеется
* М. Л. Миль и В И. Ярошенко.
«Техника воздушного флота», 1946, № 11
Аэродинамическим расчет геликоптера.
полная аналогия с крылом, где аэродинамическое качество связано с уг-
лом полной аэродинамической силы соотношением
здесь Q — лобовое сопротивление крыла, Y — его подъемная сила и К =
= —2-— аэродинамическое качество крыла.
У вертолета получится знак минус, так как сила X направлена у него
вперед, а угол т отрицателен. Заметим еще, что лопасти при наличии го-
ризонтальных шарниров будут
плоскости Окг, а в некоторой
плоскости, близкой к плоско-
сти, нормальной к силе Т.
В дальнейшем мы подробно
рассмотрим этот вопрос.
Производя аэродинамиче-
ский расчет, мы будем оп-
ределять углы т и dr, а
угол 6Б будет задан компонов-
кой машины. Исходя из этих
величин, в заключение расче-
та можно по формулам (196)
и (197) легко найти кон-
структивный угол атаки
дБ (198)
и необходимое для балан-
сировки машины отклонение
с илы Т под действием авто-
при этом вращаться ие в конструктивной
Фшг 51. Характерные углы и скорости на режиме
планирования ак>0
мата-перекоса
бдп = &х' 0 99)
На фиг. 50 несущий винт был изображен в положении нормальной ра-
боты, и конструктивный угол атаки ак и угол качества т были у него
отрицательными. На некоторых вертолетах с гребным винтом и на авто-
жирах возможен полет с положительным углом атаки. Планирование вер-
толета также происходит при положительных углах ак и т.
Все полученные нами формулы, дающие связь между углами, сохра-
няют свою силу и в этом случае благодаря стоогому соблюдению правила
знаков. На фиг. 51 изображен винт при положительном угле атаки ак.
Сразу можно написать, что т = ак 4* 6Х 4- 6^ =-- ак 4- бБ, ак — т— 6Б,
б4П dx = dB и ^ап = т- е- Ф°рмулы (196) — (199), уже полу-
ченные ранее.
Углы взлета и тангажа
На фиг. 50 даны еще два важных угла, характеризующих движение
вертолета относительно земли. Это угол взлета G, образованный ско-
ростью полета Vo с горизонтом (лииия HHf), и угол таигажа О, об-
разуемый конструктивной плоскостью вращения (линия Oxj) с горизонтом.
Из чертежа видна непосредственная связь между этими углами
G = О — ак,
или
ft = е -j-«к-
(200)
Почти всегда ось фюзеляжа, обычио проводимая параллельно полука-
бины, образует с конструктивной плоскостью вращения угол ф*. Его мы
будем называть углом установки оси фюзеляжа. Тогда наклон
пола (оси фюзеляжа) в полете будет таким:
= ft -т- Фф = 0 -г «к -г фф. (201)
Эти формулы справедливы для ак~£0 (фиг. 51).
§ 2. СКОРОСТИ ОБДУВКИ ДИСКА НЕСУЩЕГО ВИНТА
И УГОЛ СКОСА ПОТОКА
Рассмотрим струю воздуха, набегающую на работающий несущий винт,
с точки зрения импульсной теории (фиг. 50). Невозмущенный воздух на-
бегал бы иа диск винта со скоростью Уо, как показано иа чертеже. К
этой скорости прибавится индуктивная скорость у1 (скорость подсасыва-
ния), вызванная работой несущего винта. Ее значение будем брать средним
по диску, т. е. считать как бы постоянным. Произведение этой скорости
на секундную массу протекающего воздуха должно равняться действующей
силе Г. Направлена эта скорость прямо противоположно силе Т. Согласно
правилу знаков, приведенному в главе 2, эта скорость положительна прн
положительной силе Т и направлена при нормальном полете вниз.
Складывая векторно скорость невозмущенного потока Уо с индуктив-
ной скоростью получим полную скорость Ft воздуха, пересекающего диск,
т. е.
Vi =- Vo-;~ Vv (202)
Сила Т определяет направление аэродинамической оси несущего
винта ОА. Шарнирно подвешенные лопастн современных вертолетов при
косой обдувке приходят в маховое движение (см. главу 9) и, как пока-
зывают теория и опыты, начинают вращаться не около конструктивной
оси Oyit а почти в точности около аэродинамической оси ОА. Угол меж-
ду ними равен бБ.
Для аэродинамического расчета удобно разложить скорость потока
на два компонента: по аэродинамической оси — VA и по перпендикуляру к
ней — VT. Скорость VA мы будем называть скоростью протекания
воздуха через диск несущего винта, отклоненный на угол бБ = 6Х 4- бдп
от осн Oylt и скорость VT будры называть скоростью скольжения
воздуха вдоль этого диска.
Из фиг. 50 непосредственно видно, что
VA = — F sin т -г (203)
и
Vr V() cos т. (204)
В первой формуле поставлен знак минус, так как т<^0.
Полная скорость потока в плоскости диска Vi может теперь быть
представлена так:
У1= /Ул+ 14. (205)
Знаки у всех скоростей взяты по единому правилу, изложенному в
главе 1; углы т и ак в нашем случае вертолетного режима имеют знаки
минус, что и указано на чертеже. Угол между скоростями н Уо назы-
вается углом индуктивного скоса потока и обозначается в теории
индуктивного сопротивления через е/. Этот угол играет очень большую
роль как в теории крыльев, так и в теории винтов. Найдем его величину.
Угол е, = £Oad — Zead, но /_Oad = arctg-—, a ^ead = —т (фиг. 50).
Следовательно,
S; = arctg^i-I-т. (206)
Этот угол можно вычислить также приближенно с большой точностью
нз следующих соображений. Величина на всех режимах полета мала
(порядка 2,5°). Если в точке b на фиг. 50 восстановить к линии ОЬ пер-
пендикуляр Ьс, то угол abc = т, и нз полученного маленького треуголь-
ника Ьса, который можно считать прямоугольным, получим, что отрезок
be — Vi cos т,
а малый угол скоса в радианах будет равен
—<=^0ST- <207>
Формулы (206) и (207) дают практически совпадающие результаты.
Безразмерные или относительные скорости
Как мы уже знаем, в теории винтов очень удобно пользоваться вве-
денными проф. Н. Е. Жуковским и В. П. Ветчинкиным относительными
скоростями, равными по величине отношению любых скоростей к окруж-
ной скорости конца лопасти U = Все такие скорости, без исключения,
пишутся с помощью тех же букв, как именованные, но над ними ставит-
ся черта.
v
А Rm ’ J ftu) ’
Вводя эти обозначения во все выведенные формулы, путем деления их на
получим основные выражения для теории несущего винта:
VA = —(209)
VT = cos т;
(210)
ИЛИ
(211)
s, = arc tg 4-т,
vr
(212)
8/cost.
Vo
(213)
Как легко видеть, режим работы несущего виита задается дву-
мя любыми величинами: или Vo и як (или т = як 4- 6Б), или VA и VT, или
VT и як и т. д.
Отметим, что при тЗ>0 эти формулы сохраняют свою силу, как это
видно из фиг. 51.
При полете на вертолетном режиме т<4 0 и Кл^>0.
На автожирном режиме тЗ>0 и VA<Z® воздух пересекает диск снизу
вверх. При этом як = т— 6Б>-0.
Замечание об аксиальной скорости Уаи тангенциальной скорости
Vt (А. и |л)
Некоторые авторы для упрощения расчета принимают, что индуктив-
ная скорость направлена не по силе Т, а по конструктивной оси вра-
щения Or/р Тогда вместо формул (206) и (207) получится следующее вы-
ражение:
V,.. V-l
8Z = arc tg у- -р ак pr- cos як.
(214)
Здесь Vxi и Vj/i компоненты скорости Vi по осям Ох! н Оух.
Скоростями Vxi и У#! мы будем пользоваться при рассмотрении махо-
вого движения лопастей. Для упрощения написания формул мы в дальней-
шем будем писать Va вместо V^, называя ее аксиальной скоростью,
н Vt вместо Vxi, насьтая ее тангенциальной скоростью потока.
Формулы (209) и (210) напишутся в этом случае в таком виде:
Va =—I/o sin як + th = —(215)
Vt = Vo cos як = ц.
(216)
Здесь А, и ц обозначают эти скорости в англо-американском стандарте
Они встречаются и у нас в работах разных авторов (см. главу 1).
Скорости VX1 и Vyi связаны простым соотношением со скоростями VA
и VT. Проектируя обе скорости VA и VT на связанные оси координат
ОхуУь получим по фиг. 52 соответственно:
Vt Vr cos дБ — VA sin дБ;
Va = Vr sin dD 4- VA cos dB.
Угол дБ мал, обычно меньше 3°, поэтому
МОЖНО принять, ЧТО sin^g^ дБ HCOSdg^l.
Тогда получим:
Ve =7^ — Vr;
Va = Vrds + VA.
В первой формуле второй член УлбБ мал по
сравнению с первым, и его можно отбро-
сить. Окончательно получаем:
Vt = VT = ц. 1
- - - (217)
1/« = 1/л + 1/7.бБ = -;1- )
Фиг. 52 К переходу от скоро-
стей Vy и Гдк скоростям Р‘х1 =
= Vt и Кл= Va
Для аэродинамического расчета скорости VА и VT дают много преиму-
ществ и сильно упрощают все формулы, почему мы и будем имн пользо-
ваться в главах, посвященных аэродинамическому расчету и балансировке
вертолетов.
§ 3. ИНДУКТИВНАЯ СКОРОСТЬ ПРИ КОСОЙ ОБДУВКЕ
ИЗОЛИРОВАННОГО НЕСУЩЕГО ВИНТА
Для дальнейшего развития теории нам нужно научиться находить
среднюю индуктивную скорость Vi на ометаемом лопастями диске несу-
щего винта. Для этого воспользуемся теорией индуктивного сопротивле-
ния, дающей общие формулы для любых несущих систем. Эта теория
подробно излагается во всех больших курсах теоретической и экспери-
ментальной аэродинамики (см., например, Б. Н. Юрьев, Эксперименталь-
ная аэродинамика, часть II, Оборонгиз, 1938). На возможность ее приме-
нения для расчета вертолетов указали впервые Лок и Глауэрт (см.
список литературы) в 1928 г. Напомним ее основные положения.
Крыло или любая несущая система эквивалентны системе вихрей, изо-
браженных на фиг. 53. Крыло заменено здесь так называемыми присое-
диненными вихрями Жуковского, идущими по размаху крыла. Они
сбегают с крыла в виде вихревой пелены. Эти вихри создают в ок-
ружающем крыло воздухе так называемые индуктивные скорости. В слу-
чае крыла с эллиптическим законом изменения циркуляции по размаху
(«эллиптического крыла») вертикальная скорость скоса по всему разма-
ху одинакова. За крылом, на расстоянии полуразмаха, эта скорость, оста-
ваясь почти постоянной по размаху, увеличивается примерно в 2 раза,
т. е.
Vz = (218)
Теория индукции позволяет находить индуктивные скорости, т. е. ско-
рости, вызванные вихрями в любой точке пространства (х, у, г), и полу-
чить три компонента этих’ скоростей vx, vy и vz. Влияние вихрей в этой
теории хотя и простирается до бесконечности, но быстро ослабевает. По-
этому в приближенных расчетах можно считать, что несущая система дей-
ствует лишь на воздушную струю, имеющую вид трубы (фиг. 54), и вы-
зывает в ней некоторую среднюю индуктивную скорость щ в нормальном к У3
сечении, проходящем через центр несущей системы. Пусть площадь такого
Фиг. 53. Эпюра индуктивных скоро Фиг 54. Эквивалентная струя у несущей
стен и вихревая пелена \ крыла ко- системы; v\—индуктивная скорость
печного удлинения
сечения струи равна Fc. Тогда очень легко вычислить индуктивную ско-
рость по секундному импульсу подъемной силы системы, т. е. по силе Т.
Действительно, секундная масса воздуха, проходящего через струю,
равна m = изменение количества движения по вертикали в I сек.
будет равно т2цх = 2pFcV1a1; оио должно равняться импульсу силы Т за
I сек., т. е.
(219)
Отсюда
— г
01 “ '
Заметим, что совершенно такую же формулу мы уже получили для
* винта, работающего при осевой скорости. Следовательно, импульсная тео-
рия охватывает единой формулой как крыло, так и вннт в осевой и косой
обдувке. В этом, несмотря на ее приближенный характер, заключается ее
большая практическая ценность. Скорость vr вообще может сильно изме-
няться по диску, но средняя скорость вычисленная по импульсу реаль-
ной тяги Т, позволяет, как увидим далее, достаточно точно определить
мощность, потребляемую несущим винтом, как в осевой обдувке, с чем
мы уже познакомились в предыдущих главах, так и в косой.
Частным случаем осевой работы несущего винта является режим ви-
сения, когда Vo = 0. Тогда Vi = &iB и
Тв = 2pre^iD-
Индекс «в» указывает, что рассматривается режим висеиия. Отсюда иаходим
<221>
Скорость У1В играет большую роль в теории винтов, и мы будем называть
ее характеристической скоростью несущего винта. Какова
же площадь сечения струи Fc? Оказывается, что для идеального крыла
она равна площади круга с радиусом, равным полуразмаху, т. е.
= (222)
Несущий винт с точки зрения теории является также эллиптическим (кру-
говым) крылом, и для него можно было бы брать такую же площадь,
если бы ие существовало у него концевых потерь. Мы с этим вопросом
познакомились в § 6 главы 2 и потому вводим и здесь концевые потери
и считаем, что площадь струн будет несколько меньше площади описан-
ного круга, т. е.
Fc = xF = х . (223)
В дальнейшем всюду будем вводить концевые потери, заменяя Fc через
xF. Формула (220) перепишется тогда в таком виде:
она соответствует полету с горизонтальной скоростью. Для работы несу-
щего винта на висении формула (221) перепишется в таком виде:
(224)
д
или, вводя р = -g-, получим удобную расчетную формулу
(225)
Подставив в формулу (224) выражение Т через Ст, найдем
__ 1 ст
= Y V ~
(226)
Для косой обдувки примем Fc = xF, как и в случае осевой обдувки.
Ищем теперь скорость исходя из двух полученных формул, считая
тягу Т очень близкой к весу машины G и равную в обоих случаях
Т = 2pFcV1oI
(219)
Т Т. 2pFc01!„
Отсюда находим
У Л =
(227)
Подставляем сюда Vx = V Va 4- Vt и возводим полученное выражение
i квадрат:
(V.4 + Ут) vl
Чодставляя теперь в эту формулу VA = —Vosinr4-^i и Уг = У0со5т,
юлучаем после сокращения н раскрытия скобок:
ulVo — 2Voul sin т 4- vl — vlD = 0.
Для удобства составления обобщенных графиков вводим в это уравнение
ювые безразмерные скорости, отнеся нх к характеристической скорости
>1В. Такой прием впервые предложил в теории винтов проф. В. П. Вет-
4инкин. Будем обозначать такие безразмерные скорости волнистой чер-
ой сверху, т. е.
”1В °1В
(228)
Оделив полученное уравнение иа vlB, получим:
v{V20 __ 2Vovl sin т -I- vl — 1 = 0. (229)
?ешать это уравнение относительно неудобно. Проще всего решать его,
<ак квадратное, относительно Уо; тогда получим:
Уо = vL sin т +1 f sin2 т — vl -|- Д- , (230)
Тользуясь этой формулой, легко построить график, связывающий Уо с их
I sinr (фиг. 55). Пользуются им так: зная для частного случая величину
>1В, угол т _ ак + и скорость полета Уо, находим сначала
Уо
V1B
< по графику, зная т, получаем и затем находим индуктивную скорость
= ^1в-
(231)
Заметим, что в диапазоне Уо — 0<-2, при т = — 90’, мы получим ре-
кимы вихревого кольца и авторотации. Теория, как мы видели в § 3 гла-
1Ы 5, здесь оказывается неприменимой. Мы поэтому нанесли пунктиром при-
мерные кривые для т = 4- 90° и 4-60°, исходя нз фиг. 43. Они имеют, по-
мятно, лишь примерный вид.
Точки с т < 0 соответствуют вертолетному режиму полета, а точки
с т>0 — автожирному. При скоростях полета Vo> 2 все кривые ноч-
ей сливаются н влияние угла т делается малозаметным. Обычно при рас-
чете вертолетов интепесуются или вертикальным движением или гори-
зонтальным полетом с большими скоростями ^0>*2, причем угол т<6°.
В этом случае можно находить Vi, не пользуясь фиг. 55, так как в фор-
мулу
ViVj. = His
можно подставить для этого случая и тогда
VIB glB
Vi
(232)
или в безразмерном виде
Такой формулой пользуются многие авторы, она очень упрощает все
расчеты. Для малых скоростей (примерно Vg < 1,5) она дает малую точ-
ность. Угол скоса при больших .скоростях VQ можно найти, согласно
фиг. 56, по формуле
Фиг. 56. Угол скоса е, при больших
скоростях полета
Указанные формулы относились
к изолированному несущему винту, т.е.
такому, у которого нет заметного
влияния соседних виитов н крыльев.
К такому случаю относятся вертолет одновинтовой схемы и двухвинтовой
вертолет поперечной схемы с сильно разнесенными несущими винтами.
Вопрос о том, как использовать выведенные формулы в более сложных
системах, мы рассмотрим в следующем параграфе.
Отметим еще, что индуктивная скорость их прн больших горизонталь-
ных скоростях полета вертолета, обычно близких к Уо=О,25 и Ро =5, при-
мерно в 5 раз меньше индуктивной скорости и1в при висении. Так, если
и1в = Ю м/сек, то ut === 2 м/сек. Это показывает, что влияние этих скоро-
стей делается малым, и расчет по средией скорости по диску оказывается
достаточно точным.
Второй вид графика индуктивных скоростей
Скорость vL нужна главным образом для вычисления скорости протека-
ния, т. е. скорости У4. Так как
VA — VosinT Ч- ир
то, разделив эту формулу на и1в, получим
УА — — Уо sinx 4- Up
(234)
Очень легко, пользуясь этой формулой и графиком, приведенным иа фиг. 55,
построить новый график, изображенный на фиг. 57. По оси ординат отло-
жена величина Уд, по оси абсцисс V • С помощью этого графика по т и
V’o = сразу получается величина УА; далее находится скорость про-
и1в
текания
= VAvle,
(235)
входящая в очень многие формулы теории несущего винта.
_ Заметим еще, что все эти выводы применимы для скоростей полета
Vo <0,3—0,4; при больших скоростях получается асимметрия скоростного
поля в плоскости диска и точность формул уменьшается. Строго говоря,
излагавшаяся теория относилась к соосной схеме несущих винтов со столь
близкими ометаемыми площадями, что они сливаются в один диск. Тем не
менее, указанный метод расчета в различных его модификациях постоянно
применяется при расчете
несущих винтов и дает
достаточно удовлетвори-
тельные результаты. Это
объясняется тем, что при
больших скоростях полета
индуктивные скорости де-
лаются малыми и вызывае-
мая ими асимметрия по-
тока мало влияет на тягу
и мощность винта, так
как они зависят от общего
импульса всей струи, а не
от распределения импуль-
сов по диску винта. Послед-
ний фактор влияет на Ст
и тл очень слабо.
На самом деле, величина
индуктивной скорости за-
висит и от радиуса и от ази-
мута, т. е.
»1 = /(Г, И>).
Однако до сих пор эту
скорость удавалось полу-
чить как теоретическим,
так и опытным путем лишь
как среднюю скорость для
фиксированной на диске
точки. Для уточнения же
расчетов нужно было бы
получить скорость на самой
лопасти, чего до сих пор
Фиг. 57. Зависимость скорости протекания V
от Vo и т
сделать не удалось. Поэтому пользование
средними индуктивными скоростями вполне допустимо в аэродинамическом
расчете вертолетов, но для расчета устойчивости оно недостаточно точно.
§ 4. ВЗАИМНОЕ ВЛИЯНИЕ НЕСУЩИХ ВИНТОВ И КРЫЛЬЕВ
У сложных систем вертолетов, имеющих несколько несущих вннтов,
а иногда и крылья, возникает взаимодействие между всеми несущими эле-
ментами вертолета.
Самым надежным способом учета этих влияний являются опыты, про-
веденные с моделями таких вертолетов в аэродинамических трубах, или
натурные опыты. Однако в первом приближении эти влияния можно оце-
нить теоретически с помощью теории индуктивного сопротивления.
И* Для изучения вопроса о взаимном влиянии несущих винтов и крыльев
не приходится создавать новую теорию, так как хорошо разработанная еще
25 Б. Н. Юрьев, т. I
в 1918 г. теория сложных коробок крыльев, так называемая теория
полиплаиов, полностью может быть перенесена и на этот случай.
Как мы знаем, крыло и винт можно заменить при полете с горизонталь-
ной скоростью вихревой системой, изображенной на фиг. 53. Эта вихревая
система, согласно законам теоретической аэродинамики, вызывает во всем
окружающем воздухе индуктивные скорости, в частности на самом крыле
или винте скорость vlt а за ним на расстоянии, большем 1/2, скорость 2vt.
Прн наличии нескольких таких вихревых систем каждая из них вызывает
такие индуктивные скорости, как если бы других вихревых систем не су-
ществовало: это так называемый закон независимости действия вихрей или
принцип наложения скоростных полей.
Индуктивные скорости при этом складываются векторно, и в любой
точке воздушного пространства получится результирующая индуктивная
скорость
v V1 4- v2 -Г • • • (236)
где Vi, v2, .. ., vn — индуктивные скорости, вызванные в данной точке от-
дельными вихревыми системами.
Полная скорость потока в этой точке будет равна
V = Ц, + I»! + + . .. + к„,
(237)
где — скорость невозмущенного потока, равно-противоположная скорости
полета машины.
Для оценки взаимных влияний с точки зрения индукции нужно найти
индуктивные скорости, вызванные как своей вихревой системой, так и со-
седними. Для удобства расчетов будем применять у скоростей двойные
индексы: первый дает номер рассматриваемой несущей системы, а второй--
номер той системы, влияние которой рассматривается. Следовательно, полу-
чим у продольной двухвинтовой системы: v11uv22 — индуктивные скорости
от самоиндукции, т. е. вызванные у них своими же вихревыми системами,
t?i 2 — индуктивная скорость от влияния второй системы на первую и —
индуктивная скорость от влияния первой системы на вторую. Следовательно,
в этом случае
о, = Oi.i + с, 2; (238)
о, = о2.2 -1-02Д. (239)
Скорости в плоскости дисков будут равны
Vo + г1Л 4- 2 (240)
и
К2 = Ко + 1»2.2 + ®2.1- (241)
Скорости ©1Л и v2.2 мы уже научились находить по правилам, изложен-
ным в § 3.
Следовательно, для учета взаимных влияний нужно расчет несущих
систем и крыльев вести исходя не нз скорости иевозмущенного воздуха, а
из скоростей подходящего воздуха:
VM = Vq + ^1-21
(242)
V02 = Vo + гг2Л, (243)
т. e. нужно к скорости невозмущенного воздуха прибавить скорость от
взаимоиндукции. Это правило относится к любому числу несущих элемен-
тов.
Скорости ®1ф2 и ^2.1 малы по сравнению со скоростью Уо н имеют как
вертикальную, так и горизонтальную составляющие. Обычно эти скорости
разлагают по скоростным осям координат и получают составляющие по
скорости полета г>х1.2, п₽1.2 н пл21» vy-2.i- Скорости ил1.2 и ил211 изменяют
величину скоростей набегающего потока, делая нх равными
Vol = vo + vxi.2 (244)
и
V02 = vo + vX21, (245)
а скорости Vjfi.4 н ay2.i лишь поворачивают скорости VOi н V&2 на малые
углы
н
(247)
'02
Эти углы называются углами скоса потока от взаимоиндукции несущих
систем. В таком виде эти формулы могут применяться для любых, напри-
мер очень больших, углов атаки ак.
Однако на практике обычно интересуются малыми углами атаки, и тогда
предыдущие формулы можно упростить, так как обычно vAi2 и ux2i малы
по сравнению с 14 и их можно отбросить и считать, что в сложной системе
скорость потока, набегающего на отдельные несущие винты и крылья,
всегда равна Vo и лишь изменяет направление на некоторый угол е. Тогда
для двух несущих винтов можно написать
н
Следовательно, задача учета взаимных влияний сводится к нахождению
индуктивных скоростей или углов скоса, возникающих от влияния соседних
вихревых систем.
Формулы (203) и (204) могут применяться и в этом случае, но в таком
виде:
а) для первого несущего винта
Kn = — (Vo + ^1.2) sin (Та + е, а) + «ы = 1
~ — Vo sin (т, + в,о,.,; I (248)
Vn — (Vo + и..,.2) cos (г, + ег2)як Vo cos (т, + в,.,); J
б) для второго несущего вннта
Vh2 = — (V„ + 1) sin (т2 + 62.1) +
+ V2.2 — Vo sin (т3 ч- е2Л) + с2.2;
VT2 = (Vo + ux2.i) cos (т2 + е2Л) Vo cos (t2 + e211).
(249)
В соответствии с этим можно пользоваться графиками, приведенными
на фиг. 55 н 57, только вместо т нужно брать углы тх + е12 и т2 + 82.x.
Продольная двухвинтовая система
В случае продольной схемы задний несущий винт попадает в след пе-
реднего виита. Заменяя передний несущий винт вихревой пеленой, мы смо-
жем получить для^всякой точки, лежащей в плоскости, перпендикулярной
Фиг 58 Зависимость индуктивной скорости моноплана от координат
при х — О
!
< скорости У0'и проходящей через присоединенные вихри первой системы
1ля любых координат, скорости иу. Для этого удобно пользоваться так
называемым графиком Польгаузена (фнг. 58), дающим зависимость --- от
безразмерных координат z~—у— и у =, где I — размах несущей си-
2 2
стемы (т. е. диаметр виита). График составлен для крыла с эллиптическим
законом изменения циркуляции по размаху. В этом случае прн у — О,
(52-) = 1 и постоянно по размаху. При удалении от крыла в точке
'01-Г
с координатами z и у мы найдем по кривым величину ——-j и, зная для
изолированного крыла нли несущего виита величину 15 находим vy =
Присоединенный вихрь заднего винта можно считать прохо-
дящим через его втулку, горизонтальным и перпендикулярным к скорости
При этом х = I. Если провести через него плоскость, перпендикулярную.
к Vo, т° в любой ее точке с координатами z и у вихревая пелена перед-
него винта вызовет индуктивную скорость (——\ == f (z, у), причем можно
\ 1 /
считать ^при , что эти скорости будут в 2 раза больше скоростей
в поперечной плоскости переднего винта. Это следует из известной теоремы
аэрогидродинамики о том, что действие вихрей в 2 раза больше действия
полувихрей. Из этого следует, что в случае, когда задний несущий винт
лежит в плоскости переднего винта, индуктивная скорость от влияния пе-
реднего виита равна n2.i = 2^ i и полная индуктивная скорость у заднего
виита будет равна u2 = v2 2 + v.2 Р Если же задний несущий винт располо-
жен выше переднего, то, взяв кривую, соответствующую у = ——,мысмо-
2
жем иаити величину ------: она сильно меняется по «размаху» второго
винта. Для упрощения расчетов следует брать ее среднее значение, напри-
мер для четырех точек, лежащих накрест на диске несущего вннта и имею-
щих г = 0,7. На основании таких расчетов ниже приводим средние вели-
2 - У У
чины----- в зависимости от у = —;— =
»>> J_ R
2
7= . 0,0 0,05 0,1 0,2 0,3
- к
~ .... 2,0 1,78 1,64 1,35 1,13
У современных вертолетов продольной схемы задний несущий винт имеет
превышение, равное примерно от ]/б до 1/3о радиуса винтов. Тогда из
приведенных данных получаем в среднем и полная индуктив-
ная скорость у заднего винта будет равна
^2 — ^2 2
Дополнительный скос у заднего вннта будет, например прн Уо = 60 м/сек
и и1Л 2 м/сек, равен
. 1,5ц, ,
8ЗЛ = -2^-57,3 ^—^57,3^3°,
Vo 60
т. е. величине сравнительно большой, что сильно ухудшает работу заднего
несущего винта. Влияние заднего несущего винта на передний очень неве-
лико; обычно нм можно пренебрегать и считать, что и12 = 0.
Двухвинтовая поперечная система
В случае двухвинтовой системы с расположенными поперек винтами
как видно из гоанка фщ. 53, получаются сильно изменяющиеся отрица-
тельные скооости от действия соседнего несущего винта. Это улучшает
работу винтов. Находим вел 14 а ну с <оса в зависимости от расстояния между
втулками несущих винтов 1Ъ. П аи этом нужно учесть, что современные несущие
винты имеют угол конусности Поэтому на графике Польгаузена
нужно брать в этом случае не h = 0, а примерно /гср = 0,05. Введя без-
размерные расстояния 1В = и приняв определение средних скоростей
индукции по этому графику по четырем накрест лежащим точкам на г — 0,7
- 1В
мы получим зависимость средней индуктивной скорости от/в = —— дляпо-
перечной двухвинтовой схемы вертолетов.
У = -Г-.... 2,5 2,0 1,8;
R
— .....—0,12 —0,25 —0,42.
и11
При /в=2 несущие винты не пересекаются. При ZB<2 они пересекаются
и изложенная теория дает лашь приближенные результаты.
Опыты показывают, что в зависимости от формы лопастей виитов нан-
выгоднейшее расстояние между втулками получается при /в= 1,8 —1,6,
т. е. при перекрывающихся несущих винтах. Мы снова вернемся к этому
вопросу в главе 10. Теперь же отметим еще раз, что в поперечной схеме
взаимные влияния при полете с горизонтальной скоростью несколько улуч-
шают работу винтов.
О четырехвннтовой схеме
В случае четырех несущих винтов у них взаимные влияния просто
складываются, и задача их вычисления сводится к уже разобранным слу-
чаям (§ 5 главы 7).
Расчет взаимных влияний прн использовании
П-образной схемы вихрей
Изображенная на фиг. 53 схема является идеальной. На самом деле
вихревая пелена неустойчива небыстро сворачивается в два отдельных вих-
ревых шнура, в так называемые вих’
ревые усы (фиг. 59). Их действие не'
сколько отлично от действия вихре’
вой пелены, но для средних скоростей
индукции разница получается сравни-
тельно небольшая. Расстояние G меж-
ду вихревыми усами для крыла с
эллиптическим законом изменения
циркуляции скорости по размаху
оказывается равным величине*
1^—1^0,781.
4
Фиг. 54. Свертывание вихревой пе-
пены в лв i вихревых шнура. Экви-
валентная П-образная система
вихрей
'8 D. Для вычисления вертикальной
у и z) можно пользоваться формулой
Поэтому расчет индуктивных скоро-
стей можно делать, исходя ’ также
из П-образных вихрей, взяв расстоя-
ние между вихревыми усами равным О,
скорости для любого положения точек (
(250)
Эта формула может применяться и к несущим винтам, и к крыльям. Осн
координат в ней взяты стандартные: х — по скорости полета, у—вверх и
г—в правую сторону.
В эту формулу входит циркуляция скорости Го у центрального сечения.
Для крыла с эллиптическим законом изменения циркуляции («эллиптического»
крыла), как доказывается в аэродинамике, подъемная сила Т связана с
этой циркуляцией простой формулой
Т --- 4-PW.
4
(251)
где I — размах крыла. Несущий винт также является эллиптическим (кру-
говым) крылом, и мы можем воспользоваться для него этой формулой. Из
* Б. Н. Юрьев. Экспериментальная аэродинамика, ч. II, стр. 45 и 245.
нее находим^для несущего винта:
Г<
pV»i .
4 Сг’ТрЛ4“2
pV02fl
Ст
= —£-^3.
Vo
(252)
Л
Вместо Ст в эту формулу можно подставить характеристическую скорость
1 / СТ Г) Т
— 1 / — кы. 1 огда получим:
У х
Фиг. 60 Вычисление средних скоростей
от взаимоиндукции по четырем точкам
V*
Го = 4х R 4z»,R. (253)
Vo
Последнее выражение применимо
при больших скоростях полета
вертолета, т. е. Уо^>0,1.
Следовательно, для вычисления
циркуляции скорости у вихревых
шнуров при эквивалентной П-образ-
ной схеме можно пользоваться
любым из выражений:
= 4x^-R = 4x^7?.
Vo
(254)
В качестве средней индуктивной
скорости, вызванной соседним внн
том, иногда берут скорость в центре несущего виита, у втулки. Это очень при-
ближенно. Более правильно вычислять среднюю скорость по четырем
накрест лежащим на радиусах г — 0,7 точкам, как это изображено на
фиг. 60 для случая четырехвинтового вертолета
Вычислив
^2 1 =
fl ~}~ Ч; -j- р8 vi
4
получаем более правильную величину среднего скоса от влияния соседнего
несущего винта.
Применение приближенных формул в этих расчетах вполне оправды-
вается тем, что скорости эти малы, хотя их влияние и существенно.
Не вполне точное их определение на окончательном результате сказы-
вается мало.
Кроме того, вся теория несущего винта приближенна и исходит из сред-
них скоростей, тогда как на самом деле все скорости пульсируют н дви-
жение воздуха и лопастей является неу становившимся. В главе 10 мы рас-
смотрим еще один прием учета индуктивных скоростей
§ 5. О БАЛАНСИРОВОЧНОМ УГЛЕ дБ ВЕРТОЛЕТА
Рассмотренный в § 1 угол балансировки бБ входит в ряд важных фор-
мул, необходимых для аэродинамического расчета вертолета; кроме того,
знание его необходимо для правильной компоновки машины.
Найдем его величину, взяв для определенности одновинтовую систему
с рулевым винтом (фиг. 61). Напомним, что балансировочным углом бБ мы
будем называть угол, образуемый полной силой тягн Т с направлением
(%г 0) при Висений
Фиг 61 Схема балансировки одновинтового вертолета
конструктивной осн вращения несущего винта Оуи при котором получается
в продольной плоскости уравновешивание, «балансировка», вертолета, н
полный аэродинамический момент /И2, действующий на него, равен нулю.
Угол бБ мал (порядка 2—3°) н ось 0ххх, проведенная через центр тяжести
машины (точка ц. т.), будет почти перпендикулярна к силе Т. Поэтому
можно принять, что при высоте центра втулки над осью 0гхъ равной h,
отрезки хт = Ор и хц т = (\с можно рассматривать как дуги, описанные
радиусом h из центра втулки, т. е.
хт = hdB, хц т = Абц
где бц т — угол центра тяжести или центровки вертолета. Сила Т дей-
ствует по отношению к центру тяжести с на плече хт— хцт и вызывает
момент
Мт = Т (х-г — Гц т) = Th (6б — бц т)-
(255)
Если бы вертолет не имел стабилизатора и хвостового винта и момент
фюзеляжа был бы малым, то Мт = 0 и бБ —бцт = 0, т. е. тогда бв = бцт
и балансировочный угол равнялся бы углу центровки.
В общем случае момент Мт должен уравновешивать действующие на
вертолет моменты. Таких моментов будет у бескрылого вертолета три.
Момент от горизонтального оперения можно представить так:
ру*
Я.0 = /г.О^-Г.О = ~~ Су г.О--- Sr.oLr.o, (256)
где Л.о—подъемная сила оперения, a LT.O —плечо этой силы относительно
ц. т. Момент от хвостового винта
где Мх.в — мси’рссть этсго еинта и — число его оборотов в минуту.
Знак момента ааггснт от направления вращения хвостового винта. Момент
от фюзеляжа будет
рУ;
/Иф = -+- С,п ф5ф/ф (258)
где Зф — площадь миделевсго сечення фюзеляжа, Стф— коэффициент мо-
мента фюзеляжа относительно ц. т., /ф — длина фюзеляжа. Эта величина
обычно очень мала при горизонтальном полете.
Для вертикальной обдувки во время висения можно писать:
/Иф == Q$Iq, (259)
где фф — лобовое сопротивление и Zq— плечо этой силы относительно ц.т.
Следовательно, условие балансировки, т. е. Мт = SA1, можно написать
в таком виде:
/ h (&б — бц.т) Мг.о + АФх.в + Мф.
Отсюда
Мго Мхв
Подставляя в последнее выражение найденную величину моментов по фор-
мулам (256) — (258), получим в общем виде:
рУ* 5ГДГП 716,2Л/ R ру2
бв = бц.т-± + С,„ф5ф/ф|^, (261)
4ЛИ
бБ = бц.т Н- бг.о бх.в -Ь бф. (262)
Каждый члеи правой части этого выражения можно рассматривать как
^который угол поворота силы Т, необходимый для балансировки. Поря*
рок этих величии такоз: второй член правой части мэжзт изменяться в раз-
[ых схемах от 0 до —3°, тргтий член мал и имеет пэмщзк о<оло
[ри направлении вращения хвостового винта, указанном иа фиг. 61, и
юследний член может иметь порядок от 0 до 4-3°. Величина бБ в среднем
»авна 1 — 3°.
Наиболее важно соблюсти условия балансировки для полета с макси*
(альной горизонтальной скоростью и для висения: тогда в промежуточных
лучаях легко сбалансировать машину с помощью малых углов б ап.
В первом случае очень мал последний член, а дляс^г.о можно восполь-
зоваться выражением
СуГ,О~' ^г.о^г.о»
de
где Яго — Угол атаки оперения и Дг.о = , г,о~4. Тогда для горизонталь-
ааг о
кого полета можно написать:
бв — бц.т
А, о«г.о с г , 716Ж.В
771 2 г'° г'0± Т/гпх
(263)
Здесь скорость обдувки
Фиг. 62. Схема обдувки вертолета струей воздуха
сверху на режиме висения
Во втором случае, при висении, обдувка части фюзеляжа и оперения
происходит сверху со скоростью 2vlB (фиг. 62). Для вычисления момента
/Иф для второго случая, т. е. для вертикальной обдувки, можно принять,
что для оперения сх ~ 1,2 (угол аг.о = —90°), а для фюзеляжа, обдувае-
мого поперек, как для цилиндра, сх = 0,4 (числа Re > 1 000 000). При вы-
за несущим винтом сжимается и
-^—^0,71 R н внутренний /"01 =
числении А4ф нужно помнить, что струя
ее радиусы будут равны: внешний =
= ~г^0,71го. По эскизу нужно найти обдуваемую сверху площадь фюзе-
ляжа 5ф и определить ее центр Ф. Найдя расстояние от центра площади до
центра тяжести машины, т. е. длину Iq, можно вычислить момент от силы
лобового сопротивления фюзеляжа по формуле
Он положителен, так как стремится повернуть машину на кабрирование.
Следовательно, для висения условие балансировки будет таким:
Л я VsrxA-.o р(Чв)3
0Б.в — Оц.т — 2
0,4Sta/e Р(2»1е)’ , W.2N^
Th 2 Х
Углы 6б и бБ.в в общем случае могут быть различными.
Мы здесь предполагали, что стабилизатор помещен в самой струе
несущего вннта с целью получения при висении момента «на кабрирова-
ние», а при горизонтальном полете —
«на пикирование». Это выгодно для
уменьшения угла бдп.
Как видно из фиг. 63, для балан-
сировки машины нужно с помощью
автомата-перекоса повернуть силу Т
наследующие углы: при полете с мак-
симальной горизонтальной скоростью
на угол
— бдп = бх—бБ (265)
и при висении на угол
бдп.в бБ.в. (266)
Большие величины бдп требуют боль-
шего поворота кольца автомата-пере-
коса, равного примерно от одно- до
двукратной величины бдп- При боль-
ших отклонениях легко возникают
вибрации в системе головки несущего
вннта, а на ручке управления — боль-
Фиг. 63. Углы балансировки при висении шие усилия и рывки (см. список ли-
3Бви на максимальной скорости полета <3Б тераТурЫ? работы В. Е. Касторского).
Поэтому желательно иметь величи-
ну бдп порядка Р/г — 3°, тогда кольцо автомата-перексса нужно будет
отклонять для балансировки на угол в 2—4°, н останется еще достаточ-
ный запас иа управление машиной.
Центровка вертолета
Скажем несколько слов о рациональных способах центровки машин.
Если нет стабилизатора, а момент фюзеляжа и эффект хвостового винта
малы, то лучше всего помещать центр тяжести так, чтобы 6б = бц.т = — бх
(фиг. 64). Тогда по формулам (265) и (266) получим:
4
бдп = бБ — бх = — дх — бх = — —;
. _А __ 1 .
бдп.в — об.в — -гр- бх,
т. е. угол бБ будет в среднем иметь величину
В каждом частном случае легко найти эти углы. При правильной уста-
новке стабилизатора углы бдп н бдп.в могут быть еще более уменьшены.
Можно даже так сбалансировать вертолет, что не потребуется для балан-
сировки прибегать к автомату-перекосу. Для этого нужно соответствующим
образом выбрать величины Sr.o и аг.о- Для этого нужно получить в обоих
случаях (Уо = 0 и Vo = Vmax) балансировку машины на этих двух режимах
без действия АП, что требует, как видно из формул (265) и (266), соблю-
дения следующих условий:
бдп = бв — бх = 0;
бдп.в — бв.в — О-
Отсюда для указанного случая необходимо соблюсти условия
бБ = б.
бв.в = 0.
Подставляя сюда в развернутом виде значения бБ и бБ.Е по формулам
(263) и (264), получим для висения:
. А Р(2^1в)2 (Шф'о , 716,2^.в
0R в ~ Отт Т " "* гт* г V.
“ Th 2 Th 2 ~ Thn^
Решая это уравнение, находим необходимую площадь оперения Sr.o.
Из второго условия получаем:
. . , 716,ЙУ,.В
б Б — бц.т — ’ — —I ---------- — бх-
Th 2 ~ ThnK B
Подставляя сюда найденное значение Sr.o, получаем из этого уравнения
величину необходимого угла атаки аг.о. Угол установки оперения <рг.о будет,
равен, очевидно,
фг.О =•• ёг.О Ч- <Хт-,О»
где ег.о—скос потока у оперения от взаимоиндукции, равный приблизи-
тельно двойному скосу потока у несущего винта е/.
При таких параметрах оперения автомат-перекос в обоих случаях стоит
нейтрально. Летчики, однако, предпочитают такое управление, чтобы по-
лету с горизонтальной скоростью соответствовало отклонение ручки вперед,
для чего при установке стабилизатора его площадь берут несколько мень-
шей расчетной величины, и тогда указанное условие соблюдается.
В нашу задачу не входит подробный анализ управляемости и устойчи-
вости вертолетов, и мы ограничимся лишь вопросами балансировки, непо-
средственно связанными с аэродинамическим расчетом.
Фиг. 64. Схема балансировки машины
без добавочных моментов
Укажем только, как приходится в первом приближении балансировать
в продольной плоскости вертолет продольной схемы (фиг. 65). Будем счи-
тать, что с помощью изменения шага вн нов летчик обеспечивает равен-
ство сил тяги у переднего и заднего несущих винтов, т. е. ~ Т2.
1 сгда ] авнодействующая этих сил
будет приложена в средней точке
прямой, соединяющей центры вту-
лок обоих винтов. Эта равнодей-
ствующая получится сложением сил
тяги по правилу ромба, так как эти
силы равны. Следовательно, равно-
действующая пойдет по биссектрисе
угла между силами 7\ и Г2.
«Средняя» ось 0у1ср пойдет так-
же по биссектрисе направлений
осей Оуц н 0у1.2- Тогда средний
угол отклонения бхср равнодей-
ствующей силы 2Т можно ис-
пользовать для приложенного ра-
счета балансировки, следуя опи-
санной для одного винта методике; получатся те же углы бБср, бц.т.ср >
тср, ак.Ср и т. д., но взятые как средние для обоих несущих винтов. Здесь
получается полная аналогия с методом, применяемым прн балансировке
самолетов-бипланов,исходящим из средней аэродинамической хорды САХ.
Фиг. 65. К расчету центровки по методу сред-
ней фиктивной втулки
Здесь в качестве такой хорды служит прямая линия, соединяющая центры
обеих втулок. Точку пересечения этой линии с равнодействующей тяг на-
зовем центром условной втулки (ЦУВ)
В главе 10 мы покажем, как можно найти среднюю величину бЛ по
приближенным методам для сложных комбинаций несущих вннтов и
крыльев.
От’em л ‘не, чго некоюрые старые вертолеты центрировались непра-
вильно: чаще всего центр тяжести помещался на конструктивной оси Oyf.
Тогда при горизонтальном полете с максимальной скоростью летчику при-
ходилось отклонять силу Т на угол бдп = бЛ, т. е. примерно на 4—8°,
что вызывало вибрации и получалось сильное давление на ручке управления.
Такие машины летали при сильно «задранном» вверх хвосте.
Положение осей вертолета при висеиии
и вертикальном взлете
Рассмотрим, как располагаются оси вертолета при вертикальном движе-
нии. Ось Ох всегда напоавлена
вертикальна, а следовательно,
Тяга Т будет направлена
вертикально вверх и урав-
новесит силу веса G и вред-
ные лобозые сопротив ления
вертолета QBp. Она образ к.
по
ось
скорости полета Уо, т. е. она будет
Оу будет горизонтальной (фиг. 66).
ет с конструктивной осью
Oyi угол дв.в. При этом,
как видно из чертежа, 9 =
90е, т = — 90; следова-
тельно,
ак = т — бь.в = — 90° —
— 6бв, (267 )
т. е. при внеенин угол
ак^90°. Угол тангажа
У, \
#б.&.
оси фюзеляжа при внеенни
будет равен у
'Э’ф.в— 9 4- Як.в 4- Фф—90е—
— 90° — бв.в 4~ Фф>
фиг. 66. Схема действия сил на вертолет
при вертикальном взлете и висении
или
#ф.в = — бв.в 4- Фф-
(268)
При компоновке вертолета нужно стремиться, чтобы прн полете с макси
мальной горизонтальной скоростью ось фюзеляжа была приблизительно го
ризонтальна, а при висении и на стоянке — фюзеляж образовывал бы не
большой угол с горизонтом. Для этого берут Фф —7°. У вертолета
продольной схемы, изменяя дифференциально тягу переднего и заднего вин-
тов, можно получить очень большие продольные моменты и сбалансиро-
вать машину для любых условий; в частности, можно получить и взлет и
полет с максимальной скоростью при горизонтальном фюзеляже (Оф -•=
— ОфВ = 0). В некоторых схемах крылатых вертолетов фюзеляж повора-
чивается на 90°. Тогда приходится устраивать поворотные сиденья или
поворотные кабины.
Глава 7
СИЛЫ, ДЕЙСТВУЮЩИЕ НА НЕСУЩИЙ ВИНТ,
И ПОТРЕБЛЯЕМАЯ ИМ МОЩНОСТЬ
§ 1. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ НЕСУЩЕГО ВИНТА
Несущий винт, как мы видели в предыдущей главе, при косой обдувке
является как бы крылом.
Если бы несущий винт не обдувался косым потоком, а работал на ре-
жиме висения, то его тяга была бы направлена по его конструктивной или
связанной оси При косой обдувке, т. е. при полете с горизонтальной
скоростью, поток набегающего воздуха поворачивается на некоторый не-
большой угол скоса 8(, подобно тому, как это происходит у крыла. Этот
поворот потока, как учит теория индуктивного сопротивления, вызывает
такой же поворот всех действующих на несущую систему сил
Фиг. 67. К' расчету индуктивного сопротивления Qi
(фиг. 67). Сила Т, следовательно, отклонится назад иа малый угол £/, что
вызовет, подобно тому, как это получается у крыла, индуктивное сопро-
тивление в плоскости вращения винта, т. е. направленное по осн OXj.
Q,- = Т е,-.
(269)
Разделив это выражение на —р7?4со2, получим слева винтовой коэффи-
циент индуктивного сопротивления, а справа—коэффициент подъемной силы,
т. е.
CQi = CT&l. (270)
Легко'понять физическую причину ' возникновения индуктивного сопро-
тивления .
На фиг. 68 изображены два противоположных сечения жесткого несу-
щего винта, лзжащие на одном и том же радиусе г. Одно из них, чэриое,
движется вперед, и скорость набегающего на него воздуха прн висении
Фиг. 68. Определение индуктивного
сопротивления у жесткого
несущего винта
Фиг. 69. Определение индуктивного
сопротивления у несущего винта
с машущими лопастями
равна гео, а при косой обдувке она равна приблизительно го -|~ VT. Лопасть,
изображенная пунктиром, идет назад. При висении скорость обдувки рав-
на гео, а прн горизонтальном полете го> — VT. Поэтому при висении оба
элемента дадут равные силы dY, равнодействующая которых будет направ-
лена по оси Oyt. При косой обдувке лопасть, идущая вперед, разовьет го-
раздо большую силу dYn (подъемную силу элемента), чем идущая назад,
дающая силу dY3, так как эти силы пропорциональны (гео 4- Vy)2 и (го>—Vr)2;
происходящее при этом малое изменение величины су влияет мало. Проек-
тируя эти подъемные силы на плоскость вращения, получим избыток силы
от профиля, идущего вперед; это и есть индуктивное сопротивление. Мы
здесь указали лишь на схему явления. На самом деле, при вращении не-
сущего винта величина и направление этих сил изменяются, но схема яв-
ления неизменна. Следовательно, косая обдувка виита неизбежно вызывает
сопротивление, завися цее от подъемных сил элементов.
В случае шарнирной подвески лопастей при работе на месте они не-
сколько отклоняются вверх; получается так называемый конус лопастей
(фиг. 69). Сила тяги направлена по оси этого конуса. Если произвести
косую обдувку такого несущего винта, то ось конуса лопастей «завали-
вается» назад приблизительно на угол ez, а сила тяги оказывается направ-
ленной почти точно по новому направлению оси конуса. Это и вызывает
отклонение назад силы Т и связанное с этим возникновение силы индук-
тивного сопротивления несущего винта Q,.
Величину угла скоса ег вычисляем по индуктивной скорости и, или по
осевой Уд по формулам (206) и (207), или при скоростях полета Уо 0,1
по приближенной формуле (233).
В эти формулы -МОЖНО- подставлять как именованные скорости, так и
относительные Уо, и1В и vt.
§ 2. ПРОФИЛЬНОЕ СОПРОТИВЛЕНИЕ НЕСУЩЕГО ВИНТА
В ЦЕЛОМ
Кроме рассмотренного индуктивного сопротивления, у несущего винта
в косой обдувке возникает еще действующее в плоскости вращения про-
фильное сопротивление. Оно получается как разность профильных сопротив-
Фиг. 70. Определение профильного со-
противления элемента лоласти при
полете с горизонтальной скоростью
лении у лопастей, идущих вперед и на-
зад. Иногда его называют продоль-
ной силой. Для его вычисления вы-
делим на лопасти элемент, лежащий на
некотором радиусе г н имеющий ширину
b и длину dr.
На фиг. 70 изображена конструктив-
ная плоскость вращения несущего винта
Положение лопастн будем задавать
углом азимута ф, отсчитывая его от
заднего, «флюгерного», положения лопа-
сти. Скорость Wx потока, набегающего
на вырезанный элемент, если пренебречь
ничтожным влиянием скорости Va и угла
6б, как видно из чертежа, будет равна
Wx = го 4- Vt sin ф.
Здесь мы считаем, что Vxi = Vp (см. § 3
главы 6). У элемента лопасти возникает
профильное сопротивление
dQp.e = схр bdr схр (гео + Ут-зтф)2^. (271 >
Оно направлено по скорости Wx, т. е. по окружной скорости.
Для получения мгновенгего префгльвего сопротивления для' несу-
щего винта нужно это сопротивление спроектировать иа ось Охг. Тогда
получим:
dQp = dQp.e sin ф =- -у- (геи 4- Vt sin ф )2 sin ф dr.
Для получения полного сопротивления от одной лопастн для данного ее
положения ф нужно предыдущее выражение проинтегрировать по всей
длине лопасти, т. е. от г = 0 до г = R. Однако у несущего винта нас
интересует не мгновенная величина сопротивления, а среднее сопротивление
всех k лопастей за полный оборот винта. Для вычисления средней величи-
ны Qp за оборот применим весьма употребительный в теории несущего
винта прием, для чего напишем равенство импульса силы dQp за период
оборота винта, равный tn = с интегральным импульсом силы сопро-
w
тивлення лопастн, т. е.
2л с С С W Г
— Qp = k J dt\ dQp = k $ — j) dQp,
0 0 0 0
где dt = —i—время поворота лопасти на угол dip, k — число лопастей.
а>
Сокращая <о, получим употребительную формулу осреднения различных
величин за один оборот несущего винта
(272)
В нашем случае мы имеем
, 2Л R
k р р -jb
= 2п” J J <r® + Vt sln sin dr'
Раскрывая скобки и изменяя порядок интегрирования, получим для
^-лопастного несущего винта:
Л . . 2Л
г» ph 1 Г»
Qo _= k Схр ~2 {^r2 sin ip -Ь 2го sin2 хрРт + V'j. sin3 ip) dip. (273)
о о
Вычисляем сначала внутренний интеграл, разбив его на трн, и тогда полу-
чаем:
§ г2»2 sin ip dip = г2со21 — cos ip — 0;
о
f V г sina -ф d-ф = Vt $ (— -^ 5>п,3ф + -3- sin -ф ) = 0;
о o'
2Л 2Л
2rcoVr sin3 ф dip = 2г(оУт § sin2 ip dip =
о о
2Л j
= 2rwVr§ ---------— cos2ip ) dip = л2г(оУГ-
о
Следовательно, формула (273) примет теперь вид:
Qp = k Схр r^Vrdr.
Выносим средине значения схр и b (обычно нх берут на радиусе г = 0,7).
Тогда, вычислив интеграл, получим:
с .kb~
Qp = ^-~pVTR2^.
Перейдем к отвлеченным величинам, разделив обе части последнего выра-
жения на р/?4со2. Тогда получим весьма употребительную формулу
(274)
26’
Здесь нужно отметить, что профильное сопротивление несущего винта про-
порционально первой степени Vt-
С. помощью Cqp можно вычислять Qp, пользуясь формулой
= Свд7^1/г -^-рЦУ. (275)
§ 3. СВЯЗЬ УГЛОВ 8р, 5Л. и гБ с СИЛАМИ,
ДЕЙСТВУЮЩИМИ НА НЕСУЩИЙ ВИНТ
Эффект добавления профильного сопротивления Qp к силе Тв удобнее
всего представлять как поворот вектоэа поп ной силы тяги Т на некоторый
малый угол (фиг. 71). Сила ТВ^Т отменяется, не изменяя практически
величины, на два угла: на угол инду<тивного скоса et
и иа угол провального сэлрзгизландл ер, т. е.
Ъ «Р
Фш 71 Схема от
клонения вектора
силы тяги Т на
углы Ft и ер
Эти углы в градусах равны: ег 1,5—2,5° и ео^0,5—
0,75й. Ввиду малости можно вычислять их упрощен-
но, считая tg 8 8.
Полный угол отклонения силы Т от конструктивной
оси несущего винта будет равен
dr = е, + Бр (277)
Теперь можем написать эту формулу в разверну-
том виде, пользуясь формулами (206) и (207), и по-
лучить-
= е, + е„ = arc tg 4- т q----(278)
или приближенно
дх ~ -Й- cos т + — (279)
2 Сг
При скоростях полета V’03>0,1 можно получ1ть еще более простое выра-
жение
вх = е,+ер^^ + -р^-’А (280)
что -L — (67).
4 х
Напомним,
О выборе величин схгп и х мы скажем в конце § 4.
Угол Ьх при Уо = 0,25 лежит обычно в пределах 2,5—3,5°. При
Нии дх = 0.
висе-
у о углов ьр, <зх и <зБ с силами
405
Для балансировки машины на двух крайних режимах (иа режимах го-
ризонтального полета с Vn sx и висения) в случае, если ие применены дру-
гие стабилизирующие приспособления, летчику приходится отклонять силу Т
с помощью автомата-перекоса на угол балансировки 6б- При этом
6б = + 6ап-
Так как при больших отклонениях автомата-перекоса у несущего винта
возникают вибрации и иа ручку управления начинают действовать большие
силы, желательно иметь возможно малую величину бдп- Если взять угол 6в рав-
ным приблизительно , то при висении придется отклонять кольцо автомата-
-перекоса приблизительно иа 3° назад, давая отклонение силы Т всего на
1,2 — 2° (в среднем на 1,5°). При полете с максимальной горизонтальной
скоростью придется отклонять кольцо вперед примерно на тот же угол.
При наличии же различных стабилизирующих поверхностей и рулевого винта
нужно каждый раз внимательно проверять балансировку вертолета на этих
режимах. Здесь на этих вопросах мы останавливаться ие будем.
В § 1 главы 6 была получена формула
т — оск -р- •
(281)
Отсюда следует, что в среднем при 6б = 1,5°
т = + 1,5°,
(282)
т. е т близко по величине к конструктивному углу атаки.
§ 4. ПОТРЕБЛЯЕМАЯ НЕСУЩИМ, ВИНТОМ МОЩНОСТЬ
ПРИ КОСОЙ ОБДУВКЕ
Получаемая от двигателя мощность L расходуется у несущего винта
на преодоление профильного сопротивления и на проталкивание воздуха
через диск виита. Первую часть называют иногда потерями на трение
лопастей о воздух, а вторую — вентиляторной мощностью.
Найдем сначала мощность профильных потерь. Обратимся снова к фиг. 70
На выделенный элемент лопасти действует, как мы видели, сила dQpe (271).
Этот элемент вращается с окружной скоростью г<о, и, следовательно, сила
dQpe производит работу торможения, равную
dl^p —• r to dQpe.
Подставляя сюда найденное значение dQpe, получим:
dLp = схр —-(гю + Иг$1пф)1 2Г(о dr
Полная мощность получится путем интегрирования элементарных мощ-
ностей по радиусу лопасти, т. е. от г — 0 до г — R, и «осреднения» мощ-
ности за один оборот приемом, описанным в § 3, т. е.
1 Р р pb
Lp = fe — у dty \ — ц- Vt sin ф)2 га dr.
о о
Раскрывая скобки и изменяя порядок интегрирования, получаем для fe-ло-
пастного несущего винта:
с рь 1 ? „
Lp = k у схр —гы dr —у (г2(о2 + 2гыУт sin ф 4. Kf sin2 ф) dip.
Вычисляем сначала внутренний интеграл, разбив его на три; тогда по-
лучаем:
г3от2 dip — г2<о22л;
о
2Л
\ 2гыУт sin ip dip = 0;
о
2Л 2Л 1 1
\ Vrsinai|) di|- = Vt ---------~cos 2-ф ) dip = nV}.
о О '' '
Следовательно, выражение для Lp примет теперь вид:
R , / 1’2 \
1 iA рЬ , М,
Lp = k } схр — гы \г о) — j dr.
Вынося средние значения схр и Z? за знак интеграла и интегрируя по г,
получим окончательно:
Для расчетов удобно пользоваться аэродинамическим коэффициентом
крутящего момента от профильного сопротивления, т. е. величиной щк.р
В нашей системе этот коэффициент является одновременно и коэффициен-
том мощности. Для получения тлр делим обе части полученного выражения
для Lp на ~ р%5ы3, получаем широко применяющуюся формулу
"’кр- -^(1 + Ут)- (283)
Мощность профильных потерь будет равна
= тк.р р^ы3 = (1 + V/) pR-W. (284)
Найдем теперь вентиляторную работу несущего винта. Воздух в пло-
скости диска имеет осевую скорость Va- Тяга несущего винта равна Т.
Поэтому затрачиваемая на преодоление перепада давления мощность, каза-
лось бы, должна равняться TVa- Одиако мы в § 7 главы 2, рассматривая
коицевые потери несущего винта, показали, что для учета этих потерь
мощность нужно вычислять, считая, что вннт работает без концевых
потерь, вычисляя же тягу Т, мы должны эти потери вводить.
Следовательно, вычисляя мощность, нужно брать не тягу Т, а ту тягу
Р, которая получилась бы, если бы несущий винт не имел концевых потерь.
Так как Т = хР, то
Р=-^Т. (285)
Следовательно, вентиляторные потери несущего винта будут равны
L , (286)
Этой формулой постоянно приходится пользоваться в теории вертолета.
Удобно применять ее в безразмерных обозначениях, для чего нужно ее раз-
делить иа -^-pR5<o3. Тогда получим:
«к t = ~CtVa. (287)
Полная мощность, потребляемая несущим винтом при косой обдувке, будет
суммой обеих мощностей; следовательно,
1 cr„b,k<osRi { Vr \
L = Lt-У =— ТУ а -^4--------------( 1 -L ) Р, (288)
или в л. с.
В безразмерном написании получим полный коэффициент мощности
т„ = -^С7¥лЧ--^р(1 +14)-
(289)
Полученные формулы находят очень широкое применение при расчете вер-
толетов. Они, конечно, являются приближенными, ио при правильном вы-
боре величии х и сАР7 они дают достаточно точный для целей практики ко-
личественный ответ.
Величину х здесь следует понимать в более широком смысле: это и по-
правка иа концевые потери, и фактор, учитывающий неравномерность ско-
ростного поля у несущего винта. Средний коэффициент профильного сопро-
тивления схр нужно брать, учитывая и продувки профиля, и поправки
иа критерии подобия, т. е. иа числа М и Re. Так как эти величины изме-
няются в зависимости от азимута лопасти, то следует брать четыре накрест
лежащие сечения лопасти, расположенные на г = 0,9 с азимутом ф = 0, 90,
180, 270°, и вычислять среднее значение схр7. При полете с горизонтальной
скоростью наблюдается еще одно сложное явление: обтекание сечений не-
сущего винта потоком с углом скольжения [3 (фчг. 72). На конце лопасти,
в момент, когда она находится в азимуте ф = 180°, поток набегает по на-
правлению скорости У/, получающейся векторным сложением окружной ско-
рости Ru) и скорости потока Ут , лежащей в плоскости диска. Сле-
довательно, скорость W образует с нормальным к оси лопастн сечением
угол Р, тангенс которого равен
tg 3180°
Ут
Ru)
(290)
Так как при максимальной скорости полета вертолетов обычно V’t-^0.25. то угол
р иа конце лопастн равен р
горизонтал-.ной скоростью
Vr=const
iso0 — arc tg I г 14°. При азимуте ф — 0 ско-
рость W отклонится в противоположную
стор'ону и общая амплитуда изменения угла
р на конце лопасти будет равна
Р = 2р180°^28°.
На любом радиусе г мы будем иметь соот-
ветственно
tg ^180°
VT VT vr
ru) rRti) r
что даст для того же значения Vt = 0,25
следующие углы:
7 1,0 0,7 0,5 0,25
₽*мо 14 19 26,5 45
23180° 28 38 53 90
Следовательно, набегающий на элемент
лопасти поток сильно колеблется по направ-
лению. Это вызывает, во-первых, наруше-
ния в пограничном слое у профилей лопасти,
что может уменьшить сутях и увеличить схр,
а, во-вторых, лопасть работает как бы с
некоторой стреловидностью, что ослабляет
влияние сжимаемости воздуха. Получается
в некоторых случаях своего рода компенса-
ция, но все же характеристики профилей прн
этом заметно изменяются. Приходится, как это предлагает большинство
авторов, увеличивать схр профилей в 1,5 — 2 раза по сравнению с
исправленными на число Re продувками.
Обработка статистики вертолетов показывает, что можно ориентировочно,
для предварительных расчетов, у несущего винта средней формы (см. § 3
главы 3) брать следующие значения х и схр: значение х^: 0,92; при висении
Схр = 0,008 — 0,01; при горизонтальном полете с Vo 0,25 и MmaX =----—-
Мкр значение слр = 0,01—0,012;при Мтях = значение схр = 0,012 —
0,015; при /Итах>/ИКр значение схр = 0,015— 0,03 н более.
Первые цифры относятся к очень гладкой поверхности лопастей, вто-
рые—к несколько шероховатой (плохая окраска, швы, слой пыли или сне-
га и т. д.).
Необходимая мощность двигателя в л. с. получится по формуле
где z — число несущих вннтов на один двигатель, £— коэффициент исполь-
зования мощности в данной схеме.
Другие выражения для коэффициента мощности
В тех случаях, когда в расчетах пользуются ие скоростями Va и Vt, а
у t и формула для коэффициента мощности принимает несколько иной
внД- Найдем вид этой формулы.
Вентиляторная мощность, т. е. работа полной силы Т за 1 сек., полу-
чится в этом случае в виде скалярного произведения вектора Т и вектора
Vb т. е.
Lr=-i-(TV,) (291)
илн, переходя к координатам.
Здесь Тух — проекция силы Т иа ось Оус- она очень близка по величине
к силе Т. Величина Тр1<5в = Тбв дает проекцию силы на ось О*'—она от-
рицательна. Переходя к безразмерным величинам и пользуясь обозначениями
Vxi = Vt н Vti = Va, получим:
«< т= 4- стУа — Ст^- (292)
Профильные потери запишутся теперь в таком внде:
= ^f^(l + V}). (293)
Полная величина коэффициента мощности будет равна
тк = ткг+ткр = -4сг170^-4-с’'17< + --Т^(1 + ^)- (294)
Очень часто прн написании такого выражения упускают второй член
— Cj-i//нлн берут его с неверным знаком, что уменьшает точность этой форму-
лы. В англо-американских обозначениях оиа имеет такой вид:
тк=------Lq/. --+ !‘2)-
Если в формулу (294) подставим вместо Va н V/ скорости Va и Vt, вос-
пользовавшись формулами (217), то получим:
мк = — Ст (Иа -г Иубв)---— CtVt^c Ч—(1 + Ит)=
^-(1 +Ут),
т. е. уже найденное выражение (289) для тк: оио проще и нагляднее, чем
выражение (294), поэтому им и удобнее пользоваться при аэродинамиче-
ском расчете вертолетов.
§ 5. РАСЧЕТ СЛОЖНЫХ СИСТЕМ
ПО СРЕДНЕЙ СКОРОСТИ ВЗАИМНЫХ ВЛИЯНИИ
При производстве аэродинамического расчета первого приближения у вер-
толетов сложной формы очень выгодно, чтобы избежать громоздких и дли-
тельных вычислений, пользоваться ос ре дне н ным несущим винтом
системы, т. е. таким, у которого индуктивная скорость взаимных влия-
ний от соседних винтов берется средняя. Так, например, для двухвиитовой,
системы получается
а для четырехвинтовой
°1. 2+3+4 + V2 1+3+4 + 1+2+4 + V4. l+2+з
Vcp---------------------£-------------------- .
Эта скорость изменит у осредненного несущего виита скорость набегающе-
го потока V’o на некоторую величину t>cp. Сложение этих векторов даст ре-
зультирующую скорость. Однако вектор t>cp обычно мал и почти перпенди-
кулярен к скорости 1/0. Поэтому можно принять, что взаимные влияния при
больших скоростях 170, не изменяя абсолютной величины скорости, повора-
чивают ее на малый угол еср, равный по фиг. 56
Тогда
Тер = т -|- еср;
^ср = сс -|- 8ср и т. д.
Пользуясь этими величинами, можно применить все известные формулы,
выведенные для одиночного несущего виита. Из фиг. 55 и 57 определим
t»icp и найдем:
161 ср — Vo sin Тер 4- и1ср; (295)
Ут ср Ио COS тЧ1 (296)
При больших скоростях, как мы видим, для определения можно было
пользоваться приближенной формулой (232). Она совершенно не учитывает
влияния угла т. В нашем случае для осредненного несущего винта можно
писать ее в таком виде:
Р?_
укр — —И уср, (297)
*0
т. е. прибавлять к ней индуктивную скорость от взаимоиндукции. Лучше
всего для нахождения Илср и Vrcp пользоваться графиками, приведенными
иа фиг. 55 и 57, исходя из Vo и тср.
Найдя Ул ср и Р7ср, переходим к вычислению мощности. Сначала нахо-
дим:
ткгр = —Ср.рУлср !- ХР^'! (14- Vt ср)
и
Ncv = тк ср-^-р/?ьш3.
Полная тяга и мощность для z несущих внитов на двигатель будут,
очевидно, равны
ГПОлН = 72 (298)
N=~NCP. (299)
Следовательно, расчет многовиитовой системы в первом приближении может
быть произведен как расчет одновинтовой системы, но со скоростью набе-
гающего потока, повернутой на дополнительный угол efp. Точность при этом
получается достаточная для компоновочных расчетов. Далее всегда возможно
уточнить расчет, учтя индивидуальные особенности обдувки каждого винта
и крыльев в отдельности. Имея компоновку и приближенные, но достаточ-
но точные, величины первого приближения, такой уточненный расчет сделать
легко. Получатся некоторые индивидуальные поправки к работе изолиро-
ванного одиночного несущего винта.
На основании изложенного, получим (например, для продольной двух-
винтовой системы) в среднем:
Для поперечной системы получится в среднем:
е1 з + е2 1^(-°Л-°,4)о1 1 плУ11
®ср“ 2 ~ 2И„ °’4 V»
Здесь скос улучшает работу несущих винтов.
В случае четырехвинтовой схемы получим в среднем:
еср^(0,4-0,2)^р,
Уо
и при сближенных несущих виитах можно получить еср^г 0,2. Более точный
прием будет указан в главе 10.
В предыдущих формулах = в
Глава 8
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВЕРТОЛЕТА
НА ВСЕХ РЕЖИМАХ
§ 1. ЗАДАЧА АЭРОДИНАМИЧЕСКОГО РАСЧЕТА ВЕРТОЛЕТА
Целью аэродинамического расчета вертолета является определение
летных свойств вертолета по его конструктивным параметрам с одно-
временным исследованием вопросов его балансировки. Последние во-
просы, как увидим, очень тесно связаны с самим процессом аэродина-
мического расчета вертолета.
Предлагалось множество различных приемов этого расчета. Неко-
торые из них исходили из продувочных поляр виита, другие носили
характер упрощенной теории, исходящей из средних величин; сущест-
вовали приемы расчета, рассматривавшие с самого начала маховое
движение лопастей. Первые методы оказались неудобными, так как для
их применения было необходимо иметь подробные испытания несущих
винтов и притом проведенные на больших числах Re и М. Практически
для их осуществления требовались для каждого винта целые альбомы
аэродинамических диаграмм. Все это привело к тому, что эти методы
оказались мало применимыми на практике.
Введение в аэродинамический расчет махового движения лопастей
в явном виде давало весьма сложные и трудоемкие расчетные приемы,
притом мало наглядные. Кроме того, обычное упрощение, вводимое в
расчет махового движения, а именно оставление лишь первых гармоник,
снижало точность расчетов.
Поэтому за последнее десятилетие появилось много работ, в которых
авторы пытались, исходя из физической картины полета вертолета, раз
Работать простой и наглядный метод расчета У иас по такому пути
юшли раньше, чем за границей. Методы таких расчетов излагались в
Работах Б. Я. Жеребцова, М. Л. Миля, Б. Н. Юрьева, В. Н. Ярошенко
i др. Много работал в этом направлении Л. С. Вильдгрубе. За грани-
гей расчеты, близкие к нашим, предложили Уольд, Янг, Никольский
I др.
Все эти работы были написаны в самых различных обозначениях, и
юлученные формулы не всегда доводились до наипростейшей формы
i этой книге автор использовал в основном опубликованные советские
'аботы, подвергнув их методической переработке. Иностранными ма-
ериалами в этой части автору почти не пришлось пользоваться.
Как известно, основы аэродинамического расчета самолетов разра-
ботал Н. Е. Жуковский в 1916 г. Он показал, что этот расчет можно
ести двумя приемами, применяя или более точный метод тяг или менее
точный, но более простой метод мощностей. Все это почти полностью
применимо к вертолетам, и мы изложим далее оба эти метода. Но
прежде чем изложить расчет, нам необходимо рассмотреть уравнения
движения вертолета, летящего под углом к горизонту, и получить вы-
ражения для вредного лобового сопротивления.
§ 2. УРАВНЕНИЯ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ
ВЕРТОЛЕТА
На фиг. 73 изображены силы, действующие на вертолет, летящий под
углом 6 к горизонту. На несущие винты действует полная сила тяги от z
винтов zT, на корпус действует вредное лобовое сопротивление QBp и в цент-
ре тяжести вертолета приложена сила тяжести G. На чертеже нанесены
подробно рассмотренные
нами в § 1 главы 6 харак-
терные углы бц, т, ак и
б. Движение считаем пло-
ским и установившимся;
следовательно, силы инер-
ции отсутствуют. В случае
z винтов берем средние
значения всех углов в со-
ответствии с § 5 главы 7.
Маховое движение учтено
углом бв-
Напишем условия равно-
весия сил.
Проекция сил на ось
О у дает уравнение
Фиг. 73 Схема сил, действующих на вертолет
при полете с горизонтальной скоростью
(в сложных схемах углы берутся осредненные)
zT cos тср = Geos 9.
Отсюда
„ cos 0 •
(300)
Проекция сил на ось Ох, т. е. на направление скорости полета Уо, дает
уравнение
— zTsin-rCp = QBP+GsinS. (301)
Подставляя сюда по первому уравнению zT = G cos - и разделив обе части
полученного уравнения на Geos0, находим:
-tgrcp= б^:-(302)
Третье уравнение — это условие равенства нулю моментов. Как мы уже
указывали, для балансировки вертолета необходимо, чтобы сила zT была
отклонена от конструктивной оси на угол балансарэзси бв ср для чего, как
было показано в § 1 главы 6, должно соблюдаться условие
®к*ср — Тгр ббср’
(303)
что требует отклонения силы zT с помощью автомата-перекоса на угол бАП,
равный
бдп ср ~ ср б* ср- (304)
Угол бв может быть найден предварительным подсчетом по схеме вер-
толета. Обычно он близок к 1,5°. О вычислении углов 6Х = et -]- ер н дв
было подробно сказано в § 5 главы 6 и § 3 главы 7.
Кроме того, нужно обеспечить равенство крутящего момента, подведен-
ного к валу от двигателя, моменту аэродинамического сопротивления ло-
пастей. Последнее достигается тем, что угол установки лопастей <р7 всегда
подбирается так, что это условие соблюдается. Число оборотов несущего
винта считаем постоянным. Мощность, потребляемая осредненным несущим
винтом, будет, согласно § 4 главы 7, равна
^кср= — СгсрУл ср Н------(1 -J- Vkp) (289)
и
д; ,ПК СР Л ns о
“ •
Мощность же двигателя при z винтах будет равна
В частных случаях эти уравнения сильно упрощаются. Так, при гори-
зонтальном полете
угол и = и и т мало; тогда получим:
гТ = ^~а’ О05)
(306)
Tc^-arctg^-^—(307)
полете 0 = 90“ и г -=—90“. Из уравнения (301) полу-
zT = QBp-|-G. (308)
г = — 50°.
или
Прн вертикальном
чаем
При этом, так как
ак. в = — тв - Se. п -= — 90° — бв. в- (267)
н
бдп. в — ^Б. в — &х “ бв. в- (266)
Углы балансировки 6Б при наличии стабилизатора и рулевых винтов мо-
гут несколько отличаться в полете и при висении.
В дальнейшем для упрощения формул мы не всегда будем писать в
формулах индекс «ср»; нужно лишь помнить, что в случае сложной систе-
мы все величины берутся осреднение.
§ 3. ВРЕДНОЕ ЛОБОВОЕ СОПРОТИВЛЕНИЕ ВЕРТОЛЕТА
Фюзеляж и другие ненесущие детали вертолета дают вредное лобовое
сопротивление QBP. Скорость потока в плоскости диска несущего винта, как
мы знаем, равна V = V Va + Vt, и лобовое сопротивление омываемых пото-
ком частей направлено приблизительно по этой скорости. Кроме того, неко-
торые детали могут давать небольшую подъемную силу, перпендикулярную
Фиг. 74. Поляра круглого и квадратного фюзеляжей при больших углах
атаки
к этой скорости. Однако угол между скоростями Vo и Vt мал и равен ско-
су потока &!, т. е. 2 — 3°. Подъемные силы деталей очень малы. Все это
позволяет считать, что сила QBp направлена по скорости 170 невозмущенного
потока, ио величину скорости набегающего потока нужно считать равной
Vi для малых углов ак и равной V2 для близких к ак^ — 90°. Каждая
отдельная я-ная деталь вертолета, омываемая потоком, дает вредное со-
противление QBpn, причем
QbP п — Схп^п — s
(309)
Полное сопротивление будет равно
QbP <3l0}
В дальнейшем индексы «я» и «т» мы будем опускать. Обдувка фюзе-
ляжа и других частей вертолета происходит при углах атаки, изменяю-
щихся в пределах от нескольких градусов до —90°. На максимальной
скорости QBP получается так же, как на самолете, но на режиме висения
или вертикального взлета ак —90° и фюзеляж обдувается потоком
сверху вниз, т. е. поперек. Поэтому для уточнения расчета необходимо
строить график, дающий величину ZcxS в зависимости от угла атаки ак.
Сопротивление фюзеляжей очень сильно возрастает даже при небольших
углах ак (фиг. 74). На вертолетах нередко применяются короткие фюзеля-
жи-кабины, близкие по форме к шару или слегка вытянутому эллипсоиду
(фиг. 75). У последних наблюдается сильное влияние числа Re. К сопро-
тивлению фюзеляжа нужно добавить влияние различных «шероховато-
стей»— окон, лесенок, люков и т. д., что, как известно, сильно увели-
чивает его сопротивление (примерно в 1% раза). Остальные детали
учитываются по правилам экспериментальной аэродинамики. Для оценки
общего сопротивления составляется так называемая сводка лобовых сопро-
тивлений, т. е. перечень всех деталей, дающих сопротивление. Ее пример-
ный вид дан в табл- 4. Эту сводку нужно составлять для горизонтального
полета (ах0) и для вертикального (ак — 90°). Желательно иметь и
промежуточные углы.
Таблица 4
Сводка лобовых сопротивлений вертолета
Детали
Фюзеляж.............. .
Надстройки и головки несу-
щих винтов ..............
Охлаждение ..............
Мотогондолы..............
Шасси: стойки............
колеса ........
Стабилизаторы ...........
Кили и ограждения . . . .
Задний винт .............
Фары.....................
Антенны..................
При вычислении вредного сопротивления при взлетз и висении необхо-
димо по эскизу вертолета в плане (фиг. 62) брать отдельно те детали или
их части, которые попали в струю несущего винта, и те, которые лежат
вне ее. Первые обдуваются со скоростью потока V2, вторые — со скоростью
Vy = Уо. Обычно скорость подъема вертолетов невелика и лежит в преде-
лах 1,5—4 м/сек. Скорость в струе V2, как мы показали в § 3 главы 5,
практически постоянна и близка к 2t>iB, т. е. около 15—20 м/сек; следова-
тельно, детали, отмеченные индексом «1» и лежащие вне струи, обдуваются
со скоростью, значительно меньшей, чем детали, отмеченные индексом «2»
и находящиеся в струе. Можно принять в среднем, что полное лобовое
сопротивление при вертикальном полете будет равно
(311)
Первый член в этой формуле мал, а при висении вертолета он равен нулю
так как Vy — 0.
На основании таких подсчетов нужно построить график (фиг. 76)
изменение 2-сЛ-д и (^вр в за-
висимости от ак. Если нет точных
данных о промежуточных углах ата-
ки, то можно построить эту кривую
приближенно, по эллиптическому за-
кону. Для этого, зная (ScvS)a 0= и
(2c.vS)a_эо0’ можно построить, как
показано на фиг. 76, на этих осях
эллипс. Это упрощение не влечет боль-
ших погрешностей, так как у верто-
летов важно рассчитать точно мак-
симальную скорость горизонтального
полета и скорость при вертикальном
взлете, а промежуточные значения
могут быть найдены более грубо.
Если есть более подробные материалы,
то можно найти более точные и про-
межуточные значения.
Часто, как это принято и в расчете
самолетов, вредные сопротивления
оценивают не величиной а вели-
чиной площади вредной эквивалентной
плоской пластинки <5вр, т. е. такой,
которая при той же скорости полета,
дает такое же сопротивление, как и
□V;
1,28звр -
Фиг. 76. Приближенная зависимость
от ак вредного сопротивления Ji’xS и
QBpкорпуса вертолета при разных
углах атаки
будучи^нерпендикулярной к потоку,
все части вертолета, т. е.
Здесь принимают обычно для пластинки су = 1,28. Отсюда
3Вр
1,28
(312)
У вертолетов приходится различать звр для горизонтального полета и для
вертикального взлета.
27 Б- Н. Юрьев, т I
Если отнести эту пластинку к ометаемой несущим винтом площади, то
получится вредная относительная плоская пластинка
Звр = —-р (313)
Эта величина у хорошо обтекаемых конструкций вертолетов равна для
горизонтального полета примерно = 0,5% =0,005, а у менее обтекае-
мых = 1 % =0,01,
В среднем --~100- -0,75 %.
При подсчете вредного сопротивления фюзеляжа нужно учитывать на-
личие различных щелей, дверок, люков, волнистости обшивки и т. д.
Все это может увеличивать сопротивление фюзеляжа при ак ~0° примерно
в 1,5 раза.
В общем полный коэффициент вредного сопротивления обычных одно-
винтовых вертолетов, отнесенный к миделю самого фюзеляжа, лежит в
пределах от 0,3 до 0,5. У продольных ои несколько меньше и равен при-
мерно 0,2—0,4. Более точную величину можно найти, рассчитав сопротив-
ление фюзеляжа и прочих деталей по правилам экспериментальной аэро-
динамики.
Отметим еще, что иногда фюзеляж вертолета делается очень похожим
на автомобиль. Коэффициент сопротивления современного, хорошо обтекае-
мого легкового автомобиля получается около 0,25—0,3. Добавляя к этой
цифре еще сопротивление надстроек и хвостовой балки, получим и для
таких машин ск^0,4—0,5.
Следовательно, сопротивление современных вертолетов по сравнению
с самолетами еще велико и может быть значительно уменьшено.
К указанным сопротивлениям нужно еще прибавить около 10% от со-
противления фюзеляжа на прохождение охлаждающего воздуха, отдающего
фюзеляжу свое количество движения, н сопротивление, вызванное задним
винтом. Это сопротивление можно вычислить по обычной формуле несу-
щего винта
<Х.» — л.в(е,„ + е,„. в) « Тх. Д, (314)
где ег—скос потока от индукции и — от профильного сопротивления
у хвостового винта; индекс «х.в» обозначает хвостовой винт.
Остальные коэффициенты можно прямо брать по любому авиационному
справочнику или курсу аэродинамического расчета самолетов.
§ 4. АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВЕРТОЛЕТА
ПО МЕТОДУ ТЯГ
Рассмотрим сначала более точный метод тяг, в котором уравнения
движения вертолета строго соблюдаются. Мы будем излагать его для на-
глядности как бы для одновинтовой схемы, хотя ои полностью применим
и к любым сложным системам вертолетов, если пользоваться осредненным
винтом, как указано в § 5 главы 7. Отметим еще, что на практике чаще
пользуются более простым методом мощностей, который мы подробно
изложим в § 5.
Аэродинамический расчет полностью основан на материалах глав 6 и 7.
Для удобства использования материалов этих глав на практике мы из-
ложим метод тяг по пунктам, дающим последовательные этапы расчета.
1) Задание. При проведении расчета считаются заданными: вес вер-
толета в полете G, радиус несущего винта угловую скорость его вра-
щения со, мощность двигателя Л;м и эскиз машины. Очень часто задают
несколько вариантов решения задачи, поставленной перед конструктором,
и тогда весь расчет приходится повторять несколько раз.
При проведении аэродинамического расчета приходится задаваться рядом
величин, иапрнмер, высотой полета И, углом взлета 0 и скоростью полета
по траектории Vo. Исходя из этих величии, иаходят потребную мощность
двигателя угол атаки ак, угол оси фюзеляжа с горизонтом Фф и др.
Совокупность всех этих величин дает так называемую «точку расчета».
Полный аэродинамический расчет требует вычисления ряда точек для
разных высот полета И, скоростей Уо и углов 9. Другими словами, расчет
состоит из ряда повторных расчетов, идущих по одном}' и тому же
трафарету.
2) Определяем Вредное сопротивление. Выбрав точку ра-
счета Н, 0 и Уо, находим величину вредного сопротивления, составив
сводку лобовых сопротивлений и построив график (фнг. 76) как
указано в § 3. Наметив приблизительные величины ак и (здесь ие тре-
буется большая точность), находим и вычисляем QBp:
Эту величину можно в дальнейшем уточнить, получив из расчета ак н
В первом приближении ак — 9 и
3) Находим углы ти ак. С помощью уравнения (307)
находим величину т, и после этого вычисляем угол атаки ак по формуле
ак = т — бг>.
(198)
Величина 6б для машин без стабилизатора в среднем равна 1,5°, а со
стабилизатором может быть найдена по методу, изложенному в § 5 главы 6;
в среднем она равна 0,5°. Выбор величины угла <5в иа результаты расчета
почти не оказывает влияния, и его можно брать приближенно.
4) Находим тягу несущего винта Т н ряд связанных
с ней величии:
„ cos о
л
p£4w3
5) Обдувка несущего винта и скорость VQ. По формуле
(227) находим индуктивную скорость
Зная vlt Vy и х, находим скорость полета по траектории с помощью
соотношения
V? = Va Vr' (205)
куда подставляем
Va = — V„ sint -Ь Of, (203)
Vt = Vo cost, (204)
и получаем после упрощения
Vi = Уо — 21/0f i sin x + у2.
Решая это уравнение относительно Уо, находим:
Vo = UisinX + у/ v'isin2x + У2 —-у, .
Вместо решения этого уравнения можно воспользоваться графиком, при-
веденным на фиг. 55, и по ух = и х найти величину V’o = Уос»18. Поле-
У1В
ту вертолета соответствует перед корнем знак плюс (Vo^>0). Зная Vo,
находим Va и Vt по формулам (203) и (204). В случае сложных систем
вертолетов нужно пользоваться указаниями, данными в главе 6. Удобно
вести расчет по средним индуктивным скоростям, как будет указано в
главе 10. Тяга, приходящаяся на каждый винт, может быть принята прн
~ G
z винтах равной Т = .
6) Мощность двигателя. Вычисляем потребную на валу несущего
винта мощность
N = TVA + (1 + V1) 4 pR6w3.
Потребная мощность двигателя прн z несущих винтов на один двигатель
при коэффициенте использования мощности схемой и, будет равна
•V„ = 4 -V.
Расчет можно вести, вычисляя относительные скорости Va и Vt и вычисляя
сначала коэффициент крутящего момеита или мощности:
«К = 4 Ст^А + (1 + ^) . (289)
а затем найти
Ум = рУ&<-’3.
7) Сетка Жуковского. Сделав расчет для ряда точек в и Vo,
нужно построить сетку потребных мощностей для полета на данной высо-
те Н (фиг. 77).
Фиг. 77. Сетка потребных мощностей в зависимо-
сти от Vo и 0 для /7=0
Проведя на этой диаграмме горизонтальную линию, дающую мощность
двигателя, развиваемую на этой высоте, получим в точках пересечения этой
линии с кривыми 0 = const скорости полета по траектории V’o и углы
взлета 0. По этим данным из фиг. 78 находим горизонтальную и верти-
Фиг. 78. Разложение скорости Vo по траектории
на горизонтальную и вертикальную компоненты
Vx и Vy
кальную скорости полета машины
Vx = V0cosG, = ycsin 0
и определяем наклон пола фюзеляжа (тангаж фюзеляжа) для характерных
режимов — для полета с максимальной скоростью у земли и на рабочей
высоте по формуле
+ (201)
и на режиме висения по формуле
#Ф-Фф — &в. Б. (268
Подробно эти материалы изложены в § 5 главы 6. Нужно стремиться по-
лучить малые наклоны пола и при висенин и в полете.
Примечание. Хотя в п. 6 и 7 мы и сделали переход к мощностям, тем не
менее мы сохранили название у этого способа расчета «метод тяг», гак как в его
основу положена точная увязка всех сил, действующих на вертолет, чего нет и из-
лагаемом далее «методе мощностей».
8) Эффект автомата-перекоса. Находим необходимый для по-
лета иа этом режиме угол отклонения силы Т с помощью автомата-перекоса.
Для этого сначала вычисляем
— ег 4
-= arctg —R т 4
’ а VT '
или упрощенно
6, .-^-eosr 4<-?-4
V2 2 Сг
После этого находим:
бдп - дв — 6Л.
(278)
(279)
(199)
Отклонение ручки управления в зависимости от параметров передачи полу-
чается в 2—3 раза больше. Заметим, что указанный ход расчета охватывает
Фиг. 79. Указательница скоростей
у вертолета
все режимы полета, начиная от висения
или вертикального взлета до полета с мак-
симальной скоростью.
Построив сетку для отрицательных
значений 0, мы получим при Л\, — 0 режимы
планирования. Сетка эта позволяет сразу
получить решение вопроса о том, что по-
лучится у многомоторного вертолета в
случае остановки одного двигателя. Для
этого нужно лишь взять меиьшую вели-
чину располагаемой мощности Л4. р. В
некоторых случаях вертолет сможет про-
должать в таких условиях горизонтальный
полет, в других он сможет лететь, лишь
постепенно снижаясь.
Следовательно, указанный расчет является универсальным. Его нужно
повторить для нескольких высот полета, беря мощность по высотной
характеристике двигателя.
9)Указательницей скоростей называется кривая, дающая го-
юграф скоростей самолета или вертолета, т. е. полярная диаграмма век-
'ора скорости Vo. Зная компоненты скорости полета н Vy или Уо и 9,
•е очеиь легко построить по точкам (фиг. 79). Обычно наносят на одну
диаграмму несколько кривых для разных высот полета Н. У вертолета до
[екоторой высоты до так называемого потолка висения (статического по-
олка) имеется вертикальная скорость Уу при Vx 0. На фиг. 79 Нст =
- 2000 м. При полете с горизонтальной скоростью потолок увеличивается
2—3 раза: это так называемый потолок вертолета на скорости или дина-
нческий потолок. На фиг. 79 Ятах = 4000 м. Горизонтальная скорость
ри этом меньше максимальной в 1,5—2 раза. Так как вблизи потолка
корость взлета очень мала и машина почти не поднимается, то часто
читают потолком такую высоту, где скорость вертикального взлета падает
1 1
о величины -j- — м/сек. Такие потолки называют практическими
этолком висения и потолком вертолета иа скорости. По указательнице
юростей непосредственно видно, при какой скорости Ух получится макси-
альная скорость Д^я этого достаточно провести горизонтальные
касательные к кривым. На фиг. 79 пунктирная кривая соединяет точки,
где получается V,, тах.
10) Кривая скороподъемности и барограмма взлета.
Пользуясь указательницей скоростей (фиг. 79), легко построить кривую
скороподъемности (фиг. 80), дающую
Vy max f (Н).
Для увеличения скороподъемности верто-
летов обычно у земли пользуются взлетной
мощностью двигателя, т. е. форсируют его.
Если этого не делать, то скороподъемность
на малых высотах сильно уменьшится, как
показано на чертеже пунктиром. Нужно по-
мнить, что такое форсирование двигателя
допускается обычно не более 5 мин.
Получив кривую скороподъемности, легко
построить по изложенным в § 5 главы 4
правилам, барограмму набора высоты. Мож-
но применять способ «змейки» и способ гра-
фического интегрирования.
11) Аэродинамический паспорт
вертолета. На основании этих расчетов
можно построить весьма полезный для экс-
плуатации сводный график, дающий основ-
Фиг. 80. Кривая скороподъ-
емности вертолета
ные летные данные вертолета для разных высот (фиг. 81).
На такой диаграмме видно, где получается наибольшая горизонтальная
скорость полета (точка А); непосредственно видно, что на высотах, больших
потолка висения (линия ВС), вертолет может летать, подобно самолету, имея
Фиг. 81. Аэродинамический паспорт вертолета
/ — барограмма взлета с горизонтальной скоростью; 2 — барограмма
вертикального взлета
лишь горизонтальную скорость, лежащую между VAmin и Кешах- На диаг-
рамму наносят пунктиром кривую горизонтальных скоростей Vx наб, соответ-
ствующих максимальной вертикальной скорости набора высоты. По баро-
грамме непосредственно видно, сколько времени потребуется для подъема
на заданную высоту, и т- д.
Такой аэродинамический паспорт весьма желательно нметь|для несколь-
ких вариантов нагрузки. Это позволит сознательно планировать н рассчи-
тывать эксплуатационные задания.
§ 5. АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВЕРТОЛЕТА
ПО .МЕТОДУ МОЩНОСТЕЙ
Описанный в предыдущем параграфе «метод тяг» требует большой вы-
числительной работы, так как много расчетных точек 9, Vo, нужных для
построения кривых, в расчете оказываются неиспользованными. Поэтому
на практике обычно предпочитают пользоваться более простым и нагляд-
ным «методом мощностей», хотя он и менее точен, чем первый метод.
Мы его излагаем по отдельным пунктам, в соответствии с последователь-
ностью расчета.
Горизонтальный полет аертолета
В основу метода мощностей положен расчет горизонтального полета,
который ведем, задаваясь скоростью Vo и высотой полета Я.
1) Характерные углы. Сначала находим по сводке лобовых сопро-
тивлений величину для ак—О и вычисляем QBp:
Р V? \ 1
Q»p--=-4 l310>
Уравнение движения (302) в нашем случае упрощается, так как 9 = 0. и
1римет вид уравнения (306) или (307).
В сложной системе к значению т нужно прибавить средний скос от
взаимной индукции, т. е.
еСр = 4г- (233)
'огда можно пользоваться осредненным винтом, беря у него, согласно § 5
лавы 7,
Тср = t -J- 8ср
тягу
1
T = -~-G.
г
осле этого можно найти средний угол атаки:
#к. ср = Тер — ср- (198)
глицину бв. ср нужно брать, как указано в § 5 главы 6, пользуясь поня-
гем «центр условной втулки» (ЦУВ).
2) Скорости обдувки диска несущего винта. Находим спа-
ла индуктивную скорость у изолированного несущего винта на режиме
юения viB, исходя из силы тяги Т = Скорость Vi находим по опи-
йному в предыдущих параграфах методу, а именно находим сначала
-1 1 /Ст
в»= г ^ = — 1
затем вычисляем индуктивную скорость и' считая винт изолированным, по
формуле (232)
Прибавляем к ней среднюю величину индуктивной скорости от взаимной
индукции с»ср, после чего определяем индуктивную скорость осредненного
винта, т. е.
После этого находим скорость набегающего потока, исходя из очередной
зависимости
vi = vi н- ui,
и получаем:
v» =
После этого вычисляем по формулам (203) и (204) скорости обдувки
Va ср и Vt ср:
Va ср = — Vq sill Тер -[-Уь
Vt ср = Cos тср.
3) Потребная мощность двигателя. После этого можно вычис-
лить потребную для горизонтального полета мощность на валу осредиен-
ного несущего виита
N ~~ ср 4^75 (1 + гср) ~ Р^5(°3
и мощность двигателя
Для исследования общих вопросов и для контроля величии и здесь можно
сначала находить коэффициент мощности
Ст^ =<= + '<•)’ (289)
а затем вычислять
'v« mh-4-p^5<o3.
4) Кривая потребных для горизонтального полета
мощностей. Сделав указанный расчет для нескольких скоростей и полу-
чив парные значения Vo и Nu, строят кривую потребных мощностей, т. е.
jVM.n = f(V0). Она обычно имеет вид, показанный на фиг. 82. Индексом «п»
обозначим потребную мощность. Если нанести на эту же диаграмму распо-
лагаемую мощность двигателя, т. е. NM.p, то получится линия Л/И, кото-
рую при малых скоростях следует проводить горизонтально. При больших
же скоростях полета Ух = Уо > 250 км/час нужно учитывать небольшое
увеличение мощности за счет скоростного напора засасываемого двигате-
лем воздуха. Делается это по правилам, излагаемым во всех курсах авиа-
ционных двигателей. Для получения полного эффекта от наддува, необхо-
димо делать вынесенные из фюзе-
ляжа всасывающие патрубки напра-
вленными вперед.
В точке ,'И получается равенство
потребной и располагаемой мощно-
стей, т. е. Л;м.п -= Мм.р. Эта точка
соответствует максимальной ско-
рости полета на данной высоте.
Точка В соответствует режиму
висения. Точка Э соответствует
минимальной потребной мощно-
сти; этой точке соответствует
экономическая скорость полета V3-
Режим такого полета называется
Фиг. 82. Диаграмма потребных
и располагаемых мощностей при
горизонтальном полете
режиму,
единицу
денного
экономическим.
Если провести из начала коорди-
нат к кривой NM.n касательную пря-
мую, то точка касания И будет
соответствовать наивыгоднейшему
будет не мощность (т. е. работа в
при котором минимальной
времени), а минимальная работа, затрачиваемая на единицу прой-
вертолетом пути (работа на 1 км или иа 1 м).
Доказательство этого очень просто. Работа, затраченная на любом
режиме за dt сек., равна 75 Л'М.ПЛ, а вертолет за это время пролетит рас-
стояние VodZ. Следовательно, затрата работы иа единицу пути равна
V*dt
75WM
= 75tgr,
где у — угол наклона прямой линии, соединяющей любую точку кривой
Жп с началом координат. Наименьшее значение эта величина получит
тогда, когда у будет минимально возможной, а линия ОН коснется кри-
вой Л^м.п- Скорость полета Рн, соответствующая этому режиму, называется
наивыгоднейшей.
5) И с п о л ь з ов а н и е на практике экономического и наи-
выгоднейшего режимов. Полет на экономическом режиме соответ-
ствует при заданном запасе топлива 6Г максимальной продолжительности
полета, а полет на наивыгоднейшем режиме — наибольшей дальности. При
этом двигатель нужно дросселировать до мощности ЛД.Э и Л/м.и, и все
рассуждение пригодно лишь для двигателей с идеально отрегулированным
расходом топлива и смазки, у которых обеспечивается неизменный удель-
ный расход Сг.
На практике обычно этого не бывает, и расход сильно изменяется при
дросселировании. Для уточнения расчета нужно поэтому находить эти ре-
жимы не по кривой мощности, а по кривой расхода топлива, у которой
по оси ординат отложена величина CTN№ п, а по оси абсцисс скорости
полета Vx = Vo (фиг. 83). Найдя по этой кривой точки Э и Н по прежнему
правилу, получим V, и VH с учетом изменения Сг двигателя.
При расчете длительных полетов нужно учитывать еще выгорание топ-
лива. У современных вертолетов запас топлива невелик и составляет обычно
10—15°6веса машины в полете. Поэтому, подобно тому, как это делается и
при расчете самолетов, это проще всего учесть, сделав аэродинамический расчет
для среднего в полете веса машины. Если машина при вылете имела вес
(j, то ее нужно рассчитывать на
вес
6с1,-<5 —(315)
Такой прием вообще следует ре-
комендовать при расчете вертоле-
тов, так как при расчете «на вес
при взлете» почти все летные дан-
ные несколько занижаются, и если
расчет проводился для Gma.x, то
полезно сделать расчет машины с
выгоревшим наполовину запасом
топлива.
В случае вертолетов с очень
большим запасом топлива, проще
Фиг. 83, Диаграмма часового расхода топ-
лива при горизонтальном полете. Экономи-
ческая и наивыгоднейшая точки при учете
изменяемости удельного расхода топлива
всего для заданной высоты построить ряд кусочных кривых для разных
весов машины и путем проб получить правильное течение кривых. Су-
ществуют и аналитические методы, на которых мы здесь останавливаться
не будем.
Для обычного, малого, запаса топлива получаем на экономическом режи-
ме время полета в часах
^э,ч = д? (316)
ЬГ.ЭАМ э
и пройденный при этом путь в км
°’=-ТбйГ 3'61/’4- <317>
Здесь Уэ взято в м/сек и t9 — в сек.
Для полета на иаивыгоднейшем режиме получим соответственно
a = w = 3'6W" <319)
При этом и £)Э<Д|.
Для полного расчета вертолета нужно построить кривые потребных
мощностей для ряда высот полета: Н = 0, 1000, 2000, 4000, 6000 м и так
далее и ряда нагрузок.
6) Определение скороподъемности по методу мощно-
стей. Вертикальная скорость вертолета определяется по избытку мощно-
сти .Мизб., т. е. по разности между располагаемой мощностью и мощностью,
потребной для горизонтального полета (фиг. 84):
Л^цзб — —Л^м.п- (320)
Предполагается, что весь этот избыток с учетом всех потерь £х может
быть использован на подъем машины, т. е.
Фиг. 84. Определение избытка мош- Фиг. 85. Указательнлца скоростей. Скорости
ности (УИЗбЛ'м.п) при получены по данным главы 4
/5Л^ИЗб«х — GVy,
откуда получается скорость взлета
Здесь £ — коэффициент использования мощности данной схемой и х— коэф-
фициент концевых потерь. Наибольшая скорость Vy получится прн таком
расчете на экономическом режиме полета. Угол взлета 6 получится из фнг. 78
sin 6 = —- , (322)
следовательно,
Vx = 1Л, cos 9 = V V') - 1Л) . (323)
По этим данным можно построить указательницу скоростей, барограмму
взлета и аэродинамический паспорт машины, как это делалось в предыду-
щем параграфе (фиг. 85).
Дополнение. Ввиду того, что при вычислении скорости Vy часто допу-
скаются ошибочные суждения, мы приведем дополнительный подробный
вывод формулы для Vy. При полете с малым углом взлета (или снижения)
9 можно принять, что sin 6 = 6 н sinr = т. Тогда уравнение движения верто-
лета примет вид:
Отсюда
Ф--0.
Найдем величину скорости V,i по формуле (203), куда подставляем най-
денное значение т, и получаем:
1Л4--У0г-'г ^+V09 + v,.
Замечая, что V'o() = V и Фо ф- Vi = Ул г, где УА г — скорость УА при
горизонтальном полете, можем написать:
Ул = Ул г -г У у-
Вычисляем теперь потребную мощность двигателя на режиме взлета по
обычной формуле
75,v„, -L1/Л ( + ф 2V ,.= _L 1/л rG X [/„о X л,р.
Замечая, что
фК4гО+фл?Р = 75Л/,,г,
получим уже найденное выражение для У у.
Заметим, что в указанном методе прн определении вертикальных скоро-
стей не учитывалось изменение режима работы несущего винта, т. е. вели-
чины ак илн т. Это не вносит больших погрешностей при У0'у> 0,1, но прн
меиьших скоростях получаются заметные отклонения от более точного мето-
да тяг. Поэтому кривая — указательиица скоростей на участке 0 0,1
должна проводиться пунктиром, как это сделано на фнг. 85. Рекоменду-
ется поэтому для Фо = 0, т. е. для режима висеиия, вычислять вертикаль-
ные скорости по главе 10 н через полученные таким образом точки рекомен-
дуется провести кривую (на глаз) до сопряжения ее со сплошной кривой.
Пунктирная часть лишь поможет такому проведению кривой для малых
скоростей (Фо <У 0,1).
Полный расчет требует повторения описанной процедуры для ряда высот,
что сильно увеличивает объем расчетной работы.
Замечание. Кривая потребных мощностей (см. фиг. 77 и 82) была построена у
нас в натуральных величинах: она давала зависимость W (| = /(Vo)- Иногда ее строят
в безразмерном виде, откладывая по оси ординат величину тк , а по оси абсцисс Vo
(иногда Vr иди ц). Тогда располагаемый коэффициент мощности будет, очевидно, равен
В остальном ход расчета остается неизменным. Расчет в натуральных величинах бо-
лее нагляден, что очень важно при компоновке машины, почему мы и изложили его в
этой главе.
§ в. ПЛАНИРОВАНИЕ ВЕРТОЛЕТА
Планированием вертолета называется спуск под углом к горизонту с
неработающим двигателем на авторотации. Вертикальный спуск, иногда
называемый парашютированием, мы подробно рассмотрели в главах 4 н 5.
Как мы видели, при таком спуске получается очень большая скорость сни-
жения, требующая для обеспечения безопасного спуска применения шасси
с очень большим ходом и
применения специального, трудного ма-
невра— «подрыва». В случае полого-
' го планирования скорость снижения зна-
чительно уменьшается, и возможна по-
садка даже без выравнивания вертолета
у земли. Поэтому многие конструкторы
отказываются от вертикального спуска на
авторотации н считают, что нормальной
посадкой прн отказе двигателя является
планирование вертолета. Это, однако,
как увидим далее, сильно ограничивает
применение вертолетов, так как при ви-
сении на малой высоте вертолет может
получить достаточную скорость полета
Фиг 86. Определение скоростей пла лишь после потери большой высоты,
нировгнпя по кривой потребных мощ- порадка 150—200 м и более.
ногтей ‘ г1
Скорость снижения при планировании
можно найти или по описанному в § 4 главы 8 методу сеток Н. Е. Жу-
ковского, или по методу мощностей, или по способу, описанному ниже. Ско-
рость Vy в этом случае нужно считать отрицательной, гак как V„ обозна-
чает в общем случае скорость взлета.
Проще всего исходить из метода мощностей, дающего хорошие резуль-
таты для скоростей порядка Vo^>O,l.
При пологом планировании потребная для полета мощность получается
за счет работы веса машины при снижении. При скорости снижения Vy и
весе машины G сила тяжести совершает в секунду работу, равную GVy кгм/сек.
На диаграмме потребных мощностей (фнг. 86) у нас даны мощности
отнесенные к валу двигателя, т. е. NM
. Поэтому мощность силы
веса будет эквивалентна мощности на валу двигателя и равна
оу„
75?
(324)
При установившемся пологом планировании эта мощность должна равнять-
ся потребной для полета мощности .V... т. е.
ov„
75S
— А^М-П'
Отсюда
J и
Если на фиг. 86 проведем горизонтальную линию, то получим в общем
случае две точки пересечения 1 и 2. в которых мощность будет одинако-
и
вой и, следовательно, по формуле (325) получатся одинаковые скорости
снижения, но будут различные скорости полета на траектории V01 и У02.
Это дает два режима планирования, точно так же, как это получается и у
самолета.
Наименьшая скорость снижения получится в точке, характеризующей
экономический режим полета, так как величина будет в этом случае
минимальной потребной мощностью, и мы можем написать:
(326)
По этой простой формуле скорость снижения получается достаточно точ-
ной, если взяты точные величины X и для данной машины.
Для прикидочных и предварительных расчетов можно принять, что в
среднем у вертолетов Мэ~-у-Лгн0М, т. е. равна половине номиналь-
ной мощности у земли; величина * % 0,78 для одновинтовой и £^0,85
для многовинтовой схем; в среднем ее можно принять равной 0,8. Тогда
можно написать:
75-0,8-0,5jV 30JVhom
Vy ---------------ъ= — -dHOM . (327)
Отношение <yitoM кг!л. с., т. е. равно номинальной нагрузке на 1 л. с.
Она известна с самого начала расчета вертолета. Следовательно, можно
для быстрых расчетов пользоваться формулой
V, =-------------- . (328)
‘’НОМ
Таким образом, при номинальной нагрузке на 1 л. с., равной 4 кг, полу-
чится наименьшая скорость снижения пру планировании, примерно равная
7,5 м/сек, а при нагрузке <?110м = 5 кг/л. с. вертикальная скорость будет
равна 6 м/сек.
Скорость снижения можно еще выразить через нагрузку р кг/м2- на
ометасмую площадь, так как имеется зависимость
'Аюм 1/ д ’
откуда получаем, что вблизи земли, когда А = 1,
Ч"°" vi
Подставляя это выражение в формулу (328), получаем:
(329)
беря среднее значение Ем = 20, получим окончательно:
(330)
Напомним, что при вертикальном спуске на авторотации мы получили
и, следовательно, наименьшая скорость снижения прн планировании почти
в 2% раза меньше скорости вертикального спуска на авторотации. Живая
сила, которую должна поглотить амортизация шасси, уменьшается при этом
почти в 9 раз, что позволяет применять шасси малого хода.
Указательиица скоростей при планировании
Получив Vy и зная Vo из диаграммы потребных мощностей, находим
горизонтальную проекцию скорости полета по очевидной (фиг. 87) фор-
муле
Vx -j/ Vo — V*-
(331)
Наклон траектории к горизонту получится по формуле
V V
О = arc tg arc sin . (332)
Прн пологом планировании угол 9 — мал;
тогда V0^Vx, tg 6 6 и можно вы-
числять 6 по более простой формуле
е = i. (ззз)
Фиг. 87. Угол планирования о Пользуясь последними формулами,
нужно помнить, что Vy <С 0 в случае
спуска. Задаваясь рядом значений Ng,
будем получать с помощью диаграм-
мы, приведенной на фиг. 86, по два значения скоростей Vx„ Vy, и V.r, н Vy2,
причем Vy, = Vy,. По этим точкам строим указательницу скоростей; она
имеет примерно внд, изображенный на фиг. 88.
По оси абсцисс отложены скорости Vx, а по оси ординат скорости Vz/;
угол между горизонтальной осью ОН и вектором скорости Vo есть угол
снижения 9. Наименьшей скорости снижения соответствует точка Э при
экономическом режиме полета, наименьшему углу снижения на наивыгод-
нейшем режиме — точка И; этим режимам будут соответствовать горизон-
тальные проекции скорости полета Vx$ и VXH. Каждой скорости снижения
у будут в общем случае соответствовать две горизонтальных скорости VX1 и Vxz
и два угла снижения и (V.
Прн планировании на авторотации выгодно допускать несколько боль-
шую скорость снижения, чем Vymin, так как тогда сильно уменьшается
Vx и увеличивается угол 0 и спуск машины приближается к вертикальному.
Пробег по земле благодаря малости Vx делается весьма небольшим, а при
наличии колес с тормозами или шассн с полозьями он может н совершенно
отсутствовать.
При наклонном спуске не возникает вихревое кольцо и связанное с ним
раскачивание машины.
Обычно летчик не допускает, чтобы вертолет касался земли даже на
скорости Vyy применяя самолетный прием посадки и выравнивая траекторию
Фиг. 88. Указательнина скоростей планярован1Ия
вертолета на авторотации
у'земли, переходя на горизонтальный полет и даже делая перед спуском
«горку», после чего машина «проваливается» и касается земли с очень ма-
лыми скоростями Vx и Vy
Фиг. 89. Определение безопасной высоты (//$ез )
для спуска вертолета при аварийной остановке двигателя
Иногда применяют еще подрыв несущего винта, т. е. увеличивают его
шаг у земли. Обычно посадка делается против ветра, и спуск вертолета
на планировании_еще более приближается к вертикальному (фиг. 89).
Безопасная высота вертолета
Недостатком" вынужденного спуска вертолета по способу планирования
является то, что" висящий в воздухе вертолет не может начать планировать
без потери высоты. Дело в том, что висящий неподвижно в воздухе вер-
толет не имеет кинетической энергии поступательного движения, а плани-
рующий вертолет должен иметь скорость планирования 1/опл и, следова-
ml/2
тельно, кинетическую энергию, равную —. Если не заимствовать эту
ОЙ К W Юо.
энергию у вращающегося по инерции несущего вннта, т. е. сохранять
число оборотов последнего неизменным, то получить эту энергию вертолет
может лишь от работы собственного веса G, которая при спуске с высоты
Н н будет равиа GH. Эта энергия может быть передана вертолету лишь
с некоторым к. п. д., равным в этих условиях приблизительно 0,5. Кроме
того, во время спуска затрачивается еще эиергия на вредное лобовое со
противление, на обслуживание вертолета электроэнергией, иа составление
самого несущего винта и так далее, на что затрачивается примерно около
половины располагаемой энергии..Кроме того, нельзя использовать всю энер-
гию несущего винта, так как он должен все время вращаться, как мы
видели в § 5 главы 5.
В общем нужно считать, что на создание скорости удается использовать
лишь около ’/5 полной потенциальной энергии веса. Будем обозначать эту
величину через Zg- Приравнивая эту энергию кинетической энергии при
планировании, получим уравнение
&GH
2g
Отсюда находим:
Н = 2j”2- . . (334)
Безопасная высота Н^ез будет несколько большей, так как летчик не
сразу переведет машину на переходный режим; кроме того необходимо
иметь запас высоты у земли на выравнивание машины или для маневра
«горка». Оценить эту добавочную высоту можно приблизительно в 10 лк
тогда получим:
= 10. (335)
lo2S
При , н считая 2g:->.'20, получим:
ю. (336)
4
Если машина в момент остановки двигателя двигалась со скоростью
то из потребной работы нужно вычесть соответствующую энергию —— .
Тогда формула 335 примет вид:
и безопасная высота Н^з соответственно уменьшится.
Не останавливаясь на подробностях, можно аналогичным приемом иссле-
довать и спуск с малых высот, учитывая «подрыв несущего винта».
Более точно расчет таких маневров можно сделать, разбив траекторию
спуска на элементы и вычислив движение на таком элементе, как происхо-
дящее при среднем значении действующих сил, как это мы делали в § 5
главы 5, изучая подрыв несущего винта вертолета.
На фиг. 90 даиа заимствованная у Р. А. Янга диаграмма безопасных
высот спуска иа авторотации для среднего американского вертолета. Мы
видим, что опасная зона попадает в область, представляющую наибольший
интерес для эксплуатации вертолета. С этим неприятным ограничением
борются известными приемами: установкой двух и более независимых дви-
гателей и использованием кинетиче-
ской энергии несущего винта путем
подрыва, для чего необходимо иметь
более тяжелые несущие винты.
Планирование вертолета
в общем случае
Более точно, особенно в области,
где < 0,1, расчет планирования
вертолета может быть сделан по
способу тяг, в котором учитываются
характерные углы силы Т с осями
координат.
Исходим нз условия авторотации
несущего виита, т. е. считаем тк — 0,
и тогда получаем:
Фиг. 9П. Диаграмма безопасных
высот спуска на авторотаичи
по Р А, Янгу (р = 14 кг/м2)
mK —CTVA 4- 1,2 V't) = о.
х 4
Здесь множитель 1,2 при тк р вводит потери на рулевой винт, на тренне
в трансмиссиях, на работу масляного насоса, электрогенератора и т. д.
Из этого уравнения находим, задавшись величиной Vt, скорость Va'
Va = — z.0,3
cxmei + vt )
Ст
(338)
Зная величины Vt и Va, по формуле (205), находим Vi и получаем точное
значение индуктивной скорости по формуле (203).
Далее, пользуясь известными формулами (203) и (204), н переписывая
их в виде:
sin т =- — Va J- Vo cos т — Vt.
находим:
tgT =
т — arc tg
(339)
(340)
(341)
Кроме того, находим
28*
Теперь пользуемся уравнением движения вертолета (302), которое можно
переписать в виде:
О
— tg т cos 6 = —SI -j- sin О, (342)
G
откуда видим, что все величины, входящие в это выражение, нам известны,
кроме угла 0. Величина
Qbp cxS
находится по сводке лобовых сопротивлений.
Следовательно, задача сводится к решению уравнения (342) относительно
0. Его можно решать^или графически, путем засечки, или аналитически.
угла планирования скоростей планирования вертолета
ЭД*В первом случае удобнее задаваться величиной 0 и находить соответ-
ствую цую вел тчдау т' (фиг. 91). Там, где т'= т, и получится нужная
величина 0. Нужю помнить, что пэч планировании величина 0<Ои, кроме
того, одному т соответствуют при выбранном Vt два значения 0.
Для аналитического решения в формулу (342) нужно подставить cosO=)/" 1 —siп20,
изолировать радиол и возвести полученное выражение в квадрат. После
этого получится уравнение второй степени:
sin2 9(1-}- tg2 т) + sin 02 -^2 т = о.
v 6 ' G G1 *
Решая его, получим:
sin О
G V G1
l + ts2^
(343)
Для каждой скорости планирования, т. е. |/0, мы получим в общем случае
два значения угла планирования 0, что ясно видно из фиг. 92. Задавшись
§7.0 методах второго приближения
437
каким-либо значением V'o и очертив из начала координат окружность с ра-
диусом ]/0, показанную тонкой линией, мы получим у нес две точки пере-
сечения с указательницсй скоростей планирования, которые и дадут два
угла планирования G и две скорости снижения V&. В точке получится
минимальная скорость по траектории VOmm. обеспечивающая установившееся
планирование.
Этот режим представляет большой интерес, так как при полете на нем
скорость сниж?ння мало отличается от наименьшей возможной скорости
на экономическом режиме, а скорость по траектории значительно меньше.
л GVo
следовательно, значительно меньше будет и кинетическая энергия —
_ 2ё
вертолета. Это позволяет в случае внезапной остановки двигателя быстро
набрать необходимую скорость VOmin и начать установившееся планирова-
ние. Этот прием снижает безопасную высоту, и им пользуются опытные
летчики, умеющие делать безопасные посадки при крутом планировании.
При этом сильно уменьшается и горизонтальная скорость при посадке.
На автожирах такая посадка применялась очень часто. Кроме того, при
такой посадке не возникает вихревое кольцо.
Углы атаки и тангажа при планировании
При пологом планировании балансировочный угол б б близок к тому,
который соответствует режиму полета с большой горизонтальной скоростью.
У одновинтовой схемы хвостовой виит дает очень малый момент Мхв.
и ему соответствует, согласно § 5 главы 6, изменение балансировочного
угла, равное всего лишь около 1/л°. При крутом планировании нужно
определять балансировочный угол заново, по уже известной методике, учи-
тывая влияние стабилизирующих поверхностей.
Угол атаки определится по известной формуле (198).
Угол тангажа фюзеляжа при планировании определится по формуле (201).
При этом угол G отрицателен, а угол ак положителен; получается некото-
рая компенсация, и угол тангажа фюзеляжа получается при пологом пла-
нировании малым. Это подтверждает давно известное наблюдение, что ось
фюзеляжа на обычных режимах полета вертолета почти горизонтальна.
В некоторых типах вертолетов н конвертопланов ось фюзеляжа на
обычных режимах может поворачиваться на 90°. Такие схемы требуют
каждый раз специального рассмотрения, и здесь нельзя дать общих правил.
В заключение заметим, что сложные типы вертолетов можно рассчиты-
вать по описанной методике, если пользоваться осредненным винтом, т- е.
величиной тСр, согласно § 5 главы 7.
§ 7. О МЕТОДАХ ВТОРОГО ПРИБЛИЖЕНИЯ
Разобранные здесь методы позволяют сделать полный аэродинамический
расчет и найти все основные данные проектируемого вертолета. В нем
с самого начала учитывается условие балансировки вертолета и маховое
движение лопастей (угол 6б)- Однако они основаны на вычислениях, в ко-
торые вводились средние значения многих величин. Так, не учитывалось
изменение величин и схр. Совершенно не учитывались радиальные ско-
рости потока, набегающего на лопасти, хотя оин очень велики - и их вли-
яние должно быть заметным. Индуктивные скорости вводились в виде
средней величины по диску винта. На самом деле они изменяются. Правда,
для аэродинамического расчета это допущение не дает больших погрешно-
стей, так как сила тяги считается равной приросту количества движения
в струе, а средняя скорость определяется по импульсу. Но при этом воз-
никают вторичные явления (например, изменение махового движения), что
несколько изменяет действующие на несущий винт силы.
Очень важно в уточненных расчетах обеспечить соблюдение уравнения
моментов (величины 6б), так как несоблюдение этого условия вносит до-
вольно заметные погрешности.* К сожалению, до сих пор не разработан
еще метод нахождения истинных индуктивных скоростей на самих лопастях
(относительное движение воздуха), и обычно находят путем опытов или
теоретически лишь средние скорости на диске, а не истинные скорости на
лопасти. Кроме того, как увидим далее, теория винтов с машущими ло-
пастями разработана еще слабо, с рядом грубых допущений. Таким образом,
нужно признать, что теоретически обоснованный метод второго приближе-
ния в настоящее время еще не создан.
Взамен этого можно легко уточнить расчет первого приближения, поль-
зуясь результатами экспериментальных исследований. Обычно каждое кон-
структорское бюро придерживается одной формы лопастей у своих верто-
летов, и постепенно накапливается большой запас материалов по испыта-
ниям машин в полете или в аэродинамических трубах. Это позволяет вос-
пользоваться экспериментально полученными полярами. Если иметь проде-
ланный расчет по описанным методам, то будут известны Ио, ак, Сг,
и тогда можно на основании графиков получить уточненную величину угла
установки лопастей <р- и найти надежную величину тк, после чего можно
найти /Vn и по ряду точек построить уточненную, второго приближения,
кривую потребных мощностей. Таков в основном метод Л. М. Миля
и В. Н. Ярошенко, в котором было указано удобство использования угла т.
Таким образом, уточнение аэродинамического расчета вертолета в на-
стоящее время возможно лишь с помощью экспериментальных кривых. Надо
заметить, что и при аэродинамическом расчете самолета приходится поль-
зоваться такими же приемами. Ни один ответственный проект самолета не
обходится без многочисленных продувок его моделей. То же получается
и для более сложной машины, т. е. для вертолета. Поэтому надо принять
за правило тщательную разработку проекта вертолета на моделях в аэро-
динамических трубах и иа свободно летающих в воздухе моделях с двига-
телями.
Глава 9
МАХОВОЕ ДВИЖЕНИЕ ЛОПАСТЕЙ
И КОЭФФИЦИЕНТ ТЯГИ НЕСУЩЕГО ВИНТА
ПРИ КОСОЙ ОБДУВКЕ В ПЕРВОМ ПРИБЛИЖЕНИИ
§ 1. ПОСТАНОВКА ЗАДАЧИ
До сих пор мы не рассматривали в явном виде маховое движе-
ние шарнирно подвешенных лопастей, какие теперь применяются
только на вертолетах. Учет же этого движения совершенно необходим для
получения коэффициента тяги Ст при полете с горизонтальной скоростью
и для решения ряда важных вопросов.
Рассмотрим этот вопрос в упрощенной, но весьма наглядной постановке,
с тем, чтобы вернуться в главах 11 и 12 к более точной, ставшей ныне
классической, постановке, но значительно
более сложной и требующей громоздких
вычислений.
Будем считать, что боковой завал не-
сущего винта мал и уничтожается нетчиком
путем малого отклонения автомата-переко-
са вбок.
Основной гипотезой является положение
о том, что истинная плоскость вращения
лопастей перпендикулярна к полной силе тя-
ги несущего винта Г (фиг. 93). Это допу-
щение будем Называть центрирующим эффек-
том силы тягн. Классическая теория под-
тверждает это положение как достаточно
близкое к действительности. Опыты также
дают близкий к этому результат.
Сила Т образует с конструктивной
осью угол 6б = 6х4~6ап- Углом конус-
ности лопастей ввиду его малости будем
Va и V/
.___ ... ... ... ... ____ пренебрегать при вычисле-
нии силы тяги, как это делается и в классической теории. Об этом будет
сказано в § 3.
Для расчета махового движения удобно исходить не из скоростей Уд и
Что очень упрощает аэродинамический расчет, а из скоростей К и Vt,
взятых по связанным осям 0хг и Oyi (см. фиг. 93). Для такого перехода
проектируем скорости УА и Vr на новые оси и получаем, считая бв малым
углом.
Уа = уА 4- Vrfi
(344)
и
Vt = —Va^ + Vt^Vt- (345)
Эти формулы мы уже получили в § 2 главы 6.
В безразмерных обозначениях ЖукоЕского-Ветчиикииа их можно напи-
сать в таком виде:
Va = VA + VW (346)
и
Vf = — VW +Vr. (347)
В аигло-америкаиских стандартах применяются еще такие обозначения:
X = — Va; ц = Vt. (348) (349)
Полная скорость обдувки диска Vi получится, очевидно, из соотношения
V1= V VW Vt. (350)
§ 2. КОЭФФИЦИЕНТ ТЯГИ НЕСУЩЕГО ВИНТА
В КОСОЙ ОБДУВКЕ
Выделим у лопасти иа радиусе г элемент с хордой b и длиной по раз-
маху dr (фиг. 94) и рассмотрим его обтекание при маховом движении. Ре-
Фиг. 94, Завал плоскости вращения несу-
щего винта в приближенной теории
зультирую’цая скорость набега-
ющего потока составится из че-
тырех скоростей: rw, Va, \н и fp.
Первые три мы уже умеем вы-
числять. Скорость же Пр возни-
кает при маховом движении лопас-
ти. Цеитр выделенного на фиг. 94
элемента лопасти (точка а) бу-
дет то подниматься, то опускать-
ся над конструктивной плоско-
стью вращения. Его высота пусть
будет равна уе. Плоскость истин-
ного движения лопастей будет
пересекаться с конструктивной
плоскостью по линии Ozu и ,в за-
штрихованной части диска выде-
ленный элемент будет находить-
ся выше конструктивной плоскос-
ти, а в незаштрихованной—ниже.
Угол между этими плоскостями
равен дв. Длина перпендикуля-
ра ар, опущенного из точки а
иа линию 0гг, равна, как видно
из чертежа, г cos у. н тогда
Уе = — 6бГ COS ф.
Скорость взмаха будет равна , а относительная скорость потока ив
dt
будет иметь обратное направление, но тот же знак. Следовательно,
fp = н---- = <Wsinip~ .
dt
. т d’lb
Но -x- — co и, следовательно.
dt
op = 6Бга> simp.
(351)
Таким образом, относительная скорость IF = lFr потока, набегаю цего
на выделенный элемент, будет равна [как было уже получено в § 2 главы
7 и как непосредственно видно из чер-
тежа. (см. фиг. 94)],
Wx — rw + 14 sin ф. (352)
Осевая компонента скорости W будет
равна (фиг. 95)
= Уд + дв H0sini|>. (353)
Угол, образуемый притекающим к
элементу потоком, т. е. скоростью IV
с плоскостью вращения, будет равен
о W и + бБг о sin ф Фиг. д5. Силы и скорости у элемента
~ ’ ™+yfSind, ' ( > лопасти
Здесь угол Ре считается малым, и
Угол атаки аР сечения будет равен
a« = q> — fc = q> — (355)
Угол установки ср в нашем случае можно представить в таком виде:
ф = ф0 — Фап cos ф. (356)
Здесь ф0 — общий угол установки лопастей, а величина фхпсозср пред-
ставляет собой добавочный угол установки, возникаю ций от действия
автомата-перекоса, работающего у нас лишь в продольной плоскости. Для
ф = 0 эта формула дает ф == ф0 — фдп; для ф — 90° угол ф = Фо; для
ф = 180° угол ф •-= ф0 + фдп, т. е. при подъеме переднего края АП угол уста-
новки спереди увеличивается, а позади уменьшается.
Угол атаки сечения будет равен, следовательно.
«» = Фо — Фап COS ф-----, (357)
а коэффициент подъемной силы сечения может быть (подобно тому, как
это давалось в § 5 главы 2) написан в таком виде:
/ W \
Су = Act., = А I '1ЛП cos ф----2- \ . (358)
Вычислим тягу вырезанного элемента лопасти (см. фиг. 95), считая, что
dTe = dYe, (359)
т. е. сила тяги элемента равна его подъемной силе, что можно делать,
допуская, что угол мал. Это допущение всегда делается в теории несу-
щего винта.
Тогда получим:
dTe-=dYe = A (ф-^’) '^bdr =
= A(<tW‘--Vx№’y)^dr .
(360)
Подставляя сюда найденные значения Wx н IFj, по формулам (352) и (353)
и величину ф по формуле (356), получаем для /г-лопастного несущего
винта среднюю за оборот тягу Т:
= k\^dr— [ [фХ— Фап^соэФ- WxWs]dty =
J 2 2л J
о о
R . . .2%
= k £ dr — С (ф0г2ш2 + фс2Кга> sin ф +
J 2 2л J
о о
+ Фо W эш2ф — Фапг2(х>2 cos ф — фдп 27/гсо sin ф cos ф —
— ФапУ/ $ш*ф cos ф — г2о)26б sin ф — 14г(о —
— бьгсо1// sin2 ф — VaVt sin ф) с£ф. (361)
•После интегрирования по ф получим;
т = + —у™7')*'' <362)
Член с фдп нз формулы выпал, так как множитель при фдп оказался
после интегрирования равным нулю.
Для дальнейшего интегрироваиия по г нужно иметь зависимость b и ф0
от г.
В простейшем случае, часто встречающемся на практике, b = const и
ф0 = const. Тогда получим:
г Apkb I Rs:d2 . V'fR VaR2v R2o> \
T= 2 (‘b — +q’»^----------2----«б—V, j. <363)
Хотя эта формула и выведена для b = const и ф0 = const, ею или анало-
гичными формулами пользуются и для расчета любых несущих винтов,
вводя в нее значения Ь7 и ф7, взятые иа г — 0,7. Это, понятно, упрощает
все расчеты, но вводит в них погрешность. Сравнение с более точными
методами показывает, что до V/<10,25 погрешность невелика, особенно
если учесть грубость многих допущений, вводимых вообще в теорию несу-
щего винта.
Разделив обе части полученного выражения на~рЯ4(±)2, получим вели-
чину Ст, выраженную через безразмерные величины:
(364)
При расчете вертолетов величины Ст, Vt, Va и 6б получаются из аэродина-
мического расчета (см. § 4 и 5 главы 8), а величина ср- остается неизвест-
ной. Из выведенной формулы легко найти <р-, т. е.
ст | Т, | V,
1 V?
—F —
3 2
Формула (364) практически совпадает с формулой (366):
Сг= А37[1’(1 +, (360)
которую дает классическая теория для несущего винта без АП. Все отли-
чие формулы (364) от формулы (366) в том, что в формуле (364) имеется
добавочный члеи —-—. Это объясняется тем, что в первой формуле было
принято заранее, что летчик с помощью АП ставит силу тяги Т в пло-
скость полета и отклоняет ее на заданный балансировочный угол бБ. При
свободном несущем винте и нейтральном АП сила Т отклоняется назад на
б,
угол и вбок, в сторону оси Ozi на угол'5г~— .
Работа АП входит в формулу (364) через дБ, так как этот угол, как
известно, связан с дх и 6АП формулой (196), т. е.
бв = бх + б.Ш-
Тогда формулу (364) можно переписать в таком виде:
Формула эта показывает, что действие АП сравнительно мало влияет на
величину Ст-
Учет коицевых потерь
Выведенной формулой для Ст часто пользуются на практике. В нее ие
были введены концевые потери винта. Не представляет никакого труда
ввести эти потери, для чего лишь нужно интегрирование вести не в пре-
делах от 0 до а от R^ до R^. Тогда получим:
, ущпи у. тихивие движение лопастей и коэффициент тяги
Z 4 J
Выиося общий множитель — Bi -- х(см. § 6 главы 2), получим;
п л Г4” (1 3 g2— £i—Л V 6J-V'/1
с’“лЧ11 + ^'Ч-т4 <368>
Выражение в скобках можно упростить, воспользовавшись тем, что член
1 у* = А__1__р;
2 2 b-Hi
значительно меньше единицы н в него можно ввести среднее значение
£2 +£1^1’23; тогда получим окончательно:
Ст = Ав,х (1 + 1,2V?) —. (369)
Сравнение формул (364) н (369) показывает, что неучет коицевых потерь
прн х^0,9 — 0,92 дает по формуле (364) преувеличение на 10% значения
Ст, почему и нужно в расчетах пользоваться формулой (369), как более
точной.
Более сложный несущий винт
Предыдущие формулы были выведены для случая, когда b = const и
Фо = const. Пользование величинами Ь? н Ф7 позволяет их применять и к
более сложным случаям, ио, конечно, такой прием дает малую точность и
пригоден лишь для вычислений первого приближения.
Не представляет никакого труда вывести выражения для любого закона
изменения шнрниы b н угла <р вдоль по лопасти. Для примера возьмем
винт, у которого ширина b и угол ф изменяются по простому закону:
Ьр
й = ; (370)
Ч> = Ч>« + -3:. (371)
Г
Здесь и фя даны для коицевого радиуса R, а величина Ф представляет
собой коэффициент закрутки лопасти. На практике удобно пользоваться
значениями 67 и Ф7. Для перехода к этим величинам иапншем предыдущие
формулы для г = 0,7 и получим:
й, = —~ , илн bR = й, /0J ,
Уо,7
и
ф, Фя + —, или ф/? = ф7 ——
Введя полученные значения b# и ф/< в предыдущие формулы, получим:
b - Ь7
и
Ф . Ф . Ф X . Ф
<р = 'р’-0-5 + Т = 1Л:“0-^+Т-
При работе АП получим для угла установки сечеиия, лежащего иа радиусе
г, при азимуте <р, следующее выражение:
I Ф \ Ф
ф / ф. — —- + ~ — фАП СО8ф.
Полученные значения b и ф нужно подставить в общую формулу тяги
{см. формулу (360)] и проинтегрировать ее по ф и г. Интегрирование по
ф приведет к формуле (352). Но интегрирование этой формулы по г дает
более сложный результат. Проделав вычисление, получим теперь:
2 2 _ бк К ’I
+ ~Ф — ФУ,2----------Ув-----*-£. . (372)
3 3 3
Эту формулу можно также переписать в таком виде:
Ст - As, 0,7 <р, ( 1 11/,2) -1 к
Из нее видио, что эффект крутки сводится к добавлению к Ст иезакручен-
иой лопасти (первый члеи) еще второго слагаемого, пропорционального коэф-
фициенту крутки лопасти. Здесь не были учтены концевые потерн. Про-
делав интегрирование в пределах от г Rc,2 До R^i, получим еще более
сложное выражение:
С,--.Ао,0,7^Й
й ) ф,-
“(а—а а)(й)к-
1
3
(й-й Rv,].
(373;
И эту формулу можно разбить иа два слагаемых: первое — не зави-
сящее от крутки, и второе — пропорциональное коэффициенту Ф. Такие
формулы могут быть получены для любого закона изменения b и Ф. Не-
которая неточность получается во всех таких формулах из-за введения в
них средней скорости Va, вычисленной по импульсной теории. Однако для
Ст это вносит малую погрешность, так как индуктивные скорости малы
и, кроме того, они вычислялись по силе тяги. Это еще более уменьшает
ошибку.
§ 3. УГОЛ КОНУСНОСТИ И МАХОВОЕ ДВИЖЕНИЕ ЛОПАСТЕЙ
До сих пор мы считали, что лопасти движутся по плоскости перпенди-
кулярно к полной силе тяги. Это получалось бы в случае несущего винта
с качающейся втулкой или сквозными лонжеронами. В этих условиях лопа-
Фиг. 96. Вычисление угла конусности ло-
пастей
сти лишь вращались около оси
Oyi и делали взмахи вверх и
вниз в плоскости меридиаиа по
закону —cosip.
При обычной же независимой
шарнирной подвеске лопастей
они буду г еще отклоняться вверх
под действием силы тяги Т н
будут образовывать с конструк-
тивной плоскостью вращения
угол конусности а0, к которому
прибавятся колебательные дви-
жения лопасти; угол их откло-
нения будет равен для азимута
-ф величиие
3 - а0 — 5бcosip. (374)
Угол а0 практически, как увидим далее, ие зависит от высоты и режима
полета, и мы можем его вычислить для простейшего случая, а именно для
висения вертолета иа месте.
На фнг. 96 изображена лопасть в меридиональной плоскости. Будем
считать, что горизонтальный шарнир (ГШ) лежит не иа оси вращения не-
сущего винта, а вынесен на расстояние, равное гш. Лопасть при висении
ие будет иметь махового движения, а лишь отклонится вверх иа угол а0.
Условие равновесия лопасти во вращающихся осях координат сведется к
равенству нулю момента всех действующих на лопасть енл относительно
горизонтального шаоиира (ГШ), так как шарнир не может передавать мо-
мента ко втулке. Лопасть будем считать твердым телом, угол а, — малым;
sina0^r«0, a cosa0st:l. На нее будут действовать три момента.
От силы тяги момент
где k — число лопастей и Гт — плечо силы тяги; от веса лопасти получится
момент (?л1 (гцт — г1Ц), где — вес одной лопасти, гцт — радиус центра
тяжести лопасти и, наконец, получится момеит от центробежных сил.
Найдем величину последнего момента. Выделим на произвольном ра-
диусе г элемент лопасти с длиной dr н массой dm. На иего действует
центробежная сила
= dm га)2 на плече (г — гш) tg а0^(г — гш) а0
н вызывает момеит относительно ГШ, равный
(г — гш) а0 == dm гео2 (г — гш)а0.
Полный момент центробежной силы будет равен
я я к
Мц = ао^ dm гш2 (г — гш) = о)2ао dm г2 — Л0Гш J г dm.
О 0 0
Интеграл первого члена дает величину момента инерции лопастн Jo отно-
сительно центра втулки, т. е.
Я G
Л) =Д dm г2 - тг* =г\ , (375)
о
где т = —-----масса лопасти, а г< — радиус инерции. Второй член, но
известной теореме о центре тяжести, может быть представлен так:
г G
m \ dm т — со2СуГц.т — co2Qq — гц.т гш, (376)
о 8
Приравняв нулю выражение полного момента, действующего около гори-
зонтального шарнира, можно написать:
г‘ o0ci)2 гшгц.т -И {г гш) — Сл1 (гц.т гш) =0.
Положительный знак у моментов брался в сторону увеличения а0. Решая
полученное уравнение относительно са и учитывая, что при висении тяга
Т почти равна полетному весу G, находим: •
(ГТ гш) ^л1(гцт
Введя сюда относительные радиусы го гш, гт н гц.т, получим окончательно:
G _ _ _ _
а kG (Ги-т
п„ .= —в--------!-------------------
Влияние на а0 мало, так как гш обычно ие превосходит 0,1 -—0,2 м,
а 10 м, и им обычно пренебрегают. Полагая гш = 0, получим рабочую
формулу;
G - -
= g t('" Гт f"T == g а______________г2______g См
° 7? ква -г ш’-R -р
Величина —~ есть относительный вес лопастей; ои обычно лежит в пре-
делах 0,05 — 0,07 н, следовательно, величина
— 20 - 15.
Второй член в формуле (378) мал, и при легких лопастях им можно
пренебрегать в предварительных расчетах. Тогда формула (378) будет
иметь простой вид:
g а \
~г> (379>
Угол Со = 57,3ао получается обычно равным 4—6°
Крайнее положение лопастей
В излагаемой теории предполагается, что летчик с помощью АП при-
водит ось конуса вращения лопастей, с которой мы здесь считаем совпа-
дающей тягу несущего винта Т, в плоскость полета и отклоняет ее на
заданный схемой’’угол балансировки бв. В этих условиях в моменты нахож-
дения на азимутах ф = 90° и ф = 270° лопасти будут образовывать с
конструктивной плоскостью вращения углы = [1„0° =-= а0. В заднем поло-
жении при ф = 0° лопасть будет образовывать с этой плоскостью угол
Зо° = Со — бв, а в переднем положении — угол Зио0 — о0 + бв (фиг. 97).
При полете в «болтанку» лопасти от порывов ветра и от работы АГТ
сильно раскачиваются и дополнительный угол доходит до 5—10°. Легкие
лопасти раскачиваются сильнее, а тяжелые меньше.
Компонуя вертолет, необходимо наносить на его эскиз крайние положе-
ния лопастей, оставляя еще просвет в 3—5°. Это необходимо делать во
избежание ударов лопастей о корпус и коисоли вертолета, что может вы-
звать катастрофу. Кроме того, лопасти, проходя близко к частям вертолета,
получают аэродинамические удары от местного изменения скорости Va, что
может вызвать тряску машииы.
У автожиров и у вертолетов без АП, но с гребными виитами сила Т
отклоняется на угол бх в плоскости Полета и иа угол, близкий к у бх,
вбок, в сторону оси Oz. Тогда
бБ = б*,
и для балансировки машины нужно соблюсти условие
бБ = бц т 4” &Г.0»
из которого и можно получить необходимую величину площади и угла
установки горизонтального оперения.
Раднус инерции лопастей
Для вычисления а0 иужио знать, кроме G, Сл, R и со, радиусы гр, гц.т
и г/. Радиус гт (см. § б главы 3) обычно близок к г = 0,7—0,8.
Радиусы гцти г, зависят от распределения масс вдоль лопасти.
Мы имеем осиовиое выражение
где------масса, приходящаяся иа 1 пог. м радиуса винта; ее часто иазы-
dr
вают лииейиой плотностью. Далее находим механические характеристики
лопастей:
статический момент
момент инерции
am ,
— r dr :
dr •
R
я j
e dm „ ,
\ — r2 dr;
J dr
радиус ц. т.
= Uo
m
два
J0
i. Пусть — = — = const; это близко
радиус ииерции
Рассмотрим
к тому, что имеется у лопастей постоянной ширины и одинакового профиля
29 В. Н. Юрьев, т. I !»*, f 1!
речений Тогда получаем-
. г,,т
’7. > ' -SlZii;
JR 3 Зе
о s
r2 R^
tn 3
ИЛИ )
(380)
у тйких ‘лойастей
Гт ~ 0,8.
Второй случай соответствует расширяющимся ко втулке лопастям.
« Предположим, что —— изменяется по линейному закону (фиг. 98) и тогда
Фиг 98 Эпюра распределения
масс по длине лопасти
dm __ tn tn / г
dr ~~ R R \R
(381)
где ц —• коэффициент весовой трапеце-
видное™. Примем его в этом примере
равным единице: тогда у втулки — бу-
Jp
дет в три раза больше, чем на конце
~ dm tn / , _ г \
лопасти. Тогда — = —1,5-------------I и
dr R \ R >
момент ииерции будет равен
Статический момент будет равен
<4
Отсюда
^иг. = «
4 2
'А
ш 12
У таких несущих винтов, близких по форме к винту НЕЖ, гг~0,7
На основании таких расчетов получаем следующие данные:
Лопасть гт ГЦ Т г- '1
Постоянной ширины профиля . . , и 0,8 0,5 0.333 0,577 0,67
Трапецевидная . . . . . 0,7 0,415 0,25 0,5 0,60
Средний несущий винт . 0,75 0,46 0,3 0,55 0,65
I. !
При окончательной увязке проекта и наличии чертежа лопасти иужно
величины G„, Jo, гц.т и rt вычислять по весу отдельных ее элементов,
разбивая ее по длине на несколько частей. Если части берутся длинные,
то нужно применять известную теорему механики о том, что момент инер-
ции тела относительно произвольной оси равен моменту относительно парал-
лельной ей линии, проходящей через центр тяжести элемента, плюс момент
инерции его массы, сосредоточенной в его центре тяжести, т е.
Jo = А т + тг^ т.
Обозначив через J'a т, tn’ и г т величины, относящиеся к отдельным
частям лопасти, получим для полного момента инерции лопасти следую-
щее выражение:
Jo = Sj; т J- Sm’ (г; т)2 (382)
При вычислении Jo и t/0 мы брали нижний преде^ интегралов, равный
нулю, а ие так как в центре имеется тяжелый лоижефои Лопасти и
Фяг 99 Определение момента центробежных сил
при помощи центра качания
детали втулки, колеблющиеся вместе с лопастью. Момент инерции этих
частей близок к тому, который получится, если продолжить фиктивно ло-
пасть до оси вращения несущего винта.
Иногда момент центробежных сил лопасти подсчитывают, исходя из
величины полной центробежной силы Fa = mr-d тсо2. Одиако в этом случае
иа лопасть в ее центре тяжести действует добавочный момент центробеж-
ных сил, равный
Мху = <МХу, (383)
где
J ху = \ dm ху
— это так называемый центробежный момент инерции (илн произведение
инерции).
Тогда
Мц = ГцйоГц т + &zJxy. (384)
Вместо этого можно подсчитывать момент центробежных сил, прикладывая
полную центробежную силу не в центре тяжести, т. е. не в точ<е центра
тяж'сти, а в центре качания лопасти, лежащей на радиусе гА (фдг. 99).
Тогда можно написать:
Л4ц — F^Clgfк — Oq/72W Гц, ffк.
(385)
Величину гк легко найти, так как можно написать по-прежнему:
44ц = Jow2a0 = mr*w2a0.
Сравнивая эти выражения, получаем:
Фиг. 100 Графическое нахождение центра
качения
отсюда
Гк = . (386)
гц. т
Величину гк можно найтн простым
геометрическим построением (фиг. 100).
Из точки центра тяжести нужно вос-
становить перпендикуляр СР, н ради-
усом ОД — гг сделать циркулем засеч-
ку на линии СР; получится точка А
Восстановив в ней перпендикуляр к линии ОА и продолжив его до Пересе
чения с осью лопасти 00 lt получим в точке /С центр качания. Отрезок
ОК = г«.
Справедливость этого построения следует из того, что rt, как в-щно и
чертежа, будет средней пропорциональной величиной между гц. г и гк, т. е
Отсюда
гк = -— •
И Т
Центробежную силу в формуле нужно вычислять по радиусу гц.т, а не
по гк.
Заметим, что отрезок АС дает величину г; ц. т — радиуса инерции лопа-
сти относительно ее центра тяжести.
Выше (385) приведена величина гк для типичных случаев.
Как видно, гк ~ 0,65, а гц. т = 0,46; следовательно, приложив при вы-
числении Л4ц силу Лц в точке, лежащей на радиусе т, а не гк, мы
сделаем ошибку в отношении = 1,41, т. е. ошибка получится
гц. т ’
в 40% в сторону занижения Л4Ц.
i и, о или>.лис I и вращения
Фиг. 101. Отклонение оси лопасти
в плоскости вращения при ВШ
§ 4. ОТКЛОНЕНИЕ ОСИ ЛОПАСТИ
В ПЛОСКОСТИ ВРАЩЕНИЯ
ПРИ НАЛИЧИИ ВЕРТИКАЛЬНОГО ШАРНИРА
Очень часто у лопастей устраивают вертикальные шарниры. При работе
на режиме висения ось такой лопасти несколько отклоняется назад, а при
полете с горизонтальной скоростью она приходит в колебательное движе-
ние в плоскости вращения. Чтобы лопасть
не слишком сильно раскачивалась в пло-
скости вращения, у нее устраивают раз-
личного типа демпферы.
Рассмотрим равновесное положениеосн
лопасти на режиме висення.
На фиг. 101 изображена лопасть'в от-
клоненном на угол fr положении; в точке
С находится центр тяжести лопастн. Ради-
ус ОС = Гц.т, соединяющий центр тяжести
с осью вращения несущего вннта, образует
с линией, перпендикулярной к оси ГШ, угол у.
Найдем углы & и р Раднус гц.т ввиду ма-
лости величин отрезка а и угла 8 от угла у
практически не зависит.
Центробежная сила действует по ра-
диусу и равна
Момент этой силы около ВШ равен
Мц = Fuh,
де h — длина перпендикуляра, опушенкго
На каждую нз k лопастей действует еще момент аэродинамических сил,
равный крутящему моменту, приходящемуся на одну лопасть. Последний
можно найти по известной формуле механики
Мл = фмк = 716,2-^- . (389)
Прн равновесном положении на режиме висения эти моменты равны
н тогда
м = 716,2-^ .
Отсюда '
* = 716,2-^4-. (390)
Угол у находится непосредственно, так как
“гц. ти2- (387)
(388)
из сси ЕШ на радиус гц. т.
sin г = —
1 а
(391)
h
г = arc sin — .
* a
(392)
Угол 8 всегда мал, и можно принять, что е = ; тогда по фиг. 101
злучим:
(393)
хе отрезок ОЕ2 — а2 — h2.
Зная углы у и £, вычисляем угол ft как прилежащий угол треугольника
SC, т. е.
ft = Y + е. (394)
одставляя сюда найденные выражения, получим в развернутом виде
ft = arc sin — Н-------h . (395)
а гц.т — —v '
ри легких лопастях угол ft довольно велик: около 14—16°; прн более
1жзлых лопастях его значение лежит обычно в пределах 8—12°.
При гидравлическом демпфере лопасть встанет при висении вертолета
мио на этот угол. При фрикционном же демнфере вследствие трения
/дет иметься некоторый «угол трения* ft/, соответствую ций моменту тре-
ня Mf от затяж<и демпфера. Его можно учесть, подставив в формулу (389)
за значения Ма 4- .И/ и /Ид — И/: по ним получатся два значения н
. н два угла ft! и ft2- Приближенно можно написать, что arc sin—
z, , и тогда формула (395) примет вид:
е. угол ft пропорционален действующему моменту. Отсюда можно по-
зжить, что
ft/ _ Mf
ft — л/
ледовательно, отношение угла трения к углу отклонения лопасти без
рения прибл is стельно поо юоциоиально отношению момента трепля к пере-
зваемому моменту. Обычно загяжта равна 8—12% от крутящего момен-
I М, н тогда при ft ^15° получим:
ледовательно, пои фрикционных демпферах может получиться большая
►асденгровка» соседних лмазгей — до 3°, что может вызвать сильные
1брации нз-за нэсоаланслрозаниосги лопастей у несущего вннта.
' При полете с горизонтальной скоростью аэродинамический момент зави-
сит от угла ф, и лопасть приходит в колебательное движение.' Расчет
этого движения очень сложен из-за трудности определения демпфирующего
момента самой лопасти. Мы этот вопрос здесь рассматривать не будем.
Отметим лишь, что иногда собственный период колебаний лопастей совпа-
дает с числом оборотов винта; тогда получается опасный резоиаис, и ло-
пасти начинают сильно колебаться.
Иногда у лопастей получается резонанс на земле с колебаниями всей
машины около продольной оси вследствие упругости шасси. В этом случае
вертолет начинает сильно качаться около продольной оси и делать прыжки
из стороны в сторону, чем нарушается правильный взлет машины.
§ 5. УГОЛ АТАКИ ПРОФИЛЕЙ
Угол атаки профилей лопасти легко находится, когда известны скорости
Wx и Wy. Впервые эта задача была решена в 1927 г. в классической тео-
рии несущего винта в общем виде. Формулы получаются громоздкие из-за
довольно сложного вида выражений для скоростей Wx и Wu.
Эти углы можно найти и по приближенной теории, и особенно просто
получить их для азимутов ф = 90 и 270°, которые представляют наиболь-
ший интерес для конструктора.
Мы уже получили выражение (354) для (Зе. Для указанных азимутов
получим соответстненио
У 4- -I- 6К г
^ = -^v-----------------(398)
и I _________
. „ К,-вв7
tgPrao- — _ 7 (399)
Угол установки сечения равен, как мы видели в формуле (356),
Ф = Фо — ФапСоэФ- г. n.^v
; 1 (
В нашем упрошенном случае созф — 0, так как ф = 90 и 270°.
Угол атаки равен всегда
ае = ф — & = ф0 — р„ (400)
или в развернутом виде
®е90* — ф —
(401)
Здесь в общем случае ф может быть переменным по радиусу. Таким об-
разом, после аэродинамич.ского расчета, когда все входящие сюда величи-
ны известны, определение угла атаки не представляет никаких затруднений.
Для наглядности полезно строить для азимутов 90 и 270° диаграмму,
дающую углы Зе и ф для разных относительных радиусов, причем справа
даны величины для ф =90°, а слева — для 270°. Она полностью соответ-
ствует диаграммам, приведенным на фнг. 13 и 14 для осевого движения
винта. Примерный внд такой диаграммы при косой обдувке дан на фнг. 102.
На левой части, в точке с абсциссой г = Vt, величина tg [Зе.270о = ое, и угол
Зе270о =- 90°. На правой части, при г = — Vt, получается также tg3flJoe = O
и 3^0= = 90°. _
У обычных несущих вннтов на-всех рабочих радиусах (г = от 1 до 0,30)
угол Зе невелик, и допустимо считать Зе tg Зе! однако у втулки такое
упрощение недопустимо. Прн больших Vt, например = —, уже начи-
__ -j
ная с г — — и до втулки углы делаются очень большими.
Фиг. 102. Углы ср, и ае для сечений лопасти
при ф = 90 и 270°
Угол атаки ае получается как разность ординат и £е; на чертеже
эта разность отмечена штриховкой. Картина получается весьма несиммет-
ричная, и угол атаки у лопасти, идущей вперед, значительно меньше, чем
у лопасти, идущей назад.
На участке с двойной штриховкой у лопасти, идущей назад, получаются
отрицательные углы атаки. Имея продувку профиля, можно сразу найтн ра-
диусы, где возможен срыв потока, н, изменив там угол ср, устранить его.
Впрочем, малые области срыва у втулки не всегда опасны, и встречаются
на практике такие формы лопасти, у которых заведомо имеется срыв, а
вибрации машины не превосходят допустимых пределов.
Напомним, что здесь мы рассматривали этот вопрос лишь с точки зре-
ния упрощенной теории. Классическая теория, излагаемая в § 3 и 4 главы 11.
позволяет найти углы Зе точнее: с учетом работы автомата-перекоса в двух
плоскостях н с учетом угла конусности лопастей. Изменения Va оиа также
не учитывает.
Эпюра С. К. Джевецкого для несущего винта
Формулы (398) и (399) можно применить для графического нахождения
ае, воспользовавшись эпюрой С. К- Джевецкого, построенной им для внн-
тов, работающих в осевой обдувке. Там скорость набегающего потока 1Г
находилась векторным сложением скоростей Уа и гю; здесь же нужно до-
бавить скорости Vt н гр — dj/sini|>, что для выбранных азимутов даст
в безразмерном виде:
(402)
Отложив скорости Va Н Vt, как показано на фиг. 103, откладываем от по-
лученной точки Ог вверх и вниз по вертикали величину бв и разбиваем
Ф.иг. 103. Эпюра С. К. Джевецкого для несущего винта
в косой обдувке
полученный отрезок на части, равные 6бГ. Если любую точку, лежащую
на радиусе несущего винта г = ОА, соединить с точкой В на отрезке бв
с такой же отметкой радиуса г, то линия АВ даст величину н направле-
ние скорости набегающего на элемент лопасти потока. Таким образом, мы
получим Зе и UZ. Нанеся хорды профилей, т. е. линии с наклоном ср, по-
лучим угол атаки как разность ср и Зе- Эпюры С. К. Джевецкого весьма
наглядны, но обладают тем недостатком, что углы Зе У несущего винта
малы, обычно порядка 3—4° на r~ 1, что делает трудным точные отсче-
ты. Для устранения этого недостатка следует вычерчивать эту диаграмму
в достаточно большом масштабе.
Можно также увеличивать вертикальный масштаб скоростей в несколько
раз, ио тогда будут получаться не углы Зе, a tg Зе, и угол атаки нужно
будет находить по формуле
= <р — arc tg. (403)
В случае жестких лопастей, не имеющих махового движения,
W V
о _ Lf
47 — _1_ 1/
W х гш + Vt sin гр
Чо для получения угла бв и выравнивания момента, кренящего несущий
1инт вбок, кривая ф дается несимметричной вследствие действия автомата-
терекоса, движение которого задается в этом случае более сложно, а именно:
Ф = фо — Фап л cos гр — фАп г sin гр,
де фАп х и фдп г — отклонения ф под действием АП в азимутах гр = 0°
гр .-= 90°.
Этот вопрос мы рассмотрим далее в § 2 и 3 главы 13 при разборе
классической теории*.
* Материалы об угле атаки профилей приведены в книге А. Гессоу и Г Мейерса
Аэродинамика вертолета» (Оборочгиз. 1954).
Глава 10
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ
И СРАВНЕНИЕ ВЕРТОЛЕТОВ РАЗНЫХ СХЕМ
§ 1. ОСНОВЫ ПРИБЛИЖЕННОЙ ТЕОРИИ ИНДУКЦИИ для сложных
«КОРОБОК КРЫЛЬЕВ»
Конструктивная форма у современных вертолетов еще не установи-
лась, и многие конструкторы и изобретатели предлагают самые причуд-
ливые системы, состоящие из расположенных в пространстве вннтов и
крыльев.
Выведенные нами в § 3 главы 6 формулы относились к одиночному
изолированному несущему винту. В § 4 главы 6 и § 5 главы 7 было по-
казано, что для расчета сложных комбинаций, несущих винтов пол-
ностью применима хорошо разработанная еще в 1918 г. проф. Л. Пран-
дтлем теория сложных комбинаций крыльев. Дело сводилось к определе-
нию добавочных индуктивных скоростей, возникших от взаимовлияния
винтов и крыльев. Однако учет этих скоростей требует длительных рас-
четов, а во многих случаях для общих соображений и грубых прикидок
желательно иметь еще более простой способ расчета. Такой способ
имеется и давно (с 1918 г.) применяется при расчете коробок крыль-
ев,— это замена вихрей условной струей воздуха, набегающего на не-
сущую систему. Мы пользовались этим методом в § 3 главы 6 для
расчета одиночного крыла и несущего вита; в таких случаях струя
имела круговое поперечное сечение. В случае же комбинаций крыльев
эта струя имеет более сложнхю форму поперечного сечения (см. далее
фиг. 106, 108, 109, 111, 112 и др.).
С точки зрения индукции, как мы уже указывали, безразлично,
чем создана струя — крылом или несущим винтом. Теория индукции
охватывает едиными формулами оба случая.
Прежде чем перейти к рассмотрению теории струи, нужно напом-
нить о двух весьма важных теоремах теории индукции, показывающих,
как нужно рассчитывать коробки крыльев и винтов «с выносом», т. е
с расположенными друг за другом несущими элементами. Заметим, что
все приведенные здесь рассуждения относятся к полету с большой го-
ризонтальной скоростью, когда можно считать УовИ-
Теорема 1. Любую несущую систему с выносом
(фиг. 104) можно заменить системой без выноса, если
сохранить у нее прежнее распределение подъемных
сил, и ее индуктивное сопротивление при этом не
изменится.
Следовательно, для общего индуктивного сопротивления несущест-
венно продольное размещение несущих винтов и крыльев, а важен лишь
вид системы спереди, если смотреть иа нее вдоль вектора скорости Vo.
Теорема 2. Общую среднюю индуктивную скорость
Vi у сложной системы можно
вычислить по импульсу
общей подъемной силы
Y (у нас Т), считая, что
влияние системы про-
стирается на струю
воздуха с эффективным
сечением Fc н шириной,
равной размаху систе-
мы I (фнг. 105).
Теория индукции (см. курсы
теоретической и эксперимен-
тальной аэродинамики) решает
задачу в этом случае, исходя из
Фиг. 104. Эквивалентность коробки крыль- так называемого наивыгодней-
ев с выносом и коробки без выноса Шего закона изменения цирку-
ляции по размаху. В этом слу-
чае вихревая пелена движется
сверху вниз, как твердая пластинка. Это позволяет найти индуктивные
скорости, постоянные по размаху, пользуясь хорошо разработанной
теорией обтекания пластинок потоком, текущим снизу вверх. Было по-
казано (Л. Прандтль, 1918 г.), что в этих условиях подъемную силу
крыла можно рассматривать как результат отклонения ограниченной
струи, охватывающей несущую систему. Так, в случае моноплана
Фиг. 105. Общая струя воздуха у сложной системы
без выноса при больших скоростях полета
(фнг. 160) получается указанное на чертеже обтекание вихревой не
лены, а эквивалентная струя имеет круговое сечение, н ее диаметр-
равен «размаху», т. е. l=2R. Площадь этой струи равна
г. лР лР1
f =
В случае более сложных систем можно получить аналогичным способом
соответствующую площадь сечения эквивалентной струи FCt ио она будет
иметь другую форму и величину сечения, и можно написать, что
<404>
где х, — коэффициент индукции коробки в целом. Заметим еще, что орди-
наты заштрихованной площади на фиг. 106, фиг.
котором масштабе величину циркуляции скорости
вокруг сечения крыла иа данной точке размаха.
Так, для моноплана получается эллиптический за-
кон изменения циркуляции скорости и х( = 1.
Для применения этих формул на практике
нужно иметь готовые величины коэффициента
индукции х( для разных комбинаций крыльев;
вихревая пелена в этом случае повторяет форму
«коробки крыльев», как она видна, если смотреть
иа коробку вдоль скорости полета Vo. Следова-
тельно, для индукции важен вид на коробку спе-
реди, а не в плане. Соосные и продольные сис-
108 и других дают в не-
темы несущих винтов полностью эквивалентны
при горизонтальном полете биплану (фиг. 107).
На фиг. 108 изображено соответствующее обте-
кание двойной вихревой пелены и форма получа-
ющегося эквивалентного сечения струи. Для три-
плана с равной нагрузкой крыльев получим в
этом случае струю, представленную на фиг. 109.
Величина х( в этих случаях очень сильно
зависит от относительной высоты коробки, т. е.
/г , ,
от отношения —; для таких коробок мы будем
обозначать ее через хЛ, чтобы подчеркнуть зави-
Фиг 106. Сечение струи
у моноплана
симзеть х/i от h.
Нафиг. ПО пр1ведед график, дающий зависимость х,, от—для типич-
ных коробок крыльев: для моноплана, для моноплана с концевыми шайба-
Фиг 107 Соосная и продольная схемы, эквивалентные
биплану
ми, для биплана, для триплана с равной нагрузкой крыльев, для триплана с
наивыгоднейшим распределением подъемной силы и для наивыгодизйшей ко-
робки крыльев Последняя может иметь вид нли биплан? с боковыми
Фиг. 108. Сеиение струи
у бипланнык систем
Фиг 109. Сечение струи
у трипланов
Фиг ПО Зависимость х от относительной высоты несущей
системы и ее типа
/—моноплан. 2 — биплан. <3 — триплан с равномерным
распределением подъемной силы. 4 — нанвыгоднейший
триплан 5 — наивыгоднейшая несущая система
стенками, или решетки с бесконечным числом крыльев (фиг. 111). Такими
«решетками» являются многовинтовые вертолеты.
Как мы видим из фиг. ПО, увеличение
высоты коробки заметно увеличивает площадь
струи
F______F 1 л/3____1 лРа
с ~ хл “ хл 4 ~ xh 4
и тем уменьшает индуктивное сопротивление.
Эффект щели
Иногда «крылья» имеют продольную щель,
например в месте крепления их к фюзеляжу;
несущие винты вертолета могут быть расста-
влены в поперечном направлении так, что
между ними получится просвет.
Влияние щели оказывается весьма замет-
ным. Пусть щель (фиг. 112) имеет вели-
чину s, а отдельное крыло имеет размах
тогда общий размах системы будет равен
I =-- 2ZX -F s (406)
Фиг 11. Наивыгоднейшая
несущая система
На фиг. 112 изображено обтекание вихревой пелены у такого крыла, а на
фиг. ИЗ дана величина в зависимости от величины
4=* <407>
Здесь площадь струи уменьшается по сравне’
нию с площадью струи, соответствующей
моноплану с размахом /, a xs > 1.
Ниже приведены величины х.$ в зависимо-
сти от величины S.
S . . . о 0,001 о 01 о,1 1,0
х5 ... 1 1,312 1,489 1,763 2
Для случая сложной коробки крыльев
можно считать, что каждый фактор, т. е.
h s
— и —, действует независимо,
эффективной струи будет равна
Фиг. 112 Сечение струи у крыла
со щелью в центре
площадь
л/2
(408)
где / — полный размах системы.
Обращаясь к фиг. 105, можем написать по-прежнему, что секундный
импульс суммарной силы S71 равен секундному приросту количества дви-
жения, т. е.
ST ~ mvit
где т = pfcVo н у2 = 2wf, и тогда
ЪТ = 2PFJ><.
F,
Но Fc ------ и, следовательно,
xs
S7'“-vV2₽w»°>
ХЛ >
Отсюда получаем среднюю индуктивную скорость всей системы:
2Т G
°' = W' = х‘х’ ~^F,VT •
Средний полный угол скоса потока будет равен
е,
vc G
~2vFlVl ’
и полное индуктивное сопротивление
Gi
2^Ло
(409)
(410)
(411)
Q, = Ge{ . . хдх.
Формулы эти относились к изолированным коробкам крыльев. Фюзеляж,
как показывают опыты, вносит заметное ухудшение в работу коробки
крыльев. В аэродинамическом расчете самолетов эту поправку вводят,
уменьшая размах системы. Будем считать, что влияние фюзеляжа умень-
шает площадь струи и вводит коэффициент потерь на фюзеляж Хф. Тогда
прежние формулы примут вид:
к,. %, хй п
’=vw=vw' <412>
—ь Хф G (413)
Q, = Ge, = G2 (414)
Хф 2pFtV‘
Величина «ф в среднем равна 0,9.
§ 2. ПЕРЕХОД К НЕСУЩИМ ВИНТАМ
Выведенные формулы полностью применимы и для несущих винтов. В
них нужно лишь ввести с помощью величины х = — Ц концевые потери
(см. § 6 главы 2), для чего нужно умножить площадь струи на х н вве-
сти во все формулы, вместо площади Fc, площадь %FC. Так как у крыла
Хф^ х, то можно принять, что для любой комбинации крыльев и несущих
винтов, развивающих общую тягу G—zT и имеющих размах /, можно поль-
зоваться формулами:
- с 1
‘ « 2pFIV„ ’
z Zp/Wf
_°L
Таким образом, формулы индуктивного сопротивления у несущих винтов и
у крыльев практически полностью совпадают.
Для расчета поэтам формулам можно брать х = Хф^0,9, а величину x/t мож-
но находить с помощью графика, приведен-
ного на фиг. 110. Величину хг, оцениваю-
щую эффект щели, для крыльев молено
брать по графику, приведенному на фиг.
113. Однако применять его непосред-
ственно к несущим винтам неудобно, так
как у разнесенных несущих винтов «щель»
имеет переменную ширину, н для приме-
нения этого графика нужно пользоваться
какой-то эквивалентной (или средней)
щелью, что вносит в расчет нечто весьма
условное.
Про це для вычисления величины х,
воспользоваться найденными нами в § 4
главы б и § 5 главы 7 средними ско-
ростями скоса. Пользуясь данными,
(416)
(417)
Фиг 113 Определение эффекта
щели
Приведенными на стр. 392 можем получить величину в зависимо-
сти от /в = ^. Там расчет вели, исходя из размаха системы, равного 2R,
н мы вычисляем скорость ащ по формуле
(220)
а скорость от взаимоиндукции находим по формуле
(418)
Полная индуктивная скорость считалась тогда равной
»< = 01.1 + о2.1 = ( 1 01 i ( 1 + —'i —— . (419)
V "и > \ "1 Л х2р/% '
Теперь мы будем вычислять эту скорость, исходя из полного размаха си-
стемы I = /в + 2R, где /Б — расстояние между втулками, пользуясь фор-
мулой
J0 Б Н Юрьев, т 1
(420)
1ак как результат должен быть в обоих случаях одинаковым, то. сравни-
вая эти формулы для vt, получим:
х2^//0
Отсюда получаем:
Но так как
= _£_ = +2)2
"г ~
где /в —безразмерное расстояние между нтулками, то окончательно по-
лучим:
(421)
Пользуясь дачными, приведенными на стр. 392,
выч Келлэм по этой формуле коэффициент
влияния расстояния zK на индуктивное сопро-
тизлзние в пэ Iерзч юл схеме вертолета (ве-
личину xs) для разных 1в.
1В . . 2,5 2 1.8 1,7
х5 . . . 2,22 1,48 1,05 1,0
ние системы уменьшается и
Эти дачные и построенный на их осно-
вании график (фиг. 114) показывают, что
при расстоянии, близком к 1,8, величина xs
близка к единице. Это значит, что при сближе-
нии несущих винтов индуктивное соиротивле-
при расстоянии между втулками, равно.м при-
мерно 1а = 1,8, «эффект шелк» пропадает и несущие винты работают как
сплошное крыло. Опыты хорошо подтверждают этот вывод, но наивыгод-
нейшее расстояние между втулками получается различное, в зависимости
от формы лопастей, н заключается оно в узких пределах от /в =» 1,8
До 1,6.
Полное сопротивление сложной комбинации крыльев
и несущих винтов
Полисе сопротивлэние сложной несущей системы будет состоять из
двух частей: индуктивного и профильного. Индуктивное сопротивление мо-
жно подсчитывать для всей системы как единого целого ио формула (414),
а профильное сопротивление будем подсчитывать по обычным формулам:
для крыла
для несущих винтов
Тогда
<? = q< + 2Qp-
(422)
§ 3. СРАВНЕНИЕ РАЗЛИЧНЫХ СХЕМ ВЕРТОЛЕТОВ
НА БОЛЬШИХ ГОРИЗОНТАЛЬНЫХ СКОРОСТЯХ ПОЛЕТА
Теория индукции позволяет сравнивать различные системы вертолетов
по потрсбляеусн ими мсщнссти при заданной скорости горизонтального по-
лета. Скорость будем предполагать большой и У0>0,2. Расчет будем ве-
сти в натуральных величинах. Для вычисления мощности будем пользо-
ваться формулой
; 75У = + -
где
А';, = -^(1 + 775 ₽R5“3
есть мощность, затраченная на преодоление профильного сопротивления
вращению несущего винта. Систему будем поиводить к системе без выно-
са; среднюю индуктивную скорость будем обозначать через vt и вычгслять
по формуле (412). Ход расчета по методу мощностей иам известен (фгг.
§ 5, гл. 8). Рассмотрим последовательно типичные схемы вертолетов. При
г винтах следует пользоваться осредиенными величинами по § 5, гл. 7.
1. Обычная «пропульсивная» схема. Для такой схемы (флг. 115), мо
жно, задавшись скоростью полета Уо, вычислить QBP и иайти
При больших скоростях, как изнестно,
Уд - — Уот -р vt - Уо + ut. (4231
Следовательно, потребная мощность двигателя Ум при числе z несущих
виитов, если считать скорости Уд и vt осредиенными, получится из соот-
ношения:
75^V м 1 1 Gv = — GV а -!- 15zNp = — Qupy0 + 7§zNp (424)
и будет равна 75A7. = 1qb^ + ^+^, (425)
30’
В этой формуле первый член в ее правой части дает затрату мощности
двигателя на преодоление вредных сопротивлений, второй — на преодоление
индуктивного сопротивления, а третий—на преодоление профильного соп-
ротивления лопастей. Уравнение дает баланс энергии у пропульсивного
вертолета.
2. Автожнрный режим. При переходе на чисто автожирный режим для
горизоиталы ого полета нужно иметь гребной винт, на который передается
вся мощность двигателя; мощность двигателя для автожнрного полета
Фиг. 115. Схема сил. действующих
на вертолет пропульсивного типа
Фиг. 116 Схема сил, действующих
на вертолет с гребным винтом
на автожирном режиме
обозначим через Nma (фиг. 116). Винт имеет некоторый к. п. д. т); в усло-
виях вертолета, т. е. при сравнительно малых скоростях полета н прн боль-
шом числе детален, попадающих в струю, этот к. п. д. будет не бо-
лее 0,8.
В этих условиях тяга гребного винта будет равна
Условия авторотации будут таковы (см. § 6 главы 8);
757Vma = iGVa + 75Л> 1,2 - 0.
Отсюда находим
х75Лп2.1,2
Va =----------о----;
но так как
Ул = — Уот 4- vt.
(426)
то нз двух псследннх уравнений получаем
Z75-1.2A',/
Gk0 V'o
(427)
Приравняем теперь тягу винта Р в установившемся движении сумме
сопротивлений: вредного QBP и сопротивления несущего винта Gt, т. е.
Р — Qbp + Gr.
Подставив в это равенство найденные значения т и Р, получим:
75М,. x75-l,2W„z v G
n — = Q»P +------|Z—- + — .
VO '0 ^0
ИЛИ
75.У„Л = ~4 75 1,2Npz. (428)
3. Сравнение пропульсивного и автожирного режимов. Вычислим разность
потребных мощностей для разобранных режимов, считая, что у сравнива-
емых вертолетов будут равные вес, диаметры несущих винтов и вредное
сопротивление QBp. Тогда из формул (425) и (428) получаем разность мо-
щностей:
75^-^) = (^-1)^"+^-1)J +
Это выражение можно переписать в таком виде:
—„----? - р----1+0,2 —• 42 9
лм (ч ) ’ ч N„ '
Если в правой части получится нуль, то автожирный и пропульсивный ре-
жимы потребуют одинаковой мощности двигателя. Если правая часть бу-
дет больше нуля, то автожирный режим будет хуже, если меньше нуля,
то автожирный режим будет лучше, чем пропульсивный.
о х N г
Величина 0,2—— мала и мало изменяется. Приняв, что в среднем
М гЛ'
х = 0,92; т| = 0,8 и беря = 0,3, получим эту величину равной
'“м
х z/V,,
0,2— -гт— 0,06. Тогда выражение (429) можно писать в таком виде:
ч
= _ о 94. (430)
Следовательно, автожирный режим будет хуже тогда, когда
~ > 0,94. (431)
У двухвинтовой поперечной схемы обычно ~ 0,9, х = 0,9, т) = 0,8;
tx .
тогда —st 1, т. е. пропульсивный режим выгоднее.
У хороших одновинтовых вертолетов можно принять £ = 0,8 и, остав-
ляя прежние значения х = 0,9 и т) = 0,8, получим
Ех _ 0.8-0,9 _ q g
1) — О,У “ ' ’
т. е. в этом случае на автожириом режиме получается очень небольшой
выигрыш. Здесь не учитывалось увеличение веса машины вследствие установки
гребного винта, удлинительного вала, редуктора, муфты сцепления и т. д.
Некоторые конструкторы предлагали не делать муфты у такого гребного
винта, а просто уменьшать на вертикальном взлете или висении его шаг
до получения нулевой тяги. Однако в этих условиях винт требует до
5—6% от полной мощности двигателя, что сильно ухудшает взлетные ка-
чества вертолета.
Общие выводы
Пропульсивный полет вообще выгоднее полета со специальным гребным
винтом на режиме авторотации. Лишь однозинтовая схема уступает немно-
го автожнрной из-за больших потерь на хвостовой винт и на редуктор.
Однако если учесть увелшениз веса из-за установки гребных винтов, она
не дает большого выигрыша. Лишь в особых случаях установка гребных
винтов на вертолете может быть оправдана, например, прн использовании
реактивного винта для взлета и висения и при переходе на автожирный
режим для горизонтального полета (французская система «Аонэль» и до.)
В некоторых случаях у скоростных вертолетов получаются очень боль-
шие отрицательные углы т и ак, что затрудняет компоновку машины.
При переходе на автожнрный режим эти углы делаются полэж {тельны-
ми и малыми, и компоновка машины облегчается. Иногда предлагают для
этого применять промежуточные режимы, когда и несущий и гребной вин-
ты развивают тягу. В этом случае также улучшается компоновка маши-
ны, ио заметного энергетического выигрыша нет.
§ 4. КРЫЛАТЫЕ ВЕРТОЛЕТЫ
У некоторых вертолетов, делаются крылья для улучшения летных дан-
ных при гсрисснтальюм г.слсте (фгг. 117). И здесь теория индукции по-
зволяет получить ответ о потребнай мощности двигателя. Для вычтслзиия
средней индуктивной скорости система
и здесь приводится к системе без выно-
са, причем мы будем считать, что осред-
ненная подъемная сила несущего вннта
равна Т, а крыла Y; полный вес машины
6 = zT + Y. Рассмотрим горизонтальный
полет.
Уравнение проекции силы на ско
рость полета будет в этом случае
иметь вид:
' Фиг. 117. Схема сил. действующих
в полете па крь-латый вертолет
пропульсивного типа
— zTx — QBp 4- Q,
.1 кр •
Отсюда
Qbo Q-жр Чкр
zT гТ гТ
(432)
Средняя осевая скорость потока у несущего винта равна
Ул = — У<Д + »,
= ~тг + ~^т~ + “гТ“ + и-
«о так как
Q, кР - У v,o ,
Находим теперь потребную мощность двигателя:
75,VM£ = 1 zTVA -Н 75zNp --= QopV'0 -f- ^QpKPV0 +
4--^ Yut + —zTbi -4 75iVpZ.
1 i v,
Замечая, что — Yvt 4- — zTvt = — G, получим окончательно:
75NK = + 4 G«. + + 75;Vp2.
Лэ Xfe X5
Сравнение крылатого вертолета с бескрылым
Написав по-прежнему разность модностей у крылатого и бескрылого
вертолетов, считая у них равными G, QBP, / и Np и учитывая, что при на-
личия крыльев высота « огобки крылыв» h. будет больше, а следовательно,
Хй будет обычно меньше, чем прн чисто вертолетной х'(, получим, обозна-
чив индуктивную скорость у бескрылого вертолета через vlt
£75 (tfM кр — Л\>) = -i QpKPVO - ~ (v, - 4- 75Npz — ~°7-.
Здесь
Ws (*h Л
ut — V! = - — Vl ~ vL I —----1 .
x \ хл J
Отношение --------- дает еозмсжиссть оценить разные величины коэффици-
ента заполнения а7кр и в„ так как у крылатого вертолета можно брать
несколько меньшую величину заполнения.
Окончательно получаем:
£75 (jVm кр — А^м) = — QapVo Ч-Qpk₽Vo4-( -7- — 1 'j 4“
х х х \ хл ;
+ 75^^=^. (434)
В этом случае может получиться заметный выигрыш как в результате уве-
личения высоты «коробки крыльев», вызывающего уменьшение х*, так и
вследствие малого профильного сопротивления крыльев, так как
Qp кр = РкрУ,
где цкр^=0,02— обратное качество крыльев, отнесенное к профильному
сопротивлению (индуктивное сопротивление вошло в третий член формулы
(434)], поэтому, даже сохраняя о7кр = j7, обычю получаем заметный выиг-
рыш. Общий результат зависит'от параметров машины.
В качестве примера возьмем двухвинтовой вертолет со следующими дан-
ными: G = 7000 кг-, Vn = 50 м/сек, Y = 3000 кг, площадь крыльев S =
= 32л?, цкр — • Тогда получим:
г, \/ 3000
хркр — Гцкр — — 60,
т. е. величину очень малую. Индуктивные потери могут уменьшиться бла-
годаря так называемому «эффекту биплаиности» : •= 1, а х = 0,8 прн
— = 01. Сохранив о7 = <з7кр, получим, проделав числовые вычисления
/., ... 33 — 40—120 127 ,.п
(Л/мкр — Л/м) =----£---------- —jj-g л. с. = — 143 л.с., т. е. при
»т G 7000 . .
N„ = — = -j— = 1400л. с.
153
получим выигрыш 100=г= 10%, что позволит увеличить скорость поле-
та примерно на 3%. При этом, однако, крылья увеличат вес н уменьшат
-подъемную силу вертолета на взлете из-за обдувки крыла сверху струей
несущего винта,
У скоростных вертолетов крыло, кроме того, уменьшает нагрузку не-
сущего винта, и винт работает на малых Ст, что в свою очередь устраня-
ет опасность срыва потока у лопастей.
Предлагались еще более сложные схемы вертолетов — с крыльями и
гребиыми винтами. На основании указанных примеров легко рассмотреть с
точностью первого приближения такие схемы и сделать их сравнительный
анализ.
В общем, простые пропульсивные схемы оказываются экономичнее, чем
более сложные. Этим и объясняется их болзе широкое распространение,
чем крылатых схем и схем с гребными винтамн, которые до 1955 г. еще
не вышли из стадии опытных.
§ 5. СРАВНЕНИЕ ВЕРТОЛЕТА И САМОЛЕТА
Этот вопрос представляет большой практический н теоретический инте-
рес, вследствие чзго он н привлзк внимание многих исследователей как у
нас, так и за границей. Первые исследования этого вопроса были сделаны
еще в 1910 г. (проф. Г. Взлльнер и др.). Затем они продолжались до са-
мого последнего времени. Общие выводы этих исследований совпадают:
при равных значениях скорости полета Уо, полетного веса G, размаха
I = D и вредного сопротивления QBp обычный вертолет требует примерно в
2 раза большей мощности двигателя, чем самолет.
Для самолета можно написать баланс мощности в таком виде:
n75,VM.c = QBPVO + СркгЛ + G ^-Vo, (435)
’О
где JVk.c — потребная мощность двигателя для самолета; QpKp — профиль-
vt
ное сопротивление крыльев; G р------индуктивное сопротивление крыльев.
Для вертолета мы имели формулу (425). Разность этих мощностей со-
ставит:
75/Vpz
+ —---------------—•
Это выражение можно переписать еще в таком виде:
Qp. Vn / Гх \ Gv, / Сх \
75 (А'„.е - ад = - 1) + (- -1 ) +
—75Л’2ад <4зе>
Отсюда
/Сх \ х
75 (yvB.e - ад - 75ЛЦ - - 1 j + - 75ад - .
Относительная разность будет такой:
Д'.. с — У',, _ Е* И„СР0 _ A’.zz
Л + 75r|ZVM л„м
Оценим основные величины, входящие в эту формулу:
£ = <7„ = 5 кг/л. с., % 0,3; ? =. 0,85
'* м ;v м
(437)
1
(у одновинтовой схемы £--0,78, х = 0.9, т] =0,85, Цоо = 0,02; скорость!
горизонтального полета берем равной 50 м/сек.}. Тогда получим:
для числа несущих винтов z 2
NMC-NM 0,85-0,9
0,85
0,02-5.50
7о-и,й5
-0’3<^ = -°’36-
1
+
для одновинтовой схемы при £ -= 0,78
Nvc— /V,
= — 0,43.
Следовательно, мощность двигателя самолета иа 36—43% меньше мощно-
сти двигателя вертолета. Если относить мощность двигателя вертолета к
мощности двигателя самолета NM с, то получим для числа несущих винтов
в схеме г 2
Ли
^м.с
1 — и,^ь 0,ь4 1’6’
а для одновинтовой схемы
При этом мы не учитывали, что вредное сопротивление QB? самолета
может быть значительно меньшим, чем вертолета. Более подробные
подсчеты этого сопротивления
и приводят к общепризнанному
выводу о том, что вертолет тре-
бует в 1,8—2 раза большей
мощности, чем самолет.
Причиной этого, как ясно
видно из формулы (437), яв-
ляется большой расход мощно-
сти на преодоление момента
профильного сопротивления са-
мого несущего винта. Умень-
шить и даже совсем устранить
эти потери в горизонтальном
полете можно лишь или убрав
несущий винт внутрь фюзеля-
жа, или обратив его лопасти в
неподвижные крылья. Такие
Фиг. 118. Срзвяепк? самолета (7), вертолета
(2) и крылатого вертолета (3). Дана ско-
рость горизонтального полета п зависимости
от высоты Н Нагрузка па I i с. считалась
одинаковой и равной 5 кг/л. с.
системы называют обычно
«конвертопланами». Возникли
эти системы очень давно, но в
последние 10 лет они снова
начинают привлекать внимание
многих изобретателей и конст-
рукторов. Основной трудностью для их осуществления является пробле-
ма складывания лопастей при полете с большой скоростью, что застав-
ляет делать очень прочные и, следовательно, очень тяжелые механизмы
складывания. Трудной проблемой является также управление такими
машинами, особенно в процессе перехода с вертикального режима по-
лета на самолетный. Тем не меиее, развернувшаяся всюду работа над
такими машинами позволяет надеяться на успех и в этой трудной обла-
сти вертолетостроения.
На фиг. 118 приведен схематический сравнительный график скоро-
стей горизонтального полета вертолета, крылатого вертолета и самолета
прн д~5 кг/л. с. Скорости горизонтального полета даны в зависимости
от высоты полета при одинаковом двигателе для всех трех случаев.
В последние годы были построены по весьма старой схеме самоле
ты-вертолеты (фиг. 119) с очень хорошими данными. Эту схему нельзя
было осуществить с поршневыми двигателями вследствие их большого
удельного веса. Теперь, прн наличии мощных турбовинтовых двигате
лей эта задача оказалась вполне разрешимой, и при ^~2 кг/л. с. удает
ся построить винты, хорошо работающие как на режиме висения, так и
при больших скоростях на режиме гребного винта. Получаются быстро-
ходные машины, со скоростями порядка 7С0 км/час, могущие взлетать и
садиться вертикально. В Америке такие машины были построены в
конце 1954 г. фирмами Локхид н Конвер для военно-морского флота
США.
Фиг. 119. Самолет-вертолет с универсальными винтами
* * *
В заключение отметим, что все выводы здесь носят ориентировочный ха-
рактер, так как они основаны на теории индукции, не учитывающей
ряда факторов, например, неравномерного распределения скоростей по
диску несущего виита и разного веса машин, построенных по разным
схемам. Для более точных выводов необходимо проводить детальные
расчеты сравниваемых вертолетов.
При расчете балансировки этой теорией можно пользоваться лишь
для обших соображений и компоновки машин, пользуясь понятием
сусловной втулки» системы. Более точный расчет нужно вести по мето-
дам, изложенным н § 4 главы 6.
Часть III
КЛАССИЧЕСКАЯ ТЕОРИЯ НЕСУЩЕГО ВИНТА
Глава II
МАХОВОЕ ДВИЖЕНИЕ ЛОПАСТЕЙ
§ 1. ИСТОРИЯ ВОПРОСА
В аэродинамическом расчете (глава 9) мы уже касались вопросов
махового движения. Там оии рассматривались в упрощенном виде *
пон хсловии балансировки машины летчиком на всех режимах полета.
Истинная плоскость вращения считалась перпендикулярной к полной
силе Т. Боковой завал несущего виита, получающийся в этих условиях,
там не рассматривался, так как принималось, что ои устранен летчи-
ком. Это позволило получить все необходимые для аэродинамического
расчета формулы, но не давало возможности более глубоко рассмот-
реть происходящие при маховом движении явления.
В этой части книги мы рассмотрим так называемую классическую
теорию несущего винта. Как мы указали, боковая обдувка несущего
винта впервые была изучена проф. Н. Е Жуковским. Под его руковод-
ством в 1906 г. в Кучинском аэродинамическом институте были прове-
дены опыты в аэродинамической трубе, а в 1909 г. он дал теорию прос-
тейшего элементарного винта, работающего при боковой обдувке.
Впервые тогда было обнаружено сложное воздействие воздуха на несу-
щий винт: получились три силы и три момента.
Дальнейшее продвижение вперед было стелано через 18 лет в Анг-
лии, где Глауэрт и Локк дали в 1927 г. теорию несущего виита авто-
жира. При этом они учли индуктивные скорости и маховое движение
лопастей. В своем анализе они использовали широко применяющийся
теперь метод тригонометрических рядов.
В 1932 г. И. П. Братухин значительно упростил эту теорию и привел
ее к удобной для инженерных расчетов форме. Л1иого улучшений в эгу
теорию внесли А. П. Проскуряков и М. Л. Миль. Последний впервые
изучил неустановившееся движение несущего винта и получил ряд цен-
ных результатов.
А М Михайлов в 1940 г. исследовал теоретически действие автома-
та-перекоса на автожире. В. Е. Касторский и А. М Школьников иссле-
довали экспериментально работу несущего винта вертолета и дали тео-
рию работы автомата-перекоса в этих весьма сложных условиях.
Ряд ценных теоретических исследований провел А. П. Проскуряков
Он углубил теорию несущего винта с АП, исследовал колебания лопа-
стей около вертикальных шарниров и первый начал исследование во-
просов устойчивости движения лопастей. Много работ по теории несу-
щего винта было опубликовано Л. С. Вильдгрубе, разработавшим ряд
вопросов приближенной теории несущего винта вертолета. В результате
всех этих исследований указанная теория приобрела стройный и закон
ценный вид.
Обычно эта теория рассматривает сначала свободное движение
лопастей, что может встретиться лишь на автожирах и на некоторых
многовинтовых схемах вертолетов. Угол же балансировки бв.как пра-
вило, бывает задан, и это упрощает расчеты. Далее в эту теорию вво-
дят эффект АП и РВ и учитывают изменение ширины и закрутку у ло-
пастей При этом формулы очень усложняются.
В. Е. Касторский показал, что эффект АП можно рассматривать
отдельно и прибавлять его к расчетным величинам, полученным для не-
сущего винта со свободными лопастями, с нейтральной установкой
кольца АП.
При расчете вертолетов обычно ограничиваются рядами Фурье с пер-
выми гармониками угла азимута лопастей ф. Если в эти ряды ввести
вторые гармоники, то получаются необычайно сложные формулы с де-
сятками членов. Они весьма ненаглядны и дают малую точ-
ность из-за необходимости при пользовании ими вычислять малые раз-
ности между большими числами Поэтому обычно расчет ведут, ограни-
чиваясь первыми гармониками. Мы также не будем от этого отступать и
высшие гармоники будем применять лишь в некоторых отдельных слу-
чаях
§ 2. СКОРОСТЬ ОБДУВКИ ДИСКА НЕСУЩЕГО ВИНТА
Поток воздуха, пересекающий диск несущего вннта, движется со ско-
ростью I/,. При изучении махового движения ее удобно разлагать на ком-
поненты Уа и Vt, как было указано в § 2 главы 6
При этол считают т^ак:
Va = — VosinaK + Vi (215)
и
V/ —V0cosaK- (216)
Скорость в этом случае можно брать из аэродинамического расчета вер-
тол ета.
В случае сложных схем вертолетов нужно учесть взаимоиндукцию не-
сущих влчтоз, как было указано в § 4 главы 6. Это сводится к добавле-
нию к индуктивной скорости от самоиндукции еще скорости от взаимоин-
дукции, т. е.
п
= i>i + 2 ”»
Мы будем обозначать полную скорость индукции через ц,. Разлагая
скорость V- по связанным осям координат, получим ее компоненты va и v,,
которые и нужно вводить в случае расчета сложных коробок в приведен-
ные формулы (215) и (216), т. е. нужгэ птсать, чго
Va = — Vo sin aK + v,
Vt — Vocos aK vf
(438)
(439)
Скорость vt обычно мала по сравнению с первым членом, и ею обычно
пренебрегают.
Можно в этом случае, как мы видели в § 4 главы 6, пользоваться фор-
мулами (215) и (216), вводя в иих вместо ак угол ак + е, где е— угол
добавочного скоса от взаимоиндукции для данного несущего виита.
§ 3. ЗАДАНИЕ МАХОВОГО ДВИЖЕНИЯ ЛОПАСТЕЙ
Маховое движение лопасти совершается в общем случае в двух плос-
костях. Будем предстазлягь его. рядом Фурь? в таком виде:
3 = с70 —Qicos ф — Z^sin ф — а2соз2ф — 62sin 2ф —
— а3совЗф—638(пЗф. (440>
Здесь 3 — угол взмаха и ф — угол азимута ^см. главу 1 и 9).
Фиг. 120. К вычислению махового движения лопастей
Обычно этот ряд пишется в усеченном виде, и в ием сохраняются лишь
первые гармоники угла азимута ф. Мы будем рассматривать здесь лишь
усеченный ряд, имеющий вид:
3 = <«’о — Qi cos ф — bi sinip. (441)
На фиг. 120 изображено движение лопастей, описываемое этой форму-
лой. При азимуте ф —0° величина Зо° = — ар при ф = 90° величина
Зво0 = й0 — Ьи при ф ~ 180° величина 3J80o =- а0 -|- а, и при ф = 270° вели-
чина Згто0 — а0 4- Ь|. Это движение можно рассматривать как вращение ло-
пастей по конусу с углом конусности а0 вокруг оси Оуд, отклонившейся от.
конструктивной оси Otji назад иа малый угол cii и вбок иа малый угол bv
Знаки всех углов берутся в строгом соответствии с осями координат. По
ложительные направления углов и bi соответствуют тому, что получа-
ется прн свободно машущих лопастях у несущего винта: конус лопастей
(«тюльпан») заваливается назад и в сторону лопастн, идущей вперед (ази-
мут ф = 90°).
Легко найти азимуты фм, при которых получаются максимальная и ми-
нимальная величины угла взмаха р. Для этого дифференцируем выраже-
ние (441) по ф и приравниваем его нулю. Получаем:
— = а-, ьшф —diCosAb — 0.
dip 1 v i 't-
отсюда находим:
(«2)
Следовательно,
rfi = arc tg + 180°. (443)
Таким образом, максимальное и минимальное отклонения лопастей полу-
чатся на диаметре ЛШХ (см. фиг. 120).
При некотором угле ф0 угол отклонения лопастей будет равен углу
конусности а0. Находим его из формулы (441), положив в ией р = а0,
тогда
3 = а0 — cos ф0 — bt sin ф0 = °о
и, следовательно,
tgn>»= 5!"-^- =-21. (444)
Отсюда
ф* = —arc tg у- + 180°. (445)-
Таким образом, отклонения лопастей, равные углу конусности а0, нахо-
дятся на азимутах ф° и ф^± 180°, лежащих на диаметре MVx (см. фиг. 120).
На заштрихованном участке диска лопасть имеет а на остальных
азимутах р<.я0. Так как
tg 1|!о = — ~ = etg (90» — Ц!-),
то диаметры ММг и AWt взаимно перпендикулярны.
В дальнейшем нам при изучении махового движения придется пользо-
ваться производными по времени от угла р. Найдем эти производные:
р = KL = (о, sin Цз — b, cos if) .
Величина =. со, и формула окончательно напишется в таком виде:
3 = = со (aL sin ф—6Lcosip). (446)
Далее находим Вторую производную: __
3 = ~ = ы^соэф -J-ZjiSintp). (447)
Этими формулами мы будем часто пользоваться в дальнейшем.
§ 4. СКОРОСТЬ ОБДУВКИ ЭЛЕМЕНТОВ ЛОПАСТИ
Найдем скорости IF( н обдувки сечения лопасти для данного зна-
чения азимута ф. На фиг. 121 изображена лопасть в положении, заданном
азнмутом ф, спроектированная на кбпстоуктивнюу плоскость вращения Ох^.
Фиг. 121. Скорость обдувки элемента логасти
Справа вверху дана совмеденная проекция лопасти на меридиональную
плоскость лопасти.
Рассмотрим составляюдие скорости относительного движения для эле-
мента лопасти, л^жа ц°го на некотором радиусе г. Угол 3 будем считать
лалым, sin 3 = 3, a cosp^rl.
Скорость 1УХ получится сразу по фиг. 121 и будет равна
Wx = 4- Vt sin ф. (448)
Мы ее уже получили в § 2 главы 7.
Скорость Wu получится из сложения проекций на ось О;уе элемента
шнта следующих скоростей: осевой скорости потока Va> скорости, обрат-
юй скорости взмаха лопасти гр, и пэоэкции скорости Vt, равной, как вид-
ю из чертежа, У/созф-р. Следовательно,
УГу = Va +тЗ + УгРсоэф. (449)
При производстве расчетов удобнее пользоваться безразмерными выра-
жениями для и 1ГУ. Разделив формулы (448) и (449) на Яо>, получим:
=?Н-Vfslnip; (450)
-Ь г -А pjpcosip. (451)
Зная эти скорости, находим угол притекания потока к элементу (фиг. 122)
и получаем:
= (452)
ИЛИ
IF
= arctg
V + 7 А + КЗ cos
(1)
(453)
При малых углах Зе можно пи-
сать приближенно, что
Фиг. 122. Скоростной треугольник
у элемента ломсти и действующие
на тего силы
У а 4- г — 4- V43 COS -ф
О)
(454).
г 4- Vt sin 4)
Угол атакп элемента ае, отсчитываемый
получится по фиг. 122 в таком виде:
от аэродинамической хорды,
□св = фе —ре. (455)
Величину коэффициента подъемной силы будем находить по формуле
/ IF \
Ааг = А (фе — &) = А .
(456)
Такая линейная зависимость получается у профилей лишь до критического
(«посадочного») угла атаки, когда = сутах- Далее наступает срыв потока.
Этот угол у обычных профилей невелик и равен 12—14°.
§5. МЕТОД ОТБРАСЫВАНИЯ ВЫСШИХ ГАРМОНИК
Для дальнейшего развития теории нам придется в найденные выраже-
ния скоростей li<v и подставлять выражения для р, р и р. Тогда полу-
чатся двойные произведения типа sin ф cos ф, sin2 ф cos2 ф и т. д. Во мно-
гие расчетные формулы скорости Ц?х и входят в виде произведений
W'xW'ff и степеней Wx и Ц/J. Тогда при развертывании таких выражений в
3] Б Н Юрьев, т. I
них получатся члены типа sinn фсоз"*ф. Возникает вопрос: как с наиболь-
шей точностью привести эти выражения к виду, содержащему лишь пер-
вые гармоники, т. е. члены с sinip и cos гр? Для этого применяют следую-
щий прием: сначала вычисляют формулу без упрощений и лишь после этого
делают тригонометрические преобразования, заменяющие степени и произве-
дения тригонометрических величин тригонометрическими величинами кратных
дуг, после чего можно отбросить высшие гармоники.
Приведем основные формулы упрощения, которыми мы будем пользо-
ваться в дальнейшем:
1) вт2ф = -^-(1 —cos 2ф)
2) cos2 ф = ~ (1 4- cos 2ф) у- ;
3) sin ф cos ф— 8ш2ф 0;
1 3
4) sin3 ф — — (Зэшф— sin Зф) — sin ф;
1 3
5) cos3 ф — — (3 cos ф + cos Зф) —созф;
6) sin ф cos2 ф = sin ф (1 — sin2 ф) = sin ф — sin3 ф == sin ф -J-
, 1 • о , 1
4—sin Зф ~ Ф.
7) sin2 ф cos ф = cos ф (1 — cos2 ф) cos ф — cos3 ф — ~созф —
1 1
---4- cos Зф cos ф;
8) sin4 ф = -L- (cos 4ф — 4 cos 2ф -г 3) ;
1 3
9) cos4 ф = -g- (cos 4ф 4- 4 cos 2ф 4- 3) -g-:
10) sin2 ф cos2 ф =-- sin2 ф (1 — sin2 ф) = sin2 ф —sin4 гр - -1- = :
11) sin ф cos3 ф — sin ф со$ф (1 — sin2 ф)
= -£- sin 2ф (1--~ cos 2ф)^ 0
и т. д.
Для удобства дальнейших расчетов даем сводную таблицу таких упро-
щений:
Формулы отбрасывания высших гармоник
1
sin2 ф sz -у ;
1
cos2 ф ж ,
sin ф cos ф г 0;
1
sin ф cos2 ф ж sin ip;
1
sin2 ip cos ip z. —£~ cos ip;
sir*3 ф — sinip,
cos3 ip zz — cos ip;
sin4 ip ~"g~ ;
3
cos4 ip zz ;
1
sin2 ip COS2 ip SZ. -g- ;
sin ip cos3 ip cz 0;
sin3 ip cos ip zz 0;
Отбрасывание высших гармоник, естественно, уменьшает точность упро-
щенных формул. Опыты показали, что, например, вторая гармоника угла
взмаха 3 иногда имеет амплитуду порядка 20—30% от первой и она мо-
жет оказать заметное влияние на окончательные результаты вычислений.
Тем не менее очень редко пользуются более длинным рядом, так как при
этом все формулы очень сильно осложняются. Кроме того, эта теория
делает много других упрощающих предположений, например, введение в
расчеты скоростей Va и Vt средним значением, допущение малости угла 3,
вычисление коэффициента подъемной силы профиля по линейной формуле
су — Да£, постоянство сгр, пренебрежение радиальной скоростью обдувки
и т. д.
Все эти допущения очень грубы, но если их не вводить в теорию, то
формулы приобретают крайне громоздкий и мало пригодный для расче-
тов вид.
Эти общие соображения и оправдывают применение в классической тео:
рии приведенных в этом параграфе тригонометрических упрощений.
§ 6. ВЫЧИСЛЕНИЕ РАЗВЕРНУТЫХ ВЫРАЖЕНИИ
ДЛЯ ил. wy> IV’, и Wx Wy
Во многих формулах теории несущего вннта встречаются указанные
комбинации скоростей Wx и Wц. Их удобно вычислять заранее, используя
указанные в предыдущем параграфе формулы упрощения.
Ход вычисления будет следующий: сначала в нужные формулы подста-
вим выражения махового движения, т. е. • •
3 — njcos ф — б^шф (441}
и
р = — (й (а2 sinnjp — bicosip); (446}
затем будем упрощать полученный результат согласно таблице.
Выражение для ]VX. Оно не требует вычислений, так как в него
входит лишь первая гармоника
НЛ = г + Vt sin ф. (44,8)’
31*
Выражение для W !Г В формулу --
= Va г +• V/3 cos Ip (449)
подставляем величины [3 и [3 по формулам (441) н (446) и получаем:
\Vy = Va + rai sin ф — rbi cos ф ф- Vta0 cos ф — cos2 ф — Vtbt sin ф cos ф.
(457)
Сделав упрощения по приведенной выше сводной таблице упрощений, окон-
чательно получаем такой результат:
— _ И/Qi — -
= Va----2---Ь (^ао — cos rai sin Ф- (458)
Выражение для UZ|. •
W* = (г + Vt sin ф)2 = г2 -И 2г Vt sin ф + Vt sin2 ф. (459)
Упрощая, получим:
__ _ 7? __
UZ2 = r2 + _^__р 2r ^sin ф.
При пользовании усеченными выражениями для скоростей следует пом-
нить, что они не точны. Они дают хороший результат для средних по
обороту несущего винта величин, но для мгновенных значений для данно-
го азимута даюг заметную погрешность. Так, полученное выражение дает
для азимута ф° = 0° следующую величину UZ*:
__ _ V:
ivi = гг + ~,
а точная формула (459) дает
Г* = ?.
Скорость Vt доходит в среднем до величины 0,3, н тогда
= о,О45.
На конце лопасти, где г == 1, эта погрешность равна 4,5%. Однако у втул-
ки при г — 0,3 она достигает 50%. Поэтому всегда следует помнить, что
упрощенные формулы классической теории могут иногда давать весьма за-
метные математические погрешности. Особенно это огноснтся к определе-
нию мгновенных снл и моментов, действующих на несущий винт. Здесь
нужно по возможности исходить из точных выражений для IVX и IVP-
Выражение для 1У^. Пользуясь полной формулой (457), дающей
иеусеченное выражение для 1У^, получаем:
UZj = (Уа 4- rat sin ф — fbi cos ф + Vta0 cos ф — Угах cos2 ф —
— Vtbi sin ф cos ф)а = Va + г2а* sin2 ф f£bi cos2 ф 4- V;c?Q cos2 ф 4-
4“ Vtaf cos4 ф - Vtbl sin2 ф cos2 ф + 2Varaj sin ф — 2УдГ&х cos ф 4-
4- 2УаУ/а0 cos ф — 2УаУ/а1 cos3 ф — 2УаУ(&х sin ф cos ф —
— 2г2аД sin ф cos ф 4- 2г Vta^ sin ф cos ф — 2rz'tV/ sin ф cos2 ф —
— 2га1У/Ь1 sin2 ф cos ф — 2гЬхУ/а0 cos2 ф 4~ 2г6хУгах cos3 ф -}-
4- 2rb\Vi sin ф cos2 ф — 2Уга0а1 cos3 ф — 2V|a0bx sin ф cos2 ф 4-
4- 2У<а1д1 sin ф cos3 ф.
С помощью сводной таблицы упрощений производим упрощение этой фор-
мулы, отбрасывая все гармоники, кроме первой, и группируем в скобках
члены с cos ф н с sin. ф. Получаем следующий окончательный результат:
W* =и 4- 4- Ра? + 4 гЧ>1 + ~ ^а» + A V?a; + 4 V& -
— rbjVtao — и<Й,а, 4- (— 21V&1 + ----|-'/iaoai + rb1alVt^cos if +
+ (2l'arai----ra^V, + 4 rb’pt-----sin if. (460)
Как видим, для U/J получается очень длинное выражение, что усложняет
многие формулы классической теории. Если бы мы взяли усеченное выраже-
ние для 1У₽ по формуле (458), то получили бы более простое, ио менее
точное выражение:
=vi+4йа:+4- +4 - ^,а>- F,a«6i~+
+ 4 r*ai + (2VaVla0 — 2УагЬг — Vfa^ + ^аДг) cos if +
4- (2Vara1 — У/iifг) sin ф. (461)
В этом случае число членов в постоянной части уменьшилось с восьми до
семи, в скобках при созф оно осталось прежним, а в скобке у эшф оио
уменьшилось с четырех до двух. Как видно, более точное решение не на-
много сложнее упрощенного.
Выражение для \X/xWy. Это выражение встречается в очень многих
формулах, в частности в уравнении махового движения и в выражении для
Ст при косой обдувке.
Сначала пишем:
1Ух^р = (г 4- Vt sin ф) (ya 4-7ах sin ф —~rbi cos ф 4- Vtao cos ф —
— VtQi cos2 ф — Vtbx sin ф cos ф) = r Va 4- r2Qt sin ф — r2bi cos ф 4-
4- r Vtao cos ip — r Vtaj cos2 ip — r Vtbx sin ip cos ip -r VaVt sin ip 4-
4- гаУ( sin2 ip —rbyt sin ip cos ip 4- Via0 sin ip cos ip — V^i sin ip cos2 ip—
— Vtbi sin3 tp cos ip. (462)
Упрощая по сводной таблице упрощений, получим окончательно:
UZVUZ,; = г Va 4- f Vta0 — r2bi — -у- ) cos ip 4-
+ (Pa, + КУ, — - V;u, )sinx|:. (463)
Заметим, что если бы при вычислении Wx \Vy мы взяли не полное выра-
жение для \Vy по формулам (457), а усеченное выражение (458), то мы
потеряли бы в окончательном результата члены н что
дало бы ошибку в окончательном результате порядка 3—6%.
Из формулы (462) видно, что в точное выражение для WXV/и войдут
третьи гармоники из-за наличия в нем членов sin ip cos2 ip и sin2 ip cosip.
Глава 12
НЕСУЩИЙ ВИНТ
СО СВОБОДНОМАШУЩИМИ ЛОПАСТЯМИ
§ 1. МАХОВОЕ ДВИЖЕНИЕ СВОБОДНОЙ ЛОПАСТИ
Сначала рассмотрим более простой случай свободного движения ло-
пасти, т. е. такого, когда нет работы автомата-перекоса и регулятора
взмаха. Такой случай встречается на автожирах и многовннтовых вер-
толетах.
На фиг. 123 изображена лопасть в некоторый момент движения в мери-
диональной плоскости. Выделим на лопасти элемент, на радиусе г длиной
по радиусу dr и массой dm. На этот элемент будут действовать силы:
Фиг. 126 Схема сил, действующих на элемент
лопасти в плоскости потока
элементарная тяга dTe, элементарная центробежная сяла~dFe = dm гео2, вес
элемента dGn = gdm и сила инерции от взмаха PH=dmr$. Направление
сил показано на фиг. 123 стрелками.
Мы можем написать теперь для лопасти выражение момента, действую-
щего относительно горизонтального шарнира лопасти. Этот момент должен
быть равным нулю, так как шарнир не может передавать моменты. Шар-
нир будем считать расположенным на оси главного вала. Из чертежа ви-
дим, что
/Игш рГ. r~$dF‘ r~SdP" r = 0- (464)
ОС 0 0
Здесь
я
I) ^dTe г - МА — аэродинамический момент;
о
R £
2) гр = 3 ( (dm гео2) г — ЗоЛ/ — момент центробежной силы,
о о
R.
где J = у dm г2 — момент инерции всей лопасти относительно ГШ;
о
R
3) J dGj! г = ОлГц.т — момент от силы веса лопасти Ол (гц.т — радиус ее
о
центра тяжести);
л л
4) J dPK г = ^(dtn гр) г — —момент от сил инерции махового движения,
о о
Теперь выражение (464) можно написать в таком виде:
R *
Мгш = J dTe г - — Олга.т — jV = 0. (465)
о
Отсюда аэродинамический момент МА равен
МА = jjdTe r=Jrf (|3 + А) + ОлгЦгТ. (466)
о
Для удобства дальнейших расчетов мы будем писать формулу (466) в
безразмерном виде, введя в нее коэффициент аэродинамического момента
лопасти тА относительно горизонтального шарнира. Следовательно, мы бу-
дем писать:
МА = тА pW2. (467)
Тогда формула (466) может быть переписана в виде:
тл PRW ( 0 + jr) + Ол..,-
Отсюда
тА = -А_ ((3 -F -4'1 -г ^л''?,т •
At>7 Ab7pP6 \ & ' Лс7р/?5<02
Множитель —_- при тА выгодно оставить, так как при вычислении коэф-
фициента тА перед ним получается обратная величина , которая и со-
кращается.
Вводим в формулу две важных безразмерных величины:
т„ - (468)
— так называемую безразмерную инерционную
лопасти, и
_ °ЛГЦ.Т
Тв Joj2
характеристику
(469)
— безразмерную весовую характеристику лопасти. С помощью
этих величин пишем уравнение махового движения в таком виде:
тА
Ab?
(470)
Аэродинамический момент при сохранении первых гармоник
В случае сохранения в формулах лишь первых гармоник, аэроди-
намический момент МА лопасти остается неизменным
при всех азимутах.
Для доказательства этого подставляем в формулу (466) выражения для
р и [3 при сохранении первых гармоник и получаем:
я
МА = ^dTe г = J®2 (aQ — a, cos гр — bj sin гр -|- сц cos ip + b{ sin гр) -p блГц.т.
о
Отсюда
R
MA = ^dTer = a0a2J 4-блгц.т. (471)
0
Из этой формулы выпал азимут гр, и, следовательно, МА = const во время
всего оборота несущего вннта.
В безразмерном виде эта формула написалась бы в таком виде:
При учете высших гармоник такая простая зависимость не получается.
Вычисление аэродинамического момента
Найдем развернутое выражение для аэродинамического момента МА-
Для этого сначала найдем выражение для элементарной тяги dTe. Пользу-
ясь уже применявшимся в § 2 главы 9 приемом, пишем:
dYe % dTe = су -£-b dr = A (ере — Ре) ~~ b dr.
Вводя сюда и раскрывая скобки, получим:
dTe = A UZ..UZ,) dr. (473)
Следовательно, элементарный момент будет равен
ЛМа = dTe г = А?- — w.W,) br dr.
Переходим к безразмерным величинам, разделив обе части найденного
выражения иа -^-рЯ5со2, после чего получим:
dmA = — WxW„)7d7.
Здесь через dmA обозначен коэффициент аэродинамического момента эле-
мента относительно ГШ. Переходя от элемента ко всей лопасти и, поль-
зуясь готовыми усеченными выражениями для и WjWy, получаем-
тА = 4$ Ш®7’- WxW„)7d7 = -А 4 I" -
— ( r Vta0 — r2bj--- Vjb-^ cos ф —
— (r2^ + VaVf--— 2r Vt<pe) sin ipj r dr. (474)
Это выражение применимо для любых лопастей с любым законом измене-
ния b и <ре по радиусу лопасти. В него нужно лишь перед интегрированием
подставить зависимости
b=fb (г) и фг = (г).
Сначала рассмотрим простейшую лопасть, имеющую b — b7 = const и
<Ре = <Р? = const. Для нее получим после интегрирования по г:
тл = 4 [4 ч”+4- - 4 - (4 г'а» - 4 - 4 cos -
—(4 «I ч- 4 4 ^ia‘—4 sin 4
Возвращаемся теперь к уравнению махового движения (472). Получим-
4 ч>7+4 ч17®' —г у* ~ (4?'а» ~ 4ь> —г ^bi)cos
- (4Я> + 4^>й-------г VJ01 + 4 V,(p,) sin Ч> - 4 + 4 • (475)
Последнее уравнение и решает задачу о маховом движении. Для получения
полной характеристики этого движения нам нужно найти три неизвест-
и ы х: ац, ах н bt. Оказывается, что полученное тригонометрическое уравнение
распадается на три независимых. Действительно, оно должно соблюдаться
для всех значений азимута ф, а это возможно лишь тогда, когда множн
тели при sin ф и созф равны нулю и равны постоянные члены в правой и
левой частях формулы (475).
Следовательно, уравнение распадается на следующие три:
4^о-4ь,- 4^. о.
4 “i+4- v‘Vt -4- l/-ui 4
4^+4'^-4^ -4+4-
Решая эти уравнения относительно а0, ах и blf получим
".’т.4^1 +^)-44~тв; (476>
27, (4ф,- 4
а, =--------, (477)
Полученные формулы полностью описывают маховое движение лопастей
с точностью до первых гармоник. Этими формулами как приближенными
можно пользоваться и для лопастей любой формы, вводя в формулы Ь? и
Ф-, взятые на г = 0,7. Точность получается при этом достаточная для
расчетов первого приближения.
Рассмотрим более подробно полученные формулы. Угол конусности at
в формуле (476) зависит от режима полета, а при выводе приближенного
значения а0 в § 3 главы 9 мы считаем его постоянным. Дело в том, что
там мы считали постоянной тягу несущего винта, равную почти точно весу
машины, а здесь эта тяга изменяется со скоростью полета. Ограничение
на тягу в ней не наложено. На самом деле, летчик, сохраняя величину Ст,
измеииет в полете угол ф? и const.
Угол продольного завала оси конуса лопастей аг не зависит от угла
конусности а0.
Угол бокового завала bt прямо пропорционален углу конусности а0.
— 1
Величина bt на больших скоростях полета вертолета, когда — , равна
1
примерно — aQ. Боковой завал bi зависит лишь от тангенциальной скорости
Vi и ие зависит от аксиальной скорости Уа.
§ 2. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА ТЯГИ Ст
Мы уже получили выражение для элементарной силы тягн:
dT„ = A(<feWx — WxWf}^dr. (473)
Подставив в него dTe = dCT1 -у рА>4(4, где Сп и dCn относятся к одной
лэпэсти, мы получим после сокращений:
dCn = - — iPx^„) b dr.
Л
Отсюда
Сп = — ? (<Р,^ — ИОД b dr.
Л J
0
Обычно в классической теории интегрируют в пределах г — 0 и г -= 1,
хотя было бы правильнее вести интегрирование в пределах от до £2-
как это мы делали ранее.
Примем опять, что b = b7 = const и <рв = <р7 = const и вычислим выра-
жение для Ст, пользуясь готовыми выражениями для и
Получим:
СГ1 = А ь7 [ (ф,Wi- иШ,)37 = а 6, f [ф,? + 1 yfo - Wa -
л J л J 2
о о
— (rVta„ — ггЬ, — -^Vjb, j cos if - S pa, 4- vav, — -1 vja, —
- 2rV/(p7)sin ip J dr. (479>
Интегрируя по г, получаем;
/- Ab? I 1 > 1 Г72 1 «7
CT, — n [ 3 4,7 + 2 '/'4’7 2
— (y Vta0 — jb, — 1 V?b,)cosif —
— (01 + VaVt — у V?a, — V(<p7 ) sin if J . (480}
Эта формула показывает, что сила тяги, создаваемая одной лопастью, не-
постоянна и изменяется по закону
СГ1 == Ао— Дсоэф—Bjsinip, (481)
где коэффициенты Ао, Ах и Вг — сокращенные обозначения многочленов в
формуле (480). Для получения средней тягн за один оборот несущего вин-
та при числе лопастей, равном k, нужно воспользоваться формулой осред-
нения (см. § 2 главы 9), т. е.
CT=k—[C r,dif. (482}
2л J 1
о
рн таком интегрирования в выражении (480) пропадут члены с sin гр и
cosxp и останется следующее выражение:
Cr»i4O,[<p7(A + iw)-^], (483)
де ~ — коэффициент заполнения несущего винта.
Эта формула является основной в теории несущего винта. Мы получи-
ли в § 2 главы 9 очень близкие выражения 1см. формулу (364)], исходя
из заданного значения бБ.
Формулой (483) пользуются и для несущих винтов с переменными по
радиусу величинами b и <р, вводя в нее Ь7 и <р7. Этот прием дает лишь
первое приближение.
Обычно величина Ст известна из аэродинамического расчета, и форму-
лой (483) пользуются для нахождения угла установки лопастей <р7. Решая
уравнение (483) относительно ср7, получим:
(484)
Влияние числа лопастей иа тягу
У вертолетов встречается самое различное число лопастей, начиная от
одной.
Мгновенная тяга лопасти пропорциональна Сг ; следовательно, тяга из-
меняется по закону, выражаемому формулой (481,) т. е. она очень сильно
Фиг. 124. Изменения силы тяги на разных азимутах
для несущих винтов с числом лопастей Л = |, 2 и 3
при учсте высших гармоник
изменяется в зависимости от азимута. При двух лопастях мгновенная сум-
марная тяга будет равна
= Ао — Л1 costp — Bt sin ф + Ао — Дсо5(ф° + 180э) —
— sin (ф° 4- 180°) = 2Ап — Ау созф — Bt sin ф ф-
+ Ах cos ф ф- Bi sin ф -= 2А0.
Таким образом, с точностью до первых гармоник уже при двухлопаст-
ном несущем винте переменные части в выражении тяги взаимно уравно-
вешиваются, и на втулку передается постоянная тяга. Легко убедиться в
том, что при большем числе лопастей получается такой же эффект. На
самом деле существуют высшие гармоники, и прн двух лопастях сила тяги
будет несколько пульсировать. Так как в формулу (462), дающую произ-
ведение входят третьи гармоники, если даже само маховое движе-
ние задано первой гармоникой, относительное постоянство тяги получается
лишь при трех и более лопастях. Следует помнить, что пульсация тяги мо-
жет вызвать вибрацию в различных деталях вертолета, поэтому у несуще-
го винта со свободномашущими лопастями нужно применять не менее трех
лопастей. Как увидим далее, этого же результата можно достигнуть и при
двух лопастях с качающейся втулкой.
На фиг. 124 приведена полная сила тяги в зависимости от азимута пер-
вой лопасти для числа лопастей k — 1, 2 и 3. Средняя тяга принята рав-
ной единице.
На вопросе уравновешивания гармоник на втулке несущего винта мы
подробнее остановимся в § 4 главы 15.
§ 3. СИЛЫ И МОМЕНТЫ, ДЕЙСТВУЮЩИЕ НА ЛОПАСТИ
И НА НЕСУЩИЙ ВИНТ В ЦЕЛОМ
Вычислим теперь силы, действующие на элемент лопасти (фиг. 125).
Подъемная сила элемента dYе действует перпендикулярно к продоль-
ной оси лопасти и к скорости набегающего на элемент потока Wj. Следо-
вательно, она отклонена на угол 3 от оси 0ух в меридиональной плоскости
и на угол Зе от оси Оух в плоскости нормального к оси лопасти сечения
(фиг. 125). Так как углы 3 и Зе малы, то можно принять, что sin 3 = 3,
sin Зе = Зе, cosp-= 1 и cos За - 1- Такое допущение всегда делается в тео-
рии несущего винта. В этом случае проекции силы тяги на ось 0ух и на
направление окружной скорости будут равны:
dTe -=dYe cos Зе = dYe, (485)
dYe cos Зе cos 3 dTe cos 3 ~ dTe
dQie=dYe Sin Зе = Зе ^Ye, . (486)
где dTe — тяга элемента и dQle — его индуктивное сопротивление. Кроме
того, на элементе возникнет сила профильного сопротивления dQpe, дей-
ствующая по направлению скорости Ее проекцию на ось 0ух можно
считать равной нулю, так как сила dQpe мала и мал угол Зе (см. § 4 гла-
вы 2). Ее проекция на плоскость вращения будет равна самой силе и будет
направлена по окружной скорости элемента.
Таким образом, на элемент лопасти будут действовать следующие силы:
по оси 0yt проекция силы dYe~^dTs,
по оси лопасти ОМ сила fidTe и
по направлению окружной скорости U окружная сила
dQue dTe sin Зе + dQpe Зе dTe -Ь dQpe.
Для расчетов нам нужны проекции этих сил на связанные оси коорди-
нат OXji/jZp Пользуясь фиг. 125, можем сразу написать для этих сил, со-
блюдая правило знаков, следующие выражения:
Фи: 125. Схема сил, действующих на элемент лспасти
dX} ~ —dQpe sin ф — dTe sinip -h $dTe cos ф; (487)
dYr = dTe. (488)
dZx = — dQpe созф — Зе dTe cos ф — $dTe simp. (489)
Элементарные аэродинамические моменты
Для вычисления этих моментов воспользуемся основными формулами
механики, служащими для определения компонентов момента по компонен-
там силы, т. е.
= yidZl—z1dY^,
dMyr = - dMK - r dQUe = - r dQpe - 3e dTe - r;
dMzl - XidY-t — yv dXx.
(490)
силы мы уже нашли, а координаты xL, и zx легко найти по фиг. 125.
Они таковы:
Xi = — г cos ф; )
У1 = г^; (491)
гг — г sin гр. J
Элементарные силы dTe и dQpe, входящие во все формулы, получим, рас-
смотрев элемент лопасти как крыло шириной b и длиной по радиусу dr.
Тогда получим:
р№2 { № \ pW?2
dTedYe — Су b dr = A — b dr =
= 4^(<pM-riW's)(lr (492)
И
pW*
dQpe = Схр —bdr. (493)
Дальнейший ход вычисления полных сил и моментов ясен: нужно в
формулы (487) — (489) подставить найденные значения dTe и dQpe и вве-
сти в них развернутые выражения для скоростей IVX, WXV/у, Wy и для уг-
лов и р. После упрощения получается развернутое выражение для эле-
ментарных сил. Полные мгновенные силы получаются путем интегрирова-
ния этих выражений по г. Для получения средних за оборот несущего винта
сил нужно проинтегрировать эти выражения для &-лопастного несущего
винта, умножив их предварительно на <2ф, по ф в пределах от 0 до 2л и
разделить результаты на 2л. Мы этот процесс «осреднения» проделали со
всеми подробностями при вычислении Ст и CQ в § 2 главы 9. Поэтому
здесь мы не будем производить подробных выкладок и дадим готовые ре-
зультаты, приведя их к безразмерной форме. В приведенных здесь форму-
лах лопасть имела <рв = <р, = const и b = b1 = const.
Коэффициент продольной силы Qi, действующей по оси
9x1.
Знак «-]-» у нее совпадает с направлением скорости потока Vt:
Св1 = -с« = А°’ |Р<(+ ^Va) +1 (1 + jVi)-
+ 1 (494)
4 о 4 J
Коэффициент силы тяги Г. Этот коэффициент был нами получен
з выражения (483).
Коэффициент боковой силы Zx. Знак «-{-» берем при направле-
ии силы ПО ОСИ Ozx;
Ся - Ла7 Г 7 у a„VaV/ 7 у Via^ 7
7 aiW - + Ч>7 - J -Ф у Ь, 7 | б.Р?) J . (495)
Напомним, что некоторые наши авторы придерживаются американских
•означений и пишут коэффициенты продольной силы в виде Сн (индекс от
ова «Head» — лобовое сопротивление), и коэффициент боковой силы в виде
? (индекс от слова «Side» — боковой). Скорости потока в этих случаях обо-
зиачаются так:
Va = —• л (иногда х)
и
Мы здесь строго придерживаемся обозначений, связанных с координатами,
и не нарушаем правил знаков.
Аэродинамические моменты, действующие на несущий винт
Проделав такие же вычисления для моментов, получим, исходя из тех
же предположений, следующие коэффициенты:
Коэффициент момента крена тХ1. Ввиду того что угол взмаха
В мал, а следовательно, мало плечо yt силы dZlt выражение для d\4xl при-
мет вид:
(495)
тогда
тЛ1 = — Аа, ^1ф7 —— ia, (1 — i . (496)
Коэффициент момеита рыскания:
тп = — m„ = — Аз, gp (' + + у Фт^» — у ~
Г 1 2 , 1,2. 1 .-уа / 2 . 3 з , 1 , з\
1 1 Т7'(а" + та1 + 761)^
^£у,(_й1уа_|аА VI. (497)
\ 3 ) J )
Мы уже получили величину коэффициента крутящего момеита (он же коэф-
фициент мощности) — формулы (289) и (294) в главе 7. Там мы исходили
из общих механических принципов. При выводе последней формулы (497)
мы не учитывали концевых потерь и считали движение лопастей совершен-
но свободным; тогда бь =- av Если формулу (497) переписать в таком виде:
™« = ^(1 VVI) + А3;{[ф, ( ± + Ай)-1р„]ув-
- aiCT Vt + | V^-ya + atCrVt-^ VaVtat + | Vtajh -
1 2 1/2 1 Tri t 2. ?’ 2 I 1 L2 \ I 'J
--------------Qi---bt----V «o”i— a! H----bi] [ J-,
то оказывается, что выражение в последних квадратных скобках обычно
очень мало по сравнению с первыми, и его можно отбросить. Но тогда по-
лучится
(1 + Vl) -t- CTVa - afirVt.
32 Б. Н. Юоьев т Т
Если в него ввести коэффициент концевых потерь л/.; то получится прежнее
выражение. Следовательно, простая формула (289), которой мы широко
пользовались в аэродинамическом расчете, может быть получена и из клас-
сической теории. Можно показать, что и форма лопасти мало сказывается
иа окончательном результате, если брать схр ио яа г = 0,7. Следователь-
но, формулу (289) можно считать универсальной, особенно если ее уточ-
нять с помощью взятых из опытов значений схр1 и х.
Коэффициент момента тангажа т21. Аналогично вычислению
коэффициента момента тГ1, считаем dM?i --- XidYi и тогда получаем:
(498)
Все эти формулы выведены для свободномашущей лопасти с b ~ const
и <р = const. Ими иногда пользуются для лопастей любой формы и вводят
в иих Ь1 и ф7. В этом случае формулы дают лишь первое приближение к
действительным значениям аэродинамических коэффициентов. Мгновенное
значение коэффициентов сил и моментов для одной лопасти мы здесь не
приводим ввиду крайней громоздкости получающихся результатов при со-
хранении двух и более гапмоник. Приводить же значения для одной лопа-
сти с первыми гармониками бесполезно, так как при вычислении мгновен-
ной величины полных сил и моментов Для всего несущего виита с /г лопа-
стями первые гармоники пропадают, и все зависит от вторых, третьих, а
иногда и от еще более высших гармоник.
Кроме того, окончательные формулы зависят от закона изменения ши-
рины лопасти b=fi)(Y), крутки лопасти, коэффициента передачи в меха-
низме РВ и установки автомата-перекоса п ср2. Поэтому в тех случаях,
когда требуются такие коэффициенты, иужно лишь проделать для данного
частного случая уже описанный при получении Ст путь. При этом полу-
чаются очень длинные формулы, содержащие иногда до сотни членов. Мы
дадим лишь мгновенное значение тк с точностью до первых гармоник, так
как им приходится пользоваться при расчете втулок. При это.м берем усе-
ченное значение W*, и
= (2. схр -И ~ сх,У1 г А ^<р7 ~ К, — ~ V‘ — У 7oi7<ai +
+ И»: + — Vial — ~ Vta^pi г 61 т 1 +
о 4 3 о о J
+ Л Г- ФтК/Оо — ф7 —bi — -|- — УаЬ1 ф
L з 4 з
+ 4 — т I COS Ф а Л I ~7/ -г 0^7 +
4 3 J I Л 3 3
+ ~?VaVt'^— + т'7,а‘ Isin’l’}-<”и. (499),
2 4 3 3 J J л
§ 4. ОБТЕКАНИЕ СВОБОДНОМАШУЩИХ ЛОПАСТЕЙ
ПО КЛАССИЧЕСКОЙ ТЕОРИИ
Мы уже рассмотрели в главе 9 обтекание профилей для несвободных ло-
пастей. Там мы считали, что у несущего винта угол dR задан, и летчик с
помощью АТ осуществляет это условие. При этом мы ограничивались по-
ложениями лопасти на азимутах ф — 90° и ф — 270°.
В классической теории можно найти угол атаки на лобом азимуте и
радиусе. Для определения угла X мы уже имел! формулы (453) и (454).
Подставив в формулу (453) выражения (441) и (446), получим:
& -
Va + г (Qi sin — £»i cos ф) + V(a0 cos ip — Vtax cos2 ip ~Vtbi sin ip cos ip
r -j- Vf Sin ip
(500)
Часто пользуются усеченным выражением, беря скорости и и/у по
§ 6 главы 11. Тогда получают:
___ VjQj ---------- -- -----------
V —_L______4- (Vta0 —rbt) cos ip+ rat sin ip
™ Vy sin ip
(501)
Однако последняя формула значи-
тельно менее точна, чем первая,
так как в нее входят дополнитель-
ные слагаемые, не имеющие физи-
ческого смысла для мгновенных
значений величии. Поэтому для
определения следует пользовать-
ся формулой (500).
Зная угол установки лопастей,
например, считая, что фс — Ф —
= const, получаем угол атаки эле-
мента
ае =- ф<- — Ре-
По формуле (500) можно под-
считать угол атаки профиля на
любом радиусе г и на любом ази-
муте ф. Результаты получаются
довольно близкие к действительно-
сти за исключением сечений, лежа-
щих близко к втулке.
На фиг. 126 даны на диске линии
постоянного значения угла атаки ае.
В общем наименьшие углы атаки
а наибольшие — на ф — 270°. Это и
рамм, приведенных на фиг. 102 и 10.
Фиг 126. Углы атаки у несущего винта
по Р. А Янгу для одного частного
случая:
"bi = 0,06, Vt - 0.2;
р = 11,8 кг/м*, лопасти с фанерным
покрытием
лежат приблизительно на ф— 90°,
было учтено при построении диаг-
§ 5. УЧЕТ КОНЦЕВЫХ ПОТЕРЬ В ТЕОРИИ НЕСУЩЕГО ВИНТА
Самым простым приемом учета концевых потерь является введение по-
правочных множителей и, которые можно ввести во все формулы, дающие
те или другие расчетные величины. Эти коэффициенты можно брать для
данного типа несущего винта из опытов, и тогда получаемые по таким фор-
мулам данные будут достаточно точными. В них в неявном виде войдут и
другие поправки.
Более рациональным методом является отбрасывание при интегрировании
по радиусу г элементарных сил и моментов концов лопастей. Этот прием
ведет свое начало из классических работ Н. Е. Жуковского и В. П. Вет-
чинкина. В случае его применения интегрирование сил ведется в пределах
радиусов г = и г = Мы широко пользовались этими приемами. При
этом в окончательном результате получаются множители вида с> — £х;
£2 — й; Й/г— йЛ и т. д. Обычно наибольшее влияние оказывают множи-
тели Й — й и Й — й; они обычно близки по величине и мы их обозначим
буквой х. Не представляет никакого труда вводить эти множители во все
формулы при интегрировании по г. Однако мы это делали не всегда из-за
громоздкости получающихся при этом результатов и предлагали применять
(по первому способу) простые поправочные множители.
В американской и английской литературе встречается еще один прием,
основанный на понятии «эффективный радиус винта». Под ним понимается
величина
/?эф = BR,
где В — коэффициент концевых потерь. В этом случае при интегрировании
по г берут пределы нуль и В. По сути дела, эта величина является отвле-
ченным радиусом s2. взятым с некоторым уменьшением, для оценки неучи-
тываемой центральной нерабочей части, равной й- Этот прием весьма ис-
кусственен, так как ^«=0,2—0,25, а й^0,98, т. е. центральная нера-
бочая часть занимает гораздо большее протяжение, чем коицевая.
При использовании этого приема в окончательный результат всех фор-
мул входит вместо гп величина Вп. Мы этим способом пользоваться не бу-
дем ввиду его явной неточности.
Заметим еще следующее: в главе 8 мы показали, что концевые потери
зависят от угла атаки профиля. У несущего винта при косой обдувке угол
атаки изменяется в весьма широких пределах и концевые потери зависят от
азимутального положения лопастей. Учет этого трудно осуществить, почему
и приходится пользоваться описанными простейшими приемами такого учета.
Глава 13
РАБОТА НЕСУЩЕГО ВИНТА С АВТОМАТОМ-ПЕРЕКОСОМ
И РЕГУЛЯТОРОМ ВЗМАХА
§ I. КИНЕМАТИКА АВТОМАТА-ПЕРЕКОСА
И РЕГУЛЯТОРА ВЗМАХА
Большинство современвых вертолетов имеют АП и РВ. Их”действие
сказывается на угле установки лопастей. Все они работают’по одному в
тому же принципу, и иам достаточво разобрать длы вывода вужных фор-
мул простейшую форму таких устройств, приведенную в перспективе и
в плайе (фиг. 127 и 128).
Фиг. 127. Схема простейшего механизма Ф-иг. 128 Схема механизма АП и РВ
АП с суммирующим рычагом снизу в плане
Лопасть Л имеет поводок с длиной е (кривошип), соединенвый тя-
гой tx с управляющей точкой А. Эга точка находится ва конце суммирую-
щего рычага S. Шарвир 1 у этого рычага может подниматься и опускаться
с помощью муфты М (с прорезью), связанной с рычагом измеиевия общего
шага лопастей. Шарнир 2 соединен тягой t2 с внутренним кольцом АП.
что позволяет при наклонах этого кольца передать на суммирующий рычаг .S
циклическое изменение шага. В точке А получается сумма или разность
этих команд.
Пусть плоскость кольца АП отклонена иа фиг. 128 иа_некоторый угол
назад и вправо (положительные вращения). Углы эти будем считать ма-
лыми. В результате этих поворотов плоскость диска, описываемого точкой А,
лежащей иа радиусе гд, наклонится иа некоторый угол 9 около линии ТТ\,
образующей угол т с осью Ох,.
Таким образом, летчик, управляя машиной, может поднимать и опускать
точку А с помощью механизма общего шага иа некоторую высоту hH. от
нейтрального положения и поворачивать кольцо АП, задавая его положе-
ние двумя углами т и 0. Эти три величины: /?ш, т и 0 назовем установ-
кой АП.
При нейтральном положении кольца АП угол установки лопастей, ко-
торый обычно берут на г 0,7, равен некоторой величине Рассмотрим
сначала лопасть без РВ. Найдем изменение высоты точки А при установке
кольца АП, заданной углами тиО (см. фиг. 128). Пусть положение лопа-
сти задано углом азимута -ф, угол называется углом конструктивного опе-
режения поводка, а т — угол азимутальной установки кольца.
Опустим из точти А на линию Т1\ перпендикуляр AN (см. фиг. 128).
Его длина будет равна r^sin(—ту -}- ф). Так как описываемый радиу-
сом ОА диск наклонен по отношению к его нейтральному положению иа
малый угол 0, то точка А опустится на высоту, равную
гд 0 sin (— т + Y -|- ф).
Следовательно, подъем точки А будет при установках АП, заданных ве-
гичииами /гш, т и 0, равен
Лл = hlt, — rA0 sin (— т -Н у 4- ф).
5 результате подъема точки А лопасть повернется иа малый угол фАп,
эавный
h, ГД
фАП -- — - --------—0sin(— т + т -н ф).
Эту формулу можно переписать, заменив в ней синус суммы его разверну-
•ым выражением; тогда получим:
Фап = -------~ 0 sin ф cos (у — т)-^0 cos ф sin (у — т).
Вводим следующие обозначения: фш — угол изменения шага.
— О sin (у — т) -.ZL (р¥ — угол поворота лопасти от действия АП, когда ф = 0.
О— cos (у— т) — <р2 — угол поворота лопасти от действия АП, когда
> =90°.
Теперь предыдущее выражение примет вид:
фдп = фш — Фх COS ф — ф2 sin ф. (502)
1,и этом угол установки характерного сечеиия будет равен
Ф" = ЧЧ» + ФАП = <Р;.О + <Рш — фл COS ф — фг sin ф. (503)
Для лопасти с круткой фкр нужно знать закон изменения фкр в зависи-
мости от г. Простейшей зависимостью является линейная зависимость вида
Ф^== Ф(0,7-7) (504)
и
фг = Ф7 + Ф(0,7—7), (505)
где Ф — коэффициент закрутки.
Теперь мы можем окончательно написать для любого радиуса г и угла
азимута ф для лопасти без регулятора взмаха следующее выражение:
Фе Фт.о 4- фщ — фхcosip — фг5Ш1р + Ф (0,7 — г). (506)
Случай, когда имеется регулятор взмаха
При отклонении лопасти вверх на угол 3 при заданной установке тяги
точка В лопасти поднимается по отношению к точке поводка на
высоту Z3 (см. фиг. 128), что вызывает поворот лопасти на отрицательный
малый угол
фр.в ' — == — /3,
е
где f -- —-передаточный коэффициент регулятора взмаха.
е
Он дает величину поворота лопасти при взмахе на 1°.
Подставляя сюда развернутое выражение для 3, получим:
Фр.в = — Мо 4- Mi cos ф 4- Mi sin ф. (507)
Следовательно, угол установки сечения на любом радиусе несущего вннта
будет в общем случае равен
ф^ = Ф7.0 4- Фш — Фх cos ф — фг sin ф 4- Ф (О,7 — г) —
— Мо 4- Mj cos Ф 4- Mi sin ф,
или
Фе -= Ф7 0 4 - фш + Ф (0,7 — г) — fa0 —
— (ф.г — Ml) COS ф — (фг — Ml) S*n Ф •
В дальнейшем мы будем вводить в это уравнение эффективный угол
установки лопасти на радиусе г — 0,7, определяя его формулой
Ф7 = Фт-о 4-Фш — Мо- (508)
Это — истинный угол установки характерного сечения, получившийся после
установки шагового угла фш и отклонения лонастн на угол конусности а0.
Величина этого угла известна, так как в полете величина
— — р/?Ъ)г
известна, а Ст связано с <р7 приближенным соотношением (484). Следова-
тельно, мы будем всегда знать в первом приближении величину ф7.
Основное выражение для сре примет теперь вид:
= ф7 + Ф(0,7 — г) — (фЛ —/а^соэф — (фг — /£>2) sin -ф. (509)
Таким образом, угол установки профиля на любом радиусе изменяется
по гармоническому закону с постоянной величиной ф7 4- ф (0,7 — г). Это
получается в том случае, когда углы 9 н все отклонения рычагов АП
малы, порядка 5°. При больших углах неизбежно входят высшне гармо-
ники, н формулы для фе очень сильно осложняются.
Проведенные во многих странах опыты по изучению угла фе в полете
показали, что лопасть под действием аэродинамических сил деформируется.
Она сильно изгибается в меридиональной плоскости и закручивается около
своей продольной осн. Угол закручивания достигает иногда нескольких
градусов (1—5°), что сильно изменяет картину обтекания лопасти. Введе-
ние в расчет этих углов делает формулы еще более громоздкими и крайне
неудобными для расчетов. Поэтому приходится считать лопасть абсолютно
твердой и затем после расчета увеличивать или уменьшать угол ф7 на не-
которую величину, взятую нз опытов с несущими вннтамн с аналогичными
конструктивными формами. У хороших, жестких на кручение лопастей эта
величина составляет около 4~ 1° н иногда доходит до -42°.
§ 2. МАХОВОЕ ДВИЖЕНИЕ ЛОПАСТЕЙ В ОБЩЕМ СЛУЧАЕ
ПРИ РАБОТЕ АП И РВ
Рассмотрим теперь движение лопасти при наличии регулятоэа взмаха и
отклонения автомата-перекоса, заданного углами фх и фг. Лопасть будем
считать постоянной ширины, и крутку лопасти заданной по линейному
закону. Не представляет никакого труда ввести в формулы н более слож-
ный закон изменения b и фкр, так как интегрирование по г всегда осу-
ществимо Мы уже получили в § 1 главы 12 формулу (474), дающую вели-
чину аэродинамического момента около горизонтального шарнира. В эту фор-
мулу нужно теперь подставить мгновенную величину угла установки любого
элемента лопасти фв, которая находится по формуле
Фе = Ф: + ф (0,7 — Г) — (ф^ — Ml)cosф — (фг — f6i) sin ф. (509)
После подстановки получим следующее выражение:
гпа = — Ф7га + г2Ф (0,7 — г) — г2(фх — ffli)cos ф — г2 (ф2 — f^sinip 4*
+ Уаф7 4- У/Ф (0,7 — г)---------- V, (фх - - fat) cos ф —
---~-V2t (фг — fbr) sin ф — rVa — j rVtaQ — ггЬг-- V^b^ соэф —
— + VaVt-----sin ф 4- 2гУ,ф7 sin ф 4- 2гУ/Ф (0,7 — г) вшф —
— 2rVt (фл — Mi) sin ф cos ф — 2rVt (Ф? — fbi) sin2 ф r dr.
Упрощая это выражение, приняв sin ф cos ф = 0 и sin2 ф = , и интегри-
руя по г в пределах от 0 до 1, получаем:
,Пл = Т L 4"<р’ + ^‘<р’ ~ — "Г (<Рг +
+ 4“ф(О'7-т) + ТР'ф (°’7~Т^ +
4-4^(<Р.-М.) + трйя»------r6i--jcos if —
4 3 4 8 J
- Г— (фг - fbj ч- -i- Vl (ф2 - fb + -L a, + 4- VOV(-- Vfa +
|_ 4 4 4 2 8
+ 4P'^ + 4PW0-7~-7-')'lsin’l’ = + (510)
3 3 \ 4 / J \ in Th / л
Мы приравняли здесь величину тА выражению ( —4-— согласно
\ Тк Тк у Л
формуле (472). Полученное уравнение нужно соблюдать для всех азимутов,
что возможно только в том случае, если коэффициенты при sin ф и cos ф
будут равны нулю. Тогда получим три уравнения, как в § 1 главы 12, но
более сложные:
4-^+4- —г - мо+4 ф I °’7 —У +
+ АИФ (0,7-4-)=^ + ^;
4- (<рх—f<h)+4- й (ч>»—мо+4“ ^,а« ~
4 4 3
---------Lj^6l = 0;
4 8
4- (<ь - мо ч- ф v < (Фг - /м)+4- «1+4- - 4- ?'ai+
4 4 4 2 о
+4- р'ф’ + 4-^ф (°-7—г)=°-
Решать эти уравнения в общем виде неудобно из-за громоздкости получаю-
щихся формул. На практике почти все члены задаются и их удобно вычислить
заранее.
Таким образом, мы можем ввести следующие обозначения:
£>=+4-- 4-г»- !г'7,ф;+
4 4 3 3
+±ф (0,7-44+4-7?® 1'0,7-444
4 \ 5/4 \ 3 ' 1 и
Ф*+4-
4 4
=4-^+4- +4 +
4 4 2
+ Ау,ф;Н. Ар/Ф (oj-A);
Ci = —;
Ти
Ct = -±-Vt;
С3 = 0;
Л, =0;
л=4^+4^;
4 4
Лз = +Ар?-А;
3 8 4
а2 = +4- + 4-7?:
4 о
в3=+4-/+4-т?/.
4 4
(511)
Пользуясь этими величинами, переписываем наши три уравнения в таком
виде:
Cia0 + = Ei, j
C2a„ + +.K, + B2bj = £2; I (512)
A3at + BJ>! = E„. J
Детерминант этой системы будет равен:
0
^2
С2
0
Bi
~ CiA^B3 + C^A^Bi — CiA3Bz.
Следовательно, решения этих
уравнений будут:
Е1А2В3 — Е1АяВ2 + Е.А3В1 — Е3АгВх
CiA2B3 -р С2А3В1 — Cj <4зВ3
(513)
CiE2B3— CjE3B2 C2E\B3—C2E3B\ (514)
1 С^А2В3 + — С1А3В2
_ С^Нз-СМзНз+СИзЕ, 5
1- Cj^Ba + CaA.Bi-Ci^A ' '
Таким образом, мы получим ответ о маховом движении лопастей любой
формы при работе АП и РВ с точностью до первых гармоник.
Видно, что эффект «командных» углов ф7, фх и фг входнт в формулы
линейно. Линейно входит и величина крутки, заданная коэффициентом Ф.
Действительно, эти углы входят только в члены Ег, Е2 и £3. Поэтому,
написав в сокращенном виде выражения для
Е} -= ф-Е1Л — фг£] 2 — Ф£1.з — £1.4,
£2 ф.гЕ2л
и
Е3 --- ф7£31 -}- фг£з.г 4~£"зз,
где коэффициенты не зависят непосредственно от ф7, фг, <рл и S, мы смо-
жем записать решения для а0, aY и bi в таком виде:
ао = Ci дФ? "I' £1.2фх 4~ £1.зфх 4~ С1.4Ф Ч- Ci.5;
~ £«.1ф7 Съ.гфх т Сл.зф? 4“ С2 4Ф
— С3.1Ф7 4_ Е3 зф.с -[ Сз.зФ? 4- С3.4Ф _1“ Е3 5.
Величину коэффициентов СГ1, Сал, С31 н так далее легко подсчитать для
каждого частного случая.
Таким образом, каждый командный параметр и крутка входят в фор-
мулы линейно, если ограничиваться расчетом с сохранением первых гармо-
ник. Это позволяет упрощать расчеты и, например, эффект автомата-пере-
коса просто прибавлять к величинам, полученным для свободномашущих
лопастей.
Особенно подробно изучил работу АП и РВ В. Е. Касторский, опубли-
ковавший ряд работ по этому вопросу (см. список литературы). Он пришел
к таким выводам:
1) при работе на месте угол а0 пропорционален ф7;
2) при работе на месте, при отклонении кольца АП угол отклонения
оси истинного вращения несущего винта пропорционален углу отклонения
кольца; для получения чисто продольного или поперечного управления не-
сущим винтом нужно соответствующим образом подобрать угол конструк-
тивного опережения; у несущих винтов без РВ угол отклонения оси истин-
ного вращения равен углу наклона кольца АП; другими словами, плоскость
вращения в этом случае при работе на месте параллельна плоскости кольца;
3) при полете с горизонтальной скоростью в коэффициенты махового
движения входят линейно добавочные члеиы; это позволяет прибавлять эф-
фект «команд» к данным, полученным для нейтрального положения кольца
автомата-перекоса;
4) поворот оси истинного вращения при полете с горизонтальной ско-
ростью ие совпадает по направлению с наклоном кольца АП; при этом
получается сдвиг фазы управления на угол, зависящий от ряда параметров
н в первую очередь от У?; следовательно, управление вертолетом на ско-
рости будет затруднено сдвигом его управления по фазе.
Приведенные в этой книге формулы позволяют вычислить действие АП
и РВ лишь при сохранении первых гармоник. Поэтому они являются лишь
первым приближением к действительности. Кроме того, онн относятся
к установившемуся движению лопастей, когда углы а0, н не зависят
от времени. На самом деле приблизительно установившееся движение лопа-
стей несущего вннта начинается лишь после полутора-двух оборотов вала;
и в первый момент, как показывает детальный анализ, вертолет прн резком
отклонении ручки начинает поворачиваться в направлении, составляющем
с направлением отклонения ручкн угол около 90°, и лишь затем движение
делается установившимся и угол отклонения получается в соответствии
с выведенными формулами (513), (514) н (515). Все это сильно усложняет
управление вертолетом.
§ 3. КОЭФФИЦИЕНТ ТЯГИ ПРИ РАБОТЕ АП И РВ
Для вычисления Ст воспользуемся выражением (479), в которое вместо
ср7 подставим сре. Тогда получим сначала
P _ __ __ __ __ А (*_____ Г 1 __ ___
Сп = — р (фМ - lt/X) dr =~\b\ ч>еГ* + Т Vfoe
о о L
— (rVta0 — rzbL---У/th) cos ф — ( г2аг 4- VaVt — У2^ —
— 2г У/сре)sin ф j rfr.
Подставляя сюда развернутое выражение (509) для сре и считая
b = b- = const, получим:
АЬ? с— - -
Сп = \ [г2Фт 4- г2Ф (0,7 — г) — г2 (срх — fai) cos ф —
— Г2 (ф, — fbi) sin Ч) + -|- Г;<р, + Л-Т?Ф (0,7 — 7) —
---1— (фл — Ml) cos Ф---Y Vf (ф2 — fbi) sin ф — rVa —
— (rVia„ — r26,---— VMi 'l cos i|> — (r2a, 4- VM-— Via,) sin A +
\ 4/V 4 /
4- 2гУ/ф7 sin ф -L- 2гУгФ (0,7 — r )sin ф — 2rVt (<px — fajcos ф sin ф —
— 2rVt (фг — fb^ sin2 ф] dr.
Упрощая формулу, приняв sin2 ф = — и со5ф51‘пф = 0, согласно свод-
ной таблице упрощений, и интегрируя по г, получим:
Сп = 44 4 Фт +4-Ф (°>7 — -J-) —-3-(Фл: — fa,) cost —
— -1-((рг— fbj)sinф + ~ + -J- У*® (0>7---M —
---— Vf (<px — fcM COS V--(фг — fbt) sin ф L ya _
2 2 <.
- I A Vta0 — J- 61----- VjMcos*— (-^ + VaV<- -‘-V,2a3sin4? +
\ 2 3 4 / \ 3 4 У
+ V('(>,sin ф + V,® ^0,7--|-j sin-ф--
Таково выражение для мгновенной силы тяги одно;! лопасти.
Для среднего Ст за оборот для /г-лопастного несущего винта получим
сокращение всех периодических членов; тогда
k Г 1 1 i 3 \ 1 _п
Ст = 2Я ) CTidty = Аз71 з Ф? + з Ф I 0,7—• ) 4* ~ Vftp? ф-
о '
+ А^ф ^0,7— ----1_у0__к7,(фг-/61)
“ [ф, (4 + 4 Vp - 4 к] + Ла; [4 Ф (0,7-А; +
+ Ау~ф(о,7~АрАй(Фг-(б1)‘|,
н окончательно
Ст = Аз, |ф7 (А + А-тр - А к] + Ло,Ф(-0,02 + О, IV?) -
— fbi)- (517)
Первый член дает основную величину коэффициента тяги, зависящую
от истинного нлн эффективного угла установки характерного сечення несу-
щего вннта (с учетом РВ н фш), а второй член дает добавок, получаю-
щийся от закрутки. Этот член обычно мал и часто не превосходит прн
линейной закрутке 1—2% от первого члена. Третий член дает малое влия-
ние АП.
Влияние регулятора взмаха входит в выражение для ф7, так как
Фт — Ф? О + Фш — fa„, (508)
а летчик устанавливает этот угол автоматически, стремясь получить необ-
ходимую для полета величину Ср.
Мы не будем выводить всех формул для отдельных сил н моментов,
так как они очень длинны, хотя по существу не содержат никаких слож-
ных вычислений. На Практике, когда нх приходится решать для частных
случаев, задача упрощается, так как коэффициенты имеют численное вы-
ражение.
Более подробные указания можно получить из работ М. Л. Миля,
А. Н. Михайлова, В. Е. Касторского, А. П. Проскурякова и др.
§ 4. КРИТИЧЕСКИЕ ЗАМЕЧАНИЯ
к классической теории несущего винта
Изложенная здесь теория несущего вннта позволяет единым методом
находить все величины, интересующие конструктора и исследователя в об-
ласти вертолетостроения. В этом ее положительное значение.
Однако, несмотря на очень громоздкие и длинные формулы, она оказы-
вается во многих случаях грубопрнблнженной н дает весьма заметные
ошибки. Происходит это из-за того, чго в нее вводятся в весьма упрощен-
ном виде многие основные факторы и делается ряд грубых упрощении, а
также из-за отбрасывания высших гармоник при вычисленин тригонометри-
ческих рядов. Укажем на ряд упрощений, вводимых в эту теорию.
1) Угол притекания потока к элементу лопасти ft. вычисляется грубо-
приближенно. Его истинная величина
W
& - - arc tg
заменяется упрощенным выражением
Такая замена допустима для углов ft <40°. Однако у несущего вннта
получается круговая обдувка проф гл ей на все 360°. Угол ft, достигает
величины 90° на идущей иазад лопасти на раднусе г - Vt = ц, а так как
у современных вертолетов Vt достигает значения 0,3 н более, то на ’/3
радиуса уже получается совершенно неверный результат. Даже на радиусе
г — 0,5 ft. равно 20° при ft- на конце лопасти, равном 10°.
Интегрируя все величины в пределах радиусов от г — 1 до г -= 0, полу-
чают заведомо неточный результат. Он маскируется другими допущениями,
искажающими вычисления в другую сторону. Происходит во многих случаях
некоторая компенсация ошибок, н опыты с несущими винтами дают для
суммарных величин достаточно близкие результаты. Но отдельные,
промежуточные величины часто резко отличаются от теоретических (напри-
мер, углы атаки сечений).
2) Входящий во все выражения этой теории коэффициент подъемной
силы сечений су вводится в них в виде линейной зависимости
су — Аосе,
на самом же деле он изменяется так. как показано иа фиг. 129,
кривая •?. Только до критического угла атаки, имеющего Для про-
филей обычно величину 10—12°, можно пользоваться этой форму-
лой, так как при больших углах атаки начинается резкий срыв по-
тока, и су быстро падает.
Однако на это обстоятельство прн интегрировании не обращают
внимания, хотя при этом величина а.е изменяется на все 360°, и
величина су будет местами достигать совершенно невозможных
значений: 5, 10 н т. д.
3) Угол взмаха лопастей ft считается малым, и в большинстве
формул принимают, что sinft^ft и cosft=l. На самом деле этот
угол в некоторых случаях достигает величины в 15°. Прн этом
даже радиус г элемента изменяется на 34%, так как cos 15° =
= 0,9659. Это упрощение вносит заметную погрешность в вычи-
сления.
4) В этой теории пренебрегают радиальными скоростями, а сни, как мы
показали в § 4 главы 7 (см.фиг.72), достигают очень большой величины, и угол
скольжения потока по радиусу достигает в середине лопасти при г —- 0,5
величин порядка+ 25— + 30°, а в центре вннта при г 0,25 этот угол
делается весьма большим, порядка + 45°. При этом этот угол при каждом
обороте изменяет свой знак. Совершенно очевидно, что обтекание сечений
и образование пограничного слоя происходят в условиях неустановившегося
движения, пои совершенно других условиях,
дувке профилей лопасти в аэродинамиче-
ской трубе.
В таких условиях величины схр и с,/т„х
должны сильно изменяться.
5) Не учитывается влияние скорости
изменения угла атаки проф 1ля на величину
подъемной силы. Как показывают опыты,
при возрастании угла атаки кривая су
идет выше, чем при его уменьшении. Это
явление иногда называется в аэродинами-
ке эффектом Фаррона, или аэро-
динамическим гистерезисом.
de da
В этом случае величина — зависит от
dae dt
чем те, какие были при про-
Фиг. 129. Аэродинамический гисте-
резис у профиля лопасти
а су характеризуется кривыми / и 2, изображенными на фиг. 129. Такое
явление «затягивания», или «гистерезиса» потока весьма заметно изменяет и
величину Супих- Все это должно заметно влиять на аэродинамику поофилей.
6) В классической теории или совсем не учитываются, или учитываются
грубо основные аэродниахнческне критерии подобия Re и М. Они сильно
изменяются во время полета с горизонтальной скоростью. Следовательно,
и величины коэффициентов схр, су и tnz не остаются постоянными, а сильно
изменяются во время оборота, что Hi учитывается в указанной теории.
7) В этой теории не учитывают изменение индуктивной скорости
на ометаемом лопастями диске и берут ее соедним значением.
Но, как показывают произведенные опыты и более глубокие теоретические
соображения, она заметно изменяется.
Делались попытки уточнить величину щ и вводить ее в расчет как
величину, зависящую от г и ф. Но и в таких случаях ее берут за оборот
несущего винта средним значением. На самом деле нужно было бы делать
расчеты, исходя из «относительной» теории винтов и вычислять или брать
нз опытов индуктивные скорости дня точек, лежащих на самой лопасти н
вращающихся вместе с ней. Этого, однако, ие делают нз-за сложности
получающихся выражений.
Ошибки, получающиеся при этом для нормальных режимов полета,
оказываются малыми, так как скорость Vi оказывается малой, и закон ее
изменения по диску мало влияет на окончательный результат. Поэтому
при расчете максимальных скоростей полета можно брать величину щ по-
стоянной во всех точках диска, что мы н делали в настоящей книге. При
расчете же ненормальных режимов (крутой взлет, очень большая ско-
рость горизонтального полета н др.) ошибка может получаться довольно
большая.
8) Принимается, что автомат-перекос поворачивает лопасти по гармони-
ческому закону с первыми гармониками. На самом деле при больших
отклонениях АП он вызывает вторые гармоники и все явление очень сильно
осложняется.
9) Метод отбрасывания высших гармоник дает заметную ошибку. Она
особенно велика для мгновенных значений всех величин. Мы уже показали,
как искажается величина HZ*, если ее брать по приближенной формуле
(см- § 6 главы И).
10) Еще нет точных методов учета взаимного влияния несущих вннтов
друг на друга и влияния фюзеляжа и крыльев на несущий винт.
11) Все опыты показывают, что лопасть иногда очень сильно изгибается
под действием воздушных н инерционных нагрузок и сильно закручивается,
что должно заметно искажать аэродинамику несущего винта.
12) Большим недостатком теории является и сама структура получа-
ющихся формул. Они имеют иногда десятки, а прн учете деформации ло-
пастей свыше 100 членов. Вследствие этого онн весьма ненаглядны и трудны
для вычислении.
ВЫВОДЫ
Несмотря на все указанные грубые упрощения, эта теория, как пока-
зывают опыты, дает во многих случаях результаты, довольно близкие к
действительности. Вычисленные и полученные нз опытов величины рас-
ходятся обычно на 10—15%, а в более трудных случаях на 20—25%.
По-внднмому, это происходит из-за взаимной нейтрализации ошибок и поло-
женных в основу теории допущений. Одни допущения увеличивают, а дру-
гие уменьшают истинную величину; получается некоторая компенсация.
Поэтому данную теорию можно применять для расчета несущих вннтов,
но нужно помнить, что она является только первым приближением в изу-
чении столь сложного явления, как работа несущего винта в косом потоке.
Глава 14
ОСОБЫЕ ФОРМЫ НЕСУЩИХ ВИНТОВ
§ 1. НЕСУЩИЙ ВИНТ С КАЧАЮЩЕЙСЯ ВТУЛКОЙ,
БЕЗ УГЛА КОНУСНОСТИ
В настоящее время наравне с несущими винтами со свободномашущими
лопастями широко применяются двухлопастные винты с качающейся втул-
кой (фиг. 130).
Вертолеты с такими несущими винтами выпускаются серийно в Америке
фирмами Белл и Хиллер. У таких винтов довольно хорошо уравновешива-
ются аэродинамические силы. Вертолеты с такими винтами весьма компактны
на стоянке, так как позволяют устанавливать лопасти несущих винтов
вдоль фюзеляжа. Особо компактной делается при этом одновинтовая схема,
где для установки лопастей вдоль фюзеляжа не требуется никаких доба-
вочных приспособлений.
Эта схема может быть простои (фиг. 130) и сложной (фиг. 131 и 132).
В первом случае втулка качается около оси OiO2> 11 угол установки ло-
пастей управляется обычным автоматом-перекосом. На фиг. 130 поводки
П поставлены так, что не получается эффекта регулятора взмаха. На фиг.
131 втулка осуществлена в виде подвеса кардана с помощью кольца К.
Точка Aj соединена с обычным автоматом-перекосом, управляющим углом
дифференциальной установки лопастей. Общий шаг управляется с помощью
проходящей через вал штанги Н и поводков П.
Наконец, в эту схему вводят иногда элементы автоматической стабили-
зации. На фнг. 132 введен гироскопический горизонт, состоящий из штаиги
33 Б. Н Юрьев, т. I
4,
Фиг. 131. Схема качающейся втулки с карданным
подвесом
R с укрепленными на ее концах грузами G. Прн’кренах аппарата плоскость
вращения этой штанги сохраняется, н она посредством суммирующего рычага
S управляет с помощью тягн t углом установки лопастей. Суммирующий
рычаг передает команды йш, Ф* н Фг от автомата-перекоса АП с помощью
штанг t и 4 и шарниров _ А, Ах и Л2 непосредственно и независимому
Фиг. 132. Схема несущего винта с гироскопическим
горизонтом
положения рычага R к лопастям несущего винта Л. Общий шаг изменяется
с помощью скользящей по валу муфты /И н качалки Н. Иногда вместо
грузов G на штанге R устанавливают серворулн.
Имеется много других схем, использующих качающуюся втулку.
В качестве особенности таких устройств необходимо отметить, что когда
первая лопасть находится на азимуте ф, то вторая лопасть имеет азимут
фх = ф 4- л. Кроме того, когда первая лопасть поднимается вверх на угол
взмаха, то вторая лопасть опускается на такой же угол вниз; следовательно,
у нее 31 = — 3-
Это свойство качающейся втулки упрощает многие расчетные формулы.
Рассмотрим простейший случай, когда втулка осуществлена по схеме,
приведенной на фнг. 130, и имеет нейтральную установку АП.
Простейший вывод формул для несущего виита
с качающейся втулкой
Рабочие формулы для такого несущего винта можно получить при со-
хранении первых гармоник сразу из формул, выведенных ранее для сво-
бодных лопастей. Действительно, в этом случае а9 = 0, и тогда маховое
движение представится формулой
р= —OjCosip — sin -ф. (518)
Если в нее подставить вместо ф величину ф + л, то знак р в этой фор-
муле изменится, а величина 0 останется неизменной; т. е. условия работы
качающейся втулки правильно описываются выведенной формулой при а0 = 0.
Отсюда все полученные ранее формулы могут быть использованы для этого
случаи.
Так, для махового движения сразу найдем по формулам (477) н (478)
при о0 = 0:
— , 4 _ \
2 V{ Va\
=; (519)
1 — —
2 '
Ьг = 0. (520)
Тогда cos i(.. Отсюда находим все коэффициенты сил:
CQ = Ас7 + <р7к,) + Ачзд (1 + | И(2)-
^V,a2i, (521)
4 4
Сг = Л3,[срЦ|5Дк2')-Айор (522)
Сг = 0. (523)
Коэффициенты моментов будут такими:
тп = - Ло7 ^-1- ср, - Й - {«i ( 1 - у V?)] ; (524)
= - mK = - As, (1 + V? ) + ±<р7К - -
- Г| °*++4 <525)
L о lb j J
m21 = 0. (526)
Аналогично можно написать выражения для мгновенных сил и момен-
тов, воспользовавшись формулами, приведенными в главе 12. Однако нуж-
но всегда помнить, что полученные формулы выведены, исходя из усечен-
ного ряда Фурье, и что на самом деле существуют высшие гармоники,
способные вызывать вибрации. Для осредненных за оборот значений эти
гармоники несущественны, так как при этом онн из уравнения выпадают.
Для рассмотрения же более подробной картины силового воздействия
на лопасти нужно подробно рассматривать сначала маховое движение и
вычислять по полученным результатам силы и моменты.
Однако в данном случае, как увидим далее, в уравнении махового дви-
жения уравновешенными оказываются вторые гармоники, что делает полу-
ченные в общем виде формулы с первыми гармониками точными для ка-
чающейся втулки и до вторых гармоник.
Теория несущего винта с качающейся втулкой
с учетом вторых гармоник
Мы рассмотрим сначала маховое движение парных лопастей, причем
будем учитывать и вторые гармоники. Исходным уравнением у нас будет
выражение (470). *
В нашем случае обе лопастн колеблются как одио твердое тело, причем
З2 = — Зь З2 = — Зь ао — 0, ф2 = Ф1 -• Вес лопастей здесь всегда урав-
новешен и момента не дает. Следовательно, формула (470) будет иметь вид;
~ ("U1 - тЯ2) = — ( ₽ + ДЛ • (527)
аь7 тй\ «2/
Величина т» вычислена здесь для одной лопастн. Найдем теперь вели-
чину ntAi — тд3 по уже известным формулам (474):
— тА2 = — £>7 (<p7^i — 1^л-1^)7 dr —
л J
о
- - бД (<Р, W7;, - ~rTr =
Л J
о
= -&Д [<р7 (Fi -
л J
о
Вводя сюда выражения для Wxi и Wxi^yi по формулам (459) и (463) и ис-
пользуя соотношения функций углов ф н ф 4- л, получим:
Wxi — ~ г2 -j- 2rVt sin ф 4- У, sin2 ф —
— г4 5 4- 2г7/зшф — V/sin2 ф = 4гУ/зшф;
iPjVTi - = (V,, + 7 £ + V,(3 cos -ф W + V, sin м>) —
— ( Va — 7 £ + COS Ф \ (7 - Vt Sin ф) = ~rVa + 7 £ +
\ (d J co
4- rV& cos ф 4- VaVf sin ф 4- Vtr - sin ф 4-- Vft sin ф cos ф — rVa 4"
co
+ r2~ — гк'/рcos if: — |70Vzsinip— rVt L sinip -i- V'ts3inip cosip =
• (i) (O
= 2ra^- -- 2VaVzsinip + 2y$sin ip cos ip.
co
Формула для угла взмаха со второй гармоникой и Oq = 0 будет иметь вид:
3 -- —cos ip — bisinip —a3cos2ip —b2sin2ip,
а ее производные таковы:
3 = co (Gi sin ip — b, cos ip +- 2a2 sin 2ip — 2b2 cos 2ip)
и
3 — со2(ахcosip -r biSinip + 4a2cos2ip 4- 4b2sin2ip).
В выражение для —Мк2и/уг входит член 3 sin ip cos ip: мы его
вычислим отдельно таким путем;
3 sin ip cosip = (—cosip — bi sin ip) sin ip cosip 4- (—a2cos 2ip —
— b2 sin 2тр) у sin 2ip =- — Ox cos2 ip sin ip — bt sin2 ip cos ip—
1 1
— у a2 cos 2ip sin 2ip — — b2 sin22ip.
Пользуясь сводной таблицей упрощений и отбрасывая гармоники выше
второй, получим:
3 sin ip cos ip = —- — Ь2 —• — sin ip — — cos ip,
4 4 4
т. е. из этого выражения выпала вторая гармоника. Это, как мы покажем
далее и в § 4 главе 15, получается всегда при вычитании вторых гармоник
функций, аргументы которых отличаются на 180°. Следовательно,
= 2л2 (cii sin ip — bi cos ip -h 2a, sin 2ip — 2b2 cos 2ip) 4-
4 2Va14sinip 4- 2Vj I — — b2 —• — sin ip — — cos ip')
\ 4 4 4 '
Возвращаясь к уравнению (527) и подставив в него найденные выраже-
ния, получим после приведения тригонометрических коэффициентов:
|4 Ь.у, — (~2г"-ь, — I cos4’ —
О
— [ ~ (р74г 2г2О1 — у V/ 4- 2УаУг | sin ip — 4r2aa sin 2ip 4~
4- 4r2b2 cos 2тр 1 rdr ~ (3a2 cos 2ip 1 - 362 sin 2ip).
34 Б H. Юрьев, T. I
Интегрируя по г и приравнивая коэффициенты при одинаковых тригоно-
метрических величинах, получим пять уравнений:
4
--ft,— -0;
2 4
- -= °;
3 2 4
— а,— — 3&>; Ь2 -~3а„.
Ти Тц ’
Решая их, находим:
bt -= 0;
2V/ ( уф7-
а ------12----
1 — -V;
2 '
а2 = ь2 - 0.
(528)
(529)
мы получили прямо из формул (477) и (478) для
Этот же результат
свободномашущей лопасти; эти формулы можно считать универсальными.
Следовательно, несущий винт с качающейся втулкой при нейтральной
установке АП лишь заваливается назад на угол аъ и маховое движение
совершается по закону
3 = — Gj cos ф.
(530)
Мы таким законом уже пользовались в главе 9.
Зная величину коэффициента а2 и помня, что а2 = bt = b2 = 0, можно
прямо воспользоваться готовыми выражениями по формулам (521)—(526).
Для мгновенных значений сил и моментов можно использовать аналогичные
формулы, приведенные в главе 12.
Более общий случай
Более общим случаем является такой, когда имеется крутка лопасти,
ширина лопасти изменяется по радиусу и работает автомат-перекос. В этом
случае расчеты нужно вести с учетом третьих гармоник и вводить величину
(ре по формуле (509). В нашем случае будет отсутствовать регулятор взмаха
(РВ). Кроме того, для получения более точного результата нужно вести
вычисление интегралов в пределах от г = g2 до г = L для учета конце-
вых потерь. Все это приводит к весьма громоздким формулам, если все
расчеты вести в алгебраической форме. Если же сначала решить уравнение
махового движения, то далее расчеты можно упростить, вычислив Wy,
IV'x, u/y и МхМу для заранее выбранных значений азимута, изменяющихся
через 45 или 30°. Тогда можно построить для всех интересующих нас ве-
личин графики в функции азимута ф, что даст точное мгновенное значение
всех величин. Для получения средних за оборот значений нужно определить
площадь, охваченную этими кривыми, осью абсцисс и крайними ординатами,
и разделить ее на 2л. Такой способ вычисления очень нагляден, и задача
решается быстрее.
§ 2. НЕСУЩИЙ ВИНТ С ЖЕСТКОЙ ВТУЛКОЙ
Такие несущие винты могут применяться лишь в многовинтовых систе-
мах или в таких, где опрокидывающие несущий винт моменты как-то урав-
новешиваются. В случае применения автомата-перекоса можно строить даже
одновинтовые вертолеты с жесткими лопастями. У такого жесткого несу-
щего винта отсутствует угол конусности, и лопасти не имеют махового
движения. Тогда а0 = = 0, ? = 0, £ = р = 0. Это сильно упрощает
все формулы. Нет надобности выводить их снова, так как изучаемый слу-
чай является частным случаем для выведенных ранее более общих формул.
Для рассмотрения вопроса о пульсациях силы тяги такого винта сделан
вывод Ст с сохранением всех гармоник.
Тогда получим для скоростей ЙД, UZ^, UZ* и УЛЙД следующие простые
выражения:
ИД = г + Vt sin ф;
UZ; = г2 -f- 2rVt sin ф /- Vf sin2 ф,
Wy=Va‘,
КУ/sin ф-
С их помощью вычисляем мгновенное значение Стц считая b — b7 = const
и <pj = <р? = const. Получаем:
СГ1 = - С b-, (Ч> ж2 — dr =.
Л
о
~~7 (QV2 -г v72rKsini[) ср7К2 sin2 ф — rVa — КУ/sin ф) dr =--
о
= [ — (р7 — ср/// sin ф cp7l// sin2 ф — — 1Д VaVt sin ф | =
” L з 2 J
~ Д<Р; — Д« + (<P?V( — VaY,', sin 4- <г-Уг sin2J . (531)
Из этой формулы видно, что у двухлопастного винта пульсации полу-
чаются по второй гармонике от члена с зт2ф. Полное уничтожение пуль-
саций Ст у жесткого винта получается при четырех лопастях, что легко
вывести, сложив
Cti. 1 + Cti. 2 + Си. з + Сп. 4
Средний за оборот коэффициент тяги будет равен
т. е. получается такое же выражение, как и для несущих винтов. Его
можно уточнить, учтя концевые потери, оцениваемые коэффициентом х, и
введя любой закон изменения ширины лопасти b = ft> (г), переменный угол
установки лопасти <рс и крутку лопасти. Для обычных расчетов можно
брать средние значения <з7 и <р7 и исправлять результат на коэффициент
потерь х, взятый из опытов с аналогичными несущими винтами, т. е. писать
выражение для Ст в таком виде:
Ст ~ х/4<57
mi
V;
Коэффициент крутящего момента тк вычисляют обычно по известным фор-
мулам (289) н (294). Пользуясь формулами, выведенными для махового
движения, получим сразу результат для жесткого несущего винта, положив
в них а0 = а± = -- 0.
Таким образом, для средних за оборот силовых и моментных коэффи-
циентов из формул (483), (495)—(499) получим:
CQ,--~ Ся, = Аз,
- Ао, [чъ (1 + ;
£21- 0;
тХ1= ;
‘f.O'J (v и • • н ।
««, -mK=- - Vt) ;
mZi 0.
Следует еще раз напомнить, что полученные формулы являются лишь пер-
вым приближением и их точность невел-гха. Они дают лшь ооиентнровоч-
ные значения величины. Точные результаты могут быть получены лишь
в опытах с моделями несущих винтов или путем летных испытаний верто-
летов.
Глава 15
ИНЕРЦИОННЫЕ НАГРУЗКИ ЛОПАСТЕЙ
§ 1. ЦЕНТРОБЕЖНАЯ СИЛА
Кроме аэродинамических усилий, на лопасти вертолета действуют
еще инерционные силы и моменты. Мы уже встретились с этим вопро-
сом в § 1 главы 12 при изучении махового движения лопастей. При
выводе этих формул мы сделали ряд упрощающих предположений; в
частности, мы, считали угол 0 очень малым. Однако это допущение мож-
но принимать с известной осторожностью, так как этот угол часто дости-
гает величины 12°, а иногда доходит до 15°. Мы рассмотрим теперь,
какие погрешности вызывает такое допущение в различных случаях.
Общая постановка будет такой: движение лопастей рассматривается
во вращающейся около оси Оу\ системе координат, а само маховое дви-
жение задано законом.
3 = cos ф — 6i sin ф.
Тогда на элементы лопастей будут действовать центробежная сила,
кориолисова сила и сила инерции от махового движения. Начнем их
рассмотрение с центробежной силы.
Следует помнить, что силы инерции здесь определяются по заданно-
му движению лопастей, а ие по действующим силам. Силы же, как это
видно из уравнения махового движения, всегда содержат высшие гар-
моники. Поэтому в классической теории получаются небольшие неувяз-
ки сил инерции с действующими на лопасти силами.
Учет сил инерции нужен для расчета лопастей на прочность. Рас-
смотрение вопросов прочности не входит в задачу этой книги, и мы ие
будем здесь рассматривать эти вопросы подробно; отметим только, что
лопасть в работе нагружена как внешними аэродинамическими силами,
так и инерционными. Поэтому приходится вести расчет, исходя из
алгебраической суммы этих сил, и не вполне точная увязка инерцион-
ных и аэродинамических сил заметно снижает точность таких расчетов.
Центробежная сила и момеит
Как мы знаем (см. § 3 главы 9), на лопасть в целом действует центро-
бежная сила
Л'ц = — Гц.тоА
g
Она вызывает относительно горизонтального шарнира момент, равный
тгкр(о2.
ё
° '“l ° 7
Замечая, что гц Ггк = г;, а — rt - Jo, получаем выражение
ё
Л/ц = ЛР(О2.
Как мы уже упоминали, центробежную силу нужно вычислять по радиусу
гцл., но прикладывать ее нужно на радиусе центра качания гк.
Однако столь простое выра-
Фиг, 133. Вычисление центробежной силы
жение мы получили потому,
что приняли cos р = 1 (фиг. 133)
На самом деле радиус элементов
лопасти при ее отклонении на
угол р будет меньше и равен
г cos р. В частности, и центр
тяжести лопасти будет лежать
на радиусе гц,т cos р. Следова-
тельно, написанные ранее фор-
мулы нужио писать в таком
виде:
Гц.тШ3 cos р = Гц.тсо3 У1 — sin2 [3. (532)
Совершенно аналогично, для момеита центробежной силы мы Должны
вписать:
/Иц — гц TrKpw2cos В = ~ /-ц тгк3й)2 V 1 —sin2 р. (533)
ё ё
’ак как угол р мал, то sinpanp. Согласно известной формуле приближен-
ью вычислений, выражение У1 — sin2 Р — У1 — р2 можно заменить более
ростым: 1 —Тогда предыдущие формулы запишутся в таком виде:
Рц-^гцт^(1-£) (534)
Мц. = — ГцтГкШ2^
ё
?)•
(535)
Величина р° Достигает значения До ~15° или Pas —. Следовательно,
4
В2 1
ибка получается для силы и момента порядка — —ал 0,03 или 3%.
[ужно заметить, что в заднем положении лопасти р°«0, и, следовательно,
ри работе несущего винта возникают пульсации центробежной силы в 3%-
§ 2 Кориолисова сила и ее момент
523
Центробежная сила у несущих винтов велика и доходит до десятков тонн,
а пульсация силы может достигнуть 1000 /с?, что в свою очередь может
вызвать вибрации в ряде конструктивных элементов вертолета.
Характер этих вибраций легко получить, подставив в предыдущие фор-
мулы величину З2 в развернутом виде:
р2 = (а0 — av cos ф — bL sin ф)2 =
о , № ьгД
= ао -г y + у — 2a0«i cos ф — 2аод! sin ф -J- I ~ I cos 2ф 4-
+ a1£>1sin2ip, (536)
г е. величина Р2 изменяется, имея первые и вторые гармоники. Если у не-
сущего винта а0 = 0, как это имеет место прн качающейся втулке, то
остаются лишь вторые гармоники. Следовательно, опасными могут быть не
только те детали вертолета, у которых собственная частота равна числу
оборотов несущего винта, но и вторые и даже высшие гармоники.
Если ввести более сложные выражения для в расчет, то уравнение
махового движения нужно будет писать с тремя и даже четырьмя гармо-
никами, что чрезвычайно осложняет все формулы. Поэтому на практике
ограничиваются обычно первыми гармониками и лишь иногда пользуются
вторыми, а расчеты уточняют с помощью поправочных коэффициентов.
§ 2. КОРИОЛИСОВА СИЛА И ЕЕ МОМЕНТ
Кориолисовы силы инерции связаны с наличием у элементов лопасти
линейных скоростей взмаха Ур, равных гр. Мы здесь считаем, что верти-
кальные шарниры у лопастей отсутствуют. Скорость гр образует с векто-
ром о» угол р (фиг. 134).
Величину силы Кориолиса,
действующей на элемент, нахо-
дим по известной формуле
dK = dm 2wVpsinp,
или
dK = dm 2u) rp sin p. (537)
Положительное направление этой
силы считаем совпадающим с
направлением вращения элемента
около оси Oyi.
Ввиду малости угла Р последнее выражение можно переписать в таком
виде:
dK = 2wppr dm,
и полная сила будет равна
К = 2(оРР \ г dm = 2o)Ppt7o.
(538;
Здесь Uq — статический момент масс лопасти около оси ГШ несущего
винта. Его можно вычислить по формуле
и
и0 — гц.т •
g
Момент этой силы относительно оси несущего винта будет равен
* . g
= j г cos [Ж = 2ыЗЁЦ г2dm.
о о
Замечая, что
* G
V r2dtn =
J g
о
получим окончательно:
Мк = 2./ошЗЗ == 2 (539)
Из выражения для силы К и ее момента Мд- видно, что ее, как и
центробежную силу, нужно вычислять по радиусу гц.т, но прикладывать
надо в центре качания.
Эту формулу можно написать в развернутом виде, введя в нее вели-
чины 3 и 3, т. е.
= (а0 — аг cos ф — di sin ф) (ах sin ф — bi cos ф) =
со
— — aob! cos ф -J- а0С! sin ф -j- axbi cos 2ф +
a,)sin2xp. (540)
Таким образом, полная сила Кориолиса и ее момент пульсируют по первой
и второй гармоникам. На фиг. 135 построены кривые 3, —, — и — для
со со2 <о
частного случая, когда а0 = 0,155, щ = 0,11 и bj — 0,055. Как видим, вели-
чина — достигает примерно максимальных значений —=0,022 приф = 150°
со со
и = - 0,022 при ф = 270°.
СО
Возьмем в качестве примера несущий винт с такими параметрами:
D — 20 м, N = 1200 л. с., Сл - 150 кг, со — 20 1/сек, п^г200 об/мин,
г? = 30 м2.
Момент кориолисовой силы очень велнк, и для указанного примера ои
доходит до значения
Мк = 2 —г^2^- —30-202-0,022 ^8000 кгм.
g со 9,81
За время оборота эта величина изменяется в пределах
Мк = +8000 кгм.
Средний крутящий момент у несущего винта с указанными параметрами
равен
Л1К = 716,2- = 716,2 —ж 4300 кгм.
п 200
Следовательно, момент кориолисовых сил для одной лопастн имеет порядок
двойной величины среднего крутящего момента на валу несущего винта.
m=0,155; ai = 0,ll; bi=0,055
По принципу Даламбера мы можем написать, что сумма мгновенных
значений крутящего Ик, кориолисова /Ик и ‘аэродинамического моментов
равна нулю, т. е.
Мк + + Alyi — 0.
(541)
Отсюда мгновенный крутящий момент, действующий на одну лопасть, бу-
дет равен
Л4К =——Myi-
(542)
Величины Мк. и Л1^1 нужно брать с нх знаками, и тогда окончательный
результат представится как алгебраическая сумма моментов снл аэро-
динамических и кориолисовых. Получающийся результат зависит О'”
формы несущего винта и конкретных значений всех величин, входя-
щих в формулы для Мк И [см. формулы (539) и (499)].
Подробный разбор получающихся при этом соотношений составляет
задачу расчета несущего винта на прочность н в этой книге рассматри-
ваться не будет.
Заметим, что д.ъя уменьшения эффекта сил Кориолиса часто делают у
лопастей несущих винтов вертикальные шарниры. Теория движения лопа-
стей с вертикальным итапниром и демпфером очень сложна, так как силы
Кориолиса в этом случае будут во время движения лопасти изменять свое
направление, а демпфер, особенно фрикционный, вносит большие матема-
тические осложнения во все формулы. Наиболее полное исследование таких
лопастей было проведено А. П. Проскуряковым * в его работе.
Примечание. Момент от сил Кориолисч при отсутствии ВШ легко найти по
теореме о производной главного момента количества дгижения масс несущего винта
Этот момент L равен, как известно,
где /0{Л —момент инерции лопасти относительно оси Crt. Если обозначить момент не
(тклоненной на угол 3 лопасти через Jo. то У отклоненной лопает он будет равен
J = Jo cos8 [3- Возникающий при этом момент сил Корго/леа будет равен
dL d о'Й
Al - =— = — J0o cos- 8 = J0<o 2 cos В s'n 3 — •
Л dt dt ' dt
dR
Величина — — (3, cos 3^1, sing^S, и мы получаем.
т- е. прежнюю формулу (539).
Мк - 2 Jo<o30,
§ 3. СИЛА ИНЕРЦИИ ОТ ВЗМАХА ЛОПАСТЕЙ
Эта сила действует перпендикулярно к оси лопастей.' Она, очевидно,
равна для элемента лопасти
dPn = — dm гр.
Знак минус показывает, что эта сила направлена обратно ускорению эле-
мента rj.
Для всей лопасти получи^:
..
Ри = — 3 dm г — $U0,
о
где Uo — статический момент лопасти, равный —
g
в формулы для Ри, получим окончательно:
Гц.т- Введя эту величину
Пи-- — Гц.т р. (543)
g
* А. П. Проскуряков. Колебание лопасти автожира относительно вертикаль-
ного шарнира. Труды ЦАГИ, вып. 379, 1938.
Элементарный момент силы dPK относительно горизонтального шарнира
будет таким:
dMp = rdP^ — — dmr2^,
и полный момент найдется из выражения
R
Мр = — 3 J г2 dm = — Jop
о
(544)
Эту величину мы уже получили ранее [см. формулу (465)]. Подставляя в
нее и в формулу для силы Рк выражение 3 = со2(а1со5ф 4- 5xsin ф), полу-
чим окончательно:
Рн =----Гц.т о)2 («j cos ф 4- sin ф) (545)
и
Мр = — — Г/ со2 (с?! cos ф by sin ф), (546)
т. е. и сила Ри, и ее момент Мр изменяются по первой гармонике. Сила
Р(. должна, как и центробежная Сила, вычисляться по Гц.т, но приклады-
ваться в центре качания, т. е. на радиусе гк --.
гц.т
Порядок этой силы для того же примера таков:
Ря = — гцт - — 5 • 400 0,1228^3750 кг,
g OJ2 g
т. е. величина порядка силы тяги, приходящейся на одну лопасть.
Если обозначить мгновенную силу, действующую по оси Оуу на гори-
зонтальный шарнир, через Ргш, то на лопасть будет действовать обратная
сила — Ргш и, применяя принцип Даламбера, можно написать:
— ^гш + Ту 4- Р„ = 0.
Здесь мы приняли, что cos£ = 1. Отсюда
Ргш - Ту 4- Pv.
Мгновенная сила тяги Ту и инерционная сила Рк направлены почти всюду
в разные стороны, и их эффект в значительной мере компенсируется. Окон-
чательный результат зависит от частных условий работы несущего виита,
веса его лопастей, снимаемой с него тяги и от того, со сколькими гармо-
никами велся расчет силы тяги и аэродинамического момента.
§ 4. УРАВНОВЕШИВАНИЕ ГАРМОНИК НА ВТУЛКЕ
НЕСУЩЕГО ВИНТА
В предыдущих разделах этой книги мы определяли мгновенную величину
различных сил и моментов, действующих на отдельные лопасти. Эти силы
и моменты можно было, как мы видели, представлять в виде усеченного
тригонометрического ряда, т. е. любая величина Q разлагалась на гармо-
ники и представлялась в виде:
Q = Ао — Л1 cos -ф — Bi sini|5
— А.2 cos — В2 sin 2ip —
— Ал cos —B3sin3ip— ... (547)
Обычно брались первая, вторая и третья гармоники, в зависимости от слож-
ности величины. Эти величины обычно разлагались по осям координат. При
наличии k лопастей на втулку несущего винта действовало k таких сил и
моментов. Суммируя их величину, мы получали частичное уравновешива-
ние, и остаток всех этих воздействий позволял судить о степени баланси-
ровки несущего винта той или иной системы.
Мы рассмотрим теперь, что получается прн таком суммировании прн
k = 2, 3 и 4.
Двухлопастный несущий винт
Обозначим азимуты первой лопасти через ip; тогда вторая лопасть,
идущая впереди, будет иметь азимут ip 4- л. Вычислим теперь суммарный
эффект лопастей и получим:
Q = Qi Q2 ~ 2А0 —
— [cos ip 4- cos (ip л)] —
— [sin ip 4~ sin (ip -Ь л)] —
— A2 [cos 2ip + cos (2ip г 2л)] —
- B3 [sin 2ip 4- sin (2ip -|- 2 л)] —
— A3 [cos 3 ip 4- cos (3ip 4- 3л)] —
— B3 [sin 3ip 4- sin (3ip 4- 3л)] — ...
Замечая, что
sin (ip 4- л) = — sin ip,
cos (ip 4- л) = — cos ip,
sin(2ip 4- 2л) — sin 2ip,
cos (2ip 4- 2л) == cos 2ip,
sin (3ip 4- 3 л) = — sin 3ip,
cos (3ip 4-3 л) = —cos3ip и т. д.,
получим окончательно:
Q' = 2Л0 — 2A cos 2ip — 2B3 sin 2ip — 2Л4 cos 4ip — 2/>4 sin 4ip — . . . ,
т. e. в этом случае останется постоянная часть и четные гармоники.
Если бы требовалось вычислить разность усилий (например, моментов)
двух лопастей, то получилось бы:
Q’ = Qt — Q2 — — 2.4 j cos ф — 2e!sinip —
— 2A3 cos Зф — 2B3 sin Зф —
— 2Лб cos 5ф — 2B5 sin 5ф — ... ,
т. e. пропал бы постоянный член и остались бы нечетные гармо-
ники. Мы уже встретились с таким случаем у несущего виита с качаю-
щейся втулкой, где остались лишь третьи гармоники.
Трехлопастный несущий винт
Когда первая лопасть имеет азимут ф, вторая будет иметь ф -J-— и
третья ф -|- — л. Тогда при суммировании получим:
Q -- Qi + Q2 л- Q3 - —
— А3 (cos Зф -J- cos (Зф -4- 2тс) ф- cos (Зф ф- 4к)] —
— В3 [sin Зф 4- sin (Зф 4- 2л) 4 sin (Зф ф- 4~)] — ...
Развернув косинусы и синусы сумм, получим после простых вычисле-
ний:
Q' Qi ~г Q-г Qs ~ ЗЛ0 — ЗА3 cos Зф — ЗВ3 sin Зф,
т. е. в сумме выпали все гармоники, кроме третьей и кратных ей. Легко
показать, что это получается при любом числе лопастей k-.k-тая и кратные
ей гармоники сохраняются, если Ak и Вк не равны нулю.
Действительно, угол между лопастями будет в этом случае равен
у = —, и для £-той гармоники можно написать:
Льсовйф J- Ль cos k
Развертывая синус и косииус сумм, получим:
— Ац [соз&ф (cos 2л -J- cos 4“ ф-...) — sin Лгф (sin 2- -j-
4- sin 4л 4- ...)] — Вл [соэ2ф (cos 2л ф- cos 4~ ф-...) — соэ2ф (sin 2г 4.
+ sin 4- ф-...)] = —kAKcoskty —kBKsinkty.
Следовательно, при сложении всегда сохраняется £-тая и кратные ей гар-
моники, если только Аь и Bh не равны нулю.
Изображение гармоннк с помощью вращающегося вектора
Очень часто, как известно, периодически изменяющиеся величины пред-
тавляют с помощью векторных диаграмм. Особенно удобен этот способ
ля изображения функций, разлагаемых в ряды Фурье. Некоторые авторы
[Ироко применяют такой прием в теории несущего винта.
Пусть какая-либо функция задана выражением
Q = Qo -h At cos ф -J- sin ф 4 А2 cos 2ф •- В2 sin 2ф 4- . . .
водим величины:
G = V aj + В?; С, _ vА‘ + в»; . . с„ - //Ц + в»,
пишем предыдущее выражение в таком виде:
Q — Q + — cos ф + Ct — sin ф 4- Cj ~ cos 2ф + С2 — sin 2ф 4- . . .
Ci С| С2 С2
и, вь
. . . |- Си — соэ&ф -4 Ck — sin &ф.
cii
ведем следующие обозначения:
Л, . . Bi . До . л
~.1 = 5шф1; ^- = со5фх; — -51п2ф2;
— = cos 2ф2 - - . — sin £фь и — = cos /гф/;.
С2 Cft Ch
го всегда можно сделать, выбрав фазовые углы фп ф2... фь из соотно-
ений:
д л Д.
tg4>i = g;tg2^ tg^,<
J этих же формул видно, что
С1 = /<4; + в;; с2 =. + • • •; I
G = j
помощью этих величин выражение для Q получит вид:
Q = Qo 4- Ci (sin Ф1 cos ф 4- cos ф1 sin ф) 4-
4- С2 (sin 2ф2 cos 2ф 4- cos 2ф.3 sin 2ф) 4- • • • 4-
4- Си (sin kx'jk cos &ф — cos&<PhSin^).
о выражение можно переписать окончательно в таком виде:
Q Qo + С, sin (i|) + >h) J- C2 sin 2 (ф 4- ip.) + ... +
+ GsinAfip 4- фи).
а формула может быть очень наглядно представлева геометрически
ir. 136). Если отложить по оси ординат на прямоугольных осях коор-
дннат величину Qo и очертить около точки Ot окружность радиусом
Ci = Vто радиус OtM, образующий с осью абсцисс угол ф + г|>и
дает проекцию sin (ф + г^), а полная ордината ОР проекции точки М
на ось Oyi дает величину
Qo Ci sin (гр -Ь гр^.
Следовательно, подвижная точка
И будет при вращении со ско-
ростью со давать величину Q с
точностью до первых гармоник.
Такой же результат получится и
для второй гармоники, но вектор
С2 будет вращаться с двойной
угловой скоростью, так как его
аргумент равен 2 (гр гр2).
При определении суммарного
эффекта от k лопастей нужно
сложить проекции k точек Mi
М2, ...» Мь, образующих друг
с другом угол, равный для первой
2л
гармоники и = —
Фиг. 136. Графическое изображение
функции Q = Qo -f- С] sin (ф -|- ф4)
для второй гармоники = 2 — =2ухн для й-той гармо-
k
инки rk = — 2ТС.
• h
>v = 2; 7=180°
1-я гармоника^
Н=3; 7-120°
1-я гормоника=Ъ
Ь 3
2
1-я гармоника^
г
4
2-я гармоника^
1 4.
77
2-я гармоникой
4 2 /
м v
Фиг 137. Сложение гармоник на втллке
H=1f - 7=00°
Вместо проектирования точек Mlt /VL..... М& можно сложить векторы
геометрически и проектировать суммарный вектор на ось оодччат. Вращая
такой вектор для первой гармоники со скоростью со, для второй со ско-
ростью 2со и так далее, мы можем сразу судить, уравновешиваются ли
передающиеся на втулку воздействия отдельных лопастей или не уравно-
вешиваются.
На фиг. 137 изображены результаты для разного числа лопастей. Из
расположения векторов С1г С2 и так далее видим, что прн двух лопастях
Т = — = л и четные гармоники будут складываться, а нечетные будут
k
уравновешены. При трех лопастях у - и 70 = 120°. Суммарный вектор
для первых гармоник для второй и третьей лопастей равен Ci и направлен
прямо противоположно вектору Сг первой лопасти. Следовательно, при k = 3
первые гармоники полностью уравновешены, вторые гармоники оказываются
также уравновешенными, но третьи гармоники складываются.
У четырехлопастного несущего винта Ti = — — —, т. е. — 90°,
4 2
Т2° = 180° и т. д. Как видно из фиг. 137, здесь все гармоники, кроме
гармоник, кратных четырем, уравновешены.
Этот способ изображения сложения различных гармоник очень нагляден.
Однако степень неуравновешенности зависит от величины если с по-
мощью соответствующего подбора параметров несущего винта она сделана
близкой к нулю, то н суммарный вектор будет малым и не сможет выз-
вать заметных вибраций.
Окончательный результат /
На крепления лопасти ко втулке будут действовать н аэродинамические
силы и инерционные. И те и другие зависят от азимута, причем в неко-
торых случаях существенными являются в их выражениях члены с третьей
гармоникой. Это очень усложняет все точные расчеты. Кроме того, эти
выражения зависят от формы лопасти, ее закрутки, угла <р7, установки
автомата-перекоса (<рЛ н <рг) и от распределения масс в самой лопасти.
Поэтому дать готовые окончательные результаты не представляется воз-
можным и нужно в каждом частном случае выводить описанными мето-
дами величину всех сил и моментов.
§ 5. МОМЕНТ СИЛ ИНЕРЦИИ
ОТНОСИТЕЛЬНО ПРОДОЛЬНОЙ оси лопасти
Центробежные силы, действующие на элементы лопасти, вызывают
скручивающий лопасть момент, стремящийся поставить ее на меньший угол
установки.
На фиг. 138 изображен выделенный на радиусе г элемент лопасти с
длиной dr. Он вращается около оси несущего виита Оух с угловой скоро-
стью со. Если на этом профиле выделить элемент объема dxdydr с массой
dm, то на него будет действовать по направлению радиуса (а не г)
центробежная сила, равная
dFe -- dm rjco2.
Проекцию dFx этой силы на ось Ох получим, рассмотрев геометрически
подобные треугольники, заштрихованные на фиг. 138, для чего пишем:
dFx : dFe = х : гг;
'‘они провальной оси лопасти
533
отсюда
~dFe.
Подставляя в это выражение силу dFe = dm г^2, получим:
dFx — dm хсо2.
Эта сила дает относительно оси лопасти Oz момент, равный
dMxy = dFx у = dm хуы2.
Фиг. 188. Определение скручивающего момента
центробежных сил
Полный момеит получится суммированием моментов по всем сечениям и
по длине лопасти, т. е.
я
Мху = со2 dm ху = <лЧху.
г f
(548)
Последняя величина Jxy представляет собой центробежный момент
всех масс выделенной радиусами R и г части лопасти. Беря разные значе-
ния г, можно получить изменение скручивающего момеита по длние
лопасти.
Для практических расчетов удобно писать последнее выражение, под-
ставив в иего массу элементарного объема в таком виде:
dm = pmdx dy dr,
где Pm — массовая плотность, обычно средняя для выделенного элемента
лопасти, так как рт несколько изменяется по длине лопасти, a dxdydr —
объем этого элемента.
Подставляя это выражение в формулу (548), получим:
R.
Мху = о3 J dr pm § dx dy ху,
Величина
dxdyxy = Jfxy
есть центробежный момент площади сечеиия профиля. На практике,
чтобы не пользоваться средним для всей лопасти значением prt, обычно
лопасть разбивают на несколько частей, и тогда
Л rt
Mas = p^Ar/f г9+ Ш2 ^PmArJ, ... = ы!
В работе лопасть изгибается, и тогда ее сечеиия отходят от ее про-
дольной оси. Пусть момент J(y0 обозначает центробежный момент инерции
относительно оси, проходящей через центр тяжести сечения; а и Ъ— коор-
динаты этого центра относительно произвольной оси и f — площадь этого
Фиг. 139. Определение центробеж-
ного момента лопасти относитель-
но ее продольной оси
Фиг. 140. Схема установки
контргрузов на лопастях
сечеиия (фиг. 139). Тогда, как известно из механики, центробежный момент
инерции сечеиия относительно оси будет равен
Jxy Jxy о _г F ab.
Следовательно, прогиб лопасти может очень сильно изменить а и b и
величину Jxy, а следовательно, и Мху. Поэтому рассчитывать Мху нужно,
задавшись хотя бы приблизительно величиной прогиба лопасти. Этот момент
прибавляется алгебраически к аэродинамическому скручивающему моменту
и может вызвать заметное дополнительное закручивание лопастей и нару-
шение всей аэродинамики несущего винта.
Наибольшей величины Мху достигает у втулки. Ои сильно нагружает
механизм АП. Для уменьшения этого момента иа лонжероне лопасти у
втулки устанавливают иногда контргрузы (фиг. 140) с массами tn. Тогда
они дадут центробежный момент обратного знака, равный
Mg = 2mab(iA (549)
Если обозначить расстояние, на котором находятся эти грузы от про*
дольной осн, через с, то прн отклонении их на угол ф, мы получим:
а = с81пф, b ~ ссозф,
и тогда
Mg == 2mca(oa sin ф cos ф = тс2 со2 sin 2<р. (550)
Этот момент достигает максимальной величины при ф = 45®. Такие контр-
грузы встречаются на некоторых тяжелых вертолетах и у гребных винтов.
Приложение I
График определения силтяги по формуле Н. Е. Жуковского
со степенью 2/з при ам=18
Приложение II
КРАТКОЕ ОПИСАНИЕ ГЕЛИКОПТЕРА
СИСТЕМЫ Б. Н. ЮРЬЕВА, ТИП II * **
Геликоптер состоит из следующих главных частей.
1) Винтов.
Большого винта V, служащего для поддержания аппарата в воздухе.
Винт сделан по типу аэропланных крыльев, т. е. из деревянного карка-
са, обтянутого материей. Мотор т приводит его во вращение с по-
мощью зубчаток z и Z. Автомат-перекос А служит для приведения ло-
пастей большого винта в колебательное движение.
Малого винта и, удерживающего аппарат от вращения под дейст-
вием большого винта и служащего, кроме того, рулем направления.
Вращается он ременной передачей S.
2) Фермы.
I ондола g служит помещением для авиатора. В ней находятся ап-
параты управления большим и малым винтами и мотором. Хвост х,
передающий усилие малого винта v к центральным частям аппара-
та. К нему прикреплен киль Q, служащий для торможения вращения
аппарата в случае обрыва передаточного ремня и остановки малого
винта
3) Мотора т и зубчаток z и Z, помещенных для безопасности в мо-
торную коробку А4, затянутую сеткой.
' Мотор имеет двойной комплект отказывающих частей, т. е. 2 магне-
то и 2 карбюратора.
4) Шасси В, п, состоящего из передней колесной рамы и заднего
полозка п, служащего для принятия ударов при падении и при спуске
аппа[ ата, а также для перемещения аппарата по земле. Полозок л,
кроме того, защищает малый винт от поломок, не давая ему доходить
до земли.
Взлет. Мотор пускается в ход вращением или малого винта v, илн
специальной рукояткой г. Последний способ позволяет пускать мотор
с-амо.му летчику, не сходя со своего места. Перед полетом следует испы-
тать мотор на полный ход. Для этого несколько человек держат гели-
коптер, не давая ему улететь. При этом летчик несколько раз переклю-
чает мотор с одного комплекта карбюратора и зажигания на другой.
Оба комплекта должны работать одинаково хорошо. После испытания
мотор останавливают и производят осмотр геликоптера. Мотор регули-
* Текст литографированной листовки, раздававшейся всем желающим в 1912 г1
на Международной выставке воздухоплавания и автомобилизма в Москве студенче-
ским «Воздухоплавательным кружком» Н. Е. Жуковского. На листовке указана дата
вппуска. 5 мая 1911 г.
** Привилегия заявлена. Охранное свидетельство X» 45212 . - •
35 Б. Н. Юрьев, т. «
руется рычагом k на колонке К Для взлета геликоптера нам усилить
работу мотора с помощью рычага k до нужной величины.
Примечание Во время вращения большого винта ферма стремится вращаться в
противоположную сторону Этому противодействует малый винт, на что идет около^7%
рабош мотора
Повороты У малого винта лопасти могут менять свой наклон по
желанию авиатора, .что достигается с помощью педали Р (схема тит
Блерио), благодйр’я'Этому изменяется сила тяги вннта против нормаль-
ной, чем и производится поворот аппарата в соответствующую сторону
(пересиливает малый вннт или большой). Аппарат может повернуться
и во время неподвижного висения в воздухе
Сх е j* а. о Kuнпо?ою гел.и копin.cpct
СЛ*С*П Зэ.ТОвъеба,тпиль п
Одновинтовой вертолет продольной схемы с рмевым винтом и автоматом
перекосом (прообраз современных одновинтовых вертолетов) Чертеж взят
из листовки Б Н Юрьева, датированной 5 мая 1911 г
Равновесие 1 ели аппарат получил крен, то выравнивание до
стигается летчиком движением колонки К в противоположную сторону
Этим лопасти большого виита приводятся в колебательное движение
таким образом, что они пробегают опустившуюся сторону опорного кру
га большого винта под большим углом и дают там большую силу,
благодаря чему эта сторона поднимается до положения равновесия
Колебательное движение лопастей большого винта получается с по
мощью автомата-перекоса А
Висение в воздухе Высота полета регулируется работой мо
тора Если при этом геликоптер будет двигаться относительно земли, то
Для неподвижного висения летчик отклоняет аппарат при помощи
коленки /С назад на некоторый угол до поекращення этого движения
Поступательное движение Достигается наклоном всего
аппарата вперед с помощью колонки К В этом случае сила большого
винта действует наклонно и дает тве силы — подъемную и тягу, и аппа-
рат начинает двигаться поступательно По мере увеличения скорости
движения лопасти большого вннта начинают работать неравномерно
Лопасть, идущая вперед, действует сильнее идущей назад Но двигая
колонку в сторону, летчик заставляет лопасть колебаться, и ее дейст
вне этим выравнивается, аппарат будет лететь ровно (плюс скорости
компенсируется минусом угла наклона, и наоборот) Чем больше накпоы
аппарата, тем больше скорость полета Поступательное движение может
быть получено по любому направлению, например, перпендикулярно
ферме (с меньшей скоростью), т е для аппарата возможно «боковое
примыкание»
Спуск
Аппарат ставят наклонно против ветпа, до тех пор пока он не по-
виснет неподвижно в воздухе и затем медленно опускаются на выбран-
ное место Коснувшись земли, останавливают мотор.
Остановка мотора в воздухе и планирующий спуск.
В случае внезапной остановки мотора летчик быстро с помощью
переключателя переводит мотор на второй комплект карбюратора и вос-
пламенения и тотчас же спускается на землю для осмотра аппарат1»
Если же мотор не пойдет со второго комплекта, то это покажет, что
произошла серьезная поломка мотора (весьма редкий случай), и тогда
летчик должен принять меры к безопасному спуску на землю Для этого
он с помощью рычага 7? уменьшает шаг большого винта до нуля и за-
тем постепенно, по мере уменьшения скорости вращения делает шаг
большого вннта отрицательным. Тогда аппарат спускается планируя,
причем большой винт вертится, как ветряная мельница С помощью ко-
лонки К можно заставить геликоптер спуститься на землю не только-
вертикально, но и наклонно, что позволит выбирать место для спуска.
Удар при спуске принимается резиновыми амортизаторами шасси,
имеющими большой ход Кроме того, для большей безопасности спуска
аппарат может быть снабжен и веерообразным парашютом D
35*
ЛИТЕРАТУРА
Александров В.Л. Приложение теории решеток к винту. Труды ЦАГИ, вып 6.
1924.
Александров В.Л. Воздушные вичты. М., Оборонгиз, 1951. Атлас вентиля
торов и дефлекторов. Под редакцией К. А. Ушакова. Труды НАГИ. № 172, 1934.
Батурина Т А. Влияние формы капота и размеров кока на его к. п. д. Труды
ЦАГИ, № 392, 1939.
Баршевский В, Б. Вертолет в полете. М, ДОСААФ, 1951.
Белкин С. Л., Дружинин А. С. Практический метод подсчета характеристик
кинтов. Труды ЦАГИ, № 429, 1939.
Боднер В. А Анализ основных схем регулирования автоматических ВИШ. Труды
ВВИА. № 221, 1947,
Ботезат Г. А. Исследование явления работы лопастного винта. Главный аэро-
дром УВВФ, Пг., 1917.
Братухин И. П. Аэродинамический расчет автожира. «Техника воздушного
флота», 1934, № 3.
Братухин И. П. Автожиры. М,— Л., Госмашметиздат, 1934.
Бычков А. Г. Осевые вентиляторы ЦАГИ серии V. Труды ЦАГИ, вып. 362,
(938.
Вагнер Р., Коментц К. и К у харе кий В. Направляющие аппараты греб-
ных винтов. Гострансиздат, М, 1932.
Вальтер П. А. К расчету гребных винтов. «Техника воздушного флота». 1928, №9
В ед ров В. С. Относительный коэффициент полезною действия гребного винта
«Техника воздушного флота», 1927, № 4.
ВедровВС. и ОстославскийИ. В. Расчет обдувки монопланных крыль-
ев с винтами перед крылом Труды ЦАГИ, № 232, 1935.
Вельнер Г. Летательные машины. Расчет аэропланов и геликоптеров. Перевод
анж. В. Арефьева, СПб., 1910.
Веселовский МН, Новая система характеристических коэффициентов греб-
ного винта. М.. журн. «Война и техника», 192,7, № 1.
Ветчинкин В.П, Расчет гребного вита М. «Бюллетени Политехнич. об-ва»,
1913, № 5.
Ветчинкин В.П. Об инвариантах гребного винта. Труды Отд, физич. наук
Общества любителей естествознания, т. XVII, вып. I, 1914.
Ветчинкин В.П. Приложение теории идеального пропеллера к исследованию
а расчету гребных винтов. (Литография ) М., Изд. Кратких теоретич. курсов авиации,
W16. при МВТУ.
ветчинкин В.П, О методе предварительного определения к. п. д. гребного
Ъинта при производстве аэродинамического расчета аэроплана. (Литография.) Изд
ЦАГИ. 1918.
Ветчинкин В.П. Расчет гребного виита. Труды Авиационного расчетно-испы-
гательного бюро при МВТУ, вып. 3 и 4. (Литография.) М., 1918.
Ветчинкин В.П. Теория гребных винтов. (Литография.) Изд-во Воен, воздуш
академии РККА. 1926.
*' Ветчинкин В.П. Динамика самолета. ОЖИ, 1933.
Ветчин кин В. П. и Поляхов Н. Н. Теория и расчет воздушного гребного
винта. Оборонгиз, 1940.
Вильдгрубе Л. С. Некоторые графические приемы аэродинамических расчетов
«Техника воздушного флота», 1945, № 4.
'Вильдгрубе Л. С. Оптимальные параметры геликоптера на режимах вертикаль-
ного полета. «Техника воздушного флота», 1946, № 3 и 5.
Вильдгрубе Л.С. Определение летных характеристик геликоптера на всех ре-
жимах и высотах и выбор его параметров при проектировании. «Техника воздушного
флота». 1947, № 6.
Гессоу А. и Мейерс Г. Аэродинамика вертолета. Оборонгиз, 1954.
Глауерт Г. Основы теории крыльев и винта. М.— Л., ГНТИ, 1931.
Го рошен ко Б. Т. Расчет максимальной скорости полета. Оборонгиз. 1944.
Горошенко Б. Т. Аэродинамика скоростного самолета. Оборонгиз, 1948.
Джевецкий С. К. Теория воздушных винтов и способ их вычисления Киев,
1910.
Доллежаль В. А. Редукторы числа оборотов авиационных двигателей. М., Мань-
издат, 1936.
Дудаков В. И. Пересчет воздушной характеристики пропеллера при изменении
шага. «Техника воздушного флота», 1929, № 9.
Дюрэнд В. Ф. Аэродинамика, т. 2 и 4. Оборонгиз, 1939,
Егоров Б. Н., Кузнецов В А. 1. Исследование работы винтов тандем в при-
сутствии крыла. 2. Приложение вихревой теории к расчету заднего винта в комбинат
ции тандем. Труды ЦАГИ, вып. 87, 1932.
Егоров Б. Н. Испытания винтов на больших окружных скоростях. Труды ЦАГИ,
№ 158. 1933.
Жуковский Н. Е. К теории летания. М., изд. Русского физико-химич. об-ва, часть
физическая, 1890; Собр. соч., т. VI. ОНТИ, 1937; Собр. соч., т. IV. Гостехиздат, 1949.
Жуковский Н. Е. О крылатых пропеллерах. «Воздухоплавание и исследование
атмосферы», вып. 4. СПб., изд. Русского те.хнич. об-ва, 1898; Собр. соч., т. VI. ОНТИ,
1937. Собр. соч., т. IV. Гостехиздат, 1949.
Жуковский Н. Е. О полезном грузе, поднимаемом геликоптером. СПб., «Воз-
духоплаватель», 1904, № 2; Собр. соч., т. VI. ОНТИ. 1937; Собр. соч., т. IV. Гостехиздат,
1949.
Жуковский Н. Е. Теория гребного винта с большим числом лопастей, т. XIII,
вып. 2, М., Труды Отд. физич на}'к об-ва любителей естествознания, Отд. физич. наук,
1907; Собр. соч., т. VI. ОНТИ, 1937; Собр. соч., т. IV. Гостехиздат, 1949.
Жуковский Н. Е. Опыт теоретического определения эффекта ветра, дующего
в плоскости геликоптерного винта. Собр. соч., т. VI. ОНТИ, 1937; Собр. соч., т. 1V.
Гостехиздат. 1949.
Жуковский Н. Е. Теоретические основы воздухоплавания. М., изд. студенче-
ского общества при Импер. Моск. Техн, училище, 1911. Собр. соч., добавочный том.
М.— Л., ОНТИ, 1938: Собр. соч., т. 6. Гостехиздат, 1950.
Жуковский Н. Е. Вихревая теория гребного винта. Статьи 1, 2, 3, 4. Собр.
соч., т. VI, ОНТИ, 1937; Собр. соч, т. IV, Гостехиздат, 1949
Жуковский Н. Е. Аэродинамический расчет медленно движущихся ветряных
мельниц. Труды ЦАГИ, 1920; Собр. соч., т. VI, ОНТИ, 1937; Собр. соч., т. VH,
Гостехиздат, 1950.
Жуковский Н.Е. Тихоходная ветряная мельница. Труды ЦАГИ, 1920; Собр.
соч.. т. VI. ОНТИ, 1937; Сбор, соч., т. VII, Гостехиздат, 1950.
Жуковский Н.Е. Ветряная мельница типа НЕЖ. Труды ЦАГИ, 1920; Собр.
соч., т. V11, ОНТИ, 1937; Собр. соч., т. VII. Грстехиздат, 1950.
Изаксон А'/М; Работа воздушного винта на режиме авторотации. ГИТИ. Труды
ЦАГИ, № 47, 1930.
Изаксон А;М. Геликоптеры. ГНТИ. 1931.
, Изаксон А. М., Антонов Д И. Работа воздушных винтов с элеронами на
режиме авторотации. Труды ЦАГИ, № 127, 1932,
Изаксон А М. Работа на месте воздушных винтов С элеронами. «Техника воз
душного флота», 1933, № 10.
Изаксон А. М. Исследование работы взаимно перекрывающихся воздушных
винтов. «Техника воздушного флота», 1933, № 3.
Изаксон А. М., Лаписов В. П. Работа воздушного винта на режиме косой
обдувки. «Техника воздушного флота», 1934, № 8.
Изаксон AM. 1 еликоптеры Оборонгиз, 1947.
Камов И. И. Военное применение автожиров «Весгник воздушного флота», 1935.
№ 11 и 12
Камов Н. И. Развитие конструктивных форм винтовых летательных аппаратов
«Техника воздушного флота», 1945, Xs 7.
Камов Н. И. Винтовые летательные аппараты. Оборонгиз, 1948,
Калинушкин М.П. Вентиляторы осевые ЦАГИ и центробежные низкого
и среднего давления. Технич. заметки ЦАГИ, Xs 157, 1937.
Калинушкин М.П. Осевые вентиляторы ЦАГИ. Технич. заметки ЦАГИ, № 63,
1935.
Касторский В.Е. Оптический метод исследования макового движения шарнир
но подвешенной лопасти геликоптера Труды ВВИА, № 115, 1944.
Касторский В Е. Графо-аналитический метод определения коэффициента про-
текания геликоптерного винта. Труды ВВИА, № 121, 1944.
Касторский BE. Расчет коэффициента махового движения шарнирно подве
щепной лопасти геликоптерного ротора с автоматом-перекосом. Труды ВВИА. № 125.
1945.
* Касторский В. Е Оценка влияния шероховатости на аэродинамику воздушного
винта. Труды ВВИА, № 143, 1945.
Касторский В Е. Сравнение геликоптерного винта типа НЕЖ с вариацион
ным винтом. Труды ВВИА, №-144. 1945.
Келдыш М. В и Ф р а н к е л ь Ф. И. Строгое обоснование теории винта Жуковско-
го. Математический сборник, т. 42, Xs 2, 1935 Изд. Московского математич об-ва.
Козлов С. Г. Воздушные гребные винты. Библиотека авиационного инженера
«Самолетостроение», ГНТИ, 1931.
Козлов С. Г. Воздушные гребные винты. Изд. ВВИА. Сборник. 1931.
- Кожевников В А. Влияние близости земли на аэродинамические характери-
стики несущего винта геликоптера. «Техника воздушного флота», 1947, № 4.
Ко ч и н Н. Е., К и б е л ь И. А. и Розе Н. В. Теоретическая гидромеханика, т. 1
ГоС. Изд-во технико-теоретич. лит-ры, 1948; т 2, Гостехизлат, 1948.
Кравец АС. Тормозное действие авторотирующего и остановленного винта
Труды ВВИА, 1945.
Кузьмин Г. И. Пересчет характеристики винта на другое перекрытие. «Техника
воздушного флота», 1928, Xs 12.
Кузьмин Г. И. Диаграмма для проектирования воздушных винтов. Трхды ЦАГИ
№ 38, 1929.
Кузьмин Г. И. Исследование работы воздушных винтов. Труды ЦАГИ, Xs 45
too.
Кузьмин Г. И. Расчет винта по вихревой теории Труды ЦАГИ, № 132, 1932
Кузьмин Г. И. и ХалезовД. В. Влияние формы профиля и толщины лопасти
на характеристику винта. Труды ЦАГИ. Xs 129, 1932.
Кузьмин Г. И. и ХалезовД. В. Диаграммы для проектирования воздушных
аинтсв с профилями ВС-2. Труды ЦАГИ, № 137, 1933.
Кузьмин Г. И. Винты регулируемого шага. Труды ВВИА, 1934.
Курочкин Ф. П. Соосные винты ИВС. Труды ВВИА, 1941.
Лесникова Н.П, Графики для расчета гребных винтов. Авиаиздат, 1932. t
' Листопадов В К. Распределение давления по сечениям лопасти воздушного
винта. Труды ВВИА, № 4. 1947.
Мартынов А. К. Экспериментальная аэродинамика Оборонгиз, 1950.
Майкапар Г. И,, Л е п и л к и н А. М., Халезов Д. В Аэродинамический расчет
знмтов по лопастной теории. Труды ЦАГИ. № 529, 1940.
Майкапар Г.И К теории тонкого крыла. Приложения вихревой теории винта
Труды ЦАГИ, № 613, 1947.
Мейл ер М. А Основы теории и проектирования гребного винта. Военмориздат
1940.
Миль М. Л. О работе автожира. «Техника воздушного флота», 1934. № 5.
'Миль М Л. О динамическом закручивании лопастей ротора автожира в полете
«Техника гоздушного флота», 1937, № 2.
Миль'М Л. Аэродинамика несущего винта с шарнирным креплением лопастей при
криволинейном движении. Труды ЦАГИ, № 465. 1940.
Миль М.Л. и Ярошенко В. Н. Аэродинамический расчет геликоптера. «Тех-
ника воздушного флота». 1946. № 11
Минухин Б. А. Расчет винта по относительной теории Труды ЦАГИ, М 401, 1939.
Михайлов А. Н. Теория ротора автожира с переменным углом установки. «Тех-
ника воздушного флота». 1940. № 3.
Мои и а Т. Индуктивная скорость и характеристика пропеллера. Бюллетень ЦАГИ.
Л"2 20. 1933.
Мориа Т. Диаграммы индуктивной скорости и метод расчета аэродинамических
характеристик винта. Технич. записки ЦАГИ, № 119. 1936.
Николаев Д. Н Приведение коэффициента полезного действия винта к стан-
дартныг» атмосферным условиям. Технич. записки ВВИА, № 3, 1945.
Оглоблин А. П. Оснозы гидромеханики. Оборонгиз, 1945.
Остославский И В и Халезов Д. В. Взаимное влияние винта и самолета.
Труды ЦАГИ, № 213, 1935.
Остославский И. В и Матвеев В. Н. О работе винта, помешенного в коль-
це. Труды ЦАГИ, № 248. 1935.
Остославский И. В. и Халезов _Д В Характеристика трехлопастных ме-
таллических винтов З-СМВ-2 ЦАГИ. Труды ЦАГИ, 1936.
Остославский И. В. и Халезов Д. В Характеристики винтовых профилей
типа Кларк Y. Технич. записки ЦАГИ, № 154, 193.7.
Остославский И. В. и Титов В. М. Аэродинамический расчет самолета.
Оборонгиз, 1947
Панов ДЮ. Расчет воздушного винта на прочность. Труды ЦАГИ, вып. 288,
1937.
Поликовский В. И. Вентиляторы, воздуходувки и компрессоры. ОНТИ, 1935.
Поляхов Н. Н. К теории гребного винта. Труды ЦАГИ, Хе 184, 1935.
Полях ов Н.Н. Теория винта с конечным числом лопастей, Труды ЦАГИ, № 324,
1937.
Поляхов Н.Н. О наивыгоднейшем винте. Труды ЦАГИ, № 455, 1939
История воздухоплавания и авиации в СССР. Под редакцией В. А. Попова. Обо-
ронгиз, 1944
Проскура Г. Ф. Воздушные винты. Теория и расчет воздушных винтов. Харьков.
Изд. Авиасекиии Харьковского технолог, ин та, 1927.
Проскуряков А. П- Колебания лопастей автожира относительно вертикального
шарнира. Труды ЦАГИ, № 379, 1938.
Проскуряков А. П. Влияние нестационарности потока на аэродинамику лопа-
сти автожира. Труды ЦАГИ, № 460. 1939.
Проскуряков А. П. Характеристические числа решений дифференциального
уравнения 2-го порядка с периодическими коэффициентами. Прикладная математика
и механика, т. X, вып. 5—6. 1946. М-. Изд. Ин-та матем. и мех. АН СССР, 1946.
Проскуряков А.П. Аэродинамииескпй расчет несущего винта с переменным
по азимуту углом установки лопастей Труды ЛИИ, № 16, 1946.
Проскуряков А. П. Динамическая-устойчивость несущего винта при наличии
горизонтальных шарнипов у лопастей. Труды ЛИИ. № 22. 1947.
’Пышнов В. С. Аэродинамика самолета. Оборонгиз, 1943.
Ря.бушинский Д.П. Теоретичссксс 'исследование о винтах. Изд. Кучинского
аэроданамич. ин-та. 1912.
Сабинин Г. X. Концевые потери у гребного вицта. Приложение к журналу
«Вестник воздушного флота», 1924. № 3.
Сабинин Г. X. Теория идеального ветряка. Труды ЦАГИ. № 32, 1927.
Сабинин Г. X. Теория и аэродинамический расчет ветряных двигателей. Труды
ЦАГИ, К’ 104, 1931.
. „СкржинскийН.К. Геликоптеры. Журнал «Самолет», 1936, № 16.
Стр Ижевск ий С. Я- К аэродинамике подъемного винта. Труды ВВИА, № 6,
1944,
Стрижевский С. Я. Теория и расчет воздушных винтов. Труды ВВИА, 1948.
Струве Э.Э. К вопросу о поверочном расчете осевого вентилятора. Труды ЦАГИ,
№ 326, 1937.
Сборник статей по Промышленной аэродинамике и вентиляторостроению. Труды
ЦАГИ, рып 211, 1935.
Табачников В. Г. Боковая сила ротэпа автожира. Труды ЦАГИ, № 456. 1939.
Toy ш. В Л. .и Сидоров И. А. Общий курс воздушных винтов. Оборонгиз,
1943.
ТеушВ.Л.,а Чернобыльский М. Б. Работа воздушного винта. Оборонгиз,
1946.
Ушаков К. А. Аэродинамический расчет осевого вентилятора. Труды ЦАГИ,
№ 277. 1936.
Ушаков К. А. Красильщиков П П., Волков А. К-. Г ржегоржевский
А. Н- Атлас аэродинамических характеристик профилей крыльев. Труды ЦАГИ
1940.
ХалезовД. В. и ОстославскийИ. В Характеристики двухлопастных и че-
тырехлопасткых винтов ЦАГИ. Труды ЦАГИ, 1935.
Халезов Д. В. К вопросу о соосных винтах. Труды ЦАГИ, № 386, 1939.
Халезов Д. В и Остославский И. В. Характеристики трехлопастных ме-
таллических винтов. Труды ЦАГИ, № 300.
ЧерновДК О наступлении возможности механического воздухоплавания. СПб.,
Изд-во Сойкина, 1894.
Чудаков Е.А. Расчет автомобиля, ч. I. Изложение расчетов трансмиссий авто-
мобиля, весьма близких к трансмиссиям геликоптеров. Госмашметиздат, 193G.
Штейнен. Естественный метод расчета гребных винтов. Гострансиздат, 1932.
Юрьев Б Н. О наибольшем полезном грузе, поднимаемом аэропланами и ге-
ликоптерами. Жури. «Автомобиль и воздухоплавание», 19'1, № 6 и 11.
Юрьев Б.Н. Графо-аналитический метод расчета винта. М., Изд. Высшего воен-
ного редакц. Совета, 1922.
ЮрьевБ Н. О современном положении теории гребного винта. «Вестник воздушно-
го флота», 1923, № 5.
Юрьев Б. Н Воздушные гребные винты (пропеллеры). Труды ЦАГИ, № 10, 1925.
е Юрьев Ц..Н Воздушные вингы. ОНТИ, 1934.
Юрьев Б. Н. Современное положение аэродинамической теории воздушного винта.
1-я„В<?ес. конференция по воздушны?л и водяным винтам. Труды ЦАГИ, 1934.
Юрьев Б Н Некоторые вопросы теории геликоптера. 3-я Всес. конференция по
(аэродинамике/Труды ЦАГИ, 1935. , ' „ ".
Юрьев Б. Н. Геликоптеры. Труды ВВИА, 1935 г. (Доклад на конференции ЁВА.
1932). ?:• ) , ;.. ... ,s:.. .... _,.uu .. .
Юр ье а Б. H. Пределы современной авиацид, и способы их преодоления. Труды
ЦАГИ. 1936-.
Юрьев Б. Н. Экспериментальная аэродинамика, ч. 2. Оборонгиз, 1938.
. Юрьев Б.Н. Экспериментальная аэродинамика, ч. 1. Оборонгиз, 1939.
Юрьев Б. Н. Исследование летных свойств геликоптера. Труды ВВИА, вып. № 49
1939. ’ ' ' ’
Юрьев Б.Н. Проблема геликоптера. Труды научно-технич. конференции ВВИА
(1944). 1945. (Сокращенное изложение данов Известиях АН СССР, ОТН, К® 6.
1945).
Юрьев Б.Н. Вихревая теория винтов. Труды ВВИА, 1947.
Юрьев Б. Н. и Воробьев Б. Н. Работы Леонардо да Винчи в области меха-
ники и авиации. Известия АН СССР, ОТН, № 7, 1952.
Яблонев А. Воздухоплавание. Устройство автомобиля. М, Изд. Кушнарева
1903.
Я н г Р. А. Теория и расчет геликоптера. Оборонгиз, 1951.
В е п d е ш а п п F. Luftschrauben Untersuchungen. В. 1912.
Bendemann F. Luftschrauben Untersuchungen. В. 1918.
Crowe J. H. The problem of vertical flight. «Aircraft Engineering,» L., 1934, v. 6.
N 69, p. 292—296, ill., N 70, p 315—318, ill.
Diehl W. S. The application ot propeller test data to design and performance cal-
culations. «NACA Rep», 1924, N 186.
Diehl W. S. The general efficiency curve lor air propellers. «NACA Rep.», 1923,
N 168.
Durand W. F. The aerodynamic laboratory at Lenand Stanford Junior University
and the equipment installed with special reference to tests on air propellers. «NACA Rep.»,
1917, N 14.
Durand W. F. Experimental research on air propellers. IL «NACA Rep.», 1918,
N 30.
Durand W. F. Experimental research on air propellers. V. «NACA Rep.», 1922,
N 141.
Durand W. F. a. Lesley E.P. Experimental research on air propellers. 111.
«NACA Rep », 1920, N 64.
Durand W. F. a. L e s 1 e у E. P. Experimental research on air propellers. IV. «NACA
Rep.», 1920, N 109.
D u г a ii d \V. F. a. Lesley E.P. Comparison of tests on air propellers in Hight with
wind tunnel model tests on similar forms. «NACA Rep.» 1926, N 220.
Fage A., Lock C.N.H., Howard R.G. a. Bateman H. Experiments with
a family of airscrew. Part I. Experiments wiih the family of airscrews mounted in front
of a small body. «ARC R. & M.», L., 1922, N 829.
Fla mm O. Die Schiffsschraube und ihre Wirkung in dem Wasser. «Jahrbuch der
Schiffbautechn. Gesellschaft», Berlin, 1909, v 9
Glauert H. An aerodynamic theory of the airscrew. «ARC R. & M.», L., 1922,
N 786.
Glauert H. A general theory ol the autogyro, «ARC R. & M.», L., 1926,
N 1111.
Glauert H. Vertical ascent of a helicopter. «ARC R. & M », L., 1927, N 1132.
Glauert H. On the horisontal flight of a helicopter. «ARC R. & M.», L., 1928,
N 1157.
Lame M. Le Vol vertical, p. 1926.
Lauchcster F.M. Aerodynamics. L., 1907, 442 p, ill.
Lichteu R. L. Some aspects of convertible aircraft design. «JAS», 1949, X, v. 16,
N iO. p. 611—622, ill.
Lock C. N. H. Further development of autogiro theory. «ARC R. & M.», L.. 1927,
N t!27.
' Mat gout is W. S. Les hellcopteres. P„ 1922.
Margoulis W. Nouvelles recherches experimentales sur les helices d’helicopteres.
«Compres Rendus de L’Acad, des Sciences*, P„ 1927, v. 184, N 12, p. 735—737.
Munk M. Analysis of W F Durand’s and S. P Lesley’s propeller tests. «NACA
Rep.», Г923, N 175.
Nikolsky A. A. Notes on helicopter design theory. L„ 1945. 228 p., ill.
Offermann E. Reisenflugzeuge. B., 1927, 518 p
Renard C. Sur la qualite des helices sustentatrices «Comptes Rendus de 1’Acad des
Sciences», P. 1903, N 21, p. 970.
Riaoouchinsky D. Recherches sur les helices aeriennes «Bull. de 1’lnstitut
Aerodynamique de Koutchino», M., 1909, fasc. 11, p. 3—102 ill.
Stssingh G. Contribution to the aerodynamics of rofating wing aircraft. <NACA
ТМ», 1939; N 921; 1941, N 990 (Перевод из «I ultfahtforschung», Munch., 1938, Juni 6
v. XI, N 6, p. 290-302, ill.; 1940, Juni 20, v. XVII, \ 7, p. 196—203, ill).
Theodorsen T. Theory of propellers. N. Y.— Toronto—L, 1948, 164 p.
Wald O. A method for rapid estimation of helicopter performance. «JAS», 1943, IV,
v 10. N 4, p 131—135, ill.
Wein j ng F. Aerodynamik der Luitschraube. B, 1940.
W b e a 11 e у J B. An aerodynamic analysis of the autogiro rotor with a comparison
between calculated and experimental results «NACA Rep», 1934, N 487
ОГЛАВЛЕНИЕ
Предисловие . . . . ..................................... 3
Борис Николаевич Юрьев (Очерк жизни и деятельности) ........................... 7
Раздел 1
ВОЗДУШНЫЕ ВИНТЫ
ИМПУЛЬСНАЯ ТЕОРИЯ ВОЗДУШНЫХ винтов
Глава 1. Основные формулы импульсной теории винта . .25
§ I. Скорости в струе, создаваемой винтом . ... .25
§ 2. Уравнение связи............................................. 30
§ 3 Сили, действующие на элемент лопасти, и мощность, необходимая
для его вращения................................................33
Глава 2. Поверочный расчет винта.......................................... 36
§ 1. Графо-аналитический метод поверочного расчета винта в нату-
ральных величинах на одном режиме . . .... 39
§ 2. Расчет винта на всех режимах в натуральных величинах . 36
§ 3 Работа винта на 20 режимах ............... . 43
§ 4. Форма струи винта на разных режимах .... ... 45
§ 5. Характеристики профиля, приспособленные к расчету винтов . 47
§ 6. Упрощенное уравнение связи и его аналитииеское решение . . 50
Глава 3 Расчет винта в отвлеченных обозначениях............................57
§ 1. Отвлеченные величины в теории винта...........................57
§ 2. Тригонометрические выражения для скоростей в струе винта . . 60
§ 3. Тригонометрическая форма уравнения связи......................62
§ 4. Поверочный расчет винта в отвлеченных обозначениях . . 65
§ 5. Расчет винта для всех режимов одновременно в отвлеченных обо-
значениях ................................................' . . 68
§ 6. О точности и пределах применения изложенной теории ... 72
Глава 4. Нормальный винт . . ... . .... 75
§ 1. Скорость потока у нормального винта...........................75
§ 2. Формулы силы тяги >и мощности нормального винта .... 78
§ 3. Расчет нормального винта......................................81
§ 4. Форма лопасти у нормального винта........................ ... 85
Глава 5. Приближенный расчет винта-пропеллера произвольной формы . . 88
§ 1. Осреднение скоростей и упрошенные формулы тяги и мощности 88
§ 2. Факторы скорости, тяги и мощности.........................90
Глава 6. Общий анализ импульсной теории винтов.............................93
§ 1. Основные формулы Уравнение связи — основа теории .... 93
§ 2. Уравнение связи по осевому импульсу.......................97
S 3. Решение уравнения связи........................................98
Выводы....................................................... 100
уточнение импульсной теории винтов
§ 1. Скорость вращения в струе винта ... ............102
§ 2. Вычисление скорости вращения Uj..............................104
§ 3. Давления в уходящей струе воздуха .
§ 4, Вычисление осевой индуктивной скорости
ВИХРЕВАЯ ТЕОРИЯ ВИНТОВ
Глава 1. Скорости в струе винта .... ......................
§ 1. Скорость потока, набегающего на лопасть винта.............
§ 2. Схема вихрей, сбегающих с винта. Струя винта ....
§ 3. Скачок окружной скорости..................................
§ 4. Давления в горловом сечении струи винта ..................
§ 5. Осевая скорость потока ...................................
§ 6. Поверхностное условие и скорость отбрасывания у винта типа НЕЖ
§ 7. Теорема Фруда — Фннстервальдера—Жуковского................
§ 8. Скоростное поле винта.....................................
113
117
119
120
122
124
- -125
Глава 2 Тяга, мощность и к.пд. винта....................
§ I. Силы, действующие на элемент винта
§ 2. Отвлеченные обозначения ...................
§ 3. Переход к отвлеченным обозначениям . . . .
§ 4. Сила тяги, мощность -и к.п.д. винта типа НЕЖ .
105
106
112
112
127
127
130
132
135
Глава 3. Расчет -и компоновка винтов.................................. . 139
§ I. Подбор циркуляции винта НЕЖ для заданных условий работы . 139
§ 2. Расчет и компоновка винта НЕЖ и винта с переменной по радиусу
циркуляцией................................................. ... 141
§ 3. Учет прочности винта при его компоновке........................145
§ 4. Поверочный расчет вннта........................................149
§ 5. Понятие о наивыгоднейшем винте.................................153
Глава 4. Особые случаи работы винтов.................................. . 160
§ 1. Расчет геликоптерных винтов....................................160
§ 2. Расчет осевых вентиляторов............................ . . z 163
§ 3. Ветряные двигатели .... -.......................................167
§ 4. Теория решеток ............................................... 170
§ 5. Контрпропеллер..................................................176
§ 6. Соосные винты...................................................183
Приложение 1. Характеристики винтовых профилей........................ , 188
Приложение II. Подбор циркуляции с помощью логарифмической диаграммы 192
О СОВРЕМЕННОМ ПОЛОЖЕНИИ ТЕОРИИ ГРЕБНОГО ВИНТА
§ 1. Обзор характерных теорий винта..............................196
§ 2. Основные положения новой теории вннтов......................203
Раздел П
ВЕРТОЛЕТЫ
ИССЛЕДОВАНИЕ ЛЕТНЫХ СВОЙСТВ ГЕЛИКОПТЕРОВ
Глава 1. Висение в воздухе................................................... 215
§ I. Аэродинамические свойства винтов, работающих на месте . . 215
$ 2. Трансмиссии геликоптера....................................... 226
§ 3. Вес редукторов и трансмиссий . ........................232
§ 4. Вес Винтов и роторов.....................................- ' . 237
§ 5. Полный вес геликоптеров.....................................1 . 239
§ 6. Статический потолок геликоптера...........................«' . 241
Глава 2. Вертикальное движение геликоптера . .....................246
§ 1. Взлет геликоптера. Графическое решение задачи .... 246
§ 2. Графический расчет взлета геликоптера с интегрированием по спо-
собу Маделунга................................................... . ' . 249
§ 3. Аналитическое решение задачи о взлете геликоптера . . . ‘ . 251
Глава в. Движение геликоптера с горизонтальной скоростью . . . 256
§ I. Планирование геликоптера.......................................256
§ 2. Поляры роторов . ................................. • 260
§ 3. Горизонтальный полет геликоптера без пропеллера................263
§ 4. Аэродинамический расчет беспропеллерного геликоптера, летящего
под углом к горизонту..............................» . . 265
§ 5. Горизонтальный полет геликоптера с пропеллером................268
§ 6. Геликоптеры, превращающиеся в аэропланы . . .... 273
Выводы........................................................... . 276
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ ВЕРТОЛЕТОВ
Часть I. Теория винтов и вертикальный полет вертолета.......................277
Глава L Основные термины и обозначения, принятые в книге....................277
§ 1. Общие указания и пояснения................................... 277
§ 2. Пояснения к некоторым терминам.................................279
§ 3. Основные обозначения......................................... 280
Глава 2 Импульсная теория несущего вннта при осевом движении (общая тео-
рия несущего винта)....................................................287
, s § I. История разработки импульсной теории винтов.....................287
\ § 2. Струя воздуха, создаваемая реальным винтом в общем случае . . 288
у § 3. Элементарные сила тяги и мощность, вычисленные по струе. Без-
у размерные величины..............................................291
(• " § 4. Элементарные сила тяги и мощность, вычисленные по профилю
лопасти.........................................................292
§ 5 Уравнение связи . 295
§ 6. Концевые потери у винтов.................................... 298
{,р; § 7. Интегральные формулы для тяги и мощности несущего винта при
осево.м движении................................................301
§ 8. Замечание об индуктивной скорости у винтов.....................302
Глава 3. Рабочие формулы импульсной теории..................................303
§ I. Несущий винг типа НЕЖ..........................................303
§ 2. Несущий винт с a — const и Cy=const............................308
§ 3. Несущий вицт средней формы.....................................311
§ 4. Одночленные формулы с использованием относительного к.п.д. т]о 315
§ 5 Двучленные формулы для расчета несущих винтов на режиме
висения.............................................................318
§ 6. Формулы для расчета многовинтовых вертолетов...................323
§ 7. Поверочный расчет несущего винта любой формы...................324
Глава 4. Вертикальный полет вертолета ......................................329
§ 1. Значение вертикального полета вертолета ...................... 329
§ 2. Определение высоты потолка висения и скороподъемности вертолета
по избытку мощностей...............................................330
§ 3. Расчет скороподъемности и потолка висения на основе опытных
данных........................................................... 333
§ 4. Расчет скороподъемности на основе теоретических формул . . . 335
§ 5. Кривая скороподъемности и построение барограммы вертикального
взлета.............................................................337
' § 6. Скорость вертикального спуска на авторотации по опытным данным 340
. § 7. Предельная нагрузка вертолета.................................. 341
Глава 5. Режим вертикального спуска вертолета с работающим двигателем я
на авторотации ........................................................344
§ 1. Безопасиость спуска вертолета................................ 344
§ 2. Струя у несущего винта на разных режимах вертикального полета
Режим вихревого кольца............................................ 345
; • § 3. Использование кривей и7в) ..... 353
§ 4. Шасси вертолета............................................... 360
§ 5. Вертикальная посадка вертолета «с подрывом» несущего винта . 362
‘•f' § 6. Специальные мероприятия по улучшению вертикального спуска
вертолета ... . . 370
Часть II. Полет с горизонтальной скоростью ......... 373
Глава 6. Характеристические углы и скорость у несущего винта при полете
с горизонтальной скоростью ...................................... ....... 373
§ J. Углы, образованные полной силой тяги Т с осями координат . . 373
§ 2. Скорости обдувки диска несущего винта и угол скоса потока 376
§ 3. Индуктивная скорость при косой обдувке изолированного несущего
винта.............................................................379
§ 4. Взаимное влияние несущих винтов и крыльев...................385
§ 5. О балансировочном угле дБ вертолета.........................393
Глава 7. Силы, действующие на несущий винт, и потребляемая им мощность 400
§ I. Индуктивное сопротивление несущего винта....................' 40^
§ 2. Профильное сопротивление несущего винта в целом .... 402
§ 3. Связь углов ei, ер, дх, дБ с силами, действующими на несущий винт 404
§ 4. Потребляемая несущим винтом мощность при косой обдувке . . 405
§ 5. Расчет сложных систем по средней скорости взаимных влияний 410
Глзва 8. Аэродинамический расчет вертолета на всех режимах .... 412
§ 1. Задача аэродинамического расчета вертолета..................412
§ 2. Уравнения установившегося движения вертолета................413
§ 3. Вредное лобовое сопротивление вертолета .................... 415
§ 4. Аэродинамический расчет вертолетов по методу тяг ..... 413
§ 5. Аэродинамический расчет вертолета по методу мощностей . . . 424
§ 6. Планирование вертолета......................................430
§ 7. О методах второго приближения • . •.........................437
Глава 9. Маховое движение лопастей и коэффициент тяги несущего винта при
косой обдувке в первом приближении......................................439
§ 1. Постановка задачи ................................................439
§ 2. Коэффициент тяги несущего винта в косой обдувке .... 440
§ 3. Угол конусности и маховое движение лопастей.......................446
§ 4. Отклонение оси лопасти в. плоскости вращения при наличии вер*
тикального шарнира..................................................45.3
§ 5. Угол атаки, профилей..............................................455
Глава 10. Аэродинамический расчет и сравнение вертолетов разных схем 459
§ 1. Основы приближенной теории индукции для сложных «коробок
крыльев»............................................................459
§ 2. Переход к несущим винтам..........................................464
§ 3. Сравнение различных схем вертолетов на больших горизонталь-
ных скоростях полета ... 467
§ 4. Крылатые вертолеты .............................................. 470
§ 5. Сравнение вертолета и самолета....................................472
Часть III, Классическая теория несущего винта ........ 476
Глава И. Маховое движение лопастей.......................................476
§ 1. История вопроса . . •. . ................476
§ 2. Скорость обдувки диска несущего -винта......................477
§ 3. Задание махового движения лопастей............................ 478
§ 4. Скорость обдувки элементов лопасти..........................480
§ 5. Метод отбрасывания высших гармоник..............................481
§ 6. Вычисление развернутых выражений типа IF*,Ifp и W’x.W'i/
Глава 12. Несущий винт со свободномашущими лопастями.....................487
§ 1. Маховое движение свободной лопасти..........................487
§ 2. Вычисление коэффициента тяги Су* . . ............. 491
§ 3. Силы и моменты, действушие ка лопасти и на несущий винт
в целом .... ....... ................ 494
§ 4. Обтекание свободномашущих лопастей по ’ классической теории 499
§ 5. Учет концевых потерь в теории несущего винта ...... 499
Глава 13. Работа несущего винта с автоматом-перекосом и регулятором взмаха 501
§ I. Кинематика автомата-перекоса и регулятора взмаха .... 501
§ 2. Маховое движение лопастей в общем случае при работе АП и РВ 504
§ 3. Коэффициент тяги при работе АП и РВ.............................. 508
§ 4. Критические замечания к классической теории несущего винта . 510
Выводы............................................................... 512
Глава 14. Особые формы несущих винтов 513
§ I. Несущий винт с качающейся втулкой, без угла конусности . . 513
§ 2. Несущий винт с жесткой втулкой . '...............519
Глава 15. Инерционные нагрузки лопастей........................................521
§ I. Центробежная сила ................................................521
§ 2. Кориолисова сила и ее момент ...............523
§ 3. Сила инерции от взмаха лопастей...............................526
§ 4 Уравновешивание армоник на втулке несущего винта .... 527
§ 5. Момент сил инерции относительно продольной оси лопасти . . 532
Приложение 1. Г рафик для определения силы тяги по формуле Н. Е. Ж у ков-
ского со степенью 2/з при ам = 18.......................................536
Приложение И. Краткое описание геликоптера системы Б. Н. Юрьева, тип II 537
Литература . . ....................................................540
Борис Николаевич Юрьев
Избранные тр>ды, том 1
Воздушные винты. Вертолеты
Утверждено к печати Отделением технических наук
Академий наук СССР
Редактор издательства Г. Б. Горшков
Технический редактор В. Г. Лаут
Корректор В. Т. МакарОь
РИСО АН СССР № 18-7В. Сдано в набор 8/V 1961 г
Подписан» к Пэтти 15/XI 19SJ г. Формат 70х108’/|,
Печ л. 34.25+4 вкл. (0,5 печ. л.); усл печ. л 47,60.
уч -издат л 32,1 /31 4+07 вкл.). Тираж 1500 экз
Изд № 5351 Тип зак № 3905
Цена 2 р. 44 к
Издательство Академии наук СССР.
Москва, Б-62, Подсосенский пер.. 21
2-я типография Издатстьства
Москва. Г-99, Шубинский пер, 10
ИСПРАВЛЕНИЯ И ОПЕЧАТКИ
Страница Строка Напечатано Должно быть
22 9 св. тех- техники
30 Ф-ла (t2) 1®. 1 |®,|
44 20 св. получить вихревые кольца получить режим вихревого
кольца
04 5 сн, uj.br Ujdr
122 2 си. Ра 2rt Ра 2
126 Ф-ла (24) 1/J
137 Ф-ла (78) Ч« = По «=
137 8 си. Ло И Лр. П) и т)и
137 Ф-ла (79) ча
-=-(гт д ——jr Г
155 16 св. dl дГ 1
а д
7Г12Г ~дТ 11’
155 Ф-ла (109; + 2^- -2€
г
204 2 сн. ф
204 1 си. COS ф COS
ь. н. Юрьев, т. I