QUANTUM FIELDS IN
CURVED SPACE
N. D. Birrell
Consultant, Communications Group, Logica Lid
and
P. С W. Davies
Professor of Theoretical Physics,.
University of Newcastle upon Tyne
CAMBRIDGE UNIVERSITY PRESS
Cambridge London New York New Rochelle Melbourne Sydney
1982

Н. БИРРЕЛЛ, П.ДЕВИС
КВАНТОВАННЫЕ
ПОЛЯ
В ИСКРИВЛЕННОМ
ПРОСТРАНСТВЕ-
ВРЕМЕНИ
Перевод с английского
д-ра физ.-мат. наук
Д. В. Гальцова
под редакцией
д-ра физ.-мат. наук
Я. А. Смородинского
МОСКВА «МИР» 1984

ББК 22.31
Б64
УДК 530.145
Биррелл Н., Девис П.
Б64 Квантованные поля в искривленном пространстве-вре-
пространстве-времени. Пер. с англ. — М.: Мир, 1984. — 356 с, ил.
Книга английских авторов посвящена снстеиатнческому изложению кванто-
квантовой теории поля в искривленном пространстве-времени, возникшей в результате
объединения принципов квантовой теории полей и общей теории относительности.
Большое внимание уделяется методам расчета перенормнрованных средних зна-
значений тензора энергнн-нмпульса, пострренню эффективною лагранжиана грави-
гравитационного поля в однопетлевом приближении, а также приложениям теории
к космологии н черным дырам. Сформулированы принципы построения теории
взаимодействующих полей.
Книга рассчитана на специалистов в области теоретической физнкн, матема-
математиков, а также студентов старших курсов и аспирантов соответствующих спе-
специальностей. Оиа дает возможность читателю не только ознакомиться с уже
имеющимися результатами в дайкой области, но и получить представление о еще
KS решенных проблемах и тенденциях «того бурно развивающегося направле-
направления теоретической физики.
17Q4020000-128 ББК 22.31
Б ' Ь41@1)-84 se-84> ч- ' 530.1
Редакция литературы по физике
Cambridge University Press, 1982
Перевод на русский язык, «Мир», 1984

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В ноябре 1915 г. Эйнштейн на четырех заседаниях Прусской
Академии наук выступил с сообщением об уравнениях общей
теории относительности (ОТО) и о наблюдаемых эффектах: дви-
движении перигелия Меркурия и отклонении луча света в поле мас-
массивного тела. С этих работ ведет свое начало классическая элек-
электродинамика в искривленном пространстве.
В течение многих лет эффекты ОТО рассматривались в связи
с теорией классических полей. Возможность объединения ОТО и
теории квантованных полей была лишь далекой целью. Для вы-
выполнения такой программы не только не было технических
средств, но было даже не вполне ясно, в какой реальной обла-
области такая объединенная теория может оказаться полезной.
И хотя в разных работах обсуждался эффект рождения пар в
гравитационных полях, только замечательная работа Хокинга
о спектре излучения черной дыры открыла путь в совершенно
новую область квантовых эффектов, в формулы для которых
входят одновременно и постоянная тяготения Эйнштейна и по-
постоянная Планка. Неожиданным в этих формулах оказалось
проявление статистических свойств в системах, описываемых
уравнениями механики. Необходимость теории квантованных
полей в искривленном пространстве стала очевидной. Само гра-
гравитационное поле также стало объектом квантования, правда
только в том ограниченном числе случаев, когда квантовыми
считаются лишь малые колебания метрики относительно более
или менее гладкого метрического фона.
Книга английских физиков Биррелла и Девиса содержит ре-
результаты, полученные в этом направлении за последние десять
лет. Хотя материал еще не принял форму последовательной тео-
теории, авторам удалось собрать практически все важные резуль-
результаты в хорошо организованном обзоре, дополненном большим
количеством ссылок на литературу1). Эта книга сейчас практи-
чески единственное введение в новую область теоретической
') В нашем издании переводчик добавил список литературы, содержащий
наиболее важные новые работы, появившиеся после выхода английского из-
издания книги. Ссылки на эти работы даиы цифрами со звездочками.

6 Предисловие редактора перевода
физики, доступную всем, кто знаком с обычной теорией реля-
релятивистских полей.
Следует помнить, конечно, что задача квантования произ-
произвольного гравитационного поля, когда квантовые флуктуации не
малы, остается нерешенной. Этот вопрос, по-видимому, примы-
примыкает к более трудному вопросу о том, как в очень ранней вселен-
вселенной возникла сама метрика. Последний вопрос тесно связан с
двумя возможными взглядами на гравитацию: как на геометри-
геометрический объект и как на релятивистское поле — систему квантов-
гравитонов. По этому поводу пока не существует сколько-нибудь
установившейся точки зрения. Наверно в теориях супергравита-
супергравитации ответ может стать более яс,ным. В рамках книги Биррелла и
Девиса квантовая часть гравитации — это малая добавка к клас-
классическому полю. Сейчас закончился первый этап развития такой
теории, и появление перевода данной книги на русский язык
должно быть полезным для тех, кто начинает работать в этой
почти фантастической области.
#. Смородинский

ПРЕДИСЛОВИЕ
За последнее десятилетие квантовая теория поля в искрив-
искривленном пространстве-времени приобрела важное значение как
некоторое приближение к пока не существующей квантовой тео-
теории гравитации. В этой книге сделана попытка собрать воедино
большое число работ, внесших вклад в быстрое развитие этой
области исследований. Часть материала книги основана на ис-
исследованиях авторов, в особенности это касается моделей детек-
детекторов частиц и адиабатических состояний.
Изложение преследует как педагогические, так и историко-
научные цели. Предварительное знакомство с предметом не
предполагается, но желательно, чтобы читатель знал основы
квантовой теории поля на уровне книги Бьеркена и Дрелла [49]
и общую теорию относительности на уровне книг Вейнберга
[494] или Мизнера, Торна и Уилера [363]. Теория формулирует-
формулируется, начиная с ее первооснов, многие детали собраны здесь вме-
вместе впервые. Обращаем внимание читателя на список обозначе-
обозначений и сокращений, а также на обширную библиографию.
При подготовке этой книги был использован материал ра-
работ большого числа авторов. В отдельных случаях мы внесли не-
некоторые поправки (в том числе и в работы авторов данной кни-
книги), иногда не предупреждая читателя о тех отличиях, которые
имеются в книге по сравнению с первоначальными публика-
публикациями.
Основная часть книги написана во время нашей совместной
работы в отделе математики Королевского колледжа в Лондоне.
Мы чувствуем себя в большом долгу перед нашими коллегами
из этого и других научных центров за оказанную поддержку.
Мы хотим выразить особую благодарность Т. С. Банчу, С. М. Кри-
стенсену, Н. А. Дути, Дж. С. Даукеру, М. Дж. Даффу, Л. X. Фор-
Форду, С. А. Фуллингу, К- Дж. Айшему, Г. Кеннеди, Л. Паркеру и
Р. М. Уолду за критические замечания по отдельным разделам
рукописи.
Наконец, мы хотели бы поблагодарить г-жу Дж. Банн за
перепечатку рукописи и Совет по научным исследованиям за фи-
финансовую помощь.

ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
Обозначения величин, относящихся к квантовой теории поля,
в основном соответствуют книге Бьеркена и Дрелла [49]. Выбор
знаков у компонент метрики и тензора кривизны соответствует
( ) в терминологии Мизнера, Торна и Уилера [363].
А именно, сигнатура метрики (-] ); #apYe = derapY —...;
R\j.v = Ranav Переход от используемой здесь системы величин к
.часто применяемой системе (+ + +). принятой в книге [363],
производится путем замены знаков у величин g^, ? = g^V^Wv,
^ R Т /?
у у g^ g^v,
pY Ry.v, Ту?, в то время как величины /?apYe, Ru.v, R и Т^
остаются неизменными. В большей части книги используется си-
система единиц, в которой Н = с = G = 1.
Используются следующие специальные символы и сокраще-
сокращения:
комплексное сопряжение
эрмитово сопряжение
дираково сопряжение
частная производная
ковариантная производная
вещественная (мнимая) часть
след
натуральный логарифм
постоянная Больцмана
постоянная Эйлера
АВ-ВА
АВ + ВА
~2 (an. v + av. v)
приближенно равно
оценка по порядку величины
асимптотически приближается
равно по определению
нормальное упорядочение
*
t
д
дх»
Va
Re(
tr
In
kB
V
[A,
{A,
-, дп или
или ;ц
Im)
В]
В)
11

Глава 1
ВВЕДЕНИЕ
Последнее десятилетие ознаменовалось замечательными до-
достижениями в построении объединенной теории фундаменталь-
фундаментальных сил природы. Электромагнитные и слабые взаимодействия
были описаны единым образом теорией Вейнберга — Салама
[493, 413], а так называемые теории великого объединения
([228], см. также обзор [120]), по-видимому, открывают путь
к включению в более широкую калибровочную теорию и сильных
взаимодействий, описываемых квантовой хромодинамикой.
В это последовательное объединение не входит гравитация.
Тяготение не только оказывается в стороне от трех остальных
сил природы, но и упорно не поддается попыткам истолкования
с точки зрения квантовой теории. В течение последних сорока
лет (см. обзоры [309, 310, 314]) с большой изобретательностью
и настойчивостью предпринимались усилия в направлении кван-
квантования гравитации, но полностью удовлетворительной кванто-
квантовой теории гравитации до сих пор не создано. По-видимому, наи-
наибольшие надежды в настоящее время возлагаются на теории су-
супергравитации, в которых гравитон является лишь одной части-
частицей более широкого мультиплета калибровочных частиц, вклю-
включающего как бозоны, так и фермионы [148, 214] (см. также об-
обзор [571*] и книги [475, 572*—575*]).
В отсутствие жизнеспособной квантовой теории гравитации
можно ли вообще что-либо сказать о влиянии гравитационного
поля на квантовые явления? В первые годы развития квантовой
теории был предпринят ряд расчетов, в которых электромаг-
электромагнитное поле рассматривалось как классическое внешнее поле,
взаимодействующее с квантованной материей. Такое полуклас-
полуклассическое приближение позволяет сразу получить некоторые
результаты, находящиеся в полном согласии с точной квантовой
электродинамикой (см., например, [418], гл. 11). Поэтому мож-
<ио надеяться, что подобное соответствие имеет место и для тех
квантовых аспектов гравитации, в которых гравитационное поле
рассматривается как классический фон, в то время как мате-
материальные поля квантованы обычным образом. Принимая в каче-
качестве классической теории гравитации эйнштейновскую общую
теорию относительности, приходим к квантовой теории полц

10 Глава 1
в искривленном фоновом пространстве-времени, которая и со-
составляет содержание этой книги.
Как впервые показал Планк [399], из мировых постоянных
G, Н и с можно составить комбинации, имеющие смысл новых
фундаментальных единиц длины (планковская длина (Gh/c3)'ll=
= 1,616-10~33 см) и времени (планковское время (Gft/c5)'/a =
= 5,39-10~44 с). Если рассматривать гравитационное поле как
малое возмущение и попытаться его квантовать, следуя образцу
квантовой электродинамики (КЭД), то в роли константы взаи-
взаимодействия будет выступать квадрат планковской длины. Но в
отличие от КЭД, в которой константа связи е2/Нс безразмерна
(и мала по сравнению с единицей), планковская длина имеет
размерность. Если пространственные или временные масштабы
интересующих нас квантовых процессов становятся меньше со-
соответствующих планковских величин, то квантовые эффекты мо-
могут быть велики. В этом случае высшие порядки теории возму-
возмущений будут сравнимы, с низшим порядком, и вся концепция
разложения по малым возмущениям теряет смысл.
Таким образом, планковские величины обозначают границу,
за которой должна привлекаться полная, по-видимому, непертур-
бативная по своему характеру квантовая теория гравитации. Тем
не менее можно надеяться, что в случаях, когда расстояния и
времена, характерные для рассматриваемых процессов, намного
больше планковских величин, квантовые эффекты гравитацион-
гравитационного поля будут пренебрежимо малыми. Поскольку планковская .
длина весьма мала (в десять в двадцатой степени раз меньше
размера атомного ядра), очевидно, остается широкая область,
в которой возможно применение полуклассической теории.
Но, продолжая рассуждать в том же духе, мы сталкиваемся
со следующей проблемой. Согласно принципу эквивалентности,
лежащему в самом основании метрических теорий гравитации,
все виды материи и энергии в одинаковой степени подвержены
тяготению. Сюда, конечно, следует включить и гравитационную
энергию, иными словами, «гравитация гравитирует». В терми-
терминах квантовой теории можно сказать, что гравитационное поле
действует на гравитон так же, как, скажем, на фотон. Следова-
Следовательно, всякий раз, когда класическое гравитационное поле при-
приводит к существенным эффектам, в которых участвуют (реаль-
(реальные или виртуальные) фотоны, необходимо учитывать также
аналогичные процессы с участием гравитонов. Отсюда следует,
что если возникают представляющие интерес квантовые эффек-
эффекты, то квантовая гравитация должна проявиться нетривиальным
образом во всех масштабах расстояний и времени. Таким обра-
образом, лежащая в основе гравитационного взаимодействия нели-
нелинейность срывает любые попытки пренебрежения квантовой гра-
гравитацией [186]

Введение 11
Несмотря на это затруднение, полуклассическос описание
все же возможно. В классической общей теории относительно-
относительности рассматривается распространение гравитационных волн на
фоне искривленного пространства-времени. В основе такого рас-
рассмотрения лежат вакуумные уравнения Эйнштейна, но малое воз-
возмущение метрики g^v, вызываемое гравитационной волной, мож-
можно отделить от метрики g0^ фонового пространства-времени:
gp.v = g'nv + gp.v (LI)
Тогда гравитационные волны можно рассматривать как изотроп-
изотропную жидкость, подобную любой другой жидкости, а их вклад в
левую часть уравнений Эйнштейна преобразовать к виду, в ко-
котором его можно перенести в правую часть, интерпретируя как
часть источника, т. е. часть Т^.
В духе этих рассуждений кажется разумным предположить,
что поле «гравитонов», соответствующее линеаризованным воз-
возмущениям фонового пространства-времени, можно трактовать
наряду с другими квантованными полями как часть материи, а
не как геометрию. Можно ожидать, что такая линеаризованная
теория будет справедлива вдали от планковской области. Однако
пока не создана законченная квантовая теория гравитации, "во-
"вопрос о справедливости данного приближения остается открытым.
(Спорным, конечно, остается и вопрос о том, можно ли называть
«полуклассической» теорию, использующую представление о гра-
гравитонах.) Такой подход аналогичен рассмотрению испускания
фотонов атомом, находящимся во внешнем электрическом или
магнитном поле. •
Де Витт [154, 155] использовал A.1) в качестве отправной
точки подхода к полному квантованию гравитации, получившего
название метода фонового поля. В этом подходе g?v представ-
представляет собой классическую метрику некоторого фонового простран-
пространства-времени, a g^v описывает квантованное поле, распростра-
распространяющееся на этом фоне. Эйнштейновское действие и действия
для материальных полей могут быть разложены по степеням g^v
относительно gcy.v, что позволяет вывести соответствующие пра-
правила Фейнмана. Квантовые процессы низшего порядка — одно-
петлевые— изображаются фейнмановскими диаграммами, пока-
показанными на рис. 1. Волнистая линия представляет пропагатор
поля gjxv, распространяющегося на фоне g0^, ровная линия —
соответствующий пропагатор материального поля. Так как ни
¦<рис. \,а, ни рис. 1,6 не содержат гравитонных вершин, обе эти
диаграммы определяют выражения, не зависящие от гравита-
гравитационной постоянной G и, следовательно, сравнимые по величине.
Таким образом, оказывается, что на однопетлевом уровне кван-
квантование гравитационного поля на фоне gVv столь же существен-
существенно, как и квантование полей материи.

12 Глава 1
Рис. 1. Вклад низшего порядка
(однопетлевой), даваемый в энер-
энергию вакуума материальными по-
полями (а) и линеаризованными
гравитонами (б), распространяю-
распространяющимися в заданном фоновом гра-
гравитационном поле.
С физической точки зрения изолированные замкнутые петли
представляют бесконечную вакуумную, или нулевую, энергию,
которая в случае плоского пространства-времени (т. е. в обыч-
обычной квантовой теории поля) искусственно устраняется с по-
помощью вычитаний или так называемого нормального упорядоче-
упорядочения (см. разд. 2.4). Но, если фоновое пространство искривлено,
необходима более тонкая процедура, учитывающая динамику
гравитационного поля. Этот прием, называемый перенормиров-
перенормировкой, известен из КЭД, где также возникают расходимости.
В этом последнем случае расходимости устраняются в резуль-
результате перенормировки масс, зарядов и волновых функций частиц.
Важно, что лишь конечное число величин подвергается перенор-
перенормировке — особенность, которая придает К.ЭД статус перенор-
перенормируемой теории. Перенормируемость КЭД критически связана
с фактом безразмерности константы связи е2/%с. Напротив, G
имеет размерность квадрата длины (в единицах, в которых Ь, =
= с = 1), что приводит, как видно из простого подсчета степе-
степеней, к бесконечной последовательности новых расходимостей в
каждом порядке теории возмущений. Члены высших порядков в
разложении гравитационного действия по степеням g дают мно-
многопетлевые гравитационные фейнмановские диаграммы
(рис. 2, а). Между степенью расходимости и числом петель в
диаграмме существует простое соотношение (см., например,
[184]), согласно которому увеличение числа петель сопровож-
сопровождается появлением все более опасных расходимостей. Это об-
обстоятельство делает квантовую гравитацию неперенормируе-
мой — в каждом следующем порядке теории возмущений нужно
вводить новые величины, чтобы поглотить бесконечности. Имен-
Именно по этой причине не было успешно выполнено квантование гра-
гравитационного поля.
Если в квантовой теории гравитации с учетом материи огра-
ограничиться некоторым заданным числом петель, то остается конеч-
конечное число расходимостей, которые могут быть устранены пере-
перенормировкой конечного числа физических величин. Например,
как мы увидим в гл. 6, чтобы сделать теорию конечной на одно-
петлевом уровне, достаточно перенормировать G, космологиче-
космологическую постоянную А и константы связи двух вновь вводимых тен-

Введение 13
зоров. Таким образом, в некотором смысле эта усеченная теория
может рассматриваться как перенормируемая.
Следует отметить, что если пытаться квантовать гравитацион-
гравитационное поле, используя разложение на фоне плоского пространства-
времени, т.е. выбирая в A.1) g0^ = х\^ (метрика пространства
Минковского), то перенормировку нельзя выполнить общекова-
риантным образом (см., например, [184]). По этой причине, а
также в связи с другими трудностями такого подхода [118] целе-
целесообразно рассматривать поля, распространяющиеся на фоне
пространства с произвольной метрикой g0^.
В большей части этой книги мы рассматриваем квантовую
теорию гравитации с учетом материи в однопетлевом приближе-
приближении. Многопетлевые диаграммы для свободных материальных
полей вообще отсутствуют, в рис. 1,а изображает точный вклад
этих полей (в эффективное действие, вводимое в гл. 6). На
рис. 1,6 показан вклад гравитонов нулевого порядка по G. По-
Поскольку разложение по чиолу петель есть разложение по Ь, [367],
однопетлевая теория, совпадающая с точной теорией с учетом
величин порядка ft, представляет собой первую квантовую по-
поправку к общей теории относительности.
При включении в теорию самодействующих или взаимодей-
взаимодействующих полей однопетлевые вклады материальных полей, изо-
изображенные на рис. 1,а, более не являются точными ввиду пояр-
ления многопетлевых диаграмм, содержащих вершины (рис.2, 6).
Так как в лабораторных экспериментах чаще всего наблюдают-
наблюдаются именно эффекты взаимодействий между материальными по-
полями («частицами»), такие многопетлевые диаграммы для мате-
материальных полей также должны быть включены в рассмотрен^.
Разумеется, если мы хотим сохранить все члены определенного
порядка по %, то следует включить и гравитационные диаграммы
Рис. 2. а — многопетлевые грави-
тЬнные диаграммы, содержащие
вершины; они представляют вкла-
вклады в энергию вакуума, которые
имеют более сильные расходимо-
расходимости, чем диаграммы на рис. 1,6,
что и делает квантовую гравита-
гравитацию неперенормируемой; б — есл»
вводятся негравитационные взаи-
взаимодействия, на диаграммах мате-
материальных полей также могут по-
появиться множественные петли.

14 Глава 1
с произвольным числом петель, но при этом мы столкнемся с не-
перенормируемостью гравитации. Однако каждая дополнитель-
дополнительная гравитационная петля в связной фейнмановской диаграмме
вносит, вообще говоря, множитель G, в то время как соответ-
соответствующая материальная петля дает множителем характерную
константу связи (например, e2/hc). Если / — типичный простран-
пространственный или временной масштаб рассматриваемой системы, то
при условии l~2G ¦< е2 вклад дополнительных гравитонных пе-
петель будет пренебрежимо малым по сравнению с вкладом доба-
добавочных материальных петель. Таким образом, даже в случае
взаимодействующих материальных полей использование одно-
петлевой квантовой теории гравитации оправданно в достаточно
широкой области.
Допустим, что мы располагаем по крайней мере некоторым
разумным приближением к теории, описывающей влияние тяготе-
тяготения на квантованные поля. Насколько существенными являются
описываемые таким образом процессы? Грубо говоря, нетриви-
нетривиальные гравитационные эффекты должны проявляться для тех
мод квантованного поля, длина волны которых сравнима с ха-
характерным масштабом изменения фонового пространства-време-
пространства-времени. Так, вблизи черной дыры радиуса г моды с длиной волны боль-
больше г будут заметно искажаться дырой. Аналогично, если грави-
гравитационное поле изменяется за характерное время t, то полевые
моды частоты <Zt~* будут испытывать значительное возмущение.
Следовательно, если для пространственного и временного мас-
масштабов, характеризующих основные квантовые процессы, при-
принять значения 10~13 см и Ю-23 с, то мы приходим к выводу, что
существенных квантовых эффектов можно ожидать лишь в ок-
окрестности микроскопических черных дыр или на самой ранней
стадии расширения вселенной.
Таким образом, слабость гравитационного взаимодействия
препятствует возможности изучения рассматриваемых эффектов
в лабораторных условиях, и, если только микроскопические чер-
черные дыры не являются гораздо более многочисленными, чем сле-
следует из существующих оценок, прямая экспериментальная про-
проверка теории совершенно исключена. Квантовой теории поля в
искривленном пространстве-времени, по-видимому, суждено по-
покоиться на чисто теоретических основаниях.
Ввиду ограниченных возможностей экспериментальной про-
проверки особое значение приобретают результаты Хокинга [278].
Выполненное им исследование квантовых процессов в черных
дырах и открытие их теплового излучения составляют краеуголь-
краеугольный камень развиваемой в этой книге теории. Результат Хо-
Хокинга приковывает к себе внимание по двум причинам. Во-пер-
Во-первых, это фундаментальный физический результат, который может
быть получен несколькими различными способами. Во-вторых, он

Введение 15
устанавливает тесную связь между физикой черных дыр и тер-
термодинамикой, о существовании которой строили догадки еще до
попыток применения квантовой теории к черным дырам. Не-
Невольно напрашивается мысль, что эффект Хокинга лишь при-
приоткрыл завесу над новой широкой областью фундаментальной
физики, в которой тесно переплетены гравитация, квантовая тео-
теория поля и термодинамика. Если это так, то синтез этих теорий,
несомненно, приведет к развитию новых физических представ-
представлений, некоторые из которых могут иметь экспериментально на-
наблюдаемые следствия.
Эту ситуацию можно сравнить с ранним периодом развития
кинетической теории. В середине девятнадцатого века атомная
гипотеза фактически не могла быть прямо проверена экспери-
экспериментально ввиду малости атомных эффектов. Тем не менее пол-
полностью разработанная теория приводила к следствиям, выходя-
выходящим за рамки собственно атомной области, и предсказывала но-
новые явления в динамике газов, которые могли быть проверены.
Аналогично можно надеяться, что правильно сформулированная
квантовая теория гравитации сможет проникнуть в другие, бо-
более доступные области физики.
Начало исследованию влияния гравитации на квантовые про-
процессы было положено еще работой Шредингера [420]. После
второй мировой войны интерес к квантованию гравитационного
поля значительно возрос, но прямое изучение эффектов рожде-
рождения частиц в классическом гравитационном поле началось с ра-
работы Паркера в конце 60-х годов, за которой последовали ра-
работы Зельдовича с сотрудниками. В этих первых работах рассма-
рассматривались космологические следствия рождения частиц. Даль-
Дальнейшее продвижение затруднялось отсутствием систематических
методов изучения тензора энергии-импульса Т^ гравитационно-
возмущенных квантованных полей. Тензор энергии-импульса
важен по двум причинам. Он может быть использован для оцен-
оценки роли квантовых эффектов в динамике самого гравитационного
поля (т. е. при решении проблемы обратного воздействия рож-
рождающихся частиц на метрику пространства-времени). Кроме
того, тензор энергии-импульса часто более адекватно отражает
физическую реальность, чем число частиц. В области сильного
гравитационного поля эффекты поляризации вакуума, так же
как в КЭД, могут быть существенными даже при отсутствии фак-
фактического рождения частиц.
, В середине 70-х годов большие усилия были направлены на
развитие строгих методов расчета (.Т^у. Методы перенормиров-
перенормировки для устранения формальных бесконечностей заимствовались
как из обычной квантовой теории поля (в пространстве Минков-
ского), так и из квантовой гравитации, наряду с чем были раз-
развиты и новые методы.

16 Глава 1
Важной особенностью этих методов является то, что они при-
приводят к ковариантно сохраняющемуся (с равной нулю диверген-
дивергенцией) <7^>, который благодаря этому является подходящим
кандидатом для правой части полуклассических уравнений Эйн-
Эйнштейна. Может показаться, что в условиях рождения пар частиц
из вакуума <7Vv> не должен сохраняться. В самом деле, Хокинг
[274] показал, что сохранение {Т^у при выполнении условия
энергодоминантности (сводящегося в основном к требованиям
положительности энергии и давления — см. [287]) несовместимо'
с рождением частиц. Выяснилось, однако, что нетривиальной
особенностью квантовой теории поля в искривленном простран-
пространстве-времени является возможность отрицательных значений
энергии-импульса вакуума за счет кривизны пространства-вре-
пространства-времени и, следовательно, нарушения условия энергодоминантности
в обход результата Хокинга [502]. Таким образом, рождение
частиц не противоречит сохранению <Гцу>- Возможность нару-
нарушения энергетических условий также открывает путь к построе-
построению моделей, в которых удается избежать пространственно-
временных сингулярностей (см. разд. 7.4).
После открытия Хокингом теплового излучения черных дыр и
возникновения более совершенных методов расчета <Г^> кван-
квантовая теория-поля в искривленном пространстве-времени, или од-
нопетлевая квантовая гравитация, пережила период бурного раз-
развития, когда было опубликовано несколько сотен работ. Хотя вы-
выводы некоторых работ носили спорный характер (наиболее при-
примечательными с физической точки зрения были дискуссии о ча-
частицах и <7Vv>, ° роли пространственно-временных сингулярно-
сингулярностей, о существовании так называемых конформных аномалий
и о критериях для выяснения физического смысла тех или иных
квантовых состояний), теперь имеется общее согласие между
техническими результатами большей части расчетов. Интерпре-
Интерпретация результатов в последующих главах неизбежно несет на
себе отпечаток мнения авторов, но мы, насколько возможно, пы-
пытались придерживаться суждений, представляющих, как мы счи-
считаем, «точку зрения большинства». Мы старались избегать неяс-
неясных утверждений о физической природе «частиц» и «энергии»,
везде, где это возможно, формулируя наши выводы в операцион-
операционных терминах, т. е. описывая результаты, к которым пришел бы
гипотетический наблюдатель, движущийся определенным обра-
образом и пользующийся определенным прибором.
Порядок изложения материала в книге традиционный. В гл.2
дается обзор основных понятий обычной квантовой теории поля
в пространстве Минковского и устанавливаются принятые нами
обозначения. В гл. 3 эти понятия обобщаются на случай искрив-
искривленного пространства-времени и вводится представление о ро-
рождении частиц гравитационными полями. Дается также наибо.*

Введение 17
лее полное на настоящий момент описание адиабатических со-
состояний и детекторов частиц. В гл. 4 и 5 на детально разрабо-
разработанных конкретных примерах излагаются применения теории к
плоскому и искривленному пространству-времени.
В гл. 6, являющейся центральной частью книги, исчерпываю-
исчерпывающим образом рассматриваются методы регуляризации и пере-
перенормировок. Мы предприняли попытку не только обсудить все
описанные в литературе методы перенормировок (с примерами),
но и, насколько возможно, изложить их с единой точки зрения.
Вооружившись этими результатами, читатель может приступить
к изучению гл. 7, в которой описанные в предыдущей части книги
методы применяются к ряду конкретных задач.
Развитые в предшествующих главах методы вычислений в
полном объеме используются для детального обсуждения проб-
проблемы черных дыр, занимающего всю гл. 8. Недостаток места вы-
вынудил нас ограничиться лишь ссылками на литературу при об-
обсуждении многих важных и завораживающих воображение фи-
физических следствий теории. В частности, нам не удалось ни
достаточно подробно остановиться на термодинамических аспек-
аспектах физики черных дыр,-включая возможные обобщения на гра-
гравитационные поля более общего вида, ни детально коснуться
таких вопросов, как временная асимметрия, циклы Пуанкаре,
соотношение черные дыры — белые дыры, влияние квантовых
эффектов на пространственно-временные сингулярности. Кроме
того, опущено почти все, касающееся астрофизических и космо-
космологических следствий квантовых процессов в черных дырах.
В последней гл. 9 мы попытались выйти за рамки того, что
можно назвать «первым кругом» результатов в области кванто-
квантовой теории поля в искривленном пространстве-времени. Здесь
мы кратко описываем обобщение теории, необходимое для того,
чтобы учесть негравитационные взаимодействия полей между со-
собой. Особое внимание уделяется изучению влияния взаимодей-
взаимодействия и самодействия полей на рождение частиц и поляризацию
вакуума, а также обсуждению вопроса о том, остается ли тео-
теория, перенормируемая в пространстве Минковского, такая, как
КЭД или теория Я^>4, перенормируемой при наличии нетривиаль-
нетривиальной топологии или пространственно-временной кривизны.
В книге такого рода неизбежны несколько размытые очерта-
очертания. Данная область исследований продолжает быстро разви-
развиваться, и в ней еще много белых пятен, которые предстоит запол-
заполнить. Тем не менее последний год явился периодом осмысления
и кристаллизации основных идей, что позволило нам дать здесь
достаточно последовательное и полное изложение предмета.

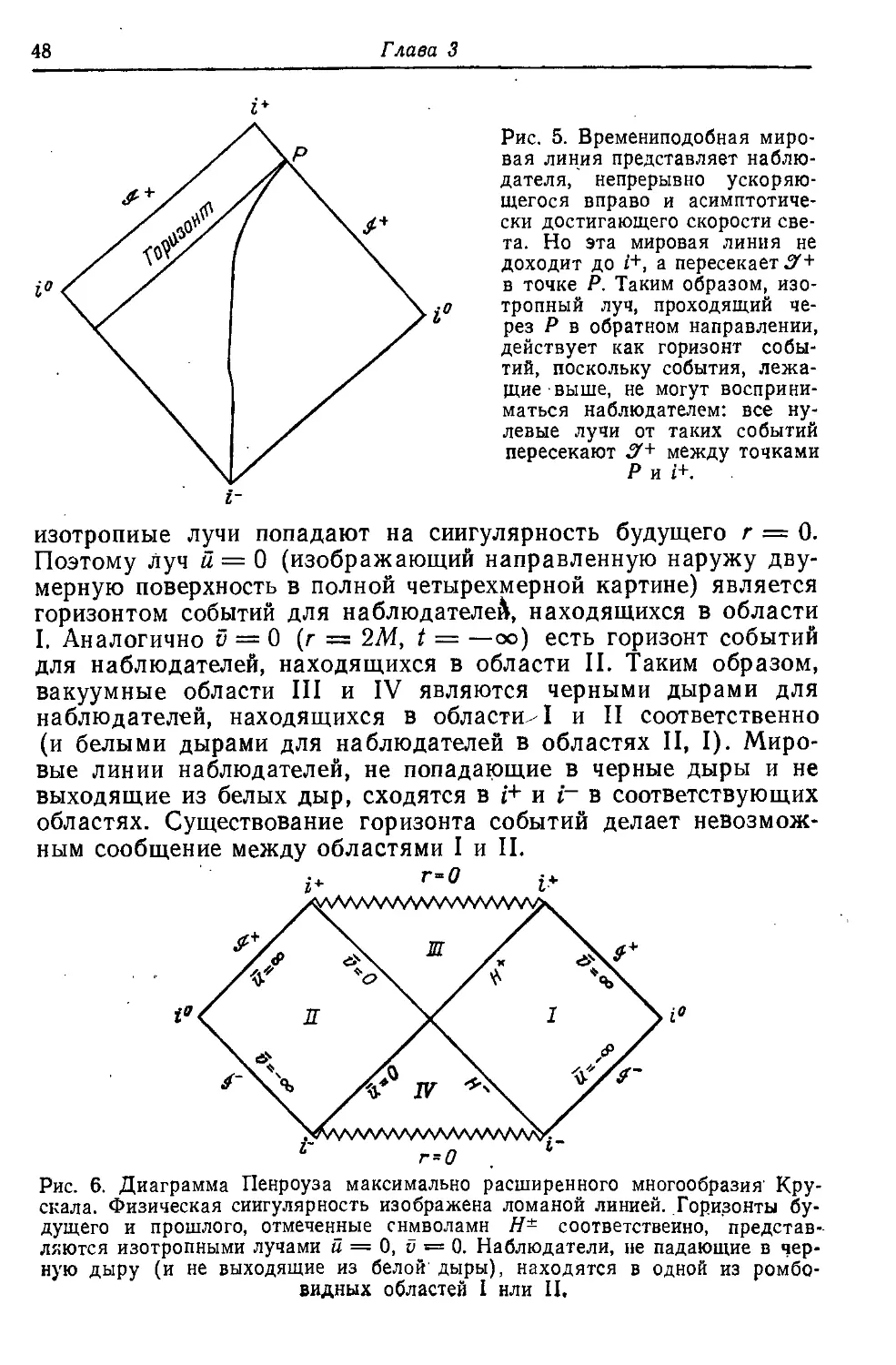
Глава 3
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ
В ПРОСТРАНСТВЕ МИНКОВСКОГО
В этой главе мы даем резюме основных положений обычной
квантовой теории поля в пространстве Минковского, с которой,
как мы предполагаем, читатель знаком по опыту работы. Значи-
Значительная часть этого формализма может быть перенесена на слу-
случай искривленного пространства-времени и нетривиальной топо-
топологии почти или вовсе без изменений. В последующих главах мы
будем следовать данной здесь трактовке.
Большая часть подробных выкладок относится к скалярному
полю, но приводятся также основные результаты для полей выс-
высших спииов. Это ограничение позволяет с минимальными мате-
математическими сложностями выявить существенные особенности
квантовой теории поля в искривленном пространстве.
Многое из того, что изложено в этой главе, известно из таких
учебников, как книга Бьеркена и Дрелла [49], но читателю сле-
следует обратить особое внимание на результаты, касающиеся вы-
вычисления среднего значения тензора эиергии-импульса и расхо-
расходимости энергии вакуума (разд. 2.4), которые будут играть в
дальнейшем центральную роль. Особое значение также придает-
придается функциям Грина, подробно рассматриваемым в разд. 2.7. Чи-
Читатель возможно не знаком а тепловыми функциями Грина и ев-
клидизацией метрики. Поскольку это существенно для понима-
понимания квантовых черных дыр, мы коротко останавливаемся здесь
на этих вопросах.
Наконец, хотя основная часть формализма развивается без
помощи фейнмановского интегрирования по траекториям, мы ис-
используем представление о континуальном интеграле при обсуж-
обсуждении перенормировок в гл. 6, а также в гл. 9, посвященной вза-
взаимодействующим полям в искривленном пространстве. Хотя от
читателя ие требуется основательного знакомства с формулиров-
формулировкой теории в терминах интегралов по траекториям, очерк основ-
основных положений этого подхода, данный в разд. 2.8, может ока-
оказаться полезным.
2.1. Скалярное поле
" Рассмотрим скалярное поле <]>(t,x), заданное во всех точках
(t,x) n-мерного простраиства-времени Мииковского и удовлетво-
удовлетворяющее волновому уравнению
. (р+т2)^ = 0, B.1)

Квантовал тебрия полк й пространстве Минковского
где ? г= ц^дцд?, r\^v — метрический тензор Минковского. Вели-
Величину пг следует интерпретировать как массу полевого кванта во
вторично-квантованном варианте теории. В дальнейшем точки
пространства-времени (t, x) = (х°, х) мы часто обозначаем крат-
кратко СИМВОЛОМ X.
Уравнение B.1) можно получить из плотности лагранжиана
±(ч^ф,аф,р-т*ф*), B.2)
если построить действие
S = ^2 (х) dnx B.3)
и наложить требование, чтобы вариация по ф была равна нулю:
6S = 0. B.4)
Один из возможных наборов решений уравнения B.1) имеет
вид
Ub(t, х)~е1к-*~ш, B.5)
где
со _ (k2 + т2)\ k - | к | = (IE к*У , B.6), B.7)
и декартовы компоненты вектора к принимают значения —оо <
< ki < оо, i = 1, ..., п — 1. Моды B.5), являющиеся собствен-
собственными функциями оператора d/dt, называются положительно-ча-
положительно-частотными по отношению к /:
-^ ик (t, х) = - to«k (t, х), о > 0. B.8)
Определим скалярное произведение
(х) - [&fr (х)] ф1(х)} dn-xx =
{х)<1п-'х, B.9)
где t обозначает пространственноподобную гиперповерхность од-
одновременных событий в момент времени t По отношению к это-
этому скалярному произведению функции B.5) ортогональны:
(Ик, «к-) = 0, к =5*= к'. B.10)
Если выбрать
uk = [2coBJt)n-I]-Vkx-'0". B.11)
то функции «it будут нормированы условием
(«к, ык') = 6п-1(к-к/). B.12)

20 Глава 2
Для многих задач решения ык удобнее ограничить внутрен-
внутренностью пространственноподобного (п—1)-мерного тора со сто-
стороной L (т. е. выбрать периодические граничные условия). Тогда
¦\aybetk-x-totf B.13)
где
ki = 2nji/L, }t = Q, ±1, ±2 /=1, ..., n— 1.
Следовательно,
("к, "к') = бкк'. B.14)
Для перехода от нормировки непрерывного спектра к дискрет-
дискретной нормировке в ящике следует заменить \ dn~lk на
2.2. Квантование
При каноническом квантовании системы поле </> следует рас-
рассматривать как оператор, удовлетворяющий следующим одновре-
одновременным перестановочным соотношениям:
[ф((, х), ф((, х')] = 0,
[n(t, x), n(t, x0] = 0, B.15)
, х), n(t, x')] = ibn-i(x-x'),
^ переменная я, канонически сопряжеиная ф, определяется вы-
выражением
Л ^'- BЛ6)
Полевые моды B.11) или B.13) и комплексно-сопряженные
о ними образуют ортонормированныи базис со скалярным произ-
произведением B.9), поэтому поле </> может быть представлено в виде
разложения
Ф (t, х) = ^ [акик(t, x) + atui (t, x)]. B.17)
Одновременные коммутационные соотношения для ф и я эквива-
эквивалентны Следующим соотношениям:
К, ак'] = 0,
[at аМ = 0, B.18)
[ак, ак'] = 6кк'.

Квантовая теория поля в пространстве Минковского 21
В представлении Гейзенберга квантовые состояния образуют
гильбертово пространство. В этом гильбертовом пространстве
удобно использовать фоковский базис. Нормированные базисные
кет-векторы, обозначаемые символом | >, могут быть построены,
исходя из вакуумного,состояния |0>, физический смысл которого
обсуждается ниже. Состояние JO> определяется тем, что оно об-
обращается в нуль всеми операторами ак:
ак|0> = 0, Vk. B.19)
Состояние, получающееся в результате действия на |0> опе-
оператора aj, называется одночастичным состоянием и обозначает-
обозначается |1к>:
|1к) = ак|0>. B.20)
Подобным же образом можно построить многочастичные состоя-
состояния
|1к„ 1ц, -.., .!*,) = <<... <|0>, B.21)
к2,
если все ki, k2, ..., к/ различны. Если некоторые операторы а\
повторяются, то
X «)'» RJ» ... (ay» |0>, B.22)
где множители п\ необходимы для того, чтобы удовлетворить
статистике Бозе для тождественных скалярных частиц. При этом
a?l"k> = (tt+iI/2|(tt+l)k>, B.23)
ak\nk) = n4*\(n—l)k). B.24)
Базисные векторы нормированы соотношением
, 2п
kl k2
lm f, 2m /, ..., и
Kl k2 k
Л
s/
B<25)
где суммирование ведется по всем перестановкам а индексов
1 s.
* 2.3. Энергия и импульс
Для выяснения физического смысла фоковских состояний це-
целесообразно рассмотреть оператор Гамильтона и оператор им-
импульса поля. Эти величины можно построить с помощью тензора
энергии-импульса Т^. Тензор ГцУ может быть получен стандарт-

22 Глава 2
ным способом (см. C.189)) в виде
B.26)
откуда находим для плотности гамильтониана
и для плотности импульса
/=1„..., п-1, B.28)
в координатах Минковского.
Подставляя ф из B.17) в B.27) и B.28) и интегрируя по все-
всему пространству, находим
Я - J Г„ d-'jc = ^ (atok + akaj) со, B.29)
t k
Pf= J Ttidn-lx = J^aUkki B.30)
/ k
для гамильтониана и операторов компонент импульса соответ-
соответственно. С помощью коммутационных соотношении B.18) выра-
выражение B.29) может быть представлено в более наглядной форме
( j) B.31)
k
Ясно, что обе величины Я и Pi коммутируют с операторами
[N, H] = [N, Pt] = 0. B.33)
Смысл оператора Af выявляется, если вычислить его среднее зна-
значение в фоковских состояниях. Из B.19) и B.24) получаем
<О|ЛГк|О) = О, Vk; B.34)
<1лк,, 2Пк2, .... 'пк11 Л^к/1 lnki, 2nkt, .... 'п*,) = 'я. B.35)
Таким образом, среднее значение оператора Л^ есть целое
число % входящее в выражение для кет-вектора с индексом к,-.
Просуммировав Nkl в B.35) по всем i, найдем
Zln. B.36)

Квантовая теория поля в пространстве Минковского 23
Это простое соотношение между N^ и п позволяет назвать
yVk оператором числа частиц моды к, a N— оператором полного
числа частиц. В силу соотношений B.33) собственные состояния
N являются также собственными состояниями операторов Я и Р.
При возрастании каждого из чисел 1п на единицу средние <|Я|>
и <| Р|> возрастают на со* и к,- соответственно. Следовательно, мы
можем интерпретировать 'п как число квантов, каждый из кото-
которых несет энергию и, и импульс к». Поэтому состояние IW,,
2Дк2, • • -.'«к,) есть состояние, содержащее 'и квантов моды с им-
импульсом кь 2п квантов моды с импульсом к2 и т. д.
Возвращаясь к соотношениям B.23) и B.24), можем дать фи-
физическую интерпретацию операторов ак и а^. Первый из них
уменьшает число квантов моды к на единицу, в то время как вто-
второй увеличивает это число на едицицу. Поэтому ak называют
оператором уничтожения, а а\. — оператором рождения квантов
моды к.
2.4. Расходимость энергии вакуума
Особый интерес вызывает состояние |0>. Это вакуумное со-
состояние, не содержащее частиц. Оно имеет нулевой импульс
<0|Р|0> = 0, B.37)
что непосредственно следует из B.30). Можно было бы ожидать,
что оно несет и нулевую энергию, поскольку кванты поля отсут-
отсутствуют. Но в выражении B.31) имеется член '/г^к©, поэтому
- со, B.38)
где использовано условие нормировки <0|0> = 1.
Правая часть B.38) не только отлична от нуля; на самом
деле она бесконечна:
= (/,2/4я)("-1)/2Г((га^1)/2) $ (k2 + mf' kn~2 dk, B.39)
Г((га^1)/2)
о
так как интеграл расходится как kn при больших k. Эту расхо-
расходимость удобно анализировать, выполнив интегрирование в
B.39) при п, не равном целому числу, что приводит к-резуль-
тату
1п1П2п

24 Глава 2
Функция Г имеет полюсы при всех четных целочисленных зна-
значениях п ^ 0. Такой метод временного превращения бесконеч-
бесконечных величин в конечные путем продолжения размерности про-
пространства-времени на нецелочисленные значения является основ-
вой размерной регуляризации (см. гл. 6).
Может показаться, что бесконечность выражения B.39) озна-
означает, что вакуум обладает бесконечной плотностью энергии. Это
затруднение происходит из-за нулевой энергии гармонического
осциллятора V20), ассоциируемого с каждой модой скалярного
поля. Поскольку частота со не ограничена сверху, нулевая энер-
энергия каждого осциллятора может быть произвольно большой. Это
проблема, которая постоянно возникает в квантовой теории поля
в искривленном пространстве-времени. В плоском пространстве-
времени она разрешается просто. Энергия, как таковая, в негра-
негравитационной физике неизмерима, и мы можем изменить — пере-
перенормировать — начало отсчета энергии даже на бесконечную ве-
величину, не изменяя значений наблюдаемых величин. Этого мож-
можно достичь отбрасыванием члена '/22кш в B.31) или, в более
изящной форме, вводя операцию нормального упорядочения опе-
операторов, обозначаемую символом ::, которая означает, что в
любом произведении операторов рождения и уничтожения по-
последние следует поставить справа от первых. Применительно к
выражению B.29) нормальное упорядочение подразумевает, что
:акак = а\ак, B.40)
откуда следует
S 4 B.41)
и вызывающий трудности член '/г© исчезает.
Наконец, вернемся к тензору Т^у и выражению B.26). Ис-
Используя разложение B.17) для ф по модам uk, имеем
Из B.19) и соответствующего условия
@14 = 0 ' 2.42)
с учетом соотношения
получаем
В общем случае
=ЕгврК ик\, B.43)

Квантовая теория Лоля в пространстве Минковскогд 25
где Та$[ф, ф] обозначает билинейную форму B.26) для
Аналогично
Г[(, 4J. B.44)
2.5. Дираковское спинорное поле
До сих пор мы ограничивались скалярным полем (со спином,
равным нулю). Квантование полей высших спинов проводится
аналогично. В частности, фермионное поле \|> спина 1/2 имеет
функцию Лагранжа
SB = 41 (чЛа ~ +л\°*) - »»ФФ, B.45)
где ф —спинор, дираковски сопряженный к t|) (т. е. ¦ф+70), и
матрицы Дирака у* удовлетворяют антикоммутационным соотно-
соотношениям
{Ya, vp} = 2ri«P. B.46)
(Свойства у-матриц в пространстве п измерений см., например,
в работе [141].)
Варьирование действия 5= \ S?dnx по ф приводит к уравне-
уравнению Дирака
г'УЧа — /пф = 0, B.47)
описывающему частицу с массой т. Поле tf> имеет спинорный ин-
индекс (it>°), который в приведенных формулах опущен. Подобным
же образом мы опускаем индексы матриц Дирака (уаь).
Полный набор решений уравнения Дирака в дискретной нор-
нормировке дается формулами
vk,s(t, x) =
где
\BLn-rxl\ m-0. }
Известные постоянные спиноры с положительной и отрицатель-
отрицательной энергией ы(к, s), v(k, s) (см., например, [49], гл. 3 и 10) су-
существуют для двух независимых спиновых состояний и нормиро-
нормированы согласно равенствам
{((о/

26 Глава 2
Мы можем поэтому разложить поле 1]з следующим образом:
(s)uk.s(t, х) + 4(s)t>k,stf, x)] B.51)
)ZS
±s к
и нормировать в соответствии со скалярным произведением
(Ф, Ф) = J dn-'x^ (t, x) yo^ С x). B.52)
t
Все операторы bt(s), dk(s), bl(s), dt(s) антикоммутируют,
за исключением
К (s), ^' (sO) = {rfk (s), rfj- («')} = 6SS'6kk'. B.53)
Построив гамильтониан, а также операторы импульса и угло-
углового момента и вычислив их математические ожидания в фоков-
ских состояниях, найдем, что bt(s) есть оператор рождения
кванта с импульсом к, энергией со и спином s, в то время как
dk(s) уничтожает квант моды с импульсом (—к), энергией (—со)
и спином s. Физически операторы bk(s) и dl(s) представляют со-
собой операторы рождения для электрона и позитрона соответ-
соответственно, a bk(s)adk(s) — соответствующие операторы уничтоже-
уничтожения.
Более подробное исследование тензора энергии-импульса для
поля Дирака мы откладываем до изложения теории в искривлен-
искривленном пространстве-времени в разд. 3.8.
2.6. Электромагнитное поле
Электромагнитное (безмассовое со спином 1) поле описывает-
описывается плотностью лагранжиана
где
/?ч, = Ах.э-Лр.а . B.55)
— максвелловский тензор поля. Варьирование действия 5 =
= \ 3?dnx дает
Fap,p = 0, B.56)
что вместе с тождеством
составляет уравнения Максвелла.

Квантовая теория поля в пространстве Минковского 27
Тензор поля B.55) и, следовательно, лагранжиан B.54) ин-
инвариантны относительно локальных калибровочных преобразова-
преобразований
Аа-»Ай=*Аа + даА(х), B.58)
где А(х)—произвольная дифференцируемая скалярная функ-
функция. Калибровочная инвариантность препятствует возможности
прямого квантования теории, и ее следует нарушить, что обычно
достигается добавлением к лагранжиану слагаемого, фиксирую-
фиксирующего калибровку:
^ = -jr'№aJ. B.59)
где ? — параметр, определяющий выбор калибровки; ? = 1 со-
соответствует калибровке Фейнмана, ?-*0— калибровке Ландау.
Введение члена, нарушающего калибровку, приводит к урав-
уравнениям поля
hapn-(i-rWpMe = o. B.60)
В фейнмановской калибровке эти уравнения сводятся к уравне-
уравнению
аАа=0, B.61)
решения которого имеют вид
Аа (t, х) = ? клик* (t, х) + a\*f&(t, x)], B.62)
где плосковолновые моды ы? определяются выражением
«?х (t, х) = BL"-'(o)-^ е^е1к-х~ш, B.63)
а векторы поляризации е?К, Я, = 1, 2, 3, 4, задают независимые
состояния поляризации моды к. Эти векторы можно выбрать так,
что они образуют ортонормированную систему
¦Парек^А/ = Ли'. B.64)
Квантование поля проводится в основном так же, как кван-
квантование скалярного поля, но поскольку физический фотон имеет
только две независимые (поперечные) степени свободы, а при
сделанном выше выборе лоренц-ковариантной калибровки все че-
тьфе компоненты потенциала Аа равноправны, получаемые та-
таким путем результаты не сразу приобретают физический смысл.
Для физической интерпретации квантованной теории, можно ис-
использовать формализм Гупты—Блейлера ([52, 258], см. так-
также учебники [56, 318, 423]). Мы не будем привлекать здесь этот

28 Глава 2
формализм, а проведем квантование электромагнитного поля ме-
методом интегрирования по траекториям, при котором появляется
новая особенность — так называемые духовые поля, что важно
при построении теории в искривленном пространстве-времени.
Но прежде следует ввести аппарат функций Грина.
2.7. Функции Грина
Вакуумные математические ожидания различных произведе-
произведений операторов свободного поля могут быть отождествлены с
различными функциями Грина волнового уравнения. Сначала мы
рассмотрим случай скалярного поля, где особое значение имеют
математические ожидания коммутатора и антикоммутатора по-
полей, обозначаемые соответственно как
iG(x, *0 = <0| [*(*), *(*0]|0>, B.65)
G(l)(x, *') = <0|{*(*), ф(х'))\О). B.66)
Функция G известна как функция Паули — Йордана или Швин-
гера, a GA) иногда называют элементарной функцией Адамара.
Эти функции Грина могут быть разбиты на положительно- и от-
отрицательно-частотные части:
10 (х, х') = G+ (х, х') - G- (х, х%
G<]> (х, х') = G+ (х, х') + Q- {х, х'),
где функции Вайтмана G± имеют вид
G+(x, *0=<0|*(*Ж*')|0>,
G~(x, х') = @\ф(х')ф(х)\0). (Z-bb>
Фейнмановский пропагатор GF определяется как хронологически
упорядоченное произведение полей
iGF{x, х') = Ш{ф{х)ф{х'))Щ =
= Q(t-tf)G+(x, x') + W-t)G-{x, x'), B.69)
Наконец, запаздывающая и опережающая функции Грина
определяются соответственно как
GR(x, x') = -Q(t-t')G{x, x%
GA{x, x')=Q(t'-t)G(x, x%
а их полусумма, обозначаемая
О(х, х') = |[GR(х, х') + GA (х, х% B.71)

Квантовая теория поля в пространстве Минковского 29
связана с Gf соотношением
OF{x, x') = -G(x, x')-jiGm(x, x'). BJ2)
Из уравнений поля B.1) ясно, что G, GO, G± удовлетворяют
однородному уравнению
х') = 0 B.73)
С другой стороны, используя соотношение dtQ(t — f) = b{t —
— t') и одновременные коммутаторы B.15), получаем следую-
следующие уравнения для Gf> GR и GA:
(ая + /n2) GP (x, x') = -8n(x- x'), B.74)
(П, + m2) G*. A (x, x') = 6n(x- xr). B.75)
Функции Грина Qf,r,a описывают распространение возмущений
поля при различных граничных условиях.
Интегральные представления для функций Грина можно по-
получить, подставляя разложение по модам B.17) для ф в опреде-
определения функций Грина как вакуумных,ожиданий. Получим, что
все функции Грина могут быть представлены в виде
<Й(Х х'\ - /дяч-п Г exp [Ik • (х - х') - Ц° (t - t')] .„.
&(Х, х) — (zn) ^ (fe0J — | к Р — от2 \4.1Ъ)
Интеграл имеет полюсы при k° = ±(]к]2 + /n2)l/s. Рассматривая
интегрирование по k° как контурное интегрирование в комплекс-
комплексной плоскости, можно выполнить его, деформируя контур вблизи
полюсов. Характер этой деформации (рис. 3) зависит от нала*
гаемых на поле граничных условий и определяет, какая из past
личных функций Грина будет получена с помощью B.76).
Например, контур интегрирования, соответствующий Gf, при-
приводит к выражению
^Г2)/4^1{[2т2(а-/е)П B.77)
где о = 7г (х — *'J = !/2Лар (х<* — дс'«) (jcP — ж'Р), а Ж2> — функ-
функция Ханкеля второго рода. Добавка — ie к о показывает, что Gp
фактически представляет собой граничное значение функции,
аналитической в нижней полуплоскости а.
В безмассовом пределе функции Грина обычно обозначаются
символом D вместо G. В этом пределе фейнмановский пропага-
тор для четырехмерного случая приводится к виду
DF(x, x') = (i/8n2o) — A/8я)б(а), B.78)
а элементарная функция Адамара равна
Da) (x, х') = — 1/4л2а. B.79)

30
Глава 2
Рис. 3. Контуры в комплексной
плоскости переменной k°, которым
отвечают различные функции Гри-
Грина. Полюса иа вещественной оси
k° = ±(|*|* + л»*I/а отмечены
крестиками. Открытые контуры
могут рассматриваться как зам-
замкнутые бесконечно удаленными
полуокружностями в верхней или
нижней полуплоскости.
удовлетворяющие уравнениям
ae - tn) SF (x, x')
- x'\
Для полей со спином х/2 и 1 мы приведем здесь лишь неко-
некоторые функции Грина. Для дираковского спинорного поля вво-
вводятся функции
iSF(x, jc') = <01Г (-ф (х) -ф (jc')) 10>» B-80)
' 5A)(лг, х') = @\№(х), Ъ(х')]\О), B.81)
нениям
B.82)
B.83)
которые могут быть выражены через GF и G<'> следующим обра-
образом:
Sp(x, x') = {iyada + m)GF(x, x'), B.84)
5A) {х, х') = - (i\ada + m) GA) {х, х'). B.85)
Заметим, что, например, SF есть матрица по спинорным индек-
индексам полей в B.80), в полной записи имеющая вид
iSF (х, x')ab = <01 фв (*I>J (хг) 10) (v°)C6 б (/ - f) -
- (о | tf W) *«(*) I o> (y°)c» 0 V - 0-

Квантовая теория поля в пространстве Минковского 31
Фейнмановский пропагатор электромагнитного поля опреде*
ляется выражением
lDPafi(х, х') = <0|7-(Аа(х)Лр(*')I0>, B.86)
которое, очевидно, калибровочно неинвариантно. С помощью
B.60) находим
Ы Ш - 0 - Г1) дхад?\ Df (х, х') = браб" {х - х'), B.87)
что дает для пропагатора интегральное представление
-B«Г \ {~^\lZ\lla4'k2] ехР № •(Х -Х'> - ik° « - Wdnk.
B.88)
Контур интегрирования по k° в B.88) тот же, что и для GF
(рис. 3). В частности, в фейнмановской калибровке (?, = 1)
DFafi (х, х') = - г^рР (х, х'). B.89)
Заметим также, что если нарушающий калибровочную симме-
симметрию член удалить, полагая ?->°о> то B.88) становится беско-
бесконечным. Это значит, что в отсутствие слагаемого, нарушающего
калибровочную инвариантность, дифференциальный оператор в
левой части B.87) необратим.
Исследование интегральных представлений фейнмановских
функций Грина, таких, как B.76) и B.88), выявляет полезное
математическое свойство, часто используемое в практических вы-
вычислениях. Рассмотрение контуров для Of в комплексной пло-
плоскости k° показывает, что топологическое соотношение между
контуром (который подразумевается замкнутым полуокруж-
полуокружностью на бесконечности) и полюсами остается неизменным,
если повернуть контур на 90° против часовой стрелки, чтобы он
совпал с мнимой осью k° от —too до too. Если теперь провести
замену переменных и = — ik°, 0 = — it ит' = —it', то контур ин-
интегрирования будет снова лежать на вещественной оси, но уже
не будет пересекать полюсов.
Например, в скалярном случае получаем
О, (/, х; f, х') = - ШБ (ix, x; tV, x'), B.90)
где
Здесь Ge — «евклидова» функция Грина, удовлетворяющая урав-
уравнению
(D* - w2) GF (x, х') = -6п(х- х'). B.92)

52 Глава 5
В B.92) ? — эллиптический оператор
представляющий собой оператор Даламбера в «-мерном евкли-
евклидовом пространстве, а не в пространстве Минковского. Это соот-
соответствует рассмотрению поля ф в евклидовом пространстве.
Преимущество евклидовой теории поля в том, что эллипти-
эллиптический оператор имеет единственный хорошо определенный об-
обратный оператор, поскольку полюса в интегральном представ-
представлении B.91) лежат на мнимой, а не на вещественной оси. По-
Поэтому часто с точки зрения математики удобнее работать в ев-
евклидовом пространстве, «поворачивая» обратно к псевдоевкли-
псевдоевклидову пространству с помощью B.90) в конце вычислений. Гра-
Граничные условия для фейнмановского пропагатора этой процеду-
процедурой накладываются автоматически. (Заметим, что ни один из
других контуров, изображенных на рис. 3, нельзя повернуть та-
таким способом, не пересекая полюсов.) Более детальное обсужде-
обсуждение вопроса (для случая искривленного пространства-времени)
можно найти в работах [94, 486].
Введенные выше функции Грина были определены как мате-
математические ожидания произведений операторов поля в чистом
состоянии, а именно в состоянии вакуума. Эти функции Грина
пригодны для описания систем при нулевой температуре. Но си-
система при ненулевой температуре находится не в чистом состоя-
состоянии, а представляет собой статистическую смесь чистых состоя-
нийпПоэтому функции Грина для систем при ненулевой темпера-
температуре определяют средним по всем чистым состояниям от мате-
математического ожидания произведений полевых операторов в этих
состояниях [3, 192, 319, 354].
Предположим, что |г|)<>— чистое собственное состояние га-
гамильтониана B.41), принадлежащее собственному значению
энергии Ей Тогда оно будет также и собственным состоянием
оператора полного числа частиц N B.32) с некоторым собствен-
собственным значением т. Так как и число частиц и энергия могут изме-
изменяться, равновесное состояние при температуре Т описывается
большим каноническим ансамблем состояний. Вероятность того,
что система будет находиться в состоянии |i|)«>, определяется
выражением
Pt ¦=* е~р (B«~|MI«)/Z, B.93)
где
Р = l/kBT, • B.94)
ke — постоянная Больцмана, \х — химический потенциал,
= e-pQ B.95)

Квантовая теория поля в пространстве Минковского 33
— большая статистическая сумма и Q — термодинамический по-
потенциал. Таким образом, среднее по ансамблю при температуре
Т = (kB$)~l от любого оператора А равно
М)р = Z Pi ('Фг I А | г^). B.96)
Вводя квантовую матрицу плотности
B.97)
имеем
Р* = <Ч>« I P I Ч>*>- B.98)
Требование равенства полной вероятности единице записывается
в виде
trp=?<4>,|pl4>i> = l, B.99)
i
а B.96) сводится к равенству
<Л>р = 1грЛ. B.100)
Теперь можно ввести функции Грина при ненулевой темпера-
температуре (называемые также тепловыми или температурными функ-
функциями Грина) с помощью простой замены вакуумного ожидания
в определении функций Грина при нулевой температуре средним
по ансамблю < >р. Например, исходя из B.68), в случае скаляр-
скалярных полей имеем
Gt(x, х') = (ф(х)ф(х%,
Оз(*, *') = <*(*')*(*)>,>.
Принимая временно, что химический потенциал равен нулю,
получаем следующее важное соотношение для тепловых функций
Грина:
Of (t, x; f, х') = Gj (t + ф, х; f, x'). B.102)
Это соотношение получается из гейзенберговских уравнений
движения
°> B.103)
следующим образом:
Gt (t, x; f, x') = tr [е~ея ф (t, x) ф (f, x')]/tr (е"ря) =
tr[*(* + #, х)е-»Иф(?, x)]/tr(в-(»») =
(^, xO^(^ + tP, x)]/tr(e-Pff)==
, x; t', x') (9.104a)

34 Глава 2
и аналогично для Gp. При выводе этого результата было исполь-
использовано соотношение tr АВ = tr BA. Из B.102) можно вывести
подобные соотношения для других функций Грина, например, из
B.67) следует
GjJ>(/, x; /', x') = GjJ>(/ + /p, х; /', х'). B.1046)
Если удерживать химический потенциал, то это приводит лишь
к появлению множителя е^ в правой части. Заметим однако, что
«GpU, *')=т И? (**') = [*(*). ф(х% B.105)
поскольку коммутатор свободных скалярных полей есть с-число
(это следует из B.18)), и его статистическое и вакуумное ожи-
ожидания равны между собой. Для теорий с взаимодействием это,
вообще говоря, неверно, так как соответствующий коммутатор
(при неравных временах) может быть оператором.
Используя B.105) и соотношения типа B.104) для других
функций Грина, можно получить интегральные представления
для тепловых функций Грина. С помощью B.105) находим
фурье-образ функции Gp:
Ю(х, х') = Юр(х, x') = (l/2n) Jdcoc(«; x, х^е-**»-*1*, B.106)
где с (со; х, х') легко вычислить, исходя из B.76), при соответ-
соответствующем выборе контура интегрирования:
с (со; х, *') = BяI-"$ dn-xkbW -| kf - m2) X
Х[0(ю)— Э(— (o)]eik-<x-*'K B.107)
Если записать также фурье-образ функции Gf в виде
G$(x, x') = (l/2n) J dcog±(co)e-iM(i-''), B.108)
' ~°°
то из B.67) найдем
C(co) = g+(co)-g-(co). B.109)
Из соотношения B.104а) следует g+(co) = еРи?~(<й), что вместе
счB.109) дает
g± (а) = ± с (со) A - \
приводя к интегральному представлению
Gt(x. *0-± ] ^Т

Квантовая теория поля в пространстве Минковского 35
На основе этой формулы могут быть получены представления
для других функций Грина. В частности, вычислив явно интегра-
интегралы и разложив множители A — етР@)~' по степеням ет0(О, найдем
G<" (/, х; /', х') = ? Gto(t + ik$,x; t', x'), B.111)
k= — оо
т. е. тепловая функция Грина может быть записана в виде бес-
бесконечной суммы функций Грина при нулевой температуре, взя-
взятых в моменты времени, сдвинутые на мнимую величину.
В случае спина 7г ввиду того, что поля не коммутируют, а
антикоммутируют, находим, что аналог B.81) при температуре,
не равной нулю, SJ}' удовлетворяет условию антипериодичности
SjJ>(/, x; С, хО = -5Ц'(/ + »р, х; /', х'), B.112)
заменяющему условие периодичности B.104). Далее получаем
представление в виде суммы, аналогичное B.111), в котором ан-
антипериодичность проявляется в наличии множителя (—l)k:
Sg)(/, x; /', х')= Z (-l)*S<'>(f+ i*p, x; f, x'). B.113)
Случай коммутирующих полей спина 1 аналогичен скаляр-
скалярному случаю (см., например, [66]).
2.8. Квантование методом интегрирования
по траекториям
Схема канонического квантования, кратко описанная в
разд. 2.1, представляет собой лишь один из различных подхо-
подходов, существующих в квантовой теории поля. Можно, например,
исходить из ковариантных коммутационных соотношений
1Ф[х), *{х')] = Ю{х,х') B.114)
(вспомним B.65), учитывая, что G есть с-число) вместо канони-
канонических коммутационных соотношений B.15). Такой путь ближе
по духу к общей теории относительности, поскольку в B.114)
время / не играет выделенной роли. Он немедленно приводит к
тем ж€ коммутационным соотношениям B.18) для операторов
рождения и уничтожения. В случае глобально гиперболического
пространства-времени (см. разд. 3.1) ковариантный и канониче-
канонический подходы эквивалентны.
Другая схема квантования, применяемая в квантовой теории
поля, наиболее близкая к строгой трактовке в функциональном
анализе, — это метод С*-алгебр Сигала [430] (обзор примене-
применения этого подхода к случаю искривленного пространства-вре-
пространства-времени, см. в работе [310]).
2*

36 Глава 2
Наконец, фейнмановский подход к квантованию с помощью
интегралов по траекториям [194] является эффективным мето-
методом в квантовой теории гравитации и при квантовании взаимо-
взаимодействующих полей с присущими им проблемами перенормиро-
перенормировок. Более подробное изложение можно найти в работах [1, 211,
317, 373,411,452].
Основным объектом теории является функциональный инте-
интеграл для поля ф, обладающего действием S,
Z [J] = (out, 0 10, in) = \® [ф] ехр { iS [ф] + / \ dnxJ (х) ф(х)},
B.115)
который вычисляют по пространству функций ф с надлежащей
мерой. Величина Z известна как производящий функционал тео-
теории; она дает амплитуду перехода из начального вакуумного со-
состояния |0, in) в конечное вакуумное состояние |0, out) в при-
присутствии источника частиц J(x). При выключении источника оба
вакуума сводятся к обычному вакууму пространства Минков-
ского без источников, и мы имеем
Z[0] = <0|0) B.116)
(что обычно нормируется на единицу).
Можно показать, что функциональные производные Z по /
дают связные, хронологически упорядоченные функции Грина
<2Л17)
(индекс с означает, что в теории возмущений учитываются толь-
только связные фейнмановские диаграммы).
В качестве примера рассмотрим случай свободного скаляр-
скалярного поля, обладающего действием
5 [ф] = \
dnx [ <?„ (х) + y *
где 2?о — лагранжиан свободного поля B.2), а инфинитезималь-
ный фактор (связанный с граничными условиями для ф) введен
для того, чтобы сделать функциональный интеграл сходящимся.
Подставляя вместо i?o выражение B.2) и интегрируя по частям,
приводим действие к виду
SM=\dn х[-±ф(П +т2-1г)ф], B.118)
где опущен поверхностный член. С помощью B.118) экспоненту
в B.115) можно записать в более удобной для интерпретации
форме
- 1 \ йпхс1пуф (х) Кхуф (У) + J / (х) ф (х) <Г х, B.119)

Квантовая теория поля в пространстве Минковского 37
где симметрический оператор
x-y) B.120)
формально можно считать симметричной матрицей К с непре-
непрерывно изменяющимися индексами х, у, обладающей свойствами
\ B.121)
^ = б"(х - г), B.122)
в(ху), B.123)
где последний результат получен путем обращения определения
фейнмановского пропагатора B.74). Эти равенства становятся
хорошо определенными при подстановке их в функциональный
интеграл-по 2)[ф].
Вводя вместо ф новую переменную интегрирования
B.124)
запишем квадратичную форму B.119) с учетом B.121) — B.123)
в виде
~~ 7 \ d"x \?' № ~ ) d"yJ № % ух12] — j) dnxdnyj (x) GP (x,.
B.125)
После подстановки B.125) в экспоненту в функциональном
интеграле второй член, не зависящий от ф, можно вынести за
знак интеграла, а первый член приводит к интегралу гауссова
типа, взятие которого дает численный коэффициент.
Таким образом,
Z(J) ~ (det/C1/2)~'exp[--|-/ J dnxdnyJ(x)GP(x, y)J (у)], B.126)
где
(det /A/2Г' = [det (- GP)]m = exp ri tr In (- GF)] B.127)
— якобиан, возникающий вследствие замены переменной B.124).
Из формулы B.126) следует, например,
а/У
в соответствии с определением B.69).
"lG*

38 Глава 2
Для поля 1|э спина '/г производящий функционал Z выбирают
в виде
Z (ть ij) = $ Ф Ц>] 0 № ехр {/ J <Гх[Я?0 (*)+Ч (*) * (jc)+tj (х) ф (*
B.128)
где tj, fj— антиком мутирующие внешние токи, а лагранжиан i?o
определен формулой B.45). Вместо B.126) получаем
-^ йпхц (x)SF (х, у) г\(у)]. B.129)
В случае электромагнитного поля возникают некоторые ус-
усложнения, связанные с калибровочной симметрией. Действитель-
Действительно, рассмотрим аналог выражения B.115)
Z (/) = \Ф [Аа] ехр { I \ dnx [ <?0 (х) + /Р (*) Лр (х)]} , B.130)
где 3?о(х) определен формулой B.54). Действие, входящее в экс-
экспоненту в B.130), может быть представлено в виде
a»F^dax = - y $ daxdayAa (х) K$At (у),
B.131)
К$ = Ыа*Пх-а№)Ьа{х-у). B.132)
Из формул B.87), B.88) следует, что в пределе ?-*-°° величина
К = Dp (С -*- °°) сингулярна. Поэтому, как мы увидим ниже,
квантование электромагнитного поля непосредственно с по-
помощью описанной процедуры выполнить не удается. Эта труд-
трудность была отмечена в связи с калибровочной инвариантностью
на стр. 27, где в лагранжиан введен фиксирующий калибровку
член B.59) (исчезающий в пределе ?->- с»), благодаря которому
волновой оператор становится обратимым и может быть опреде-
определена функция Грина B.88) для конечных %.
Поскольку лагранжиан S'o явно калибровочно инвариантен,
он не зависит от продольной и временной компонент Аа, т. е.
К выделяет поперечные компоненты поля. Следовательно, любое
изменение продольной и временной компонент Аа будет остав-
оставлять 3?о неизменным. Вообще переход к новому потенциалу Аа,
связанному с первоначальным Аа преобразованием калибровки
B.58), не будет изменять лагранжиана 3?0.
Если представить себе пространство всех функций Аа, то под
действием калибровочного преобразования B.58) точка (т. е.
функция Аа) этого пространства будет отображаться в точки на
линии, изображающей другие функции, которые связаны с исход-
исходной функцией Аа непрерывным калибровочным преобразованием.
Такая линия называется орбитой калибровочной группы, ассо?

Квантовая теория поля в пространстве Минковского 39
циируемой с преобразованием B.58). Трудность с функциональ-
функциональным интегрированием возникает из-за того, что изменение Аа в
?D[Aa] вдоль орбит не вызывает каких-либо изменений Я?о(х).
Чтобы убедиться в этом, достаточно заметить, что функциональ-
функциональный интеграл в B.130) вычисляется по бесконечному объему в
функциональном пространстве, поэтому для сходимости инте-
интеграла необходимо стремление 3?о(х) —>- оо при Аа—>-оо, обеспе-
обеспечивающее экспоненциальное спадание. Однако, если Аа-*- °°
вдоль орбиты калибровочной группы, то j?o остается постоянным
(и, следовательно, конечным), что не обеспечивает требуемой
сходимости. Так как объем занимаемого орбитой подпростран-
подпространства также бесконечен, функциональный интеграл остается неоп-
неопределенным, пока не найден способ перенормировать его путем
деления на этот бесконечный объем.
Один из способов преодоления этой трудности был указан
Фаддеевым и Поповым [190], развившими более ранние работы
Фейнмана [193] и де Витта [153, 155]. Требуется, чтобы измене-
изменение Аа было ограничено лишь функциями, принадлежащими раз-
различным орбитам. Этого можно добиться, выбирая в пространстве
Аа «гиперповерхность», пересекающую каждую орбиту лишь
один раз. Далее, вместо того чтобы интегрировать по всему про-
пространству, вычисляют интеграл только по гиперповерхности.
Уравнение такой гиперповерхности можно записать в виде
F[Aa] = 0, B.133)
поэтому можно было бы предположить, что достаточно лишь
ввести в подынтегральное выражение в B.130) дельта-функцию
б[/г(Ла)]. Но чтобы обеспечить калибровочную инвариантность,
нужно действовать более осторожно. Две соседние гиперповерх-
гиперповерхности связаны соотношением
F(A$ (х)) = F (Аа (х)) + \ dnyMxyA (у) + О (Л2), B.134)
где Л параметризует калибровочное преобразование, F(Aa) =
==¦ [У?(Л^)]Л=0, а М зависит от выбора калибровки. Например,
в калибровке Ландау /г(Ла) = Ла1 а, поэтому
F{A?) = Aa,a+nh = F(Aa) + nA, B.135)
откуда следует
Мху=ПЬп(х-у). B.136)
* Удобно ввести величину AF(Aa) с помощью соотношения
l B.137)
которое, как легко показать, является калибровочно инвариант-
инвариантным. На гиперповерхности B.133) первый член в правой части

40 - '' Глава 2
B.134) исчезает, поэтому в символической записи F (а?) = МА.
Тогда интегрирование в B.137) может быть выполнено с по-
помощью перехода от переменной Л к переменной МЛ.:
д^1 (Аа) = (det My1 = ехр (- tr In M), B.138)
где (det М)~х — якобиан, возникающий в результате этой замены
переменной.
Возвращаясь к функциональному интегралу B.130) (с /, рав-
равным нулю), вызвавшему эти усложнения, учитывая B.137),
можно, не изменяя результата, подставить в подынтегральное
выражение единичный оператор AF (Aa)\& [Л] 6 [^(Ла)]. Учиты-
Учитывая независимость величины Af от выбора калибровки, можно
заменить ее аргумент на Аа, и далее, сделав замену переменной
интегрирования, переписать функциональный интеграл в виде
J Й> [Аа] \®[A]\F (Аа) 6 [F (Аа)] ехр [/ \ <?0 (*) сГх] ,B.139)
откуда ясно, что подынтегральное выражение в интеграле по
3) [Л] не зависит от Л и, следовательно, может быть вынесено
за знак интеграла. Результирующий интеграл, хотя и бесконе-
бесконечен, не зависит от полей Аа, поэтому разделив на него B.139),
приходим к новому определению величины Z, которое уже не
приводит к сингулярностям:
1 ехР {l \ л №<> W+/a W л« W -'tr ln м!
B.140)
При получении B.140) учтено, что множитель 8[F(Aa)] в под-
подынтегральном выражении в B.139) ограничивает А^ гиперповерх-
гиперповерхностью B.133), что позволяет использовать результат B.138).
Таким образом, ограничение интегрирования гиперповерх-
гиперповерхностью F(Aa) = 0 не только означает введение в подынтеграль-
подынтегральное выражение множителя 8\F(Aa)], но также приводит к по-
появлению дополнительного члена в действии для поля. Этот
добавочный вклад может рассматриваться как происходящий от
дополнительного фиктивного поля. Действительно, нетрудно
показать, что в калибровке Ландау
JJ0 [с] Ф \с\ ехр (i jp^cdpc'^expt-trlnM), B.141)
где с и с* — безмассовые скалярные поля, удовлетворяющие, од-
однако, антикоммутационным соотношениям, ввиду чего они полу-
получили название «духовые поля фаддеева — Попова». Поскольку
они не связаны с векторным полем Аа, эти поля обычно опускают
в квантовой теории поля в плоском пространстве-времени. Но в
искривленном пространстве-времени они играют важную роль.

Квантовая теория поля в пространстве Минковского 41
Векторную часть интеграла по траекториям можно далее уп-
упростить в калибровке Ландау, выражая fifF^a)] = 6(Ла,а) в
виде экспоненты:
B.142)
Сравнение с B.59) показывает, что эта экспонента в калибровке
Ландау (?-»-0) есть просто iSa- Следовательно, производящий
функционал для векторного поля равен
[Аа] exp [i \ dnx Bо + 3?о)\ ¦ B.143)
¦ Этот функциональный интеграл может быть вычислен с по-
помощью тех же приемов, что и в случае скалярного поля; он ока-
оказывается пропорциональным выражению
х-У)*» (У)]. B-144)
где D'fP определяется формулой B.88).
Хотя полный производящий функционал, представляющий
собой произведение B.144) и B.141), был получен в калибровке.
Ландау ?->-0, найденное выражение остается справедливым при
любом ?.
Закончим эту главу краткими замечаниями о сходимости
функционального интеграла B.115). Поскольку действие S веще-
вещественно, экспонента в подынтегральном выражении является чи-
чисто мнимой, вследствие чего интеграл по всему функциональному
пространству не является хорошо определенным. В предшество-
предшествовавшем изложении это положение было исправлено введением
множителя is. Как было замечено в разд. 2.7, использование ie
в определении фейнмановских функций Грина эквивалентно пе-
переходу к описанию в мнимом времени, когда поле рассматри-
рассматривается в евклидовом пространстве, а не в пространстве Минков-
Минковского. Если вакуумные ожидания от произведений хронологиче-
хронологически упорядоченных полей, такие, как B.117), аналитичны в ком-
комплексной плоскости t, то можно проводить квантование в евклидо-
евклидовом пространстве, в котором интегралы по траекториям стано-
становятся хорошо определенными сильно сходящимися интегралами
гауссова типа (по крайней мере для широкого класса лагран-
лагранжианов), а затем вернуться к теории в пространстве Минков-
Минковского, «поворачивая» назад от it к t. Такой метод часто исполь-
используют на практике, Однако при переходе к искривленному про-
1 странству может случиться, что «евклидизированное» (т. е.
имеющее положительно определенную метрику) пространство-
время, соответствующее исходному псевдориманову простран-
пространству-времени, вообще не существует.

Глава 3
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ
В ИСКРИВЛЕННОМ ПРОСТРАНСТВЕ-ВРЕМЕНИ
В настоящей главе проводится обобщение формализма кван-
квантовой теории поля на случай искривленного пространства-вре-
пространства-времени. Предварительно кратко обсуждаются основные понятия
псевдоримановой геометрии. Это введение не претендует на пол-
полноту; более полное изложение читатель может найти в книгах
[287, 313, 494]. Тем, кто не знаком с конформными преобразова-
преобразованиями и диаграммами Пенроуза, советуем внимательно прочи-
прочитать разд. 3.1.
Обобщение понятия частиц на искривленное пространство-
время технически осуществляется довольно просто. Однако фи-
физическое истолкование возникающего формализма встречает за-
затруднения. По поводу смысла и содержания понятия частиц при
наличии фонового гравитационного поля высказывались противо-
противоречивые суждения. В некоторых случаях, например в статиче-
статическом пространстве-времени, понятие частиц кажется хорошо оп-
определенным, в других (если пространство допускает существова-
существование замкнутых времениподобных линий или не обладает всюду
поверхностями Коши) оно может показаться безнадежно неяс-
неясным. Здесь мы ограничиваемся «хорошими» пространствами и
не предаемся философским рассуждениям о смысле понятия ча-
частиц. Вместо этого формализм непосредственно связывается с
теми величинами, которые могли бы быть измерены в интересую-
интересующем нас квантовом состоянии с помощью некоторого прибора.
Понятие частиц в искривленном пространстве-времени исполь-
используется здесь именно в таком операционном смысле. Такой под-
подход и ранее обсуждался в литературе, но в этой книге представ-
представления о детекторах частиц развиты более детально, чем это было
до сих пор.
Используя конкретный пример рождения частиц переменным
фоновым гравитационным полем, мы проводим подробный и уг-
углубленный анализ адиабатичности и на нем основываем пред-
представление о частицах в квазистатическом пространстве-времени.
Именно здесь следует ожидать соприкосновения с обычной кван-
квантовой теорией поля, которая, как известно, является хорошим
приближением для (относительно) медленно расширяющейся
вселенной, где мы находимся. Из анализа следует, что поведение

Квантовая теория поля в искривленном пространстве-времени 43
высокочастотной части поля не зависит от квантового состояния
или глобальной структуры пространства-времени, а определяется
только его локальной геометрией. Это обстоятельство является
решающим при проведении программы регуляризации и пере-
перенормировок в последующих главах.
В разд. 3.5 мы попытались дать полное изложение представ-
представления об адиабатических состояниях, и этот раздел требует
тщательного изучения. Наиболее существенным моментом яв-
является применение адиабатического предельного перехода к
фейнмановскому пропагатору, что проводится в разд. 3.6. «Вер-
«Вершиной» формализма можно считать так называемое представ-
представление де Витта — Швингера для функции Грина GF, определяе-
определяемое разложением C.141). Важность этого разложения в теории
перенормировок трудно переоценить. Рекомендуем читателю
сначала ознакомиться с разд. 3.5, обращая внимание на заме-
замечания физического характера, и вернуться к более детальному
изучению этого раздела после того, как будут рассмотрены по-
последующие приложения.
Раздел 3.7, посвященный конформному вакууму, значительно
легче для восприятия. Он необходим для дальнейших приложе-
приложений, в частности при проведении конкретных расчетов космоло-
космологического рождения частиц и квантового натяжения вакуума.
Последний раздел, посвященный полям высших спинов в ис-
искривленном пространстве, содержит лишь краткое изложение
стандартного формализма, но приводимые здесь выражения
C.190) — C.195) для тензоров энергии-импульса будут часто ис-
использоваться.
3.1. Структура пространства-времени
Мы принимаем определение пространства-времени как п-мер-
ного, глобально гиперболического псевдориманова многообразия
класса С°° (более подробное обсуждение можно найти в работе
[287]). Такое определение может оказаться более ограничитель-
ограничительным, чем это необходимо для построения жизнеспособной кван-
квантовой теории поля (пример теории в пространстве-времени, не
удовлетворяющем условию глобальной гиперболичности, см. в
работе [16]). Условия дифференцируемое™ обеспечивают суще-
существование дифференциальных уравнений, а глобальная гипербо-
гиперболичность — существование поверхностей Коши.
, Псевдориманова метрика g^v, ассоциируемая с элементом
длины
(х) dx» dx\ \i, v =<0, 1, ..., (« — О,
имеет сигнатуру п — 2. Для покрытия полного многообразия мо-
может понадобиться несколько координатных сеток с соответствую-

44 Глава 3
щими guv. Детерминант определим следующим образом:
Мы будем часто использовать конформные диаграммы Пен-
роуза [394] для изображения причинной структуры простран-
пространства-времени. Этот метод позволяет представить все бесконечное
пространство-время в виде конечной диаграммы (компактного
многообразия) с помощью конформного преобразования мет-
метрики. Конформные преобразования, сжимающие или растягиваю-
растягивающие многообразие, следует отличать от преобразований коорди-
координат x^-^x'v-, которые лишь изменяют обозначения точек на не-
некоторой карте, оставляя геометрию без изменений. Конформное
преобразование метрики имеет вид
г„у(*)->?|«-(*) = О2 (*)?.«(*), C-1)
где п(х) — некоторая непрерывная, неисчезающая, конечная, ве-
вещественная функция.
Исходя из этого преобразования метрики, можно вывести
трансформационные свойства различных физических величин от-
относительно конформных преобразований. Например, символы
Кристоффеля, тензор Риччи и скалярная кривизна преобразуют-
преобразуются соответственно как
О;а), C.2)
R\-и. R\ = Q-*R\ - (n - 2) Q-' (О'1); wgpv +
+ (n- 2) О"» (Q"-2); pagpa6\, C.3)
R->R = Q-2R + 2{n-l)Q-*Q;^ + (n-l)(n-4)X
XQQ;^Q;vguv, C.4)
откуда можно получить следующее полезное преобразование:
[|] C.5)
где
1%[Ч] C.6)
C.7)
В качестве простой иллюстрации построения диаграмм Пен-
роуза рассмотрим двумерное пространство Минковского с эле-
элементом длины
ds2 = dt2-dx2. C.8)

Квантовая теория поля в искривленном пространстве-времени 45
Мы часто используем также изотропные координаты
u = t — х,
v^ + x. C-9)
в которых элемент длины C.8) имеет вид
(ЗЛО)
так что
»«-нг а- <з">
Допустим, что мы совершаем преобразование координат
и' = 2 arctg и,
г о * C-12)
v =2 arctg v, '
где
— я<ы', и'<я. ' C.13)
Тогда из C.10) получаем
ds2 = -j-cos-21 и' cos-2 i-o'Ai'do', C.14)
так что
i4l[J J] C.15)
Если теперь провести конформное преобразование метрики с по-
помощью функции
=(|cos i-и'cos-if'
(«', оо=4-[° J]
то
и связанный конформным преобразованием элемент длины при-
принимает вид
ds2=du'dv'. C.17)
Он имеет тот же вид, что и элемент длины в первоначальном
пространстве Минковского C.10), но покрывает только ком-
компактную область C.13), как показано на рис. 4. Действие кон-
конформного преобразования C.16) состоит в «подтягивании» бес-
бесконечности к граничным линиям на диаграмме.
Границы на рис. 4 обладают рядом интересных особенностей.
Прежде всего заметим, что все изотропные лучи остаются на
диаграмме Пенроуза лежащими под углом 45°: конформные пре-
преобразования .оставляют инвариантными изотропные конусы.
Поэтому анализ причинных отношений можно проводить с

46 Глава 3
помощью изотропных линий, изображаемых так же, как в обыч-
обычном пространстве Минковского. Ясно, что все изотропные линии
оканчиваются на граничных диагоналях, отмеченных символами
3+ и 3~ и называемых соответственно изотропной бесконеч-
бесконечностью будущего и прошлого. Асимптотически времениподобные
линии сходятся к точкам, обозначенным i+ (времениподобная
бесконечность будущего) и i~ (времениподобная бесконечность
прошлого). Аналогично асимптотически пространственноподоб-
ные линии сходятся к i° (пространственноподобной бесконечно-
бесконечности).
Изложенный анализ применим и к случаю четырехмерного
пространства Минковского, если каждую точку диаграммы рас-
рассматривать как двумерную сферу, за исключением точек на
вертикальной оси, и Р, изображающих отдельные простран-
пространственно-временные точки. Таким образом, линии 3+ и Э~ в
действительности представляют собой трехмерные изотропные
поверхности.
Времениподобная линия, являющаяся асимптотически изо-
изотропной, может возникнуть, если некоторая частица испытывает
постоянное равномерное ускорение и ее скорость приближается
к скорости света при t-*-oo. Мировая линия такой частицы изо-
изображена на рис. 5. Изотропная асимптота обладает тем свой-
свойством, что лежащие выше ее события не могут быть причинно
связаны с ускоряющейся частицей. Иначе говоря, сигнал от этих
событий не может достигать частицы (хотя обратное может быть
неверным). Изотропная асимптота является поэтому горизонтом
событий для ускоренной частицы, хотя и не является горизонтом
для неускоренной частицы.
В качестве другой- иллюстрации применения диаграмм Пен-
роуза рассмотрим четырехмерное пространство-время Шварц-
шильда, описываемое элементом длины
ds2 = A — 2M/r)dt2-{l — 2M/r)~[ dr2 - г2 (d& + sin29d<f>2). C.18)
Это пространство-время представляет собой единственное сфери-
сферически симметричное вакуумное решение уравнений Эйнштейна и
часто используется для изображения пустой пространственной
области, окружающей сферическую звезду или коллапсирующее
тело массы М.
После перехода к координатам Крускала [334]
ы = — 4Ме-"'ш,
где u = t — r*, v = t + r* и r*=r + 2M ln\(r/2M) — 1|, эле-
элемент длины C.18) можно представить в виде
ds*— {2M/r)e-r'2Mdudv - r2{d& + sin29u^2). C.20;

Квантовая теория поля в искривленном пространстве-времени 47
Рис. 4. Конформная диаграмма
Пенроуза пространства Минков-
ского. Компактная область
—я ^ и', v' ^ л является кон-
конформным изображением всего про-'
странства Минковского (—оо ^ и,
v sg оо). Изотропные лучи и, v =
= const остаются под углом 45°.
Показана мировая линия асимпто-
асимптотически времениподобного наблю-
наблюдателя.
Часть этой метрики, содержащая произведение du dv, конформно
эквивалентна метрике двумерного пространства Минковского
C.10), которое в свою очередь может быть компактифицировано
координатными и конформными преобразованиями C.12) и
C.16). Результирующая диаграмма Пенроуза идентична изобра-
изображенной на рис. 4. Но левый край ромба в этом случае не есть Э,
так как из C.19) следует, что переменные ы и v определены
лишь в квадранте — оо ¦< п ^ 0, 0 =^ и ^ оо. Таким образом,
левый край изображает области й = 0и» = 0 или г = 2М, t =
= ±оо. Координатная система и, v (или t, r) имеет здесь сингу-
сингулярность, которая отсутствует для координат п, v, в чем легко
убедиться, сравнивая метрики C.18) и C.20). Поэтому простран-
пространство-время можно аналитически продолжить за левый край, ис-
используя координаты Крускала п, v, определенные на всей пло-
плоскости —оо < п, v < оо. Результирующая диаграмма Пенроуза
показана на рис. 6, и это пространство-время известно как мак-
максимально расширенное многообразие Крускала.
Горизонтальные зигзагообразные линии изображают точку
г = 0 в прошлом и будущем. Здесь метрика Крускала C.20)
имеет особенность, которая является истинной особенностью про-
пространства-времени, как следует из рассмотрения тензора Римана.
Многообразие не может быть аналитически продолжено за эти
края. В левой части диаграммы имеется другая пространственно-
временная область II, асимптотически представляющая собой
пространство Минковского, которая содержит поверхности 9
"при п= +оо, 5 = —оо. Эта половина многообразия геометриче-
геометрически тождественна правому ромбу I с точностью до изменения на-
направления времени (/-*—t).
Изотропный луч м = 0 (г = 2М, t = +°°) представляет со-
собой последний нулевой луч, достигающий У+: при п > 0 все

48
Глава 3
Рис. 5. Времениподобная миро-
мировая линия представляет наблю-
наблюдателя, непрерывно ускоряю-
ускоряющегося вправо и асимптотиче-
асимптотически достигающего скорости све-
света. Но эта мировая линия не
доходит до (+, а пересекает У+
в точке Р. Таким образом, изо-
изотропный луч, проходящий че-
через Р в обратном направлении,
действует как горизонт собы-
событий, поскольку события, лежа-
лежащие выше, не могут восприни-
восприниматься наблюдателем: все ну-
нулевые лучи от таких событий
пересекают 2/+ между точками
Р и (+.
изотропные лучи попадают на сиигулярность будущего г = 0.
Поэтому луч п = 0 (изображающий направленную наружу дву-
двумерную поверхность в полной четырехмерной картине) является
горизонтом событий для наблюдателей, находящихся в области
I. Аналогично v = 0 (г = 2М, t = —оо) есть горизонт событий
для наблюдателей, находящихся в области II. Таким образом,
вакуумные области III и IV являются черными дырами для
наблюдателей, находящихся в области,-1 и II соответственно
(и белыми дырами для наблюдателей в областях II, I). Миро-
Мировые линии наблюдателей, не попадающие в черные дыры и не
выходящие из белых дыр, сходятся в i+ и i~ в соответствующих
областях. Существование горизонта событий делает невозмож-
невозможным сообщение между областями I и II.
Рис. 6. Диаграмма Пенроуза максимально расширенного многообразия Кру-
скала. Физическая сиигулярность изображена ломаной линией. Горизонты бу-
будущего и прошлого, отмеченные символами Н± соответственно, представ--
ляются изотропными лучами п = 0, v = 0. Наблюдатели, не падающие в чер-
черную дыру (и не выходящие из белой1 дыры), находятся в одной из ромбо-
ромбовидных областей I нли II.

Квантовая теория поля в искривленном пространстве-времени 49
Максимально расширенное пространство-время Крускала яв-
является всюду (кроме точки г = 0) решением вакуумных уравне-
уравнений Эйнштейна. В реальном мире, где черные дыры, вероятно,
образуются при схлопывании звезды, вакуумные уравнения опи-
описывают лишь область вне звезды, и, следовательно, к этому слу-
случаю относится только часть рис. 6. Тем не менее, как показано
в гл. 8, для наблюдателей, находящихся в области I, различие
становится несущественным в поздние моменты времени (t-*-
-*¦ оо) после схлопывания.
Наше рассмотрение, как правило, будет ограничено простран-
пространствами, обладающими определенной геометрической симметрией.
Симметрии могут быть описаны с помощью векторов Киллинга
?•*, которые являются решениями уравнений Киллинга
2teiiv(*) = 0, C.21)
где &\ — производная Ли вдоль векторного поля \*. Уравнение
C.21) может быть записано в виде
Нас также будут интересовать симметрии, связанные с кон-
конформно-плоским характером метрики, когда пространство-время
конформно-эквивалентно пространству Минковского. Такая гео-
геометрия допускает конформное векторное поле Киллинга, удовле-
удовлетворяющее конформному обобщению C.21)
2tei«(*) = M*)g|iv(*). C-23)
где К(х) — некоторая (несингулярная, неисчезающая) скалярная
функция.
3.2. Квантование скалярного поля
Формально квантование поля в искривленном пространстве-
времени проводится аналогично случаю пространства Минков-
Минковского. Мы исходим из плотности лагранжиана (разд. 3.8)
C.24)
где ф(х) —скалярное поле.т — масса кванта поля. Связь между
скалярным и гравитационным полями, представленная членом-
|/?^>2, где| — некоторый численный множитель, a R(x)—ска-
R(x)—скалярная кривизна Риччи, введена как единственно возможная ло-
локальная скалярная связь с правильной размерностью. Соответ-
Соответствующее действие имеет вид
dnx, C.25)

50 Глава 3
где п — размерность пространства-времени. Принимая, что ва-
вариация действия по ф равна нулю, приходим к уравнению для
скалярного поля
= 0, C.26)
где оператор ? задан выражением C.6).
Два значения параметра | представляют особый интерес:
значение |=0, соответствующее так называемой минимальной
связи, и значение
| = i-[(n-2)/(n-l)]^i(rt) C.27)
для конформной связи. В последнем случае действие и, следова-
следовательно, уравнения поля при т=0 инвариантны относительно
конформных преобразований C.1), если считать, что поле преоб-
преобразуется согласно C.7). Действительно, из C.5) следует, что если
то
Скалярное произведение B.9) обобщается следующим обра-
образом:
(Фи *,) = -' $ Фх (*) W*)[-ixM]Vld»\ C-28)
2
где d2,v- = nPdZt пУ- — направленный в будущее единичный век-
вектор, ортогональный пространственноподобной гиперповерхности
2, a d2 —элемент объема на 2. Гиперповерхность 2 выбирается
как поверхность Коши в (глобально гиперболическом) простран-
пространстве-времени, и можно показать с помощью теоремы Гаусса (см.,
[287], § 2.8), что значение (ф\, фг) не зависит от 2.
Существует полный набор решений щ(х) уравнения C.26),
ортогональных в смысле скалярного произведения C.28), т. е.
удовлетворяющих соотношениям
Индекс i представляет набор величин, необходимых для разли-
различения мод. Поле ф может быть разложено аналогично B.17):
ф (х) = Z [atut (x) + ар\ (*)], C.30)
Ковариантное квантование теории осуществляется наложением
коммутационных соотношений B.18)
[а,, а+] = в„ и т. д. C.31)

Квантовая теория поля в искривленном пространстве-времени 51
Построение вакуумного состояния, пространства Фока и т. д.
можно далее проводить точно так же, как это было сделано в
случае пространства Минковского в разд. 2.1. Но теперь в фор-
формализме возникает внутренняя неоднозначность [221]. В про-
пространстве Минковского существует естественный набор мод, а
именно B.11), который связан с естественной ортогональной си-
системой координат (t, х, у, z). В свою очередь эти координаты ас-
ассоциируются с группой Пуанкаре, оставляющей инвариантным
элемент длины в пространстве Минковского. В частности, вектор
d/dt является вектором Киллинга пространства Минковского, ор-
ортогональным пространственноподобным гиперповерхностям t =
= const, а моды B.11) представляют собой собственные функ-
функции этого вектора Киллинга с собственными значениями — tea
при со > 0 (положительно-частотные решения). Вакуум инва-
инвариантен относительно группы Пуанкаре.
В искривленном пространстве-времени группа Пуанкаре уже
не является группой симметрии (см. в этой связи [469]). Дей-
Действительно, в общем случае векторы Киллинга, с помощью кото-
которых можно было бы определить положительно-частотные реше-
решения, вообще не существуют. Для некоторых специальных клас-
классов пространств могут существовать симметрии относительно ог-
ограниченных преобразований, например вращений, трансляций
или группы де Ситтера» В этих случаях могут быть выбраны
«естественные» координаты, ассоциируемые с векторами Кил-
Киллинга, аналогичные галилеевым координатам в пространстве
Минковского. Но даже в том случае, когда такие координаты су-
существуют, они не играют в квантовой теории поля той решающей
роли, которую играют в пространстве Минковского. В общем же
случае такие привилегированные системы координат отсут-
отсутствуют, и естественного разложения поля ф, основанного на раз-
разделении переменных в волновом уравнении C.26) в таких коор-
координатах, не существует. В самом деле, основная идея общей тео-
теории относительности заключеиа в принципе общей ковариантно-
ковариантности, означающем, что выбор координатных систем не является
физически существенным.
Рассмотрим поэтому другой ортонормированный набор реше-
решений п,(х). Поле ф может быть также разложено по этому на-
набору:
(х) + а]щ (х)]- C.32)
Это разложение ф определяет новое состояние вакуума |0>:
S,|0> = 0, V/. C.33)
и новое пространство Фока

52 Глава 3
Так как оба набора решений полны, новые моды щ могут
быть выражены через старые:
«/ = Z (<*/*«' + Р//И*)- C.34)
И наоборот,
"i = Z (<*/*«/ — Ругй/). C.35)
Эти соотношения известны как преобразования Боголюбова [55].
Матричные элементы осу, Р;/ называют коэффициентами Боголю-
Боголюбова; с помощью C.34) и C.29) они могут быть представлены
в виде
щ! = {щ,и!), р(/ = —(й,, и?). C.36)
Приравнивая разложения C.30) и C.32), а также используя
C.34), C.35) и условие ортонормированности решений C.29),
получаем
at = Z (а,/й/ + Р;,а;), C.37)
Коэффициенты Боголюбова обладают следующими свойствами:
О. C.40)
Из соотношения C.37) немедленно следует, что два фоков-
ских пространства, основанные на выборе разных наборов мод
щ и п/, являются различными до тех пор, пока Р/* # 0. Напри-
Например, состояние |0> не уничтожается оператором ас.
а«|0>=Ер;/|Т,)#0 C.41)
в противоположность C.33). В действительности математическое
ожидание оператора Ni = a*ai числа частиц моды щ в состоя-
состоянии |0> есть
<0|ЛМ0>=Е|Р/г|2. C.42)
т. е. можно сказать, что вакуум мод п/ содержит.?] | р/г |2 ча-
частиц моды щ.
Заметим, что если ы; — положительно-частотные решения по
отношению к некоторому времениподобному векторному полю

Квантовая теория поля в искривленном пространстве-времени 53
Киллинга |, которые удовлетворяют уравнению
?хщ = — юи,, ш > 0 C.43)
(для сравнения заметим, что B.8) можно переписать в виде
3?дМъ = —ноык), и б* являются линейными комбинациями толь-
только функций Ы/ (не включая Ыу), т. е. содержат лишь положитель-
положительные частоты по отношению к |, то коэффициенты p/fe = 0. В этом
случае а*]0> = 0 и одновременно а/|0> = 0. Следовательно, два
набора мод ы; и пи имеют общее вакуумное состояние. Если не-
некоторые из коэффициентов 0/* Ф О, то пи будет содержать смесь
положительно-частотных (и,-) и отрицательно-частотных (ы*) ре-
решений и частицы будут присутствовать.
В более общем случае фоковское пространство, основанное
на |0>, может быть связано с пространством, построенным на
|0> с помощью соотношений, выражающих полноту (Ьоковского
базиса:
00
вЕтг Z М/Л/.
*=о /l...,k
Например, в используемых обозначениях имеем
где символ 1/, повторяется xnt раз. Матричный элемент
A/,, Т/2, ..., \,k11ni], 2щг, ...) можно понимать как амплитуду
перехода или элемент S-матрицы для _ перехода из состояния
!'««,» 2«(j, •-.) в состояние IT/,, \,2, ..., T/fc). Эти матричные
элементы S-матрицы могут быть выражены через коэффициенты
Боголюбова. В частности, для амплитуд перехода из вакуума
в многочастичные состояния находим [156]
;*/2<o|0>
0
г*/2<0|0>
0
Z лР]р2...
0
Z~l ' 0,f>2 ' * '
P
AP*-.Pft
k четное»
k нечетное,
C.45)
k четное,
k нечетное,
C.46)

54 Глава 3
где р обозначает все различные перестановки индексов {/i ... jk}
и
^-?fw- C-47)
Амплитуды перехода между многочастичными состояниями при-
приведены в работе [48]. Рассмотрение амплитуд перехода ва-
вакуум — вакуум мы откладываем до гл. 6.
Помимо векторов состояний частиц и коэффициентов Бого-
Боголюбова, необходимо построить функции Грина, введенные в
разд. 2.7. Будут использоваться те же определения и обозначе-
обозначения, что и в разд. 2.7, с той разницей, что поле ф (х) теперь удо-
удовлетворяет волновому уравнению в искривленном пространстве-
времени C.26), и необходимо соблюдать осторожность в выборе
вакуумного состояния H>. Обобщение уравнений для функций
Грина B.73) —B.75) на случай искривленного пространства осу-
осуществляется с помощью C.26). Например, для фейнмановского
пропагатора
ЮР(х, х') = (О\Т(ф(х) f (x')) |0> C.48)
находим
[?* + m2 + IR (х)] GF (x, х') = -[-g (*)Г'А 6п (х - х') C.49)
вместо B.74). Важно подчеркнуть, что само уравнение C.419)
не определяет вакуумного состояния |0>, фигурирующего в
C.48)', и не обеспечивает характера решения, как связанного
именно с хронологически упорядоченным произведением полей.
Для фиксации состояния вакуума и введения хронологического
упорядочения на решения уравнения C.49) необходимо нало-
наложить граничные условия. В пространстве Минковского эти гра-
граничные условия выражаются в форме выбора контура интегри-
интегрирования в B.76). В искривленном пространстве выбор гранич-
граничных условий не является столь же простой задачей и зависит от
глобальных свойств пространства в каждом конкретном случае.
(Например, излучение, являющееся «запаздывающим» вблизи
источника, перестает быть таковым на некотором расстоянии от
него вследствие обратного рассеяния на кривизне пространства-
времени.) Детальное обсуждение распространения волн в ис-
искривленном пространстве-времени и свойств функций Грина мо-
можно найти, например, в работах [158, 216]. ;
3.3. Смысл понятия частиц: детекторы частиц
Возникает естественный вопрос: какой набор мод обеспечи-
обеспечивает «наилучшее» описание физического вакуума, т. е. наиболее
точно соответствует нашему обычному представлению об отсут-
отсутствии частиц? Оказывается, что в такой постановке на этот во-

Квантовая теория поля в искривленном пространстве-времени 55
прос ответить нельзя, если не указать конкретный процесс кван-
квантового измерения, используемый для обнаружения квантов.
В частности, состояние движения измерительного прибора влияет
на то, наблюдаются или нет частицы. Например, свободно па-
падающий детектор не всегда будет обнаруживать ту же плотность
частиц, что и неинерциальный, ускоренный детектор. В действи-
действительности это верно уже в пространстве Минковского: ускорен-
ускоренный детектор будет регистрировать кванты даже в вакуумном
состоянии, определенном условием B.19).
Особенностью пространства Минковского является не то, что
для него существует единственное состояние вакуума (это не-
неверно), а то, что обычное вакуумное состояние, определяемое мо-
модами B.11), является истинным вакуумом для всех инерциаль-
инерциальных наблюдателей во всем пространстве-времени. Причина со-
состоит в том, что вакуум, заданный условием B.19), инвариантен
относительно группы Пуанкаре и таким же свойством обладает
множество инерциальных наблюдателей в пространстве Минков-
Минковского.
Одним из уроков, который удалось извлечь в результате раз-
развития квантовой теории поля в искривленном пространстве, было
осознание неуниверсальности понятия частиц. Частицы могут ре-
регистрироваться одними детекторами и не восприниматься дру-
другими, так что суждение о них в известной степени зависит от на-
наблюдателя. Можно, конечно, доказывать существование частиц,
но если при этом не уточнять характер движения детектора, то
от этого утверждения мало пользы даже в случае пространства
Минковского.
Отчасти причина расплывчатости понятия частиц состоит в
его глобальном характере. Полевые моды определены во всем
пространстве-времени (или по крайней мере в широкой обла-
области), поэтому разложение поля по модам, соответствующее вы-
выбранному наблюдателю, а значит, и оператор числа частиц, опи-
описывающий отклик детектора частиц, зависит от всей истории
этого наблюдателя в прошлом. Для более объективного отраже-
отражения состояния поля следует строить величины, определяемые ло-
локально, такие, как <if|Т^(х) |г|з>, принимающие определенное
значение в точке х пространства-времени. Тензор энергии-им-
энергии-импульса является объективной характеристикой в том смысле, что
для заданного состояния |г|л> результаты, даваемые различными
измерительными приборами, могут быть связаны между собой с
помощью обычных правил преобразования тензоров. Например,
есл"и <я|)| r^v(х) |я|)>= 0 для одного наблюдателя, то эта вели-
величина будет равной нулю и для всех остальных наблюдателей.
В противоположность этому один наблюдатель может не детек-
детектировать частиц, в то время как другой будет обнаруживать их
присутствие.

56 Глава 3
Во многих интересующих нас задачах пространство-время мо-
может считаться асимптотически плоским (пространством Минков-
ского) в отдаленном прошлом и (или) будущем. В этих условиях
выбор «естественного» вакуума Минковского, определенного
соотношением B.19), имеет ясный физический смысл: в этом
состоянии частицы отсутствуют для всех инерциальных наблюда-
наблюдателей в асимптотической области — что и лежит в основе обще-
общепринятого представления о вакууме. Отдаленное прошлое и бу-
будущее мы будем называть in- и out-областями соответственно.
Эта терминология заимствована из квантовой теории поля в про-
пространстве Минковского, где предполагается, что при /-»-±оо
взаимодействие полей исчезает. Здесь аналогично предполагает-
предполагается, что in- и out-области пространства-времени допускают есте-
естественное определение состояний частиц и выделенного вакуум-
вакуумного состояния. Это может быть либо пространство Минков-
Минковского, либо другое пространство-время, обладающее высокой
симметрией, такое, как статическая вселенная Эйнштейна. Ответ
на вопрос, имеет, ли данное пространство-время подходящие in-
и out-области, зависит и от того, какое именно квантованное
поле нас интересует. В случае безмассовых полей с конформной
связью этому требованию удовлетворяет конформно-плоское про-
пространство-время, хотя оно и не является статическим (см. § 3.7).
Поскольку используется гейзенберговская картина, то если
мы выбираем состояние квантованного поля в in-области в ка-
качестве вакуумного, это состояние остается неизменным в течение
всей последующей эволюции. Однако, как будет показано ниже,
в последующие моменты времени, вне in-области, свободно па-
падающий детектор частиц может все еще регистрировать частицы
в этом вакуумном состоянии. В частности, если имеется также
out-область, то in-вакуум может не совпадать с out-вакуумом.
В этом случае естественный, например инерциальный, наблюда-
наблюдатель в out-области будет обнаруживать присутствие частиц.
Поэтому мы можем сказать, что частицы были «рождены» за-
зависящим от времени внешним гравитационным полем. Такое
описание особенно полезно, если in- и out-области представляют
собой пространство Минковского, так что все инерциальные на-
наблюдатели в out-области обнаруживают присутствие частиц.
Аналогичные процессы рождения частиц внешними электромаг-
электромагнитными полями хорошо известны (см., например, [245], где
имеются ссылки на более ранние работы). Возможность рожде-
рождения частиц из-за кривизны пространства-времени обсуждалась
более сорока лет назад Шредингером [421]; из других ранних
работ отметим работы де Витта [152], Такахаши и Умэдзавы
1449] и Имамуры [308]. Впервые строгая трактовка рождения
частиц внешним гравитационным полем была дана Паркером
[379—381] и Секслем и Урбантке [431, 432].

Квантовая теория поля в искривленном пространстве-времени 57
Для иллюстрации этих сообоажений рассмотрим модель де-
детектора частиц, предложенную Унру [468] и де Виттом [157].
Детектор представляет собой идеализированную точечную ча-
частицу с внутренними уровнями энергии Е, связанную монополь-
монопольным взаимодействием со скалярным полем ф. Будем рассматри-
рассматривать случай четырехмерного пространства Минковского.
Предположим, что детектор частиц движется вдоль мировой
линии ^(т), где т — собственное время детектора. Взаимодей-
Взаимодействие детектор — поле описывается лагранжианом ст(х)ф[х(х)],
где с — малая константа связи, am — оператор монопольного
момента детектора. Предположим, что поле находится в вакуум-
вакуумном состоянии |0м>, заданном условием B.19), где индекс М
обозначает вакуум Минковского. В общем случае произвольной
траектории движения детектор не будет оставаться в своем ос-
основном состоянии ?0, а перейдет в возбужденное состояние
Е > Ео, в то время как поле перейдет в возбужденное состояние
|i|)>. При достаточно малом с амплитуда этого перехода будет
определяться первым порядком теории возмущений (см. § 9.1)
в виде
ic(E, 1|>| \ m{xL>[x(x)]dx\0M, ?„>
(Пределы интегрирования можно ограничить и меньшим интер-
интервалом времени, предполагая, что взаимодействие детектора с по-
полем адиабатически выключается вне этого интервала.)
С помощью уравнения, описывающего временную эволюцию
т(х):
где Н0\Е) = Е\Е}, амплитуда перехода факторизуется, прини-
принимая вид
/с (Е | т @) | ?0) \ ei <*-'•> * <ф | ф (х) \ 0M) dr. C.50)
— оо
Если поле ф разложено по стандартным плосковолновым мо-
модам B.17), то в этом порядке теории возмущений могут проис-
происходить переходы только в состояние | ¦»(>) = | Ц), содержащее один
кцант частоты со = (|к|2 + /и2I'2 для некоторого к. Тогда (в не-
непрерывной нормировке B.11))
C.51)

58 Глава 3
Теперь следует принять во внимание, что х в C.51) не яв-
является независимой переменной, но определяется траекторией де-
детектора. Предположим, что детектор движется по инерции, т. е.
х = х0 + v/ = х0 + vt A - о2)"''2. C-52)
где х0 = const, v = const, |v| < 1; тогда интеграл в C.50) (при
Ф =1 Ik) равен
' (?-?о)Ут(a-k-v) A-o!)"VsdT =
= Dясо)-1/2е-'к'Хоб (Е - Ео + (со - к • v) (I - v2)''1') C.53)
Но, поскольку k-v^|k||v|<;co и Е > Ео, аргумент б-функции
всегда положителен и амплитуда перехода равна нулю. Пере-
Переход запрещен из соображений сохранения энергии, что является
прямым следствием пуанкаре-инвариантности.
Если, с другой стороны, вместо C.52) выбрана более слож-
сложная траектория, то интеграл C.50) не сводится к б-функции, и
результат отличен от нуля. В таком случае представляет инте-
интерес рассчитать вероятность перехода во все возможные состоя-
состояния \Е) и г|з, которая получится, если квадрат модуля C.50)
просуммировать по всем ? и по полному набору г|з, что дает
с2 ? I (Е \т @) | Ео) fT(E- EQ), C.54)
где
&-{Е)= \dx J dx'e-^H-OQ+ixix), дг(т')). C.55)
— 00 —ОО
Функция отклика детектора &~(Е) не зависит от деталей его
устройства и определяется положительно-частотной вайтманов-
ской функцией Грина G+, введенной в B.68). Она описывает
море «частиц», которые эффективно действуют на детектор бла-
благодаря его движению. Остающийся множитель в C.54) опре-
определяет избирательность детектора и, очевидно, зависит от его
внутренней структуры.
Для тех траекторий движения детектора в пространстве
Минковского, для которых
О+(дг(т),д:(т0) = я(Ат)> C.56)
Лт^т-т' C.57)
(g—некоторая функция), система инвариантна относительно
временных трансляций в системе отсчета детектора (т->-т-|-
4- const). Это означает, что детектор находится в равновесии с

Квантовая теория поля в искривленном пространстве-времени 59
полем <j> и число частиц, поглощаемых им в единицу времени т,
постоянно. Если скорость поглощения отлична от нуля, то пол-
полная вероятность перехода бесконечна, поскольку амплитуда
перехода C.54) подсчитывается для всего бесконечного интер-
интервала времени. Это непосредственно видно из C.55), так как
функция Вайтмана зависит только от разности х — т' и двойной
интеграл сводится к произведению фурье-образа двухточечной
функции на бесконечный интеграл по времени.
Такая ситуация часто возникает в квантовой теории, и здесь
можно использовать адиабатическое выключение взаимодей-
взаимодействия при т-»-±оо либо вместо этого рассматривать вероятность
перехода в единицу собственного времени
00
с2 ? | (Е \ m @) | ?0> ? \ d (Ат) е~* <*-*»> *Ю+ (Лт). C.58)
Е -оо
Для упрощения дальнейших примеров ограничимся случаем
безмассового скалярного поля ф. Тогда положительно-частотная
функция Вайтмана может быть найдена из B.76) с использо-
использованием соответствующего контура, показанного на рис. 3:
D+ (х, х') = - 1/4л2 [(t — t' — itJ -1 х - х' |2], C.59)
где малую мнимую добавку /е, е > 0, можно интерпретировать,
используя соотношение
\/(х Т /е) = (Р/х) ± ind (x). C.60)
В случае инерциального детектора C.52) равенство C.59) при-
принимает вид
2ieJ C.61)
(где положительный множитель A—vz)~'b включен в е) и ин-
интеграл в C.58) может быть вычислен как контурный интеграл
с помощью замыкания контура бесконечно удаленной полу-
полуокружностью в нижней полуплоскости переменной Лт, так как
Е — ?0 > 0. Поскольку полюс подынтегрального выражения
Ат = is находится в верхней полуплоскости, интеграл равен
нулю, как и следовало ожидать. Частицы не регистрируются.
В качестве другого примера такого состояния равновесия
рассмотрим детектор, движущийся вдоль гиперболической тра-
траектории в плоскости (t, z):
4 х = у = 0, z = (t2 + a2)'1', a = const, . C.62)
с постоянным ускорением а~1 в собственной системе отсчета
(см., например, [405]). Собственное время детектора т связано
с t соотношением
/ = ash (т/а), C.63)

60 Глава 3
поэтому из C.59) получаем
C-64)
где некоторая положительная функция т, V включена в е. Ис-
Используя соотношение
оо
__±_. = я-2 ? (x — k)~'\ C.65)
&--00
перепишем C.64) в виде
оо
D+(At) = — Dit2)"' ? (Лт — 2me + 2niak)~2. C.66)
^ ft™ —ОО
Подставляя это выражение в C.58) и выполняя преобразование
Фурье с помощью контурного интегрирования,, находим
il V (? - ?о) I (? I m @) | ?р) \2 ,_ fi7
Е
Появление планковского множителя [е2я(?-Е»'а — 1]~' в
C.67) указывает на то, что равновесие между ускоренным детек-
детектором и полем ф в состоянии |0м> имеет такой же характер, как
и для инерциального детектора, помещенного в термостат, за-
заполненный тепловым излучением при температуре
Т = l/2nakB = ускорение/2л;^в, C.68)
где fiB — постоянная Больцмана.
К такому же заключению можно прийти и на основании рас-
рассмотрения тепловой функции Грина для инерциального детек-
детектора [169]. Выше рассмотрена соответствующая связь для G1^
B.111) (аналогичный вывод для Gg более сложен). Подстановка
х = х'= 0, t = x, t'= %' в B.111) и использование B.79) для
безмассового поля приводит к выражению
X (Ат + ikfif2, C.69)
где особенность понимается в смысле главного значения.
Сравним этот результат с функцией ?>A) для ускоренного
наблюдателя, движущегося в квантованном поле, находящемся
в состоянии вакуума Минковского. Она может быть получена
из D+ с помощью соотношения B.67) в форме
/)A) (Ат) = D+ (At) + D+ (— At).
Применяя это соотношение в C.66) с учетом C.60), находим

Квантовая теория поля в искривленном пространстве-времени 61
где р = 1/keT, a T определено формулой C.68). Следовательно,
вакуумная функция Грина для детектора, движущегося с по-
постоянным ускорением, совпадает с тепловой функцией Грина
для инерциально движущегося детектора.
Что это означает физически? Часто утверждают, что равно-
равномерно ускоренный наблюдатель будет «видеть» тепловое излу-
излучение [128, 468], несмотря на то что поле ф находится в вакуум-
вакуумном состоянии |0м> и инерциальные наблюдатели не регистри-
регистрируют никаких частиц. Конечно, ускоренный детектор поглощает
энергию и переходит в возбужденные состояния так же, как
если бы он находился в равновесии с тепловым излучением.
Однако, как было установлено в § 2.4, <0м|: Т^ : |0м> = 0. Пе-
Переход к ускоренно движущейся системе отсчета с помощью
обычного закона преобразования тензоров также дает
(®м\ '• ^v • j0а*^ === 0, поэтому как ускоренный, так и инерциаль-
ный наблюдатели согласятся с тем, что тензор энергии-импульса
поля ф равен нулю. Это привело к употреблению терминов
«квази» или «фиктивных» частиц для квантов, возбуждающих
ускоренно движущийся детектор, но в действительности это яв-
явление скорее указывает на то, что традиционное представление
о квантовых частицах применимо лишь при весьма сильных огра-
ограничениях.
Если состояние |0м> не может служить источником энергии,
необходимой для возбуждения детектора, как можно примирить
его возбуждение с законом сохранения энергии? Более того, пе-
переход,, который увеличивает энергию детектора от Ео до Е, со-
сопровождается появлением кванта поля ^(|0м)-*| Ik)). Это зна-
значит, что и детектор, и поле одновременно приобретают энергию.
Для объяснения этого кажущегося противоречия следует рас-
рассмотреть воздействие ускорения на сам детектор. Когда детектор
ускоряется, его взаимодействие с полем ф вызывает излучение
квантов, которые создают силу реакции, направленную против
ускоряющей силы. Работа, производимая внешней силой на
преодоление этого сопротивления, обеспечивает недостающую
энергию, которая передается полю посредством испускаемых
детектором квантов, а также детектору, одновременно испыты-
испытывающему переходы вверх. В целом же, если интересоваться со-
состоянием детектора, суммарным эффектом является поглощение
квантов, распределенных по тепловому закону.
Возвращаясь к проблеме определения вакуумного состояния
и фоковского пространства, следует задуматься, существуют ли
доводы в пользу того, что такие определения для ускоренных
систем могут претендовать на ту же роль, что и традиционные
построения в пространстве Минковского? В ответ можно было
бы возразить, что связывать эти понятия с ускоренными систе-
системами неправомерно вбиду того выделенного положения, которое

62 Глава 3
занимают инерциальные наблюдатели в большинстве физи-
физических теорий. Следовательно, что касается пространства Мин-
ковского, то вакуумное состояние |0м> является сильнейшим
претендентом на роль «правильного» или «физического» ва-
вакуума— наблюдения же из ускоренных систем отсчета «иска-
«искажены» вследствие неравномерного движения последних. Труд-
Трудность в том, что при наличии гравитационных полей инерциаль-
инерциальные наблюдатели становятся свободно падающими, и, вообще
говоря, не существует двух различных свободно падающих
наблюдателей, для которых вакуум был бы одним и тем же.
Лишь в исключительных случаях пространств с высокой сте-
степенью симметрии существует некоторое множество траекторий
детекторов, которые не регистрируют частиц, причем они могут
и не являться свободно падающими (например, ускоренные
наблюдатели, находящиеся в стационарном режиме вблизи сфе-
сферической звезды, см. разд. 8.4).
Нетрудно обобщить формулу, описывающую показания де-
детектора, на случай искривленного пространства-времени, заме-
заменив G+ соответствующей величиной для искривленного про-
пространства (см. с. 54), а вакуумное состояние |0м> — некоторым
вакуумом более общего вида. Примеры будут даны в разд. 3.6
и 3.7.
Интересно также рассмотреть случай, когда квантовое поле
находится не в вакуумном, а в многочастичном состоянии B.22)
(или аналогичном состоянии в искривленном пространстве).
В этом случае G+ следует заменить на
= G+ (х, х') + S lnuk.(х)ul {х') + S lnuL(x)ик.{х'). C.70)
* ' ' t ' '
При переходе к непрерывному спектру правая часть C.70)
принимает вид
G+(x, x') + \dn-lknkuk(x)uUx')+\dn-lknbui(x)uk(x'), C.71)
где пк — плотность квантов в ^-пространстве.
Для инерциального детектора, движущегося вдоль траекто-
траектории C.52) в n-мерном пространстве Минковского, лишь послед-
последний член в C.71) дает вклад в функцию отклика -детектора
C.55):
X ехр [i (со - к • v) Дт A — v2)-'1'] «к, C.72)

Квантовая теория поля в искривленном пространстве-времени 63
где Т — полное время, в течение которого детектор остается
включенным. Если v = 0, то интегрирование по Ат дает
2л8(Е — ш). Если к тому же кванты распределены изотропно, то
п\. = Пк и интегрирование по d"~1k приводит к выражению
дг (Е) __ 22-V3-" 2 ауя-з)/2
Т — г ((«— 1)/2) ^ ' n(E'-
При подстановке C.73) в C.54) следует обратить внимание на
функцию Э(? — Ео— т), которая показывает, что поглощение
детектором единичного кванта массы т не может происходить
до тех пор, пока расстояние между уровнями энергии детектора
Е — Ео не станет по крайней мере равным энергии покоя ча-
частицы т. Из C.73) следует также, что скорость квантовых пе-
переходов, испытываемых детектором в море квантов, пропорцио-
пропорциональна числу квантов интересующей нас моды, чего и можно
было ожидать на основании физических соображений. Но зави-
зависимость от энергии сложным образом связана со спектром
частиц и дополнительно усложняется из-за избирательности де-
детектора (энергетической зависимости матричного элемента в
C.54)).
При v=7^=0 сначала следует проинтегрировать в C.72) по
углам. Затем интегрирование по т дает разность двух Э-функций
(а не б-функцию), ограничивающую область интегрирования по
dk. В четырехмерном безмассовом случае получаем
где ?± = ?[A±и)/A:Р»)]''1. Это выражение легко истолко-
истолковать физически. При движении детектора в изотропном поле
излучения некоторый переход с энергией Е — Ео будет отвечать
квантам не одной моды, а целой области, начиная от испыты-
испытывающих голубое смещение низкочастотных квантов, движущихся
в направлении вперед, до испытывающих красное смещение
квантов более высокой частоты, движущихся в направлении
назад. В величинах [A + v)/{l — v)] ''• и [A — v)/(l + и)]1/*
нетрудно узнать обычные доплеровские множители голубого и
красного смещения соответственно, и, следовательно, функция
отклика пропорциональна полному числу квантов в области
¦резонансных частот в пределах доплеровского уширения.
4 Учитывая неопределенность представления о частицах в бо-
более общих случаях, следует выяснить, какой смысл можно при-
придать коэффициентам Боголюбова аир, введенным в предыду-
предыдущей главе, в частности, что подразумевается под математиче-
математическим ожиданием числа квантов моды i, даваемым выражением
C.42).

64 Глава 3
Вообще говоря, не существует простого соотношения между
> и числом частиц, измеряемым некоторым детектором, даже
свободно падающим. Однако в одном частном случае такое со-
соотношение имеется. Рассмотрим пространство-время, асимптоти-
асимптотически статическое в отдаленном прошлом и будущем, и построим
вакуумное состояние в in-области, связывая его со стандарт-
стандартными плоско-волновыми модами типа B.11). Это обычное фи-
физическое состояние без частиц, и инерциальный наблюдатель,
конечно, не будет обнаруживать кванты в in-области.
Конечно, если пространство-время является статическим
лишь в асимптотических областях, верхние пределы в интегра-
интегралах C.55), строго говоря, уже нельзя считать бесконечными.
Мы делаем предположение, что монопольное взаимодействие де-
детектора адиабатически выключается до того, как детектор вхо-
входит в нестатическую область. Подобным же образом в out-об-
out-области детектор будет адиабатически включаться после пре-
прекращения движений пространства-времени. Это позволяет нам
по-прежнему использовать в качестве пределов ±оо, как если
бы пространство-время было всюду статическим. Как уже отме-
отмечалось, предположения такого рода — ограничение взаимодей-
взаимодействия конечным временем с помощью адиабатического выклю-
выключения— обычны для квантовой теории, и до тех пор, пока время
взаимодействия много больше, чем (Е — Eq)~\ возбуждение
детектора самим процессом выключения можно считать прене-
пренебрежимо малым.
В out-области in-моды, вообще говоря, уже не будут пло-
плоскими волнами определенной частоты типа B.11). Что же тогда
будет регистрировать детектор в out-области, если поле нахо-
находится в состоянии in-вакуума? Ясно, что инерциальный детектор
не будет обнаруживать частиц, если поле находится в состоянии
out-вакуума, ассоциируемого с модами вида B.11) в out-об-
out-области. Однако он будет регистрировать присутствие квантов/
если поле находится в состоянии in-вакуума. .
Для того чтобы выяснить, что будет регистрировать детек-
детектор, нужно проанализировать (в связи с равенством C.55)) функ-
функцию Вайтмана G+ (построенную с использованием in-вакуума)
в out-области. Как правило, она оказывается сложной функцией
пространственных переменных х, х'. Однако в простом случае
однородной вселенной, такой, как асимптотически статическая
пространственно-плоская модель Робертсона — Уокера, функция.
G+ будет инвариантна относительно пространственных трансля-
трансляций и вращений. Ограничим обсуждение этим простым случаем.
Если in-моды обозначить через м'кп, а in-вакуум — через
|0, in>, то
GUx, *') = <in, 0\ф(х)ф(х')\0, in) = \и?(х)и?(х')сГ-1к, C-75)

Квантовая теория Поля в иСКривЛённбм ПространСтбе-времени 65
где обе точки х и х' находятся в out-области. Обозначая out-
моды (т. е. моды, которые редуцируются к стандартным плоским
волнам B.11) в out-области) через «?"*, можно использовать
C.34) для разложения и'кп по функциям w?ut. Благодаря про-
пространственной однородности оба набора мод «?"' и нкп будут
оставаться плоскими волнами (т. е. ~etkx) всюду, хотя и с дру-
другой зависимостью от времени. Поэтому скалярные произведения
(«kn, «?"') и (икП> ик"'*) будут пропорциональны бкк' и б_кк' соот-
соответственно (см. C.28)). Из C.36) следует, что преобразование
Боголюбова будет диагональным и изотропным, т. е. имеет вид
акк' = а*бкк', C.76)
Ркк' = М-кк" C-77)
где k = |k|, так что
«к1 (*) = <rf' (х) + М-к* (x). C.78)
Подстановка C.78) в C.75) дает
G+ =- \ da~'k [ | а* |2 «Г (х) «
Г
+ Pfta>°_T (*) uf (x') + | Рk |2 u°X (x) if% («О]- C.79)
Анализ выражения C.79) показывает, что, поскольку «к имеет
зависимость видае'кх, функция G+ зависит от координат только
через разность х — х', т. е., как и ожидалось, инвариантна отно-
относительно пространственных трансляций. Отсюда сразу следует,
что, если х и х' ограничены инерциальными траекториями де-
детектора C.52), зависимость G+ от координат исчезает. Поэтому
отклик детектора C.55) не зависит от его положения, чего и
следовало ожидать из соображений однородности.
В out-области «Ц^-моды представляют собой обычные пло-
плоские волны, поэтому интегрирование по т и т' в C.55) выпол-
выполняется сразу и дает б-функции. Единственный неисчезающий
вклад дает последний член в C.79).
Функция отклика детектора В единицу времени принимает
вид
где Для простоты мы ограничились случаем скорости детектора
V == 0 и выбрали масштабный множитель Робертсона — Уокера
в out-области равным единице. Эта функция отклика не
3 Зак, Ш

66 thaea 3
отличается от функции отклика детектора в изотропном море
квантов с |р*|2 частицами моды k в статическом пространстве-
времени, что устанавливается путем сравнения C.80) с C.73).
Простой вид этого результата делает вполне убедительной
интерпретацию |Р*|2 как числа частиц моды k, рождаемых в
ходе космологической эволюции. Конечно, использование детек-
детектора не единственный критерий, с помощью которого устанавли-
устанавливается физическая разумность этой интерпретации. Вычисление
<?Vv> также выявляет в out-области наличие энергии, соответ-
соответствующей |р*|2 частицам моды k в статическом пространстве-
времени.
3.4. Космологическое рождение частиц:
простой пример
Для того чтобы проследить, как практически может происхо-
происходить рождение частиц в пространстве-времени, являющемся
пространством Минковского в in и out-областях, рассмотрим
простой пример двумерной вселенной Робертсона — Уокера с
элементом длины
ds2 = df-~a2(t)dx2, C.81)
пространственные сечения которой однородно расширяются
(или сжимаются) в соответствии с поведением единственной
скалярной функции a(t). Определяя новый временной параметр
(так называемое конформное время) соотношением dr\ = dt/a,
так что
t tl
f~\a (т)') dr\', C.82)
Можно переписать C.81) в виде
ds2 = а2 (т)) (drf — dx2) = С (r\) (dt\2 - dx2), C.83)
где введен «конформный масштабный множитель» C(t])= а2(ц).
В этой форме элемент длины имеет явно конформно-плоский
вид (см. разд. 3.1).
Предположим, что
С(ц) == А + В th pri, А, В, р== const; C.84)
тогда, в отдаленном прошлом и будущем пространство-время
становится плоским, поскольку
С{ц)->А±В, т)^±со
(рис. ?). Рассмотрим рождение массивных минимально сёязЯн-
ных скалярных частиц в этом пространстве-времени (это было
впервые сделано Бернардом и Дунканом [34]). Заметим, что

Квантовая теория поля в искривленном пространстве-времени 67
А+В
in-области
out- область
А-В
Рис. 7. Конформный масштабный множитель С(г\) = А + В th рц описывает
асимптотически статическую вселенную, претерпевающую гладкое расширение
в промежуточной области.
в пространстве двух измерений минимальная и конформная
связи эквивалентны (см. C.27)).
Поскольку С(г\) не зависит от пространственной переменной
х, пространственные трансляции являются преобразованиями
симметрии; поэтому для скалярных мод в C.30) переменные
разделяются:
«ft \ Ь X) —¦ \Zti\j с Л? \Ц)* (o.oOJ
Подставляя C.85) вместо Ф в уравнение C.26) для скалярного
поля с ? = 0 и метрикой C.83), получаем обыкновенное диффе-
дифференциальное уравнение для %к{ц)'
C.86)
X* (Л) + (k2 + С (ц) m2) xj (ц) = 0.
Это уравнение можно решить с помощью гипергеометрических
функций. Нормированные моды, которые ведут себя как поло-
положительно-частотные моды B.11) пространства Минковского в
отдаленном прошлом (i\, t^>—оо), имеют вид
М1ЛП (х\, х) = Dя(от) ~Vl exp {ikx — /(o+Ti — (/©_/р) In [2 ch (p, ti)]} X
+ (/co_/p), гсо_/р; 1 — (icoin/p); - A + thpii)) >
где
Y . C.88)
С другой стороны, моды, которые ведут себя как положи-
положительно-частотные в пространстве Минковского при r\-*--\-odt
3*

68 Глава 3
оказываются равными
и*1' (Л, *) = Dя»Out)~l/j exp {ikx - to+л - (/о>_/р) in [2 ch (рт))]} X
XзР\ (l + (to-/p), fto-/p; 1 + (icoout/p);y(l -'
C.89)
Очевидно, что ulg и «Jut не совпадают; это означает, что коэф-
коэффициент Боголюбова р в C.34) должен быть не равным нулю.
Чтобы убедиться в этом явно, можно воспользоваться свойст-
свойствами гипергеометрических функций при линейных преобразо-
преобразованиях (см., например, [2], A5.3.6), A5.3.3)), чтобы выразить
ttjf через u°kat (ср. C.78)) следующим образом:
и? (Л. х) = aft«°ut (т), х) + р^ы^' (т), д:), C.90)
где
(- «co+/p) Г A -
Сравнение C.90) с C.34) приводит к выражениям для бо-
голюбовских коэффициентов (ср. C.76), C.77))
Чк' = «A*- Pftft'=P*s-*ft» C.93)
Из C.91) и C,92) находим
sh2 (яш+/р)
sh(ncuin/p)sh(ncuout/p) '
sh»(TO_/p)
Sh (ЯШ^р) Sh (ЯС0ои4/р) '
откуда немедленно следует (см. C.39)) соотношение норми-
нормировки
|a*P-IP*P-l- C.96)
Рассмотрим случай, когда квантованное поле находится в со-
состоянии |0, in>, определяемом C.33) в терминах мод и'ла (отож-
(отождествляемых с модами пк, разд. 3.2). В отдаленном прошлом,
когда пространство-время было плоским, все инерциальные де-
детекторы указывали на отсутствие частиц, так что неускоренные
наблюдатели должны были идентифицировать это квантовое
состояние как физический вакуум.

Квантовая теория поля в искривленном пространстве-времени 69
В out-области (т)-»-+оо) пространство-время также плоское,
а квантованное поле также находится в состоянии |0, in> (ис-
(используем гейзенберговскую картину движения), но в противо-
противоположность ситуации в in-области состояние |0, in> не будет вос-
восприниматься инерциальными наблюдателями в out-области как
физический вакуум; эта роль принадлежит состоянию |0, outX
определенному в терминах мод u°kat. Действительно, неускорен-
неускоренные детекторы частиц в этой области будут обнаруживать при-
присутствие квантов (см. C.80)). Ожидаемое число квантов моды k
дается формулой C.95). Поэтому такую эволюцию квантовой
системы можно назвать рождением частиц моды k вследствие
космологического расширения.
3.5. Адиабатический вакуум
Результаты предыдущего раздела нетрудно истолковать в
более наглядных физических терминах. В безмассовом пределе
ю_->-0 правая часть C.95) обращается в нуль: рождения частиц
нет. Это пример конформно тривиальной ситуации — конформна-
инвариантного поля в пространстве-времени, конформном про-
пространству Минковского (см. разд. 3.1). Рождение частиц про*-
исходит лишь тогда, когда конформная симметрия нарушена
наличием массы, задающей в теории масштаб длины. Процесс
рождения можно рассматривать как результат воздействия рас-
расширения пространства-времени на квантованное поле через
массу. Изменяющееся гравитационное поле подпитывает энер-
энергией возмущенные скалярные моды.
Если рождение квантов, поля приписывать изменяющемуся
гравитационному полю, то кажется естественным считать, что
частицы появляются в течение периода расширения. Ясно, что
частицы не рождаются в асимптотически статических областях.
Более того, если C.95) дает конечную плотность для частиц,
которые отсутствовали в in-области, то можно ожидать, что
измерение в промежуточный момент времени в период расши-
расширения даст плотность частиц где-то между нулем и значением
C.95).
К сожалению, эти представления не оправдываются при бо-
более тщательном рассмотрении. Как было объяснено в разд. 3.3,
в искривленном пространстве-времени, вообще говоря, ие су-
существует естественного определения понятия частиц. Тем не
менее благодаря симметрии пространства-времени Робертса-
Аа — Уокера в нем можно ввести привилегированный класс
наблюдателей, а именно сопутствующих наблюдателей, кото-
которые видят вселенную расширяющейся строго изотропно. По-
Поэтому возникает желание идентифицировать частицы в период
расширения с возбуждениями сопутствующих детекторов

70 Глава 3
частиц. Этот аспект проблемы будет рассмотрен в следующем
разделе.
Но, даже если можно ввести специальное определение поня-
понятия частиц на основе соображений симметрии, как это предло-
предложено выше, число частиц не будет постоянным, что делает про-
процесс измерения этой величины внутренне неопределенным. Если
средняя скорость рождения частиц в интервале Д* равна Л, то
для точного измерения числа частиц нужно выбрать Д/ таким,
чтобы |Л|Д?<;1. Но существует еще неопределенность числа
частиц (mAt)-\ обусловленная соотношением неопределенностей
Гейзенберга. Таким образом, полная неопределенность числа
частиц при измерении за время Д^ [381]
AN ^ (т ДО"' +1А | At.
Последняя величина имеет минимальное значение 2(|Л|//пI/2
при At = (т\А\)~'/г. Если |Л|=5>*=0 или m=fcoot эта внутренняя
неопределенность числа N не обращается в нуль.
Но успешное применение квантовой теории поля в простран-
пространстве Минковского говорит о том, что в,искривленном простран-
пространстве-времени должно существовать некоторое приближение, в
котором понятие частиц «почти осмысленно»; в конце концов мы
живем в расширяющейся вселенной. Приведенные выше физи-
физические аргументы подсказывают, что если скорость рождения
частиц мала, или их масса велика, то представление об опреде-
определенном числе частиц становится полезным.
Как можно придать этим соображениям более точный смысл?
Плотность частиц и скорость их рождения, очевидно, зави-
зависят от скорости расширения. В пределе очень медленного рас-
расширения можно ожидать уменьшения скорости рождения до
нуля в соответствии с результатом теории в пространстве Мин-
Минковского. Из C.95) видно, что |Р&|2 ~ В2->0, если полное рас-
расширение (т. е. полное изменение радиуса пространства) стре-
стремится к нулю, чем обеспечивается переход к пространству Мин-
Минковского. Но рождение частиц прекращается гораздо быстрее,
если скорость расширения стремится к нулю. Скорость расши-
расширения в нашем случае определяется параметром р, и при р->0
имеет место экспоненциальное спадание
; I Р* I2 -> е-2™'"/" -> 0. C.97)
Соответствующий параметр «медленности» p/coin становится,
малым, если р ^ k или щ. Это условие вполне понятно физи-
физически. Следует ожидать, что расширение будет возбуждать по-
полевые моды, для которых и меньше или порядка скорости рас-
расширения. Для значений и, существенно превышающих эту ве-
величину, рождение частиц экспоненциально подавлено. Таким
образом, моды с высокими k возбуждаются весьма незначи-

Квантовая Теория ЛоАя в искривленном пространстве-времени 71
тельно. Аналогично рождение частиц большой массы экспонен-
экспоненциально мало, поскольку для создания массы покоя необходимо
отобрать от гравитационного поля большую энергию.
Столь сильное подавление рождения квантов с большими k
или m означает, что в out-области (т)->оо) инерциальные де-
детекторы частиц будут регистрировать кванты высокоэнергетиче-
высокоэнергетических мод лишь крайне редко. Поле, находящееся в состоянии
вакуума при г\-*-—оо для всех мод, остается в «почти» вакуум-
вакуумном состоянии для высокоэнергетических мод. Чем медленнее
расширение в промежуточной стадии, тем больше вероятность
того, что данная мода не будет содержать частиц. Так как
эта вероятность уменьшается с энергией экспоненциально при
больших k и пг, приближение, в котором рождением частиц пре-
небрегается, с ростом энергии становится все более точным.
Если высокоэнергетическая in-мода остается вакуумной с
большой вероятностью в out-области, то кажется очевидным, что
она должна быть вакуумной и в промежуточной области (в пе-
период расширения). Но, чтобы придать этому утверждению
строгий смысл, необходимо уточнить движение детектора ча-
частиц. В следующем разделе мы покажем, что сопутствующий
детектор действительно в течение промежуточной фазы расши-
расширения почти не регистрирует квантов, принадлежащих высоко-
высокоэнергетическим модам.
Эти замечания, основанные на примере, рассмотренном в
предыдущем разделе, остаются справедливыми для любого про-
пространства-времени Робертсона — Уокера с гладким (С°°) мас-
масштабным фактором С(ц). В частности, быстрое прекращение
рождения частиц при m или &->-оо представляет собой общую
закономерность.
В случае модельной вселенной Робертсона — Уокера со ста-
статическими in- и out-областями ситуация ясна. Если в качестве
состояний квантованного поля выбраны вакуумные in- или
out-состояния, то сопутствующий детектор частиц почти не
будет регистрировать высокоэнергетических квантов вдоль всей
своей мировой линии. До тех пор пока частота моды много боль-
больше, чем скорость расширения, вероятность нулевого отклика де-
детектора будет оставаться очень близкой к единице. Но для низ-
низших мод кванты будут регистрироваться, что сигнализирует о
нарушении приближения, в котором состояние поля понимается
как вакуумное. (Аналогичные замечания относятся и к случаю,
цогда поле выбирается в многочастичном in- или out-состоянии.)
Более того, поскольку вакуумные состояния in и out ведут себя
в этом смысле одинаково, любая линейная комбинация этих
состояний будет давать такие же предсказания относительно
поведения детектора.
Если статических in- и out-областей нет, то приближенное

72 Глава 3
определение понятия частиц не может основываться на таком
построении. Вместо этого следует указать метод выбора тех из
точных модовых решений уравнений поля, которые в определен-
определенном смысле наиболее близки к соответствующим решениям в
пределе пространства Минковского. Физически это можно себе
представить как построение минимального возмущения поля при
расширении, приводящее к такому определению частиц, при
котором рождение частиц при изменении геометрии минималь-
минимально. Такое построение было дано Паркером [379—383] и в даль-
дальнейшем развито в работах [36, 75, 76, 223, 225, 302, 303, 350].
Для придания этим соображениям точного математического
смысла необходимо провести разложение полевых мод, спра-
справедливое при больших массах. Здесь мы рассмотрим случай
конформного скалярного поля в пространственно-плоских мо-
моделях Робертсона — Уокера. Более общий случай исследовался
в цитированных выше работах.
Элемент длины в рассматриваемом пространстве имеет вид
ds2 = С (л) Ш - Z (dxlf\, C.98)
где предполагается, что С(х\)—функция класса С°° конформного
времени г\. В силу однородности пространственных сечений ме-
методом разделения переменных можно найти решения для вол-
волновых мод
ик = Bя)A-")/2 С<2-")/4 (г,) elk*Xk (т,), C.99)
где А = |к|. Для конформного поля функция %k удовлетворяет
уравнению
-?fXk(r\) + <»l(r\)%kD) = 0, C.100)
где
'(ц)т2. ' C.101)
Уравнение C.100) напоминает классическое уравнение для
гармонического осциллятора с частотой, зависящей от времени,
например для- математического маятника, длина подвеса кото-
которого медленно укорачивается, вызывая изменение периода коле-
колебаний. В терминах квантовой теории ясно, что энергия Е кванта
колебаний (hv) недостаточна для формирования нового кванта
при возрастании частоты v. Действительно, Эйнштейн показал,
что если длина маятника уменьшается бесконечно медленно, то ,
E/v является адиабатическим инвариантом, и число квантов со-
сохраняется независимо от полного изменения длины маятника
(см., например, [106]).
В космологической задаче мы покажем, что подобным же
образом число квантов (т. е. число частиц) является адиабати-
адиабатическим инвариантом независимо от полной величины космоло-

Квантовая теория поля в искривленном пространстве-времени 73
гического расширения, если скорость расширения бесконечно
мала.
Уравнение C.100) имеет формальное ВКБ-решение
%k = BWkr4' ехр Г - / J Wk (ri') dx{ j , C.102)
где функция Wk удовлетворяет нелинейному уравнению
C.103)
В выражении C.102) неявно присутствует произвольный фазо-
фазовый множитель, который можно задать выбором, нижнего пре-
предела интегрирования.
Если пространство-время эволюционирует медленно, то члены
с производными в C.103) будут малы по сравнению с со|, по-
поэтому в нулевом приближении можно в подынтегральном выра-
выражении C.102) положить
<Мч)- C.104)
Это решение, очевидно, сводится к стандартным модам про-
пространства Минковского, поскольку С (tj)-*- const.
Решений уравнения C.103) могут бытв получены с помощью
итераций, причем W$ выбирается в качестве нулевого прибли-
приближения ([73], этот прием эквивалентен методу Лиувилля [431],
см. также [105]). Для выявления характера «медленности»
удобно ввести параметр адиабатичности Т. Если временно за-
заменить ц на х\/Т (полагая Т = 1 в конце вычисления), то адиа-
адиабатический предел медленного расширения можно исследовать,
рассмотрев, что происходит при Т-*-оо.
Воспользовавшись этим приемом, можно переписать C.100)
в виде
где Tii = х\/Т. Очевидно,
^^^ (злоб)
,так что в пределе Т-*-оо функция С(г\\) и все ее производные
по т) изменяются бесконечно медленно. Таким образом, можно
воспроизвести влияние медленного изменения С(г\), рассматри-
рассматривая приближение больших Т.
В разложении по обратным степеням Т член, пропорциональ-
пропорциональный Т~п, будет называться членом я-го адиабатического

74 . Глава 3
порядка. Из C.106) ясно, что адиабатический пврядок эквива-
эквивалентен числу производных от С. Из соображений размерности
следует, что если некоторая величина имеет размерность тй, то
член адиабатического порядка Л в ее разложении будет содер-
содержать А — d степеней т~} и к~х.
Следующая итерация в C.103) дает
f) (ЗЛ07)
куда входят две производные от со& и, следовательно, от С, так
что это член второго адиабатического порядка в приближении
медленных движений. А-я итерация дает член адиабатического
порядка 2А. (При подстановке W$ в C.102) с целью получения
разложения до второго порядка в разложении квадратного
корня из выражения C.107) необходимо удержать члены также
до второго порядка по адиабатическому параметру.) Ниже
мы будем обозначать А-Pi порядок разложения по адиабатиче-
адиабатическому параметру через %(АЛ), а соответствующие моды C.99) —
через и^К
Предположим, что вместо точного решения JU» задаваемого
формулой C.102), использовано адиабатическое приближение
нулевого порядка, получаемое заменой Wk на Wy- В in-области,
в которой пространство является статическим, оба выражения
приводят к обычным решениям уравнения с постоянной часто-
частотой в пространстве Минковского. По мере расширения вселен-
вселенной точное и приближенное решеиия перестают быть совпадаю-
совпадающими, но различие будет проявляться только в членах второго
порядка по адиабатическому параметру, и это остается справед-
справедливым, сколь бы сильно ни расширилась вселенная.
В качестве иллюстрации рассмотрим закон расширения
C(ti)=1+e<"i, a = const, r\ < 0, C.108)
для которого существует асимптотически статическая in-область
и далее следует период расширения. Точное решение, сводя-
сводящееся к обычному положительно-частотному решению для про-
пространства Минковского в отдаленном прошлом, имеет вид [37]
гA-(»^/а))/»уЦ»7' (зл09)
где /—функция Бесселя и со^ = coft(— oo) =(?2-f m2f\ С дру-
другой стороны, адиабатическое решение нулевого порядка (кото-
(которое также сводится к стандартным положительно-частотным мо-

Квантовая теория поля в искривленном пространстве-времени 75
дам пространства Минковского в in-области) имеет вид
'1' (k2 + m2 + mVY" exp { - Ц- [(k2 + m2 + mV)V
Точное решение и решение нулевого порядка по адиабатиче-
адиабатическому параметру согласуются в отдаленном прошлом, когда
расширение происходит бесконечно медленно. Используя стан-
стандартное асимптотическое разложение функций C.109) для боль-
больших ш, нетрудно проверить, что с точностью до несущественного
фазового множителя (соответствующего неопределенному ниж-
нижнему пределу в интеграле C.102)) C.109) сводится к C.110)
с точностью до членов более высокого порядка по адиабатиче-
адиабатическому параметру независимо от значения ц.
В общем случае справедливо следующее соотношение:
«к = а</> (т,) и<Л) + pjf > (т,) и<Л)\ C.111)
выражающее точные полевые моды (т. е. точные решения волно-
волнового уравнения) через решения, найденные в адиабатическом
приближении ы?*>. Ясно, что а^' и р^' должны быть постоян-
постоянными с точностью до членов порядка Л, поскольку и^ и «(^ —
решения полевого уравнения соответствующего порядка. Допу-
Допустим, что заданы конкретные значения
(ЗЛ12)
для некоторого фиксированного момента времени т\о. Тогда из
наших рассуждений следует, что аир, определенные форму-
формулами C.112) при г| = г|0, будут удовлетворять C.112) в любой
момент времени. Моды «к, заданные соотношениями C.111),
C.11.2), называются адиабатическими положительно-частотными
модами порядка А. Важно заметить, что, несмотря на такое на-
название, эти моды являются не приближенными, а точными реше-
решениями волнового уравнения. Но они не определены однозначно
заданием условий C.111) и C.112). Существует бесконечное
множество таких мод, соответствующих различному выбору т]о.
Особое внимание следует обратить на точные моды м'кп,
которые сводятся к стандартным плосковолновым положитель-
положительно-частотным решениям в статичесйвй in-области. Другой на-
набор мод Mj[ut сводится к стандартной форме в статической

76
out-области. В обеих статических областях все члены ненуле-
ненулевого порядка разложения по адиабатическому параметру в ы(кд'
обращаются в нуль, так что эти точные моды являются также
и адиабатическими положительно-частотными модами бесконеч-
бесконечного порядка. Таким образом, как следует из обсуждения соот-
соотношений C.112), коэффициент Боголюбова р, связывающий два
набора мод «'kn и «?ut, должен убывать в адиабатическом пре-
пределе Т -*¦ оо быстрее любой обратной степени Т. Это действи-
действительно имело место в рассмотренном в предыдущем разделе
примере. Следовательно, число частиц, найденное на основе
квантования с использованием любого из этих наборов мод, бу-
будет адиабатическим инвариантом в период космологического
расширения в полной аналогии с задачей о маятнике перемен-
переменной длины.
Если вместо набора точных полевых мод, сводящихся к стан-
стандартному виду, скажем в in-области, использовать точные ре-
решения, сшитые с приближенными адиабатическими модами по-
порядка Л в некоторый последующий момент тH с помощью C.111)
(«к и dujdt приравнены и^ и du^jdt с точностью до членов
порядка Л по адиабатическому параметру при л —Ло), то в
in-области эти точные решения уже не будут сводиться к стан-
стандартной форме, а будут, вообще говоря, представлять собой ли-
линейную комбинацию положительно- и отрицательно-частотных
нлосковолновых мод. Поэтому состояние вакуума, построенное
е использованием, этих «искаженных» мод, ие будет совпадать
е обычным вакуумным состоянием в in-области. Это значит, что
инерциальный детектор частиц укажет на присутствие частиц
в состоянии «искаженного» вакуума. Тем не менее спектр этих
квантов будет всегда спадать при больших энергиях как k~(A+
(или т~(Д+1)), что является отражением того факта, что эти
моды сшиты е приближенными модами, отличающимися от стан-
стандартных jn-мод лишь членами адиабатического порядка A -f- 1
и выше. Таким образом, «искаженный» вакуум можно рассма-
рассматривать как адиабатическое приближение для in-вакуума. В со-
состоянии адиабатического вакуума высокоэнергетические моды
с большой вероятностью остаются вакуумными, поэтому сопут-
сопутствующий детектор с большой вероятностью даст нулевое зна-
значение для числа квантов этих мод. Но вероятность того, что
любая наперед заданная мода не будет содержать квантов в
течение всего времени, не столь велика, как в случае вакуум-
вакуумных состояний in и out с характерным для них более быстрым
спаданием при высоких энергиях (быстрее любой степени k
или пг).
Следует правильно понимать две особенности понятия адиа-
адиабатического вакуума. Во-первых, как уже отмечалось, адиаба-

Квантовая теория поля в искривленном пространстве-времени 77
тический вакуум не является некоторым приближенным состоя-
состоянием, связанным с приближенными полевыми модами. Конечно,
адиабатические моды сами по себе являются лишь приближен-
приближенными решениями полевого уравнения (с точностью до членов
порядка Л), но они используются лишь как математический
шаблон, с которым сравниваются точные решения в некоторый
момент ц = у\0. Квантуются именно сами точные моды. Соот-
Соответствующее состояние вакуума (т. е. адиабатический вакуум
порядка Л) для этих точных мод является вполне приемлемым
претендентом на роль вакуумного состояния. Правда, оно мо-
может не отражать показаний сопутствующего детектора так же
хорошо, как, скажем, вакуумные (Л + 1)-адиабатическое или
in-состояния, но вполне удовлетворяет общим принципам кван-
квантовой теории поля.
Во-вторых, адиабатическое вакуумное состояние порядка А
не единственно, так как процедура сшивания может осущест-
осуществляться при любом Т)о. Соответствующие точные моды будут от-
отличаться во все остальные моменты времени только членами
более высокого порядка малости по адиабатическому параметру,
так что все они могут быть использованы при квантовании и
построении адиабатического вакуума порядка А. Все такие ва-
вакуумные состояния будут иметь сходное поведение при больших
энергиях, но, вообще говоря, различную структуру низкоэнерге-
низкоэнергетических мод.
Хотя адиабатический вакуум менее точно определен, чем
вакуумное состояние, связанное со статическими in- и out-обла-
out-областями, соответствующее представление о физических частицах
(в смысле показаний сопутствующего детектора) является тем
не менее наилучшим в случае пространства-времени, не имею-
имеющего статических in- и out-областей. Согласно современным кос-
космологическим теориям, именно такой является реальная все-
вселенная.
Для иллюстрации использования адиабатического прибли-
приближения в асимптотически нестатических четырехмерных космо-
космологических моделях выберем масштабный фактор
-oo<n<oo, C.113)
где а и Ь — постоянные [11]. В асимптотических областях
¦П-»-±оо эта модель соответствует радиационно-доминированнои
Фридманов с кой космологии, причем
a(t)*=C4'{t)~t4'. C.114)
Симметрия относительно изменения направления времени, при-
присущая (ЗЛ13), означает, что пространство сжимается до мини-
минимального масштабного фактора при т) =» 0, «отражается» и
вновь расширяется (рис. 8).

78
Глава 3
Рис. 8. Конформный масштабный
фактор С(т|) = а2 + 62Т]2 описы
вает вселенную, сжимающуюся до
минимального «размера» и затем
снова расширяющуюся симметрич-
симметричным образом. При больших ц ее
поведение соответствует радиаци-
онно-доминированной модели
Фридмана.
Хотя это пространство-время не является статическим в
асимптотических областях, его можно рассматривать как мед-
медленно изменяющееся при т]-»-±оо, поскольку
— (С/С) --> О, / > О.
C.115)
Таким образом, в пределе скорость расширения стремится к
нулю, и адиабатическое приближение становится точным, по-
поэтому приближения разных порядков будут приводить к одина-
одинаковому результату при tj->-±oo.
Адиабатическое приближение нулевого порядка остается хо-
хорошим приближением до тех пор, пока частота
Фк (Л) = (k2 + mW + mWrft
велика по сравнению с производными в левой части C.115).
Чтобы найти условия, при которых это справедливо, достаточно
обратиться к C.105), записывая множитель ^^(^i) в виде
где
= шЬТ2К
Я. == {ma2/b) + (k2/mb).
C.116)
Поскольку производная С/С ведет себя как Т~\ нетрудно ви-
видеть, что для фиксированного rii = r\/T адиабатическое прибли-
приближение нулевого порядка справедливо при больших К или х\, или
mb, либо для больших значений одновременно нескольких из
этих величин.
Рассмотрим предел больших К при фиксированных mb и х\.
Подставляя
в C.102), получаем
Dт6Я)"'/4ехр [- / {тЬХ)ъ
C.117)

Квантовая теория поля в искривленном пространстве-времени 79
где ц фиксировано. Для сравнения построим точные решения
уравнения C.100), сводящиеся к C.117) с точностью до членов
порядка О(Т~1) (т. е. О(я~'/2)) в пределе больших К:
%ibD) = Bmb)-'l<e-nmD_{l_a)n[(i-l)(mb)>l*i]} при т, < 0, C.118)
ХГ4(Т1)=--4П(-Л)* при ц>0. C.119)
(Это можно проверить, выражая функцию параболического ци-
цилиндра D через функции Уиттекера W и используя асимптоти-
асимптотическое разложение функций Уиттекера для больших индексов;
см., например, [68], с. 99, уравнение A9а)).
Можно также проверить, что предельное значение C.102)
при больших |т)|
Х(о, (ч) Л±±^ {2mb I r, | Г* е*"« C.120)
совпадает с пределом %'? при ti->-—оо и с пределом %°kat при
г]-*-+оо.
Подставляя C.118) в C.99), получим адиабатические поло-
положительно-частотные моды и^ \х), с помощью которых разло-
разложим поле ф:
^ = ?(« + ^4"*) C.121)
к
и введем соответствующее адиабатическое вакуумное состояние
|0in), определенное соотношением
акп|0?„> = 0. C.122)
Аналогично можно с помощью C.119) ввести другое адиаба-
адиабатическое вакуумное состояние того же адиабатического порядка
0. C.123)
Поскольку %'fcn сшиты с х^при г\ = —оо,когда все адиабатиче-
адиабатические поправки более высокого порядка-исчезают в силу C.115),
при у\ = —оо это состояние оказывается сшитым с х^ для про-
произвольного Л. Таким образом, вакуум |0т) является адиабати-
адиабатическим in-вакуумом бесконечного порядка адиабатичности. Точ-
Точно так же состояние |0out) представляет собой адиабатический
out-вакуум бесконечного порядка. Чтобы убедиться в этом явно,
.достаточно вычислить коэффициенты преобразования Боголю-
Боголюбова между ы'кп и M°ut:
„out _ ie-n\%ouf (з. 124)
AA-/Я))

80 Глава 3
(см., например, [47], формула (9.248C))). Следовательно, если
задано квантовое состояние 10in), сопутствующий детектор ча-
частиц в out-области будет регистрировать спектр
I2 = ехр {- я [(k*/mb) + (та*/Ь)]), C.125)
который при больших энергиях действительно спадает быстрее,
чем любая обратная степень k или т. Спектр спадает быстрее
любой положительной степени b (параметра «медленности»)
при 6->-0. Заметим также, что выражение C.125) остается
конечным при а-*-0, что соответствует космологической модели
с прохождением через сингулярность при г\ = 0.
Как было отмечено в работе [10], распределение C.125) сов-
совпадает со спектром нерелятивистского газа находящихся в теп-
тепловом равновесии частиц с импульсом &С~'''(т)) при зна-
значении химического потенциала — Х1чта С~ (г)) и температуре
b/BnCkB), где kB, как и раньше, обозначает постоянную Больц-
мана.
Альтернативная формулировка задачи рождения частиц гра-
гравитационным полем, называемая методом диагонализации га-
гамильтониана, основана на определении состояний частиц в каж-
каждый момент времени по аналогии с определением в пространстве
Минковского (см.; например, [33, 103, 104, 260—254, 308]). В об-
общем случае эта процедура приводит к предсказанию значи-
значительно более интенсивного рождения частиц, чем методы, ис-
использованные здесь, и не дает отмеченного выше быстрого спа-
спадания числа частиц при больших k. В работе [417], например,
предсказывается скорость рождения частиц, равная 16 части-
частицам в 1 км3 в год, — на много порядков больше значения, кото-
которого можно было ожидать на основании физических соображе-
соображений. Диагонализация гамильтониана была подвергнута сущест-
существенной критике, в частности, в работе Фуллинга [223] (см.
также [401])').
Анализ концептуальных оснований понятия частиц в искрив-
искривленном пространстве-времени проведен в работах [8, 9, 264,
352,478]).
3.6. Адиабатическое разложение функций Грина
В предыдущем разделе было показано, что высокочастотное
поведение массивного скалярного поля относительно нечувстви-
') В работе [4,17] при вычислении скорости рождения частиц допущена
ошибка, на которую указано в работе С. Г. Мамаева и В. М. Мостепаненко
(Phys. Lett., 1978, A vol. 67, p. 165). Правильный расчет методом диагонали-
диагонализации дает требуемое быстрое убывание .импульсного спектра рожденных ча-
частиц при к-*- оо (см. [253, 254]); приведено также выражение для полного
тензора энергии-импульса с учетом вклада рожденных частиц и поляризация
вакуума — Прим. перев.

Квантовая теория поля в искривленном пространстве-времени 81
тельно к крупномасштабной временной зависимости фонового
пространства-времени Робертсона — Уокера. Причина состоит в
том, что высокочастотные компоненты поля чувствительны лишь
к геометрии в непосредственной близости от интересующей нас
точки, а в этой ограниченной области метрика изменяется мало.
В противоположность этому длинноволновые низкочастотные
моды чувствительны к полному многообразию, и их структура
зависит от геометрии и, следовательно, от конкретного адиаба-
адиабатического построения.
Для некоторых приложений, например связанных с регуля-
регуляризацией ультрафиолетовых расходимостей, представляет инте-
интерес только высокочастотное поведение поля. В этом случае
можно ограничиться приближением высоких частот. Поскольку
высокие частоты чувствительны к малым расстояниям, мы при-
приходим к необходимости построения приближения, справедли-
справедливого для малых расстояний.
Особый интерес представляет поведение функций Грина, на-
например Gf(x, x), в пределе х-*-х'. Здесь мы будем следовать
работе [83], в которой было получено, адиабатическое разло-
разложение GF-
Вводя нормальные римановы координаты у* для точки х
с началом в точке х! [333, 398], можно получить следующее
разложение метрики:
20 ^novp- у8 + 45"
['20
где ч\^у— метрический тензор Минковского, и все коэффициенты
вычислены при у = 0.
Вводя функцию
9Р (х, А = (- g (x)Lt GF (х, х'), C.126)
и ее фурье-образ
9, {х, х') = Bя)"" J dake~lku9P (k), C.127)
где ky =¦ rf$kay&, можно перейти к некоторому локальному им-
импульсному пространству. Разлагая C.49) в нормальных коор-
координатах и переходя к ^-пространству, можно найти 9f{1i) путем
итераций с точностью до любого адиабатического порядка. При-
Приведем результат с точностью до четвертого порядка (т. е,

82 Глава 3
с учетом четырех производных от метрики):
9, (к) ~ (k2 - т2)-' - A - 6) R (k2 - тГ2 + ±1 D - б) Я. аХ
х a«(tf - тТ2 - ja<*dad* (k2 - m2y2 +
+ [(^-lfR2 + ia\](k2-mr\ C.128)
где
C.129)
"op = У {} * 6"J Я; „р + 720" ^: аР ~ Ж ^af»; Л ~ зо" ^а ^а
и символом « обозначено асимптотическое разложение. Для
того чтобы выражение C.127) действительно представляло со-
собой хронологически упорядоченное произведение (типа C,48)),
достаточно проводить интегрирование по k° вдоль соответствую-
соответствующего (фейнмановского) контура на рис. 3. Это эквивалентно
замене т2 на т? — гг. Аналогично получим адиабатические раз-
разложения для остальных функций Грина, используя другие кон-
контуры на рис. 3.
Подстановка C.128) в C.127) дает
9Ах. *') - J -щг е~">У [а0 (х, *') + щ (х, х') (- ±?) +
+ a2(x,x')(-±i)*](k2-m2)-\ C.130)
где
aQ{x,x')^\ C.131)
и с точностью до четвертого адиабатического порядка
:a/-j«^V. C-132)
а2 (х, х') = 1 (j - if R2 +1 а\, C.133)
причем все геометрические величины в правой части должны
быть ваяты в точке х'.
Если в C.130) использовать интегральное представление
/в)--/Г**"(*-"Ч!« C.134)

Квантовая теория поля в искривленном пространстве-времени 83
то, изменив порядок интегрирования по dnk и ds и выполнив
явно интегрирование по dnk, получим
00
9р(х, х')^-/Dя)-п/2 \ ids(is)~n/2exp[-itns+(a/2is)]F{x, х'\ is),
S
C.135)
где величина а определена как
±а C.136)
т. е. представляет собой половину квадрата расстояния между
х и х', а функция F имеет следующее адиабатическое разло-
разложение:
F (х, х'; is) ~ а0 (х, х') + а, (х, х') is + а2 (х, х') (isJ + ... . C.137)
С учетом C.126) равенство C.135) дает представление для
функции GF(x, x'), первоначально полученное де Виттом [153,
156] с помощью метода Швингера [427] (отсюда индекс DS;
см. также [199, 366])
оо
G$s(x, x')=z-iA'l2(x, х')Dлуп12 [ ids(is)~n'2X
i
Xexp[-im2s + (a/2is)]F(x, x'\ is), C.138)
где Д — определитель ван-Флека [476]
Д(х, *') = - йе1[д^а(х, х')][ё(х)ё(х')Г'к. C.139)
В нормальных координатах с началом в точке х', которые здесь
используются, Д сводится к[—g (х)]~ . В трактовке де Витта
асимптотическое разложение C.137) с учетом всех порядков
адиабатичности записывается в виде
оо
F (х, х'\ is) « Е а/ (х, х') (isI, C.140)
/-о
где ао(х, х')= 1, а все прочие коэффициенты а/ определяются
рекуррентными соотношениями, позволяющими найти их асимп-
тртические разложения [113]. Следует отметить, что так назы-
называемое представление «собственного времени» де Витта —
Швингера C.138) является точным представлением для фейнма-
новского пропагатора. Разложения же C.137) и C.140) пред-
представляют собой лишь асимптотические приближения, справед-
справедливые в пределе больших значений параметра адиабатичности Т.

84 Глава 3
Если подставить C.140) в C.138), то можно вычислить ин-
интеграл и получить адиабатическое разложение фейнмановского
пропагатора в координатном пространстве1):
C.141)
в котором подразумевается, что величина а имеет мнимую
часть te.
Поскольку мы не накладывали глобальных граничных усло-
условий на функции Грина как решения уравнения C.49), разло-
разложение C.141) не определяет выбора какого-либо вакуумного
состояния в C.48). В частности, добавка te в разложении GP
означает только, что C.141) представляет собой математическое
ожидание хронологически-упорядоченного произведения полей
на некотором множестве состояний. При некоторых условиях
использование добавки te в точном представлении C.138) может
дать добавочную информацию о глобальной природе состояний
(см., например, обсуждение на стр. 54). Иначе говоря, то же
самое высокочастотное поведение C.48) имеет место почти при
любом выборе вакуумного состояния — факт, который, как мы
vувидим ниже, играет очень важную роль.
В пространстве-времени Робертсона — Уокера фейнманов-
ская функция Грина, вычисленная в состоянии адиабатического
вакуума {№): ¦
iGUx, х') = @А\Т(ф(х)ф(х'))\0А), C.142)
должна иметь разложение вида C.138), C.140). Вакуум |
определен с помощью набора адиабатических положительно-
частотных мод «к, задаваемых соотношениями C.111), C.112)
для некоторого цо, так что C.142) можно переписать в виде
iGAF (х, х') =0(х° - х*')\ dn~lkuk(х)ик(*') +
n~l kuUx)uk(x'). C.143)
Чтобы получить разложение C.143) с точностью до членов по-
порядка А по адиабатическому параметру, достаточно разложить
Ик до этого порядка, т. е. вычислить C.133), заменив мк на и?
*) С помощью функционального интегрирования можно расширить об-
область применимости адиабатического приближения [593*]. — Прим. перев.

Квантовая теория Поля в искривленном пространстве-времени 85
Выполнив это, можно явно проверить, что C.142) и C.143) со-
согласуются с точностью до членов порядка А [36, 76, 83]. В част-
частности, можно проверить, что добавка te необходима, чтобы обес-
обеспечить временное упорядочение в C.142) и C.143).
Обсудим теперь вопрос о реакции детектора на адиабатиче-
адиабатическое вакуумное состояние порядка А. Для этой цели следует
подставить
G+A (х (т), х (т')) ^ @А | ф (х (т)) ф (х (т'))! 0д> ¦ C.144)
в C.55) и найти функцию отклика детектора, движущегося
вдоль мировой линии х(х). Если ограничиться вкладом в ве-
вероятность членов до адиабатического порядка А в точной двух-
двухточечной функции, то для произвольного пространства-времени
можно рассчитать этот вклад с помощью адиабатического раз-
разложения «{/" для мод. Как и для Gf, разложение функции G\
эквивалентно учету членов до порядка А в представлении
де Витта — Швингера Gds- Разложение Gdsможет быть вычис-
вычислено в импульсном представлении как
iGis(x, х') = [-ё(х)]-'14$+(х, х'),
где с точностью до четвертого порядка по параметру адиабатич-
ности $+ дается правой частью C.130), причем интегрирование
по k° проводится вдоль контура, показанного на рис. 9. Исполь-
Используя разложение для [— g(x)]~l/t в нормальных координатах с
началом в точке х', замечаем, что G+ (с точностью до произ-
произвольного адиабатического порядка) представляет собой сумму
членов вида
(ЗЛ45>
где 5 — некоторый тензор, построенный из геометрических ве-
величин, a yvt как и выше, нормальные координаты точки х отно-
относительно точки х''. В результате интегрирования по k° вдоль
контура, показанного на рис. 9, получаем линейную комбинацию
величин вида
где гид — целые числа.
В дальнейшем мы ограничимся сопутствующими детекторами,
для которых мировые линии х{х) таковы, что х1 = const и т = /
(космологическое время Робертсона — Уокера). Используя
свойства нормальных координат, перепишем Gds (х (т). ¦* (т')) в
виде линейной комбинации членов типа C.146) с у = 0, у0 — t.

86 Глава 3
"&* Рис. 9. Контур в плоскости комп-
комплексной переменной k°, который ис-
пользуется при вычислении инте-
интеграла, определяющего &+. Крести-
Крестиком отмечен полюс в точке ft" =
= (|k|2 + m2) 'I'.
Подстановка такого члена в C.55) даег интеграл вида
e-i«o+E-E0)T(T)(rfT (/ целое).
Поскольку со + Е — Ео > 0, все интегралы такого типа обра-
обращаются в нуль, так как представляют собой производные от
6(ш+? — ?0).
В заключение можно сказать, что адиабатический вакуум
Л-го порядка есть состояние, в котором сопутствующий детектор
частиц остается невозбужденным с вероятностью, отличающейся
от единицы лишь членами порядка А-\- 1. Это означает, что ве-
вероятность регистрации частицы с энергией ш в ультрафиолетовом
пределе стремится к нулю быстрее, чем А-я обратная степень со,
или как А-я степень некоторого параметра «медленности». Тем
самым доказано утверждение Паркера [381] о том, что адиаба-
адиабатические частицы (хотя такой термин обычно не употребляется,
см. [390]) удовлетворяют критерию «наблюдаемости в медленно
расширяющейся вселенной с помощью тех же приборов, что и в
статическом случае». Паркер доказал это совершенно другим
путем [375].
Чем выше выбирается порядок А при этом построении, тем
более вероятно, что высокочастотные моды окажутся в вакуум-
вакуумном состоянии. Конечно, при этом все еще будут регистрировать-
регистрироваться частицы низкочастотных мод; проведенное здесь высокоча-
высокочастотное разложение не позволяет детально проследить за ними.
Если же детектор не является сопутствующим, то, вообще го-
говоря, будут регистрироваться частицы и в высокочастотных мо-
модах, которые спадают медленнее, чем Т~А.
3.7. Конформный вакуум
Несмотря на всю привлекательность адиабатических вакуум-
вакуумных состояний, факт остается фактом, что в искривленном про-
пространстве-времени некоторый специальный набор решений урав-
уравнений поля и соответствующие вакуумное и многочастичные со-
состояния в общем случае не имеют прямого физического смысла.
В частности, «вакуумное» состояние вовсе не обязательно ока-

Квантовая теория поля в искривленном пространстве-времени 87
зывается лишенным частиц, даже если измерения производятся
свободно падающим детектором. Тем не менее, если интересую-
интересующее нас пространство-время имеет геометрические симметрии, то
можно указать выделенный набор мод, и соответствующие со-
состояния частиц становятся в некотором смысле «естественными».
Один из специальных случаев, к которому мы будем часто
обращаться, это случай конформно-тривиальной ситуации, т. е.
конформно-инвариантного поля в конформно-плоском простран-
пространстве-времени (конформном пространству Минковского). Симме-
Симметрия таких пространств проявляется в существовании конформ-
конформного вектора Киллинга, удовлетворяющего уравнению C.23).
Примерами конформно-плоских пространств могут служить все
двумерные пространства, а также пространственно-плоские кос-
космологические модели Робертсона — Уокера. Метрические тен-
тензоры таких пространств всегда могут быть представлены в виде
Q!WV C-147)
где т]цу — метрический тензор пространства Минковского.
Волновое уравнение для конформно-инвариантного скаляр-
скалярного поля получается при m = 0 и при указанном в C.27) вы-
выборе параметра |:
] = 0. C.148)
При конформном преобразовании
из C.1), C.5) и C.148) находим
? ^П^дЛ(й(п-2)/240 = О, C.150)
так как R = 0 в пространстве Минковского. Показатель степени
(п — 2)/2 величины Q представляет собой конформный вес ска-
скалярного поля. Уравнение C.150) имеет обычные решения для ф
в пространстве Минковского (см. B.11))
пк(х) = [2ыBл)п-*Г1'ге-1к-х, к° = ы. C.151)
Эти моды являются положительно-частотными по отношению к
времениподобному конформному вектору Киллинга дп:
&о& М = - to"k M« а>>°- C.152)
Замечая на основании уравнения C.150), что ф = QB-")/2 ф,
мы можем записать разложение C.30) по модам для ф в виде
А (х) = QB-")/2 (x) Z [акпк (х) + atih (x)], C.153)

88 Глава 3
где йк определено C.151). Ассоциируемое с этими модами ва-
вакуумное состояние, определяемое условием flk I 0) = 0, называют
конформным вакуумом. Подобные состояния существуют также
для безмассового поля со спином '/2 и для электромагнитного
поля (см. разд. 3.8).
Аналогично можно рассмотреть уравнение для функций Гри-
Грина C.49). После применения преобразования C.5) уравнение
[п, + ^ (* - 2)R (х)/(п - 1)] DF(x, *') = - [- g (х)]-'1' б" (х - х')
принимает вид
Q-(n+2)/2 (x) rf\dv (Q(n-2)/2 (x) DF (x, x')) = -О"" (x) 6" (x - x').
Таким образом,
tTVv (Q(n)/2 (*) °p (*. *')) = - Q<2~n)/2 (*) б" (* - *') =
= -d2-n)l2{x')bn(x-x%
откуда следует
DP (x, x') = Q<2-")/2 (x) DP (x, x') QB-n)/2 (x% C.154)
где Dp{x, x') —фейнмановская функция Грина для безмассового
поля в пространстве Минковского, удовлетворяющая уравнению
B.74). Это соотношение может быть также получено на основе
определения C.48) функции Грина в терминах полей. Подобные
соотношения существуют и для других функций Грина скаляр-
скалярного поля. Для безмассовых полей со спином '/г и 1 выполняют-
выполняются аналогичные соотношения, в которых степень Q определяется
конформным весом данного поля (см. разд. 3.8).
Применим теперь эти результаты для анализа показаний де-
детектора частиц во вселенной Робертсоиа — Уокера с элементом
длины C.98), предполагая, что поле находится в состоянии кон-
конформного вакуума. Будем рассматривать случай четырех изме-
измерений.
Сопутствующая геодезическая х = const в пространстве-вре-
пространстве-времени Робертсона — Уокера при конформном преобразовании
C.149) отображается в геодезическую х = const пространства
Минковского. Но собственное время т вдоль этих геодезических,
совпадающее с космическим временем t, не совпадает с конформ-
конформным временным параметром х° = х\ в C.98) (см. также C.82)).
Вдоль сопутствующей геодезической функция Грина D+(x,x)
сводится к
где использованы соотношения C.59) и C.154) с заменой Gf на
Р+ и положено Q2 = С. Подставляя это выражение в функцию

Квантозая Теория ПоЛя в искривлённом ttpoctpaHctee-времени 89
отклика C.55) и используя C.82) для перехода от интегрирова-
интегрирования по т к интегрированию по т), получим выражение
-IE J С'А (т,*) Л,"
которое, вообще говоря, не обращается в нуль из-за наличия мно-
множителя С"'2 в показателе экспоненты. В разд. 5.3, 5.4 приведены
примеры.
Таким образом, даже сопутствующий детектор частиц — бли-
ближайший аналог в пространстве-времени Робертсона — Уокера
инерциального наблюдателя пространства Минковского, — вооб-
вообще говоря, будет регистрировать присутствие частиц в состоянии
конформного вакуума. С другой стороны, из соотношения C.152)
следует, что моды, которые являются положительно-частотными
по отношению к конформному времени в некоторый момент вре-
времени, остаются такими при всех значениях времени. Следова-
Следовательно, если поле, удовлетворяющее конформно-инвариантному
волновому уравнению в конформно-плоском пространстве-вре-
пространстве-времени, находится в состоянии конформного вакуума в некоторый
момент времени, оно будет находиться в этом состоянии все вре-
время, и рождения частиц происходить не будет [379—384] (см.
также с. 198). Это верно для нейтрино (если они безмассовы) и
фотонов, но не имеет места для гравитонов [255, 256]. Утвержде-
Утверждение об отсутствии рождения частиц нужно понимать в следую-
следующем смысле. Если космологическое расширение останавливается
(гладким образом), то инерциальный детектор, адиабатически
включающийся после остановки расширения, не будет обнаружи-
обнаруживать частиц. Положительный отклик детектора при его включе-
включении во время расширения можно поэтому интерпретировать как
ложный, хотя на самом деле это лишь еще одно проявление того
факта, что в областях с ненулевой кривизной пространства-вре-
пространства-времени понятие частиц теряет значительную часть смысла, интуи-
интуитивно в него вкладываемого.
Конформный вакуум для несколько более общего класса про-
пространств обсуждается в разд. 5.2 (см. также [31]).
3.8. Поля произвольного спина
в искривленном пространстве-времени
В теории поля в пространстве Минковского спиновые свой-
свойства поля определяются его поведением при бесконечно малых
лоренцевых преобразованиях
ха->*а^А\х* = (Ь% + <»%)х\ C.157)
%-~<V 1«>ае1<1- C.158)

ЙО Глава S
(Мы ограничимся здесь случаем четырехмерного пространства
Минковского.)
Многокомпонентное поле общего вида TY '"x(x) преобразует-
преобразуется согласно
\ C.159)
p. C.160)
Для того чтобы преобразования Лоренца образовывали группу,
антисимметричные величины 2ар (называемые генераторами
группы) должны удовлетворять коммутационным соотношениям
р Yp -f Пвр2г« — Пба2ур, C.161)
или, что эквивалентно,
aXa = fa, bXb = tb, [а„й,] = 0, C.162)
где
at = j(-ie*%i + Zto), bj = j(-ie'!%i-Zio). C.163)
Соотношения C.162) представляют собой коммутационные соот-
соотношения для двух независимых операторов углового момента
а и Ь. Каждый из них может быть представлен бесконечными
матрицами, сводящимися к конечномерным матрицам, опреде-
определяемым целыми или полуцелыми числами А к В, где
а2 = Л(Л + 1), Ь2 = В(В+1), C.164)
которые действуют в векторном пространстве 2Л + 1 и 25 -f 1
измерений соответственно. Эти неприводимые представления, бу-
будучи скомбинированы в прямое произведение, дают представле-
представления группы Лоренца, задаваемые парой целых или полуцелых
чисел (А, В), которые действуют в пространстве BЛ -f- 1) BS -j-
+ 1) измерений.
Например, векторное поле 7*v преобразуется какАууТу, по-
поэтому с учетом C.157) и C.160) имеем
[2аРГ6 = баЧв-йрЧв. C-165)
что дает в соответствии с C.164) Л = '/г, В = у2. Таким обра-
образом, векторное поле может классифицироваться как неприводи-
неприводимое представление ('/2, '/г) группы Лоренца. Это поле имеет
спин '/г + 'А — 1-
Подобным образом находим, что скалярное поле, для кото-
которого очевидно Sap = 0, может быть отождествлено с неприводи-
неприводимым представлением @,0), т. е. с полем спина нуль. Тензорное

Квантовая теория поля в искривленном пространстве-времени 91
поле второго ранга преобразуется как Ау УА6йТу6, следовательно,
D(A) есть произведение двух преобразований D(A) для вектор-
векторного поля. Произведение представлений ('/2, ^/2)®{!/2, '/г) раз-
разлагается на четыре неприводимых представления A,1), A,0),
@, 1) и @,0). Поэтому тензорное поле содержит компоненты со
спинами 2, 1 и 0.
Наконец, для дираковского спинорного поля нужно выбрать
2ap = T[Ya, Yp], • C.166)
где у — матрицы Дирака, что ассоциируется с представлениями
('/г, 0) и @,'/г)—неприводимыми представлениями для спи-
спина 1/г-
Эту теорию можно обобщить на случай искривленного про-
пространства-времени, не теряя связи с группой Лоренца. Этого
можно достичь с помощью так называемого тетрадного форма-
формализма (см., например, [446, 494]), который легко может быть
приспособлен и для п измерений. Сущность такого подхода со-
состоит во введении нормальных координат уах в каждой точке
пространства-времени X. В терминах координат уах метрика в
точке X есть просто г]а$. В терминах более общей системы ко-
координат метрический тензор имеет более сложный вид, но свя-
связан с г\ар соотношением
^vW^O^vWv (зле?)
где величины
, o = 0, 1,2, 3,
образуют тетраду. Заметим, что индекс а относится к локально-
инерциальной системе координат, связанной с нормальными ко-
координатами уах в точке X, в то время как ц относится к общей
системе координат х^. В этом разделе индексы первого типа мы
будем обозначать начальными буквами греческого алфавита, а
индексы второго типа — буквами из второй половины того же
алфавита.
Так как общая система координат произвольна, можно рас-
рассматривать изменение х^, оставляя фиксированными уах. Тогда
величины Fa,i преобразуются как ковариантный вектор:
'?." C.168)
Очевидно, координаты t^x можно также подвергать преобра-
преобразованию Лоренца, зависящему от пространственно-временной
точки Х\
C.169)

92 Глава 3
В этом случае величины Уа^ преобразуются'как лоренцев кон-
травариантный вектор
V\(X) ^ A\(X)V\(X), C.170)
что, очевидно, оставляет метрику C.167) инвариантной.
Если общековариантный вектор Лц скалярно умножить на
Va11, то результирующий объект
при общих преобразованиях координат преобразуется как сово-
совокупность четырех скаляров, в то время как при локальных ло-
ренцевых преобразованиях C.169) он ведет себя как вектор. Та-
Таким образом, с помощью тетрады можно превращать общекоор-
общекоординатные тензоры в локальные преобразующиеся по Лоренцу
тензоры, перенося дополнительную координатную зависимость на
тетрадные векторы.
Если выражение C.159) записать схематически как ?)(Л)г|),
где ф —тензорное поле, то производные да$ также будут тен-
тензорными полями в пространстве Минковского. При преобра-
преобразованиях Лоренца daty переходит в Aap<D(A)dpiJ>. При переходе
к искривленному пространству-времени производную да можно
обобщить до ковариантной производной Va, но сохранить этот
простой закон преобразования для произвольных локальных ло-
ренцевых преобразований в каждой пространственно-временной
точке:
> Лар (х) D (Л (х)) УЭФ (х). C.171)
Этого можно достичь, определяя коварйантную производную со-
соотношением
Уа=^(<Зц + ГД C.172.)
где связность
Г, W = lEaVavw(^rF3v (я)); C.173)
здесь 2аР — генератор группы Лоренца, ассоциируемый с вы-
выбранным представлением D(A), по которому преобразуется i|),
а VPv = g^Vp.
Польза, которую можно извлечь из соотношения C.171), со-
состоит в том, что любая функция $ и Vai|>, являющаяся скаляром
при лоренцевых преобразованиях в пространстве Минковского,
остается скаляром при локальном преобразовании тетрады, рав-
равно как и при общих преобразованиях координат. Поэтому лаг-
лагранжиан поля может быть обобщен на случай искривленного
пространства-времени заменой производных да на Va и превра-

Квантовая теория поля в искривленном пространстве-времени 93
щением всех векторов, тензоров и т. д. в величины: Аа -> V^a^v-
и т. д.
Например, для скалярного поля г|) спин равен нулю и 2ар =
= 0, поэтому C.172) дает Va = да. Следовательно, лагранжиан
B.2) принимает вид
g (х) = 1 (_ gf (ца?Уа^фУ\д^ф - пг2ф2). C.174)
Множитель [—#(*)]''• = det(FaM.) введен для того, чтобы 3?(х)
было скалярной плотностью и соответственно чтобы действие
было скаляром. С учетом C.167) выражение C.174) сводится
к C.24) с ? = 0. Член IR в плоском пространстве-времени обра-
обращается в нуль; он является единственным геометрическим ска-
скаляром, который можно добавить в лагранжиан.
Плотность лагранжиана поля со спином 7г в пространстве
Минковского дается выражением B.45). В искривленном про-
пространстве-времени с учетом выражения C.166) для 2ар в C.173)
она принимает вид
S (х) = det V {1 i [WaX* ~ V<? <Vt>) Y4] - mw } =
' C.176)
где yv-= Vv-aya — зависящие от координат матрицы, представ-
представляющие собой обобщение дираковских матриц у на искривлен-
искривленное пространство, которые, как следует из C.167), удовлетво-
удовлетворяют соотношениям
(V", VV} = 2^v, C.177)
обобщающим B.46) на искривленное пространство-время.
Лагранжиан C.176), который также может быть использо-
использован в пространстве п измерений, является конформно-инвариант-
конформно-инвариантным в безмассовом пределе, если принять закон преобразования
C.178)
при преобразованиях C.1).
Варьирование действия 5 по г); приводят к ковариантному
уравнению Дирака
'Ац* — "*¦ = 0 C.179)
[23, 198,200,420].
Следующим является электромагнитное поле F^v, имеющее
спин 1. Выражение B.54), используемое в пространстве

94 Глава 3
Мннковского совместно с дополнительным членом, нарушающим
калибровочную симметрию, и лагранжианом духов, нужно обоб-
обобщить путем замены Аа на ^аЛд и д? на Va, где Гд определяется
формулой C.173). В этом случае Еар задается выражением
C.165) для представления ('/г,'/г) группы Лоренца. В резуль-
результате получим максвелловский лагранжиан
^(*)==-т(-?I/2/>^. C.180)
Г]х\== ^ц; v ^v; ц== ^ц, v "v, ц. C.181)
(вклады связностей сокращаются),, и нарушающий калибровоч-
калибровочную симметрию дополнительный член
?а = -уГ'С4%J. C.182)
Духовое поле описывается обычной скалярной плотностью ла-
лагранжиана (см, B.141))
(V. C.183)
Варьирование действия S = \ {ЗЕ + 9?Q) dAx по отношению к
А и, дает
^v;V + r1(^Viv);tl = 0» C-184)
ИЛИ
/ln:vV + /?nPy4p~A ~S~1)^v;(lv = 0. C.185)
Важно отметить, что эта теория является конформно-инвариант-
конформно-инвариантной только в случае четырех измерений.
Детальное обсуждение полей спина 1 в искривленном про-
пространстве-времени дано Шредингером [421], Паркером [383] и
Машуном [353].
Использованный выше метод обобщения теорий полей со спи-
спином 0, 7г и 1 на случай искривленного пространства-времени мо-
может быть применен также для полей произвольного спина. Такие
теории в плоском пространстве-времени исследовались, напри-
например, Дираком [160], Фирцем [195], Фирцем и Паули [196], а
также в работах [26, 165, 166, 456, 490—492] (см. также обзор
[364]).
Следствия теорий произвольного спина в. искривленном про-
пространстве-времени были рассмотрены, например, в работах [31,
38, 115, 117, 168, 182, 273, 349, 395]. Мы не будем здесь больше
касаться этого интересного направления.
Как и для скалярных полей, можно обобщить на случай ис-
искривленного пространства-времени функции Грина и соответст-
соответствующие уравнения для полей ненулевого спина. Например, фейн-

Квантовая теория поля в искривлённом пространстве-времени 95
мановские пропагаторы для спинов '/г и I по-прежнему будут
иметь форму B.80) и B.86) соответственно, но теперь они удо-
удовлетворяют уравнениям (ср. B.82), B.87))
= [-§(х)Г'1'Ьп(х- х'), C.186)
- A - Г') Vj<I Д? (x, xf) =
]4ttWl(x-x'), C.187)
которые выводятся с помощью C.179) и C.185) соответственно.
В случае спина '/г обобщение B.84) на искривленное простран-
пространство-время имеет вид
SF (x, x') = [*/ (х) V? + m] GF (x, x'), C.188)
где QF— би-спинор '), удовлетворяющий уравнению C.49) с | =
= 'Д и ?x = g*tv(*)V?V*, что следует из подстановки C.188) в
C.186).
Заметим, что, как и в скалярном случае, если не налагать гра-
граничных условий, дифференциальные уравнения для пропагаторов
не определяют состояний вакуума, фигурирующих в вариантах
выражений B.80) или B.86) для искривленного пространства-
времени. Эти граничные условия зависят от конкретной рассма-
рассматриваемой физической системы. Так же как и в скалярном слу-
случае, можно получить адиабатические разложения (де Витта —
Швингера) для пропагаторов. Для спина Уг такое разложение
было построено Банчем и Паркером [83] с помощью импульс-
импульсного представления, рассмотренного в предыдущем разделе. Ре-
Результаты для спинов Уг и 1 в рамках метода собственного вре-
времени де Витта — Швингера были получены Кристенсеном [114]
(см. также [5, 153, 158]). Отдельные члены (имеющие отноше-
отношение к конформным аномалиям, см. разд. 6.3) в адиабатических
разложениях пропагаторов полей высших спинов были получены
Кристенсеном и Даффом [115, 117] и Бирреллом [38].
В заключение отметим, что тензор энергии-импульса поля
произвольного спина в искривленном пространстве-времени мо-
может быть построен путем варьирования действия по метрике:
7Vv(*)= f_e(fe),.A bfp4x) = det[V(x)] 6V7W" 9)
(множитель (—g)~'/! введен для того, чтобы сделать эту вели-
величину тензором, а не тензорной плотностью). В частности,
*) Термин би-спннор (билинейная функция двух 4-компонентных спино-
спиноров) следует отли4ать от термина биспинор D-компонентный спинор). — Прим.
перев.

96 Глава 3
тензоры энергии-импульса полей 0, '/2 и 1 равны
^v (s - 0) = A - 2|) ф. ^. v
[т04) ] '*.«* (ЗЛ90)
T' l^Vv»^ - (V>) Y^*]. C-191)
T^ (s = 1) = С" + ^v + 7$x, C.192)
1 ppop p pp . /
0; op + j (^1P: PJ] }, C.194)
Эти выражения получены из C.189) с плотностями лагранжиа-
лагранжианов C.24) и C.176) для s —0 и s = '/« соответственно, а ре-
результат для спина 1 получен из суммы плотностей лагранжиа-
лагранжианов C.180), C.182) и C.183). При выводе выражений для спи-
спинов 0 и '/г результаты приведены к симметричной форме с по-
помощью соответствующих уравнений поля; в случае спинов 7s н
1 использовалось интегрирование по частям. Выпишем также не-
некоторые формулы варьирования, полезные при выводе приведен-
приведенных выше формул:
(- g)'>* =±(- gf fTug^,
Г ,v + 4,,, ov> (
6Vpa.

Глава 4
ПРИМЕРЫ ДЛЯ ПЛОСКОГО
ПРОСТРАНСТВА-ВРЕМЕНИ
После того как было потрачено столько усилий на построение
квантовой теории поля в искривленном пространстве-времени,
читатель, возможно, будет разочарован возвращением к плоско-
плоскому пространству. Однако плоское пространство еще не означает
пространство Минковского.
Здесь будут рассмотрены три основные ситуации, в которых
общий формализм квантовой теории поля в искривленном про-
пространстве-времени дает нетривиальные результаты даже, когда
геометрия является плоской. При этом удается исследовать но-
новые геометрические эффекты благодаря упрощениям, вносимым
плоским характером геометрии. В частности, в ряде случаев мо-
можно найти <Гцд,>, не прибегая к полной теории регуляризации и
перенормировок в искривленном пространстве, которая развита
в гл. 6.
Первый тип эффектов связан с нетривиальной топологией.
Здесь не будет обсуждаться рождение частиц, и рассмотрение бу-
будет касаться только (Т^У, который оказывается отличным от
нуля даже в состоянии вакуума. Это один из немногих случаев
рассматриваемой теории, когда имеется непосредственная связь
с экспериментом, поскольку возмущение электромагнитного ва-
вакуума, создаваемое двумя параллельными проводящими пласти-
пластинами, действительно наблюдаемо. Явление притяжения между
пластинами, получившее название эффекта Казимира, широко
обсуждалось в литературе.
Исследование эффектов, связанных с ограничивающими по-
поверхностями, приводит естественным образом к очень простой, но
крайне полезной модели, заслуживающей детального изучения.
Речь идет о «движущихся зеркалах» — модели, в которой поверх-
поверхности, ограничивающие квантованные поля, находятся в движе-
движении. Вследствие движения возникает рождение частиц, изучение
которого имеет важное эвристическое значение для понимания
рассматриваемых далее более сложных ситуаций. В частности,
испаряющиеся черные дыры имеют ряд черт, характерных для
модели движущихся зеркал определенного вида. Рекомендуем чи-
читателю детально разобраться в вычислении коэффициентов пре-
преобразования Боголюбова D.60), которые совпадают с соответ-
4 Зак. 674

98 Глава 4
ствующими величинами для черных дыр и поэтому их расчет не
повторяется в гл. 8.
Третий вопрос, на котором мы останавливаемся в этой главе,
также тесно связан с испарением черных дыр, но помимо этого
представляет и самостоятельный интерес. Он касается реакции
наблюдателя (детектора частиц), движущегося с постоянным
ускорением, на вакуум Минковского. Результат — тот факт, что
ускоренный наблюдатель воспринимает это состояние как запол-
заполненное излучением с тепловым спектром,— является весьма ин-
интригующим и проливает свет на взаимосвязь между горизонтами
событий, квантовой теорией поля и энтропией. Здесь также ос-
основное внимание сосредоточено на обсуждении преобразования
Боголюбова (последние три страницы данной главы). Хотя этот
вопрос может показаться несколько техническим, он (в особен-
особенности это касается аналитических свойств полевых мод) имеет
прямое отношение к черным дырам и заслуживает вниматель-
внимательного изучения.
4.1. Двумерное цилиндрическое
пространство-время
Простейшее обобщение квантовой теории поля в пространстве
Минковского состоит во введении в локально плоское простран-
пространство нетривиальной топологии. Наиболее просто такое обобще-
обобщение осуществляется в двумерном пространстве-времени /?' X S1
с компактными (замкнутыми) пространственными сечениями.
Расстояние в нем определено как в пространстве Минковского
C.8) или C.10), но пространственные точки х и x-\-L отождест-
отождествлены (L —длина периодичности — «длина окружности вселен-
вселенной») (рис. 10).
Вследствие замкнутости пространственных сечений полевые
моды B.11) ограничены дискретным множеством (ср. B.13)) ,
*fr-BLJ-V <**-«, D.1)
где k = 2nn/L, n = 0, ±1, ±2, .... В безмассовом случае ю =
= \k\ моды exp[ik(x — t)] с положительными значениями п
описывают волны, движущиеся слева направо, а Mojxhiexp[ik(x -f-
+ t)] с отрицательными п — волны, движущиеся справа налево.
При получении D.1) были наложены граничные условия пе-
периодичности Uk(t, x) = Uk(t, JC-f-nL). Можно также наложить
условия антипериодичности uk{t, х) — (—l)nuk(t, x + nL), что
снова приводит к модам D.1), но с k = 2п(п -\- l/2)/L, п = 0,
±1, ±2 .... В последнем случае скалярное поле можно связать
с сечением в расслоении, не являющимся прямым произведением;
его иногда называют скрученным (twisted) полем (см. [311]).

Примеры для плоского пространства-времени
99
Вследствие ограничения дискретным мно-
множеством мод энергия поля изменяется. В рас-
рассматриваемом двумерном случае с помощью
B.26) получаем декартовы компоненты тензо-
тензора энергии-импульса в виде
D.3)
дФ дФ
ki
Рис. 10. Двумер-
Будем вычислять <0t | Т^ 10L>, где |0L> —ва- ное пространство-
куум, ассоциируемый с дискретными модами ®Ремм„я спк°""^'
D.1). Это состояние, очевидно, удовлетворяет ственнымн сече-
условию |0i>->|0> при L —* оо, где |0>— ннями (^X-S1).
обычный вакуум пространства Минковского Длнна окружно-
(см. [221] по поводу неэквивалентности |0L) с™. . «или»ДРа
и |0t.> при ЪфЬ'). Р
Воспользовавшись B.43) и подставляя моды D.1), соответ-
соответствующие вакууму |0t>, получим выражение
@L \Ttt\0L} = ( 1/2L)
k | -
2) ? n,
re=0
D.4)
которое, очевидно, бесконечно. Этого и следовало ожидать, ибо
в пространстве Rl X S1 рассматриваемая система имеет те же
расходимости, что и в пространстве Минковского. Компактифи-
кация пространственных сечений может сказаться на низкоча-
низкочастотных модах, но поведение в ультрафиолетовой области не
должно измениться.
При расчете энергии вакуума в пространстве Минковского
(см. разд. 2.4) ультрафиолетовая расходимость устранялась с
помощью нормального упорядичения операторов рождения и уни-
уничтожения, связанных с модами B.11). Для произвольного со-
состояния |г|з> в фоковском пространстве нормальное упорядочение
сводится к вычитанию
- <0 |Гав 10),
D.5)
которое, в частности, обеспечивает равенство <0| :Гар:|О> = 0.
Если считать пространство Минковского накрывающим про-
пространством для R1 X S\ то |0i> можно рассматривать как одно
из возможных состояний в фоковском пространстве, порождае-
порождаемом модами B.11) [221], и для устранения расходимости в
<0l|7"<xp|0i> применить D.5). (Более строгое обоснование дано

100 Глава 4
в работе [320].) В частности,
@L |: Ttt :\0L)^@L\Ttt\0L)- <0|7-„|0> =
= Фь I Tti 10L) - lim Фи I Ttt I Or). D.6)
L'-*oo
Поскольку оба слагаемых в правой части D.6) расходятся по
отдельности, вычитание требует дополнительного исследования.
Подробное обсуждение дано в гл. 6. Здесь мы воспользуемся
процедурой, основанной на введении обрезающего множителя
e-aifti в расходящиеся суммы типа D.4), полагая а->0в конце
вычисления. Эта процедура получает оправдание в более стро-
строгом подходе, развиваемом ниже.
После введения обрезающего множителя сумма D.4) стано-
становится конечной и легко вычисляется:
Фь I Ttt 10L> = Bn/L2) ? ne-amn/L _ Bя/1
D.7)
Полученное выражение можно разложить в окрестности a = 0i
@l I Tti 10L> = A/2яа2) - (n/6L2) + О (а3).
В аналогичном виде можно представить и фи \ Ttt \ 0z/>- Тогда
lim @^|^|0г>=1/2яа2.
Подставляя эти выражения в D.6) и переходя к пределу при
a -*- 0, находим
С помощью аналогичных вычислений можно показать, что
<Ql\:TIx:\0l>^0.
Хотя величина <Гар> для каждого из состояний |0> и \0L}
расходится, разность между двумя расходящимися суммами ока-
оказывается конечной. Таким образом, если потребовать, чтобы
<0|: Та$ :|0> = 0, то состояние \0L} будет обладать конечной от-
отрицательной плотностью энергии
D.8)
и давлением
P = <0L|:r^:|0L) = -n/6L2. D.9)
Эта отрицательная вакуумная энергия распределена с одинако-
одинаковой плотностью в пространстве Rl 'X S1 и соответствует полной
энергии —n/6L.

Примеры для плоского пространства-времени 101
Аналогично можно рассчитать энергию вакуума для скручен-
скрученного поля [311]. Вместо D.7) в этом случае имеем
= 2 [2n/BLJ] ? ne-2nan/BL) _ Bл/?2) ? пе-2ла^, D.10)
где вторая строчка получается с учетом того, что сумма по не-
нечетным п равна сумме по всем п минус сумма по четным п. По-
Последний член в D.10) совпадает с суммой D.7), взятой с обрат-
обратным знаком, а предыдущий член — с удвоенной суммой D.7), в
которой следует заменить L на 2L. Поэтому конечную часть р
можно получить непосредственно из формулы D.8) в виде
р = - 2л/6 BLJ + n/6L2 = n/\2L2. D.11)
Энергия вакуума для скрученного скалярного поля оказывается
равной половине соответствующей энергии для нескрученного
поля, взятой с обратным знаком.
Наконец, для безмассового поля со спином 7г с помощью со-
соотношений B.51) и C.191) в плоском пространстве-времени на-
находим [139]
Фь 17"nv I °i> — Yl Z Z I6*- s'Vdi.^w*, s — d{vvk, s\v,wft. s], D.12)
±s ft
откуда, воспользовавшись формулами B.48) и B.50), получаем
<0L ITH |0L) = - A/21) ? jy (*, s) v (k, s) -
±s ft
— (8ji/L2) ? n (нескрученное поле),
— Bn/L2) Y* I 2n + 1 | (скрученное поле).
D.13)
В обоих случаях результат равен просто соответствующему ре-
результату для скалярного поля, умноженному на минус четыре.
Спинорные скрученные поля могут быть введены тем же спо-
способом, что и скалярные [13, 14, 312]; вакуумная энергия для них
была рассчитана в случае различных топологий в работах [20,
159]. В работах [13, 14] доказывается, что в большинстве про-
пространств с нетривиальной топологий, для которых производящий

102 Глава 4
вакуумный функционал Z@,0) (см. B.129)) инвариантен отно-
относительно преобразований Лоренца C.170) тетрады, необходимо
включать в рассмотрение как спинорные нескрученные поля, так
и скрученные поля. Таким образом, скрученные поля следует
рассматривать не как математический курьез, а как поля, вы-
выступающие наравне с обычными.
4.2. Использование функций Грина
Вместо того чтобы непосредственно вычислять тензор энер-
энергии-импульса Tjxv D.2), D.3) и использовать некоторую обрезаю-
обрезающую функцию при суммировании по модам, результаты преды-
предыдущего раздела можно получить более изящным способом с по-
помощью функций Грина, введенных в разд. 2.7.
При вычислениях удобно использовать изотропные коорди-
координаты и и v C.9). Соответствующие компоненты Т^(и, v) для
безмасеового скалярного поля в двумерном случае имеют про-
простой вид
Тии*=ФиФУ> D.14)
Tvv = (djf, D.15)
TUv *= Tvu — ~2 диФ^иФ- D.16)
Имеют место соотношения
Ти — Т + Tv + 2Г„ , D.17)
Т — Ти + Т ^-2Ти , D.18)
т —т —т т /д 1 о\
* IX XI W UU' \~* Ai7/
Из формул D.14) и B.66) следует
<0? I Тии (и, v) | (k) = lim lim ди«ди-1 ?>?> {и", v"; и', v'), D.20)
о", »'->» и", и'-* и л
где введен индекс L у Dw, чтобы показать, что эта функция вы-
вычисляется в состоянии вакуума JOz.> пространства R1 X S1, по-
построенном в предыдущем разделе. (Напомним, что через D обо-
обозначают функции Грина для безмассовых полей.) Выражение
D.20) приведено к форме, симметричной относительно замены
(и", v") иа (и', v'). Можно также построить «термодинамическое
состояние» |Pl> при температуре T = (kB$)~ с помощью термо-
термодинамической функции Грина ?>!% (обобщая B.111) на случай
пространства Rl X S1) вместо D{l:
причем D.21) сводится к D.20) при |3->-оо (Г-*-0).

Примеры для плоского пространства-времени 103
Построим сначала функцию Грина при нулевой температуре,
воспользовавшись модами D.1). Получим
Dt} (и", v"; и!, vf) = <0д | {ф [и", v"), ф (и', v')} \ 0L) =
оо
= ? ["*(""> v")u\(u'< v') + компл. сопр.] =
со
где Au = u"~ u', Av = v" — v'. При выводе D.22) бесконеч-
бесконечный член с п = 0 в сумме был опущен. Эта инфракрасная рас-
расходимость (при нулевой частоте) является особенностью безмас-
безмассового поля в двумерном пространстве-времени. Опущенный член
в любом случае исчезает при дифференцировании в D.21), если
оно проводится до перехода к безмассовому пределу.
Поскольку показатели экспонент в D.22) чисто мнимые,
сумма абсолютно не сходится. Функцию Грина D(l следует оп-
определить более точно в смысле обобщенных функций; этот воп-
вопрос рассмотрен в работе [76]. Здесь мы ограничимся введением
в показатель экспоненты бесконечно малой вещественной части
соответствующего знака, чтобы сделать сумму абсолютно сходя-
сходящейся. В рассматриваемых ниже случаях эта операция оказы-
оказывается достаточной.
Выполнив суммирование в D.22), находим
DlV. v"; и', y')' = -(l/4:*)ln[16sin2^Au/L)sin2(nAy/L)]. D.23)
Для скрученного скалярного поля функция D{i определяется
выражением во второй строке в D.22) с заменой п на п + Уг-
(Заметим, что в этом случае инфракрасная расходимость отсут-
отсутствует.) Получаем
?>Г (и", v"; uf, v') = - A/4я) In [tg2 (я A«/2L) tg2 (я Av/2L)]. D.24)
Термодинамическая функция Грина может быть теперь по-
построена по известной D(l в результате суммирования с по-
помощью соотношения B.111):
оо
О2!р«= —A/4я) ? \п {16 sin2 [л (Аи+ im$)/L]X
X sin2 [я (Аи + imf>)jL\ (нескрученное поле), D.25)
In {tg2 [я (Аи -j- in
ГП** — оо
X tg2 [я (Аи +/mP)/2L]} (скрученное поле). D.26)

104 Глава 4
Слагаемое cm = 0 представляет собой функцию Грина D^l при
нулевой температуре.
Тензор энергии-импульса теперь строится с помощью D.21):
Wl\Tuu\$l)= Hm [-
-\-(n/2L2) Yi sh~2(nmP/L) (нескрученное поле),
m=l
оо
~{n/8L2) ? [ch~2(nmP/2L) + sh(nmP/2i.)] (скрученное поле).
В пределе нулевой температуры (р-»-оо) остаются только
первые, (не зависящие от т) члены. Как и следовало ожидать,
они расходятся как (Д«)~; в пределе Ды-»-0. Это соответствует
бесконечной энергии вакуума. Для перенормировки нужно вы-
вычесть
@1 Тиа 10) «= Hm (Ох, | Таа 10L) = - 1/4я А«2.
L-»oo
Переходя к пределу при Ды->0, получаем конечный результат
— (nfl2L2)-\-(n/2L2) ^sh~2(nm$/L) (нескрученное поле),
!
D.27)
(n/24L2) + (n/8L2) S [ch2 2]
1
(скрученное поле).
Из симметрии /Э^р относительно замены ы на v немедленно
следует
(pjruJPL>. D.28)
Учитывая также, что М^р можно представить в виде суммы
функции, не зависящей от v, и функции, не зависящей от и, с по-
помощью D.16) находим
<Ptir«.lPt>-<Pi.l*\,elPx.>-0. D.29)
Тогда с учетом D.17) получаем, что плотность энергии выра-
выражается величинами D.27), умноженными на два, что согласуется
6 пределе нулевой температуры (р-»-оо) с формулами D.8) и
D.11).

Примеры для плоского пространства-времени 105
4.3. Влияние границ
До сих пор мы ограничивались многообразиями без границ.
Но, даже если пространство само по себе не имеет границ, кван-
квантованное поле может быть ограничено некоторой областью бла-
благодаря присутствию материальных ограничивающих поверхно-
поверхностей. Например, для электромагнитного поля такие ограничения
могут возникать при наличии проводящих поверхностей. Это от-
открывает реальную возможность лабораторной проверки некото-
некоторых геометрических эффектов, характерных для квантовой тео-
теории поля в искривленном пространстве.
Как отмечалось в предыдущем разделе, вакуумное ожидание
тензора энергии-импульса Т^ формально расходится даже в слу-
случае плоского пространства-времени. Если топология нетривиаль-
нетривиальна, разность вакуумных средних для данной топологии и три-
тривиальной топологии оказывается конечной и не равной нулю.
Подобным же образом проводящие поверхности изменяют топо-
топологию полевых конфигураций, что также приводит к ненулевым
вакуумным средним тензора энергии-импульса.
Рассмотрим сначала безмассовое скалярное поле, на кото-
которое наложено условие исчезновения на бесконечной плоскости в
неограниченном четырехмерном пространстве Минковского [156,
157] (граничные условия Дирихле). Благодаря отражению от по-
поверхности, в качестве которой выберем плоскость х3 = 0, поле-
полевые моды не будут иметь форму B.5). Вместо этого следует ис-
использовать функции
sin I kz | х8е|*«*+"л-й|1, D.30)
которые обращаются в нуль при х$ = 0. Соответствующее ваку-
вакуумное состояние также изменится.
Вместо выражения B.79) для функции Грина с помощью ме-
метода изображений найдем следующее представление:
)- ъ?\ о, - *о
- *зJ - и -
(, \уB 4) Од2 -и- f
Эта функция обращается в нуль при Хз —0 и л:з = 0. Первый
член в {4.31) совпадает с функцией Грина в пространстве Мин-
Минковского, он имеет квадратичную расходимость при х-+х'; по-
после дифференцирования для получения <0|7^|0> D.31) будет
давать расходимость четвертого порядка. Влияние границы мо-
можно выделить путем вычитания из D.31) выражения B.79) для
функции Грина неограниченного пространства Минковского,
иначе говоря, путем отбрасывания первого слагаемого. Остаю-

106 Глава 4
щийся член в пределе х-*-х' остается конечным. Его следует
теперь подставить в четырехмерный аналог формулы D.20).
С помощью B.27), например, получаем (т = 0)
@ |Г„ 10>, - Iim 1(<V<V + d,fx[ + дфг + дф^ X
t, X,, Х2,
X [?>J}> (*", *') - D<» (*", *')] = - 1/16я2х*. D.32)
Аналогично @\Тн\ 0}в = + A6я2х34)~! (все другие компоненты
равны нулю).
Вдали от границы (я3->оо) вакуумные средние, как и следо-
следовало ожидать, обращаются в нуль. Однако вблизи нее они суще-
существенно изменяются. Более того, величина D.32) расходится на
границе (хз->-0). Интегрирование по всему пространству приво-
приводит к бесконечной энергии вакуума на единицу площади гранич-
граничной поверхности, несмотря на то что мы уже вычли из <Г^> бес-
бесконечную энергию вакуума в пространстве Минковского.
Нетрудно понять причину появления этой бесконечной по-
поверхностной энергии. Функция Грина D.31) построена так, что
на границе х3 = 0 она обращается в нуль, даже когда х-+х'.
С другой стороны, функция ?>A)(*, х'), задаваемая выражением
B.79), очевидно, обращается в бесконечность на границе при
х ->¦ х'. Поэтому при попытке сделать функцию Грина конечной
путем вычитания последнего выражения из первого, разность
также становится расходящейся на границе. Из формулы D.31)
видно, что второе слагаемое действительно расходится при Хз =
= 0, когда х-+х'. Таким образом, простое вычитание бесконеч-
бесконечных членов, ассоциируемых с безграничным пространством Мин-
Минковского, позволяет избавиться от расходимости четвертого по-
порядка всюду, кроме точек на границе, где эта расходимость
остается в виде члена *з.
Из этих рассуждений ясно, что бесконечная поверхностная
энергия будет возникать всегда, если требовать исчезновения
поля на граничной поверхности, независимо от ее формы. Однако
из того, что величина Db1 — D(U расходится на границе, не обяза-
обязательно следует существование расходимости <Г^>, поскольку
эта последняя величина получается из первой после выполнения
довольно сложных операций.
Чтобы исследовать этот вопрос подробнее, выясним общий
вид тензора <7Vv> в окрестности единственной плоской границы
при х% = 0 [157]. Из соображений симметрии ясно, что этот тен-
Зор может быть построен из г)^ и ЦЦ, где Ц— единичный век-

Примеры для плоского прЬстранбтва-времени
тор, нормальный к границе. Более того, он может зависеть толь-
только от х%. Следовательно,
<7Г> = /(*3)тГ + ?(*з)«- D-33)
Если наложить ковариантное условие сохранения (см.
разд. 6.3)
cV<rv> = 0, D.34)
то можно прийти к выводу, что fug могут различаться только
на постоянную. Таким образом, правая часть D.33) должна
иметь вид
где а — постоянная. След этой величины равен 3g (x3)-{-4а.
Если потребовать, чтобы тензор энергии-импульса имел нулевой
след, то получим g(xs) = —4а/3 = const. Поскольку перенор-
перенормированный тензор эиергии-импульса вакуума должен обра-
обращаться в нуль вдали от границы, эта постоянная должна быть
равна нулю. Следовательно, перенормированные вакуумные сред-
средние Ту.ч обращаются в нуль для поля, тензор энергии-импульса
которого имеет нулевой след. Это справедливо для электромаг-
электромагнитного поля и безмассового нейтринного поля, но не для без-
безмассового скалярного поля с Т^, задаваемым формулой B.26).
В разд. 3.2 отмечалось, что в искривленном пространстве-вре-
пространстве-времени скалярное уравнение может содержать дополнительный
член \R. Соответствующий оператор тензора энергии-импульса
определяется формулой C.190). Даже в случае плоского про-
пространства-времени формула C.190) не сводится к B.26), если
| ф 0. (Этот любопытный факт становится менее удивительным,
если вспомнить, что Т^ получается с помощью варьирования
метрики g^v в лагранжиане поля; поэтому даже в пределе g\iv-*-
-> ri^., к которому следует перейти в конце вычисления, остается
вклад в 7Vv от члена lR<j>2 в C.24).) При выборе значения | =
= '/б, соответствующего конформно-инвариантному скалярному
уравнению, след Т^ обращается в нуль:
0=т) = т *. Л. v - т
Г%«=0. D.36)
Иногда выражение D.35) называют «новым улучшенным
тензором энергии-импульса» [86, ПО]. В этом случае и для ска-
скалярного поля <0| 7Vv|0> = 0 вблизи плоской границы.

108 Глава 4
Хотя из приведенных соображений следует, что для конформ-
конформно-инвариантного поля при наличии плоской границы бесконеч-
бесконечная энергия вакуума отсутствует, этот вывод существенно связан
с симметрией граничной поверхности. Если граница искрив-
искривлена, бесконечная поверхностная энергия появляется вновь. Мо-
Можно показать, что в общем случае вблизи искривленной границы
[151, 323]
<7Vv> ~ е~ V + О (е-*)
для конформно-инвариантного поля, где е — (малое) расстояние
до граничной поверхности, a %nv — ее вторая фундаментальная
форма. Мы вернемся к обсуждению этого вопроса и выяснению
физического смысла бесконечной поверхностной энергии в
разд. 6.6.
Ограничиваясь здесь рассмотрением конформно-инвариант-
конформно-инвариантных полей и плоских поверхностей, обобщим задачу на случай,
когда имеется несколько таких поверхностей. Вакуумная энергия
электромагнитного поля, заключенного в области между двумя
параллельными отражающими плоскостями, была вычислена Ка-
Казимиром [102]. Ограничения, накладываемые условиями сохра-
сохранения и обращения в нуль следа, приводят к выражению •
где А — постоянная, а плоскости считаются ортогональными x$.
Из соображений размерности А ~ а~4, где а — расстояние ме-
между плоскостями. Расчет [102] показывает, что
Л = -я2/180а4 D.37)
для вакуумного состояния.
Постоянная А отлична от нуля, так как присутствие гранич-
граничных плоскостей делает полевые моды дискретными по кванто-
квантовому числу, ассоциируемому с направлением х3. В этом случае
поле испытывает такую же топологическую деформацию, что и
в модели fl'XS1, рассмотренной в разд. 4.1, и постоянная А мо-
может быть вычислена тем же методом. Другой способ состоит в
нахождении функции Грина D{b в виде бесконечной суммы по
изображениям (соответствующим бесконечному числу отраже-
отражений между плоскостями).
В случае скалярного поля
-** - Ч>2 - (* - * У
D-38)
н - <2 -Ь-

Примеры для плоского пространства-времени 109
обращается в нуль при хъ или *з = 0 и хъ или х'г = а; что и тре-
требуется в задаче. Бесконечная энергия вакуума устраняется пу-
путем отбрасывания слагаемого с п = 0. Воспользовавшись далее
выражением D.35), находим
г 1 0 0 Он
-я2
<°I^vI0)b=1440^
0-1 0 0
0 0-10
L0 0 0 3-
D.39)
в декартовых координатах. Коэффициент в D.39) равен поло-
половине соответствующей величины для электромагнитного поля, по-
поскольку скалярное поле имеет вдвое меньше мод (одно поляри-
поляризационное состояние вместо двух).
Если квантованное поле находится не в чистом вакуумном
состоянии, а при конечной температуре Г, то можно заменитьD{b
в D.38) термодинамической функцией Грина, т. е. заменить ? — f
на t — f — imp (где |i = \/kBT) и просуммировать по всем m
от —оо до +°°- Соответствующая плотность энергии между пла-
пластинами равна
[л2 + 4?2т2]*
т, п=\
и g = ?вГа. В пределе малых значений произведения Та темпе-
температурная поправка к плотности энергии равна (кТ)%C)/2ла, где
? — дзета-функция; для больших Та поправка имеет вид
A/30)я2(?ГL. Для электромагнитного поля соответствующие
значения в два раза больше; подробные вычисления можно най-
найти в работе [66].
Существование вакуумных натяжений между параллельными
граничными поверхностями приводит к появлению силы притя-
притяжения между двумя электрически нейтральными проводящими
поверхностями. Расчет Казимира (см. D.37)) дает для силы,
приходящейся на единицу площади поверхности, выражение F =
= —дЕ/да = —я2/B40а4). Возникающие благодаря этому меха-
механизму силы были измерены экспериментально (см., например,
[438, 447]). «Эффект Казимира» явился предметом многочислен-
многочисленных исследований; особенно подробный анализ проведен в рабо-
работах [18, 19, 339].
Другая задача с плоскими граничными поверхностями была
рассмотрена в работах [151, 178]; для вакуумных средних тен-
тензора энергии-импульса конформного скалярного поля в области
клиновидной формы между двумя наклонными плоскостями было

по
Глава 4
получено выражение
1
1440л4о2
/ Л2 О*_\
v о2 "я5";
-1
0
0
-0
0
-1
0
0
0
0
3
0
0-
0
0
1 -
где а — угол между плоскостями, г — расстояние от линии пере-
пересечения до рассматриваемой точки; для пространственной части
тензора использованы цилиндрические координаты.
Для случая электромагнитного поля получено выражение
[151]
~а* + П) ("о5" ~~ Ч
-1
0
0
-0
0
-1
0
0
0
0
3
0
о-
0
0
-1 -
В обоих случаях конечный результат можно получить с по-
помощью обычной процедуры вычитания бесконечных вакуумных
средних, вычисляемых в безграничном пространстве Минков-
ского1).
4.4. Движущиеся зеркала
Во всех рассмотренных выше примерах системы были стати-
статическими, поэтому вносимые возмущения квантовых состояний
приводили к появлению поляризации вакуума, но не к рождению
частиц. Если параллельные пластины, описанные в предыдущем
разделе в связи с эффектом Казимира, заставить быстро дви-
двигаться, то возникнет необратимое изменение энтропии и между
пластинами появятся новые кванты. Частицы будут рождаться,
даже если движется одна отражающая пластина (зеркало).
Мы рассмотрим эту задачу подробно для двумерного случая,
когда можно использовать конформную тривиальность ситуации.
Явных примеров для четырехмерного пространства довольно ма-
мало [93, 95, 590*—592*]. Мы будем следовать здесь работам [135,
224].
Предположим, что зеркало (которое в двумерном случае вы-
вырождается в точку) движется вдоль мировой линии
х = *(*), 14@ К 1, 2@ = 0,
D.40)
1) Эффект Казимира с учетом реальных граничных условий на поверх-
поверхности металлов (диэлектриков) рассматривается в работе [589*]. — Прим.
пврев.

Примеры для плоского пространства-времена
111
Рис. 11. Излучение от движу-
движущегося зеркала. Скалярное по-
поле удовлетворяет нулевому
граничному условию на грани-
границе x = z(t). Изотропные лучи,
выходящие из Zf~, такие, как
Y, отражаются от зеркала и
уходят в 9+. Волны, отражен-
отраженные после момента времени
/ = 0, испытывают доплеров-
скнй сдвиг частоты вследствие М' \ х
движения зеркала.
Безмассовое скалярное поле ф, удовлетворяющее волновому
уравнению
и граничному условию отражения
ф (t, г @) = 0, D.42)
имеет следующий набор решений:
ujj1 (и, v) = I DжоГ1/2 {е~ш - е'ш Bт«-и)), D.43)
где со= |&| и значением» определяется
D.40) из уравнения
для мировой линии
D.44)
Решения D.43) справедливы в области справа от зеркала. Вхо-
Входящие (распространяющиеся налево) волны e-"*v соответствуют
стандартным экспоненциальным решениям всюду между 2f~
(рис. 11) и поверхностью зеркала, но волны, распространяющие-
распространяющиеся направо (отраженные) имеют более сложный вид из-за доп-
леровского сдвига при отражении от движущегося зеркала. Эта
асимметрия между и и v соответствует условию запаздывания
(отсутствуют кванты, приходящие из Sf~).
В области справа от зеркала поле ф с граничным условием
D.42) можно разложить по модам D.43):
f at (uf) ] D.45)
k>0
И ввести in-вакуум с помощью соотношения
D.46)

112 Глава 4
Это состояние и моды D.43) выбраны в качестве «входящих»,
поскольку при t ^ 0 зеркало находится в покое в точке 2 = 0
в системе координат (и, v). Тогда ти = и, и D.43) сводится к
выражению
uin = / Dлсо)-'/г (е~Ше - еШи) = (жо)'1'' sin (ахе'ш, (< 0, D.47)
которое является положительно-частотным по отношению ко
времени t Минковского.
Состояние |0, in> может рассматриваться как не содержа-
содержащее частиц при t < 0. Действительно, функция Вайтмана в in-
области имеет вид
(in,
«= — A/4л) In [(Ди - ie) (До - ie)/(v - и' — ie) {u — vf- /e)], D.48)
где Аи = и — и', &v = v — v' и t, t' •< 0. Подставив D.48) в
C.55), нетрудно убедиться в том, что, несмотря на более слож-
сложный вид аргумента под знаком логарифма, инерциальный детек-
детектор частиц, движущийся вдоль мировой линии C.52), который
адиабатически выключается вне in-области, не будет регистри-
регистрировать частиц. Присутствие зеркала не будет возбуждать детек-
детектор, даже если зеркало движется по отношению к детектору с
постоянной скоростью.
Если зеркало в течение некоторого периода времени движется
ускоренно (t > 0), полевые моды при и > 0 будут искажаться
по сравнению со стандартной формой D.47), принимая общий
вид D.43). Таким образом, движущееся зеркало выполняет ту
.же роль, что и изменяющаяся геометрия пространства-времени
(т. е. гравитационное поле). Заметим, однако, что функция
2%и — ив D.43) остается неизменной вдоль изотропного луча
и = const от поверхности зеркала до ЗГ+. Искажение мод проис-
происходит внезапным образом (при отражении), а не постепенно в
течение времени, когда происходят возмущения геометрии, как
это было в гравитационном случае.
Рассмотрим часть решения D.43), соответствующую волне,
движущейся направо, ехр[—коBти—и)]. В области и •< 0 эта
функция сводится к стандартному выражению егШи, поэтому при
t <C 0 она ассоциируется с обычным физическим вакуумным со-
состоянием, задаваемым соотношением D.46). С другой стороны,
в области и > 0 это уя--е не будет обычная плоская волна, рас-
распространяющаяся направо. Поэтому состояние |0, in> в этой об-
области уже будет не состоянием физического вакуума, а состоя-
состоянием, содержащим частицы. Таким образом, доплеровское
искажение, описываемое более сложной экспонентой в D.43),со-
D.43),соответствует возбуждению полевых мод и рождению частиц. С фи-
физической точки зрения это означает, что движущееся зеркало

Примеры для плоского пространства-времени 113
рождает частицы, уходящие направо вдоль изотропных лучей
и = const.
Чтобы убедиться в физической реальности этих частиц, про-
проанализируем показания инерциального детектора частиц в обла-
области и > 0. Функция Вайтмана в состоянии in-вакуума имеет вид
D+(u, v; и', о') =
= - A/4я) In [(р (и) - р («') - 1в) (v-v'- ie)/(v - р («') - ie) X
X(pM-v'-ie)], D.49)
где принято
/?(ы) = 2т„ — и. D.50)
Для функции x(t) и, следовательно, р(и) общего вида фурье-
образ выражения D.49) отличен от нуля, поэтому при подста-
подстановке D+ в формулу C.55) получаем ненулевое значение отклика
детектора.
В качестве примера рассмотрим движение зеркала по закону,
задаваемому в асимптотической области выражением
z (/)-> - / - Ае-ы + В, t-*oo, D.51)
где А, В, к— положительные постоянные. Поведение этой функ-
функции в более ранние моменты времени оказывается несуществен-
несущественным для вычисления потока частиц в асимптотической области
f->oo. Пример мировой линии, которая сшивается гладким об-
образом (С) со статической мировой линией при t <c 0 дает функ-
функция z(t) = — ln(ch xt).
Класс траекторий D.51) представляет особый интерес по-
потому, что отражение от зеркала испытывают только лучи ср<
<С В. Все лучи с v > В распространяются без возмущения в ле-
левую часть 3f+ (рис. 12). Поэтому луч с v = B представляет со-
собой линию горизонта, причем расположенные эквидистантно лу-
лучи с постоянным и при их продолжении в направлении ?Г~ обра-
образуют семейство линий, сгущающихся к горизонту v — В. В гл. 8
мы увидим, что аналогичная картина имеет место при коллапсе
звезды с образованием черной дыры.
Из формул D.44) и D.51) находим
ы->оо. D.52)
Предположим, что детектор движется по закону
= const. D.53)
Выражение D.49) для D+ можно переписать в виде суммы четы-
четырех слагаемых, факторизуя аргумент под знаком логарифма.
Если в качестве р(и) подставить выражение D.52) и возникаю-
возникающую при этом функцию D+ использовать в формуле C.55),

114
Глава 4
Рис. 12. Мировая линия зеркал z(/) =• — t — Ae-™t + В асимптотически при-
приближается к изотропному лучу v = В. Поверхности постоянной фазы из 9+
при больших значениях времени (эквидистантные изотропные лучи и = const)
после отражения от зеркала сгущаются около линии v = В. Опережающие
(движущиеся влево) лучи, мировые линии которых лежат правее прямой
v = В, не встречаются с зеркалом. Излучение, возбуждаемое из вакуума при
таком движении зеркала, имеет тепловой спектр при больших значениях
времени.
определяющей отклик детектора (в предположении адиабатиче-
адиабатического включения при Малых значениях времени), то три из этих
слагаемых обращаются в нуль. Остающийся член, в который вхо-
входит разность р(и') — р{и), приводит к выражению
ff~ (?)/(ед. времени) =
D.54)
m-l
С помощью тождества
оо
sh х = х JJ (тп — ix) (тп + ix)/(mnf
и соотношения
J ( -Рей
1пШ

Примеры для плоского пространства-времени 115
где y — постоянная Эйлера, правая часть D.54) приводится к
виду
(.п.. о
Изменив порядок интегрирования, получаем сумму двух дельта-
функций, лишь одна из которых дает вклад в интеграл пою,при-
пою,приводя к выражению
&"{Е) в единицу времени = , ?/йдГ г-> D.55)
Е\е — \)
где
kBT = (и/2я) [A - w)l{\ + w)]\ D.56)
Этот результат означает, что детектор воспринимает постоян-
постоянный поток частиц от зеркала, распространяющийся в направле-
направлении и и имеющий тепловой спектр с температурой D.56). Множи-
Множитель [A — ш)/A + w)Yk дает доплеровский сдвиг, возникаю-
возникающий из-за движения детектора со скоростью w по отношению к
излучению (красное и голубое смещение температуры). Если де-
детектор покоится относительно выделенной системы отсчета, в ко-
которой зеркало неподвижно на начальной стадии процесса (т. е.
w = 0), то
D.57)
Тепловая природа потока излучения от зеркала, движущегося
по закону D.51), может быть также установлена путем непосред-
непосредственного вычисления коэффициентов боголюбовского преобразо-
преобразования между in- и out-модами. Решения м'йп D.43) имеют про-
простой вид на Э', ио после отражения от зеркала они становятся
сложными функциями на Зг+. С другой стороны, можно ввести
моды u?ut, представляющие собой плоские волиы на 3f+, но
сложные функции в in-области, т. е. на Э~. Преобразование Бо-
Боголюбова между u'fen и u°kut может быть рассчитано для любой про-
странственноподобной поверхности; для асимптотически изотроп-
изотропной траектории D.51) удобно вычислять коэффициенты преоб-
преобразования при / = 0 в in-области. Тогда моды ы'й" имеют простой
вид D.47), а функции u°kui — более сложную форму.
Для нахождения вида функций м?и* при t = 0 заметим, что
стандартные движущиеся вправо плоские волны е~'ши иа 9+ при
продолжении назад по времени и отражении от зеркала в in-об-
ласть имеют форму волн, распространяющихся влево с более
сложной зависимостью от v, а именно г'"'!'1, Волны е~ш\ соот-
соответствующие более поздним моментам времени и, имеют на Э~

116 Глава 4
форму волн, движущихся влево, причем соответствующие лучи
сгущаются к изотропной асимптоте v = В. Поэтому f(v) будет
быстро меняющейся функцией v в этой области. Из соображе-
соображений симметрии ясно, что функция f обратна функции р D.52);
это означает, что
f{v) ¦x-4n[{B-v)/A] — B, v<B, D.58)
в области V-+-B. Волны, движущиеся влево в области v > В,
нас здесь не интересуют, так как они остаются невозмущенными
вплоть до &+ и не дают вклада в тепловое излучение. Поэтому
можно положить u?ut = 0 при v ^ В.
Таким образом, достаточно вычислить коэффициенты преоб-
преобразования Боголюбова между uj," и той частью u°kui, которая со-
соответствует волнам e~imu, движущимся вправо по направлению
к У+, т. е. частью e~itofiv) в области v < В. Воспользовавшись
формулами C.36), выражающими эти коэффициенты через ска-
скалярные произведения (п = и1" и и = uout), вычисляем интегралы
при t = 0 и v = В. После интегрирования по частям находим
ч В
„"'* } = ±Bя)~' *(а>7в>)'А [ e±{<*fW-Wx dx. D.5^)
Поскольку функция f(x) быстро изменяется в окрестности точки
х = В, основной вклад в интеграл дает именно эта область; по-
поэтому в D.59) опущен граничный член при х = 0. Можно также
использовать асимптотическую формулу D.58) для аппроксима-
аппроксимации функции f(x) в D.59) при всех значениях х. Получаемые при
этом выражения для коэффициентов Боголюбова хорошо аппро-
аппроксимируют поток излучения при поздних временах (больших и)
в out-области. После этих упрощений интеграл может быть явно
вычислен в терминах неполных Г-функций. Более того, поскольку
быстро меняющаяся форма волны в окрестности точки v = В
соответствует высоким частотам, можно положить м'->оо и вы-
выразить коэффициенты через обычную Г-функцию:
где D = угЧпА — В. Отсюда следует, что
где keT определяется формулой D.57). Этот результат согласует-
согласуется со спектром излучения D.55).

Примеры для плоского пространства-времени 117
Заметим, что величина
оо
5 fWW D.62)
логарифмически расходится. Дело в том, что ускорение зеркала
продолжается бесконечное время, а поток излучения не зависит
от времени, поэтому в каждой моде накапливается бесконечное
число квантов. Результат можно представить в форме плотности
квантов на интервале с?со в единицу времени, если вместо пло-
плоских волн рассматривать волновые пакеты. Мы вернемся к об-
обсуждению этого вопроса в гл. 8.
В качестве другого примера расчета коэффициентов Бого-
Боголюбова для движущихся зеркал рассмотрим гиперболическое
движение зеркала назад с постоянным ускорением. Зададим за-
закон движения в виде
-(B2 + t2)y\ t>0,
<4вз>
где В — постоянная. Качественно этот случай не отличается от
изображенного на рис. 12; здесь также имеется изотропная
асимптота v = В. При продолжении out-решений назад во вре-
времени к точке t = О для !)<В возникает зависимость вида
e-«<af(o)_ Поэтому для расчета коэффициентов Боголюбова можно
по-прежнему использовать выражение D.59), беря в качестве
f (х) функцию, соответствующую траектории D.63). Повторяя
приведенные выше рассуждения, находим f(x) = Вх/(В — х),
откуда следует
«V» = I (В/п) е-1 «¦>+<*'> ВК\ B1В (<о»')'А). D.64)
Р*. = (В/л) е' «¦>-<¦>'> % B5 (ако'I/2), D.65)
где /Ci — модифицированная функция Бесселя. Мы вернемся к
этому примеру в разд. 7.1.
Оказывается возможным также подробно исследовать рожде-
рождение частиц в области между двумя движущимися зеркалами
[224,365].
4.5. Квантовая теория поля
в пространстве Риндлера
В двух из рассмотренных выше примеров детектор регистри-
регистрирует излучение с тепловым спектром. В разд. 3.3 было показано,
что движущийся с постоянным ускорением детектор восприни-
воспринимает обычное пространство Минковского, как термостат, запол-

118 ' Глава 4
ненный излучением, а в предыдущем разделе было установлено,
что инерциальный детектор регистрирует тепловой поток излу-
излучения от зеркала, движение которого описывается формулой
D.51). С физической точки зрения эти две ситуации различны,
и обычно считается, что во втором случае тепловое излучение яв-
является в некотором смысле более реальным, чем в первом. Это
подтверждается вычислением (Т^} для обоих случаев (см.
разд. 7.1). Но, несмотря на различный физический статус, эти
два примера тесно связаны геометрически. Конформное преобра-
преобразование, «выпрямляющее» мировую линию D.51), одновременно
превращает прямолинейную траекторию инерциального детек-
детектора в гиперболическую [135].
Тепловое излучение, воспринимаемое в равномерно ускорен-
ускоренной системе отсчета, можно описать совершенно другим спосо-
способом, проливающим свет на тесную связь между понятием кванто-
квантовой частицы и причинной и топологической структурой простран-
пространства-времени, что важно при обсуждении квантовых черных дыр.
(Подробности, относящиеся к материалу настоящего раздела,
можно найти в работах [89, 128, 221, 222, 293, 466, 468].)
Рассмотрим двумерное пространство Минковского с метрикой
C.8) или C.10), т. е.
ds2 = dudv = dp — dx2. D.66)
(Черта над буквами п, v, обозначающими изотропные коорди-
координаты в пространстве Минковского, введена для того, чтобы отли-
отличить их от величин, используемых далее.) Под действием коор-
координатного преобразования
r\, D.67)
* = a-'eschar), D.68)
а = const > 0 и —оо < т), | < оо, или, что то же самое,
п = -а~]е-аи, D.69)
v = a-{ea°, D.70)
где и = г) — I. ^ = ч + 1> выражение D.66) принимает вид
ds2 = e2a| du dv = e2al {drf - df). D.71)
Координаты (т), |) покрывают лишь один квадрант простран-
пространства Минковского, а именно клин х > \t\, изображенный иа
рис. 13. Линии постоянного г) — прямые (х ~ t), а линии по-
постоянного | — гиперболы
= const D.72)

Примеры для плоского пространства-времени
119
Рис. 13. Координаты Риндлера в про-
пространстве Минковского. В областях
R и L линии, отвечающие постоянной
временной координате ц = const, —
прямые, проходящие через начало ко-
координат, линии | = const — гипербо-
гиперболы (соответствующие мировым лини-
линиям равноускоренных наблюдателей),
имеющие изотропные асимптоты
п = О, v = 0, которые играют роль
горизонтов событий. Четыре области
R, L, F и Р должны быть покрыты
отдельными картами. Координаты
Риндлера неаналитичны при п = 0 и
v = 0.
Они представляют собой мировые линии равноускоренных на-
наблюдателей, таких, как в разд. 3.3. Сравнение C.62) с D.72) по-
показывает, что
ае-а\ = а = собственное ускорение. D.73)
Таким образом линии, отвечающие большим положительным |
(вдали от точки х = t = 0), соответствуют слабо ускоренным
наблюдателям, в то время как гиперболы, близко подходящие к
точке х = t = 0, соответствуют большим отрицательным | и,
следовательно, большому ускорению. Все гиперболы асимптоти-
асимптотически приближаются к изотропным лучам п = 0, v = 0 (или
и = оо, v = —оо), что означает стремление скорости наблюдате-
наблюдателей к скорости света при т)-»-±оо. Собственное время ускорен-
ускоренных наблюдателей т связано с | и т) соотношением
х = еа^г]. D.74)
Координаты (т), I) образуют систему координат Риндлера [404],
а часть пространства Минковского Jt^li1! известна как ринд-
леровский клин. Равномерно ускоренных наблюдателей иногда
называют риндлеровскими наблюдателями.
Второй клин Риндлера х < 11 \ можно получить, отражая
сначала ось t, а затем ось х. Для этого достаточно изменить
знаки в правых частях уравнений преобразования D.67) — D.70).
Будем обозначать левый и правый клинья через L и R соответ-
соответственно. Заметим, что изменение знаков координат в L означает
изменение направления времени: возрастание t соответствует
убыванию tj.
Интересна причинная структура клина Риндлера. Поскольку
риндлеровские наблюдатели (находящиеся при постоянном зна-
значении пространственной координаты |) приближаются, но не пе-
пересекают изотропных лучей и = оо, у = —оо, эти лучи являются

120
Глава 4
Призонт
S-const
Рис. 14. Конформная диа-
диаграмма системы Риндлера.
Области R, L, F и Р на диа-
диаграмме имеют вид ромбов.
Временнподобная линия | =
= const пересекает &*, а
не /*. Ясно, что события в
области L не могут быть на-
наблюдаемы нз R, поэтому
изотропный луч п = 0 (и =
= оо) играет роль горизон-
горизонта событий.
горизонтами событий. Например, никакое событие в L нельзя на-
наблюдать из R и наоборот, так как события в L могут быть свя-
связаны с событиями в R лишь мировыми линиями, являющимися
на некотором участке пространственноподобными. Поэтому об-
области L и R представляют собой две причинно не связанные все-
вселенные. На рис. 13 отмечены также остающиеся области буду-
будущего (F) и прошлого (Р). События в Р и F могут быть связаны
изотропными лучами с событиями в L и R.
Эта причинная структура может быть также изображена на
конформной диаграмме Пенроуза, как показано на рис. 14. Ринд-
леровские наблюдатели пересекают 9±, а не i-, как асимптоти-
асимптотически инерциальные наблюдатели. Поэтому изотропный луч и =
= оо является горизонтом событий будущего, а события в обла-
области F не могут быть причиной событий в имеющей форму ромба
области R.
Обратимся к квантованию безмассового скалярного поля в
двумерном пространстве Минковского. Волновое уравнение
i D.75)
дпдО
имеет стандартные ортонормированные решения в виде плоских
волн
мА = Dяоо) !ге D.76)
(т. е. B.11) при п = 2), где ю = |й|> 0 и —оо < k < оо. Эти
решения являются положительно-частотными по отношению к

Примеры для плоского пространства-времени 121
времениподобному вектору Киллинга dt, т. е. они удовлетворяют
уравнению
D.77)
Решения при k > О представляют собой волны
{4ла)-ч'еш, D.78)
движущиеся направо вдоль лучей п = const, а решения при
k < 0 — волны, движущиеся налево вдоль v = const
Dяи)-'/ге-'™. D.79)
Вакуумное состояние Минковского |0м> и соответствующее про-
пространство Фока получаются в результате разложения ф по мо-
модам пи, как было объяснено в разд. 2.2.
В риндлеровских областях R и L можно принять другой спо-
способ квантования, основанный на использовании не мод пк, а их
риндлеровских двойников ик. Метрика D.71) конформна всему
пространству Минковского, так как при конформном преобра-
преобразовании g».v -> e~2a%g)s.\ выражение D.71) сводится к drf — dt?
при —оо •< т), | •< оо. Поскольку волновое уравнение конформ-
конформно-инвариантно, мы можем переписать его в координатах Ринд-
лера (см. C.150)) в виде
а соответствующие решения представить в виде
uk = Dяга) /!еь , co = |ft|>O, — оо < ft < оо. D.81)
Верхний знак в D.81) относится к области L, а нижний — к
области R. Изменение знака можно понимать как обращение
направления времени в L либо как выражение того, что волна,
движущаяся в области R направо, переходит в область возра-
возрастающих %, в области L такая же волна перемещается в область
убывающих g. В любом случае моды D.81) удовлетворяют усло-
условию ортонормированности C.29). Они являются положительно-
частотными по отношению к времениподобному вектору Кил-
линга -f C,1 в R и — дт, в L, удовлетворяя уравнению
2±д uk = — iauk D.82)
(в R и L соответственно) вместо D.77).
Совпадение функционального вида D.81) и D.76) есть след-
следствие конформной тривиальности системы (пространство Ринд-
лера конформно пространству Минковского, а волновое урав-
уравнение B.1) конформно-инвариантно).

122 Глава 4
Введем функции
( Dлсо)-'/2 е'«-*»ч в области R,
4=1 « * D-83)
* (.0 в области L, ч '
( Dлч>)-'1гет+1т в области L,
Ч = I * n D-84)
* 1.0 в области R.
Набор решений D.83) является полным в риндлеровской об-
области R, в то время как набор D.84) — полным в области L, но
ни один из них в отдельности не полон во всем пространстве
Минковского. Однако оба набора вместе образуют полную си-
систему в пространстве Минковского, причем линии ц = const, пе-
пересекающие обе области, являются поверхностями Коши для
всего пространства-времени. Поэтому моды D.83) и D.84)
можно аналитически продолжить также в области F и Р [59,
60] (а становится мнимым). Таким образом, риндлеровские
моды оказываются столь же пригодными в качестве базиса при
квантовании поля ф, как и обычные моды D.76) в пространстве
Минковского.
Квантованное поле можно представить в виде разложения по
любому набору
ф= Z (ukuk + atuk) D.85)
ft--oo
(см. B.17)) либо
*- Z (b(l)Luk + b(rLUk + bf«uk + b(rRuk), D.86)
6--00
что приводит к двум различным фоковским пространствам и
двум вакуумным состояниям |0ж> и |0«> (индексы М и R соот-
соответствуют пространствам Минковского и Риндлера), которые
определены соотношениями
D.87)
0. D.88)
Неэквивалентность этих вакуумных состояний следует из
структуры риндлеровских мод D.81). Вследствие изменения
знака в показателе экспоненты при « = fJ = 0 (точка «перекры-
«перекрытия» областей L и R) функции RUk не переходят гладким обра-
образом в Luk при переходе из R в L. Это означает, что при переходе
отк<0кн>0 (или от v <. 0 к v > 0) моды, распространяю-
распространяющиеся вправо (или влево), не аналитичны в этой точке. В про-
противоположность этому положительно-частотные моды Минков-
Минковского D.78) и D.79) аналитичны не только на вещественной

Примеры для плоского пространства-времени 123
оси п (или v), но являются аналитическими и ограниченными
функциями во всей нижней полуплоскости комплексной пере-
переменной п (или v). Это свойство аналитичности остается спра-
справедливым для любых положительно-частотных решений, т. е.
любых линейных комбинаций положительно-частотных мод
Минковского. Поэтому риндлеровские моды в силу их неанали-
неаналитичности при ы = п = 0 не могут быть линейной комбинацией
лишь положительно-частотных мод Минковского, но должны
также содержать примесь отрицательных частот. Напомним, что
перемешивание положительных и отрицательных частот, как
было показано в разд. 3.2, означает, что вакуум не может быть
тем же самым, т. е. вакуум, связанный с одним набором мод,
содержит частицы, ассоциируемые с другим набором решений.
Чтобы выяснить, какие из риндлеровских частиц присут-
присутствуют в вакууме Минковского, нужно построить преобразование
Боголюбова между двумя наборами решений. Это можно сде-
сделать, воспользовавшись выражениями C.36), представляющими
собой по существу фурье-образы риндлеровских мод. Другой,
более изящный способ, предложенный Унру [468], основан на
наблюдении, что хотя Luk и *ы* неаналитичны, две (ненормиро-
(ненормированные) линейные комбинации
*. D-89)
D.90)
аналитичны и ограничены для всех вещественных п и v и всюду
в нижних полуплоскостях комплексных переменных п и v.
Чтобы убедиться в этом, перепишем D.89) и D.90) в коорди-
координатах Минковского, в которых эти выражения оказываются про-
пропорциональными
йш1а, k>0,
€-<°><а, k<0, D'91)
vi<ala, k > 0,
(со = |&[) соответственно для всех п, V в области от —оо до оо
(т. е. как в L, так ив/?); они явно аналитичны и в точке п =
= v = 0. Они также аналитичны в нижних полуплоскостях
комплексных переменных н и 5, если выбрать разрез по пере-
переменным, стоящим в показателях степеней в D.91) и D.92), ле-
лежащим в верхней полуплоскости (т. е. 1п(—1)= —/я, что опре-
определяет знаки показателей экспонент е±яи'а в D.89) и D.90)).
Поскольку моды D.89) и D.90) обладают теми же аналити-
аналитическими свойствами, что и моды Минковского пи, ассоциируемое
с ними вакуумное состояние должно совпадать с [0ж> (см.

124 Глава 4
замечание на с. 53). Таким образом, вместо D.85) поле ф мож-
можно разложить по величинам D.89) и D.90):
+ df {е~ш12а.V_» + еп<л/2аLuk)} + эрмит. сопр., D.93)
где операторы уничтожения теперь удовлетворяют соотношениям
Л1) 42)|0Л1> = 0 D.94)
и введен нормировочный множитель. Операторы 6*'2) можно
связать с операторами dk } с помощью скалярных произведе-
произведений (ф, Ruk), (ф, Luk), подставляя сначала ф, заданное разложе-
разложением D.86), а затем разложением D.93). Получаем
[2 sh (nco/a)]-1'' [e^^df + e'^dV *], D.95)
r}. D.96)
Эти преобразования Боголюбова определяют искомую связь
между состояниями |0«> и [0м>.
Рассмотрим теперь ускоренную риндлеровскую систему от-
отсчета при I = const, Из соотношения D.74) видно, что собствен-
собственное время в такой системе пропорционально ц. Поэтому для
риндлеровских наблюдателей вакуумным состоянием будет
10«>, ассоциируемое с положительно-частотными модами по
отношению кт). Таким образом, согласно D;86), риндлеровский
наблюдатель в L (соответственно в R) будет обнаруживать
частицы, для которых оператор числа квантов есть btf^btf (со-
(соответственно bi^b^). Если поле находится в состоянии |0ai>
(т. е. лишено обычных частиц в пространстве Минковского), то
воспользовавшись соотношениями D.95) и D.96) можно пока-
показать, что риндлеровский наблюдатель обнаружит
(Ом I bl-2) 41-2) | ОМ) = <Г™'7[2 sh (ясо/а)] = (е*™'а - l) D.97)
частиц в состоянии k. Это выражение представляет собой в точ-
точности планковский спектр для излучения при температуре 7"о =
= a/2nkB. Температура Т, воспринимаемая ускоренным наблю-
наблюдателем, дается соотношением Толмена
T = (g00V'/'To D.98)
(см., например, [335, 460] или [17]). Здесь goo—компонента
метрики D.71), в которой ускоренный наблюдатель имеет по-
постоянную пространственную координату.. Воспользовавшись со-
соотношениями D.73) и D.98), получим Т «= l/BnakB) в точном

Примеры для плоского пространства-времени 125
согласии с формулой C.68), найденной для ускоренного детек-
детектора в пространстве Минковского. Частицы, обнаруживаемые
таким наблюдателем, часто называют риндлеровскими части-
частицами. Квантовая теория поля для ускоренных наблюдателей и
соответствующие термодинамические эффекты рассмотрены с
большой общностью в работе [416]. Возможные физические
эффекты исследованы в работах [25, 207].
Здесь предсказывается тепловой спектр частиц с точки зре-
зрения ускоренного наблюдателя в плоском пространстве, но с по-
помощью конформного преобразования можно получить такой же
тепловой спектр для инерциального наблюдателя в искривлен-
искривленном пространстве. В этом состоит так называемый эффект Хо-
кинга (гл. 8).

Глава б
ПРИМЕРЫ ДЛЯ ИСКРИВЛЕННОГО
ПРОСТРАНСТВА-ВРЕМЕНИ
Эта глава посвящена прямым применениям квантовой теории
поля в искривленном пространстве-времени, развитой в гл. 3.
Рассматривается рождение частиц зависящими от времени гра-
гравитационными полями на примерах различных расширяющихся
и сжимающихся космологических моделей. Большинство моде-
моделей относится к типу однородных изотропных пространств Ро-
бертсона — Уокера, выбор которых обусловлен либо их просто-
простотой, либо стремлением проиллюстрировать определенные аспек-
аспекты формализма.
Здесь приведены все основные случаи, которые рассматри-
рассматривались в литературе. Вселенная Милна (с технической точки
зрения плоское пространство) и пространство де Ситтера осо-
особенно полезны при выяснении роли принципа адиабатичности в
приписывании некоторому квантовому состоянию физического
содержания. Пространство де Ситтера замечательно также тем,
что это единственная космологическая модель с зависимостью
от времени, для которой удается явно рассчитать всеми извест-
известными методами как рождение частиц, так и поляризацию ва-
вакуума (что отложено до разд. 6.4).
Небольшой, но важный разд. 5.5 посвящен классификации
и установлению соотношений между вакуумными состояниями
в пространствах, связанных конформными преобразованиями.
Этот вопрос также имеет отношение к «тепловым» аспектам
теории. Мы будем возвращаться к нему при вычислении <7'liV>
в пространствах Робертсона —Уокера в гл. 6 и 7.
Последний раздел представляет собой попытку выхода за
рамки простых моделей Робертсона — УОкера; он относится к
анизотропной космологии. Этот вопрос — один из центральных
в современной космологической теории, поскольку наблюдаемая
высокая степень изотропии вселенной не имеет адекватного
объяснения. Здесь теория снова входит в контакт с реальным
миром, хотя и довольно ограниченным и модельно-зависимым
образом. Представляется вероятным, что квантовое рождение
частиц играло важную роль в формировании состава и опреде-
определении физического состояния первичной космологической мате-
материи. Более того, обратное воздействие квантовых эффектов на

Примеры для искривлённого Нространства-времени 12?
гравитационную динамику, обсуждаемое в гл. 6 и 7, играло
важную роль в сглаживании первичной анизотропии. Возникаю-
Возникающая в результате энтропия, определяемая квантовыми части-
частицами, остается и сейчас, что приводит к наблюдаемым ограни-
ограничениям на квантовые модели ранней вселенной.
5.1. Пространства Робертсона—Уокера
Большинство примеров, рассматриваемых в этой главе, отно-
относится к полям в пространствах Робертсона — Уокера специаль-
специального вида. Эти пространства важны, поскольку соответствующие
космологические модели хорошо согласуются с наблюдениями.
Пространства Робертсона —Уокера с плоскими пространствен-
пространственными .сечениями обсуждались в разд. 3.4—3.6. Мы начинаем со
сводки основных соотношений для них и далее проводим обоб-
обобщение на случай гиперболических и сферических пространствен-
пространственных сечений. Рассматриваются скалярные поля, обобщение на
поля высших спинов может быть проведено аналогично тому,
как это сделано в разд. 3.8.
Элемент длины для n-мерных пространств Робертсона —
Уокера с плоскими пространственными сечениями имеет вид
t l\ E.1)
Разложение поля ф по модам C.30) записывается в виде
ф(х)=\ dn~xk [акик (х) + at ик (х)} E.2)
Моды можно представить после разделения переменных в виде
An>Vk<2)/4h), E.3)
-\ у/*
где fc = |k| = (?fcjl , з. %k удовлетворяет уравнению
-$- + {k2 + С (Л) [т2 + (| -1 (n)) R (л)]} X* = 0, E.4)
1(п)^\[(п~2)/(п-1)}. E.5)
Условие нормировки C.29) сводится к условию на вронскиан
решений х4
хДх;-Х*Лх*-*\ E.6)
Эти соотношения нетрудно обобщить на случай, пространств Ро-
Робертсона — Уокера с искривленными пространственными сечения-
сечениями. Для простоты ограничимся четырехмерными пространства-
пространствами; уравнения, которые допускают обобщение на произвольное

128 Глава 5
число измерений, могут быть найдены в работе [21]. Элемент
длины Робертсона — Уокера в общем случае имеет вид
ds2 = dt2-a2{t) E hudx'dx', E.7)
где
? h,i dx' dx1 = A - Кг2)'' dr- + r2 {dtf + sin29<ty2) =
d2 f2()B + 2Qd42) E.8)
sinx,
= \ X. 0<X<°°, K^O, E.9)
Выражение E.8) дает элемент длины для гиперболического,
плоского и замкнутого пространственных сечений при К = —1,
О, 1 соответственно. Вводя C(r\) = a2(t), где г| —параметр кон-
конформного времени, задаваемый выражением
-'(ОЛ'. E.10)
можно переписать элемент длины E.7) в форме
? hudx'dx1.). E.11)
Вводя величины Т = A —Кг2)~} и D = С/С, где точка обо-
обозначает производную по л. запишем отличные от нуля символы
Кристоффеля для метрики E.11) (индексы 0, 1, 2, 3 соответ-
соответствуют т), г, 9, ф соответственно) в виде
= /-Г,
22 = Г?з=1/г, E-12)
r23==ctg9.
С помощью E.12) можно вычислить ненулевые компоненты
тензора Риччи и скалярную кривизну:
(o.l о)
11111' r R\i> А33== sin 6a22>
| ] E.14)

Примеры для искривленного пространства-времени 129
Скалярное поле ф удовлетворяет уравнению C.26) с R, да-
даваемым формулой E.14). Его разложение по модам можно
представить в виде
Ф{х) = J dp(k)[ak«k (х) + atul(x)], E.15)
где мера р(&) будет определена ниже. Разделение переменных
осуществляется следующим образом:
'их)хк(ц), E.16)
где х = (г, 9, ф) или (х, 9. Ф), a Vv (х) — решение уравнения
Л(Х (х) = № - К) <Ук (х). E.17)
В E.17) АC) — лапласиан в трехмерном пространстве с метри-
метрикой Л//:
C) '
h — det(ft//). При этом функции х* удовлетворяют уравнению
E.4) при п = 4, (|D)='/в)- Далее, если функции fyk норми-
нормировать соотношением
J <ЛсЛ*<Ук (х) ук, (х) = б (к, к'), E.19)
где б (к, к') — дельта-функция по отношению к мере ii:
k') = / (k), E.20)
то условие нормировки C.29) снова сводится к E.6).
Собственные функции Щк трехмерного лапласиана имеют
вид [390]
(В,ф), k = (k,J,M) (К =
где
— оо < k{ < оо, k = \k\ (К = 0),
M=—J, —/+ 1 /;
'io, I;;;;; J<i;<rli2 (?i-u. <5-22>
Здесь Yf — сферические гармоники. Функции П'"^ определены
соотношением (см., например, [21, 163])
E.23)
5 Зак. 674

130 Глава 8
Функции ПИ' (х) можно получить из Пи/' (х) заменой k на — ik
и х на —fX (CM-> например, [340]).
В соответствии с этими определениями мера Д (k) задается
следующим образом:
E.24)
I.M
В заключение заметим, что пространственную часть разложе-
разложения по модам можно также записать в полиномах Гегенбауэра
вместо функций П(+) (см., например, [202]).
5.2. Статические пространства
Робертсона — Уокера
Простейшими примерами, к которым можно применить полу-
полученные выше соотношения, являются статические пространства,
для которых С(ц) = с =* а2 = const. Статическое пространство
с плоскими пространственными сечениями (К = 0) есть, конеч-
конечно, пространство Минковского, которое мы не будем более здесь
рассматривать. Рассмотрим случай замкнутой (К— 1) эйнштей-
эйнштейновской вселенной [188] и случай статического пространства-
времени с гиперболическими пространственными сечениями
(К = -1).
Для этих пространств скалярная кривизна F.14) сводится к
E.26)
что позволяет сразу записать нормированные решения уравне-
уравнения F.4) в четырехмерном случае:
E.26)
где
©I = k2 + И2 = k2 + cm2 + F1 - 1) К. F.27)
Из соотношения E.10) следует, что т) == t/a, поэтому решения
E.26) являются положительно-частотными по отношению к век-
векторам Киллинга дц и dt. Поскольку пространства статические и
имеют глобальные времениподобные векторы Киллинга, опре-
определение частиц здесь столь же однозначно, как и в пространстве
Минковского. В частности, используя E.16) и E.26) для по-
построения положительно-частотных решений
ик (х) = Bс(о,)-'л Щк (х) e-'W E.28)

Примеры для искривленного пространства-времени 131
в разложении E.15), определяем вакуумное состояние |0> тре-
требованием
ак|0) = 0. E.29)
Можно ожидать, что этот вакуум будет физически аналогичен
вакууму в пространстве Микковского; в справедливости этого
предположения можно непосредственно убедиться, рассматри-
рассматривая детекторы частиц. Функция Вайтмана в эйнштейновской
вселенной вычислена Даукером [167] (см. также [77, 124, 174]),
который получил
G+ (х, х') — 8пс sin (Дх) X
(*Х + 2яя) flf> {у. [(At) - Uf
nk~ [<Ат,-*е)>-(Ах+ *«)«]*
E.30)
где Н — функция Ханкеля. Здесь, как обычно, введены обозна-
обозначения
Дх=»х-х'. Дл = л-тГ E.31)
и без потери общности, ввиду изотропии пространства, оси коор-
координат выбраны так, что ф = ф', 9 == 9'. Функция Вайтмана пред-
представляет собой сумму положительно-частотных вайтмановских
функций в пространстве Минковского (ср. B.77)). Используя
это обстоятельство, нетрудно показать с помощью C.55), что
детектор, находящийся в покое в системе координат (х> ^Т. не
будет регистрировать частиц.
Для последующих приложений отметим, что в предельном
случае безмассового поля с конформной связью (m-»-0, l-^'/e.
следовательно, ц-*-0) выражение E.30) сводится к
времени была вычислена Банчем [70]:
. E.32)
Функция Вайтмана для безмассового скалярного поля с кон-
конформной связью в статическом гиперболическом пространстве-
F.83)
для массивного поля при произвольном | можно получить
—I).
(8.84)

132 Глава 5
Здесь опять сходство с вайтмановской функцией в пространстве
Минковского гарантирует, что детектор, находящийся в состоя-
состоянии покоя в системе (х, л), не будет регистрировать частиц.
Если пространство-время не статическое, решения уравнения
E.4) построить трудно; это удается выполнить только в спе-
специальных случаях или с помощью приближенных методов. Од-
Однако для безмассового поля с конформной связью можно сразу
записать решения, воспользовавшись конформной инвариант-
инвариантностью уравнений поля; они будут иметь вид E.28), где с сле-
следует заменить на С(г\). Это аналогично пространственно-пло-
пространственно-плоскому случаю, рассмотренному в разд. 3.7, а получаемые таким
путем решения, как и в разд. 3.7, являются положительно-ча-
положительно-частотными по отношению к конформному вектору Киллинга дп.
С помощью построенных таким путем мод можно без труда
найти функции Грина в состоянии конформного вакуума. На-
Например, для /(=±1, функция G+ в состоянии конформного
вакуума получается заменой с на d>(г\) С»(if) в E.32) и E.33).
5.3. Вселенная Милна
Случай пространства Робертсона — Уокера с a(t)=:t пред-
представляет особый интерес не только потому, что для него, су-
существуют точные решения уравнения конформно-нетривиаль-
конформно-нетривиального поля (тфО), но и потому, что он проливает свет на при-
природу соотношения между конформным и адиабатическим
вакуумами [69, 70, 76, 136, 225].
Четырехмерное гиперболическое пространство-время са(/) =
= t (известное как вселенная Милна [359]) и его двумерный
аналог в действительности являются лишь необычной коорди-
координатной формой плоского пространства-времени, подобной
системе Риндлера (разд. 4.5). Тем не менее, как и в случае систе-
системы Риндлера, модель Милиа приводит к нетривиальным кванто-
квантовым эффектам и проясняет особенности однородных расширяю-
расширяющихся космологических моделей с К = 0 и 1 (которые уже не
являются просто замаскированными плоскими).
Элемент длины двумерного пространства Милна имеет вид
ds2 — dt2 - аН2 dx2 = в*«ч (drJ - dx2), E.35)
де |/| ==а~1еач, a — достоянная. С помощью преобразования
координат
'V E.36)
выражение E.35) приводится к виду
ds2 = {dy*f - W?> 0<y°<oo, -oo<t/I<oo E.37)
(рис. 151.

Примеры для искривленного пространства-времени
133
Рис. 15. Вселенная Милна. Координа-
Координаты t, х покрывают клин в простран-
пространстве Минковского, соответствующий
области F на рис. 13. Эта область
представляет собой наружную часть
риндлеровского клина. Линии х =
= const, выходящие из начала коор-
координат, — мировые линии наблюдате-
наблюдателей, которые видят изотропное рас-
расширение вселенной после большого
взрыва в начале координат.
Волновое уравнение для массивного поля с | = 0 и С =
имеет решения в функциях Бесселя и Ханкеля, из которых мож-
можно построить два полных набора ортонормированных мод
{йк, йк} и {кк, кк} в форме E.3) с функциями %k вида
X, = [Bа/я) sh (лк/а)Г'<> I _Ща (mt),
?ш№) (*>0).
E.38)
E.39)
Эти два полных набора связаны между собой преобразованием
Боголюбова
Х* = «Л + РД;. E-40)
где
/a)\<°, E.41)
откуда видна аналогия со случаем Риндлера (ср. E.41) с
D.96)).
Из соотношения E.40) следует, что состояние |0>, опреде-
определяемое с помощью C.32) и C.33) по отношению к модам пк,
не эквивалентно состоянию 10>, определяемому по отношению
к модам «к- Поэтому снова возникает вопрос: какому вакууму
следует отдать предпочтение?
Вопрос несколько проясняется с помощью перехода к без-
безмассовому пределу в E.38):
*'**/Bк)\ E.42)
где 8 — некоторая не зависящая от ц фаза. Ясно, что в безмас-
безмассовом случае x,ft является положительно-частотной функцией по
отношению к конформному времени ц, поэтому |0> может быть.

134 Глава 5
отождествлено в этом пределе с состоянием конформного ва-
вакуума (разд. 3.7).
Воспользовавшись интегральным представлением для функ-
функции Ханкеля в E.39), можно записать [225]
«к (х) = (8я2а)~'/! [ йре-ш (р) «V(р) yYikpla, E.43)
— 00
где у0 и у1 определяются формулами E.36) и введены величины
Очевидно «к есть суперпозиция положительно-частотных мод по
отношению ко времени у° в пространстве Минковского [161,
437]. Поэтому, если пространство E.35) погрузить в двумерное
йространство Минковского, вакуум |0>, определенный по отно-
отношению к модам «к, будет совпадать с обычным вакуумом Мин-
Минковского. Далее, поскольку сопутствующий наблюдатель имеет
собственное время t, он не будет обнаруживать частиц в этом
состоянии.
Другое важное свойство мод иу выясняется при сравнении
их с положительно-частотными адиабатическими модами, осно-
основанными на соотношении C.102) (которое в случае конформной
связи остается справедливым и для двух измерений). В нулевом
порядке
что после подстановки в C.105) дает, величину
Ясно, что частота ю* становится большой по сравнению с произ-
производными от С/С = О(Т~1) (при фиксированном t)i = r\/T), если
k, m, г\ возрастают по отдельности или вместе.
В пределе больших х\
что при подстановке в C.102) дает
>! т]->оо E.45)
(индекс А указывает, что это соотношение справедливо с точ-
йостью до любого адиабатического порядка; все поправки выс-
высших порядков исчезают при т]->оо). С другой стороны, восполь-
воспользовавшись асимптотическим разложением функций Ханкеля,
легко показать, что (с точностью до постоянного фазового мно-
множителя) в пределе больших ц (б.ольщих \t\) выражение F.39)

Примеры для искривленного пространства-времени 1^5
сводится к E.45). Можно также проверить, что в пределе боль-
больших k или больших k и m E.39) совпадает с соответствующим
пределом C.102).
Таким образом, моды Кк оказываются положительно-частот-
положительно-частотными по отношению к определению, данному в разд. 3.5 на
основе принципа адиабатичности, а вакуум |0> является адиа-
адиабатическим вакуумом бесконечного порядка. Поэтому в данном
случае адиабатическое определение положительно-частотных ре-
решений естественным образом согласуется с определением в про-
пространстве Минковского. Более того, инерциальный детектор ча-
частиц не только не будет обнаруживать квантов с точностью до
любого конечного адиабатического порядка, но и вообще не
будет регистрировать в этом вакуумном состоянии никаких
частиц.
Поскольку инерциальный детектор не обнаруживает частиц
в состоянии |0>, из соотношения E.40) ясно, что он должен
регистрировать частицы в состоянии |0>. Применительно к без-
безмассовому случаю это означает, что сопутствующий детектор
регистрирует частицы в конформном милновском вакууме, чего
и следовало ожидать почти для любого конформного вакуума
(разд. 3.7).
Наличие частиц в состоянии конформного вакуума можно
выявить и другим способом — путем вычисления среднего зна-
значения тензора энергии-импульса в этом состоянии <0[Г^у|0>.
Чтобы выполнить это строго [136], необходимо использовать
методы регуляризации и перенормировок, излагаемые в следую-
следующей главе и применяемые к этой задаче в разд. 7.1. Однако и
без использования этих методов можно вычислить конечную раз-
разность средних значений Т„.ч в состояниях [0> и [0>. В безмас-
безмассовом пределе получаем [69, 76]
_ I) dq = - l/24nt2, E.46)
где использованы коэффициенты E.41).
Далее можно воспользоваться тем, что вакуум |0> эквива-
эквивалентен обычному вакууму Минковского, поэтому перенормиро-
перенормированное (нормально упорядоченное) среднее <0[Г«[0> должно
быть равно нулю, и, следовательно^ выражение E.46) дает пере-
перенормированное среднее значение <0|Г«|0>. (Этому утверждению
удается придать более строгий смысл в гл. 6.) Таким обра-
образом; конформный вакуум обладает отрицательной плотностью

136 Глава 5
энергии излучения с планковским спектром при температуре
Bnt)~l. Соотношение между этими двумя вакуумными состоя-
состояниями, следовательно, вполне аналогично соотношению между
вакуумами Минковского и Риндлера вплоть до термодинамиче-
термодинамических ассоциаций.
Этот явный пример хорошо иллюстрирует физическое разли-
различие между состояниями адиабатического и конформного ва-
куумов. Различие становится менее удивительным, если вспом-
вспомнить, что первый строится на основе анализа поведения поля
в пределе больших масс, в то время как второй связан с кон-
конформной симметрией в безмассовом пределе.
В случае четырехмерного (/(=—1) пространства Милна
ситуация аналогична. Выражения E.38) и E.39) по-прежнему
дают решения уравнения поля для конформной связи (| = '/6).
Состояния |0> и |0> также являются адиабатическим и кон-
конформным (в безмассовом пределе) вакуумными состояниями
соответственно. В действительности подобные результаты имеют
место и для моделей с К = О и 1 при a(t)= t, несмотря на то
что для выяснения смысла состояния |0> уже нельзя обращаться
к связи с пространством Минковского.
Модель с К = 0 иллюстрирует любопытное явление, касаю-
касающееся безмассового предела в состоянии адиабатического ва-
вакуума. В этом случае уравнение E.4) сводится к
_1+[6 + F|-1)а]х* = 0. (б-47)
Пропорциональный кривизне член F| — 1)а2 входит в это урав-
уравнение так же, как и массовый член. Однако при ? < '/в он
становится отрицательным (соответствует массе тахиона), что
обычно интерпретируется как неустойчивость вакуумного со-'
стояния. Если к лагранжиану поля добавить член, описываю-
описывающий взаимодействие, такой, как %ф*, возникает спонтанное
нарушение симметрии [246]. Эта особенность возникает также
в других космологических моделях (разд. 5.4); она отмечалась
в работах Фролова, Гриба и Мостепаненко [217, 218].
Тот факт, что состояния частиц при | < 'Д становятся плохо
определенными, можно также установить из рассмотрения мас-
массивных адиабатических мод в случае К = 0:
^ F.48)
Решение F.48), сводящееся к E.45) при больших \t\, можно
использовать для построения адиабатического вакуума обычным

Примеры для искривленного пространства-времени 137
способом. Но в пределе малых масс %и сводится к выражению
которое расходится при т-»-0, если ? < '/б> k2/a2 < 1 —6|.
Рождение частиц в этой модели было подробно рассмотрено
Читром и Хартлем [111] с помощью методов, основанных на
аналитическом продолжении (разд. 8.5).
5.4. Пространство де Ситтера
Пространство де Ситтера [149, 150] всегда привлекало к себе
особое внимание специалистов в области квантовой теории поля
(см. библиографию и приводимые ниже ссылки на литературу).
Причина состоит в том, что пространство де Ситтера является
единственным искривленным пространством с максимальной
симметрией (см., например, [494]). Оно обладает той же сте-
степенью симметрии, что и пространство Минковского (десять век-
векторов Киллинга), что весьма сильно облегчает расчеты в кван-
квантовой теории поля. Наличие кривизны и нетривиальных глобаль-
глобальных свойств обусловливает при этом ряд новых особенностей
при квантовании полей в пространстве де Ситтера. В этом раз-
разделе мы' ограничимся скалярными полями, хотя поля высших
спинов также рассмотрены во многих цитируемых работах, в
частности поля произвольного спина в пространстве де Ситтера
обсуждались в работах [38, 149, 171, 172], см. также разд. 6.4.
Четырехмерное пространство де Ситтера проще всего пред-
представить как гиперболоид
Z02_Zl2_222_Z32_Z42=_a2 E49)
в пятимерном пространстве Минковского с метрикой
ds2 = dz02 - dzx2 — dz22 — dz32 - dz42 E.50)
(см., например, [287, 422], и особенно [220], где обсуждается
связь между геометрией пространства де Ситтера и квантовой
теорией поля).
Из формулы уравнения E.49) ясно, что группой симметрии
пространства де Ситтера является десятипараметрическая груп-
группа SO A, 4) однородных «преобразований Лоренца» в пятимер-
пятимерном пространстве (см., например, [259]), известная как группа
де Ситтера. Точно так же, как группа Пуанкаре играет цен-
центральную роль при квантовании полей в пространстве Минков-
Минковского, группа де Ситтера важна при квантовании в пространстве
де Ситтера.

138
Глава 5
Рис. 16. Пространство де Ситтера, представленное как гиперболоид, погру-
погруженный в пятимерное плоское пространство-время (два измерения опущены).
Изображенные координаты покрывают только полупространство, называемое
стационарной вселенной, причем границами служат изотропные лучи
2э + 24 = 0 (t = —оо). Трехмерное пространство при t = const плоское, рас-
расширяющееся с ростом t.
Первый этап квантования скалярного поля, как обычно, со-
состоит в построении решений волнового уравнения C.26). Для
получения решений необходимо ввести специальную систему
координат. Из обсуждения пространств Риндлера и Милна ясно,
что выбор специальной системы координат' может привести к
естественному выбору «вакуумного» состояния (возможно не
единственному). Например, риндлеровский вакуум, определяе-
определяемый положительно-частотными модами D.81), является наибо-
наиболее естественным для системы координат D.71), в то время как
для координат D.66) естественным будет вакуум Минковского.
Таким образом, мы приходим к необходимости изучить последо-
последовательно три широко используемые системы координат на десит-
теровском гиперболоиде и. обсудить свойства соответствующих
решений волнового уравнения.
Рассмотрим сначала систему координат (t, x), определенную
соотношениями
E.51)
/=1,2,3, -
х{<оо,
которая покрывает половину многообразия де Ситтера при
2о-|_г4;>о (рис. 16). В этих координатах элемент длины E.50)
принимает вид
ds2 = dt2
? (dx1J,
2-1
E.52)

Примеры для искривленного пространства-времени 139
что представляет собой элемент длины в стационарной вселен-
вселенной Бонди — Голда [58] и Хойла [298]. Выраженный через кон-
конформное время
т) = — ае-"а, — oo<ti<0, E.53)
элемент длины E.52) принимает вид
= (а2/Л2) [dy]2 - Z (d*'J]. E.54)
Z
откуда следует, что эта часть пространства де Ситтера кон-
конформна части пространства Минковского. Остающаяся поло-
половина пространства де Ситтера может быть параметризована с
помощью соотношений E.51) с заменой знака в правых частях
либо охвачена путем расширения области изменения конформ-
конформного времени т\ до всей вещественной оси —оо •< ц •< оо.
Поскольку выражение E.54) имеет форму элемента длины
пространственно-плоской модели Робертсона — Уокера E.1) при
C() (/02 ф . 5.1. С
р р р () р
(l) = (a/T02. можно использовать формализм разд. 5.1. Ска-
Скалярная кривизна, рассчитанная с помощью соотношения E.14),
равна
Я=12сГ2, E.55)
что при подстановке в E.4) приводит к уравнению для завися-
зависящей от т) функции %k в выражении для полевых мод. Решение
этого уравнения выражается через функции Бесселя и Ханкеля.
Определенные линейные комбинации, используемые в' качестве
«положительно-частотных» решений, определяют выбор ва-
вакуума. Поскольку
можно ожидать, что адиабатический вакуум будет соответство-
соответствовать физическому состоянию без частиц при i\-*- ±°° (разд. 3.5).
Выберем точные решения равными (в хорошем приближении)
адиабатическим модам C.102) при условии, что величина
«V/if + 12 (| - D/rj? E.57)
велика по сравнению с С/С = О(Т~1) для фиксированного
— ц/Т. В этом случае
F.88)
при больших k или tj. Легко проверить, что правильно нормиро-

140 Глава 5
ванные точные решения, обладающие этим свойством, имеют
вид
11/12) E.69)
где #—функция Ханкеля и
B/? + i). E.60)
Заметим, что выражение E.59) сводится к E.58) в безмас-
безмассовом пределе в случае конформной связи (?='/б). Следова-
Следовательно, в противоположность модели Милна здесь конформный
вакуум совпадает с адиабатическим вакуумом в безмассовом
пределе.
Поскольку выражение E.59) имеет асимптотический ч вид
адиабатических мод E.58) как при г|->+<», так и при г|->— <х>,
рождение частиц не имеет места, даже если масштабный фак-
фактор проходит через координатную особенность при г\ = 0. Этого
и следовало ожидать для вакуумного состояния, инвариантного
относительно группы де Ситтера. Однако, так же как инвариант-
инвариантность относительно группы Пуанкаре вакуума в пространстве
Минковского не гарантирует его единственности, инвариант-
инвариантность относительно группы де Ситтера не определяет единствен-
единственным образом состояние вакуума в пространстве де Ситтера
'[ПО]. Поэтому для выбора положительно-частотных решений
необходимо было привлекать соображения, основанные на ана-
анализе адиабатичности, чтобы выделить это вакуумное состояние
из различных состояний, инвариантных относительно группы де
Ситтера.
Чтобы проверить, насколько выбранный вакуум соответ-
соответствует представлению о состоянии, не содержащем частиц с точ-
точки зрения сопутствующего наблюдателя, необходимо найти по-'
ложительно-частотиую вайтмановскую функцию G+ для этого
вакуумного состояния. Это сделано с помощью суммирования
по мОдам с использованием E.59) в ряде работ (см., например,
[69, 79, 124, 419]), где было получено
G+ (х, хг) = (Гбяа2)-1 (-j - v2) secjiv X
+ v, ±-v; 2; 1 + <А""'*7<*>' ); E.61)
здесь F — гипергеометрическая функция. В пределе безмассо-
безмассового поля с конформной связью выражение E.61) сводится к
D (х, х ) = 4f[2a2 |(Дч _ .gJ _ | Дх р] . E.62)
откуда видна конформная связь с функцией Вайтмана C.59) в
лространстве Минковского (разд. 3.7).

Примеры для искривленного пространства-времени 141
Подставляя E.62) в C.55) и полагая Ах=0, можно вычис-
вычислить функцию отклика сопугствующего детектора с собствен-
собственным временем t в состоянии конформного (совпадающего с
адиабатическим) вакуума. Ограничиваясь «стационарной» ча-
частью пространства де Ситтера, определяемой условием E.53),
находим
00 00 IT? Ki
) L ) aal
П» —oo—oo
[(i At/2an) + e -
Вычислив интеграл по At путем замыкания контура интегриро-
интегрирования в нижней полуплоскости комплексной переменной At
(Е > 0), находим
V (Е)/(ед. времени) = (Е/2п) (е2аяВ - 1)"J, E.63)
что соответствует тепловому спектру при температуре Т ==
в*= 1/Bлакв). Таким образом, хотя частицы не рождаются, со-
сопутствующий наблюдатель, движущийся в этой области про-
пространства де Ситтера, воспринимает тепловое излучение. Это
другой пример общего явления, обсуждавшегося в разд. 3.7,
когда сопутствующий детектор имеет ненулевой отклик в со-
состоянии конформного вакуума.
Полученный результат не противоречит тому, что конформ-
конформный вакуум также является адиабатическим вакуумом произ-
произвольного порядка, поскольку в разд. 3.6 показано, что вероят-
вероятность детектирования частицы с энергией Е сопутствующим де-
детектором в таком вакууме должна стремиться к нулю быстрее
любой обратной степени Е при больших Е (см. стр. 86). Выра-
Выражение E.63) удовлетворяет этому требованию. Подобным же
образом оно стремится к нулю быстрее любой обратной степени
адиабатического параметра а, являющегося мерой кривизны
пространства (R = 12/а2).
Другая часто используемая система координат {t, %, 8, ф)
вводится соотношениями
20 = a sh (//а),
Zi = а ch (//а) cos %,
г2 =>= а ch (tfa) sin % cos©, <6.64)
z3•= « ch ({(a) sin % sinScosi>,
Zi = a ch (t/a) sin % sin 8 sin $,

142
Глава 5
X=const
t=const
Рис. 17. Пространство де Ситтера,
представленное как сжимающееся и
расширяющееся компактное про-
пространство с метрикой E.65).
а соответствующий элемент
длины E.50) принимает вид
rfs2 = dt2 — a2 ch2 (Ца) [d%2 +
+ sin2/(cfe2 + sin2Q dj>% E.65)
Если —oo </<oo, 0 ^ % ^
< я, 0 ^ 9 ^ n, 0 < <f> ^ 2я,
то эти координаты покрывают
все многообразие де Ситтера.
Метрика E.65) отвечает (зам-
(замкнутому) пространству Ро-
бертсона — Уокера с К = +1
(рис. 17).
Вводя конформное время
0 < п < я,
E.66)
можно привести элемент длины E.65) к виду, явно конформному
пространству Эйнштейна:
ds2 = о2sin-2ri [dr\2 - d%2 - sin2% (d92 + sin29 dj>2)]. E.67)
Воспользовавшись этим представлением, уравнение E.4) приве-
приведем к форме
-^ + { k2 + cosec2 r, [m2a2 + 12 (g - j)] } %k = 0, E.68)
допускающей явные решения в функциях Лежандра [124, 448]
E.69)
где в соответствии с E.22) k = 1, 2, 3,..., а v определяется фор-
формулой E.60). Выбор постоянных А, В фиксирует состояние ва-
•
куума. К сожалению, поскольку С/С = —2ctgr]-»-±°o при t->-
->±оо, пространство-время нельзя рассматривать как медленно
расширяющееся в этих предельных случаях, и ввести физически
оправданные состояния in- и out-вакуума невозможно.
Эта трудность проявляется наиболее отчетливо, если для ре-
решения уравнения E.68) используется преобразование Лиувилля
[341] (см. также [223]). Это преобразование в Данном случае
соответствует замене переменной г\ на t и введению функции
в результате чего уравнение E.68) принимает вид
E.70)

Примеры для искривленного пространства-времени 148
В отдаленном прошлом и будущем (^->±оо) это уравнение
сводится к
и имеет решение
Xi ~ «-**»,. E.71)
которое является положительно-частотным по отношению к t
(при v2 < 0, Im v > 0). Некоторые авторы (например, [124, 260,
408, 409], см. также [171]) определяют вакуумные состояния,
вводя в качестве положительно-частотных решений уравнений
E.68) и E.70) решения, имеющие асимптотику E.71) при боль-
больших |/|. При таком определении in- и out-вакуумы оказываются
неэквивалентными, а связывающее их преобразование Боголю-
Боголюбова — не зависящим от частоты, что приводит к бесконечному
числу рождающихся частиц. (Замечание об ошибочности такого
определения вакуума, по-видимому, впервые было высказаьо
Фуллингом [220]; см. также [416]). Этот патологический ре-
результат объясняется тем, что области f->±oo И) следовательно,
определенные выше вакуумные состояния не являются адиаба-
адиабатическими. Однако из разд. 3.5 следует, что если потребовать
достаточно быстрого убывания коэффициента Боголюбова [3*
при больших k, чтобы гарантировать конечность полной плот-
плотности частиц, то необходимо использовать адиабатический ва-
вакуум не ниже второго порядка.
Хотя адиабатических in- и out-областей не существует, но мо-
можно определить адиабатические состояния вакуума, как те со-
состояния, которые не содержат частиц с большими импульсами.
Напомним, что адиабатические решения C.102) становятся хо-
хорошим приближением для точных адиабатических положительно-
частотных мод, когда величина
[()] E.72)
делается большой по сравнению с производными от С/С при фик-
фиксированном Tii = ц/Т. Очевидно, это выполняется для больших k,
m или а (при фиксированном ц), но не имеет места для больших
\t\, т. е. т]->0 или я при Г->0, п/ци Например, при г)->я, Г->
->я/тI выражение E.72) становится бесконечным, возрастая с
т;ой же скоростью, что и dl(C/C)/dlt\ при /^ 1 и более медленно
для / > I.
В пределе больших k выражение C.102) в нулевом порядке
дает
e-'*"/Bi*i)Vl- с5-73)

144 Глава 5
Выбирая постоянные А, В так, чтобы правильно нормированиое
решение E.69) сводилось к E.73) при больших k, находим
[ПО, 448]
Хк (Л) = sin7' л [яГ (* + -i - у)/4Г (k + | + v)]'A X
X еш'2 [Pl-Vl (- cos ti) - Bi/n) Ql-y, (- cos r,)]. E.74)
Поскольку решение E.74) в пределе больших k сводится к
E.73) независимо от величины ц, оно задает адиабатический
вакуум при всех значениях времени. Таким образом, как и в
случае координат E.51) в пространстве де Ситтера, рождение
частиц отсутствует, выражение E.74) соответствует устойчи-
устойчивому адиабатическому состоянию вакуума. Далее, в случае без-
безмассового поля с конформной связью решения E.74) сводятся
к правой части E.73), поэтому опять конформный вакуум сов-
совпадает с адиабатическим вакуумом в безмассовом пределе.
Теперь можно воспользоваться выражением E.74) для вы-
вычисления положительно-частотной вайтмановской функции для
адиабатического вакуума [448]. Она оказывается в точности
такой же функцией координат гй пространства, в которое по-
погружено пространство де Ситтера, что и E.61). Таким образом,
вакуум, определенный в координатах E.54), совпадает с ва-
вакуумом, определенным в координатах E.67). Более того, ока-
оказывается, что детектор, находящийся в покое в этой системе
координат, воспринимает такое вакуумное состояние как тер-
термостат, заполненный тепловым излучением при температуре
Т = l/Bnake), точно как и в стационарном случае (см. E.63)).
Этот результат впервые был получен Гиббонсом и Хокингом
[236], использовавшим его в качестве аргумента, свидетель-
свидетельствующего о том, что определение понятия частицы в квантовой
гравитации зависит от наблюдателя.
Последняя система координат, которую мы рассмотрим
здесь, — статические координаты, определяемые соотношениями
zo=(a2-r2)'/2sh(//a),
z, = (a2-r2)'/2ch(*/a),
Z2=r sin Э cos ф, E.75.)
2»3=r si
Z4 = r cos 6,
и покрывающие лишь половину многообразия де Ситтера с
Zo + Zj > 0 (рис. 18).. В этих координатах элемент длины E.50)
принимает вид
rfs2 = [ 1 - (r2/a2)] dt2 - [ 1 - (г2/а2)] ~' d>2 -
22 E.76)

Примеры для искривленного пространства-времени 145
Рис. 18. Пространство де Ситтера как
статическое пространство с метрикой
E.76).
r=const
t'cansf
Метрика E.76) обладает координатной особенностью при г = а,
где находится горизонт событий для наблюдателя, мировая ли-
линия которого следует траектории вектора Киллинга dt при
г = 0. Выражение E.76) напоминает элемент длины в простран-
пространстве Шварцшильда C.18), и квантование поля можно проводить
аналогичным образом [236, 337, 342, 343] (см. также [265]).
Соответствующая формулировка квантовой теории поля в
пространстве де Ситтера, выбор полевых мод и вакуумного со-
состояния, ассоциируемых с системой координат E.75), имеют
уже иной физический статус, нежели обсуждавшиеся выше, по-
поскольку вакуумное состояние оказывается неинвариантным от-
относительно группы де Ситтера (см. [ПО]). Действительно, как
мы увидим в разд. 6.3, среднее значение тензора энергии-им-
энергии-импульса в этом квантовом состоянии обращается в бесконечность
на горизонте событий г =¦ а. Поскольку положение горизонта
зависит от выбора начала радиальной координаты, каждая
точка в пространстве де Ситтера (т. е. каждый наблюдатель)
ассоциируется с различным выбором вакуумного состояния.
Следовательно, такая схема квантования приводит к вакууму,
который не инвариантен даже относительно трансляций и вос-
воспринимается сопутствующим наблюдателем как резервуар с теп-
тепловым излучением. (Свойства статической системы координат
обсуждались Шредингером [442], § 1.4.)
5.5. Классификация состояний конформного вакуума
Прежде чем переходить к более общему типу пространств,
объединим полученные в предыдущих разделах результаты в
рамках классификации, предложенной Канделасом и Даукером
[91}. Этот подход также оказывается полезным при обсуждении
свойств тензора энергии-импульса в различных пространствах.
Идея классификации конформных вакуумных состояний, ас-
ассоциируемых с различными пространствами, формулируется
следующим образом. Пусть М — некоторое искривленное про-

146
Глава 5
I ~"~'4
Рнс. 19. Изображение
вселенной Эйнштейна в
виде цилиндра. Коорди-
Координаты в и Ф опущены, t из-
изменяется в вертикальном
направлении от —оо до
+оо, % отсчитывается
вдоль окружности цн-
лнндра.
странство-время, конформно отображае-
отображаемое на плоское пространство-время М (не
обязательно совпадающее с неограничен-
неограниченным пространством Минковского),- и
пусть 2 — глобальная гиперповерхность
Коши в М, отображаемая при конформ-
конформном преобразовании в глобальную гипер-
гиперповерхность Коши 2 в М; тогда для каж-
каждого глобального времениподобного век-
вектора Киллинга в М существует глобаль-
глобально времениподобный конформный вектор
Киллинга в М. Таким образом, состояния
конформного вакуума, определяемые по
отношению к конформному вектору Кил-
Киллинга, можно классифицировать, обра-
обращаясь к вакуумным состояниям, задан-
заданным на М. В частности, если fit— про-
пространство Минковского, то поскольку для
него существует единственный глобаль-
глобальный времениподобный вектор Киллинга,
вакуум, определенный по отношению к
вектору Киллинга dt, будет единствен-
единственным; если же М — пространство Риндлера, то имеются два ва-
вакуумных состояния, одно из которых определяется по отноше-
отношению к dt, а второе—по отношению к д^ (см. D.82)).
Свойства глобальных гиперповерхностей Коши в различных
пространствах Робертсона — Уокера, с которыми мы встреча-
встречались, проще всего обсуждать с помощью конформных диаграмм
Пенроуза (см. [287], гл. 5), получаемых при конформном
отображении этих пространств в статическую вселенную Эйн-
Эйнштейна (разд. 5.2) с элементом длины
ds2 = dt2 —d%2-sin2%(dB2 + sin2Bd<t>2). E.77)
Опуская координаты 0, ф, эйнштейновскую вселенную можно
изобразить в виде цилиндра, как показано на рис: 19. Развер-
Развертывание цилиндра дает область —со < t < со, 0 ^ % < я, на
плоскости t, %. Конформные образы каждого кз пространств
в этой области и образуют диаграммы Пенроуза, к которым мы
обратимся.
Различные типы пространств Робертсона — Уокера показаны
на рис. 20.
Для случаев пространств Робертсона — Уокера с /С=1, 0,
—1 (рис. 20, б, г и е соответственно) точная область изменения
конформного времени г\ зависит от вида функции С(г\) в E.11).
Мы ограничимся значениями tj > 0, но если опустить это огра-
ограничение и рассматривать пространства, продолжаемые через

Примеры для искривленного пространства-времени
147
t-tt
t-Я
Рис. 20. Конформные образы различных пространств на эйнштейновском ци-
цилиндре. Координата t совпадает с временной координатой на цилиндре Эйн-
Эйнштейна (рнс. 19). а — пространство Мннковского, б —пространство де Снт-
тера и пространство Робертсона — Уокера при К = 1, в — стационарная все-
вселенная, г — пространство-время Робертсона — Уокера прн К = 0, д — клин
Ринддлера, статическое пространство де Снттера, открытая вселенная Эйн-
Эйнштейна и вселенная Милна, е — пространство-время Робертсона — Уокера при
К=-1 [91].
сингулярность в точке г\ = 0, то верхнюю часть диаграммы
можно получить путем отражения относительно линии t = 0.
Так, например, если стационарная вселенная E.54) продолжена
на всю область —оо < г\ < оо, то верхняя половина рис. 20, в
получается отражением относительно линии ? = 0.
Важной особенностью этих диаграмм является то, что все
пространства, изображенные на рис. 20, а—г, имеют в качестве
конформного образа глобальной гиперповерхности Коши поверх-
поверхность ? = 0, 0 ^ % <С.п, а пространства, изображенные на
рис. 20, д, е,— поверхность t = я/2, 0 ^ % < я/2.
Поэтому изображенные на рис. 20 пространства можно раз-
разделить на два класса: 1) пространства на рис. 20, а—г, для ко-
которых имеется лишь один конформный вакуум, соответствую-
соответствующий конформному вектору Киллинга, связанному конформным
преобразованием с времениподобным вектором Киллинга dt

148 Глава 5
пространства Минковского (/—время Минковского), и 2) про-
пространства на рис. 20,5, е, для которых имеются два конформных
вакуума по отношению к конформным векторам Киллинга, свя-
связанным с времениподобными векторами Киллинга dt и дц про-
пространства Риндлера.
Поскольку й пространство Минковского и пространство
Риндлера являются плоскими, эта классификация конформных
состояний вакуума имеет чисто топологический характер. Раз-
Различные топологии можно охарактеризовать инвариантной вели-
величиной, называемой характеристикой Эйлера — Пуанкаре (см.
[242]), использованной в работе [116] для классификации
(евклидизированных) состояний вакуума Минковского и Ринд-
Риндлера. Она принимает значение 1 для пространства Минковского
(топология /?4) и 0 для пространства Риндлера (топология
R3XSl).
Что означает физически эта топологическая классификация?
В разд. .4.5 показано, что вакуум Минковского содержит тепло-
тепловой спектр частиц Риндлера при температуре a/2nkB. Можно
также убедиться в том, что функции Грина в вакууме Минков-
Минковского совпадают с риндлеровскими тепловыми функциями Грина
(разд. 2.7). Аналогичным образом можно связать между собой
вакуумные состояния в других показанных на рис. 20 простран-
пространствах, имеющих одинаковую геометрию, но различную тополо-
топологию. Например, статическое пространство де Ситтера E.76) и
пространство де Ситтера E.65) имеют одинаковую кривизну, но
статическое пространство де Ситтера относится к классу Ринд-
Риндлера (рис. 20, д), в то время как пространство де Ситтера —
к классу Минковского (рис. 20,6). Отсюда можно сделать вы-
вывод, что деситтеровский конформный вакуум является терма-
лизацией статического деситтеровского вакуума по отношению
к конформному вектору Киллинга, связанному с дц, при темпе-'
ратуре l/2mx?s. Аналогично конформный вакуум эйнштейнов-
эйнштейновской вселенной представляет собой термализацию при мнимой
температуре T=l/2nikB конформного вакуума, связанного с
дц, для открытой вселенной Эйнштейна (дальнейшее обсужде-
обсуждение см. в работе [91]).
Эти результаты суммированы на рис 21, где вертикальные
стрелки обозначают конформные преобразования, а горизон-
горизонтальные— термализацию при указанной температуре. В допол-
дополнение к этому из обсуждения поведения детекторов частиц ц
стационарной вселенной (см. E.63)) мы знаем, что конформный'
вакуум в стационарной вселенной может быть получен из ва-
вакуума Минковского термадизацией при температуре l/2nak&.
Это значит, что вертикальное конформное соотношение между
вакуумами пространства Минковского и стационарной вселен-
вселенной на диаграмме в этом случае является также соотношением

Примеры для искривленного пространства-времени
149
¦Клин Риндлера
\
Статическое пространство
де Ситтера
I
Открытая вселенная Эйнштейна
4
Пространства РоЬ~ертсана-Уоша
при И—1
г
Вселенная Милна
(Zffa)
-1
Btri)
-t
Пространство МинкаВскаго
\
Пространство дв Ситтера
\
Вселенная Эйнштейна
\
Пространство РоЬ*ертсона-
Уокера при К' 1
¦
Пространство Родертсана-
Уокера при К" О
' \
Стационарная вселенная
Рис. 21. Термодннамнческне н конформные соотношения между различными
пространствами. Вертикальные стрелки означают, что пространства связаны
конформными преобразованиями, горизонтальные стрелки соответствуют тер-
малнзацин при указанной температуре [91].
термализации. Можно проверить, что подобное соотношение
имеет место для эйнштейновского и деситтеровского (с элемен-
элементом длины E.65)) конформных вакуумов.
5.6. Пространства типа Бианки I
и теория возмущений
До сих пор все наши примеры ограничивались случаем изо-
изотропных пространств. Такие пространства особенно интересны,
поскольку в настоящее время вселенная, согласно наблюдениям,
является изотропной с высокой точностью. Источник этой изо-
изотропии в течение долгого времени был загадкой для космологов
(см., например, обзор [349]). Среди других предположений
Зельдович (см. [408]) выдвинул гипотезу, что первоначально
вселенная была анизотропна^ но быстро изотропизировалась
из-за квантовых эффектов на начальной стадии расширения.
Исследование этого предположения технически довольно слож-
сложно, так как требует учета обратного воздействия квантово-поле-
вых эффектов, индуцируемых пространственно-временной кри-
кривизной, на динамику гравитационного Поля. Мы еще вернемся
к этому вопросу в конце гл. 7 после обсуждения расчета тензора
энергии-импульса. Здесь мы ограничимся общим -построением
квантовой теории поля в анизотропном пространстве-времени.
Рассмотрим четырехмерное {прострайственно-плоское) про-
пространство типа Бианки I [35] с элементом длины
-Za* @ dx\.
E.78)

150 Глава 5
(Квантовая теория поля в замкнутой анизотропной вселенной
типа Бианки IX построена в работах [299—301, 305]; см. также
[33].)
Введем величину
[a (t)]2 = С (t) a (a, W* = (САСз)'\ E.79)
где C^Hsa^. Новый временной параметр ц удобно определить
соотношением
t
E.80)
в изотропном пределе а.\ = Яг = Яз = # он сводится к обычному
конформному времени E.10). Если ввести также величины
di=Ci/Ch E.81)
где точка над буквой обозначает дифференцирование по % и
з
г) V/7 ГЧС (К Я9\
i-1
(d, - djf, E.83)
«</
то отличные от нуля символы Кристоффеля для метрики E.78)
будут иметь вид
Отсюда можно найти ненулевые компоненты тензора Риччи"
(см., например, [225]):
m ^ Rtt^-^C'Ctidt + dtD), E.85)
л скалярную кривизну
6Q]. E.86)
Вводя далее величины
5

Примеры для искривленного пространства-времени 151
можно представить квадрат тензора Вейля в виде
Ca*v*Capv5 = 4С~2 C?/ - 45 + 12Q2). E.88)'
Эта величина служит мерой анизотропии пространства-времени.
Поскольку пространство не является конформно-плоским, мы не
можем ввести состояния конформного вакуума для полей, обла-
обладающих конформно-инвариантными лагранжианами, как это де-
делалось в пространствах Робертсона — Уокера. Однако адиаба-
адиабатические состояния вакуума построить можно [223, 225, 302].
Разложение по модам C.30) с мерой, отвечающей плоским
пространственным сечениям, имеет вид
3k [акик (х) + aUl (x)}. E.89)
Поскольку модели типа Бианки I симметричны относительно
пространственных трансляций, решения для мод можно по-
построить методом разделения переменных (ср. E.3)):
ик (х) = Bя)~ Vk-xC-'/s (г,) Хк (Ч). E.90)
Подставляя это разложение в C.26), получаем уравнение для
Хк (ср. E.4)):
E.91)
В соответствии с C.28) условие нормировки принимает вид
(СР- E6)) ¦ . .,
У я у* — у*д у, = /. E 92)
Как и в разд. 3.5, положительно-частотное обобщенное ре-
решение типа ВКБ уравнения E.91) имеет вид
I — i:\ Wk(x\')dr\'\. E.93)
где величина Wk может быть найдена с точностью до любого
адиабатического порядка А (и обозначается W^\ /j^) с помо-
помощью итераций, опирающихся на нулевое приближение
E.94)
Далее можно ввести адиабатические состояния вакуума с по-,
мощью процедуры, применявшейся в моделях Робертсона —
Уокера, т. е. путем сшивания точных положительно-частотных
решений уравнения E.91) с построенными приближенными ре-
решениями в некоторый момент времени.

152 Глава 5
К сожалению, найти точные решения уравнения E.91) очень
трудно. Но это удается сделать в одном простом случае, когда
ax{f) = t, а2 = а3=1, 0<t<oo, — оо<*'<оо. E.95)
Такое пространство-время аналогично вселенной Милна
(разд. 5.3), в чем можно убедиться с помощью преобразований
yu = Lc\ix\ yi = tshxi, у2 = х2, у3 = х3, E.96)
приводящих элемент длины E.78) при выборе E.95) к соответ-
соответствующей величине в пространстве Минковского с ограничением
у° > I у11.
В этом простом случае решение уравнения E.91) может быть
выражено через функции Бесселя и Ханкеля [225, 369—372].
Можно показать, что решение, выражающееся через функцию
Ханкеля #B), является положительно-частотным в смысле адиа-
адиабатического определения. Как и в случае вселенной Милна, ока-
оказывается, что оно также положительно-частотное в смысле обыч-
обычного определения в накрывающем пространстве Минковского.
Ввиду затруднений при отыскании точных решений уравне-
уравнения E.91) естественно пытаться применить для его решения
приближенные методы. Один из таких методов, использованный
в первоначальных работах Зельдовича и Старобинского [503,
504] и далее развитый Биррелом и Дэвисом [43], состоит в ре-
решении уравнения E.91) для малых анизотропных возмущений
пространства-времени Робертсона—Уокера (см. также разд. 7.3).
Опишем коротко этот метод. Элемент длины E.78) сначала
приводится к виду
ds2 = С (ту) { drf - g [I + ht (ti)J (dx1J |; E.97)
далее предполагается, что
max|Mn)t« 1, E.98)
и для- упрощения последующих рассуждений принимается
а
?a{(ti) = O. E.99)
Теперь можно разложить уравнение E.91) с точностью до ли-
линейных членов по hi, что дает
2хк Г
W + «2С (Л) + (l - |)С (т,) R
<-'

Примеры для искривленного пространства-времени 163
где Ri — скалярная кривизна изотропного пространства-времени
при hi = 0:
#/ = С [3D + 4^]. E.101)
Налагая дополнительные условия
1) А/(т])->0 при т]-> ± cxs,
2) ССп)/?(т1)-*0 при п->±оо, если |=^-|-.
3) С{у\)-*С(оо) = С{—оо)<оо при г1->±оо,еслит^=0) E.102)
нетрудно показать, что нормированные положительно-частот-
положительно-частотные решения уравнения E.100) при х\-*-—оо имеют вид
xjn (т,) = B(о) -'he- '«п, E.103)
где
со2 = ?2 + т?С (оо). E.104)
Метод, позволяющий ослабить второе и третье условия с по-
помощью преобразования Лиувилля, был предложен Бирреллом
[37, 39].
При выполнении начальных условий E.102) уравнение
E.100) можно представить в виде интегрального уравнения
ХЬ (Л) - ЗСкп (Л) + и» \ Vk (nO sin [© (л - л01 ЗСк (Л0 </л'. E.105)
—оо
где
Iе (°°) - с Ml - (б - т
E.106)
Йри больших значениях времени уравнение E.105) имеет
решение
ХГ (Л) = eyef (Л) + Рьз4я* <Л), E.107)
где коэффициенты Боголюбова равны
к О?) </Л. E.108)
h - -' S XL" (л) ^к (ч) ЗСк A1) di\. E.109)
Если рассматривать величину Vk (л) как малую, можно по-
построить итерационное решение уравнения E.105). В низшем
порядке по Vk имеем %к (г\) = зс'кп 0l)> что после подстановки в
F.108) и E.109) приводит к следующим выражениям для коэф-

'54 Глава 5
фициентов Боголюбова в первом порядке по Vk'-
00
Ok—1 + 0/2») J Vk(i\)di\, E.110)
pk =x — (//2to) J e~2i^Vk (л) dr\. E.111)
— 00
Такой метод также можно использовать в космологических мо-
моделях вблизи сингулярности при ц = 0, если Vk(f\) обращается
в нуль при т]->0. Для этого достаточно заменить нижний предел
интегрирования по ц на нуль.
Эта процедура может рассматриваться как применение тео-
теории возмущений при нарушении конформной тривиальности
вследствие анизотропии пространства-времени. Метод можно
обобщить на случай нарушения конформной симметрии при на-
наличии (малой) массы или (малой) неконформной связи. Тогда
при т'= О, 1 = 'Д условие малости Vk соответствует условию
слабой анизотропии E.98). Если же тф§, \Фх/ъ, то малость
Vk означает, что т мало и 1 =; !Д- При А, = 0 эти условия
означают малое нарушение конформнойг инвариантности в про-
пространстве-времени Робертсона — Уокера с масштабным факто-
() С1М)
A) М,)
Если выбранное квантовое состояние совпадает с состоянием
in-вакуума, то в out-области (tj-»- оо) плотность числа частиц
(в единице собственного объема) равна (ср. C.42))
$ E.112)
а плотность энергии —
р = Bя)~3а~4 ^ I Pk |2<orf3^. E.113)
Подставляя E.111) и E.106) в E.112) и интегрируя по им-
импульсам [43], во втором порядке (по Vk) для плотности частиц
получаем
00
п - (ЭбОяаГ1 J [С2 (т,) Са™СЧУб + 60К2 (ч)] d4 +
— оо
+ т(960а3)-1 \ di), \ йц2 Ь(т(ч, - r\2))\- 60F(т,,) V
-оо —оо ^
8т4 - 6от2аяЛ2 + | д\д\) ^ Л, (л,) Kt (П2>1 -
- 42»[
-/,BЛ(Л. - 42»[60V Ы V (п2) + j%h, (тц)А",Ы11. E.114)

Примеры для искривленного пространства-времени 155
где
m2 = C(oo)m2, E.115)
V (л) - rri1 [С (оо) - С (л)] - (l -1) С (л) /?; ft), E.116)
F()(l)[/B)#( ] E.117)
(Н —функции Струве, / — функции Бесселя). Мы также вос-
воспользовались тем, что с точностью до второго порядка по hi вы-
выражение E.88) сводится к СаЭувСарув=-|с~2 ? (А,J. В без-
безмассовом пределе E.114) принимает вид
1J$]л E.118)
и имеет чисто геометрический характер. При получении выра-
выражений E.114) и E.118) в дополнение к E.102) было наложено
условие
ht(л). Мл)->0 при г1-*±оо. E.119)
Если далее потребовать, чтобы
МЛ)-* 0 при л-*±°°. E.120)
то аналогичным образом можно вычислить из E.113) плотность
энергии
оо оо
X Г 1207 Ы К Ы + (дчАь - 4m2J J А, (Л1) А, (л2I, E.121)
где /Со — модифицированная функция Бесселя.
В безмассовом пределе выражение E.121) сводится к
р = - C840HV)-1 J di|i J йл2 In
X 112QV Ы К (Л.) + 2 А| (Л,) А, (ть)| . E.122)
*
| .
В *этом выражении ц — произвольная малая масса, значение
которой можно изменять, не меняя р, поскольку

156 Глава 5
К сожалению, явно выразить интегралы E.114) или E.121)
через известные функции удается лишь для некоторых значении
hi и V, но полученные выражения могут использоваться для
численных расчетов. Метод численного (а иногда и аналитиче-
аналитического) построения точных решений был предложен Бирреллом
[37, 39]
Более широкий класс задач удается решить в замкнутом
виде, возвратившись к E.111) и проводя интегрирование по tj
до вычисления пирс помощью E.112) и E.113). В качестве
примера рассмотрим пространство-время, обладающее элемен-
элементом длины E.97), при
+ 6<), E.123)
где а, р, 8i — постоянные; для выполнения условия E.99) пред-
предполагается, что фазы 6i отличаются друг от друга на 2я/3.
Из формул E.106) » E.U1) получаем вклад в коэффициент
Боголюбова (Jk, обусловленный анизотропией:
Подставляя это выражение в формулу E.113), найдем соответ-
соответствующий вклад в плотность энергии в out-области
ш2 (rt2 _J_. ft2\ h ' f Qs****2 \
п т *** -Г р ; ^-3amg/faa4.ft^U7 I ^a^ I /С 1 ОС\
р *~~" -—1/4 2 ~* /2> Vз \ о о2 /'* ^v* I eU||
где W — функция Уиттекера. В предельном случае 1 ='Д.
от з= О этот вклад является единственным и сводится к
4^- <*•*»
Поскольку в этом случае требуется выполнение лишь первого
условия в E.102), выражение для плотности энергии E.126)
оказывается справедливым при любом выборе масштабного фак-
фактора а (г\) = С'1'(ц), что позволяет использовать его при срав-
сравнении различных космологических гипотез ([43J, см. также
разд. 7.4).

Глава в
ПЕРЕНОРМИРОВКА ТЕНЗОРА
ЭНЕРГИИ-ИМПУЛЬСА
В предшествовавших главах подробно исследовано рождение
частиц переменным гравитационным полем. Как отмечалось,
лишь в исключительных случаях понятие частиц в искривленном
пространстве-времени в достаточной степени, соответствует ин-
интуитивным физическим представлениям об элементарных части-
частицах. Вообще говоря, естественного определения понятия частиц
не существует, а реакция детектора оказывается такой, что ее
трудно интерпретировать в терминах частиц.
Для некоторых задач более целесообразно рассматривать
средние значения других наблюдаемых. Затруднения в опреде
лении понятия частицы отчасти связаны с глобальным характе-
характером этого понятия, опирающегося на представление о полевых
модах, которые зависят от крупномасштабной структуры про
странства-времени. В отличие от этого реальные детекторы ча-
частиц по крайней мере квазилокальны Поэтому правильнее рас-
рассматривать не глобальные физические величины, а величины,
имеющие локальный характер, т. е. определенные в отдельной
точке пространства-времени. Одним из таких объектов, пред-
представляющих физический интерес, является тензор энергии-им-
энергии-импульса Tliv(x), заданный в точке х. Особое значение тензора
энергии-импульса состоит в том, что он не только описывает
физическую структуру квантового поля в точке х, но и служит
источником гравитационного поля в уравнениях Эйнштейна.
Поэтому он играет важную роль во всех попытках, построения
модели самосогласованной динамики гравитационного поля,
взаимодействующего с квантованными материальными полями.
Для многих приложений, в частности астрофизических, основ-
основной интерес представляет обратное воздействие квантовых про-
процессов на геометрию пространства-времени.
В этой главе будет сформулирован аппарат, позволяющий
рарсчитывать <7\лУ> для различных квантованных полей. В таких
расчетах имеется ряд необычных моментов, требующих особого
внимания. Большая часть главы посвящена подробному обсуж-
обсуждению различных методов регуляризации для получения конеч-
конечного перенормированного <7^> из бесконечных величин, на пер-
первый взгляд не имеющих смысла. Хотя читатель, вероятно, знаком

168 Глава 6
из опубликованных работ с этими разнообразными мето-
методами, мы хотим подчеркнуть, что окончательные результаты не
зависят от конкретного метода регуляризации. Здесь представ-
представлены все основные методы регуляризации не только для
полноты, но и для того, чтобы продемонстрировать их взаимо-
взаимосвязь и согласованность. Для понимания содержания последую-
последующих разделов, где рассматриваются приложения к частным
случаям фоновых метрик, представляющих особый интерес, вла-
владения всеми этими методами не требуется.
Как правило, мы будем работать с эффективным действием
а не с Tpv, что позволяет добиться некоторых упрощений, в осо-
особенности когда применяемые аналитические методы достаточно
сложны. Однако подход остается весьма формальным и часто
требует манипулирования величинами, смысл которых в рас-
рассматриваемой задаче не совсем ясен. Возможно, читатель будет
испытывать неудобства, встречаясь с такими необычными вели-
величинами, как In Gf, и предпочел бы рассчитывать <7^> непосред-
непосредственно, особенно если при этом используются иеаналитические
методы регуляризации.
Наряду с гл. 3 данная глава составляет основу рассматри-
рассматриваемого предмета. Она значительно длиннее и содержит больше
технических деталей, чем другие главы книги. Мы рекомендуем
при первом чтении обратить внимание на метод регуляризации
с помощью аналитического продолжения по размерности, а так-
также на конформные аномалии. Затем, освоив применение размер-
размерной регуляризации для перенормировок и ознакомившись с кон-
конкретными примерами, такими, как пространство де Ситтера в
разд. 6.4, читатель, по-видимому, захочет изучить и другие
методы регуляризации. В частности, регуляризация с помощью
раздвижки точек и адиабатическая регуляризация являются
наилучшими отправными пунктами для тех, кто пожелает про-
провести вычисления для конкретных моделей. Эта глава содержит
всю основную информацию, необходимую для проведения таких
расчетов.
Последний раздел данной главы может быть с пользой про-
прочитан и без глубокого понимания теории регуляризации и пере-
перенормировок.
Более раннее обсуждение регуляризации в квантовой теории
поля в искривленном пространстве можно найти в работах
Утиямы и де Витта [471J и Халперна [267]. Некоторые физиче-
физические предположения были, высказаны Сахаровым [412] и раз-'
виты Грибом и Мамаевым {250].
Формализм, несколько отличающийся от описываемого здесь,
развит в работах [326, 402] на основании нелинейного обобще-
обобщения квантовой механики, предложенного Кибблом [325].

Перенормировка тензора энергии-импульса 169
6.1. Основная проблема
Как было отмечено в разд. 2.4, математическое ожидание
оператора Я в вакуумном состоянии бесконечно даже в про-
пространстве Минковского. В разд. 4.1—4.3 мы также обнаружили,
что величина <0|ГцУ|0> имеет ультрафиолетовые расходимости.
Такое поведение симптоматично для всех задач, в которых пы-
пытаются вычислить среднее значение оператора, квадратичного
по напряженности поля. Например, величина @\<jP(x) |0> может
быть найдена как предел при х'-*-х функции Грина G<l)(x, x')
(см. B.66)). Однако из разложения де Витта — Швингера
C.141) следует, что в общем случае GF (и, следовательно, G''1)
при ог-»-0 расходится как а<2-">/2 (или как lncr для п = 2).
В квантовой теории поля в пространстве Минковского эту
расходимость легко исключить, например, с помощью нормаль-
нормального упорядочения операторов (см. B.41)). Если топология
пространства нетривиальна, но геометрия по-прежнему плоская,
как в случаях, рассмотренных в разд. 4.1, 4.2, для обрезания
ультрафиолетовой расходимости можно использовать регуляри-
зующую функцию e~a|kl, a затем взять разность величины <7\iV>
в интересующей нас топологии и соответствующей (обрезанной)
величины в пространстве Минковского, полагая а-»-0 в конце
вычисления. Можно также, используя метод функции Грина, вы-
вычесть неограниченную величину GA)(x, x/), построенную в про-
пространстве Минковского, из функции GO, вычисленной в рассма-
рассматриваемой топологии, и лишь затем перейти к пределу при
х-*-х?.
В искривленном пространстве-времени эти простые приемы
не заслуживают доверия по следующим двум причинам. Первая
касается роли тензора Т^ в теории гравитации. В негравита-
негравитационной физике наблюдаема лишь разность энергий, поэтому
бесконечная энергия вакуума никого не смущает — достаточно
сдвинуть начало- отсчета на бесконечную величину. При учете
гравитации эта процедура становится неудовлетворительной.
Энергия является источником тяготения и изменяет кривизну
самого пространства-времени, влияние которого мы и пытаемся
изучать. Она не может быть просто отброшена: мы не имеем
права изменять начало отсчета энергии. Вместо этого требуется
менее формальная схема перенормировок, учитывающая дина-
динамику гравитационного поля.
Вторая причина затруднений может быть проиллюстриро-
проиллюстрирована на простом примере. Рассмотрим пространственно-плоскую
модель Робертсона — Уокера с масштабным фактором
a(t) = (\-A2t2Li, А = const, F,1)
имеющим физические особенности при t = ±A~l

160 Глава 6
Безмассовое скалярное поле, в случае четырех измерений
удовлетворяющее волновому уравнению
?^ = 0, F.2)
не является конформно-связанным, но удается найти решения
для полевых мод [80)
ик та Aбя3Гэ/2С-''°(ч) (k* + Л2)-'''ехр [ft • х - / (k2 + A*)\], F.3)
где C(r\) = a2(Ti) = cos2 Ar\ и Ti — конформное время.
С помощью мод F.3) можно построить пространство Фока
и использовать вакуумное состояние |0> при вычислении
<0|Гц,у|0>. Из выражения C.190) находим тензор энергии-им-
энергии-импульса для случая минимальной связи 1 = 0:
Т^ = ф. »Ф, v - 4 S^gaof. аФ. р> F.4)
который имеет ту же форму, что и выражение B.26) для пло-
плоского пространства-времени при m = 0. Используя формулу
B.43) (которая справедлива и в искривленном пространстве),
для плотности энергии получаем
@ | Го ° 10) = A/32яЗС2) \ d3k [(k* + A2)'h + (k2 +1 D2) (?2+Л2Г'/г],
F.5)
где D fa) = С" 1дС/дч\.
Как и следовало ожидать, этот интеграл имеет расходимость
четвертой степени. Если ввести в F.5) обрезающий множитель
ехр[—a(k2 + А2L»], интеграл можно выразить через функции
Макдональда. Разлагая полученное выражение по степеням pt,
яаходим
ра4 = C2Я2) [48/а4 + (D2 — вЛ2)/^ + А2 (-| О2 - Л2) In а]+О (а°),
F.6)
где плотность энергии обозначена через р, а С2 — через а4. Ле-
Левая часть F.6) представляет собой энергию безмассового излу-
излучения в объеме a* i учетом красного смещения при расширении
вселенной.
Чтобы получить соответствующий результат в пространстве
Минковского, достаточно положить в F.6) а = 1 и D = А = 0.
Отличным от нуля остается лишь первое слагаемое в правой
части F.6). Следовательно, если даже отбросить этот член,
в искривленном пространстве-времени величина ра4 все еще
будет расходиться в пределе при а-»-0. Иначе говоря, разность
нулевых энергий во вселенной Робертсона — Уокера и в про-
пространстве Минковского по-прежнему бесконечна. Мы не сможем

Перенормировка тензора энергии-импульса 161
избавиться от расходимости в выражении для <0|ГОо|0>, просто
отбрасывая бесконечный член, характерный для пространства
Минковского.
Из выражения F.6) видно, что помимо ожидаемой расходи-
расходимости четвертого порядка имеются также квадратичная и лога-
логарифмическая расходимости. Поэтому выделение бесконечностей
в <?Vv> требует более внимательного подхода, нежели в случае
плоского пространства-времени.
Каким образом можно выяснить физический смысл расходя-
расходящегося выражения? Очевидно, для получения конечного ответа
необходимо вычитание бесконечных величин, но это можно
сделать бесконечным числом способов. Для того чтобы получить
однозначный ответ, необходимо наложить дополнительные тре-
требования. Расходимости имеются и в квантовой теории поля в
пространстве Минковского, в особенности это касается случая
взаимодействующих полей. В квантовой электродинамике мож-
можно выполнить бесконечные вычитания систематически и полу-
получить конечные результаты, согласующиеся с экспериментом, при
условии, что вычитания проводятся ковариантным образом
(см., например, [427, 472—474]). Поэтому, имея дело с беско-
бесконечностями в <7^у>, следует прежде всего пытаться сохранить
общую ковариантность теории. Помимо требования общей кова-
ковариантности, необходимо также потребовать выполнения ряда
«физически разумных» условий на <7"^>- Если наложить на
<^nv> достаточное число таких условий, то процедура вычитаний
становится однозначной. Мы увидим в разд. 6.6, что такой под-
подход действительно может быть осуществлен.
Альтернативная стратегия состоит в рассмотрении <7ЦУ> как
величины, входящей в более широкую динамическую теорию,
включающую гравитацию. В рассматриваемой в данной книге
полуклассической теории гравитационное поле считается клас-
классическим, в то время как материальные поля (включая грави-
гравитоны в однопетлевом приближении, см. гл. 1) трактуются кван-
квантовым образом. Это напоминает полуклассическую теорию,
успешно применявшуюся в электродинамике, где классическое
электромагнитное поле связывалось со средним значением опе-
оператора электромагнитного тока. По аналогии мы строим тео-
теорию, основанную на уравнениях Эйнштейна
Jfc + A? 8яОГ, F.7)
в, которых тензор энергии-импульса, являющийся источником
поля, теперь рассматривается как квантовое среднее значение:
\ OVv). F.8)
Космологическая постоянная Л и гравитационная постоянная G
снабжены индексом В по причине, которая будет ясна из
А Яак. 674

162 Глава 6
дальнейшего. В этой главе мы будем явно выписывать гравита-
гравитационную постоянную G, которая в других разделах книги пола-
полагается равной единице.
Классическое уравнение Эйнштейна F.7) может быть полу-
получено из действия
S = Sg + Sm F.9)
с помощью вариационного принципа
Первый член в правой части F.9) представляет собой дей-
действие для гравитационного поля
Sg= J Lg(-gL'dnx = J (-g)'h№nGB)-1 (R - 2A)dnx, F.11)
и вариационная производная 2(— g) bSg/bgw дает левую часть
F.7). Второй член в F.9) есть классическое действие мате-
материальных полей, варьирование которого
__JL__J^_==7'liV F.12)
приводит к правой части F.7).
Как можно использовать эту процедуру для полуклассиче-
полуклассического уравнения F.8)? Можно попытаться построить величину
W, называемую эффективным действием для квантованных ма-
материальных полей, варьирование которой давало бы {Гцу):
. \ч, А1=<^> (ел?)
(точный смысл операции усреднения < >, применяемой к Т^
будет выяснен ниже).
Для изучения структуры W вернемся к основным принципам
теории, вспомнив процедуру квантования с помощью интегралов
по траекториям, коротко описанную в разд. 2.8. Наши рассужде-
рассуждения непосредственно относятся к скалярному полю, но фор-
формально выкладки не отличаются и для полей высших спинов.
В разд. 2.8 производящий функционал
\} F.14),
был интерпретирован физически как амплитуда вероятности ва-
вакуумного перехода (out, 010, in>. Наличие внешнего тока /
делает начальное состояние вакуума нестабильным, т. е. приво-
приводит к рождению частиц. В плоском пространстве в пределе
/ = 0 частицы не рождаются, и мы имеем условие нормировки

Перенормировка тензора энергии-импульса 163
=(out, О |О, in>y_0 = <О 10> == 1. F.15)
Однако в искривленном пространстве-времени, как мы видели,
вообще говоря, |0, out>=^=|0, in> даже в отсутствие источника /.
Поэтому условие F.15) становится неприменимым.
Квантование с помощью интегралов по траекториям при-
пригодно и в искривленном пространстве-времени; достаточно счи-
считать 5т в F.14) действием для материальных полей в искрив-
искривленном пространстве, а 7(а') — соответствующей плотностью
тока (скалярной плотностью в случае скалярного поля). По-
Поэтому можно положить / = 0 в F.14) и рассматривать вариа-
вариацию Z [0]:
Ы [0] = l\& [ф] eSme15*[ф] = i (out, 016Sm 10, in) F.16)
в соответствии с вариационным принципом Швингера [428]. Со-
Сопоставляя F.16) и F.12), будем иметь
Поскольку материальное действие Sm появляется в F.14)
в показателе экспоненты, можем отождествить ¦
Z[0] = e'^, F.18)
или, иначе
W = -/ln<out, 0 |0, in); F.19)
тогда из F.17) найдем
2 6W =<out, 0[ГЦу|0, in)
(-g)'1' W (out, 010, in) ' { ' '
Функционал Z[0] строится по той же схеме, что и в случае
плоского пространства-времени (см. с. 36). Но при этом нужно
1) заменить dnx на ковариантную меру dnx[—gOc)]1'2; 2) заме-
заменить б"(х — у) произведением б"(л: — у) [—g(y))~'l!, для кото-
которого инвариантный интеграл
и 3) вместо B.120) ввести оператор
Kxy = (nx + m2-ie + lRNn(x-y)[-g(y)]-\ F.21)
для которого с учетом соотношения
dny [- g iy)f KXUK^ = б (х - z){- g (г)]'11' F.22)

164 Глава б
и формулы C.49) находим
г-1
Kxz=-GF(x,z) F.23)
(ср. B.123)). С помощью выкладок, аналогичных выполненным
на с. 37, найдем (как и в плоском пространстве-времени)
Z[O]~[det(-GF)]''\ F.24)
причем коэффициент пропорциональности, не зависящий от
метрики, не существен. В результате мы приходим к формуле
W = -i\nZ[O] = -±itr[[n(-GF)]. F.25)
В этой формуле Gf можно рассматривать как оператор, дей-
действующий в пространстве векторов \х), нормированных усло-
условием
(х | Xе) = б" (х - х') [- g (x)] -1/l F.26)
так, что
GF{x,x') = (x\GF\xr). F.27)
След оператора М, действующего в этом пространстве, опреде-
определен как
tr М = J сГх[-g(х)]ъМхх«, J dnx[-g(x)f (x\M\x). F.28)
Чтобы придать смысл формальному выражению F.23), не-
необходимо использовать некоторое представление для фейманов-
ской функции Грина Gf. Мы воспользуемся представлением
де Витта — Швингера в терминах интеграла по собственному
времени C.138). Записав операторный аналог соотношения
F.23) в виде
00
GF = - /Г1 = -1 J e-iKsds, F.29)
из C.138) будем иметь
(х | e~lKs | *') = l DяГ"/2 А1'' (х, х') e-im's+°l2is X
XF(x, x';is)(isym. F.30)
Далее, предполагая, что К имеет малую отрицательную мнимую
часть, найдем
5 e~iKs {is)~x ids = - Ei (- iKK). F.31)
A
Здесь Ei — интегральная показательная функция, для которой
цри малых значениях аргумента справедливо разложение

Перенормировка тензора энергии-импульса 165
где у — постоянная Эйлера. Подставляя F.32) в F.31) и по-
полагая Л->-0, будем иметь
оо
S K4 F.33)
что верно с точностью до не зависящей от метрики (бесконеч-
(бесконечной) константы, которая для дальнейшего не существенна. Та-
Таким образом, в представлении де Витта — Швингера F.30) (или
C.138)) имеем
оо
(х | In (- G$s) | xf) = - J O?s (x, x') dm2, F.34)
где интеграл по переменной mz сокращает добавочный множи-
множитель (is)-1 в F.33).
Возвращаясь к выражению F.25) для W, из F.28) и F.34)
находим
сю
W = -J- i[ dnx [- g (х)]Уг lim [ dm2GpS (x, x'). F.35)
Изменяя порядок интегрирования и переходя к пределу при
х'-*-х, получаем
00
W = 4 i \ dm2 J dnx [- g (x)]'1' G?s (x, x),
m1
где интеграл по dnx, как нетрудно видеть, представляет собой
выражение, описываемое однопетлевой фейнмановской диаграм-
диаграммой, изображенной на рис. \,а (о правилах Фейнмана см. гл. 9).
Поэтому величина W получила название однопетлевого эффек-
эффективного действия. В случае фермионов эффективное действие
содержит также след по спинорным индексам.
С помощью F.35) можно ввести плотность эффективного
лагранжиана ^эфф, исходя из соотношения
W = \ &т (х) dnx ^\[-g (x)]'1' Lm (x) dnx. F.36)
Для этой величины находим
4 00
1/==-5-/ lim [ dm2G?s (x,xf). F.37)
Использование выражений C.137) и C.138) показывает, что
ф расходится на нижнем пределе интеграла по s, поскольку

166 Глава б
сглаживающий множитель o/2s в показателе экспоненты в пре-
пределе х'-*-х исчезает. (Сходимость на верхнем пределе гаранти-
гарантируется добавкой —ie, которая в представлении де Витта —
Швингера для GF неявно включена в т2.) В четырехмерном
случае потенциально расходящимися в разложении де Витта —
Швингера для 1Эфф являются члены
X [а0 (х, х') + а, (х, х?) is + а2 (х, xf) (isJ], F.38)
где функции ао, а\ и а2 определяются формулами C.131) —
C.133). Остальные члены в асимптотическом разложении, на-
начиная с аз, в пределе х' -*-х конечны.
Расходимости в ?Эфф конечно те же, что и для <7*wv>. Из
формул C.131) — C.133) следует, что в пределе х'-^-х выраже-
выражение в квадратных скобках в F.38) имеет чисто геометрический
характер, т. е. построено из компонент локального тензора i?WV0T
и его производных. Эта особенность не случайна, как видно из
следующих соображений. Расходимости возникают вследствие
«плохого» поведения мод в ультрафиолетовом пределе. Все
короткие волны чувствительны лишь к локальной геометрии в
окрестности точки х и нечувствительны к глобальным свойствам
пространства-времени, таким, как топология или.поведение в
прошлом. Ниже мы увидим, что расходимости не зависят и от
выбора квантового состояния поля.
Поскольку Lpacx имеет чисто геометрический характер, -эту
величину следует скорее рассматривать как вклад в гравита-
гравитационный лагранжиан, чем в лагранжиан материальных полей.
Хотя величина Lpacx обусловлена действием для квантового ма-
материального поля, она зависит только от переменных, описы-
описывающих гравитационное поле. Конечно, это не справедливо для
остальных конечных членов в Lэфф, учитывающих и длинновол-
длинноволновый вклад. Они чувствительны к крупномасштабной струк-
структуре многообразия и зависят от выбора квантового состояния.
6.2. Перенормировка в эффективном действии
Обратимся к отысканию точной формы геометрических чле-1
нов Lpacx, чтобы сравнить их с обычным гравитационным лагран-.
жианом Lg, фигурирующим в F.11). Эта задача требует осто-
осторожности, поскольку выражение F.38) расходится. Фактически
нам необходимо показать, что расходящаяся часть может быть
представлена в виде произведения оо X геометрический объект.
Это можно сделать различными способами.

Перенормировка тензора энергии-импульса 167
Например, в случае п измерений асимптотическое (адиабати-
(адиабатическое) разложение ?Эфф имеет вид
. *') f С*)'-1-'2.-1 ^-^>*Л. F.39)
f
где первые л/2 + 1 члена расходятся при а-»-0. Если л рассма-
рассматривать как переменную, которая может быть аналитически
продолжена в комплексную плоскость, то можно перейти к пре-
пределу при х?-**х\
оо со
?эфф « j Dя)-"/2 ? а/ (х) J (is)'~1~n/2 e-lm'si ds = F.40)
/-0 0
¦ с»
1п12^2п12'п/2), F.41)
/-о
где
a,(x)^ai(x, x).
В дальнейшем удобно сохранить для ?Эфф размерность (дли-
(длина) даже в случае пф\. Для этого следует ввести произволь-
произвольный масштаб массы ц и переписать F.41) в виде
с»
^эфф ~ J Dя)""/2 (m/fx)"-4 ? а, (х) т4/Г (/ - п/2). F:42)
/-о
При л->-4 первые три члена в F.42) расходятся из-за нали-
наличия полюсов у Г-функций:
F.43)
Обозначая эти первые три члена Lpacx, получаем [72]
где мы использовали разложение
( f-)" - 1 + ? </» - 4) In (i-г) + О ((« - 4J) F'45)
и опустили в F.43) члены, исчезающие при я->4.

168 Глава б
Функции ао, а{ и а2 получаются в пределе совпадающих то-
точек из выражений C.131) —C.133) и C.129):
¦оо(*)-=1, «.(*)=(!-!)#, F.46), F.47)
n IY\— { в r>aPv« I noPn
Теперь очевидно, что выражение Lpacx F.44) представляет собой
чисто геометрическую величину. Здесь уместно напомнить, что
/,Эфф является лишь частью полного лагранжиана, помимо кото-
которой имеется гравитационная часть. Поскольку LpaCx имеет чисто
геометрический характер, можно попытаться включить его в
гравитационный лагранжиан.
Используя F.11), представим плотность полного гравита-
гравитационного лагранжиана в виде произведения (—g)'11 на
{^r |[ (f)]}. (в.49)
где
Первый член в F.49) есть постоянная. Вклад от LPaCx (т. е.
величина А) физически неотличим от Лв. Эта часть гравита-
гравитационного лагранжиана приводит к возникновению так назы-
называемого космологического члена Agwv в уравнениях гравита-
гравитационного поля F.8). Таким образом, влияние скалярного кван-
квантованного поля состоит в изменении или перенормировке значе-
значения космологической постоянной Лв:
Поскольку физические наблюдения всегда будут давать лишь
перенормированное значение Л, величиной Ав можно не интере-
интересоваться и не беспокоиться о том, что при п—*-4 величина в ква-
квадратных скобках в F.50) расходится (мы никогда не сможем
измерить эту величину отдельно). Такой метод включения бес-

Перенормировка тензора энергии-импульса 169
конечностей в перенормировочные физические величины обычен
в квантовой теории поля. Например, в квантовой электродина-
электродинамике электрон оказывается одетым в «шубу» виртуальных фото-
фотонов, которые дают (бесконечный) вклад в полную массу элек-
электрона. Измеримой является лишь перенормированная масса
электрона (которая, безусловно, конечна). Электрон неотделим
от своей фотонной шубы, и мы никогда не сможем измерить
«голую» массу. Используя эту терминологию, мы можем ска-
сказать, что «голая» космологическая постоянная Лв также не-
наблюдаема (индекс В означает «bare» — голая).
Обращаясь ко второму члену в F.49) находим, что LpaCx
также перенормирует ньютоновскую гравитационную постоян-
постоянную, превращая GB в
). F.51)
Последний член в F.49) в обычном эйнштейновском лагран-
лагранжиане отсутствует. Функция а.2{х) — величина четвертого адиа-
адиабатического порядка, поскольку она содержит четыре производ-
производных от метрики (см. F.48)). Ее следует рассматривать как
поправку высшего порядка к лагранжиану общей теории отно-
относительности, в который входят лишь вторые производные от ме-
метрики. Если включить этот добавочный член в Sg, левая часть
уравнений для гравитационного поля принимает вид
Яцу - у ^iiv + Aguv + аA»Я^ + РB)#nv + Y#nv> F.52)
где
= 2R-, „v - 2gnV aR-j g^R2 + 2/?/?|xv, F.53)
j
va п/?^ - у g^ nR + 2^Xv ~ T 8»Х*К<#> F-54)
Wv°PV - 4 °^v + Щ ,v - 4/?^°v + 4/?°4,Pv. F-55)
Заметим, что в случае п = 4 обобщенная теорема Гаусса —
Боннэ [108, 109] утверждает, что величина
\d\x)[-g (*)]''• Uaj3Y5*afiYe + Я2 - 4/?арЯор) F.56)

170 Глава 6
является топологическим инвариантом (называемым числом
Эйлера), так что ее вариация по метрике тождественно равна
нулю. Тогда-из F.53) — F.55) следует
Н^-т^+А^Н^. F.57)
Коэффициенты а, р и v B F.52) содержат множитель
1/(л— 4) и, следовательно, расходятся, когда п стремится к фи-
физической размерности пространства-времени п = 4. Поэтому мы
должны ввести в исходный гравитационный лагранжиан члены
четвертого адиабатического порядка с «голыми» коэффициен-
коэффициентами ав, Ьв, св, которые затем используются для поглощения
бесконечных членов, пропорциональных a, (J, у, и дают перенор-
перенормированные значения а, Ь, с. Поскольку при п = 4 ввиду F.57)
лишь два из этих коэффициентов независимы, мы можем поло-
положить с = 0. Значения постоянных а и & могут быть найдены
только из эксперимента. Чтобы избежать противоречия с наблю-
наблюдениями,- следует предположить, что численные значения а и b
весьма малы (см., например, [215, 442, 443]). В принципе нет
причины, по которой эти перенормированные величины нельзя
положить равными нулю, что возвращает нас к эйнштейновской
теории. Квантовая теория поля лишь указывает, что члены,
включающие высшие производные метрики, априори могут при-
присутствовать в лагранжиане1).
Прием, состоящий в аналитическом продолжении размер-
размерности пространства-времени п иа область нефизических значе-
значений, позволяет сделать формально расходящуюся часть Lpacx
временно конечной, так что с отдельными вкладами в эту вели-
величину можно проводить осмысленные действия и включить их'
в гравитационный лагранжиан. Такое преобразование фор-
формально расходящихся выражений называется регуляризацией.
Использованный выше подход известен как размерная регуля-
регуляризация; он был впервые использован в теориях взаимодейст-
взаимодействующих квантованных полей в пространстве Минковского [7,
57, 458]. В конце вычислений, после того как выполнена пере-
перенормировка затравочных констант, регуляризация может быть
снята, т. е. п-*-4.
После удаления LpaCx из /,Эфф остающаяся часть становится
конечной и представляет собой перенормированный эффектив-
эффективный лагранжиан
— Lpacx. F.58)
•) Обсуждение теорий с высшими производными см. в работах [676*—
578*]. Такие теории перенормируемы [442] и асимптотически свободны
{578*1, хотя в теории возмущений появляются тахионы и духи. См, также
[67' ~
&79*—682*], — Прим. перев.

Перенормировка тензора энергии-импульсй 171
В случае четырех измерений асимптотическое разложение ?рен
содержит все члены с / ^ 3 в F.40). Полагая я = 4 и xf = х,
можем записать это асимптотическое разложение в виде
0 /=.3
или, проинтегрировав трижды по частям (см. C.140)),
оо
EF 5 In (Is) -дщг [F (х, x; is) е-"*1] d (is) +
~ism^lds- F-60)
Последний конечный член перенормирует Л, G, а, Ъ в с на ко-
конечные величины; он имеет ту же форму, что и LpaCx, и содер-
содержит функции const X О/ при / = 0, 1,2. Очевидно, перенормиро-
перенормированный лагранжиан всегда будет определен с точностью до
членов такого типа — конечных перенормировочных членов, по-
поэтому мы можем опустить второе слагаемое в F.60).
По той же причине можно не заботиться о выборе масштаба
массы \х, введенного в F.42). Изменение параметра ц, приведет
к конечной перенормировке Lpacx, в результате которой изме-
изменятся коэффициенты в геометрических членах ао, а\ и а2. Прак-
Практически следует выбрать некоторое фиксированное значение ц
и затем использовать результаты какого-либо расчета с этим
значением ц для градуировки измерительного прибора, приме-
применяемого для определения констант Л, G, а и Ь. Используя изме-
измеренные этим прибором константы, можно провести дальнейшие
расчеты с тем же значением параметра ц,, причем получаемые
предсказания следует проверять экспериментально с помощью
тех же проградуированных ранее приборов. Если изменить зна-
значение ц,,1 необходимо заново ттроградуировать приборы или за-
заменить параметры Л, G, а и Ь; в результате предсказания тео-
теории остаются неизменными. Такой анализ изменения констант
при замене масштаба ц в теориях взаимодействующих полей в
пространстве Минковского приводит к уравнению ренормгруппы
([457], см. также разд. 9.2). С учетом сказанного вместо F.60)
можно написать
* оо
причем подразумевается, что к этому выражению могут быть
добавлены любые конечные комбинации ао, а.\ и а^. Будучи

172 Глава 6
полученным из асимптотического разложения для F, выражение
F.61) не может рассматриваться как полный лагранжиан, ассо-
ассоциируемый с физическим перенормированием <Tnv>. построение
которого откладывается до разд. 6.4. Мы представили LpeH в
такой форме лишь для полноты. Следует, однако, заметить,
что в принципе полный перенормированный лагранжиан можно
было бы найти из F.61), если располагать точным выражением
для F.
Помимо размерной регуляризации существуют и другие спо-
способы регуляризации. Рассмотрим разложение по собственным
функциям для оператора К~1:
К--1 г VI т)(т\
К =-Gf= 2,—ЦТ"' F.62)
т
где
= б„т> F.63)
?|/n)<m|=l. F.64)
т
Тогда
Kv\m)^Kl\m), F.65)
так что
(-Gf)v = I>m-v|/n)<m| F.66)
т
и, следовательно,
tr (- OP)V J d'x [- g (x)]11' 2 & (х | т) (т \х) = J] Ж, F.67)
где мы использовали условие полноты
4» [-*(*)]*!*><* 1-1. F.68)
Правая часть F.67) .напоминает ^-функцию Римана
?m=i m~v и может быть использована для введения обобщен-
обобщенной ^-функции [171, 172, 175, 231, 281]:
tr (- GFj* = Ц ЛГ *= I (v). F.69)
m
Выразим теперь эффективное действие F.25) через обобщен-
обобщенную 5-функцию. Прежде всего заметим, что аргумент логарифма
в F.25) должен быть безразмерным. Поскольку GF(x, xr) имеет
размерность (масса)"-2, а \х} в F.26) имеет размерность
(масса)п/2, из F.27) видно, что оператор Gf имеет размерность
(масса). Поэтому мы можем сделать аргумент логарифма в

Перенормировка тензора энергии-импульса 173
F.25) безразмерным для всех п, вставляя множитель ц2:
W = -±itr [In (- y.zGF)]. F.70)
Фактически мы уже ввели аналогичную константу, переходя от
F.24) к F.25). Параметр ц в методе регуляризации с помощью
^-функции выполняет ту же роль, что и величина (л, введенная
в F.42) в схеме размерной регуляризации. Как и выше, измене-
изменение ц приводит лишь к конечным изменениям коэффициентов
в перенормировочных членах, которые неоднозначны по своей
природе.
Эффективное действие F.70), выраженное через обобщенную
^-функцию, принимает вид
W = - 4 / Hm tr ¦?- (-n2Gf)v = Hm {- 1 /ц2* [?'(v) + I (v) In ц2]} .
• F.71)
Введение обобщенной ^-функции следует понимать как чн-
сто формальную операцию. Выражение F.69), вообще говоря,
не сходится при всех значениях v. Но эту величину можно опре-
определить как аналитическое продолжение из области, в которой ряд
сходится. Тогда мы найдем, что ?@) и ?'@) конечны, и можно
написать
Таким образом, с помощью формального аналитического про-
продолжения расходимости в выражении для эффективного дейст-
действия W устранены. Этот результат можно сопоставить с соответ-
соответствующим свойством ^-функции Римана: ряд ?m_i tn~v, очевид-
очевидно, расходится, если положить v = 0, но ^-функция Римана,
определяемая этим рядом при v > 1, будучи аналитически
продолжена в точку v = 0, имеет конечное, значение 1/2.
Чтобы показать конечность величин ?@) и ?'@), фигурирую-
фигурирующих в F.72), вычислим их явно в представлении собственного
времени де Витта — Швингера. Заметим предварительно, что
(tay-le-iK*d (is) = K~VT (v), F.73)
откуда следует
оо
(- GPf = /C~v = [r (vJJ-1 \ (is)v-le-iKsida. F.74)

174 Глава 6
Используя теперь F.69) и F.30), для случая четырех измерений
получаем
С(v) = i [Г (v)]-1 Dя)-2 \d\\-g(х)]'АX
(isy-3e~im'sF (х, х; is) ids. F.75)
Если Re v > 2, мы можем трижды проинтегрировать по частям.
Вспоминая, что т2 понимается как m2— ie, находим, что подста-
подстановки обращаются в нуль, и в результате получаем
х S № w^F {х' *'is) e~ism'^[ds> FJ6)
S
о
откуда находим
5 @) = I Dя)-2 \<tx[-g (x)]'A [^ m4 - /nV (х) + а2 (*)], F.77)
где использовано разложение C.140) для вычисления
¦3jj&[F(x, x; to)e''#M1.-o-
Поскольку Ц0) содержит лишь конечные перенормировочные
члены, теперь ясно, что изменение (л в F.72) приведет лишь
к конечному изменению перенормировочных коэффициентов
в полном действии. Таким образом, для'наших целей членом,
содержащим ?@) в F.72), можно пренебречь.
Дифференцирование F.76) по v дает
С @) = -J- i Dя)-2 { (у - у) \d\ [- g {x)f X
X [ j m - m\ (x) + a2 (x)] - \ d*x [- g (x)]'A J In (to) ^-^ X
X [P (x, x; is) e - »•»'] / rfs }, F.78)
т. е. конечную величину. Первый интеграл в этом выражении
содержит лишь конечные перенормировочные члены, которыми
также можно пренебречь. Подставляя оставшийся член в F.72)
и используя определение F.36), получаем
оо
ln <'"*) W [F (х, х; is) е-"-] i ds =
о
конечные перенормировочные члены, F.79)

Перенормировка тензора энергии-импульса 175
что согласуется с результатом F.61), найденным методом раз-
размерной регуляризации.
Заметим, что описанный здесь метод ^-функции не требует
явной перенормировки констант связи в гравитационном лагран-
лагранжиане, в отличие от метода, примененного Даукером и Кричли
[171, 172, 175]. Аналитическое продолжение позволяет получить
конечный результат из явно расходящегося ряда (например, ряд
2m=i/n~v ПРИ v==0 становится равным 1/2. Ясно, что беско-
бесконечный член был отброшен с помощью этой формальной про-
процедуры.
Можно предположить поэтому, что разные варианты этого
метода будут давать разные ответы. Например, если вместо
F.71) подставить логарифм в F.70) в виде lim[v~'(—
*0
v], то мы получим
W = - 1 Him v-'? @) -11 [?' @) +1 @) In ц2] + c, F.80)
где с — бесконечная не зависящая от метрики константа, кото-
которую можно опустить. Выражение F.80) отличается от F.72)
только в первом слагаемом, которое, как видно из сопоставле-
сопоставления с формулой F.77), описывает бесконечную перенормировку
гравитационного действия. Таким образом, перенормированное
эффективное действие остается тем же самым независимо от
того, выполнялась ли бесконечная перенормировка или нет.
Все же может возникнуть некоторое сомнение по поводу од-
однозначности перенормированного эффективного действия. Можно
ли быть уверенным, что перенормировочные процедуры, вклю-
включающие сомнительные формальные манипуляции с расходящи-
расходящимися величинами, всегда приводят к «правильному» ответу?
Чтобы ответить на этот вопрос, необходимо, во-первых, устано-
установить, каким физическим требованиям должен удовлетворять
«правильный» ответ (мы займемся этим в разд. 6.6). Во-вторых,
нужно дать строгое математическое обоснование использован-
использованным формальным манипуляциям. В случае плоского простран-
пространства такая трактовка квантовой теории поля дана в работах
[84,450,451].
В другом часто используемом методе регуляризации исполь-
используется расщепление, или раздвижка точек. Основная идея
.состоит в возвращении к F.37), где точки х' и х остаются раз-
разделенными некоторым бесконечно малым расстоянием в неизо-
неизотропном направлении. Пока а не равно нулю, ?Эфф остается ко-
конечным, и интеграл в F.38) может быть выражен через функции
Ханкеля. (Тот же результат можно получить также, подставив
первые три члена суммы C.138) в формулу F.37).) Используя

176 Глава б
асимптотическое разложение функций Ханкеля по степеням а
и оставляя только члены, не исчезающие при 0->О, получим в
случае четырех измерений [114]
Lpacx= lim A/8я2)Д1/2(х, х'){ао(х,
F.81)
Величины a0 (*>*')> fli (*>*')> fl2 (*>*') и А.(х,х') теперь можно
разложить по степениям а. Основной член результирующего раз-
разложения F.81) расходится как а~2. Коэффициенты разложения
имеют геометрический характер и определяются тензором Ри-
мана и его производными, но, как показывают выражения
C.132) и 3.133), эти коэффициенты содержат векторные вели-
величины, обусловленные наличием множителей у*. Исходя из
C.136), или из общей теории [153], эти векторы можно предста-
представить с помощью а как
/ = а:1* = <Л F.82)
откуда для C.136) имеем
о = ±оу. F.83)
Степень расходимости удобно параметризовать с помощью ве-
величины е, пропорциональной геодезическому расстоянию между
х' и х, выделяя (неизотропное) направление расщепления по-
посредством единичного вектора t» (рис. 22). Для этого запишем
аи = 2е^, F.84)
где
W[iSS2 = ±l F.85)
в зависимости от того, является ли вектор № времениподобным
или пространственноподобным. Тогда F.83) принимает вид
сг = 2е22 , F.86)
(множитель 2 введен в F.86) для удобства в дальнейших вы-
вычислениях). При такой параметризации главная особенность
в Lpacx ведет себя как е~4, а типичный зависящий от направ-
направления коэффициент имеет вид RilvRpaM'vtPtom (Дальнейшие под-
подробности даны в разд. 6.4.) Такие члены нельзя устранить с, по-

Перенормировка тензора энергии-импульса
177
Рис. 22. Точки х", х', лежащие на ие-
изотропной геодезической, проходя-
проходящей через точку х, параметризован-
параметризованные с помощью вектора <*\ на соб-
собственном расстоянии е от х.
мощью перенормировок, поскольку вектор f- имеет искусствен-
искусственный характер, а не определяется из динамики.
Чтобы освободить теорию от членов, зависящих от направ-
направления, можно усреднить по всем направлениям, используя под-
подходящую меру [5]. Тогда такие члены сводятся к комбинациям
R, R2, Ra$Ra^ и /?<xpY6#aPY6> которые устраняются обычным спо-
способом путем перенормировки Л, G, a, b и с в гравитационном
действии. Конечный остаток LpeH = ?эфф — ?расх, очевидно, вос-
воспроизводит формулы F.59) и F.61) и, таким образом, согла-
согласуется с результатами как размерной, так и ^-регуляризации.
Если нас интересуют уравнения поля, а не само действие, пере-
перенормировки постоянной с не требуется. Причина состоит в том,
что метод расщепления точек с самого начала используется для
случая четырех измерений, когда величина F.56) является то-
топологическим инвариантом и, следовательно, не дает вклада
в уравнения поля при подстановке в функциональную произ-
производную F.10). Это может быть использовано для исключения
одной из констант а, Ь или с из уравнений поля.
Полезно рассмотреть подробнее тесную взаимосвязь мето-
методов расщепления точек и размерной регуляризации. Исходным
пунктом обоих методов является представление де Витта —
Швингера F.39), в котором можно выполнить интегрирование
по s (вспомним C.141)). Рассмотрим простейший случай про-
пространства Минковского. Тогда ао(х,х') = 1, a.j(x,х') = 0, />0.
Вклад дает только первый член ряда; из C.141) и F.37) на-
находим
F.87)
Если используется размерная регуляризация, то мы хотим
иметь возможность положить о = 0 в F.87) и разложить

178 Глава 6
результат в окрестности п = 4. Из асимптотических формул
Rev>0, F.88а)
г->0
{!ln)e-™T(-v)[jzy, Rev<0, F.886)
ясно, что, для того чтобы сделать F.87) конечным при a-vO,
нужно продолжить это выражение по п в область веществен-
вещественных отрицательных значений; тогда
тпГ
( п\
^ 1)
2
»¦¦¦ 32я2(я-4)
С другой стороны, если используется метод расщепления точек,
то мы хотим иметь возможность положить п = 4 с самого на-
начала, используя в качестве регуляризатора а. В этом случае
можно воспользоваться формулой F.88а) и мы найдем
г . (-11
Заметим, что в безмассовом случае расходящийся член при раз-
размерной регуляризации полностью исчезает, и перенормировка
не требуется. В противоположность этому при использовании
метода расщепления точек зависимость от т исчезает, и ?эфф
по-прежнему расходится как а~2 в безмассовом пределе. По-
Поэтому при таком способе регуляризации необходима перенор-
перенормировка.
В случае двумерного пространства-времени исследование
выражения F.41) показывает, что при п = 2 потенциально рас-
расходящимися в ряду де Витта — Швингера являются лишь чле-
члены с / = 0 и /=1. Эти члены можно устранить с помощью
перенормировки Л и G в эффективном действии, как и выше.
Следует заметить, что величина \ d2x[— g (x)]'hR(x) в двумер-
двумерном случае есть топологический инвариант, и ее вариация
в эффективном действии не дает вклада в двумерное «уравне-
«уравнение Эйнштейна». Иначе говоря-, двумерный тензор Эйнштейна
Rpv—о" ^SVv тождественно равен нулю. Но мы должны вклю-
включить член, содержащий R, в эффективное действие, чтобы мож-
можно было устранить расходимости с помощью перенормировок.
Перенормированный эффективный лагранжиан (ср. F.61))
имеет вид
оо
Lpea = —щг J In (is) зщг[р (х, х; is) e-'"»1] d (is). F.89)

Перенормировка тензора энергии-импульса 179
В случае полей высших спинов изложенное выше повто-
повторяется почти без изменений. Для спинорных полей эффектив-
эффективное действие может быть записано с помощью би-спинора Gf,
определенного соотношением C.188):
Ww = ±nr[ln(-GF)], F.90)
где след теперь берется также и по спинорным индексам. Раз-
Различие в знаках между F.90) и F.25) непосредственно следует
из антикоммутативности спинорных полей в противоположность
коммутативности для скалярного поля. Случай электромагнит-
электромагнитного поля усложняется из-за наличия полей духов (разд. 2.8).
Методом интегрирования по траекториям находим
itv[\n(D)] + Wuyx, F.91)
где Df определено соотношением C.187), a Wayx равно умно-
умноженному на —2 эффективному действию для скалярного поля
с минимальной связью (множитель —2 возникает из-за того;
что имеются два антикоммутирующих скалярных поля духов).
Для расчета эффективного действия F.90), F.91) в терми-
терминах разложений де Витта — Швингера необходимы соответст-
соответствующие коэффициенты щ. Они были найдены де Виттом [153]
и Кристенсеном [П4], которые также подробно рассмотрели
перенормировку эффективного действия методом раздвижки то-
точек. (В электромагнитном случае, для того чтобы можно было
воспользоваться методом де Витта — Швингера, необходимо
временно ввести в лагранжиан массовый член.) Здесь мы при-
приводим только предельные значения коэффициентных функций
в совпадающих точках, которые встречаются в расходящихся
членах в четырехмерном случае. Для спина '/г коэффициенты
п разложении Gf в C.188) и F.90) представляют собой сле-
следующие матрицы:
()I
«2 (X) = (Tjgjj- R2 + -J20 П^ ~ 180 ^V^nv + -fifi R^""
^-S-VSpa^VV F-92)
1 — единичная матрица, а
(уи — зависящие от координат матрицы Дирака для искрив-
искривленного пространства-времени, введенные на с, 93, Eag дается

180 Глава 6
формулой C.166)). Для последующих применений мы приве-
приведем выражения для следов по спинорным индексам в F.92):
tr а0 (х) = tr 1 = д,
tr а2 (х) = ^ б[| R2 + 6 aR -\ tf^Xvpa - 4/?*Xv]. F.93)
где й — число компонент спиноров (т. е. размерность гамма-
матриц). Коэффициенты в разложении Df^ в C.187) и F.91)
являются тензорами, которые в фейнмановской калибровке
t = 1 имеют вид
i "g" ? °[iv i ~2 ^[ip^ v [2" R [lAtopv r
TW ^ ^P" "^ 180" ^ ^?p(AmJff(iv F.94)
В заключение этого раздела, носящего несколько техниче-
технический характер, сформулируем основные выводы. Метод пере-
перенормировки позволяет ввести действие для .связанной системы,
состоящей из гравитационного поля и квантованных материаль-
материальных полей, в форме
S S + W
и 'расходящиеся члены в W включить в достаточно общее вы-
выражение для Sg, так что все бесконечности оказываются погло-
поглощенными перенормированными константами связи. Таким об-
образом,
¦S = (¦Sg)peH + W рен>
где Eг)рен содержит перенормированные "физические констан-
константы, a WpeH теперь конечно. Подстановка S в F.10) приводит
к полуклассическому уравнению (в четырехмерном случае)
(out, 0|Г |0, in)peH
==~83tG
(out, 0 | 0, in)
где правая часть теперь конечна, а постоянные Л, а, Ь и G
должны быть определены из эксперимента.
При выполнении перенормировок не потребовалось явного
использования состояний |0, out) или |0, in>. В частности, не
возникло необходимости в предположении, что существуют

Перенормировка тензора энергии-импульса 181
асимптотические in- и out-области, в которых понятие вакуума
возникает естественно, либо вводится с помощью дополнитель*
ных физических соображений; вакуумные in- и out-состояния
появляются здесь чисто формально. Возникновение величины
<out, 0|Г[^|0, in>, а не какой-либо другой комбинации вакуум-
вакуумных состояний, связано с граничными условиями, заложенными
в представлении де Витта — Швингера для фейнмановского
пропагатора Gf, выполнение которых обеспечивается введением
множителя ie (см. с. 84). В^ряде случаев нас более интересует
величина <in, 01 Tuvj 0, in> (или, возможно, <out, 01Гuv10, out>).
Эффективное действие, которое приводит к таким вакуумным
математическим ожиданиям, можно получить, используя F.25)
с GF, записанным в терминах соответствующих вакуумных ожи-
ожиданий (например, для <in, 0| У^у! О, in> следует взять GF(x, х') —
= — i<in, О\Т(ф (х) ф {х')) |0, in>). К счастью, нам не придется
обсуждать перенормировки для каждого случая отдельно. Рас-
Расходимости обусловлены поведением пропагатора на малых рас-
расстояниях (при больших импульсах) (см. разд. 3.6), которое не
зависит от глобальных эффектов и выбора квантового состоя-
состояния. Поэтому следует ожидать, что расходимости для всех трех
форм <7nv> будут одинаковыми [156]. Это можно видеть, если
с помощью C.45), C.46) выразить |0, out) через многочастич-
многочастичные in-состояния. Величину (lllt 1/2, 1/3, ..., \jk, т|Г[м,|0, in)
можно найти, разлагая Гцу по произведениям операторов рож-
рождения и уничтожения, действующим на |0, in>. После проведе-
проведения этих выкладок приходим к результату
1 Г.,„ 10, in)
и-п, и и'п.,), F.96)
а
где «in, i — моды для in-области, а обозначения, использован-
использованные для записи последнего члена, объяснены на с. 25. Анало-
Аналогичная формула имеет место для <out, 0|Г^|0, out) с заменой
Ас/ на Vij из C.46) и заменой ищ на «out- Последний член в
F.96) конечен. Следовательно, имеющиеся в <in, 0|Гцу|0, in)
расходимости являются теми же самыми, что и в
<out, 0|Г^|0, in>/<out, 0|0, in>.
* 6.3. Конформные аномалии и безмассовый случай
Особый интерес вызывают теории поля, в которых класси-
классическое действие S инвариантно относительно конформных пре-
преобразований (разд. 3.1)
)-^D F.97)

182 Глава 6
Из определения вариационной производной имеем
, F.98)
откуда, используя 6§^ (х) = — 2{t4{x)Q~l {х)Ш(х) и F.12), на-
находим
5 [g^] = 5 [gviV] -\[-g (x)]'u Tpp [g^v (x)] Q-1 (л;) 6Q (л;) dnx. F.99)
Из этого уравнения немедленно получаем
F.100)
0-1
откуда ясно, что если классическое действие инвариантно от-
относительно конформных преобразований F.97), то след клас-
классического тензора энергии-импульса равен нулю. Это нетрудно
проверить в явном виде, используя формулы C.190), C.191) и
C.193) для безмассового скалярного поля с | = |(/г), безмас-
безмассового поля со спином 7г и электромагнитного поля в четы-
четырехмерном пространстве соответственно. Поскольку конформ-
конформные преобразования представляют собой преобразования длин
в каждой пространственно-временной точке х, наличие массы,
а следовательно, шкалы расстояний в теории всегда приводит
к нарушению конформной инвариантности. Таким образом, мы
приходим к проблеме безмассового предела при проведении
процедур регуляризации и перенормировок, использованных
в предыдущем разделе. При этом мы сталкиваемся с некото-
некоторыми тонкостями.
Несмотря на то что все члены высокого порядка (/ > 2)
в разложении де Витта - Швингера для эффективного лагран-
лагранжиана F 42) содержат инфракрасные расходимости при т->-0
в случае п = 4, мы по-прежнему можем использовать это раз-
разложение для членов, содержащих ультрафиолетовые расходи-
расходимости / = 0, 1 и 2 в четырехмерном случае. В членах с / = 0
и 1 можно сразу положить т = 0, поскольку они содержат по-
положительные степени разности п — 4. Следовательно, эти чле-
члены обращаются в нуль. Таким образом, единственное потен-
потенциально расходящееся в ультрафиолетовой области слагаемое
возникает при /' = 2:
; F.101)
оно требует тщательного исследования.
Подставляя для а2(х) при |=|(п) выражение из F.48),
после перегруппировки членов перепишем расходящееся ела*

Перенормировка тензора энергии-импульса 183
гаемое эффективного действия, связанное с F.101), в следую-
следующем виде:
Wpacx = у Dя)"П/2 (у)" Г B - т) J Л [- ff (*)]'* а2 (л;) =
F.102)
Ц Dя)-/2 (f )""' Г B -1) J rf»(х) [- g {x)f X
X[aF(*) + PG(*)] + O(n-'4), F.103)
где
+1 R2, F.104)
% + ^ F.105)
причем коэффициенты равны
a = 1/120, p = — 1/360. F.106)
При получении F.103) мы опустили члены UR и R2 в а2(х):
первый потому, что он представляет собой полную производную
и, следовательно, не дает вклада в действие, а второй потому,
что коэффициент перед ним пропорционален (п — 4J для слу-
случая конформной связи, когда | = |(п) ='/4(п — 2)/(п—1).
В пределе л-»-4 этот коэффициент подавляет особенность
(n — 4)-1, которую имеет Г-функция в F.43), в результате чего
данный член обращается в нуль.
Разбиение функции а2 на F и G связано с тем, что в четы-
четырехмерном случае (и только в этом случае) F представляет
собой квадрат тензора Вейля Са^уйСа^уй. С другой стороны,
интеграл \ (— g)'/a Qd4x есть топологический инвариант (см.
F.66)). Обе эти величины инвариантны относительно конформ-
конформных преобразований. Отсюда следует, что при п = 4 в безмас-
безмассовом пределе теории с конформной связью Wpacx инвариантно
относительно конформных преобразований.
Однако мы не должны снимать регуляризацию и переходить
к пределу п = 4 до того, как будут вычислены интересующие
нас физические величины, а вне точки п = 4 величина Wpacx
не является конформно-инвариантной (в противоположность W).
Мы увидим, что это нарушение конформной инвариантности
отражается на физических величинах даже после того, как
в конце вычисления положено п = 4.
* Чтобы убедиться в этом, воспользуемся тождествами [185]
F.107)
F.108)

184 Глава 6
которые позволяют сразу получить вклад Wpacx в след тензора
энергии-импульса
)
2 DЯ) ^—J D П) X
X Г B -1) [a (F - 4 п#) + PG] + О (п - 4). F.109)
Из F.43) видно, что множители (п — 4), возникающие из
F.107) и F.108), уничтожают расходимость (п — 4) от
ГB — п/2), приводя в пределе п->-4 к выражению
F.110)
Поскольку этот результат не зависит от отношения т/\к, кото-
которое было удержано в F.109) для обрезания в инфракрасной
области, в окончательном выражении F.110) мы можем поло-
положить т ¦= 0. Заметим, что локальность величины №расх и неза-
независимость от выбора состояния влечет за собой такие же свой-
свойства и для величины <Гц^>расх. Последняя также зависит толь-
только от геометрических величин, характеризующих пространство-
время в точке х.
Так как действие W в безмассовом пределе для случая кон-
конформной связи является конформно-инвариантным, среднее зна-
значение следа полного тензора энергии-импульса равно нулю:
= 0. F.1 Н)
"»-0, l-'/s. Q-1
Следовательно, если расходящаяся часть приобрела ненулевой
след F.110), то конечный перенормированный остаток (Г^рен
также должен иметь ненулевой след — выражение F.110) со
знаком минус:
0Wh= -0/16я2)[а (F - -| d#) + PG]= F.112)
F.113)
?/?]= F.114)
— -д" /? — D/?J• F.115)
След F.112)—F.115) появился в теории, несмотря на то
что классический тензор энергии-импульса является бесследо-
бесследовым, и обе величины W и U7pacx остаются конформно-инвариант-
конформно-инвариантными в четырехмерном случае. Ненулевой след появился вслед-
вследствие неконформной природы №'Расх (в отличие от W) вне точки
п = 4, которая оставляет свой отпеч'аток и при п==4 из-за рас-

Перенормировка тензора энергии-импульсп 185
ходимости UPpacx типа (п — 4)-1. Этот факт известен как кон-
конформная аномалия, или аномалия следа. Аналогичное наруше-
нарушение симметрии, получившее название аксиально-векторной ано-
аномалии, было ранее обнаружено [4] в квантовой электродина-
электродинамике.
Существование аномального члена DR в выражении для
следа было первоначально найдено Каппером и Даффом [98,
99]. За этим последовало указание [147] на возможное суще-
существование других членов, и в ряде более поздних работ
(см. библиографию) были установлены коэффициенты при
этих членах. Некоторые из ранних работ содержали ошибки и
противоречия (см. [72]). Но теперь известно, что все схемы
регуляризации предсказывают одинаковую конформную анома-
аномалию для скалярного поля.
Появление аномального следа тесно связано со скейлинго-
выми свойствами эффективного действия и, следовательно,
с ренормгруппой (см. гл. 9). Чтобы исследовать эту связь под-
подробнее, обратимся к методу ^-регуляризации. С помощью рас-
рассуждений, аналогичных приведенным на с. 88, найдем, что при
конформном преобразовании F.97) фейнмановский пропагатор
безмассового конформно-связанного скалярного поля преобра-
преобразуется к выражению Q~in~2)l2 (x) G P (х, x')Q-{n-2)l2(x'). Из соот.
ношения F.26) следует, что \х) преобразуется в Q~nl2(x) \x),
поэтому видно, что оператор GF, определенный формулой F.27),
переходит в Q2Gf. Применяя этот результат к F.70), получаем
W [?nvl =» - у'tr On [- (цОJ С,]}, F.116)
где Й появляется только в комбинации ^Q. Поэтому, восполь-
воспользовавшись формулой F.100) для W, можем написать
Q.I
Ц-1
, F.117)
где величина ц временно рассматривается как функция х, а
W — как функционал от ц. Учитывая это, мы можем теперь
применить соотношения F.72) и F.77), чтобы записать без-
безмассовый предел Wв виде
W = - j К' @) + A/32я2) J d*x [- g (x)]>k a2 (x) In [ц2 (*)], F.118)
что после подстановки в F.117) дает
(Т^(х))рек = ~а2(х)!Ш2. F.119)
Очевидно, аналитическое продолжение по v, используемое в ме-
методе g-функции, не только делает W конечным, но и приводит
к нарушению конформной инвариантности, давая отличный от

186 Глава 6
нуля след F.119). Это выражение для следа в точности соот-
соответствует F.113), полученному с помощью размерной регуля-
регуляризации.
Нетрудно рассчитать аномалию следа и в пространстве-вре-
пространстве-времени с числом измерений, отличным от 4 [114]. Прежде всего
заметим, что при нечетном п эффективный лагранжиан /.эфф,
определенный соотношением F.42), является конечным. От-
Отсюда можно сделать вывод, что в пространстве-времени не-
нечетной размерности нет конформных аномалий.
Для четных п, равных по, расходящимися в ультрафиолето-
ультрафиолетовой области являются только первые 1 + по/2 членов в F.42),
для которых соответствующие Г-функции имеют полюсы при
п = По. Из этих членов все, кроме а„п/2, обращаются в нуль
в точке п — щ при т-*-0. Последний член содержит множи-
множитель тч-"° и не обращается в нуль. Этот член приводит к ано-
аномальному следу
Г/2. F-120)
Такой результат подтверждается при использовании .^-регуля-
.^-регуляризации.
Представляет интерес случай п0 = 2, для которого
? F.121)
где мы использовали F.47) при | = 0 (чт<* соответствует кон-
конформному характеру связи для двух измерений).
Возникает вопрос: нельзя ли избавиться от аномальных сле-
следов, добавляя соответствующий контрчлен в эффективный лаг-
лагранжиан? Оказывается, что локальных геометрических величин,
варьирование которых в эффективном действии давало бы
вклад в (Г^рен, след которого уничтожал бы аномалию пол-
полностью, не существует. Однако конформные аномалии можно
устранить в динамической теории, допускающей действие более
общего вида [67, 210]. Можно также устранить член ?/? из
F.114) или F.115) с помощью тождества
-*>*«'Лв-12п* FЛ22>
(см. F.53)). Добавлением члена R2 к ЬЭфф (напомним, что
в соответствии с F.104) — F.106) величина aF + PG не содер-
содержит члена /?2) коэффициент при DR в выражении для аномаль-
аномального следа может быть сделан равным любой наперед задан-
заданной величине, в частности равным нулю. Конечно, добавление
члена R2 в 1Эфф означает, что №эфф уже не будет инвариант-
инвариантным относительно конформных преобразований. Разумно это
или нет, можно выяснить только с помощью эксперимента. По-

Перенормировка тензора энергии-импульса 187
видимому, не существует убедительных теоретических причин,
по которым конформную симметрию динамики следует искус-
искусственно нарушать, поэтому в дальнейшем мы будем оставлять
в выражениях для аномальных следов член OR (см., однако,
[295]).
Обратимся теперь к аномалиям следов для полей высших
спинов. До тех пор пока мы требуем, чтобы величина W была
конформно-инвариантной, аномальный след будет иметь вид
F.112) с некоторыми значениями аир. Но, если W не являет-
является конформно-инвариантным (например, скалярное поле при
ЪФЦп)), аномальный след может содержать добавочные
члены вида OR и R2. Он будет, конечно, содержать также обыч-
обычные, т. е. неаномальные, компоненты, зависящие от квантового
состояния поля. Эти величины, вообще говоря, уже не будут
иметь геометрической природы и могут быть даже нелокаль-
нелокальными (см. явные примеры в гл. 7). Аномальная же часть следа
не зависит от состояния, локальна и имеет геометрический ха-
характер.
Как было отмечено выше, появление конформных аномалий
с точки зрения размерной регуляризации можно понять как
следствие того, что действие №расх конформно-инвариантно
лишь в четырехмерном случае, хотя W конформно-инвариантно
при всех п. При аналитическом продолжении по размерности
пространства-времени к п нарушение конформной инвариант-
инвариантности вдали от п = 4 сказывается на значении <f ц^расх и, сле-
следовательно, (ТуНУрен при п = 4. Можно было бы спорить по
поводу теорий, в .которых не только №расх, но и само W яв-
является конформно-инвариантным лишь в пространстве-времени
некоторой фиксированной размерности. Двумя примерами та-
таких теорий могут служить случай скалярного поля с |, фикси-
фиксированным независимо от п, и случай электромагнитного поля,
для которого конформная инвариантность имеется лишь в че-
четырехмерном пространстве. В этих случаях размерная регуля-
регуляризация дает иные результаты, нежели другие схемы регуля-
регуляризации. Но различие возникает лишь в коэффициенте при
OR, который, как мы видели, можно изменить добавлением
контрчлена. R2 в ?эфф и, следовательно, нужно определять
экспериментально.
Обобщение результата F.119) на поля произвольного спина
было дано Кристенсеном и Даффом [115]:
( y tra2 (А, В), F.123)
где индексы (А, В) характеризуют представление группы Ло-
Лоренца, по которому преобразуется рассматриваемое поле (см.
C.164)). Этот след можно записать с помощью четырех

188
Глава б
параметров в виде
0W. - B880Я2) {
-1R2) +
F.124)
Коэффициенты а, Ь, с и d могут быть выражены в виде поли-
полиномов от Л и В. Общие формулы даны в работе [117] для не-
некоторых значений высших спинов. В табл. 1 приведены некото-
некоторые из наиболее важных результатов для полей спина
Таблица 1. Коэффициенты в выражении для аномального следа F.124)
для полей с различным спнном. В случае спина '/з приведены
результаты дли двухкомпонентных спиноров;
для четырехкомпонентных спиноров коэффициенты
следует умножить на 2. Крестнкн показывают, что условия
согласованности для полей высших спинов требуют
исчезновения соответствующего геометрического объекта
в выражении для аномального следа [118]
(А, В)
.@,0)
A/2, 0) -
A/2, 1/2)
A,0)
A. 1/2)
A.1)
а
— 1
-7/4
11
—33
291/4
—189
ь
—1
— 11/2
—64
27
X
X
с
F-301)
3
—6
12
X
X
й
-90 (t - 1/6J
0
¦"-— О
-5/2
61/8
—747/4
Отметим, что табл. 1 дает только аномальные вклады. Если
поле не является конформно-инвариантным, то, как отмеча-
отмечалось выше, будут также дополнительные неаномальные вкла-
вклады. В частности, в скалярном случае при | =^= '/6 имеется неано-
неаномальный вклад
F--J-
6*
FЛ25)
зависящий от выбора квантового состояния. Результаты для
скалярного поля, поля спина '/г, преобразующегося по представ-
представлению ('/г, 0) и поля спина 1, преобразующегося по представ-
представлению ('/г, '/г), могут быть получены из формул F.48), F.93)
и F.94) соответственно.
В общем случае физические поля высших спинов могут соот-
соответствовать не какому-то одному представлению (Л, В) группы
Лоренца, но линейной комбинации нескольких таких представ-
представлений. Например, электромагнитное поле содержит вклады
скалярных духов, поэтому, чтобы получцть, электромагнитнукз

Перенормировка тензора энергии-импульса
189
аномалию, нужно вычесть из аномалии для поля ('/2> '/г)
удвоенную аномалию для поля @,0). В табл. 2 приведены раз-
различные физические комбинации для безмассовых полей со спи-
спинами ^2. Эти результаты были получены с помощью регуля-
регуляризации методом ^-функции. Как. отмечалось, применение раз-
размерной регуляризации изменяет коэффициент при OR в случае
электромагнитного поля; Браун и Кассиди [64] получили зна-
значение с = 12.
Таблица 2. Коэффициенты аномалий следов для физических
безмассовых полей спина < 2. В случаях спинов 1 и 2
обозначение @, 0) соответствует скалярному полю
с минимальной связью (| = 0). Крестики имеют
тот же смысл, что и в табл. 1
Спнн
0
1/2
1
3/2
2
(А, В)
@, 0)
A/2, 0)
A/2, 1/2) - 2 @, 0)
A. 1/2)-2 A/2, 0)
A, 1) +@,0)-2 A/2. 1/2)
а
— 1
-7/4
13
233/4
-212
Ь
-1
-11/2
-62
X
X
с
F-30|)
3
—18
X
X
й
-90 A - 1/6J
0
0
61/8
-717/4
Существует полезное условие согласованности между коэф-
коэффициентами а, Ь, с и d, возникающее при использовании раз-
размерной регуляризации в теории, которая конформно-инвариант-
конформно-инвариантна в п- измерениях [185]. Сравнение F.112) и F.124) показы-
показывает, что
а=- 180(а + р), fe = 360p, с=120а, d = 0, F.126)
откуда получаем условия
2a + fe + 3c = 0, d = 0. F.127)
Остается найти лишь два из четырех коэффициентов а, Ь, с
и d.
Аномалии следов особенно важны в частном случае кон-
конформно-плоского фонового пространства-времени. Если кванто-
квантованное поле также конформно-инвариантно, то мы имеем кон-
конформно-тривиальную ситуацию (разд. 3.7). В этом случае ока-
оказывается, что аномальный след определяет, полный тензор
энергии-импульса в заданном состоянии квантового поля [63,
7§, 130, 131].
Чтобы убедиться в этом, используем F.99) с заменой S на
WpeH [gllv\ -\[-
X <V
X
*) Ш (X)
. 128)

190 Глава б
Далее, используя F.13), а также соотношение
получаем
» X
/)^V. F.129)
Для конформно-инвариантных теорий поля след под знаком
интеграла в правой части этого равенства чисто аномальный;
он, как мы знаем, локален и не зависит от квантового состоя-
состояния. Следовательно, независимо от выбора состояния в левой
части можно выполнить вариационное интегрирование [63, 157].
Или же в рамках метода размерной регуляризации можно рас-
рассуждать так. Учитывая замечания, сделанные при выводе фор-
формул F,111) — F.115), можно записать соотношение
Щ
[-IW]1'' вам
подстановка которого в F.129) позволяет выполнить интегри-
интегрирование и найти
< V [&* (*)]>рен = (f)'/! (У"
FЛ31)
Сначала применим этот результат к двумерному случаю.
Воспользовавшись F.41) и F.47) при | = |B)=0, а также
соотношением ГA —п/2) =2/B — п) + 0A), получаем
- [ 1/24я (tt - 2)] J [- ff (*')]"/! ^ (д;') rf V, F.132)

Перенормировка тензора энергии-импульса 191
где члены порядка п — 2 опущены. Подставляя F.132) и со-
соответствующее выражение для gK\ в F.131), получаем
< V [&А М1>Рен = (gig)''' < V [^ (*)]>рен +
' FЛЗЗ>
что при использовании выражений C.3) и C.4) для #uv и R
дает
'/j < V [ft* WDpeH +
4 ) PV /pCT X
F.134)
С помощью F.93) нетрудно показать, что F.132) и, следова-
следовательно, F.134) выполняются также для двухкомпонентных спи-
норных полей со спином '/г.
Любое двумерное пространство-время является конформно-
плоским: gyiv= С(х)у]^. Поэтому соотношение F.134) с gKx —
= г\к\ и О = СЧ' позволяет записать среднее значение тензора
энергии-импульса в любом двумерном искривленном простран-
пространстве-времени через соответствующее значение в плоском про-
пространстве. Особенно простую форму этот результат имеет в
изотропных координатах C.9)
ds2 = C(u, v)dudv, F.135)
для которых F.134) дает [131]
<V [g* (*)]>Рен = (- §У'1г <V [*W (*)]>рен + б/ - A/48Я) R&/,
F.136)
где
1
/% F.137)
о о __ о
vuv оцц и.
Если состояние, в котором вычисляется среднее значение в
плоском пространстве-времени, является вакуумным, то состоя-
состояние, фигурирующее в соответствующем среднем в искривлен-
искривленном пространстве, представляет собой конформный вакуум. Как
отмечалось в разд. 5.5, ответ на вопрос, будет ли вакуум в пло-
плоском пространстве обычным вакуумом Минковского, зависит
от того, является ли искривленное пространство-время кон-
конформным всему пространству Минковского или же только его
части. Если оно конформно всему пространству Минковского,
то это действительно обычный вакуум и первый член в правой

192 Глава 6
части F.136) обращается в нуль, В противном случае это сла-
слагаемое дает ненулевой вклад. Ниже мы остановимся на этом
подробнее.
Обратимся теперь к четырехмерному конформно-тривиаль-
конформно-тривиальному случаю. Из формулы F.103) находим
й^расх = ~ П/16Я2 (П - 4)] J СГХ [- g (x))'h [OF (X) + PG (*)] + О A).
F.138)
Подставляя F.138) в F.131) с заменой gK% на gK% и gK% на
ён.% — метрику плоского пространства (например, г\кх) и выпол-
выполняя функциональное дифференцирование [64, 72], получаем
<V [Ы>рен = (gig)''' <V [&*1>рея ~
1)Я/ + 2РC)Я/}, F.139)
где величина A)Я^ определяется формулой F.53) и
- %RooRpag*v + 7Лц». F.140)
В скалярном случае аир определены F.106) и
<V [Ы>рен = (Ш)У> <Т^ [#Л])р.я -
- A/2880я2)[76A>Я/ -C)ЯД F.Н1)
Для других конформно-инвариантных теорий аир могут быть
выражены через коэффициенты аномалий а, Ь, с и d в F.124)
с помощью F.126).
Соотношение F.139) было получено менее формальным спо-
способом в работе Банча и Дэвиса [78]. Учитывая, что использо-
использованный ими метод более тесно связан с физикой рассматривае-
рассматриваемых явлений, мы опишем здесь кратко основные этапы этого
подхода.
Прежде всего заметим, что, поскольку среднее значение
H получено из эффективного действия Wpta, оно автома-
автоматически удовлетворяет ковариантному условию сохранения
Далее учтем, что если квантовое Состояние представляет,
собой конформный вакуум или любое из соответствующих воз-
возбужденных состояний, то величина <Гцу>рен должна быть ло-
локальным тензором, т. е. зависеть только от геометрии в точке
х. Это следует из локального характера величины Gf (которую
можно построить с помощью простого конформного преобразо-
преобразования из пространства Минковского, где эта величина явно

Перенормировка тензора энергии-импульса
локальна; см., например, C.154)). Более того, дифференциро-
дифференцирование GF, используемое при получении {Т^УРен, и процедура
перенормировки также являются локальными (и ковариант-
ными) операциями.
Имея в виду два этих ограничения мы попытаемся построить
в наиболее общем виде локальный сохраняющийся тензор тре-
требуемой размерности (длина)-4. Из соотношения
Rafiy6 == Y (S«Y^08 ga&R^y ~~ g$yRa& "^ 8 $6 Ray) "Т"
+  ^ (gofigfly — gaygfiu) + Сарув F.143)
ясно, что в конформно-плоском пространстве, в котором
Capve = 0, тензор Римана полностью определяется тензором
Риччи и его свертками. Учитывая далее вырождение, связанное
с конформной симметрией [137], найдем следующие шесть не-
независимых геометрических величин требуемой размерности:
F.144)
Нам необходимы коварйантно сохраняющиеся линейные
комбинации этих тензоров. Два локально сохраняющихся тен*
зора C'#nV й B)//цУ уже известны; но в конфорМно-плоских про»
странствах они не являются независимыми:
С пОМоЩый F.142) Легко проверить, что единственным Другим
Локальным сохраняющимся тензором является C)ЯЦу, опреде-
определенный соотношением F.140). Хотя этот Тензор имеет чисто
геометрический характер, он сохраняется лишь й конформно'
Плоских пространствах, т. е. йё может быть получен Ёарьиро^
ЬанйеМ какой-либо геометрической величины ё действии и не
Является Пределом тензора, сохраняющегося ё неконформно-
Плоском пространстве [244].
Помимо этих двух геометрических тенЗорОв Возможен еще
Локальный, но не Геометрический тензор, т. е. тензор, пол-
полностью определяемый локальной геометрией, нО не вь!ражак>
Шийся через Ra$ и R. Обозначим его D)Яцу- Таким образом,
<^%я = ^0)Я/ + ЯC)#/ + D)Я/, F.146)
We А и В — некоторые постоянные. След от F.146) имеет вид
<W» = - &А nR - В (R4RaSi - j R2) + D)Я/, F.147)
Сравнивая С F.112) (напомним, что F = Ca$y6Ca№ =0), на-
находим
Л = -а/144я2, В=-р/8л2, D)Я/ = 0. F.148)
7 Зак. 674

194 Глава 6
Следовательно, аномальный след определяет <Гцу>рен с точ-
точностью до локального сохраняющегося бесследового тензора
<4>#uv, значения которого, во всяком случае, должны зависеть
от выбора квантового состояния. Сопоставление F.139) с
F.148) показывает, что D>Я^ следует отождествить с «гранич-
«граничным» ЧЛеНОМ (|/ЯI/г<ТУ [1и*]>рен.
Применим теперь формулу F.139) к некоторым специаль-
специальным случаям, а именно к моделям Робертсона — Уокера, об-
обсуждавшимся в разд. 5.5. Любое однородное и изотропное рас-
распределение материи (в том числе в состоянии конформного
вакуума) для этого класса пространств имеет одинаковые геомет-
геометрические симметрии. Это накладывает на (Г^рен следующие
ограничения:
<7У
<W.-o, ,*». «¦'•>
Используя координаты, в которых метрика имеет вид E.11), и
принимая во внимание E.13)Гполучаем •
">Я00 = С [- 9DD + ~D* + ~ D* + 9К& - Ж2],
<'>#„ = С~'Г [бО - 3DD + 4 ZJ - 9DD2 + -| D4 -
- 12/сЬ + 3KD2 - 6/С2]; F.150)
F.151)
*//„ =СТ[- i-?>D2 + -1D4 - 2/С?> + 1 /(?J + К2].
Для пространств, изображенных на рис. 20, а — г, конформ-
конформный вакуум совпадает с вакуумом пространства Минковского,
поэтому первый член в правой части F.239) обращается в нуль,
и математическое ожидание тензора энергии-импульса в со-
состоянии конформного вакуума определяется полностью выра-
выражениями F.150) и F.151). В частности, для вселенной
Эйнштейна, для которой C = a2s=const, D = 0 (разд. 5.2), по-
получаем
'-!- -т- -4)'
где p(s) —зависящий от спина коэффициент, который прини-
принимает значения р@)=='/240, ре/2)='Yeeo, p(l)= n/i2o. (Слу-
(Случай вселенной Эйнштейна с отождествленными точками см.
в работе |324].) В закрытом пространстве-времени де Ситтера

Перенормировка тензора энергии-импульса 195
E.65) или в стационарной вселенной E.52) находим
v
стационарн. 960я2<Х4 И > V
где 9@)= 1, 9('А)= "А, ?(!)== 62.
Для пространств, показанных на рис. 20, д, е, конформный
вакуум может быть связан с вакуумом Минковского или ва-
вакуумом Риндлера (разд. 4.5). В последнем случае первый член
в правой части F.139) не обращается в нуль. Элемент длины
в четырехмерном пространстве Риндлера можно записать в
виде
ds2 = ^dy\2-dl2-dy2~dz2 @ < ? < оо), F.154)
что представляет собой четырехмерное обобщение выражения
D.71) при ? = а-1еа* и с заменой ц на а~% С помощью преоб-
преобразования координат
у = rXVj sin 8 cos <j> A - rt1' cos б), F Л 55)
г = rt'1 sin9sin ф (l - rtu cos9)~\
где величина Y принимает значение A+г2)-1, соответствую-
соответствующее К = —1> выражение F.154) приводится к виду
F.156)
откуда видна конформная связь пространств Риндлера и Ро-
бертсона — Уокера при К = —1. Канделас и Дейч [89, 90] вы-
вычислили среднее значение тензора энергии-импульса в состоя-
состоянии вакуума Риндлера и получили интересный результат
Xdiag(-1, Vs, Vs. 7з), FЛ57)
где h(s)—число спиральных состояний поля со спином s.
Теперь довольно просто получить <Г/>Рен для статической
открытой вселенной (разд. 5.2). Геометрические вклады ОЯ/.
<3>//uv будут теми же самыми, что и для эйнштейновской все-
вселенной, поэтому
Последнее равенство следует из возможности представления
p{s) в F.152) в виде

196 Глава 6
С другой стороны, можно получить соотношение F.158) из не-
независимых соображений [70] (разд. 7.2) и, таким образом,
прийти к F.157). Термодинамические соотношения между раз->
личными вакуумными состояниями, схематически изображенные
на рис. 21, непосредственно вытекают из вида интегралов план-
ковского типа FЛ57) и F.159).
Наконец статическая форма пространства де Ситтера E.76)
представляет собой еще один интересный пример пространства,
конформно-связанного с пространством Риндлера. Метрика
E.76), записанная в виде
ds2 = [ 1 - (r2/a2)} {dt2 - [ 1 - (г2/а2)] dr2 -
- г2 [1 - (г2/а2]-' Ш + sin29 йф2)}
после замены переменной г/а = г'[1 -|- (г'J] приводится к виду
cfs2 = (а2 - г2) [(dt2/a2) - Y dr'2 - г'2 (dQ2.+ sin29 d<f>2)], F.160)
где Y = [1 +(О23~1> что имеет явную конформную связь с
F.156), если положить r\ = t/a. Вклад геометрических членов в
F.139) не зависит от координат и поэтому будет таким же, как
и в случае стационарной вселенной F.153). Таким образом, для
среднего значения тензора энергии-импульса в статическом кон*
формном вакууме пространства де Ситтера (пространства Ринд«
лера) сразу же получаем выражение
/т v\ =?4(a2 r2\~2 IT v) 4- (Т Л
V ц /стат. де Ситтер » V / ч I* /Рнндлер • \ Ц /стацнонарн. .
-Уз, -'/а, ~'/з) +
»|Л F.161)
которое, очевидно, имеет особенность на горизонте (г = сс). Это
нежелательная черта, присущая «зависящему от наблюдателя»
вакууму де Ситтера, как отмечено в конце разд. 5.4.
Полезное соотношение между конформной аномалией и пол-
полным тензором энергии-импульса в простанствах Робертсона —
Уокера было получено Паркером [388]. Пространства Роберт-
Робертсона— Уокера обладают конформным векторным полем Кил«
линга gi* (разд. 3.1):
F.162)
где а = С'1г, и величина А, из C.23) равна
Я = 2а'@ F.163),

Перенормировка тензора энергии-импульса 197
(штрих обозначает дифференцирование по t). Из условий сохра-
сохранения F.142) и C.23) находим
рена v = (Ope- 6(v; * = Т Л (^ W|«- F-164)
Интегрируя F.164) по 4-объему, ограниченному гиперповерх-
гиперповерхностями постоянного времени t\ и jf2, получаем
F.165]
где мы воспользовались теоремой о дивергенции. Поскольку
<Г^> является функцией одного лишь t, F.165) приводится к
виду
'«
Р (t2) a* (t2) = р (<,) а* (<,) - J а3а' <V>pe. Л, F-166]
где р = <Г">рен представляет собой собственную плотность
энергии, измеренную сопутствующим наблюдателем, и исполь-
использованы равенства F.162) и F.163).
Если применить F.166) отдельно к члену WH^, то из усло-
условия равенства нулю следа найдем
^Я,1 = - 1 D)Я/ = -1 р @ - а @, F.167]
откуда видно, что тензор D)ЯЦУ описывает классическое безмас-
безмассовое излучение с характерным красным смещением при расши-
расширении вселенной: полная энергия в сопутствующем объеме
WHttO? уменьшается как стх. Условие сохранения F.142) в этом
случае принимает простой вид
+ d(pa3)=0, F.168]
где давление р =
Если применить F.166) к полному тензору энергии-импульса
<Г^>рен, даваемому формулой F.146), то следует учесть нену-
ненулевой след F.147). С помощью формул E.13),' переписанных
в виде
jDD2 +~D* + 6KD + GKD2+ 12tf2],
F.169]
x F.170]

198 Глава 6
легко проверить, что подынтегральное выражение в F.166)
представляет собой полную производную по времени.. Интегри-
Интегрирование вклада, который дает след, приводит к выражению
3 [В (а'4 + 2Ка'2) + 12Л (- а2а'а"' - ш'Ч" +
] F.171)
где А, В определяются формулами F.148).
В случае асимптотически статического пространства-времени
выражение F.171) обращается в нуль и F.166) приводит к со-
' отношению
р (in) a4 (in) = p (out) a4 (out), F.172)
выражающему тот факт, что первоначальная энергия поля любо-
любого происхождения (например, возникающая из-за кривизны или
присутствия квантов) испытывает в out-области красное сме-
смещение, такое же, как и классическое излучение. В процессе
расширения не происходит ни возрастания, ни убывания энер-
энергии поля. Это совсем не удивительно для конформно-травиаль-
иой ситуации. В самом деле, мы уже знаем из результатов ¦
разд. 3.7, что в процессе расширения не происходит рождения
квантов, если поле находится в состоянии конформного вакуума.
Соотношение F.172) является лишь другим выражением того
же факта.
6.4. Расчет перенормированного тензора
энергии-импульса
В предшествующих разделах этой главы продемонстрирова-
продемонстрировано, как расходящаяся величина <7Vv> может быть сделана ко-
нечной с помощью перенормировки констант связи в гравитаци-
гравитационном действии, т. е. введения бесконечных контрчленов, име*
ющих чисто геометрическую природу, которые можйо считать
обусловленными динамикой гравитационного поля. Разумеется,
интерес представляют не сами расходимости, а конечные вели-
величины, которые остаются после их устранения, поскольку именно
они имеют физический смысл. В частности <Гцу>реи является
величиной, которая должна находиться в правой части обобщен-,
ных уравнений Эйнштейна F.95). Если для некоторых конформ-
но-тривиальных систем величина (Т^Урен может быть рассчитав
на полностью по известной конформной аномалии (разд. 6.3) ,
то в общем случае такой простой способ расчета отсутствует и
необходимо применять трудоемкие методы «грубой силы». В
этом разделе мы коротко опишем применение таких методов.

Перенормировка тензора энергии-импульса
Прежде всего выясним, какую величину следует вычислять.
Стандартное применение представления де Витта — Швингера
приводит к величине
<out, Oir^jO, in)
(out, 0|0, in) ' ({5Л'д>
которая, очевидно, не является математическим ожиданием.
Эта роль принадлежит величинам типа <^|7\и.|^>. В рамках
гейзенберговской картины естественно выбрать квантовое состо-
состояние в in-области, например <in,0| Tlxv(x) |0, in>, где х может
обозначать любую точку пространства-времени. Как показно
в конце разд. 6.2, расходимости и, следовательно, перенормиров-
перенормировки для . различных вакуумных ожиданий одинаковы. Различа-
Различаются лишь конечные остатки.
В принципе можно пытаться вычислить (^l^vl ¦»!>>, пользуясь
перенормированным эффективным лагранжианом LpSH, и рассчи-
рассчитать коэффициенты Л в F.96). Но помимо технической сложно-
сложности представление де Витта — Швингера не заслуживает дове-
доверия в области больших длин волн, если пользоваться асимпто-
асимптотическим разложением того же типа, что и при получении F.61).
Вместо этого лучше сразу же вычислять величину <ip| ГЦЛ,|ф>,
прибегая к представлению де Витта — Швингера лишь при про-
проведении перенормировок.
Поскольку <Гц„>Рен определяется низкоэнергетической длин-
длинноволновой частью <TWv>, эта величина зависит от глобальной
структуры пространственно-временного многообразия и выбора
квантового состояния поля. Поэтому она уже не будет иметь
чисто геометрический вид и даже не будет локальной. Суще-
Существуют различные методы расчета <7^>рен в зависимости от
принятого способа регуляризации.
Хотя формальное обсуждение перенормировок было основано
на функционале действия, при практическом проведении расче-
расчетов следовать этому пути не удается. Причина состоит в том,
что для осуществления функционального дифференцирования
WPeH no guv с целью получения <Гцу>рен, вообще говоря, нужно
знать №рен для всех геометрий guv. Эту задачу решить невоз-
невозможно. Есть, правда, одно исключение, а именно конформно-
тривиальный случай, в котором полный тензор энергии-импуль-
энергии-импульса полностью определяется своими конформными свойствами.
Во всех остальных случаях необходимо непосредственно вычис-
вычислить <7Vv>-
Число явных примеров, в которых могут быть использованы
аналитические методы регуляризации, довольно ограничено, по-
поскольку мало пространств, допускающих точное решение волно-
волнового уравнения в п. измерениях или приведение расходящихся
величин к виду, соответствующему обобщенным ^-функциям.

200 Глава 6
Один из интересных случаев, в котором благодаря высокой
степени геометрической симметрии может успешно применять-
применяться размерная регуляризация, представляет собой пространство
де Ситтера. Если выбранное вакуумное состояние инвариантно
относительно группы де Ситтера (разд. 5.4), то поскольку един-
единственным (максимально) форм-инвариантным тензором второго
ранга является ^ц.у (см., например, [494], §13,4). мы должны
иметь
(T^^Tg^/n, F.174)
где Т — след тензора энергии-импульса:
T~*(Tf). F.175)
Для массивного скалярного поля, воспользовавшись уравне-
уравнением C.26), из C.190) получим
V = тУЧ (я- I)R-6(я)] п**; F.176)
следовательно, на основании B.66) имеем
^ 1 *). F.177)
Величина G(l)(x, х) расходится при п<=4, но может быть
Конечной при п ф- 4. Она была получена для всех п Канделасом
й Рэйном [92] (ё случае |*=0) й Даукером й Кричли [172].
Результат имеет вид
,л -^ 2tt2 - г (у I") ~ Уз + "/2) Г (- v jn) - 4i + Ф\ r r 1 „.к
F.178)
Где а — радиус вселенной де СиТтёра (см. E.49)) И
[V (п)]2 =± -J. {П - IJ- /rtW — %п(п - 1) F.179)
(ср. (S.60)). Отметим, что, taK как G<!> не зэёисйт of x, вклад
в след тензора энергии-импульса дает только первый член в
F.177):
T = ±m2G{x, X). F.180)
Выражение F.178) имеет полюс при rt = 4. Особенность
можно устранить, разлагая GA> в ряд в окрестности « = 4 и вы*
' читая адиабатическое разложение G(ds, оборванное на соответ*
ствующем порядке аДиабатйчности А, которое также следует
разложить около «==4. Оборванное разложение де Витта —
Швингера мы будем обозначать далее через {A)G(ds- Смысл этой
процедуры в том, что именно низшие члены в адиабатическом

Перенормировка тензора энергии-импульса 201
разложении G^ds в соответствии с F.37) дают вклад в
Вычитание этих членов из G<'> эквивалентно перенормировке
Z/эфф через F.58).
Для того чтобы определить порядок адиабатичности А, на
котором следует оборвать разложение G(ds, заметим, что в LpaCx
имеются члены четвертого порядка (в виде Gds)- Следователь-
Следовательно, мы должны удерживать в G'ds те члены, которые при под-
подстановке в Lpacx будут давать члены до четвертого адиабатиче--
ского порядка. Но в случае пространства де Ситтера из F.177)'
и F.180) видно, что при подстановке в (Tuv} производные от
GA> не возникают. Поскольку адиабатический порядок (Т^У
тот же, что и для Lpacx, это означает, что разложение G^ds долж-
должно быть оборвано на четвертом порядке (для п измерений — на
адиабатическом порядке п). В явном виде, воспользовавшись
C.135) и C.137) и повторяя выкладки, приведшие к F.41), по-
получаем
WG% = 2m"-4 (Ы)'п12 {а0 (х) m2Y(\ - п/2) +
F.181)
где для n-мерного пространства де Ситтера ай{х)= 1, а\{х) =
= ('/б — ?)п(п— 1)а~2> а функция п2, необходимая только в че-
четырехмерном случае, дается выражением
Вычитая F.181) из F.178) и разлагая результат вблизи
п = 4, получаем
G(!) (х, х) - (i)G% (x, x) = G8я2а2) {mW +12E- 2) [ф C/2 + v) +
+ у C/2 _ v) - In {tn2a?) - 1] + m2a? - 2/з - (a/mJ a2} + О {п — 4).
F.182)
Далее, воспользовавшись F.180) и F.174), можно получить пе-
перенормированный тензор энергии-импульса при дг = 4 [ 172]j
(TWpeH = (Я^/64я2) {m2 [m + (Е - Vie) R] N> C/2 + v) + * C/2 - v) -
*где использовано соотношение R = 12a~2. Заметим, что в безмас-
безмассовом пределе в случае конформной связи (|—7б) след F.183),
определяемый выражением F.180) для перенормированных ве«
личин, полностью обусловлен последним членом в F.182): Грен=.
== —а2/16я2 в согласии с F.120),

202 - Глава 6
Обратимся теперь к примеру использования ^-регуляризации
[170]. В разд. 5.2 мы получили решения для нормальных мод
безмассового скалярного уравнения с конформной связью в. ста-
статической вселенной Эйнштейна (см. E.28)). Поскольку прост-
пространственные сечения компактны, полная перенормированная
энергия вакуума, обусловленная кривизной пространства-време-
пространства-времени и нетривиальной топологией, будет конечна. Поэтому можно
вычислить эту величину вместо плотности энергии, а затем, вос-
воспользовавшись пространственной однородностью, благодаря ко^
торой плотность энергии постоянна, рассчитать <0|Г00|0>, раз-
разделив на полный объем пространства 2я2а3.
Полная энергия определяется выражением
0), F.184)
которое для конформно-связанного безмассового скалярного
поля во вселенной Эйнштейна равно
, F.185)
где мы воспользовались соотношениями C.190), E.15), E.28),"
и E.19). Это выражение аналогично результату для простран-
пространства Минковского B.38); причем lk{kla) представляет собой
собственное значение энергии мод, характеризуемых индексом
k. С помощью E.24) находим
оо ft —1 I оо
/=0 M--J
откуда видно, что вклад в энергию от вырожденных состояний
с заданным k пропорционален k2. Сумма в F.186) расходится
как k*. Для регуляризации заменим собственное значение энер-
энергии k/2a на (k/2a)~s; тогда
оо
Я= lim У k2(k/2ays. F.187)
Теперь сумма в F.187) пропорциональна ^-функции Римана,
а именно
(s-2). F.188)
Но эта величина при аналитическом продолжении к точке s =
.««=—1 остается конечной. Поэтому из F.187) имеем
? = S(-3)/2a=l/24Oa, F.189)

Перенормировка тензора энергии-импульса 203
Разделив Е на собственный объем пространства, найдем про»
стое выражение для плотности энергии
р=1/480я2а4; F.190)
поскольку аномальный след во вселенной Эйнштейна обращается
в нуль, из F.190) можно найти полный перенормированный тен-
тензор энергии-импульса:
k' -'/з. -7з, -7з). F.191)
Этот результат впервые был получен Фордом [202] с помощью
обрезания суммы по модам; он находится в согласии с F.152)
(см. также [173]).
В качестве последнего примера использования аналитиче-
аналитического метода регуляризации вычислим «казимировскую» плот-
плотность энергии в плоском пространстве с топологией RlX,Sl для
безмассового конформно-связанного скалярного поля [311].
Плотность энергии вакуума равна (разд. 4.1)
оо оо
Bя/12)?л и (я/L2) ?|п+±| F.192)
/1=0 П = — оо
для нескрученного и скрученного полей соответственно. С помо-
помощью замены пи \п + 7г| на n~s и | п + 7г l~s можно выразить
F.192) через ^-функции, аналитически продолженные назад к
точке s = —1:
BЯ/12) ? (- 1) = - я/612, F.193)
(я/LJ [? (-1, V2) + Б (~ 1, -72) + Yal = я/12L2 F.194)
соответственно, где
00
?(*. Я)s Z (? + «P. Res>l, F.195)
«-о
и значение ^(—1, q) дается, например, в работе [247], (9.531).
Равенства F.193) и F.194) находятся в согласии с равенствами
D.8) и D.11), полученными методом обрезания.
Заметим, что ни в одном из двух последних примеров не воз-
возникло необходимости в явной перенормировке каких-либо вели-
величин. Аналитическое продолжение позволяет просто отбросить
расходящиеся члены, Получая конечный ответ. Всегда ли при
этом опускаются именно нужные члены (т. е. такие, которые в
другой схеме регуляризации были бы поглощены при перенор-
перенормировке констант связи), доказано не было, хотя обычно счита-
считается, что это так.

204 Глава 6
С точки зрения практических вычислений, по-видимому, на-
наиболее эффективным методом регуляризации является расщеп-
расщепление (раздвижка) точек. При этом снова в общем случае ока-
оказывается невозможным получить <Г|ХУ>рен с помощью функцио-
функционального дифференцирования эффективного действия. Вместо
этого приходится работать непосредственно с (Т^) или, что
предпочтительнее, с более простой функцией GA)(jc, х'). Пере-
Перенормировка <7Vv> выполняется путем вычитания членов вплоть
до адиабатического порядка п в разложении (T^ds, получае-
получаемом дифференцированием G^six, x'). Эти члены возникают из
Z>pacx, и их вычитание эквивалентно перенормировке констант
в обобщенном эйнштейновском действии. Можно также постро-
построить <Г,л,у>рен, действуя на
О(р'1н (х, х') = G(" (х, х') - (n)G% (x, х') F.196)
Дифференциальным оператором, получаемым из C.190) спосо-
способом, который коротко описывается ниже. В {n)G% удерживают
только члены, которые дают вклад в тензор энергии-импульса
адиабатического порядка я и ниже. Это члены порядка п или
ниже в '"'Go'si хотя следует соблюдать осторожность, поскольку
при дифференцировании адиабатический порядок величин мо-
может изменяться. Таким образом, процедура расчета перенорми-
перенормированного тензора энергии-импульса с помощью расщепления
точек в целом выглядит так:
1) Из уравнений поля находят полный набор нормальных
мод, с помощью которых можно определить состояния частиц.
2) Строят Gm(x, x') в виде суммы по модам.
3) Находят GpeHi согласно F.196), обрывая разложение
^ds на порядке п.
4) Действуют на Оре'н соответствующим оператором, чтобы
найти <0|Гц,г(х, х/)|0>Рен, отбрасывая члены адиабатического
порядка выше п, которые возникают прн дифференцировании
членов в {n)Gys.
5) Полагают х'-*-х и записывают окончательный результат
для<0|Г^(л:)|0>ре„.
Состояние |0> будет зависеть, конечно, от определения «по-
«положительно-частотных» мод на первом этапе расчета.
Дифференцирование GA>(a:,x'), вообще говоря, является:
Сложной процедурой. Формально мы имеем
Vv ()> ^i»v («. «0 G0) (x. *')• F-197)
х'->х
Функция Грина GA>(x, x') является не скалярной функцией х,
а бискалярной функцией двух пространственно-временных точек

Перенормировка тензора энергии-импульса 205
х и х', т. е. преобразуется как скаляр в каждой точке1). (Поля
высших спинов приводят к би-спинорам, би-векторам и т. д.)
Следовательно, дифференциальный оператор D^ (x, х') являет-
является нелокальным. Например, первый член в C.190) приводит к
среднему значению
F.198)
которое в методе расщепления точек понимается как
lim \{\ -2l)[V^v + Vh-VvItG'V x'), F.199)
где штрих у производной указывает на то, что она действует на
х'', а не на х. Это означает, что возникающий объект является
не тензором, а би-вектором. (Выражение F.199) записано в на-
наиболее симметричном виде, хотя это и не существенно.)
Чтобы построить тензор из би-вектора и восстановить требуе-
требуемую ковариантность, необходимо осуществить параллельный пе-
перенос дифференцируемых векторов (спиноров и т. д.) в одну
пространственно-временную точку, в качестве которой можно
взять среднюю точку отрезка между х и х', один из концов этого
отрезка (например, х) или какую-нибудь другую точку. Разли-
Различия между перенесенными параллельно и не перенесенными ве-
величинами остается и в пределе совпадающих точек х и х'\ оно
обусловлено множителем о в разложении G(l)(x, x') для по-
поправок порядка а при параллельном переносе. К счастью, эти
сложные поправки были вычислены раз и навсегда в работах
f[5, 6, 69, 137, 413, 414], и мы не будем обсуждать эти подроб-
подробности.
Следует, однако, заметить, что если сначала перенормиро-
перенормировать G<'> (до дифференцирования, приводящего к <7VV>), сог-
согласно F.196), то все члены типа а будут заведомо устранены,
поэтому любые поправки порядка а, возникающие при парал-
параллельном переносе, исчезают при ст->0 в конце вычисления. Та-
Таким образом, при практических вычислениях эффекты парал-
параллельного переноса следует учитывать только в том случае, если
сначала строится неперенормированныи тензор энергии-импульса.
Мы рассмотрим симметричный случай, когда строится функ-
функция Gw{x", x') от двух точек х", х', лежащих на (малом) оди-
одинаковом собственном расстоянии от интересующей нас точки х
с каждой стороны вдоль некоторой неизотропной геодезической,
проходящей через х (рис. 22). Симметризация, хотя и не явля-
является необходимой, упрощает некоторые выражения. В конце вы-
вычисления обе точки х" и х' устремляются к х. Собственное
. (малое) расстояние между х и х' обозначается через е, а
') См. примечание на с. 95.

206 Глава 6
направление геодезической параметризуется касательным век-
вектором № в точке х. (Если разделенные точки х", х' остаются
в нормальной окрестности точки х, эта геодезическая будет
единственной.)
Для применения формализма в качестве первого шага сле-
следует превратить GA> в функцию еиС вместо х" и х'. Для этого
необходимо решить уравнения геодезической, соединяющей точ-
точки х", л; и/, относительно еиСс помощью рядов по е вплоть
до порядка еп+|. Соответствующие результаты имеются для двух
важных случаев: двумерного пространства-времени и четырех-
четырехмерных пространств Робертсона— Уокера. Для двумерного слу»
чая [136]
+ j С[С~3(ЗС% - СС. иа) t"-j Rtv] (tuf e3 + ..., F.200)
где использованы изотропные координаты и и v и метрика
F.135). Аналогичное выражение справедливо для v(e) с заме-
заменой и на v и обратно. Подразумевается, что функция С и ее
производные вычислены в средней точке х=(и, v). Конечные
точки задаются соотношениями х' = (ы(е), v(e)), x" = (u(—е),
v(-e)).
Для пространства-времени Робертсона — Уокера с элементом
длины E.7), не ограничивая общности, можно выбрать 9" =
= 9' = Э, ф" = ф' = ф, поскольку пространство изотропно. Тог-
Тогда требуется знать только т](е).и г (г), определяемые выраже-
выражениями [69, 77]
,v , г , 1 2-r, 1 .,' 1 4, , (б-201)
\ / i ' 2! ' 3! ' 41
где
X г OYJ + (т od - -|z>3) Y (О4.

Перенормировка тензора энергии-импульса 207
й = (-?)+ 5Z>?> - 3?K)(/Т1K *r + (*DKr - QD2Kr) Y (/VJ +
4- BZ)Z) - 3D3 + 6W) Г/4 0гK + (- 2D2Kr + К2г) Y2 (tr)\
& = (_. ^ Ь> -» Щ) + -?- ZJ - f- ?>ZJ + |- D4) (f *)» + F.202)
i. S + ^. i)Z) + 5D2 - 32Z)ZJ + 15?>4) Y (^K (frJ +
r) Y (^)
| DD + 2D2 - ^ DD2 + 15Z>4
+ (- lODDKr + 2QD3Kr - WDK*r) Y2/"(t'Y +
+ (- Ш2 + 4 D< - 5D2A: + /C2) Y2 (ЛM.
Обозначения здесь те же, что в E.12), и положено № = t°, tr =
= /'ит.д.
После того как GO переписано в терминах е, №, для про-
проверки вычислений полезно удостовериться в том, что расходя-
расходящиеся члены согласуются с соответствующими членами в
G1ds(x, x'). Главные члены в Go's для скалярного случая
имеют вид [69]
G& (в, П = -A/я) { [1 - (m2 + IR) e2S] (Y +1 In | mV | ) +
+ т (б - т) т/?+e2s h2 + т (s - т)Л]} + ° (е2г) +
+ О (е4) + О (Г) F.203)
для двух измерений и [69,80]
- 2m2/?ap -^ - 6 (б - ~) m?R
360т2 (Б - j) ^ + 60m2/?up -^- + б^ар; уб

208 Глава б
л
X [/Л„р - т^2 - ? R + зо 0 - {Jа R + 90 (I - -^J r2] +
+ О(е4) + 0(Г-6) F.204)
в конформно-плоских четырехмерных пространствах. В этих
выражениях вектор Р нормирован, согласно F.85), и, как и
выше, символ О(Т~Р) обозначает члены адиабатического по-
порядка р (т. е. содержащие р-е производные от метрики).
Теперь можно выполнить перенормировки G^{x", x'). Запи-
Записав эту величину как функцию е и Р, следует просто вычесть
из нее все выражение F.203) для двумерного случая и F.204)
для четырехмерного. Но пока нельзя переходить к пределу при
е-*-0, несмотря на то что GplH(x", x') остается конечной при
х",х'-*-х. Сначала нужно продифференцировать получившееся
выражение и получить <0|Г,«(*", х') |0>рен, отбросив все члены
адиабатического порядка выше п, которые возникают при диф-
дифференцировании некоторых членов из F.203) или F.204).
Для выражения общего вида
F.205)
где аи^- постоянные, а с, f, r, еа& и qa$ могут быть функ-
функциями х, результирующий тензор энергии импульса в пределе
совпадающих точек имеет вид [80, 137] ¦
- т (т - о]
2 6
[^(^)]^, F.206)
где
4 Vag j; ^suv —2~J 4 (na' fv)
X (^v + -^).+ |c;,v - -i-^v ~ у fe,»v. F-207)
¦ —?%* <6-208)

Перенормировка тензора энергии-импульса 209
В случае конформйой связи | = %{п) выражение F.206) имеет
отличный от нуля след ЦчП^с. Заметим, что члены порядка е2
в G*1' дают конечный вклад в <Г^> после дифференцирования.
Анализ выражения F.206) показывает, что вклад в <Г^>рен
адиабатического порядка выше п дают только те члены в
F.203) и F.204), которые имеют порядок т~2. При этом вклад
достаточно низкого адиабатического порядка, который не сле-
следует отбрасывать при выполнении описанной процедуры, воз-
возникает лишь при подстановке этих членов в качестве с в пос-
последнее слагаемое в F.206). Таким образом, вклад членов, про-
пропорциональных гп-2, в <7^>рен оказывается порядка т°, по-
поэтому переход в случае необходимости к безмассовому пределу
в <7'|xv>peH не вызывает затруднений. Массу следует сохранить
отличной от нуля до того, как будет выполнено дифференци-
дифференцирование, чтобы избежать появления инфракрасных расходимо-
стей на промежуточных этапах вычислений.
В качестве примера этой довольно громоздкой процедуры
вычислим <7^>Рен для безмассового скалярного поля с кон-
конформной связью в двумерном пространстве-времени в состоя-
состоянии конформного вакуума (другие примеры даны в следующей
главе). Эта конформно-тривиальная ситуация уже рассматри-
рассматривалась' в разд. 6.3 (см, F.136)). Для того чтобы первое сла-
слагаемое в правой части F.136) было отличным от нуля, прове-
проведем компактификацию пространственных сечений. Функции
Грина для нескрученных и скрученных полей определяются вы-
выражениями D.23) и D.24) соответственно:
{ — A/4яIп[1б8т2(яДн//,)8т2(я Au/L)] (нескрученное поле),
— A/4яIп [tg2^A«/2L)tg2(n &v/2L)] (скрученное поле),
где Дн = н(е)—ы(—е), До = v(е) — v(—е). Хотя в разд. 4.2
эти функции Грина были построены для плоского пространства-
времени, они остаются теми же самыми и в рассматриваемом
случае, поскольку пространство-время конформно-плоское и
конформный вес для скалярного поля в двумерном случае ра-
равен нулю (см. C.154)).
Воспользовавшись F.200), можно сразу же построить раз-
разложение в-ряд по е для функции D{l{x", x'):
censt - A/2я) 1п | е2С-' | + (е2/2я) {-~ R2 + -| (ая2//,2) [{ff +
+ (О2] +тс~2 (сс. щ ~ зс?«) (/ИJ + т с~

210 Глава 6
где а = 1 для нескрученного поля и а — —7г Для скрученного
поля, и использовано условие нормировки F.85), которое для
метрики F.135) имеет вид
Ctutv = Z. F.209)
Для выполнения перенормировки необходимо вычесть вы-
выражение F.203), полагая ? = 0 (конформная связь) а т = 0
всюду, за исключением члена m~2R (см. замечания выше).
В результате, помимо члена m~2R, остается выражение
const + A/2я) 1п С + е22 {(яа/312) Е [(/«J + (И2] +
+ A/12я)ЗГ1*:(СС. „„ - ЗС2„)(О2 + A/12я)Е-'С-2Х
X (СС. т - ЗС?0) (ff - A/24я) /?} + О (е2).
Отсюда можно получить скалярные функции с и /и бесследо*
вый тензор е„р с компонентами
ецц = (яа/312) + -{у С (СС, ии- ЗС2Д
еРВ ^= (яа/312) + -^ С (СС. 00 - 3CfD),
л — о — П
которые следует подставить в общую формулу F.205). Все
остальные члены равны нулю.
Из F.206) —F.208) при п = 2 получаем
<0|Ги„|0)рен = —r^+^[-%^-i-JL]. F.210)
w I ' w 1 и/рен 12U ' 24?
Член —R/I2nm? не дает вклада в эти компоненты тензора
энергии-импульса при его подстановке в качестве с в последнее
слагаемое в F.206) (так как guu = gvv = 0), но он приводит
к возникновению компонент
рр
= ^ С @1 Таа | 0)рен = - /?С/96я. F.212)
Отсюда ясно, что член, пропорциональный т~2, дает вклад
в аномальный след. Эти результаты находятся в полном согла-
согласии с формулой F.136), где при построении <Г^ 1цх\] >рен ис-
использован неисчезающий при нулевой температуре (главный)
член в D.27)—D.29),

^)
Перенормировка тензора энергии-импульсй 211
Мы показали, как может быть получен <7'^>рен из построен-
построенного первоначально <Г,^> путем регуляризации и вычитания
<7'iXV>ds, составленного из соответствующих членов разложения
де Витта — Швингера. Практически это было сделано путем
построения GC, регуляризации, вычитания из этой величины
соответствующих членов в G{os и последующего дифференциро-
дифференцирования для получения тензора энергии-импульса. Вычитания
были эквивалентны перенормировке коэффициентов в обобщен-
обобщенном эйнштейновском действии, что свелось к вычитанию всех
членов в <7nv>fls До адиабатического порядка п (в случае п
измерений).
Может показаться неестественным нахождение перенорми-
перенормированного <r^v> путем рассмотрения G<'> и /,эфф вместо урав-
уравнений гравитационного поля, в которые <Г^> входит в каче-
качестве правой части. В конце концов можно было бы попытаться
включить все бесконечности непосредственно в геометрические
члены в левой части обобщенных уравнений Эйнштейна F.95),
перенормируя константы G, Л, а и Ь. Но на этом пути возникает
одна трудность, которую полезно подчеркнуть для лучшего по-
понимания причины появления конформных аномалий.
Рассмотрим сначала метод размерной регуляризации. Пов-
Повторяя выкладки разд. 6.2 для произвольного поля, имеющего
tr а0 — s, tr a, = zR,
tr а2 = wRa™Ra&yu + xRa*R4 + yR2,
получаем
<т„А.„ — -^ [^+i (v + m (f))] X
v ( 4sm* 4m*z (D 1
X \ ~ n(n-2) 8v* * (n-2) V^v ~ T 8^K
}F.214)
Эти члены следует устранить из <Г^>, включая их в соответ-
соответствующие слагаемые в обобщенном уравнении Эйнштейна, ле-
левая часть которого имеет вид F.52). Сопоставление F.213)
с F.123) и F.124) позволяет выразить w, x, у через коэффи-
коэффициенты аномалий а, Ь, с, d для поля, преобразующегося по
представлению (А, В) группы Лоренца:
х = _ (ISO) (_1JЛ+2В (Ь - 2а), F.215)
у = - (ISO) (- lfA+2B (d-±b+±a).

212 Глава 6
Выражение F.214) удобно переписать в виде [72]
( ) 2{Aw + x)A^ + A>Я^ X
Dш + x){ - ^jy +
^]} F.216)
где бесследовый тензор А^ определен как
л п (\)и , B)н (п — 2) (»— 4)
^Jiv— 4(п—1) n^v"T "nv 4 (и — 3)
а WHyy представляет собой обобщение F.140) на случай /г-мер-
ного пространства-времени, не являющегося конформно-плос-
конформно-плоским:
C)w _ 4(n-3) „ Рд 2и(и —3)
(„_2J ^ ^pv („_!)(„_ 2K
2(я-3) n „pa , (я + 2) (я - 3) _2
(п-2J ^Pa/< ^у+ 2(и-1)'(и-2J ^S
F.218)
При получении F.217) использовано также тождество
?= ^ар\8 (ге 2) (ga&R$y + ^pv^ae SayR(,6
+ (n - I) (л - 2) (gavgpe - ga&g^) R. F.219)
В конформно-инвариантном случае выражение F.216) уп-
упрощается, поскольку можно использовать условия F.127). Это
приводит к соотношению w -\- х = —Зг/, благодаря которому
расходящийся член в F.216), пропорциональный A)//цУ, обра-
обращается в нуль. Если затем перейти к безмассовому пределу, то
единственными неисчезающими членами, расходящимися при
п-*-4, будут A^v и члены, содержащие тензор Вейля. Первый
имеет, нулевой след, а след последних порядка О(п — 4). При
умножении на (га — 4)-1 получим конечный след. Добавление
его к следу (конечных) членов A)Я^ и C)Я^ в F.216) приво-
приводит к известной аномалии следа со знаком минус. Отсюда сле-
следует, что при вычитании <Г^>расх из бесследового <ruv> полу-

Перенормировка тензора энергии-импульса 213
чим (У^рен, который приобретет аномальный след. Таким об-
образом, нет никаких препятствий для проведения размерной ре-
регуляризации и перенормировки <ГцУ> в самих уравнениях гра-
гравитационного поля.
Но если пытаться повторить эти рассуждения, используя
регуляризацию методом расщепления точек, то ситуация ока-
окажется иной. В четырехмерном случае левая часть уравнений
Эйнштейна имеет вид
R** ~ i /fcnv + A^v + а»»Я^ + ргоя^. F.220)
Здесь тензор Н^ отсутствует, поскольку в случае четырех из-
измерений можно воспользоваться соотношением F.57). Приме-
Применяя F.81) для построения регуляризованного расщеплением
точек эффективного действия и выполнив функциональное диф-
дифференцирование, чтобы найти <7'(iv>pacx, можно убедиться в том,
что все расходящиеся члены действительно устраняются при
перенормировке коэффициентов в обобщенных уравнениях
Эйнштейна с левой частью F.220). Но возникает новая проб-
проблема. В пределе безмассового поля с конформной связью по-
получаем [114]
<7Vv>p.c, = - A/480Я2) ((Xv - Т °4v) (v + уln | T A | ) +
-f (геометрические члены, которые остаются конечными
при а->0); F.221)
здесь еще раз проведено усреднение по направлениям вектора
расщепления, а (х — произвольный параметр инфракрасного об-
обрезания.
Первое слагаемое в F.221) устраняется путем перенорми-
перенормировки а и р в F.220), но оказывается, что остальные (конеч-
(конечные) члены при этом не исчезают. Однако из F.53) и F.54)
видно, что след расходящейся части F.221) пропорционален
DR, поэтому устранение первого слагаемого в F.221) не может
дать полную аномалию следа F.113) — F.115). Оказывается,
что конечные геометрические члены в {6.221}, не устраняемые
перенормировкой, и дают недостающую часть конформной ано-
аномалии. В противоположность этому если перенормировка
производится в действии, то весь член Wpacx, включая части,
приводящие к конечным членам в F.221), устраняется из W,
что.приводит к обычной аномалии следа. Таким' образом, ре-
результирующий <rM,v>PeH существенно зависит от того, проводит-
проводится ли перенормировка до или после дифференцирования при
получении тензора энергии-импульса.

214 Глава 6
Более детальное исследование позволяет понять причину
этого. Перенормированное гравитационное действие имеет вид
5Грав. рен = \ (- ёI' {A6Я0Г1 (Я - 2Л) + aR2 +
Здесь а, Ъ и с (не путать с коэффициентами в F.124I) не яв-
являются строго постоянными при использовании метода рас-
расщепления точек. Они содержат расходимости, зависящие от а,
например как ст~2 и In о, которые возникают из F.81) и являют-
являются как функциями х, так и функционалами метрики. При сня-
снятии регуляризации и переходе к пределу совпадающих точек
зависимость этих величин от х исчезает. Так получается, если
выполнить перенормировку для действия. С другой стороны,
если требуется перенормировать уравнения гравитационного
поля, то, как и в случае размерной регуляризации, снятие ре-
регуляризации может проводиться лишь после перенормировки,
иначе некоторые члены могут быть потеряны. Следовательно,
нужно выполнить функциональное дифференцирование W при
о Ф 0. Таким образом, W представляет собой нелокальный
функционал от метрики, поскольку а есть би-скаляр а(х, х').
Добавочные конечные члены появляются из-за дифференциро-
дифференцирования величин, зависящих от о, причем они оказываются в точ-
точности теми геометрическими членами в F.221) (в случае без-
безмассового конформно-связанного скалярного поля), которые
обеспечивают недостающий вклад в аномальный след тензора
энергии-импульса.
Чтобы убедиться в этом явно, рассмотрим часть эффектив-
эффективного действия для безмассового поля, обусловленную последним
слагаемым в Lpacx в формуле F.81):
- A/32я2) \ (- g)'1' а2 (х, х') In 14- т2а (х, х') | d'x. F.222)
Здесь т удерживается отличным от нуля для обеспечения ин-
инфракрасного обрезания. Если перенормировать действие и по-
положить а->•(), этот член будет устранен из W, что и приводит
к появлению аномального следа, пропорционального а2(х,х).
Но, если сначала выполнить функциональное дифференциро-
вание,1 мы получим конечный вклад в <Г^> от о, равный
*. * F.223)
где использовано соотношение [114]

Перенормировка тензора энергии-импульса 215
и проведено усреднение по (Гц. Если удержать этот член в
<7Vv>peH, аргументируя это тем,.что он конечен и не имеет вида
ни одного из тензоров в F.'220), то <Г^>рен будет оставаться
бесследовым. Но если рассматривать его как часть расходяще-
расходящегося вклада (поскольку он возникает при функциональном диф-
дифференцировании расходящегося члена в Lvacx, то этот член сле-
следует отбросить, что приведет к правильному выражению для
следа <Г^>рен. Именно этого требует предписание, сформулиро-
сформулированное на с. 204, поскольку вклад F.223) имеет адиабатический
порядок четыре и должен вычитаться.
Заметим, что если согласиться с возможностью появления
нелокальных членов в действии даже после снятия регуляри-
регуляризации, то, как показывает проведенный расчет, к выражению ¦
для -следа <Г^>рён можно добавить величину, кратную а2(х).
Как было отмечено в работе [67], для полного устранения кон-
конформных аномалий необходимо использовать нелокальное дей-
действие.
6.5. Другие методы регуляризации
Хотя метод расщепления точек и аналитические методы
представляют собой наиболее разработанные способы регуля-
регуляризации, было предложено и много других методов. В прост-
пространствах* Робертсона — Уокера эти методы связаны с так на-
называемой схемой адиабатической регуляризации Паркера и
Фуллинга [391], которую мы рассмотрим в первую очередь.
Адиабатическая регуляризация по существу представляет
собой некорректное название схемы вычитаний, которая может
включать расщепление точек, размерную регуляризацию или
любой другой способ регуляризации. Вместо вычитания адиа-
адиабатического разложения G*ds для получения перенормирован-
перенормированной функции Грина, как это было сделано в предыдущем раз-
разделе, адиабатическая регуляризация основана на вычитаниях
из адиабатических разложений отдельных мод. Возможнсть та-
такого способа действий вытекает из соотношения, обсуждавше-
обсуждавшегося в разд. 3.6:
*", х') = <0А | {ф (х"), ф (*')} 0А> |(А>, F.224)
где левая часть есть разложение G'ds вплоть до адиабатиче-
адиабатического порядка А, а правая часть — разложение до того же по-
порядка среднего значения произведения полей в адиабатиче-
адиабатическом вакуумном состоянии порядка А, Поскольку правая часть
требуется лишь с .точностью порядка А; точное решение для
поля ф можно заменить его разложением Ф(А) с точностью до
порядка А, которое можно построить в терминах разложения

216 Глава 6
по модам и? из разд. 3.5. Таким образом,
А = <0л
¦ = J d» (k) КА) (*") «Г (*') + «Г (х") «Г И) 1(А>, F.225)
где интегрирование ведется по мере, заданной E.24). В случае
обладающих пространственной кривизной моделей Робертсо-
на—Уокера с К~±1 построение адиабатического формализ-
формализма требует лишь очевидных изменений по сравнению с рас-
рассмотренным в разд. 3.5 случаем К = 0. Символ |(Л) в F.225)
означает, что перекрестные члены от произведений полей, имею-
имеющие порядок выше А, должны быть опущены.
Как отмечалось выше, регуляризация и перенормировка ме-
методом расщепления точек состоит в вычитании адиабатического
разложения из З'эфф, из <Г^> или из G<'>. В последнем случае
левая часть F.225) при А = п выражается в виде ряда де Вит-
та — Швингера и вычитается из GA'(x", x'). Вместо этого мож-
можно было бы работать непосредственно с правой частью, т. е.
с суммой по адиабатическим модам, вычитая ее из GO. Преи-
Преимущество вычислений непосредственно с адиабатическими мо-
модами (а не с адиабатическим разложением точной GA>) состоит
в том, что в некоторых случаях удается добиться взаимного
сокращения расходимостей до интегрирования по модам; тогда
потенциально расходящиеся члены вовсе не появляются в рас-
расчетах и все интегралы оказываются конечными. Таким образом,
никакой явной регуляризации не потребуется. Точки х" и х'
могут быть с самого начала приняты совпадающими. (Если
нужно вычислить (Гцд,), то дифференцирование GA)(x", x')
должно быть выполнено прежде, чем х", х' -*¦ х.)
Для иллюстрации применения метода адиабатической регу-
регуляризации рассмотрим безмассовое скалярное поле с конформ-
конформной связью в двумерной модели Робертсона — Уокера с топо-
топологией R2 [67, 71]. Следуя трактовке, данной в разд. 4.1, 4.2
и используя конформный вакуум, получим
оо
^\dk, F.226)
F.227)
где заранее взяты совпадающие точки в надежде на то, что
интегралы по модам будут сходящимися.
В двумерном случае адиабатическое приближение для мод
описывается выражением (см., например, C.86))
uiA) (х) = Bя)~* elk%A) (г0, F.228)

Перенормировка тензора энергии-импульса 217
где функции Xft41 определены формулой C.102), в которой сле-
следует выполнить разложение до порядка А. Подставляя F.228)
в F.225) и выполняя дифференцирование, получаем
F.229)
A)
'-<ол|гВи1оА)(Л) = —S
F.230)
(Л)
F.231)
В. соответствии с принятым методом адиабатического вычита-
вычитания (основанном на стремлении получить тот Же результат, что
и с помощью перенормировки эффективного Лагранжиана),
вычтем F.229) —F.231) при А =±=2 из соответствующих Вели-
Величин в F.226), F.227), находя W%} с помощью итераций
(см. с. 74). Получив для W^ Выражение
^ ш, - Щ. + ^f-i F.232)
и подставляя его в F.229) й F.230), найдем
0А=21 Тии 10А=2> |B) = <0А=21 Tvb 10л=2> |12) ^
8л J | s a; 8 cot 8 atl 32 а^
^ _8_ CWm* 1 dk_ (Q233)
32 «7 J
Вычитание этого выражения из7 F.226) дает
Ч _/Г ч _ 1 f (COft - fej2 .. .,
/рен W ог/рен 8л \ ть ««"Г
--^-+- t2kY\dk> F-234)
4 coft 4 Юз у
Где в окончательном результате следует перейти к пределу при
/я->-0. Как и ожидалось, оба интеграла оказываются
4

218 _ Глава в
конечными. Первый интеграл обращается в нуль при m-»-0, a
второй равен
V ии)рен = V оо)рен == дбя \"С 2" "С5/ ~ ии == 0I" F-235)
где 0UV определено формулой F.137).
Подобным же образом находим
^ Г° dk , 5СС2от8 Г dfc __
¦1 / С С» \ _ J? .
1 )^ Л
Следовательно,
(TVvVh^V-C48*)^. F.237)
что представляет собой частный случай выражений F.136) и
F.210) — F.212), полученных другими методами. Аналогичные
вычисления для четырехмерного пространства были проведены
Банчем [69, 70] и привели к согласию с результатом F.141).
В большинстве случаев точные выражения для мод оказы-
оказываются слишком сложными, чтобы можно было уничтожить
потенциально расходящиеся члены До суммирования по модам.
В таких случаях должна применяться явная регуляризация.
Если воспользоваться методом расщепления точек или размер-
размерной регуляризацией, то по существу мы возвращаемся к тех-
технике, описанной в предшествовавших разделах. Однако преи-
преимуществом выражения F.225) является то, что оно позволяет
применять различные методы регуляризации заранее зная, что
окончательный результат будет совпадать с результатом пере-
перенормировки констант.связи в обобщенном уравнении Эйнштей-
Эйнштейна. При этом регуляризация используется лишь для удобства
расчетов с величиной, о конечности которой известно заранее.
В частности, можно прибегать к нековариантной регуляриза-
регуляризации, которая представляет.удобства в вычислительном отноше-
отношении по сравнению с ковариантными схемами. Например, Бир-
релл [36] применил экспоненциальное обрезание e~ak, что
позволило сильно упростить вычисления, а Банч [73] — некова-
риантную форму размерной регуляризации при исследовании'
расходимостей <0л|Гц?|0/1>. С другой стороны, Ху [303] исполь-
использовал форму записи F.225) для получения формальной пара-
параметризации ф^\Т^\ОА'у с помощью одного простого логариф-
логарифмически расходящегося интеграла; такой метод ранее приме-
применялся также в пространствах типа Бианки I [302] на основе
формализма, предложенного Паркером, Фуллингом и Ху [391]'.

Перенормировка тензора энергии-импульса 219
Наконец, схема адиабатической регуляризации особенно
удобна при проведении численных расчетов [36], где можно
действовать следующим образом. Продифференцировав выра-
выражение F.225) и получив тензор энергии-импульса, в пределе
совпадающих точек будем иметь
@А | 7Vv (х) 10А> fA) = \ # (?) 7$ (к; х), F.238)
где величина Т^{к; х) определена через моды и]^{х). Анало-
Аналогично среднее значение точного тензора энергии-импульса в ин-
интересующем нас пространстве-времени можно записать в виде
(например, F.226), F.227))
<7VV (х)) = J dp (k).T^ (к; х), F.239)
где тензор Т^(к,х) задан с помощью точных мод Ик(я). То-
Тогда перенормированное среднее значение равно
<Гду>рен = <?Vv (X)) - @* | 7VV (х) | 0^> |Л
d\i (k) [Т^ (к, х) - Г$ (к, хI F.240)
причем в га-мерном пространстве-времени А = п. Если известны
моды и их производные (либо в виде аналитических выраже-
выражений, либо из численного решения уравнения поля), то вели-
величина Т11У(к; х) может быть рассчитана численно без особых
затруднений; величина же Г$ прн А = 2 или 4 вообще вы-
вычисляется элементарно. Поскольку потенциально расходящиеся
члены в F.240) должны взаимно уничтожаться по построению
этого выражения, результирующий интеграл конечен и может
быть вычислен с помощью прямых квадратурных методов. Чис-
Численный расчет с использованием методов размерной регуляри-
регуляризации или расщепления точек оказывается невозможным ввиду
невозможности численного перехода к пределу п^-п0 (физи-
(физической размерности) или х" ->• х' соответственно.
С адиабатической регуляризацией тесно связаны /г-волновая
регуляризация и метод Паули — Вилларса. Метод /г-волновой
регуляризации был предложен Зельдовичем и Старобинским
[503] как вариант схемы Паули — Вилларса; как было пока-
показано Паркер.ом и Фуллингом [390], он эквивалентен адиаба-
адиабатической регуляризации. Здерь мы ограничимся обсуждением
собственно метода Паули — Вилларса.
Этот прием в течение долгого времени использовался в тео-
теории взаимодействующих полей в пространстве Минковского
в качестве метода регуляризации [393]. Основная, идея состоит
в добавлении к лагранжиану интересующего нас физического

220 Глава 6
поля вкладов от дополнительных фиктивных полей, и такой
подгонке параметров теории, чтобы расходящиеся выражения,
обусловленные фиктивными полями, в точности сокращались
бы с расходимостями, связанными с физическим полем, делая
теорию конечной. Для устранения всех расходимостей может
потребоваться несколько фиктивных полей. Чтобы избежать
появление фиктивных частиц в начальном и конечном состоя-
состояниях системы (и, следовательно, нарушения унитарности), в
конце вычисления регуляризация должна сниматься путем
устремления масс фиктивных частиц к бесконечности. Расходи-
Расходимости, которые могут при этом снова появиться, устраняются
с помощью перенормировки, как и в других схемах устранения
бесконечностей. Тогда потенциально расходящиеся члены стано-
становятся функциями масс фиктивных частиц. Если некоторые из
фиктивных скалярных полей антикоммутируют, а не коммути-
коммутируют (либо в случае спинорных полей коммутируют, а не анти-
антикоммутируют), то их вклад в тензор энергии импульса стано-
становится отрицательным и они сокращаются с расходимостями про-
противоположного знака от физического поля.
Этот метод применялся Виленкиным [477] при расчете ано-
аномалии следа для скалярного поля с конформной связью и Бер-
Бернардом и Дунканом [34], детально обсуждавшим проблему ре-
регуляризации тензора энергии-импульса. Идея использования
приближения больших масс для изоляции и вычитания чисто
геометрических расходящихся членов в <7\iv> по существу сов-
совпадает с той, которая используется в адиабатическом подходе
и при использовании разложения де Витта — Швингера по сте-
степеням т~1. Таким образом, регуляризация Паули — Вилларса
в принципе не отличается от других методов, используемых для,
проведения перенормировки [76].
Разложение де Витта — Швингера F.39) в пределе совпа-
совпадающих точек х = х' (а — 0) приводит, к следующему выраже-
выражению для эффективного лагранжиана:
Y\. F.241)
где проведена замена переменной интегрирования s — m2s.
Здесь первые га/2 членов имеют ультрафиолетовые расходимо-
расходимости. Если добавить к ЬЭфф вклады от фиктивных скалярных ре-
гуляризующих полей в определенной комбинации, эти расходи-
расходимости можно формально уничтожить. В двумерном случае, tfa-
пример, требуются три дополнительных поля: коммутирующее
поле с массой {2М2— т2)'1' и два антикоммутирующих поля,
каждоес массой М. (В конце вычисления полагаем М->оо.) Ко-
Коэффициент в расходящемся интеграле лидирующего порядка

Перенормировка тензора энергии-импульса 221
(квадратичного) в F.241) тогда равен айт2-{-aQBM2 — т2)—
— 2ааМ2 = О, а коэффициент перед следующим (логарифмиче-
(логарифмически) расходящимся интегралом равен ао + ао — 2ао = 0.
В четырехмерном случае необходимо ввести пять дополни-
дополнительных скалярных полей, например, два антикоммутирующих
с массами (М2-{-т2)'1', одно с массой DА12.+ т2I'2 и Два ком-
коммутирующих с массами (ЪМ2-\-т2У!*. Нетрудно проверить, что
при таком соотношении происходит точное сокращение в выра-
выражении F.241) членов, содержащих ай, а\ и аг-
Хотя описанная процедура формально уничтожает ультра-
ультрафиолетово-расходящиеся члены в F.241), замена переменной
s — m2s, строго говоря, не является законной для расходящихся
членов с / = 0 и 1. В самом деле, если сохранить переменную
s, полный интеграл с учетом вклада регуляризующих полей для
п = 2 будет иметь вид
Г (isI
о
'2 [е~im2s + е~' BM!-m2) s - 2е- ш^ ds =
= _ 4 [ (isf e~m's sin2 [i- (M2 - т2) s] ds. F.242)
Этот интеграл легко вычислить. Для / > 1 он стремится к ну-
нулю при Af-»-oo. Для / = 0, 1 в пределе М^-оо он расходится.
Эти расходимости были потеряны при замене переменной ин-
интегрирования на s. Появления таких расходимостей и следует
ожидать при снятии регуляризации; они устраняются перенор-
перенормировкой обобщенного эйнштейновского действия (или урав-
уравнений гравитационного поля) обычным образом. В конце этого
раздела будет дан пример практических вычислений, в котором
зависящие от М расходимости будут представлены в виде явных
выражений.
Полезно, однако, сначала проследить более детально, как
появляются конформные аномалии в методе Паули — Вилларса.
След классического выражения, для Tuv, в случае конформной
связи (I = ?(«)) равный т2ф2, очевидно, обращается в нуль при
т = 0. Но (Гц*1) не обращается в нуль, поскольку в эту вели-
величину следует включить вклады регуляризующих полей, для ко-
которых М-*-оо, а не к нулю. Так в двумерном случае имеем
@17/1 0) = M2Gi%, (х, х) - M2G% (x, x), F.243)
где т = 0и использовано соотношение GA>(x, .jc)=2<O|^2(x) |0>
Используя разложение де Витта — Швингера для GA>,

222 Глава б
находим
00 00
(О | Т/1 0) = (М212п) ? а, (х) J (is)'-' [e~2iM's - в"'"'1] /da. F.244)
/-0 О
Рассматривая этот интеграл, так же как F.242), нетрудно
установить, что расходящимся при М->-оо является лишь член
ао. Эта расходимость устраняется с помощью перенормировки
космологической постоянной Л в F.220). Вычислив остальные
интегралы, находим, что при М->оо все члены разложения об-
обращаются в нуль, кроме члена, содержащего а\, что дает
<° IСI °>р*н i^T - fli W/4" F-245)
в согласии с F.121).
В четырехмерном случае аналогично находим, что единст*
венным неисчезающим членом после перенормировки и снятия
регуляризации (Af->oo) является член, пропорциональный гп~2,
в GA), от которого остается известное выражение —аг/16я2.
В пространствах нечетной размерности членов, пропорциональ-
пропорциональных пг~2, в Gos нет, поэтому аномалия следа не возникает.
В качестве иллюстрации использования метода Паули —
Вилларса в практических вычислениях приведем пример, рас-
рассмотренный Бернардом и Дунканом [34]. Этот пример уже
обсуждался в разд. 3.4 в связи с рождением частиц.
Рассмотрим массивное скалярное поле с конформной связью
в двумерном пространстве Робертсона — Уокера с метрикой,
определяемой соотношениями C.83) и C.84). В области
г)->-—оо отклонение метрики от плоской можно считать ма-
малым. Если выбрать А = 1 + Ь/2, В = Ь/2, то конформный фак-
фактор
C(ti)='l+-jft(l+thpTi)«-l+fte*1> F.246)
при рг| —*—оо. Величину р-1 можно рассматривать как адиаба-
адиабатический параметр Т, введенный в разд. 3.5.
С точностью до первого порядка по величине бе2* моды
C.87) сводятся к
где теперь ю^ = k2 + tn2.
Из соотношения C.190), полагая п = 2, ? = 0, находим
7V= Ф; A; v - -• g^'f; оф; р + j mg^\ F.248)

Перенормировка тензора энергии-импульса 223
Воспользовавшись теперь формулой B.43) (которая остается
верной и в искривленном пространстве-времени) и подставляя
решения F.247), в первом порядке получаем
<in, 0 | Тщ 10, in) = -fc \ (k* + m2)'1' dk +
— 00
+ wiypn J г dk 2 ,/a , F.249)
— 00
00. ' OO
<in, 01 Txx'\ 0, in) = — [ (k2 + m2)''2 dk — —[ ^—r
**' ' 4я J 4я J (fe2 + m2)A
— 00 -OO '
«26е2Р1 Г <ffe
С dk I w4&e2pT1 Г
J (fe2 + m2I/' 8я J (p2 + feJ
— OO — 00
8я- J (fe2 + m2I/' 8я J (p2 + feJ + m2) (fe2 + m2I^ '
— OO — 00
F.250)
Эти выражения содержат обычные квадратичные и логариф-
логарифмические расходимости, для уничтожения которых нужно вве-
ввести регуляризующие поля. При добавлении вкладов от этих по-
полей к выписанным интегралам получаем
\ № + т2I'' + (k2 + 2М2 -т*)'1' - 2{k2 + M2)'*]dk =
— оо
. =-? т2 In [BM2 - /п2)/т2] + М2 In [М2/BМ2 - т2)], F.251)
/п2 (k2 + т2)-'/! + BМ2 - т2) (й2 + 2М2 - т2)/г - .
- 2М2 (fe2 + М2)~1/!] dk = /и2 In [BM2 - mz)lm2] +
+ 2М2 In [M7BM2 - т2)] F.252)
для слагаемых, которые раньше имели"квадратичные и логариф-
логарифмические расходимости соответственно. Подставляя выражения
F.251) и F.252) в F.249) и F.250) (вместе с соответствую-
соответствующими выражениями для регуляризующих полей), с точностью
до членов рассматриваемого порядка получаем
(tn, 0\Tm\0, in) = (C/8n){m2In[BM2-m2)/m2} +
¦ . +2M2ln[M2/BM2-m2)]}, F.253)
<in, 01 Тхх 10, in) = - (С/8я) {m2 In [BM2 - m2)/tn2} +
+ 2М2 In [М2/BМ2 - т2)]} + / (т2) + / BМ2 - т2) - 2/ (М2), F.254)

224 Глава 6
где
/(m2)= '" ""¦ ¦ f dk
8я J (ft2 + p2 + m2) (ft2 + m2I/2
— ,n vn т п -г f I F_255)
8лр (m2 + p2) '2 L (m2 + p2)li — p J
Замечая, что (Г^*) —(ТХГ]у = 0, можем записать эти выра-
выражения в общем виде
(in, 0 | Т^ 10, in) = (?^/8я) {m2 In [BAf2 - m2)/tn2} +
+ 2М2 In [М2/BМ2 - т2)]} + ti^tivi If itn2) +
* + f BM2- m2) - 2/ (M2)]. F.256)
Первое слагаемое в правой части F.256) поглощается перенор-
перенормировкой космологической постоянной Л в уравнении Эйнштей-
Эйнштейна (оно расходится при Af->oo). Перенормировки, связанной
с щ, в эффективном лагранжиане Не требуется, так как это сла-
слагаемое дает вклад в уравнение гравитационного ноля, пропор-
пропорциональный тензору Эйнштейна, который тождественно равен
нулю в двумерном случае. Остающееся слагаемое в F.256) ко-
конечно при М-уоо и в этом пределе легко вычисляется. В ре-
результате имеем
Jgpn
(in, 0 | Гц, | 0, in)peH *= - Ti^tiv, -1S- X
Заметим, что при m = 0 след выражения F.257) с точностью
До низшего порядка по величине be2w дает правильную величи-
величину конформной аномалии:
(in, 01 Г,/10, itl)peH = - Й^рпрз/бя « - /?/24я4 F.258)
Недостатком метода регуляризации Паулй — Вйлларса яй-
Лйется необходимость работать с массивными полйми (пусть
даже в некотором Приближении). Во многих вычислениях урав-
уравнения для безмассового поля оказываются значительно более
простыми, чем соответствующие уравнения дли массивных
Полей.
6.6. Физический смысл тензора энергйи-имПульса
Огромные усилия, затраченные на разработку методой рас-
расчета <ГA%,>рен, заставляют нас обратиться к более подробному
обсуждению физического смысла этой величины. В предшеству-

Перенормировка тензора энергии-импульса 225
ющих разделах показано, каким образом с помощью различных
математических приемов можно из формально расходящейся
величины <Г|м,> получить некоторый остаток, который, по край-
крайней мере в явно рассмотренных случаях, может серьезно претен-
претендовать на роль правой части в уравнении гравитационного поля.
Несмотря на физическую осмысленность получаемых ре-
результатов, метод построения (Т^)рен с помощью бесконечной
перенормировки постоянных гравитационного взаимодействия
остается открытым для критики. Интеграл де Витта — Швинге-
ра по собственному времени, разложение Gf по обратным мас-
массам, а также многие более формальные манипуляции, проделан-
проделанные в разд. 6.1 и 6.2 (такие, как операции с tr\nGF), являют-
являются в лучшем случае плохо определенными для операторов ги-
гиперболического типа, а в некоторых случаях, возможно, и вовсе
не существуют. Строго доказанных результатов имеется доволь-
довольно мало.
Помимо этих математических проблем возникает также воп-
вопрос, имеет ли вообще смысл полуклассическая теория. Как
следует измерять <7'(lv>? Когда справедливо полуклассическое
приближение? Если <?VV> можно измерить лишь гравитацион-
гравитационными методами (т. е. через вклад этой величины в уравнения
поля), то можно ли пренебрегать вкладами высших порядков
(двухгравитонными и т. д.)? Каково отношение поправок выс-
высших порядков к эвристически ожидаемому результату, что
GVv)B) должно быть много меньше, чем <Гц?>, если эта послед-
последняя величина правильно аппроксимирует некоторое среднее рас-
распределение квантового тензора энергии-импульса? В каком слу-
случае можно, и можно ли вообще хотя бы приближенно описы-
описывать «обратную реакцию» (т. е. изменение гравитационного
поля, за счет индуцируемого гравитацией <Гцу>) с помощью
<7Vv)peH, вычисленного на однопетлевом уровне? Опасения по
этому поводу высказывались многими авторами (см., например,
[186]). Ответить на многие из этих вопросов могла бы точная
квантовая теория гравитации (пока не существующая), по от-
отношению к которой полуклассическая теория являлась бы не-
некоторым приближением.
Один из подходов к проблеме "установления физического
смысла <r(lV> состоит в том, чтобы вообще отказаться от пере-
перенормировок и поставить вопрос о том, каким критериям должен
удовлетворять <7VV> в полуклассической теории. Если такие
критерии будут слишком ограничительными, то эта величина
мд*жет вовсе не существовать, если слишком широкими — она
может оказаться не единственной.
Подход, целью которого является определение единствен-
единственного ненулевого <7'(lv> путем наложения чисто физических тре-
требований («аксиом»), был предложен Кристенсеном [112] и
8 Зак. 674

226 Глава 6
затем успешно развит в работах Уолда [482—484], послужив-
послуживших существенным подкреплением программы перенормировок.
В слабой системе аксиом Уолда на любой физически осмыслен-
осмысленный объект <Гцу> предлагается наложить по крайней мере сле-
следующие четыре разумных условия:
1) ковариантное сохранение,
2) выполнение условия причинности,
3) стандартные результаты для «недиагональных» элемен-
элементов,
4) обычные свойства в пространстве Минковского.
Первое условие представляет собой требование выполнения
соотношения F.142), необходимого для того, чтобы <7Vv> мож-
можно было ввести в правую часть уравнения гравитационного поля,
левая часть которого имеет равную нулю дивергенцию.
Аксиома причинности содержит некоторую тонкость. Точная
формулировка такова: «для фиксированного in-состояния зна-
значение <r,j,v> в точке р пространства-времени зависит от геомет-
геометрии пространства-времени только в причинном прошлом точки
р». Под этим понимается, что изменение метрической структуры
пространства вне светового конуса прошлого с вершиной в точке
р не должно сказываться на <Грд,> до тех пор, пока квантовое
состояние поля в отдаленном прошлом остается прежним. (Мо-
(Можно представить себе некоторые изменения геометрии вне све-
светового конуса прошлого, которые влияют на фоковское прост-
пространство, построенное на базе in-мод. Но это не допускается.) Со-
Соответствующее обращенное во времени утверждение применимо
к out-состояниям и возможным изменениям геометрии вне све-
светового конуса будущего.
Третье условие состоит просто, в том, что величина
<Фмм^|ЧО должна быть заведомо конечной для ортогональных
состояний, <Ф|ЧО = 0, причем в этом случае ее значения долж-
должны совпадать с формальным результатом. Под четвертым усло-
условием понимается, что в пространстве Минковского справедлива
процедура нормального упорядочения (разд. 2.4).
Теперь можно доказать важное утверждение: если тензор
(T'uv) удовлетворяет первым трем из приведенных четырех ус-
условий, то он является единственным с точностью до некоторого
сохраняющегося тензора.
Доказательство состоит в следующем (подробности см. в
[482]). Если Гцу и fp.v — два (перенормированных) оператора
тензора энергии-импульса, удовлетворяющие первым трем ус-
условиям, то нам нужно показать, что среднее значение оператора
Уру — Т^-Т^ F.259)
есть локальный сохраняющийся тензор.

Перенормировка тензора энергии-импульса - 227
Заметим сначала, что при выполнении третьего условия мат-
матричный элемент Uuv между ортогональными состояниями дол-
должен быть равен нулю (поскольку <Ф| T^W) = <Ф| f(iv|Y>).
Далее, полагая | П±) = 2~'/г(| W) + | Ф», где | Ф> и |?> — орто*
нормированные состояния, находим
<n+|t/|lv|n_>=o
и, значит,
Ф. F-260)
т. е. все диагональные элементы (средние значения) равны. Это
означает, что ?/wv кратен единичному оператору:
^v = «|Av/. F-261)
где «wv—обычное с-числовое тензорное поле.
Теперь можно убедиться в том, что «wv является локальным
тензором, ибо среднее значение Uuv в некотором нормированном
in-состоянии равно
(т\и^(р)\\п)=^и^(р). F.262)
То же самое должно быть верно и для out-состояний:
<out|t/|4V(p)|out)==«liV(p). F.263)
Поскольку второе условие требует, чтобы тензор uuv(p) в
F.262) зависел лишь от геометрии в причинном прошлом точ-
точки р, a «uv(P) B F.263) подобным же образом ограничен гео-
геометрией причинного будущего, эти две величины могут совпа-
совпадать лишь в том случае, если они зависят от геометрии только
в пересечении световых конусов прошлого и будущего, т. е.
в самой точке р. Следовательно, uWv(p) есть локальный тензор
в точке р.
Наконец, благодаря первому условию локальный тензор и^
должен быть сохраняющимся:
«¦*. v = 0. F.264)
Таким образом, тензор <Гр,у> является единственным с точно-
точностью до локального сохраняющегося тензора. Однако любой
сохраняющийся тензор, зависящий только от локальной гео-
геометрии, относится к левой части уравнений гравитационного
поля и его следует рассматривать как величину, описывающую
динамику гравитационного поля, а не приписывать квантовому
полю.
В теории перенормировок как раз имеется свобода в выборе
локального сохраняющегося тензора (например (I)//nV), кото-
который можно ввести в правую часть уравнений поля. Возникаю-
Возникающая неоднозначность может быть разрешена путем эксперимент
в»

228 Глава 6
тального измерения коэффициента при этом члене в уравнении.
С другой стороны, можно попытаться дать обоснование тому, что
такого члена не должно быть из физических соображениий (т. е.
коэффициент при нем равен нулю). Так Уолд [482] предложил
пятое условие, основанное на критерии устойчивости гравитаци-
гравитационной динамики, которое вместе с четвертым условием одно-
однозначно фиксирует ицу = 0. В настоящее время это условие ка-
кажется сомнительным, о чем будет сказано ниже.
Возникает вопрос: удовлетворяет ли описанная в предыду-
предыдущих разделах программа перенормировок условиям Уолда? Ес-
Если да, то имеются все основания верить полученным результа-
результатам независимо от того, рассматривается ли отбрасывание бес-
бесконечностей как законная перенормировка гравитационных кон-
констант связи или же как специально вводимое предположение.
В особенности это важно для метода расщепления точек, по-
поскольку в этом случае невозможно последовательно осуществить
перенормировку <2"M,V> в уравнениях гравитационного поля и
приходится (основываясь на результатах перенормировки эф-
эффективного действия) отбрасывать некоторый член, чтобы полу-
получить полную конформную аномалию (см. обсуждение на с. 214).
Более того, процедура усреднения по направлениям вектора
расщепления ty, до перенормировки вызывает возражения, по-
поскольку однозначно определенной меры в пространстве направ-
направлений не существует—выбирается лишь наиболее «естествен-
«естественная» мера.
Отправной точкой метода расщепления точек является раз-
разложение де Витта —Швингера для Gw{x, х'). Если это разло-
разложение существует, то из соотношения C.141) можно заключить,
что в четырехмерном случае оно должно иметь следующую об-
общую форму:
S (х, х') = (U/a) + V In a + W, F.265)
где U = U(x, х1) и
ОО ОО
V {х, х') =ZVi (х, х') о1, W (х, х') = ? Wt (x, х') о1. F.266)
/-0 1=0
Функция Грина, представленная в такой форме, ноеит на-
название элементарного решения Адамара в связи с исчерпываю-
исчерпывающей работой Адамара [262]^ о структуре сингулярностей эллип-
эллиптических и гиперболических уравнений второго порядка. Во-
Вопрос о том, когда функция G^(x, x')= <0| {ф(х), ^(*')}|°>
имеет вид элементарного решения Адамара (т. е. для каких
пространств и векторов состояний |0>), остается открытым, но
обычно предполагают, что она имеет такой вид для широкого
класса пространств и интересующих нас граничных условии.

Перенормировка тензора энергии-импульса 229
В частности, Фуллинг, Свини и Уолд [226] доказали, что если
GO имеет структуру' сингулярностей типа Адамара в некото-
некоторой открытой окрестности поверхности Коши, то она имеет та-
такую форму всюду. Следствием этого является утверждение,
что если в прошлом от некоторой поверхности Коши простран-
пространство-время плоское, то функция GO, вычисленная в состоянии
m-вакуума, имеет форму решения Адамара всюду, поскольку
она заведомо имеет такую форму в обычной квантовой теории
поля в плоском пространстве.
Коэффициенты в F.266) можно найти, подставляя F.265)
в уравнение поля и решая его методом последовательных при-
приближений [5, 158, 227]. С помощью этой процедуры V опре-
определяется однозначно. Более того, если задать W0(x,х'), то и W
будет определена однозначно. Это доопределение можно рас-
рассматривать как наложение граничного условия на поле, и оно
однозначно характеризует функцию S(x, x'). Общая нормиров-
нормировка затем фиксирует U.
Решение Адамара удобно записать в следующем несколько
измененном виде:
5 (*, х') = [2/DяJ] Д'/г [- B/а) + v In б + w], F.267)
где величина &(х,х') определена соотношением C.139), а для
v и w имеются разложения, аналогичные F.266). При разло-
разложении решения F.267) по обратным степеням массы воспроиз-
воспроизводится разложение де Витта — Швингера функции Грина
G% C.141), которое было использовано в качестве основы
программы перенормировок. В четырехмерном случае из
GW(x,x?) вычитали первые три члена разложения по обрат-
обратным степеням массы (члены до четвертого адиабатического
порядка) функции Go's. Но для выяснения совместности с ак-
аксиомами Уолда предпочтительнее иметь дело не с оборванным
разложением по обратной массе, а с точной формой Адамара
F.267). Особенно это необходимо в безмассовом пределе, ког-
когда коэффициенты разложения де Витта — Швингера для w
расходятся (поскольку это разложение по m~l). Ниже мы рас-
рассмотрим связь между перенормировками, основанными на
5 (х, х') и на Gfls (х, х').
Функция Грина G<l)(x, x') является основной величиной,
из которой можно построить <0|7V|0> путем дифференциро-
дифференцирования. При проведении практических вычислений будем пред-
предполагать, что GW имеет форму решения Адамара. Функция
G^{x,х1), согласно своему определению, должна быть симмет-
симметричной по х и х' и, следовательно, удовлетворять уравнению
поля по обеим переменным. Для решения Адамара F.267)
можно показать [226], что Д и v действительно симметричны

230 Глава 6
в общем случае. Но для w такого заключения сделать нельзя,
поскольку эта несингулярная часть определяется заданием
wo(x,x/) и может изменяться в зависимости от граничных ус-
условий. Таким образом, хотя для GO (я, х') функция w(x,x/)
должна быть симметричной по построению, в общем случае
это не так. Поэтому мы приходим к заключению, что в общем
случае функция S(x, x') не удовлетворяет полевым уравнениям
по переменной х', хотя она удовлетворяет им по переменной х.
Мы хотим найти способ устранения полюсных вкладов из
G0)(x, x') при соблюдении аксиом Уолда, гарантирующих по-
получение (почти) однозначного результата для <7Vv(*)> в ре-
результате дифференцирования. Один из таких способов состоит
в вычитании из G^(x,x') решения Адамара S(x,x') [5, 482,
483]. Для доопределения этой процедуры следует выбрать, гра-
граничные условия для S, т. е. задать wo(x,x/). Поскольку в слу-
случае безмассовых полей в пространстве Минковского -DO имеет
форму B.79), т. е. до = 0 (в массивном .случае до = const),
в соответствии с четвертым условием предположим, что
wo(x,х'\ = 0 для S. Из проведенных выше рассуждений ясно,
что для любого другого выбора wQ, совместного со всеми че-
четырьмя условиями, результат будет отличаться от результата,
получаемого при шо = О, не более чем на локальный сохраняю-
сохраняющийся тензор.
Выбирая до0 = 0, будем иметь
GB = G^-S, F.268)
где G3 (индекс В обозначает часть, зависящую от выбора гра-
граничных условий) — гладкая однозначно определенная функция
х и х1. С помощью этой функции можно построить (r°v) путем
дифференцирования (детали построения см. в разд. 6.4).
Результат, очевидно, удовлетворяет второму условию Уолда,
так как обе части GO и S, из которых он строится, удовлет-
удовлетворяют условию причинности: GO — потому, что условие при-
причинности выполняется для поля ф, а 5 — потому, что является
чисто локальной величиной, не зависящей от геометрии вне
светового конуса. При х'-*-х GB зависит только от геометрии
на световом конусе вокруг точки х и внутри него.
Легко показать, что третье условие также выполняется.
С помощью соотношения F.260). матричные элементы Tj^v
между ортогональными состояниями можно представить в виде
\Т[ ф> -
^ *Vv (Pv ~ G&) - j Hm^ 9>„ (Ov - СФ), F.269)

Перенормировка тензора энергии-импульса 231
где 3),jv — оператор, введенный на с. 204, а через dp й т. д.
обозначены величины вида (Л?\{Ф(х),Ф(х')}\у?). Последнее
равенство в B.269) следует из того, что из Gy и Go вычитает-
вычитается одна и та же функция S(x, х') в соответствии с предполо-
предположением о перенормировке F.268). Согласно третьему условию,
выражение F.269) должно быть «обычным» (формальным,
«неперенормированным») выражением, каковым оно и является
в действительности, поскольку не зависит от S.
К сожалению, предположение F.268) не удовлетворяет пер-
первому условию Уолда. Как отмечалось выше, функция S(x, x'),
вообще говоря, не удовлетворяет уравнению поля по обеим
переменным х и х'. При выборе граничного условия wQ = 0
она действительно не удовлетворяет этому уравнению по х'.
Расчет для безмассового случая приводит к следующему вы-
выражению для дивергенции тензора энергии-импульса:
Vv <7U> = i Hm V* \аХ' + i- R (*0l GB (x, х'), F.270)
откуда видно, что тензор (т^) не сохраняется, если не удов-
удовлетворяется полевое уравнение по х'. Правая часть F.270)
явно вычислена Уолдом [482] и равна
V^ (х)/64я2, F.271)
где а2(х)—обычный коэффициент разложения де Витта —
Швингера. Таким образом, чтобы построить сохраняющийся
тензор <7Vv>, который удовлетворял бы второму, третьему и
четвертому условиям Уолда, нужно взять
<?Vv (*)> = (Г?, (*)) - а2 (х) g^ (х)/64я2. F.272)
Поскольку g*v G>v) = 0 по построению, находим
F.273)
в согласии с конформной аномалией F.119). Так как наш ре-
результат является единственным с точностью до локального
сохраняющегося тензора, а тензора со следом, равным F.273),
не существует, можно прийти к заключению, что конформная
аномалия является неизбежным следствием локальной полу-
полуклассической теории. Конечно, при этом остается свобода в вы-
выборе коэффициента при DR путем добавления некоторой ли-
линейной комбинации локальных сохраняющихся тензоров <'>#,«
и B>ЯцУ.
Первоначально Уолд предложил еще основанное на сообра-
соображениях об устойчивости пятое условие, состоящее в требова-
требовании отсутствия в <r,j,v> слагаемых выше третьего адиабатиче-
адиабатического порядка (которые дают величину П^ в выражении для

232 Глава 6
следа). Однако можно показать, что в общем случае тензор
энергии-импульса будет содержать нелокальные члены, вклю-
включающие вклады высших адиабатических порядков, которые не
могут быть устранены введением (локальных) контрчленов,
пропорциональных A)Я^ и B)Я^. Горовиц [294] предположил,
что для безмассовых полей наличие нелокальных членов с выс-
высшими производными приведет к неустойчивости относительно
плоского пространства-времени. Следствия таких результатов
для полуклассической теории полностью еще не выяснены.
Какова связь между функцией S(x, х'), использованной
здесь для обеспечения конечности GA), и функцией де Витта —
Швингера G{ds(x, х'), применявшейся выше для перенормиров-
перенормировки GO? Предварительно заметим, что (в четырехмерном слу-
случае) нас интересуют только члены разложения G[>s не выше
четвертого адиабатического порядка и порядка не выше о. Сла-
Слагаемые высших порядков по о не дают вклада в <7"uv> при
<т->0. Из. формулы C.141) в явном виде находим
GA) (х, х') = (Л1/2/4я2) { а0 [ - A/о) + m2L (l - «Дт2*) - х\2т +
-~ т2а] - a, [L A - 1/2т2а) + 1/2т2а] - а2а [l/2L - '/4] +
F.274)
где L = у -\- ]/2\п\ ]/2т2а\, у — постоянная Эйлера.
Ясно, что расходящиеся и логарифмические члены в F.274)
имеют форму решения Адамара F.267)'' и ввиду их однознач-
однозначности должны согласовываться с соответствующими членами
в разложении S (х, х/). Более того, поскольку Gds удовлетворяет
уравнениям поля в любом адиабатическом порядке и для каж-
каждой степени о, определение коэффициентов при членах а0т2,
аот*а, а^ггРа и а2а не зависит от членов, пропорциональных т.-2
и более высоким степеням m-1. Следовательно, эти коэффициен-
коэффициенты должны совпадать с соответствующими величинами для ре-
решения Адамара S(x, x'). Это подтверждается и прямым вычисле-
вычислением [5]. Таким образом, разность между G(bs и 5 есть «ано-
«аномальный член», т. е. последний член в F.274), стремящийся
к а2/(8п2т2) при дс'-vjt. В практических расчетах перенорми-
перенормировка <Т|j,v> осуществляется путем вычитания выражения F.274)
из GO и опускания после дифференцирования всех членов адиа-
адиабатического порядка выше четвертого, которые происходят от
F.274). Как отмечалось на с. 215, эта процедура эквивалентна
') Более детальное обсуждение характера сингулярности двухточечной
функции Грнна массивного скалярного поля содержится в работе [595*].—•
Прим. перев.

Перенормировка тензора энергии-импульса 233
вычитанию последнего члена в F.274) только через его вклад
вида 2{'/4—[—(l/rt)]i}m2g^v^2 в C.190). Таким образом,
в четырехмерном безмассовом случае, с конформной связью по-
последний член в F.274) дает в <7"uv> лишь вклад —a2g uV/F4я2)
и в этом состоит единственное различие в выражении для <TUV>»
которое получается при вычитании величины Gds вместо 5. Но
в методе, в котором вычитается 5, в точности такой член добав-
добавляется в F.272) для обеспечения ковариантного сохранения.
(Необходимость добавления такого члена можно видеть из того
факта, что G'1' удовлетворяет уравнению поля по переменной х
шаг за шагом по параметру адиабатичности. Аналогичный ха-
характер имеет и закон сохранения для <ГЦУ>- Следовательно, для
получения сохраняющегося <ГЦУ> нужно учитывать все члены
соответствующего адиабатического порядка. Член ш2ф2, не со-
содержащий производных, должен учитываться с точностью до
двух более высоких порядков по параметру адиабатичности, чем
остальные члены, содержащие две производных.) Поэтому мож-
можно прийти к заключению, что способ перенормировок методом
расщепления точек, сформулированный в разд. 6.2 и 6.4, эквива-
эквивалентен методу вычитаний Уолда с использованием функции Ада-
мара, который, как было показано выше, приводит к (почти)
однозначному результату (обсуждение двумерного случая
см. в работе [76]). Таким образом, метод расщепления точек
так же, как и другие способы перенормировки, которые, как мы
показали, тесно связаны с ним, могут применяться с уверен-
уверенностью, что даваемые ими результаты согласуются с физически
весьма правдоподобными и однозначными (с точностью до ло-
локальных сохраняющихся тензоров) четырьмя условиями Уолда.
Это означает, что получаемое перенормированное среднее зна-
значение тензора энергии-импульса <7"цу>рен представляет собой
физически правильное решение, если полуклассическая теория
вообще имеет какой-то смысл.
В заключение коснемся еще одного аспекта физической ин-
интерпретации среднего значения <ГЦУ>. связанного с граничными
условиями. Обычно предполагается, что пространство-время
не имеет границ. Но материальные поверхности могут действо-
действовать как эффективные границы, например на поверхности про-
проводников электромагнитное поле должно исчезать (если пре-
пренебречь глубиной проникновения). Общая математическая тео-
теория эллиптических операторов в римановом пространстве
, [241, 242, 322, 355, 360, 444] и соответствующих волновых опе-
операторов в псевдоримановом пространстве-времени учитывает
влияние границы дМ многообразия М на разложение де Вит-
та — Швингера и его эквивалент в эллиптическом случае. Ока-
Оказывается, что при наличии границы к эффективному действию,
даваемому формулами F.36) и F.40), следует добавить

234 Глава 6
поверхностное эффективное действие (см., например, [323])
= J da-xx(±hLtLs{x), F.275)
s
дМ
где h — определитель метрики кц, индуцируемой на границе
метрикой пространства-времени g^v (знаки ± в зависимости от
того, является ли граница дМ времениподобной или пространст-
венноподобной соответственно), а асимптотическое разложение
(ср. с F.40)) имеет вид
оо
F.276)
/-о
Явный вид коэффициентов Ъ зависит от характера граничных
условий, налагаемых на поле на границе дМ. В случае скаляр-
скалярного поля с граничными условиями Дирихле
Ф (х) = 0, х е= дМ, F.277)
первые несколько коэффициентов записываются в виде
ьч, = -ч&\ б, = 7зх,
И = -пи Я>А I3 <3 ~ 32&) х2 + бAб|— 1) х^зГ -
- 16 A - 6|) R - 24 (8? - 1) R^nW], F.278)
где Пц — единичный вектор на дМ, направленный внутрь, %^ и
X == Хн1* — вторая фундаментальная форма дМ и ее след, R —
скаляр Риччи индуцируемой метрики h^ (см., например, [287],
§ 2.7). Для граничных условий Робина
№(х) + п»Ч11]ф(х) = 0 F.279)
получаем
6
Ш п>1' IШ^2 + 96*х + 3
6 C - 16?) ХцУХцу + 16A- 6|) ? - 24 A - 8?) Л^п»]. F.280)
Ясно, что слагаемые с /' < (п—1)/2 в F.276) являются
расходящимися. В предыдущих разделах расходящиеся вели-
величины сначала подвергались некоторой регуляризации, а затем
бесконечности устранялись путем перенормировки. Поверхности
ное эффективное действие F.275) также можно регуляризовать
с помощью сформулированных выше методов и далее исследо-
исследовать возможность устранения расходимостей посредством пере-
перенормировки констант в действии для гравитационного поля.

Перенормировка тензора энергии-импульса 235
Обобщенное гравитационное действие, которое было пере-
перенормировано в разд. 6.2, не предусматривает поверхностных
расходимостей, поэтому на первый взгляд кажется, что наличие
границы дМ, на которой накладываются граничные условия на
поле, приводит к истинной бесконечности для натяжений ваку-
вакуума на границе. В работе [151] приведены аргументы, говоря-
говорящие о том, что такие поверхностные расходимости представляют
собой реальный эффект в теории квантованных полей. Во вся-
всяком случае, существование границ пространства-времени пред-
представляет собой настолько патологическое явление, что возникно-
возникновение расходимостей в <7"ду> не вызывает особого удивления.
В случае материальных поверхностей следует учитывать, что
замена их границами многообразия представляет собой некото-
некоторую идеализацию. Например, в электромагнитном случае конеч-
конечная проводимость реальных проводников приводит к тому, что
вещество становится прозрачным при очень высоких частотах,
что обеспечивает ультрафиолетовое обрезание при интегрирова-
интегрировании по модам. (Параметр обрезания, применявшийся в разд. 4.1
как чисто математическое средство, в этом случае имеет физи-
физическое истолкование.) Следовательно, кажущиеся расходимости
на материальных поверхностях на самом деле представляют
собой очень большие, но конечные вклады в <ГЦУ>- Дойч и Кан-
делас [151] отметили, что любое изменение проводимости веще-
вещества приведет к большому и, возможно, измеримому изменению
С другой стороны, если допустить, что обобщенное эйнштей-
эйнштейновское действие может содержать поверхностные члены, такие,
как в F.278) и F.280), то расходимости, возникающие в (по-
(поверхностном) действии для материальных полей, можно устра-
устранить путем перенормировки. Такой подход развит в работе [323].
Необходимость добавления к обычному эйнштейновскому
действию 5g F.11) поверхностного члена отмечена в другом
контексте Гиббонсом и Хокингом [237]. Они указали, что дей-
действие F.11) недостаточно для того, чтобы для всех вариаций
метрики, исчезающих на дМ, стационарность Sg приводила
к уравнениям Эйнштейна. Причина состоит в том, что вариации
членов в Sg, которые происходят от тех членов в R, которые*
линейны по вторым производным метрики, можно преобразовать
с помощью интегрирования по частям в интеграл по дМ, зави-
зависящий от нормальных производных метрики на поверхности.
Если не требовать исчезновения нормальных производных на
дМ, то необходимо добавить в F.11) член, сокращающий этот
поверхностный интеграл. Гиббоне и Хокинг получили для него
выражение .
()$(А) d" х + с <
дМ

236 Глава 6
где С зависит только от h, но не от g. Если граница может быть
погружена в плоское пространство и имеет вторую фундамен-
фундаментальную форму x°v, естественный выбор значення С таков
d*~lx, . F.282)
8jiG
д'М
так что поверхностное действие обращается в нуль в плоском
пространстве-времени. Важность учета члена F.281) в кванто-
квантовой гравитации подчеркнул Хокинг [285] (см. также разд. 8.5),

Глава 7
ПРИМЕНЕНИЯ МЕТОДОВ ПЕРЕНОРМИРОВОК
Эта короткая глава посвящена примерам использования тео-
теории регуляризации и перенормировок, развитой в гл. 6. Число
случаев, для которых <7"цу> можно вычислить в простых функ-
функциях, весьма ограничено, и, вероятно, они все рассмотрены либо
здесь, либо в работах, на которые мы даем ссылки.
Особое внимание уделяется моделям Робертсона — Уокера,
как в связи с их важностью для космологии, так и потому, что,
будучи конформно-плоскими, они могут служить хорошей иллю-
иллюстрацией роли конформных аномалий. Но именно вследствие их
простоты эти модели не отражают общей нелокальной структу-
структуры тензора энергии-импульса; поэтому в разд. 7.3 мы кратко
обращаемся к менее изящному, но более реалистическому при-
примеру анизотропной однородной космологической модели.
Хотя основная задача этой книги состоит в изложении теории
квантованных полей в заданном фоновом пространстве-времени,
мотивировка этого направления в значительной степени связана
с возможными астрофизическими и космологическими приложе-
приложениями, в которых должна учитываться динамика гравитацион-
гравитационного поля. Например, многие специалисты в области космологии
считают, что обратная реакция квантовых эффектов, порождав:
мых фоновым гравитационным полем, может оказывать глубокое
воздействие на динамику ранней вселенной, приводя, в частно-
частности, к ее изотропизации. Мы не углубляемся в детали этой тео-
теории, имеющей важное самостоятельное значение, но отметим, что
представленные здесь результаты являются отправной точкой
для таких исследований. Краткое обсуждение широкого круга
космологических приложений дано в разд. 7.4.
7.1. Двумерные модели
Перенормированный тензор энергии-импульса для конформ-
конформно-тривиального случая безмассового скалярного поля с |= О
в двумерном пространстве-времени получен в разд. 6.3 и 6.4.
Мы используем элемент длины
= C(u, v)dudv, G.1)

238 Глава 7
для которого скалярная кривизна равна
# = ШпС. G.2)
В плоском пространстве-времени R = 0, поэтому
Следовательно,'
C = F(u)G(v), G.4)
где F и О — произвольные дифференцируемые функции.
Одно из решений уравнения G.4) имеет вид F = G = 1, что
возвращает нас к метрике пространства Минковского
ds2=*dudv. G.5)
Другое решение можно получить из G.5) преобразованием ко-
координат и-*¦ п, v -> v, таким, что
и = /(й), ?> = *, G.6)
которое превращает G.5) в
ds2 = f'(u)dudv. - G.7)
Здесь штрихом обозначена производная функции по ее аргу>
менту.
Если выбрать функцию f так, чтобы
{ } G.8)
где
F = 1F + 0) G.9)
есть временная координата для переменных п, v, то соотношение
G.8) можно понимать как сужение к точке х = 0 соотношения
{l } G.10)
где
x = ±{v-u) G.11)
есть пространственная координата для системы п, v.
В системе координат (м, v) соотношение G.10) принимает
вид
x = z(t). G.12)
Его можно рассматривать как изображающее движение зеркала
в задаче, исследованной в разд. 4.4. В системе координат (м, v)
зеркало находится в точке х — 0. В силу равенства G.7) систе-

Применения методов перенормировок 239
ма, в которой зеркало движется, конформно связана с системой
покоя, поэтому можно воспользоваться общим соотношением
F.136), связывающим <Г^> для конформно-связанных вакуум-
вакуумных состояний. В разд. 4.3 показано, что для конформно-связан-
конформно-связанного безмассового поля в четырехмерном случае <7"цу> в полу-
полупространстве, ограниченном статической плоской поверхностью,
обращается в нуль. Тот же результат можно получить и для
двумерного случая. Поэтому первое слагаемое в правой части вы-
выражения F.136) можно опустить. Соответствующий конформный
фактор С, как видно из формулы G.7),» равен /'(«); поэтому,
вспоминая, что R = 0, из выражения F.137) для средних зна-
.чений компонент тензора энергии-импульса в состоянии «кон-
«конформного вакуума» получаем [137]
V пй/рен == '¦¦ пп/рен == V 55/рен == 0.
Переходя к системе координат (и, v), будем иметь
ГЧгд1{ГУч\ G.13)
(Tuv)Pea = (Tvu)Pe9 = <Tvv)pea = 0. G.14)
Аргумент функции f в G.13) равен
й = Г1(и) = 2т||-и = р(и) G.15)
(см. D.44) и D.50)). Выражая G.13) через р(и), получаем
(Тии)реа = A/12я) {p'f сЦ (рУ1'- GЛ6)
Поскольку <Гии>Рен зависит только от и, эта величина постоянна
вдоль запаздывающих изотропных лучей и = const от ЗГ+ до
поверхности зеркала. Это означает, что энергия создается самим
зеркалом и затем распространяется вправо без затухания. Заме-
Заметим, что хотя точно указать, в каких точках рождаются отдель-
отдельные кванты, невозможно, источник энергии можно выявить
однозначно. Действительно, потока энергии справа налево нет.
Эта асимметрия возникла в силу выбора граничного условия
запаздывания, подразумевавшегося при преобразовании коор-
координат G.6). В случае когда существуют статические in- и out-об-
out-области, это эквивалентно выбору в качестве квантового состояния
|0, in>, а не |0, out). Чтобы убедиться в этом, предположим,
что z(t) = const .при t < t0, что задает in-область (t <.t0). Тогда
из G.8) следует, что /'(м)=1 при t <. t0, и ясно, что «конформный
вакуум», введенный в терминах координат G.7), соответствует
in-вакууму, совпадающему с обычным вакуумным состоянием
для статической системы. Поменяв местами координаты и и v

240 Глава 7
в G.6), можно получить аналогичное соотношение между опере-
опережающим граничным условием и out-вакуумом [224].
Преобразуя выражения G.14) и G.16) к координатам (t,x)
и пользуясь соотношениями D.44) и G.15), чтобы выразить ре-
результат через траекторию зеркала z(xu), получаем
(Тн)рен = (ТХх)рен = ~ (Txt)peH = ~ (Ttx)ptH =
_ 1 A - г*)''' d
12я A-iJ dxt
Здесь z = z(xu), а точка обозначает производную по ти. Пара-
Параметр хи (введенный в D.44)) фактически представляет собой
временную координату зеркала в момент пересечения его траек-
траектории с запаздывающим изотропным лучом и. Заметим, что
для нерелятивистского движения выражение G.17) сводится к
— (\2п)-1г. Правую часть G.17) можно записать в виде
Gт
12я A-кJ dxu ' к-10)
где v — скорость зеркала z, a a — собственное ускорение в соб-
собственной системе отсчета. При \v\ < 1 знак выражения G.18)
зависит от того, является ли а возрастающей или убывающей
функцией времени. Таким образом, зеркало может излучать
отрицательную энергию, если ускорение возрастает, будучи
направленным вправо, или убывает, будучи направленным вле-
влево. Излучение отрицательной энергии — чисто квантовое явление.
Оно делает возможными необычные физические эффекты, не
встречающиеся в классической теории. В следующей главе мы
увидим, что потоки отрицательной энергии играют важную роль
при квантовом испарении черной дыры. Можно предположить,
что движущееся зеркало можно использовать для охлаждения
нагретого тела потоком отрицательной энергии в нарушение
второго закона термодинамики. Но если "выражение G.17) про-
проинтегрировать по времени между двумя стационарными поло-
положениями зчеркала, то результат будет положительно определен-
определенным, т. е. поток отрицательной энергии ограничен конечными
интервалами времени [224]. Форд [203] показал, что потоки
отрицательной энергии невозможно поддерживать достаточно
долго, чтобы уменьшение энтропии нагретого тела превысило
уровень, соответствующий обычным тепловым флуктуациям.
Представляет интерес случай гиперболической траектории
зеркала, когда а = const, т. е. ускорение постоянно в собствен-
собственной системе отсчета. Из выражения G.18) тогда следует, что
<7'uv>peH = 0, т. е. энергия не излучается в течение промежутков
времени, когда ускорение постоянно. Но, как было показано
в разд. 4.4, в этом случае преобразование Боголюбова D.64) и

Применения методов перенормировок 241
D.65) недиагонально. Отсюда следует, что зеркало испускает
частицы, ибо, как видно из обсуждения формулы C.80), детек-
детектор частиц реагирует на них. Тем не менее энергия не излучает-
излучается. Этот пример особенно отчетливо иллюстрирует нетривиаль-
нетривиальность соотношения между энергией-импульсом поля и части-
частицами. Наличие частиц еще не означает наличия энергии.
Может показаться парадоксальным, что детектор частиц,
несмотря на отсутствие энергии поля, поглощает кванты и пере-
переходит в возбужденное состояние. Разгадка состоит з том, что
при этом сам детектор испускает отрицательную энергию, ком-
компенсирующую изменение энергии поля. Испускание отрицатель-
отрицательной энергии зеркалами и детекторами имеет прецеденты в кван-
квантовой теории поля. И в отсутствие зеркал или детекторов ча-
частиц можно построить многочастичные состояния с нулевым или
отрицательным потоком энергии [189] (см. также [135]).
Еще одна траектория зеркала D.51) интересна тем, что при-
приводит к тепловому потоку излучения в более поздние моменты
времени. Применяя формулу G.16) к D.52), находим
(^)Рен = ^Г. t-+OO, G.19)
что представляет собой выражение для потока теплового излу-
излучения с температурой и/2я. Этот результат находится в полном
согласии с расчетом теплового спектра частиц, выполненным
в разд. 4.4. Действительно, для теплового спектра D.61)
ГГЛ=^ <7-20>
откуда видно, что вероятность рождения частицы с частотой со
равна A/2я)(е2я(й/* — I). (Для получения этого результата из
D.61) нужно использовать волновые пакеты, чтобы перейти от
числа частиц в данной моде |РИй/12 к соответствующей скорости
рождения, см. разд. 8.1.)
Полезно отметить, что в соответствии с формулой G.20) в
случае теплового спектра излучения энергия излучения пред-
представляет собой произведение числа частиц на энергию квантов
to, просуммированное по всем модам. В общем случае, как мы
убедились, простого соотношения между числом частиц и энер-
энергией не существует. Но для теплового излучения наивное пред-
представление об энергии «Йю на один квант» остается справедли-
справедливым. Это можно интерпретировать как результат отсутствия
корреляций между модами в тепловом спектре (см. т^кже
гл. 8). Для произвольных траекторий зеркал такое заключение
неверно.

242 Глава 7
Можно также рассмотреть задачу о двух зеркалах, одно из
которых неподвижно, а другое движется; при этом возникает
«возмущенный казимировский» вклад от первого члена в правой
части формулы F.136). В результате находим [224]
<Г»)рен = а«>рен = Л (U) + Л (V),
(TixheH = (Txi)peH = A(v)-A(u), G.21)
Л = - A/24я) [(#"'/#) - у (R"/R') + л2 (R'f/2L2]. G.22)
Здесь штрихи обозначают производные по аргументу, а функ-
функция R определена уравнением
R[t + z(t)] = R(t-z(t)] + 2L G.23)
через траекторию зеркала z(t). Покоящееся зеркало находится
в точке х = 0, а второе зеркало находится в точке х = L до мо-
момента времени ^ = 0. Вакуум определен в in-области (t<CO).
Заметим, что выражения G.21) соответствуют суперпозиции
потоков, движущихся вправо и влево. Так получается потому,
что поток излучения от движущегося зеркала отражается не-
неподвижным зеркалом. В частном случае z(t) = L при всех зна-
значениях t из уравнения G.23) находим R(u)=u и выражение
G.21) дает <Г»> ==— n/B4L2), т. е. казимировскую энергию для
двух пластин, находящихся на расстоянии L. Этот результат
равен одной четвертой от D.8); различие связано с использова-
использованием граничных условий исчезновения поля вместо периодиче-
периодических граничных условий.
Еще один интересный случай соответствует F (х) = G (х) =
= ехр(ал:), а = const в формуле G.4) Это снова плоское прост-
пространство с метрикой ds2 = e2ari(dff — dx2), т. е. вселенная Милна,
рассмотренная в разд. 5.3. Подставляя С = e2ai в общую фор-
формулу F.136) и полагая первый член в правой части равным
нулю, поскольку двумерное пространство Милна конформно
всему двумерному пространству Минковского, находим
<Г»'>рен = -<Г/>рен--1/24п/* G.24)
в согласии с E.46).
Число конформно-нетривиальных двумерных точно решаемых
примеров невелико. Один из таких примеров представляет со-
собой пространство де Ситтера, которое можно рассматривать по
аналогии с четырехмерным случаем, исследованным в" разд. 6.4.
Другой пример — пространство Робертсона — Уокера с кон-
конформным фактором
С (л) - &¦*, а = const. G.25)

Применения методов перенормировок 243
При таком выборе RC = 2а и нормированные решения безмас-
безмассового уравнения E.4) при |(п) =|B)=0 и произвольном |
имеют вид
Dп^-'''е1(кх-^\ G.26)
где
со2 = ?2+02, р2=2а;. G.27)
Таким образом, для вакуумного состояния, связанного с по-
положительно-частотными модами G.26), получаем
+ 00
>-1е1к*х-ША*с1к= G.28)
= A/л) Re Ко [Ф (А« At>)'A]. G.29)
где Аи=(ц" — ч')~(х" — х'), Аи = (ц" — л') +.(*". — х').
Разложение G.29) по степеням АыАи дает
GA) (л:", жО - A/") {- У - Y In (j Р2 Аи До) +
]} G.30)
Теперь можно использовать разложение F.200) и аналогич-
аналогичное разложение с заменой и на у для приведения G.30) к яв-
явно геометрическому виду
GO (*", х') = - A/я) {A - еЗД [Y + -i- In |e^ |] +
+ гЪ(Аа/?2-1-1Я)}, G.31)
где Лар —тензор с компонентами
Auu = Avv = -&(-b + 2I?), Auv = Avu = -±-D. G.32)
В соответствии с установленной процедурой перенормировок
из выражения G.31) необходимо вычесть члены до второго ади-
адиабатического порядка в разложении де Витта — Швингера, т.е.
члены, приведенные в F.203). Логарифмически расходящиеся
ч-дены взаимно уничтожаются, и остается выражение
- A/*) { Y A - еЭД I" I Шт~21 + е22 Uo/Лг1 -
) ( ) }G.33)

244 Глава 7
Сравнивая G.33) с формулой F.205) и опуская члены
О(т2), находим
с = - A/2я) [ In |
далее с помощью F.206) получаем следующее выражение для
перенормированного тензора энергии-импульса в безмассовом
пределе:
<01Т^ 10)рен = - A/48я) [
-(R;»R;JR2) + jRg»vl G.34)
где S^v — тензор, имеющий нулевой след,
9,v = -4Т { AW ~ 7 ^Xv - Т И«; .v/^) - № Л v/tf2)] "
—fRgv»}- G-35)
а члены выше второго адиабатического порядка, возникающие
при дифференцировании слагаемых в разложении де Витта —
Швингера, как объяснено в гл. 6, опущены. (При этом исклю-
исключается член, пропорциональный ш~2.) При получении выражения
G.34) мы также воспользовались тем, что в двумерном прост-
пространстве-времени R^—2"gnv# = 0 и в рассматриваемом кон-
конкретном примере П1п^ =—1пС = —R. Заметим, что при | = 0
след выражения G.34), как и следовало ожидать, равен
—R/24n, причем тензор 0Uv в G.35) совпадает с тензором Q^v,
определяемым формулой F.137). Таким образом, слагаемое,
пропорциональное |, в G.34) можно рассматривать как поправ-
поправку к формуле F.136), возникающую в случае неконформной
связи.
7.2. Модели Робертсона — Уокера
Большое внимание уделялось расчету тензора энергии-им-
энергии-импульса для квантованных полей в фоновых пространствах Ро-
Робертсона— Уокера. Интерес к ним связан как с высокой сте-
степенью симметрии этих моделей, так и с их значением для кос-
космологии.
В качестве первого примера рассмотрим четырехмерное ста-
статическое гиперболическое (/( = —1) пространство-время Роберт-
Робертсона— Уокера, которое обсуждалось в разд. 5.2. Будем иссле-
исследовать случай безмассового скалярного поля с конформной

Применения методов перенормировок 245
связью [70]. Функция Грина D'1' определяется из формулы
E.33), в которой следует опустить te и ввести множитель 2.
Разлагая shA% до величин порядка (АхN и используя разложе-
разложения F.201), получаем
G.36)
С помощью E.13) находим R^ = 0, /?ии = 2; поэтому выраже-
выражение G.36) можно переписать в явно геометрической форме
1
G.37)
Сравнивая G.37) с выражением F.204) для статической ги-
гиперболической модели, можно убедиться в том, что безмассовые
вклады совпадают. Более того, коэффициент при (последнем)
слагаемом в F.204), пропорциональном пг2, в рассматриваемом
случае обращается в нуль; поэтому конформная аномалия от-
отсутствует. Следовательно, если вычесть G(I) из DO для полу-
получения перенормированного выражения, то мы получим точно
нуль.
Таким образом, мы приходим к следующему результату:
<0|7Vv|0>peB = 0 G.38)
для состояния конформного вакуума, определенного с помощью
положительно-частотных мод E.28) и ассоциируемого с кон-
конформным вектором Киллинга, связанным с вектором Киллинга
дц в пространстве Риндлера (разд. 5.5). К этому результату мы
уже пришли обходным путем, используя риндлеровский тензор
энергии-импульса, в разд. 6.3 F.158). С другой стороны, теперь
можно воспользоваться проведенным расчетом и формулой
F.158), чтобы получить тензор энергии-импульса Риндлера
F.157).
В качестве второго примера рассмотрим модели с /( = 0 я
К = +1, но с С, зависящим от времени. Функцию D'1* в состоя-
состоянии конформного вакуума можно получить с помощью конформ-
конформного масштабного преобразования B.79) и E.32) соответствен-
соответственно (полагая е = 0 и удваивая последнее выражение). Результат
в обоих случаях имеет вид
1 ' Х ] 4я2 [cos (К1'' Дт)) - cos (/Г1* ДхI' ( '
где, не теряя общности, мы выбрали раздвижку точек х" и я' в
плоскости (т), %).

246 Глава 7
Воспользовавшись разложениями F.201) и соотношением
±Ь-±
X i№2 + ( - -?¦ DD2 + ± Z>4) Y2 (/!L] } + О (e6), G.40)
которое выполняется в любом пространстве Робертсона — Уо-
кера, находим
. к')-
±D + -L
XWLY2]}. G.41)
Если теперь использовать линейные комбинации геометриче-
геометрических тензорных величин с точностью до соответствующего адиа-
адиабатического порядка, можно представить G.41) в чисто геомет-
геометрической форме:
?Х"{х", х') = — + [#
G.42)
Заметим, что два других возможных члена типа /?ар/?ав и
здесь не появляются. Тот факт, что выражение G.42) имеет чи-
чисто геометрический характер, объясняется конформной тривиаль-
тривиальностью рассматриваемого примера.
Для получения перенормированного выражения необходимо
вычесть члены вплоть до четвертого адиабатического порядка
в разложении де Витта — Швингера F.204). Расходящиеся чле-

Применения методов Перенормировок 247
ны и слагаемые, содержащие произведения четырех векторов /°,
взаимно уничтожаются, и остается выражение
* I ^ 17 2RKR 4- — RR -R Л—-
144я2 + 1440Я2 1Л *а **Р+ 3 ^ар ^"Pj 2
- 4 Я2 + ? R + Лор] - -п?г (ЛаР - j tf - ? R) • G.43)
Сопоставляя с формулой F.205), находим, что здесь присутст-
присутствуют члены вида с, еа$ и f, поэтому с помощью F.206) (опуская
члены выше четвертого адиабатического порядка, возникающие
при дифференцировании Gds). получаем для перенормирован-
перенормированного тензора энергии-импульса следующее выражение:
@17V, 10)рен = A/2880Я2) [(- jR-,^ +
== ~ Ч 2880Я2 ) 16 V-4 ~ '" livj* G-44)
которое находится в согласии с F.141), если учесть, что первый
член в правой части обращается в нуль, поскольку конформный
вакуум для пространств с К = 0 и К = + 1 связан с вакуумом
Минковского (см. разд. 5.5 и рис. 20). Результат G.44) для
/С = 0 был получен данным методом в работе [137], а для К = 0
и К = +Т — в работе [77].
Подобный расчет можно проделать и для случая К = —1
при том же выборе конформного вакуума, что и в G.38). Ока-
Оказывается, что к чисто геометрическому вкладу G.42) в /)<" в
этом случае добавляется локальный член, не имеющий геомет-
геометрического характера, который после подстановки в F.206) дает
вклад (?/а(л)L<7'цу>Риндлер, фигурирующий в F.141) (см.
F.158) и соответствующее обсуждение).
Банч и Дэвис [78] выполнили расчет для безмассового ска-
скалярного поля с неконформной связью в пространстве Робертсо-
на — Уокера для некоторых масштабных факторов специального
вида, допускающего вычисление функции Грина D^ в терминах
известных функций. Например, при К = 0 и
a(t) = atc. G.45)
(а, с — постоянные) имеем
а2/A-с) A - cf/A-<Ус/('-с). G.46)
и уравнение для поля с минимальной связью П^ = 0 имеет точ-
точные решения E.3) с я = 4 и [207]
(Л) = С* (л) ( | Ъ | фЪIиь [С1Я,A) (fct)) + c2tfvw#t))]. G.47)

248 Глава 7
где #<¦>, #B) — функции Ханкеля, k =» | k | и
Ъ = A - с)/A - Зс), v = 1/B1 Ъ\), а0 = а [а3 A - 3c)fA-3c). G.48)
Коэффициенты cj и с2 — комплексные числа, связанные усло-
условием постоянства вронскиана E.6), которое здесь сводится к
условию ¦ -
k2|2-.k,P==n/4&. G.49)
Скалярное поле с минимальной связью можно использовать для
описания линеаризованных гравитонов в модели вселенной Ро-
бертсона — Уокера [255,256].
Выберем вакуумное состояние заданием Ci=0; это состоя*
ние сводится к вакууму Минковского в пределе с-»-0. Функцию
Грнна ЪA)(л:", х') .нетрудно вычислить как интеграл по модам
", х') = \ [ик (*")«; (*') + и\ (*") ик (*')] d3k =
X F {% + у, % - у; 2; 1 + (Ati2 - AzWV). G.50)
где F — гипергеометрическая функция, и раздвижка точек вы-
выбрана в плоскости (т), z), причем Дт] = т|" — т]', Дг ==» z" — z' =
Теперь следует разложить выражение G.50) по степеням в
до порядка е2, используя F.201) с заменой г на 2 и учитывая
равенство G.40). Выражая результат через линейные комбина-
комбинации геометрических тензорных величин в соответствующем ади-
адиабатическом порядке, будем иметь
Первое слагаемое в правой части представляет собой выра-
выражение для функции D<'> (/', х') в случае конформной связи
| = '/б! мы видим, что при | = 0 появляется дополнительный
вклад. Хотя функция D^ по-прежнему является локальным би-
скаляром, теперь она содержит негеометрические члены, не име-
имеющие тензорного (геометрического) характера, например член,
содержащий ц-2, который возникает вследствие отклонения от

Применения методов перенормировок 249
конформной тривиальности. Заметим, что при R = 0 добавочные
члены исчезают. В этом случае нет различия между конформ-
конформной и минимальной связью.
Перенормировка осуществляется вычитанием из G.51) чле-
членов разложения де Витта — Швингера F.204) при g = 0. Так
как результат вычитания выражения F.204) при | = у6 из кон-
конформной функции й^Цх", л;'), т. е. первый член в G.51), нам
уже известен, то теперь мы получим выражение G.44) плюс
дополнительные Слагаемые в G.51), а также члены, возникаю-
возникающие из-за различий между конформной и минимальной G{oh
@ 17Vv I 0)рен = - ( 2880я2 ) [j (l)#„,v — <3)#nv] -
- (w) X* [ln Wm2> + * D +v) + ¦ (f -v) + t
^crf. G-52)
Логарифмический член, который всегда появляется при на-
нарушении конформной тривиальности, содержит произвольный
масштаб массы т. Изменение этого масштаба приводит к до-
добавке к G.52), пропорциональной сохраняющемуся тензору
A)#,iv Однако, как отмечалось в разд. 6.2, при получении пере-
перенормированного тензора энергии-импульса всегда имеется про-
произвол в добавлении членов, пропорциональных A)Яцу, посколь-
поскольку такой член появляется в левой части уравнений гравитаци-
гравитационного поля. Таким образом, можно устранить все члены вида
A)#nv в G.52), перенормируя величину а в F.220). Поэтому при
переходе к безмассовому пределу (т-»-0) не возникает труд-
трудностей; достаточно лишь выполнить дополнительную (на этот раз
инфракрасную) перенормировку а. Заметим, что негеометриче-
негеометрические члены, содержащие ¦ф-функции, и множитель 4/з можно
включить в новое значение массы т.
Оставшиеся в выражении G.52) члены все локальны; неко-
некоторые из них «случайно» имеют геометрический характер бла-
благодаря высокой степени симметрии задачи, а последний член
является негеомётрическим. При этом отсутствует возможность
перенесения всех добавочных геометрических членов в левую
часть уравнений гравитационного поля, поскольку они не со-
сохраняются без учета слагаемых, содержащих 1п# и тр2."
В более общем или менее симметричном случае можно ожи-
ожидать появления не только негеометрических вкладов в (.Т^}рен,
но и нелокальных членов: например, если выбрать квантовое со-
состояние более сложного вида или рассматривать анизотропное
пространство-время. В разд. 7.3 обсуждается пример, когда не-
нелокальные члены возникают в явном виде.

250 Глава 7
7.3. Расчет тензора энергии-импульса
методом теории возмущений
Точно решаемые модели, полезные для педагогических целей,
не очень интересны с точки зрения практических расчетов. Что-
Чтобы выйти за рамки таких моделей, приходится обращаться либо
к численным расчетам, либо, как в разд. 5.6, к приближенным
методам.
Метод теории возмущений, обсуждавшийся в разд. 5.6, оказы-
оказывается особенно полезным при вычислении <Гцу>Рен. Нужно по-
построить итерационное решение уравнения E.105) для функций
Хь которые сводятся в in-области к функциям %^, представля-
представляющим собой положительно-частотные решения по отношению к
конформному вектору Киллинга д„ в in-области (см. E.103)).
Далее можно воспользоваться этими решениями для построе-
построения функции Грина G^(x",x') =<in, 0\{ф(х"), ф(х')}\0, in>, где
|0, in> — конформный вакуум в in-области, которую затем сле-
следует перенормировать и продифференцировать для нахождения
вакуумного среднего от тензора энергии-импульса обычным спо-
способом. Дэвис и Унру [140] рассчитали <in, Ol^^O, in>peH для
ht = O, m = 0 с точностью до второго порядка по (| — '/б) и по-
получили выражение
(in, 0 | Т^ 10, in)peH =
+ 10 (g - j) (Xv + 180 (Б - DTXv A + In С') +
С~1 $ 7/(Th)In0i|Ti-T
— оо
+1 e^C-lV (т,) \ V' Ы In (ц | т, - т,,
— оо
Ч Л Ч -1 Ч
d4l \ dn2V' Ы V' М In (ц | п, - ц21) [, G.53)
-оо / J )
где V (ц) = R (ц) С(ц), ц — произвольный масштаб массы, e^v —
тензор, диагональный в декартовых координатах с компонента-
компонентами еоо=1. еи = '/з", штрихом обозначено дифференцирование
функций по их аргументам. Тензорный оператор Ж^ определен
следующим образом: 2 (v^Vv — g^v П + #nv — -j Rg^J • так что
(Tl) (см. F.53)). Наконец, С^ — локаль-

Применения методов перенормировок 251
ный но негеометрический тензор с компонентами
Схх = Суу = Сгг = С FDD + | Ь2 +1 Z)D2 - -? Z
Выражение G.53), которое нелокально лишь во втором по-
порядке по (I—'/б), сводится в E.122) (при Л( = т = 0)'в out-
области т)->-оо, если воспользоваться соотношениями E.102) и
р = <7У>> = С-'<Гоо>.
Одним из преимуществ метода теории возмущений являетсй
то, что в каждом новом порядке по возмущению поправка к
X* появляется с дополнительным множителем ©~' (см. E.105)).
Это означает, что расходимости в <7VV> могут возникать лишь
в членах до второго порядка по возмущению. Все более высо-
высокие порядки приводят к конечным выражениям, не требующим
регуляризации, что делает возможным проведение численных
расчетов.
Альтернативный подход состоит в использовании теории воз-
возмущений для расчета эффективного действия [197, 268, 269, 271,
304]. Рассмотрим метрику несколько более общего вида
ds2 = C(n)[drJ-{e^^dx1 dx'l '. G.54)
где р(т))—симметричная матрица 3X3 с нулевым следом. За^
метим, что с точностью до первого порядка 2J3« = hi.
Фейнмановская функция Грина для безмассового поля с
конформной связью в этом пространстве-времени удовлетворяет
уравнению вида
F (х, х') = - [~ё(х)ГЧ\х - х')^ VDF(x, x% G.55)
где Ох—волновой, оператор, fli — скалярная кривизна Риччи
в приближении точной изотропии, а оператор V обозначает
(малые) поправки к этим величинам при учете анизотропии.
Уравнение G.55) имеет формальное решение вида
DF = DM + DfVDF,, ' G.56)
гд$ D(p)— фейнмановский пропагатор в состоянии конформно-
конформного вакуума (т. е. C.154) при я = 4);. эта величина является
естественным пропагатором в пределе точной изотропии. Вы-
Выражение для DF можно аппроксимировать с помощью итераций:
Df — Df> -h DfVDf + DfVDfVDf +•.'.'. G.57)

252 Глава 7
и воспользоваться им в F.25) для разложения ln(—DF), чтобы
получить ряд теории возмущений для эффективного действия
: • W = Z W®, G.58)
г-о
где
± G.59)
(^) G.60)
WB> = - -J-1 tr (V&pVDf). G.61)
Член нулевого порядка Wm рассматривался в разд. 6.3 и давал
выражение для тензора энергии-импульса F.141). Поскольку
регуляризованное продолжением по размерности выражение для
Dfix, х) -обращается в нуль (см. с. 178), то. в первом порядке
W{i) = 0. Но величина W{2) будучи квадратичной ~по D/?, имеет
отличное от нуля значение, регуляризованное продолжением по
размерности. Выписывая часть размерно-регуляризованного WB\
имеющую второй порядок по ($ (в G.61) присутствуют также
члены третьего и четвертого порядков), получаем [271]
Чл$
'Р Ol) Kim (x — х') ря' (т|'), G.62)
где
Kijki{k)== — A/1920я ) \bijbki -Ь bikbji -\- 6u6jk\ (к —ko) X
X [1/(л- 4) + у In (к2 - kl) - const + O(n -4)] +
+ (члены, не дающие вклада в W2)). G.64)
При получении формулы G.64) был использован явный вид. G(p
(в n-мерном случае) и Ун результат был разложен в ряд отно-
относительно точки п = 4. Вычисление полюсного вклада приводит
к выражению.
- [1/1 &20*2 (п - 4)] J dnx{- g}'1'

Применения методов перенормировок 253
где (—g)'1* и CapY6 — четырехмерные величины. Это выраже-
выражение можно переписать в виде (ср. F.138))
(x)+O(l), G.65)
где (—g)'1' и F (см. F.104)) построены из /г-мерных величин, а
а определяется формулой F.106). Полюсный член в G.65) мож-
можно устранить с помощью перенормировок, как обсуждалось в
разд. 6.2, 6.3, что приводит к конечному W-2), в который дают
вклад логарифмический член в G.64) и конечные члены в G.65)
порядка 0A). Расчет показывает, что
W«, = G/2880я2) | \йц[-(а/а + а*/а2)fj/' +
V -оо
+ 00 +oa .
+ 3 [4 in + In a] р„р"] - 3 \ dT\ \ d^n (г,) К (л - Ч') p" W) i _
— 00 —OO )
G.66)
00
г
где V — объем пространства, а К (л) = A/л;) \ cos (©л) In (оо/ц) do
(м- — произвольный масштаб массы, введенный при перенорми-
перенормировке).
С помощью функционального дифференцирования ряда тео-
теории возмущений для W можно построить вакуумное среднее от
тензора энергии-импульса. Оно будет содержать обычные ано-
аномальные члены для изотропного случая F.141), которые обус-
обусловлены U7(°), а также анизотропные поправки к этим аномаль-
аномальным членам от G.65) и, наконец, неаномальные члены, возни-
возникающие от G.66), которые можно рассматривать как описыва-
описывающие вклад частиц, рождающихся за счет возмущения. Эти ре-
результаты в явном виде приведены Хартлем и Ху [271].
До сих пор мы не рассматривали граничные условия, содер-
содержащиеся неявно в формальном (интегральном) уравнении
G.56) вследствие выбора в качестве Dp фейнмановского пропа-
гатора в состоянии конформного вакуума. Это условие, опреде-
определяет, по какому вакуумному состоянию усредняется тензор энер-
энергии-импульса, математическое ожидание которого получается
при варьировании G.58).
Чтобы выяснить этот вопрос, предположим, что анизотропия
исчезает в далеком прошлом и будущем и существуют .конформ-
.конформно-плоские in- и out-области и соответствующие in- и out-кон-
out-конформные состояния вакуума. Для установления характера гра-
граничных условий, содержащихся в G.56), получим уравнение
для оператора поля $>(х)у а не для функции Гранд.; , , ._-

254 Глава 7
Воспользовавшись теоремой Гаусса, можем записать
- \ dny [- g Ш'г [KyDf] (х, у)] Т (ф (у) ф (х1)) =
= - \ dny [- g (у))'1' Df (x, у) КУТ (ф (у) ф (х')) +
+ \ d% [- g (У)]"' Df (x, y)vl (Ф (У) ф (*')) -
у°-Юо
- \ d2y-[-g(y)}'kDpx,yOyA1>(x')i>(y)) G.67)
j/°-*-a>
(обозначения см. в C.28)); для общности рассматривается
случай п измерений и
G.68)
Грина Df, определенная в C
удовлетворяет уравнению
Таким образом, функция Грина Df, определенная в C.154),
k6n(x-y). G.69)
Мы также предполагаем для простоты, что поля исчезают на
пространственноподобной бесконечности, так что граничные
(пространственные) члены можно опустить.
В конформно-плоских in- и out-областях поле ф имеет раз-
разложение по модам вида C.153):
* (У) -уТ^Г ? М + в*«И. G.70)
где ы^0' — положительно-частотные моды по отношению к кон-
конформному времени г\, связанные конформным преобразованием
с модами C.151) в плоском пространстве-времени:
uV = C^n)liuk. ¦ G.72)
Поскольку между in- и out-областями имеется анизотропная
область, операторы а^ и by не совпадают. Если использовать их
для построения конформных in- и out-состояний вакуума
flk|0, in) = 0, МО, out> = 0, G.73)
то это не будет одно и то же состояние. .

Применения методов перенормировок 255
Воспользовавшись разложением по модам для фейнманов-
ского пропагатора в плоском пространстве, запишем выражение
C.154) в виде
iDf (х, у) = 6 (х° - у0) Z «Г (*) «Г (У) +
к
»'-*-«
G.74)
Используя G.70), G.71) и G.74) в поверхностных членах в
G.67), применяя условия ортонормированности C.29) и под-
подставляя G.69) в левую часть G.67), получаем
Т (ф (х) ф (х')) = ~\dny [-g Ш'г D$ (х, у) КУТ (ф (у) ф (х')) +
+ Z «к0) * (х) Ь\ф (х') + Z «Г (х) ф (х')ак. G.75)
Если теперь вычислить вакуумное ожидание G.75) вида
<out, 0|...|0, in>, то два последних члена обратятся в нуль
в силу G.73) и останется выражение
Dp (х, х') =.-\dny\-g {y)t Df (x, у) KyDF (у, хг), G.76)
где
DF (х, х') = (out, 0 | Т (ф (х) ф (х')) 10, in). G.77)
Эта величина удовлетворяет n-мерному обобщению уравнения
G.55), а именно
KXDP (х, х') = - [-g (х)Г'и б" (х - *0 - VDP (x, x'). G.78)
Подставляя G.78) в G.76), окончательно получаем
DF (х, х') = Dp (х, х') + \ dny [- g {y)f Df (x, у) VDF (у, х'\
G.79)
что представляет собой явную форму записи уравнения G.56).
Если бы взяли средние значения от G.75) вида <in, 0| ... |0, in>
или <out, 0| ... |0, out), то один из двух-поверхностных членов
не обратился бы в нуль, и результирующеее уравнение отлича-
отличалось бы от G.56).
Изложенное выше можно обобщить на случай пространств
более сложного вида с сохранением основного результата, т. е.

256 Глава 7
вывода о том, что уравнение вида G.56) определяет пропага-
тор из семейства <out, 0| ... |0, in>. Причина состоит в исполь-
использовании фейнмановского пропагатора, что формально обеспечи-
обеспечивается введением добавочного члена (—ге) в левую часть G.55)
(см. обсуждение на стр. 84).
Методы решения интегральных уравнений для пропагаторов
типа <out| ... |in> или <inj ... |in> в импульсном представлении
разработаны Бирреллом [391 (см. также [37], где рассматрива-
рассматривается только случай <out| ...|in>).
Наконец, совсем иной подход к построению теории возмуще-
возмущений был предложен Горовицем [294], который использовал ак-
аксиомы Уолда, изложенные в разд. 6.6, для получения ограниче-
ограничений на структуру (общих) возмущений первого порядка отно-
относительно пространства Минковского для тензора энергии-им-
энергии-импульса безмассового скалярного поля с конформной связью. Ес-
Если предположить, что тензор <Гц„> не содержит членов выше
четвертого адиабатического порядка (например, членов вида
ORguv), то можно получить однозначный нелокальный резуль-
результат в виде некоторого интеграла по изотропному конусу прошло-
прошлого относительно интересующей нас точки пространства-времени.
Этот результат в рамках теории возмущений для (ТПУ) был
ранее получен в импульсном представлении в работе [100], а
его обобщение на случай произвольных возмущений конформно-
плоских пространств дано в работе [296] '>.
7.4. Приложения к космологии
Как уже отмечалось в гл. 1, гравитационные эффекты в кван-
квантовой теории поля, вероятно, могут быть наблюдаемы лишь
вблизи микроскопических черных дыр или на ранних стадиях
развития вселенной. Ввиду отсутствия наблюдательных данных,
касающихся черных дыр, мы сосредоточим внимание на след-
следствиях квантовой теории поля в искривленном пространстве-вре-
пространстве-времени для физической космологии.
Большинство специалистов по космологии в настоящее вре^
мя считают, что вселенная возникла из сингулярности около
15 млрд. лет назад, причем эпоха, начавшаяся через 1 с после
большого взрыва, характеризовалась изотропным расширением
и термодинамическим равновесием.-,В предыдущих разделах бы-
было показано, что плотность энергии вакуума в космологическом
гравитационном поле пропорциональна величинам типа R2, ко*
торые становятся сравнимы с гравитационными членами в
уравнениях Эйнштейна лишь при планковских значениях време-
времени A0~43 с). Надежная информация о ранней вселенной не рас-
>) В этой работе есть ошибка, исправленная авторами в работе [633*]
(см. также [635*]). — Прим. перев.

Применения методов Перенормировок 257
пространяется на моменты времени, предшествующие значению
1 с после начала расширения из гипотетического сингулярного
состояния; поэтому обсуждаемые в этой книге эффекты вряд
ли когда-либо будут непосредственно наблюдаемыми. Но суще-
существуют косвенные методы проверки некоторых из модельных
предсказаний.
Квантово-гравитационные эффекты для ранней вселенной
приводят к возрастанию энтропии вследствие рождения частиц.
Кроме того, обратное воздействие квантовых эффектов через
индуцируемый гравитационным полем тензор энергии-импульса
изменяет динамику расширения. В частности, любая начальная
анизотропия и неоднородность, по-видимому, должна приводить
к более обильному рождению частиц (разд. 5.6) и к более силь-
сильной поляризации вакуума (разд. 7.3). Поэтому обратное воз-
воздействие должно приводить к сильному затуханию начальной
турбулентности и нерегулярности. Высокая степень крупно-
крупномасштабной однороднегсти и изотропии вселенной, наблюдаемая
в настоящее время, означает, что либо начальная анизотропия
и неоднородность были эффективно сглажены, либо расширение
с самого начала характеризовалось столь высокой степенью од-
однородности и изотропии, которая кажется априори совершенно
невероятной [397].
Бэрроу и Мацнер [24] на основании весьма общих соображе-
соображений показали, что производство энтропии на один барион при
диссипации космологической анизотропии сильно зависит от то-
того, в какой момент времени начинается эпоха диссипации. Ани-
Анизотропные возмущения можно рассматривать как некоторую
жидкость, плотность энергии которой изменяется с космологи-
космологическим масштабным фактором как <зг6 [361]. С другой стороны,
плотность энергии излучения ведет себя как cri. Следовательно,
энтропия, возникающая при затухании анизотропии, изменяется
как а~2. Чем раньше начинается эпоха диссипации, тем больше
производство энтропии.
Эффективность квантово-гравитационных процессов, как
объяснялось выше, возрастает с приближением к сингулярности
(а->0), откуда следует, что эти эффекты будут приводить к
большому производству энтропии при очень малых значениях
времени (оценки см. в работах [219, 350]). Поскольку второе
начало термодинамики запрещает последующее уменьшение
этой космической энтропии, наблюдаемое значение энтропии,
приходящейся на один барион, можно использовать для получе-
получения ограничений на начальную анизотропию. (Мы предполагаем,
что вселенная имеет фиксированное число барионов, отличное
от нуля. Некоторые из современных калибровочных теорий
предсказывают несохранение барионного заряда в условиях,
которые должны были иметь место в ранней вселенной.
9 Зак. 674

258 Глава 7
В таком случае величина энтропии, приходящейся на один ба-
рион, перестает быть параметром, по которому можно судить
о начальной анизотропии.)
Для оценки порядка интересующих нас величин можно вос-
воспользоваться результатами теории возмущений, развитой в
разд. 5.6. Выражение E.122) определяет плотность энергии рож-
рожденных безмассовых частиц в out-области, когда анизотропия Л,-
и неконформная связь V исчезают. Если Л, и V заметно отличны
от нуля лишь на некотором малом "интервале конформного
времени около т]о, то медленным изменением логарифмического
множителя в подынтегральном выражении можно пренебречь,
и в результате приближенного интегрирования в E.122) найти
ра4 - const X [60 (| - 7еJ Я2 Ы + СаМ Ы СаМ (т|0)],
где постоянная представляет собой численный множитель поряд-
порядка единицы.
На основании элементарных соображений трудно себе пред-
представить, чтобы пространство-время могло избежать появления в
планковскую эпоху значений R2 и CaPveCapYe, сравнимых с план-
ковскими значениями, просто за счет квантовых флуктуации
метрики. Поэтому даже пренебрегая последующим нарушением
конформной симметрии, можно ожидать, что р будет иметь по-
порядок планковской плотности энергии в планковский момент
времени с соответствующим красным смещением к настоящему
моменту времени (по крайней мере для гравитонов, см. [32,
257]). В термодинамических терминах планковская температура
A032 К) в планковский момент времени, испытав красное сме-
смещение, приводит к температуре теплового фона в настоящее
время порядка нескольких Кельвинов [386], которая действи-
действительно наблюдается для реликтового излучения. Таким обра-
образом, можно прийти к заключению, что наблюдаемое значение
энтропии, приходящейся на один барион, не на много превышает
минимальное значение, соответствующее квантовым флуктуаци-
ям метрики в планковскую эпоху.
Дальнейшее подтверждение, того, что крупномасштабные не-
нерегулярности не могут сохраняться за пределами планковской
эпохи, следует из вычислений эффектов обратной реакции, про-
проведенных рядом авторов [272, 306, 345, 503] (см. также [269,
304]). Как показано в этих работах, для анизотропных моделей
пространства-времени затухание происходит очень быстро, за
время порядка планковского.
Иногда квантово-полевые эффекты привлекаются при попыт-
попытках найти механизм, благодаря которому вселенная могла бы из-
избежать первоначальной сингулярности [130, 358, 368, 389, 392,
410]. Конечно, такая вселенная имела бы бесконечный возраст
со всеми вытекающими отсюда термодинамическими проблема-

Применения методов перенормировок
259
Рис. 23. Зависимость плотности энергии
конформно-связанных скалярных частиц,
рожденных в космологической модели с
временной зависимостью G.80), от мас-
массы частицы.
-4,0 -
'5,0
-6,0
О 1,0 2,0
та
ми (см., например, [ 127]). Теоремы Хокинга — Пенроуза (об-
(обзор и ссылки см. в работе [287]) существенно опираются на так
называемые энергетические условия. В пространствах Роберт-
сона — Уокера одно из таких условий сводится к требованию
р -f- Зр > 0. Но, как мы видели, квантовые эффекты делают
возможными появление при определенных условиях отрицатель-
отрицательных значений р и р, и можно предположить, что при достаточно
большой плотности вселенная испытывает «отскок», вместо того
чтобы достигать сингулярности. Такие модели рассмотрены в
разд. 3.4, 3.5.
При отсутствии в теории другого параметра с размерностью
длины кажется вероятным, что «отскок» может происходить
при временах порядка планковского. К сожалению, это тот слу-
случай, когда однопетлевое приближение перестает быть надеж-
надежным. Делались попытки найти решения уравнений гравитацион-
гравитационного поля с источником <7VV> для безмассового конформно-ин-
конформно-инвариантного поля, выражение для которого получено в разд. 6.3
[130, 197, 440]. Анализ существенно усложняется из-за наличия
членов вида A)Яцу и B)#ц„.
Если в теории имеется другой масштаб длины, помимо план-
планковского, то «отскок» может произойти и вне планковской об-
области. На первый взгляд не равная нулю масса полевых квантов
(типичное значение 10~24 г, что соответствует комптоновскому
времени 10~23 с) могла бы привести к существенному изменению
динамики гравитационного поля на расстояниях и при време-
временах, на много порядков величины превышающих планковские
значения. Действительно, как было показано в работе. [389], при
специальном выборе квантового состояния такая возможность
может осуществляться. Но в общем случае влияние массы пре-
пренебрежимо мало по сравнению с другими механизмами наруше-
нарушения конформной инвариантности [43]. Причина состоит в том,
что члены в <ГЦу> вида m2R превышают члены вида R2 лишь
при т2 > R ~ t~2, т. е. когда t больше комптоновского времени
9*

260 Глава 7
частицы. Но в столь поздние моменты времени квантово-грави-
тационные эффекты оказываются в любом случае пренебрежи-
пренебрежимо малыми.
Своего рода резонансный эффект возникает при t ~ тгх.
Этот резонансный эффект можно исследовать, воспользовавшись
теорией возмущений, развитой в разд. 5.6, на примере модели
массивного скалярного поля с конформной связью в простран-
пространственно-плоской вселенной Робертсона — Уокера с масштабным
фактором
а (т|) = 1 - 1 <х2/(а2 + тJ), а = const. G.80)
Это пространство-время сжимается до минимального значения
масштабного фактора, «отскакивает» и затем снова расширя-
расширяется, испытывая наиболее быстрое расширение (со скоростью
~а~1) при ц ~ а. Подставив выражение E.106) при С = а2
(Л»- = 0, g = Ve) в E.111), найдем коэффициент Боголюбова р и
получим для плотности энергии следующее выражение [43]:
р = J?fl (Iа3 ¦?¦ [а-'/d Dта)] + 7 -|- NCi Dта)]. + 49/Сх Dта)|.
v 2048 14 да21 1V " ' да l ' v " ' lv ')
G.81)
График зависимости <х4р от та приведен на рис. 23; на нем ви-
виден резонанс при та ~ 1. Это означает, что плотность энергии
максимальна, если время наиболее быстрого расширения (т.е.
наиболее интенсивного рождения частиц) порядка комптонов-
ского времени.
Фундаментальная длина может войти в теорию и другим пу-
путем, если учитывать негравитационные взаимодействия. Напри-
Например, в феноменологической теории распада я-мезона вводится
константа связи, имеющая размерность длины. Влияние обрат-
обратной реакции таких взаимодействий на гравитационное поле мо-
может стать большим при масштабах, соответствующих этой ха-
характерной длине, а не планковской длине [45].
Величина квантовых эффектов для ранней вселенной до из-
известной степени зависит от выбора квантового состояния, о ко-
котором мы ничего не знаем. В отсутствие каких-либо наблюда-
наблюдательных данных приходится прибегать к чисто математическим
критериям (см., например., работу [111], где для выбора опре-
определенного квантового состояния использовалось аналитическое
продолжениеI).
В современную эпоху рождение частиц и вакуумные эффекты
пренебрежимо малы [380—382].
*) В последнее время разработаны более детальные «сценарии» развития
ранней вселенной с учетом рождения частиц и поляризации вакуума [634*.
636*] (см. также библиографию). — Прим. перев.

Глава S
КВАНТОВЫЕ ЧЕРНЫЕ ДЫРЫ *
В январе 1974 г. Хокинг [277] сформулировал свое знаме-
знаменитое утверждение, что черные дыры на самом деле не совсем
черные, а вследствие квантовых эффектов испускают излучение
с тепловым спектром. Этот результат оказался важнейшим
событием в развитии теории квантованных полей в искривлен-
искривленном пространстве-времени и привлек внимание многих исследо-
исследователей к этому вопросу. Посвящая квантовым черным дырам
целую главу, мы учитываем широкий интерес к замечательному
открытию Хокинга.
Завершив представление всех основных аспектов квантовой
теории свободных полей в искривленном пространстве-времени,
мы здесь используем различные методы, описанные в предыду-
предыдущих главах. Основной результат, а именно, что гравитационное
возмущение, создаваемое коллапсирующей звездой, приводит к
появлению выходящего теплового потока излучения, легко вос-
воспроизвести. Длина волны излучения, покидающего поверхность
звезды, коллапсирующей с образованием черной дыры, как хо-
хорошо известно, экспоненциально возрастает. Поэтому представ-
представляется вероятным, что стандартные моды входящего поля после
прохождения внутренней области звезды и выхода с противопо-
противоположной стороны также будут испытывать экспоненциальное
красное смещение. Не представляет труда показать, что боголю-
бовское преобразование между этими модами, испытавшими
экспоненциальное красное смещение, и стандартными выходя-
выходящими комплексными экспоненциальными модами имеет план-
ковскую структуру. Это означает, что состояние in-вакуума со-
содержит тепловой поток уходящих частиц.
К сожалению, решения волнового уравнения в фоновой мет-
метрике коллапсирующей звезды не удается выразить через извест-
известные функции, поэтому для выявления экспоненциального крас-
красного смещения уходящих мод мы воспользуемся двумя упро-
упрощенными моделями. Первая представляет собой двумерную
модель гравитационного коллапса, в которой выбрана метрика,
соответствующая сферически-симметричному телу, сжимающе-
сжимающемуся по произвольному закону с уходом под горизонт событий.
•Вторая модель возникает в результате пренебрежения обратным
рассеянием в четырехмерной картине.

262 Глава 8
Двумерная модель обладает тем дополнительным преимуще-
преимуществом, что для нее можно вычислить перенормированный тензор
энергии-импульса во всех точках пространства-времени, что
способствует пониманию физических явлений, связанных с эф-
эффектом Хокинга вблизи горизонта и внутри черной дыры. Она
также приводит к любопытной связи эффекта Хокинга с кон-
конформной аномалией. Мы отводим место также обсуждению воп-
вопросов о том, где рождаются частицы и каким образом черная
дыра теряет массу.
Представлена также более изящная теория квантовых черных
дыр, в которой не рассматривается фаза коллапса, а вместо,
этого вводятся соответствующие граничные условия на горизонте
прошлого для максимально расширенного многообразия. Это
позволяет глубже понять тесную связь между существованием
горизонта событий и тепловыми свойствами черных дыр, а так-
также приводит к установлению аналогии между черной дырой
и рассмотренной в гл. 4 системой Риндлера. Хотя наибольший
интерес к квантовым черным дырам связан с астрофизическими
и термодинамическими приложениями, мы ограничились при об-
обсуждении этих вопросов лишь краткими замечаниями. В то же
время мы даем многочисленные ссылки на оригинальные ра-
работы.
8.1. Рождение частиц коллапсирующим
сферическим телом
Рассмотрим сферически-симметричное тело в свободном про-
пространстве. Во внешней области единственное сферически-сим-
сферически-симметричное решение уравнений Эйнштейна есть решение Шварц-
шильда, описываемое метрикой C.18). Мы не интересуемся
здесь метрикой внутреннего решения, поскольку она оказывает-
оказывается в данной задаче несущественной.
Известно (см., например, [363] гл. 31), что если тело имеет
достаточно малый радиус, то оно начинает катастрофически
сжиматься, образуя шварцшильдову черную дыру. Внешняя
метрика в процессе коллапса не изменяется, но моды квантован-
квантованного поля, проходящие через внутренность шара, испытывают
сильные возмущения. Поэтому можно ожидать, что будет иметь
место рождение частиц.
Если предположить, что в отдаленном прошлом шар доста-
достаточно велик, так что пространство-время приближенно можно
считать плоским, то можно построить стандартное состояние
вакуума в пространстве Минковского. После коллапса прост-
пространство-время будет шварцшильдовым, и в этой out-области
вакуум уже не будет совпадать с вакуумом Минковского, по-
построенным в in-области, Для расчета рождения частиц необхо-

Квантовые черные дыры 263
димо вычислить коэффициенты боголюбовского преобразования,
связывающего вакуумные in- и out-состояния.
Мы будем следовать здесь работам Хокинга [278] и Паркера
[385, 387], ограничивая рассмотрение случаем безмассового ска-
скалярного поля. Поскольку для пространства Шварцшильда # = 0
(и результаты не зависят от метрики внутри шара), при расчете
коэффициентов Боголюбова нет необходимости различать слу-
случаи конформной и минимальной связи.
Моды, представляющие собой решения волнового уравнения
= 0 в пространстве-времени Шварцшильда, имеют вид
r-lR*i{r)Ylm{B, ф)е~™, ¦ (8.1)
где Yim — сферические гармоники, а радиальные функции R
удовлетворяют уравнению
~Т + К -Щ1+ О г'2 + 2Мг-*] [ 1 - 2Л1/-']} Ral = 0 (8.2)
(координата г* определена на с. 46). В асимптотической области
г->оо уравнение (8.2) имеет решения е±'0)Л, и выражение (8.1)
в изотропных координатах, и = t — г*, v — t-\- r* принимает вид
г-%те-*°» и г-1уше-ш, (8>3)) (8.4)
Из-за наличия «потенциала» в квадратных скобках в (8.2)
стандартные входящие волны (8.4) частично рассеиваются на-
назад гравитационным полем, превращаясь в суперпозицию пада-
падающих и отраженных волн. К счастью, если мы ограничиваемся
наблюдениями в асимптотической области (г->оо), то построе-
построение точного решения уравнения (8.2) оказывается излишним.
Следуя общей теории, развитой в гл. 3, разложим поле ф по
полному набору положительно-частотных мод, которые обозна-
обозначим /ш/
(a®lmfalm + flllm/Ilm). (8.5)
Ф = 2] \
где моды faim нормированы в соответствии с условием C.29), т. е.
(/coi/im,, fanhmi) = б (©, — ©2) Ьифт,т„ (8.6)
и выбраны так, что в отдаленном прошлом они переходят в схо-
сходящиеся сферические волны (8.4). В качестве квантового состо-
состояния выбираем in-вакуум, определяемый условием
«o>zm|O> = O, Vco, I, m, (8.7)
которое соответствует отсутствию входящих частиц из Sf-.
Чтобы найти вид решений faim в будущем, заметим сначала,
что входящие волны (8.4) сходятся к центру шара, через

264
Глава 8
Гориаонт
событий
Коллапсирующее
тело
Рис. 24. По мере приближения коллап-
сирующего сферического тела к сиигу-
лярирсти сходящиеся из 3f~ к его цен-
центру изотропные лучи претерпевают иска-
искажение. Один из иих Y образует горизонт
событий, представляющий собой грани-
границу между предшествующими лучами, ко-
которые уходят на 3f+, и более поздними
лучами, которые попадают иа сингуляр-
сингулярность. Лучи, эквидистантные на 3f+ в
поздние моменты времени, сгущаются во-
вокруг луча y вблизи Sf~\
который они проходят, превращаясь в расходящиеся сфериче-
сферические волны. Приближаясь к поверхности шара, падающие
волны испытывают голубое смещение, а при выходе после
прохождения сквозь шар —красное смещение. В случае ста-
статического тела эти два эффекта в точности компенсируют
друг друга, а волны достигают ЗГ+, имея форму (8.3). Но
если тело коллапсирует, то за время, пока волны распростра-
распространяются внутри него, оно сжимается, и его поверхностная грави-
гравитация возрастает. Поэтому выходящие волны испытывают боль-
большее красное смещение, чем это требуется для компенсации
голубого смещения на входе. Если тело испытывает полный
гравитационный коллапс с образованием черной дыры, времен-
временной масштаб сжатия имеет тот же порядок величины., что и
время прохождения света через тело; поэтому избыточное крас-
красное смещение становится заметным. Мы увидим ниже, что крас-
красное смещение возрастает экспоненциально, причем время изме-
изменения в е раз оказывается порядка времени прохождения.
Эта ситуация схематически изображена на рис. 24, где пока-
показан шар, коллапсирующий с образованием сингулярности. Не-
Некоторые входящие изотропные лучи показаны проходящими
через центр коллапсирующего тела и выходящими с противопо-
противоположной стороны. Существует последний выходящий луч, обоз-
обозначенный через у, который еще успевает пройти через коллап-
коллапсирующее тело и достичь &+ с противоположной стороны. Этот
луч образует горизонт событий вокруг черной дыры. Более позд-
поздние лучи проходят через горизонт, но уже не достигают &+, а
попадают в сингулярность. Важно отметить, что прямым взаимо-
взаимодействием квантованного поля с веществом коллапсирующего

Квантовые черные дыры 265
тела мы здесь пренебрегаем. Роль вещества в этой модели выра-
выражается лишь в создании соответствующего гравитационного
поля.
Чтобы найти вид мод, испытавших красное смещение и до-
достигающих 9+, опустим угловые переменные и рассмотрим дву-
двумерную модель коллапсирующего тела, которая оказывается
весьма полезной. Вне шара элемент длины имеет вид
ds2 = C(r)dudv, (8.8)
где теперь
и = t - г* + Rl, v = t + r'-R0, (8.9)
-Ыг, (8.10)
R*q — const. Внутри шара возьмем элемент длины общего вида
ds2=*A(U, V)dUdV, (8.11)
где А— произвольная гладкая несингулярная функция, а
U = x-r + RQ, V = x + r-RQ. (8.12)
Связь между #о и R*o такая же, как и между г и г* (8.10).
Внешняя метрика (8.8) выбирается так, что С-*-1 и дС/дг-~*-0
при г->оо. Горизонт событий находится при некотором значе-
значении переменной г, для которого С = 0 (предполагается, что
пространство-время несингулярно вне горизонта). Например, для
С= 1 — 2Мг~г горизонт событий расположен при r= 2M, что
представляет собой двумерную модель шварцшильдовой черной
дыры. Аналогично С = 1—2Мг~[ -f- е2г~2 моделирует черную
дыру Рейсснера — Нордстрема. Однако на этом этапе рассуж-
рассуждений нет необходимости уточнять вид функции С (г).
До момента т = 0 шар находится в покое, и его поверхность
соответствует г = Ro- При т > 0 будем считать, что поверхность
сжимается вдоль мировой линии r=R (т). Оказывается, что для
поздних моментов времени на 3f+ (т. е. при больших и) точная
форма функций A(U, V) и R{%) несущественна. Координаты (8.9)
и (8.12) выбраны так, чтобы в момент начала коллапса т = / =
= 0 на. поверхности шара и — U = v = V = Q.
Для того, чтобы смоделировать сферическую симметрию че-
четырехмерного случая, можно применить отражение метрики
(8.8) и (8.11) относительно начала пространственных координат
г = 0. Иначе можно ограничить изменение этой координаты
областью г^О и отражать изотропные лучи в точке г = 0.
Это воспроизводит прохождение радиального луча через центр
шара с выходом наружу. Такое отражение достигается в
результате наложения граничного условия ф = 0 при г = 0,

266 Глава 8
Уравнения, выражающие связь внутренних и внешних коор-
координат, запишем в виде
?/ = сф), (8.13)
(8-14)
пренебрегая эффектами отражения на поверхности шара. Точ-
Точная форма функций аир будет определена ниже. Центр шара
находится на линии
V = U-2RQ. (8.15.)
Нам нужно построить решения Двумерного волнового уравне-
уравнения
обращающиеся в нуль вдоль линии (8.15) и сводящиеся к стан-
стандартным экспонентам на Sf~. Построение решения облегчается
благодаря конформной симметрии. Заметив, что, согласно (8.15),
при г = О , ¦
v = Р (V) = Р (С/ - 2Я0) = Р [а (и) - 2/?0],
и учитывая D.43), можем записать решение в виде
i Dяю)-'/2 (е-1™ - е-'6* [« <«>-2«°]). (8.16)
Таким образом, оказывается, что простая «входящая» (движу-
(движущаяся влево) волна е~1<а" превращается коллапсирующим телом
в сложную «выходящую» (движущуюся вправо) волну
ехр{—i©p[a(u) —2До]}.
Из физических соображений можно ожидать, что фазовый
множитель р[сс(и)—2R0] должен соответствовать стационарно
возрастающему красному смещению, когда поверхность шара
приближается к горизонту событий. Для нахождения формы
этого множителя, описывающего красное смещение, необходимо
сшить внутреннюю и внешнюю метрики на поверхности коллап-
сирущего тела r — R(%). Это приводит к уравнениям
а' (") = ^- = A -
^ - R2) + R2}'1' - Я}, (8.17)
Р'W=-Jr=c~*u + яг1 {[лсA-я8)+ № + *}, <8Л8>
где R обозначает dR/dx, а U, V и С берутся при r==R(x). Заме-
Заметим, что для коллапсирующего тела R<iO, поэтому (R2)^— —R.
Когда поверхность шара приближается к горизонту собы-
событий, С стремится к нулю, а уравнения (8.17), (8.18) упрощаю?'

Квантовые черные дыры 267
ся и принимают вид
^^(*>, - (8Л9)
Вблизи точки С = 0 можно разложить R(x) в ряд:
R (т) = Rh + v (т„ -х) +0 ((xh - тJ), (8.21)
где R = Rh на горизонте, т = xh при R{x) = Rh, а —v =
= R(xh). Тогда, проинтегрировав (8.19), с точностью до O(xh —
— т) получаем
хи = - In | U + Rh — Ro + xh | + const, (8.22)
где величина
1 дС
2 дг
/¦-Л.
(8.23)
называется поверхностной гравитацией черной дыры [101]..
Из соотношения (8.22) видно, что при U-*-Xh-{- Ro — Rh име-
имеем «->оо. Обращение этого соотношения дает
U ~ е~ки + const (8.24)
для поздних моментов времени на &+.
Эта ситуация показана на диаграмме Пенроуза (рис. 25).
Изотропный луч и = оо, изображающий горизонт событий чер-
черной дыры, соответствует внутри коллапсирующего тела изотроп-
изотропному лучу U = тй + /?о — Rh- Соответствующий «входящий» луч
из Э~, помеченный символом у, является последним лучом, ко-
который может пройти через точку г = 0 и достичь &+. Лучи,
отвечающие более поздним моментам времени, попадают в син-
сингулярность. Изотропные лучи и = const, взятые при больших
значениях и, при их продолжении назад во времени и отражении
в сторону &~ сгущаются около последнего луча у (что напоми-
напоминает рис. 12). Наоборот, очень узкая область значений v и V
отвечает целой асимптотической области на &+, соответствую-
соответствующей поздним моментам времени. Следовательно, рассматривая
картину с точки зрения асимптотического наблюдателя в позд-
поздние моменты времени и, мы можем при интегрировании урав-
уравнения (8.20) считать величину А постоянной: в результате
.получим
о ~ const — AV(l +v)/2v. (8.25)
Подставляя (8.24) и (8.25) в (8.16), найдем выражение для
мод в поздние моменты времени
4K"d) (8-26)

268
Глава 8
Сингулярность^
Черная
дыра
Мировая линия
наблюдателя
Коллалсирующая,
звезда
Рис. 25. Диаграмма Пенроуза пространства-времени звезды, коллапси-
рующей с образованием черной дыры. Внешняя область представляет собой
часть пространства, изображенного на рис. 6, включая участки областей I и
III. Изотропный луч у проходит через центр звезДы и, выходя из нее,
образует горизонт событий (и = оо), обозначенный Н+, как на рис. 24.
Луч y' (штриховая линия), непосредственно предшествующий y на
/~, достигает /+ при конечном и. С учетом конформного сжатия ? оче-
очевидно, что все бесконечное будущее наблюдателя, находящегося вне чер-
черной дыры, соответствует узкой полосе изотропных лучей между y и y'>
отвечающей малому промежутку времени на ?~. Следовательно, беско-
бесконечное число эквидистантных изотропных лучей и = const в поздние
моменты времени при продолжении назад через звезду иа f~ будут сгу-
сгущаться около Y внутри этой узкой полосы.
где с и d — постоянные. Нетрудно видеть, что «выходящие»
изотропные лучи испытывают экспоненциально возрастающее
красное смещение с увеличением в е раз за время к~\ что в точ-
точности соответствует красному смещению излучения, испускаемо-
испускаемого с поверхности коллапсирующего шара (см., например, [363],
§32.3).
Выражение (8.26) имеет тот же вид, что и результат,подста:
новки формулы D.52) в D.43) для зеркала, движущегося вдоль
траектории с асимптотикой вида D.51). Преобразование Бого-
Боголюбова в обоих случаях одно и то же. Причину можно усмот-
усмотреть в том, что в случае черной дыры расчет основывается на
геометрической оптике. Распространение полевых мод внутри
коллапсирующей «звезды» аналогично с геометрической точки
зрения их отражению от удаляющегося зеркала. В последнем
случае доплеровский сдвиг воспроизводит тот же эффект, к ко-
которому приводит гравитационное красное смещение для мод
поля. Более того, функция In ch, задающая траекторию зеркала
с асимптотикой вида D.51), совпадает с траекторией частицы,
падающей в черную дыру, в координатах (г*, t) [135].
Из общей теории, развитой в гл. 3, следует, что, поскольку
полевые моды сводятся к стандартной форме на У~, инерциаль-

Квантовые черные дыры 269
ный детектор в области Э~ не будет обнаруживать частиц в
вакуумном состоянии, построенном с их помощью |т. е. в состо-
состоянии in-вакуума). Однако в силу более сложной формы волн
(8.26) инерциальный детектор на &+ в out-области будет реги-
регистрировать частицы в этом состоянии. Более того, поскольку
сложный фактор, соответствующий красному смещению, содер-
содержит лишь часть решения, зависящую от и, эти частицы будут
выходящими (т. е. движущимися вправо в двумерной модели),
что соответствует потоку частиц от черной дыры наружу.
Спектральное распределение этого излучения может быть
рассчитано обычным образом с помощью боголюбовского пре-
преобразования между модами (8.26) и стандартными экспоненци-
экспоненциальными решениями в out-области. Впервые это было сделано
Хокингом [277, 278]. Нет необходимости повторять здесь эти
вычисления, поскольку они математически тождественны с про-
проведенными в разд. 4.4 для случая попятно движущегося зеркала
(см. сделанные выше замечания). Из формулы D.61) мы знаем,
что ожидаемый спектр будет планковским, соответствующим
тепловому излучению черного тела при температуре
(8.27)
Для вычисления боголюбовскдх коэффициентов в разд. 4.4
оказалось удобно выбрать поверхность интегрирования лежащей
в in-области. Это означает, что функцию р(и) следовало об-
обратить, чтобы получить f(v) в D.58). Физически это соответст-
соответствует выбору стандартных выходящих волн на 3f+, которые на
&~ принимают вид более сложных функций координаты v. Об-
Обращая функцию (8.26) (с точностью до фазового множителя),
для мод такого типа получим выражение
1п [<во-
_ е- ши^ D <- Oqj (8.28)
где vo—постоянная, соответствующая последнему изотропному
лучу у. Сгущение входящих лучей около у выражается в быст-
быстром изменении фазы в (8.28) при v->-vq.
Расчет для четырехмерного случая, выполненный в работе
Хокинга [278], по существу не отличается от приведенного вы-
выше для двумерной модели. Основной результат — существование
потока частиц от черной дыры с тепловым спектром при темпе-
температуре (8.27) —остается тем же. Однако в четырехмерном слу-
¦чае возникает ряд технических усложнений, на которых мы крат-
кратко остановимся здесь. Решения Rai(r) радиального уравнения
(8.2) оказывается невозможным выразить через известные
функции, хотя свойства этих решений были исчерпывающим
обр-азом изучены в работах [59, 60, 88, 375, 400, 407, 441, 453,
454] (см. также [60] для случая спина '/2).

270 ' Рлава 8 _
Уравнение (8.2) имеет вид одномерного волнового уравнения
с потенциалом (квадратные скобки). С физической точки зре-
зрения этот потенциал приводит к возникновению отраженных
волн, что можно понимать как обратное рассеяние полевых мод
на кривизне пространства-времени. В случае коллапсирующего
шара некоторые входящие возмущения будут превращаться в
выходящие в результате обратного рассеяния, а не после про-
прохождения через внутреннюю область шара. Поскольку интере-
интересующий нас эффект связан именно с вкладом проходящих волн,
мы временно пренебрежем обратным рассеянием, опуская по-
потенциал в (8.2). Тогда радиальные функции сводятся к обычным
экспонентам, и нормированные моды принимают простой вид
Ущ F, Ф) у f g~ to", (8.29)
(8jAoL \e-iw>, . (8.30)
который при больших г совпадает с соответствующей формой
для плоского пространства-времени, когда и = /— r*—*t — г,
v==t-\-r*^t-\-r.
Нас интересуют^специальные линейные комбинации мод
(8.30), которые совпадают со стандартными модами на &+. Ес-
Если продолжить эти решения назад во времени [378] через кол-
лапсирующее тело и далее вдоль входящего изотропного луча
на Sf+, то для моды, которая на 2f+ имеет вид (8.29), получим
^ln[fo,-*Vc]>. v<v0, (83i)
0, v > v0
(с — постоянная) вблизи последнего входящего луча у на
рис. 24. Сходство между (8.31) и (8.28) очевидно.
Обычный in-вакуум определяется по отношению к модам
(8.30). Коэффициенты Боголюбова, связывающие (8.30) и
(8.31), определяются выражениями
v Но
а<т' } = A/2я) \ dv(mr/taL4!±b'*exp{4Mfaln[(v0-v)/c]}. - (8.32)
Ниш') J
Интегралы в правой части можно вычислить в терминах Г-функ-
ций [278]; ответ совпадает с D.60). В этом случае также на-
наличие множителя {а>')~'1г приводит к логарифмической расходи-
расходимости выражения иНшш'р^®'- Число частиц в каждой моде на
Sf' оказывается бесконечным. Расходимость здесь связана с нор-
нормировкой мод (8.29) — (8.31) непрерывного спектра. Коллапси-
рующее тело дает постоянный поток излучения на У+, поэтому
полное число частиц за все время бесконечно велико. Больший

Квантовые черные дыры 271
интерес представляет число частиц, испускаемых в единицу вре-
времени. Эту величину можно найти, рассматривая систему, поме-
помещенную в ящик с периодическими граничными условиями, что
делает моды дискретными [375]. *
В этом случае из условия постоянства вронскиана C.39) на-
находим
?2-IPa*,'l2)=l- (8.33)
Вычисление интегралов в (8.32) показывает, что (см. D.60))
|о«/|2 = евя*|*1Р<ш'|2 (8.34)
(соображения об аналитичности, приводящие к множителю е8яМш,
аналогичны рассмотренным на с. 124).
Чтобы подсчитать поток частиц, попадающих на &+ в позд-
поздние моменты времени, заметим, что число состояний внутри сфе-
сферы радиуса R с центром, совпадающим с центром коллапсирую-
щего шара, равно Rd<o/2n (для фиксированных I, пг). Как сле-
следует из (8.33) и (8.34), число частиц в каждой моде равно
= X I Рс**' I2 = 1/(е*"М* - 1), (8.35)
поэтому число частиц, испускаемых в единицу времени в ин-
интервале частот от сэ до сэ + dm, которые проходят через поверх-
поверхность сферы, равно
(йсо/2я) (е8"Мй> — I)-1, (8.36)
где мы воспользовались тем, что время, за которое частица до-
достигает поверхности сферы, равно R. Это планковский спектр
излучения черного тела с температурой (8.27), совпадающей с
температурой в двумерном случае. Альтернативный способ вы-
вывода этой формулы основан на рассмотрении волновых пакетов
в качестве базисных состояний вместо (8.29) — (8.31) [278].
На этом этапе следует учесть обратное рассеяние, которым
мы до сих пор пренебрегали. Равенство (8.33) можно интерпре-
интерпретировать как условие сохранения вероятности. Влияние обрат-
обратного рассеяния сводится к появлению множителя 1 — Гш в выра-
выражении для потока уходящих частиц, описывающего отражение
частиц назад в черную дыру. Поэтому правая часть (8.33) должна
быть заменена на Га, в результате чего множитель Гщ появится
,в выражении (8.36). Поскольку эта величина зависит от ©, спектр
излучения не будет чисто планковским. Но его тем не менее
можно считать «тепловым» в следующем смысле. Если поме-
поместить черную дыру в термостат, заполненный излучением при
температуре (8.27), то обратное рассеяние от черной дыры ис-
испытает та же доля 1— Тщ падающего излучения, что и для

272 Глава 8
выходящего потока. Поэтому лишь доля Га падающего излуче-
излучения моды со будет поглощаться черной дырой. Следовательно,
соотношение между излучением и поглощением в каждой моде
не зависит от Га и совпадает с тем, которое получилось бы при
замене черной дыры на черное тело. Таким образом, черная дыра
остается в термодинамическом равновесии с термостатом, не-
несмотря на искажение ее спектра.
Полная светимость черной дыры определяется интегралом
от величины (8.36) по всем модам
^ (8.37)
/=о о
j-де мы ввели множитель Г, а также учли зависимость от /.
В случае фермионов благодаря антикоммутативности в ус-
условии нормировки (8.33) перед |РШ@, |2 будет стоять знак плюс
(см., например, [156, 382]). Поэтому в выражении для спектра
появится множитель еЪяМа-\-1, чего и следовало ожидать для
случая статистики Ферми.
Вычисление L для реалистической модели черной дыры тре-
требует рассмотрения реальны* квантованных полей. Хотя до сих
пор мы ограничивались рассмотрением безмассового скалярного
поля, общие соображения остаются справедливыми для любых
полей. В частности, кванты электромагнитного и нейтринного из-
излучений и линеаризованные гравитоны будут иметь тепловое
распределение с температурой (8.27). Основное различие заклю-
заключается в величине множителей Г, которая существенно зависит
от спина. Детальные вычисления требуют исследования ради-
радиального уравнения типа (8.2) и проведения численных расче-
расчетов.
Пэйдж [375] (см. также [376, 377]) получил оценку
L = C,4- 1046)(М/1гГ2 эрг (8.38)
для шварцшильдовой черной дыры массы много больше 1017г,
причем излучение содержит 81% нейтрино (четырех типов), 17%
фотонов и 2% гравитонов. (Подавление высших спинов свя-
связано с увеличением барьера, обусловленного угловым моментом.)
Выражение (8.27) для температуры можно записать в виде
Г = A,2-1026К)Aг/М), (8.39)
что для объекта солнечной массы дает 6 • Ю-8 К. Для такого
объекта возможно испускание лишь безмассовых частиц. Но
для Л1.<С1017 г температура Г^,109К и становится возмож-
возможным тепловое рождение электрон-позитронных пар. При еще
меньших массах могут испускаться и другие типы элементарных

Квантовые черные дыры 273
частиц. Детали этого высокотемпературного режима зависят от
взаимодействия между частицами. Заметим, что черная дыра
массы 1015 г имеет радиус около одного ферми, т. е. близкий к
радиусу сильного взаимодействия. Но хотя из-за усложнений,
связанных с учетом взаимодействия, точно вычислить скбрость
потери энергии не удается, все же можно говорить о термоди-
термодинамической природе квантового рождения частиц.
До сих пор мы ограничивались сферически-симметричным
случаем. Если допускается вращение, то черная дыра будет опи-
описываться аксиально-симметричным семейством решений Керра,
для которого метрика характеризуется еще одним параметром
Q, имеющим смысл угловой скорости вращения горизонта со-
событий.
Решение волнового уравнения в метрике Керра сложнее,
нежели в шварцшильдовом случае (подробности см., например,
в работе [156]). Сферические гармоники Ytm в (8.1) заменяются
на аксиально-симметричные сфероидальные гармоники, а потен-
потенциал в радиальном уравнении становится более сложным. Но
при больших г переход к метрике Керра сводится к замене со
на со — mQ, где m— азимутальное квантовое число для сферо-
сфероидальных гармоник (играющее роль m для Yim). Таким обра-
образом, для расчета излучения на &+ достаточно заменить со на
со — mQ в выражении для планковского множителя в (8.36) или
(8.37):
1/{ехр[2ях-' (со — mQ)] ± 1}. (8.40)
Следовательно, вращение влияет на тепловой спектр так же,
как химический потенциал. Расчеты светимости черной дыры,
проведенные Пэйджем [376], показали, что вращение приводит
к существенному увеличению вероятности испускания частиц
высших спинов.
Поскольку вероятность испускания зависит от азимутального
квантового числа т, процесс не является аксиально-симметрич-
аксиально-симметричным. Множитель (8.40) больше для положительных т, чем для
отрицательных, в силу чего более вероятно испускание квантов
с угловым моментом, параллельным моменту вращения дыры,
чем с противоположно направленным угловым моментом. Это
означает, что испускание частиц приводит к систематической по-
потере углового момента вращающейся черной дырой, т. е. замед-
замедлению ее вращения.
, В случае бозонов (знак минус в (8.40)) при w<mQ выра-
выражение (8.40) становится отрицательным. Более того, даже в
пределе М->-оо (Г->0), когда хокинговское тепловое излучение
коллапсирующего тела исчезает, величина (8. 40) остается ко-
конечной и равна —1 для со < mQ (она стремится к нулю для
со >_mQ и, следовательно, для всех со в шварцшильдовом случае,

274 Глава 8
когда Q = 0). Отрицательный поток излучения имеет следую-
следующий смысл: если низкочастотная классическая волна (с по-
положительным т) падает на вращающуюся черную дыру, вра-
вращение приводит к усилению волны, вследствие чего волна от-
отражается с большей энергией — явление, получившее название
«сверхизлучения» [362, 400, 499, 500] '>. На квантовом языке
это соответствует процессу индуцированного излучения. Поэ-
Поэтому вероятность поглощения этих мод черной дырой становится
отрицательной. Сверхизлучение не связано с механизмом Хо-
кинга (обусловленным распространением волн через коллапси-
рующее тело); оно имеет место и для обычных вращающихся
звезд [9]. Квантовый расчет сверхизлучения был выполнен до
открытия эффекта Хокинга Старобинским [439] и Унру [467]
(см. также [201]).
Представляет интерес также рассмотреть влияние электри-
электрического заряда на тепловое излучение черной дыры. Сначала
рассмотрим случай электрически нейтрального поля в метрике
Рейсснера — Нордстрема, описывающей (невращающуюся) чер-
черную дыру с зарядом е. Элемент длины
ds2 = [1 - BМ/г) + (е2/'2)] dt2 - [1 - BМ/г) + (^/г2)] dr2 —
- г2 (dB2+sin2 В dj>2) (8.41)
соответствует горизонту событий при
r = r+ = M + (M2-e2)v'. (8.42)
Воспользовавшись значением (8.42) для Rh в (8.23), найдем по-
поверхностную гравитацию и для метрики (8.41). Тогда равен-
равенство (8.27) приводит к следующему выражению для темпера-
температуры заряженной черной дыры:
Т = (l/8nkBM) A - 16я2е4/^2), (8.43)
где s4> = 4лг2+ — площадь поверхности горизонта событий.
Из формулы (8.43) следует, что наличие заряда уменьшает
температуру черной дыры. В экстремальном случае е2 = М2
(максимально заряженная дыра) Т = 0. Из выражений (8.41)
и (8.42) следует, что при е2 > М2 горизонта событий не суще-
существует: в точке г = 0 находится голая сингулярность. Таким об-
образом, гипотеза «космической цензуры» [369], согласно кото-
которой при гравитационном коллапсе не могут образовываться го-
голые сингулярности, приобретает термодинамический смысл тре-
требования Т >• 0, которое можно интерпретировать как третий
закон термодинамики применительно к черным дырам [101].
Однако более тщательное рассмотрение [133, 191] показывает,
') Для массивных полей имеются также «сверхизлучательные» квази-
СЕязанные состояния [601*, 605*, §06*, 614*—616*]. — Прим. перед.

Квантовые Черные дыры 275
что вопрос о возможности в принципе достижения температуры
Т = О остается открытым.
Если черная дыра достаточно мала, она оказывается настоль-
настолько горячей, что рождаются электрон-позитронные пары. Рожде-
Рождение заряженных частиц черной дырой Рейсснера — Нордстрема
усложняется наличием электрического поля дыры. Детальное
обсуждение этого вопроса дано Гиббонсом [230]. -
Хорошо известно, что в фоновом электрическом поле могут
рождаться пары заряженных частиц даже в отсутствие грави-
гравитационного поля. Это следует уже из полуклассической дира-
ковской модели рождения пар. Состояния с положительной и
отрицательной энергией свободного дираковского поля разде-
разделены промежутком 2т. Для частиц с зарядом q во внешнем
электрическом поле Е градиент потенциальной энергии равен
qE. Если появляется виртуальная электрон-позитронная пара,
то электрическое поле ускоряет частицы пары в противополож-
противоположных направлениях. Если расстояние между частицами Ajc доста-
достаточно велико к моменту их предполагаемой аннигиляции, то
энергия, приобретаемая частицами за счет электрического поля,
становится достаточной, чтобы сделать эти частицы реальными.
Это происходит, если qEAx « 1т. Данный эффект можно также
понимать как прохождение (туннелирование) частицы через по-
полосу запрещенных энергий 2т, в результате чего возникает пара
частица — античастица. Это явление получило название пара-
парадокса Клейна [331]; оно приводит к противоречию с предполо-
предположением об устойчивости вакуума.
Если учесть также гравитационное поле черной дыры, то
ситуация несколько усложняется, в особенности когда дыра
вращается [126, 146, 230]). Возникает тенденция к быстрому
электрическому разряду черной дыры вследствие преимущест-
преимущественного испускания заряженных частиц того же знака заряда,
что и заряд черной дыры, по сравнению с античастицами проти-
противоположного знака. Возникает явление «сверхизлучения заряда»
для частиц с энергией со < тп + ^Ф, где Ф —электростати-
—электростатический потенциал горизонта событий [278]. Таким образом,
электрический зар.яд также дает вклад в «химический потен-
потенциал» черной дыры.
Из-за наличия электрического поля, стимулирующего рож-
рождение пар частиц, испускание электронов и позитронов может
иметь место и для очень массивных черных дыр, имеющих весь-
весьма низкую температуру. В таком режиме преобладает рождение
пар электрическим полем (парадокс Клейна). Рождение заря-
заряженных частиц подавлено лишь при М » 105Мо. В противопо-
противоположном предельном случае при М .<: 1015 г гравитационное (хо-
кинговское) рождение доминирует над рождением частиц элек-
электрическим полем.

276 Глава 8
8.2. Физические аспекты испускания
частиц черными дырами
На первый взгляд излучение черной дыры кажется парадок-
парадоксальным, поскольку ничто, очевидно, не может выходить из об-
области внутри горизонта событий. Но из выражения (8.36) сле-
следует, что средняя длина волны испускаемых квантов порядка М,
т. е. сравнима с размерами черной дыры. Поскольку локализо-
локализовать квант в области порядка длины волны невозможно, бес-
бессмысленно говорить о том, что частицы возникают в какой-либо
выделенной области вблизи горизонта. Представление о ча-
частицах, имеющее глобальный характер, оказывается полезным
лишь в области вблизи 3f+. В окрестности черной дыры кри-
кривизна пространства-времени сравнима с длиной волны излуче-
излучения в интересующем нас диапазоне энергий, и представление о
локализованных частицах теряет смысл.
Эвристически можно представить себе, что возникающие
кванты «туннелируют» из-под горизонта событий [282]. Для
объяснения излучения Хокинга можно также использовать пред-
представление о непрерывном возникновении виртуальных пар ча-
частиц и античастиц в окрестности черной дыры. Частицы вир-
виртуальной пары образуются с длиной волны X на расстоянии по-
порядка X. При Я порядка размера черной дыры (Я « М) дей-
действуют большие приливные силы, препятствующие аннигиляции
частиц. Одна из частиц уходит на бесконечность с положитель-
положительной энергией, что и создает хокинговский поток, а соответству-
соответствующая античастица попадает в черную дыру на времениподобную
траекторию в глубокой потенциальной яме, соответствующую
отрицательной энергии по отношению к бесконечности (см., на-
например, [234]). Таким образом, черная дыра излучает кванты
с длиной волны порядка М.
Несмотря на неопределенность представления о частицах
вблизи горизонта, ясно, что тепловое излучение будет уносить
энергию на Sf+, и возникает вопрос об источнике этой энергии.
Она может отбираться только у гравитационного поля, которое
вследствие этого должно терять массу. Чтобы выявить это ста-
стационарное убывание массы-энергии, необходимо рассмотреть
среднее значение тензора энергии-импульса <Уцу(*)> в окрест-
окрестности черной дыры. В противоположность частицам, тензор
энергии-импульса является локальным объектом, и его можно
использовать для выяснения физической стороны процесса и в
непосредственной близости к черной дыре и даже внутри ее.
В двумерной модели <ГЦУ> можно рассчитать явно для кон-
конформно-инвариантного поля (разд. 6.3). Рассмотрим статиче-
статический шар, описываемый статической метрикой общего вида (8.8).
Волновое уравнение имеет решения -'ши и e~iw(rjxe и и v за-

Квантовые черные дыры 277
даны формулами (8.9)), которые являются положительно-ча-
положительно-частотными по отношению к глобальному времениподобному век-
вектору Киллинга dt. Вакуумное состояние, построенное по от-
отношению к этим модам, является устойчивым: частицы не рож-
рождаются, и система симметрична относительно обращения вре-
времени.
Но вследствие поляризации вакуума, вызываемой кривизной
пространства-времени, среднее значение тензора энергии-им-
энергии-импульса отлично от нуля; оно получается при подстановке С (г)
в F.136):
-C'2], (8.44)
<01 Гяо 10> = A/96я) СС, (8.45)
где функционал F определен выражением
РАу) = 1Ууу^(У-Ч (8.46)
а штрих обозначает дифференцирование по г.
В качестве примера рассмотрим двумерный аналог прост-
пространства-времени Рейсснера — Нордстрема (8.41), для которо-
которого С(г) = A — 2Мг~1 -\- е2г~2). С помощью формул (8.44) нахо-
находим
(8.47)
что соответствует статическому облаку энергии, имеющему осо-
особенность при г = О и отрицательному вне горизонта событий
г = г+.
Предположим теперь, что «звезда» претерпевает гравита-
гравитационный коллапс при начальном радиусе Ro, как описано на
с. 265. Хотя метрика (8.8) правильно описывает геометрию во
внешней области, координаты г* и t (или и и v) уже нельзя
использовать для записи простого экспоненциального решения
волнового уравнения, так как «уходящие» моды е~Ши превра-
превращаются в сложные функции (8.28) на &~. Вместо этого мы
выберем такие координаты, в которых «входящие» моды и,
следовательно, вакуумное состояние (обозначаемое через |0>)
имеют стандартную форму Минковского на ЗГ- (т. е. является
обычным вакуумным in-состоянием). Как объяснено в преды-
предыдущем разделе, это означает использование вместо и и v ко-
координат
й = Р [а (и) - 2Я0], i> = и, (8.48), (8.49)

278 Глава 8
где аир заданы соотношениями (8.13) и (8.14). В этих коор-
координатах метрика (8,8) принимает вид
6)dud6, (8.50)
С(й, б) = С(г)|^. (8.51)
Вычисляя du/du с помощью (8.17) и (8.18) и dv/dd с по-
помощью (8.49) и подставляя в F.136), найдем [129] (см. также
[138, 289—292]
(О I Тии I б> = (8.44) + Ю2 Fu (Р') + Fu (a'), (8.52)
где а = а(ы), p = P(L/—2R0), а штрих обозначает дифференци-
дифференцирование функций по их аргументам. Выражения для <0|Гоо|б>
и <б|Гщ,|6> совпадают с (8.44) и (8.45) соответственно.
Выражение (8.52) описывает область вне коллапсирующего
тела. Во внутренней области, где метрика имеет форму (8.11),
имеем
6 (P')-fl/(^), (8.53)
(t')-Fv(A), (8.54)
где р = $(U—2Ro) и р == р(К) соответственно.
Общая формула F.136) применительно к координатам й, v
(8.48) и (8.49) дает <6| 7>|б>. При получении (8.52) —(8.54)
мы переходили к координатам v, и или U, V с помощью обыч-
обычных правил преобразования компонент тензоров. Эти результаты
показывают, что вследствие коллапса к статической энергии
вакуума (8.44) добавляется выходящий (запаздывающий) поток
излучения, постоянный на запаздывающих изотропных лучах
и или U (в рассматриваемом случае обратного рассеяния нет).
Во внутренней области имеются как падающий, так и уходя-
уходящий потоки излучения, зависящие сложным образом от внут-
внутренней метрики А и траектории коллапса R(i). Они описывают
частицы, рождающиеся внутри вещества коллапсирующей «звез-
«звезды» и на ее поверхности. Например, F»(P') в (8.54) соответ-
соответствует излучению, возникающему на поверхности и распростра-
распространяющемуся в направлении к г = 0, в то время как /чу(Р') в
(8.53) описывает то же излучение, возвращающееся назад после
прохождения через центр тела. Тот же поток, выходящий (без
изменения) во внешнюю область, описывается членом, пропор-
пропорциональным (а'J в (8.52). В дополнение к этому выходящему
потоку, возникающему после «отскока», имеется вклад, описы-
описываемый последним членом в (8.52), который также можно про-
продолжить назад до поверхности коллапсирующего тела, но кото-
который является с самого начала выходящим.

Квантовые черные дыры 279
Если функцию а'(и) выразить через т как функцию v(T)>
то с помощью (8.17) можно показать, что при приближении
поверхности тела к горизонту событий (R-^-Rh, С-*-0, и-*<х>)
справедливы следующие предельные соотношения:
\->0 как е~*а, у-> — A — R)x, уу-*О
(здесь точка обозначает дх), из которых следует, что средний
член в правой части (8.52), измеренный удаленным наблюда-
наблюдателем в координатах и, v, экспоненциально быстро исчезает.
Таким образом, этот член представляет собой короткий импульс
излучения, который экспоненциально затухает по тому же за-
закону, что и излучение с поверхности коллалсирующего тела.
Последний член в (8.52) можно записать в виде
(8.55)
24я1_A — RJ A —ЛK A — ЯJ J 48я
что в точности соответствует потоку (в двух измерениях) от
теплового излучателя с температурой T = %/2nkB (см. D.27)
для случая L—>-oo), совпадающей с хокинговской температурой
(8.27). Следовательно, этот член описывает излучение Хокинга.
Заметим, что он не зависит от деталей коллапса и полностью
определяется единственным параметром х — поверхностной гра-
гравитацией возникающей черной дыры. Излучение, зависящее от
деталей коллапса, целиком описывается экспоненциально зату-
затухающим средним членом в (8.52).
Для поздних моментов времени в асимптотической области
г->оо вклад поляризации вакуума (8.47) исчезает, и тензор
энергии-импульса сводится к
<0|Гии|0> = х2/48я, <0|Гоо|0) = (б|Гио|0) = 0. (8.56)
Явная асимметрия этого выражения относительно обращения
времени (имеется лишь запаздывающее излучение) отражает
необратимую природу коллапса за горизонт событий.
Хотя различные члены в (8.52) — (8.54) имеют легко вы-
выясняемое происхождение, каждому из них в отдельности не
следует придавать слишком большое физическое значение. На-
Например, было бы неверным заключение, что поток Хокинга ис-
исходит с поверхности коллапсирующего тела. Нужно помнить,
что экспериментатор не сможет различить отдельные вклады;
цогут быть измерены лишь компоненты полного тензора энер-
энергии-импульса. Разбиение, проведенное здесь, соответствует вы-
выбору специальной координатной системы и, v (или U, V), но эта
система сингулярна на горизонте событий.
Чтобы определить, что будет измерять наблюдатель в дей-
действительности, нужно задать мировую линию измерительного

280 Глава 8
прибора. Если вектор мгновенной скорости наблюдателя есть и^,
то его измерительный прибор будет регистрировать в качестве
энергии величину <Гцу>"и "v. а в качестве потока энергии
<ГцУ>"и«у, где ы^Лц = 0. Например, наблюдатель, находящийся
в точке с фиксированным г, имеет 2-скорость С~'/а A, 0) (в коор-
координатах t, r*) и будет измерять плотность энергии C-^lTttfty,
где Ttt определяется с помощью D.17). Эта величина обраща-
обращается в бесконечность на горизонте, где С = 0, что отражает
тот факт, что мировая линия наблюдателя, находящегося при
фиксированном г, по мере приближения к горизонту событий все
больше отклоняется от мировой линии свободно падающего
наблюдателя.
Более реалистическим является рассмотрение свободно па-
падающего наблюдателя. В случае метрики Шварцшильда наибо-
наиболее подходящими будут координаты Крускала (которые не-
несингулярны на горизонте — см. разд. 3.1), Используя преобра-
преобразования C.19) и конформный множитель С = 2Mr-ie~rl2M из
C.20), найдем, что наблюдатель, движущийся вдоль мировой
линии постоянного г с 2-скоростью С~'/2A, 0) (в координатах
J, r); i = 7г (у + и), г — 7г (v — и)) измеряет плотность энергии
С (б | Ttt 10) = @ | Tue + Гбй + 27У 10), .(8.57)
где
бф BЫГ1Же~ГЩ ( ^ ^) (8.58)
±-%.), (8.59)
(8.60)
Ясно, что выражение (8.57) конечно (при п-»-оо), поскольку v
остается конечным на горизонте будущего. Таким образом, мы
приходим к заключению, что наблюдатель, пересекающий го-
горизонт событий вдоль мировой линии с постоянным значением
крускаловской пространственной координаты, измеряет конеч-
конечную плотность энергии.
Этот анализ позволяет разрешить кажущийся парадокс, ка-
касающийся эффекта Хокинга. Собственное время, требуемое сво-
свободно падающему наблюдателю для достижения горизонта со-
событий из точки, находящейся на конечном расстоянии от дыры,
конечно, но время этого свободного падения, измеренное по ча-
часам бесконечно удаленного наблюдателя (в координатах и, v),
бесконечно. Если пренебречь реакцией излучения, черная дыра
успевает излучить бесконечную энергию за то время, пока сво-
свободно падающий, наблюдатель С точки зрения, системы обсчета.

КвантоМе чернЫё дыры 281
на бесконечности достигнет горизонта событий. Поэтому может
показаться, что в падающей системе отсчета наблюдатель за
конечное время встретит бесконечный полный поток излучения,
который должен привести к его гибели. С другой стороны, го-
горизонт событий представляет собой глобальную конструкцию,
не имеющую локального смысла [276]; поэтому абсурдно ду-
думать, что он может действовать как физический барьер для сво-
свободно падающего наблюдателя.
Парадокс разрешается, если тщательно учитывать различие
между числом частиц и плотностью энергии. Когда наблюдатель
приближается к горизонту, представление об определенном
числе частиц теряет смысл для интересующих нас длин волн
хокинговского излучения (см. с. 276); наблюдатель оказывается
«внутри» частиц. Следовательно, мы не должны беспокоиться о
том, что наблюдатель столкнется с бесконечным числом частиц.
С другой стороны, энергия имеет локальный смысл. В этом слу-
случае, хотя поток Хокинга и расходится при приближении к го-
горизонту, но то же самое происходит с вкладом статической по-
поляризации вакуума, причем последняя отрицательна. Падающий
наблюдатель не сможет отличить поток энергии, связанный с
уходящим излучением Хокинга, от потока энергии, обусловлен-
обусловленного тем, что он пересекает «облако» поляризованного ваку-
вакуума. Результирующий эффект состоит в сокращении бесконеч-
бесконечных членов на горизонте событий и появлении конечных вели-
величин, таких, как (8.57) — (8.60). (Точные значения зависят от
траектории падения.)
Проведенный анализ позволяет разрешить также загадку о
том, как черная дыра может терять массу, хотя вещество не
пересекает горизонта событий из внутренней области наружу.
Можно показать, что на горизонте событий <б|Гоо|б> оказыва-
оказывается равным величине
- A/192») (дС/дгJ \r=Rk = - х2/48я,
которая всегда отрицательна и равна потоку Хокинга на бес-
бесконечности со знаком минус. Это с необходимостью должно
быть так, поскольку при построении величины <ГЦУ> было зало-
заложено условие ковариантного сохранения. Поскольку (Tvvy пред-
представляет собой изотропный поток, пересекающий горизонт со-
событий, легко видеть, что постоянная потеря энергии-массы за
счет потока Хокинга уравновешивается таким же потоком отри-
отрицательной энергии, падающим на черную дыру снаружи. Таким
образом, черная дыра теряет массу не путем испускания кван-
квантов, а вследствие поглощения отрицательной энергии. Идея
потока отрицательной энергии уже встречалась нам в связи с
задачей о движущихся зеркалах в разд. 7.1.

282
Глава 8
В приведенных рассуждениях предполага-
предполагалось, что квантовое состояние представляет
собой обычный вакуум в in-области. Можно
задать вопрос: в какой степени изменит эф-
эффект Хокинга присутствие квантов в началь-
начальном состоянии [481]? Из формулы B.44) (ко-
(которая справедлива и в искривленном прост-
пространстве-времени) можно найти вклад в <7UV>
в out-области, обусловленный наличием л
квантов моды а в начальном состоянии. В слу-
случае бозонов вследствие индуцированного из-
излучения в out-области появится дополнитель-
дополнительный поток энергии [30]. Форма уходящих мод
в out-области дается вторым членом в (8.26),
откуда легко видеть, что последний член в
B.44) экспоненциально затухает по и со вре-
временем убывания в е раз Bх)-', т. е. характер-
характерным временем коллапса. Таким образом, влия-
влияние первоначально присутствующих квантов
экспоненциально затухает за то же время, что
и поверхностная светимость, и черная дыра
быстро приходит в состояние теплового равно-
равновесия, «забывая» детали начального состоя-
состояния. Поэтому мы приходим к заключению, что
эффект Хокинга является чрезвычайно общим
и не зависит от выбора физически разумного
начального квантового состояния.
Эти общие черты, характеризующие излу-
излучение черной дыры, сохраняются и в полной
четырехмерной трактовке.
Потеря массы черной дырой порождает
проблему обратной реакции излучения на
структуру самой черной дыры. Предполагая,
что фоновую метрику по-прежнему можно рас-
рассматривать как классическую, приходим к за-
заключению, что поток отрицательной энергии
будет вызывать уменьшение площади поверх-
поверхности горизонта событий. Это показано схема-
схематически на рис. 26 для шварцшильдовой дыры.
По мере уменьшения поверхности горизонта
и массы черной дыры ее температура (8.39)
и светимость (8.38) возрастают. Следова-
Следовательно, шварцшильдовы черные дыры имеют отрицательную
теплоемкость: они излучают и при этом нагреваются — пове-
поведение, типичное для самогравитирующих систем [348].
Имея выражение для <7 Цу> на горизонте событий, можно по-
Рис. 26. Испаре-
Испарение черной дыры.
Нижняя часть
рисунка соответ-
соответствует рис. 24.
Поток отрица-
отрицательной энергии
через горизонт
событий в чер-
иую дыру (пря-
(прямые стрелки) по-
постепенно приво-
приводит к сокраще-
сокращению площади по-
поверхности гори-
горизонта. Скорость
этого процесса
нарастает до тех
пор, пока не про-
происходит быстрое
сжатие горизон-
горизонта до сингуляр-
сингулярности, сопрово-
сопровождаемое взрыв-
взрывным испусканием
квантов.

Квантовые черные дыры 283
пытаться исследовать обратную реакцию более детально путем
интегрирования уравнений Эйнштейна. Таким путем можно опи-
описать эволюцию горизонта событий. В частности, в адиабатиче-
адиабатическом приближении, когда схлопывание черной дыры не учиты-
учитывается при расчете {Т^У, можно ожидать, что горизонт будет
сокращаться в соответствии с потерей массы черной дырой.
К сожалению, уравнение эволюции горизонта нелинейно, и оно
не было решено. Но если пренебречь некоторыми членами выс-
высшего порядка, то скорость схлопывания действительно соответ-
соответствует тому, чего можно ожидать, исходя из примитивных пред-
представлений [88]. Тем не менее пока неясно, является ли влияние
членов высшего порядка пренебрежимо малым и действительно
ли форма схлопывающегося горизонта на рис. 26 правильна
[266,459] ').
По мере того как дыра становится горячее, она начинает
испускать элементарные частицы большей массы. При темпе-
температуре выше 1010 К испускаются электроны и позитроны, и лю-
любой остаточный заряд черной дыры быстро исчезнет. Более
того, эффекты сверхизлучения приводят к потере черной дырой
углового момента, и она медленно приближается к шварцшиль-
довой.
Продолжение процесса Хокинга приводит к тому, что дыра
испаряется все быстрее. Ее конечная судьба не может быть
предсказана в рамках существующей теории: когда
Ж^~^~М-', (8.61)
дыра схлопывается со скоростью, сравнимой с частотой излуче-
излучения. В этой ситуации уже нельзя говорить о термодинамическом
равновесии, нельзя считать хорошим приближением представ-
представление о фиксированном фоновом пространстве-времени. Условие
(8.61) достигается, когда
или
т. е. когда М ~ 1 (масса Планка ~ Ю-5 г), где мы использо-
использовали закон излучения Стефана и выражение для площади по-
поверхности si- шварцшильдовой черной дыры 16яМ2. На этой
стадии черная дыра имеет планковские размеры A0~33 см), и
квантово-гравитационные эффекты высшего порядка, несомнен-
несомненно, становятся существенными.
, Были высказаны предположения, что конечной стадией ис-
испарения черной дыры является ее взрывное исчезновение [281],
образование голой сингулярности [156, 397] или, возможно,
') В работе [459] допущена ошибка, исправленная в [597*]. — Прим,
перев.

284
Глава 8
Видимый ВзрыЬ
черной дыры
Рис. 27. Диаграмма Пенроуза испаряющей-
испаряющейся черной дыры. Нижняя часть диаграммы
соответствует рис. 25. Однако при учете
Черная $^У"$* / обратной реакции черная дыра испаряется
дыра л/л$ / и ГОРИЗОИТ пересекает Sf+ в конечный мо-
Ч/ > • мент времени после прохождения через го-
голую сингулярность (отмеченную вопроси-
вопросительным знаком), Область, лежащая выше,
предположительно является пространством
Минковского.
объекта планковской массы. На рис. 27 показана возможная
диаграмма Пенроуза для этих ситуаций, где точка представляет
одну из упомянутых выше трех возможностей. Следует заме-
заметить, однако, что, согласно Герлаху [229], горизонт вообще не
будет образовываться. Каков бы ни был конечный исход, де-
детальное поведение дыры на конечных стадиях испарения зави-
зависит от природы элементарных частиц при высоких энергиях.
Например, если число истинно элементарных частиц невелико,
скорость излучения не будет возрастать столь быстро, как в
случае, когда число сортов частиц быстро растет при больших
массах, как предполагает Хагедорн [263]. Это может привести
и к наблюдаемым следствиям [50, 403]. Таким образом, ис-
исследование испарения черных дыр дает уникальную возмож-
возможность проникновения в физику частиц сверхвысоких энергий.
В течение последней десятой доли секунды своего существо-
существования черная дыра высвобождает энергию 1030 эрг, что эквива-
эквивалентно взрыву 106 мегатонных термоядерных бомб, причем зна-
значительная доля ее испускается в виде у-квантов. С помощью
существующих у-телескопов такие вспышки не были зарегист-
зарегистрированы, хотя величина потока, необходимого для их обнару-
обнаружения с помощью существующего оборудования, намного пре-
превышает величину, которой можно ожидать, исходя из других
соображений [51]. Более обещающим является поиск радио-
радиовспышек, вызываемых взрывным впрыскиванием плазмы из чер-
черной дыры в межзвездное магнитное поле [403]. Тот факт, что
такие вспышки не были обнаружены с помощью существующих
установок, дает верхнюю оценку числа взрывов черных дыр гго-
рядка Ю-5 пс-3 в год [357].
Предполагая, что гравитационные поправки высших поряд-
порядков несущественны, время жизни испаряющейся черной дыры
можно вычислить исходя из ее светимости (8.38). В результате
получим оценку 10-26(ЛГ/1 гK с; следовательно, для черной дыры

Квантовые черные дыры 285
размера порядка 1 ферми A0~13 см) с массой около 1015 г вре-
время жизни сравнимо с возрастом вселенной. Маловероятно, что-
чтобы такие черные минидыры могли образовываться когда-либо,
кроме начальной стадии существования вселенной; это означа-
означает, что к настоящему времени черные дыры с массой меньше
1015 г должны уже исчезнуть в результате испарения.
Несмотря на то что квантовые черные дыры рождают
элементарные частицы и античастицы парами, некоторые из за-
законов сохранения оказываются нарушенными. Например, чер-
черная дыра, возникающая в результате коллапса звезды, погло-
поглощает в основном барионы, а испускает преимущественно нейт-
нейтрино и фотоны, поскольку в течение большей части времени ее
существования температура слишком мала для испускания
массивных частиц. Таким образом, теряет обычный смысл закон
сохранения барионного числа. (Следует напомнить, что, несмот-
несмотря на испарение черной дыры, остается еще сингулярность, че-
через которую барионы могут покидать наше пространство-
время.)
Тот факт, что существование квантовых черных дыр приво-
приводит к прекращению действия некоторых законов физики эле-
элементарных частиц, означает возможность осуществления в ее
присутствии процессов, которые иначе были бы запрещены. Мо-
Можно даже предположить, что некоторые реакции могут идти че-
через образование виртуальных черных дыр в качестве промежу-
промежуточных состояний. Например, Хокинг [286] обсуждал процесс
ц*—>¦ черная дыра—>е± + \
(реакция ц-+е-\-у запрещена законом сохранения лептонноге
квантового числа мюона).
Несомненно, наиболее убедительным аргументом, говорящим
о том, что к хокинговскому излучению следует относиться серь-
серьезно, является глубокая связь, которую устанавливает этот эф-
эффект между физикой черных дыр и термодинамикой. Еще до
появления работы Хокинга было замечено, что в теории черных
дыр имеются четыре закона, аналогичные четырем началам
термодинамики [22]. Существование параметра поверхностной
гравитации к, постоянного на горизонте событий, напоминает
«нулевой закон» термодинамики, требующий постоянства тем-
температуры для системы, находящейся в тепловом равновесии.
Сохранение энергии при столкновениях черных дыр и в процес-
процессах типа процесса Пенроуза (с. 274) и сверхизлучения, в кото-
рнх происходит извлечение энергии из черной дыры, либо пере-
передача энергии дыре, эквивалентно первому началу термодина-
термодинамики. Более того, уже упоминалось (с. 274), что существует
аналог и третьего закона, запрещающий приближение к случаю
экстремальной черной дыры Керра — Ньюмена,

286 Глава 8
Второе начало термодинамики, требующее необратимого
увеличения энтропии, находит естественную аналогию в теореме
Хокинга [275], согласно которой поверхность горизонта собы-
событий s4- не может убывать
uW>0 . (8.62)
во всех процессах с черными дырами при выполнении слабого
энергетического условия Хокинга — Пенроуза [288]. Это силь-
сильный аргумент в пользу отождествления s4- с энтропией 91.
Существование энтропии черной дыры следует также из
известного соотношения между энтропией и информацией [433]
(см. также обзор [489]). Если звезда сжимается и образует
черную дыру, вся информация о микроскопических состояниях
звезды оказывается скрытой за горизонтом событий. Считая для
грубой оценки, что на одну элементарную частицу приходится
один бит информации, получаем полную потерю информации
в черной дыре порядка М/т, где М — масса дыры, т — м.асса
характерной элементарной частицы, из которых было построено
коллапсирующее тело. Соответствующая энтропия 91 ~ Mke/m.
Может показаться, что в принципе не существует нижнего
предела для т, поэтому величина & должна быть неограничен-
неограниченной. (Это согласуется с тем фактом, что классическая черная
дыра, будучи абсолютно черной, имеет нулевую температуру.)
Однако, как было впервые отмечено Бекенштейном [27, 28],
существует нижняя граница для т, обусловленная тем, что
комптоновская длина волны составляющих частиц не должна
превышать радиуса черной дыры, т. е. быть ,<jW, чтобы такая
частица могла «уместиться» в дыре. Следовательно, макси-
максимальная потеря информации ~M2/ti, так что 9? ~ M2kB/ti =
= M2ke ~ kBk- в используемой системе единиц. Очевидно, 9?
становится бесконечной в классическом пределе (Й-»-0).
Работа Хокинга поставила догадку Бекенштейна на прочный
теоретический фундамент, причем точное соотношение имеет
вид (см., например, [156])
\ (8.63)
Таким образом, закон возрастания поверхности горизонта собы-
событий (8.62) оказывается лишь частным случаем второго начала
термодинамики й9* ^ 0.
При испарении черной дыры, когда поверхность горизонта
событий сокращается, условие (8.62) нарушается. Это стано-
становится возможным вследствие нарушения лежащего в основании
теоремы слабого энергетического условия из-за отрицательной
энергии вакуума. Однако при этом не происходит нарушения
второго начала термодинамики, поскольку энтропия окружаю-
окружающей среды возрастает вследствие испускания теплового излу-.

Квантовые черные дыры 287
чения. Полная энтропия по-прежнему возрастает. Оказывается
невозможным и искусственное нарушение второго начала путем
впрыскивания в черную дыру отрицательной энергии (например,
от движущихся зеркал, см. разд. 7.1) [203].
Можно развить полную термодинамическую теорию черных
дыр [132, 133, 279, 307], включая фазовые переходы, циклы
Карно, анализ устойчивости и даже обобщения на случай не-
неравновесных ситуаций [96, 429] (см. также [505]). Но некото-
некоторые проблемы остаются нерешенными, например каково соот-
соотношение между потерей информации при коллапсе звезды и
внутренними микросостояниями вечной черной дыры, такой, как
черная дыра, описываемая решением Крускала (см. следующий
раздел), которое является всюду вакуумным решением урав-
уравнений Эйнштейна [29]. Можно ли распространить понятие
энтропии черной дыры на произвольные гравитационные поля
[127, 134, 378]? Будет ли хокинговское излучение всегда точно
тепловым даже при наличии взаимодействий (разд. 9.3) и при
учете реакции самой дыры [378] ? Означает ли процесс Хркин-
га нарушение симметрии относительно обращения времени в
квантовой гравитации [487] ? Многие из этих вопросов еще на-
находятся в стадии исследования (см. также [617* — 625*]).
8.3. Вечные черные дыры
В предыдущих разделах рассматривалось поведение кван-
квантованного поля в фоновом пространстве-времени коллапсирую-
щего тела. Но, как оказалось, основные закономерности эффек-
эффекта Хокинга не.зависят от деталей коллапса, что наводит на
мысль, что этот эффект в большей степени связан с причинной
и топологической структурой пространства-времени, чем с его
конкретной геометрией. Оказывается, что это действительно так.
Поэтому можно попытаться полностью забыть о коллапсирую-
щем теле и построить квантовую теорию поля в максимально
расширенном многообразии, которое всюду является решением
вакуумных уравнений Эйнштейна (разд .3.1).
Начнем с обсуждения двумерной модели шварцшильдовой
черной дыры, полагая С=A—2 Мг~[) в (8.8). Результаты
легко обобщить на случай черной дыры Рейсснера — Нордстре-
ма [133]. Диаграмма Пенроуза для этого многообразия пока-
показана на рис. 6. В координатах Крускала й, v, введенных в
C.19), элемент длины имеет вид
dsi = 2Mr-le-r'!lM dudv; (8.64)
он регулярен всюду, кроме точки г = 0, где имеется физическая
особенность. Отметим, что хотя метрика пространства-времени
симметрична относительно обращения времени, выбираемо?

288 Глада 8
квантовое состояние не обязательно должно обладать этим
свойством.
Существуют два естественных набора мод для безмассового
скалярного поля, которые пропорциональны либо е~Ши, е~ш
в изотропных шварцшильдовых координатах и и .у, либо
e-'*>", е~ш5в изотропных координатах Крускала C.19). Первый
набор имеет бесконечно быстрые осцилляции на горизонте со-
событий, второй набор является регулярным во всем многообра-
многообразии. Этим наборам соответствуют вакуумные состояния, кото-
которые мы будем обозначать |0s> и |0к> соответственно. Скаляр-
Скалярные функции Грина в каждом случае определяются в терминах
функций Грина пространства Минковского D.23) при ?->-оо
с помощью соотношения вида C.154) при п = 2. Опуская, как
обычно, бесконечную постоянную (инфракрасная расходимость),
получаем
?<'>(", лО = —A/2яIпДиДо, (8.65)
?", х') = -A/2яIпД(Ш. (8.66)
Преобразовав D'k к шварцшильдовым координатам, будем
иметь
D») (#', хг) = - A/2я) In [ch x (f - t') - ch x (r*" - r*')] +
+ функция от (г", /), (8.67)
что явно инвариантно относительно преобразования t"-*-t"-\-.
-\-2лт/к (п — целое число), где и = DМ)~1 — поверхностная
гравитация. Это означает, что 0$ периодична по мнимому
шварцшильдову времени с периодом 2я/х. Как объяснено в
разд. 2.7 (см. B.104)), эта особенность характерна для тепло-
тепловых функций Грина. В данном случае температура равна
х/2я&в, что совпадает с температурой Хокинга (8.27). Анало-
Аналогичное условие периодичности имеет место и в четырехмерном
случае, даже если дыра вращается [270]. Например, для мод
с азимутальным квантовым числом т
о) (t" _ f _|_ 2nin/x; г", /-')=* e2nmQ/*D?>(*"-^; Л г'), (8.68)
что подтверждает аналогию между /nQ и химическим потенци-
потенциалом (см. замечание после формулы B.104)). Эти представле-
представления также обобщаются на случай электрически заряженных
черных дыр и испускаемых частиц [239, 240].
Вдали от дыры функция Грина (8.65) сводится к обычной
функции D<"> для плоского пространства-времени; в этой обла-
области |0s> — обычное вакуумное состояние. Очевидно, наблюда-
наблюдатель, находящийся в этой области, будет рассматривать |0к>:
как термодинамическое состояние с температурой и/2я&в, а-

Квантовые черные дыры 289
D{k — как тепловую функцию Грина для черной дыры, по-
погруженной в термостат с тепловым излучением при хокингов-
ской температуре. Действительно, как показывает подробный
анализ [41], вдали от дыры D^ можно записать в виде бес-
бесконечной суммы B.111) функций Грина D{s, что потверждает
тепловой характер этой функции. Выражение (8.67), очевидно,
инвариантно относительно обращения времени, поэтому помимо
хокинговского потока излучения, уходящего на 5Г+, имеется та-
такой же по величине поток, падающий на дыру из Sf~. Этот вы-
вывод подтверждается вычислением <Оаг| 7Vv|0/c> стандартным спо-
способом с использованием D^', в результате которого плотность
энергии на 2f_- оказывается равной х2/24я. Таким образом,
вакуум |0/с> описывает состояние установившегося термодина-
термодинамического равновесия между черной дырой и окружающей сре-
средой, такое, которое получалось бы, если бы черная дыра была
погружена в полость*с идеально отражающими стенками. (Если
полость слишком велика, равновесие будет неустойчивым; см.,
например, [133].) Состояние |0к> известно как вакуум Харт-
ля — Хокинга [270] или вакуум Израэля [316].
Сравнение C.19) с D.69) и D.70) при а = х=DМ)~1 по-
показывает, что состояние |0s> аналогично состоянию |0«>, свя-
связанному с ускоренно движущейся системой отсчета в области
риндлеровского клина в пространстве Минковского. Подобным
же образом \0к) соответствует ]0м>- Это неудивительно, посколь-
поскольку структуры горизонтов риндлеровского клина и шварцшильдо-
вой черной дыры совпадают. Сравнение рис. 6 и 14 показывает,
что область R пространства Минковского находится в том же
причинном отношении к области L, что и область I (представ-
(представляющая вселенную, внешнюю по отношению к черной дыре)
к области II («зеркальной» вселенной). Точно так же, как в
разд. 4.5, моды, заданные на расширенном многообразии, мож-
можно связать с модами, определенными лишь в областях I и II 'по
отдельности [468]. Поскольку математическая связь между
координатами и, v и п, v в обоих примерах одинакова, нет не-
необходимости повторять здесь выкладки, и можно сразу выпи-
выписать боголюбовские преобразования, связывающие оба набора
мод. Формально они совпадают с D.95) и D.96), где теперь
bki2) — оператор уничтожения для мод в шварцшильдовой об-
области I (уничтожение частиц в «нашей» вселенной вне черной
дыры), а ^О — оператор' уничтожения в области II. Операторы
d'k аналогично связаны с крускаловскими модами.
Как было показано в разд. .4.5, преобразование Боголюбова
приводит к тепловому спектру D.97) с температурой a/2nke =
= х/2я?в, чего и следовало ожидать. Но это преобразование на
самом деле содержит больше информации. Полагая фа> = е-яа/а,
1/.)П Зак 67*

290 Глава 8
из D.95) и D.96) получаем
«A) I] <A) — I] /о сп\
о\==е dye , (.о.оу/
где со = | k |,
/___ X ч "JL /t(l) TtB) Т 1»(^) f.(*)\ /О Т/\Ч
== ^, t^ffl \O-k Ok — D-kOk ) (O./U)
и использованы коммутационные соотношения.
Из определений вакуумных состояний
0, (8.71).
4I0к) = 42>Юк) = 0 (8.72) ¦
и равенства е""'7^! 0$) =dit)e~'/| 05>, следующего из (8.69),
имеем
(8.73)!
После разложения экспоненты и перегруппировки слагаемых:
находим • ¦ ¦
(8.74);
в терминах состояний, содержащих п^ квантов области I и njj):
квайтов в области II [316, 468]. ¦
Если наблюдатель ограничен областью I (вне черной дыры)
и не имеет доступа в область II, он не сможет измерить \п(^у
Если такой наблюдатель измеряет некоторую величину А, опи-;
сываемую оператором А в квантовом состоянии 10Ку, то часть
(8.74), связанная с |п^, выделяется в виде отдельного множи-
множителя:
@к|А\ ОК) = ? П<«РIА !п?)ехр(- 2nkn<*/x)X
nk k
X [1 - ехр (- 2дао/и)] = tr (Ар); (8.75),
здесь р можно записать в виде
<8'7в>;
Z
m-o

Квантовые черные дыры 291
где En = «со, р = 2я/х, и рассматривать как матрицу плотности,
соответствующую термодинамическому усреднению (разд. 2.7)
при температуре и/2я&в. В частности, если А — оператор числа
квантов моды а, то получим
00 / ОО
/л иг in \ V -РЕ* / V — В?~ 1 К Вю i\ (Я T7\
n-0 / m=0
т. е. планковский спектр.
Тот факт, что чистое состояние |ОК>, заданное на полном
многообразии, представляется наблюдателю, ограниченному об-
областью I, как смешанное состояние с матрицей плотности (8.76),
не вызывает удивления. Наличие горизонта событий приводит
к тому, что информация о модах в области II теряется, и эта
потеря информации естественно сопровождается появлением не-
ненулевой энтропии в области I (энтропия чистого состояния рав-
равна нулю). В самом деле, соотношение (8.76) не только приводит
к тепловому спектру, но и определяет полностью тепловое из-
излучение, т. е. полное отсутствие корреляции между испущенны-
испущенными квантами [280, 385, 480]. Например, вероятность того, что
|0к> содержит ltik, квантов моды k\, гпы квантов моды k2 и
т. д. в области I, равна
(8-78)
где Р ('tik,) — вероятность того, что мода k\ содержит ;дй
частиц. Тот факт, что все P({nk.) входят в это выражение в
виде произведения, показывает полную статистическую неза-
независимость этих вероятностей.
Соображения, касающиеся матрицы плотности и тепловых
состояний, непосредственно обобщаются на случай четырех из-
измерений и применимы также к однородно ускоренным системам
отсчета. Делались также попытки [143, 144, 236, 337, 342, 343]
распространить их на случай горизонтов, не связанных с чер-
черными дырами, таких, как в пространстве де Ситтера, хотя в
этом случае физический смысл тепловой структуры менее ясен.
При получении этих результатов обратной реакцией рожде-
рождения частиц на фоновое пространство-время пренебрегалось. От-
Отдача при испускании черной дырой квантов с необходимостью
должна приводить к корреляциям между испущенными кван-
квантами, если излучается лишь небольшая часть полной энергии
VilQ*

292 Глава 8
[378]. Это, конечно, относится к любому нагретому телу и яв-
является следствием того, что дыра не находится в термодинами-
термодинамическом равновесии с окружающей средой.
Хотя приведенные рассуждения основаны на использовании
максимально расширенного многообразия Крускала, тепловая
природа излучения и отсутствие корреляций имеют место и в
более реалистической модели коллапса. В случае безмассового
поля 2f- является поверхностью Коши для пространства-време-
пространства-времени коллапсирующего тела, но ?7+ не является поверхностью Ко-
Коши; необходимо также учесть распространение поля за горизонт
событий будущего Н+. Объединение 3+ и Н+ является поверх-
поверхностью Коши (рис. 25). Следовательно, для получения полного
набора мод в out-области необходимо к стандартным экспо-
экспоненциальным модам на &+ добавить моды, связанные с Н+.
Явное построение такого полного набора было выполнено Уол-
дом [480]. Но результаты измерений, выполняемых на &+, не
зависят от деталей, связанных с модами на горизонте. Если ог-
ограничиться измерениями на ?У+и отказаться от информации о
модах на горизонте, то мы снова получим матрицу платности
вида (8.76). Моды на горизонте можно представлять себе как
описывающие кванты, падающие в черную дыру. Таким обра-
образом, мы приходим к модели процесса Хокинга, упомянутой на
с. 276: пары частиц рождаются вблизи горизонта, одна из ча-
частиц движется к &+ (в пренебрежении обратным рассеянием),
а вторая попадает в черную дыру. Отказываясь от информации
о частицах, падающих в черную дыру, приходим к необходимо-
необходимости описывать частицы на бесконечности с помощью смешанно-
смешанного состояния (т. е. использовать матрицу плотности). Таким
образом, независимо от того, исследуется ли эффект Хокинга
в полном многообразии Крускала или в поле коллапсирующе-
коллапсирующего тела, результаты измерений на 3+ будут иметь тепловой ха-
характер.
До сих пор мы обсуждали свойства двух «вакуумных» со-
состояний |0к> и |0s>, первое из которых соответствует термоста-
термостату с тепловым излучением, а второе сводится к обычному ваку-
вакуумному состоянию Минковского на больших расстояниях от
дыры. Как всегда в квантовой теории, необходимо привлечь
дополнительные физические соображения, чтобы установить,
какое квантовое состояние соответствует интересующей нас си-
ситуации. Когда во вселенной имеется вечная черная дыра, только
наблюдения могут выявить, какое квантовое состояние дейст-
действительно реализуется. Но состояние |0к> явно воспроизводит
физическую картину, которая возникает, если черную дыру, об-
образовавшуюся в результате коллапса, поместить в ящик с от-
отражающими стенками и дождаться установления теплового
равновесия.

Квантовые черные дыры 293
На максимально расширенном многообразии можно постро-
построить еще одно «вакуумное» состояние, которое будет воспроизво-
воспроизводить излучение коллапсирующего тела, т. е. несимметричный во
времени тепловой поток от дыры, а не излучение в термостате.
Это состояние было открыто Унру [468].
Заметим, что состояние |0s> связано с модами, которые яв-
являются положительно-частотными по отношению к вектору Кил-
линга dt (см. D.77)), в то время как состояние | 0#> определено
для положительно-частотных мод относительно вектора <?(-, где
i — время Крускала (? = l/2(u-\-v)) (см. D.82)). Как видно из
рис. 6, изотропные линии и = const, соответствующие поверхно-
поверхностям постоянной фазы стандартных экспоненциальных мод
(е~Ши) пространства Минковского на &+, будучи продолжен-
продолженными назад во времени, в отутствие коллапсирующего тела пе-
пересекают горизонт прошлого Н~ расширенного многообразия
Крускала. В картине коллапса (рис. 25) изотропный луч у (по-
(последний луч, проходящий через коллапсирующее тело, который
при выходе из него остается лежащим на горизонте будущего
Н+) выполняет роль, аналогичную Н- на рис. 6. Лучи, входящие
немного раньше у, отражаются от начала координат и пересе-
пересекают у на пути к &+ вблизи Н+. Эти лучи соответствуют вол-
волнам, которые являются положительно-частотными по отноше-
отношению к аффинному параметру вдоль у [278] (см. также [235,
387]). Для лучей, очень близких к #+, этот аффинный параметр
с хорошей точностью совпадает с аффинным параметром п на
горизонте прошлого расширенного многообразия (рис. 6). Сле-
Следовательно, геометрические эффекты при коллапсе, можно ими-
имитировать, выбирая in-моды, имеющие формуе~1<вй на Н~ и е-'1
па 3~. Моды е~Шй являются положительно-частотными по от-
отношению к вектору ди, который является вектором Киллинга
па Н~ [468]. Далее можно забыть о коллапсирующем теле и
работать только с расширенным многообразием Крускала. Ва-
Вакуумное состояние, ассоциируемое с таким выбором мод в прош-
прошлом, получило название вакуума Унру; мы будем обозначать
его |0у>. Оно соответствует тепловому потоку частиц, выходя-
выходящих из области, где находится черная дыра. Обращенное во
времени состояние, соответствующее модам е~ш на Н+ и е~ш
па &+, описывает стационарный поток теплового излучения, па-
падающего в черную дыру.
Дальнейшие сведения о свойствах вакуумных состояний
[ ] |
0s>
(иногда называемого вакуумом Булвара [59, 60]), |0#> и
можно получить, анализируя показания детектора частиц в точ-
точке с фиксированной щварцшильдовой радиальной координатой
г = R. Для безмассового поля в двумерном случае можно найти
функцию отклика детектора C.55) в явном виде, воспользовав-

294 Глава 8
шись вайтмановскими функциями
D$ (х, х') = - -?- In [(Ди - it) (Аи - &)], (8.79)
Dt (x, x')^-~- In [(Дм - й) (A3 - /е)], (8.80)
/#(*, х') = --^г М(Дм — fe)(Ao —ie)].: (8.81)
Собственное время детектора, находящегося в точке г = R, опре-
определяется соотношением
dx = (l-2M/R)'hdt, (8.82)
причем Дм = Ду = Д< и, как следует из C.19),
Дй = — 4Ме«*'ш (е-''4М — е-«'/«*), (8.83ч
4)
(8.84)
Подстановка выражения (8.79) для вакуума Булвара в фор-
формулу для функции отклика детектора C.55) приводит к выра-
выражению, в точности совпадающему с соответствующей величиной
для детектора, покоящегося в двумерном пространстве Минков-
ского в случае обычного вакуумного состояния поля. Так же
как и в этом случае, находим, что @~ (Е) =0 при Е > 0, т. е.
детектор не обнаруживает частиц в состоянии |0s>.
В случае вакуума Унру подстановка (8.81) в C.55) с учетом
соотношений (8.82) и (8.84) приводит к функции отклика в еди-
единицу собственного времени, совпадающей с D.54) при w = О
и х= [16AI2(l — 2Af//?)]-'/' .Таким образом,
&~и (?)/ед. собств. времени = 1/? (еЕ/квТ — l), (8.85)
где /гвГ= [64л2М2A —2M/R)]~'!'. Так же как и в случае уско-
ускоренно движущегося зеркала, для которого было получено выра-
выражение D.54), детектор регистрирует поток частиц с видимой тем-
температурой Т при T0=l/8nkBM, определяемой соотношением Тол-
мена D.98). Этот вывод согласуется с (8.27), если учесть, что
x = DiW)-1 для шварцшильдовой черной дыры. По мере при-
приближения детектора к горизонту (R-+-2M) температура воспри-
воспринимаемого им потока бесконечно растет. Это связано с тем, что
детектор, находящийся на фиксированном расстоянии от черной
дыры, является неинерциальным. Величина ускорения по, от-
отношению к локальной свободной падающей системе отсчета
равна iW/f^2(l—2M/RY1']. Это ускорение приводит к тому, что
детектор дополнительно регистрирует частицы, как в случае
пространства Минковского (разд. 3.3). По мере приближения
к горизонту ускорение стремится к бесконечности; то же проис^
ходит с температурой (ср. C.68)). ;

Квантовые черные дыры 295
Для случая вакуума |ОК> расчет аналогичен; он приводит к
результату, отличающемуся от (8.85) коэффициентом 2, что со-
соответствует термостату с излучением при видимой темпера-
температуре Т.
Отклик детектора частиц в четырехмерном случае исследо-
исследовался приближенно Унру [468] и Кднделасом [88]. В частно-
частности, Канделас вычислил функцию отклика при R-*-2M и R-*-oo
для каждого из трех вакуумных состояний, рассмотренных вы-
выше, и получил результаты, согласующиеся с результатами рас-
расчетов для двумерной модели.
Подробный анализ свойств вакуумных состояний |0s>, |0/(> и
|0f/> дан в работе Фуллинга [222].
8.4. Исследование тензора энергии-импульса
Вычисление <7'piv> в построенном выше «вакуумном» состо-
состоянии с помощью теории, развитой в гл. 6, не вызывает принци-
принципиальных затруднений. В двумерном случае результаты удает-
удается получить в замкнутой форме. Но сначала полезно провести
общее исследование (Т^у в духе аксиом Уолда (разд. 6.6). Это
было сделано Кристенсеном и Фуллингом [119].
Начнем с двумерного «шварцшильдова» случая. Подставив
С=A—2М/г) в (8.8), ковариантное условие сохранения
F.142) приведем к виду
(Trt) = const, (8.86)
где &~ — след <ГA^>, и предполагается, что все компоненты
<7'м.у> не зависят от времени. Интегрируя (8.87) с учетом
<7У> = ^~ — <7У>, находим
M = (f\") + (fV) + (fV), (8.88)
где в координатах (t, r*)
(8.92)
10*

296 Глава 8
причем постоянные К и Q определяются выбором квантового
состояния.
Рассмотрим сначала состояние |0s>. Этот случай был под-
подробно исследован Блюмом [54] и Булваром [59, 61). На Sf±
это состояние совпадает с обычным вакуумом в пространстве
Минковского |0м>, поэтому излучение на бесконечности отсут-
отсутствует. Следовательно, можно положить К. = 0 и Q = M2H(oo),
так что (8.88) обращается в нуль при больших г. Воспользо-
Воспользовавшись формулами F.121) и G.2), получим
Т (г) = - М/блг3 (8.93)
и, подставляя это выражение в (8.92), найдем
Н(г) = ~ A/384лМ2) + (М2/24лг4). (8.94)
Таким образом, для состояния |0s> Q = 1/384л и <7'M.V> сво-
сводится к выражению (8.47) (с е = 0). Следовательно, |0s> —
Состояние вакуума около статической звезды.
Но оно не может соответствовать случаю черной дыры, на
что указывают следующие соображения. Заметим, (ср. D.17) —
D.19)). что
Тип = \ (Ttt + Tr<r* - 27V), (8.95)
и из (8.88) —(8.91) находим
(Тиа) = -±(Н + Q/M2) +1 A - 2М/г)Г->- Q/2M2 (8.96)
при г-*-2М. Но координаты Шварцшильда сингулярны на го-
горизонте. Для исследования поведения тензора энергии-импуль-
энергии-импульса вблизи горизонта перейдем к координатам Крускала C.19),
регулярным в этой области. В координатах Крускала будем
иметь
(Тпп) = - (Q/32M4) e"r/V A - Г/2МУ2. (8.97)
Это выражение расходится при r-v2M, за исключением случая
Q = 0. Величина <Гйй> описывает физическую ситуацию на го-
горизонте событий, т. е. то, что измеряет свободно падающий
наблюдатель [222]. Следовательно, состояние |0s> является
нефизическим, если метрика имеет шварцшильдову форму
в окрестности точки г =¦ 2М. Иначе говоря, если попытаться
создать такое квантовое состояние в присутствии черной дыры,
то обратная реакция приведет к существенному изменению гра-
гравитационного поля в окрестности г = 2М.
Обращаясь к другому выбору постоянных, рассмотрим слу-
случай симметрии во времени, когда требуется, чтобы <7VV> было
регулярным как на горизонте прошлого, так и на горизонте

Квантовые черные дыры 297
будущего. Анализ выражения <Гаа> при г-*2М показывает,
что в этом случае необходимо положить К = Q = 0. Тогда
<7VV> = <7"V>> и ПРИ г-+ОО эта величина сводится к
(8.98)
где 7= l/8kBM = x/2nkB. Это выражение представляет собой
тензор энергии-мпульса равновесного теплового излучения при
температуре Г; следовательно, выбранное квантовое состоя-
состояние соответствует вакууму Израэля — Хартля — Хокинга |0&>.
Наконец, чтобы описать процесс испарения Хокинга, необ-
необходимо, чтобы присутствовал лишь уходящий поток теплового
излучения, для которого тензор энергии-импульса при боль-
больших г имеет вид
/Л 14
(8.99)
где Т = \/%nkeM. Таким образом, требуется, чтобы плотность
и поток энергии совпадали, для чего необходимо (при Q = 0)
выполнение соотношения
оо
К = у М2 [Я (оо) - Г (оо)] = 1 М3 J Г (р) р dp, (8.100)
2М
если заметить, что ?Г(оо)=0. Это замечательное соотношение
дает поток Хокинга при г = оо (т. е. величину К/М2) в виде
интеграла от следа тензорл энергии-импульса. Поскольку мы
знаем, что в силу тепловой природы боголюбовского преобра-
преобразования К Ф 0 (должен быть поток энергии, если спектр тепло-
тепловой), это доказывает существование аномального следа W.
В гл. 6 существование аномального следа было установлено
из более тонких соображений, связанных с перенормировкой
(Т^у. Теперь, следуя работе Кристенсена и Фуллинга [119],
мы установили его необходимость совершенно иначе, не прибе-
прибегая к соображениям о перенормировке.
Конечно, получить величину ZT из соотношения (8.100) не-
невозможно, хотя, если предположить, что она должна иметь
чисто геометрический вид, можно заключить, что ?7" ~ /?, по-
поскольку R является единственным геометрическим скаляром
размерности (длина) в двумерном случае. Поэтому, зная К,
можно найти аномальный коэффициент и наоборот. Из соотно-
соотношения (8.99) или (8.93) имеем К==—G68л), следовательно,
0" = —R/24n. Мы потребовали, чтобы Q = 0, поэтому тензор
энергии-импульса будет регулярным на горизонте будущего #+,
что соответствует вакууму Унру |0у>. Но тензор энергии-им-
энергии-импульса не регулярен на Н-.

298
Глава 8
Рис. 28. Диаграмма Пен-
роуза сферической звез-
звезды, коллапсирующей с
образованием заряжен-
заряженной черной дыры Рейсс-
нера — Нордстрема. (Ср.
с рнс. 25. Изображенное
многообразие ие полно и
может быть продолжено
в вертикальном направ-
направлении. Но такое продол-
продолжение несущественно для
данного рассмотрения.)
Сингулярность имеет вре-
мениподобиый характер.
Изотропные лучи, падаю-
падающие из Э~ в поздние мо-
моменты времени, сгущают-
сгущаются, испытывая голубое
смещение, около г_.
Для которой С == A
имеет два горизонта:
один горизонт в точке
Заметим, что в случае безмассового
фермионного поля изменение планков-
ского множителя на (еа1квТ + l) приво-
приводит к появлению коэффициента 'Д в
(8.98) и (8.99). Если же учесть, что в
этом случае имеются два состояния с
различной спиральностью, то результи-
результирующие выражения окажутся совпадаю-
совпадающими с соответствующими величинами
для скалярного случая. Таким образом,
мы заключаем, что в двумерном случае
конформные аномалии и хокинговский
поток одинаковы для спинов 0 и '/2. что
согласуется с результатами, полученны-
полученными в гл. 6.
В четырехмерном случае требований
сферической симметрии независимо от
времени и ковариантного сохранения ока-
оказывается недостаточно для того, чтобы
однозначно связать след с потоком Хо-
кинга; дополнительный произвол возни-
возникает для угловых компонент <Гее> =
=<ГфЧ)>. Этот случай подробно рассмот-
рассмотрен Кристенсеном и Фуллингом [119],
которые привели аргументы, указываю-
указывающие на качественные ограничения на
<Гее>. Сделанные в этой работе предпо-
предположения об асимптотической форме тен-
тензора энергии-импульса при г-*-оо или
2УИ для каждого из трех «вакуумных»
состояний были подтверждены явными
вычислениями Канделаса [88].
В заключение этого раздела- рассмот-
рассмотрим снова кратко двумерную модель
черной дыры Рейсснера — Нордстрема,
- 2Mr~i -\- е2г~2). Это пространство-время
г+, задаваемый формулой (8.42), и еще
r_=M-(M2~e2)'h,
(8.101)
в которой функция С также обращается в нуль. Этот внутрен-
внутренний горизонт является горизонтом Коши, но он не является
горизонтом событий для рассматриваемого пространства-време-
пространства-времени (см., например, [287], гл. 5). Соответствующая конформная
диаграмма показана на рис. 28, где видно с учетом конформ»
рого сжатия 9', что г_ представляет собой поверхность беско,»

Квантовые черные дыры 299
нечного голубого смещения, так как изотропные лучи из 3~
сгущаются около г_ внутри черной дыры.
Расчет <r,j.v> во внутренней области дыры для состояний
|0{/> и |0к> не представляет затруднений [133]. Оказывается
[289—291], что <Гц7> расходится на г_ даже в системе коорди-
координат, которая регулярна в этой области. Общие соображения
показывают, что этот результат остается верным и в четырех-
четырехмерном случае [42, 291]. Можно сделать вывод, что обратное
воздействие поляризации вакуума приводит к разрушению
внутренней геометрии черной дыры и, вероятно, на горизонте
Коши возникает сингулярность, препятствующая возможности
аналитического продолжения многообразия в другие асимпто-
асимптотические плоские области пространства-времени [356, 436].
Наконец, в работе [125] показано, что в случае вращаю-
вращающейся черной дыры внутренний горизонт можно интерпретиро-
интерпретировать как поверхность отрицательной температуры (в смысле
Хокинга), удовлетворяющую некоторому аналогу теоремы
о поверхности горизонта (8.62) и связанную с понятием спино-
спиновой температуры (см. также [87]).
8.5. Дальнейшее развитие теории
Выполненные детальные исследования квантовых аспектов
физики черных дыр и замечательное согласие результатов са-
самых различных теоретических подходов воодушевило многих
авторов использовать черные дыры в качестве отправной точки
более широкого поиска в квантовой теории поля в искривлен-
искривленном пространстве и даже в квантовой гравитации. В частности,
Хокинг с сотрудниками составили обширную программу иссле-
исследований, в которой центральную роль играют тепловые аспекты
физики черных дыр (см. обзор [285]).
Значительная часть последующих работ была связана со
свойством периодичности функции Грина в вакуумном состоя-
состоянии Израэля — Хартля — Хокинга |0к> (или его обобщении для
других пространств) по мнимому шварцшильдову времени (см.
с. 288). Учитывая это свойство, предлагается ввести новую коор-
координату х = it и вместо пространства-времени Шварцшильда
рассматривать связанное с ним риманово пространство (с отри-
отрицательно определенной метрикой в противоположность псевдо-
риманову пространству с метрикой неопределенного знака),
имеющее элемент длины вида Крускала
где
X = AM [r/2M - 1 ]Vt ег'ш cos m,
Y = 4M [r/2M - 1 ]v' erm sin xt.

300 Глава 8
Это пространство имеет нулевой тензор Риччи и топологию
R2 X S2. Вектор Киллинга ах порождает вращения вокруг
точки Х=У —0. Эта вращательная симметрия придает пере-
переменной т характер угловой координаты, что влечет за собой
требование периодичности: точки, для которых х отличается
на 2я/х, отождествляются. Начдло координат X = Y = 0 соот-
соответствует г = 2М, т. е. горизонту событий. Область, отвечаю-
отвечающая внутренней части черной дыры, в частности сингулярность
г = 0, в этом римановом пространстве отсутствует. Хартль и
Хокинг [270] использовали это обстоятельство для введения
естественной функции Грина, которая при аналитическом про-
продолжении назад в псевдориманово пространство Шварцшильда
совпадает с функцией Грина, ассоциируемой с вакуумом |0к>.
Тем самым устанавливается красивое соотношение между гео-
геометрической симметрией риманова многообразия относительно
вращений в плоскости X—У и тепловым характером излучения
Хокинга. Эти выводы непосредственно обобщаются на случай
черных дыр КеРРа — Ньюмена [239, 240].
Замена / на ix напоминает способ построения фейнманов-
ского пропагатора в обычной квантовой теории поля в про-
пространстве Минковского (см. с. 31). В разд. 2.8 объяснено, как
можно облегчить решение проблемы сходимости в функциональ-
функциональном подходе к квантованию с помощью формальной замены t
на ix в функциональном интеграле B.115). При этом экспо-
экспонента приобретает показатель —3 вместо iS, где 5—действие
в евклидовом пространстве. Эти соображения можно обобщить
на случай риманова пространства.
Если для построения производящего функционала Z[J]
в виде функционального интеграла по полям, обладающего
свойством периодичности по переменной т с периодом р, ис-
использовать действие S в римановом многообразии, то функции
Грина, получаемые с помощью B.117), будут не обычными
вакуумными функциями Грина, а тепловыми функциями с тем-
температурой Т=\/кв$.
Связь между функциональным подходом и термодинамикой
становится еще более ясной, если заметить, что амплитуда пе-
перехода между состояниями поля ф\ в момент t\ и ф2 в момент t2
определяется выражением
\>[ф]е*М, (8.103)
где интеграл берется по всем значениям поля, заданного в на-
начальный и конечный моменты времени. В картине Шредингера
эту амплитуду можно представить в виде <^>2|ехр[—iH(t2 —
]|^ где Н — гамильтониан. Полагая t2 — ^i ==—ф и

Квантовые черные дыры 301
фъ = ф\ и суммируя по полному набору полевых конфигураций,
находим Z = 5]е~ря", где Еп — энергия, соответствующая кон-
конфигурации поля ф„. Сравнивая с B.95), нетрудно видеть, что
Z можно отождествить с термодинамической статистической
суммой при температуре 7" = 1/&в|3 и нулевом значении хими-
химического потенциала. С другой стороны, из формулы (8.103)
имеем
9[</>]e-sM, (8.104)
где интеграл берется по всем полям, удовлетворяющим усло-
условию периодичности по т с периодом р. Таким образом, с по-
помощью этого функционального интеграла в римановом много-
многообразии можно вычислить статистическую сумму и рассмотреть
термодинамические свойства системы. (Строгую трактовку со-
соотношения между термодинамикой и функциональным интег-
интегралом в пространстве Минковского можно найти, например,
в работе [243].)
Этот результат был применен Гиббонсом и Хокингом [236]
к самому гравитационному полю (см. также [284]). Если для
квантования гравитации применить метод фонового поля
(см. гл. 1), то метрику следует представить В виде guv = gcnv +
+ guv, где gCiiv — решение классических уравнений Эйнштейна,
a fuv описывает квантовые флуктуации относительно фона.
Разлагая действие в функциональный ряд Тейлора относитель-
относительно классического фонового поля в виде S[g] = В [gc] + S2[g]
+ члены высших порядков, где 52 квадратично по g, для ста-
статистической суммы получаем выражение
In Z = - S[gc] + In \ 0[g]exp(- S2[g]) +
+ члены высших порядков. (8.105)
Первое слагаемое в правой части представляет собой вклад
классического гравитационного поля, второе слагаемое дает
однопетлевые поправки, возникающие за счет гравитонов; его
можно трактовать аналогично случаю материальных полей,
рассмотренному в гл. 6. Члены высших порядков дают вклад
многопетлевых гравитонных фейнмановских диаграмм; их по-
последовательный расчет затруднителен ввиду неперенормируе-
мости квантовой гравитации.
Пренебрегая далее всеми слагаемыми, кроме первого (клас-
(классического) в правой части (8.105), запишем действие в виде
(см. разд. 6.6, где нужно положить G=l в используемых
в этой главе единицах)
^4]^^^^' (8Л06>

302 Глава 8
где g — определитель римановой метрики, h — определитель
метрики, индуцируемой на границе многообразия, а х и х° опре-
определены на с. 234. Выбирая в качестве фонового пространство-
время Шварцшильда с римановой метрикой (8.102), будем
иметь R=A — 0, и S[gc] сводится к 4яМ2 [237] (см. также
[232]). Таким образом, классический вклад в статистическую
сумму определяется выражением
(8.107)
откуда можно получить .температуру Г— \/kB$ = 1/8лквМ,
среднюю энергию <?>р, энтропию У с помощью обычных тер-
термодинамических соотношений (см., например, [315], § 3.2):
9> = kBf> <Е>„ + kB In Z = 4nkBM2 = j kBs4-,
что совпадает с (8.63).
Этот результат представляется особенно замечательным по-
потому, что он получен из действия для самого классического
гравитационного поля, а не путем рассмотрения квантованных
материальных полей, как делалось выше. В самом деле, тот
факт, что 91 оказывается чисто геометрической величиной (пло-
(площадь поверхности горизонта), не зависящей от типов мате-
материальных полей, что обычно имеет место для энтропии, указы-
указывает на более фундаментальный характер понятия энтропии
черной дыры, чем самой квантовой теории поля в искривлен-
искривленном пространстве-времени, и как подтверждает приведенный
расчет, энтропия в действительности является внутренним, свой-
свойством черной дыры. Впервые в физике появилось понятие
энтропии, как объективного внутреннего свойства. В тради-
традиционном подходе понятие энтропии содержит в себе элемент
субъективности, связанный с «крупнозернистостью» описания
или нашим неумением различать отдельные микроскопические
состояния.
Развитие метода «риманизированного» квантования грави-
гравитационного поля привело к установлению связи между чер-
черными дырами и инстантонами [107, 238, 283] (см. также [241]
относительно обобщения этой идеи на другие пространства) и
более глубокому пониманию связи между топологией простран-
пространства-времени и квантовой теорией поля [285]. Методы, анало-
аналогичные обсуждавшимся выше, были применены к пространст-
пространствам де Ситтера [237] и Бертотти — Робинсона [336], в которых
также возникают тепловые эффекты. Дальнейшее обсуждение
этих вопросов выходит за рамки настоящей книги, и мы отсы-
отсылаем читателя к цитированной литературе.

Квантовые черные дыры 303
Вопрос о рождении частиц вблизи пространственно-времен-
пространственно-временных сингулярностей также привлек к себе внимание. Сильные
квантовые эффекты, сопровождающие возрастание кривизны
пространства-времени, по-видимому, могут приводить к боль-
большой обратной реакции, что существенно при обсуждении во-
вопроса о «космической цензуре». Форд и Паркер [208] исследо-
исследовали вопрос о возможности предотвращения образования
идеализированной голой сингулярности при сжатии сильно заря-
заряженного (е2 > М2) тела вследствие квантовой обратной реак-
реакции. Квантование полей вблизи «белых дыр» обсуждали Зель-
Зельдович, Новиков и Старобинский [501] и Уолд и Рамасвами
[488].
Если допустить, что может образовываться сингулярность,
вопрос о рождении частиц в ее окрестности усложняется нару-
нарушением предцказуемости [287]. В частности, неизвестно, какие
граничные условия следует накладывать на квантованные поля
в сингулярных точках. Эта проблема также возникает в космо-
космологическом случае, как отмечалось в разд. 7.4.
Хокинг [280] пытался связать случайный характер теплово-
теплового испускания черной дыры с граничными условиями на сингу-
сингулярности, исходя из того, что рождение пары частиц вблизи
горизонта снаружи от черной дыры с последующим удалением
частицы на бесконечность и «туннелированием» античастицы
в дыру, где она затем попадает в сингулярность, можно рас-
рассматривать в духе фейнмановского представления об антича-
античастицах как частицах, движущихся «назад во времени». Можно
представить себе, что испускаемая частица образуется в сингу-
сингулярности, движется назад во времени до горизонта, рассеи-
рассеиваясь затем на гравитационном поле в направлении вперед во
времени, и становится частицей в хокинговском потоке. Таким
способом Хокинг приписывает тепловой характер излучения
самой сингулярности. Обобщение этой идеи на произвольные
сингулярности привело к формулировке «принципа стохастич-
ности», согласно которому граничные условия в сингулярности
должны соответствовать полностью случайному влиянию сингу-
сингулярности на все, происходящее вне ее. Эта идея, возможно, бу-
будет иметь приложения к космологии и белым дырам.

Глава 9
ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
После того как была построена теория свободных кванто-
квантованных полей в искривленном пространстве-времени, ее наибо-
наиболее естественным развитием явилось включение в рассмотрение
эффектов, обусловленных самодействием и взаимодействием
полей негравитационной природы. Хотя это направление только
начинает развиваться, основные рамки теории установлены до-
достаточно четко, и в этой заключительной главе описаны фор-
формальные приемы расчета процессов рождения частиц и пере-
перенормировки <rwv>-
При учете взаимодействия между полями сразу возникают
два вопроса. Первый из них — в какой мере взаимодействие
может стимулировать или подавлять рождение частиц гравита-
гравитационным полем по сравнению со случаем свободных полей.
Конечно, взаимодействия могут привести и к негравитационно-
негравитационному рождению частиц, но нас будут в большей степени интере-
интересовать процессы, которые запрещены в пространстве Минков-
ского, такие, как одновременное рождение фотона и злектрон-
позитронной пары.
Второй вопрос касается перенормируемости теории. Будет
ли теория (например, квантовая электродинамика), перенорми-
перенормируемая в пространстве Минковского, оставаться перенормируе-
перенормируемой в пространстве, имеющем нетривиальную топологию или
кривизну? Этот вопрос имеет важнейшее значение, ибо если
теория теряет свою предсказательную силу, как только учиты-
учитываются слабые гравитационные возмущения, ее справедливость
представляется сомнительной. Довольно трудно дать общее до-
доказательство перенормируемости, и до настоящего времени
существенное продвижение было связано с теорией скалярного
поля с взаимодействием Яср4 '>.
Третий круг вопросов, вызывающих большой интерес, свя^
зан с излучением черных дыр. Остается ли процесс Хокинга
тепловым при учете взаимодействий? Если нет, то кажется воз-
') Перенормировка в квантовой электродинамике в искривленном про-
пространстве-времени рассматривалась в работе [648*] (см. также [639*, 640*,
643*, 644*, 647*]. — Прим. перев.

Взаимодействующие поля ¦ 305
можным нарушение второго закона термодинамики. Мы обсу-
обсудим некоторый модельный расчет, в котором тепловой характер
излучения действительно сохраняется.
Эта глава имеет целью лишь ввести читателя в круг задач
теории взаимодействующих полей в искривленном простран-
пространстве-времени. Мы не пытались дать исчерпывающий обзор и
ограничились лишь отдельными конкретными примерами.
9.1. Расчет матричных элементов
S-матрицы
Расмотрим общий случай взаимодействующих полей, опи-
описываемых плотностью лагранжиана
i? = i?o + i?/. (9.1)
где Э?й — лагранжиан свободного поля, например типа обсуж-
обсуждавшихся в разд. 3.2 и 3.8, а 27 — лангранжиан взаимодейст-
взаимодействия, содержащий произведения полей порядка выше квадратич-
квадратичного. Предположим, как и прежде, что пространство является
глобально гиперболическим и выбран параметр х°, имеющий
смысл времени.
Предположим далее, что взаимодействие (9.1) адиабати-
адиабатически выключается в отдаленных прошлом и будущем, где
поля, которые мы будем в общем случае изображать симво-
символом ф, сводятся к свободным полям фт и ^out соответственно:
Пт ф(х) = ф1а{х), (9.2)
»-»--оо
lim 4>{x)=*4>oat{x), (9.3)
°
причем предел понимается в смысле слабой операторной схо-
сходимости. Эти асимптотические условия, необходимые для вве-
введения представления о частицах, в квантовой теории поля
в пространстве Минковского оправданы тем, что в типичной
задаче рассеяния частицы в начальном и конечном состояниях
действительно находятся на достаточном удалении друг от
друга вне области взаимодействия. Лишь в промежуточные
моменты времени, когда частицы сближаются, взаимодействие
между ними становится существенным. Аналогичные сообра-
соображения можно использовать и в случае искривленного простран-
пространства-времени. Но нетрудно представить себе пространства, для
которых асимптотические условия (9.2) и (9.3) не могут быть
выполнены. Например, в пространстве-времени, обладающем
замкнутыми пространственными сечениями, частицы не могут
быть бесконечно удалены друг от друга, и асимптотические
условия можно рассматривать лишь как приближенные. Кроме

306 Глава 9
того, пространство-время может иметь сингулярности, которые
ограничивают его в прошлом или будущем, и асимптотические
области во времени не существуют. В этом случае можно по-
попытаться прибегнуть к другим физическим или математическим
критериям или пытаться иначе сформулировать квантовую тео-
теорию поля (см., например, [321]).
Поскольку ф-ш и ^>out — свободные поля, для них справедли-
справедливо все, что сказано в разд. 3.2. В частности, эти поля можно
представить в виде разложения по полным наборам мод C.30).
Ка'к выяснено в гл. 3, определение положительно-частотных ре-
решений в отдаленном прошлом и будущем может быть различ-
различным; поэтому будем считать, что и™ и u?ut представляют со-
собой положительно-частотные моды в этих областях, выбранные,
например, с использованием адиабатического определения.
Тогда ф(П и cpout можно разложить по каждому из наборов мод:
&п (х) = ? W"u{" (х) + аТ f"!"* (#)) = (9.4а)
La I I
i
= ? (аТ1иТ1 (х) + af Vut* (x)). (9.56)
i
Поскольку в общем случае и\п не совпадают с u°ut, а связа-
связаны с ними некоторым преобразованием Боголюбова вида C.34),
то а\п с а\" и a?ut с a?ut также связаны соответствующими пре-
преобразованиями C.37). Таким образом, в общем случае сущест-
существуют четыре неэквивалентных вакуумных состояния, определен-
определенные соотношениями (ср. B.19), C.33)):
а\"\0, in) = 0, V*> (9-6)
а? |0, in) = 0, V'. (9.7)
a?ut I 0, out) = 0, V*"> (9.8)
'S?Btl0, out) = 0, V». (9.9)
с каждым из которых ассоциируется пространство Фока. Про-
Пространство Фока, построенное^ на базе |0, in), связано с прост-
пространством, построенным на |0, in), элементами 5-матрицы типа
C.45), которые могут быть полностью выражены через боголю-
бовские коэффициенты. Таким же способом можно связать меж-
между собой пространства Фока, построенные на |0, out) и |0, out).
Но связь между пространствами Фока, построенными на |0, in)

Взаимодействующие поля 307
и |О, out), зависит от взаимодействия. При выключении взаимо-
взаимодействия эти пространства становятся эквивалентными.
Поскольку вакуум |0, in> определен по отношению к поло-
положительно-частотным модам в отдаленном прошлом, где точное
поле ф с учетом взаимодействия совпадает с фш, этот вакуум
определяет «физическое» пространство Фока в прошлом. Ана-
Аналогично, вакуум |0, out), определенный по отношению к поло-
положительно-частотным модам в будущем, где ф сводится к фОпь
задает «физическое» пространство Фока в этой области. Поэто-
Поэтому физические взаимодействия «частиц» в искривленном про-
пространстве-времени описываются элементами S-матрицы, связы-
связывающими между собой пространства Фока, построенные на
|0, in> и |0, out).
Заметим, что все проблемы, связанные с определением со-
состояний частиц в искривленном пространстве-времени, которые
обсуждались в гл. 3, остаются и прн учете взаимодействия;
лишь в частных случаях, например, когда возможно адиаба-
адиабатическое определение положительных частот или может быть
использована конформная симметрия, выбор «in и «?ut будет
однозначным.
Предположим, что выбрано некоторое определение состоя-
состояний частиц; тогда возникает проблема вычисления матричных
элементов S-матрицы (амплитуд рассеяния) между in- и out-
состояниями (разд. 3.2). Некоторое in-состояние | хпи, 2nil, ...
..., in)будет переходить в некоторое out-состояние! xmu, 2mh,...
..., ои^либо вследствие наличия кривизны пространства-вре-
пространства-времени, либо из-за взаимодействия. Оказывается удобным раз-
разделить эти два эффекта с помощью следующего приема. Раз-
Разложим состояние | ltntl, 2thh, ..., out) по полному набору out-
состояний без черты сверху аналогично C.41). Тогда соответ-
соответствующий элемент S-матрицы запишется в виде
(out, ..., 2mtl, хти\хпь, 2nh in) =
со
= Zii Z <out' •••- *"Ч' 1™h\1'i' lU 4. out)X
fc=o il...lk
X<out, Iv .... l/f, I/J'ni,,»*,, •••, in). (9.10)
Существование S-матрицы в искривленном пространстве-времени
исследовал Уолд [485, 486]. Вероятность перехода между вы-
выбранными in- и out-состояниями есть
(out 2thi2, lmil\inh, 2nh, ..., in)p. (9.11)
Амплитуда (out, ..., 2mh, lmh\\,v l/2 l/ft, out) пол-
полностью описывается боголюбовскими коэффициентами (см.

308 Глава 9
C.44)) и не зависит от деталей взаимодействия. С другой сто-
стороны, амплитуда (out, llk, ..., l/s, l/J'ra,,, 2nh, ..., in) оп-
определяется взаимодействием, но этот матричный элемент связы-
связывает состояния, основанные на одном и том же определении
положительных частот. Поэтому его можно вычислять, исполь-
используя обычные методы, применяемые в случае пространства Мин-
ковского. Здесь мы обсудим два различных метода.
Превый — метод редукции матричных элементов S-матрицы,
называемый методом ЛСЦ (Лемана —Симанчика — Циммер-
Циммермана) [338]. Вывод редукционных формул проводится по суще-
существу так же, как и в случае пространства Минковского (см.,
например, [49], § 16.7). В частности, для скалярного поля с са-
самодействием, когда S'o задается выражением C.24), получаем
(ср. [49] формула A6.81))
(out, 1Р], ..., 1P,|1V ..., 1„т, in)/(out, 0|0, in) =
т I
= im+l Д \ dnxt [- g {Xi)\h Д \ dnyi [- g iytf* uqi (x{) uPj (y,) X
i-\ /-1 , ¦
X [axi + m2 + %R (x{)] [ayi + m2 + tR (г//)] т (г/, yh x{ ..., xm),
(9.12)
где принято pi ф q/ V/, / и введена функция Грина
X{XU X2, ..., Хт) (out, 0 | 0, in) • ^Лд>
Детали вывода соотношений типа (9.12) имеются в работах [39,
48], в которых получены редукционные формулы _для полной
амплитуды (9.11) в терминах функций Грина <out, 0) ... |0, in>
и боголюбовских коэффициентов.
При выводе соотношения (9.12) два момента заслуживают
специального внимания. Во-первых, в отличие от случая прост-
пространства Минковского, для которого |0, out>=|0, in> (с точ-
точностью до фазового множителя), вакуумное состояние |0, in>
в искривленном простраьстве-времени в общем случае неустой-
неустойчиво, т. е. <out, 0|0, in>=?M. Эта неустойчивость связана не с
различным определением положительных частот (состояния
|0, in) и |0, out) основаны на одном и том же определении), а с
иеинвариантностью относительно группы Пуанкаре в искрив-
искривленном пространстве-времени, которая может приводить к до-
дополнительному рождению частиц по сравнению с рассмотрен-
рассмотренным в гл. 3. Этот вопрос будет рассмотрен в разд. 9.3.
Второе замечание относится к использованию теоремы Га-
Гаусса при выводе соотношения (9.12), когда были опущены по-
поверхностные члены на пространственноподобной бесконечности.

Взаимодействующие поля 309
Если пространство-время имеет пространственноподобные гра-
границы, эти поверхностные члены необходимо удерживать, исполь-
используя физически обоснованные граничные условия.
Построим теперь функции Грина (9.13). В практических
расчетах найти точные выражения, как правило, не удается,
и приходится использовать некоторые приближенные методы,
например теорию возмущений. Это можно сделать, вводя так
называемую матрицу эволюции U [187] (см., например, [49],
гл. 17), которая приводит к практически такому же ряду теории
возмущений для 5, что и представление взаимодействия, к ко-
которому мы обратимся ниже.
Альтернативный метод состоит в использовании формулиров-
формулировки теории с помощью интегралов по траекториям (разд. 2.8)
и построении производящего функционала для функций Грина
с учетом взаимодействия в виде
(9.14)
Если плотность лагранжиана взаимодействия — полиномиаль-
полиномиальная функция полей, то выражение (9.14) можно переписать в
виде
(9.15)
Функциональный интеграл в (9.15) теперь есть просто сво-
свободный производящий функционал, который мы обозначим
Zo[/]. Таким образом,
{\[]?]}0[J]. (9.16)
Для скалярных полей Zo определяется выражением B.126),
которое справедливо и в искривленном пространстве-времени.
Следовательно, в этом случае
[det (- GF)]'h exp {i \s, [\ -^-] dnx } X
(y)GF(y, z)J{z)dnydnz), (9.17)
гДе коэффициент пропорциональности не зависит от метрики
и тока 7 и не влияет на функции Грина. Разлагая в ряд экспо-
экспоненты в (9.17) и выполняя функциональное дифференцирование,
получаем разложение теории возмущений для Z, полностью
выраженное через фейнмановский пропагатор для свободного

310 Глава 9
поля. Это разложение можно использовать в B.117) с целью по-
получения разложений для точных функций Грина.
Важно иметь в виду, что граничные условия, закладываемые
в функции Грина взаимодействующих полей, порождаемые вы-
выражением (9.17), зависят от выбора фейнмановского пропага-
тора Gf. Поскольку мы хотим получить функции Грина (9.13),
соответствующие одному определению положительно-частотных
мод Ui, фейнмановский пропагатор Gf нужно задавать в этих
модах:
iGF (х, у) = 0 (х° - у0) Z Щ (х) и\ (у) + 6 (у° - х°) ? и- {Х) U( (у)
(9.18)
(ср. G.74)). При таком выборе пропагатора будем иметь
т.(*„ х* .... ^ = r-[6/UiN6;(y^6/Um)]^o, (9.19)
где индекс с при хс означает, что в разложении по теории воз-
возмущений величины (9.17) в (9.19) учтены лишь связные фейн-
мановские диаграммы. Это нетрудно проверить в явной форме
для некоторых конкретных лагранжианов; в следующем разде-
разделе будет рассмотрен пример.
Метод исследования взаимодействующих квантованных полей
в искривленном пространстве-времени, используемый уже до-
довольно долго [213, 470], состоит в разложении производящего
функционала (или функций Грина) в функциональные степен-
степенные ряды (ряды Вольтерра) по отклонению метрики от метрики
Минковского. Каждый член разложения можно далее рассмат-
рассматривать в рамках обычной теории возмущений в пространстве
Минковского, разлагая по степеням константы взаимодействия.
Вместо разложения величины Z[J] на практике удобнее
записывать разложение для lnZ, входящего в (9.19). Полагая
(ср. F.25))
W[J; g^] = -i\nZ[J;gllv], (9.20)
где
gnv(x) = %v + hllv{x), - (9.21)
можно записать разложение W в ряд Вольтерра (см., например,
[411],§1,2):
[J; guv] =ZMli йПх1Н^1 {Xi) X
X IFn.ViV, wm \-J> xi> *2> • • ¦. *«I), (9.22)

Взаимодействующие поля 311
где
№V,v,. n2v2 nmvm i'I
= Г
L
,i,v, цЛ, (g 23)
При 7 = 0 выражение (9.22) определяет разложение эффек-
эффективного действия в теории с учетом взаимодействия, причем
первый член этого разложения, как видно из формулы F.13),
содержит вакуумное среднее значение тензора энергии-импуль-
энергии-импульса
HW0] = <0|7VlVl|0> (9.24)
взаимодействующего поля в пространстве Минковского. Эта ве-
величина исследовалась многими авторами [86, 122, 212, 215].
Члены более высокого порядка имеют более сложную структуру
и помимо вкладов типа @|7VlV,, 7V2v2, •••, ^nmvm|0) содержат
также вклады типа «чайки», которые возникают при функци-
функциональном дифференцировании T^v [guv] [213].
Этот метод построения теорий взаимодействующих полей
в искривленном пространстве-времени имеет три недостатка:
1) вычисления удается выполнить лишь в случае небольших от-
отклонений метрики пространства-времени от плоской, 2) метод не
дает информации об эффектах, обусловленных топологией про-
пространства-времени (см., например, [180]), 3) крайне трудно
определить, какое квантовое состояние вакуума при этом ис-
используется. Поэтому мы не будем развивать здесь этот подход
и, основываясь на формулировке теории с помощью функцио-
функциональных интегралов, будем рассматривать лишь разложения
теории возмущений по степеням константы взаимодействия, та-
такие, как (9.17).
Как уже упоминалось, в пространстве Минковского сущест-
существует другой метод вычисления амплитуд <out, ljk,..., xj2, lj\\lnll,
2nt2, ..., in); фигурирующих в (9.11), который легко приме-
применить и в данном случае. Это расчеты в картине взаимодействия,
в которой поля удовлетворяют свободным уравнениям, а ди-
динамическая информация содержится в векторах состояний си-
системы. (См., например, [406], гл. 4, где дана ковариантная
формулировка подхода в пространстве Минковского. Формули-
Формулировка картины взаимодействия в искривленном пространстйе-
вр*емени дана в работах [46, 82].)
В картине взаимодействия состояния |ij)> удовлетворяют
уравнению Шредингера
(9-25)

312 Глава 9
где 36i — плотность гамильтониана взаимодействия, которая
в случае связи без производных равна
ЗЮ, = — 2„ (9.26)
а 2 (х) — пространственноподобная гиперповерхность Коши,
проходящая через точку х. Для случая поверхности постоянно-
постоянного времени (9.25) имеет вид
3®1(х)\Ъ(х°)) = 1д]*}?У> ¦ (9.27)
Решение уравнения (9.25) записывается с помощью унитар-
унитарного оператора U, определяемого соотношением
|Ф[2]> = */[2, ЗоЛФРУ), (9.28)
который, как следует из уравнения (9.25), удовлетворяет урав-
уравнению Томонага — Швингера [424—426, 461]
с начальным условием
С/[20>20] = 1. (9.296)
Записывая соотношения (9.29) в виде интегрального уравнения
s
U [2, So] = 1 -1 \ Ж, (x') U [S't So] dV, (9.30)
s»
можно с помощью итераций найти следующее решение в замк-
замкнутой форме:
U [2, So] = Рехр | - i J 5», (xf) dvl,
J (9.31)
где символ упорядочения Р имеет тот же смысл, что и символ
хронологического упорядочения Т, с той лишь разницей, что
для фермионных полей при перестановках не следует изменять
знак.
Согласно теореме Хаага [261], величина U не может быть
хорошо определенным оператором в гильбертовом пространстве
состояний (см., например, [406], § 8.4), поэтому мы будем по-
понимать (9.31) как чисто формальное выражение, используемое
для получения 5-матрицы, определяемой как
S = ?/[S0Ut, SIn]. (9.32)
Здесь Sout — поверхность в out-области в бесконечно далеком
будущем, а 21п — поверхность в in-области в бесконечно уда-

Взаимодействующие поля 313
ленном прошлом. Тогда из (9.28) получаем
№°ut]) = S №'"]), (9.33)
и в соответствии с (9.31) S имеет разложение
5== Е SC»>, (9.34)
где
S<°!=1, (9.35)
5'm) =±^Г- \ Р №'{х^ Ж1 ^ ••¦Ж1 (*m)) dnx{dnx2. ... dnxm.
(9.36)
Выберем теперь состояние |i|)[2in]>, принадлежащее прост-
пространству Фока, построенному с помощью гейзенберговского ва-
вакуума |0, in) (см. (9.6)). Тогда можно утверждать, что на
поверхности Sin поле ф в картине взаимодействия должно сов-
совпадать с гейзенберговским полем. Но на 21п гейзенберговское
поле сводится к свободному полю ф\п (см. (9.2)). Следователь-
Следовательно, то же самое относится и к полю в картине взаимодействия.
Поскольку поле в представлении взаимодействия удовлетворяет
уравнению для свободного, поля, отсюда следует, что оно
должно совпадать с ф\п в любой момент времени.
Рассмотрим, в частности, начальное состояние
) = |l/,) l/2 l/,,in). (9.37)
Тогда соотношение (9.33) имеет вид
|1У1, 1/2, ..., l/fc;out) = S|l/l, 1/2, ..., llk, in). (9.38)
Заметим, что поскольку оператор 5 описывает лишь эффекты,
обусловленные взаимодействием, вектор |\J)[2out]> в левой
части (9.38) определен в терминах out-состояний без черты
сверху. Поэтому мы получаем другую возможность расчета
части амплитуды (9.10), не зависящей от преобразования Бого-
Боголюбова. С помощью (9.38) находим
(out, l,k, .... 1/2> l/J'm,, %г, ..., in) =
= <in, l/ft l/2, 1/JS+IV 2n,2, .... in). (9.39)
Правая часть (9.39) может быть рассчитана с точностью до
любого порядка теории возмущений с помощью (9.34), причем
Mi в (9.36) строится из полей <f>in, записанных в виде (9.4).
Независимо от того, используется ли картина взаимодейст-
взаимодействия или применяется метод редукции и квантование с помощью

314 Глава 9
функционального интеграла, в теории возникают расходимости,
которые следует устранить с помощью перенормировок. Приме-
Применение описан-ных выше методов расчета и последующая регу-
регуляризация и перенормировка бесконечных величин лучше всего
иллюстрируется примером, к которому мы теперь переходим.
9.2. Скалярное поле с самодействием
в искривленном пространстве-времени
Рассмотрим теорию скалярного поля с самодействием, опи-
описываемую плотностью лагранжиана (9.1); где 2'о дано выраже-
выражением C.24), a Si имеет вид
#/=-ж(-*>1/1Я*4- (9-40>
Это так называемая теория кф*.
Особый интерес представляют амплитуды перехода из на-
начального вакуумного состояния в конечное многочастичное со-
состояние, так как такие процессы не могут иметь места
в пространстве Минковского. Рассмотрение таких амплитуд
позволяет продемонстрировать методы перенормировок, приме-
применяемые и в других случаях. Полагая в (9.10) | 'и^, 2in2 in)=
= | 0, in), находим
<out, ,.., 2т{„ хти |0, in) =
оо
¦ =Y,T\ 2 <out 2/й'.1/й'.М/1. 1/2 4>out)X
fc-0 /,.../fc
X(out, l/fc, ..., 1,2, 1Л|0, in). (9.41)
Первая амплитуда в правой части лег!ко строится с помощью
боголюбовских коэффициентов; она является конечной. Рас-
Рассмотрим поэтому первые несколько вкладов от второй ампли-
амплитуды.
Чтобы показать подробнее применение двух методов рас-
расчета, описанных выше, рассмотрим сначала вычисление ампли-
амплитуды (out, lBl, lpJO, in) в теории возмущений. Редукционная
формула (9.12) в методе ЛСЦ приводит к следующему выра-
выражению для этой амплитуды:
(out, lpi, 1„|0. in)
<out, 010, in)
= \ dnyidny2[-g(Xl)]y>[-g(х2)?> uPl (y{)иРг(у2) X
X / [Dyi + m2 + IR (</,)] i [Ojri + m2 + IR (у,)] х (yv y2). (9.42)

Взаимодействующие поля 315
J_
2
Рис. 29. Фейнмановские диаграммы для вкладов нулевого и первого порядка
в полный связный пропагатор tc(yi,y%) в теории А,Ф4.
Необходимо, следовательно, построить функцию Грина %{у\,у2),
называемую также точным пропагатором (с учетом взаимодей-
взаимодействия). ,
Подставляя (9.40) в (9.27) и разлагая экспоненты, нетрудно
найти члены в любом порядке по к, которые дают в выражении
для 1п2[/] вклад, квадратичный по /. Именно такие члены
вносят неисчезающий вклад в величину
(9-43)
(см. (9.19)). Несвязные диаграммы дают вклад в т, который
можно рассчитать, комбинируя связные компоненты; мы не бу-
будем касаться этого вопроса, заметим лишь, что несвязные диаг-
диаграммы дают вклад в полную амплитуду.
В первом порядке по X, воспользовавшись формулами (9.17)
и (9.43), получаем выражение
т:с(У\, У*) = Юр (Уи У2) —
-jk\GP(yu х) GF (х, х) GP Ос, у2) [- g (*)]*'• d"x, (9.44)
которое сводится к iGF{yuy2) при Я = 0, чего и следовало ожи-
ожидать (ср. (9.13) и B.69)). Выражения типа (9.44) удобно
изображать с помощью диаграмм Фейнмана. Изображая \
в виде вершины, a iGF(x,y)—с помощью линии, получаем
диаграммы, соответствующие (9.44), как показано на рис. 29,
где подразумевается интегрирование по координатам точки при
вершине.
В редукционную формулу (9.42) функция Грина входит
в виде комбинации
V О/,, У2) - i [П„ + m* + \R (У1)] I [пуг + m* + lR (y2)] T (yit y2).
(9.45)
Подставляя (9.44) в (9.45) и воспользовавшись формулой
C.49), получаем
Ye (</,> У2) = *У1У, + Т Wf (Ух> У'О S {Ух - У»I[- 8 0/.)]'/г. (9-46)

316 Глава 9
где К определяется формулой F.21) или F.23). Величина у
называется усеченной функцией Грина, поскольку ее диаграм-
диаграммное изображение получается из хс (рис. 29) отсечением внеш-
внешних линий. Подставляя (9.46) в (9.42), окончательно находим
d'V + OU1). (9.47)
Первое слагаемое в (9.46) не дает вклада в (9.47), так как
моды удовлетворяют уравнению свободного поля.
Прежде чем переходить к обсуждению этого результата,
а также поправок более высокого порядка и других амплитуд,
покажем, как можно получить его в картине взаимодействия.
Будем исходить из формулы (9.39), которая в этом случае дает
(out, 1Р1, 1р,|0, in> = <in, 1Р„ 1P,|S+|O, in), (9.48)
и, ограничиваясь первым порядком по К, подставим первые два
члена разложения (9.34) для S. Первый член вклада не дает,
поэтому остается (с учетом (9.26) и (9.40)) величина
(out, 1Р„ 1Ра|0, in) =
l, lP,\T(p(x))\0, in)[-g(x))'hdnx+O(X2). (9.49)
Матричный элемент в подынтегральном выражении (9.49)
можно вычислить, подставляя (9.4а) для ф (напомним, что
в картине взаимодействия 0 = ^|П), или с помощью теоремы
Вика [497] (см.. например, [406], гл. 4). В обоих случаях по-
получаем
(in, 1Р„ 1р,\Т(ф*(х))\0, in) =
= 12ы; (х)«; (х) iGF (х, х) (in, 010, in), (9.50)
где GF определяется формулой (9.18). Подставляя это выраже-
выражение в (9.49) и замечая, что
(out, 0|0, in) = (in, 0|0, in)+O(X), (9.51)
приходим снова к формуле (9.47). При таком методе расчета
учитываются (в высших порядках) как связные, так и несвяз-
несвязные диаграммы. Деление на (9.51) устраняет несвязные петле-
петлевые диаграммы, не содержащие внешних линий (см., напри-
например, [49], § 17.6 или [423], § 146).
Анализ выражения (9,47) сразу приводит к затруднению,
так как величина Gp(y,y) бесконечна при и->4. В самом деле,
мы считали п произвольным в (9.47), предвидя необходимость

Взаимодействующие поля 317
регуляризации этого выражения, что наиболее просто осущест-
осуществляется с помощью продолжения по размерности. Природа по-
полюсного члена может быть установлена с помощью разложения
де Витта —Швингера для GF. Из C.138) или F.29) находим
G» (у> у)-
где величина G?0He4H(«/, у) конечна при n-М. Полюсные члены
можно устранить с помощью перенормировки констант в лаг-
лагранжиане, как в случае пространства Минковского. Но есть
очевидное различие, проявляющееся в наличии члена, пропор-
пропорционального скалярной кривизне Риччи R. Мы увидим, что
этот дополнительный полюсный член можно устранить пере-
перенормировкой постоянной 1, отсутствующей в теории поля в про-
пространстве Минковского.
Метод перенормировок, основанный на размерной регуляри-
регуляризации, был продолжен т'Офтом [457] и исследован в работах
[121, 123], где бъгла выполнена в явном виде перенормировка
в теории Кф4 с точностью до четвертого порядка в пространстве
Минковского (см. также [373]). Полный лагранжиан (9.1)
имеет вид
31 = т (-ёУ<> [§^Ф, »Ф, v - К + № (*)) *У -
W + J (S/n2 + W ^2]• (9-53)
где tnR и \r — «перенормированные константы», связанные
с «голыми константами» m и | соотношениями
m% = m2-6m2, 1л=|-6|. (9.54), (9.55)
Для сокращения записи здесь опущены индексы В у голых ве-
величин. Первый член в (9.53), содержащий перенормированные
величины, мы будем рассматривать теперь |как плотность сво-
свободного лагранжиана 3?о, а второй член — как новую плот-
плотность лагранжиана взаимодействия. Цель состоит в сокраще-
сокращении полюсных членов в S-матрице с помощью подходящего
выбора dm2 и б|. Предполагая, что это возможно, запишем
4
00 00 ОО
Ьт = m%Z Z *v/4 in - 4)"v = mR ? 6V (KR) (n - 4)~v, (9.56)
v=-l /=-v v=-l
8|=ZZ dvAfe (n - 4)"v = f dv (Як) (ft - 4)-v, (9.57)
V=-i /-V V = l

318 ¦ Глава 9
где также предусмотрена возможность перенормировки кон-
константы связи с помощью соотношения
v=l /-v
aH4"%+E avW(ft-4)"v. (9.58)
Как и в разд. 6.2, здесь введен произвольный масштаб массы \i,
.чтобы сделать полное действие безразмерным.
Необходимо также принять во внимание возможную пере-
перенормировку поля («волновой функций»), при которой
ф->фк = г~ч*ф, (9.59)
где
00 00 ОО
— 1 + Zj 2-1 Cvi^R (tt — 4) =; 2j cv (Xr) (n — 4) . (9.oU)
v-l /=v v=l
Теория перенормируема, если все полюсные члены в элементах
5-матрицы могут быть устранены с помощью некоторого вы-
выбора величин avj, bVj, cv/ и dv,-.
Если второй член в (9.53) рассматривать как лагранжиан
взаимодействия, т. е.
] (9.61)
то легко вычислить усеченную функцию Грина ус:
I v=l
[-g (У1у'<> 6n (yx - y2)] + О(%2R) (9.62)
n -
вместо (9.46). При получении этого выражения использованы
представления (9.56) — (9.58) и удержаны лишь члены, линей-
линейные по Xr. Все величины в (9.62) выражены через перенорми-
перенормированные константы lR и mR, а не через «голые» параметры,
как это было раньше. Поскольку функция Грина Гс(УиУ2) пред-
представляет собой вакуумное среднее от произведения двух по-
полей ф (см. (9.13)), можно ожидать, что из-за перенормировки
полей хс будет умножено на Z~2. Но при построении усеченной
функции Грина выражение дважды делится на Gf и, следова-
следовательно, на Z4. Таким образом, выражение (9.62) следует умно-
умножить на Z2. Единственный вклад в элементы 5-матрицы по-
порядка XR, который возникает в результате этого умножения,

Взаимодействующие поля 319
дает первый член в правой части (9.62):
= ikR ? cv, (я - 4)~v[?„ + m\ + 1RR (У1)] [- g (</,)Г'/г X
X5"(</,-</2). (9.63)
Подставляя (9.52) (с заменой m->mR, 1-»-|к) в (9.62), не-
нетрудно убедиться, что все полюсные члены могут быть устра-
устранены из ус{У\, Уъ), если выбрать
cvl=0, yv; rfvi ==6Vi =0, vv =^ 1;
(9'64)
ft,,—1/16Я»; du = -(iR--i
При таком выборе параметров подстановка (9.62) в редукцион-
редукционные формулы теперь приводит к амплитудам, конечным при
+ (бд - 1) /? (у)] In (г } [- g (у)]'1' d4y. (9.65)
Появление произвольного массового параметра ji в этой ам-
амплитуде связано с неоднозначностью перенормировочной про-
процедуры, присущей любой схеме перенормировок. Изменение
масштаба ц изменяет соотношение между голыми и перенорми-
перенормированными константами, что отражает необходимость фиксиро-
фиксирования значений XR, mR и |R с помощью эксперимента. (См. об-
обсуждение на с. 171. В связи с перенормировкой тензора энер-
энергии-импульса мы вернемся к этому вопросу ниже.)
Аналогично рассчитываются многочастичные амплитуды
[40, 47, 81—83]. Расходимости имеет лишь четырехчастичная
амплитуда, ее перенормировка изложенным методом фиксирует
коэффициенты aV; в (9.58). Таким образом, перенормировка
двухчастичных и четырехчастичных амплитуд определяет все
коэффициенты в выражениях (9.56) — (9.58) и (9.60) и, следо-
следовательно, в лагранжиане скалярного поля. Но, как мы увидим
ниже, остается еще расходимость амплитуд вакуум — вакуум,
i Чтобы выяснить, как устранить эту расходимость с помо-
помощью переномировки, напомним, что эффективное действие
W[g^] = W[0; gp.v] (см. (9.20)) связано с вакуумной амплиту-
амплитудой соотношением
W [*,„] — - / In «out, 010, in» — - /In Z [0]. (9.66)

320 Глава 9
Поэтому следует ожидать, что эта добавочная расходимость
может быть устранена перенормировкой констант в обобщенном
эйнштейновском действии так же, как и в случае свободных
полей, рассмотренном в разд. 6.2. Что это действительно так,
было проверено Банчем и Панангаденом [81] с точностью до
второго порядка по \R. Аналогичные перенормировки оказались
необходимы и в безмассовой квантовой электродинамике в про-
пространстве де Ситтера [65, 180, 434, 435].
Здесь мы рассмотрим перенормировку амплитуды вакуум —
вакуум с точностью до первого порядка по kR. Выбирая кар-
картину взаимодействия, можем записать
(out, 0|0, in) = (in, 0|5|0, in) =
= (in, 010, in) + (in, 0 | SO 10, in) + О (Ц), (9.67)
где использовано разложение (9.34). Подстановка в (9.66)
с учетом разложения логарифма дает
Заметим, что величина <in, 0 | 0, in) не предполагалась норми-
нормированной на единицу. Это лишь вопрос удобства; если считать,
что норма этого вектора равна величине
(in, 0 10, in) = [det (- О,)], (9.69)
входящей в выражение (9.17) (без учета взаимодействия), то
Wo = — / In ((in, 0 10, in)) (9.70)
и при подстановке Wo в F.13) будем иметь <in, 0|7цУ|0, in>/
/<in, 010, in).
Но если величина W не предназначается для вычисления
среднего значения тензора энергии-импульса, то можно норми-
нормировать <in,0|0, in) на единицу; тогда первый член в (9.68)
обращается в нуль.
Воспользовавшись формулами (9.26), (9.36) и выражением
(9.61) для плотности лаграижиаиа взаимодействия, получим
<in, о | S"> | о, in) _ Г ,п , , цу. f Я 2 , ._
(in, 010, in) t)ax[ g(x)\ [&uF(x,x)
-1 (б/и2 + 6|Я) GF (x, x)} = / J d"x [- g (x))'h X
), (9.71)

Взаимодействующие поля 321
где во втором слагаемом использованы выражения (9.56) —
(9.58) с коэффициентами (9.64). Воспользовавшись формулой
(9.52) для Gf, будем иметь
<in. 0|3<"|0, in) _ г а , ,./,
(in, 0|0, in) — 1 )а х[ S{x)l X
8 I0" (X> X)i + 512л;* (я - 4J
Полюсные члены, пропорциональные (и —4)-1, сократились
в этом выражении после перенормировки параметров m и |.
Но остается еще двойной полюс, который нельзя устранить та-
таким способом и который приводит к появлению двойного по-
полюса в эффективном действии (9.68). Эта расходимость может
быть устранена перенормировкой констант в обобщенном эйн-
эйнштейновском лагранжиане. Для этого необходима перенорми-
перенормировка ньютоновской постоянной, космологической постоянной и
коэффициента перед R2.
Доказательство того, что описанная схема перенормировок
позволяет устранить все расходимости, возникающие в теории
с взаимодействием Кф* во всех порядках теории возмущений,
нетривиально уже в случае пространства Минковского (см.,
например, [62]; а также [351], где показано, что вычитания,
предложенные в [62], эквивалентны перенормировке констант
в действии). В искривленном пространстве-времени такое до-
доказательство оказывается еще более сложным не только из-за
технических трудностей, но и в связи с некоторыми принци-
принципиальными проблемами [48]. В частности, упрощения, дости-
достигаемые путем использования инвариантности относительно
группы Пуанкаре, которые важны при доказательстве перенор-
перенормируемости теории в пространстве Минковского (см., например,
[406], § 4.2 и 5.1), невозможны в искривленном пространстве-
времени. Одним из непосредственных следствий этого, с кото-
которым мы уже столкнулись, является возникновение полюсных
членов, пропорциональных скалярной кривизне, и связанная
с этим необходимость перенормировки параметра ?[674*]. Од-
Однако R не единственный новый скаляр, который может поя-
появиться. Например, полюсный член, пропорциональный G^OHe4H,
возникает из члена Qp в (9.71). Этот скаляр в общем случае
* представляет собой крайне сложную нелокальную функцию
геометрии пространства-времени. (Конечно, асимптотическое
разложение <з?онечн в первой строчке формулы (9.52) локально.)
На языке диаграмм Фейнмана член типа Q% в (9.71)
представляется диаграммой, показанной на рис. 30. Полюс,

322 Глава 9
Рис. 30. Фейнмановская диаграмма для
вклада первого порядка в амплитуду ва-
вакуум — вакуум в теории Кф*.
пропорциональный G?OHe4H, возникает в результате умножения
полюса, ассоциируемого с одной из петель, на конечную часть
другой петли. Эта расходимость известна как расходимость «пе-
«перекрытия», и ее уничтожение существенно для возможности по-
построения перенормируемого эффективного действия W в терми-
терминах чисто локальных величин. В случае (9.71) эта расходимость
уничтожается членом, возникающим при перенормировке т и
|. Сокращение расходимостей перекрытия необходимо также
в двухчастичных элементах S-матрицы, если их конечность
должна обеспечиваться (локальной) перенормировкой парамет-
параметров т и |. Банч показал, что такое сокращение действительно
имеет место и что теория Я^4 остается перенормируемой
в искривленном пространстве-времени.
Тот факт, что при включении взаимодействия, вообще го-
говоря, необходимы дополнительные зависящие от I перенорми-
перенормировки констант в обобщенном эйнштейновском действии, наво-
наводит на мысль, что должен существовать зависящий от X вклад
в конформную аномалию. Для изучения этого вопроса удобно
использовать методы ренормгруппы в формулировке т'Офта
[457], основанной на размерной регуляризации (см. также
[123]).
Основная идея метода уже упоминалась в разд. 6.2. Теория
может предсказывать элементы S-матрицы лишь при условии
фиксации произвольного масштаба массы ц. Это вносит внут-
внутреннюю неопределенность в значения перенормированных кон-
констант, которые практически не удается определить из экспе-
эксперимента. При изменении ц необходимо изменить значения
перенормированных констант таким образом, чтобы эле-
элементы S-матрицы сохраняли физические наблюдаемые зна-
значения.
Следуя т'Офту, эти изменения, например, для Kr и mR (па-
(параметр |я или любая другая константа, трактуется аналогично
mR) можно установить, выразив (фиксированные) голые кон-
константы Хит, определяемые формулами (9.54), (9.55), (9.58),
через новый масштаб массы ц', связанный с ц бесконечно ма-
малым преобразованием
ц'-(Ц-в)ц.' (9.73)

Взаимодействующие поля 323
Из формулы (9.58) с точностью до первого порядка по е на-
находим
К = (^-"[1 + г (п - 4)] { XR + ? av (XR) (n - 4)~
= (»')*-" \ е (п - 4) kR + lR + ea, (ЯЛ) + ?
(. v=l
р| (9.74)
Поскольку это разложение содержит член, пропорциональный
(п — 4), оно не совпадает с исходным разложением (9.58).Сла-
(9.58).Слагаемые такого типа всегда можно добавить к разложениям го-
голых констант в терминах перенормированных констант, по-
поскольку они исчезают для физической размерности пространст-
пространства-времени я = 4; это отражает обычную неопределенность при
перенормировках. Но если бы мы начинали проводить перенор-
перенормировки, имея масштаб массы ц' вместо ц, мы не получили бы
членов, пропорциональных (п — 4), так как таких членов нет
в исходном выражении (9.58). Поэтому мы устраним член,
пропорциональный (п — 4), в (9.74) с помощью преобразо-
преобразования
lR = lR-e(n-4)lR, (9.75)
которое является нетривиальным лишь вне точки п = 4. В ре-
результате этого преобразования (9.74) принимает вид
4" \~kR + ea, (kR) - екк^
(9.76)
Точно так же преобразование (9.75) в (9.56) приводит к но-
новому разложению для параметра т:
dXR
v=l
т\ У(п- 4)-v(bv (lR) - bIr а\+' {Xr) ) + О (в2). (9.77)
Чтобы привести выражения (9.76) и (9.77) снова к стан-
стандартному виду (9.56) и (9.58) (с заменой ц на ц'), который мы

324 Глава 9
получили бы, используя с самого начала параметр р/, введем
величины
= lR + в (ах (lR) - lR *"' (*д)), (9.78)
%
(m'Ry = m% - гт\1к ^М . (9.79)
Так как параметры кит фиксированы, для сохранения пере-
перенормированных значений элементов S-матрицы при использо-
использовании масштаба ,и/ вместо ц следует перейти к новым величи-
величинам XR и mR, согласно соотношениям (9.78) и (9.79), которые
при п = 4 сводятся к
К = h +е («. (К) -
С помощью этих соотношений для бесконечно малых преобра-
преобразований Ад и mR можно получить следующие дифференциаль-
дифференциальные уравнения:
_А = а1(Я,я)Лд^^Р(Ы (9.82)
(9-83)
Функции й и Ym иногда называют й- и у-функциями Каллана —
Симанчика из-за их роли в уравнениях ренормгруппы, впервые
установленной Калланом [85] и Симанчиком [445]. Мы уви-
увидим, что аналогичную роль эти функции выполняют и в связи
с конформными аномалиями [44, 65, 181].
Лагранжева плотность для свободного скалярного поля
C.24) в случае четырех измерений инвариантна относительно
конформных преобразований C.1) и C.7) при условии, что
т = 0 и % = '/в. Плотность лагранжиана взаимодействия (9.40)
также инвариантна относительно этих преобразований в четы-
четырехмерном случае. Как отмечалось в разд. 6.3, эта инвариант-
инвариантность формально гарантирует исчезновение следа вакуумного
среднего значения тензора энергии-импульса. Мы уже видели,
что перенормировка констант в обобщенном эйнштейновском
действии приводит к нарушению конформной инвариантности
и сопровождается появлением аномального следа даже в слу-
случае свободных полей. Аномалию следа для свободного поля

Взаимодействующие поля 325
можно отделить от вклада взаимодействия, так как эффектив-
эффективное действие (9.66) для взаимодействующего поля в соответст-
соответствии с (9.17) может быть записано в виде суммы
W = WQ + W,, (9.84)
где Wo — эффективное действие для свободного поля F.25),
a Wi — часть, зависящая от взаимодействия:
Xexp[—ji\ /(У) ОР(у, г) J(z)dny dnz]]j=o. (9.85)
Поэтому, используя соотношение (см. F.117))
(V (*)> = -
г P^v]
(9.86)
получаем
/f1 ц\ ___ /71 ц\ L /71 Ы\ tQ Q*7\
\ ц / — v И /О ~Т~ \ ц /1> ^У.о/ I
\
где (Г^о — аномалия следа свободного поля, a <T(x^>i — вклад,
зависящий от взаимодействия, возникающий при подстановке
W, вместо W ъ (9.86).
В случае взаимодействующих полей, вообще говоря, невоз-
невозможно сохранить конформную инвариантность не только эф-
эффективного действия, но и просто действия. Причина состоит
в том, что необходимо перенормировать параметры ти |, поэто-
поэтому они не могут сохранить значения т = 0 и 1 = 'Д, необходи-
необходимые для обеспечения конформной инвариантности. Эти пара-
параметры становятся неопределенными, и лишь перенормированные
константы m.R и lff можно определить с помощью эксперимента.
В некоторой выбранной схеме регуляризации голые и перенор-
перенормированные константы можно связать соотношениями (9.54) и
(9.55), где 8т2 и 61 имеют вполне определенные значения. Напри-
Например, в схеме т'Офта при условии, что доказана возможность
успешной перенормировки массы на основе (9.56), равенство
нулю mR означает, что т=0. Но в общем случае 61 и 6т2 совер-
совершенно произвольны, и если используется другая схема регуля-
регуляризации, то равенство mR — Q не обязательно влечет за собой
Ыр. = 0. Так будет, например, в случае регуляризации с по-
помощью раздвижки точек [46].
Поскольку в схеме т'Офта условие mR = 0 влечет за собой
бш2 = 0, можно поставить вопрос о том, существует ли такое
?я, для которого 61 = 0. Из соотношения (9.64) следует, что
если g = '/в, то 65 = 0 с точностью до первого порядка по А,«.

326 Глава 9
Но вычисления показывают [40, 81], что во втором порядке это
соотношение нарушается. Если же изменить схему т'Офта, до-
допустив зависимость |R от п, то, как показано в работах [65,
122], выбор значения ?* = ?(«) (см. C.27)) приводит к 61 = 0
с точностью до третьего, но не более высоких порядков по KR.
Выбор |R = ?(n) эквивалентен выбору 1 = :Д в (9.57) и по-
последующему добавлению членов, пропорциональных п — 4, т. е.
использованию обсуждавшейся выше неоднозначности перенор-
перенормировочной процедуры.
Поскольку 8|#0 в четвертом и более высоких порядках и
так как действие не является конформно-инвариантным, нельзя
ожидать, что вакуумное среднее от тензора энергии-импульса
будет хотя бы формально бесследовым. Но полный след можно
представить в виде суммы аномальной и неаномальной частей.
Аномальная часть возникает из следующих трех источников: из
аномалии следа свободного поля, которая, как было показано
выше, может рассматриваться отдельно; из перенормировки
констант в обобщенном эйнштейновском действии, зависящей
от константы связи Я«. Это дает также и неаномальную часть,
но аномальный вклад возникает так же, как и в случае свобод-
свободного поля. Третий источник аномалии, пожалуй, наиболее ин-
интересен; он связан с тем, что выражение (9.40) является кон-
конформно-инвариантным лишь в случае четырех измерений.
В случае п измерений при преобразованиях C.1) и C.7)
выражение (9.40) преобразуется к виду
=W" тг U*+Ё «*
(9.88)
где использовано соотношение (9.58). Поскольку функция Q{x)
входит в (9.88) только в виде комбинации jiQ, вариацию по Q
можно заменить вариацией по ц в (9.86), рассматривая времен-
временно ц. как функцию х:
Величину (9.89) можно вычислить, воспользовавшись тем, что
нам известно изменение XR и ?R, в точности компенсирующее из-
изменение ix. Пусть XR(x) и lR{x) выбраны так, что компенсируют
вариацию ц(х). Тогда
(9.90)

Взаимодействующие поля 327
где Q = 1 также означает, что \х(х) = ц, Яя(х) =%R, Ir(x) = |r.
С помощью соотношения (9.82) и аналогичного (9.83) соотноше-
соотношения
преобразуем (9.90) к виду
тег+р М -фт т }
(9.92)
напоминающему по форме уравнение ренормгруппы (см., на-
например, [123], уравнение A1)). Воспользовавшись равенством
(9.92) для вычисления • (9.89), найдем для соответствующего
вклада в <r^>/ выражение
[-«'<*)]* [Р ^"бГ^Г~%(Ч) -SfToo"] Х
\ , (9.93)
На практике удобнее не вычислять след тензора энергии-
импульса по частям, как это было сделано выше, а пытаться
найти его целиком. Но выражение (9.93) иллюстрирует важное
различие аномальных следов для свободного поля и для вклада
взаимодействия. В то время как аномалия следа для свободного
поля не зависит от квантового состояния и локальна, след, воз-
возникающий за счет взаимодействия, определяется всей соответ-
соответствующей частью эффективного действия и, вообще говоря, за-
зависит от состояния поля и не является локальным. В частно-
частности, подстановка (Т„,*у в F.166) в общем случае приводит к
увеличению плотности энергии со временем, что ассоциируется
с процессом рождения частиц в отличие от случая свободного
поля, рассмотренного на с. 198. Рождение частиц за счет взаи-
взаимодействия в таком подходе обсуждалось Бирреллом и Девисом
[44] •). В следующем разделе мы рассмотрим влияние взаимо-
взаимодействия на рождение частиц с другой точки зрения.
9.3. Рождение частиц
5а счет взаимодействия
При наличии взаимодействий рождение частиц может быть
связано с двумя причинами. Во-первых, как и в случае свободно-
свободного поля, определение положительных частот может различаться
*) См. также [642*. 650*]. —Прим. перев.

328 Глава 9
для in- и out-областей. Во-вторых, отсутствие инвариантно-
инвариантности относительно группы Пуанкаре делает возможным возникно-
возникновение энергии и импульса из вакуума. Воспользовавшись ре-
результатами, полученными в предыдущих разделах, нетрудно
рассчитать число частиц, рождающихся благодаря этим эффек-
эффектам.
Если выбрать гейзенберговскую картину, то состояние си-
системы будет оставаться фиксированным в течение всего времени.
Выберем в качестве такого состояния физический вакуум при
малых временах |0, in>. В этой картине операторы описывают
динамику поля, в частности операторы числа частиц в ранние
и поздние моменты времени различны..При малых временах one-,
ратор, описывающий число частиц моды i, связанной с поло-
положительно-частотной функцией и\п (см. (9.4а)), имеет вид
Nf = aT"aT (9.94).
и (in, 0|Mn|0, in) = 0. В поздние моменты времени поле имеет,
положительно-частотные моды «?ut и описывается разложением
(9.5); поэтому физический оператор числа частиц есть
ЫТ1 = аТХ1гаТХ. (9.95)
Таким образом, число частиц, рожденных в состоянии вакуума
|0, in>, равно _
(in, 0|/V°ut|0, in). (9.96)
Это среднее значение можно вычислить разными способами.
Во-первых, можно записать
00
10, in)^^^ 2 IT/,, .... 1,е out)(out, Т,,, .... f/,|0, in),
г-о /,.../[
(9.97)
что в результате подстановки в (9.96) дает произведение сред-
средних вида
/out, Т, Т ATutIf./,..., T/, out\ (9.98)
с амплитудами, имеющими вид (9.41). Средние значения (9.98)
находятся тривиальным образом, поскольку состояния out-про-
out-пространства Фока с чертой сверху определены по отношению к
операторам Щи1, фигурирующим в (9.95); поэтому вся инфор-
информация заключена в амплитудах (9.41). В этих амплитудах раз-
разделены два источника рождения частиц: эффекты перемешива-

Взаимодействующие поля 329
ния положительных и отрицательных частот сосредоточены в
первой амплитуде в правой части, в то время как вторая ампли-
амплитуда может быть отличной от нуля лишь при отсутствии инва-
инвариантности относительно группы Пуанкаре, за исключением
тривиального случая перехода вакуум—вакуум.
Поскольку амплитуды, определяемые с помощью боголю-
бовских коэффициентов, представляют собой довольно сложные
выражения, практически удобнее пользоваться другим спосо-
способом вычислений, разлагая в ряд в виде
оо
'°>{П> = ЕТ! ? I1/,----' 1П> °ut)<out, 1,,, .... Iyi|0, in),
(9.99)
откуда
(in, olivrMo, in) =
= ?тг?^Г ? ? (in, 0Щ,,..., Um, out)X
/-0 m = 0 /,...;, kx...km
X(out, 1/, 1/, I 0, in) (out, Um,..., Ujivr'l h? •••• l/,.out)
(9.100)
Здесь первые два сомножителя в правой части, вообще говоря,
отличны от нуля в отсутствие пуанкаре-инвариаитности, а по-
последний содержит информацию о рождении частиц вследствие
премешивания положительных и отрицательных частот. Пос-
Последняя амплитуда рассчитывается наиболее просто, если с помо-
помощью боголюбовского преобразования C.38) переписать (9.95)
в терминах операторов af11, по отношению к которым определе-
определены векторы пространства Фока без черты сверху. Для простоты
ограничимся пространственно-плоскими моделями Робертсона—
Уокера, для которых коэффициенты Боголюбова имеют вид
C.76), C.77). Тогда с помощью C.38) запишем
a°ut = а]а™1 — р *a°_uJ+; (9.101)
следовательно,
„ N°tai *= | at р №iat +1 Pi I*a™\a™\+ - а$\аГ' V_u*+ - alpЛ?и',
(9.102)
где
tf?ut = a?ut+a?ut. . (9.103)
П Зак. 674

330 Глава 9 ',
Подстановка (9.102) в (9.100) с учетом лишь членов, дающих
ненулевой вклад в сумму, приводит к выражению
(in, 0|tf?ut|0, in) = IM2 +
оо
+ Ei E {K<out- ч,•••• то. in)i»x
m = 0 ft, -. - *m
X(out, lkm, ..., Ц|ЛС'|Ц, .... \km, out)-
-2Re[a.p;(in, 0|l,, 1_,, lkj, ..., l'v out)X
X(out, \km, ..., Щ0, in)(out, 1кт, •-.,
1*,, l-i, h|a?utW|lv ..., Um, out)]}. (9.104)
При получении первого слагаемого в правой части мы предпо-
предположили, что амплитуда <in, 0|0, in> нормирована на единицу
(см. с'. 320). Это первое слагаемое совпадает с числом частиц,
рожденных в отсутствие взаимодействия (ср. C.42)).
Остальные слагаемые возникают из-за взаимодействия и мо-,
гут быть рассчитаны в рамках теории возмущений. Мы приве-
приведем соответствующие выражения лишь с точностью до первого
порядка по Ir. Член, содержащий |(out, lkm, ..., U,|0, in)|2,
в (9.104) не дает вклада порядка ниже %\, и мы опустим его.
С другой стороны, член, содержащий боголюбовский коэффи-
коэффициент р, дает вклад порядка %я в первое слагаемое с т = 0
в сумме:
— 2Re[a,p)(in,. 0|1,, !_,, out)(out, 0|0, in)X
X (out, 1 _ t, 111 af + a™l + j 0, out)] =
= —2Не[агр;Aп, 0|I,, l_f, out)<out, 0|0, in)]. (9.105)
Как было показано в предыдущем разделе, первая амплитуда'
в (9.105) порядка Яя, в то время как <out, 0|0, in> = 1 + 0(%R)
(в принятой выше нормировке). Поэтому с точностью до перво-
первого порядка по Я,я подстановка (9.65) в (9.105) приводит к Сле-
Следующему выражению для перенормированного среднего:
(in, О|ЛГГ|О, in)peH=| p, |s-R
- (г/8я2) (m| + (U -|)/? (У)) In-ц] [- g (у)]'Ы4у] . (9.106)
Заметим, что вклад первого порядка возникает как комбинация
боголюбовского преобразования и взаимодействия. В частности,
если р* = 0, рождения частиц в первом порядке не происходит.

Взаимодействующие поля 331
Возможность рождения частиц в первом порядке по взаимо-
взаимодействию означает, что даже для достаточно слабой связи (т. е.
малых kR) вклад взаимодействия в полное число частиц будет
существенным по сравнению с вкладом |р,|2 от свободного поля.
Существование вклада первого порядка было замечено Лотцем
[344], Бирреллом и Фордом [46] и Банчем, Панангаденом и
Паркером [82], вычислившим среднее значение тензора энер-
энергии-импульса в out-области. Численные примеры рождения ча-
частиц за счет взаимодействия были приведены в работах [45,
46].
9.4. Другие эффекты взаимодействия 4
Аппарат, развитый в предыдущем разделе, можно без осо-
особого труда применить к случаю вечной черной дыры [48], но
он не позволяет сразу сделать вывод о том, остается ли хокин-
говское излучение тепловым при учете взаимодействий. Ввиду
важности тепловой природы хокинговского излучения с точки
зрения второго начала термодинамики (разд. 8.2) желательно
проверить, что взаимодействия не разрушают это свойство.
Аргументы в пользу того, что излучение Хокинга остается
тепловым и при учете взаимодействий, были высказаны Гиб-
бонсом и Перри [239, 240], а затем развиты Хокингом [286].
Вспомним (разд. 8.3), что в случае свободного поля скалярная
функция Грина G в состоянии крускаловского вакуума совпа-
совпадает с тепловой функцией Грина, ассоциируемой со шварцшиль-
довыми координатами. В частности, она периодична во мни-
мнимом шварцшильдовом времени. Гиббоне и Перри отметили, что
в теории возмущений функции Грина взаимодействующих полей
строятся с помощью функций Грина, соответствующих сво-
свободным полям, поэтому функция Грина, связанная с координа-
координатами Крускала, обладает тем же свойством периодичности по
мнимому времени, автоматически заложенным в ней. Посколь-
Поскольку соображеиия о периодичирсти во времени, сформулированные
на с. 33, не зависят от того, являются ли Н и ф свободными или
взаимодействующими, эта функция Грина обладает теми же
тепловыми свойствами, что и в случае свободного поля.
Если пытаться выйти за рамки теории возмущений, то воз-
возникают серьезные технические трудности. Даже в случае про-
пространства Минковского свойства точных квантово-полевых мо-
моделей (вне теории возмущений) удается исследовать лишь в об-
общих чертах (например, используя спектральные представления
для пропагаторов). В искривленном пространстве-времени в
отсутствие инвариантности относительно группы Пуанкаре про-
продвижение еще более затруднительно.
К счастью, существуют некоторые теоретико-полевые мо-
модели, которые можно обобщить на случай искривленного

332 Глава 9
пространства-времени, не прибегая к теории возмущений или ка-
каким-либо приближениям. Одной из них является безмассовая
модель Тирринга [455, 456], которая была подробно изучена
в случае пространства Минковского (см., например, [330]). Эта
модель имеет точные решения, которые можно распространить
на случай искривленного пространства-времени [41, 415].
Модель Тирринга представляет собой теорию безмассового
поля со спином Уг в двумерном пространстве-времени. Она пе-
переносится из пространства Минковского в искривленное прост-
пространство-время с помощью метода, использованного для спи*
норного поля в разд. 3.8. Для лагранжевой плотности получаем
сумму плотности лагранжиана C.176) при т = 0 и лагранжиа-
лагранжиана взаимодействия
^«(det^U^, (9.107)
где
/» = $/1|> (9.108)
(.уи — гамма-матрицы Дирака в искривленном пространстве-
времени, см. с. 93).
Построение точного решения в двумерном искривленном
пространстве-времени оказывается возможным благодаря кон-
конформной инвариантности теории; при этом конформный вес по-
поля равен У2. Поэтому операторное решение уравнения поля,
получаемого варьированием действия в пространстве с элемен-
элементом длины G.1), имеет вид
где г|) — решение в пространстве Минковского [330].
С помощью (9.109) легко получить выражения для функ-
функций Грина в пространстве-времени вечной черной дыры в тер-
терминах функций Грина в пространстве Минковского, приведен-
приведенных Клайбером [330]. В частности, используя координаты Кру-
скала для построения функции Грина в состоянии вакуума |0*>
(как и в свободном случае, см. с. 288), находим, что вдали от
черной дыры эти функции Грина, рассматриваемые как функции
шварцшильдовых координат, соответствуют тепловым функциям
Грина в модели Тирринга, построенным Дабином [183]. Это под-
подтверждает в случае модели Тирринга предположение о том, что
взаимодействия не разрушают теплового характера излучения
Хокинга.
Модель Тирринга является для теории взаимодействующих
полей в искривленном пространстве-времени исключением, по-
поскольку она имеет точные решения. В общем случае очень труд-
трудно построить решения даже в рамках теории возмущений из-за
сложного вида фейнмановских пропагаторов в искривленном

Взаимодействующие поля 333
пространстве-времени. Но эффекты, обусловленные топологией,
для взаимодействующих полей можно исследовать в случае,
когда геометрия пространства остается плоской. В разд. 4.1,
например, построена теория свободного квантованного поля в
двумерном плоском пространстве-времени, имеющем топологию
i?'X5'. Нетрудно обобщить эту задачу на случай взаимодей-
взаимодействия, воспользовавшись теорией возмущений в импульсном
представлении, как это делается в пространстве Минковского.
Покажем это на примере плоского пространства с топо-
топологией /?3Х5'. Фейнмановский пропагатор имеет тот же вид,
что и в пространстве Минковского, а именно (р2 — т2 -j- ie)~l,
но компонента импульса р3 (соответствующая измерению, свя-
связанному с топологией 51) принимает дискретные значения
нескрученное поле,
скрученное поле,
где } = 0, ±1, ±2 L — длина периодичности (разд. 4.1).
Таким образом, расчет фейнмановских диаграмм можно прово-
проводить в импульсном представлении с помощью методов (таких,
как фейнмановская параметризация), развитых в теории поля
в пространстве Минковского.
Рассчитаем, например, вклад первого порядка в усеченную
функцию Грина (9.62) с помощью размерной регуляризации.
Чтобы вычислить Gf(x, х) в случае п измерений, будем счи-
считать, что дополнительные п — 4 измерений связаны с топо-
топологией R1, т. е. найдем фейнмановский пропагатор в плоском
пространстве-времени с топологией R3 X Sl X Rn~4- He сущест-
существует глубокой причины, заставляющей считать, что дополнитель-
дополнительные измерения имеют топологию R1; столь же естественно было
бы рассматривать для них топологию S1. В схеме размерной
регуляризации этот выбор всегда произволен. Но различие то-
топологий для дополнительных измерений может сказываться
только в членах в Gf(x, х), пропорциональных п — 4, оставляю-
оставляющих (9.62) инвариантным. В высших порядках теории возмуще-
возмущений это различие, как легко показать, может сказаться лишь на
членах, в любом случае подвергающихся перенормировке, т. е.
тех, которые должны определяться из эксперимента (обычная
неопределенность перенормировочной процедуры — см. с. 323).
При сделанном выборе топологии «-мерного пространства
получаем
/— »

334 Глава 9
Интеграл можно вычислить с помощью полезной формулы [458]
рг'~?* г V* (91I2)
(m' + ЛТ""'* Г (а) %
а сумму можно упростить различными способами (см., напри-
например, [205], дополнение Б). В пределе тц = 0 выражение (9.111)
после взятия интеграла принимает вид
оо
? I / Г~3 для нескрученных полей,
оо
У* \i' + -г П Для скрученных полей.
В этом случае сумма выражается через ^-функцию Римана,
что дает фейнмановский пропагатор
( 1 для нескрученных полей,
\B3~" — 1) для скрученных полей, * .
имеющий конечный предел при п->4:
( ~ i/(\2L2) для нескрученных полей,
gf(x> *)ТП}\ j/B4L2) для скрученных полей. (9Л14)
Конечный характер этого' результата типичен для безмассовой
теории; его можно было предвидеть, если учесть, что в этом слу-
случае полюсный член в (9.62), пропорциональный bvU обращается
в нуль (величина R в этом случае также, конечно, равна нулю).
Подставляя (9.114) и (9.62) (и полагая п = 4), можно заме-
заметить, что это приводит к тому же результату, что и добавление
конечной величины к биг2 (см. (9.56)). В случае нескрученных
полей добавка равна Ял/B4?2), в случае скрученных полей она
равна —XK/D8L2). Таким образом, поле,, являющееся безмас-
безмассовым на беспетлевом уровне, приобретает эффективную массу
m,L в однопетлевом приближении благодаря влиянию топологии:
ml = А,д/B4/,2) нескрученное поле,
2 // 2\ (9.115)
mL = — Xr/\48L ) скрученное поле.
Явление генерации массы в теории Кф4 было замечено и иссле-
исследовано в работах [47, 143, 209, 462—464], а аналогичное явле-
явление в других теориях рассматривалось в работах [144, 205, 374,
465]. Оно тесно связано с первой поправкой к энергии Кази-
Казимира [204, 320].

Взаимодействующие поля 335
При Xr ~> О масса, генерируемая в случае нескрученных по-
полей, вещественная, а для скрученных полей мнимая (тахион-
(тахионная). Наличие тахионной массы обычно означает, что теория не-
неустойчива [206] относительно спонтанного нарушения симмет-
симметрии (см., например, [246]).
Для нескрученных полей.в плоском пространстве-времени с
топологией R3 X «S1 влияние топологии подобно влиянию темпе-
температуры. В частности, в теории Кф4 при ненулевой темпера-
температуре также имеет место генерация массы и при достаточно
высокой температуре восстановление нарушенных симметрии
[162,327, 328, 329, 495].
В случае скрученных полей между топологическими и тем-
температурными эффектами нет простого соотношения, и исследо-
исследование спонтанного нарушения симметрии значительно услож-
усложняется тем, что классические решения полевых уравнений с
тахионной массой не могут.быть постоянными (как для нескру-
ченного поля) из-за необходимости удовлетворить антипериоди-
антипериодическим граничным условиям [12].
Совместное влияние топологии, ненулевой температуры и
кривизны в теориях со спонтанным нарушением симметрии, по-
видимому, имело важное значение на ранних стадиях эволюции
вселенной. Некоторые возможные следствия обсуждаются," на-
например, в работах [53, 97, 164, 179, 217, 218, 233, 332], где мож-
можно найти ссылки на более ранние работы (см. также с. 137).

ЛИТЕРАТУРА
1. Abers Е. S., Lee В. W., Phys. Rep., 9C. 1 A973).
2. Abramowitz M., Stegun I. A., eds., Handbook of Mathematical Functions,
Dover, New York, 1965. [Имеется перевод: Справочник по специальным
функциям, под ред. Абрамовича М. и Стиган И. — М.: Наука, 1979.]
3. Абрикосов А. А., Горькое Л. П., Дзялошинский И. Е. Методы квантовой
теории поля в статистической физике. — М.: Физматгиз, 1962.
4. Adler S. L, Phys. Rev., 177, 2426 A969).
5. Adler S. L, Lieberman I., Ng Y. J., Ann. Phys. (USA), 106, 279 A977).
6. Adter S. L, Lieberman I., Ng Y. I., Ann. Phys. (USA), 113, 294 A978).
7. Ashmore J. F., Lett. Nuovo Cimento, 4, 289 A972).
8. Ashtekar A., Magnoti A., Proc. Roy. Soc. London, A346, 375 A975),
9. Ashtekar A., Magnon A., С R. Acad. Sci., Ser. A, 281, 875 A975).
10. Audretsch I., Schafer G., Phys. Lett, 66A, 459 A978).
11. Audretsch /., Schafer G., Journ. Phys. A: Gen. Phys., 11, 1583 A978).
12. Avis S. !., Isham C. /., Proc. Roy. Soc. London, A363, 581 A978).
13. Avis S. J., Isham С J., Nucl. Phys., B156, 441 A979).
14. Avis S. J., Isham C. I., Quantum field theory and fibre bundles in a ge-
general spacetime, в книге: Recent Developments in Gravitation — Cargese
1978, eds., Levy M., Deser S., Plenum Press, New York, 1979.
15. Avis S. J., Isham C. I., Commun Math. Phys., 72, 103 A980).
16. Avis S. J., Isham С I., Storey D., Phys. Rev. D, 18, 3565 A978).
17. Balazs N. L, Astrophys. Journ., 128, 398 A958).
18. Balian R., Duplantier В., Ann. Phys. (USA), 104, 300 П977).
19. Balian R., Duplantier В., Ann. Phys. (USA), 112, 165 A978).
20. Banach R., Dowker J. S., Journ. Phys A: Gen Phys., 12, 2527, 2545
A979).
21. Bander M., Itzykson C, Rev. Mod. Phys.. 38, 346 A966).
22. Bardeen J. W., Carter В., Hawking S. W., Commun. Math. Phys., 31, 161
A973).
23. Bargmann V., Sitz. Preuss. Akad Wiss., 346 A932).
24. Barrow J. D., Matzner R. A., Mon. Not. Roy. Astron. Soc, 181, 719 A977).
25. Barshay S., Troost W., Phys. Lett. 73B, 437 A978).
26. Barut A. O., Muzinich I. !., Williams D. N., Phys. Rev., 130, 442 A963).
27. Bekenstein J. D., Lett. Nuovo Cimento, 4, 7371 A972).
28. Bekenstein J. D., Phys. Rev. D, 7, 2333 A973).
29. Bekenstein J. D., Phys Rev. D, 12, 3077 A975).
30. Bekenstein J. D., Meisels A., Phys. Rev. D, 15, 2775 A977).
31. Bellfante F. I., Physica (Utrecht), 7, 305 A940). " '
32. Berger В., Ann. Phys. (USA), 83, 458 A974).
33. Berger В., Phys. Rev. D, 12, 368 A975).
34. Bernard C, Duncan A., Ann. Phys. (USA), 107, 201 A977).
35. Bianchi L., Lezioni Sulla Teoria dei Gruppi Continui Finiti Transforma-
zioni, Pisa: Spoerri, 1918.
36. Birrell N. D., Proc. Roy. Soc. London, A361, 513 A978).
37. Birrell N. D., Proc. Roy. Soc. London, A367, 123 A979).

Литература 337
38. Birrell N. D., Journ. Phys. A: Gen. Phys., 12, 337 A979).
39. Birrell N. D., Ph. D. Thesis, King's College, London, 1979.
40. Birrell N. D., Journ. Phys. A: Gen. Phys., 13, 569 A980).
41. Birrell N. D., Davies P. С W., Phys. Rev. D, 18, 4408 A978).
42. Birrell N. D., Davies P. С W., Nature (London), 272, 35 A978).
43. Birrell N. D., Davies P. С W., Journ. Phys. A: Gen. Phys., 13, 2109
A980).
44. Birrell N. D., Davies P. С W., Phys. Rev. D, 22, 322 A980).
45. Birrell N. D., Davies P. С W. Ford L. H., Journ. Phys. A: Gen. Phys., 13,
961 A980).
46. Birrell N. D., Ford L. H., Ann. Phys. (USA), 122, I A979).
47. Birrell N. D., Ford L H., Phys. Rev- D, 22, 330 A980).
48. Birrell N. D. Taylor J. G., Journ. Math. Phys. (USA), 21, 1740 A980).
49. Bjorken J. D., Drell S. D., Relativists Quantum Mechanics (Chs. I—10)
and Relativistic Quantum Fields (Chs. П—19), New York: McGraw-Hill,
1965. [Имеется перевод: Релятивистская квантовая теория, т. I, II. — М.:
Наука 1978.]
50. Blandford R. D., Mon. Not. Roy. Astron. Soc, 181, 489 A977).
51. Blandford R. D., Thome K. S., в книге: General Relativity: An Einstein
Centenary Survey, eds. S. W. Hawking, W. Israel, Cambridge: Cambridge
University Press, 1979.
52. Bleuler K., Helv. Phys. Acta, 23, 567 A950).
53. Bludman S. A., Ruderman M. A., Phys. Rev Lett., 38, 255 A977).
54. Blum B. S., Ph. D. Thesis, Brandeis University, 1973.
55. Боголюбов H. H. — ЖЭТФ, 1958, т. 34, с. 58.
56. Боголюбов Н. Н., Шцрков Д. В. Введение в теорию квантованных по-
полей. — М.: Наука, 1976.
57. Bollini С. G., Giambiagi J. J., Phys. Lett., 40B, 566 A972).
58. BondiH., Gold Т., Mon. Not. Roy. Astron. Soc., 108, 252 A948).
59. Boulware D. G., Phys. Rev. D, 11, 1404 A975).
60. Boulware D. G., Phys. Rev. D, 12, 350 A975).
61. Boulware D. G., Phys. Rev. D, 13, 2169 A976).
62. Breitenlohner P., Maison D., Commun. Math. Phys., 52, 11 A977).
63. Brown L. S., Cassidy J. P., Phys. Rev. D, 16, 1712 A977).
64. Brown L. S., Cassidy J. P., Phys. Rev. D, 15, 2810 A977).
65. Brown L S., Collins J. C, Ann. Phys. (USA), 130, 215 A980).
66. Brown L. S., Maclay G. J., Phys. Rev., 184, 1272 A969).
67. Brown M. R., Dutton С R., Phys. Rev. D, 18, 4422 A978).
68. Bucholz H., The Confluent Hypergeometric Function, Berlin: Springer-Ver-
lag, 1969.
69. Bunch T. S., Ph. D. Thesis, King's College, London, 1977.
70. Bunch T. S., Phys. Rev. D, 18, 1844 A978).
71. Bunch T. S., Journ. Phys. A: Gen. Phys., 11, 603 A978).
72. Bunch T. S., Journ. Phys. A: Gen. Phys., 12, 517 A979).
73. Bunch T. S., Journ. Phys. A: Gen. Phys., 13, 1297 A980).
74. Bunch T. S., Gen. Relativ. Gravit., 1981.
75. Bunch T. S., Ann. Phys. (USA), 131, 118 A981).
76. Bunch T. S., Christensen S. M., Fulling S. A., Phys. Rev. D, 18, 4435
A978).
477. Bunch T. S,, Davies P. С W., Proc. Roy. Soc. London, A357, 381 A977).
78. Bunch T. S., Davies P. С W., Proc. Roy. Soc. London, A356, 569 A977).
79. Bunch T. S., Davies P. С W., Proc. Roy. Soc. London, A360, 117 A978).
80. Bunch T. S., Davies P. C. W., Journ. Phys. A: Gen. Phys., 11, 1315 A978).
81. Bunch T. S., Panangaden P., Journ. Phys. A: Gen. Phys., 13, 919 A980).
82. Bunch T. S., Panangaden P., Parker L, Journ. Phys. A: Gen. Phys., 13,
901 A980). ¦
83. Bunch T. S., Parker L, Phys. Rev. D, 20, 2499 A979).

338 Литература
84. Caianello Е. R., Combinatorics and Renormalization in Quantum Field
Theory, New York: W. A. Benjamin, 1973.
85. Callan С G., Phys. Rev. D, 2, 1541 A970).
86. Callan C. G., Coletnan S., Jackiw R., Ann. Phys. (USA), 59, 42 A970).
87. Calvani M., Francaviglia M., Acta Phys. Pol., B9, 11 A978).
88. Candelas P., Phys. Rev. D, 21, 2185 A980).
89. Candelas P., Deutsch D., Proc. Roy. Soc. London, A354, 79 A977).
90. Candelas P., Deutsch D., Proc. Roy. Soc. London, A362, 251 A978).
91. Candelas P., Dowker J. S., Phys. Rev. D, 19, 2902 A979).
92. Candelas P., Raine D. /., Phys. Rev. D, 12, 965 A975).
93. Candelas P., Raine D. J., Journ. Math. Phys. (USA) 17, 2101 A976).
94. Candelas P., Raine D. J., Phys. Rev. D, 15, 1494 A977).
95. Candelas P., Raine D. /., Proc. Roy. Soc. London, A354, 79 A977).
96. Candelas P., Sciama D. W., Phys. Rev. Lett., 38, 1372 A977).
97. Canute V., Lee J. F., Phys. Lett., B72, 281 A977).
98. Capper D. M., Duff M. J., Nuovo Cimento, A23, 173 A974).
99. Capper D. M., Duff M. /, Phys. Lett, 53A, 361 A975).
100. Capper D. M., Duff M. J., Halpern L, Phys. Rev. D, 10, 461 A974).
101. Carter В. в книге: Black Holes, eds. С DeWitt, B. S. DeWitt, New York:
Gordon and Breach, 1975.
102. Casifhir H. B. G., Proc. Ron. Ned. Akad. Wet., 51, 793 A948).
103. Castagnino M., Verbeure A., Weder R. A., Phys. Lett., 8A, 99 A974).
104. Castagnino M., Verbeure A., Weder R. A., Nuovo Cimento, 26B, 396 A975).
105. Chakraborty В., Journ. Math. Phys. (USA), 14, 188 A973).
106. Chandrasekhar S. в книге: The Plasma in a Magnetic Field,
ed. R. К. М. Landshoff, Stanford, California: Stanford University Press,
1958.
107. Charap J. M., Duff M. J., Phys. Lett., 69B, 445; 71B, 219 A977).
108. Chern S. S,, Hamburg Abh., 20, 177 A955).
109. Chern S. S., Journ. Soc. Indust. Appi. Math., 10, 751 A962).
110. Chernikov N. A., Tagirov E. A., Ann. Inst. Henri Poincare, 94, 109 A968).
111. Chitre D. M., Hartle J. В., Phys. Rev. D, 16, 251 A977).
112. Christensen S. M., Bull. Am. Phys. Soc., 20, 99 A975).
113. Christensen S. M., Phys. Rev. D, 14, 2490 A976).
114. Christensen S M., Phys. Rev. D, 17, 946 A978).
115. Christensen S. M., Duff M. J., Phys. Lett, 76B, 571 A978).
116. Christensen S. M., Duff M. J., Nucl. Phys., B146, 11 A978).
117. Christensen S. M., Duff M. ]., Nucl. Phys., B154, 301 A979).
118. Christensen S. M., Duff M. J., Nucl. Phys., B170 FSI, 480 A980).
119. Christensen S. M., Fulling S. A., Phys. Rev. D, 15, 2088 A977).
120. Cline D. В., Mills F. E. (eds.), Unification of Elementary Forces and Gauge
Theories, London: Harwood Academic Publ., 1978.
121. Collins J. C, Phys. Rev. D, 10, 1213 A974).
122. Collins J. C, Phys. Rev. D, 14, 1965 A976).
123. Collins J. C, Macfarlane A. J., Phys. Rev., 10, 1201 A974).
124. Critchley R., Ph. D. Thesis, University of Manchester, 1976.
125. Curir A., Francaviglia M., Acta Phys. Pol., B9, 3 A978).
126. Damour Т. в книге: Recent Developments in the Fundamentals ox General
Relativity, ed. R. Ruffini, Amsterdam: North-Hoiland, 1977.
127. Davies P. С W., The Physics of Time Asymmetry, London: Surrey Uni-
University Press; Berkeley and Los Angeles: University of California Press,
1974. .
128. Davies P. С W., Journ. Phys. A: Gen. Phys., 8, 365 A975).
129. Davies P. С W., Proc. Roy. Soc. London, A351, 129 A976).
130. Davies P. С W., Phys. Lett., 68B, 402 A977).
131. Davies P. С W., Proc. Roy. Soc. London, A354, 529 A977).
132. Davies P. C. W., Proc. Roy. Soc. London, A353, 499 A977),

Литература' 339
133. Davies P. С. W., Rep. Prog. Phys., 41. 1313 A978).
134. Davies P. С W., в книге: Quantum Gravity II: A Second Oxford Sympo-
Symposium, eds. С J. Isham, R. Penrose, D. W. Sciama, Oxford: Clarendon, 1981.
135. Davies P. С W., Fulling S. A., Proc. Roy. Soc. London, A356, 237 A977).
136. Davies P. С W., Fulling S. A., Proc. Roy. Soc. London, A354, 59 A977).
137. Davies P. С W., Fulling S. A., Christensen S. M., Bunch T. S., Ann. Phys.
(USA), 109, 108 A977).
138. Davies P. С W., Fulling S. A., Unruh W. G., Phys. Rev. D., 13, 2720
A976).
139. Davies P. С W., Unruh W. G., Proc. Roy. Soc. London, A356, 569 A977).
140. Davies P. С W., Unruh W. G., Phys. Rev. D., 20, 388 A979).
141. Delbourgo R., Prasad V. В., Nuovo Cimento, 21A, 32 A974). .
142. Denardo G., Spallucci E., Nuovo Cimento, 53B, 334 A979).
143. Denardo G., Spallucci E., Nuovo Cimento, 55B, 97 A980).
144. Denardo G., Spallucci E., Nucl. Phys., B169, 514 A980).
145. Denardo G.,-Spaltucci E., Nuovo Cimento, ,59A, 1 A980).
146. Deruelle N.. Ruffini R., Phys. Lett., 57B, 248 A976).
147. DeserS., Duff M. /., Isham С I., Nucl. Phys., Bill, 45 A976).
148. Deser S., Zumino В., Phys. Lett., 62B. 335 A976).
149. de Sitter W., Proc. Kon. Ned. Akad. Wet., 19, 1217 A917).
150. de Sitter W., Proc. Kon. Ned. Akad. Wet., 20, 229 A917).
151. Deutsch D., Candelas P., Phys. Rev. D, 20, 3063 A979).
152. DeWitt B. 5., Phys. Rev., 90, 357 A953).
153. DeWitt B. S., The dynamical theory of groups and fields в книге: Relati-
Relativity, groups and Topology, eds. B. S. DeWitt, С DeWitt, New York: Gor-
Gordon and Breach, 1965.
154. DeWitt B. 5., Phys. Rev., 160, 1113 A967).
155. DeWitt B. S., Phys. Rev., 162, 1195, 1239 A967).
156. DeWitt B. S., Phys. Rep., 19C, 297 A975).
157. DeWitt B. S., в книге: General Relativity, eds. S. W. Hawking, W. Israel,
Cambridge: Cambridge University Press, 1979.
158. DeWitt B. S., Brehme R. W., Ann. Phys. (USA), 9, 220 A960).
159. DeWitt B. S., Hart С F., Isham С J. в книге: Themes in Contemporary
Physics, ed. S. Deser, Amsterdam: North-Holland, 1960.
160. Dirac P. A. M., Proc. Roy. Soc. London, A155, 447 A936).
161. di SessaA., Journ. Math. Phys, (USA), 15, 1892 A974).
162. Dolan L., Jackiw R., Phys. Rev. D, 9, 3320 A974).
163. Долгинов A. 3., Топтыгин И. Н. — ЖЭТФ, 1959, т. 37, с. 141. .
164. Dotnokos G., Janson M. M., Kovesi-Domokos S., Nature (London), 257, 203
165. Dowker J. S., Proc. Roy. Soc. London, A297, 351 A967).
166. Dowker I. S., Supp.'Nuovo Cimento, 5, 734 A967).
167. Dowker J. 5., Ann. Phys. (USA), 62, 361 A971).
168. Dowker J. S., Ann. Phys. (USA), 71, 577 A972).
169. Dowker J. S., Journ. Phys. A: Gen. Phys., 10, 115 A977).
170. Dowker J, S., Banach R., Journ. Phys. A: Gen. Phys., 11, 2255 A978).
171. Dowker J. S., Critchley R., Phys. Rev. D, 13, 224 A976).
172. Dowker J. 5., Critchley R., Phys. Rev. D, 13, 3224 A976).
173. Dowker J. S., Critchley R., Journ. Phys. A: Gen. Phys., 9, 535 A976).
174. Dowker J. 5., Critchley R., Phys. Rev. D, 15, 1484 A977).
'175. Dowker J. S., Critchley R., Phys. Rev. D, 16, 3390 A977).
176. Dowker I.'S., Dowker Y. P., Proc. Roy. Soc. London, A294, 175 A966).
177. Dowker J. S., Dowker Y. P., Proc. Roy. Soc. London, 87, 65 A966).
178. Dowker J. S., Kennedy G., Journ. Phys. A: Gen. Phys., 11, 895 A978).
179. Dreitlein J., Phys. Rev. Lett., 33, 1243 A974).
180. Drummond I. Т., Hathrell 5. /., Phys. Rev. D, 21, 958 A980).
181. Drummond I. Т., Shore G. M., Phys. Rev. D, 19, 1134 A979).

340 Литература
182. Дуан И. С —ЖЭТФ, 1956, т. 31, с. 1098.
183. Dubin D. A., Ann. Phys. (USA), 102, 71 A976).
184. Duff M. J. в книге: Quantum Gravity: An Oxford Symposium, eds.
С J. Isham, R. Penrose, D. W. Sciama, Oxford: Clarendon, 1975.
185. Duff M. J., Nucl. Phys., В125, 334 A977).
186. Duff M. I. в книге: Quantum Gravity II: A Second Oxford Symposium,
eds. C. J. Isham, R. Penrose, D. W. Sciama, Oxford: Clarendon, 1981.
187. Dyson F. J., Phys. Rev., 75, 486, 1736 A949).
188. Einstein A., Sitz. Preuss. Akad. Wiss., 142 A917).
189. Epstein H., Gaser V., Jaffe A., Nuovo Cimento, 36, 1016 A965).
190. Fadeev L. D., Popov V. N., Phys. Lett., 25B, 29 A967).
191. Farrugia С J., Hajicek P., Commun. Math. Phys., 68, 291 A980).
192. Fetter A. L, Walecka J. D., Quantum Theory of Many-Particle Systems,
' New York: McGraw-Hill, 1971.
193. Feynman R. P., Acta Phys. Pol. 24, 697 A963).
194. Feynman R. P., Hibbs A. R., Quantum Mechanics and Path Integrals, New
•York: McGraw-Hill, 1965. [Имеется перевод. Фейнман Р. П., Хиббс Д. Р.
Квантовая механика и интегралы по траекториям. — М.: Мир, 1968.]
195. Fierz M., Helv. Phys. Acta, 12, 3 A939).
196. Fierz M., Pauli W., Proc. Roy. Soc. London, A173, 211 A939).
197. Fischetti M. V., Hartle J. В., Ни В. L, Phys. Rev. D, 20, 1757 A979).
198. Fock V. A., Zs. Phys., 57, 261 A929).
199. Fock V. A., Phys. Zs. Sow. 12, 404 A937).
200. Fock Y. A., Ivanenko D., Zs Phys., 54, 798 A929).
201. Ford L. Я., Phys. Rev D, 12, 2963 A975).
202. Ford L. H., Phys. Rev. D, 14, 3304 A976).
203. Ford L. H., Proc. Roy. Soc. London A364, 227 A978).
204. Ford L. H., Proc. Roy Soc. London, A368, 305 A979).
205. Ford L. H., Phys. Rev. D, 21, 933 A980).
206. Ford L. H., Phys. Rev. D 22, 3003 A980).
207. Ford L. H., Parker L, Phys. Rev. D, 16, 245 A977).
208. Ford L. //., Parker L, Phys. Rev. D, 17, 1485 A978).
209. FordL. H., Yoshimura Т., Phys. Lett., 70A, 89 A979).
210. Fradkin E. S., Vilkovisky G. S., Phys. Lett., 73B, 209 A978).
211. Frampton P. H., Lectures on Gauge Field Theories. Part Two: Quantiza-
Quantization, University of California at Los Angeles publication UCLA/77/TEP/21,
1977.
212. Freedman D. Z., Muzinich I. J., Weinberg E. J.. Ann. Phys. (USA), 87, 95
A974).
213. Freedman D. Z., Pi S-Y., Ann. Phys. (USA), 91, 442 A975).
214. Freedman D. Z., van Mieuwenhuizen P., Ferrara S., Phys. Rev. D, 13, 3214
A976).
215. Freedman D. Z., Weinberg E. J., Ann. Phys (USA) 87, 354 A974).
216. Friedlander F. G., The Wave Equation в книге: Curved Space-Time, Cam-
Cambridge: Cambridge University Press, 1975.
217. Фролов В. М., Гриб А. А:, Мостепаненко В. М. — ТМФ, 1977, т. 33, с. 42.
218. Frolov V. М., Grib A. A., Mostepanenko V. М., Phys. Lett., 65A, 282
A978).
219. Frolov V. М., Mamaev S. G., Mostepanenko V. M., Phys. Lett., 55A, 389
A976).
220. Fulling S. A., Ph. D. Thesis, Princeton University, 1972.
221. Fulling S. A., Phys. Rev. D, 7, 2850 A973).
222. Fulling S. A., Journ. Phys. A: Gen. Phys., 10, 917 A977).
223. Fulling S. A., Gen. Relativ. Gravit. 10, 807 A979).
224. Fulling S. A., Davies P. С W., Proc. Roy. Soc. London, A348, 393 A976).
225. Fulling S. A , Parker L, Ни В. L, Phys. Rev. D, 10, 3905; erratum ibid
11, 1714 A974).

Литература 341
226. Fulling S. A., Sweeny M., Wald R. M., Commun. Math. Phys. 63, 257
A978).
227. Garabedian P. R., Partial Differential Equations, New York: Wiley, 1964.
228. Georgi H., Glashow S. L, Phys. Rev. Lett., 32, 438 A974).
229. Gerlach U., Phys. Rev. D, 14, 1479 A976).
230. Gibbons G. W., Commun. Math. Phys., 44, 245 A975).
231. Gibbons G. W., Phys. Lett., 60A, 385 A977).
232. Gibbons G. W., Phys. Lett., 61A, 3 A977).
233. Gibbons G. W., Journ. Phys. A: Gen. Phys., 11, 1341 A978).
234. Gibbons G. W. в книге: General Relativity: An Einstein Centenary Survey,
eds. S. W. Hawking, W. Israel, Cambridge: Cambridge University Press,
1979.
235. Gibbons G. W., Ann. Phys. (USA), 125, 98 A980).
236. Gibbons G. W., Hawking S. W., Phys. Rev. D, 15, 2738 A977).
237. Gibbons G. W., Hawking S. W., Phys. Rev. D, 15, 2752 A977).
238. Gibbons G. W., Hawking S. W., Commun. Math. Phys., 66, 291 A979).
239. Gibbons G. W., Perry M. J., Phys. Rev. Lett., 36, 985 A976).
240. Gibbons G. W., Perry M. J., Proc. Roy. Soc. London, A358, 467 A978).
241. Gibbons G. W., Pope С N., Commun. Math. Phys., 61, 239 A978).
242. Gilkey P. В., Adv. Math., 15, 334 A975).
243. Ginibre J. в книге: Statistical Mechanics and Quantum Field Theory,
eds. С DeWitt, R. Stora, New York: Gordon and Breach, 1971.
244. Гинзбург В. Л., Киржниц Д. А., Любушин А. А. — ЖЭТФ, 1971, т. 60,
с. 451.
245. Gitman D. M., Journ. Phys. A: Gen. Phys., 10, 2007 A977).
246. Goldstone J., Nuovo Cimento, 19, 154 A961).
247. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и про-
произведений.— М.: Наука, 1971.
248. Greiner P., Archs. Ration. Mech. Analysis, 41, 163 A971).
249. Grensing G., Journ. Phys. A: Gen. Phys., 10, 1687 A977).
250. Гриб А. А., Мамаев С. Г.— Ядерная физика, 1969, т. 10, с. 1276.
251. Гриб А. А., Мамаев С. Г.— Ядерная физика, 1971, т. 14, с. 800.
252. Grib A. A., Matnaev S. G., Mostepanenko V. M., Gen. Relativ. Gravit., 7,
535 A976).
253. Grib A. A., Matnaev S. G., Mostepanenko V. M., Journ. Phys. A: Gen.
Phys., 13,2057 A980)
254. Гриб А. А., Мамаев С. Г., Мостепаненко В. М. — Квантовые эффекты в
сильных внешних полях. — М.: Атомиздат, 1980.
255. Грищук Л. Я- —ЖЭТФ, 1974, т. 67, с. 825.
256. Grishchuk L. P., Lett. Nuovo Cimento, 12, 60 A975).
257. Grishchuk L. P., Graviton creation in the eaiiy universe в книге: Eighth
Texas Symposium on Relativistic Astrophysics, ed. M. D. Papagiannis, New
York: New York Academy of Sciences, 1977.
258. Gupta S. N., Proc. Phys. Soc. (London), A63, 681 A950).
259. Gursey F., Introduction to group theory в книге: Relativity, Groups and
Topology, eds. B. S. DeWitt, С DeWitt, New York: Cordon and Breach,
1964.
260. Gutzwiller M., Helv. Phys. Acta, 29, 313 A956).
261. Haag R., Kgl. Danske Videnskah Selskah, Mat-Fys. Medd., 29, No. 12
A955).
262. Hadamard J., Lectures on Cauchy's Problem в книге: Linear Partial Dif-
Differential Equations, New Haven: Yale University Press, 1923.
263. Hagedorn R., Supp. Nuovo Cimento, 3, 147 A965).
264. Hdji6ek P., Nuovo Cimento. 33B, 597 A976).
265. Hdjicek P., Phys. Rev. D, 15, 2757 A977).
266. HdjU^k P., Israel W., Phys. Lett., 80A, 9 A980).
267. Halpem L, Ark. Eys., 34, 539 A967).

342 Литература
268. Hartle J. P., Phys. Rev. Lett., 39, 1373 A977).
269. Hartle J. В. в книге: Quantum Gravity II: A Second Oxford Symposium,
eds. C. J. Isham, R.. Penrose, D. W. Sciama, Oxford: Clarendon, 1981.
270. Hartle I. В., Hawking S. W., Phys. Rev. D, 13, 2188 A976).
271. Hartle J. В., Ни В. L, Phys. Rev. D, 20, 1772 A979).
272. Hartle J. В., Ни В. L., Phys. Rev. D, 21, 2756 A981).
273. Hatalkar M. AT, Phys. Rev., 94, 1472 A954).
274. Hawking S. W., Commun. Math. Phys., 18, 301 A970).
275. Hawking S. W., Commun. Math. Phys., 25, 152 A972).
276. Hawking S. W., 'The event horizon' в книге: Black Holes, eds. С DeWitt,
B. S. DeWitt, New York: Gordon and Breach, 1973.
277. Hawking S. W., Nature (London), 248, 30 A974).
278. Hawking S. W., Commun. Math. Phys., 43, 199 A975).
279. Hawking S. W., Phys. Rev. D, 13, 191 A976).
280. Hawking S. W., Phys. Rev. D, 14, 2460 A976).
281. Hawking S. W., Commun. Math. Phys., 55, 133 A977).
282. Hawking S. W., Sci. Am., 236, 34 A977).
283. Hawking S. W., Phys. Lett., 60A, 81 A977).
284. Hawking S. W., Phys. Rev. D, 18, 1747 A978).
285. Hawking S. W., The path-integral approach to quantum gravity в книге:
General Relativity: An Einstein Centenary Survey, eds. S. W. Hawking,
W. Israel, Cambridge: Cambridge University Press, 1979.
286. Hawking S. №., Acausal propagation in quantum gravity в книге: Quan-
Quantum Gravity II: A Second Oxford Symposium, eds. С J. Isham, R. Pen-
rose, D. W. Sciama, Oxford: Clarendon, 1981.
287. Hawking S. W., Ellis G. F. R., The Large Scale Structure of Space-Time,
Cambridge: Cambridge University Press, 1973. [Имеется перевод: Хо-
кинг С, Эллис Дж. Крупномасштабная структура пространства-време-
пространства-времени.— М.: Мир, 1977.]
288. Hawking S. W., Penrose R., Proc. Roy. Soc. London, A314, 529 A970).
289. Hlscock W. A., Phys. Rev. D, 15, 3054 A977).
290. Hiscock W. A., Phys. Rev. D, 16, 2673 A977).
291. Hiscock W. A., Ph. D. Thesis, University of Maryland, 197.9.
292. Hiscock №. A., Phys. Rev. D, 21, 2063 A980).
293. Horibe M., Prog. Theor. Phys., ftl, 661 A979).
294. Horowitz G. Т., Phys. Rev. D, 21, 1445 (^80).
295. Horowitz G. Т., Wald R. M., Phys. Rev. D, 17, 414 A978).
296. Horowitz G. Т., Wald R. M., Phys. Rev. D, 21, 1462 A980).
297. Hosoya A., Prog. Theor. Phys., 61, 280 A979).
298. Hoyle F., Mon. Not. Roy. Astron. Soc, 108, 372 A948).
299. Ни В. L, Ph. D. Thesis, Princeton University 1972.
300. Ни В. L, Phys. Rev. D, 8, 1048 A973).
301. Ни В. L, Phys. Rev. D, 9, 3263 A974).
302. Ни В. L, Phys. Rev. D, 18, 4460 A978).
303. Ни B.-L, Phys. Lett., 71 A, 169 A979).
304. Ни В. L., Quantum field theories and relativistic cosmology в книге: Re-
Recent Developments in General Relativity, ed, R. Ruffini, Amsterdam: North-
Holland, 1980.
305. Ни В. L, Fulling S. A., Parker L, Phys. Rev. D, 8, 2377 A973).
306. Ни В. L, Parker L, Phys. Rev. D, 17, 933 A978).
307. Hut P., Mon. Not. Roy. Astron. Soc, 180, 379 A977).
308. Imamura Т., Phys. Rev., 118, 1430 A960).
309. Isham С !., An introduction to quantum gravity в книге: Quantum Gra-
Gravity: An Oxford Symposium, eds. С J. Jsham, R. Penrose, D. W. Sciama,
Oxford: Clarendon, 1975. - ,
310. Isham C. I., Quantum field theory in a curved spacetime — a general ma-
mathematical framework в книге: Proceedings of the Bonn Conference on

Литература 843
Differential Geometrical Methods in Mathematical Physics, eds. K. Bleuler,
. H. R. Petry, A. Reetz, New York: Springer-Verlag, 1978.
311. Isham С J., Proc. Roy. Soc. London, A362, 383 A978).
312. Isham С J., Proc. Roy. Soc. London, A364, 591 A978).
313. Isham С J., Proc. Roy. Soc. London, A368, 33 A979).
314. Isham С /., Quantum gravity—an overview в книге: Quantum Gravity II:
A Second Oxford Symposium, eds. С J. Isham. R. Penrose, D. W. Sciama,
Oxford: Clarendon, 1981.
315. Isihara A., Statistical Physics, New York: Academic Press, 1971.
316. Israel W., Phys. Lett., 57A, 107 A976).
317. Itzykson C, Zuber J.-C, Quantum Field Theory, New York: McGraw-Hill,
1980.
318. Jauch J. M., Rohrlich F., The Theory of Photons and Electrons, Reading,
Mass.: Addison-Wesley, 1955.
319. Kadanoff L. P., Baym G, Quantum Statistical Mechanics, Menlo Park,
California: Benjamin, 1962.
320. Kay B. S., Phys. Rev. D, 20, 3052 A979).
321. Kay B. S., Commun. Math. Phys., 71, 29 A980).
322. Kennedy G, Journ. Phys. A: Gen. Phys., 11, L173 A978)..
323. Kennedy G., Critchley R., Dowker J. S., Ann. Phys. (USA), 125, 346
A980).
324. Kennedy G., Unwin S. D., Journ. Phys. A: Gen. Phys., 13, L253 A980).
325. Kibble f. W. В., Commun. Math. Phys., 64, 73 A978).
326. Kibble T. W. В., Randjbar-Daemi S., Journ. Phys. A: Gen. Phys., 13, 141
A980).
327. Kirzhnits D. A., Linde A. D., Phys. Lett., 42B, 471 A972).
328. Kirzhnits D. A., Linde A. D., Ann. Phys. (USA), 101, 195 A976).
329. Kislinger M. В., Morley P. D., Phys. Rev. D, 13, 2771 A976).
330. Klaiber В. в книге: Lectures in Theoretical Physics, Vol. XA, eds. A. O. Ba-
rut, W. E. Britten, New York: Gordon and Breach, 1968.
331. Klein O., Zs. Phys., 53, 157 A929).
332. Kobsarev I. Yu., Okun L. В., Zel'dovich Ya. В., Phys. Lett., 50B, 340
A974).
333. Kreyszlg E., Introduction to Differential Geometry and Riemannian Geo-
Geometry, Toronto: University of Toronto Press, 1968.
334. Kruskal M. ?>., Phys. Rev., 119, 1743 A960).
335. Landau L. D., Lifshitz E. M., Statistical Physics, London: Pergamon, 1958.
336. Lapedes A. S., Phys. Rev. D, 17, 2556 A978).
337. Lapedes A. S., Journ. Math. Phys. (USA), 19, 2289 A978).
338. Lehmann #., Symanzik K., Zimmetmann W., Nuovo Cimento, 1, 1425
A955).
339. Лифшиц E. M. — ЖЭТФ, 1955, т. 29, с. 94.
340. Lifshitz E. M., Khalatnikov I. M., Adv. Phys., 12, 185 A963).
341. Liouville J., Journal de Math., 2, 24 A837).
342. Lohiya D., Panchapakesan N., Journ. Phys. A: Gen. Phys., 11, 1963 A978).
343. Lohiya D., Panchapakesan N., Journ. Phys. A: Gen. Phys., 12, 523 A979).
344. Lotze K.-H., Acta Phys. Pol, B9, 665, 677 A978).
345. Лукаш В. Н., Новиков И. Д., Старобинский А. Л.—ЖЭТФ, 1975, т. 69,
. с. 1484.
346. Lukash V. N., Novikov I. D., Starobinsky A. A., Zel'dovich Ya. В., Nuovo
Cimento, 35B, 293 A976).
347. Лукаш В. Н., Старобинский А. А. — ЖЭТФ, 1974, т. 66, с. 515.
348. Lynden-Bell ?>., Wood R., Mon Not. Roy. Astron. Soc, 136, 107 A967).
349. MacCallum M. A. #., Anisotropic and inhomogenous relativistic cosmolo-
cosmologies в книге: General Relativity: An Einstein Centenary Survey,
eds. S. W. Hawking, W. Israel, Cambridge: Cambridge University Press,

344 Литература
350. Мамаев С. Г., Мостепаненко В. М., Старобинский А. А. — ЖЭТФ, 1976,
т. 70, с. 1577.
351. Manoukian Е. В., Nuovo Cimento, 53A, 345 A979).
352. Martellini M., Sodano P., Vitiello G., Nuovo Cimento, 48A, 341 A978).
353. Mashhoon В., Phys. Rev. D, 8, 4297 A973).
354. Mattuck R. D., A Guide to Feynman Diagrams in the Many-Body Problem,
London: McGraw-Hill, 1967.
355. McKean H. P., Singer I. M., Journ. Diff. Geom., 1, 43 A967).
356. McNamara J. M., Proc. Roy. Soc. London, A358, 499 A978).
357. Meikle W. P. S., Nature (London), 269, 41 A977).
358. Melnikov V. N., Orlov S. V., Phys. Lett., 70A, 263 A979).
359. Milne E. A., Nature (London), 130, 9 A932).
360. Minakshlsundaram S., Pleijel A., Can. Journ. Math., 1, 242 A949).
361. Misner С W., Astrophys. Journ. 151, 431 A968).
362. Misner С W., Phys. Rev. Lett., 28, 994.A972).
363. Misner C. W., Thome K. S., Wheeler J. A., Gravitation, San Francisco:
Freeman, 1973. [Имеется перевод: Мизнер Ч. В., Торн К. С, Уилер Дж. А.
Гравитация, т. 1—III. — М.: Мир, 1977.]
364. Mohan G. в книге: Lectures in Theoretical Physics, Vol. XB, eds. A. O. Ba-
rut.-W. E. Britten, New York: Gordon and Breach, 1968.
365. Moore G. Т., Journ. Math. Phys. (USA), 9, 2679 A970).
366. Nambu Y., Prog. Theor. Phys., 5, 82 A950).
367. Nambu Y., Phys. Lett., 26B, 626 A966).
368. Nariai H., Prog. Theor. Phys., 46, 433, 776 A971).
369. Nariai #., Nuovo Cimento, 35B, 259 A976).
370. Nariai H., Prog. Theor. Phys., 57, 67 A977).
371. Nariai H., Prog. Theor. Phys., 58, 560 A977).
372. Nariai H., Prog. Theor. Phys., 58, 842 A977).
373. Nash C, Relativistic Quantum Fields, London: Academic Press, 1978.
374. Omero C, Percacci R., Nucl. Phys., B165, 351 A980).
375. Page D. N., Phys. Rev. D, 13, 198 A976).
376. Page D. N., Phys. Rev. D, 14, 3260 A976).
377. Page D. N., Phys. Rev. D, 16, 2402 A977).
378. Page D. N., Phys. Rev. Lett., 44, 301 A980).
379. Parker L, The Creation of Particles in an Expanding Universe, Ph. D. The-
Thesis, Harvard University (available from: University Microfilms Library
Service, Xerox Corp., Ann. Arbor, Michigan, USA), 1966.
380. Parker L, Phys. Rev. Lett., 21, 562 A968).
381. Parker L, Phys. Rev. 183, 1057 A969).
3.82. Parker L, Phys. Rev. D, 3, 346 A971).
383. Parker L, Phys. Rev. D., 5, 2905 A972).
384. Parker L, Phys. Rev. D, 7, 976 A973).
*385. Parker L, Phys. Rev. D, 12, 1519 A975).
386. Parker L, Nature (London), 261, 20 A976).
387. Parker L., The production of elementary particles by strong gravitational
fields в книге: Asymptotic Structure of Space-Time, eds. F. P. Esposito,
L. Witten, New York: Plenum, 1977.
388. Parker Ц., Aspects of quantum field theory in curved spacetime: effective-
action and energy — momentum tensor в книге: Recent Developments in
Gravitation, eds. S. Deser, M. Levy, New York: Plenum, 1979.
389. Parker L, Fulling S. A., Phys. Rev. D, 7, 2357 A973).
390. Parker L, Fulling S. A., Phys. Rev. D, 9, 341 A974).
391. Parker L, Fulling S. А., Ни В. L, Phys. Rev. D, 10, 3905 A974).
392. Parnovsky S. L, Phys. Lett., 73A, 153 A979).
393. Pauli W., Villars F., Rev. Mod. Phys., 21, 434 A949).
394. Penrose R., Conformal treatment of infinity в книге: Relativity, Groups
and Topology, eds. B. S. DeWitt, Q. DeWitt, New York: Gordon gnq|

Литература 345
Breach, 1964. [Имеется перевод: В сб.: Гравитация и топология, под ред.
Д. Д. Иваненко. — М.: Мир, 1966, с. 152.]
395. Penrose R., Proc. Roy. Soc. London, A284, 159 A965).
396. Penrose R., Riv. Nuovo Cimento, 1, 252 A969).
397. Penrose R., Singularities and time-asymmetry в книге: General Relativity:
An Einstein Centenary Survey, eds. S. W. Hawking, W. Israel, Cambridge:
Cambridge University Press. 1979.
398. Петров A. 3. Пространства Эйнштейна. — M.: ГИФМЛ, 1961.
399. Planck М. К. Е. L, Sitz. Deut. Akad. Wiss. Berlin, Kl. Math.-Phys. Tech,
440 A899).
400. Press W. H., Teukolsky S. A., Nature (London), 238, 211 A972).
401. Raine D. /., Winlove C. P., Phys. Rev. D, 12, 946 A975). '
402. Randjbar-Daemi S., Kay B. S., Kibble T. W. В., Phys. Lett., 91B, 417
A980).
403. Rees M. /., Nature (London), 266, 333 A977).
404. Rindler W., Am. Journ. Phys., 34, 1174 A966). Many features of this work
were anticipated in a paper by Max Born, Ann. Phys. (Leipzig), 30, 1
A909).
405. Rindler W., Essential Relativity, New York: Van Nostrand, 1969.
406. Roman P., Introduction to Quantum Field Theory, New York: Wiley, 1969.
407. Rowan D. I., Stephenson G., Journ. Phys. A: Gen. Phys., 9, 1631 A976).
408. Rumpf H., Phys. Lett., 61B, 272 A976).
409. Rumpf H., Nuovo Cimento, 35B, 321 A976).
410. Рузмайкина Т. В., Рузмайкин А. А. — ЖЭТФ, 1970, т. 57, с. 680.
411. Rzewuski ]., Field Theory, Vol. II, London: Iliffe Books, 1969.
412. Сахаров А. Д. — ДАН СССР, 1967, т. 177, с. 70.
413. Salam A., Weak and electromagnetic interactions в книге: Elementary Par-
Particle Theory, ed. N. Svartholm, Stockholm: Almquist, Forlag AB, p. 367,
1963.
414. Sanchez N.. Phys. Lett., 87B, 212 A979).
415. Scarf F. L, A soluble quantum field theory in-curved space в книге: Les
Theories Relativistes de la Gravitation, Paris: Centre National de Recher-
Recherche Scientifique, 1962.
416. Schafer G., Journ. Phys. A: Gen. Phys., 11, L179 A978).
417. Schafer G., Dehnen H., Astron. Astrophys., 54, 823 A977).
418. Schiff L. /., Quantum Mechanics, New York: McGraw-Hill, 1949. [Имеется
перевод: Шифф Л. И. Квантовая механика. — М.: ИЛ, 1959.]
419. Schomblond С, Spindel P., Ann. Inst. Henri Poincare, 25A, 67 A976).
420. Schrodinger E., Sitz. Preuss. Akad. Wiss., 105 A932).
421. Schrodinger E., Physica (Utrecht), 6, 899 (Ш?).
422. Schrodinger E., Expanding Universes, Cambridge: Cambridge University
Press, 1956.
423. Schweber S., An> Introduction to Relativistic Quantum Field Theory, New
York: Harper and Row, 1961. [Имеется перевод: Швебер С. Введение в
квантовую теорию поля. — М.: ИЛ, 1963.]
424. Schwinger /., Phys. Rev., 74, 1439 A948).
425. Schwinger /., Phys. Rev., 75, 651 A949).
426. Schwinger /., Phys. Rev., 76, 790 A949).
427. Schwinger I., Phys. Rev., 82, 664 A951).
428. Schwinger J., Proc. Nat. Acad. Sci. (USA), 37, 452 A951).
429. Sciama D. W., Vistas in Astron., 19, 385 A976).
430. Segal I. E. в книге: Applications of Mathematics to Problems in Theore-
Theoretical Physics, ed. F. Luciat, New York: Gordon and Breach, 1967. [Имеется
перевод: Сигал И. Е. Математические проблемы релятивистской физи-
физики.—М.: Мир, 1968.]
431. Sexl R. U., Urbantke H. К., Acta Phys. Austriaca, 26, 339 A967).
4.32. Sexl R. U., Urbantke H. K., Phys. Rev., 179, 1247 A969).

346 Литература
433. Shannon С, Weaver W., The Mathematical Theory of Communication,
Urbana: University of Illinois Press, 1949.
434. Shore G. M., Phys. Rev. D, 21, 2226 A980).
435. Shore G. M., An. Phys. (USA), 128, 376 A980).
436. Simpson M., Penrose R., Int. Journ. Theor. Phys., 7, 183 A973).
437. Sommerfield С Al.,-Ann. Phys. (USA), 84, 285 A974).
438. Sparnaay M. J., Physica (Utrecht), 24, 751 A958). .
439. Старобшский A. A. — ЖЭТФ, 1973, т. 64, с. 48.
440. Starobinsky A. A., Phys. Lett., 91B, 99 A980).
441. Старобшский А. А., Чу рилов С. М. — ЖЭТФ, 1973, т. 65, с. 3.
442. Stelle К. S., Phys. Rev. D, 16, 953 A977).
443. Stelle K. S., Gen. Relativ. Gravit., 9, 353 A978).
444. Stewartson K., Waechter R. Т., Proc Camb. Phil. Soc, 69, 353 A971).
445. Symanzik K., Commun. Math. Phys., 18, 48 A970). .
446. Synge I. L., Relativity. The General Theory, Amsterdam: North-Holland,
1960. [Имеется перевод: Синг Дж. Л. Общая теория относительности.—
М.: ИЛ, 1962.]
447. Tabor ?>.. Winterton R. H. S., Proc. Roy. Soc. London, A312, 435 A969).
448. Tagirov E. A., Ann. Phys. (USA), 76, 561 A973).
449. Takqhashi Y., Umezawa H., Nuovo Cimento, 6, 1324 A957).
450. Taylor J. C, Nuovo Cimento, 17, 695 A960).
451. Taylor J. C, Supp. Nuovo.Cimento, 1, 857 (953).
452. Taylor J. C, Gauge Theories of Weak Interactions, Cambridge: Cambridge
University Press, 1976.
453. Teukolsky S. A., Astrophys. Journ., 185, 635 A973).
454. Teukolsky S. A., Press W. H., Astrophys. Journ., 193, 443 A974).
455. Thlrring W. E., Ann. PUys. (USA), 3, 91 A958).
456. Thirring W. E., Nuovo Cimento, 9, 1007 A958).
457. '/ Hooft G., Nucl. Phys., B61, 455 A973).
458. 't Hooft G., Veltman M., Nucl. Phys., B44, 189 A972).
459. Tipler F,, Phys. Rev. Lett, 45, 949 A980).
460. Tolman R. C., Relativity, Thermodynamics, and Cosmology, Oxford: Cla-
Clarendon, 1934.
461. Tomonaga S., Prog. Theor. Phys., 1, 27 A946).
462. Toms D, J., Phys. Rev. D, 21, 928 A980).
463. Toms D. I., Phys. Rev. D, 21, 2805 A980). •
464. Toms D. J., Ann. Phys. (USA), 129, 334 A980).
465. Toms D. J., Phys. Lett., 77A, 303 A980).
466. Troost W., van Dam H., Phys. Lett, 71B, 149 A977).
467. Uhruh W. G., Phys. Rev. D, 10, 3194 A974).
468. Unruh W. G., Phys. Rev. D, 14, 870 A976). ,
469. Urbantke H. K., Nuovo Cimento, 63B, 203 A969).
470. Utiyama R., Phys. Rev., 125, 1727 A962).
471. Utiyama R., DeWitt B. S., Journ. Math. Phys. (USA), 3, 608 A962).
472. Valatin J. G., Proc. Roy. Soc. London, A222, 93 A954).
473. Valatin J. G., Proc. Roy. Soc. London A222, 228 A954).
-474. Valatin J. G., Proc. Roy. Soc. London, A225, 535 A954).*
475. van Nieuwenhuizen P., Freedman D. Z. (eds.), Supergravity, Amsterdam:
North-Holland, 1979.
476. Van Vleck, Proc. Nat. Acad. Sci. (USA), 14, 178 A928):
477. Vilenkin A., Nuovo Cimento, 44A, 441 A978).
478. Воловин И. В., Загребное В. А., Фролов В. П. — ТМФ, 1977, т. 33, с-а
479. Waechter R. Т., Proc. Camb. Phil. Soc, 72, 439 A972).
480. Wald R. M., Commun. Math. Phys., 45, 9 A975),
481. Wald R. M., Phys. Rev. D, 13, 3176 A976).
482. Wald R. M., Commun. Math. Phys., 54, 1 A977).
483. Wald R. M., Phys. Rev. D, 17, 1477 A978).

Литература 347
484. WaldR. M., Ann. Phys. (USA), 110, 472 A978).
485. Wald R. M., Ann. Phys.. (USA), 118, 490 A979).
486. Wald R. M., Commun. Math. Phys., 70, 221 A979).
487. Wald R. M., Phys. Rev. D, 21, 2742 A980).
488. Wald R. M., Ramaswamy S., Phys. Rev. D, 21, 2736 A980).
489. Wehrl A., Rev. Mod. Phys. 50, 221 A978).
490. Weinberg S., Phys. Rev., 133, B1318. A964).
491. Weinberg S., Phys. Rev., 134, B882 A964).
492. Weinberg S., The quantum theory of massless particles в книге: Lectures
on Particles and Field Theory. Vol. II, eds. K. A. Johnson and others,
Englewood Cliffs, N. J.: Prentice-Hall, 1964.
493 .Weinberg S., Phys. Rev. Lett, 19, 1264 A967).
494. Weinberg S., Gravitation and Cosmology: Principles and Applications of
the General Theory of Relativity, New York: Wiley, 1972. [Имеется пере-
перевод: Вейиберг С. Гравитация и космология. — М.: Мир, 1975.]
495. Weinberg S., Phys. Rev. D, 9, 3357 A974).
496. Wichmann E. H., Selected Topics in the Theory of Particles and Fields,
Copenhagen: Nordita, 1962.
497. Wick G. C, Phys. Rev., 80, 268 A950).
498. Зельдович Я. Б. — Письма в ЖЭТФ, 1970, т. 12, с. 443.
499. Зельдович Я- б.— Письма в ЖЭТФ, 1971, т. 14, с. 270.
500. Зельдович Я. Б. —ЖЭТФ, 1972, т. 62, с. 2076.
501. Зельдович Я. Б., Новиков И. Д., Старобинский А. Л.— ЖЭТФ, 1974,
т. 66, с. 1897. "
502. Zel'dovich Ya. В., Pitaevsky L. P., Commun. Math. Phys., 23, 185 A971).
503. Зельдович Я- Б., Старобинский А. Л.—ЖЭТФ, 1971, т. 61, с. 2161.
504. Зельдович Я. Б., Старобинский А. Л.— Письма в ЖЭТФ, 1977, т. 26,
с. 373.
505. Zurek W. H., Phys. Lett., 77A, 399 A980).
КОНФОРМНЫЕ АНОМАЛИИ
506. Adler S. L, Lieberman J., Ng Y. J., Ann. Phys. (USA), 106, 279 A977).
507. Bernard C, Duncan A., Ann. Phys. (USA), 107, 201 A977).
508. Brown L. S., Phys. Rev. D, 15, 1469 A977).
509. Brown L. S., Cassidy J. P., Phys. Rev. D, 15, 2810 A977).
510. Brown L. S., Cassidy J. P., Phys. Rev. D, 16, 1712 A977).
511. Bunch T. S., Journ. Phys., AH, 603 A978).
512. Bunch T. S., Journ. Phys., A12, 517 A979).
513. Capper D. M., Duff M. J., Nuovo Cimento, A23, 173 A974).
514. Capper D. M., Duff M. J., Phys. Lett., 53A, 361 A975).
515. Christensen S. M., Phys. Rev. D, 14, 2490 A976).
516. Christensen S. M., Phys. Rev. D, 17, 946 A978).
517. Christensen S. M., Duff M. J., Phys. Lett., 76B, 571 A978).
518. Christensen S. M., Duff M. /.,-Nucl. Phys., B146, 11 A978).
519. Christensen S. M., Fulling S. A., Phys. Rev., D, 15, 2088 A977).
520. Critchley R., Phys. Rev. D, 18, 1849 A978).
521. Critchley R., Phys. Lett., 78B, 410 A978).
522. Davies P. C. W., Stress tensor calculations and conformal anomalies в
книге: Eighth Texas Symposium on Relativistic Astrophysics, ed. M. D. Pa-
« pagiannis, New York: New York Academy of Sciences, 1977.
523. Davies P. С W., Fulling S. A., Proa. Roy. Soc. London, A354, 59 A977).
524. Davies P. C. W., Fulling S. A., Unruh W. G., Phys. Rev. D, 13, 2720
A976).
525. Deser S., Duff M. J., lsham С J., Nucl. Phys. Bill, 45 A976).
526. Dowker L S., Critchley R., Phys. Rev. D, 13, 3224 A976).
527. Dowker J. S., Critchley R., Phys. Rev. D, 16, 3390 A977).

348 Литература
528. Duncan A., Phys. Lett., 66B, 170 A977).
529. Duff M. J., Nucl. Phys., B125, 334 A978).
530. Eguchi Т., Freund P. G. O., Phys. Rev. Lett., 37, 125 A976).
531. Fradkin E. S., Vilkovisky G. A., Phys. Lett., 73B, 209 A978).
632. Hawking S. W., Commun. Math. Phys., 55, 133 A977).
533. Ни В. L, Phys. Rev. D, 18, 4460 A978).
534. Ни В. L, Phys. Lett, 71A, 169 A979).
535. Perry M. I., Nucl. Phys., B143, 114 A978).
536. Tsao H. S., Phys. Lett., 68B, 79 A977).
537. Wald R. M., Commun. Math. Phys., 54, 1 A977).
538. Wald R. M., Ann. Phys. (USA), 110, 472 A978).
•539. Wald R. M), Phys. Rev. D, 17, 1477 A978).
540. Vilenkin A., Nuovo Cimento, 44A, 441 A978)
ПРОСТРАНСТВО де СИТТЕРА
541. Adler S. L, Phys. Rev. D, 6, 3445 A972).
542. Adler S. L, Phys. Rev. D, 8, 2400 A973).
543. Birrell N. D., Proc. Roy, Soc. London, A361, 513 A978).
544. Birrell N. D., Journ. Phys. A: Gen. Phys., 12, 337 A979).
545. Borner G., Durr H. P., Nuovo Cimento, 64, 669 A969).
546. Bunch T. S., Davies P. С W,. Proc. Roy. Soc. London, 360, 117 A978).
547. Candelas P., Raine D. J., Phys Rev. D, 12, 965 A975).
548. Chernikov N. A., Tagirov E. A., Ann. Inst. Henri Poincare, 9A, 109 A968).
549. Dtrac P. A. M., Ann. Math., 36, 657 A935).
550. Dowker I. S, Critehley R., Phys. Rev. D, 13, 224 A976).
551. Dowker I. S., Gritchley R., Phys. Rev. D, 13, 322 A976).
552. Drummond I. T., Nucl. Phys. B94, 115 A975).
553. Drummond l. Т., Shore G. M., Phys. Rev. D, 19, П34 A979).
554. Figari R., Hoegh-Krohn R., Nappi C, Commun. Math. Phys., 44, 265
A975).
555. Fronsdal C, Rev. Mod. Phys., 37, 221 A965).
556. Fronsdal C, Phys. Rev. D, 10, 589 A974).
557. Fronsdal C, Haugen R. В., Phys. Rev. D, 12, 3810 A975).
558. Fulling S. A., Ph Thesis, Princeton University. 1972.
559. Gehenian J., Schomblond C, Acad. Roy. de Belgique, Bull. Cl. des Sciences,
54, 1147 A968).
560. Gibbons G. W., Hawking S. W., Phys. Rev. D, 15, 2738 A977).
561. 'Grensing G., Journ. Phys. A: Gen. Phys., 10, 1687 A977).
562. Lohiya D., Journ. Phys. A: Gen. Phys., 11, 1335 A978).
563. Lohiya D., Panchapakesan N., Journ. Phys. A: Gen. Phys., 11, 1963 A978).
564. Lohiya D., Panchapakesan N.. Journ. Phys. A: Gen. Phys., 12, 533 (Ш9).
565. Nachtmann O., Commun. Math. Phys. 6, 1 A967).
566. Rumpf H., Gen. Relativ. Gravit, 10, 647 A979).
567. Schomblond C, Spindel P., Ann. Inst. Henri Poincare, 25A, 67 A976).
568. Shore G. M., Ann. Phys. (USA), 117, 89 A979).
569. Shore G. M., Phys. Rev. D, 21, 2226 A980).
570. Tagirov E. A., Ann. Phys. (USA), 76, 561 A973).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
СУПЕРГРАВИТАЦИЯ
571*. van Nieuwenhuizen P. — Phys. Rep., 1981, v. 68C, p. 189.
572*. Supergravity'81. Lectures at 1981 Triest Sch. on Supergravity. Eds. Fer-
rara S., Taylor J. G. — Cambridge, 1982.

Литература 349
573*. Superspace and Supergravity. Eds. Hawking S. W., Ro?ek M. — Cam-
Cambridge, 1981.
574*. Quantum structure of space and time. Proc. of the Nuffield Workshop,
3—21 Aug. 1981. Eds. Duff M. J., Isham С J. — Cambridge, 1982.
575*. Квантовая гравитация. (Труды II Межд семинара по квантовой грави-
гравитации. Москва, 13—15 окт. 1981 г.). —М.': ИЯИ, 1983.
КВАДРАТИЧНЫЕ ТЕОРИИ
576*. Julve Л, Tonin M. — Nuovo Cimento, 1978, vol. 46B, p. 137.
577*. Salam A., Strathdee /. —Phys. Rev., 1978, v. 18D, p. 4480.
578*. Fradkin E. S., Tseytlin A. A. — Phys. Lett., 1981, v. 104B, p. 377; 1982,
, v. HOB, p. 117.
ИНДУЦИРОВАННАЯ ГРАВИТАЦИЯ
579*. Adler S. — Phys. Rev. Lett, 1980, v. 44, p. 1567; Phys. Lett., 1980,
v. 95B, p. 241; Rev. Mod. Phys.,' 1982, v. 54, p. 729.
580*. Hasslacher В., Mottola E. — Phys. Lett., 1980, v. 95B, p; 237; 1981,
v. 99B, p. 221.
581*. KhuriN. N. — Phys. Rev. Lett., 1982, v. 49, p 513.
582*. Zee A. — Phys. Rev. Lett., 1979, v. 42, p. 417; Phys. Rev., 1981, v. 23D,
p. 858; Phys. Lett., 1982, p. 109B, p 183.
ОБЩИЕ ВОПРОСЫ КВАНТОВАНИЯ В ИСКРИВЛЕННОМ
ПРОСТРАНСТВЕ-ВРЕМЕНИ
583*. Davies Р. С. V., Fang J. — Proc. Roy. Soc. Lond., 1982, v. 381A, p. 469.
584*. Ceccatto H., Foussats A., Giacomini H.. Zandron 0. — Phys. Rev., 1981,
v. 24D, p. 2576.
585*. Ikuo Ichinose. — Phys. Rev., 1982, v 25D, p. 365
586*. Kay B. S. — Lecture notes in Mathematics, 1982, v. 905, p. 272.
587*. Martellini M. — Nuovo Cimento, 1982, v. 67A, p. 305
588*. Харьков А. А.— ЖЭТФ, 1981, т. 80, с. 19. Яд. физ., 1982, т. 35, с. 1350;
Phys. Lett., 1982, v 88A, p. 109
ЭФФЕКТ КАЗИМИРА, ДВИЖУЩИЕСЯ ЗЕРКАЛА
589*. Candelas P. Confining the Aether. В книге: Quantum Electrodynamics
of Strong Fields. Ed. Greiner W. — Nato Adv. Study Inst., 1983, v. 80B,
p. 817.
590*. Nugayev R. M. — Phys. Lett., 1982, v. 91A, p. 216.
561*. Ford L H., Vilenkin A., Qauntum radiation by moving mirrors, Tufts
Univ. Preprint TUTP-82-1.
592*. Walker W. R., Davies P. С W. — Joum. of Phys., 1982, v. 15A, p. 474.
* ФУНКЦИИ ГРИНА
593*. Beckenstein J. D., Parker L. — Phys Rev., 1981, v. 23D p. 2850.
594*. Gal'tsov D. V. — Joum. of Phys., 1982, v. 15A p. 3737.
.595*. Fulling S. A., Narcowich F /., Wald R. M. —Ann of Phys (USA) 1981,
v. 136, p. 243.
596*. Gilkey P. В. —Joum. Diff. geom., 1975, v. 10, p. 601.

350 Литература.
ПОЛЯРИЗАЦИЯ ВАКУУМА
И КВАНТОВЫЕ ПРОЦЕССЫ В ЧЕРНЫХ ДЫРАХ
597*. Bardeen I. Н. — Phys. Rev. Lett., 1981, v. 46, p. 382.
598*. Balbinot R., Bergamini R.— Lett. Nuovo Cim., 1981, v. 30, p. 13. J
599*. Candelas P., Chrzanowski P., Howard K- W. — Phys. Rev., 1981, v. 24ЕЁ
p. 297. ' 1
600*. Dolgov A. D. — Phys. Rev., 1981, v. 24D, p. 1042. ?.
601*. DetweilerS. —Phys. Rev., 1980, v. 22D, p. 2323. .<
602*. Fawcett M. S., Whiting B. F., Spontaneons symmetry breaking near S
black hole, в книге Quantum structure of space and time, Cambridge;
1982. '
603*. Гальцов Д. В., Померанцева Г. В., Чижов Г. А. ¦— Изв. высш. уч. зай4
сер. физика, 1983, № 8, с. 75.
604*. Frolov V. P., Zelnikov A. /. — Phys. Lett., 1982, v. 115В, p. 372. . г
605*. Gal'tsov D. V., Chizhov G. A., Pomeranlseva G. V. — Phys. Lett., 1984,
606*. Тайна А. Б., Чижов Г. А. —Изв. высш. уч. зав., сер. физика, 1980, № 4,
с. 120.
607*. Hiscock W. Л. —Phys. Rev., 1981, v. 23D, p. 2813; 2823.
608*. Hawking S. L— Comm. Math. Phys., 1981, v 80, p. 421.
609*. Elster Т. — Journ. Phys., 1983, v. 16A, p. 985.
610*: Kofman L A. — Phys. Lett., 1982, v. 87A, p. 281.
611*. Page D. — Phys. Rev., 1981, v. 25D, p. 1499; Gen. Rel. and Grav., 1981,;
v. 13, p. 1117.
612*. Piran Tsvi, Wald R. M. — Phys. Lett., 1982, v. 80A, p. 9.
613*. Elster Г-Phys. Lett., 1982, v 89A, p. 125.
614*. Тернов И. М., Халилов В. Р., Чижов Г. А., Гаина А. Б. — Изв. высш;
уч. зав., сер. физика, 1978, № 9, с. 109.
6J5*. Тернов И. М., Гаина, А. Б., Чижов Г. А.—Изв. высш. уч. зав., сер.
физика, 1980, № 8, с. 56.
616*. Zouros Т., Eardley D. M. — Ann. of Phys. (USA), 1979, v. 118, p. 139.
ТЕРМОДИНАМИКА
617*. Curir A^Gen. Rev. and Grav., 1981, v. 13, p. 417.
618*. Гальцов Д. В. Симметрия SUB,1) уравнений Эйнштейна — Максвелла
и термодинамика черных дыр в магнитном поле. В книге: Теоретико-
групповые методы в физике. — М.: Наука, 1980, с. 183.
6!9*. Kasya M. — Phys. Lett., 1982, v. 115В, p. 104.
620*. Magnon-Ashtekar Л.— Journ. Math. Phys., 1981, v. 22, p. 2012.
621*. Мамаев С. Г., Трунов Н. Я.— Яд. физ., 1981, т. 34, с. 1142; Изв. высш.
уч. зав., сер. физика, 1982, № 5, с. 82.
622*. Sciama D, W., Candelas P., Deutsch D. — Adv. Phys., 1981, v. 30, p. 327.
623*. Unruh №., Wald R. M. — Phys. Rev., 1982, v. 25D, p. 942.
624*. Wald R. M. — Phys. Rev., 1979, V..20D, p. 1271.
625*. Zannias Т., Israel W. — Phys. Lett., 1981, v. 86A, p. 82.
КВАНТОВЫЕ ЭФФЕКТЫ В КОСМОЛОГИИ
626*. Бейлин В. А., Верешков Г. М., Гришкан Ю. С, Нестеренко В. А., Пол-
Полтавцев Н. А. — ЖЭТФ, 1980,. т. 68, с. 2081.
627*. Верешков Г. М., Гришкан Ю. С, Иванов С. В., Нестеренко В. А., Пол-
Полтавцев Н. Л. —ДАН СССР, 1976, т. 231, с. 578; ЖЭТФ, 1977, т! 73,
с. 1985. •¦ ' .
628*. Верешков Г. М., Гришкан Ю. С, Иванов С. В., Полтавцев Н. А. —
ЖЭТФ, 1981, т. 80, с. 1665.
629*. Гурович В. Ц., Старобинский А. А —ЖЭТФ, 1979, т. 77, с. 1683.

Литература 351
630*. Guth А. Я. —Phys. Rev., 1981, v. 23D. p. 347.
631*. Dolgov A. D., Zel'dovich Y. В. —Rev. Mod. Phys., 1981, v. 53, p. 1.
632*. Зельдович Я. Б. — Письма в ЖЭТФ, 1981, т. 7, с. 579.
6S3*. Horowitz G. Т., Wald R. М.— Phys. Rev., 1982, v. 25D, с. 3408.
634*. My ханов В. Ф., Чибисов Г. В. — Письма в ЖЭТФ, 1981, т. 33, с. 549.
635*. Старобинский А. А. — Письма' в ЖЭТФ, 1981, т. 34, с. 460.
636*. Старобинский.А. Л.— Письма в ЖЭТФ, 1983, т.'37, с. 55.
637*. Станюкович К- П., Мельников В. Н. Гидродинамика, поля и константы
в теории гравитации. — М.: Эиергоатомиздат, 1983, с. 256.
638*. Пономарев В. Н., Барвинский А. О. — Теор. и мат. физ., 1978, т. 38,
с. 224.
ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
В ИСКРИВЛЕННОМ ПРОСТРАНСТВЕ-ВРЕМЕНИ
639*. Bunch Т. S. — Gen. Rel. and Grav., 1981, v. 13, p. 711.
640*. Bunch T. S. — Ann. Phys. (USA), 1981, v. 131, p. 118.
641*. Gal'tsov D. V., Petukbov V. I. Quantum Electrodynamics in Plane Gravi-
Gravitational wave. GR-.10 Abstracts, Padova 1983; Гальцов Д. В., Грац Ю. В.,
Петухов В. И. Излучение гравитационных волн электродинамическими
системами. М.: изд. МГУ, 1984, гл. 7.
642*. Долгов А. Д. —Письма в ЖЭТФ, 1980, т. 32, с. 673.
643*. Denardo G., Spallucci E. — Lett. Nuovo Cim., 1982, v. 33, p. 336; 1982,
v. 34, p. 284; Nuovo Cim., 1981, v 64A, p. 27.
644*. Drummond I. Т., Hathrell S. 1. — Phys. Rev., 1980, v. 22D, p. 342.
645*. Isham С /. — Phys. Lett, 1981, v. 102B, p. 251; Journ. Phys., 1981,
v. 14A, p. 2943.
64.6*. Hathrell S. I. —Ann. of Phys. (USA), 1982, v. 139, p. 136.
647*. Nelson B. L, Panangaden P. — Phys. Rev., 1982, v. 25D, p. 1019.
648*. Panangaden P. — Phys. Rev., 1981, v. 23D, p. 1735.
649*. Parker L, Pimentel L O. —Phys: Rev., 1982, v. 25D, p. 3180.
650*. Spokoiny B. L. — Phys. Lett., 1982, v. 87A, p. 211.
651*. Toms D. /. — Phys. Rev., 1982, v. 26D, p. 2713.
ГОЛЫЕ СИНГУЛЯРНОСТИ, КРУЧЕНИЕ
652*. Hiscock W. A., Williams L. G., Eardley D. M. — Phys. Rev., 1982, v. 26D,
p. 751.
653*. lvanenko D. D., Sardanshvili G. A. — Lett. Nuovo Cim., 1981, v. 30,
p. 220.
654*. Nieh H. Т., Yan M. L. — Ann. of Phys. (USA), 1982, v. 138, p. 237.
655*. Парновский С. Л. —ЖЭТФ, 1981, т. 80, с. 1261; Gen. Rel. and Grav.,
1981, v. 13, p. 853.
656*. Пономарев В. Н., Пронин П. И. -= Теор, и матем. физика, 1979, т, 39,
с. 425.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адамара функция 28, 29, 228, 229
Адиабатическая регуляризация см.
Регуляризация
Адиабатические состояния 17, 43, 136
Адиабатический вакуум 69, 76, 77,
84, 135, 136, 144, 151
— инвариант 72, 76
— порядок 73—77, 82—85, 134, 135,
151, 169, 170, 200, 204, 209, 215,
232, 243, 256
Адиабатическое выключение 57, 59,
64, 112, 305
— приближение 76
— разложение 80—86, 95, 167, 200,
215, 216
Аксиально-векторная аномалия 185
Аналитическое продолжение 137, 158,
202, 203, 260
Анизотропная космология 126, 149,
251, 257, 258
Аномалии см. Конформные аномалии,
Аксиально-векторная аномалия
Антикоммутаторы 26, 28, 40
Антнпернодические граничные усло-
условия 98, 335. См. такжъ Скручен-
Скрученные поля
Белые дыры 48, 303
Бианки I пространства 14Э
Бн-вектор 205
Бискаляр 204, 248
Бн-спинор 95
Боголюбова коэффициенты 52, 53,
68, 76, 115-117, 153, 154, 260,
263, 269, 314, 329
— преобразования 52, 65, 115, 123,
124, 133, 143, 240, 269, 313, 329,
330
Бозе статистика 21
Бозоны 9, 273, 282
Больцмана постоянная 32
большой взрыв 13?
Вакуумное состояние 23
адиабатическое определние 69—
80, 132
конформное 86—88, 132
in- и out- 36, 260, 263
Взаимодействующие поля 13, 14, 17,
18, 273, 304—335
Гамильтониан 21, 22, 26, 32, 312
—. диагонализацня 80
Гаусса — Бонна теорема 169
Гейзенберга представление 21, 313,
328
— соотношение неопределенностей 70
Гильберта пространство 21
Глобальная гиперболичность 35, 43.
50
Горизонт событий 46, 48, 119, 120,
145, 264, 265, 267, 274
Гравитационная постоянная 161, 169,
321
Гравитация 9, 10, 159—161
— квантовая см. Квантовая гравита-
гравитация
Гравитоны 10, 13, 89, 248, 272
Границы 97, 105—110, 233—236, 309
Грина функции 18, 28—35, 80—84,
102—104, 299, 300
для взаимодействующих полей
308—310
¦ тепловые (термодинамические)
18, 33—35, 98, 99, 109, 148, 288
усеченные 316
Движущиеся зеркала 97, ПО—117,
240, 294
Де Витта — Швингера представление
43, 83, 85, 164—166, 173, 177,
181, 199
разложение 95, 159, 178, 179,
182, 200, 211, 243, 244, 246
Де Ситтера группа. 51, 137, 140, 145,
20Q

Предметный указатель
353
Де Сип ера пространство 126, 137—
145, 147, 148, 194, 196, 200, 242,
291, 302, 320
Действие 12, 13, 19, 25, 26, 36, 38,
50, 93, 162, 163, 213, 214, 235,
300
— эффективное 158, 162, 165, 166,
192, 214, 233—235, 251, 252, 311,
319-325
Детекторы частиц 54—66, 293—295
Дирака матрицы 25, 91
— поле 26, 91
— уравнение 25, 93
Дираковски сопряженный спинор 25
Духовые поля 28, 40, 94, 179, 188
Импульс 21, 23, 26
Иистаитоиы 3Q2
Интегралы по " траекториям 18, 28,
35—41, 300, 301, 314,
Казимира эффект 97, 109, ПО, 334
Калибровочные преобразования 27,
38, 39
Квантовая гравитация 9—17, 225, 236,
283
— электродинамика (КЭД) 10, 12,
Квантовые черные дыры 261
Керра черная дыра 273
— Ньюмена черная дыра 285, 300
Киллинга векторы 49, 51—53, 121,
130, 137, 145, 147, 293, 300
Ковариантность общая 51
Коллапс звезды 46, 113, 261—275,277,
292, 293
Коммутаторы 28, 34, 35
Коммутационные соотношения 20, 35,
50, 90, 290
Конформная инвариантность 69, 87,
89, 132, 181—197, 212, 325—327,
332
— связь (скалярного поля) 50, 56, 67,
131
Конформное время 66, 89, 133, 160
Конформно-плоское простраиство-вре-
мя 56, 69, 87, 89, 190-192
Конформно-тривиальная ситуация 69,
87, 189, 199, 246
„Конформные аномалии 16, 95, 181—
197, 245, 297
— диаграммы (Пенроуза) 42, 44—48,
120, 146, 268, 284, 298
— преобразования 42, 44, 45, 47, 87,
88, 118, 121, 125, 148, 149, 181—
185
Конформный вакуум 43, 86—89, 145—
148, 191, 209, 239
— вектор Киллинга 49, 87, 132, 147,
148, 196, 245
Космическая цензура 274, 303
Космологическая постоянная 12, 161,
169, 224, 321
Крускала координаты 46, 47, 280, 296
— многообразие 48, 49, 292
Лагранжиан для детектора частиц 57
— скалярного поля 19, 49, 93, 96,
107, 305, 317
— спинориого поля 25, 93, 96
— электромагнитного поля 26, 93, 94
— эффективный 165, 199, 217
Ландау калибровка 27, 39, 40
Лоренца группы представление 90—
92, 187, 188
— преобразования 89—92, 137
ЛСЦ метод 308, 314
Максвелла уравнения 26
S-матрица 53, 305—307
Матрица плотности 33, 291, 292
Милна вселенная 122, 132, 133, 140,
152, 252
Минковского пространство 15, 16,
18—41, 44—47, 56, 89, 97—99
Нейтрино 89, 107
Нормальное упорядочение 12, 24, 226
Нормировка 19, 25, 50, 121, 127
Обратное воздействие (квантовых эф-
эффектов) 126, 149, 157, 225, 282,
283
— рассеяние 261, 270, 271, 278
Общая теория относительности 9, И,
51
Одиопетлевое приближение 11, 12,
161, 259
Оператор числа частиц 23, 32, 52
Паули — Вилларса регулиризацня см.
Регуляризация
Перенормировка 12—14, 24, 36, 43,
104, 135, 157—199, 203, 317
Плоское простраиство-время 97
Причинность 226
Производящий функционал 36, 38,
101, 102, 309
Пуанкаре инвариантность 51, 55, 58,
137, 140, 308, 321

354
Предметный указатель
Размерное продолжение 24, 158. См.
также Регуляризация
Расходимости 12, 13, 23, 99, 160
Расходимость инфракрасная 103, 182
— поверхностная 106
— ультрафиолетовая 99, 182
Регуляризация 17, 43, 81, 97, 157, 158
— адиабатическая 158, 216—219
— методом дзета-функции 172—175,
185, 189, 202
— Паули — Вилларса 219—222
— размерная 158, 219, 317
Римана многообразие 300, 301
Риндлера координаты 119, 121
— пространство 117 124, 132,
146—149
Робертсона — Уокера вселенная 64,
66, 69, 71, 72, 126—130
Рождение пар 272, 275, 285
— частиц 42, 56, 69—72
— — движущимися границами 97,
112; Ш
черными дырами см. Черные
дыры
Сверхизлучение 274
Скалярное поле 18, 19, 28, 49—51, 90
— — в искривленном пространстве
49—51, 87. 93
— произведение 19, 20, 26, 50, 65
Скрученные поля 98, 101, 102, 203,
209, 335
След тензора энергии-импульса 107,
200
Спин 1В, 25, 26, 89—95
Спинорное поле 25, 30, 101, 102, 191
Спиноры 25
Статистическая сумма 32, 33, 301
Супергравитация 9
Термодинамика 256, 272, 274, 300
Тирринга модель 332
Томонага — Швингера уравнение 312
Топология (нетривиальная) 97, 98,
118, 147, 148, 159
Угловой момент 26, 90
Уничтожения и рождения операторы
23—26, 99
Ускоренный наблюдатель (детектор)
46, 48, 55, 59—62, 98, 117, 124,
125 -
Фейнмана .калибровка 27, 31
— пропагатор 28, 29, 31, 37 %
Фермиоиы 9, 272, 298
Фока базис 21
Фонового поля метод 11
Фотон 27, 89, 285 '¦'¦.
Фридмана модель 78 ' '!
Функция отклика (детектора) 58, 62,^
141, 294
Хокинга теорема 286
— эффект 14, 15, 125, 331, 332. См.
также Черные дыры
Частицы в искривленном простран-
пространстве 42, 54, 55, 72
Черные дыры 14, 47, 48, 98, 113, 256,
261—303
вечные 287—294
взрыв 283, 284
— — вращающиеся 273, 288, 299
заряженные 274, 275, 288, 298
излучение 271, 272, 282
испарение 240, 281—284 :
квантовые 261—303
сверхизлучение 274, 283, 285
температура 269, 274, 282
термодинамика 285, 286
— — энтропия 286, 287, 302
Шварцшильда пространство-время 46,
262, 263, 280, 296
Швингера вариационный принцип 163
Эйлера — Пуанкаре характеристика
148
Эйнштейна вселенная 56, 130, 131,
142, 194, 202, 203
— уравнения 11, 14, 46, 49, 161, 162,
198, 211, 283
Электромагнитное поле 26—28, 38,
88, 93, 105, 109
Энергни-импульса тензор 16, 18, 95,
135, 157, 198, 237
Энергия 21—23
— вакуума 12, 13, 23, 24, 99, 101,
106
— отрицательная 100, 240, 241
Энтропия 98, 110, 127
— в космологии 257, 258
— черной дыры 286, 287, 302
Эффективное действие см. Действие
Эффективный лагранжиан см. Лаг-
Лагранжиан

ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 7
Глава 1. ВВЕДЕНИЕ . 9
Глава 2. КВАНТОВАЯ ТЕОРИЯ ПОЛЯ В ПРОСТРАНСТВЕ МИН-
КОВСКОГО -18
2.1. Скалярное поле . . . 18
2.2. Квантование ....:. 20
2.3. Энергия и импульс 21
2.4. Расходимость энергии вакуума 23
2.5. Дираковское спинорное поле 25
2.6. Электромагнитное поле , 26
2.7. Функции Грина 28
2.8. Квантование методом интегрирования по траекториям . . 35
Глава 3. КВАНТОВАЯ ТЕОРИЯ ПОЛЯ В ИСКРИВЛЕННОМ" ПРОСТ-
ПРОСТРАНСТВЕ-ВРЕМЕНИ .... 42
3.1. Структура пространства-времени 43
3.2. Квантование скалярного поля . 49
3.3. Смысл понятия частиц: детекторы частиц 54
3.4. Космологическое рождение частиц: простой пример .... 66
3.5. Адиабатический вакуум 69
3.6. Адиабатическое разложение функций Грина 80
3.7. Конформный вакуум 86
3.8. Поля произвольного спина в искривленном пространстве-
времени 89
Глава 4. ПРИМЕРЫ ДЛЯ ПЛОСКОГО ПРОСТРАНСТВА-ВРЕМЕНИ 97.
4.1. Двумерное цилиндрическое пространство-время 98
4.2. Использование функций Грина 102
4.3. Влияние границ 105
4.4. Движущиеся зеркала НО
4.5. Квантовая теория поля в пространстве Риидлера . . . .117
Глава 5. ПРИМЕРЫ ДЛЯ ИСКРИВЛЕННОГО ПРОСТРАНСТВА-
ВРЕМЕНИ 126
5.1. Пространства, Робертсона — Уокера 127
5.2. Статические пространства Робертсона —Уокера 130
5.3. Вселенная Милиа 132
5.4. Пространство де Ситтера 137
5.5. Классификация состояний конформного вакуума .... 145
5.6. Пространства типа Бианки I и теория возмущений .... 149

356 Оглавление
Глава 6. ПЕРЕНОРМИРОВКА ТЕНЗОРА ЭНЕРГИИ-ИМПУЛЬСА . . 15?J
6.1. Основная проблема . 1Щ
6.2. Перенормировка в эффективном действии 16$
6.3. Конформные аномалии и безмассовый случай \Щ
6.4. Расчет перенормированного тензора энергии-импульса . . . 19#
6.5. Другие методы регуляризации 215;
6.6. Физический смысл тензора энергни-импульса 224J
Глава 7. ПРИМЕНЕНИЯ МЕТОДОВ ПЕРЕНОРМИРОВОК .... 237:
7.1. Двумерные модели 237
7.2. Модели Робертсона — Уокера 244
7.3. Расчет тензора энергии-импульса методом теории возмуще-
возмущений 2Щ
7.4. Приложения к космологии 25в
Глава 8. КВАНТОВЫЕ. ЧЕРНЫЕ ДЫРЫ 261
8.1. Рождение частиц коллапсирующим сферическим телом . . 262
8.2. Физические аспекты испускания частиц черными дырами 276
8.3. Вечные черные дыры 28/
8.4. Исследование тензора энергии-импульса 295
8.5. Дальнейшее развитие теории 29&
Глава 9. ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ 304
9.1. Расчет матричных элементов S-матрицы 304
9.2. Скалярное поле с самодействием в искривленном простран-
пространстве-времени 314
9.3. Рождение частиц за счет взаимодействия 327
9.4. Другие эффекты взаимодействия 331
Литература 336
Предметный указатель ¦ 352

УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании кни-
книги, ее оформлении, качестве перевода и
другие просим присылать по адресу:
129820, Москва, И-ПО, ГСП, 1-й Риж-
Рижский пер., д. 2, изд-во «Мир».
Биррелл Н., ДевиеП.
КВАНТОВАННЫЕ ПОЛЯ В ИСКРИВЛЕННОМ
ПРОСТРАНСТВЕ-ВРЕМЕНИ
Ст. научн. редактор Н. Телеснин
Мл. научн. редакторы Г. Сорокина, В. Цлаф
Художник Е. Волков Художественный редактор В. Шаповалов
Технический редактор И. Кренделева Корректор С. Денисова
ИБ № 3745
Сдано в набор 18.05.83. Подписано к печати 09.01.84.
Формат бОхЭО'/щ. Бумага'.типографская № 2. Бум л. 11,25.
Гарнитура латинская. Печать высокая.
Усл. печ. л. 22,5. Усл. кр.-отт. 22,5. Уч.-изд. л. 21,89.
Изд. № 2/2715. Тираж 4400 экз. Зак. 674. Цеиа 3 р. 60 к.
ИЗДАТЕЛЬСТВО «МИР» Москва. 1-й Рижский пер., 2.
Ленинградская типография Mi 2 головное предприятие ордена Трудового
Красного Знамени Ленинградского объединения «Техническая книга»
им. Евгении Соколовой Союзполиграфпрома при Государственном комитете
СССР по делам издательств, полиграфии и книжной торговли.
198052, г. Ленинград, Л-52, Измайловский проспект, 29.