Планиметрия. Пособие для углубленного изучения математики - Бутузов В.Ф., Кадомцев С.Б., Шестаков С.А., Юдина И.И., Позняк Э.Г.

Автор: Бутузов В.Ф. Кадомцев С.Б. Шестаков С.А. Юдина И.И. Позняк Э.Г.

Теги: геометрия топология математика планиметрия общая геометрия физматлит

ISBN: 5-9221-0635-Х

Год: 2005

Похожие

Дидактические материалы по геометрии для 8 класса с углубленным изучением математики

ЕГЭ 2019. Математика. Геометрия. Планиметрия

Геометрия, пробный учебник, 6 класс.

Геометрия. 9 класс.

Текст

УДК 514.1 Книга подготовлена под научным руководством
ББК 22.151 академика РАН В. А. Садовничего в рамках прог-
прогул 13 раммы «МГУ — школе»
Планиметрия. Пособие для углубленного изучения математики /
В. Ф. Бутузов, СБ. Кадомцев, Э. Г. Позняк, С. А. Шестаков, И. И. Юдина. —
М.: ФИЗМАТЛИТ, 2005. - 488 с. - ISBN 5-9221-0635-Х.
В настоящем пособии дается систематическое изложение углубленного
курса планиметрии. Наряду с основными геометрическими сведениями, входя-
входящими в стандартную школьную программу по геометрии, содержится большой
дополнительный материал, расширяющий и углубляющий основные сведения.
Стиль изложения, принятый в пособии, заметно отличается от традиционного:
теорема — доказательство. В ряде случаев авторы не формулируют теоремы
и аксиомы заранее, а ищут их формулировки вместе с читателем. Такой
подход объясняется желанием авторов дать представление о том, как строится
математика и как работают математики.
В книге значительное внимание уделяется геометрии Лобачевского, кривым
постоянной ширины, изопериметрическим задачам, доказывается целый ряд
замечательных теорем планиметрии.
Пособие ориентировано на учащихся, проявляющих повышенный интерес
к математике, а также всех, кого привлекает красота геометрии. Оно может
использоваться в классах с углубленным изучением математики, в работе мате-
математических кружков и факультативов, служить основным учебником в школах
физико-математического профиля.
© ФИЗМАТЛИТ, 2005
© В. Ф. Бутузов, С. Б. Кадомцев,
Э. Г. Позняк, С. А. Шестаков,
ISBN 5-9221 -0635-Х И. И. Юдина, 2005

Предисловие
Настоящее пособие ориентировано на учащихся, проявляющих по-
повышенный интерес к математике, и предназначено, прежде всего, для
классов с углубленным изучением математики, для математических
кружков и факультативов. Оно состоит из 13 глав, соответствующих
главам учебника «Геометрия 7-9» Л.С. Атанасяна, В.Ф. Бутузова,
СБ. Кадомцева, Э.Г. Позняка, И.И. Юдиной (М.: Просвещение, 1990 г.
и последующие издания). Вместе с тем пособие вполне автономно,
что позволяет использовать его как в тех классах, где преподавание
геометрии ведется по другим учебникам, так и в качестве основного
учебника в школах физико-математического профиля.
Следует отметить, что стиль изложения, принятый в пособии, от-
отличается от традиционного: теорема — доказательство. В ряде случаев
мы не формулируем теоремы и аксиомы заранее, а ищем их формули-
формулировки вместе с читателем. Такой подход объясняется желанием авторов
дать представление о том, как строится математика и как работают
математики.
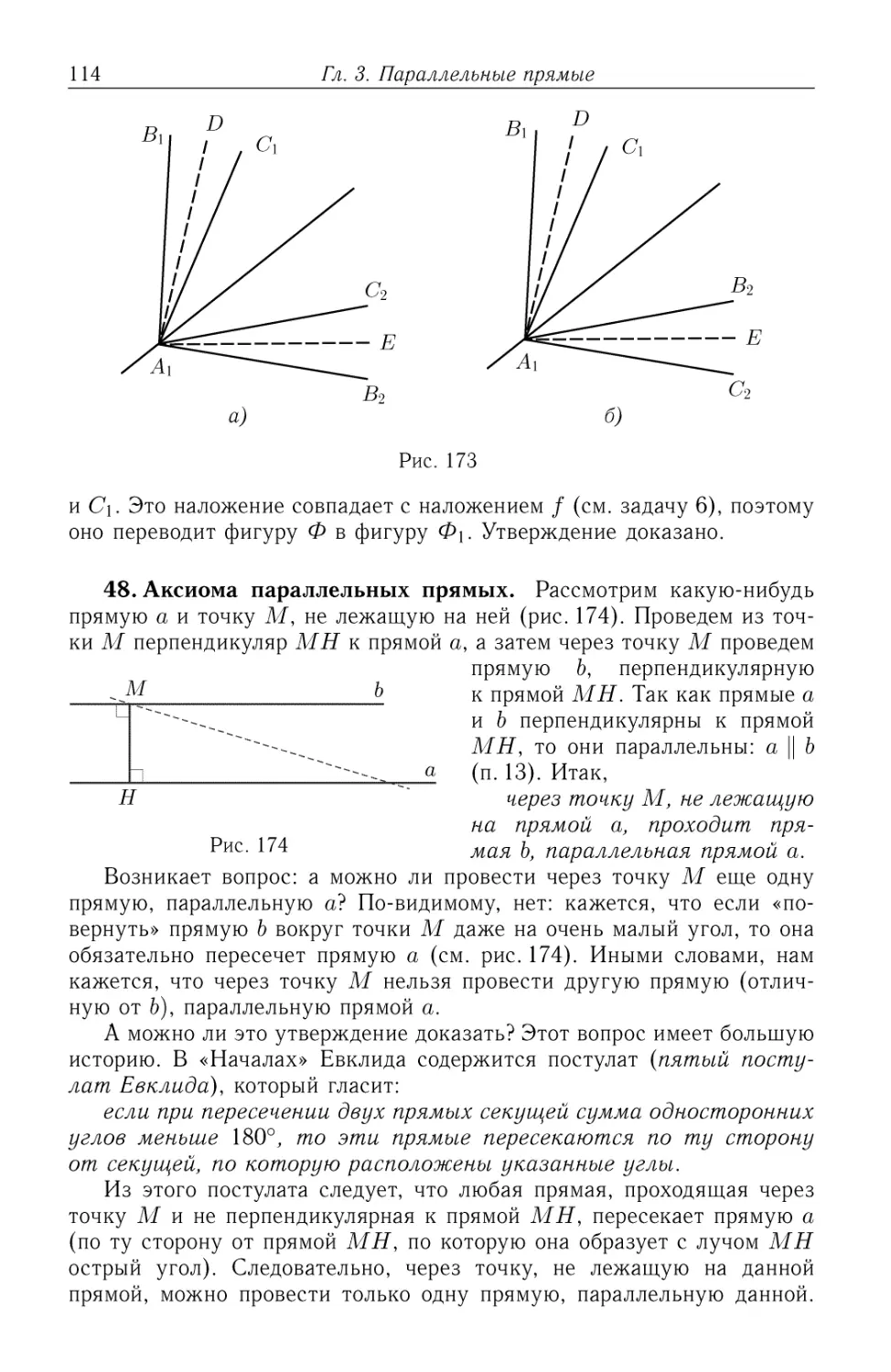
В пособии наряду с основными геометрическими сведениями, вхо-
входящими в стандартную школьную программу по геометрии, содержит-
содержится большой дополнительный материал, расширяющий и углубляющий
основные сведения. В частности, значительное внимание уделяется
теории параллельных прямых и дается представление о связанной
с ней геометрии Лобачевского. Так, уже в первой главе наряду с тра-
традиционным материалом, относящимся к начальным геометрическим
сведениям, вводится понятие параллельных прямых, рассматриваются
признаки параллельности прямых и обсуждается вопрос о существова-
существовании квадрата.
Вторая глава посвящена изучению тех свойств треугольников, кото-
которые справедливы как в геометрии Евклида, так и в геометрии Лобачев-
Лобачевского (т.е. в абсолютной геометрии). Здесь рассматриваются разнооб-
разнообразные (в том числе нетрадиционные) признаки равенства треугольни-
треугольников, соотношения между сторонами и углами треугольника, свойства
серединного перпендикуляра к отрезку и биссектрисы угла, взаимное
расположение прямой и окружности и двух окружностей, теорема
об окружности, вписанной в треугольник, задачи на построение.
В третьей главе изучаются параллельные прямые. Здесь рассматри-
рассматриваются аксиомы и основные понятия геометрии, приводятся примеры
решения задач на основе аксиом, подробно обсуждается связь меж-
между аксиомой параллельных прямых, фактом существования квадрата,
пятым постулатом Евклида и связанной с ним задачей о построении

Предисловие
треугольника по стороне и двум прилежащим углам. Здесь же впервые
заходит речь о геометрии Лобачевского.
Четвертая глава существенно расширяет и углубляет геометриче-
геометрические сведения о треугольниках. Здесь практически единым рассужде-
рассуждением одновременно доказываются теорема о сумме углов треугольника
и две теоремы о средней линии треугольника (свойство и признак),
весьма подробно обсуждается специфика геометрии Лобачевского (на-
(например, объясняется, почему в этой геометрии имеет место признак
равенства треугольников по трем углам), приводятся доказательства
теорем о замечательных точках треугольника и об окружности, опи-
описанной около треугольника.
В пятой главе наряду с традиционным изучением параллелограмма
и трапеции рассматриваются замкнутые выпуклые линии, вписанные
и описанные по отношению к ним многоугольники, характеристические
свойства некоторых четырехугольников (например, выпуклого четы-
четырехугольника), доказываются теорема Жордана (о внутренней области
многоугольника), теоремы Вариньона и Гаусса.
В шестой главе, посвященной измерению площадей, вводятся по-
понятия равновеликих и равносоставленных многоугольников и в связи
с этим рассматривается ряд задач на разрезание многоугольников,
а также приводится доказательство теоремы Бойяи-Гервина. Здесь же
представлены задачи о площадях некоторых фигур, расположенных
на целочисленной решетке. Особого внимания заслуживает теорема
об отношении площадей треугольников, имеющих по равному углу:
с ее помощью удается построить треугольник по двум сторонам и бис-
биссектрисе, проведенным из одной вершины (причем как на евклидовой
плоскости, так и на плоскости Лобачевского), вывести формулу Герона,
дать три нетрадиционных доказательства теоремы Пифагора (всего
в главе приведено девять различных доказательств этой теоремы),
а позже (в главе «Окружность») вывести формулу, выражающую пло-
площадь треугольника через его стороны и радиус описанной окружности,
что, в свою очередь, позволяет дать простое доказательство теоремы
синусов в ее усиленной формулировке.
В седьмой главе рассматриваются разнообразные (в том числе
нетрадиционные) признаки подобия треугольников, тригонометриче-
тригонометрические функции острого угла, обобщенная теорема Фалеса, теорема
о пропорциональных отрезках в треугольнике, теоремы Чевы и Мене-
лая, ряд теорем о свойствах замечательных точек треугольника.
Восьмая глава посвящена изучению углов, связанных с окружно-
окружностью, и примыкающих к этой теме теорем (например, теоремы Паскаля
о вписанном шестиугольнике). Здесь же рассказывается о кривых по-
постоянной ширины, что выходит за рамки обычной школьной геометрии.
Изложение темы «Векторы» в девятой главе отличается от традици-
традиционного, главным образом, пунктуальностью при доказательстве теорем,
в частности, дано обоснование транзитивности сонаправленности.

Предисловие
В десятой главе рассматриваются вопросы, так или иначе связанные
с методом координат: уравнения прямой и окружности, радикальная
ось и радикальный центр, теорема Брианшона для описанного шести-
шестиугольника, построение касательной при помощи одной линейки.
В одиннадцатой главе выводятся теоремы синусов и косинусов, ос-
основные тригонометрические формулы, изучаются свойства скалярного
произведения и в связи с этим доказывается ряд классических теорем
геометрии (Эйлера, Лейбница, Морлея, Брахмагупты и др.).
В двенадцатой главе вводятся понятия длины линии (в частности,
окружности), площади фигуры (в частности, круга), рассматриваются
теорема Барбье, первый замечательный предел и изопериметрическая
задача.
Последняя, тринадцатая глава книги посвящена изучению геомет-
геометрических преобразований (движений, центрального подобия и инвер-
инверсии) и их использованию при решении задач и доказательстве теорем,
в том числе: при решении задачи Аполлония, при доказательстве тео-
теорем Наполеона, Птолемея, Фейербаха, теорем о прямой Симеона, о пря-
прямой и окружности Эйлера, об окружностях Аполлония, при выводе
формулы Эйлера. Приложения в конце книги существенно расширяют
и углубляют сведения учащихся о геометрии Лобачевского и теории
вещественных чисел.
В каждой главе по мере изложения теоретического материала да-
даются задачи с решениями, иллюстрирующие применение тех или иных
утверждений. К каждому параграфу главы даны задачи для само-
самостоятельной работы, снабженные ответами и указаниями. Наиболее
трудные задачи и разделы отмечены звездочкой. Имеется также пред-
предметный указатель, позволяющий легко ориентироваться в книге.
Мы надеемся, что наша книга окажется интересной не только для
учителей и учеников из классов с углубленным изучением математики,
но и для всех, кого привлекает красота геометрии.
Авторы

Глава 1
НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ
§ 1. Точки, прямые, отрезки
1. Точка. Что такое точка? Наверное каждый ответит, что это
нечто совсем маленькое. Возьмем остро отточенный карандаш и при-
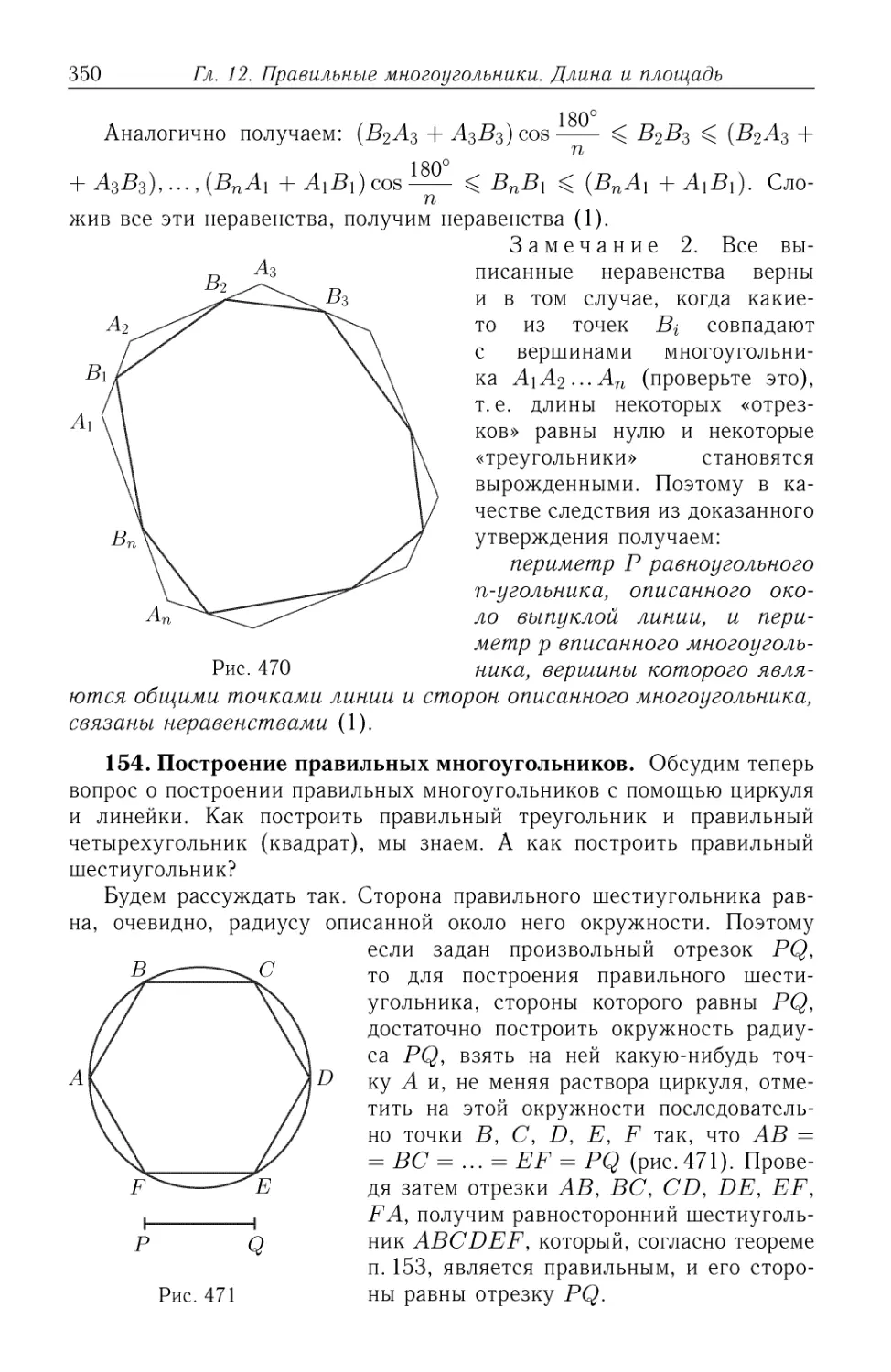
прикоснемся им к бумаге (рис. 1). Получим изображение точки. Это
действительно только изображение точки, а сама
точка еще меньше. Если мы посмотрим на рису-
рисунок 1 в увеличительное стекло, то увидим, что
наша точка довольно большая. Есть предметы, ко-
которые вообще не видны невооруженным глазом,
их можно увидеть только в микроскоп (напри-
(например, бактерии). Но и это еще не точки. Бактерии
хотя и маленькие, но имеют размеры. Точки же
не имеют размеров, настолько они малы. В окру-
окружающем нас мире таких объектов, разумеется, нет.
И все же каждый из нас отчетливо представляет,
что такое точка — это геометрическая фигура,
не имеющая размеров.
Обычно точки обозначают большими буквами латинского алфавита:
А, В и т.д. Точка — самая простая геометрическая фигура.
2. Прямая линия. Что такое линия? Можно сказать так: линия —
это геометрическая фигура, не имеющая ширины.
Прямая дорога в степи, уходящая
т за горизонт, дает представление о пря-
Ш мой линии. Как и дорога, прямая линия
V представляется нам безграничной.
На рисунке мы не можем изобразить
всю прямую линию. Но часть ее изоб-
изобразить можно. Для этого надо взять ли-
линейку, приложить ее к бумаге и провести
вдоль края линейки карандашом (рис.2).
Рис. 1. Изображе-
Изображение точки
1 I I I I I I Г
Рис. 2. Изображение прямой
Этим способом изображения прямых пользуются, например, в черче-
черчении. Как правило, прямые обозначаются малыми латинскими буквами:
а, Ь и т. д.

/. Точки, прямые, отрезки
На рисунке 3 изображена линия. Эта ли-
линия искривленная. Когда мы говорим о прямой,
то представляем себе линию, не имеющую ис-
искривлений.
Отметим на листе бумаги две точки — Aw В.
Через точки А и В с помощью линейки проведем
линию. Затем перевернем линейку (перевернутая
линейка на рисунке 4 изображена пунктиром)
и снова через точки Aw В проведем линию. Если
обе линии совпадают, то линейка не искривлена.
Если же проведенные таким способом линии не совпадают, то этот
край линейки искривлен и не пригоден для проведения прямых линий.
Рис. 3. Изображение
линии
L
1
А
т
1 1
В
т
I I
О
1
О
\ А _—
--я о;
Рис.4
Тем самым мысль о том, что прямая линия не имеет искривлений,
можно выразить такой фразой:
через любые две точки 0 прохо-
проходит прямая и притом только од-
одна (рис.5).
Если на прямой отмечены две точ-
точки, обозначенные, например, буквами А
и В, то прямую можно обозначить этими
двумя буквами: АВ или В А (рис.5).
А
В
Рис. 5. Через две точки А и В
проходит только одна прямая
Две прямые могут пересекать-
пересекаться, т. е. иметь общую точку, а мо-
могут не пересекаться. На рисунке 6
прямые р и q пересекаются, а пря-
прямые а и Ъ не пересекаются. Если
две прямые не пересекаются, то они
называются параллельными. Ино-
Иногда вместо слов «прямые а и Ъ па-
параллельны» используют следующее
обозначение: а || Ъ.
Прямые р и q на рисунке 6 пе-
пересекаются в точке А. Но, может
быть, они пересекаются еще в од-
одной точке? Конечно, нет! В другой
Рис. 6. Прямые р и q пересекаются
в точке А. Прямые а и Ь не пересе-
пересекаются, они параллельны
х) Говоря «две точки», «три прямые» и т.д., мы считаем, что эти точки,
прямые и т. д. различны.

Гл. 1. Начальные геометрические сведения
точке В прямые р и q пересекаться не могут — тогда через точки А и В
проходили бы две прямые, а этого не может быть. Теперь совершенно
ясно, что
две прямые могут пересекаться только в одной точке.
Обратите внимание на то, что это свойство прямых мы установи-
установили путем рассуждений. Такие рассуждения называются доказатель-
доказательством. Мы доказали, что две прямые могут пересекаться только в од-
одной точке.
Как уже отмечалось, прямые а и Ь, изображенные на рисунке 6,
не пересекаются, т.е. параллельны. А можно ли это проверить? Это
трудный вопрос. Ведь на рисунке изображены только части прямых а
и Ь. Полностью их изобразить невозможно, так как прямые безгранич-
безграничны. А, может быть, и вообще нет параллельных прямых, т. е. любые
две прямые пересекаются? На этот вопрос мы пока не можем ответить,
но постараемся ответить тогда, когда будем знать больше о свойствах
геометрических фигур. С подобной ситуацией нам предстоит столк-
столкнуться неоднократно. Поэтому советуем Вам завести специальный
блокнот, чтобы записывать туда все вопросы — и те, которые возникнут
у Вас, и те, на которые мы обратим Ваше внимание. В качестве первого
мы рекомендуем записать такой вопрос:
есть ли параллельные прямые?
Рассмотрим на прямой а какие-нибудь три точки: А, В и С (рис. 7).
Из этих точек только одна (в данном случае В) лежит между двумя
другими (между А и С). Таким образом,
из любых трех точек прямой только одна лежит между двумя
другими.
На первый взгляд кажется, что это, вроде бы, очевидное свойство
можно не выделять. Но посмотрите на рисунок 8, где изображена
окружность (замкнутая линия) и
А В С ТрИ точки А, Б и С на ней. Мож-
Можно ли сказать, что из трех то-
Рис. 7. Точка В лежит между точ- чек на окружности только одна ле-
леками А и С жит между двумя другими? Конеч-
Конечно, нет! Наоборот, каждая из трех
точек на окружности (а также на любой замкнутой линии, рис.9)
лежит между двумя другими.
Сказанное можно проиллюстрировать таким примером: если трое
ребят сидят за круглым столом, то каждый из них сидит между двумя
другими. Но если они сидят на скамейке, то только один из них
сидит между двумя другими. Теперь понятно, в чем дело: выделенное
нами свойство прямой указывает на то, что прямая — незамкнутая
линия.
Иногда вместо слов «точка В лежит между точками А и С» ис-
используют слова «точки А и С лежат по разные стороны от точки В»
или «точки А и В лежат по одну сторону от точки С».

/. Точки, прямые, отрезки
А
Рис. 8. Каждая из трех точек А,
В и С на окружности располо-
расположена между двумя точками
Рис. 9. Каждая из трех точек на лю-
любой замкнутой линии лежит между
двумя другими точками
З.Луч и отрезок. Любая точка О прямой разделяет ее на две
части (рис. 10). Каждая из этих частей называется лучом, исходящим
из точки О — начала луча. Отметим очевидное свойство двух лучей,
на которые прямая разделяется точ-
точкой О: О
любые две точки одного и то-
того же луча лежат по одну сторону Рис. 10. Точка О разделяет пря-
от точки О, а любые две точки раз- мую на два луча. Один из них
ных лучей лежат по разные стороны выделен жирной линией
от точки О.
Обычно луч обозначают либо малой ла-
_ тинской буквой (например, луч h на рисун-
рисунке 11, а), либо двумя большими латинскими
буквами, первая из которых обозначает на-
— чало луча, а вторая — какую-нибудь точку
на этом луче (например, луч О А на рисун-
рисунке 11, б).
а)
О
А
б)
Рис. 11
Обратимся к рисунку 7, на котором изображены два луча с общим
началом {ВА и ВС), лежащие на одной прямой. В таком случае говорят,
что каждый из этих лучей является продолжением другого луча.
Перейдем теперь к отрезкам. Каждый отрезок получается так:
на прямой берут две точки А и В (рис. 12). Их называют концами
отрезка. Сам же отрезок состоит
из этих выделенных точек А и В
и всех точек прямой, лежащих меж-
между ними. Точки, лежащие между
концами отрезка, называются внут-
внутренними точками отрезка. Отре-
Отрезок с концами А и В обозначается
АВ или ВА.
А С
В
Рис. 12. Точки А и В — концы
отрезка. Любая точка С, лежащая
между точками А и В, — внутрен-
внутренняя точка отрезка

10
Гл. 1. Начальные геометрические сведения
4. Несколько задач.
Задача 1. Даны четыре попарно пересекающиеся прямые (т.е.
каждая прямая пересекается с любой другой). Известно, что через
точку пересечения любых двух из них проходит по крайней мере
еще одна из данных прямых. Найти число точек пересечения этих
прямых.
Решение. Обозначим данные прямые через а\, а,2, аз> а4- Рас-
Рассмотрим прямые а\ и а^. По условию они пересекаются в некоторой
точке М, и через эту точку проходит по крайней мере еще одна
из данных прямых. Пусть, например, через точку М проходит пря-
прямая аз (рис. 13, а).
а3
а\
а\
б)
Рис. 13
Если прямая а± не проходит через точку М, то она пересекает
прямые а\, а^ и аз в точках М\, М^ и Мз (рис.13, б). Рассмотрим
одну из них, например точку М\. Через нее проходят прямые а\ и сц,
и не проходят прямые а^ и аз. Но по условию задачи через точку
пересечения прямых а\ и а\ должна проходить по крайней мере еще
одна из данных прямых, а такой третьей прямой для точки М\ нет.
Что же это означает? Это означает, что прямая а\ должна проходить
через точку М, иначе получается противоречие с условием задачи.
Таким образом, все данные прямые проходят через точку М, т. е.
имеют только одну точку пересечения.
Задача 2. На плоскости проведены п прямых. Каждые две
из них пересекаются. Кроме того, через точку пересечения каждых
двух прямых не проходит больше ни одной из наших прямых. Найти
число всех точек пересечения этих прямых.
Решение. Будем рассуждать так. Проведем первую прямую
(рис. 14, а). Затем проведем вторую прямую (рис. 14, б). Появится одна
точка пересечения. Проведем третью прямую (рис. 14, в). Она пересе-
пересечется с первой и второй прямыми, поэтому общее число точек пересече-
пересечения станет равным 1 +2. Проведем четвертую прямую (рис. 14, г). Она
пересечется с первой, второй и третьей. Количество точек пересечения
станет равным 1+2 + 3. После проведения пятой прямой число точек

/. Точки, прямые, отрезки 11
г)
Рис. 14
пересечения станет равным 1 +2 + 3 + 4 (рис. 14, д). Теперь ясно, что
поскольку всего проведено п прямых, то число точек пересечения равно
1 + 2 + 3 + 4 + ... + (п - 3) + (п - 2) + (п - 1).
Замечание. С практической точки зрения выведенная нами фор-
формула не очень удобна — слишком громоздкая. Например, при п = 101
в ней 100 слагаемых! Можно ли получить более удобную формулу?
Оказывается, можно.
Рассказывают, что однажды учителю младших классов гимназии
в немецком городе Брауншвейге понадобилось по каким-то делам уйти
с урока арифметики. Чтобы не оставлять класс без дела, он, недолго
думая, предложил учащимся решить такую задачу: найти сумму всех
целых чисел от 1 до 100. Будучи абсолютно уверенным в том, что
теперь до конца урока можно заниматься своими делами, он уже
сделал несколько шагов по направлению к выходу, как вдруг один
из учеников поднял руку.
— У тебя какой-то вопрос? — спросил учитель.
— Нет, — ответил тот. — Я решил задачу. У меня получилось 5050.
— Как ты получил это число?! — спросил совершенно ошарашенный
учитель.
— Очень просто, — сказал ученик и написал две строчки, одну под
другой. — Теперь совершенно ясно, что наша сумма равна 5050.
Изумленный учитель некоторое время молча смотрел на написан-
написанные строчки, а затем произнес:
— Ты станешь великим математиком!
И не ошибся. Этот 9-летний ученик — Карл Фридрих Гаусс A777—
1855) — действительно стал одним из величайших математиков.

12
Гл. 1. Начальные геометрические сведения
Какие же две строчки написал Гаусс? Не можем ли мы применить
ту же идею к решению нашей задачи? Давайте попробуем. Поступим
так. Запишем нашу формулу еще раз и под ней запишем ее же, но взяв
слагаемые в обратном порядке:
1 + 2 + 3 + ... +
(п-1) + (п-2) + (п-3) + ... +
-З) + (п-2) + (п-1)
3 + 2 + 1.
на
Сложим теперь эти две суммы следующим
способом. Сначала сложим первое слагаемое 1
в первой строчке с первым слагаемым (п — 1)
во второй строчке. Получим в сумме п. За-
Затем ко второму слагаемому 2 в первой строчке
прибавим второе слагаемое (п — 2) во второй
строчке. Опять получим п. И так далее. В ре-
результате получим:
п-\-п-\-п-\-...-\-п-\-п-\-п = (п — \)п.
п-1
Итак, мы сложили две наши суммы и по-
получили число (п — \)п. Следовательно, наша
сумма в два раза меньше этого числа, т. е. рав-
. Например, для пяти прямых, т. е. когда п = 5, число точек
пересечения равно -——— = 10 (см. рис. 14, д), а для 101 прямой
A01-1I01 СГкСГк
число точек пересечения равно —— = 5050.
Задача 3* Точка С лежит на прямой между точками А и В,
а точка D лежит между точками А и С. Лежит ли точка D между
точками А и В?
Решение. Проведем прямую, отметим на ней точки А и В, а затем
С, лежащую между точками А и В, и точку D, лежащую между
А и С (рис. 15). Мы лежит между точками А видим, что точка D
и В. Тем самым ответ на вопрос
A d с В задачи получен. Но давайте этим
не ограничимся, а поставим во-
Рис. 15 прос так: можно ли путем рас-
рассуждений (а не с помощью ри-
рисунка) обосновать тот факт, что точка D лежит между А и В?
Оказывается, можно. Но рассуждения не очень простые. Попытайтесь
в них разобраться, чтобы проводить потом аналогичные рассуждения
в других задачах. Будем рассуждать следующим образом.
По условию точка С лежит между А и В. Как уже отмечалось
ранее, это можно выразить другими словами:
1° точки А и В лежат по разные стороны от точки С.

/. Точки, прямые, отрезки
13
Также по условию точка D лежит между А и С, что можно
выразить так:
2° точки А и С лежат по разные стороны от точки D,
или так:
3° точки А и D лежат по одну сторону от точки С.
Сопоставим утверждения 1° и 3°. Можно сделать вывод, что точ-
точки В и D лежат по разные стороны от точки С, т. е. точка С лежит
между В и D, а значит,
4° точки В и С лежат по одну сторону от точки D.
Сопоставим теперь утверждения 2° и 4°. Из них следует, что
точки А и В лежат по разные стороны от точки D, т. е. точка D лежит
между А и В.
Итак, тот факт, что точка D лежит между А и В, мы обосновали
путем рассуждений. Иначе говоря, мы доказали, что точка D лежит
между А и В.
5. Угол. Геометрическая фигура, состо-
состоящая из точки и двух лучей, исходящих
из этой точки, называется углом. Лучи
называются сторонами угла, а их общее
начало — вершиной угла. На рисунке 16
изображен угол с вершиной О, на сторо-
сторонах h и к которого отмечены точки А и В.
Этот угол можно обозначить разными спо-
способами: Zhk, или ZAOB, или АО, или /Л.
Рис. 16
Р
С
Рис. 17. Развернутый угол
Если стороны угла лежат на одной
прямой, то угол называют развернутым
(рис. 17). Можно сказать, что каждая сто-
сторона развернутого угла является продол-
продолжением другой стороны.
Каждый угол разделяет плоскость на две части. Если угол нераз-
неразвернутый, то одна из этих частей называется внутренней, а другая —
внешней областью этого угла. На рисун-
рисунке 18 изображен угол и указаны его внут-
внутренняя и внешняя области. Фигуру, состо-
состоящую из угла и его внутренней области,
также называют углом.
Если луч исходит из вершины нераз-
неразвернутого угла и проходит внутри это-
этого угла (т.е. в его внутренней области),
то он делит угол на два угла, внутрен-
внутренние области которых лежат по разные сто-
стороны от этого луча. На рисунке 19, а
луч ОС делит угол АОВ на два угла:
ZAOC и АСОВ. Если угол АОВ - раз-
развернутый, то любой луч ОС, не совпа-
Внешняя
область
угла
Внутренняя
область угла
Рис. 18

14
Гл. 1. Начальные геометрические сведения
О
А
В О
А
а)
Рис. 19. Луч ОС делит угол АОВ на два угла: ZAOC и АСОВ
дающий с лучами ОА и ОВ, делит этот угол на два угла: ZAOC
и АСОВ (рис. 19, б).
6. Полуплоскость. Наше представление о внутренней и внешней
областях угла наглядное, оно связано с рисунком — изображением
угла. А как описать словами, что такое внутренняя область угла? Это
можно сделать с помощью понятия полуплоскости.
Любая прямая разделяет плоскость на две части, каждая из кото-
которых называется полуплоскостью, а сама прямая служит границей этих
полуплоскостей. На рисунке 20, а одна из полуплоскостей с границей а
заштрихована. Отметим такое очевидное свойство полуплоскостей:
полуплоскость
А
а)
б)
Рис. 20. а) Прямая а разделяет плоскость на две полуплоскости; б) если
точки А и В лежат в одной полуплоскости с границей а, то отрезок АВ не
пересекается с прямой а; в) если точки А и В лежат в разных полуплоскостях
с границей а, то отрезок АВ пересекается с прямой а
если две точки А и В лежат в одной полуплоскости с грани-
границей а, то отрезок АВ не пересекается с прямой а (рис. 20, б), а если
в разных полуплоскостях, то отрезок АВ пересекается с прямой а,
т. е. имеет внутреннюю точку, общую с прямой а (рис.20, в).
В первом случае говорят, что точки А и В лежат по одну сторону
от прямой а (рис.20, б), а во втором — что точки А и В лежат
по разные стороны от прямой а (рис.20, в).
Обратимся теперь к рисунку 21. На нем изображен угол hk, внут-
внутренняя область которого заштрихована. Эту область можно получить
так. Разрежем плоскость по прямой а, содержащей сторону h. Мы ви-
видим, что после разреза внутренняя область угла останется в полу-
полуплоскости а, которая содержит сторону к. Затем разрежем плоскость

/. Точки, прямые, отрезки
15
Полуплоскость а
с границей а,
содержащая сторону к
Внутренняя область
\ угла hk — общая часть
полуплоскостей а и J3
h
Полуплоскость f3
с границей Ь,
содержащая сторону h
Рис. 21. Выделение внутренней области угла с помощью полуплоскостей
по прямой Ь, содержащей сторону к. После этого разреза внутренняя
область угла останется в полуплоскости /3, которая содержит луч h.
Теперь ясно, что внутренняя область угла — это общая часть полу-
полуплоскостей а и /3.
Разрезы, которые мы проводили,
можно рассматривать как отреза-
отрезание всего лишнего, того что не со-
содержит точек внутренней области
угла.
Давайте теперь обсудим такой
вопрос. Пусть точки А и В распо-
расположены во внутренней области угла
hk (рис.22). Как Вы думаете, бу-
будет ли отрезок АВ также целиком
расположен во внутренней области
угла hk? Посмотрим еще раз на ри-
рисунок. Мы видим, что действитель-
действительно отрезок АВ целиком располо-
расположен во внутренней области угла hk. А можно ли путем рассуждений
убедиться в том, что это действительно так? Мы только что обсудили,
как с помощью полуплоскостей выделить внутреннюю область угла.
Может быть, этим и воспользоваться? Попробуем.
Мы уже отмечали, что если две точки А и В лежат в одной
полуплоскости с границей а, то отрезок АВ не пересекается с пря-
прямой а, и следовательно, весь отрезок АВ лежит в этой полуплоскости.
Ну, теперь все ясно! Ведь внутренняя область угла — это общая
часть полуплоскостей а и /3 (рис.22). Так как отрезок АВ лежит и в
полуплоскости а, и в полуплоскости /3, то он целиком расположен в их
общей части, т. е. во внутренней области угла.
У Вас может возникнуть вопрос: а зачем нужно объяснять словами,
что такое внутренняя область угла? Почему нельзя сказать просто:
Рис. 22

16
Гл. 1. Начальные геометрические сведения
внутренняя область угла — это то, что изображено на рисунке 18?
Но любая ли фигура, изображенная на рисунке, есть изображение
какой-то действительно существующей фигуры? Посмотрите на рисун-
рисунки 23 и 24. На первом из них изображен куб, сделанный из деревянных
реек. А что изображено на втором рисунке? Не знаете? То-то и оно!
Оказывается, нарисовать можно такое, чего нет на самом деле.
Рис. 23. Куб из реек
Рис. 24. А что изображено на этом
рисунке?
Задачи
1. Даны четыре точки. Известно, что прямая, проходящая через
любые две из них, содержит по крайней мере еще одну из данных
точек. Докажите, что все данные точки лежат на одной прямой.
2. Даны пять попарно пересекающихся прямых. Известно, что через
точку пересечения любых двух из них проходит по крайней мере еще
одна из данных прямых. Докажите, что все данные прямые проходят
через одну точку.
3! Решите задачу 1 для случая, когда даны пять точек.
4. Точки О, А и В лежат на одной прямой, причем точки А и В
лежат по разные стороны от точки О. Лежат точки А и В на одном
луче или на разных лучах с началом О? Ответ обоснуйте.
5! Точка В лежит между точками А и С, а точка С лежит между
точками В и D. Лежит ли точка С между точками А и D? Ответ
обоснуйте.
6! Точка N лежит между точками М и О, а точка О лежит между
точками М и Р. Лежит ли точка О между точками N и Р? Ответ
обоснуйте.
7* Точка М — внутренняя точка отрезка АВ. Докажите, что: а) все
точки отрезка AM принадлежат отрезку АВ; б) отрезки AM и MB
не имеют общих внутренних точек.
8. Отрезок АВ пересекается с прямой а, а отрезок АС не пересе-
пересекается с этой прямой. Пересекается ли отрезок ВС с прямой а? Ответ
обоснуйте.

2. Измерение отрезков и углов
17
9! Даны четыре точки А, В, С, D и прямая а, не проходящая
ни через одну из этих точек. Известно, что отрезки АВ и CD пересе-
пересекаются с прямой а, а отрезок ВС не имеет общих точек с этой прямой.
Пересекается ли отрезок AD с прямой а? Ответ обоснуйте.
§ 2. Измерение отрезков и углов
7. Равенство геометрических фигур. Среди окружающих нас
предметов встречаются такие, которые имеют одинаковую форму
и одинаковые размеры (одинаковые листы бумаги, книги, автомобили
и т.п.). В геометрии две фигуры, имеющие одинаковую форму и оди-
одинаковые размеры, называют равными.
Каким образом можно проверить равенство фигур Ф\ и Ф^ (рис.25
и 26)? Можно представить себе, что фигура Ф\ накладывается на фи-
фигуру 02 той или другой стороной. Если в результате фигуры Ф\ и Ф^
совместятся, то они равны.
ф\
02
Ф\
Ф2
Рис. 25. Фигуры 0i и 02 равны
Рис. 26. Фигуры 0i и 02 также рав-
равны. Подумайте, как совместить их
наложением
Итак, две геометрические фигуры называются равными, если
их можно совместить наложением.
8. Сравнение отрезков и углов. Пусть даны два отрезка
(рис.27, а, б). Наложим один отрезок на другой так, чтобы
конец одного отрезка совместился с концом другого. Если при
этом совместятся и два других конца этих отрезков, то отрезки
совместятся, и значит, они равны (рис.27, а); если же два других
конца не совместятся, то меньшим считается тот отрезок, который
составит часть другого (рис.27, б).
Обратимся теперь к углам. Пусть даны два неразвернутых уг-
угла (углы 1 и 2 на рисунке 28). Наложим один угол на другой так,
В А
В
С
а)
D С
D
Рис. 27. а) АВ = CD; б) CD < АВ

18
Гл. 1. Начальные геометрические сведения
1
а) б)
Рис. 28. a) Zl = Z2; б) Zl < Z2
чтобы сторона одного угла совместилась со стороной другого, а две
другие стороны оказались по одну сторону от совместившихся сторон.
Если при этом две другие стороны также совместятся, то и углы
совместятся — значит, они равны (на рисунке 28, a Zl = Z2). Если же
две другие стороны не совместят-
совместятся, то меньшим считается тот угол,
который составит часть другого (на
рисунке 28, б Zl < Z2).
Неразвернутый угол является
частью развернутого угла (рис.29).
Поэтому развернутый угол больше
любого неразвернутого угла. Лю-
Любые два развернутых угла, очевид-
Рис. 29. ZAOC < ZAOB, ZBOC <
<ZAOB
но, равны.
9. Середина отрезка и биссектриса угла. Точка отрезка, де-
делящая его пополам, т. е. на два равных отрезка, называется се-
серединой этого отрезка (рис.30, а). Чтобы найти середину отрезка
АВ, изображенного на листе бумаги, можно поступить так: пере-
перегнуть лист таким образом, чтобы точки А и В совместились. Ес-
А
М
В
А
М
В
а) б)
Рис. 30. AM = MB. Точка М — середина отрезка АВ

2. Измерение отрезков и углов
19
ли теперь разогнуть лист и отметить точку М пересечения отрез-
отрезка АВ с линией сгиба (рис.30, б), то эта точка и будет середи-
серединой отрезка АВ. В самом деле, при повторном перегибании листа
точка М останется на месте, а точ-
точки А и В совместятся. Следователь-
Следовательно, отрезок МА совместится с от-
отрезком МБ, а значит, МА = МБ,
т. е. точка М — середина отрез-
отрезка АВ.
Луч, исходящий из вершины уг-
угла и делящий его на два равных уг-
угла, называется биссектрисой этого
угла (рис.31). Как провести биссек-
биссектрису угла, изображенного на листе
бумаги (рис. 32, а)? Можно посту-
поступить таким образом: перегнуть этот лист так, чтобы стороны р и q
угла совместились (рис.32, б). Тогда линия сгиба будет биссектрисой
угла pq. Докажите это самостоятельно.
h
О
Рис. 31. Zhl = Zlk. Луч I - бис-
биссектриса угла hk
Р
б)
Рис. 32. Сторона q угла pq совпадает с нижним краем листа бумаги (а). После
перегибания листа бумаги, сторона q должна совместиться со стороной р (б).
Тогда линия сгиба — биссектриса угла pq
10. Измерение отрезков и углов. Как измеряются отрезки?
Пусть AqBq — измеряемый отрезок, PQ — выбранная единица изме-
измерения отрезков. На луче AqBq отложим отрезок AqA\ = PQ, на луче
А\Во — отрезок А\А2 = PQ и т.д. до того момента, когда либо
точка Ап совпадет с точкой Бо, либо точка Бо окажется лежащей
между Ап и Ап+\ (рис.33). В первом случае говорят, что длина
отрезка AqBq при единице измерения PQ выражается числом п (или
что отрезок PQ укладывается в отрезке AqBq n раз). Во втором случае
можно сказать, что длина отрезка AqBq при единице измерения PQ
приближенно выражается числом п. Для более точного измерения
отрезок PQ делят на равные части, обычно на 10 равных частей,

20 Гл. 1. Начальные геометрические сведения
Рис. 33
и с помощью одной из этих частей измеряют описанным способом
остаток АпВо. Если при этом десятая часть отрезка PQ не укла-
укладывается целое число раз в измеряемом остатке, то ее также делят
на 10 равных частей и продолжают процесс измерения. Таким способом
можно измерить любой отрезок, т. е. выразить его длину при данной
единице измерения конечной или бесконечной десятичной дробью.
Иными словами,
при выбранной единице измерения отрезков длина каждого от-
отрезка выражается положительным числом.
Измерение углов аналогично измерению отрезков и основано
на сравнении их с углом, принятым за единицу измерения. Обычно
за единицу измерения углов принимают градус (°) — угол, равный ——-
180
части развернутого угла. — часть градуса называется минутой
('), а — минуты — секундой (/х). Градусной мерой угла называют
положительное число, которое показывает, сколько раз градус и его
части укладываются в данном угле.
Развернутый угол равен 180° (так как градус — это ——- часть
180
развернутого угла). Неразвернутый угол меньше 180°.
Угол называется прямым, если он равен 90°. Угол, который мень-
меньше прямого, называется острым, а угол, который больше прямого,
но меньше развернутого, — тупым (рис.34).
Прямой угол равен 90° Острый угол мень- Тупой угол больше 90°,
ше 90° но меньше 180°
Рис. 34
11.0 числах. Мы говорили, что при выбранной единице изме-
измерения длина отрезка выражается некоторым положительным числом.
Таким образом, при измерении отрезков используются числа. В этом
пункте мы поговорим о числах.

2. Измерение отрезков и углов 21
Вам знакомы разные числа. Это, прежде всего, целые положи-
положительные числа: 1, 2, 3 и т. д. Их называют также натуральными
числами. Они возникли из потребностей счета. Можно сказать, что
натуральные числа понадобились для измерения количества предме-
предметов. Если, например, на книжной полке находится какое-то количество
книг, то измерить его (это количество) можно с помощью натураль-
натурального числа: на этой полке находится 20 книг, а на другой полке —
23 книги.
Натуральных чисел для измерений недостаточно. Если разрезать
яблоко пополам, то каждая половина равна - яблока. Если же раз-
разрезать яблоко на четыре равные части, то каждая часть равна -
яблока. Обозначение - показывает, что 1 (одно яблоко) разделили
3
на 4 части. Число - получается, если 3 разделить на 7. Такого рода
числа, когда в числителе и в знаменателе стоят натуральные числа,
называют рациональными положительными (рацио — значит деление).
Итак, рациональные положительные числа — это числа вида -, где р
и q — натуральные числа.
На практике часто использу-
используют десятичные дроби, в частно- и * см
сти, они появились у нас при ^ ^
измерении отрезков. Так, на ри- С D
сунке 35 длина отрезка АС рав-
равна 3,4 см, а длина отрезка AD Рис- 35- Ав = 2 см> АС = 3>4 см>
приближенно равна 3,8 см. Чис- = ' см
ло 3,8 — десятичная дробь. Его
Q О О
можно записать в виде 3,8 = 3 + — = —, поэтому десятичная
дробь 3,8 — это рациональное число. Любая другая десятичная дробь
также является рациональным числом. Например, 4,79 = 4 + — +
9 479
+ -— = -—, т.е. число 4,79 — рациональное число.
100 100
При измерении отрезков с определенной точностью, например с точ-
точностью до миллиметра, мы получаем их длины в виде рациональных
чисел. Итак,
рациональных чисел достаточно для приближенных измерений
с любой заданной точностью.
Но оказывается, что точное значение длины отрезка может не быть
рациональным числом. Приведем пример.
Вспомним, что такое квадрат. Это четырехугольник, у которого
стороны равны и все четыре угла — прямые (рис.36, а). Из курса
математики 6 класса известно, что площадь квадрата со стороной а
равна а2. Например, квадрат со стороной 10 мм имеет площадь 100
мм2, что можно увидеть на миллиметровой бумаге (рис.36, б).

22
Гл. 1. Начальные геометрические сведения
а
а)
f
(\
\\
\
/
/
/
}
1
ч
i
\
\
\
б)
Рис. 36. а) Квадрат со стороной а, его площадь равна а2; б) квадрат со
стороной 10 мм имеет площадь 100 мм2
Пусть имеются два одинако-
одинаковых квадрата, стороны которых
равны 1 (рис.37). Разрежем каж-
каждый квадрат по диагонали (они
проведены пунктиром) на два
треугольника, а затем составим
из получившихся четырех тре-
треугольников новый квадрат, кото-
который изображен на рисунке 38.
Если мы обозначим длину диа-
диагонали квадрата на рисунке 37
буквой а, то площадь квадрата
Рис. 37. Квадраты со стороной 1. Пло-
Площадь каждого из них равна 1. Число
а — длина диагонали, по которой раз-
разрезается каждый квадрат
на рисунке 38 будет равна а . С другой
стороны, площадь этого квадрата равна
сумме площадей двух квадратов, изобра-
изображенных на рисунке 37, т. е. равна 2. Итак,
= 2.
A)
Докажем, что число а не является
рациональным.
Будьте внимательны — может быть,
это первое в Вашей жизни не простое до-
доказательство! Напомним, что рациональ-
рациональное положительное число получается пу-
путем деления одного натурального числа
на другое натуральное число. Например,
3
число - получается, когда натуральное
число 3 делят на натуральное число 7.
Отметим, что числитель (число 3) и зна-
знаменатель (число 7) не имеют общих мно-
множителей (отличных от единицы). А вот
\ а
\
\
¦&
Рис. 38. Из треугольников,
на которые разрезаны квад-
квадраты на рис.37, составлен
новый квадрат со стороной
а. Площадь этого квадрата
равна а2 и, конечно, равна 2
(сумме площадей квадратов
на рис. 37)

2. Измерение отрезков и углов 23
о
у рационального числа - числитель (число 8) и знаменатель (число 6)
имеют общий множитель 2, так как 8 = 2-4и6 = 2-3. На этот общий
множитель числитель и знаменатель можно сократить, так что
8 _ 2-4 _ 4
6 ~ 2^3 ~ 3'
Дальше сокращать невозможно, так как у числителя и знаменателя
нет общих множителей.
Рассмотрим еще один пример. Число — путем сокращения числи-
числителя и знаменателя на общие множители можно привести к виду, когда
у числителя и знаменателя нет общих множителей:
30 _ 2-3-5 _ 5
48 ~ 2-3-8 ~ 8'
Таким способом — путем сокращения на общие множители чис-
числителя и знаменателя — можно привести любое данное рациональное
число к несократимому виду (у числителя и знаменателя нет общих
множителей).
Посмотрим теперь, что получится, если мы предположим, что чис-
число а, квадрат которого равен 2, — рациональное. При этом, конечно,
можно считать, что число а приведено к несократимому виду:
где числа р и q не имеют общих множителей. Из равенства B) полу-
получаем: 2
2 V V V
Q Q q
2
Но a2 = 2 (см. A)). Поэтому ^ = 2, т. е.
q
P2 = 2q2. C)
Из равенства C) можно сделать вывод: число р делится на 2.
Действительно, число р2 делится на 2, так как оно равно числу 2,
умноженному на натуральное число q2. Но р2 = р • р, и если бы число р
не делилось на 2, то и число р2 не делилось бы на 2. Значит, число р
делится на 2, и его можно записать в виде
р = 2г, D)
где г — натуральное число. Подставим это выражение для р в левую
часть равенства C). Получим:
BrJ = 2q\
Но BгJ = 2г • 2г = 2 ¦ 2 • г2, поэтому

24 Гл. 1. Начальные геометрические сведения
Сократим на общий множитель 2 левую и правую части этого
равенства. После этого оно запишется так:
2r2 = q\
откуда следует, что q2 делится на 2, а значит, и q делится на 2.
Что же мы получили? Мы предположили, что число а, квадрат
которого равен 2, рациональное, т.е. равно -, причем числа р и q
не имеют общих множителей. После этого путем рассуждений мы до-
доказали, что числа р и q имеют общий множитель — число 2. Но
это противоречит нашему предположению. Следовательно, наше пред-
предположение не верно, и поэтому число а не является рациональным.
Итак, кроме рациональных чисел есть еще и другие числа. Их на-
называют иррациональными. Приставка «ир» в переводе означает «не».
Примером такого числа служит наше число а, равное длине стороны
квадрата, площадь которого равна 2. Это число обычно обозначают
так: а = у/2 (читается «корень из двух»).
Естественно возникает вопрос: как записать число л/2 с помощью
десятичной дроби? Иными словами, есть ли способ, с помощью кото-
которого можно найти:
1) целую часть числа л/2;
2) число десятых числа л/2;
3) число сотых числа л/2 и т.д.?
Такой способ есть. Он заключается вот в чем: будем подбирать де-
десятичные дроби, квадраты которых будут все ближе и ближе к числу 2.
Так как квадрат числа л/2 равен 2, то целая часть должна быть
меньше 2, и значит, равна 1. Итак, л/2 = 1,...
Далее, мы знаем, что A,4J = 1,96 < 2, A,5J = 2,25 > 2. Следова-
Следовательно, л/2 = 1,4...
Возьмем теперь числа 1,41 и 1,42. Имеем: A,41J = 1,9881 < 2,
A,42J = 2,0164 > 2. Поэтому л/2 = 1,41...
Ясно, что таким способом можно найти любой десятичный знак
числа л/2- Найдите самостоятельно третий после запятой десятичный
знак этого числа.
Задачи
10. Пусть а — число, выражающее длину отрезка АВ при единице
измерения CD, а Ъ — число, выражающее длину отрезка CD при
единице измерения АВ. Как связаны между собой числа а и Ы
11. Длина отрезка АВ при единице измерения .Ei.Fi выражается
числом т, а при единице измерения E^F^ — числом п. Каким числом
выражается длина отрезка E\F\ при единице измерения E^Ffi
12. Точки А, В и С лежат на одной прямой, точки М и N —
середины отрезков АВ и АС. Докажите, что ВС = 2MN.
13! На луче с началом А отмечены последовательно точки В, С,
D, Е и F. Длина отрезка AF равна 7а, расстояние между середина-

3. Перпендикулярные и параллельные прямые
25
ми отрезков АВ и EF равно 6а, а между серединами отрезков ВС
и DE — 4а. Найдите длину отрезка CD.
14! Из вершины угла в 160° проведены три луча, разделяющие
данный угол на четыре части. Угол между биссектрисами крайних
частей равен 140°. Найдите угол между биссектрисами средних частей.
15! Докажите, что число а, удовлетворяющее условию а2 = 3,
является иррациональным числом.
3
16. Запишите число - с помощью десятичной дроби.
17. Напишите три десятичных знака числа а, удовлетворяющего
условию а2 = 3.
§ 3. Перпендикулярные и параллельные прямые
12. Перпендикулярные прямые. Два угла, у которых одна сто-
сторона — общая, а две другие являются продолжениями друг друга,
называются смежными (рис.39). Рассуждения, приведенные под ри-
рисунком 39, показывают, что
сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла
являются продолжениями сторон другого. На рисунке 40 углы 1 и 3,
а также углы 2 и 4 — вертикальные. Рассуждения, приведенные под
рисунком 40, показывают, что
вертикальные углы равны.
Две пересекающиеся прямые образуют четыре неразвернутых уг-
угла (углы 1, 2, 3, 4 на рисунке 40). Если один из них — прямой,
то и остальные — прямые (рис.41). Докажите это.
Две прямые называются перпендикулярными (или взаимно пер-
перпендикулярными), если они образуют четыре прямых угла.
Перпендикулярность прямых АС и BD обозначается так: AC _l_ BD
(читается: «прямая АС перпендикулярна к прямой BD»). Отрезки
С
О
А
Рис. 39. Углы АОВ и ВОС -
смежные. Общая сторона ОВ этих
углов делит развернутый угол АОС
на два смежных угла. Поэтому сум-
сумма смежных углов равна 180°
Рис. 40. Углы 1 и 3 — вер-
вертикальные. Углы 2 и 4 —
также вертикальные. Z1 +
+ Z2 = 180° и Z2 + Z3 =
= 180°. Поэтому Zl = Z3.
Точно также доказывается,
что Z2 = Z4

26
Гл. 1. Начальные геометрические сведения
называются перпендикулярными, если
они лежат на перпендикулярных пря-
прямых (рис.42). Аналогично можно опреде-
определить перпендикулярные лучи, луч и от-
. резок, луч и прямую, отрезок и прямую
-Щ (см. рис.42).
Рассмотрим прямую а и точку А,
не лежащую на ней (рис.43). Отре-
Отрезок, соединяющий точку А с точкой Н
Рис.41. Перпендикулярные прямой а, называется перпендикуляром,
прямые проведенным из точки А к прямой а,
если прямые АН и а перпендикулярны.
При этом точка Н называется основанием перпендикуляра или про-
проекцией точки А на прямую а.
а) б) в)
Рис. 42. а) Перпендикулярные отрезки; б) перпендикулярные лучи; в) перпен-
перпендикулярные отрезок и прямая
Мы ввели понятие
ки к данной прямой.
Н
Рис. 43. Отрезок
АН — перпендикуляр,
проведенный из точки
А к прямой а, а точка
Н — основание этого
перпендикуляра
перпендикуляра, проведенного из данной точ-
А есть ли такой перпендикуляр? И если есть,
то сколько перпендикуляров можно провести
из данной точки к данной прямой? Чтобы от-
ответить на эти вопросы, необходимо провести
рассуждения.
В математике каждое утверждение, спра-
справедливость которого устанавливается путем
рассуждений, называется теоремой, а са-
сами эти рассуждения называются доказатель-
доказательством теоремы. Обычно сначала формулиру-
формулируют теорему (т. е. то утверждение, которое хо-
хотят доказать), а затем ее доказывают. Напри-
Например, когда мы рассматривали число а, удовле-
удовлетворяющее условию а2 = 2, то сначала сформу-
сформулировали теорему (хотя и не называли ее тео-
теоремой): число а не является рациональным. За-
Затем мы привели доказательство этой теоремы.

3. Перпендикулярные и параллельные прямые
27
Докажем теперь теорему о перпендикуляре к прямой.
Теорема. Из точки, не лежащей на прямой, можно провести
перпендикуляр к этой прямой и притом только один.
Доказательство. Пусть А — точка, не лежащая на данной
прямой а (рис.44). Докажем сначала, что из точки А можно провести
перпендикуляр к прямой а. Мысленно перегнем плоскость по пря-
прямой а и отметим точку А\, на которую наложится при этом точка А.
Проведем через точки А и А\ прямую и обозначим буквой Н точку
пересечения прямых АА\ и а. При перегибании плоскости по прямой а
все точки этой прямой останутся на месте, а луч НА совместится с лу-
лучом НА\. Следовательно, угол 1 совместится с углом 2. Таким образом,
эти углы равны, а поскольку они являются смежными, то каждый
из них — прямой. Итак, отрезок АН — перпендикуляр к прямой а.
Докажем теперь, что из точки А нельзя провести другой перпен-
перпендикуляр к прямой а. Предположим, что можно провести еще один
перпендикуляр АВ (рис.45). При перегибании плоскости по прямой а
точка В останется на месте, а точка А наложится на точку А\, поэтому
луч В А совместится с лучом ВА\, и следовательно, прямой угол 3
совместится с углом 4. Таким образом, угол 4 — также прямой, а зна-
значит, угол АВА\ — развернутый. Отсюда следует, что точки А, В и А\
лежат на одной прямой. Тем самым, мы получили, что через точки А
и А\ проходят две прямые (одна из них пересекается с прямой а
в точке Н, а другая — в точке В). Но через две точки проходит только
одна прямая. Следовательно, наше предположение неверно, а значит,
из точки А можно провести только один перпендикуляр к прямой а.
Теорема доказана.
Н
Ах
Рис. 44. После перегибания плос-
плоскости по прямой а точка А нало-
наложится на точку А\
НВ\
Ах
Рис. 45

28
Гл. 1. Начальные геометрические сведения
Замечание. Мы сказали, что обычно сначала формулируют тео-
теорему (т.е. то утверждение, которое хотят доказать), а затем ее до-
доказывают. На самом деле это не совсем так. Ведь тому, кто впервые
формулирует и доказывает теорему, заранее неизвестна ее формули-
формулировка! В действительности все начинается с того, что в виде гипотезы
формулируется утверждение, которое кажется правильным. Это утвер-
утверждение пытаются доказать на «черновике». Если в ходе доказательства
выясняется, что утверждение ошибочно, то возвращаются назад, т. е.
формулируют новую гипотезу с учетом допущенных ошибок и вновь
пытаются доказать ее справедливость. Иногда этот процесс повто-
повторяется многократно. Когда же, наконец, доказательство истинности
очередной гипотезы удается провести до конца, ее формулируют в виде
теоремы и доказывают на «чистовике».
13. Признаки параллельности двух прямых. Теперь мы можем
утвердительно ответить на один из поставленных ранее вопросов:
а есть ли параллельные прямые? В самом деле, рассмотрим две
прямые а и Ь, каждая из кото-
которых перпендикулярна к прямой с
(рис.46). Если бы прямые а и Ъ
пересекались, то из точки их пе-
пересечения оказались бы проведен-
проведенными два перпендикуляра к пря-
прямой с, что невозможно. Следова-
Следовательно, прямые а и Ъ не пересека-
пересекаются, т.е. параллельны. Итак,
две прямые, перпендикулярные
к третьей прямой, параллельны.
Сформулированное утверждение выражает признак (перпендику-
(перпендикулярность двух прямых к третьей прямой), по которому можно сделать
вывод о параллельности двух прямых, или, коротко говоря, признак
параллельности двух прямых.
Рассмотрим теперь прямые а и Ь, а также прямую с, которая
пересекает их в точках А и В (рис.47). Прямую с назовем секущей
по отношению к прямым а и Ь,
а углы 1 и 2 и также углы 3
и 4 на рисунке 47 — накрест
лежащими углами. Глядя на ри-
рисунок, можно предположить, что
если накрест лежащие углы рав-
равны, то прямые а и Ъ параллельны.
Но так ли это?
Давайте рассуждать. Если
накрест лежащие углы — пря-
прямые (рис.46), то прямые а и Ъ
перпендикулярны к прямой с и
ь /
Рис. 46
А.
Рис. 47. Прямая с — секущая. Углы 1
и 2 — накрест лежащие. Углы 3 и 4 —
накрест лежащие

3. Перпендикулярные и параллельные прямые
29
поэтому параллельны, это мы знаем. А можно ли это доказать, не ссы-
ссылаясь на теорему о перпендикуляре к прямой? Можно, и весьма просто.
Если мысленно перегнуть плоскость по прямой с (см. рис.46), то одна
половина рисунка совместится с другой. Поэтому если бы прямые а
и Ъ пересекались по одну сторону от прямой с, то они пересекались бы
и по другую сторону от этой прямой, чего не может быть, так как через
две точки можно провести только одну прямую.
Допустим теперь, что накрест лежащие углы 1 и 2 равны,
но прямыми не являются. Ясно, что смежные с ними накрест ле-
лежащие углы 3 и 4 также равны (рис.48, а). Разрежем плоскость
по прямой с (рис.48, б) и повернем одну из половин рисунка
на 180° (рис.48, в). Теперь наложим одну половину на другую так,
В
а)
б)
А
А, В
в) г)
Рис. 48. a) Zl = Z2, поэтому Z3 = Z4; б) разрезали плоскость по прямой с;
в) правую половину рисунка повернули на 180°; г) совместили две половины
рисунка
чтобы точка А на одной половине совместилась с точкой В на другой
половине, и наоборот (рис.48, г). Поскольку углы 1 и 2 равны, то они
совместятся. По аналогичной причине совместятся углы 3 и 4. Таким
образом, одна половина рисунка полностью совместится с другой его
половиной. Теперь все ясно! Осталось сформулировать теорему и, поль-
пользуясь нашими наблюдениями, доказать ее.
Теорема. Если при пересечении двух прямых секущей накрест
лежащие углы равны, то эти прямые параллельны.
Доказательство. Пусть при пересечении прямых а и Ъ секу-
секущей АВ накрест лежащие углы 1 и 2 равны. Тогда смежные с ними
углы 3 и 4 также равны (рис.49, а). Мысленно разрежем плоскость
по прямой АВ, повернем одну из полуплоскостей на 180° и наложим ее
на вторую полуплоскость так, чтобы точки А и В на ней совместились
соответственно с точками В и А на второй полуплоскости. Поскольку

30
Гл. 1. Начальные геометрические сведения
а)
Д В
С, D\
А, В
С \
углы 1 и 2 равны, то угол 1 совместит-
совместится с углом 2. Углы 3 и 4 также равны,
поэтому и они совместятся.
Если предположить, что прямые а
и Ъ пересекаются в точке С одной
из полуплоскостей, то точка D, с ко-
которой совместится точка С при на-
нашем наложении, также окажется об-
общей точкой прямых а и Ь (рис.49, б).
Тем самым окажется, что через точ-
точки С и D проходят две различные
прямые — а и Ъ (рис.49, в). Но это-
этого не может быть — через две точки
проходит только одна прямая. Следо-
Следовательно, прямые а и Ъ параллельны.
Теорема доказана.
в)
Рис.49, a) Zl = Z2, поэтому
Z3 = Z4; б) совместили две по-
половины рисунка. Если С — об-
общая точка прямых а и Ь, то
точка D, которая на нее нало-
жилась, — также общая точка
прямых а и 6; в) через точки С
и D проходят две прямые — а
и Ь, чего не может быть
Доказанная теорема является еще
одним признаком параллельности
двух прямых, причем ранее установ-
установленный признак является его частным
случаем. В самом деле, если две пря-
прямые перпендикулярны к третьей пря-
прямой, то накрест лежащие углы, образо-
образованные при пересечении этих двух пря-
прямых третьей, равны (эти углы — пря-
прямые), поэтому прямые параллельны.
Прежде чем сформулировать еще
два признака параллельности прямых,
обратимся к рисунку 50, на котором
прямые а и Ъ пересечены секущей с. Образовавшиеся при этом углы
обозначены цифрами. Назовем углы 1 и 5, 4 и 8, 2 и 6, 3 и 7
соответственными, а углы 4 и 5, 3 и 6 — односторонними.
Утверждения, которые непо-
непосредственно вытекают из теоремы,
называют следствиями. Из дока-
доказанной теоремы вытекают такие
следствия.
Если при пересечении двух пря-
прямых секущей соответственные
углы равны, то эти прямые па-
параллельны.
Если при пересечении двух пря-
прямых секущей сумма односторон-
односторонних углов равна 180°, то эти пря-
прямые параллельны.
5/6
рис 50

3. Перпендикулярные и параллельные прямые
31
Доказательства этих утверждений приведены под рисунками 51
и 52.
3/2
Рис. 51. Пусть соответственные уг-
углы Z1 и Z2 равны: Zl = Z2. Так
как Z2 = Z3 (как вертикальные уг-
углы), то Zl = Z3, т. е. равны накрест
лежащие углы. Следовательно, а \\ Ъ
Рис. 52. Пусть сумма односторон-
односторонних углов 1 и 2 равна 180°. Так как
сумма смежных углов 3 и 2 также
равна 180°, то Zl = Z3, т.е. рав-
равны накрест лежащие углы. Следова-
Следовательно, а II Ъ
14. Практические способы построения параллельных прямых.
Признаки параллельности двух прямых лежат в основе практических
способов построения параллельных прямых с помощью различных ин-
инструментов. Рассмотрим, например, способ построения параллельных
прямых с помощью чертежного угольника и линейки.
Чтобы построить прямую, проходящую через точку М и парал-
параллельную данной прямой а, сначала приложим чертежный угольник
к прямой а, а к нему линейку так, как показано на рисунке 53. Затем,
передвигая угольник вдоль линейки, добьемся того, чтобы точка М
оказалась на стороне угольника, и проведем прямую Ь. Прямые а и Ь
параллельны, так как соответственные углы, обозначенный на рисун-
рисунке 53 буквами а и /3, равны.
На рисунке 54 показан способ построения параллельных прямых
при помощи рейсшины. Этим способом пользуются в чертежной прак-
практике.
М
Рис. 53
Рис. 54

32
Гл. 1. Начальные геометрические сведения
Рис. 55
Аналогичный способ применяется при столяр-
столярных работах, где для разметки параллельных пря-
прямых используется малка, представляющая собой
две деревянные планки, скрепленные шарниром
(рис. 55).
15. А есть ли квадрат?. Вернемся к нашим
геометрическим конструкциям, связанным с чис-
числом у/2 (см. п. 11). Мы разрезали каждый из двух
одинаковых квадратов с площадью 1 по диагонали
и из получившихся четырех треугольников соста-
составили квадрат с площадью 2 (см. рис.37 и 38).
А почему получился квадрат? Если внимательно
посмотреть на рисунок 38, то видно, что стороны получившегося че-
четырехугольника одинаковы, так как каждая из них равна диагонали а
исходного квадрата. Но ведь четырехугольник, все стороны которого
равны, может и не быть квадратом (рис.56). У квадрата каждый
из углов — прямой. А вот являются ли у составленного нами четырех-
четырехугольника все углы прямыми? Это нужно доказать!
Можно поступить так. Разрежем квадрат ABCD со стороной 1
по диагонали (рис.57). Докажем, что полученные при этом треуголь-
треугольники ABD и CBD равны. Для этого треугольник ABD наложим
на треугольник CBD так, чтобы прямой угол при вершине А совме-
совместился с прямым углом при вершине С (рис.58). Тогда сторона АВ
совместится со стороной СВ, а сторона AD совместится со сторо-
стороной CD. Теперь уже ясно, что треугольник ABD полностью совместит-
совместится с треугольником CBD. Следовательно, эти треугольники равны.
Поэтому ZABD = ZCBD (эти углы отмечены дугами на рисунках 57
и 58) и ZADB = ZCDB. Равенство этих углов означает, что диагональ
квадрата делит пополам каждый из углов квадрата, через вершины
В
Рис. 56. Четырехуголь-
Четырехугольник, у которого все сто-
стороны равны, называет-
называется ромбом. Ромб может
и не быть квадратом
Рис. 57. Квадрат ABCD
разрезан по диагонали на
два треугольника ABD
и CBD

3. Перпендикулярные и параллельные прямые
33
D
Рис. 58. На этом рисунке по-
показан процесс наложения тре-
треугольника ABD на треугольник
CBD. Начальное и промежу-
промежуточное положения треугольни-
треугольника ABD показаны пунктиром.
Стрелками указан путь вершин
которых она проходит. Взглянув теперь
еще раз на рисунок 38, мы сразу уви-
увидим, что углы при вершинах построен-
построенного нами четырехугольника (он изоб-
изображен штрихами) — прямые, так как
каждый из них составлен из двух по-
половинок прямого угла. Стороны же че-
четырехугольника равны, и поэтому этот
четырехугольник — квадрат.
Но возникает другой вопрос. При
конструировании квадрата со сторо-
стороной а мы исходили из того, что у нас
есть квадрат со стороной 1, т.е. есть
четырехугольник, все стороны которо-
которого равны 1 и все углы — прямые.
А есть ли такой четырехугольник, т. е.
есть ли квадрат со стороной 1? И во-
вообще, существует ли квадрат с дан-
данной стороной d? Можно попытаться
ответить на этот вопрос так: попро-
попробовать построить квадрат со сторо-
стороной d.
Рассмотрим отрезок AD длины d (рис.59). Через точку А под
прямым углом к прямой AD проведем луч h и отложим на нем от-
отрезок АВ = d. Через точку В под прямым углом к лучу h проведем
луч к и отложим на нем отрезок ВС = d. Далее через точку С под
прямым углом к лучу к про-
проведем луч /. Теперь на этом
луче отложим отрезок CD\ =
= d. Наше построение завер-
завершено, но что мы получили?
Если точка D\ совпадет с точ-
точкой D, то мы получим четы-
четырехугольник с равными сто-
сторонами. Но откуда следует,
что угол при вершине D этого
четырехугольника будет пря-
прямым? А может быть и точ-
точка D\ не совпадет с точкой D.
Тогда даже четырехугольник
не получится.
Можно предложить иную
конструкцию — через точку С
не проводить луч / под пря- Рис. 59. Построение квадрата с заданной
мым углом к лучу fc, а просто стороной d
соединить точки С и D отрез-
к
2 С. Б. Кадомцев

34 Гл. 1. Начальные геометрические сведения
ком. Но будет ли сторона CD равна d и будут ли углы при верши-
вершинах С и D прямыми? Самое удивительное, что без дополнительных
предположений нельзя ответить ни на один из этих вопросов. Эти
предположения мы обсудим в нашей книге позже и тогда докажем, что
квадрат с заданной стороной есть, он существует. А пока запишите
в свой блокнот вопрос:
есть ли квадрат?
16. Заключительные замечания. Мы познакомились с некоторы-
некоторыми начальными геометрическими понятиями. И уже появились вопро-
вопросы, на которые мы пока не знаем ответа. Например, мы не знаем, есть
ли квадрат.
В наших доказательствах мы широко ис-
использовали рисунки. Хотя, наверное, Вы почув-
почувствовали, что рисунки только поясняют суть
дела, но не заменяют рассуждения. К рисункам
надо относиться с осторожностью. Об этом уже
говорилось в пункте 6. Вот еще два рисунка —
60 и 61, показывающие, что рисункам можно
доверять далеко не всегда.
Геометрия развивает наши пространствен-
пространственные представления. Но не только для этого
она нужна. Она важна для нашей практической
деятельности. Но, пожалуй, и это не главное.
Наполеон Доказывая что-то, решая задачи, мы учимся
рассуждать, а это важно в любом деле. Геомет-
Геометрия, как мы вскоре увидим, поражает воображение тем, что путем
рассуждений в ней устанавливаются совершенно неожиданные факты.
Не удивительно, что на протяжении многих столетий люди самых раз-
разнообразных профессий посвящали часы досуга занятиям геометрией.
Даже Наполеон Бонапарт, будучи императором и великим полковод-
полководцем, оставил свой след в геометрии в виде теоремы Наполеона.
Задачи
18. Докажите, что если биссектрисы углов ABC и CBD перпенди-
перпендикулярны, то точки А, В и D лежат на одной прямой.
19. Пусть Zhk — меньший из двух смежных углов hk и hi. Дока-
Докажите, что Zhk = 90° - \{Zhl - Zhk), a Zhl = 90° + \{Zhl - Zhk).
20. Докажите, что биссектрисы вертикальных углов лежат на одной
прямой.
21. Пять прямых пересекаются в одной точке (рис.62). Найдите
сумму углов 1, 2, 3, 4 и 5.
22. Даны две пересекающиеся прямые а и Ь и точка А, не лежа-
лежащая на этих прямых. Через точку А проведены прямые тип так,
что т JL а, п ±Ь. Докажите, что прямые т и п не совпадают.
23. Квадрат разрезан по диагонали. Докажите, что сумма углов
в каждом из полученных треугольников равна 180°.

3. Перпендикулярные и параллельные прямые
35
Рис. 60. Такая пространственная
фигура невозможна. А на рисунке
она есть. Этот рисунок придумал
ученый Р. Пенроуз
Рис. 61. Лестница Схоутена (по име-
имени ученого, придумавшего этот ри-
рисунок). Звездочкой отмечена стена, в
которую упирается лестница. Повер-
Поверните рисунок на 180° и посмотрите,
во что превратится стена, отмеченная
звездочкой
24. Прямоугольник, составленный из двух равных квадратов
(рис.63), разрезан по диагонали на два треугольника (один из них
на рисунке 63 заштрихован). Докажите, что эти треугольники равны.
Докажите также, что сумма углов каждого из этих треугольников
равна 180°.
25. На рисунке 64 прямые а и Ъ пересечены секущей с. Докажите,
что а || Ь, если: a) Z1 = 37°, Z7 = 143°; б) Zl = Z6; в) Z1 = 45°, a Z7
в три раза больше Z3.
26. Дан квадрат ABCD. Докажите, что АВ \\ CD и AD \\ ВС.
Рис. 62

36
Гл. 1. Начальные геометрические сведения
V
1\2
Рис. 63
7\6
Рис. 64
27. На рисунке 65 ABAC = ABC А и ZDCE = ZDEC. Докажите,
что АВ || DE.
28. Исходя из рисунка 66, докажите, что: а) ВС \\ DE; б) прямые,
содержащие биссектрисы углов ABC и DEF, параллельны.
А
Е
D
Рис. 65
Рис. 66
29. Исходя из рисунка 67, докажите, что прямая, содержащая
биссектрису угла BCD, параллельна прямой АВ.
А
С
Рис. 67
D
D
Рис. 68
30. На рисунке 68 луч BD — биссектриса угла ABC. Докажите,
что AD || ВС.

Глава 2
ТРЕУГОЛЬНИКИ
§ 1. Треугольники и их виды
17. Треугольник. Вспомним, что такое треугольник. Это фигура,
состоящая из трех отрезков — сторон треугольника, соединяющих
три точки — вершины треугольника. К этому надо добавить еще, что
вершины треугольника не должны лежать на одной прямой. Итак, тре-
треугольником называется геометрическая фигура, состоящая из трех
отрезков, соединяющих три точки, не лежащие на одной пря-
прямой. Треугольник с вершинами А, В и С условимся обозначать
так: ААВС (рис.69).
Углы ABAC, ZCBA и ZACB называют углами треугольни-
треугольника ABC. Эти углы часто обозначают одной буквой: /.A, ZB и Z.C.
Сумма трех сторон треугольника называется его периметром.
Каждый треугольник разделяет плоскость на две части: внутрен-
внутреннюю и внешнюю области (рис.70). Как сказать словами, что такое
внутренняя область треугольника? Можно сказать так: это общая
часть внутренних областей трех его углов (рис.71). Фигуру, состоя-
состоящую из сторон треугольника и его внутренней области, также называ-
называют треугольником.
Внешняя
7\
область ~/ \ треугольника
/ \
Внутренняя
область >v
треугольника
А В
Рис. 69. Треугольник ABC Рис. 70

38
Гл. 2. Треугольники
Внутренняя
область
угла А
Внутренняя
область
угла С
Внутренняя область
треугольника ABC
Внутренняя
область
угла В
Рис. 71. Внутренняя область треугольника ABC — общая часть внутренних
областей трех углов А, В и С этого треугольника
18. Внешний угол треугольника. В следующих пунктах мы полу-
получим ряд важных соотношений между сторонами и углами треугольни-
треугольника. При выводе этих соотношений нам понадобится понятие внешнего
угла треугольника и его свойство.
Внешним углом треугольника называется угол, смежный с каким-
нибудь углом этого треугольника. При каждой вершине треугольника
имеются два внешних угла. На рисунке 72 изображены внешние углы
треугольника ABC.
Докажем теорему о внешнем угле треугольника.
Теорема. Внешний угол треугольника больше каждого угла
треугольника, не смежного с этим внешним углом.
Доказательство. Рассмотрим треугольник ABC (рис. 73) и до-
докажем, например, что внешний угол BCD больше угла В. Проведем
луч ВА\ так, чтобы углы А\ВС и BCD оказались равными накрест
2/4
Рис. 72. Углы 1, 2, 3, 4, 5, б — внеш-
внешние углы треугольника ABC
С
А
Рис. 73

/. Треугольники и их виды
39
лежащими углами, образованными при пересечении прямых А\В и CD
секущей ВС. По признаку параллельности двух прямых прямые А\В
и CD параллельны.
Следовательно, угол BCD не может быть равен углу В. Иначе пря-
прямая А\В совпала бы с прямой АВ и потому не была бы параллельной
прямой CD, поскольку прямая АВ пересекает прямую CD в точке А.
Если бы угол BCD, а значит и равный ему угол А\ВС, был меньше
угла В, то луч ВА\ делил бы угол В на два угла и, следовательно,
пересекал бы отрезок АС, а значит, и прямую CD. Этого также
не может быть, поскольку прямые А\В и CD параллельны. Поэтому
угол BCD больше угла В. Теорема доказана.
Следствие. Сумма двух углов треугольника меньше 180°.
В самом деле, рассмотрим треугольник ABC и докажем, например,
что А А + /Б < 180°. Внешний угол при вершине А равен 180° —
— /.А. Поскольку этот угол больше угла В, то 180° — ZА > ZB,
откуда 180° > ZA + ZB, или ZA + ZB < 180°.
19. Классификация треугольников.
Из теоремы о внешнем угле треугольника
следует, что если в треугольнике один
из углов — прямой или тупой, то два
других угла — острые. В самом деле,
пусть в треугольнике ABC угол А —
прямой или тупой (рис.74). Тогда внеш-
внешний угол BAD — прямой или острый. ^^_^^_^_^^_^^^^
По теореме о внешнем угле треугольника С A D
углы В и С треугольника ABC меньше
угла BAD, поэтому они — острые. Таким
образом,
в любом треугольнике либо все три угла — острые, либо два
угла — острые, а третий — прямой или тупой.
Если все углы треугольника — острые, то его называют остро-
остроугольным (рис.75, а). Если один из углов треугольника — прямой,
то его называют прямоугольным (рис.75, б), а если один из углов
Рис. 74
а)
б)
в)
Рис. 75. а) Остроугольный треугольник — все его углы острые; б) прямоуголь-
прямоугольный треугольник — у него один угол прямой; в) тупоугольный треугольник —
у него один угол тупой

40
Гл. 2. Треугольники
треугольника — тупой, то тупоугольным
(рис.75, в). Сторону прямоугольного тре-
треугольника, лежащую против прямого угла,
называют гипотенузой, а две другие сто-
стороны — катетами (рис.76).
Эта классификация треугольников, т. е.
разделение их на три вида (класса), ос-
основана на сравнении углов треугольника.
Можно дать классификацию треугольни-
треугольников, опираясь на сравнение их сторон.
Если длины всех сторон треугольни-
треугольника разные, то его называют разносторон-
разносторонним (рис.77, а). Если две стороны равны, то треугольник называют
равнобедренным (рис.77, б). Равные стороны равнобедренного тре-
треугольника обычно называют боковыми сторонами, а третью сторо-
сторону — основанием. Треугольник, у которого все стороны равны, назы-
называют равносторонним (рис.77, в).
катет
Рис. 76. Прямоугольный
треугольник
основание
а)
б)
Рис. 77. а) Разносторонний треугольник — длины всех его сторон разные;
б) равнобедренный треугольник — у него две стороны равны; в) равносторон-
равносторонний треугольник — у него все стороны равны
20. Медианы, биссектрисы и высоты треугольника. С каждым
треугольником связаны несколько отрезков, которые имеют специаль-
специальные названия.
Отрезок, соединяющий вершину треугольника с серединой проти-
противоположной стороны, называется медианой треугольника (рис.78, а).
Отрезок биссектрисы угла, соединяющий вершину с точкой
противоположной стороны, называется биссектрисой треугольника
(рис. 79, а).
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой треуголь-
треугольника (рис.80, а).
Посмотрим на рисунки 78, 79, 80. Мы видим, что три медианы
треугольника на рисунке 78, б пересекаются в одной точке, три бис-

/. Треугольники и их виды
41
М
а)
В
м2
м1
с
Рис. 78. a) AM — медиана треугольника; б) АМ\, ВМ2, СМ^ — медианы
треугольника ABC
сектрисы на рисунке 79, б пересекаются в одной точке, три высоты или
их продолжения на рисунках 80 б, в, г также пересекаются в одной
точке. Случайно ли это, или так будет в любом треугольнике? Пока
мы не можем ответить на эти вопросы, поэтому запишем их в блокнот:
Верно ли, что три медианы треугольника пересекаются в одной
точке}
Верно ли, что три биссектрисы треугольника пересекаются
в одной точке?
Верно ли, что три высоты треугольника или их продолжения
пересекаются в одной точке}
А
D
С
б)
— биссектриса треугольника ABC; б) СС\, DD\, EE\ —
биссектрисы треугольника CDE
Задачи
31. Может ли в треугольнике один угол быть острым, другой —
прямым, а третий — тупым? Ответ обоснуйте.
32. В треугольнике ABC угол А — прямой. Докажите, что внешние
углы при вершинах В и С — тупые.
33. Докажите, что в любом треугольнике сумма двух внешних
углов при разных вершинах больше 180°.

42
Гл. 2. Треугольники
В
Н
В
а)
С В
А
н.
с в Hl
С
Рис. 80. а) АН — высота треугольника; б), в), г) АН\, ВЩ, СЩ — высоты
треугольника ABC
34. В прямоугольном треугольнике ABC с прямым углом С точ-
точка D лежит на катете ВС. Докажите, что ZADB > ZABC и ZADB >
> ABAC.
35! Точка М лежит во внутренней области треугольника ABC.
Докажите, что ABAC < ZBMC.
36. Вершина С треугольника ABC лежит между вершиной В
и основанием высоты АН. Докажите, что углы А и В — острые.
37. Периметр равнобедренного треугольника ABC с основани-
основанием ВС равен 40 см, а периметр равностороннего треугольника BCD
равен 45 см. Найдите стороны АВ и ВС.
38. В равнобедренном треугольнике ABC с основанием ВС про-
проведена медиана AM. Найдите AM, если периметр треугольника ABC
равен 32 см, а периметр треугольника АВМ равен 24 см.
39. Основание равнобедренного треугольника равно 8 см. Меди-
Медиана, проведенная к боковой стороне, разбивает треугольник на два
треугольника так, что периметр одного треугольника на 2 см больше
периметра другого. Найдите боковую сторону данного треугольника.
40! Докажите, что в остроугольном треугольнике основания высот
лежат на сторонах треугольника и не совпадают с его вершинами.
41! Докажите, что в тупоугольном треугольнике основание высоты,
проведенной из вершины тупого угла, лежит на стороне треугольника,
а основания высот, проведенных из вершин острых углов, — на про-
продолжениях сторон.

2. Равнобедренный треугольник
43
§ 2. Равнобедренный треугольник
21. Теорема об углах равнобедренного треугольника.
Теорема. Углы при основании равнобедренного треугольника
равны.
Доказательство. Рассмотрим равнобедренный треугольник
ABC с основанием ВС (рис.81, а) и докажем, что АВ = Z.C.
В
а)
С
б)
Рис. 81
Мысленно наложим на рисунок 81, а прозрачный лист, скопируем
рисунок, перевернем лист (рис.81, б) и вновь наложим на рисунок так,
чтобы вершина А на листе совместилась с вершиной А на рисунке,
а луч АВ на листе совместился с лучом АС на рисунке. Ясно, что
при этом луч АС на листе совместится с лучом АВ на рисунке,
а поскольку АВ = АС, то точка В совместится с точкой С, а точ-
точка С — с точкой В. Иными словами, треугольник на листе полностью
совместится с треугольником на рисунке. При этом угол В совместится
с углом С, а значит, эти углы равны. Теорема доказана.
22. Признак равнобедренного треугольника.
Теорема. Если два угла треугольника
равны, то такой треугольник — равнобед-
равнобедренный.
Доказательство. Рассмотрим треуголь-
треугольник ABC, углы В и С которого равны (рис. 82),
и докажем, что АВ = АС.
Воспользуемся идеей доказательства теоре-
теоремы об углах равнобедренного треугольника.
Мысленно наложим на рисунок 82 прозрач-
прозрачный лист, скопируем рисунок, перевернем лист
и вновь наложим на рисунок так, чтобы вер-
вершина В на листе совместилась с вершиной С
на рисунке, а вершина С на листе — с вер- В
шиной В на рисунке. Поскольку углы В и С
равны, то луч В А на листе совместится с лу-
С
Рис. 82

44
Гл. 2. Треугольники
чом С А на рисунке, а луч С А на листе — с лучом В А на рисунке.
Поэтому треугольник на листе полностью совместится с треугольни-
треугольником на рисунке. При этом сторона АВ совместится со стороной АС,
а значит, эти стороны равны. Теорема доказана.
Таким образом, равенство у треугольника двух углов является
признаком, по которому можно сделать вывод о том, что этот треуголь-
треугольник — равнобедренный, т. е. доказанная теорема выражает признак
равнобедренного треугольника.
23. Теорема о высоте равнобедренного треугольника.
Теорема. Высота равнобедренного треугольника, проведенная
к основанию, является медианой и биссектрисой.
Доказательство. Рассмотрим равнобед-
равнобедренный треугольник ABC, в котором АН —
высота, проведенная к основанию ВС (рис.83).
Докажем, что отрезок АН является также ме-
медианой и биссектрисой треугольника ABC.
Мысленно наложим на треугольник ABC
прозрачный лист, скопируем треугольник и от-
отрезок АН, перевернем лист и вновь наложим
на треугольник ABC так, чтобы вершины А,
В и С на листе совместились соответственно
с вершинами А, С и В треугольника (см. до-
доказательство теоремы об углах равнобедренно-
равнобедренного треугольника). Из точки А можно провести
только один перпендикуляр к прямой ВС. Сле-
Следовательно, отрезок АН на листе совместится
с высотой АН треугольника ABC. Поэтому
отрезок ВН совместится с отрезком СН, а угол ВАН — с углом САН.
Значит, ВН = СН и ZBAH = АСАН. Из этого следует, что отре-
отрезок АН является медианой и биссектрисой треугольника ABC. Теоре-
Теорема доказана.
Итак, мы установили, что высота, медиана и биссектриса равнобед-
равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому
следствиями из доказанной теоремы являются следующие утвержде-
утверждения:
1° биссектриса равнобедренного треугольника, проведенная к ос-
основанию, является высотой и медианой]
2° медиана равнобедренного треугольника, проведенная к осно-
основанию, является биссектрисой и высотой.
Задача. Доказать, что если в треугольнике биссектриса явля-
является медианой, то этот треугольник — равнобедренный.
Решение. Рассмотрим треугольник ABC, в котором биссектри-
биссектриса AM является одновременно медианой (рис.84, а), т.е. Zl = Z2
и MB = МС. Требуется доказать, что АВ = АС.
В
Н
Рис. 83
С

2. Равнобедренный треугольник
45
В
М
а)
С В
Рис. 84
Попробуем рассуждать так. Мысленно перегнем плоскость по пря-
прямой AM так, чтобы треугольник АВМ наложился на треуголь-
треугольник АСЫ. При этом луч АВ совместится с лучом АС, посколь-
поскольку Z1 = Z2, и, следовательно, точка В совместится с какой-то точкой
на луче АС. Если мы докажем, что точка В совместится с точкой С,
то из этого будет следовать, что АВ = АС, т. е. треугольник ABC —
равнобедренный, и тем самым задача будет решена.
Но как доказать, что точка В совместится с точкой С? Допустим,
что точка В совместится не с точкой С, а с какой-то другой точкой В'
на луче АС. Предположим сначала, что точка В' лежит между А
и С (рис.84, б). Поскольку в результате перегибания угол АВМ
совмещается с углом АВ'М, то ZABM = ZAB'M, т. е.
ZB = ZAB'M.
A)
Отрезок MB совмещается с отрезком MB', поэтому MB' = МБ,
а так как по условию MB = МС, то MB' = МС. Это означает, что
треугольник MB'С — равнобедренный и, следовательно, его углы при
основании В'С равны:
ZC = ZCB'M. B)
Заметим теперь, что углы АВ'М и СВ'М — смежные, поэто-
поэтому ZAB'M + ZCB'M = 180°. Из этого равенства, учитывая равен-
равенства A) и B), получаем:
= 180°.
C)
Итак, мы получили, что сумма двух углов треугольника ABC
равна 180°. Но этого не может быть — сумма двух углов треугольника
меньше 180° (см. п. 18).
Таким образом, наше предположение о том, что в результате пе-
перегибания по прямой AM точка В совместится с точкой В', лежа-
лежащей между А и С, привело к противоречию с установленным ранее
свойством углов треугольника. Это означает, что наше предположение
не верно.
Если мы предположим, что точка В совместится с такой точкой В',
что точка С лежит между точками А и В' (рис. 84, в), то снова придем

46 Гл. 2. Треугольники
к равенству C), которое не может быть выполнено. Рассуждения для
этого случая проведите самостоятельно.
Следовательно, в результате перегибания точка В обязательно сов-
совместится с точкой С. Поэтому АВ = АС, т. е. треугольник ABC —
равнобедренный, что и требовалось доказать.
Задачи
42. Докажите, что в равностороннем треугольнике все углы равны.
43. Медиана AM треугольника ABC равна отрезку ВЫ. Докажи-
Докажите, что один из углов треугольника ABC равен сумме двух других
углов.
44. На рисунке 85 АВ = ВС,
CD = DE. Докажите, что ABAC =
= ZCED.
45. В треугольнике ABC ZA =
= 38°, ZB = 110°, АС = 32°. На
стороне АС отмечены точки D и Е
так' что точка D лежит на отрез-
ке АЕ, BD = DA, BE = ЕС. Най-
дите ZDBE.
46* Даны три точки А, В и С,
рис g? лежащие на одной прямой, и точ-
точка D, не лежащая на этой прямой.
Докажите, что по крайней мере два из трех отрезков AD, BD, CD
не равны друг другу.
47. В равнобедренном треугольнике ABC с основанием АС биссек-
биссектрисы углов А и С пересекаются в точке О. Докажите, что треуголь-
треугольник АОС — равнобедренный.
48. В равнобедренном треугольнике DEK с основанием DK от-
отрезок ЕЕ — биссектриса, DK = 16 см, ZDEF = 43°. Найдите KF,
ZDEK, ZEFD.
49! Докажите, что если медиана треугольника совпадает с его
высотой, то этот треугольник — равнобедренный.
50. Докажите, что если в треугольнике ABC стороны АВ и АС
не равны, то медиана AM этого треугольника не является его высотой.
51! Докажите, что если биссектриса треугольника является его
высотой, то этот треугольник — равнобедренный.
§ 3. Соотношения между сторонами и углами
треугольника
24. Теорема о соотношениях между сторонами и углами тре-
треугольника. Рассмотрим треугольник ABC. Если стороны АВ и АС
равны, т. е. треугольник равнобедренный, то, как мы знаем, углы В
и С также равны. А что можно сказать об углах В и С, если стороны
АВ и АС не равны? Пусть, например, сторона АВ больше стороны

3. Соотношения между сторонами и углами треугольника
47
А'
В
Рис. 86. Если АВ > АС, то АС > АВ:
против большей стороны лежит боль-
больший угол
АС (рис.86). Тогда лежащие
против этих сторон углы С и В
также не равны. В самом деле,
если эти углы равны, то тре-
треугольник ABC — равнобедрен-
равнобедренный, а стороны АВ и АС —
его равные боковые стороны,
т. е. АВ = АС, что противоре-
противоречит условию.
Итак, если сторона АВ
больше стороны АС, то углы С
и В не равны друг другу. А ка-
какой из этих углов больше? На нашем рисунке видно, что больше
угол С, т.е. тот угол, который лежит против большей стороны. А все-
всегда ли это так? Оказывается, всегда. Докажем это утверждение.
Теорема. В треугольнике против большей стороны лежит
больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ боль-
больше стороны АС. Докажем, что АС > АВ (рис.86).
Отложим на луче АВ от-
отрезок AD, равный стороне АС
(рис.87). Так как AD < АВ,
то точка D лежит между точ-
точками А н В. Следовательно,
угол 1 является частью уг-
угла С, а значит, АС > А\.
Но А\ = Z2 (как углы при А _
основании CD равнобедренно-
равнобедренного треугольника ACD), поэто- Рис. 87
му АС > Z2.
Рассмотрим теперь треугольник BCD. Так как угол 2 — внешний
угол этого треугольника, то Z2 > АВ. Таким образом, АС > Z2,
a Z2 > АВ, поэтому АС > АВ. Теорема доказана.
25. Обратные теоремы. Во всякой теореме различают две части:
условие и заключение. Условие теоремы — это то, что дано, заключе-
заключение — то, что требуется доказать.
Рассмотрим, например, теорему об углах равнобедренного треуголь-
треугольника. Для того чтобы выделить условие теоремы, сформулируем ее так:
«если треугольник равнобедренный, то углы при его основании рав-
равны». В этой теореме условием является первая часть утверждения:
«если треугольник равнобедренный», а заключением — вторая часть:
«то углы при его основании равны». Иными словами, дан равнобед-
равнобедренный треугольник и требуется доказать, что углы при его основании
равны.

48 Гл. 2. Треугольники
Теоремой, обратной данной, называется такая теорема, в которой
условием является заключение данной теоремы, а заключением —
условие данной теоремы. Теоремой, обратной теореме об углах рав-
равнобедренного треугольника, является теорема о признаке равнобед-
равнобедренного треугольника: если два угла треугольника равны, то этот
треугольник — равнобедренный.
Отметим, что если доказана прямая теорема, то отсюда еще не сле-
следует справедливость обратной теоремы. Более того, обратная теорема
не всегда имеет место. Приведем простой пример. Мы знаем, что
если а2 = 2, то число а — иррациональное. Обратное утверждение:
«если число а — иррациональное, то а2 = 2», конечно же, неверно (см,
например, задачу 15).
Докажем теорему, обратную теореме предыдущего пункта.
Теорема. В треугольнике против большего угла лежит
большая сторона.
Доказательство. Пусть в
треугольнике ABC угол С больше
угла В. Докажем, что АВ > АС
(рис.88).
Допустим, что это не так. То-
, ^ гда либо АВ = АС, либо АВ <
< АС. В первом случае тре-
Рис. 88. Если ZC > ZB, то АВ > У™льник ABC - равнобедренный,
> АС: против большего угла лежит а значит, ZC = ZB. Во втором слу-
большая сторона чае по теореме предыдущего пунк-
пункта ZC < ZB. И то, и другое проти-
противоречит условию теоремы: ZC > ZB. Поэтому сторона АВ не может
быть равной стороне АС и не может быть меньше стороны АС. Следо-
Следовательно, АВ > АС. Теорема доказана.
Следствие. В прямоугольном треугольнике гипотенуза больше
катета.
В самом деле, гипотенуза лежит против прямого угла, а катет —
против острого. Так как прямой угол больше острого, то гипотенуза
больше катета.
Замечание. При доказательстве теоремы мы использовали спо-
способ рассуждений, который называется методом доказательства
от противного. Мы предположили, что АВ ^ АС, т. е. предположили
противоположное (противное) тому, что хотим доказать. Исходя из это-
этого предположения, путем рассуждений мы пришли к противоречию
с условием теоремы. Это означает, что наше предположение неверно,
а значит, АВ > АС.
Такой способ рассуждений часто используется в математике при
доказательстве утверждений. Может быть Вы заметили, что мы уже
неоднократно им пользовались.

3. Соотношения между сторонами и углами треугольника
49
В
М
Рис.
С
Задача 1. Отрезок соединяет вершину треугольника с внут-
внутренней точкой противоположной стороны. Доказать, что этот
отрезок меньше большей из двух других сторон.
Решение. Рассмотрим треугольник ABC, в котором отрезок AM
соединяет вершину А с точкой М стороны ВС (рис.89). Пусть АВ >
> АС. Требуется доказать, что AM < АВ.
Отрезки AM и АВ являют-
являются сторонами треугольника АМВ.
В треугольнике же из двух сто-
сторон та больше, которая лежит про-
против большего угла. Поэтому если
мы докажем, что АВ < Z1, то из
этого будет следовать, что AM <
<АВ.
Сравнить углы В и 1 можно та-
таким образом. Угол В меньше уг-
угла С (так как АС < АВ по усло-
условию), а угол С меньше угла 1, так
как угол 1 — внешний угол треугольника АМС. Итак, ZB < ZC
и ZC < Z1. Следовательно, ZB < Z1, поэтому AM < АВ, что и тре-
требовалось доказать.
26. Неравенство треугольника. Теперь мы знаем несколько со-
соотношений между сторонами и углами треугольника. А существует
ли какое-нибудь соотношение между тремя сторонами треугольника
или между тремя его углами? Начнем со сторон, а вопрос о соотноше-
соотношении между тремя углами запишем пока в блокнот.
Нарисуем треугольник ABC (рис. 90, а) и представим себе, что нам
нужно по кратчайшему пути вдоль сторон треугольника ABC пройти
из точки А в точку В. Как мы пойдем: по стороне АВ, или сначала
по АС, а затем по СВ? Ясно, что по АВ — этот путь короче. Вот
мы и получили соотношение между тремя сторонами треугольника:
каждая сторона треугольника меньше суммы двух других сторон.
Сформулируем это утверждение в виде теоремы и докажем ее.
Теорема. Каждая сторона треугольника меньше суммы двух
других сторон.
С
А
а)
С
б)
D
Рис. 90

50
Гл. 2. Треугольники
Доказательство. Рассмотрим треугольник ABC и докажем,
например, что АВ < АС + СВ. Отложим на продолжении стороны
АС отрезок CD, равный стороне СВ (рис.90, б). Так как треуголь-
треугольник BCD — равнобедренный (ВС = CD), то Zl = Z2, а посколь-
поскольку ZABD > Z1, то ZABD > Z2. В треугольнике ABD против боль-
большего угла лежит большая сторона, поэтому АВ < AD. Но AD = АС +
+ CD = АС + СБ. Следовательно, АЕ> < АС + СБ. Теорема доказана.
Доказанную теорему можно сформулировать иначе:
для любых трех точек А, В и С, не лежащих на одной прямой,
справедливы неравенства:
АВ <АС + СВ, ВС <ВА + АС, СА<СВ + В А.
Каждое из этих неравенств называется неравенством треугольни-
треугольника.
Воспользуемся неравенством треугольника для решения такой за-
задачи.
Задача 2. Доказать, что
если точка М лежит внутри
треугольника ABC, то MB +
+MC <АВ + АС.
Решение. Обратимся к ри-
рисунку 91, на котором отре-
отрезок MD является продолжением
отрезка ВЫ. Воспользуемся нера-
неравенством треугольника примени-
тельно к треугольникам ABD
и MDC. В треугольнике ABD
BD < АВ + AD, или MB +
+ MD < АВ + AD. Отсюда полу-
полуВ
С
Рис. 91
чаем:
MB <AB + AD-MD.
В треугольнике MDC
МС < MD + DC.
A)
B)
Ясно, что сумма слагаемых, стоящих в левых частях неравенств A)
и B), меньше суммы слагаемых, стоящих в правых частях этих нера-
неравенств, т. е. MB + МС < АВ + AD - MD + MD + DC, или MB +
+ МС <AB + AD + DC. Но AD + DC = АС, поэтому MB + МС <
< АВ + АС, что и требовалось доказать.
Задачи
52. Докажите, что в равнобедренном треугольнике отрезок, соеди-
соединяющий любую точку основания, отличную от вершины, с противопо-
противоположной вершиной, меньше боковой стороны.

3. Соотношения между сторонами и углами треугольника 51
53. Докажите, что медиана треугольника не меньше высоты, про-
проведенной из той же вершины.
54! Высота АА\ треугольника ABC не меньше стороны ВС, а вы-
высота ВВ\ не меньше стороны АС. Докажите, что треугольник ABC —
равнобедренный и прямоугольный.
55. Дан треугольник ABC с тупым углом С, К — произвольная
внутренняя точка стороны АС. Докажите, что ВК > ВС и ВК < АВ.
56! Докажите, что любой отрезок с концами на разных сторонах
треугольника не больше наибольшей из сторон этого треугольника.
57! Внутри треугольника ABC взята такая точка D, что AD = АВ.
Докажите, что АС > АВ.
58. Отрезок ВВ\ — биссектриса треугольника ABC. Докажите,
что В А > ВХА и ВС > ВХС.
59. Отрезок АН — перпендикуляр к прямой а, точки М\ и М2,
отличные от точки Я, лежат на прямой а. Докажите, что: а) если
НМХ = НМ2, то АМХ = АМ2, б) если НМХ < НМ2, то АМХ < АМ2,
в) если АМ\ = АМ2, то НМ\ = НМ2, г) если АМ\ < АМ2, то НМ\ <
<НМ2.
60! Отрезок AD — биссектриса треугольника ABC, АВ > АС.
Докажите, что ZADB > ZADC и BD > CD.
61. В треугольнике ABC проведены биссектриса AD и высота АН,
АВ < АС. Докажите, что точка Н лежит на луче DB.
62! Отрезки AM, AD и АН — медиана, биссектриса и высота
треугольника ABC, АВ ф АС. Докажите, что точка D лежит между
точками М и Я.
63. Найдите сторону равнобедренного треугольника, если две дру-
другие стороны равны: а) 8 см и 2 см; б) 10 см и 5 см; в) 5 см и 3 см.
64. Докажите, что каждая сторона треугольника больше разности
двух других сторон.
65. Докажите, что если АВ = АС + СВ, то точки А, В и С лежат
на одной прямой.
66. Периметр равнобедренного треугольника равен 25 см, разность
двух сторон равна 4 см, а один из его внешних углов — острый.
Найдите стороны треугольника.
67. На сторонах ВС, С А и АВ треугольника ABC отмечены
соответственно точки А\, В\ и С\, отличные от вершин треугольника.
Докажите, что периметр треугольника А\В\С\ меньше периметра тре-
треугольника ABC.
68. Стороны ВС и AD треугольников ABC и ABD пересекаются.
Докажите, что ВС + AD > АС + BD.
69. Одна сторона треугольника равна 1,9 дм, а другая — 0,7 дм.
Найдите третью сторону, зная, что ее длина в дециметрах выражается
целым числом.
70. Докажите, что сумма расстояний от любой точки, лежащей
внутри треугольника, до его вершин меньше периметра треугольника.

52 Гл. 2. Треугольники
71! Через вершину А треугольника ABC проведена прямая, пер-
перпендикулярная к биссектрисе его угла А, и на этой прямой взята
произвольная точка М, отличная от А. Докажите, что периметр тре-
треугольника МВС больше периметра треугольника ABC.
72! Точки В и С лежат по одну сторону от прямой а. Укажите
на прямой а такую точку А, что сумма АВ + АС меньше суммы MB +
+ МС, где М — любая точка прямой а, отличная от А.
§ 4. Признаки равенства треугольников
27. Три признака равенства треугольников. Рассмотрим три
признака равенства треугольников.
Теорема 1 (первый признак равенства треугольников). Если
две стороны и угол между ними одного треугольника соответ-
соответственно равны двум сторонам и углу между ними другого треуголь-
треугольника, то такие треугольники равны.
Доказательство. Рассмотрим треугольники ABC и А\В\С\,
у которых АВ = А\В\, АС = А\С\, ZА = /_А\ (рис.92). Докажем,
что эти треугольники равны. Мысленно наложим треугольник ABC
на треугольник А\В\С\ так, чтобы вершина А совместилась с верши-
вершиной А\, а стороны АВ и АС на-
ложились на лучи А\В\ и А\С\.
Это можно сделать, так как углы
А и А\ равны. Поскольку АВ =
= А\В\ и АС = А\С\, то сторо-
сторона АВ совместится со стороной
А\В\, а сторона АС совместится
со стороной А\С\, в частности,
совместятся точки В и В\, С
и С\. Следовательно, совместят-
совместятся стороны ВС и В\С\. Итак,
треугольники полностью совме-
совместятся, а значит, они равны. Тео-
рис 92 Рема доказана.
Теорема 2 (второй признак равенства треугольников). Если
сторона и два прилежащих к ней угла одного треугольника соот-
соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники равны.
Доказательство. Рассмотрим треугольники ABC и А\В\С\,
у которых АВ = А\В\, ZA = ZA\, ZB = /_В\ (рис.93). Докажем,
что эти треугольники равны. Мысленно наложим треугольник ABC
на треугольник А\В\С\ так, чтобы вершина А совместилась с вер-
вершиной А\, сторона АВ — с равной ей стороной А\В\, а вершины С
и С\ оказались по одну сторону от прямой А\В\. Так как АА = /_А\
и /Б = ZB\, то сторона АС наложится на луч А\С\, а сторона ВС —

4. Признаки равенства треугольников
53
на луч В\С\. Поэтому вершина С — общая точка сторон АС и ВС —
совместится с общей точкой сторон А\С\ и В\С\, т. е. с точкой С\. Зна-
Значит, стороны АС и ВС совместятся соответственно со сторонами А\С\
и В\С\. Итак, треугольники полностью совместятся, и следовательно,
они равны. Теорема доказана.
Теорема 3 (третий признак равенства треугольников). Если
три стороны одного треугольника соответственно равны трем
сторонам другого треугольника, то такие треугольники равны.
Доказательство. При доказательстве двух предыдущих теорем
мы накладывали один треугольник на другой так, чтобы совместились
их равные углы. Но сейчас нам ничего не известно об углах данных
треугольников. Поэтому мы окажемся в затруднительном положении,
если попытаемся совместить их наложением.
Попробуем рассуждать иначе. Рассмотрим треугольники ABC
и А\В\С\, у которых АВ = АхВи ВС = Bid, С А = СХАХ (рис.94).
Ах
Вх
Рис. 93
Рис. 94
Приложим треугольник ABC к треугольнику А\В\С\ так, чтобы вер-
вершины А и А\, В и В\ совместились, а вершины С и С\ оказа-
оказались по разные стороны от прямой А\В\ (рис.95). Проведем отре-
С
с
с
а/
Ах\
Л
^\. В
^^Вх
с, <
а)
ч
\
/
Ж-
Рис
Al ^
б)
.95
\^В
^Вх
А/
<
в)
В
Вх

54
Гл. 2. Треугольники
зок СС\. В результате получим два равнобедренных треугольника:
А\С\С и В\С\С (рис.95, а, б), или один равнобедренный треуголь-
треугольник (рис.95, в; этот случай рассмотрите самостоятельно). Следова-
Следовательно, Z1 = Z2 и Z3 = Z4, а значит, ZC = АСХ. Итак, АС = А\С\,
ВС = В\С\ и АС = ZCi, поэтому треугольники ABC и А\В\С\ равны
по первому признаку равенства треугольников. Теорема доказана.
Воспользуемся признаками равенства треугольников для решения
двух задач.
Задача 1. На сторонах угла MON отмечены точки А, В, С
и D так, что О А = OB, AC = BD (рис.96, а). Отрезки AD и ВС
пересекаются в точке Е. Доказать, что луч ОЕ — биссектриса
угла MON.
Решение. Глядя на рисунок 96, а, можно предположить,
что АОАЕ = АОВЕ, АОСЕ = AODE, ААСЕ = ABDE. Но как
доказать хотя бы одно из этих равенств? Ни одним из признаков
равенства треугольников здесь воспользоваться не удается.
Приглядимся к рисунку внимательнее. Рассмотрим треугольни-
треугольники OAD и ОВС. Эти треугольники равны по первому признаку ра-
равенства треугольников. В самом деле, угол О у них общий, О А = ОВ
по условию, OD = OB + BD = О А + АС = ОС. Из равенства этих
треугольников следует, что (рис. 96, б)
ZOAD = ZOBC, ZODA = ZOCB.
A)
Теперь мы можем доказать одно из выписанных выше равенств:
ААСЕ = ABDE. Действительно, АС = BD по условию, ZOCB =
= ZODA, ZCAD = 180° - ZOAD = 180° - ZOBC = ZDBC (см. A)).
Следовательно, треугольники АСЕ и BDE равны по второму признаку
равенства треугольников. Поэтому СЕ = DE (рис.96, в).
Теперь мы видим, что треугольники ОСЕ и ODE равны по третье-
третьему признаку равенства треугольников. Из этого следует, что ZEOC =
= ZEOD, т. е. луч ОЕ — биссектриса угла M0N, что и требовалось
доказать.

4. Признаки равенства треугольников
55
На этой задаче основан один из способов построения биссектрисы
угла (рис. 97).
Один из способов построения середины отрезка (рис. 98) основан
на следующей задаче.
А
О
В
Рис. 97. Луч ОЕ — биссектриса
угла MON
Рис. 98. Точка О — середина
отрезка АВ
Задача 2. Точки С и D лежат по разные стороны от пря-
прямой АВ и расположены так, что АС = BD и ABAC = ZABD
(рис.99, а). Доказать, что отрезки АВ и CD пересекаются и точ-
точкой пересечения делятся пополам.
А
а)
В
С
О
D
с
К
г)
В
Рис. 99

56 Гл. 2. Треугольники
Решение. Проведем отрезок CD, обозначим буквой О точку
пересечения этого отрезка с прямой АВ и попытаемся сравнить тре-
треугольники АСО и BDO (рис.99, б). В этих треугольниках АС = BD,
А А = АВ (по условию) и Zl = Z2 (как вертикальные углы). Можно
ли на основании этих равенств сделать вывод о равенстве треугольни-
треугольников АСО и BDO1 Мы знаем признак равенства двух треугольников
по стороне и двум прилежащим к ней углам. Но в данном случае угол 1
является не прилежащим, а противолежащим стороне АС (и точно
также угол 2 — противолежащий стороне BD). Поэтому на основе
этих равенств мы не можем сделать заключение о равенстве треуголь-
треугольников АСО и BDO. Кроме того, на нашем рисунке отрезки АВ и CD
пересекаются в точке О. Но всегда ли так будет? Не может ли в каком-
то случае получиться так, что отрезок CD пересечет прямую АВ
в точке О, лежащей вне отрезка АВ (рис. 99, в)? В таком случае
углы 1 и 2 окажутся вовсе не вертикальными, а смежными. Итак,
рассмотренный подход не привел нас к решению задачи.
Попробуем применить другой способ. Отметим середину К отрез-
отрезка АВ (рис.99, г) и соединим ее с точками С и D. Получим тре-
треугольники АСК и BDK. Они равны по двум сторонам и углу между
ними (АС = BD и /.САК = /DBK по условию, АК = KB, поскольку
точка К — середина отрезка АВ). Следовательно, С К = DK и Z1 =
= Z2. Угол СКВ является смежным с углом 1, поэтому АС К В + Z1 =
= 180°, а так как Zl = Z2, то АС К В + Z2 = 180°. Отсюда следует, что
угол CKD — развернутый, а значит, точки С, К и D лежат на одной
прямой.
Таким образом, отрезки АВ и CD пересекаются в точке К и де-
делятся этой точкой пополам, что и требовалось доказать.
Замечание. При решении этой задачи мы столкнулись с весьма
любопытной ситуацией. Путем рассуждений мы установили, что сере-
середина К отрезка АВ на рисунке 99, г и точка О пересечения прямой АВ
с отрезком CD на рисунке 99, б — это одна и та же точка. Иными
словами, указанные рисунки отличаются друг от друга только обозна-
обозначениями. Тем не менее, первый рисунок не привел нас к доказательству
утверждения, а второй — привел. Подумайте об этом. Как ни странно,
подобные ситуации в математике встречаются довольно часто.
28. Есть ли другие признаки равенства треугольников?. При
решении задачи 2 предыдущего пункта мы сначала провели от-
отрезок CD и обозначили буквой О точку его пересечения с пря-
прямой АВ (рис.99, б). В результате образовались два треугольника,
причем сторона и два угла — прилежащий и противолежащий для этой
стороны — одного треугольника оказались соответственно равными
стороне и двум углам — прилежащему и противолежащему для этой
стороны — другого треугольника (если, конечно, углы 1 и 2 — верти-
вертикальные, как на рисунке 99, б, а не смежные, как на рисунке 99, в). Пу-
Путем сложных рассуждений мы доказали, что эти треугольники равны.

4. Признаки равенства треугольников 57
Может быть, мы обнаружили новый признак равенства треугольников?
Давайте поставим вопрос шире.
Условимся называть стороны и углы треугольника элементами
этого треугольника. Каждый из трех известных нам признаков равен-
равенства треугольников позволяет сделать вывод о равенстве двух тре-
треугольников, если установлено, что три элемента одного треугольника
соответственно равны трем элементам другого треугольника. В первом
признаке такими элементами были две стороны и угол между ними,
во втором — сторона и два прилежащих к ней угла, в третьем — три
стороны. Возникает вопрос: а будут ли равны два треугольника, если
какие-то другие три элемента одного треугольника равны соответству-
соответствующим элементам другого треугольника? Иначе говоря, есть ли другие
признаки равенства двух треугольников по трем элементам?
Сначала подумаем, какие еще есть возможности. Если взять одну
сторону и два угла, то оба они могут быть прилежащими к этой
стороне (такой случай рассматривается во втором признаке равенства
треугольников), и может быть другой вариант: один из углов является
прилежащим, а другой — противолежащим для этой стороны (с этим
мы столкнулись при решении задачи 2). Таким образом, возможен
признак равенства треугольников по стороне и двум углам, один из ко-
которых является прилежащим, а другой — противолежащим для этой
стороны.
Далее, если взять две стороны и угол, то он может быть заключен
между этими сторонами (такой случай рассматривается в первом при-
признаке равенства треугольников), а может быть противолежащим одной
из сторон. Тем самым, возникает вопрос о признаке равенства тре-
треугольников по двум сторонам и углу, противолежащему одной из них.
Наконец, в качестве трех элементов треугольника можно взять три
угла и рассмотреть вопрос о признаке равенства треугольников по трем
углам.
Итак, есть три возможности. Посмотрим, какие из них дают при-
признаки равенства треугольников. Начнем с первой.
Гипотеза. Если сторона и два угла — прилежащий и проти-
противолежащий для этой стороны — одного треугольника соответ-
соответственно равны стороне и двум углам — прилежащему и противо-
противолежащему для этой стороны — другого треугольника, то такие
треугольники равны.
Попробуем доказать, что эта гипотеза верна. Рассмотрим треуголь-
треугольники ABC и А\В\С\, у которых АВ = А\В\, ZA = ZAU ZC =
= ZC\ (рис. 100, а). Мы хотим доказать, что эти треугольники равны.
Мысленно наложим треугольник ABC на треугольник А\В\С\ так,
чтобы вершина А совместилась вершиной А\, а стороны АВ и АС
наложились на лучи А\В\ и А\С\. Это можно сделать, так как уг-
углы А и А\ равны. Поскольку АВ = А\В\, то сторона АВ совместится
со стороной А\В\, в частности, совместятся вершины В и В\. Остается
доказать, что вершины С и С\ также совместятся. Если предположить,

58 Гл. 2. Треугольники
(А)АХ
а) б)
Рис. 100. а) АВ = АхВх, АА = ZAU ZC = ZC\
что вершина С совместится не с точкой Сь ас какой-то другой точ-
точкой Съ на луче А\С\ (рис. 100, б), то получится треугольник В\С\С^
у которого внешний угол равен углу треугольника, не смежному с этим
внешним углом (на рисунке 100, б Zl = Z2). Но этого не может
быть, поэтому вершина С совместится с вершиной С\. Следовательно,
совместятся стороны ВС и В\С\. Итак, треугольники ABC и А\В\С\
полностью совместятся, а значит, они равны.
Таким образом, наша гипотеза оказалась верной: имеет место еще
один признак равенства треугольников — по стороне и двум углам,
один из которых является прилежащим, а другой — противолежащим
для этой стороны. Назовем его четвертым признаком равенства
треугольников.
Попробуем теперь доказать следующее утверждение.
Гипотеза. Если две стороны и угол, противолежащий одной
из этих сторон, одного треугольника соответственно равны двум
сторонам и углу другого треугольника, то такие треугольники
равны.
Попробуем доказать, что эта гипотеза верна. Рассмотрим треуголь-
треугольники ABC и А\В\С\, у которых АВ = А\В\, АС = А\С\ и ZC =
= ZC\ (рис.101, а). Мысленно наложим треугольник ABC на тре-
треугольник А\В\С\ так, чтобы вершина С совместилась с вершиной С\,
а стороны С А и С В наложились на лучи С\А\ и С\В\. Это можно
сделать, так как углы С и С\ равны. Поскольку АС = А\С\, то сторо-
сторона АС совместится со стороной А\С\, в частности, совместятся верши-
вершины А и А\. Остается доказать, что вершины В и В\ также совместятся.
Но так ли это? Допустим, что точка В совместилась не с точкой В\,
а с какой-то другой точкой Б2 на луче С\В\ (рис.101, б). Тогда
треугольник А\В\В^ — равнобедренный.

4. Признаки равенства треугольников
59
В
а)
JD
Рис. 101
Сх
Вх
В2
Поскольку углы при основании равнобедренного треугольника —
острые, то смежные с ними углы — тупые. Поэтому либо угол В\
треугольника А\В\С\ — тупой (если точка В\ лежит между С\ и Б2),
либо угол B<i треугольника АхВ^Сх — тупой (если точка В^ лежит
между Сх и Вх). Принимая во внимание соотношение между сторонами
и углами треугольника, и в том и в другом случае получаем: АхВх =
= АхВ2 < АхСх. Следовательно, если АхВх > АхСх, то точки В и Вх
должны совместиться. Таким образом, треугольники ABC и АхВхСх
полностью совместятся, а значит, они равны.
Если же АхВх < АхСх (и следовательно, АВ < АС) (рис. 101, в),
то никакого противоречия не видно. Похоже, что в этом случае наша
гипотеза неверна. Попробуем это доказать, т. е. указать два таких
треугольника, которые удовлетворяют всем нашим условиям, но не
равны друг другу.
Рассмотрим какой-нибудь равнобедренный треугольник ABC с ос-
основанием ВС (рис. 102, а). Продолжим сторону ВС, возьмем на ее
продолжении произвольную точку D (рис. 102, б) и проведем отре-
отрезок AD. Мы получим два треугольника: ABD и ACD, у которых
общие сторона AD и угол D и, кроме того, равны стороны АВ
и АС. Таким образом, стороны AD и АВ и угол D, противолежащий
стороне АВ, треугольника ABD соответственно равны сторонам AD

60 Гл. 2. Треугольники
А
В С В с D
а) б)
Рис. 102
и АС и углу D, противолежащему стороне АС, треугольника ACD.
Однако сами треугольники, очевидно, не равны.
Итак, наша гипотеза в том виде, как мы ее сформулировали, не вер-
верна. Вместе с тем мы доказали, что
признак равенства треугольников по двум сторонам и углу, про-
противолежащему одной из них (назовем его пятым признаком равен-
равенства треугольников), имеет место в том случае (и, как мы увидим
в п. 41, только в этом случае), когда сторона, противолежащая
этому углу, не меньше второй из данных сторон. В частности, он
имеет место тогда, когда указанный угол — прямой или тупой.
Осталось выяснить, имеет ли место признак равенства треуголь-
треугольников по трем углам. На первый взгляд кажется, что этот признак
не имеет места. В самом деле, рассмотрим два неравных квадра-
квадрата (рис. 103, а). Проведем диагонали АС и А\С\ и рассмотрим тре-
треугольники ABC и А\В\С\ (рис. 103, б). Углы этих треугольников
соответственно равны: в каждом треугольнике один угол — прямой,
а два другие по 45°. Но сами треугольники, очевидно, не равны.
А теперь откроем наш блокнот. Мы видим в нем такой вопрос: есть
ли квадрат? На этот вопрос мы пока не нашли ответа. Следовательно,
проведенное только что рассуждение не дает ответа и на вопрос о спра-
справедливости признака равенства треугольников по трем углам. Поэтому,
пока наш блокнот открыт, запишем в него еще один вопрос:
имеет ли место признак равенства треугольников по трем уг-
углам!
Замечание 1. Мы обнаружили, что вторая из наших гипотез
(в том виде, как она была сформулирована) неверна: мы привели
пример двух неравных треугольников, которые, однако, удовлетворяют
всем нашим условиям. Такой пример, который показывает, что какое-то
утверждение неверно, называется контрпримером для этого утвержде-
утверждения.
Замечание 2* Вспомним задачу, которую мы решили в пунк-
пункте 23: «Доказать, что если в треугольнике биссектриса является ме-
медианой, то этот треугольник — равнобедренный». Решив эту зада-

4. Признаки равенства треугольников
61
В ,
С
А
D
Ах
а)
Рис. 103. ABCD и AxBxCxDx - квадраты, АВ ф АХВХ
чу, мы фактически доказали, что треугольники АВМ и АСЫ рав-
равны (см. рис.84). При этом мы пользовались тем, что в этих треуголь-
треугольниках Zl = Z2, MB = МС и сторона AM — общая. Таким образом,
мы исходили из того, что две стороны (MB и AM) и угол, проти-
противолежащий одной из этих сторон (стороне MB), одного треугольника
соответственно равны двум сторонам и углу другого треугольника,
т. е. исходили из условий, которые сформулированы в пятом признаке
равенства треугольников. Но пятый признак равенства треугольников
имеет место только в том случае, когда сторона, противолежащая
данному углу, не меньше второй из данных сторон. В нашем же случае
неравенство MB ^ AM может и не выполняться. Почему же, несмотря
на это обстоятельство, нам удалось доказать равенство указанных
треугольников?
Разгадка здесь состоит вот в чем. Помимо упомянутых соотноше-
соотношений между элементами треугольников АВМ и АСМ, нам было дано
еще одно равенство: ZAMB + ZAMC = 180°. Попробуйте самостоя-
самостоятельно разобраться в том, к чему это приводит.
29. Признаки равенства треугольников, использующие медиа-
медианы, биссектрисы и высоты. Количество признаков равенства тре-
треугольников возрастает, если наряду с элементами (сторонами и углами)
треугольника использовать другие отрезки, связанные с треугольни-
треугольником: медианы, биссектрисы и высоты. Рассмотрим несколько примеров.

62 Гл. 2. Треугольники
Задача 3. Доказать, что два треугольника равны, если две
стороны и медиана, проведенная из общей вершины этих сто-
сторон, одного треугольника соответственно равны двум сторонам
и медиане, проведенной из общей вершины этих сторон, другого
треугольника.
Решение. Рассмотрим треугольники ABC и А\В\С\, у кото-
которых АВ = А\В\, АС = А\С\, AM = А\М\, где AM и А\М\ — медианы
этих треугольников (рис. 104). Докажем, что эти треугольники равны.
Рис. 104
На продолжениях медиан AM и А\М\ отметим точки D и D\ так,
что DM = AM = A\M\ = D\M\. Треугольники ABM и С DM равны
по двум сторонам и углу между ними (AM = DM по построению;
ВМ = СМ, так как точка М — середина отрезка ВС; углы с верши-
вершиной М в этих треугольниках равны как вертикальные). Поэтому АВ =
= CD.
Аналогично, из равенства треугольников А\В\М\ и C\D\M\ следу-
следует, что А\В\ = C\D\, а так как АВ = А\В\, то CD = C\D\.
Треугольники ACD и A\C\D\ равны по трем сторонам (АС =
= А\С\ по условию; CD = C\D\ согласно доказанному; AD = 2AM =
= 2А\М\ = A\D\). Поэтому ZCAD = ZC\A\D\. Следовательно, тре-
треугольники САМ и С\А\М\ равны по двум сторонам и углу между
ними, а значит, СМ = С\М\. Из этого следует, что ВС = 2СМ =
= 2СХМХ =ВХСХ.
Итак, в треугольниках ABC и А\В\С\ имеем: АВ = А\В\, АС =
= А\С\ и ВС = В\С\. Следовательно, треугольники ABC и А\В\С\
равны по трем сторонам. Утверждение доказано.
Замечание. Мы установили, что имеет место признак равенства
треугольников по двум сторонам и медиане, проведенным из одной
вершины. Возникает такой вопрос: а что, если медиану в этом признаке
заменить на биссектрису или на высоту — сохранится ли признак
равенства треугольников? Иначе говоря, справедливы ли следующие
утверждения:
1° если две стороны и биссектриса, проведенная из общей вершины
этих сторон, одного треугольника соответственно равны двум сторонам
и биссектрисе, проведенной из общей вершины этих сторон, другого
треугольника, то такие треугольники равны;
2° если две стороны и высота, проведенная из общей вершины
этих сторон, одного треугольника соответственно равны двум сторо-

4. Признаки равенства треугольников
63
нам и высоте, проведенной из общей вершины этих сторон, другого
треугольника, то такие треугольники равны?
Попробуем доказать эти утверждения. Начнем с первого.
1°. Рассмотрим треугольники ABC и А\В\С\ с биссектрисами AM
и АХМХ, у которых АВ = АХВХ, АС = АХСХ, AM = АХМХ (рис. 105, а).
Если бы удалось доказать, что углы А и Ах или стороны ВС и ВХСХ
равны, то эти треугольники оказались бы равными по первому или
третьему признакам равенства треугольников. Интуитивно понятно,
что если стороны АВ и АС треугольника ABC сдвинуть или раздви-
раздвинуть (рис. 105, б), то точки В, С и М перестанут лежать на одной
прямой, поэтому углы А и Ах, а также стороны ВС и ВХСХ не могут
быть неравными. Но как это доказать?
Допустим, что углы А и Ах не равны друг другу. Пусть, например,
ZA < ZAX, АВ = АХВХ, АС = АХСХ. Попробуем доказать, что в этом
случае AM ^ АМХ.
Мысленно наложим треугольник ABC на треугольник АХВХСХ так,
чтобы луч AM наложился на луч АХМХ, а вершины В и Вх оказались
лежащими по одну сторону от отрезка AM (рис. 105, в). Обозначим
буквами Р и Q точки пересечения отрезка ВХСХ с лучами АВ и АС.
В треугольнике APQ хотя бы один из углов Р, Q — острый. Если,
например, угол Р — острый, то смежный с ним угол АРВХ — тупой.
Поэтому сторона АВХ треугольника АРВХ больше, чем АР. Но АВХ =
= АВ. Следовательно, АВ > АР, а значит, точка Р лежит на отрез-
отрезке АВ. Если и угол Q треугольника APQ — острый, то точка Q лежит
А
А
В м С Вх М]
В
г)
Рис. 105

64
Гл. 2. Треугольники
на отрезке АС — это доказывается аналогично. Итак, в этом случае
точки Р и Q лежат по одну сторону от прямой ВС. Поэтому точка М\
пересечения отрезка В\С\ с лучом AM является внутренней точкой
отрезка AM, т.е. AM ^ АМ\, что и требовалось доказать.
Наши рассуждения останутся в силе и в том случае, когда
угол Q треугольника APQ — прямой (объясните, почему). Но ес-
если этот угол — тупой, то ничего не получится: точки Р и Q
в этом случае могут оказаться лежащими по разные стороны от пря-
прямой ВС (рис. 105, г). Здесь требуются какие-то другие, более сложные
рассуждения. Обратим внимание и на такое обстоятельство: мы фак-
фактически не пользовались тем, что луч AM — биссектриса угла А\
По-существу, нам важно было лишь, что точки В\ и С\ лежат вне
угла ВАС. Ясно, что для доказательства нашего утверждения в общем
случае нужно знать какие-то свойства биссектрисы угла, которые нам
пока не известны. Поэтому откроем блокнот и запишем в него вопрос:
имеет ли место признак равенства треугольников по двум сто-
сторонам и биссектрисе, проведенным из одной вершины?
Обратимся ко второму утверждению.
2°. Рассмотрим треугольники ABC и А\В\С\ с высотами АН
и AiHi, у которых АВ = АХВХ, АС = АХСХ, АН = АХНХ (рис. 106).
Попробуем доказать, что углы А и А\ этих треугольников равны,
а затем воспользуемся первым признаком равенства треугольников.
Прямоугольные треугольники АВН и А\В\Н\ равны по пятому
признаку равенства треугольников {АВ = А\В\, АН = А\Н\, ZAHB =
= ZA\H\B\ = 90°). Следовательно, ZBAH = ZB\A\H\. Аналогично
доказывается, что ZCAH = АС\А\Н\. Казалось бы, из этого можно
сделать такой вывод: А А = ZBAH + ZCAH = /_В\А\Н\ + Z.C\A\H\ =
= ZA\. Но не может ли получиться так, например, что ZA = ZBAH +
+ ZCAH, a ZA\ = ZB\A\H\ — ZC\A\H\? Если может, то треугольни-
треугольники ABC и А\В\С\ окажутся неравными, а утверждение 2° — ошибоч-
ошибочным!
Попробуем привести контрпример для утверждения 2°, основанный
на наших соображениях. Рассмотрим произвольный равнобедренный
треугольник ABC, в котором АВ = АС, отрезок АН — высота тре-
треугольника (рис. 107). Отметим на продолжении стороны ВС какую-
В
Н
С Вх
Рис. 106
Сх

4. Признаки равенства треугольников
65
нибудь точку D. Тогда в треугольниках ABD и ACD имеем: АВ =
= AC, AD — общая сторона, АН — общая высота. Таким образом,
треугольники ABD и ACD удовле-
удовлетворяют условию утверждения 2°, А
но при этом сами треугольники,
очевидно, не равны. Следовательно,
утверждение 2° ошибочно.
Приведем теперь пример при-
признака равенства треугольников, в
формулировке которого использу-
используются не только отрезки, но и углы.
Задача А. Доказать, что два и С
треугольника равны, если сторо-
сторона, прилежащий к ней угол и вы-
высота, проведенная к этой стороне, одного треугольника соответ-
соответственно равны стороне, прилежащему к ней углу и высоте, прове-
проведенной к этой стороне, другого треугольника.
Решение. Рассмотрим треугольники ABC и А\В\С\, у кото-
которых АС = АХС\, АА = ZAU ВН = В{Ни где ВН и ВХНХ - высоты
треугольников (рис. 108). Докажем, что эти треугольники равны.
В Вх
D
Н
В
Рис. 107
А(Н)
С
Сх
Рис. 108
3 С. Б. Кадомцев

66
Гл. 2. Треугольники
Рассмотрим сначала случай, когда углы А и А\ — острые
(рис. 108, а). В этом случае треугольники АВН и А\В\Н\ равны
по четвертому признаку равенства треугольников (ВН = В\Н\,
ZBHA = /_В\Я\А\ = 90°, ZA = /.А\). Отсюда следует, что АВ =
Так как АВ = А\В\, АС = А\С\, ZA = ZA\, то треугольники ABC
и А\В\С\ равны по двум сторонам и углу между ними.
Если углы А и А\ — тупые (рис. 108, б), то снова треугольни-
треугольники АВН и А\В\Н\ равны по четвертому признаку равенства треуголь-
треугольников, но только теперь равенство углов ВАН и В\А\Н\ не является
данным по условию задачи, а следует из того, что эти углы — смежные
с равными углами CAB и С\А\В\. Дальнейший ход рассуждений
такой же, как и в случае, когда углы А и А\ — острые.
Наконец, если углы А и А\ — прямые (рис. 108, в), то высота ВН
совпадает со стороной В А треугольника ABC (т. е. совпадают точки Я
и А), а высота В\Н\ совпадает со стороной В\А\ треугольника А\В\С\.
В этом случае треугольники ABC и А\В\С\ равны по двум сторонам
и углу между ними (АВ = А\В\, АС = А\С\, ZА = АА\).
Итак, во всех случаях треугольники ABC и А\В\С\ равны. Утвер-
Утверждение доказано.
Задачи
73. На сторонах равностороннего треугольника ABC отложены
равные отрезки AD, BE и CF так, как показано на рисунке 109. Точ-
Точки D, Е и F соединены отрезками. Докажите, что треугольник DEF —
равносторонний.
74. Стороны равностороннего треугольника ABC продолжены так,
как показано на рисунке ПО, на равные отрезки BD, СЕ и AF.
Докажите, что треугольник DEF — равносторонний.
75. Докажите, что в равных треугольниках: а) медианы, проведен-
проведенные к равным сторонам, равны; б) биссектрисы, проведенные из вер-
Е
F
D
С
Рис. 109
Рис. ПО

4. Признаки равенства треугольников 67
шин равных углов, равны; в) высоты, проведенные из вершин равных
углов, равны.
76. Докажите, что в равнобедренном треугольнике: а) медианы,
проведенные к боковым сторонам, равны; б) биссектрисы, проведенные
из вершин основания, равны; в) высоты, проведенные из вершин осно-
основания, равны.
77. Точки М и Р лежат по одну сторону от прямой Ь. Перпендику-
Перпендикуляры MN и PQ, проведенные к прямой Ь, равны. Точка О — середина
отрезка NQ. Докажите, что ZOMP = ZOPM; найдите ZNOM, ес-
если ZMOP= 105°.
78. Начертите равнобедренный треугольник ABC с основани-
основанием АС, проведите медиану BD и отметьте на сторонах АВ и СВ
точки Е и F так, что АЕ = CF. Проведите отрезки ED и FD и назо-
назовите все пары равных треугольников, которые получились на рисунке.
Ответ обоснуйте.
79. Начертите отрезки АС и BD, пересекающиеся в точке О
и делящиеся этой точкой пополам. Проведите отрезки АВ, ВС, CD,
DA и назовите все пары равных треугольников, которые получились
на рисунке. Ответ обоснуйте.
80. Начертите угол с вершиной А и отметьте на одной его стороне
точки Б и С, а на другой — точки Е и D так, что АВ = АЕ,
АС = AD > АВ. Проведите отрезки BD, CE, CD, обозначьте точку
пересечения отрезков BD и СЕ буквой О и назовите все пары равных
треугольников, которые получились на рисунке. Ответ обоснуйте.
81. В треугольниках ABC и ADC стороны ВС и AD равны
и пересекаются в точке О, ZOAC = /.ОСА. Докажите, что треуголь-
треугольники АВО и CDO равны.
82. На рисунке 111 /DBC = /DAC, ВО = АО. Докажите,
что АС = /D и АС = BD.
83. На рисунке 112 АВ = CD, AC = BD. Назовите все пары рав-
равных треугольников, изображенных на этом рисунке. Ответ обоснуйте.
84. На рисунке 113 АВ = CD, AD = ВС, BE — биссектриса
угла ABC, DF — биссектриса угла ADC. Назовите все пары равных
треугольников, изображенных на этом рисунке. Ответ обоснуйте.
с
А В A D
Рис.111 Рис.112

68
Гл. 2. Треугольники
D
Рис. 113
С
85. Отрезки АВ и CD пересека-
пересекаются в их общей середине О. На от-
отрезках АС и BD отмечены точки К
и К\ так, что АК = ВК\. Докажите,
что: а) ОК = ОК\\ б) точка О лежит
на прямой КК\.
86. На рисунке 114 ОС = OD,
ОВ = ОЕ. Докажите, что АВ = EF.
Объясните способ измерения ширины озера (отрезка АВ), основанный
на этом факте.
87. Отрезки АВ и CD пе-
пересекаются в точке О. До-
Докажите, что ОС = OD, ес-
если АС = АО = ВО = BD.
88. Докажите, что тре-
треугольники ABC и А\В\С\ рав-
равны, если АА = ZA\, ZB =
= ZB{ и ВН = В{Ни где ВН
и В\Н\ — высоты треугольни-
треугольников ABC и АХВ\С\.
89* Докажите, что если
угол, прилежащая к нему сто-
сторона и сумма двух других сто-
сторон одного треугольника соответственно равны углу, прилежащей
к нему стороне и сумме двух других сторон другого треугольника,
то такие треугольники равны.
90! Две стороны треугольника не равны друг другу. Докажите, что
медиана, проведенная из их общей вершины, составляет с меньшей
из сторон больший угол.
91! В треугольнике ABC проведен отрезок AM, соединяющий
вершину А с произвольной точкой М стороны ВС. Докажите, что
если АВ ^ АС, то треугольники АМВ и АМС не равны друг другу.
Рис. 114
§ 5. Признаки равенства прямоугольных
треугольников
30. Пять признаков равенства прямоугольных треугольников.
В прямоугольном треугольнике угол между катетами — прямой, а лю-
любые два прямых угла равны. Поэтому из первого признака равенства
треугольников следует:
1° если катеты одного прямоугольного треугольника соответ-
соответственно равны катетам другого, то такие треугольники рав-
равны (рис. 115).
Из второго признака равенства треугольников следует:

5. Признаки равенства прямоугольных треугольников
69
В
А
С Ах
Сх
Рис. 115. Прямоугольные треугольники ABC и АхВхСх равны по двум катетам
(АВ = АхВх, АС = АхСх)
2° если катет и прилежащий к нему острый угол одного пря-
прямоугольного треугольника соответственно равны катету и при-
прилежащему к нему острому углу другого, то такие треугольники
равны (рис. 116).
С
Сх
А
В Ах
Вх
Рис. 116. Прямоугольные треугольники ABC и АхВхСх равны по катету
и прилежащему острому углу (АВ = АхВх, ZB = ZBx)
Из четвертого признака равенства треугольников следуют сразу два
признака равенства прямоугольных треугольников:
3° если гипотенуза и острый угол одного прямоугольного тре-
треугольника соответственно равны гипотенузе и острому углу дру-
другого, то такие треугольники равны (рис. 117);
С
В Ах
Вх
Рис. 117. Прямоугольные треугольники ABC и АхВхСх равны по гипотенузе
и острому углу (ВС = ВхСх, ZB = АВХ)
4° если катет и противолежащий ему угол одного прямоуголь-
прямоугольного треугольника соответственно равны катету и противолежа-
противолежащему ему углу другого, то такие треугольники равны (рис. 118).

Гл. 2. Треугольники
В,
Рис. 118. Прямоугольные треугольники ABC и А\В\С\ равны по катету
и противолежащему углу (АВ = А\В\, АС = Z.C\)
Вспомним теперь пятый признак равенства треугольников —
по двум сторонам и углу, противолежащему одной из них. Этот
признак имеет место, в частности, в том случае, когда указанный
угол — прямой или тупой. Поскольку один из углов прямоугольного
треугольника — прямой, а сторона, противолежащая этому углу, — ги-
гипотенуза, то мы получаем еще один признак равенства прямоугольных
треугольников:
5° если гипотенуза и катет одного прямоугольного треугольни-
треугольника соответственно равны гипотенузе и катету другого, то такие
треугольники равны (рис. 119).
Ах
Вх
Рис. 119. Прямоугольные треугольники ABC и АхВхСх равны по гипотенузе
и катету {ВС = В{Си АВ = АХВХ)
Задача. Доказать, что два остроугольных треугольника равны,
если сторона и высоты, проведенные из концов этой стороны,
одного треугольника соответственно равны стороне и высотам,
проведенным из концов этой стороны, другого треугольника.
Решение. Рассмотрим остроугольные треугольники ABC и
А\В\Си У которых АВ = АхВи АН = АхНи В К = ВхКи где АН,
В К и А\Н\, В\К\ — высоты треугольников (рис. 120). Требуется
доказать, что ААВС = АА\В\С\.
Отметим, что так как данные треугольники — остроугольные, то ос-
основания их высот (точки Н, К, Н\, К\) лежат на соответствующих
сторонах, а не на продолжениях сторон (см. задачу 40).

5. Признаки равенства прямоугольных треугольников
71
Н
К
К
А
В Ах
Рис. 120
Вх
Рассмотрим прямоугольные треугольники АВК и А\В\К\. Они
равны по гипотенузе и катету (АВ = А\В\ и В К = В\К\ по условию).
Следовательно, АА = /_А\.
Аналогично из равенства прямоугольных треугольников АВН
и А\В\Н\ (они равны также по гипотенузе и катету) следует, что АВ =
= ZB,.
Итак, АВ = Ai^i, ZA = ZA\, ZB = Zi?i, поэтому треугольни-
треугольники ABC и А\В\С\ равны по второму признаку равенства треугольни-
треугольников. Утверждение доказано.
Замечание. Обратим внимание на то, что по условию треуголь-
треугольники ABC и А\В\С\ — остроугольные. В ходе решения мы дей-
действительно использовали этот факт. Возникает, однако, такой вопрос:
если в формулировке задачи опустить слово «остроугольных», будет ли
утверждение верным?
Попробуем привести контрпример. Рассмотрим треугольник ABC
с тупым углом А и проведем его высоты АН и ВК (рис.121, а).
На стороне ВС возьмем произвольную точку С\ и рассмотрим тре-
Н
Рис. 121

72
Гл. 2. Треугольники
угольники ABC и АВС\ (рис.114, б). Сторона АВ и высота АН
у этих треугольников — общие. Поэтому если нам удастся выбрать
точку С\ так, чтобы высоты ВК и ВК\ оказались равными, то контр-
контрпример (треугольники ABC и АВС\) будет построен.
Давайте рассуждать. Из равенства ВК = ВК\ следует, что пря-
прямоугольные треугольники АВК и АВК\ равны по гипотенузе и ка-
катету, поэтому ZBAK = АВАК\. Теперь все ясно: нужно провести
луч АС\ так, чтобы ZBAK = АВАК\. Тогда прямоугольные треуголь-
треугольники АВК и АВК\ окажутся равными по гипотенузе и острому
углу, откуда и будет вытекать равенство ВК = ВК\. Таким образом,
неравные треугольники ABC и АВС\ будут удовлетворять всем усло-
условиям задачи. Следовательно, если в условии задачи опустить слово
«остроугольных», то утверждение станет неверным.
31. Серединный перпендикуляр к отрезку. Осевая симмет-
симметрия. Серединным перпендикуляром к отрезку называется пря-
прямая, проходящая через середину этого отрезка и перпендикулярная
к нему (рис. 122).
Докажем теорему о серединном перпендикуляре к отрезку.
Теорема 1. Каждая точка середин-
серединного перпендикуляра к отрезку равно-
равноудалена от концов этого отрезка.
Доказательство. Пусть прямая
т — серединный перпендикуляр к отрез-
отрезку АВ, точка О — середина этого отрез-
отрезка (рис. 123). Возьмем произвольную точ-
точку М на серединном перпендикуляре т
и докажем, что MA = MB.
Если точка М совпадает с точкой О,
то это равенство верно, поскольку О —
середина отрезка АВ. Если же точка М
не совпадает с точкой О, то рассмот-
рассмотрим прямоугольные треугольники АОМ
и ВОМ. Эти треугольники равны по двум
катетам: АО = ОВ, ОМ — общий катет.
Отсюда следует, что MA = MB. Теорема
доказана.
А ь
н в
т
Рис. 122. Прямая т — сере-
серединный перпендикуляр к от-
отрезку АВ
Докажем теперь обратную теорему.
Теорема 2. Каждая точка, равноудаленная от концов отрез-
отрезка, лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Рассмотрим произвольную точку М, равно-
равноудаленную от концов отрезка АВ (рис. 124). Докажем, что она лежит
на серединном перпендикуляре к этому отрезку.
Если точка М лежит на прямой АВ, то она совпадает с серединой О
отрезка АВ. Если же точка М не лежит на прямой АВ, то треуголь-
треугольник МАВ — равнобедренный, поскольку MA = MB. Следовательно,

5. Признаки равенства прямоугольных треугольников
73
Рис. 123
т
Рис. 124
медиана МО этого треугольника является также высотой, а значит,
прямая МО — серединный перпендикуляр к отрезку АВ. Итак, точ-
точка М лежит на серединном перпендикуляре к отрезку АВ. Теорема
доказана.
Две точки А и А\ называются симметричными относительно
прямой а, если эта прямая является серединным перпендикуляром
к отрезку АА\ (рис. 125, а). При этом каждая точка прямой а считается
Ах
а)
Рис. 125
симметричной самой себе. На рисунке 125, б точки М и М\, N и N\
симметричны относительно прямой Ь, а точка Р симметрична самой
себе относительно этой прямой.
Фигура называется симметричной относительно прямой а, если
для каждой точки фигуры симметричная ей точка относительно пря-
прямой а также принадлежит этой фигуре. Прямая а называется осью
симметрии фигуры. Говорят также, что фигура обладает осевой сим-
симметрией.
На рисунке 126 изображена фигура, обладающая осевой симметри-
симметрией. Если перегнуть этот рисунок по оси симметрии (прямой а), то ле-
левая по отношению к прямой а часть фигуры в точности совместится

74
Гл. 2. Треугольники
Рис. 126
с правой частью фигуры, в частности, произ-
произвольная точка А фигуры наложится на сим-
симметричную ей точку А\.
Приведем примеры фигур, обладающих
осевой симметрией (рис. 127). У неразвернуто-
неразвернутого угла одна ось симметрии — прямая, на кото-
которой расположена биссектриса угла. Равнобед-
Равнобедренный (но не равносторонний) треугольник
имеет также одну ось симметрии, а равно-
равносторонний треугольник — три оси симметрии.
Имеются фигуры, у которых нет ни одной
оси симметрии, например разносторонний тре-
треугольник.
Рис. 127
Изображения на плоскости многих предметов окружающего нас
мира имеют ось симметрии. Некоторые листья деревьев и лепестки
цветов симметричны относительно стебля (рис. 128). С симметрией
мы встречаемся в искусстве, архитектуре, технике, быту. Так, фасады
многих зданий обладают осевой симметрией (рис. 129). В большинстве
случаев симметричны относительно оси узоры на коврах, тканях, ком-
комнатных обоях.
Рис. 128
Рис. 129

5. Признаки равенства прямоугольных треугольников
75
рис
32. Расстояние от точки до прямой. Рассмотрим произвольную
прямую а и точку А, не лежащую на ней. Пусть точка Н — основание
перпендикуляра, проведенного из точки А к прямой а, а М — любая
другая точка прямой а (рис. 130). Отре-
Отрезок AM называется наклонной, проведен-
проведенной из точки А к прямой а.
Перпендикуляр АН является кате-
катетом, а наклонная AM — гипотенузой
прямоугольного треугольника АНМ. Так
как в прямоугольном треугольнике ка-
катет меньше гипотенузы, то перпендику-
ляр, проведенный из точки к прямой,
меньше любой наклонной, проведенной
из той же точки к этой прямой.
Длина перпендикуляра, проведенного из точки к прямой, назы-
называется расстоянием от этой точки до прямой.
Ясно, что расстояние от точки до прямой равно наименьшему
из расстояний между данной точкой и всевозможными точками этой
прямой.
33. Свойство биссектрисы угла. Докажем теорему о биссектри-
биссектрисе угла.
Теорема 1. Любая точка биссектрисы неразвернутого угла
равноудалена от его сторон.
Доказательство. Рассмотрим не-
неразвернутый угол А и возьмем произволь-
произвольную точку М на его биссектрисе. Про-
Проведем из точки М перпендикуляры MB
и МС к сторонам угла (рис. 131). Требу-
Требуется доказать, что MB = МС.
Рассмотрим прямоугольные треуголь-
треугольники АМВ и АМС. Они равны по гипо-
тенузе и острому углу {AM — их общая
гипотенуза, Zl = Z2, так как луч AM —
биссектриса угла А). Отсюда следует,
что MB = МС. Теорема доказана.
A
Рис. 131
Замечание 1. На рисунке 131 основания перпендикуляров MB
и МС (точки В и С) лежат на сторонах угла А. Возникает вопрос:
не может ли получиться так, что основание перпендикуляра, проведен-
проведенного к стороне неразвернутого угла из точки его биссектрисы, окажется
не на стороне угла, а на ее продолжении (рис. 132)? Докажем, что этого
не может быть.
Предположим, что основание перпендикуляра MB лежит на про-
продолжении стороны угла А. Тогда получится прямоугольный треуголь-
треугольник АВМ (см. рис. 132), у которого угол В — прямой, а внешний
угол 1 — острый, так как он равен половине неразвернутого угла.

76
Гл. 2. Треугольники
Таким образом, окажется, что внешний угол треугольника меньше
угла треугольника, не смежного с этим внешним углом. Но этого
не может быть. Поэтому основание перпендикуляра MB, проведенного
из точки М биссектрисы неразвернутого угла к его стороне, всегда
лежит на самой стороне, а не на ее продолжении.
Задача-загадка. Рассмотрим треугольник ABC, в кото-
котором АВ ф ВС (рис. 133). Проведем биссектрису угла В, серединный
В
А
Рис. 132
Рис. 133
перпендикуляр к стороне АС и обозначим буквой О точку их пересе-
пересечения (на рисунке 133 точка М — середина отрезка АС). Из точки О
проведем перпендикуляры ОН и ОК к прямым АВ и ВС.
Так как точка О лежит на серединном перпендикуляре к сто-
стороне АС, то О А = ОС, а поскольку она лежит также на биссектрисе
угла В, то ОН = ОК. Следовательно, прямоугольные треугольни-
треугольники АОН и СОК равны по гипотенузе (АО = ОС) и катету (ОН =
= ОК), а значит,
АН = СК. A)
Прямоугольные треугольники ВОН и ВОК также равны (объяс-
(объясните, почему), откуда следует, что
нв = кв.
Складывая равенства A) и B), получаем:
АН + НВ = СК + КВ,
B)
т. е. АВ = ВС. Но по условию задачи АВ ф ВС\ Значит, в наших
рассуждениях где-то имеется ошибка. Постарайтесь ее найти.
Докажем теперь теорему, обратную теореме о биссектрисе угла.
Теорема 2. Любая точка, лежащая внутри неразвернутого
угла и равноудаленная от сторон этого угла, лежит на его биссек-
биссектрисе.
Доказательство. Пусть точка М лежит внутри угла А и рав-
равноудалена от его сторон. Докажем, что луч AM — биссектриса угла А.

5. Признаки равенства прямоугольных треугольников
77
Рис. 134
Проведем перпендикуляры MB и МС к сторонам угла (рис. 134)
и рассмотрим прямоугольные треугольники АМВ и АМС. Они рав-
равны по гипотенузе и катету {AM — общая гипотенуза, MB = МС
по условию). Отсюда следует, что Zl = Z2, т. е. луч AM — биссектриса
угла А. Теорема доказана.
Замечание 2. В ходе доказатель-
доказательства мы фактически предполагали, что
основания перпендикуляров MB и МС
(точки В и С) лежат на сторонах угла
(см. рис. 134). Снова возникает вопрос:
а не может ли получиться так, что осно-
основание какого-то из перпендикуляров, про-
проведенных из точки М к сторонам угла,
окажется не на стороне, а на ее продолже-
продолжении или совпадет с точкой А? Докажите
самостоятельно, что этого не может быть.
Помните при этом, что точка М — не произвольная точка, лежащая
внутри угла, а равноудаленная от его сторон (т. е. от прямых, содержа-
содержащих стороны угла).
34. Теорема о пересечении биссектрис треугольника. Теперь
мы можем ответить на один из вопросов, записанных в блокноте.
Теорема. Три биссектрисы треугольника пересекаются в одной
точке.
Доказательство. Рассмотрим произвольный треугольник ABC.
Обозначим буквой О точку пересечения его биссектрис АА\ и ВВ\
(рис. 135). Проведем из точки О перпендикуляры OK, OL и ОМ
к прямым АВ, ВС и С А. Так как
любая точка биссектрисы угла рав-
равноудалена от его сторон, то ОК =
= ОМ и OK = OL. Отсюда сле-
следует, что ОМ = OL. Таким обра-
образом, точка О лежит внутри угла С
и равноудалена от его сторон АС
и ВС. Следовательно, точка О ле-
лежит на биссектрисе угла С. Но это
и означает, что все три биссектри-
биссектрисы треугольника ABC пересекаются
в точке О. Теорема доказана.
А
МВХ
Рис. 135
С
Замечание. Ясно, что точка пересечения биссектрис треугольни-
треугольника равноудалена от его сторон. Справедливо и обратное утверждение:
если точка лежит внутри треугольника и равноудалена от его
сторон, то она является точкой пересечения биссектрис этого
треугольника.

78
Гл. 2. Треугольники
В самом деле, указанная точка должна лежать на каждой из бис-
биссектрис треугольника, т.е. совпадать с точкой их пересечения.
Задачи
92. В треугольниках ABC и А\В\С\ углы А и А\ — прямые, BD
и B\D\ — биссектрисы. Докажите, что ААВС = АА\В\С\, если ZB =
= ZB{ и BD = B\D\.
93. Докажите, что треугольники равны, если сторона и проведен-
проведенные к ней высота и медиана одного треугольника соответственно равны
стороне и проведенным к ней высоте и медиане другого треугольника.
94. Серединные перпендикуляры к сторонам АВ и АС треугольни-
треугольника ABC пересекаются в точке D стороны ВС. Докажите, что: a) D —
середина стороны ВС] б) АА = АВ -\- Z.C.
95. Серединный перпендикуляр к стороне АВ равнобедренного
треугольника ABC пересекает сторону ВС в точке Е. Найдите основа-
основание АС треугольника, если периметр треугольника АЕС равен 27 см,
а АВ = 18 см.
96. Равнобедренные треугольники ABC и ABD имеют общее ос-
основание АВ. Докажите, что прямая CD — серединный перпендикуляр
к отрезку АВ.
97. Высоты АА\ и ВВ\ равнобедренного треугольника ABC, про-
проведенные к боковым сторонам, пересекаются в точке М. Докажите,
что прямая МС — серединный перпендикуляр к отрезку АВ.
98. Серединные перпендикуляры к двум сторонам треугольника
пересекаются в некоторой точке. Докажите, что серединный перпенди-
перпендикуляр к третьей стороне проходит через эту точку.
99. Точка О — середина отрезка АВ, ОМ — прямая, не пер-
перпендикулярная к прямой АВ. Докажите, что если точка X лежит
на прямой ОМ и отлична от точки О, то АХ ф ХВ.
100. Прямая а — серединный перпенди-
перпендикуляр к отрезку АВ, М — точка, принадле-
принадлежащая той же полуплоскости с границей а,
что и точка А. Докажите, что MA < MB.
101. На рисунке 136 АВ = АС, АР =
= AQ, отрезки BQ и СР пересекают-
пересекаются в точке О. Докажите, что: а) тре-
треугольник ВОС — равнобедренный; б) пря-
прямая АО — серединный перпендикуляр к сто-
стороне ВС.
102. Через середину отрезка проведена
прямая. Докажите, что концы отрезка рав-
равноудалены от этой прямой.
103. Докажите, что серединный перпен-
перпендикуляр к отрезку является осью симметрии
этого отрезка.
А
Рис. 136

6. Задачи на построение 79
104. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
105. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е,
О, F?
106. Докажите, что прямая, содержащая биссектрису равнобедрен-
равнобедренного треугольника, проведенную к основанию, является осью симмет-
симметрии этого треугольника.
107. Из точки М биссектрисы неразвернутого угла О проведе-
проведены перпендикуляры МА и MB к сторонам этого угла. Докажите,
что АВ JL ОМ.
108. Что представляет собой множество всех точек плоскости,
равноудаленных от двух данных пересекающихся прямых?
109* Отрезок ВС — основание равнобедренного треугольни-
треугольника ABC. Серединный перпендикуляр к стороне АС пересекает
прямую ВС в точке D так, что точка В лежит между С и D.
На прямой AD взята точка Е так, что АЕ = BD и точка А
лежит между точками Е и D. Докажите, что треугольник CDE —
равнобедренный.
110. Биссектрисы треугольника ABC пересекаются в точке О,
а биссектрисы треугольника А\В\С\ — в точке О\. Известно, что АВ =
= АХВ\, АО = А\ОХ иВО = ВХОХ. Докажите, что ААВС = АА{В{С{.
111. Точка пересечения биссектрис треугольника лежит на его
высоте. Докажите, что этот треугольник — равнобедренный.
112. Точка пересечения биссектрис треугольника лежит на его
медиане. Докажите, что этот треугольник — равнобедренный.
§ 6. Задачи на построение
35. Окружность. Центральная симметрия. Предложение, в кото-
котором разъясняется смысл того или иного выражения или названия, на-
называется определением. Мы уже встречались с определениями, напри-
например с определением угла, смежных углов, равнобедренного треуголь-
треугольника и т. д. Дадим определение еще одной геометрической фигуры —
окружности.
Определение. Окружностью называется геометрическая фи-
фигура, состоящая из всех точек плоскости, расположенных на за-
заданном расстоянии от данной точки.
Данная точка называется центром окружности, а отрезок, соеди-
соединяющий центр с какой-либо точкой окружности, — радиусом окруж-
окружности (рис. 137). Часть плоскости, ограниченная окружностью, назы-
называется кругом (рис. 138).
Отрезок, соединяющий две точки окружности, называется ее хор-
хордой. Хорда, проходящая через центр окружности, называется диамет-
диаметром.
На рисунке 139 отрезки АВ и ЕЕ — хорды окружности, отре-
отрезок CD — диаметр окружности.

80
Гл. 2. Треугольники
Рис. 137. Окружность с
центром О радиуса г
Рис. 138
Любые две точки окружности делят ее на две части. Каждая
из этих частей называется дугой окружности. На рисунке 140 ALB
и АМВ — дуги, ограниченные точками А и В.
Рис. 139. АВ и EF - хор-
хорды, CD — диаметр окруж-
окружности
Рис. 140. Точки А и В де-
делят окружность на две ду-
дуги. Одна из них выделена
жирной линией
Отметим, что окружность симметрична относительно любой пря-
прямой, проходящей через ее центр. Докажите это утверждение самосто-
самостоятельно.
Две точки А и А\ называются симметричными относительно
точки О, если точка О — середина отрезка АА\ (рис. 141, а). Точка О
считается симметричной самой себе. На рисунке 141, б точки М
и Mi, N и N\ симметричны относительно точки О, а точки Р и Q
не симметричны относительно этой точки.
Фигура называется симметричной относительно точки О, если
для каждой точки фигуры симметричная ей точка относительно точ-
точки О также принадлежит этой фигуре. Точка О называется центром
симметрии фигуры. Говорят также, что фигура обладает централь-
центральной симметрией.

6. Задачи на построение
81
О
а)
М
N
б)
Рис. 141
Рис. 142
На рисунке 142 изображена фигура, обладающая центральной сим-
симметрией. Если повернуть эту фигуру на 180° вокруг центра сим-
симметрии — точки О, то она совместится сама с собой, в частности,
произвольная точка А фигуры перейдет
в симметричную ей точку А\, а точ-
точка А\ — в точку А.
Примером фигуры, обладающей цен-
центральной симметрией, является окруж-
окружность. Центром симметрии окружно-
окружности является центр окружности. Пря-
Прямая также обладает центральной сим-
симметрией, однако в отличие от окружно-
окружности, которая имеет только один центр
симметрии, у прямой их бесконечно
много — любая точка прямой является ее центром симметрии. Приме-
Примером фигуры, не имеющей центра симметрии, является треугольник.
36. Взаимное расположение прямой и окружности. Выясним,
сколько общих точек могут иметь прямая и окружность в зависимости
от их взаимного расположения. Рассмотрим прямую р и окружность
радиуса г с центром О. Допустим сначала, что прямая р не прохо-
проходит через точку О. Проведем из точки О перпендикуляр ОН к пря-
прямой р (рис. 143) и обозначим длину этого перпендикуляра, т.е. рассто-
расстояние от точки О до прямой р, буквой d. Возможны три случая.
1°. d > г. Поскольку перпендикуляр ОН, проведенный из точки О
к прямой р, меньше любой наклонной, проведенной из той же точ-
точки О к прямой р, то для каждой точки А прямой р О А ^ ОН =
= d (рис. 143, а). Но d > г, поэтому О А > г. Следовательно, точка А
не лежит на окружности. Таким образом,
если расстояние от центра окружности до прямой больше ради-
радиуса окружности, то прямая и окружность не имеют общих точек.
2°. d = r. Поскольку ОН = d = г, то точка Я лежит на окружности,
т.е. является общей точкой прямой и окружности (рис.143, б). Для
любой другой точки А прямой р О А > ОН = г, так как перпенди-
перпендикуляр ОН меньше наклонной О А. Следовательно, точка А не лежит
на окружности. Таким образом,

82
Гл. 2. Треугольники
А
Н
Н
Ах
а) б) в)
Рис. 143. а) ОН = d> г; общих точек нет; б) ОН = d = r; одна общая точка
точка Я; в) ОЯ = d < г; две общие точки — точки А и В
если расстояние от центра окружности до прямой равно ради-
радиусу окружности, то прямая и окружность имеют единственную
общую точку.
3°. d < г. Поскольку ОН = d < г, то точка Н лежит внутри круга,
ограниченного данной окружностью. Отметим на прямой р точку М,
для которой МН = г (рис. 143, в). Гипотенуза ОМ прямоугольного
треугольника МОН больше катета МН, поэтому ОМ > г, а значит,
точка М лежит вне круга, ограниченного данной окружностью. Таким
образом, один конец отрезка МН (точка Я) лежит внутри указанного
круга, а другой (точка М) — вне этого круга. Следовательно, на от-
отрезке МН должна быть точка А, являющаяся общей точкой прямой р
и окружности.
На луче НМ не может быть другой общей точки прямой р
и окружности. В самом деле, допустим, что такая точка А\ на-
нашлась (см. рис. 143, в). Тогда ОА\ = О А = г, следовательно, прямо-
прямоугольные треугольники АНО и А\НО равны по гипотенузе (ОА =
= ОА\) и катету (ОН — общий катет). Поэтому НА = НА\, и значит,
точка А\ совпадает с точкой А. Итак, на луче НМ есть только одна
общая точка прямой р и окружности — точка А.
Точка В, симметричная точке А относительно прямой ОН, также
является общей точкой прямой р и окружности (объясните, почему).
Таким образом,
если расстояние от центра окружности до прямой меньше ради-
радиуса окружности, то прямая и окружность имеют ровно две общие
точки.

6. Задачи на построение 83
Ясно, что если прямая р проходит через центр О окружности, то она
пересекает окружность в двух точках — концах диаметра окружности,
лежащего на этой прямой.
Замечание 1. Если прямая и окружность имеют только одну
общую точку, то говорят, что окружность касается прямой, прямая
называется касательной к окружности, а общая точка касательной
и окружности называется точкой касания. Из наших рассуждений
следует, что
если d = г, т. е. если прямая проходит через конец радиуса, лежа-
лежащий на окружности, и перпендикулярна к этому радиусу, то она
является касательной;
и обратно: если прямая является касательной, то d = г, т. е. ка-
касательная к окружности перпендикулярна к радиусу, проведенному
в точку касания.
Отметим еще один факт, связанный с касательной. Для этого
рассмотрим две касательные к окружности с центром О, проходящие
через точку А и касающиеся окружности в точках В и С (рис. 144).
Отрезки АВ и АС назовем от-
отрезками касательных, прове-
проведенными из точки А. Они обла-
обладают следующим свойством:
отрезки касательных к ок-
окружности, проведенные из од-
одной точки, равны и состав-
составляют равные углы с прямой,
проходящей через эту точку
и центр окружности.
Для доказательства этого
утверждения обратимся к рисун-
рисунку 144. Поскольку углы 1 и 2 — Рис- 144
прямые, то треугольники АВО
и АСО — прямоугольные. Они равны, так как имеют общую гипоте-
гипотенузу О А и равные катеты ОВ и ОС. Следовательно, АВ = АС и Z3 =
= Z4, что и требовалось доказать.
Замечание 2. При рассмотрении случая 3° (d < г) может воз-
возникнуть вопрос: нельзя ли более точно найти местоположение точки А
на луче НМ, например выразить длину отрезка АН через d и г?
Пока ответить на этот вопрос мы не можем. Впрочем, можно указать
способ, позволяющий найти длину отрезка АН с любой точностью.
Разделим отрезок НМ (напомним, что НМ = г) точками на 10 равных
частей и выберем из этих точек две соседние точки А\ и В\, для
которых ОА\ ^ г, а ОВ\ ^ г. Тогда можно сказать так: длина отрез-
отрезка АН приближенно равна длине отрезка А\Н. Так, на рисунке 145
длина отрезка АН приближенно равна 0JHM = 0,7г. Если требуется
найти длину отрезка АН с большей точностью, то можно разделить
отрезок А\В\ точками на 10 равных частей и выбрать из этих точек

84
Гл. 2. Треугольники
-М
Рис. 145
две соседние точки А^ и В^, для которых ОА^ ^ г, а О?>2 ^ г. Тогда
можно будет сказать, что длина отрезка АН приближенно равна длине
отрезка А^Н и т. д.
37. Окружность, вписанная в треугольник. Если все стороны
треугольника касаются окружности, то окружность называется впи-
вписанной в треугольник, а треугольник — описанным около этой окруж-
окружности. На рисунке 146 треугольник ABC описан около окружности
радиуса г с центром О. Приглядимся к этому рисунку. Что можно ска-
сказать о точке О? Из результатов предыдущего пункта следует, что эта
точка находится на расстоянии г от каждой из сторон треугольника.
Тем самым, точка О равноудалена от сторон треугольника ABC.
Рассмотрим теперь произвольный треугольник и поставим такой
вопрос: можно ли вписать в этот треугольник окружность? Чтобы
ответить на этот вопрос, нужно прежде всего понять, существует
ли точка, равноудаленная от сторон этого треугольника? Как мы знаем,
такая точка существует, и притом только одна — точка пересечения

6. Задачи на построение
85
биссектрис треугольника. Это наводит на мысль о том, что должна
быть верна следующая теорема.
Теорема. В любой треугольник можно вписать окружность,
и притом только одну.
Доказательство. Рассмотрим произвольный треугольник ABC
и обозначим буквой О точку пересечения его биссектрис. Проведем
из точки О перпендикуляры OK, OL и ОМ к сторонам АВ, ВС
и С А (рис. 147). Поскольку точка О равноудалена от сторон треуголь-
треугольника ABC, то OK = OL = ОМ. Поэтому окружность с центром О
радиуса ОК проходит через точки К, L и М. Стороны треугольни-
треугольника ABC находятся от точки О на расстоянии, равном радиусу этой
окружности. Следовательно, указанная окружность касается сторон
треугольника ABC, т. е. является окружностью, вписанной в этот
треугольник.
Рис. 146
Допустим, что в треугольник ABC можно вписать еще одну окруж-
окружность. Тогда центр этой окружности равноудален от сторон треуголь-
треугольника и, следовательно, совпадает с точкой О пересечения биссектрис
треугольника ABC, а ее радиус равен расстоянию от точки О до сто-
сторон этого треугольника. Тем самым, эта окружность совпадает с первой
окружностью. Теорема доказана.
Замечание. Как мы только что обнаружили, центр окружности,
вписанной в треугольник, совпадает с точкой пересечения биссектрис
этого треугольника. По этой причине точку пересечения биссектрис
треугольника часто называют центром вписанной окружности.
38. Взаимное расположение двух окружностей. Начнем с такого
вопроса: могут ли две окружности иметь три общие точки? Видимо,
нет. Во всяком случае, нарисовать такой рисунок не удается. Тогда
попробуем доказать, что не могут.
Теорема. Две окружности не могут иметь три общие точки.
Доказательство. Допустим, что две окружности имеют три
общие точки — А, В и С. Что можно сказать о центре и радиусе

86
Гл. 2. Треугольники
С
В
А
первой окружности (рис. 148)? По-
Поскольку центр этой окружности
равноудален от точек А и В, то он
лежит на серединном перпендику-
перпендикуляре к отрезку АВ. По аналогичной
причине он лежит и на серединном
перпендикуляре к отрезку ВС. Сле-
Следовательно, центр О первой окруж-
окружности — это точка пересечения се-
серединных перпендикуляров к отрез-
отрезкам АВ и ВС. А чему равен радиус
этой окружности? Он равен, напри-
например, расстоянию от точки О до точ-
точки А.
Теперь применим те же рассуж-
рассуждения ко второй окружности. В ре-
результате мы обнаружим, что центр этой окружности совпадает с точ-
точкой О пересечения серединных перпендикуляров к отрезкам АВ и ВС,
а ее радиус равен расстоянию от точки О до точки А. Таким образом,
центры и радиусы наших окружностей совпадают, а значит, совпадают
и сами окружности.
Итак, если две окружности имеют три общие точки, то эти окруж-
окружности обязательно совпадают. Но это и означает, что две (различные)
окружности не могут иметь три общие точки. Теорема доказана.
Рис. 148
Следствие. Две окружности не могут иметь более двух общих
точек.
Перейдем теперь к решению следующего вопроса: как могут быть
расположены относительно друг друга две окружности?
Рассмотрим две окружности радиусов г\ и Г2, центры О\ и 0%
которых находятся на расстоянии d друг от друга (рис. 149). Для
определенности будем считать, что r\ ^ г^.
Начнем со случая, когда d > г\ + т^ (рис. 149, а), т.е. d — т^>
> г\. Так как для каждой точки А второй окружности, в соответ-
соответствии с неравенством треугольника, выполняется неравенство О\А +
+ Г2 ^ d (знак равенства возможен в том случае, когда точка А лежит
на отрезке O1O2), то О\А ^ d — т^ > т\. Следовательно, все точки вто-
второй окружности лежат вне круга, ограниченного первой окружностью.
В этом случае говорят, что одна окружность лежит вне другой.
Пусть d = г\ + Г2 (рис. 149, б), т. е. d — г^ =г\. Так как для каждой
точки А второй окружности О\А -\- Г2 ^ d, то О\А ^ d — т^ = п,
причем знак равенства возможен только в том случае, когда точка А
лежит на прямой О\О^ между точками О\ и 0%. Следовательно, наши
окружности имеют единственную общую точку, а все остальные точки
второй окружности лежат вне круга, ограниченного первой окружно-

6. Задачи на построение
87
а)
б)
Р
D
д)
е)
Рис. 149. a) d > п + Г2\ б) d = п + Г2; в) d < п + Г2 и d > п — г^\ г) d < п +
+ Г2 и d > п — Г2\ д) d = п — Г2\ е) d < п — Г2
стью. В этом случае говорят, что окружности касаются друг друга
извне.
Далее, если d < г\ + т^ и d > г\ — т^ (рис. 149, в, г), т.е. d —
— Г2 < г\ и d -\- Г2 > г\, то для точки А второй окружности, лежа-
лежащей на прямой О\О^ по ту же сторону от точки 0%, что и О\,
получаем: либо О\А = d — т^ <т\ (рис. 149, в), либо О\А = т^ — d <
< Г2 < г\ (рис. 149, г), т. е. точка А лежит внутри круга, ограниченного
первой окружностью. Для точки В второй окружности, расположен-
расположенной на прямой О\О<2 так, что точка 0% лежит между точками О\
и В (см. рис. 149, в, г), получаем: О\В = d + т^ > п, т.е. точка Б
лежит вне круга, ограниченного первой окружностью. Таким образом,
часть точек второй окружности лежит внутри круга, ограниченного
первой окружностью, а часть — вне этого круга. Следовательно, на вто-
второй окружности есть такая точка С, отличная от А и В, которая
лежит на первой окружности. Иными словами, точка С является общей
точкой наших окружностей, не лежащей на прямой О\О^. Точка D,

Гл. 2. Треугольники
симметричная точке С относительно прямой О\О^, также является
общей точкой наших окружностей (объясните, почему). Поскольку две
окружности не могут иметь более двух общих точек, то можно сделать
вывод: в этом случае окружности пересекаются в двух точках.
Допустим теперь, что Т\ > т^. Если d = г\ — т^ (рис. 149, д), т.е.
d -\- Г2 = г\, то для каждой точки А второй окружности О\А ^ d +
+ Г2 = г\, причем знак равенства возможен только в том случае, когда
точка А расположена на прямой О\О^ так, что точка О^ лежит между
точками О\ и А. Следовательно, наши окружности имеют единствен-
единственную общую точку, а все остальные точки второй окружности лежат
внутри круга, ограниченного первой окружностью. В этом случае го-
говорят, что окружности касаются друг друга изнутри.
Наконец, если d < г\ — т^ (рис. 149, е), т.е. d -\- Г2 < г\, то для
каждой точки А второй окружности О\А ^ d-\-Г2 < г\. Следователь-
Следовательно, все точки второй окружности лежат внутри круга, ограниченного
первой окружностью. В этом случае говорят, что одна окружность
лежит внутри другой. В частности, если центры окружностей совпа-
совпадают (случай d = 0), то окружности называются концентрическими.
Назовем линией центров двух неконцентрических окружностей
прямую, на которой лежат центры этих окружностей. Тогда получен-
полученные нами результаты можно кратко сформулировать так:
если расстояние между центрами двух окружностей больше
суммы их радиусов или меньше разности радиусов, то окружности
общих точек не имеют]
если расстояние между центрами двух окружностей равно сум-
сумме их радиусов или равно разности радиусов, то окружности име-
имеют ровно одну общую точку, лежащую на линии центров]
если расстояние между центрами двух окружностей меньше
суммы их радиусов, но больше разности радиусов, то окружности
имеют равно две общие точки, не лежащие на линии центров.
39. Построение треугольника по трем сторонам. В геометрии
принято выделять те задачи на построение, которые решаются с помо-
помощью только циркуля и линейки без масштабных делений. Их называют
задачами на построение. При этом предполагается, что:
линейка позволяет провести произвольную прямую, а также постро-
построить прямую, проходящую через две данные точки;
с помощью циркуля можно провести окружность произвольного
радиуса, а также окружность с центром в данной точке и радиусом,
равным данному отрезку.
Из всевозможных задач на построение можно выделить несколько
основных — тех, которые используются при решении других, более
сложных задач. Важнейшей из основных задач является следующая.
Задача 1. Построить треугольник по трем сторонам.
Решение. Эту задачу нужно понимать так: даны три отрезка —
MN, PQ и RS (рис. 150, а); требуется построить треугольник, стороны

R. /// .S
6. Задачи на построение 89
N
А в
А В
а) б) в)
Рис. 150. а) Данные отрезки MN, PQ и RS; б) на прямой отложили отрезок
АВ = MN; в) окружность радиуса PQ с центром А и окружность радиуса RS
с центром В пересекаются в точке С. Треугольник ABC искомый: АВ = MN,
АС = PQ, ВС = RS
которого соответственно равны этим трем отрезкам.
Построение искомого треугольника можно провести следующим
образом. Проведем произвольную прямую, отметим на ней точку А
и отложим отрезок АВ, равный MN (рис. 150, б). Затем построим две
окружности: радиуса PQ с центром в точке А и радиуса RS с центром
в точке В. Одну из точек пересечения этих окружностей обозначим
буквой С (рис. 150, в). Соединив точку С отрезками с точками А
и В, получим искомый треугольник ABC. В самом деле, в этом
треугольнике по построению АВ = MN, AC = PQ, ВС = RS, т. е.
треугольник ABC удовлетворяет условию задачи.
Исходную прямую и точку А на ней можно выбрать произвольно,
поэтому существует бесконечно много треугольников, удовлетворяю-
удовлетворяющих условию задачи. Однако все эти треугольники равны друг другу
по третьему признаку равенства треугольников, поэтому принято гово-
говорить, что данная задача имеет единственное решение.
Замечание 1. Обычно когда говорят: «Построить треугольник
по каким-то его элементам», то имеют в виду, что данные элементы —
отрезки, углы и т. д. — действительно являются элементами некоторого
треугольника. Иными словами, считают, что треугольник, который тре-
требуется построить, существует. Можно, однако, встать на другую точку
зрения — считать, что заранее неизвестно, существует ли треугольник
с данными элементами. В этом случае может оказаться, что задача
на построение не имеет решения, или имеет решение, но не всегда.
Например, если в нашей задаче заранее неизвестно, что искомый
треугольник существует, то данная задача не всегда имеет решение.
Действительно, в треугольнике каждая сторона меньше суммы двух
других сторон. Поэтому если какой-нибудь из данных отрезков больше
или равен сумме двух других, например MN > PQ + RS, то нельзя
построить треугольник, стороны которого равны данным отрезкам.
Если мы попытаемся это сделать, то обнаружим, что окружности
с центрами А и В не пересекутся (рис. 151).
Возникает вопрос: а имеет ли задача решение, если каждый из дан-
данных отрезков меньше суммы двух других, т. е. MN < PQ + RS, PQ <

90 Гл. 2. Треугольники
М> >• ¦ N
R ¦ /// ¦ S
Рис. 151. Если MN > PQ + RS, то окружности с центрами А и В и радиусами
PQ и ii^ не пересекаются
< RS + MTV, i^g < MTV + PQ? На этот вопрос можно ответить утвер-
утвердительно — задача имеет решение. В самом деле, в этом случае рассто-
расстояние MN между центрами наших окружностей меньше суммы PQ +
+ RS их радиусов, но больше их разности: MN < PQ + RS и MN >
> RS — PQ. Следовательно, эти окружности пересекаются в двух
точках, причем эти точки не лежат на прямой АВ (п. 38).
Замечание 2. Если требуется выяснить, существует ли тре-
треугольник, стороны которого равны данным отрезкам MN, PQ и RS,
то не обязательно проверять справедливость всех трех неравенств:
MN < PQ + RS, PQ < RS + MN, RS < MN + PQ. Действительно,
пусть, например, MN ^ PQ и MN ^ RS. Тогда неравенства PQ <
< RS + MN и RS < MN + PQ выполняются автоматически (объяс-
(объясните, почему), поэтому остается проверить справедливость только од-
одного неравенства: MN < PQ + RS. Таким образом, если наибольший
из трех данных отрезков меньше суммы двух других, то существу-
существует треугольник, стороны которого равны данным отрезкам.
Замечание 3. Возьмем три произвольных отрезка с длинами х,
у, z и положим
а = у + z, b = z + x, c = x + y. A)
Ясно, что выполняются неравенства а + Ъ > с, Ъ + с > а, с + а > Ь,
поэтому
для любых положительных х, у и z существует треугольник,
стороны а, Ь и с которого выражаются формулами A).
Верно и обратное утверждение:
если a, b и с — стороны данного треугольника ABC, то су-
существуют такие положительные величины х, у и z, что а, Ъ и с
выражаются формулами A).
Чтобы убедиться в этом, нужно из уравнений A) выразить х, у и z
через а, Ъ и с. В результате получим:
х = -(Ъ + с-а)=р-а, у = -(с + а-Ъ)=р-Ъ,
B)

6. Задачи на построение
91
где р = -(а + Ъ + с) — полупериметр треугольника ABC. Так как
стороны a, b и с треугольника ABC удовлетворяют неравенству тре-
треугольника, т. е. а < Ъ + с, 6 < с + а, с < а + 6, то найденные х, у и z,
как видно из формул B), положительны.
Возникает вопрос: как гео-
геометрически связаны отрезки х,
у, z с треугольником ABC? Что-
Чтобы ответить на этот вопрос, от-
отметим точки К, L и М касания
вписанной в треугольник окруж-
окружности со сторонами АВ, ВС
и СА, равными соответствен-
соответственно с, а и Ъ (рис. 152). Посколь-
Поскольку отрезки касательных, про-
К
А
М
С
Рис. 152. АВ = с, ВС = а,СА = Ъ
веденные из одной точки, рав-
равны, то АК = AM, BK = BL
и CL = СМ. Если теперь поло-
положить х = AM, у = BK, z = CL,
то получим: а = у + z, Ъ = z + х, с = х -\- у, откуда следует, что х, у
и z выражаются через а, Ъ и с формулами B).
40. Основные задачи на построение. К числу основных задач
на построение обычно относят еще четыре задачи: 1) построение угла,
равного данному; 2) построение биссектрисы данного угла; 3) постро-
построение серединного перпендикуляра к данному отрезку; 4) построение
прямой, проходящей через данную точку и перпендикулярной к данной
прямой.
Решения первых двух задач приведены на рисунках 153 и 154.
Обратим особое внимание на то, что в основе этих решений лежит по-
а)
Рис. 153
строение треугольника по трем сторонам. Займемся теперь следующей
задачей.
Задача 2. Построить серединный перпендикуляр к данному
отрезку.
Решение. Данный отрезок АВ изображен на рисунке 155, а.
Проведем две окружности радиуса АВ с центрами А и В. Они

92
Гл. 2. Треугольники
а)
Рис. 154
пересекутся в двух точках: М\ и М2 (рис. 155, б). Проведем пря-
прямую MiM2 (рис. 155, в). Она и является искомым серединным перпен-
перпендикуляром к отрезку АВ.
В самом деле, точки М\ и М2 по построению равноудалены от кон-
концов отрезка АВ (АМ\ = ВМ\ = АМ2 = ВМ^) и поэтому лежат на се-
серединном перпендикуляре к этому отрезку. Таким образом, серединный
перпендикуляр к отрезку АВ проходит через точки М\ и М2, т.е.
совпадает с прямой M\M<i.
Замечание 1. Построив серединный перпендикуляр к данному
отрезку АВ, мы решили попутно еще одну задачу: разделить данный
отрезок АВ пополам, т. е. найти его середину. Действительно, точка О
пересечения серединного перпендикуляра с отрезком АВ и есть сере-
середина этого отрезка (см. рис. 155, в).
Если отрезки АО и ОВ также разделить пополам, то отрезок АВ
будет разделен на четыре равные части. Возникает вопрос: а можно
ли с помощью циркуля и линейки разделить данный отрезок на три
равные части, на пять равных частей и вообще на произвольное чис-
а)
Рис. 155

6. Задачи на построение
93
ло п равных частей? Сейчас мы не можем ответить на этот вопрос,
но вернемся к нему в дальнейшем. А пока запишем его в блокнот.
Отметим, что аналогичный вопрос для углов (можно ли с помощью
циркуля и линейки разделить данный угол на произвольное число п
равных частей?) решается отрицательно. Например, с помощью цир-
циркуля и линейки нельзя осуществить трисекцию угла, т. е. разделить
любой данный угол на три равных угла. Это было доказано француз-
французским математиком Пьером Лораном Ванцелем A814-1848) в 1837 году,
когда ему было 23 года. Правда, некоторые углы, например углы в 135°
и 54°, можно разделить с помощью циркуля и линейки на три равных
угла. Подумайте, как это сделать.
Невозможность трисекции угла стала, по-видимому, одной из при-
причин, по которым до начала XX века оставался незамеченным такой
удивительный факт. Если через вершины произвольного треугольни-
треугольника ABC провести лучи АВ\, АС\, ВА\, ВС\, СА\, СВ\, делящие
каждый из его углов на три равные части (так, как показано на ри-
рисунке 156), то точки А\, В\ и С\ их пересечения окажутся вершина-
вершинами равностороннего треугольника. Эта теорема называется теоремой
Морлея в честь открывшего ее в 1904 году американского математика
Франка Морлея A862-1937). Пока мы не можем ее доказать. Поэтому
запишем в блокнот вопрос:
как доказать теорему Морлея!
Перейдем теперь к последней из перечисленных основных задач
на построение.
Задача 3. Через данную точку провести прямую, перпендику-
перпендикулярную к данной прямой.
Решение. Данная точка может лежать на данной прямой и может
не лежать на ней. В любом из этих двух случаев построение прямой,
А
С
Рис. 156. Треугольник А\В\С\ — равносторонний

94
Гл. 2. Треугольники
проходящей через данную точку перпендикулярно к данной прямой,
можно свести к построению серединного перпендикуляра к отрезку.
Рассмотрим данную точку М и данную прямую р (на рисунке 157, а
точка М не лежит на прямой р, а на рисунке 157, б — лежит на пря-
прямой р). Построим окружность с центром в точке М, пересекающую
Р
М
Р
а)
Рис. 157
прямую р в двух точках: А и В (рис. 157, в). Точка М равноудалена
от точек А и В (так как MA = MB) и, следовательно, лежит на сере-
серединном перпендикуляре к отрезку АВ. Остается построить серединный
перпендикуляр к отрезку АВ (как это сделать, мы знаем). Он и будет
искомой прямой, проходящей через данную точку М перпендикулярно
к данной прямой р (рис. 157, г).
Замечание 2. Теперь мы можем построить с помощью циркуля
и линейки биссектрисы, высоты и медианы данного треугольника,
а также построить треугольник по двум сторонам и углу между ними
или по стороне и двум прилежащим к ней углам. Объясните, как вы-
выполнить соответствующие построения. Отметим, что последняя из пе-
перечисленных задач, в отличие от остальных, может и не иметь решения
(если заранее неизвестно, что искомый треугольник существует). На-
Например, если заданные углы составляют в сумме 180°, или их сумма
больше 180°, то эта задача решений не имеет, поскольку в каждом
треугольнике сумма двух углов меньше 180°. Возникает вопрос: а если
сумма данных углов меньше 180°, можно ли утверждать, что наша
задача всегда имеет решение? Пока мы не можем ответить на этот
вопрос, так что запишем его в блокнот.
41. Еще несколько задач на построение треугольника.
Задача 4. Построить треугольник по стороне, прилежащему
к ней углу и биссектрисе треугольника, проведенной из вершины
этого угла.
Решение. Эту задачу нужно понимать так. Даны два отрезка MN
и PQ и угол hk (рис. 158, а). Требуется с помощью циркуля и ли-

6. Задачи на построение
95
> N
D
А
В
а)
б)
К/
D
А
В
А
В
г)
К
А
В
В
д)
Рис. 158
нейки построить такой треугольник ABC, у которого одна сторона,
например АВ, равна отрезку MN, один из прилежащих к ней углов,
например угол А, равен углу hk, а биссектриса AD равна отрез-
отрезку PQ (рис. 158, б).
Давайте подумаем, как это можно сделать. Поступим так, как обыч-
обычно делают, когда ищут путь решения задачи на построение. Предполо-

96 Гл. 2. Треугольники
жим, что мы уже построили искомый треугольник ABC. Рассматривая
этот треугольник и обращая внимание на те его элементы, которые
нам заданы по условию задачи, попытаемся отыскать ход построе-
построения. Ясно, что мы можем провести произвольную прямую, отложить
на ней отрезок АВ, равный данному отрезку MN, а затем построить
угол КАВ, равный данному углу hk. На рисунке 158, в изображен
результат этого этапа построения. Что же делать дальше? Как найти
положение точки С на луче АК? Давайте посмотрим, что нам еще
дано. Нам дан отрезок PQ, которому должна равняться биссектри-
биссектриса AD искомого треугольника ABC. Поэтому нужно поступить так:
построить биссектрису угла КАВ (как это сделать, мы знаем) и отло-
отложить на ней отрезок AD, равный данному отрезку PQ (рис. 158, г).
После этого остается провести прямую BD и обозначить буквой С
точку пересечения этой прямой с лучом АК. Получившийся треуголь-
треугольник ABC (рис. 158, д) и есть искомый треугольник. В самом деле,
в этом треугольнике по построению сторона АВ равна отрезку MN,
угол А — углу hk, а биссектриса AD — отрезку PQ.
Итак, мы указали способ построения искомого треугольника. За-
Заметим, что поскольку прямая BD не может пересечь луч АК в двух
точках, то данная задача имеет единственное решение.
Отметим еще один момент. Если заранее неизвестно, существует
ли искомый треугольник, то может получиться так, что прямая BD
не пересечется с лучом АК (см. рис. 158, е) — данный отрезок PQ
слишком велик. В таком случае невозможно построить треуголь-
треугольник ABC, у которого сторона АВ, биссектриса AD и угол А рав-
равнялись бы заданным отрезкам и углу, т. е. треугольника с такими
элементами не существует.
Задача 5. Построить треугольник по стороне, прилежащему
к ней углу и сумме двух других сторон.
Решение. Эту задачу нужно понимать так. Даны два отрезка MN
и PQ и угол hk (рис. 159, а). Требуется с помощью циркуля и ли-
линейки построить такой треугольник ABC, у которого одна сторона,
например АВ, равна отрезку MN, один из прилежащих к ней углов,
например угол А, равен углу hk, а сумма АС + С В равна отрезку PQ
(рис. 159, б).
Допустим, что искомый треугольник ABC уже построен. Продол-
Продолжим сторону АС на отрезок CD, равный С В (рис. 159, в). В полу-
получившемся треугольнике ABD мы знаем две стороны (АВ и AD =
= АС + СВ = PQ) и угол между ними, поэтому этот треугольник
мы можем построить. Осталось понять, как на его стороне AD найти
такую точку С, что CD = СВ, т. е. точку С, равноудаленную от концов
отрезка BD. Как это сделать, тоже ясно — нужно провести серединный
перпендикуляр к отрезку BD.
Итак, приступим к построению. Построим сначала треуголь-
треугольник ABD, угол А которого равен данному углу hk, а стороны АВ
и AD соответственно равны данным отрезкам MN и PQ (рис. 159, г).

6. Задачи на построение
97
В
г)
е)
Затем построим серединный перпендикуляр к отрезку BD и обозначим
буквой С точку его пересечения с отрезком AD (рис. 159, д).
Поскольку ВС = CD, то треугольник ABC — искомый.
Если заранее неизвестно, что искомый треугольник существует,
то данная задача может не иметь решения. Так, если PQ < MN,
то искомый треугольник не существует, поскольку сторона АВ тре-
треугольника ABC должна быть меньше суммы двух других его сторон.
Если выполнить наше построение в этом случае, то мы обнаружим, что
серединный перпендикуляр к отрезку BD не пересекает отрезок AD
(рис. 159, е). Если же PQ > MN, то данная задача имеет решение.
В самом деле, из условия PQ > MN следует, что в треугольни-
треугольнике ABD AD > АВ, и поэтому угол В больше угла D. Следовательно,
ZDBC = ZD < АВВА (рис. 159, д). Это означает, что луч ВС прохо-
проходит внутри угла DBA, поэтому он пересекает отрезок AD.
Из построения ясно также, что данная задача имеет единственное
решение, поскольку серединный перпендикуляр к отрезку BD не мо-
может пересечь прямую AD в двух точках.
Замечание 1. Задачи на построение интересны еще и тем, что
они в ряде случаев помогают найти формулировку теоремы или уста-
установить, что какое-то утверждение правильным не является. Приведем
пример. Как мы помним, признак равенства треугольников по двум
сторонам и углу, противолежащему одной из них, имеет место только
в том случае, когда сторона, противолежащая этому углу, не меньше
второй из данных сторон. Попробуем установить это путем построений.
Для этого сформулируем такую задачу.
Задача 6. Построить треугольник по двум сторонам и углу,
противолежащему одной из них.
4 С. Б. Кадомцев

98
Гл. 2. Треугольники
Решение. На рисунке 160 изображены два данных отрезка MN
и PQ и данный угол hk, причем на рисунке 160, a PQ < MN, на ри-
рисунке 160,6 PQ = MN, а на рисунке 160, в PQ > MN. Требуется
М-
Р-
М-
Р-
а)
Рис. 160
построить треугольник ABC, в котором АВ = M7V, ??С = PQ, ZA =
= Zhk. Имея в виду нашу цель, будем исходить из того, что искомый
треугольник существует.
Возьмем произвольный луч, начало которого обозначим буквой А,
и отложим от него угол, равный данному углу hk (рис. 161). На одной
из сторон этого угла отложим отрезок АВ, равный MN, и проведем
окружность с центром В радиуса PQ. Поскольку по предположению
искомый треугольник существует, то проведенная окружность либо
пересекает прямую, содержащую вторую сторону угла, в двух точках
С\ и С2, либо касается этой прямой. Рассмотрим сначала первый
случай. Если PQ < MN, то точка А лежит вне круга, ограниченного
этой окружностью, поэтому точки С\ и Съ лежат на одном луче
с началом А, т. е. на второй стороне построенного угла (рис. 161, а).
Следовательно, каждый из треугольников АВС\ и АВС^ является ис-
искомым. Эти треугольники не равны друг другу, поскольку АС\ Ф АС^.
Таким образом, наша задача имеет два решения. Теперь совершенно
ясно, что признак равенства треугольников по двум сторонам и углу,
противолежащему одной из них, в этом случае не имеет места. Иначе
по этому признаку треугольники АВС\ и АВС^ были бы равны друг
а)

6. Задачи на построение 99
другу, а это не так. Если же PQ = MN или PQ > MN, то точка А
лежит на границе или внутри проведенной окружности (рис. 161,6, в).
Следовательно, эта окружность пересекает вторую сторону угла только
в одной точке (точка С% на рисунках 161,6, в). В этом случае наша
задача имеет единственное решение, поэтому признак равенства тре-
треугольников по двум сторонам и углу, противолежащему одной из них,
имеет место.
Рассмотрим теперь случай, когда окружность радиуса PQ с цен-
центром В касается прямой, содержащей сторону угла в некоторой точке
С. Тогда задача на построение имеет единственное решение, причем
угол С искомого треугольника ABC оказывается прямым. Заметим,
однако, что в этом случае постановка задачи отличается от нашей:
требуется построить треугольник по двум сторонам и углу, проти-
противолежащему одной из них, если известно, что существует прямо-
прямоугольный треугольник, острый угол которого равен данному углу,
противолежащий ему катет равен одной из данных сторон, а ги-
гипотенуза — другой стороне. Ясно, что эта задача уже не является
задачей 6.
Замечание 2. Решив задачи 4 и 5, мы фактически обнаружили
еще два признака равенства треугольников:
если сторона, прилежащий к ней угол и биссектриса, проведен-
проведенная из вершины этого угла, одного треугольника соответственно
равны стороне, прилежащему к ней углу и биссектрисе, проведенной
из вершины этого угла, другого треугольника, то такие треуголь-
треугольники равны]
если сторона, прилежащий к ней угол и сумма двух других сто-
сторон одного треугольника соответственно равны стороне, прилежа-
прилежащему к ней углу и сумме двух других сторон другого треугольника,
то такие треугольники равны.
Попробуйте объяснить, как доказать эти утверждения, опираясь
на наши построения.
Задачи
113. Докажите, что перпендикуляр, проведенный из центра окруж-
окружности к хорде, делит эту хорду пополам.
114. Отрезки АВ и CD — диаметры окружности с центром О.
Найдите периметр треугольника AOD, если СВ = 13 см, АВ = 16 см.
115. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара
пересекающихся прямых?
116. Какие из следующих букв имеют центр симметрии: А, О, М,
X, К?
117. Приведите примеры фигур, имеющих бесконечно много цен-
центров симметрии.
118. Расстояние от точки А до центра окружности меньше радиуса
окружности. Докажите, что любая прямая, проходящая через точку А,
пересекает окружность в двух точках.

100 Гл. 2. Треугольники
119. Окружность касается прямых АВ и АС в точках В и С. Через
произвольную точку дуги ВС проведена касательная к окружности,
пересекающая отрезки АВ и АС в точках М и Р. Найдите периметр
треугольника AMP, если АВ = а.
120. Прямая пересекает две концентрические окружности. Дока-
Докажите, что отрезки прямой, заключенные между этими окружностями,
равны.
121* Окружность пересекает одну из двух концентрических окруж-
окружностей в точках А и В, а другую — в точках С и D. Докажите,
что АВ || CD.
122. Окружности с центрами О\ и 0% касаются друг друга извне,
и каждая из них касается изнутри окружности радиуса 10 см с цен-
центром Оз. Найдите периметр треугольника ОхО^О^.
123. Дан тупой угол АОВ. Постройте луч ОХ так, чтобы уг-
углы ХОА и ХОВ были равными тупыми углами.
124. Постройте равнобедренный треугольник по боковой стороне
и углу при основании.
125* Постройте треугольник: а) по двум сторонам и высоте, прове-
проведенной к третьей стороне; б) по двум сторонам и медиане, проведенной
к третьей стороне; в) по стороне, высоте и медиане, проведенным
к этой стороне; г) по углу, высоте и биссектрисе, проведенным из вер-
вершины этого угла.
126. На данной окружности постройте точку, равноудаленную
от двух данных пересекающихся прямых. Сколько решений может
иметь задача?
127. Даны прямая а и две точки А и В, лежащие по одну сторону
от нее. На прямой а постройте точку М, равноудаленную от точек А
и В. Всегда ли задача имеет решение?
128. Даны точки А, В, С и отрезок PQ. Постройте такую точку М,
чтобы выполнялись равенства: AM = ВМ и СМ = PQ. Сколько ре-
решений может иметь задача?
129. Даны угол и отрезок. Постройте точку, лежащую внутри угла,
равноудаленную от его сторон и равноудаленную от концов данного
отрезка.
130. Точки А и В лежат по одну сторону от прямой а. Постройте
точку М прямой а так, чтобы сумма AM + MB была бы меньше
суммы АХ + ХВ, где X — любая точка прямой а, отличная от М.
131* Постройте прямую, которая проходит через данную точку М,
лежащую вне данной окружности, и пересекает эту окружность в та-
таких точках А и В, что AM = АВ.

Глава 3
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
§ 1. Аксиома параллельных прямых
42. Аксиомы. Изучая свойства геометрических фигур, мы дока-
доказали ряд теорем. При этом мы опирались, как правило, на доказан-
доказанные ранее теоремы. Например, в п. 34 мы доказали такую теорему:
три биссектрисы треугольника пересекаются в одной точке. При этом
мы опирались на ранее доказанные теоремы о свойствах биссектрисы,
но не только на них. Прочитав еще раз доказательство, мы обнару-
обнаружим, что в наших рассуждениях использовался такой факт: биссектри-
биссектрисы АА\ и ВВ\ треугольника ABC пересекаются в некоторой точке.
А как это доказать? Видимо, нужно сначала вспомнить определение
биссектрисы треугольника: отрезок биссектрисы угла, соединяющий
вершину с точкой противоположной стороны, называется биссектрисой
треугольника. Но откуда следует, что биссектриса угла треугольника
пересекает противоположную сторону? Давайте вспомним, что такое
биссектриса угла: луч, исходящий из вершины угла и делящий его
на два равных угла, называется биссектрисой угла. Будем теперь
рассуждать так. Поскольку биссектриса АА\ угла ВАС делит этот
угол на два угла, то стороны АВ и АС лежат по разные стороны
от прямой АА\ (рис. 162), или, иными сло-
словами, стороны АВ и АС лежат в разных
полуплоскостях с границей АА\. Тем са-
самым, если мы хотим доказать, что пря-
прямая АА\ пересекает отрезок ВС, то нам
нужно доказать следующее утверждение:
если точки В и С лежат в различных В
полуплоскостях с границей АА\, то пря-
прямая АА\ пересекает отрезок ВС. ИС"
А как доказать это утверждение? С одной стороны, сам факт, вроде
бы, не вызывает сомнений. С другой стороны, как это доказать —
не ясно. Все это наводит на мысль, что не все утверждения можно
доказать. Некоторые из них, самые очевидные, следует принять на веру
в качестве исходных положений, а затем уже на их основе доказывать

102 Гл. 3. Параллельные прямые
теоремы и вообще строить всю геометрию. Такие исходные положения
называются аксиомами.
Некоторые аксиомы были сформулированы еще в первой главе
(хотя и не назывались там аксиомами). Например, аксиомой является
утверждение:
через любые две точки проходит прямая, и притом только одна.
Многие другие аксиомы, хотя и не были выделены особо, фактиче-
фактически использовались в наших рассуждениях. Это относится, в частно-
частности, к аксиомам о наложении и равенстве отрезков и углов. Так, срав-
сравнение двух отрезков основано на наложении одного отрезка на другой.
Возможность такого наложения вытекает из следующей аксиомы:
на любом луче от его начала можно отложить отрезок, равный
данному, и притом только один.
Сравнение углов основано на аналогичной аксиоме:
от любого луча в заданную сторону можно отложить угол,
равный данному неразвернутому углу, и притом только один.
Отметим, наконец, что сформулированное выше утверждение выте-
вытекает из следующей аксиомы:
каждая прямая а разделяет плоскость на две части (полуплос-
(полуплоскости) так, что любые две точки А и В одной и той же полу-
полуплоскости лежат по одну сторону от прямой а (т. е. отрезок АВ
не пересекается с прямой а), а любые две точки С и D разных полу-
полуплоскостей лежат по разные стороны от прямой а (т. е. отрезок CD
пересекается с прямой а).
Мы видим, что все перечисленные аксиомы являются наглядно оче-
очевидными и не вызывают сомнений. Само слово «аксиома» происходит
от греческого «аксиос», что означает «ценный», «достойный».
43. Основные понятия. Возникает еще один вопрос. Можно
ли дать определения всем понятиям, которыми мы пользуемся в гео-
геометрии? Например, треугольником мы назвали геометрическую фигуру,
которая состоит из трех отрезков, соединяющих три точки, не лежащие
на одной прямой. Тем самым понятие треугольника вводится с помо-
помощью следующих трех понятий: «точка», «прямая», «отрезок». А что
такое отрезок? Вспомним, что отрезком АВ называется геометрическая
фигура, состоящая из точек А и В и всех точек прямой АВ, лежащих
между ними. Итак, отрезок определяется с помощью понятий: «точка»,
«прямая», «лежать между». Конечно, когда мы говорим: «Точка М
лежит между точками А и Б», то наглядно себе представляем, что
это означает (рис.163), однако никакого определения этому понятию
мы не даем. Аналогично обстоит де-
А У В ло с понятиями «точки» и «прямой».
Правда, может показаться, что точку
Рис. 163. Точка М лежит между и ПРЯМУЮ мы определили в первой
точками А и В главе. Но вдумаемся в эти определе-
определения. Мы сказали, что точка — это

/. Аксиома параллельных прямых 103
геометрическая фигура, не имеющая размеров, а что такое «размеры»?
Мы сказали, что линия — это геометрическая фигура, не имеющая
ширины, а прямая линия безгранична и не имеет искривлений. Но что
такое «ширина», что такое «искривление» и что означает «безгранич-
«безгранична»? Определений этих понятий не было. Но предположим, что такие
определения мы дадим. Тогда в них обязательно будут использоваться
другие понятия, которые, в свою очередь, также будут нуждаться
в определениях. Ясно, что эта цепь не может продолжаться бесконечно,
где-то она должна иметь начало (подобно тому, как цепь вытекающих
друг из друга теорем имеет своим началом аксиомы). Таким началом
должны служить понятия, определения которым не даются — так
называемые основные понятия.
Но здесь возникает сомнение: ведь если мы не определяем основные
понятия, то как ими пользоваться? Вроде бы получается, что про ос-
основные понятия мы вообще ничего не знаем! На самом деле это не так.
Свойства основных понятий как раз и выражаются в аксиомах, и тем
самым основные понятия как бы определяются аксиомами. Рассмотрим,
например, понятия «точка», «прямая» и «лежать между». Эти понятия
естественно считать основными и определений им не давать. Означает
ли это, что про них мы ничего не знаем? Конечно же, нет! Мы знаем,
например, аксиому: через две точки проходит прямая, и притом только
одна. Приведем еще три аксиомы о взаимном расположении точек
и прямых:
на каждой прямой имеются по крайней мере две точки)
имеются по крайней мере три точки, не лежащие на одной
прямой)
из трех точек прямой одна и только одна лежит между двумя
другими.
Вот и получается, что мы уже кое-что знаем о наших основных
понятиях.
К числу основных понятий естественно отнести также понятие
«наложение». В главе 1 мы сказали: две фигуры называются равными,
если их можно совместить наложением. При этом мы опирались на на-
наглядные представления о наложении фигур и допускали, что всякая
геометрическая фигура может перемещаться как единое целое, напо-
наподобие того, как перемещаются материальные тела. Но геометрические
фигуры — не материальные тела, а воображаемые объекты, поэтому
наложение геометрических фигур следует понимать в особом смысле.
Чтобы выяснить этот смысл, заметим, что при наложении фигу-
фигуры Ф на равную ей фигуру Фь как мы представляем его наглядно,
каждая точка фигуры Ф накладывается на некоторую точку фигуры
Ф\. Иначе говоря, каждая точка фигуры Ф сопоставляется некоторой
точке фигуры Ф\. Но мы можем сопоставить каждую точку фигуры
Ф некоторой точке фигуры Ф\ и без непосредственного наложения
Ф на Ф\ (рис. 164). Такое сопоставление называется отображением
фигуры Ф на фигуру Ф\ (при этом подразумевается, что каждая точка

104
Гл. 3. Параллельные прямые
Ах
Ф
М9
Mi
Фх
А
Вх
Рис. 164
фигуры 0i оказывается сопоставленной некоторой точке фигуры Ф).
Под наложением фигуры Ф на фигуру Ф\ мы понимаем отображение
Ф на Ф\. Более того, мы считаем, что при этом не только точки
фигуры Ф, но и любая точка плоскости отображается на определенную
точку плоскости, т. е. наложение — это отображение плоскости
на себя. Однако не всякое отображение плоскости на себя мы называем
наложением. Наложения — это такие отображения плоскости на себя,
которые обладают свойствами, выраженными в аксиомах. Приведем
одну из них:
если при наложении совмещаются концы двух отрезков, то сов-
совмещаются и сами отрезки.
Такой подход к построению геометрии, когда
сначала формулируются исходные положения —
аксиомы, а затем на их основе путем логических
рассуждений доказываются другие утверждения,
зародился еще в глубокой древности и был изло-
изложен в знаменитом сочинении «Начала» древнегре-
древнегреческого ученого Евклида (ок. 365-300 гг. до н. э.).
Некоторые из аксиом Евклида (часть из них
он называл постулатами) и сейчас используются
в курсах геометрии в современной формулировке,
Евклид а сама геометрия, изложенная в
вается евклидовой геометрией.
Сколько же аксиом и основных понятий нужно
для построения геометрии? Этот вопрос был де-
детально исследован великим немецким математиком
Давидом Гильбертом A862-1943), который, в част-
частности, привел полный список аксиом и основных
понятий геометрии, или, как говорят, построил си-
систему аксиом геометрии.
44. Система аксиом планиметрии. Итак, ак-
аксиомами называются те основные положения гео-
геометрии, которые принимаются в качестве исходных.
Вместе с основными понятиями они образуют фун-
«Началах», назы-
Д. Гильберт

/. Аксиома параллельных прямых 105
дамент для построения геометрии. Определения основных понятий
не даются, а их свойства выражаются в аксиомах. Используя основные
понятия и аксиомы, мы даем определения новых понятий, формулируем
и доказываем теоремы и таким образом изучаем свойства геометриче-
геометрических фигур.
В нашей системе аксиом (несколько отличной от системы аксиом
Гильберта) основных понятий четыре: «точка», «прямая», «лежать меж-
между» и «наложение».
Первыми основными понятиями, с которыми мы познакомились,
были понятия точки и прямой. В соответствии с этим первые три
аксиомы характеризуют взаимное расположение точек и прямых:
1° каждой прямой принадлежат по крайней мере две точки 0;
2° имеются по крайней мере три точки, не принадлежащие
одной прямой;
3° через любые две точки проходит прямая, и притом только
одна.
Следующие три аксиомы связаны с понятием «лежать между»,
относящемуся к трем точкам, лежащим на одной прямой.
4°. Из трех точек прямой одна и только одна лежит между
двумя другими.
Говоря: «Точка В лежит между точками А и С», мы имеем в виду,
что А, В, С — различные точки прямой и точка В лежит между С
и А. Иногда вместо этих слов мы говорим, что точки А и В лежат
по одну сторону от точки С (аналогично точки В и С лежат по одну
сторону от точки А) или что точки А и С лежат по разные стороны
от точки В.
5°. Каждая точка О прямой разделяет ее на две части (два
луча) так, что любые две точки одного и того же луча лежат
по одну сторону от точки О, а любые две точки разных лучей
лежат по разные стороны от точки О.
При этом точка О не принадлежит ни одному из указанных лучей.
Напомним, что отрезком АВ называется геометрическая фигура,
состоящая из точек Aw В и всех точек прямой АВ, лежащих между А
и В. Если отрезок АВ не имеет общих точек с прямой а, то говорят,
что точки А и В лежат по одну сторону от прямой а; если же
отрезок АВ пересекается с прямой а (в некоторой точке С, лежащей
между А и В), то говорят, что точки А и В лежат по разные стороны
от прямой а.
6°. Каждая прямая а разделяет плоскость на две части (две
полуплоскости) так, что любые две точки одной полуплоскости
х) Такие понятия, как «принадлежать», «множество», «отображение», отно-
относятся не только к геометрии, но и к другим разделам математики. Поэтому
мы считаем их известными и не относим к числу основных понятий геометрии.

106 Гл. 3. Параллельные прямые
лежат по одну сторону от прямой а, а любые две точки разных
полуплоскостей лежат по разные стороны от прямой а.
Прямая а называется границей каждой из указанных полуплоско-
полуплоскостей; ее точки не принадлежат ни одной из этих полуплоскостей.
Следующие аксиомы связаны с понятием «наложение». Как уже
отмечалось в п. 43, наложения — это такие отображения плоскости
на себя, которые обладают свойствами, выраженными в аксиомах.
Чтобы сформулировать эти аксиомы, введем понятие равенства фигур.
Пусть Фи 0i - две фигуры. Если существует наложение, при котором
фигура Ф отображается на фигуру Ф\, то мы говорим, что фигуру
Ф можно совместить наложением с фигурой Ф\, или что фигура
Ф равна фигуре Ф\. Сформулируем теперь аксиомы о свойствах нало-
наложений:
7° любая фигура равна самой себе]
8° если фигура Ф равна фигуре Ф\, то фигура Ф\ равна фигуре
Ф;
9° если фигура Ф\ равна фигуре Ф% а фигура Ф^ равна фигуре
Фз, то фигура Ф\ равна фигуре Фз;
10° если при наложении совмещаются концы двух отрезков,
то совмещаются и сами отрезки)
11° на любом луче от его начала можно отложить отрезок,
равный данному, и притом только один) это означает, что если
даны какой-то отрезок АВ и какой-то луч h с началом в точке О,
то на луче h существует, и притом только одна, точка С такая, что
отрезок АВ равен отрезку ОС;
12° от любого луча в данную полуплоскость можно отложить
угол, равный данному неразвернутому углу, и притом только один;
это означает, что если даны какой-то луч О А и какой-то неразвер-
неразвернутый угол hk, то в каждой из двух полуплоскостей с границей О А
существует, и притом только один, луч ОВ такой, что угол АОВ равен
углу hk)
13° любой угол hk можно совместить наложением с равным
ему углом h\k\ двумя способами: 1) так, что луч h совместится
с лучом h\, а луч к — с лучом к\) 2) так, что луч h совместится
с лучом к\, а луч к — с лучом h\.
Следующие две аксиомы связаны со сравнением отрезков. Множе-
Множество точек, лежащих на одной прямой, называется ограниченным, если
существует отрезок, содержащий все эти точки.
14°. Для любого ограниченного множества точек, лежащих
на одной прямой, существует наименьший отрезок, содержащий
все эти точки.
Иными словами, существует такой отрезок АВ, что все точки
данного ограниченного множества ему принадлежат, а для любого
отрезка CD, меньшего АВ (см. п. 8), в данном множестве найдется
хотя бы одна точка, не принадлежащая отрезку CD.

/. Аксиома параллельных прямых 107
Рассмотрим теперь произвольный отрезок АВ. На продолжении лу-
луча В А отложим отрезок ВВ\ = АВ, на продолжении луча В\А — отре-
отрезок B\B2 = АВ, ..., на продолжении луча Вп_\А — отрезок Вп_\Вп =
= АВ (рис. 165). Говорят, что отрезок ВВп равен произведению отрез-
отрезка АВ на число п: ВВп = пАВ.
А В Вх В2 Вп-х Вп
Y
пАВ
Рис. 165
15°. Для любых двух отрезков АВ и CD существует такое
натуральное число п, что пАВ > CD.
Эту аксиому связывают с именем древнегреческого ученого Архи-
Архимеда (ок.287-212 до н.э.). Отметим, что аксиома Архимеда позволяет
осуществить процесс измерения отрезков, описанный в п. 10.
Систему аксиом планиметрии завершает аксиома параллельных
прямых, речь о которой пойдет в п. 48.
Замечание 1. Как уже отмечалось, система аксиом Гильберта
отличается от нашей. Несколько иные системы аксиом используются
в других учебниках геометрии (например, в учебнике А. В. Погорело-
ва). Но все эти системы аксиом эквивалентны друг другу, т. е. приводят
к одним и тем же выводам.
Замечание 2. Иногда стремятся к тому, чтобы аксиомы были
независимы, т. е. ни одну из них нельзя было вывести из остальных.
Мы не ставили перед собой такой цели. Например, утверждение акси-
аксиомы 5° может быть доказано на основе остальных аксиом, т. е. факти-
фактически это утверждение является теоремой, а не аксиомой. Подумайте,
как доказать эту теорему.
Замечание 3. При доказательстве некоторых утверждений (тео-
(теоремы о перпендикуляре к прямой в п. 12 и утверждения задачи п. 23)
мы использовали термин «перегибание плоскости по прямой». При
этом мы исходили из наглядных представлений о перегибании плоско-
плоскости рисунка. С точки зрения аксиом, перегибание плоскости по пря-
прямой представляет собой наложение, которое определяется следующим
образом. Рассмотрим произвольную пря-
прямую а. На этой прямой есть по крайней
мере две точки (аксиома 1°), обозначим
их буквами А и В. Кроме того, существу-
существует по крайней мере одна точка, не ле-
лежащая на прямой а (аксиома 2°), обо-
обозначим ее буквой С. Прямая а разделяет
плоскость на две полуплоскости (аксио-
(аксиома 6°). В ту из них, которая не содержит
точку С (рис. 166), отложим от луча АВ

108 Гл. 3. Параллельные прямые
угол BAD, равный углу ВАС (аксиома 12°). Согласно аксиоме 13°
существует такое наложение, при котором луч АВ накладывается
на луч АВ (т.е. луч АВ остается на месте), а луч АС накладывается
на луч AD. Это наложение и называется перегибанием плоскости
по прямой а. Оно вполне соответствует нашим наглядным представле-
представлениям о перегибании плоскости рисунка.
Отметим, что при перегибании плоскости по прямой а каждая точка
плоскости переходит в точку, симметричную ей относительно прямой а.
По этой причине перегибание плоскости по прямой а обычно назы-
называют осевой симметрией, прямую а — осью симметрии, а фигуры,
совмещающиеся этим наложением — симметричными относительно
прямой а.
45. Два следствия из аксиом. Выведем два наглядно очевидных
следствия из наших аксиом.
Следствие 1. На каждом луче есть хотя бы одна точка.
В самом деле, рассмотрим луч с началом А, являющийся частью
прямой а (на рисунке 167 он выделен жирной линией). На прямой а
есть хотя бы одна точка В, отличная от точки А (аксиома 1°). Если
точка В лежит на нашем луче (рис. 167, а), то она и является той
точкой, существование которой мы доказываем. Если же точка В
лежит на продолжении нашего луча (рис. 167, б), то поступим так:
на нашем луче от его начала отложим отрезок АС, равный АВ. Это
можно сделать согласно аксиоме 11°. Тогда точка С будет лежать
на нашем луче, что и доказывает справедливость утверждения.
Следствие 2. Если точка А лежит на прямой а, а точка В
не лежит на этой прямой, то все точки луча АВ лежат в одной
полуплоскости с границей а.
Действительно, пусть С — произвольная точка луча АВ, отличная
от В (а есть ли такая точка? Положительный ответ на этот вопрос
обоснуйте самостоятельно). Докажем, что точка С лежит в той же
полуплоскости с границей а, что и точка В (рис. 168). Прежде всего
отметим, что прямые ВС и а пересекаются в точке А. Но поскольку
точки В и С лежат по одну сторону от точки А, то согласно аксио-
аксиоме 4°, точка А не лежит на отрезке ВС. Следовательно, отрезок ВС
не пересекается с прямой а. Если же мы предположим, что точки В
В
а)
б)
В
А
Рис. 167
С
а
а
Рис. 168

/. Аксиома параллельных прямых 109
и С лежат в разных полуплоскостях с границей а, то по аксиоме 6°
отрезок ВС будет пересекаться с прямой а. Полученное противоречие
означает, что наше предположение ошибочно, т. е. точки В и С лежат
в одной полуплоскости с границей а, что и требовалось доказать.
46. О теоремах. Как мы только что видели, опираясь на аксиомы,
можно доказывать утверждения без привлечения наглядных представ-
представлений о свойствах геометрических фигур. Это относится, в частности,
ко всем рассмотренным ранее теоремам. Возьмем, например, теорему,
выражающую первый признак равенства треугольников. Ее доказатель-
доказательство опиралось на наглядные представления о наложении и равенстве
фигур, понятие «аксиомы» тогда еще не было введено. Напомним
это доказательство и рассмотрим его с точки зрения принятых нами
аксиом.
Нужно было доказать, что если АВ = А\В\, АС = А\С\ и А А =
= /.А\, то треугольники ABC и А\В\С\ равны. С этой целью мы рас-
рассматривали такое наложение, при котором вершина А совмещается
с вершиной А\, а стороны АВ и АС треугольника ABC накладываются
соответственно на лучи А\В\ и А\С\. При этом мы опирались на оче-
очевидный факт, что такое наложение существует, поскольку углы А и А\
равны. Теперь можно сказать, что существование такого наложения
следует из аксиомы 13°. Далее мы рассуждали так: поскольку АВ =
= А\В\, АС = А\С\, то сторона АВ совместится со стороной А\В\,
а сторона АС — со стороной А\С\, в частности совместятся точки В
и В\, С и С\. Как обосновать этот факт, опираясь на аксиомы? Очень
просто. По аксиоме 11° на луче А\В\ от точки А\ можно отложить
только один отрезок, равный отрезку АВ. Но по условию теоре-
теоремы АВ = А\В\, поэтому при нашем наложении точка В совместится
с точкой В\. Аналогично точка С совместится с точкой С\. Остается
сослаться на аксиому 10°, чтобы обосновать тот факт, что сторона ВС
совместится со стороной В\С\. Теперь можно сделать вывод: треуголь-
треугольники ABC и А\В\С\ полностью совместились и, следовательно, они
равны, что и требовалось доказать.
Отметим, что на той же идее основаны доказательства теорем
об углах и высоте равнобедренного треугольника (проведите эти дока-
доказательства, опираясь на аксиомы).
Рассмотрим теперь теорему, выражающую второй признак равен-
равенства треугольников. Требуется доказать, что если АВ = А\В\, ZA =
= АА\ и АВ = ZB\, то треугольники ABC и А\В\С\ равны. Как
и прежде, рассмотрим такое наложение, при котором луч АВ наложит-
ся на луч А\В\, а луч АС — на луч А\С\ (такое наложение существует
в силу аксиомы 13°). При этом точка В совместится с некоторой
точкой В<2 луча А\В\, а точка С — с некоторой точкой С% луча А\С\.
Поскольку АВ = А\В\, то А\В2 = А\В\. Следовательно, точка В%
совпадает с точкой В\ (аксиома 11°). Далее, точка С^, а значит и все
точки луча В\С2, лежат в полуплоскости с границей А\В\, содержа-

ПО Гл. 3. Параллельные прямые
щей точку С\ (и то, и другое утверждение вытекает из следствия 2
п.45), причем АА\В\С^ = /.А\В\С\. Поэтому (аксиома 12°) луч В\С^
совпадает с лучом В\С\. Итак, точка С^ лежит как на прямой А\С\,
так и на прямой В\С\, откуда по аксиоме 3° следует, что эта точка сов-
совпадает с точкой С\. Таким образом, при рассматриваемом наложении
треугольники ABC и А\В\С\ полностью совместятся (аксиома 10°),
что и требовалось доказать.
По существу, на той же идее основаны доказательства теорем,
выражающих признак параллельности двух прямых и признак рав-
равнобедренного треугольника (проведите эти доказательства, опираясь
на аксиомы).
Приведенные примеры показывают, что доказательства теорем
о первом и втором признаках равенства треугольников, опирающиеся
на аксиомы, по сути, не отличаются от наших прежних доказательств,
основанных на наглядных представлениях. Аналогично обстоит дело
и с остальными ранее доказанными утверждениями (проверьте это).
Исключения здесь составляют лишь доказательства двух утвержде-
утверждений — о взаимном расположении прямой и окружности и двух окруж-
окружностей, где требуются более аккуратные рассуждения (см. раздел «Сно-
«Снова о числах» в конце книги).
47*. Несколько задач. Попробуем теперь доказать те два утвер-
утверждения, которые были упомянуты в начале главы:
биссектриса угла треугольника пересекает противоположную
сторону этого треугольника;
любые две биссектрисы треугольника пересекаются.
Начнем с трех вспомогательных задач.
Задача 1. Доказать, что если луч исходит из вершины нераз-
неразвернутого угла и проходит через точку внутренней области этого
угла, то все точки луча лежат во внутренней области угла.
Решение. Рассмотрим угол АОВ и луч ОС, проходящий через
точку С внутренней области этого угла (рис. 169). Поскольку точка С
принадлежит полуплоскости с гра-
границей ОА, содержащей точку В,
то все точки луча ОС также
принадлежат этой полуплоскости
(следствие 2 п. 45). По аналогич-
аналогичной причине все точки луча ОС
принадлежат полуплоскости с гра-
границей ОВ, содержащей точку А.
О а Следовательно, все точки луча ОС
принадлежат общей части указан-
указание- I69 ных полуплоскостей, т.е. внутрен-
внутренней области угла АОВ.

/. Аксиома параллельных прямых
111
Задача 2. Доказать, что если прямая а пересекает сторо-
сторону АВ треугольника ABC и не проходит через вершину этого тре-
треугольника, то она пересекает либо сторону ВС, либо сторону АС.
Решение. Данная прямая а разделяет плоскость на две полуплос-
полуплоскости (аксиома 6°), причем точки А и В лежат в разных полуплоско-
полуплоскостях (рис. 170). Поэтому если точка С лежит в одной полуплоскости
А
7
В
А
\
В
а)
Рис. 170
с точкой А, то точки В и С лежат в разных полуплоскостях, а значит,
прямая а пересекает отрезок ВС (рис. 170, а). Если же точка С лежит
в одной полуплоскости с точкой В, то точки А и С лежат в разных по-
полуплоскостях, а значит, прямая а пересекает отрезок АС (рис. 170, б).
Задача 3. Доказать, что если точка С лежит во внутренней
области неразвернутого угла АОВ, то луч ОС пересекает отре-
отрезок АВ.
Решение. Пусть D — произвольная точка луча, являющегося
продолжением луча О А (рис. 171). Прямая ОС пересекает сторону AD
треугольника ABD и не проходит через его вершину. Следовательно,
она пересекает либо сторону АВ, либо сторону BD (см. задачу 2)
в точке, лежащей на луче ОС (поскольку точки В и С лежат в одной
В
D
О
Рис. 171

112 Гл. 3. Параллельные прямые
полуплоскости с границей AD). Но точка D не лежит во внутренней
области угла АОВ — она лежит в полуплоскости с границей ОВ,
не содержащей точку А. Поэтому все точки луча BD не принадлежат
внутренней области угла АОВ (следствие 2 п. 45), а значит, луч ОС
не может пересечь сторону BD — все точки этого луча принадлежат
внутренней области угла АОВ (см. задачу 1). Следовательно, он пере-
пересекает сторону АВ, что и требовалась доказать.
Задача 4. Доказать, что биссектриса угла треугольника пере-
пересекает противоположную сторону этого треугольника.
Решение. Биссектриса AD делит угол А треугольника ABC
на два угла (рис. 172, а). Следовательно, лучи АВ и АС, а значит,
и точки В и С лежат по разные стороны от прямой AD. Иными сло-
А
С А В
а) б)
Рис. 172
вами, прямая AD пересекает отрезок ВС. Поскольку все внутренние
точки отрезка ВС лежат во внутренней области угла ВАС, то и точка
пересечения отрезка ВС с прямой AD лежит во внутренней области
угла ВАС, т. е. на луче AD.
Задача 5. Доказать, что любые две биссектрисы треугольника
пересекаются.
Решение. Рассмотрим треугольник ABC и проведем биссектрису
угла А (рис. 172, б). Эта биссектриса пересекает сторону ВС в некото-
некоторой точке А\ (см. задачу 4). Аналогично биссектриса угла В пересекает
сторону АС в некоторой точке В\. Луч АА\ является биссектрисой
угла А треугольника АВВ\, поэтому он пересекает сторону ВВ\
этого треугольника. Следовательно, общая точка прямых АА\ и ВВ\
лежит на отрезке ВВ\. Аналогично луч ВВ\ является биссектрисой
угла В треугольника АВА\, поэтому он пересекает сторону АА\
этого треугольника. Значит, общая точка прямых АА\ и ВВ\ лежит
на отрезке АА\. Итак, общая точка прямых АА\ и ВВ\ лежит как
на отрезке ВВ\, так и на отрезке АА\. Поэтому отрезки АА\ и ВВ\ —
биссектрисы треугольника ABC — пересекаются, что и требовалось
доказать.
Замечание. Мы начали решение задачи 5 с того, что провели
биссектрису угла А. Тем самым мы исходили из того, что у каждого

/. Аксиома параллельных прямых 113
угла есть биссектриса. А откуда это следует, как это доказать? Вспом-
Вспомните теорему о высоте равнобедренного треугольника и попробуйте
провести доказательство самостоятельно.
Решим теперь две задачи, связанные с понятием «наложение».
Задача 6. Доказать, что наложение, при котором точки А,
В и С, не лежащие на одной прямой, переходят соответственно
в точки А\, В\ и С\, определяется единственным образом.
Решение. Допустим, что есть два наложения, удовлетворяющих
условию задачи. Тогда существует по крайней мере одна точка М,
которая при одном наложении отображается на некоторую точку М\,
а при другом — на какую-то другую точку М2. Поскольку А\М\ =
= AM и А\М2 = AM, то А\М\ = А\М2. Следовательно, точка А\
лежит на серединном перпендикуляре к отрезку М\М2. Аналогично
доказывается, что точки В\ и С\ лежат на указанном серединном
перпендикуляре. Но это противоречит условию задачи — точки А,
В и С, г значит и точки А\, В\ и С\, не лежат на одной прямой
(докажите это). Полученное противоречие доказывает справедливость
утверждения, сформулированного в задаче.
Задача 7. Доказать, что любые две равные фигуры можно
совместить не более, чем тремя осевыми симметриями (см. п. 44).
Решение. Рассмотрим две равные фигуры Ф и Ф\, совмещаю-
совмещающиеся некоторым наложением /. Пусть А, В и С — какие-нибудь
три точки фигуры Ф, не лежащие на одной прямой (случай, когда все
точки фигуры Ф лежат на одной прямой, рассмотрите самостоятельно),
А\, В\ и С\ — точки, на которые они отображаются при наложении
/. Тогда АВ = АхВи АС = АХСХ, ABAC = АВХАХСХ. При осевой
симметрии относительно серединного перпендикуляра к отрезку АА\
(если точки А и А\ совпадают, то этот этап рассуждений пропус-
пропускается) точка А переходит в точку А\, а точки В и С — в какие-
то точки В2 и С2. При этом АВ = А\В2 = А\В\, АС = А\С2 =
= А\С\, ABAC = АВ2А\С2 = АВ\А\С\. Проведем биссектрисы A\D
и А\Е углов В\А\С\ и В2А\С2 (если они совпадают, то следующий
этап рассуждений пропускается). При осевой симметрии относительно
прямой, содержащей биссектрису угла DA\E, луч А\Е накладывается
на луч A\D, поэтому угол В2А\С2 накладывается на равный ему угол
Bi^iCi (докажите это). Возможны два случая: 1° лучи А\В2 и А\С2
накладываются соответственно на лучи А\В\ и А\С\, и тогда точка
В2 совмещается с точкой В\, а точка С2 — с точкой С\ (рис. 173, а);
2° лучи А\В2 и А\С2 накладываются соответственно на лучи А\С\
и А\В\ (рис. 173, б). Во втором случае нужно выполнить далее осевую
симметрию относительно прямой A\D, в результате чего точка В2
перейдет в точку В\, а точка С2 — в точку С\.
Итак, в результате последовательного выполнения не более, чем
трех осевых симметрии, получилось наложение (докажите это), при
котором точки А, В и С отобразились соответственно в точки А\, В\

114
Гл. 3. Параллельные прямые
Рис. 173
и С\. Это наложение совпадает с наложением / (см. задачу 6), поэтому
оно переводит фигуру Ф в фигуру Ф\. Утверждение доказано.
48. Аксиома параллельных прямых. Рассмотрим какую-нибудь
прямую а и точку М, не лежащую на ней (рис. 174). Проведем из точ-
точки М перпендикуляр МН к прямой а, а затем через точку М проведем
прямую Ь, перпендикулярную
к прямой МН. Так как прямые а
и Ъ перпендикулярны к прямой
МН, то они параллельны: а || b
(п. 13). Итак,
через точку М, не лежащую
на прямой а, проходит пря-
мая ^ параллельная прямой а.
М
Н
с- 174
Возникает вопрос: а можно ли провести через точку М еще одну
прямую, параллельную а? По-видимому, нет: кажется, что если «по-
«повернуть» прямую b вокруг точки М даже на очень малый угол, то она
обязательно пересечет прямую а (см. рис. 174). Иными словами, нам
кажется, что через точку М нельзя провести другую прямую (отлич-
(отличную от Ь), параллельную прямой а.
А можно ли это утверждение доказать? Этот вопрос имеет большую
историю. В «Началах» Евклида содержится постулат (пятый посту-
постулат Евклида), который гласит:
если при пересечении двух прямых секущей сумма односторонних
углов меньше 180°, то эти прямые пересекаются по ту сторону
от секущей, по которую расположены указанные углы.
Из этого постулата следует, что любая прямая, проходящая через
точку Мине перпендикулярная к прямой МН, пересекает прямую а
(по ту сторону от прямой МН, по которую она образует с лучом МН
острый угол). Следовательно, через точку, не лежащую на данной
прямой, можно провести только одну прямую, параллельную данной.

/. Аксиома параллельных прямых 115
Однако возникает вопрос: а не является ли пятый постулат теоремой,
которую Евклид не сумел доказать и поэтому включил ее в число
аксиом?
Многие математики, начиная с древних времен, предпринимали
попытки доказать пятый постулат Евклида, т. е. вывести его как тео-
теорему из других аксиом Евклида. Однако эти попытки каждый раз
оказывались неудачными: в предложенных доказательствах либо об-
обнаруживались ошибки, либо пятый постулат неявно заменялся дру-
другой аксиомой, эквивалентной этому постулату. Так, древнегреческий
ученый Посидоний (I в. до н.э.) строил доказательство пятого по-
постулата на том, что множество всех точек плоскости, равноудаленных
от данной прямой, представляет собой две прямые; древнегреческий
ученый Прокл (V в. н.э.) исходил из того, что если две прямые
параллельны, то расстояния от точек одной прямой до другой прямой
не может неограниченно увеличиваться; персидский поэт и ученый
Омар Хайям (XI—XII в. н.э.) в своих рассуждениях опирался на то,
что две сближающиеся прямые не могут с некоторого момента начать
расходиться. Но каждое из этих утверждений формулировалось без
доказательства, т. е. по существу принималось за новую аксиому. Лишь
в XIX веке ответ на вопрос о доказательстве пятого постулата был
получен. Огромную роль в решении этого вопроса сыграл великий
русский математик Николай Иванович Лобачевский A792-1856).
Вся творческая жизнь Н. И. Лобачевского была
связана с Казанским университетом, где он учился,
затем был профессором, а с 1827 года — ректором
университета. Его очень рано заинтересовала гео-
геометрия, и он, как и многие его предшественники,
пытался доказать пятый постулат Евклида. Рассуж-
Рассуждения Н. И. Лобачевского были основаны на мето-
методе доказательства от противного. Он предположил,
что через данную точку, не лежащую на данной
прямой, можно провести несколько прямых, не пе-
пересекающих данную. Исходя из этого, он пытался тт тх „ ^
^ Н И Лобачевский
получить утверждение, которое противоречило бы
другим аксиомам или полученным из них теоремам. Если бы такое
утверждение удалось получить, то это означало бы, что его предполо-
предположение неверно, а верно утверждение о единственности прямой, прохо-
проходящей через данную точку параллельно данной прямой. Тем самым,
как мы увидим в п. 49, пятый постулат Евклида был бы доказан.
Но Н.И. Лобачевский не получил утверждения, противоречаще-
противоречащего другим аксиомам. Более того, он понял, что такое утверждение
и нельзя получить! Из этого он сделал замечательный вывод: если
вместо пятого постулата Евклида принять в качестве аксиомы про-
противоположное утверждение, то можно построить другую геометрию,
отличную от геометрии Евклида. Такая геометрия им была построена.
Ее называют теперь геометрией Лобачевского. В настоящее время она

116 Гл. 3. Параллельные прямые
широко используется не только в математике, но и в физике, в химии,
в биологии и других разделах естествознания.
Другой вывод, вытекающий из исследований Н. И. Лобачевского,
состоит в том, что утверждение о единственности прямой, проходящей
через данную точку параллельно данной прямой (или эквивалентный
этому утверждению пятый постулат Евклида), не может быть доказано
на основе остальных аксиом Евклида, а само является аксиомой евкли-
евклидовой геометрии.
Итак, в качестве еще одного из исходных положений мы принимаем
аксиому параллельных прямых:
16° через точку, не лежащую на данной прямой, проходит толь-
только одна прямая, параллельная данной.
До сих пор мы не пользовались этой аксиомой, поэтому все ра-
ранее установленные нами факты верны как в геометрии Евклида, так
и в геометрии Лобачевского. Рассмотрим теперь некоторые следствия
из аксиомы параллельных прямых:
1° если прямая пересекает одну из двух параллельных прямых,
то она пересекает и другую]
2° если две прямые параллельны третьей прямой, то они парал-
параллельны]
3° если прямая перпендикулярна к одной из параллельных пря-
прямых, то она перпендикулярна и к другой прямой]
4° если две параллельные прямые пересечены секущей, то на-
накрест лежащие углы равны]
5° если две параллельные прямые пересечены секущей, то соот-
соответственные углы равны]
6° если две параллельные прямые пересечены секущей, то сумма
односторонних углов равна 180°.
Пользуясь методом доказательства от противного, докажите эти
утверждения самостоятельно, а также сравните с утверждениями п. 13.
49.0 пятом постулате Евклида. Как мы уже отмечали, если
принять пятый постулат Евклида за аксиому, то из него можно вывести
как теорему аксиому параллельных прямых. В свою очередь, если
принять аксиому параллельных прямых, то пятый постулат Евклида
может быть доказан как теорема. В самом деле, вспомним формули-
формулировку этого постулата: если при пересечении двух прямых секущей
сумма односторонних углов меньше 180°, то эти прямые пересека-
пересекаются по ту сторону от секущей, по которую расположены указанные
углы. Докажем это утверждение методом от противного. Допустим,
что указанные прямые параллельны. Тогда сумма односторонних уг-
углов равна 180° (следствие 6° п. 48), а это противоречит условию.
Если же предположить, что эти прямые пересекаются, но по ту сторону
от секущей, по которую сумма односторонних углов больше 180°,
то получится треугольник, в котором сумма двух углов больше 180°.

/. Аксиома параллельных прямых 117
Этого также не может быть (п. 18). Тем самым пятый постулат Евклида
доказан.
Теперь мы можем ответить еще на один из вопросов, записанных
в нашем блокноте: всегда ли можно построить треугольник по стороне
и двум прилежащим к ней углам, если сумма этих углов меньше 180°?
Ответ на этот вопрос дает пятый постулат Евклида — такая задача
на построение всегда имеет решение (обоснуйте это).
50. Еще раз о существовании квадрата. Опираясь на свойства
параллельных прямых, мы можем ответить еще на один вопрос из на-
нашего блокнота, а именно доказать существование квадрата со сто-
стороной, равной данному отрезку. В самом деле, пусть АВ — данный
отрезок. Проведем через точку В луч, перпендикулярный к АВ, и от-
отложим на нем отрезок ВС = АВ (рис. 175). Далее, через точку С
(в соответствующую сторону) проведем луч,
перпендикулярный к ВС, и отложим на нем
отрезок CD = АВ. Соединим точки А и D
и докажем, что четырехугольник ABCD —
квадрат, т. е. докажем, что углы А и D —
прямые, а сторона AD равна АВ.
Проведем диагональ АС и рассмотрим
треугольники ABC и ADC. Эти треуголь-
треугольники равны по двум сторонам и углу меж-
между ними: АВ = DC по построению, сто-
сторона АС — общая, а углы ВАС и ACD
равны, так как являются накрест лежащи-
лежащими углами, образованными при пересече- рис 175
нии параллельных прямых АВ и CD секу-
секущей АС (прямые АВ и CD перпендикулярны к прямой ВС, поэтому
они параллельны). Из равенства треугольников следует, что AD =
= ВС = АВ и ZD = АВ = 90°. Осталось доказать, что угол А —
прямой. Это следует из того, что прямая AD, перпендикулярная
к прямой CD, перпендикулярна также и к параллельной ей пря-
прямой АВ (следствие 3° п. 48).
Замечание. Существование квадрата со стороной, равной данно-
данному отрезку, мы доказали, опираясь на свойство параллельных прямых,
т. е. равенство накрест лежащих углов, образованных при пересечении
двух параллельных прямых секущей. В свою очередь это свойство
доказывается на основе аксиомы параллельных прямых. Французский
математик Алексис Клод Клеро A713-1765) обнаружил, что мож-
можно поступить и наоборот: используя факт существования квадрата,
доказать утверждение о единственности прямой, проходящей через
данную точку и параллельной данной прямой. Другими словами, акси-
аксиому параллельных прямых можно заменить утверждением: существует
хотя бы один квадрат. Из этого следует, что в геометрии Лобачевского
нет ни одного квадрата! К этому вопросу мы еще вернемся в п. 55.

118
Гл. 3. Параллельные прямые
Задачи
132. Прямые а и Ъ пересекаются. Можно ли провести такую пря-
прямую, которая пересекает прямую а и параллельна прямой Ы Ответ
обоснуйте.
133. Даны две прямые — а и Ь. Докажите, что если любая прямая,
пересекающая прямую а, пересекает и прямую Ь, то прямые а и Ь
параллельны.
134. Концы отрезка АВ лежат на параллельных прямых а и Ь. Пря-
Прямая, проходящая через середину О этого отрезка, пересекает прямые а
и Ь в точках С и В. Докажите, что СО = ОВ.
135. На рисунке 176 СЕ = ЕВ, BE = EF и КЕ \\ АВ. Докажите,
что КЕ || ВС.
136. Через конец В биссектрисы AD треугольника ABC проведена
прямая, параллельная АВ и пересекающая сторону АС в точке М.
Докажите, что AM = MB.
137. На рисунке 177 луч BE — биссектриса угла ABF. По данным
рисунка найдите углы треугольника ABE.
138. Угол ABC равен 70°, а угол ВСВ равен 110°. Могут ли пря-
прямые АВ и СВ быть: а) параллельными; б) пересекающимися?
139! Докажите, что если стороны одного угла соответственно па-
параллельны сторонам другого угла, то такие углы либо равны, либо
в сумме составляют 180°.
140* Докажите, что если стороны одного угла соответственно пер-
перпендикулярны к сторонам другого угла, то такие углы либо равны,
либо в сумме составляют 180°.
141* На гипотенузе АВ прямоугольного треугольника ABC от-
отмечена точка В так, что ZA = ZACB. Через вершину С проведена
прямая MN, параллельная гипотенузе АВ, причем точки А и М лежат
по одну сторону от прямой СВ, а точки N и В — по другую. Докажите,
что: а) лучи С А и СВ — биссектрисы смежных углов МСВ и NCB;
6) отрезок СВ — медиана треугольника ABC.
142. Докажите, что медиана прямоугольного треугольника, прове-
проведенная к гипотенузе, равна половине гипотенузы.
143. Докажите, что если биссектриса внешнего угла треугольника
параллельна стороне треугольника, то треугольник — равнобедренный.
Е
А
D
F
Рис. 176

2. Свойства параллельных прямых
119
144. Через точку пересечения биссектрис треугольника ABC про-
проведена прямая, параллельная прямой ВС и пересекающая стороны АВ
и АС в точках М и N. Докажите, что MN = ВЫ + CN.
145. Через точку пересечения прямых, содержащих биссектрисы
внешних углов при вершинах В w С треугольника ABC, проведена
прямая, параллельная прямой ВС и пересекающая прямые АВ и АС
соответственно в точках М и N. Докажите, что MN = ВЫ -\- CN.
146. На рисунке 178 лучи ВО и СО -
биссектрисы углов В и С треугольни-
треугольника ABC, OE || АВ, OD || АС. Докажите,
что периметр треугольника OED равен
длине отрезка ВС.
147* Отрезки АА\, ВВ\, СС\ попарно
параллельны и равны. Точки А, В и С
лежат на прямой а, а точки А\, В\ и С\ —
в одной полуплоскости с границей а. До-
Докажите, что точки А\, В\ и С\ лежат
на одной прямой.
148* Четырехугольник называется прямоугольником, если все его
углы — прямые. Докажите, что: а) существует прямоугольник ABCD,
стороны АВ и AD которого равны данным отрезкам; б) если ABCD —
прямоугольник, то ААВС = ACDA, АВ = CD, AD = ВС.
149. Внутри угла дана точка А. Постройте прямую, проходящую
через точку А и отсекающую на сторонах угла равные отрезки. Все-
Всегда ли задача имеет решение?
150*. Даны три попарно пересекающиеся прямые, не проходящие
через одну точку. Постройте точку, равноудаленную от этих прямых.
Сколько решений имеет задача?
В
Е
D
С
Рис. 178
А
§ 2. Свойства параллельных прямых
51. Расстояние между параллельными прямыми.
одно из важнейших свойств параллельных прямых.
Теорема. Все точки каждой
из двух параллельных прямых рае- __
ноудалены от другой прямой.
Доказательство. Пусть а
и Ь — параллельные прямые. От-
Отметим на прямой а какую-нибудь
точку А и проведем из этой
точки перпендикуляр АВ к пря- —
мой Ъ (рис. 179). Докажем, что рас-
расстояние от любой точки X прямой а
до прямой Ь равно АВ.
В
Рассмотрим
X
Рис. 179

120
Гл. 3. Параллельные прямые
Проведем перпендикуляр XY из точки X к прямой Ъ. Так
как XY _l_ b, то XY _1_ а. Прямоугольные треугольники ABY и YXA
равны по гипотенузе и острому углу (АУ — общая гипотенуза, углы 1
и 2 равны как накрест лежащие углы, образованные при пересечении
параллельных прямых а и Ь секущей AY). Следовательно, XY =
= АВ. Итак, любая точка X прямой а находится на расстоянии АВ
от прямой Ь. Очевидно, что все точки прямой Ь находятся на таком же
расстоянии от прямой а. Теорема доказана.
Расстояние от произвольной точки одной из параллельных пря-
прямых до другой прямой называется расстоянием между этими пря-
прямыми.
Ясно, что расстояние между параллельными прямыми равно наи-
наименьшему из всевозможных расстояний между двумя точками, одна
из которых лежит на одной, а другая — на другой из параллельных
прямых.
52. Еще один способ построения параллельных прямых. Вся-
Всякий, кто наблюдал за работой столяра, видел инструмент, называемый
рейсмусом (рис. 180, а). Рейсмус используется для разметки на по-
а)
Рис. 180. Рейсмус
верхности деревянного бруска прямой, параллельной краю бруска. При
передвижении рейсмуса вдоль края бруска его металлическая игла
прочерчивает отрезок, параллельный краю бруска (рис. 180, б).
На каком свойстве параллельных прямых основан такой способ
их построения? В первый момент может показаться, что здесь ис-
используется теорема из п.51: все точки одной из двух параллельных
прямых равноудалены от другой прямой. Однако если подумать, то
можно заметить, что это не совсем так. Действительно, с помощью
рейсмуса строится множество точек, равноудаленных от данной прямой
и находящихся по одну сторону от нее. Мы хотим доказать, что это
множество точек есть прямая, параллельная данной. Тем самым, речь

M
Q
2. Свойства параллельных прямых 121
здесь идет об обратном утверждении по отношению к теореме из п. 51.
Сформулируем его в виде теоремы и попробуем доказать.
Теорема. Множество всех точек плоскости, расположенных
по одну сторону от данной прямой и равноудаленных от нее, есть
прямая, параллельная данной.
Доказательство. Пусть а — данная прямая, Ф — множество
всех точек плоскости, расположенных по одну сторону от прямой а
и таких, что расстояние от каждой точки этого множества до прямой а
равно заданной величине d. Через какую-нибудь точку А множества Ф
проведем прямую Ь, параллельную прямой а (рис. 181). Докажем, что
множество Ф совпадает с прямой Ъ. Так как расстояние от точки А
до прямой а равно d, то, со-
согласно теореме п. 51, расстояние
от любой точки прямой Ъ до пря- ъ
мой а также равно d, поэтому
любая точка прямой Ъ принад- ^~ф"
лежит множеству Ф. Обратно,
пусть М — произвольная точка а
множества Ф, а ММ\ — пер-
перпендикуляр, проведенный из точ- 1
ки М к прямой а (см. рис. 181). рис jgj
Прямая ММ\ перпендикулярна
к прямой а, поэтому она пересекает прямую Ъ в некоторой точке Q. Так
как QM\ = d и ММ\ = d, то точки Q и М совпадают, т. е. точка М
лежит на прямой Ъ. Теорема доказана.
Замечание. Множество всех точек, обладающих каким-либо
геометрическим свойством, иногда называют геометрическим местом
точек. Можно сказать, например, что
геометрическое место точек плоскости, равноудаленных от концов
данного отрезка, есть серединный перпендикуляр к этому отрезку;
геометрическое место точек плоскости, расположенных внутри угла
и равноудаленных от его сторон, есть биссектриса этого угла;
геометрическое место точек плоскости, расположенных по одну
сторону от данной прямой и равноудаленных от нее, есть прямая,
параллельная данной.
53. Задачи на построение. Пользуясь свойствами параллельных
прямых, решим несколько задач на построение с помощью циркуля
и линейки.
Задача 1. Даны прямая а и точка М, не лежащая на этой
прямой. Построить прямую, проходящую через точку М и парал-
параллельную прямой а.
Решение. Рассмотрим два способа решения этой задачи.
Первый способ. Этот способ основан на утверждении о параллель-
параллельности двух прямых, перпендикулярных к третьей прямой.

122
Гл. 3. Параллельные прямые
\/
л
\ ^
\
м
ъ
\/
/
р
а
Через точку М проведем пря-
прямую Ь, перпендикулярную к пря-
прямой а, а затем через точку М
проведем прямую р, перпендику-
перпендикулярную к прямой Ъ (как это сде-
сделать с помощью циркуля и ли-
линейки, описано в п. 40; соответ-
соответствующее построение выполнено
на рисунке 182). Прямая р — ис-
искомая: она проходит через точ-
точку М, и так как р _1_ Ъ и а _1_ Ь,
то р || а.
Очевидно, задача имеет един-
единственное решение, так как по ак-
аксиоме параллельных прямых че-
через точку М проходит только
одна прямая, параллельная пря-
прямой а.
Второй способ. Этот способ основан на признаке параллельности
двух прямых, связанном с накрест лежащими углами.
Проведем окружность с центром М так, чтобы она пересекала
прямую а в двух точках: Р и Q (рис. 183). Затем проведем окружность
радиуса РМ с центром Р. Пусть N — одна из точек пересечения
этой окружности с прямой а. Если теперь провести окружность радиу-
радиуса MN с центром Р, то эта окружность пересечет первую окружность
радиуса МР с центром М в двух точках, одна из которых (точка R
на рисунке 183) лежит на искомой прямой. В самом деле, треуголь-
треугольники PNM и MPR равны по трем сторонам (PN = МР, РМ = MR
и NM = PR по построению), поэтому Zl = Z2. Так как углы 1 и 2
Рис. 182
Рис. 183

2. Свойства параллельных прямых
123
являются накрест лежащими углами при пересечении прямых а и MR
секущей РМ, то MR || а, т.е. прямая MR — искомая.
Замечание. Второй способ решения задачи более громоздкий,
но он интересен тем, что построение точки R, лежащей на искомой
прямой, осуществляется с помощью одного циркуля, без линейки.
Задача 2. Даны прямая а и отрезок АВ. Построить прямую р,
параллельную прямой а, так, чтобы расстояние между прямыми а
и р было равно АВ.
Решение. Отметим на прямой а какую-нибудь точку С и прове-
проведем через нее прямую Ь, перпендикулярную к прямой а (рис. 184, а).
Затем на одном из лучей прямой Ь, исходящих из точки С, отложим
отрезок CD, равный отрезку АВ. Через точку D проведем прямую р,
перпендикулярную к прямой Ь. Прямая р — искомая. В самом деле,
прямые р и а параллельны, так как они перпендикулярны к прямой Ъ.
По построению CD = АВ, поэтому расстояние от точки D до прямой а
равно АВ. Следовательно, и расстояние между прямыми аир рав-
равно АВ.
Как видно из построения, задача имеет два решения (прямые р и р\
на рисунке 184, б).
Задача 3. Построить прямоугольный треугольник по катету
и противолежащему углу.
Решение. Эту задачу нужно понимать так. Даны отрезок PQ
и острый угол hk (рис. 185, а). Требуется построить прямоугольный
треугольник ABC с прямым углом С так, чтобы один из катетов,
например ВС, был равен данному отрезку PQ, а противолежащий
угол А — данному углу hk.
Построим угол XAY, равный данному углу hk. Для построения
точки В на луче АХ заметим, что расстояние от нее до прямой AY
должно равняться PQ. Поэтому точка В лежит на прямой р, па-
параллельной прямой AY, причем расстояние между прямыми р и AY
равно PQ. Следовательно, искомая точка В есть точка пересечения
D
L
Г
С
b
р
а
D
С
Dx
b
Р
а
Pi
а)
а)
Рис. 184

124
Гл. 3. Параллельные прямые
а)
А
л
1
В
г
С
X
V
Y
Рис. 185
прямой р и луча АХ. Построение прямой р выполнено на рисун-
рисунке 185, б (см. задачу 2).
Проведем теперь через точку В прямую, перпендикулярную к пря-
прямой AY. Эта прямая пересекается с прямой AY в точке С. Треуголь-
Треугольник ABC — искомый.
Из четвертого признака равенства прямоугольных треугольни-
треугольников (п. 30) следует, что задача имеет единственное решение.
Задача 4. Построить треугольник по стороне, прилежащему
к ней углу и высоте, проведенной к этой стороне.
Решение. Даны отрезки P\Q\ и P2Q2 и угол hk (рис.186, а).
Требуется построить треугольник ABC, у которого АВ = P\Q\, ZA =
= Zhk и высота СН равна P^Qi-
Построим угол XAY, равный данному углу hk, и отложим на лу-
луче АХ отрезок АВ, равный данному отрезку P\Q\ (рис. 186, б). Оста-
Остается найти положение точки С на луче AY. Заметим, что расстояние
от точки С до прямой АВ равно P^Qi- Поэтому точка С лежит
на прямой р, параллельной прямой АВ, причем расстояние между пря-
прямыми р и АВ равно P^Qi- Следовательно, искомая точка С есть точка
пересечения прямой р и луча AY. Построение прямой р выполнено
на рисунке 186, б.
Очевидно, треугольник ABC удовлетворяет всем условиям задачи:
АВ = PiQi, ZA = Zhk, СН = P2Q2-
Л-
P
H
В X
a)
Рис. 186

2. Свойства параллельных прямых
125
с
Сам ход построения показывает, что при любых данных отрез-
отрезках P\Q\, P2Q2 и угле hk можно построить искомый треугольник. Ясно
также, что задача имеет единственное решение (докажите это).
Задача 5. Построить треугольник по стороне, высоте, прове-
проведенной к ней, и медиане, проведенной к одной из двух других сторон.
Решение. Построим отрезок АВ, равный данной стороне
(рис. 187), и проведем прямую а, параллельную прямой АВ и нахо-
находящуюся от нее на расстоянии, равном данной высоте (см. задачу 2).
Затем проведем прямую Ь, параллельную АВ и равноудаленную
от прямых АВ и а. Далее, по-
построим окружность с центром А,
радиус которой равен данной /
медиане, и отметим точку М
пересечения этой окружности М Hi
с прямой Ъ. Наконец, проведем
прямую ВЫ. Она пересекается
с прямой а в точке С. Треуголь-
Треугольник ABC — искомый. А
В самом деле, проведем
из точек В и С перпендикуля-
перпендикуляры ВН\ и СН2 к прямой Ъ и рассмотрим прямоугольные треугольни-
треугольники ВМН\ и СМЩ. Углы этих треугольников с вершиной М равны
как вертикальные, катеты ВН\ и СЩ равны по построению. Следо-
Следовательно, рассматриваемые треугольники равны по катету и противо-
противолежащему углу, а значит, ВЫ = МС, т. е. отрезок AM — медиана
треугольника ABC.
Из построения ясно, что задача может иметь два решения (тре-
(треугольники ABC и АВС\ на рисунке 188, а), одно решение (рис. 188, б)
и может не иметь решений (рис. 188, в).
Задача 6. Построить треугольник по периметру, одному из уг-
углов и высоте, проведенной из вершины другого угла.
Решение. Пусть даны ZA, высота ВН искомого треугольни-
треугольника ABC и отрезок PQ, длина которого равна периметру иско-
искомого треугольника. Рассмотрим случай, когда данный угол А —
острый (остальные случаи рассмотрите самостоятельно). Построим
В
Рис. 187
С
С
А
а)
b
X
в
\
)
Рис.
\м
\^
А
б)
188
b
В
1
А
в)
b
В

126
Гл. 3. Параллельные прямые
А
Н /С
D
Е
Рис. 189
прямоугольный треугольник АВН
по острому углу А и катету ВН
(рис. 189). На луче АН отложим
отрезок АЕ, равный данному от-
отрезку PQ, а затем на луче ЕА
отложим отрезок ED = АВ. Про-
Проведем отрезок BD и построим се-
серединный перпендикуляр а к этому
отрезку. Точку пересечения прямой а и прямой AD обозначим бук-
буквой С. Треугольник ABC — искомый.
Действительно, угол А равен данному углу по построению, ВН —
заданная высота, ВС = CD (по свойству серединного перпендикуляра),
DE = АВ по построению. Поэтому АС + ВС + АВ = АС + CD +
+ DE = PQ, т. е. периметр треугольника ABC равен длине данного
отрезка PQ.
Задачи
151* Две окружности с центрами О\ и О^ пересекаются в точках А
и В. Через точку А проведена прямая, пересекающая эти окружности
в точках М и Р. Докажите, что отрезок МР будет наибольшим в том
случае, когда МР || О\О^.
152. Прямые а и Ъ параллельны. Докажите, что середины всех от-
отрезков XY, где X G a, Y G Ъ, лежат на прямой, параллельной прямым а
и Ъ и равноудаленной от этих прямых.
153. Что представляет собой множество всех точек плоскости,
равноудаленных от двух данных параллельных прямых?
154. Что представляет собой множество всех точек плоскости,
находящихся на данном расстоянии от данной прямой?
155. Даны пересекающиеся прямые а и Ъ и отрезок PQ. На пря-
прямой а постройте точку, удаленную от прямой Ъ на расстояние PQ.
156* Дан треугольник ABC. Постройте отрезок DE, параллельный
прямой АС, так, чтобы точки D и Е лежали соответственно на сторо-
сторонах АВ и ВС и чтобы выполнялось равенство: DE = AD + СЕ.
157. На данной окружности постройте точку, равноудаленную
от двух данных параллельных прямых. Сколько решений может иметь
задача?
158* Постройте треугольник: а) по стороне, прилежащему к ней
углу и противолежащему ей углу; б) по углу, биссектрисе, проведенной
из вершины этого угла, и высоте, проведенной из вершины другого
угла; в) по двум сторонам и высоте, проведенной к одной из этих
сторон; г) по углу, медиане, проведенной из вершины этого угла,
и высоте, проведенной из вершины другого угла; д) по стороне, высо-
высоте, проведенной к другой стороне, и медиане, проведенной к третьей
стороне.

Глава 4
ДАЛЬНЕЙШИЕ СВЕДЕНИЯ О ТРЕУГОЛЬНИКАХ
§ 1. Сумма углов треугольника. Средняя линия
треугольника
54. Задача о разрезании треугольника. Можно ли разрезать про-
произвольный треугольник на четыре равных треугольника? Попробуем.
Рассмотрим произвольный треугольник ABC, отметим середи-
середины А\, В\, С\ сторон ВС, С А, АВ и соединим их отрезками (рис. 190).
В результате треугольник ABC окажет-
окажется разделенным на четыре треугольни-
треугольника. Глядя на рисунок, можно предполо-
предположить, что эти треугольники равны друг
другу. Но как это доказать? Ведь мы по-
почти ничего не можем сказать об их уг-
углах! Давайте подумаем, что можно вы-
вывести из того, что точки А\, В\ и С\ —
середины отрезков ВС, С А и АВ. А ' ^ "' С
Начнем с более простой задачи. Про-
Проведем прямую а, пересекающую какой- Рис. 190
нибудь отрезок АВ в его середине М
(рис. 191), и докажем, что концы отрезка равноудалены от этой прямой.
Если прямая а перпендикулярна к отрезку АВ, то точки А и В,
Ах
А
1 м
а
i
i
В
А
В
В
а)
б)
Рис. 191

128
Гл. 4. Дальнейшие сведения о треугольниках
очевидно, равноудалены от нее (рис. 191, а). Если же она не пер-
перпендикулярна к АВ (рис. 191, б), то проведем перпендикуляры АА\
и ВВ\ к прямой а (рис. 191, б). Тогда образуются два прямоугольных
треугольника — АА\М и ВВ\М, равных друг другу по гипотенузе
и острому углу (углы 1 и 2 равны как вертикальные). Следовательно,
АА\ = ВВ\. Мы видим, что и в этом случае концы отрезка АВ
равноудалены от прямой а.
Вернемся теперь к нашей задаче. Поскольку прямая А\С\ проходит
через середину отрезка АВ, то точки А и В равноудалены от этой
прямой. По аналогичной причине равноудаленными от прямой А\С\
оказываются точки В и С. Поэтому точки А и С также равноудалены
от прямой А\С\, причем лежат по одну сторону от нее (рис. 192, а).
С А
Сх
Вх
С
А
Вх
в)
С
А
Вх
г)
С
Рис. 192
Отсюда следует, что точки А и С лежат на прямой, параллель-
параллельной А\С\ (см. п. 52). Иными словами, прямые АС и А\С\ параллельны.
Аналогично получаем: АВ || А\В\, ВС || В\С\.
Теперь мы обнаруживаем, что некоторые углы равны друг другу как
соответственные углы, образованные при пересечении параллельных
прямых секущими. Эти углы отмечены на рисунке 192, б. Из равенства
указанных углов следует, что три «крайних» треугольника — АВ\С\,
ВС\А\ и СА\В\ — равны друг другу по стороне и двум прилежа-
прилежащим к ней углам (рис. 192, в). Но тогда и «центральный» треуголь-
треугольник А\В\С\ равен каждому из них по трем сторонам (рис. 192, г).
Таким образом, если разрезать треугольник ABC по отрезкам А\В\,

/. Сумма углов треугольника. Средняя линия треугольника
129
В\С\ и С\А\, то получатся четыре рав-
равных треугольника: АВХСХ, ВСХАХ, СА\В\
и АХВХСХ (рис. 193).
55. Сумма углов треугольника. Раз-
Разрезав произвольный треугольник на четыре
равных треугольника, мы получили воз-
возможность доказать сразу несколько важ-
важных теорем. Первую из них обсудим в этом
пункте, другие — в следующем.
С
А Вх С
Рис. 193
Обратимся к рисунку 193. Мы видим, что ZAXBXC + ААХВХСХ +
+ ZABXCX = 180°, причем ZAXBXC = ZA, ZAXBXCX = ZB, ZABXCX =
= Z.C. Следовательно, ZА + ZB + ZC = 180°. Итак, мы доказали
теорему о сумме углов треугольника:
сумма углов треугольника равна 180°.
Эта теорема является одной из самых важных теорем геометрии.
Сформулируем несколько следствий из нее.
Следствие 1. Внешний угол треугольника равен сумме двух
углов треугольника, не смежных с этим внешним углом (рис. 194).
Вспомним свойство внешнего угла треугольника, которое мы об-
обнаружили ранее, в п. 18: внешний угол треугольника больше каждого
угла треугольника, не смежного с ним. Мы видим, что следствие 1
позволяет установить, на сколько внешний угол треугольника больше
не смежного с ним угла треугольника: на величину другого угла
треугольника, не смежного с данным внешним углом.
Следствие 2. Сумма двух острых углов прямоугольного тре-
треугольника равна 90° (рис. 195).
Рис. 194. Zl + Z2 + Z3 =
= 180°, Z4 + Z3 = 180°,
поэтому Z4 = Zl + Z2
Рис. 195. Zl + Z2
= 90°
Следствие 3. Катет прямоугольного треугольника, лежащий
против угла в 30°, равен половине гипотенузы] обратно: если катет
прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
Пользуясь рисунком 196, на котором к данному прямоугольному
треугольнику ABC приложен равный ему треугольник ABD, выведите
это следствие самостоятельно.
5 С. Б. Кадомцев

130
Гл. 4. Дальнейшие сведения о треугольниках
С
А
а)
С
Рис. 196
А
D
Задача 1. Доказать, что угол треугольника является острым,
прямым или тупым, если медиана, проведенная из вершины этого
угла, соответственно больше, равна или меньше половины проти-
противоположной стороны.
Решение. Рассмотрим треугольник ABC с медианой AM и дока-
докажем сначала, что если AM > -ВС, то ZA < 90° (рис. 197, а).
Поскольку ВМ = МС = \вС, то AM > ВМ и AM > МС.
Применив теорему о соотношениях между сторонами и углами тре-
треугольника к треугольникам АВМ и АСМ, получим: ZBAM <
< ZB и АСАМ < Z.C. Поэтому АА = ZBAM + АСАМ < ZB + ZC.
Но ZB + ZC = 180° - ZA. Следовательно, ZA < 180° - ZA, откуда
находим: ZA < 90°.
Аналогично, если AM = -ВС (рис. 197, б) или AM < -ВС
(рис. 197, в), то ZA = 180° - ZA или ZA > 180° - ZA, откуда находим:
ZA = 90° или ZA > 90°. Утверждение доказано.
А
В
м
а)
С
В
м
б)
с
в
м
в)
С
Рис. 197. a) AM > -ВС; б) AM = -ВС; в) AM < -ВС

/. Сумма углов треугольника. Средняя линия треугольника 131
Замечание 1. Теорема о сумме углов треугольника тесно связана
с аксиомой параллельных прямых. Вы можете сказать, что в дока-
доказательстве теоремы сама аксиома параллельных прямых не исполь-
использовалась. Это верно, но в доказательстве использовалось равенство
соответственных углов, образованных при пересечении двух парал-
параллельных прямых секущей (обратите еще раз внимание на это место
доказательства). А равенство соответственных углов следует из аксио-
аксиомы параллельных прямых (см. п. 48). Таким образом, теорема о сумме
углов треугольника фактически основана на аксиоме параллельных
прямых. До введения аксиомы параллельных прямых мы не смогли бы
доказать эту теорему.
Давайте теперь вспомним задачи 23 и 24, связанные с суммой
углов треугольника, которые были предложены в конце §3 первой
главы. В первой задаче нужно было доказать, что сумма углов каждого
из треугольников, которые получаются, если разрезать квадрат по диа-
диагонали, равна 180°. Во второй задаче рассматривались треугольники,
которые получаются при разрезании по диагонали прямоугольника, со-
составленного из двух равных квадратов (рис.63). Нужно было доказать,
что сумма углов каждого из этих треугольников также равна 180°.
Вы можете спросить: как же так? В тот момент мы еще ничего не знали
об аксиоме параллельных прямых. Как же мы решали (и решили!)
те две задачи, если без аксиомы параллельных прямых этого сделать
нельзя? Разгадка здесь вот в чем: в условии тех двух задач предпо-
предполагалось, что есть квадрат (квадрат существует). Считая, что нам дан
квадрат, мы разрезали его (или прямоугольник, составленный из двух
равных квадратов) по диагонали на два треугольника и доказали, что
сумма углов в каждом из получившихся треугольников равна 180°.
Таким образом, мы опирались на то, что квадрат есть, квадрат суще-
существует. А утверждение о существовании квадрата равносильно аксиоме
параллельных прямых — об этом говорилось в п. 50.
Замечание 2. Возникает такой вопрос: что можно сказать о сум-
сумме углов треугольника, если вместо нашей аксиомы параллельных пря-
прямых принять противоположное утверждение: через точку, не лежащую
на данной прямой, проходит более одной прямой, не пересекающей
данную прямую. Именно это утверждение, как мы помним, было при-
принято Н.И. Лобачевским за аксиому в его исследованиях. Оказывается,
что тогда формула суммы углов треугольника принимает иной вид,
а именно
АА + АВ + АС = 180° - kS, A)
где S — площадь треугольника ABC, k — некоторый положительный
коэффициент (один и тот же для всех треугольников). Эта форму-
формула показывает, что в геометрии Лобачевского сумма углов любого
треугольника меньше 180°. Более того, она зависит от площади S
треугольника. Чем больше S, тем меньше сумма углов треугольника.

132 Гл. 4. Дальнейшие сведения о треугольниках
Из формулы A) следует и другой удивительный факт: в геометрии
Лобачевского площадь любого треугольника меньше величины ——!
/с
А нельзя ли, измерив сумму углов произвольного треугольника,
экспериментально установить, какой из двух геометрий описывается
окружающий нас Мир? Это непростой вопрос. Ведь из формулы A)
следует, что чем меньше площадь треугольника, тем ближе к 180° сум-
сумма его углов. Поэтому выбранный треугольник должен быть достаточ-
достаточно большим. Подобная ситуация хорошо известна нам из опыта. Так,
путешествуя по озеру, мы можем считать его поверхность плоской и,
выбирая маршрут, исходить из евклидовой геометрии. Другое дело —
океан: здесь мореплаватель, пользующийся евклидовой геометрией,
и считающий поверхность океана плоской, а не сферической, не сможет
привести свой корабль в нужное место.
Сам Лобачевский, опираясь на результаты астрономии XIX века,
обнаружил, что в пределах ошибок измерительных приборов сумма
углов треугольника равна 180°. Однако по современным оценкам есть
основания считать, что в масштабах Вселенной сумма углов треуголь-
треугольника может быть существенно меньше 180°, следовательно, наше про-
пространство может описываться геометрией Лобачевского.
Итак, в геометрии Лобачевского сумма углов треугольника мень-
меньше 180°. Следовательно, рисунок 193 в ней невозможен.
Замечание 3. Теперь совершенно ясно, почему в геометрии
Лобачевского нет квадрата. Действительно, если разрезать квадрат
по диагонали, то получатся два треугольни-
треугольника, в каждом из которых сумма углов равна
90° +45° +45° = 180° (рис. 198). Но в гео-
геометрии Лобачевского таких треугольников
нет (в ней сумма углов любого треугольника
меньше 180°), поэтому нет и квадрата.
Замечание 4. Доказав теорему о сум-
сумме углов треугольника, мы ответили на один
из вопросов, записанных в нашем блокно-
блокноте: «Существует ли какое-нибудь соотно-
соотношение между тремя углами треугольника?»
рис ^98 Вслед за ним записан другой вопрос: «Имеет
ли место признак равенства треугольников
по трем углам?» Теперь мы знаем, что из аксиомы параллельных
прямых следует существование квадрата со стороной, равной данному
отрезку, а значит, и существование неравных друг другу треугольников
с соответственно равными углами (п. 28). Таким образом, в евклидовой
геометрии признак равенства треугольников по трем углам не име-
имеет места.
А что можно сказать об этом признаке в геометрии Лобачевского?
Давайте подумаем. Рассмотрим два треугольника ABC и А\В\С\,
углы которых соответственно равны: ZA = ZA\, ZB = ZB\, ZC =

/. Сумма углов треугольника. Средняя линия треугольника
133
= /_С\ (рис. 199, а). Из формулы A) следует, что площади этих тре-
треугольников равны: S = S\.
Докажем, что имеет место еще одно равенство: АВ = А\В\. В са-
самом деле, допустим, что АВ ф А\В\. Пусть, например, АВ > А\В\.
Наложим треугольник ABC на треугольник А\В\С\ так, чтобы вер-
вершина А совместилась с вершиной А\, а стороны АВ и АС наложились
на лучи А\В\ и А\С\ (это можно сделать, поскольку ZА = ZA\).
При этом точки В и С наложатся на какие-то точки В2 и С2 этих
лучей (рис. 199, б). Так как АХВ2 = АВ и ZB2 = ZB, то АХВ2 > АхВи
а соответственные углы В\ и В2, образованные при пересечении пря-
прямых В\С\ и В2С2 секущей В\В2, равны, и поэтому прямые В\С\
и В2С2 параллельны. Следовательно, площадь треугольника А\В2С2
больше площади треугольника А\В\С\ (треугольник А\В2С2 состав-
составлен из треугольника А\В\С\ и четырехугольника В\В2С2С\). Но тре-
треугольник А\В2С2 равен треугольнику ABC, поэтому его площадь
равна S. Мы получили неравенство S > S\, что противоречит равен-
равенству S = S\. Полученное противоречие означает, что наше предполо-
предположение ошибочно и стороны АВ и А\В\ не могут быть неравными друг
другу.
Итак, АВ = А\В\. Следовательно, треугольники ABC и А\В\С\
равны по второму признаку равенства треугольников. Тем самым
мы доказали, что в геометрии Лобачевского имеет место признак
равенства треугольников по трем углам\
А
СХ
а)
Рис. 199

134 Гл. 4. Дальнейшие сведения о треугольниках
56. Средняя линия треугольника. Отрезок, соединяющий сере-
середины двух сторон треугольника, называется средней линией этого
треугольника.
Разрезав произвольный треугольник на четыре равных треуголь-
треугольника (п. 54), мы получили возможность доказать еще одну важную
теорему — теорему о средней линии треугольника. Чтобы ее сфор-
сформулировать, обратимся к рисунку 193. Отрезки А\В\, В\С\ и С\А\
на этом рисунке — средние линии треугольника ABC. Мы установили,
что А\В\ || АВ, ВХСХ || ВС, С\АХ || С А и, кроме того, АХВХ = \аВ,
В\С\ = -БС, С\А\ = -zCA. Тем самым мы доказали теорему о сред-
средней линии треугольника:
средняя линия треугольника параллельна одной из его сторон
и равна половине этой стороны.
Замечание 1. В п. 55 (замечание 2) мы отмечали, что рису-
рисунок 193 в геометрии Лобачевского невозможен. Следовательно, в этой
геометрии неверна и теорема о средней линии треугольника (объясни-
(объясните, почему).
Замечание 2. Ясно, что справедлива и такая теорема:
прямая, проходящая через середину стороны треугольника и па-
параллельная другой его стороне, делит третью сторону пополам.
В самом деле, по аксиоме параллельных прямых через середину сто-
стороны треугольника можно провести только одну прямую, параллель-
параллельную другой его стороне. Но такой прямой является прямая, содержащая
среднюю линию нашего треугольника. Иными словами, указанная пря-
прямая проходит через середину третьей стороны, т.е. делит ее пополам.
Эту теорему можно сформулировать иначе:
отрезок, соединяющий середину стороны треугольника с точкой
другой стороны и параллельный третьей стороне, является средней
линией этого треугольника.
В такой формулировке теорема выражает признак средней линии
треугольника.
57. Теорема Фалеса. Обратимся к рисунку 200, а. На этом ри-
рисунке сторона АВ треугольника ABC разделена точками D, Е и F
на четыре равные части. Проведем через эти точки прямые, парал-
параллельные стороне АС и пересекающие сторону ВС в точках D\, E\
и F\ (рис.200, б). Теперь несколько раз воспользуемся признаком сред-
средней линии (рис.200, в, г, д). Мы видим (рис.200, е), что сторона ВС
делится точками D\, Е\ и F\ на четыре равные части.
Случайно ли это? Видимо, нет. По всей видимости, имеет место
следующая теорема.
Теорема. Если на одной из двух прямых отложить последо-
последовательно несколько равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую, то они отсе-
отсекут на второй прямой равные между собой отрезки.

/. Сумма углов треугольника. Средняя линия треугольника 135
В В В
\ XV1 / X
„ ' \Е'
А
С А
С А
С
а)
б)
в)
В
В
В
А
С А
г)
Е/ \
D/ ^
д)
Рис. 200
\
и
Цг
У
Л
/
е)
\ F>\
ч1,
и
Доказательство. Рассмотрим прямую а, на которой отложены
равные друг другу отрезки А\А2, А2Л3, A3A4, ... Через их концы про-
проведены параллельные прямые l\, \<i, h, h, ¦••, пересекающие прямую b
в точках В[, В2, Б3, В4, ... (рис.201, а). Требуется доказать, что
отрезки В\В2, -В2-В3, B3-B4, ¦•• равны друг другу.
Л/
А2/
V
м/
м/
\в2
\В3
\в4
\в5
B
h
m/\ b2
A3/ \ Въ
a)
, М\ Гв
1 М\ /В2
h
a/
Z
Z
/ \
6)
At/
и
к
Мт
/
i
sP \в2
\
\
e)
Рис. 201

136
Гл. 4. Дальнейшие сведения о треугольниках
Докажем сначала, что В\В2 = В2В^. Если точки А\ и В\ или
точки Аз и В^ совпадают (рис.201, б, в), то В\В2 = В2Вз по признаку
средней линии треугольника. Если же указанные точки не совпадают,
то поступим так. Проведем отрезок А\В% и обозначим буквой С точку
его пересечения с прямой 12 (такая точка С существует, поскольку
точки А\ и Дз лежат по разные стороны от прямой 12). Прямая А2С
проходит через середину А2 стороны А\А% треугольника А\А%Въ и па-
параллельна стороне А3В3 этого треугольника, поэтому точка С является
серединой отрезка А\Щ (рис.201, г). Прямая СВ2 проходит через
середину С стороны А\В% треугольника А\В\В% и параллельна сто-
стороне А\В\ этого треугольника, поэтому точка В2 является серединой
отрезка В\В%. Итак, В\В2 = В2Дз-
Точно так же доказывается, что В2ВЪ = В^В^ и т.д. Следовательно,
все отрезки B\B2, B2B^, В^В^, ... равны друг другу. Теорема доказана.
По мнению многих историков, эту теорему впервые открыл древне-
древнегреческий ученый Фалес Милетский (ок.625-547 гг. до н.э.). И хотя
единого мнения на этот счет нет, ее называют теоремой Фалеса.
Решим теперь такую задачу.
Задача 2. С помощью циркуля и линейки разделить данный
отрезок на п равных частей.
Решение. Пусть АВ — данный отрезок, п — данное нату-
натуральное число, большее единицы. Проведем луч АХ, не лежащий
на прямой АВ, и на нем от точки А отложим последовательно п
равных отрезков АА\, А\А2, ..., Ап_\Ап (рис.202), т.е. столько рав-
равных отрезков, на сколько равных частей нужно разделить данный
отрезок АВ (на рисунке 202 задача решается для п = 5). Проведем
прямую АпВ (точка Ап — конец последнего отрезка) и построим
прямые, проходящие через точ-
точки А\, А2, ..., Ап-\ и параллель-
параллельные прямой АпВ. По теореме
Фалеса эти прямые пересекают
отрезок АВ в точках В\, В2, ...,
Бп_ь которые делят отрезок АВ
на п равных частей.
Таким образом, мы ответили
еще на один из вопросов, запи-
записанных в нашем блокноте: мож-
можно ли с помощью циркуля и ли-
линейки разделить данный отрезок
на п равных частей? Мы видим,
что эта задача имеет решение
для любого натурального чис-
Рис. 202 ла п.
58. Неожиданный факт. Рассмотрим треугольник ABC со сто-
сторонами АВ = 12 см, ВС = 18 см, С А = 27 см (рис.203). Сразу же
В

/. Сумма углов треугольника. Средняя линия треугольника
137
возникает вопрос: а существует
ли такой треугольник? Большая
из сторон треугольника ABC
равна 27 см, а сумма двух дру-
других сторон равна 12 см + 18 см =
= 30 см > 27 см. Следователь-
Следовательно, такой треугольник существу-
существует (см. замечание 2 п. 39).
Разделим сторону ВС этого
треугольника точками А\ и А2
на три равные части и проведем через точки А\ и А2 прямые, па-
параллельные стороне АВ, до пересечения со стороной АС в точках В\
и В2 (см. рис.203).
Рассмотрим треугольники ABC и А\В\С. Угол С у них общий,
АА = /-В\, поскольку эти углы являются соответственными углами,
образованными при пересечении параллельных прямых АВ и А\В\
секущей АС. По аналогичной причине АВ = АА\. Таким образом, углы
треугольника ABC соответственно равны углам треугольника А\В\С.
Сравним теперь стороны этих треугольников. По построению
2
А\С = -ВС = 12 см. По теореме Фалеса АВ\ = В\В2 = В2С, поэтому
о
ВХС = \АС = 18 см.
Что же получилось? Углы треугольника ABC соответственно равны
углам треугольника А\В\С, ВС = В\С = 18 см, АВ = А\С = 12 см.
Таким образом, пять (из шести!) элементов треугольника ABC равны
соответствующим элементам треугольника А\В\С, но сами треуголь-
треугольники, очевидно, не равны друг другу. Не правда ли, удивительный
факт?
Задачи
159. На рисунке 204 AD || BE, AC = AD и ВС = BE. Докажите,
что угол DCE — прямой.
160. На рисунке 205 АВ = АС, АР = PQ = QR = RB = ВС.
Найдите угол А.
161. Через каждую верши-
вершину треугольника проведена пря- А,
мая, перпендикулярная к бис-
биссектрисе треугольника, исходя-
исходящей из этой вершины. Отрезки
этих прямых вместе со сторона-
сторонами данного треугольника образу-
образуют три треугольника. Докажите,
что углы этих треугольников со-
соответственно равны. Рис. 204
С
В

138
Гл. 4. Дальнейшие сведения о треугольниках
Р
Рис. 205
162. В каждом из следующих случаев опреде-
определите вид треугольника: а) сумма любых двух углов
больше 90°; б) каждый угол меньше суммы двух
других.
163. Докажите, что если один из внешних уг-
углов треугольника в два раза больше угла треуголь-
треугольника, не смежного с ним, то этот треугольник —
равнобедренный. Верно ли обратное утверждение?
164. Окружность с центром О касается пря-
прямых АВ и АС в точках В и С. Через произ-
произвольную точку дуги ВС проведена касательная
к окружности, пересекающая отрезки АВ и АС
в точках М и Р. Найдите угол МОР, если угол А
равен а.
165. В прямоугольном треугольнике проведена высота из вершины
прямого угла. Докажите, что данный треугольник и два образовавших-
образовавшихся треугольника имеют соответственно равные углы.
166. Из середины D стороны ВС равностороннего треугольни-
треугольника ABC проведен перпендикуляр DM к прямой АС. Найдите AM,
если АВ = 12 см.
167. Прямоугольный треугольник с острым углом в 30° разрежьте:
а)* на три равных прямоугольных треугольника; б) на четыре равных
прямоугольных треугольника.
168. Высоты, проведенные к боковым сторонам АВ и АС остро-
остроугольного равнобедренного треугольника ABC, пересекаются в точ-
точке М. Найдите углы треугольника, если ZBMC = 140°.
169. В треугольнике ABC с прямым углом А проведены высота АН
и медиана AM. Угол В равен а, причем а < 45°. Найдите АН AM.
170. В треугольнике с неравными сторонами АВ и АС проведены
высота АН и биссектриса AD. Докажите, что угол HAD равен полу-
полуразности углов В и С.
171. Докажите, что в прямо-
прямоугольном треугольнике с неравными
катетами биссектриса прямого угла
делит угол между высотой и меди-
медианой, проведенными из той же вер-
вершины, пополам.
172. На гипотенузе АВ прямо-
прямоугольного треугольника ABC от-
отмечены точки D и Е так, что
АЕ = АС и BD = ВС. Найди-
Найдите ZDCE.
173. Найдите сумму углов, обо-
обозначенных на рисунке 206 цифрами.
174! Медиана и высота тре-
треугольника, проведенные из одной
Рис. 206

2. Четыре замечательные точки треугольника 139
вершины, делят угол треугольника на три равных угла. Докажите, что
этот треугольник — прямоугольный.
175* Внутри равнобедренного треугольника ABC с основанием ВС
взята такая точка М, что AM ВС = 30°, ZMCB = 10°. Найдите
угол АМС, если ABAC = 80°.
176* В треугольнике ABC ZB = 70°, ZC = 50°. На сторонах АВ
и АС взяты точки М и N так, что АМС В = 40° и /ЛГБС = 50°.
Найдите ZNMC.
177*. На боковых сторонах В А и ?>С равнобедренного треугольни-
треугольника ABC с углом В, равным 20°, взяты соответственно точки Q и Р
так, что ZACQ = 60° и ZCAP = 50°. Найдите ZAPQ.
178. С помощью циркуля и линейки постройте угол, равный: а) 30°;
б) 60°; в) 15°; г) 120°; д) 150°; е) 135°; ж) 165°; з) 105°.
179* Постройте треугольник по периметру и двум углам.
180* Постройте треугольник по стороне, разности углов при этой
стороне и сумме двух других сторон.
181. Сторона АВ треугольника ABC разделена на четыре равные
части, через точки деления проведены прямые, параллельные сто-
стороне ВС. Стороны АВ и АС треугольника отсекают на этих парал-
параллельных прямых три отрезка. Длина наименьшего из получившихся
отрезков равна 3,4. Найдите длины двух других отрезков.
182. Точки А и В расположены в одной полуплоскости с грани-
границей а. Из точек А, В и середины О отрезка АВ проведены перпендику-
перпендикуляры АА\, ВВ\ и ОО\ к прямой а. Докажите, что 2ОО\ = АА\ + ВВ\.
183. Точки М и N симметричны точкам В и С относительно
середин сторон АС и АВ треугольника ABC. Докажите, что точки М,
N и А лежат на одной прямой.
184. Постройте треугольник, если даны середины его сторон.
§ 2. Четыре замечательные точки треугольника
59. Теорема о пересечении серединных перпендикуляров к сто-
сторонам треугольника. В п. 34 мы доказали, что биссектрисы треуголь-
треугольника пересекаются в одной точке. Докажем теперь, что аналогичным
свойством обладают серединные перпендикуляры к сторонам треуголь-
треугольника.
Теорема. Серединные перпендикуляры к сторонам треугольни-
треугольника пересекаются в одной точке.
Доказательство. Обозначим буквой О точку пересечения се-
серединных перпендикуляров т и п к сторонам АВ и ВС треугольни-
треугольника ABC (рис.207). Согласно теореме о серединном перпендикуляре
к отрезку (п. 31) имеют место равенства: О А = ОВ и ОВ = ОС. Отсю-
Отсюда следует, что О А = ОС, т. е. точка О равноудалена от концов отрез-
отрезка АС. Поэтому точка О лежит на серединном перпендикуляре р к от-
отрезку АС (теорема 2 п. 31). Таким образом, точка О лежит на каждом

140
Гл. 4. Дальнейшие сведения о треугольниках
из трех серединных перпендикуляров к сторонам треугольника ABC,
а это и означает, что все три серединных перпендикуляра га, п и р
пересекаются в одной точке. Теорема доказана.
Замечание. Написав слова «Теорема доказана», мы допустили
неточность. Действительно, мы начали доказательство теоремы с того,
что обозначили буквой О точку пересечения серединных перпендику-
перпендикуляров га и п к сторонам АВ и ВС. Возникает вопрос: а не может
ли случиться так, что эти серединные перпендикуляры не пересека-
пересекаются, т.е. га || п? Докажем, что этого не может быть. Доказательство
проведем методом от противного. Предположим, что в каком-то тре-
треугольнике ABC серединные перпендикуляры га и п к сторонам АВ
и ВС параллельны: га || п (рис.208). Тогда прямая ВС, перпендикуляр-
перпендикулярная к прямой п, будет перпендикулярна также и к прямой га (следствие
3° п. 48). Таким образом, мы получаем, что через точку В проходят
две прямые (АВ и ВС), перпендикулярные к прямой га. Но этого
не может быть. Следовательно, наше предположение о параллельности
прямых тип неверно, а значит, серединные перпендикуляры тип
к сторонам АВ и ВС треугольника ABC пересекаются в некоторой
точке. Теперь мы можем сказать, что теорема о пересечении трех
серединных перпендикуляров к сторонам треугольника в одной точке
полностью доказана.
Отметим также, что в п. 31, где была доказана теорема о сере-
серединном перпендикуляре к отрезку, мы не могли доказать теорему
о пересечении серединных перпендикуляров к сторонам треугольника
в одной точке именно по той причине, что в то время мы не смогли бы
доказать, что два серединных перпендикуляра к сторонам треугольника
пересекаются в некоторой точке. Доказательство этого факта, как
мы только что видели, основано на свойстве параллельных прямых:
если прямая перпендикулярна к одной из параллельных прямых, то она
перпендикулярна и к другой прямой. В свою очередь, это утверждение
нельзя доказать, не приняв аксиому параллельных прямых — в гео-
А
С
Р
Рис. 207
Рис. 208

2. Четыре замечательные точки треугольника 141
метрии Лобачевского оно неверно. Но в п. 31 аксиомы параллельных
прямых мы еще не знали, поэтому и теорему о пересечении серединных
перпендикуляров к сторонам треугольника доказать не могли.
60. Окружность, описанная около треугольника. Окружность,
проходящая через все три вершины треугольника, называется опи-
описанной около этого треугольника, а сам треугольник называется
вписанным в окружность. На рисунке 209 окружность с центром О
описана около треугольника ABC. Поскольку точка О равноудалена
от всех вершин этого треугольника, то она является точкой пересече-
пересечения серединных перпендикуляров к сторонам треугольника ABC. Если
еще немного приглядеться к рисунку, то станет ясно, что имеет место
следующая теорема.
Теорема. Около любого треугольника можно описать окруж-
окружность, и притом только одну.
Доказательство. Рассмотрим произвольный треугольник ABC.
Обозначим буквой О точку пересечения серединных перпендикуляров
к его сторонам и проведем отрезки О А, ОВ и ОС (рис.210). Точка О
равноудалена от вершин треугольника ABC, т. е. О А = ОВ = ОС.
Поэтому окружность с центром О радиуса О А проходит через все три
вершины треугольника и, следовательно, является описанной около
треугольника ABC. Итак, около треугольника ABC можно описать
окружность.
Около треугольника ABC можно описать только одну окружность,
поскольку две окружности не могут иметь три общие точки — А, В
и С (п. 38). Теорема доказана.
Замечание 1. Как мы только что установили, центр окружно-
окружности, описанной около треугольника, совпадает с точкой пересечения
серединных перпендикуляров к сторонам этого треугольника. По этой
причине точку пересечения серединных перпендикуляров к сторонам
треугольника часто называют центром описанной окружности.
С А
Рис. 209 Рис. 210

142 Гл. 4. Дальнейшие сведения о треугольниках
Замечание 2. Рассмотрим три произвольные точки, не лежащие
на одной прямой. Соединив эти точки отрезками, получим треуголь-
треугольник, около которого, согласно доказанной теореме, можно описать
окружность, и притом только одну. Таким образом, мы приходим к сле-
следующему выводу:
через любые три точки, не лежащие на одной прямой, проходит
окружность, и притом только одна.
61. Теорема о пересечении высот треугольника. Если мы за-
заглянем в наш блокнот, то увидим в нем следующие вопросы, ответы
на которые мы пока не нашли:
верно ли, что три медианы треугольника пересекаются в одной
точке; верно ли, что три высоты треугольника или их продолжения
пересекаются в одной точке?
Попытаемся ответить на эти вопросы. Начнем с высот.
Рассмотрим произвольный треугольник ABC и проведем его сред-
средние линии А\В\, В\С\ и С\А\ (рис.211). Далее, проведем высоту А\А2
треугольника А\В\С\. Мы видим,
что прямая A\A<i является сере-
серединным перпендикуляром к стороне
ВС треугольника ABC. Но сере-
серединные перпендикуляры к сторо-
сторонам треугольника ABC пересекают-
пересекаются в одной точке. Следовательно,
и высоты треугольника А\В\С\ (или
^ их продолжения) пересекаются в од-
А В\ С ной точке!
Теперь уже ясно, что так будет
Рис. 211 не только в треугольнике А\В\С\,
но и в любом другом треугольнике.
Теорема. Высоты треугольника (или их продолжения) пересе-
пересекаются в одной точке.
Доказательство. Рассмотрим произвольный треугольник ABC
и докажем, что прямые АА\, ВВ\ и СС\, содержащие его высоты,
пересекаются в одной точке (рис.212).
Через каждую вершину треугольника ABC проведем прямую, па-
параллельную противоположной стороне, и обозначим точки пересечения
этих прямых (объясните, почему проведенные прямые пересекаются)
через А2, В2, С2 (см. рис.212).
Треугольники ABC и А2СВ равны по стороне и двум прилежащим
к ней углам {ВС — общая сторона, ZABC = ZA2CB, так как эти
углы — накрест лежащие при пересечении параллельных прямых АВ
и А2В2 секущей ВС; ZACB = ZA2BC, так как эти углы — на-
накрест лежащие при пересечений параллельных прямых АС и А2С2
секущей ВС). Из равенства треугольников ABC и А2СВ следует,
что А2С = АВ.

2. Четыре замечательные точки треугольника
143
Рис. 212
Аналогично треугольники ABC и СВ2А равны по стороне и двум
прилежащим к ней углам {АС — общая сторона, ABAC = ZB2CA,
ABC A = ZB2AC), поэтому В2С = АВ.
Из равенств А2С = АВ и В2С = АВ получаем: А2С = В2С,
т.е. точка С — середина стороны А2В2 треугольника А2В2С2. Так
как А2В2 || АВ (по построению) и СС\ JL АВ, то СС\ JL A2B2, т.е.
прямая СС\ — серединный перпендикуляр к стороне А2В2 треугольни-
треугольника А2В2С2.
Аналогично доказывается, что прямые АА\ и ВВ\ — серединные
перпендикуляры к сторонам В2С2 и А2С2 треугольника А2В2С2. Сле-
Следовательно, прямые АА\, ВВ\ и СС\ пересекаются в одной точке.
Теорема доказана.
Замечание. Точку пересечения высот треугольника или их про-
продолжений для краткости называют ортоцентром 0 этого треуголь-
треугольника.
62. Размышления о точке пересечения медиан треугольника.
Займемся теперь медианами треугольника. Как доказать, что они пе-
пересекаются в одной точке (если, конечно, это так)? С чего начать?
Рассмотрим треугольник ABC и проведем его медианы АА\, ВВ\
и СС\ (рис.213, а). Пусть О, Р и Q — точки их пересечения (на
рисунке они не отмечены). Мы хотим доказать, что эти три точки
совпадают.
Попробуем уточнить место расположения точек О, Р и Q. Прежде
всего ясно, что эти точки находятся внутри треугольника ABC (объ-
(объясните, почему). Далее, обратим внимание на такой интересный факт:
1) Греческое слово «орто» означает «прямой»: здесь имеются в виду прямые
углы между высотами и соответствующими им сторонами треугольника (или
их продолжениями).

144
Гл. 4. Дальнейшие сведения о треугольниках
В
а)
б)
Рис. 213
медиана АА\ делит среднюю линию В\С\ пополам. В самом деле,
по свойству средней линии В\С\ || ВС, поэтому признак средней линии
применительно к треугольникам АСА\ и АВА\ дает равенства: В\ А2 =
= -цСА\ = -цА\В = А^С\. Иными словами, отрезок А\А2 медианы АА\
является медианой треугольника А\В\С\. По аналогичной причине
отрезки В\В% и С\С2 также являются медианами этого треугольника.
Следовательно, точки О, Р и Q лежат внутри треугольника А\В\С\.
Применив такие же рассуждения к треугольнику А\В\С\, мы об-
обнаружим, что его медианы А\А^, В\В^ и С\С^ пересекаются внутри
треугольника А^В^С^ (рис.213, б) и т.д.
Таким образом, мы получаем бесконечную последовательность
уменьшающихся треугольников АпВпСп (по свойству средней ли-
линии стороны каждого следующего треугольника вдвое меньше сторон
предыдущего треугольника), причем точки О, Р и Q лежат внутри
каждого из этих треугольников. Ясно, что такое возможно только в том
случае, когда точки О, Р и Q совпадают. Следовательно, все три
медианы АА\, ВВ\ и СС\ пересекаются в точке О, что и требовалось
доказать.
В принципе, на этом можно было бы и закончить, так как своей
цели мы достигли. Но давайте еще немного поразмышляем. Нельзя
ли как-то уточнить место расположения точки О на медиане АА\?
Попробуем.
Из нашего построения вытекает, что А\О = А\А% + А^А^ + A$Aj +
Но А^Аъ = -тА\Аъ (объясните, почему). Точно так-
так= - • -АХА3, А7А9 = ^А5А7 = - • - • -А{А3,...,
же АЪА7 = ^

2. Четыре замечательные точки треугольника 145
поэтому
С другой стороны, АО = АА2 + А2А4 + A4Aq + Аб^8 + ..., при-
причем А2А4 = ^АА2, А4А6 = ^А2А4 = ^ • ^АА2, Л^8 = ^А4А6 = i x
х - • jAA2,..., поэтому
Но АА2 = 2А\А% (докажите это). Следовательно, АО = 2А\О. Ана-
Аналогично доказывается, что ВО = 2В\О и СО = 2CiO. Итак, мы устано-
установили замечательный факт: точка пересечения медиан треугольника
делит каждую медиану в отношении 2 : 1, считая от вершины\
Замечание. Попутно мы фактически решили еще одну, весьма
непростую задачу: чему равна сумма ^ = 0 + т + т*т + т*т*т +
+ ...)? Имеем: АА\ = ЗА\О = ЗА\Ао, • S. С другой стороны, АА\ =
= 4т41т4з. Приравнивая эти выражения для АА\, получим: 3S = 4,
откуда S = -.
о
63. Теорема о пересечении медиан треугольника. Теперь, когда
мы уже знаем, где находится точка пересечения медиан треугольника,
нетрудно придумать и более простые доказательства теоремы об этой
точке. Сформулируем теорему о пересечении медиан треугольника
и приведем одно из доказательств этой теоремы.
Теорема. Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2 : 1, считая от вер-
вершины.
Доказательство. Рассмотрим произвольный треугольник ABC
и обозначим буквой О точку пересечения его медиан АА\ и ВВ\
(рис.214, а). Проведем средние линии треугольников АВВ\ и СВВ\,
параллельные стороне ВВ\ (рис.214, б). Вместе с отрезком ВВ\ эти
средние линии делят сторону АС треугольника ABC на четыре равные
М / / \Ау
А Вх С А~ • ' Вх ' ! с
а) б)
Рис. 214

146
Гл. 4. Дальнейшие сведения о треугольниках
части. Следовательно, по теореме Фалеса медиана АА\ оказывается
разделенной ими и медианой ВВ\ на три равные части. Поэтому АО =
= 20Аи или АО : ОАХ =2:1.
Итак, точка О пересечения медиан АА\ и ВВ\ делит медиану АА\
в отношении 2:1, считая от вершины. Аналогично доказывается,
что точка О делит медиану ВВ\ также в отношении 2:1, считая
от вершины, т. е. ВО : ОВ\ =2:1.
Рассмотрим теперь точку О\ пересечения медиан АА\ и СС\. Та-
Таким же образом, как и для медиан АА\ и ВВ\, можно доказать, что
точка О\ делит каждую из медиан АА\ и СС\ в отношении 2:1,
считая от вершины. В частности, АО\ : О\А\ =2:1. Следовательно,
точка О\ совпадает с точкой О.
Итак, три медианы треугольника пересекаются в одной точ-
точке (рис.215) и каждая медиана делится этой точкой в отношении 2:1,
считая от вершины. Теорема доказана.
Замечание 1. К рассмотренной теореме можно прийти значи-
значительно проще, чем в п. 62, если вспомнить некоторые сведения из физи-
физики. Действительно, представим себе, что в каждой вершине треуголь-
треугольника ABC находится точечная масса в 1 г. Как найти центр тяжести
системы этих трех масс? Сначала нужно взять какие-нибудь две массы,
например массы в точках А и В. Их центр тяжести находится в се-
середине С\ отрезка АВ (рис.216). Далее следует рассмотреть систему
двух масс: массы 1 г в точке С и массы 2 г в точке С\. Их центр
тяжести находится в точке О отрезка СС\, т.е. на медиане СС\ тре-
треугольника ABC, причем СО = 2ОС\. Путем аналогичных рассуждений
можно установить, что АО = 20А\ и ВО = 2ОВ\, где точки А\ и В\ —
середины сторон ВС и АС. Таким образом, все три медианы АА\,
ВВ\ и СС\ треугольника ABC пересекаются в точке О и каждая
медиана делится этой точкой в отношении 2:1, считая от вершины.
В связи с этим рассуждением становится ясно, почему точку пересе-
В
Сх
Ах
Вх С
Рис. 215
Рис. 216. Точка О — центр тя-
тяжести треугольника ABC

2. Четыре замечательные точки треугольника 147
чения медиан треугольника часто называют центром тяжести этого
треугольника.
Замечание 2. Итак, с каждым треугольником связаны четыре
точки: центр вписанной окружности — точка пересечения биссектрис
треугольника; центр описанной окружности — точка пересечения се-
серединных перпендикуляров к сторонам треугольника; ортоцентр —
точка пересечения высот треугольника или их продолжений; центр
тяжести — точка пересечения медиан треугольника. Эти четыре точки
называются замечательными точками треугольника.
В равностороннем треугольнике роль каждой из четырех заме-
замечательных точек играет одна и та же точка. Эта точка называется
центром равностороннего треугольника.
Задачи
185* Серединные перпендикуляры к сторонам треугольника ABC
пересекаются в точке О, лежащей внутри треугольника ABC, а се-
серединные перпендикуляры к сторонам треугольника А\В\С\ пере-
пересекаются в точке О\, лежащей внутри треугольника А\В\С\. Из-
Известно, что АО = А\О\, ZA = ZA\, ZAOB = АА\О\В\. Докажите,
что ААВС = АА{В{С{.
186. Докажите, что: а) точка пересечения серединных перпенди-
перпендикуляров к сторонам прямоугольного треугольника является серединой
гипотенузы; б) радиус окружности, описанной около прямоугольного
треугольника, равен половине гипотенузы.
187* Центр описанной около треугольника окружности лежит
на его медиане. Определите вид этого треугольника.
188. Докажите, что ортоцентр равнобедренного треугольника ле-
лежит на серединном перпендикуляре к основанию этого треугольника.
189. Ортоцентр треугольника совпадает с одной из его вершин.
Докажите, что этот треугольник — прямоугольный.
190. Докажите, что если две замечательные точки треугольника
совпадают, то совпадают все четыре замечательные точки, и треуголь-
треугольник является равносторонним. Рассмотрите все возможные случаи.
191. Докажите, что радиус окружности, описанной около равно-
равностороннего треугольника, в два раза больше радиуса окружности,
вписанной в этот треугольник.
192. С помощью циркуля и линейки через три данные точки про-
проведите окружность. Всегда ли эта задача имеет решение?
ПОДВЕДЕМ ИТОГИ
Итак, что нового о свойствах геометрических фигур мы узнали?
Очень многое! Раньше нам казалось, что про треугольник мы знаем
все. Это и не удивительно — казалось бы, у столь простой геомет-
геометрической фигуры каким-то неожиданным свойствам взяться просто
неоткуда! Теперь мы знаем, что это не так. Мы обнаружили целый ряд
неожиданных свойств треугольника. Напомним некоторые из них.
Сумма углов любого треугольника равна 180°.

148
Гл. 4. Дальнейшие сведения о треугольниках
Средняя линия треугольника параллельна одной из его сторон
и равна половине этой стороны.
С каждым треугольником связаны четыре замечательные точки:
центр вписанной окружности — точка пересечения биссектрис тре-
треугольника; центр описанной окружности — точка пересечения середин-
серединных перпендикуляров к сторонам треугольника; ортоцентр — точка пе-
пересечения высот треугольника или их продолжений; центр тяжести —
точка пересечения медиан треугольника.
Означает ли это, что теперь про треугольник мы знаем все? Конечно
же, нет! Оказывается, например, что в произвольном неравностороннем
треугольнике:
1° центр тяжести лежит на отрезке, соединяющем ортоцентр с цен-
центром описанной окружности, и делит этот отрезок в отношении 2:1,
считая от ортоцентра (рис.217, а, где G — центр тяжести, Н —
ортоцентр, О — центр описанной оружности);
б)
Рис. 217. а) Точка О — центр описанной окружности, точка G — центр
тяжести, точка Н — ортоцентр треугольника; GH : GO = 2:1
2° девять точек: середины сторон, основания высот и середины
отрезков, соединяющих ортоцентр с вершинами — лежат на одной
окружности (рис.217, б).
Если мы откроем наш блокнот, то обнаружим, что не на все по-
поставленные вопросы найден ответ. Так, мы пока не знаем, как доказать
теорему Морлея. Нет ответа и на такой вопрос: имеет ли место признак
равенства треугольников по двум сторонам и биссектрисе, проведен-
проведенным из одной вершины. Запишем еще один вопрос: как построить
треугольник по двум сторонам и биссектрисе, проведенным из одной
вершины? Запишем также в виде вопросов утверждения 1° и 2°.
Итак, многого мы пока не знаем. И все же мы уже не те, что
прежде. Теперь мы поняли главное — при помощи рассуждений можно

2. Четыре замечательные точки треугольника 149
установить совершенно неожиданные факты. Нам ясно, что самый
трудный этап рассуждений — это, как правило, поиск формулировки
теоремы. Иногда ее можно увидеть на рисунке (именно рисунки на-
навели нас на мысль о замечательных точках треугольника), но далеко
не всегда это так. Вспомним теорему о сумме углов треугольника:
сколько бы мы ни разглядывали даже очень аккуратно нарисованный
треугольник, мы бы не смогли увидеть, чему равна сумма его углов.
Часто формулировка теоремы находится путем весьма сложных рас-
рассуждений, но когда она уже найдена, обнаруживаются более простые
методы доказательства (вспомним теорему о пересечении медиан тре-
треугольника). Впрочем, бывает и такое: формулировка теоремы вроде бы
ясна, но найти правильный ход рассуждений весьма непросто — с этим
мы столкнулись, например, при решении задачи 2 п. 27.
Особого внимания заслуживают наши размышления, связанные
с параллельными прямыми. Прежде никто из вас, по-видимому, даже
не задумывался над таким вопросом: а есть ли квадрат? Но что самое
удивительное — ответ на этот вопрос зависит от нашего выбора. Если
мы примем за аксиому, что квадрат есть (в п. 60 мы говорили о том,
что аксиома параллельных прямых эквивалентна утверждению о суще-
существовании квадрата), то он будет; если же, следуя Н. И. Лобачевскому,
мы примем за аксиому противоположное утверждение: квадрата нет,
то его и не будет!
Геометрия — наука древняя, она зародилась в XVII веке до нашей
эры. Многое из того, что мы изучаем, было известно еще древним
грекам. Но обратим внимание вот на какой факт. В нашей книге
наряду с именами Фалеса (VII в. до н.э.), Евклида (III в. до н.э.),
Архимеда (II в. до н.э.), Посидония (I в. до н.э.) встречаются имена
Наполеона (XIX в.), Лобачевского (XIX в.), Морлея (XX в.). Это
наводит на мысль о том, что не только мы с вами, но и вообще никто
не может похвастаться тем, что знает все про треугольник! Возможно,
многие свойства треугольника еще не открыты. Во всяком случае
вопросов, над которыми можно поразмышлять, масса!

Глава 5
МНОГОУГОЛЬНИКИ
§ 1. Выпуклый многоугольник
64. Ломаная. Рассмотрим фигуру, составленную из отрезков
А^Аъ,..., Ап_\Ап. Точки А\ и Ап могут быть различными (рис.218, а)
и могут совпадать (рис.218, б). Будем считать, что соседние отрезки
не лежат на одной прямой (в противном случае их можно объединить
в один отрезок). Такая фигура, составленная из отрезков, называется
ломаной А\А^... Ап, а отрезки, из которых составлена ломаная, назы-
называются ее звеньями. Если точки А\ и Ап различные, то говорят, что
ломаная соединяет точки А\ и Ап, а если точки А\ и Ап совпадают,
то ломаная называется замкнутой. Два соседних звена ломаной имеют
общий конец. Ломаная называется простой, если ее несоседние звенья
не имеют общих точек. Ломаные на рисунках 218, а и 218, б —
простые, а ломаная на рисунке 218, в — непростая.
Рассмотрим какую-нибудь ломаную А\А^ ... Ап, соединяющую точ-
точки А\ и Ап (рис.218, а, в). Интуитивно ясно, что длина отрезка А\Ап
меньше суммы длин всех звеньев этой ломаной. Но как это доказать?
Возьмем ломаную, состоящую из двух звеньев — А\А2 и А2А3
(т. е. п = 3). В этом случае справедливость неравенства А\ А% < А\ А% +
следует из неравенства треугольника.
А...
Ах /Ап
а)
Рис. 218

/. Выпуклый многоугольник
151
Пусть п = 4, т.е. ломаная состоит из трех звеньев — А\А2, А2А^
и А^А\ (рис. 219, а). Рассмотрим сначала ломаную А\А2А^. Она состо-
состоит из двух звеньев. Поэтому, согласно доказанному, А\А^ < А\А2 +
+ А2А3. С другой стороны, А\АА < А\А% + А^А^ (объясните, почему).
Следовательно, А\А^ < А\ А2 + А2А3 + Аз А*.
Итак, для п = 4 утверждение доказано. Далее аналогичным образом
можно доказать это утверждение для п = 5, затем для п = 6 и т. д.
Общее рассуждение, позволяющее доказать наше утверждение для
любого п, проводится с помощью так называемого метода матема-
математической индукции. Поясним на примере нашей задачи, в чем состоит
этот метод.
Мы знаем, что наше утверждение верно при п = 3.
Предположим, что оно верно при п = к, где к — некоторое целое
число, большее или равное 3, и докажем, что тогда оно верно и при п =
Рассмотрим ломаную А\А%... ^U+i (рис. 219, б). Отбросим послед-
последнее звено AkAk+\. Останется ломаная, у которой п = к. Поэтому,
согласно нашему предположению, А\А^ < А\А^ + А^А^ + ... + А^-\А^.
С другой стороны, в силу неравенства треугольника A\Ak+\ < A\Ak +
+ AkAk+\. Следовательно,
АхАк+х < А{А2 + А2А3 + ... + Ак_хАк + AfcAfc+i.
Итак, если наше утверждение верно при некотором п = к ^ 3,
то оно верно и при п = /с + 1. Из этого можно сделать вывод: утвержде-
утверждение верно при любом п. В самом деле, оно верно при п = 3. Но тогда
оно верно и при п = 3 + 1 = 4, а значит, и при п = 4+1=5ит. д.
Метод математической индукции состоит в следующем. Если тре-
требуется доказать, что данное утверждение справедливо для любого
натурального числа п, то поступают так:
1° проверяют справедливость этого утверждения для самого ма-
маленького п, при котором утверждение имеет смысл (в нашем случае
для п = 3);
а)
б)
Рис. 219

152
Гл. 5. Многоугольники
2° доказывают, что если утверждение верно для п = к, то оно верно
и для п = к + 1.
Из этого делают вывод: утверждение справедливо для любого п.
65. Многоугольник. Простая замкнутая ломаная называется мно-
многоугольником. Звенья такой ломаной называются сторонами, а концы
звеньев — вершинами многоугольника. Сумма длин всех сторон на-
называется периметром многоугольника. Две вершины многоугольника,
принадлежащие одной стороне, называются соседними. Отрезок, со-
соединяющий любые две несоседние вершины, называется диагональю
многоугольника.
Интуиция подсказывает, что каждый многоугольник разделяет
плоскость на две части — внутреннюю и внешнюю. Но как это дока-
доказать? Сначала, конечно, следует понять, что именно мы хотим доказать.
Обратимся к рисунку 220, на котором изображен весьма причудли-
причудливый многоугольник. Какой области многоугольника принадлежит точка
М — внешней или внутренней? Сразу и не скажешь. Поступим так:
проведем какой-нибудь луч с началом М, не проходящий через верши-
вершины многоугольника, и отметим точки М\, М^, ..., Мп пересечения это-
этого луча со сторонами многоугольника. Поскольку за точкой Мп точек
многоугольника нет, то все точки проведенного луча, лежащие за этой
точкой, принадлежат, как нам представляется, внешней области много-
многоугольника. Поэтому если наша гипотеза о существовании внутренней
и внешней областей верна, то все внутренние точки отрезка Mn_iMn
лежат во внутренней области многоугольника, все внутренние точки
отрезка Мп_2Мп_\ — во внешней области и т.д. Таким образом, точка
Рис. 220

/. Выпуклый многоугольник 153
М лежит во внешней или внутренней области в зависимости от того,
четным или нечетным является число п.
Отметим, что если наша гипотеза верна, то четность числа к точек
пересечения продолжения проведенного луча (см. рис.220) должна
совпадать с четностью числа п. Иначе получилось бы, что точка
М, с одной стороны, принадлежит внешней области многоугольника,
а с другой — его внутренней области. Таким образом, нам представля-
представляется, что число п + к должно быть четным. Иными словами,
число общих точек прямой и многоугольника четно.
Но так ли это? Для произвольной прямой это не так. Например,
если прямая содержит сторону многоугольника, то общих точек прямой
и многоугольника бесконечно много. Этот случай следует исключить.
Сверх того будем считать, что рассматриваемая прямая а не параллель-
параллельна ни одной из сторон и диагоналей многоугольника (такая прямая
существует, поскольку число сторон и диагоналей многоугольника
конечно). При этом условии любая прямая, параллельная а, не может
содержать более одной вершины многоугольника. Далее, если прямая а
проходит через вершину Аш многоугольника, то возможны два случая:
1° стороны угла Аш лежат по одну сторону от прямой а (рис.221, а);
2° стороны угла Аш лежат
по разные стороны от пря- /
мой а (рис.221, б). В пер- Аш а Аш/ а
вом случае, двигаясь по пря-
мой а и проходя точку Ат,
мы, как нам представляется,
не попадаем в другую область,
во втором — попадаем. В свя- р 291
зи с этим условимся называть
точкой пересечения прямой а и многоугольника их общую точку,
не являющуюся вершиной, соответствующей случаю 1°.
Теперь мы можем сформулировать нашу гипотезу в уточненном
виде:
число точек пересечения многоугольника и прямой а (удовлетво-
(удовлетворяющей указанным условиям) четно.
Попробуем доказать это утверждение. Через произвольную точку А
прямой а, не принадлежащую многоугольнику, проведем какую-нибудь
прямую АВ, отличную от а и не содержащую ни одной из вершин.
Пусть В\, В%,... — точки пересечения прямой АВ с прямыми, парал-
параллельными а и проходящими через вершины многоугольника (рис.222).
Начнем двигаться по лучу АВ и через каждую точку этого луча
будем проводить прямую, параллельную а. Ясно, что в процессе это-
этого движения четность числа точек пересечения проводимых прямых
и многоугольника может меняться только при переходе через точки Bi.
Но, как видно из нашего определения точек пересечения, при переходе
через точки Bi четности числа точек пересечения проводимых прямых
и многоугольника также не меняются (на рисунке 222 при переходе

154 Гл. 5. Многоугольники
Рис. 222
через точку В^ число точек пересечения не меняется, при переходе
через точку В% увеличивается на 2, при переходе через точку В\ умень-
уменьшается на 2 и т.д.). Следовательно, эти четности одни и те же для
всех проводимых прямых. После прохождения последней из точек В{
мы начнем проводить прямые, не имеющие с многоугольником ни одной
общей точки. Число точек пересечения, таким образом, станет четным.
Поэтому число точек пересечения прямой а и многоугольника также
четно. Утверждение доказано.
Эти рассуждения допускают дальнейшее развитие. Рассмотрим про-
произвольную точку М, не принадлежащую многоугольнику, и проведем
из нее какой-нибудь луч, параллельный прямой а. Четность числа
точек пересечения проведенного луча с многоугольником назовем чет-
четностью точки М (т.е. точку М назовем «четной», если указанное
число четно, и «нечетной» в противоположном случае). Отметим, что
это определение не зависит от того, какой из двух лучей проводится
(объясните, почему). Из наших рассуждений следует, что
если отрезок АВ не имеет общих точек с многоугольником, то
все его точки имеют одну и ту же четность.
Если же отрезок АВ имеет с многоугольником общую точку, то при
переходе через нее на лучах, параллельных а и лежащих по одну
сторону от прямой АВ, число точек пересечения изменяется ровно на 1
(см. рис.222). Следовательно,
при переходе через общую точку отрезка АВ и многоугольника
четность точек отрезка меняется на противоположную.
Назовем множество всех «четных» точек плоскости внешней обла-
областью многоугольника, а множество всех «нечетных» точек — внут-
внутренней областью многоугольника. Тогда про каждую точку, не при-

/. Выпуклый многоугольник 155
надлежащую многоугольнику, мы сможем сказать, какой из обла-
областей — внутренней или внешней — она принадлежит. Этого, однако,
еще не достаточно. Когда мы говорим: «Каждый многоугольник раз-
разделяет плоскость на две части — внутреннюю и внешнюю», то имеем
в виду, что любые две точки одной и той же области можно соединить
ломаной, не имеющей общих точек с многоугольником, а любая лома-
ломаная, соединяющая две точки разных областей, имеет с многоугольни-
многоугольником хотя бы одну общую точку. Попробуем это доказать.
Мы знаем, что если отрезок АВ не имеет общих точек с мно-
многоугольником, то все его точки имеют одну и ту же четность и,
следовательно, лежат в одной и той же области. Из этого следует, что
любая ломаная, соединяющая две точки разных областей, имеет
с многоугольником хотя бы одну общую точку. В противном случае
указанные точки лежали бы в одной области.
Рассмотрим теперь точки А и В, лежащие в одной и той же об-
области, и докажем, что их можно соединить ломаной, не имеющей
общих точек с многоугольником. При этом можно считать, что отрезок
АВ не содержит ни одной из вершин многоугольника. В противном
случае в качестве точки В можно взять близкую к ней точку С
так, чтобы отрезок ВС не имел общих точек с многоугольником,
а отрезок АС не содержал ни одной из вершин многоугольника. Пусть
С\,С2,... ,Ck — точки пересечения отрезка АВ со сторонами много-
многоугольника, взятые последовательно. Выберем одну из двух ломаных,
образованных сторонами многоугольника и соединяющих точку С\
с точкой Ck, и обозначим буквой d наименьшее расстояние между
парами точек ее несоседних звеньев. Ясно, что, двигаясь параллельно
какому-либо звену ломаной на расстоянии d\ ^ d от прямой, содержа-
содержащей это звено, мы либо «наткнемся» на соседнее с ним звено (т. е.
точки этого звена окажутся лежащими от нас на расстоянии, меньшем
d\), либо «потеряем нашу сторону из виду» (т.е. ее точки окажутся
лежащими от нас на расстоянии, большем d\). Воспользуемся этим
наблюдением. Сначала приблизимся по отрезку АВ к точке С\ на рас-
расстояние d\ ^ d, затем будем двигаться на расстоянии d\ от того звена
ломаной, на которое мы «наткнулись», до тех пор, пока не «потеряем
это звено из виду» или не «наткнемся» на соседнее с ним звено, после
чего начнем двигаться па-
параллельно соседнему звену
на расстоянии d\ от него
и т.д. (рис.223). Обойдя
ломаную, мы окажемся в
какой-то точке М прямой
АВ, лежащей в той же об-
области, что и точка А. Бу- * ^Г //cfc_i ск М Ъ
дем считать, что величина / /
d\ столь мала, что MCk <
< Ck-\Ck, следовательно, Рис.223

156 Гл. 5. Многоугольники
точки М и Ck лежат по одну сторону от точки Ck-\. При этом
точка М не может лежать между точками С^-\ и С&, так как иначе
концы отрезка MB имели бы разную четность, а значит, точки А
и В имели бы разную четность, что противоречит условию (точки А
и В лежат в одной и той же области). Следовательно, точки М и В
лежат по одну сторону от точки Ck. Осталось провести отрезок MB,
и ломаная, соединяющая точки А и В и не имеющая общих точек
с многоугольником, построена.
Итак, мы доказали, что любые две точки одной и той же области
можно соединить ломаной, не имеющей общих точек с многоугольни-
многоугольником, а любая ломаная, соединяющая две точки разных областей, имеет
с многоугольником хотя бы одну общую точку. Подводя итог, можно
сказать:
каждый многоугольник разделяет плоскость на две области
{внутреннюю и внешнюю) так, что две точки можно соединить ло-
ломаной, не имеющей общих точек с многоугольником, в том и только
в том случае, когда эти точки лежат в одной и той же области
(теорема Жордана 0).
Отметим, что теорема Жордана верна не только для многоугольни-
многоугольника, но и для любой замкнутой линии без самопересечений (рис.224),
но доказательство в этом случае на-
намного сложнее. Его можно найти лишь
в некоторых курсах высшей матема-
математики (см., например, Валле-Пуссен
де ла Ш. Ж. Курс анализа бесконечно
малых. - Л.-М.: ГТТИ, 1933).
Из теоремы Жордана, в частности,
Рис. 224 следует, что любая прямая, не содер-
содержащая стороны многоугольника (в
том числе параллельная какой-либо его стороне или диагонали), пе-
пересекает многоугольник в четном числе точек. Подумайте, как это
доказать.
Решим теперь такую задачу.
Задача 1. Доказать, что в каждом многоугольнике найдется
диагональ, все внутренние точки которой лежат во внутренней
области многоугольника.
Решение* Попробуем сначала понять, какие соображения можно
положить в основу наших рассуждений. Представим себе, что мы на-
находимся в углу А\ многоугольной комнаты А\А^ ... Ап. Если при этом
мы видим какую-нибудь вершину Ат C ^ т ^ п — 1), то диагональ
А\Ат является искомой (рис.225). Возможно, однако, что мы не видим
ни одной из указанных вершин так как мешают стены А\Аъ и А\Ап
ОЖордан Камилл A838-1922) — французский математик, иностранный
член-корреспондент Петербургской академии наук.

/. Выпуклый многоугольник
157
(рис.226). Но тогда, как нам представляется, искомой является диаго-
диагональ А^Ап. Руководствуясь этими соображениями, перейдем к реше-
решению задачи.
Рассмотрим произвольный многоугольник А\Аъ ... Ап и допустим,
что ни одна из его диагоналей, выходящих из вершины А\, не обладает
указанным свойством. Проведем через точку А\ какую-нибудь прямую
а, делящую угол А^АхАп на два угла и не проходящую ни через
одну из остальных вершин многоугольника. Поскольку при переходе
через точку А\ четность точек прямой а меняется на противополож-
противоположную, то один из ее лучей с началом А\ «входит» во внутреннюю
область многоугольника, а другой — «выходит» из нее. Выберем тот
из лучей, который «входит» во внутреннюю область многоугольника.
Он пересекает многоугольник в нескольких точках. Пусть М — та из
них, которая ближе всех к А\ (рис.225). Луч А\М не проходит через
вершины многоугольника, поэтому все внутренние точки отрезка А\М
лежат во внутренней области многоугольника, а точка М является
внутренней точкой какой-то стороны AkAk+\. Отметим все вершины
многоугольника, лежащие внутри и на границе треугольника А\А^М,
и проведем через них лучи с началом А\. Выберем из проведенных
лучей тот луч А\Ат, для которого точка Р пересечения с лучом
MAk расположена ближе всех к М. На луче А\Ат может оказаться
несколько вершин многоугольника. В этом случае будем считать, что
Ат — та из них, которая ближе всех к А\. По построению внутри
треугольника А\РМ нет ни одной из вершин многоугольника. Более
того, внутри этого треугольника нет ни одной из точек многоуголь-
многоугольника, поскольку никакая сторона многоугольника не может пересе-
пересекать ни отрезок А\М, ни отрезок МР (являющийся частью стороны
AkAk+\). Если каждая внутренняя точка отрезка А\Ат не является
точкой многоугольника, то она является точкой внутренней области
многоугольника, так как ее можно соединить с точкой, лежащей меж-
Аи
Ак+\
Рис. 225
Рис. 226

158 Гл. 5. Многоугольники
ду А\ и М, отрезком, целиком принадлежащим внутренней области
многоугольника. В этом случае отрезок А\Ат является диагональю,
все внутренние точки которой лежат во внутренней области много-
многоугольника, что противоречит нашему предположению. Следовательно,
внутри отрезка А\Ат существует хотя бы одна точка многоугольника.
Сторона, содержащая эту точку, не может пересекать отрезок А\Ат
(объясните, почему), и ни один из ее концов не лежит между точками
А\ и Аш (так выбиралась вершина Ат). Это означает, что указанная
сторона содержит отрезок А\Ат, т.е. отрезок А\Ат является не диа-
диагональю многоугольника, а его стороной А\А^.
Итак, исходя из нашего предположения, мы доказали, что луч А\А^
пересекает сторону А^А^+х в точке Р так, что точка А% принадлежит
отрезку А\Р, а все внутренние точки треугольника А\РМ и его сто-
стороны А\М лежат во внутренней области многоугольника. Аналогично
доказывается, что луч А\Ап пересекает сторону А^А^+х в такой точке
Q, что точка Ап принадлежит отрезку A\Q, а все внутренние точки
треугольника A\QM лежат во внутренней области многоугольника
(рис.226). Следовательно, в этой области лежат и все внутренние
точки диагонали А^Ап. Таким образом, либо все внутренние точки
одной из диагоналей A\Ai, либо все внутренние точки диагонали А^Ап
лежат во внутренней области многоугольника. Утверждение доказано.
В заключение отметим, что фигуру, состоящую из сторон мно-
многоугольника и его внутренней области, также называют многоуголь-
многоугольником.
66. Выпуклый многоугольник.
Многоугольник называется выпуклым, если все его точки лежат
по одну сторону от каждой прямой, проходящей через две его сосед-
соседние вершины. При этом, конечно, имеются в виду те точки, которые
не лежат на указанной прямой. На рисунке 227 многоугольник F\ —
выпуклый, а многоугольник F% — невыпуклый.
Рассмотрим выпуклый n-угольник А\А^ ...Ап (рис.228). Поскольку
он лежит по одну сторону от прямой А^А^ и по одну сторону от пря-
прямой АпА\, то кроме точек стороны А\А2 никакие другие точки пря-
прямой А\А2 не принадлежат многоугольнику. Следовательно,
все точки выпуклого многоугольника, не лежащие на его сто-
стороне, лежат по одну сторону от прямой, содержащей эту сторону.
Проведем через произвольную точку А многоугольника прямую а,
не содержащую ту из сторон многоугольника, на которой лежит эта
точка. Скажем, что прямая а пересекает многоугольник в точке А,
если точка А является точкой пересечения прямой а и многоугольника
(см. п. 65).
Рассмотрим прямую а, пересекающую выпуклый многоугольник
в некоторой точке А. В соответствии с доказанным, эта прямая
не может содержать ни одной из сторон многоугольника (объясните,
почему). Далее, поскольку число точек пересечения многоугольника

/. Выпуклый многоугольник
159
Рис. 227
Рис. 228
с прямой а четно (см. п. 65), то есть еще одна общая точка прямой
а и многоугольника — обозначим ее буквой В. Других общих точек
у многоугольника и прямой а нет. В самом деле, предположим, что
на прямой а лежит еще одна точка многоугольника — обозначим
ее буквой С. Пусть, например, точка С лежит между А и В. Тогда
точки А и В многоугольника лежат по разные стороны от прямой,
содержащей сторону многоугольника и проходящей через точку С.
Но этого не может быть, так как весь многоугольник лежит по одну
сторону от указанной прямой. Итак,
любая прямая, пересекающая выпуклый многоугольник, имеет
с ним ровно две общие точки.
Углами выпуклого n-угольника А\А2...Ап называются углы
АпА\А2, А1А2А3,..., Ап_\АпА\. Поскольку данный многоугольник
лежит по ту сторону от прямой А\А^, где находится точка Ап, а также
по ту сторону от прямой А\Ап, где находится точка А^, то он лежит
внутри угла АпА\А2. Таким образом,
выпуклый многоугольник лежит внутри каждого из его углов
(точнее, внутри каждого угла расположены все точки многоугольника,
кроме тех его точек, которые лежат на сторонах этого угла). Из этого
следует, что
внутренняя область выпуклого многоугольника является общей
частью внутренних областей его углов.
В самом деле, если точка М принадлежит внутренней области
многоугольника, то луч А\М пересекает многоугольник в некоторой
точке, лежащей внутри угла АпА\А2, поэтому точка М также лежит
внутри этого угла. Аналогично доказывается, что точка М лежит
внутри остальных углов многоугольника. Осталось доказать, что если
точка М лежит внутри всех углов многоугольника, то она лежит в его
внутренней области. Докажем это. Рассмотрим произвольную точку N,

160 Гл. 5. Многоугольники
лежащую во внутренней области многоугольника и, следовательно,
также лежащую внутри каждого из его углов. Поскольку точки М и N
лежат по одну сторону от каждой из прямых, содержащих стороны
многоугольника, то отрезок MN не пересекает многоугольник. Поэто-
Поэтому точка М, как и N, лежит во внутренней области многоугольника.
Утверждение доказано.
Рассмотрим теперь выпуклый n-угольник А\А2 ... Ап, где п ^ 4.
Прямая А\А% не имеет общих точек с многоугольником, отличных
от А\ и A3. Следовательно, прямая А\А% разделяет многоугольник
на треугольник А\А2А% и выпуклый
А... (п — 1)-угольник А\А% ... Ап (объяс-
(объясните, почему он выпуклый). Если
^ 4 теперь применить те же рассужде-
рассуждения к многоугольнику А\А%... Ап
(при п ^ 5), затем к многоугольни-
ку АхАА...Ап (при п > 6) и т.д.
(рис.229), то окажется, что
диагонали выпуклого п-уголь-
ника, проведенные из одной вер-
вершины, разделяют его на (п — 2)
Рис. 229 треугольника.
Замечая, что сумма углов этих треугольников равна сумме углов
данного n-угольника, мы приходим к еще одному важному выводу:
сумма углов выпуклого п-уголъника равна (п — 2) • 180°.
Решим теперь такую задачу.
Задача 2. Один выпуклый многоугольник лежит внутри друго-
другого выпуклого многоугольника (т. е. все точки первого многоугольника
лежат во внутренней области или на сторонах второго многоугольни-
многоугольника). Доказать, что периметр первого многоугольника меньше, чем
периметр второго.
Решение. Рассмотрим выпуклый многоугольник А\А^... Ап,
лежащий внутри выпуклого многоугольника B\B^ ...Вш (рис.230).
Разрежем плоскость по прямой А\А^ и отбросим ту полуплоскость,
в которой нет точек многоугольника А\А^... Ап. Если при этом
от многоугольника B\B^ ...Вш отрежется какая-то ломаная, то пери-
периметр оставшейся части этого многоугольника уменьшится, поскольку
длина этой ломаной больше длины отрезка, соединяющего ее концы.
Проводя далее разрезы по прямым А2А^,... ,АпА\ (первые два разреза
изображены на рисунке 230) и отбрасывая те части плоскости,
которые не содержат точек многоугольника А\А2... Ап, мы превратим
многоугольник В\В2... Вт в многоугольник А\А2... Ап. Так как
по условию эти многоугольники не совпадают, то хотя бы на одном
шаге от многоугольника В\В2...ВШ окажется отрезанной какая-то
ломаная. Следовательно, периметр многоугольника А\А2 ...Ап меньше,
чем периметр многоугольника В\В2 ...Вт, что и требовалось доказать.

/. Выпуклый многоугольник
161
В...
Рис.230. 1-й разрез: Рахсхв2...вгп_х < Рвхв2...вт, 2-й разрез:
PAxA2C2B3...Brn_x < PAxCxB2...Bm_x
67. Выпуклая линия. Понятие выпуклости можно ввести не толь-
только для многоугольников, но и для произвольных линий 0 , в том числе
для незамкнутых линий. Назовем опорной прямой данной линии L
такую прямую а, которая имеет с L хотя бы одну общую точку, причем
все точки линии L, не лежащие на прямой а, лежат по одну сторону
от а (рис.231, а). Линия называется выпуклой, если через любую
ее точку проходит хотя бы одна опорная прямая. Линии, изображенные
на рисунках 231, а, б и в, — выпуклые, а линия, изображенная на ри-
рисунке 231, г, — невыпуклая, так как через ее точку М не проходит
ни одной опорной прямой. Нетрудно доказать (сделайте это самостоя-
самостоятельно), что если многоугольник является выпуклым по определению
данному в п. 66, то он будет выпуклым и по общему определению
выпуклой линии, и наоборот.
а)
Рис. 231. а) Прямая а — опорная прямая линии L; б) и в) а и Ь — опорные
прямые; г) L — невыпуклая линия: любая прямая, проходящая через точку М,
не является опорной
1) Здесь и далее под словом «линия» подразумевается линия без самопере-
самопересечений.
6 С. Б. Кадомцев

162
Гл. 5. Многоугольники
Рис. 232. а и Ь — опорные пря-
прямые, М — угловая точка ли-
линии L
\L
Точка линии L называется угловой,
если через нее проходят по крайней
мере две опорные прямые (рис.232).
Ясно, что любая вершина выпуклого
многоугольника является его угловой
точкой.
Выпуклые линии обладают следую-
следующим свойством:
если три точки выпуклой линии
лежат на одной прямой, то эта пря-
прямая является опорной.
В самом деле, допустим, что
какие-то три точки А, В и С
выпуклой линии L лежат на од-
одной прямой. Докажем, что прямая АС является опорной.
Для определенности будем считать, что точка В лежит между А
и С (рис.233). Проведем через точку В опорную прямую а. Она
не может пересекать прямую АС, так
как в противном случае окажется,
что точки А и С линии L лежат
по разные стороны от опорной пря- ^ 7j ^
мой а. Следовательно, она совпада-
совпадает с прямой АС, т. е. прямая АС — рис 233
опорная. Утверждение доказано.
68. Замкнутая линия. В дальнейшем нас будут интересовать,
главным образом, замкнутые линии. При движении по такой линии L
от какой-либо ее точки А мы проходим через
каждую точку линии, а затем возвращаемся
в исходную точку А. Если в процессе этого
движения отметить какую-нибудь промежу-
промежуточную точку В, то линия L окажется разде-
разделенной на две части — путь от А до В и путь
от В до А (рис.234, а). Таким образом,
любые две точки замкнутой линии раз-
разделяют ее на две части.
Эти части называют дугами линии L.
В п. 2 мы говорили о том, что каждая
из трех точек А, В и С замкнутой линии
лежит между двумя другими. Теперь ясно,
из-за чего так получается. Действительно,
точки В и С разделяют линию на две дуги,
поэтому точка А лежит на одной из них, т. е.
лежит между точками В и С (рис.234, б).
По аналогичной причине точка В лежит
между А и С, г точка С — между А и В.
А
Рис. 234. а) Точки А
и В разделяют замкну-
замкнутую линию L на две дуги;
б) точка А лежит между
В и С, точка В лежит
между А и С, точка С
лежит между А и В

/. Выпуклый многоугольник 163
Замкнутые линии обладают следующим свойством:
если прямая и замкнутая линия имеют ровно одну общую точку,
то эта прямая — опорная.
В самом деле, если прямая а, проходящая через точку А замкнутой
линии L, не является опорной, то на линии L найдутся две точки —
В и С, лежащие по разные стороны от прямой а (рис.235). Поэтому
на дуге ВС, не содержащей точки А,
найдется точка D, лежащая на пря-
прямой а. Таким образом, если прямая,
проходящая через точку замкнутой ли-
линии L, не является опорной, то она
имеет с линией L по крайней мере еще
одну общую точку. Из этого и вытекает
справедливость нашего утверждения.
Примером замкнутой линии явля-
является окружность. Прямая, имеющая Рис. 235
с окружностью ровно одну общую точ-
точку, называется, как мы знаем, касательной к окружности. Из доказан-
доказанного утверждения следует, что касательная к окружности является
опорной прямой этой окружности. Верно и обратное: опорная пря-
прямая окружности является касательной к этой окружности (дока-
(докажите это утверждение).
69. Замкнутая выпуклая линия. Рассмотрим замкнутую выпук-
выпуклую линию L и прямую а, проходящую через точку А этой линии.
В соответствии с результатами пунктов 68 и 67 справедливы следую-
следующие утверждения:
если А — единственная общая точка прямой а и линии L,
то прямая а — опорная]
если прямая а и линия L имеют еще две общие точки В
и С (см. рис.233), то прямая а — опорная.
Осталось выяснить такой вопрос: что можно сказать о прямой а
в том случае, когда она имеет с линией L ровно две общие точки —
А и В? Оказывается, что в этом случае прямая а не является опорной,
что вытекает из следующего утверждения:
если замкнутая выпуклая линия и опорная прямая к ней имеют
две общие точки А и В, то все точки отрезка АВ принадлежат
этой линии.
Доказательство этого утверждения проведем методом от противно-
противного. Допустим, что на отрезке АВ существует точка С, не принадле-
принадлежащая данной линии L. Проведем через точку С прямую а, отличную
от АВ. Поскольку точки А и В лежат по разные стороны от а,
то прямая а пересекает одну из двух дуг АВ в некоторой точке М,
а другую — в некоторой точке N (рис.236). При этом точки М
и N лежат на одном луче с началом С (объясните, почему). Пусть,
например, точка М лежит между точками С и N и, следовательно,

164
Гл. 5. Многоугольники
Рис. 236
внутри треугольника ABN. Тогда лю-
любая прямая Ъ, проходящая через точ-
точку М, пересекает треугольник ABN
в двух точках, и поэтому какие-то
две вершины этого треугольника (т. е.
две точки линии L) оказываются ле-
лежащими по разные стороны от пря-
прямой Ъ. Это означает, что через точ-
точку М не проходит ни одной опорной
прямой линии L, что противоречит
условию (линия L — выпуклая). По-
Полученное противоречие и доказывает
наше утверждение.
Прямая, проходящая через точку линии, называется секущей по от-
отношению к линии, если эта прямая не является опорной. Мы доказали,
что
если прямая и замкнутая выпуклая линия имеют ровно две
общие точки, то эта прямая — секущая.
Справедливо и обратное утверждение:
секущая по отношению к замкнутой выпуклой линии имеет
с этой линией ровно две общие точки.
В самом деле, секущая не может иметь с линией только одну общую
точку, иначе она была бы опорной прямой, а это противоречит опре-
определению секущей. Следовательно, секущая и линия имеют по крайней
мере две общие точки. С другой сто-
стороны, если предположить, что общих
точек три, то секущая вновь окажется
опорной прямой, т. е. опять получится
противоречие. Таким образом, общих
точек ровно две, что и требовалось до-
доказать.
Рассмотрим теперь какую-нибудь
замкнутую выпуклую линию и секу-
секущую, пересекающую ее в точках А и В.
Фигура, состоящая из отрезка АВ и од-
одной из двух дуг АВ, называется кри-
криволинейным сегментом (рис.237). При
этом отрезок называется хордой криво-
криволинейного сегмента, а дуга — дугой
криволинейного сегмента.
70. Вписанный многоугольник. Многоугольник называется впи-
вписанным в замкнутую линию, если все его вершины лежат на этой
линии (рис.238, а). Что можно сказать об этом многоугольнике, если
данная линия — выпуклая? Ответ на этот вопрос дает следующая
теорема.
Рис. 237. При пересечении
замкнутой выпуклой линии се-
секущей получились два криво-
криволинейных сегмента. Один из
них выделен жирной линией.
Он состоит из отрезка (хорды)
АВ и дуги АВ

/. Выпуклый многоугольник
165
An A...
а) б) в)
Рис. 238. а) Многоугольник вписан в замкнутую линию
Теорема. Многоугольник, вписанный в замкнутую выпуклую
линию, является выпуклым.
Доказательство. Воспользуемся методом математической ин-
индукции. Рассмотрим сначала вписанный в замкнутую выпуклую ли-
линию L четырехугольник А1А2А3А4 и докажем, что этот четырех-
четырехугольник — выпуклый, т. е. лежит по одну сторону от любой пря-
прямой, проходящей через две его соседние вершины. Допустим, что это
не так. Пусть, например, точки Аз и А\ лежат по разные стороны
от прямой А\А2. Тогда прямая А\А^ пересекает отрезок А3А4 в неко-
некоторой точке М и не является опорной прямой линии L (рис.238, б).
Поскольку точки А2, А% и А4 лежат по одну сторону от опорной
прямой а к линии L в точке Аь то точка М лежит на луче AiA2.
По аналогичной причине точка М лежит на луче А2Аь Следовательно,
точка М лежит на отрезке А\А2, а это означает, что стороны А\А2
и А3А4 четырехугольника пересекаются в точке М. Но этого не может
быть, поэтому наше предположение ошибочно, точки Аз и А^ лежат
по одну сторону от прямой А\А2. Таким образом, весь многоуголь-
многоугольник А1А2А3А4 лежит по одну сторону от прямой А\А2. Аналогично
доказывается, что он лежит по одну сторону от прямых А2А%, А3А4
и А4А1, т.е. является выпуклым.
Предположим теперь, что теорема доказана для п-угольника
при некотором п ^ 4, и докажем, что тогда она верна и для
(п + 1)-угольника. Рассмотрим (п + 1)-угольник А\А2 ... Ап+\,
вписанный в замкнутую выпуклую линию, и проведем прямую А1А2
(рис.238, в). Согласно нашему предположению вписанный п-угольник
А\А2... Ап — выпуклый, поэтому его вершины Аз,...,Ап лежат
по одну сторону от прямой А1А2. По той же причине выпуклым
является n-угольник AiA2A4... Ап+Ь следовательно, его верши-
вершины А4,..., An+i также лежат по одну сторону от прямой А1А2. Таким
образом, все вершины A3, A4,...,An+i лежат в одной полуплоскости
с границей А1А2 (в той, в которой лежит точка А4), т.е. многоуголь-
многоугольник А1А2 ... An_|_i лежит по одну сторону от прямой А\А2. Аналогично
доказывается, что он лежит по одну сторону и от любой другой
прямой, проходящей через две соседние вершины. Но это и означает,
что многоугольник А\А2... Ап+\ — выпуклый. Теорема доказана.

166
Гл. 5. Многоугольники
71. Описанный многоугольник. Выпуклый многоугольник назы-
называется описанным около замкнутой линии L, если любая его сторона
лежит на опорной прямой этой линии и каждая точка линии лежит
либо на стороне многоугольника, либо в его внутренней области. Мно-
Многоугольники, изображенные на рисунках 239, а, б, являются описан-
описанными, а изображенные на рисунках 239, в, г не являются описанными
а)
б)
г)
Рис. 239
около данной линии: на рисунке 239, в одна из сторон многоугольника
не лежит на опорной прямой, а на рисунке 239, г многоугольник
не является выпуклым.
Если линия L не имеет угловых точек, то общие точки этой линии
и сторон описанного многоугольника не совпадают с вершинами много-
многоугольника (объясните, почему), а лежат между ними (см. рис.239 а, б).
Рассмотрим четырехугольник ABCD, описанный около окружно-
окружности. Так как опорные прямые к окружности являются касательными,
то все стороны этого четырехугольника касаются окружности 0 . Обо-
Обозначим равные отрезки касательных одними и теми же буквами так,
как это сделано на рисунке 240, а. Мы видим, что АВ + CD = а -\-Ь +
+ с + d, ВС + AD = а + Ъ + с + d, т. е. АВ + CD = ВС + AD. Итак,
если четырехугольник описан около окружности, то суммы его
противоположных сторон равны.
с С
D А
D
D' А
а)
Рис. 240
1) Обратно, если все стороны четырехугольника касаются окружности,
то этот четырехугольник — выпуклый (докажите это) и, следовательно, явля-
является описанным.

/. Выпуклый многоугольник 167
Из этого следует, что если суммы противоположных сторон четы-
четырехугольника не равны, или четырехугольник — невыпуклый, то в него
нельзя вписать окружность. В связи с этим возникает вопрос: можно
ли вписать окружность в любой выпуклый четырехугольник, у кото-
которого суммы противоположных сторон равны? Оказывается, можно:
если четырехугольник — выпуклый, и суммы его противополож-
противоположных сторон равны, то в него можно вписать окружность.
Пользуясь рисунками 240, б, в, докажите это утверждение само-
самостоятельно методом от противного (предполагается, что на этих рисун-
рисунках АВ + CD = ВС + AD, но окружность с центром О, касающаяся
сторон AD, АВ и ВС, не касается стороны CD, а касательная CD'
параллельна CD).
Задачи
193. Докажите, что длина любой диагонали многоугольника мень-
меньше половины его периметра.
194. Докажите, что сумма расстояний от любой точки плоскости
до вершин многоугольника больше полупериметра этого многоуголь-
многоугольника.
195. Может ли сумма расстояний от некоторой точки, лежащей
внутри четырехугольника, до его вершин быть больше периметра этого
четырехугольника? Ответ обоснуйте.
196. Докажите, что сумма расстояний от любой точки плоскости
до вершин пятиугольника больше полусуммы длин диагоналей этого
пятиугольника.
197. В выпуклом четырехугольнике ABCD диагональ АС равна
стороне AD. Докажите, что ВС меньше BD.
198. Докажите, что два выпуклых многоугольника равны, если
их стороны и углы соответственно равны.
199* Из точки внутренней области выпуклого многоугольника про-
проведены перпендикуляры к прямым, содержащим его стороны. Дока-
Докажите, что хотя бы одно из оснований этих перпендикуляров лежит
на самой стороне, а не на ее продолжении.
200* Докажите, что в любом выпуклом n-угольнике при п ^ 5
найдутся п диагоналей, сумма длин которых больше периметра этого
n-угольника, но меньше его удвоенного периметра.
201. Докажите, что сумма расстояний от произвольной точки О, ле-
лежащей внутри выпуклого многоугольника А\А2...Ап с периметром Р,
Р{п- 1)
до его вершин меньше величины —^——-.
202. Можно ли выпуклый стоугольник разрезать на 97 треуголь-
треугольников?
203. Докажите, что в любом выпуклом n-угольнике при п ^ 5
найдется не более трех нетупых углов.
204. Все углы выпуклого шестиугольника ABCDEF равны друг
другу. Докажите, что АВ + ВС = DE + EF.

168
Гл. 5. Многоугольники
205. Докажите, что для любого выпуклого семиугольника найдутся
такие две прямые, содержащие его диагонали, что либо угол между
ними меньше 13°, либо они параллельны.
206. Четырехугольник ABCD описан около окружности с цен-
центром О. Найдите сумму ZAOD + ZBOC.
207. Окружность отсекает на сторонах четырехугольника четыре
равные хорды. Докажите, что в этот четырехугольник можно вписать
окружность.
208. Докажите, что: а) если в выпуклом четырехугольнике ABCD
окружности, вписанные в треугольники ABC и ACD, касаются диа-
диагонали АС в одной точке, то в этот четырехугольник можно впи-
вписать окружность; б) если в четырехугольник ABCD можно вписать
окружность, то окружности, вписанные в треугольники ABC и ACD,
касаются диагонали АС в одной точке.
§ 2. Четырехугольники
72. Свойство диагоналей выпуклого четырехугольника. На ри-
рисунке 241 диагонали АС и BD выпуклого четырехугольника ABCD
пересекаются в точке О, а диагонали EG и FH невыпуклого четырех-
четырехугольника EFGH не пересекаются. Это наводит на мысль о справед-
справедливости следующей теоремы.
Теорема. Диагонали выпуклого четырехугольника пересека-
пересекаются, а невыпуклого — не пересекаются.
Доказательство. Рассмотрим выпуклый четырехугольник
ABCD (рис.241) и докажем, что его диагонали АС и BD
пересекаются. Диагональ АС разделяет четырехугольник на два
треугольника (см. п.66), поэтому прямая АС пересекает отрезок BD
в некоторой точке О. Точка О, будучи внутренней точкой диагонали
BD, лежит во внутренней области четырехугольника. Следовательно,
она лежит на отрезке АС, т. е. диагонали АС и BD пересекаются
в точке О.
Рассмотрим теперь невыпуклый четырехугольник EFGH. В таком
четырехугольнике какие-то две соседние вершины лежат по разные
В
Е

2. Четырехугольники 169
стороны от прямой, проходящей через две другие соседние вершины.
Пусть, например, вершины F и G лежат по разные стороны от прямой
ЕН (рис.241). Тогда лучи HF и EG лежат в разных полуплоскостях
с границей ЕН и, следовательно, не имеют общих точек. Значит,
и отрезки HF и EG не имеют общих точек, т. е. диагонали HF и EG
четырехугольника EFGH не пересекаются. Теорема доказана.
Следствие. Если диагонали четырехугольника пересекаются,
то этот четырехугольник — выпуклый.
Замечание. Мы знаем, что в каждом четырехугольнике най-
найдется диагональ, все внутренние точки которой лежат во внутренней
области многоугольника (задача 1 п. 65). Прямая, содержащая эту
диагональ, пересекает четырехугольник в двух точках (см. п. 65), т. е.
делит каждый из углов с вершинами в концах диагонали на два угла.
Следовательно,
в каждом четырехугольнике найдется диагональ, разделяющая
его на два треугольника (так, что внутренние области треугольников
лежат по разные стороны от прямой, содержащей эту диагональ).
Ясно, что в выпуклом четырехугольнике этим свойством облада-
обладают обе диагонали. Рассмотрим невыпуклый четырехугольник EFGH,
диагональ FH которого разделяет его на два треугольника (рис.241).
Прямая FH пересекает диагональ EG в точке, не лежащей на отрезке
FH, т. е. в точке внешней области четырехугольника. Следовательно,
все внутренние точки диагонали EG также принадлежат внешней
области многоугольника. Поэтому лучи EF, EH, GF и GH, а значит
и внутренние области треугольников EFG и EHG, лежат по одну
сторону от прямой EG. Иными словами, диагональ EG не разделяет
четырехугольник EFGH на два треугольника.
Воспользуемся нашими наблюдениями для решения такой задачи.
Задача 1. Доказать, что четырехугольник, две стороны кото-
которого параллельны, является выпуклым.
Решение. Рассмотрим четырех-
четырехугольник ABCD, стороны AD и ВС
которого параллельны (рис.242). Пусть,
например, диагональ АС разделяет его
на два треугольника. Тогда прямая АС
пересекает отрезок BD в некоторой точ-
точке О. Точка О, будучи точкой отрезка у ]j
BD, принадлежит полуплоскости с гра-
границей AD, содержащей точку В. Этой
же полуплоскости принадлежит точка С
(поскольку ВС || AD). Поэтому точка О лежит на луче АС. Ана-
Аналогично доказывается, что она лежит на луче С А. Следовательно,
точка О лежит на отрезке АС. Таким образом, диагонали АС и BD
четырехугольника ABCD пересекаются в точке О, а значит, этот
четырехугольник — выпуклый. Утверждение доказано.

170 Гл. 5. Многоугольники
73. Характеристическое свойство фигуры. В п. 72 было доказа-
доказано, что диагонали выпуклого четырехугольника пересекаются, и обрат-
обратно, если диагонали четырехугольника пересекаются, то этот четырех-
четырехугольник — выпуклый. Таким образом, выпуклые четырехугольники
обладают определенным свойством, которое выделяет их среди всех
четырехугольников, отличает от других (невыпуклых) четырехуголь-
четырехугольников. Такое свойство геометрических фигур называется характери-
характеристическим свойством.
Характеристическое свойство может быть положено в основу опре-
определения геометрической фигуры. Например, можно дать такое опре-
определение выпуклого четырехугольника: четырехугольник называется
выпуклым, если его диагонали пересекаются.
Это определение равносильно «старому» определению выпуклого
четырехугольника, данному в п. 65 (напомним, что «старое» определе-
определение относилось к любым многоугольникам, в том числе и к четырех-
четырехугольникам). В самом деле, если четырехугольник является выпуклым
по «старому» определению, то по доказанной в п. 72 теореме его диа-
диагонали пересекаются, и значит, он является выпуклым по «новому»
определению. И обратно, если четырехугольник является выпуклым
по «новому» определению, т. е. его диагонали пересекаются, то соглас-
согласно следствию из той же теоремы он является выпуклым и по «старому»
определению.
Утверждение о характеристическом свойстве фигуры можно сфор-
сформулировать с использованием словосочетания «тогда и только тогда».
Например:
диагонали четырехугольника пересекаются тогда и только то-
тогда, когда он является выпуклым.
В этом предложении содержатся два утверждения. Первое (оно свя-
связано со словом «тогда») выражает свойство выпуклого четырехуголь-
четырехугольника: если четырехугольник выпуклый, то его диагонали пересекают-
пересекаются. Второе (обратное) утверждение связано со словами «только тогда»,
оно выражает признак выпуклого четырехугольника: если диагонали
четырехугольника пересекаются, то четырехугольник — выпуклый.
74. Параллелограмм. Параллелограммом называется четырех-
четырехугольник, у которого противоположные стороны попарно параллель-
параллельны (рис.243). Параллелограмм является выпуклым четырехугольни-
четырехугольником (см. задачу 1 п. 72). Иногда одну из сторон параллелограмма
называют основанием, а перпендикуляр, проведенный из произвольной
точки противоположной стороны к прямой, содержащей основание —
высотой параллелограмма (рис.243, б).
Сформулируем несколько свойств и признаков параллелограмма.
Свойства параллелограмма. В параллелограмме:
1° противоположные стороны равны)
2° противоположные углы равны]

2. Четырехугольники
171
С
М
С
А
А
а)
N
б)
D
Рис. 243. а) АВ || CD, ВС || AD, четырехугольник ABCD — параллелограмм;
б) AD — основание, MN — высота параллелограмма
3° диагонали пересекаются и точкой пересечения делятся по-
пополам.
Признаки параллелограмма. Если в четырехугольнике:
4° две стороны равны и параллельны, или
5° диагонали пересекаются и точкой пересечения делятся попо-
пополам, или
6° противоположные стороны попарно равны,
то этот четырехугольник — параллелограмм.
Для доказательства утверждений 1°, 2° и 4° следует провести
диагональ (рис.244, а, б), для доказательства утверждений 3° и 5° —
две диагонали (рис.245), а для доказательства утверждения 6° —
ту из диагоналей, которая разделяет четырехугольник на два тре-
треугольника (рис.244, в). Соответствующие рассуждения проведите
самостоятельно.
Нетрудно заметить, что каждому из утверждений 1° и 3° о свой-
свойствах параллелограмма соответствует обратное утверждение, выража-
выражающее признак параллелограмма (подумайте, как сформулировать при-
признак параллелограмма, соответствующий свойству 2°). Таким образом,
каждое из этих свойств является характеристическим свойством парал-
параллелограмма. Можно объединить каждое из свойств с соответствующим
признаком в одно утверждение с использованием слов «тогда и только
тогда»:
противоположные стороны четырехугольника попарно равны
тогда и только тогда, когда четырехугольник — параллелограмм;
JC В
Рис. 244. a) AABD = ACDB, поэтому: 1° АВ = CD; 2° ZA = ZC;
б) AABD = ACDB, поэтому Zl = Z2, и, следовательно, AD \\ ВС;
в) AABD = ACDB, поэтому Zl = Z2, и, следовательно, AD \\ ВС

172
Гл. 5. Многоугольники
В
С
В
с
D
А
D
а)
Рис. 245. a) AD = ВС (см. 1°), поэтому AADO = АСВО и, следовательно,
АО = ОС, ВО = OD; б) AADO = АСВО, поэтому Zl = Z2 и, следователь-
следовательно, AD || ВС
диагонали четырехугольника пересекаются и точкой пересече-
пересечения делятся пополам тогда и только тогда, когда этот четырех-
четырехугольник является параллелограммом.
Заметим также, что каждое из этих утверждений допускает и иную
формулировку. Например, первое из них можно сформулировать так:
четырехугольник является параллелограммом тогда и только
тогда, когда его противоположные стороны попарно равны.
75. Теоремы Вариньона и Гаусса. Рассмотрим произвольный че-
четырехугольник ABCD, диагональ АС которого разделяет его на два
треугольника. Отметим середины К и L сторон АВ и ВС (рис.246).
Поскольку отрезок KL — сред-
средняя линия треугольника ABC, то
KL
1
АС и KL = -АС. Но то же
2
самое можно сказать и о сред-
средней линии NM треугольника ADC:
NM || АС и NM = ^
Сле-
Следовательно, KL \\ NM и KL =
= NM, т. е. две стороны четы-
четырехугольника KLMN равны и па-
параллельны. Значит, четырехуголь-
рис 246 ник KLMN — параллелограмм. Тем
самым мы доказали такую замеча-
замечательную теорему.
Теорема. Середины сторон произвольного четырехугольника
являются вершинами параллелограмма.
Эту теорему часто связывают с именем французского математика
и механика Пьера Вариньона A654-1722).
Вернемся к произвольному четырехугольнику ABCD с середи-
серединами сторон К, L, М и N (рис.247, а). Поскольку четырехуголь-
четырехугольник KLMN — параллелограмм, то отрезки КМ и LN пересекаются
в некоторой точке О, причем КО = ОМ и LO = ON. Отметим теперь
середины Р и Q диагоналей АС и BD (рис.247, б). Отрезок LP —

2. Четырехугольники
173
М
а)
средняя линия треугольника ABC, поэтому LP || АВ и LP = -
Аналогично из треугольника ABD находим: NQ || АВ и NQ = -i
Следовательно, LP || NQ (случай, когда прямые LP и NQ совпа-
совпадают, рассмотрите самостоятельно) и LP = NQ, поэтому четырех-
четырехугольник LPNQ — параллелограмм. Отсюда следует, что середина
отрезка PQ совпадает с серединой О отрезка LN. Кроме того, точка О
является серединой отрезка КМ. Таким образом, отрезки KM, LN
и PQ имеют общую середину — точку О. Тем самым, мы доказали
утверждение, которое называется теоремой Гаусса.
Теорема. В произвольном четырехугольнике три отрезка, два
из которых соединяют середины противоположных сторон, а тре-
третий — середины диагоналей, имеют общую середину.
Замечание. Отрезок, соединяющий середины диагоналей четы-
четырехугольника, может вырождаться в точку. Это будет в том случае,
когда данный четырехугольник — параллелограмм.
Отметим также, что справедливость теоремы Гаусса можно устано-
установить из физических соображений, если заметить, что точка О является
центром тяжести системы четырех одинаковых масс, расположенных
в точках А, В, С и D (объясните, почему это так).
76. Прямоугольник, ромб и квадрат.
Прямоугольником называется параллелограмм, у которого все
углы — прямые.
В этом определении слово «параллелограмм» можно заменить сло-
словами «выпуклый четырехугольник», т.е. можно дать такое опреде-
определение:
прямоугольником называется выпуклый четырехугольник, у ко-
которого все углы — прямые.
Если же оставить в первом определении слово «параллелограмм»,
то можно не требовать, чтобы все углы были прямыми. Достаточно
потребовать, чтобы всего лишь один из углов был прямым. Иначе
говоря, определение прямоугольника можно дать и в такой форме:

174 Гл. 5. Многоугольники
прямоугольником называется параллелограмм, у которого один
из углов — прямой.
Попробуйте доказать равносильность этих трех определений.
Заметим, что каждое из данных определений использует то или
иное характеристическое свойство прямоугольника, выделяющее его
из всех параллелограммов (первое и третье определения) или даже
из всех выпуклых четырехугольников (второе определение). Все эти
характеристические свойства связаны с углами прямоугольника. У пря-
прямоугольника есть и характеристическое свойство, связанное не с угла-
углами, а с отрезками, именно с его диагоналями:
диагонали прямоугольника равны (свойство прямоугольника);
если диагонали в параллелограмме равны, то этот параллело-
параллелограмм — прямоугольник (признак прямоугольника).
Докажите эти утверждения самостоятельно.
Ясно, что свойство и признак прямоугольника можно объединить
в одном утверждении:
параллелограмм является прямоугольником тогда и только то-
тогда, когда его диагонали равны.
Перейдем теперь к определению ромба и его характеристическим
свойствам.
Ромбом называется параллелограмм, у которого все стороны
равны.
В этом определении слово «параллелограмм» можно заменить сло-
словом «четырехугольник». Получится такое определение:
ромбом называется четырехугольник, у которого все стороны
равны.
Если же оставить в первом определении слово «параллелограмм»,
то можно не требовать равенства всех сторон. Достаточно потребовать,
чтобы были равны какие-то две смежные стороны, т. е. можно дать
и такое определение:
ромбом называется параллелограмм, у которого две смежные
стороны равны.
Докажите самостоятельно равносильность этих трех определений.
Рассмотрим характеристические свойства ромба, связанные с его
диагоналями. Прежде всего заметим, что
диагонали ромба:
а) взаимно перпендикулярны;
б) делят его углы пополам (пользуясь рисунком 248, докажите эти
утверждения самостоятельно).
Сформулируем и докажем обратные утверждения (признаки ромба).
Задача 2. Доказать, что параллелограмм является ромбом,
если выполнено любое из следующих условий:
1° диагонали параллелограмма взаимно перпендикулярны]
2° диагональ параллелограмма делит пополам углы при верши-
вершинах, которые она соединяет.

2. Четырехугольники
175
Решение. 1°. Пусть в параллелограмме ABCD диагонали АС
и BD взаимно перпендикулярны (рис.249, а). Так как точкой пересече-
пересечения они делятся пополам, то прямоугольные треугольники АОВ, ВОС,
COD и DO А равны друг другу по двум катетам. Отсюда следует, что
гипотенузы этих треугольников равны: АВ = ВС = CD = DA, т.е.
равны стороны параллелограмма, и значит, параллелограмм ABCD —
ромб.
в
D
а) б)
Рис. 249
2°. Пусть диагональ BD параллелограмма ABCD делит углы В
и D пополам (рис.249, б). Так как противоположные углы В и D
параллелограмма равны, то углы 1, 2, 3 и 4 равны друг другу.
Следовательно, равнобедренные треугольники ABD и CBD равны
по стороне (BD — общая сторона) и двум прилежащим углам. Отсюда
следует, что АВ = ВС = CD = DA, т. е. параллелограмм ABCD —
ромб, что и требовалось доказать.
Теперь можно сформулировать такое утверждение о характеристи-
характеристических свойствах ромба:
параллелограмм является ромбом тогда и только тогда, когда
выполнено любое из следующих условий:
1° его диагонали взаимно перпендикулярны;
2° его диагональ делит пополам углы при вершинах, которые
она соединяет.
Квадрат является и прямоугольником, и ромбом. Поэтому квадрат
обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Можно дать различные определения квадрата, например:
1° квадратом называется прямоугольник, у которого все сторо-
стороны равны]
2° квадратом называется ромб, у которого все углы прямые.
Придумайте сами еще несколько определений квадрата и докажи-
докажите их равносильность. Сформулируйте также несколько утверждений
о характеристических свойствах квадрата.

176
Гл. 5. Многоугольники
А
Рис. 250
Характеристические свойства ромба часто используются при реше-
решении задач. Приведем пример.
Задача 3. Доказать, что диагонали четырехугольника равны
тогда и только тогда, когда отрезки, соединяющие середины его
противоположных сторон, взаимно перпендикулярны.
Решение. Рассмотрим четырехугольник ABCD, в котором точ-
точки К, L, М, N - середины сторон АВ, ВС, CD, DA (рис.250).
1°. Пусть KM JL LN. Дока-
Докажем, что АС = BD. Четырехуголь-
г> ^Т^Г / ник KLMN — параллелограмм (по
теореме Вариньона), причем KL = ^АС,
LM = -BD (по теореме о средней линии
треугольника). Так как диагонали КМ
и LN параллелограмма KLMN взаимно
перпендикулярны, то KLMN — ромб (за-
(задача 2 этого пункта), значит, KL = LM.
Следовательно, АС = BD.
2°. Обратно, пусть АС = BD. Докажем, что KM JL LN. Снова
воспользуемся тем, что четырехугольник KLMN — параллелограмм
(по теореме Вариньона), причем KL = ^AC, LM = -BD (по теореме
о средней линии треугольника). Так как АС = BD, то KL = LM,
значит, KLMN — ромб. Поэтому его диагонали взаимно перпендику-
перпендикулярны: KM JL LN.
77. Трапеция. Трапецией называется четырехугольник, у которого
две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются ее основаниями, а две
другие стороны — боковыми сторонами (рис.251, а). Перпендикуляр,
проведенный из произвольной точки одного из оснований к прямой, со-
содержащей другое основание, называют высотой трапеции. Трапеция —
выпуклый четырехугольник (см. задачу 1 п. 72).
Трапеция называется равнобедренной, если ее боковые стороны
равны (рис.251, б). Трапеция, один из углов которой — прямой, на-
в м с
в)
Рис. 251. а) Трапеция ABCD: AD и ВС — основания, АВ и CD — боковые
стороны, MN — высота; б) равнобедренная трапеция; в) прямоугольная тра-
трапеция

2. Четырехугольники 177
зывается прямоугольной (рис.251, в). Отметим, что в прямоугольной
трапеции ровно два угла являются прямыми. Эти углы прилегают
к боковой стороне, перпендикулярной к основаниям трапеции.
Средней линией трапеции
называется отрезок, соединя-
соединяющий середины ее боковых
сторон. Что можно сказать
о средней линии MN трапе- Mj.
ции ABCD (рис.252)?
Прежде всего, если провести
через точку М прямую, парал-
параллельную основаниям трапеции, " ~
то эта прямая, согласно теоре- рис 252
ме Фалеса, разделит отрезок CD
пополам, т. е. пройдет через точку N. Следовательно, средняя ли-
линия MN параллельна основаниям трапеции.
Далее, проведем диагональ АС. По теореме Фалеса прямая MN
делит отрезок АС пополам, т. е. проходит через середину Р этого
отрезка. Поэтому отрезки МР и PN — средние линии треугольни-
треугольников ABC и ACD. Пользуясь свойством средней линии треугольника,
получаем:
мр = ±вс, pn = -L
Следовательно,
MN = МР + PN = ЬвС + AD).
Итак,
средняя линия трапеции параллельна ее основаниям и равна
их полусумме.
Замечание. Свойство средней линии трапеции мы установили,
опираясь на свойство средней линии треугольника. В свою очередь,
свойство средней линии треугольника может быть выведено из свой-
свойства средней линии трапеции следующим образом. Пусть в трапе-
трапеции ABCD (см. рис. 252) вершины А, В и D неподвижны, а вершина С
приближается к В. При любом положении вершины С справедливы
соотношения: «
MN || AD и MN = ^(ВС + AD).
Когда вершина С совпадет с вершиной Б, трапеция ABCD перей-
перейдет в треугольник ABD, а ее средняя линия MN — в среднюю линию
этого треугольника. При этом ВС станет равным нулю и мы получим:
MN || AD и MN = X-AD,
т. е. средняя линия MN треугольника ABD параллельна стороне AD
этого треугольника и равна ее половине. Тем самым, можно сказать,

178 Гл. 5. Многоугольники
что теорема о средней линии трапеции является (в указанном смысле)
обобщением теоремы о средней линии треугольника.
Задачи
209. Внутри выпуклого четырехугольника укажите точку, сумма
расстояний от которой до вершин четырехугольника имеет наименьшее
значение.
210. Докажите, что сумма двух противоположных сторон выпукло-
выпуклого четырехугольника меньше суммы длин его диагоналей.
211. Докажите, что сумма длин диагоналей выпуклого четырех-
четырехугольника больше полупериметра, но меньше периметра этого четы-
четырехугольника.
212. Дан выпуклый четырехугольник ABCD. Периметр треуголь-
треугольника ABD меньше периметра треугольника ACD. Докажите, что АВ
меньше АС.
213. Докажите, что в любом выпуклом пятиугольнике найдутся
три диагонали, из которых можно составить треугольник.
214. Длины сторон выпуклого четырехугольника выражаются раз-
различными целыми числами. Докажите, что хотя бы одна из его диаго-
диагоналей больше -.
215. Докажите, что прямые, содержащие стороны параллелограм-
параллелограмма, отсекают на прямой, параллельной одной из его диагоналей, равные
отрезки.
216. Докажите, что если в шестиугольнике ABCDEF АВ = DE,
ВС = ЕЕ, CD = FA, АВ \\ DE, ВС \\ ЕЕ, CD \\ FA, то диагона-
диагонали AD, BE и CF пересекаются в одной точке.
217. Точки М и Т — середины сторон AD и ВС параллелограм-
параллелограмма ABCD. Докажите, что прямые AT и СМ делят диагональ BD
на три равных отрезка.
218. Середины сторон АВ и CD, ВС и ED выпуклого пятиуголь-
пятиугольника ABCDE соединены отрезками, точки Н и К — середины этих
отрезков. Докажите, что отрезок НК параллелен АЕ и равен одной
четверти АЕ.
219. Постройте отрезок с концами на сторонах данного угла так,
чтобы он делился данной точкой, лежащей внутри этого угла, на два
равных отрезка.
220. Даны три точки А, М и Р, не лежащие на одной прямой.
Постройте параллелограмм ABCD так, чтобы точки М и Р оказались
серединами сторон ВС и CD.
221. Найдите множество середин всех отрезков, концы которых
лежат на двух данных непараллельных отрезках (по одному на каждом
отрезке.)
222. Центром окружности, вписанной в четырехугольник, является
точка пересечения его диагоналей. Докажите, что этот четырехуголь-
четырехугольник — ромб.

2. Четырехугольники 179
223. Диагонали выпуклого четырехугольника разбивают его на че-
четыре треугольника с равными периметрами. Докажите, что этот четы-
четырехугольник — ромб.
224. Две окружности пересекаются в точках А и В. а) Докажите,
что если через точки А и В провести две параллельные прямые,
то части этих прямых, заключенные внутри окружностей, окажутся
равными, б) С помощью циркуля и линейки проведите через точку А
прямую, часть которой, заключенная внутри данных окружностей,
равна данному отрезку.
225. В прямоугольнике ABCD АВ : AD =1:3. Сторона AD
точками Е и М делится на три равные части. Найдите сумму ABE A +
+ ZBMA + АВВА.
226. Отрезок, соединяющий середины диагоналей выпуклого че-
четырехугольника ABCD, равен отрезку, соединяющему середины сто-
сторон ВС и AD. Найдите угол между прямыми АВ и CD.
227. Докажите, что трапеция является равнобедренной тогда
и только тогда, когда: а) углы при одном из оснований трапеции равны;
б) диагонали трапеции равны.
228. На основании AD трапеции ABCD имеется такая точка Е,
что периметры треугольников ABE, ВСЕ и CDE равны. Докажите,
что AD = 2BC.
229. В трапеции ABCD с основаниями ВС и AD биссектрисы
углов А и В пересекаются в точке М, а биссектрисы углов С и D —
в точке Т. Докажите, что отрезок МТ параллелен основаниям трапе-
трапеции, и найдите его длину, если AD + ВС = а, АВ + CD = Ъ.
230. Диагонали трапеции взаимно перпендикулярны, а длина
ее средней линии равна с. Найдите длину отрезка, соединяющего
середины оснований трапеции.
231. Основания трапеции равны а и Ъ (а > Ь). Найдите: а) длину
отрезка, высекаемого диагоналями на средней линии; б) длину отрезка,
соединяющего середины оснований, если дополнительно известно, что
сумма углов при одном из них равна 90°.
232. Докажите, что если стороны одной трапеции соответственно
равны сторонам другой трапеции, то такие трапеции равны.
233. Внутри равностороннего треугольника ABC взята произволь-
произвольная точка М. Докажите, что из отрезков MA, MB и МС можно
составить новый треугольник, вписанный в треугольник ABC так,
что на каждой стороне треугольника ABC будет лежать ровно одна
вершина нового треугольника.
234. Постройте трапецию: а) по четырем сторонам; б) по двум
основаниям и двум углам при одном из них; в) по двум основаниям
и двум диагоналям.

Глава 6
ПЛОЩАДЬ
§ 1. Равносоставленные многоугольники
78. Задачи на разрезание многоугольников. Пусть М и N —
какие-нибудь точки, лежащие на сторонах многоугольника. Если все
точки ломаной (или отрезка), соединяющей точки М и N (кроме
самих точек М и N), лежат внутри много-
многоугольника, то говорят, что ломаная (отре-
(отрезок) разбивает многоугольник на два мно-
многоугольника. На рисунке 253 ломаная MN
разбивает многоугольник F на многоуголь-
многоугольники F\ и F2. На рисунке 254, а много-
многоугольник F разбит на многоугольники F\,
F2, F3, а на рисунке 254, б шестиугольник
разбит на треугольники Ai, A2, A3, А4.
Пусть многоугольник F разбит
на многоугольники F\, F2,..., F^. Рас-
Рассмотрим какие-нибудь многоугольни-
многоугольники F[, FrJ,..., F^, соответственно равные F\, F2,..., F^. Говорят, что
многоугольник F можно разрезать на многоугольники F{, F2X,..., F^,
а из многоугольников F[, F^,..., F^ можно составить многоуголь-
многоугольник F. Задачи, в которых требуется разрезать данный многоугольник
на какие-то определенные части (многоугольники) или, наоборот, со-
составить из данных многоугольников новый многоугольник с заданными
Рис. 253
Рис. 254

/. Равно со став ленные многоугольники
181
свойствами, называются задачами на разре-
разрезание многоугольников. Рассмотрим несколько
примеров таких задач.
Задача 1. Разрезать треугольник на че-
четыре равных треугольника.
Решение. Как решить эту задачу, мы зна-
знаем. Проведем средние линии данного треуголь-
треугольника (рис.255). В результате треугольник ока-
окажется разрезанным на четыре равных треуголь-
треугольника. Рис- 255
Задача 2. Из квадрата со стороной а вырезан квадрат со сто-
стороной - так, как показано на рисунке 256, а. Разрезать полученную
а
а)
Рис. 256
фигуру на четыре равных многоугольника.
Решение. Данная фигура состоит из трех квадратов со сто-
стороной -. Разрежем каждый из них на четыре квадрата со сторо-
стороной - (рис.256, б). В результате наша фигура окажется разрезанной
на четыре равные части, каждая из которых состоит из трех квадратов
со стороной -.
Задача 3. Доказать, что любой многоугольник можно раз-
разрезать на треугольники, вершинами которых являются вершины
многоугольника.
Решение. Если данный многоугольник А\А^ ... Ап — выпуклый,
то для доказательства этого утверждения достаточно провести его
диагонали, имеющие общий конец (рис.257, а). Если же данный мно-
многоугольник — невыпуклый, то будем рассуждать так.
Воспользуемся методом математической индукции. Поскольку все
внутренние точки одной из диагоналей четырехугольника AxAzA^A^
лежат в его внутренней области, то эта диагональ разрезает четырех-
четырехугольник на два треугольника с вершинами А\, А^ Лз и А±. Таким
образом, при п = 4 утверждение верно. Допустим, что оно доказано
для всех п, удовлетворяющих неравенствам 4 ^ п ^ /с, и докажем,

182
Гл. 6. Площадь
А.
Ап
Рис. 257
что в таком случае оно верно и для п = к + 1. Пусть, например, все
внутренние точки диагонали А\Ат многоугольника А\Аъ... Ап лежат
в его внутренней области (см. задачу 1 п.65). Тогда эта диагональ
разрезает многоугольник на m-угольник А\А^... Аш и (п — т + 2)-
угольник А\Ат... Ап (рис.257, б). При этом т < п, т > 2, следова-
следовательно, п — m + 2 < п. Таким образом, в каждом из полученных мно-
многоугольников число сторон не превосходит к. Следовательно, каждый
из них можно разрезать на треугольники, вершинами которых явля-
являются вершины этих многоугольников, т. е. вершины многоугольника
А\А2... Ап. Утверждение доказано.
Отметим, что задачи на разрезание не всегда имеют единствен-
единственное решение. Так, рисунок 258, а, б, в иллюстрирует три различных
решения задачи о разрезании данного квадрата на четыре равные
части (доказательство проведите самостоятельно).
В задачах 1, 2 и 3 требовалось разрезать данный многоугольник
на какие-то определенные части. Приведем пример обратной задачи:
из данных многоугольников требуется составить многоугольник с за-
заданными свойствами.
Задача 4. На рисунке 259 изображен квадрат ABCD, разре-
разрезанный на четыре части (точки Р, М, N и Q — середины его сторон,
б)
Рис. 258

/. Равно со став ленные многоугольники
183
L — середина отрезка PQ). Составить из этих частей равнобедрен-
равнобедренный треугольник.
Решение. Обратимся к рисунку 260. По условию АР = ВР =
= ВЫ = CM = CN = DN = DQ = AQ, углы А, В, С и D - прямые,
ZAPQ + ZBPL =180°, ZAQP + ZDQL =180°, ZLMB + ZLMC =
= 180°, ZLND + ZLNC = 180°. Поэтому если сдвинуть четырех-
четырехугольники в направлениях, указанных стрелками, то они составят
с треугольником APQ один равнобедренный треугольник с основа-
основанием, вдвое большим, чем PQ, и следовательно, равным диагонали
квадрата.
79. Равносоставленные многоугольники. Задача на разрезание
многоугольника существенно усложнится, если поставить ее так: раз-
разрезать данный многоугольник на такие части, из которых можно соста-
составить другой многоугольник с определенными свойствами. Например,
задачу 4 из предыдущего пункта можно переформулировать так: разре-
разрезать квадрат на такие части, из которых можно составить равнобедрен-
равнобедренный треугольник с основанием, равным диагонали квадрата. Решить
такую задачу значительно труднее — ведь надо еще догадаться, как
именно разрезать квадрат!
Если один многоугольник разрезать на части и составить из них
другой многоугольник, то такие многоугольники называются равносо-
ставленными. Например, рассмотренные в задаче 4 квадрат и равно-
равнобедренный треугольник являются равносоставленными.
Отметим, что
если каждый из двух многоугольников равносоставлен с тре-
третьим многоугольником, то они равносоставлены.
В самом деле, пусть каждый из многоугольников Р и Q равносо-
равносоставлен с многоугольником F. Разрежем многоугольник F следующим
образом: сначала проведем все разрезы, необходимые для составления
В М с
м
D
М
Q
Рис. 259
Рис. 260

184 Гл. 6. Площадь
многоугольника Р, а затем все разрезы, необходимые для составления
многоугольника Q. В результате многоугольник F окажется разрезан-
разрезанным на части, из которых можно составить как многоугольник Р, так
и многоугольник Q. Но это и означает, что многоугольники Р и Q
равносоставлены.
Рассмотрим два примера равносоставленных многоугольников.
Задача 5. Доказать, что треугольник равносоставлен с парал-
параллелограммом, у которого основание совпадает с данной стороной
треугольника, а высота равна половине соответствующей высоты
треугольника.
Решение. Проведем среднюю линию DE треугольника ABC, па-
параллельную данной стороне АС, и продолжим ее до пересечения в точ-
точке F с прямой CF, параллельной АВ (рис.261). Треугольник DBE
равен треугольнику FCE (объясните почему), следовательно, паралле-
параллелограмм ADFC равносоставлен с треугольником ABC, причем высота
параллелограмма равна половине высоты треугольника (докажите это).
Задача 6. Доказать, что
параллелограмм равносостав-
равносоставлен с прямоугольником, одна
из смежных сторон которого
равна данной стороне паралле-
параллелограмма, а другая — высоте
параллелограмма, проведенной
к этой стороне.
Решение. Пусть AD —
данная сторона параллелограм-
параллелограмма ABCD. Примем эту сторо-
сторону за основание и проведем вы-
Рис- 261 соты ВН и СК. Докажем, что
параллелограмм ABCD равносо-
равносоставлен с прямоугольником НВСК, сторона ВС которого равна ос-
основанию AD параллелограмма, а сторона ВН является высотой па-
параллелограмма. Возможны два случая: 1° проекция одной из вершин
параллелограмма на прямую, содержащую основание (т. е. одна из то-
точек Н, К), принадлежит основанию; 2° проекция ни одной из вершин
параллелограмма на прямую, содержащую основание, не принадлежит
основанию. Рассмотрим эти случаи в отдельности. Для определенности
будем считать, что угол BAD — острый. При этом условии точка К
не принадлежит отрезку AD, а точка Н может либо принадлежать,
либо не принадлежать ему.
1°. Точка Н принадлежит отрезку AD (рис.262, а). В этом слу-
случае равносоставленность параллелограмма ABCD и прямоугольника
НВСК вытекает из равенства прямоугольных треугольников АВН
и DC К (они равны по гипотенузе и катету).
2°. Точка Н не принадлежит отрезку AD, т. е. АН > AD. Разделим
сторону АВ на п равных отрезков и через их концы проведем прямые,

/. Равно со став ленные многоугольники
185
В
В С
A D
б)
Рис. 262
параллельные AD (рис.262, б). В результате параллелограмм ABCD
окажется разрезанным на п параллелограммов с основаниями, равными
AD. Если число п достаточно велико (п ^ x{j)> то в каждом из этих
параллелограммов проекция одной из вершин на прямую, содержащую
основание, принадлежит основанию (пользуясь теоремой Фалеса, дока-
докажите это самостоятельно). Следовательно, согласно доказанному в 1°,
каждый из них равносоставлен с прямоугольником, одна из смежных
сторон которого равна основанию параллелограмма, а другая является
его высотой. Но указанные прямоугольники равносоставлены с пря-
прямоугольником НВСК (рис.262, в, г). Следовательно, параллелограмм
ABCD также равносоставлен с этим прямоугольником. Утверждение
доказано.
Задачи на разрезание допускают дальнейшее усложнение: требуется
разрезать несколько данных многоугольников на части и составить
из них новый многоугольник определенного вида. Или, наоборот, тре-
требуется разрезать данный многоугольник на части и составить из них
несколько новых многоугольников. Эти задачи обычно формулируют
так: доказать, что многоугольник F равносоставлен с многоугольника-
многоугольниками F\, F2,..., .Ffc. Приведем пример такой задачи.
Задача 7. Доказать, что пять равных квадратов
равносоставлены с одним квадратом.
Решение. Возьмем четыре из пяти данных квадра-
квадратов и разрежем каждый из них на треугольник и трапе-
трапецию так, как показано на рисунке 263. Четыре трапеции
приложим к сторонам пятого квадрата так, как пока-
показано на рисунке 264. Наконец приложим треугольники
катетами к основаниям трапеций (рис.265). Полученная
фигура — квадрат (докажите это).
80. Разрезание квадрата на неравные квадраты. Из всевозмож-
всевозможных задач на разрезание многоугольников следует выделить задачу
о разрезании квадрата на меньшие квадраты, любые два из которых
не равны друг другу. Эта простая по формулировке задача оказалась
в действительности очень трудной. До конца 30-х годов XX в. многие
геометры считали, что она вообще не имеет решения. Лишь в 1939 г.
Рис. 263

186
Гл. 6. Площадь
Рис. 264
Рис. 265
немецкий математик Р. Шпраг сумел разбить квадрат на 55 попарно
неравных квадратов. Приблизительно в это же время группа ученых
Кембриджского университета в Англии установила связь между зада-
задачей о разрезании квадрата и теорией электрических цепей в физике 0 .
Это позволило им в 1940 г. разрезать квадрат на 28 попарно нерав-
неравных квадратов, чуть позже — на 26. Наконец в 1948 г. англичанин
Ф. Г. Уилкокс сумел уменьшить число квадратов до 24. Это разбиение
квадрата изображено на рисунке 266 (число внутри квадрата означает
длину его стороны).
А
А
55
56
39
164-
3
18
1
20
38
64
31
33
8
30
29
35
1
51
/ 8
43
С
16
с
4
3
\
5
1 20
14
В
Рис. 266. Квадрат ABCD со стороной АВ = 175 разбит на 24 попарно нерав-
неравных квадрата; числа указывают длины сторон соответствующих квадратов
х) Об этом можно прочитать в книге Б. А. Кордемского и Н.В. Русалева
«Удивительный квадрат» (М.: Столетие, 1994).

/. Равно со став ленные многоугольники 187
Любопытно, что аналогичная задача о разбиении куба на попарно
неравные кубы меньших размеров значительно проще. Ответ здесь от-
отрицательный, т. е. такое разбиение невозможно. Докажем это методом
от противного. Предположим, что на столе перед нами лежит куб, раз-
разбитый на попарно неравные кубики. Ясно, что нижняя грань куба будет
при этом разбита нижними кубиками на попарно неравные квадраты.
Самый маленький из этих квадратов не может прилегать к стороне
нижней грани куба, так как в противном случае
нельзя будет заполнить зазор между прилегаю-
прилегающими к нему большими квадратами (рис.267).
Следовательно, самый маленький из кубиков,
примыкающих к нижнему основанию, окружен
со всех сторон кубами больших размеров. Эти
кубы создают вокруг него своеобразный «забор»,
поэтому сверху на него могут опираться только
кубы еще меньших размеров. Выберем из них
самый маленький и применим к нему те же рас-
рассуждения, что и к его предшественнику. Мы по- ^ис- ^67. Нижняя
лучим, что он тоже должен быть обложен куба- грань куба„ и лежа"
ми больших размеров, создающими вокруг него щие на не^ основа"
^ r r ' rJ ния кубиков
«забор», и т.д. Повторяя рассуждения, мы по-
получим неограниченную последовательность все меньших и меньших
кубов. Но это противоречит нашему предположению о том, что куб
разбит на конечное число попарно неравных кубиков. Следовательно,
наше предположение ошибочно: куб нельзя разбить на попарно нерав-
неравные кубы.
Задачи
235. Докажите, что трапеция равносоставлена с параллелограммом,
основание которого равно средней линии трапеции, а высота — высоте
трапеции.
236* В шестиугольнике ABCDEF АВ = ^EF, ВС = ^AF, ZA =
= ZB = ZBCD = ZD = ZE = ZF = 90° (рис.268). Разрежьте его
на четыре равных многоугольника, из которых можно составить пря-
прямоугольник.
237. Разрежьте произвольный треугольник на три таких много-
многоугольника, из которых можно составить прямоугольник.
238. Прямоугольный треугольник с острым углом в 30° разрежьте:
а) на три равных прямоугольных треугольника; б) на четыре равных
прямоугольных треугольника.
239. Прямоугольник, стороны которого равны 4 и 9, разрежьте
на два равных многоугольника так, чтобы из них можно было соста-
составить квадрат.
240. Даны два квадрата со сторонами 6 и 8. Разрежьте каждый
из квадратов на два многоугольника так, чтобы из полученных четырех
частей можно было составить квадрат со стороной 10.

188
Гл. 6. Площадь
241* Фигуру, составленную из пяти равных квадратов, изображен-
изображенную на рисунке 269, разрежьте на части, из которых можно составить
квадрат.
F Е
С
D
А В
Рис. 268
С
D
Рис. 269
242* Докажите, что разносторонний треугольник нельзя разрезать
на два равных треугольника.
243. Через вершины А и D параллелограмма ABCD проведены две
параллельные прямые — АЕ и DK, где Е и К — точки прямой ВС.
Из точек А и Е проведены перпендикуляры AF и EG к прямой DK.
Докажите, что параллелограмм ABCD и прямоугольник AEGF рав-
носоставлены.
§ 2. Понятие площади
81. Измерение площади многоугольника. Измерение площадей
многоугольников проводится аналогично измерению длин отрезков.
За единицу измерения площадей принимается квадрат, сторона ко-
которого равна единице измерения отрезков. Площадь этого квадрата
считается равной единице. Измерить площадь многоугольника — зна-
значит узнать, сколько раз единица измерения и ее части укладываются
в данном многоугольнике. Это число и принимается за его площадь
при данной единице измерения.
Практически измерение площади многоугольника можно осуще-
осуществить так. Расчертим лист бумаги на квадраты со стороной, равной
единице измерения отрезков, и наложим на него данный многоуголь-
многоугольник. Пусть т — число квадратов, полностью покрытых многоуголь-
многоугольником, an — число квадратов, покрытых многоугольником лишь
частично (рис.270). Число S, выражающее площадь многоугольника,
заключено, таким образом, между числами s\ = т и S\ = т + п:

2. Понятие площади
189
Каждое из чисел s\ и S\ может рассматри-
рассматриваться как приближенное значение числа S (s\ —
с недостатком, S\ — с избытком). Для более точ-
точного измерения площади многоугольника разобьем
каждый из п частично покрытых квадратов на 100
равных квадратиков. Ясно, что сторона каждого
из этих квадратиков равна 1/10, площадь каждого
из них равна 1/100. Пусть т\ — число квадра-
квадратиков, полностью покрытых нашим многоугольни-
многоугольником, щ — число частично покрытых квадратиков.
Теперь можно сказать, что число S заключено между числами 52 =
= га +
Рис. 270
ГП\ а .7711+711 / о / о гт
—— и ^2 = тп Н 77-—, т. е. 52 < о < О2- При этом, очевидно,
100 100
52 > 5ь С другой стороны, S2 ^ S\, поскольку фигура с площадью S\
содержит все квадратики, на которые разбиты п квадратов, а фигура
с площадью $2 — только те из этих квадратиков, которые полностью
или частично покрыты данным многоугольником. Итак,
51 < 52 < 54 #2 < S\.
Разобьем теперь каждый из щ частично покрытых квадратиков
на 100 еще меньших равных квадратиков со стороной —^ и повторим
наши рассуждения. Получим новые неравенства: 53 ^ S ^ S$, при-
причем 5з > 52, а S3 ^ S2, поэтому
si <S2<s3<5<53<52<5i.
Вновь повторим аналогичные рассуждения и т. д. Для любого нату-
натурального числа к получатся неравенства:
52
Sk < S < Sk
причем разность Sk — Sk при неограниченном увеличении к будет
стремиться к нулю. Это следует из того, что разность Sk — Sk равна
-I
площади фигуры, составленной из квадратиков со стороной —^—р и по-
покрывающей ломаную, ограничивающую многоугольник (на рисунке 271
данный многоугольник изображен в увеличенном масштабе). С уве-
увеличением к эта фигура все ближе и ближе «сжимается» к ломаной
и поэтому ее площадь стремится к нулю (см. замечание 1 в конце
пункта). Следовательно, числа Sk и Sk будут стремиться к S. В этом
и состоит процесс измерения площади многоугольника, позволяющий
найти приближенное значение S с произвольной точностью 0 .
1) Существование точного значения S вытекает из теоремы Вейерштрасса,
доказанной в приложении 1 «Снова о числах» в конце книги.

190
Гл. 6. Площадь
х
х
х
X
х
X
х
У
<
к
К
%
ДА,
щ
ЛЛ
i
W
ЛЛ
Лл
YY
W
xV
YY
YY
ЛЛ
/У4
Vx
ЛЛ
ЛЛ
YY
88
i<Y;
ЛЛ
щ
ЛЛ
со
Рис. 271
В связи с описанным процессом измерения площади многоугольни-
многоугольника возникает вопрос: а если положить данный многоугольник на рас-
расчерченный лист бумаги иначе (рис.272), будет ли результат измерения
тот же? В частности, верно ли, что в результате измерения площади
квадрата со стороной 1, изображенного на рисунке 273, получится
\
>
\
Рис. 272
Рис. 273
число 1? Интересующий нас вопрос можно сформулировать следующим
образом: если на расчерченном листе лежат два равных многоуголь-
многоугольника (рис.274), то можно ли утверждать, что результат измерения
их площадей будет одним и тем же, т. е. можно ли утверждать, что
их площади равны? Ответ оказывается положительным:
1° равные многоугольники имеют равные площади.
Однако доказать это утверждение не очень просто (см. замечание 2
в конце пункта).
Рассмотрим теперь многоугольник F, составленный из многоуголь-
многоугольников F\ и F<}. При измерении его площади каждый квадрат, со-
содержащийся целиком в многоугольнике F, либо целиком содержит-
содержится в одном из многоугольников F\, F2, либо часть его содержится

2. Понятие площади
191
У
1
1
\
\
\
\
У
Рис. 274
в многоугольнике F\, а другая часть — в многоугольнике ?%. То же
относится и к частям квадратов, содержащихся в многоугольнике F
лишь частично (рис.275). Поэтому:
2° если многоугольник составлен из двух многоугольников,
то его площадь равна сумме площадей этих многоугольников.
Из этого следует:
если многоугольник разбит на несколько многоугольников, то его
площадь равна сумме площадей этих многоугольников.
Так, на рисунке 276 многоугольник составлен из двух четырех-
четырехугольников, каждый из которых, в свою очередь, составлен из двух
треугольников. Поэтому, согласно свойству 2°, его площадь равна
сумме площадей (S\ + S2) и (S3 + S4), а значит, равна S\ + S2 + S3 +
+ S4.
Свойства 1° и 2° часто называют основными свойствами пло-
площадей, поскольку на основе этих свойств можно вывести формулы,
выражающие площади многоугольников через их элементы.
Замечание 1! Описывая процесс измерения площади много-
многоугольника, мы сказали, что площадь фигуры, составленной из квадра-
1
тиков со стороной —?—у и покрывающей ломаную, ограничивающую
многоугольник (см. рис. 271), при неограниченном увеличении к стре-
стремится к нулю. Докажем это.
Рис. 275
Рис. 276

192 Гл. 6. Площадь
Рассмотрим одну из сторон многоугольника. Проведя через ее кон-
концы прямые, параллельные сторонам квадратиков, получим прямоуголь-
прямоугольный треугольник с катетами а и Ь, гипотенуза с которого представляет
собой рассматриваемую сторону. Пусть п — количество квадратиков,
покрывающих сторону с. Обойдем эти квадратики ходом шахмат-
шахматной ладьи. Тогда количество N пройденных квадратиков окажется
не меньше, чем п: N ^ п (см. рис.271). С другой стороны, если путь
от одного конца стороны с к другому концу проделать лишь двумя
ходами ладьи, то количество пройденных квадратиков также окажется
равным N (объясните, почему). Из этого следует, что
ЛГ<С (а- Ю^1 +2)+ F- Ю^1 + 1) = (а + Ь)\Ок-1 +3.
Поскольку в прямоугольном треугольнике гипотенуза больше кате-
катета, то а ^ с и Ь ^ с, а значит, а + Ь ^ 2с. Таким образом,
n^N <2с- Ю^1 +3.
Будем считать, что число к столь велико, что каждая сторона
данного многоугольника больше стороны квадратика, в частности, с >
> —:—г. Тогда можно написать такое неравенство:
10fc-i
п < 2с • Юк~1 + Зс • Ю* = 5с • Ю*.
Итак, количество квадратиков, покрывающих сторону с многоуголь-
многоугольника, меньше 5с- Ю^. Применяя аналогичные рассуждения к осталь-
остальным сторонам и складывая полученные неравенства, мы приходим
к выводу: количество квадратиков, покрывающих ломаную, ограничи-
ограничивающую многоугольник, меньше 5р • \0к~\ где р — периметр много-
многоугольника. Следовательно, площадь фигуры, состоящей из этих квад-
ратиков, меньше эр- 10 • I —^—р 1 = —^rf, поэтому при неограни-
неограниченном увеличении числа к она стремится к нулю.
Замечание 2! Докажем, что площади равных многоугольников
(измеренные описанным в этом пункте способом) равны. Поскольку
любые два равных многоугольника совмещаются друг с другом не бо-
более, чем тремя осевыми симметриями (см. задачу 7 п. 47), то до-
достаточно доказать это утверждение для двух многоугольников, сим-
симметричных относительно некоторой прямой. Для краткости условимся
называть лист бумаги, расчерченный на квадраты со стороной 1, сетью
N (от слова «net» — сеть). Один из этих квадратов обозначим буквой К.
Рассмотрим произвольный многоугольник Ф и многоугольник 01,
симметричный многоугольнику Ф относительно некоторой прямой а.
Пусть S и S\ — их площади, измеренные описанным в этом пункте
способом. Числа S и S\, таким образом, показывают, сколько раз квад-
квадрат К и его части укладываются в многоугольниках Ф и Ф\. Докажем,
что S\ = S. С этой целью рассмотрим сеть N\, симметричную сети N

2. Понятие площади
193
относительно прямой а. Ясно, что квадрат К\ этой сети, симметричный
квадрату К сети N относительно прямой а, и его части укладываются
в многоугольнике Ф\ столько же раз, сколько раз квадрат К укладыва-
укладывается в многоугольнике Ф (так как при симметрии относительно прямой
а многоугольник Ф и сеть N переходят в многоугольник Ф\ и сеть N\),
т. е. S раз. Таким образом, если X — число, показывающее, сколько
раз квадрат К и его части укладываются в квадрате К\, то S\ = SX.
Итак, для любого многоугольника Ф с площадью S (измеренной
описанным в этом пункте способом) площадь S\ симметричного ему
относительно прямой а многоугольника Ф\ равна SX, где X — пло-
площадь квадрата К\, симметричного квадрату К относительно прямой
а. В частности, площадь квадрата К^, симметричного квадрату К\
относительно прямой а, равна XX = X2. Но квадратом К^ является
квадрат К, площадь которого равна 1. Следовательно, Х2=1, откуда
X = 1. Таким образом, для любого многоугольника с площадью S
и симметричного ему относительно прямой а многоугольника с площа-
площадью S\ имеет место равенство: S\ = S. Утверждение доказано.
82. Площадь произвольной фигуры. Для измерения площади
произвольной фигуры F поступают так. Рассматривают множество
всех многоугольников, целиком содержащихся в фигуре F, и мно-
множество всех многоугольников, целиком содержащих в себе фигу-
фигуру F (рис.277). Ясно, что площадь каждого многоугольника из первого
множества не превосходит площади лю-
любого многоугольника из второго мно-
множества (объясните почему). Если су-
существует величина S, для которой как
в первом, так и во втором множестве
найдутся многоугольники, площади ко-
которых сколь угодно мало отличаются
от S, то величина S и принимается
за площадь данной фигуры.
В качестве иллюстрации понятия
площади произвольной фигуры решим
задачу, которую часто называют за-
задачей Минковского 0 . Представим се-
себе, что плоскость разбита на квадраты
со стороной, равной единице измерения
отрезков (рис. 278). Вершины этих квадратов образуют так называемую
целочисленную решетку и называются узлами решетки (рис.279).
Сформулируем теперь нашу задачу.
Задача. Дана произвольная фигура, площадь которой (при вы-
выбранной единице измерения) меньше 1. Доказать, что эту фигуру
Рис. 277
ОМинковский Герман A864-1909) — немецкий математик
7 С. Б. Кадомцев

194
Гл. 6. Площадь
Рис. 278
Рис. 279
можно расположить так, что ни один из узлов целочисленной
решетки не попадет на фигуру.
Решение. Представим себе, что решетка нарисована на прозрач-
прозрачной бумаге. Наложим эту бумагу на фигуру произвольным образом,
скопируем на нее данную фигуру и закрасим копию в какой-то цвет.
Затем разрежем бумагу на квадратики вдоль линий решетки (рис.280),
аккуратно, не поворачивая, положим эти квадратики один на дру-
другой (наподобие колоды карт) и посмотрим на образовавшуюся стопку
квадратиков на просвет. Мы увидим что в некоторых местах закра-
закрашенные области квадратиков накладываются друг на друга, в других
местах закрашенную область имеет лишь один квадрат, и обязательно
найдутся прозрачные области, поскольку площадь каждого из квад-
квадратиков равна 1, а площадь фигуры меньше 1. Вооружимся иголкой
и проткнем все наши квадратики в какой-нибудь точке прозрачной
области.
Теперь разложим все квадратики так, как они лежали до разреза-
разрезания (рис.281). Мы увидим в каждом квадратике один след от нашего
прокола, расположенный одинаковым образом во всех квадратиках.
Следы эти образуют новую целочисленную решетку (объясните по-
почему), причем ни один из узлов этой новой решетки не попадает
на фигуру. Утверждение доказано.
Е
?Е
•
•
• 111=
-
•
•
•
•
•
•
Рис. 280
Рис. 281

2. Понятие площади
195
7Z
7L
1
Рис. 282
83*. Площадь многоугольника с вершинами в узлах целочис-
целочисленной решетки. На рисунке 282 изображен десятиугольник, все
вершины которого являются узлами це-
целочисленной решетки. Ясно, что пло-
площадь каждой клетки равна 1. Чему
равна площадь десятиугольника? Ответ
на этот вопрос можно дать почти сразу,
проделав небольшие вычисления в уме.
Для этого нужно воспользоваться сле-
следующей теоремой.
Теорема. Площадь многоуголь-
многоугольника, все вершины которого явля-
являются узлами целочисленной решет-
( . п 1
ки, выражается числом ( т + — — 1
где т — количество узлов, находя-
находящихся внутри многоугольника, а п —
количество узлов, лежащих на его
границе.
Доказательство. Для многоугольника с вершинами в уз-
узлах целочисленной решетки условимся обозначать буквой R число
га+ - — 1 ], а буквой S — число, выражающее его площадь. Наша
задача, тем самым, — доказать, что для любого многоугольника ука-
указанного вида эти числа совпадают: R = S.
Центральное место в наших рассуждениях будет занимать следу-
следующий факт. Если два данных многоугольника с вершинами в узлах
целочисленной решетки составляют один многоугольник, то соответ-
соответствующие им числа R\ и R% связаны с числом R для многоугольника,
составленного из двух данных, равенством: R = R\ + i?2-
Докажем это утверждение. Пусть (к + 2) — количество узлов ре-
решетки, лежащих на общей ломаной двух данных многоугольников (два
конца и к внутренних точек этой ломаной).
Тогда внутри большого многоугольника ока-
окажется (mi + ТП2 + к) узлов, где т\ — число
узлов, лежащих внутри первого, а Ш2 — внут-
внутри второго многоугольника (рис.283), т.е.
m = гп\ +
к.
На границу большого многоугольника по-
попадут два конца ломаной, а также все уз-
узлы, лежащие на границах данных многоуголь-
многоугольников, за исключением (к + 2) узлов, на-
находящихся на общей ломаной. На границе
первого многоугольника таких узлов будет
Рис. 283. m = 7; m =
= 7П\ + 7712 + к

196
Гл. 6. Площадь
(п\ — к — 2), на границе второго многоугольника — (п2 — к — 2). Таким
образом,
п = 2 + (щ - /с - 2) + (п2 - к - 2) = щ + п2 - 2fc - 2.
В результате для числа Д получаем равенства:
= \mi + -^-
Итак,
it — ill + it2- (Ij
Перейдем теперь непосредственно к доказательству
теоремы. Прежде всего заметим, что для квадрата со сто-
стороной 1 (рис.284)
Рис. 284 Но и площадь S этого квадрата равна 1. Следователь-
Следовательно, для такого квадрата R = S.
Рассмотрим теперь прямоугольник, составленный из N единичных
квадратов, стороны которого лежат на линиях решетки (рис.285).
В силу доказанного равенства A) число R для такого прямоугольника
равно A + 1 + ... + 1) = N. Но и площадь S прямоугольника равна N.
Поэтому для такого прямоугольника R = S. Из этого следует, что
аналогичное равенство имеет место и для прямоугольного треуголь-
треугольника, катеты которого лежат на линиях решетки (рис.285), так как
рассмотренный прямоугольник состоит из двух таких треугольников
с общей гипотенузой.
Следовательно, равенство R = S верно и для любого треугольни-
треугольника (рис.286), так как его можно получить из прямоугольника, последо-
последовательно отсекая от него прямоугольные треугольники, катеты которых
лежат на линиях решетки.
Для завершения доказательства осталось вспомнить, что любой
многоугольник можно разрезать на треугольники, вершинами кото-
которых являются вершины многоугольника (задача 4 п. 78). Следователь-
Рис. 285
Рис. 286

3. Площадь треугольника
197
но, для многоугольника соотношение R = S также верно. Теорема
доказана.
Вернемся теперь к десятиугольнику, изображенному на рисун-
рисунке 282. Для него т = 12, п = 12, следовательно,
5= 12 +у- 1 = 17.
Таким образом, площадь этого десятиугольника легко вычисляется
в уме.
Задачи
244. Каждая из трех прямых на рисунке 287 делит площадь много-
многоугольника пополам. Докажите, что площадь треугольника, образован-
образованного этими прямыми, не превосходит - площади многоугольника.
245. Площадь произвольной фигу-
фигуры при выбранной единице измерения
меньше целого числа к. Докажите, что
на нее можно наложить целочисленную
решетку так, что не более (к — 1) точек
решетки попадет на фигуру.
246. Площадь произвольной фигу-
фигуры при выбранной единице измерения
больше целого числа к. Докажите, что
на нее можно наложить целочисленную
решетку так, что по крайней мере к
точек решетки попадет на фигуру.
Рис. 287
§ 3. Площадь треугольника
84. Площади прямоугольника, параллелограмма и треугольни-
треугольника. Вы, конечно, знаете, что площадь S прямоугольника ABCD
со сторонами АВ = а и AD = Ъ выражается формулой S = аЪ. Давайте
подумаем, как это доказать.
Рассмотрим сначала прямоугольник AB\C\D, сторона АВ\ которо-
которого равна единице измерения отрезков (рис.288, а). Ясно, что единица
измерения площадей (т.е. квадрат со стороной 1) и ее части укла-
укладываются в этом прямоугольнике столько раз, сколько раз единица
измерения отрезков и ее части укладываются в отрезке AD, т. е. Ь
раз. Следовательно, площадь S\ этого прямоугольника выражается
числом Ъ\ S\ = Ъ.
Аналогично прямоугольник AB\C\D и его части укладываются
в прямоугольнике ABCD столько раз, сколько раз единица измере-
измерения отрезков (т.е. отрезок АВ\) и ее части укладываются в отрез-
отрезке АВ (рис.288, б), т.е. а раз. Следовательно, площадь S прямоуголь-
прямоугольника ABCD равна aS\, т. е. S = аЪ. Итак:

198
Гл. 6. Площадь
1
1
D
A D
а) б)
Рис. 288. a) AD = Ъ, Sx = Ъ; б) АВ = a, AD = Ъ, S = aSx = ah
площадь прямоугольника равна произведению его смежных сто-
сторон.
Далее, рассмотрим параллелограмм и примем какую-нибудь его
сторону за основание. Этот параллелограмм равносоставлен с прямо-
прямоугольником, одна из смежных сторон которого равна основанию парал-
параллелограмма, а другая — его высоте (задача 6 п. 79). Следовательно,
площадь параллелограмма равна произведению его основания
на высоту.
Рассмотрим теперь треугольник, выберем одну из его сторон и на-
назовем ее основанием. Под словом «высота» условимся понимать ту из
высот треугольника, которая проведена к основанию. Поскольку тре-
треугольник равносоставлен с параллелограммом, основание которого сов-
совпадает с основанием треугольника, а высота равна половине высоты
треугольника (задача 5 п. 79), то
площадь треугольника равна половине произведения его основа-
основания на высоту.
85. Равновеликие многоугольники. Два многоугольника называ-
называются равновеликими, если их площади равны. Примером равновеликих
многоугольников могут служить (согласно свойству 1° площадей) лю-
любые равные многоугольники. Обратное утверждение, конечно, неверно:
равновеликие многоугольники могут быть неравными. Так, изображен-
изображенные на рисунке 289 прямоугольник и квадрат равновелики (площадь
каждого из них равна 4 см2), но они, очевидно, не равны друг другу.
В силу свойства 2° площадей два равносоставленных многоуголь-
многоугольника равновелики. А верно ли обратное утверждение: любые два
равновеликих многоугольника равносоставлены? Оказывается, верно.
Это утверждение называется теоремой Бойяи-Гервина. Ф. Бойяи —
венгерский математик — доказал эту теорему в 1832 г., а П. Гервин —
немецкий математик-любитель — независимо от Ф. Бойяи доказал
ее в 1833 году.
Докажем сначала теорему Бойяи-Гервина для равновеликих пря-
прямоугольников со смежными сторонами а, Ъ и а\, Ъ\. Пусть для опре-
определенности а > Ь, а\ > Ъ\. Тогда а\ > а\Ъ\ = аЪ > Ь2, откуда а\ > Ъ.

3. Площадь треугольника
199
Построим параллелограмм со смежными сторонами а и а\ и высотой
Ь, проведенной к стороне а (рис.290). Его площадь равна ab, поэтому
высота, проведенная к стороне а\, равна Ъ\. Этот параллелограмм
равносоставлен как с одним, так и с другим прямоугольником (см.
задачу 6 п. 79). Следовательно, рассматриваемые прямоугольники рав-
носоставлены, что и требовалось доказать.
1 см
1 см
Рис. 289
Рис. 290
Рассмотрим теперь два равновеликих многоугольника с площадью
S и докажем, что они равносоставлены. Возьмем один из них и раз-
разрежем на треугольники с площадями S\, #2,..., Sn (рис.291). Каждый
из треугольников равносоставлен с параллелограммом, основание ко-
которого совпадает с основанием треугольника, а высота равна половине
высоты треугольника. Параллелограмм, в свою очередь, равносостав-
равносоставлен с прямоугольником, одна из смежных сторон которого равна осно-
основанию параллелограмма, а другая — его высоте, поэтому треугольник
также равносоставлен с этим прямоугольником. Следовательно, г-ый
треугольник равносоставлен и с прямоугольником, смежные стороны
S-
которого равны заданному отрезку длины а и отрезку длины —. Из та-
таких прямоугольников можно составить один прямоугольник со сторо-
стороной а и площадью S (рис.292). Таким образом, выбранный нами мно-
многоугольник равносоставлен с этим прямоугольником. Аналогично до-
доказывается, что и другой многоугольник равносоставлен с указанным
прямоугольником, поэтому данные многоугольники равносоставлены.
Теорема доказана.
Рис. 291
а
Рис. 292

200
Гл. 6. Площадь
86. Метод Евклида. Для нахождения площади произвольного
многоугольника можно разрезать его на треугольники и найти пло-
площадь каждого из них. Сумма площадей этих треугольников равна
площади данного многоугольника. Этот прием, в частности, можно
использовать для вывода формул площадей параллелограмма и трапе-
трапеции (рис.293 а, б).
Е
h
В
/
[у
_ i
о
а
а • /г/
У
h
С
\
h \
п \
D
А
D
а)
б)
1
1
Рис. 293. a) Sabcd = S\ + S2 = -ah + -ah = ah, площадь параллелограмма
равна произведению его основания на высоту; б) Sabcd = S\ + S2 = -(а +
+ b)h, площадь трапеции равна произведению полусуммы ее оснований на
высоту
Площадь многоугольника можно найти и другими способами. Один
из таких способов был указан Евклидом. Он состоит в построении тре-
треугольника, площадь которого равна площади данного многоугольника.
Поясним этот способ на примере выпуклого пятиугольника ABCDE,
изображенного на рисунке 294.
Построим треугольник, площадь которого равна площади пяти-
пятиугольника ABCDE. Для этого через вершину В проведем прямую, па-
параллельную диагонали АС пятиугольника. Она пересекает прямую АЕ
в точке F. Треугольники ABC и AFC равновелики, так как у них
общее основание АС, а вершины В и F лежат на прямой, параллель-
параллельной АС, и поэтому высоты, проведенные из этих вершин к основа-
основанию АС, равны.
Итак, треугольник ABC можно заменить равновеликим треуголь-
треугольником AFC. В результате получим четырехугольник FCDE, равнове-
равновеликий данному пятиугольнику. Далее аналогичным образом заменим
треугольник CDE на равновеликий ему треугольник СЕК. Получив-
Получившийся в итоге треугольник CFK равновелик пятиугольнику ABCDE.
Применяя метод Евклида к трапеции, получаем другой способ вы-
вывода формулы площади трапеции. Действительно, рассмотрим трапе-
трапецию ABCD с основаниями AD = а, ВС = Ъ и высотой h (рис.295).
Проведем через вершину С прямую, параллельную диагонали BD,
и обозначим буквой Е точку пересечения этой прямой с прямой AD.
Тогда Sabcd = Sabe- Четырехугольник ВС ED — параллелограмм,

3. Площадь треугольника
201
В
D
В
FA E К
Рис. 294
поэтому DE = ВС = b. Итак,
Sabcd = Sabe = ^ (а + fyh.
87. Две теоремы об отношении площадей треугольников.
Из формулы площади треугольника следует, что
площади треугольников, имеющих равные основания, относятся
как их высоты)
площади треугольников, имеющих равные высоты, относятся
как их основания.
Рассмотрим треугольник ABC с площадью S и отметим на луче АВ
какую-нибудь точку В\ (рис.296, а). Треугольники ABC и АВ\С
имеют общую высоту СЕ., поэтому
S АВ
Sabxc АВх'
Отметим теперь на луче АС произвольную точку С\ (рис.286, б).
Треугольники АВ\С и АВ\С\ имеют общую высоту В\Н\, поэтому
Sab у
АС
АСХ'
Sabxcx
Перемножая два равенства, получаем:
S АВ-АС
Таким образом, мы приходим к следующей теореме.
Теорема 1 . Если угол одного треугольника равен углу друго-
другого треугольника, то площади этих треугольников относятся как
произведения сторон, заключающих равные углы.
Доказательство. Пусть S и S\ — площади треугольников ABC
и А\В\С\, у которых ZA = /_А\ (рис.286, в). Наложим треуголь-
треугольник ABC на треугольник А\В\С\ так, чтобы вершина А совместилась
с вершиной А\, а стороны АВ и АС наложились соответственно

202
Гл. 6. Площадь
С
Н
А
Н В Вх
А
Вх
а)
б)
С/
Вх Ах
В
Вх
Рис. 296
на лучи А\В\ и А\С\ (рис.286, г). Как мы только что установили,
S АВ-АС
S_ _ АВ-АС
Sx ~ АхВх -АхСх'
Теорема доказана.
Докажем еще одну теорему, являющуюся, по-существу, следствием
только что доказанной теоремы.
Теорема 2. Если угол одного треугольника составляет в сумме
с углом другого треугольника 180°, то площади этих треугольни-
треугольников относятся как произведения сторон, заключающих указанные
углы.
Доказательство. Пусть S и S\ — площади треугольников ABC
и А\В\С\, у которых ZA + ZA\ = 180° (рис.297, а). Докажем, что
S _ АВ-АС
- АхСх'
Продолжим сторону АВ за точку А на отрезок AD = АВ
(рис.297, б). Треугольники ABC и ADC имеют равные основания АВ

3. Площадь треугольника
203
Bx D
А
В
Рис. 297
и AD, а также общую высоту, проведенную из вершины С. Поэтому
их площади равны, т. е. площадь треугольника ADC равна S.
Поскольку ABAC + AD АС =180°, то ZDAC = ААХ. Следователь-
Следовательно, по теореме 1 ^ ^ АР ¦ Ж7
С Л D Л Г^
или, с учетом равенства AD = АВ,
_S_ _ АВ-АС
Sx AxBx • АхСх
Теорема доказана.
88. Две теоремы о биссектрисах треугольника. Рассмотрим тре-
треугольник ABC с биссектрисой AD (рис.298). Треугольники ABD
и ACD имеют общую высоту АН, по-
поэтому А
Sacd DC
С другой стороны, эти же треуголь-
треугольники имеют по равному углу (Zl = Z2),
поэтому
Sabd _ AB-AD _ АВ_
Sacd ~ АС • AD ~ АС
Из двух равенств для отношения
площадей получаем:
BD AB BD DC
— = АСИШ
Н D
Рис. 298
DC AC ™" AB АС
т. е. отрезки BD и DC пропорциональны отрезкам АВ и АС.
Итак, мы доказали такую теорему — назовем ее теоремой о бис-
биссектрисе треугольника:
биссектриса треугольника делит противоположную сторону
на отрезки, пропорциональные прилежащим сторонам треуголь-
треугольника.

204
Гл. 6. Площадь
С
При доказательстве этой теоремы
мы опирались на теорему 1 п. 87. Ис-
Используя теорему 2 п. 87, можно ана-
аналогичным образом доказать теорему
о биссектрисе внешнего угла тре-
треугольника:
если биссектриса внешнего угла
при вершине А треугольника ABC
пересекает прямую ВС в точке D,
BD DC
В
А
Рис. 299
Проведите доказательство само-
самостоятельно.
89. Признак равенства треугольников по двум сторонам и бис-
биссектрисе, проведенным из одной вершины. Теперь, когда в нашем
распоряжении оказались новые сведения о биссектрисе треугольника,
попытаемся ответить на два вопроса, записанных в блокноте:
имеет ли место признак равенства треугольников по двум сто-
сторонам и биссектрисе, проведенным из одной вершины]
как построить треугольник по двум сторонам и биссектрисе,
проведенным из одной вершины?
Если данные стороны равны друг другу, то ответить на оба вопроса
легко (объясните, как). Поэтому будем считать, что они не равны друг
другу.
Рассмотрим треугольник ABC с биссектрисой AD. Для удобства
введем следующие обозначения: АС = b, AB = с. Пусть, например,
Ъ > с (рис.300, а). Из теоремы о биссектрисе треугольника следует,
BD с
ЧТ° DC = Ъ'
На стороне АС отложим отрезок АЕ = с (рис.300, б). Треугольни-
Треугольники ABD и AED равны по первому признаку равенства треугольников,
С
D
а)
В С
D
В С
D
в)
В
Рис. 300. АЕ = с, DF _L AD

3. Площадь треугольника
205
поэтому BD = DE и ZADB = ZADE, т. е. луч DA — биссектриса
угла BDE.
Проведем через точку D прямую, перпендикулярную к AD и пере-
пересекающую АС в точке F (рис.300, в). Поскольку луч DA — биссек-
биссектриса угла BDE, a DF JL AD, то луч DF — биссектриса угла CDE,
смежного с углом BDE, поэтому отрезок DF — биссектриса тре-
угольника CDE. По теореме о биссектрисе треугольника -^ = -^.
с
Ь'
ТТ ПГ ПП BD С Г EF
Но DE = BD, а —— = -. Следовательно, ——
JJC о г С
FC
Полученное соотношение позволяет выразить AF через Ъ и с. В са-
мом деле, ЕЕ = AF — с, ЕС = Ь — AF, поэтому
— = -, откуда
о — Ar b
AF =
2Ьс
A)
Мы приходим к совершенно неожиданному выводу: длина отрез-
отрезка AF не зависит от угла А треугольника АВС\ Еще более удивитель-
удивительно то, что это утверждение, как показывают выкладки, справедливо
и в геометрии Лобачевского, хотя формула, аналогичная формуле A),
имеет там значительно более сложный вид.
Теперь мы можем ответить на оба интересующих нас вопроса.
Сформулируем их в виде задач и приведем решения.
Задача 1. Доказать, что если две стороны и биссектриса, про-
проведенные из одной вершины, одного треугольника соответственно
равны двум сторонам и биссектрисе, проведенным из одной верши-
вершины, другого треугольника, то такие треугольники равны.
Решение. Рассмотрим треугольники ABC и А\В\С\ с биссек-
биссектрисами AD и A\D\, у которых АВ = А\В\, АС = А\С\ и AD =
= A\D\. Через точки D и D\ проведем прямые, перпендикулярные
к AD и A\D\ и пересекающие большие из данных сторон треуголь-
треугольников в точках F и F\ соответственно (рис.301). Поскольку АВ =
= А\В\ и АС = А\С\, то, как следует из формулы A), AF = A\F\.

206
Гл. 6. Площадь
Следовательно, прямоугольные треугольники ADF и A\D\F\ равны
по гипотенузе и катету (AF = AXFX, AD = A\D\). Поэтому ZDAF =
= ZDXAXFX, а значит, ABAC = 2ZDAF = 2ZDXAXFX = ZBXAXCX. Тем
самым, треугольники ABC и АХВХСХ равны по первому признаку
равенства треугольников. Утверждение доказано.
Задача 2. Построить треугольник по двум сторонам и биссек-
биссектрисе, проведенным из одной вершины.
Решение. Построим сначала какой-нибудь треугольник АХВХСХ,
стороны АХВХ и А\С\ которого равны данным сторонам, и проведем его
биссектрису A\D\. Через точку Dx проведем прямую, перпендикуляр-
перпендикулярную к AXDX, и отметим точку Fx пересечения этой прямой с большей
из сторон АХВХ и А\С\ (рис.302, а).
Bi D
Рис.302. AF =
б)
Построим теперь прямоугольный треугольник ADF с гипо-
гипотенузой AF = A\F\ и катетом AD, равным данной биссектри-
биссектрисе (рис.302, б). Как следует из решения задачи 1, угол DAF
этого прямоугольного треугольника равен половине угла искомого
треугольника, заключенного между данными сторонами. Построим
угол, вдвое больший угла DAF, и тогда построение искомого
треугольника сведется к построению треугольника по двум данным
сторонам и углу между ними.
Задачи
247. Две стороны треугольника равны а и Ь, а высоты, проведенные
к этим сторонам, равны ha и /i&. Докажите, что а : Ь = hb : ha (отно-
(отношение двух сторон треугольника обратно пропорционально отношению
высот, проведенных к этим сторонам).
248. Может ли площадь треугольника быть: а) меньше 2 см2, если
любая его высота больше 2 см; б) больше 100 см2, если любая его
высота меньше 1 см; в) больше площади второго треугольника, если

3. Площадь треугольника 207
каждая сторона первого меньше 1 см, а каждая сторона второго больше
1 км?
249. Многоугольник описан около окружности. Докажите, что:
а) его площадь равна половине произведения периметра на радиус
вписанной окружности; б) любая прямая, проходящая через центр
вписанной окружности, делит его площадь и периметр в равных отно-
отношениях.
250. Внутри треугольника ABC взята точка М. Докажите, что
площади треугольников ВАМ и ВСМ равны тогда и только тогда,
когда точка М лежит на медиане треугольника ABC, проведенной
из вершины В.
251. Докажите, что медианы треугольника разбивают его на шесть
равновеликих треугольников.
252. Сумма длин двух сторон треугольника равна р. Найдите наи-
наибольшее возможное значение его площади.
253. Докажите, что: а) сумма расстояний от любой точки основа-
основания равнобедренного треугольника до его боковых сторон равна высоте
треугольника, проведенной к боковой стороне; б) разность расстояний
от любой точки, лежащей на продолжении основания равнобедренного
треугольника, до прямых, содержащих его боковые стороны, равна
высоте треугольника, проведенной к боковой стороне; в) сумма рассто-
расстояний от любой точки, лежащей внутри равностороннего треугольника,
до его сторон равна высоте треугольника.
254. Диагонали выпуклого четырехугольника делят его на четыре
треугольника, площади которых, взятые последовательно, равны S\,
S2, S3, S4. Докажите, что S\S% = S2S4.
255. Сторона АВ треугольника ABC продолжена за точку А на от-
отрезок AD, равный АС. На продолжении отрезка AD за точку D
отмечена точка К, а на продолжении стороны ВС за точку С — точ-
точка М так, что площади треугольников BDM и ВКС равны. Найдите
угол ВКМ, если ABAC = а.
256. На стороне АВ треугольника ABC взята точка К, а на
стороне ВС — точка М так, что ВК : К А = 2:5, ВЫ : МС =
= 7:3. Найдите отношение площади треугольника ВКМ к площади
четырехугольника АКМС.
257. Точки К, М и Р лежат соответственно на сторонах АВ, ВС
и С А треугольника ABC, причем АК = \кВ, ВЫ = \мС, СР =
1
= jPA. Найдите отношение площадей треугольников МРК и ABC.
258. Дан треугольник ABC. На продолжениях стороны АВ за точ-
точку В, стороны ВС за точку С и стороны С А за точку А отмечены
соответственно точки С\, А\ и В\ так, что АВ = ВС\, ВС = СА\,
С А = АВ\. Докажите, что отношение площадей треугольников ABC
и А\В\С\ равно 1 : 7.

208 Гл. 6. Площадь
259* Докажите, что из медиан данного треугольника можно по-
построить треугольник, и найдите отношение его площади к площади
данного треугольника.
260. На сторонах АС и ВС треугольника ABC взяты точ-
точки М и К, а на отрезке МК — точка Р так, что AM : МС =
= СК : KB = МР : РК = т : п. Найдите отношение площадей тре-
треугольников AMP и ВКР.
261* Через вершины треугольника ABC проведены параллель-
параллельные друг другу прямые, пересекающие противоположные стороны или
их продолжения соответственно в точках А\, В\, С\. Найдите отноше-
отношение площади треугольника ABC к площади треугольника А\В\С\.
262. Точки М и К — середины сторон ВС и AD выпуклого
четырехугольника ABCD, отрезки AM и ВК пересекаются в точке Р,
отрезки DM и КС пересекаются в точке Т. Докажите, что площадь
четырехугольника РМТК равна сумме площадей треугольников АВР
и CDT.
263* Прямая, проходящая через середину диагонали BD выпуклого
четырехугольника ABCD и параллельная диагонали АС, пересекает
сторону AD в точке Р, а сторону CD — в точке Q. На отрезке PQ
отмечена произвольная точка М. а) Докажите, что площадь четырех-
четырехугольника АВСМ равна площади четырехугольника ADCM. б) Най-
Найдите множество всех точек М, для которых выполняется равенство
пункта а), в) Найдите внутри четырехугольника ABCD такую точку,
что отрезки, соединяющие эту точку с серединами сторон четырех-
четырехугольника, делят его на четыре равновеликие части.
264. Через середину О диагонали BD выпуклого четырехугольни-
четырехугольника ABCD проведена прямая, параллельная диагонали АС и пересе-
пересекающая сторону AD в точке Е. Докажите, что площади треугольни-
треугольника CDE и четырехугольника АВСЕ равны.
265. Середины двух боковых сторон трапеции являются вершинами
параллелограмма, две другие вершины которого лежат на прямой,
содержащей основание трапеции. Докажите, что площадь параллело-
параллелограмма равна половине площади трапеции.
266. Точка О лежит на прямой, содержащей диагональ АС па-
параллелограмма ABCD. Докажите, что площади треугольников АОВ
и AOD равны.
267. Внутри параллелограмма ABCD взята произвольная точка К.
Докажите, что Sad к + SBck = Sab к + SDCk-
268. Через точку D стороны ВС треугольника ABC проведены
прямые, параллельные двум другим сторонам и пересекающие сто-
стороны АВ и АС в точках Е и Р соответственно. Докажите, что
треугольники CDE и BDP равновелики.
269. Найдите площадь параллелограмма, вершинами которого яв-
являются середины сторон выпуклого четырехугольника с площадью S.
270. Точки Р, Q, R и Т — соответственно середины сторон АВ,
ВС, CD и DA параллелограмма ABCD. Докажите, что при пересече-

3. Площадь треугольника 209
нии прямых AQ, BR, СТ и DP образуется параллелограмм, и найдите
отношение его площади к площади параллелограмма ABCD.
271. Внутри выпуклого четырехугольника ABCD взята точка М.
Докажите, что площадь четырехугольника, вершинами которого яв-
являются точки, симметричные точке М относительно середин сторон
четырехугольника ABCD, вдвое больше площади четырехугольни-
четырехугольника ABCD.
272. Отрезки, соединяющие середины противоположных сторон
выпуклого четырехугольника, равны. Найдите площадь четырехуголь-
четырехугольника, если: а) его диагонали равны а и Ь; б) указанные отрезки взаимно
перпендикулярны и равны с.
273. Диагонали четырехугольника равны. Найдите его площадь,
если отрезки, соединяющие середины его противоположных сторон,
равны а и Ъ.
274. Площади двух треугольников с общим основанием равны S\
и $2, причем 5i ф $2- Найдите площадь четырехугольника с вершина-
вершинами в серединах их боковых сторон.
275. На каждой стороне параллелограмма взято по одной точке.
Одна из диагоналей четырехугольника с вершинами в этих точках
параллельна стороне параллелограмма. Докажите, что площадь четы-
четырехугольника равна половине площади параллелограмма.
276. Сторона АВ параллелограмма ABCD продолжена на отре-
отрезок BE, а сторона AD — на отрезок DK, причем точка С не лежит
на прямой КЕ. Прямые ED и ВК пересекаются в точке О. Докажите,
что четырехугольники ABOD и СЕОК равновелики.
277. Через середину М стороны ВС параллелограмма ABCD пло-
площади S и вершину А проведена прямая, пересекающая диагональ BD
в точке О. Найдите площадь четырехугольника OMCD.
278. В параллелограмме ABCD точки Р и К делят диагональ BD
на три равные части, точки М и Е — середины сторон DC и СВ.
Найдите отношение площади четырехугольника МЕРК к площади
параллелограмма.
279. Докажите, что площадь трапеции равна произведению длин
боковой стороны и перпендикуляра, проведенного из середины другой
боковой стороны к прямой, содержащей первую сторону.
280. Середина М боковой стороны CD трапеции ABCD соединена
отрезками с вершинами А и В. Докажите, что площадь треугольни-
треугольника АМВ равна половине площади трапеции.
281. Диагонали трапеции ABCD с основаниями AD и ВС пере-
пересекаются в точке О. а) Докажите, что площади треугольников АОВ
и COD равны, б) Найдите площадь трапеции, если площади треуголь-
треугольников ВОС и AOD равны S\ и^2.
282. Найдите площадь равнобедренной трапеции, диагонали кото-
которой взаимно перпендикулярны, а длина средней линии равна га.

210
Гл. 6. Площадь
283* Каждая диагональ выпуклого пятиугольника отсекает от него
треугольник, площадь которого равна 1. Найдите площадь пятиуголь-
пятиугольника.
284. В параллелограмме ABCD точки М и К — середины сто-
сторон CD и AD соответственно, Р — точка пересечения отрезков AM
и ВК. Найдите отношение площади треугольника АРК к площади
параллелограмма.
285. В ромбе ABCD угол А равен 60°, серединный перпендикуляр
к стороне AD пересекает диагональ АС в точке М, а серединный
перпендикуляр к стороне CD пересекает АС в точке Р. Найдите
отношение площади треугольника DMP к площади ромба.
§ 4. Формула Герона и ее приложения
90. Формула Герона. Рассмотрим треугольник ABC со сторона-
сторонами АВ = с, ВС = а и С А = Ь. Попытаемся выразить его площадь S
через a, b и с.
Из точки О пересечения биссектрис треугольника ABC про-
проведем перпендикуляры OK, OL и ОМ к его сторонам АВ, ВС
и С А (рис. 303). Ясно, что ОК =
= OL = ОМ = г, где г — ради-
радиус окружности, вписанной в тре-
треугольник ABC.
Для удобства воспользуем-
воспользуемся обозначениями, принятыми
на рисунке 303. Четырехуголь-
Четырехугольник АКОМ составлен из двух
равных прямоугольных треуголь-
треугольников с катетами х и г, поэтому
его площадь S\ выражается фор-
формулой
Si=xr. A)
Аналогично S^ = yr, S% =
= zr. Следовательно, S = S\ +
-\- S2 + S% = xr -\- yr -\- zr, т. e.
M/
О
A
x/
f
Sx
\ >
/ \
\
\
\
\
r
~l
\y
\
\
К
в
Рис. 303
С другой стороны, S\ = Sakm
5 = (ж + у + *)r. B)
- Но по теореме 1 п. 87
-, а по теореме 2 п. 87
Sokm
Sakm _ ж_
(поскольку АКОМ = 360° - 90° - 90° - ZA = 180° - ZA). Поэтому,
складывая два последних равенства, получаем:

4. Формула Герона и ее приложения 211
Подставляя в это равенство выражения A) и B) для S\ и S и умно-
умножая обе его части на (х + у)(х + z)(x + у + z), приходим к равенству:
х(х + у)(х + z) = ж2(ж + у + ^) + г2(ж + у + z),
откуда
2 ж?/? / xyz
г = или г = ' —
Используя формулу B), находим:
5= у/(х + 2/ + г)ж2/* .
Остается вспомнить, что х = р — а, у = р — b, z = р — с, где р =
= ~—9—~ ~~ П0ЛУпеРиметР треугольника (см. замечание 3 п. 39),
и учесть, что х -\- у -\- z = р. В результате получаем формулу, выража-
выражающую площадь треугольника через его стороны:
S = у/р(р-а)(р-Ъ)(р-с).
Эту формулу обычно связывают с именем Герона Александрийско-
Александрийского — древнегреческого математика и механика, жившего, вероятно,
в 1 в. н.э. (годы его жизни точно не установлены). Однако по мне-
мнению некоторых математиков она была известна еще древнегреческому
ученому Архимеду (ок.287-212 до н.э.). Если подставить в формулу
~ а + Ь + с ^
1ерона вместо р выражение и раскрыть скобки, то получится
следующая формула:
S = V-^2a42 + 2Ь2с2 + 2с2а2 - а4 - б4 - с4 . C)
Следствие. Квадрат высоты АН треугольника ABC выража-
выражается через его стороны АВ = с, ВС = а и С А = Ъ формулой
AH2 = -L- BаЧ2 + 2ЬЧ + 2с2а2 - а4 - Ъ4 - с4). D)
4а
В самом деле, S = -а • АН, поэтому АН2 = —~~. Подставляя сюда S
* а
из формулы C), приходим к формуле D).
91. Теорема о медиане. Выразим теперь квадрат медианы AM
треугольника ABC через его стороны АВ = с, ВС = а и С А = Ъ.
Треугольники АВМ и АСЫ имеют равные основания ВЫ и МС
и общую высоту (рис.304), поэтому их площади равны. Пользуясь
формулой C) п.90, получаем:
^-Ь2 + 2Ъ2АМ2 + 2АМ^ ^
4 4 16
= j\2°Tc2 + ^c2AM2 + 2AM2°j- - (- - с4 - AM4 .
4 V 4 4 16

212
Гл. 6. Площадь
с в
а/2 М а/2
а)
Рис. 304. а) Ъ ф с; б) Ъ = с
Умножая обе части равенства на 4 и возводя в квадрат, преобразуем
его к виду:
2АМ2(Ъ2 - с2) = \а\с2 - Ь2) + (Ь2 - с2)(Ь2 + с2).
Если Ъ ф с, то из этого равенства находим:
AM2 = 2(Ь2 + с2)-а\
E)
Если же Ъ = с (рис.304, б), то медиана AM является высотой.
В этом случае формула E) получается из формулы D), посколь-
поскольку 2Ъ2с2 — Ь4 — с4 = 0. Итак, в том и другом случае
квадрат медианы AM треугольника ABC выражается через его
стороны АВ = с, ВС = а и С А = Ъ формулой E).
Это утверждение называется теоремой о медиане.
92. Формула биссектрисы треугольника. Теперь мы знаем, как
выразить высоту АН и медиану AM треугольника ABC через его
стороны АВ = с, ВС = а и С А =
= Ъ. А как выразить через а, Ъ и с
его биссектрису AD? Давайте по-
подумаем. Обратимся к рисунку 305.
По теореме о биссектрисе треуголь-
С
D а
Рис. 305
В
ника -—- = -. Кроме того, CD +
DB с
= а. Из этих двух равенств
находим:
аЬ
CD =
DB =
F)
Теперь мы можем, пользуясь формулой C), выразить площади тре-
треугольников ABD и ACD через а, Ь, с, AD, a затем учесть, что эти

5. Теорема Пифагора 213
треугольники имеют равные углы при вершине А, и поэтому
с
= -. Это и даст нам возможность выразить AD через а, Ъ и с.
Записывая соотношение между площадями в виде №S\BD • Ъ2 =
= 16S\CD • с2 и подставляя в него выражения для Sabd и Sacd,
после несложных преобразований приходим к равенству AD4(c2 —
/ 2 \ 2
— б2) = Ь2с2(с2 — Ь2) ( 1 — ?г 1 . В соответствии с неравенством
треугольника 1 — ^ > О, поэтому при с ф Ъ получаем:
AD2 = bc(\ °-^). G)
При с = Ь биссектриса AD является медианой, и справедливость
формулы G) вытекает из формулы E) (проверьте это). Следовательно,
формула G) верна при любых Ъ и с.
Замечание. Если воспользоваться формулами F), то формулу G)
можно переписать так: AD2 = be — CD • DB.
Задачи
286. Найдите площадь треугольника, если его высоты равны 3 см,
4 см и 6 см.
287. В треугольнике ABC АВ = 13 см, ВС = 14 см, АС =
= 15 см. Внутри треугольника взята точка М, расположенная на рас-
расстоянии 6 см от прямой АВ и на расстоянии 3 см от прямой ВС.
Найдите расстояние от точки М до прямой АС.
288. Найдите площадь треугольника, если его медианы равны 9 см,
12 см и 15 см.
289. В треугольнике ABC АВ = 13 см, ВС = 14 см, АС =
= 15 см, AD — биссектриса треугольника. Найдите площадь треуголь-
треугольника ACD.
290. Биссектрисы BD и СЕ треугольника ABC пересекаются
в точке О, АВ = 14, ВС = 6, АС = 10. Найдите OD.
§ 5. Теорема Пифагора
93. Обобщенная теорема Пифагора. Рассмотрим треуголь-
треугольник ABC с медианой AM и сторонами АВ = с, ВС = а и С А =
= Ь (рис.304). Вспомним утверждение, сформулированное в задаче 1
п. 55:
угол треугольника является острым, прямым или тупым, ес-
если медиана, проведенная из вершины этого угла, соответственно
больше, равна или меньше половины противоположной стороны.
Теорема о медиане дает возможность заменить в этом утверждении
соотношение между медианой и противоположной стороной на соот-

214
Гл. 6. Площадь
ношение между сторонами треугольника. В самом деле, согласно этой
теореме (см. формулу E) в п. 91)
Ь2 + с - а2
Следовательно,
угол А треугольника ABC со сторонами АВ = с, ВС = а и С А =
= Ъ является острым, прямым или тупым, если выражение Ъ2 + с2 —
— а2 соответственно больше, равно или меньше нуля.
Следствие 1. Если квадрат одной из сторон треугольника ра-
равен сумме квадратов двух других сторон, то этот треугольник —
прямоугольный.
Следствие 2. В прямоугольном треугольнике квадрат гипоте-
гипотенузы равен сумме квадратов катетов. В самом деле, если предпо-
предположить, что квадрат гипотенузы меньше или больше суммы квадратов
катетов, то окажется, что угол, противолежащий гипотенузе, острый
или тупой.
Следствия 2 и 1 называют теоремой Пифагора и теоремой, об-
обратной теореме Пифагора, а то утверждение, из которого мы их
вывели, назовем обобщенной теоремой Пифагора.
Теорема Пифагора (ок. 580-ок. 500
до н.э.) является одной из самых важ-
важных (если не самой важной) в евклидо-
евклидовой геометрии. В настоящее время из-
известно более ста ее доказательств.
Рисунок 306 иллюстрирует сразу
два доказательства теоремы Пифагора,
в каждом из которых фигурируют пло-
площади четырех равных друг другу пря-
прямоугольных треугольников и двух квад-
квадратов.
Еще одно доказательство связано
с идеей, использованной при выводе
формулы Герона. Обратимся к рисун-
рисунку 307, на котором два треугольника
с катетами а, Ъ и гипотенузой с прило-
приложены друг к другу сперва равными ка-
катетами, а затем — гипотенузами, и вос-
воспользуемся обозначениями, принятыми
Q 2 Q
на этом рисунке. По теореме 1 п. 87 —J- = -^, а по теореме 2 п. 87 -^ =
b2 Si+S2 а* + 62 ы с ,
— = »—. Но *Si +
а /
/с
а — Ь
Ь ^^^.
а ^^^
а — Ъ /
/с
/ ъ
Рис. 306. Г (а + ЬJ = с2 +
+ 4^ => с2 = а2 + Ь2; 2° с2 =
= (а - ЬJ + 4— => с2 = а2 +
+ Ь2
= -z. Складывая эти выражения, получаем: —-— =
с ^ с
+ #2 = S. Следовательно, с2 = а2 + Ъ2.
Наконец, приведем еще одно доказательство теоремы Пифагора.
Пусть СН — высота прямоугольного треугольника ABC, проведенная

5. Теорема Пифагора
215
Рис. 307
из вершины прямого угла (рис.308), S, S\ и $2 — площади треуголь-
треугольников ABC, ВСН и АСН. Угол А треугольника ABC равен углу С
треугольника ВСН (каждый из них в сумме с углом В составляет
90°), поэтому ^ = °~^- Но S =
1 , 1 ab
= -ао = -с • СН, откуда СН = —.
Следовательно, —^ = -s-. Аналогично
S2 b п
находим: — = — Складывая эти ра-
Ь с
венства и учитывая, что S\ + S^ = S,
получаем:
Si +S2 a + b2
S
= 1, т.е.
Рис. 308
94. Задача о разрезании квадратов. Теорему Пифагора можно
сформулировать и так:
площадь квадрата, построенного на гипотенузе прямоугольно-
прямоугольного треугольника, равна сумме площадей квадратов, построенных
на катетах.
Иными словами, квадрат, построенный на гипотенузе прямоуголь-
прямоугольного треугольника, равновелик с двумя квадратами, построенными
на катетах. Но согласно теореме Бойяи-Гервина (п. 85) любые два
равновеликих многоугольника равносоставлены. Следовательно, два
квадрата, построенные на катетах прямоугольного треугольника, мож-
можно разрезать на части, из которых можно составить один квадрат,
построенный на его гипотенузе. Но как это сделать?
Сформулируем наше утверждение в виде задачи и решим ее.
Задача. Разрезать два квадрата, построенные на катетах
прямоугольного треугольника, на такие части, из которых можно
составить квадрат, построенный на его гипотенузе.
Решение. Рассмотрим прямоугольный треугольник с катетами
a, b и гипотенузой с. Можно, конечно, воспользоваться идей дока-

216 Гл. 6. Площадь
зательства теоремы Бойяи-Гервина: разрезать квадраты с сторонами
а и Ъ на части так, чтобы из частей первого квадрата составить
2
„а
параллелограмм с основанием с и высотой —, из частей второго —
„ ь2
параллелограмм с основанием с и высотой —, затем построить пря-
прямоугольники, соответственно равносоставленные с параллелограмма-
параллелограммами, и, наконец, из этих прямоугольников составить прямоугольник
со сторонами си 1 . Тогда, согласно теореме Пифагора, этот
прямоугольник и будет искомым квадратом. Возникает, однако, вопрос:
а нельзя ли решить нашу задачу без ссылки на теорему Пифагора?
Ведь если бы это удалось, то мы получили бы еще одно доказательство
теоремы Пифагора! Оказывается, можно. Для этого достаточно заме-
заметить, что высоты параллелограммов с основанием с, равносоставленных
с данными квадратами, равны отрезкам, на которые высота данного
треугольника делит его гипотенузу, поэтому сумма этих высот равна
с. Соответствующее доказательство проведите самостоятельно.
Нашу задачу можно решить и проще. Пусть, например, а > Ъ.
Расположим квадраты так, как показано на рисунке 309, а, и отрежем
от них два равных прямоугольных треугольника с катетами а и Ъ (на
рисунке эти треугольники заштрихованы). Поскольку эти треугольни-
треугольники равны, то длина каждой из линий разреза равна их гипотенузе с,
а угол между линиями разреза равен 90°. Повернем теперь каждый
из отрезанных треугольников вокруг их вершин на угол 90° так, как
показано на рисунках 309 б, в. Тогда вместе с неподвижной частью
они образуют квадрат со стороной с.
Итак, при а > Ь мы разрезали квадрат со стороной а на три части,
квадрат со стороной Ь — на две части, и составили из этих частей
квадрат со стороной с, равной гипотенузе прямоугольного треугольни-
треугольника с катетами а и Ъ. Если а = Ь, то каждый квадрат окажется разре-
разрезанным на две части (рис.309, г), и мы придем к способу разрезания,
описанному в п. 11.
Таким образом, мы указали два способа решения задачи, а заодно
придумали еще два доказательства теоремы Пифагора.
Можно указать и другие способы решения этой задачи. Один
из них иллюстрирует рисунок 310. На этом рисунке через центр
левого квадрата (т. е. через точку пересечения диагоналей квадрата)
проведены два взаимно перпендикулярных разреза, один из которых
параллелен гипотенузе треугольника. Примечательно, что из двух
квадратов один вообще не разрезается, а другой разрезается на четыре
равные части. Более того, если эти части укладывать так, как показано
на рисунке, то каждую из частей не нужно даже поворачивать (дока-
(доказательство проведите самостоятельно).
Интересно, что это доказательство теоремы Пифагора было опуб-
опубликовано лишь в 1873 году. Его автор — лондонский биржевой маклер

5. Теорема Пифагора
217
b
а
а)
к
с м
у"
\с
6)
г)
Рис. 309
Генри Перигел — был в таком восторге от своего открытия, что
приказал отпечатать схему с разрезанием квадрата на своей визитной
карточке.
Задачи
291. Точка А лежит внут-
внутри угла С, равного 60°. Рас-
Расстояния от точки А до сторон
этого угла равны а и Ь. Най-
Найдите: а) расстояние от точки А
до вершины С; б) площадь четы-
четырехугольника ABCD, если АВ
и AD — перпендикуляры, прове-
проведенные к сторонам угла.
292. В треугольнике ABC
проведена высота BD. Отре-
Отрезок АК перпендикулярен пря-
прямой АВ и равен DC, отре-
отрезок СМ перпендикулярен ВС
и равен AD. Докажите, что от-
отрезки ВЫ и ВК равны.
Рис. 310

218 Гл. 6. Площадь
293. Внутри прямоугольника ABCD взята точка М так, что МА =
= a, MB = Ъ, МС = с. Найдите MD.
294. Найдите площадь квадрата, вписанного в равносторонний
треугольник со стороной а так, что две вершины квадрата лежат на од-
одной стороне треугольника, а две другие — на двух других сторонах
квадрата.
295. Докажите, что сумма квадратов четырех сторон параллело-
параллелограмма равна сумме квадратов его диагоналей.
296. Внутри прямоугольного треугольника ABC с гипотенузой АВ
выбрана точка О так, что площади треугольников АОВ, ВОС и АОС
равны. Докажите, что О А2 + ОВ2 = ЪОС2.
297. Докажите, что квадрат стороны треугольника, лежащей про-
против острого (тупого) угла, равен сумме квадратов двух других сторон
минус (плюс) удвоенное произведение какой-нибудь из этих сторон
на длину отрезка, соединяющего вершину указанного угла и основание
высоты, проведенной к этой стороне.
298. В трапецию ABCD с основаниями АВ и CD (АВ > CD)
вписана окружность. Найдите площадь трапеции, если CD = a, DK =
= Ъ и АК = d, где К — точка касания окружности и стороны AD.
299. Докажите, что для любой точки М, лежащей на высоте АН
треугольника ABC, выполняется равенство: MB2 + АС2 = МС2 +
2
300. В треугольнике ABC медианы AM и BN взаимно перпен-
перпендикулярны. Найдите площадь треугольника ABC, если AM = 3 см,
BN = 4 см.
301. Диагонали трапеции равны 6 см и 8 см, а отрезок, соединяю-
соединяющий середины ее оснований, равен 5 см. Найдите площадь трапеции.
302. Диагонали трапеции взаимно перпендикулярны, одна из них
равна 6 см. Найдите другую диагональ, если отрезок, соединяющий
середины оснований, равен 4,5 см.

Глава 7
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
§ 1. Признаки подобия треугольников
95. Подобие и равенство треугольников. Два треугольника на-
называются подобными, если их углы соответственно равны и стороны
одного треугольника пропорциональны сходственным сторонам другого
треугольника. Другими словами, два треугольника подобны, если для
них можно ввести обозначения ABC и А\В\С\ так, что
= BxCx = CXAX
AB ВС С А '
Число к, равное отношению сходственных сторон треугольни-
треугольников (т.е. к = l l), называется коэффициентом подобия треугольни-
треугольников. ЛВ
Подобие треугольников ABC и А\В\С\ обозначается так: A ABC ~
~ АА\В\С\. На рисунке 311 изображены подобные треугольники ABC
и AiBiCi.
Если два треугольника равны, то их углы и стороны соответствен-
соответственно равны. На рисунке 312 изображены равные треугольники ABC
и AiBid, у которых ZA = ZAU ZB = ZBU ZC = ZCU AB = A{BU
ВС = В\С\, С А = С\А\. Следовательно,
А С Ax
Рис. 311. AABCoo AAxBxCx, ZA = ZA{, ZB = ZB{, ZC = ZCX,
—-—- = ——- = k, k — коэффициент подобия треугольников

220
Гл. 7. Подобные треугольники
АХВХ
ВХСХ
СхАх
= 1.
АВ ВС СА
Эти соотношения показывают, что
равные треугольники являются подобными, причем коэффици-
коэффициент подобия равен 1.
Очевидно, верно и обратное:
если два треугольника подобны и коэффициент подобия равен \,
то эти треугольники равны.
Таким образом, в евклидовой геометрии равенство треугольников
можно рассматривать как частный случай подобия треугольников, ко-
когда коэффициент подобия равен 1.
С Ах
Рис. 312. ААВС = ААхВхСх
Сх
В геометрии Лобачевского нет подобных и неравных друг другу
треугольников, поскольку в ней, как мы отмечали, имеет место признак
равенства треугольников по трем углам.
В евклидовой геометрии каждому признаку равенства треугольни-
треугольников соответствует признак подобия треугольников, в котором вместо
равенства каких-либо отрезков требуется их пропорциональность. Так,
первому признаку равенства треугольников соответствует такой при-
признак подобия треугольников:
если две стороны одного треугольника пропорциональны двум
сторонам другого треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники подобны (обычно его
называют вторым признаком подобия треугольников).
Второму признаку равенства треугольников соответствует следую-
следующий признак подобия треугольников (его называют первым признаком
подобия треугольников):
если два угла одного треугольника соответственно равны двум
углам другого треугольника, то такие треугольники подобны.
Подумайте и объясните, почему здесь, в отличие от второго призна-
признака равенства треугольников, ничего не говорится о сторонах треуголь-
треугольников.
Третьему признаку равенства треугольников соответствует третий
признак подобия треугольников:
если три стороны одного треугольника пропорциональны трем
сторонам другого треугольника, то такие треугольники подобны.

/. Признаки подобия треугольников
221
Четвертому признаку равенства треугольников соответствует уже
сформулированный первый признак подобия треугольников.
Наконец, пятому признаку равенства треугольников соответствует
признак подобия треугольников, который назовем четвертым призна-
признаком:
если две стороны одного треугольника пропорциональны двум
сторонам другого треугольника и угол, противолежащий не мень-
меньшей из этих сторон, одного треугольника равен соответствующе-
соответствующему углу другого треугольника, то такие треугольники подобны.
Докажем сначала утверждение о первом признаке подобия тре-
треугольников. Пусть ABC и А\В\С\ — два треугольника, у кото-
которых ZA = ZAU ZB = ZBX (рис.313).
А
В Ах
Рис. 313
Требуется доказать, что ААВС ~ АА\В\С\.
Согласно теореме о сумме углов треугольника ZC = 180° — ZA —
- ZB, ZCX = 180° - ZA\ - ZBi, откуда следует, что ZC = ZCX. Таким
образом, углы треугольника ABC соответственно равны углам тре-
треугольника А\В\С\.
Докажем, что сходственные стороны треугольников ABC и А\В\С\
пропорциональны. Так как ZA = ZA\ и ZC = ZC\, то, применяя
теорему об отношении площадей треугольников, имеющих по равному
углу, получаем:
Sabc AB-AC Sabc CA-CB
Saxbxcx C\A\ • С\В\
ВС
Saxbxcx A\B\ • А\С\
Из этих равенств следует, что
АВ
АХВХ ВхСх'
Аналогично, используя равенства ZA = ZA\, ZB = ZB\, получаем:
ВС _ С А
ВхСх ~ СхАх'
Итак, углы треугольника ABC соответственно равны углам тре-
треугольника А\В\С\, а сходственные стороны этих треугольников про-
пропорциональны, т.е. треугольники ABC и А\В\С\ подобны, что и тре-
требовалось доказать.

222
Гл. 7. Подобные треугольники
Остальные утверждения о признаках подобия треугольников высту-
выступают как следствия из доказанного утверждения и соответствующей
теоремы о равенстве треугольников. Поясним, о чем идет речь.
Возьмем, например, утверждение о четвертом признаке подобия
треугольников и докажем его, опираясь на первый признак подобия
треугольников и пятый признак равенства треугольников. Пусть даны
два треугольника ABC и АхВхСх, у которых
АВ АС /U /U АЯ< АГ
——— = . _ , /-В = /-t>\, AJd ^ АС,
АхВх АхСх
и, следовательно, А\В\ ^ А\С\ (рис.314, а).
Докажем, что АА\В\С\ ~ ААВС.
Рассмотрим треугольник А2В2С2, у которого ZA2 = ZA, ZB2 = ZB,
А2С2 = АхСх (рис.314, б). Треугольники ABC и А2В2С2 подобны
по первому признаку подобия
треугольников, поэтому
АВ _ АС
А2В2 ~ А2С2'
Но А2С2 = АхСх. Значит,
АВ _ АС
А2В2 ~ АхСх'
С другой стороны, по уело-
вию
АВ
АС
АхВх АхСх
Рис. 314
Из этих двух равенств полу-
получаем: А2В2 = А\В\.
Итак, А2В2 = АхВи А2С2 =
АВ2 = ZB = ZBx,
АхСх. Следовательно,
треугольники АхВхСх и А2В2С2 равны по пятому признаку равенства
треугольников. Но АА2В2С2 ~ ААВС. Поэтому и ААхВхСх ~ ААВС.
96. Другие признаки подобия треугольников. Опираясь на приз-
признаки равенства треугольников, использующие медианы, биссектрисы
и высоты, можно сформулировать аналогичные утверждения о призна-
признаках подобия треугольников и доказать их аналогично тому, как был
доказан четвертый признак подобия треугольников. Но сначала решим
такую задачу.
Задача 1. Доказать, что в подобных треугольниках:
а) отношение сходственных биссектрис равно коэффициенту подо-
б) отношение сходственных медиан равно коэффициенту подобия;
в) отношение сходственных высот также равно коэффициенту
подобия треугольников.

/. Признаки подобия треугольников
223
Решение. Пусть AD и A\D\ — сходственные биссектрисы
(рис.315, a), AM и А\М\ — сходственные медианы (рис.315, б), АН
и А\Н\ — сходственные высоты (рис.315, в) в подобных треугольниках
ABC и А\В\С\, у которых А А = ZA\, АВ = ZB\, а коэффициент
подобия равен к.
С
Рис. 315. a) AD и A\D\ — биссектрисы; б) AM и А\М\ — медианы; в) АН
и А\Н\ — высоты
а) Треугольники ABD и A\B\D\ (рис.315, а) подобны по двум уг-
углам (ZDAB = ZD\A\B\, так как эти углы равны половинам равных
углов А и А\; ZB = /-В\). Из подобия треугольников ABD и A\B\D\
следует, что
У
AD AB
Но отношение х 1 равно коэффициенту к подобия треугольни-
/\ Г)
ков ABC и А\В\С\. Следовательно,
AD
= к.
б) Рассмотрим треугольники АВМ и А\В\М\ (рис.315, б). В этих
треугольниках
АВ
откуда следует, что
= к,
В1М1 _ 2ВхСх _
ВМ
_ РЮ1 _ ,
АВ ВМ
= к.

224 Гл. 7. Подобные треугольники
Кроме того, АВ = /_В\. Следовательно, треугольники АВМ
и А\В\М\ подобны по второму признаку и коэффициент подобия этих
треугольников равен к. Отсюда следует, что
AM -*'
Отметим, что полученное равенство можно вывести и из теоремы
о медиане, воспользовавшись формулой E) п. 91.
в) Пусть равные углы В и В\ — острые (рис.315, в). Рассмотрим
треугольники АВН и А\В\Н\. Эти треугольники подобны по двум
углам (ZB = ZBu ZAHB = ZAXHXBX = 90°). Следовательно,
АН АВ
Если же равные углы В и В\ — прямые или тупые, то равен-
равенство l l = к следует из подобия треугольников АСН и А\С\Н\.
Итак, отношение сходственных биссектрис, медиан и высот равно
коэффициенту подобия треугольников, что и требовалось доказать.
Теперь можно обнаружить целый ряд новых признаков подобия
треугольников. Приведем пример.
Задача 2. Доказать, что если две стороны и биссектриса,
проведенная из общей вершины этих сторон, одного треугольника
соответственно пропорциональны двум сторонам и биссектрисе,
проведенной из общей вершины этих сторон, другого треугольника,
то такие треугольники подобны.
Решение. Пусть в треугольниках ABC и А\В\С\ с биссектриса-
биссектрисами AD и A\D\ выполнены равенства:
АВ AC AD m
АхСх
Докажем, что AA{B{Ci ~ ААВС.
Рассмотрим треугольник А^В^С^ с биссектрисой A2D2,
у которого ZA2 = ZA, ZB2 = ZB, A2C2 = АХСХ (рис.316, б).
Треугольники ABC и А2В2С2 подобны по двум углам, поэтому
АВ _ АС _ AD
А2В2 ~ АхСх ~ A2D2
(поскольку А2С2 = А\С\). Сопоставляя эти равенства с равенства-
равенствами A), приходим к выводу: А\В\ = А2В2, A\D\ = A2D2. Так как,
кроме того, А\С\ = А2С2, то треугольники А\В\С\ и А2В2С2 рав-
равны по двум сторонам и биссектрисе, проведенным из одной верши-
вершины (п. 89). Но АА2В2С2 - ААВС. Поэтому и АА{В{С{ - ААВС.
Утверждение доказано.
97. Тригонометрические функции. Рассмотрим прямоугольный
треугольник ABC с прямым углом С (рис.317, а). Катет ВС этого

/. Признаки подобия треугольников
225
Рис. 316
треугольника является противолежащим углу А, а катет АС — приле-
прилежащим к этому углу.
Синусом острого угла прямоугольного треугольника называется
отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называ-
называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называ-
называется отношение противолежащего катета к прилежащему.
Котангенсом острого угла прямоугольного треугольника назы-
называется отношение прилежащего катета к противолежащему.
Синус, косинус, тангенс и котангенс угла а обозначаются символа-
символами sin a, cos а, tga и ctga (читается: «синус альфа», «косинус альфа»,
«тангенс альфа» и «котангенс альфа») и называются тригонометри-
А
а)
В
С
Ах
Вх
Сх
Рис. 317. Z А = /_А\\ sin A = sinAi, cos A = cos Ax, tg A = tg Ax, ctgA = ctg A\
8 С. Б. Кадомцев

226 Гл. 7. Подобные треугольники
ческими функциями 0 . На рисунке 317
sin A -
cos A ¦
tgA--
ctgA-
Из формул B) и C) получаем:
sin А ВС АВ ВС
cos А АВ АС АС
_ ВС
АС
АВ'
ВС
" АС
_ АС
~ ~ВС'
cos A
sin A
Сравнивая эти формулы с формулами D)
tgA =
ctgA =
sin A
cos A'
cos A
АС АВ
АВ ВС
АС
ВС
и E), находим:
B)
C)
D)
E)
F)
G)
т.е.
тангенс угла равен отношению синуса к косинусу этого угла)
котангенс угла равен отношению косинуса к синусу этого угла.
Докажем, что
если острый угол одного прямоугольного треугольника равен
острому углу другого прямоугольного треугольника, то синусы
этих углов равны, косинусы этих углов равны, тангенсы этих углов
равны и котангенсы этих углов равны.
В самом деле, пусть ABC и А\В\С\ — два прямоугольных тре-
треугольника с прямыми углами С и С\ и равными острыми углами А
и А\ (рис.317 а, б). Треугольники ABC и А\В\С\ подобны по первому
признаку подобия треугольников, поэтому
АВ ВС СА
Из этих равенств следует, что
ВС ВхСх . л . л
-jB = ^r-F^' T-e- sinA = sinAi.
, т. е. cos A = cos A\,
Аналогично
АС АхСх
АВ хх
-"¦¦*'» =
х) Слово «тригонометрия» в переводе с греческого языка означает «измере-
«измерение треугольников».

/. Признаки подобия треугольников
227
Доказанные утверждения позволяют говорить: «синус острого угла,
косинус острого угла, тангенс острого угла, котангенс острого угла»,
не указывая при этом, об остром угле какого именно прямоугольного
треугольника идет речь. Воспользуемся этим наблюдением для вывода
так называемых формул приведения:
sin(90° - А) = cos A, cos(90° - А) = sin А.
Обратимся к рисунку 317, а. Поскольку ZB = 90° — /.А, то
sin(90° - А) = sin В = ^ = cos A,
cos(90° — А) = cos В = —— = sin A,
что и требовалось доказать.
Выведем еще одну важную формулу. Используя равенства B) и C),
получаем:
. 2 л , 2 л ВС2 , АС2 ВС2 + АС2
sin A + cos А = т + 5- = ^ .
АВ2 АВ2
По теореме Пифагора ВС2 + АС2 =
= АВ2, поэтому
sin2 A + cos2 A = 1. (8)
Равенство (8) называется основным
тригонометрическим тождеством.
Решим теперь такую задачу.
Задача 3. В треугольнике ABC
АВ = с, ВС = а, С А = Ъ. Доказать, что
(Ь + с) sin —,
(9)
причем равенство имеет место только
в том случае, когда Ъ = с.
Решение. Проведем биссектрису
AD. Если 6 = с, т. е. треугольник ABC —
равнобедренный, то биссектриса AD яв-
является также высотой (рис.318, а). Тогда
из прямоугольных треугольников ADC
и ADB получаем: DC = hsin—, BD =
= с sin—. Следовательно, а = БС =
= ED + DC = (Ъ + с) sin —, т. е. неравен-
неравенство (9) в этом случае превращается в ра-
равенство.
С
б)
Рис.318, а) Ъ = с; б) Ьф с

228 Гл. 7. Подобные треугольники
Если же b ^ с (рис. 318, б), то биссектриса AD не перпендикулярна
к стороне ВС. Проведем перпендикуляры ВН и СК к прямой AD.
Из прямоугольных треугольников АВН и АСК имеем:
В прямоугольном треугольнике BHD гипотенуза BD больше кате-
катета ВН, т. е. ,
BD>csmj.
По аналогичной причине
DC > b sin j.
Складывая эти два неравенства, получаем:
BD + DC > F + c)sin^,
т. е. а > (Ь + с) sin —, что и требовалось доказать.
Задачи
303. Докажите, что прямая, пересекающая две стороны треуголь-
треугольника, параллельна третьей его стороне тогда и только тогда, когда она
отсекает на этих двух сторонах отрезки, пропорциональные данным
сторонам.
304. На основании AD трапеции ABCD взяты точки К и Т так,
что АК = TD. Отрезки АС и ВТ пересекаются в точке М, отрез-
отрезки КС и BD — в точке Р. Докажите, что отрезок МР параллелен
основаниям трапеции.
305* Через точку Р, лежащую вне окружности, проведены две
прямые, касающиеся этой окружности в точках А и В. Отрезок АС —
перпендикуляр к диаметру BD. Докажите, что прямая PD делит
отрезок АС пополам.
306. В выпуклом четырехугольнике ABCD углы ABD и ACD
равны, диагонали АС и BD пересекаются в точке О. Докажите, что
треугольники ВОС и AOD подобны.
307. Вершины А, В, С треугольника ABC лежат на сторонах А\В\,
В\С\, С\А\ треугольника А\В\С\ соответственно. Докажите, что если
углы В\АВ, С\ВС и А\СА равны, то треугольники ABC и А\В\С\
подобны.
308. Отрезки АН и ВР — высоты треугольника ABC. Докажите,
что треугольники РСН и ABC подобны.
309. Отрезок ВН — высота треугольника ABC, точки К и М —
основания перпендикуляров, проведенных из точки Н к прямым АВ
и СВ соответственно. Докажите, что треугольники МВК и ABC
подобны.
310. На биссектрисе угла взята точка Р. Прямая, проходящая через
точку Р, отсекает на сторонах угла отрезки с длинами а и Ь. Докажите,

/. Признаки подобия треугольников 229
что величина - + т не зависит от выбора прямой.
311. Прямая, проходящая через вершину неравнобедренного тре-
треугольника, разбивает его на два подобных треугольника. Найдите
величину угла, через вершину которого проведена эта прямая.
312. Прямая, проходящая через вершину треугольника, разбивает
его на два подобных треугольника с коэффициентом подобия л/3.
Найдите углы данного треугольника.
313. Докажите, что треугольники ABC и А\В\С\ подобны, если:
ч АВ AC AM Л,, , ,,
а) . _ = -j-ft = л ъ* > гДе AM и А\М\ — медианы треугольников;
А\В\ А\С\ А\М\
s<\ ВС AM АН Л Ъ /Г Л Ъ /Г Л ТТ Л ТТ
б) = = , где AM и А\М\ — медианы, АН и А\Н\ —
В\С\ А\М\ А\Н\
высоты треугольников;
АН AD
в) ZA = ZAU -^Ц- = -р^-, где АН и АХНХ - высоты, AD и AXDX -
А\Н\ A\D\
биссектрисы треугольников;
ч ?7li 7712 W&3 л т->^1
г) —— = -— = —, где пг\, ni2, ^з — длины медиан треугольника ABC,
l\ h h
h, h, h — длины медиан треугольника А\В\С\.
О1Л U /Л /Л АВ АС + СВ
314. Докажите, что если ZA = /_АХ и = ——— , то тре-
угольники ABC и А\В\С\ подобны.
315* В равнобедренном треугольнике ABC из середины Н основа-
основания ВС проведен перпендикуляр НЕ к прямой АС. Точка О — сере-
середина отрезка НЕ. Докажите, что прямые АО и BE перпендикулярны.
316* Из точки М внутренней области угла АО В проведены перпен-
перпендикуляры МР и MQ к прямым О А и ОВ. Из точек Р и Q проведены
перпендикуляры PR и QS соответственно к ОВ и О А. Докажите, что
прямая RS перпендикулярна к ОМ.
317. На сторонах АВ, ВС, CD и DA параллелограмма ABCD взя-
взяты точки М, К, Т, Р соответственно, причем AM : СТ = АР : С К ф 1.
Докажите, что четырехугольник МКТР — трапеция.
318. Дан параллелограмм ABCD. Отрезки AM и АР — перпенди-
перпендикуляры, проведенные к прямым ВС и CD. Докажите, что треугольни-
треугольники MAP и ABC подобны.
319. Диагонали трапеции взаимно перпендикулярны. Докажите,
что произведение длин оснований трапеции равно сумме произведений
длин отрезков одной ее диагонали и длин отрезков другой ее диагона-
диагонали, на которые диагонали делятся точкой пересечения.
320* Докажите, что если в треугольнике ABC угол А в два раза
больше угла В, то ВС2 = АС2 + АС • АВ.
321* В треугольнике ABC углы А, В и С равны соответственно а,
/3 и 7, причем За + 2/3 = 180°. Докажите, что ВС2 + АВ • АС = АВ2.
322. Докажите, что отношение площадей подобных треугольников
равно квадрату коэффициента подобия.

230 Гл. 7. Подобные треугольники
323. Прямая, параллельная основанию треугольника с площа-
площадью S\, отсекает от него треугольник с площадью S^. Найдите площадь
четырехугольника, три вершины которого совпадают с вершинами
меньшего треугольника, а четвертая вершина лежит на основании
большего треугольника.
324. Через точку, взятую на стороне треугольника, проведены пря-
прямые, параллельные двум другим его сторонам. Эти прямые разбивают
треугольник на параллелограмм и два треугольника, площади которых
равны S\ и^2. Найдите площадь параллелограмма.
325. Через точку, лежащую внутри треугольника, проведены три
прямые, параллельные его сторонам. Площади образовавшихся при
этом треугольников равны S\, S2, S3. Найдите площадь данного тре-
треугольника.
326. Биссектриса угла А параллелограмма ABCD пересекает сто-
сторону ВС в точке Р, а диагональ BD — в точке Т. Известно,
что АВ : AD = k < 1. Найдите отношение площадей треугольни-
треугольника ВТР и параллелограмма ABCD.
327. Основания трапеции равны а и Ъ (а > Ь). Прямые, соединя-
соединяющие середину большего основания с концами меньшего, пересекают
диагонали в точках М и Р. Найдите длину отрезка МР.
328. Найдите синус, косинус, тангенс и котангенс углов А и В
прямоугольного треугольника ABC с прямым углом С, если: а) ВС =
= 8, АВ = 17; б) ВС = 21, АС = 20; в) ВС = 1, АС = 2; г) АС = 24,
АВ = 25.
329. Найдите значения синуса, косинуса, тангенса и котангенса для
углов 30°, 45°, и 60°.
330. Основания трапеции равны 1 и 3 + 2л/3, а боковые стороны
равны 2л/2 и 4. Найдите углы трапеции.
331. Докажите, что: а) если тангенс одного острого угла равен
тангенсу другого острого угла, то эти углы равны; б) если синус одного
острого угла равен синусу другого острого угла, то эти углы равны;
в) если косинус одного острого угла равен косинусу другого острого
угла, то эти углы равны.
332. Два острых угла равны а и /3. Докажите, что: а) если а > /3,
то sin а > sin/З, и обратно: если sin а > sin/З, то а > /3; б) если а > /3,
то cos а < cos/3, и обратно: если cos а < cos/З, то а > /3; в) если а > /3,
то tga > tg/З, и обратно: если tga > tg/З, то а > /3; г) если а > /3,
то ctga < ctg/З, и обратно: если ctga < ctg/З, то а > /3.
§ 2. Применение подобия к доказательству теорем
и решению задач
98. Обобщенная теорема Фалеса. Доказательства нескольких
важных теорем геометрии основаны на следующем факте.

2. Применение подобия к доказательству теорем и решению задач 231
Теорема. Три параллельные прямые, пересекающие две дан-
данные прямые, отсекают на этих двух прямых пропорциональные
отрезки.
Доказательство. Обратимся к рисунку 319, а, на котором
прямая а рассечена параллельными прямыми на отрезки А\А2 и А2А%,
а прямая Ь — на отрезки В\В2 и В2В%. Требуется доказать, что
А\А2 _ В\В2
А2А3 ~ В2В3'
A)
Возможны два случая.
1°. Прямые а и Ъ параллельны (рис.319, б). Тогда четырехугольни-
четырехугольники А\А2В2В\ и А2А^В^В2 — параллелограммы. Поэтому А\А2 = В\В2
и А2А^ = В2В%, откуда и следует равенство A).
2°. Прямые а и Ъ не параллельны. Если при этом точки А2 и В2
не совпадают (рис.319, в), то через точку А2 проведем прямую с, па-
параллельную прямой Ь. Она пересечет прямые А\В\ и А3Д3 B некоторых
точках С\ и Со,. Треугольники А\С\А2 и А2А^С^ подобны по двум
б)
Рис. 319

232 Гл. 7. Подобные треугольники
углам (ZA\C\A2 = ZA2C3A3 и ZC\A\A2 = ZA2A3C3 как накрест ле-
лежащие углы при пересечении параллельных прямых А\В\ и А3В3
секущими С\С% и А\А% соответственно), поэтому
А2А3 А2С3'
Но С\А2 = В\В2, А2С3 = В2В3 (как противоположные стороны
параллелограммов А2С1Б1Б2 и А^С^В^В^), и мы снова приходим к ра-
равенству A).
Если же точки А% и В% совпадают (рис.319, г), то равенство A)
непосредственно следует из подобия треугольников А\В\А<2 и А^В^А^.
Теорема доказана.
Замечание. Доказанная теорема называется обобщенной теоре-
теоремой Фалеса, поскольку теорема Фалеса содержится в ней как частный
случай. В самом деле, если отрезки А\А2 и А2А3 равны, то из A)
следует, что отрезки B\B2 и Б2Б3 также равны. Это и есть теорема
Фалеса.
99. Следствие из обобщенной теоремы Фалеса. Рассмотрим
какую-нибудь прямую а и выберем на ней две точки — А и В. Инту-
Интуитивно ясно, что на прямой а можно выбрать два направления — от А
к В и от В к А. Чтобы различать эти
. . щ а направления, поступим так. При выбран-
С A D н°й единице измерения отрезков поста-
поставим в соответствие отрезку АВ два числа,
а) каждое из которых по модулю равно числу,
выражающему длину отрезка АВ, но зна-
¦ ¦ * ки у них различные. Обозначим эти чис-
А С D ла так: АВ и В А. Таким образом, АВ =
^ч = —ВА. Какое из этих обозначений отно-
относится к положительному числу, а какое —
к отрицательному, для нас не будет иметь
' ' ' значения. Пусть, например, число АВ —
положительное. Тогда АВ = АВ. Для лю-
в\ бой точки М, лежащей на прямой а и от-
отличной от А, положим AM = AM, ec-
С ли точки В и М лежат по одну сторону
1 " от точки А, и AM = —AM в противопо-
ложном случае. Условимся считать также,
г\ что АА = 0. Наконец, для произвольных
точек С и D прямой а положим
Рис- 32° ~СВ = ~AD - ~AC. B)
Отметим, что если А лежит между точками С и D (рис.320, а), то
= \\AC\ + \AD\\ = \AD-AC\,

2. Применение подобия к доказательству теорем и решению задач 233
так как числа АС и AD имеют разные знаки. В противном слу-
случае (рис. 320, б, в, г)
CD= \\AD\-\AC\\ = [AD-AC\,
поскольку знаки чисел АС и AD совпадают. Таким образом, и в том,
и в другом случае CD = [AD - ~АС\ = [CD\.
Итак, каждому отрезку CD прямой а мы поставили в соответствие
два числа — CD и DC; при этом \CD\ = CD, DC = —CD. Этот способ
сопоставления отрезку двух чисел предложил великий английский
физик Исаак Ньютон A643-1727).
Задача 1. Доказать, что для любых трех точек А\, А2 и А&
лежащих на одной прямой, имеет место равенство'.
Решение. Используя равенство B), получаем:
А\ А2 + А2А3 = АА2 - АА\ + АА3 - АА2 = АА3 - АА\ = А\ А3,
что и требовалось доказать.
Замечание 1. Доказанное утверждение называется теоремой
Шаля по имени открывшего эту теорему французского математика
и историка математики Мишеля Шаля A793-1880). Отметим, что
теорема Шаля верна и в том случае, когда какие-то из данных точек
совпадают, если условиться, что формула B) верна и в том случае,
когда точки С и D совпадают. Убедитесь в этом самостоятельно.
Замечание 2. Из теоремы Шаля следует, что если точка А2
лежит между точками А\ и А3 (рис.321, а), то числа А\А2, А2А3
и А\А3 имеют одинаковые знаки. В самом деле, пусть, например,
А\А2 = А\А2 (случай А\А2 = —А\А2 рассмотрите самостоятельно). То-
Тогда, согласно теореме Шаля, А\А2 -\- А2А3 = А\А3. Вычитая равенство
А\А2 + А2А3 = А\А3, получаем:
А2АЪ - А2А3 =
Если предположить, что А2А3 = —А2А%, то получим: —2А2А3 =
= А\А3 — А\Аз, т. е. либо А2А% = 0 (при А\А3 = А\Аз), либо А2А^ =
= А\Аз (при А\А% = —А\А%). И то и другое противоречит тому,
Ах А2 А3
а)
Ах Аз А2
б)
Рис. 321

234
Гл. 7. Подобные треугольники
что точка А2 лежит между А\ и A3. Следовательно, А2А% = А2А%.
Но тогда, согласно нашему равенству, А\А% = А\А%. Таким образом,
числа А\А2, А2А% и А\А% имеют одинаковые знаки, что и требовалось
доказать.
Замечание 3. Отметим, что если лучи А\А2 и A\A% совпадают,
то числа А\А2 и А\А% имеют одинаковые знаки. В самом деле, если
точка А2 лежит между точками А\ и А% (рис.321, а), то знаки чи-
чисел А\А2, А2А3 и А\А3 совпадают; если же точка А% лежит между
точками А\ и А2 (рис.321, б), то знаки чисел А\А3, А%А2 и А\А2
совпадают. И в том и в другом случае числа А\А2 и А\А3 имеют
одинаковые знаки.
Выведем теперь важн�