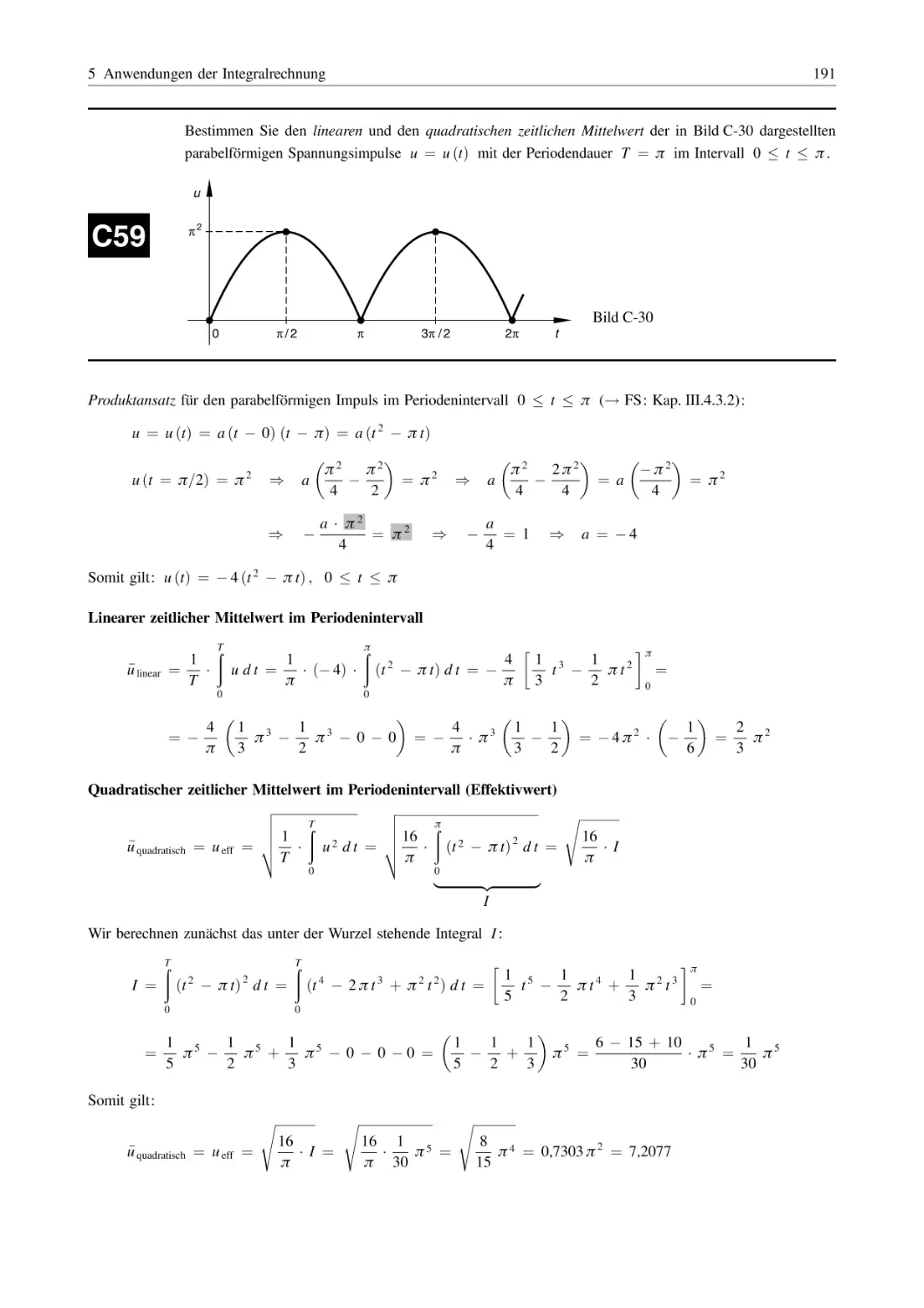
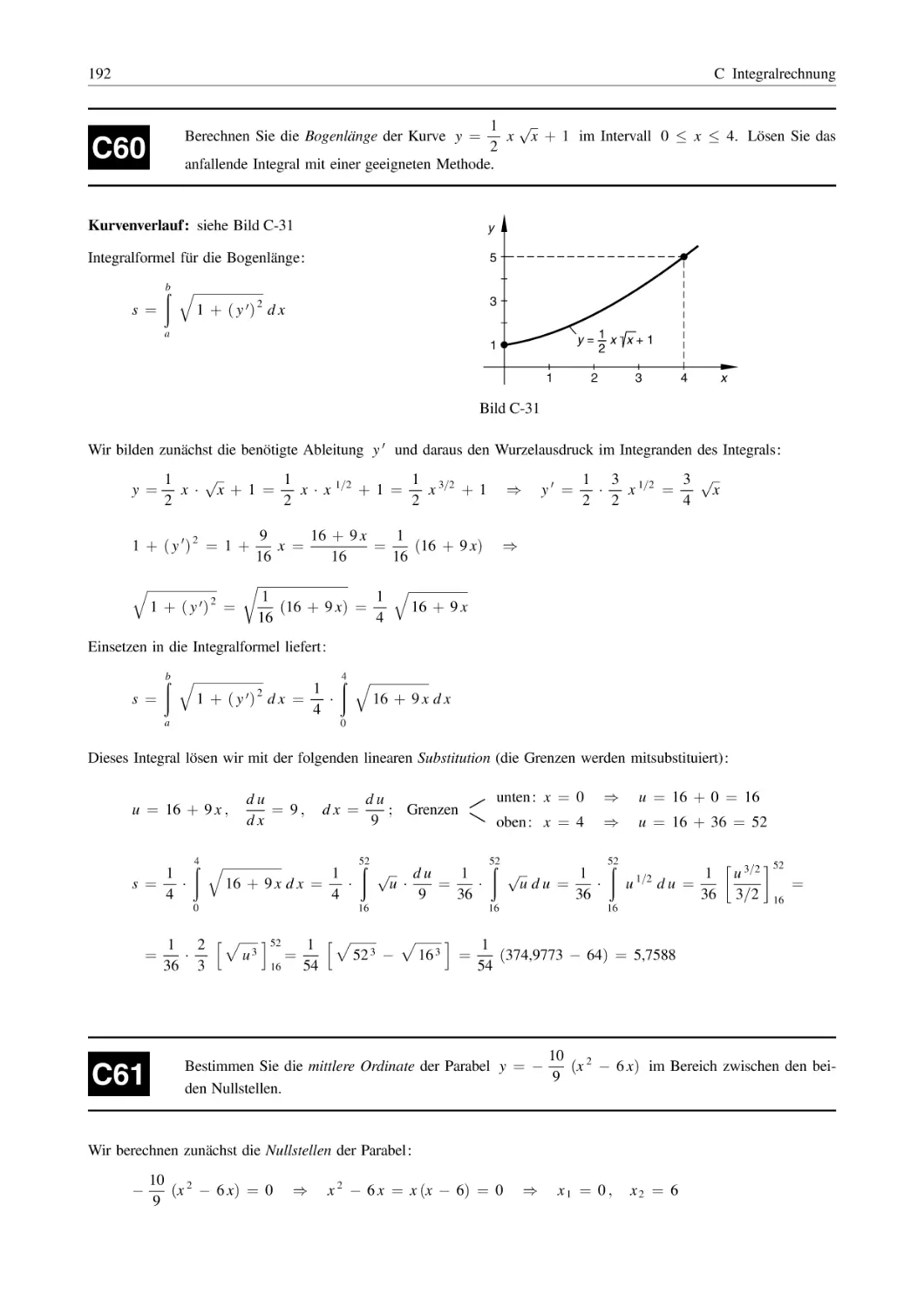
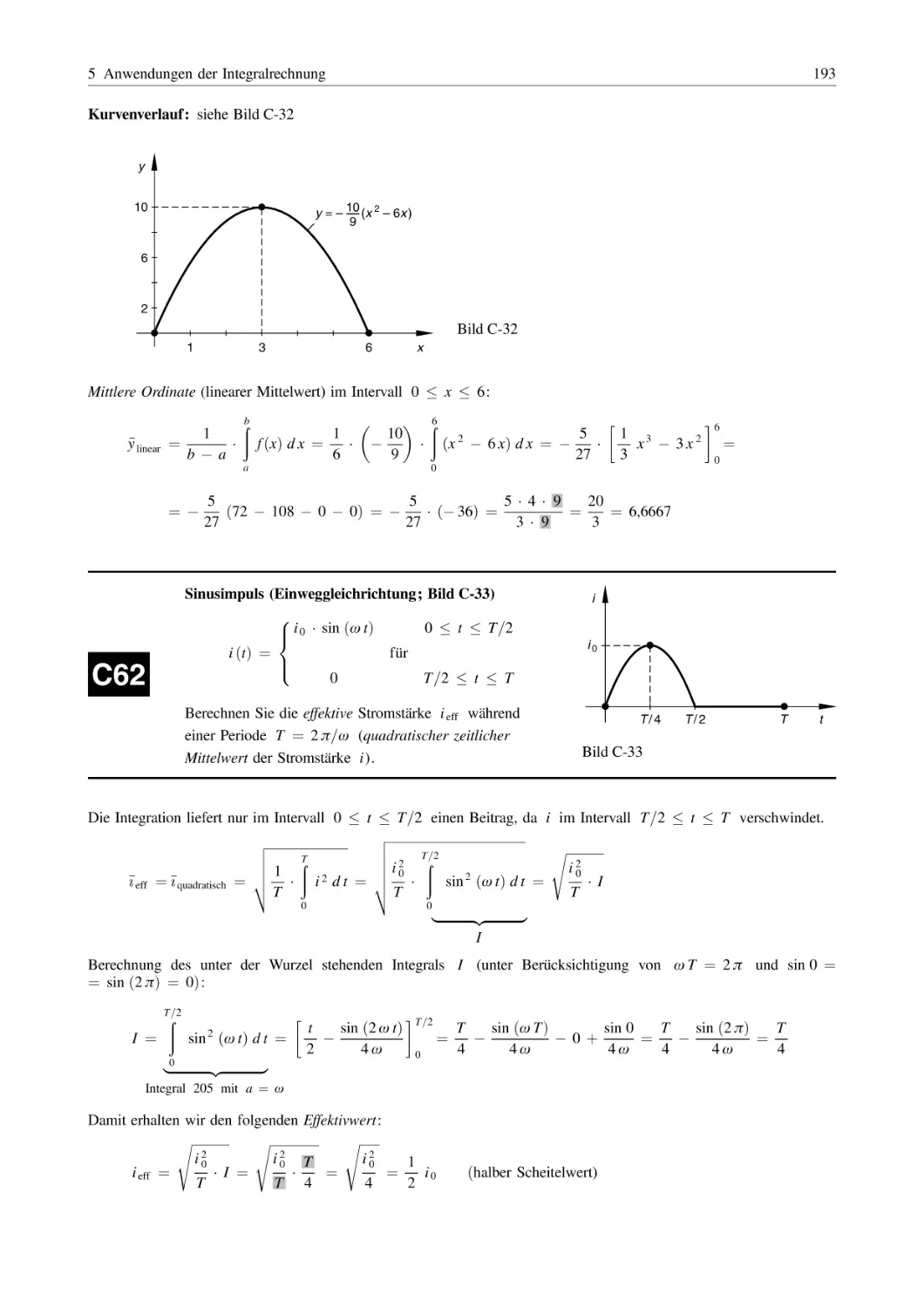
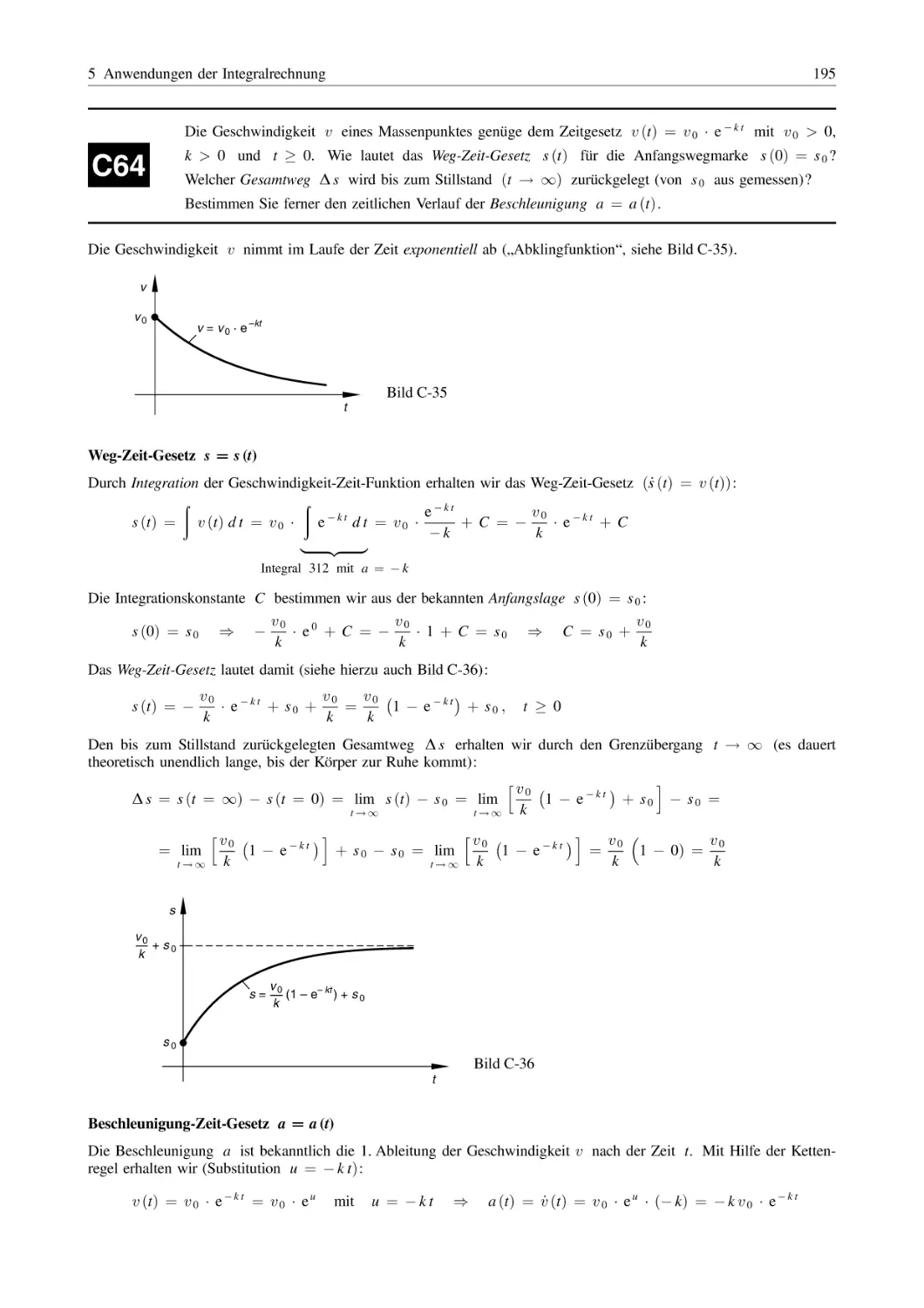
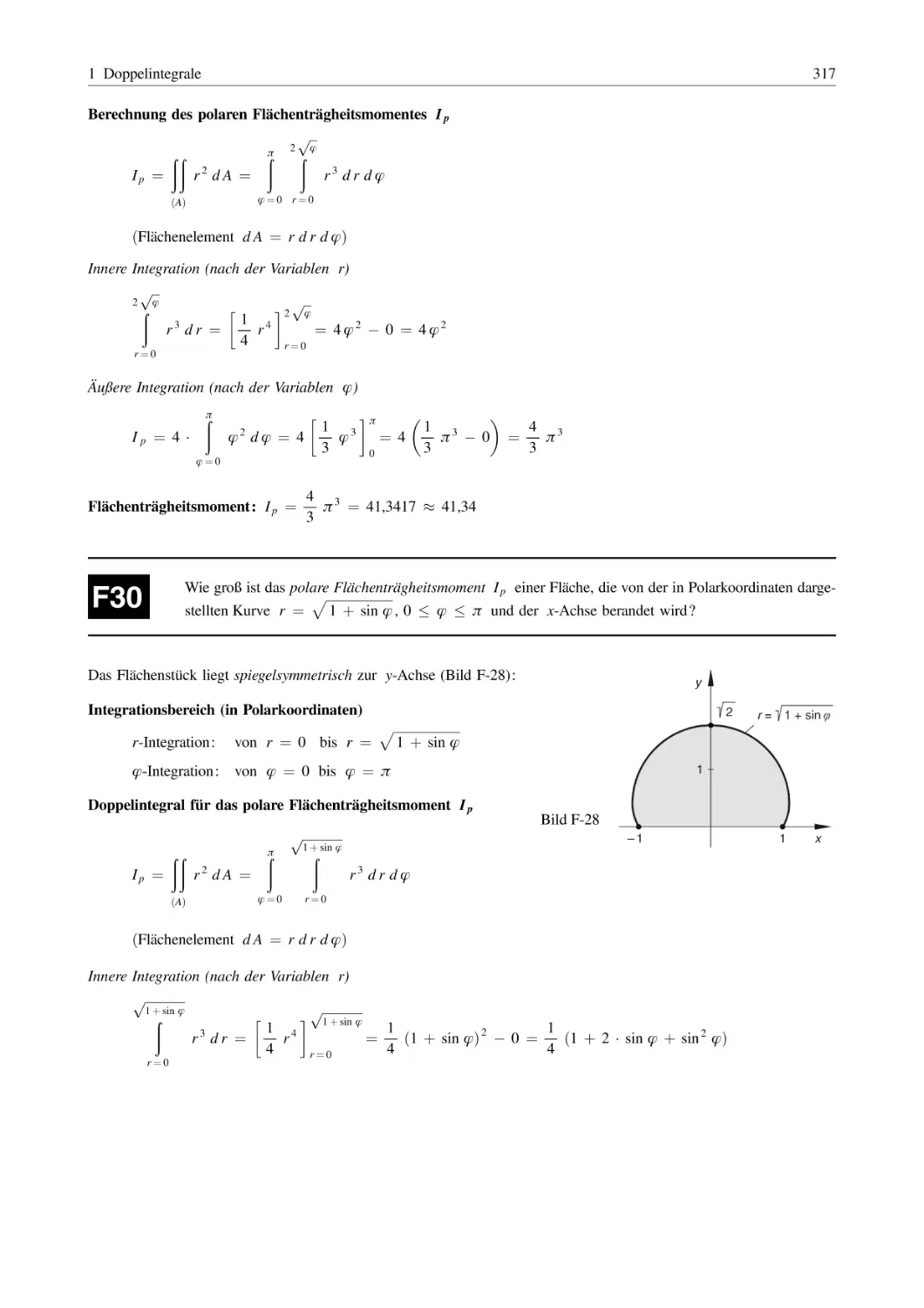
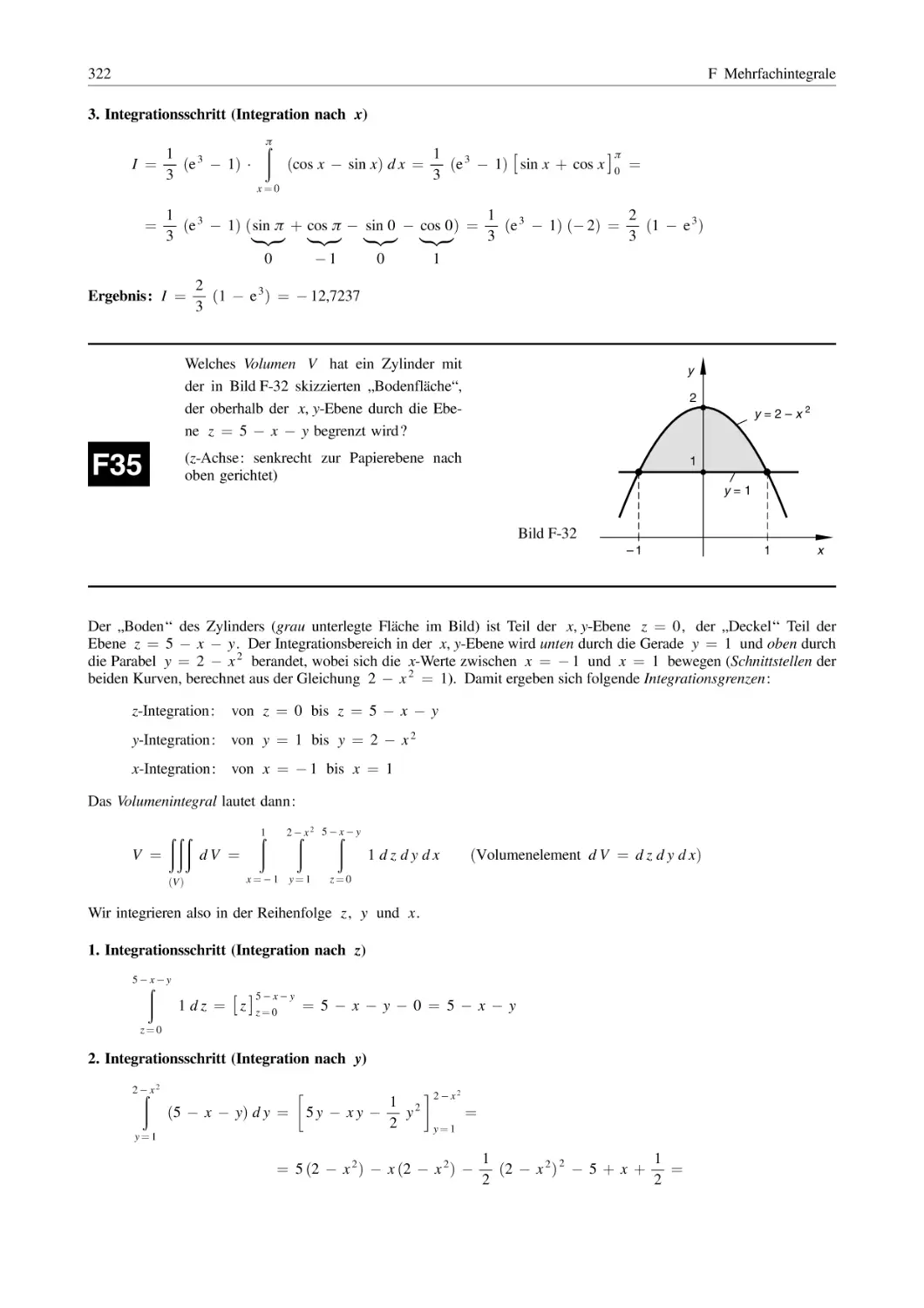
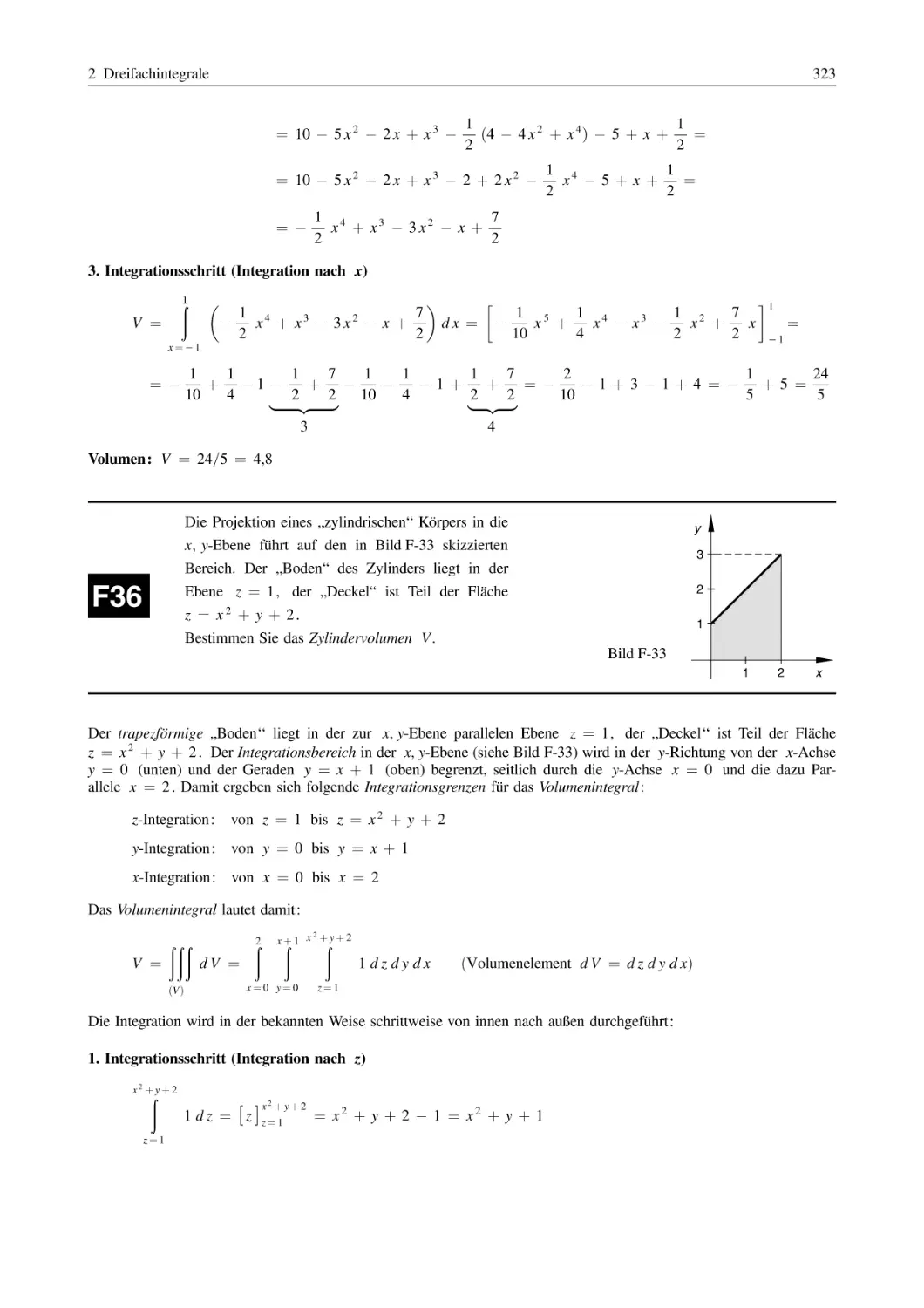
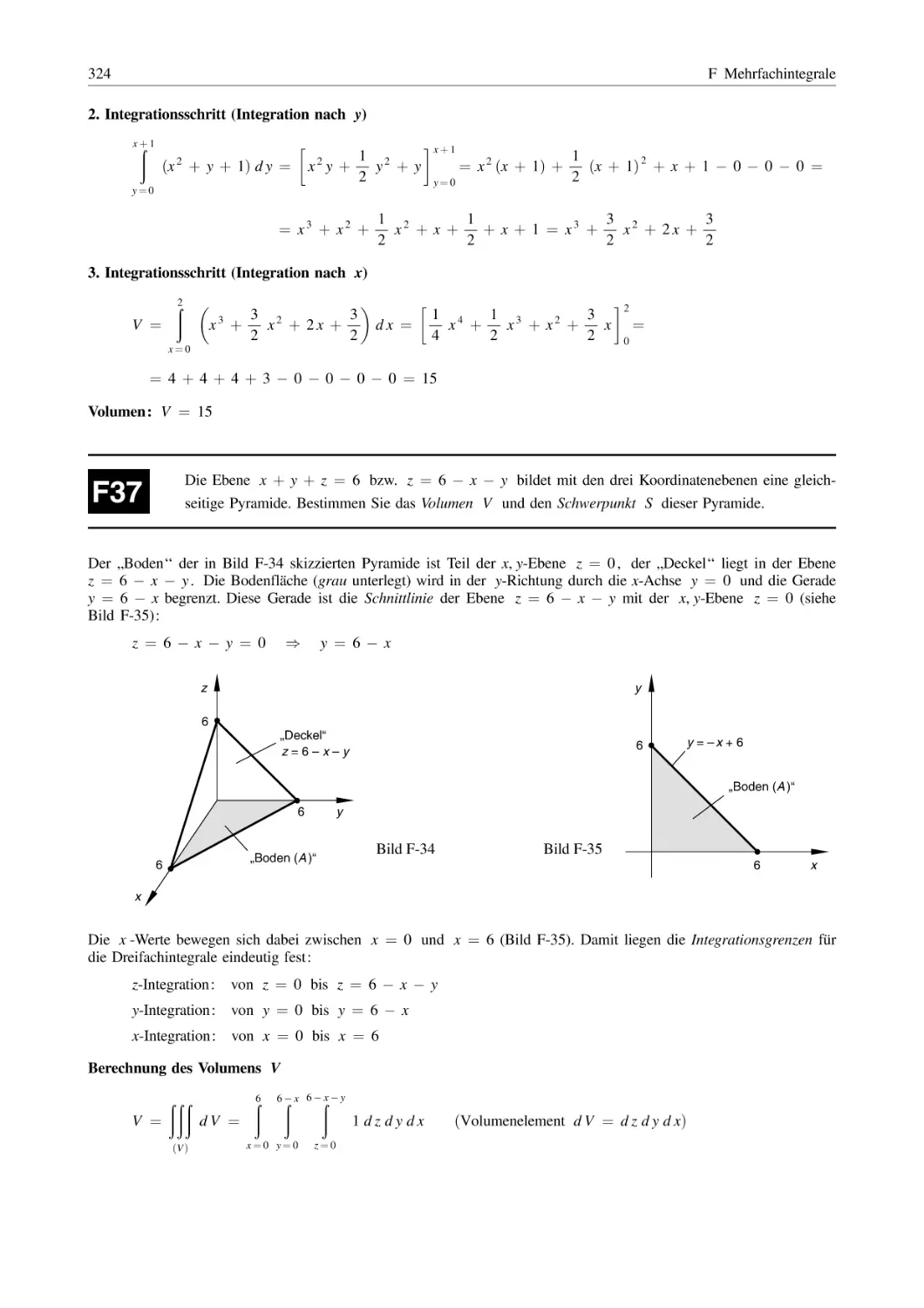
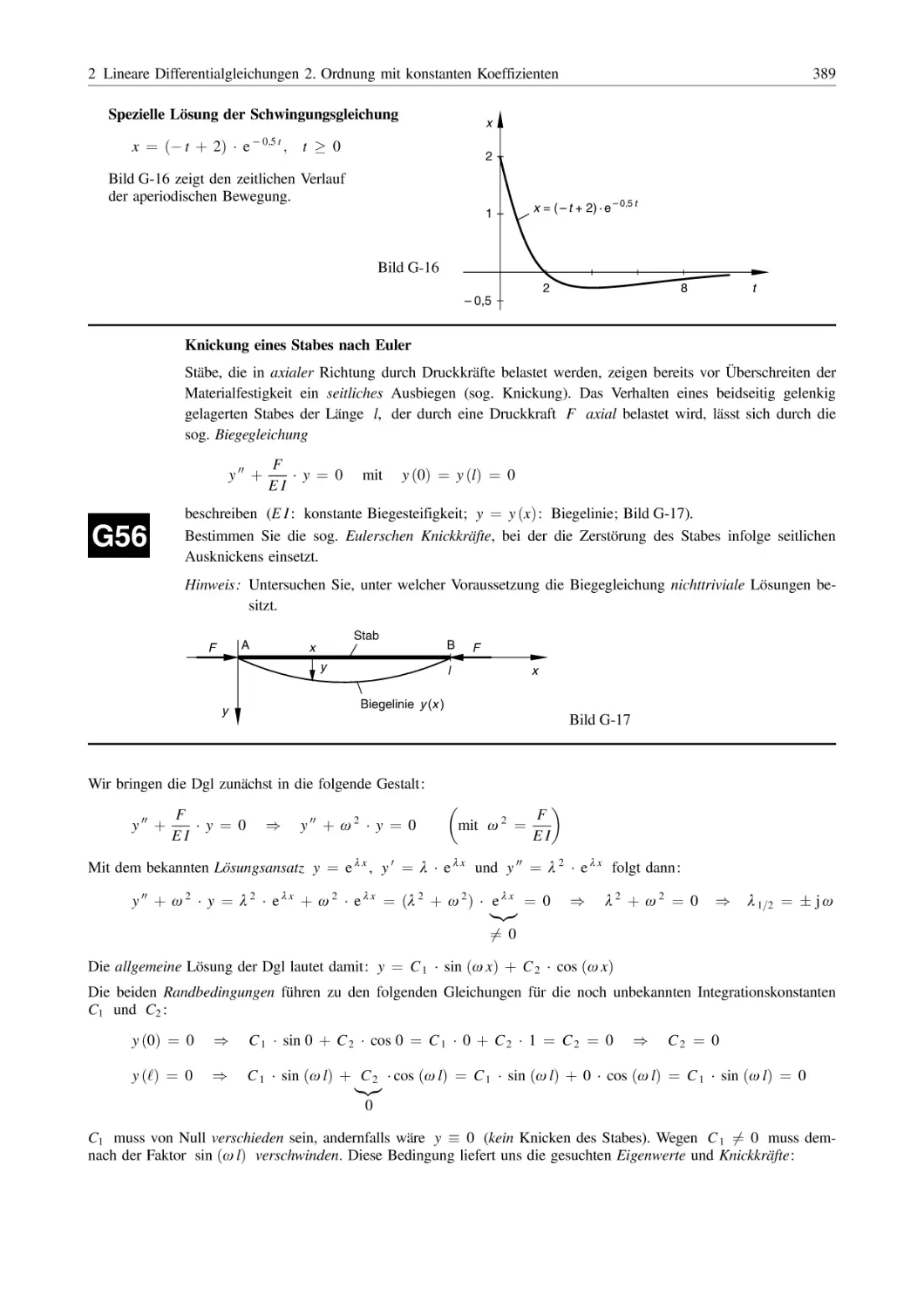
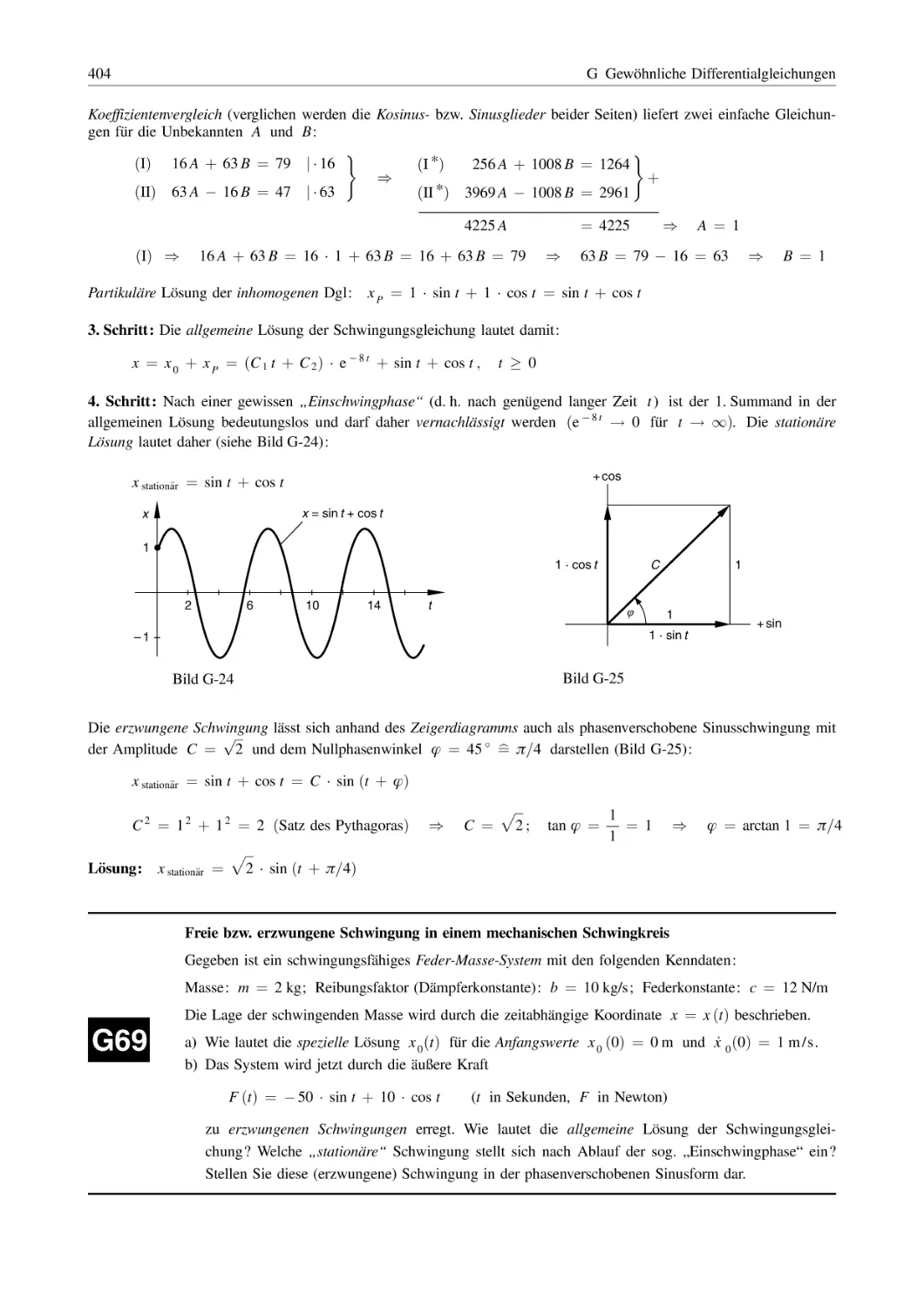
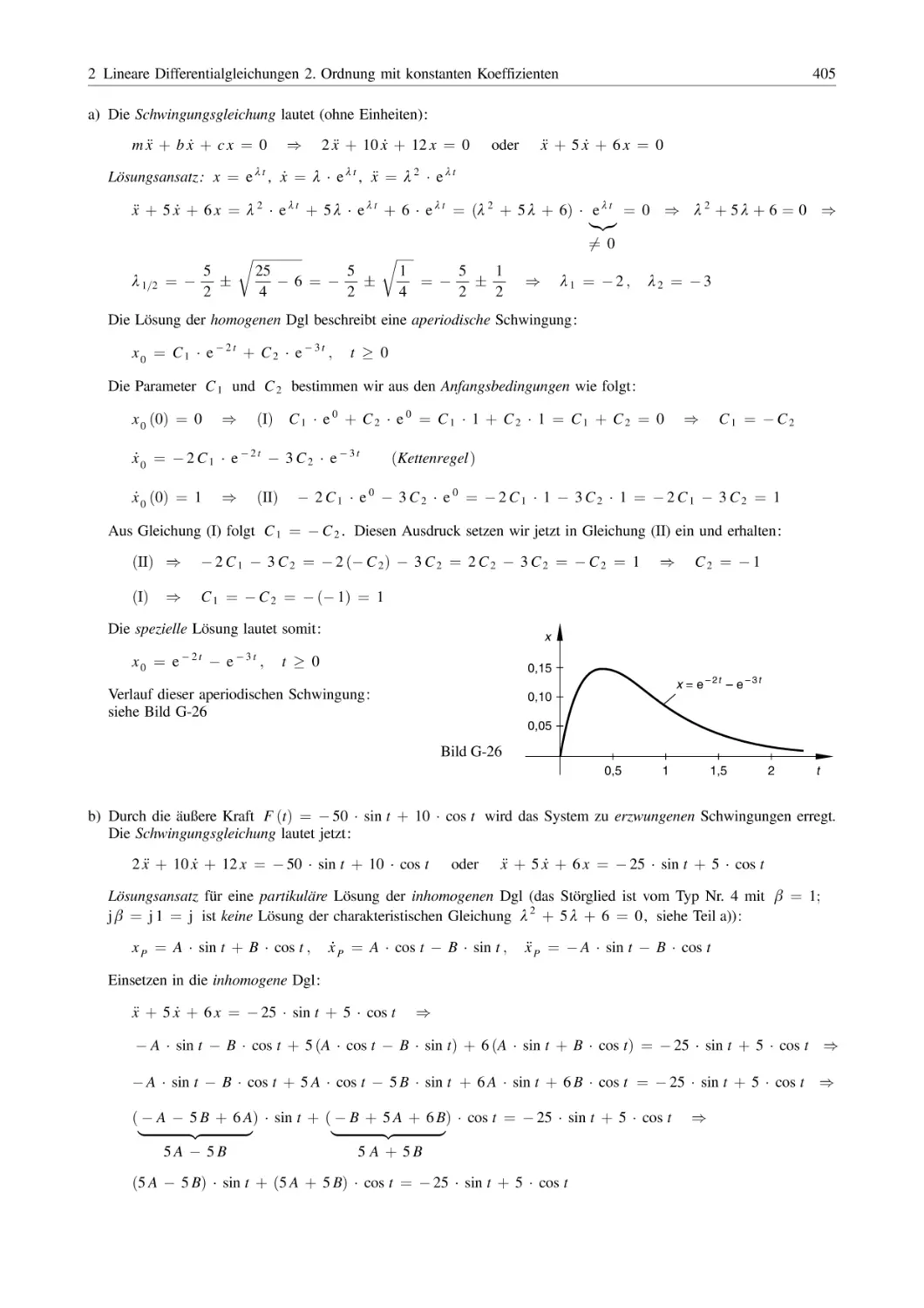
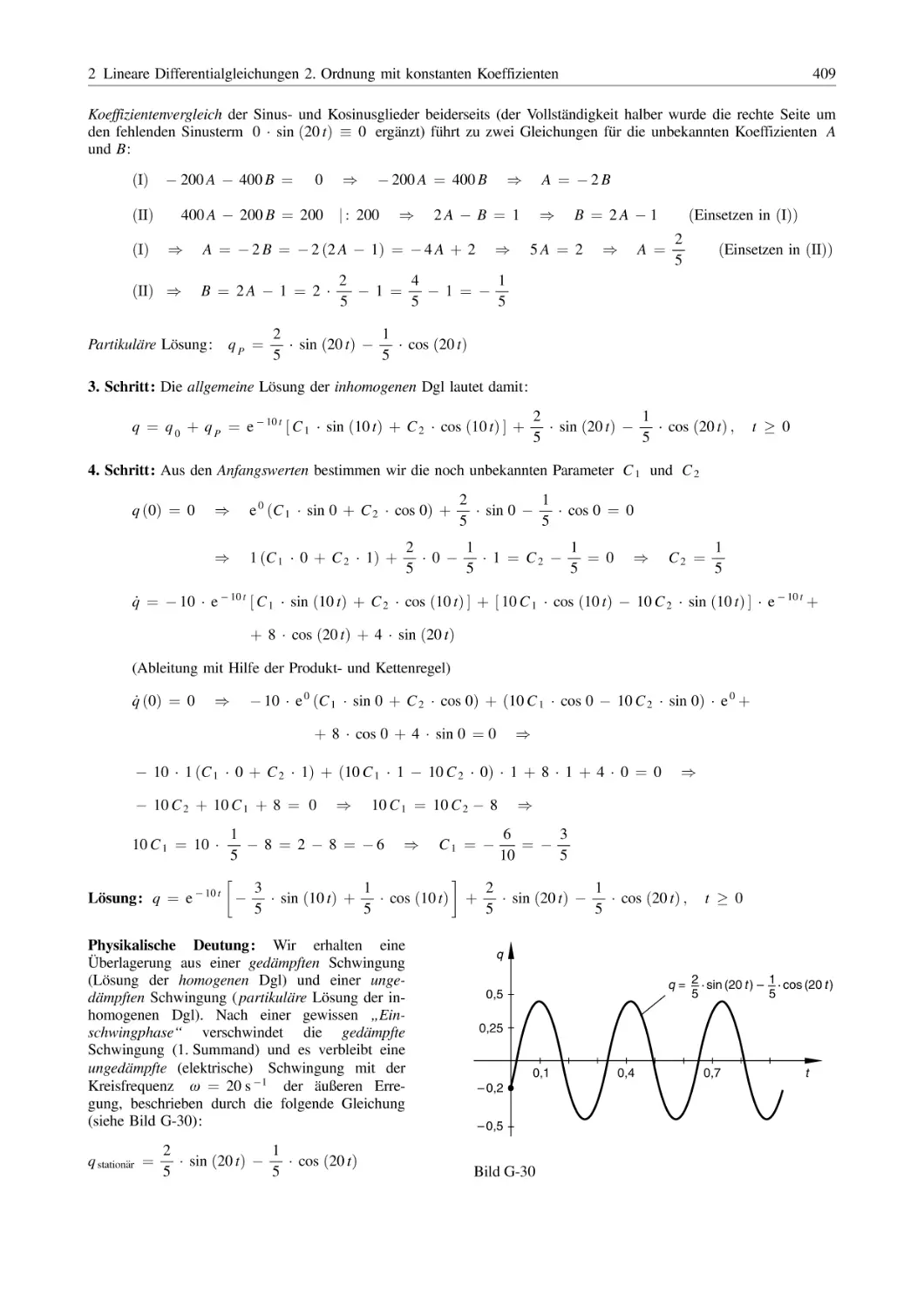
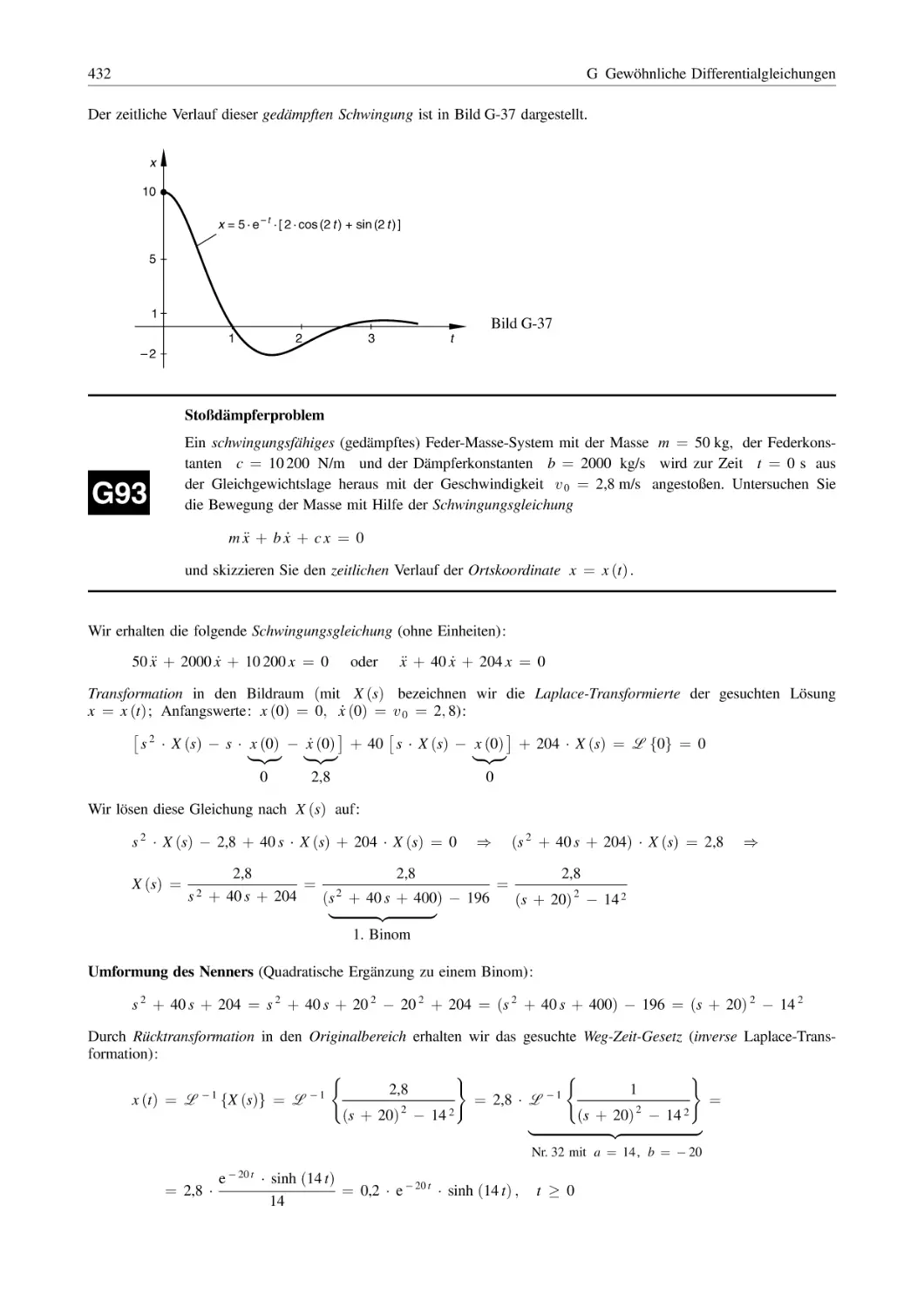
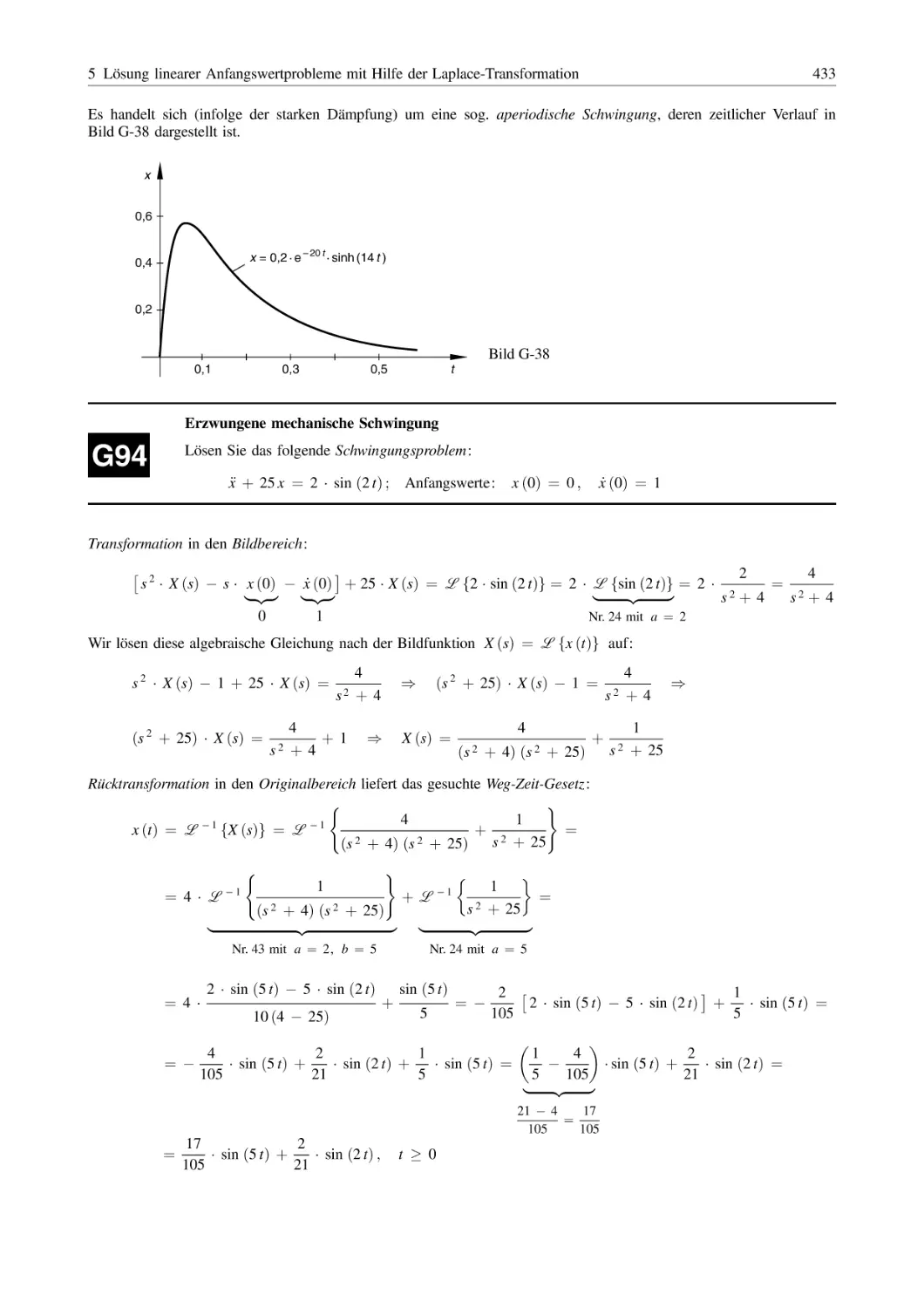
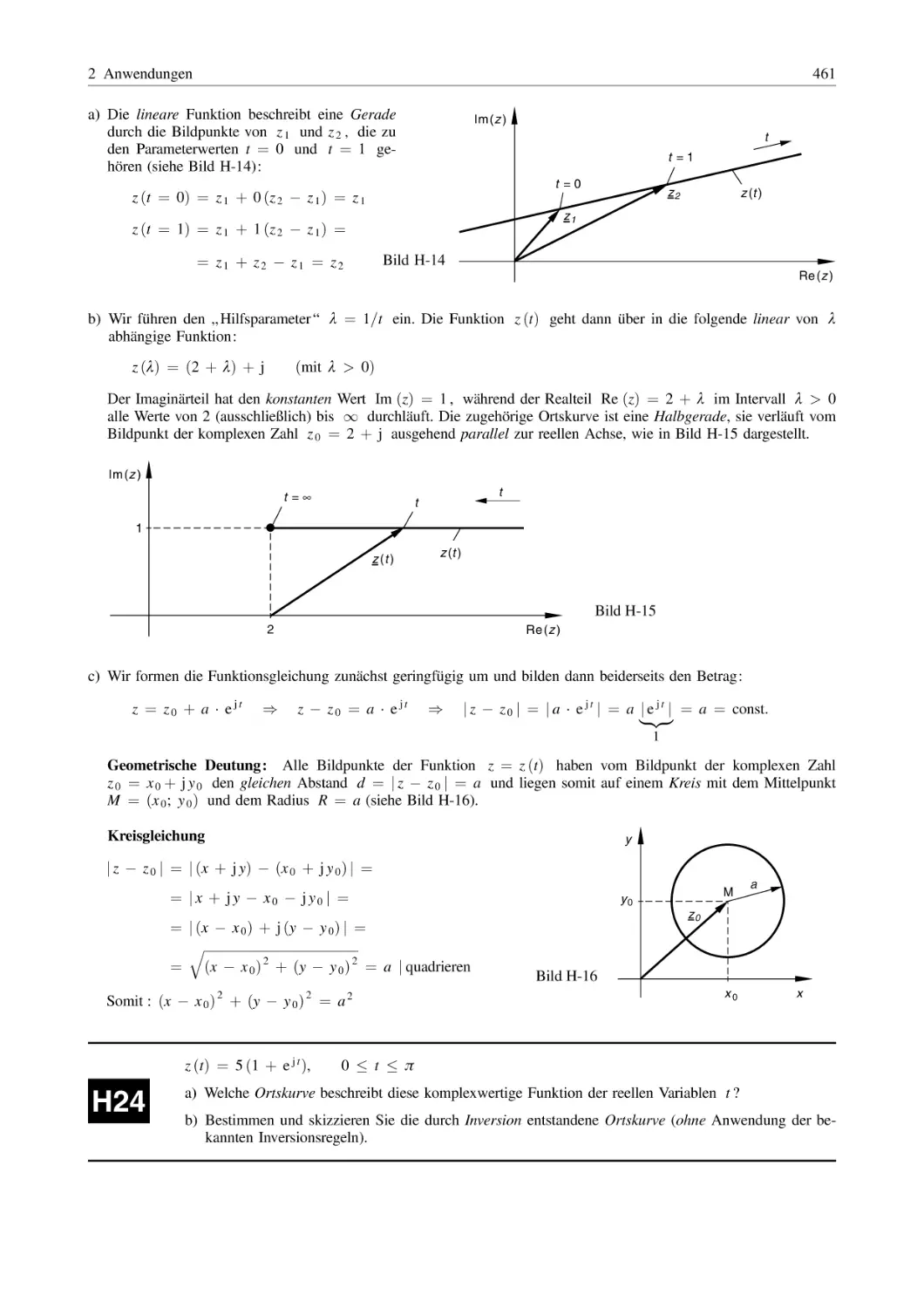
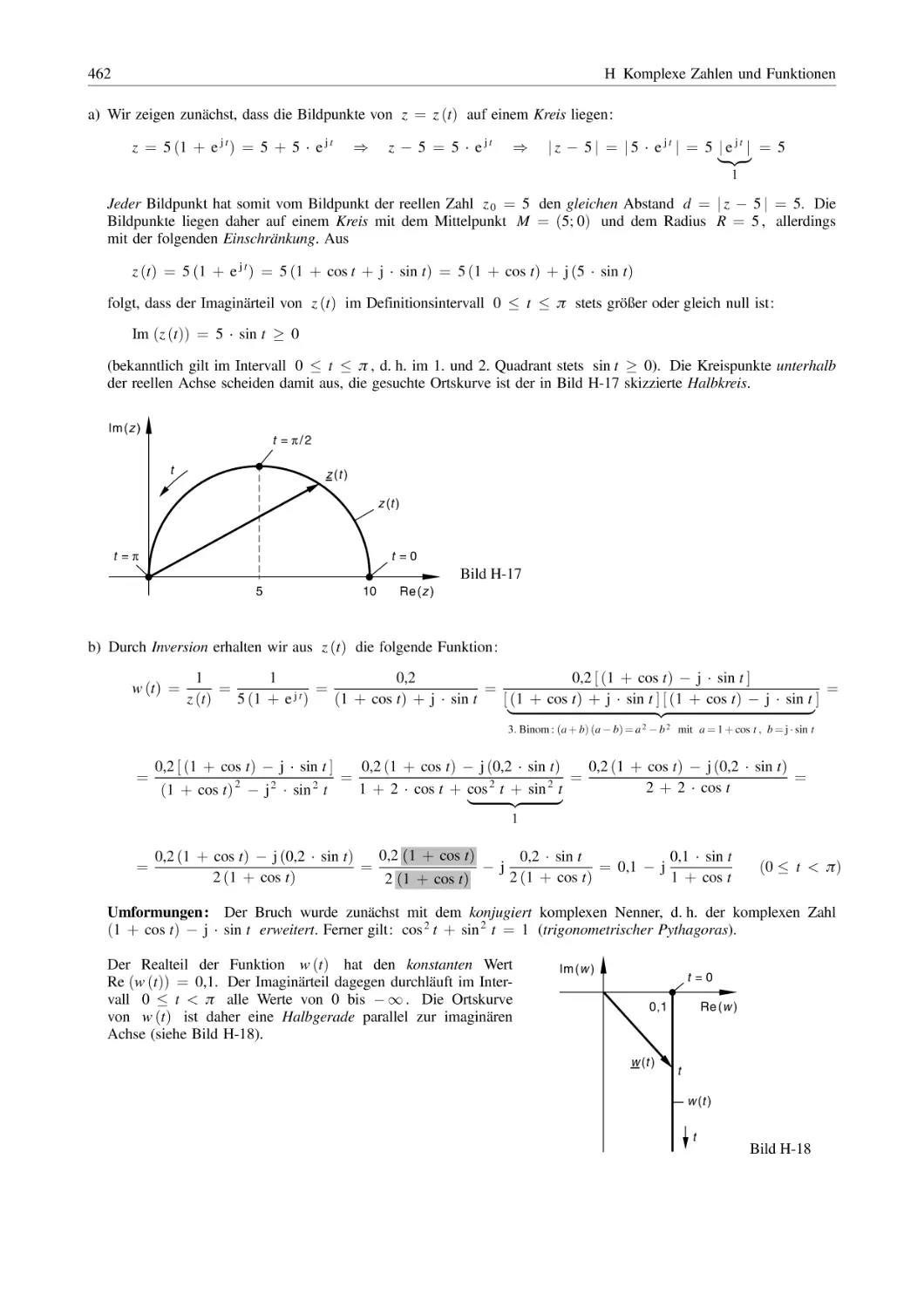
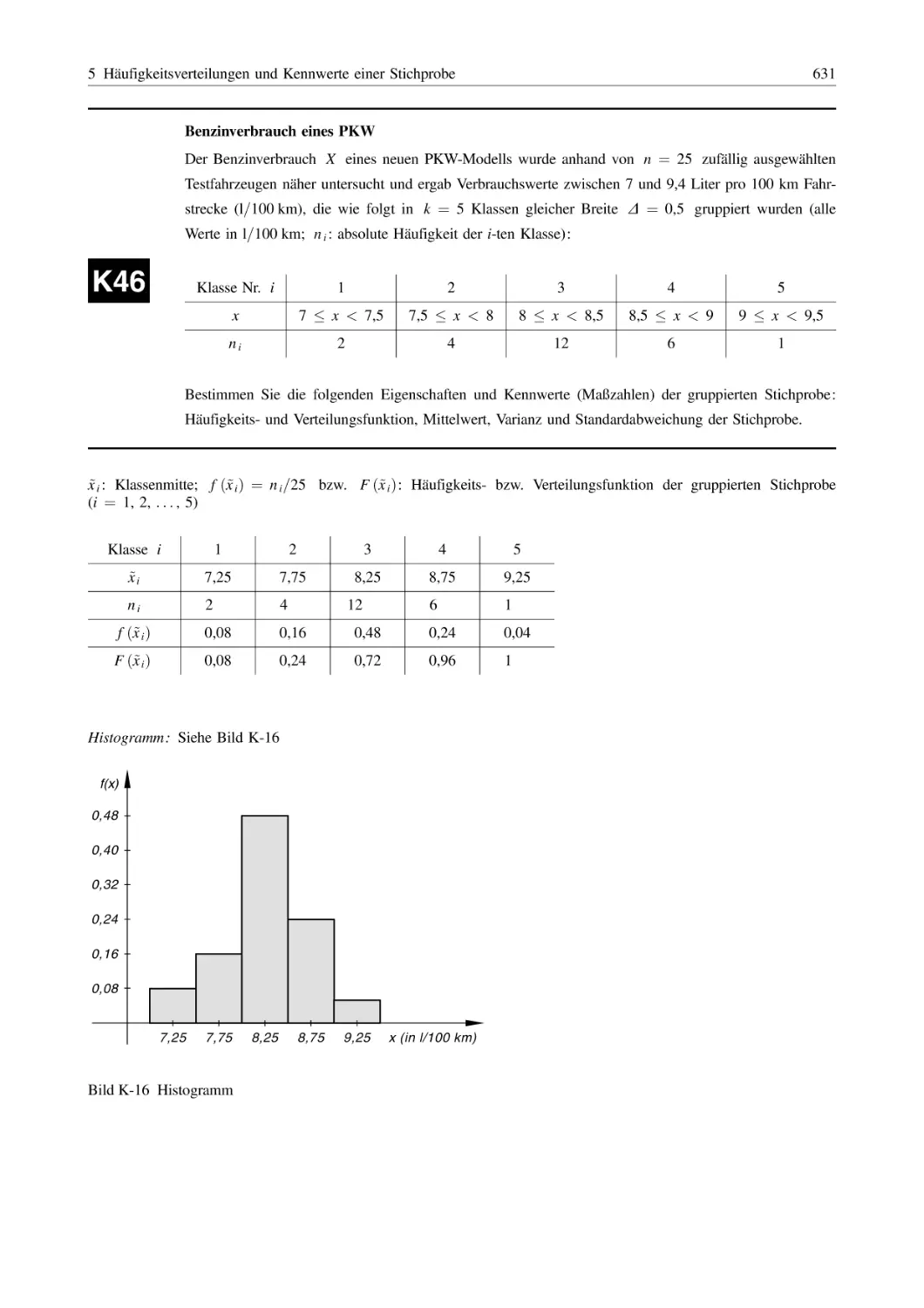
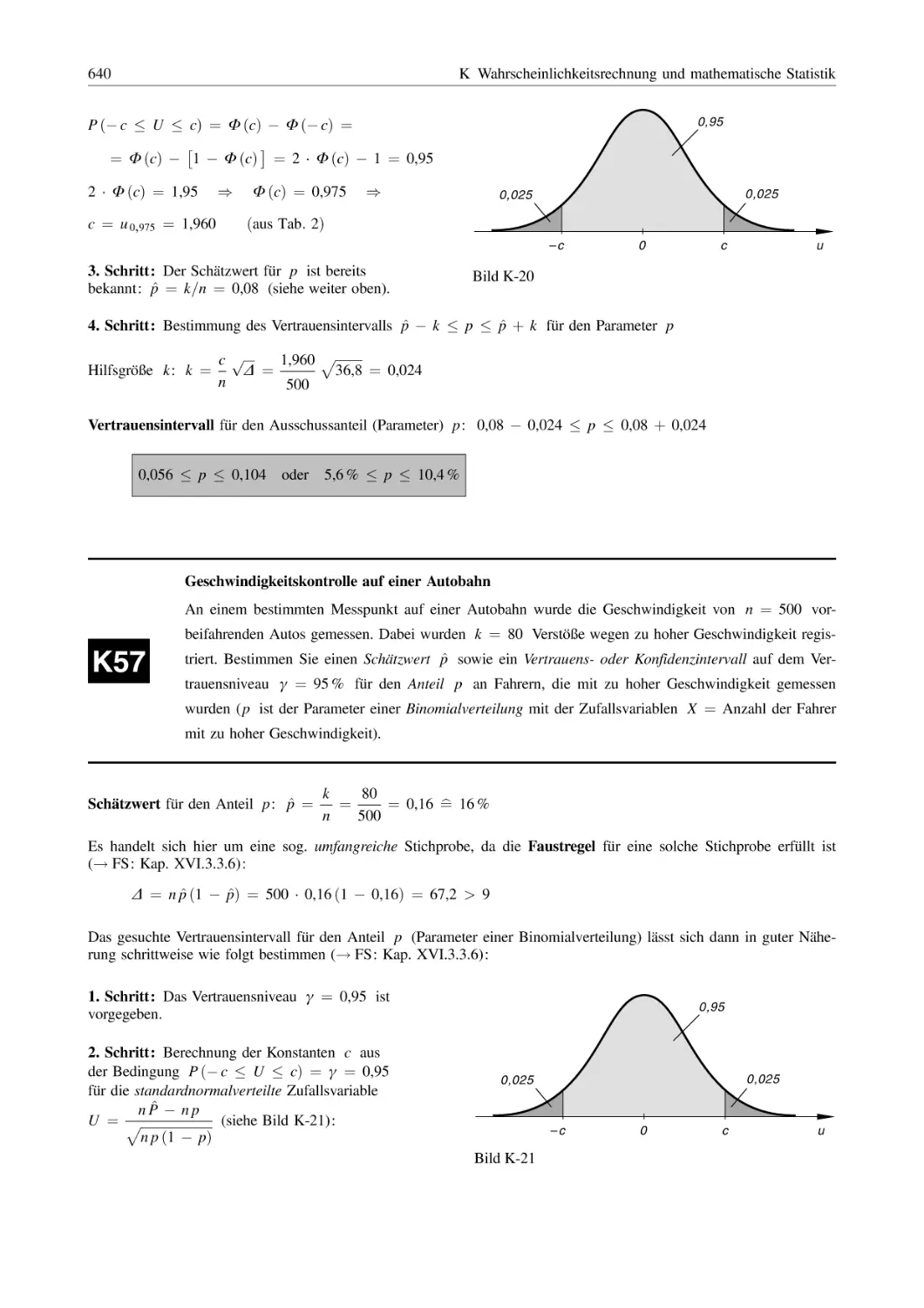
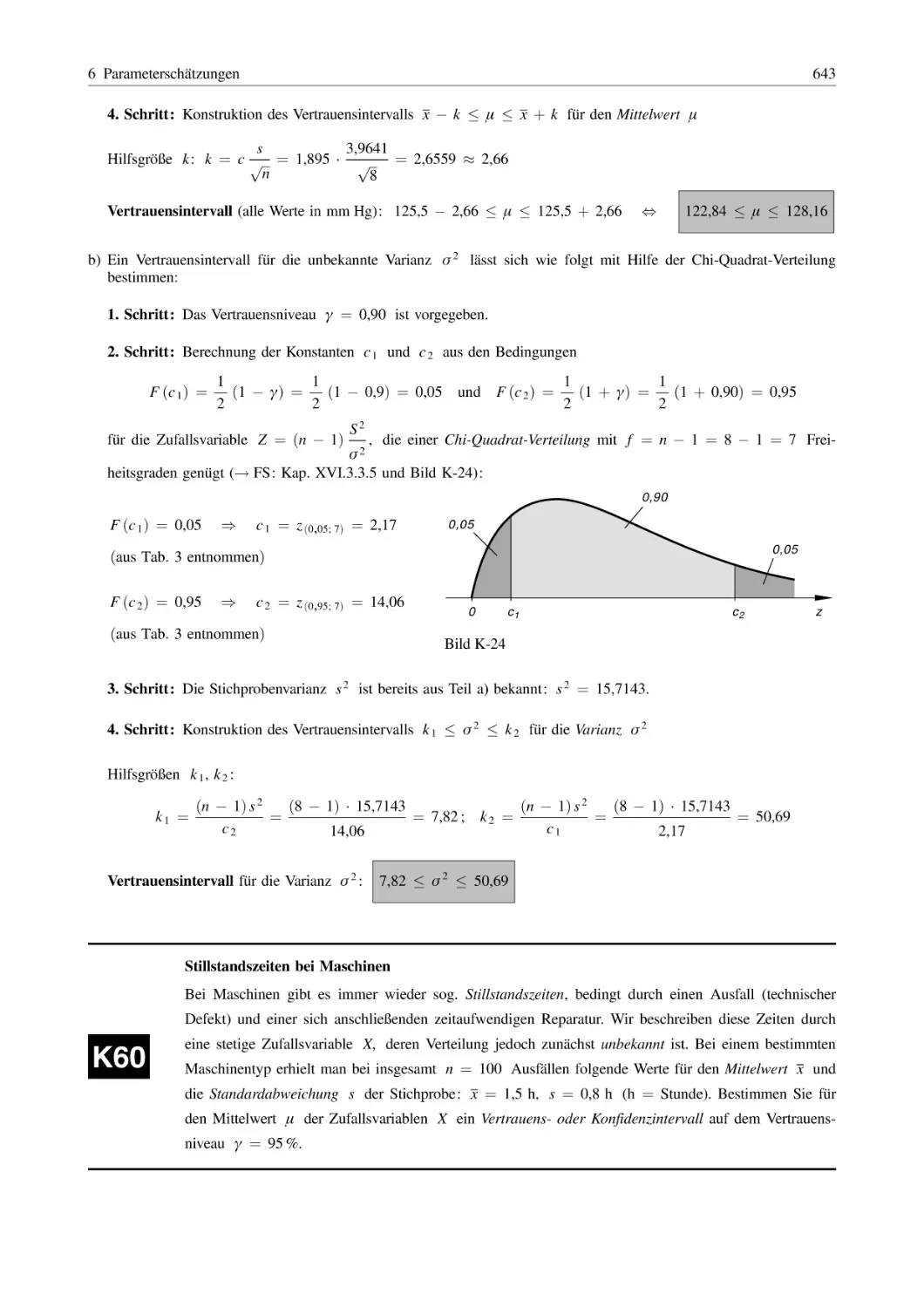
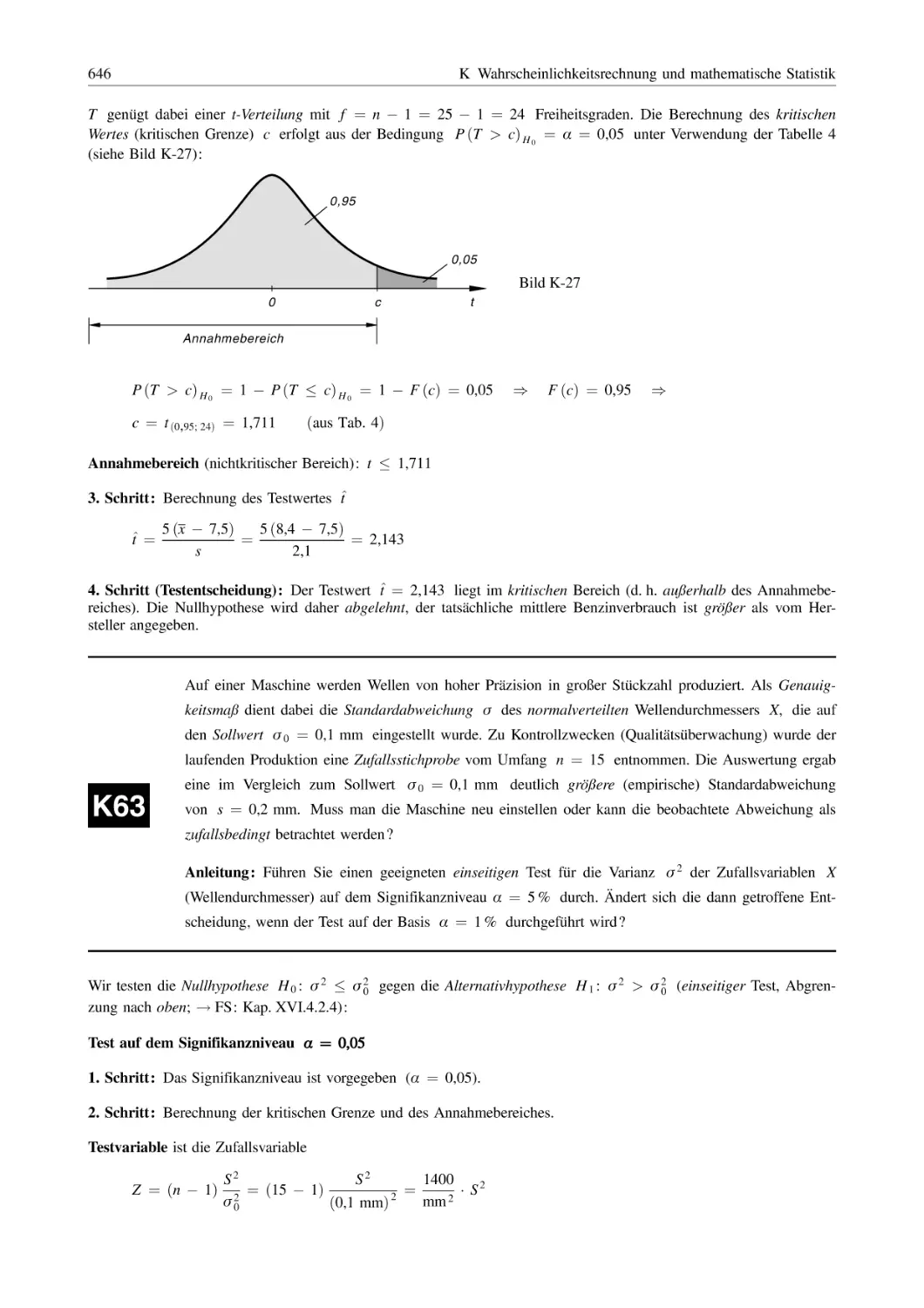
Похожие
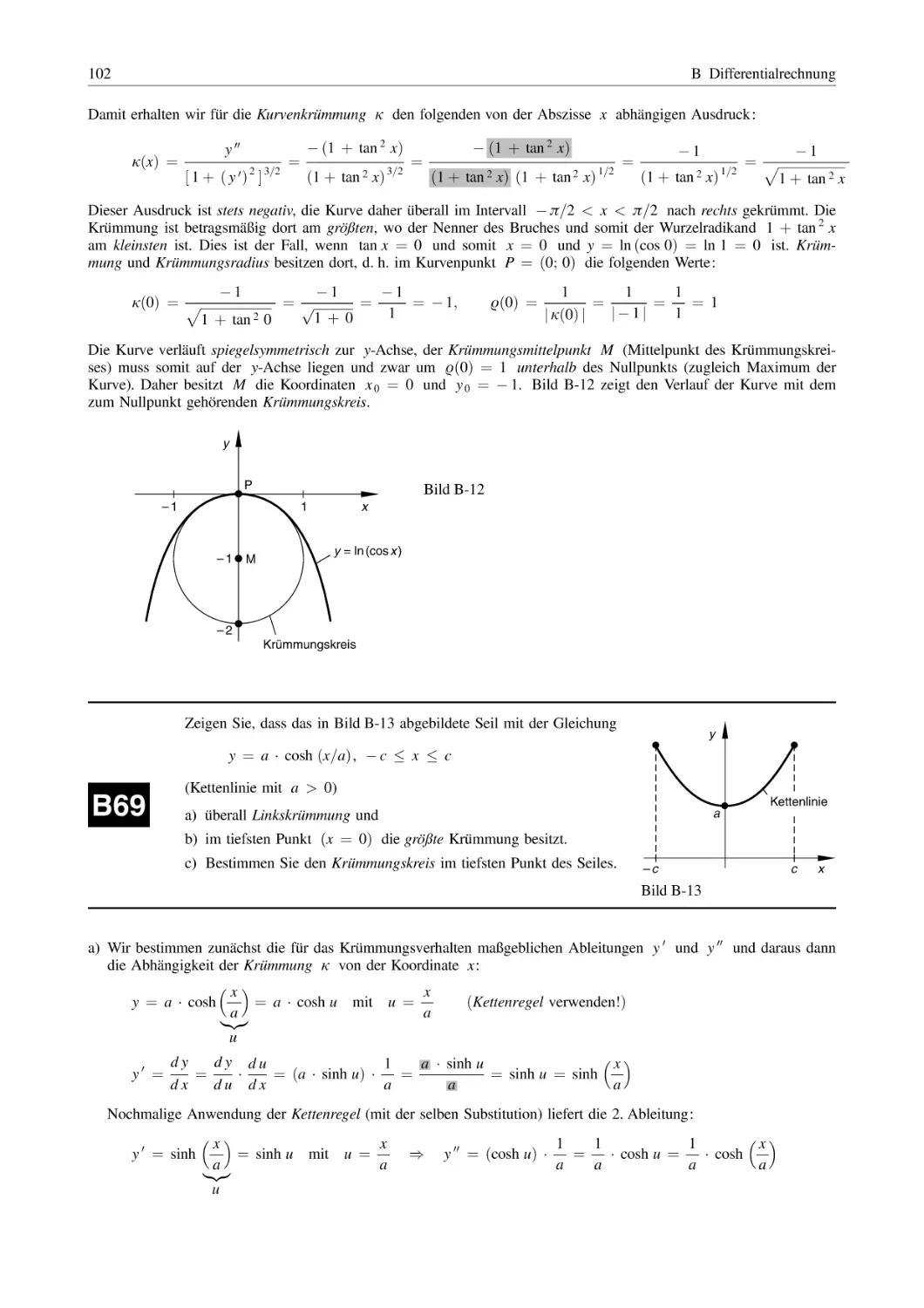
Текст
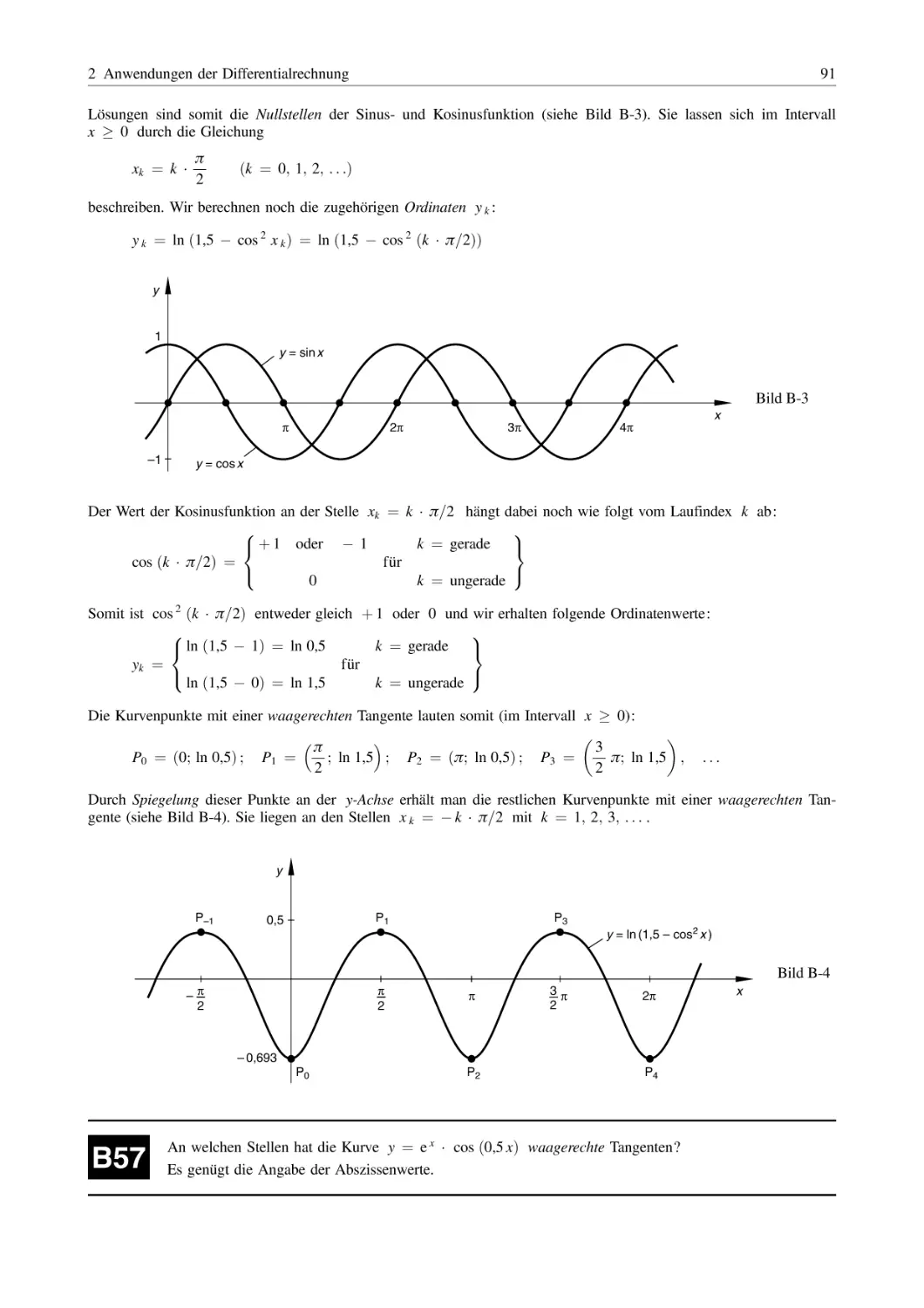
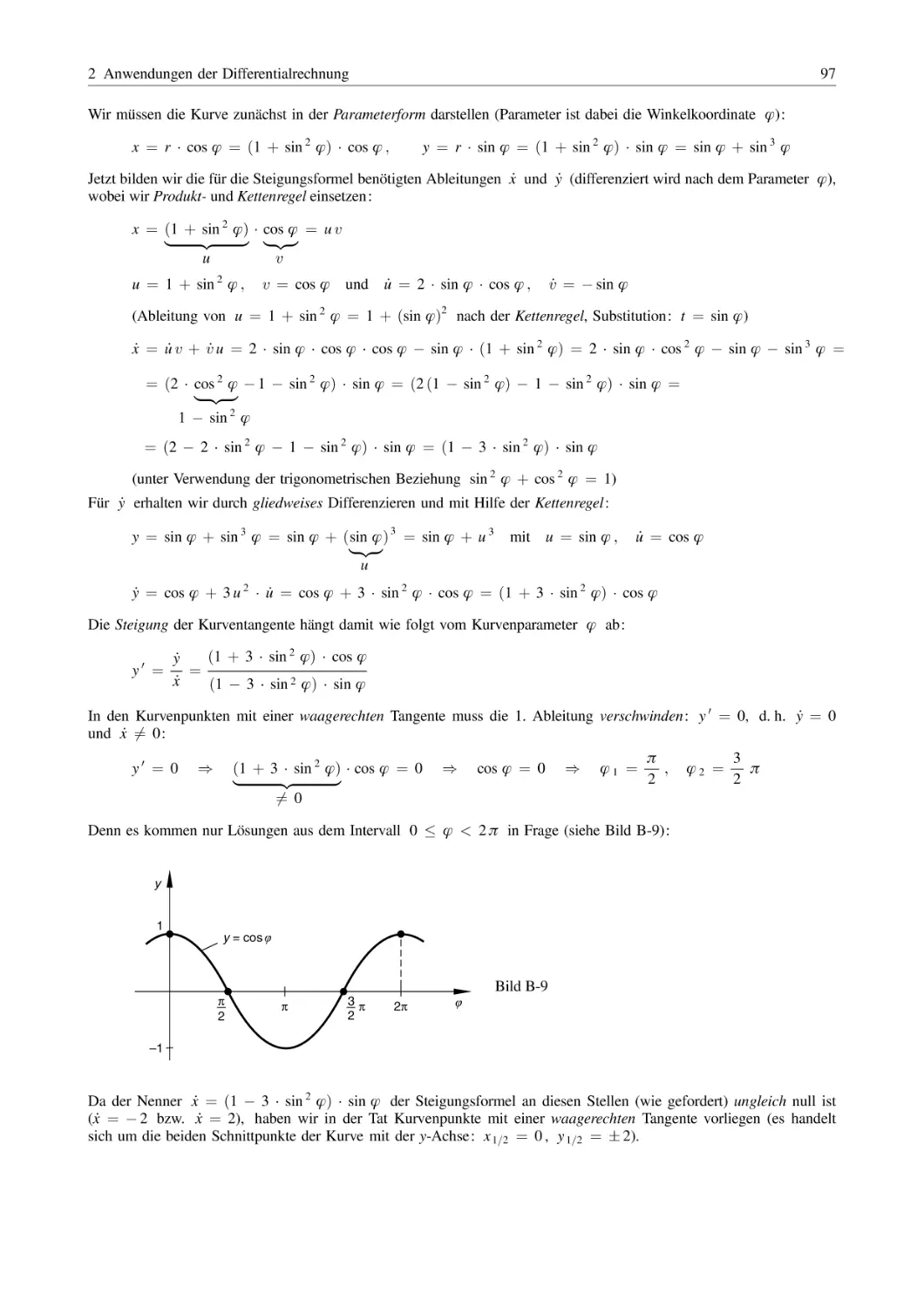
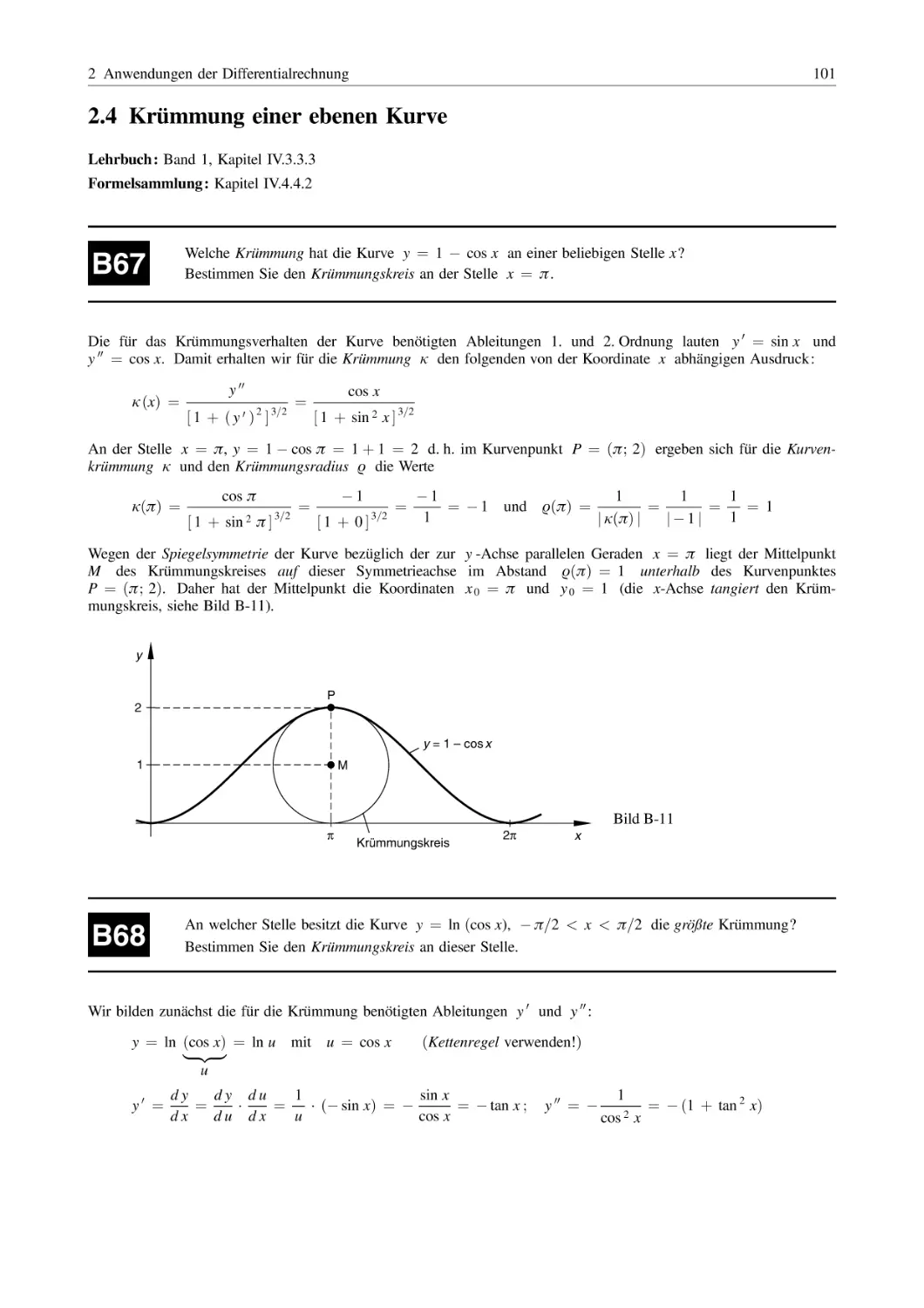
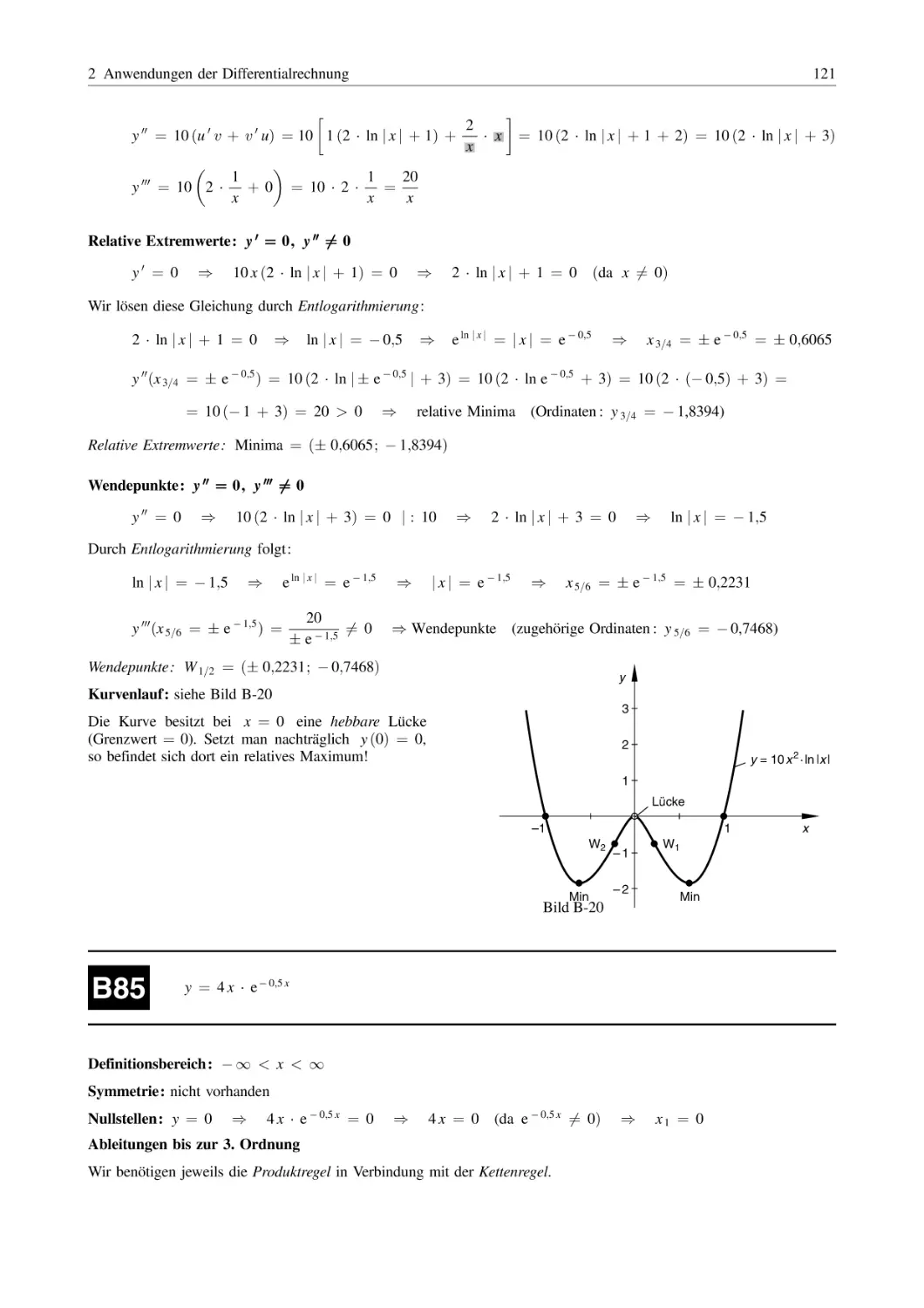
Lothar Papula
Mathematik für Ingenieure
und Naturwissenschaftler –
Klausur- und Übungsaufgaben
711 Aufgaben mit ausführlichen Lösungen
zum Selbststudium und zur Prüfungsvorbereitung
6. Auflage
Mathematik für Ingenieure und
Naturwissenschaftler –
Klausur- und Übungsaufgaben
Das sechsbändige Lehr- und Lernsystem Mathematik für Ingenieure und Naturwissenschaftler umfasst neben
dem Buch mit Klausur- und Übungsaufgaben die folgenden Bände:
Papula, Lothar
Mathematik für Ingenieure und Naturwissenschaftler Band 1
Ein Lehr- und Arbeitsbuch für das Grundstudium
Mit 643 Abbildungen, 500 Beispielen aus Naturwissenschaft und Technik
sowie 352 Übungsaufgaben mit ausführlichen Lösungen
Mathematik für Ingenieure und Naturwissenschaftler Band 2
Ein Lehr- und Arbeitsbuch für das Grundstudium
Mit 345 Abbildungen, 300 Beispielen aus Naturwissenschaft und Technik
sowie 324 Übungsaufgaben mit ausführlichen Lösungen
Mathematik für Ingenieure und Naturwissenschaftler Band 3
Vektoranalysis, Wahrscheinlichkeitsrechnung, Mathematische Statistik, Fehler- und Ausgleichsrechnung
Mit 550 Abbildungen, zahlreichen Beispielen aus Naturwissenschaft und Technik und
295 Übungsaufgaben mit ausführlichen Lösungen
Mathematische Formelsammlung
für Ingenieure und Naturwissenschaftler
Mit über 400 Abbildungen und zahlreichen Rechenbeispielen
und einer ausführlichen Integraltafel
Mathematik für Ingenieure und Naturwissenschaftler –
Anwendungsbeispiele
222 Aufgabenstellungen mit ausführlichen Lösungen
Mit 369 Bildern und einem Anhang mit Physikalischen Grundlagen
Lothar Papula
Mathematik für Ingenieure
und Naturwissenschaftler –
Klausur- und
Übungsaufgaben
711 Aufgaben mit ausführlichen Lösungen
zum Selbststudium und zur
Prüfungsvorbereitung
6., erweiterte und überarbeitete Auflage
Lothar Papula
Wiesbaden, Deutschland
ISBN 978-3-658-30271-9
ISBN 978-3-658-30270-2
https://doi.org/10.1007/978-3-658-30271-9
(eBook)
Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie; detaillierte bibliografische
Daten sind im Internet über http://dnb.d-nb.de abrufbar.
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2004, 2007, 2008, 2010, 2018, 2020
Das Werk einschließlich aller seiner Teile ist urheberrechtlich geschützt. Jede Verwertung, die nicht ausdrücklich
vom Urheberrechtsgesetz zugelassen ist, bedarf der vorherigen Zustimmung des Verlags. Das gilt insbesondere für
Vervielfältigungen, Bearbeitungen, Übersetzungen, Mikroverfilmungen und die Einspeicherung und Verarbeitung in
elektronischen Systemen.
Die Wiedergabe von allgemein beschreibenden Bezeichnungen, Marken, Unternehmensnamen etc. in diesem Werk bedeutet
nicht, dass diese frei durch jedermann benutzt werden dürfen. Die Berechtigung zur Benutzung unterliegt, auch ohne gesonderten
Hinweis hierzu, den Regeln des Markenrechts. Die Rechte des jeweiligen Zeicheninhabers sind zu beachten.
Der Verlag, die Autoren und die Herausgeber gehen davon aus, dass die Angaben und Informationen in diesem Werk
zum Zeitpunkt der Veröffentlichung vollständig und korrekt sind. Weder der Verlag, noch die Autoren oder die Herausgeber übernehmen, ausdrücklich oder implizit, Gewähr für den Inhalt des Werkes, etwaige Fehler oder Äußerungen.
Der Verlag bleibt im Hinblick auf geografische Zuordnungen und Gebietsbezeichnungen in veröffentlichten Karten
und Institutionsadressen neutral.
Lektorat: Thomas Zipsner
Bilder: Graphik & Text Studio Dr. Wolfgang Zettlmeier, Barbing
Springer Vieweg ist ein Imprint der eingetragenen Gesellschaft Springer Fachmedien Wiesbaden GmbH und ist ein Teil von
Springer Nature.
Die Anschrift der Gesellschaft ist: Abraham-Lincoln-Str. 46, 65189 Wiesbaden, Germany
V
Vorwort
Entwicklung und Erwerb der Fähigkeit, die im Grundstudium vermittelten mathematischen Kenntnisse auf Problemstellungen aus Naturwissenschaft und Technik erfolgreich anwenden zu können,
sind ein wesentliches Ziel der Grundausbildung und somit zugleich auch Voraussetzung für ein erfolgreiches Studium. Dieses Ziel ist aber nur erreichbar durch ständiges und intensives Training
(ben), zumal die Defizite der Studienanfänger in den Grundlagenfächern wie Mathematik nach wie
vor enorm sind.
Die vorliegende Sammlung enthält 711 ausführlich und vollständig gelöste bungs- und Klausuraufgaben und bietet dem Studienanfänger Hilfestellung und Unterstützung auf dem Wege zum genannten Ziel. Dieses Buch ermöglicht
als ständiger Begleiter zur Vorlesung das intensive Einüben und Vertiefen des Vorlesungsstoffes,
eine gezielte und optimale Vorbereitung auf die Prüfungen und Klausuren des Grundstudiums
und eignet sich in besonderem Maße zum Selbststudium.
Die Lösung der Aufgaben wird dabei Schritt für Schritt vorgeführt, der Lösungsweg ist damit leicht
nachvollziehbar. Alle verwendeten Regeln werden genannt und erklärt, wobei besondere Sorgfalt auf
die elementaren Rechenschritte gelegt wird. Denn die tägliche Arbeit mit den Anfangssemestern
bringt es immer wieder zu Tage: Die größten Probleme treten meist im Bereich der Elementarmathematik auf (Wer kann heutzutage noch fehlerfrei mit Logarithmen, Wurzeln und Potenzen umgehen? Wie werden eigentlich Brüche addiert?). Daher werden in diesem Buch auch die beim Lösen
einer Aufgabe auftretenden elementarmathematischen Probleme behandelt und alle nötigen Rechenschritte besprochen.
Welche Stoffgebiete wurden berücksichtigt?
Die Auswahl der Stoffgebiete ist im Wesentlichen auf die Mathematikvorlesungen im Grundstudium
abgestimmt. Zahlreiche der 711 Aufgaben sind dabei anwendungsorientiert formuliert und beschreiben einfache Problemstellungen aus Naturwissenschaft und Technik. Berücksichtigt wurden folgende Gebiete:
Funktionen und Kurven
Differentialrechnung
Integralrechnung
Taylor- und Fourier-Reihen
Partielle Differentiation
Mehrfachintegrale
Gewöhnliche Differentialgleichungen
Laplace-Transformationen (im Zusammenhang mit
linearen Differentialgleichungen)
Komplexe Zahlen und Funktionen
Vektorrechnung
Lineare Algebra
Wahrscheinlichkeitsrechnung und mathematische
Statistik
Neu aufgenommen wurden 79 Aufgaben aus der Wahrscheinlichkeitsrechnung und mathematischen
Statistik.
VI
Hinweise für den Benutzer
Ein Wort des Dankes . . .
. . . an den Cheflektor Herrn Thomas Zipsner vom Springer Vieweg Verlag für die hervorragende Unterstützung bei der Erstellung dieses Werkes.
Wiesbaden, im Herbst 2020
Lothar Papula
Hinweise für den Benutzer
Die bungs- und Klausuraufgaben sind kapitelweise durchnummeriert.
Zu Beginn eines jeden Kapitels bzw. Abschnitts finden Sie Hinweise auf das Lehrbuch
„ Mathematik für Ingenieure und Naturwissenschaftler“ (Band 1––3) sowie auf die Mathematische Formelsammlung des Autors. Hier können Sie die zum Lösen der Aufgaben benötigten
mathematischen Hilfsmittel nachlesen und gegebenenfalls nacharbeiten. Beachten Sie auch die
weiteren nützlichen Informationen.
Die vollständige Lösung der jeweiligen Aufgabe finden Sie direkt im Anschluss an die Aufgabenstellung. So wird lästiges Blättern vermieden.
Folgen Sie meiner Empfehlung:
Versuchen Sie zunächst, die Aufgaben selbst zu lösen (Lösungsteil vorher abdecken). Skizzen
erleichtern dabei in vielen Fällen den Lösungsweg. Vergleichen Sie dann „ Ihre“ Lösung mit der
angegebenen Lösung. Sollten Sie bei einem Zwischenschritt „ hängen bleiben“, so greifen Sie auf
die vorgegebene Lösung zurück und versuchen einen neuen Start. Denn auch aus Fehlern lernt
man.
Verwendete Abkürzungen
Bd. 1
FS
Dgl
LGS
! Band 1 des Lehr- und Lernsystems „ Mathematik für Ingenieure und Naturwissenschaftler“ des Autors
! Mathematische Formelsammlung des Autors
! Differentialgleichung
! Lineares Gleichungssystem
VII
Inhaltsverzeichnis
A Funktionen und Kurven
..................................................
1
1
Ganzrationale Funktionen (Polynomfunktionen) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
Gebrochenrationale Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
3
Trigonometrische Funktionen und Arkusfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
4
Exponential- und Logarithmusfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
5
Hyperbel- und Areafunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
6
Funktionen und Kurven in Parameterdarstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
7
Funktionen und Kurven in Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
B Differentialrechnung
.........................................................
57
1
Ableitungsregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1 Produktregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Quotientenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Kettenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4 Kombinationen mehrerer Ableitungsregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5 Logarithmische Ableitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6 Implizite Differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.7 Differenzieren in der Parameterform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.8 Differenzieren in Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
57
60
62
67
72
75
78
80
2
Anwendungen der Differentialrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1 Einfache Anwendungen in Physik und Technik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Tangente und Normale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Linearisierung einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Krümmung einer ebenen Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5 Relative Extremwerte, Wende- und Sattelpunkte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6 Kurvendiskussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.7 Extremwertaufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.8 Tangentenverfahren von Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.9 Grenzberechnung nach Bernoulli und de L’Hospital . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
83
83
89
99
101
105
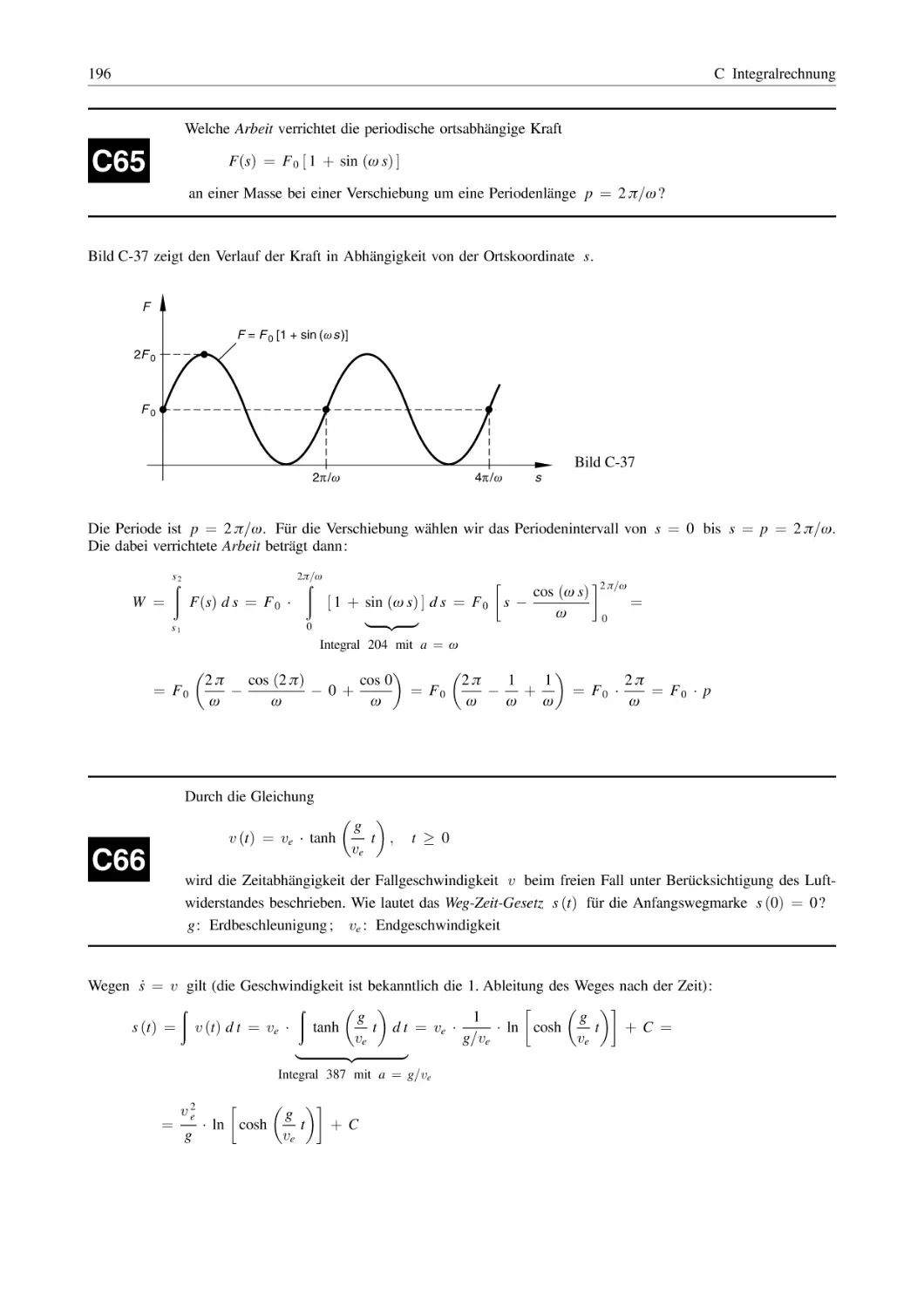
112
123
134
138
VIII
Inhaltsverzeichnis
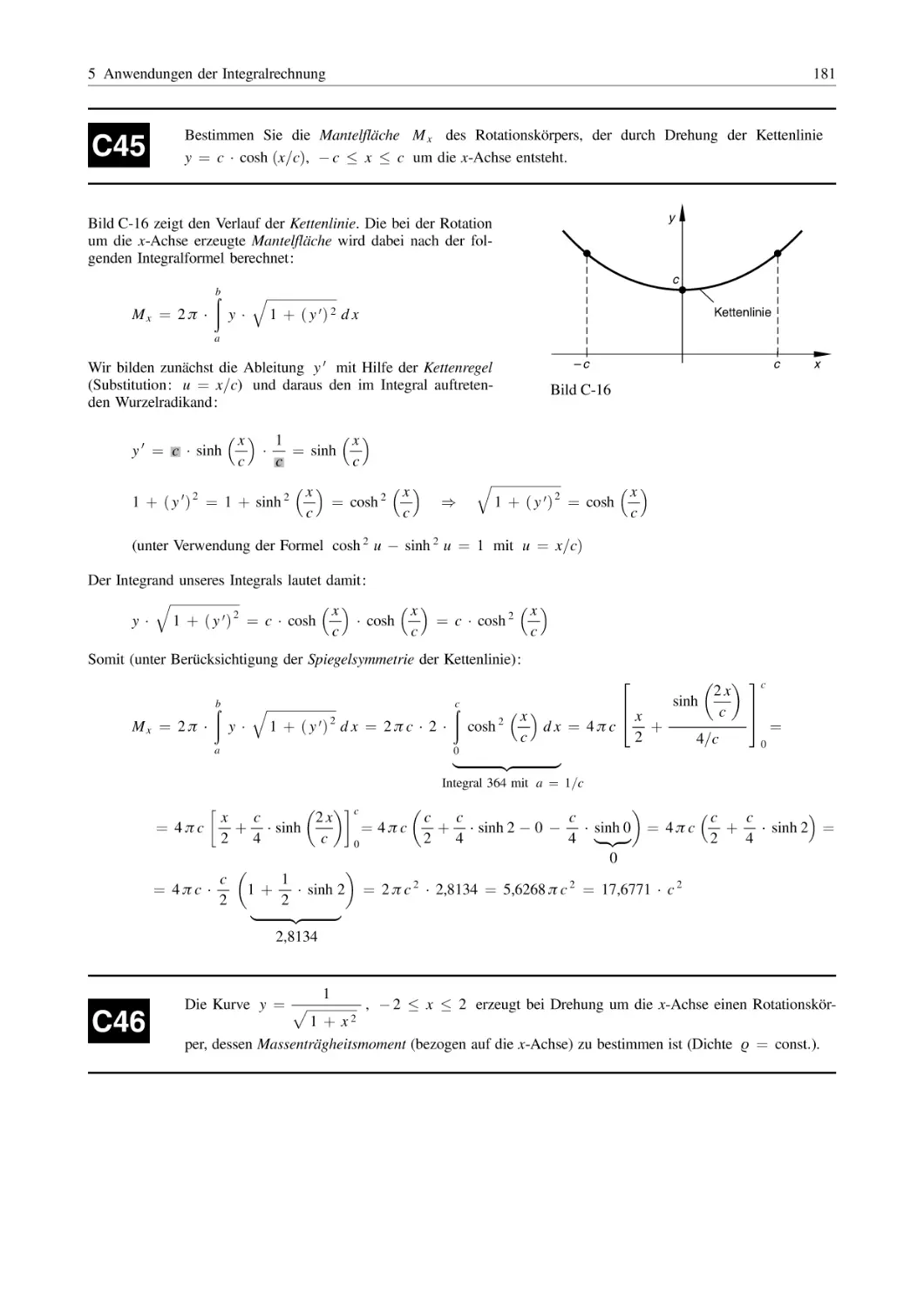
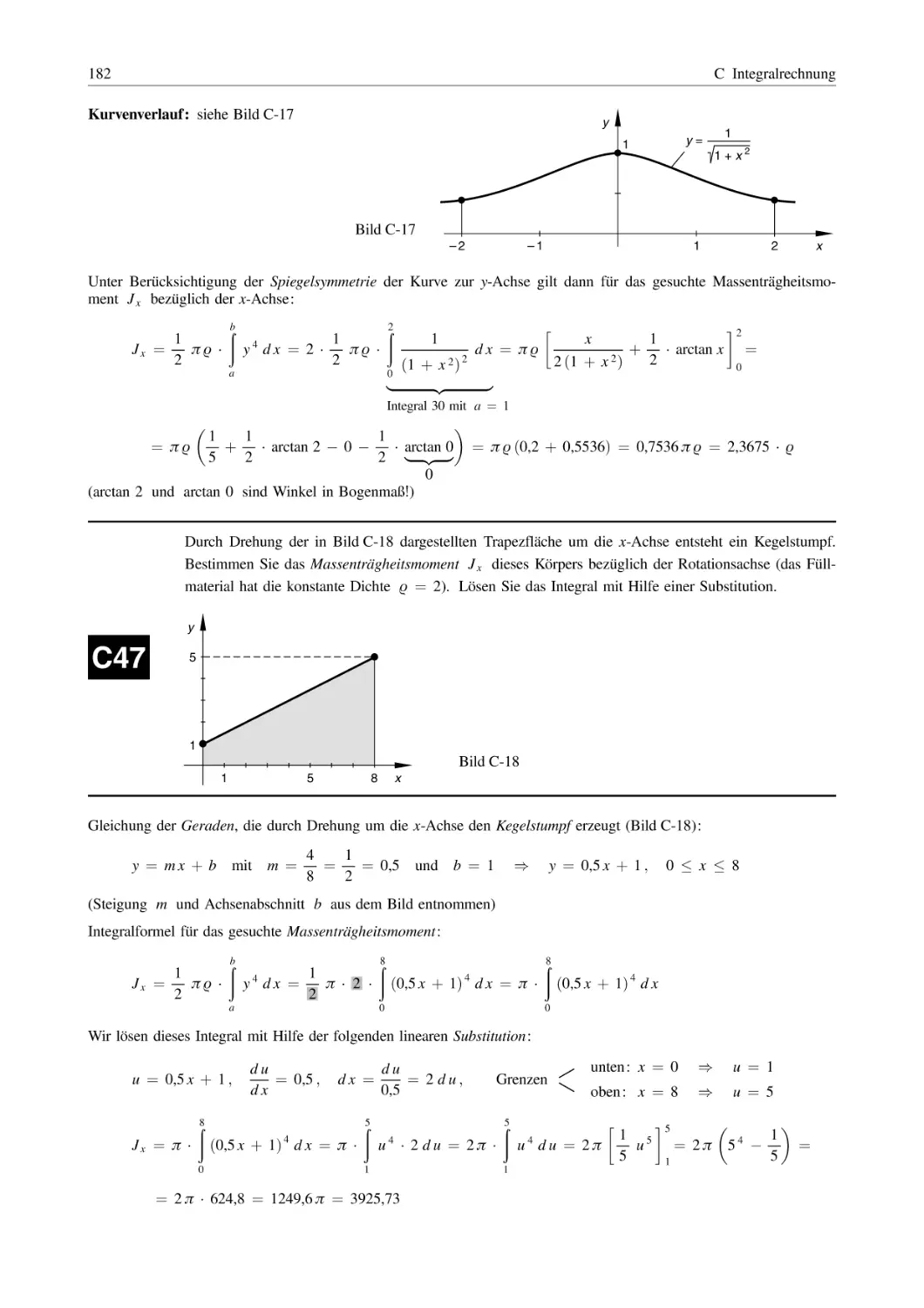
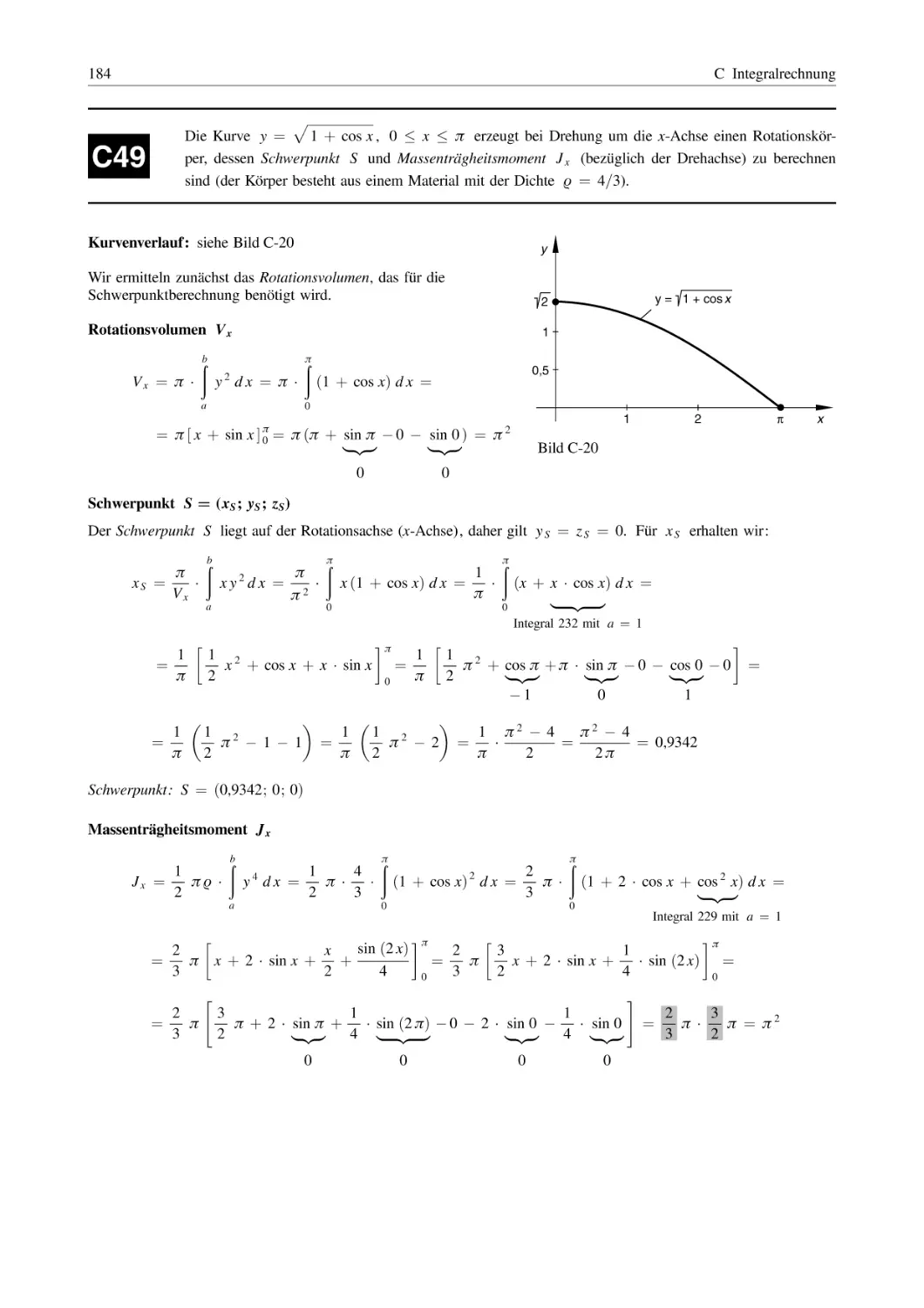
C Integralrechnung
...............................................................
143
1
Integration durch Substitution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
143
2
3
Partielle Integration (Produktintegration) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Integration einer echt gebrochenrationalen Funktion
durch Partialbruchzerlegung des Integranden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
152
4
Numerische Integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
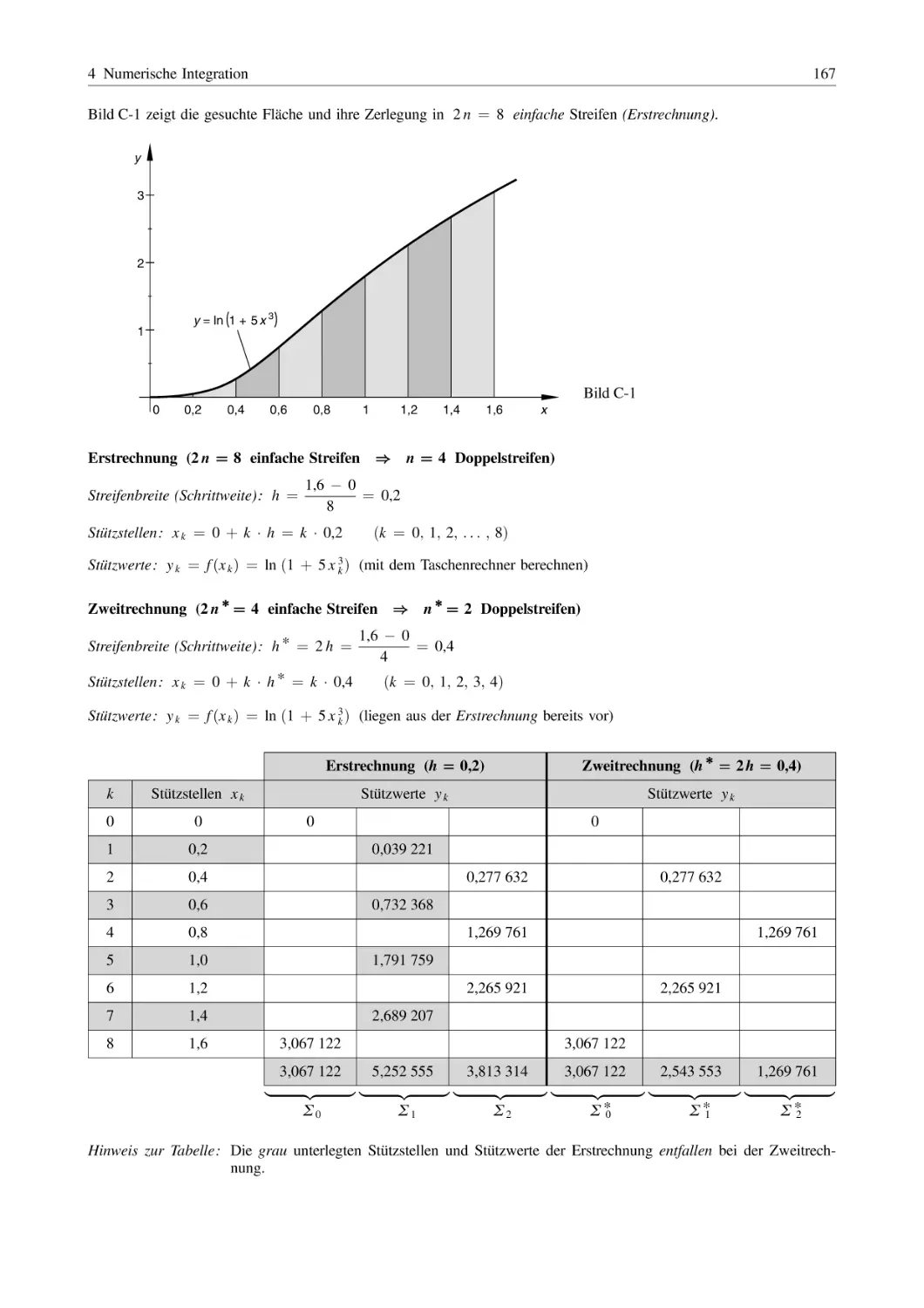
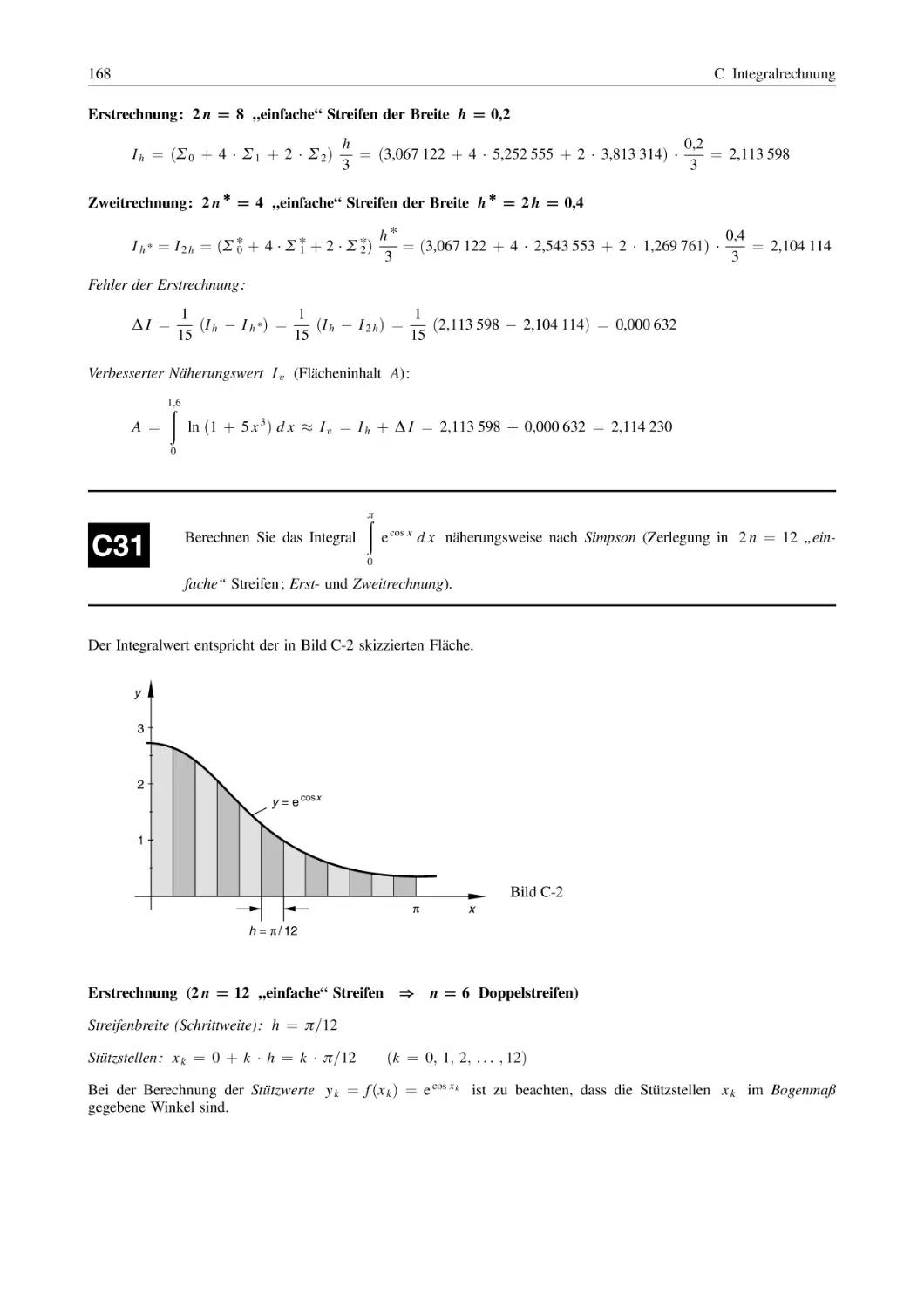
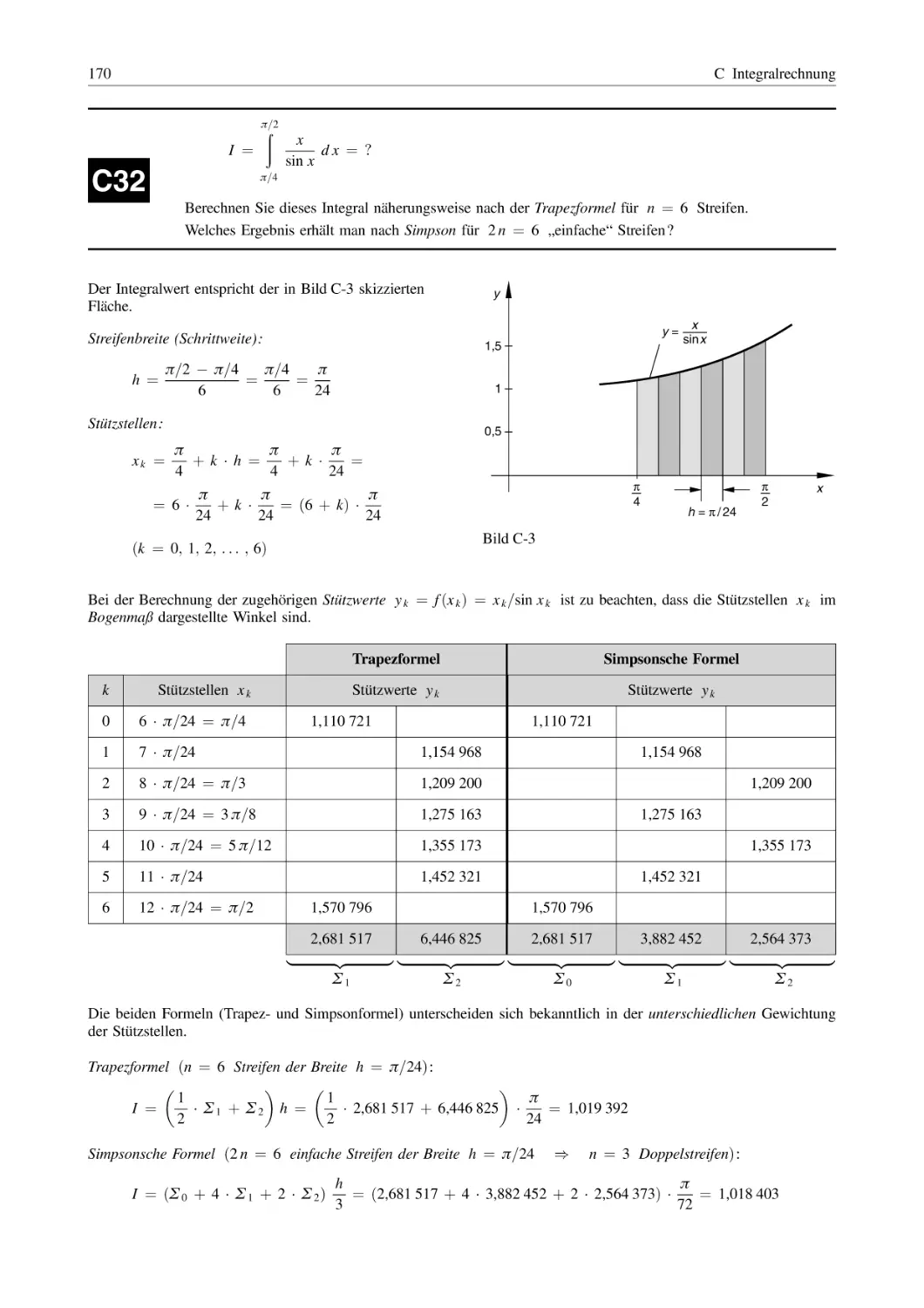
166
5
Anwendungen der Integralrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
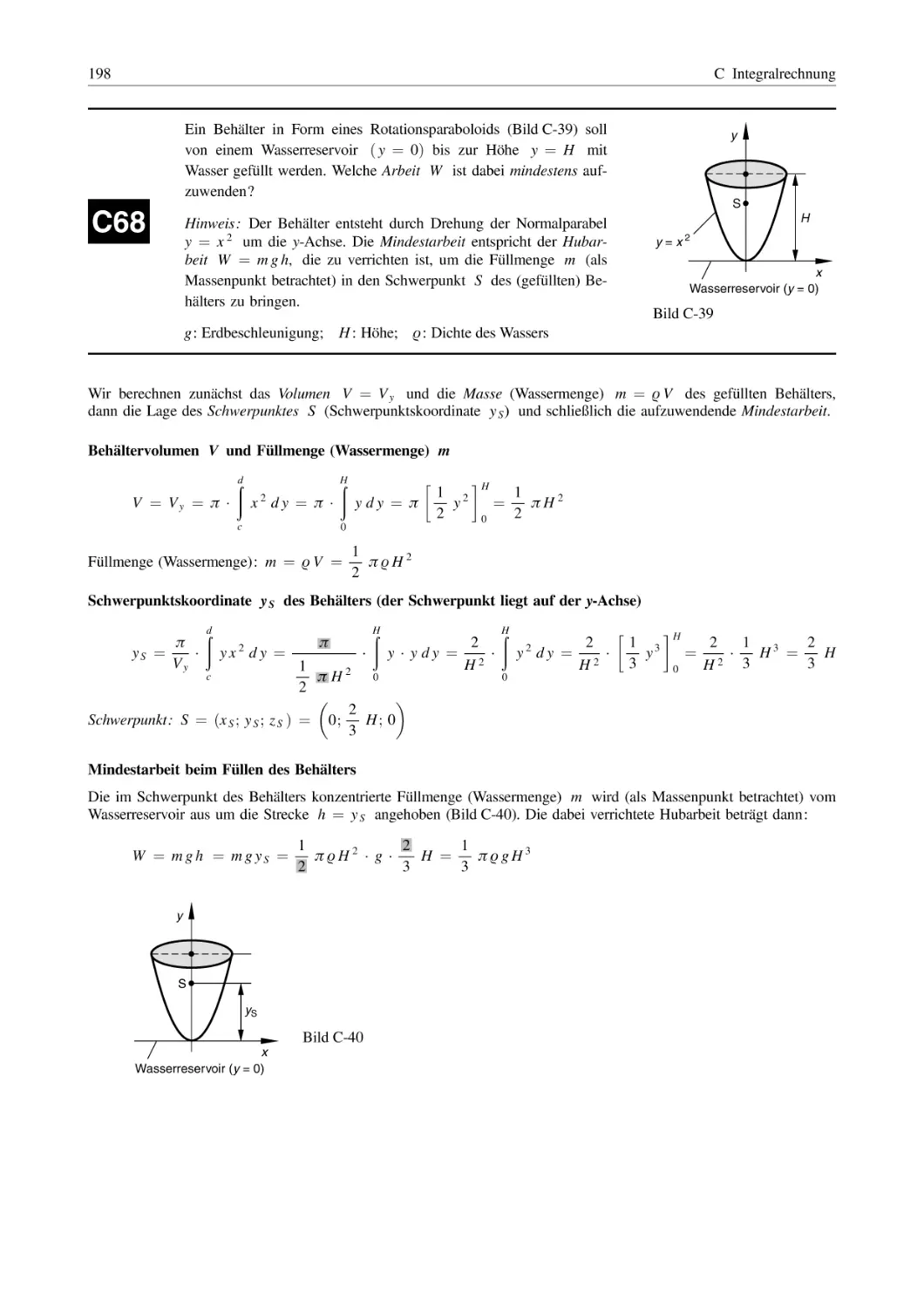
171
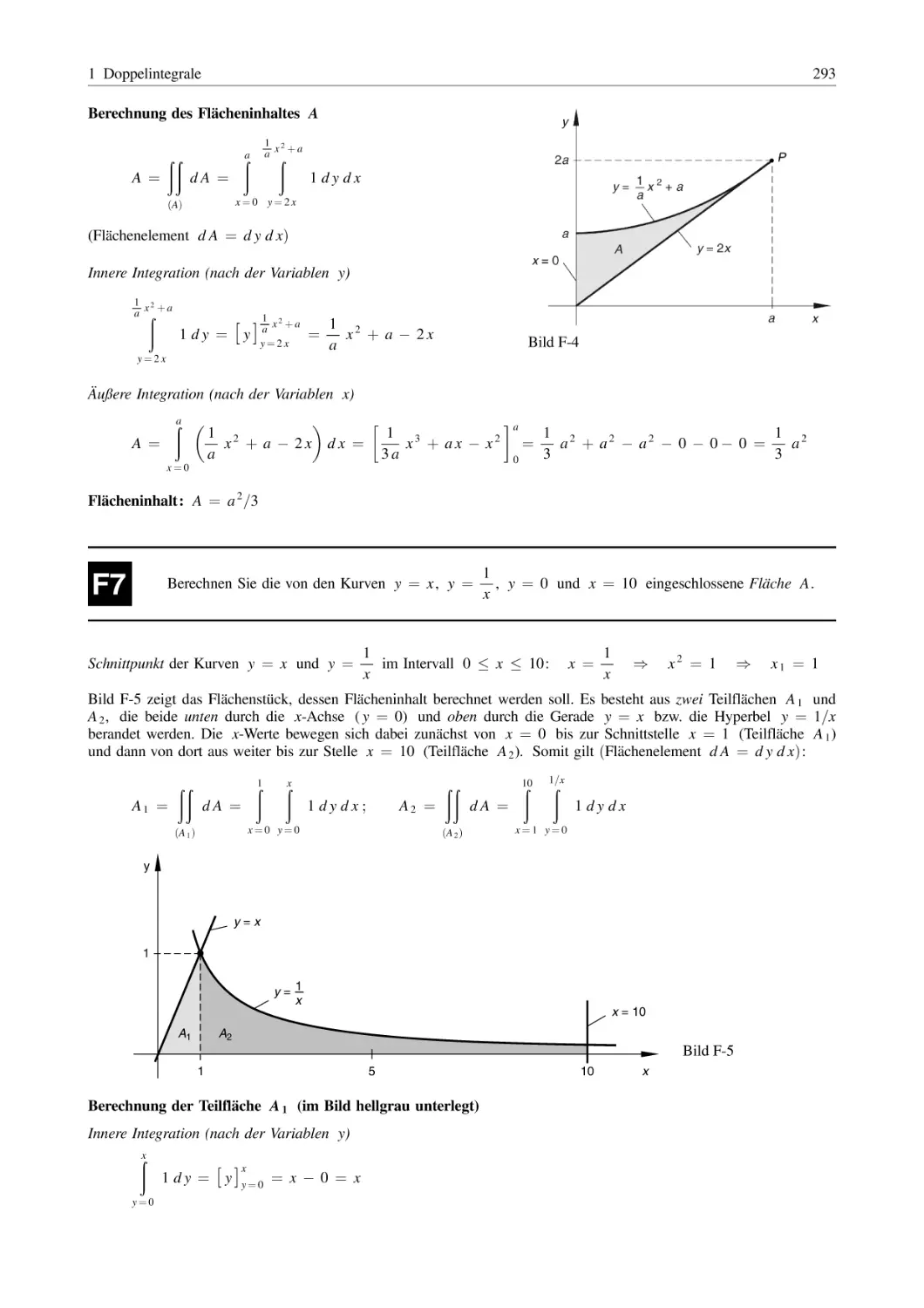
5.1
5.2
171
5.3
5.4
Flächeninhalt, Flächenschwerpunkt, Flächenträgheitsmomente . . . . . . . . . . . . . . . . . . . .
Rotationskörper
(Volumen, Mantelfläche, Massenträgheitsmoment, Schwerpunkt) . . . . . . . . . . . . . . . . .
Bogenlänge, lineare und quadratische Mittelwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Arbeitsgrößen, Bewegungen (Weg, Geschwindigkeit, Beschleunigung) . . . . . . . . . .
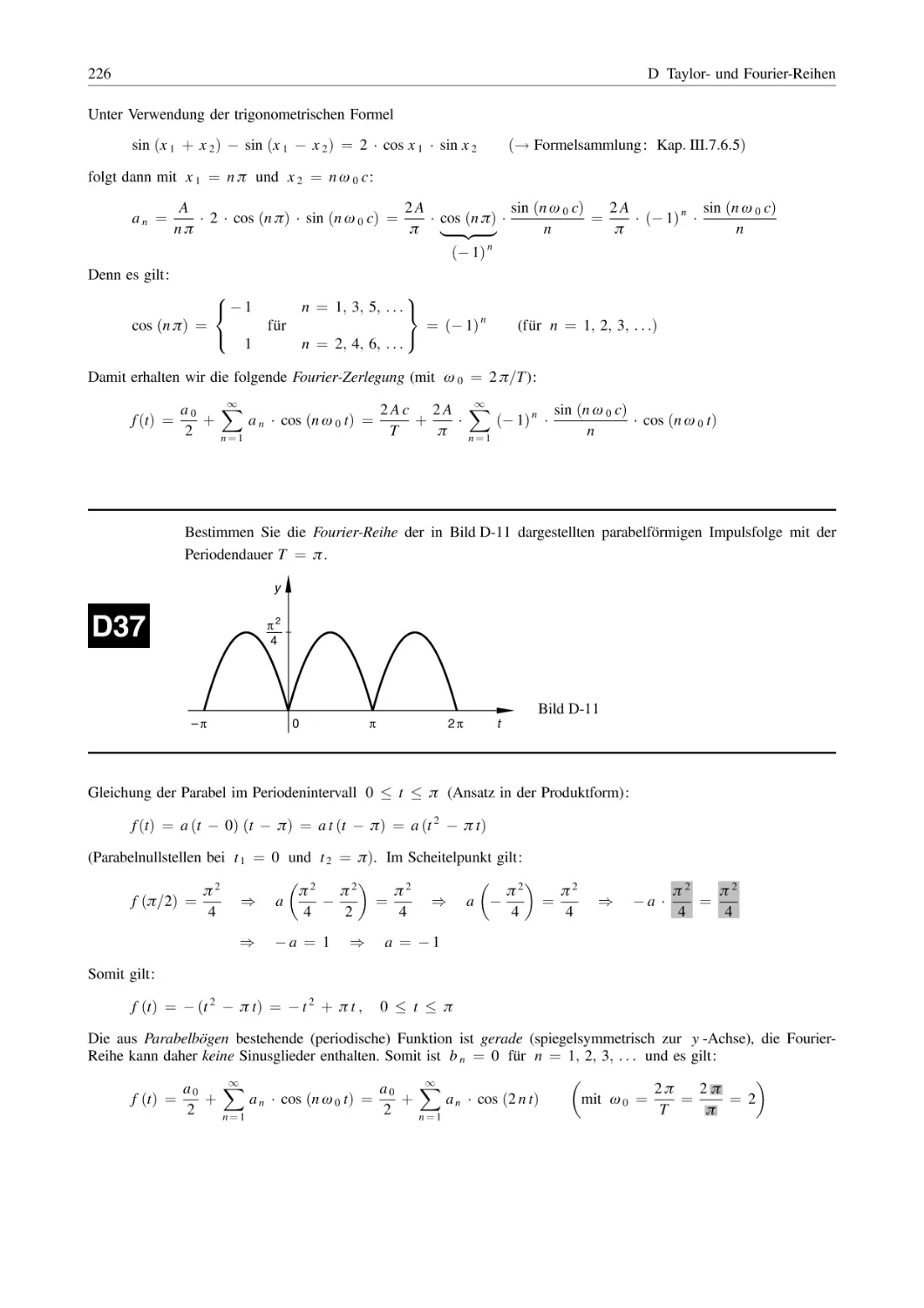
D Taylor- und Fourier-Reihen
159
177
187
194
............................................
199
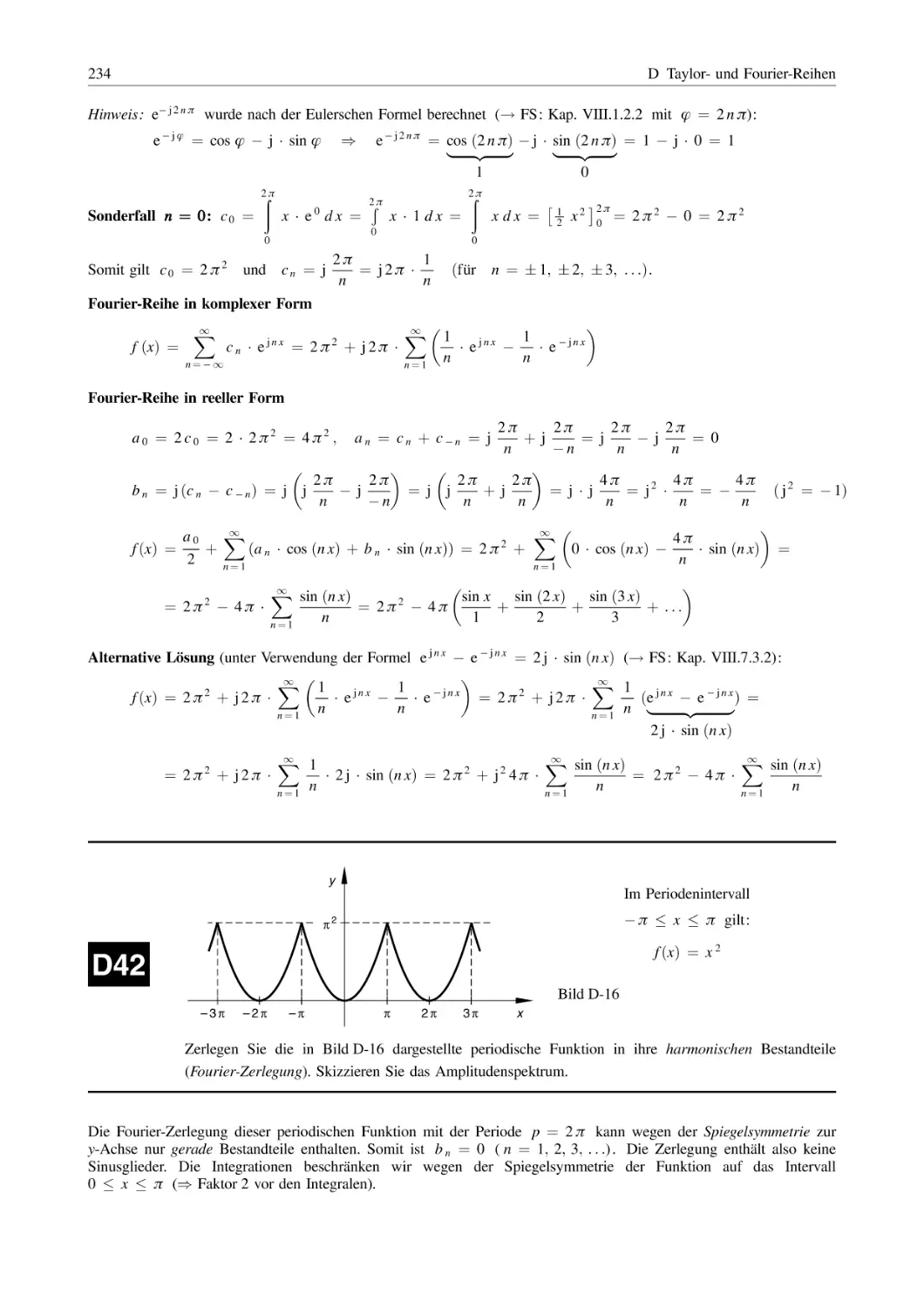
Potenzreihenentwickungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
199
1.1
1.2
Mac Laurinsche und Taylor-Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
199
210
Fourier-Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
225
E Partielle Differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
237
1
Partielle Ableitungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
237
2
Differentiation nach einem Parameter (Kettenregel) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
252
3
Implizite Differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
257
4
Totales oder vollständiges Differential einer Funktion
(mit einfachen Anwendungen) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
261
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1 Linearisierung einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Lineare Fehlerfortpflanzung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3 Relative Extremwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4 Extremwertaufgaben mit und ohne Nebenbedingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
269
269
273
278
282
1
2
5
Inhaltsverzeichnis
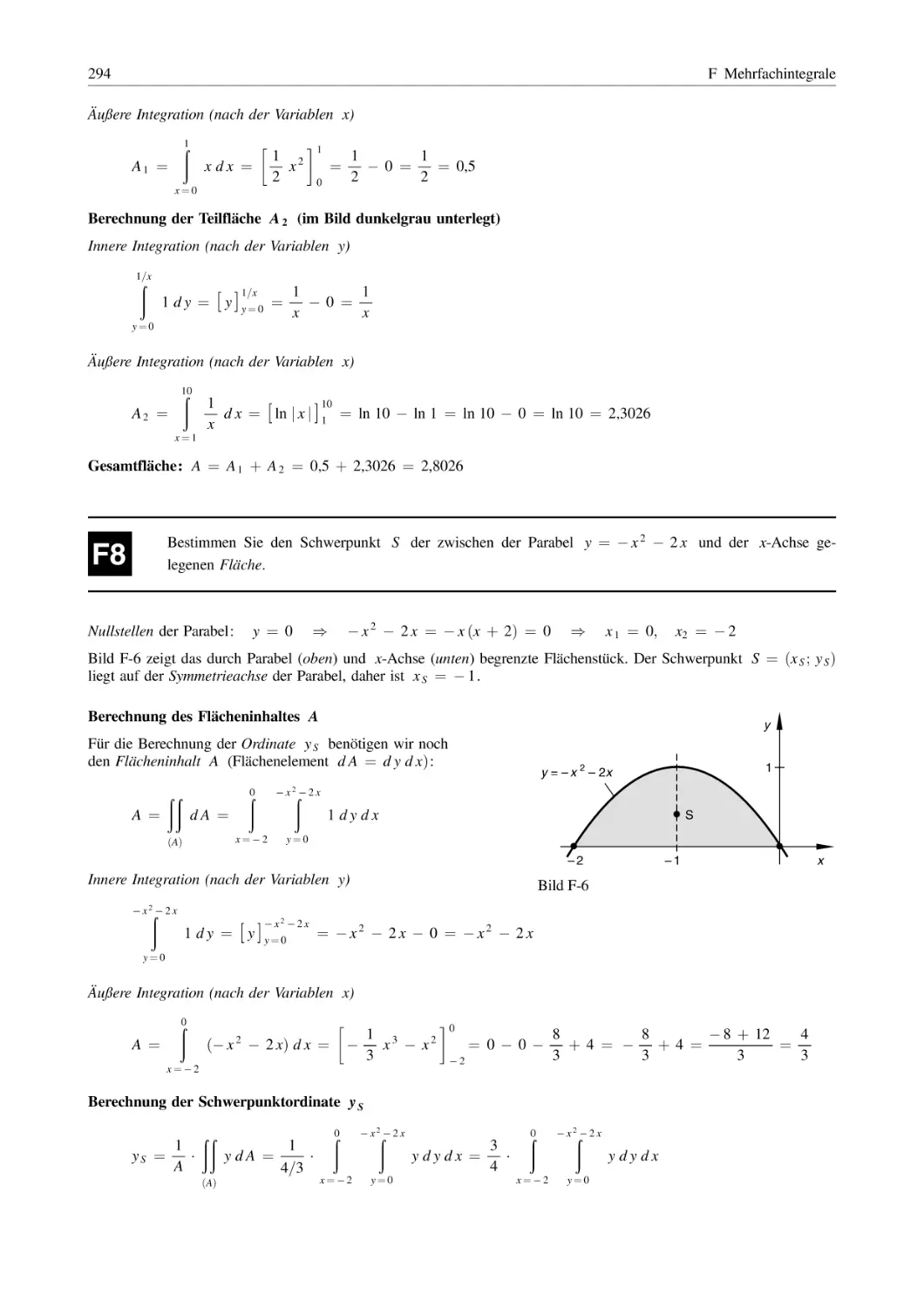
F Mehrfachintegrale
IX
.............................................................
289
Doppelintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
289
1.1
1.2
Doppelintegrale in kartesischen Koordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Doppelintegrale in Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
289
304
Dreifachintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
321
2.1
2.2
Dreifachintegrale in kartesischen Koordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dreifachintegrale in Zylinderkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
321
327
G Gewöhnliche Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
344
Differentialgleichungen 1. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
344
1.1
1.2
1.3
1.4
1.5
Differentialgleichungen mit trennbaren Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Integration einer Differentialgleichung durch Substitution . . . . . . . . . . . . . . . . . . . . . . . . .
Lineare Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lineare Differentialgleichungen mit konstanten Koeffizienten . . . . . . . . . . . . . . . . . . . .
Exakte Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
344
352
361
367
379
Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten . . . . . . . . .
387
2.1
2.2
Homogene lineare Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Inhomogene lineare Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
387
391
3
Integration von Differentialgleichungen 2. Ordnung durch Substitution . . . . . . . . . . .
410
4
Lineare Differentialgleichungen 3. und höherer Ordnung
mit konstanten Koeffizienten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
414
4.1
4.2
Homogene lineare Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Inhomogene lineare Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
414
418
Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation . . . .
424
5.1
5.2
Lineare Differentialgleichungen 1. Ordnung mit konstanten Koeffizienten . . . . . . .
Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten . . . . . . .
425
431
H Komplexe Zahlen und Funktionen ................................
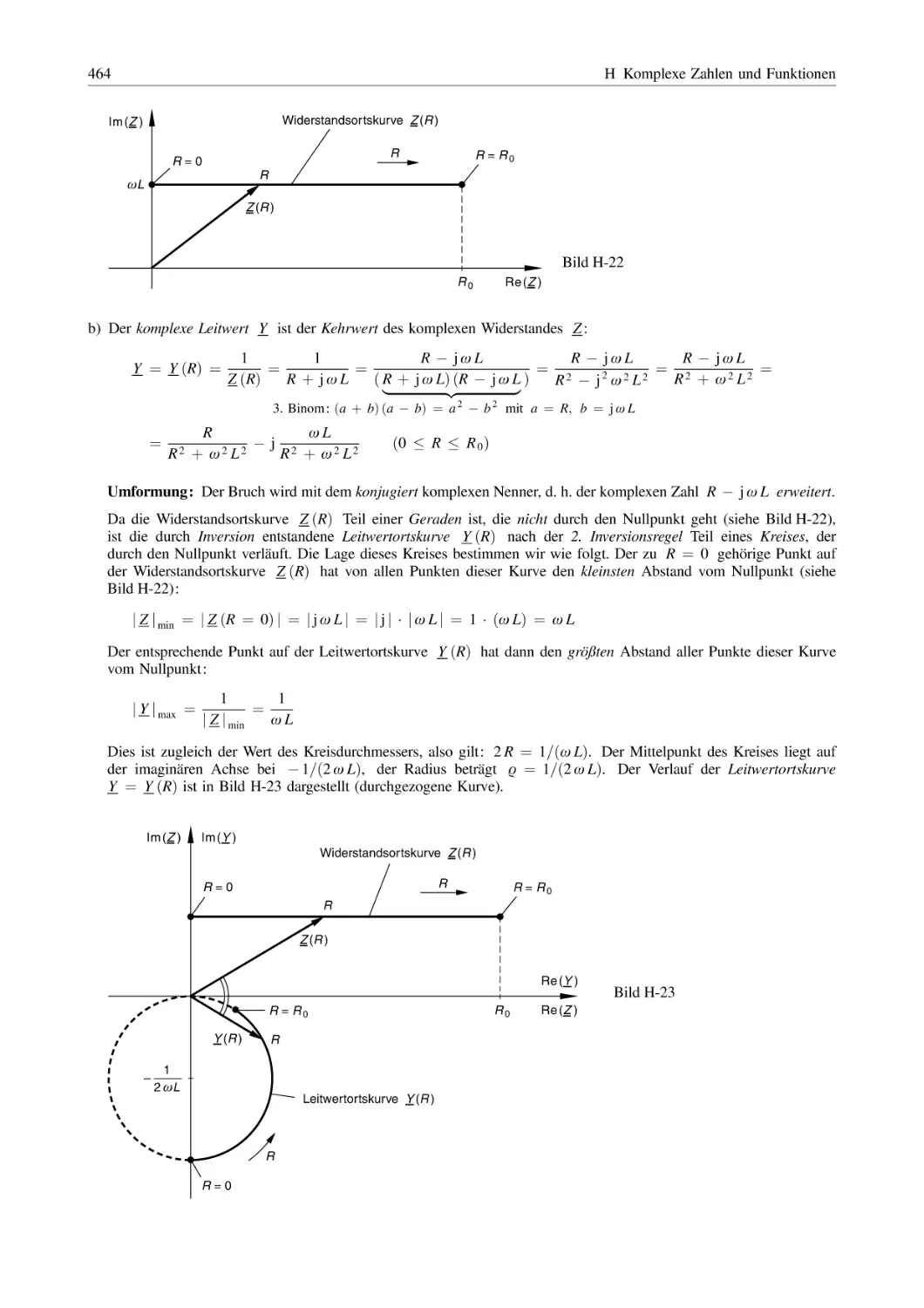
436
Komplexe Rechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
436
1.1
Grundrechenarten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
436
1.2
Potenzen, Wurzeln, Logarithmen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
442
1.3
Algebraische Gleichungen, Polynomnullstellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
447
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
453
2.1
berlagerung von Schwingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
453
2.2
Komplexe Widerstände und Leitwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
457
2.3
Ortskurven, Netzwerkfunktionen, Widerstands- und Leitwertortskurven elektrischer
Schaltkreise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
460
1
2
1
2
5
1
2
X
Inhaltsverzeichnis
I
Vektorrechnung
.................................................................
467
1
Vektoroperationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
467
2
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
479
J
Lineare Algebra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
503
1
Matrizen und Determinanten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
503
1.1
1.2
1.3
Rechenoperationen mit Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Determinanten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spezielle Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
503
511
525
2
Lineare Gleichungssysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
545
3
Eigenwertprobleme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
567
K Wahrscheinlichkeitsrechnung und mathematische
Statistik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
591
1
Wahrscheinlichkeit von Ereignissen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
591
2
Wahrscheinlichkeitsverteilungen einer Zufallsvariablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
598
3
Spezielle Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
608
3.1
3.2
3.3
Diskrete Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Stetige Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Approximationen diskreter Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . .
608
614
618
4
Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen . . . . . . . . . . . . . . . . . . . .
623
5
Häufigkeitsverteilungen und Kennwerte einer Stichprobe . . . . . . . . . . . . . . . . . . . . . . . . . . . .
628
6
Parameterschätzungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
633
6.1
6.2
Punktschätzungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Intervallschätzungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
633
637
7
Parametertests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
644
8
Chi-Quadrat-Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
652
9
Ausgleichskurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
661
1
A Funktionen und Kurven
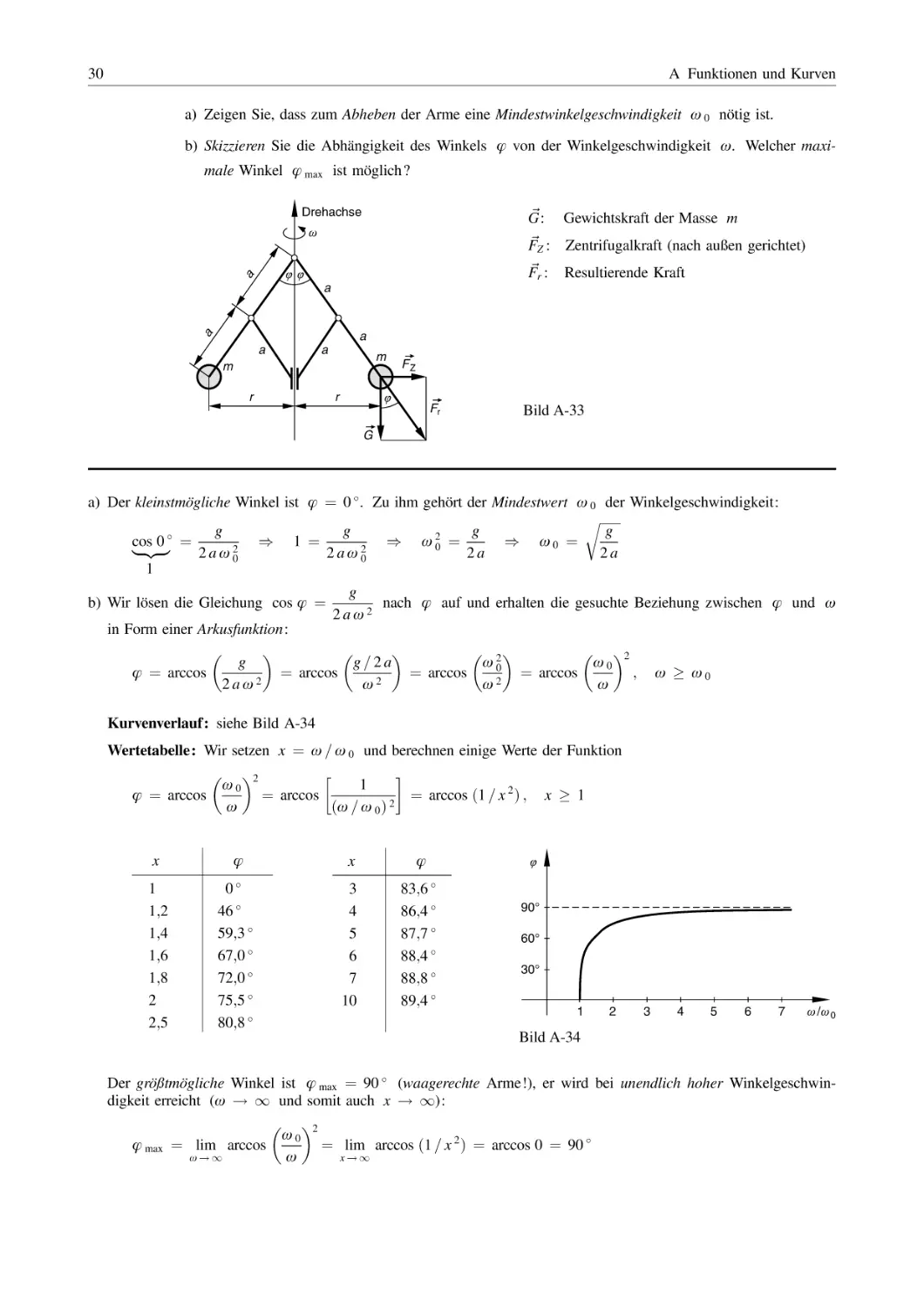
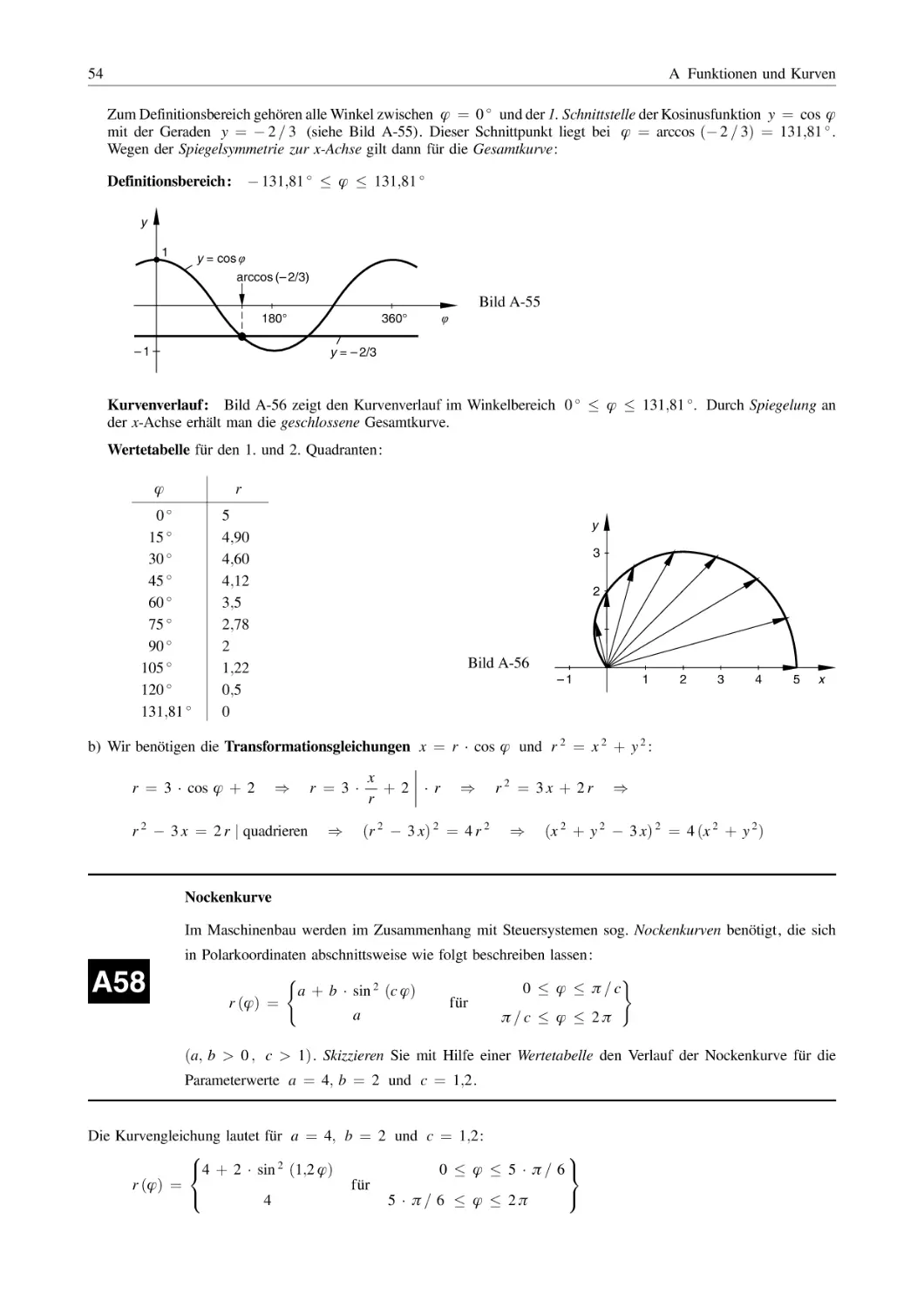
1 Ganzrationale Funktionen (Polynomfunktionen)
Lehrbuch: Band 1, Kapitel III.5
Formelsammlung: Kapitel III.4
Zerlegen Sie die folgenden ganzrationalen Funktionen (Polynomfunktionen) in Linearfaktoren:
a) y ¼ 2 x 3 þ 20 x 2 24 x 144
A1
b) y ¼ 2 x 4 þ 12 x 3 44 x þ 30
c) y ¼ 3 x 5 þ 3 x 4 36 x 3 36 x 2 þ 81 x þ 81
d) y ¼ x 5 þ 4 x 4 þ 4 x 3 6 x 2 37 x 30
Lösungsweg: Durch Probieren eine Nullstelle bestimmen, dann das Polynom mit Hilfe des Horner-Schemas reduzieren. Das Verfahren so lange wiederholen, bis man auf eine quadratische Gleichung stößt, aus der man die restlichen
Nullstellen erhält. Fehlen Potenzen (ist also das Polynom unvollständig), so sind im Horner-Schema die entsprechenden
Koeffizienten gleich Null zu setzen.
a) Eine Nullstelle liegt bei x 1 ¼ 2; das Polynom ist vollständig:
2
x1 ¼ 2
2
20
24
144
4
48
144
24
72
0
) 1. reduziertes Polynom: 2 x 2 þ 24 x 72
Restliche Nullstellen: 2 x 2 þ 24 x 72 ¼ 0 j : ð 2Þ ) x 2 12 x þ 36 ¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
x 2=3 ¼ 6 36 36 ¼ 6 0 ¼ 6 0 ¼ 6
Nullstellen: x 1 ¼ 2 ;
x2 ¼ 6;
)
x3 ¼ 6
Produktform (Zerlegung in Linearfaktoren): y ¼ 2 ðx þ 2Þ ðx 6Þ ðx 6Þ ¼ 2 ðx þ 2Þ ðx 6Þ 2
b) Eine Nullstelle liegt bei x 1 ¼ 1; das Polynom ist unvollständig (es fehlt das quadratische Glied):
2
x1 ¼ 1
2
12
0
44
30
2
14
14
30
14
14
30
0
) 1. reduziertes Polynom: 2 x 3 þ 14 x 2 þ 14 x 30
Eine weitere Nullstelle liegt bei x 2 ¼ 1; das 1. reduzierte Polynom ist vollständig:
2
x2 ¼ 1
2
14
14
30
2
16
30
16
30
0
) 2. reduziertes Polynom: 2 x 2 þ 16 x þ 30
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_1
2
A Funktionen und Kurven
Restliche Nullstellen: 2 x 2 þ 16 x þ 30 ¼ 0 j : 2 ) x 2 þ 8 x þ 15 ¼ 0 )
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 3=4 ¼ 4 16 15 ¼ 4 1 ¼ 4 1 ) x 3 ¼ 3 ;
Nullstellen: x 1 ¼ 1 ;
x2 ¼ 1;
x3 ¼ 3;
x4 ¼ 5
x4 ¼ 5
Produktform (Zerlegung in Linearfaktoren):
y ¼ 2 ðx 1Þ ðx 1Þ ðx þ 3Þ ðx þ 5Þ ¼ 2 ðx 1Þ 2 ðx þ 3Þ ðx þ 5Þ
c) Eine Nullstelle liegt bei x 1 ¼ 1; das Polynom ist vollständig:
3
36
36
81
81
3
0
36
0
81
0
36
0
81
0
3
x1 ¼ 1
3
) 1. reduziertes Polynom: 3 x 4 36 x 2 þ 81
Die restlichen Nullstellen erhalten wir aus der biquadratischen Gleichung 3 x 4 36 x 2 þ 81 ¼ 0; die wir durch
die Substitution u ¼ x 2 wie folgt lösen:
3 x 4 36 x 2 þ 81 ¼ 0 j : 3 ) x 4 12 x 2 þ 27 ¼ 0 ) u 2 12 u þ 27 ¼ 0 )
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
u 1=2 ¼ 6 36 27 ¼ 6 9 ¼ 6 3 ) u 1 ¼ 9 ; u 2 ¼ 3
pffiffiffi
Rücksubstitution: x 2 ¼ u 1 ¼ 9 ) x 2=3 ¼ 3 ; x 2 ¼ u 2 ¼ 3 ) x 4=5 ¼ 3
pffiffiffi
pffiffiffi
Nullstellen: x 1 ¼ 1 ; x 2 ¼ 3 ; x 3 ¼ 3 ; x 4 ¼ 3 ; x 5 ¼ 3
pffiffiffi
pffiffiffi
Produktform (Zerlegung in Linearfaktoren): y ¼ 3 ðx þ 1Þ ðx 3Þ ðx þ 3Þ ðx 3Þ ðx þ 3Þ
d) Eine Nullstelle liegt bei x 1 ¼ 1 ; das Polynom ist vollständig:
4
4
6
37
30
1
3
1
7
30
3
1
7
30
0
1
x1 ¼ 1
1
) 1. reduziertes Polynom:
x 4 þ 3 x 3 þ x 2 7 x 30
Eine weitere Nullstelle liegt bei x 2 ¼ 2 ; das 1. reduzierte Polynom ist vollständig:
1
x2 ¼ 2
1
3
1
7
30
2
10
22
30
5
11
15
0
) 2. reduziertes Polynom: x 3 þ 5 x 2 þ 11 x þ 15
Eine weitere Nullstelle liegt bei x 3 ¼ 3 ; das 2. reduzierte Polynom ist vollständig:
1
x3 ¼ 3
1
5
11
15
3
6
15
2
5
0
) 3. reduziertes Polynom: x 2 þ 2 x þ 5
Es gibt keine weiteren Nullstellen, da die Gleichung x 2 þ 2 x þ 5 ¼ 0 keine reellen Lösungen hat (die Parabel
y ¼ x 2 þ 2 x þ 5 liegt oberhalb der x-Achse). Der quadratische Faktor x 2 þ 2 x þ 5 lässt sich daher nicht
weiter zerlegen.
Produktform (Zerlegung in Linearfaktoren): y ¼ ðx þ 1Þ ðx 2Þ ðx þ 3Þ ðx 2 þ 2 x þ 5Þ
1 Ganzrationale Funktionen (Polynomfunktionen)
3
y
36
3
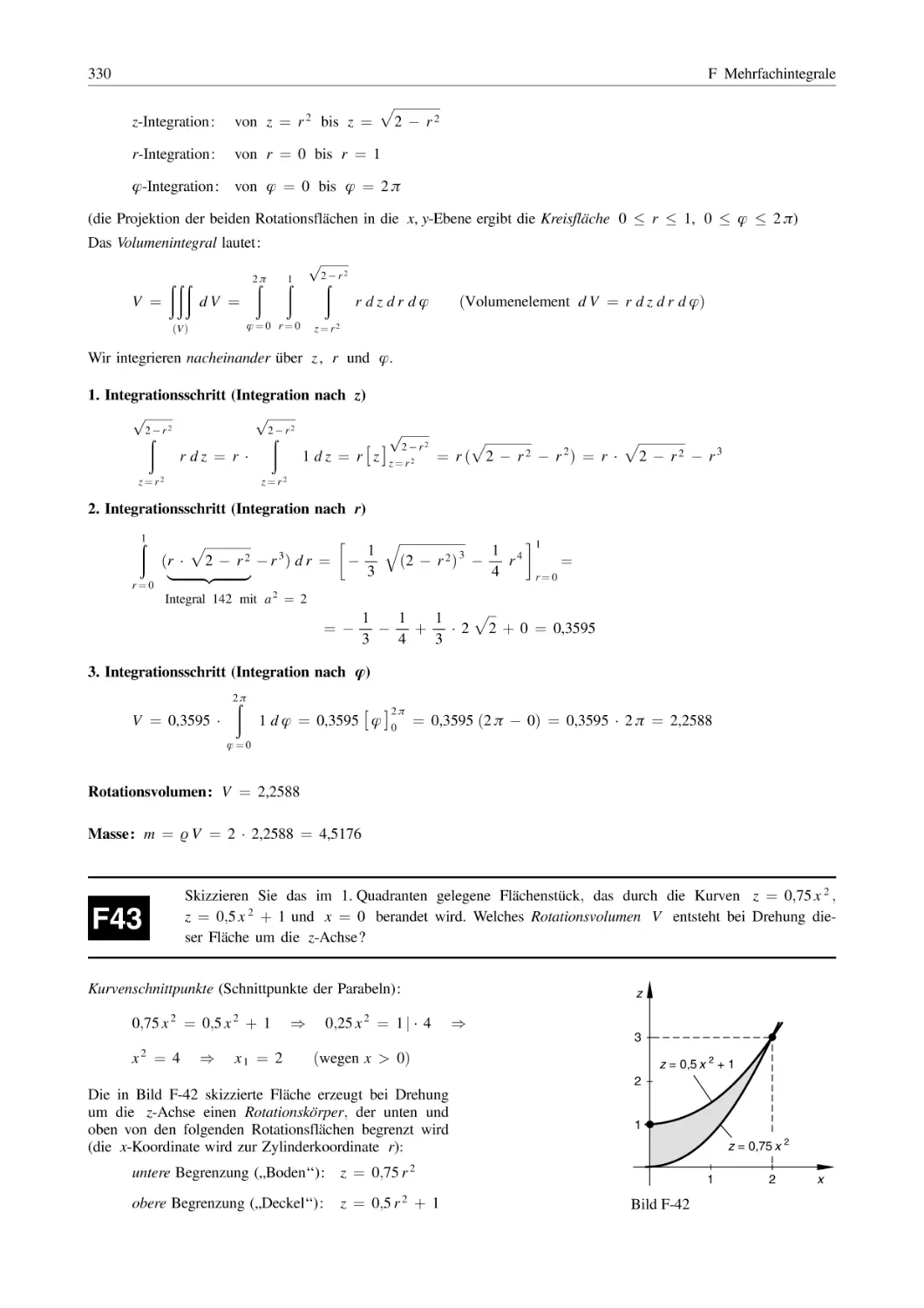
Wie lautet die Gleichung der in Bild A-1
skizzierten Polynomfunktion 3. Grades?
A2
x2
–3
x
– 72
Bild A-1
A
Bei x 1 ¼ 3 liegt eine doppelte Nullstelle (relatives Minimum, Berührungspunkt), eine weitere einfache Nullstelle
gibt es bei x 2 (noch unbekannt, 0 < x 2 < 3). Wir verwenden den Produktansatz (Zerlegung in Linearfaktoren)
y ¼ a ðx þ 3Þ 2 ðx x 2 Þ
ðmit a 6¼ 0Þ
und bestimmen die noch unbekannten Konstanten a und x 2 aus der Schnittstelle der Kurve mit der y-Achse und
dem Kurvenpunkt A wie folgt:
y ðx ¼ 0Þ ¼ 36
)
a ð3Þ 2 ð x 2 Þ ¼ 9 a x 2 ¼ 36 j : ð 9Þ
)
ðIÞ
A ¼ ð3 ; 72Þ
)
a ð3 þ 3Þ 2 ð3 x 2 Þ ¼ 36 a ð3 x 2 Þ ¼ 72 j : 36
ax2 ¼ 4
)
ðIIÞ
a ð3 x 2 Þ ¼ 2
Gleichung (I) in Gleichung (II) einsetzen:
ðIIÞ
)
a ð3 x 2 Þ ¼ 3 a a x 2 ¼ 3 a þ 4 ¼ 2
|{z}
4
ðIÞ
)
ax2 ¼ 4
Ergebnis:
)
2x2 ¼ 4
)
)
3a ¼ 6
)
a ¼ 2
x2 ¼ 2
y ¼ 2 ðx þ 3Þ 2 ðx 2Þ ¼ 2 ðx 2 þ 6 x þ 9Þ ðx 2Þ ¼
¼ 2 ðx 3 þ 6 x 2 þ 9 x 2 x 2 12 x 18Þ ¼ 2 ðx 3 þ 4 x 2 3 x 18Þ
y ¼ 2 x 3 þ 12 x 2 þ 19 x þ 9
A3
a) Zeigen Sie mit Hilfe einer Koordinatentransformation, dass diese ganzrationale Funktion bezüglich des
Kurvenpunktes A ¼ ð 2 ; 3Þ punktsymmetrisch verläuft.
b) Wo liegen die Nullstellen? Wie lautet die Produktdarstellung der Funktion?
a) Wir führen eine Parallelverschiebung des x; y-Koordinatensystems
durch, wählen dabei den Punkt A als Nullpunkt des neuen u; vKoordinatensystems. Die Transformationsgleichungen können wir
aus Bild A-2 ablesen:
y
v
P
v
u ¼ x þ 2;
v ¼ y3
u
u
bzw.
x ¼ u 2;
3
A
y
3
y ¼ vþ3
–2
Bild A-2
0
2
x
x
4
A Funktionen und Kurven
Gleichung der Polynomfunktion im neuen u; v-System ðx durch u 2 ; y durch v þ 3 ersetzenÞ:
y ¼ 2 x 3 þ 12 x 2 þ 19 x þ 9
)
v þ 3 ¼ 2 ðu 2Þ 3 þ 12 ðu 2Þ 2 þ 19 ðu 2Þ þ 9 ¼
¼ 2 ðu 3 6 u 2 þ 12 u 8Þ þ 12 ðu 2 4 u þ 4Þ þ 19 u 38 þ 9 ¼
¼ 2 u 3 12 u 2 þ 24 u 16 þ 12 u 2 48 u þ 48 þ 19 u 29 ¼ 2 u 3 5 u þ 3
v ¼ f ðuÞ ¼ 2 u 3 5 u
Ergebnis:
Diese Funktion enthält nur ungerade Potenzen (ungerade Funktion) und verläuft somit punktsymmetrisch:
f ð uÞ ¼ 2 ð uÞ 3 5 ð uÞ ¼ 2 u 3 þ 5 u ¼ ð2 u 3 5 uÞ ¼ f ðuÞ
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
f ðuÞ
b) Durch Probieren finden wir eine Nullstelle bei x 1 ¼ 1 : Mit dem Horner-Schema erhalten wir das 1. reduzierte
Polynom und daraus die restlichen Nullstellen:
2
x1 ¼ 1
12
19
9
2
10
9
10
9
0
2
) 1. reduziertes Polynom: 2 x 2 þ 10 x þ 9
Restliche Nullstellen: 2 x 2 þ 10 x þ 9 ¼ 0 j : 2 ) x 2 þ 5 x þ 4;5 ¼ 0 )
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
x 2=3 ¼ 2;5 6;25 4;5 ¼ 2;5 1;75 ¼ 2;5 1;3229 ) x 2 ¼ 1;1771 ;
Nullstellen:
x1 ¼ 1;
Produktdarstellung:
x 2 ¼ 1;1771 ;
x 3 ¼ 3;8229
x 3 ¼ 3;8229
y ¼ 2 ðx þ 1Þ ðx þ 1;1771Þ ðx þ 3;8229Þ
Die Flugbahn eines Geschosses laute wie folgt:
A4
y ¼
1
ðx 2 100 x 416Þ
58
ðx; y in mÞ
(Abschussort: x ¼ 0Þ. Bestimmen Sie Flugweite W und Steighöhe (maximale Höhe) H .
Die Flugbahn ist eine nach unten geöffnete Parabel (Bild A-3). Wir berechnen zunächst die Nullstellen und den Scheitelpunkt S ¼ ðx 0 ; y 0 Þ der Parabel und daraus dann die gesuchten Größen.
Nullstellen:
x 1=2
y ¼ 0
) x 2 100 x 416 ¼ 0 )
pffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ 50 2500 þ 416 ¼ 50 2916 ¼ 50 54
x1 ¼ 4;
S
y
Flugbahn
H y0
x 2 ¼ 104
Abschussort
Flugweite:
W ¼ x 2 ¼ 104
ðin mÞ
x1
Die Steighöhe H ist die Ordinate y 0 des Scheitelpunktes S,
der genau in der Mitte zwischen den beiden Nullstellen liegt:
x0 ¼
x1 þ x2
4 þ 104
¼
¼ 50
2
2
H ¼ y 0 ¼ y ðx 0 ¼ 50Þ ¼
x0
W
Bild A-3
ðin mÞ
1
ð50 2 100 50 416Þ ¼ 50;28
58
ðin mÞ
x2
x
1 Ganzrationale Funktionen (Polynomfunktionen)
5
Welche zur y-Achse spiegelsymmetrische Polynomfunktion 6. Grades besitzt bei x 1 ¼ 2 ; x 2 ¼ 3 und
A5
x 3 ¼ 5 jeweils (einfache) Nullstellen und schneidet die y-Achse an der Stelle y ð0Þ ¼ 450?
Wegen der Spiegelsymmetrie können nur gerade Potenzen auftreten, die gesuchte Funktion hat also die Form
y ¼ ax6 þ bx4 þ cx2 þ d
Zu jedem Kurvenpunkt gibt es ein Spiegelbild. Dies gilt auch für die Nullstellen, d. h. es gibt weitere Nullstellen bei
x 4 ¼ 2, x 5 ¼ 3 und x 6 ¼ 5. Damit kennen wir sämtliche Nullstellen der noch unbekannten Polynomfunktion
6. Grades. Sie lauten also (in neuer paarweiser Nummerierung):
x 1=2 ¼ 2 ;
x 3=4 ¼ 3 ;
x 5=6 ¼ 5
Als Lösungsansatz für die Funktionsgleichung verwenden wir jetzt zweckmäßigerweise den Produktansatz (mit a 6¼ 0Þ:
y ¼ a ðx 2Þ ðx þ 2Þ ðx 3Þ ðx þ 3Þ ðx 5Þ ðx þ 5Þ ¼ a ðx 2 4Þ ðx 2 9Þ ðx 2 25Þ
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
x2 9
x 2 25
x2 4
Die durch Klammern gekennzeichneten Produkte wurden nach dem 3. Binom berechnet.
Die Berechnung von a erfolgt aus der Schnittstelle mit der y-Achse:
y ð0Þ ¼ 450
Ergebnis:
)
a ð 4Þ ð 9Þ ð 25Þ ¼ 900 a ¼ 450
)
a ¼ 0;5
y ¼ 0;5 ðx 2 4Þ ðx 2 9Þ ðx 2 25Þ ¼ 0;5 ðx 4 4 x 2 9 x 2 þ 36Þ ðx 2 25Þ ¼
¼ 0;5 ðx 4 13 x 2 þ 36Þ ðx 2 25Þ ¼ 0;5 ðx 6 13 x 4 þ 36 x 2 25 x 4 þ 325 x 2 900Þ ¼
¼ 0;5 ðx 6 38 x 4 þ 361 x 2 900Þ ¼ 0;5 x 6 þ 19 x 4 180;5 x 2 þ 450
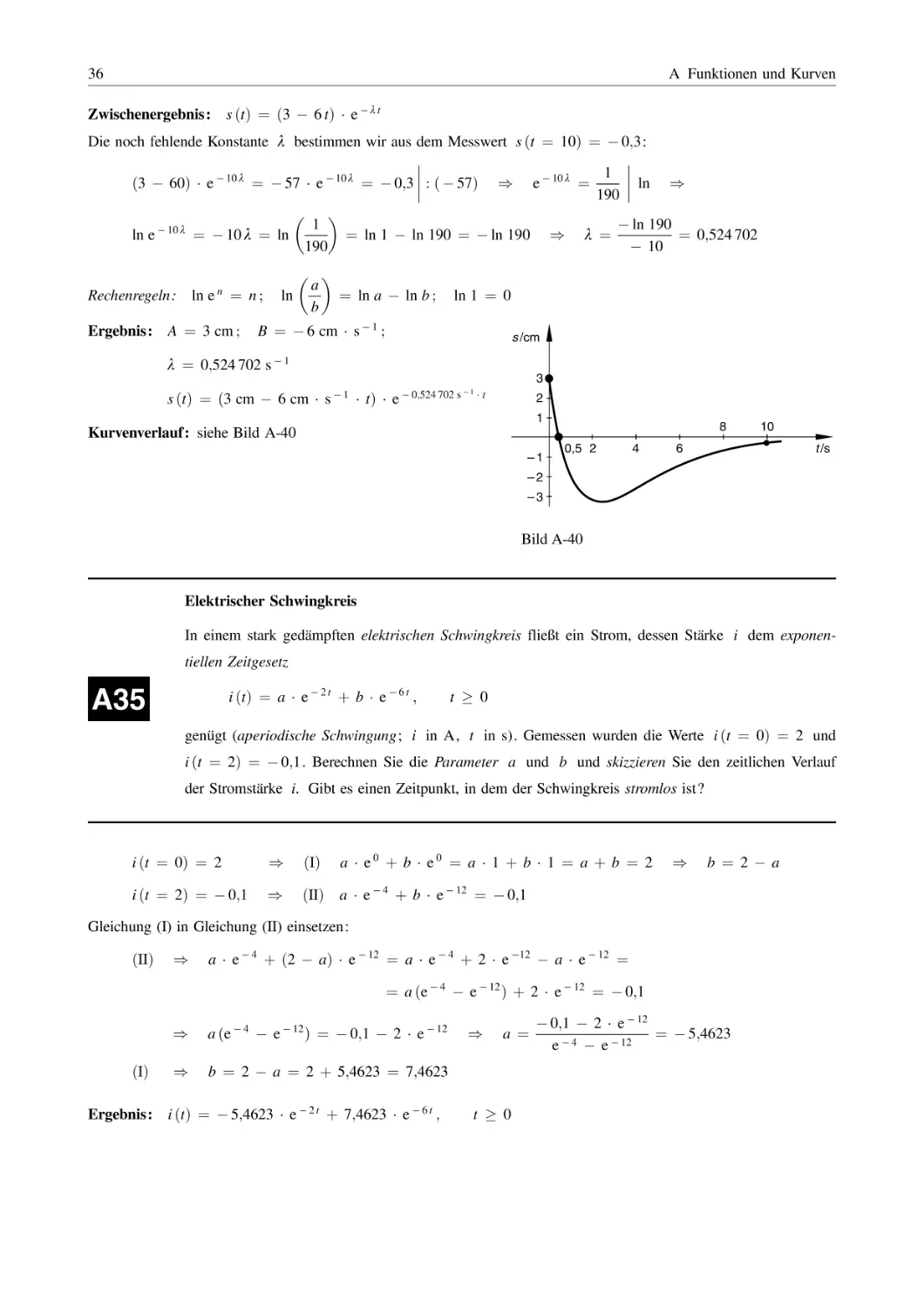
Kennlinie einer Glühlampe
Eine Glühlampe stellt einen nichtlinearen elektrischen Widerstand dar. Aus einer Messung sind die folgenden Strom-Spannungs-Wertepaare bekannt ( I : Stromstärke in Ampere; U : Spannung in Volt):
A6
I /A
0
0,1
0,2
0,5
U /V
0
21,0
48,0
225,0
a) Bestimmen Sie aus diesen Messwerten ein Näherungspolynom 3. Grades für die unbekannte Kennlinie
U ¼ f ðIÞ der Glühlampe.
b) Welcher Spannungsabfall ist bei einer Stromstärke von I ¼ 0;3 A zu erwarten?
Anleitung: Verwenden Sie die Interpolationsformel von Newton (! Band 1: Kap. III.5.6 und FS:
Kap. III.4.7.3)
a) Interpolationsformel von Newton:
U ¼ f ðIÞ ¼ a 0 þ a 1 ðI I 0 Þ þ a 2 ðI I 0 Þ ðI I 1 Þ þ a 3 ðI I 0 Þ ðI I 1 Þ ðI I 2 Þ ¼
¼ a 0 þ a 1 ðI 0Þ þ a 2 ðI 0Þ ðI 0;1Þ þ a 3 ðI 0Þ ðI 0;1Þ ðI 0;2Þ ¼
¼ a 0 þ a 1 I þ a 2 I ðI 0;1Þ þ a 3 I ðI 0;1Þ ðI 0;2Þ
6
A Funktionen und Kurven
Berechnung der Koeffizienten a 0 ; a 1 ; a 2 und a 3 aus dem folgenden Steigungs- oder Differenzenschema:
k
Ik
Uk
a0
0
0
0
1
0,1
21
2
0,2
48
3
0,5
225
a1
a2
210
300
270
800
590
Somit:
a3
1000
a0 ¼ 0;
a 1 ¼ 210 ;
a 2 ¼ 300 ;
a 3 ¼ 1000
Näherungspolynom 3. Grades für die unbekannte Kennlinie U ¼ f ðIÞ:
U ¼ f ðIÞ ¼ 0 þ 210 I þ 300 I ðI 0;1Þ þ 1000 I ðI 0;1Þ ðI 0;2Þ ¼
¼ 210 I þ 300 I 2 30 I þ 1000 I ðI 2 0;1 I 0;2 I þ 0;02Þ ¼
¼ 180 I þ 300 I 2 þ 1000 I ðI 2 0;3 I þ 0;02Þ ¼
¼ 180 I þ 300 I 2 þ 1000 I 3 300 I 2 þ 20 I ¼ 200 I þ 1000 I 3
Unter Berücksichtigung der Einheiten:
U ¼ f ðIÞ ¼ 200
U /V
V
V
I þ 1000 3 I 3
A
A
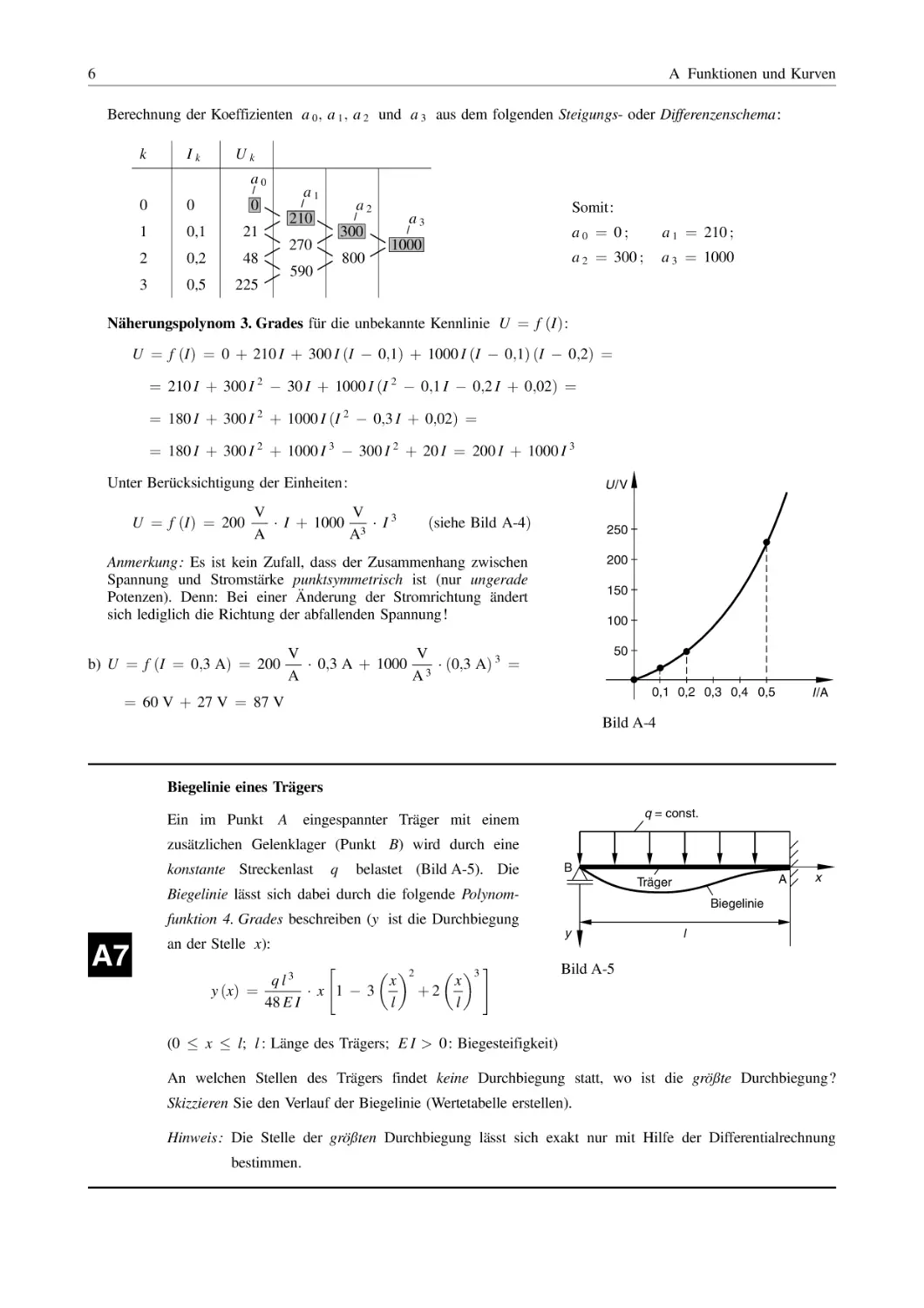
ðsiehe Bild A-4Þ
250
200
Anmerkung: Es ist kein Zufall, dass der Zusammenhang zwischen
Spannung und Stromstärke punktsymmetrisch ist (nur ungerade
Potenzen). Denn: Bei einer nderung der Stromrichtung ändert
sich lediglich die Richtung der abfallenden Spannung!
b) U ¼ f ðI ¼ 0;3 AÞ ¼ 200
150
100
50
V
V
0;3 A þ 1000 3 ð0;3 AÞ 3 ¼
A
A
0,1 0,2 0,3 0,4 0,5
¼ 60 V þ 27 V ¼ 87 V
I /A
Bild A-4
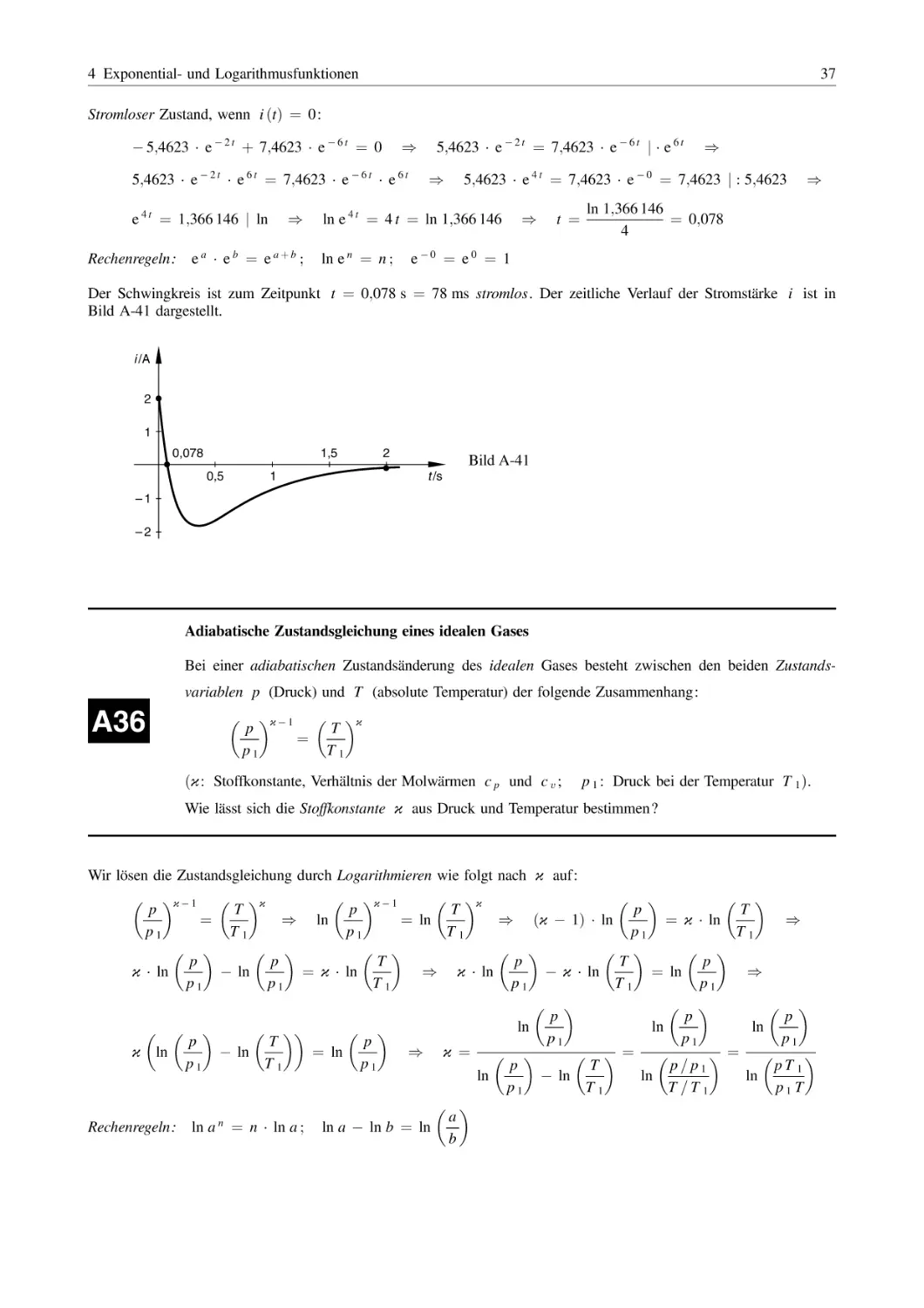
Biegelinie eines Trägers
q = const.
Ein im Punkt A eingespannter Träger mit einem
zusätzlichen Gelenklager (Punkt B) wird durch eine
konstante Streckenlast
q
belastet (Bild A-5). Die
B
A
Träger
Biegelinie lässt sich dabei durch die folgende Polynom-
x
Biegelinie
funktion 4. Grades beschreiben (y ist die Durchbiegung
A7
an der Stelle x):
"
2
3 #
ql3
x
x
y ðxÞ ¼
þ2
x 13
48 E I
l
l
y
l
Bild A-5
(0 x l; l : Länge des Trägers; E I > 0: Biegesteifigkeit)
An welchen Stellen des Trägers findet keine Durchbiegung statt, wo ist die größte Durchbiegung?
Skizzieren Sie den Verlauf der Biegelinie (Wertetabelle erstellen).
Hinweis: Die Stelle der größten Durchbiegung lässt sich exakt nur mit Hilfe der Differentialrechnung
bestimmen.
1 Ganzrationale Funktionen (Polynomfunktionen)
7
Zur Vereinfachung führen wir eine neue Variable u ¼ x = l mit 0 u 1 ein. Die Gleichung der Biegelinie lautet
dann (wir erweitern zunächst den Faktor vor der Klammer mit l ):
"
2
3 #
"
2
3 #
ql3
x
x
ql4
x
x
x
y ðxÞ ¼
¼
)
þ2
þ2
x 13
13
48 E I
48 E I
l
l
l
l
l
y ðuÞ ¼ K u ð1 3 u 2 þ 2 u 3 Þ ¼ K u ð2 u 3 3 u 2 þ 1Þ
mit K ¼
ql4
> 0
48 E I
und 0 u 1
Berechnung der Nullstellen im Intervall 0 u 1
Aus physikalischen Gründen ist einleuchtend, dass in den Randpunkten A und B keine Durchbiegung stattfinden
kann. Somit sind u 1 ¼ 0 und u 2 ¼ 1 Nullstellen der Biegelinie. Sämtliche Nullstellen erhält man aus der Gleichung y ðuÞ ¼ 0 , d. h.
u ¼ 0 ) u1 ¼ 0
K u ð2 u 3 3 u 2 þ 1Þ ¼ 0
2u3 3u2 þ 1 ¼ 0
u 1 ¼ 0 ist dabei die (bereits bekannte) Lösung der linearen Gleichung u ¼ 0 , u 2 ¼ 1 eine Lösung der kubischen
Gleichung 2 u 3 3 u 2 þ 1 ¼ 0 (ebenfalls schon bekannt). Die restlichen Lösungen der kubischen Gleichung erhalten wir mit Hilfe des Horner-Schemas durch Reduzierung des Polynoms 2 u 3 3 u 2 þ 1 (Abspaltung des Linearfaktors u 1; das Polynom ist unvollständig, das lineare Glied fehlt):
2
u2 ¼ 1
2
3
0
1
2
1
1
1
1
0
) 1. reduziertes Polynom: 2 u 2 u 1
2 u 2 u 1 ¼ 0 j : 2 ) u 2 0;5 u 0;5 ¼ 0 )
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ 0;25 0;0625 þ 0;5 ¼ 0;25 0;5625 ¼ 0;25 0;75 ) u 3 ¼ 1 ;
Restliche Nullstellen:
u 3=4
u 4 ¼ 0;5
Am Ort der Einspannung (Punkt A) liegt somit eine doppelte Nullstelle ðu 2=3 ¼ 1Þ, der Wert u 4 ¼ 0;5 dagegen
hat keine physikalische Bedeutung (er liegt außerhalb des Trägers). Zwischen den Randpunkten A und B des Trägers
gibt es keine weiteren Stellen ohne Durchbiegung.
Ort der maximalen Durchbiegung
Eine exakte Berechnung dieser Stelle ist nur mit Hilfe der Differentialrechnung über die 1. und 2. Ableitung der Biegelinie möglich:
y ¼ K ð2 u 4 3 u 3 þ uÞ
)
y 0 ¼ K ð8 u 3 9 u 2 þ 1Þ ;
y 00 ¼ K ð24 u 2 18 uÞ
Aus der notwendigen Bedingung y 0 ¼ 0 erhalten wir eine kubische Gleichung, von der wir bereits eine Lösung
kennen (nämlich u 1 ¼ 1 ; an dieser Stelle besitzt die Biegelinie bekanntlich eine doppelte Nullstelle!):
y0 ¼ 0
)
K ð8 u 3 9 u 2 þ 1Þ ¼ 0 j : K
)
8u3 9u2 þ 1 ¼ 0
Die restlichen Lösungen dieser Gleichung bestimmen wir mit Hilfe des Horner-Schemas (Abspalten des Linearfaktors
u 1; das Polynom ist unvollständig, das lineare Glied fehlt):
8
u1 ¼ 1
8
0
1
8
1
1
1
1
0
) 1. reduziertes Polynom: 8 u 2 u 1
1
1
u ¼ 0 )
8
8
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
1
1
1
1
1 þ 32
1
33
1 33
1 5;7446
¼
¼
¼
¼
¼
þ
2
2
2
16
16
8
16
16
16
16
16
16
Restliche Nullstellen:
u 2=3
9
u 2 ¼ 0;4215 ;
8u2 u 1 ¼ 0 j : 8
u 3 ¼ 0;2965 < 0
)
u2
)
(ohne physikalische Bedeutung, liegt außerhalb des Definitionsbereichs)
8
A Funktionen und Kurven
Umformungen: Brüche des Radikanden gleichnamig machen (Hauptnenner: 16 2 ), den 2. Bruch also mit 2 16 ¼ 32
erweitern, dann Teilwurzeln ziehen.
Wegen y 00 ðu 2 ¼ 0;4215Þ ¼ K ð 3;3231Þ ¼ 3;3231 K < 0 liegt ein Maximum vor. Die größte Durchbiegung findet daher an der Stelle u 2 ¼ 0;4215 und somit x 2 ¼ 0;4215 l statt. Sie hat den Wert
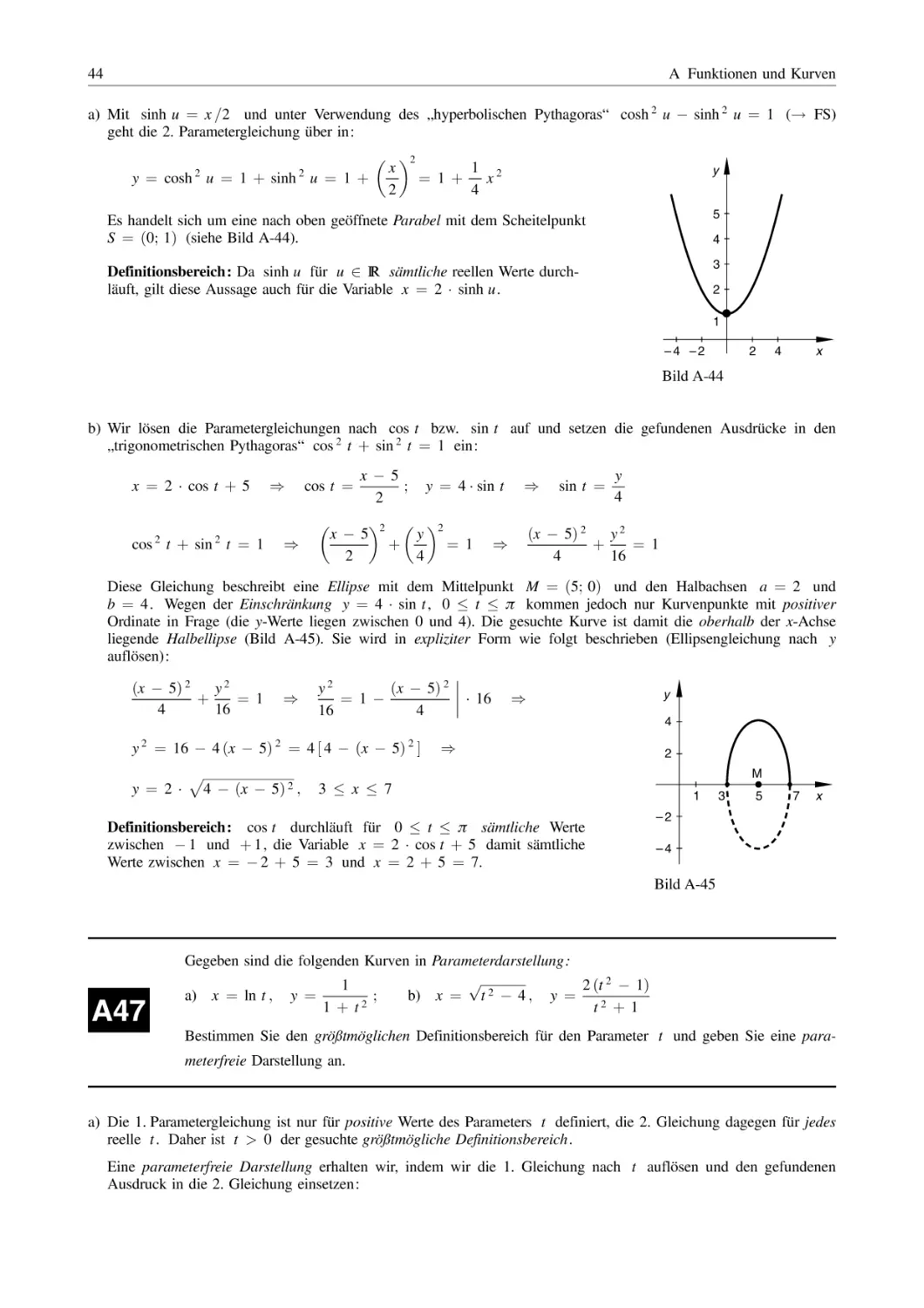
y ðu 2 ¼ 0;4215Þ ¼ 0;2600 K. An der Stelle u 1 ¼ 1 (Punkt A) liegt ein Minimum (keine Durchbiegung).
Der Kurvenverlauf (ermittelt mit Hilfe der folgenden Wertetabelle) bestätigt diese Ergebnisse (Bild A-6).
Wertetabelle (ohne den Faktor K > 0Þ:
u
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
y
0
0,097
0,179
0,235
0,259
0,25
0,211
0,151
0,083
0,025
0
0,4215
1 u
0,5
Bild A-6
Biegelinie
y
2 Gebrochenrationale Funktionen
Lehrbuch: Band 1, Kapitel III.6
Formelsammlung: Kapitel III.5
y ¼
A8
ðx 1Þ ðx þ 5Þ
ðx þ 1Þ 2 ðx 3Þ
Bestimmen Sie folgende Eigenschaften: Definitionslücken, Nullstellen, Pole, Asymptoten, Schnittpunkt
mit der y-Achse. Skizzieren Sie den Kurvenverlauf.
Definitionslücken:
Nullstellen:
Pole:
Nenner ¼ 0
Zähler ¼ 0 ,
Nenner ¼ 0 ,
) ðx þ 1Þ 2 ðx 3Þ ¼ 0
Nenner 6¼ 0
Zähler 6¼ 0
)
) ðx 1Þ ðx þ 5Þ ¼ 0
) ðx þ 1Þ 2 ðx 3Þ ¼ 0
)
x ¼ 1;
)
x ¼ 3
x1 ¼ 1;
x 3=4 ¼ 1 ;
x2 ¼ 5
x5 ¼ 3
Bei 1 liegt ein Pol ohne Vorzeichenwechsel (doppelte Nennernullstelle), bei 3 ein solcher mit Vorzeichenwechsel
(einfache Nennernullstelle).
Polgeraden (senkrechte Asymptoten):
x ¼ 1;
x ¼ 3
Verhalten der Funktion im „Unendlichen“
Die Funktion ist echt gebrochen (Zähler: quadratisch, Nenner: kubisch), sie nähert sich daher für x ! 1 asymptotisch der x-Achse ðy ¼ 0Þ.
Asymptote im „Unendlichen“:
y ¼ 0
2 Gebrochenrationale Funktionen
y ð0Þ ¼
Schnittpunkt mit der y-Achse:
Kurvenverlauf:
9
ð1Þ ð5Þ
5
¼
3
ð1Þ 2 ð 3Þ
siehe Bild A-7
Die Kurve nähert sich für x ! 1 von unten der x-Achse, links von der Nullstelle x 2 ¼ 5 besitzt sie daher
noch ein relatives Minimum (die genaue Lage lässt sich nur mit Hilfe der Differentialrechnung bestimmen).
y
2
5/3
1
Bild A-7
–8
–6
–4
–2
1
2
4
x
x=3
–1
x = –1
6
–2
Diskutieren Sie den Verlauf der gebrochenrationalen Funktion
y ¼
A9
2 x 4 2 x 3 20 x 2 þ 8 x þ 48
x3 þ x2 4x 4
(Definitionslücken, Nullstellen, Pole, Asymptoten, Schnittpunkt mit der y-Achse). Gibt es hebbare Definitionslücken? Wie lautet gegebenenfalls die „erweiterte“ Funktion? Skizzieren Sie den Kurvenverlauf.
Sinnvoller Weise zerlegen wir zunächst Zähler und Nenner in Linearfaktoren.
Zähler:
Z ðxÞ ¼ 2 x 4 2 x 3 20 x 2 þ 8 x þ 48 ¼ 0
Durch Probieren findet man die Lösung x 1 ¼ 2, mit dem Horner-Schema wird dann reduziert:
2
2
20
8
48
4
4
32
48
2
16
24
0
x1 ¼ 2
2
) 1. reduziertes Polynom: 2 x 3 þ 2 x 2 16 x 24
Eine weitere Nullstelle liegt bei x 2 ¼ 3:
2
x2 ¼ 3
2
2
16
24
6
24
24
8
8
0
Restliche Zählernullstellen:
Zähler:
) 2. reduziertes Polynom: 2 x 2 þ 8 x þ 8
2x2 þ 8x þ 8 ¼ 0 j : 2
)
x 2 þ 4 x þ 4 ¼ ðx þ 2Þ 2 ¼ 0
Z ðxÞ ¼ 2 x 4 2 x 3 20 x 2 þ 8 x þ 48 ¼ 2 ðx 2Þ ðx 3Þ ðx þ 2Þ 2
)
x 3=4 ¼ 2
10
A Funktionen und Kurven
N ðxÞ ¼ x 3 þ x 2 4 x 4 ¼ 0
Nenner:
Durch Probieren erhält man die Lösung x 1 ¼ 1, mit dem Horner-Schema wird reduziert:
1
4
4
1
0
4
0
4
0
1
x1 ¼ 1
1
x2 4 ¼ 0
Restliche Nennernullstellen:
Nenner:
)
) 1. reduziertes Polynom: x 2 4
x2 ¼ 4
)
x 2=3 ¼ 2
N ðxÞ ¼ x 3 þ x 2 4 x 4 ¼ ðx þ 1Þ ðx 2Þ ðx þ 2Þ
Die (unecht) gebrochenrationale Funktion lässt sich damit auch wie folgt darstellen:
y ¼
2 x 4 2 x 3 20 x 2 þ 8 x þ 48
2 ðx 2Þ ðx 3Þ ðx þ 2Þ 2
¼
3
2
ðx þ 1Þ ðx 2Þ ðx þ 2Þ
x þ x 4x 4
ðx 6¼ 1; 2; 2Þ
Es gibt drei Definitionslücken bei 1, 2 und 2 (dort wird der Nenner jeweils gleich Null). Zähler und Nenner
haben bei x ¼ 2 und x ¼ 2 gemeinsame Nullstellen, diese Definitionslücken sind jedoch beide behebbar, da die
jeweiligen Grenzwerte vorhanden sind:
lim
2 ðx 2Þ ðx 3Þ ðx þ 2Þ 2
2 ðx 3Þ ðx þ 2Þ 2
2 ð 1Þ ð4Þ 2
8
¼ lim
¼
¼
3
ðx þ 1Þ ðx 2Þ ðx þ 2Þ
ðx
þ
1Þ
ðx
þ
2Þ
ð3Þ
ð4Þ
x!2
lim
2 ð x 2Þ ðx 3Þ ðx þ 2Þ ðx þ 2Þ
2 ðx 2Þ ðx 3Þ ðx þ 2Þ 2
¼ lim
¼
ðx þ 1Þ ðx 2Þ ðx þ 2Þ
ðx þ 1Þ ðx 2Þ ðx þ 2Þ
x!2
x!2
x ! 2
¼ lim
x ! 2
2 ðx 2Þ ðx 3Þ ðx þ 2Þ
2 ð 4Þ ð 5Þ ð0Þ
¼
¼ 0
ðx þ 1Þ ðx 2Þ
ð 1Þ ð 4Þ
„Erweiterte“ Funktion und ihre Eigenschaften
Die „erweiterte“ Funktion y * erhalten wir durch Kürzen der gemeinsamen Faktoren:
y ¼
2 ðx 2Þ ðx 3Þ ðx þ 2Þ ðx þ 2Þ
2 ðx 3Þ ðx þ 2Þ
! y* ¼
x þ1
ðx þ 1Þ ðx 2Þ ðx þ 2Þ
ðx 6¼ 1Þ
Wir bestimmen zunächst die Eigenschaften dieser Funktion.
Definitionsbereich:
Nullstellen:
Pole:
x 6¼ 1
2 ðx 3Þ ðx þ 2Þ ¼ 0
x þ1 ¼ 0
)
x3 ¼ 1
Polgerade (senkrechte Asymptote):
)
x1 ¼ 3;
x2 ¼ 2
(Pol mit Vorzeichenwechsel)
x ¼ 1
Verhalten im „Unendlichen“
Die Funktion ist unecht gebrochenrational (Grad des Zählers > Grad des Nenners). Wir zerlegen sie durch Polynomdivision wie folgt:
y* ¼
y* ¼
2 ðx 3Þ ðx þ 2Þ
2 ðx 2 3 x þ 2 x 6Þ
2 ðx 2 x 6Þ
2 x 2 2 x 12
¼
¼
¼
x þ1
x þ1
x þ1
x þ1
ð2 x 2 2 x
ð2 x 2 þ 2 xÞ
4x
ð 4 x
12Þ : ðx þ 1Þ ¼ 2 x 4
12
4Þ
8
8
x þ1
|fflffl{zfflffl}
echt gebrochen
2 Gebrochenrationale Funktionen
11
Für große x-Werte (d. h. für x ! 1) wird der echt gebrochenrationale Anteil vernachlässigbar klein (er strebt
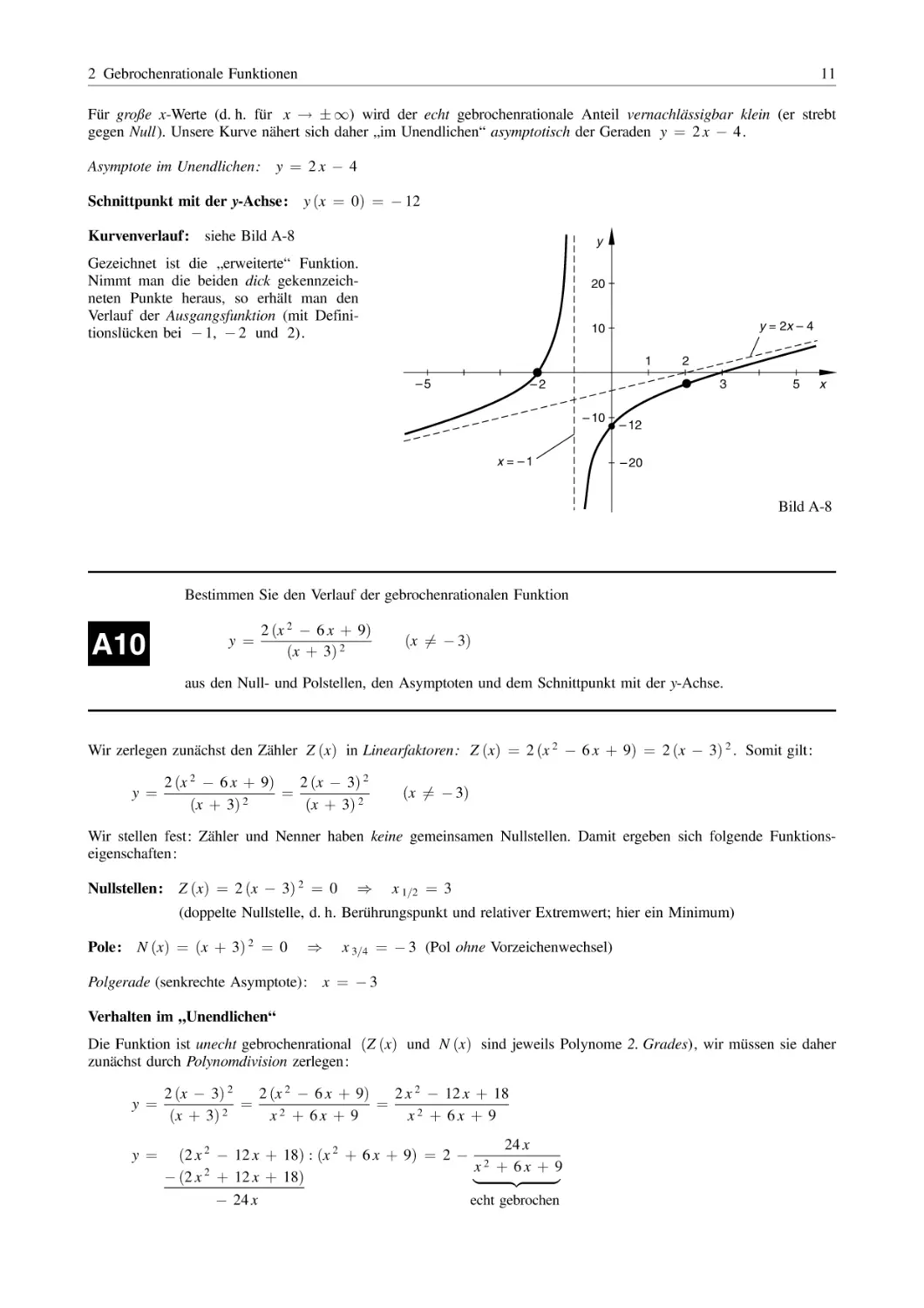
gegen Null). Unsere Kurve nähert sich daher „im Unendlichen“ asymptotisch der Geraden y ¼ 2 x 4.
y ¼ 2x 4
Asymptote im Unendlichen:
Schnittpunkt mit der y-Achse:
Kurvenverlauf:
y ðx ¼ 0Þ ¼ 12
siehe Bild A-8
y
Gezeichnet ist die „erweiterte“ Funktion.
Nimmt man die beiden dick gekennzeichneten Punkte heraus, so erhält man den
Verlauf der Ausgangsfunktion (mit Definitionslücken bei 1, 2 und 2).
20
y = 2x – 4
10
1
–5
2
3
–2
– 10
x = –1
5
x
– 12
– 20
Bild A-8
Bestimmen Sie den Verlauf der gebrochenrationalen Funktion
A10
y ¼
2 ðx 2 6 x þ 9Þ
ðx þ 3Þ 2
ðx 6¼ 3Þ
aus den Null- und Polstellen, den Asymptoten und dem Schnittpunkt mit der y-Achse.
Wir zerlegen zunächst den Zähler Z ðxÞ in Linearfaktoren: Z ðxÞ ¼ 2 ðx 2 6 x þ 9Þ ¼ 2 ðx 3Þ 2 . Somit gilt:
y ¼
2 ðx 2 6 x þ 9Þ
2 ðx 3Þ 2
¼
ðx þ 3Þ 2
ðx þ 3Þ 2
ðx 6¼ 3Þ
Wir stellen fest: Zähler und Nenner haben keine gemeinsamen Nullstellen. Damit ergeben sich folgende Funktionseigenschaften:
Nullstellen:
Z ðxÞ ¼ 2 ðx 3Þ 2 ¼ 0
)
x 1=2 ¼ 3
(doppelte Nullstelle, d. h. Berührungspunkt und relativer Extremwert; hier ein Minimum)
Pole:
N ðxÞ ¼ ðx þ 3Þ 2 ¼ 0
)
Polgerade (senkrechte Asymptote):
x 3=4 ¼ 3 (Pol ohne Vorzeichenwechsel)
x ¼ 3
Verhalten im „Unendlichen“
Die Funktion ist unecht gebrochenrational ðZ ðxÞ und N ðxÞ sind jeweils Polynome 2. Grades), wir müssen sie daher
zunächst durch Polynomdivision zerlegen:
y ¼
y ¼
2 ðx 3Þ 2
2 ðx 2 6 x þ 9Þ
2 x 2 12 x þ 18
¼
¼
ðx þ 3Þ 2
x2 þ 6x þ 9
x2 þ 6x þ 9
24 x
ð2 x 2 12 x þ 18Þ : ðx 2 þ 6 x þ 9Þ ¼ 2 2
x þ 6x þ 9
ð2 x 2 þ 12 x þ 18Þ
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
echt gebrochen
24 x
12
A Funktionen und Kurven
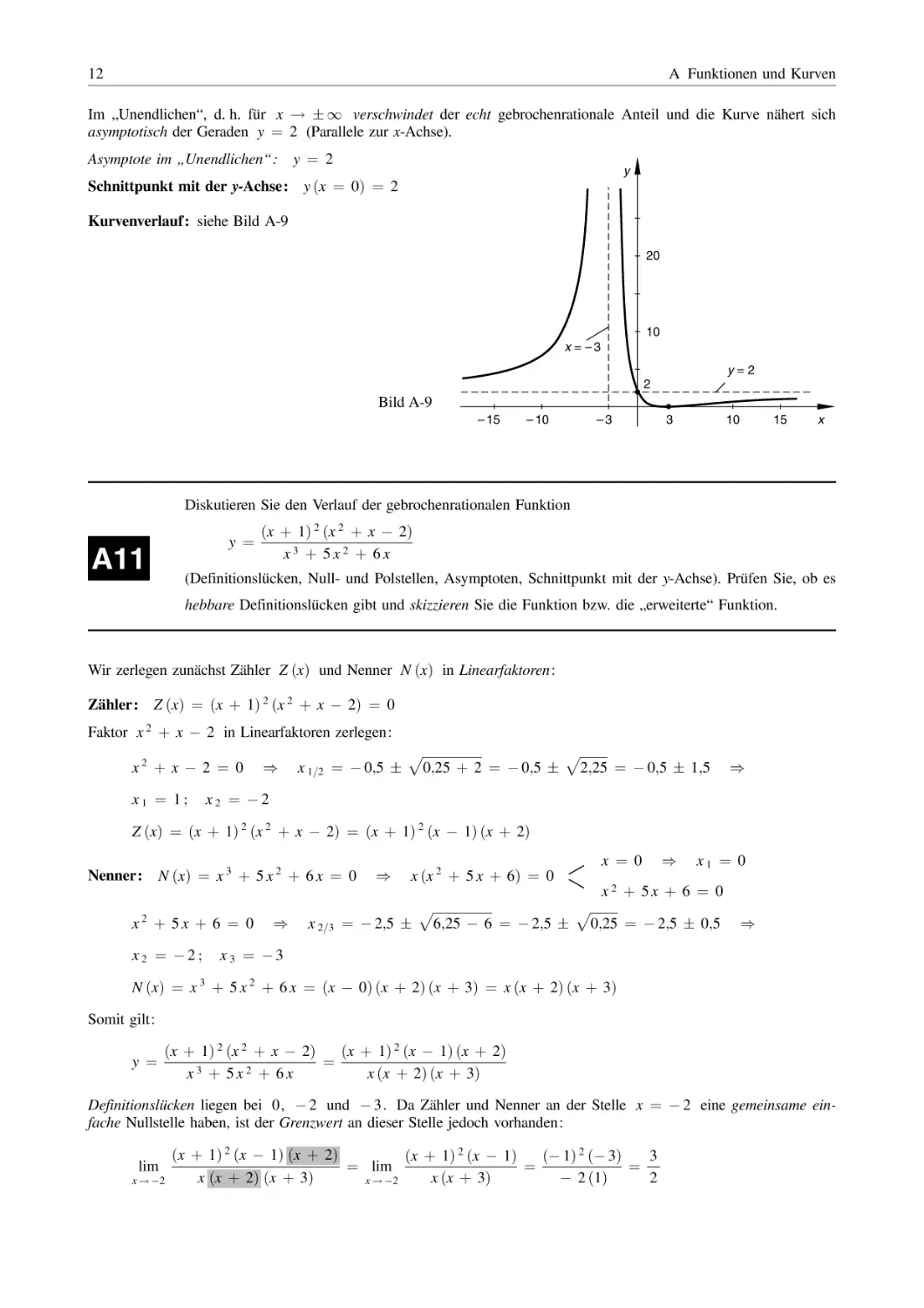
Im „Unendlichen“, d. h. für x ! 1 verschwindet der echt gebrochenrationale Anteil und die Kurve nähert sich
asymptotisch der Geraden y ¼ 2 (Parallele zur x-Achse).
Asymptote im „Unendlichen“:
Schnittpunkt mit der y-Achse:
y ¼ 2
y
y ðx ¼ 0Þ ¼ 2
Kurvenverlauf: siehe Bild A-9
20
10
x = –3
y=2
2
Bild A-9
– 15
– 10
–3
3
10
15
x
Diskutieren Sie den Verlauf der gebrochenrationalen Funktion
y ¼
A11
ðx þ 1Þ 2 ðx 2 þ x 2Þ
x3 þ 5x2 þ 6x
(Definitionslücken, Null- und Polstellen, Asymptoten, Schnittpunkt mit der y-Achse). Prüfen Sie, ob es
hebbare Definitionslücken gibt und skizzieren Sie die Funktion bzw. die „erweiterte“ Funktion.
Wir zerlegen zunächst Zähler Z ðxÞ und Nenner N ðxÞ in Linearfaktoren:
Z ðxÞ ¼ ðx þ 1Þ 2 ðx 2 þ x 2Þ ¼ 0
Zähler:
Faktor x 2 þ x 2 in Linearfaktoren zerlegen:
x2 þ x 2 ¼ 0
x1 ¼ 1;
)
x 1=2 ¼ 0;5
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
0;25 þ 2 ¼ 0;5 2;25 ¼ 0;5 1;5
)
x2 ¼ 2
Z ðxÞ ¼ ðx þ 1Þ 2 ðx 2 þ x 2Þ ¼ ðx þ 1Þ 2 ðx 1Þ ðx þ 2Þ
Nenner:
N ðxÞ ¼ x 3 þ 5 x 2 þ 6 x ¼ 0
x2 þ 5x þ 6 ¼ 0
x2 ¼ 2;
)
x 2=3
)
x ðx 2 þ 5 x þ 6Þ ¼ 0
x ¼ 0
)
x1 ¼ 0
x2 þ 5x þ 6 ¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
¼ 2;5 6;25 6 ¼ 2;5 0;25 ¼ 2;5 0;5
)
x3 ¼ 3
N ðxÞ ¼ x 3 þ 5 x 2 þ 6 x ¼ ðx 0Þ ðx þ 2Þ ðx þ 3Þ ¼ x ðx þ 2Þ ðx þ 3Þ
Somit gilt:
y ¼
ðx þ 1Þ 2 ðx 2 þ x 2Þ
ðx þ 1Þ 2 ðx 1Þ ðx þ 2Þ
¼
3
2
x þ 5x þ 6x
x ðx þ 2Þ ðx þ 3Þ
Definitionslücken liegen bei 0, 2 und 3. Da Zähler und Nenner an der Stelle x ¼ 2 eine gemeinsame einfache Nullstelle haben, ist der Grenzwert an dieser Stelle jedoch vorhanden:
lim
x ! 2
ðx þ 1Þ 2 ðx 1Þ ðx þ 2Þ
ðx þ 1Þ 2 ðx 1Þ
ð 1Þ 2 ð 3Þ
3
¼ lim
¼
¼
x ðx þ 2Þ ðx þ 3Þ
x ðx þ 3Þ
2 ð1Þ
2
x ! 2
2 Gebrochenrationale Funktionen
13
Die Definitionslücke bei x ¼ 2 lässt sich daher beheben, in dem wir nachträglich diesen Grenzwert zum Funktionswert an der Stelle x ¼ 2 erklären. Wir erhalten dann die „erweiterte“ Funktion
y* ¼
ðx þ 1Þ 2 ðx 1Þ
x ðx þ 3Þ
ðx 6¼ 0 ; 3Þ
(sie entsteht aus der Ausgangsfunktion durch Kürzen des gemeinsamen Faktors x þ 2). Diese Funktion besitzt nur
noch zwei Definitionslücken bei 0 und 3. Wir ermitteln nun die Eigenschaften der „erweiterten“ Funktion y * .
Definitionslücken:
Nullstellen:
x ¼ 0;
x ¼ 3
Z ðxÞ ¼ ðx þ 1Þ 2 ðx 1Þ ¼ 0
)
x 1=2 ¼ 1 ;
x3 ¼ 1
Die doppelte Nullstelle x 1=2 ¼ 1 ist zugleich ein Berührungspunkt mit der x-Achse und somit ein relativer Extremwert (hier ein relatives Minimum).
Pole:
N ðxÞ ¼ x ðx þ 3Þ ¼ 0
)
Polgeraden (senkrechte Asymptoten):
x4 ¼ 0;
x ¼ 0
x 5 ¼ 3 (bei Pole mit Vorzeichenwechsel)
ðy-AchseÞ ;
x ¼ 3
Verhalten im „Unendlichen“
Die Funktion ist unecht gebrochenrational (Grad des Zählers > Grad des Nenners), wir zerlegen sie daher zunächst mit
Hilfe der Polynomdivision in einen ganzrationalen und einen echt gebrochenrationalen Anteil:
y* ¼
y* ¼
ðx þ 1Þ 2 ðx 1Þ
ðx 2 þ 2 x þ 1Þ ðx 1Þ
x3 þ 2x2 þ x x2 2x 1
x3 þ x2 x 1
¼
¼
¼
2
2
x ðx þ 3Þ
x þ 3x
x þ 3x
x2 þ 3x
5x 1
ðx 3 þ x 2 x 1Þ : ðx 2 þ 3 xÞ ¼ x 2 þ 2
x
þ 3x
ðx 3 þ 3 x 2 Þ
|fflfflfflfflffl{zfflfflfflfflffl}
2x2 x 1
echt gebrochen
ð 2 x 2 6 xÞ
5x 1
Für x ! 1 verschwindet der echt gebrochenrationale Anteil, die Kurve nähert sich dann asymptotisch der Geraden
y ¼ x 2.
Asymptote im „Unendlichen“:
y ¼ x 2
Schnittpunkt mit der y-Achse: nicht vorhanden (Polstelle bei x ¼ 0Þ
Funktionsverlauf: siehe Bild A-10
y
Gezeichnet wurde die „erweiterte“ Funktion y * .
Die Ausgangsfunktion y hat an der fett gezeichneten Stelle ðx ¼ 2Þ eine weitere Definitionslücke, ansonsten aber den gleichen Verlauf wie die
„erweiterte“ Funktion.
10
5
–8
–6
–4
–2 –1
2
–5
y=x–2
x = –3
– 10
Bild A-10
4
x
14
A Funktionen und Kurven
Eine gebrochenrationale Funktion besitzt an den Stellen x 1 ¼ 2 und x 2 ¼ 5 einfache Nullstellen
A12
und bei x 3 ¼ 0 und x 4 ¼ 6 Pole 1. Ordnung. Für große x-Werte, d. h. für x ! 1 nähert sie
sich asymptotisch der Geraden y ¼ 2. Durch welche Gleichung lässt sich diese Funktion beschreiben? Skizzieren Sie den Kurvenverlauf.
Die Nullstellen der gesuchten Funktion sind die Nullstellen des Zählerpolynoms Z ðxÞ, die Pole die Nullstellen des
Nennerpolynoms N ðxÞ (gemeinsame Nullstellen gibt es nicht). Wir wählen daher für Zähler und Nenner den Produktansatz:
y ¼
Z ðxÞ
a ðx þ 2Þ ðx 5Þ
a ðx þ 2Þ ðx 5Þ
¼
¼
N ðxÞ
ðx 0Þ ðx 6Þ
x ðx 6Þ
ðx 6¼ 0 ; 6Þ
Die Asymptote im „Unendlichen“, deren Gleichung bekannt ist ðy ¼ 2Þ, erhält man durch Polynomdivision. Sie
entspricht dabei dem ganzrationalen Anteil, der bei dieser Division entsteht:
y ¼
a ðx þ 2Þ ðx 5Þ
a ðx 2 þ 2 x 5 x 10Þ
x 2 3 x 10
¼
¼ a
2
x ðx 6Þ
x 6x
x2 6x
Polynomdivision (der Faktor a 6¼ 0 wird zunächst weggelassen):
3 x 10
ðx 2 3 x 10Þ : ðx 2 6 xÞ ¼ 1 þ 2
x 6x
ðx 2 6 xÞ
3 x 10
Damit erhalten wir die folgende Zerlegung:
x 2 3 x 10
3 x 10
¼
a
1
þ
y ¼ a
x2 6x
x2 6x
|fflfflfflfflffl{zfflfflfflfflffl}
echt gebrochen
Im „Unendlichen“ verschwindet der echt gebrochenrationale Anteil und die Funktion nähert sich asymptotisch der
Geraden y ¼ a (Parallele zur x-Achse). Sie ist identisch mit der Geraden y ¼ 2, woraus folgt: a ¼ 2. Die
gesuchte Funktionsgleichung lautet somit:
y ¼
2 ðx þ 2Þ ðx 5Þ
2 ðx 2 3 x 10Þ
¼
x ðx 6Þ
x2 6x
ðx 6¼ 0 ; 6Þ
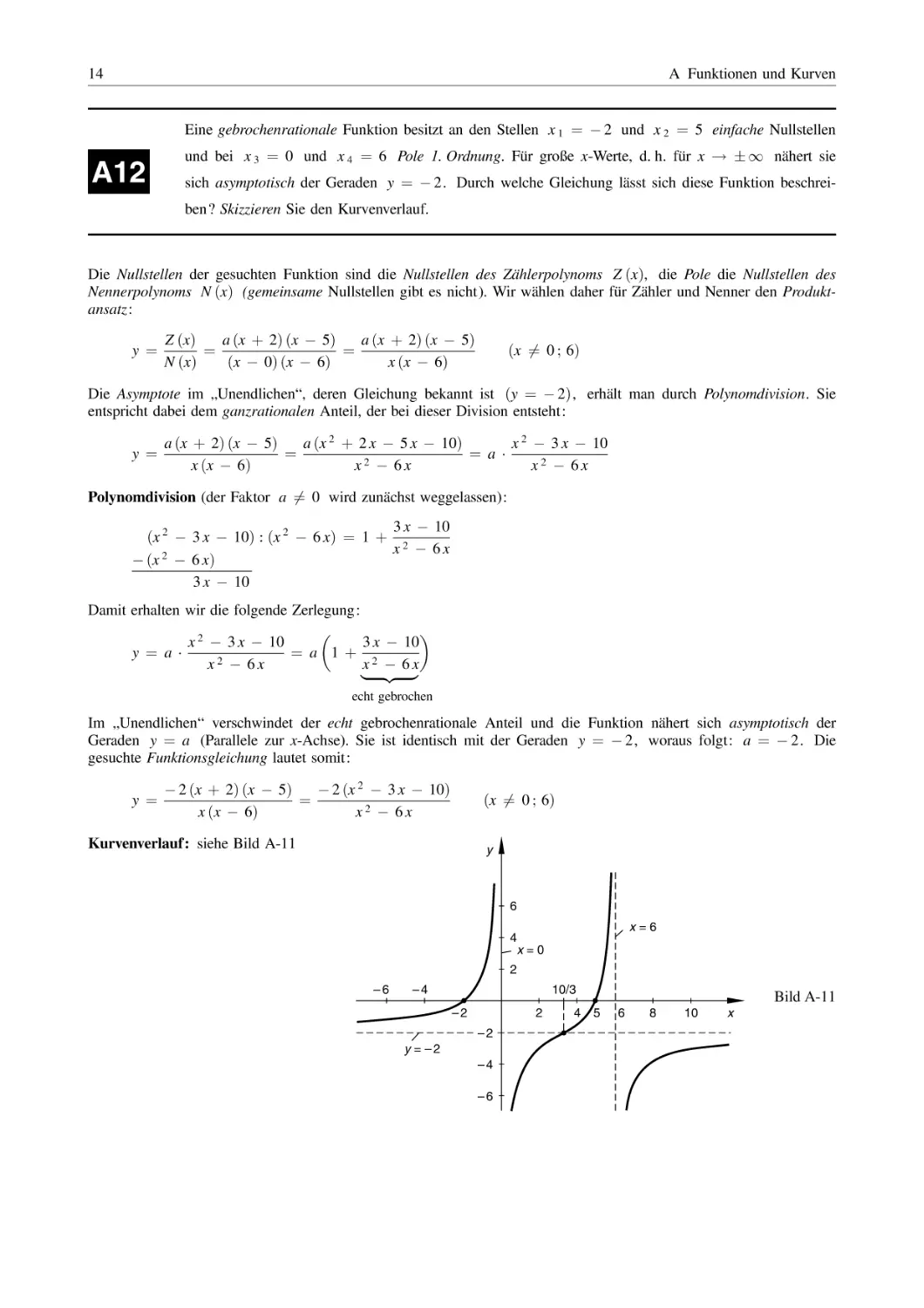
Kurvenverlauf: siehe Bild A-11
y
6
x=6
4
x=0
2
–6
10/3
–4
–2
2
–2
y = –2
–4
–6
4
Bild A-11
5
6
8
10
x
2 Gebrochenrationale Funktionen
15
Eine echt gebrochenrationale Funktion besitze folgende Eigenschaften:
Doppelte Nullstelle bei x 1=2 ¼ 2 ;
Einfache Polstellen bei x 3 ¼ 4; x 4 ¼ 0 und x 5 ¼ 10 ;
A13
Punkt P ¼ ð1; 0;2Þ liegt auf der Kurve;
Nennerpolynom vom Grade 3.
a) Wie lautet die Funktionsgleichung?
b) Skizzieren Sie den Kurvenverlauf.
a) Die Nullstellen der gesuchten Funktion sind die Nullstellen des Zählerpolynoms, die Polstellen dagegen die Nullstellen des Nennerpolynoms. Die Linearfaktorenzerlegung von Zähler und Nenner ist somit (bis auf einen noch
unbekannten Faktor a 6¼ 0) bekannt. Wir wählen daher den folgenden Ansatz (Zähler und Nenner jeweils in der
Produktform):
y ¼ a
ðx 2Þ ðx 2Þ
ðx 2Þ 2
¼ a
x ðx þ 4Þ ðx 10Þ
ðx þ 4Þ ðx 0Þ ðx 10Þ
ðx 6¼ 4 ; 0 ; 10Þ
Die Konstante a bestimmen wir aus dem Kurvenpunkt P ¼ ð1 ; 0;2Þ:
y ðx ¼ 1Þ ¼ 0;2
)
y ¼ 9
Funktionsgleichung:
b) Nullstellen:
Pole:
ð 1Þ 2
¼ 0;2
1 ð5Þ ð 9Þ
a
)
ðx 2Þ 2
x ðx þ 4Þ ðx 10Þ
1
a ¼ 0;2
45
)
a ¼ 9
ðx 6¼ 4 ; 0 ; 10Þ
x 1=2 ¼ 2 (Berührungspunkt und relativer Extremwert, hier ein Minimum)
x3 ¼ 4;
x4 ¼ 0;
Asymptote im „Unendlichen“:
x 5 ¼ 10 (alle mit Vorzeichenwechsel)
y ¼ 0 (die Funktion ist echt gebrochenrational)
Schnittpunkt mit der y-Achse: nicht vorhanden (Polstelle bei x ¼ 0Þ
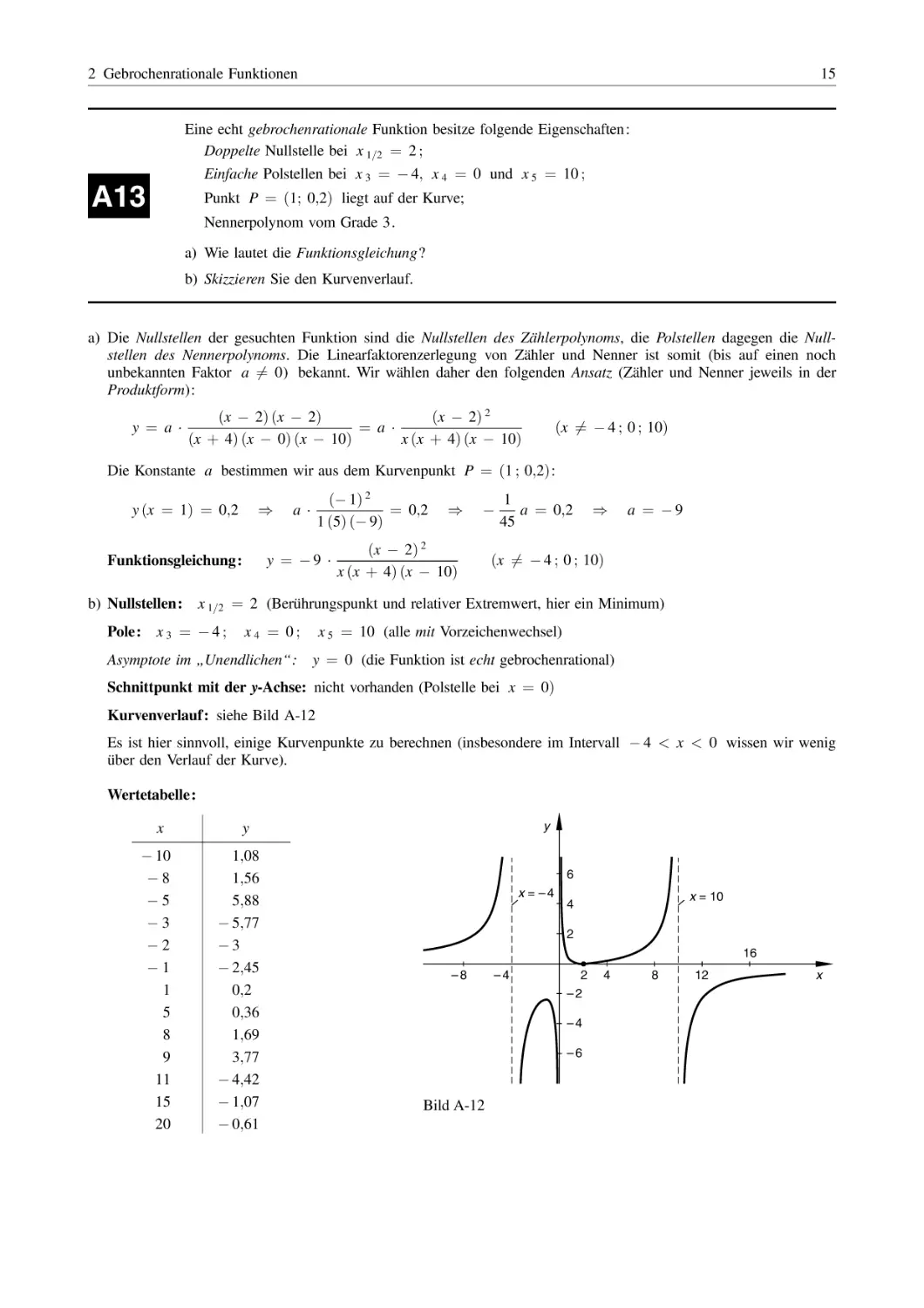
Kurvenverlauf: siehe Bild A-12
Es ist hier sinnvoll, einige Kurvenpunkte zu berechnen (insbesondere im Intervall 4 < x < 0 wissen wir wenig
über den Verlauf der Kurve).
Wertetabelle:
x
10
8
5
3
2
1
1
5
8
9
11
15
20
y
y
1;08
1;56
5;88
5;77
3
2;45
0;2
0;36
1;69
3;77
4;42
1;07
0;61
6
x = –4
x = 10
4
2
16
–8
–4
2
–2
–4
–6
Bild A-12
4
8
12
x
16
A Funktionen und Kurven
Eine gebrochenrationale Funktion y ¼ Z ðxÞ = N ðxÞ schneide die y-Achse bei 3. Sämtliche Nullstellen
des Zählerpolynoms Z ðxÞ und des Nennerpolynoms N ðxÞ sind bekannt:
A14
Z ðxÞ :
x1 ¼ 2;
x2 ¼ 1;
N ðxÞ :
x 3=4 ¼ 1 ;
x5 ¼ 4
a) Bestimmen Sie die Gleichung dieser Funktion und skizzieren Sie den Kurvenverlauf.
b) Wie lautet die Partialbruchzerlegung der Funktion?
a) Zähler und Nenner können in der Produktform angesetzt werden, da alle Nullstellen des Zähler- und Nennerpolynoms bekannt sind:
y ¼
a ðx 2Þ ðx þ 1Þ
a ðx 2Þ ðx þ 1Þ
¼
ðx 1Þ ðx 1Þ ðx 4Þ
ðx 1Þ 2 ðx 4Þ
ðx 6¼ 1 ; 4Þ
Die Berechnung der Konstanten a 6¼ 0 erfolgt aus dem (bekannten) Schnittpunkt mit der y-Achse:
y ðx ¼ 0Þ ¼ 3
)
Funktionsgleichung :
a ð 2Þ ð1Þ
2a
a
¼
¼ 3
¼
2
ð 1Þ ð 4Þ
4
2
y ¼
6 ðx 2Þ ðx þ 1Þ
ðx 1Þ 2 ðx 4Þ
)
a ¼ 6
ðx 6¼ 1 ; 4Þ
Eigenschaften der Funktion
Nullstellen:
Pole:
x1 ¼ 2;
x2 ¼ 1
x 3=4 ¼ 1 (Pol ohne Vorzeichenwechsel);
Polgeraden (senkrechte Asymptoten):
Asymptote im „Unendlichen“:
x ¼ 1;
x 5 ¼ 4 (Pol mit Vorzeichenwechsel)
x ¼ 4
y ¼ 0 (die Funktion ist echt gebrochenrational)
Schnittpunkt mit der y-Achse:
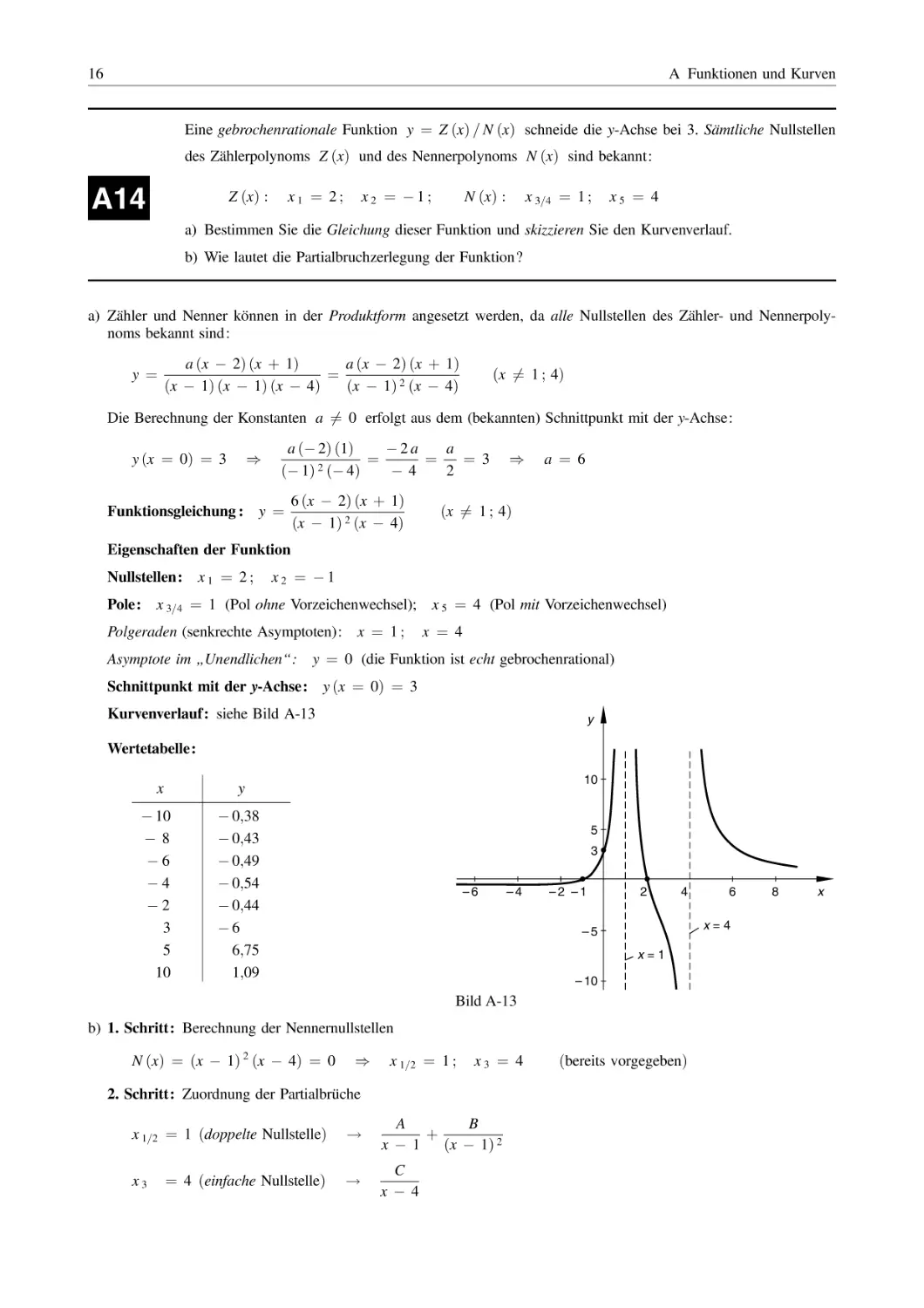
y ðx ¼ 0Þ ¼ 3
Kurvenverlauf: siehe Bild A-13
y
Wertetabelle:
x
y
10
8
6
4
2
3
5
10
0;38
0;43
0;49
0;54
0;44
6
6;75
1;09
10
5
3
–6
–4
–2 –1
2
4
x=4
–5
x=1
– 10
Bild A-13
b) 1. Schritt: Berechnung der Nennernullstellen
N ðxÞ ¼ ðx 1Þ 2 ðx 4Þ ¼ 0
)
x 1=2 ¼ 1 ;
x3 ¼ 4
2. Schritt: Zuordnung der Partialbrüche
x 1=2 ¼ 1 ðdoppelte NullstelleÞ
!
A
B
þ
x 1
ðx 1Þ 2
¼ 4 ðeinfache NullstelleÞ
!
C
x 4
x3
6
ðbereits vorgegebenÞ
8
x
2 Gebrochenrationale Funktionen
17
3. Schritt: Partialbruchzerlegung (Ansatz)
6 ðx 2Þ ðx þ 1Þ
A
B
C
¼
þ
þ
ðx 1Þ 2 ðx 4Þ
x 1
ðx 1Þ 2
x 4
4. Schritt: Alle Brüche werden gleichnamig gemacht, d. h. auf den Hauptnenner ðx 1Þ 2 ðx 4Þ gebracht.
Dazu müssen die Teilbrüche der rechten Seite der Reihe nach mit ðx 1Þ ðx 4Þ, ðx 4Þ bzw. ðx 1Þ 2
erweitert werden:
6 ðx 2Þ ðx þ 1Þ
A ðx 1Þ ðx 4Þ þ B ðx 4Þ þ C ðx 1Þ 2
¼
ðx 1Þ 2 ðx 4Þ
ðx 1Þ 2 ðx 4Þ
Da die Nenner beider Seiten übereinstimmen, gilt dies auch für die Zähler:
6 ðx 2Þ ðx þ 1Þ ¼ A ðx 1Þ ðx 4Þ þ B ðx 4Þ þ C ðx 1Þ 2
Um die drei Konstanten A; B und C zu bestimmen, benötigen wir drei Gleichungen. Diese erhalten wir durch
Einsetzen der Werte x ¼ 1; x ¼ 4 (es sind die Nullstellen des Nenners) und x ¼ 0:
x ¼ 1
6 ð 1Þ ð2Þ ¼ 3 B
x ¼ 4
6 ð2Þ ð5Þ ¼ 9 C
x ¼ 0
6 ð 2Þ ð1Þ ¼ A ð 1Þ ð 4Þ 4 B þ C
)
4 A ¼ 12 þ 16
Ergebnis:
y ¼
)
3 B ¼ 12
9 C ¼ 60
)
)
B ¼ 4
C ¼
60
20
¼
9
3
)
4A 4B þ C ¼ 4A 4 4 þ
20
20
12 20
8
¼ 4
¼
¼
3
3
3
3
)
A ¼
20
¼ 12
3
)
2
3
6 ðx 2Þ ðx þ 1Þ
2
1
4
20
1
þ
¼
þ
2
2
ðx 1Þ ðx 4Þ
3 x 1
ðx 1Þ
3 x 4
Magnetfeld in der Umgebung einer stromdurchflossenen elektrischen Doppelleitung
Die in Bild A-14 skizzierte elektrische Doppelleitung besteht aus zwei langen parallelen Leitern, deren
Durchmesser gegenüber dem Leiterabstand d ¼ 2 a vernachlässigbar klein ist. Die Ströme in den
beiden Leitern L 1 und L 2 haben die gleiche Stärke I, fließen jedoch in entgegengesetzte Richtungen. Der Verlauf der magnetischen Feldstärke H längs der Verbindungslinie der beiden Leiterquerschnitte (x-Achse) wird durch die Gleichung
A15
H ðxÞ ¼
Ia
1
;
p a2 x2
j x j 6¼ a
beschrieben. Bestimmen Sie die wesentlichen Eigenschaften dieser gebrochenrationalen Funktion und
skizzieren Sie den Feldstärkeverlauf.
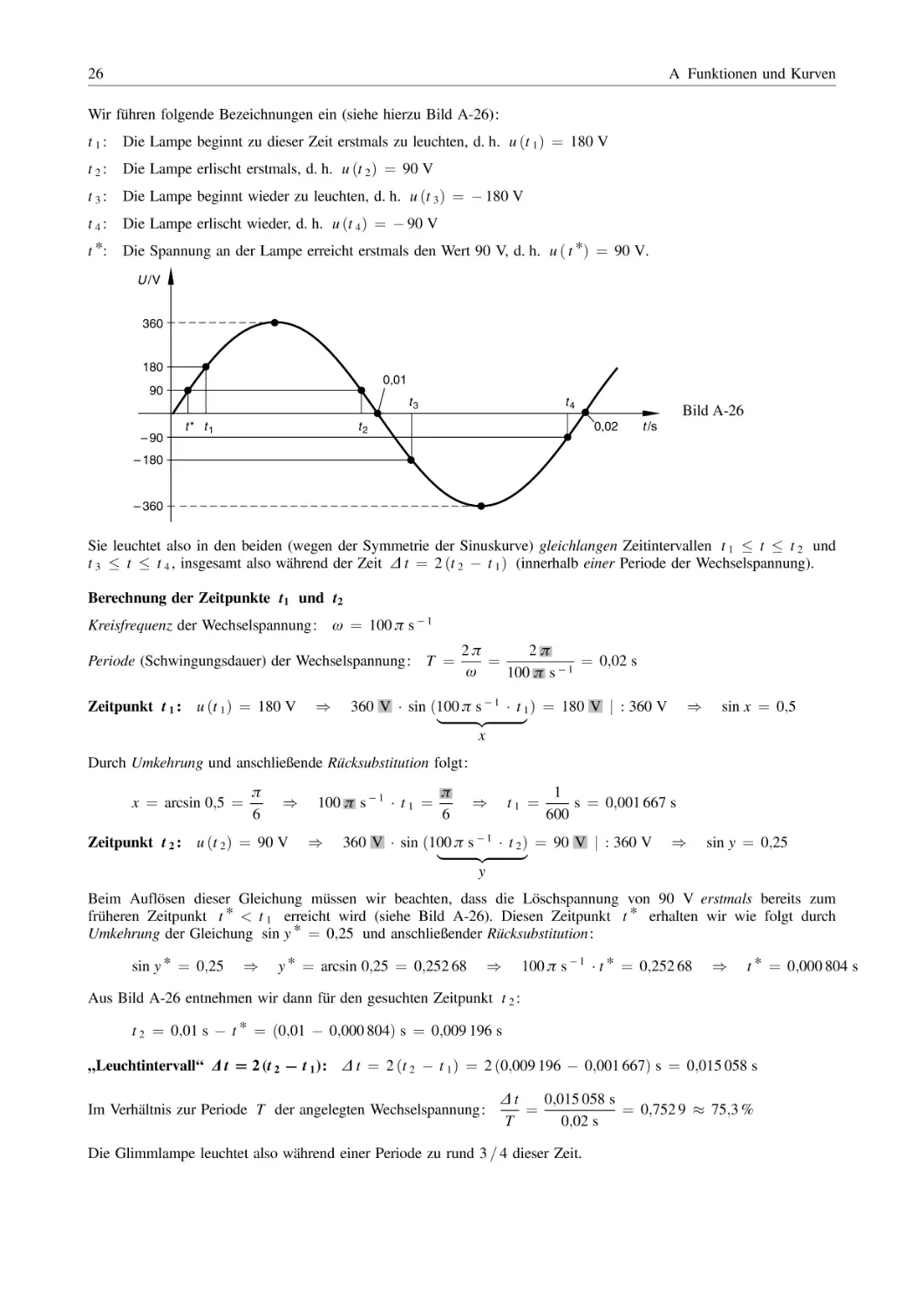
Strom fließt senkrecht
zur Papierebene nach unten
H
H (x )
L1
L2
Bild A-14
x
x = –a
2a
x=a
x
Strom fließt senkrecht
zur Papierebene nach oben
18
A Funktionen und Kurven
j x j 6¼ a (am Ort der beiden Leiter verschwindet der Nenner)
Definitionsbereich:
Symmetrie: Nur gerade Potenzen ) Spiegelsymmetrie zu H-Achse
Nullstellen: keine
Pole:
a2 x2 ¼ 0
)
x 1=2 ¼ a (Pole mit Vorzeichenwechsel)
Physikalische Deutung: Die magnetische Feldstärke wird unendlich groß am Ort der Leiter und ändert ihr Vorzeichen
(Richtungsänderung), wenn man auf die andere Seite des Leiters geht!
Polgeraden (senkrechte Asymptoten): x ¼ a
Schnittpunkt mit H-Achse:
H ðx ¼ 0Þ ¼
Ia 1
I
2 ¼
p a
pa
Verhalten im „Unendlichen“
Die Funktion ist echt gebrochenrational (Zähler: konstante Funktion; Nenner: quadratische Funktion), für große Werte
von x, d. h in großer Entfernung von der Doppelleitung nimmt die magnetische Feldstärke H rasch gegen Null ab.
Asymptote im „Unendlichen“:
H ¼ 0 (x-Achse)
Verlauf der magnetischen Feldstärke: siehe Bild A-15
H
Deutung aus physikalischer Sicht
x=a
Kleinster Wert (Minimum) zwischen den beiden Leitern
I
genau in der Mitte ðx ¼ 0Þ : H ðx ¼ 0Þ ¼
pa
H nimmt in Richtung der Leiter zunächst zu, wird am Ort
der Leiter unendlich groß ðPolstellen x 1=2 ¼ aÞ und
fällt dann nach außen hin gegen Null ab, wobei sich gleichzeitig die Richtung des Feldstärkevektors umkehrt:
H ðxÞ > 0
f ür
jxj < a
H ðxÞ < 0
f ür
jxj > a
L1
I /πa
–a
L2
a
x
x = –a
Bild A-15
3 Trigonometrische Funktionen und Arkusfunktionen
Lehrbuch: Band 1, Kapitel III.9 und 10
Formelsammlung: Kapitel III.7 und 8
A16
Zeige:
sin ðarccos xÞ ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 x2;
1 x 1
Wir setzen y ¼ arccos x ðmit 0 y pÞ: Durch Umkehrung folgt x ¼ cos y. Dann gilt:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sin ðarccos xÞ ¼ sin y ¼ 1 cos 2 y ¼ 1 x 2
(unter Berücksichtigung der trigonometrischen Bezeichnung sin 2 y þ cos 2 y ¼ 1 und sin y 0 im Intervall
0 y pÞ. Damit ist die Formel bewiesen.
3 Trigonometrische Funktionen und Arkusfunktionen
19
Welche Lösungen besitzen die folgenden trigonometrischen Gleichungen?
A17
a) 2 ðsin x þ cos 3 xÞ ¼ sin x sin ð2 xÞ
b) cos ð2 xÞ ¼ 2 sin 2 x
a) Unter Verwendung der trigonometrischen Formeln sin 2 x þ cos 2 x ¼ 1 und sin ð2 xÞ ¼ 2 sin x cos x
werden beide Seiten zunächst wie folgt umgeformt (! FS: Kap. III.7):
Linke Seite:
2 ðsin x þ cos 3 xÞ ¼ 2 sin x þ 2 cos 3 x ¼ 2 sin x þ 2 cos x cos 2 x ¼
|fflffl{zfflffl}
1 sin 2 x
¼ 2 sin x þ 2 cos x ð1 sin 2 xÞ ¼ 2 sin x þ 2 cos x 2 cos x sin 2 x
Rechte Seite:
sin x sin ð2 xÞ ¼ sin x ð2 sin x cos xÞ ¼ 2 cos x sin 2 x
|fflfflffl{zfflfflffl}
2 sin x cos x
Die trigonometrische Gleichung 2 ðsin x þ cos 3 xÞ ¼ sin x sin ð2 xÞ geht damit über in:
2 sin x þ 2 cos x 2 cos x sin 2 x ¼ 2 cos x sin 2 x
sin x þ cos x ¼ 0
)
sin x ¼ cos x j : cos x
)
)
2 sin x þ 2 cos x ¼ 0 j : 2
)
sin x
¼ tan x ¼ 1
cos x
ðunter Berücksichtigung der trigonometrischen Beziehung tan x ¼ sin x = cos xÞ
Die Lösungen dieser Gleichung lassen sich anhand einer Skizze leicht bestimmen (Bild A-16). Sie entsprechen den
Schnittstellen der Tangenskurve mit der Geraden y ¼ 1 (Parallele zur x-Achse).
y
y = tan x
arctan (– 1)
–π
π
Bild A-16
x
2π
A
y = –1
π
Der Schnittpunkt A liegt dabei an der Stelle x ¼ arctan ð 1Þ ¼ p = 4, die weiteren Schnittpunkte im Abstand
von ganzzahligen Vielfachen der Periode p ¼ p links und rechts von A. Wir erhalten somit folgende Lösungen:
x k ¼ arctan ð 1Þ þ k p ¼ p = 4 þ k p
ðmit k 2 ZÞ
b) Unter Verwendung der trigonometrischen Beziehungen cos ð2 xÞ ¼ cos 2 x sin 2 x und sin 2 x þ cos 2 x ¼ 1
lässt sich die linke Seite der Gleichung wie folgt umformen (! FS: Kap. III.7):
cos ð2 xÞ ¼ cos 2 x sin 2 x ¼ ð1 sin 2 xÞ sin 2 x ¼ 1 2 sin 2 x
|fflffl{zfflffl}
1 sin 2 x
Somit folgt aus cos ð2 xÞ ¼ 2 sin 2 x :
1 2 sin 2 x ¼ 2 sin 2 x
)
4 sin 2 x ¼ 1
)
sin 2 x ¼ 0;25
)
sin x ¼
pffiffiffiffiffiffiffiffiffi
0;25 ¼ 0;5
Wir untersuchen zunächst die Lösungen dieser beiden einfachen trigonometrischen Gleichungen im Periodenintervall 0 x < 2 p . Sie entsprechen den Schnittstellen der Sinuskurve mit den beiden zur x-Achse parallelen
Geraden y ¼ 0;5 bzw. y ¼ 0;5 (siehe Bild A-17).
20
A Funktionen und Kurven
2π – arcsin 0,5
y
Symmetrieachse
π + arcsin 0,5
y = sin x
1
y = 0,5
A
B
Bild A-17
π
2π
B*
y = – 0,5
–1
x
A*
arcsin 0,5
π – arcsin 0,5
sin x ¼ 0;5
Die Umkehrung dieser Gleichung im Intervall 0 x p liefert die Lösung x ¼ arcsin 0;5 ¼ p = 6
(Punkt A), eine weitere Lösung liegt spiegelsymmetrisch zur eingezeichneten Symmetrieachse an der Stelle
x ¼ p arcsin 0;5 (Punkt B). Somit ergeben sich für die Gleichung sin x ¼ 0;5 insgesamt folgende Lösungen:
9
x 1 k ¼ arcsin 0;5 þ k 2 p ¼ p = 6 þ k 2 p
>
=
mit k 2 Z
p
5
þ k 2p ¼
p þ k 2p>
x 2 k ¼ ðp arcsin 0;5Þ ¼ p
;
6
6
Denn wegen der Periodizität der Sinusfunktion wiederholen sich die Schnittstellen im Abstand von ganzzahligen
Vielfachen der Periode p ¼ 2 p .
sin x ¼ 0;5
Die Lösungen dieser Gleichung erhalten wir aus den Lösungen der ersten Gleichung sin x ¼ 0;5
durch eine einfache Symmetriebetrachtung. Die im Periodenintervall 0 x < 2 p gelegenen Schnittstellen A * und
B * liegen bezüglich der Nullstelle x ¼ p der Sinusfunktion punktsymmetrisch zu den Punkten A und B (siehe
Bild A-17). Der Schnittpunkt B * liegt daher an der Stelle x ¼ p þ arcsin 0;5; der Schnittpunkt A * bei
x ¼ 2 p arcsin 0;5. Weitere Schnittstellen ergeben sich, wenn wir wiederum ganzzahlige Vielfache der Periode
p ¼ 2 p addieren oder subtrahieren:
9
p
7
>
>
þ k 2p ¼
p þ k 2p
x 3 k ¼ ðp þ arcsin 0;5Þ þ k 2 p ¼ p þ
>
=
6
6
mit k 2 Z
>
p
11
>
>
x 4 k ¼ ð2 p arcsin 0;5Þ þ k 2 p ¼ 2 p
þ k 2p ¼
p þ k 2p ;
6
6
Lösungsmenge der Ausgangsgleichung (mit k 2 Z):
x 1k ¼
p
þ k 2p;
6
x 2k ¼
5
p þ k 2p;
6
x 3k ¼
7
p þ k 2p;
6
x 4k ¼
11
p þ k 2p
6
Bestimmen Sie sämtliche Nullstellen der periodischen Funktion
1
1
p
y ¼ 5 sin
x 3 cos
x
2
2
3
a) unter Verwendung des Additionstheorems der Kosinusfunktion,
A18
b) mit Hilfe des Zeigerdiagramms.
Hinweis zu b): Fassen Sie die beiden Summanden als gleichfrequente (mechanische) Schwingungen
auf ðx : Zeit; y: Auslenkung; Kreisfrequenz: w ¼ 1 = 2Þ und ersetzen Sie die beiden
Einzelschwingungen durch eine resultierende Sinusschwingung gleicher Frequenz,
deren Nullstellen dann leicht bestimmt werden können.
3 Trigonometrische Funktionen und Arkusfunktionen
21
1
1
p
x 3 cos
x
¼ 0 )
2
2
3
1
1
p
p
) 5 sin u ¼ 3 cos u
x ¼ 3 cos
x
5 sin
2
2
6
6
|fflffl{zfflffl}
|{z}
u
u
a) Nullstellen:
y ¼ 0
)
5 sin
Substitution : u ¼
1
x
2
Mit dem Additionstheorem der Kosinusfunktion erhalten wir (! FS: Kap. III.7.6.1):
5 sin u ¼ 3 cos ðu p = 6Þ ¼ 3 ½ cos u cos ðp = 6Þ þ sin u sin ðp = 6Þ ¼
¼ 3 cos ðp = 6Þ cos u þ 3 sin ðp = 6Þ sin u ¼ 2;5981 cos u þ 1;5 sin u
3;5 sin u ¼ 2;5981 cos u j : 3;5 cos u
)
sin u
2;5981
¼
cos u
3;5
)
)
tan u ¼ 0;7423
(unter Verwendung der trigonometrischen Beziehung tan u ¼ sin u = cos u)
Die Lösungen der Gleichung tan u ¼ 0;7423 entsprechen den Schnittstellen der Tangenskurve mit der zur
u-Achse parallelen Geraden y ¼ 0;7423 und lassen sich aus Bild A-18 leicht ermitteln:
y
y = tan u
y = 0,7423
A
π
–π
Bild A-18
π
2π
u
arctan 0,7423
Lösung im Periodenintervall p = 2 < u < p = 2 (Punkt A in Bild A-18): u ¼ arctan 0;7423 ¼ 0;6386
Weitere Lösungen liegen im Abstand von ganzzahligen Vielfachen der Periode p ¼ p :
u k ¼ arctan 0;7423 þ k p ¼ 0;6386 þ k p
ðk 2 ZÞ
Durch Rücksubstitution erhalten wir die gesuchten Nullstellen ðx ¼ 2 uÞ:
x k ¼ 2 u k ¼ 2 ð0;6386 þ k pÞ ¼ 1;2772 þ k 2 p
ðk 2 ZÞ
b) Die gleichfrequenten Einzelschwingungen
1
1
p
1
p
x
und y 2 ¼ 3 cos
x
¼ 3 cos
x
y 1 ¼ 5 sin
2
2
3
2
6
ergeben bei ungestörter berlagerung eine gleichfrequente resultierende Schwingung in der Sinusform
1
+ cos
y ¼ y 1 þ y 2 ¼ A sin
x þj
ðmit A > 0Þ
2
Zunächst aber müssen wir die Kosinusschwingung y 2 in eine Sinusschwingung mit positiver Amplitude verwandeln. Dies geschieht besonders anschaulich mit Hilfe des Zeigerdiagramms (Bild A-19):
Drehwinkel:
240
¼
b
y 2 ¼ 3 cos
240°
4
p
3
1
p
x
2
6
3 · sin
¼ 3 sin
1
4
x þ
p
2
3
Auf die Berechnung der Amplitude A können wir verzichten, da
diese keinen Einfluss auf die Lage der Nullstellen hat.
3
30°
– 3 · cos
y2
Bild A-19
+ sin
22
A Funktionen und Kurven
Berechnung des Nullphasenwinkels j (! FS: Kap. III.7.7.3)
Mit A 1 ¼ 5; A 2 ¼ 3; j 1 ¼ 0
tan j ¼
und j 2 ¼ 240
folgt dann:
A 1 sin j 1 þ A 2 sin j 2
5 sin 0 þ 3 sin 240
¼
A 1 cos j 1 þ A 2 cos j 2
5 cos 0 þ 3 cos 240
¼
0 2;5981
¼ 0;7423
5 1;5
Aus dem Zeigerdiagramm entnehmen wir, dass der resultierende Zeiger
im 4. Quadranten liegt (siehe Bild A-20). Somit gilt:
tan j ¼ 0;7423
3
)
Bild A-20
j ¼ arctan ð 0;7423Þ ¼ 0;6386
y ¼ y 1 þ y 2 ¼ A sin
Resultierende Schwingung:
y1
5
f
1
x 0;6386
2
30°
A
y
y2
ðmit A > 0Þ
Die Nullstellen der Funktion sin u liegen bekanntlich an den Stellen u k ¼ k p mit k 2 Z. Somit besitzt die
resultierende Schwingung genau dort Nullstellen, wo ihr Argument u ¼ x = 2 0;6386 einen der Werte k p
annimmt:
1
x k 0;6386 ¼ k p
2
1
x k ¼ 0;6386 þ k p
2
)
)
x k ¼ 1;2772 þ k 2 p
ðmit k 2 ZÞ
Das Weg-Zeit-Gesetz einer periodischen Bewegung laute wie folgt:
A19
s ðtÞ ¼ 2 sin 2 t cos t ;
t 0
(s: Auslenkung; t : Zeit). Zu welchen Zeiten hat die Auslenkung den Wert s ¼ 2?
Uns interessieren also die positiven Lösungen der trigonometrischen Gleichung 2 sin 2 t cos t ¼ 2 : Umformung
mit Hilfe des „trigonometrischen Pythagoras“ sin 2 t þ cos 2 t ¼ 1 führt zu:
2 sin 2 t cos t ¼ 2
)
2 cos 2 t cos t ¼ 0
2 ð1 cos 2 tÞ cos t ¼ 2
)
)
2 2 cos 2 t cos t ¼ 2
cos t ð 2 cos t 1Þ ¼ 0
)
cos t ¼ 0
2 cos t 1 ¼ 0
Wir erhalten zwei einfache trigonometrische Gleichungen:
cos t ¼ 0
)
Lösungen sind die positiven Nullstellen des Kosinus : t 1 k ¼
2 cos t 1 ¼ 0
oder
cos t ¼ 0;5
p
þk p
2
) Die Lösungen dieser Gleichung entsprechen den Schnittpunk-
ten der Kosinuskurve mit der zur Zeitachse parallelen Geraden y ¼ 0;5 (Bild A-21):
y
2π – arccos (– 0,5)
arccos (– 0,5)
1
y = cos t
Bild A-21
π
A
–1
2π
B
y = – 0,5
Symmetrieachse
p = 2π
ðk 2 NÞ
3π
t
3 Trigonometrische Funktionen und Arkusfunktionen
23
Im Periodenintervall 0 t < 2 p gibt es genau zwei Lösungen (Punkte A und B). Die erste Lösung (Punkt A) erhalten wir aus der Gleichung cos t ¼ 0;5 durch Umkehrung: t ¼ arccos ( 0;5). Die zweite Lösung (Punkt B) liegt
bezüglich der eingezeichneten Symmetrieachse spiegelsymmetrisch zur ersten Lösung bei t ¼ 2 p arccos ( 0;5).
Wegen der Periodizität der Kosinusfunktion liegen weitere Lösungen rechts der Punkte A bzw. B im Abstand jeweils
ganzzahliger Vielfacher der Periode p ¼ 2 p. Damit ergeben sich insgesamt folgende Lösungen:
9
2
>
>
t 2 k ¼ arccos ð 0;5Þ þ k 2 p ¼
p þ k 2p
>
=
3
mit k 2 N
>
2
4
>
>
t 3 k ¼ ð2 p arccos ð 0;5ÞÞ þ k 2 p ¼ 2 p
p þ k 2p ¼
p þ k 2p ;
3
3
Lösungsmenge der Ausgangsgleichung:
t 1k ¼
A20
p
þ k p;
2
t 2k ¼
2
p þ k 2p;
3
t 3k ¼
4
p þ k 2p
3
ðk 2 NÞ
Bestimmen Sie auf elementarem Wege die Nullstellen und relativen Extremwerte der Funktion
pffiffiffi
y ¼ sin x þ 3 cos x .
Hinweis: Bringen Sie die Funktion zunächst auf die Sinusform y ¼ A sin ðx þ jÞ mit A > 0
und 0 j < 2 p .
Wir fassen die Funktionsgleichung als eine harmonische Schwingung auf, die durch ungestörte berlagerung zweier
gleichfrequenter Schwingungen entstanden ist (Periode: p ¼ 2 p ; Winkelgeschwindigkeit: w ¼ 1). Aus dem
Zeigerdiagramm können wir die „Amplitude“ A und den „Nullphasenwinkel“ j leicht berechnen“ (siehe Bild A-22):
pffiffiffi
+ cos
y 1 ¼ 1 sin x; y 2 ¼ 3 cos x; y ¼ y 1 þ y 2 ¼ A sin ðx þ jÞ
y2
Satz des Pythagoras (im grau unterlegten Dreieck):
pffiffiffi
pffiffiffi
A2 ¼ 12 þ ð 3Þ2 ¼ 1 þ 3 ¼ 4 ) A ¼ 4 ¼ 2
pffiffiffi
pffiffiffi
pffiffiffi
3
tan j ¼
¼ 3 ) j ¼ arctan 3 ¼ 60 ¼
b p=3
1
pffiffiffi
y ¼ y 1 þ y 2 ¼ sin x þ 3 cos x ¼ 2 sin ðx þ p = 3Þ
y
A
3
3
f
Bild A-22
+ sin
1
y1
Die Resultierende ist also eine um p = 3 nach links verschobene Sinuskurve mit der „Amplitude“ A ¼ 2 und der
Periode p ¼ 2 p (siehe Bild A-23). Die Lage der Nullstellen und relativen Extremwerte lässt sich unmittelbar ablesen
ðk 2 ZÞ:
Nullstellen:
x 1k ¼
Relative Maxima:
p
þk p
3
x 2k ¼
y
p
þ k 2p;
6
Max
Max
2
y 2k ¼ 2
Relative Minima:
x 3k ¼
7
p þ k 2p;
6
7·
–
y 3k ¼ 2
π
3
π
6
π
π
2·
3
6
5·
π
3
x
–2
Min
Bild A-23
p = 2π
Min
24
A Funktionen und Kurven
berlagerung gleichfrequenter Wechselspannungen
Wie groß ist der Scheitelwert u 0 und der Nullphasenwinkel j einer Wechselspannung, die durch
ungestörte berlagerung der gleichfrequenten Wechselspannungen
A21
u 1 ðtÞ ¼ 100 V sin ðw t p = 6Þ
und u 2 ðtÞ ¼ 200 V cos ðw t p = 4Þ
mit w ¼ 100 s 1 entsteht?
a) Zeichnerische Lösung im Zeigerdiagramm.
b) Rechnerische Lösung. Verwenden Sie den folgenden Lösungsansatz:
u ðtÞ ¼ u 1 ðtÞ þ u 2 ðtÞ ¼ u 0 sin ðw t þ jÞ
mit
u0 > 0
und 0 j < 2 p .
a) Zeigerdiagramm: Bild A-24
abgelesene Werte:
u2
+ cos
0
45°
u
V
20
246 V
j
22 ðim Bogenmaß: j
0,38Þ
u0
f
+ sin
30°
10
u0
0V
u1
Bild A-24
b) Die kosinusförmige Wechselspannung u 2 ðtÞ bringen wir zunächst mit Hilfe des Zeigerdiagramms (Bild A-24) auf
die Sinusform (Drehung des entsprechenden Sinuszeigers aus der unverschobenen Position um 45 ¼
b p = 4):
u 2 ðtÞ ¼ 200 V cos ðw t p = 4Þ ¼ 200 V sin ðw t þ p = 4Þ
Berechnung von Scheitelwert u 0 und Nullphasenwinkel j (! FS: Kap. III.7.7.3)
Somit gilt:
u 01 ¼ 100 V ;
u 02 ¼ 200 V ;
j1 ¼ p=6 ¼
b 30 ;
j2 ¼ p=4 ¼
b 45
u 20 ¼ u 201 þ u 202 þ 2 u 01 u 02 cos ðj 2 j 1 Þ ¼
¼ ð100 VÞ 2 þ ð200 VÞ 2 þ 2 ð100 VÞ ð200 VÞ cos ð45 þ 30 Þ ¼
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
75
¼ ð10 000 þ 40 000 þ 10 352;76Þ V 2 ¼ 60 352;76 V 2
tan j ¼
¼
)
u 0 ¼ 245;67 V
u 01 sin j 1 þ u 02 sin j 2
ð100 VÞ sin ð 30 Þ þ ð200 VÞ sin 45
¼
ð100 VÞ cos ð 30 Þ þ ð200 VÞ cos 45
u 01 cos j 1 þ u 02 cos j 2
¼
ð 50 þ 141;4214Þ V
91;4214
¼ 0;4009
¼
ð86;6025 þ 141;4214Þ V
228;0239
Da der gesuchte Nullphasenwinkel j im 1. Quadranten liegt (siehe Zeigerdiagramm, Bild A-24), gilt:
j ¼ arctan 0;4009 ¼ 21;85
Ergebnis:
¼
b 0;3813
u ðtÞ ¼ u 1 ðtÞ þ u 2 ðtÞ ¼ 245;67 V sin ðw t þ 0;3813Þ
ðmit w ¼ 100 s 1 Þ
3 Trigonometrische Funktionen und Arkusfunktionen
25
Superposition gedämpfter Schwingungen gleicher Frequenz
Die gedämpfte mechanische Schwingung mit der Funktionsgleichung
y ðtÞ ¼ 5 cm e 0;1 t = s ½ 2 sin ð2 s 1 tÞ þ 3 cos ð2 s 1 tÞ ;
A22
t 0s
kann als berlagerung zweier gleichfrequenter gedämpfter Schwingungen aufgefasst werden. Bringen
Sie diese Schwingung mit Hilfe des Zeigerdiagramms auf die folgende „Sinusform“:
y ðtÞ ¼ A e 0;1 t = s sin ð2 s 1 t þ jÞ
ðmit A > 0 und 0 j < 2 pÞ
Aus der Gleichung
5 cm e 0;1 t = s ½ 2 sin ð2 s 1 tÞ þ 3 cos ð2 s 1 tÞ ¼ A e 0;1 t = s sin ð2 s 1 t þ jÞ
folgt unmittelbar durch Kürzen der e-Funktion:
5 cm ½ 2 sin ð2 s 1 tÞ þ 3 cos ð2 s 1 tÞ ¼ 10 cm sin ð2 s 1 tÞ þ 15 cm cos ð2 s 1 tÞ ¼
¼ A sin ð2 s 1 t þ jÞ
Die beiden gleichfrequenten ungedämpften Einzelschwingungen
x 1 ðtÞ ¼ 10 cm sin ð2 s 1 tÞ
und x 2 ðtÞ ¼ 15 cm cos ð2 s 1 tÞ
können durch die resultierende Sinusschwingung
x ðtÞ ¼ x 1 ðtÞ þ x 2 ðtÞ ¼ A sin ð2 s 1 t þ jÞ
ersetzt werden, deren Amplitude A und Nullphasenwinkel j sich wie folgt aus dem Zeigerdiagramm berechnen
lassen (Bild A-25):
Satz des Pythagoras (im grau unterlegten Dreieck):
¼ ð10 cmÞ þ ð15 cmÞ ¼ ð100 þ 225Þ cm
pffiffiffiffiffiffiffiffi
A ¼ 325 cm ¼ 18;03 cm
A
2
2
tan j ¼
15 cm
¼ 1;5
10 cm
2
)
+ cos
2
¼ 325 cm
j ¼ arctan 1;5 ¼ 56;31
10 cm
2
x
x2
¼
b 0;983
A
15 cm
Somit gilt: x ðtÞ ¼ x 1 ðtÞ þ x 2 ðtÞ ¼ 18;03 cm sin ð2 s 1 t þ 0;983Þ
Bild A-25
15 cm
f
+ sin
10 cm
x1
Darstellung der gedämpften Schwingung in der Sinusform:
y ðtÞ ¼ e 0;1 t = s x ðtÞ ¼ e 0;1 t = s 18;03 cm sin ð2 s 1 t þ 0;983Þ ¼
¼ 18;03 cm e 0;1 t = s sin ð2 s 1 t þ 0;983Þ
ðt 0 sÞ
Zünd- und Löschspannung einer Glimmlampe
Eine Glimmlampe liegt an der Wechselspannung
A23
u ðtÞ ¼ 360 V sin ð100 p s 1 tÞ ;
t 0s
Sie beginnt zu leuchten, wenn die Zündspannung u Z ¼ 180 V erreicht wird und sie erlischt bei
Unterschreitung der Löschspannung u L ¼ 90 V. Wie lange leuchtet sie (bezogen auf eine Periode der
angelegten Wechselspannung)?
26
A Funktionen und Kurven
Wir führen folgende Bezeichnungen ein (siehe hierzu Bild A-26):
t 1:
Die Lampe beginnt zu dieser Zeit erstmals zu leuchten, d. h. u ðt 1 Þ ¼ 180 V
t 2:
Die Lampe erlischt erstmals, d. h. u ðt 2 Þ ¼ 90 V
t 3:
Die Lampe beginnt wieder zu leuchten, d. h. u ðt 3 Þ ¼ 180 V
t 4:
Die Lampe erlischt wieder, d. h. u ðt 4 Þ ¼ 90 V
t *:
Die Spannung an der Lampe erreicht erstmals den Wert 90 V, d. h. u ð t *Þ ¼ 90 V.
U /V
360
180
0,01
90
– 90
t3
t* t1
t4
t2
Bild A-26
0,02
t /s
– 180
– 360
Sie leuchtet also in den beiden (wegen der Symmetrie der Sinuskurve) gleichlangen Zeitintervallen t 1 t t 2 und
t 3 t t 4 , insgesamt also während der Zeit D t ¼ 2 ðt 2 t 1 Þ (innerhalb einer Periode der Wechselspannung).
Berechnung der Zeitpunkte t1 und t2
w ¼ 100 p s 1
Kreisfrequenz der Wechselspannung:
Periode (Schwingungsdauer) der Wechselspannung:
Zeitpunkt t 1 :
u ðt 1 Þ ¼ 180 V
)
T ¼
2p
2p
¼
¼ 0;02 s
w
100 p s 1
360 V sin ð100 p s 1 t 1 Þ ¼ 180 V j : 360 V
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
x
)
sin x ¼ 0;5
Durch Umkehrung und anschließende Rücksubstitution folgt:
x ¼ arcsin 0;5 ¼
Zeitpunkt t 2 :
p
6
)
u ðt 2 Þ ¼ 90 V
100 p s 1 t 1 ¼
)
p
6
)
t1 ¼
1
s ¼ 0;001 667 s
600
360 V sin ð100 p s 1 t 2 Þ ¼ 90 V j : 360 V
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
y
)
sin y ¼ 0;25
Beim Auflösen dieser Gleichung müssen wir beachten, dass die Löschspannung von 90 V erstmals bereits zum
früheren Zeitpunkt t * < t 1 erreicht wird (siehe Bild A-26). Diesen Zeitpunkt t * erhalten wir wie folgt durch
Umkehrung der Gleichung sin y * ¼ 0;25 und anschließender Rücksubstitution:
sin y * ¼ 0;25
)
y * ¼ arcsin 0;25 ¼ 0;252 68
)
100 p s 1 t * ¼ 0;252 68
)
t * ¼ 0;000 804 s
Aus Bild A-26 entnehmen wir dann für den gesuchten Zeitpunkt t 2 :
t 2 ¼ 0;01 s t * ¼ ð0;01 0;000 804Þ s ¼ 0;009 196 s
„Leuchtintervall“ D t == 2 (t 2 — t 1 ):
D t ¼ 2 ðt 2 t 1 Þ ¼ 2 ð0;009 196 0;001 667Þ s ¼ 0;015 058 s
Im Verhältnis zur Periode T der angelegten Wechselspannung:
Dt
0;015 058 s
¼
¼ 0;752 9
T
0;02 s
Die Glimmlampe leuchtet also während einer Periode zu rund 3 = 4 dieser Zeit.
75;3 %
3 Trigonometrische Funktionen und Arkusfunktionen
27
+ cos
a) Wie lauten die Gleichungen der in Bild A-27 durch Zeiger
y1
dargestellten gleichfrequenten zeitabhängigen Schwingungen
5
cm
(Kreisfrequenz: w; t 0 s)?
b) Bestimmen Sie zeichnerisch die durch ungestörte Super-
A24
45°
+ sin
15°
5 cm
position erzeugte resultierende Schwingung.
y2
c) Wie lautet die Gleichung der resultierenden Schwingung
Bild A-27
(elementare Berechnung ohne fertige Formeln).
Hinweis: Alle Schwingungen sind in der Sinusform mit positiver Amplitude anzugeben.
a) Zeiger y 1 :
A 1 ¼ 5 cm ;
j 1 ¼ 45
¼
b p=4
)
y 1 ¼ 5 cm sin ðw t þ p = 4Þ ;
Zeiger y 2 :
A 2 ¼ 5 cm ;
j 2 15
¼
b p = 12
)
y 2 ¼ 5 cm sin ðw t p = 12Þ ;
t 0s
t 0s
b) Zeigerdiagramm: siehe Bild A-28
+ cos
abgelesene Werte:
y1
cm
5
45°
A
8;7 cm
j
15
y
A
f
+ sin
15°
5 cm
y2
Bild A-28
c) Darstellung der resultierenden Schwingung in der Sinusform:
y ¼ y 1 þ y 2 ¼ A sin ðw t þ jÞ
ðmit A > 0 und t 0 sÞ
Das aus den Zeigern y 1 und y 2 aufgespannte Parallelogramm ist eine Raute (Rhombus) mit der Seitenlänge 5 cm
und Innenwinkeln von 60 und 120 (siehe Bild A-29). Da die Diagonalen einer Raute bekanntlich die Innenwinkel
halbieren, muss der gesuchte Phasenwinkel j ¼ 15 ¼
b p = 12 betragen. Die Berechnung der Amplitude A erfolgt
aus dem in Bild A-29 grau unterlegten gleichschenkligen Dreieck mit Hilfe des Kosinussatzes (! FS: Kap. I.6.7):
A 2 ¼ ð5 cmÞ 2 þ ð5 cmÞ 2 2 ð5 cmÞ ð5 cm Þ cos 120 ¼
pffiffiffiffiffi
¼ ð25 þ 25 þ 25Þ cm 2 ¼ 75 cm 2 ) A ¼ 75 cm ¼ 8;66 cm
5 cm
cm
120°
cm
5
y ¼ y 1 þ y 2 ¼ 8;66 cm sin ðw t þ p = 12Þ ;
5
60°
Ergebnis:
60°
A
t 0s
5 cm
120°
Bild A-29
Gegeben sind die gleichfrequenten Sinusschwingungen mit den Gleichungen
A25
y 1 ¼ 5 cm sin ð2 s 1 t þ p = 3Þ
und y 2 ¼ A 2 cos ð2 s 1 t þ 4 p = 3Þ
ðt 0 sÞ. Bestimmen Sie (zeichnerisch und rechnerisch) die Amplitude A 2 > 0 so, dass die durch
Superposition entstandene resultierende Schwingung zu einem unverschobenen Sinuszeiger mit positiver Amplitude A führt. Wie groß ist A?
28
A Funktionen und Kurven
Für die resultierende Schwingung gilt also ðj ¼ 0Þ:
y ¼ y 1 þ y 2 ¼ 5 cm sin ð2 s 1 t þ p = 3Þ þ A 2 cos ð2 s 1 t þ 4 p = 3Þ ¼ A sin ð2 s 1 tÞ
Zeigerdiagramm: siehe Bild A-30
abgelesene Werte:
+ cos
y1
A
A2
m
A2
5c
240°
60°
y
8;7 cm
+ sin
5c
m
A
30°
10 cm
A2
y2
Bild A-30
Berechnung der Amplituden A 2 und A
Aus dem Zeigerdiagramm entnehmen wir: die Zeiger y 1 und y 2 stehen senkrecht aufeinander, das Parallelogramm
ist somit ein Rechteck und wir können daher auf fertige Berechnungsformeln verzichten. Aus dem grau unterlegten
rechtwinkligen Dreieck folgt dann:
tan 60
¼
A2
5 cm
)
A 2 ¼ 5 cm tan 60
cos 60
¼
5 cm
A
)
A ¼
Resultierende Schwingung:
5 cm
cos 60
¼ 8;66 cm
¼ 10 cm
y ¼ y 1 þ y 2 ¼ 10 cm sin ð2 s 1 tÞ ;
t 0s
berlagerung sinusförmiger Wechselströme
Wie lauten die Funktionsgleichungen der in Bild A-31 dargestellten Wechselströme? Durch welche
Gleichung lässt sich der Gesamtstrom beschreiben, der durch ungestörte berlagerung der beiden
Einzelströme entsteht?
Hinweis: Sämtliche Ströme sind in der Sinusform i ðtÞ ¼ i 0 sin ðw t þ jÞ anzugeben mit i 0 > 0
und 0 j < 2 p .
A26
i /A
i1
6
i2
4
π
4
–4
–6
π
2
3π
4
π
5π
4
Bild A-31
t /s
3 Trigonometrische Funktionen und Arkusfunktionen
29
Wechselstrom i 1 (t) == i 01 sin (w 1 t + j 1 )
Scheitelwert: i 01 ¼ 6 A ; Nullphasenwinkel: j 1 ¼ 0 ; Schwingungsdauer: T 1 ¼ p s
Kreisfrequenz: w 1 ¼
2p
2p
¼ 2 s 1
¼
T1
ps
Somit gilt: i 1 ðtÞ ¼ i 01 sin ðw 1 t þ j 1 Þ ¼ 6 A sin ð2 s 1 tÞ ;
t 0s
Wechselstrom i 2 (t) == i 02 sin (w 2 t + j 2 )
Scheitelwert: i 02 ¼ 4 A ; Schwingungsdauer: T 2 ¼ p s ; Kreisfrequenz: w 2 ¼
2p
2p
¼ 2 s 1
¼
ps
T2
Die Sinuskurve
i 2 ðtÞ ¼ i 02 sin ðw 2 t þ j 2 Þ ¼ 4 A sin ð2 s 1 t þ j 2 Þ
ist auf der Zeitachse um t 0 ¼ p = 4 s nach rechts verschoben. Daraus lässt sich der Nullphasenwinkel j 2 wie folgt
bestimmen:
p
p
1
i 2 ðt 0 ¼ p = 4 sÞ ¼ 0 ) 4 A sin 2 s
s þ j 2 ¼ 4 A sin
þ j2 ¼ 0 j : 4 A )
4
2
p
p
p
þ j2 ¼ 0 )
þ j2 ¼ 0 ) j2 ¼
sin
2
2
2
|fflfflfflfflffl{zfflfflfflfflffl}
0
Somit gilt: i 2 ðtÞ ¼ 4 A sin ð2 s 1 t p = 2Þ ;
t 0s
berlagerung der Teilströme i 1 (t) und i 2 (t)
Da die Teilströme gleiche Schwingungsdauer und damit gleiche Kreisfrequenz haben ðw 1 ¼ w 2 ¼ 2 s 1 Þ, entsteht
bei der berlagerung ebenfalls ein Wechselstrom der Kreisfrequenz w ¼ 2 s 1 :
i ðtÞ ¼ i 1 ðtÞ þ i 2 ðtÞ ¼ 6 A sin ð2 s 1 tÞ þ 4 A sin ð2 s 1 t p = 2Þ ¼ i 0 sin ð2 s 1 t þ jÞ
Die Berechnung des Scheitelwertes i 0 und des Nullphasenwinkels j erfolgt anhand des Zeigerdiagramms (Bild A-32).
Die Zeiger der beiden Teilströme stehen aufeinander senkrecht, das Parallelogramm ist somit ein Rechteck. i 0 und j
lassen sich daher elementar wie folgt berechnen:
+ cos
Satz des Pythagoras (im grau unterlegten Dreieck):
pffiffiffiffiffi
i 20 ¼ ð4 AÞ 2 þ ð6 AÞ 2 ¼ 52 A 2 ; i 0 ¼ 52 A ¼ 7;211 A
4A
2
2
¼
tan a ¼
) a ¼ arctan
¼ 0;588
3
3
6A
Phasenwinkel:
Ergebnis:
6A
a
4A
i0
+ sin
4A
i
i2
j ¼ 2 p a ¼ 2 p 0;588 ¼ 5;695
i ðtÞ ¼ i 1 ðtÞ þ i 2 ðtÞ ¼ 7;211 A sin ð2 s 1 t þ 5;695Þ ;
i1
t 0s
6A
Bild A-32
Zentrifugalkraftregler
Bild A-33 zeigt den prinzipiellen Aufbau eines Zentrifugalkraftreglers. An den (als masselos angenommenen) Armen der Länge 2a hängt jeweils eine punktförmige Masse m, die mit der Winkelgeschwin-
A27
digkeit w um die eingezeichnete Drehachse rotiert. Zwischen dem Winkel j, unter dem sich infolge
der Zentrifugalkräfte die Arme gegenüber der Achse einstellen, und der Winkelgeschwindigkeit w besteht dabei der folgende Zusammenhang:
cos j ¼
g
2aw2
ðg : ErdbeschleunigungÞ
30
A Funktionen und Kurven
a) Zeigen Sie, dass zum Abheben der Arme eine Mindestwinkelgeschwindigkeit w 0 nötig ist.
b) Skizzieren Sie die Abhängigkeit des Winkels j von der Winkelgeschwindigkeit w. Welcher maximale Winkel j max ist möglich?
Drehachse
v
a
ff
~:
G
Gewichtskraft der Masse m
~Z :
F
Zentrifugalkraft (nach außen gerichtet)
~r :
F
Resultierende Kraft
a
a
a
a
a
m
m
r
FZ
f
r
Fr
Bild A-33
G
a) Der kleinstmögliche Winkel ist j ¼ 0 . Zu ihm gehört der Mindestwert w 0 der Winkelgeschwindigkeit:
rffiffiffiffiffiffiffi
g
g
g
g
2
)
w
cos 0 ¼
)
1
¼
)
w
¼
¼
0
0
|fflffl{zfflffl}
2 a w 20
2 a w 20
2a
2a
1
b) Wir lösen die Gleichung cos j ¼
g
nach j auf und erhalten die gesuchte Beziehung zwischen j und w
2aw2
in Form einer Arkusfunktion:
2
2
g
g=2a
w0
w0
;
¼
arccos
¼
arccos
¼
arccos
j ¼ arccos
w2
w
2aw2
w2
w w0
Kurvenverlauf: siehe Bild A-34
Wertetabelle: Wir setzen x ¼ w = w 0 und berechnen einige Werte der Funktion
2
w0
1
¼ arccos ð1 = x 2 Þ ; x 1
¼ arccos
j ¼ arccos
ðw = w 0 Þ 2
w
x
1
1;2
1;4
1;6
1;8
2
2;5
j
x
j
0
46
59;3
67;0
72;0
75;5
80;8
3
4
5
6
7
10
83;6
86;4
87;7
88;4
88;8
89;4
f
90°
60°
30°
1
2
3
4
5
6
7
v /v 0
Bild A-34
Der größtmögliche Winkel ist j max ¼ 90 (waagerechte Arme!), er wird bei unendlich hoher Winkelgeschwindigkeit erreicht (w ! 1 und somit auch x ! 1):
2
w0
¼ lim arccos ð1 = x 2 Þ ¼ arccos 0 ¼ 90
j max ¼ lim arccos
w!1
x!1
w
4 Exponential- und Logarithmusfunktionen
31
4 Exponential- und Logarithmusfunktionen
Lehrbuch: Band 1, Kapitel III.11 und 12
Formelsammlung: Kapitel III.9 und 10
Zeigen Sie: Die Funktion y ¼ 3 2 3 x þ 1 5 3 x 1 ;
A28
1 < x < 1 ist umkehrbar. Wie lautet die
Umkehrfunktion?
Zunächst bringen wir die Funktion auf eine „günstigere“ Form:
6
y ¼ 3 2 3xþ1 5 3x1 ¼ 3 2 3x 2 1 5 3x 5 1 ¼ 3 2 5 1 2 3x 5 3x ¼
ð2 5Þ 3 x ¼ 1;2 10 3 x
|fflffl{zfflffl}
|fflffl{zfflffl}
|fflfflfflfflffl{zfflfflfflfflffl}
5
2 3x 2 1
5 3x 5 1
ð2 5Þ 3 x
a mþn ¼ a m a n ;
Rechenregeln:
a n b n ¼ ða bÞ n
Es handelt sich also um eine streng monoton wachsende Exponentialfunktion, die bekanntlich umkehrbar ist. Wir lösen
die Funktionsgleichung nun nach x auf, indem wir beide Seiten logarithmieren (Zehnerlogarithmus verwenden):
y ¼ 1;2 10 3 x j lg
)
lg y ¼ lg ð1;2 10 3 x Þ ¼ lg 1;2 þ lg 10 3 x ¼ lg 1;2 þ 3 x lg 10 ¼ lg 1;2 þ 3 x 1 ¼ lg 1;2 þ 3 x
3 x ¼ lg y lg 1;2 j : 3
)
1
1
1
lg y
lg 1;2 ¼
lg y 0;0264
3
3
3
x ¼
lg ða bÞ ¼ lg a þ lg b ;
Rechenregeln:
)
lg a n ¼ n lg a ;
lg 10 ¼ 1
Durch Vertauschen der beiden Variablen erhalten wir schließlich die gesuchte Umkehrfunktion:
y ¼
1
lg x 0;0264 ;
3
x > 0
Aufladen eines Kondensators
Beim Aufladen eines Kondensators steigt die Kondensatorspannung u im Laufe der Zeit t nach dem
Exponentialgesetz
A29
u ðtÞ ¼ 100 V ð1 e t = t Þ ;
t 0s
ðt > 0: Zeitkonstante, noch unbekanntÞ.
a) Bestimmen Sie die Zeitkonstante t aus dem Messwert u ðt ¼ 2 sÞ ¼ 80 V:
b) Welchen Endwert u E erreicht die am Kondensator liegende Spannung? Nach welcher Zeit wird der
halbe Endwert erreicht? Skizzieren Sie den Spannungsverlauf am Kondensator.
c) Berechnen Sie die Kondensatorspannung zum Zeitpunkt t ¼ 5 s:
a) u ðt ¼ 2 sÞ ¼ 80 V
0;2 ¼ e 2 s = t j ln
Rechenregel:
)
)
ln e n ¼ n
100 V ð1 e 2 s = t Þ ¼ 80 V j : 100 V
ln 0;2 ¼ ln e 2 s = t ¼
2s
t
)
t ¼
)
1 e 2 s = t ¼ 0;8
2 s
¼ 1;242 67 s
ln 0;2
)
32
A Funktionen und Kurven
b) Der Endwert u E wird erst nach unendlich langer Zeit, d. h. für t ! 1 erreicht. Er beträgt:
u E ¼ lim u ðtÞ ¼ lim 100 V ð1 e t = 1;242 67 s Þ ¼ 100 V
t!1
t!1
(die streng monoton fallende e-Funktion verschwindet für t ! 1). Der halbe Endwert, also u ¼ 50 V, wird zum
Zeitpunkt t ¼ T erreicht:
u ðt ¼ TÞ ¼ 50 V
)
0;5 ¼ e T = 1;242 67 s j ln
100 V ð1 e T = 1;242 67 s Þ ¼ 50 V j : 100 V
ln 0;5 ¼ ln e T = 1;242 67 s ¼
)
1 e T = 1;242 67 s ¼ 0;5
)
T
1;242 67 s
)
)
T ¼ ð 1;242 67 sÞ ln 0;5 ¼ 0;8614 s
Rechenregel:
ln e n ¼ n
Spannungsverlauf: siehe Bild A-35
u /V
u ðtÞ ¼ 100 V ð1 e t = 1;242 67 s Þ ¼
¼ 100 V ð1 e 0;804 72 s
1
t
100
80
Þ
60
ðfür t 0 sÞ
40
c) u ðt ¼ 5 sÞ ¼ 100 V ð1 e 0;804 72 s
1
5s
20
Þ ¼
¼ 100 V ð1 e 4;023 60 Þ ¼ 98;21 V
1
2
3
4
5
6
7
t /s
Bild A-35
Abkühlungsgesetz von Newton
Ein Körper besitzt im Zeitpunkt t ¼ 0 die Temperatur T 0 ¼ 30 C und wird dann durch einen Luftstrom der konstanten Temperatur T L ¼ 20 C gekühlt, wobei für den Temperaturverlauf
T ðtÞ ¼ ðT 0 T L Þ e k t þ T L ;
A30
t 0 min
gilt ðT ðtÞ: Körpertemperatur zum Zeitpunkt t; k > 0: Konstante).
a) Nach 5 min beträgt die Körpertemperatur 28 C. Bestimmen Sie aus diesem Messwert die
Konstante k.
b) Welche Temperatur besitzt der Körper nach 60 min?
c) Wann ist der Abkühlungsprozess beendet, welche Temperatur T E besitzt dann der Körper?
Skizzieren Sie den Temperaturverlauf.
Das Abkühlungsgesetz lautet für die vorgegebenen Werte wie folgt:
T ðtÞ ¼ ð30 C 20 CÞ e k t þ 20 C ¼ 10 C e k t þ 20 C ;
a) T ðt ¼ 5 minÞ ¼ 28 C
)
10 C e ð5 minÞ k þ 20 C ¼ 28 C
ln e ð5 minÞ k ¼ ð5 minÞ k ¼ ln 0;8
Rechenregel:
ln e n ¼ n
t 0 min
)
)
10 C e ð 5 minÞ k ¼ 8 C j : 10 C
k ¼
ln 0;8
¼ 0;044 63 min 1
5 min
)
e ð5 minÞ k ¼ 0;8 j ln
)
4 Exponential- und Logarithmusfunktionen
b) T ðtÞ ¼ 10 C e 0;044 63 min
1
t
33
þ 20 C ;
T ðt ¼ 60 minÞ ¼ 10 C e 0;044 63 min
1
t 0 min
60 min
þ 20 C ¼
¼ 10 C e 2;677 8 þ 20 C ¼ 0;687 C þ 20 C ¼ 20;687 C
c) Der Abkühlungsprozess ist (theoretisch) erst nach unendlich langer Zeit beendet ðt ! 1Þ. Der Körper hat dann
die Temperatur der Luft angenommen:
T E ¼ lim T ðtÞ ¼ lim ½ 10 C e 0;044 63 min
t!1
1
t!1
t
þ 20 C ¼ 20 C ¼ T L
(die streng monoton fallende e-Funktion verschwindet für t ! 1)
Aus physikalischer Sicht: Der Abkühlungsprozess ist beendet,
wenn (auf Grund gleicher Temperaturen) kein Wärmeaustausch
mehr stattfindet (Körpertemperatur ¼ Lufttemperatur).
T /°C
30
Temperaturverlauf: siehe Bild A-36
T ðtÞ ¼ 10 C e
0;044 63 min 1 t
25
20
þ 20 C
15
(für t 0 min)
10
5
Bild A-36
10
20
30
40
50
60
t /min
Fallschirmspringer
Beim Fallschirmspringen gilt unter der Annahme, dass der Luftwiderstand R der Fallgeschwindigkeit
v proportional ist ðR
v ðtÞ ¼
A31
v , d. h. R ¼ c vÞ, das folgende Geschwindigkeit-Zeit-Gesetz:
mg
ð1 e ðc = mÞ t Þ ;
c
t 0
(m: Masse des Fallschirmspringers incl. Fallschirm; g: Erdbeschleunigung; c > 0: Reibungsfaktor,
abhängig von den äußeren Umweltbedingungen).
a) Welche Endgeschwindigkeit v E erreicht der Fallschirmspringer?
Annahme: Der Sprung erfolgt aus großer Höhe, der Fallschirmspringer ist also lange unterwegs.
b) Skizzieren Sie das Geschwindigkeit-Zeit-Gesetz.
c) Nach welcher Zeit t wird die halbe Endgeschwindigkeit erreicht?
Wir setzen im Exponenten c = m ¼ a und beachten dabei, dass a > 0 ist:
v ðtÞ ¼
mg
mg
ð1 e ðc = mÞ t Þ ¼
ð1 e a t Þ ;
c
c
t 0
a) Die streng monoton fallende e-Funktion besitzt für große Fallzeiten vernachlässigbar kleine Werte. Bei (theoretisch)
unendlich langer Fallzeit ðt ! 1Þ erreicht der Fallschirmspringer folgende Endgeschwindigkeit:
v E ¼ lim v ðtÞ ¼ lim
t!1
t!1
mg
mg
ð1 e a t Þ ¼
c
c
Dieses Ergebnis ist physikalisch gesehen einleuchtend: Die Endgeschwindigkeit v E wird erreicht, wenn der Fallschirmspringer kräftefrei fällt. Dies aber ist genau dann der Fall, wenn Gewicht G ¼ m g und der entgegen wirkende Luftwiderstand R ¼ c v sich gerade kompensieren:
G ¼ R
)
mg ¼ cvE
)
vE ¼ mg=c
34
A Funktionen und Kurven
b) Geschwindigkeit-Zeit-Gesetz in „neuer Schreibweise“
(siehe Bild A-37):
v ðtÞ ¼ v E ð1 e a t Þ ;
v
t 0
vE
ðmit v E ¼ m g = c und a ¼ c = mÞ
1
v
2 E
1
1
vE )
v E ) v E ð1 e a t Þ ¼
2
2
1
1
1 e at ¼
) e at ¼
j ln )
2
2
1
ln 2
m
ln e a t ¼ a t ¼ ln
¼ ln 1 ln 2 ¼ ln 2 ) t ¼
¼ ðln 2Þ
a
c
2
a
¼ ln a ln b ; ln 1 ¼ 0
Rechenregeln: ln e n ¼ n ; ln
b
c) v ðt ¼ tÞ ¼
Gaußsche Glockenkurve:
A32
y ¼ a e b ðx cÞ ;
2
t
t
Bild A-37
1 < x < 1
Bestimmen Sie die Kurvenparameter a > 0; b > 0 und c so, dass das Maximum an der Stelle
x ¼ 10 angenommen wird und die Punkte A ¼ ð5 ; 8Þ und B ¼ ð12 ; 10Þ auf der Kurve liegen.
Skizzieren Sie den Kurvenverlauf.
Das Maximum wird an der Stelle x ¼ c angenommen ðx ¼ c ist Symmetrieachse, die Kurve fällt auf beiden Seiten
gleichmäßig streng monoton gegen Null abÞ. Somit ist c ¼ 10.
Berechnung der Kurvenparameter a und b
A ¼ ð5 ; 8Þ
)
y ðx ¼ 5Þ ¼ 8
)
ðIÞ
a e b ð5 10Þ ¼ a e 25 b ¼ 8
B ¼ ð12 ; 10Þ
)
y ðx ¼ 12Þ ¼ 10
)
ðIIÞ
a e b ð12 10Þ ¼ a e 4 b ¼ 10
2
2
Wir dividieren Gleichung (I) durch Gleichung (II) (linke Seite durch linke Seite, rechte Seite durch rechte Seite), dabei
kürzt sich der Faktor a heraus:
a e 25 b
8
¼ e ð 25 b þ 4 bÞ ¼
10
a e 4b
21 b ¼ ln 0;8
Rechenregeln:
)
b ¼
)
e 21 b ¼ 0;8 j ln
)
ln e 21 b ¼ ln 0;8
)
ln 0;8
¼ 0;010 626
21
em
¼ e mn ;
en
ln e n ¼ n
Diesen Wert setzen wir für b in Gleichung (II) ein:
ðIIÞ
)
a e 4 0;010 626 ¼ a e 0;042 504 ¼ a 0;958 387 ¼ 10
)
a ¼ 10;4342
Gaußsche Glockenkurve:
y ¼ 10;4342 e 0;010 626 ðx 10Þ
y
2
(für 1 < x < 1Þ
10
8
Kurvenverlauf: siehe Bild A-38
Max B
A
5
Bild A-38
–5
5
10 12
15
20
25
x
4 Exponential- und Logarithmusfunktionen
35
Barometrische Höhenformel
Zwischen dem Luftdruck p und der Höhe h (gemessen gegenüber dem Meeresniveau) gilt unter der
Annahme konstanter Lufttemperatur der folgende Zusammenhang:
A33
p ðhÞ ¼ p 0 e h = a ;
h 0 ðin mÞ
ðp 0 ¼ 1;013 bar : Luftdruck an der Erdoberfläche; a ¼ 7991 mÞ.
a) Geben Sie die Höhe als Funktion des Luftdruckes an und skizzieren Sie den Funktionsverlauf.
b) In welcher Höhe hat sich der Luftdruck halbiert?
c) Wie groß ist der Luftdruck in 10 km Höhe?
a) Gleichung zunächst geringfügig umformen, dann logarithmieren:
p
p
h
h=a
h = a
¼ ln e h = a ¼
p ¼ p0 e
)
¼ e
: p0
ln ) ln
p0
p0
a
p
p0
¼ a ð ln p ln p 0 Þ ¼ a ð ln p 0 ln pÞ ¼ a ln
h ¼ a ln
p0
p
a
¼ ln a ln b
Rechenregeln: ln e n ¼ n ; ln
h /km
b
Ergebnis:
h ð pÞ ¼ a ln
p0
p
20
1;013 bar
¼ 7991 m ln
p
10
ðf ür 0 < p p 0 Þ
5,54
Kurvenverlauf: siehe Bild A-39
b) h ð p ¼ p 0 = 2Þ ¼ a ln
)
Bild A-39
!
p0
p0 =2
¼ a ln
0,290 0,507
1
1=2
1,013
¼ a ln 2 ¼ ð7991 mÞ ln 2 ¼ 5538;9 m
p /bar
5;54 km
c) p ðh ¼ 10 000 mÞ ¼ 1;013 bar e 10 000 m = 7991 m ¼ 1;013 bar e 1;251 408 ¼ 0;290 bar
Aperiodischer Grenzfall einer Schwingung
Die Bewegung eines stark gedämpften Federpendels lässt sich im sog. aperiodischen Grenzfall durch
das Weg-Zeit-Gesetz
A34
s ðtÞ ¼ ðA þ B tÞ e l t ;
t 0
beschreiben (s: Auslenkung in cm; t : Zeit in s). Es liegen drei Messwertpaare vor:
t=s
0
0,5
10
s = cm
3
0,0
0,3
Bestimmen Sie die drei Kurvenparameter A; B und l und skizzieren Sie den „Schwingungsverlauf“.
Wir führen die Zwischenrechnungen ohne Einheiten durch.
s ðt ¼ 0Þ ¼ 3
)
ðA þ 0Þ e 0 ¼ A 1 ¼ 3
s ðt ¼ 0;5Þ ¼ 0
)
ðA þ 0;5 BÞ e 0;5 l ¼ ð3 þ 0;5 BÞ e 0;5 l ¼ 0
|fflffl{zfflffl}
6¼ 0
)
A ¼ 3
)
3 þ 0;5 B ¼ 0
)
B ¼ 6
36
A Funktionen und Kurven
s ðtÞ ¼ ð3 6 tÞ e l t
Zwischenergebnis:
Die noch fehlende Konstante l bestimmen wir aus dem Messwert s ðt ¼ 10Þ ¼ 0;3:
1
10 l
10 l
10 l
ð3 60Þ e
¼ 57 e
¼ 0;3 : ð 57Þ ) e
¼
ln )
190
1
ln 190
¼ ln 1 ln 190 ¼ ln 190 ) l ¼
¼ 0;524 702
ln e 10 l ¼ 10 l ¼ ln
190
10
Rechenregeln:
Ergebnis:
ln e
n
¼ n;
A ¼ 3 cm ;
a
¼ ln a ln b ;
ln
b
ln 1 ¼ 0
B ¼ 6 cm s 1 ;
s /cm
l ¼ 0;524 702 s 1
3
s ðtÞ ¼ ð3 cm 6 cm s 1 tÞ e 0;524 702 s
1
t
2
1
8
Kurvenverlauf: siehe Bild A-40
–1
0,5 2
4
10
t /s
6
–2
–3
Bild A-40
Elektrischer Schwingkreis
In einem stark gedämpften elektrischen Schwingkreis fließt ein Strom, dessen Stärke i dem exponentiellen Zeitgesetz
A35
i ðtÞ ¼ a e 2 t þ b e 6 t ;
t 0
genügt (aperiodische Schwingung; i in A, t in s). Gemessen wurden die Werte i ðt ¼ 0Þ ¼ 2 und
i ðt ¼ 2Þ ¼ 0;1. Berechnen Sie die Parameter a und b und skizzieren Sie den zeitlichen Verlauf
der Stromstärke i. Gibt es einen Zeitpunkt, in dem der Schwingkreis stromlos ist?
i ðt ¼ 0Þ ¼ 2
)
ðIÞ
a e0 þ b e0 ¼ a 1 þ b 1 ¼ a þ b ¼ 2
i ðt ¼ 2Þ ¼ 0;1
)
ðIIÞ
a e 4 þ b e 12 ¼ 0;1
)
b ¼ 2a
Gleichung (I) in Gleichung (II) einsetzen:
ðIIÞ
)
a e 4 þ ð2 aÞ e 12 ¼ a e 4 þ 2 e 12 a e 12 ¼
¼ a ðe 4 e 12 Þ þ 2 e 12 ¼ 0;1
ðIÞ
Ergebnis:
)
a ðe 4 e 12 Þ ¼ 0;1 2 e 12
)
b ¼ 2 a ¼ 2 þ 5;4623 ¼ 7;4623
i ðtÞ ¼ 5;4623 e 2 t þ 7;4623 e 6 t ;
)
a ¼
t 0
0;1 2 e 12
¼ 5;4623
e 4 e 12
4 Exponential- und Logarithmusfunktionen
37
Stromloser Zustand, wenn i ðtÞ ¼ 0:
5;4623 e 2 t þ 7;4623 e 6 t ¼ 0
)
5;4623 e 2 t e 6 t ¼ 7;4623 e 6 t e 6 t
e 4 t ¼ 1;366 146 j ln
Rechenregeln:
)
e a e b ¼ e aþb ;
5;4623 e 2 t ¼ 7;4623 e 6 t j e 6 t
)
5;4623 e 4 t ¼ 7;4623 e 0 ¼ 7;4623 j : 5;4623
ln e 4 t ¼ 4 t ¼ ln 1;366 146
ln e n ¼ n ;
)
)
t ¼
)
ln 1;366 146
¼ 0;078
4
e 0 ¼ e 0 ¼ 1
Der Schwingkreis ist zum Zeitpunkt t ¼ 0;078 s ¼ 78 ms stromlos. Der zeitliche Verlauf der Stromstärke i ist in
Bild A-41 dargestellt.
i /A
2
1
0,078
1,5
0,5
2
Bild A-41
t /s
1
–1
–2
Adiabatische Zustandsgleichung eines idealen Gases
Bei einer adiabatischen Zustandsänderung des idealen Gases besteht zwischen den beiden Zustandsvariablen p (Druck) und T (absolute Temperatur) der folgende Zusammenhang:
A36
p
p1
k 1
¼
T
T1
k
ðk: Stoffkonstante, Verhältnis der Molwärmen c p und c v ;
p 1 : Druck bei der Temperatur T 1 Þ.
Wie lässt sich die Stoffkonstante k aus Druck und Temperatur bestimmen?
Wir lösen die Zustandsgleichung durch Logarithmieren wie folgt nach k auf:
k 1 k
k 1
k
p
T
p
T
p
T
¼ k ln
)
¼
) ln
¼ ln
) ðk 1Þ ln
p1
T1
p1
T1
p1
T1
p
p
T
p
T
p
k ln
ln
¼ k ln
) k ln
k ln
¼ ln
)
p1
p1
T1
p1
T1
p1
p
p
p
ln
ln
ln
p
p
p
1
1
1
p
T
p
k ln
ln
¼ ln
) k ¼
¼
¼
p1
T1
p1
p
T
p=p1
pT 1
ln
ln
ln
ln
T =T 1
p1T
p1
T1
a
Rechenregeln: ln a n ¼ n ln a ; ln a ln b ¼ ln
b
38
A Funktionen und Kurven
5 Hyperbel- und Areafunktionen
Lehrbuch: Band 1, Kapitel III.13
Formelsammlung: Kapitel III.11 und 12
A37
Zeigen Sie: Für jedes reelle x gilt
Unter Verwendung der Definitionsformeln
cosh 2 x sinh 2 x ¼
Rechenregeln:
cosh 2 x sinh 2 x ¼ 1
cosh x ¼
1 x
ðe þ e x Þ
2
und
(„hyperbolischer Pythagoras“).
sinh x ¼
1 x
ðe e x Þ
2
erhalten wir:
1 x
1 x
1
ðe þ e x Þ 2
ðe e x Þ 2 ¼
½ ðe x þ e x Þ 2 ðe x e x Þ 2 ¼
4
4
4
¼
1
½ e 2 x þ 2 e 0 þ e 2 x ðe 2 x 2 e 0 þ e 2 x Þ ¼
4
¼
1 2x
1
ðe þ 2 þ e 2 x e 2 x þ 2 e 2 x Þ ¼
4 ¼ 1
4
4
ðe a Þ n ¼ e n a ;
e a e b ¼ e aþb ;
e0 ¼ 1
Beweisen Sie das sogenannte Additionstheorem für den Sinus hyperbolicus:
A38
sinh ðx þ yÞ ¼ sinh x cosh y þ cosh x sinh y
1 x
1 x
ðe þ e x Þ und sinh x ¼
ðe e x Þ lässt sich die rechte Seite
2
2
der Gleichung schrittweise wie folgt umgestalten:
Mit Hilfe der Definitionsformeln cosh x ¼
sinh x cosh y þ cosh x sinh y ¼
1 x
1 y
1 x
1 y
ðe e x Þ
ðe þ e y Þ þ
ðe þ e x Þ
ðe e y Þ ¼
2
2
2
2
1
x
x
y
y
x
x
y
y
ðe e Þ ðe þ e Þ þ ðe þ e Þ ðe e Þ ¼
¼
4
¼
¼
1 x
ðe e y e x e y þ e x e y e x e y þ e x e y þ e x e y e x e y e x e y Þ ¼
4
¼
1 xþy
e x þ y þ e x y e x y þ e x þ y þ e x þ y e x y e x yÞ ¼
ðe
4
¼
1
1 xþy
1 xþy
e x yÞ ¼
e ðx þ yÞ Þ
ð2 e x þ y 2 e x y Þ ¼
ðe
ðe
4
2
2
Rechenregel:
e a e b ¼ e aþb
Der letzte Ausdruck ist definitionsgemäß der Sinus hyperbolicus von u ¼ x þ y :
1 xþy
1 u
ðe
ðe e u Þ ¼ sinh u ¼ sinh ðx þ yÞ
e ðx þ yÞ Þ ¼
2
2
Damit ist das Additionstheorem bewiesen.
5 Hyperbel- und Areafunktionen
A39
39
Beweisen Sie die Formel cosh 2 x ¼
1
½ cosh ð2 xÞ þ 1 :
2
Wir ersetzen auf der linken Seite der Gleichung cosh x mit Hilfe der Definitionsformel cosh x ¼
1 x
ðe þ e x Þ und
2
erhalten nach einigen Umformungen genau den Ausdruck auf der rechten Seite der Gleichung:
cosh x ¼
2
¼
1 x
1 2x
1 2x
ðe þ e x Þ 2 ¼
ðe þ 2 e 0 þ e 2 x Þ ¼
ðe þ 2 þ e 2 x Þ ¼
4
4
4
¼
1
1 2x
1
1 1 2x
1
½ ðe 2 x þ e 2 x Þ þ 2 ¼
ðe þ e 2 x Þ þ
¼
ðe þ e 2 x Þ þ
¼
4
4
2
2 |fflfflfflfflfflfflfflfflfflfflfflffl
2
2
ffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
cosh ð2 xÞ
¼
1
1
1
cosh ð2 xÞ þ
¼
½ cosh ð2 xÞ þ 1
2
2
2
e a e b ¼ e aþb ;
ðe a Þn ¼ e n a ;
Rechenregeln:
2
1 x
ðe þ e x Þ
2
e0 ¼ 1
2 cosh ð2 xÞ þ 3 sinh ð2 xÞ ¼ 3
A40
Lösen Sie diese Gleichung unter Verwendung der Definitionsformeln der Hyperbelfunktionen.
Substitution:
u ¼ 2x
Mit
)
2 cosh ð2 xÞ þ 3 sinh ð2 xÞ ¼ 2 cosh u þ 3 sinh u ¼ 3
e u e u
folgt:
2
e u þ e u
e u e u
2 cosh u þ 3 sinh u ¼ 2
þ3
¼ e u þ e u þ 1;5 ðe u e u Þ ¼
2
2
cosh u ¼
e þe
2
u
u
und
sinh u ¼
¼ e u þ e u þ 1;5 e u 1;5 e u ¼ 2;5 e u 0;5 e u ¼ 3
Wir multiplizieren beide Seiten mit e u :
ð2;5 e u 0;5 e u Þ e u ¼ 2;5 e u e u 0;5 e u e u ¼ 2;5 ðe u Þ 2 0;5 ¼ 3 e u
|fflfflfflfflffl{zfflfflfflfflffl}
e uþu ¼ e 0 ¼ 1
Mit der Substitution z ¼ e u erhalten wir schließlich eine quadratische Gleichung:
2;5 z 2 0;5 ¼ 3 z ) 2;5 z 2 3 z 0;5 ¼ 0 j : 2;5 )
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
z 1 = 2 ¼ 0;6 0;36 þ 0;2 ¼ 0;6 0;56 ¼ 0;6 0;7483
Rücksubstitution:
e 2 x ¼ z 2 ¼ 0;1483
Lösung:
)
z 1 ¼ 1;3483 ;
)
z 2 ¼ 0;1483
z ¼ e u ¼ e 2x
e 2 x ¼ z 1 ¼ 1;3483 j ln
Rechenregel:
z 2 1;2 z 0;2 ¼ 0
ln e n ¼ n
x 1 ¼ 0;1494
)
)
ln e 2 x ¼ 2 x ¼ ln 1;3483
nicht lösbar; da stets
e 2x > 0
)
ist
x1 ¼
ln 1;3483
¼ 0;1494
2
40
A Funktionen und Kurven
berlandleitung (Kettenlinie)
Die in Bild A-42 skizzierte berlandleitung wird zwi-
y /m
schen zwei aufeinander folgenden Strommasten durch die
30
Kettenlinie
A41
y ðxÞ ¼ 1000 m cosh ð0;001 m 1 xÞ 980 m
20
Strommast
mit 150 x = m 150 beschrieben. Berechnen Sie
Leitung
Strommast
10
die Höhe der Strommasten sowie den Durchhang H in
der Mitte der Leitung.
– 150
– 50
50
150
x /m
Bild A-42
Höhe der Strommasten:
y ðx ¼ 150 mÞ ¼ 1000 m cosh ð0;001 m 1 150 mÞ 980 m ¼ ð1000 cosh 0;15 980Þ m ¼ 31;27 m
Höhe in der Mitte der Leitung
(x == 0 m):
y ðx ¼ 0 mÞ ¼ 1000 m cosh 0 980 m ¼ 1000 m 1 980 m ¼ 20 m
Durchhang:
H ¼ y ðx ¼ 150 mÞ y ðx ¼ 0 mÞ ¼ 31;27 m 20 m ¼ 11;27 m
Die Hyperbelfunktion y ¼ sinh x setzt sich definitionsgemäß aus Exponentialfunktionen wie folgt
zusammen:
A42
y ¼ sinh x ¼
1 x
ðe e x Þ ;
2
1 < x < 1
Zeigen Sie, dass sich ihre Umkehrfunktion y ¼ arsinh x durch eine logarithmische Funktion darstellen
lässt.
Wir multiplizieren die Funktionsgleichung beiderseits mit 2 e x , führen dann die Substitution u ¼ e x durch und
lösen die erhaltene quadratische Gleichung:
y ¼
1 x
ðe e x Þ j 2 e x
2
)
|{z}
u
2yu ¼ u 1
2
)
1
ðe x e x Þ 2 e x ¼ e x e x e 0 ¼ ðe x Þ 2 1
|{z}
2
u
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
) u 1=2 ¼ y y 2 þ 1
2y ex ¼
u 2yu 1 ¼ 0
2
)
Daffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
wegen u ¼ e x > 0 nur positive Lösungen in Frage kommen, scheidet u 2 < 0 als Lösung aus (beachte:
p
y 2 þ 1 > j y j für y 6¼ 0). Somit gilt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u ¼ ex ¼ y þ y2 þ 1
Diese Gleichung lösen wir durch Logarithmieren nach x auf:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ln e x ¼ x ¼ ln ðy þ y 2 þ 1 Þ
Rechenregeln:
e a e b ¼ e aþb ;
e0 ¼ 1;
ln e n ¼ n
Durch Vertauschen der beiden Variablen erhalten wir die Umkehrfunktion von y ¼ sinh x; also die Funktion
y ¼ arsinh x; in der gewünschten logarithmischen Darstellungsform:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ arsinh x ¼ ln ðx þ x 2 þ 1 Þ ; 1 < x < 1
5 Hyperbel- und Areafunktionen
A43
41
Zeige: Die Funktion y ¼
1
ln
2
1þx
;
1x
jxj < 1
ist die Umkehrfunktion von y ¼ tanh x:
Wenn diese Aussage zutrifft, muss die logarithmische Funktion identisch sein mit der Areafunktion y ¼ artanh x: Es
genügt daher zu zeigen, dass die Umkehrung der logaritmischen Funktion auf den Tangens hyperbolicus führt.
1þx
Wir setzen u ¼
und lösen dann die Funktionsgleichung durch Entlogarithmieren nach u auf:
1x
1
1þx
1
ln
) y ¼
ln u j 2 ) 2 y ¼ ln u ) e 2 y ¼ u
y ¼
2
1x
2
Rechenregel:
ln a ¼ b
)
a ¼ eb
Die aus u ¼ e 2 y durch Rücksubstitution erhaltene Gleichung lösen wir nach x auf:
1þx
u ¼ e 2y )
¼ e 2 y j ð1 xÞ ) 1 þ x ¼ ð1 xÞ e 2 y )
1x
x þ x e 2y ¼ e 2y 1
)
x ð1 þ e 2 y Þ ¼ e 2 y 1 j : ð1 þ e 2 y Þ
)
1 þ x ¼ e 2y x e 2y
x ¼
e 2y 1
e 2y 1
¼ 2y
2
y
1þe
e þ1
Durch Vertauschen der Variablen erhalten wir die Umkehrfunktion, die in der Tat auf den Tangens hyperbolicus führt:
y ¼
e 2x 1
ðe 2 x 1Þ e x
e 2x e x e x
e x e x
¼
¼
¼ tanh x
¼
ðe 2 x þ 1Þ e x
e 2x e x þ e x
e x þ e x
e 2x þ 1
Umformungen: Gleichung zunächst mit e x erweitern, dann die Rechenregel e a e b ¼ e a þ b anwenden.
Freier Fall unter Berücksichtigung des Luftwiderstandes
Berücksichtigt man beim freien Fall den Luftwiderstand durch eine dem Quadrat der Fallgeschwindigkeit v proportionale Reibungskraft R ¼ k v 2 ; so ergeben sich für Fallweg s und Fallgeschwindig-
A44
keit v die folgenden (komplizierten) Zeitgesetze:
rffiffiffiffiffiffiffiffiffi
m
mg
s ðtÞ ¼
ln ½ cosh ða tÞ ; v ðtÞ ¼
tanh ða tÞ ;
k
k
(m: Masse;
g: Erdbeschleunigung;
k > 0: Reibungsfaktor;
t 0
pffiffiffiffiffiffiffiffiffiffiffiffiffi
a ¼ gk=mÞ
a) Welcher Zusammenhang besteht zwischen der Fallgeschwindigkeit v und dem Fallweg s?
b) Welche Endgeschwindigkeit v E wird erreicht?
c) Welche Strecke muss der Körper fallen, um die halbe Endgeschwindigkeit zu erreichen? Wie lange
ist er dann bereits unterwegs?
sinh x
und cosh 2 x sinh 2 x ¼ 1 (! FS) lässt sich die im Geschwindigkeitcosh x
Zeit-Gesetz auftretende Funktion tanh ða tÞ wie folgt durch cosh ða tÞ ausdrücken, wobei wir vorübergehend
x ¼ a t setzen ðx 0Þ:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh 2 x 1
cosh 2 x
cosh 2 x 1
sinh x
1
1
tanh x ¼
¼
¼
¼
1
¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
2
cosh x
cosh x
cosh 2 x
cosh x
cosh x
cosh 2 x
a) Mit Hilfe der Formeln tanh x ¼
Umformungen:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
cosh 2 x sinhp
1 ) sinh x ¼ cosh 2 x 1 ;
ffiffixffi ¼ r
ffiffiffiffiffi
a
a
anwenden ða; b > 0Þ.
Rechenregel: pffiffiffi ¼
b
b
cosh x ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh 2 x ;
)
42
A Funktionen und Kurven
Damit erhalten wir:
rffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffi sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
mg
mg
1
1
v ¼
tanh ða tÞ ¼
k
k
cosh 2 ða tÞ
Das Weg-Zeit-Gesetz lösen wir durch Entlogarithmierung wie folgt nach cosh ða tÞ auf:
k
m
k
ln ½ cosh ða tÞ
)
s ¼ ln ½ cosh ða tÞ ) e ðk = mÞ s ¼ e ln ½ cosh ða tÞ ¼ cosh ða tÞ
s ¼
k
m
m
Diesen Ausdruck setzen wir in das Geschwindigkeit-Zeit-Gesetz ein und erhalten die gesuchte Abhängigkeit der
Fallgeschwindigkeit v vom Fallweg s:
rffiffiffiffiffiffiffiffiffi sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffi rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
mg
1
mg
1
mg
1 ðk = mÞ s 2 ¼
1 ð2 k = mÞ s ¼
1 e ð2 k = mÞ s ;
v ðsÞ ¼
s 0
k
½e
k
e
k
ln a ¼ b
Rechenregeln:
)
e ln a ¼ a ¼ e b ;
ðe a Þ n ¼ e n a ;
1
¼ e a
ea
b) Endgeschwindigkeit (nach unendlich langer Fallzeit und damit auch unendlich langem Fallweg):
rffiffiffiffiffiffiffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffi rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffi
mg
mg
mg
ð2
k
=
mÞ
s
ð2
k
=
mÞ
s
¼
Þ ¼
v E ¼ lim v ðsÞ ¼ lim
1e
lim ð1 e
s!1
s!1
s!1
k
k
k
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
Umformungen: Der Grenzübergang s ! 1 darf unter
der Wurzel vorgenommen werden; die streng monoton
fallende e-Funktion verschwindet für s ! 1.
v
vE
Damit können wir den Zusammenhang zwischen v und s
auch wie folgt darstellen (Bild A-43):
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
v ðsÞ ¼ v E 1 e ð2 k = mÞ s
1
v
2 E
ðmit s 0Þ
Bild A-43
0,1438 · m /k
c) Fallweg bis zum Erreichen der halben Endgeschwindigkeit:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ð2
k
=
mÞ
s
¼
)
1e
quadrieren )
2
2k
3
ð2 k = mÞ s
s ¼ ln
)
¼
ln e
m
4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
) v E 1 e ð2 k = mÞ s ¼
vE
2
1
3
ð2 k = mÞ s
ð2 k = mÞ s
) e
¼
¼
1e
ln )
4
4
m
3
m
s ¼
ln
¼ 0;1438
2k
4
k
1
v ðsÞ ¼
vE
2
Rechenregel:
ln e n ¼ n
Fallzeit t bis zum Erreichen der halben Endgeschwindigkeit:
rffiffiffiffiffiffiffiffiffi
mg
tanh ða tÞ ¼ v E tanh ða tÞ
v ðtÞ ¼
k
v ðtÞ ¼
1
vE
2
)
v E tanh ða tÞ ¼
1
vE
2
)
tanh ða tÞ ¼
1
2
Auflösen dieser Gleichung durch bergang zur Umkehrfunktion Areatangens hyperbolicus:
rffiffiffiffiffiffiffiffi
artanh ð1 = 2Þ
0;5493
m
¼
¼ 0;5493
a t ¼ artanh ð1 = 2Þ ) t ¼
a
a
gk
s
6 Funktionen und Kurven in Parameterdarstellung
43
6 Funktionen und Kurven in Parameterdarstellung
Lehrbuch: Band 1, Kapitel III.1.2.4
Formelsammlung: Kapitel III.1.2.2
Wie lauten die folgenden in der Parameterform dargestellten Funktionen in der expliziten kartesischen
Darstellungsform y ¼ f ðxÞ ?
A45
t
1þt
; y ðtÞ ¼
; t 6¼ 1
1t
1t
1
2
ln t ; y ðtÞ ¼ 1
; t > 0
b) x ðtÞ ¼
t þ1
2
a) x ðtÞ ¼
Jeweils die erste Parametergleichung nach dem Parameter t auflösen, den gefundenen Ausdruck dann in die zweite
Gleichung einsetzen.
t
a)
x ¼
ð1 tÞ ) x ð1 tÞ ¼ t ) x x t ¼ t ) x t þ t ¼ x )
1t
t ðx þ 1Þ ¼ x j : ðx þ 1Þ
1þt
y ¼
¼
1t
1þ
1
x
x þ1
x
x þ1
)
t ¼
x
x þ1
x þ1þx
¼
x þ1
x þ1x
x þ1
¼
ðx 6¼ 1Þ
2x þ 1
x þ1
1
x þ1
¼
2x þ 1 x þ 1
¼ 2x þ 1
x þ1
1
Umformungen: Zunächst im Zähler und Nenner die jeweiligen Brüche auf den Hauptnenner x þ 1 bringen, dann
den Zählerbruch mit dem Kehrwert des Nennerbruches multiplizieren und den gemeinsamen Faktor x þ 1 kürzen.
Lösung:
y ¼ 2x þ 1;
x 6¼ 1
b) Die 1. Parametergleichung wird durch Entlogarithmierung nach t aufgelöst:
1
ln t j 2 ) ln t ¼ 2 x ) e ln t ¼ t ¼ e 2 x
2
2
ðt þ 1Þ 2
t þ12
t 1
y ¼ 1
¼
¼
¼
¼
t þ1
t þ1
t þ1
t þ1
x ¼
¼
ðRechenregel:
ln a ¼ b
)
a ¼ e bÞ
e 2x 1
ðe 2 x 1Þ e x
e 2x e x e x
e x e x
¼
¼
¼
¼ tanh x
e 2x þ 1
ðe 2 x þ 1Þ e x
e 2x e x þ e x
e x þ e x
Umformungen: Brüche zunächst auf den Hauptnenner t þ 1 bringen, t durch e 2 x ersetzen, Bruch dann mit
e x erweitern, Rechenregel e a e b ¼ e a þ b anwenden.
Lösung:
y ¼ tanh x ;
1 < x < 1
Die nachstehenden in der Parameterform vorliegenden Funktionen sind in der expliziten kartesischen
Form y ¼ f ðxÞ darzustellen. Um welche Kurven handelt es sich dabei? Bestimmen Sie den Defini-
A46
tionsbereich und skizzieren Sie den Kurvenverlauf.
a) x ðuÞ ¼ 2 sinh u ;
y ðuÞ ¼ cosh 2 u ;
b) x ðtÞ ¼ 2 cos t þ 5 ;
u 2 R
y ðtÞ ¼ 4 sin t ;
0 t p
44
A Funktionen und Kurven
a) Mit sinh u ¼ x =2 und unter Verwendung des „hyperbolischen Pythagoras“ cosh 2 u sinh 2 u ¼ 1 (! FS)
geht die 2. Parametergleichung über in:
2
x
1 2
y ¼ cosh u ¼ 1 þ sinh u ¼ 1 þ
x
¼ 1þ
2
4
2
y
2
Es handelt sich um eine nach oben geöffnete Parabel mit dem Scheitelpunkt
S ¼ ð0; 1Þ (siehe Bild A-44).
5
Definitionsbereich: Da sinh u für u 2 R sämtliche reellen Werte durchläuft, gilt diese Aussage auch für die Variable x ¼ 2 sinh u.
3
4
2
1
–4 –2
2
x
4
Bild A-44
b) Wir lösen die Parametergleichungen nach cos t bzw. sin t auf und setzen die gefundenen Ausdrücke in den
„trigonometrischen Pythagoras“ cos 2 t þ sin 2 t ¼ 1 ein:
x ¼ 2 cos t þ 5
)
cos t ¼
cos t þ sin t ¼ 1
2
2
)
x 5
;
2
y ¼ 4 sin t
2
x 5 2
y
þ
¼ 1
2
4
)
)
sin t ¼
y
4
ðx 5Þ 2
y2
þ
¼ 1
4
16
Diese Gleichung beschreibt eine Ellipse mit dem Mittelpunkt M ¼ ð5; 0Þ und den Halbachsen a ¼ 2 und
b ¼ 4. Wegen der Einschränkung y ¼ 4 sin t , 0 t p kommen jedoch nur Kurvenpunkte mit positiver
Ordinate in Frage (die y-Werte liegen zwischen 0 und 4). Die gesuchte Kurve ist damit die oberhalb der x-Achse
liegende Halbellipse (Bild A-45). Sie wird in expliziter Form wie folgt beschrieben (Ellipsengleichung nach y
auflösen):
ðx 5Þ 2
y2
y2
ðx 5Þ 2
y
¼ 1
þ
¼ 1 )
16 )
4
16
16
4
4
y 2 ¼ 16 4 ðx 5Þ 2 ¼ 4 ½ 4 ðx 5Þ 2
y ¼ 2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 ðx 5Þ 2 ;
)
2
M
3 x 7
Definitionsbereich: cos t durchläuft für 0 t p sämtliche Werte
zwischen 1 und þ 1, die Variable x ¼ 2 cos t þ 5 damit sämtliche
Werte zwischen x ¼ 2 þ 5 ¼ 3 und x ¼ 2 þ 5 ¼ 7.
1
3
5
7
x
–2
–4
Bild A-45
A47
Gegeben sind die folgenden Kurven in Parameterdarstellung:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2 ðt 2 1Þ
2 4;
a) x ¼ ln t ; y ¼
;
b)
x
¼
t
y
¼
1 þ t2
t2 þ 1
Bestimmen Sie den größtmöglichen Definitionsbereich für den Parameter t und geben Sie eine parameterfreie Darstellung an.
a) Die 1. Parametergleichung ist nur für positive Werte des Parameters t definiert, die 2. Gleichung dagegen für jedes
reelle t . Daher ist t > 0 der gesuchte größtmögliche Definitionsbereich.
Eine parameterfreie Darstellung erhalten wir, indem wir die 1. Gleichung nach t auflösen und den gefundenen
Ausdruck in die 2. Gleichung einsetzen:
6 Funktionen und Kurven in Parameterdarstellung
x ¼ ln t
y ¼
)
e x ¼ e ln t ¼ t
ðEntlogarithmierung: ln a ¼ b ) a ¼ e b Þ
1
1
1
¼
¼
2
x
2
1þt
1 þ ðe Þ
1 þ e 2x
Rechenregel:
45
ðmit x 2 RÞ
ðe a Þ n ¼ e n a
b) Der Radikand der Wurzel muss größer oder gleich Null sein:
t2 4 0
)
t2 4
)
jtj 2
Da es für die 2. Parametergleichung keine Einschränkung gibt (der Nenner t 2 þ 1 ist stets ungleich 0),
ist j t j 2 der gesuchte größtmögliche Definitionsbereich.
Parameterfreie Darstellung
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x ¼ t 2 4 quadrieren
y ¼
)
x2 ¼ t2 4
2 ðt 2 1Þ
2 ðx 2 þ 4 1Þ
2 ðx 2 þ 3Þ
¼
¼
2
2
t þ1
x þ4þ1
x2 þ 5
)
t2 ¼ x2 þ 4
ðmit x 0Þ
Die Parameterdarstellung einer Kurve lautet wie folgt:
A48
x ðuÞ ¼ a cot u ;
y ðuÞ ¼ b = sin u ;
0 < u < p
ða; b > 0Þ
Eliminieren Sie den Parameter u und beschreiben Sie die Kurve in kartesischer Form. Skizzieren Sie
den Kurvenverlauf.
Die 1. Parametergleichung quadrieren, dann cot u mit Hilfe der trigonometrischen Beziehungen cot u ¼ cos u = sin u
und sin 2 u þ cos 2 u ¼ 1 durch sin u ausdrücken:
cos u 2 a 2 cos 2 u
a 2 ð1 sin 2 uÞ
x ¼ a cot u ) x 2 ¼ a 2 ðcot uÞ 2 ¼ a 2
¼
¼
sin u
sin 2 u
sin 2 u
Die 2. Parametergleichung nach sin u auflösen ðsin u ¼ b = yÞ, den gefundenen Ausdruck in die (quadrierte) 1. Gleichung einsetzen:
b2
2
!
a 1 2
2
2
2
2
2
y
a
ð1
sin
uÞ
b
y
y
¼
¼ a2 1 2 2 ¼ a2
1
)
x2 ¼
y
b
b2
b2
sin 2 u
y2
x2
y2
¼
1
a2
b2
)
y2
x2
¼ 1
b2
a2
Umformungen: Zählerbruch mit dem Kehrwert des Nennerbruches
multiplizieren, gliedweise ausmultiplizieren und dann beide Seiten
durch a 2 dividieren.
y
b
Es handelt sich um eine um 90 gedrehte Ursprungshyperbel (siehe
Bild A-46).
Asymptote
Bild A-46
x
Asymptote
46
A Funktionen und Kurven
Schiefer Wurf mit und ohne Berücksichtigung des Luftwiderstandes
Die Bewegung eines Körpers, der von der Erdoberfläche aus mit der Geschwindigkeit v 0 unter dem
Winkel a schräg nach oben geworfen wird, lässt sich durch die Parametergleichungen
x ðtÞ ¼ ða v 0 cos aÞ t b
y ðtÞ ¼ ða v 0 sin aÞ t b
und
1
gt2
2
mit t 0 beschreiben (Bild A-47).
A49
y
Flugbahn
v0
a
t:
Zeit
x; y:
Kartesische Koordinaten des Körpers zum Zeitpunkt t
a; b:
Positive, von den äußeren Bedingungen abhängige Konstanten
Bild A-47
x
W
a) Wie lautet die Bahnkurve in explizieter Form?
b) Berechnen Sie Flugzeit t und Wurfweite W .
c) Welche Ergebnisse erhält man im luftleeren Raum (dort gilt a ¼ b ¼ 1) ? Welche maximale Höhe
erreicht der Körper (Wurfhöhe H )?
a) Wir lösen die 1. Gleichung nach t auf und setzen den gefundenen Ausdruck in die 2. Gleichung ein:
x ¼ ða v 0 cos aÞ t b
)
tb ¼
ðbeide Seiten mit 1 = b potenzieren:
x
a v 0 cos a
)
t ¼
1 = b
x
a v 0 cos a
ðt b Þ 1 = b ¼ t b 1 = b ¼ t 1 ¼ tÞ
1
x
1
y ¼ ða v 0 sin aÞ t
g t 2 ¼ ða v 0 sin aÞ
g
a
v
cos
a
2
2
0
b
¼
"
x
a v 0 cos a
1 = b #2
¼
2 = b
sin a
1
x
g
¼ ðtan aÞ x
x 2=b
x
g
2
cos a
a v 0 cos a
2 ða v 0 cos aÞ 2 = b
Bahnkurve:
y ðxÞ ¼ ðtan aÞ x
Umformungen:
tan a ¼
sin a
;
cos a
g
x 2=b ; x 0
2 ða v 0 cos aÞ 2 = b
n
a
an
¼ n
ða m Þ n ¼ a m n ;
b
b
b) Berechnung der Flugzeit t
Die Parametergleichung y ðtÞ beschreibt die Höhe des Körpers zur Zeit t . Sie ist genau Null im Augenblick des
Abwurfs ðt ¼ 0Þ und im Augenblick des Auftreffens auf dem Erdboden ðt ¼ t > 0Þ. Aus der Bedingung
y ¼ 0 berechnen wir die gesuchte Flugzeit t wie folgt:
y ðtÞ ¼ 0
)
ða v 0 sin aÞ t b
1
2b
gt
¼ 0
t a v 0 sin a
2
1
gt2 ¼ 0
2
tb ¼ 0
)
)
ða v 0 sin aÞ t b
1
tb
gt2 b ¼ 0
2
t
t 1 ¼ 0 ðZeitpunkt des AbwurfsÞ
b
a v 0 sin a
1
g t 2b ¼ 0
2
(der 2. Summand wurde zunächst mit t b erweitert, dann der gemeinsame Faktor t b ausgeklammert)
)
6 Funktionen und Kurven in Parameterdarstellung
47
Die untere Gleichung liefert die Flugzeit t :
1
g t 2b ¼ 0 )
2
2 a v 0 sin a 1 = ð2 bÞ
¼ t ¼
g
a v 0 sin a
t2
1
g t 2 b ¼ a v 0 sin a
2
)
t 2b ¼
2 a v 0 sin a
g
)
(beide Seiten wurden mit 1 = ð2 bÞ potenziert)
Berechnung der Wurfweite W
Die Wurfweite W entspricht der x-Koordinate zum Zeitpunkt t ¼ t :
W ¼ x ðt ¼ tÞ ¼ ða v 0 cos aÞ t b ¼
"
#b
2 a v 0 sin a 1 = ð2 bÞ
2 a v 0 sin a b = ð2 bÞ
¼ ða v 0 cos aÞ
¼ ða v 0 cos aÞ
g
g
Rechenregel:
ða m Þ n ¼ a m n
c) Sonderfall luftleerer Raum ða ¼ b ¼ 1Þ
Bahnkurve:
y
g
y ðxÞ ¼ ðtan aÞ x
x2;
2 ðv 0 cos aÞ 2
x 0
S
y0
Wurfparabel
y0 = H
Die Flugbahn ist eine Parabel (auch „Wurfparabel“ genannt,
siehe Bild A-48).
x0
x
Wurfweite W
Flugzeit t und Wurfweite W
t ¼
Bild A-48
2 v 0 sin a
g
W ¼ v 0 cos a
2 v 0 sin a
2 v 20 cos a sin a
v 2 sin ð2 aÞ
¼
¼ 0
g
g
g
(unter Verwendung der trigonometrischen Beziehung sin ð2 aÞ ¼ 2 sin a cos aÞ
Wurfhöhe H
Die Wurfhöhe H ist durch die Ordinate y 0 des Scheitelpunktes S ¼ ðx 0 ; y 0 Þ der Wurfparabel gegeben, wobei
x 0 die halbe Wurfweite ist (wegen der Symmetrie der Flugbahn):
x0 ¼
W
v 2 sin a cos a
¼ 0
;
2
g
H ¼
sin a v 20 sin a cos a
g
v 4 sin 2 a cos 2 a
0
¼
g
g2
cos a
2 v 20 cos 2 a
H ¼ y 0 ¼ y ðx ¼ x 0 Þ ¼ ðtan aÞ x 0
g
x 20
2 ðv 0 cos aÞ 2
¼
g v 20 v 20 sin 2 a
v 20 sin 2 a
g v 40 sin 2 a
v 20 sin 2 a
¼
¼
g
g
2 g 2 v 20
2 g g v 20
¼
v 20 sin 2 a
v 2 sin 2 a
2 v 20 sin 2 a v 20 sin 2 a
v 2 sin 2 a
0
¼
¼ 0
2g
g
2g
2g
(unter Berücksichtigung der trigonometrischen Beziehung tan a ¼ sin a = cos a)
48
A Funktionen und Kurven
Lissajous-Figuren
Durch ungestörte berlagerung der beiden zueinander senkrechten Schwingungen mit den Gleichungen
x ðtÞ ¼ a sin t
A50
und
y ðtÞ ¼ a sin ð2 t þ jÞ
entsteht eine sog. Lissajous-Figur ða > 0; t 0 : ZeitÞ: Beschreiben Sie die Bahnkurve in kartesischen Koordinaten für a ¼ 2 und
a) j ¼ 0 ;
b) j ¼ p = 2
und skizzieren Sie die Kurven.
a) Die Parametergleichungen lauten für a ¼ 2 und j ¼ 0 wie folgt:
x ðtÞ ¼ 2 sin t ;
y ðtÞ ¼ 2 sin ð2 tÞ ;
t 0
Unter Verwendung der trigonometrischen Formeln sin ð2 tÞ ¼ 2 sin t cos t und sin 2 t þ cos 2 t ¼ 1 (! FS)
lässt sich die 2. Parametergleichung wie folgt durch sin t ausdrücken:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ 2 sin ð2 tÞ ¼ 4 sin t cos t ¼ 4 sin t 1 sin 2 t ; t 0
Die 1. Parametergleichung wird nach sin t aufgelöst, der gefundene Ausdruck sin t ¼ x = 2 dann in die 2. Gleichung eingesetzt:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 x2
x
x2
4 x2
1
¼ 2x
¼ x 4 x2
¼ 2x
ð 2 x 2Þ
y ¼ 4
2
4
4
2
Wir erhalten somit zwei (ungerade) Funktionen, die durch Spiegelung an der x-Achse ineinander übergehen und die
in Bild A-49 skizzierte geschlossene Kurve ergeben. Diese sog. Lissajous-Figur ist sowohl zur x-Achse als auch zur
y-Achse spiegelsymmetrisch.
y
A4
Wertetabelle (1. Quadrant):
x
y
0
0,5
1
1,5
2
0
0,97
1,73
1,98
0
A1
2
1
Bild A-49
B2
–2
B1
–1
0
1
2
x
–1
–2
A3
A2
Die geschlossene Kurve wird dabei innerhalb der
Periode 0 t < 2 p wie folgt durchlaufen:
Startpunkt 0 ! A 1 ! B 1 ! A 2 ! 0 ! A 4 ! B 2 ! A 3 ! 0
b) Parametergleichungen für a ¼ 2 und j ¼ p = 2:
x ðtÞ ¼ 2 sin t ;
y ðtÞ ¼ 2 sin ð2 t p = 2Þ ;
t 0
Die 2. Gleichung lässt sich unter Verwendung des Additionstheorems der Sinusfunktion und der Formel
cos ð2 tÞ ¼ 1 2 sin 2 t (! FS) wie folgt darstellen:
y ¼ 2 sin ð2 t p = 2Þ ¼ 2 ½ sin ð2 tÞ cos ðp = 2Þ cos ð2 tÞ sin ðp = 2Þ ¼
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflffl{zfflfflfflfflffl}
0
1
¼ 2 ½ 0 cos ð2 tÞ ¼ 2 cos ð2 tÞ ¼ 2 ð1 2 sin 2 tÞ ¼ 2 ð2 sin 2 t 1Þ ;
t 0
7 Funktionen und Kurven in Polarkoordinaten
49
Aus der 1. Parametergleichung folgt sin t ¼ x = 2 und durch Einsetzen in die 2. Gleichung somit
2
x2
x
y ¼ 2 ð2 sin 2 t 1Þ ¼ 2 2
1 ¼ 2
1 ¼ x2 2
ð 2 x 2Þ
4
2
Die (periodische) Bewegung verläuft längs der in Bild A-50 skizzierten
Parabel zwischen den Punkten A und B: Startpunkt ist dabei der
Scheitelpunkt S mit den Koordinaten
x ðt ¼ 0Þ ¼ 2 sin 0 ¼ 0 ;
|ffl{zffl}
0
y
B
y ðt ¼ 0Þ ¼ 2 sin ð p = 2Þ ¼ 2
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
1
1
–2
Die geschlossene Kurve wird innerhalb einer Periode 0 t 2 p wie
folgt durchlaufen (Startpunkt ist der Scheitelpunkt S):
S ! A ! S ! B ! S
A
2
–1
1
2
x
–1
–2 S
Bild A-50
7 Funktionen und Kurven in Polarkoordinaten
Lehrbuch: Band 1, Kapitel III.3.3.2
Formelsammlung: Kapitel I.9.1.3.2 und III.1.2.3
A51
Gegeben sind folgende Kurven in Polarkoordinatendarstellung:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a) r ðjÞ ¼ 4 sin 2 j þ 2 cos 2 j
b) r ðjÞ ¼ a tan j sin j ;
Für welche Winkel aus dem Intervall 0
j < 360
a > 0
sind diese Kurven definiert ? Wie lauten die
Gleichungen der Kurven in kartesischen Koordinaten?
Zur Erinnerung: Es sind (definitionsgemäß) nur solche Winkel zugelassen, für die r 0 ist.
Die benötigten Transformationsgleichungen lauten:
cos j ¼ x = r ;
sin j ¼ y = r ;
r2 ¼ x2 þ y2
a) Unter Verwendung des „trigonometrischen Pythagoras“ sin 2 j þ cos 2 j ¼ 1 lässt sich die Gleichung wie folgt
umschreiben (wir beschränken uns zunächst auf den Radikand der Wurzel):
4 sin 2 j þ 2 cos 2 j ¼ 4 sin 2 j þ 2 ð1 sin 2 jÞ ¼ 4 sin 2 j þ 2 2 sin 2 j ¼ 2 ðsin 2 j þ 1Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Somit: r ¼
2 ðsin 2 j þ 1Þ
Definitionsbereich:
r 0
)
2 ðsin 2 j þ 1Þ 0 j : 2
Diese Bedingung ist für jeden Winkel aus dem Intervall 0
Quadrat einer reellen Zahl kann nicht negativ sein).
)
sin 2 j þ 1 0
j < 360
)
sin 2 j 1
erfüllt, da sogar sin 2 j 0 gilt (das
Kurvengleichung in kartesischen Koordinaten
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼
2 ðsin 2 j þ 1Þ quadrieren )
r
2
y2
¼ 2 ðsin j þ 1Þ ¼ 2
þ1
r2
2
ðx 2 þ y 2 Þ 2 ¼ 2 ðy 2 þ x 2 þ y 2 Þ
!
y2 þ r2
¼ 2
r2
)
!
2 ðy 2 þ r 2 Þ
¼
r2
ðx 2 þ y 2 Þ 2 ¼ 2 ðx 2 þ 2 y 2 Þ
r2
)
r 4 ¼ 2 ðy 2 þ r 2 Þ
)
50
A Funktionen und Kurven
b) Unter Verwendung der Beziehung tan j ¼ sin j = cos j lässt sich die Kurvengleichung wie folgt umschreiben:
r ¼ a tan j sin j ¼ a
sin j
sin 2 j
sin j ¼ a
cos j
cos j
Definitionsbereich: Die Bedingung r 0 ist wegen a > 0 und sin 2 j 0 nur erfüllt, wenn der Nenner
des Bruches (also cos j) negativ ist: cos j < 0 ) 90 < j < 270
ð2: und 3: QuadrantÞ
Kurvengleichung in kartesischen Koordinaten
sin 2 j
r ¼ a
cos j ) r cos j ¼ a sin 2 j
cos j
|fflfflfflfflffl{zfflfflfflfflffl}
x
xr2 ¼ ay2
)
)
y 2
x ¼ a 2 r2
r
)
x ðx 2 þ y 2 Þ ¼ a y 2
Wie lauten die Gleichungen der nachfolgenden Kurven in Polarkoordinaten? Welche Aussagen lassen
A52
sich über den Definitionsbereich (Winkelbereich) machen?
x y þ c ¼ 0 ðmit c > 0Þ
a) Gerade:
b) Rechtwinklige Hyperbel:
y2 ¼ 2px
c) Parabel:
y ¼ 8=x;
x > 0
ðmit p > 0Þ
Wir benötigen die Transformationsgleichungen x ¼ r cos j und y ¼ r sin j:
a) x y þ c ¼ 0
)
r cos j r sin j þ c ¼ 0
r ðcos j sin jÞ ¼ c
Definitionsbereich:
)
r 0
r ¼
)
)
r ðcos j sin jÞ þ c ¼ 0
)
c
c
¼
cos j sin j
sin j cos j
sin j cos j > 0
ðda c > 0Þ
)
sin j > cos j
45 < j < 225 (in diesem Winkelbereich liegt die Sinuskurve oberhalb der Kosinuskurve)
8
b) y ¼
x ) x y ¼ 8 ) ðr cos jÞ ðr sin jÞ ¼ 8 ) r 2 cos j sin j ¼ 8
x
8
28
16
4
r2 ¼
¼
¼
) r ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cos j sin j
2 cos j sin j
sin ð2 jÞ
sin ð2 jÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
sin ð2 jÞ
)
)
ðunter Verwendung der Beziehung sin ð2 jÞ ¼ 2 sin j cos j ! FS : Kap: III:7:6:3Þ
Definitionsbereich:
c) y 2 ¼ 2 p x
)
r 0
)
0
< j < 90
ðr sin jÞ 2 ¼ 2 p ðr cos jÞ
r sin 2 j ¼ 2 p cos j
Definitionsbereich:
90
)
r ¼
ð1. QuadrantÞ
)
ðwegen x > 0 und somit y ¼ 8 = x > 0Þ
r 2 sin 2 j ¼ 2 p r cos j j : r
)
2 p cos j
sin 2 j
j 90 ;
j 6¼ 0
ð1. und 4. QuadrantÞ
ðdie Bedingung r 0 ist nur für cos j 0 erfüllt und somit nur für Winkel aus dem 1. und 4. Quadranten
außerdem muss der Nenner sin 2 j 6¼ 0 und damit j 6¼ 0 seinÞ
Wie lauten die folgenden Kurvengleichungen in Polarkoordinaten?
A53
x3 þ y3 3xy ¼ 0
a) Cartesisches Blatt:
b) Konchoide: ðx 2 þ y 2 Þ ðx bÞ 2 ¼ a 2 x 2
c) Zissoide: x þ y ðx aÞ ¼ 0
3
2
ða > 0; b > 0Þ
7 Funktionen und Kurven in Polarkoordinaten
51
Transformationsgleichungen:
x ¼ r cos j ;
a) x 3 þ y 3 3 x y ¼ 0
r 3 cos 3 j þ r 3 sin 3 j 3 ðr cos jÞ ðr sin jÞ ¼ 0
)
y ¼ r sin j ;
r ðcos j þ sin jÞ 3 r cos j sin j ¼ 0 j : r
x2 þ y2 ¼ r2
)
) r ðcos j þ sin jÞ 3 cos j sin j ¼ 0
3 cos j sin j
r ðcos 3 j þ sin 3 jÞ ¼ 3 cos j sin j ) r ¼
cos 3 j þ sin 3 j
b) ð x 2 þ y 2 Þ ðx bÞ 2 ¼ a 2 x 2 ) r 2 ðr cos j bÞ 2 ¼ a 2 r 2 cos 2 j : r 2 )
pffiffiffi
ðr cos j bÞ 2 ¼ a 2 cos 2 j j
) r cos j b ¼ a cos j )
3
3
3
2
r cos j ¼ b a cos j
c) x 3 þ y 2 ðx aÞ ¼ 0
)
)
r ¼
2
3
)
3
b a cos j
b
¼
a
cos j
cos j
r 3 cos 3 j þ r 2 sin 2 j ðr cos j aÞ ¼ 0 j : r 2
r cos 3 j þ sin 2 j ðr cos j aÞ ¼ 0
0
1
)
)
r cos 3 j þ r cos j sin 2 j a sin 2 j ¼ 0
r cos j@cos 2 j þ sin 2 j A a sin 2 j ¼ 0 ) r cos j ¼ a sin 2 j
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
a sin 2 j
sin j
¼ a sin j
¼ a sin j tan j
r ¼
cos j
cos j
)
)
ðunter Verwendung des „trigonometrischen Pythagoras“ sin 2 j þ cos 2 j ¼ 1 und der Beziehung
tan j ¼ sin j = cos j ! FS: Kap. III.7)
Charakterisieren und skizzieren Sie die Kurven, die durch die folgenden Gleichungen in Polarkoordina-
A54
ten beschrieben werden:
a) r ¼
2
;
cos j
0 j < p=2
b)
r ¼
1
;
sin j
p < j
3
p
2
Anleitung: Gehen Sie zunächst zu kartesischen Koordinaten über.
Benötigte Transformationsgleichungen:
2
cos j
a) r ¼
cos j
)
x ¼ r cos j und y ¼ r sin j
r cos j ¼ 2
|fflfflfflfflffl{zfflfflfflfflffl}
x
)
y
x ¼ 2
)
r sin j ¼ 1
|fflfflfflfflffl{zfflfflfflfflffl}
y
)
x=2
2
(y ≥ 0)
1
Die Gleichung x ¼ 2 beschreibt eine Parallele zur y-Achse (im Abstand
d ¼ 2 rechts von dieser Achse). Wegen 0 j < p = 2 kommt nur der
im 1. Quadranten gelegene Teil x ¼ 2, y 0 in Frage (Halbgerade,
siehe Bild A-51):
1
b) r ¼
sin j
sin j
3
1
x
Bild A-51
y
y ¼ 1
Durch die Gleichung y ¼ 1 wird eine Parallele zur x-Achse
beschrieben, die im Abstand d ¼ 1 unterhalb dieser Achse
verläuft. Wegen p < j 3 p = 2 kommt nur der im 3. Quadranten gelegene Teil in Frage (Halbgerade y ¼ 1; x 0;
siehe Bild A-52).
2
–3
–2
–1
x
–1
y = –1
(x ≤ 0)
Bild A-52
52
A Funktionen und Kurven
Strophoide:
ðx þ aÞ x 2 þ ðx aÞ y 2 ¼ 0 ðmit a > 0Þ
a) Beschreiben Sie diese Kurve durch explizite Funktionen (in kartesischen Koordinaten) und zeichnen
A55
Sie den Kurvenverlauf für den Parameterwert a ¼ 3.
b) Bringen Sie die Kurvengleichung in die Polarkoordinatenform r ¼ r ðjÞ und bestimmen Sie den
zulässigen Winkelbereich (im Intervall 0
j < 360 ).
a) Wir lösen die Kurvengleichung nach y auf und erhalten zwei Funktionen, die durch Spiegelung an der x-Achse
ineinander übergehen:
ðx þ aÞ x 2 þ ðx aÞ y 2 ¼ 0
y
2
)
ðx aÞ y 2 ¼ ðx þ aÞ x 2
ðx þ aÞ x 2
ðx þ aÞ x 2 ð 1Þ
ðx þ aÞ x 2
¼
¼
¼
x a
ax
ðx aÞ ð 1Þ
Umformungen:
)
)
rffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x þa
y ¼ x
;
ax
a x < a
Bruch mit 1 erweitern, dann Teilwurzel ziehen.
Kurvenverlauf (für a == 3):
siehe Bild A-53
Wir erstellen eine Wertetabelle für die Funktion
rffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ3
; 3 x < 3
y ¼ þx
3x
y
6
Wertetabelle:
Asymptote
4
x
y
3
2;5
2
1;5
1
0;5
0
0
0;75
0;89
0;87
0;71
0;42
0
x
y
0;5
1
1;5
2
2;5
2;9
2
0;59
1;41
2;60
4;47
8;29
22;28
Bild A-53
–3
3
–2
–4
–6
b) Kurvengleichung in Polarkoordinaten
Unter Verwendung der Transformationsgleichungen x ¼ r cos j und y ¼ r sin j folgt:
ðx þ aÞ x 2 þ ðx aÞ y 2 ¼ 0
)
ðr cos j þ aÞ r 2 cos 2 j þ ðr cos j aÞ r 2 sin 2 j ¼ 0 j : r 2
ðr cos j þ aÞ cos 2 j þ ðr cos j aÞ sin 2 j ¼ 0
r cos 3 j þ r cos j sin 2 j ¼ a sin 2 j a cos 2 j
)
)
r cos 3 j þ a cos 2 j þ r cos j sin 2 j a sin 2 j ¼ 0
r cos j ðcos 2 j þ sin 2 jÞ ¼ a ðsin 2 j cos 2 jÞ
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
cos ð2 jÞ
)
)
)
(unter Verwendung der Formeln cos 2 j þ sin 2 j ¼ 1 und cos ð2 jÞ ¼ cos 2 j sin 2 j ! FS)
r cos j ¼ a cos ð2 jÞ
)
r ¼
a cos ð2 jÞ
cos j
x=3
x
7 Funktionen und Kurven in Polarkoordinaten
53
Bestimmung des Definitionsbereiches (Winkelbereiches)
Wir wissen bereits, dass die Kurve spiegelsymmetrisch zur x-Achse verläuft, können uns daher bei den weiteren
Untersuchungen auf den 1. und 2. Quadranten beschränken. Wegen der Bedingung r 0 und da nach Voraussetzung a > 0 ist müssen cos j und cos ð2 jÞ unterschiedliche Vorzeichen haben. Wir unterteilen den Winkelbereich 0 j 180 in vier gleiche Teilbereiche, in denen cos j und cos ð2 jÞ folgende Vorzeichen besitzen:
0 45
45 90
90 135
135 180
cos j
þ
þ
cos ð2 jÞ
þ
þ
Winkelbereich
Somit sind nur Winkel zwischen 45 und 90 bzw. zwischen 135 und 180 zulässig ðj 6¼ 90 wegen
cos j 6¼ 0Þ. Für die Gesamtkurve ergibt sich daher wegen der Spiegelsymmetrie zur x-Achse der folgende
Definitionsbereich: 45 j < 90 , 135 j 225 , 270 < j 315 .
Zeigen Sie, dass durch die Gleichung r ðjÞ ¼ 2 a sin j, 0
A56
j < 180
ein Kreis beschrieben
wird ða > 0Þ. Bestimmen Sie den Mittelpunkt M und den Radius R des Kreises.
Anleitung: Gehen Sie von den Polarkoordinaten über zu den kartesischen Koordinaten.
Mit den Transformationsgleichungen y ¼ r sin j und r 2 ¼ x 2 þ y 2 erhalten wir zunächst:
y
r ) r2 ¼ 2ay ) x2 þ y2 ¼ 2ay
r ¼ 2 a sin j ) r ¼ 2 a
r
Der y-Term wird quadratisch ergänzt:
x þ ðy 2ayÞ ¼ 0
2
2
)
y
x þ ðy 2ay þ a Þ ¼ a
2
2
2
2
)
x 2 þ ð y aÞ 2 ¼ a 2
a
Dies ist die Gleichung eines verschobenen Kreises mit dem Mittelpunkt
M ¼ ð0; aÞ auf der y-Achse und dem Radius R ¼ a (Bild A-54).
M
Bild A-54
x
Kurvengleichung in Polarkoordinaten: r ðjÞ ¼ 3 cos j þ 2
A57
a) Bestimmen Sie den Definitionsbereich (Winkelbereich) und skizzieren Sie den Kurvenverlauf mit
Hilfe einer Wertetabelle (Schrittweite: D j ¼ 15 ).
b) Wie lautet die Kurvengleichung in kartesischen Koordinaten in impliziter Form?
a) Definitionsbereich ðr 0Þ
r 0
)
3 cos j þ 2 0
)
3 cos j 2
)
cos j 2 = 3
Wegen der Spiegelsymmetrie der Kurve bezüglich der x-Achse (r ändert sich nicht, wenn wir den Winkel nach
unten, d. h. in Uhrzeigerrichtung abtragen, da cos j eine gerade Funktion ist) beschränken wir uns zunächst auf
das oberhalb der x-Achse gelegene Kurvenstück (1. und 2. Quadrant).
54
A Funktionen und Kurven
Zum Definitionsbereich gehören alle Winkel zwischen j ¼ 0 und der 1. Schnittstelle der Kosinusfunktion y ¼ cos j
mit der Geraden y ¼ 2 = 3 (siehe Bild A-55). Dieser Schnittpunkt liegt bei j ¼ arccos ð 2 = 3Þ ¼ 131;81 .
Wegen der Spiegelsymmetrie zur x-Achse gilt dann für die Gesamtkurve:
131;81
Definitionsbereich:
j 131;81
y
1
y = cos f
arccos (– 2/3)
Bild A-55
180°
–1
360°
f
y = – 2/3
Kurvenverlauf: Bild A-56 zeigt den Kurvenverlauf im Winkelbereich 0
der x-Achse erhält man die geschlossene Gesamtkurve.
j 131;81 . Durch Spiegelung an
Wertetabelle für den 1. und 2. Quadranten:
j
r
0
15
30
45
60
75
90
105
120
131;81
5
4;90
4;60
4;12
3;5
2;78
2
1;22
0;5
0
y
3
2
Bild A-56
–1
1
2
3
4
5
x
b) Wir benötigen die Transformationsgleichungen x ¼ r cos j und r 2 ¼ x 2 þ y 2 :
x
r ¼ 3 cos j þ 2 ) r ¼ 3
þ 2 r ) r 2 ¼ 3 x þ 2 r )
r
r 2 3 x ¼ 2 r j quadrieren
)
ðr 2 3 xÞ 2 ¼ 4 r 2
)
ðx 2 þ y 2 3 xÞ 2 ¼ 4 ðx 2 þ y 2 Þ
Nockenkurve
Im Maschinenbau werden im Zusammenhang mit Steuersystemen sog. Nockenkurven benötigt, die sich
A58
in Polarkoordinaten abschnittsweise wie folgt beschreiben lassen:
(
)
0 j p=c
a þ b sin 2 ðc jÞ
f ür
r ðjÞ ¼
a
p=c j 2p
ða; b > 0 ; c > 1Þ. Skizzieren Sie mit Hilfe einer Wertetabelle den Verlauf der Nockenkurve für die
Parameterwerte a ¼ 4; b ¼ 2 und c ¼ 1;2.
Die Kurvengleichung lautet für a ¼ 4; b ¼ 2 und c ¼ 1;2:
8
9
<4 þ 2 sin 2 ð1;2 jÞ
0 j 5 p= 6=
r ðjÞ ¼
f ür
:
;
4
5 p= 6 j 2p
7 Funktionen und Kurven in Polarkoordinaten
55
Diese Nockenkurve besteht aus zwei Teilen, die wir jetzt genauer untersuchen.
Im Winkelbereich von 5 p = 6 bis 2 p, d. h. im Bereich von 150
bis 360
verläuft die Nockenkurve kreisförmig:
r ¼ const: ¼ 4 (Ursprungskreis mit dem Radius R ¼ 4).
Im restlichen Winkelbereich von 0
bis 150
r ðjÞ ¼ 4 þ 2 sin 2 ð1;2 jÞ ;
lautet die Gleichung der Nockenkurve:
0 j 5 p= 6
oder
j 150
0
In den beiden Randpunkten gilt:
r ðj ¼ 0Þ ¼ 4 þ 2 sin 2 0 ¼ 4 ;
|fflfflffl{zfflfflffl}
r ðj ¼ 5 p = 6 Þ ¼ 4 þ 2 sin 2 ð1;2 5 p = 6 Þ ¼ 4 þ 2 sin 2 p ¼ 4
|fflfflffl{zfflfflffl}
0
0
Die beiden Teile der Kurve gehen also in den Randpunkten stetig ineinander über.
Verlauf der Nockenkurve:
siehe Bild A-57
Wertetabelle für das Intervall 0
y
j 150 :
60°
j
0
30
45
60
90
120
135
150
120°
r
4
4,69
5,31
5,81
5,81
4,69
4,19
4
6
30°
150°
Bild A-57
–4
4
x
–4
Bestimmen Sie die Gleichung einer Kurve mit den folgenden Eigenschaften: Ist P ein beliebiger Punkt
der Kurve und bezeichnet man die Abstände dieses Punktes von zwei festen Punkten P 1 und P 2 im
A59
Abstand P 1 P 2 ¼ 2 e mit r 1 und r 2 , so soll das Produkt dieser Abstände stets konstant e 2 betragen. Bestimmen Sie die Kurvengleichung
a) in kartesischen Koordinaten (in impliziter Form),
b) in Polarkoordinaten.
c) Skizzieren Sie den Kurvenverlauf für e 2 ¼ 8.
y
Wir wählen das kartesische Koordinatensystem so, dass
die Punkte P 1 und P 2 auf der x-Achse liegen und die
Mittelsenkrechte auf P 1 P 2 die y-Achse bildet (siehe
Bild A-58). Die Punkte P 1 ; P 2 und P haben dann
folgende Koordinaten:
P 1 ¼ ð e ; 0Þ ;
P 2 ¼ ðe ; 0Þ
P
r1
Bild A-58
P1
–e
P ¼ ðx ; yÞ
e
y
x
r2
e–x
A
P2
e
x
a) Die Kurvenpunkte erfüllen die Bedingung r 1 r 2 ¼ const: ¼ e 2 : Aus den beiden rechtwinkligen Dreiecken
P 1 A P und A P 2 P in Bild A-58 erhalten wir mit dem Satz des Pythagoras:
r 21 ¼ ðe þ xÞ 2 þ y 2
und
r 22 ¼ ðe xÞ 2 þ y 2
56
A Funktionen und Kurven
Aus der Bedingung r 1 r 2 ¼ e 2 folgt dann:
r 1 r 2 ¼ e 2 j quadrieren
)
r 21 r 22 ¼ e 4
)
½ðe þ xÞ 2 þ y 2 ½ ðe xÞ 2 þ y 2 ¼ e 4
ðe þ xÞ 2 ðe xÞ 2 þ y 2 ðe xÞ 2 þ y 2 ðe þ xÞ 2 þ y 4 ¼ e 4
)
½ ðe þ xÞ ðe xÞ 2 þ y 2 ½ ðe xÞ 2 þ ðe þ xÞ 2 þ y 4 ¼ e 4
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
)
)
3. Binom: e 2 x 2
ðe 2 x 2 Þ 2 þ y 2 ðe 2 2 e x þ x 2 þ e 2 þ 2 e x þ x 2 Þ þ y 4 ¼ e 4
e 4 2 e 2 x 2 þ x 4 þ y 2 ð2 e 2 þ 2 x 2 Þ þ y 4 ¼ e 4
2 e2 x2 þ x4 þ 2 e2 y2 þ 2x2 y2 þ y4 ¼ 0
)
)
)
2 e 2 x 2 þ 2 e 2 y 2 þ x 4 þ 2 x 2 y 2 þ y 4 ¼ 2 e 2 x 2 þ 2 e 2 y 2 þ ðx 2 þ y 2 Þ 2 ¼ 0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
)
1. Binom: ðx 2 þ y 2 Þ 2
2 e 2 ðx 2 y 2 Þ þ ðx 2 þ y 2 Þ 2 ¼ 0
ðx 2 þ y 2 Þ 2 ¼ a 2 ðx 2 y 2 Þ
)
ðx 2 þ y 2 Þ 2 ¼ 2 e 2 ðx 2 y 2 Þ
)
ðmit a 2 ¼ 2 e 2 Þ
b) Mit Hilfe der Transformationsgleichungen x ¼ r cos j ; y ¼ r sin j und x 2 þ y 2 ¼ r 2 erhalten wir
aus der hergeleiteten Kurvengleichung in kartesischer Form die folgende Darstellung in Polarkoordinaten:
ðx 2 þ y 2 Þ 2 ¼ a 2 ðx 2 y 2 Þ
)
ðr 2 Þ 2 ¼ a 2 ðr 2 cos 2 j r 2 sin 2 jÞ
r 2 r 2 ¼ a 2 r 2 ðcos 2 j sin 2 jÞ
r ¼ a
)
)
r 2 ¼ a 2 ðcos 2 j sin 2 jÞ ¼ a 2 cos ð2 jÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
cos ð2 jÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cos ð2 jÞ
)
ðunter Verwendung der trigonometrischen Beziehung cos ð2 jÞ ¼ cos 2 j sin 2 j ! FSÞ
c) Kurvenverlauf für e2 == 8:
a 2 ¼ 2 e 2 ¼ 2 8 ¼ 16
siehe Bild A-59
)
a ¼ 4
Kurvengleichung in Polarkoordinaten: r ðjÞ ¼ 4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cos ð2 jÞ
Wir müssen die Winkelbereiche von 45 bis 135 und 225 bis 315 ausklammern, da dort cos ð2 jÞ < 0
gilt. Die Kurve ist geschlossen und sowohl zur x-Achse als auch zur y-Achse spiegelsymmetrisch, da die kartesische Kurvengleichung nur gerade Potenzen der Koordinaten x und y enthält (Vorzeichenänderung bei x bzw. y
bewirkt keine nderung der anderen Koordinate). Wir können uns daher bei der Wertetabelle auf den Winkelbereich
0 j 5 beschränken:
Wertetabelle:
j
r
0
7;5
15;0
22;5
30
37;5
45
4
3;93
3;72
3;36
2;83
2;03
0
y
2
1
–4
–3
–2
–1
1
–1
–2
Bild A-59
2
3
4
x
57
B Differentialrechnung
1 Ableitungsregeln
1.1 Produktregel
Wir verwenden die Produktregel in der folgenden Form:
y ¼ uv
)
y 0 ¼ u 0v þ v 0 u
ðu; v : Funktionen von xÞ
Lehrbuch: Band 1, Kapitel IV.2.3
Formelsammlung: Kapitel IV.3.3
B1
y0 ¼ ?
y ¼ ð5 x 3 4 xÞ ðx 2 þ 5 xÞ ;
Die vorliegende Funktion ist ein Produkt aus zwei Faktoren u und v, die jeweils von der Variablen x abhängen:
y ¼ ð5 x 3 4 xÞ ðx 2 þ 5 xÞ ¼ u v
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
u
v
Somit gilt: u ¼ 5 x 3 4 x ;
v ¼ x2 þ 5x
und
u 0 ¼ 15 x 2 4 ;
v0 ¼ 2x þ 5
Die Produktregel liefert dann die gesuchte Ableitung:
y 0 ¼ u 0 v þ v 0 u ¼ ð15 x 2 4Þ ðx 2 þ 5 xÞ þ ð2 x þ 5Þ ð5 x 3 4 xÞ ¼
¼ 15 x 4 þ 75 x 3 4 x 2 20 x þ 10 x 4 8 x 2 þ 25 x 3 20 x ¼ 25 x 4 þ 100 x 3 12 x 2 40 x
Anmerkung: Diese Funktion lässt sich auch ohne Produktregel differenzieren (Klammern ausmultiplizieren, anschließend gliedweise differenzieren).
B2
y ¼ x 5 ln x
ðx > 0Þ;
y0 ¼ ?
Die Funktion ist ein Produkt der beiden Faktorfunktionen u ¼ x 5 und v ¼ ln x :
f
y ¼ x 5 ln x ¼ u v mit
|{z}
u
v
u ¼ x5;
v ¼ ln x
und u 0 ¼ 5 x 4 ;
v0 ¼
1
x
Die Produktregel liefert die gesuchte Ableitung:
y 0 ¼ u 0 v þ v 0 u ¼ 5 x 4 ln x þ
1
x 5 ¼ 5 x 4 ln x þ x 4 ¼ x 4 ð5 ln x þ 1Þ
x
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_2
58
B Differentialrechnung
B3
y ¼ 4 sin x tan x ;
y0 ¼ ?
Wir „zerlegen‘‘ die Funktion wie folgt: y ¼ 4 sin x tan x ¼ 4 ðu vÞ
|ffl{zffl} |ffl{zffl}
u
v
Der konstante Faktor 4 bleibt beim Differenzieren erhalten. Die Produktregel lautet daher in diesem Beispiel wie folgt:
y 0 ¼ 4 ðu 0 v þ v 0 uÞ
mit u ¼ sin x ;
v ¼ tan x
und u 0 ¼ cos x ;
v0 ¼
1
cos 2 x
1
sin x
sin x
sin x ¼ 4 cos x
¼
y ¼ 4 ðu v þ v uÞ ¼ 4 cos x tan x þ
þ
cos x
cos 2 x
cos 2 x
sin x
1
cos 2 x þ 1
4 sin x ðcos 2 x þ 1Þ
¼
¼ 4 sin x þ
¼ 4 sin x 1 þ
¼ 4 sin x
cos 2 x
cos 2 x
cos 2 x
cos 2 x
0
0
0
Anmerkung: Sie können den konstanten Faktor 4 auch in den Faktor u oder v einbeziehen, z. B.:
y ¼ 4 sin x tan x ¼ ð4 sin xÞ tan x
|fflfflfflffl{zfflfflfflffl} |ffl{zffl}
u
v
B4
y ¼ ðcos x sin xÞ e x ;
mit
u ¼ 4 sin x
und v ¼ tan x
y0 ¼ ?
„Zerlegung‘‘ der Funktion in ein Produkt aus zwei Faktorfunktionen u und v:
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
u
u ¼ cos x sin x ;
v ¼ e x und u 0 ¼ sin x cos x ;
f
y ¼ ðcos x sin xÞ e x ¼ u v mit
v
Mit Hilfe der Produktregel erhalten wir dann:
y 0 ¼ u 0 v þ v 0 u ¼ ð sin x cos xÞ e x þ e x ðcos x sin xÞ ¼
¼ ð sin x cos x þ cos x sin xÞ e x ¼ 2 sin x e x
B5
y ¼ 2 e x arcsin x ;
y0 ¼ ?;
y 0 ð0Þ ¼ ?
f
„Zerlegung‘‘ der Funktion in ein Produkt: y ¼ 2 e x arcsin x ¼ 2 ðe x arcsin xÞ ¼ 2 ðu vÞ
u
Der konstante Faktor 2 bleibt beim Differenzieren erhalten. Mit
u ¼ ex ;
v ¼ arcsin x
und
u0 ¼ ex ;
1
v 0 ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 x2
erhalten wir mit Hilfe der Produktregel die folgende Ableitung:
|fflfflfflffl{zfflfflfflffl}
v
v0 ¼ ex
1 Ableitungsregeln
0
59
0
1
e arcsin x þ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi e x
1 x2
0
y ¼ 2 ðu v þ v uÞ ¼ 2
x
!
¼ 2e
x
1
arcsin x þ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 x2
!
y 0 ð0Þ ¼ 2 e0 ðarcsin 0 þ 1Þ ¼ 2 1 ð0 þ 1Þ ¼ 2
B6
y ¼
pffiffiffi
x arctan x ;
y0 ¼ ?
Wir „zerlegen‘‘ die Funktion wie folgt:
pffiffiffi
x arctan x ¼ u v
f
y ¼
u
|fflfflfflfflffl{zfflfflfflfflffl}
mit
u ¼
pffiffiffi
x;
v ¼ arctan x
und
u0 ¼
v
1
pffiffiffi ;
2 x
v0 ¼
1
1 þ x2
Mit Hilfe der Produktregel erhalten wir die gesuchte Ableitung:
pffiffiffi
x
ð1 þ x 2 Þ arctan x þ 2 x
pffiffiffi
1
1
arctan x
þ
x ¼
¼
y ¼ u v þ v u ¼ pffiffiffi arctan x þ
pffiffiffi
pffiffiffi
1 þ x2
1 þ x2
2 x
2 x
2 x ð1 þ x 2 Þ
pffiffiffi
pffiffiffi
Umformungen: Hauptnenner 2 x ð1 þ x 2 Þ bilden, d. h. die Brüche mit ð1 þ x 2 Þ bzw. 2 x erweitern.
0
B7
0
0
y ¼ x 4 e x cosh x ;
y0 ¼ ?
Die vorliegende Funktion ist ein Produkt aus drei Faktorfunktionen u, v und w, die alle von der Variablen x abhängen:
u
u ¼ x ;
4
f
f
y ¼ x 4 e x cosh x ¼ u v w
v
|fflfflffl{zfflfflffl}
w
v ¼ ex ;
w ¼ cosh x
und u 0 ¼ 4 x 3 ;
v0 ¼ ex ;
w 0 ¼ sinh x
Mit Hilfe der Produktregel für drei Faktoren erhalten wir die folgende Ableitung:
y 0 ¼ u 0 v w þ u v 0 w þ u v w 0 ¼ 4 x 3 e x cosh x þ x 4 e x cosh x þ x 4 e x sinh x ¼
¼ x 3 e x ð4 cosh x þ x cosh x þ x sinh xÞ
B8
y ¼ 5 ðx 2 1Þ ð2 x þ 1Þ sin x ;
y0 ¼ ?
Wir könnten diese Funktion mit Hilfe der Produktregel für drei Faktoren differenzieren:
y ¼ 5 ðx 2 1Þ ð2 x þ 1Þ sin x ¼ 5 ðu v wÞ
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl} |ffl{zffl}
u
v
w
Günstiger ist es jedoch, die Funktion zunächst zu vereinfachen (ausmultiplizieren der ersten beiden Faktoren):
y ¼ 5 ðx 2 1Þ ð2 x þ 1Þ sin x ¼ 5 ð2 x 3 þ x 2 2 x 1Þ sin x
60
B Differentialrechnung
Wir haben jetzt ein Produkt aus nur zwei Faktorfunktionen (der konstante Faktor 5 bleibt beim Differenzieren erhalten):
y ¼ 5 ð2 x 3 þ x 2 2 x 1Þ sin x ¼ 5 ðu vÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |ffl{zffl}
u
v
u ¼ 2x3 þ x2 2x 1;
v ¼ sin x
und
u 0 ¼ 6 x 2 þ 2 x 2 ¼ 2 ð3 x 2 þ x 1Þ ;
Die Produktregel für zwei Faktoren liefert jetzt die gewünschte Ableitung:
y 0 ¼ 5 ðu 0 v þ v 0 uÞ ¼ 5 ½ 2 ð3 x 2 þ x 1Þ sin x þ cos x ð2 x 3 þ x 2 2 x 1Þ
1.2 Quotientenregel
Wir verwenden die Quotientenregel in der folgenden Form:
y ¼
u
v
)
y0 ¼
u0 v v0 u
v2
ðu; v : Funktionen von xÞ
Lehrbuch: Band 1, Kapitel IV.2.4
Formelsammlung: Kapitel IV.3.4
B9
y ¼
x2
;
1 x2
y0 ¼ ?
Die vorliegende Funktion ist der Quotient aus u ¼ x 2 und v ¼ 1 x 2 :
y ¼
x2
u
¼
2
v
1x
mit
u ¼ x 2;
v ¼ 1 x2
und u 0 ¼ 2 x;
v 0 ¼ 2 x
Die Quotientenregel liefert dann:
y0 ¼
B10
2 x ð1 x 2 Þ ð 2 xÞ x 2
u0v v0u
2x 2x3 þ 2x3
2x
¼
¼
¼
2
2
2
v
ð1 x 2 Þ
ð1 x 2 Þ
ð1 x 2 Þ 2
y ¼
cos x
;
x2
y0 ¼ ?;
y 0 ðpÞ ¼ ?
Die vorliegende Funktion ist der Quotient der Funktionen u ¼ cos x und v ¼ x 2 :
y ¼
cos x
u
¼
x2
v
mit
u ¼ cos x ;
v ¼ x2
und
u 0 ¼ sin x ;
v0 ¼ 2x
Die Quotientenregel führt zu der folgenden Ableitung:
y0 ¼
¼
ðsin xÞ x 2 2 x cos x
u0v v0u
x 2 sin x 2 x cos x
¼
¼
¼
v2
x4
x4
ðx sin x 2 cos xÞ x
x3 x
¼
x sin x 2 cos x
x sin x þ 2 cos x
¼
x3
x3
v 0 ¼ cos x
1 Ableitungsregeln
61
Ableitung an der Stelle x ¼ p : y 0 ðpÞ ¼
B11
ln x
y ¼ pffiffiffi
x
p 0 þ 2 ð1Þ
p sin p þ 2 cos p
2
2
¼
¼
¼
3
p
p3
p3
p3
y0 ¼ ?
ðx > 0Þ;
Zähler u und Nenner v dieses Quotienten sind elementare Funktionen mit bekannten Ableitungen:
u ¼ ln x ;
v ¼
pffiffiffi
x
)
u0 ¼
1
;
x
v0 ¼
1
pffiffiffi
2 x
Die gesuchte Ableitung erhalten wir mit Hilfe der Quotientenregel:
1 pffiffiffi
1
1
1
2 ln x
x pffiffiffi ln x
pffiffiffi pffiffiffi ln x
pffiffiffi
x
2 x
x
2 x
2 x
u vv u
2 ln x 1
2 ln x
0
y ¼
¼
¼
¼
¼
¼
pffiffiffi
pffiffiffi
pffiffiffi 2
2
x
x
x
v
2 x
2x x
ð xÞ
1
pffiffiffi
Umformungen: Brüche im Zähler zunächst auf den Hauptnenner 2 x bringen, dann den Zählerbruch mit dem Kehrwert des Nennerbruches multiplizieren.
0
B12
0
y ¼
2 cos x sin x
;
cos x þ 2 sin x
y0 ¼ ?;
y 0 ðp=2Þ ¼ ?
Die vorliegende Funktion ist der Quotient aus den Funktionen u ¼ 2 cos x sin x und v ¼ cos x þ 2 sin x :
y ¼
2 cos x sin x
u
¼
cos x þ 2 sin x
v
Somit gilt:
u ¼ 2 cos x sin x ;
v ¼ cos x þ 2 sin x und u 0 ¼ 2 sin x cos x ;
v 0 ¼ sin x þ 2 cos x
Bei genauerer Betrachtung der Ableitungen u 0 und v 0 fällt auf, dass u 0 ¼ v und v 0 ¼ u ist:
u 0 ¼ 2 sin x cos x ¼ ð2 sin x þ cos xÞ ¼ ðcos x þ 2 sin xÞ ¼ v
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
v
v 0 ¼ sin x þ 2 cos x ¼ 2 cos x sin x ¼ u
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
u
Die Quotientenregel lautet dann unter Berücksichtigung dieser Beziehungen wie folgt:
ð vÞ v u u
ðv 2 þ u 2 Þ
u0v v0u
v 2 u 2
u2 þ v2
y ¼
¼
¼
¼
¼
v2
v2
v2
v2
v2
0
Für den Zähler dieser Bruches erhalten wir unter Verwendung des „trigonometrischen Pythagoras‘‘ sin 2 x þ cos 2 x ¼ 1:
u 2 þ v 2 ¼ ð2 cos x sin xÞ 2 þ ðcos x þ 2 sin xÞ 2 ¼
¼ 4 cos 2 x 4 cos x sin x þ sin 2 x þ cos 2 x þ 4 cos x sin x þ 4 sin 2 x ¼
¼ 5 cos 2 x þ 5 sin 2 x ¼ 5 ðcos 2 x þ sin 2 xÞ ¼ 5
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
62
B Differentialrechnung
Die gesuchte Ableitung lautet damit:
y0 ¼
u2 þ v2
5
¼
v2
ðcos x þ 2 sin xÞ 2
y 0 ðp=2Þ ¼
B13
y ¼
y ¼
5
½ cos ðp=2Þ þ 2 sin ðp=2Þ
x3 2x þ 5
;
x2 4x þ 1
x3 2x þ 5
u
¼
2
v
x 4x þ 1
2
¼
5
ð0 þ 2 1Þ
2
¼
5
4
y0 ¼ ?
mit u ¼ x 3 2 x þ 5 ;
u0 ¼ 3x2 2;
v ¼ x2 4x þ 1;
v0 ¼ 2x 4
Die Quotientenregel liefert die gesuchte Ableitung:
y0 ¼
¼
¼
¼
ð3 x 2 2Þ ðx 2 4 x þ 1Þ ð2 x 4Þ ðx 3 2 x þ 5Þ
u0v v0u
¼
¼
v2
ðx 2 4 x þ 1Þ 2
3 x 4 12 x 3 þ 3 x 2 2 x 2 þ 8 x 2 ð2 x 4 4 x 2 þ 10 x 4 x 3 þ 8 x 20Þ
ðx 2 4 x þ 1Þ 2
3 x 4 12 x 3 þ x 2 þ 8 x 2 ð2 x 4 4 x 3 4 x 2 þ 18 x 20Þ
ðx 2 4 x þ 1Þ 2
3 x 4 12 x 3 þ x 2 þ 8 x 2 2 x 4 þ 4 x 3 þ 4 x 2 18 x þ 20
ðx 2 4 x þ 1Þ
2
¼
¼
¼
x 4 8 x 3 þ 5 x 2 10 x þ 18
ðx 2 4 x þ 1Þ 2
1.3 Kettenregel
Die Kettenregel ist eine Substitutionsregel. Mit Hilfe einer geeigneten Substitution u ¼ uðxÞ wird die vorgegebene
Funktion y ¼ f ðxÞ zunächst in eine elementar differenzierbare Funktion y ¼ F ðuÞ der „Hilfsvariablen‘‘ u übergeführt. Dann gilt (Kettenregel):
y0 ¼
dy
dy du
¼
dx
du dx
oder
y 0 ¼ F 0 ðuÞ u 0 ðxÞ
(,,äußere Ableitung mal innere Ableitung‘‘)
Anschließend wird rücksubstituiert. In einigen Fällen müssen mehrere Substitutionen nacheinander durchgeführt werden, bis man auf eine elementar differenzierbare Funktion stößt.
Lehrbuch: Band 1, Kapitel IV.2.5
Formelsammlung: Kapitel IV.3.5
B14
y ¼ ð4 x 2 2 x þ 1Þ 5 ;
y0 ¼ ?
1 Ableitungsregeln
63
Durch die Substitution u ¼ 4 x 2 2 x þ 1 wird die vorliegende Funktion in eine elementare Potenzfunktion übergeführt:
y ¼ ð4 x 2 2 x þ 1Þ 5
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
u
!
y ¼ u5
u ¼ 4x2 2x þ 1
mit
y ¼ u 5 ist dabei die äußere, u ¼ 4 x 2 2 x þ 1 die innere Funktion. Beide Funktionen sind elementar differenzierbar. Mit Hilfe der Kettenregel erhalten wir zunächst:
y0 ¼
dy
dy du
¼
¼ 5 u 4 ð8 x 2Þ ¼ 5 u 4 2 ð4 x 1Þ ¼ 10 ð4 x 1Þ u 4
dx
du dx
Rücksubstitution ðu ¼ 4 x 2 2 x þ 1Þ führt zur gesuchten Ableitung:
y 0 ¼ 10 ð4 x 1Þ u 4 ¼ 10 ð4 x 1Þ ð4 x 2 2 x þ 1Þ 4
Anmerkung: Die Funktion lässt sich auch ohne Kettenregel differenzieren (Binom auflösen, dann gliedweise differenzieren). Dieser Weg ist jedoch aufwendig und daher nicht zu empfehlen (überzeugen Sie sich selbst).
B15
y ¼ ln
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4x x2 ;
y0 ¼ ?
Wir vereinfachen die Funktion zunächst wie folgt:
y ¼ ln
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
4 x x 2 ¼ ln ð4 x x 2 Þ 1=2 ¼
ln ð4 x x 2 Þ
2
(Rechenregel : ln a n ¼ n ln aÞ
Mit Hilfe der Substitution u ¼ 4 x x 2 zerlegen wir die Funktion in ihre elementaren Bestandteile:
y ¼
1
ln ð4 x x 2 Þ
2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
u
!
y ¼
1
ln u
2
mit
u ¼ 4x x2
(äußere und innere Funktion). Die Kettenregel liefert dann (nach erfolgter Rücksubstitution):
y0 ¼
B16
2 ð2 xÞ
dy
dy du
1 1
4 2x
2x
¼
¼
¼
ð4 2 xÞ ¼
¼
dx
du dx
2 u
2u
2 ð4 x x 2 Þ
4x x2
1
y ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
a þ bx2
ða; b : KonstantenÞ ;
y0 ¼ ?
Die Funktion lässt sich auch als Potenz darstellen:
1
1
y ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
¼ ða þ b x 2 Þ 1=3
1=3
3
2
ða þ b x Þ
a þ bx2
Durch die Substitution u ¼ a þ b x 2 wird die Funktion in zwei elementare Funktionen zerlegt:
äußere Funktion: y ¼ u 1=3 ;
innere Funktion: u ¼ a þ b x 2
Die Kettenregel führt dann zu dem folgenden Ergebnis (zunächst wird y nach u, dann u nach x differenziert):
y0 ¼
dy
dy du
1
2
¼
¼ u 4=3 ð2 b xÞ ¼ b x u 4=3
dx
du dx
3
3
64
B Differentialrechnung
Durch Rücksubstitution ðu ¼ a þ b x 2 Þ folgt schließlich:
y0 ¼
B17
2
2
x
2bx
¼
b x ða þ b x 2 Þ 4=3 ¼ b
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4=3
3
3
3
ða þ b x 2 Þ
3 ða þ b x 2 Þ 4
y ¼ 4 e cos x sin x ;
y0 ¼ ?;
y 0 ðpÞ ¼ ?
Durch die Substitution u ¼ cos x sin x führen wir die vorliegende Exponentialfunktion auf die elementare e-Funktion zurück:
y ¼ 4 e cos x sin x
!
y ¼ 4 eu
mit
u ¼ cos x sin x
Beide Funktionen (äußere und innere) sind elementar differenzierbar. Die Kettenregel liefert dann (äußere Ableitung
mal innere Ableitung):
y0 ¼
dy
dy du
¼
¼ 4 e u ð sin x cos xÞ ¼ 4 ðsin x þ cos xÞ e u
dx
du dx
Durch Rücksubstitution ðu ¼ cos x sin xÞ erhalten wir die gewünschte Ableitung:
y 0 ¼ 4 ðsin x þ cos xÞ e cos x sin x
y 0 ðpÞ ¼ 4 ðsin p þ cos pÞ e cos p sin p ¼ 4 ð0 1Þ e 1 0 ¼ 4 e 1 ¼ 1;4715
B18
y ¼ 4
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
x2 þ x ;
y0 ¼ ?;
y 0 ðx ¼ 1Þ ¼ ?
pffiffiffi
Mit der Substitution u ¼ x 2 þ x (Wurzelradikand) erreichen wir unser Ziel: die Funktion wird in zwei elementar
differenzierbare Bestandteile (äußere und innere Funktion) zerlegt:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
y ¼ 4 x2 þ x
! y ¼ 4 u mit u ¼ x 2 þ x
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
Wir wenden die Kettenregel an (äußere Ableitung mal innere Ableitung)
pffiffiffi
pffiffiffi
pffiffiffi
4x x þ 1
4x x þ 1
4x x þ 1
dy
dy du
1
1
4
y ¼
¼
¼ 4 pffiffiffi 2 x þ pffiffiffi ¼ pffiffiffi
¼ pffiffiffi pffiffiffi ¼
pffiffiffi
pffiffiffiffiffiffi
dx
du dx
2 x
x u
xu
4 x
2 u
u
p
ffiffi
ffi
Rücksubstitution ðu ¼ x 2 þ x Þ liefert das gewünschte Ergebnis:
pffiffiffi
pffiffiffi
pffiffiffi
4x x þ 1
4x x þ 1
4x x þ 1
0
y ¼
¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffi
pffiffiffi
pffiffiffi
xu
x ðx 2 þ x Þ
x3 þ x x
0
Ableitung an der Stelle x ¼ 1:
pffiffiffi
pffiffiffi
41 1þ1
4þ1
5
5 2
5 pffiffiffi
0
y ðx ¼ 1Þ ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffi ¼ pffiffiffi ¼ pffiffiffi pffiffiffi ¼
2 ¼ 3;5355
pffiffiffi
2
2
2
2 2
3
1 þ1 1
1 Ableitungsregeln
B19
65
Zeigen Sie: y ¼ ½ f ðxÞ n
)
y 0 ¼ n ½ f ðxÞ n 1 f 0 ðxÞ
Wenden Sie diese Ableitungsformel auf die Funktion y ¼ sin 4 x an.
Mit der Substitution u ¼ f ðxÞ wird die gegebene Funktion auf die elementar differenzierbare Potenzfunktion y ¼ u n
zurückgeführt:
y ¼ ½ f ðxÞ n
|ffl{zffl}
u
!
y ¼ un
u ¼ f ðxÞ
mit
y ¼ u n ist dabei die äußere, u ¼ f ðxÞ die innere Funktion. Mit Hilfe der Kettenregel erhalten wir:
y0 ¼
dy
dy du
¼
¼ n u n 1 f 0 ðxÞ
dx
du dx
Rücksubstitution u ¼ f ðxÞ führt dann zu dem gewünschten Ergebnis:
y 0 ¼ n u n 1 f 0 ðxÞ ¼ n ½ f ðxÞ n 1 f 0 ðxÞ
Anwendungsbeispiel:
B20
y ¼ sin 4 x ¼ ð sin x Þ 4
|ffl{zffl}
u
y ¼ cos ð5 x 2 3 x þ 1Þ ;
)
y 0 ¼ 4 ðsin xÞ 3 cos x ¼ 4 sin 3 x cos x
y0 ¼ ?
Mit der Substitution u ¼ 5 x 2 3 x þ 1 erreichen wir unser Ziel: die vorliegende Funktion wird in die elementare
Kosinusfunktion übergeführt:
y ¼ cos ð5 x 2 3 x þ 1Þ
!
y ¼ cos u mit
u ¼ 5x2 3x þ 1
Dabei ist y ¼ cos u die äußere und u ¼ 5 x 2 3 x þ 1 die innere Funktion. Die Kettenregel liefert dann (erst
wird y nach u, dann u nach x differenziert):
y0 ¼
dy
dy du
¼
¼ ð sin uÞ ð10 x 3Þ ¼ ð10 x 3Þ sin u
dx
du dx
Die Rücksubstitution u ¼ 5 x 2 3 x þ 1 führt zur gesuchten Ableitung:
y 0 ¼ ð10 x 3Þ sin u ¼ ð10 x 3Þ sin ð5 x 2 3 x þ 1Þ
B21
y ¼ ln ½ cos ð1 x 2 Þ ;
y0 ¼ ?
Diese Aufgabe unterscheidet sich von den bisherigen dadurch, dass sie nicht mit Hilfe einer einzigen Substitution
lösbar ist. Wir benötigen insgesamt zwei Substitutionen, die wir nacheinander von innen nach außen ausführen, um
unser Ziel zu erreichen:
1. Substitution:
mit
y ¼ ln ½ cos u ¼ ln v mit v ¼ cos u
|ffl{zffl}
v
y ¼ ln v mit v ¼ cos u und u ¼ 1 x 2
2. Substitution:
Somit gilt:
y ¼ ln ½ cos ð1 x 2 Þ ¼ ln ½ cos u
|fflfflfflffl{zfflfflfflffl}
u
u ¼ 1 x2
66
B Differentialrechnung
Alle drei Bestandteile (Funktionen) sind elementar differenzierbar. Die Kettenregel liefert dann (erst wird y nach v,
dann v nach u und schließlich u nach x differenziert):
y0 ¼
dy
dy dv du
1
2 x sin u
¼
¼
ð sin uÞ ð 2 xÞ ¼
dx
dv du dx
v
v
Rücksubstitution ðv ! u ! xÞ liefert das gewünschte Ergebnis (mit sin u=cos u ¼ tan u):
y0 ¼
B22
2 x sin u
2 x sin u
¼
¼ 2 x tan u ¼ 2 x tan ð1 x 2 Þ
v
cos u
y ¼ A eax þ B ebxþc
2
ðA; B; a; b; c : KonstantenÞ ;
y0 ¼ ?;
y 0 ðx ¼ 0Þ ¼ ?
Es wird gliedweise differenziert. Die e-Funktionen werden dabei durch die Substitutionen u ¼ a x 2
v ¼ b x þ c in elementare Funktionen übergeführt:
1: Summand:
y 1 ¼ A eax
2: Summand:
y 2 ¼ B ebxþc
2
)
y1 ¼ A eu
mit
u ¼ ax2
)
y2 ¼ B ev
mit
v ¼ bx þ c
bzw.
Die Kettenregel liefert dann:
y 01 ¼
d y1
d y1 d u
¼ A e u ð 2 a xÞ ¼ 2 a A x e u
¼
dx
du dx
y 02 ¼
d y2
d y2 d v
¼ B e v ð bÞ ¼ b B e v
¼
dx
dv dx
Nach Rücksubstitution erhalten wir schließlich die gewünschte Ableitung. Sie lautet:
y 0 ¼ y 01 þ y 02 ¼ 2 a A x e u b B e v ¼ 2 a A x e a x b B e b x þ c
2
Ableitung an der Stelle x ¼ 0:
B23
y ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cos ð5 x 2 Þ ;
y 0 ðx ¼ 0Þ ¼ 2 a A 0 e 0 b B e c ¼ b B e c
y0 ¼ ?
Mit Hilfe von zwei Substitutionen gelingt es, die vorliegende Funktion in ihre elementaren Bestandteile zu zerlegen
(wir substituieren von innen nach außen):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi pffiffiffiffiffiffiffiffiffiffiffi
1. Substitution: y ¼ cos ð5 x 2 Þ ¼ cos u mit u ¼ 5 x 2
|ffl{zffl}
u
pffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
2. Substitution: y ¼ cos u ¼ v mit v ¼ cos u
|ffl{zffl}
v
pffiffiffi
Aus y ¼ v mit v ¼ cos u und u ¼ 5 x 2 folgt dann mit Hilfe der Kettenregel:
y0 ¼
dy
dy dv du
1
5 x sin u
¼ pffiffiffi ð sin uÞ 10 x ¼
¼
pffiffiffi
dx
dv du dx
2 v
v
1 Ableitungsregeln
67
Rücksubstitution in der Reihenfolge v ! u ! x führt zur gesuchten Ableitung:
y0 ¼
5 x sin ð5 x 2 Þ
5 x sin u
5 x sin u
¼
¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
v
cos u
cos ð5 x 2 Þ
B24
y 0 ð1Þ ¼ ?
y ¼ ln ða x þ e x Þ 4 ;
ða > 0 : KonstanteÞ
Zunächst vereinfachen wir die Funktion unter Verwendung der logarithmischen Rechenregel ln c n ¼ n ln c:
y ¼ ln ða x þ e x Þ 4 ¼ 4 ln ða x þ e x Þ
Die Substitution u ¼ a x þ e x führt dann zum Ziel:
y ¼ 4 ln ða x þ e x Þ
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
u
!
y ¼ 4 ln u mit
u ¼ ax þ ex
Anwendung der Kettenregel und Rücksubstitution:
y0 ¼
4 ða þ e x Þ
4 ða þ e x Þ
dy
dy du
1
¼ 4
ða þ e x Þ ¼
¼
¼
u
u
ax þ ex
dx
du dx
)
y 0 ð1Þ ¼
4 ða þ e 1 Þ
a þ e1
¼ 4
1.4 Kombinationen mehrerer Ableitungsregeln
Sie benötigen beim Lösen der folgenden Aufgaben stets mehrere Ableitungsregeln, meist die Produkt- oder Quotientenregel in Verbindung mit der Kettenregel.
Lehrbuch: Band 1, Kapitel IV.2.3 bis 2.6
Formelsammlung: Kapitel IV.3.3 bis 3.5
B25
y ¼ e x cos x ;
y0 ¼ ?
Wir substituieren den Exponenten, setzen also t ¼ x cos x und erhalten die elementare e-Funktion:
y ¼ e x cos x
!
y ¼ et
mit
t ¼ x cos x
Die Kettenregel führt zunächst zu:
y0 ¼
dy
dy dt
dt
¼
¼ et
dx
dt dx
dx
Die innere Ableitung, d. h. die Ableitung von t ¼ x cos x nach x bilden wir mit Hilfe der Produktregel:
f
t ¼ x cos x ¼ u v mit
|ffl{zffl}
u
v
u ¼ x;
v ¼ cos x
und u 0 ¼ 1 ;
v 0 ¼ sin x
dt
¼ u 0 v þ v 0 u ¼ 1 cos x þ ð sin xÞ x ¼ cos x x sin x
dx
Die gesuchte Ableitung lautet damit (nach erfolgter Rücksubstitution):
y0 ¼ et
dt
¼ e t ðcos x x sin xÞ ¼ ðcos x x sin xÞ e t ¼ ðcos x x sin xÞ e x cos x
dx
68
B Differentialrechnung
B26
y ðtÞ ¼ A e d t sin ðw t þ jÞ
ðA; d; w; j : KonstantenÞ ;
y 0 ðt ¼ 0Þ ¼ ?
A bleibt als konstanter Faktor beim Differenzieren erhalten, das Produkt aus Exponential- und Sinusfunktion wird
nach der Produktregel differenziert:
y ¼ A e d t sin ðw t þ jÞ ¼ A ðu vÞ
|ffl{zffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
u
v
y 0 ¼ A ðu 0 v þ v 0 uÞ
)
Die dabei benötigten Ableitungen der Faktorfunktionen u ¼ e d t und v ¼ sin ðw t þ jÞ bilden wir wie folgt mit
Hilfe der Kettenregel:
u ¼ e dt ¼ e z
mit
z ¼ dt
)
u0 ¼
v ¼ sin ðw t þ jÞ ¼ sin z mit z ¼ w t þ j
du
du dz
¼
¼ e z ð dÞ ¼ d e d t
dt
dz dt
)
v0 ¼
dv
dv dz
¼
¼ ðcos zÞ w ¼ w cos ðw t þ jÞ
dt
dz dt
Die gesuchte Ableitung lautet damit:
y 0 ¼ A ðu 0 v þ v 0 uÞ ¼ A ½ d e d t sin ðw t þ jÞ þ w cos ðw t þ jÞ e d t ¼
¼ A e d t ½ d sin ðw t þ jÞ þ w cos ðw t þ jÞ
f
y 0 ðt ¼ 0Þ ¼ A e 0 ½ d sin j þ w cos j ¼ A ð d sin j þ w cos jÞ
1
B27
y ¼ e x ln ðx 3 þ 1Þ ;
2
y0 ¼ ?
Es liegt ein Produkt aus zwei Faktoren u und v vor:
y ¼ e x ln ðx 3 þ 1Þ ¼ u v
|ffl{zffl} |fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
u
v
2
Wir benötigen daher die Produktregel, beim Differenzieren der beiden Faktorfunktionen u ¼ e x und v ¼ ln ðx 3 þ 1Þ
jeweils auch die Kettenregel:
2
u ¼ e x ¼ e t
2
mit
t ¼ x 2
v ¼ ln ðx 3 þ 1Þ ¼ ln z
mit
)
u0 ¼
z ¼ x3 þ 1
du
du dt
2
¼
¼ e t ð 2 xÞ ¼ 2 x e x
dx
dt dx
)
v0 ¼
dv
dv dz
1
3x2
3x2
¼
¼
3x2 ¼
¼
dx
dz dx
z
z
x3 þ 1
Unter Berücksichtigung dieser Ableitungen liefert dann die Produktregel das gewünschte Ergebnis:
3x2
3x2
2
2
2
e x ¼ 2 x ln ðx 3 þ 1Þ þ
e x
y 0 ¼ u 0 v þ v 0 u ¼ 2 x e x ln ðx 3 þ 1Þ þ
x3 þ 1
x3 þ 1
B28
y ¼ arctan
1þx
;
1x
y 0 ð3Þ ¼ ?
1 Ableitungsregeln
69
1þx
und zerlegen damit die vorliegende Funktion in eine elementare äußere und
1x
eine (gebrochenrationale) innere Funktion:
1þx
1þx
! y ¼ arctan z mit z ¼
y ¼ arctan
1x
1x
dy
1
¼
. Die Ableitung der inneren FunkDie äußere Funktion y ¼ arctan z besitzt bekanntlich die Ableitung
dz
1 þ z2
tion erhalten wir mit Hilfe der Quotientenregel:
Wir wählen die Substitution z ¼
z ¼
1þx
u
¼
1x
v
u ¼ 1 þ x;
mit
v ¼ 1x
und u 0 ¼ 1 ;
v0 ¼ 1
1 ð1 xÞ ð 1Þ ð1 þ xÞ
dz
u0v v0u
1x þ1þx
2
¼
¼
¼
¼
2
2
dx
v2
ð1 xÞ
ð1 xÞ
ð1 xÞ 2
Mit der Kettenregel folgt dann:
y0 ¼
dy
dy dz
1
2
2
¼
¼
¼
2
2
dx
dz dx
2
1þz
ð1 xÞ
ð1 þ z Þ ð1 xÞ 2
1þx
führt schließlich zur gesuchten Ableitung (wir bringen zunächst den im Nenner auftreten1x
den Ausdruck 1 þ z 2 auf eine möglichst einfache Form):
Rücksubstitution z ¼
ð1 þ xÞ 2
ð1 xÞ 2 þ ð1 þ xÞ 2
1þx 2
¼ 1þ
¼
¼
1x
ð1 xÞ 2
ð1 xÞ 2
1 þ z2 ¼ 1 þ
¼
1 2x þ x2 þ 1 þ 2x þ x2
ð1 xÞ 2
¼
2 þ 2x2
ð1 xÞ 2
¼
2 ð1 þ x 2 Þ
ð1 xÞ 2
Umformungen: Der erste Summand wird mit ð1 xÞ 2 erweitert.
y0 ¼
2
ð1 þ
z 2Þ
ð1 xÞ
2
¼
2
2 ð1 þ x Þ
2
ð1 xÞ
B29
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a þ x2 þ 5
y ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5 a þ x2
2
¼
ð1 xÞ 2
ða : KonstanteÞ ;
1
1þ
x2
)
y 0 ð3Þ ¼
1
1þ
32
¼
1
10
y0 ¼ ?
Zähler und Nenner despBruches
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi enthalten den gleichen Wurzelausdruck. Wir versuchen daher, diese Aufgabe mit Hilfe
der Substitution z ¼ a þ x 2 zu lösen:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
zþ5
a þ x2 þ 5
! y ¼
mit z ¼ a þ x 2
y ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5z
5 a þ x2
Die äußere Ableitung erhalten wir mit der Quotientenregel, die innere Ableitung über die Kettenregel:
ußere Ableitung:
y ¼
zþ5
u
¼
5z
v
mit u ¼ z þ 5 ;
v ¼ 5z
und
u0 ¼ 1;
1 ð5 zÞ ð1Þ ðz þ 5Þ
dy
u0 v v0 u
5zþzþ5
10
¼
¼
¼
¼
2
2
2
dz
v
ð5 zÞ
ð5 zÞ
ð5 zÞ 2
v0 ¼ 1
70
B Differentialrechnung
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffi
a þ x2 ¼ t
|fflfflfflffl{zfflfflfflffl}
t
z ¼
Innere Ableitung:
t ¼ a þ x2
mit
dz
dz dt
1
x
x
¼
¼ pffi 2 x ¼ pffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx
dt dx
t
2 t
a þ x2
ðnach erfolgter Rücksubstitution t ¼ a þ x 2 Þ
Die Ableitung der Ausgangsfunktion erhalten wir mit Hilfe der Kettenregel (erst y nach z differenzieren, dann z
nach x) mit anschließender Rücksubstitution:
y0 ¼
dy
dy dz
10
x
10 x
¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
2
dx
dz dx
ð5 zÞ
ð5 zÞ 2 a þ x 2
a þ x2
B30
y ¼
ln ðx 2 þ 1Þ
y0 ¼ ?
;
x3
10 x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5 a þ x2 a þ x2
Die vorliegende Funktion ist ein Quotient und lässt sich daher nach der Quotientenregel differenzieren:
y ¼
ln ðx 2 þ 1Þ
x3
¼
u
v
mit
u ¼ ln ðx 2 þ 1Þ ;
v ¼ x3
und
u0 ¼ ?;
v0 ¼ 3x2
Die noch fehlende Ableitung der Zählerfunktion u ¼ ln ðx 2 þ 1Þ erhalten wir mit Hilfe der Kettenregel:
u ¼ ln ðx 2 þ 1Þ ¼ ln t
|fflfflfflfflffl{zfflfflfflfflffl}
t
t ¼ x2 þ 1
mit
)
u0 ¼
du
du dt
1
2x
2x
¼
¼
2x ¼
¼
2
dx
dt dx
t
t
x þ1
(nach erfolgter Rücksubstitution t ¼ x 2 þ 1) . Somit gilt zusammenfassend:
u ¼ ln ðx 2 þ 1Þ ;
v ¼ x3
und
u0 ¼
2x
;
þ1
x2
v0 ¼ 3x2
Die Quotientenregel liefert dann die gewünschte Ableitung:
y0 ¼
0
0
u vv u
¼
v2
2x
x 3 3 x 2 ln ðx 2 þ 1Þ
þ1
x2
x6
¼
2x4
3 x 2 ln ðx 2 þ 1Þ
þ1
x2
x6
¼
2 x 4 3 x 2 ðx 2 þ 1Þ ln ðx 2 þ 1Þ
x2 þ 1
¼
¼
6
x 2 ½ 2 x 2 3 ðx 2 þ 1Þ ln ðx 2 þ 1Þ
x
1
¼
x 2 ½ 2 x 2 3 ðx 2 þ 1Þ ln ðx 2 þ 1Þ
ðx 2 þ 1Þ x 4 x 2
¼
x2
þ1
1
¼
x6
2 x 2 3 ðx 2 þ 1Þ ln ðx 2 þ 1Þ
ðx 2 þ 1Þ x 4
Umformungen: Im Zähler des Gesamtbruches den Hauptnenner x 2 þ 1 bilden, den 2. Summand also mit x 2 þ 1
erweitern ! Nenner x 6 als Bruch schreiben: x 6 ¼ x 6 =1 ! im Zähler den gemeinsamen Faktor x 2 ausklammern
! Zählerbruch mit dem Kehrwert des Nennerbruches multiplizieren ! gemeinsamen Faktor x 2 kürzen.
B31
y ¼
x sin x þ cos x
;
x cos x sin x
y0 ¼ ?
1 Ableitungsregeln
71
Der Quotient aus u ¼ x sin x þ cos x und v ¼ x cos x sin x wird nach der Quotientenregel differenziert.
Die dabei benötigten Ableitungen u 0 und v 0 erhalten wir wie folgt mit Hilfe der Summen- und Produktregel:
0
0
f
u ¼ x sin x þ cos x ¼ a b þ cos x
Zähler:
|ffl{zffl}
a
b
mit
a ¼ x;
und a 0 ¼ 1 ;
b ¼ sin x
b 0 ¼ cos x
0
u ¼ a b þ b a sin x ¼ 1 sin x þ ðcos xÞ x sin x ¼ x cos x
v ¼ x cos x sin x ¼ a b sin x
f
Nenner:
|ffl{zffl}
a
b
mit a ¼ x ;
b ¼ cos x
und
a0 ¼ 1;
b 0 ¼ sin x
v 0 ¼ a 0 b þ b 0 a cos x ¼ 1 cos x þ ðsin xÞ x cos x ¼ x sin x
Somit gilt zusammenfassend:
u ¼ x sin x þ cos x ;
v ¼ x cos x sin x
und u 0 ¼ x cos x ;
v 0 ¼ x sin x
Die Quotientenregel liefert dann die gesuchte Ableitung:
y0 ¼
¼
¼
x cos x ðx cos x sin xÞ ð x sin xÞ ðx sin x þ cos xÞ
u0v v0u
¼
¼
2
v
ðx cos x sin xÞ 2
x 2 cos 2 x x cos x sin x þ x 2 sin 2 x þ x sin x cos x
ðx cos x sin xÞ 2
x 2 ðcos 2 x þ sin 2 xÞ
ðx cos x sin xÞ 2
¼
x2 1
ðx cos x sin xÞ 2
¼
¼
x 2 cos 2 x þ x 2 sin 2 x
ðx cos x sin xÞ 2
¼
x2
ðx cos x sin xÞ 2
(unter Verwendung des „trigonometrischen Pythagoras‘‘ cos 2 x þ sin 2 x ¼ 1).
B32
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 a2
y ¼
ða : KonstanteÞ ;
a2 þ x2
y0 ¼ ?
Wir substituieren den Radikand der Wurzel und führen damit die gegebene Funktion auf eine elementare Wurzelfunktion zurück:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffi
x2 a2
x2 a2
y ¼
! y ¼ z mit z ¼
a2 þ x2
a2 þ x2
|fflfflfflfflffl{zfflfflfflfflffl}
z
Die gesuchte Ableitung erhalten
pffiffi wir dann mit Hilfe der Kettenregel (erst y nach z differenzieren, dann z nach x).
Die „äußere‘‘ Funktion y ¼ z ist elementar differenzierbar:
0
1
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffi
2
2
B
C
dy
1
1
1
a þx
BRechenregel: r1ffiffiffi ¼ bC
¼ pffiffi ¼
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
@
2
2
a
dz
2
aA
2 z
x a
x2 a2
2
b
a2 þ x2
Die Ableitung der gebrochenrationalen „inneren‘‘ Funktion erfolgt mit der Quotientenregel:
z ¼
x2 a2
u
¼
2
2
v
a þx
mit
u ¼ x2 a2;
v ¼ a2 þ x2
und u 0 ¼ 2 x ;
v0 ¼ 2x
2 x ða 2 þ x 2 Þ 2 x ðx 2 a 2 Þ
dz
u0 v v0 u
2a2 x þ 2x3 2x3 þ 2a2 x
4a2 x
¼
¼
¼
¼ z0 ¼
dx
v2
ða 2 þ x 2 Þ 2
ða 2 þ x 2 Þ 2
ða 2 þ x 2 Þ 2
72
B Differentialrechnung
Mit der Kettenregel folgt dann:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2
4a2 x
a2 þ x2
2a2 x ¼
¼
x 2 a 2 ða 2 þ x 2 Þ 2
ðx 2 a 2 Þ ða 2 þ x 2 Þ 4
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
1
2
¼ 2a x
¼ 2 a 2 x qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
3
2
2
2
2
ðx a Þ ða þ x Þ
ðx 2 a 2 Þ ða 2 þ x 2 Þ ða 2 þ x 2 Þ 2
dy
dy dz
1
y0 ¼
¼
¼
dx
dz dx
2
¼
2a2 x
2a2 x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ x 4 a 4
ða 2 þ x 2 Þ ðx 2 a 2 Þ ða 2 þ x 2 Þ
Umformungen: ða 2 þ x 2 Þ 2 mit ða 2 þ x 2 Þ 4 unter die Wurzel bringen ! dann durch a 2 þ x 2 kürzen ! aus
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffi
pffiffiffi
dem verbliebenen Faktor ða 2 þ x 2 Þ 3 die Teilwurzel ziehen (Rechenregel: b 3 ¼ b 2 b ¼ b b ) ! Wurzelradikand vereinfachen (3. Binom):
ðx 2 a 2 Þ ða 2 þ x 2 Þ ¼ ðx 2 a 2 Þ ðx 2 þ a2 Þ ¼ x 4 a 4
1.5 Logarithmische Ableitung
Die Funktion wird zunächst logarithmiert, dann differenziert.
Lehrbuch: Band 1, Kapitel IV.2.7
Formelsammlung: Kapitel IV.3.6
B33
y ¼
2þ
1
x
x
;
y0 ¼ ?
1. Schritt: Beide Seiten logarithmieren:
1 x
1
ln y ¼ ln 2 þ
¼ x ln 2 þ
x
x
ðRechenregel : ln a n ¼ n ln aÞ
2. Schritt: Beide Seiten nach x differenzieren:
Linke Seite:
z ¼ ln y
y ¼ f ðxÞ
mit
Da y eine von x abhängige Funktion ist, muss nach der Kettenregel differenziert werden:
y0
dz
dz dy
1
¼
¼
y0 ¼
dx
dy dx
y
y
1
¼ u v mit
Rechte Seite: z ¼ x ln 2 þ
x
f
z0 ¼
u
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
u ¼ x;
v ¼ ln
1
2þ
und
x
u0 ¼ 1;
v0 ¼ ?
v
Die Funktion z ¼ uv wird mit Hilfe der Produktregel differenziert. Vorher müssen wir noch die Ableitung v 0 des
rechten Faktors bestimmen. Dies geschieht wie folgt nach der Kettenregel:
1
¼ ln ð2 þ x 1 Þ ¼ ln t mit t ¼ 2 þ x 1
v ¼ ln 2 þ
x
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
t
d
v
d
v
d
t
1
x 2
1
1
1
v0 ¼
¼
¼
¼
¼
¼
ð x 2Þ ¼
2
1
2
2
t
dx
dt dx
t
t x
ð2 þ x Þ x
2x þ x
1 Ableitungsregeln
73
Damit gilt: u ¼ x ;
v ¼ ln
2þ
1
x
und
u0 ¼ 1;
v0 ¼
1
1
¼
2x2 þ x
x ð2 x þ 1Þ
Wir erhalten schließlich mit Hilfe der Produktregel die folgende Ableitung für die rechte Seite der logarithmierten
Funktionsgleichung:
1
1
1
1
x ¼ ln 2 þ
z 0 ¼ u 0 v þ v 0 u ¼ 1 ln 2 þ
x ð2 x þ 1Þ
x
x
2x þ 1
Somit gilt:
y0
1
1
¼ ln 2 þ
)
y
x
2x þ 1
1
1
1
1
1 x
0
y ¼ ln 2 þ
y ¼ ¼ ln 2 þ
2þ
x
2x þ 1
x
2x þ 1
x
z0 ¼
B34
y ¼ x cos x
ðx > 0Þ ;
y0 ¼ ?
Die vorliegende Funktion ist weder eine Potenz- noch eine Exponentialfunktion, da Basis (x) und Exponent (cos x)
von der Variablen x abhängen. Wir können daher weder die Potenzregel noch die Ableitungsregel für Exponentialfunktionen anwenden.
1. Schritt: Durch Logarithmieren beider Seiten lässt sich der Potenzausdruck der rechten Seite in ein Produkt verwandeln, das dann mit Hilfe der Produktregel differenziert werden kann:
ln y ¼ ln x cos x ¼ cos x ln x
ðRechenregel : ln a n ¼ n ln aÞ
2. Schritt: Beide Seiten werden nach x differenziert. Beim Differenzieren der linken Seite ist zu beachten, dass y
eine von x abhängige Funktion ist ð y ¼ f ðxÞÞ. Der Term z ¼ ln y muss daher nach der Kettenregel differenziert
werden (zunächst z nach y differenzieren, dann y nach x):
z ¼ ln y
mit
y ¼ f ðxÞ
)
z0 ¼
y0
dz
dz dy
1
¼
¼
y0 ¼
y
dx
dy dx
y
Die Ableitung der rechten Seite erfolgt mit Hilfe der Produktregel:
z ¼ cos x ln x ¼ u v
|ffl{zffl} |{z}
u
v
mit u ¼ cos x ;
z 0 ¼ u 0 v þ v 0 u ¼ sin x ln x þ
v ¼ ln x
und
u 0 ¼ sin x ;
v0 ¼
1
x
1
x sin x ln x þ cos x
cos x ¼
x
x
Damit gilt:
z0 ¼
y0
x sin x ln x þ cos x
¼
x
y
y0 ¼
x sin x ln x þ cos x
x sin x ln x þ cos x
y ¼
x cos x ¼
x
x
)
¼ ð x sin x ln x þ cos xÞ x 1 x cos x ¼ ð x sin x ln x þ cos xÞ x ðcos x 1Þ
B35
y ¼ e x cos x ;
y0 ¼ ?;
y 0 ðpÞ ¼ ?
74
B Differentialrechnung
1. Schritt: Beide Seiten logarithmieren:
ln y ¼ ln e x cos x ¼ ðx cos xÞ ln e ¼ x cos x
ðRechenregel : ln e n ¼ nÞ
2. Schritt: Jetzt beide Seiten der logarithmierten Gleichung nach x differenzieren:
Linke Seite: Kettenregel anwenden, da y von x abhängt:
z ¼ ln y
mit
y ¼ f ðxÞ
z0 ¼
)
y0
dz
dz dy
1
¼
y0 ¼
¼
dx
dy dx
y
y
Rechte Seite: Produktregel anwenden:
f
z ¼ x cos x ¼ u v mit
|fflffl{zfflffl}
u
v
u ¼ x;
v ¼ cos x
und u 0 ¼ 1 ;
v 0 ¼ sin x
z 0 ¼ u 0 v þ v 0 u ¼ 1 cos x þ ð sin xÞ x ¼ cos x x sin x
Somit ist:
y0
¼ z 0 ¼ cos x x sin x
y
)
y 0 ¼ ðcos x x sin xÞ y ¼ ðcos x x sin xÞ e x cos x
y 0 ðpÞ ¼ ðcos p p sin pÞ e p cos p ¼ ð 1 p 0Þ e p ð 1Þ ¼ e p
Anmerkung: Diese Aufgabe lässt sich auch mit Hilfe der Ketten- und Produktregel lösen (siehe Aufgabe B 25).
B36
y 2 ðsin xÞ ln x ¼ 0 ðx > 0Þ;
y0 ¼ ?
Zunächst stellen wir die Gleichung wie folgt um: y 2 ¼ ðsin xÞ ln x
1. Schritt: Beide Seiten werden logarithmiert:
ln y 2 ¼ ln ðsin xÞ ln x
)
2 ln y ¼ ln x ln ðsin xÞ
ðRechenregel : ln a n ¼ n ln aÞ
2. Schritt: Jetzt werden beide Seiten der logarithmierten Gleichung nach x differenziert:
Linke Seite: Kettenregel anwenden, denn y ist eine von x abhängige Funktion:
z ¼ 2 ln y
mit
y ¼ f ðxÞ
z0 ¼
)
2y0
dz
dz dy
1
¼
y0 ¼
¼ 2
dx
dy dx
y
y
Rechte Seite: Produktregel anwenden:
z ¼ ln x ln ðsin xÞ ¼ u v mit
|{z} |fflfflfflfflffl{zfflfflfflfflffl}
u
v
u ¼ ln x ;
v ¼ ln ðsin xÞ
und
u0 ¼
1
;
x
v0 ¼ ?
Die noch unbekannte Ableitung v 0 des rechten Faktors erhalten wir mit der Kettenregel:
v ¼ ln ðsin xÞ ¼ ln t
|fflfflffl{zfflfflffl}
t
mit
t ¼ sin x
Die Produktregel liefert dann mit u ¼ ln x ;
der rechten Seite:
z0 ¼ u0 v þ v0 u ¼
)
v0 ¼
dv
dv dt
1
cos x
cos x
¼
¼
cos x ¼
¼
¼ cot x
dx
dt dx
t
t
sin x
v ¼ ln ðsin xÞ
und
u0 ¼
1
;
x
v 0 ¼ cot x die gesuchte Ableitung
ln ðsin xÞ þ x cot x ln x
1
ln ðsin xÞ þ cot x ln x ¼
x
x
1 Ableitungsregeln
75
Somit erhalten wir für y 0 den folgenden Ausdruck:
ln ðsin xÞ þ x cot x ln x
2y0
¼
x
y
)
y0 ¼
ln ðsin xÞ þ x cot x ln x
2x
y
y 0 hängt noch von x und y ab. Durch Auflösen der vorgegebenen Funktionsgleichung nach y folgt:
y ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðsin xÞ ln x
Diesen Ausdruck setzen wir in die Ableitungsformel ein und erhalten y 0 in Abhängigkeit von x:
y0 ¼
ln ðsin xÞ þ x cot x ln x
2x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðsin xÞ ln x
1.6 Implizite Differentiation
Die in der impliziten Form Fðx; yÞ ¼ 0 vorliegende Funktion wird gliedweise mit Hilfe der bekannten Ableitungsregeln nach der Variablen x differenziert. Dabei ist zu beachten, dass y eine Funktion von x ist. Terme mit der
Variablen y müssen daher nach der Kettenregel differenziert werden. Die (differenzierte) Gleichung wird anschließend
nach y 0 aufgelöst. Die Ableitung hängt dabei von x und y ab.
Lehrbuch: Band 1, Kapitel IV.2.9
Formelsammlung: Kapitel IV.3.8
B37
y0 ¼ ?
x3 þ y3 3xy ¼ 0;
Es wird gliedweise nach x differenziert.
1. Summand:
z1 ¼ x 3
)
z 01 ¼ 3 x 2
2. Summand:
z2 ¼ y 3
mit
y ¼ f ðxÞ
z 2 ¼ y 3 ist die äußere, y ¼ f ðxÞ die innere Funktion. Die Kettenregel liefert dann (zunächst y 3 nach y, dann y
nach x differenzieren):
z 02 ¼ 3 y 2 y 0
u
v ¼ y und u 0 ¼ 1 ;
v0 ¼ 1 y0 ¼ y0
f
z 3 ¼ 3 x y ¼ 3 ð x y Þ ¼ 3 ðu vÞ mit u ¼ x ;
f
3. Summand:
v
Mit der Produktregel erhalten wir (der rechte Faktor v ¼ y wurde nach der Kettenregel differenziert):
z 03 ¼ 3 ðu 0 v þ v 0 uÞ ¼ 3 ð1 y þ y 0 xÞ ¼ 3 ð y þ x y 0 Þ
Die gliedweise Differentiation der impliziten Funktion führt damit zu dem folgenden Ergebnis:
z 01 þ z 02 þ z 03 ¼ 3 x 2 þ 3 y 2 y 0 3 ð y þ x y 0 Þ ¼ 0
j: 3
)
x 2 þ y 2 y 0 ð y þ x y 0 Þ ¼ x 2 þ y 2 y 0 y x y 0 ¼ ð y 2 xÞ y 0 þ x 2 y ¼ 0
ð y 2 xÞ y 0 ¼ y x 2
)
y0 ¼
y x2
y2 x
¼
x2 y
ðy x 2 Þ ð1Þ
¼
ðy 2 xÞ ð1Þ
x y2
)
76
B Differentialrechnung
B38
y0 ¼ ?;
ðx þ 2Þ x 2 þ ðx 2Þ y 2 ¼ 0 ;
y 0 ðx ¼ 1; y ¼
pffiffiffi
3Þ ¼ ?
Wir bringen die Funktion zunächst auf eine für das implizite Differenzieren günstigere Form:
x 3 þ 2 x 2 þ ðx 2Þ y 2 ¼ z 1 þ z 2 ¼ 0
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
z2
z1
Es wird gliedweise nach x differenziert, der zweite Summand z 2 dabei nach der Produktregel (in Verbindung mit der
Kettenregel).
z1 ¼ x 3 þ 2 x 2
)
2. Summand:
z 2 ¼ ðx 2Þ y 2 ¼ u v
|fflfflffl{zfflfflffl}
u
v
z 01 ¼ 3 x 2 þ 4 x
u ¼ x 2;
mit
v ¼ y2
und
u0 ¼ 1;
v0 ¼ 2y y0
f
1. Summand:
Die Ableitung des rechten Faktors v ¼ y 2 erfolgte nach der Kettenregel, da y von x abhängt (zunächst y 2 nach y
differenzieren, dann y nach x). Somit gilt:
z 02 ¼ u 0 v þ v 0 u ¼ 1 y 2 þ 2 y y 0 ðx 2Þ ¼ y 2 þ 2 ðx 2Þ y y 0
Die gliedweise Differentiation der vorgegebenen impliziten Funktion führt schließlich zu dem folgenden Ergebnis (wir
lösen die Gleichung noch nach y 0 auf):
z 01 þ z 02 ¼ 3 x 2 þ 4 x þ y 2 þ 2 ðx 2Þ y y 0 ¼ 0
)
2 ðx 2Þ y y 0 ¼ 3 x 2 4 x y 2 ¼ ð3 x 2 þ 4 x þ y 2 Þ
)
y0 ¼
3x2 þ 4x þ y2
2 ðx 2Þ y
pffiffiffi
pffiffiffi
3þ4þ3
10
5
5 3
5 pffiffiffi
y ðx ¼ 1; y ¼ 3 Þ ¼
3 ¼ 2;8868
pffiffiffi ¼
pffiffiffi ¼ pffiffiffi ¼ pffiffiffi pffiffiffi ¼
3
3
2 ð1 2Þ 3
2 3
3 3
0
B39
ð y xÞ 3 þ sin 2 y ¼ 0 ;
y0 ¼ ?
Die Funktionsgleichung wird gliedweise nach x differenziert, beide Summanden dabei jeweils nach der Kettenregel:
1. Summand:
z 1 ¼ ð y xÞ 3 ¼ u 3
|fflfflfflffl{zfflfflfflffl}
u
mit
u ¼ yx
und y ¼ f ðxÞ
z 01 ¼ 3 u 2 u 0 ¼ 3 u 2 ð1 y 0 1Þ ¼ 3 ð y xÞ 2 ð y 0 1Þ
Bei der Ableitung der inneren Funktion u ¼ y x musste der Summand y nach der Kettenregel differenziert werden (zunächst y nach y, dann y nach x differenzieren).
2. Summand:
z 2 ¼ sin 2 y ¼ ð sin y Þ 2 ¼ u 2
|ffl{zffl}
u
mit
u ¼ sin y
und
y ¼ f ðxÞ
Die Kettenregel (für zwei Substitutionen) führt zu:
z 02 ¼
dz2
dz2 du dy
¼ 2 u ðcos yÞ y 0 ¼ 2 sin y cos y y 0 ¼ sin ð2 yÞ y 0
¼
dx
du dy dx
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
sin ð2 yÞ
(unter Verwendung der trigonometrischen Beziehung sin ð2 yÞ ¼ 2 sin y cos y). Damit erhalten wir:
1 Ableitungsregeln
77
z 01 þ z 02 ¼ 3 ð y xÞ 2 ð y 0 1Þ þ sin ð2 yÞ y 0 ¼ 3 ð y xÞ 2 y 0 3 ð y xÞ 2 þ sin ð2 yÞ y 0 ¼ 0
½ 3 ð y xÞ 2 þ sin ð2 yÞ y 0 ¼ 3 ð y xÞ 2
)
y0 ¼
3 ð y xÞ 2
3 ð y xÞ 2 þ sin ð2 yÞ
Bestimmen Sie die Tangentensteigung der Kardioide y 2 þ 2 x ðx 2 þ y 2 Þ ðx 2 þ y 2 Þ 2 ¼ 0 :
Wie groß ist die Steigung im Kurvenpunkt P ¼ ð0; 1Þ?
B40
Es wird gliedweise nach der Variablen x differenziert.
1. Summand:
z1 ¼ y 2
y ¼ f ðxÞ
mit
Differenziert wird nach der Kettenregel, da y von x abhängt (zuerst y 2 nach y differenzieren, dann y nach x):
z 01 ¼
d z1
d z1 d y
¼ 2y y0
¼
dx
dy dx
z 2 ¼ 2 x ðx 2 þ y 2 Þ ¼ 2 ðu vÞ mit u ¼ x ;
f
2. Summand:
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
u
v ¼ x 2 þ y 2 und u 0 ¼ 1 ;
v0 ¼ 2x þ 2y y0
v
Differenziert wird nach der Produktregel, wobei der Summand y 2 im rechten Faktor v nach der Kettenregel zu
differenzieren ist:
z 02 ¼ 2 ðu 0 v þ v 0 uÞ ¼ 2 ½ 1ðx 2 þ y 2 Þ þ ð2 x þ 2 y y 0 Þ x ¼ 2 ðx 2 þ y 2 þ 2 x 2 þ 2 x y y 0 Þ ¼
¼ 2 ð3 x 2 þ y 2 þ 2 x y y 0 Þ
3. Summand:
2
z 3 ¼ ðx 2 þ y 2 Þ ¼ u 2
|fflfflfflfflffl{zfflfflfflfflffl}
u
mit
u ¼ x2 þ y2
Die Kettenregel liefert dann:
z 03 ¼
d z3
d z3 d u
¼ 2 u u 0 ¼ 2 u ð2 x þ 2 y y 0 Þ ¼ 2 ðx 2 þ y 2 Þ 2 ðx þ y y 0 Þ ¼
¼
dx
du dx
¼ 4 ðx 2 þ y 2 Þ ðx þ y y 0 Þ
Bei der Ableitung der inneren Funktion u ¼ x 2 þ y 2 wurde dabei berücksichtigt, dass der Summand y 2 nach der
Kettenregel zu differenzieren ist ( y hängt ja von x ab). Damit erhalten wir das folgende Ergebnis:
z 01 þ z 02 þ z 03 ¼ 2 y y 0 þ 2 ð3 x 2 þ y 2 þ 2 x y y 0 Þ 4 ðx 2 þ y 2 Þ ðx þ y y 0 Þ ¼ 0
j: 2
y y 0 þ 3 x 2 þ y 2 þ 2 x y y 0 2 ðx 2 þ y 2 Þ ðx þ y y 0 Þ ¼
¼ y y 0 þ 3 x 2 þ y 2 þ 2 x y y 0 2 ðx 2 þ y 2 Þ x 2 ðx 2 þ y 2 Þ y y 0 ¼
¼ ½ y þ 2 x y 2 ðx 2 þ y 2 Þ y y 0 þ 3 x 2 þ y 2 2 ðx 2 þ y 2 Þ x ¼ 0
Wir lösen diese Gleichung noch nach y 0 auf und erhalten:
y0 ¼
2 ðx 2 þ y 2 Þ x 3 x 2 y 2
y þ 2 x y 2 ðx 2 þ y 2 Þ y
¼
2 x ðx 2 þ y 2 Þ 3 x 2 y 2
y ½ 1 þ 2 x 2 ðx 2 þ y 2 Þ
Steigung der Kurventangente in P ¼ ð0; 1Þ: y 0 ðPÞ ¼
0 ð0 þ 1Þ 0 1
1 ½ 1 þ 0 2 ð0 þ 1Þ
¼
1
1 ð 1Þ
¼ 1
78
B Differentialrechnung
1.7 Differenzieren in der Parameterform
Die Funktion bzw. Kurve liegt in der Parameterform x ¼ xðtÞ, y ¼ yðtÞ vor (t: Parameter). Die ersten beiden Ableitungen werden wie folgt gebildet:
y0 ¼
y_
;
x_
y 00 ¼
x_ y€ y_ x€
Die Striche kennzeichnen die Ableitungen nach der Variablen x,
die Punkte die Ableitungen nach dem Parameter t.
x_ 3
Lehrbuch: Band 1, Kapitel IV.2.12
Formelsammlung: Kapitel IV.3.9
Bestimmen Sie den Anstieg der Kurve mit der Parameterdarstellung x ¼ 4 cos 3 t þ 3 cos t,
y ¼ 2 sin ð2 tÞ þ 3 sin t, 0 t 2 p für den Parameterwert t ¼ p=2.
B41
Beide Gleichungen werden gliedweise und mit Hilfe der Kettenregel wie folgt nach dem Parameter t differenziert:
x ¼ 4 cos 3 t þ 3 cos t ¼ 4 ð cos t Þ 3 þ 3 cos t ¼ 4 u 3 þ 3 cos t
|ffl{zffl}
u
mit
u ¼ cos t
x_ ¼ 12 u 2 ð sin tÞ 3 sin t ¼ 12 cos 2 t sin t 3 sin t ¼ 3 sin t ð4 cos 2 t þ 1Þ
y ¼ 2 sin ð2 tÞ þ 3 sin t ¼ 2 sin v þ 3 sin t
|{z}
v
mit v ¼ 2 t
y_ ¼ 2 cos v 2 þ 3 cos t ¼ 4 cos ð2 tÞ þ 3 cos t
Der Kurvenanstieg in Abhängigkeit vom Kurvenparameter t beträgt dann:
y0 ¼
4 cos ð2 tÞ þ 3 cos t
y_
¼
x_
3 sin t ð4 cos 2 t þ 1Þ
Somit gilt an der Stelle t ¼ p=2:
y 0 ðt ¼ p=2Þ ¼
B42
x ¼
4 cos p þ 3 cos ðp=2Þ
3 sin ðp=2Þ ð4
t2 1
;
t
y ¼ ln t ;
cos 2
ðp=2Þ þ 1Þ
t > 0;
¼
y 0 ðtÞ ¼ ? ;
4 ð 1Þ þ 3 0
þ 1Þ
¼
3 1 ð4
02
y 00 ðtÞ ¼ ? ;
y 0 ð2Þ ¼ ? ;
4
4
¼
3
3
Wir bilden zunächst die benötigten Ableitungen x_ , x€, y_ und y€ :
x ¼
t2 1
1
¼ t
¼ t t 1
t
t
y ¼ ln t
)
y_ ¼
1
¼ t 1;
t
)
x_ ¼ 1 þ t 2 ;
x€ ¼ 2 t 3
y€ ¼ t 2
Damit erhalten wir für y 0 und y 00 , jeweils in Abhängigkeit vom Parameter t:
y0 ¼
y_
t 1
t 1 t 2
t
¼
¼
¼
2
2
2
2
x_
t þ1
1þt
ð1 þ t Þ t
(der Bruch wurde mit t 2 erweitert)
y 00 ð2Þ ¼ ?
1 Ableitungsregeln
y 00 ¼
¼
79
x_ y€ y_ x€
x_ 3
¼
t 4 t 2
ðt 2 þ 1Þ 3
ð1 þ t 2 Þ ð t 2 Þ t 1 ð 2 t 3 Þ
¼
¼
ð1 þ t 2 Þ 3
ðt 4 t 2 Þ t 6
ðt 2 þ 1Þ 3
¼
t 2 t 4 þ 2 t 4
t 4 t 2
¼
3
3 ¼
1
t2 þ 1
1þ
t2
t2
t2 t4
ðt 2 þ 1Þ 3
t6
y 0 ð2Þ ¼
2
22
þ1
¼
2
;
5
y 00 ð2Þ ¼
ð2 2 2 4 Þ
ð2 2
þ
1Þ 3
¼
4 16
12
¼
53
125
bringen ! Zähler mit dem Kehrwert des Nenners
Umformungen: Brüche im Nenner auf den Hauptnenner t 2
multiplizieren ! Zähler ausmultiplizieren.
B43
Gegeben ist die folgende Parameterform einer Kurve:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x ¼ 2 sin t þ 1 ; y ¼ 2 cos 2 t ; 0 t p
Bestimmen Sie den Kurvenanstieg in Abhängigkeit vom Parameter t. Wie groß ist die Steigung der
Kurventangente für den Parameterwert t ¼ p=2?
Beide Parametergleichungen werden nach der Kettenregel differenziert:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
x ¼ 2 sin t þ 1 ¼ u mit u ¼ 2 sin t þ 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
u
x_ ¼
dx
dx du
1
cos t
cos t
¼
¼ pffiffiffi 2 cos t ¼ pffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dt
du dt
2 u
u
2 sin t þ 1
y ¼ 2 cos 2 t ¼ 2 ð cos t Þ 2 ¼ 2 v 2
|ffl{zffl}
v
y_ ¼
mit
v ¼ cos t
dy
dy dv
¼ 4 v ð sin tÞ ¼ 4 v sin t ¼ 4 cos t sin t
¼
dt
dv dt
Kurvenanstieg in Abhängigkeit vom Parameter t:
y_
4 cos t sin t
y ¼
¼
¼ 4 cos t sin t
x_
cos t
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 sin t þ 1
0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 sin t þ 1
¼ 4 sin t 2 sin t þ 1
cos t
An der Stelle t ¼ p=2 gilt:
y 0 ðt ¼ p=2Þ ¼ 4 sin ðp=2Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
2 sin ðp=2Þ þ 1 ¼ 4 1 2 1 þ 1 ¼ 4 3
Welchen Anstieg besitzt die Kurve mit der Parameterdarstellung
B44
x ¼ cos t sin ð2 tÞ ;
y ¼ 2 cos 2 t þ sin ð3 tÞ
in Abhängigkeit vom (reellen) Parameter t ?
Bestimmen Sie die Steigung der Kurventangente für den Parameterwert t ¼ p .
Wie lautet die Gleichung der dortigen Tangente?
80
B Differentialrechnung
Beim Differenzieren der beiden Parametergleichungen benötigen wir neben der Summenregel jeweils die Kettenregel:
x ¼ cos t sin ð2 tÞ ¼ cos t sin u
|{z}
u
mit u ¼ 2 t
x_ ¼ sin t ðcos uÞ 2 ¼ sin t 2 cos ð2 tÞ
y ¼ 2 cos 2 t þ sin ð3 tÞ ¼ 2 ð cos t Þ 2 þ sin ð3 tÞ ¼ 2 v 2 þ sin w
|ffl{zffl}
|{z}
v
w
mit
v ¼ cos t
und
w ¼ 3t
y_ ¼ 4 v ðsin tÞ þ ðcos wÞ 3 ¼ 4 v sin t þ 3 cos w ¼ 4 cos t sin t þ 3 cos ð3 tÞ ¼
¼ 2 ½ 2 cos t sin t þ 3 cos ð3 tÞ ¼ 2 sin ð2 tÞ þ 3 cos ð3 tÞ
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
sin ð2 tÞ
(unter Verwendung der trigonometrischen Beziehung sin ð2 tÞ ¼ 2 sin t cos t)
Der Anstieg der Kurve hängt damit wie folgt vom Kurvenparameter t ab:
y0 ¼
2 sin ð2 tÞ þ 3 cos ð3 tÞ
2 sin ð2 tÞ 3 cos ð3 tÞ
y_
¼
¼
x_
sin t 2 cos ð2 tÞ
sin t þ 2 cos ð2 tÞ
Somit gilt an der Stelle t ¼ p :
y 0 ðt ¼ pÞ ¼
2 sin ð2 pÞ 3 cos ð3 pÞ
sin p þ 2 cos ð2 pÞ
¼
2 0 3 ð 1Þ
0þ21
¼
Tangentenberührungspunkt P ¼ ðx 0 ; y 0 Þ:
x 0 ¼ x ðt ¼ pÞ ¼ cos p sin ð2 pÞ ¼ 1 0 ¼ 1
y 0 ¼ y ðt ¼ pÞ ¼ 2 cos 2 p þ sin ð3 pÞ ¼ 2 ð 1Þ 2 þ 0 ¼ 2
Tangentensteigung: m ¼ y 0 ðt ¼ pÞ ¼
3
2
)
P ¼ ð 1 ; 2Þ
3
2
Tangentengleichung:
y y0
¼ m
x x0
)
y2
3
¼
x þ1
2
)
y2 ¼
3
3
3
ðx þ 1Þ ¼
x þ
2
2
2
)
y ¼
3
7
x þ
2
2
1.8 Differenzieren in Polarkoordinaten
Sie müssen die in Polarkoordinaten r, j dargestellte Kurve mit der Gleichung r ¼ r ðjÞ zunächst in die Parameterform bringen:
x ðjÞ ¼ r ðjÞ cos j ;
y ðjÞ ¼ r ðjÞ sin j
ðParameter : Winkel jÞ
Die Ableitungen der winkelabhängigen kartesischen Koordinaten x ðjÞ und y ðjÞ erhalten Sie dann wie in Abschnitt 1.7
beschrieben, sie sind ebenfalls Funktionen des Winkelparameters j.
Lehrbuch: Band 1, Kapitel IV.2.13
Formelsammlung: Kapitel IV.3.10
Bestimmen Sie den Anstieg der Kurve
B45
r ¼ 1 þ e j,
j 0
in Abhängigkeit vom Winkel j. Welche Steigung m besitzt die Kurventangente für j ¼ p ?
1 Ableitungsregeln
81
Die Kurve wird zunächst in die Parameterform gebracht:
x ¼ r cos j ¼ ð1 þ e j Þ cos j ;
y ¼ r sin j ¼ ð1 þ e j Þ sin j
Die benötigten Ableitungen x_ und y_ nach dem Winkelparameter j erhalten wir mit der Produktregel:
x ¼ ð1 þ e j Þ cos j ¼ u v mit
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflffl{zfflffl}
u
v
u ¼ 1 þ ej;
v ¼ cos j und
u_ ¼ e j ;
v_ ¼ sin j
x_ ¼ u_ v þ v_ u ¼ e j cos j sin j ð1 þ e j Þ ¼ e j cos j ð1 þ e j Þ sin j
y ¼ ð1 þ e j Þ sin j ¼ u v
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |ffl{zffl}
u
v
mit u ¼ 1 þ e j ;
v ¼ sin j
u_ ¼ e j ;
und
v_ ¼ cos j
y_ ¼ u_ v þ v_ u ¼ e j sin j þ cos j ð1 þ e j Þ ¼ e j sin j þ ð1 þ e j Þ cos j
Steigung der Kurventangente in Abhängigkeit vom Winkel j:
e j sin j þ ð1 þ e j Þ cos j
y_
y ¼
¼
x_
e j cos j ð1 þ e j Þ sin j
0
Dividiert man die Summanden in Zähler und Nenner jeweils durch cos j und beachtet dabei die trigonometrische
sin j
, so lässt sich die Steigungsformel auch wie folgt schreiben:
Beziehung tan j ¼
cos j
y0 ¼
e j sin j þ ð1 þ e j Þ cos j
e j cos j ð1 þ e j Þ sin j
¼
e j tan j þ 1 þ e j
e j ð1 þ e j Þ tan j
Steigung der Tangente für j ¼ p :
m ¼ y 0 ðt ¼ pÞ ¼
B46
r ¼
e p tan p þ 1 þ e p
e p ð1 þ e p Þ tan p
sin 2 j
;
cos j
¼
p
p
< j <
2
2
ep 0 þ 1 þ ep
e p ð1 þ e p Þ 0
¼
1 þ ep
¼ 1,0432
ep
(„Zissoide“)
Bestimmen Sie die Tangentensteigung dieser Kurve in Abhängigkeit vom Winkel j.
Wir stellen die Kurve zunächst in der Parameterform dar (mit dem Winkel j als Kurvenparameter):
x ¼ r cos j ¼
sin 2 j
cos j ¼ sin 2 j ;
cos j
y ¼ r sin j ¼
sin 2 j
sin 3 j
sin j ¼
cos j
cos j
Die benötigten Ableitungen x_ und y_ erhalten wir wie folgt:
x ¼ sin 2 j ¼ ðsin j Þ 2 ¼ u 2
|ffl{zffl}
u
mit
u ¼ sin j
Die Kettenregel liefert dann (nach erfolgter Rücksubstitution):
x_ ¼
dx
dx du
¼
¼ 2 u cos j ¼ 2 sin j cos j
dj
du dj
Die zweite Parametergleichung wird mit Hilfe der Quotientenregel differenziert:
y ¼
sin 3 j
ðsin jÞ 3
u
¼
¼
cos j
cos j
v
mit u ¼ ðsin jÞ 3 ;
v ¼ cos j
und
u_ ¼ ? ;
v_ ¼ sin j
82
B Differentialrechnung
Die noch unbekannte Ableitung von u ¼ ðsin jÞ 3 erhalten wir mit der Kettenregel:
u ¼ ðsin j Þ 3 ¼ t 3
|ffl{zffl}
t
mit t ¼ sin j
u_ ¼
)
du
du dt
¼
¼ 3 t 2 cos j ¼ 3 sin 2 j cos j
dj
dt dj
Die Quotientenregel liefert dann mit
u ¼ ðsin jÞ 3 ¼ sin 3 j ;
v ¼ cos j und u_ ¼ 3 sin 2 j cos j ;
v_ ¼ sin j
die gesuchte Ableitung y_ :
y_ ¼
¼
3 sin 2 j cos j cos j ð sin jÞ sin 3 j
3 sin 2 j cos 2 j þ sin 4 j
u_ v v_ u
¼
¼
¼
cos 2 j
cos 2 j
v2
sin 2 j ð3 cos 2 j þ sin 2 jÞ
cos 2 j
¼
sin 2 j ð3 cos 2 j þ 1 cos 2 jÞ
cos 2 j
¼
sin 2 j ð2 cos 2 j þ 1Þ
cos 2 j
(unter Verwendung der Formel sin 2 j þ cos 2 j ¼ 1). Die Steigungsformel lautet damit:
sin 2 j ð2 cos 2 j þ 1Þ
y0 ¼
¼
y_
¼
x_
cos 2 j
¼
2 sin j cos j
sin 2 j ð2 cos 2 j þ 1Þ
2 sin j cos 3 j
¼
sin 2 j ð2 cos 2 j þ 1Þ
cos 2
j
sin j sin j ð2 cos 2 j þ 1Þ
2 sin j cos 3 j
1
¼
2 sin j cos j
¼
sin j ð2 cos 2 j þ 1Þ
2 cos 3 j
Umformungen: Zählerbruch mit dem Kehrwert des Nennerbruches multiplizieren, dann den gemeinsamen Faktor
sin j kürzen.
Welche Steigung hat die Tangente an die Kurve mit der Gleichung
B47
r ¼
1
;
2þj
0 j 2p
im Schnittpunkt mit der negativen x-Achse? Wie lautet die Gleichung dieser Tangente?
Darstellung der Kurve in der Parameterform mit dem Winkelparameter j:
x ¼ r cos j ¼
cos j
1
;
cos j ¼
2þj
2þj
y ¼ r sin j ¼
sin j
1
sin j ¼
2þj
2þj
Beide Parametergleichungen werden mit Hilfe der Quotientenregel nach j differenziert:
x ¼
cos j
u
¼
2þj
v
x_ ¼
sin j ð2 þ jÞ 1 cos j
ð2 þ jÞ sin j cos j
u_ v v_ u
¼
¼
2
2
v
ð2 þ jÞ
ð2 þ jÞ 2
y ¼
sin j
u
¼
v
2þj
y_ ¼
cos j ð2 þ jÞ 1 sin j
ð2 þ jÞ cos j sin j
u_ v v_ u
¼
¼
v2
ð2 þ jÞ 2
ð2 þ jÞ 2
mit
mit
u ¼ cos j ;
u ¼ sin j ;
v ¼ 2þj
und u_ ¼ sin j ;
v ¼ 2 þ j und
u_ ¼ cos j ;
v_ ¼ 1
v_ ¼ 1
2 Anwendungen der Differentialrechnung
83
Die Steigung der Kurventangente berechnet sich damit wie folgt:
ð2 þ jÞ cos j sin j
y0 ¼
ð2 þ jÞ cos j sin j
ð2 þ jÞ 2
ð2 þ jÞ 2
y_
¼
¼
¼
x_
ð2 þ jÞ sin j cos j
ð2 þ jÞ sin j cos j
ð2 þ jÞ 2
ð2 þ jÞ 2
¼
ð2 þ jÞ cos j sin j
ð2 þ jÞ sin j cos j
¼
sin j ð2 þ jÞ cos j
ð2 þ jÞ sin j þ cos j
¼
tan j ð2 þ jÞ
ð2 þ jÞ tan j þ 1
Umformungen: Zählerbruch mit dem Kehrwert des Nennerbruches multiplizieren ! gemeinsamen Faktor ð2 þ jÞ 2
kürzen ! Bruch mit 1 erweitern ! alle Summanden in Zähler und Nenner durch cos j dividieren ! trigonometrische Beziehung tan j ¼ sin j=cos j beachten.
Steigung der Kurventangente für den Winkel j ¼ p (Schnittstelle mit der negativen x -Achse):
y 0 ðj ¼ pÞ ¼
tan p ð2 þ pÞ
ð2 þ pÞ tan p þ 1
¼
0 ð2 þ pÞ
ð2 þ pÞ 0 þ 1
¼
ð2 þ pÞ
¼ ð2 þ pÞ ¼ 5,1416
1
Tangentenberührungspunkt P ¼ ðx 0 ; y 0 Þ ðwegen j ¼ p liegt dieser Punkt auf der negativen x-AchseÞ:
j ¼ p
)
r ðj ¼ pÞ ¼
1
¼ 0;1945
2þp
x 0 ¼ r ðj ¼ pÞ ¼ 0;1945 ;
y0 ¼ 0
)
P ¼ ð 0;1945 ; 0Þ
Tangentengleichung ðmit der Steigerung m ¼ y 0 ðj ¼ pÞ ¼ 5;1416Þ:
y y0
¼ m
x x0
)
y0
¼ 5;1416
x þ 0;1945
)
y ¼ 5;1416 ðx þ 0;1945Þ ¼ 5;1416 x 1
2 Anwendungen der Differentialrechnung
In diesem Abschnitt finden Sie anwendungsorientierte Aufgaben zu folgenden Themen:
Einfache Anwendungen in Physik und Technik
Tangente und Normale
Linearisierung einer Funktion
Krümmung einer ebenen Kurve
Relative Extremwerte, Wende- und Sattelpunkte
Kurvendiskussion
Extremwertaufgaben
Tangentenverfahren von Newton
Grenzwertberechnung nach Bernoulli und de L’Hospital
2.1 Einfache Anwendungen in Physik und Technik
Lehrbuch: Band 1, Kapitel IV.2.14.1
Formelsammlung: Kapitel IV.4.1
B48
Die Ladung q eines Kondensators genüge dem Zeitgesetz qðtÞ ¼ q 0 e sin t mit t 0.
Bestimmen Sie den Ladestrom i ¼ iðtÞ ð q 0 : Ladung zu Beginn, d. h. zur Zeit t ¼ 0Þ.
84
B Differentialrechnung
Die Stromstärke i ist die zeitliche Ableitung der Ladung q. Differenziert wird nach der Kettenregel:
q ¼ q 0 e sin t ¼ q 0 e u
i ¼ q_ ¼
mit
u ¼ sin t
dq
dq du
¼
¼ q 0 e u cos t ¼ q 0 e sin t cos t
dt
du dt
Beim freien Fall unter Berücksichtigung des Luftwiderstandes gilt das Weg-Zeit-Gesetz
rffiffiffiffiffiffiffiffi
v 2e
mg
g
s ¼ sðtÞ ¼
t ; t 0 mit v e ¼
ln cosh
ve
g
k
B49
(g: Erdbeschleunigung; m: Masse; k : Reibungskoeffizient).
Bestimmen Sie Geschwindigkeit v und Beschleunigung a als Funktionen der Zeit.
Welcher Kraft unterliegt der frei fallende Körper?
Geschwindigkeit-Zeit-Gesetz u = s_
Die Geschwindigkeit v ist die 1. Ableitung des Weges s nach der Zeit t. Mit Hilfe der Kettenregel erhalten wir (es
sind zwei Substitutionen durchzuführen):
v 2e
v 2e
g
ln cosh
ln ½ cosh u ¼
ln w
t
¼
s ¼
ve
g
g
g
|fflfflfflffl{zfflfflfflffl}
|fflfflffl{zfflfflffl}
w
u
v 2e
v ¼ s_ ¼
¼ ve
mit
w ¼ cosh u und
u ¼
g
t
ve
v 2e 1
v 2e g sinh u
v e v e g sinh u
ds
ds dw du
g
¼
¼
ðsinh uÞ
¼
¼
¼
dt
dw du dt
ve
w
w
g w
g ve
g ve
sinh u
sinh u
¼ ve
¼ v e tanh u ¼ v e tanh
w
cosh u
g
t
ve
ðZur Erinnerung: tanh u ¼ sinh u=cosh uÞ. Wegen
g
g
lim v ðtÞ ¼ lim v e tanh
t ¼ v e lim tanh
t ¼ ve 1 ¼ ve
ve
ve
t!1
t!1
t!1
ist v e die Endgeschwindigkeit (die theoretisch erst nach unendlich langer Fallzeit erreicht wird).
Bild B-1 zeigt das Geschwindigkeit-Zeit-Diagramm.
Beschleunigung-Zeit-Gesetz a = u_ = s€
Die Beschleunigung a ist die 1. Ableitung der Geschwindigkeit v nach der Zeit t. Die Kettenregel liefert:
g
g
v ¼ v e tanh
t ¼ v e tanh u mit u ¼
t
ve
ve
|fflfflffl{zfflfflffl}
u
dv
dv du
g
¼
¼ v e ð1 tanh 2 uÞ
¼
dt
du dt
ve
g
¼ g ð1 tanh 2 uÞ ¼ g 1 tanh 2
t
ve
v
ve
v = ve · tanh
g
t
ve
a ¼ v_ ¼
t
Bild B-1
2 Anwendungen der Differentialrechnung
85
Diese Gleichung lässt sich noch aussagekräftiger gestalten, wenn man die aus dem Geschwindigkeit-Zeit-Gesetz folgende Beziehung
rffiffiffiffiffiffiffiffiffi
g
mg
v
tanh
t ¼
mit v e ¼
ve
k
ve
beachtet:
v2
a ¼ g 1
v 2e
!
¼ g
gv2
v 2e
¼ g
gv2
k
kv2
2
¼ g
¼ g gv
mg
mg
m
k
Durch Multiplikation dieser Gleichung mit der Masse m erhält man die beschleunigende Kraft F:
kv2
F ¼ ma ¼ m g
¼ mg kv2
m
Physikalische Bedeutung der beiden Summanden:
m g: Gewichtskraft (Gravitationskraft)
k v 2 : Luftwiderstand (proportional dem Geschwindigkeitsquadrat), wirkt der Gewichtskraft entgegen
Die Gleichung
B50
x ¼ ð4 t 2Þ e 0;5 t ;
t 0
beschreibe die aperiodische Schwingung eines Feder-Masse-Schwingers ðx : Auslenkung; t : Zeit).
Bestimmen Sie die Geschwindigkeit v und die Beschleunigung a in Abhängigkeit von der Zeit.
Nach welcher Zeit ist die Auslenkung x am größten?
Geschwindigkeit u = x_
Mit Hilfe der Produkt- und Kettenregel erhalten wir:
x ¼ ð4 t 2Þ e 0;5 t ¼ u w
|fflfflfflfflffl{zfflfflfflfflffl} |fflffl{zfflffl}
u
w
w ¼ e 0;5 t
mit u ¼ 4 t 2 ;
und
u_ ¼ 4 ;
w_ ¼ 0,5 e 0;5 t
(w wurde dabei nach der Kettenregel differenziert, Substitution: z ¼ 0,5 t)
v ¼ x_ ¼ u_ w þ w_ u ¼ 4 e 0;5 t 0,5 e 0;5 t ð4 t 2Þ ¼ ½ 4 0,5 ð4 t 2Þ e 0;5 t ¼
¼ ð4 2 t þ 1Þ e 0;5 t ¼ ð5 2 tÞ e 0;5 t
Beschleunigung a = u_ = x€
Wir differenzieren das Geschwindigkeit-Zeit-Gesetz v ¼ v ðtÞ nach der Zeit t unter Verwendung von Produkt- und
Kettenregel:
v ¼ ð5 2 tÞ e 0;5 t ¼ u w
|fflfflfflfflffl{zfflfflfflfflffl} |fflffl{zfflffl}
u
w
mit
w ¼ e 0;5 t
u ¼ 5 2t;
und u_ ¼ 2 ;
w_ ¼ 0,5 e 0;5 t
a ¼ v_ ¼ u_ w þ w_ u ¼ 2 e 0;5 t 0;5 e 0;5 t ð5 2 tÞ ¼ ½ 2 0;5 ð5 2 tÞ e 0;5 t ¼
¼ ð 2 2;5 þ tÞ e 0;5 t ¼ ðt 4;5Þ e 0;5 t
Maximale Auslenkung: x_ ¼ v ¼ 0 , x€ ¼ v_ ¼ a < 0
x_ ¼ v ¼ 0
)
ð5 2 tÞ e 0;5 t ¼ 0
|fflffl{zfflffl}
6¼ 0
)
5 2t ¼ 0
)
t 1 ¼ 2,5
86
B Differentialrechnung
x€ ðt1 ¼ 2,5Þ ¼ a ðt1 ¼ 2,5Þ ¼ 2 e 1;25 < 0
)
Maximum
xmax ¼ x ðt1 ¼ 2,5Þ ¼ 8 e 1;25 ¼ 2,2920
Das Weg-Zeit-Gesetz ist in Bild B-2 bildlich dargestellt.
x
Max
2,29
x = (4t – 2) · e– 0,5 t
1
Bild B-2
1
–1
2
3
4
5
6
7
8
9
t
2,5
–2
Das Weg-Zeit-Gesetz einer erzwungenen Schwingung laute wie folgt:
B51
s ¼ sðtÞ ¼ e t cos ð5 tÞ þ sin ð2 t þ pÞ ; t 0
Bestimmen Sie die Geschwindigkeit v sowie die Beschleunigung a zu Beginn der Bewegung ðt ¼ 0Þ.
Wegen v ¼ s_ und a ¼ v_ ¼ s€ müssen wir das Weg-Zeit-Gesetz zweimal nacheinander nach t differenzieren.
1. Ableitung u = s_ (Geschwindigkeit)
Wir differenzieren das Weg-Zeit-Gesetz gliedweise mit Hilfe von Produkt- und Kettenregel:
s ¼ e t cos ð5 tÞ þ sin ð2 t þ pÞ ¼ x y þ z
|{z} |fflfflfflffl{zfflfflfflffl} |fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
x
y
z
Der 1. Summand x y wird dabei nach der Produktregel differenziert, die dabei benötigten Ableitungen x_ und y_ der
beiden Faktoren erhält man jeweils nach der Kettenregel (Substitutionen: u ¼ t bzw. u ¼ 5 t). Die Ableitung des
2. Summanden z erfolgt mit der Kettenregel (Substitution: u ¼ 2 t þ p). Somit gilt:
x ¼ e t ;
y ¼ cos ð5 tÞ ;
x_ ¼ e t ;
y_ ¼ 5 sin ð5 tÞ ;
z ¼ sin ð2 t þ pÞ ;
z_ ¼ 2 cos ð2 t þ pÞ
s_ ¼ x_ y þ y_ x þ z_ ¼ e t cos ð5 tÞ 5 sin ð5 tÞ e t þ 2 cos ð2 t þ pÞ ¼
¼ ½ cos ð5 tÞ 5 sin ð5 tÞ e t þ 2 cos ð2 t þ pÞ
Damit erhalten wir das folgende Geschwindigkeit-Zeit-Gesetz:
v ¼ s_ ¼ ½ cos ð5 tÞ 5 sin ð5 tÞ e t þ 2 cos ð2 t þ pÞ
Geschwindigkeit zum Zeitpunkt t ¼ 0:
v ðt ¼ 0Þ ¼ s_ ðt ¼ 0Þ ¼ ½ cos 0 5 sin 0 e 0 þ 2 cos p ¼ ð 1 5 0Þ 1 þ 2 ð 1Þ ¼ 3
2. Ableitung a = u_ = s€ (Beschleunigung)
Wir benötigen (analog wie bei der Bildung der 1. Ableitung) Produkt- und Kettenregel:
s_ ¼ ½ cos ð5 tÞ 5 sin ð5 tÞ e t þ 2 cos ð2 t þ pÞ ¼ x y þ z
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z} |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
x
y
z
x_ ¼ 5 sin ð5 tÞ 25 cos ð5 tÞ ;
y_ ¼ e t
und
z_ ¼ 4 sin ð2 t þ pÞ
2 Anwendungen der Differentialrechnung
87
€
s ¼ x_ y þ y_ x þ z_ ¼ ½ 5 sin ð5 tÞ 25 cos ð5 tÞ e t e t ½ cos ð5 tÞ 5 sin ð5 tÞ 4 sin ð2 t þ pÞ ¼
¼ ½ 5 sin ð5 tÞ 25 cos ð5 tÞ þ cos ð5 tÞ þ 5 sin ð5 tÞ e t 4 sin ð2 t þ pÞ ¼
¼ ½ 10 sin ð5 tÞ 24 cos ð5 tÞ e t 4 sin ð2 t þ pÞ
Das Beschleunigung-Zeit-Gesetz lautet somit:
a ¼ v_ ¼ €s ¼ ½ 10 sin ð5 tÞ 24 cos ð5 tÞ e t 4 sin ð2 t þ pÞ
Beschleunigung zum Zeitpunkt t ¼ 0:
a ðt ¼ 0Þ ¼ €s ðt ¼ 0Þ ¼ ð10 sin 0 24 cos 0Þ e 0 4 sin p ¼ ð10 0 24 1Þ 1 4 0 ¼ 24
Die Bahnkurve eines Massenpunktes in der x; y -Ebene wird durch die Gleichungen
B52
x ¼ x ðtÞ ¼ ðsin tÞ e t ;
y ¼ y ðtÞ ¼ ðcos tÞ e t ;
t 0
beschrieben. Bestimmen Sie Geschwindigkeit v und Beschleunigung a zur Zeit t ¼ p .
Wir benötigen die ersten beiden Ableitungen der Parametergleichungen. Differenziert wird jeweils nach der Produktregel in Verbindung mit der Kettenregel:
x ¼ ðsin tÞ e t ¼ u v
|fflffl{zfflffl} |{z}
u
v
mit u ¼ sin t ;
v ¼ e t
und u_ ¼ cos t ;
v_ ¼ e t
(Ableitung von v nach der Kettenregel, Substitution: z ¼ t)
x_ ¼ u_ v þ v_ u ¼ ðcos tÞ e t e t sin t ¼ ðcos t sin tÞ e t
x_ ¼ ðcos t sin tÞ e t ¼ u v mit u ¼ cos t sin t ;
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |{z}
u
v
v ¼ e t und u_ ¼ sin t cos t ;
v_ ¼ e t
x€ ¼ u_ v þ v_ u ¼ ð sin t cos tÞ e t e t ðcos t sin tÞ ¼
¼ ð sin t cos t cos t þ sin tÞ e t ¼ 2 ðcos tÞ e t
Analog erhält man y_ und y€:
y ¼ ðcos tÞ e t ¼ u v mit
|fflfflffl{zfflfflffl} |{z}
u
v
u ¼ cos t ;
v ¼ e t
und
u_ ¼ sin t ;
v_ ¼ e t
y_ ¼ u_ v þ v_ u ¼ ð sin tÞ e t e t cos t ¼ ð sin t cos tÞ e t
y_ ¼ ð sin t cos tÞ e t ¼ u v mit u ¼ sin t cos t;
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
u
v
v ¼ e t und u_ ¼ cos t þ sin t; v_ ¼ e t
y€ ¼ u_ v þ v_ u ¼ ð cos t þ sin tÞ e t e t ð sin t cos tÞ ¼
¼ ð cos t þ sin t þ sin t þ cos tÞ e t ¼ 2 ðsin tÞ e t
Geschwindigkeit v ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x_ 2 þ y_ 2 (die Geschwindigkeitskomponenten x_ und y_ stehen senkrecht aufeinander)
v 2 ¼ x_ 2 þ y_ 2 ¼ ðcos t sin tÞ 2 e 2 t þ ð sin t cos tÞ 2 e 2 t ¼
¼ ½ ðcos t sin tÞ 2 þ ð sin t cos tÞ 2 e 2 t ¼
¼ ðcos 2 t 2 sin t cos t þ sin 2 t þ sin 2 t þ 2 sin t cos t þ cos 2 tÞ e 2 t ¼
¼ ð2 cos 2 t þ 2 sin 2 tÞ e 2 t ¼ 2 ðcos 2 t þ sin 2 tÞ e 2 t ¼ 2 1 e 2 t ¼ 2 e 2 t
88
B Differentialrechnung
(unter Verwendung des trigonometrischen Pythagoras cos 2 t þ sin 2 t ¼ 1). Somit gilt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
ðe 2 t ¼ e t e t ¼ ðe t Þ 2 Þ
v ¼ 2 e 2 t ¼ 2 e t ) v ðt ¼ pÞ ¼ 2 e p ¼ 0,0611
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x€ 2 þ y€ 2 (die Beschleunigungskomponenten x€ und y€ stehen senkrecht aufeinander)
Beschleunigung a ¼
a 2 ¼ x€ 2 þ y€ 2 ¼ 4 ðcos 2 tÞ e 2 t þ 4 ðsin 2 tÞ e 2 t ¼ 4 ðcos 2 t þ sin 2 tÞ e 2 t ¼ 4 e 2 t
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a ¼ 4 e 2 t ¼ 2 e t ) a ðt ¼ pÞ ¼ 2 e p ¼ 0,0864
Ein Rad mit dem Radius R ¼ 1 rollt reibungsfrei auf einer Geraden (x-Achse) und beschreibt dabei
eine sog. Rollkurve oder gewöhnliche Zykloide mit der folgenden Parameterdarstellung:
B53
x ¼ t sin ðp tÞ ;
y ¼ 1 cos ðp tÞ
ðt 0 : ZeitÞ
Bestimmen Sie Geschwindigkeit v und Beschleunigung a in Abhängigkeit von der Zeit.
Nach welcher Zeit erreicht die Geschwindigkeit erstmals ihren größten Wert?
Wir bilden zunächst die benötigten Ableitungen x_ , x€, y_ und y€ (gliedweises Differenzieren in Verbindung mit der
Kettenregel):
x ¼ t sin ðp tÞ ¼ t sin u
|ffl{zffl}
u
mit
x_ ¼ 1 p cos ðp tÞ ¼ 1 p cos u
|ffl{zffl}
u
y ¼ 1 cos ðp tÞ ¼ 1 cos u
|ffl{zffl}
u
mit
u_ ¼ p
u ¼ p t;
u ¼ pt
mit
u ¼ p t;
y_ ¼ p sin ðp tÞ ¼ p sin u mit u ¼ p t
|ffl{zffl}
u
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Geschwindigkeit v ¼
x_ 2 þ y_ 2
)
)
)
u_ ¼ p
)
x_ ¼ 1 ðcos uÞ p ¼ 1 p cos ðp tÞ
x€ ¼ 0 p ð sin uÞ p ¼ p 2 sin ðp tÞ
y_ ¼ 0 þ ðsin uÞ p ¼ p sin ðp tÞ
y€ ¼ p ðcos uÞ p ¼ p 2 cos ðp tÞ
v 2 ¼ x_ 2 þ y_ 2 ¼ ½ 1 p cos ðp tÞ 2 þ p 2 sin 2 ðp tÞ ¼
¼ 1 2 p cos ðp tÞ þ p 2 cos 2 ðp tÞ þ p 2 sin 2 ðp tÞ ¼
¼ 1 2 p cos ðp tÞ þ p 2 ðcos 2 ðp tÞ þ sin 2 ðp tÞÞ ¼ 1 2 p cos ðp tÞ þ p 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
2
2
(unter Verwendung der Beziehung cos u þ sin u ¼ 1 mit u ¼ p tÞ. Somit gilt:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
v ¼ 1 2 p cos ðp tÞ þ p 2 ; t 0
Das Geschwindigkeitsmaximum wird erreicht, wenn cos ðp tÞ den kleinsten Wert 1 annimmt:
cos ðp tÞ ¼ 1
f ür
pt ¼ p;
d: h: t1 ¼ 1
Nach einer halben Drehung des Rades, d. h. im höchsten Bahnpunkt ist die Geschwindigkeit am größten. Sie beträgt:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
v max ¼ v ðt1 ¼ 1Þ ¼ 1 2 p ð 1Þ þ p 2 ¼ 1 þ 2 p þ p 2 ¼ ð1 þ pÞ 2 ¼ 1 þ p
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1. Binom : ð1 þ pÞ 2
2 Anwendungen der Differentialrechnung
Beschleunigung a ¼
89
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x€ 2 þ y€ 2
a 2 ¼ x€ 2 þ y€ 2 ¼ p 4 sin 2 ðp tÞ þ p 4 cos 2 ðp tÞ ¼ p 4 ½ sin 2 ðp tÞ þ cos 2 ðp tÞ ¼ p 4 ¼ const:
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
2
Die Bewegung erfolgt also mit konstanter Beschleunigung: a ¼ p :
2.2 Tangente und Normale
Lehrbuch: Band 1, Kapitel IV.3.1
Formelsammlung: Kapitel IV.4.2
B54
Wie lauten die Gleichungen der Tangente und Normale im Punkt P ¼ ð6; 6Þ der in der impliziten
Form gegebenen Kurve x 3 12 x y þ y 3 ¼ 0 ?
Für die Berechnung der Steigungswerte von Tangente und Normale benötigen wir die 1. Ableitung der impliziten Funktion. Die Funktionsgleichung wird daher gliedweise nach x differenziert. Dabei ist y als eine Funktion von x zu
betrachten, d. h. Terme mit der Variablen y müssen nach der Kettenregel differenziert werden (zunächst nach y
differenzieren, dann y nach x):
f
f
d
ðx 3 12 x y þ y 3 Þ ¼ 3 x 2 12 ðu 0 v þ v 0 uÞ þ 3 y 2 y 0 ¼
dx
u v
¼ 3 x 2 12 ð1 y þ 1 y 0 xÞ þ 3 y 2 y 0 ¼
¼ 3 x 2 12 ð y þ x y 0 Þ þ 3 y 2 y 0 ¼ 0
Der 2. Summand 12 x y ¼ 12 ðx yÞ wurde dabei nach der Produktregel differenziert (mit u ¼ x, v ¼ y
und u 0 ¼ 1, v 0 ¼ 1 y 0 ¼ y 0 ). Wir lösen jetzt diese Gleichung schrittweise nach y 0 auf (zunächst wird durch 3
dividiert):
x 2 4 ð y þ x y 0 Þ þ y 2 y 0 ¼ x 2 4 y 4 x y 0 þ y 2 y 0 ¼ y 0 ð 4 x þ y 2 Þ þ x 2 4 y ¼ 0
y 0 ð 4 x þ y 2 Þ ¼ x 2 þ 4 y
y0 ¼
)
x2 þ 4y
4x þ y2
¼
ð x 2 þ 4 yÞ ð1Þ
ð 4 x þ y 2 Þ ð1Þ
¼
x2 4y
4x y2
Gleichung der Tangente in P == (x 0 ; y 0 ) == (6; 6)
m t ¼ y 0 ðx 0 ¼ 6; y 0 ¼ 6Þ ¼
y y0
¼ mt
x x0
Tangente:
)
36 24
12
¼
¼ 1
24 36
12
y6
¼ 1;
x 6
y 6 ¼ 1 ðx 6Þ ¼ x þ 6
y ¼ x þ 12
Gleichung der Normale in P == (x 0 ; y 0 ) == (6; 6)
mn ¼
Normale:
1
1
¼
¼ 1
mt
1
y ¼ x
)
y y0
¼ mn
x x0
)
y6
¼ 1;
x 6
y 6 ¼ 1 ðx 6Þ ¼ x 6
90
B Differentialrechnung
B55
Bestimmen Sie die Tangente der Funktion y ¼ e 2 x cos ð4 x þ pÞ an der Stelle x 0 ¼ 0.
Tangentenberührungspunkt: x 0 ¼ 0 ;
y 0 ¼ e 0 cos ð0 þ pÞ ¼ 1 cos p ¼ 1 ð 1Þ ¼ 1 ) P ¼ ð0; 1Þ
Steigung m der Kurventangente in P == (0; – 1)
Die benötigte Ableitung erhalten wir mit der Produktregel, wobei beide Faktoren mit Hilfe der Kettenregel zu differenzieren sind:
y ¼ e 2 x cos ð4 x þ pÞ ¼ u v
|ffl{zffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
u
v
u ¼ e 2x ¼ e t
mit
t ¼ 2x
v ¼ cos ð4 x þ pÞ ¼ cos z
)
u 0 ¼ e t ð 2Þ ¼ 2 e 2 x
mit z ¼ 4 x þ p
)
v 0 ¼ ð sin zÞ 4 ¼ 4 sin ð4 x þ pÞ
y 0 ¼ u 0 v þ v 0 u ¼ 2 e 2 x cos ð4 x þ pÞ 4 sin ð4 x þ pÞ e 2 x ¼
¼ 2 e 2 x ½ cos ð4 x þ pÞ þ 2 sin ð4 x þ pÞ
m ¼ y 0 ð0Þ ¼ 2 e 0 ½ cos p þ 2 sin p ¼ 2 1 ð 1 þ 2 0Þ ¼ 2 1 ð 1Þ ¼ 2
Gleichung der Tangente in P == (x 0 ; y 0 ) == (0; – 1)
y y0
¼ m
x x0
B56
)
yþ1
¼ 2
x 0
)
y þ 1 ¼ 2x
)
y ¼ 2x 1
Wo besitzt die Kurve y ¼ ln ð1,5 cos 2 xÞ waagerechte Tangenten?
Wegen der Spiegelsymmetrie der Kurve zur y-Achse dürfen wir uns zunächst auf das Intervall x 0 beschränken.
Die benötigte 1. Ableitung der Funktion bilden wir wie folgt mit Hilfe der Kettenregel, wobei zwei Substitutionen
nacheinander durchzuführen sind (von innen nach außen).
1. Substitution:
y ¼ ln ð1,5 cos 2 xÞ ¼ ln ð1,5 cos x Þ 2 ¼ ln ð1,5 u 2 Þ
|ffl{zffl}
u
2. Substitution:
y ¼ ln ð1,5 u 2 Þ ¼ ln v mit
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
v
Somit gilt: y ¼ ln v
mit v ¼ 1,5 u 2
mit
u ¼ cos x
v ¼ 1,5 u 2
und u ¼ cos x
Die Kettenregel liefert dann die gewünschte Ableitung:
y0 ¼
dy
dy dv du
1
2 u sin x
2 u sin x
2 cos x sin x
¼
ð 2 uÞ ð sin xÞ ¼
¼
¼
¼
2
v
v
dx
dv du dx
1,5 u
1,5 cos 2 x
In den Kurvenpunkten mit einer waagerechten Tangente muss die 1. Ableitung verschwinden (Zähler ¼ 0):
y0 ¼ 0
)
2 cos x sin x ¼ 0
cos x ¼ 0
)
x ¼ p=2;
sin x ¼ 0
)
x ¼ 0;
3 p=2;
p;
2 p;
5 p=2;
...
...
2 Anwendungen der Differentialrechnung
91
Lösungen sind somit die Nullstellen der Sinus- und Kosinusfunktion (siehe Bild B-3). Sie lassen sich im Intervall
x 0 durch die Gleichung
xk ¼ k
p
2
ðk ¼ 0; 1; 2; . . .Þ
beschreiben. Wir berechnen noch die zugehörigen Ordinaten y k :
y k ¼ ln ð1,5 cos 2 x k Þ ¼ ln ð1,5 cos 2 ðk p=2ÞÞ
y
1
y = sin x
Bild B-3
x
π
–1
2π
3π
4π
y = cos x
Der Wert der Kosinusfunktion an der Stelle xk ¼ k p=2 hängt dabei noch wie folgt vom Laufindex k ab:
8
9
k ¼ gerade =
< þ 1 oder 1
cos ðk p=2Þ ¼
f ür
:
;
0
k ¼ ungerade
Somit ist cos 2 ðk p=2Þ entweder gleich þ 1 oder 0 und wir erhalten folgende Ordinatenwerte:
8
9
k ¼ gerade =
< ln ð1,5 1Þ ¼ ln 0,5
yk ¼
f ür
:
;
ln ð1,5 0Þ ¼ ln 1,5
k ¼ ungerade
Die Kurvenpunkte mit einer waagerechten Tangente lauten somit (im Intervall x 0):
p
3
P0 ¼ ð0; ln 0,5Þ ; P1 ¼
; ln 1,5 ; P2 ¼ ðp; ln 0,5Þ ; P3 ¼
p; ln 1,5 ;
2
2
...
Durch Spiegelung dieser Punkte an der y-Achse erhält man die restlichen Kurvenpunkte mit einer waagerechten Tangente (siehe Bild B-4). Sie liegen an den Stellen x k ¼ k p=2 mit k ¼ 1; 2; 3; . . . .
y
P–1
P1
0,5
P3
y = ln (1,5 – cos2 x )
Bild B-4
–π
2
π
2
π
3π
2
2π
– 0,693
P0
B57
P2
P4
An welchen Stellen hat die Kurve y ¼ e x cos ð0,5 xÞ waagerechte Tangenten?
Es genügt die Angabe der Abszissenwerte.
x
92
B Differentialrechnung
Die Funktion wird nach der Produktregel differenziert, wobei die Ableitung des rechten Faktors in der angedeuteten
Weise mit Hilfe der Kettenregel erfolgt:
y ¼ e x cos ð0,5 xÞ ¼ u v
f
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
mit u ¼ e x ;
u0 ¼ ex ;
v ¼ cos ð0,5 xÞ und
v 0 ¼ 0,5 sin ð0,5 xÞ
v
u
(Ableitung von v ¼ cos ð0,5 xÞ nach der Kettenregel, Substitution: t ¼ 0,5 x)
y 0 ¼ u 0 v þ v 0 u ¼ e x cos ð0,5 xÞ 0,5 sin ð0,5 xÞ e x ¼ e x ½ cos ð0,5 xÞ 0,5 sin ð0,5 xÞ
Für einen Kurvenpunkt mit waagerechter Tangente gilt y 0 ¼ 0:
)
e x ½ cos ð0,5 xÞ 0,5 sin ð0,5 xÞ ¼ 0
f
y0 ¼ 0
)
cos ð0,5 xÞ 0,5 sin ð0,5 xÞ ¼ 0
6¼ 0
Diese Gleichung stellen wir zunächst wie folgt um:
cos ð0,5 xÞ ¼ 0,5 sin ð0,5 xÞ
)
2 cos ð0,5 xÞ ¼ sin ð0,5 xÞ
)
sin ð0,5 xÞ
cos ð0,5 xÞ
¼ tan ð0,5 xÞ ¼ 2
( Zur Erinnerung: tan a ¼ sin a=cos a; hier mit a ¼ 0,5 x )
Wir substituieren z ¼ 0,5 x und erhalten die einfache trigonometrische Gleichung tan z ¼ 2. Die Lösungen sind die
Schnittstellen der elementaren Tangensfunktion y ¼ tan z mit der zur z-Achse parallelen Geraden y ¼ 2 (siehe
Bild B-5):
y
y = tan z
y=2
2
1
Bild B-5
–2
2
4
6
8
10
z
1,107
Die 1. positive Schnittstelle erhalten wir durch Umkehrung der Gleichung tan z ¼ 2 im Intervall p=2 < z < p=2.
Sie liegt bei z 0 ¼ arctan 2 ¼ 1,107. Wegen der Periodizität der Tangensfunktion gibt es unendlich viele weitere
Lösungen im Abstand von jeweils einer Periode p ¼ p. Die Lösungen lauten somit:
z k ¼ arctan 2 þ k p ¼ 1,107 þ k p
ðk ¼ 0; 1; 2; . . .Þ
Rücksubstitution liefert uns dann die gesuchten x-Werte der Kurvenpunkte mit einer waagerechten Tangente:
z ¼ 0,5 x
)
x ¼ 2z
)
x k ¼ 2 z k ¼ 2 ð1,107 þ k pÞ ¼ 2,214 þ k 2 p
ðk ¼ 0; 1; 2; . . .Þ
Bestimmen Sie die Gleichung der Tangente der in der Parameterform
B58
x ðtÞ ¼ sin ð2 tÞ þ 2 cos 2 t ;
y ðtÞ ¼ 2 sin t cos ð2 tÞ
dargestellten Kurve für den Parameterwert t 0 ¼ p .
Wir berechnen zunächst die kartesischen Koordinaten zum Parameterwert t 0 ¼ p :
)
x 0 ¼ sin ð2 pÞ þ 2 cos 2 p ¼ 0 þ 2 ð 1Þ 2 ¼ 2
) P ¼ ðx 0 ; y 0 Þ ¼ ð2; 1Þ
y 0 ¼ 2 sin p cos ð2 pÞ ¼ 2 0 1 ¼ 1
2 Anwendungen der Differentialrechnung
93
Steigung der Kurventangente in P == (2; – 1)
Wir benötigen die Ableitungen der beiden Parametergleichungen nach dem Parameter t, die wir mit Hilfe der Kettenregel wie folgt erhalten:
x ¼ sin ð2 tÞ þ 2 cos 2 t ¼ sin ð2 tÞ þ 2 ð cos t Þ 2 ¼ sin u þ 2 v 2
|{z}
|ffl{zffl}
u
v
mit
u ¼ 2t;
v ¼ cos t
x_ ¼ ðcos uÞ 2 þ 2 2 v ð sin tÞ ¼ 2 cos ð2 tÞ 4 sin t cos t ¼ 2 cos ð2 tÞ 2 sin ð2 tÞ
(unter Verwendung der trigonometrischen Beziehung sin ð2 tÞ ¼ 2 sin t cos t)
y ¼ 2 sin t cos ð2 tÞ ¼ 2 sin t cos u
|{z}
u
u ¼ 2t
mit
y_ ¼ 2 cos t þ ðsin uÞ 2 ¼ 2 cos t þ 2 sin ð2 tÞ
Für die Steigung der Kurventangente in Abhängigkeit vom Parameter t erhalten wir damit:
2 cos t þ 2 sin ð2 tÞ
cos t þ sin ð2 tÞ
y_
¼
¼
x_
2 cos ð2 tÞ 2 sin ð2 tÞ
cos ð2 tÞ sin ð2 tÞ
y0 ¼
Im Punkt P ¼ ð2; 1Þ, d. h. für t 0 ¼ p gilt dann:
cos p þ sin ð2 pÞ
m ¼ y 0 ðt 0 ¼ pÞ ¼
cos ð2 pÞ sin ð2 pÞ
¼
1 þ 0
¼ 1
10
Gleichung der Kurventangente in P == (x 0 ; y 0 ) == (2; – 1)
y y0
¼ m
x x0
yþ1
¼ 1
x 2
)
)
y þ 1 ¼ 1 ðx 2Þ ¼ x þ 2
)
y ¼ x þ 1
2t2
6t
Wie lautet die Tangente an die Kurve mit der Parameterdarstellung x ¼
, y ¼
, t 6¼ 1
3
1 t3
1t
an der Stelle t 0 ¼ 1?
B59
Wir berechnen zunächst die zum Parameterwert t 0 ¼ 1 gehörenden kartesischen Koordinaten des Tangentenberührungspunktes P ¼ ðx 0 ; y 0 Þ:
x0 ¼
2 ð 1Þ 2
1 ð 1Þ
3
¼
21
1 ð 1Þ
¼
2
¼ 1;
2
y0 ¼
6 ð 1Þ
1 ð 1Þ
3
¼
6
¼ 3
2
)
P ¼ ð1; 3Þ
Die für die Tangentensteigung benötigten Ableitungen der Parametergleichungen nach dem Parameter t erhalten wir
jeweils mit Hilfe der Quotientenregel:
x ¼
2t2
u
¼
3
v
1t
x_ ¼
4 t ð1 t 3 Þ ð 3 t 2 Þ 2 t 2
4t 4t4 þ 6t4
4t þ 2t4
u_ v v_ u
¼
¼
¼
v2
ð1 t 3 Þ 2
ð1 t 3 Þ 2
ð1 t 3 Þ 2
y ¼
6t
u
¼
3
v
1t
y_ ¼
6 ð1 t 3 Þ ð 3 t 2 Þ 6 t
6 6 t 3 þ 18 t 3
6 þ 12 t 3
u_ v v_ u
¼
¼
¼
v2
ð1 t 3 Þ 2
ð1 t 3 Þ 2
ð1 t 3 Þ 2
mit
mit
u ¼ 2t2;
u ¼ 6t;
v ¼ 1 t3
v ¼ 1 t3
und
und
u_ ¼ 4 t ;
u_ ¼ 6 ;
v_ ¼ 3 t 2
v_ ¼ 3 t 2
94
B Differentialrechnung
Tangentensteigung in Abhängigkeit vom Parameter t
6 þ 12 t 3
y0 ¼
3 2
6 ð1 þ 2 t 3 Þ
ð1 t 3 Þ 2
6 þ 12 t 3 ð1 t Þ
6 þ 12 t 3
y_
3 ð1 þ 2 t 3 Þ
¼
¼
¼
¼
¼
4
4
4
3
x_
2 t ð2 þ t Þ
4t þ 2t
t ð2 þ t 3 Þ
4t þ 2t
ð1 t 3 Þ 2 4 t þ 2 t
ð1 t 3 Þ 2
Steigung im Punkt P ¼ ð1; 3Þ, d. h. für t 0 ¼ 1:
m ¼ y 0 ðt 0 ¼ 1Þ ¼
3 ð1 þ 2 ð 1Þ 3 Þ
3
1 ð2 þ ð 1Þ Þ
¼
3 ð1 þ 2 ð1ÞÞ
1 ð2 1Þ
¼
3 ð1 2Þ
¼
1 1
3
¼ 3
1
Gleichung der Kurventangente in P == (x 0 ; y 0 ) == (1; – 3)
y y0
¼ m
x x0
)
yþ3
¼ 3
x 1
)
y þ 3 ¼ 3 ðx 1Þ ¼ 3 x 3
)
y ¼ 3x 6
Wo besitzt die Kurve mit der Parameterdarstellung
B60
x ¼ t e t ;
y ¼ cos t e t ;
1 < t < 1
waagerechte bzw. senkrechte Tangenten?
Wir bilden zunächst die 1. Ableitung der beiden Parametergleichungen unter Verwendung von Produkt- und Kettenregel:
mit
f
x ¼ t e t ¼ u v
|{z}
u v
u ¼ t;
v ¼ e t
und u_ ¼ 1 ;
v_ ¼ e t
(Ableitung von v ¼ e t mit der Kettenregel, Substitution z ¼ t)
x_ ¼ u_ v þ v_ u ¼ 1 e t e t t ¼ ð1 tÞ e t
y ¼ cos t e t ¼ u v
|ffl{zffl} |{z}
u
v
mit u ¼ cos t ;
v ¼ e t
und u_ ¼ sin t ;
v_ ¼ e t
y_ ¼ u_ v þ v_ u ¼ sin t e t e t cos t ¼ ð sin t cos tÞ e t
Kurvenanstieg in Abhängigkeit vom Parameter t
y0 ¼
ð sin t cos tÞ e t
y_
sin t cos t
ð sin t cos tÞ ð 1Þ
sin t þ cos t
¼
¼
¼
¼
x_
1t
ð1 tÞ ð1Þ
t 1
ð1 tÞ e t
Kurvenpunkte mit waagerechter Tangente: y 0 == 0, d. h. y_ == 0 und x_ 6¼ 0
y0 ¼ 0
)
sin t þ cos t ¼ 0
ðf ür t 6¼ 1Þ
Diese trigonometrische Gleichung formen wir wie folgt um:
sin t ¼ cos t
)
sin t
¼ tan t ¼ 1
cos t
Die Lösungen lassen sich anhand einer Skizze leicht bestimmen, es sind die Abszissenwerte der Schnittpunkte der
Tangenskurve y ¼ tan t mit der konstanten Funktion y ¼ 1 (Parallele zur t-Achse; siehe Bild B-6). Die im Intervall p=2 < t < p=2 liegende Schnittstelle ist t 0 ¼ arctan ð 1Þ ¼ p=4. Wegen der Periodizität der Tangensfunktion gibt es weitere Lösungen im jeweiligen Abstand von genau einer Periode p ¼ p. Die unendlich vielen
Lösungen lassen sich durch die Formel
t k ¼ arctan ð 1Þ þ k p ¼
p
þk p
4
ðk ¼ 0; 1; 2; . . .Þ
beschreiben. An diesen Stellen verlaufen die Kurventangenten waagerecht ( t k 6¼ 1).
2 Anwendungen der Differentialrechnung
95
y
y = tan t
1
– π/4
Bild B-6
–π
π
0
2π
3π
t
y = –1
Kurvenpunkte mit senkrechter Tangente (parallel zur y-Achse): y 0 == 1, d. h. x_ == 0 und y_ 6¼ 0
y0 ¼ 1
)
t 1 ¼ 0
)
t1 ¼ 1
Wegen
y_ ðt 1 ¼ 1Þ ¼ sin 1 þ cos 1 ¼ 0,8415 þ 0,5403 ¼ 1,3818 6¼ 0
verläuft die Kurventangente an dieser Stelle parallel zur y-Achse. Weitere Lösungen gibt es nicht.
Durch ungestörte berlagerung der beiden zueinander senkrechten Schwingungen mit den Gleichungen
x ðtÞ ¼ a sin t und y ðtÞ ¼ a sin ð2 tÞ ða > 0; t 0Þ entsteht eine sog. Lissajous-Figur
(Frequenzverhältnis 1 : 2). Bestimmen Sie die Stellen mit einer waagerechten bzw. senkrechten Tangente im Periodenintervall 0 t < 2 p .
B61
Wir bestimmen zunächst die benötigten Ableitungen x_ und y_ (letztere erhält man mit der Kettenregel):
x ¼ a sin t
x_ ¼ a cos t
)
y ¼ a sin ð2 tÞ ¼ a sin u
|{z}
u
mit
u ¼ 2t
)
y_ ¼ a cos u u_ ¼ a cos ð2 tÞ 2 ¼ 2 a cos ð2 tÞ
Für den Kurvenanstieg (Steigung der Tangente) erhalten wir in Abhängigkeit vom Parameter t:
y0 ¼
2 a cos ð2 tÞ
2 cos ð2 tÞ
y_
¼
¼
x_
cos t
a cos t
Kurvenpunkte mit waagerechter Tangente: y 0 == 0, d. h. y_ == 0 und x_ 6¼ 0
y0 ¼ 0
)
2 cos ð2 tÞ ¼ 0
)
cos ð2 tÞ ¼ cos u ¼ 0
|{z}
u
(Substitution u ¼ 2 t). Die Lösungen sind die Nullstellen der Kosinusfunktion y ¼ cos u (siehe Bild B-7):
uk ¼
p
þk p
2
ðk ¼ 0; 1; 2; . . .Þ
y
1
y = cos u
–π
2
π
2
–1
Bild B-7
3π
2
5π
2
7π
2
u
96
B Differentialrechnung
Rücksubstitution ergibt:
u ¼ 2t
)
t ¼
1
u
2
)
tk ¼
1
1
uk ¼
2
2
p
þk p
2
¼
p
p
þk
4
2
ðk ¼ 0; 1; 2; . . .Þ
Wegen der Beschränkung auf das Periodenintervall 0 t < 2 p gibt es nur vier Lösungen:
t0 ¼
p
;
4
t1 ¼
p
p
3
þ1
¼
p;
4
2
4
t2 ¼
p
p
5
þ2
¼
p;
4
2
4
p
p
7
þ3
¼
p
4
2
4
t3 ¼
Der Nenner cos t der Steigungsformel ist an diesen Stellen von null verschieden. Es gibt somit genau vier Kurvenpunkte mit einer waagerechten Tangente. Wir berechnen noch die kartesischen Koordinaten dieser Punkte:
)
(
x 0 ¼ a sin ðp=4Þ ¼ a 0,707 ¼ 0,707 a
p
) A 0 ¼ ð0,707 a; aÞ
t0 ¼
)
4
y 0 ¼ a sin ðp=2Þ ¼ a 1 ¼ a
Wegen der Spiegelsymmetrie der Lissajous-Kurve bezüglich beider Achsen gilt für die vier Kurvenpunkte mit waagerechter Tangente (ohne Rechnung; siehe Bild B-8):
A 0 ¼ ð0,707 a; aÞ ;
A 1 ¼ ð0,707 a; aÞ ;
A 2 ¼ ð 0,707 a; aÞ ;
A 3 ¼ ð 0,707 a; aÞ
Kurvenpunkte mit senkrechter Tangente: y 0 == 1, d. h. x_ == 0 und y_ 6¼ 0
y0 ¼ 1
)
cos t ¼ 0
)
tk ¼
p
þk p
2
ðk ¼ 0; 1; 2; . . .Þ
(Nullstellen der Kosinusfunktion, siehe hierzu auch Bild B-7). Uns interessieren aber nur die im Periodenintervall
0 t < 2 p liegenden Werte. Sie lauten:
t0 ¼
p
2
und
t1 ¼
p
3
þ1p ¼
p
2
2
Der Zähler x_ ¼ 2 cos ð2 tÞ der Steigungsformel ist an diesen Stellen (wie gefordert) von null verschieden. Es gibt
somit genau zwei Kurvenpunkte mit einer senkrechten Tangente. Wir berechnen noch die kartesischen Koordinaten
dieser Punkte:
(
)
x 0 ¼ a sin ðp=2Þ ¼ a 1 ¼ a
p
) B 0 ¼ ða; 0Þ
t0 ¼
)
2
y 0 ¼ a sin p ¼ a 0 ¼ 0
Der zweite Punkt liegt spiegelsymmetrisch zur y-Achse bei B 1 ¼ ð a; 0Þ.
Bild B-8 zeigt den Verlauf der geschlossenen Kurve mit
den vier waagerechten und den zwei senkrechten Tangenten.
y
A2
a
A0
B1
–a
B0
a
Bild B-8
–a
A3
B62
x
A1
In welchen Punkten hat die in Polarkoordinaten definierte Kurve r ¼ 1 þ sin 2 j, 0 j < 2 p
waagerechte Tangenten?
2 Anwendungen der Differentialrechnung
97
Wir müssen die Kurve zunächst in der Parameterform darstellen (Parameter ist dabei die Winkelkoordinate j):
x ¼ r cos j ¼ ð1 þ sin 2 jÞ cos j ;
y ¼ r sin j ¼ ð1 þ sin 2 jÞ sin j ¼ sin j þ sin 3 j
Jetzt bilden wir die für die Steigungsformel benötigten Ableitungen x_ und y_ (differenziert wird nach dem Parameter j),
wobei wir Produkt- und Kettenregel einsetzen:
x ¼ ð1 þ sin 2 jÞ cos j ¼ u v
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl} |fflffl{zfflffl}
u
v
u ¼ 1 þ sin 2 j ;
v ¼ cos j
und
u_ ¼ 2 sin j cos j ;
v_ ¼ sin j
(Ableitung von u ¼ 1 þ sin 2 j ¼ 1 þ ðsin jÞ2 nach der Kettenregel, Substitution: t ¼ sin j)
x_ ¼ u_ v þ v_ u ¼ 2 sin j cos j cos j sin j ð1 þ sin 2 jÞ ¼ 2 sin j cos 2 j sin j sin 3 j ¼
¼ ð2 cos 2 j 1 sin 2 jÞ sin j ¼ ð2 ð1 sin 2 jÞ 1 sin 2 jÞ sin j ¼
|fflfflffl{zfflfflffl}
1 sin 2 j
¼ ð2 2 sin 2 j 1 sin 2 jÞ sin j ¼ ð1 3 sin 2 jÞ sin j
(unter Verwendung der trigonometrischen Beziehung sin 2 j þ cos 2 j ¼ 1)
Für y_ erhalten wir durch gliedweises Differenzieren und mit Hilfe der Kettenregel:
y ¼ sin j þ sin 3 j ¼ sin j þ ðsin j Þ 3 ¼ sin j þ u 3
|ffl{zffl}
u
mit
u ¼ sin j ;
u_ ¼ cos j
y_ ¼ cos j þ 3 u 2 u_ ¼ cos j þ 3 sin 2 j cos j ¼ ð1 þ 3 sin 2 jÞ cos j
Die Steigung der Kurventangente hängt damit wie folgt vom Kurvenparameter j ab:
y0 ¼
ð1 þ 3 sin 2 jÞ cos j
y_
¼
x_
ð1 3 sin 2 jÞ sin j
In den Kurvenpunkten mit einer waagerechten Tangente muss die 1. Ableitung verschwinden: y 0 ¼ 0, d. h. y_ ¼ 0
und x_ 6¼ 0:
y0 ¼ 0
)
ð1 þ 3 sin 2 jÞ cos j ¼ 0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
6¼ 0
)
cos j ¼ 0
)
j1 ¼
p
;
2
j2 ¼
3
p
2
Denn es kommen nur Lösungen aus dem Intervall 0 j < 2 p in Frage (siehe Bild B-9):
y
1
y = cos f
π
2
Bild B-9
π
3π
2
2π
f
–1
Da der Nenner x_ ¼ ð1 3 sin 2 jÞ sin j der Steigungsformel an diesen Stellen (wie gefordert) ungleich null ist
(x_ ¼ 2 bzw. x_ ¼ 2), haben wir in der Tat Kurvenpunkte mit einer waagerechten Tangente vorliegen (es handelt
sich um die beiden Schnittpunkte der Kurve mit der y-Achse: x 1=2 ¼ 0 , y 1=2 ¼ 2).
98
B Differentialrechnung
Archimedische Spirale: r ðjÞ ¼ 2 j , 0 j p
B63
a) In welchen Punkten gibt es waagerechte bzw. senkrechte Tangenten?
b) Bestimmen Sie die Tangentengleichung im Schnittpunkt mit der y-Achse.
Wir bringen zunächst die Kurve in die Parameterform:
x ¼ r cos j ¼ 2 j cos j ;
y ¼ r sin j ¼ 2 j sin j
ð0 j pÞ
Die für die Steigungsformel benötigten Ableitungen x_ und y_ erhalten wir mit der Produktregel:
f
x ¼ 2 j cos j ¼ 2 ð j cos jÞ ¼ 2 ðu vÞ
u
|fflffl{zfflffl}
u ¼ j;
mit
v ¼ cos j
und
u_ ¼ 1 ;
v_ ¼ sin j
v
x_ ¼ 2 ðu_ v þ v_ uÞ ¼ 2 ð1 cos j ðsin jÞ jÞ ¼ 2 ðcos j j sin jÞ
f
y ¼ 2 j sin j ¼ 2 ð j sin jÞ ¼ 2 ðu vÞ
u
|fflffl{zfflffl}
u ¼ j;
mit
v ¼ sin j
und u_ ¼ 1 ;
v_ ¼ cos j
v
y_ ¼ 2 ðu_ v þ v_ uÞ ¼ 2 ð1 sin j þ ðcos jÞ jÞ ¼ 2 ðsin j þ j cos jÞ
Damit erhalten wir für den Kurvenanstieg y 0 in Abhängigkeit vom Winkelparameter j den folgenden Ausdruck:
y0 ¼
2 ðsin j þ j cos jÞ
sin j þ j cos j
tan j þ j
y_
¼
¼
¼
cos j j sin j
1 j tan j
x_
2 ðcos j j sin jÞ
Wir haben am Schluss noch gliedweise in Zähler und Nenner durch cos j dividiert und dabei beachtet, dass
sin j=cos j ¼ tan j ist.
a) Kurvenpunkte mit einer waagerechten Tangente: y 0 == 0, d. h. y_ == 0 und x_ 6¼ 0
y0 ¼ 0
)
tan j þ j ¼ 0
)
tan j ¼ j
Diese trigonometrische Gleichung besitzt im vorgegebenen Intervall 0 j p genau eine Lösung. Sie lautet:
j 1 ¼ 2,0288 (entspricht 116,24 ; siehe hierzu Aufgabe B-98). Der Nenner ist an dieser Stelle (wie gefordert) von
null verschieden (Nenner ¼ 5,1155).
Kurvenpunkte mit einer senkrechten Tangente: y 0 == 1, d. h. x_ == 0 und y_ 6¼ 0
y0 ¼ 1
)
1 j tan j ¼ 0
)
tan j ¼
1
j
Diese trigonometrische Gleichung wird in Aufgabe B-99 nach dem Tangentenverfahren von Newton gelöst. Sie besitzt
im Intervall 0 j p genau eine Lösung j 2 ¼ 0,8603 (im Gradmaß: 49,29 ). Da der Zähler tan j þ j der
Steigungsformel an dieser Stelle (wie gefordert) ungleich Null ist (Zähler ¼ 2,0226), besitzt die Kurve dort eine senkrechte Tangente.
Bild B-10 zeigt den Kurvenverlauf und die beiden Kurvenpunkte mit einer waagerechten bzw. senkrechten Tangente.
y
A:
A
π
r = 2f
P
B:
2
B
1
Bild B-10
– 2π
–5
–4
–3
–2
–1
j ¼ 116,24 ; r ¼ 4,0576
x ¼ 1,794; y ¼ 3,639
1
x
j ¼ 49,29 ;
r ¼ 1,7206
x ¼ 1,222;
y ¼ 1,304
2 Anwendungen der Differentialrechnung
99
b) Schnittpunkt mit der positiven y-Achse: j 0 ==
x0 ¼ 2
p
cos
2
p
2
¼ p 0 ¼ 0;
p
2
y0 ¼ 2
Steigung der Tangente in P ¼ ð0; pÞ, d. h. für j 0 ¼
p
:
2
p
2
¼
p
cos
2
1þ
y0 j0
p
¼
2
sin
p
cos
2
p
sin
2
þ
p
2
p
2
p
sin
2
p
2
¼ p 1 ¼ p
)
P ¼ ð0; pÞ
p
0
2
1
2
¼
¼
¼
p
p
p
0
1
2
2
Gleichung der Tangente in P == (x 0 ; y 0 ) == (0; p)
y y0
¼ m
x x0
)
yp
2
¼
x 0
p
)
yp ¼
2
x
p
)
y ¼
2
x þp
p
2.3 Linearisierung einer Funktion
Lehrbuch: Band 1, Kapitel IV.3.2
Formelsammlung: Kapitel IV.4.3
B64
Linearisieren Sie die Funktion y ¼
p2
in der Umgebung der Stelle x 0 ¼ p. Bestimmen Sie
sin x x
ferner den exakten Wert sowie den Näherungswert an der Stelle x ¼ 3.
Berechnung des „Arbeitspunktes‘‘ (Tangentenberührungspunktes) P ¼ ðx0 ; y0 Þ :
x0 ¼ p;
y0 ¼
p2
p2
¼
¼ p
sin p p
0p
)
P ¼ ðp; pÞ
Tangentensteigung m
Die benötigte Ableitung der Funktion bilden wir mit Hilfe der Kettenregel (Alternative: Quotientenregel mit konstantem Zähler):
y ¼
y0 ¼
p2
¼ p 2 ðsin x x Þ 1 ¼ p 2 u 1
sin x x
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
u ¼ sin x x
mit
p 2 ðcos x 1Þ
p 2 ðcos x 1Þ
dy
dy du
¼
¼ p 2 ð u 2 Þ ðcos x 1Þ ¼
¼
dx
du dx
u2
ðsin x xÞ 2
m ¼ y 0 ðpÞ ¼
p 2 ðcos p 1Þ
ðsin p pÞ 2
¼
p 2 ð 1 1Þ
ð0 pÞ 2
¼
2 p2
p2
¼ 2
Gleichung der Tangente in P == (x 0 ; y 0 ) == (p ; p)
y y0
¼ m
x x0
)
yþp
¼ 2
x p
)
y þ p ¼ 2 ðx pÞ ¼ 2 x 2 p
In der Umgebung des „Arbeitspunktes‘‘ P ¼ ðp; pÞ linearisierte Funktion: y ¼
Exakter Funktionswert an der Stelle x ¼ 3:
Näherungswert an der Stelle x ¼ 3:
y ¼
p2
¼ 3,4523
sin 3 3
y ¼ 2 3 3 p ¼ 3,4248
)
y ¼ 2x 3p
p2
¼ 2x 3p
sin x x
100
B Differentialrechnung
B65
Linearisieren Sie die Funktion y ¼ ln
1 þ x2
2x
in der Umgebung der Stelle x 0 ¼ 1.
Wir ersetzen die nur für x < 2 definierte Kurve in der Umgebung der Stelle x 0 ¼ 1 durch die dortige Tangente.
Zunächst wird die zugehörige Ordinate y 0 des „Arbeitspunktes‘‘ P berechnet:
1 þ 12
1þ1
¼ ln
y 0 ¼ ln
¼ ln 2 ) P ¼ ðx 0 ; y 0 Þ ¼ ð1; ln 2Þ
21
1
Bevor wir die Ableitung bilden, bringen wir die Funktion noch in eine für das Differenzieren günstigere Form:
1 þ x2
y ¼ ln
¼ ln ð1 þ x 2 Þ ln ð2 xÞ ¼ ln u ln v mit u ¼ 1 þ x 2 und v ¼ 2 x
2x
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
u
v
a
Rechenregel: ln
¼ ln a ln b . Gliedweise Differentiation unter Verwendung der Kettenregel (in der durch die
b
Substitutionen angedeuteten Weise) führt dann zu:
y0 ¼
1
1
2x
1
þ
2x
ð 1Þ ¼
2
u
v
2x
1þx
)
m ¼ y 0 ð1Þ ¼
2
1
þ
¼ 1þ1 ¼ 2
1þ1
21
Gleichung der Tangente in P == (x 0 ; y 0 ) == (1; ln 2)
y y0
¼ m
x x0
)
y ln 2
¼ 2
x 1
)
y ln 2 ¼ 2 ðx 1Þ
Gleichung der linearisierten Funktion (in der Umgebung von x 0
B66
Ersetzen Sie die Funktion y ¼
)
y ¼ 2 x 2 þ ln 2 ¼ 2 x 1,3069
1 þ x2
¼ 2 x 1,3069
¼ 1): y ¼ ln
2x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 e 2 x in der Umgebung von x 0 ¼ 0 durch eine lineare Funktion.
Berechnung des Tangentenberührungspunktes („Arbeitspunktes‘‘) P ¼ ðx 0 ; y 0 Þ:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 0 ¼ 0 ; y 0 ¼ 2 e 0 ¼ 2 1 ¼ 1 ) P ¼ ð0; 1Þ
Berechnung der Tangentensteigung m
Die Funktion wird mit Hilfe der Kettenregel wie folgt differenziert (dabei sind zwei Substitutionen durchzuführen):
pffiffiffi
y ¼ u mit u ¼ 2 e v und v ¼ 2 x
y0 ¼
dy
dy du dv
1
2 ev
ev
ev
e 2x
¼
¼ pffiffiffi ð e v Þ ð 2Þ ¼ pffiffiffi ¼ pffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx
du dv dx
2 u
2 u
u
2 ev
2 e 2x
e0
1
1
m ¼ y 0 ð0Þ ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
¼ 1
1
21
2 e0
Gleichung der Tangente in P == (x 0 ; y 0 ) == (0; 1)
y y0
¼ m
x x0
)
y1
¼ 1
x 0
)
y 1 ¼ 1 ðx 0Þ ¼ x
Linearisierte Funktion (in der Umgebung von x 0 ¼ 0): y ¼
)
y ¼ x þ1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 e 2x ¼ x þ 1
2 Anwendungen der Differentialrechnung
101
2.4 Krümmung einer ebenen Kurve
Lehrbuch: Band 1, Kapitel IV.3.3.3
Formelsammlung: Kapitel IV.4.4.2
Welche Krümmung hat die Kurve y ¼ 1 cos x an einer beliebigen Stelle x?
Bestimmen Sie den Krümmungskreis an der Stelle x ¼ p .
B67
Die für das Krümmungsverhalten der Kurve benötigten Ableitungen 1. und 2. Ordnung lauten y 0 ¼ sin x und
y 00 ¼ cos x. Damit erhalten wir für die Krümmung j den folgenden von der Koordinate x abhängigen Ausdruck:
j ðxÞ ¼
y 00
2 3=2
½1 þ ðy0 Þ
¼
cos x
½ 1 þ sin 2 x 3=2
An der Stelle x ¼ p, y ¼ 1 cos p ¼ 1 þ 1 ¼ 2 d. h. im Kurvenpunkt P ¼ ðp; 2Þ ergeben sich für die Kurvenkrümmung j und den Krümmungsradius r die Werte
jðpÞ ¼
cos p
½ 1 þ sin 2 p
3=2
¼
1
½1 þ 0
3=2
¼
1
¼ 1
1
und
rðpÞ ¼
1
1
1
¼
¼
¼ 1
1
j jðpÞ j
j1j
Wegen der Spiegelsymmetrie der Kurve bezüglich der zur y -Achse parallelen Geraden x ¼ p liegt der Mittelpunkt
M des Krümmungskreises auf dieser Symmetrieachse im Abstand rðpÞ ¼ 1 unterhalb des Kurvenpunktes
P ¼ ðp; 2Þ. Daher hat der Mittelpunkt die Koordinaten x 0 ¼ p und y 0 ¼ 1 (die x-Achse tangiert den Krümmungskreis, siehe Bild B-11).
y
P
2
y = 1 – cos x
1
M
Bild B-11
π
B68
Krümmungskreis
2π
x
An welcher Stelle besitzt die Kurve y ¼ ln ðcos x), p=2 < x < p=2 die größte Krümmung?
Bestimmen Sie den Krümmungskreis an dieser Stelle.
Wir bilden zunächst die für die Krümmung benötigten Ableitungen y 0 und y 00 :
y ¼ ln ðcos xÞ ¼ ln u
|fflfflffl{zfflfflffl}
u
y0 ¼
mit
u ¼ cos x
ðKettenregel verwenden!Þ
dy
dy du
1
sin x
¼
¼
ð sin xÞ ¼
¼ tan x ;
dx
du dx
u
cos x
y 00 ¼
1
¼ ð1 þ tan 2 xÞ
cos 2 x
102
B Differentialrechnung
Damit erhalten wir für die Kurvenkrümmung j den folgenden von der Abszisse x abhängigen Ausdruck:
jðxÞ ¼
y 00
½1 þ
ð y 0 Þ 2 3=2
¼
ð1 þ tan 2 xÞ
ð1 þ
tan 2
xÞ
3=2
ð1 þ tan 2 xÞ
¼
ð1 þ
tan 2
xÞ ð1 þ
tan 2
xÞ
1=2
¼
1
ð1 þ
tan 2
xÞ
1=2
1
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ tan 2 x
Dieser Ausdruck ist stets negativ, die Kurve daher überall im Intervall p=2 < x < p=2 nach rechts gekrümmt. Die
Krümmung ist betragsmäßig dort am größten, wo der Nenner des Bruches und somit der Wurzelradikand 1 þ tan 2 x
am kleinsten ist. Dies ist der Fall, wenn tan x ¼ 0 und somit x ¼ 0 und y ¼ ln ðcos 0Þ ¼ ln 1 ¼ 0 ist. Krümmung und Krümmungsradius besitzen dort, d. h. im Kurvenpunkt P ¼ ð0; 0Þ die folgenden Werte:
1
1
1
¼ 1;
jð0Þ ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
1
1þ0
1 þ tan 2 0
rð0Þ ¼
1
1
1
¼
¼ 1
¼
j1j
1
j jð0Þ j
Die Kurve verläuft spiegelsymmetrisch zur y-Achse, der Krümmungsmittelpunkt M (Mittelpunkt des Krümmungskreises) muss somit auf der y-Achse liegen und zwar um rð0Þ ¼ 1 unterhalb des Nullpunkts (zugleich Maximum der
Kurve). Daher besitzt M die Koordinaten x 0 ¼ 0 und y 0 ¼ 1. Bild B-12 zeigt den Verlauf der Kurve mit dem
zum Nullpunkt gehörenden Krümmungskreis.
y
P
–1
Bild B-12
1
–1
x
y = ln (cos x )
M
–2
Krümmungskreis
Zeigen Sie, dass das in Bild B-13 abgebildete Seil mit der Gleichung
y
y ¼ a cosh ðx=aÞ, c x c
B69
(Kettenlinie mit a > 0)
Kettenlinie
a
a) überall Linkskrümmung und
b) im tiefsten Punkt ðx ¼ 0Þ die größte Krümmung besitzt.
c) Bestimmen Sie den Krümmungskreis im tiefsten Punkt des Seiles.
–c
c
x
Bild B-13
a) Wir bestimmen zunächst die für das Krümmungsverhalten maßgeblichen Ableitungen y 0 und y 00 und daraus dann
die Abhängigkeit der Krümmung j von der Koordinate x:
y ¼ a cosh
y0 ¼
x
¼ a cosh u mit
a
|{z}
u
u ¼
x
a
ðKettenregel verwenden!Þ
dy
dy du
1
a sinh u
¼
¼ ða sinh uÞ
¼
¼ sinh u ¼ sinh
dx
du dx
a
a
x
a
Nochmalige Anwendung der Kettenregel (mit der selben Substitution) liefert die 2. Ableitung:
y 0 ¼ sinh
x
¼ sinh u mit
a
|{z}
u
u ¼
x
a
)
y 00 ¼ ðcosh uÞ
1
1
1
¼
cosh u ¼
cosh
a
a
a
x
a
2 Anwendungen der Differentialrechnung
103
Kurvenkrümmung in Abhängigkeit von der Abszisse x
jðxÞ ¼
¼
y 00
½ 1 þ ð y 0 Þ 2 3=2
¼
1
cosh ðx=aÞ
a
½ 1 þ sinh 2 ðx=aÞ 3=2
¼
cosh ðx=aÞ
1
1 cosh ðx=aÞ
¼
¼
a ½ cosh 2 ðx=aÞ 3=2
a cosh 3 ðx=aÞ
cosh ðx=aÞ
1
1
1
1
¼
¼
2
a cosh ðx=aÞ cosh ðx=aÞ
a cosh 2 ðx=aÞ a cosh 2 ðx=aÞ
(unter Verwendung der Beziehung cosh 2 u sinh 2 u ¼ 1
)
cosh 2 u ¼ 1 þ sinh 2 u mit u ¼ x=a)
Wegen a > 0 und cosh 2 ðx=aÞ > 0 ist der Nenner stets positiv und daher auch j > 0. Dies aber bedeutet Linkskrümmung an jeder Stelle der Kettenlinie.
b) Die Krümmung ist im tiefsten Kurvenpunkt (d. h. an der Stelle x ¼ 0) am größten, da dort der Nenner des
Bruches seinen kleinsten Wert hat ( cosh 2 0 ¼ 1, sonst cosh 2 x > 1).
c) Krümmungskreis im tiefsten Punkt P == (0; a)
Krümmung bzw. Krümmungsradius in P:
jð0Þ ¼
1
1
1
¼
¼
2
a
1
a
a cosh 0
)
rð0Þ ¼
1
1
¼
¼ a
j j ð0Þ j
1=a
Der Krümmungsmittelpunkt M muss auf der Symmetrieachse (d. h. y-Achse) liegen, und zwar im Abstand
rð0Þ ¼ a oberhalb von P ¼ ð0; aÞ. M hat somit die Koordinaten x 0 ¼ 0 und y 0 ¼ 2 a .
Krümmungskreis:
Mittelpunkt M ¼ ð0; 2 aÞ;
Radius r ¼ a
Die gewöhnliche Zykloide (Rollkurve) lässt sich in der Parameterform
x ¼ Rðt sin tÞ ; y ¼ Rð1 cos tÞ
B70
(Parameter : Drehwinkel t 0)
darstellen (R > 0Þ.
a) Bestimmen Sie die Krümmung der Kurve in Abhängigkeit vom Parameter (Drehwinkel) t.
b) Wo im Periodenintervall 0 j 2 p ist der Krümmungsradius r am größten? Bestimmen Sie
den zugehörigen Krümmungskreis.
a) Wir benötigen für die Berechnung der Krümmung die ersten beiden Ableitungen der Parametergleichungen. Sie
lauten:
x_ ¼ R ð1 cos tÞ ;
x€ ¼ R ð0 þ sin tÞ ¼ R sin t ;
y_ ¼ R ð0 þ sin tÞ ¼ R sin t ;
y€ ¼ R cos t
Für die Abhängigkeit der Krümmung j vom Parameter t entnehmen wir der Formelsammlung die folgende Berechnungsformel:
jðtÞ ¼
x_ y€ x€ y_
ðx_ 2 þ y_ 2 Þ 3=2
ð! FS : Kap: XIV:1:5Þ
Der besseren bersicht wegen berechnen wir Zähler und Nenner getrennt und vereinfachen dabei so weit wie
möglich:
x_ y€ x€ y_ ¼ Rð1 cos tÞ R cos t R sin t R sin t ¼ R 2 ðcos t cos 2 tÞ R 2 sin 2 t ¼
¼ R 2 ðcos t cos 2 t sin 2 t Þ ¼ R 2 ðcos t 1Þ ¼ R 2 ð1 cos tÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
(unter Verwendung der trigonometrischen Beziehung cos 2 t þ sin 2 t ¼ 1)
104
B Differentialrechnung
x_ 2 þ y_ 2 ¼ R 2 ð1 cos tÞ 2 þ R 2 sin 2 t ¼ R 2 ð1 2 cos t þ cos 2 tÞ þ R 2 sin 2 t ¼
¼ R 2 ð1 2 cos t þ cos 2 t þ sin 2 t Þ ¼ R 2 ð2 2 cos tÞ ¼ 2 R 2 ð1 cos tÞ
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1
ðx_ 2 þ y_ 2 Þ 3=2 ¼ ½ 2 R 2 ð1 cos tÞ 3=2 ¼ ð2 R 2 Þ 3=2 ð1 cos tÞ 3=2 ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
¼ 2 3=2 ðR 2 Þ 3=2 ð1 cos tÞ 1 ð1 cos tÞ 1=2 ¼ 2 2 R 3 ð1 cos tÞ 1 cos t
pffiffiffi
(2 3=2 ¼ 2 1 2 1=2 ¼ 2 2 ). Einsetzen dieser Ausdrücke in die Krümmungsformel ergibt (mit R 3 ¼ R R 2 Þ:
j ðtÞ ¼
x_ y€ x€ y_
ðx_ 2 þ y_ 2 Þ 3=2
¼
R 2 ð1 cos tÞ
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffi
pffiffiffi
2 2 R 1 cos t
2 2 R R 2 ð1 cos tÞ 1 cos t
Die Krümmung ist im Intervall 0 < t < 2 p stets negativ, die Kurve somit nach rechts gekrümmt (1 cos t > 0).
b) Für den Krümmungsradius r in Abhängigkeit vom Parameter t gilt dann:
rðtÞ ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
1
1
¼
¼ 2 2 R 1 cos t
j K ðtÞ j
1
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 2 R 1 cos t
Der größte Wert für r liegt vor, wenn der Wurzelradikand 1 cos t am größten wird. Dies ist der Fall, wenn
cos t den kleinsten Wert 1 annimmt. Dieser Wert wird bekanntlich an der Stelle t ¼ p erreicht. Der Krümmungsradius r hat also für t ¼ p seinen größten Wert (dies entspricht einer halben Drehung des Rades und somit
der höchsten Stelle der Rollkurve, siehe hierzu auch Bild B-14).
Krümmungskreis für t == p
(
t ¼ p
)
x ¼ R ðp sin pÞ ¼ R ðp 0Þ ¼ p R
y ¼ R ð1 cos pÞ ¼ R ð1 þ 1Þ ¼ 2 R
)
)
P ¼ ðp R; 2 RÞ
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
rmax ¼ rðt ¼ pÞ ¼ 2 2 R 1 cos p ¼ 2 2 R 1 þ 1 ¼ 2 2 R 2 ¼ 4 R
Da die Rollkurve spiegelsymmetrisch bezüglich der Geraden x ¼ p R ðParallele zur y-Achse durch den höchsten
Punkt P ¼ ðp R; 2 RÞÞ verläuft, liegt auch der Krümmungsmittelpunkt M auf dieser Geraden und zwar um die
Strecke rmax ¼ 4 R unterhalb des Punktes P:
Krümmungskreis in P ¼ ðp R; 2 RÞ : Mittelpunkt M ¼ ðp R; 2 RÞ; Radius r ¼ 4 R
Bild B-14 zeigt den Verlauf der Rollkurve im Parameterintervall 0 t 2 p und den Krümmungskreis im
höchsten Kurvenpunkt.
y
P = (π R ; 2 R )
2R
Krümmungskreis
Rollkurve
Bild B-14
0
πR
2πR
x
2 Anwendungen der Differentialrechnung
105
2.5 Relative Extremwerte, Wende- und Sattelpunkte
Lehrbuch: Band 1, Kapitel IV.3.4
Formelsammlung: Kapitel IV.4.5 und 4.6
B71
Bestimmen Sie die relativen Extremwerte der Funktion y ¼ x arctan ð2 xÞ.
Wir bilden zunächst die benötigten Ableitungen y 0 und y 00 .
y ¼ x arctan ð2 xÞ ¼ x arctan u
|ffl{zffl}
u
mit
u0 ¼ 2
u ¼ 2x;
Summen- und Kettenregel liefern:
y0 ¼ 1
1ð1 þ u 2 Þ 2
1
1 þ u2 2
u2 1
4x2 1
¼
2 ¼
¼
¼
1 þ u2
1 þ u2
u2 þ 1
1 þ u2
4x2 þ 1
Mit Hilfe der Quotientenregel bilden wir die 2. Ableitung:
y0 ¼
4x2 1
u
¼
2
v
4x þ 1
y 00 ¼
8 x ð4 x 2 þ 1Þ 8 x ð4 x 2 1Þ
u0v v0u
32 x 3 þ 8 x 32 x 3 þ 8 x
16 x
¼
¼
¼
2
2
2
2
2
v2
ð4 x þ 1Þ
ð4 x þ 1Þ
ð4 x þ 1Þ 2
mit
u ¼ 4x2 1;
v ¼ 4x2 þ 1
und u 0 ¼ 8 x ;
v0 ¼ 8x
Wir berechnen jetzt die Kurvenpunkte mit einer waagerechten Tangente (notwendige Bedingung für einen relativen
Extremwert):
y0 ¼ 0
)
4x2 1
¼ 0
4x2 þ 1
)
4x2 1 ¼ 0
)
x2 ¼
1
4
)
x 1=2 ¼
1
2
Die 2. Ableitung muss ungleich Null sein und entscheidet mit ihrem Vorzeichen über die Art des Extremwertes (hinreichende Bedingung für einen Extremwert):
1
8
8
00
y
¼
¼ 2 > 0 ) relatives Minimum
x1 ¼
¼
2
2
4
ð1 þ 1Þ
1
8
8
y
¼
¼ 2 < 0
x2 ¼
¼
2
2
4
ð1 þ 1Þ
00
)
relatives Maximum
Wir berechnen noch die zugehörigen Ordinaten:
y1 ¼
1
1
p
arctan 1 ¼
¼ 0,2854 ;
2
2
4
y2 ¼
1
1
p
arctan ð 1Þ ¼
þ
¼ 0,2854
2
2
4
Es gibt somit zwei Extremwerte. Sie lauten:
Min ¼ ð0,5; 0,2854Þ;
B72
Max ¼ ð 0,5; 0,2854Þ
Bestimmen Sie die relativen Extremwerte der Funktion y ¼ ln
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ x 2 þ arctan x .
106
B Differentialrechnung
Wir vereinfachen zunächst die Funktion unter Verwendung der logarithmischen Rechenregel ln a n ¼ n ln a:
y ¼ ln
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
1 þ x 2 þ arctan x ¼ ln ð1 þ x 2 Þ 1=2 þ arctan x ¼
ln ð1 þ x 2 Þ þ arctan x
2
Die 1. Ableitung erhalten wir durch gliedweise Differentiation, wobei der 1. Summand nach der Kettenregel zu differenzieren ist:
y ¼
y0 ¼
1
1
ln ð1 þ x 2 Þ þ arctan x ¼
ln u þ arctan x
2
2
|fflfflfflfflffl{zfflfflfflfflffl}
u
mit
u ¼ 1 þ x2;
u0 ¼ 2x
1 1
1
1
1
1
x
1
x þ1
¼
2x þ
¼
þ
¼
u0 þ
2 1 þ x2
2 u
1 þ x2
1 þ x2
1 þ x2
1 þ x2
1 þ x2
Die 2. Ableitung bilden wir mit Hilfe der Quotientenregel:
y0 ¼
x þ1
u
¼
v
1 þ x2
y 00 ¼
1 ð1 þ x 2 Þ 2 x ðx þ 1Þ
u0v v0u
1 þ x2 2x2 2x
1 x2 2x
¼
¼
¼
2
2
2
v
ð1 þ x 2 Þ
ð1 þ x 2 Þ
ð1 þ x 2 Þ 2
mit
u ¼ x þ 1;
v ¼ 1 þ x2
und u 0 ¼ 1 ;
v0 ¼ 2x
Berechnung der relativen Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
x þ1
¼ 0
1 þ x2
)
)
x þ1 ¼ 0
)
x1 ¼ 1
Die Kurve besitzt also an der Stelle x 1 ¼ 1 eine waagerechte Tangente. Wie verhält sich die 2. Ableitung an dieser Stelle?
y 00 ðx 1 ¼ 1Þ ¼
11þ2
ð1 þ 1Þ
2
¼
2
1
¼
> 0
4
2
)
relatives Minimum
Die Kurve ist demnach an der Stelle x 1 ¼ 1 nach links gekrümmt und besitzt daher dort ein relatives Minimum.
Zugehöriger Ordinatenwert: y 1 ¼
1
1
p
ln ð1 þ 1Þ þ arctan ð 1Þ ¼
ln 2
¼ 0,4388
2
2
4
Ergebnis: Relatives Minimum in ð 1; 0,4388Þ
B73
Wo besitzt die Funktion y ¼ 2
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1 x þ 2 x þ 1 , 1 x 1 relative Extremwerte ?
Bildung der benötigten Ableitungen y 0 und y 00
Die 1. Ableitung erhalten wir durch gliedweise Differentiation, wobei beide Summanden nach der Kettenregel zu differenzieren sind:
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
y ¼ 2 1 x þ 2 x þ 1 ¼ 2 u þ 2 v mit u ¼ 1 x ; v ¼ x þ 1 und u 0 ¼ 1 ; v 0 ¼ 1
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
y0 ¼ 2
2
1
1
1
1
1
1
pffiffiffi u0 þ 2 pffiffiffi v0 ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ð 1Þ þ pffiffiffiffiffiffiffiffiffiffiffiffiffi 1 ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi þ pffiffiffiffiffiffiffiffiffiffiffiffiffi
u
2 v
1x
x þ1
1x
x þ1
Bevor wir die 2. Ableitung bilden, verwandeln wir die Wurzelausdrücke in Potenzen mit negativ gebrochenen Exponenten, die mit Hilfe der Kettenregel leicht zu differenzieren sind:
y0 ¼
1
ð1 xÞ
u ¼ 1 x;
1=2
þ
1
ðx þ 1Þ
v ¼ x þ1
1=2
¼ ð1 xÞ 1=2 þ ðx þ 1Þ 1=2 ¼ u 1=2 þ v 1=2
|fflfflfflffl{zfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
u
v
und u 0 ¼ 1 ;
v0 ¼ 1
2 Anwendungen der Differentialrechnung
107
1
1 3=2
1 3=2
1 3=2
1
1
y 00 ¼
v0 ¼
ð 1Þ
1 ¼
¼
u 3=2 u 0
v
u
v
3=2
2
2
2
2
2u
2 v 3=2
¼
0
1
1
1
1
1
1
1
1
¼
¼
þ
pffiffiffiffiffiffi
pffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi A
2 @qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi3ffi
2 u3
2 v3
2 ð1 xÞ 3
2 ðx þ 1Þ 3
ð1 xÞ
ðx þ 1Þ 3
Berechnung der relativen Extremwerte: y 0 == 0, y 00 6¼ 0
1
1
1
1
pffiffiffiffiffiffiffiffiffiffiffiffiffi þ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 0 ) pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi
)
1x
x þ1
x þ1
1x
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1 x ¼ x þ 1 j quadrieren ) 1 x ¼ x þ 1 ) 2 x ¼ 0 )
y0 ¼ 0
)
x1 ¼ 0
Der gefundene Wert x 1 ¼ 0 erfüllt die Wurzelgleichung und ist daher eine Lösung (die Kurve hat an dieser Stelle
eine waagerechte Tangente). Anhand der 2. Ableitung prüfen wir die Art der Kurvenkrümmung (Rechts- oder Linkskrümmung):
!
1
1
1
1
1
y 00 ðx 1 ¼ 0Þ ¼
ð1 þ 1Þ ¼
2 ¼ 1 < 0 ) relatives Maximum
¼
pffiffiffiffiffi þ pffiffiffiffiffi
2
2
2
3
3
1
1
Zugehöriger Ordinatenwert: y 1 ¼ 2
pffiffiffi
pffiffiffi
1þ2 1 ¼ 2þ2 ¼ 4
Ergebnis: Relatives Maximum in ð0; 4Þ
Bremskraft K einer Wirbelstrombremse in Abhängigkeit von der Geschwindigkeit v:
v
ða > 0; v 0Þ
KðvÞ ¼
2
v þ a2
B74
Bei welcher Geschwindigkeit erreicht die Bremskraft ihren größten Wert?
Wir bilden zunächst die benötigten Ableitungen 1. und 2. Ordnung, jeweils mit Hilfe der Quotientenregel:
KðvÞ ¼
v
a
¼
v2 þ a2
b
K 0 ðvÞ ¼
K 0 ðvÞ ¼
a0 b b0 a
b2
a2 v2
ðv 2
þ
a 2Þ 2
a ¼ a2 v2;
¼
¼
mit
a ¼ v;
b ¼ v2 þ a2
1 ðv 2 þ a 2 Þ 2 v v
ðv 2 þ
a 2Þ 2
¼
und
a0 ¼ 1;
v2 þ a2 2v2
ðv 2 þ
a 2Þ 2
¼
b0 ¼ 2v
a2 v2
ðv 2 þ a 2 Þ 2
a
b
b ¼ ðv 2 þ a 2 Þ 2
und
a0 ¼ 2v;
b 0 ¼ 2 ðv 2 þ a 2 Þ 2 v ¼ 4 v ðv 2 þ a 2 Þ
( b wurde dabei nach der Kettenregel differenziert, Substitution: t ¼ v 2 þ a 2 )
K 00 ðvÞ ¼
¼
a0 b b0 a
b2
¼
2 v ðv 2 þ a 2 Þ 2 4 v ðv 2 þ a 2 Þ ða 2 v 2 Þ
ðv 2 þ a 2 Þ 4
ðv 2 þ a 2 Þ ½ 2 v ðv 2 þ a 2 Þ 4 v ða 2 v 2 Þ
ðv 2 þ a 2 Þ ðv 2 þ a 2 Þ 3
¼
¼
2v3 2a2 v 4a2 v þ 4v3
ðv 2 þ a 2 Þ 3
Umformungen: Im Zähler den gemeinsamen Faktor v 2 þ a 2 ausklammern, dann kürzen.
¼
2v3 6a2 v
ðv 2 þ a 2 Þ 3
108
B Differentialrechnung
Berechnung des gesuchten Maximums: K 0 (u) == 0, K 00 (u) < 0
K 0 ðvÞ ¼ 0
a2 v2
)
ðv 2
þ
a 2Þ 2
¼ 0
)
a2 v2 ¼ 0
)
v 1=2 ¼ a
Wegen v 0 kommt nur der positive Wert v 1 ¼ a infrage. An dieser Stelle gilt:
K 00 ðv 1 ¼ aÞ ¼
2a3 6a3
¼
ða 2 þ a 2 Þ 3
4a3
1
¼
< 0
2a3
8a6
(wegen a > 0 nach Aufgabenstellung). Die hinreichende Bedingung für ein Maximum ist damit erfüllt.
Ergebnis: Für v ¼ a wird die Bremskraft am größten. Sie beträgt dann:
Kmax ¼ K ðv ¼ aÞ ¼
B75
a2
a
a
1
¼
¼
2
2
2
a
2a
þa
Zeigen Sie: Die Funktion y ¼ 3 þ
Maximum.
x
ðx þ aÞ 2
mit a > 0 besitzt an der Stelle x 1 ¼ a ein relatives
Wir müssen zeigen, dass an der Stelle x 1 ¼ a die folgenden hinreichenden Bedingungen für ein relatives Maximum
erfüllt sind:
y 0 ðx 1 ¼ aÞ ¼ 0 ðwaagerechte TangenteÞ;
y 00 ðx 1 ¼ aÞ < 0
ðRechtskr ümmung der KurveÞ
Daher bilden wir zunächst die benötigten Ableitungen y 0 und y 00 , jeweils mit Hilfe der Quotientenregel in Verbindung mit der Kettenregel:
y ¼ 3þ
x
ðx þ aÞ
2
¼ 3þ
u
v
mit
u ¼ x;
v ¼ ðx þ aÞ 2
und
u0 ¼ 1;
v 0 ¼ 2 ðx þ aÞ
(die Ableitung von v ¼ ðx þ aÞ 2 erhalten wir mit der Kettenregel, Substitution: t ¼ x þ a)
1 ðx þ aÞ 2 2 ðx þ aÞ x
ðx þ aÞ ½ ðx þ aÞ 2 x
u0 v v0 u
x þ a 2x
ax
¼
¼
¼
¼
y ¼ 0þ
2
4
3
3
v
ðx þ aÞ
ðx þ aÞ ðx þ aÞ
ðx þ aÞ
ðx þ aÞ 3
0
y0 ¼
ax
ðx þ aÞ
3
¼
u
v
mit
u ¼ a x;
v ¼ ðx þ aÞ 3
und
u0 ¼ 1;
v 0 ¼ 3 ðx þ aÞ 2
(v 0 haben wir mit Hilfe der Kettenregel gebildet, analog wie bei der 1. Ableitung, Substitution: t ¼ x þ a)
y
00
1 ðx þ aÞ 3 3 ðx þ aÞ 2 ða xÞ
ðx þ aÞ 2 ½ ðx þ aÞ 3 ða xÞ
u0v v0u
¼
¼
¼
¼
v2
ðx þ aÞ 6
ðx þ aÞ 2 ðx þ aÞ 4
¼
x a 3a þ 3x
ðx þ aÞ
4
¼
2x 4a
ðx þ aÞ 4
Einsetzen des Wertes x 1 ¼ a in y 0 und y 00 :
y 0 ðx 1 ¼ aÞ ¼
y 00 ðx 1 ¼ aÞ ¼
aa
ða þ aÞ
3
2a 4a
ða þ aÞ
4
¼
0
¼ 0
8a3
¼
2a
1
¼
< 0
4
16 a
8a3
)
waagerechte Tangente
ðwegen a > 0Þ
)
relatives Maximum
2 Anwendungen der Differentialrechnung
109
Damit haben wir die Behauptung als richtig nachgewiesen. Die zugehörige Ordinate lautet:
y1 ¼ 3 þ
a
ða þ aÞ
2
¼ 3þ
Ergebnis: Relatives Maximum in
B76
a
1
12 a þ 1
¼ 3þ
¼
2
4a
4a
4a
ða gekürztÞ
12 a þ 1
a;
4a
Bestimmen Sie die relativen Extremwerte, Wende- und Sattelpunkte der Funktion y ¼ x 3 e 2 x .
Bildung aller benötigten Ableitungen (bis zur 3. Ordnung)
Wir benötigen jeweils Produkt- und Kettenregel.
1. Ableitung
f
y ¼ x 3 e 2 x ¼ u v mit
u
|fflffl{zfflffl}
v ¼ e 2x
u ¼ x3;
und
u0 ¼ 3x2 ;
v 0 ¼ 2 e 2x
v
(Ableitung von v ¼ e 2 x nach der Kettenregel, Substitution: t ¼ 2 x)
y 0 ¼ u 0 v þ v 0 u ¼ 3 x 2 e 2 x 2 e 2 x x 3 ¼ ð3 x 2 2 x 3 Þ e 2 x
2. Ableitung
y 0 ¼ ð3 x 2 2 x 3 Þ e 2 x ¼ u v ;
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |ffl{zffl}
u
v
u ¼ 3 x 2 2 x 3;
v ¼ e 2x ;
u0 ¼ 6x 6x2 ;
v 0 ¼ 2 e 2x
y 00 ¼ u 0 v þ v 0 u ¼ ð6 x 6 x 2 Þ e 2 x 2 e 2 x ð3 x 2 2 x 3 Þ ¼
¼ ½ 6 x 6 x 2 2 ð3 x 2 2 x 3 Þ e 2 x ¼ ð6 x 6 x 2 6 x 2 þ 4 x 3 Þ e 2 x ¼
¼ ð4 x 3 12 x 2 þ 6 xÞ e 2 x
3. Ableitung
y 00 ¼ ð4 x 3 12 x 2 þ 6 xÞ e 2 x ¼ u v
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |ffl{zffl}
u
v
u ¼ 4 x 3 12 x 2 þ 6 x ;
v ¼ e 2x
und u 0 ¼ 12 x 2 24 x þ 6 ;
v 0 ¼ 2 e 2 x
y 000 ¼ u 0 v þ v 0 u ¼ ð12 x 2 24 x þ 6Þ e 2 x 2 e 2 x ð4 x 3 12 x 2 þ 6 xÞ ¼
¼ ½ 12 x 2 24 x þ 6 2 ð4 x 3 12 x 2 þ 6 xÞ e 2 x ¼
¼ ð12 x 2 24 x þ 6 8 x 3 þ 24 x 2 12 xÞ e 2 x ¼ ð 8 x 3 þ 36 x 2 36 x þ 6Þ e 2 x
Berechnung der Extremwerte: y 0 == 0, y 00 6¼ 0
y 0 ¼ 0 ) ð3 x 2 2 x 3 Þ e 2 x ¼ 0 ) 3 x 2 2 x 3 ¼ x 2 ð3 2 xÞ ¼ 0
|fflffl{zfflffl}
6¼ 0
x2 ¼ 0
x 1=2 ¼ 0
3 2 x ¼ 0 ) x 3 ¼ 1,5
Wir prüfen jetzt über die 2. Ableitung, ob an diesen Stellen relative Extremwerte vorliegen:
y 00 ðx 1=2 ¼ 0Þ ¼ ð4 0 12 0 þ 6 0Þ e 0 ¼ 0 1 ¼ 0
)
110
B Differentialrechnung
An der Stelle x1=2 ¼ 0 ist die hinreichende Bedingung für einen Extremwert ð y 00 6¼ 0Þ nicht erfüllt. Es kann sich
hier aber um einen Sattelpunkt handeln (siehe spätere Berechnung der Wende- und Sattelpunkte).
y 00 ðx 3 ¼ 1,5Þ ¼ ð13,5 27 þ 9Þ e 3 ¼ 4,5 e 3 < 0
)
relatives Maximum
y 3 ¼ ð1,5Þ 3 e 3 ¼ 0,1680
Die Koordinaten des Maximums lauten: x 3 ¼ 1,5;
Relative Extremwerte: Max ¼ ð1,5; 0,1680Þ
Berechnung der Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
ð4 x 3 12 x 2 þ 6 xÞ e 2 x ¼ 0
|ffl{zffl}
6¼ 0
)
x ð4 x 2 12 x þ 6Þ ¼ 0
x ¼ 0
)
4 x 3 12 x 2 þ 6 x ¼ 0
)
x4 ¼ 0
4 x 12 x þ 6 ¼ 0
2
)
x 5 ¼ 2,3660;
x 6 ¼ 0,6340
(bitte nachrechnen!). Wir prüfen jetzt, ob an diesen Stellen die hinreichende Bedingung für einen Wendepunkt erfüllt ist:
y 000 ðx 4 ¼ 0Þ ¼ 6 e 0 ¼ 6 1 ¼ 6 6¼ 0
)
Wendepunkt
y 000 ðx 5 ¼ 2,3660Þ ¼ ð 105,9581 þ 201,5264 85,1760 þ 6Þ e 4,7320 ¼
¼ 16,3923 e 4,7320 6¼ 0
)
Wendepunkt
y 000 ðx 6 ¼ 0,6340Þ ¼ ð 2,0387 þ 14,4704 22,8240 þ 6Þ e 1,2680 ¼
¼ 4,3923 e 1,2680 6¼ 0
)
Wendepunkt
Es gibt somit drei Wendepunkte: W 1 ¼ ð0; 0Þ; W 2 ¼ ð2,3660; 0,1167Þ; W 3 ¼ ð0,6340; 0,0717Þ
Der Wendepunkt W 1 ist sogar ein Sattelpunkt, denn die dortige Tangente verläuft waagerecht (was wir bereits weiter
vorne vermutet haben): y 0 ð0Þ ¼ 0 e 0 ¼ 0 1 ¼ 0
B77
y ¼ ðx 1Þ e 2 x
Bestimmen Sie die relativen Extremwerte, Wendepunkte und Wendetangenten dieser Funktion.
Wir bilden zunächst die benötigten ersten drei Ableitungen (mit Hilfe von Produkt- und Kettenregel).
1. Ableitung (Produkt- und Kettenregel)
y ¼ ðx 1Þ e 2 x ¼ u v mit
|fflfflfflffl{zfflfflfflffl} |ffl{zffl}
u
v
u ¼ x 1;
v ¼ e 2x
und u 0 ¼ 1 ;
v 0 ¼ 2 e 2x
(der Faktor v ¼ e 2 x wurde dabei nach der Kettenregel differenziert, Substitution: t ¼ 2 x)
y 0 ¼ u 0 v þ v 0 u ¼ 1 e 2 x 2 e 2 x ðx 1Þ ¼ ½ 1 2 ðx 1Þ e 2 x ¼ ð3 2 xÞ e 2 x
2. Ableitung (Produkt- und Kettenregel)
y 0 ¼ ð3 2 xÞ e 2 x ¼ u v mit
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |ffl{zffl}
u
v
u ¼ 3 2x;
v ¼ e 2x
und u 0 ¼ 2 ;
v 0 ¼ 2 e 2x
y 00 ¼ u 0 v þ v 0 u ¼ 2 e 2 x 2 e 2 x ð3 2 xÞ ¼ ½ 2 2 ð3 2 xÞ e 2 x ¼ ð 8 þ 4 xÞ e 2 x
2 Anwendungen der Differentialrechnung
111
3. Ableitung (Produkt- und Kettenregel)
y 00 ¼ ð 8 þ 4 xÞ e 2 x ¼ u v mit
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl} |ffl{zffl}
u
v
v ¼ e 2x
u ¼ 8 þ 4x;
u0 ¼ 4;
und
v 0 ¼ 2 e 2x
y 000 ¼ u 0 v þ v 0 u ¼ 4 e 2 x 2 e 2 x ð 8 þ 4 xÞ ¼ ½ 4 2 ð 8 þ 4 xÞ e 2 x ¼ ð20 8 xÞ e 2 x
Berechnung der Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
ð3 2 xÞ e 2 x ¼ 0
|ffl{zffl}
6¼ 0
)
)
3 2x ¼ 0
y 00 ðx 1 ¼ 1,5Þ ¼ ð 8 þ 6Þ e 3 ¼ 2 e 3 < 0
)
)
y 1 ¼ 0,5 e 3 ¼ 0,0249
x 1 ¼ 1,5 ;
relatives Maximum
Extremwerte: Max ¼ ð1,5; 0,0249Þ
Berechnung der Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
ð 8 þ 4 xÞ e 2 x ¼ 0
|ffl{zffl}
6¼ 0
)
)
8 þ 4x ¼ 0
y 000 ðx 2 ¼ 2Þ ¼ ð20 16Þ e 4 ¼ 4 e 4 6¼ 0
)
)
x2 ¼ 2 ;
y 2 ¼ e 4 ¼ 0,0183
Wendepunkt
Wendepunkte: W ¼ ð2; 0,0183Þ
Wendetangente in W == (x 2 ; y 2 ) == (2; 0,0183)
Steigung in W : m ¼ y 0 ðx 2 ¼ 2Þ ¼ ð3 4Þ e 4 ¼ e 4 ¼ 0,0183
Gleichung der Wendetangente (Ansatz in der Punkt-Steigungs-Form):
y y2
¼ m
x x2
)
y 0,0183
¼ 0,0183
x 2
)
y 0,0183 ¼ 0,0183 ðx 2Þ ¼ 0,0183 x þ 0,0366
Wendetangente: y ¼ 0,0183 x þ 0,0549
B78
Wo besitzt die Funktion y ¼ 2 x 2 ln
pffiffiffi
x , x > 0 relative Extremwerte bzw. Wendepunkte?
Die Funktion wird zunächst wie folgt vereinfacht:
y ¼ 2 x 2 ln
pffiffiffi
1
ln x ¼ x 2 ln x
x ¼ 2 x 2 ln x 1=2 ¼ 2 x 2
2
ðRechenregel: ln a n ¼ n ln aÞ
Ableitungen 1. bis 3. Ordnung (Produktregel)
f
y ¼ x 2 ln x ¼ u v mit
u
|{z}
u ¼ x2;
v ¼ ln x
und
u0 ¼ 2x;
v
1
x 2 ¼ 2 x ln x þ x
x
y 0 ¼ 2 x ln x þ x ¼ u v þ x
mit
f
y 0 ¼ u 0 v þ v 0 u ¼ 2 x ln x þ
u
|{z}
v
y 00 ¼ u 0 v þ v 0 u þ 1 ¼ 2 ln x þ
y 000 ¼ 2
1
2
¼
x
x
u ¼ 2x;
v ¼ ln x
v0 ¼
1
x
und u 0 ¼ 2 ;
v0 ¼
1
x
1
2 x þ 1 ¼ 2 ln x þ 2 þ 1 ¼ 2 ln x þ 3
x
112
B Differentialrechnung
Berechnung der Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
2 x ln x þ x ¼ 0
)
x ð2 ln x þ 1Þ ¼ 0
)
2 ln x þ 1 ¼ 0
f
)
> 0
Diese logarithmische Gleichung lösen wir wie folgt durch Entlogarithmieren (Rechenregel: e ln z ¼ z für z > 0):
2 ln x þ 1 ¼ 0
)
ln x ¼ 0,5
e ln x ¼ x ¼ e 0,5
)
)
x 1 ¼ e 0,5
Es gibt somit nur einen Kurvenpunkt mit waagerechter Tangente. Wegen
y 00 ðx 1 ¼ e 0,5 Þ ¼ 2 ln e 0,5 þ 3 ¼ 2 ð 0,5Þ þ 3 ¼ 1 þ 3 ¼ 2 > 0
liegt ein relatives Minimum vor. Die zugehörigen Koordinaten lauten:
x 1 ¼ e 0,5 ¼ 0,6065;
y 1 ¼ ðe 0,5 Þ 2 ln e 0,5 ¼ e 1 ð 0,5Þ ¼ 0,5 e 1 ¼ 0,1839
Relative Extremwerte: Min ¼ ð0,6065; 0,1839Þ
Berechnung der Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
2 ln x þ 3 ¼ 0
y 000 ðx 2 ¼ e 1;5 Þ ¼
)
ln x ¼ 1,5
2
¼ 2 e 1;5 6¼ 0
e 1;5
)
)
e ln x ¼ e 1;5
|{z}
x
)
x 2 ¼ e 1;5
Wendepunkt
Die Koordinaten des Wendepunktes sind:
x 2 ¼ e 1;5 ¼ 0;2231;
y 2 ¼ ðe 1;5 Þ 2 ln e 1;5 ¼ e 3 ð 1;5Þ ¼ 1;5 e 3 ¼ 0,0747
Wendepunkte: W ¼ ð0;2231; 0;0747Þ
2.6 Kurvendiskussion
Diskutieren Sie den Verlauf der Funktionen und Kurven nach dem folgenden Schema: Definitionsbereich, Symmetrie,
Nullstellen, Pole, Ableitungen (in der Regel bis zur 3. Ordnung), relative Extremwerte, Wende- und Sattelpunkte,
Verhalten „im Unendlichen‘‘. Am Schluss ist eine saubere Skizze des Kurvenverlaufs anzufertigen.
Lehrbuch: Band 1, Kapitel IV.3.6
Formelsammlung: Kapitel IV.4.7
B79
y ¼ x4 x3 3x2 þ 5x 2
Definitionsbereich: 1 < x < 1
Symmetrie: nicht vorhanden
Nullstellen: x 1 ¼ 1 (durch Probieren gefunden)
Horner-Schema (Abspalten des Linearfaktors x 1):
1
x1 ¼ 1
1
1
3
5
2
1
0
3
2
0
3
2
0
) 1. reduziertes Polynom: x 3 3 x þ 2
2 Anwendungen der Differentialrechnung
113
Eine weitere Nullstelle liegt bei x 2 ¼ 1 (durch Probieren gefunden).
Horner-Schema (Abspalten des Linearfaktors x 1):
1
x2 ¼ 1
1
0
3
2
1
1
2
1
2
0
Restliche Nullstellen: x 2 þ x 2 ¼ 0
x3 ¼ 1 ;
) 2. reduziertes Polynom: x 2 þ x 2
)
x 3=4 ¼ 0,5
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
0,25 þ 2 ¼ 0,5 2,25 ¼ 0,5 1,5
)
x4 ¼ 2
Die Funktion besitzt also eine dreifache Nullstelle bei x 1=2=3 ¼ 1 und eine einfache Nullstelle bei x 4 ¼ 2.
Ableitungen (bis zur 3. Ordnung)
y0 ¼ 4x3 3x2 6x þ 5;
y 00 ¼ 12 x 2 6 x 6 ;
y 000 ¼ 24 x 6
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
4x3 3x2 6x þ 5 ¼ 0
)
x5 ¼ 1
ðdurch Probieren gefundenÞ
Horner-Schema (Abspalten des Linearfaktors x 1):
4
x5 ¼ 1
4
3
6
5
4
1
5
1
5
0
4x2 þ x 5 ¼ 0 j : 4
x 6=7
)
) 1. reduziertes Polynom: 4 x 2 þ x 5
x 2 þ 0,25 x 1,25 ¼ 0
)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ 0,125 0,015 625 þ 1,25 ¼ 0,125 1,265 625 ¼ 0,125 1,125 )
x 6 ¼ 1 ; x 7 ¼ 1,25
Die Kurve besitzt also an den Stellen x 5=6 ¼ 1 und x 7 ¼ 1,25 waagerechte Tangenten. Ob es sich dabei auch
um Extremwerte handelt, entscheidet die 2. Ableitung:
y 00 ðx 5=6 ¼ 1Þ ¼ 12 6 6 ¼ 0
Die hinreichende Bedingung für einen Extremwert ist somit an der Stelle x5=6 ¼ 1 nicht erfüllt (später zeigt sich,
dass dort ein Sattelpunkt liegt).
y 00 ðx 7 ¼ 1,25Þ ¼ 18,75 þ 7,5 6 ¼ 20,25 > 0
)
relatives Minimum
Ordinate des relativen Minimums: y 7 ¼ 8,543
Relative Extremwerte: Min ¼ ð 1,25; 8,543Þ
Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
x 8=9 ¼ 0,25
12 x 2 6 x 6 ¼ 0 j : 12
)
x 2 0,5 x 0,5 ¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0,0625 þ 0,5 ¼ 0,25 0,5625 ¼ 0,25 0,75
y 000 ðx 8 ¼ 1Þ ¼ 24 6 ¼ 18 6¼ 0
)
)
)
x8 ¼ 1 ;
x 9 ¼ 0,5
Wendepunkt
y 000 ðx 9 ¼ 0,5Þ ¼ 12 6 ¼ 18 6¼ 0
)
Wendepunkt
Die zugehörigen Ordinaten sind y 8 ¼ 0 und y 9 ¼ 5,0625.
Wendepunkte: W 1 ¼ ð1; 0Þ und W 2 ¼ ð 0,5; 5,0625Þ
Wegen y 0 ð1Þ ¼ 4 3 6 þ 5 ¼ 0 ist W 1 ein Sattelpunkt (wie bereits weiter oben vermutet).
114
B Differentialrechnung
Bild B-15 zeigt den Verlauf der Polynomfunktion.
y
4
y = x 4 – x 3 – 3x 2 + 5x – 2
2
W1
–2
–1
Bild B-15
1
2
x
–2
–4
W2
–6
–8
Min
B80
y ¼
– 10
ðx 2Þ 2
x þ2
Definitionsbereich: x þ 2 6¼ 0
)
x 6¼ 2
Symmetrie: nicht vorhanden
Nullstellen: Zähler ¼ 0, Nenner 6¼ 0
)
ðx 2Þ 2 ¼ 0
)
x 1=2 ¼ 2
ðdoppelte NullstelleÞ
Die Kurve berührt an dieser Stelle die x-Achse, d. h. es liegt ein Extremwert vor (! relative Extremwerte).
Pole: Nenner ¼ 0, Zähler 6¼ 0
)
x þ2 ¼ 0
)
x3 ¼ 2
ðPol mit VorzeichenwechselÞ
Polgerade (senkrechte Asymptote): x ¼ 2
Ableitungen (bis zur 3. Ordnung)
y ¼
ðx 2Þ 2
ðx 2Þ 2
x2 þ 4x 4
¼
¼
x þ2
x þ2
x þ2
1. Ableitung (Quotientenregel)
y ¼
y0 ¼
¼
x2 þ 4x 4
u
¼
x þ2
v
mit
u ¼ x2 þ 4x 4;
v ¼ x þ2
und u 0 ¼ 2 x þ 4 ;
v0 ¼ 1
u0 v v0 u
ð 2 x þ 4Þ ðx þ 2Þ 1 ð x 2 þ 4 x 4Þ
¼
¼
v2
ðx þ 2Þ 2
2x2 4x þ 4x þ 8 þ x2 4x þ 4
ðx þ 2Þ 2
¼
x 2 4 x þ 12
ðx þ 2Þ 2
2. Ableitung (Quotienten- und Kettenregel)
y0 ¼
x 2 4 x þ 12
ðx þ 2Þ
2
¼
u
; u ¼ x 2 4 x þ 12 ; v ¼ ðx þ 2Þ 2 und u 0 ¼ 2 x 4 ; v 0 ¼ 2 ðx þ 2Þ
v
ðv ¼ ðx þ 2Þ 2 wurde nach der Kettenregel differenziert, Substitution: t ¼ x þ 2Þ
2 Anwendungen der Differentialrechnung
y 00 ¼
¼
¼
115
ð 2 x 4Þ ðx þ 2Þ 2 2 ðx þ 2Þ ð x 2 4 x þ 12Þ
u0v v0u
¼
¼
v2
ðx þ 2Þ 4
ðx þ 2Þ ½ ð 2 x 4Þ ðx þ 2Þ 2 ð x 2 4 x þ 12Þ
¼
ðx þ 2Þ ðx þ 2Þ 3
2 x 2 4 x 4 x 8 þ 2 x 2 þ 8 x 24
ðx þ 2Þ
3
¼
ð 2 x 4Þ ðx þ 2Þ 2 ð x 2 4 x þ 12Þ
ðx þ 2Þ 3
¼
32
ðx þ 2Þ 3
Wegen y 00 6¼ 0 (Zähler 6¼ 0) kann es keine Wendepunkte geben, die dritte Ableitung wird daher nicht benötigt.
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
x 2 4 x þ 12
ðx þ 2Þ
¼ 0
2
)
x 2 4 x þ 12 ¼ 0
)
x4 ¼ 2 ;
x5 ¼ 6
Es gibt somit zwei Kurvenpunkte mit waagerechter Tangente. Wir prüfen über die 2. Ableitung, ob die hinreichende
Bedingung für relative Extremwerte erfüllt ist:
y 00 ðx 4 ¼ 2Þ ¼
32
ð2 þ 2Þ
y 00 ðx 5 ¼ 6Þ ¼
3
¼
32
32
1
¼
< 0
¼
64
2
43
32
ð 6 þ 2Þ
Zugehörige Ordinaten: y 4 ¼
3
¼
32
ð 4Þ
ð2 2Þ 2
2þ2
3
¼
¼ 0;
)
32
1
¼
> 0
64
2
y5 ¼
relatives Maximum
)
ð 6 2Þ 2
6 þ 2
relatives Minimum
¼
ð 8Þ 2
4
¼
64
¼ 16
4
Relative Extremwerte: Max ¼ ð2; 0Þ; Min ¼ ð 6; 16Þ
Wendepunkte: y 00 == 0, y 000 6¼ 0
Wegen y 00 6¼ 0 ist die notwendige Bedingung für Wendepunkte nicht erfüllbar, d. h. es gibt keine Wendepunkte.
Verhalten im Unendlichen
Die Funktion ist unecht gebrochen (Grad des Zählers > Grad des Nenners). Wir zerlegen sie durch Polynomdivision:
16
x þ2
|fflfflffl{zfflfflffl}
echt gebrochen
y ¼ ð x 2 þ 4 x 4Þ : ðx þ 2Þ ¼ x þ 6
ð x 2 2 xÞ
6x 4
ð6 x þ 12Þ
16
Für große x-Werte dürfen wir den echt gebrochenen Anteil vernachlässigen (er strebt gegen
Null). Die Kurve nähert sich daher „im Unendlichen‘‘ asymptotisch der Geraden y ¼ x þ 6.
y
Polgerade
24
20
Asymptote im Unendlichen: y ¼ x þ 6
16
Bild B-16 zeigt den Verlauf der Kurve mit ihren
beiden Asymptoten.
Min
12
8
Asymptote y = –x + 6
6
6
Max
Bild B-16
– 12
–8
–4
2
–8
12
y=
(x – 2)
x+2
2
x
116
B Differentialrechnung
B81
y ¼
3x3 þ 3x 6
x
Definitionsbereich: x 6¼ 0
Symmetrie: nicht vorhanden
) 3x3 þ 3x 6 ¼ 0 j : 3
Nullstellen: Zähler ¼ 0, Nenner 6¼ 0
)
x3 þ x 2 ¼ 0
Durch Probieren findet man die Lösung x 1 ¼ 1, mit dem Horner-Schema erhält man dann das 1. reduzierte Polynom, dessen Nullstellen (falls vorhanden) weitere Lösungen liefern:
1
x1 ¼ 1
1
0
1
2
1
1
2
1
2
0
)
x2 þ x þ 2 ¼ 0
) keine reellen Lösungen
Es gibt nur eine Nullstelle bei x 1 ¼ 1.
Pole: Nenner ¼ 0 ; Zähler 6¼ 0 )
x ¼ 0
x2 ¼ 0
)
Bei x 2 ¼ 0 liegt eine Polstelle mit Vorzeichenwechsel (der Zähler ist dort ungleich Null).
Polgerade: x ¼ 0 (y-Achse)
Ableitungen 1. bis 3. Ordnung
Durch Polynomdivision lässt sich die unecht gebrochenrationale Funktion auf eine für das Differenzieren günstigere
Form bringen:
y ¼
3x3 þ 3x 6
6
¼ 3x2 þ 3
¼ 3 x 2 þ 3 6 x 1
x
x
Gliedweise differenzieren:
y 0 ¼ 6 x þ 0 6 ð x 2 Þ ¼ 6 x þ 6 x 2
oder
y 00 ¼ 6 þ 6 ð 2 x 3 Þ ¼ 6 12 x 3 ¼ 6
y 000 ¼ 12 ð 3 x 4 Þ ¼ 36 x 4 ¼
y0 ¼ 6x þ
6
6x3 þ 6
¼
x2
x2
12
6 x 3 12
¼
x3
x3
36
x4
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
6x3 þ 6 ¼ 0 j : 6
y 00 ðx 3 ¼ 1Þ ¼
)
6 12
¼ 18 > 0
1
x3 þ 1 ¼ 0
)
)
x3 ¼ 1
relatives Minimum
)
x3 ¼ 1
(Ordinate : y 3 ¼ 12)
Relative Extremwerte: Min ¼ ð 1; 12Þ
Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
y 000 ðx 4 ¼
p
3 ffiffiffi
2Þ ¼
6 x 3 12 ¼ 0 j : 6
36
6¼ 0
p
3 ffiffiffi 4
ð 2Þ
Wendepunkte: W ¼ ð1,260; 3Þ
)
)
x3 2 ¼ 0
)
x3 ¼ 2
Wendepunkt (Ordinate : y 4 ¼ 3)
)
x4 ¼
p
3 ffiffiffi
2 ¼ 1,260
2 Anwendungen der Differentialrechnung
117
Verhalten im Unendlichen
y ¼
y
3x þ 3x 6
6
¼ 3x2 þ 3
x
x
3
40
Der echt gebrochenrationale Anteil 6=x wird
für große x-Werte verschwindend klein und darf
dann vernachlässigt werden. Die Kurve zeigt daher „im Unendlichen‘‘ nahezu das gleiche Verhalten wie die Parabel y ¼ 3 x 2 þ 3.
Asymptote im Unendlichen: y ¼ 3 x 2 þ 3
32
Polgerade
24
16
Asymptote
(Parabel)
Min
y=
3x 3 + 3x – 6
x
8
W
Bild B-17 zeigt den Verlauf der Kurve.
–3
–2
–1
1
2
3
x
–8
Bild B-17
B82
y 2 ¼ ð4 xÞ 2 ðx þ 2Þ
Die Kurve besteht aus zwei zur x-Achse spiegelsymmetrischen Teilen, die durch die Funktionen
pffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ ð4 xÞ x þ 2 ;
x 2
beschrieben werden. Es genügt daher, den Verlauf des Kurvenstücks mit der Gleichung y ¼ ð4 xÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ 2 zu
untersuchen.
Definitionsbereich: x þ 2 0
)
x 2
Symmetrie: nicht vorhanden
4 x ¼ 0 ) x1 ¼ 4
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ 2 ¼ 0 )x þ 2 ¼ 0
|fflffl{zfflffl}
0
Zwei Nullstellen in x 1 ¼ 4 und x 2 ¼ 2 .
Nullstellen: ð4 xÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ2 ¼ 0
)
x 2 ¼ 2
Ableitungen 1. bis 3. Ordnung
y ¼ ð4 xÞ
|fflfflffl{zfflfflffl}
u
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ 2 ¼ uv
|fflffl{zfflffl}
v
mit u ¼ 4 x ;
v ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ 2 und u 0 ¼ 1 ;
|fflffl{zfflffl}
t
v0 ¼
1
pffiffiffiffiffiffiffiffiffiffiffiffiffi
2 x þ2
(die Ableitung v 0 erhalten wir in der angedeuteten Weise mit der Kettenregel, Substitution: t ¼ x þ 2)
Die Produktregel liefert dann:
y0 ¼ u0 v þ v0 u ¼ 1
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x þ2þ
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1
4x
pffiffiffiffiffiffiffiffiffiffiffiffiffi ð4 xÞ ¼ x þ 2 þ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
2 x þ2
2 x þ2
2 ðx þ 2Þ þ 4 x
2x 4 þ 4 x
3x
3
x
¼
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
2 ðx þ 2Þ 1=2
2 x þ2
2 x þ2
2 x þ2
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
Umformungen: Hauptnenner bilden ð2 x þ 2 Þ, also den 1. Summand mit 2 x þ 2 erweitern.
¼
118
B Differentialrechnung
Die 2. Ableitung wird mit Hilfe der Quotientenregel gebildet:
y0 ¼
3
x
3 u
¼
1=2
2 ðx þ 2Þ
2 v
mit
u ¼ x;
v ¼ ðx þ 2Þ 1=2
|fflffl{zfflffl}
t
u0 ¼ 1;
und
v0 ¼
1
ðx þ 2Þ 1=2
2
(v 0 erhalten wir in der angedeuteten Weise mit der Kettenregel, Substitution: t ¼ x þ 2)
y 00
y
00
3 u0 v v0 u
3
¼
¼
2
2
2
v
1 ðx þ 2Þ 1=2
1
ðx þ 2Þ 1=2 x
2
ðerweitern mit 2 ðx þ 2Þ 1=2 Þ
ðx þ 2Þ 1
1
1=2
1
0
2 ðx þ 2Þ 1=2 x ðx þ 2Þ 1=2 2 ðx þ 2Þ 1=2
3 ðx þ 2Þ
3 2 ðx þ 2Þ x ðx þ 2Þ
2
¼
¼
¼
2
2
ðx þ 2Þ 1 2 ðx þ 2Þ 1=2
2 ðx þ 2Þ 3=2
¼
1
3 2 ðx þ 2Þ x 1
3 2x þ 4 x
3
x þ4
¼
¼
3=2
3=2
2
4
4
2 ðx þ 2Þ
ðx þ 2Þ
ðx þ 2Þ 3=2
Rechenregeln: a m a n ¼ a m þ n ; a 0 ¼ 1
Die 3. Ableitung wird nicht benötigt, da es keine Wendepunkte geben kann (warum?).
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
3
x
¼ 0
2 ðx þ 2Þ 1=2
)
x ¼ 0
3
4
3
¼ pffiffiffi < 0 )
3=2
4 2
2 2
pffiffiffi
Relative Extremwerte: Max ¼ ð0; 4 2 Þ ¼ ð0; 5,66Þ
y 00 ðx 3 ¼ 0Þ ¼
)
x3 ¼ 0
relatives Maximum (Ordinate : y 3 ¼ 5,66)
Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
3
x þ4
¼ 0
4 ðx þ 2Þ 3=2
)
x þ4 ¼ 0
)
x4 ¼ 4
Dieser Wert liegt außerhalb des Definitionsbereiches, daher gibt es keine Wendepunkte (die 3. Ableitung wird also ––
wie bereits vorher erwähnt –– nicht benötigt).
Zusammenfassung
y
Die Gesamtkurve mit der Gleichung y 2 ¼ ð4 xÞ 2 ðx þ 2Þ
ist nur für x 2 definiert und verläuft spiegelsymmetrisch
zur x-Achse (Bild B-18). Sie besitzt folgende Eigenschaften:
5,66
Nullstellen: x 1 ¼ 4; x 2 ¼ 2
4
Extremwerte: Max ¼ ð0; 5,66Þ; Min ¼ ð0; 5,66Þ
2
–2
–1
–2
Max
1
4
–4
– 5,66 Min
Bild B-18
y 2 = (4 – x )2 (x + 2)
x
2 Anwendungen der Differentialrechnung
B83
119
y ¼ 1 þ sin 2 x ¼ 1 þ ðsin xÞ 2
Diese überall definierte Funktion ist periodisch mit der Periode p ¼ p und verläuft spiegelsymmetrisch zur y-Achse.
Wir beschränken uns daher zunächst auf das Periodenintervall 0 x p .
Nullstellen: Wegen 1 þ sin 2 x ¼ 1 þ ðsin xÞ 2 1 gibt es keine Nullstellen.
Ableitungen bis zur 3. Ordnung
Gliedweise Differentiation unter Verwendung der Kettenregel:
y ¼ 1 þ ð sin x Þ 2 ¼ 1 þ u 2
|ffl{zffl}
u
mit
u ¼ sin x
)
y 0 ¼ 0 þ 2 u cos x ¼ 2 sin x cos x ¼ sin ð2 xÞ
(unter Verwendung der trigonometrischen Formel sin ð2 xÞ ¼ 2 sin x cos x)
y 0 ¼ sin ð2 xÞ ¼ sin u
|{z}
u
mit
u ¼ 2x
y 00 ¼ 2 cos ð2 xÞ ¼ 2 cos u mit
|{z}
u
)
y 00 ¼ ðcos uÞ 2 ¼ 2 cos ð2 xÞ
u ¼ 2x
)
y 000 ¼ 2 ð sin uÞ 2 ¼ 4 sin ð2 xÞ
sin u ¼ 0
mit
u ¼ 2x
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
sin ð2 xÞ ¼ 0
|{z}
u
)
Lösungen sind die Nullstellen von sin u im Periodenintervall 0 u 2 p . Sie lauten: u 1 ¼ 0, u 2 ¼ p, u 3 ¼ 2 p
(durch die Substitution u ¼ 2 x geht das Periodenintervall 0 x p in das Periodenintervall 0 u 2 p über).
Durch Rücksubstitution ðx ¼ u=2Þ folgt dann:
x1 ¼ 0 ;
x 2 ¼ p=2 ;
x3 ¼ p
An diesen Stellen besitzt die Kurve nicht nur waagerechte Tangenten, sondern auch Extremwerte, da dort y 00 6¼ 0 ist:
y 00 ðx 1 ¼ 0Þ ¼ 2 cos 0 ¼ 2 1 ¼ 2 > 0
)
relatives Minimum
(Ordinate : y 1 ¼ 1)
y 00 ðx 2 ¼ p=2Þ ¼ 2 cos p ¼ 2 ð 1Þ ¼ 2 < 0
)
y 00 ðx 3 ¼ pÞ ¼ 2 cos ð2 pÞ ¼ 2 1 ¼ 2 > 0
relatives Minimum
)
relatives Maximum
(Ordinate : y 2 ¼ 2)
(Ordinate : y 3 ¼ 1)
Relative Extremwerte im Periodenintervall 0 x p : Min ¼ ð0; 1Þ; Max ¼ ðp=2; 2Þ; Min ¼ ðp; 1Þ
Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
2 cos ð2 xÞ ¼ 0
|ffl{zffl}
u
)
2 cos u ¼ 0
)
cos u ¼ 0
mit u ¼ 2 x
Lösungen sind die Nullstellen von cos u im Periodenintervall 0 u 2 p . Sie lauten u 1 ¼ p= 2 und u 2 ¼ 3 p=2.
Rücksubstitution ðx ¼ u=2Þ führt dann zu:
x 1 ¼ p=4 ;
x 2 ¼ 3 p=4
An diesen Stellen ist die 3. Ableitung von Null verschieden:
y 000 ðx 1 ¼ p=4Þ ¼ 4 sin ðp=2Þ ¼ 4 1 ¼ 4 6¼ 0
)
y 000 ðx 2 ¼ 3 p=4Þ ¼ 4 sin ð3 p=2Þ ¼ 4 ð 1Þ ¼ 4 6¼ 0
Wendepunkt
)
Wendepunkt
Wendepunkte im Periodenintervall 0 x p : W 1 ¼ ðp=4; 1,5Þ, W 2 ¼ ð3 p=4; 1,5Þ
120
B Differentialrechnung
Zusammenfassung
Die periodische Funktion y ¼ 1 þ sin 2 x ist überall definiert und verläuft spiegelsymmetrisch zur y-Achse, da
1 þ sin 2 ð xÞ ¼ 1 þ sin 2 x ist. Es gibt keine Nullstellen, jedoch unendlich viele relative Extremwerte und Wendepunkte an den folgenden Stellen (Kurvenverlauf: siehe Bild B-19):
Minima:
x ¼ 0; p; 2 p; . . .
Maxima:
x ¼
Wendepunkte:
(Ordinate : jeweils y ¼ 1Þ
p
3
5
;
p;
p; . . . (Ordinate : jeweils y ¼ 2Þ
2
2
2
p
3
5
x ¼ ;
p;
p; . . . (Ordinate : jeweils y ¼ 1,5Þ
4
4
4
y
Max
Max
Max
Max
Max
y = 1 + sin2 x
2
W
W
W
W
W
W
W
W
W
W
1
Min
Min
Min
Min
π
2π
Bild B-19
–π
– 2π
B84
x
y ¼ 10 x 2 ln j x j
Definitionsbereich: x 6¼ 0
Symmetrie: Wegen 10 ð xÞ 2 ln j x j ¼ 10 x 2 ln j x j ist die Funktion gerade, d. h. die Kurve verläuft spiegelsymmetrisch zur y-Achse.
Nullstellen: y ¼ 0
)
10 x 2 ln j x j ¼ 0
|ffl{zffl}
6¼ 0
)
ln j x j ¼ 0
Wir lösen diese Gleichung wie folgt durch Entlogarithmieren (Rechenregel: e ln z ¼ z für z > 0):
e ln j x j ¼ j x j ¼ e 0 ¼ 1
)
jxj ¼ 1
)
x 1=2 ¼ 1
Nullstellen: x 1=2 ¼ 1
Ableitungen bis zur 3. Ordnung
Wir differenzieren im Wesentlichen mit Hilfe der Produktregel:
y ¼ 10 x 2 ln j x j ¼ 10 ðu vÞ
f
|fflfflffl{zfflfflffl}
mit
u ¼ x2;
v ¼ ln j x j
und u 0 ¼ 2 x ;
v
u
v0 ¼
1
x
1
2
¼ 10 ð2 x ln j x j þ xÞ ¼ 10 x ð2 ln j x j þ 1Þ
x
y ¼ 10 ðu v þ v uÞ ¼ 10 2 x ln j x j þ
x
0
0
0
f
y 0 ¼ 10 x ð2 ln j x j þ 1Þ ¼ 10 ðu vÞ
u
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
v
mit
u ¼ x;
v ¼ 2 ln j x j þ 1
und u 0 ¼ 1 ;
v0 ¼
2
x
2 Anwendungen der Differentialrechnung
121
2
y 00 ¼ 10 ðu 0 v þ v 0 uÞ ¼ 10 1 ð2 ln j x j þ 1Þ þ
x ¼ 10 ð2 ln j x j þ 1 þ 2Þ ¼ 10 ð2 ln j x j þ 3Þ
x
1
1
20
þ 0 ¼ 10 2
¼
y 000 ¼ 10 2
x
x
x
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
10 x ð2 ln j x j þ 1Þ ¼ 0
)
2 ln j x j þ 1 ¼ 0
ðda x 6¼ 0Þ
Wir lösen diese Gleichung durch Entlogarithmierung:
2 ln j x j þ 1 ¼ 0
)
ln j x j ¼ 0;5
)
e ln j x j ¼ j x j ¼ e 0;5
x 3=4 ¼ e 0;5 ¼ 0;6065
)
y 00 ðx 3=4 ¼ e 0;5 Þ ¼ 10 ð2 ln j e 0;5 j þ 3Þ ¼ 10 ð2 ln e 0;5 þ 3Þ ¼ 10 ð2 ð 0;5Þ þ 3Þ ¼
¼ 10 ð 1 þ 3Þ ¼ 20 > 0
)
relative Minima
(Ordinaten : y 3=4 ¼ 1,8394)
Relative Extremwerte: Minima ¼ ð 0;6065; 1;8394Þ
Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
10 ð2 ln j x j þ 3Þ ¼ 0 j : 10
)
2 ln j x j þ 3 ¼ 0
)
ln j x j ¼ 1;5
Durch Entlogarithmierung folgt:
ln j x j ¼ 1;5
e ln j x j ¼ e 1;5
)
y 000 ðx 5=6 ¼ e 1;5 Þ ¼
20
6¼ 0
e 1;5
)
j x j ¼ e 1;5
) Wendepunkte
)
x 5=6 ¼ e 1;5 ¼ 0;2231
(zugehörige Ordinaten : y 5=6 ¼ 0,7468)
Wendepunkte: W 1=2 ¼ ð 0;2231; 0;7468Þ
y
Kurvenlauf: siehe Bild B-20
3
Die Kurve besitzt bei x ¼ 0 eine hebbare Lücke
(Grenzwert ¼ 0). Setzt man nachträglich y ð0Þ ¼ 0,
so befindet sich dort ein relatives Maximum!
2
y = 10 x 2 · ln |x |
1
Lücke
–1
1
W2
Min
–1
–2
Bild B-20
B85
W1
Min
y ¼ 4 x e 0;5 x
Definitionsbereich: 1 < x < 1
Symmetrie: nicht vorhanden
Nullstellen: y ¼ 0
)
4 x e 0;5 x ¼ 0
)
4x ¼ 0
(da e 0;5 x 6¼ 0Þ
Ableitungen bis zur 3. Ordnung
Wir benötigen jeweils die Produktregel in Verbindung mit der Kettenregel.
)
x1 ¼ 0
x
122
B Differentialrechnung
f
y ¼ 4 x e 0;5 x ¼ u v
v ¼ e 0;5 x
u ¼ 4x;
mit
|fflfflffl{zfflfflffl}
und
u0 ¼ 4;
v 0 ¼ 0,5 e 0;5 x
v
u
(die Ableitung des Faktors v ¼ e 0;5 x wurde dabei mit Hilfe der Kettenregel gebildet, Substitution:
t ¼ 0;5 x)
y 0 ¼ u 0 v þ v 0 u ¼ 4 e 0;5 x 0;5 e 0;5 x 4 x ¼ 4 e 0;5 x 2 x e 0;5 x ¼ ð4 2 xÞ e 0;5 x
y 0 ¼ ð4 2 xÞ e 0;5 x ¼ u v
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflffl{zfflfflffl}
u
v
u ¼ 4 2x;
mit
v ¼ e 0;5 x
und u 0 ¼ 2 ;
v 0 ¼ 0;5 e 0;5 x
y 00 ¼ u 0 v þ v 0 u ¼ 2 e 0;5 x 0;5 e 0;5 x ð4 2 xÞ ¼ ½ 2 0,5 ð4 2 xÞ e 0;5 x ¼
¼ ð 2 2 þ xÞ e 0;5 x ¼ ðx 4Þ e 0;5 x
y 00 ¼ ðx 4Þ e 0;5 x ¼ u v mit
|fflfflfflffl{zfflfflfflffl} |fflfflffl{zfflfflffl}
u
v
u ¼ x 4;
v ¼ e 0;5 x
und u 0 ¼ 1 ;
v 0 ¼ 0;5 e 0;5 x
y 000 ¼ u 0 v þ v 0 u ¼ 1 e 0;5 x 0;5 e 0;5 x ðx 4Þ ¼ ½ 1 0;5 ðx 4Þ e 0;5 x ¼
¼ ð1 0;5 x þ 2Þ e 0;5 x ¼ ð3 0;5 xÞ e 0;5 x
Relative Extremwerte: y 0 == 0, y 00 6¼ 0
y0 ¼ 0
)
ð4 2 xÞ e 0;5 x ¼ 0
y 00 ðx 2 ¼ 2Þ ¼ 2 e 1 < 0
)
)
4 2x ¼ 0
(da e 0;5 x 6¼ 0Þ
)
x2 ¼ 2
relatives Maximum
Relative Extremwerte: Max ¼ ð2; 2;9430Þ
Wendepunkte: y 00 == 0, y 000 6¼ 0
y 00 ¼ 0
)
ðx 4Þ e 0;5 x ¼ 0
y 000 ðx 3 ¼ 4Þ ¼ 1 e 2 ¼ e 2 6¼ 0
)
)
x 4 ¼ 0
(da e 0;5 x 6¼ 0Þ
)
x3 ¼ 4
Wendepunkt
Wendepunkte: W ¼ ð4; 2,1654Þ
Verhalten im Unendlichen
Wegen
lim 4 x e 0;5 x ¼ lim
x!1
x!1
ð4 xÞ 0
4x
4
8
¼ lim
¼ lim
¼ lim
¼ 0
e 0;5 x
x ! 1 ðe 0;5 x Þ 0
x ! 1 0,5 e 0;5 x
x ! 1 e 0;5 x
nähert sich die Kurve im „Unendlichen‘‘ asymptotisch der x -Achse (siehe Bild B-21). Den Grenzwert, der zunächst
auf den unbestimmten Ausdruck 1=1 führt, haben wir nach der Regel von Bernoulli und de L’Hospital berechnet (!
FS: Kap. III.3.4).
y
Max
3
W
y = 4x · e– 0,5 x
2
1
Bild B-21
–1
1
–1
2
4
5
10
x
2 Anwendungen der Differentialrechnung
123
2.7 Extremwertaufgaben
Lehrbuch: Band 1, Kapitel IV.3.5
Formelsammlung: Kapitel IV.4.5
Der Querschnitt eines Tunnels besteht aus einem Rechteck mit aufgesetztem Halbkreis. Wie müssen die
Abmessungen gewählt werden, damit bei fest vorgegebenem Umfang U ¼ const: ¼ c die Querschnittsfläche möglichst groß wird?
B86
Für den Flächeninhalt A des Tunnelquerschnitts gilt die Formel
x
1
px2
A ¼ 2xy þ
2
ðsiehe Bild B-22)
x
y
A hängt also zunächst von zwei Größen, nämlich x und y ab.
Diese sind jedoch nicht unabhängig voneinander, sondern über die Nebenbedingung
U ¼ 2 x þ 2 y þ p x ¼ const: ¼ c
x
A
y
2x
ðmit c > 0Þ
Bild B-22
miteinander verknüpft. Denn es kommen nach der Aufgabenstellung nur solche Querschnitte infrage, deren Umfang U
die konstante Länge c besitzt. Wir lösen die Nebenbedingung zweckmäßigerweise nach y auf, setzen dann den
gefundenen Ausdruck in die Flächenformel ein und erhalten den Flächeninhalt A in Abhängigkeit vom Radius x des
aufgesetzten Halbkreises:
y ¼
c 2x px
2
)
A ðxÞ ¼ 2 x y þ
1
c 2x px
1
1
px2 ¼ 2 x
px2 ¼ cx 2x2
px2
þ
2
2
2
2
Mit Hilfe der Differentialrechnung bestimmen wir jetzt das absolute Maximum dieser Funktion, wobei die Lösung
zwischen x ¼ 0 und x ¼ c=ð2 þ pÞ liegen muss (die Randwerte kommen nicht infrage). Wir bilden zunächst die
benötigten ersten beiden Ableitungen:
A 0 ðxÞ ¼ c 4 x p x ¼ c ð4 þ pÞ x ;
A 00 ðxÞ ¼ ð4 þ pÞ < 0
Aus der notwendigen Bedingung A 0 ðxÞ ¼ 0 erhalten wir den folgenden Wert:
A 0 ðxÞ ¼ 0
)
c ð4 þ pÞ x ¼ 0
)
x ¼
c
4þp
Dieser Wert liegt im Gültigkeitsbereich der Funktion und ist das gesuchte (absolute) Maximum, da die 2. Ableitung
überall, also auch an dieser Stelle negativ ist (die hinreichende Bedingung für ein Maximum ist somit erfüllt). Wir
berechnen noch die zum Maximum gehörenden Werte für y und A:
2 y ¼ c 2 x p x ¼ c ð2 þ pÞ x ¼ c ð2 þ pÞ
¼
Amax
½ 4 þ p ð2 þ pÞ c
4þp
¼ A x ¼
¼
c
4þp
¼
¼
4þp
¼
2c
4þp
)
y ¼
c
4þp
c2
2c2
pc2
2 ð4 þ pÞ c 2 4 c 2 p c 2
¼
¼
4þp
ð4 þ pÞ 2
2 ð4 þ pÞ 2
2 ð4 þ pÞ 2
ð8 þ 2 p 4 pÞ c 2
2 ð4 þ pÞ 2
ð4 þ p 2 pÞ c
ð4 þ pÞ c ð2 þ pÞ c
c
¼
¼
4þp
4þp
¼
ð4 þ pÞ c 2
2 ð4 þ pÞ ð4 þ pÞ
¼
c2
2 ð4 þ pÞ
Umformungen: Brüche auf den Hauptnenner 2 ð4 þ p 2 Þ bringen.
Lösung: Bei gegebenem Umfang U ¼ const: ¼ c ist die Querschnittsfläche des Tunnels am größten, wenn Radius x
und Seitenhöhe y übereinstimmen.
124
B Differentialrechnung
Zur Zeit t ¼ 0 startet von A aus ein Fahrzeug 1 mit der konstanten Geschwindigkeit v 1 in Richtung B. Zur gleichen Zeit setzt sich ein Fahrzeug 2 von B aus mit der konstanten Geschwindigkeit
v 2 in Richtung C in Bewegung (Bild B-23).
Nach welcher Zeit besitzen die beiden Fahrzeuge den geringsten Abstand voneinander?
B87
A B ¼ e ¼ 700 m
C
a ¼ 60
v2
v1
v 1 ¼ 10 m/s,
a
A
v 2 ¼ 5 m/s
Bild B-23
B
Fahrzeug 1 bewegt sich in der Zeit t von A nach A*, Fahrzeug 2 in der gleichen Zeit von B nach B* (Bild B-24). Die
dabei zurückgelegten Wege x bzw. y betragen (wir rechnen ohne Einheiten):
x ¼ v 1 t ¼ 10 t
C
y ¼ v2 t ¼ 5 t
Die Seiten im Dreieck A* B B* haben damit folgende Längen:
B*
d
A* B ¼ A B A A* ¼ e x ¼ 700 10 t;
a
A
B B* ¼ y ¼ 5 t ;
A* B* ¼ d ;
y
x
a ¼ 60
A*
e–x
B
Bild B-24
Der Kosinussatz liefert dann den folgenden Zusammenhang (! FS: Kap. I.6.7):
d2 ¼
A* B
2
þ B B*
2
2 A* B
B B*
cos a ¼
¼ ð700 10 tÞ 2 þ 25 t 2 2 ð700 10 tÞ 5 t cos 60 ¼ ð700 10 tÞ 2 þ 25 t 2 ð700 10 tÞ 5 t ¼
|fflfflffl{zfflfflffl}
1=2
¼ 700 2 14 000 t þ 100 t 2 þ 25 t 2 3 500 t þ 50 t 2 ¼ 175 t 2 17 500 t þ 490 000
Wenn der Abstand d einen kleinsten Wert annimmt, dann gilt dies auch für das Abstandsquadrat d 2 . Es genügt
daher, das absolute Minimum der „Zielfunktion‘‘
z ðtÞ ¼ d 2 ¼ 175 t 2 17 500 t þ 490 000
im Zeitintervall t 0 zu bestimmen. Mit
z 0 ðtÞ ¼ 350 t 17 500
und z 00 ðtÞ ¼ 350 > 0
folgt dann aus der für ein Minimum notwendigen Bedingung z 0 ðtÞ ¼ 0:
z 0 ðtÞ ¼ 0
)
350 t 17 500 ¼ 0
)
t 0 ¼ 50 ðin sÞ
Wegen z 00 ðtÞ ¼ 350 und somit auch z 00 ðt 0 Þ ¼ 350 > 0 handelt es sich um ein (relatives) Minimum. Der Abstand
der beiden Fahrzeuge zur Zeit t 0 ¼ 50 s beträgt dann (in der Einheit m):
d 2 ðt 0 ¼ 50Þ ¼ 175 50 2 17 500 50 þ 490 000 ¼ 52 500
)
d ðt 0 ¼ 50Þ ¼ 229,13
Da der Abstand zu Beginn (t ¼ 0) größer ist (er beträgt e ¼ 700 m), ist dieser Wert der kleinste Abstand der beiden
Fahrzeuge.
Lösung: Nach genau 50 s ist der Abstand der beiden Fahrzeuge am kleinsten. Er beträgt dann dmin ¼ 229,13 m .
2 Anwendungen der Differentialrechnung
125
Der in Bild B-25 skizzierte Körper vom Gewicht G soll durch eine schräg nach oben angreifende
konstante Kraft F gerade in Bewegung gesetzt werden. Wählen Sie den Angriffswinkel a so, dass die
Kraft möglichst klein wird.
B88
R ¼ mN :
F
a
S
Bild B-25
R
Reibungskraft
N:
Normalkraft
m:
Reibungskoeffizient (m > 0)
S:
Schwerpunkt
G
Welchen Winkel a 0 erhält man für den speziellen Reibungskoeffizienten m ¼ 0,2 ?
Wir zerlegen die im Schwerpunkt S angreifende Kraft F zunächst in eine Horizontal- und eine Normalkomponente
(Bild B-26):
F
FN
Horizontalkomponente :
FH ¼ F cos a
Normalkomponente :
FN ¼ F sin a
a
Bild B-26
S
FH
Die Normalkraft N, die den Körper auf die Ebene drückt, ist die Differenz aus der Gewichtskraft G und der Normalkomponente FN . Die Haftreibungskraft R berechnet sich damit wie folgt:
R ¼ m N ¼ m ðG FN Þ ¼ m ðG F sin aÞ
Der Körper setzt sich in Bewegung, wenn die Horizontalkomponente FH die Haftreibung R gerade überwindet.
Somit gilt:
FH ¼ R
)
F cos a ¼ m ðG F sin aÞ ¼ m G m F sin a
Diese Gleichung lösen wir nach F auf und erhalten dann für diese Kraft in Abhängigkeit vom Winkel a:
F cos a þ m F sin a ¼ F ðcos a þ m sin aÞ ¼ m G
)
F ¼ FðaÞ ¼
mG
cos a þ m sin a
Wir bestimmen jetzt den im Intervall 0 < a < 90 liegenden Winkel so, dass die angreifende Kraft F den kleinstmöglichen Wert annimmt. Die dafür benötigten Ableitungen 1. und 2. Ordnung erhalten wir wie folgt:
F ðaÞ ¼
mG
mG
¼
¼ m G u 1
cos a þ m sin a
u
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
u
mit
u ¼ cos a þ m sin a
Die Kettenregel liefert dann:
F 0 ðaÞ ¼
sin a m cos a
dF
dF du
¼
¼ m G ð u 2 Þ ð sin a þ m cos aÞ ¼ m G
da
du da
ðcos a þ m sin aÞ 2
Aus der für ein Minimum notwendigen Bedingung F 0 ðaÞ ¼ 0 folgt dann:
sin a m cos a ¼ 0
)
sin a ¼ m cos a
)
sin a
¼ tan a ¼ m
cos a
)
a 0 ¼ arctan m
Dass für diesen Winkel der Kraftaufwand am kleinsten ist, lässt sich aus physikalischer Sicht leicht nachvollziehen.
Trotz des relativ hohen Rechenaufwands wollen wir zeigen, dass auch die hinreichende Bedingung für ein Minimum
erfüllt ist. Den Nachweis F 00 ða 0 Þ > 0 führen wir wie folgt: Zunächst differenzieren wir F 0 ðaÞ nach der Quotientenregel:
0
F ðaÞ ¼
m G ðsin a m cos aÞ
ðcos a þ m sin aÞ 2
¼
u ðaÞ
v ðaÞ
)
00
F ðaÞ ¼
u 0 ðaÞ v ðaÞ v 0 ðaÞ u ðaÞ
½ v ðaÞ 2
126
B Differentialrechnung
An der Stelle a 0 ist F 0 ða 0 Þ ¼ 0 und somit auch u ða 0 Þ ¼ 0. Damit erhalten wir für die 2. Ableitung an der
gleichen Stelle den folgenden Ausdruck:
F 00 ða 0 Þ ¼
u 0 ða 0 Þ v ða 0 Þ v 0 ða 0 Þ u ða 0 Þ
½ v ða 0 Þ 2
u 0 ða 0 Þ v ða 0 Þ v 0 ða 0 Þ 0
¼
½ v ða 0 Þ 2
¼
u 0 ða 0 Þ v ða 0 Þ
½ v ða 0 Þ 2
¼
u 0 ða 0 Þ
v ða 0 Þ
Mit u 0 ðaÞ ¼ m G ðcos a þ m sin aÞ und v ðaÞ ¼ ðcos a þ m sin aÞ 2 folgt dann:
F 00 ða 0 Þ ¼
u 0 ða 0 Þ
v ða 0 Þ
¼
m G ðcos a 0 þ m sin a 0 Þ
ð cos a 0 þ m sin a 0 Þ
2
¼
mG
> 0
cos a 0 þ m sin a 0
Anmerkung: Da der Winkel a 0 im 1. Quadrant liegt, ist sowohl cos a 0 als auch sin a 0 positiv!
In unserem Beispiel ist m ¼ 0,2 und somit a 0 ¼ arctan 0,2 ¼ 11,31 .
Bei einer Feuerwehrübung soll mit einer Wasserspritze eine e ¼ 15 m weit entfernte Wand möglichst
weit oben getroffen werden. Wie muss der „Abspritzwinkel“ a eingestellt werden, wenn der Wasserstrahl eine Anfangsgeschwindigkeit von v 0 ¼ 20 m/s besitzt?
Anleitung: Behandeln Sie das Problem als einen schiefen Wurf mit dem Abwurfwinkel a (gegenüber
der Horizontalen) im luftleeren Raum (Erdbeschleunigung g ¼ 9,81 m=s 2 ).
B89
Bild B-27a) zeigt die vom Wasserstrahl beschriebene Bahnkurve. Die Geschwindigkeit v0 zerlegen wir wie folgt in
Komponenten (siehe hierzu Bild B-27b)):
v 0 x ¼ v 0 cos a und v 0 y ¼ v 0 sin a
y
y
Wand
Wasserstrahl
P
v0
h
y
v0
v 0y
a
a
e
x
v 0x
x
a)
x
b)
Bild B-27
a) Bahnkurve des Wasserstrahls
b) Zerlegung der Geschwindigkeit in Komponenten
In der x-Richtung bewegt sich ein Wasserteilchen mit der konstanten Geschwindigkeit v 0 x und legt daher in der Zeit t
den Weg x ¼ v 0 x t zurück. Nach oben, d. h. in der y-Richtung überlagert sich der konstanten Geschwindigkeit v 0 y
der freie Fall, sodass wir hier den Fallweg abziehen müssen. Die Gesamtbewegung wird daher durch die folgenden Parametergleichungen beschrieben (g: Erdbeschleunigung):
x ¼ v 0 x t ¼ ðv 0 cos aÞ t ;
y ¼ v0y t
1
1
g t 2 ¼ ðv 0 sin aÞ t
gt2
2
2
ðt 0Þ
Die Bahnkurve in expliziter Form erhalten wir, indem wir die erste Gleichung nach t auflösen und den gefundenen
Ausdruck für t in die zweite Gleichung einsetzen:
t ¼
x
v 0 cos a
)
y ¼ v 0 sin a
v0
gx2
x
1
x2
¼ ðtan aÞ x
g 2
2
cos a
v 0 cos 2 a
2 v 20 cos 2 a
2 Anwendungen der Differentialrechnung
127
Die Bahnkurve ist also eine nach unten geöffnete Parabel (in diesem Zusammenhang auch als „Wurfparabel‘‘ bezeichnet).
Die im Abstand e befindliche Wand wird damit in der Höhe
h ¼ y ðx ¼ eÞ ¼ ðtan aÞ e
g e2
g e2
ðcos aÞ 2
¼
e
tan
a
2 v 20 cos 2 a
2 v 20
getroffen. Mit Hilfe der Differentialrechnung bestimmen wir den Winkel a so, dass die Wand in möglichst großer
Höhe getroffen wird, wobei die Lösung im Intervall 0 < a < 90 liegen muss. Die (zunächst) benötigte 1. Ableitung erhalten wir durch gliedweises Differenzieren unter Verwendung der Kettenregel:
hðaÞ ¼ e tan a
h 0 ðaÞ ¼ e
¼
g e2
g e2
ðcos aÞ 2 ¼ e tan a
u 2
2
2 v 0 |ffl{zffl}
2 v 20
u
mit
u ¼ cos a ;
u 0 ¼ sin a
1
g e2
e
g e2
2 ðcos aÞ 3 sin a ¼
ð 2 u 3 Þ ð sin aÞ ¼
2
2
2
cos a
cos a
2 v0
v0
e v 20 cos a g e 2 sin a
e
g e 2 sin a
e v 20 cos a g e sin a
2
¼
¼
v 20 cos 3 a
cos 3 a
cos 2 a
v 0 cos 3 a
v 20
(der 1. Bruch wurde mit v 20 cos a erweitert)
Aus der für ein Maximum notwendigen Bedingung h 0 ðaÞ ¼ 0 folgt dann:
v 20
cos a g e sin a ¼ 0 )
!
v 20
v 20
v 20
sin a
sin a ¼
cos a )
) a 0 ¼ arctan
¼ tan a ¼
ge
ge
ge
cos a
Aus physikalischer Sicht kann es sich bei diesem Wert nur um das gesuchte Maximum handeln, sodass wir auf den
Nachweis h 00 ða 0 Þ < 0 verzichten können. Die Wand wird dabei in der folgenden Höhe getroffen:
hmax ¼ h ða ¼ a 0 Þ ¼ e tan a 0
¼ e tan a 0
¼
g e2
2 v 20
cos 2
a0
¼ e tan a 0
v 20
g e2
g e2
2
ð1
þ
tan
a
Þ
¼
e
0
ge
2 v 20
2 v 20
g e2
1
¼
cos 2 a 0
!
v 40
v 20
v 40
g e2
g e2
1þ
¼
¼
g
g2 e2
2 v 20
2 v 20 g 2 e 2
2 v 20
v 20
g e2
v 20
v 40 g 2 e 2
g v 20 v 20
v 20
g e2
2 v 40 g 2 e 2 v 40
¼
¼
¼
g
g
2g
2 v 20
2 g v 20
2 v 20
2 g v 20
2 v 20 g g
ðv 0 >
pffiffiffiffiffiffi
geÞ
1
Umformungen: Verwendung der trigonometrischen Beziehung cos 2 a ¼
(! FS: Kap. III.7.5) !
1 þ tan 2 a
v 20
ersetzen ! Klammer ausmultiplizieren, gemeinsame Faktoren in Zähler und Nenner kürzen !
tan a 0 durch
ge
Hauptnenner 2 g v 20 bilden.
Die Wand wird nur dann getroffen, wenn die Bedingung h max > 0 erfüllt ist:
pffiffiffiffiffiffi
h max > 0 ) v 40 g 2 e 2 > 0 ) v 40 > g 2 e 2 ) v 0 > g e
Diese Bedingung ist für die vorgegebenen Werte v 0 ¼ 20 m=s, e ¼ 15 m und g ¼ 9,81 m=s 2 erfüllt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffi
pffiffiffiffiffiffi
g e ¼ 9,81 15 m=s ¼ 12,13 m=s ) v 0 > g e ¼ 12,13 m=s
v 0 ¼ 20 m=s ;
Die Wand wird dann in der folgenden Höhe getroffen:
h max ¼
v 40 g 2 e 2
2 g v 20
¼
20 4 9,81 2 15 2
2 9,81 20 2
m ¼ 17,63 m
Der „Abspritzwinkel“ a 0 beträgt dann:
!
v 20
20 2
a 0 ¼ arctan
¼ arctan
¼ arctan 2,7183 ¼ 69,80
ge
9,81 15
128
B Differentialrechnung
Ein beiderseits aufliegender Balken mit einem rechteckigen Querschnitt wird durch eine konstante
Streckenlast q ¼ const: belastet (Bild B-28). Die Durchbiegung y des Balkens an der (festen) Stelle x
ist dabei umgekehrt proportional zum Flächenmoment
q = constant
1
ab3
12
9
a : Breite =
des Balkens
b : Dicke
;
l : Länge
I ¼
B90
Der Balken soll aus einem kreisrunden Baumstamm vom Radius R herausgeschnitten werden und zwar so, dass die Durchbiegung des
(belasteten) Balkens möglichst klein wird.
Wie sind a und b zu wählen?
Balken
Balken
x
y
l
x
Biegelinie
y
Bild B-28
Da die Durchbiegung y dem Flächenmoment I umgekehrt proportional ist, ist y genau dann am kleinsten, wenn I
den größten Wert annimmt. Da der Balken aus einem kreisrunden Baumstamm vom Durchmesser 2 R herausgeschnitten werden soll, sind Breite a und Dicke b nicht unabhängig voneinander, sondern –– wie man Bild B-29 entnehmen
kann –– über den Satz des Pythagoras miteinander verknüpft (Balkenquerschnitt grau unterlegt):
a2 þ b2 ¼ 4 R2
Diese Nebenbedingung lösen wir nach a auf:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a ¼ 4 R2 b2
2R
Einsetzen in die Formel für das Flächenmoment liefert dann:
pffiffiffiffiffi
1
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ab3 ¼
4 R2 b2 b 3 ¼
4 R2 b2 b6 ¼
12
12
12
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
p
1
1
¼
ð4 R 2 b 2 Þ b 6 ¼
4 R2 b 6 b 8
12
12
M
b
a
IðbÞ ¼
Bild B-29
pffiffiffi pffiffiffi
pffiffiffiffiffiffi
(Rechenregel:
u v ¼ u v). Damit hängt I nur noch von der einen Variablen b ab. Wir müssen b so
bestimmen, dass das Flächenmoment den größtmöglichen Wert annimmt. Die Lösung muss dabei im offenen Intervall 0 < b < 2 R liegen (die Werte b ¼ 0 bzw. b ¼ 2 R und damit a ¼ 2 R bzw. a ¼ 0 geben keinen Sinn).
Es genügt im Folgenden, das absolute Maximum der unter der Wurzel stehenden „Zielfunktion‘‘ (Wurzelradikand)
z ðbÞ ¼ 4 R 2 b 6 b 8 ;
0 < b < 2R
zu bestimmen. Die dabei benötigten Ableitungen lauten:
z 0 ðbÞ ¼ 24 R 2 b 5 8 b 7 ;
z 00 ðbÞ ¼ 120 R 2 b 4 56 b 6
Die hinreichenden Bedingungen z 0 ðbÞ ¼ 0 und z 00 ðbÞ < 0 führen zu folgender Lösung:
z 0 ðbÞ ¼ 0
)
24 R 2 b 5 8 b 7 ¼ 8 b 5 ð3 R 2 b 2 Þ ¼ 0
|{z}
6¼ 0
)
3 R2 b2 ¼ 0
(der negative Wert scheidet dabei wegen b > 0 aus)
pffiffiffi
z 00 ðb 1 ¼ 3 RÞ ¼ 120 R 2 9 R 4 56 27 R 6 ¼ 432 R 6 < 0 )
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffi
Zugehörige Balkenbreite: a ¼ 4 R 2 b12 ¼ 4 R 2 3 R 2 ¼ R 2 ¼ R
)
pffiffiffi
b 1=2 ¼ 3 R
Maximum
Lösung: Die Durchbiegung des Balkens ist am kleinsten, wenn Balkenbreite a und Balkendicke b die Werte a ¼ R
pffiffiffi
und b ¼ 3 R annehmen.
2 Anwendungen der Differentialrechnung
129
Bild B-30 zeigt den Querschnitt einer kreisförmigen Transformatorspule mit einem kreuzförmigen Eisenkern. Die Querschnittsfläche A des Eisenkerns (im Bild grau unterlegt) soll
dabei möglichst groß werden.
Wie sind die Abmessungen zu wählen, wenn die Spule den
Querschnittsradius r besitzt?
B91
r
f
Anleitung: Machen Sie den Flächeninhalt A vom eingezeichneten Winkel j abhängig.
b
a
Bild B-30
Die Querschnittsfläche A des kreuzförmigen Eisenkerns erhalten wir anhand von Bild B-31, wenn wir aus dem eingeab
zeichneten Quadrat mit der Seitenlänge a die vier grau unterlegten kongruenten Quadrate mit der Seitenlänge
2
herausnehmen:
A ¼ a2 4
ab
2
2
(a – b) / 2
¼ a 2 ða bÞ 2 ¼
(a – b) / 2
¼ a ða 2 a b þ b Þ ¼ 2 a b b
2
2
2
2
r
Die Größen a und b lassen sich dabei durch den Radius r
und den eingezeichneten Winkel j ausdrücken:
cos j ¼
a=2
a
¼
r
2r
)
a ¼ 2 r cos j
sin j ¼
b
b=2
¼
2r
r
)
b ¼ 2 r sin j
f
a
a/2
b/2
b
a
Bild B-31
Für den Flächeninhalt A erhalten wir damit in Abhängigkeit vom Winkel j:
AðjÞ ¼ 2 a b b 2 ¼ 2 ð2 r cos jÞ ð2 r sin jÞ ð2 r sin jÞ 2 ¼
¼ 8 r 2 sin j cos j 4 r 2 sin 2 j ¼ 4 r 2 ð2 sin j cos j sin 2 jÞ ¼ 4 r 2 ðsin ð2 jÞ sin 2 jÞ
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
sin ð2 jÞ
(unter Verwendung der trigonometrischen Beziehung sin ð2 jÞ ¼ 2 sin j cos jÞ
Wir bestimmen das Maximum dieser Flächenfunktion im Intervall 0 < j p45
ffiffiffi (j ¼ 0 bedeutet a ¼ 2 r und
b ¼ 0; für j ¼ 45 erhalten wir als Grenzfall ein Quadrat mit a ¼ b ¼ 2 r). Die benötigten Ableitungen erhalten wir in der angedeuteten Weise mit Hilfe der Kettenregel:
A ðjÞ ¼ 4 r 2 ½ sin ð 2 j Þ ðsin j Þ 2 ¼ 4 r 2 ½ sin u v 2 mit u ¼ 2 j ; v ¼ sin j ; u 0 ¼ 2 ; v 0 ¼ cos j
|{z}
|ffl{zffl}
u
v
A 0 ðjÞ ¼ 4 r 2 ½ ðcos uÞ 2 2 v cos j ¼ 4 r 2 ½ 2 cos ð2 jÞ 2 sin j cos j ¼
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
sin ð2 jÞ
¼ 4 r 2 ½ 2 cos ð2 jÞ sin ð2 jÞ
A 0 ðjÞ ¼ 4 r 2 ½ 2 cos ð2 jÞ sin ð2 jÞ ¼ 4 r 2 ½ 2 cos t sin t
|ffl{zffl}
|ffl{zffl}
t
t
mit
t ¼ 2j;
A 00 ðjÞ ¼ 4 r 2 ½ 2 ð sin tÞ 2 ðcos tÞ 2 ¼ 8 r 2 ½ 2 sin ð2 jÞ þ cos ð2 jÞ
t0 ¼ 2
130
B Differentialrechnung
Aus der für ein Maximum notwendigen Bedingung A 0 ðjÞ ¼ 0 folgt:
4 r 2 ½ 2 cos ð2 jÞ sin ð2 jÞ ¼ 0 ) 2 cos ð2 jÞ sin ð2 jÞ ¼ 0 ) sin ð2 jÞ ¼ 2 cos ð2 jÞ
)
sin ð2 jÞ
¼ tan ð2 jÞ ¼ 2
cos ð2 jÞ
)
2 j ¼ arctan 2 ¼ 63,435
)
j 0 ¼ 31,72
Ohne Rechnung sehen wir, dass die 2. Ableitung für diesen Winkel negativ ist, da sin ð2 j 0 Þ und cos ð2 j 0 Þ beide
positiv sind (der Winkel 2 j 0 ¼ 63,435 liegt im 1. Quadrant):
A 00 ðj 0 Þ ¼ 8 r 2 ½ 2 sin ð2 j 0 Þ þ cos ð2 j 0 Þ < 0
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl}
> 0
> 0
)
Maximum
Der Flächeninhalt beträgt dann:
A ðj 0 ¼ 31,72 Þ ¼ 4 r 2 ½ sin 63,435 sin 2 ð31,72 Þ ¼ 4 r 2 ð0,8944 0,2764Þ ¼ 2,472 r 2
Ein Vergleich mit der Fläche im Intervallrandpunkt j ¼ 45 (der Flächeninhalt beträgt dann A ¼ 2 r 2 ) zeigt, dass
j 0 das gesuchte absolute Maximum ist.
Lösung: Für j 0 ¼ 31,72
hat der dem Kreis einbeschriebene kreuzförmige Querschnitt den größten Flächeninhalt:
Amax ¼ A ðj 0 ¼ 31,72 Þ ¼ 2,472 r 2
Welcher Punkt der gleichseitigen Hyperbel x 2 y 2 ¼ 1 hat den kleinsten Abstand vom Punkt
B92
Q ¼ ð0; 2Þ?
Der Abstand des Hyperbelpunktes P ¼ ðx; yÞ vom Punkt
Q ¼ ð0; 2Þ beträgt nach Bild B-32:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
d ¼ x 2 þ ð2 yÞ 2
y
2 Q
2–y
oder
x2 ¼ 1 þ y2
–1
Damit ist der Abstand d nur noch von der Ordinate y
des Hyperbelpunktes P abhängig:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
d ðyÞ ¼ x 2 þ ð2 yÞ 2 ¼ 1 þ y 2 þ ð2 yÞ 2 ¼
¼
P
x
Da P ein Punkt der Hyperbel ist, gilt die Nebenbedingung
x2 y2 ¼ 1
d
Hyperbel
1
y
x
Hyperbel
Bild B-32
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ y2 þ 4 4 y þ y2 ¼ 2 y2 4 y þ 5
y muss nun so bestimmt werden, dass der Abstand d seinen kleinstmöglichen Wert annimmt. Dies ist der Fall,
wenn der unter der Wurzel stehende Ausdruck z ð yÞ ¼ 2 y 2 4 y þ 5 den kleinsten Wert annimmt. Mit Hilfe der
Differentialrechnung lässt sich das (absolute) Minimum dieser „Zielfunktion‘‘ wie folgt bestimmen:
z 0 ð yÞ ¼ 4 y 4 ;
z 0 ð yÞ ¼ 0
)
z 00 ð yÞ ¼ 4 > 0
4y 4 ¼ 0
)
y ¼ 1
Wegen z 00 ð yÞ ¼ 4 und somit auch z 00 ð 1Þ ¼ 4 > 0 handelt es sich bei diesem Extremwert um das gesuchte absolute Minimum.
Aus der Nebenbedingung erhalten wir für die Abszisse des Hyperbelpunktes P zwei Werte
pffiffiffi
x ¼ 2 . pEs
ffiffiffi gibt also wegen der Spiegelsymmetrie der Hyperbel bezüglich der y-Achse genau zwei Punkte
P 1=2 ¼ ð 2; 1Þ, die vom Punkt Q ¼ ð0; 2Þ den kleinstmöglichen Abstand haben. Dieser beträgt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
dmin ¼ d ð y ¼ 1Þ ¼ 2 4 þ 5 ¼ 3
2 Anwendungen der Differentialrechnung
131
I
Ein veränderlicher Verbraucherwiderstand Ra wird von
einer Spannungsquelle mit der Quellenspannung U0
und dem Innenwiderstand Ri gespeist (Bild B-33).
Bestimmen Sie den Verbraucherwiderstand so, dass er
die größtmögliche Leistung
B93
Ri
U0
Ra
P ¼ Ra I 2
aufnimmt (I : Stromstärke).
Bild B-33
Ri und Ra sind in Reihe geschaltet, sodass der Gesamtwiderstand R ¼ Ri þ Ra beträgt (bei Reihenschaltung addieren sich die Einzelwiderstände). Aus dem Ohmschen Gesetz folgt für die Stromstärke I:
U0
I
R ¼
)
I ¼
U0
U0
¼
R
Ri þ Ra
Die vom Widerstand Ra aufgenommene Leistung P ist dann nur noch von Ra abhängig:
P ¼ P ðRa Þ ¼ Ra I 2 ¼ Ra
U 02
ðRi þ Ra Þ
2
¼ U 02
Ra
ðRi þ Ra Þ 2
ðRa > 0Þ
Da der positive konstante Faktor U 02 keinen Einfluss auf die Art und Lage der Extremwerte hat, beschränken wir uns
bei den weiteren Untersuchungen auf die „Zielfunktion“
y ¼
Ra
ðR i þ R a Þ 2
;
Ra > 0
Wir bestimmen jetzt Ra so, dass die größtmögliche Leistung aufgenommen wird. Die dafür benötigten ersten beiden
Ableitungen erhalten wir wie folgt mit Hilfe von Quotienten- und Kettenregel (der besseren bersicht wegen setzen wir
vorübergehend Ra ¼ x):
y ¼
x
ðRi þ xÞ
2
¼
u
v
mit
und u 0 ¼ 1 ;
v ¼ ðRi þ xÞ 2
u ¼ x;
v 0 ¼ 2 ðRi þ xÞ
(Ableitung von v ¼ ðRi þ xÞ 2 mit der Kettenregel, Substitution: t ¼ Ri þ xÞ
1 ðRi þ xÞ 2 2 ðRi þ xÞ x
ðRi þ xÞ ½ ðRi þ xÞ 2 x
u0v v0u
Ri x
¼
¼
¼
y ¼
2
4
3
v
ðRi þ xÞ
ðRi þ xÞ ðRi þ xÞ
ðRi þ xÞ 3
0
y0 ¼
Ri x
ðRi þ xÞ
3
¼
u
v
mit u ¼ Ri x ;
v ¼ ðRi þ xÞ 3 und u 0 ¼ 1 ;
v 0 ¼ 3 ðRi þ xÞ 2
(Ableitung von v ¼ ðRi þ xÞ 3 mit der Kettenregel, Substitution: t ¼ Ri þ x)
y
00
ðRi þ xÞ 2 ½ ðRi þ xÞ 3 ðRi xÞ
1 ðRi þ xÞ 3 3 ðRi þ xÞ 2 ðRi xÞ
u0v v0u
¼
¼
¼
¼
v2
ðRi þ xÞ 6
ðRi þ xÞ 2 ðRi þ xÞ 4
¼
Ri x 3 Ri þ 3 x
ðR i þ xÞ
4
¼
4 Ri þ 2 x
ðRi þ xÞ 4
Berechnung des Maximums: y 0 ¼ 0 , y 00 < 0
y0 ¼ 0
)
y 00 ðx ¼ Ri Þ ¼
Ri x
ðRi þ xÞ 3
¼ 0
4 Ri þ 2 Ri
ðRi þ Ri Þ
4
¼
)
Ri x ¼ 0
2 Ri
ð2 Ri Þ
4
¼
)
x ¼ Ri
2 Ri
1
¼
< 0
4
8 R 3i
16 R i
)
Maximum
Lösung: Die vom Verbraucherwiderstand Ra aufgenommene Leistung wird am größten, wenn x ¼ Ra ¼ Ri ist.
132
B Differentialrechnung
B94
Einer Ellipse mit den Halbachsen a ¼ 6 und b ¼ 3 ist ein achsenparalleles Rechteck größten Flächeninhalts einzubeschreiben. Bestimmen Sie Breite und Höhe dieses Rechtecks.
Bild B-34 zeigt die Ursprungsellipse mit dem einbeschriebenen Rechteck. Wir müssen die Koordinaten x und y des
im 1. Quadranten gelegenen Eckpunktes P so bestimmen, dass der Flächeninhalt A des Rechtecks seinen größten
Wert annimmt (0 < x < 6, 0 < y < 3). Wegen der Spiegelsymmetrie bezüglich beider Achsen gilt dann:
A ¼ A ðx; yÞ ¼ 4 x y
y
3
Die Fläche hängt zunächst von x und y,
d. h. von zwei Variablen ab.
P = (x ; y )
y
x
–6
6
x
Bild B-34
–3
Die Koordinaten x und y genügen dabei der Ellipsengleichung, da der Punkt P ¼ ðx; yÞ auf der Ellipse liegt. Dies
liefert die benötigte Nebenbedingung, die wir nach y auflösen:
x2
y2
þ
¼ 1
36
9
)
y2
x2
36 x 2
¼ 1
¼
9
36
36
)
y ¼
)
y2 ¼
9
1
ð36 x 2 Þ ¼
ð36 x 2 Þ
36
4
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi2
36 x
2
Es kommt nur das positive Vorzeichen infrage, da der Punkt P auf der oberen Halbellipse im 1. Quadrant liegt.
Diesen Ausdruck setzen wir für y in die Flächenformel ein und erhalten den Flächeninhalt A in Abhängigkeit von
der Koordinate x:
pffiffiffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi2
36 x ¼ 2 x 36 x 2 ¼ 2 x 2 36 x 2 ¼
A ðxÞ ¼ 4 x y ¼ 4 x
2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð0 < x < 6Þ
¼ 2 x 2 ð36 x 2 Þ ¼ 2 36 x 2 x 4
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
pffiffiffi pffiffiffi
Mathematischer „Trick‘‘: x ¼ x 2 ! Rechenregel
a b ¼ a b anwenden. Das Maximum dieser Wurzelfunktion liegt an der gleichen Stelle wie das Maximum der unter der Wurzel stehenden „Zielfunktion‘‘ (Wurzelradikand)
z ¼ z ðxÞ ¼ 36 x 2 x 4 ;
0 < x < 6
Mit den Ableitungen
z 0 ðxÞ ¼ 72 x 4 x 3
und z 00 ðxÞ ¼ 72 12 x 2
lässt sich die Lösung dieser Extremwertaufgabe wie folgt bestimmen:
pffiffiffi
pffiffiffiffiffi
72 x 4 x 3 ¼ 4 x ð18 x 2 Þ ¼ 0 ) x 1 ¼ 0 ; x 2=3 ¼ 18 ¼ 3 2
pffiffiffi
Nur die Lösung x 2 ¼ þ 3 2 ¼ 4,2426 liegt im Gültigkeitsbereich 0 < x < 6. An dieser Stelle liegt das gesuchte
Maximum, denn es gilt:
pffiffiffi
pffiffiffi
z 00 ðx 2 ¼ 3 2 Þ ¼ 72 12 ð3 2 Þ 2 ¼ 72 12 18 ¼ 144 < 0 ) relatives Maximum
z 0 ðxÞ ¼ 0
Lösung:
)
pffiffiffi
x ¼ 3 2,
1
y ¼
2
Amax ¼ 4 x y ¼ 4 3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi 2
pffiffiffi
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 pffiffiffiffiffi
1
3 pffiffiffi
36 ð3 2Þ ¼
36 18 ¼
18 ¼
3 2 ¼
2,
2
2
2
2
pffiffiffi 3 pffiffiffi
43 2 3
2
¼ 36
2 ¼
2
2
2 Anwendungen der Differentialrechnung
B95
133
Einer Kugel vom Radius R soll ein gerader Kreiskegel mit möglichst kleinem Volumen umbeschrieben
werden. Wie ist dieser Kegel zu dimensionieren (Radius r, Höhe hÞ?
1
p r 2 h hängt zunächst
3
sowohl vom Radius r als auch von der Höhe h und somit von zwei Variablen ab. Diese sind jedoch nicht unabhängig
voneinander, sondern über eine Neben- oder Kopplungsbedingung miteinander verknüpft, die wir wie folgt durch eine
geometrische Betrachtung erhalten.
Bild B-35 zeigt einen ebenen Schnitt längs der Symmetrieachse. Das Kegelvolumen V ¼
A
a
D
R
b
Kegel
D*
h–R
M
R
b
Kugel
B
r
C
Bild B-35
B*
r
Die rechtwinkligen Dreiecke A B C und A D M in Bild B-35 sind ähnlich, da sie in zwei Winkeln (und damit auch
im 3. Winkel) übereinstimmen: gemeinsamer Winkel a in A, ein rechter Winkel in C bzw. D. Damit sind auch die
Winkel in B bzw. M gleich (b ¼ 90 a). Wir betrachten jetzt die den Winkeln a und b jeweils gegenüber
liegenden Seiten in beiden Dreiecken. Dem Winkel a liegen die Seiten B C ¼ r und D M ¼ R gegenüber, dem
Winkel b entsprechend die Seiten A C ¼ h und A D. Es gilt dann:
ð*Þ
B C : D M ¼ A C : A D oder
r : R ¼ h : AD
Im rechtwinkligen Dreieck A D M liefert der Satz des Pythagoras:
2
2
¼ AM
2
AD ¼ AM DM
2
2
2
AD þ DM
AD ¼
mit
D M ¼ R und
AM ¼ AC M C ¼ h R
¼ ðh RÞ 2 R 2 ¼ h 2 2 R h þ R 2 R 2 ¼ h 2 2 R h ¼ h ðh 2 RÞ
)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
h ðh 2 RÞ
Die Nebenbedingung ð*Þ lautet damit:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð*Þ r : R ¼ h : h ðh 2 RÞ
)
Rh
r ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
h ðh 2 RÞ
Diesen Ausdruck setzen wir in die Volumenformel für r ein und erhalten das Kegelvolumen V in Abhängigkeit von
der Höhe h:
VðhÞ ¼
1
1
R2 h2
1
h2
h ¼
pr2 h ¼
p
p R2
h ðh 2 RÞ
h 2R
3
3
3
ðh > 2 RÞ
Da der (positive) konstante Faktor keinen Einfluss auf die Lage der Extremwerte hat, beschränken wir die weiteren
Untersuchungen auf die „Zielfunktion‘‘
zðhÞ ¼
h2
h 2R
ðh > 2 RÞ
deren Ableitungen z 0 ðhÞ und z 00 ðhÞ sich wie folgt mit Hilfe von Quotienten- und Kettenregel bilden lassen:
134
B Differentialrechnung
zðhÞ ¼
h2
u
¼
v
h 2R
u ¼ h2 ;
mit
v ¼ h 2R
und u 0 ¼ 2 h ;
v0 ¼ 1
2 h ðh 2 RÞ 1 h 2
u0 v v0 u
2 h2 4 R h h2
h2 4 R h
¼
¼
¼
v2
ðh 2 RÞ 2
ðh 2 RÞ 2
ðh 2 RÞ 2
z 0 ðhÞ ¼
h2 4 R h
z 0 ðhÞ ¼
ðh 2 RÞ
2
¼
u
v
mit
u ¼ h2 4 R h ;
v ¼ ðh 2 RÞ 2
und
u 0 ¼ v 0 ¼ 2 ðh 2 RÞ
(Ableitung von v ¼ ðh 2 RÞ 2 mit der Kettenregel, Substitution: t ¼ h 2 R)
z 00 ðhÞ ¼
¼
2 ðh 2 RÞ ðh 2 RÞ 2 2 ðh 2 RÞ ðh 2 4 R hÞ
u0 v v0 u
¼
¼
v2
ðh 2 RÞ 4
2 ðh 2 RÞ ½ ðh 2 RÞ 2 ðh 2 4 R hÞ
ðh 2 RÞ ðh 2 RÞ 3
¼
2 ðh 2 4 R h þ 4 R 2 h 2 þ 4 R hÞ
ðh 2 RÞ 3
¼
8 R2
ðh 2 RÞ 3
Berechnung des Minimums: z 0 ðhÞ ¼ 0, z 00 ðhÞ > 0
z 0 ðhÞ ¼ 0
)
h2 4Rh
ðh 2 RÞ
2
h 4 R ¼ 0 ðda h 6¼ 0Þ
z 00 ðh ¼ 4 RÞ ¼
8 R2
ð4 R 2 RÞ 3
¼ 0
)
¼
)
h 2 4 R h ¼ h ðh 4 RÞ ¼ 0
)
h ¼ 4R
8 R2
ð2 RÞ 3
¼
8 R2
1
> 0
¼
R
8 R3
)
Minimum
Lösung: Wählt man die Höhe h ¼ 4 R, so hatpder
ffiffiffi Kegel das kleinstmögliche Volumen. Der aus der Nebenbedingung (*)
berechnete Radius beträgt dann r ¼ 2 R . Das Volumen hat dann den folgenden Wert:
Vmin ¼ V ðh ¼ 4 RÞ ¼
pffiffiffi
1
1
1
8
pr2 h ¼
p ð 2 RÞ 2 4 R ¼
p 2R2 4R ¼
p R3
3
3
3
3
2.8 Tangentenverfahren von Newton
Das Tangentenverfahren von Newton liefert Näherungswerte für die Nullstellen einer Funktion y ¼ f ðxÞ. Die (zu
lösende) Gleichung muss daher in der Form f ðxÞ ¼ 0 vorliegen bzw. auf diese Form gebracht werden.
Lehrbuch: Band 1, Kapitel IV.3.7
Formelsammlung: Kapitel I.4.5
B96
Bestimmen Sie die Lösungen der Gleichung 2,4 ln x þ 0,5 x 2 þ 1 ¼ 0 auf mindestens 5 Stellen
nach dem Komma genau.
Bestimmung des Startwertes x 0
Wir stellen die Gleichung f ðxÞ ¼ 2,4 ln x þ 0,5 x 2 þ 1 ¼ 0 zunächst wie folgt um:
2,4 ln x ¼ 0,5 x 2 1
2 Anwendungen der Differentialrechnung
135
Dann zeichnen wir die Kurven y ¼ 2,4 ln x und
y ¼ 0,5 x 2 1 (sie entsprechen der linken bzw. rechten
Seite der Gleichung) und entnehmen der Skizze, dass es genau
einen Schnittpunkt in der Nähe von x ¼ 0,6 gibt (Bild B-36).
Diesen Wert wählen wir als Startwert für die Newton-Iteration: x 0 ¼ 0,6.
y
0,5
–1
f ðxÞ ¼ 2,4 ln x þ 0,5 x 2 þ 1 ;
f 0 ðxÞ ¼
2,4
þ x;
x
f 00 ðxÞ ¼
y = 2,4 · ln x
≈ 0,6
1
y = – 0,5 x 2 – 1
–1
2,4
þ1
x2
x
Bild B-36
Zunächst prüfen wir noch, ob der gewählte Startwert x 0 ¼ 0,6 „geeignet‘‘ ist, d. h. die Konvergenzbedingung erfüllt:
f ðx Þ f 00 ðx Þ
f ð0,6Þ f 00 ð0,6Þ
ð 0,045 981Þ ð 5,666 667Þ
0
0
¼ 0,012 314 < 1
¼
¼
½ f 0 ðx Þ 2
½ f 0 ð0,6Þ 2
4,6 2
0
Folgerung: Der Startwert x 0 ¼ 0,6 ist geeignet.
Der 1. Iterationsschritt liefert dann den folgenden (verbesserten) Näherungswert:
x1 ¼ x0
f ðx 0 Þ
f
0 ðx
0Þ
¼ 0,6
f ð0,6Þ
f 0 ð0,6Þ
¼ 0,6
0,045 981
¼ 0,609 996
4,6
Mit diesem Wert als Startwert berechnen wir die 2. Näherung:
x2 ¼ x1
f ðx 1 Þ
f
0 ðx
1Þ
¼ 0,609 996
f ð0,609 996Þ
f 0 ð0,609 996Þ
¼ 0,609 996
0,000 279
¼ 0,610 057
4,544 448
Der Start in die 3. Iteration zeigt dann, dass dieser Näherungswert sogar auf 6 Dezimalstellen nach dem Komma
genau ist. Die gesuchte Lösung ist somit x ¼ 0,610 057.
B97
Ein liegender zylindrischer Behälter mit einem Volumen von Vz ¼ 2000 ‘ ist zu drei viertel mit Heizöl gefüllt. Berechnen Sie die Füllhöhe h des Behälters.
Hinweis: Radius r und Länge l des Zylinders sind (zahlenmäßig) nicht bekannt. Die gesuchte Füllhöhe h wird daher noch von r bzw. l abhängen.
Bild B-37 zeigt den liegenden Zylinderkessel mitsamt der kreisförmigen Querschnittsfläche.
Kreissegment
Zylinderkessel
y
f
2r
M
A
l
a)
Bild B-37
b)
a) Zylinderkessel
b) Querschnitt des Kessels
2r
h
136
B Differentialrechnung
Das Füllvolumen erhalten wir (formelmäßig), wenn wir die im Bild dunkelgrau unterlegte Querschnittsfläche A mit
der Zylinderlänge l multiplizieren. Die Querschnittsfläche A wiederum ist die Differenz zwischen der Kreisfläche
p r 2 und der Fläche des hellgrau unterlegten Kreissegments. Aus der Formelsammlung entnehmen wir (Kap. I.7.10):
A ¼ pr2
1 2
1 2
r ðj sin jÞ ¼
r ð2 p j þ sin jÞ ;
2
2
0 < j < p
Damit gilt für das Füllvolumen (der Behälter ist zu drei viertel gefüllt ) V ¼ 1500 ‘):
ð*Þ
V ¼ Al ¼
1 2
r l ð2 p j þ sin jÞ ¼ 1500
2
Radius r und Länge l des Kessels sind zwar unbekannt, hängen jedoch wie folgt zusammen (Zylindervolumen
Vz ¼ 2000 ‘):
Vz ¼ p r 2 l ¼ 2000
)
2000
p
r2 l ¼
Diesen Wert setzen wir in Gleichung ð*Þ ein und erhalten eine Bestimmungsgleichung für den noch unbekannten
Zentriwinkel j, aus dem wir dann die gesuchte Füllhöhe ermitteln können:
1 2
1 2000
1000
r l ð2 p j þ sin jÞ ¼
ð2 p j þ sin jÞ ¼
ð2 p j þ sin jÞ ¼ 1500
2
2
p
p
2 p j þ sin j ¼ 1,5 p
oder
)
sin j ¼ j 0,5 p
Da der Behälter zu drei viertel gefüllt ist, muss die Füllhöhe h zwischen r und 2 r und der Zentriwinkel j demnach zwischen 0 und p liegen. Wir suchen also die Lösung der Gleichung sin j ¼ j 0,5 p im Intervall
0 < j < p. Anhand einer Skizze erkennen wir, dass sich die Kurven y ¼ sin j und y ¼ j 0,5 p in der Nähe
von j ¼ 2,3 schneiden (Bild B-38). Wir wählen daher j 0 ¼ 2,3 als Startwert für das Tangentenverfahren:
y
f ðjÞ ¼ sin j j þ 0,5 p
y = sin f
y = f – 0,5π
f 0 ðjÞ ¼ cos j 1
0,5 π
π
f
≈ 2,3
Bild B-38
1. Näherung:
j1 ¼ j0
2. Näherung:
j2 ¼ j1
f ðj 0 Þ
f
0 ðj
0Þ
f ðj 1 Þ
f
0 ðj
1Þ
¼ 2,3
f ð2,3Þ
¼ 2,3
f 0 ð2,3Þ
¼ 2,309 904
0,016 502
¼ 2,309 904
1,666 276
f ð2,309 904Þ
f
0 ð2,309
904Þ
¼ 2,309 904
0,000 038
¼ 2,309 881
1,673 629
Wegen f ðj 2 Þ ¼ f ð2,309 881Þ ¼ 7,69 10 7 ist dieser Näherungswert bereits auf 6 Stellen nach dem Komma genau. Somit ist j ¼ 2,309 881 die gesuchte Lösung (im Gradmaß: j ¼ 132,346 ).
Die Berechnung der Füllhöhe erfolgt nach der Formel
h ¼ 2 r y ¼ 2 r r ½ 1 cos ðj=2Þ ¼ 2 r r þ r cos ðj=2Þ ¼ r þ r cos ðj=2Þ ¼ r ½ 1 þ cos ðj=2Þ
(mit y ¼ r ½ 1 cos ðj=2Þ ! FS: Kap. I.7.10 und Bild B-37 b). Wir erhalten:
h ¼ r ½ 1 þ cos ðj=2Þ ¼ r ð1 þ cos 66,173 Þ ¼ 1,404 r
2 Anwendungen der Differentialrechnung
B98
137
Bestimmen Sie die Lösungen der Gleichung tan j ¼ j im Intervall 0 < j < p (auf mindestens
4 gültige Stellen nach dem Komma).
Der Schnittpunkt der beiden Kurven y ¼ tan j und y ¼ j im Intervall 0 < j < p liegt in der Nähe von
j ¼ 2. Er dient uns als Startwert für die Newton-Iteration: j 0 ¼ 2 (Bild B-39). Auf die berprüfung der Konvergenzbedingung wollen wir dabei verzichten.
f ðjÞ ¼ tan j þ j
y
f 0 ðjÞ ¼ ð1 þ tan 2 jÞ þ 1 ¼ 2 þ tan 2 j
y = tan f
1
≈2
1. Näherung:
j1 ¼ j0
¼ 2
2. Näherung:
f ðj 0 Þ
f 0 ðj 0 Þ
¼ 2
f ð2Þ
f 0 ð2Þ
–1
f ðj 1 Þ
f 0 ðj 1 Þ
f
y = tan f
y = –f
0,185 040
¼ 2,027 315
6,774 399
j2 ¼ j1
π
1
¼
–2
Bild B-39
¼ 2,027 315
f ð2,027 315Þ
f 0 ð2,027 315Þ
¼ 2,027 315
0,008 846
¼ 2,028 754
6,145 951
Wegen f ðj 2 Þ ¼ f ð2,028 754Þ ¼ 0,000 023 und f 0 ðj 2 Þ ¼ f 0 ð2,028 754Þ ¼ 6,115 938 bringt die 3. Iteration keine
Veränderung mehr in der 4. Stelle nach dem Komma. Der Näherungswert x 2 ist sogar auf 5 Nachkommastellen genau.
Ergebnis: j ¼ 2,02875.
B99
Welche Lösungen besitzt die Gleichung x tan x 1 ¼ 0 im Intervall 0 x p ?
Wir stellen zunächst die Gleichung wie folgt um:
x tan x 1 ¼ 0
,
tan x ¼
y
1
x
y = tan x
2
Der Schnittpunkt der beiden Kurven y ¼ tan x und y ¼ 1=x liegt
nach Bild B-40 in der Nähe von x ¼ 0,9 und liefert uns den für das
Newton-Verfahren benötigten Startwert: x 0 ¼ 0,9
f ðxÞ ¼ x tan x 1 ¼ u v 1
|{z}
u
v
y=1
x
1
≈ 0,9
π/2
f
Bild B-40
π
y = tan x
Die benötigte Ableitung f 0 ðxÞ erhalten wir mit der Produktregel:
f 0 ðxÞ ¼ u 0 v þ v 0 u 0 ¼ 1 tan x þ
1. Näherung:
x1 ¼ x0
2. Näherung:
x2 ¼ x1
f ðx 0 Þ
f 0 ðx 0 Þ
f ðx 1 Þ
f 0 ðx 1 Þ
1
x
x ¼ tan x þ
2
cos x
cos 2 x
¼ 0,9
f ð0,9Þ
f 0 ð0,9Þ
¼ 0,862 628
¼ 0,9
0,134 142
¼ 0,862 628
3,589 357
f ð0,862 628Þ
f 0 ð0,862 628Þ
¼ 0,862 628
0,007 333
¼ 0,860 341
3,206 688
x
138
B Differentialrechnung
3. Näherung:
x3 ¼ x2
f ðx 2 Þ
f ð0,860 341Þ
0,000 024
¼ 0,860 341 0
¼ 0,860 341
¼ 0,860 333
0
f ðx 2 Þ
f ð0,860 341Þ
3,185 083
Die Ergebnisse stellen wir in einer Tabelle wie folgt zusammen:
n
xn1
f ðx n 1 Þ
f 0 ðx n 1 Þ
xn
1
0,9
0,134 142
3,589 357
0,862 628
2
0,862 628
0,007 333
3,206 688
0,860 341
3
0,860 341
0,000 024
3,185 083
0,860 333
Ergebnis: x ¼ 0,8603
2.9 Grenzwertberechnung nach Bernoulli und de L’Hospital
Lehrbuch: Band 1, Kapitel VI.3.3.3
Formelsammlung: Kapitel III.3.4
B100
lim
x!0
ax bx
¼ ?
tan x
ða > 0
und b > 0Þ
Zähler und Nenner des Bruches streben für x ! 0 jeweils gegen Null, der Grenzwert führt also zunächst zu einem
unbestimmten Ausdruck vom Typ 0=0, auf den die Grenzwertregel von Bernoulli und de L’Hospital anwendbar ist:
ða x b x Þ 0
ðln aÞ a x ðln bÞ b x
ðln aÞ a 0 ðln bÞ b 0
ax bx
¼
¼
¼ lim
¼ lim
lim
tan x
1 þ tan 2 x
1 þ tan 2 0
x!0
x!0
x!0
ðtan xÞ 0
¼
B101
g ¼ lim
x!0
ðln aÞ 1 ðln bÞ 1
1þ
02
ex x 1
ðe x 1Þ x
¼ ln a ln b ¼ ln
a
b
Rechenregel : ln
a
¼ ln a ln b
b
¼ ?
Der Grenzwert führt zunächst auf den unbestimmten Ausdruck 0=0, da Zähler und Nenner für x ! 0 gegen Null
streben:
lim ðe x x 1Þ ¼ e 0 0 1 ¼ 1 1 ¼ 0 ;
x!0
lim ðe x 1Þ x ¼ ðe 0 1Þ 0 ¼ 0
x!0
Die Grenzwertregel von Bernoulli und de L’Hospital führt ebenfalls auf den unbestimmten Ausdruck 0=0:
ðe x x 1Þ 0
ex x 1
ex 1
ex 1
0
g ¼ lim
!
¼ lim
¼
lim
¼
lim
x þ ex 1
x
x
0
x
x
x
e
0
x ! 0 ðe 1Þ x
x ! 0 ½ ðe 1Þ x
x ! 0 e x þ 1 ðe 1Þ
x!0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Produktregel
(Zähler ! e 0 1 ¼ 1 1 ¼ 0; Nenner ! 0 e 0 þ e 0 1 ¼ 0 þ 1 1 ¼ 0)
2 Anwendungen der Differentialrechnung
139
Nochmalige Anwendung der Grenzwertregel führt schließlich zu dem folgenden Ergebnis:
g ¼ lim
x!0
ðe x 1Þ 0
ex x 1
ex 1
¼
lim
¼
lim
¼
x
x
ðe x 1Þ x
x!0 x e þ e 1
x ! 0 ðx e x þ e x 1Þ 0
|fflffl{zfflffl}
Produktregel
¼ lim
x!0
B102
1
ex
ex
ex
ex
1
1
1
¼ lim
¼ lim
¼ lim
¼
¼
x
x
x
x
þe x þe
2þ0
2
x!0 2 e þ x e
x ! 0 e x ð2 þ xÞ
x!0 2 þ x
sin ð3 tÞ
g ¼ lim pffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi ¼ ?
t!0
t þ2 2
Bei der Grenzwertbildung streben Zähler und Nenner jeweils gegen Null, der Bruch damit gegen den unbestimmten
Ausdruck 0=0. Die Grenzwertregel von Bernoulli und de L’Hospital ist daher anwendbar und führt zu folgendem
Ergebnis (Ableitungen von Zähler und Nenner jeweils mit Hilfe der Kettenregel, Substitutionen: u ¼ 3 t bzw.
v ¼ t þ 2):
pffiffiffiffiffiffiffiffiffiffiffiffi
2 t þ2
sin ð3 tÞ
ðsin ð3 tÞÞ 0
3 cos ð3 tÞ
g ¼ lim pffiffiffiffiffiffiffiffiffiffiffiffi
¼
¼ lim 3 cos ð3 tÞ
pffiffiffi 0 ¼ lim
pffiffiffi ¼ lim pffiffiffiffiffiffiffiffiffiffiffiffi
1
1
t!0
t!0 ð t þ 2
t!0
t !0
2Þ
t þ2 2
pffiffiffiffiffiffiffiffiffiffiffiffi 1
2 t þ2
pffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
¼ 6 lim cos ð3 tÞ t þ 2 ¼ 6 cos 0 2 ¼ 6 1 2 ¼ 6 2
t!0
B103
x 1
¼ ?
g ¼ lim x ln
x þ1
x!1
Der Grenzwert führt zu dem folgenden unbestimmten Ausdruck:
x 1
x 1
1 1=x
g ¼ lim x ln
! 1 ln 1 ¼ 1 0
ln
¼ ln
! ln 1 f ür x ! 1
x þ1
x þ1
1 þ 1=x
x!1
Auf diese Form ist die Grenzwertregel von Bernoulli und de L’Hospital nicht anwendbar, wir können diesen
unbestimmten Ausdruck jedoch durch eine elementare Umformung auf
den zulässigen Typ 0=0 zurückführen
1
1
mathematischer Trick: Faktor x ist der Kehrwert von
, d. h. x ¼
:
x
1=x
0
1
1
1
B
xC
C
ln B
@
A
x 1
1
ln
1
þ
x 1
ln 1
0
x þ1
x
¼ lim
!
g ¼ lim x ln
¼ lim
¼
x þ1
0
0
x!1
x!1
x
!
1
1
1
x
x
Jetzt dürfen wir die Grenzwertregel anwenden. Die dabei benötigte Ableitung der Zählerfunktion erhalten wir wie folgt
mit Hilfe von Ketten- und Produktregel:
x 1
x 1
u
¼ ln z mit z ¼
y ¼ ln
¼
ðu ¼ x 1; v ¼ x þ 1 und u 0 ¼ v 0 ¼ 1Þ
x þ1
x þ1
v
140
B Differentialrechnung
y0 ¼
¼
dy
dy dz
dy u0v v0u
1 1 ðx þ 1Þ 1 ðx 1Þ
1 x þ1x þ1
¼
¼
¼
¼
¼
2
2
dx
dz dx
dz
z
z
v
ðx þ 1Þ
ðx þ 1Þ 2
1
2
1
2
2
2
2
¼
¼
¼
¼
2
2
z ðx þ 1Þ 2
x 1 ðx þ 1Þ
x 1
ðx 1Þ ðx þ 1Þ
ðx 1Þ ðx þ 1Þ ðx þ 1Þ
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
x þ1
x þ1
3. Binom
Die Grenzwertregel führt jetzt zu dem folgenden Ergebnis:
0
x 1
x 1 0
2
ln
ln
x þ1
x þ1
B x2 1
g ¼ lim
¼ lim
¼ lim B
0
@
1
x!1
x!1
x!1
1
1
x2
x
x
0
¼ lim
x!1
B
2x2
x2
¼ 2 lim
¼ 2 lim B
@
2
2
x 1
x!1 x 1
x!1
1
C
2
C ¼ lim
A
x!1 x2 1
x2
¼
1
1
C
C ¼ 2 1 ¼ 2
1 A
1
x2
1
Umformungen: Zählerbruch mit dem Kehrwert des Nennerbruches multiplizieren ! Zähler und Nenner vor der
Grenzwertbildung noch gliedweise durch x 2 dividieren.
B104
g ¼ lim x
1
x1
¼ ?
x!1
1
¼ 1 führt der Grenzwert g zunächst auf den unbestimmten Ausdruck 1 1 ,
x!1
x!1 x 1
für den die Grenzwertregel von Bernoulli und de L’Hospital nicht anwendbar ist. Wir können diesen Ausdruck jedoch
durch elementare Umformungen auf die Form 0=0 zurückführen. Wegen z ¼ e ln z für z > 0 gilt:
Wegen lim x ¼ 1 und lim
x
1
x 1
¼ e
1
x 1
ln x
¼ e
1
ln x
x 1
¼ e
ln x
x 1
(Rechenregel : ln a n ¼ n ln a)
Somit lässt sich der Grenzwert auch wie folgt darstellen:
g ¼ lim x
1
x 1
¼ lim e
x!1
ln x
x 1
lim
¼ e
x!1
x!1
ln x
x 1
Dabei haben wir bereits berücksichtigt, dass die Grenzwertbildung im Exponenten vorgenommen werden darf (siehe
Rechenregeln für Grenzwerte: Band 1, Kap. III.4.2.3 und Formelsammlung, Kap. III.3.3).
ln x
führt zunächst zu dem unbestimmten Ausdruck 0=0, da Zähler und Nenner für x ! 1
Der Grenzwert lim
x!1 x 1
gegen Null streben (ln 1 ¼ 0). Die Grenzwertregel von Bernoulli und de L’Hospital ist daher anwendbar und führt zu
dem folgenden Ergebnis:
lim
x!1
ln x
x 1
¼ lim
x!1
ðln xÞ
!
0
ðx 1Þ
0
¼ lim
x!1
1
x
1
!
¼ lim
x!1
1
¼ 1
x
Damit haben wir die gestellte Aufgabe gelöst, der gesuchte Grenzwert beträgt
g ¼ lim x
x!1
1
x 1
ln x
x!1 x 1
lim
¼ e
¼ e1 ¼ e
2 Anwendungen der Differentialrechnung
B105
g ¼ lim
x!1
1
1
þ
ln x
1x
141
¼ ?
ðx > 1Þ
Der Grenzwert führt zunächst auf einen unbestimmten Ausdruck, auf den die Grenzwertregel von Bernoulli und de
L’Hospital nicht anwendbar ist:
1
1
g ¼ lim
þ
! 11
ln x
1x
x!1
Wir müssen daher den in der Klammer stehenden Ausdruck vor dem Grenzübergang umformen (Hauptnenner bilden:
ð1 xÞ ln x). Die Grenzwertbildung führt dann zu dem unbestimmten Ausdruck 0=0, den wir mit der Grenzwertregel weiter behandeln können:
1
1
ð1 xÞ þ ln x
ð1 1Þ þ ln 1
0þ0
0
þ
¼ lim
!
¼
¼
g ¼ lim
ln x
1x
00
0
ð1 1Þ ln 1
x!1
x ! 1 ð1 xÞ ln x
x þ 1
x
¼ lim
¼
¼ lim
g ¼ lim
0
x ! 1 ðð1 xÞ ln xÞ
x!1
x ! 1 x ln x þ 1 x
1
ð1
xÞ
1
ln
x
þ
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
x
x
1 þ
ð1 x þ ln xÞ 0
1
x
Produktregel
x!1
x þ 1
x
x þ 1
1 þ 1
0
¼ lim
!
¼
x ln x x þ 1
1 ln 1 1 þ 1
0
x
x ! 1 x ln x x þ 1
f
¼ lim
0
Umformungen: Im Zähler und Nenner jeweils den Hauptnenner x bilden ! den Zählerbruch mit dem Kehrwert des
Nennerbruches multiplizieren ! Faktor x kürzen.
Nochmalige Anwendung der Grenzwertregel führt schließlich zum Ziel:
ð x þ 1Þ 0
1
1
¼ lim
¼
¼ lim
ð x ln x x þ 1Þ 0
1
x!1
x ! 1 ln x 1 1
ð x Þ 1
1 ln x þ
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
x
g ¼ lim
x!1
Produktregel
x!1
1
1
1
1
1
¼ lim
¼
¼
¼
ln x 2
ln
x
þ
2
ln
1
þ
2
0
þ
2
2
x!1
f
¼ lim
0
Die Tangentensteigung der Kardioide r ¼ 1 þ cos j, 0 j 2 p wird nach der Formel
y 0 ðjÞ ¼
B106
2 cos 2 j cos j þ 1
sin j þ sin ð2 jÞ
berechnet. An der Stelle j ¼ p erhält man zunächst den unbestimmten Ausdruck 0=0. Zeigen Sie
mit Hilfe der Grenzwertregel von Bernoulli und de L’Hospital, dass die Kurventangente an dieser
Stelle waagerecht verläuft.
Die Steigungsformel führt beim Grenzübergang j ! p zunächst auf einen unbestimmten Ausdruck:
m ¼ lim y 0 ðjÞ ¼ lim
j!p
¼
2 cos 2 j cos j þ 1
j!p
2 ð 1Þ 2 þ 1 þ 1
0þ0
sin j þ sin ð2 jÞ
¼
2 þ 2
0
¼
0
0
!
2 cos 2 p cos p þ 1
¼
sin p þ sin ð2 pÞ
142
B Differentialrechnung
Mit Hilfe der Grenzwertregel von Bernoulli und de L’Hospital lässt sich der Grenzwert wie folgt bestimmen:
m ¼ lim
j!p
¼ lim
j!p
¼
ð 2 cos 2 j cos j þ 1Þ 0
ðsin j þ sin ð2 jÞÞ
0
4 cos j sin j þ sin j
cos j þ 2 cos ð2 jÞ
ð4 ð 1Þ þ 1Þ 0
1 þ 2 1
¼
¼ lim
2 2 cos j ð sin jÞ þ sin j
cos j þ 2 cos ð2 jÞ
j!p
¼ lim
j!p
ð4 cos j þ 1Þ sin j
cos j þ 2 cos ð2 jÞ
ð 3Þ 0
0
¼
¼ 0
1 þ 2
1
)
¼
¼
ð4 cos p þ 1Þ sin p
cos p þ 2 cos ð2 pÞ
¼
waagerechte Tangente
ðdie Ableitungen von cos 2 j und sin ð2 jÞ erhält man mit Hilfe der KettenregelÞ
Die Tangente im Nullpunkt ðd. h. für j ¼ p und r ¼ 0Þ verläuft daher –– wie behauptet –– waagerecht.
B107
Beim freien Fall unter Berücksichtigung des Luftwiderstandes besteht der folgende komplizierte Zusammenhang zwischen der Fallgeschwindigkeit v und dem Fallweg s:
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0
1
u
2ks
m : Masse des frei fallenden Körpers
u
m
1
e
u
@
A
;
s 0
g : Erdbeschleunigung
v ¼ tmg
k
k : Reibungskoeffizient (k > 0)
Wie lautet dieses Gesetz im luftleeren Raum (k ¼ 0)?
Anleitung: Betrachten Sie v als eine Funktion des Reibungskoeffizienten k und bilden Sie dann
den Grenzwert für k ! 0.
Die Abhängigkeit der Fallgeschwindigkeit v vom Fallweg s im luftleeren Raum erhalten wir durch den Grenzübergang k ! 0. Mit der Abkürzung a ¼ 2 s=m und unter Beachtung der Rechenregeln für Grenzwerte (hier: der
Grenzwert darf „unter der Wurzel‘‘ ausgeführt werden) erhalten wir zunächst:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
1 e ak
1 e ak
v k ¼ 0 ¼ lim v ðkÞ ¼ lim
¼ m g lim
mg
k
k
k!0
k!0
k!0
Berechnung des Grenzwertes
Der Grenzwert führt zunächst auf einen unbestimmten Ausdruck:
lim
k!0
1 e ak
1 e0
11
0
¼
!
¼
0
0
k
0
Mit der Grenzwertregel von Bernoulli und de L’Hospital erreichen wir unser Ziel:
ð1 e a k Þ 0
1 e ak
a e ak
2s
¼ lim
¼ lim a e a k ¼ a e 0 ¼ a 1 ¼ a ¼
¼
lim
lim
0
m
k
1
k!0
k!0
k!0
k!0
ðkÞ
ðAbleitung von e a k nach der Kettenregel, Substitution: t ¼ a kÞ
Wir erhalten damit im luftleeren Raum die folgende Abhängigkeit der Fallgeschwindigkeit v vom Fallweg s:
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
2s
vk¼0 ¼
mg
¼ 2gs;
s 0
m
v
a)
mg
k
Bild B-41 zeigt den Zusammenhang zwischen v und s im
luftleeren Raum (Kurve a) bzw. unter Berücksichtigung des
Luftwiderstandes (Kurve b) .
b)
s
Bild B-41
143
C Integralrechnung
1 Integration durch Substitution
Alle Integrale in diesem Abschnitt lassen sich mit Hilfe einer geeigneten Substitution auf Grund- oder Stammintegrale
zurückführen. Bei einem bestimmten Integral kann auf die Rücksubstitution verzichtet werden, wenn die Integrationsgrenzen mit Hilfe der Substitutionsgleichung mitsubstituiert werden.
Lehrbuch: Band 1, Kapitel V.8.1
Formelsammlung: Kapitel V.3.1
Tabelle der Grund- oder Stammintegrale: Band 1, Kapitel V.5 und Formelsammlung, Kapitel V.2.3
ð1
C1
x
I ¼
ð1 þ x 2 Þ 2
0
dx ¼ ?
Durch die Substitution u ¼ 1 þ x 2 wird der Nenner des Integranden vereinfacht und wir erhalten nach Durchführung der vollständigen Substitution ein Grundintegral (die Integrationsgrenzen werden hier mitsubstituiert). Die Substitutionsgleichungen lauten:
u ¼ 1 þ x2;
du
¼ 2x;
dx
dx ¼
du
;
2x
Grenzen
unten: x ¼ 0
)
u ¼ 1þ0 ¼ 1
oben: x ¼ 1
)
u ¼ 1þ1 ¼ 2
Durchführung der Integralsubstitution:
ð1
I ¼
0
ð2
x
ð1 þ
x 2Þ 2
dx ¼
u¼1
x du
1
¼
2
2
2
x
u
ð2
1
du
u2
1
Integration (Potenzregel der Integralrechnung):
I ¼
1
2
ð2
1
1
du ¼
2
u2
1
ð
C2
I ¼
ð2
u 2 d u ¼
1
2
1
u 1
1
2
¼
1
1
2
1
u
2
¼
1
1
2
1
1 1
1
þ1 ¼
¼
2
2 2
4
3x8
dx ¼ ?
x3 þ 1
Sinnvoll erscheint die Substitution u ¼ x 3 þ 1; da sie den Nenner des Integranden vereinfacht. Mit
u ¼ x3 þ 1;
du
¼ 3x2 ;
dx
dx ¼
du
3x2
erhalten wir zunächst:
ð
I ¼
3x8
dx ¼
x3 þ 1
ð
3x8 du
¼
u
3x2
ð
3x2 x6 du
¼
u
3x2
ð
x6
du
u
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_3
144
C Integralrechnung
Die Durchführung der Integralsubstitution ist jedoch unvollständig, denn das neue Integral enthält noch die alte Variable x. Wir müssen diese daher noch durch die neue Variable u ausdrücken. Dies geschieht mit Hilfe der Substitutionsgleichung u ¼ x 3 þ 1, die nach x 3 aufgelöst und anschließend quadriert wird:
x3 ¼ u 1
)
x 6 ¼ ðu 1Þ 2 ¼ u 2 2 u þ 1
Damit geht das Integral über in:
ð 6
ð 2
ð
x
u 2u þ 1
1
1 2
I ¼
du ¼
du ¼
u2þ
du ¼
u 2 u þ ln j u j þ C
u
u
u
2
Rücksubstitution ðu ¼ x 3 þ 1Þ führt schließlich zur Lösung dieser Aufgabe:
I ¼
1 3
1
ðx þ 1Þ 2 2 ðx 3 þ 1Þ þ ln j x 3 þ 1j þ C ¼
ðx 6 þ 2 x 3 þ 1Þ 2 x 3 2 þ ln j x 3 þ 1 j þ C ¼
2
2
1 6
1
1 6
3
x þ x3 þ
2 x 3 2 þ ln j x 3 þ 1 j þ C ¼
x x 3 þ ln j x 3 þ 1 j
þC ¼
2
2
2
2
1 6
3
C* ¼
¼
x x 3 þ ln j x 3 þ 1 j þ C *
þC
2
2
¼
C3
ð
I ¼
e 2x
dx ¼ ?
1 þ ex
Die Substitution u ¼ 1 þ e x führt zu einer Vereinfachung im Nenner des Integranden. Somit gilt (versuchsweise):
u ¼ 1 þ ex ;
du
¼ ex ;
dx
dx ¼
du
ex
Durchführung der Integralsubstitution:
ð
ð 2x
ð x
ð x
e 2x
e
du
e ex du
e
I ¼
du
d
x
¼
¼
¼
1 þ ex
u
u
u
ex
ex
Um die alte Variable x vollständig aus dem Integral zu entfernen, lösen wir die Substitutionsgleichung u ¼ 1 þ e x
nach e x auf und setzen den gefundenen Ausdruck e x ¼ u 1 ein. Das Integral I lässt sich jetzt leicht lösen:
ð x
ð
ð
e
u1
1
du ¼
1
d u ¼ u ln j u j þ C
I ¼
du ¼
u
u
u
Nach der Rücksubstitution u ¼ 1 þ e x erhält man die folgende Lösung:
ð
e 2x
I ¼
d x ¼ ð1 þ e x Þ ln j 1 þ e x j þ C ¼ e x ln ð1 þ e x Þ þ C *
1 þ ex
C4
ðC * ¼ 1 þ CÞ
ð
I ¼
sin 3 x cos 3 x d x ¼ ?
Wir versuchen, das Integral mit der folgenden Substitution zu lösen:
u ¼ sin x ;
du
¼ cos x ;
dx
dx ¼
du
cos x
Durchführung der Integralsubstitution führt zunächst zu:
ð
ð
ð
ð
du
du
I ¼ sin 3 x cos 3 x d x ¼ u 3 cos 3 x
¼ u 3 cos 2 x cos x
¼ u 3 cos 2 x d u
cos x
cos x
1 Integration durch Substitution
145
Die Substitution ist offensichtlich unvollständig, da die alte Variable x immer noch im Integral vorhanden ist. Den
Faktor cos 2 x im Integral können wir jedoch unter Verwendung der trigonometrischen Formel sin 2 x þ cos 2 x ¼ 1
wie folgt durch die neue Variable u ausdrücken:
cos 2 x ¼ 1 sin 2 x ¼ 1 u 2
Das Integral I geht dann in Grundintegrale über:
ð
ð
ð
1 4
1 6
u
u þC
I ¼ u 3 cos 2 x d u ¼ u 3 ð1 u 2 Þ d u ¼ ðu 3 u 5 Þ d u ¼
4
6
Durch Rücksubstitution ðu ¼ sin xÞ erhalten wir die gesuchte Lösung. Sie lautet:
ð
1
1
sin 4 x
sin 6 x þ C
I ¼ sin 3 x cos 3 x d x ¼
4
6
Anmerkung: Auch die Substitution u ¼ cos x führt zum Ziel!
ð
C5
I ¼
dx
pffiffiffiffiffiffiffiffiffiffiffi ¼ ?
tan x
cos 2 x
1
. Wir wählen daher versuchsweise die folgende
Der Integrand enthält die Funktion tan x und deren Ableitung
cos 2 x
Substitution:
u ¼ tan x ;
du
1
;
¼
dx
cos 2 x
d x ¼ cos 2 x d u
Sie führt (wie erhofft) zu einem Grundintegral:
ð
I ¼
dx
pffiffiffiffiffiffiffiffiffiffiffi ¼
2
cos x tan x
ð
cos 2 x d u
pffiffiffi ¼
cos 2 x u
ð
du
pffiffiffi ¼
u
ð
du
¼
u 1=2
ð
u 1=2 d u ¼
pffiffiffi
u 1=2
þC ¼ 2 uþC
1=2
Nach der Rücksubstitution u ¼ tan x erhalten wir die Lösung:
ð
pffiffiffiffiffiffiffiffiffiffiffi
dx
I ¼
¼ 2 tan x þ C
p
ffiffiffiffiffiffiffiffiffiffi
ffi
cos 2 x tan x
C6
ð
I ¼
arctan x
dx ¼ ?
1 þ x2
Wir schreiben den Integrand als Produkt und erkennen, dass der rechte Faktor genau die Ableitung des linken Faktors ist:
ð
ð
ð
arctan x
1
1
d x ¼ arctan x
d x ¼ f ðxÞ f 0 ðxÞ d x mit f ðxÞ ¼ arctan x und f 0 ðxÞ ¼
2
1 þ x2
1
þ
x
1
þ
x2
|fflfflfflffl{zfflfflfflffl} |fflfflffl{zfflfflffl}
f ðxÞ
f 0 ðxÞ
Ein solches Integral wird bekanntlich durch die Substitution u ¼ f ðxÞ gelöst (! FS: Kap. V.3.1.2, Integraltyp B).
Wir setzen daher u ¼ arctan x und erhalten folgende Substitutionsgleichungen:
u ¼ arctan x ;
du
1
;
¼
dx
1 þ x2
d x ¼ ð1 þ x 2 Þ d u
146
C Integralrechnung
Nach der Durchführung dieser Integralsubstitution erhalten wir ein Grundintegral:
ð
ð
ð
arctan x
u
1 2
I ¼
dx ¼
ð1 þ x 2 Þ d u ¼ u d u ¼
u þC
2
2
1þx
1 þ x2
Die Rücksubstitution u ¼ arctan x führt schließlich zur gesuchten Lösung:
ð
arctan x
1
ðarctan xÞ 2 þ C
I ¼
dx ¼
2
2
1þx
ð
C7
I ¼
8 x 3 20 x
dx ¼ ?
x4 5x2 þ 4
Eine genaue Betrachtung des echt gebrochenrationalen Integranden zeigt, dass im Zähler genau die Ableitung des
Nenners steht (bis auf den konstanten Faktor 2, den wir vor das Integral ziehen):
ð
I ¼
8 x 3 20 x
dx ¼
x4 5x2 þ 4
ð
2 ð4 x 3 10 xÞ
x4 5x2 þ 4
ð
dx ¼ 2
4 x 3 10 x
dx ¼ 2
x4 5x2 þ 4
ð
f 0 ðxÞ
f ðxÞ
dx
Zähler: f 0 ðxÞ ¼ 4 x 3 10 x
Nenner: f ðxÞ ¼ x 4 5 x 2 þ 4
Ein solches Integral wird durch die Substitution u ¼ f ðxÞ gelöst (! FS: Kap. V.3.1.2, Integraltyp E). Wir setzen
daher u ¼ x 4 5 x 2 þ 4 und erhalten folgende Substitutionsgleichungen:
u ¼ x4 5x2 þ 4;
du
¼ 4 x 3 10 x ;
dx
dx ¼
du
4 x 3 10 x
Durchführung der Integralsubstitution:
ð
ð
ð
4 x 3 10 x
4 x 3 10 x
du
1
dx ¼ 2
d u ¼ 2 ln j u j þ C
¼ 2
I ¼ 2
4
2
3
u
u
x 5x þ 4
4 x 10 x
Rücksubstitution und Lösung:
ð
8 x 3 20 x
d x ¼ 2 ln j x 4 5 x 2 þ 4 j þ C
I ¼
x4 5x2 þ 4
ð
C8
I ¼
x2
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ ?
x2 þ 1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Das Integral enthält einen Wurzelausdruck vom allgemeinen Typ
x 2 þ a 2 . Aus der Formelsammlung entnehmen
wir für ein solches Integral die hyperbolische Substitution x ¼ a sinh u, die den Wurzelausdruck beseitigt (! FS:
Kap. V.3.1.2, Integraltyp G). In diesem speziellen Fall ist a ¼ 1 und die Substitutionsgleichungen lauten:
x ¼ sinh u ;
dx
¼ cosh u ;
du
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 þ 1 ¼ sinh 2 u þ 1 ¼ cosh 2 u ¼ cosh u
d x ¼ cosh u d u ;
(unter Verwendung der Beziehung cosh 2 u sinh 2 u ¼ 1 ) sinh 2 þ 1 ¼ cosh 2 uÞ: Wir erhalten ein Grundintegral:
ð
I ¼
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
x2 þ 1
x2
ð
cosh u d u
sinh 2
u cosh u
ð
¼
1
d u ¼ coth u þ C
sinh 2 u
1 Integration durch Substitution
147
Vor der Rücksubstitution drücken wir diese Lösung noch wie folgt durch sinh u aus (dies ist wegen der Rücksubstitution x ¼ sinh u sinnvoll):
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh u
sinh 2 u þ 1
I ¼ coth u þ C ¼
þC
þC ¼
sinh u
sinh u
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh u
2
2
unter Verwendung der Beziehungen coth u ¼
sinh 2 u þ 1
und cosh u sinh u ¼ 1 ) cosh u ¼
sinh u
Rücksubstitution ðx ¼ sinh uÞ und Lösung:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
x2 þ 1
dx
þC
I ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
x
x2
x2 þ 1
ð
C9
I ¼
x arcsin ðx 2 Þ
dx ¼ ?
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 x4
Dieses komplizierte Integral lässt sich schrittweise durch zwei Substitutionen auf ein Grundintegral zurückführen. Zunächst einmal erreichen wir mit Hilfe der Substitution u ¼ x 2 eine Vereinfachung im Zähler des Integranden:
u ¼ x2;
ð
I ¼
du
¼ 2x;
dx
dx ¼
x arcsin ðx 2 Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d x ¼
1 x4
ð
du
;
2x
u2 ¼ x4
x arcsin u d u
1
¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2x
2
1 u2
ð
arcsin u
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d u
1 u2
Bedauerlicherweise
liegt noch kein Grundintegral vor. Eine genauere Betrachtung zeigt jedoch, dass dieses Integral
Ð
vom Typ
f ðuÞ f 0 ðuÞ du ist. Dazu formen wir den Integranden wie folgt in ein Produkt aus zwei Faktoren um:
arcsin u
1
0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ ðarcsin uÞ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ f ðuÞ f ðuÞ
2
2
1u
1u
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
f ðuÞ
f 0 ðuÞ
Wir erkennen: Der rechte Faktor ist genau die Ableitung des linken Faktors. Für ein solches Integral entnehmen wir
aus der Formelsammlung die Substitution v ¼ f ðuÞ, hier also v ¼ arcsin u (! FS: Kap. V.3.1.2, Integraltyp B).
Die Substitutionsgleichungen lauten somit:
v ¼ arcsin u ;
dv
1
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ;
du
1 u2
du ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 u2 dv
Wir erhalten jetzt ein Grundintegral:
ð
ð
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
arcsin u
1
v
1
1 2
2
I ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d u ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
v dv ¼
v þC
1 u dv ¼
2
2
2
4
1 u2
1 u2
Bei der Rücksubstitution ðv ! u ! xÞ ersetzen wir zunächst v durch arcsin u und anschließend u durch x 2 .
Damit erhalten wir folgende Lösung:
ð
I ¼
x arcsin ðx 2 Þ
1 2
1
1
v þC ¼
ðarcsin uÞ 2 þ C ¼
½ arcsin ðx 2 Þ 2 þ C
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d x ¼
4
4
4
4
1x
148
C Integralrechnung
ð
C10
I ¼
ðln xÞ 3
x
dx ¼ ?
du
1
¼
;
dx
x
Mit der naheliegenden Substitution u ¼ ln x ;
ð
I ¼
ðln xÞ 3
dx ¼
x
ð
u3
x du ¼
x
ð
u3 d u ¼
d x ¼ x d u erreichen wir unser Ziel:
1 4
u þC
4
Die Lösung lautet somit nach vollzogener Rücksubstitution u ¼ ln x wie folgt:
ð
I ¼
ðln xÞ 3
1
ðln xÞ 4 þ C
dx ¼
4
x
ð
C11
I ¼
cos 5 x d x ¼ ?
Wir zerlegen den Integrand cos 5 x zunächst wie folgt in ein Produkt aus zwei Faktoren:
ð
ð
5
I ¼ cos x d x ¼ cos 4 x cos x d x
Der rechte Faktor cos x ist dabei bekanntlich die Ableitung von sin x. Sollte es uns gelingen, den linken Faktor
cos 4 x durch sin x auszudrücken, dann hilft uns die Substitution u ¼ sin x (voraussichtlich) weiter. Unter Verwendung der Beziehung sin 2 x þ cos 2 x ¼ 1 und damit cos 2 x ¼ 1 sin 2 x erreichen wir unser Ziel:
cos 4 x ¼ ðcos 2 xÞ 2 ¼ ð1 sin 2 xÞ 2
Das vorgegebene Integral I geht damit über in
ð
ð
I ¼ cos 4 x cos x d x ¼ ð1 sin 2 xÞ 2 cos x d x
Es lässt sich mit Hilfe der bereits weiter oben erwähnten Substitution u ¼ sin x in ein Grundintegral verwandeln:
u ¼ sin x ;
du
¼ cos x ;
dx
dx ¼
ð
ð
ð1 sin 2 xÞ 2 cos x d x ¼
I ¼
ð
¼
du
cos x
ð1 2 u 2 þ u 4 Þ d u ¼ u
ð1 u 2 Þ 2 cos x
du
¼
cos x
ð
ð1 u 2 Þ 2 d u ¼
2 3
1 5
u þ
u þC
3
5
Durch Rücksubstitution u ¼ sin x erhalten wir schließlich die folgende Lösung:
ð
2
1
I ¼ cos 5 x d x ¼ sin x
sin 3 x þ
sin 5 x þ C
3
5
C12
ð
I ¼
ðx þ 2Þ 2
ðx 10Þ 2
dx ¼ ?
1 Integration durch Substitution
149
Mit der Substitution u ¼ x 10 wird der Nenner des Integranden vereinfacht, was sicher sinnvoll ist. Gleichzeitig
ersetzen wir im Zähler die alte Variable x durch u þ 10 (Auflösen der Substitutionsgleichung nach x). Die vollständige
Integralsubstitution lautet also:
du
¼ 1;
dx
u ¼ x 10 ;
dx ¼ du;
x ¼ u þ 10
Sie führt zu Grundintegralen:
ð
I ¼
¼
ð
ðx þ 2Þ 2
ðx 10Þ 2
ðu þ 10 þ 2Þ 2
dx ¼
u2
ð
du ¼
ðu þ 12Þ 2
u2
ð
du ¼
u 2 þ 24 u þ 144
du ¼
u2
ð
ð
24
144
24
144
þ
þ 144 u 2 d u ¼ u þ 24 ln j u j
þC
du ¼
1þ
1þ
2
u
u
u
u
Rücksubstitution ðu ¼ x 10Þ und Lösung:
I ¼ x 10 þ 24 ln j x 10 j
C13
ð
I ¼
144
144
þ C ¼ x þ 24 ln j x 10 j
þ C * ðC * ¼ C 10Þ
x 10
x 10
2 e 2 x þ 1 cosh x d x ¼ ?
Der Integrand lässt sich wesentlich vereinfachen, wenn man sich an die Definitionsformel der Hyperbelfunktion
cosh x erinnert. Sie lautet (! FS: Kap. III.11.1):
cosh x ¼
1
ðe x þ e x Þ
2
Umformung des Integranden mit Hilfe dieser Formel und der Rechenregel e m e n ¼ e m þ n ergibt:
2 e 2 x þ 1 cosh x ¼ 2 e 2 x þ 1
1
ðe x þ e x Þ ¼ e 2 x þ 1 ðe x þ e x Þ ¼ e 3 x þ 1 þ e x þ 1
2
Das Integral I lässt sich dann wie folgt in zwei Teilintegrale I 1 und I 2 aufspalten:
ð
ð
ð
ð
2xþ1
3xþ1
xþ1
3xþ1
I ¼ 2e
cosh x d x ¼ ðe
þe
Þ dx ¼ e
d x þ e xþ1 d x ¼ I1 þ I2
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
I1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
I2
Diese sind durch einfache Substitutionen leicht lösbar:
Integral I 1 : u ¼ 3 x þ 1 ;
ð
I1 ¼
e 3xþ1
Integral I 2 : v ¼ x þ 1 ;
ð
I2 ¼
e xþ1
du
du
¼ 3; dx ¼
dx
3
ð
ð
du
1
1
1
¼
eu du ¼
e u þ C1 ¼
e 3xþ1 þ C1
dx ¼ eu
3
3
3
3
dv
¼ 1; dx ¼ dv
dx
ð
d x ¼ e v d v ¼ e v þ C2 ¼ e xþ1 þ C2
In beiden Integralen wurde die Rücksubstitution bereits durchgeführt. Für das Integral I erhalten wir damit:
I ¼ I1 þ I2 ¼
1
1
e 3xþ1 þ C1 þ e xþ1 þ C2 ¼
e 3xþ1 þ e xþ1 þ C
3
3
ðC ¼ C 1 þ C 2 Þ
150
C Integralrechnung
ð
C14
dx
mit Hilfe einer geeigneten trigonometrischen Umformung
sin ð2 xÞ
Lösen Sie das Integral I ¼
(! Formelsammlung) und der sich anschließenden Substitution u ¼ tan x .
Wir drücken den Integrand zunächst durch elementare trigonometrische Funktionen aus. Dabei verwenden wir die
Beziehung sin ð2 xÞ ¼ 2 sin x cos x (! FS: Kap. III.7.6.3). Das Integral I nimmt dann die folgende Gestalt an:
ð
ð
ð
dx
dx
1
dx
¼
I ¼
¼
2 sin x cos x
2
sin x cos x
sin ð2 xÞ
du
1
; d x ¼ cos 2 x d u wird daraus zunächst
¼
dx
cos 2 x
ð
ð
ð
ð
1
dx
1
cos 2 x d u
1
cos x cos x
1
cos x
¼
¼
du
du ¼
I ¼
2
sin x cos x
2
sin x cos x
2
sin x cos x
2
sin x
Mit der (vorgegebenen) Substitution u ¼ tan x ;
cos x
1
Der Integrand ist wegen der trigonometrischen Beziehung
¼ cot x ¼
der Kehrwert von tan x und somit
sin x
tan x
der Kehrwert der neuen Variablen u:
I ¼
1
2
ð
cos x
1
du ¼
sin x
2
ð
1
1
du ¼
tan x
2
ð
1
du
u
Die Substitution führt damit zu einem Grundintegral und schließlich nach erfolgter Rücksubstitution ðu ¼ tan xÞ zur
Lösung dieser Aufgabe:
ð
1
1
1
1
I ¼
du ¼
ln j u j þ C ¼
ln j tan x j þ C
2
u
2
2
ð
C15
Lösen Sie das Integral I ¼
cos 4 x d x mit Hilfe einer geeigneten trigonometrischen Umformung
(! Formelsammlung) und anschließender Substitution. berprüfen Sie das Ergebnis.
Mit Hilfe der trigonometrischen Beziehung cos 4 x ¼
1
½ cos ð4 xÞ þ 4 cos ð2 xÞ þ 3
8
(! FS : Kap. III.7.6.4)
lässt sich das Integral in drei einfache Teilintegrale aufspalten:
ð
ð
1
I ¼ cos 4 x d x ¼
½ cos ð4 xÞ þ 4 cos ð2 xÞ þ 3 d x ¼
8
ð
cos ð4 xÞ d x þ
1
2
ð
cos ð2 xÞ d x þ
f
1
8
f
¼
3
8
ð
1 dx
v
u
Das letzte Integral ist bereits ein Grundintegral, die beiden übrigen lassen sich in der angedeuteten Weise wie folgt
durch einfache Substitutionen in solche überführen:
du
¼ 4;
dx
u ¼ 4x;
I ¼
¼
1
8
ð
cos u
dx ¼
du
1
þ
4
2
du
4
bzw:
ð
cos v
v ¼ 2x;
dv
¼ 2;
dx
dv
3
1
þ
x ¼
2
8
32
1
1
3
sin u þ
sin v þ
x þC
32
4
8
dx ¼
dv
2
ð
cos u d u þ
1
4
ð
cos v d v þ
3
x ¼
8
1 Integration durch Substitution
151
Durch Rücksubstitution ðu ¼ 4 x; v ¼ 2 xÞ erhalten wir die gesuchte Lösung:
ð
1
1
3
I ¼ cos 4 x d x ¼
sin ð4 xÞ þ
sin ð2 xÞ þ
x þC
32
4
8
¼
f
f
Wir überprüfen das Ergebnis (die 1. Ableitung der rechten Seite muss den Integrand cos 4 x ergeben):
d
1
1
3
1
1
3
sin ð4 xÞ þ
sin ð2 xÞ þ
x þC ¼
4 cos ð4 xÞ þ
2 cos ð2 xÞ þ
þ0 ¼
d x 32
4
8
32
4
8
u
v
1
1
3
1
cos ð4 xÞ þ
cos ð2 xÞ þ
¼
½ cos ð4 xÞ þ 4 cos ð2 xÞ þ 3 ¼ cos 4 x
8
2
8
8
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
cos 4 x
(unter Verwendung der Kettenregel, Substitutionen: u ¼ 4 x bzw. v ¼ 2 x)
C16
ð
I ¼
x
dx ¼ ?
x 2 2 x þ 10
Der Nenner des Integranden muss zunächst durch elementare Umformungen auf die einfachere Form u 2 þ 1 gebracht werden. Dies geschieht auf folgende Weise:
9
1
x 2 2 x þ 10 ¼ ðx 2 2 x þ 1Þ 1 þ 10 ¼ ðx 1Þ 2 þ 9 ¼
ðx 1Þ 2 þ 9 ¼ 9
ðx 1Þ 2 þ 1 ¼
|fflfflfflffl{zfflfflfflffl}
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
9
9
quadratische
ðx 1Þ 2
Ergänzung
"
¼ 9
#
x 1 2
þ 1 ¼ 9 ðu 2 þ 1Þ
3
|fflfflfflffl{zfflfflfflffl}
u
mit
u ¼
x 1
1
¼
ðx 1Þ
3
3
Durch die (vollständige) Substitution
u ¼
1
ðx 1Þ ;
3
du
1
¼ ;
dx
3
dx ¼ 3 du;
3u ¼ x 1
)
x ¼ 3u þ 1
geht das Integral I über in:
ð
ð
ð
x
3u þ 1
1
3u þ 1
dx ¼
3 du ¼
du
I ¼
2
2
3
x 2 x þ 10
9 ðu þ 1Þ
u2 þ 1
Aufspaltung in zwei Teilintegrale:
1
I ¼
3
ð
3u
1
du þ
2
3
u þ1
ð
1
du ¼
2
u þ1
ð
ð
u
1
1
1
du þ
d u ¼ I1 þ
I2
2
2
3
3
u þ1
u þ1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
I 2 ¼ arctan u þ C 2
I1
I 2 ist bereits ein Grundintegral und führt auf den Arkustangens. Das Integral I 1 lösen wir mit der Substitution
v ¼ u2 þ 1;
dv
¼ 2u;
du
du ¼
dv
2u
(im Zähler steht –– vom fehlenden Faktor 2 abgesehen –– die Ableitung des Nenners ! FS: Kap. V.3.1.2, Integraltyp E):
ð
ð
ð
u
u dv
1
1
1
1
dv ¼
ln j v j þ C 1 ¼
ln j u 2 þ 1 j þ C 1
du ¼
¼
I1 ¼
v 2u
2
v
2
2
u2 þ 1
(nach erfolgter Rücksubstitution v ¼ u 2 þ 1Þ. Somit gilt:
152
C Integralrechnung
I ¼ I1 þ
1
1
I2 ¼
ln ðu
3
2
2
þ 1Þ þ C 1 þ
1
ðarctan u þ C 2 Þ ¼
3
1
1
1
1
1
1
ln ðu 2 þ 1Þ þ C 1 þ
arctan u þ
C 2 ¼ ln ðu 2 þ 1Þ þ
arctan u þ C 1 þ
C2 ¼
2
3
3
2
3
3
1
1
1
2
ln ðu þ 1Þ þ
arctan u þ C
mit C ¼ C 1 þ
C2
¼
2
3
3
¼
Rücksubstitution: u ¼
1
ðx 1Þ ;
3
u2 þ 1 ¼
x 2 2 x þ 10
9
Die gesuchte Lösung lautet dann:
2
1
x 2 x þ 10
1
1
I ¼
ln
þ
arctan
ðx 1Þ þ C
2
9
3
3
2 Partielle Integration (Produktintegration)
Alle Integrale in diesem Abschnitt lassen sich durch Partielle Integration lösen. Wir verwenden die folgende Formel:
ð
ð
f ðxÞ d x ¼
|{z}
uv0
uv0 dx ¼ uv
ð
u0 v dx
ðu; v : Funktionen von xÞ
|fflfflfflfflffl{zfflfflfflfflffl}
„Hilfsintegral“
In einigen Fällen muss man mehrmals hintereinander partiell integrieren, ehe man auf ein Grundintegral stößt.
Häufig führt die Partielle Integration zwar auf ein einfacheres Integral, das aber noch kein Grundintegral darstellt.
Dann muss dieses „Hilfsintegral“ nach einer anderen Integrationsmethode (meist mit Hilfe einer Substitution) weiter
behandelt werden, bis man auf ein Grundintegral stößt.
Lehrbuch: Band 1, Kapitel V.8.2
Formelsammlung: Kapitel V.3.2
Tabelle der Grund- oder Stammintegrale: Band 1, Kapitel V.5 und Formelsammlung, Kapitel V.2.3
C17
ð
I ¼
ð1 þ 2 xÞ e x d x ¼ ?
Zerlegung des Integranden f ðxÞ ¼ ð1 þ 2 xÞ e x in zwei Faktoren u und v 0
f ðxÞ ¼ ð1 þ 2 xÞ e x
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |{z}
u
v0
mit
u ¼ 1 þ 2x;
v 0 ¼ e x
und
u0 ¼ 2;
v ¼ e x
Die Stammfunktion zu v 0 ¼ e x haben wir dabei mit Hilfe der folgenden Substitution erhalten:
dt
¼ 1; dx ¼ dt
dx
ð
ð
ð
ð
v ¼ v 0 d x ¼ e x d x ¼ e t ð d tÞ ¼ e t d t ¼ e t þ K ¼ e x þ K
t ¼ x;
(die Integrationskonstante K wird für die partielle Integration nicht benötigt und daher weggelassen).
2 Partielle Integration (Produktintegration)
153
Die Formel der partiellen Integration führt dann zu der folgenden Lösung:
ð
ð
ð
ð
I ¼ ð1 þ 2 xÞ e x d x ¼ u v 0 d x ¼ u v u 0 v d x ¼ ð1 þ 2 xÞ ð e x Þ 2 ð e x Þ d x ¼
¼ ð1 þ 2 xÞ e x þ 2
ð
e x d x ¼ ð1 þ 2 xÞ e x þ 2 ð e x þ CÞ ¼
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
e x þ C
¼ ð1 þ 2 xÞ e x 2 e x þ 2 C ¼ ð3 þ 2 xÞ e x þ C *
ðC * ¼ 2 CÞ
ð
C18
I ¼
x n ln x d x ¼ ?
ðn 6¼ 1Þ
Zerlegung des Integranden f ðxÞ ¼ x n ln x in zwei Faktoren u und v 0 :
f ðxÞ ¼ x n ln x ¼ ðln xÞ x n ¼ u v 0
f
|ffl{zffl}
u ¼ ln x ;
mit
v0 ¼ xn
und
u0 ¼
v0
u
1
;
x
v ¼
x nþ1
nþ1
Begründung: Die ebenfalls denkbare Zerlegung in die Faktoren u ¼ x n und v 0 ¼ ln x kommt nicht infrage, da wir
keine Stammfunktion zu v 0 ¼ ln x angeben können!
Partielle Integration führt dann zu einem Grundintegral:
ð
I ¼
¼
C19
ð
x n ln x d x ¼
ð
ðln xÞ x n d x ¼
x n þ 1 ln x
1
n þ1
n þ1
ð
xn dx ¼
uv0 dx ¼ uv
ð
u 0 v d x ¼ ln x
x nþ1
n þ1
x n þ 1 ln x
1
x nþ1
x nþ1
þC ¼
n þ1
n þ1
n þ1 n þ1
ð
ln x
1 x nþ1
dx ¼
x n þ1
1
n þ1
þC
ð
I ¼
x arctan x d x ¼ ?
Zerlegung des Integranden f ðxÞ ¼ x arctan x in zwei Faktoren u und v 0 :
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
mit
u ¼ arctan x ; v 0 ¼ x
f
f ðxÞ ¼ x arctan x ¼ ðarctan xÞ x ¼ u v 0
v0
und
u0 ¼
1
1 2
x
; v ¼
2
2
1þx
Begründung: Die auch mögliche Zerlegung in umgekehrter Reihenfolge ðu ¼ x, v 0 ¼ arctan xÞ scheidet aus, da wir
keine Stammfunktion zu v 0 ¼ arctan x angeben können!
Die Formel der partiellen Integration liefert dann:
ð
ð
ð
ð
1 2
1
1 2
I ¼ ðarctan xÞ x d x ¼ u v 0 d x ¼ u v u 0 v d x ¼ ðarctan xÞ
x
x dx ¼
2
1 þ x2 2
1 2
1
x arctan x
¼
2
2
ð
x2
1 2
1
x arctan x
I1
dx ¼
2
2
2
1þx
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
I1
154
C Integralrechnung
Das „Hilfsintegral“ I 1 der rechten Seite ist leider kein Grundintegral, lässt sich aber auf solche zurückführen. Aus
diesem Grund zerlegen wir den unecht gebrochenrationalen Integrand durch Polynomdivision wie folgt:
ðx 2
Þ : ðx 2 þ 1Þ ¼ 1
ðx 2 þ 1Þ
1
1
¼ 1
x2 þ 1
1 þ x2
1
Damit erhalten wir für das Hilfsintegral I 1 die folgende Lösung:
ð
ð
ð
ð
x2
1
1
dx ¼ 1 dx
dx ¼
1
d x ¼ x arctan x þ C
I1 ¼
2
2
1þx
1 þ x2
1þx
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Grundintegral
Die Lösung der gestellten Aufgabe lautet dann:
ð
I ¼
1 2
1
1 2
1
x arctan x
I1 ¼
x arctan x
ðx arctan x þ CÞ ¼
2
2
2
2
x arctan x d x ¼
1 2
1
1
1
1 2
1
1
1
x arctan x
x þ
arcxtan x
C ¼
x arctan x þ
arctan x
x
C ¼
2
2
2
2
2
2
2
2
1
1
1
1
1
1
2
2
*
*
¼
arctan x ðx þ 1Þ
x
C ¼
ðx þ 1Þ arctan x
x þC
C ¼
C
2
2
2
2
2
2
¼
ð
I ¼
C20
ð
cos n x d x ¼
cos n 1 x cos x d x ¼ ?
|fflfflfflfflffl{zfflfflfflfflffl} |ffl{zffl}
u
v0
Leiten Sie mit Hilfe der angedeuteten Zerlegung des Integranden eine Rekursionsformel für das Integral I
her und wenden Sie diese auf den Fall n ¼ 3 an.
Aufgrund der vorgegebenen Zerlegung gilt:
u ¼ cos n 1 x ¼ ðcos xÞ n 1 ;
v 0 ¼ cos x
)
u 0 ¼ ðn 1Þ sin x cos n 2 x ;
v ¼ sin x
(die Ableitung von u ¼ ðcos xÞ n 1 erhält man mit der Kettenregel, Substitution: t ¼ cos xÞ
Die Formel der partiellen Integration liefert dann:
ð
ð
ð
ð
I ¼ cos n x d x ¼ cos n 1 x cos x d x ¼ u v 0 d x ¼ u v u 0 v d x ¼
¼ cos n 1 x sin x þ ðn 1Þ
¼ sin x cos n 1 x þ ðn 1Þ
ð
ð
sin x cos n 2 x sin x d x ¼
sin 2 x cos n 2 x d x ¼ sin x cos n 1 x þ ðn 1Þ I 1
ð*Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I1
Unter Verwendung der trigonometrischen Beziehung sin 2 x þ cos 2 x ¼ 1 und damit sin 2 x ¼ 1 cos 2 x lässt
sich das „Hilfsintegral“ I 1 wie folgt aufspalten:
ð
ð
ð
I 1 ¼ sin 2 x cos n 2 x d x ¼ ð1 cos 2 xÞ cos n 2 x d x ¼ ðcos n 2 x cos n xÞ d x ¼
ð
¼
cos n 2 x d x
ð
ð
cos n x d x ¼
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
I
cos n 2 x d x I
2 Partielle Integration (Produktintegration)
155
Dabei haben wir bereits berücksichtigt, dass es sich beim zweiten Integral der rechten Seite um das gesuchte Integral I
handelt. Gleichung (*Þ geht damit über in:
ð
I ¼ sin x cos n 1 x þ ðn 1Þ I 1 ¼ sin x cos n 1 x þ ðn 1Þ
cos n 2 x d x I ¼
ð
¼ sin x cos n 1 x þ ðn 1Þ cos n 2 x d x ðn 1Þ I
Durch „Rückwurf“ erhalten wir aus dieser Gleichung die gesuchte Rekursionsformel (der Summand ðn 1Þ I der
rechten Seite enthält die Unbekannte I und wird „zurückgeworfen“, d. h. auf die linke Seite gebracht):
ð
n1
x þ ðn 1 Þ cos n 2 x d x
I þ ðn 1Þ I ¼ I þ n I I ¼ n I ¼ sin x cos
I ¼
sin x cos n 1 x
n1
þ
n
n
ð
cos n 2 x d x
Somit gilt die folgende Rekursionsformel:
ð
ð
sin x cos n 1 x
n1
n
cos x d x ¼
þ
cos n 2 d x
n
n
Das Integral der rechten Seite ist vom gleichen Typ wie das Ausgangsintegral I, besitzt aber einen um 2 kleineren
Exponenten im Integranden ðn ! n 2Þ. Durch wiederholte Anwendung dieser Rekursionsformel lässt sich der
Exponent der Potenz cos n x schrittweise reduzieren, bis man auf ein Grundintegral stößt.
Anwendungsbeispiel für n == 3:
ð
ð
sin x cos 2 x
2
1
2
cos 3 x d x ¼
þ
cos x d x ¼
sin x cos 2 x þ
sin x þ C
3
3
3
3
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
Grundintegral
C21
ð
ðln xÞ 2 d x ¼ ?
I ¼
Zerlegung des Integranden f ðxÞ ¼ ðln xÞ 2 in ein Produkt aus zwei Faktoren u und v 0 :
mit
u ¼ ðln xÞ 2 ;
f
f ðxÞ ¼ ðln xÞ 2 ¼ ðln xÞ2 1
|fflffl{zfflffl}
u
v0
v 0 ¼ 1 und
u0 ¼
2 ln x
;
x
v ¼ x
(mathematischer „Trick“: Faktor 1 ergänzen; u ¼ ðln xÞ 2 wird nach der Kettenregel differenziert, Substitution:
t ¼ ln x) .
Begründung: Die ebenfalls mögliche (und zunächst nahe liegende) Zerlegung in zwei gleiche Faktoren u ¼ ln x und
v 0 ¼ ln x führt nicht zum Ziel, da wir keine Stammfunktion zu v 0 ¼ ln x angeben können!
Die Formel der partiellen Integration führt mit der gewählten Zerlegung auf ein einfacher gebautes Integral vom gleichen Typ, das jedoch noch kein Grundintegral ist:
ð
ð
ð
ð
2 ln x
I ¼ ðln xÞ 2 1 d x ¼ u v 0 d x ¼ u v u 0 v d x ¼ ðln xÞ 2 x
x dx ¼
x
ð
2
¼ x ðln xÞ 2
ln x d x ¼ x ðln xÞ 2 2 I 1
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
I1
156
C Integralrechnung
Was hat die partielle Integration bisher gebracht? Aus dem Integral
(Absenkung des Exponenten um 1):
ð
ð
ðln xÞ 2 d x ! ðln xÞ 1 d x
Ð
ðln xÞ 2 d x wurde das Integral
Ð
ðln xÞ 1 d x
f
Ð
Ð
Ð
Wir vermuten daher: Das „Hilfsintegral“ I 1 ¼ ln x d x geht in das Grundintegral
ðln xÞ 0 d x ¼ 1 d x über,
wenn wir auf I 1 die gleiche Methode (bei sinngemäß gleicher Zerlegung) anwenden:
ð
ð
1
; v ¼ x
I 1 ¼ ln x d x ¼ ðln xÞ 1 d x mit u ¼ ln x ; v 0 ¼ 1 und u 0 ¼
x
|ffl{zffl}
0
u
v
ð
I1 ¼
ð
ðln xÞ 1 d x ¼
uv0 dx ¼ uv
ð
u 0 v d x ¼ ðln xÞ x
ð
1
x dx ¼
x
ð
¼ x ln x
1 d x ¼ x ln x x þ C
Unsere Vermutung hat sich also bestätigt. Durch zweimalige Anwendung der partiellen Integration haben wir unser
Ziel endlich erreicht. Die Lösung lautet damit:
ð
I ¼ ðln xÞ 2 d x ¼ x ðln xÞ 2 2 I 1 ¼ x ðln xÞ 2 2 ðx ln x x þ CÞ ¼
¼ x ðln xÞ 2 2 x ln x þ 2 x 2 C ¼ x ½ðln xÞ 2 2 ln x þ 2 þ C *
C22
ðC * ¼ 2 CÞ
ð
I ¼
artanh x d x ¼ ?
Wir ergänzen zunächst im Integrand f ðxÞ ¼ artanh x den Faktor 1 (der ja nichts verändert) und zerlegen dann wie
folgt in zwei Faktoren u und v 0 :
f
f ðxÞ ¼ artanh x ¼ ðartanh xÞ 1 ¼ u v 0
|fflfflfflfflffl{zfflfflfflfflffl}
u
v0
Begründung: Die ebenfalls mögliche Zerlegung u ¼ 1 und v 0 ¼ artanh x kommt nicht infrage, da wir zu
v 0 ¼ artanh x keine Stammfunktion angeben können (eine solche Stammfunktion soll ja gerade bestimmt werden).
Mit der gewählten Zerlegung
u ¼ artanh x ;
v0 ¼ 1
und damit
u0 ¼
1
;
1 x2
v ¼ x
liefert die partielle Integration ein „Hilfsintegral“, das zwar kein Grundintegral ist, aber mit Hilfe einer Substitution
gelöst werden kann:
ð
ð
ð
ð
0
I ¼ artanh x d x ¼ ðartanh xÞ 1 d x ¼ u v d x ¼ u v u 0 v d x ¼
ð
¼ ðartanh xÞ x
1
x d x ¼ x artanh x
1 x2
ð
x
d x ¼ x artanh x I 1
1 x2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
I1
Das „Hilfsintegral“ I 1 lösen wir mit der folgenden Substitution (im Zähler steht –– vom fehlenden Faktor 2 abgesehen –– die Ableitung des Nenners ! FS: Kap. V.3.1.2, Integraltyp E):
u ¼ 1 x2;
du
¼ 2x;
dx
dx ¼
du
2x
2 Partielle Integration (Produktintegration)
ð
I1 ¼
x
dx ¼
1 x2
ð
157
x
du
1
¼
u 2 x
2
ð
1
1
1
du ¼
ln j u j þ C ¼
ln j 1 x 2 j þ C
u
2
2
Die gesuchte Lösung lautet damit:
ð
1
I ¼ artanh x d x ¼ x artanh x I 1 ¼ x artanh x
ln j 1 x 2 j þ C ¼
2
¼ x artanh x þ
C23
ð
I ¼
1
1
ln j 1 x 2 j C ¼ x artanh x þ
ln j 1 x 2 j þ C *
2
2
x
dx ¼ ?
cos 2 x
Wir zerlegen den Integrand f ðxÞ ¼
„Verifizieren“ Sie anschließend das Ergebnis.
x
wie folgt in ein Produkt aus zwei Faktoren u und v 0 :
cos 2 x
x
1
¼ x
¼ uv0
2
cos x
cos 2 x
|fflfflffl{zfflfflffl}
u
v0
f
f ðxÞ ¼
ðC * ¼ CÞ
Begründung: Diese Zerlegung hat Aussicht auf Erfolg, da v 0 ¼
Mit der gewählten Zerlegung
u ¼ x;
v0 ¼
1
cos 2 x
und damit
u0 ¼ 1;
1
bekanntlich die Ableitung von tan x ist.
cos 2 x
v ¼ tan x
führt die partielle Integration zu folgendem Ergebnis:
ð
ð
ð
ð
ð
x
1
0
0
I ¼
dx ¼ x
d x ¼ u v d x ¼ u v u v d x ¼ x tan x 1 tan x d x ¼
cos 2 x
cos 2 x
ð
¼ x tan x
tan x d x ¼ x tan x I 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
I1
Das „Hilfsintegral“ I 1 ist zwar kein Grundintegral, lässt sich aber durch eine Substitution leicht lösen, wenn man die
sin x
trigonometrische Beziehung tan x ¼
beachtet:
cos x
ð
ð
sin x
dx
I 1 ¼ tan x d x ¼
cos x
Im Zähler steht –– vom Vorzeichen abgesehen –– die Ableitung des Nenners, das Integral I 1 ist daher durch die Substitution u ¼ cos x wie folgt lösbar (! FS: Kap. V.3.1.2, Integraltyp E):
du
du
¼ sin x ; d x ¼
dx
sin x
ð
ð
ð
ð
sin x
sin x
du
1
I 1 ¼ tan x d x ¼
¼
dx ¼
d u ¼ ln j u j þ C ¼ ln j cos x j þ C
cos x
u
sin x
u
u ¼ cos x ;
Für das vorgegebene Integral I erhalten wir damit die Lösung
ð
x
d x ¼ x tan x I 1 ¼ x tan x ð ln j cos x j þ CÞ ¼ x tan x þ ln j cos x j C ¼
I ¼
cos 2 x
¼ x tan x þ ln j cos x j þ C *
ðC * ¼ CÞ
158
C Integralrechnung
Wir „verifizieren“ das Ergebnis, indem wir zeigen, dass die 1. Ableitung des unbestimmten Integrals zum Integranden führt. Dabei verwenden wir in der angedeuteten Weise die Produktregel (1. Summand) und die Kettenregel
(2. Summand):
f
I ¼ x tan x þ ln j cos x j þ C * ¼ u v þ ln j t j þ C *
|{z}
|{z}
u
v
t
I 0 ¼ u0 v þ v0 u þ
1
1
1
x
x
t 0 ¼ 1 tan x þ
ð sin xÞ ¼ tan x þ
x þ
tan x ¼
t
cos 2 x
cos x
cos 2 x
cos 2 x
(unter Verwendung der trigonometrischen Beziehung sin x=cos x ¼ tan x)
ð
I ¼
x
cos x
dx ¼ ?
sin 3 x
|fflffl{zfflffl}
u
v0
Lösen Sie dieses Integral in der angedeuteten Weise durch partielle Integration. Die benötigte Stammfunktion zum Faktor v 0 erhalten Sie durch eine geeignete Substitution.
f
C24
Die vorgegebene Zerlegung des Integranden lautet:
u ¼ x;
v0 ¼
cos x
sin 3 x
und
u0 ¼ 1;
v ¼ ?
cos x
erhalten wir mit Hilfe der folgenden Substitution (im
sin 3 x
Zähler steht genau die Ableitung von sin x ! FS: Kap. V.3.1.2, Integraltyp C mit f ðxÞ ¼ sin x und n ¼ 3Þ:
Die zunächst noch unbekannte Stammfunktion zu v 0 ¼
t ¼ sin x ;
ð
v ¼
¼
dt
¼ cos x ;
dx
v0 dx ¼
ð
dx ¼
cos x
dx ¼
sin 3 x
ð
dt
cos x
cos x
dt
¼
cos x
t3
ð
1
dt ¼
t3
ð
t 3 d t ¼
t 2
þK ¼
2
1
1
þK ¼
þK
2
2t
2 sin 2 x
Die Integrationskonstante K ist für die partielle Integration ohne Bedeutung und wird daher weggelassen. Mit der
jetzt vollständigen Zerlegung
u ¼ x;
v0 ¼
cos x
sin 3 x
und
u0 ¼ 1;
v ¼
1
2 sin 2 x
führt die partielle Integration zu einem Grundintegral und damit zur gesuchten Lösung:
ð
ð
ð
ð
cos x
1
1
0
0
d
x
¼
u
v
d
x
¼
u
v
u
v
d
x
¼
x
I ¼ x
1
dx ¼
sin 3 x
2 sin 2 x
2 sin 2 x
¼
x
1
þ
2
2
2 sin x
ð
1
x
1
ð cot x þ CÞ ¼
dx ¼
þ
2
2
2
sin x
2 sin x
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
cot x þ C
x
1
1
x
1
¼
cot x þ
C ¼
cot x þ C *
2
2
2
2
2
2 sin x
2 sin x
1
C* ¼
C
2
3 Integration einer echt gebrochenrationalen Funktion durch Partialbruchzerlegung des Integranden
159
3 Integration einer echt gebrochenrationalen Funktion
durch Partialbruchzerlegung des Integranden
Alle Integrale in diesem Abschnitt lassen sich durch Partialbruchzerlegung des echt gebrochenrationalen Integranden
auf Grund- oder Stammintegrale zurückführen. Ist der Integrand jedoch unecht gebrochenrational, so muss er zunächst
(z. B. durch Polynomdivision) in eine ganzrationale und eine echt gebrochenrationale Funktion zerlegt werden. Der
echt gebrochenrationale Anteil wird dann (vor der Integration) in Partialbrüche zerlegt.
Lehrbuch: Band 1, Kapitel V.8.3
Formelsammlung: Kapitel V.3.3
C25
ð
I ¼
8 x 2 2 x 43
ðx þ 2Þ 2 ðx 5Þ
dx ¼ ?
Der Integrand ist echt gebrochenrational (Zähler: Polynom vom Grad m ¼ 2; Nenner: Polynom vom Grad n ¼ 3;
m < n) und wird in Partialbrüche zerlegt. Zunächst benötigen wir die Nullstellen des Nenners:
ðx þ 2Þ 2 ðx 5Þ ¼ 0
)
x 1=2 ¼ 2 ;
x3 ¼ 5
Ihnen ordnen wir folgende Partialbrüche zu:
x 1=2 ¼ 2 (doppelte Nullstelle) !
A
B
þ
x þ2
ðx þ 2Þ 2
x3 ¼ 5
C
x 5
ðeinfache Nullstelle) !
Der Partialbruchansatz lautet damit:
8 x 2 2 x 43
2
ðx þ 2Þ ðx 5Þ
¼
A
B
C
þ
þ
2
x þ2
x 5
ðx þ 2Þ
Um die unbekannten Konstanten A, B und C bestimmen zu können, müssen die Brüche zunächst gleichnamig
gemacht werden (Hauptnenner: ðx þ 2Þ 2 ðx 5ÞÞ. Die Brüche der rechten Seite müssen daher der Reihe nach mit
ðx þ 2Þ ðx 5Þ, ðx 5Þ und ðx þ 2Þ 2 erweitert werden:
8 x 2 2 x 43
ðx þ 2Þ 2 ðx 5Þ
¼
A ðx þ 2Þ ðx 5Þ þ B ðx 5Þ þ C ðx þ 2Þ 2
ðx þ 2Þ 2 ðx 5Þ
Da die Brüche der beiden Seiten im Nenner übereinstimmen, müssen sie auch im Zähler übereinstimmen:
8 x 2 2 x 43 ¼ A ðx þ 2Þ ðx 5Þ þ B ðx 5Þ þ C ðx þ 2Þ 2
Diese Gleichung gilt für alle reellen x-Werte. Wir setzen jetzt der Reihe nach die Werte x ¼ 2, x ¼ 5 (d. h. die
Nennernullstellen unserer gebrochenrationalen Funktion) und zusätzlich den Wert x ¼ 0 ein und erhalten ein gestaffeltes lineares Gleichungssystem für die drei Unbekannten A, B und C :
160
C Integralrechnung
x ¼ 2
)
7 ¼ 7 B
)
B ¼ 1
x ¼
5
)
147 ¼ 49 C
)
C ¼ 3
x ¼
0
)
43 ¼ 10 A 5 B þ 4 C ¼ 10 A 5 1 þ 4 3 ¼ 10 A þ 7
43 ¼ 10 A þ 7
)
10 A ¼ 7 þ 43 ¼ 50
)
)
A ¼ 5
Somit gilt A ¼ 5, B ¼ 1 und C ¼ 3, die Partialbruchzerlegung lautet daher:
8 x 2 2 x 43
5
1
3
þ
þ
2
x þ2
x
5
ðx þ 2Þ
¼
2
ðx þ 2Þ ðx 5Þ
Die Integration der Partialbrüche führt auf drei einfache Integrale, die mit den angedeuteten Substitutionen gelöst
werden:
!
ð
ð
ð
ð
5
1
3
dx
dx
dx
þ
dx ¼ 5
þ
þ
þ3
I ¼
2
2
x þ2
x
5
x
þ
2
x
5
ðx þ 2Þ
ðx þ 2Þ
|fflffl{zfflffl}
|fflffl{zfflffl}
|fflffl{zfflffl}
u
u
v
du
¼ 1;
dx
u ¼ x þ 2;
ð
I ¼ 5
ð
¼ 5
dx
þ
x þ2
du
þ
u
¼ 5 ln j u j
ð
dx ¼ du
ð
u
ð
dx
ðx þ 2Þ
2
und
2
þ3
ð
du þ 3
v ¼ x 5;
dx
¼ 5
x 5
ð
dv
¼ 1;
dx
du
þ
u
ð
dx ¼ dv
du
þ3
u2
ð
dv
¼
v
dv
u 1
þ 3 ln j v j þ C ¼
¼ 5 ln j u j þ
1
v
1
þ 3 ln j v j þ C
u
Durch Rücksubstitution ðu ¼ x þ 2, v ¼ x 5Þ erhalten wir schließlich die folgende Lösung:
ð
8 x 2 2 x 43
1
þ 3 ln j x 5 j þ C
d x ¼ 5 ln j x þ 2 j
I ¼
2
x
þ
2
ðx þ 2Þ ðx 5Þ
C26
ð
I ¼
2 x 3 12 x 2 þ 20 x 2
dx ¼ ?
x2 6x þ 9
Der Integrand ist unecht gebrochenrational (Zählerpolynom vom Grad 3, Nennerpolynom vom Grad 2) und muss zunächst (durch Polynomdivision) zerlegt werden:
ð2 x 3 12 x 2 þ 20 x 2Þ : ðx 2 6 x þ 9Þ ¼ 2 x þ
ð2 x 3 12 x 2 þ 18 xÞ
x2
2x 2
6x þ 9
2x 2
2x 2
Der echt gebrochenrationale Bestandteil
x2
6x þ 9
wird dann schrittweise wie folgt in Partialbrüche zerlegt.
3 Integration einer echt gebrochenrationalen Funktion durch Partialbruchzerlegung des Integranden
161
Partialbruchzerlegung
1. Schritt: Berechnung der Nennernullstellen
x 2 6 x þ 9 ¼ ðx 3Þ 2 ¼ 0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
2. Binom
)
x 1=2 ¼ 3
2. Schritt: Zuordnung der Partialbrüche
A
B
þ
x 3
ðx 3Þ 2
x 1=2 ¼ 3 (doppelte Nullstelle) !
3. Schritt: Partialbruchzerlegung (Ansatz)
2x 2
x2
6x þ 9
¼
2x 2
ðx 3Þ
¼
2
A
x 3
þ
B
ðx 3Þ 2
4. Schritt: Berechnung der Konstanten A und B
Die Brüche werden gleichnamig gemacht ðHauptnenner: ðx 3Þ 2 Þ: Der erste Partialbruch muss daher mit x 3
erweitert werden:
2x 2
ðx 3Þ 2
¼
A ðx 3Þ þ B
ðx 3Þ 2
Da die Nenner beider Brüche übereinstimmen, gilt diese Aussage auch für die Zähler:
2 x 2 ¼ A ðx 3Þ þ B ¼ A x 3 A þ B
Durch Koeffizientenvergleich erhalten wir zwei Gleichungen für die Unbekannten A und B mit folgender Lösung:
A ¼ 2;
3A þ B ¼ 2
)
B ¼ 2 þ 3A ¼ 2 þ 3 2 ¼ 2 þ 6 ¼ 4
Die Partialbruchzerlegung ist damit abgeschlossen:
2x 2
x2
6x þ 9
¼
2
4
þ
x 3
ðx 3Þ 2
Durchführung der Integration
ð
I ¼
ð
dx ¼
2x þ
2 x 3 12 x 2 þ 20 x 2
x2
ð
¼ x þ
2
6x þ 9
2
4
þ
x 3
ðx 3Þ 2
2x 2
x2
!
6x þ 9
ð
dx ¼ x þ 2
2
ð
ð
dx ¼
dx
þ4
x 3
ð
2x dx þ
2x 2
x2
6x þ 9
dx ¼
dx
ðx 3Þ 2
Das erste Integral der rechten Seite ist bereits ein Grundintegral, die beiden restlichen werden mit Hilfe der Substitution
u ¼ x 3;
in solche übergeführt:
I ¼ x2 þ 2
du
¼ 1;
dx
ð
dx ¼ du
dx
þ4
x 3
ð
¼ x 2 þ 2 ln j u j þ 4
ð
ð
dx
ðx 3Þ
2
¼ x2 þ 2
du
þ4
u
u 2 d u ¼ x 2 þ 2 ln j u j þ 4
ð
du
u2
¼
u 1
4
þ C ¼ x 2 þ 2 ln j u j
þC
u
1
Durch Rücksubstitution ðu ¼ x 3Þ erhalten wir schließlich die gesuchte Lösung:
I ¼ x 2 þ 2 ln j x 3 j
4
þC
x 3
162
C Integralrechnung
ð
C27
I ¼
x3
x3 þ 2x 2 x 2
dx ¼ ?
Der Integrand ist unecht gebrochenrational (Zähler- und Nennerpolynom sind jeweils vom Grad 3) und muss daher zunächst (durch Polynomdivision) wie folgt zerlegt werden:
ðx 3
Þ : ðx 3 þ 2 x 2 x 2Þ ¼ 1 þ
ðx 3 þ 2 x 2 x 2Þ
2x2 þ x þ 2
x3 þ 2x 2 x 2
2x2 þ x þ 2
Der echt gebrochenrationale Bestandteil
2x2 þ x þ 2
x3 þ 2x 2 x 2
wird schrittweise in Partialbrüche zerlegt.
Partialbruchzerlegung
1. Schritt: Nullstellenberechnung des Nenners
x3 þ 2x 2 x 2 ¼ 0
)
x1 ¼ 1
(durch Probieren)
Die restlichen Nullstellen (falls überhaupt vorhanden) erhält man nach Abspalten des Linearfaktors x 1 (mit Hilfe
des Hornerschemas) aus dem 1. reduzierten Polynom:
1
x1 ¼ 1
1
2
1
2
1
3
2
3
2
0
)
x2 þ 3x þ 2 ¼ 0
)
x2 ¼ 1 ;
x3 ¼ 2
2. Schritt: Zuordnung der Partialbrüche
Den einfachen Nennernullstellen x 1 ¼ 1, x 2 ¼ 1 und x 3 ¼ 2 werden der Reihe nach die folgenden Partialbrüche zugeordnet:
A
;
x 1
B
;
x þ1
C
x þ2
3. Schritt: Partialbruchzerlegung (Ansatz)
2x2 þ x þ 2
x3
þ
2x2
x 2
¼
2x2 þ x þ 2
ðx 1Þ ðx þ 1Þ ðx þ 2Þ
¼
A
B
C
þ
þ
x 1
x þ1
x þ2
4. Schritt: Alle Brüche werden auf den Hauptnenner ðx 1Þ ðx þ 1Þ ðx þ 2Þ gebracht. Dazu müssen die drei Teilbrüche der rechten Seite der Reihe nach mit ðx þ 1Þ ðx þ 2Þ, ðx 1Þ ðx þ 2Þ bzw. ðx 1Þ ðx þ 1Þ erweitert werden:
2x2 þ x þ 2
ðx 1Þ ðx þ 1Þ ðx þ 2Þ
¼
A ðx þ 1Þ ðx þ 2Þ þ B ðx 1Þ ðx þ 2Þ þ C ðx 1Þ ðx þ 1Þ
ðx 1Þ ðx þ 1Þ ðx þ 2Þ
Die Brüche stimmen im Nenner, somit auch im Zähler überein:
2 x 2 þ x þ 2 ¼ A ðx þ 1Þ ðx þ 2Þ þ B ðx 1Þ ðx þ 2Þ þ C ðx 1Þ ðx þ 1Þ
Um drei Gleichungen für die drei Unbekannten A, B und C zu erhalten, setzen wir für die Variable x drei (verschiedene) Werte ein. Günstig sind die Werte der drei Nennernullstellen des Integranden (das lineare Gleichungssystem
ist dann gestaffelt und leicht zu lösen). Wir erhalten:
x ¼
1
)
x ¼ 1
x ¼ 2
1 ¼
6A
)
A ¼
1=6
)
1 ¼ 2 B
)
B ¼
1=2
)
8 ¼
)
C ¼ 8=3
3C
3 Integration einer echt gebrochenrationalen Funktion durch Partialbruchzerlegung des Integranden
163
Die Partialbruchzerlegung lautet somit:
2x2 þ x þ 2
x3
þ
x 2
2x2
¼
1=6
x 1
þ
1=2
þ
x þ1
8=3
x þ2
¼
1
1
1
1
8
1
þ
6 x 1
2 x þ1
3 x þ2
Durchführung der Integration
Der Integrand des gesuchten Integrals I lässt sich jetzt wie folgt darstellen:
x3
x3
þ
2x2
x 2
¼ 1þ
2x2 þ x þ 2
x3
þ
2x2
x 2
¼ 1þ
1
1
1
1
8
1
þ
6 x 1
2 x þ1
3 x þ2
Gliedweise Integration führt auf ein Grundintegral und drei einfache Integrale, die in der angedeuteten Weise mit Hilfe
einfacher Substitutionen gelöst werden:
ð
ð
ð
ð
1
dx
1
dx
8
dx
þ
I ¼ 1 dx þ
6
2
3
x 1
x þ1
x þ2
|fflffl{zfflffl}
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
w
du
¼ 1;
dx
u ¼ x 1;
ð
I ¼
1 dx þ
1
6
ð
dx ¼ du;
du
1
þ
u
2
ð
analog: v ¼ x þ 1; d x ¼ d v und
dv
8
v
3
ð
w ¼ x þ 2;
dx ¼ dw
dw
1
1
8
¼ x þ
ln j u j þ
ln j v j
ln j w j þ C
w
6
2
3
Durch Rücksubstitution ðu ¼ x 1, v ¼ x þ 1, w ¼ x þ 2Þ erhält man die gesuchte Lösung:
I ¼ x þ
1
1
8
ln j x 1 j þ
ln j x þ 1 j ln j x þ 2 j þ C
6
2
3
ð
C28
I ¼
4 x 4 x 3 38 x 2 þ 9 x þ 45
ðx 2 9Þ ðx þ 1Þ
dx ¼ ?
Da der Integrand unecht gebrochenrational ist (Zählerpolynom vom Grad m ¼ 4, Nennerpolynom vom Grad
n ¼ 3; m > n), müssen wir ihn zunächst zerlegen (Polynomdivision).
Nenner: ðx 2 9Þ ðx þ 1Þ ¼ x 3 þ x 2 9 x 9
ð4 x 4
x 3 38 x 2 þ 9 x þ 45Þ : ðx 3 þ x 2 9 x 9Þ ¼ 4 x 5 þ
ð4 x 4 þ 4 x 3 36 x 2 36 xÞ
5 x 3 2 x 2 þ 45 x þ 45
3x2
ðx 2 9Þ ðx þ 1Þ
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
echt gebrochen
ð 5 x 3 5 x 2 þ 45 x þ 45Þ
3x2
Partialbruchzerlegung (des echt gebrochenrationalen Anteils)
1. Schritt: Berechnung der Nennernullstellen
ðx 2 9Þ ðx þ 1Þ ¼ 0
x2 9 ¼ 0
)
x1=2 ¼ 3
x þ1 ¼ 0
)
x3 ¼ 1
2. Schritt: Zuordnung der Partialbrüche
Den drei einfachen Nennernullstellen x 1 ¼ 3, x 2 ¼ 3 und x 3 ¼ 1 werden der Reihe nach folgende Partialbrüche zugeordnet:
A
;
x 3
B
;
x þ3
C
x þ1
164
C Integralrechnung
3. Schritt: Partialbruchzerlegung (Ansatz)
3x2
ðx 2 9Þ ðx þ 1Þ
¼
3x2
A
B
C
¼
þ
þ
x 3
x þ3
x þ1
ðx 3Þ ðx þ 3Þ ðx þ 1Þ
4. Schritt: Alle Brüche werden gleichnamig gemacht, d. h. auf den Hauptnenner ðx 3Þ ðx þ 3Þ ðx 1Þ gebracht.
Dazu müssen die Teilbrüche der rechten Seite der Reihe nach mit ðx þ 3Þ ðx 1Þ, ðx 3Þ ðx 1Þ bzw.
ðx 3Þ ðx þ 3Þ erweitert werden:
3x2
ðx 3Þ ðx þ 3Þ ðx þ 1Þ
A ðx þ 3Þ ðx þ 1Þ þ B ðx 3Þ ðx þ 1Þ þ C ðx 3Þ ðx þ 3Þ
¼
ðx 3Þ ðx þ 3Þ ðx þ 1Þ
Da die Nenner beider Brüche übereinstimmen, gilt dies auch für die Zähler. Somit ist:
3 x 2 ¼ A ðx þ 3Þ ðx þ 1Þ þ B ðx 3Þ ðx þ 1Þ þ C ðx 3Þ ðx þ 3Þ
Durch Einsetzen der Werte x ¼ 3, x ¼ 3 und x ¼ 1 (es sind die Nennernullstellen des Integranden!) erhalten
wir ein leicht lösbares gestaffeltes lineares Gleichungssystem:
3
)
27 ¼ 24 A
)
A ¼
27
9
¼
24
8
x ¼ 3
)
27 ¼ 12 B
)
B ¼
27
9
¼
12
4
x ¼ 1
)
3 ¼ 8C
)
C ¼
x ¼
3
8
Die Partialbruchzerlegung lautet damit:
3 x2
ðx 2
9Þ ð x þ 1Þ
¼
9=8
x 3
þ
9=4
x þ3
þ
3=8
x þ1
¼
9
1
9
1
3
1
þ
8 x 3
4 x þ3
8 x þ1
Durchführung der Integration
Der Integrand des gesuchten Integrals I lässt sich jetzt in der folgenden Form darstellen:
4 x 4 x 3 38 x 2 þ 9 x þ 45
ðx 2 9Þ ð x þ 1Þ
¼ 4x 5 þ
¼ 4x 5 þ
3 x2
ðx 2 9Þ ð x þ 1Þ
¼
9
1
9
1
3
1
þ
8 x 3
4 x þ3
8 x þ1
Gliedweise Integration führt auf ein Grundintegral und drei weitere durch die angedeuteten Substitutionen leicht lösbare Integrale:
ð
ð
ð
ð
9
dx
9
dx
3
dx
I ¼ ð4 x 5Þ d x þ
þ
8
4
8
x 3
x þ3
x þ1
|fflffl{zfflffl}
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
w
u ¼ x 3;
du
¼ 1;
dx
ð
I ¼
ð4 x 5Þ d x þ
¼ 2x2 5x þ
dx ¼ du;
9
8
ð
analog: v ¼ x þ 3 ;
du
9
þ
u
4
ð
dv
3
v
8
ð
d x ¼ d v und
w ¼ x þ 1;
dw
¼
w
9
9
3
ln j u j þ
ln j v j
ln j w j þ C
8
4
8
Rücksubstitution ðu ¼ x 3, v ¼ x þ 3, w ¼ x þ 1Þ führt schließlich zur gesuchten Lösung:
I ¼ 2x2 5x þ
9
9
3
ln j x 3 j þ
ln j x þ 3 j ln j x þ 1 j þ C
8
4
8
dx ¼ dw
3 Integration einer echt gebrochenrationalen Funktion durch Partialbruchzerlegung des Integranden
ð
C29
I ¼
165
5 x 2 7 x þ 20
dx ¼ ?
x 3 3 x 2 þ 12 x 10
Der echt gebrochenrationale Integrand (Zählerpolynom vom Grad m ¼ 2, Nennerpolynom vom Grad n ¼ 3,
m < n), wird in Partialbrüche zerlegt.
1. Schritt: Berechnung der Nennernullstellen
x 3 3 x 2 þ 12 x 10 ¼ 0
)
x1 ¼ 1
(durch Probieren)
Die restlichen Nullstellen sind die Nullstellen des 1. reduzierten Polynoms, das wir mit Hilfe des Horner-Schemas
ermitteln:
1
x1 ¼ 1
1
3
12
10
1
2
10
2
10
0
)
)
x 2 2 x þ 10 ¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffi
x2=3 ¼ 1 1 10 ¼ 1 9 ¼ 1 3 j
2. Schritt: Zuordnung der Partialbrüche
x 1 ¼ 1 (einfache reelle Nullstelle) !
A
x 1
x 2=3 ¼ 1 3 j (konjugiert komplexe Nullstellen) !
Bx þ C
x2
2 x þ 10
3. Schritt: Partialbruchzerlegung (Ansatz)
5 x 2 7 x þ 20
x 3 3 x 2 þ 12 x 10
¼
5 x 2 7 x þ 20
ðx 1Þ ðx 2 2 x þ 10Þ
¼
A
Bx þ C
þ
x 1
x 2 2 x þ 10
4. Schritt: Alle Teilbrüche werden auf den Hauptnenner ðx 1Þ ðx 2 2 x þ 10Þ gebracht. Sie müssen daher der
Reihe nach mit x 2 2 x þ 10 bzw. x 1 erweitert werden:
5 x 2 7 x þ 20
ðx 1Þ ðx 2 2 x þ 10Þ
¼
A ðx 2 2 x þ 10Þ þ ðB x þ CÞ ðx 1Þ
ðx 1Þ ðx 2 2 x þ 10Þ
Die Brüche auf beiden Seiten dieser Gleichung stimmen im Nenner überein und somit auch im Zähler:
5 x 2 7 x þ 20 ¼ A ðx 2 2 x þ 10Þ þ ðB x þ CÞ ðx 1Þ
Wir benötigen drei Gleichungen für die drei Unbekannten A, B und C und setzen daher für die Variable x drei
verschiedene Werte ein: x ¼ 1 (reelle Nennernullstelle), x ¼ 0 und x ¼ 2. Das bereits gestaffelte lineare Gleichungssystem führt zu der folgenden Lösung:
x ¼ 1
) 18 ¼ 9 A ) A ¼ 2
x ¼ 0
) 20 ¼ 10 A C ) C ¼ 10 A 20 ¼ 10 2 20 ¼ 20 20 ¼ 0
x ¼ 2
) 26 ¼ 10 A þ 2 B þ C ) 2 B ¼ 26 10 A C ¼ 26 10 2 0 ¼ 6 ) B ¼ 3
Die Partialbruchzerlegung besitzt damit die folgende Gestalt:
5 x 2 7 x þ 20
x3
3x2
þ 12 x 10
¼
2
3x
þ
2
x 1
x 2 x þ 10
166
C Integralrechnung
Durchführung der Integration
Gliedweise Integration der Partialbrüche führt zu
ð
ð
ð
5 x 2 7 x þ 20
dx
x
þ3
d x ¼ 2 I1 þ 3 I2
I ¼
dx ¼ 2
2
3
2
x 1
x 2 x þ 10
x 3 x þ 12 x 10
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I1
I2
Das Teilintegral I 1 wird durch eine einfache Substitution gelöst:
du
¼ 1; dx ¼ du
dx
ð
ð
dx
du
I1 ¼
¼
¼ ln j u j þ C 1 ¼ ln j x 1 j þ C 1
x 1
u
u ¼ x 1;
Das Teilintegral I 2 lässt sich nach einigen elementaren Umformungen im Nenner ebenfalls durch Substitution lösen.
Wir haben dieses Integral bereits in der eigenständigen Aufgabe C16 ausführlich behandelt. Die Lösung lautete:
2
ð
x
1
x 2 x þ 10
1
1
þ
I2 ¼
ln
arctan
ðx 1Þ þ C 2
dx ¼
2
3
3
x 2 2 x þ 10
9
Damit erhalten wir für das Integral I folgende Lösung:
2
1
x 2 x þ 10
1
1
ln
þ
arctan
ðx 1Þ þ C 2 ¼
I ¼ 2 I 1 þ 3 I 2 ¼ 2 ð ln j x 1 j þ C 1 Þ þ 3
2
3
3
9
2
3
x 2 x þ 10
1
¼ 2 ln j x 1 j þ 2 C 1 þ
þ arctan
ln
ðx 1Þ þ 3 C 2 ¼
2
3
9
3
1
2
¼ 2 ln j x 1 j þ 2 C 1 þ
ln ð x 2 x þ 10Þ ln 9 þ arctan
ðx 1Þ þ 3 C 2 ¼
2
3
3
1
3
ln ð x 2 2 x þ 10Þ þ arctan
ðx 1Þ þ 2 C 1
ln 9 þ 3 C 2 ¼
2
3
2
3
1
3
ln ðx 2 2 x þ 10Þ þ arctan
ðx 1Þ þ C *
C * ¼ 2 C1 þ 3 C2
ln 9
¼ 2 ln j x 1 j þ
2
3
2
¼ 2 ln j x 1 j þ
4 Numerische Integration
Lehrbuch: Band 1, Kapitel V.8.4
Formelsammlung: Kapitel V.3.5
Bestimmen Sie mit der Simpsonschen Formel für 2 n ¼ 8 einfache Streifen einen Näherungswert für
den Flächeninhalt A zwischen der Kurve y ¼ ln ð1 þ 5 x 3 Þ, 0 x 1,6 und der x-Achse (Erstund Zweitrechnung mit halber Streifenzahl).
C30
Die Flächenberechnung erfolgt durch das folgende Integral:
1;6
ð
A ¼
ln ð1 þ 5 x 3 Þ d x
0
4 Numerische Integration
167
Bild C-1 zeigt die gesuchte Fläche und ihre Zerlegung in 2 n ¼ 8 einfache Streifen (Erstrechnung).
y
3
2
y = ln 1 + 5 x 3
1
Bild C-1
0
0,2
0,4
0,6
0,8
1
1,2
Erstrechnung (2 n = 8 einfache Streifen )
Streifenbreite (Schrittweite): h ¼
1,4
1,6
x
n = 4 Doppelstreifen)
1,6 0
¼ 0,2
8
Stützstellen: x k ¼ 0 þ k h ¼ k 0,2
ðk ¼ 0; 1; 2; . . . ; 8Þ
Stützwerte: y k ¼ f ðx k Þ ¼ ln ð1 þ 5 x 3k Þ (mit dem Taschenrechner berechnen)
Zweitrechnung (2 n * = 4 einfache Streifen )
Streifenbreite (Schrittweite): h * ¼ 2 h ¼
Stützstellen: x k ¼ 0 þ k h * ¼ k 0,4
n * = 2 Doppelstreifen)
1,6 0
¼ 0,4
4
ðk ¼ 0; 1; 2; 3; 4Þ
Stützwerte: y k ¼ f ðx k Þ ¼ ln ð1 þ 5 x 3k Þ (liegen aus der Erstrechnung bereits vor)
k
Stützstellen x k
0
0
1
0,2
2
0,4
3
0,6
4
0,8
5
1,0
6
1,2
7
1,4
8
1,6
Erstrechnung (h = 0,2)
Zweitrechnung (h * = 2 h = 0,4)
Stützwerte y k
Stützwerte y k
0
0
0,039 221
0,277 632
0,277 632
0,732 368
1,269 761
1,269 761
1,791 759
2,265 921
2,265 921
2,689 207
3,067 122
3,067 122
3,067 122
5,252 555
3,813 314
3,067 122
2,543 553
1,269 761
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
S0
S1
S2
S *0
S *1
S *2
Hinweis zur Tabelle: Die grau unterlegten Stützstellen und Stützwerte der Erstrechnung entfallen bei der Zweitrechnung.
168
C Integralrechnung
Erstrechnung: 2 n = 8 „einfache“ Streifen der Breite h = 0,2
I h ¼ ðS 0 þ 4 S 1 þ 2 S 2 Þ
h
0,2
¼ ð3,067 122 þ 4 5,252 555 þ 2 3,813 314Þ
¼ 2,113 598
3
3
Zweitrechnung: 2 n * = 4 „einfache“ Streifen der Breite h * = 2 h = 0,4
h*
0,4
I h * ¼ I 2 h ¼ ðS *0 þ 4 S *1 þ 2 S *2 Þ
¼ ð3,067 122 þ 4 2,543 553 þ 2 1,269 761Þ
¼ 2,104 114
3
3
Fehler der Erstrechnung:
1
1
1
ðI h I h *Þ ¼
ðI h I 2 h Þ ¼
ð2,113 598 2,104 114Þ ¼ 0,000 632
15
15
15
DI ¼
Verbesserter Näherungswert I v (Flächeninhalt A):
1;6
ð
ln ð1 þ 5 x 3 Þ d x
A ¼
I v ¼ I h þ D I ¼ 2,113 598 þ 0,000 632 ¼ 2,114 230
0
ðp
C31
e cos x d x näherungsweise nach Simpson (Zerlegung in 2 n ¼ 12 „ein-
Berechnen Sie das Integral
0
fache“ Streifen; Erst- und Zweitrechnung).
Der Integralwert entspricht der in Bild C-2 skizzierten Fläche.
y
3
2
y = e cos x
1
Bild C-2
π
x
h = π / 12
Erstrechnung (2 n = 12 „einfache“ Streifen )
n = 6 Doppelstreifen)
Streifenbreite (Schrittweite): h ¼ p=12
Stützstellen: x k ¼ 0 þ k h ¼ k p=12
ðk ¼ 0; 1; 2; . . . ; 12Þ
Bei der Berechnung der Stützwerte y k ¼ f ðx k Þ ¼ e cos x k ist zu beachten, dass die Stützstellen x k im Bogenmaß
gegebene Winkel sind.
4 Numerische Integration
169
Zweitrechnung (2 n * = 6 „einfache“ Streifen ) n * = 3 Doppelstreifen)
Streifenbreite (Schrittweite): h * ¼ 2 h ¼ p=6
Stützstellen: x k ¼ 0 þ k h ¼ k p=6
ðk ¼ 0; 1; 2; . . . ; 6Þ
Stützwerte: y k ¼ f ðx k Þ ¼ e cos x k (liegen aus der Erstrechnung bereits vor)
k
Erstrechnung (h = p /12)
Zweitrechnung (h * = 2 h = p /6)
Stützwerte y k
Stützwerte y k
Stützstellen x k
0
0
2,718 282
1
1 p=12 ¼ p=12
2
2 p=12 ¼ p=6
3
3 p=12 ¼ p=4
4
4 p=12 ¼ p=3
5
5 p=12
6
6 p=12 ¼ p=2
7
7 p=12
8
8 p=12 ¼ 2 p=3
9
9 p=12 ¼ 3 p=4
10
10 p=12 ¼ 5 p=6
11
11 p=12
12
12 p=12 ¼ p
2,718 282
2,627 219
2,377 443
2,377 443
2,028 115
1,648 721
1,648 721
1,295 399
1
1
0,771 963
0,606 531
0,606 531
0,493 069
0,420 620
0,420 620
0,380 631
0,367 879
0,367 879
3,086 161
7,596 396
6,053 315
3,086 161
3,798 063
2,255 252
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
S0
S1
S2
S *0
S *1
S *2
Hinweis zur Tabelle: Die grau unterlegten Stützstellen und Stützwerte der Erstrechnung entfallen bei der Zweitrechnung.
Erstrechnung: 2 n = 12 „einfache“ Streifen der Breite h = p /12
I h ¼ ðS 0 þ 4 S 1 þ 2 S 2 Þ
h
p
¼ ð3,086 161 þ 4 7,596 396 þ 2 6,053 315Þ
¼ 3,977 464
3
36
Zweitrechnung: 2 n * = 6 „einfache“ Streifen der Breite h * = 2 h = p /6
h*
p
¼ ð3,086 161 þ 4 3,798 063 þ 2 2,255 252Þ
¼ 3,977 416
I h * ¼ I 2 h ¼ ðS *0 þ 4 S *1 þ 2 S *2 Þ
3
18
Fehler der Erstrechnung:
DI ¼
1
1
1
ðI h I h *Þ ¼
ðI h I 2 h Þ ¼
ð3,977 464 3,977 416Þ ¼ 0,000 003
15
15
15
Verbesserter Näherungswert I v :
ðp
e cos x d x
0
I v ¼ I h þ D I ¼ 3,977 464 þ 0,000 003 ¼ 3,977 467
170
C Integralrechnung
ð
p=2
I ¼
C32
x
dx ¼ ?
sin x
p=4
Berechnen Sie dieses Integral näherungsweise nach der Trapezformel für n ¼ 6 Streifen.
Welches Ergebnis erhält man nach Simpson für 2 n ¼ 6 „einfache“ Streifen?
Der Integralwert entspricht der in Bild C-3 skizzierten
Fläche.
y=
Streifenbreite (Schrittweite):
h ¼
y
1,5
p=2 p=4
p=4
p
¼
¼
6
6
24
x
sin x
1
Stützstellen:
0,5
p
p
p
xk ¼
þk h ¼
þk
¼
4
4
24
π
4
p
p
p
¼ 6
þk
¼ ð6 þ kÞ
24
24
24
h = π / 24
π
2
x
Bild C-3
ðk ¼ 0; 1; 2; . . . ; 6Þ
Bei der Berechnung der zugehörigen Stützwerte y k ¼ f ðx k Þ ¼ x k =sin x k ist zu beachten, dass die Stützstellen x k im
Bogenmaß dargestellte Winkel sind.
k
Stützstellen x k
Trapezformel
Simpsonsche Formel
Stützwerte y k
Stützwerte y k
0
6 p=24 ¼ p=4
1
7 p=24
1,154 968
2
8 p=24 ¼ p=3
1,209 200
3
9 p=24 ¼ 3 p=8
1,275 163
4
10 p=24 ¼ 5 p=12
1,355 173
5
11 p=24
1,452 321
6
12 p=24 ¼ p=2
1,110 721
1,570 796
1,110 721
1,154 968
1,209 200
1,275 163
1,355 173
1,452 321
1,570 796
2,681 517
6,446 825
2,681 517
3,882 452
2,564 373
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
S2
S0
S1
S2
S1
Die beiden Formeln (Trapez- und Simpsonformel) unterscheiden sich bekanntlich in der unterschiedlichen Gewichtung
der Stützstellen.
Trapezformel ðn ¼ 6 Streifen der Breite h ¼ p=24Þ:
1
1
p
S1 þ S2 h ¼
2,681 517 þ 6,446 825
¼ 1,019 392
I ¼
2
2
24
Simpsonsche Formel ð2 n ¼ 6 einfache Streifen der Breite h ¼ p=24
I ¼ ðS 0 þ 4 S 1 þ 2 S 2 Þ
)
n ¼ 3 DoppelstreifenÞ:
h
p
¼ ð2,681 517 þ 4 3,882 452 þ 2 2,564 373Þ
¼ 1,018 403
3
72
5 Anwendungen der Integralrechnung
171
5 Anwendungen der Integralrechnung
In diesem Abschnitt finden Sie ausschließlich anwendungsorientierte Aufgaben zu folgenden Themen:
Flächeninhalt, Flächenschwerpunkt, Flächenträgheitsmomente (Flächenmomente)
Rotationskörper (Volumen, Mantelfläche, Massenträgheitsmoment, Schwerpunkt)
Bogenlänge, lineare und quadratische Mittelwerte
Arbeitsgrößen, Bewegungen (Weg, Geschwindigkeit, Beschleunigung)
Fertigen Sie zu jeder Aufgabe eine Skizze an, sie erleichtert Ihnen den Lösungsweg und führt zu einem besseren
Verständnis.
Alle anfallenden Integrale dürfen der Integraltafel entnommen werden. Bei der Lösung der Integrale wird die jeweilige
Integralnummer aus der Integraltafel der Mathematischen Formelsammlung des Autors mit den entsprechenden Parameterwerten angegeben („gelbe Seiten“, z. B. Integral 313 mit a ¼ 2). Selbstverständlich dürfen Sie die Integrale
auch „per Hand“ lösen (zusätzliche bung).
5.1 Flächeninhalt, Flächenschwerpunkt, Flächenträgheitsmomente
Lehrbuch: Band 1, Kapitel V.10.2 und 10.8
Formelsammlung: Kapitel V.5.4 bis 5.6
Welcher Flächeninhalt A wird von der Kurve y 2 ¼ 9 x 2 x 4 eingeschlossen?
Das dabei anfallende Integral ist mit einer geeigneten Integrationsmethode zu lösen.
C33
y
Wir lösen die Kurvengleichung nach y auf und erhalten
zwei zur x-Achse spiegelsymmetrische Funktionen:
y 2 = 9x 2 – x 4
4
y 2 ¼ 9 x 2 x 4 ¼ x 2 ð9 x 2 Þ
)
2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ x
9 x2;
3 x 3
–3
Bild C-4 zeigt die eingeschlossene Fläche, die sowohl zur
x- als auch zur y-Achse symmetrisch ist. Bei der Integration können wir uns daher auf den 1. Quadrant beschränken
(dunkelgrau unterlegte Fläche):
ðb
A ¼ 4
ð3
y dx ¼ 4
a
x
–2
–1
1
2
3
x
–2
–4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
9 x2 dx
Bild C-4
0
Das Integral lösen wir mit Hilfe der folgenden Substitution (die Grenzen werden mitsubstituiert):
du
¼ 2x;
dx
u ¼ 9 x2;
ð3
A ¼ 4
dx ¼
¼ 2
Grenzen
unten: x ¼ 0
)
u ¼ 90 ¼ 9
oben: x ¼ 3
)
u ¼ 99 ¼ 0
ð9
ð0
ð0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
du
2
u d u ¼ 2 u 1=2 d u ¼
¼ 2
x
9 x dx ¼ 4 x u
2 x
0
du
;
2x
9
3=2 9
u
3=2
0
¼
4 hpffiffiffiffiffi3 i 9
4
u
¼
0
3
3
9
u
pffiffiffi 9
4
u 0¼
ð27 0Þ ¼ 36
3
0
172
C Integralrechnung
Bestimmen Sie den Flächeninhalt A, den die Kurve y ¼ x 3 6 x 2 4 x þ 24 mit der x-Achse im
Bereich der beiden am weitesten außen gelegenen Schnittstellen einschließt.
C34
Wir benötigen die Nullstellen der Funktion:
x 3 6 x 2 4 x þ 24 ¼ 0
)
x1 ¼ 2
(durch Probieren)
Abspalten des zugehörigen Linearfaktors x 2 mit dem Horner-Schema, Berechnung der restlichen Nullstellen aus
dem 1. reduzierten Polynom:
1
6
x1 ¼ 2
4
8 24
2
1
24
4
12
0
)
x 2 4 x 12 ¼ 0
Die Polynomfunktion besitzt den in Bild C-5 dargestellten Verlauf. Die gesuchte Fläche A ergibt sich dann als
Summe der skizzierten Teilflächen A 1 und A 2 :
)
x2 ¼ 6 ;
x3 ¼ 2
y
30
20
A ¼ A1 þ A2
10
y = x 3 – 6x 2 – 4x + 24
A1
Bild C-5
–2
–1
– 10
1
2
3
4
5
6
x
A2
– 20
Teilfläche A 1 : Die Kurve liegt oberhalb der x-Achse. Daher gilt:
ðb
ð2
A1 ¼
y dx ¼
ðx 3 6 x 2 4 x þ 24Þ d x ¼
2
a
– 30
1 4
x 2 x 3 2 x 2 þ 24 x
4
2
¼
2
¼ ð4 16 8 þ 48Þ ð4 þ 16 8 48Þ ¼ 28 þ 36 ¼ 64
Teilfläche A 2 : Die Kurve liegt unterhalb der x-Achse. Daher gilt jetzt:
ðc
A2 ¼
y dx ¼
b
ð6
ðx 3 6 x 2 4 x þ 24Þ d x ¼
1 4
x 2 x 3 2 x 2 þ 24 x
4
2
6
¼
2
¼ ½ ð324 432 72 þ 144Þ ð4 16 8 þ 48Þ ¼ ½ 36 28 ¼ ð 64Þ ¼ 64
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
36
28
Gesamtfläche A:
C35
A ¼ A 1 þ A 2 ¼ 64 þ 64 ¼ 128
1 2
x þ 2 x eingeschlossene
Berechnen Sie für das von den Parabeln y ¼ x 2 4 x und y ¼
5
Flächenstück Flächeninhalt A und Flächenschwerpunkt S.
Wir berechnen zunächst die benötigten Schnittpunkte der beiden Parabeln:
1 2
x þ 2x
x 4x ¼
5
2
)
6 2
x 6x ¼ 6x
5
1
x 1 ¼ 0
5
6 x ¼ 0 ) x1 ¼ 0
1
x 1 ¼ 0 ) x2 ¼ 5
5
5 Anwendungen der Integralrechnung
173
Aus Bild C-6 entnehmen wir die folgenden Randkurven:
y
1 2
x þ 2x
5
obere Randkurve:
yo ¼
untere Randkurve:
yu ¼ x 2 4 x
5
1
yo = – x 2 + 2x
5
A
1
Bild C-6
1
–1
A ¼
–4
a
0
2 3
x þ 3x2
5
Schwerpunkt S = (xS; yS)
ðb
1
xS ¼
A
0
5
¼ 50 þ 75 0 0 ¼ 25
0
(Lage im 1. Quadrant, siehe Bild C-6)
1
x ð y o y uÞ d x ¼
25
ð5
a
1 2
2
x
x þ 2 x ðx 4 xÞ d x ¼
5
0
ð5
1
¼
25
0
1 2
1
x þ 2 x x 2 þ 4 xÞ d x ¼
x@
5
25
0
¼
4
ð5
ð5
1 2
6 2
2
x þ 2 x ðx 4 xÞ d x ¼
x þ 6x dx ¼
ð y o y uÞ d x ¼
5
5
¼
3
ð5
6 2
x þ 6x dx ¼
x
5
0
5
ð5
6 3
1
3 4
x þ 6x2 dx ¼
x þ 2x3 ¼
5
25
10
0
1
25
0
¼
1
25
375
1 375 þ 500
1 125
5 25
5
¼
þ 250 0 0 ¼
¼
¼
¼ 2,5
25 2
2
25
2
25
2
2
ðb
1
yS ¼
2A
1
ð y 2o y 2u Þ d x ¼
50
a
1
¼
50
#
2
ð5 "
1 2
2
dx ¼
x þ 2 x ðx 2 4 xÞ
5
0
ð5
1 4
4 3
x
x þ 4x2
25
5
ðx 4 8 x 3 þ 16 x 2 Þ d x ¼
0
1
¼
50
ð5
1 4
4 3
x
x þ 4 x 2 x 4 þ 8 x 3 16 x 2
25
5
dx ¼
0
1
¼
50
ð5
24 4
36 3
x þ
x 12 x 2
25
5
dx ¼
1
50
24 5
9 4
x þ
x 4x3
125
5
0
¼
5
yu = x 2 – 4 x
Flächeninhalt A
ðb
2
1
1
1
ð 600 þ 1125 500 0 0 0Þ ¼
25 ¼
¼ 0,5
50
50
2
Schwerpunkt: S ¼ ð2,5; 0,5Þ
5
¼
0
x
174
C Integralrechnung
C36
Bestimmen Sie den Flächeninhalt A und den Flächenschwerpunkt S des Flächenstücks, das von der
Kurve y ¼ x e x mit der positiven x-Achse eingeschlossen wird.
Wir berechnen zunächst den Flächeninhalt A des in Bild C-7
dargestellten Flächenstücks und anschließend die Lage des
Flächenschwerpunktes S.
y
0,4
0,3
y = x · e–x
Flächeninhalt A
1
ð
ðb
f ðxÞ d x ¼
A ¼
a
x e x d x ¼ lim
0,2
ðl
l!1
0
A
x ex d x
0,1
0
1
2
3
4
x
5
Bild C-7
Dieses uneigentliche Integral wird wie folgt berechnet: Zunächst wird von x ¼ 0 bis x ¼ l > 0 integriert, anschließend der Grenzwert l ! 1 gebildet (! FS: Kap. V.4.1):
ðl
AðlÞ ¼
x ex d x ¼
ð x 1Þ e x
l
0
¼ ð l 1Þ e l þ 1 e 0 ¼ ð l 1Þ e l þ 1
0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ 1
A ¼ lim AðlÞ ¼ lim
l!1
l!1
ð l 1Þ e l þ 1
¼ 0þ1 ¼ 1
Hinweis: Für ein beliebiges Polynom PðlÞ gilt: lim P ðlÞ e l ¼ 0
ðf ür l > 0Þ
l!1
Schwerpunkt S = (xS ; yS)
xS ¼
1
A
ðb
xy dx ¼
a
1
1
1
ð
x 2 e x d x ¼ lim
ðl
l!1
0
x 2 e x d x ¼ lim
l!1
x2 þ 2x þ 2
ex
1
0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Integral 314 mit a ¼ 1
¼ lim
l!1
1
yS ¼
2A
ðx 2 þ 2 x þ 2Þ e x
ðb
1
y dx ¼
21
0
1
ð
x e
2
a
l
2
0
¼ lim
l!1
2x
ðl 2 þ 2 l þ 2Þ e l þ 2
1
dx ¼
lim
2 l!1
ðl
¼ 0þ2 ¼ 2
x 2 e2x d x ¼
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 314 mit a ¼ 2
¼
2
l
l
1
4x þ 4x þ 2
1
lim
e2x ¼
lim ð4 x 2 þ 4 x þ 2Þ e 2 x 0 ¼
2 l!1
8
16 l ! 1
0
¼
1
1
1
lim ð4 l 2 þ 4 l þ 2Þ e 2 l 2 ¼
ð0 2Þ ¼
¼ 0,125
16 l ! 1
16
8
Schwerpunkt: S ¼ ð2; 0,125Þ
l
¼
0
5 Anwendungen der Integralrechnung
175
Ein Flächenstück wird berandet durch die folgenden Kurven: y 2 ¼ ðx 2 þ 1Þ 2 , x ¼ 0, x ¼ 3.
Bestimmen Sie den Flächeninhalt A sowie die Lage des Schwerpunktes S.
C37
Die Fläche verläuft spiegelsymmetrisch zur x-Achse (Bild C-8). Bei der Integration beschränken wir uns auf den im
1. Quadrant gelegenen Teil der Fläche.
y
x=0
10
x=3
yo = x 2 + 1
5
Randkurven
obere Randkurve: y o ¼ x 2 þ 1
1
–5
2
untere Randkurve: y u ¼ x 2 1
x
3
yu = –x 2 – 1
– 10
Bild C-8
Flächeninhalt A
ðb
A ¼
ðb
ð yo yu Þ d x ¼ 2
a
ð3
yo d x ¼ 2
a
ðx 2 þ 1Þ d x ¼ 2
1 3
x þx
3
0
3
¼ 2 ½ 9 þ 3 0 0 ¼ 24
0
Schwerpunkt S = (xS ; yS)
Aus Symmetriegründen liegt der Schwerpunkt auf der x-Achse, d. h. y S ¼ 0. Für x S erhalten wir:
1
xS ¼
A
ðb
1
x ð y o yu Þ d x ¼ 2
A
a
¼
1
12
ðb
1
x yo d x ¼ 2
24
a
1 4
1 2
x þ
x
4
2
3
¼
0
1
12
ð3
1
x ðx þ 1Þ d x ¼
12
ð3
ðx 3 þ xÞ d x ¼
2
0
0
81
9
1 81 þ 18
99
33
þ
00 ¼
¼
¼
¼ 2,0625
4
2
12
4
48
16
Schwerpunkt: S ¼ ð2,0625; 0Þ
C38
4
Bestimmen Sie den Schwerpunkt S der Fläche zwischen der Kurve y ¼
und der x-Achse im
4 þ x2
Intervall 2 x 2.
Die Fläche verläuft spiegelsymmetrisch zur y-Achse (Bild C-9). Wir beschränken daher die anfallenden Integrationen
auf das Intervall von x ¼ 0 bis x ¼ 2 (Faktor 2). Zunächst berechnen wir den benötigten Flächeninhalt A.
y
1
y=
4
4 + x2
0,5
Bild C-9
–2
–1
1
2
x
176
C Integralrechnung
Flächeninhalt A
ð2
ðb
y dx ¼ 2
A ¼
a
0
ð2
4
dx ¼ 8
4 þ x2
1
dx ¼ 8
4 þ x2
0
1
arctan
2
x
2
2
h
¼ 4 arctan
x i2
¼
2 0
0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral 29 mit a ¼ 2
p
0
4
¼ 4 ðarctan 1 arctan 0Þ ¼ 4
¼ p
(Winkel im Bogenmaß!)
Schwerpunkt S = (xS ; yS)
Wegen der Spiegelsymmetrie liegt der Schwerpunkt auf der y-Achse, d. h. x S ¼ 0. Für y S erhalten wir:
ðb
1
yS ¼
2A
1
y dx ¼
2
2p
ð2
2
a
0
16
16
dx ¼
2
p
ð4 þ x 2 Þ
ð2
1
dx ¼
2Þ 2
ð4
þ
x
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 30 mit a ¼ 2
¼
¼
16
p
16
p
x
1
þ
arctan
2
16
8 ð4 þ x Þ
1
1 p
þ
32
16 4
¼
16
p
x
2
2
¼
0
16
p
1
1
1
þ
arctan 1 0
arctan 0
32
16 |fflfflfflffl{zfflfflfflffl}
16 |fflfflfflffl{zfflfflfflffl}
p=4
0
¼
1
p
16 2 þ p
16 ð2 þ pÞ
2þp
¼
þ
¼
¼
¼ 0,4092
32
64
p
64
4p
p 4 16
Schwerpunkt: S ¼ ð0; 0,4092Þ
Die nach rechts geöffnete Parabel y 2 ¼ 2 p x schließt mit der Geraden x ¼ const: ¼ 2 p ein Flächenstück ein ð p > 0Þ. Berechnen Sie die Flächenträgheitsmomente (Flächenmomente) I x , I y und Ip .
C39
Durch Auflösen nach y erhalten wir die beiden zur x-Achse spiegelsymmetrischen Funktionen
pffiffiffiffiffiffiffiffiffiffi
(obere und untere Halbparabel, siehe Bild C-10).
y ¼ 2 p x ¼ ð2 p xÞ 1=2
y
2p
yo = 2px
Randkurven
p
x = 2p
p
2p
oben: y o ¼ ð2 p xÞ 1=2 ¼ ð2 pÞ 1=2 x 1=2
x
unten: y u ¼ ð2 p xÞ 1=2 ¼ ð2 pÞ 1=2 x 1=2
–p
yu = – 2px
– 2p
Bild C-10
Wir beschränken uns bei den Integrationen auf den 1. Quadranten (hellgrau unterlegte Fläche).
5 Anwendungen der Integralrechnung
177
Flächenmoment I x
ðb
1
Ix ¼
3
ð y 3o
y 3u Þ
1
dx ¼ 2
3
a
¼
ðb
2
dx ¼
3
a
2
ð2 pÞ 3=2
3
x 5=2
5=2
2p
¼
0
ð
2p
y 3o
ð
2p
ð2 pÞ
3=2
x
3=2
2
dx ¼
ð2 pÞ 3=2
3
x 3=2 d x ¼
0
0
h
i2p
4
4
4
64 4
ð2 pÞ 3=2 x 5=2
ð2 pÞ 3=2 ½ ð2 p Þ 5=2 0 ¼
ð2 pÞ 4 ¼
p
¼
0
15
15
15
15
Flächenmoment I y
ðb
Iy ¼
ðb
x ð y o y uÞ d x ¼ 2
a
ð
x 7=2
7=2
2p
¼
0
2p
x ð2 pÞ
2
a
¼ 2 ð2 pÞ 1=2
ð
2p
x yo d x ¼ 2
2
2
1=2
x
1=2
d x ¼ 2 ð2 pÞ
0
1=2
x 5=2 d x ¼
0
h
i2p
4
4
4
64 4
¼
ð2 pÞ 1=2 x 7=2
ð2 pÞ 1=2 ½ ð2 p Þ 7=2 0 ¼
ð2 pÞ 4 ¼
p
0
7
7
7
7
Polares Flächenmoment I p
Es gilt:
64 4
64 4
Ip ¼ Ix þ Iy ¼
p þ
p ¼ 64 p 4
15
7
1
1
þ
15
7
¼ 64 p 4
7 þ 15
22
1408 4
¼ 64 p 4
¼
p
105
105
105
5.2 Rotationskörper (Volumen, Mantelfläche, Massenträgheitsmoment,
Schwerpunkt)
Lehrbuch: Band 1, Kapitel V.10.3, 10.5, 10.8.3 und 10.9
Formelsammlung: Kapitel V.5.8 bis 5.11
C40
1 2
x gelegene Flächenstück erzeugt
6
bei Drehung um die y-Achse einen Rotationskörper. Wie groß ist das Rotationsvolumen V y ?
Das zwischen dem Kreis x 2 þ y 2 ¼ 16 und der Parabel y ¼
Wir berechnen zunächst die benötigten Kurvenschnittpunkte P 1 und P 2 :
y ¼
1 2
x
6
)
x2 ¼ 6y
x 2 þ y 2 ¼ 6 y þ y 2 ¼ 16
y1 ¼ 2 ;
y2 ¼ 8
Zugehörige x-Werte: x 2
(in Kreisgleichung einsetzen)
)
y 2 þ 6 y 16 ¼ 0
)
)
y 1=2 ¼ 3
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
9 þ 16 ¼ 3 5
(der zweite Wert ist eine Scheinlösung und scheidet somit aus)
pffiffiffi
pffiffiffi
¼ 6 y ¼ 6 2 ¼ 12 ) x1=2 ¼ 2 3 ) P 1=2 ¼ ð 2 3 ; 2Þ
)
178
C Integralrechnung
Aus Bild C-11 entnehmen wir, dass der Rotationskörper
aus zwei Teilen besteht. Diese Teilkörper entstehen durch
Drehung der hell- bzw. dunkelgrau unterlegten Flächenstücke um die y-Achse:
y
4
Kreis
3
P1 Parabel
2
P2
1
Bild C-11
–2 3
–1
2 3
1
x
V 1 : Volumen des Rotationskörpers, der durch Drehung der Parabel x 2 ¼ 6 y, 0 y 2 um
die y-Achse entsteht (hellgraue Unterlegung im Bild)
ðd
V1 ¼ p
ð2
x2 dy ¼ p
c
6y dy ¼ p 3y2
2
0
¼ p ð12 0Þ ¼ 12 p
0
V 2 : Volumen des Rotationskörpers, der durch Drehung des Kreises x 2 þ y 2 ¼ 16 , 2 y 4 um die y-Achse
entsteht (dunkelgraue Unterlegung im Bild)
ðd
V2 ¼ p
ð4
x dy ¼ p
2
c
2
1 3 4
64
8
ð16 y 2 Þ d y ¼ p 16 y
¼ p 64
y
32 þ
¼
3
3
3
2
56
96 56
40
¼ p
¼
p
¼ p 32
3
3
3
Gesamtvolumen V y :
C41
V y ¼ V 1 þ V 2 ¼ 12 p þ
40
36 p þ 40 p
76
p ¼
¼
p
3
3
3
pffiffiffi
x
Bestimmen Sie das Rotationsvolumen V x des Körpers, der durch Drehung der Kurve y ¼
,
1 þ x2
x 0 um die x-Achse erzeugt wird.
Bild C-12 zeigt den Kurvenverlauf. Die Volumenberechnung
führt auf ein uneigentliches Integral (unendlicher Integrationsbereich):
ðb
Vx ¼ p
1
ð
y dx ¼ p
2
a
0
y
0,5
x
y=
dx
ð1 þ x 2 Þ 2
x
1+x
2
0,1
Bild C-12
l
x
Dieses Integral wird berechnet, indem man zunächst von x ¼ 0 bis x ¼ l ðmit l > 0Þ integriert und dann den
Grenzwert für l ! 1 bildet (! FS: Kap. V.4.1):
1
ð
Vx ¼ p
0
x
ð1 þ x 2 Þ 2
ðl
d x ¼ p lim
l!1
x
d x ¼ p lim
2Þ 2
l!1
ð1
þ
x
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 33 mit a 2 ¼ 1
¼ p lim
l!1
1
1
þ
2
2
2 ð1 þ l Þ
¼ p
1
0þ
2
¼
p
2
1
2 ð1 þ x 2 Þ
l
¼
0
5 Anwendungen der Integralrechnung
179
Welches Volumen V x hat das Fass, das durch Drehung
y
der in Bild C-13 dargestellten Parabel um die x-Achse
0,5
Parabel
entsteht?
C42
P1
Parabelpunkt P 1 ¼ ð1; 0,25Þ
Bild C-13
–1
1
x
– 0,5
Wir müssen zunächst die Gleichung der zur y-Achse spiegelsymmetrischen Parabel bestimmen.
y ¼ a x 2 þ b ¼ a x 2 þ 0,5
Ansatz :
Den ffnungsparameter a bestimmen wir aus den Koordinaten des Parabelpunktes P 1 ¼ ð1; 0,25Þ:
1
ðx 2 2Þ
4
Bei der Berechnung des Rotationsvolumens beschränken wir die Integration wegen der Symmetrie der Parabel auf das
Intervall von x ¼ 0 bis x ¼ 1 (Faktor 2):
a 1 2 þ 0,5 ¼ 0,25
)
ðb
ð1
Vx ¼ p
y dx ¼ p
2
1
a
¼
C43
p
8
a ¼ 0,25
)
y ¼ 0,25 x 2 þ 0,5 ¼ 0,25 ðx 2 2Þ ¼
1
1
ðx 2 2Þ 2 d x ¼ 2 p
16
16
1 5
4 3
x
x þ 4x
5
3
ð1
ðx 4 4 x 2 þ 4Þ d x ¼
0
1
¼
0
p
8
1
4
p 3 20 þ 60
p 43
43
þ40 ¼
¼
¼
p
5
3
8
15
8 15
120
Die in der Parameterform x ¼ a cos t, y ¼ b sin t, 0 t 2 p vorliegende Ellipse erzeugt bei
Drehung um die y-Achse ein sog. Rotationsellipsoid. Bestimmen Sie das Volumen V y dieses Drehkörpers.
Da die rotierende Kurve in der Parameterform vorliegt,
erfolgt die Volumenberechnung durch das Integral
y
b
x = a · cos t, y = b · sin t
ð
t2
x 2 y_ d t
Vy ¼ p
t1
–a
(! FS: Kap. V.5.8). Wegen der Spiegelsymmetrie der
Ellipse (bezüglich beider Achsen) beschränken wir uns bei
der Rotation auf die im 1. Quadranten gelegene Viertelellipse
(in Bild C-14 grau unterlegt; Faktor 2 im Integral). Mit
y_ ¼ b cos t ;
x ¼ a cos t ;
a
x
–b
Bild C-14
0 t p=2
erhalten wir das folgende Rotationsvolumen:
ð
ð
p=2
Vy ¼ 2 p
a cos t b cos t d t ¼ 2 p a b
2
0
p=2
2
2
sin 3 t
cos t d t ¼ 2 p a b sin t
3
3
p=2
¼
2
0
0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 230 mit a ¼ 1
¼ 2pa b
2
sin 3 ðp=2Þ
sin 3 0
sin 0 þ
sin ðp=2Þ
3
3
!
¼ 2pa2 b
1
4
1
0þ0 ¼
pa2b
3
3
180
C Integralrechnung
Durch Drehung der Kurve y ¼
C44
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ x 2 , 0 x 3 um die x-Achse wird ein Rotationskörper
erzeugt. Welche Mantelfläche M x besitzt dieser Körper?
Die Berechnung der Mantelfläche, die die in Bild C-15 skizzierte Kurve
bei Drehung um die x-Achse erzeugt, erfolgt durch das Integral
ðb
Mx ¼ 2 p
y
3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y
1 þ ð y 0Þ 2 d x
y= 1+ x2
2
a
1
0
Wir bilden zunächst die benötigte Ableitung y mit Hilfe der Kettenregel
(Substitution: u ¼ 1 þ x 2 ) und daraus den im Integral auftretenden
Wurzelradikand:
y0 ¼
1
3
x
Bild C-15
1
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2 x ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
1 þ x2
2
1þx
1 þ ð y 0Þ 2 ¼ 1 þ
ð1 þ x 2 Þ þ x 2
x2
1 þ 2x2
¼
¼
1 þ x2
1 þ x2
1 þ x2
Der Integrand unseres Integrals lautet damit:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2x2
1 þ 2x2
2
0
2
2
¼
y
1 þ ðy Þ ¼
1 þ x pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
1þx
1 þ 2x2
2
1þx
2
1þx
pffiffiffi
rffiffiffiffiffi
a
a
Rechenregel:
¼ pffiffiffi
b
b
Wir formen den Integrand noch geringfügig um (der Wurzelausdruck wird auf den einfacheren Typ
rück geführt):
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
1
2
0
2
2
2
y 1 þ ðy Þ ¼
¼ 2
0,5 þ x 2
2
1 þ 2x ¼
þ 2x ¼
þx
2
2
Rechenregel:
2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 þ x 2 zu-
pffiffiffiffiffiffiffiffiffiffi
pffiffiffi pffiffiffi
ab ¼ a b
Für die Mantelfläche (Rotationsfläche) M x erhalten wir dann mit Hilfe der Integraltafel das folgende Ergebnis:
ðb
Mx ¼ 2 p
3
ð3 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffi ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
0
2
1 þ 2x dx ¼ 2p 2
y
1 þ ðy Þ dx ¼ 2p
0,5 þ x 2 d x ¼
a
0
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 116 mit a 2 ¼ 0,5
¼ 2
pffiffiffiffi
2p
1
2
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0,5 þ x 2
0,5 þ x 2 þ 0,5 ln x þ
3
¼
0
¼
h
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi i 3
pffiffiffiffi
0,5 þ x 2
¼
2p x
0,5 þ x 2 þ 0,5 ln x þ
¼
pffiffiffiffi
pffiffiffiffi
2 p ð9,2466 þ 0,9027 0 þ 0,1733Þ ¼ 2 p 10,3226 ¼ 14,5983 p
0
45;86
5 Anwendungen der Integralrechnung
C45
181
Bestimmen Sie die Mantelfläche M x des Rotationskörpers, der durch Drehung der Kettenlinie
y ¼ c cosh ðx=cÞ, c x c um die x-Achse entsteht.
y
Bild C-16 zeigt den Verlauf der Kettenlinie. Die bei der Rotation
um die x-Achse erzeugte Mantelfläche wird dabei nach der folgenden Integralformel berechnet:
ðb
Mx ¼ 2 p
c
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y
1 þ ð y 0Þ 2 d x
Kettenlinie
a
Wir bilden zunächst die Ableitung y 0 mit Hilfe der Kettenregel
(Substitution: u ¼ x=c) und daraus den im Integral auftretenden Wurzelradikand:
y 0 ¼ c sinh
x
c
1
¼ sinh
c
1 þ ð y 0 Þ 2 ¼ 1 þ sinh 2
x
c
–c
c
x
Bild C-16
x
c
¼ cosh 2
x
c
)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ ð y 0 Þ 2 ¼ cosh
x
c
(unter Verwendung der Formel cosh 2 u sinh 2 u ¼ 1 mit u ¼ x=cÞ
Der Integrand unseres Integrals lautet damit:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x
y
1 þ ð y 0 Þ 2 ¼ c cosh
cosh
c
x
c
x
c
¼ c cosh 2
Somit (unter Berücksichtigung der Spiegelsymmetrie der Kettenlinie):
2
ðb
Mx ¼ 2 p
y
a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ ð y 0Þ 2 d x ¼ 2 p c 2
ðc
cosh 2
x
c
dx ¼ 4pc
6
4x
þ
2
sinh
0
3c
2x
7
c
5
4=c
¼
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 364 mit a ¼ 1=c
c
x
c
2x
c
c
c
¼ 4pc
þ sinh
þ sinh 2 0
sinh 0 ¼ 4 p c
2
4
c
2
4
4 |fflffl{zfflffl}
0
0
c
1
1þ
sinh 2 ¼ 2 p c 2 2,8134 ¼ 5,6268 p c 2 ¼ 17,6771 c 2
¼ 4pc
2
2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
2,8134
¼ 4pc
C46
c
c
þ
sinh 2 ¼
2
4
1
Die Kurve y ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi , 2 x 2 erzeugt bei Drehung um die x-Achse einen Rotationskör1 þ x2
per, dessen Massenträgheitsmoment (bezogen auf die x-Achse) zu bestimmen ist (Dichte r ¼ const:).
182
C Integralrechnung
Kurvenverlauf: siehe Bild C-17
y
1
y=
1
1+x2
Bild C-17
–2
–1
1
2
x
Unter Berücksichtigung der Spiegelsymmetrie der Kurve zur y-Achse gilt dann für das gesuchte Massenträgheitsmoment J x bezüglich der x-Achse:
Jx ¼
1
pr
2
ðb
y4 dx ¼ 2
ð2
1
pr
2
1
dx ¼ pr
ð1 þ x 2 Þ 2
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
a
x
1
þ
arctan x
2
2 ð1 þ x 2 Þ
2
¼
0
Integral 30 mit a ¼ 1
1
1
1
þ
arctan 2 0
arctan 0
5
2
2 |fflfflfflffl{zfflfflfflffl}
0
(arctan 2 und arctan 0 sind Winkel in Bogenmaß!)
¼ p r ð0,2 þ 0,5536Þ ¼ 0,7536 p r ¼ 2,3675 r
¼ pr
Durch Drehung der in Bild C-18 dargestellten Trapezfläche um die x-Achse entsteht ein Kegelstumpf.
Bestimmen Sie das Massenträgheitsmoment J x dieses Körpers bezüglich der Rotationsachse (das Füllmaterial hat die konstante Dichte r ¼ 2). Lösen Sie das Integral mit Hilfe einer Substitution.
y
C47
5
1
Bild C-18
1
5
x
8
Gleichung der Geraden, die durch Drehung um die x-Achse den Kegelstumpf erzeugt (Bild C-18):
y ¼ mx þ b
m ¼
mit
4
1
¼
¼ 0,5
8
2
und
b ¼ 1
)
y ¼ 0,5 x þ 1 ;
0 x 8
(Steigung m und Achsenabschnitt b aus dem Bild entnommen)
Integralformel für das gesuchte Massenträgheitsmoment:
1
pr
Jx ¼
2
ðb
1
y dx ¼
p 2
2
ð8
a
ð8
4
ð0,5 x þ 1Þ 4 d x
ð0,5 x þ 1Þ d x ¼ p
4
0
0
Wir lösen dieses Integral mit Hilfe der folgenden linearen Substitution:
u ¼ 0,5 x þ 1 ;
du
¼ 0,5 ;
dx
dx ¼
ð8
ð0,5 x þ 1Þ d x ¼ p
0
Grenzen
ð5
4
Jx ¼ p
du
¼ 2 du;
0,5
unten : x ¼ 0
)
u ¼ 1
oben : x ¼ 8
)
u ¼ 5
ð5
u 2 du ¼ 2p
u du ¼ 2p
4
1
¼ 2 p 624,8 ¼ 1249,6 p ¼ 3925,73
4
1
1 5
u
5
1
4
¼
¼ 2p 5
5
1
5
5 Anwendungen der Integralrechnung
183
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Für den durch Drehung der Kurve y ¼ 2
1 þ 3 x 2 , 0 x 1 um die y-Achse entstandenen
Rotationskörper sind (bei konstanter Dichte r) folgende Größen zu ermitteln: Volumen V y , Schwerpunkt S und Massenträgheitsmoment J y (Bezugsachse ist die Rotationsachse).
C48
Kurvenverlauf: siehe Bild C-19
y
Für die anfallenden Integrale benötigen wir die Auflösung der Kurvengleichung nach x bzw. x 2 :
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ 2
1 þ 3 x 2 ) y 2 ¼ 4 ð1 þ 3 x 2 Þ ¼ 4 þ 12 x 2 )
4
y = 2 · 1 + 3x 2
3
2
12 x 2 ¼ y 2 4 ) x 2
1
¼
ð y 2 4Þ
12
1
Die Integrationen werden zwischen y ¼ 2 und y ¼ 4 vorgenommen.
0,5
Rotationsvolumen V y
Bild C-19
ðd
ð4
Vy ¼ p
x dy ¼ p
2
c
¼
p
12
1
p
ð y 2 4Þ d y ¼
12
12
2
1
ð4
ð y 2 4Þ d y ¼
p
12
1 3
y 4y
3
4
2
¼
2
64
8
p 56
p 56 24
p 32
4 8
8
p ¼
16
þ8 ¼
8 ¼
¼
¼
p
3
3
12 3
12
3
12 3
9
4 33
Schwerpunkt S = (xS ; yS ; zS )
Der Schwerpunkt liegt auf der y-Achse (Rotationsachse). Somit gilt x S ¼ 0 und z S ¼ 0. Für y S erhalten wir:
p
yS ¼
Vy
ðd
yx dy ¼
2
c
3 3
¼
84 3
p
8
p
9
1 4
y 2y2
4
ð4
1
9
1
y
ð y 2 4Þ d y ¼
12
8 12
2
ð4
ð y 3 4 yÞ d y ¼
2
4
3
3
3 4 9
27
¼
ð64 32 4 þ 8Þ ¼
36 ¼
¼ 3,375
32
32
8
4 8
¼
2
Schwerpunkt: S ¼ ð0; 3,375; 0Þ
Massenträgheitsmoment J y
1
pr
Jy ¼
2
ðd
1
pr
x dy ¼
2
c
1
¼
pr
288
1
¼
pr
288
ð4
4
1
1
ð y 2 4Þ 2 d y ¼
pr
144
288
2
1 5
8 3
y
y þ 16 y
5
3
992
448
þ 32
5
3
¼
ð4
ð y 4 8 y 2 þ 16Þ d y ¼
2
4
1
¼
pr
288
2
1024
512
32
64
þ 64
þ
32
5
3
5
3
¼
1
2976 2240 þ 480
1
1216
pr
¼
p r ¼ 0,8843 r
288
15
288
15
x
184
C Integralrechnung
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Die Kurve y ¼
1 þ cos x , 0 x p erzeugt bei Drehung um die x-Achse einen Rotationskörper, dessen Schwerpunkt S und Massenträgheitsmoment J x (bezüglich der Drehachse) zu berechnen
sind (der Körper besteht aus einem Material mit der Dichte r ¼ 4=3).
C49
Kurvenverlauf: siehe Bild C-20
y
Wir ermitteln zunächst das Rotationsvolumen, das für die
Schwerpunktberechnung benötigt wird.
2
Rotationsvolumen V x
1
ðb
ðp
Vx ¼ p
y dx ¼ p
0,5
ð1 þ cos xÞ d x ¼
2
a
y = 1 + cos x
0
1
¼ p ½ x þ sin x p0 ¼ p ðp þ sin p 0 sin 0 Þ ¼ p 2
|ffl{zffl}
|ffl{zffl}
0
π
2
Bild C-20
0
Schwerpunkt S = (xS ; yS ; zS )
Der Schwerpunkt S liegt auf der Rotationsachse (x-Achse), daher gilt y S ¼ z S ¼ 0. Für x S erhalten wir:
p
xS ¼
Vx
ðb
p
xy dx ¼
p2
ðp
2
a
1
x ð1 þ cos xÞ d x ¼
p
0
ðp
0
ðx þ x cos xÞ d x ¼
|fflfflfflfflffl{zfflfflfflfflffl}
Integral 232 mit a ¼ 1
¼
1
p
1
¼
p
p
1 2
x þ cos x þ x sin x
2
1 2
p 11
2
1
¼
p
¼
0
1
p
1 2
p þ cos p þ p sin p 0 cos 0 0
2
|fflffl{zfflffl}
|ffl{zffl}
|ffl{zffl}
1
0
1
¼
1 2
1 p2 4
p2 4
p 2 ¼
¼
¼ 0,9342
2
p
2
2p
Schwerpunkt: S ¼ ð0,9342; 0; 0Þ
Massenträgheitsmoment J x
1
Jx ¼
pr
2
ðb
1
4
y dx ¼
p
2
3
a
2
p
¼
3
2
¼
p
3
"
ðp
2
ð1 þ cos xÞ d x ¼
p
3
ðp
2
4
0
0
sin ð2 xÞ
x
x þ 2 sin x þ
þ
2
4
p
0
2
p
¼
3
ð1 þ 2 cos x þ cos 2 xÞ d x ¼
|fflfflffl{zfflfflffl}
Integral 229 mit a ¼ 1
3
1
x þ 2 sin x þ
sin ð2 xÞ
2
4
3
1
1
p þ 2 sin p þ
sin ð2 pÞ 0 2 sin 0
sin 0
2
4 |fflfflfflfflffl{zfflfflfflfflffl}
4 |ffl{zffl}
|ffl{zffl}
|ffl{zffl}
0
0
0
0
#
¼
p
¼
0
2
3
p
p ¼ p2
3
2
x
5 Anwendungen der Integralrechnung
185
Wo liegt der Schwerpunkt S eines Körpers mit der konstanten Dichte r, der durch Drehung der
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Kurve y ¼
x 4 þ 1 , 0 x 1 um die x-Achse erzeugt wurde?
C50
Kurvenverlauf: siehe Bild C-21
y
Wir berechnen zunächst das benötigte Volumen des Rotationskörpers:
ðb
Vx ¼ p
y dx ¼ p
¼ p
y= x4+1
ðx þ 1Þ d x ¼
2
a
1,5
ð1
4
1
0
1 5
x þx
5
1
¼ p
0
1
þ100
5
0,5
6
¼
p
5
0,5
1
x
Bild C-21
Die Lage des Schwerpunktes S ¼ ðx S ; y S ; z S Þ auf der Drehachse (x-Achse) wird durch die Koordinate x S eindeutig
beschrieben. Es gilt:
p
xS ¼
Vx
ðb
ð1
p
5
x ðx þ 1Þ d x ¼
6
ð1
5
ðx þ xÞ d x ¼
6
6
p
0
0
5
5
1
1
5
1
3
5 4
5 4
5
¼
¼
¼
þ
00 ¼
þ
¼
6
6
2
6
6
6
6 6
9
2 3 2 3
xy dx ¼
2
4
5
1 6
1 2
x þ
x
6
2
a
1
¼
0
Schwerpunkt: S ¼ ð5=9; 0; 0Þ
Wo liegt der Schwerpunkt des homogenen Rotationskörpers, der durch Drehung der Kurve
pffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ x 4 x im Bereich zwischen ihren beiden Nullstellen um die x-Achse entsteht?
C51
Wir berechnen zunächst die Nullstellen der Kurve :
pffiffiffiffiffiffiffiffiffiffiffiffiffi
x 4x ¼ 0
x ¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffi
4x ¼ 0
y
y = x· 4 – x
)
x1 ¼ 0
3
)
x2 ¼ 4
2
1
Bild C-22 zeigt den Kurvenverlauf zwischen den beiden Nullstellen.
1
Berechnung des benötigten Rotationsvolumens:
ðb
Vx ¼ p
y dx ¼ p
a
¼ p
ð4
ð4
ð4 x x Þ d x ¼ p
2
0
3
Bild C-22
x ð4 xÞ d x ¼ p
2
2
2
0
256
256 192
64
64 0 0 ¼ p
¼
p
3
3
3
3
4 3
1 4
x
x
3
4
4
¼
0
4
x
186
C Integralrechnung
Schwerpunkt S = (xS ; yS ; zS )
Der Schwerpunkt liegt auf der x-Achse (Rotationsachse), somit gilt y S ¼ z S ¼ 0. Für x S erhalten wir:
ð4
ð4
p
3
3
1 5 4
¼
x x 2 ð4 xÞ d x ¼
ð4 x 3 x 4 Þ d x ¼
x4
x
64
64
5
64
0
p
a
0
0
3
3
1024
3 1280 1024
3 256
3 4 64
12
¼
256
00 ¼
¼
¼
¼
¼ 2,4
64
5
64
5
64
5
5
5
64
xS ¼
ðb
p
Vx
xy2 dx ¼
Schwerpunkt: S ¼ ð2,4; 0; 0Þ
Durch Drehung der Kurve y ¼
C52
x þ1
pffiffiffi , 1 x 4 um die x-Achse entsteht ein (homogener) Rota2 x
tionskörper, dessen Volumen und Schwerpunkt zu bestimmen ist.
Kurvenverlauf: siehe Bild C-23
y
1,5
Rotationsvolumen V x
ðb
ð4
Vx ¼ p
y dx ¼ p
2
a
¼
x+1
2 x
1
1
ð4
p
4
ðx þ 1Þ 2
dx ¼
4x
y=
0,5
x2 þ 2x þ 1
dx ¼
x
1
2
3
4
1
¼
p
4
ð4
x þ2þ
1
x
Bild C-23
dx ¼
1
¼
p
4
1 2
x þ 2 x þ ln j x j
2
4
¼
1
p
4
1
8 þ 8 þ ln 4
2 ln 1 ¼ 3,7216 p
2
|{z}
0
11,69
Schwerpunkt S = (xS ; yS ; zS )
Der Schwerpunkt liegt auf der Drehachse (x-Achse). Daher ist y S ¼ z S ¼ 0. Für die x-Koordinate erhalten wir:
p
xS ¼
Vx
ðb
p
xy dx ¼
3,7216 p
a
ð4
ðx 2 þ 2 x þ 1Þ d x ¼
1
1
14,8864
ðx þ 1Þ 2
1
dx ¼
x
4x
3,7216 4
1
1
¼
14,8864
¼
ð4
2
ð4
ðx þ 1Þ 2 d x ¼
1
1
14,8864
1 3
x þ x2 þ x
3
4
¼
1
64
1
1
þ 16 þ 4
11 ¼
39 ¼ 2,6198
3
3
14,8864
Schwerpunkt: S ¼ ð2,62; 0; 0Þ
2,62
x
5 Anwendungen der Integralrechnung
187
5.3 Bogenlänge, lineare und quadratische Mittelwerte
Lehrbuch: Band 1, Kapitel V.10.4 und 10.7
Formelsammlung: Kapitel V.5.3 und 5.7
Bestimmen Sie den linearen Mittelwert der Funktion y ¼ A cos 2 ðw tÞ im Periodenintervall
0 t T mit der Periode T ¼ p=w ðA > 0, w > 0Þ.
C53
Linearer zeitlicher Mittelwert der in Bild C-24 dargestellten periodischen Funktion während einer Periode T ¼ p=w:
y linear
1
¼
T
ðT
ð
p=w
1
f ðtÞ d t ¼
A
p=w
0
cos 2 ðw tÞ d t ¼
Aw
p
t
sin ð2 w tÞ
þ
2
4w
p=w
0
¼
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 229 mit a ¼ w
Aw
¼
p
sin ð2 pÞ
p
sin 0
þ
0
2w
4w
4w
Aw
p
¼
Quadratischer zeitlicher Mittelwert
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
ðT
u
u1
y quadratisch ¼ t ½ f ðtÞ 2 d t ¼
T
p
þ000
2w
¼
Aw
p
A
¼
2w
2
p
y
A
y = A · cos2 (vt )
0
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
p=w
u
uw A 2 ð
¼ u
cos 4 ðw tÞ d t ¼
u p
t
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
3pj8w
T/2
T
Bild C-24
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffi
w A2 3 p
3 2
3
¼
¼
A ¼
A
p
8w
8
8
Berechnung des Integrals (sin p ¼ sin ð2 pÞ ¼ sin 0 ¼ 0 ; cos 0 ¼ 1 ; cos p ¼ 1)
p=
ðw
cos ðw t Þ d t ¼
4
cos ðw tÞ d t
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
¼
2
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
p=w
ð
cos 3 ðw t Þ sin ðw t Þ
3
þ
4w
4
0
Integral 229 mit a ¼ w
Integral 231 mit n ¼ 4; a ¼ w
¼
¼
cos 3 ðw t Þ sin ðw t Þ
3
þ
4w
4
cos 3 p sin p
3
þ
4w
4
¼ 0þ
3
4
p
þ0
2w
p=w
t
sin ð2 w t Þ
¼
þ
2
4w
0
p
sin ð2 pÞ
þ
2w
4w
0
cos 3 0 sin 0
3
4w
4
3
3
p
3p
ð0 þ 0Þ ¼
¼
4
4 2w
8w
0þ
sin 0
4w
¼
t
188
C Integralrechnung
C54
Welche mittlere Ordinate hat die Kurve y ¼
1
im Intervall 1 x 1?
1 þ x2
Kurvenverlauf: siehe Bild C-25:
y
Die mittlere Ordinate im Intervall 1 x 1 entspricht
dem linearen Mittelwert der Funktion in diesem Intervall.
Unter Berücksichtigung der Spiegelsymmetrie der Kurve gilt:
y linear
1
¼
ba
ðb
1
f ðxÞ d x ¼
2
a
1
¼ 2
2
ð1
0
ð1
1
y=
1
1+x2
0,5
1
dx ¼
1 þ x2
1
1
d x ¼ ½ arctan x 0 ¼
1 þ x2
¼ arctan 1 arctan 0 ¼
1
–1
– 0,5
0,5
x
1
Bild C-25
p
0 ¼ 0,7854
4
(die Werte der Arkustangensfunktion sind Winkel und müssen hier im neutralen Bogenmaß angegeben werden).
Die in Bild C-26 skizzierte Kurve (sog. Astroide) wird
durch die folgenden Parametergleichungen beschrieben:
x ¼ a cos 3 t ;
C55
y
a
y ¼ a sin 3 t
Astroide
ða > 0; 0 t 2 pÞ
a
–a
Wie groß ist der Umfang (Bogenlänge) dieser Kurve?
x
Hinweis: Die Berechnung der Bogenlänge erfolgt durch
ðt 2 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x_ 2 þ y_ 2 d t :
die Integralformel s ¼
–a
Bild C-26
t1
Für den Wurzelausdruck im Integranden benötigen wir die Ableitungen x_ und y_ der beiden Parametergleichungen.
Mit Hilfe der Kettenregel erhalten wir (Substitutionen: u ¼ cos t bzw. v ¼ sin t):
x ¼ a cos 3 t ¼ a u 3
)
x_ ¼ a 3 cos 2 t ð sin tÞ ¼ 3 a sin t cos 2 t
y ¼ a sin 3 t ¼ a v 3
)
y_ ¼ a 3 sin 2 t cos t ¼ 3 a sin 2 t cos t
Somit ist:
x_ 2 þ y_ 2 ¼ 9 a 2 sin 2 t cos 4 t þ 9 a 2 sin 4 t cos 2 t ¼
¼ 9 a 2 sin 2 t cos 2 t ðcos 2 t þ sin 2 tÞ ¼ 9 a 2 sin 2 t cos2 t
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
9 a 2 sin 2 t cos 2 t ¼ 3 a sin t cos t
x_ 2 þ y_ 2 ¼
(unter Verwendung des „trigonometrischen Pythagoras“ sin 2 t þ cos 2 t ¼ 1Þ
5 Anwendungen der Integralrechnung
189
Wegen der Spiegelsymmetrie der Astroide sowohl zur x- als auch zur y-Achse beschränken wir uns bei der Integration
auf den 1. Quadranten, d. h. auf das Intervall 0 t p=2 () Faktor 4):
p=2
p=2
p=2
ðt 2 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ð
1
3 a sin t cos t d t ¼ 12 a
sin t cos t d t ¼ 12 a
¼
s ¼
sin 2 t
x_ 2 þ y_ 2 d t ¼ 4
2
0
0
t1
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 254 mit a ¼ 1
p=2
¼ 6 a sin 2 t
0
¼ 6 a sin 2 ðp=2Þ sin 2 0
¼ 6 a ð1 0Þ ¼ 6 a
Die auf einen Körper einwirkende Kraft F hängt wie folgt von der Ortskoordinate s ab:
C56
FðsÞ ¼ F 0 ½ 1 cos ðw sÞ , F 0 > 0 , w > 0,
s 0
Wie groß ist die mittlere Kraft im Wegintervall (Periodenintervall) 0 s p mit p ¼ 2 p=w?
Kraft-Weg-Diagramm: siehe Bild C-27
F
Die mittlere Kraft ist der lineare Mitttelwert im Periodenintervall:
F linear
1
¼
p
2 F0
ðP
F = F0 [1 – cos (vs )]
F ðsÞ d s ¼
F0
0
ð
2 p=w
1
F0
¼
2 p=w
0
½ 1 cos ðw sÞ d s ¼
|fflfflfflfflffl{zfflfflfflfflffl}
π /v
sin ðw sÞ
s
w
2 p=w
0
w F0
¼
2p
s
Bild C-27
Integral 228 mit a ¼ w
w F0
¼
2p
2 π /v
sin ð2 pÞ
2p
sin 0
0þ
w
w
w
¼
w F0 2 p
¼ F0
2p
w
ðsin ð2 pÞ ¼ sin 0 ¼ 0Þ
t
Die Gleichung v ðtÞ ¼ v 0 ð1 e t Þ mit v 0 > 0, t > 0, t 0 beschreibt die Geschwindigkeit
eines Körpers in Abhängigkeit von der Zeit. Bestimmen Sie die durchschnittliche (mittlere) Geschwindigkeit im Zeitintervall 0 t t.
C57
Bild C-28 zeigt den zeitlichen Verlauf der Geschwindigkeit v („Sättigungsfunktion“).
v
v0
v = v 0 (1 – e –t / t )
0,63 v 0
Bild C-28
t
t
Der gesuchte Mittelwert der Geschwindigkeit v im Zeitintervall 0 t t ist der wie folgt berechnete lineare
Mittelwert der Geschwindigkeit-Zeit-Funktion:
190
C Integralrechnung
1
¼
t
v linear
ðt
1
v ðtÞ d t ¼
v0
t
0
ðt
1
v0
dt ¼
t
t
e t
|{z}
0
"
t
e t
t
1=t
#t
¼
0
t it
v0 h
t þ t e t ¼
0
t
Integral 312 mit a ¼ 1=t
¼
v0
v0
t þ t e1 0 t ¼
t e 1 ¼ v 0 e 1 ¼ 0,3679 v 0
t
t
Gegeben ist die Kettenlinie mit der Gleichung
x
, c x c (mit c > 0 ).
y ¼ c cosh
c
Bestimmen Sie die Länge dieser Kurve sowie die mittlere Ordinate.
C58
Bild C-29 zeigt den Verlauf der Kettenlinie.
y
Bogenlänge s
Die Berechnung der Bogenlänge erfolgt durch
das bestimmte Integral
c
ðb qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s ¼
1 þ ð y 0Þ 2 d x
Kettenlinie
Bild C-29
a
–c
x
c
Wir bilden zunächst die benötigte Ableitung y 0 und daraus den im Integral auftretenden Wurzelausdruck:
y 0 ¼ c sinh
x
c
1
¼ sinh
c
1 þ ð y 0 Þ 2 ¼ 1 þ sinh 2
x
c
x
c
ðKettenregel, Substitution: u ¼ x=cÞ
¼ cosh 2
x
c
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ ð y 0 Þ 2 ¼ cosh
)
x
c
(unter Verwendung des „hyperbolischen Pythagoras“ cosh 2 u sinh 2 u ¼ 1 mit u ¼ x=cÞ. Für die Bogenlänge
erhalten wir dann (wegen der Spiegelsymmetrie der Kettenlinie zur y-Achse beschränken wir uns bei der Integration auf
das Intervall von x ¼ 0 bis x ¼ c ) Faktor 2):
2
x 3c
ðb qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
ðc
sinh
h
x
x
x ic
4
c 5
1 þ ð y 0Þ 2 d x ¼
s ¼
cosh
¼ 2 c sinh
¼
d x ¼ 2 cosh
dx ¼ 2
c
c
c 0
1=c
0
c
a
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 363 mit a ¼ 1=c
¼ 2 c ðsinh 1 sinh 0Þ ¼ 2 c ð1,1752 0Þ ¼ 2,3504 c
Mittlere Ordinate
Die mittlere Ordinate der Kettenlinie im Intervall c x c entspricht dem dortigen linearen Mittelwert:
y linear
1
¼
ba
ðb
1
f ðxÞ d x ¼
c
2c
a
2
¼
4
sinh
1=c
x 3c
c 5
0
ðc
cosh
c
x
c
1
dx ¼ 2
2
ðc
cosh
0
x
c
ðc
dx ¼
cosh
x
c
dx ¼
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 363 mit a ¼ 1=c
h
¼ c sinh
x ic
¼ c ðsinh 1 sinh 0Þ ¼ c ð1,1752 0Þ ¼ 1,1752 c
c 0
5 Anwendungen der Integralrechnung
191
Bestimmen Sie den linearen und den quadratischen zeitlichen Mittelwert der in Bild C-30 dargestellten
parabelförmigen Spannungsimpulse u ¼ u ðtÞ mit der Periodendauer T ¼ p im Intervall 0 t p .
u
C59
π2
Bild C-30
π/2
0
π
3π / 2
t
2π
Produktansatz für den parabelförmigen Impuls im Periodenintervall 0 t p (! FS: Kap. III.4.3.2):
u ¼ u ðtÞ ¼ a ðt 0Þ ðt pÞ ¼ a ðt 2 p tÞ
u ðt ¼ p=2Þ ¼ p 2
2
p
p2
¼ p2
4
2
)
a
)
a p2
¼ p2
4
)
)
a
2
p
2p2
p2
¼ a
¼ p2
4
4
4
a
¼ 1
4
)
a ¼ 4
Somit gilt: u ðtÞ ¼ 4 ðt 2 p tÞ ; 0 t p
Linearer zeitlicher Mittelwert im Periodenintervall
u linear
1
¼
T
ðT
1
ð 4Þ
u dt ¼
p
0
4
¼
p
ðp
ðt 2 p tÞ d t ¼
4
p
1 3
1
t
pt2
3
2
0
p
¼
0
1 3
1 3
4
1
1
1
2 2
3
2
¼ 4p
¼
p
p 00 ¼
p
p
3
2
p
3
2
6
3
Quadratischer zeitlicher Mittelwert im Periodenintervall (Effektivwert)
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffi
u
u
ðT
ðp
u
u
16
16
u1
u
2
ðt 2 p tÞ d t ¼
I
u quadratisch ¼ u eff ¼ t u 2 d t ¼ t
T
p
p
0
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
I
Wir berechnen zunächst das unter der Wurzel stehende Integral I :
ðT
I ¼
ðT
2
ðt p tÞ d t ¼
2
0
ðt 2 p t þ p t Þ d t ¼
4
3
2 2
1 5
1
1 2 3
t
pt4 þ
p t
5
2
3
0
1 5
1 5
1 5
p
p þ
p 0 0 0 ¼
¼
5
2
3
1
1
1
þ
5
2
3
p5 ¼
¼
0
6 15 þ 10
1 5
p5 ¼
p
30
30
Somit gilt:
u quadratisch ¼ u eff
p
sffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffi
16
16 1 5
8 4
¼
I ¼
p ¼
p ¼ 0,7303 p 2 ¼ 7,2077
p
p 30
15
192
C Integralrechnung
1 pffiffiffi
x x þ 1 im Intervall 0 x 4. Lösen Sie das
2
anfallende Integral mit einer geeigneten Methode.
Berechnen Sie die Bogenlänge der Kurve y ¼
C60
Kurvenverlauf: siehe Bild C-31
y
Integralformel für die Bogenlänge:
5
ðb qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s ¼
1 þ ð y 0Þ 2 d x
3
y=1x x+1
2
a
1
1
2
3
4
x
Bild C-31
Wir bilden zunächst die benötigte Ableitung y 0 und daraus den Wurzelausdruck im Integranden des Integrals:
y ¼
pffiffiffi
1
1
x x þ1 ¼
x x
2
2
1 þ ð y 0Þ 2 ¼ 1 þ
1 3=2
x
þ1
2
)
9
16 þ 9 x
1
x ¼
¼
ð16 þ 9 xÞ
16
16
16
)
1=2
þ1 ¼
y0 ¼
1 3 1=2
3 pffiffiffi
x
x
¼
2 2
4
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
1
2
0
ð16 þ 9 xÞ ¼
16 þ 9 x
1 þ ðy Þ ¼
16
4
Einsetzen in die Integralformel liefert:
ðb qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð4 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
0
s ¼
16 þ 9 x d x
1 þ ðy Þ dx ¼
4
a
0
Dieses Integral lösen wir mit der folgenden linearen Substitution (die Grenzen werden mitsubstituiert):
u ¼ 16 þ 9 x ;
s ¼
1
4
du
¼ 9;
dx
C61
du
; Grenzen
9
unten : x ¼ 0
)
u ¼ 16 þ 0 ¼ 16
oben : x ¼ 4
)
u ¼ 16 þ 36 ¼ 52
52
52
52
52
ð4 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ð
ð
pffiffiffi d u
pffiffiffi
1
1
1
1 u 3=2
16 þ 9 x d x ¼
¼
u 1=2 d u ¼
¼
u
u du ¼
4
9
36
36
36 3=2 16
0
¼
dx ¼
16
16
16
pffiffiffiffiffiffiffiffiffi i
1 2 h pffiffiffiffiffiffi3 i 52
1 h pffiffiffiffiffiffiffiffi3ffi
1
u
52
ð374,9773 64Þ ¼ 5,7588
¼
16 3 ¼
16
36 3
54
54
10 2
ðx 6 xÞ im Bereich zwischen den beiBestimmen Sie die mittlere Ordinate der Parabel y ¼
9
den Nullstellen.
Wir berechnen zunächst die Nullstellen der Parabel:
10 2
ðx 6 xÞ ¼ 0
9
)
x 2 6 x ¼ x ðx 6Þ ¼ 0
)
x1 ¼ 0 ;
x2 ¼ 6
5 Anwendungen der Integralrechnung
193
Kurvenverlauf: siehe Bild C-32
y
10
y = – 10 (x 2 – 6x )
9
6
2
Bild C-32
1
3
x
6
Mittlere Ordinate (linearer Mittelwert) im Intervall 0 x 6:
y linear ¼
1
ba
ðb
1
f ðxÞ d x ¼
6
a
¼
6
ð6
10
5
1 3
2
2
¼
ðx 6 xÞ d x ¼
x 3x
9
27
3
0
0
5
5
54 9
20
¼
ð72 108 0 0Þ ¼
ð 36Þ ¼
¼ 6,6667
27
27
3 9
3
Sinusimpuls (Einweggleichrichtung; Bild C-33)
i ðtÞ ¼
C62
8
>
< i 0 sin ðw tÞ
0 t T=2
i0
f ür
>
:
i
T=2 t T
0
Berechnen Sie die effektive Stromstärke i eff während
einer Periode T ¼ 2 p=w (quadratischer zeitlicher
Mittelwert der Stromstärke i).
T/4
T/2
T
t
Bild C-33
Die Integration liefert nur im Intervall 0 t T=2 einen Beitrag, da i im Intervall T=2 t T verschwindet.
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
sffiffiffiffiffiffiffiffiffiffiffiffi
u
u 2 T=2
T
ð
u
ui0 ð
i 20
u1
{ eff ¼ { quadratisch ¼ t i 2 d t ¼ u
I
sin 2 ðw tÞ d t ¼
t
T
T
T
0
0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
I
Berechnung des unter der Wurzel stehenden Integrals I (unter Berücksichtigung von w T ¼ 2 p und sin 0 ¼
¼ sin ð2 pÞ ¼ 0Þ:
ð
T=2
sin 2 ðw tÞ d t ¼
I ¼
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
t
sin ð2 w tÞ
2
4w
T=2
¼
0
T
sin ðw TÞ
sin 0
T
sin ð2 pÞ
T
0þ
¼
¼
4
4w
4w
4
4w
4
Integral 205 mit a ¼ w
Damit erhalten wir den folgenden Effektivwert:
sffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
i 20
i 20 T
i 20
1
i eff ¼
¼
i0
I ¼
¼
2
T
T 4
4
ðhalber Scheitelwert)
194
C Integralrechnung
5.4 Arbeitsgrößen, Bewegungen (Weg, Geschwindigkeit, Beschleunigung)
Lehrbuch: Band 1, Kapitel V.10.1.1 und 10.6
Formelsammlung: Kapitel V.5.1 und 5.2
C63
Die Beschleunigung eines Massenpunktes in Abhängigkeit von der Zeit genüge der Gleichung
a ðtÞ ¼ a 0 ð1 e t Þ mit a 0 > 0, t 0. Bestimmen Sie Geschwindigkeit v und Weg s als Funktionen der Zeit für die Anfangswerte v ð0Þ ¼ 0 und s ð0Þ ¼ 0.
Die Beschleunigung a wächst im Laufe der Zeit von Null auf den Endwert a 0 („Sättigungsfunktion“, siehe Bild C-34).
Es gilt dann (v ¼ s_ und a ¼ v_ ):
a
ð
ð
v ðtÞ ¼ v_ ðtÞ d t ¼ a ðtÞ d t
a
0
ð
s ðtÞ ¼
ð
s_ ðtÞ d t ¼
a = a 0 (1 – e –t )
v ðtÞ d t
Bild C-34
t
Geschwindigkeit-Zeit-Gesetz u = u ðtÞ
ð
ð
v ðtÞ ¼ a ðtÞ d t ¼ a 0 ð1 e t Þ d t ¼ a 0 ðt þ e t þ C 1 Þ
|{z}
Integral 312 mit a ¼ 1
Die Integrationskonstante C 1 ermitteln wir aus der bekannten Anfangsgeschwindigkeit v ð0Þ ¼ 0:
v ð0Þ ¼ 0
)
a 0 ð0 þ 1 þ C 1 Þ ¼ a 0 ð1 þ C 1 Þ ¼ 0 j : a 0
)
1 þ C1 ¼ 0
)
C1 ¼ 1
Damit erhalten wir das folgende Geschwindigkeit-Zeit-Gesetz:
v ðtÞ ¼ a 0 ðt þ e t 1Þ ¼ a 0 ðt 1 þ e t Þ ;
t 0
Weg-Zeit-Gesetz s = s (t)
ð
ð
1 2
s ðtÞ ¼ v ðtÞ d t ¼ a 0 ðt 1 þ e t Þ d t ¼ a 0
t t e t þ C2
2
|{z}
Integral 312 mit a ¼ 1
Aus der Anfangsposition s ð0Þ ¼ 0 bestimmen wir die noch unbekannte Konstante C 2 :
s ð0Þ ¼ 0
)
a 0 ð0 0 1 þ C 2 Þ ¼ a 0 ð 1 þ C 2 Þ ¼ 0 j : a 0
Das Weg-Zeit-Gesetz lautet somit:
1 2
1 2
t
t
s ðtÞ ¼ a 0
;
t t e þ 1 ¼ a0
t t þ1e
2
2
)
t 0
1 þ C2 ¼ 0
)
C2 ¼ 1
5 Anwendungen der Integralrechnung
195
Die Geschwindigkeit v eines Massenpunktes genüge dem Zeitgesetz v ðtÞ ¼ v 0 e k t mit v 0 > 0,
k > 0 und t 0. Wie lautet das Weg-Zeit-Gesetz s ðtÞ für die Anfangswegmarke s ð0Þ ¼ s 0 ?
C64
Welcher Gesamtweg D s wird bis zum Stillstand ðt ! 1Þ zurückgelegt (von s 0 aus gemessen)?
Bestimmen Sie ferner den zeitlichen Verlauf der Beschleunigung a ¼ a ðtÞ.
Die Geschwindigkeit v nimmt im Laufe der Zeit exponentiell ab („Abklingfunktion“, siehe Bild C-35).
v
v0
v = v 0 · e –kt
Bild C-35
t
Weg-Zeit-Gesetz s = s (t)
Durch Integration der Geschwindigkeit-Zeit-Funktion erhalten wir das Weg-Zeit-Gesetz ðs_ ðtÞ ¼ v ðtÞÞ:
ð
ð
e kt
v0
e kt d t ¼ v0
þC ¼
e kt þ C
s ðtÞ ¼ v ðtÞ d t ¼ v 0
k
k
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
Integral 312 mit a ¼ k
Die Integrationskonstante C bestimmen wir aus der bekannten Anfangslage s ð0Þ ¼ s 0 :
v0
v0
v0
s ð0Þ ¼ s 0 )
e0 þ C ¼
1 þ C ¼ s0 ) C ¼ s0 þ
k
k
k
Das Weg-Zeit-Gesetz lautet damit (siehe hierzu auch Bild C-36):
s ðtÞ ¼
v0
v0
v0
e kt þ s0 þ
¼
1 e kt þ s0 ;
k
k
k
t 0
Den bis zum Stillstand zurückgelegten Gesamtweg D s erhalten wir durch den Grenzübergang t ! 1 (es dauert
theoretisch unendlich lange, bis der Körper zur Ruhe kommt):
hv
i
0
D s ¼ s ðt ¼ 1Þ s ðt ¼ 0Þ ¼ lim s ðtÞ s 0 ¼ lim
1 e kt þ s0 s0 ¼
k
t!1
t!1
¼ lim
t!1
hv
0
k
1 e kt
i
þ s 0 s 0 ¼ lim
hv
t!1
0
k
1 e kt
i
¼
v0
k
1 0Þ ¼
v0
k
s
v0
+ s0
k
s=
v0
(1 – e– kt ) + s 0
k
s0
Bild C-36
t
Beschleunigung-Zeit-Gesetz a = a (t)
Die Beschleunigung a ist bekanntlich die 1. Ableitung der Geschwindigkeit v nach der Zeit t. Mit Hilfe der Kettenregel erhalten wir (Substitution u ¼ k tÞ:
v ðtÞ ¼ v 0 e k t ¼ v 0 e u
mit
u ¼ kt
)
a ðtÞ ¼ v_ ðtÞ ¼ v 0 e u ð kÞ ¼ k v 0 e k t
196
C Integralrechnung
Welche Arbeit verrichtet die periodische ortsabhängige Kraft
C65
FðsÞ ¼ F 0 ½ 1 þ sin ðw sÞ
an einer Masse bei einer Verschiebung um eine Periodenlänge p ¼ 2 p=w?
Bild C-37 zeigt den Verlauf der Kraft in Abhängigkeit von der Ortskoordinate s.
F
F = F 0 [1 + sin (v s )]
2F 0
F0
2 π /v
Bild C-37
4 π /v
s
Die Periode ist p ¼ 2 p=w. Für die Verschiebung wählen wir das Periodenintervall von s ¼ 0 bis s ¼ p ¼ 2 p=w.
Die dabei verrichtete Arbeit beträgt dann:
ð
ð
s2
2p=w
W ¼
FðsÞ d s ¼ F 0
0
s1
½ 1 þ sin ðw sÞ d s ¼ F 0
|fflfflfflfflffl{zfflfflfflfflffl}
s
cos ðw sÞ
w
2 p=w
¼
0
Integral 204 mit a ¼ w
¼ F0
2p
cos ð2 pÞ
cos 0
2p
1
1
2p
0þ
¼ F0
þ
¼ F0
¼ F0 p
w
w
w
w
w
w
w
Durch die Gleichung
v ðtÞ ¼ ve tanh
C66
g
t ;
ve
t 0
wird die Zeitabhängigkeit der Fallgeschwindigkeit v beim freien Fall unter Berücksichtigung des Luftwiderstandes beschrieben. Wie lautet das Weg-Zeit-Gesetz s ðtÞ für die Anfangswegmarke s ð0Þ ¼ 0?
g: Erdbeschleunigung ; ve : Endgeschwindigkeit
Wegen s_ ¼ v gilt (die Geschwindigkeit ist bekanntlich die 1. Ableitung des Weges nach der Zeit):
ð
ð
g
1
g
tanh
t d t ¼ ve
ln cosh
t
þC ¼
s ðtÞ ¼ v ðtÞ d t ¼ ve
ve
g=ve
ve
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 387 mit a ¼ g=ve
¼
g
t
þC
ln cosh
ve
g
v 2e
5 Anwendungen der Integralrechnung
197
Die Integrationskonstante C bestimmen wir aus dem Anfangswert s ð0Þ ¼ 0:
s ð0Þ ¼ 0
v 2e
v 2e
ln ðcosh 0Þ þ C ¼
ln 1 þ C ¼ 0 þ C ¼ 0
g
g |{z}
|fflfflfflffl{zfflfflfflffl}
1
0
)
)
C ¼ 0
Der Fallweg s genügt somit dem folgenden Weg-Zeit-Gesetz:
s ðtÞ ¼
v 2e
g
ln cosh
g
t
ve
;
t 0
Das Geschwindigkeit-Zeit-Gesetz einer Bewegung laute:
C67
v ðtÞ ¼
30 t 2
;
100 þ t 3
t 0:
Bestimmen Sie das Weg-Zeit-Gesetz s ¼ s ðtÞ für die Anfangswegmarke s ð0Þ ¼ 0.
Das anfallende Integral soll per Hand mit einer geeigneten Substitution gelöst werden.
Bild C-38 zeigt den zeitlichen Verlauf der Geschwindigkeit v ¼ s_ .
v
3
v=
30 t 2
100 + t 3
2
1
Bild C-38
10
20
t
30
Durch Integration erhalten wir das Weg-Zeit-Gesetz s ¼ s ðtÞ:
ð
ð
ð
t2
s ðtÞ ¼ v ðtÞ d t ¼ s_ d t ¼ 30
dt
100 þ t 3
Das Integral lässt sich leicht lösen mit Hilfe der folgenden Substitution:
u ¼ 100 þ t 3 ;
ð
s ðtÞ ¼ 30
du
¼ 3t2;
dt
dt ¼
t2
d t ¼ 30
100 þ t 3
ð
du
3t2
t2 du
1
¼ 30
3
u 3 t2
ð
1
d u ¼ 10
u
ð
1
du ¼
u
¼ 10 ln j u j þ C ¼ 10 ln ð100 þ t 3 Þ þ C
Aus der Anfangslage berechnen wir die Integrationskonstante C :
s ð0Þ ¼ 0
)
10 ln 100 þ C ¼ 0
)
C ¼ 10 ln 100
Somit lautet das Weg-Zeit-Gesetz wie folgt:
s ðtÞ ¼ 10 ln ð100 þ t 3 Þ 10 ln 100 ¼ 10 ½ ln ð100 þ t 3 Þ ln 100 ¼ 10 ln
¼ 10 ln ð1 þ 0,01 t 3 Þ ;
Rechenregel : ln a ln b ¼ ln
a
b
t 0
100 þ t 3
¼
100
198
C Integralrechnung
Ein Behälter in Form eines Rotationsparaboloids (Bild C-39) soll
von einem Wasserreservoir ð y ¼ 0Þ bis zur Höhe y ¼ H mit
Wasser gefüllt werden. Welche Arbeit W ist dabei mindestens aufzuwenden?
C68
y
S
H
Hinweis: Der Behälter entsteht durch Drehung der Normalparabel
y ¼ x 2 um die y-Achse. Die Mindestarbeit entspricht der Hubarbeit W ¼ m g h, die zu verrichten ist, um die Füllmenge m (als
Massenpunkt betrachtet) in den Schwerpunkt S des (gefüllten) Behälters zu bringen.
y=x
2
x
Wasserreservoir (y = 0)
Bild C-39
g: Erdbeschleunigung; H : Höhe; r: Dichte des Wassers
Wir berechnen zunächst das Volumen V ¼ V y und die Masse (Wassermenge) m ¼ r V des gefüllten Behälters,
dann die Lage des Schwerpunktes S (Schwerpunktskoordinate y S ) und schließlich die aufzuwendende Mindestarbeit.
Behältervolumen V und Füllmenge (Wassermenge) m
ðd
V ¼ Vy ¼ p
ðH
x dy ¼ p
y dy ¼ p
2
c
0
Füllmenge (Wassermenge): m ¼ r V ¼
1 2
y
2
H
¼
0
1
pH2
2
1
prH2
2
Schwerpunktskoordinate y S des Behälters (der Schwerpunkt liegt auf der y-Achse)
p
yS ¼
Vy
ðd
yx dy ¼
2
p
ðH
2
y y dy ¼
H2
1
c
pH2 0
2
2
Schwerpunkt: S ¼ ðx S ; y S ; z S Þ ¼ 0;
H; 0
3
ðH
y2 dy ¼
0
2
H2
1 3
y
3
H
¼
0
2
1 3
2
H ¼
H
3
H2 3
Mindestarbeit beim Füllen des Behälters
Die im Schwerpunkt des Behälters konzentrierte Füllmenge (Wassermenge) m wird (als Massenpunkt betrachtet) vom
Wasserreservoir aus um die Strecke h ¼ y S angehoben (Bild C-40). Die dabei verrichtete Hubarbeit beträgt dann:
W ¼ m g h ¼ m g yS ¼
1
2
1
H ¼
prgH3
prH 2 g
3
3
2
y
S
yS
Bild C-40
x
Wasserreservoir (y = 0)
199
D Taylor- und Fourier-Reihen
1 Potenzreihenentwicklungen
1.1 Mac Laurinsche und Taylor-Reihen
Alle Potenzreihen sollen mindestens bis zur 3. Potenz (einschließlich) entwickelt werden.
Die Potenzreihe einer Funktion, die als Produkt zweier Funktionen darstellbar ist, lässt sich meist schneller durch
Multiplikation der (als bekannt vorausgesetzten) Reihen der Faktorfunktionen gewinnen (sog. „Reihenmultiplikation‘‘).
Diese dürfen der Formelsammlung entnommen werden.
Lehrbuch: Band 1, Kapitel VI.2 und 3
Formelsammlung: Kapitel VI.2 und 3
2x þ 3x2 þ 4x3 þ 5x4 þ 6x 5 þ ...
Welchen Konvergenzbereich besitzt diese Potenzreihe?
D1
Das Bildungsgesetz für den Koeffizienten a n der n-ten Potenz lautet: a n ¼ n þ 1 (für n ¼ 1; 2; 3; . . .). Mit
a n ¼ n þ 1 und a n þ 1 ¼ n þ 2 erhalten wir für den Konvergenzradius r der Potenzreihe den folgenden Wert:
1
1þ
n
þ
1
1
n
¼ lim
¼
¼ lim
¼ 1
1
n!1 n þ 2
n!1
nþ1
2
1þ
n
an
r ¼ lim
n!1 a
(alle Glieder im Zähler und Nenner des Bruches wurden dabei vor der Grenzwertberechnung durch n dividiert)
In den Randpunkten x ¼ 1 und x ¼ 1 ergeben sich folgende Zahlenreihen:
x ¼ 1
2 þ 3 4 þ 5 6 þ ...
x ¼ 1
2 þ 3 þ 4 þ 5 þ 6 þ ...
Die Glieder einer konvergenten Reihe müssen notwendigerweise eine Nullfolge bilden. Diese Bedingung ist in beiden
Fällen nicht erfüllt, die Potenzreihe divergiert daher in beiden Randpunkten. Konvergenzbereich ist daher das offene
Intervall j x j < 1 .
D2
1þ
x1
52
þ
x2
52 3
þ
x3
53 4
an ¼
x4
54 5
þ ...
Bestimmen Sie den Konvergenzbereich dieser Potenzreihe.
Bildungsgesetz für die Koeffizienten: a n ¼
Mit
þ
1
5n
ðn þ 1Þ
und a n þ 1 ¼
1
5n
ðn þ 1Þ
1
5 nþ1
ðn þ 2Þ
ðf ür n ¼ 0; 1; 2; . . .Þ
erhalten wir den folgenden Konvergenzradius:
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_4
200
D Taylor- und Fourier-Reihen
an
r ¼ lim
n!1 a
nþ1
¼ lim
n!1
¼ lim
n!1
5 n 5 ðn þ 2Þ
5n
ðn þ 1Þ
5n
1
ðn þ 1Þ
1
n
þ
1
5
ðn þ 2Þ
¼ lim
n!1
¼ lim
5 ðn þ 2Þ
nþ1
n!1
5 n þ 1 ðn þ 2Þ
1
¼
1
5 n ðn þ 1Þ
nþ2
¼ 5 lim
¼ 5 lim
n!1 n þ 1
n!1
1þ
1þ
lim
n!1
2
n
1
n
5 n þ 1 ðn þ 2Þ
5 n ðn þ 1Þ
¼ 5
¼
1
¼ 51 ¼ 5
1
Umformungen: Zähler mit dem Kehrwert des Nenners multiplizieren ! Kürzen durch 5 n ! Zähler und Nenner
gliedweise durch n dividieren.
Wir untersuchen noch das Verhalten der Potenzreihe in den Randpunkten x ¼ 5 und x ¼ 5:
x ¼ 5
1
1
1
1
þ
þ ...
2
3
4
alternierende harmonische Reihe
x ¼ 5
1þ
1
1
1
þ
þ
þ ...
2
3
4
harmonische Reihe
)
)
konvergent
divergent
Konvergenzbereich der Reihe: 5 x < 5
D3
1
X
Berechnen Sie den Konvergenzradius r der Potenzreihe
xn
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi .
n2 1
n¼2
1
Das Bildungsgesetz für den Koeffizienten a n der n-ten Potenz lautet: a n ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi (für n ¼ 2; 3; 4; . . .)
n2 1
1
1
1
Mit a n ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi und a n þ 1 ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi erhalten wir für den Konvergenzradius r
n2 1
n2 þ 2 n
ðn þ 1Þ 2 1
den folgenden Wert:
an
r ¼ lim
n!1 a
nþ1
¼ lim
¼ lim
n!1
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n2 þ 2 n
n!1
n2 1
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n2 1
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n2 þ 2 n
1
¼ lim pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n!1
n2 1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n2 þ 2 n
n2 þ 2 n
¼ lim pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
1
n!1
n2 1
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
u
2
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
rffiffiffiffiffi
1þ
u
2
pffiffiffi
n þ 2n
1
n
u
¼ 1 ¼ 1
¼ u lim
¼
lim
¼
2
1
tn ! 1
n!1 n 1
1
1
2
n
rffiffiffiffiffiffi
pffiffiffi
a
a
Umformungen: Zähler mit dem Kehrwert des Nenners multiplizieren ! Rechenregel für Wurzeln: pffiffiffi ¼
b
b
! Grenzwert darf unter der Wurzel gebildet werden ! Vor der Grenzwertbildung Zähler und Nenner gliedweise
durch n 2 dividieren.
D4
Welchen Konvergenzbereich besitzt die Potenzreihe
1
X
ðx 1Þ n
?
n!
n¼0
1 Potenzreihenentwicklungen
201
1
1
Das Bildungsgesetz für den Koeffizienten a n der n-ten Potenz ðx 1Þ n lautet: a n ¼
. Somit gilt a n ¼
und
n!
n!
1
und wir erhalten den folgenden Konvergenzradius:
anþ1 ¼
ðn þ 1Þ !
1
an
ðn þ 1Þ !
n ! ðn þ 1Þ
n
!
¼ lim
¼ lim
¼ lim ðn þ 1Þ ¼ 1
¼ lim
r ¼ lim
n
!
a
1
n!
n!1
n!1
n!1
n!1
n!1
nþ1
ðn þ 1Þ !
Die Potenzreihe konvergiert daher beständig, d. h. für jedes reelle x.
Umformungen: Zunächst wird der Zähler mit dem Kehrwert des Nenners multipliziert, dann wird die höhere Fakultät
ðn þ 1Þ ! in das Produkt ðn þ 1Þ ! ¼ n ! ðn þ 1Þ zerlegt und schließlich der gemeinsame Faktor n ! gekürzt (siehe
hierzu Bild D-1).
(n + 1) ! = n ! (n + 1)
Bild D-1
1
2
n
3
n+1
Zahlenstrahl
n!
D5
e x
Entwickeln Sie durch Reihenmultiplikation die Funktion f ðxÞ ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi
1x
eine Potenzreihe bis zum kubischen Glied.
um die Stelle x 0 ¼ 0
in
Wir bringen die Funktion zunächst in die Produktform (Wurzel vorher in eine Potenz umwandeln):
e x
ex
¼ e x ð1 xÞ 1=2
f ðxÞ ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
1=2
ð1
xÞ
1x
Aus der Formelsammlung entnehmen wir für die beiden Faktorfunktionen folgende Potenzreihenentwicklungen (Mac
Laurinsche Reihen ! FS: Kap. VI.3.4):
e x ¼ 1
x1
x2
x3
1 2
1 3
þ
þ ... ¼ 1 x þ
x
x þ ...
1!
2!
3!
2
6
ð1 xÞ 1=2 ¼ 1 þ
ðj x j < 1Þ
1
13 2
135 3
1
3 2
5 3
x þ
x þ
x þ ... ¼ 1 þ
x þ
x þ
x þ ...
2
24
246
2
8
16
ðj x j < 1Þ
Durch gliedweises Multiplizieren dieser Reihen erhalten wir die gewünschte Potenzreihenentwicklung der Ausgangsfunktion, wobei der Aufgabenstellung entsprechend nur Glieder bis zur 3. Potenz berücksichtigt werden. Die Potenzreihe beginnt wie folgt:
1 2
1 3
1
3 2
5 3
f ðxÞ ¼ e x ð1 xÞ 1=2 ¼ 1 x þ
x
x þ ... 1 þ
x þ
x þ
x þ ... ¼
2
6
2
8
16
1
3 2
5 3
1 2
3 3
1 2
1 3
1 3
x þ
x þ
x x
x
x þ
x þ
x
x þ ... ¼
2
8
16
2
8
2
4
6
1
3
1
1
5
3
1
1
2
1 x þ
þ
x þ
þ
x3 þ ... ¼
¼ 1þ
2
8
2
2
16
8
4
6
|fflfflffl{zfflfflffl}
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1=2
3=8
1=48
¼ 1þ
¼ 1
1
3 2
1 3
x þ
x þ
x þ ...
2
8
48
Konvergenzbereich: 1 < x < 1
(da die Reihe des Faktors ð1 xÞ 1=2 nur für j x j < 1 konvergiert)
202
D6
D Taylor- und Fourier-Reihen
Gesucht ist die Mac Laurinsche Reihe von f ðxÞ ¼ ðe x 1Þ 2 bis zur 4. Potenz. Die Reihe soll
a) durch Reihenmultiplikation,
b) auf direktem Wege über die Ableitungen hergeleitet werden.
a) Die Funktion ist ein Produkt aus zwei gleichen Faktoren e x 1, deren Reihenentwicklung unter Verwendung
der bekannten Reihe von e x (aus der Formelsammlung entnommen) wie folgt lautet:
x1
x2
x3
x4
1 2
1 3
1 4
x
x
x þ
x þ ...
e
þ
þ
þ ... 1 ¼ x þ
1 ¼ 1
2
6
24
1!
2!
3!
4!
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Mac Laurinsche Reihe von e x
Durch gliedweise Multiplikation erhalten wir die gesuchte Reihenentwicklung um den Nullpunkt (es werden dabei
nur Glieder bis einschließlich der 4. Potenz berücksichtigt):
f ðxÞ ¼ ðe x 1Þ 2 ¼ ðe x 1Þ ðe x 1Þ ¼
¼
1 2
1 3
1 4
1 2
1 3
1 4
x þ
x
x þ
x þ ... x þ
x
x þ
x þ ... ¼
2
6
24
2
6
24
1 3
1 4
1 3
1 4
1 4
x þ
x
x þ
x þ
x þ ... ¼
2
6
2
4
6
1
1
1
7 4
2
3
¼ x x þ
þ
þ
x4 þ ... ¼ x2 x3 þ
x þ ...
6
4
6
12
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
7=12
¼ x2
Konvergenzbereich: j x j < 1 (da die Reihen beider Faktoren überall konvergieren)
b) Wir benötigen die ersten vier Ableitungen, wobei wir jeweils in der angedeuteten Weise die Kettenregel verwenden:
f ðxÞ ¼ ðe x 1 Þ 2 ¼ u 2
|fflfflfflfflffl{zfflfflfflfflffl}
u
mit u ¼ e x 1 ;
u 0 ¼ e x
f 0 ðxÞ ¼ 2 u u 0 ¼ 2 ðe x 1Þ ð e x Þ ¼ 2 ð e 2 x þ e x Þ
f 00 ðxÞ ¼ 2 ð2 e 2 x e x Þ ;
f 000 ðxÞ ¼ 2 ð 4 e 2 x þ e x Þ ;
f
ð4Þ
ðxÞ ¼ 2 ð8 e 2 x e x Þ
(Ableitungen der Summanden e 2 x und e x mit der Kettenregel, Substitutionen: t ¼ 2 x bzw. t ¼ x)
An der Stelle x 0 ¼ 0 gilt dann ðe 0 ¼ 1Þ:
f ð0Þ ¼ ðe 0 1Þ 2 ¼ 0 ;
f 0 ð0Þ ¼ 2 ð e 0 þ e 0 Þ ¼ 0 ;
f 000 ð0Þ ¼ 2 ð 4 e 0 þ e 0 Þ ¼ 2 ð 3Þ ¼ 6 ;
f
ð4Þ
f 00 ð0Þ ¼ 2 ð2 e 0 e 0 Þ ¼ 2 1 ¼ 2 ;
ð0Þ ¼ 2 ð8 e 0 e 0 Þ ¼ 2 7 ¼ 14
Damit erhalten wir die folgende Mac Laurinsche Reihe (in bereinstimmung mit dem Ergebnis aus a)):
f ðxÞ ¼ ðe x 1Þ 2 ¼ f ð0Þ þ
¼ 0þ
f 0 ð0Þ 1
f 00 ð0Þ 2
f 000 ð0Þ 3
f ð4Þ ð0Þ 4
x þ
x þ
x þ
x þ ... ¼
1!
2!
3!
4!
0 1
2 2
6 3
14 4
7 4
x þ
x þ
x þ
x þ ... ¼ x2 x3 þ
x þ ...
1!
2!
3!
4!
12
ðj x j < 1Þ
1 Potenzreihenentwicklungen
D7
203
Leiten Sie durch Reihenmultiplikation die Potenzreihenentwicklung von f ðxÞ ¼
den Nullpunkt x 0 ¼ 0 her (bis zur 4. Potenz einschließlich).
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ x cos ð2 xÞ um
Aus der Formelsammlung entnehmen wir für die beiden Faktorfunktionen folgende Potenzreihenentwicklungen (die
Reihe für cos ð2 xÞ erhalten wir dabei aus der Mac Laurinschen Reihe von cos u mit Hilfe der Substitution u ¼ 2 x):
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1
11 2
113 3
1135 4
1 þ x ¼ ð1 þ xÞ 1=2 ¼ 1 þ
x
x þ
x
x þ ... ¼
2
24
246
2468
¼ 1þ
1
1 2
1 3
5 4
x
x þ
x
x þ ...
2
8
16
128
f
cos ð2 xÞ ¼ cos u ¼ 1
u
¼ 1 2x2 þ
ðj x j 1Þ
ð2 xÞ 2
ð2 xÞ 4
4x2
16 x 4
u2
u4
þ
þ ... ¼ 1
þ
þ ... ¼ 1
þ
þ ... ¼
2!
4!
2
24
2
24
2 4
x þ ...
3
ðj x j < 1Þ
Durch gliedweise Multiplikation der beiden Reihen erhält man die gesuchte Entwicklung:
pffiffiffiffiffiffiffiffiffiffiffiffiffi
f ðxÞ ¼ 1 þ x cos ð2 xÞ ¼ ð1 þ xÞ 1=2 cos ð2 xÞ ¼
1
1 2
1 3
5
2 4
4
2
¼ 1þ
x
x þ
x
x þ ... 1 2x þ
x þ ... ¼
2
8
16
128
3
2 4
1
1 2
1 4
1 3
5
x þ
x x3
x þ
x þ
x
x4 þ ... ¼
3
2
8
4
16
128
1
1
1
2
1
5
2
3
¼ 1þ
x þ 2
x þ 1 þ
x þ
þ
x4 þ ... ¼
2
8
16
3
4
128
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
17=8
15=16
337=384
¼ 1 2x2 þ
¼ 1þ
D8
1
17 2
15 3
337 4
x
x
x þ
x þ ...
2
8
16
384
ðj x j 1Þ
Wie lautet die Mac Laurinsche Reihe von f ðxÞ ¼ ln ðcosh xÞ bis zum x 4 - Glied?
Bildung aller benötigten Ableitungen
1. Ableitung (Kettenregel): f ðxÞ ¼ ln ðcosh xÞ ¼ ln u
|fflfflfflffl{zfflfflfflffl}
u
f 0 ðxÞ ¼
mit
u ¼ cosh x ;
u 0 ¼ sinh x
1
1
sinh x
u0 ¼
sinh x ¼
¼ tanh x
u
cosh x
cosh x
2. Ableitung: f 00 ðxÞ ¼ 1 tanh 2 x
3. Ableitung (Kettenregel):
f 00 ðxÞ ¼ 1 tanh 2 x ¼ 1 ðtanh xÞ 2 ¼ 1 u 2
|fflffl{zfflffl}
u
mit u ¼ tanh x ;
u 0 ¼ 1 tanh 2 x
f 000 ðxÞ ¼ 0 2 u u 0 ¼ 2 tanh x ð1 tanh 2 xÞ ¼ 2 tanh x þ 2 tanh 3 x
204
D Taylor- und Fourier-Reihen
4. Ableitung (Kettenregel):
f 000 ðxÞ ¼ 2 tanh x þ 2 tanh 3 x ¼ 2 tanh x þ 2 ðtanh xÞ 3 ¼ 2 tanh x þ 2 u 3
|fflffl{zfflffl}
u
mit
f
ð4Þ
u ¼ tanh x
und u 0 ¼ 1 tanh 2 x
ðxÞ ¼ 2 ð1 tanh 2 xÞ þ 6 u 2 u 0 ¼ 2 ð1 tanh 2 xÞ þ 6 tanh 2 x ð1 tanh 2 xÞ ¼
¼ ð1 tanh 2 xÞ ð 2 þ 6 tanh 2 xÞ
(der gemeinsame Faktor 1 tanh 2 x wurde ausgeklammert)
Ableitungswerte an der Entwicklungsstelle x 0 ¼ 0 (unter Berücksichtigung von cosh 0 ¼ 1 und tanh 0 ¼ 0Þ:
f 0 ð0Þ ¼ tanh 0 ¼ 0 ;
f ð0Þ ¼ ln ðcosh 0Þ ¼ ln 1 ¼ 0 ;
f 000 ð0Þ ¼ 2 tanh 0 þ 2 tanh 3 0 ¼ 0 ;
f
ð4Þ
f 00 ð0Þ ¼ 1 tanh 2 0 ¼ 1 ;
ð0Þ ¼ ð1 tanh 2 0Þ ð 2 þ 6 tanh 2 0Þ ¼ 1 ð 2Þ ¼ 2
Mac Laurinsche Reihe von f (x) = ln (cosh x)
f ðxÞ ¼ ln ðcosh xÞ ¼ f ð0Þ þ
¼ 0þ
f 0 ð0Þ 1
f 00 ð0Þ 2
f 000 ð0Þ 3
f ð4Þ ð0Þ 4
x þ
x þ
x þ
x þ ... ¼
1!
2!
3!
4!
0 1
1 2
0 3
2 4
1 2
1 4
x þ
x þ
x þ
x þ ... ¼
x
x þ ...
1
2
6
24
2
12
ð j x j < 1Þ
1
Bestimmen Sie die Taylorsche-Reihe von f ðxÞ ¼ pffiffiffi um das Entwicklungszentrum x 0 ¼ 1 bis zur
x
4. Potenz (einschließlich).
D9
Wir bilden zunächst die benötigten Ableitungen bis zur 4. Ordnung:
1
1
f ðxÞ ¼ pffiffiffi ¼
¼ x 1=2 ;
x 1=2
x
3
f ðxÞ ¼
4
000
1
f ðxÞ ¼ x 3=2 ;
2
0
5 7=2
15 7=2
x
x
¼
;
2
8
f
ð4Þ
1
f ðxÞ ¼
2
00
15
ðxÞ ¼
8
3 5=2
3
x
x 5=2 ;
¼
2
4
7 9=2
x
2
¼
105 9=2
x
16
Ableitungswerte an der Entwicklungsstelle x 0 ¼ 1:
f ð1Þ ¼ 1 ;
f 0 ð1Þ ¼
1
;
2
f 00 ð1Þ ¼
3
;
4
f 000 ð1Þ ¼
15
;
8
f
ð4Þ
ð1Þ ¼
105
16
Taylor-Reihe um das Entwicklungszentrum x 0 = 1
f 0 ð1Þ
f 00 ð1Þ
f 000 ð1Þ
f ð4Þ ð1Þ
1
f ðxÞ ¼ pffiffiffi ¼ f ð1Þ þ
ðx 1Þ 1 þ
ðx 1Þ 2 þ
ðx 1Þ 3 þ
ðx 1Þ 4 þ . . . ¼
1!
2!
3!
4!
x
¼ 1þ
1=2
3=4
15=8
105=16
ðx 1Þ 1 þ
ðx 1Þ 2 þ
ðx 1Þ 3 þ
ðx 1Þ 4 þ . . . ¼
1
2
6
24
¼ 1
1
3
5
35
ðx 1Þ 1 þ
ðx 1Þ 2
ðx 1Þ 3 þ
ðx 1Þ 4 þ . . .
2
8
16
128
Konvergenzbereich: 0 < x < 2
1 Potenzreihenentwicklungen
205
Entwickeln Sie die Funktion f ðxÞ ¼ 4 x um x 0 ¼ 2 in eine Taylorsche Reihe.
Wie lautet das Bildungsgesetz für die Koeffizienten?
D10
Ableitungen bis zur 3. Ordnung
f 0 ðxÞ ¼ ðln 4Þ 4 x ;
f ðxÞ ¼ 4 x ;
f 00 ðxÞ ¼ ðln 4Þ ðln 4Þ 4 x ¼ ðln 4Þ 2 4 x ;
f 000 ðxÞ ¼ ðln 4Þ 2 ðln 4Þ 4 x ¼ ðln 4Þ 3 4 x
Ableitungswerte an der Entwicklungsstelle x 0 ¼ 2:
f ð2Þ ¼ 4 2 ¼ 16 ;
f 0 ð2Þ ¼ ðln 4Þ 4 2 ¼ 16 ðln 4Þ 1 ;
f 00 ð2Þ ¼ ðln 4Þ 2 4 2 ¼ 16 ðln 4Þ 2 ;
f 000 ð2Þ ¼ ðln 4Þ 3 4 2 ¼ 16 ðln 4Þ 3
Taylor-Reihe von f (x) = 4 x um das Entwicklungszentrum x 0 = 2
f ðxÞ ¼ 4 x ¼ f ð2Þ þ
f 0 ð2Þ
f 00 ð2Þ
f 000 ð2Þ
ðx 2Þ 1 þ
ðx 2Þ 2 þ
ðx 2Þ 3 þ . . . ¼
1!
2!
3!
16 ðln 4Þ 2
16 ðln 4Þ 3
16 ðln 4Þ 1
ðx 2Þ 1 þ
ðx 2Þ 2 þ
ðx 2Þ 3 þ . . . ¼
1!
2!
3!
!
ðln 4Þ 1
ðln 4Þ 2
ðln 4Þ 3
2
3
1
1þ
ðx 2Þ þ
ðx 2Þ þ
ðx 2Þ þ . . .
ð j x j < 1Þ
1!
2!
3!
¼ 16 þ
¼ 16
Bildungsgesetz für die Koeffizienten: a n ¼ 16
D11
ðln 4Þ n
n!
ðf ür n ¼ 0; 1; 2; . . .Þ
Bestimmen Sie die Taylor-Reihe von f ðxÞ ¼ ln
1 þ x2
; x 6¼ 0 um die Stelle x 0 ¼ 1.
x2
Wir bringen die Funktion zunächst auf eine für das Differenzieren günstigere Form:
1 þ x2
f ðxÞ ¼ ln
¼ ln ð1 þ x 2 Þ ln x 2 ¼ ln ð1 þ x 2 Þ 2 ln j x j
x2
Rechenregeln:
ln
a
¼ ln a ln b
b
und
ln a 2 ¼ 2 ln j a j
1. Ableitung (der 1. Summand wird nach der Kettenregel differenziert):
f ðxÞ ¼ ln ð1 þ x 2 Þ 2 ln j x j ¼ ln u 2 ln j x j mit u ¼ 1 þ x 2 ; u 0 ¼ 2 x
|fflfflfflfflffl{zfflfflfflfflffl}
u
2 x x 2 ð1 þ x 2 Þ
1
1
2x
2
2x2 2 2x2
2
¼
¼
f 0 ðxÞ ¼
u0 2
¼
¼
2
2
3
u
x
x
1þx
x þ x3
ð1 þ x Þ x
x þx
2. Ableitung (Kettenregel):
2
¼ 2 ðx þ x 3 Þ 1 ¼ 2 u 1 mit u ¼ x þ x 3 ; u 0 ¼ 1 þ 3 x 2
x þ x3
|fflfflffl{zfflfflffl}
u
2 ð1 þ 3 x 2 Þ
2u0
2 þ 6x2
00
2
0
2
0
u ¼
¼
¼
f ðxÞ ¼ 2 ð u Þ u ¼ 2 u
u2
ðx þ x 3 Þ 2
ðx þ x 3 Þ 2
f 0 ðxÞ ¼
206
D Taylor- und Fourier-Reihen
3. Ableitung (Quotienten- und Kettenregel):
f 00 ðxÞ ¼
2 þ 6x2
ðx þ
x 3Þ 2
¼
u
v
v ¼ ðx þ x 3 Þ 2 ¼ t 2
|fflfflffl{zfflfflffl}
t
u ¼ 2 þ 6x2 ;
und
u 0 ¼ 12 x ;
v 0 ¼ 2 t t 0 ¼ 2 ðx þ x 3 Þ ð1 þ 3 x 2 Þ
(Ableitung von v in der angedeuteten Weise mit der Kettenregel, Substitution t ¼ x þ x 3 ; t 0 ¼ 1 þ 3 x 2 )
f 000 ðxÞ ¼
12 x ðx þ x 3 Þ 2 2 ðx þ x 3 Þ ð1 þ 3 x 2 Þ ð2 þ 6 x 2 Þ
u0 v v0 u
¼
¼
v2
ðx þ x 3 Þ 4
¼
ðx þ x 3 Þ ½ 12 x ðx þ x 3 Þ 2 ð1 þ 3 x 2 Þ 2 ð1 þ 3 x 2 Þ
ðx þ x 3 Þ ðx þ x 3 Þ 3
¼
12 x ðx þ x 3 Þ 4 ð1 þ 3 x 2 Þ 2
ðx þ x 3 Þ 3
(Im Zähler den gemeinsamen Faktor ðx þ x 3 Þ ausklammern, dann kürzen)
Ableitungswerte an der Stelle x 0 ¼ 1:
f ð1Þ ¼ ln 2 ;
f 0 ð1Þ ¼ 1 ;
f 00 ð1Þ ¼ 2 ;
f 000 ð1Þ ¼ 5
Die Taylor-Reihe um den Entwicklungspunkt x 0 ¼ 1 lautet damit:
f 0 ð1Þ
f 00 ð1Þ
f 000 ð1Þ
1 þ x2
f ðxÞ ¼ ln
¼ f ð1Þ þ
ðx 1Þ 1 þ
ðx 1Þ 2 þ
ðx 1Þ 3 þ . . . ¼
1!
2!
3!
x2
¼ ln 2 þ
1
2
5
ðx 1Þ 1 þ
ðx 1Þ 2 þ
ðx 1Þ 3 þ . . . ¼
1
2
6
¼ ln 2 ðx 1Þ 1 þ ðx 1Þ 2
Konvergenzbereich: 0 < x < 2
D12
5
ðx 1Þ 3 þ . . .
6
(Symmetrisches Intervall mit dem Radius r ¼ 1 und x 0 ¼ 1)
Die Funktion f ðxÞ ¼ x sin x ist um die Stelle x 0 ¼ p nach Taylor in eine Potenzreihe zu entwickeln.
Ableitungen bis zur 3. Ordnung
Wir verwenden jeweils in der angedeuteten Weise die Produktregel.
f 0 ðxÞ ¼ u 0 v þ v 0 u ¼ 1 sin x þ ðcos xÞ x ¼ sin x þ x cos x
|ffl{zffl}
u
v
f
)
f
f ðxÞ ¼ x sin x
|{z}
u
v
f 00 ðxÞ ¼ cos x þ u 0 v þ v 0 u ¼ cos x þ 1 cos x þ ð sin xÞ x ¼ 2 cos x x sin x
|fflfflfflffl{zfflfflfflffl}
f ðxÞ
f 000 ðxÞ ¼ 2 sin x f 0 ðxÞ ¼ 2 sin x ðsin x þ x cos xÞ ¼ 3 sin x x cos x
Ableitungswerte an der Entwicklungsstelle x 0 ¼ p :
f ðpÞ ¼ p sin p ¼ 0 ;
|ffl{zffl}
0
f 0 ðpÞ ¼ sin p þ p cos p ¼ p ;
|ffl{zffl}
|fflffl{zfflffl}
0
1
f 000 ðpÞ ¼ 3 sin p p cos p ¼ p
|ffl{zffl}
|fflffl{zfflffl}
0
1
f 00 ðpÞ ¼ 2 cos p p sin p ¼ 2;
|fflffl{zfflffl}
|ffl{zffl}
1
0
1 Potenzreihenentwicklungen
207
Taylor-Reihe von f (x) = x . sin x um die Entwicklungsstelle x 0 = p
f ðxÞ ¼ x sin x ¼ f ðpÞ þ
f 0 ðpÞ
f 00 ðpÞ
f 000 ðpÞ
ðx pÞ 1 þ
ðx pÞ 2 þ
ðx pÞ 3 þ . . . ¼
1!
2!
3!
p
2
p
ðx pÞ 1 þ
ðx pÞ 2 þ
ðx pÞ 3 þ . . . ¼
1
2
6
p
¼ p ðx pÞ 1 ðx pÞ 2 þ
ðx pÞ 3 þ . . .
6
Konvergenzbereich: j x j < 1
¼ 0þ
D13
Entwickeln Sie die Funktion f ðxÞ ¼ ln
1þx
1x
in eine Mac Laurinsche Reihe bis zur 5. Potenz.
Wir bringen die Funktion zunächst in eine für das Differenzieren günstigere Form (mit j x j < 1):
1þx
a
¼ ln ð1 þ xÞ ln ð1 xÞ
Rechenregel: ln
¼ ln a ln b
f ðxÞ ¼ ln
1x
b
Ableitungen bis zur 5. Ordnung
Alle Ableitungen erhalten wir mit Hilfe der Kettenregel in der jeweils angedeuteten Weise:
f ðxÞ ¼ ln ð1 þ xÞ ln ð1 xÞ ¼ ln u ln v
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
f 0 ðxÞ ¼
ðu ¼ 1 þ x ;
u0 ¼ 1;
v ¼ 1 x;
v 0 ¼ 1Þ
1
1
1
1
1
1
u0
v0 ¼
1
ð 1Þ ¼
þ
¼ ð1 þ xÞ 1 þ ð1 xÞ 1
u
v
1þx
1x
1þx
1x
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
f 00 ðxÞ ¼ u 2 u 0 v 2 v 0 ¼ ð1 þ xÞ 2 1 ð1 xÞ 2 ð 1Þ ¼ ð1 þ xÞ 2 þ ð1 xÞ 2
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
f 000 ðxÞ ¼ 2 u 3 u 0 2 v 3 v 0 ¼ 2 ð1 þ xÞ 3 1 2 ð1 xÞ 3 ð 1Þ ¼ 2 ð1 þ xÞ 3 þ 2 ð1 xÞ 3
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
f
ð4Þ
ðxÞ ¼ 6 u 4 u 0 6 v 4 v 0 ¼ 6 ð1 þ xÞ 4 1 6 ð1 xÞ 4 ð 1Þ ¼
¼ 6 ð1 þ xÞ 4 þ 6 ð1 xÞ 4
|fflffl{zfflffl}
|fflffl{zfflffl}
u
v
f
ð5Þ
ðxÞ ¼ 24 u 5 u 0 24 v 5 v 0 ¼ 24 ð1 þ xÞ 5 1 24 ð1 xÞ 5 ð 1Þ ¼
¼ 24 ð1 þ xÞ 5 þ 24 ð1 xÞ 5
Ableitungswerte an der Entwicklungsstelle x 0 ¼ 0:
f ð0Þ ¼ ln 1 ln 1 ¼ 0 ;
f
ð4Þ
ð0Þ ¼ 6 þ 6 ¼ 0 ;
f 0 ð0Þ ¼ 1 þ 1 ¼ 2 ;
f
ð5Þ
f 000 ð0Þ ¼ 2 þ 2 ¼ 4 ;
ð0Þ ¼ 24 þ 24 ¼ 48
Mac Laurinsche Reihe von f (x) ¼ ln
f 00 ð0Þ ¼ 1 þ 1 ¼ 0 ;
1þx
1x
f 0 ð0Þ 1
f 00 ð0Þ 2
f 000 ð0Þ 3
f ð4Þ ð0Þ 4
f ð5Þ ð0Þ 5
1þx
¼ f ð0Þ þ
x þ
x þ
x þ
x þ
x þ ... ¼
f ðxÞ ¼ ln
1x
1!
2!
3!
4!
5!
¼ 0þ
2 1
0 2
4 3
0 4
48 5
2 3
2 5
x þ
x þ
x þ
x þ
x þ ... ¼ 2x þ
x þ
x þ ...
1
2
6
24
120
3
5
Konvergenzbereich: j x j < 1
208
D Taylor- und Fourier-Reihen
1
: Bestimmen Sie zunächst
1 þ x2
mit Hilfe der Binomischen Reihe (! Formelsammlung) die Reihenentwicklung der Ableitung und daraus durch Integration die Mac Laurinsche Reihe von arctan x (Angabe der ersten vier Glieder).
Die Ableitung von f ðxÞ ¼ arctan x lautet bekanntlich f 0 ðxÞ ¼
D14
Aus der Formelsammlung entnehmen wir die Mac Laurinsche Reihe von
1
¼ ð1 þ uÞ 1 ¼ 1 u þ u 2 u 3 þ . . .
1þu
1
¼ ð1 þ uÞ 1 . Sie lautet:
1þu
ðj u j < 1Þ
Mit der Substitution u ¼ x 2 erhalten wir daraus die Potenzreihenentwicklung der Funktion
1
¼ ð1 þ x 2 Þ 1 ¼ 1 x 2 þ x 4 x 6 þ . . .
1 þ x2
1
:
1 þ x2
ðj x j < 1Þ
Diese Reihe ist zugleich die 1. Ableitung von arctan x . Durch gliedweise Integration der Potenzreihe erhalten wir
daher die gesuchte Potenzreihenentwicklung der Arkustangensfunktion (wir ersetzen dabei die Variable x durch die
Integrationsvariable t, um Missverständnisse zu vermeiden):
x
ðx
ðx
1
1 3
1 5
1 7
2
4
6
t þ
t
t þ ... ¼
d t ¼ ð1 t þ t t þ . . .Þ d t ¼ t
arctan x ¼
3
5
7
1 þ t2
0
0
0
¼
D15
x
1 3 1 5 1 7
1 3 1 5
1 7
x þ x x þ . . . ð0Þ ¼ x
x þ x
x þ ...
3
5
7
3
5
7
ðj x j < 1Þ
Wie lautet die Mac Laurinsche Reihe von f ðxÞ ¼ ln ð1 þ e a x Þ mit a 2 R?
Bildung aller Ableitungen bis zur 3. Ordnung
1. Ableitung (Kettenregel mit zwei Substitutionen)
f ðxÞ ¼ ln ð1 þ e a x Þ ¼ ln v mit
f 0 ðxÞ ¼
v ¼ 1 þ eu
und
u ¼ ax
1
1
a eu
a eu
a e ax
ð0 þ e u Þ a ¼
eu a ¼
¼
¼
v
v
v
1 þ eu
1 þ e ax
(Zuerst ln v nach v, dann v ¼ 1 þ e u nach u und schließlich u ¼ a x nach x differenzieren)
2. Ableitung (Quotientenregel in Verbindung mit der Kettenregel)
f 0 ðxÞ ¼
a e ax
u
¼
v
1 þ e ax
mit
u ¼ a e ax ;
v ¼ 1 þ e ax
und
u 0 ¼ a2 e ax ;
v 0 ¼ a e ax
(Ableitung von e a x nach der Kettenregel, Substitution: t ¼ a x)
f 00 ðxÞ ¼
¼
u0 v v0 u
v2
¼
a 2 e a x ð1 þ e a x Þ a e a x a e a x
ð1 þ e a x Þ 2
a2 e ax
ð1 þ
Rechenregel: e m e m ¼ ðe m Þ 2 ¼ e 2 m
e a xÞ 2
3. Ableitung (Quotienten- und Kettenregel)
f 00 ðxÞ ¼
a2 e ax
ð1 þ
e a xÞ 2
¼
¼
u
v
a2 e ax þ a2 e 2ax a2 e 2ax
ð1 þ e a x Þ 2
¼
1 Potenzreihenentwicklungen
u ¼ a2 e ax ;
209
v ¼ ð1 þ e a x Þ 2 und u 0 ¼ a 3 e a x ; v 0 ¼ 2 ð1 þ e a x Þ a e a x ¼ 2 a ð1 þ e a x Þ e a x
(die Ableitung von v ¼ ð1 þ e a x Þ 2 erhält man nach der Kettenregel: v ¼ z 2
f 000 ðxÞ ¼
¼
mit
z ¼ 1 þ e t ; t ¼ a xÞ
a 3 e a x ð1 þ e a x Þ 2 2 a ð1 þ e a x Þ e a x a 2 e a x
u0 v v0 u
¼
¼
v2
ð1 þ e a x Þ 4
a 3 e a x ð1 þ e a x Þ ½ ð1 þ e a x Þ 2 e a x
ð1 þ e a x Þ3 ð1 þ e a x Þ
¼
a 3 e a x ð1 e a x Þ
ð1 þ e a x Þ 3
Umformungen: Im Zähler zunächst den Faktor a 3 e a x ð1 þ e a x Þ ausklammern, dann 1 þ e a x kürzen.
Ableitungswerte an der Stelle x 0 ¼ 0:
f ð0Þ ¼ ln ð1 þ e 0 Þ ¼ ln ð1 þ 1Þ ¼ ln 2 ;
f 00 ð0Þ ¼
a2 e 0
ð1 þ e 0 Þ 2
¼
a2 1
ð1 þ 1Þ 2
¼
a2
;
4
f 0 ð0Þ ¼
f 000 ð0Þ ¼
a e0
a1
a
¼
¼
;
1þ1
2
1 þ e0
a 3 e 0 ð1 e 0 Þ
ð1 þ e 0 Þ 3
¼
a 3 1 ð1 1Þ
ð1 þ 1Þ 3
¼ 0
Mac Laurinsche Reihe von f (x) = ln (1 + e a x )
f ðxÞ ¼ ln ð1 þ e a x Þ ¼ f ð0Þ þ
¼ ln 2 þ
f 0 ð0Þ 1
f 00 ð0Þ 2
f 000 ð0Þ 3
x þ
x þ
x þ ... ¼
1!
2!
3!
a=2 1
a 2 =4 2
0 3
a
a2 2
x þ
x þ
x þ 0 x3 þ ...
x þ . . . ¼ ln 2 þ
x þ
1
2
8
6
2
Konvergenzbereich: j x j < 1
D16
1
¼ 1 þ x 1 þ x 2 þ x 3 þ . . . þ x n þ . . . ðj x j < 1Þ
1x
die Mac Laurinsche Reihe von f ðxÞ ¼ ð1 xÞ 3 her. Wie lautet das Bildungsgesetz für die Koeffi-
Leiten Sie aus der geometrischen Reihe
zienten dieser Reihe?
Wir zeigen zunächst (mit Hilfe der Kettenregel), dass die Funktion f ðxÞ ¼ ð1 xÞ 3 bis auf einen konstanten Fak1
tor genau die 2. Ableitung von y ¼
ist:
1x
1
¼ ð1 xÞ 1 ¼ u 1 mit u ¼ 1 x ; u 0 ¼ 1
y ¼
1x
|fflffl{zfflffl}
u
y 0 ¼ u 2 u 0 ¼ ð1 xÞ 2 ð 1Þ ¼ ð1 xÞ 2 ¼ u 2
|fflffl{zfflffl}
u
mit u ¼ 1 x ;
u0 ¼ 1
y 00 ¼ 2 u 3 u 0 ¼ 2 ð1 xÞ 3 ð 1Þ ¼ 2 ð1 xÞ 3 ¼ 2 f ðxÞ
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
f ðxÞ
Daraus folgt (wie behauptet):
f ðxÞ ¼ ð1 xÞ 3 ¼
1
y 00
2
mit
y ¼ ð1 xÞ 1 ¼
1
1x
Die gesuchte Potenzreihe von f ðxÞ ¼ ð1 xÞ 3 erhalten wir daher, indem wir die bekannte Potenzreihe von
y ¼ ð1 xÞ 1 zweimal nacheinander gliedweise nach x differenzieren und den gefundenen Ausdruck dann in diese
Gleichung einsetzen:
210
D Taylor- und Fourier-Reihen
y ¼ ð1 xÞ 1 ¼ 1 þ x 1 þ x 2 þ x 3 þ x 4 þ . . . þ x n þ x n þ 1 þ x n þ 2 þ . . .
y 0 ¼ 1 þ 2 x 1 þ 3 x 2 þ 4 x 3 þ . . . þ n x n 1 þ ðn þ 1Þ x n þ ðn þ 2Þ x n þ 1 þ . . .
y 00 ¼ 2 1 þ 3 2 x 1 þ 4 3 x 2 þ . . . þ n ðn 1Þ x n 2 þ ðn þ 1Þ n x n 1 þ ðn þ 2Þ ðn þ 1Þ x n þ . . .
Somit gilt:
1 00
y ¼
2
f ðxÞ ¼ ð1 xÞ 3 ¼
¼
1
2 1 þ 3 2 x 1 þ 4 3 x 2 þ . . . þ n ðn 1Þ x n 2 þ ðn þ 1Þ n x n 1 þ ðn þ 2Þ ðn þ 1Þ x n þ . . .
2 |{z} |{z}
|{z}
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
a1
a2
a n2
a n1
an
a0
Das Bildungsgesetz für die Koeffizienten lautet (bis auf den gemeinsamen Faktor 1=2):
a n ¼ ð n þ 2Þ ðn þ 1Þ
für
n ¼ 0; 1; 2; . . .
Damit erhalten wir die folgende Potenzreihenentwicklung für f ðxÞ ¼ ð1 xÞ 3 (in der Summenschreibweise):
f ðxÞ ¼ ð1 xÞ 3 ¼
1
1 P
ðn þ 2Þ ðn þ 1Þ x n
2 n¼0
Die Reihe konvergiert wie die geometrische Reihe für j x j < 1.
1.2 Anwendungen
Lehrbuch: Band 1, Kapitel VI.3.3
Formelsammlung: Kapitel VI.3
D17
Bestimmen Sie mit Hilfe der Potenzreihenentwicklung eine Näherungsparabel der Funktion
pffiffiffiffiffiffiffiffiffiffi
f ðxÞ ¼ ln cos x in der Umgebung der Stelle x 0 ¼ 0.
Wir entwickeln die Funktion in eine Mac Laurinsche Reihe, brechen diese nach dem quadratischen Glied ab und
erhalten eine Näherung in Form einer Parabel:
f ðxÞ ¼ ln
pffiffiffiffiffiffiffiffiffiffi
cos x
f ð0Þ þ
f 0 ð0Þ 1
f 00 ð0Þ 2
x þ
x
1!
2!
Ableitungen 1. und 2. Ordnung
Die 1. Ableitung erhalten wir mit Hilfe der Kettenregel:
pffiffiffiffiffiffiffiffiffiffi
1
1
cos x ¼ ln ðcos xÞ 1=2 ¼
ln ðcos x Þ ¼
ln u
2
2
|ffl{zffl}
u
Rechenregel: ln a n ¼ n ln a
f ðxÞ ¼ ln
f 0 ðxÞ ¼
mit
u ¼ cos x ;
u 0 ¼ sin x
1 1
1
1
1 sin x
1
u0 ¼
ð sin xÞ ¼
¼
tan x
2 u
2 cos x
2 cos x
2
f 00 ðxÞ ¼
1
ð1 þ tan 2 xÞ
2
Ableitungswerte an der Stelle x 0 ¼ 0 (unter Berücksichtigung von cos 0 ¼ 1; tan 0 ¼ 0):
f ð0Þ ¼ ln
pffiffiffiffiffiffiffiffiffiffiffi
cos 0 ¼ ln 1 ¼ 0 ;
f 0 ð0Þ ¼
1
tan 0 ¼ 0 ;
2
f 00 ð0Þ ¼
1
1
ð1 þ tan 2 0Þ ¼
2
2
1 Potenzreihenentwicklungen
211
Näherungsparabel (in der Umgebung von x 0 = 0)
f ðxÞ ¼ ln
pffiffiffiffiffiffiffiffiffiffi
cos x
f ð0Þ þ
f 0 ð0Þ 1
f 00 ð0Þ 2
0 1
1=2 2
1 2
x þ
x ¼ 0þ
x þ
x ¼
x
1!
2!
1
2
4
Bild D-2 zeigt den Verlauf der Näherungsparabel.
y
Bild D-2
–3
–2
–1
1
2
x
3
– 0,5
Näherungsparabel
– 1,5
y = ln cos x
1
soll in der Umgebung der Stelle x 0 ¼ 0 durch eine Parabel ersetzt
1 sin x
werden. Welchen Näherungswert liefert diese Parabel an der Stelle x ¼ 0;2?
Die Funktion f ðxÞ ¼
D18
Lösungsweg: f ðxÞ wird nach Mac Laurin in eine Potenzreihe entwickelt, die Reihe dann nach dem quadratischen
Glied abgebrochen.
Ableitungen 1. und 2. Ordnung
1. Ableitung (Kettenregel):
f ðxÞ ¼
1
¼ ð1 sin xÞ 1 ¼ u 1
1 sin x
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
mit u ¼ 1 sin x ;
f 0 ðxÞ ¼ 1 u 2 u 0 ¼ ð1 sin xÞ 2 ð cos xÞ ¼
u 0 ¼ cos x
cos x
ð1 sin xÞ 2
2. Ableitung (Quotienten- und Kettenregel):
cos x
f 0 ðxÞ ¼
ð1 sin xÞ
u ¼ cos x ;
2
¼
u
v
v ¼ ð1 sin xÞ 2
und u 0 ¼ sin x ;
v 0 ¼ 2 ð1 sin xÞ cos x
(v wurde nach der Kettenregel differenziert, Substitution: t ¼ 1 sin x mit t 0 ¼ cos x)
sin x ð1 sin xÞ 2 þ ½ 2 ð1 sin xÞ cos x cos x
u0 v v0 u
¼
¼
f ðxÞ ¼
v2
ð1 sin xÞ 4
00
¼
ð1 sin xÞ ½ sin x ð1 sin xÞ þ 2 cos 2 x
ð1 sin xÞ ð1 sin xÞ 3
¼
sin x ð1 sin xÞ þ 2 cos 2 x
ð1 sin xÞ 3
Umformungen: Im Zähler zunächst den gemeinsamen Faktor 1 sin x ausklammern, dann kürzen.
Ableitungswerte an der Stelle x 0 ¼ 0 (unter Berücksichtigung von sin 0 ¼ 0, cos 0 ¼ 1):
f ð0Þ ¼
1
¼ 1;
1 sin 0
f 0 ð0Þ ¼
cos 0
ð1 sin 0Þ 2
¼ 1;
f 00 ð0Þ ¼
sin 0 ð1 sin 0Þ þ 2 cos 2 0
ð1 sin 0Þ 3
¼ 2
212
D Taylor- und Fourier-Reihen
Näherungsparabel in der Umgebung von x 0 = 0 (siehe Bild D-3)
1
1 sin x
f ðxÞ ¼
f ð0Þ þ
f 0 ð0Þ 1
f 00 ð0Þ 2
1 1
2 2
x þ
x ¼ 1þ
x þ
x ¼ 1 þ x þ x2
1!
2!
1
2
Exakter Wert an der Stelle x ¼ 0;2:
f ð0;2Þ ¼
y
1
¼ 1;2479
1 sin 0;2
Näherungswert an der Stelle x ¼ 0;2:
f ð0;2Þ
y=
1
1 – sin x
4
3
Näherungsparabel
2
1 þ 0;2 þ 0;2 2 ¼ 1;24
Näherungsparabel
1
Bild D-3
– 1,5
D19
–1
– 0,5
0,5
1
1,5
x
Bestimmen Sie durch Reihenentwicklung eine Näherungsparabel der Funktion f ðxÞ ¼ e x cos ðx=2Þ
für die Stelle x 0 ¼ 0. Die Reihenentwicklung soll
a) auf direktem Wege über die Ableitungen,
b) durch Reihenmultiplikation gewonnen werden.
a) Wir entwickeln f ðxÞ nach Mac Laurin in eine Potenzreihe und brechen diese nach dem quadratischen Glied ab.
Zunächst aber bestimmen wir die dabei benötigten Ableitungen f 0 ðxÞ und f 00 ðxÞ.
1. Ableitung (Produkt- und Kettenregel)
f
1
f ðxÞ ¼ e x cos ðx=2Þ ¼ u v mit u ¼ e x ; v ¼ cos ðx=2Þ und u 0 ¼ e x ; v 0 ¼
sin ðx=2Þ
|fflfflfflfflffl{zfflfflfflfflffl}
2
u
v
(v wurde nach der Kettenregel differenziert, Substitution: t ¼ x=2)
1
1
f 0 ðxÞ ¼ u 0 v þ v 0 u ¼ e x cos ðx=2Þ
sin ðx=2Þ e x ¼ e x cos ðx=2Þ
sin ðx=2Þ
2
2
f
2. Ableitung (Produkt- und Kettenregel)
1
f 0 ðxÞ ¼ e x cos ðx=2Þ
sin ðx=2Þ ¼ u v
2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
u
v
1
sin ðx=2Þ und
u ¼ e x ; v ¼ cos ðx=2Þ
2
u0 ¼ ex ;
v0 ¼
1
1
sin ðx=2Þ
cos ðx=2Þ
2
4
(die beiden Summanden in v wurden jeweils mit Hilfe der Kettenregel differenziert, Substitution: t ¼ x=2)
1
1
1
f 00 ðxÞ ¼ u 0 v þ v 0 u ¼ e x cos ðx=2Þ
sin ðx=2Þ þ
sin ðx=2Þ
cos ðx=2Þ e x ¼
2
2
4
1
1
1
3
x
x
¼ e cos ðx=2Þ
sin ðx=2Þ
sin ðx=2Þ
cos ðx=2Þ ¼ e
cos ðx=2Þ sin ðx=2Þ
2
2
4
4
Ableitungswerte an der Stelle x 0 ¼ 0 (unter Berücksichtigung von e 0 ¼ 1, cos 0 ¼ 1 und sin 0 ¼ 0Þ:
1
3
3
f ð0Þ ¼ e 0 cos 0 ¼ 1 ; f 0 ð0Þ ¼ e 0 cos 0
sin 0 ¼ 1 ; f 00 ð0Þ ¼ e 0
cos 0 sin 0 ¼
2
4
4
1 Potenzreihenentwicklungen
213
Näherungsparabel in der Umgebung von x 0 = 0
f ðxÞ ¼ e x cos ðx=2Þ
f ð0Þ þ
f 0 ð0Þ 1
f 00 ð0Þ 2
3=4 2
1 1
3 2
x þ
x ¼ 1þ
x ¼ 1þx þ
x þ
x
1!
2!
2
1
8
b) Aus der Formelsammlung entnehmen wir die folgenden Mac Laurinschen Reihen:
ex ¼ 1 þ
x1
x2
1 2
þ
þ ... ¼ 1 þ x þ
x þ ...
1!
2!
2
und
cos z ¼ 1
z2
þ ...
2!
Die Kosinusreihe geht durch die Substitution z ¼ x=2 über in:
cos ðx=2Þ ¼ 1
ðx=2Þ 2
1 2
þ ... ¼ 1
x þ ...
2!
8
Reihenmultiplikation liefert dann das gewünschte Ergebnis:
1 2
1 2
f ðxÞ ¼ e x cos ðx=2Þ ¼ 1 þ x þ
x þ ... 1
x þ ... ¼
2
8
1 2
1 2
3 2
x þx þ
x þ ... ¼ 1 þ x þ
x þ ...
8
2
8
3 2
Näherungsparabel: f ðxÞ ¼ e x cos ðx=2Þ
x
1þx þ
8
ð j x j < 1Þ
¼ 1
D20
1
Die Funktion f ðxÞ ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi soll in der Umgebung von x 0 ¼ 0 durch ein Polynom 6. Grades
1 x3
ersetzt werden. Welchen Näherungswert liefert diese Näherungsfunktion an der Stelle x ¼ 0,2? Wie
lässt sich der Fehler (größenordnungsmäßig) abschätzen?
Hinweis: Die benötigte Potenzreihenentwicklung der Funktion lässt sich aus der Binomischen Reihe
(! Formelsammlung) leicht herleiten.
Wir benötigen für die Herleitung der Näherungsfunktion (Polynomfunktion 6. Grades) die Mac Laurinsche Reihe der
vorgegebenen Funktion. Diese lässt sich mit Hilfe der Substitution u ¼ x 3 aus der folgenden (als bekannt vorausgesetzten und der Formelsammlung entnommenen) Binomischen Reihe gewinnen:
1
1
1
13 2
135 3
¼ ð1 uÞ 1=2 ¼ 1 þ
uþ
u þ
u þ ... ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
1=2
2
2
4
246
1u
ð1 uÞ
¼ 1þ
1
3 2
5 3
uþ
u þ
u þ ...
2
8
16
ð j u j < 1Þ
(das kubische Glied benötigen wir für die Fehlerabschätzung!)
Die Substitution u ¼ x 3 führt zu der Mac Laurinschen Reihe der Ausgangsfunktion:
1
1
3
5
1 3
3 6
5 9
ðx 3 Þ 1 þ
ðx 3 Þ 2 þ
ðx 3 Þ 3 þ . . . ¼ 1 þ
x þ
x þ
x þ ...
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 1 þ
2
8
16
2
8
16
1 x3
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflffl{zfflfflffl}
Näherungsfunktion
Näherungsfunktion:
f ðxÞ ¼ 1 þ
1 3
3 6
x þ
x
2
8
Fehler
(in der Umgebung von x 0 ¼ 0Þ
Das erste in der Reihenentwicklung weggelassene Glied bestimmt dabei die Größenordnung des Fehlers. An der Stelle
x ¼ 0,2 erhalten wir:
Näherungswert: f ð0,2Þ
1þ
1
3
0,2 3 þ
0,2 6 ¼ 1,004 024;
2
8
1
Exakter Funktionswert: f ð0,2Þ ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 1,004 024 161
1 0,2 3
Fehler:
5
0,2 9 ¼ 1,6 10 7
16
214
D Taylor- und Fourier-Reihen
Die Funktion f ðxÞ ¼ ð1 þ e x Þ 2 soll in der Umgebung von x 0 ¼ 0 durch eine Polynomfunktion
D21
3. Grades angenähert werden. Welchen Näherungswert erhält man an der Stelle x ¼ 0;1 im Vergleich
zum exakten Funktionswert?
Wir entwickeln die Funktion um die Stelle x 0 ¼ 0 in eine Potenzreihe (Mac Laurinsche Reihe) und brechen diese
nach dem kubischen Glied ab. Zunächst aber bilden wir die benötigten Ableitungen bis einschließlich 3. Ordnung:
f ðxÞ ¼ ð1 þ e x Þ 2 ¼ u 2
|fflfflffl{zfflfflffl}
u
u ¼ 1 þ ex ;
mit
u0 ¼ ex
f 0 ðxÞ ¼ 2 u u 0 ¼ 2 ð1 þ e x Þ e x ¼ 2 ðe x þ e 2 x Þ
f 00 ðxÞ ¼ 2 ðe x þ 2 e 2 x Þ ;
ðKettenregel!Þ
f 000 ðxÞ ¼ 2 ðe x þ 4 e 2 x Þ
(die Ableitung von e 2 x erfolgte nach der Kettenregel, Substitution: t ¼ 2 x)
Ableitungswerte an der Stelle x 0 ¼ 0 (unter Berücksichtigung von e 0 ¼ 1):
f ð0Þ ¼ ð1 þ 1Þ 2 ¼ 4 ;
f 0 ð0Þ ¼ 2 ð1 þ 1Þ ¼ 4 ;
f 00 ð0Þ ¼ 2 ð1 þ 2Þ ¼ 6 ;
f 000 ð0Þ ¼ 2 ð1 þ 4Þ ¼ 10
Näherungspolynom 3. Grades in der Umgebung der Stelle x 0 = 0
f ðxÞ ¼ ð1 þ e x Þ 2
¼ 4þ
f ð0Þ þ
f 0 ð0Þ 1
f 00 ð0Þ 2
f 000 ð0Þ 3
x þ
x þ
x ¼
1!
2!
3!
4 1
6 2
10 3
5 3
x þ
x þ
x ¼ 4 þ 4x þ 3x2 þ
x
1
2
6
3
Näherungswert an der Stelle x ¼ 0;1:
Exakter Wert an der Stelle x ¼ 0;1:
D22
f ð0;1Þ
4 þ 0;4 þ 0;03 þ 0;00166 ¼ 4;43166
4;4317
f ð0;1Þ ¼ ð1 þ e 0;1 Þ 2 ¼ ð1 þ 1;10517Þ 2 ¼ 2;10517 2 ¼ 4;43174
Bestimmen Sie für die Funktion f ðxÞ ¼
4;4317
cos ð2 xÞ
das Mac Laurinsche Näherungspolynom 4. Grades.
ð1 xÞ 2
Die Potenzreihenentwicklung soll dabei durch Reihenmultiplikation erfolgen.
Wir schreiben zunächst die Funktion als Produkt:
f ðxÞ ¼
cos ð2 xÞ
ð1 xÞ
2
¼ cos ð2 xÞ ð1 xÞ 2
Aus der Formelsammlung entnehmen wir die Mac Laurinschen Reihen von cos u und ð1 xÞ 2 , wobei wir in der
Kosinusreihe u durch 2 x substituieren:
cos u ¼ 1
u2
u4
u2
u4
þ
þ ... ¼ 1
þ
þ ...
2!
4!
2
24
)
ðSubstitution u ¼ 2 xÞ
ð2 xÞ 2
ð2 xÞ 4
2 4
cos ð2 xÞ ¼ 1
þ
þ ... ¼ 1 2x2 þ
x þ ...
2
24
3
ð1 xÞ 2 ¼ 1 þ 2 x þ 3 x 2 þ 4 x 3 þ 5 x 4 þ . . .
ðj x j < 1Þ
ð j x j < 1Þ
1 Potenzreihenentwicklungen
215
Durch Reihenmultiplikation folgt dann (es werden nur Glieder bis einschließlich x 4 berücksichtigt):
f ðxÞ ¼
cos ð2 xÞ
2
¼ cos ð2 xÞ ð1 xÞ 2 ¼
ð1 xÞ
2 4
x þ . . . ð1 þ 2 x þ 3 x 2 þ 4 x 3 þ 5 x 4 þ . . .Þ ¼
¼ 1 2x2 þ
3
¼ 1 þ 2x þ 3x2 þ 4x3 þ 5x4 2x2 4x3 6x4 þ
Näherungspolynom 4. Grades: f ðxÞ ¼
cos ð2 xÞ
ð1 xÞ
2
1 þ 2x þ x2
2 4
1 4
x þ ... ¼ 1 þ 2x þ x2
x þ ...
3
3
1 4
x
3
(in der Umgebung von x 0 ¼ 0Þ
Gegeben ist die Kurve mit der Gleichung
y ¼ a ½ x b ð1 e x=b Þ
D23
(a > 0; b > 0: reelle Konstanten)
Bestimmen Sie mit Hilfe der Potenzreihenentwicklung die Näherungsparabel dieser Kurve in der Umgebung von x 0 ¼ 0.
Hinweis: Die Potenzreihenentwicklung lässt sich aus der bekannten Mac Laurinschen Reihe der
e-Funktion gewinnen.
Wir gehen von der aus der Formelsammlung entnommenen Mac Laurinschen Reihe von eu aus, ersetzen dort u durch
x=b, brechen dann die Entwicklung nach dem quadratischen Glied ab und setzen schließlich den gefundenen Ausdruck in die vorgegebene Funktion ein:
x
x2
þ ...
þ
b
2 b2
x
x2
x
x2
x=b
y ¼ a ½ x b ð1 e
Þ ¼ a x b 1 1 þ
þ ...
¼ a xb
þ ...
¼
b 2 b2
b 2 b2
2
x2
x
a 2
x þ ...
ð j x j < 1Þ
þ ... ¼ a
þ ... ¼
¼ a x x þ
2b
2b
2b
eu ¼ 1 þ
u1
u2
þ
þ ...
1!
2!
Näherungsparabel: y ¼
)
e x=b ¼ 1
x
1
þ
b
2
x
b
a 2
x
2b
2
þ ... ¼ 1
y
(in der Umgebung von x ¼ 0; siehe Bild D-4)
3
Näherungsparabel
2
y = a [x – b (1 – e – x / b )]
1
Bild D-4
–1
D24
Durch die Gleichung
R
U
t
L
I ðtÞ ¼
;
1e
R
1
2
x
t 0
wird die zeitliche Abhängigkeit der Stromstärke I in einem RL-Stromkreis beschrieben. Linearisieren
Sie diese Funktion für t 0 ¼ 0.
( R: Ohmscher Widerstand; U : angelegte Spannung; L: Induktivität; t : Zeit)
216
D Taylor- und Fourier-Reihen
In der als bekannt vorausgesetzten Mac Laurinschen Reihe von e x (! Formelsammlung) substitutieren wir
R
x ¼
t , brechen die Reihe nach dem linearen Glied ab und ersetzen die Exponentialfunktion durch diesen lineaL
ren Ausdruck:
R
x1
R
R
t
t þ ...
1
t
þ ... ¼ 1 þ x þ ... ) e L ¼ 1
L
L
1!
R
U
U
R
U
R
U
R
U
t
L
I ¼
1e
1 1
t
¼
11þ
t ¼
t ¼
t
R
R
R
L
R
L
L
L
ex ¼ 1 þ
Linearisierte Funktion:
U
t
L
I
(für kleine Zeitwerte t 0)
Anmerkung: Die „Sättigungsfunktion‘‘ (exakte Funktion) wurde durch die Tangente in t ¼ 0 ersetzt (siehe Bild D-5):
I
I= U t
L
U
R
I= U
R
1– e
–R t
L
Bild D-5
t
D25
Bestimmen Sie mit Hilfe der Potenzreihenentwicklung eine Näherungsparabel für die Kosinusfunktion
in der Umgebung der Stelle x 0 ¼ p .
Die Näherungsparabel erhalten wir, indem wir die Kosinusfunktion zunächst um die Stelle x 0 ¼ p in eine TaylorReihe entwickeln und diese dann nach dem quadratischen Glied abbrechen. Mit
f ðxÞ ¼ cos x ;
f 0 ðxÞ ¼ sin x ;
f 00 ðxÞ ¼ cos x
und somit
f ðpÞ ¼ cos p ¼ 1 ;
f 0 ðpÞ ¼ sin p ¼ 0 ;
f 00 ðpÞ ¼ cos p ¼ 1
folgt dann:
f ðxÞ ¼ cos x ¼ f ðpÞ þ
¼ 1 þ
f 0 ðpÞ
f 00 ðpÞ
ðx pÞ 1 þ
ðx pÞ 2 þ . . . ¼
1!
2!
0
1
1
ðx pÞ 1 þ
ðx pÞ 2 þ . . . ¼ 1 þ
ðx pÞ 2 þ . . .
1
2
2
Näherungsparabel (siehe Bild D-6):
ð j x j < 1Þ
y
1
ðx pÞ 2
y ¼ 1 þ
2
1
(in der Umgebung von x 0 ¼ p )
Näherungsparabel
y = cos x
p
Bild D-6
p/2
–1
3p/2
x
1 Potenzreihenentwicklungen
217
Lösen Sie die Gleichung e x ¼ sinh x þ 3 näherungsweise mit Hilfe der Potenzreihenentwicklung.
D26
Hinweis: Verwenden Sie die Mac Laurinschen Reihen von e x und sinh x und brechen Sie diese nach
der 5. Potenz ab.
Aus der Formelsammlung entnehmen wir die folgenden beständig konvergierenden Potenzreihen:
sinh x ¼
x1
x3
x5
1 3
1
x þ
x5 þ ...
þ
þ
þ ... ¼ x þ
6
120
1!
3!
5!
ex ¼ 1 þ
x1
x2
x3
x4
x5
1 2
1 3
1 4
1
þ
þ
þ
þ
þ ... ¼ 1 þ x þ
x þ
x þ
x þ
x5 þ ...
1!
2!
3!
4!
5!
2
6
24
120
Mit den nach der 5. Potenz abgebrochenen Reihen erhält man eine leicht lösbare Näherungsgleichung:
1 2
1 3
1 4
1
1 3
1
x þ
x þ
x þ
x5 ¼ x þ
x þ
x5 þ 3 )
2
6
24
120
6
120
1 2
1 4
1 4
1 2
1þ
x þ
x ¼ 3 )
x þ
x 2 ¼ 0 24 ) x 4 þ 12 x 2 48 ¼ 0
2
24
24
2
1þx þ
Diese biquadratische Gleichung wird durch die Substitution u ¼ x 2 wie folgt gelöst:
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u 2 þ 12 u 48 ¼ 0 ) u 1=2 ¼ 6 36 þ 48 ¼ 6 84 ¼ 6 9,16515
u 1 ¼ 3,16515 ;
u 2 ¼ 15,16515 < 0
)
ðdieser Wert scheidet wegen u ¼ x 2 > 0 ausÞ
Rücksubstitution liefert aus dem positiven Wert u 1 zwei Lösungen:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 ¼ u 1 ¼ 3,16515 ) x 1=2 ¼ 3,16515 ¼ 1,77909
1,779
Anmerkung: Die Gleichung lässt sich unter Verwendung der Definitionsformeln für die Hyperbelfunktionen sinh x
und cosh x auch wie folgt exakt lösen (! FS: Kap. III.11.1):
e x ¼ sinh x þ 3
ex
)
ex ¼
1
1
ex þ
ex ¼ 3
2
2
cosh x ¼ 3
)
1
ðe x e x Þ þ 3
2
)
x ¼ arcosh 3
)
ex ¼
1
1
ex þ
ex ¼ 3
2
2
1
1
ex
ex þ 3
2
2
)
1
ðe x þ e x Þ ¼ 3
2
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
cosh x
1,763
Bild D-7 zeigt die grafische Lösung (Schnittpunkte der Kurven y ¼ e x und y ¼ sinh x þ 3) .
y
6
4
y = sinh x + 3
2
y = ex
Bild D-7
– 1,2 – 0,6
» – 1,8
0,6
1,2
x
» 1,8
)
)
218
D Taylor- und Fourier-Reihen
D27
1
Welche Näherungsformeln erhält man für den Ausdruck pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi für j x j
1 x2
wicklung und Abbruch nach dem 1. bzw. 2. nichtkonstanten Glied?
1 durch Reihenent-
Wir gehen von der bekannten Binomischen Reihe für ð1 uÞ 1=2 aus (! Formelsammlung):
ð1 uÞ 1=2 ¼ 1
1
13 2
uþ
u
2
24
... ¼ 1
1
3 2
uþ
u
2
8
...
ðj u j < 1Þ
Durch die Substitution u ¼ x 2 erhalten wir hieraus die Mac Laurinsche Reihe unserer Ausgangsfunktion:
1
1
1
3
ðx 2 Þ 1 þ
ðx 2 Þ 2
¼ ð1 x 2 Þ 1=2 ¼ 1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
1=2
2
8
2Þ
ð1
x
1 x2
1 2
3 4
¼ 1
x þ
x
...
ðj x j < 1Þ
2
8
... ¼
Durch Abbruch nach dem 1. bzw. 2. nichtkonstanten Glied erhalten wir die gesuchten Näherungsformeln. Sie lauten
wie folgt ðj x j
1Þ:
1. Näherung: ð1 x 2 Þ 1=2
1
1 2
x
2
2. Näherung: ð1 x 2 Þ 1=2
1
1 2
3 4
x þ
x
2
8
Die Masse m eines Elektrons nimmt nach der Relativitätstheorie mit der Geschwindigkeit v zu. Es gilt:
D28
m0
m ¼ m ðvÞ ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 ðv=cÞ 2
m 0 : Ruhemasse des Elektrons
c:
Lichtgeschwindigkeit
Entwickeln Sie mit Hilfe der Potenzreihenentwicklung eine Näherungsformel für die Abhängigkeit zwischen Masse und Geschwindigkeit unter der Annahme v
c.
Wir gehen von der Wurzelschreibweise zur Potenzschreibweise über:
m0
m0
¼ m 0 ½ 1 ðv=cÞ 2 1=2
m ¼ m ðvÞ ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
2
1=2
½ 1 ðv=cÞ
1 ðv=cÞ 2
Der Ausdruck ½ 1 ðv=cÞ 2 1=2 entspricht der aus der Formelsammlung entnommenen Binomischen Reihe
ð1 xÞ 1=2 ¼ 1 þ
1 1
13 2
1
3 2
x þ
x þ ... ¼ 1 þ
x þ
x þ ...
2
24
2
8
ðj x j < 1Þ
wenn wir dort x durch ðv=cÞ 2 ersetzen (substituieren):
½ 1 ðv=cÞ 2 1=2 ¼ 1 þ
1
2
v
c
2
þ
3
8
v
c
4
þ ... ¼ 1 þ
1
3
v2 þ
v4 þ . . .
2
2c
8 c4
v
< 1
c
Diese Entwicklung brechen wir nach dem 1. nichtkonstanten Glied ab und erhalten für die Masse m in Abhängigkeit
von der Geschwindigkeit v folgende Näherungsformel:
1
m ¼ m 0 ½ 1 ðv=cÞ 2 1=2
ðv
cÞ
m0 1 þ
v2
2 c2
Begründung: Wegen v
werden.
c sind die weggelassenen Glieder verschwindend klein und dürfen daher vernachlässigt
1 Potenzreihenentwicklungen
219
Lösen Sie näherungsweise die Gleichung cosh x þ x 2 ¼ 4 , indem Sie die Hyperbelfunktion durch
ihr Mac Laurinsches Näherungspolynom 4. Grades ersetzen. Sie erhalten eine leicht lösbare Näherungsgleichung.
D29
Wir verschaffen uns zunächst einen berblick über die zu erwartenden Lösungen, indem wir die Gleichung geringfügig umstellen: cosh x ¼ 4 x 2 . Die Lösungen dieser Gleichung sind die Schnittstellen der Kurven y ¼ cosh x
und y ¼ 4 x 2 . Aus der Zeichnung (Bild D-8) ergeben sich genau zwei spiegelsymmetrisch zueinander liegende
Werte in der Nähe von x 1=2 ¼ 1,4 .
y
y = 4 – x2
4
1
y = cosh x
Bild D-8
–1
x
1
≈ – 1,4
≈ 1,4
Bei der näherungsweisen Lösung dieser Gleichung ersetzen wir die Hyperbelfunktion durch die zugehörige nach der 4.
Potenz abgebrochene Mac Laurinsche Reihe (! Formelsammlung) und lösen dann die erhaltene biquadratische Gleichung in der bekannten Weise mit Hilfe einer Substitution:
cosh x
1þ
x2
x4
1 2
1 4
x þ
x
þ
¼ 1þ
2
24
2!
4!
cosh x þ x 2 ¼ 4
)
cosh x þ x 2 4 ¼ 0
1 4
3 2
x þ
x 3 ¼ 0 24
24
2
)
)
1þ
1 2
1 4
x þ
x þ x2 4 ¼ 0
2
24
)
x 4 þ 36 x 2 72 ¼ 0
Substitution: u ¼ x 2 ) u 2 þ 36 u 72 ¼ 0
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u 1=2 ¼ 18 324 þ 72 ¼ 18 396 ¼ 18 19;8997
)
u 1 ¼ 1;8997 ;
u 2 ¼ 37;8997
Rücksubstitution führt zu folgenden Näherungslösungen (u 2 < 0 scheidet wegen u ¼ x 2 > 0 aus):
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 ¼ u 1 ¼ 1;8997 ) x 1=2 ¼ 1;8997 ¼ 1;3783
D30
lim
x!0
cosh x 1
¼ ?
5x2
Berechnen Sie diesen Grenzwert mit Hilfe der Potenzreihenentwicklung.
Mit Hilfe der aus der Formelsammlung entnommenen Mac Laurinschen Reihe von cosh x lässt sich der Zähler des
Bruches wie folgt darstellen:
x2
x4
x6
x2
x4
x6
þ
þ
þ ... 1 ¼
þ
þ
þ ...
cosh x 1 ¼ 1 þ
2!
4!
6!
2!
4!
6!
220
D Taylor- und Fourier-Reihen
Wir dividieren beide Seiten gliedweise durch x 2 und erhalten (diese Division ist wegen x 6¼ 0 und somit
x 2 6¼ 0 erlaubt):
x2
x4
x6
þ
þ
þ ...
cosh x 1
1
x2
x4
2!
4!
6!
¼
¼
þ
þ ...
þ
4!
6!
2!
x2
x2
ðx 6¼ 0Þ
Jetzt lässt sich der Grenzwert leicht bestimmen:
cosh x 1
1
cosh x 1
1
lim
¼
¼
lim
lim
2
2
5 x!0
5 x!0
5x
x
x!0
1
x2
x4
1 1
1
þ
þ ... ¼
þ
¼
4!
6!
2!
5 2!
10
Unter Berücksichtigung des Luftwiderstandes besteht zwischen der Fallgeschwindigkeit v und dem
Fallweg s der folgende (komplizierte) Zusammenhang:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
2ks
mg
m
;
1e
v ¼ v ðsÞ ¼
k
D31
m : Masse des Körpers
g : Erdbeschleunigung
k : Reibungskoeffizient ðk > 0Þ
s 0
Wie lautet dieses Fallgesetz im luftleeren Raum ðk ¼ 0Þ?
Hinweis: Betrachten Sie v in Abhängigkeit vom Reibungskoeffizienten k und bestimmen Sie mit
Hilfe der Potenzreihenentwicklung den Grenzwert für k ! 0.
Wir betrachten die Geschwindigkeit v als eine vom Reibungskoeffizienten k abhängige Funktion. Alle übrigen Größen (also auch der Fallweg s) werden als Konstanten (Parameter) angesehen. Wir müssen dann den folgenden Grenzwert bestimmen:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
2ks
mg
m
v ðk ¼ 0Þ ¼ lim v ðkÞ ¼ lim
1e
k
k!0
k!0
Nach den Rechenregeln für Grenzwerte dürfen wir die Grenzwertbildung unter dem Wurzelzeichen vornehmen, außerdem darf der konstante Faktor m g vor den Grenzwert gezogen werden (! Bd. 1: Kap. III.4.2.3 und FS:
Kap. III.3.3):
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2ks
u
2ks
mg
1 e m
1 eak
t
m
1e
¼
m g lim
¼
m g lim
v ðk ¼ 0Þ ¼
lim
k
k
k!0 k
k!0
k!0
2s
gesetzt. Die direkte Berechnung des Grenzwertes
m
0
unter der Wurzel führt zu dem unbestimmten Ausdruck „ ‘‘ (mit k ! 0 strebt auch der Zähler gegen null:
0
1 e a k ! 1 e 0 ¼ 1 1 ¼ 0Þ. Wir schlagen daher den in der Aufgabenstellung bereits vorgegebenen Lösungsweg ein. In der Mac Laurinschen Reihe von e x (der Formelsammlung entnommen) ersetzen wir x durch a k :
Der besseren bersicht wegen haben wir (vorübergehend) a ¼
e x ¼ 1
x1
x2
x3
þ
þ ...
1!
2!
3!
)
e ak ¼ 1
ak
a2 k2
a3 k3
þ ...
þ
2!
3!
1!
Dann gilt (am Schluss wird noch gliedweise durch k dividiert):
1e
k
ak
1
¼
¼ a
ak
a2 k2
a3 k3
þ
þ ...
1
1!
2!
3!
k
a2
a3 2
k þ
k þ ...
2
6
¼
ak
a2 k2
a3 k3
þ
þ ...
2!
3!
1!
k
¼
1 Potenzreihenentwicklungen
221
Jetzt lässt sich der Grenzwert leicht bestimmen:
1 e ak
a2
a3 2
2s
k þ
k þ ... ¼ a ¼
lim
¼ lim a
m
2
6
k!0
k!0
k
Im luftleeren Raum hängt die Fallgeschwindigkeit damit wie folgt vom Fallweg s ab:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
1 e ak
2s
v ðk ¼ 0Þ ¼
m g lim
¼
¼ 2gs
ðs 0Þ
mg
m
k!0
k
Dieses Gesetz kennen Sie sicher aus der Schulphysik. Bild D-9
zeigt den zeitlichen Verlauf der Geschwindigkeit mit und ohne Berücksichtigung des Luftwiderstandes (Kurve a): luftleerer Raum;
Kurve b): mit Luftwiderstand).
v
a)
b)
mg
k
Bild D-9
s
0;3
ð
D32
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ x2 dx ¼ ?
0
a) Entwickeln Sie den Integranden zunächst in eine Potenzreihe (Abbruch nach dem 4. Glied) und
integrieren Sie dann gliedweise.
b) Welchen exakten Integralwert erhält man mit der Integraltafel?
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a) Der Integrand f ðxÞ ¼ 1 þ x 2 lässt sich aus der Binomischen Reihe von
1 þ u (! Formelsammlung) mit
Hilfe der Substitution u ¼ x 2 wie folgt als Potenzreihe darstellen:
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1
11 2
113 3
u
u þ
u þ ... ¼
1 þ u ¼ ð1 þ uÞ 1=2 ¼ 1 þ
2
24
246
¼ 1þ
Substitution
1
1 2
1 3
u
u þ
u þ ...
2
8
16
u ¼ x2
)
ðj u j 1Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2
1 4
1 6
1 þ x2 ¼ 1 þ
x
x þ
x þ ...
2
8
16
Gliedweise Integration führt zu dem folgenden Ergebnis (Näherungswert):
0;3
ð
0;3
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2
1 4
1 6
1þ
1 þ x2 d x ¼
x
x þ
x þ ... dx ¼
2
8
16
0
0
¼
1 3
1 5
1
x þ
x
x þ
x7 þ ...
6
40
112
0;3
¼
0
1
1
1
3
5
7
¼ 0;3 þ
0;3
0;3 þ
0;3 þ . . . 0 ¼
6
40
112
¼ 0;3 þ 0;0045 0;000 061 þ 0;000 002 þ . . .
0;304 441
ðj x j 1Þ
222
D Taylor- und Fourier-Reihen
b) Aus der Integraltafel der Formelsammlung entnehmen wir (Integral 116 mit a ¼ 1):
0;3
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi i 0;3
1 h
x 1 þ x 2 þ ln x þ 1 þ x 2
¼
1 þ x2 d x ¼
0
2
0
¼
pffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
1
½ 0;3 1;09 þ ln ð0;3 þ 1;09Þ 0 ln 1 ¼ 0;304 441
2
Berechnen Sie das uneigentliche Integral
ð
0;1
D33
e2x 1
dx
x
0
mit Hilfe der Potenzreihenentwicklung (auf 4 Stellen nach dem Komma genau).
Da der Integrand an der unteren Integrationsgrenze x ¼ 0 nicht definiert ist (an dieser Stelle verschwindet der Nenner), müssen wir (definitionsgemäß) zunächst von x ¼ l > 0 bis x ¼ 0,1 integrieren und dann den Grenzwert für
l ! 0 bilden:
0;1
ð
e2x 1
d x ¼ lim
x
l!0
0;1
ð
0
e2x 1
dx
x
ðl > 0Þ
l
Wir greifen auf die Mac Laurinsche Reihe von e u zurück und substituieren dort u ¼ 2 x (! Formelsammlung):
eu ¼ 1 þ
u1
u2
u3
u4
1 2
1 3
1 4
þ
þ
þ
þ ... ¼ 1 þ u þ
u þ
u þ
u þ ...
1!
2!
3!
4!
2
6
24
e 2x ¼ 1 þ 2 x þ
ðj u j < 1Þ
1
1
1
4 3
2 4
ð2 xÞ 2 þ
ð2 xÞ 3 þ
ð2 xÞ 4 þ . . . ¼ 1 þ 2 x þ 2 x 2 þ
x þ
x þ ...
2
6
24
3
3
Das Problem ist, dass wir an dieser Stelle noch nicht wissen, wie viele Glieder für die vorgegebene Genauigkeit benötigt werden (gegebenenfalls können wir weitere Glieder anschreiben). Die Potenzreihe für e 2 x setzen wir in die Integrandfunktion ein und erhalten:
4 3
2 4
4 3
2 4
x þ
x þ ... 1
1 þ 2x þ 2x2 þ
x þ
x þ ...
2x þ 2x2 þ
3
3
e 2x 1
3
3
¼
¼
¼
x
x
x
¼ 2 þ 2x þ
4 2
2 3
x þ
x þ ...
3
3
ðx 6¼ 0Þ
Die gliedweise Division durch x ist wegen x > 0 erlaubt. Wir integrieren jetzt diese Potenzreihe gliedweise in den
Grenzen von x ¼ l > 0 bis x ¼ 0,1:
0;1
ð
l
e 2x 1
dx ¼
x
0;1
ð
l
4 2
2 3
x þ
x þ ...
2 þ 2x þ
3
3
4 3
1 4
x þ
x þ ...
dx ¼ 2x þ x þ
9
6
0;1
¼
2
l
4
1
4 3
1 4
2
2
3
4
¼ 2 0;1 þ 0;1 þ
0;1 þ
0;1 þ . . . 2 l þ l þ
l þ l þ ...
9
6
9
6
1 Potenzreihenentwicklungen
223
Der Grenzübergang l ! 0 liefert dann den gesuchten Näherungswert unseres Integrals:
0;1
ð
e2x 1
d x ¼ lim
x
l!0
0
0;1
ð
e2x 1
dx ¼
x
l
¼ lim
l!0
¼
2 0;1 þ 0;1 2 þ
4
1
4 3
1 4
0;1 3 þ
0;1 4 þ . . . 2 l þ l 2 þ
l þ
l þ ...
¼
9
6
9
6
4
1
2 0;1 þ 0;1 2 þ
0;1 3 þ
0;1 4 þ . . . 0 ¼ 0;2 þ 0;01 þ 0;000 444 þ 0;000 017 þ . . .
9
6
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl}
0;210 444
Fehler
Für die vorgegebene Genauigkeit von vier Nachkommastellen benötigen wir die ersten drei Glieder, das vierte Glied
bewirkt in der vierten Nachkommastelle keine Veränderung mehr und bestimmt die Größenordnung des Fehlers. Somit
gilt:
0;1
ð
e 2x 1
d x ¼ 0,210 444
x
0,2104
(Abbruch nach der 4. Nachkommastelle)
0
Berechnen Sie das Integral
0;5
ð
D34
pffiffiffi
cosh ð x Þ d x
0
durch Reihenentwicklung des Integranden und Abbruch der Reihe nach dem 3. Glied.
Gehen Sie dabei von der als bekannt vorausgesetzten Reihe von cosh u aus (! Formelsammlung).
Wir gehen von der Mac Laurinschen Reihe
u2
u4
u6
1 2
1 4
1
u þ
u þ
u6 þ ...
þ
þ
þ ... ¼ 1 þ
2
24
720
2!
4!
6!
pffiffiffi
aus (! Formelsammlung), substituieren dann u durch x :
cosh u ¼ 1 þ
pffiffiffi
1
cosh ð x Þ ¼ 1 þ
2
pffiffiffi
x
2
þ
1 pffiffiffi
x
24
4
þ
1 pffiffiffi
x
720
6
þ ... ¼ 1 þ
ðj u j < 1Þ
1
1 2
1
x þ
x þ
x3 þ ...
2
24
720
Gliedweise Integration in den Grenzen von x ¼ 0 bis x ¼ 0,5 führt zu dem folgenden Ergebnis:
0;5
ð
pffiffiffi
cosh ð x Þ d x ¼
0
0;5
ð
0
¼
0;5
1
1 2
1 3
1 2
1 3
1
4
1þ
¼
xþ
x þ
x þ ... dx ¼ x þ x þ
x þ
x þ ...
2
24
720
4
72
2880
0
1
1
1
0;5 2 þ
0;5 3 þ
0;5 4 þ . . .
0;5 þ
4
72
2880
¼ 0;5 þ 0;0625 þ 0;001 736 þ 0;000 022 þ . . .
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl}
Näherungswert 0;564 236
Der Wert ist auf 4 Stellen nach dem Komma genau.
Fehler
0 ¼
0;5642
224
D Taylor- und Fourier-Reihen
0;1
ð
e x sinh x d x
Berechnen Sie das Integral
0
D35
a) durch Potenzreihenentwicklung des Integranden (bis einschließlich x 3 -Glied),
b) mit Hilfe der Integraltafel (exakter Wert).
a) Wir entwickeln die Integrandfunktion f ðxÞ ¼ e x sinh x auf direktem Wege in eine Mac Laurinsche Reihe bis
zum kubischen Glied. Alle dabei benötigten Ableitungen erhalten wir mit der Produktregel:
f ðxÞ ¼ e x sinh x ¼ u v mit
|fflffl{zfflffl}
u
v
f
u ¼ ex ;
v ¼ sinh x
u0 ¼ ex ;
und
v 0 ¼ cosh x
f
f 0 ðxÞ ¼ u 0 v þ v 0 u ¼ e x sinh x þ cosh x e x ¼ e x ðsinh x þ cosh xÞ ¼ u v
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
u
v
u ¼ ex ;
v ¼ sinh x þ cosh x
und
u0 ¼ ex ;
v 0 ¼ cosh x þ sinh x
f 00 ðxÞ ¼ u 0 v þ v 0 u ¼ e x ðsinh x þ cosh xÞ þ ðcosh x þ sinh xÞ e x ¼
¼ e x ðsinh x þ cosh x þ cosh x þ sinh xÞ ¼ e x ð2 sinh x þ 2 cosh xÞ ¼
¼ 2 e x ðsinh x þ cosh xÞ ¼ 2 f 0 ðxÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
f 0 ðxÞ
f 000 ðxÞ ¼ 2 f 00 ðxÞ ¼ 2 2 f 0 ðxÞ ¼ 4 f 0 ðxÞ
Ableitungswerte an der Stelle x 0 ¼ 0 (unter Berücksichtigung von e 0 ¼ 1 , sinh 0 ¼ 0 , cosh 0 ¼ 1):
f ð0Þ ¼ e 0 sinh 0 ¼ 1 0 ¼ 0 ;
f 0 ð0Þ ¼ e 0 ðsinh 0 þ cosh 0Þ ¼ 1 ð0 þ 1Þ ¼ 1 ;
f 00 ð0Þ ¼ 2 f 0 ð0Þ ¼ 2 1 ¼ 2 ;
|fflffl{zfflffl}
1
f 000 ð0Þ ¼ 4 f 0 ð0Þ ¼ 4 1 ¼ 4
|fflffl{zfflffl}
1
Mac Laurinsche Reihe von f ðxÞ ¼ e x sinh x bis zur 3. Potenz
f ðxÞ ¼ e x sinh x ¼ f ð0Þ þ
¼ 0þ
f 0 ð0Þ 1
f 00 ð0Þ 2
f 000 ð0Þ 3
x þ
x þ
x þ ... ¼
1!
2!
3!
1
2 2
4 3
2 3
x þ
x þ
x þ ... ¼ x þ x2 þ
x þ ...
1
2
6
3
ðj x j < 1Þ
Gliedweise Integration liefert den folgenden Näherungswert für das Integral:
0;1
ð
0;1
ð
e sinh x d x ¼
x
0
0
¼
0;1
2 3
1 2
1 3
1 4
2
x þx þ
¼
x þ ... dx ¼
x þ
x þ
x þ ...
3
2
3
6
0
1
1
1
0,1 2 þ
0,1 3 þ
0,1 4 þ . . . 0 ¼
2
3
6
¼ 0,005 þ 0,000 333 þ 0,000 017 þ . . .
0,005 350
Hinweis: Die Reihenentwicklung des Integranden f ðxÞ ¼ e x sinh x erhält man bequemer durch Reihenmultiplikation, sofern die Reihen von e x und sinh x bekannt sind.
b) Aus der Integraltafel der Formelsammlung entnehmen wir (Integral 326 mit a ¼ 1):
0;1
ð
e sinh x d x ¼
x
0
e 2x
x
2
4
0;1
¼
0
0
e 0;2
0,1
e
0 ¼ 0;255 351 0;25 ¼ 0;005 351
2
4
4
2 Fourier-Reihen
225
2 Fourier-Reihen
Lehrbuch: Band 2, Kapitel II.1 und 2
Formelsammlung: Kapitel VI.4
Die in Bild D-10 dargestellte Impulsfolge wird im Periodenintervall 0 t < T durch die Funktion
(
)
T=2 c t T=2 þ c
A ¼ const:
f ür
f ðtÞ ¼
alle übrigen t
0
beschrieben. Wie lautet die Fourier-Zerlegung dieser Funktion?
D36
y
A
c
c
c
T/2
T
c
Bild D-10
3T/2
2T
t
Die Fourier-Reihe enthält keine Sinusglieder, da die Funktion gerade ist (Spiegelsymmetrie zur y -Achse). Daher gilt
b n ¼ 0 für n ¼ 1; 2; 3; . . . und somit
f ðtÞ ¼
1
X
a0
a n cos ðn w 0 tÞ
þ
2
n¼1
ðmit w 0 ¼ 2 p=TÞ
Berechnung des Fourier-Koeffizienten a 0
a0
2
¼
T
ð
T=2 þ c
2
f ðtÞ d t ¼
A
T
ðTÞ
ð
T=2 þ c
2A
2A
1 dt ¼
½ t T=2 c ¼
T
T
T
T
4Ac
þc
þc ¼
2
2
T
T=2 c
Berechnung der Fourier-Koeffizienten an ( n = 1, 2, 3, . . . )
an
2
¼
T
ð
T=2 þ c
2
A
f ðtÞ cos ðn w 0 tÞ d t ¼
T
ðTÞ
ð
2A
cos ðn w 0 tÞ d t ¼
T
T=2 c
sin ðn w 0 tÞ
nw0
T=2 þ c
¼
T=2 c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 228 mit a ¼ n w 0
2A
¼
n w0 T
T=2 þ c
½ sin ðn w 0 tÞ T=2 c
2A
¼
nw0 T
nw0 T
nw0 T
þ n w 0 c sin
sin
nw0 c
2
2
Unter Berücksichtigung von w 0 T ¼ 2 p erhalten wir:
2A
n 2p
n 2p
¼
an ¼
sin
þ n w 0 c sin
n w0 c
2
2
n 2p
¼
A
½ sin ðn p þ n w 0 cÞ sin ðn p n w 0 cÞ
np
226
D Taylor- und Fourier-Reihen
Unter Verwendung der trigonometrischen Formel
sin ðx 1 þ x 2 Þ sin ðx 1 x 2 Þ ¼ 2 cos x 1 sin x 2
ð! Formelsammlung : Kap: III:7:6:5Þ
folgt dann mit x 1 ¼ n p und x 2 ¼ n w 0 c:
an ¼
A
2A
sin ðn w 0 cÞ
2A
sin ðn w 0 cÞ
2 cos ðn pÞ sin ðn w 0 cÞ ¼
cos ðn pÞ
¼
ð 1Þ n
np
p |fflfflfflfflffl{zfflfflfflfflffl}
n
p
n
n
ð 1Þ
Denn es gilt:
cos ðn pÞ ¼
8
<1
:
9
n ¼ 1; 3; 5; . . . =
f ür
n ¼ 2; 4; 6; . . .
1
;
¼ ð 1Þ n
(f ür n ¼ 1; 2; 3; . . .Þ
Damit erhalten wir die folgende Fourier-Zerlegung (mit w 0 ¼ 2 p=T):
f ðtÞ ¼
1
1
X
a0
2Ac
2A X
sin ðn w 0 cÞ
þ
cos ðn w 0 tÞ
a n cos ðn w 0 tÞ ¼
ð 1Þ n
þ
T
p n¼1
n
2
n¼1
Bestimmen Sie die Fourier-Reihe der in Bild D-11 dargestellten parabelförmigen Impulsfolge mit der
Periodendauer T ¼ p.
y
D37
π2
4
–π
π
0
2π
Bild D-11
t
Gleichung der Parabel im Periodenintervall 0 t p (Ansatz in der Produktform):
f ðtÞ ¼ a ðt 0Þ ðt pÞ ¼ a t ðt pÞ ¼ a ðt 2 p tÞ
(Parabelnullstellen bei t 1 ¼ 0 und t 2 ¼ pÞ. Im Scheitelpunkt gilt:
2
p2
p
p2
p2
p2
p2
) a
¼
) a
¼
f ðp=2Þ ¼
4
4
2
4
4
4
)
a ¼ 1
)
)
a
p2
p2
¼
4
4
a ¼ 1
Somit gilt:
f ðtÞ ¼ ðt 2 p tÞ ¼ t 2 þ p t ;
0 t p
Die aus Parabelbögen bestehende (periodische) Funktion ist gerade (spiegelsymmetrisch zur y -Achse), die FourierReihe kann daher keine Sinusglieder enthalten. Somit ist b n ¼ 0 für n ¼ 1; 2; 3; . . . und es gilt:
1
1
X
X
a0
a0
2p
2p
¼
þ
þ
¼ 2
a n cos ðn w 0 tÞ ¼
a n cos ð2 n tÞ
mit w 0 ¼
f ðtÞ ¼
T
2
2
p
n¼1
n¼1
2 Fourier-Reihen
227
Berechnung des Fourier-Koeffizienten a 0
a0
ð
2
¼
T
2
f ðtÞ d t ¼
p
ðTÞ
2
¼
p
ðp
2
ð t þ p tÞ d t ¼
p
2
1 3
1
t þ
pt2
3
2
p
¼
0
0
1 3
1 3
2 1 3
2p3
ð2 p Þ p 2
1 2
¼
¼
p þ
p 00 ¼
p ¼
p
6p
3
2
p 6
3
3 ð2 pÞ
Berechnung der Fourier-Koeffizienten a n (n = 1, 2, 3, . . .)
an
2
¼
T
ð
2
f ðtÞ cos ðn w 0 tÞ d t ¼
p
ðTÞ
ðp
ð t 2 þ p tÞ cos ð2 n tÞ d t ¼
0
9
8 p
ðp
ð
=
2 <
2
¼
t 2 cos ð2 n tÞ d t þ p t cos ð2 n tÞ d t ¼
ð I 1 þ p I 2 Þ
;
p :
p
0
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I2
Berechnung der Teilintegrale I 1 und I 2 :
"
ðp
I1 ¼
t cos ð2 n tÞ d t ¼
2
2 t cos ð2 n tÞ
4 n2
þ
ð4 n 2 t 2 2Þ sin ð2 n tÞ
#p
8 n3
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
¼
0
Integral 233 mit a ¼ 2 n
¼
2 p cos ð2 n pÞ
4 n2
þ
ð4 n 2 p 2 2Þ sin ð2 n pÞ
8 n3
0þ
2 sin 0
2p
p
¼
þ00þ0 ¼
3
2
8n
4n
2 n2
(unter Berücksichtigung von cos ð2 n pÞ ¼ 1 und sin ð2 n pÞ ¼ sin 0 ¼ 0)
"
ðp
I2 ¼
t cos ð2 n tÞ d t ¼
cos ð2 n tÞ
4 n2
þ
t sin ð2 n tÞ
2n
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
#p
¼
0
Integral 232 mit a ¼ 2 n
¼
cos ð2 n pÞ
4 n2
þ
p sin ð2 n pÞ
cos 0
1
1
0 ¼
þ0
0 ¼ 0
2n
4 n2
4 n2
4 n2
(wegen cos ð2 n pÞ ¼ cos 0 ¼ 1 und sin ð2 n pÞ ¼ 0)
Damit erhalten wir für die Fourier-Koeffizienten a n folgende Werte:
2
2
p
2
p
1
ð I 1 þ p I 2 Þ ¼
¼
þp 0 ¼
an ¼
2
2
p
p
p
2n
n2
2n
Die Fourier-Reihe der parabelförmigen Impulsfolge lautet daher wie folgt (w 0 ¼ 2):
1
1
X
X
a0
1 2
1
p
þ
a n cos ð2 n tÞ ¼
cos ð2 n tÞ ¼
2
6
2
n
n¼1
n¼1
1 2
1
1
1
¼
cos ð2 tÞ þ
cos ð4 tÞ þ
cos ð6 tÞ þ . . .
p
6
12
22
32
f ðtÞ ¼
228
D Taylor- und Fourier-Reihen
Zerlegen Sie die in Bild D-12 dargestellte „Sägezahnschwingung“ nach Fourier in ihre harmonischen
Bestandteile (Grund- und Oberschwingungen).
y
Funktionsgleichung:
A
f ðtÞ ¼
2A
t;
T
T
T
t
2
2
D38
–T/2
T/2
t
Bild D-12
–A
Die ungerade Funktion hat die Schwingungsdauer (Periode) T, die Kreisfrequenz der Grundschwingung ist daher
w 0 ¼ 2 p=T. Die gesuchte Fourier-Reihe kann wegen der Punktsymmetrie der Kurve nur Sinusglieder enthalten.
Somit gilt a n ¼ 0 für n ¼ 0; 1; 2; . . . und
f ðtÞ ¼
1
X
b n sin ðw 0 tÞ
(mit w 0 ¼ 2 p=TÞ
n¼1
Berechnung der Fourier-Koeffizienten b n (n = 1, 2, 3, . . .)
bn
ð
2
¼
T
ð
ð
T=2
2 2A
f ðtÞ sin ðn w 0 tÞ d t ¼
T
T
ðTÞ
T=2
t sin ðn w 0 tÞ d t ¼
T=2
4A
T2
t sin ðn w 0 tÞ d t
T=2
Weil der Integrand t sin ðn w 0 tÞ eine gerade Funktion ist, dürfen wir die Integration auf das Intervall 0 t T=2
beschränken () Faktor 2 vor dem Integral):
ð
T=2
bn ¼ 2
4A
T2
t sin ðn w 0 tÞ d t ¼
0
8A
"
sin ðn w 0 tÞ
n 2 w 20
T2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
t cos ðn w 0 tÞ
nw0
# T=2
¼
0
Integral 208 mit a ¼ n w 0
8A
¼
T2
sin ðn w 0 T=2Þ
8A
¼
T2
sin ðn w 0 T=2Þ
n 2 w 20
n 2 w 20
T cos ðn w 0 T=2Þ
2nw0
T cos ðn w 0 T=2Þ
¼
sin ðn pÞ
n 2 w 20
4 A ð 1Þ n
n 2p
¼ ð 1Þ 1
0
¼
!
w 0 T=2 ¼ p ;
!
T cos ðn pÞ
2nw0
n 2 w 20
2nw0
Unter Berücksichtigung von w 0 T ¼ 2 p ;
8A
bn ¼
T2
!
sin 0
8A
¼
T2
2 A ð 1Þ n
np
0
¼
sin ðn pÞ ¼ 0 und cos ðn pÞ ¼ ð 1Þ n folgt weiter:
T ð 1Þ n
2nw0
!
¼
2 A ð 1Þ 1 ð 1Þ n
np
8 A T ð 1Þ n
2nw0 T 2
¼
¼
2 A ð 1Þ n þ 1
np
¼
8 A T ð 1Þ n
2 n ðw 0 TÞ T
nþ1
2 A ð 1Þ
p
n
¼
2 Fourier-Reihen
229
Damit erhalten wir die folgende Zerlegung in eine sinusförmige Grundschwingung mit der Kreisfrequenz w 0 und
sinusförmige Oberschwingungen mit den Kreisfrequenzen 2 w 0 ; 3 w 0 ; 4 w 0 ; . . .:
1
X
f ðtÞ ¼
b n sin ðn w 0 tÞ ¼
n¼1
sin ðw 0 tÞ
2A
¼
p
1
1 ð 1Þ n þ 1
1
2A X
2A X
sin ðn w 0 tÞ
ð 1Þ n þ 1
¼
sin ðn w 0 tÞ ¼
p n¼1
p n¼1
n
n
sin ð2 w 0 tÞ
2
þ
sin ð3 w 0 tÞ
3
sin ð4 w 0 tÞ
4
!
þ ...
y
A
c
D39
c
c
T/2
T
c
Bild D-13
3T/2
2T
t
–A
Wie lautet die Fourier-Reihe dieser Rechteckkurve mit der Periodendauer T und der Kreisfrequenz
w 0 ¼ 2 p=T (Bild D-13)?
Die Kurve lässt sich im Periodenintervall 0 t T abschnittsweise durch die folgenden Gleichungen beschreiben:
8
9
A
T=2 c t < T=2 >
>
>
>
<
=
f ðtÞ ¼ A f ür T=2 t < T=2 þ c
>
>
>
>
:
;
0
alle übrigen t
Wegen der Punktsymmetrie der Kurve können in der Fourier-Zerlegung nur Sinusglieder auftreten. Somit gilt a n ¼ 0
für n ¼ 0; 1; 2; . . . und
f ðtÞ ¼
1
X
b n sin ðn w 0 tÞ
ðmit w 0 ¼ 2 p=TÞ
n¼1
Berechnung der Fourier-Koeffizienten bn (n = 1, 2, 3, . . .)
Die Integration muss abschnittsweise durchgeführt werden (Integral 204 mit a ¼ n w 0 ):
8
9
T=2
T=2 þ c
>
>
ð
ð
ð
<
=
2
2
A
f ðtÞ sin ðn w 0 tÞ d t ¼
sin ðn w 0 tÞ d t A
sin ðn w 0 tÞ d t ¼
bn ¼
>
T
T >
:
;
ðTÞ
T=2 c
8"
# T=2
cos ðn w 0 tÞ
2A <
¼
T :
nw0
T=2 c
¼
2A
nw0 T
¼
2A
nw0 T
T=2
"
T=2
# T=2 þ c 9
=
cos ðn w 0 tÞ
nw0
T=2
T=2 þ c
½ cos ðn w 0 tÞ T=2 c þ ½ cos ðn w 0 tÞ T=2
;
¼
¼
cos ðn w 0 T=2Þ þ cos ðn w 0 T=2 n w 0 cÞ þ cos ðn w 0 T=2 þ n w 0 cÞ cos ðn w 0 T=2Þ
230
D Taylor- und Fourier-Reihen
Wegen w 0 T ¼ 2 p und somit w 0 T=2 ¼ p folgt weiter:
bn ¼
¼
2A
n 2p
A
np
cos ðn pÞ þ cos ðn p n w 0 cÞ þ cos ðn p þ n w 0 cÞ cos ðn pÞ
2 cos ðn pÞ þ cos ðn p þ n w 0 cÞ þ cos ðn p n w 0 cÞ
¼
Unter Verwendung der trigonometrischen Formel
cos ðx 1 þ x 2 Þ þ cos ðx 1 x 2 Þ ¼ 2 cos x 1 cos x 2
ð! Formelsammlung : Kap: III:7:6:5Þ
mit x 1 ¼ n p und x 2 ¼ n w 0 c erhalten wir dann:
bn ¼
¼
A
np
2 cos ðn pÞ þ 2 cos ðn pÞ cos ðn w 0 cÞ
¼
2A
cos ðn pÞ 1 þ cos ðn w 0 cÞ ¼
n p |fflfflfflfflffl{zfflfflfflfflffl}
ð 1Þ n
n
2 A ð 1Þ ðcos ðn w 0 cÞ 1Þ
p
n
Die Fourier-Reihe der Rechteckkurve lautet damit:
1
X
1 ð 1Þ n ðcos ðn w cÞ 1Þ
0
2A X
sin ðn w 0 tÞ
f ðtÞ ¼
b n sin ðn w 0 tÞ ¼
n
p
n¼1
n¼1
ðw 0 ¼ 2 p=TÞ
Bestimmen Sie die Fourier-Reihe der in Bild D-14 skizzierten periodischen Funktion mit der Periode T
und der Kreisfrequenz w 0 ¼ 2 p=T:
y
D40
Im Periodenintervall 0 t < T gilt:
8
9
0 t T=2 =
< A
f ür
f ðtÞ ¼
: 2A t þ 2A
;
T=2 t < T
T
A
T/2
T
t
Bild D-14
Alle Integrationen müssen abschnittsweise durchgeführt werden.
Berechnung des Fourier-Koeffizienten a 0
9
8
T=2
>
>
ðT
ð
ð
=
<
2
2
2A
a0 ¼
f ðtÞ d t ¼
1 dt þ
A
t þ 2A dt ¼
>
T
T >
T
;
:
ðTÞ
0
T=2
8
9
T=2
>
>
ð
ðT
<
=
2A
2
2A
¼
1dt þ
t þ 2 dt ¼
>
T >
T
T
:
;
0
¼
2A
T
t
T=2
0
1 2
þ
t þ 2t
T
T=2
1
1
T 0 T þ 2T þ
T T
2
4
¼
2A
T
1
1
T þ
T
2
4
¼
T !
¼
T=2
2A 3
3
A
T ¼
4
2
T
2 Fourier-Reihen
231
Berechnung der Fourier-Koeffizienten a n (n = 1, 2, 3, . . .)
9
8
T=2
>
>
ð
ð
ðT
=
<
2
2
2A
A
t þ 2 A cos ðn w 0 tÞ d t ¼
f ðtÞ cos ðn w 0 tÞ d t ¼
cos ðn w 0 tÞ d t þ
an ¼
>
T
T >
T
;
:
ðTÞ
0
ð
ðT
T=2
2A
¼
T
4A
cos ðn w 0 tÞ d t
T2
0
T=2
T=2
cos ðn w 0 tÞ d t ¼
T=2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I1
ðT
4A
t cos ðn w 0 tÞ d t þ
T
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I3
2A
4A
4A
I1 2 I2 þ
I3
T
T
T
¼
Auswertung der Teilintegrale I 1 , I 2 , I 3 :
Bei der Auswertung der Integrale beachten wir folgende Beziehungen:
w0T ¼ 2p;
w 0 T=2 ¼ p ;
ð
T=2
I1 ¼
cos ðn w 0 tÞ d t ¼
sin ð2 n pÞ ¼ sin ðn pÞ ¼ 0 ;
sin ðn w 0 tÞ
nw0
T=2
sin ðn w 0 T=2Þ sin 0
sin ðn pÞ sin 0
00
¼
¼
¼ 0
nw0
nw0
nw0
¼
0
0
cos ðn pÞ ¼ ð 1Þ n
cos ð2 n pÞ ¼ 1 ;
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 228 mit a ¼ n w 0
"
ðT
I2 ¼
t cos ðn w 0 tÞ d t ¼
cos ðn w 0 tÞ
n 2 w 20
T=2
þ
t sin ðn w 0 tÞ
#T
nw0
¼
T=2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 232 mit a ¼ n w 0
¼
¼
cos ðn w 0 TÞ
n2
þ
w 20
cos ð2 n pÞ
n 2 w 20
þ
T sin ðn w 0 TÞ
nw0
T sin ð2 n pÞ
nw0
"
ðT
I3 ¼
cos ðn w 0 tÞ d t ¼
cos ðn w 0 T=2Þ
n2
cos ðn pÞ
n 2 w 20
sin ðn w 0 tÞ
#T
nw0
¼
w 20
T sin ðn w 0 T=2Þ
2nw0
T sin ðn pÞ
2nw0
¼
1
n 2 w 20
¼
ð 1Þ n
n 2 w 20
sin ðn w 0 TÞ sin ðn w 0 T=2Þ
nw0
T=2
T=2
¼
¼
1 ð 1Þ n
n 2 w 20
sin ð2 n pÞ sin ðn pÞ
nw0
¼ 0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 228 mit a ¼ n w 0
Die Fourier-Koeffizienten der Kosinusglieder lauten damit (unter Berücksichtigung von w 0 T ¼ 2 p ):
an ¼
n
1 ð 1Þ n
2A
4A
4A
2A
4 A 1 ð 1Þ
4A
4A
I2 þ
þ
¼
I1
I3 ¼
0
0 ¼
T
T
T
T
T2
n 2 w 20
n2
T2
w 20 T 2
¼
4A
ðw 0 TÞ 2
1 ð 1Þ n
¼
n2
4A
ð2 pÞ 2
1 ð 1Þ n
n2
¼
4A
4 p2
1 ð 1Þ n
n2
¼
A
p2
1 ð 1Þ n
n2
Für gerades n; d. h. n ¼ 2; 4; 6; . . . ist ð 1Þ n ¼ 1 und damit a n ¼ 0 . Für ungerades n; d. h. n ¼ 1; 3; 5; . . .
ist ð 1Þ n ¼ 1 und man erhält folgende Fourier-Koeffizienten:
an ¼
A
p2
1þ1
n2
¼
2A
p2
1
n2
ðn ¼ 1; 3; 5; . . .Þ
232
D Taylor- und Fourier-Reihen
Berechnung der Fourier-Koeffizienten bn (n = 1, 2, 3, . . .)
9
8
T=2
>
>
ð
ð
ðT
=
<
2
2
2A
A
t þ 2 A sin ðn w 0 tÞ d t ¼
f ðtÞ sin ðn w 0 tÞ d t ¼
sin ðn w 0 tÞ d t þ
bn ¼
>
T
T >
T
;
:
ðTÞ
0
ð
ðT
T=2
2A
¼
T
4A
sin ðn w 0 tÞ d t
T2
0
ðT
4A
t sin ðn w 0 tÞ d t þ
T
T=2
sin ðn w 0 tÞ d t ¼
T=2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I2
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I1
¼
T=2
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I3
2A
4A
4A
I2 þ
I1
I3
T
T
T2
Auswertung der Teilintegrale I 1 , I 2 und I 3 :
Bei der Auswertung der Integrale beachten wir folgende Beziehungen:
w 0 T ¼ 2 p;
w 0 T=2 ¼ p;
"
ð
T=2
I1 ¼
sin ðn pÞ ¼ sin ð2 n pÞ ¼ 0;
sin ðn w 0 tÞ d t ¼
cos ðn w 0 tÞ
# T=2
nw0
cos ðn w 0 T=2Þ cos 0
¼
nw0
0
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
cos ð2 n pÞ ¼ cos 0 ¼ 1
¼
Integral 204 mit a ¼ n w 0
¼
cos ðn pÞ 1
nw0
¼
1 cos ðn pÞ
nw0
"
ðT
I2 ¼
t sin ðn w 0 tÞ d t ¼
sin ðn w 0 tÞ
n 2 w 20
T=2
t cos ðn w 0 tÞ
#T
¼
nw0
T=2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 208 mit a ¼ n w 0
¼
¼
sin ðn w 0 TÞ
n 2 w 20
sin ð2 n pÞ
n2
¼ 0
w 20
T cos ðn w 0 TÞ
nw0
T cos ð2 n pÞ
nw0
sin ðn w 0 T=2Þ
n 2 w 20
sin ðn pÞ
n2
w 20
þ
þ
T cos ðn w 0 T=2Þ
2nw0
T cos ðn pÞ
2nw0
"
sin ðn w 0 tÞ d t ¼
#T
cos ðn w 0 tÞ
nw0
T=2
¼
¼
cos ðn w 0 TÞ cos ðn w 0 T=2Þ
nw0
T=2
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 204 mit a ¼ n w 0
¼
¼
T cos ðn pÞ
2 T þ T cos ðn pÞ
T ðcos ðn pÞ 2Þ
T
0þ
¼
¼
2nw0
2 n w0
2nw0
nw0
ðT
I3 ¼
cos ð2 n pÞ cos ðn pÞ
nw0
¼
1 cos ðn pÞ
nw0
¼
cos ðn pÞ 1
nw0
¼
2 Fourier-Reihen
233
Damit erhalten wir für die Sinusglieder folgende Fourier-Koeffizienten:
2A
4A
4A
I2 þ
I1
I3 ¼
2
T
T
T
bn ¼
2 A 1 cos ðn pÞ
4 A T ðcos ðn pÞ 2Þ
4 A cos ðn pÞ 1
þ
¼
nw0
2nw0
nw0
T
T
T2
2A
2A
2A
1 cos ðn pÞ
cos ðn pÞ 2 þ
2 ðcos ðn pÞ 1Þ ¼
¼
nw0 T
nw0 T
nw0 T
¼
2A
2A
A 1
1 ¼
1 cos ðn pÞ cos ðn pÞ þ 2 þ 2 cos ðn pÞ 2 ¼
n ðw 0 TÞ
p n
n 2p
|{z} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
2p
1
¼
Fourier-Reihe
f ðtÞ ¼
1
X
a0
ða n cos ðn w 0 tÞ þ b n sin ðn w 0 tÞÞ ¼
þ
2
n¼1
3
2A
A
¼
4
p2
A
þ
p
cos ðw 0 tÞ
12
sin ðw 0 tÞ
1
þ
þ
cos ð3 w 0 tÞ
þ
32
sin ð2 w 0 tÞ
2
cos ð5 w 0 tÞ
52
sin ð3 w 0 tÞ
þ
3
!
þ ... þ
!
þ ...
y
Funktionsgleichung:
f ðxÞ ¼ 2 p x ;
4π 2
D41
0 x < 2p
Bild D-15
2π
4π
x
Bestimmen Sie die Fourier-Reihe der in Bild D-15 skizzierten „Sägezahn-Funktion“ mit der Periode
p ¼ 2 p und der Kreisfrequenz w 0 ¼ 2 p=p ¼ 1 in komplexer Form. Wie lautet die reelle Reihenentwicklung?
Berechnung der Fourier-Koeffizienten cn (komplexe Darstellung; mit n = 1, 2, 3, . . .)
f ðxÞ e
jnx
1
dx ¼
2p
2p
2ðp
0
x e
jnx
2ðp
dx ¼
0
x e jnx d x ¼
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ j n
¼
jnx 1
j
2
n2
e
jnx
2p
¼
0
jnx 1
n2
e
jnx
2p
¼
0
1
n2
½ðjnx
2p
þ 1Þ e j n x 0
¼
f
– 1
¼
1
n2
½ð j2np
1
1
2p
þ 1Þ e j 2 n p 1 e 0 ¼
ð j 2 n p þ 1 1Þ ¼
j2np ¼ j
|fflfflffl{zfflfflffl}
n
n2
n2
1
1
f
cn
2ðp
1
¼
2p
234
D Taylor- und Fourier-Reihen
Hinweis: e j 2 n p wurde nach der Eulerschen Formel berechnet (! FS: Kap. VIII.1.2.2 mit j ¼ 2 n p):
e j j ¼ cos j j sin j
e j 2 n p ¼ cos ð2 n pÞ j sin ð2 n pÞ ¼ 1 j 0 ¼ 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
1
0
2ðp
2ðp
2Ðp
2p
x e0 dx ¼
x 1 dx ¼
x d x ¼ 12 x 2 0 ¼ 2 p 2 0 ¼ 2 p 2
Sonderfall n ¼ 0: c 0 ¼
)
0
0
Somit gilt c 0 ¼ 2 p 2
und
0
2p
1
cn ¼ j
¼ j2p
n
n
ðf ür
n ¼ 1; 2; 3; . . .Þ:
Fourier-Reihe in komplexer Form
f ðxÞ ¼
1
X
c n e jnx ¼ 2 p2 þ j 2 p
n¼1
1
X
1
n¼1
n
1
e jnx
n
e jnx
Fourier-Reihe in reeller Form
2p
2p
2p
2p
þj
¼ j
j
¼ 0
n
n
n
n
2p
2p
2p
2p
4p
4p
4p
j
¼ j j
þj
¼ jj
¼ j2
¼
¼ j ðc n c n Þ ¼ j j
n
n
n
n
n
n
n
a0 ¼ 2c0 ¼ 2 2p2 ¼ 4p2 ;
bn
a n ¼ c n þ c n ¼ j
ð j 2 ¼ 1Þ
1
1
X
X
a0
4p
2
ða n cos ðn xÞ þ b n sin ðn xÞÞ ¼ 2 p þ
0 cos ðn xÞ
f ðxÞ ¼
þ
sin ðn xÞ ¼
2
n
n¼1
n¼1
1
X
sin ðn xÞ
sin x
sin ð2 xÞ
sin ð3 xÞ
2
¼ 2p 4p
¼ 2p 4p
þ
þ
þ ...
n
1
2
3
n¼1
2
Alternative Lösung (unter Verwendung der Formel e j n x e j n x ¼ 2 j sin ðn xÞ (! FS: Kap. VIII.7.3.2):
1
1
X
X
1
1
1
2
jnx
jnx
e
e
ðe j n x e j n x Þ ¼
¼ 2p2 þ j2p
f ðxÞ ¼ 2 p þ j 2 p
n
n
n
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
n¼1
n¼1
2 j sin ðn xÞ
¼ 2p2 þ j2p
1
1
1
X
X
X
1
sin ðn xÞ
sin ðn xÞ
2 j sin ðn xÞ ¼ 2 p 2 þ j 2 4 p
¼ 2p2 4p
n
n
n
n¼1
n¼1
n¼1
y
Im Periodenintervall
p x p gilt:
π2
f ðxÞ ¼ x 2
D42
Bild D-16
–3π
–2π
–π
π
2π
3π
x
Zerlegen Sie die in Bild D-16 dargestellte periodische Funktion in ihre harmonischen Bestandteile
(Fourier-Zerlegung). Skizzieren Sie das Amplitudenspektrum.
Die Fourier-Zerlegung dieser periodischen Funktion mit der Periode p ¼ 2 p kann wegen der Spiegelsymmetrie zur
y-Achse nur gerade Bestandteile enthalten. Somit ist b n ¼ 0 ( n ¼ 1; 2; 3; . . .) . Die Zerlegung enthält also keine
Sinusglieder. Die Integrationen beschränken wir wegen der Spiegelsymmetrie der Funktion auf das Intervall
0 x p () Faktor 2 vor den Integralen).
2 Fourier-Reihen
235
Berechnung des Fourier-Koeffizienten a 0
a0
ðp
1
¼
p
p
1
f ðxÞ d x ¼
p
ðp
2
x dx ¼
p
ðp
2
p
2
x dx ¼
p
2
1 3
x
3
p
0
0
2
¼
p
1 3
p 0
3
¼
2 2
p
3
Berechnung der Fourier-Koeffizienten a n (n = 1, 2, 3, . . .)
an
ðp
1
¼
p
p
1
f ðxÞ cos ðn xÞ d x ¼
p
ðp
2
x cos ðn xÞ d x ¼
p
ðp
x 2 cos ðn xÞ d x ¼
2
p
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 233 mit a ¼ n
2
¼
p
2
¼
p
"
2 x cos ðn xÞ
n2
þ
2 p cos ðn pÞ
n2
ðn 2 x 2 2Þ sin ðn xÞ
þ
n3
#p
¼
0
ðn 2 p 2 2Þ sin ðn pÞ
n3
2 sin 0
0
n3
!
4 ð 1Þ n
2 2 p cos ðn pÞ
¼
p
n2
n2
¼
ðunter Berücksichtigung von sin ðn pÞ ¼ sin 0 ¼ 0 und cos ðn pÞ ¼ ð 1Þ n Þ
Fourier-Zerlegung
f ðxÞ ¼
1
1
X
X
a0
1 2
cos ðn xÞ
p þ4
a n cos ðn xÞ ¼
ð 1Þ n
¼
þ
3
2
n2
n¼1
n¼1
1 2
¼
p þ4
3
cos ð2 xÞ
cos ð3 xÞ
cos x
þ
þ ...
12
22
32
Amplitudenspektrum: siehe Bild D-17
An
4
Die Amplituden lauten:
A0 ¼
1 2
p ;
3
An ¼ jan j ¼
4
n2
2
ðn ¼ 1; 2; 3; . . .Þ
Bild D-17
0
1
2
3
4
v /v 0
u
Im Periodenintervall
0 t < p gilt:
u0
f ðtÞ ¼ u 0 cos t
D43
π
– u0
2π
3π
t
Bild D-18
Zerlegen Sie den in Bild D-18 dargestellten periodischen Spannungsverlauf in seine harmonischen Bestandteile (Grund- und Oberschwingungen) und bestimmen Sie das Amplitudenspektrum.
236
D Taylor- und Fourier-Reihen
Der Spannungsverlauf wird durch eine ungerade Funktion beschrieben, es können daher nur Sinusglieder auftreten. Somit
gilt a n ¼ 0 für n ¼ 0; 1; 2; . . . . Die Schwingungsdauer ist T ¼ p , die Kreisfrequenz beträgt w 0 ¼ 2 p=T ¼
¼ 2 p=p ¼ 2 .
Berechnung der Fourier-Koeffizienten bn (n = 1, 2, 3, . . .)
bn
ð
2
¼
T
2
f ðtÞ sin ðn w 0 tÞ d t ¼
u0
p
ðTÞ
ðp
cos t sin ð2 n tÞ d t ¼
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 285 mit a ¼ 2 n ; b ¼ 1
2u0
¼
p
2u0
¼
p
"
"
cos ½ ð2 n þ 1Þ t
2 ð2 n þ 1Þ
cos ½ ð2 n 1Þ t
2 ð2 n 1Þ
#p
¼
0
cos ½ ð2 n 1Þ p
cos ½ ð2 n þ 1Þ p
cos 0
cos 0
þ
þ
2 ð2 n þ 1Þ
2 ð2 n þ 1Þ
2 ð2 n 1Þ
2 ð2 n 1Þ
#
Wegen cos ½ ð2 n þ 1Þ p ¼ cos ½ ð2 n 1Þ p ¼ cos p ¼ 1 und cos 0 ¼ 1 folgt dann:
2u0
1
1
1
1
bn ¼
þ
þ
¼
p
2 ð2 n þ 1Þ
2 ð2 n 1Þ
2 ð2 n þ 1Þ
2 ð2 n 1Þ
¼
2u0
p
1
1
1
1
þ
þ
þ
¼
2 ð2 n þ 1Þ
2 ð2 n 1Þ
2 ð2 n þ 1Þ
2 ð2 n 1Þ
ðzwei verschiedene Summanden; jeweils doppeltÞ
2u0
¼
p
¼
1
1
2u0
1
1
þ 2
¼
2
þ
¼
p
2n þ 1
2n 1
2 ð2 n þ 1Þ
2 ð2 n 1Þ
2u0 2n 1 þ 2n þ 1
2 u0
4n
8u0
n
¼
¼
p
p
p
ð2 n 1Þ ð2 n þ 1Þ
ð2 n 1Þ ð2 n þ 1Þ
ð2 n 1Þ ð2 n þ 1Þ
Umformungen: Die Brüche wurden auf den Hauptnenner ð2 n 1Þ ð2 n þ 1Þ gebracht, d. h. der Reihe nach mit
2 n 1 bzw. 2 n þ 1 erweitert.
Die Fourier-Reihe lautet somit (mit w 0 ¼ 2):
f ðtÞ ¼
¼
1
P
n¼1
1
8u0 X
n
sin ð2 n tÞ ¼
p
n ¼ 1 ð2 n 1Þ ð2 n þ 1Þ
1
2
3
sin ð2 tÞ þ
sin ð4 tÞ þ
sin ð6 tÞ þ . . .
13
35
57
b n sin ðn w 0 tÞ ¼
8u0
p
Amplitudenspektrum
Grund- und Oberschwingungen sind reine Sinusschwingungen mit den Kreisfrequenzen w 1 ¼ 2; w 2 ¼ 4;
w 3 ¼ 6; . . . ; w n ¼ 2 n; . . . und den Phasenwinkeln j n ¼ 0 . Die Amplituden An stimmen hier mit den FourierKoeffizienten überein:
An ¼ bn ¼
An
A1
8u0
n
p
ð2 n 1Þ ð2 n þ 1Þ
100 %
ðf ür n ¼ 1; 2; 3; . . .Þ
Bild D-19 zeigt das Amplitudenspektrum der Funktion.
40 %
25,7 %
19 %
Bild D-19
1
2
3
4
v /v 0
237
E Partielle Differentiation
1 Partielle Ableitungen
Alle Aufgaben in diesem Abschnitt lassen sich nur dann erfolgreich bearbeiten, wenn Sie die Ableitungsregeln (insbesondere Produkt-, Quotienten- und Kettenregel) sicher beherrschen.
Ein Faktor, der die Differentiationsvariable (das ist die Variable, nach der differenziert wird) nicht enthält, ist als
konstanter Faktor zu betrachten und bleibt daher beim Differenzieren erhalten. Ein Summand, der die Differentiationsvariable nicht enthält, ist ein konstanter Summand und verschwindet daher beim Differenzieren.
Lehrbuch: Band 2, Kapitel III.2.1 und 2.2
Formelsammlung: Kapitel IX.2.1 und 2.2
E1
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ ð2 x 3 y 2 Þ 5 .
Differenziert wird mit Hilfe der Kettenregel:
z ¼ ð2 x 3 y 2 Þ 5 ¼ u 5
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
u
mit
u ¼ 2 x 3 y2
und
@u
¼ 2;
@x
@u
¼ 6y
@y
zx ¼
@z
@z @u
¼
¼ 5 u 4 2 ¼ 10 u 4 ¼ 10 ð2 x 3 y 2 Þ 4
@x
@u @x
zy ¼
@z
@z @u
¼
¼ 5 u 4 ð 6 yÞ ¼ 30 y u 4 ¼ 30 y ð2 x 3 y 2 Þ 4
@y
@u @y
E2
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2xy y2.
Die gesuchten partiellen Ableitungen 1. Ordnung werden mit Hilfe der Kettenregel wie folgt gebildet:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
@u
@u
¼ 2y;
¼ 2x 2y
z ¼ 2 x y y 2 ¼ u mit u ¼ 2 x y y 2 und
@x
@y
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
E3
zx ¼
y
@z
@z @u
1
y
¼
¼ pffiffiffi 2 y ¼ pffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
@x
@u @x
2 u
u
2 x y y2
zy ¼
2 ðx yÞ
x y
@z
@z @u
1
¼
¼ pffiffiffi ð2 x 2 yÞ ¼
pffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
@y
@u @y
2 u
2 u
2 x y y2
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ x 2 e x y .
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_5
238
E Partielle Differentiation
Die partielle Ableitung z x erhalten wir mit der Produktregel (in Verbindung mit der Kettenregel):
f
z ¼ x2 e xy ¼ u v
u
u ¼ x2 ;
mit
|fflffl{zfflffl}
v ¼ exy
vx ¼ y exy
und u x ¼ 2 x ;
v
z x ¼ u x v þ v x u ¼ 2 x e x y y e x y x 2 ¼ ð2 x x 2 yÞ e x y
Die Ableitung v x wurde dabei wie folgt mit der Kettenregel gebildet:
v ¼ exy ¼ e t
mit
t ¼ xy
und
@t
¼ y
@x
)
vx ¼
@v
@v @t
¼
¼ e t ð yÞ ¼ y e x y
@x
@t @x
z y erhalten wir mit der Kettenregel:
z ¼ x2 e xy ¼ x2 e t
E4
mit
t ¼ xy
)
zy ¼
@z
@z @t
¼
¼ x 2 e t ð xÞ ¼ x 3 e x y
@y
@t @y
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼
2t x
.
4x þ t
Beide Ableitungen erhalten wir mit Hilfe der Quotientenregel:
z ¼
2t x
u
¼
v
4x þ t
zx ¼
zt ¼
E5
mit
u ¼ 2t x;
v ¼ 4x þ t
und u x ¼ 1 ;
ut ¼ 2 ;
vx ¼ 4 ;
vt ¼ 1
1 ð4 x þ tÞ 4 ð2 t xÞ
ux v vx u
4x t 8t þ 4x
9t
¼
¼
¼
2
2
2
v
ð4 x þ tÞ
ð4 x þ tÞ
ð4 x þ tÞ 2
ut v vt u
v2
¼
2 ð4 x þ tÞ 1 ð2 t xÞ
ð4 x þ tÞ
2
¼
8x þ 2t 2t þ x
ð4 x þ tÞ
2
¼
9x
ð4 x þ tÞ 2
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ ðx 3 y 2 Þ cosh ðx yÞ .
Differenziert wird jeweils nach der Produktregel, wobei die (partiellen) Ableitungen des Faktors cosh ðx yÞ mit Hilfe
der Kettenregel gebildet werden:
z ¼ ðx 3 y 2 Þ cosh ðx yÞ ¼ u v mit
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
v
ux ¼ 3 x2 ;
uy ¼ 2 y
und
u ¼ x3 y2
und
v ¼ cosh ðx yÞ ¼ cosh t
|ffl{zffl}
t
v x ¼ ðsinh tÞ y ¼ y sinh ðx yÞ;
t ¼ xy
v y ¼ ðsinh tÞ x ¼ x sinh ðx yÞ
z x ¼ u x v þ v x u ¼ 3 x 2 cosh ðx yÞ þ y sinh ðx yÞ ðx 3 y 2 Þ ¼
¼ 3 x 2 cosh ðx yÞ þ ðx 3 y y 3 Þ sinh ðx yÞ
z y ¼ u y v þ v y u ¼ 2 y cosh ðx yÞ þ x sinh ðx yÞ ðx 3 y 2 Þ ¼
¼ 2 y cosh ðx yÞ þ ðx 4 x y 2 Þ sinh ðx yÞ
E6
mit
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ ln ð2 x þ e 3 y Þ .
1 Partielle Ableitungen
239
Wir benötigen jeweils die Kettenregel:
z ¼ ln ð2 x þ e 3 y Þ ¼ ln u
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
u
mit
u ¼ 2 x þ e 3y
und
@u
¼ 2;
@x
zx ¼
@z
@z @u
1
2
2
¼
¼
2 ¼
¼
@x
@u @x
u
u
2 x þ e 3y
zy ¼
@z
@z @u
1
3 e 3y
3 e 3y
¼
¼
¼
3 e 3y ¼
u
@y
@u @y
u
2 x þ e3y
@u
¼ 3 e3y
@y
E7
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ arctan
xy þ 1
x þy
.
Für beide Ableitungen benötigen wir jeweils die Ketten- und Quotientenregel:
xy þ 1
xy þ 1
u
¼
z ¼ arctan
¼ arctan t mit t ¼
ðu ¼ x y þ 1 ; v ¼ x þ y ; u x ¼ y ; v x ¼ 1Þ
x þy
x þy
v
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
t
zx ¼
¼
ux v vx u
y ðx þ yÞ 1 ðx y þ 1Þ
@z
@z @t
1
1
¼
¼
¼
¼
2
2
2
@x
@t @x
1þt
1þt
v
ðx þ yÞ 2
x y þ y2 x y 1
ð1 þ t 2 Þ ðx þ yÞ 2
¼
y2 1
ð1 þ t 2 Þ ðx þ yÞ 2
Rücksubstitution und Vereinfachen des Terms 1 þ t 2 im Nenner:
1 þ t2 ¼ 1 þ
xy þ 1
x þy
2
¼ 1þ
ðx y þ 1Þ 2
ðx þ yÞ 2
¼
1 ðx þ yÞ 2 þ ðx y þ 1Þ 2
ðx þ yÞ 2
¼
ðx þ yÞ 2 þ ðx y þ 1Þ 2
ðx þ yÞ 2
Umformungen: Hauptnenner bilden, d. h. den 1. Summand mit ðx þ yÞ 2 erweitern.
Damit erhalten wir für z x den folgenden Ausdruck:
zx ¼
y2 1
ð1 þ t 2 Þ ðx þ yÞ 2
¼
y2 1
ðx þ yÞ 2 þ ðx y þ 1Þ 2
ðx þ yÞ 2
¼
ðx þ yÞ 2
y2 1
ðx þ yÞ 2 þ ðx y þ 1Þ 2
Die vorgegebene Funktion ist bezüglich der Variablen x und y symmetrisch aufgebaut, d. h. die Funktionsgleichung
verändert sich nicht beim Vertauschen dieser Variablen. Daher erhalten wir aus der partiellen Ableitung z x die (noch
unbekannte) partielle Ableitung z y , indem wir x und y miteinander vertauschen:
zy ¼
E8
@z
x2 1
x2 1
¼
¼
@y
ð y þ xÞ 2 þ ð y x þ 1Þ 2
ðx þ yÞ 2 þ ðx y þ 1Þ 2
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ ln ½ cos ð4 x 3 2 y 2 þ 1Þ .
Wir benötigen zwei Substitutionen, um die Funktion auf eine elementare Funktion zurückzuführen (hier substituieren
wir von innen nach außen):
z ¼ ln ½ cos ð4 x 3 2 y 2 þ 1Þ ¼ ln ½ cos u ¼ ln v mit
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflffl{zfflfflffl}
u
v
v ¼ cos u
und u ¼ 4 x 3 2 y 2 þ 1
240
E Partielle Differentiation
Mit Hilfe der Kettenregel erhalten wir die gewünschten Ableitungen:
zx ¼
@z
@z @v @u
1
12 x 2 sin u
¼
¼
ð sin uÞ 12 x 2 ¼
@x
@v @u @x
v
v
Wir haben dabei zuerst z nach v, dann v nach u und schließlich u partiell nach x differenziert und die drei
Ableitungen miteinander multipliziert. Rücksubstitution liefert dann (in der Reihenfolge v ! u ! x):
zx ¼
12 x 2 sin u
12 x 2 sin u
¼
¼ 12 x 2 tan u ¼ 12 x 2 tan ð4 x 3 2 y 2 þ 1Þ
v
cos u
ðunter Berücksichtigung von tan u ¼ sin u=cos uÞ . Analog erhält man z y :
zy ¼
4 y sin u
4 y sin u
@z
@z @v @u
1
¼
¼
¼
¼
ð sin uÞ ð 4 yÞ ¼
v
cos u
@y
@v @u @y
v
¼ 4 y tan u ¼ 4 y tan ð4 x 3 2 y 2 þ 1Þ
pffiffiffi
pffiffiffi
Bilden Sie für die Funktion z ¼ ln ð x þ y Þ den Differentialausdruck x z x þ y z y .
E9
Die benötigten partiellen Ableitungen 1. Ordnung erhalten wir mit Hilfe der Kettenregel:
pffiffiffi
pffiffiffi
z ¼ ln ð x þ y Þ ¼ ln u mit
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
u
zx ¼
u ¼
pffiffiffi
pffiffiffi
x þ y und
@u
1
¼ pffiffiffi ;
@x
2 x
@u
1
¼ pffiffiffi
@y
2 y
@z
@z @u
1
1
1
1
1
¼
¼
pffiffiffi ¼
pffiffiffi ¼
pffiffiffi
pffiffiffi ¼ pffiffiffi pffiffiffi
p
ffiffi
ffi
pffiffiffi
@x
@u @x
u 2 x
2u x
2 ð x þ yÞ x
2 x ð x þ yÞ
Analog (wegen der Symmetrie der Funktion bezüglich der Variablen x und y):
zy ¼
1
1
pffiffiffi ¼ pffiffiffi pffiffiffi
pffiffiffi pffiffiffi
pffiffiffi
2 y ð y þ xÞ
2 y ð x þ yÞ
Einsetzen in den vorgegebenen Ausdruck liefert das folgende Ergebnis:
x zx þ y zy ¼ x
y
1
1
x
pffiffiffi pffiffiffi
pffiffiffi þ y pffiffiffi pffiffiffi
pffiffiffi ¼ pffiffiffi pffiffiffi
pffiffiffi þ pffiffiffi pffiffiffi
pffiffiffi ¼
2 y ð x þ yÞ
2 x ð x þ yÞ
2 y ð x þ yÞ
2 x ð x þ yÞ
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
y
ð x þ yÞ
x
1
¼
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi ¼
pffiffiffi ¼ 2
pffiffiffi þ
2 ð x þ yÞ
2 ð x þ yÞ
2 ð x þ yÞ
Umformungen: Die Brüche zunächst mit
E10
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
x bzw. y erweitern, dann ð x þ yÞ kürzen.
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ 4 sin 3 ðx 2 þ y 2 Þ .
Wir benötigen die Kettenregel, wobei zunächst zwei Substitutionen nacheinander durchzuführen sind (wir substituieren
wieder von innen nach außen):
z ¼ 4 sin 3 ðx 2 þ y 2 Þ ¼ 4 ½ sin ðx 2 þ y 2 Þ 3 ¼ 4 ½ sin u 3 ¼ 4 v 3
|ffl{zffl}
|fflfflfflfflffl{zfflfflfflfflffl}
u
v
mit
v ¼ sin u und u ¼ x 2 þ y 2
1 Partielle Ableitungen
241
Die Kettenregel liefert (erst z nach v, dann v nach u und schließlich u partiell nach x differenzieren):
zx ¼
@z
@z @v @u
¼
¼ 12 v 2 cos u 2 x ¼ 24 x v 2 cos u
@x
@v @u @x
Rücksubstitution (in der Reihenfolge v ! u ! x):
z x ¼ 24 x v 2 cos u ¼ 24 x sin 2 u cos u ¼ 24 x sin 2 ðx 2 þ y 2 Þ cos ðx 2 þ y 2 Þ
Wegen der Symmetrie der Funktionsgleichung (die Variablen x und y sind miteinander vertauschbar, ohne dass sich
dabei die Funktionsgleichung ändert) erhalten wir z y , wenn wir in z x die beiden Variablen x und y miteinander
vertauschen:
z y ¼ 24 y sin 2 ð y 2 þ x 2 Þ cos ð y 2 þ x 2 Þ ¼ 24 y sin 2 ðx 2 þ y 2 Þ cos ðx 2 þ y 2 Þ
E11
Bilden Sie die partiellen Ableitungen 1. Ordnung der Funktion z ¼ arcsin ðx
pffiffiffi
y Þ.
Die gesuchten partiellen Ableitungen erhalten wir wie folgt mit Hilfe der Kettenregel:
pffiffiffi
z ¼ arcsin ðx yÞ ¼ arcsin u
|fflfflffl{zfflfflffl}
u
mit
u ¼ x
pffiffiffi
y und
pffiffiffi
@u
¼ y;
@x
@u
x
¼ pffiffiffi
@y
2 y
pffiffiffi
y
pffiffiffi
@z
@z @u
1
zx ¼
¼
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 1 y ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
@x
@u @x
1 u2
1 x2 y
zy ¼
@z
@z @u
1
1
x
x
¼
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi x pffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi pffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi pffiffiffi
@y
@u @y
2 y
2 1 u2 y
2 1 x2 y y
1 u2
Zeigen Sie: Die Funktion
E12
z ¼ x y þ x ln
y
x
ðmit x > 0 und y > 0Þ
erfüllt die Gleichung x z x þ y z y ¼ x y þ z.
Die Funktion wird vor dem Differenzieren unter Verwendung der Rechenregel ln
gere Gestalt gebracht:
z ¼ x y þ x ln
y
x
a
b
¼ ln a ln b in eine günsti-
¼ x y þ x ðln y ln xÞ ¼ x y þ x ln y x ln x ¼ x ðy þ ln yÞ x ln x
Gliedweises partielles Differenzieren nach x unter Verwendung der Produktregel liefert dann:
f
f
1
z ¼ x ð y þ ln yÞ x ln x ¼ x ðy þ ln yÞ ðu vÞ mit u ¼ x ; v ¼ ln x und u x ¼ 1 ; v x ¼
x
|fflfflfflfflffl{zfflfflfflfflffl}
konst. Faktor
u
v
1
z x ¼ 1 ð y þ ln yÞ ðu x v þ v x uÞ ¼ y þ ln y 1 ln x þ
x ¼ y þ ln y ln x 1
x
f
Die partielle Ableitung nach y lässt sich besonders einfach bilden:
1
x
0 ¼ x þ
z ¼ x ð y þ ln yÞ x ln x ) z y ¼ x 1 þ
y
y
|fflfflfflfflffl{zfflfflfflfflffl}
konst. Faktor
konst. Summand
242
E Partielle Differentiation
Wir setzen die Ausdrücke für z , z x und z y seitenweise in die vorgegebene Gleichung ein:
x
¼ x y þ x ln y x ln x x þ x y þ x ¼
Linke Seite: x z x þ y z y ¼ x ð y þ ln y ln x 1Þ þ y x þ
y
¼ 2 x y þ x ln y x ln x ¼ x ð2 y þ ln y ln xÞ
Rechte Seite: x y þ z ¼ x y þ x y þ x ln y x ln x ¼ 2 x y þ x ln y x ln x ¼ x ð2 y þ ln y ln xÞ
Ein Vergleich zeigt, dass beide Seiten übereinstimmen.
Bilden Sie alle partiellen Ableitungen 1. und 2. Ordnung von z ¼ x e y y e x .
Wie lauten die reinen partiellen Ableitungen 3. Ordnung?
E13
Alle Ableitungen erhält man durch elementare gliedweise (partielle) Differentiation.
Partielle Ableitungen 1. Ordnung
zx ¼
@
½x ey y ex ¼ 1 ey y ex ¼ ey y ex
@x
zy ¼
@
½x ey y ex ¼ x ey 1 ex ¼ x ey ex
@y
Partielle Ableitungen 2. Ordnung
@
@
zx ¼
½ey y ex ¼ 0 y ex ¼ y ex
@x
@x
zxx ¼
9
@
@
>
zx ¼
½ey y ex ¼ ey 1 ex ¼ ey ex >
=
@y
@y
>
@
@
>
zy ¼
½x ey ex ¼ 1 ey ex ¼ ey ex ;
¼
@x
@x
zxy ¼
zyx
zyy ¼
)
zxy ¼ zyx
ðSatz von SchwarzÞ
@
@
zy ¼
½x ey ex ¼ x ey 0 ¼ x ey
@y
@y
Reine partielle Ableitungen 3. Ordnung
Es wird 3-mal partiell nach x bzw. y differenziert:
zxxx ¼
E14
@
@
zxx ¼
½y ex ¼ y ex ;
@x
@x
zyyy ¼
@
@
zyy ¼
½x ey ¼ x ey
@y
@y
Bilden Sie alle partiellen Ableitungen 1. und 2. Ordnung von z ¼
x y
x2 þ y2
.
Partielle Ableitungen 1. Ordnung
Beide Ableitungen erhalten wir mit Hilfe der Quotientenregel:
z ¼
x y
x2 þ y2
zx ¼
¼
u
v
mit u ¼ x y ;
v ¼ x 2 þ y 2;
u x ¼ 1;
v x ¼ 2 x;
u y ¼ 1;
vy ¼ 2 y
1 ðx 2 þ y 2 Þ 2 x ðx yÞ
x2 þ y2 2 x2 þ 2 x y
x2 þ y2 þ 2 x y
ux v vx u
¼
¼
¼
v2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
1 Partielle Ableitungen
zy ¼
243
1 ðx 2 þ y 2 Þ 2 y ðx yÞ
x2 y2 2 x y þ 2 y2
x2 þ y2 2 x y
uy v vy u
¼
¼
¼
v2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
Partielle Ableitungen 2. Ordnung
Wir benötigen jeweils die Quotientenregel in Verbindung mit der Kettenregel.
z x x : Wir differenzieren z x partiell nach x .
x2 þ y2 þ 2 x y
zx ¼
ðx 2 þ
y 2Þ 2
¼
v ¼ ðx 2 þ y 2 Þ 2
u ¼ x2 þ y2 þ 2 x y ;
zxx ¼
¼
¼
ux v vx u
v2
¼
u
v
und u x ¼ 2 x þ 2 y ;
v x ¼ 4 x ðx 2 þ y 2 Þ
ð 2 x þ 2 yÞ ðx 2 þ y 2 Þ 2 4 x ðx 2 þ y 2 Þ ð x 2 þ y 2 þ 2 x yÞ
ðx 2 þ y 2 Þ 4
ðx 2 þ y 2 Þ ½ ð 2 x þ 2 yÞ ðx 2 þ y 2 Þ 4 x ð x 2 þ y 2 þ 2 x yÞ
ðx 2 þ y 2 Þ ðx 2 þ y 2 Þ 3
2 x3 2 x y2 þ 2 x2 y þ 2 y3 þ 4 x3 4 x y2 8 x2 y
ðx 2 þ y 2 Þ 3
¼
ðKettenregel!Þ
¼
¼
2 x3 6 x2 y 6 x y2 þ 2 y3
ðx 2 þ y 2 Þ 3
z x y : Wir differenzieren z x partiell nach y.
zx ¼
x2 þ y2 þ 2 x y
ðx 2 þ
y 2Þ 2
¼
v ¼ ðx 2 þ y 2 Þ 2
u ¼ x2 þ y2 þ 2 x y ;
zxy ¼
¼
¼
uy v vy u
v2
¼
u
v
und u y ¼ 2 y þ 2 x ;
v y ¼ 4 y ðx 2 þ y 2 Þ
ð2 y þ 2 xÞ ðx 2 þ y 2 Þ 2 4 y ðx 2 þ y 2 Þ ð x 2 þ y 2 þ 2 x yÞ
ðx 2 þ y 2 Þ 4
ðx 2 þ y 2 Þ ½ð2 y þ 2 xÞ ðx 2 þ y 2 Þ 4 y ð x 2 þ y 2 þ 2 x yÞ
ðx 2 þ y 2 Þ ðx 2 þ y 2 Þ 3
2 x2 y þ 2 y3 þ 2 x3 þ 2 x y2 þ 4 x2 y 4 y3 8 x y2
ðx 2 þ y 2 Þ 3
¼
ðKettenregel!Þ
¼
¼
2 x3 þ 6 x2 y 6 x y2 2 y3
ðx 2 þ y 2 Þ 3
z y x : Wir differenzieren z y partiell nach x .
zy ¼
x2 þ y2 2 x y
ðx 2
þ
y 2Þ 2
u ¼ x2 þ y2 2 x y ;
zyx ¼
¼
¼
ux v vx u
v2
¼
¼
u
v
v ¼ ðx 2 þ y 2 Þ 2
und u x ¼ 2 x 2 y ;
v x ¼ 4 x ðx 2 þ y 2 Þ
ð 2 x 2 yÞ ðx 2 þ y 2 Þ 2 4 x ðx 2 þ y 2 Þ ð x 2 þ y 2 2 x yÞ
ðx 2 þ y 2 Þ 4
ðx 2 þ y 2 Þ ½ ð 2 x 2 yÞ ðx 2 þ y 2 Þ 4 x ð x 2 þ y 2 2 x yÞ
ðx 2 þ y 2 Þ ðx 2 þ y 2 Þ 3
2 x3 2 x y2 2 x2 y 2 y3 þ 4 x3 4 x y2 þ 8 x2 y
ðx 2 þ y 2 Þ 3
Es gilt somit: z x y ¼ z y x (Satz von Schwarz).
¼
ðKettenregel!Þ
¼
¼
2 x3 þ 6 x2 y 6 x y2 2 y3
ðx 2 þ y 2 Þ 3
244
E Partielle Differentiation
z y y : Wir differenzieren z y partiell nach y.
zy ¼
x2 þ y2 2 x y
ðx 2
þ
y 2Þ 2
v ¼ ðx 2 þ y 2 Þ 2
u ¼ x2 þ y2 2 x y ;
zyy ¼
¼
¼
E15
uy v vy u
v2
¼
u
v
¼
und u y ¼ 2 y 2 x ;
v y ¼ 4 y ðx 2 þ y 2 Þ
ð2 y 2 xÞ ðx 2 þ y 2 Þ 2 4 y ðx 2 þ y 2 Þ ð x 2 þ y 2 2 x yÞ
¼
ðx 2 þ y 2 Þ 4
ðx 2 þ y 2 Þ ½ ð2 y 2 xÞ ðx 2 þ y 2 Þ 4 y ð x 2 þ y 2 2 x yÞ
ðx 2 þ y 2 Þ ðx 2 þ y 2 Þ 3
2 x2 y þ 2 y3 2 x3 2 x y2 þ 4 x2 y 4 y3 þ 8 x y2
ðx 2 þ y 2 Þ 3
¼
ðKettenregel!Þ
¼
2 x3 þ 6 x2 y þ 6 x y2 2 y3
ðx 2 þ y 2 Þ 3
Bilden Sie alle partiellen Ableitungen 1. und 2. Ordnung von z ¼ arctan
y
x
x ¼ 1; y ¼ 2:
an der Stelle
Partielle Ableitungen 1. Ordnung
Differenziert wird jeweils nach der Kettenregel:
z ¼ arctan
zx ¼
y
¼ arctan u
x
|{z}
u
u ¼
mit
y
¼ y x 1
x
@u
¼ y x 2 ;
@x
und
@u
¼ x 1
@y
y x 2
y
@z
@z @u
1
¼
¼
y ð 1 x 2 Þ ¼
¼
2
2
@x
@u @x
1þu
1þu
ð1 þ u 2 Þ x 2
Rücksubstitution liefert (wir berechnen zunächst den Nenner 1 þ u 2 ) :
1 þ u2 ¼ 1 þ
y
x
2
¼ 1þ
y2
x2
¼
x2 þ y2
)
x2
zx ¼
y
ð1 þ u 2 Þ x 2
y
¼
x þy
2
2
x2
¼
x2
y
x2 þ y2
Analog erhalten wir z y :
zy ¼
@z
@z @u
1
1
1
1
¼ 2
¼
¼
¼
2
2
@y
@u @y
x
1þu
x þ y2
ð1 þ u Þ x
x2
¼
x
1
x þy
x
2
¼
2
x
x2
þ y2
Partielle Ableitungen 1. Ordnung an der Stelle x == – 1 , y == 2
z x ðx ¼ 1; y ¼ 2Þ ¼
2
ð 1Þ 2
þ
22
¼
2
5
;
z y ðx ¼ 1; y ¼ 2Þ ¼
1
ð 1Þ 2
þ
22
Partielle Ableitungen 2. Ordnung
z x x : z x wird mit Hilfe der Kettenregel partiell nach x differenziert
zx ¼
y
¼ y ðx 2 þ y 2 Þ 1 ¼ y u 1
x2 þ y2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
mit
u ¼ x2 þ y2
und
@u
¼ 2x
@x
¼
1
5
1 Partielle Ableitungen
zxx ¼
245
@ zx
@ zx @ u
2xy
2xy
¼
¼
¼ y ð 1 u 2 Þ 2 x ¼ 2 x y u 2 ¼
2
@x
@u @x
u
ðx 2 þ y 2 Þ 2
Alternative: Quotientenregel verwenden, wobei der Zähler eine konstante, d. h. von x unabhängige Funktion ist.
z x y : z x wird mit Hilfe der Quotientenregel partiell nach y differenziert.
zx ¼
zxy ¼
y
u
¼
v
x2 þ y2
v ¼ x2 þ y2
mit u ¼ y ;
und
uy ¼ 1 ;
vy ¼ 2 y
uy v vy u
1 ðx 2 þ y 2 Þ 2 y ð yÞ
x2 y2 þ 2 y2
x2 þ y2
@ zx
¼
¼
¼
¼
@y
v2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
Analog wird z y x gebildet (z y partiell nach x differenzieren):
zy ¼
zyx ¼
x
u
¼
v
x2 þ y2
mit
u ¼ x;
v ¼ x2 þ y2
und u x ¼ 1 ;
vx ¼ 2 x
1 ðx 2 þ y 2 Þ 2 x x
x2 þ y2 2 x2
x2 þ y2
@ zy
ux v vx u
¼
¼
¼
¼
@x
v2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
Es gilt: z x y ¼ z y x (Satz von Schwarz).
z y y : z y wird mit der Ketten- oder Quotientenregel partiell nach y differenziert. Wir wählen hier die Quotientenregel.
zy ¼
zyy ¼
x2
x
u
¼
2
v
þy
mit
u ¼ x;
v ¼ x2 þ y2
und u y ¼ 0 ;
vy ¼ 2 y
uy v vy u
0 ðx 2 þ y 2 Þ 2 y x
2xy
@ zy
¼
¼
¼
@y
v2
ðx 2 þ y 2 Þ 2
ðx 2 þ y 2 Þ 2
Partielle Ableitungen 2. Ordnung an der Stelle x == – 1 , y == 2
z x x ðx ¼ 1; y ¼ 2Þ ¼
2 ð 1Þ 2
½ ð 1Þ 2
þ
2 2 2
¼
4
25
z x y ðx ¼ 1; y ¼ 2Þ ¼ z y x ðx ¼ 1; y ¼ 2Þ ¼
E16
;
2 ð 1Þ 2
z y y ðx ¼ 1; y ¼ 2Þ ¼
ð 1Þ 2 þ 2 2
½ ð 1Þ 2
þ
2 2 2
¼
½ ð 1Þ 2
1 þ 4
ð1 þ 4Þ
2
3
25
Bilden Sie alle partiellen Ableitungen 1. und 2. Ordnung von z ¼ ln ð2 y x 2 Þ .
Partielle Ableitungen 1. Ordnung
Wir verwenden wie folgt die Kettenregel:
@u
z ¼ ln ð2 y x 2 Þ ¼ ln u mit u ¼ 2 y x 2 und
¼ 2x;
@x
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
u
@z
@z @u
1
2x
2x
zx ¼
¼
¼
ð 2 xÞ ¼
¼
@x
@u @x
u
u
2y x2
zy ¼
¼
@z
@z @u
1
2
2
¼
¼
2 ¼
¼
@y
@u @y
u
u
2y x2
@u
¼ 2
@y
þ
2 2 2
¼
4
25
246
E Partielle Differentiation
Partielle Ableitungen 2. Ordnung
z x x erhalten wir, indem wir z x mit Hilfe der Quotientenregel partiell nach x differenzieren:
2x
u
¼
v
2y x2
zx ¼
zxx ¼
mit
u ¼ 2x;
v ¼ 2y x2
und u x ¼ 2 ;
vx ¼ 2 x
2 ð2 y x 2 Þ ð 2 xÞ ð 2 xÞ
4y þ 2x2 4x2
2x2 4y
@ zx
ux v vx u
¼
¼
¼
¼
@x
v2
ð2 y x 2 Þ 2
ð2 y x 2 Þ 2
ð2 y x 2 Þ 2
z x y erhält man aus z x durch partielles Differenzieren nach y. Wir benötigen die Kettenregel:
2x
¼ 2 x ð2 y x 2 Þ 1 ¼ 2 x u 1
2y x2
|fflfflfflfflffl{zfflfflfflfflffl}
u
zx ¼
zxy ¼
mit
u ¼ 2y x2
und
@u
¼ 2
@y
@ zx
@ zx @ u
4x
4x
¼
¼
¼ 2 x ð 1 u 2 Þ 2 ¼ 4 x u 2 ¼
@y
@u @y
u2
ð2 y x 2 Þ 2
Alternative: Sie differenzieren nach der Quotientenregel, wobei der Zähler eine konstante, d. h. von der Variablen y
unabhängige Funktion ist.
z y x erhalten wir, indem wir z y mit Hilfe der Quotienten- oder Kettenregel partiell nach x differenzieren. Wir wollen
an dieser Stelle die Quotientenregel verwenden:
2
u
¼
v
2y x2
zy ¼
zyx ¼
mit
u ¼ 2;
v ¼ 2y x2
und
ux ¼ 0 ;
vx ¼ 2 x
ux v vx u
0 ð2 y x 2 Þ ð 2 xÞ 2
@ zy
4x
¼
¼
¼
2
2
@x
2
v
ð2 y x 2 Þ 2
ð2 y x Þ
Es gilt: z x y ¼ z y x (Satz von Schwarz).
z y y erhalten wir, indem wir z y mit Hilfe der Ketten- oder Quotientenregel partiell nach y differenzieren. Wir verwenden hier die Kettenregel:
2
¼ 2 ð2 y x 2 Þ 1 ¼ 2 u 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
2y x2
u
zy ¼
zyy ¼
mit
u ¼ 2y x2
und
@u
¼ 2
@y
@ zy
@ zy @ u
4
4
¼
¼
¼ 2 ð 1 u 2 Þ 2 ¼ 4 u 2 ¼
2
@y
@u @y
u
ð2 y x 2 Þ 2
Zeigen Sie, dass die Funktion
E17
f ðx; tÞ ¼ e p
2
a2 t
sin ðp xÞ
eine Lösung der Gleichung
a 2 fxx ¼ ft
ist (a: Konstante).
Wir bilden zunächst die benötigten partiellen Ableitungen f t und f x x .
Partielle Ableitung f t
f ¼ e p
2
a2 t
sin ðp xÞ ¼ sin ðp xÞ e p
2
a2 t
¼ sin ðp xÞ e u
mit
u ¼ p2 a2 t
und
@u
¼ p2 a2
@t
Mit der Kettenregel erhält man ðsin ðp xÞ ist ein konstanter FaktorÞ:
ft ¼
@f
@f @u
2 2
¼
¼ sin ðp xÞ e u ð p 2 a 2 Þ ¼ p 2 a 2 sin ðp xÞ e u ¼ p 2 a 2 sin ðp xÞ e p a t
@t
@u @t
1 Partielle Ableitungen
247
Partielle Ableitung f x x
Wir differenzieren die Funktion f ðx; tÞ zweimal nacheinander partiell nach x, wobei wir jedes Mal die Kettenregel
2 2
benutzen (e p a t ist dabei ein konstanter Faktor):
f ¼ e p
2
a2 t
sin ðp xÞ ¼ e p
|ffl{zffl}
u
2
a2 t
sin u
mit u ¼ p x
und
@u
¼ p
@x
@f
@f @u
2 2
2 2
¼
¼ e p a t ðcos uÞ p ¼ p e p a t cos u mit
@x
@u @x
fx ¼
fxx ¼
u ¼ px
@u
¼ p
@x
und
@ fx
@ fx @ u
2 2
2 2
¼
¼ p e p a t ð sin uÞ p ¼ p 2 e p a t sin ðp xÞ
@x
@u @x
Wir multiplizieren f x x mit a 2 und erhalten:
a2 fxx ¼ a2 ½ p2 e p
2
sin ðp xÞ ¼ p 2 a 2 sin ðp xÞ e p a t ¼ f t
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
ft
a2 t
2
2
Die gegebene Funktion erfüllt somit (wie behauptet) die Differentialgleichung a 2 f x x ¼ f t .
E18
Bilden Sie alle partiellen Ableitungen 1. und 2. Ordnung von z ¼ 5 e x
2
y2
.
Partielle Ableitungen 1. Ordnung
Differenziert wird unter Verwendung der Kettenregel:
z ¼ 5 ex
2
y2
¼ 5 et
t ¼ x2 y2
mit
@t
¼ 2x;
@x
und
@t
¼ 2y
@y
zx ¼
@z
@z @t
2
2
¼
¼ 5 e t 2 x ¼ 10 x e t ¼ 10 x e x y
@x
@t @x
zy ¼
@z
@z @t
2
2
¼
¼ 5 e t ð 2 yÞ ¼ 10 y e t ¼ 10 y e x y
@y
@t @y
Partielle Ableitungen 2. Ordnung
Bei der Bildung der partiellen Ableitungen 2. Ordnung benötigen wir immer wieder die partiellen Ableitungen 1. Ord2
2
nung der Funktion e x y . Diese aber sind (bis auf den Faktor 5) identisch mit den bereits bekannten Ableitungen z x
und z y unserer Ausgangsfunktion. Somit gilt:
@
@x
ex
2
y2
¼ 2x ex
2
y2
@
@y
;
ex
2
y2
¼ 2y ex
2
y2
z x x : Die partielle Ableitung z x wird mit Hilfe der Produkt- und Kettenregel partiell nach x differenziert.
z x ¼ 10 x e x y ¼ u v mit
|{z} |fflfflffl{zfflfflffl}
u
v
2
2
z x x ¼ u x v þ v x u ¼ 10 e x
2
u ¼ 10 x ;
y2
þ 2x ex
v ¼ ex
2
y2
2
y2
und u x ¼ 10 ;
10 x ¼ ð10 þ 20 x 2 Þ e x
vx ¼ 2 x e x
2
2
y2
y2
z x y : Die partielle Ableitung z x wird partiell nach y differenziert (Kettenregel).
zxy ¼
@
@
zx ¼
@y
@y
10 x e x
2
y2
¼ 10 x
@
@y
ex
2
y2
¼ 10 x ð 2 y e x
2
y2
Þ ¼ 20 x y e x
2
y2
248
E Partielle Differentiation
z y x : Die partielle Ableitung z y wird partiell nach x differenziert (Kettenregel).
zyx ¼
@
@
zy ¼
@x
@x
10 y e x
2
y2
¼ 10 y
@
@x
ex
2
y2
¼ 10 y 2 x e x
2
y2
¼ 20 x y e x
2
y2
Erwartungsgemäß ist z x y ¼ z y x (Satz von Schwarz).
z y y : Die partielle Ableitung z y wird partiell nach y differenziert (Produkt- und Kettenregel).
z y ¼ 10 y e x y ¼ u v mit u ¼ 10 y ; v ¼ e x y und u y ¼ 10 ; v y ¼ 2 y e x
|fflffl{zfflffl} |fflfflffl{zfflfflffl}
u
v
2
2
2
2
2
2
z y y ¼ u y v þ v y u ¼ 10 e x y 2 y e x y ð 10 yÞ ¼ ð 10 þ 20 y 2 Þ e x y
2
2
2
2
2
y2
Bilden Sie zunächst die partiellen Ableitungen 1. Ordnung von w ¼ e y=x und dann unter Verwendung
der erzielten Ergebnisse die gemischten partiellen Ableitungen 2. Ordnung von z ¼ x w ¼ x e y=x .
E19
Partielle Ableitungen 1. Ordnung von w = e y/x
Mit der Kettenregel erhalten wir wie folgt die gewünschten Ableitungen:
w ¼ e y=x ¼ e t
t ¼
mit
y
¼ y x 1
x
und
@t
¼ y x2 ;
@x
@t
¼ x1
@y
wx ¼
@w
@w @t
¼
¼ e t y ð 1 x 2 Þ ¼ y x 2 e t ¼ y x 2 e y=x
@x
@t @x
wy ¼
@w
@w @t
¼
¼ e t 1 x 1 ¼ x 1 e y=x
@y
@t @y
Diese Ableitungen lassen sich wegen e y=x ¼ w auch wie folgt ausdrücken:
w x ¼ y x 2 e y=x ¼ y x 2 w ;
|{z}
w
w y ¼ x 1 e y=x ¼ x 1 w
|{z}
w
Gemischte partielle Ableitungen 2. Ordnung von z = x w = x e y/x
Mit der Produktregel erhalten wir z x :
f
f
z ¼ x w ¼ u v mit
u ¼ x;
v ¼ w
und u x ¼ 1 ;
vx ¼ wx ¼ y x 2 w
u v
z x ¼ u x v þ v x u ¼ 1 w y x 2 w x ¼ w y x 1 w ¼ ð1 x 1 yÞ w
Wiederum mit Hilfe der Produktregel bilden wir die gemischte partielle Ableitung z x y :
f
z x ¼ ð1 x 1 yÞ w ¼ u v mit u ¼ 1 x 1 y; v ¼ w und u y ¼ x 1 ; v y ¼ w y ¼ x 1 w
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
u
v
z x y ¼ u y v þ v y u ¼ x 1 w þ x 1 w ð1 x 1 yÞ ¼ x 1 w þ x 1 w x 2 y w ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
¼ x 2 y w ¼ x 2 y e y=x
Jetzt bilden wir die gemischte partielle Ableitung z y x . Zunächst differenzieren wir die Funktion z ¼ x w partiell
nach y (dabei bleibt x als konstanter Faktor erhalten):
zy ¼ x wy ¼ x x 1 w ¼ w
Wir differenzieren weiter partiell nach x:
z y x ¼ w x ¼ y x 2 w ¼ x 2 y e y=x
Die gemischten partiellen Ableitungen 2. Ordnung stimmen überein (Satz von Schwarz): z x y ¼ z y x ¼ x 2 y e y=x
1 Partielle Ableitungen
E20
249
Bilden Sie mit der Funktion w ¼ ln ðx 2 þ y 2 Þ den Differentialausdruck w x x þ w y y .
Die Funktion ist symmetrisch bezüglich der Variablen x und y ( Vertauschung dieser Variablen ändert nichts an der
Funktionsgleichung). Daher genügt es, die partielle Ableitung w x x zu bilden, aus der man dann durch Vertauschen der
beiden Variablen die Ableitung w y y erhält.
Zunächst differenzieren wir partiell nach x und verwenden dabei die Kettenregel:
w ¼ ln ðx 2 þ y 2 Þ ¼ ln t
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
t
wx ¼
mit t ¼ x 2 þ y 2
und
@t
¼ 2x
@x
@w
@w @t
1
2x
2x
¼
¼
2x ¼
¼
2
@x
@t @x
t
t
x þ y2
Die partielle Ableitung 2. Ordnung w x x bilden wir mit Hilfe der Quotientenregel:
wx ¼
2x
u
¼
v
x2 þ y2
wxx ¼
ux v vx u
v2
u ¼ 2x;
mit
¼
v ¼ x2 þ y2
2 ðx 2 þ y 2 Þ 2 x 2 x
ðx 2 þ y 2 Þ 2
¼
und u x ¼ 2 ;
2 x2 þ 2 y2 4 x2
ðx 2 þ y 2 Þ 2
¼
vx ¼ 2 x
2 x2 þ 2 y2
ðx 2 þ y 2 Þ 2
Durch Vertauschen von x und y folgt dann:
wyy ¼
2 y2 þ 2 x2
ð y 2 þ x 2Þ 2
¼
2 x2 2 y2
ðx 2 þ y 2 Þ 2
Somit gilt:
wxx þ wyy ¼
E21
z ¼
2 x2 þ 2 y2
ðx 2 þ
y 2Þ 2
þ
2 x2 2 y2
ðx 2 þ
y 2Þ 2
¼
2 x2 þ 2 y2 þ 2 x2 2 y2
ðx 2 þ
y 2Þ 2
¼
0
ðx 2 þ y 2 Þ 2
¼ 0
Die gemischte partielle Ableitung 3. Ordnung zx y x dieser Funktion
x2
soll mit möglichst wenig Rechenaufwand bestimmt werden
1 þ y2
(Satz von Schwarz verwenden).
Günstigste Differentiationsreihenfolge: x ! x ! y. Wir bilden somit zx x y :
@z
@
x2
1
@
1
2x
zx ¼
¼
x2 ¼
¼
2x ¼
2
2
@x
@ x 1 þ y2
@
x
1þy
1þy
1 þ y2
zxx
@ zx
@
¼
¼
@x
@x
2x
1 þ y2
¼
2
@
2
2
½x ¼
1 ¼
2
2
@x
1þy
1þy
1 þ y2
Diesen Ausdruck differenzieren partiell nach y unter Verwendung der Kettenregel:
zxx ¼
zxxy ¼
2
¼ 2 ð1 þ y 2 Þ 1 ¼ 2 u 1
1 þ y2
|fflfflfflfflffl{zfflfflfflfflffl}
u
mit
u ¼ 1 þ y2
und
@u
¼ 2y
@y
@ zxx
@ zxx @ u
4y
4y
¼ 2 ð 1 u 2 Þ 2 y ¼ 4 y u 2 ¼
¼
¼ zxyx
¼
2
@y
@u @y
u
ð1 þ y 2 Þ 2
250
E Partielle Differentiation
Bestimmen Sie von der Funktion z ¼ x y arctan x alle partiellen Ableitungen 1. bis 3. Ordnung
E22
(auf der Basis des Satzes von Schwarz).
Partielle Ableitungen 1. Ordnung
z x erhalten wir mit Hilfe der Produktregel:
@
@
1
½ x y arctan x ¼ y
½ x arctan x mit u ¼ x ; v ¼ arctan x und u x ¼ 1 ; v x ¼
@x
@x
1
þ
x2
|fflfflfflffl{zfflfflfflffl}
" konst. Faktor
u
v
1
x
x ¼ y arctan x þ
z x ¼ y ðu x v þ v x uÞ ¼ y 1 arctan x þ
1 þ x2
1 þ x2
f
zx ¼
zy ¼
@
@
½ x y arctan x ¼ x arctan x
½ y ¼ x arctan x 1 ¼ x arctan x
@y "
@y
"
konstante Faktoren
Partielle Ableitungen 2. Ordnung
y arctan x þ
@ zx
@
¼
@x
@x
zxx ¼
u ¼ x;
x
1 þ x2
¼ y
" konst. Faktor
v ¼ 1 þ x2
ux ¼ 1 ;
und
@
@x
arctan x þ
x
1 þ x2
¼ y
@ h
ui
arctan x þ
@x
v
vx ¼ 2 x
Es wird gliedweise differenziert, der 2. Summand dabei nach der Quotientenregel:
zxx ¼ y
¼ y
1 ð1 þ x 2 Þ þ 1 þ x 2 2 x 2
¼ y
zxy
ux v vx u
1
þ
2
1þx
v2
ð1 þ
@ zx
@
¼
¼
@y
@y
x 2Þ 2
1 ð1 þ x 2 Þ 2 x x
1
þ
1 þ x2
ð1 þ x 2 Þ 2
!
¼ y
1 þ x2 þ 1 x2
ð1 þ
!
!
x 2Þ 2
¼ y
¼
2
ð1 þ
x 2Þ 2
¼
2y
ð1 þ x 2 Þ 2
y arctan x þ
x
x
@
½y ¼
¼ arctan x þ
2
2
@
y
1þx
1þx
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
konst. Faktor
¼
zyy ¼
arctan x þ
x
1 þ x2
1 ¼ arctan x þ
x
¼ zyx
1 þ x2
ðSatz von SchwarzÞ
@ zy
@
¼
½ x arctan x ¼ 0
@y
@ y |fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
konst. Summand
Partielle Ableitungen 3. Ordnung
Wir differenzieren zunächst z x x wie folgt partiell nach x unter Verwendung der Kettenregel:
zxx ¼
zxxx ¼
2y
ð1 þ
x 2Þ 2
¼ 2 y ð1 þ x 2 Þ 2 ¼ 2 y u 2
|fflfflfflfflffl{zfflfflfflfflffl}
u
mit u ¼ 1 þ x 2
und
@u
¼ 2x
@x
@ zxx
@ zxx @ u
8xy
8xy
¼
¼
¼ 2 y ð 2 u 3 Þ 2 x ¼ 8 x y u 3 ¼
@x
@u @x
u3
ð1 þ x 2 Þ 3
1 Partielle Ableitungen
251
z x x y erhalten wir, indem wir z x x partiell nach y differenzieren:
"
#
"
#
@ zxx
@
2y
@
2
2
2
¼
y ¼
1 ¼
¼ zxyx ¼ zyxx
zxxy ¼
¼
2
2
2
@y
@ y ð1 þ x 2 Þ
@ y ð1 þ x 2 Þ
ð1 þ x 2 Þ
ð1 þ x 2 Þ 2
" konst. Faktor
Aus z y y ¼ 0 folgt z y y y ¼ 0 und z y y x ¼ 0 und somit nach dem Satz von Schwarz: z x y y ¼ z y x y ¼ z y y x ¼ 0.
E23
Zeigen Sie: Für die Funktion z ¼ e x y gilt z x x y ¼ z x y x ¼ z y x x .
Wir bilden zunächst alle benötigten partiellen Ableitungen 1. und 2. Ordnung. Dies sind: z x , z y , z x x , z x y , z y x
Partielle Ableitungen 1. Ordnung
z x erhalten wir mit Hilfe der Kettenregel:
z ¼ e xy ¼ e u
u ¼ xy
mit
und
@u
¼ y
@x
)
zx ¼
@z
@z @u
¼
¼ eu y ¼ y e xy
@x
@u @x
Analog (wegen der Symmetrie der Funktion bezüglich der Variablen x und y): z y ¼ x e y x ¼ x e x y
Diese partiellen Ableitungen werden wir im Folgenden an verschiedenen Stellen benötigen. Wir merken uns daher:
@
½ exy ¼ y exy
@x
@
½e xy ¼ x exy
@y
und
Partielle Ableitungen 2. Ordnung: z x x , z x y , z y x
z x x : Wir differenzieren z x partiell nach x (Kettenregel).
zxx ¼
@ zx
@
@
¼
½ y e xy ¼ y
½ e xy ¼ y y e xy ¼ y2 e xy
@x
@x
@x
z x y : Die Ableitung z x wird partiell nach y differenziert (Produkt- und Kettenregel).
mit
u ¼ y;
v ¼ e xy
und
uy ¼ 1 ;
vy ¼ x exy
und
ux ¼ 1 ;
vx ¼ y exy
f
@ zx
@
@
½ y exy ¼
½uv
¼
@y
@y
@y
u v
f
zxy ¼
z x y ¼ u y v þ v y u ¼ 1 e x y þ x e x y y ¼ ð1 þ x yÞ e x y
z y x : Wir differenzieren z y partiell nach x (Produkt- und Kettenregel).
u ¼ x;
mit
f
@ zy
@
@
½ x exy ¼
½uv
¼
@x
@x
@x
u v
f
zyx ¼
v ¼ e xy
z y x ¼ u x v þ v x u ¼ 1 e x y þ y e x y x ¼ ð1 þ x yÞ e x y
Partielle Ableitungen 3. Ordnung: z x x y , z x y x , z y x x
z x x y : Wir differenzieren z x x partiell nach y (Produkt- und Kettenregel).
mit
u ¼ y2 ;
v ¼ e xy
f
@ zxx
@
@
½ y2 e xy ¼
½uv
¼
@y
@y
@y
u
v
f
zxxy ¼
z x x y ¼ u y v þ v y u ¼ 2 y e x y þ x e x y y 2 ¼ ð2 y þ x y 2 Þ e x y
und u y ¼ 2 y ;
vy ¼ x exy
252
E Partielle Differentiation
z x y x : Wir differenzieren z x y partiell nach x (Produkt- und Kettenregel).
zxyx ¼
@ zxy
@
@
½ ð1 þ x yÞ e x y ¼
½ u v mit u ¼ 1 þ x y ; v ¼ e x y ; u x ¼ y ; v x ¼ y e x y
¼
@ x |fflfflfflfflfflffl{zfflfflfflfflfflffl} |{z}
@x
@x
u
v
z x y x ¼ u x v þ v x u ¼ y e x y þ y e x y ð1 þ x yÞ ¼ y e x y þ y e x y þ x y 2 e x y ¼
¼ 2 y e x y þ x y 2 e x y ¼ ð2 y þ x y 2 Þ e x y
z y x x : Wir differenzieren z y x partiell nach x (Produkt- und Kettenregel).
zyxx ¼
@ zyx
@
@
¼
½ ð1 þ x yÞ e x y ¼
½ u v mit u ¼ 1 þ x y ; v ¼ e x y ; u x ¼ y ; v x ¼ y e x y
@x
@ x |fflfflfflfflfflffl{zfflfflfflfflfflffl} |{z}
@x
u
v
z y x x ¼ u x v þ v x u ¼ y e x y þ y e x y ð1 þ x yÞ ¼ y e x y þ y e x y þ x y 2 e x y ¼
¼ 2 y e x y þ x y 2 e x y ¼ ð2 y þ x y 2 Þ e x y
Durch Vergleich stellen wir fest: z x x y ¼ z x y x ¼ z y x x ¼ ð2 y þ x y 2 Þ e x y
2 Differentiation nach einem Parameter (Kettenregel)
Lehrbuch: Band 2, Kapitel III.2.3
Formelsammlung: Kapitel IX.2.3
E24
z ¼ x2 þ 6xy þ 2y2
mit
x ðtÞ ¼ cos t , y ðtÞ ¼ sin t
Differenzieren Sie z nach dem Parameter t. Welchen Wert hat diese Ableitung an der Stelle t ¼ p=2 ?
Wir bilden zunächst die benötigten Ableitungen z x , z y , x_ und y_ und drücken diese mit Hilfe der Parametergleichungen durch den Parameter t aus:
z x ¼ 2 x þ 6 y ¼ 2 cos t þ 6 sin t ;
x_ ¼ sin t ;
z y ¼ 6 x þ 4 y ¼ 6 cos t þ 4 sin t
y_ ¼ cos t
Damit erhalten wir für die gesuchte Ableitung z_ den folgenden vom Parameter t abhängigen Ausdruck:
z_ ¼ z x x_ þ z y y_ ¼ ð2 cos t þ 6 sin tÞ ð sin tÞ þ ð6 cos t þ 4 sin tÞ cos t ¼
¼ 2 sin t cos t 6 sin 2 t þ 6 cos 2 t þ 4 sin t cos t ¼ 2 sin t cos t þ 6 ðcos 2 t sin 2 tÞ ¼
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
|fflffl{zfflffl}
sin ð2 tÞ
1 sin 2 t
2
2
2
¼ sin ð2 tÞ þ 6 ð1 sin t sin tÞ ¼ sin ð2 tÞ þ 6 ð1 2 sin tÞ
(unter Berücksichtigung der Beziehungen sin ð2 tÞ ¼ 2 sin t cos t und sin 2 t þ cos 2 t ¼ 1). Somit gilt:
z_ ðt ¼ p=2Þ ¼ sin p þ 6 ð1 2 sin 2 ðp=2ÞÞ ¼ 0 þ 6 ð1 2 1 2 Þ ¼ 6 ð 1Þ ¼ 6
2 Differentiation nach einem Parameter (Kettenregel)
z ¼ arctan ðx yÞ
E25
253
x ðtÞ ¼ e 3 t , y ðtÞ ¼ 1 e 3 t
mit
Bestimmen Sie z_ ðtÞ und z_ ðt ¼ 0Þ.
Wir benötigen die Ableitungen z x , z y , x_ und y_ . Die partiellen Ableitungen z x und z y erhalten wir mit Hilfe der
Kettenregel:
z ¼ arctan ðx yÞ ¼ arctan u mit
|fflfflfflffl{zfflfflfflffl}
u
u ¼ x y
@u
¼ 1;
@x
und
@u
¼ 1
@y
zx ¼
@z
@z @u
1
1
1
¼
¼
1 ¼
¼
2
2
@x
@u @x
1þu
1þu
1 þ ðx yÞ 2
zy ¼
@z
@z @u
1
1
1
¼
¼
ð 1Þ ¼
¼
@y
@u @y
1 þ u2
1 þ u2
1 þ ðx yÞ 2
Auch die Ableitungen x_ und y_ bilden wir mit der Kettenregel:
x ¼ e 3t ¼ e u
mit
u ¼ 3t
y ¼ 1 e 3t ¼ 1 eu
du
¼ 3
dt
und
mit u ¼ 3 t
du
¼ 3
dt
und
dx
dx du
¼
¼ e u 3 ¼ 3 e 3t
dt
du dt
x_ ¼
)
)
y_ ¼ 0 e u 3 ¼ 3 e 3 t
Damit erhalten wir für die Ableitung der Funktion z ¼ arctan ðx yÞ nach dem Parameter t den folgenden Ausdruck (für x und y werden die Parametergleichungen eingesetzt):
z_ ¼ z x x_ þ z y y_ ¼
¼
6 e 3t
1 þ ðx yÞ 2
z_ ðt ¼ 0Þ ¼
1
1 þ ðx yÞ 2
¼
6 e 3t
1 þ ðe 3 t 1 þ e 3 t Þ 2
6 e0
1 þ ð2
3 e 3t
e0
1Þ
2
¼
1
1 þ ðx yÞ 2
¼
ð 3 e 3 t Þ ¼
3 e 3t þ 3 e 3t
¼
1 þ ðx yÞ 2
6 e 3t
1 þ ð2 e 3 t 1Þ 2
61
1 þ ð2 1 1Þ
2
¼
6
6
¼
¼ 3
1þ1
2
xz
mit x ð pÞ ¼ e p ; y ð pÞ ¼ p ; z ð pÞ ¼ ln p
y
Wie lautet die Ableitung von u nach dem Parameter p? Berechnen Sie ferner u_ ð p ¼ 1Þ.
u ¼
E26
Da die Funktion von drei unabhängigen Variablen abhängt, benötigen wir folgende Ableitungen: u x , u y , uz und x_ ,
y_, z_ . Wir erhalten sie durch elementare Differentiation und drücken sie unter Verwendung der Parametergleichungen
durch den Parameter p aus:
ux ¼
ln p
z
¼
;
y
p
uy ¼
e p ln p
xz
¼
;
y2
p2
uz ¼
x
ep
¼
;
y
p
x_ ¼ e p ;
y_ ¼ 1 ;
z_ ¼
1
p
Dann gilt (alle Brüche auf den Hauptnenner p 2 bringen):
u_ ¼ u x x_ þ u y y_ þ uz z_ ¼
¼
ln p
e p ln p
e p ln p
e p ln p
ep 1
ep
¼
1þ
þ
¼
ep
p
p
p p
p2
p2
p2
p e p ln p e p ln p þ e p
u_ ð p ¼ 1Þ ¼
p2
¼
ð p ln p ln p þ 1Þ e p
ð1 ln 1 ln 1 þ 1Þ e 1
12
p2
¼
ð1 0 0 þ 1Þ e
¼ 1e ¼ e
1
254
E Partielle Differentiation
z ¼ ln ðx 2 þ y 2 Þ
E27
mit
x ¼ x;
y ¼ cos x
Bestimmen Sie die Ableitung von z nach dem Parameter x sowie z_ ðx ¼ pÞ.
Hinweis: Die Koordinate x ist zuleich der Parameter.
Wir benötigen die Ableitungen z x , z y , x_ und y_ (Parameter ist die Variable x). Mit Hilfe der Kettenregel erhalten
wir die partiellen Ableitungen z x und z y und beachten dabei die Symmetrie der Funktion bezüglich der Variablen x
und y:
@u
¼ 2x
z ¼ ln ðx 2 þ y 2 Þ ¼ ln u mit u ¼ x 2 þ y 2 und
@x
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
zx ¼
@z
@z @u
1
2x
2x
;
¼
¼
2x ¼
¼
@x
@u @x
u
u
x2 þ y2
analog : z y ¼
2y
x2 þ y2
Ferner: x_ ¼ 1, y_ ¼ sin x
Die gesuchte Ableitung von z nach dem Parameter x lautet damit (unter Berücksichtigung der Parametergleichung
y ¼ cos x):
2y
2 x 2 y sin x
2 ðx cos x sin xÞ
2x
1þ
ð sin xÞ ¼
¼
z_ðxÞ ¼ z x x_ þ z y y_ ¼
2
2
2
2
2
2
x þy
x þy
x þy
x 2 þ cos 2 x
z_ ðx ¼ pÞ ¼
E28
2 ðp cos p sin pÞ
p2
þ
cos 2
p
¼
2 ðp þ 1 0Þ
p 2 þ ð 1Þ 2
¼
2p
¼ 0,5781
p2 þ 1
Gegeben ist die Funktion z ¼ z ðx; yÞ ¼ sin ðx 2 þ yÞ. Die unabhängigen Variablen x und y hängen dabei wie folgt von den Parametern u und v ab:
x ðu; vÞ ¼ u þ v , y ðu; vÞ ¼ u 2 v 2
Berechnen Sie die partiellen Ableitungen
Wir benötigen folgende partielle Ableitungen:
@z
;
@x
@z
und
@u
@z
;
@y
@x
;
@u
@z
für das Wertepaar ðu ; vÞ ¼ ð2 ; 1Þ .
@v
@x
;
@v
@y
;
@u
@y
@v
Zunächst beschäftigen wir uns mit den beiden partiellen Ableitungen der Funktion z ¼ sin ðx 2 þ yÞ:
z ¼ sin ðx 2 þ yÞ ¼ sin t
|fflfflfflfflffl{zfflfflfflfflffl}
t
mit
t ¼ x2 þ y
und
@t
¼ 2x;
@x
@t
¼ 1
@y
Die Kettenregel liefert die gewünschten Ableitungen:
@z
@z @t
¼
¼ ðcos tÞ 2 x ¼ 2 x cos t ¼ 2 x cos ðx 2 þ yÞ
@x
@t @x
@z
@z @t
¼
¼ ðcos tÞ 1 ¼ cos t ¼ cos ðx 2 þ yÞ
@y
@t @y
Wir drücken diese Ableitungen noch durch die beiden Parameter u und v aus (Parametergleichungen für x und y
einsetzen):
@z
¼ 2 x cos ðx 2 þ yÞ ¼ 2 ðu þ vÞ cos ½ ðu þ vÞ 2 þ u 2 v 2 ¼
@x
¼ 2 ðu þ vÞ cos ðu 2 þ 2 u v þ v 2 þ u 2 v 2 Þ ¼ 2 ðu þ vÞ cos ð2 u 2 þ 2 u vÞ
@z
¼ cos ðx 2 þ yÞ ¼ cos ½ ðu þ vÞ 2 þ u 2 v 2 ¼ cos ðu 2 þ 2 u v þ v 2 þ u 2 v 2 Þ ¼ cos ð2 u 2 þ 2 u vÞ
@y
2 Differentiation nach einem Parameter (Kettenregel)
255
Die partiellen Ableitungen 1. Ordnung der Parametergleichungen lauten:
@x
¼ 1;
@u
@y
¼ 2u;
@u
@x
¼ 1;
@v
@y
¼ 2v
@v
Jetzt lassen sich die gesuchten partiellen Ableitungen
@z
@z
und
wie folgt bestimmen (Kettenregel):
@u
@v
@z
@z @x
@z @y
¼
þ
¼ 2 ðu þ vÞ cos ð2 u 2 þ 2 u vÞ 1 þ cos ð2 u 2 þ 2 u vÞ 2 u ¼
@u
@x @u
@y @u
¼ ½ 2 ðu þ vÞ þ 2 u cos ð2 u 2 þ 2 u vÞ ¼ ð2 u þ 2 v þ 2 uÞ cos ð2 u 2 þ 2 u vÞ ¼
¼ ð4 u þ 2 vÞ cos ð2 u 2 þ 2 u vÞ ¼ 2 ð2 u þ vÞ cos ð2 u 2 þ 2 u vÞ
@z
@z @x
@z @y
¼
þ
¼ 2 ðu þ vÞ cos ð2 u 2 þ 2 u vÞ 1 þ cos ð2 u 2 þ 2 u vÞ ð 2 vÞ ¼
@v
@x @v
@y @v
¼ ½ 2 ðu þ vÞ 2 v cos ð2 u 2 þ 2 u vÞ ¼ 2 u cos ð2 u 2 þ 2 u vÞ
Ableitungen an der Stelle (u; u) == (2; 1)
@z
ðu ¼ 2 ; v ¼ 1Þ ¼ 2 ð2 2 þ 1Þ cos ð2 2 2 þ 2 2 1Þ ¼ 2 5 cos ð8 þ 4Þ ¼
@u
¼ 10 cos 12 ¼ 8;4385
@z
ðu ¼ 2 ; v ¼ 1Þ ¼ 2 2 cos ð2 2 2 þ 2 2 1Þ ¼ 4 cos ð8 þ 4Þ ¼ 4 cos 12 ¼ 3;3754
@v
E29
z ¼ ex y
mit
x ðu; vÞ ¼ u v , y ðu; vÞ ¼ u 2 v 2
Welchen Wert besitzen die partiellen Ableitungen
Benötigt werden folgende partielle Ableitungen:
@z
;
@x
@z
;
@y
@z
@u
@x
;
@u
und
@x
;
@v
@z
an der Stelle u ¼ v ¼ 1 ?
@v
@y
;
@u
@y
@v
Wir beginnen mit den partiellen Ableitungen von z ¼ e x y ¼ e x e y :
@z
@
@
¼
½ e x e y ¼ e y
½ e x ¼ e y e x ¼ e xy
@x
@x
@x
@z
@
@
¼
½ e x e y ¼ e x
½ e y ¼ e x ðe y Þ ð 1Þ ¼ e x e y ¼ e x y
@y
@y
@y
(Ableitung von e y nach der Kettenregel, Substitution: t ¼ y)
Die partiellen Ableitungen der beiden Parametergleichungen lauten:
@x
¼ v;
@u
@x
¼ u;
@v
@y
¼ 2u;
@u
@y
¼ 2v
@v
Die gesuchten partiellen Ableitungen der Funktion z ¼ e x y nach den Parametern u und v lassen sich jetzt wie
folgt bilden (für x und y werden schließlich noch die Parametergleichungen eingesetzt):
@z
@z @x
@z @y
2
2
¼
þ
¼ e x y v e x y 2 u ¼ ðv 2 uÞ e x y ¼ ðv 2 uÞ e u v u þ v
@u
@x @u
@y @u
@z
@z @x
@z @y
2
2
¼
þ
¼ e x y u e x y ð 2 vÞ ¼ ðu þ 2 vÞ e x y ¼ ðu þ 2 vÞ e u v u þ v
@v
@x @v
@y @v
256
E Partielle Differentiation
An der Stelle u ¼ v ¼ 1 erhalten wir:
@z
ðu ¼ 1; v ¼ 1Þ ¼ ð1 2Þ e 1 1 þ 1 ¼ e 1 ¼ e
@u
@z
ðu ¼ 1; v ¼ 1Þ ¼ ð1 þ 2Þ e 1 1 þ 1 ¼ 3 e 1 ¼ 3 e
@v
E30
z ¼ x3 y þ xy3
mit
x ðr; jÞ ¼ r cos j ,
Bilden Sie die partiellen Ableitungen
Benötigt werden die partiellen Ableitungen
@x
¼ r sin j ;
@j
und
@z
.
@j
@y
@z @z @x @x @y
,
,
,
,
und
. Sie lauten:
@x @y @r @j @r
@j
@z
¼ 3 x 2 y þ y 3 ¼ y ð3 x 2 þ y 2 Þ ;
@x
@x
¼ cos j ;
@r
@z
@r
y ðr; jÞ ¼ r sin j
@z
¼ x 3 þ 3 x y 2 ¼ x ðx 2 þ 3 y 2 Þ
@y
@y
¼ sin j ;
@r
@y
¼ r cos j
@j
Damit lassen sich die gesuchten partiellen Ableitungen 1. Ordnung der Funktion z ¼ x y ðx 2 þ y 2 Þ mit Hilfe der
Kettenregel wie folgt bilden:
@z
@z @x
@z @y
¼
þ
¼ y ð3 x 2 þ y 2 Þ cos j þ x ðx 2 þ 3 y 2 Þ sin j ¼
@r
@x @r
@y @r
¼ r sin j ð3 r 2 cos 2 j þ r 2 sin 2 jÞ cos j þ r cos j ðr 2 cos 2 j þ 3 r 2 sin 2 jÞ sin j ¼
¼ r 3 sin j cos j ð3 cos 2 j þ sin 2 j þ cos 2 j þ 3 sin 2 jÞ ¼
¼ r 3 sin j cos j ð4 cos 2 j þ 4 sin 2 jÞ ¼ 4 r 3 sin j cos j ðcos 2 j þ sin 2 jÞ ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3
3
3
1
¼ 4 r sin j cos j ¼ 2 r 2 sin j cos j ¼ 2 r sin ð2 jÞ
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
sin ð2 jÞ
Umformungen: Zunächst den gemeinsamen Faktor r 2 und dann r 3 sin j cos j ausklammern; cos 2 j þ sin 2 j ¼ 1;
sin ð2 jÞ ¼ 2 sin j cos j.
@z
@z @x
@z @y
¼ y ð3 x 2 þ y 2 Þ ð r sin jÞ þ x ðx 2 þ 3 y 2 Þ r cos j ¼
¼
þ
@j
@x @j
@y @j
¼ r sin j ð3 r 2 cos 2 j þ r 2 sin 2 jÞ ð r sin jÞ þ
þ r cos j ðr 2 cos 2 j þ 3 r 2 sin 2 jÞ r cos j ¼
¼ r 4 sin 2 j ð3 cos 2 j þ sin 2 jÞ þ r 4 cos 2 j ðcos 2 j þ 3 sin 2 jÞ ¼
¼ r 4 ½ sin 2 j ð3 cos 2 j þ sin 2 jÞ þ cos 2 j ðcos 2 j þ 3 sin 2 jÞ ¼
¼ r 4 ð 3 sin 2 j cos 2 j sin 4 j þ cos 4 j þ 3 sin 2 j cos 2 jÞ ¼
¼ r 4 ðcos 4 j sin 4 jÞ ¼ r 4 ðcos 2 j þ sin 2 jÞ ðcos 2 j sin 2 jÞ ¼ r 4 ðcos 2 j sin 2 jÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
1
Umformungen in der letzten Zeile: 3. Binom: a 2 b 2 ¼ ða þ bÞ ða bÞ mit a ¼ cos 2 j und b ¼ sin 2 j ;
ferner: cos 2 j þ sin 2 j ¼ 1 (trigonometrischer Pythagoras).
3 Implizite Differentiation
257
3 Implizite Differentiation
Beachten Sie, dass die Gleichung der impliziten Funktion zunächst auf die Form F ðx; yÞ ¼ 0 gebracht werden muss.
Die implizite Differentiation soll jeweils mit Hilfe der partiellen Ableitungen erfolgen.
Lehrbuch: Band 2, Kapitel III.2.5.1
Formelsammlung: Kapitel IV.3.8
E31
Bestimmen Sie die Gleichung der Tangente im Punkt P ¼ ð1; 1Þ der Kurve x e 2ðx yÞ ¼ 1 .
Wir benötigen die partiellen Ableitungen 1. Ordnung F x und F y der in impliziter Form gegebenen Funktion
F ðx; yÞ ¼ x e 2 ðx yÞ 1 ¼ 0 . F x erhalten wir mit Hilfe der Produkt- und Kettenregel:
f
F ðx; yÞ ¼ x e 2 ðx yÞ 1 ¼ u v 1 mit
|fflfflffl{zfflfflffl}
u
v
u ¼ x;
v ¼ e 2 ðx yÞ
und
ux ¼ 1 ;
v x ¼ 2 e 2 ðx yÞ
ðv x erhält man mit der Kettenregel, Substitution: t ¼ 2 ðx yÞÞ
F x ¼ u x v þ v x u 0 ¼ 1 e 2 ðx yÞ þ 2 e 2 ðx yÞ x ¼ ð1 þ 2 xÞ e 2 ðx yÞ
Die Kettenregel liefert die partielle Ableitung F y :
F ðx; yÞ ¼ x e 2 ðx yÞ 1 ¼ x e t 1
Fy ¼
mit t ¼ 2 ðx yÞ
und
@t
¼ 2
@y
@F
@F @t
¼
¼ x e t 2 ð 1Þ 0 ¼ 2 x e t ¼ 2 x e 2 ðx yÞ
@y
@t @y
Kurvenanstieg in einem beliebigen Kurvenpunkt:
y0 ¼
ð1 þ 2 xÞ e 2 ðx yÞ
Fx
1 þ 2x
1 þ 2x
¼
¼
¼
2
x
2x
Fy
2
ðx
yÞ
2x e
Tangentensteigung im Kurvenpunkt P ¼ ðx 0 ; y 0 Þ ¼ ð1; 1Þ:
m ¼ y 0 ðPÞ ¼ y 0 ðx 0 ¼ 1; y 0 ¼ 1Þ ¼
1þ2
3
¼
¼ 1,5
2
2
Gleichung der Tangente in P ¼ ðx 0 ; y 0 Þ ¼ ð1; 1Þ (Ansatz in der Punkt-Steigungs-Form):
y y0
¼ m
x x0
E32
)
y1
¼ 1,5
x 1
)
y 1 ¼ 1,5 ðx 1Þ ¼ 1,5 x 1,5
)
y ¼ 1,5 x 0,5
ey þ y þ x2 x 3 ¼ 0
Wie lauten die Gleichungen der Tangenten in den Nullstellen dieser (impliziten) Funktion?
Berechnung der Nullstellen: y ¼ 0 ) e 0 þ 0 þ x 2 x 3 ¼ 1 þ x 2 x 3 ¼ 0 ) x 2 x 2 ¼ 0 )
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
x 1=2 ¼ 0,5
0,25 þ 2 ¼ 0,5
2,25 ¼ 0,5
1,5 ) x 1 ¼ 1 ; x 2 ¼ 2
Nullstellen: N 1 ¼ ð 1; 0Þ, N 2 ¼ ð2; 0Þ
Anstieg der Kurve F ðx; yÞ ¼ e y þ y þ x 2 x 3 ¼ 0:
y0 ¼
Fx
2x 1
¼ y
e þ1
Fy
258
E Partielle Differentiation
Gleichungen der Tangenten in den Nullstellen
Tangente in N 1 (Ansatz: Punkt-Steigungs-Form):
m 1 ¼ y 0 ðN 1 Þ ¼ y 0 ðx 1 ¼ 1; y 1 ¼ 0Þ ¼
N 1 ¼ ðx 1 ; y 1 Þ ¼ ð 1; 0Þ ;
y y1
¼ m1
x x1
)
y0
¼ 1,5
x þ1
)
2 1
3
3
¼
¼
¼ 1,5
1þ1
2
e0 þ 1
y ¼ 1,5 ðx þ 1Þ ¼ 1,5 x þ 1,5
Tangente in N 2 (Ansatz: Punkt-Steigungs-Form):
N 2 ¼ ðx 2 ; y 2 Þ ¼ ð2; 0Þ ;
y y2
¼ m2
x x2
)
m 2 ¼ y 0 ðN 2 Þ ¼ y 0 ðx 2 ¼ 2; y 2 ¼ 0Þ ¼
y0
¼ 1,5
x 2
)
41
3
3
¼
¼ 1,5
¼
0
1þ1
2
e þ1
y ¼ 1,5 ðx 2Þ ¼ 1,5 x þ 3
x 2 10 x þ y 2 þ 4 y þ 20 ¼ 0
E33
An welchen Stellen besitzt diese in der impliziten Form gegebene Funktion waagerechte Tangenten?
Die Steigungsformel liefert für diese implizite Funktion den folgenden Ausdruck:
y0 ¼
Fx
2 x 10
2 ðx 5Þ
x 5
5x
¼
¼
¼
¼
2y þ 4
yþ2
yþ2
Fy
2 ðy þ 2Þ
Aus der Bedingung y 0 ¼ 0 erhalten wir die Stellen mit einer waagerechten Tangente:
y0 ¼ 0
)
5x
¼ 0
yþ2
)
5x ¼ 0
ðf ür y 6¼ 2Þ
)
x1 ¼ 5
Diesen Wert setzen wir in die Funktionsgleichung ein und berechnen die zugehörigen Ordinatenwerte:
25 50 þ y 2 þ 4 y þ 20 ¼ 0
)
y2 þ 4 y 5 ¼ 0
)
y1 ¼ 1 ;
y2 ¼ 5
Es gibt somit zwei Kurvenpunkte mit waagerechter Tangente: P 1 ¼ ð5; 1Þ und P 2 ¼ ð5; 5Þ.
Hinweis: Die Kurve beschreibt einen Kreis mit dem Mittelpunkt M ¼ ð5; 2Þ und dem Radius r ¼ 3.
e y sin x þ e x cos y ¼ 0
E34
Gesucht ist die Gleichung der Tangente im Kurvenpunkt P 1 ¼ ð0; p=2Þ .
Steigung der Kurventangente im beliebigen Kurvenpunkt P ¼ ðx; yÞ:
y0 ¼
e y cos x þ e x cos y
Fx
¼ y
e sin x e x sin y
Fy
Steigung der Tangente in P 1 ¼ ðx 1 ; y 1 Þ ¼ ð0; p=2Þ:
m 1 ¼ y 0 ðP 1 Þ ¼ y 0 ðx 1 ¼ 0; y 1 ¼ p=2Þ ¼
e p=2 cos 0 þ e 0 cos ðp=2Þ
e p=2
sin 0
e0
sin ðp=2Þ
¼
e p=2 1 þ 1 0
e p=2
011
Gleichung der Tangente in P 1 ¼ ðx 1 ; y 1 Þ ¼ ð0; p=2Þ (Ansatz in der Punkt-Steigungs-Form):
y y1
¼ m1
x x1
Tangente:
p
2
x 0
y
)
y ¼ e p=2 x þ
¼ e p=2
)
y
p
¼ 4,8105 x þ 1,5708
2
p
¼ e p=2 x
2
)
y ¼ e p=2 x þ
p
2
¼ e p=2
3 Implizite Differentiation
E35
259
x4 3x2 y þ y3 3 ¼ 0
Bestimmen Sie die Gleichung der Tangente im Kurvenpunkt P 0 ¼ ð1; 2Þ .
F ðx; yÞ ¼ x 4 3 x 2 y þ y 3 3
Wir berechnen zunächst die Steigung der Kurventangente in P 0 ¼ ðx 0 ; y 0 Þ ¼ ð1; 2Þ:
y0 ¼
4x3 6x y
6x y 4x3
Fx
¼
¼
Fy
3 y2 3 x2
3 x2 þ 3 y2
)
m ¼ y 0 ðP 0 Þ ¼ y 0 ðx 0 ¼ 1; y 0 ¼ 2Þ ¼
12 4
8
¼
12 3
9
Mit der Punkt-Steigungs-Form erhalten wir die Gleichung der gesuchten Tangente:
y y0
¼ m
x x0
E36
pffiffiffi
y
)
y2
8
¼
9
x 1
)
y2 ¼
8
8
8
ðx 1Þ ¼
x
9
9
9
)
y ¼
8
10
x þ
9
9
x
3 ð y 2 1Þ p ¼ 0
y
Bestimmen Sie die Steigung dieser Kurve im Punkt P 1 ¼ ðp; 1Þ .
e
tan x þ
Für die Steigungsformel benötigen wir die partiellen Ableitungen 1. Ordnung der Funktion
pffiffiffi
x
3 ð y 2 1Þ p
F ðx; yÞ ¼ e y tan x þ
y
Die Ableitung F x ðx; yÞ erhalten wir durch gliedweise elementare Differentiation nach der Variablen x:
pffiffiffi
pffiffiffi
1
1
e y
1
¼
þ
þ
F x ðx; yÞ ¼ e y
y
y
cos 2 x
cos 2 x
Die Ableitung F y ðx; yÞ wird auf ähnliche Weise gebildet, wobei wir die Funktion vorher noch geringfügig umformen:
pffiffiffi
F ðx; yÞ ¼ ðtan xÞ e y þ x y 1 3 y 2 þ 3 p
pffiffiffi
Der 1. Summand muss dabei nach der Kettenregel differenziert werden (Substitution: u ¼
y ) ðtan xÞ e u
pffiffiffiffi
mit u ¼ y ):
pffiffiffi
pffiffiffi
ðtan xÞ e y
1
x
y
2
F y ðx; yÞ ¼ ðtan xÞ e
pffiffiffi þ x ð 1 y Þ 6 y ¼
6y
pffiffiffi
2
2 y
y
2 y
Die Steigungsformel lautet damit wie folgt:
pffiffiffi
e y
1
þ
2
y
F x ðx; yÞ
cos x
y0 ¼
¼
pffiffiffi
y
F y ðx; yÞ
ðtan xÞ e
x
6y
pffiffiffi
2
y
2 y
Steigung in P 1 ¼ ðx 1 ; y 1 Þ ¼ ðp; 1Þ:
y 0 ðP 1 Þ ¼ y 0 ðx 1 ¼ p; y 1 ¼ 1Þ ¼
ðcos p ¼ 1;
tan p ¼ 0Þ
e1
þ1
cos 2 p
ðtan pÞ e
p 6
2
1
¼
eþ1
eþ1
¼
¼ 0,4067
0p 6
p þ6
260
E Partielle Differentiation
E37
F ðx; yÞ ¼ 2 y 3 þ 6 x 3 24 x þ 6 y ¼ 0
Bestimmen Sie den Steigungswinkel der Kurventangente in den Schnittpunkten dieser Kurve mit der
x-Achse. Wie lautet die Tangentengleichung in der positiven Nullstelle?
Wir berechnen zunächst die Schnittpunkte mit der x-Achse (Nullstellen):
y ¼ 0
)
6 x 3 24 x ¼ 0 j : 6
)
x 3 4 x ¼ x ðx 2 4Þ ¼ 0
)
x1 ¼ 0 ;
x 2=3 ¼ 2
Nullstellen: N 1 ¼ ð0; 0Þ ; N 2 ¼ ð2; 0Þ ; N 3 ¼ ð 2; 0Þ
Für die Steigung der Kurventangente in einem beliebigen Kurvenpunkt P erhalten wir:
y0 ¼
Fx
18 x 2 24
6 ð3 x 2 4Þ
3x2 4
4 3x2
¼
¼
¼
¼
Fy
6 y2 þ 6
y2 þ 1
6 ðy 2 þ 1Þ
y2 þ 1
In den drei Nullstellen ergeben sich folgende Werte für Steigung m und Steigungswinkel a:
m 1 ¼ y 0 ðN 1 Þ ¼ y 0 ðx 1 ¼ 0; y 1 ¼ 0Þ ¼ 4
)
m 2=3 ¼ y 0 ðN 2=3 Þ ¼ y 0 ðx 2=3 ¼ 2; y 2=3 ¼ 0Þ ¼
tan a 2=3 ¼ m 2=3 ¼ 8
)
E38
)
)
a 1 ¼ arctan 4 ¼ 75;96
4 12
8
¼
¼ 8
0þ1
1
a 2=3 ¼ 180 þ arctan ð 8Þ ¼ 180 82,87
Tangente in der Nullstelle N 2 == (x 2 ; y 2 ) == (2; 0)
y y2
¼ m2
x x2
tan a 1 ¼ m 1 ¼ 4
y0
¼ 8
x 2
)
¼ 97;13
(Ansatz in der Punkt-Steigungs-Form)
y ¼ 8 ðx 2Þ
)
y ¼ 8 x þ 16
Wo besitzt die Funktion x 3 y 3 þ 3 y ¼ 0 waagerechte Tangenten?
F ðx; yÞ ¼ x 3 y 3 þ 3 y
Wir bestimmen zunächst den Kurvenanstieg (Tangentensteigung) in Abhängigkeit von den Koordinaten x und y eines
beliebigen Kurvenpunktes P:
y0 ¼
Fx
3x2
3 x2
x2
x2
¼
¼
¼
¼
Fy
3 y2 þ 3
3 ð y 2 þ 1Þ
y2 þ 1
y2 1
Berechnung der Kurvenpunkte mit waagerechter Tangente aus der Bedingung y 0 ¼ 0:
y0 ¼ 0
)
x2
¼ 0
y2 1
)
x2 ¼ 0
ðf ür y 2 6¼ 1Þ
)
x ¼ 0
Die zugehörigen Ordinaten erhalten wir aus der Kurvengleichung für x ¼ 0:
x ¼ 0
)
y3 þ 3 y ¼ 0
)
y 3 3 y ¼ y ð y 2 3Þ ¼ 0
Die Bedingung y 2 6¼ 1 ist jeweils erfüllt.
Es gibt somit genau drei Kurvenpunkte mit einer waagerechten Tangente:
pffiffiffi
pffiffiffi
P 1 ¼ ð0; 0Þ, P 2 ¼ ð0; 3 Þ ; P3 ¼ ð0; 3Þ
)
y1 ¼ 0 ;
pffiffiffi
y 2=3 ¼ 3
4 Totales oder vollständiges Differential einer Funktion (mit einfachen Anwendungen)
261
4 Totales oder vollständiges Differential einer Funktion
(mit einfachen Anwendungen)
Lehrbuch: Band 2, Kapitel III.2.4
Formelsammlung: Kapitel IX.2.4
E39
Bestimmen Sie das totale Differential der Funktion z ¼
x2 þ y2
:
yx
Die benötigten partiellen Ableitungen 1. Ordnung erhalten wir jeweils mit der Quotientenregel:
z ¼
x2 þ y2
u
¼
v
yx
zx ¼
zy ¼
mit u ¼ x 2 þ y 2
und v ¼ y x
2 x ð y xÞ ð 1Þ ðx 2 þ y 2 Þ
2 x y 2 x2 þ x2 þ y2
x2 þ y2 þ 2 x y
ux v vx u
¼
¼
¼
v2
ð y xÞ 2
ð y xÞ 2
ð y xÞ 2
uy v vy u
v2
¼
2 y ð y xÞ 1 ðx 2 þ y 2 Þ
ð y xÞ 2
¼
2 y2 2 x y x2 y2
ð y xÞ 2
¼
x2 þ y2 2 x y
ð y xÞ 2
Totales Differential:
d z ¼ zx d x þ zy d y ¼
¼
E40
x2 þ y2 þ 2 x y
ð y xÞ 2
dx þ
x2 þ y2 2 x y
ð y xÞ 2
dy ¼
ð x 2 þ y 2 þ 2 x yÞ d x þ ð x 2 þ y 2 2 x yÞ d y
ð y xÞ 2
Bestimmen Sie das totale Differential der Funktion w ¼ arctan ðu vÞ :
Die benötigten partiellen Ableitungen 1. Ordnung erhalten wir mit Hilfe der Kettenregel:
w ¼ arctan ðu vÞ ¼ arctan t
|ffl{zffl}
t
mit t ¼ u v
)
@w
@w @t
1
v
v
v ¼
¼
¼
¼
2
2
@u
@t @u
1þt
1þt
1 þ u2 v2
Wegen der Symmetrie der Funktion (u und v sind miteinander vertauschbar) gilt dann:
@w
u
u
¼
¼
@v
1 þ v2 u2
1 þ u2 v2
Somit lautet das totale Differential wie folgt:
dw ¼
E41
@w
@w
v
u
vdu þ udv
du þ
dv ¼
du þ
dv ¼
2
2
2
2
@u
@v
1þu v
1þu v
1 þ u2 v2
Bestimmen Sie das totale Differential der Funktion z ¼ x 2 y 2 sin ðx 3 y 3 Þ .
262
E Partielle Differentiation
Die benötigten partiellen Ableitungen 1. Ordnung erhält man mit Hilfe der Produkt- und Kettenregel. Zunächst bilden
wir z x :
z ¼ x 2 y 2 sin ðx 3 y 3 Þ ¼ u v
|ffl{zffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
u
v
u ¼ x2 y2 ;
v ¼ sin ðx 3 y 3 Þ
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
t
und
ux ¼ 2 x y2 ;
v x ¼ 3 x 2 cos ðx 3 y 3 Þ
(v wurde dabei in der angedeuteten Weise mit der Kettenregel partiell nach x differenziert; t ¼ x 3 y 3 )
z x ¼ u x v þ v x u ¼ 2 x y 2 sin ðx 3 y 3 Þ þ 3 x 2 cos ðx 3 y 3 Þ x 2 y 2 ¼
¼ 2 x y 2 sin ðx 3 y 3 Þ þ 3 x 4 y 2 cos ðx 3 y 3 Þ
Analog erhält man:
z y ¼ u y v þ v y u ¼ 2 x 2 y sin ðx 3 y 3 Þ 3 x 2 y 4 cos ðx 3 y 3 Þ
Das totale Differential lautet damit:
d z ¼ z x d x þ z y d y ¼ ½ 2 x y 2 sin ðx 3 y 3 Þ þ 3 x 4 y 2 cos ðx 3 y 3 Þ d x þ
þ ½ 2 x 2 y sin ðx 3 y 3 Þ 3 x 2 y 4 cos ðx 3 y 3 Þ d y
Bestimmen Sie das totale Differential der Funktion u ¼ u ðx; y; zÞ ¼ ln
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð2 x 2 þ 2 y 2 þ 2 z 2 Þ 3 .
Wie lautet das totale Differential an der Stelle x ¼ 1 ; y ¼ 2 ; z ¼ 2?
E42
Welchen Näherungswert für die abhängige Variable u liefert das totale Differential für die nderungen
d x ¼ 0;1; d y ¼ 0;2 und d z ¼ 0;1?
Wir bringen die Funktion zunächst in eine für das Differenzieren günstigere Form:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
u ¼ ln ð2 x 2 þ 2 y 2 þ 2 z 2 Þ 3 ¼ ln ð2 x 2 þ 2 y 2 þ 2 z 2 Þ 3=2 ¼
ln ð2 x 2 þ 2 y 2 þ 2 z 2 Þ
2
Rechenregel: ln a n ¼ n ln a
Es genügt, die partielle Ableitung u x zu bilden, denn die Funktion ist symmetrisch in den drei unabhängigen Variablen x; y und z. Die Ableitung u x erhalten wir wie folgt mit Hilfe der Kettenregel:
u ¼
3
3
ln ð2 x 2 þ 2 y 2 þ 2 z 2 Þ ¼
ln t
2
2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
t
ux ¼
mit
t ¼ 2 x2 þ 2 y2 þ 2 z2
und
@t
¼ 4x
@x
@u
@u @t
3 1
3
4x
3 4x
3x
¼
¼
4x ¼
¼
¼
2
2
2
2
2
2
2
@x
@t @x
2 t
2 2x þ 2y þ 2z
2 2 ðx þ y þ z Þ x þ y 2 þ z 2
Wegen der erwähnten Symmetrie gilt (x wird durch y bzw. z ersetzt):
uy ¼
3y
x2 þ y2 þ z2
;
uz ¼
3z
x2 þ y2 þ z2
Das totale Differential besitzt dann die folgende Gestalt:
d u ¼ u x d x þ u y d y þ uz d z ¼
¼
x2
3y
3x
3z
dx þ
dy þ
dz ¼
2
2
2
2
2
2
x þ y2 þ z2
x þy þz
þy þz
3x dx þ 3y dy þ 3z dz
3 ðx d x þ y d y þ z d zÞ
¼
2
2
2
x þy þz
x2 þ y2 þ z2
4 Totales oder vollständiges Differential einer Funktion (mit einfachen Anwendungen)
263
An der Stelle x ¼ 1 ; y ¼ 2 ; z ¼ 2 lautet das totale Differential wie folgt:
du ¼
3 ð 1 d x þ 2 d y 2 d zÞ
2
ð 1Þ þ 2 2 þ ð 2Þ
¼
2
3
1
ð d x þ 2 d y 2 d zÞ ¼
ð d x þ 2 d y 2 d zÞ
9
3
Näherungswert für d x == 0,1, d y == – 0,2 und d z == – 0,1
3
ln ½ 2 ð 1Þ 2 þ 2 2 2 þ 2 ð 2Þ 2 ¼
2
3
3
¼
ln ð2 þ 8 þ 8Þ ¼
ln 18 ¼ 4;3356
2
2
u ðx ¼ 1 ; y ¼ 2 ; z ¼ 2Þ ¼
Totales Differential für d x ¼ 0;1; d y ¼ 0;2 und d z ¼ 0;1:
du ¼
1
1
1
½ 0;1 þ 2 ð 0;2Þ 2 ð 0;1Þ ¼
ð 0;1 0;4 þ 0;2Þ ¼
ð 0;3Þ ¼ 0;1
3
3
3
Näherungswert: u þ d u ¼ 4;3356 0;1 ¼ 4;2356
Exakter Funktionswert: u ðx ¼ 0;9 ; y ¼ 1;8 ; z ¼ 2;1Þ ¼ 4;2427
E43
xy
. Berechnen Sie mit Hilfe des totalen Differentials die nderung
x y
des Funktionswertes beim bergang von der Stelle ðx; yÞ ¼ ð2; 1Þ zur Stelle ðx; yÞ ¼ ð2;1; 0,8Þ.
Wie groß ist die exakte nderung?
Gegeben ist die Funktion z ¼
Näherungsrechnung mit dem totalen Differential
Wir bilden zunächst die benötigten partiellen Ableitungen 1. Ordnung unter Verwendung der Quotientenregel:
xy
u
mit u ¼ x y ; v ¼ x y und u x ¼ y ; u y ¼ x ; v x ¼ 1 ; v y ¼ 1
¼
z ¼
v
x y
zx ¼
zy ¼
y ðx yÞ 1 x y
x y y2 x y
y2
ux v vx u
¼
¼
¼
v2
ðx yÞ 2
ðx yÞ 2
ðx yÞ 2
uy v vy u
v2
¼
x ðx yÞ ð 1Þ x y
ðx yÞ 2
¼
x2 x y þ x y
ðx yÞ 2
¼
x2
ðx yÞ 2
Das totale Differential lautet damit:
d z ¼ zx d x þ zy d y ¼
y2
ðx yÞ 2
dx þ
x2
ðx yÞ 2
dy ¼
y2 d x þ x2 d y
ðx yÞ 2
An der Stelle x ¼ 2 ; y ¼ 1 bewirken die Koordinatenänderungen d x ¼ þ 0;1 und d y ¼ 0;2 die folgende
nderung des Funktionswertes (Näherungswert):
dz ¼
1 2 0;1 þ 2 2 ð 0;2Þ
ð2 1Þ
2
¼
0;1 0;8
¼ 0;9
1
Exakte Rechnung
Wir bilden die Differenz der Funktionswerte an den Stellen x ¼ 2;1 ; y ¼ 0;8 und x ¼ 2 ; y ¼ 1:
D z ¼ z ð2;1; 0;8Þ z ð2; 1Þ ¼
E44
2;1 0;8
21
¼ 1;2923 2 ¼ 0;7077
2;1 0;8
21
Bestimmen Sie die Tangentialebene im Punkt P ¼ ð1; 0; 1Þ der Fläche z ¼ ðx 2 þ y 2 Þ e y .
264
E Partielle Differentiation
Wir bilden zunächst die partiellen Ableitungen f x und f y der Funktion z ¼ f ðx; yÞ ¼ ðx 2 þ y 2 Þ e y :
f x ðx; yÞ ¼ 2 x e y
ðe y bleibt beim Differenzieren als konstanter Faktor erhaltenÞ
u ¼ x2 þ y2 ;
v ¼ e y
und
uy ¼ 2 y ;
vy ¼ e y
f
f ¼ ðx 2 þ y 2 Þ e y ¼ u v mit
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
v
(partielle Ableitung von v nach y mit der Kettenregel, Substitution: t ¼ y)
Die Produktregel liefert dann die partielle Ableitung f y :
f y ðx; yÞ ¼ u y v þ v y u ¼ 2 y e y e y ðx 2 þ y 2 Þ ¼ ½ 2 y ðx 2 þ y 2 Þ e y ¼ ð2 y x 2 y 2 Þ e y
Steigungswerte in P ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð1; 0; 1Þ:
f x ð1; 0Þ ¼ 2 1 e 0 ¼ 2 1 ¼ 2 ;
f y ð1; 0Þ ¼ ð0 1 0Þ e 0 ¼ 1 1 ¼ 1
Gleichung der Tangentialebene in P ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð1; 0; 1Þ:
z z 0 ¼ f x ðx 0 ; y 0 Þ ðx x 0 Þ þ f y ðx 0 ; y 0 Þ ð y y 0 Þ
z 1 ¼ 2 ðx 1Þ 1 ð y 0Þ ¼ 2 x 2 y
E45
)
z ¼ 2x y 1
Wie lautet die Gleichung der Tangentialebene an die Fläche z ¼ ln ðx 3 þ y 2 Þ im Flächenpunkt
P ¼ ð2; 1; z 0 ¼ ?Þ ?
Zugehörige Höhenkoordinate: z 0 ¼ f ð2; 1Þ ¼ ln ð8 þ 1Þ ¼ ln 9
)
P ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð2; 1; ln 9Þ
Partielle Ableitungen 1. Ordnung
z ¼ f ðx; yÞ ¼ ln ðx 3 þ y 2 Þ ¼ ln u
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
u
mit
u ¼ x3 þ y2
und
@u
¼ 3x2 ;
@x
@u
¼ 2y
@y
Die Kettenregel liefert:
f x ðx; yÞ ¼ z x ¼
@z
@z @u
1
3x2
¼
¼
3x2 ¼
;
@x
@u @x
u
x3 þ y2
f y ðx; yÞ ¼ z y ¼
2y
@z
@z @u
1
;
¼
¼
2y ¼
3
@y
@u @y
u
x þ y2
f x ðx 0 ; y 0 Þ ¼ f x ð2; 1Þ ¼
f y ðx 0 ; y 0 Þ ¼ f y ð2; 1Þ ¼
34
12
4
¼
¼
8þ1
9
3
21
2
¼
8þ1
9
Gleichung der Tangentialebene in P = (x 0 ; y 0 ; z 0) = (2 ; 1 ; ln 9)
z z 0 ¼ f x ðx 0 ; y 0 Þ ðx x 0 Þ þ f y ðx 0 ; y 0 Þ ð y y 0 Þ
z ln 9 ¼
z ¼
E46
4
2
4
8
2
2
ðx 2Þ þ
ð y 1Þ ¼
x
þ
y
3
9
3
3
9
9
4
2
26
4
2
x þ
y
þ ln 9 ¼
x þ
y 0;6917
3
9
9
3
9
In welchem Punkt P 0 ¼ ðx 0 ; y 0 ; z 0 Þ der Fläche z ¼ x 2 þ y 2 7 verläuft die Tangentialebene
parallel zur Ebene z ¼ 8 x þ 2 y ? Wie lautet die Gleichung dieser Tangentialebene ?
4 Totales oder vollständiges Differential einer Funktion (mit einfachen Anwendungen)
265
Die gesuchte Tangentialebene muss in der x- bzw. y -Richtung den gleichen Anstieg haben wie die Ebene
z ¼ 8 x þ 2 y ; d. h. im (noch unbekannten) Flächenpunkt P 0 müssen die partiellen Ableitungen 1. Ordnung die
Werte f x ðx 0 ; y 0 Þ ¼ 8 und f y ðx 0 ; y 0 Þ ¼ 2 haben. Mit f x ðx; yÞ ¼ z x ¼ 2 x und f y ðx; yÞ ¼ z y ¼ 2 y folgt also:
)
f x ðx 0 ; y 0 Þ ¼ 2 x 0 ¼ 8
) x0 ¼ 4 ; y0 ¼ 1
f y ðx 0 ; y 0 Þ ¼ 2 y 0 ¼ 2
Die zugehörige Höhenkoordinate ist z 0 ¼ f ðx 0 ; y 0 Þ ¼ f ð4; 1Þ ¼ 16 þ 1 7 ¼ 10 .
Flächenpunkt:
P 0 ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð4; 1; 10Þ
Gleichung der Tangentialebene in P0 = (x 0 ; y 0 ; z 0) = (4 ; 1 ; 10)
z z 0 ¼ f x ðx 0 ; y 0 Þ ðx x 0 Þ þ f y ðx 0 ; y 0 Þ ð y y 0 Þ
z 10 ¼ 8 ðx 4Þ þ 2 ð y 1Þ ¼ 8 x 32 þ 2 y 2 ¼ 8 x þ 2 y 34
)
z ¼ 8 x þ 2 y 24
Gegeben ist die Fläche z ¼ 89 x 2 96 x y þ 61 y 2 260 x þ 70 y þ C : Bestimmen Sie die noch
E47
unbekannte Konstante C so, dass die Fläche die x, y-Ebene berührt. Wie lautet der Berührungspunkt ?
Die Fläche soll also im (noch unbekannten) Flächenpunkt P 0 ¼ ðx 0 ; y 0 ; z 0 Þ die x, y-Ebene berühren. Wir folgern
daraus: die x, y-Ebene ist demnach die Tangentialebene in P 0 . Daraus lassen sich folgende Eigenschaften ableiten:
1. P 0 liegt als Berührungspunkt in der x, y-Ebene, die Höhenkoordinate hat daher den Wert z 0 ¼ 0 .
2. Die Tangentialebene in P 0 (x, y-Ebene) hat in beiden Koordinatenrichtungen (x- und y-Richtung) den Anstieg
null, die partiellen Ableitungen 1. Ordnung der Fläche müssen daher in P 0 verschwinden:
z x ðx 0 ; y 0 Þ ¼ 0
und
z y ðx 0 ; y 0 Þ ¼ 0
Diese Bedingungen führen zu zwei Gleichungen für die noch unbekannten Koordinaten x 0 und y 0 . Sie lauten wegen
z x ðx; yÞ ¼ 178 x 96 y 260
und z y ðx; yÞ ¼ 96 x þ 122 y þ 70
wie folgt:
z x ðx 0 ; y 0 Þ ¼ 0
)
ðIÞ
178 x 0 96 y 0 260 ¼ 0
z y ðx 0 ; y 0 Þ ¼ 0
)
ðIIÞ
96 x 0 þ 122 y 0 þ 70 ¼ 0
Wir teilen zunächst beide Gleichungen durch 2, multiplizieren dann die erste Gleichung mit 61 und die zweite mit 48
und addieren schließlich die erhaltenen Gleichungen:
)
ðI*Þ
5429 x 0 2928 y 0 7930 ¼ 0
ðIÞ
89 x 0 48 y 0 130 ¼ 0 j 61
)
þ
ðIIÞ 48 x 0 þ 61 y 0 þ 35 ¼ 0 j 48
ðII*Þ 2304 x 0 þ 2928 y 0 þ 1680 ¼ 0
___________________________________
_____________________________________
3125 x 0
6250 ¼ 0
3125 x 0 ¼ 6250 ¼ 0
ðIÞ
)
89 2 48 y 0 130 ¼ 0
)
48 48 y 0 ¼ 0
)
48 y 0 ¼ 48
)
)
)
x0 ¼ 2
y0 ¼ 1
Der Berührungspunkt P 0 besitzt daher die folgenden Koordinaten: P 0 ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð2; 1; 0Þ .
Einsetzen dieser Werte in die Gleichung der Fläche liefert eine Bestimmungsgleichung für die noch unbekannte Konstante C:
89 2 2 96 2 1 þ 61 1 2 260 2 þ 70 1 þ C ¼ 0
)
Die gesuchte Fläche wird somit durch die folgende Gleichung beschrieben:
z ¼ 89 x 2 96 x y þ 61 y 2 260 x þ 70 y þ 225
225 þ C ¼ 0
)
C ¼ 225
266
E Partielle Differentiation
Das in Bild E-1 skizzierte Dreieck hat die Seiten b ¼ 5 cm, c ¼ 8 cm und den Winkel a ¼ 30 .
Der Flächeninhalt des Dreiecks wird nach der Formel
A ¼ 0,5 b c sin a
E48
a
c
berechnet. Berechnen Sie die exakte Flächenänderung,
wenn b, c und a wie folgt verändert werden:
A
a
b
D b ¼ þ 2 %, D c ¼ 3 % , D a ¼ 1 :
Bild E-1
Welchen Näherungswert erhält man mit dem totalen Differential?
Exakte Flächenänderung
Ausgangswerte:
b ¼ 5 cm , c ¼ 8 cm , a ¼ 30
A 1 ¼ 0,5 ð5 cmÞ ð8 cmÞ sin 30
¼ 10 cm 2
b ¼ 1,02 5 cm ¼ 5,1 cm , c ¼ 0,97 8 cm ¼ 7,76 cm , a ¼ 30 1
Neue Werte:
A 2 ¼ 0,5 ð5,1 cmÞ ð7,76 cmÞ sin 29
¼ 9,593 cm
¼ 29
2
Flächenänderung: D A exakt ¼ A 2 A 1 ¼ ð9,593 10Þ cm 2 ¼ 0,407 cm 2
ðAbnahme !Þ
Näherungsrechnung mit dem totalen Differential
A ¼ f ðb; c; aÞ ¼ 0,5 b c sin a
dA ¼
@A
@A
@A
db þ
dc þ
d a ¼ 0,5 c sin a d b þ 0,5 b sin a d c þ 0,5 b c cos a d a
@b
@c
@a
In der Praxis übliche Schreibweise:
D A ¼ 0,5 c sin a D b þ 0,5 b sin a D c þ 0,5 b c cos a D a
Für b, c und a sind die Ausgangswerte einzusetzen, für die nderungen dieser Größen die Werte D b ¼ þ 0,1 cm,
D c ¼ 0,24 cm und D a ¼ 1 ¼ p=180 (aus Dimensionsgründen im Bogenmaß). Wir erhalten den folgenden
Näherungswert für die Flächenänderung:
D A ¼ 0,5 ð8 cmÞ sin 30 ð0,1 cmÞ þ 0,5 ð5 cmÞ sin 30 ð 0,24 cmÞ þ
þ 0,5 ð5 cmÞ ð8 cmÞ cos 30 ð p=180Þ ¼ ð0,2 0,3 0,302Þ cm 2 ¼ 0,402 cm 2
Dieser Wert ist in guter bereinstimmung mit dem exakten Wert.
E49
Das Massenträgheitsmoment einer Zylinderwalze (Masse m ; Radius R) wird nach der Formel
J ¼ 0,5 m R 2 berechnet. Wie ändert sich das Massenträgheitsmoment, wenn man von einer Walze mit
m ¼ 100 kg und R ¼ 0,2 m ausgeht und dann die Masse um 2 kg verkleinert und gleichzeitig den
Radius um 2 % vergrößert? Welchen Näherungswert liefert das totale Differential?
Exakte nderung des Massenträgheitsmomentes
J 1 ¼ 0,5 ð100 kgÞ ð0,2 mÞ 2 ¼ 2 kg m 2
Ausgangswerte:
m ¼ 100 kg , R ¼ 0,2 m;
Neue Werte:
m ¼ 0,98 100 kg ¼ 98 kg , R ¼ 1,02 0,2 m ¼ 0,204 m;
J 2 ¼ 0,5 ð98 kgÞ ð0,204 mÞ 2 ¼ 2,0392 kg m 2
nderung:
D J ¼ J 2 J 1 ¼ ð2,0392 2Þ kg m 2 ¼ 0,0392 kg m 2
4 Totales oder vollständiges Differential einer Funktion (mit einfachen Anwendungen)
267
Näherungsrechnung mit dem totalen Differential
J ¼ f ðm; RÞ ¼ 0,5 m R 2
)
dJ ¼
@J
@J
dm þ
d R ¼ 0,5 R 2 d m þ m R d R
@m
@R
Wir verwenden die in der Praxis übliche Schreibweise:
D J ¼ 0,5 R 2 D m þ m R D R
Mit m ¼ 100 kg , R ¼ 0,2 m , D m ¼ 2 kg und D R ¼ 0,004 m erhalten wir folgenden Näherungswert für die
nderung des Massenträgheitsmomentes (in guter bereinstimmung mit dem exakten Wert):
D J ¼ 0,5 ð0,2 mÞ 2 ð 2 kgÞ þ ð100 kgÞ ð0,2 mÞ ð0,004 mÞ ¼ ð 0,04 þ 0,08Þ kg m 2 ¼ 0,04 kg m 2
pffiffiffiffiffiffiffi
Die Gleichung T ¼ 2 p L C beschreibt die Abhängigkeit der Schwingungsdauer T einer elektromagnetischen Schwingung in einem L C-Kreis mit der Induktivität L und der Kapazität C. Mit Hilfe
des totalen Differentials soll die absolute und die prozentuale nderung der Schwingungsdauer T
bestimmt werden, wenn man die Induktivität von L ¼ 1 H um D L ¼ 0,01 H und gleichzeitig die
Kapazität von C ¼ 1 mF um D C ¼ 0,02 mF erhöht.
E50
Die Schwingungsdauer T ist eine Funktion von L und C:
pffiffiffiffiffiffiffi
pffiffiffi pffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
pffiffiffi pffiffiffi
T ¼ f ðL; CÞ ¼ 2 p L C ¼ 2 p L C
Rechenregel: a b ¼ a b
Das totale Differential von T liefert dann einen Näherungswert für die nderung der Schwingungsdauer T bei
geringfügigen nderungen von Induktivität L und Kapazität C:
pffiffiffiffi
pffiffiffi
@T
@T
1
1
dL þ
d C ¼ 2 p C pffiffiffi d L þ 2 p L pffiffiffiffi d C ¼
@L
@C
2 L
2 C
!
pffiffiffi
pffiffiffiffi
CdL þ L dC
p ðC d L þ L d CÞ
L dC
C dL
¼ p
¼ p
¼
pffiffiffi þ pffiffiffiffi
pffiffiffi pffiffiffiffi
pffiffiffiffiffiffiffi
LC
C
L
L C
pffiffiffi pffiffiffiffi
pffiffiffiffiffiffiffi
pffiffiffiffi
Umformungen:
Hauptnenner
L
C
¼
L
C
bilden,
d.
h.
die
in
der
großen
Klammer
stehenden
Brüche
mit
C
pffiffiffi
bzw. L erweitern.
dT ¼
Wir gehen zu der in der Technik üblichen Schreibweise über:
DT ¼
p ðC D L þ L D CÞ
pffiffiffiffiffiffiffi
LC
Die Schwingungsdauer für die Ausgangswerte L ¼ 1 H und C ¼ 1 mF ¼ 10 6 F beträgt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
T ¼ f ðL ¼ 1 H; C ¼ 10 6 FÞ ¼ 2 p 1 10 6 s ¼ 2 p 10 3 s ¼ 2 p ms ¼ 6,283 ms
Die absolute nderung der Schwingungsdauer für D L ¼ 0,01 H und D C ¼ 0,02 mF ¼ 2 10 8 F erhalten wir
mit dem totalen Differential (Näherungswert):
DT ¼
p ð10 6 0,01 þ 1 2 10 8 Þ
p ð10 8 þ 2 10 8 Þ
p 3 10 8
s ¼
s ¼ 3 p 10 5 s ¼
s ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
10 3
10 3
1 10 6
¼ 3 p 10 2 10 3 s ¼ 3 p 10 2 ms ¼ 0,094 ms
|fflfflffl{zfflfflffl}
1 ms
Prozentuale nderung der Schwingungsdauer:
DT
0,094 ms
100 % ¼
100 % ¼ 1,5 %
T
6,283 ms
268
E Partielle Differentiation
Flächenträgheitsmoment eines Kreisringes (Bild E-2):
p
I ¼
ðR 4 r 4 Þ mit R ¼ 30 cm, r ¼ 20 cm
64
E51
R
r
M
Welchen Näherungswert für die nderung des Flächenträgheitsmomentes erhält man mit Hilfe des totalen Differentials, wenn
man den Innen- und Außenradius jeweils um 2 % vergrößert ?
Bild E-2
I ist eine Funktion der beiden Variablen R und r:
I ¼ f ðR; rÞ ¼
p
ðR 4 r 4 Þ
64
Wir bilden das totale Differential von I:
dI ¼
@I
@I
p
p
p 3
p 3
p
dR þ
dr ¼
4 R3 d R
4r3 d r ¼
R dR
r dr ¼
ðR 3 d R r 3 d rÞ
@R
@r
64
64
16
16
16
Die Differentiale d R , d r und d I fassen wir als (kleine) nderungen der drei Größen R , r und I auf und schreiben dafür (wie allgemein in der Praxis üblich) D R , D r und D I . Es gilt dann:
DI ¼
p
ðR 3 D R r 3 D rÞ
16
Mit den Ausgangswerten R ¼ 30 cm und r ¼ 20 cm und den vorgegebenen nderungen D R ¼ þ 0,6 cm und
D r ¼ þ 0,4 cm erhalten wir den folgenden Näherungswert für die absolute nderung des Flächenträgheitsmomentes I:
DI ¼
p
p
p
ð30 3 0,6 20 3 0,4Þ cm 4 ¼
ð16 200 3 200Þ cm 4 ¼
13 000 cm 4 ¼ 2 552,5 cm 4
16
16
16
Im Ausgangszustand beträgt das Flächenträgheitsmoment:
I ¼
p
p
p
ð30 4 20 4 Þ cm 4 ¼
ð810 000 160 000Þ cm 4 ¼
650 000 cm 4 ¼ 31 906,8 cm 4
64
64
64
Prozentuale nderung des Flächenträgheitsmomentes:
DI
2 552,5 cm 4
100 % ¼
100 % ¼ 8 %
I
31 906,8 cm 4
Das Volumen einer Tonne (Bild E-3) wird nach der Formel
1
p h ð2 R 2 þ r 2 Þ
V ¼
3
berechnet. Es liegen folgende Werte vor:
E52
R ¼ 1 m , r ¼ 0,8 m
und h ¼ 1,50 m .
Wie ändert sich das Volumen V, wenn man bei unveränderter
Höhe h den Radius R um 2 % vergrößert und gleichzeitig den
Radius r um 2,5 % verkleinert?
(Exakte und näherungsweise Berechnung mit dem totalen Differential).
Exakte Volumenänderung
Ausgangswerte:
R ¼ 1 m , r ¼ 0,8 m , h ¼ 1,50 m
V1 ¼
Neue Werte:
1
p 1,50 ð2 1 2 þ 0,8 2 Þ m 3 ¼ 4,1469 m 3
3
R ¼ 1,02 1 m ¼ 1,02 m , r ¼ 0,975 0,8 m ¼ 0,78 m , h ¼ 1,50 m
V2 ¼
1
p 1,50 ð2 1,02 2 þ 0,78 2 Þ m 3 ¼ 4,2242 m 3
3
2r
2R
Bild E-3
h
5 Anwendungen
269
Exakte Volumenänderung:
D V ¼ V 2 V 1 ¼ ð4,2242 4,1469Þ m 3 ¼ 0,0773 m 3
Prozentuale nderung des Volumens:
DV
0,0773 m 3
100 % ¼
100 % ¼ 1,86 %
V1
4,1469 m 3
Näherungsrechnung mit dem totalen Differential
Es ändern sich die Radien R und r, nicht aber die Höhe h der Tonne. Daher können wir in diesem Zusammenhang
das Volumen V als eine nur von R und r abhängige Funktion betrachten ( Alternative: V als eine von R , r und h
abhängige Funktion ansehen und im totalen Differential d h ¼ 0 setzen):
1
V ¼ f ðR; rÞ ¼
p h ð2 R 2 þ r 2 Þ
3
dV ¼
@V
@V
1
1
2
dR þ
dr ¼
ph 4R dR þ
ph 2r dr ¼
p h ð2 R d R þ r d rÞ
@R
@r
3
3
3
Wir verwenden noch die in der Praxis übliche Schreibweise ðd V; d R; d r ! D V; D R; D rÞ:
2
p h ð2 R D R þ r D rÞ
DV ¼
3
Mit R ¼ 1 m , r ¼ 0,8 m , h ¼ 1,50 m , D R ¼ þ 0,02 m und D r ¼ 0,02 m erhalten wir den folgenden Näherungswert für die Volumenänderung (in guter bereinstimmung mit der exakten nderung):
2
DV ¼
p 1,50 ½ 2 1 0,02 þ 0,8 ð 0,02Þ m 3 ¼ p ð0,04 0,016Þ m 3 ¼ 0,0754 m 3
3
DV
0,0754 m 3
Prozentuale nderung des Volumens:
100 % ¼
100 % ¼ 1,82 %
V1
4,1469 m 3
5 Anwendungen
5.1 Linearisierung einer Funktion
Lehrbuch: Band 2, Kapitel III.2.5.2
Formelsammlung: Kapitel IX.2.5.1
E53
x y
1
mit x > y > 0 in der Umgebung der
Linearisieren Sie die Funktion z ¼ 5 ln
5
y2
Stelle x 0 ¼ 2 , y 0 ¼ 1. Berechnen Sie mit dieser Näherungsfunktion den Wert an der Stelle x ¼ 2,1,
y ¼ 0,95 . Wie groß ist die Abweichung zum exakten Funktionswert?
Die Funktion lässt sich mit elementaren Rechenregeln für Logarithmen wie folgt vereinfachen:
x y
1
1
1
2
¼ 5 ln ðx yÞ ln y
¼ 5 ln ðx yÞ 2 ln y
¼
z ¼ f ðx; yÞ ¼ 5 ln
5
5
5
y2
¼ 5 ln ðx yÞ 10 ln y 1
Rechenregeln: ln
a
b
¼ ln a ln b und
ln a n ¼ n ln a
Linearisierung der Funktion
Höhenkoordinate z 0 des „Arbeitspunktes‘‘ P ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð2; 1; z 0 Þ:
z 0 ¼ f ðx 0 ; y 0 Þ ¼ f ð2; 1Þ ¼ 5 ln ð2 1Þ 10 ln 1 1 ¼ 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|{z}
ln 1 ¼ 0
0
)
P ¼ ð2; 1; 1Þ
270
E Partielle Differentiation
Partielle Ableitungen 1. Ordnung
z ¼ f ðx; yÞ ¼ 5 ln ðx yÞ 10 ln y 1 ¼ 5 ln u 10 ln y 1
|fflfflfflffl{zfflfflfflffl}
u
mit
u ¼ x y
Es wird gliedweise differenziert, der erste Summand dabei in der angedeuteten Weise nach der Kettenregel:
z x ¼ f x ðx; yÞ ¼ 5
1
5
5
100 ¼
¼
u
u
x y
z y ¼ f y ðx; yÞ ¼ 5
1
1
5
10
5
10
ð 1Þ 10
0 ¼
¼
u
y
u
y
x y
y
Ableitungswerte in P ¼ ðx 0 ; y 0 ; z 0 Þ ¼ ð2; 1; 1Þ:
f x ð2; 1Þ ¼
5
5
¼ 5 , f y ð2; 1Þ ¼
10 ¼ 15
21
21
Gleichung der Tangentialebene in P = (x 0 ; y 0 ; z 0) = (2 ; 1 ; 1)
z z 0 ¼ f x ðx 0 ; y 0 Þ ðx x 0 Þ þ f y ðx 0 ; y 0 Þ ð y y 0 Þ
z þ 1 ¼ f x ð2; 1Þ ðx 2Þ þ f y ð2; 1Þ ð y 1Þ
z þ 1 ¼ 5 ðx 2Þ 15 ð y 1Þ ¼ 5 x 10 15 y þ 15 ¼ 5 x 15 y þ 5
z ¼ 5 x 15 y þ 4
Linearisierte Funktion in der Umgebung des Arbeitspunktes P ¼ ð2; 1; 1Þ:
x y
1
z ¼ 5 ln
5 x 15 y þ 4
5
y2
Näherungswert an der Stelle x ¼ 2,1 , y ¼ 0,95 (Einsetzen dieser Werte in die linearisierte Funktion):
z
5 2,1 15 0,95 þ 4 ¼ 0,25
Exakter Wert (berechnet mit der Funktionsgleichung):
2,1 0,95
1
¼ 0,2117
z ¼ 5 ln
5
0,95 2
Der Näherungswert fällt um D z ¼ 0,25 0,2117 ¼ 0,0383 zu groß aus.
Der elektrische Widerstand zwischen zwei koaxialen Zylinderelektroden (Hohlzylinder) wird nach der
Formel
1
ra
; ra > ri > 0
ln
R ¼
ri
2pjl
berechnet (siehe hierzu Bild E-4; ra , ri : Außen- bzw. Innenradius; l: Länge des Hohlzylinders;
j: Leitfähigkeit des Materials zwischen den Elektroden).
E54
Linearisieren Sie diese Funktion für geringfügige nderungen der Radien r a bzw. r i um D ra bzw.
D ri bei fester Länge l.
Bild E-4
5 Anwendungen
271
Bei konstanter Länge l ist der Widerstand R eine nur von ra und ri abhängige Funktion:
1
ra
1
R ¼ f ðra ; ri Þ ¼
¼
ln
ðln ra ln ri Þ
ri
2pjl
2pjl
Rechenregel : ln
a
¼ ln a ln b
b
Bei kleinen nderungen der beiden Radien ändert sich auch der Widerstand R nur geringfügig und wir können diese
Widerstandsänderung näherungsweise mit Hilfe des totalen Differentials von R bestimmen:
@R
@R
1
1
1
1
1
d ra
d ri
d ri ¼
¼
d ra þ
d ri ¼
d ra
dR ¼
@ ra
@ ri
2 p j l ra
2 p j l ri
2 p j l ra
ri
¼
1
ri d ra ra d ri
ri d ra ra d ri
¼
2pjl
ra ri
2 p j l ra ri
Die in der Praxis verwendete Schreibweise lautet (wir ersetzen d r a , d r i , d R durch D r a , D r i , D R):
DR ¼
ri D ra ra D ri
1
¼
ðri D ra ra D ri Þ
2 p j l ra ri
2 p j l ra ri
Mit dieser linearen Beziehung lässt sich die Widerstandsänderung D R aus den vorgegebenen nderungen D ra und
D ri der beiden Radien leicht berechnen (bei fest vorgegebenen Werten für l, ra und ri ).
Reihenschaltung zweier Kapazitäten C1 und C2 (Bild E-5):
1
1
1
þ
¼
C
C1
C2
E55
Bild E-5
C1
C2
a) Lösen Sie zunächst diese Gleichung nach der Gesamtkapazität C auf und linearisieren Sie dann die
erhaltene Funktion in der Umgebung des „Arbeitspunktes“ C1 ¼ 6 mF, C2 ¼ 4 mF.
b) Wie groß ist die Kapazitätsänderung, wenn die 1. Kapazität um 0,1 mF vergrößert und gleichzeitig
die 2. Kapazität um den gleichen Betrag verkleinert wird?
(Exakter Wert und Näherungswert.)
c) Beide Kapazitäten werden um jeweils 1 % verkleinert. Wie ändert sich dann die Gesamtkapazität?
a) Wir lösen die Gleichung nach C auf:
C2 þ C1
1
1
1
C1 þ C2
þ
¼
¼
¼
C1 C2
C1 C2
C
C1
C2
)
C ¼
C1 C2
C1 þ C2
(zuerst den Hauptnenner C 1 C 2 , dann den Kehrwert bilden). Für die Linearisierung benötigen wir die partiellen
Ableitungen 1. Ordnung. Die Quotientenregel liefert das gewünschte Ergebnis:
C ¼ f ðC 1 ; C 2 Þ ¼
@C
¼
@ C1
C1 C2
u
¼
v
C1 þ C2
@u
@v
v
u
@ C1
@ C1
v2
C 12
@C
¼
@ C2
ðC1 þ C2 Þ 2
¼
mit
u ¼ C1 C2 ;
v ¼ C1 þ C2
C2 ðC1 þ C2 Þ 1 C1 C2
ðC1 þ C2 Þ 2
¼
und
@u
¼ C2 ;
@ C1
C1 C2 þ C 22 C1 C2
ðC1 þ C2 Þ 2
¼
@v
¼ 1
@ C1
C 22
ðC1 þ C2 Þ 2
(aus Symmetriegründen, C 1 und C 2 sind vertauschbar)
Die linearisierte Funktion lautet damit ðtotales Differential von C ¼ f ðC1 ; C2 ÞÞ:
C 22
C 12
C 22 D C1 þ C 12 D C2
@C
@C
DC ¼
D C1 þ
D C2 ¼
D C1 þ
D C2 ¼
@ C1
@ C2
ðC1 þ C2 Þ 2
ðC1 þ C2 Þ 2
ðC1 þ C2 Þ 2
272
E Partielle Differentiation
Dabei sind D C1 , D C2 und D C Relativkoordinaten, d. h. die nderungen der Kapazitäten gegenüber dem
„Arbeitspunkt‘‘ (Ausgangsgrößen). Für C1 und C2 werden die Ausgangswerte 6 mF bzw. 4 mF eingesetzt:
DC ¼
ð4 mFÞ 2 D C 1 þ ð6 mFÞ 2 D C 2
ð6 mF þ 4 mFÞ
2
¼
16 D C1 þ 36 D C2
¼ 0,16 D C1 þ 0,36 D C2
100
b) Wir berechnen jetzt die Kapazitätsänderung D C für D C1 ¼ þ 0,1 mF und D C2 ¼ 0,1 mF:
D C ¼ ½ 0,16 0,1 þ 0,36 ð 0,1Þ mF ¼ ð0,016 0,036Þ mF ¼ 0,020 mF
Die exakte nderung ist (betragsmäßig) geringfügig größer (für C1 ¼ 6,1 mF; C2 ¼ 3,9 mF):
D Cexakt ¼ f ð6,1; 3,9Þ f ð6; 4Þ ¼
6,1 3,9
64
¼ 2,379 2,4 ¼ 0,021 ðin mFÞ :
6,1 þ 3,9
6þ4
c) Kapazitätsänderung D C für D C 1 ¼ 0;06 mF und D C 2 ¼ 0,04 mF (Näherungswert):
D C ¼ ½ 0,16 ð 0,06Þ þ 0,36 ð 0,04Þ mF ¼ ð 0,0096 0,0144Þ mF ¼ 0,0240 mF
Exakte nderung der Kapazität C (für C1 ¼ 5,94 mF; C2 ¼ 3,96 mF):
5,94 3,96
64
¼ 2,376 2,4 ¼ 0,024
5,94 þ 3,96
6þ4
D C exakt ¼ f ð5,94 ; 3,96Þ ¼
ðin mFÞ
Linearisieren Sie die Funktion u ¼ f ðx; y; zÞ ¼ 2 x 2 y þ x y sin z an der Stelle x 0 ¼ y 0 ¼ 1 ,
E56
z 0 ¼ p=2 .
Wie ändert sich der Funktionswert näherungsweise, wenn man die unabhängigen
Koordinaten
a) um jeweils 2 % vergrößert,
b) der Reihe nach um d x ¼ 0,1, d y ¼ 0,08 und d z ¼ 0,2 verändert?
Berechnung des zugehörigen Funktionswertes u 0 ¼ f ðx 0 ; y 0 ; z 0 Þ:
u 0 ¼ f ð1; 1; p=2Þ ¼ 2 1 2 1 þ 1 1 sin ðp=2Þ ¼ 2 þ 1 ¼ 3
|fflfflfflfflffl{zfflfflfflfflffl}
1
Partielle Ableitungen 1. Ordnung
9
>
>
=
u x ¼ f x ðx; y; zÞ ¼ 4 x y þ y sin z
u y ¼ f y ðx; y; zÞ ¼ 2 x 2 þ x sin z
uz ¼ fz ðx; y; zÞ ¼ 0 þ x y cos z ¼ x y cos z
>
>
;
f x ð1; 1; p=2Þ ¼ 4 1 1 þ 1 sin ðp=2Þ ¼ 5
)
f y ð1; 1; p=2Þ ¼ 2 1 2 þ 1 sin ðp=2Þ ¼ 3
fz ð1; 1; p=2Þ ¼ 1 1 cos ðp=2Þ ¼ 0
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
0
Linearisierte Funktion
u u0 ¼ f x ðx 0 ; y 0 ; z 0 Þ ðx x 0 Þ þ f y ðx 0 ; y 0 ; z 0 Þ ð y y 0 Þ þ fz ðx 0 ; y 0 ; z 0 Þ ðz z 0 Þ
u 3 ¼ f x ð1; 1; p=2Þ ðx 1Þ þ f y ð1; 1; p=2Þ ð y 1Þ þ fz ð1; 1; p=2Þ ðz p=2Þ
u 3 ¼ 5 ðx 1Þ þ 3 ð y 1Þ þ 0 z
u ¼ 5x þ 3y 5
p
2
¼ 5x 5 þ 3y 3 ¼ 5x þ 3y 8
(in der Umgebung von x 0 ¼ y 0 ¼ 1 , z 0 ¼ p=2)
Man beachte, dass die linearisierte Funktion nicht von der Koordinate z abhängt.
a) nderung des Funktionswertes (mit Hilfe des totalen Differentials berechnet)
Wir berechnen zunächst die benötigten absoluten nderungen der drei unabhängigen Koordinaten:
d x ¼ 2 % von x 0 ¼ 1
d z ¼ 2 % von z 0 ¼ p=2
)
)
d x ¼ 0,02;
d y ¼ 2 % von y 0 ¼ 1
d z ¼ 0,0314
)
d y ¼ 0,02;
5 Anwendungen
273
Mit dem totalen Differential
d u ¼ f x ð1; 1; p=2Þ d x þ f y ð1; 1; p=2Þ d y þ f z ð1; 1; p=2Þ d z ¼ 5 d x þ 3 d y þ 0 d z ¼ 5 d x þ 3 d y
erhalten wir dann den folgenden Näherungswert für die nderung des Funktionswertes:
d u ¼ 5 0,02 þ 3 0,02 ¼ 0,1 þ 0,06 ¼ 0,16
Neuer Funktionswert (Näherung): u
u 0 þ d u ¼ 3 þ 0,16 ¼ 3,16
b) Mit d x ¼ 0,1, d y ¼ 0,08 und d z ¼ 0,2 erhalten wir mit dem unter a) bestimmten totalen Differential die
folgende nderung des Funktionswertes:
d u ¼ 5 d x þ 3 d y þ 0 d z ¼ 5 d x þ 3 d y ¼ 5 0,1 þ 3 ð 0,08Þ ¼ 0,5 0,24 ¼ 0,26
Neuer Funktionswert (Näherung): u
u 0 þ d u ¼ 3 þ 0,26 ¼ 3,26
5.2 Lineare Fehlerfortpflanzung
Die unabhängigen Messgrößen x und y müssen in der Form
x ¼ x D x
und
y ¼ y D y
vorliegen (x, y sind die Mittelwerte, D x , D y die Messunsicherheiten, d. h. die Standardabweichungen der Mittelwerte). Die lineare Fehlerfortpflanzung liefert dann die maximale Messunsicherheit (auch maximaler oder größtmöglicher Fehler genannt) der „indirekten‘‘ Messgröße z ¼ f ðx; yÞ auf der Basis des totalen oder vollständigen Differentials der Funktion z ¼ f ðx; yÞ .
Lehrbuch: Band 2, Kapitel III.2.5.5
Formelsammlung: Kapitel XI.4
Der Flächeninhalt eines Kreissegments wird nach der Formel
A
A ¼ 0,5 r 2 ðj sin jÞ
r
E57
f
berechnet (grau unterlegt in Bild E-6). Radius r und Zentriwinkel j wurden wie folgt gemessen:
M
r ¼ ð10,0 0,1Þ cm , j ¼ 60 1
Bild E-6
Wie lautet das Messergebnis für die „indirekte“ Messgröße A?
„Indirekter Messwert‘‘ (Mittelwert) für A
¼ 60
Für r und j sind die Messwerte (Mittelwerte) r ¼ 10,0 cm und j
p
¼ 0,5 r 2 ðj
sin jÞ
¼ 0,5 10,0 2
sin 60
A
3
¼ p=3 einzusetzen:
bzw. j
cm 2 ¼ 9,0586 cm 2
muss aus Dimensionsgründen im Bogenmaß angegeben werden!)
(der Summand j
Lineare Fehlerfortpflanzung mit Hilfe des totalen Differentials
A ¼ f ðr; jÞ ¼ 0,5 r 2 ðj sin jÞ
dA ¼
r
@A
@A
dr þ
d j ¼ r ðj sin jÞ d r þ 0,5 r 2 ð1 cos jÞ d j
@r
@j
9,06 cm 2
274
E Partielle Differentiation
Daraus erhalten wir den Formelausdruck für den maximalen Fehler in der praxisüblichen Schreibweise:
D A max ¼ j r ðj sin jÞ D r j þ j 0,5 r 2 ð1 cos jÞ D j j
Mit r ¼ 10,0 cm , D r ¼ 0,1 cm , j ¼ 60
D A max ¼ 10,0
p
sin 60
3
bzw. j ¼ p=3 und D j ¼ p=180 (entspricht 1 ) folgt:
0,1 cm 2 þ 0,5 10,0 2 ð1 cos 60 Þ
¼ 0,1812 cm 2 þ 0,4363 cm 2 ¼ 0,6175 cm 2
Messergebnis:
p
cm 2 ¼
180
0,62 cm 2
D A max ¼ ð9,06 0,62Þ cm 2
A ¼ A
D A max
Prozentualer Maximalfehler:
A
100 % ¼
0,62 cm 2
9,06 cm 2
100 %
6,84 %
Das Massenträgheitsmoment J eines dünnen homogenen Stabes (bezogen auf die Schwerpunktsachse
senkrecht zur Stabachse) lässt sich aus der Stabmasse m und der Stablänge l wie folgt berechnen:
1
m l2
12
In einem Experiment wurden für m und l folgende Messwerte ermittelt:
J ¼ J ðm; lÞ ¼
E58
i
1
2
3
4
5
mi (in g)
119,5
121,0
120,3
119,2
120,0
li (in cm)
19,9
19,7
20,2
20,3
19,9
a) Werten Sie die beiden Messreihen in der üblichen Weise aus (Angabe des jeweiligen Mittelwertes
und der zugehörigen Standardabweichung des Mittelwertes).
b) Welcher Mittelwert ergibt sich daraus für das Massenträgheitsmoment J ?
Welchen maximalen Fehler (maximale Messunsicherheit) liefert die lineare Fehlerfortpflanzung
unter Verwendung des totalen Differentials?
Wie lautet das („indirekte‘‘) Messergebnis für die Größe J ?
a) Auswertung der beiden Messreihen
Für jede der beiden Größen bilden wir der Reihe nach den Mittelwert, die Abweichung der einzelnen Messwerte
vom Mittelwert, die Abweichungsquadrate und mit der Summe der Abweichungsquadrate dann die Standardabweichung des Mittelwertes (wird für die Fehlerfortpflanzung benötigt). Die Anordnung der Werte erfolgt zweckmäßigerweise in Form einer Tabelle:
mi
g
mi m
g
2
ðm i mÞ
1
119,5
0,5
2
121,0
3
l i l
cm
ðl i lÞ 2
g2
li
cm
0,25
19,9
0,1
0,01
1,0
1
19,7
0,3
0,09
120,3
0,3
0,09
20,2
0,2
0,04
4
119,2
0,8
0,64
20,3
0,3
0,09
5
P
120,0
0
0
19,9
0,1
0,01
600,0
0
1,98
100,0
0
0,24
i
cm 2
5 Anwendungen
275
Messergebnis für die Größe m (Spalte 2, 3 und 4; Summenindex i von 1 bis 5)
P
X
mi
600,0 g
¼ 0 (Spalte 3)
¼ 120,0 g
Kontrolle :
ðm i mÞ
¼
m ¼
n
5
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
uP
u ðm i mÞ
2
1,98 g 2
Dm ¼ t
¼
¼ 0,31 g
54
n ðn 1Þ
D m ¼ ð120,00 0,31Þ g
m ¼ m
Messergebnis:
Messergebnis für die Größe l (Spalte 5, 6 und 7)
P
X
li
100 cm
l ¼
¼ 20 cm
Kontrolle :
ðl i lÞ ¼ 0 (Spalte 6)
¼
5
n
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
uP
u ðl i lÞ 2
0,24 cm 2
¼ 0,11 cm
Dl ¼ t
¼
54
n ðn 1Þ
l ¼ l D l ¼ ð20,00 0,11Þ cm
Messergebnis:
b) Mittelwert und maximaler Fehler der „indirekten‘‘ Messgröße J
Mittelwert:
1
1
l 2 ¼
J ¼
m
ð120 gÞ ð20 cmÞ 2 ¼ 4000 g cm 2
12
12
Lineare Fehlerfortpflanzung mit Hilfe des totalen Differentials
J ¼ f ðm; lÞ ¼
1
m l2
12
)
dJ ¼
@J
@J
1 2
1
dm þ
dl ¼
l dm þ
ml dl
@m
@l
12
6
Maximaler Fehler (in praxisüblicher Schreibweise):
1 2
@J
@ J
1
D J max ¼
D m þ
D l ¼
l D m þ m l D l
@m
@l
12
6
Mit m ¼ 120 g , l ¼ 20 cm , D m ¼ 0,31 g und D l ¼ 0,11 cm erhalten wir:
D J max ¼
1
1
ð20 cmÞ 2 0,31 g þ
ð120 gÞ ð20 cmÞ 0,11 cm ¼
12
6
¼ ð10,33 þ 44Þ g cm 2 ¼ 54,33 g cm 2
Messergebnis:
J ¼ J D J max ¼ ð4000 55Þ g cm 2
Prozentualer Maximalfehler:
E59
55 g cm 2
D J max
55 g cm 2
100 %
100 % ¼
4000 g cm 2
J
1,4 %
Die Leistung eines Gleichstroms wird nach der Formel P ¼ R I 2 berechnet. Widerstand R und
Stromstärke I wurden in einem Praktikumsversuch wie folgt gemessen:
R ¼ ð80,0 1,0Þ W ;
I ¼ ð6,2 0,1Þ A
D P max an.
Geben Sie das Messergebnis für P in der Form P ¼ P
„Indirekter Messwert‘‘ (Mittelwert) für P
¼ R
I 2 ¼ ð80,0 WÞ ð6,2 AÞ 2 ¼ 3075,2 W
P
3075 W
276
E Partielle Differentiation
Lineare Fehlerfortpflanzung mit dem totalen Differential
P ¼ f ðR; IÞ ¼ R I 2
)
dP ¼
@P
@P
dR þ
dI ¼ I2 dR þ 2RI dI
@R
@I
Maximaler Fehler (in praxisüblicher Schreibweise):
@ P
@P
DR þ
D I ¼ j I 2 D R j þ j 2 R I D I j
D Pmax ¼
@R
@I
Einsetzen der Werte R ¼ 80,0 W , I ¼ 6,2 A , D R ¼ 1,0 W und D I ¼ 0,1 A liefert:
D Pmax ¼ ð6,2 AÞ 2 1,0 W þ 2 ð80,0 WÞ ð6,2 AÞ 0,1 A ¼ ð38,44 þ 99,20Þ W ¼ 137,64 W
Messergebnis:
138 W
D P max ¼ ð3075 138Þ W
P ¼ P
Prozentualer Maximalfehler:
D Pmax
138 W
100 %
100 % ¼
3075 W
P
4,5 %
Torsionsflächenmoment eines Kreisrings (Bild E-7):
p R4 r4
W ¼
2
R
E60
R
ðR > r > 0Þ
r
M
Innen- und Außenradius wurden wie folgt gemessen:
r ¼ ð2,00 0,01 cm) ,
R ¼ ð4,00 0,02Þ cm
Bild E-7
Wie lautet das Messergebnis für die „indirekte“ Messgröße W ?
„Indirekter Messwert‘‘ (Mittelwert) für W
W ¼
4 r 4
p R
p 44 24
p 256 16
¼
cm 3 ¼
cm 3 ¼ 30 p cm 3
4
2
2
2
4
R
94,25 cm 3
Lineare Fehlerfortpflanzung mit Hilfe des totalen Differentials
Wir bilden zunächst die für das totale Differential benötigten partiellen Ableitungen 1. Ordnung der von R und r
abhängigen Funktion
W ¼ f ðR; rÞ ¼
p R4 r4
R
2
Für die partielle Ableitung nach R verwenden wir die Quotientenregel:
W ¼
p R4 r4
p u
¼
2
2 v
R
mit
u ¼ R4 r4 ;
v ¼ R und
@u
¼ 4 R3 ;
@R
@v
¼ 1
@R
@u
@v
v
u
@W
p
p 4 R 3 R 1 ðR 4 r 4 Þ
p 4 R4 R4 þ r 4
p 3 R4 þ r4
@R
@R
¼
¼
¼
¼
2
2
@R
2
2
2
2
R
R
R2
v2
Die partielle Ableitung nach r lässt sich nach einer kleinen Umformung der Funktion elementar bilden:
p R4 r4
p
r4
@W
p
4r3
2pr3
3
)
¼
W ¼
¼
R
¼
0
R
R
R
R
2
2
@r
2
Totales Differential von W:
dW ¼
@W
@W
p 3 R4 þ r4
2pr3
dR þ
dr ¼
dr
dR þ
@R
@r
2
R
R2
5 Anwendungen
277
Maximaler Fehler (in praxisüblicher Schreibweise):
@W
@W
p 3 R4 þ r4
2pr3
D Wmax ¼
D R þ
D r ¼
DR þ
Dr
@R
@r
2
R
R2
Zur Erinnerung: Alle Beiträge sind positiv infolge der Betragsbildung!. Wir setzen die Werte R ¼ 4 cm , r ¼ 2 cm ,
D R ¼ 0,02 cm und D r ¼ 0,01 cm ein und erhalten den folgenden absoluten Maximalfehler:
D Wmax ¼
p 3 44 þ 24
2 p 23
0,01 cm 3 ¼
0,02 cm 3 þ
2
4
42
¼ ð1,5394 þ 0,1257Þ cm 3 ¼ 1,6651 cm 3
Messergebnis:
1,67 cm 3
W ¼ W D Wmax ¼ ð94,25 1,67Þ cm 3
Prozentualer Maximalfehler:
D Wmax
100 % ¼
W
1,67 cm 3
94,25 cm 3
100 %
1,8 %
Die Reihenschaltung zweier elastischer Federn mit den Federkonstanten c 1 und c 2 lässt sich durch
eine Ersatzfeder mit der Federkonstanten
c ¼ f ðc 1 ; c 2 Þ ¼
c1 c2
c1 þ c2
ersetzen (Bild E-8). Für c 1 und c 2 wurden folgende
Messwerte ermittelt:
E61
c 1 ¼ ð150,0 3,0Þ N=m ;
c1
c2
Bild E-8
c 2 ¼ ð100,0 2,0Þ N=m
Wie lautet das Messergebnis für die „indirekte‘‘ Messgröße c auf der Basis der linearen Fehlerfortpflanzung?
„Indirekter Messwert‘‘ (Mittelwert) für c
c ¼
150 100 N
N
c1 c2
¼ 60
¼
m
m
150 þ 100
c1 þ c2
Lineare Fehlerfortpflanzung mit dem totalen Differential
Die benötigten partiellen Ableitungen 1. Ordnung erhalten wir mit der Quotientenregel:
c ¼ f ðc 1 ; c 2 Þ ¼
@c
¼
@ c1
c1 c2
u
¼
c1 þ c2
v
@u
@v
v
u
@ c1
@ c1
v2
c 21
@c
¼
@ c2
ðc 1 þ c 2 Þ 2
¼
mit
u ¼ c 1 c2 ;
v ¼ c1 þ c2
c 2 ðc 1 þ c 2 Þ 1 c 1 c 2
ðc 1 þ c 2 Þ 2
¼
@u
¼ c2 ;
@ c1
c 1 c 2 þ c 22 c 1 c 2
ðc 1 þ c 2 Þ 2
¼
@v
¼ 1
@ c1
c 22
ðc 1 þ c 2 Þ 2
ðwegen der Symmetrie der Funktion bezüglich der Variablen c 1 und c 2 Þ
Damit lautet das totale Differential von c wie folgt:
dc ¼
und
c 22
c 21
@c
@c
d c1 þ
d c2 ¼
d c1 þ
d c2
@ c1
@ c2
ðc 1 þ c 2 Þ 2
ðc 1 þ c 2 Þ 2
278
E Partielle Differentiation
Bei der (linearen) Fehlerfortpflanzung werden die Beträge der einzelnen Summanden addiert (ungünstigster Fall) und
wir erhalten definitionsgemäß den Maximalfehler (in praxisüblicher Schreibweise):
c 22
c 21
c 22 D c 1 þ c 21 D c 2
@c
@c
D cmax ¼
D c1 þ
D c 2 ¼
D c1 þ
D c2 ¼
ðc þ c Þ 2
ðc þ c Þ 2
@ c1
@ c2
ðc 1 þ c 2 Þ 2
1
2
1
2
Mit c 1 ¼ 150 , c 2 ¼ 100 , D c 1 ¼ 3 und D c 2 ¼ 2 (alle Werte in N/m) folgt:
D cmax ¼
Messergebnis:
100 2 3 þ 150 2 2 N
30 000 þ 45 000 N
75 000 N
N
¼
¼
¼ 1,2
2
2
m
m
m
m
62
500
ð150 þ 100Þ
ð250Þ
c ¼ c D cmax ¼ ð60,0 1,2Þ N=m
Prozentualer Maximalfehler:
D cmax
1,2 N=m
100 % ¼ 2 %
100 % ¼
c
60,0 N=m
5.3 Relative Extremwerte
Lehrbuch: Band 2, Kapitel III.2.5.3
Formelsammlung: Kapitel IX.2.5.2
E62
Bestimmen Sie die relativen Extremwerte der Funktion z ¼ x y þ
1
1
þ
x
y
ðx 6¼ 0 ; y 6¼ 0Þ .
Partielle Ableitungen 1. und 2. Ordnung:
z ¼ xy þ
1
1
þ
¼ x y þ x 1 þ y 1
x
y
zx ¼ y x 2 ;
zy ¼ x y 2 ;
z x x ¼ ð 2 x 3 Þ ¼
2
;
x3
z y y ¼ ð 2 y 3 Þ ¼
2
;
y3
zxy ¼ 1
Notwendige Bedingungen für einen relativen Extremwert: z x ¼ 0 , z y ¼ 0
zx ¼ 0
)
ðIÞ
y x 2 ¼ y
1
¼ 0
x2
)
y ¼
1
x2
zy ¼ 0
)
ðIIÞ
x y 2 ¼ x
1
¼ 0
y2
)
x y2 ¼ 1
Gleichung (I) wird nach y aufgelöst, der gefundene Ausdruck in Gleichung (II) eingesetzt:
2
1
1
1
ðIIÞ ) x y 2 ¼ x
¼ x
¼
¼ 1 ) x3 ¼ 1 ) x1 ¼ 1
x2
x4
x3
(Kürzen durch x ist wegen x 6¼ 0 erlaubt). Zugehöriger y-Wert (aus Gleichung (I) berechnet): y 1 ¼ 1 .
Wir prüfen jetzt, ob an der Stelle ðx 1 ; y 1 Þ ¼ ð1; 1Þ ein relativer Extremwert vorliegt:
z x x ð1; 1Þ ¼ 2;
z y y ð1; 1Þ ¼ 2;
z x y ð1; 1Þ ¼ 1
D ¼ z x x ð1; 1Þ z y y ð1; 1Þ z 2x y ð1; 1Þ ¼ 2 2 1 2 ¼ 3 > 0
)
relativer Extremwert
Wegen z x x ð1; 1Þ ¼ 2 > 0 handelt es sich hierbei um ein relatives Minimum: Min ¼ ð1; 1; 3Þ .
5 Anwendungen
E63
279
Wo liegen die relativen Extremwerte der Funktion z ¼ f ðx; yÞ ¼ 3 x 2 2 x
pffiffiffi
y 8x þ y þ 8?
Die benötigten partiellen Ableitungen 1. und 2. Ordnung lauten:
zx ¼ 6 x 2
zxx ¼ 6 ;
pffiffiffi
y 8;
zy ¼ 2 x
1
x
x
1=2
þ1
pffiffiffi þ 1 ¼ pffiffiffi þ 1 ¼ 1=2 þ 1 ¼ x y
y
y
2 y
1
x y 3=2
x
x
3=2
y
¼
¼ x
¼ pffiffiffiffiffi ;
¼
3=2
2
2y
2
2 y3
zyy
zxy ¼ 2
1
1
pffiffiffi ¼ pffiffiffi
y
2 y
In einem relativen Extremum müssen notwendigerweise die partiellen Ableitungen 1. Ordnung verschwinden:
pffiffiffi
pffiffiffi
pffiffiffi
zx ¼ 0 )
ðIÞ 6 x 2 y 8 ¼ 0 ) 2 y ¼ 6 x þ 8 )
y ¼ 3x 4
pffiffiffi
pffiffiffi
x
x
y ¼ x
z y ¼ 0 ) ðIIÞ pffiffiffi þ 1 ¼ 0 ) pffiffiffi ¼ 1 ) x ¼ y )
y
y
pffiffiffi
Beide Gleichungen haben wir nach
y aufgelöst. Durch Gleichsetzen folgt:
x1 ¼ 2
pffiffiffiffiffi
Zugehöriger y-Wert (aus Gleichung (II) berechnet):
y 1 ¼ x 1 ¼ 2 j quadrieren
3x 4 ¼ x
)
2x ¼ 4
)
)
y1 ¼ 4
Die partiellen Ableitungen 2. Ordnung entscheiden nun, ob ein relativer Extremwert vorliegt:
2
1
1
1
1
; z x y ð2; 4Þ ¼ pffiffiffi ¼
pffiffiffiffiffi ¼ pffiffiffiffiffi ¼
8
2
64
4
2 43
1
1 2
3
1
2
1
D ¼ z x x ð2; 4Þ z y y ð2; 4Þ z 2x y ð2; 4Þ ¼ 6
¼
¼
¼
> 0
8
2
4
4
4
2
z x x ð2; 4Þ ¼ 6 ;
z y y ð2; 4Þ ¼
Damit ist das hinreichende Kriterium für einen relativen Extremwert erfüllt. Wegen z x x ð2; 4Þ ¼ 6 > 0 liegt ein
relatives Minimum vor: Min ¼ ð2; 4; 0Þ.
pffiffiffi
Höhenkoordinate: z 1 ¼ f ðx 1 ; y 1 Þ ¼ f ð2; 4Þ ¼ 3 2 2 2 2 4 8 2 þ 4 þ 8 ¼ 12 8 16 þ 12 ¼ 0
E64
Untersuchen Sie die Funktion z ¼ f ðx; yÞ ¼ x 2 þ y 3 3 x y auf relative Extremwerte.
Die benötigten partiellen Ableitungen 1. und 2. Ordnung lauten:
zx ¼ 2 x 3 y ;
zy ¼ 3 y2 3 x ;
zxx ¼ 2 ;
zyy ¼ 6 y ;
zxy ¼ 3
Wir setzen z x ¼ 0 und z y ¼ 0 (notwendige Bedingungen für einen relativen Extremwert):
zx ¼ 0
)
ðIÞ
zy ¼ 0
)
ðIIÞ
2x 3y ¼ 0
3 y2 3 x ¼ 0 j : 3
)
y2 x ¼ 0
)
x ¼ y2
Die untere Gleichung lösen wir nach x auf, erhalten x ¼ y 2 und setzen diesen Ausdruck in Gleichung (I) ein:
ðIÞ
)
2 x 3 y ¼ 2 y2 3 y ¼ 0
)
y ð2 y 3Þ ¼ 0
Aus x ¼ y 2 berechnen wir die zugehörigen x-Werte: x 1 ¼ 0 , x 2 ¼
)
9
.
4
y1 ¼ 0 ;
y2 ¼
3
2
280
E Partielle Differentiation
Folgerung: An den Stellen ðx 1 ; y 1 Þ ¼ ð0; 0Þ und ðx 2 ; y 2 Þ ¼ ð9=4; 3=2Þ verläuft die Tangentialebene jeweils parallel zur x; y-Ebene. Die partiellen Ableitungen 2. Ordnung entscheiden darüber, ob es sich bei diesen Stellen um
relative Extremwerte handelt:
ðx 1 ; y 1 Þ ¼ ð0 ; 0Þ
z x x ð0 ; 0Þ ¼ 2 ;
z y y ð0 ; 0Þ ¼ 0 ;
z x y ð0 ; 0Þ ¼ 3
D 1 ¼ z x x ð0; 0Þ z y y ð0; 0Þ z 2x y ð0; 0Þ ¼ 2 0 ð 3Þ 2 ¼ 9 < 0
ðx 2 ; y 2 Þ ¼
9 3
;
4 2
D2 ¼ zxx
9 3
;
4 2
Da z x x
9 3
;
4 2
zxx
zyy
9 3
;
4 2
9 3
;
4 2
¼ 2;
z 2x y
zyy
9 3
;
4 2
9 3
;
4 2
¼ 6
kein Extremwert
3
¼ 9;
2
zxy
¼
9 3
;
4 2
¼ 3
¼ 2 9 ð 3Þ 2 ¼ 9 > 0 ) relativer Extremwert
¼ 2 > 0 ist, handelt es sich um ein relatives Minimum: Min ¼
9 3
;
4 2
Höhenkoordinate: z 1 ¼ f ðx 1 ; y 1 Þ ¼ f
E65
)
¼
9 3
27
;
;
4 2
16
2 3
9
3
9
3
81
27
81
þ
3
¼
þ
¼
4
2
4
2
16
8
8
81 þ 54 162
27
¼
16
16
Ermitteln Sie die relativen Extremwerte der Funktion z ¼ f ðx; yÞ ¼ ð y x 2 Þ e 2 y .
Mit Hilfe der Produkt- und Kettenregel erhalten wir die benötigten partiellen Ableitungen 1. und 2. Ordnung:
zx ¼ 2 x e 2y ;
zxx ¼ 2 e 2y ;
z x y ¼ 2 x e 2 y ð 2Þ ¼ 4 x e 2 y
(Ableitung von z x nach y mit der Kettenregel, Substitution: t ¼ 2 y)
z ¼ ðy x 2 Þ e 2 y ¼ u v
|fflfflfflfflffl{zfflfflfflfflffl} |ffl{zffl}
u
v
mit
u ¼ y x2 ;
v ¼ e 2y
und
uy ¼ 1 ;
vy ¼ 2 e 2y
z y ¼ u y v þ v y u ¼ 1 e 2 y 2 e 2 y ð y x 2 Þ ¼ ð1 þ 2 x 2 2 yÞ e 2 y
z y ¼ ð1 þ 2 x 2 2 yÞ e 2 y ¼ u v ;
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} |ffl{zffl}
u
v
u ¼ 1 þ 2x2 2y;
v ¼ e 2 y und u y ¼ 2 ;
vy ¼ 2 e 2y
z y y ¼ u y v þ v y u ¼ 2 e 2 y 2 e 2 y ð1 þ 2 x 2 2 yÞ ¼ ½ 2 2 ð1 þ 2 x 2 2 yÞ e 2 y ¼
¼ ð 2 2 4 x 2 þ 4 yÞ e 2 y ¼ ð 4 4 x 2 þ 4 yÞ e 2 y ¼ 4 ð1 þ x 2 yÞ e 2 y
Notwendige Bedingungen für einen relativen Extremwert: z x ¼ 0 , z y ¼ 0
zx ¼ 0
)
ðIÞ
2 x e 2y ¼ 0
|ffl{zffl}
6¼ 0
zy ¼ 0
)
ðIIÞ
ð1 þ 2 x 2 2 yÞ e 2 y ¼ 0
|ffl{zffl}
6¼ 0
)
2x ¼ 0
)
1 þ 2x2 2y ¼ 0
Wir lösen dieses einfache Gleichungssystem wie folgt:
ðIÞ
2x ¼ 0
)
ðIIÞ
1 þ 2x2 2y ¼ 0
x1 ¼ 0
)
ðin Gleichung ðIIÞ einsetzenÞ
1 þ 0 2y ¼ 0
)
2y ¼ 1
)
y 1 ¼ 0,5
Wir prüfen jetzt anhand der partiellen Ableitungen 2. Ordnung, ob an der Stelle ðx 1 ; y 1 Þ ¼ ð0; 0,5Þ die hinreichende
Bedingung für einen relativen Extremwert erfüllt ist:
5 Anwendungen
281
z x x ð0; 0,5Þ ¼ 2 e 1 ;
z y y ð0; 0,5Þ ¼ 4 ð1 0,5Þ e 1 ¼ 2 e 1 ;
z x y ð0; 0,5Þ ¼ 0
D ¼ z x x ð0; 0,5Þ z y y ð0; 0,5Þ z 2x y ð0; 0,5Þ ¼ ð 2 e 1 Þ ð 2 e 1 Þ 0 2 ¼ 4 e 2 > 0
Es liegt demnach ein Extremwert vor, und zwar wegen z x x ð0; 0,5Þ ¼ 2 e 1 < 0 ein relatives Maximum:
Max ¼ ð0; 0,5; 0,184Þ
Höhenkoordinate: z 1 ¼ f ðx 1 ; y 1 Þ ¼ f ð0; 0,5Þ ¼ ð0,5 0 2 Þ e 1 ¼ 0,184
z ¼ f ðx; yÞ ¼ x 2 3 x y þ x y 3 þ 1
E66
Bestimmen Sie die relativen Extremwerte und Sattelpunkte dieser Funktion.
Partielle Ableitungen 1. und 2. Ordnung:
zx ¼ 2 x 3 y þ y3 ;
zy ¼ 3 x þ 3 x y2 ;
zxx ¼ 2 ;
zyy ¼ 6 x y ;
z x y ¼ 3 þ 3 y 2 ¼ 3 ð y 2 1Þ
Notwendige Bedingungen für einen relativen Extremwert: z x ¼ 0 , z y ¼ 0
zx ¼ 0
)
ðIÞ
2 x 3 y þ y3 ¼ 0
zy ¼ 0
)
ðIIÞ
3 x þ 3 x y2 ¼ 0
)
3 x ð1 y 2 Þ ¼ 0 j : ð 3Þ
)
x ð1 y 2 Þ ¼ 0
Gleichung (I) nach x auflösen, den gefundenen Ausdruck in Gleichung (II) einsetzen:
ðIÞ
1
1
ð3 y y 3 Þ ¼
y ð3 y 2 Þ
2
2
)
2 x ¼ 3 y y3
)
1
y ð3 y 2 Þ ð1 y 2 Þ ¼ 0
x ð1 y Þ ¼
2
)
x ¼
y ¼ 0
ðIIÞ
)
3 y2 ¼ 0
2
y1 ¼ 0 ;
y2=3 ¼
pffiffiffi
3;
1 y2 ¼ 0
y4=5 ¼ 1
Zugehörige x-Werte (aus Gleichung (I) berechnet): x 1 ¼ 0 , x2=3 ¼ 0 , x4=5 ¼ 1
Als relative Extremwerte kommen daher die folgenden fünf Stellen in Frage:
pffiffiffi
pffiffiffi
ðx 1 ; y 1 Þ ¼ ð0; 0Þ ; ðx 2 ; y 2 Þ ¼ ð0; 3 Þ ; ðx 3 ; y 3 Þ ¼ ð0; 3 Þ ;
ðx 4 ; y 4 Þ ¼ ð1; 1Þ ;
ðx 5 ; y 5 Þ ¼ ð 1; 1Þ
Wir prüfen jetzt mit Hilfe der partiellen Ableitungen 2. Ordnung, für welche Stellen die hinreichende Bedingung für
einen relativen Extremwert erfüllt ist:
ðx 1 ; y 1 Þ ¼ ð0; 0Þ
z x x ð0; 0Þ ¼ 2 ;
z y y ð0; 0Þ ¼ 0 ;
z x y ð0; 0Þ ¼ 3
D 1 ¼ z x x ð0; 0Þ z y y ð0; 0Þ z 2x y ð0; 0Þ ¼ 2 0 ð 3Þ 2 ¼ 9 < 0
)
kein Extremwert ðsondern ein SattelpunktÞ
ðx 2 ; y 2 Þ ¼ ð0;
D 2 ¼ z x x ð0;
)
pffiffiffi
3Þ
z x x ð0;
pffiffiffi
3Þ ¼ 2;
z y y ð0;
pffiffiffi
3Þ ¼ 0;
z x y ð0;
pffiffiffi
pffiffiffi
pffiffiffi
3 Þ z y y ð0; 3 Þ z 2x y ð0; 3 Þ ¼ 2 0 6 2 ¼ 36 < 0
kein Extremwert ðsondern ein SattelpunktÞ
pffiffiffi
Ebenso: ðx 3 ; y 3 Þ ¼ ð0; 3 Þ ist ein Sattelpunkt.
pffiffiffi
3Þ ¼ 6
282
E Partielle Differentiation
ðx 4 ; y 4 Þ ¼ ð1; 1Þ
z x x ð1; 1Þ ¼ 2 ;
z y y ð1; 1Þ ¼ 6 ;
z x y ð1; 1Þ ¼ 0
D4 ¼ z x x ð1; 1Þ z y y ð1; 1Þ z 2x y ð1; 1Þ ¼ 2 6 0 2 ¼ 12 > 0
)
relativer Extremwert
Wegen z x x ð1; 1Þ ¼ 2 > 0 liegt ein relatives Minimum vor.
Ebenso: ðx 5 ; y 5 Þ ¼ ð 1; 1Þ ist ein relatives Minimum.
pffiffiffi
Ergebnis: Minima in ð 1; 1; 0Þ; Sattelpunkte in ð0; 0; 1Þ und ð0; 3 ; 1Þ
5.4 Extremwertaufgaben mit und ohne Nebenbedingungen
Verwenden Sie zur Lösung von Extremwertaufgaben mit Nebenbedingungen das Multiplikatorverfahren von Lagrange.
Lehrbuch: Band 2, Kapitel III.2.5.3 und 2.5.4
Formelsammlung: Kapitel IX.2.5.3
Gegeben sind vier Messpunkte, die nahezu auf einer Geraden liegen:
E67
x
0
1
2
3
y
2,90
5,10
7,10
8,80
Bestimmen Sie mit der Gauß’schen Methode der kleinsten Quadrate die zugehörige Ausgleichsgerade
y ¼ m x þ b , d. h. diejenige Gerade, die sich diesen Messpunkten optimal anpasst.
Hinweis: Eine ausführliche Beschreibung dieses Verfahrens finden Sie in Band 3, Kapitel IV.5.1 bis 5.3
(siehe auch: Formelsammlung, Kapitel XI.5.1 und 5.2).
Wir bestimmen für jeden Messpunkt die Abweichung u von der Ausgleichsgeraden in vertikaler Richtung (Differenz
der Ordinatenwerte, siehe Bild E-9). Diese Werte sind mal positiv, mal negativ, da die Messpunkte teils oberhalb, teils
unterhalb der gesuchten Geraden liegen werden. Daher werden diese Abweichungen quadratiert und dann aufaddiert.
Wir stellen diesen Vorgang übersichtlich in einer Tabelle zusammen:
i
x
y
mx þ b
u ¼ y ðm x þ bÞ
y
1
0
2,90
b
2,90 b
9
Ausgleichsgerade
8
2
1
5,10
mþb
5,10 m b
7
3
2
7,10
2m þ b
7,10 2 m b
6
4
3
8,80
3m þ b
8,80 3 m b
4
5
Messpunkt
3
2
1
Bild E-9
1
Die Summe der Abweichungsquadrate lautet damit:
S ðm; bÞ ¼ ð2,90 bÞ 2 þ ð5,10 m bÞ 2 þ ð7,10 2 m bÞ 2 þ ð8,80 3 m bÞ 2
2
3
x
5 Anwendungen
283
Sie hängt noch von m und b ab. Diese Parameter müssen nun so bestimmt werden, dass diese Summe möglichst klein
wird. Wir bilden daher zunächst die für die Lösung dieser Aufgabe benötigten partiellen Ableitungen 1. und 2. Ordnung:
Sm ¼
@S
¼ 0 þ 2 ð5,10 m bÞ ð 1Þ þ 2 ð7,10 2 m bÞ ð 2Þ þ 2 ð8,80 3 m bÞ ð 3Þ ¼
@m
¼ 2 ð5,10 m bÞ 4 ð7,10 2 m bÞ 6 ð8,80 3 m bÞ ¼
¼ 10,20 þ 2 m þ 2 b 28,40 þ 8 m þ 4 b 52,80 þ 18 m þ 6 b ¼ 28 m þ 12 b 91,4
Sb ¼
@S
¼ 2 ð2,90 bÞ ð 1Þ þ 2 ð5,10 m bÞ ð 1Þ þ 2 ð7,10 2 m bÞ ð 1Þ þ
@b
þ 2 ð8,80 3 m bÞ ð 1Þ ¼
¼ 2 ½2,90 b þ 5,10 m b þ 7,10 2 m b þ 8,80 3 m b ¼
¼ 2 ð 6 m 4 b þ 23,9Þ ¼ 12 m þ 8 b 47,8
@ Sm
¼ 28 ;
@m
Smm ¼
Sbb ¼
@ Sb
¼ 8;
@b
Smb ¼
@ Sm
¼ 12
@b
Aus den für einen Extremwert notwendigen Bedingungen S m ¼ 0 und S b ¼ 0 erhalten wir das folgende lineare
Gleichungssystem:
Sm ¼ 0
)
ðIÞ
28 m þ 12 b 91,4 ¼ 0 j 2
Sb ¼ 0
)
ðIIÞ 12 m þ 8 b 47,8 ¼ 0 j 3
Lösungsweg: Die 1. Gleichung mit 2, die 2. mit 3 multiplizieren, dann die Gleichungen voneinander subtrahieren:
)
ðI *Þ 56 m þ 24 b 182,8 ¼ 0
y
ðII *Þ 36 m þ 24 b 143,4 ¼ 0
10
39,4 ¼ 0
20 m
ðIIÞ
)
m ¼ 1,97
8
)
12 1,97 þ 8 b 47,8 ¼ 0
6
)
8 b 24,16 ¼ 0
4
)
b ¼ 3,02
2
Die Gleichung der Ausgleichsgeraden lautet somit:
y ¼ 1,97 x þ 3,02
1
3
x
Bild E-10
Bild E-10 zeigt diese Gerade mit den vier Messpunkten.
E68
2
Einer Ellipse mit den Halbachsen a und b ist ein (achsenparalleles) Rechteck größter Fläche einzubeschreiben. Wie müssen die Seitenlängen des Rechtecks gewählt werden?
Bild E-11 zeigt ein (beliebiges) einbeschriebenes Rechteck, dessen Flächeninhalt A wir wie folgt durch die Koordinaten x und y des im 1. Quadranten gelegenen Ellipsenpunktes P ausdrücken können:
A ¼ 4xy
ðx > 0 ; y > 0Þ
y
b
Da P ein Punkt der Ellipse ist, gilt die folgende Nebenbedingung:
2
P = (x ; y )
2
y
x
þ
¼ 1
2
a
b2
oder
y
b2 x2 þ a2 y2 a2 b2 ¼ 0
x
–a
(Mittelpunktsgleichung einer Ellipse).
Bild E-11
–b
a
x
284
E Partielle Differentiation
Für die Lösung unserer Aufgabe verwenden wir das Lagrangesche Multiplikatorverfahren. Wir bilden aus der Flächenfunktion A ¼ 4 x y und der Nebenbedingung j ðx; yÞ ¼ b 2 x 2 þ a 2 y 2 a 2 b 2 ¼ 0 (Ellipsengleichung in impliziter Form) die von x; y und dem Lagrangeschen Multiplikator l abhängige Hilfsfunktion
F ðx; y; lÞ ¼ A ðx; yÞ þ l j ðx; yÞ ¼ 4 x y þ l ðb 2 x 2 þ a 2 y 2 a 2 b 2 Þ
Die partiellen Ableitungen 1. Ordnung dieser Funktion werden jeweils gleich null gesetzt und liefern das folgende
Gleichungssystem für die Unbekannten x, y und l (wobei uns nur die Werte für x und y interessieren):
Fx ¼ 0
)
ðIÞ
4 y þ 2 b2 l x ¼ 0
)
l ¼
Fy ¼ 0
)
ðIIÞ
4 x þ 2 a2 l y ¼ 0
)
l ¼
Fl ¼ 0
)
ðIIIÞ
b2 x2 þ a2 y2 a2 b2 ¼ 0
2y
b2 x
2x
a2 y
Wir eliminieren den Multiplikator l, indem wir die ersten beiden Gleichungen nach l auflösen und die Ausdrücke
gleichsetzen:
2y
b2
x
¼
2x
a2 y
: ð 2Þ
y
)
b2
x
¼
x
a2 y
)
a2 y2 ¼ b2 x2
ðÞ
Die gefundene Beziehung ðÞ setzen wir in die 3. Gleichung ein und berechnen daraus x und danach y (es kommen
nur positive Werte in Frage):
ðIIIÞ
ðÞ
)
b2 x2 þ b2 x2 a2 b2 ¼ 0
)
2 x2 a2 ¼ 0
)
a2 y2 ¼ b2 x2 ¼ b2
)
x2 ¼
)
1 2
a
2
2 b 2 x 2 a 2 b 2 ¼ b 2 ð2 x 2 a 2 Þ ¼ 0 j : b 2
)
x ¼
1 2
1 2 2
a ¼
a b : a2
2
2
1 pffiffiffi
2a
2
)
y2 ¼
1 2
b
2
)
y ¼
1 pffiffiffi
2b
2
Die gesuchte Lösung lautet damit wie folgt:
x ¼
1 pffiffiffi
2 a;
2
y ¼
1 pffiffiffi
2 b;
2
A min ¼ 4 x y ¼ 4
1 pffiffiffi
1 pffiffiffi
2a
2 b ¼ 2ab
2
2
Sonderfall a = b
Aus der Ellipse wird ein Kreis mit dem Radius r ¼ a. Das einbeschriebene Rechteck mit größtmöglichem Flächen1 pffiffiffi
inhalt ist dann ein Quadrat mit der Seitenlänge x ¼ y ¼
2 a und dem Flächeninhalt A ¼ 2 a 2 .
2
E69
Wie muss man einen geraden Kreiszylinder mit aufgesetzter Halbkugel dimensionieren, damit er bei
einem vorgegebenen Volumen von V ¼ 5000 cm 3 eine möglichst kleine Gesamtoberfläche A hat?
Die Gesamtoberfläche A setzt sich aus der Grundkreisfläche des Zylinders (p r 2 ),
dem Zylindermantel (2 p r h) und der Oberfläche der Halbkugel (2 p r 2 ) zusammen
(siehe Bild E-12):
r
A ¼ A ðr; hÞ ¼ p r 2 þ 2 p r h þ 2 p r 2 ¼ 3 p r 2 þ 2 p r h
h
r : Radius der Halbkugel;
h: Zylinderhöhe
Bild E-12
5 Anwendungen
285
Das vorgegebene Volumen von 5000 cm 3 liefert die noch benötigte Nebenbedingung für die Variablen r und h. Es
gilt:
V ¼ VZylinder þ VHalbkugel ¼ p r 2 h þ
2
p r 3 ¼ 5000
3
oder (in impliziter Form, die wir für das Lagrangesche Multiplikatorverfahren benötigen)
j ðr; hÞ ¼ p r 2 h þ
2
p r 3 5000 ¼ 0
3
Wir bilden jetzt die Lagrangesche „Hilfsfunktion“:
2
2
3
F ðr; h; lÞ ¼ A ðr; hÞ þ l j ðr; hÞ ¼ 3 p r þ 2 p r h þ l p r h þ
p r 5000
3
2
Dabei ist l der sog. Lagrangesche Multiplikator, dessen Wert uns nicht weiter interessiert. Die partiellen Ableitungen
1. Ordnung der Hilfsfunktion werden jeweils gleich null gesetzt und liefern ein Gleichungssystem für die unbekannten
Größen r, h und l:
@F
¼ 0
@r
)
ðIÞ
6 p r þ 2 p h þ l ð2 p r h þ 2 p r 2 Þ ¼ 0
@F
¼ 0
@h
)
ðIIÞ
2pr þ lpr2 ¼ 0
@F
¼ 0
@l
)
ðIIIÞ
pr2 h þ
)
lpr2 ¼ 2pr
)
l ¼
2pr
2 ðp rÞ
2
¼
¼
2
r
pr
ðp r Þ r
2
p r 3 5000 ¼ 0
3
Gleichung (II) lösen wir nach l auf, erhalten l ¼ 2=r und setzen dann diesen Ausdruck in die 1. Gleichung ein:
ðIÞ
2
ð2 p r h þ 2 p r 2 Þ ¼ 6 p r þ 2 p h 4 p h 4 p r ¼ 2 p r 2 p h ¼ 0
r
)
6pr þ 2ph
)
2 p ðr hÞ ¼ 0 j : 2 p
)
r h ¼ 0
)
r ¼ h
Damit haben wir die Aufgabe bereits gelöst: die Gesamtoberfläche nimmt den kleinsten Wert an, wenn Radius und
Höhe des Zylinders übereinstimmen. Der zahlenmäßige Wert von r und h lässt sich aus der Gleichung (III) ermitteln
(unter Beachtung von r ¼ h):
ðIIIÞ
)
)
2
2
5
p r 3 5000 ¼ p r 3 þ
p r 3 5000 ¼
p r 3 5000 ¼ 0
3
3
3
rffiffiffiffiffiffiffiffiffiffiffi
5
3000
3 3000
3
3
p r ¼ 5000 ) r ¼
) r ¼
¼ 9,8475
3
p
p
pr2 r þ
Lösung der Aufgabe:
r ¼ h ¼ 9,8475 cm
9,85 cm
A min ¼ 3 p r 2 þ 2 p r r ¼ 3 p r 2 þ 2 p r 2 ¼ 5 p r 2 ¼ 5 p ð9,8475 cmÞ 2 ¼ 1523,25 cm 2
E70
Welcher Punkt P ¼ ðx; yÞ der Hyperbel x 2 y 2 ¼ 12 hat vom Punkt A ¼ ð0; 4Þ den kleinsten
Abstand d ?
Anhand der Skizze (Bild E-13) erwarten wir zwei zur y-Achse spiegelsymmetrische Lösungen. Aus der allgemeinen
Abstandsformel für zwei Punkte P 1 ¼ ðx 1 ; y 1 Þ und P 2 ¼ ðx 2 ; y 2 Þ erhalten wir in unserem Fall:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
2
2
d ¼ ðx 1 x 2 Þ þ ð y 1 y 2 Þ ¼ ðx 0Þ þ ð y 4Þ ¼ x 2 þ ð y 4Þ 2
286
E Partielle Differentiation
y
6
Hyperbel
Hyperbel
4
P = (x ; y )
2
Bild E-13
–6
–4
–2
2
4
x
6
–2
–4
–6
Diese Wurzelfunktion wird minimal, wenn der Radikand (d. h. der Ausdruck unter der Wurzel) seinen kleinsten Wert
annimmt. Es genügt also, die sog. „Zielfunktion‘‘
Z ðx; yÞ ¼ d 2 ¼ x 2 þ ð y 4Þ 2
zu untersuchen. Die Koordinaten x und y genügen dabei der Hyperbelgleichung, die somit eine Neben- oder Kopplungsbedingung liefert (in impliziter Form):
j ðx; yÞ ¼ x 2 y 2 12 ¼ 0
ðNebenbedingungÞ
Nach dem Multiplikatorverfahren von Lagrange bilden wir nun die „Hilfsfunktion‘‘
F ðx; y; lÞ ¼ Z ðx; yÞ þ l j ðx; yÞ ¼ x 2 þ ð y 4Þ 2 þ l ðx 2 y 2 12Þ
l ist dabei der Lagrangesche Multiplikator, dessen Wert uns nicht zu interessieren braucht. Wir setzen die partiellen
Ableitungen 1. Ordnung dieser Hilfsfunktion jeweils gleich null und erhalten das folgende Gleichungssystem für die
drei Unbekannten x, y und l:
Fx ¼ 0
)
ðIÞ
2x þ 2lx ¼ 0
Fy ¼ 0
)
ðIIÞ
2 ð y 4Þ 1 2 l y ¼ 2 ð y 4Þ 2 l y ¼ 0
Fl ¼ 0
)
ðIIIÞ
x 2 y 2 12 ¼ 0
Aus Gleichung (I) erhalten wir wegen x 6¼ 0:
2 x þ 2 l x ¼ 2 x ð1 þ lÞ ¼ 0 j : 2 x
)
1þl ¼ 0
)
l ¼ 1
Dann folgt aus Gleichung (II):
2 ð y 4Þ 2 ð 1Þ y ¼ 0
2y ¼ 4
)
)
2 ð y 4Þ þ 2 y ¼ 0 j : 2
)
y4þy ¼ 0
)
y ¼ 2
Die zugehörigen Abszissenwerte erhalten wir aus der 3. Gleichung (für y ¼ 2):
ðIIIÞ
)
x 2 4 12 ¼ 0
)
x 2 16 ¼ 0
)
x 2 ¼ 16
)
x 1=2 ¼ 4
Die beiden Lösungen P 1=2 ¼ ð 4; 2Þ liegen unserer Erwartung entsprechend spiegelsymmetrisch zur y-Achse.
E71
Ein quaderförmiges Schwimmbecken mit einem Fassungsvermögen (Volumen) von V ¼ 108 m 3 soll
so gebaut werden, dass die Oberfläche (Boden und Seitenwände) möglichst klein wird. Wie sind die
Abmessungen des Beckens zu wählen?
Die Kanten des quaderförmigen Beckens bezeichnen wir mit x , y und z (Bild E-14). Die Berechnung der Oberfläche (Boden plus Seitenwände) erfolgt dann nach der Formel
A ¼ A ðx; y; zÞ ¼ x y þ 2 x z þ 2 y z
5 Anwendungen
287
z
y
Bild E-14
x
Die drei Variablen x , y und z sind jedoch nicht unabhängig voneinander, sondern durch die Nebenbedingung
V ¼ const: ¼ 108 m 3 miteinander verknüpft (es kommen nach der Aufgabenstellung nur Quader mit diesem Volumen in Frage):
V ¼ x y z ¼ 108
oder
j ðx; y; zÞ ¼ x y z 108 ¼ 0
Zur Lösung der Aufgabe verwenden wir das Multiplikatorverfahren von Lagrange. Zunächst bilden wir die „Hilfsfunktion‘‘
F ðx; y; z; lÞ ¼ A ðx; y; zÞ þ l j ðx; y; zÞ ¼ x y þ 2 x z þ 2 y z þ l ðx y z 108Þ
(l: Lagrangescher Multiplikator; x > 0; y > 0; z > 0)
Die partiellen Ableitungen 1. Ordnung dieser Funktion müssen sämtlich verschwinden. Dies führt zu dem folgenden
Gleichungssystem mit den vier Unbekannten x , y, z und l:
Fx ¼ 0
)
ðIÞ
y þ 2z þ lyz ¼ 0
Fy ¼ 0
)
ðIIÞ
x þ 2z þ lxz ¼ 0
Fz ¼ 0
)
ðIIIÞ
2x þ 2y þ lxy ¼ 0
Fl ¼ 0
)
ðIVÞ
x y z 108 ¼ 0
Wir lösen die Gleichungen (I) und (II) jeweils nach l z auf und setzen die Ausdrücke gleich:
9
y þ 2z >
>
ðIÞ
) lz ¼
>
=
y þ 2z
y þ 2z
y
x þ 2z
x þ 2z
¼
¼
oder
)
y
y
x
x
>
x þ 2z >
>
;
ðIIÞ ) l z ¼
x
Daraus ergibt sich die folgende Gleichung (die linke Seite wird mit x, die rechte mit y multipliziert):
x ð y þ 2 zÞ ¼ y ðx þ 2 zÞ
)
xy þ 2xz ¼ xy þ 2yz
)
2xz ¼ 2yz
)
x ¼ y
Aus Gleichung (III) folgt dann (mit y ¼ x):
)
2 x þ 2 x þ l x x ¼ 4 x þ l x 2 ¼ x ð4 þ l xÞ ¼ 0
)
4 þ lx ¼ 0
)
lx ¼ 4
f
ðIIIÞ
6¼ 0
Diesen Ausdruck setzen wir in Gleichung (II) ein:
ðIIÞ
)
x þ 2 z þ ðl xÞ z ¼ x þ 2 z þ ð 4Þ z ¼ x þ 2 z 4 z ¼ 0
)
x 2z ¼ 0 )
x ¼ 2z
„Zwischenstand‘‘: x ¼ y ¼ 2 z
Unter Berücksichtigung dieser Beziehungen lässt sich aus Gleichung (IV) die Unbekannte z (und daraus dann x und y)
berechnen:
ðIVÞ
)
x y z 108 ¼ ð2 zÞ ð2 zÞ z 108 ¼ 4 z 3 108 ¼ 0
)
z 3 ¼ 27
)
z ¼ 3
Die Lösung dieser Aufgabe lautet damit:
x ¼ y ¼ 2z ¼ 6;
z ¼ 3
ð jeweils in mÞ
A min ¼ x y þ 2 x z þ 2 y z ¼ 6 6 þ 2 6 3 þ 2 6 3 ¼ 36 þ 36 þ 36 ¼ 108
ðin m 3 Þ
288
E Partielle Differentiation
Einem Kreis vom Radius R soll ein Rechteck so einbeschrieben werden, dass das Flächenmoment
1
I ¼
x y 3 einen möglichst großen Wert annimmt. Wie sind die Rechtecksseiten x und y zu wählen?
12
E72
Die unbekannten Seiten x und y sind über den Satz des Pythagoras miteinander verknüpft (siehe Bild E-15):
x 2 þ y 2 ¼ ð2 RÞ 2 ¼ 4 R 2
2R
oder
j ðx; yÞ ¼ x 2 þ y 2 4 R 2 ¼ 0
y
M
x
Bild E-15
Nach Lagrange bilden wir die folgende „Hilfsfunktion‘‘:
F ðx; y; lÞ ¼ I ðx; yÞ þ l j ðx; yÞ ¼
1
x y 3 þ l ðx 2 þ y 2 4 R 2 Þ
12
ð0 < x < 2 R; 0 < y < 2 RÞ
Die partiellen Ableitungen 1. Ordnung dieser Funktion werden jeweils gleich null gesetzt und liefern drei Gleichungen
für die drei Unbekannten x , y und l:
Fx ¼
1 3
y þ 2lx;
12
Fy ¼
1
xy2 þ 2ly;
4
Fx ¼ 0
)
ðIÞ
1 3
y þ 2lx ¼ 0
12
Fy ¼ 0
)
ðIIÞ
1
x y2 þ 2 l y ¼ 0
4
Fl ¼ 0
)
ðIIIÞ
x2 þ y2 4 R2 ¼ 0
F l ¼ x2 þ y2 4R2
Die ersten beiden Gleichungen werden nach l aufgelöst, die gefundenen Ausdrücke dann gleichgesetzt:
9
>
y3
>
>
ðIÞ
) l ¼
>
=
24 x
y3
xy
)
) 8 y 3 ¼ 24 x 2 y j : 8 y
¼
2
>
8
24
x
xy
xy >
>
>
ðIIÞ ) l ¼
¼
;
) ðI*Þ y 2 ¼ 3 x 2
8
8y
(Kürzen durch y ist wegen y > 0 erlaubt.)
Diese Beziehung zwischen den beiden Seiten setzen wir in Gleichung (III) ein und berechnen x und daraus dann y:
ðIIIÞ
)
x2 þ y2 4 R2 ¼ x2 þ 3 x2 4 R2 ¼ 4 x2 4 R2 ¼ 0 j : 4
x2 ¼ R2
ðI*Þ
Lösung:
)
x ¼ R
y2 ¼ 3 x2 ¼ 3 R2
x ¼ R, y ¼
I min ¼
)
)
ðin Gleichung ðI*Þ einsetzenÞ
pffiffiffi
y ¼ 3R
pffiffiffi
3 R,
pffiffiffi
1
1
1 pffiffiffi 4
1 pffiffiffi 4
x y3 ¼
R ð 3 RÞ 3 ¼
3 3R ¼
3R
12
12
12
4
)
x2 R2 ¼ 0
)
289
F Mehrfachintegrale
Hinweise für das gesamte Kapitel
(1)
(2)
Fertigen Sie zu jeder Aufgabe eine Skizze an, sie erleichtert Ihnen den Lösungsweg und führt zu einem besseren Verständnis.
Alle anfallenden (gewöhnlichen) Integrale dürfen einer Integraltafel entnommen werden. Bei der Lösung der
Integrale wird die jeweilige Integralnummer aus der Integraltafel der Mathematischen Formelsammlung des
Autors mit den entsprechenden Parameterwerten angegeben (gelbe Seiten, z. B. Integral 313 mit a ¼ 2). Selbstverständlich dürfen Sie die Integrale auch „per Hand“ lösen (zusätzliche bung).
1 Doppelintegrale
In diesem Abschnitt finden Sie (fast) ausschließlich anwendungsorientierte Aufgaben zu folgenden Themen:
Stromstärke, Flächenladung, magnetischer Fluss durch einen Leiter
Flächeninhalt, Flächenschwerpunkt, Flächenträgheitsmomente (Flächenmomente) homogener Flächen
Volumen homogener „zylindrischer“ Körper
Verwendet werden sowohl kartesische Koordinaten (Abschnitt 1.1) als auch Polarkoordinaten (Abschnitt 1.2).
1.1 Doppelintegrale in kartesischen Koordinaten
Lehrbuch: Band 2, Kapitel III.3.1.2.1 und 3.1.3
Formelsammlung: Kapitel IX.3.1.2 und 3.1.4
ð3
F1
ð
p x=2
I ¼
cos
x¼1 y¼0
y
x
dy dx ¼ ?
Innere Integration (nach der Variablen y)
ð
p x=2
cos
y¼0
y
x
h
dy ¼
x sin
h
y i p x=2
¼ x sin
x y¼0
h
y i p x=2
p
¼ x sin
x y¼0
2
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 228 mit a ¼ 1=x
ußere Integration (nach der Variablen x)
ð3
I ¼
x dx ¼
x¼1
1 2
x
2
3
¼
1
1
2
½ x2 1
3
¼
1
1
ð9 1Þ ¼
8 ¼ 4
2
2
Ergebnis: I ¼ 4
F2
1
ð
ð1
I ¼
ðu vÞ e u d v d u ¼ ?
u¼1 v¼1
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_6
sin 0
i
¼ x ð1 0Þ ¼ x
290
F Mehrfachintegrale
Innere Integration (nach der Variablen v)
ð1
ðu vÞ e
u
dv ¼ e
ð1
u
v¼1
v¼1
¼ e u
1 2 1
v
ðu vÞ d v ¼ e u u v
¼
2
v¼1
1
1
u
þuþ
¼ 2 u e u
2
2
ußere Integration (nach der Variablen u)
1
ð
2u e
I ¼
u
1
ð
du ¼ 2
u¼1
u e u d u
u¼1
Dieses uneigentliche Integral wird wie folgt berechnet (! FS: V.4.1): Zunächst integrieren wir von u ¼ 1 bis
u ¼ l (l > 1) und bilden dann den Grenzwert für l ! 1.
1
ð
ðl
u e u d u ¼ 2 lim
I ¼ 2
l!1
u¼1
u e u d u ¼ 2 lim
l!1
½ ð u 1Þ e u 1
l
¼
1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ 1
¼ 2 lim ½ ð l 1Þ e l þ 2 e 1 ¼ 2 ð0 þ 2 e 1 Þ ¼ 4 e 1
l!1
Anmerkung: Für jedes Polynom P ðlÞ gilt lim P ðlÞ e l ¼ 0 (l > 0)
l!1
Ergebnis: I ¼ 4 e
ð1
F3
1
¼ 1,4715
y2
ð
I ¼
e x=y d x d y ¼ ?
y¼0 x¼0
Bild F-1 zeigt den Integrationsbereich. Er wird in der x-Richtung durch die Kurven x ¼ 0 (y-Achse) und x ¼ y 2
(nach rechts geöffnete Parabel) und in der y-Richtung durch die Parallelen y ¼ 0 (x-Achse) und y ¼ 1 berandet.
y
Integrationsbereich
1
x=0
0,5
x=y2
Bild F-1
0,5
x
1
Innere Integration (nach der Variablen x)
y2
ð
y2
y2
e x=y d x ¼ ½ y e x=y x ¼ 0 ¼ y ½ e x=y x ¼ 0 ¼ y ðe y e 0 Þ ¼ y ðe y 1Þ ¼ y e y y
x¼0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 312 mit a ¼ 1=y
1 Doppelintegrale
291
ußere Integration (nach der Variablen y)
ð1
I ¼
ð y e y yÞ d y ¼
|fflfflffl{zfflfflffl}
y¼0
ð y 1Þ e y
1 2
y
2
1
¼ 0
0
1
1
1
þ e0 0 ¼
þ1 ¼
2
2
2
Integral 313 mit a ¼ 1
Ergebnis: I ¼ 1=2
Bild F-2 zeigt den Querschnitt eines elektrischen Leiters, der senkrecht von der ortsabhängigen Stromdichte S ðx; yÞ ¼ k x 2 y 2
durchflossen wird (mit k > 0). Berechnen Sie den durch den Leiterquerschnitt A fließenden Strom I, wenn definitionsgemäß gilt :
ðð
I ¼
S ðx; yÞ d A
F4
y
1
Leiterquerschnitt
Bild F-2
1
x
ðAÞ
Wir verwenden kartesische Koordinaten. Der Leiterquerschnitt wird unten von der x-Achse ð y ¼ 0Þ und oben von
der Geraden mit der Gleichung y ¼ x þ 1 berandet, die x-Werte liegen dabei zwischen x ¼ 0 und x ¼ 1
(siehe Bild F-2). Damit ergeben sich folgende Integrationsgrenzen:
y-Integration:
von y ¼ 0 bis y ¼ x þ 1
x-Integration:
von x ¼ 0 bis x ¼ 1
Die Berechnung der Stromstärke I erfolgt somit durch das folgende Doppelintegral:
ðð
I ¼
xðþ 1
ð1
S ðx; yÞ d A ¼ k
ðFlächenelement d A ¼ d y d xÞ
x2 y2 d y d x
x¼0 y¼0
ðAÞ
Innere Integration (nach der Variablen y)
xðþ 1
xðþ 1
x y dy ¼ x
2
2
y dy ¼x
2
y¼0
2
y¼0
¼
2
1 3
y
3
xþ1
¼ x
2
y¼0
1
ð x þ 1Þ 3 0
3
¼
1 2
x ð x þ 1Þ 3 ¼
3
1 2
1
x ð x 3 þ 3 x 2 3 x þ 1Þ ¼
ð x 5 þ 3 x 4 3 x 3 þ x 2 Þ
3
3
ußere Integration (nach der Variablen x)
1
I ¼ k
3
1
¼
k
3
ð1
ð x 5 þ 3 x 4 3 x 3 þ x 2 Þ d x ¼
x¼0
1
3
3
1
þ
þ
6
5
4
3
Ergebnis: Gesamtstrom I ¼
1
k
180
¼
1
k
3
1 6
3 5
3 4
1 3
x þ
x
x þ
x
6
5
4
3
1
10 þ 36 45 þ 20
1
1
1
k
¼
k
¼
k
3
60
3
60
180
1
¼
0
292
F Mehrfachintegrale
Die in Bild F-3 skizzierte trapezförmige Grenzfläche A zweier
dielektrischer Medien enthält die ortsabhängige Oberflächenladung s ðx; yÞ ¼ k x 2 y mit k ¼ 1,5 10 10 As=cm 5 .
Berechnen Sie die Gesamtladung Q auf der Grenzfläche nach
der Formel
ðð
s ðx; yÞ d A
Q ¼
F5
y /cm
5
Grenzfläche
1
A
Bild F-3
4
x /cm
ðAÞ
Die Grenzfläche wird unten von der x-Achse y ¼ 0 und oben von der Geraden y ¼ x þ 1 berandet ð0 x 4Þ.
Das Doppelintegral für die Gesamtladung Q auf der Grenzfläche lautet damit (wir rechnen ohne Einheiten):
ð4
ðð
Q ¼
xð
þ1
s ðx; yÞ d A ¼ k
ðFlächenelement d A ¼ d y d xÞ
x2 y d y d x
x¼0 y¼0
ðAÞ
Innere Integration (nach der Variablen y)
xð
þ1
xð
þ1
x y dy ¼ x
2
y d y ¼ x2
2
y¼0
y¼0
¼
1 2
y
2
xþ1
¼ x2
y¼0
1
ðx þ 1Þ 2 0
2
¼
1 2
x ðx þ 1Þ 2 ¼
2
1 2 2
1
x ðx þ 2 x þ 1Þ ¼
ðx 4 þ 2 x 3 þ x 2 Þ
2
2
ußere Integration (nach der Variablen x)
Q ¼ k
¼
1
2
1
k
2
ð4
ðx 4 þ 2 x 3 þ x 2 Þ d x ¼
x¼0
1 5
1 4
1 3
x þ
x þ
x
5
2
3
4
¼
0
1024
64
1
3072 þ 1920 þ 320
1
5312
2656
þ 128 þ
0 ¼
k
¼
k
¼
k
5
3
2
15
2
15
15
Gesamtladung: Q ¼
F6
1
k
2
2656
2656
k ¼
1,5 10 10 ¼ 2,656 10 8
15
15
ðin AsÞ
1 2
Ein Flächenstück wird durch die Kurven x ¼ 0, y ¼ 2 x und y ¼
x þ a berandet ða > 0Þ.
a
Berechnen Sie den Flächeninhalt A.
Wir bestimmen zunächst die Schnittpunkte der Parabel mit der Geraden y ¼ 2 x :
1 2
x þ a ¼ 2 x ) x2 þ a2 ¼ 2 a x ) x2 2 a x þ a2 ¼ 0
a
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
)
ðx aÞ 2 ¼ 0 )
x 1=2 ¼ a
2. Binom
Die Kurven berühren sich somit im Punkt P ¼ ða; 2 aÞ (doppelte Schnittstelle, siehe Bild F-4). Die Integrationsgrenzen
für die Flächenberechnung mittels Doppelintegral lauten daher wie folgt:
1 2
x þa
a
bis x ¼ a
y-Integration:
von y ¼ 2 x bis y ¼
x-Integration:
von x ¼ 0
1 Doppelintegrale
293
Berechnung des Flächeninhaltes A
ðð
1 2
a xð þ a
ða
dA ¼
A ¼
1 dy dx
x¼0 y¼2x
ðAÞ
(Flächenelement d A ¼ d y d xÞ
Innere Integration (nach der Variablen y)
1 2
a xð þ a
1
1 dy ¼
x2 þa
½ y ya¼ 2 x
¼
y¼2x
1 2
x þ a 2x
a
Bild F-4
ußere Integration (nach der Variablen x)
ða
A ¼
x¼0
1 2
x þ a 2x
a
dx ¼
1 3
x þ ax x2
3a
a
¼
0
1 2
1 2
a þ a2 a2 0 0 0 ¼
a
3
3
Flächeninhalt: A ¼ a 2 =3
F7
Berechnen Sie die von den Kurven y ¼ x , y ¼
Schnittpunkt der Kurven y ¼ x und y ¼
1
, y ¼ 0 und x ¼ 10 eingeschlossene Fläche A.
x
1
im Intervall 0 x 10:
x
x ¼
1
x
)
x2 ¼ 1
)
x1 ¼ 1
Bild F-5 zeigt das Flächenstück, dessen Flächeninhalt berechnet werden soll. Es besteht aus zwei Teilflächen A 1 und
A 2 , die beide unten durch die x-Achse ( y ¼ 0) und oben durch die Gerade y ¼ x bzw. die Hyperbel y ¼ 1=x
berandet werden. Die x-Werte bewegen sich dabei zunächst von x ¼ 0 bis zur Schnittstelle x ¼ 1 (Teilfläche A 1 )
und dann von dort aus weiter bis zur Stelle x ¼ 10 (Teilfläche A 2 ). Somit gilt ðFlächenelement d A ¼ d y d xÞ:
ðð
A1 ¼
ð1
ðx
dA ¼
ðð
1 dy dx;
A2 ¼
x¼0 y¼0
ðA 1 Þ
10
ð
ð
1=x
dA ¼
ðA 2 Þ
1 dy dx
x¼1 y¼0
y
y=x
1
y= 1
x
A1
x = 10
A2
Bild F-5
1
5
Berechnung der Teilfläche A 1 (im Bild hellgrau unterlegt)
Innere Integration (nach der Variablen y)
ðx
1 dy ¼
y¼0
½ y y¼0
x
¼ x 0 ¼ x
10
x
294
F Mehrfachintegrale
ußere Integration (nach der Variablen x)
ð1
A1 ¼
x dx ¼
x¼0
1 2
x
2
1
1
1
0 ¼
¼ 0,5
2
2
¼
0
Berechnung der Teilfläche A 2 (im Bild dunkelgrau unterlegt)
Innere Integration (nach der Variablen y)
ð
1=x
1 dy ¼
½ y y¼0
1=x
¼
y¼0
1
1
0 ¼
x
x
ußere Integration (nach der Variablen x)
10
ð
A2 ¼
x¼1
10
1
d x ¼ ½ ln j x j 1 ¼ ln 10 ln 1 ¼ ln 10 0 ¼ ln 10 ¼ 2,3026
x
Gesamtfläche: A ¼ A 1 þ A 2 ¼ 0,5 þ 2,3026 ¼ 2,8026
Bestimmen Sie den Schwerpunkt S der zwischen der Parabel y ¼ x 2 2 x und der x-Achse gelegenen Fläche.
F8
Nullstellen der Parabel:
y ¼ 0
x 2 2 x ¼ x ðx þ 2Þ ¼ 0
)
)
x 1 ¼ 0;
x2 ¼ 2
Bild F-6 zeigt das durch Parabel (oben) und x-Achse (unten) begrenzte Flächenstück. Der Schwerpunkt S ¼ ðx S ; y S Þ
liegt auf der Symmetrieachse der Parabel, daher ist x S ¼ 1.
Berechnung des Flächeninhaltes A
y
Für die Berechnung der Ordinate y S benötigen wir noch
den Flächeninhalt A (Flächenelement d A ¼ d y d xÞ:
x ð 2 x
ð0
ðð
dA ¼
A ¼
1 dy dx
x¼2
ðAÞ
S
y¼0
–2
Innere Integration (nach der Variablen y)
x ð 2 x
1
y = – x 2 – 2x
2
–1
Bild F-6
2
1 dy ¼
x2 2x
½ y y¼0
¼ x2 2x 0 ¼ x2 2x
y¼0
ußere Integration (nach der Variablen x)
ð0
A ¼
ð x 2 2 xÞ d x ¼
1 3
x x2
3
x¼2
0
¼ 00
2
8
8
8 þ 12
4
þ4 ¼
þ4 ¼
¼
3
3
3
3
Berechnung der Schwerpunktordinate y S
1
yS ¼
A
ðð
ðAÞ
1
y dA ¼
4=3
ð0
x¼2
x 2ð 2 x
y¼0
3
y dy dx ¼
4
ð0
x 2ð 2 x
y dy dx
x¼2
y¼0
x
1 Doppelintegrale
295
Innere Integration (nach der Variablen y)
x 2ð 2 x
y dy ¼
y¼0
1 2
y
2
x2 2x
¼
y¼0
1
1
ð x 2 2 xÞ 2 0 ¼
ðx 4 þ 4 x 3 þ 4 x 2 Þ
2
2
ußere Integration (nach der Variablen x)
3 1
yS ¼
4 2
ð0
3
8
ðx 4 þ 4 x 3 þ 4 x 2 Þ d x ¼
x¼2
0
¼
2
32
32
16 þ
¼
5
3
3
8
¼
3 96 240 þ 160
3 16
3 8 2
2
¼
¼
¼
¼ 0,4
8
15
8 15
5
8 3 5
¼
3
8
1 5
4 3
x þ x4 þ
x
5
3
¼
0þ0þ0þ
32
32
16 þ
5
3
Schwerpunkt: S ¼ ð 1; 0,4Þ
Ein Flächenstück wird berandet durch die nach rechts geöffnete Parabel y 2 ¼ 2 p x und die Gerade
x ¼ const: ¼ p ð p > 0Þ. Bestimmen Sie die Fläche A und den Flächenschwerpunkt S.
F9
Die nach rechts geöffnete Parabel verläuft spiegelsymmetrisch zur x-Achse (Bild F-7). Wir beschränken uns daher bei
den Integrationen auf den 1. Quadranten ( ) Faktor 2 in den Integralen):
pffiffiffiffiffiffiffiffiffi
y-Integration : von y ¼ 0 bis y ¼ 2 p x
y
x-Integration :
von x ¼ 0 bis x ¼ p
2p
y = 2 px
Berechnung des Flächeninhaltes A
pffiffiffiffiffiffiffi
ð2 p x
ðð
ðP
A ¼
dA ¼ 2
1 dy dx
x¼0
ðAÞ
P
A/2
y¼0
(Flächenelement d A ¼ d y d xÞ
– 2p
Innere Integration (nach der Variablen y)
Bild F-7
pffiffiffiffiffiffiffi
pffiffiffiffiffiffiffi
ð2 p x
pffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffi pffiffiffi
2px
1 d y ¼ ½ y y¼0 ¼ 2 p x 0 ¼ 2 p x ¼ 2 p x
y¼0
ußere Integration (nach der Variablen x)
p
p
ðp pffiffiffiffiffiffi pffiffiffi
pffiffiffiffiffiffi ð
pffiffiffiffiffiffi x 3=2 p
pffiffiffiffiffiffi ð pffiffiffi
1=2
A ¼ 2
dx ¼ 2 2p
¼
2p x dx ¼ 2 2p
x dx ¼ 2 2p x
3=2 0
x¼0
¼
x=p
A/2
0
0
qffiffiffiffiffi
qffiffiffiffiffiffiffiffiffi
4 pffiffiffiffiffiffi 3=2 p
4 pffiffiffiffiffiffi 3=2
4 pffiffiffiffiffiffi
4
4 pffiffiffi 2
2 p ½ x 0 ¼
2p ðp
2 p p3 ¼
2 p4 ¼
2p
0Þ ¼
3
3
3
3
3
x
296
F Mehrfachintegrale
Berechnung des Flächenschwerpunktes S ¼ (xS ; y S )
Der Schwerpunkt S liegt auf der Symmetrieachse der Parabel (x-Achse), d. h. y S ¼ 0. Für die Koordinate x S gilt:
pffiffiffiffiffiffiffi
pffiffiffiffiffiffiffi
ð2 p x
ð2 p x
ðp
ðp
ðð
1
1
3
x dA ¼
2
x d y d x ¼ pffiffiffi
x dy dx
xS ¼
A
2
4 pffiffiffi 2
2
2
p
2p
x¼0 y¼0
x¼0 y¼0
ðAÞ
3
Innere Integration (nach der Variablen y)
pffiffiffiffiffiffiffi
pffiffiffiffiffiffiffi
pffiffiffiffiffiffiffi
ð2 p x
ð2 p x
pffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffi pffiffiffi
pffiffiffiffiffiffi
2px
x dy ¼ x
1 d y ¼ x ½ y y ¼ 0 ¼ x ð 2 p x 0Þ ¼ x 2 p x ¼ x 2 p x ¼ 2 p x 3=2
y¼0
y¼0
ußere Integration (nach der Variablen x)
pffiffiffi pffiffiffi
ðp
pffiffiffiffiffiffi
3
2 p x 5=2 p 3 p 1=2 2
3
3= 2
x S ¼ pffiffiffi
2p
x
dx ¼
¼
pffiffiffi
5
5=2 0
2
2 p2
2
2
p
2 2 p2
x¼0
¼
3 p 1=2 p 5=2
5 p2
¼
3 p3
5 p2
¼
3
5
p ¼ 0,6 p
½ x 5=2 0
p
Rechenregeln : a m a n ¼ a m þ n ;
¼
3 p 1=2
5 p2
p 5=2 0 ¼
am
¼ amn
an
Schwerpunkt: S ¼ ð0,6 p; 0Þ
F10
Die Kurven y ¼ sin ðp xÞ und y ¼ a ðx 2 xÞ schließen ein Flächenstück ein, dessen Schwerpunkt
S auf der x-Achse liegen soll ða > 0Þ. Wie muss der Kurvenparameter a gewählt werden?
Die erste der beiden Schnittstellen liegt bei x 1 ¼ 0 (beide Kurven gehen durch den Nullpunkt). Die Funktion
y ¼ sin ðp xÞ hat die Periode p ¼ 2 p=p ¼ 2 und schneidet somit die positive x-Achse bei 1; 2; 3; . . . . Die Parabel y ¼ a ðx 2 xÞ besitzt neben x ¼ 0 noch eine weitere Nullstelle bei x ¼ 1. Beide Kurven haben also gemeinsame Nullstellen bei x 1 ¼ 0 und x 2 ¼ 1 (Bild F-8). Dies sind zugleich die beiden Schnittstellen. Die Integrationsgrenzen lauten damit wie folgt:
y-Integration :
von y ¼ a ðx 2 xÞ bis y ¼ sin ðp xÞ
x-Integration :
von x ¼ 0 bis x ¼ 1
y
Der Schwerpunkt S ¼ ðx S ; y S Þ soll auf der x-Achse liegen,
also gilt y S ¼ 0 (wegen der Spiegelsymmetrie der beiden
Randkurven bezüglich der Geraden x ¼ 0;5 ist x S ¼ 0;5):
1
yS ¼
A
ðð
1
y dA ¼
A
ðAÞ
(Flächenelement d A ¼ d y d x)
ð1
y = sin (π x )
1
sin ðp xÞ
ð
0,5
y dy dx ¼ 0
1
x ¼ 0 y ¼ a ðx 2 xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
–1
Bild F-8
y = a (x 2 – x )
x
1 Doppelintegrale
297
Wegen A > 0 und somit A 6¼ 0 muss das Doppelintegral verschwinden, die Bedingung für den Parameter a lautet
also:
sin ðp xÞ
ð1
ð
y dy dx ¼ 0
x ¼ 0 y ¼ a ðx 2 xÞ
Wir berechnen jetzt das Doppelintegral in der üblichen Weise (der Wert des Integrals wird noch vom Parameter a
abhängen) und erhalten schließlich eine Bestimmungsgleichung für den noch unbekannten Parameter a.
Innere Integration (nach der Variablen y)
sin ðp xÞ
ð
y dy ¼
1 2
y
2
sin ðp xÞ
¼
y ¼ a ðx 2
y ¼ a ðx 2 xÞ
¼
xÞ
1
2
sin ðp xÞ
½ y 2 y ¼ a ðx
2
xÞ
¼
1
½ sin 2 ðp xÞ a 2 ðx 2 xÞ 2 ¼
2
1
½ sin 2 ðp xÞ a 2 ðx 4 2 x 3 þ x 2 Þ
2
ußere Integration (nach der Variablen x)
1
2
ð1
½ sin 2 ðp xÞ a 2 ðx 4 2 x 3 þ x 2 Þ d x ¼
" Integral 205 mit
x¼0
1
2
x
sin ð2 p xÞ
a2
2
4p
1 5
1 4
1 3
x
x þ
x
5
2
3
a ¼ p
1
¼
0
1
sin ð2 pÞ
1
1
1
sin 0
2
2
a
þ
0þ
þ a ð0 0 þ 0Þ ¼
2
4p
5
2
3
4p
|fflfflfflfflffl{zfflfflfflfflffl}
|ffl{zffl}
0
0
1 1
1
1
1
1 1
6 15 þ 10
1 1
1 2
¼
¼
¼
a2
þ
a2
a
2 2
5
2
3
2 2
30
2 2
30
1
¼
2
Somit gilt für den Parameter a (das Doppelintegral muss verschwinden):
ð1
sin ð
ðp xÞ
x ¼ 0 y ¼ a ðx 2 xÞ
Lösung: a ¼
1
y dy dx ¼
2
1
1 2
¼ 0
a
2
30
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
0
)
1
1 2
a ¼ 0
2
30
)
a 2 ¼ 15
)
a ¼
pffiffiffiffiffi
15
pffiffiffiffiffi
15 ¼ 3,8730
Die in Bild F-9 skizzierte trapezförmige Fläche wird unten von der Geraden y ¼ m x berandet.
a) Wie muss man die Steigung m wählen, damit der Flächenschwerpunkt S auf der y-Achse liegt?
b) Bestimmen Sie die genaue Position des Schwerpunktes.
y
F11
2
S
y = mx
Bild F-9
–2
1
–1
3
x
298
F Mehrfachintegrale
a) Der Schwerpunkt S ¼ ðx S ; y S Þ soll auf der y-Achse liegen, also muss die x-Koordinate verschwinden: x S ¼ 0.
Die Integrationsgrenzen für die anfallenden Doppelintegrale entnehmen wir aus Bild F-9:
y-Integration :
von y ¼ m x bis y ¼ 2
x-Integration :
von x ¼ 2 bis x ¼ 3
Dann gilt (Flächenelement d A ¼ d y d xÞ:
1
xS ¼
A
ðð
1
x dA ¼
A
ðAÞ
ð2
ð3
ð3
x dy dx ¼ 0
ð2
)
x¼2 y¼mx
x dy dx ¼ 0
x¼2 y¼mx
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
Das Doppelintegral muss also verschwinden (da A > 0 und somit A 6¼ 0). Wir berechnen das Doppelintegral in
der bekannten Weise (der Wert wird noch vom Parameter m abhängen) und erhalten schließlich eine Bestimmungsgleichung für den noch unbekannten Parameter m.
Innere Integration (nach der Variablen y)
ð2
ð2
1 d y ¼ x ½ y y ¼ m x ¼ x ð2 m xÞ ¼ 2 x m x 2
2
x dy ¼ x
y¼mx
y¼mx
ußere Integration (nach der Variablen x)
ð3
ð2 x m x Þ d x ¼
2
1
x
mx3
3
3
¼ 9 9m 4
2
x¼2
2
8
8
35
m ¼ 5 9m
m ¼ 5
m
3
3
3
Somit gilt:
ð3
ð2
x dy dx ¼ 5
x¼2 y¼mx
35
m ¼ 0
3
)
35
m ¼ 5
3
)
m ¼ 5
3
5 3
3
¼
¼
35
7
5 7
Lösung: m ¼ 3=7
b) Es ist m ¼ 3=7 und somit x S ¼ 0. Für die Berechnung der Schwerpunktordinate y S benötigen wir noch den
Flächeninhalt der Trapezfläche.
Berechnung des Flächeninhaltes A
ð2
ð3
ðð
1 dA ¼
A ¼
1 dy dx
x¼2
ðAÞ
y¼3 x
7
Innere Integration (nach der Variablen y)
ð2
1 dy ¼
½ y
y¼3 x
7
2
y¼3 x
7
¼ 2
3
x
7
ußere Integration (nach der Variablen x)
ð3
2
A ¼
x¼2
3
x
7
dx ¼
2x
3 2
x
14
3
¼ 6
2
27
12
15
140 15
125
þ4þ
¼ 10
¼
¼
14
14
14
14
14
1 Doppelintegrale
299
Berechnung der Schwerpunktkoordinaten yS
1
yS ¼
A
ðð
1
y dA ¼
125=14
ðAÞ
ð2
ð3
x¼2
14
y dy dx ¼
125
y¼3 x
7
ð2
ð3
y dy dx
x¼2
y¼3 x
7
Innere Integration (nach der Variablen y)
ð2
y dy ¼
1 2
y
2
2
y¼3 x
7
y¼3 x
7
1
¼
2
½y
2 2
y¼3 x
7
1
¼
2
9 2
4
x
49
ußere Integration (nach der Variablen x)
14
yS ¼
125
ð3
x¼2
1
2
9 2
7
3 3 3
7
81
24
dx ¼
¼
4
x
4x
x
12
þ8
¼
49
125
49
125
49
49
2
7
105
7
7 15
7
15
7
140 15
7
125
20
¼
20
20
¼
¼
¼
¼ 1
¼
125
49
125
125
7
125
7
7 7
125
7
Schwerpunkt: S ¼ ð0; 1Þ
1 2
Bestimmen Sie Flächeninhalt A und Flächenschwerpunkt S der von den Kurven y ¼
x und
4
8
eingeschlossenen Fläche.
y ¼
x2 þ 4
F12
Wir berechnen zunächst die benötigten Kurvenschnittpunkte:
1 2
8
x ¼
4
x2 þ 4
x 2 ðx 2 þ 4Þ ¼ x 4 þ 4 x 2 ¼ 32
)
)
x 4 þ 4 x 2 32 ¼ 0
Diese biquadratische Gleichung wird durch die Substitution u ¼ x 2 in eine quadratische Gleichung übergeführt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u 2 þ 4 u 32 ¼ 0 ) u 1=2 ¼ 2 4 þ 32 ¼ 2 6 ) u 1 ¼ 4 ; u 2 ¼ 8
Rücksubstitution (u 2 ¼ 8 scheidet als negativer Wert aus):
x2 ¼ u1 ¼ 4
)
x 1=2 ¼ 2
Bild F-10 zeigt das von beiden Kurven eingeschlossene Flächenstück (spiegelsymmetrisch zur y-Achse), aus dem wir
die folgenden Integrationsgrenzen entnehmen (Beschränkung auf den 1. Quadranten ) Faktor 2 in den Integralen):
1 2
8
x bis y ¼
2
4
x þ4
y-Integration :
von y ¼
x-Integration :
von x ¼ 0 bis x ¼ 2
y
2
Berechnung des Flächeninhaltes A
ðð
A ¼
ð2
y= 1x2
4
–2
y ¼ x 2 =4
(Flächenelement d A ¼ d y d xÞ
–1
Bild F-10
Innere Integration (nach der Variablen y)
8=ðx 2 þ 4Þ
1 dy ¼
y ¼ x 2 =4
A/2
1 dy dx
x¼0
ð
1
8
x2+4
ð
dA ¼ 2
ðAÞ
A/2
8=ðx 2 þ 4Þ
y=
8=ðx 2 þ 4Þ
½ y y¼x
2 =4
¼
x2
8
1 2
1
1 2
x ¼ 8
x
2
4
4
x þ4
þ4
1
2
x
300
F Mehrfachintegrale
ußere Integration (nach der Variablen x)
ð2
1
1 2
x
4
x2 þ 4
|fflfflfflffl{zfflfflfflffl}
8
A ¼ 2
x¼0
1
dx ¼ 2 8
arctan
2
x
2
1 3
x
12
2
¼
0
Integral 29 mit a ¼ 2
¼ 2 4 arctan
x
2
1 3
x
12
2
2
¼ 2 4 arctan 1
4 arctan 0 þ 0 ¼ 2 p
¼ 4,9499
3
3
|fflfflffl{zfflfflffl}
|fflfflffl{zfflfflffl}
0
p=4
0
2
Berechnung der Schwerpunktkoordinaten xS und yS
xS ¼ 0
yS ¼
(wegen der Spiegelsymmetrie der Fläche zur y-Achse)
1
A
ðð
y dA ¼
1
2
4,9499
ðAÞ
8=ðx 2 þ 4Þ
ð
ð2
8=ðx 2 þ 4Þ
ð
ð2
y d y d x ¼ 0,4040
x¼0
y dy dx
x¼0
y ¼ x 2 =4
y ¼ x 2 =4
Innere Integration (nach der Variablen y)
8=ðx 2 þ 4Þ
ð
y dy ¼
1 2
y
2
8=ðx 2 þ 4Þ
y ¼ x 2 =4
y ¼ x 2 =4
1
¼
2
½
8=ðx 2 þ 4Þ
y 2 y ¼ x 2 =4
1
¼
2
64
1 4
x
2
16
2
ðx þ 4Þ
!
ußere Integration (nach der Variablen x)
1
y S ¼ 0,4040
2
ð2
x¼0
64
1 4
x
2
16
ðx 2 þ 4Þ
!
ð2
1
d x ¼ 0,2020
x¼0
1 4
x
64
2
16
ðx 2 þ 4Þ
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
!
dx ¼
Integral 30 mit a ¼ 2
"
¼ 0,2020
64
1
þ
arctan
28
2 4 ðx 2 þ 4Þ
x
8x
¼ 0,2020
þ 4 arctan
2
x þ4
¼ 0,2020
x
2
1 5
x
80
x
2
!
1 1 5
x
16 5
#2
¼
0
2
¼
0
32
2
2 þ 4 arctan 1
0 4 arctan 0 þ 0 ¼ 0,2020 2 þ p
¼ 0,9578
80
5
|fflfflffl{zfflfflffl}
|fflfflffl{zfflfflffl}
p=4
0
Schwerpunkt: S ¼ ð0; 0,9578Þ
Berechnen Sie den Flächeninhalt A und den Schwerpunkt S
y
des in Bild F-11 skizzierten (grau unterlegten) Kreissegments.
5
3
F13
?
Bild F-11
Kreissegment
y=3
5
?
x
1 Doppelintegrale
301
Wir berechnen zunächst die Schnittpunkte des Kreises x 2 þ y 2 ¼ 25 mit der Geraden y ¼ 3 (Parallele zur x-Achse):
x 2 þ y 2 ¼ x 2 þ 3 2 ¼ x 2 þ 9 ¼ 25
)
x 2 ¼ 16
)
x 1=2 ¼ 4
Schnittpunkte: (4; 3) und ( 4; 3)
Wegen der Spiegelsymmetrie des Flächenstücks zur y-Achse beschränken wir uns bei den Integrationen auf den
1. Quadranten ( ) Faktor 2 vor den Integralen). Die Integrationsgrenzen sind somit:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y-Integration : von y ¼ 3 bis y ¼ 25 x 2
von x ¼ 0 bis x ¼ 4
x-Integration :
Berechnung des Flächeninhaltes A
pffiffiffiffiffiffiffiffiffiffiffi
25 x 2
ð
ð4
ðð
dA ¼ 2
1 dy dx
A ¼
ðAÞ
ðFlächenelement d A ¼ d y d xÞ
y¼3
x¼0
Innere Integration (nach der Variablen y)
pffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
25ð x 2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
25 x 2
1 d y ¼ ½ y y¼3
¼ 25 x 2 3
y¼3
ußere Integration (nach der Variablen x)
ð4
ð
A ¼ 2
x¼0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
25 x 2 3Þ d x ¼ 2
2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
25 x 2 þ 25 arcsin
x
5
4
¼
3x
0
Integral 141 mit a ¼ 5
3
2
1
7
61
¼ 2 4 ð4 3 þ 25 arcsin 0,8 Þ 12 ð0 þ 25 arcsin 0Þ 0 5 ¼ 2 ð6 þ 11,5913 12Þ ¼ 11,1826
2
2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
0,9273 (Bogenmaß)
0
Berechnung des Flächenschwerpunktes S = (xS ; yS)
xS ¼ 0
yS ¼
1
A
(wegen der Spiegelsymmetrie der Fläche zur y-Achse)
ðð
y dA ¼
1
2
11,1826
ðAÞ
ð4
ð4
pffiffiffiffiffiffiffiffiffiffiffi
25 x 2
ð
y d y d x ¼ 0,1788
x¼0
Innere Integration (nach der Variablen y)
pffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
25 x 2
25 x 2
ð
1 2
1
y dy ¼
¼
y
2
2
y¼3
y¼3
pffiffiffiffiffiffiffiffiffiffiffi
25 x 2
ð
y¼3
x¼0
pffiffiffiffiffiffiffiffiffiffiffi
25 x 2
½ y2 y¼3
y dy dx
¼
y¼3
1
1
ð25 x 2 9Þ ¼
ð16 x 2 Þ
2
2
ußere Integration (nach der Variablen x)
y S ¼ 0,1788
1
2
ð4
x¼0
1 3 4
64
x
0 þ 0 ¼ 3,8144
ð16 x 2 Þ d x ¼ 0,0894 16 x
¼ 0,0894 64
3
3
0
Schwerpunkt: S ¼ ð0; 3,8144Þ
302
F Mehrfachintegrale
F14
Wie groß sind die Flächenträgheitsmomente (Flächenmomente) I x , I y und I p einer Fläche, die durch
die Parabel y ¼ 4 x 2 und die x-Achse begrenzt wird?
Nullstellen der Parabel: y ¼ 0
4 x2 ¼ 0
)
)
x2 ¼ 4
)
x 1=2 ¼ 2
Die Integrationsgrenzen entnehmen wir aus Bild F-12:
y-Integration :
von y ¼ 0 bis y ¼ 4 x 2
y
x-Integration :
von x ¼ 2 bis x ¼ 2
4
Berechnung des Flächenträgheitsmomentes I x
3
Unter Beachtung der Spiegelsymmetrie gilt ðd A ¼ d y d xÞ:
2
ðð
Ix ¼
ð2
4
ðx 2
1
y dA ¼ 2
2
2
y dy dx
–2
x¼0 y¼0
ðAÞ
y=4–x2
–1
1
2
x
Bild F-12
Innere Integration (nach der Variablen y)
4
ðx 2
y dy ¼
2
y¼0
1 3
y
3
4x2
¼
y¼0
1
3
4x2
½ y3 y¼0
¼
1
1
½ ð4 x 2 Þ 3 0 ¼
ð64 48 x 2 þ 12 x 4 x 6 Þ
3
3
(Binomische Formel: ða bÞ 3 ¼ a 3 3 a 2 b þ 3 a b 2 b 3 mit a ¼ 4, b ¼ x 2 )
ußere Integration (nach der Variablen x)
1
Ix ¼ 2
3
2
¼
3
ð2
2
ð64 48 x þ 12 x x Þ d x ¼
3
2
x¼0
4
6
12 5
1 7
64 x 16 x þ
x
x
5
7
2
¼
3
0
384
128
2 384
128
2 2048
128 128 þ
0000 ¼
¼
¼ 39,01
5
7
3
5
7
3
35
Berechnung des Flächenträgheitsmomentes I y
ðð
Iy ¼
ð2
4
ðx 2
x dA ¼ 2
2
x2 d y d x
x¼0 y¼0
ðAÞ
Innere Integration (nach der Variablen y)
4
ðx 2
4
ðx 2
x2 d y ¼ x2
y¼0
4x2
1 d y ¼ x 2 ½ y y ¼ 0 ¼ x 2 ð4 x 2 0Þ ¼ 4 x 2 x 4
y¼0
ußere Integration (nach der Variablen x)
ð2
Iy ¼ 2
ð4 x x Þ d x ¼ 2
2
x¼0
4
4 3
1 5
x
x
3
5
Berechnung des Flächenträgheitsmomentes I p
I p ¼ I x þ I y ¼ 39,01 þ 8,53 ¼ 47,54
2
32
32
160 96
128
¼2
00 ¼ 2
¼
¼ 8,53
3
5
15
15
0
1 Doppelintegrale
303
Welchen Wert besitzt das axiale Flächenmoment I y
y
der in Bild F-13 skizzierten Fläche (grau unterlegt)?
1
y = cos x
y = 0,5
F15
0,5
Bild F-13
–π/2
?
?
π/2
x
Wir berechnen zunächst die für die Integration benötigten Schnittstellen der beiden Randkurven:
cos x ¼ 0,5
)
x ¼ arccos 0,5 ¼ p =3
ð1. Schnittstelle im Intervall x > 0Þ
Wegen der Spiegelsymmetrie zur y-Achse liegen die beiden Schnittpunkte bei x 1=2 ¼ p=3. Die Integrationsgrenzen
entnehmen wir Bild F-13:
y-Integration :
von y ¼ 0,5 bis y ¼ cos x
x-Integration :
von x ¼ p=3 bis x ¼ p=3
Unter Beachtung der Spiegelsymmetrie zur y-Achse gilt dann (Flächenelement d A ¼ d y d x):
ðð
ð
p=3
Iy ¼
cos
ðx
x dA ¼
ð
p=3
2
x ¼ p=3 y ¼ 0,5
ðAÞ
cos
ðx
x dy dx ¼ 2
2
x2 d y d x
x ¼ 0 y ¼ 0,5
Innere Integration (nach der Variablen y)
cos
ðx
cos
ðx
x dy ¼ x
2
2
y ¼ 0,5
1 d y ¼ x 2 ½ y y ¼ 0,5 ¼ x 2 ðcos x 0,5Þ ¼ x 2 cos x 0,5 x 2
cos x
y ¼ 0,5
ußere Integration (nach der Variablen x)
ð
p=3
Iy ¼ 2
x¼0
1 3 p=3
ðx 2 cos x 0,5 x 2Þ d x ¼ 2 2 x cos x þ ðx 2 2Þ sin x
¼
x
6
0
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
Integral 233 mit a ¼ 1
¼ 2
2
p cos
3
p
3
2
p
þ
2 sin
9
p
3
1 p3
000
6 27
¼
¼ 2 ð1,0472 0,7823 0,1914Þ ¼ 0,147
Flächenmoment:
I y ¼ 0;147
Bild F-14 zeigt den halbkreisförmigen „Boden“ eines
Zylinders, dessen „Deckel“ oberhalb der x; y-Ebene
F16
liegt und Teil der Fläche z ¼ x y ist (z-Achse senkrecht
y
1
zur Papierebene nach oben gerichtet). Berechnen Sie das
1
Zylindervolumen V mit Hilfe eines Doppelintegrals.
Bild F-14
1
2
x
304
F Mehrfachintegrale
Wir bestimmen zunächst die Gleichung des skizzierten Halbkreises (Mittelpunkt M ¼ ð1; 0Þ, Radius R ¼ 1):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx 1Þ 2 þ y 2 ¼ 1 ) y 2 ¼ 1 ðx 1Þ 2 ) y ¼ þ 1 ðx 1Þ 2
Integrationsbereich in kartesischen Koordinaten (aus Bild F-14 entnommen):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y-Integration : von y ¼ 0 bis y ¼ 1 ðx 1Þ 2
von x ¼ 0 bis x ¼ 2
x-Integration :
Das Doppelintegral für das Volumen V lautet damit (Flächenelement d A ¼ d y d x):
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðð
ðð
V ¼
z dA ¼
ðAÞ
1 ðx 1Þ 2
ð
ð2
xy dA ¼
xy dy dx
x¼0
ðAÞ
y¼0
Die Berechnung erfolgt durch zwei nacheinander durchzuführende gewöhnliche Integrationen.
Innere Integration (nach der Variablen y)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 ðx 1Þ 2
1 ðx 1Þ 2
ð
ð
xy dy ¼ x
y¼0
y dy ¼ x
y¼0
¼
1 2
y
2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 ðx 1Þ 2
¼ x
y¼0
1
2
1 ðx 1Þ 2
0
¼
1
1
1
1
x 1 ðx 1Þ 2 ¼
x ð1 x 2 þ 2 x 1Þ ¼
x ð2 x x 2 Þ ¼
ð2 x 2 x 3 Þ
2
2
2
2
ußere Integration (nach der Variablen x)
1
V ¼
2
ð2
x¼0
1
ð2 x 2 x 3 Þ d x ¼
2
2 3
1 4
x
x
3
4
0
1
1 @ 16
1 4
2
4 0 0A ¼
¼
¼
2
3
2
3
3
0
|fflfflfflffl{zfflfflfflffl}
4/3
2
Volumen: V ¼ 2=3
1.2 Doppelintegrale in Polarkoordinaten
Lehrbuch: Band 2, Kapitel III.3.1.2.2 und 3.1.3
Formelsammlung: Kapitel IX.3.1.3 und 3.1.4
ðð
I ¼
F17
y
ð1 þ x þ yÞ d A ¼ ?
ðAÞ
Integrationsbereich ðAÞ:
Einheitskreis nach Bild F-15
1
Bild F-15
x
1 Doppelintegrale
305
Unter Verwendung von Polarkoordinaten transformiert sich der Integrand wie folgt (Transformationsgleichungen:
x ¼ r cos j und y ¼ r sin j):
z ¼ f ðx; yÞ ¼ 1 þ x þ y ¼ 1 þ r cos j þ r sin j
Das Flächenelement d A lautet in Polarkoordinaten d A ¼ r d r d j, die Integrationsgrenzen sind (siehe Bild F-15):
r-Integration :
von r ¼ 0 bis r ¼ 1
j-Integration :
von j ¼ 0 bis j ¼ 2 p
Damit gilt:
ðð
I ¼
2ðp
ð1
ð1 þ x þ yÞ d A ¼
ð1 þ r cos j þ r sin jÞ r d r d j ¼
j¼0 r¼0
ðAÞ
2ðp
ð1
¼
ðr þ r 2 cos j þ r 2 sin jÞ d r d j
j¼0 r¼0
Wir integrieren zunächst nach r, dann nach j.
Innere Integration (nach der Variablen r)
ð1
ðr þ r 2 cos j þ r 2 sin jÞ d r ¼
r¼0
¼
1 2
1 3
1 3
r þ
r cos j þ
r sin j
2
3
3
1
¼
r¼0
1
1
1
1
1
1
þ
cos j þ
sin j 0 0 0 ¼
þ
cos j þ
sin j
2
3
3
2
3
3
ußere Integration (nach der Variablen j)
2ðp
I ¼
j¼0
¼ p þ
2 p
1
1
1
1
1
1
þ
cos j þ
sin j d j ¼
jþ
sin j
cos j
¼
2
3
3
2
3
3
0
1
1
1
1
1
1
sin ð2 pÞ
cos ð2 pÞ 0
sin 0 þ
cos 0 ¼ p
þ
¼ p
3 |fflfflfflfflffl{zfflfflfflfflffl}
3 |fflfflfflfflffl{zfflfflfflfflffl}
3 |ffl{zffl}
3 |ffl{zffl}
3
3
0
1
0
1
Ergebnis: I ¼ p
ðð
I ¼
ð3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 þ y 2 þ 4Þ d A ¼ ?
y
ðAÞ
3
F18
Integrationsbereich ðAÞ:
Kreisring nach Bild F-16
1
Bild F-16
x
306
F Mehrfachintegrale
Die Transformationsgleichungen für den bergang von kartesischen Koordinaten zu Polarkoordinaten lauten:
x ¼ r cos j ;
y ¼ r sin j ;
dA ¼ r dr dj
Die Integrationsgrenzen des kreisringförmigen Integrationsbereiches sind (siehe Bild F-16):
r-Integration:
von r ¼ 1 bis r ¼ 3
j-Integration:
von j ¼ 0 bis j ¼ 2 p
Unter Berücksichtigung von
x 2 þ y 2 ¼ r 2 cos 2 j þ r 2 sin 2 j ¼ r 2 ðcos 2 j þ sin 2 jÞ ¼ r 2
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
transformiert sich der Integrand des Doppelintegrals wie folgt:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
z ¼ f ðx; yÞ ¼ 3 x 2 þ y 2 þ 4 ¼ 3 r 2 þ 4 ¼ 3 r þ 4
Das Doppelintegral I lautet damit in Polarkoordinaten:
ðð
I ¼
2ðp
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
ð3 x þ y þ 4Þ d A ¼
ð3
2ðp
ð3 r þ 4Þ r d r d j ¼
j¼0 r¼1
ðAÞ
ð3
ð3 r 2 þ 4 rÞ d r d j
j¼0 r¼1
Die Auswertung erfolgt in der üblichen Weise (erst nach r, dann nach j integrieren).
Innere Integration (nach der Variablen r)
ð3
ð3 r 2 þ 4 rÞ d r ¼ ½ r 3 þ 2 r 2 r ¼ 1 ¼ 27 þ 18 1 2 ¼ 42
3
r¼1
ußere Integration (nach der Variablen j)
2ðp
2ðp
I ¼
42 d j ¼ 42
j¼0
1 d j ¼ 42 ½ j 0
2p
¼ 42 ð2 p 0Þ ¼ 84 p
0
Ergebnis: I ¼ 84 p
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
2ðp
ð3
I ¼
1dj
j¼0
2p
3
3 r 2 þ 4 r d r ¼ ½ j 0 ½ r 3 þ 2 r 2 1 ¼ ð2 p 0Þ ð27 þ 18 1 2Þ ¼ 84 p
r¼1
Eine kreisförmig gebogene Leiterschleife vom Radius R wird senkrecht von einem Magnetfeld durchflutet, dessen magnetische Flussdichte B nach der Gleichung
F19
B ðrÞ ¼
B0
1 þ r2
;
r 0
ðB 0 > 0 : KonstanteÞ
in radialer Richtung nach außen abnimmt. Bestimmen Sie den magnetischen Fluss F ¼
durch die Leiterschleife.
ðð
B dA
ðAÞ
1 Doppelintegrale
307
Wir verwenden wegen der Kreissymmetrie Polarkoordinaten.
Aus Bild F-17 entnehmen wir die Integrationsgrenzen:
r-Integration:
von r ¼ 0 bis r ¼ R
j-Integration:
von j ¼ 0 bis j ¼ 2 p
y
Leiterschleife
R
Bild F-17
x
Damit gilt (Flächenelement d A ¼ r d r d j):
ðR
2ðp
ðð
B d A ¼ B0
F ¼
j¼0 r¼0
ðAÞ
1
r d r d j ¼ B0
1 þ r2
2ðp
ðR
j¼0 r¼0
r
dr dj
1 þ r2
Wir integrieren zunächst in radialer Richtung, dann in der Winkelrichtung:
Innere Integration (nach der Variablen r)
ðR
r¼0
r
dr ¼
1 þ r2
1
ln ð1 þ r 2 Þ
2
R
¼
r¼0
1
1
1
ln ð1 þ R 2 Þ
ln 1 ¼
ln ð1 þ R 2 Þ
2
2 |{z}
2
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 32 mit a ¼ 1
ußere Integration (nach der Variablen j)
1
F ¼ B0
ln ð1 þ R 2 Þ
2
¼
2ðp
1 dj ¼
j¼0
2p
1
B 0 ln ð1 þ R 2 Þ ½ j 0 ¼
2
1
B 0 ½ ln ð1 þ R 2 Þ ð2 p 0Þ ¼ B 0 p ln ð1 þ R 2 Þ
2
Magnetischer Fluss durch die Schleife: F ¼ B 0 p ln ð1 þ R 2 Þ
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
2ðp
F ¼ B0
ðR
1dj
j¼0
r¼0
¼ B 0 ð2 p 0Þ
1
2
r
d r ¼ B0
1 þ r2
½ ln
½ j 0
2p
1
ln 1 þ r 2
2
R
¼
0
1
1 þ R 2 ln 1 ¼ B 0 2 p
ln 1 þ R 2 Þ ¼ B 0 p ln 1 þ R 2 Þ
|{z}
2
0
Der in Bild F-18 skizzierte elektrische Leiter besitzt einen kreisringförmigen Querschnitt mit dem
Innenradius a und dem Außenradius 2 a. Er wird in seiner Längsrichtung von einem Strom mit der
Stromdichte
S ðrÞ ¼ S 0
F20
e r
;
r
y
a r 2a
durchflossen ðS 0 > 0 : KonstanteÞ. Berechnen Sie
die Stromstärke I durch das Doppelintegral
2a
ðð
S ðrÞ d A
I ¼
ðAÞ
Leiterquerschnitt
a
x
Bild F-18
308
F Mehrfachintegrale
Wir verwenden Polarkoordinaten. Der Integrationsbereich (Kreisring nach Bild F-18), wird dabei durch die Ungleichungen a r 2 a und 0 j 2 p beschrieben. Damit erhalten wir für die Stromstärke I das folgende
Doppelintegral (Flächenelement d A ¼ r d r d j):
2ðp
ðð
2ða
S ðrÞ d A ¼ S 0
I ¼
j¼0 r¼a
ðAÞ
e r
r dr dj ¼ S0
r
2ða
2ðp
e r d r d j
j¼0 r¼a
Wir integrieren zunächst nach r, dann nach j:
Innere Integration (nach der Variablen r)
2ða
e r d r ¼ ½ e r r¼a ¼ e2a þ e a ¼ e a e 2a
2a
r¼a
ußere Integration (nach der Variablen j)
I ¼ S 0 ðe
a
e
2a
2ðp
Þ
1 d j ¼ S 0 ðe a e 2 a Þ ½ j 0
2p
¼ S 0 ðe a e 2 a Þ ð2 p 0Þ ¼
j¼0
¼ 2 p S 0 ðe a e 2 a Þ
Stromstärke: I ¼ 2 p S 0 ðe a e 2 a Þ
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
2ðp
I ¼ S0
2ða
1dj
e r d r ¼ S 0 ½ j 0 ½ e r a ¼ S 0 ð2 p 0Þ e 2 a þ e a ¼
2p
2a
r¼a
j¼0
¼ 2 p S 0 e a e 2 a
Die Randkurve der in Bild F-19 skizzierten Fläche
y
r = 2 (cos f + sin f)
wird durch die Gleichung
2
r ¼ 2 ðcos j þ sin jÞ , 0 j p=2
F21
beschrieben (r; j: Polarkoordinaten).
1
A
Wie groß ist der Flächeninhalt A?
Bild F-19
1
Wir verwenden Polarkoordinaten. Die Integrationsgrenzen lauten dann:
r-Integration:
r ¼ 0 bis r ¼ 2 ðcos j þ sin jÞ
j-Integration:
j ¼ 0 bis j ¼ p=2
Doppelintegral für den Flächeninhalt A
p=2 2 ðcos j þ sin jÞ
ðð
A ¼
ð
ð
dA ¼
ðAÞ
r dr dj
j¼0
r¼0
ðFlächenelement d A ¼ r d r d jÞ :
2
x
1 Doppelintegrale
309
Innere Integration (nach der Variablen r)
2 ðcos j þ sin jÞ
ð
r dr ¼
r¼0
1 2
r
2
2 ðcos j þ sin jÞ
¼
r¼0
1
4 ðcos j þ sin jÞ 2 0 ¼ 2 ðcos j þ sin jÞ 2 ¼
2
¼ 2 ðcos 2 j þ 2 sin j cos j þ sin 2 jÞ ¼ 2 ½ ðcos 2 j þ sin 2 jÞ þ 2 sin j cos j ¼
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
1
sin ð2 jÞ
¼ 2 ð1 þ sin ð2 jÞÞ
(unter Verwendung der trigonometrischen Beziehungen cos 2 j þ sin 2 j ¼ 1 und sin ð2 jÞ ¼ 2 sin j cos j)
ußere Integration (nach der Variablen j)
ð
p=2
A ¼ 2
j¼0
¼ 2
cos ð2 jÞ p=2
p
cos p
cos 0
ð1 þ sin ð2 jÞÞ d j ¼ 2 j
¼ 2
0þ
¼
2
2
2
2
|fflfflfflfflffl{zfflfflfflfflffl}
0
|ffl{zffl}
|ffl{zffl}
Integral 204 mit a ¼ 2
p
1
1
þ
þ
2
2
2
¼ 2
p
þ1
2
1=2
1=2
¼ p þ2
Flächeninhalt: A ¼ p þ 2 ¼ 5,1416
F22
Berechnen Sie den Flächeninhalt A des im 1. Quadranten gelegenen Flächenstücks, das durch die
Kurve r ¼ 1 þ sin 2 j und den Einheitskreis berandet wird (r; j: Polarkoordinaten).
Es handelt sich um das in Bild F-20 skizzierte Flächenstück.
Randkurven
y
Untere Berandung: r ¼ 1 (Einheitskreis)
A
Der Integrationsbereich lautet in Polarkoordinaten:
r-Integration:
von r ¼ 1 bis 1 þ sin 2 j
j-Integration:
von j ¼ 0 bis p=2
1
r=1
Bild F-20
1
Doppelintegral für den Flächeninhalt A
p=2 1 þ sin 2 j
ðð
A ¼
ð
ð
j¼0
r¼1
dA ¼
ðAÞ
r dr dj
ðFlächenelement d A ¼ r d r d jÞ
Innere Integration (nach der Variablen r)
2
1 þ sin
ð j
r dr ¼
r¼1
¼
1 2
r
2
1 þ sin 2 j
¼
r¼1
r = 1 + sin 2 f
2
Obere Berandung: r ¼ 1 þ sin 2 j
1
2
1 þ sin 2 j
½ r2 r¼1
¼
1
½ ð1 þ sin 2 jÞ 2 1 ¼
2
1
1
ð1 þ 2 sin 2 j þ sin 4 j 1Þ ¼
ð2 sin 2 j þ sin 4 jÞ
2
2
x
310
F Mehrfachintegrale
ußere Integration (nach der Variablen j)
1
A ¼
2
1
¼
2
1
¼
2
p=2
ð
ð2 sin 2 j þ sin 4 jÞ d j ¼
"
" Integral 207 mit n ¼ 4 ; a ¼ 1 und nochmals Integral 205 mit a ¼ 1
Integral 205 mit a ¼ 1
j¼0
p=2
j
sin ð2 jÞ
sin 3 j cos j
3
j
sin ð2 jÞ
2
þ
¼
2
4
4
4
2
4
0
1
1
3
3
j
sin ð2 jÞ
sin 3 j cos j þ
j
sin ð2 jÞ
2
4
8
16
p=2
¼
0
p=2
3
1
3
1
3
jþ
j
þ
sin ð2 jÞ
sin j cos j
¼
8
2
16
4
0
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
ð11=8Þ j
11=16
p=2
1 11
11
1
¼
¼
j
sin ð2 jÞ
sin 3 j cos j
2
8
16
4
0
1
¼
2
11
11
1
11
1
3
3
p
sin p
sin ðp=2Þ cos ðp=2Þ 0 þ
sin 0 þ
sin 0 cos 0 ¼
16
16 |ffl{zffl}
4 |fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflfflfflffl{zfflfflfflfflffl}
16 |{z}
4 |fflffl{zfflffl} |ffl{zffl}
0
1
0
0
0
1
1 11
11
1
11
1
1 11
11
¼
p
0
100þ
0þ 01 ¼
p ¼
p
2 16
16
4
16
4
2 16
32
1
¼
2
Flächeninhalt: A ¼
11
p ¼ 1,0799
32
1,08
Bestimmen Sie den Flächenschwerpunkt S des
in Bild F-21 skizzierten Kreisringausschnitts:
F23
Innenradius:
r1 ¼ 2
Außenradius:
r2 ¼ 6
Winkelbereich:
0 j p
y
6
2
Bild F-21
–6
–2
2
Der Integrationsbereich für die Berechnung des Flächenschwerpunktes S ¼ ðx S ; y S Þ lautet:
r-Integration:
von r ¼ 2 bis r ¼ 6
j-Integration:
von j ¼ 0 bis j ¼ p
Der benötigte Flächeninhalt A lässt sich elementar berechnen (als Differenz zweier Halbkreisflächen):
A ¼
1
1
1
ðp r 22 p r 12 Þ ¼
p ðr 22 r 21 Þ ¼
p ð36 4Þ ¼ 16 p ¼ 50,2655
2
2
2
6
x
1 Doppelintegrale
311
Wegen der Spiegelsymmetrie der Fläche zur y-Achse liegt der Schwerpunkt auf der y-Achse. Somit ist x S ¼ 0. Die
Ordinate y S berechnen wir mit dem folgenden Doppelintegral:
1
yS ¼
A
ðð
1
y dA ¼
16 p
ðAÞ
ð6
ðp
j¼0 r¼2
1
r sin j r d r d j ¼
16 p
ð6
ðp
r 2 sin j d r d j
j¼0 r¼2
(Transformationsgleichungen: y ¼ r sin j , Flächenelement d A ¼ r d r d j)
Innere Integration (nach der Variablen r)
ð6
ð6
r 2 sin j d r ¼ sin j
r¼2
r 2 d r ¼ sin j
r¼2
1 3
r
3
6
¼
r¼2
1
208
sin j ð216 8Þ ¼
sin j
3
3
ußere Integration (nach der Variablen j)
1
208
yS ¼
16 p
3
ðp
sin j d j ¼
j¼0
p
208
13 16
13
26
ð cos p þ cos 0 Þ ¼
½ cos j 0 ¼
ð1 þ 1Þ ¼
16 3 p
3
p
3
p
16 3 p
|ffl{zffl} |ffl{zffl}
1
1
Schwerpunkt: S ¼ ð0; 26=3 pÞ ¼ ð0; 2,7587Þ
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
1
yS ¼
16 p
¼
ðp
ð6
sin j d j
j¼0
r2 d r ¼
r¼2
p
1
½ cos j 0
16 p
1 3
r
3
6
¼
2
1
1
1
1
2 13 16
26
ð cos p þ cos 0Þ
ð216 8Þ ¼
2
208 ¼
¼
16 p
3
16 p
3
3p
16 3 p
Gegeben ist die Kurve r ¼ e 0;2 j ; 0 j p=2 (dargestellt in Polarkoordinaten).
F24
a) Welche Fläche A bildet die Kurve mit der positiven x- und y-Achse?
b) Welchen Wert muss die Steigung der Geraden y ¼ m x haben, damit diese die unter a) genannte
Fläche halbiert?
a) Der Verlauf der Kurve ist in Bild F-22 dargestellt. Für
die Berechnung des Flächeninhaltes A benötigen wir
noch die Integrationsgrenzen (in Polarkoordinaten ausgedrückt). Sie lauten:
r-Integration:
von r ¼ 0 bis r ¼ e 0;2 j
j-Integration:
von j ¼ 0 bis j ¼ p=2
Berechnung des Flächeninhaltes A
p=2 e 0;2 j
ðð
ð
ð
dA ¼
A ¼
ðAÞ
r dr dj
j¼0 r¼0
(Flächenelement d A ¼ r d r d jÞ
Bild F-22
312
F Mehrfachintegrale
Innere Integration (nach der Variablen r)
e 0;2 j
ð
1 2
r
2
r dr ¼
r¼0
e 0;2 j
1
1
ðe 0;2 j Þ 2 0 ¼
e 0;4 j
2
2
¼
r¼0
ðRechenregel : ðe a Þ n ¼ e n a Þ
ußere Integration (nach der Variablen j)
ð
p=2
1
A ¼
2
1
2
e 0;4 j d j ¼
j¼0
e 0;4 j
0;4
p=2
¼
0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
p=2
1
½ e 0;4 j 0 ¼ 1;25 ðe 0;2 p e 0 Þ ¼ 1;0931
2 0;4
|{z}
1
Integral 312 mit a ¼ 0,4
Flächeninhalt: A ¼ 1;0931
b) Ansatz für die gesuchte Gerade, die das Flächenstück vom Flächeninhalt A ¼ 1;0931 halbiert (in Polarkoordinaten): j ¼ const: ¼ a (siehe Bild F-22, dunkelgrau unterlegte Fläche). Das Doppelintegral für diese Fläche A*
lautet dann:
ðð
A* ¼
ða
e 0;2 j
ð
dA ¼
1
A
2
r dr dj ¼
j¼0 r¼0
ðA*Þ
(nderung gegenüber der Gesamtfläche A: Die Integration im Winkelbereich läuft jetzt von j ¼ 0 bis j ¼ a).
Die Auswertung erfolgt wie im Teil a):
Innere Integration (nach der Variablen r)
e 0;2 j
ð
1 2
r
2
r dr ¼
r¼0
e 0;2 j
¼
r¼0
1
e 0;4 j
2
ðsiehe aÞÞ
ußere Integration (nach der Variablen j)
1
A* ¼
2
ða
e
0;4 j
j¼0
1
dj ¼
2
e 0;4 j
0;4
a
¼
0
a
1
½ e 0;4 j 0 ¼ 1;25 ðe 0;4 a e 0 Þ ¼ 1;25 ðe 0;4 a 1Þ
2 0;4
Der Steigungswinkel a der gesuchten Geraden wird aus der Bedingung
1
A* ¼
A
2
)
1;25 ðe 0;4 a 1Þ ¼
1
1;0931
2
wie folgt berechnet:
e 0;4 a 1 ¼
1;0931
¼ 0;43724
2 1;25
)
e 0;4 a ¼ 1;43724
Beide Seiten werden logarithmiert (Rechenregel: ln e n ¼ n):
ln e 0;4 a ¼ ln 1;43724
)
0;4 a ln e ¼ 0;3627
|{z}
1
) 0;4 a ¼ 0;3627
)
a ¼ 0;9068
ðBogenmaßÞ
Dieser Wert entspricht im Gradmaß einem Winkel von rund 51;96 .
Ergebnis: Der Strahl unter dem Winkel von 51;96 teilt die Ausgangsfläche A in zwei gleiche Teile. Die Gleichung der Geraden lautet in kartesischen Koordinaten wie folgt:
y ¼ m x ¼ ðtan aÞ x ¼ ðtan 51;96 Þ x ¼ 1;2781 x
1 Doppelintegrale
313
r ¼ 1 þ sin j ; 0 j p
Welchen Flächeninhalt A begrenzt die in Polarkoordinaten dargestellte Kurve mit der x-Achse?
F25
Die zur y-Achse spiegelsymmetrische Kurve ist in Bild F-23 dargestellt.
y
Integrationsbereich (aus Bild F-23 entnommen):
r-Integration:
von r ¼ 0 bis r ¼ 1 þ sin j
j-Integration:
von j ¼ 0 bis j ¼ p
2
r = 1 + sin f
1
A
Berechnung des Flächeninhaltes A (Flächenelement d A ¼ r d r d j)
ðð
ðp
A ¼
1 þ sin j
ð
dA ¼
j¼0
ðAÞ
–1
r dr dj
1
x
Bild F-23
r¼0
Innere Integration (nach der Variablen r)
1 þ sin j
ð
r dr ¼
r¼0
1 2
r
2
1 þ sin j
¼
r¼0
1
1
1
ð1 þ sin jÞ 2 0 ¼
ð1 þ sin jÞ 2 ¼
ð1 þ 2 sin j þ sin 2 jÞ
2
2
2
ußere Integration (nach der Variablen j)
1
A ¼
2
¼
1
2
j¼0
ð1 þ 2 sin j þ sin 2 jÞ d j ¼
|fflffl{zfflffl}
Integral 205 mit a ¼ 1
j 2 cos j þ
j
sin ð2 jÞ
2
4
p
¼
0
1
2
3
1
j 2 cos j
sin ð2 jÞ
2
4
3
1
1
p 2 cos p
sin ð2 pÞ 0 þ 2 cos 0 þ
sin 0
2
4
4 |ffl{zffl}
|ffl{zffl}
|fflfflfflffl{zfflfflfflffl}
|ffl{zffl}
1
0
1
0
1
3
1
3
3
¼
p þ2þ2 ¼
p þ4 ¼
p þ 2 ¼ 4,3562
2
2
2
2
4
¼
1
2
ðp
Flächeninhalt: A ¼
F26
r ¼
p
¼
0
¼
3
p þ 2 ¼ 4,3562
4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 cos j ; 0 j 2 p
Berechnen Sie die von dieser Kurve eingeschlossene Fläche A (r und j sind Polarkoordinaten).
Bild F-24 zeigt den Verlauf der geschlossenen und zur x-Achse symmetrischen Kurve. Wir beschränken uns daher bei
der Integration auf das oberhalb der x-Achse gelegene Flächenstück (Faktor 2 vor dem Doppelintegral):
314
F Mehrfachintegrale
Integrationsbereich:
r-Integration:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
von r ¼ 0 bis r ¼
2 cos j
j-Integration:
von j ¼ 0 bis j ¼ p
y
r = 2 – cos f
1
A
Bild F-24
Doppelintegral für den Flächeninhalt A
ðð
A ¼
ðp
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 cos j
ð
j¼0
r¼0
dA ¼ 2
ðAÞ
–1
x
1
–1
r dr dj
ðFlächenelement d A ¼ r d r d jÞ
Innere Integration (nach der Variablen r)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 cos j
2 cos j
ð
1 2
1
1
r
ð2 cos jÞ 0 ¼
ð2 cos jÞ
r dr ¼
¼
2
2
2
r¼0
r¼0
ußere Integration (nach der Variablen j)
1
A ¼ 2
2
ðp
j¼0
ð2 cos jÞ d j ¼ ½ 2 j sin j 0 ¼ 2 p sin p 0 þ sin 0 ¼ 2 p
|ffl{zffl}
|ffl{zffl}
0
0
p
Flächeninhalt: A ¼ 2 p ¼ 6,2832
y
Berechnen Sie das axiale Flächenträgheitsmoment I x der
in Bild F-25 dargestellten Kreissektorfläche bezüglich der
R
Symmetrieachse. Welches Ergebnis erhält man für einen
a
a
Vollkreis?
F27
r=R
x
Bild F-25
R
Die Integrationsgrenzen lauten (bei Beschränkung auf den 1. Quadrant wegen der Spiegelsymmetrie zur x-Achse):
r-Integration:
von r ¼ 0 bis r ¼ R
j-Integration:
von j ¼ 0 bis j ¼ a
Doppelintegral für das Flächenträgheitsmoment I x
ðð
Ix ¼
ðR
ða
ða
y dA ¼ 2
ðr sin jÞ r d r d j ¼ 2
j¼0 r¼0
ðAÞ
ðR
2
2
r 3 sin 2 j d r d j
j¼0 r¼0
(Transformationsgleichungen: y ¼ r sin j , Flächenelement d A ¼ r d r d j)
Innere Integration (nach der Variablen r)
ðR
r sin j d r ¼ sin j
r¼0
ðR
3
2
r 3 d r ¼ sin 2 j
2
r¼0
1 4
r
4
R
¼ sin 2 j
r¼0
1 4
1 4
R 0 ¼
R sin 2 j
4
4
1 Doppelintegrale
315
ußere Integration (nach der Variablen j)
ða
1 4
Ix ¼ 2
R
4
1 4
sin j d j ¼
R
2
2
j¼0
j
sin ð2 jÞ
2
4
a
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1 4
¼
R
2
0
a
sin ð2 aÞ
sin 0
0þ
2
4
4
|{z}
¼
0
Integral 205 mit a ¼ 1
1 4
R
¼
2
a
sin ð2 aÞ
1 4 2 a sin ð2 aÞ
1 4
¼
R
¼
R ð2 a sin ð2 aÞÞ
2
4
2
4
8
1 4
R ð2 a sin ð2 aÞÞ
8
1 4
1 4
p 4
R ð2 p sin ð2 pÞÞ ¼
R ð2 p 0Þ ¼
R
Sonderfall: 2 a = 2 p (Vollkreis): I x ¼
8
8
4
Flächenträgheitsmoment I x des Kreissektors: I x ¼
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
ða
Ix ¼ 2
sin j d j
j¼0
¼ 2
ðR
r3 d r ¼ 2
2
r¼0
j
sin ð2 jÞ
2
4
a
1 4 R
¼
r
4
0
0
a
sin ð2 aÞ
1 4
a
sin ð2 aÞ
1 4
1 4
0þ0
R 0 ¼ 2
R ¼
R ð2 a sin ð2 aÞÞ
2
4
4
2
4
4
8
Der kreisförmige „Boden“ eines zylindrischen Körpers liegt in der x; y-Ebene und wird durch die
1
Ungleichung x 2 þ y 2 1 beschrieben. Der „Deckel“ ist Teil der Fläche z ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi .
4 x2 y2
Berechnen Sie (mittels Doppelintegral) das Zylindervolumen V.
F28
Die Fläche ist rotationssymmetrisch zur z-Achse, der „Boden‘‘ des Zylinders kreisförmig. Wir verwenden daher zweckmäßigerweise Polarkoordinaten.
Integrationsbereich (Bild F-26):
0 r 1;
y
0 j 2p
1
Gleichung der Rotationsfläche in Polarkoordinaten
(x ¼ r cos j, y ¼ r sin j ) x 2 þ y 2 ¼ r 2 ):
x
1
1
1
z ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 x2 y2
4 ðx 2 þ y 2 Þ
4 r2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
r2
Bild F-26
Doppelintegral für das Volumen V (in Polarkoordinaten)
2ðp
ðð
ð1
z dA ¼
V ¼
ðAÞ
j¼0 r¼0
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi r d r d j ¼
4 r2
ðFlächenelement d A ¼ r d r d jÞ
2ðp
ð1
j¼0 r¼0
r
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d r d j
4 r2
316
F Mehrfachintegrale
Innere Integration (nach der Variablen r)
ð1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 1
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
r
2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d r ¼ ½ 4 r r ¼ 0 ¼ 3 þ 4 ¼ 3 þ 2 ¼ 2 3
4 r2
r¼0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 149 mit a ¼ 2
ußere Integration (nach der Variablen j)
2ðp
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
2p
3 Þ d j ¼ ð2 3 Þ ½ j 0 ¼ ð2 3 Þ ð2 p 0Þ ¼ 2 ð2 3 Þ p
ð2
V ¼
j¼0
Volumen: V ¼ 2 ð2
pffiffiffi
3 Þ p ¼ 1,6836
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
2ðp
ð1
1dj
V ¼
j¼0
r¼0
h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi i 1
pffiffiffi
pffiffiffi
2p
r
2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d r ¼ ½ j 0 4 r 0 ¼ ð2 p 0Þ ð 3 þ 2Þ ¼ 2 ð2 3 Þ p
4 r2
Die in Polarkoordinaten definierte Kurve r ¼ 2
F29
pffiffiffiffi
j , 0 j p bildet mit der x-Achse ein
Flächenstück, dessen Flächeninhalt A und Flächenträgheitsmoment I p bestimmt werden sollen.
Bild F-27 zeigt den Verlauf der Kurve im Intervall 0 j p. Für die Berechnung von Flächeninhalt A und
Flächenträgheitsmoment I p benötigen wir noch die Integrationsgrenzen. Sie lauten:
pffiffiffiffi
r-Integration: r ¼ 0 bis r ¼ 2 j
y
j-Integration:
j ¼ 0 bis j ¼ p
3
r=2 f
Berechnung des Flächeninhaltes A
pffiffiffi
2 j
ð
ðð
ðp
A ¼
dA ¼
r dr dj
ðAÞ
j¼0 r¼0
Innere Integration (nach der Variablen r)
pffiffiffi
2 j
pffiffiffi
ð
1 2 2 j
r
r dr ¼
¼ 2j 0 ¼ 2j
2
r¼0
r¼0
ußere Integration (nach der Variablen j)
A ¼
A
– 3,54 – 3
(Flächenelement d A ¼ r d r d j)
ðp
2
2 j d j ¼ ½ j2 0 ¼ p2 0 ¼ p2
p
j¼0
Flächeninhalt: A ¼ p 2 ¼ 9,8697
9,87
Bild F-27
–2
–1
1
1
x
1 Doppelintegrale
317
Berechnung des polaren Flächenträgheitsmomentes I p
pffiffiffi
2 j
ð
ðð
ðp
Ip ¼
r2 d A ¼
r3 d r d j
j¼0 r¼0
ðAÞ
ðFlächenelement d A ¼ r d r d jÞ
Innere Integration (nach der Variablen r)
pffiffiffi
2 j
pffiffiffi
ð
1 4 2 j
3
r dr ¼
¼ 4 j2 0 ¼ 4 j2
r
4
r¼0
r¼0
ußere Integration (nach der Variablen j)
ðp
Ip ¼ 4
j dj ¼ 4
2
j¼0
Flächenträgheitsmoment: I p ¼
F30
1 3
j
3
p
¼ 4
0
4 3
p ¼ 41,3417
3
1 3
4 3
p 0 ¼
p
3
3
41,34
Wie groß ist das polare Flächenträgheitsmoment I p einer Fläche, die von der in Polarkoordinaten dargepffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
stellten Kurve r ¼
1 þ sin j , 0 j p und der x-Achse berandet wird?
Das Flächenstück liegt spiegelsymmetrisch zur y-Achse (Bild F-28):
Integrationsbereich (in Polarkoordinaten)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ sin j
r-Integration:
von r ¼ 0 bis r ¼
j-Integration:
von j ¼ 0 bis j ¼ p
Doppelintegral für das polare Flächenträgheitsmoment I p
ðð
Ip ¼
ðp
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ sin j
ð
r dA ¼
2
ðAÞ
Bild F-28
r3 d r d j
j¼0
r¼0
ðFlächenelement d A ¼ r d r d jÞ
Innere Integration (nach der Variablen r)
pffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
1 þ sin j
pffiffiffiffiffiffiffiffiffiffiffiffi
ð
1 þ sin j
1 4
1
1
3
r dr ¼
¼
r
ð1 þ sin jÞ 2 0 ¼
ð1 þ 2 sin j þ sin 2 jÞ
4
4
4
r¼0
r¼0
318
F Mehrfachintegrale
ußere Integration (nach der Variablen j)
1
Ip ¼
4
"
1
¼
4
¼
1
4
ðp
1
ð1 þ 2 sin j þ sin j Þ d j ¼
4
|fflffl{zfflffl}
2
j¼0
1
4
j
sin ð2 jÞ
j 2 cos j þ
2
4
p
¼
0
Integral 205 mit a ¼ 1
j
jþ
2
|fflfflfflffl{zfflfflfflffl}
!
1
2 cos j
sin ð2 jÞ
4
#p
¼
1
4
3
1
j 2 cos j
sin ð2 jÞ
2
4
0
3
j
2
p
¼
0
3
1
1
p 2 cos p
sin ð2 pÞ 0 þ 2 cos 0 þ
sin 0 ¼
2
4 |fflfflfflffl{zfflfflfflffl}
4 |ffl{zffl}
|ffl{zffl}
|ffl{zffl}
1
¼
0
1
0
3
1
3
3
p þ2þ2 ¼
p þ4 ¼
p þ 1 ¼ 2,1781
2
4
2
8
Polares Flächenträgheitsmoment: I p ¼
3
p þ 1 ¼ 2,1781
8
2,18
Welches polare Flächenträgheitsmoment I p liefert die von der Kurve
p=6 j p=6 umschlossene Fläche (Bild F-29)?
r ¼ 2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cos ð3 jÞ ;
y
r = 2 cos (3 f)
0,5
F31
0,25
Bild F-29
0,5
1
1,5
2
x
– 0,25
– 0,5
Integrationsbereich (wir beschränken uns wegen der Spiegelsymmetrie zur x-Achse auf den 1. Quadranten):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r-Integration: von r ¼ 0 bis r ¼ 2
cos ð3 jÞ
j-Integration:
von j ¼ 0 bis j ¼ p=6
Doppelintegral für das polare Flächenträgheitsmoment I p
pffiffiffiffiffiffiffiffiffiffiffiffiffi
p=6 2
cos ð3 jÞ
ð
ðð
ð
2
Ip ¼
r dA ¼ 2
r3 d r d j
ðFlächenelement d A ¼ r d r d jÞ
ðAÞ
j¼0
r¼0
Innere Integration (nach der Variablen r)
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
2 cos ð3 jÞ
2 cos ð3 jÞ
ð
1
1
r4
16 cos 2 ð3 jÞ 0 ¼ 4 cos 2 ð3 jÞ
r3 d r ¼
¼
4
4
r¼0
r¼0
1 Doppelintegrale
319
ußere Integration (nach der Variablen j)
ð
p=6
Ip ¼ 2 4
cos ð3 jÞ d j ¼ 8
2
j¼0
j
sin ð6 jÞ
þ
2
12
p=6
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
p
sin p
sin 0
þ
0
¼ 8
12
12
12
|ffl{zffl}
|{z}
0
Integral 229 mit a ¼ 3
Polares Flächenträgheitsmoment: I p ¼
2
p ¼ 2,0944
3
¼ 8
p
2
p
¼
12
3
0
2,09
Oberhalb des in Polarkoordinaten dargestellten Kreises r ¼ 2 sin j , 0 j p der x; y-Ebene
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
liegt die Fläche z ¼ x 2 þ y 2 . Berechnen Sie das Volumen V des „Zylinders“, der von diesen
F32
Flächen unten und oben begrenzt wird (die Mantellinien des Zylinders verlaufen parallel zur z-Achse).
Der „Boden‘‘ entspricht der in Bild F-30 dargestellten Kreisfläche
(Integrationsbereich). Die Integrationsgrenzen sind:
r-Integration:
von r ¼ 0 bis r ¼ 2 sin j
j-Integration:
von j ¼ 0 bis j ¼ p
y
r = 2 · sin f
2
1
1
Die Fläche („Deckel‘‘ des Zylinders) besitzt in Polarkoordinaten die
Bild F-30
folgende Gleichung (Transformationsgleichungen: x ¼ r cos j ;
y ¼ r sin jÞ:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
z ¼ x 2 þ y 2 ¼ r 2 cos 2 j þ r 2 sin 2 j ¼ r 2 ðcos 2 j þ sin 2 jÞ ¼ r 2 ¼ r
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
x
(unter Verwendung des „trigonometrischen Pythagoras“ sin 2 j þ cos 2 j ¼ 1Þ
Doppelintegral für das Volumen V in Polarkoordinaten
ðp
ðð
V ¼
2 sin
ð j
z dA ¼
2 sin
ð j
r r dr dj ¼
j¼0
ðAÞ
ðp
r2 d r d j
j¼0
r¼0
ðFlächenelement d A ¼ r d r d jÞ
r¼0
Innere Integration (nach der Variablen r)
2 sin
ð j
r2 d r ¼
r¼0
1 3
r
3
2 sin j
¼
r¼0
8
8
sin 3 j 0 ¼
sin 3 j
3
3
ußere Integration (nach der Variablen j)
V ¼
8
3
ðp
sin 3 j d j ¼
j¼0
8
3
cos j þ
cos 3 j
3
p
¼
0
8
3
cos p þ
cos 3 p
cos 3 0
þ cos 0
3
3
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Integral 206 mit a ¼ 1
8
¼
3
1
1
8
2
8 62
8 4
32
1
þ1
¼
2
¼
¼
¼
3
3
3
3
3
3
3 3
9
Volumen: V ¼ 32=9 ¼ 3,5556
3,56
¼
320
F Mehrfachintegrale
Bild F-31 zeigt den in der x; y-Ebene gelegenen kreisförmi-
y
gen „Boden“ eines Zylinders, dessen „Deckel“ Teil der Fläche z ¼ e x
F33
2
þy2
ist. Die Mantellinien des Zylinders verlau-
1
Bild F-31
fen parallel zur z-Achse (senkrecht zur Papierebene nach
x
oben orientiert).
Wie groß ist das Zylindervolumen V ?
Lösen Sie das Integral mittels Substitution.
Wir verwenden Polarkoordinaten (wegen der Kreis- bzw. Rotationssymmetrie). Der kreisförmige „Boden‘‘ liefert den
Integrationsbereich (siehe Bild F-31): 0 r 1 ; 0 j 2 p . Die Rotationsfläche bildet den „Deckel‘‘ des
zylindrischen Körpers, ihre Gleichung in Polarkoordinaten erhalten wir wie folgt (Transformationsgleichungen:
x ¼ r cos j ; y ¼ r sin jÞ :
x 2 þ y 2 ¼ r 2 cos 2 j þ r 2 sin 2 j ¼ r 2 ðcos 2 j þ sin 2 jÞ ¼ r 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
)
z ¼ ex
2
þ y2
¼ er
2
(unter Verwendung des „trigonometrischen Pythagroas“ sin 2 j þ cos 2 j ¼ 1Þ. Damit gilt für das gesuchte Volumen:
ðð
ð1
2ðp
V ¼
z dA ¼
2
er r dr dj
ðFlächenelement d A ¼ r d r d jÞ
j¼0 r¼0
ðAÞ
Innere Integration (nach der Variablen r)
Wir lösen das innere Integral mit Hilfe der folgenden Substitution:
du
¼ 2r;
dr
u ¼ r2 ;
ð1
e
r2
ð1
r dr ¼
r¼0
dr ¼
du
;
2r
Grenzen
du
1
¼
e r
2r
2
)
u ¼ 0
oben : r ¼ 1
)
u ¼ 1
ð1
eu du ¼
u
u¼0
unten : r ¼ 0
u¼0
1
2
½ e u u¼0
1
¼
1
1
ðe 1 e 0 Þ ¼
ðe 1Þ
2
2
ußere Integration (nach der Variablen j)
1
ðe 1Þ
V ¼
2
2ðp
1 dj ¼
j¼0
Volumen: V ¼ ðe 1Þ p ¼ 5,3981
2p
1
1
1
ðe 1Þ ½ j 0 ¼
ðe 1Þ ð2 p 0Þ ¼
ðe 1Þ 2 p ¼ ðe 1Þ p
2
2
2
5,40
Hinweis: Das Doppelintegral lässt sich auch als Produkt zweier gewöhnlicher Integrale darstellen:
ð1
2ðp
V ¼
1dj
j¼0
r¼0
r er d r ¼ ½ j 0
2
2p
1
2
er
2
1
¼ ð2 p 0Þ
0
1
e 1 e 0 ¼ ðe 1Þ p
2
2 Dreifachintegrale
321
2 Dreifachintegrale
In diesem Abschnitt finden Sie (fast) ausschließlich anwendungsorientierte Aufgaben zu folgenden Themen:
Volumen und Masse homogener „zylindrischer“ Körper
Schwerpunkt eines homogenen Körpers
Massenträgheitsmoment eines homogenen Körpers
Verwendet werden sowohl kartesische Koordinaten (Abschnitt 2.1) als auch Zylinderkoordinaten (Abschnitt 2.2).
2.1 Dreifachintegrale in kartesischen Koordinaten
Lehrbuch: Band 2, Kapitel III.3.2.2.1 und 3.2.3
Formelsammlung: Kapitel IX.3.2.2 und 3.2.5
F34
ð
ðp
p=2
ð1
I ¼
cos ðx þ yÞ e 3 z d z d y d x ¼ ?
x¼0 y¼0 z¼0
Dieses Dreifachintegral wird durch drei nacheinander auszuführende gewöhnliche Integrationen gelöst. Wir integrieren
in der vorgegebenen Reihenfolge z, y und x (wegen der konstanten Integrationsgrenzen darf hier sogar in beliebiger
Reihenfolge integriert werden).
1. Integrationsschritt (Integration nach z)
ð1
ð1
cos ðx þ yÞ e 3 z d z ¼ cos ðx þ yÞ
z¼0
e 3 z d z ¼ cos ðx þ yÞ
z¼0
e 3z
3
1
¼
z¼0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
Integral 312 mit a ¼ 3
1
3
¼ cos ðx þ yÞ
½ e 3z z¼0
1
¼ cos ðx þ yÞ
1
1
ðe 3 e 0 Þ ¼
ðe 3 1Þ cos ðx þ yÞ
3
3
2. Integrationsschritt (Integration nach y)
Dieser Integrationsschritt gelingt mit der folgenden Substitution:
u ¼ x þ y;
du
¼ 1;
dy
ð
dy ¼ du;
y¼0
)
oben : y ¼ p=2
u ¼ x
)
u ¼ x þ p=2
x þ p=2
p=2
1
ðe 3 1Þ
3
unten : y ¼ 0
Grenzen
1 3
ðe 1Þ
cos ðx þ yÞ d y ¼
3
¼
ð
cos u d u ¼
u¼x
x þ p=2
1
ðe 3 1Þ ½ sin u u ¼ x ¼
3
1
1
ðe 3 1Þ ½ sin ðx þ p=2Þ sin x ¼
ðe 3 1Þ ðcos x sin xÞ
3
3
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
cos x
b p=2 gedreht ergibt den Kosinuszeiger)
(sin ðx þ p=2Þ ¼ cos x : Sinuszeiger im Uhrzeigersinn um 90 ¼
322
F Mehrfachintegrale
3. Integrationsschritt (Integration nach x)
1
ðe 3 1Þ
I ¼
3
¼
ðp
ðcos x sin xÞ d x ¼
x¼0
p
1
ðe 3 1Þ ½ sin x þ cos x 0 ¼
3
1
1
2
ðe 3 1Þ ðsin p þ cos p sin 0 cos 0 Þ ¼
ðe 3 1Þ ð 2Þ ¼
ð1 e 3 Þ
3
3
3
|ffl{zffl} |fflffl{zfflffl} |ffl{zffl} |ffl{zffl}
0
1
0
1
Ergebnis: I ¼
2
ð1 e 3 Þ ¼ 12,7237
3
Welches Volumen V hat ein Zylinder mit
der in Bild F-32 skizzierten „Bodenfläche“,
der oberhalb der x, y-Ebene durch die Ebene z ¼ 5 x y begrenzt wird?
F35
y
2
y=2–x2
(z-Achse: senkrecht zur Papierebene nach
oben gerichtet)
1
y=1
Bild F-32
–1
1
x
Der „Boden‘‘ des Zylinders (grau unterlegte Fläche im Bild) ist Teil der x, y-Ebene z ¼ 0, der „Deckel‘‘ Teil der
Ebene z ¼ 5 x y. Der Integrationsbereich in der x, y-Ebene wird unten durch die Gerade y ¼ 1 und oben durch
die Parabel y ¼ 2 x 2 berandet, wobei sich die x-Werte zwischen x ¼ 1 und x ¼ 1 bewegen (Schnittstellen der
beiden Kurven, berechnet aus der Gleichung 2 x 2 ¼ 1). Damit ergeben sich folgende Integrationsgrenzen:
z-Integration:
von z ¼ 0 bis z ¼ 5 x y
y-Integration:
von y ¼ 1 bis y ¼ 2 x 2
x-Integration:
von x ¼ 1 bis x ¼ 1
Das Volumenintegral lautet dann:
ððð
V ¼
2
ðx 2 5 ðx y
ð1
dV ¼
ðVÞ
1 dz dy dx
x¼1 y¼1
ðVolumenelement d V ¼ d z d y d xÞ
z¼0
Wir integrieren also in der Reihenfolge z, y und x.
1. Integrationsschritt (Integration nach z)
5xy
ð
5xy
1 d z ¼ ½ z z¼0
¼ 5x y0 ¼ 5x y
z¼0
2. Integrationsschritt (Integration nach y)
2
ðx 2
ð5 x yÞ d y ¼
y¼1
5y xy
1 2
y
2
2x2
¼
y¼1
¼ 5 ð2 x 2 Þ x ð2 x 2 Þ
1
1
ð2 x 2 Þ 2 5 þ x þ
¼
2
2
2 Dreifachintegrale
323
¼ 10 5 x 2 2 x þ x 3
1
1
ð4 4 x 2 þ x 4 Þ 5 þ x þ
¼
2
2
¼ 10 5 x 2 2 x þ x 3 2 þ 2 x 2
¼
1 4
1
x 5þx þ
¼
2
2
1 4
7
x þ x3 3x2 x þ
2
2
3. Integrationsschritt (Integration nach x)
ð1
V ¼
x¼1
1
1 4
7
1 5
1 4
1 2
7
x þ x3 3x2 x þ
dx ¼
x þ
x x3
x þ
x
¼
2
2
10
4
2
2
1
1
1
1
7
1
1
1
7
2
1
24
¼
þ
1
þ
1þ
þ
1þ31þ4 ¼
þ5 ¼
10
4
2
2
10
4
2
2
10
5
5
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
3
4
¼
Volumen: V ¼ 24=5 ¼ 4,8
Die Projektion eines „zylindrischen“ Körpers in die
y
x; y-Ebene führt auf den in Bild F-33 skizzierten
3
Bereich. Der „Boden“ des Zylinders liegt in der
F36
Ebene z ¼ 1, der „Deckel“ ist Teil der Fläche
2
z ¼ x þ y þ 2.
2
1
Bestimmen Sie das Zylindervolumen V.
Bild F-33
1
2
x
Der trapezförmige „Boden‘‘ liegt in der zur x, y-Ebene parallelen Ebene z ¼ 1, der „Deckel‘‘ ist Teil der Fläche
z ¼ x 2 þ y þ 2 . Der Integrationsbereich in der x, y-Ebene (siehe Bild F-33) wird in der y-Richtung von der x-Achse
y ¼ 0 (unten) und der Geraden y ¼ x þ 1 (oben) begrenzt, seitlich durch die y-Achse x ¼ 0 und die dazu Parallele x ¼ 2 . Damit ergeben sich folgende Integrationsgrenzen für das Volumenintegral:
z-Integration:
von z ¼ 1 bis z ¼ x 2 þ y þ 2
y-Integration:
von y ¼ 0 bis y ¼ x þ 1
x-Integration:
von x ¼ 0 bis x ¼ 2
Das Volumenintegral lautet damit:
ð2
ððð
2
xð
þ 1 x þðy þ 2
dV ¼
V ¼
ðVÞ
1 dz dy dx
x¼0 y¼0
ðVolumenelement d V ¼ d z d y d xÞ
z¼1
Die Integration wird in der bekannten Weise schrittweise von innen nach außen durchgeführt:
1. Integrationsschritt (Integration nach z)
x2 þyþ2
ð
z¼1
x2 þyþ2
1 d z ¼ ½ z z¼1
¼ x2 þ y þ 2 1 ¼ x2 þ y þ 1
324
F Mehrfachintegrale
2. Integrationsschritt (Integration nach y)
xð
þ1
ðx 2 þ y þ 1Þ d y ¼
x2 y þ
y¼0
1 2
y þy
2
¼ x3 þ x2 þ
xþ1
¼ x 2 ðx þ 1Þ þ
y¼0
1
ðx þ 1Þ 2 þ x þ 1 0 0 0 ¼
2
1 2
1
3 2
3
x þx þ
þ x þ 1 ¼ x3 þ
x þ 2x þ
2
2
2
2
3. Integrationsschritt (Integration nach x)
2
ð2
3 2
3
1 4
1 3
3
3
2
dx ¼
x þ
V ¼
x þ 2x þ
x þ
x þx þ
x ¼
2
2
4
2
2
0
x¼0
¼ 4 þ 4 þ 4 þ 3 0 0 0 0 ¼ 15
Volumen: V ¼ 15
Die Ebene x þ y þ z ¼ 6 bzw. z ¼ 6 x y bildet mit den drei Koordinatenebenen eine gleich-
F37
seitige Pyramide. Bestimmen Sie das Volumen V und den Schwerpunkt S dieser Pyramide.
Der „Boden‘‘ der in Bild F-34 skizzierten Pyramide ist Teil der x, y-Ebene z ¼ 0 , der „Deckel‘‘ liegt in der Ebene
z ¼ 6 x y . Die Bodenfläche (grau unterlegt) wird in der y-Richtung durch die x-Achse y ¼ 0 und die Gerade
y ¼ 6 x begrenzt. Diese Gerade ist die Schnittlinie der Ebene z ¼ 6 x y mit der x, y-Ebene z ¼ 0 (siehe
Bild F-35):
z ¼ 6x y ¼ 0
)
y ¼ 6x
z
y
6
„Deckel“
z=6–x–y
6
y = –x + 6
„Boden (A )“
y
6
„Boden (A )“
6
Bild F-34
Bild F-35
6
x
x
Die x -Werte bewegen sich dabei zwischen x ¼ 0 und x ¼ 6 (Bild F-35). Damit liegen die Integrationsgrenzen für
die Dreifachintegrale eindeutig fest:
z-Integration:
von z ¼ 0 bis z ¼ 6 x y
y-Integration:
von y ¼ 0 bis y ¼ 6 x
x-Integration:
von x ¼ 0 bis x ¼ 6
Berechnung des Volumens V
ððð
V ¼
ð6
6ð
x 6 ðx y
dV ¼
ðVÞ
1 dz dy dx
x¼0 y¼0
z¼0
ðVolumenelement d V ¼ d z d y d xÞ
2 Dreifachintegrale
325
1. Integrationsschritt (Integration nach z)
6 ðx y
6xy
1 d z ¼ ½ z z¼0
¼ 6x y0 ¼ 6x y
z¼0
2. Integrationsschritt (Integration nach y)
6ð
x
1 2 6x
1
y
ð6 xÞ 2 0 þ 0 þ 0 ¼
ð6 x yÞ d y ¼ 6 y x y
¼ 6 ð6 xÞ x ð6 xÞ
2
2
y¼0
y¼0
¼ 36 6 x 6 x þ x 2 18 þ 6 x
1 2
1 2
x ¼
x 6 x þ 18
2
2
3. Integrationsschritt (Integration nach x)
6
ð6
1 2
1 3
x 6 x þ 18 d x ¼
x 3 x 2 þ 18 x ¼ 36 108 þ 108 0 0 0 ¼ 36
V ¼
2
6
0
x¼0
Volumen: V ¼ 36
Berechnung des Schwerpunktes S = ( xS ; yS ; zS )
Da die Pyramide gleichseitig ist, gilt x S ¼ y S ¼ z S . Wir berechnen x S mit dem folgenden Dreifachintegral:
1
xS ¼
V
ððð
1
x dV ¼
36
ðVÞ
ð6
6ð
x 6 ðx y
x dz dy dx
x¼0 y¼0
ðVolumenelement d V ¼ d z d y d xÞ
z¼0
1. Integrationsschritt (Integration nach z)
6 ðx y
6 ðx y
6xy
x dz ¼ x
1 d z ¼ x ½ z z¼0
¼ x ½6 x y 0 ¼ 6 x x2 x y
z¼0
z¼0
2. Integrationsschritt (Integration nach y)
6ð
x
6x
1
x y2
ð6 x x 2 x yÞ d y ¼ 6 x y x 2 y
¼
2
y¼0
y¼0
1
x ð6 xÞ 2 0 0 0 ¼
2
1 3
1 3
x ¼
x 6 x 2 þ 18 x
¼ 36 x 6 x 2 6 x 2 þ x 3 18 x þ 6 x 2
2
2
3. Integrationsschritt (Integration nach x)
6
ð6
1
1 3
1
1 4
xS ¼
x 6 x 2 þ 18 x d x ¼
x 2x3 þ 9x2 ¼
36
2
36 8
0
¼ 6 x ð6 xÞ x 2 ð6 xÞ
x¼0
¼
1
1
3
ð162 432 þ 324 0 0 0Þ ¼
54 ¼
¼ 1,5
36
36
2
Schwerpunkt: S ¼ ð1,5; 1,5; 1,5Þ
F38
Der „Boden“ eines Zylinders besitzt die in Bild F-36
dargestellte dreieckige Form, der „Deckel“ ist Teil
der Fläche z ¼ x 2 y. Berechnen Sie das Volumen V
des zylindrischen Körpers.
y
2
(z-Achse: senkrecht zur Papierebene nach oben gerichtet)
Bild F-36
–2
x
326
F Mehrfachintegrale
Der „zylindrische‘‘ Körper wird oben durch die Fläche z ¼ x 2 y („Deckel‘‘) und unten durch die in der x, y-Ebene
z ¼ 0 liegende Dreiecksfläche („Boden‘‘) begrenzt. Den Integrationsbereich in der x, y-Ebene entnehmen wir Bild F-36:
Die untere Berandung ist die x-Achse ( y ¼ 0), die obere Randkurve die Gerade y ¼ x þ 2 , die x-Werte bewegen
sich dabei zwischen x ¼ 2 und x ¼ 0 . Damit ergeben sich die folgenden Integrationsgrenzen für das Volumenintegral:
z-Integration:
von z ¼ 0 bis z ¼ x 2 y
y-Integration:
von y ¼ 0 bis y ¼ x þ 2
x-Integration:
von x ¼ 2 bis x ¼ 0
Das Volumenintegral lautet dann:
ð0
ððð
2
xð
þ 2 xð y
dV ¼
V ¼
ðVolumenelement d V ¼ d z d y d xÞ
1 dz dy dx
x¼2 y¼0 z¼0
ðVÞ
Wir berechnen dieses Dreifachintegral schrittweise wie folgt (Integrationsreihenfolge: z ! y ! x):
1. Integrationsschritt (Integration nach z)
x2 y
ð
x2 y
1 d z ¼ ½ z z¼0 ¼ x2 y 0 ¼ x2 y
z¼0
2. Integrationsschritt (Integration nach y)
xð
þ2
xð
þ2
x y dy ¼ x
2
y d y ¼ x2
2
y¼0
y¼0
¼
1 2
y
2
xþ2
¼ x2
y¼0
1
ðx þ 2Þ 2 0
2
¼
1 2
x ðx þ 2Þ 2 ¼
2
1 2 2
1
x ðx þ 4 x þ 4Þ ¼
ðx 4 þ 4 x 3 þ 4 x 2 Þ
2
2
3. Integrationsschritt (Integration nach x)
1
V ¼
2
1
¼
2
ð0
1
ðx þ 4 x þ 4 x Þ d x ¼
2
4
x¼2
3
2
1 5
4 3
x þ x4 þ
x
5
3
0
¼
2
32
32
1 96 240 þ 160
1 16
8
0þ0þ0þ
16 þ
¼
¼
¼
5
3
2
53
2 15
15
Volumen: V ¼ 8=15 ¼ 0,5333
Berechnen Sie das Massenträgheitsmoment J des
z
in Bild F-37 skizzierten keilförmigen Körpers aus
2
einem homogenen Material mit der Dichte r ¼ 3 .
„Deckelfläche“
z=2–y
Bezugsachse ist die z-Achse.
F39
Bild F-37
2
y
2
2
2
2
x
„Bodenfläche“
2 Dreifachintegrale
327
Der quadratische „Boden‘‘ ist Teil der x, y-Ebene z ¼ 0, die obere Begrenzung („Deckel‘‘) Teil der Ebene
z ¼ 2 y. Der Integrationsbereich in der x, y-Ebene („Bodenfläche‘‘ des Keils) ist das achsenparallele Quadrat
0 x 2 , 0 y 2 (Bild F-38). Damit haben wir folgende Integrationsgrenzen:
z-Integration:
von z ¼ 0 bis z ¼ 2 y
y-Integration:
von y ¼ 0 bis y ¼ 2
x-Integration:
von x ¼ 0 bis x ¼ 2
y
y=2
2
„Boden“
Das Dreifachintegral für das Massenträgheitsmoment J z des keilförmigen Körpers
bezüglich der z-Achse lautet damit (Volumenelement d V ¼ d z d y d x ):
ððð
Jz ¼ r
ð2
ð2
y=0
2y
ð
ðx 2 þ y 2 Þ d V ¼ 3
ðx 2 þ y 2 Þ d z d y d x
Bild F-38
x¼0 y¼0 z¼0
ðVÞ
1. Integrationsschritt (Integration nach z)
2ð
y
2ð
y
ðx þ y Þ d z ¼ ðx þ y Þ
2
2
2
2
z¼0
2y
1 d z ¼ ðx 2 þ y 2 Þ ½ z z ¼ 0 ¼ ðx 2 þ y 2 Þ ½ 2 y 0 ¼
z¼0
¼ ðx 2 þ y 2 Þ ð2 yÞ ¼ 2 x 2 x 2 y þ 2 y 2 y 3
2. Integrationsschritt (Integration nach y)
ð2
ð2 x 2 x 2 y þ 2 y 2 y 3 Þ d y ¼
2x2 y
y¼0
1 2 2
2 3
1 4
x y þ
y
y
2
3
4
¼ 4x2 2x2 þ
2
¼
y¼0
16
4
4 0 0 0 0 ¼ 2x2 þ
3
3
3. Integrationsschritt (Integration nach x)
ð2
Jz ¼ 3
4
2x þ
3
2
x¼0
dx ¼ 3
2 3
4
x þ
x
3
3
2
¼ 3
0
16
8
þ
00
3
3
Massenträgheitsmoment: J z ¼ 24
2.2 Dreifachintegrale in Zylinderkoordinaten
Lehrbuch: Band 2, Kapitel III.3.2.2.2 und 3.2.3
Formelsammlung: Kapitel IX.3.2.3 und 3.2.5
F40
2ðp
ð1
rð2
I ¼
r z sin j d z d r d j ¼ ?
j¼p r¼0 z¼r
¼ 3
24
¼ 24
3
2
x
328
F Mehrfachintegrale
Wir integrieren in der vorgegebenen Reihenfolge (z ! r ! j):
1. Integrationsschritt (Integration nach z)
rð2
rð2
r z sin j d z ¼ r sin j
z¼r
z d z ¼ r sin j
z¼r
¼
1 2
z
2
r2
¼
z¼r
r2
1
r sin j ½ z 2 z ¼ r ¼
2
1
1
r sin j ðr 4 r 2 Þ ¼
sin j ðr 5 r 3 Þ
2
2
2. Integrationsschritt (Integration nach r)
1
sin j
2
ð1
1
ðr r Þ d r ¼
sin j
2
5
r¼0
3
1
sin j
¼
2
1 6
1 4
r
r
6
4
1
1
6
4
|fflfflfflffl{zfflfflfflffl}
1=12
1
1
¼
sin j
2
r¼0
1
¼
sin j
2
1
12
1
1
0þ0
6
4
¼
¼
1
sin j
24
3. Integrationsschritt (Integration nach j)
1
I ¼
24
2ðp
sin j d j ¼
j¼p
2p
2p
1
1
1
1
½ cos j p ¼ ½ cos j p ¼ ½ cos ð2 pÞ cos p ¼
24
24
24 |fflfflfflfflffl{zfflfflfflfflffl} |fflffl{zfflffl}
12
1
1
Ergebnis: I ¼ 1=12
F41
Welches Volumen V hat ein Körper, der durch Drehung der Kurve z ¼ 1 þ cos x , 0 x p um
die z-Achse entsteht?
Der Verlauf der rotierenden Kurve ist in Bild F-39 dargestellt, es entsteht der in Bild F-40 skizzierte Rotationskörper.
Der kreisförmige „Boden‘‘ des Körpers liegt in der x, y-Ebene z ¼ 0 und lässt sich durch die Ungleichungen
0 r p und 0 j 2 p beschreiben. Der „Deckel‘‘ dagegen ist Teil der Rotationsfläche z ¼ 1 þ cos r (die
Kurve z ¼ 1 þ cos x erzeugt bei Drehung um die z-Achse die Rotationsfläche z ¼ 1 þ cos r , in Zylinderkoordinaten ausgedrückt ! Band 2, Kap. III.3.2.2.2).
z
z
2
2
z = 1 + cos x
z = 1 + cos r
1
1
2
π
π
x
π
Bild F-39
x
Bild F-40
Damit ergeben sich folgende Integrationsgrenzen:
z-Integration:
von z ¼ 0 bis z ¼ 1 þ cos r
r-Integration:
von r ¼ 0 bis r ¼ p
j-Integration:
von j ¼ 0 bis j ¼ 2 p
y
2 Dreifachintegrale
329
Das Volumenintegral lautet:
ððð
V ¼
ðp
2ðp
1 þðcos r
dV ¼
j¼0 r¼0
ðVÞ
ðVolumenelement d V ¼ r d z d r d jÞ
r dz dr dj
z¼0
Wir integrieren der Reihe nach über z, r und j.
1. Integrationsschritt (Integration nach z)
1 þðcos r
1 þðcos r
1 þ cos r
1 d z ¼ r ½ z z¼0
r dz ¼ r
z¼0
¼ r ½ 1 þ cos r 0 ¼ r ð1 þ cos rÞ ¼ r þ r cos r
z¼0
2. Integrationsschritt (Integration nach r)
ðp
r¼0
ðr þ r cos r Þ d r ¼
|fflfflfflfflffl{zfflfflfflfflffl}
1 2
r þ cos r þ r sin r
2
p
¼
r¼0
Integral 232 mit a ¼ 1
¼
1 2
1 2
1 2
p þ cos p þ p sin p 0 cos 0 0 ¼
p 11 ¼
p 2
2
2
2
|fflffl{zfflffl}
|ffl{zffl}
|ffl{zffl}
1
0
1
3. Integrationsschritt (Integration nach j)
V ¼
2ðp
2p
1 2
1 2
1 2
p 2
p 2 ½ j 0 ¼
p 2 ð2 p 0Þ ¼ p ðp 2 4Þ
1 dj ¼
2
2
2
j¼0
Volumen: V ¼ p ðp 2 4Þ ¼ 18,4399
Die durch den Kreis x 2 þ z 2 ¼ 2 und die Parabel z ¼ x 2 begrenzte Fläche erzeugt bei Drehung
F42
um die z-Achse einen Rotationskörper, dessen Volumen V zu bestimmen ist. Welche Masse m hat
dieser Körper, wenn er mit einem homogenen Material der Dichte r ¼ 2 gefüllt wird?
Wir berechnen zunächst die Kurvenschnittpunkte (Bild F-41):
x þz ¼ zþz ¼ 2
2
2
2
z2 þ z 2 ¼ 0
)
z
)
1,5
z1 ¼ 1 ;
z2 ¼ 2
S2
(die negative Lösung scheidet aus)
Zugehörige x-Werte:
x2 ¼ z1 ¼ 1
Schnittpunkte: S 1=2 ¼ ð 1; 1Þ
)
Kreis
Parabel
S1
1
0,5
x 1=2 ¼ 1
–1
1
x
Bild F-41
Bei Drehung um die z-Achse erzeugen Normalparabel und Halbkreis folgende Rotationsflächen (x ! r):
z ¼ x2
!
x2 þ z2 ¼ 2
z ¼ r2
!
(Mantelfläche des Rotationsparaboloids)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r 2 þ z 2 ¼ 2 oder z ¼ 2 r 2
(Oberfläche der oberen HalbkugelÞ
Diese Flächen begrenzen den Rotationskörper unten bzw. oben. Sie schneiden sich in der zur x, y-Ebene parallelen
Ebene z ¼ 1 längs eines Kreises mit dem Radius R ¼ 1 (siehe auch Bild F-41). Damit ergeben sich die folgenden
Integrationsgrenzen für das Volumenintegral:
330
F Mehrfachintegrale
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 r2
z-Integration:
von z ¼ r 2 bis z ¼
r-Integration:
von r ¼ 0 bis r ¼ 1
j-Integration:
von j ¼ 0 bis j ¼ 2 p
(die Projektion der beiden Rotationsflächen in die x, y-Ebene ergibt die Kreisfläche 0 r 1, 0 j 2 p)
Das Volumenintegral lautet:
ððð
V ¼
2ðp
ð1
pffiffiffiffiffiffiffiffiffi
2r2
ð
dV ¼
r dz dr dj
j¼0 r¼0
ðVÞ
ðVolumenelement d V ¼ r d z d r d jÞ
z¼r2
Wir integrieren nacheinander über z , r und j.
1. Integrationsschritt (Integration nach z)
pffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffi
2r2
2r2
pffiffiffiffiffiffiffiffiffi
ð
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2r2
r dz ¼ r
1 d z ¼ r ½ z z ¼ r 2 ¼ r ð 2 r 2 r 2Þ ¼ r 2 r 2 r 3
z¼r2
z¼r2
2. Integrationsschritt (Integration nach r)
ð1
r¼0
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
1 4 1
ðr 2 r 2 r 3 Þ d r ¼
¼
ð2 r 2 Þ 3
r
3
4
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
r¼0
Integral 142 mit a 2 ¼ 2
¼
pffiffiffi
1
1
1
þ
2 2 þ 0 ¼ 0,3595
3
4
3
3. Integrationsschritt (Integration nach j)
2ðp
V ¼ 0,3595
1 d j ¼ 0,3595 ½ j 0
2p
¼ 0,3595 ð2 p 0Þ ¼ 0,3595 2 p ¼ 2,2588
j¼0
Rotationsvolumen: V ¼ 2,2588
Masse: m ¼ r V ¼ 2 2,2588 ¼ 4,5176
F43
Skizzieren Sie das im 1. Quadranten gelegene Flächenstück; das durch die Kurven z ¼ 0;75 x 2 ;
z ¼ 0;5 x 2 þ 1 und x ¼ 0 berandet wird. Welches Rotationsvolumen V entsteht bei Drehung dieser Fläche um die z-Achse?
Kurvenschnittpunkte (Schnittpunkte der Parabeln):
0;75 x 2 ¼ 0;5 x 2 þ 1
)
z
0;25 x 2 ¼ 1 j 4
)
3
x ¼ 4
2
)
x1 ¼ 2
ðwegen x > 0Þ
z = 0,5 x 2 + 1
2
Die in Bild F-42 skizzierte Fläche erzeugt bei Drehung
um die z-Achse einen Rotationskörper; der unten und
oben von den folgenden Rotationsflächen begrenzt wird
(die x-Koordinate wird zur Zylinderkoordinate r):
untere Begrenzung („Boden‘‘):
z ¼ 0;75 r 2
obere Begrenzung („Deckel‘‘):
z ¼ 0;5 r þ 1
2
1
z = 0,75 x 2
1
Bild F-42
2
x
2 Dreifachintegrale
331
Projiziert man diese Flächen in die x; y-Ebene; so erhält man die Kreisfläche 0 r 2 ; 0 j 2 p . Damit
sind die Integrationsgrenzen für das Volumenintegral festgelegt:
z-Integration:
von z ¼ 0;75 r 2 bis z ¼ 0;5 r 2 þ 1
r-Integration:
von r ¼ 0 bis r ¼ 2
j-Integration:
von j ¼ 0 bis j ¼ 2 p
Volumenintegral
ððð
V ¼
2ðp
ð2
0;5 rð2 þ 1
dV ¼
ðVolumenelement d V ¼ r d z d r d jÞ
r dz dr dj
j ¼ 0 r ¼ 0 z ¼ 0;75 r 2
ðVÞ
1. Integrationsschritt (Integration nach z)
0;5 rð2 þ 1
0;5 rð2 þ 1
0;5 r 2 þ 1
1 d z ¼ r ½ z z ¼ 0;75 r 2 ¼ r ½ 0;5 r 2 þ 1 0;75 r 2 ¼
r dz ¼ r
z ¼ 0;75 r 2
z ¼ 0;75 r 2
¼ r ð1 0;25 r 2 Þ ¼ r 0;25 r 3
2. Integrationsschritt (Integration nach r)
ð2
ð2
1 3
1 2
1 4 2
r
r
r
ðr 0,25 r Þ d r ¼
r
¼ 2100 ¼ 1
dr ¼
4
2
16
r¼0
3
r¼0
r¼0
3. Integrationsschritt (Integration nach j)
2ðp
V ¼
1 d j ¼ ½ j 0
2p
¼ 2p 0 ¼ 2p
j¼0
Rotationsvolumen: V ¼ 2 p ¼ 6,2832
Die durch Rotation der Gauß-Kurve z ¼ e x um die z-Achse erzeugte Rotationsfläche bildet
mit der Ebene z ¼ const: ¼ e 1 einen Rotationskörper, dessen Volumen V und Schwerpunkt S
zu berechnen sind.
2
F44
Die in Bild F-43 grau unterlegte Fläche zwischen der Gauß-Kurve z ¼ e x
Geraden z ¼ e 1 erzeugt bei Rotation um die z-Achse den Rotationskörper.
z
1
z = e–x
2
0,5
z = e –1
Bild F-43
–1
– 0,5
0,5
1
x
2
und der zur x-Achse parallelen
332
F Mehrfachintegrale
Kurvenschnittpunkte: e x ¼ e 1
2
)
x2 ¼ 1
)
x 1=2 ¼ 1
Der Rotationskörper wird unten bzw. oben durch die folgenden Flächen begrenzt:
untere Begrenzung („Boden‘‘):
z ¼ e 1
ðEbene parallel zur x; y-EbeneÞ
obere Begrenzung („Deckel‘‘):
z ¼ e r
(Rotationsfläche der Gauß-Kurve; x durch r substituiert)
2
Beide Flächen liegen über dem kreisförmigen Integrationsbereich der x, y-Ebene, der durch die Ungleichungen
0 r 1 , 0 j 2 p beschrieben wird. Die für die Dreifachintegration benötigten Integrationsgrenzen lauten
damit:
z-Integration:
von z ¼ e 1 bis z ¼ e r
r-Integration:
von r ¼ 0 bis r ¼ 1
j-Integration:
von j ¼ 0 bis j ¼ 2 p
2
Berechnung des Rotationsvolumens V
ððð
V ¼
e ðr
ð1
2ðp
2
dV ¼
r dz dr dj
ðVolumenelement d V ¼ r d z d r d jÞ
j ¼ 0 r ¼ 0 z ¼ e 1
ðVÞ
1. Integrationsschritt (Integration nach z)
e ðr
2
e ðr
2
e r
z ¼ e 1
2
1 d z ¼ r ½ z z ¼ e 1 ¼ r ðe r e 1 Þ ¼ r e r e 1 r
r dz ¼ r
2
2
z ¼ e 1
2. Integrationsschritt (Integration nach r)
ð1
ðr e
r2
e
1
ð1
rÞ d r ¼
r¼0
r e
r2
dr e
ð1
1
r¼0
r dr ¼
r¼0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
I1
1 2 1
1
1 1
¼ I1 e 1
¼ I1 e 1
r
0 ¼ I1
e
2
2
2
r¼0
Das Teilintegral I 1 lösen wir wie folgt durch eine einfache Substitution:
u ¼ r2 ;
du
¼ 2r;
dr
ð1
I1 ¼
r e
r2
r¼0
¼
1
2
dr ¼
ð1
dr ¼
0
¼
Grenzen
du
1
¼
r e
2 r
2
ð1
u
u¼0
½ e u 1
du
;
2r
unten : r ¼ 0
)
u ¼ 0
oben : r ¼ 1
)
u ¼ 1
1
e du ¼
2
ð0
eu du ¼
u
0
1
1
1
ðe 0 e 1 Þ ¼
ð1 e 1 Þ
2
2
(das Integral ändert das Vorzeichen, da wir die Grenzen vertauscht haben). Somit gilt:
ð1
r¼0
ðr e r e 1 rÞ d r ¼ I 1
2
1 1
1
1 1
1
¼
¼
e
ð1 e 1 Þ
e
ð1 2 e 1 Þ
2
2
2
2
2 Dreifachintegrale
333
3. Integrationsschritt (Integration nach j)
2ðp
1
ð1 2 e 1 Þ
V ¼
2
1 dj ¼
j¼0
2p
1
1
ð1 2 e 1 Þ ½ j 0 ¼
ð1 2 e 1 Þ ð 2 p 0Þ ¼ ð1 2 e 1 Þ p
2
2
Rotationsvolumen: V ¼ ð1 2 e 1 Þ p ¼ 0,8301
Berechnung des Schwerpunktes S = (xS ; yS ; zS )
Wegen der Rotationssymmetrie liegt der Schwerpunkt S auf der Rotationsachse (z-Achse). Somit gilt x S ¼ y S ¼ 0 .
Die Höhenkoordinate z S berechnen wir mit dem folgenden Dreifachintegral:
1
zS ¼
V
ððð
z dV ¼
ðVÞ
ð1 2 e 1 Þ p
e ðr
ð1
2ðp
1
2
ðd V ¼ r d z d r d jÞ
zr dz dr dj
j ¼ 0 r ¼ 0 z ¼ e 1
1. Integrationsschritt (nach der Variablen z)
e ðr
2
e ðr
2
zr dz ¼ r
z ¼ e 1
z dz ¼ r
1 2
z
2
e r2
z ¼ e 1
¼
z ¼ e 1
2
e r
1
1
2
r ½ z 2 z ¼ e 1 ¼
r ðe 2 r e 2 Þ
2
2
2. Integrationsschritt (Integration nach r)
1
2
¼
ð1
r ðe
2r2
e
r¼0
1
1 2
I2
e
2
2
2
1
Þ dr ¼
2
ð1
r e
2r2
r¼0
1 2
e
dr
2
ð1
r dr ¼
r¼0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
I2
1
1 2
1
1 2 1
1
1 2
¼
r
I2
e
0 ¼
I2
e
2
2
2
2
2
4
r¼0
Das Teilintegral I 2 lösen wir (ähnlich wie vorher I 1 ) mit einer Substitution wie folgt:
du
¼ 4r;
dr
u ¼ 2r2 ;
ð1
r e 2r d r ¼
r¼0
¼
ð2
2
I2 ¼
dr ¼
r eu
u¼0
du
;
4r
Grenzen
du
1
¼
4 r
4
unten : r ¼ 0
)
u ¼ 0
oben : r ¼ 1
)
u ¼ 2
ð2
eu du ¼
0
1
4
ð0
eu du ¼
2
1
4
½ e u 2
0
1
1
ðe 0 e 2 Þ ¼
ð1 e 2 Þ
4
4
Somit ergibt der 2. Integrationsschritt:
1
2
ð1
r ðe 2 r e 2 Þ d r ¼
2
r¼0
1
1 2
1
1 2
1
I2
e
ð1 e 2 Þ
e
ð1 3 e 2 Þ
¼
¼
2
4
8
4
8
3. Integrationsschritt (Integration nach j)
1
1
zS ¼
ð1 3 e 2 Þ
1
ð1 2 e Þ p 8
2ðp
1 dj ¼
j¼0
1 3 e 2
8 p ð1
2 e 1Þ
½ j 0
2p
¼
¼
334
F Mehrfachintegrale
¼
1 3 e 2
8 p ð1 2 e 1 Þ
ð2 p 0Þ ¼
ð1 3 e 2 Þ 2 p
4 2 p ð1 2 e 1 Þ
¼
1 3 e 2
4 ð1 2 e 1 Þ
¼ 0,5620
Schwerpunkt: S ¼ ð0; 0; 0,5620Þ
Dreht man die in Bild F-44 skizzierte Fläche um die z-Achse, so
entsteht ein (homogener) Zylinder mit einem kegelförmigen Einschnitt. Welches Volumen V besitzt dieser Rotationskörper, wo
liegt der Schwerpunkt S ?
F45
z
2
z = 2x
1
–1
Bild F-44
1
x
–5
Der „zylindrische‘‘ Rotationskörper wird unten bzw. oben durch folgende Flächen begrenzt (x ! r):
untere Begrenzung („Boden‘‘):
Kreisfläche vom Radius 1 in der Ebene z ¼ 5
obere Begrenzung („Deckel‘‘):
z ¼ 2r
(parallel zur x, y-Ebene)
(Mantelfläche eines Kegels)
Integrationsbereich in der x, y-Ebene ist die durch die Ungleichungen 0 r 1 und 0 j 2 p beschriebene
Kreisfläche. Damit haben wir folgende Integrationsgrenzen:
z-Integration:
von z ¼ 5 bis z ¼ 2 r
r-Integration:
von r ¼ 0 bis r ¼ 1
j-Integration:
von j ¼ 0 bis j ¼ 2 p
Berechnung des Rotationsvolumens V
2ðp
ððð
V ¼
ð1
2ðr
dV ¼
r dz dr dj
ðVolumenelement d V ¼ r d z d r d jÞ
j¼0 r¼0 z¼5
ðVÞ
1. Integrationsschritt (Integration nach z)
2ðr
2ðr
r dz ¼ r
z¼5
1 d z ¼ r ½ z z ¼ 5 ¼ r ð2 r þ 5Þ ¼ 2 r 2 þ 5 r
2r
z¼5
2. Integrationsschritt (Integration nach r)
ð1
ð2 r þ 5 rÞ d r ¼
2
r¼0
2 3
5 2
r þ
r
3
2
1
¼
r¼0
2
5
2
5
4 þ 15
19
þ
00 ¼
þ
¼
¼
3
2
3
2
6
6
3. Integrationsschritt (Integration nach j)
19
V ¼
6
2ðp
1 dj ¼
j¼0
2p
19
19
19 2 p
19 2 p
19
¼
¼
p
½ j 0 ¼ ð2 p 0Þ ¼
6
6
6
3
3 2
2 Dreifachintegrale
335
Rotationsvolumen: V ¼
19
p ¼ 19,8968
3
Berechnung des Schwerpunktes S = ( xS ; yS ; zS )
Der Schwerpunkt S liegt wegen der Rotationssymmetrie auf der z-Achse, daher sind x S ¼ 0 und y S ¼ 0. Die
dritte Koordinate z S berechnen wir mit dem Dreifachintegral
1
zS ¼
V
ððð
ðVÞ
1
z dV ¼
19 p=3
ð1
2ðp
2ðr
3
zr dz dr dj ¼
19 p
j¼0 r¼0 z¼5
2ðp
ð1
2ðr
zr dz dr dj
j¼0 r¼0 z¼5
1. Integrationsschritt (Integration nach z)
2ðr
2ðr
zr dz ¼ r
z¼5
z dz ¼ r
z¼5
1 2
z
2
2r
¼
z¼5
2r
1
1
1
r ½ z2 z¼5 ¼
r ð4 r 2 25Þ ¼
ð4 r 3 25 rÞ
2
2
2
2. Integrationsschritt (Integration nach r)
1
2
ð1
ð4 r 3 25 rÞ d r ¼
r¼0
1
2
r4
25 2
r
2
1
¼
r¼0
1
2
25
1
23
23
1
00 ¼
¼
2
2
2
4
3. Integrationsschritt (Integration nach j)
3
zS ¼
19 p
23
4
2ðp
1 dj ¼
j¼0
2p
69
69
69 2 p
69
¼
½ j 0 ¼
ð2 p 0Þ ¼
¼ 1,8158
76 p
76 p
38 2 p
38
Schwerpunkt: S ¼ ð0; 0; 1,8158Þ
F46
Ein rotationssymmetrischer Körper aus einem homogenen Material wird durch die Flächen z ¼ 3
(unten) und z ¼ 4 r 2 (Mantelfläche eines Rotationsparaboloids; oben) begrenzt. Bestimmen Sie
Volumen V und Schwerpunkt S .
Die Flächen z ¼ 4 r 2 und z ¼ 3 schneiden sich in der Ebene z ¼ 3 längs eines Kreises vom Radius 1:
4 r2 ¼ 3
)
r2 ¼ 1
)
r ¼ 1
Bild F-45 zeigt die Gestalt des Rotationskörpers. Der Integrationsbereich
in der x, y-Ebene ist die durch die Ungleichungen 0 r 1 und
0 j 2 p beschriebene Kreisfläche.
z
4
z =4–r2
Die Integrationsgrenzen lauten damit wie folgt:
z-Integration:
von z ¼ 3 bis z ¼ 4 r 2
r-Integration:
von r ¼ 0 bis r ¼ 1
j-Integration:
von j ¼ 0 bis j ¼ 2 p
3
z =3
Berechnung des Rotationsvolumens V
ððð
V ¼
2ðp
ð1
dV ¼
ðVÞ
Bild F-45
4
ðr 2
y
r dz dr dj
j¼0 r¼0 z¼3
ðVolumenelement d V ¼ r d z d r d jÞ
x
336
F Mehrfachintegrale
1. Integrationsschritt (Integration nach z)
4
ðr 2
4
ðr 2
r dz ¼ r
z¼3
4r2
1 d z ¼ r ½ z z ¼ 3 ¼ r ½4 r 2 3 ¼ r ð1 r 2 Þ ¼ r r 3
z¼3
2. Integrationsschritt (Integration nach r)
ð1
ðr r Þ d r ¼
3
r¼0
1 2
1 4
r
r
2
4
1
¼
r¼0
1
1
1
00 ¼
2
4
4
3. Integrationsschritt (Integration nach j)
1
V ¼
4
2ðp
1 dj ¼
j¼0
1
4
½ j 0
2p
¼
1
2p
p
ð2 p 0Þ ¼
¼
4
4
2
Rotationsvolumen: V ¼ p=2 ¼ 1,5708
Berechnung des Schwerpunktes S = (xS ; yS ; zS )
Wegen der Rotationssymmetrie liegt der Schwerpunkt S auf der z-Achse, also gilt x S ¼ y S ¼ 0 . Die z-Koordinate
berechnen wir mit dem Dreifachintegral
1
zS ¼
V
ððð
ðVÞ
1
z dV ¼
p=2
2ðp
ð1
4
ðr 2
j¼0 r¼0 z¼3
2
zr dz dr dj ¼
p
2ðp
ð1
4
ðr 2
zr dz dr dj
j¼0 r¼0 z¼3
1. Integrationsschritt (Integration nach z)
4
ðr 2
4
ðr 2
zr dz ¼ r
z¼3
z dz ¼ r
z¼3
¼
1 2
z
2
4r2
¼
z¼3
4r2
1
1
r ½ z2 z¼3 ¼
r ½ ð4 r 2 Þ 2 9 ¼
2
2
1
1
1
r ð16 8 r 2 þ r 4 9Þ ¼
r ð7 8 r 2 þ r 4 Þ ¼
ð7 r 8 r 3 þ r 5 Þ
2
2
2
2. Integrationsschritt (Integration nach r)
1
2
ð1
1
ð7 r 8 r þ r Þ d r ¼
2
3
r¼0
5
¼
7 2
1 6
r 2r4 þ
r
2
6
1
1
¼
2
r¼0
7
1
2þ
000 ¼
2
6
1 21 12 þ 1
1 10
5
¼
¼
2
6
2
6
6
3. Integrationsschritt (Integration nach j)
2 5
zS ¼
p 6
2ðp
1 dj ¼
j¼0
Schwerpunkt: S ¼ ð0; 0; 10=3Þ
2p
2p
2 5
5
5
10 p
10
ð2 p 0Þ ¼
¼
½ j 0 ¼
½ j 0 ¼
3p
3p
3p
3
2 3p
2 Dreifachintegrale
337
Ein
einem homogenen Material gefertigter Körper wird durch die Rotationsfläche
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
z ¼ 2 x 2 þ y 2 und die x; y-Ebene berandet. Bestimmen Sie das Volumen V und den Schwerpunkt S des Körpers.
F47
aus
Gleichung der Rotationsfläche in Zylinderkoordinaten:
x ¼ r cos j ;
z ¼ 2
y ¼ r sin j
x 2 þ y 2 ¼ r 2 cos 2 j þ r 2 sin 2 j ¼ r 2 ðcos 2 j þ sin 2 jÞ ¼ r 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
x2 þ y2 ¼ 2 r2 ¼ 2 r
Die in Zylinderkoordinaten ausgedrückte Rotationsfläche z ¼ 2 r schneidet die x, y-Ebene z ¼ 0 längs eines
Mittelpunktskreises mit dem Radius 2 (siehe Bild F-46):
2r ¼ 0
)
r ¼ 2
Kreisfläche : 0 r 2 ;
0 j 2p
Der Rotationskörper hat damit das in Bild F-46 skizzierte Aussehen.
Er wird oben von der Rotationsfläche z ¼ 2 r, unten von der
x, y-Ebene z ¼ 0 berandet.
Damit liegen die Integrationsgrenzen wie folgt fest:
z-Integration:
von z ¼ 0 bis z ¼ 2 r
r-Integration:
von r ¼ 0 bis r ¼ 2
j-Integration:
von j ¼ 0 bis j ¼ 2 p
Berechnung des Rotationsvolumens V
ð2
2ðp
ððð
dV ¼
V ¼
Bild F-46
2ð
r
r dz dr dj
ðVolumenelement d V ¼ r d z d r d jÞ
j¼0 r¼0 z¼0
ðVÞ
1. Integrationsschritt (Integration nach z)
2ð
r
2ð
r
r dz ¼ r
z¼0
2r
1 d z ¼ r ½ z z ¼ 0 ¼ r ð2 r 0Þ ¼ 2 r r 2
z¼0
2. Integrationsschritt (Integration nach r)
ð2
ð2 r r Þ d r ¼
2
r¼0
1 3
r
r
3
2
¼ 4
2
r¼0
8
8
4
00 ¼ 4
¼
3
3
3
3. Integrationsschritt (Integration nach j)
4
V ¼
3
2ðp
1 dj ¼
j¼0
4
3
½ j 0
2p
¼
4
8
ð2 p 0Þ ¼
p
3
3
Rotationsvolumen: V ¼ 8 p=3 ¼ 8,3776
Berechnung des Schwerpunktes S = (xS ; yS ; zS )
Der Schwerpunkt S liegt wegen der Rotationssymmetrie auf der z-Achse. Somit gilt: x S ¼ y S ¼ 0. Die Höhenkoordinate z S berechnen wir mit dem folgenden Dreifachintegral:
338
F Mehrfachintegrale
1
zS ¼
V
ððð
ðVÞ
1
z dV ¼
8 p=3
2ðp
ð2
2ð
r
j¼0 r¼0 z¼0
3
zr dz dr dj ¼
8p
ð2
2ðp
2ð
r
zr dz dr dj
j¼0 r¼0 z¼0
1. Integrationsschritt (Integration nach z)
2ð
r
2ð
r
zr dz ¼ r
z¼0
z dz ¼ r
z¼0
1 2
z
2
2r
¼ r
z¼0
1
ð2 rÞ 2 0
2
1
ð4 r 4 r 2 þ r 3 Þ
2
¼
2. Integrationsschritt (Integration nach r)
1
2
ð2
1
ð4 r 4 r þ r Þ d r ¼
2
2
r¼0
3
¼
1
2
4 3
1 4
2r
r þ
r
3
4
2
2
1
¼
2
r¼0
32
8
þ4000 ¼
3
32
1 36 32
1 4
2
12
¼
¼
¼
3
2
3
2 3
3
3. Integrationsschritt (Integration nach j)
3
2
zS ¼
8p 3
2ðp
1 dj ¼
j¼0
2p
1
1
2p
1
¼
½ j 0 ¼
ð2 p 0Þ ¼
¼ 0,5
4p
4p
4p
2
Schwerpunkt: S ¼ ð0; 0; 0,5Þ
F48
Der kreisförmige „Boden“ eines zylindrischen Körpers liegt in der x; y-Ebene eines kartesischen
Koordinatensystems und wird durch die Ungleichung ðx 3Þ 2 þ y 2 9 beschrieben. Der „Deckel“
(obere Randfläche) ist Teil der Rotationsfläche z ¼ x 2 þ y 2 . Welches Volumen V besitzt dieser
Körper?
Wir verwenden wegen der Kreissymmetrie der Bodenfläche und der rotationssymmetrischen oberen Randfläche Zylinderkoordinaten (Bild F-47).
y
Kreisgleichung in Polarkoordinaten (Zylinderkoordinaten):
x ¼ r cos j ;
3
y ¼ r sin j
3
ðx 3Þ 2 þ y 2 ¼ 9 ) ðr cos j 3Þ 2 þ r 2 sin 2 j ¼ 9
)
r 2 cos 2 j 6 r cos j þ 9 þ r 2 sin 2 j ¼ 9
)
r 2 ðcos 2 j þ sin 2 jÞ 6 r cos j ¼ 0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
)
r 2 6 r cos j ¼ r ðr 6 cos jÞ ¼ 0
6
x
„Bodenfläche“
Bild F-47
)
r 6 cos j ¼ 0
)
r ¼ 6 cos j
Die Lösung r ¼ 0 kommt nicht infrage. Damit ist r ¼ 6 cos j die Gleichung des Kreises ð p=2 j p=2Þ .
Die Kreisfläche lässt sich durch die Ungleichungen 0 r 6 cos j und p=2 j p=2 beschreiben.
Der kreisförmige „Boden‘‘ des Körpers liegt in der x, y-Ebene z ¼ 0 , der „Deckel‘‘ ist Teil der Fläche z ¼ x 2 þ y 2 ,
die in Zylinderkoordinaten durch die Gleichung z ¼ r 2 beschrieben wird (Transformationsgleichungen: x ¼ r cos j ,
y ¼ r sin j und x 2 þ y 2 ¼ r 2 ). Insgesamt erhalten wir damit die folgenden Integrationsgrenzen:
z-Integration:
von z ¼ 0 bis z ¼ r 2
r-Integration:
von r ¼ 0 bis r ¼ 6 cos j
j-Integration:
von j ¼ p=2 bis j ¼ p=2
2 Dreifachintegrale
339
Das Volumenintegral lautet:
ððð
6 cos
ð j
ð
p=2
V ¼
rð2
dV ¼
ðVolumenelement d V ¼ r d z d r d jÞ
r dz dr dj
ðVÞ
z¼0
r¼0
j ¼ p=2
1. Integrationsschritt (Integration nach z)
rð2
rð2
r dz ¼ r
z¼0
r2
1 d z ¼ r ½ z z ¼ 0 ¼ r ðr 2 0Þ ¼ r 3
z¼0
2. Integrationsschritt (Integration nach r)
6 cos
ð j
r3 d r ¼
r¼0
1 4
r
4
6 cos j
1
ð6 cos jÞ 4 0 ¼ 324 cos 4 j
4
¼
r¼0
3. Integrationsschritt (Integration nach j)
ð
ð
p=2
cos j d j ¼ 324 2
V ¼ 324
ð
p=2
p=2
cos j d j ¼ 648
4
j¼0
j ¼ p=2
(Integration von 0 bis p=2
)
cos 4 j d j ¼ 648 I
4
j¼0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
I
Faktor 2)
Wir können dieses Integral der Integraltafel der Formelsammlung entnehmen (Integral 231 mit n ¼ 4 , a ¼ 1 in
Verbindung mit Integral 229 mit a ¼ 1) oder mit Hilfe einer geeigneten trigonometrischen Umformung in einfache
Integrale zerlegen. Wir gehen hier den letzteren Weg. Aus der Formelsammlung entnehmen wir die Beziehung
1
½ cos ð4 jÞ þ 4 cos ð2 jÞ þ 3
8
cos 4 j ¼
ð! FS : Kap. III.7.6.4Þ
Das Integral I geht dann über in:
j¼0
½ cos ð4 jÞ þ 4 cos ð2 jÞ þ 3 d j
0
f
I ¼
ð
p=2
1
cos 4 j d j ¼
8
f
ð
p=2
v
u
Mit den Substitutionen
u ¼ 4j;
du
¼ 4;
dj
dj ¼
du
;
4
Grenzen
v ¼ 2j;
dv
¼ 2;
dj
dj ¼
dv
;
2
Grenzen
unten : j ¼ 0
)
u ¼ 0
oben : j ¼ p=2
)
u ¼ 2p
unten : j ¼ 0
)
v ¼ 0
oben : j ¼ p=2
)
v ¼ p
erhalten wir schließlich:
ð
p=2
1
I ¼
8
0
1
¼
8
2ðp
0
ð
p=2
1
cos ð4 jÞ d j þ
2
0
du
1
cos u
þ
4
2
ðp
0
ð
p=2
3
cos ð2 jÞ d j þ
8
dv
3
cos v
þ
2
8
1 dj ¼
0
ð
p=2
1 dj ¼
0
2p
1
1
½ sin u 0 þ
32
4
½ sin v 0
p
þ
3
8
½ j 0
p=2
¼
340
F Mehrfachintegrale
¼
1
1
3
ðsin ð2 pÞ sin 0Þ þ
ðsin p sin 0Þ þ
32 |fflfflfflffl{zfflfflfflffl}
4
8
|{z}
|{z}
|{z}
0
0
0
0
p
0
2
¼
3 p
3
¼
p
8 2
16
Somit liefert der 3. Integrationsschritt das folgende Volumen:
V ¼ 648 I ¼ 648
3
8 81 3 p
243
¼
p ¼
p ¼ 381,7035
16
2
8 2
Bestimmen Sie das Massenträgheitsmoment J
einer homogenen Kugel mit zylindrischer Bohrung längs der Symmetrieachse (Bild F-48).
z
Untersuchen Sie den Sonderfall a ¼ 0 .
F49
R: Radius der Kugel
a: Radius der zylindrischen Bohrung
R
Bild F-48
x
a
ð0 < a < RÞ
zylindrische Bohrung
Die Gleichung der Rotationsfläche (Kugeloberfläche) lautet für z 0 in Zylinderkoordinaten:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r 2 þ z 2 ¼ R 2 ) z 2 ¼ R 2 r 2 ) z ¼ R2 r2
Wegen der Spiegelsymmetrie des Rotationskörpers bezüglich der x; y-Ebene beschränken wir uns auf den oberhalb
der x, y-Ebene gelegenen Teil (Halbkugel mit Bohrung). Der „Boden‘‘ dieses Körpers ist eine Kreisringfläche mit dem
Innenradius a und dem Außenradius R, beschrieben durch die Ungleichungen a r R und 0 j 2 p
(Bild F-49). Er liegt in der x, y-Ebene z ¼ 0. Der „Deckel‘‘ wird gebildet durch die über diesem Kreisring liegende
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Rotationsfläche z ¼ R 2 r 2 (Oberfläche der Halbkugel).
y
Damit ergeben sich folgende Integrationsgrenzen:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
z-Integration: von z ¼ 0 bis z ¼ R 2 r 2
r-Integration:
von r ¼ a bis r ¼ R
j-Integration:
von j ¼ 0 bis j ¼ 2 p
j¼0 r¼a
a
x
Das Dreifachintegral für das Massenträgheitsmoment J z lautet:
pffiffiffiffiffiffiffiffiffiffiffi
R2 r 2
2
p
R
ð
ð
ððð
ð
r2 d V ¼ 2r
r3 d z d r d j
Jz ¼ r
ðVÞ
R
Bild F-49
ðVolumenelement d V ¼ r d z d r d jÞ
z¼0
(Faktor 2 vor dem Integral, da wir die Integration auf die oberhalb der x, y-Ebene gelegene Körperhälfte beschränkt
haben)
1. Integrationsschritt (Integration nach z)
pffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
R2 r2
R2 r2
pffiffiffiffiffiffiffiffiffiffiffi
ð
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R2 r2
3
3
3
r dz ¼ r
1 d z ¼ r ½ z z¼0
¼ r 3 ð R 2 r 2 0Þ ¼ r 3 R 2 r 2
z¼0
z¼0
2 Dreifachintegrale
341
2. Integrationsschritt (Integration nach r)
ðR
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi R
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
R2
5
2
2
2
2
ðR r Þ
r R r dr ¼
¼
ðR 2 r 2 Þ 3
5
3
r¼a
3
r¼a
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 144 mit a ¼ R
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R2
1 2 2
1
ðR 2 a 2 Þ 3 ¼
ðR 2 a 2 Þ 5 þ
R ðR a 2 Þ 3=2
ðR 2 a 2 Þ 5=2 ¼
3
3
5
1 2 2
1
1 2
1
2 3=2
2
2 3=2
2
2 1
2
2 3=2
2
2
ðR a Þ ¼ ðR a Þ
¼
R ðR a Þ
ðR a Þ
R
ðR a Þ ¼
3
5
3
5
¼ 00
1
5
¼ ðR 2 a 2 Þ 3=2
1 2
1 2
1 2
R
R þ
a
3
5
5
2 3=2
¼ ðR a Þ
2
¼
2 2
1 2
R þ
a
15
5
¼ ðR 2 a 2 Þ 3=2
2 3=2
¼ ðR a Þ
2
5 R2 3 R2
1 2
þ
a
15
5
2 R2 þ 3 a2
15
¼
¼
1
ð2 R 2 þ 3 a 2 Þ ðR 2 a 2 Þ 3=2
15
Rechenregel: u 5=2 ¼ u ð3=2 þ 2=2Þ ¼ u ð3=2 þ 1Þ ¼ u 3=2 u 1 ¼ u 3=2 u
ðhier : u ¼ R 2 a 2 Þ
3. Integrationsschritt (Integration nach j)
1
ð2 R 2 þ 3 a 2 Þ ðR 2 a 2 Þ 3=2
Jz ¼ 2 r
15
¼
1 dj ¼
j¼0
2
r ð2 R 2 þ 3 a 2 Þ ðR 2 a 2 Þ 3=2 2 p ¼
15
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
2p
4
p r ð2 R 2 þ 3 a 2 Þ ðR 2 a 2 Þ 3=2
15
Massenträgheitsmoment: J z ¼
2ðp
4
p r ð2 R 2 þ 3 a 2 Þ ðR 2 a 2 Þ 3=2
15
Sonderfall: a = 0 (Kugel vom Radius R, ohne Bohrung)
J Kugel ¼
4
4
8
p r ð2 R 2 Þ ðR 2 Þ 3=2 ¼
p r 2 R2 R3 ¼
prR5
15
15
15
Welches Massenträgheitsmoment J hat das
in Bild F-50 skizzierte Speichenrad bezüglich
der Symmetrieachse (z-Achse)?
F50
y
Untersuchen Sie den Sonderfall R 1 ¼ R 2 .
Dicke des Speichenrades: H
Dichte des homogenen Materials:
R2
Bild F-50
r
R3
R1
x
Speiche
(masselos)
342
F Mehrfachintegrale
Das Speichenrad liegt auf der x, y-Ebene z ¼ 0 („Bodenfläche‘‘), die obere Begrenzung ist die Parallelebene z ¼ H
(„Deckel‘‘). Die z-Integration verläuft daher von z ¼ 0 bis z ¼ H. Der Integrationsbereich in der x, y-Ebene besteht aus zwei Teilbereichen:
0 r R1 ;
innere Scheibe:
0 j 2p
äußerer Ring:
R2 r R3 ;
0 j 2p
Das Massenträgheitsmoment J z des Speichenrades ist die Summe der Massenträgheitsmomente von Scheibe und Ring
(Volumenelement d V ¼ r d z d r d jÞ:
ððð
Jz ¼ r
ð
2ðp
ðH
R1
2ðp
r dV ¼ r
ðH
r 3 d z d r d j ¼ J1 þ J 2
3
j¼0 r¼0 z¼0
ðVÞ
ð
R3
r dz dr dj þ r
2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
J1
j¼0 r¼R2 z¼0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
J2
Die Dreifachintegrale unterscheiden sich lediglich in der r-Integration. Wir berechnen zunächst J 1 .
Massenträgheitsmoment J 1 der inneren Scheibe (in Bild F-50 hellgrau unterlegt)
2ðp
ð
ðH
R1
J1 ¼ r
r3 d z d r d j
j¼0 r¼0 z¼0
1. Integrationsschritt (Integration nach z)
ðH
ðH
1 d z ¼ r 3 ½ z z ¼ 0 ¼ r 3 ðH 0Þ ¼ H r 3
H
r dz ¼ r
3
3
z¼0
z¼0
2. Integrationsschritt (Integration nach r)
ð
R1
H
r3 d r ¼ H
r¼0
1 4
r
4
R1
¼ H
r¼0
1 4
1
R1 0 ¼
H R 41
4
4
3. Integrationsschritt (Integration nach j)
1
H R 41
J1 ¼ r
4
2ðp
1 dj ¼
j¼0
2p
1
1
1
r H R 41 ½ j 0 ¼
r H R 41 ð2 p 0Þ ¼
p r H R 41
4
4
2
Massenträgheitsmoment der Scheibe: J 1 ¼
1
p r H R 41
2
Massenträgheitsmoment J 2 des äußeren Rings (in Bild F-50 dunkelgrau unterlegt)
2ðp
ð
R3
ðH
J2 ¼ r
r3 d z d r d j
j ¼ 0 r ¼ R2 z ¼ 0
1. Integrationsschritt (Integration nach z, wie bei J 1 )
ðH
r3 d z ¼ H r3
z¼0
2. Integrationsschritt (Integration nach r)
ð
R3
H
r3 d r ¼ H
r¼R2
1 4
r
4
R3
¼
r¼R2
R3
1
1
H ½ r 4 r ¼ R2 ¼
H ðR 43 R 42 Þ
4
4
2 Dreifachintegrale
343
3. Integrationsschritt (Integration nach j)
1
H ðR 43 R 42 Þ
J2 ¼ r
4
¼
2ðp
1 dj ¼
j¼0
2p
1
1
r H ðR 43 R 42 Þ ½ j 0 ¼
r H ðR 43 R 42 Þ ð2 p 0Þ ¼
4
4
1
p r H ðR 43 R 42 Þ
2
Massenträgheitsmoment des Ringes: J 2 ¼
1
p r H ðR 43 R 42 Þ
2
Massenträgheitsmoment J des Speichenrades
Jz ¼ J1 þ J2 ¼
1
1
1
p r H R 41 þ
p r H ðR 43 R 42 Þ ¼
p r H ðR 41 þ R 43 R 42 Þ
2
2
2
Sonderfall (Zylinderscheibe vom Radius R): R 1 = R 2 , R 3 = R
J Zylinder ¼
1
1
p r H ðR 41 þ R 4 R 41 Þ ¼
prH R4
2
2
Das Massenträgheitsmoment lässt sich auch wie folgt durch Masse m und Radius R ausdrücken:
J Zylinder ¼
1
1
1
1
prHR4 ¼
ðr p R 2 HÞ R 2 ¼
ðr VÞ R 2 ¼
mR2
2
2
2 |ffl{zffl}
2
|fflfflffl{zfflfflffl}
V
m
Hinweis: Das Dreifachintegral lässt sich auch als Produkt dreier gewöhnlicher Integrale berechnen (der Integrand
hängt nur von der einen Variablen r ab; sämtliche Integrationsgrenzen sind konstant):
2ðp
J1 ¼ r
Rð1
1dj
j¼0
¼ r ð2 p 0Þ
r dr
r¼0
ðH
3
z¼0
1 d z ¼ r ½ j 0
2p
1 4
r
4
R1
0
½ z 0 ¼
H
1 4
1 4
1
R 0 ðH 0Þ ¼ r 2 p
R H ¼
p r H R 41
4 1
4 1
2
344
G Gewöhnliche Differentialgleichungen
Hinweise für das gesamte Kapitel
(1)
(2)
(3)
(4)
Treten mehrere Integrationskonstanten auf, so werden diese (zusammen mit eventuell vorhandenen konstanten
Gliedern) zu einer Integrationskonstanten zusammengefasst (im Regelfall auf der rechten Seite der Gleichung).
Häufig erhält man bei der Integration einer Dgl „logarithmische“ Terme wie beispielsweise ln j x j oder
ln j 2 x 2 x þ 1 j . Es ist dann zweckmäßiger, die Integrationskonstante nicht in der üblichen Form, sondern in
der „logarithmischen“ Form ln j C j anzusetzen. Sie können dann mit Hilfe der elementaren Rechenregeln für
Logarithmen den Arbeitsaufwand erheblich reduzieren (Rechenregeln ! Hinweis (3)).
Beim Lösen einer Dgl werden Sie immer wieder die folgenden Rechenregeln benötigen:
a
R1
ln a þ ln b ¼ ln ða bÞ
R2
ln a ln b ¼ ln
b
n
n
ln a
R3
n ln a ¼ ln a ; ln e ¼ n
R4
e
¼ a
R5
Entlogarithmierung ln a ¼ b
R6
jxj ¼ a > 0
R7
am an ¼ amn ;
)
)
x ¼ a;
a ¼ eb ;
jxj ¼ jaj
ln a ¼ ln b
)
)
a ¼ b
x ¼ a
a m a m ¼ a m m ¼ a o ¼ 1
Alle anfallenden Integrale dürfen einer Integraltafel entnommen werden (wenn nicht ausdrücklich anders verlangt). Bei der Lösung der Integrale wird die jeweilige Integralnummer aus der Integraltafel der Mathematischen Formelsammlung des Autors mit den entsprechenden Parameterwerten angegeben („gelbe Seiten“, z. B.
Integral 313 mit a ¼ 2Þ: Selbstverständlich dürfen Sie die Integrale auch „per Hand“ lösen (zusätzliche
bung).
1 Differentialgleichungen 1. Ordnung
1.1 Differentialgleichungen mit trennbaren Variablen
Lehrbuch: Band 2, Kapitel IV.2.2
Formelsammlung: Kapitel X.2.1
G1
y 0 ¼ exy ;
Anfangswert : y ð0Þ ¼ 1
Trennen der beiden Variablen führt zu:
y0 ¼
dy
¼ exy ¼ e x e y
dx
)
ey dy ¼ ex dx
Integration auf beiden Seiten, anschließend wird die Gleichung nach y aufgelöst (Rechenregel: R3):
ð
ð
e y d y ¼ e x d x ) e y ¼ e x þ C ) ln e y ¼ ln ðe x þ CÞ ) y ¼ ln ðe x þ CÞ
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_7
1 Differentialgleichungen 1. Ordnung
345
Spezielle Lösung für den Anfangswert y ð0Þ ¼ 1:
y ð0Þ ¼ 1
)
ln ðe 0 þ CÞ ¼ ln ð1 þ CÞ ¼ 1
)
1 þ C ¼ e1 ¼ e
)
C ¼ e1
Rechenregel: R5
Lösung:
y ¼ ln ðe x þ e 1Þ
G2
y 0 ¼ ð y þ 1Þ sin x ;
Anfangswert : y ðp=2Þ ¼ 4
Trennung der beiden Variablen, dann Integration auf beiden Seiten:
y0 ¼
dy
¼ ð y þ 1Þ sin x
dx
)
dy
¼ sin x d x
yþ1
)
ð
dy
¼
yþ1
|fflfflfflfflffl{zfflfflfflfflffl}
ð
sin x d x
)
Integral 2 mit a ¼ 1 , b ¼ 1
ln j y þ 1 j ¼ cos x þ ln j C j
Auflösung der Gleichung nach y (entlogarithmieren):
y þ 1
¼ cos x
ln j y þ 1 j ln j C j ¼ ln
C
y þ 1 ¼ C e cos x ¼ K e cos x
)
)
y þ 1
cos x
C ¼ e
y ¼ K e cos x 1
)
yþ1
¼ e cos x
C
)
ðmit K ¼ C Þ
Rechenregeln: R2, R5 und R6
Bestimmung der Konstanten K aus dem Anfangswert y ðp=2Þ ¼ 4:
K e cos ðp=2Þ 1 ¼ K e 0 1 ¼ K 1 1 ¼ K 1 ¼ 4
Spezielle Lösung:
)
K ¼ 4 þ 1¼ 5
y ¼ 5 e cos x 1
Aufladung eines Kondensators mit der Kapazität C über einen ohmschen Widerstand R (Bild G-1)
Die zeitabhängige Kondensatorspannung u ¼ u ðtÞ genügt der Dgl
G3
C
R
R C u_ þ u ¼ u 0 ¼ const:
(u 0 : angelegte Gleichspannung; Anfangsspannung: u ð0Þ ¼ 0) .
i (t )
Bestimmen Sie den zeitlichen Verlauf der Spannung u .
u (t )
u0
Bild G-1
Wir trennen zunächst die Variablen:
R C u_ þ u ¼ u 0
)
RC
Beide Seiten werden jetzt integriert:
ð
ð
du
1
¼
1 dt
u u0
RC
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
du
¼ u0 u
dt
)
)
du
dt
¼
u0 u
RC
ln j u u 0 j ¼
Rechenregel: R2
t
RC
)
du
dt
1
dt
¼
¼
u u0
RC
RC
1
t
t þ ln j K j ¼
þ ln j K j
RC
RC
Integral 2 mit a ¼ 1 , b ¼ u 0
ln j u u 0 j ln j K j ¼
)
u u
t
0
ln
¼
RC
K
)
346
G Gewöhnliche Differentialgleichungen
Durch Entlogarithmierung folgt (Rechenregeln: R5 und R6):
u u
t
t
t
t
u u0
0
¼ e RC ) u u0 ¼ K e RC ¼ K * e RC
¼ e RC )
K
K
u ¼ u0 þ K * e
t
RC
)
ðmit K * ¼ KÞ
Beim Einschalten (d. h. zur Zeit t ¼ 0) ist u ¼ 0 , d. h. u ð0Þ ¼ 0 . Aus diesem Anfangswert bestimmen wir die
Konstante K * wie folgt:
u ð0Þ ¼ 0
Lösung:
)
u0 þ K * e 0 ¼ u0 þ K * 1 ¼ u0 þ K * ¼ 0
u ¼ u0 u0 e
t
RC
¼ u0
1e
t
RC
)
K * ¼ u0
, t 0
u
u0
Bild G-2 zeigt den zeitlichen Verlauf der Kondensatorspannung
(„Sättigungsfunktion‘‘).
u = u0 1 – e
–
t
RC
Bild G-2
t
G4
y 0 ¼ ð y þ 1Þ cot x ;
Anfangswert : y ðp=2Þ ¼ 0
Trennung der beiden Variablen, dann Integration auf beiden Seiten:
dy
¼ ð y þ 1Þ cot x
dx
ð
ð
dy
¼ cot x d x )
yþ1
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
y0 ¼
Integral 2 mit
a ¼ b ¼ 1
)
dy
¼ cot x d x
yþ1
C
ln j y þ 1 j ¼ ln j sin x j þ ln j C j ¼ ln j C j ln j sin x j ¼ ln
sin x
Integral 293
mit a ¼ 1
(Rechenregel: R2). Entlogarithmierung der Gleichung führt dann zur allgemeinen Lösung (Rechenregeln: R5 und R6):
C
K
) yþ1 ¼ C ¼ K
jy þ 1j ¼
) y ¼
1
ðmit K ¼ C Þ
sin x
sin x
sin x
sin x
Spezielle Lösung für den Anfangswert y ðp=2Þ ¼ 0:
y ðp=2Þ ¼ 0
G5
)
K
K
1 ¼
1 ¼ K 1 ¼ 0
1
sin ðp=2Þ
)
K ¼ 1
)
y ¼
1
1
sin x
Geschwindigkeit-Zeit-Gesetz einer beschleunigten Masse unter Berücksichtigung der Reibung
Die Bewegung einer Masse, die durch eine konstante Kraft beschleunigt wird und einer der Geschwindigkeit v proportionalen Reibungskraft unterliegt, genüge der folgenden Dgl:
10
dv
þ v ¼ 40
dt
mit
v ð0Þ ¼ 10
Wie lautet das Geschwindigkeit-Zeit-Gesetz v ¼ v ðtÞ ?
Welche Endgeschwindigkeit v E erreicht die Masse?
1 Differentialgleichungen 1. Ordnung
347
Zunächst trennen wir die Variablen, dann werden beide Seiten integriert:
10
dv
¼ 40 v ¼ ðv 40Þ
dt
ð
dv
dt
¼
¼ 0,1 d t
v 40
10
)
dv
¼ 0,1
v 40
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
)
ð
1 dt
Integral 2 mit a ¼ 1 , b ¼ 40
ln j v 40 j ¼ 0,1 t þ ln j C j
)
ln j v 40 j ln j C j ¼ 0,1 t
v 40
¼ 0,1 t
ln
C
)
(Rechenregel: R2). Durch Entlogarithmierung folgt (Rechenregeln: R5 und R6):
v 40
v 40
0;1 t
)
¼ e 0;1 t ) v 40 ¼ C e 0;1 t ¼ K e 0;1 t
C ¼ e
C
v ¼ 40 þ K e 0;1 t
)
ðmit K ¼ C Þ
Zu Beginn der Bewegung (d. h. zur Zeit t ¼ 0) beträgt die Geschwindigkeit v ð0Þ ¼ 10 . Aus dieser Anfangsgeschwindigkeit lässt sich die Integrationskonstante K wie folgt berechnen:
v ð0Þ ¼ 10
)
40 þ K e 0 ¼ 40 þ K 1 ¼ 40 þ K ¼ 10
Das gesuchte Geschwindigkeit-Zeit-Gesetz lautet damit
(siehe Bild G-3):
v ¼ 40 30 e 0;1 t ;
)
K ¼ 10 40 ¼ 30
v
40
t 0
Die Endgeschwindigkeit vE erhält man für t ! 1,
d. h. nach (theoretisch) unendlich langer Zeit:
v = 40 – 30 · e– 0,1 t
v E ¼ lim v ðtÞ ¼ lim ð40 30 e 0,1 t Þ ¼ 40
t!1
10
t!1
(e 0,1 t strebt für t ! 1 gegen 0)
10
20
30 t
Bild G-3
G6
y 0 ¼ 1 y2 ;
Anfangswert : y ð0Þ ¼ 0
Zunächst trennen wir die Variablen, dann werden beide Seiten integriert:
dy
¼ 1 y2
dx
ð
ð
dy
¼ 1 dx
1 y2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
y0 ¼
dy
)
1 y2
)
¼ dx
)
1 þ y
1
¼ x þ ln j C j
ln
1 y
2
2
)
1 þ y
¼ 2 x þ 2 ln j C j
ln
1 y
Integral 46 mit a 2 ¼ 1
1 þ y
¼ 2 x þ ln j C j 2 ¼ 2 x þ ln C 2
ln
1 y
ln
¼ 2x
C 2 ð1 yÞ
1þy
)
1 þ y
ln C 2 ¼ 2 x
ln
1 y
1þy
2x
C 2 ð1 yÞ ¼ e
1þy
¼ C2 e 2x ¼ K e 2x
1y
Rechenregeln: R2, R5 und R6
)
ðmit K ¼ C 2 Þ
)
1þy
C 2 ð1 yÞ
¼ e 2x
)
)
)
348
G Gewöhnliche Differentialgleichungen
Wir lösen diese implizite Funktionsgleichung noch nach y auf:
1 þ y ¼ K e 2 x ð1 yÞ ¼ K e 2 x K e 2 x y
y ð1 þ K e 2 x Þ ¼ K e 2 x 1
)
y ¼
)
y þ K e 2x y ¼ K e 2x 1
)
K e 2x 1
K e 2x þ 1
Die Integrationskonstante K berechnen wir aus dem Anfangswert y ð0Þ ¼ 0:
y ð0Þ ¼ 0
)
K e0 1
K 11
K 1
¼
¼ 0
¼
K 1þ1
K þ1
K e0 þ 1
)
K 1 ¼ 0
)
K ¼ 1
Die spezielle Lösung lautet damit:
y ¼
G7
e 2x 1
¼ tanh x
e 2x þ 1
tanh x ¼
2 x y þ ð1 þ x 2 Þ y 0 ¼ 0 ;
ex ex
ðe x e x Þ e x
e 2x 1
¼
¼
e 2x þ 1
ex þ ex
ðe x þ e x Þ e x
Anfangswert : y ð1Þ ¼ 10
Wir trennen zunächst die Variablen und integrieren dann beide Seiten:
2 x y þ ð1 þ x 2 Þ y 0 ¼ 2 x y þ ð1 þ x 2 Þ
ð
dy
¼ 2
y
dy
¼ 0
dx
ð
x
dx
1 þ x2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
)
ln j y j ¼ 2
)
ð1 þ x 2 Þ
dy
¼ 2xy
dx
1
ln j 1 þ x 2 j þ ln j C j
2
)
dy
2x
¼
dx
y
1 þ x2
)
Integral 32 mit a 2 ¼ 1
C
ln j y j ¼ ln j 1 þ x j þ ln j C j ¼ ln j C j ln j 1 þ x j ¼ ln
1 þ x2
2
2
(Rechenregel: R2). Durch Entlogarithmieren finden wir die allgemeine Lösung der Dgl (Rechenregeln: R5 und R6):
C
K
) y ¼ C
jyj ¼
¼
ðmit K ¼ CÞ
2
2
1þx
1þx
1 þ x2
Aus dem Anfangswert y ð1Þ ¼ 10 bestimmen wir K und damit die spezielle Lösung:
y ð1Þ ¼ 10
)
K
K
¼
¼ 10
1þ1
2
)
K ¼ 20
)
y ¼
20
1 þ x2
Zusammenhang zwischen Geschwindigkeit und Auslenkung bei einem Feder-Masse-Schwinger
Beschreiben Sie die Bewegung des in Bild G-4 dargestellten Feder-Masse-Schwingers durch eine Dgl
1. Ordnung und bestimmen Sie den Zusammenhang zwischen der Geschwindigkeit v und der Auslenkung x,
wenn die Masse m bei entspannter Feder ðx ¼ 0Þ die Geschwindigkeit v 0 besitzt.
G8
Anleitung: Nach Newton ist das Produkt aus Masse m und Beschleunigung a gleich der Summe der einwirkenden Kräfte. Reibungskräfte sollen hier unberücksichtigt bleiben. Für die
elastische Feder gilt das Hookesche Gesetz (mit der Federkonstanten c > 0). Auslenkung x und Geschwindigkeit v
sind Funktionen der Zeit t (mit t 0).
Bild G-4
Federkonstante c
x=0
x = x (t )
m
1 Differentialgleichungen 1. Ordnung
349
Die auf die Masse m einwirkende beschleunigende Kraft ist die Differenz aus dem Gewicht m g und der Rückstellkraft c x der elastischen Feder (Hookesches Gesetz). Nach Newton gilt dann:
dv
dv
ðÞ
m a ¼ m g c x oder m
¼ mg cx
a ¼ v_ ¼
; g: Erdbeschleunigung
dt
dt
(die Beschleunigung a ist die 1. Ableitung der Geschwindigkeit v nach der Zeit t). Wir suchen die Abhängigkeit der
Geschwindigkeit v von der Auslenkung x . Dabei ist zu beachten, dass x selbst von der Zeit t abhängt. Die Geschwindigkeit v ist daher eine mittelbare Funktion der Zeit t und nach der Kettenregel gilt:
dv
dv dx
dv
dv
dx
¼
¼
v ¼ v
mit v ¼
dt
dx dt
dx
dx
dt
(die Geschwindigkeit v ist bekanntlich die 1. Ableitung des Weges x nach der Zeit t). Einsetzen in Gleichung (*)
liefert eine einfache Dgl 1. Ordnung für die gesuchte Funktion v ¼ v ðxÞ , die sich leicht durch „Trennung der Variablen‘‘ lösen lässt:
dv
dv
¼ mv
¼ m g c x ) m v d v ¼ ðm g c xÞ d x )
dt
dx
ð
ð
1
1
m v d v ¼ ðm g c xÞ d x )
m v2 ¼ m g x
cx2 þ K
2
2
m
Bei entspannter Feder (x ¼ 0) bewegt sich die Masse mit der Geschwindigkeit v0 . Aus diesem Anfangswert bestimmen wir die Integrationskonstante K:
v ðx ¼ 0Þ ¼ v 0
)
1
1
m v 20 ¼ m g 0
c 02 þ K ¼ K
2
2
)
K ¼
Damit hängt die Geschwindigkeit v wie folgt von der Auslenkung x ab:
2
1
1
1
c 2
m v2 ¼ m g x
cx2 þ
m v 20
) v2 ¼ 2 g x
x þ v 20
2
2
2
m
m
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
c 2
ðmit w 20 ¼ c=mÞ
x þ v 20 ¼ 2 g x w 20 x 2 þ v 20
v ¼ 2gx
m
rffiffiffiffiffiffi
c
w0 ¼
ist dabei die Kreisfrequenz der periodischen Bewegung (Schwingung).
m
G9
y0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2 ¼ y
1
m v 20
2
)
(a: Konstante)
Zunächst trennen wir die Variablen, dann werden beide Seiten integriert:
y0
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
d y pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2 ¼ y
a2 þ x2 ¼
dx
dy
¼
y
)
dy
dx
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y
a2 þ x2
ð
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
)
ln j y j ¼ ln x þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2
)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
þ ln j C j ¼ ln C x þ a 2 þ x 2
Integral 123
(Rechenregel: R1). Wir entlogarithmieren und erhalten die allgemeine Lösung der Dgl:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
j y j ¼ C x þ a2 þ x2 ) y ¼ C x þ a2 þ x2 ¼ K x þ a2 þ x2
Rechenregeln: R5 und R6
ðK ¼ C 2 Þ
350
G Gewöhnliche Differentialgleichungen
Bimolekulare chemische Reaktion 2. Ordnung vom Typ A + B ! AB
Ein Molekül A vereinigt sich mit einem Molekül B zu einem neuen Molekül AB . Zu Beginn der
Reaktion ðt ¼ 0Þ sind von beiden Bindungspartnern jeweils c Moleküle vorhanden. Die Umsatzvariable x ¼ x ðtÞ beschreibt dann die Anzahl der zur Zeit t „verbrauchten“ Moleküle vom Typ A
bzw. B und damit die Anzahl der in dieser Zeit entstandenen neuen Moleküle AB . Sie genügt der Dgl
G10
dx
¼ k ðc xÞ 2
dt
ðk > 0 : GeschwindigkeitskonstanteÞ
Bestimmen Sie den zeitlichen Verlauf der Umsatzvariablen x . Wann kommt die chemische Reaktion
zum Stillstand?
Wir trennen zunächst die Variablen und integrieren anschließend beide Seiten:
dx
¼ k ðc xÞ 2 ¼ k ðx cÞ 2
dt
ð
ð
dx
ðx cÞ
2
¼
dx
)
¼ k dt
ðx cÞ 2
ðx cÞ 2 d x ¼ k
ð
ðx cÞ 1
)
1 dt
)
1 1
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
¼ ðx cÞ 1 ¼ k t þ K
)
Integral 1 mit a ¼ 1 , b ¼ c ; n ¼ 2
1
¼ k t þ K ð 1Þ
x c
)
1
¼ kt K
x c
Aus dem Anfangswert x ð0Þ ¼ 0 bestimmen wir die Integrationskonstante K (zu Beginn der chemischen Reaktion
gibt es noch keine „neuen“ Moleküle vom Typ A B, d. h. x ð0Þ ¼ 0Þ:
x ð0Þ ¼ 0
)
1
¼ 0K
0c
)
1
¼ K
c
)
K ¼
1
c
Somit gilt:
1
1
¼ kt
x c
c
)
1
ckt 1
¼
x c
c
)
x c ¼
c
ckt 1
(letzter Rechenschritt: Kehrwertbildung auf beiden Seiten). Wir lösen diese Gleichung nach der Umsatzvariablen x
auf und erhalten:
x ¼
c þ c ð c k t 1Þ
c
c c2 k t c
c2 k t
c2 k t
þc ¼
¼
¼
;
¼
ckt 1
ckt 1
ckt 1
ckt þ 1
ckt 1
t 0
Umformungen: Hauptnenner bilden, d. h. den Summand c mit ð c k t 1Þ erweitern.
Die chemische Reaktion kommt (theoretisch!) nach unendlich langer Reaktionszeit zum Stillstand (siehe Bild G-5):
lim x ðtÞ ¼ lim
t!1
t!1
¼
c2 k t
¼ lim
ckt þ 1
t!1
c2 k
ck þ
1
t
¼
x
c
c2 k
ck c
¼ c
¼
ck
ck
x=
Dann sind sämtliche Moleküle beider Sorten A und B
„verbraucht‘‘ und es sind genau x ¼ c Moleküle vom
Typ A B entstanden.
Umformungen: Vor der Grenzwertbildung Zähler und
Nenner gliedweise durch t dividieren.
c 2k t
ckt + 1
t
Bild G-5
1 Differentialgleichungen 1. Ordnung
351
x ðx þ 1Þ y 0 þ ðx 2Þ y 2 ¼ 0
G11
Das anfallende Integral soll dabei mit Hilfe der Partialbruchzerlegung gelöst werden.
Wir trennen zunächst die beiden Variablen:
x ðx þ 1Þ y 0 þ ðx 2Þ y 2 ¼ x ðx þ 1Þ
x ðx þ 1Þ
dy
¼ ðx 2Þ y 2
dx
)
dy
þ ðx 2Þ y 2 ¼ 0
dx
dy
y2
¼
)
x 2
dx
x ðx þ 1Þ
Integration beider Seiten:
ð
dy
y2
ð
¼
y 2 d y ¼
y1
1
¼
¼
y
1
ð
x 2
d x ð 1Þ
x ðx þ 1Þ
)
1
¼
y
ð
x 2
dx
x ðx þ 1Þ
Das Integral der rechten Seite lösen wir mittels Partialbruchzerlegung des Integranden wie folgt (die Nullstellen des
Nenners liegen bei x 1 ¼ 0 und x 2 ¼ 1):
A ðx þ 1Þ þ B x
x 2
A
B
¼
þ
¼
x
x þ1
x ðx þ 1Þ
x ðx þ 1Þ
Die Partialbrüche werden der Reihe nach mit x þ 1 bzw. x erweitert und so auf den Hauptnenner x ðx þ 1Þ gebracht. Die Brüche auf beiden Seiten der Gleichung stimmen jetzt im Nenner und somit auch im Zähler überein. Dies
liefert die folgende Bestimmungsgleichung für die unbekannten Konstanten:
A ðx þ 1Þ þ B x ¼ x 2
Wir setzen für x der Reihe nach die Werte 0 und 1 ein und erhalten für die Konstanten A und B folgende
Werte:
9
>
x ¼ 0
)
A ¼ 2
=
x 2
2
3
¼
)
þ
>
x
x þ1
x ðx þ 1Þ
x ¼ 1
) B ¼ 3 ) B ¼ 3 ;
Die Integration lässt sich jetzt leicht durchführen (das zweite Integral lösen wir durch die Substitution u ¼ x þ 1,
d x ¼ d u):
ð
ð
ð
ð
ð
ð
x 2
2
3
dx
dx
dx
du
dx ¼
þ
dx ¼ 2
þ3
¼ 2
þ3
¼
x
x þ1
x
x þ1
x
u
x ðx þ 1Þ
|fflffl{zfflffl}
u
¼ 2 ln j x j þ 3 ln j u j þ ln j C j ¼ 2 ln j x j þ 3 ln j x þ 1 j þ ln j C j ¼
¼ ln j x j 2 þ ln j x þ 1 j 3 þ ln j C j ¼ ln j x 2 j þ ln j ðx þ 1Þ 3 j þ ln j C j ¼
C ðx þ 1Þ 3
3
2
¼ ln j C ðx þ 1Þ x j ¼ ln
x2
(Rechenregeln: R3 und R1). Damit erhalten wir die folgende allgemeine Lösung:
ð
C ðx þ 1Þ 3
1
x 2
1
) y ¼
d x ¼ ln
¼
2
y
x ðx þ 1Þ
x
C ðx þ 1Þ 3
ln
x2
352
G Gewöhnliche Differentialgleichungen
1.2 Integration einer Differentialgleichung durch Substitution
Alle Differentialgleichungen in diesem Abschnitt lassen sich mit Hilfe einer geeigneten Substitution auf einfache Differentialgleichungen 1. Ordnung zurückführen, die meist durch „Trennung der Variablen“ oder „Variation der Konstanten“ lösbar sind. Wir unterscheiden dabei folgende Substitutionstypen:
Typ A
y 0 ¼ f ða x þ b y þ cÞ ;
Typ B
y0 ¼ f
Typ C
y 0 þ g ðxÞ y ¼ h ðxÞ y n
y
;
x
Substitution : u ¼ a x þ b y þ c
Substitution : u ¼
y
x
ðn 6¼ 1Þ ;
ða; b; c : KonstantenÞ
(homogene Dgl)
Substitution : u ¼ y 1 n
(Bernoullische Dgl)
Beachten Sie, dass die Substitutionsvariable u eine Funktion der Variablen x ist.
Lehrbuch: Band 2, Kapitel IV.2.3
Formelsammlung: Kapitel X.2.2
G12
2xyy0 x2 ¼ y2
oder
y0 ¼
y2 þ x2
1
¼
2
2xy
y
x
þ
x
y
Die vollständige Substitution dieser Dgl vom Typ B lautet (der 2. Summand ist der Kehrwert des 1. Summanden):
u ¼
y
;
x
y ¼ xu;
y0 ¼ 1 u þ u0 x ¼ u þ xu0
(Ableitung von y ¼ x u nach der ProduktregelÞ
Sie führt auf die folgende Dgl für u:
2 x y y 0 x2 ¼ y2
)
2 u ðu þ x u 0 Þ ¼ 1 þ u 2
2 x ðx uÞ ðu þ x u 0 Þ x 2 ¼ x 2 u 2
)
2 u2 þ 2 x u u 0 ¼ 1 þ u2
)
)
2 x 2 u ðu þ x u 0 Þ ¼ x 2 þ x 2 u 2 : x 2
2 x u u 0 ¼ 1 u2
Lösung durch „Trennung der Variablen‘‘:
du
u du
dx
¼ 1 u2 )
)
¼
2
dx
2x
1u
ð
ð
u du
1
dx
1
1
)
ln j 1 u 2 j ¼
ln j x j þ ln j C j ð 2Þ
¼
2
x
2
2
1 u2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
2xuu0 ¼ 2xu
)
Integral 49 mit a 2 ¼ 1
ln j 1 u 2 j ¼ ln j x j 2 ln j C j ¼ ln j x j ln j C j 2 ¼ ln j x j ln C 2 ¼ ðln j x j þ ln C 2 Þ ¼
¼ ln j C 2 x j ¼ 1 ln j C 2 x j ¼ ln j C 2 x j 1
(Rechenregeln: R3, R1 und nochmals R3). Durch Entlogarithmierung folgt (Rechenregeln: R5 und R6):
1
1
K
K
1
2
2
2
2
¼
j1 u j ¼ jC xj
) u ¼
1 ð 1Þ
) 1u ¼
¼
2
2
x
x
jC xj
C x
K
K
x K
þ1 ¼ 1
¼
u ¼
x
x
x
2
1
mit K ¼
C2
Rücksubstitution (u ¼ y=x) liefert die gesuchte Lösung:
2
y
y2
x K
u2 ¼
¼
¼
) y 2 ¼ x ðx KÞ ¼ x 2 K x
x
x
x2
)
y ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 K x
)
1 Differentialgleichungen 1. Ordnung
G13
y 0 ¼ ð1 þ x þ yÞ 2 ;
353
Anfangswert : y ð0Þ ¼ 2
Diese Dgl ist vom Typ A und wird durch die Substitution u ¼ 1 þ x þ y wie folgt gelöst:
u0 ¼ 0 þ 1 þ y0 ¼ 1 þ y0
u ¼ 1 þ x þ y;
y 0 ¼ ð1 þ x þ yÞ 2
)
u 0 1 ¼ u2
)
)
y0 ¼ u0 1
)
u0 ¼
du
¼ 1 þ u2
dx
)
du
¼ dx
1 þ u2
Nach der bereits vorgenommenen Trennung der Variablen werden beide Seiten integriert:
ð
ð
du
¼ 1 d x ) arctan u ¼ x þ C ) u ¼ tan ðx þ CÞ
1 þ u2
Durch Rücksubstitution erhalten wir die gesuchte allgemeine Lösung:
u ¼ 1 þ x þ y ¼ tan ðx þ CÞ
)
y ¼ tan ðx þ CÞ x 1
Aus dem Anfangswert y ð0Þ ¼ 2 bestimmen wir die spezielle Lösung:
y ð0Þ ¼ 2
)
tan C 1 ¼ 2
)
tan C ¼ 3
)
C ¼ arctan 3 ¼ 1,2490
ðBogenmaß !Þ
Lösung: y ¼ tan ðx þ 1,2490Þ x 1
G14
2yy0 þ x y2 ¼ 0
Wir bringen diese Dgl zunächst auf eine andere Form, um zu erkennen, mit welcher Substitution sie gelöst werden
kann:
1
1 x
1
y ¼
¼
x y1
2
2 y
2
1
1
Die Dgl ist also eine Bernoulli-Dgl Typ C mit g ðxÞ ¼ , h ðxÞ ¼
x und n ¼ 1 . Mit der Substitu2
2
tion u ¼ y 1 n ¼ y 1 ð 1Þ ¼ y 2 erreichen wir unser Ziel:
2 y y 0 þ x y2 ¼ 0 j : 2 y
u0 ¼
u ¼ y2 ;
)
y0 þ
1 x
1
y ¼ 0
2 y
2
)
y0
du
du dy
¼
¼ 2yy0
dx
dy dx
(u hängt von y, y wiederum von x ab ! Kettenregel anwenden). Wir setzen diese Ausdrücke in die ursprüngliche
Form der Bernoulli-Dgl ein und erhalten eine inhomogene lineare Dgl 1. Ordnung:
2 y y 0 þ x y2 ¼ 0
)
u0 þ x u ¼ 0
)
u0 u ¼ x
Diese Dgl lösen wir durch „Variation der Konstanten‘‘. Zunächst wird die zugehörige homogene Dgl durch „Trennung
der Variablen‘‘ gelöst:
u0 u ¼ 0
ð
du
¼
u
)
u0 ¼
ð
1 dx
)
du
¼ u
dx
)
du
¼ dx
u
ln j u j ¼ x þ ln j C j
)
)
u
ln j u j ln j C j ¼ ln ¼ x
C
(Rechenregel: R2). Entlogarithmierung liefert dann (Rechenregeln: R5 und R6):
u
u
ðmit K ¼ CÞ
¼ ex ) u ¼ C ex ¼ K ex
¼ ex )
C
C
354
G Gewöhnliche Differentialgleichungen
Die inhomogene lineare Dgl lösen wir durch „Variation der Konstanten‘‘ ðK ! K ðxÞÞ . Lösungsansatz (mit der
benötigten Ableitung):
u 0 ¼ K 0 ðxÞ e x þ K ðxÞ e x
u ¼ K ðxÞ e x ;
ðProduktregelÞ
Einsetzen dieser Ausdrücke in die inhomogene Dgl führt zu:
u0 u ¼ x
K 0 ðxÞ e x þ K ðxÞ e x K ðxÞ e x ¼ x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
)
)
K 0 ðxÞ e x ¼ x e x
)
K 0 ðxÞ ¼ x e x
Integration liefert:
ð
ð
0
K ðxÞ ¼ K ðxÞ d x ¼ x e x d x ¼ ð x 1Þ e x þ K 1 ¼ ðx þ 1Þ e x þ K 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ 1
Damit gilt:
u ¼ K ðxÞ e x ¼ ½ ðx þ 1Þ e x þ K 1 e x ¼ ðx þ 1Þ e x e x þ K 1 e x ¼ x þ 1 þ K 1 e x
|fflfflfflfflffl{zfflfflfflfflffl}
e0 ¼ 1
Durch Rücksubstitution finden wir für die vorgegebene Bernoulli-Dgl die folgende allgemeine Lösung:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y2 ¼ u ¼ x þ 1 þ K1 e x ) y ¼ x þ 1 þ K1 e x
ðmit K 1 2 RÞ
G15
x y 0 ¼ y ðln x ln y þ 1Þ
Diese Dgl ist vom Typ B, denn sie kann wie folgt umgeschrieben werden:
y
0
)
x y ¼ y ðln x ln y þ 1Þ ¼ y ½ 1 ðln y ln xÞ ¼ y 1 ln
x
y
y
1 ln
y ¼
x
x
0
(Rechenregel: R2). Mit der Substitution
u ¼
y
;
x
y ¼ xu
y0 ¼ 1 u þ u0 x ¼ xu0 þ u
)
(Ableitung mit der Produktregel Þ
erhalten wir eine Dgl für u , die sich durch „Trennung der Variablen‘‘ lösen lässt:
y
y
1 ln
) x u 0 þ u ¼ u ð1 ln uÞ ¼ u u ln u
y0 ¼
x
x
x u 0 ¼ u ln u
ð
du
¼
u ln u
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
ð
)
dx
x
x
)
du
¼ u ln u
dx
)
du
dx
¼
u ln u
x
)
)
C
ln j ln u j ¼ ln j x j þ ln j C j ¼ ln j C j ln j x j ¼ ln
x
Integral 343
(Rechenregel: R2). Wir entlogarithmieren und erhalten (Rechenregeln: R5, R6 und nochmals R5):
C
C
K
ðmit K ¼ CÞ
j ln u j ¼ ) ln u ¼
¼
) u ¼ e K=x
x
x
x
Rücksubstitution führt schließlich zur gesuchten Lösung:
y ¼ x u ¼ x e K=x
ðK 2 RÞ
1 Differentialgleichungen 1. Ordnung
G16
355
x 2 y 0 ¼ y ðx yÞ
Durch eine geringfügige Umstellung erkennt man, dass diese Dgl vom Typ B ist:
2
x y y2
y
y2
y
y
¼
¼
x 2 y 0 ¼ y ðx yÞ ¼ x y y 2 ) y 0 ¼
x
x
x
x2
x2
Sie lässt sich also durch die folgende Substitution in eine durch „Trennung der Variablen‘‘ lösbare Dgl überführen:
y
; y ¼ xu ) y0 ¼ 1 u þ u0 x ¼ u þ xu0
(Ableitung mit der Produktregel Þ
x
2
y
y
du
du
dx
y0 ¼
) u þ x u 0 ¼ u u2 ) x u 0 ¼ x
¼
¼ u2 )
x
x
dx
x
u2
u ¼
Integration beider Seiten führt zur Lösung für die Hilfsvariable u:
ð
ð
ð
ð
du
dx
dx
u1
1
2
)
u du ¼
)
¼ ln j x j þ C ð 1Þ
¼
¼
2
x
x
u
1
u
1
¼ ln j x j C
u
)
u ¼
1
ln j x j C
)
(nach Kehrwertbildung)
Durch Rücksubstitution erhalten wir die gesuchte Lösung:
y ¼ xu ¼ x
G17
1
¼
ln j x j C
xy0 þ y ¼ xy2
x
ln j x j C
oder
y0 þ
ðmit C 2 RÞ
1
y ¼ y2 ;
x
Anfangswert: y ð1Þ ¼ 0,2
Mit Hilfe der Substitution u ¼ y 1 2 ¼ y 1 lässt sich diese Bernoulli-Dgl ðTyp C mit g ðxÞ ¼ 1=x , h ðxÞ ¼ 1
und n ¼ 2Þ auf eine lineare Dgl zurückführen:
u ¼ y1 ¼
1
y
)
y ¼
1
¼ u1
u
)
y0 ¼
dy
dy du
u0
¼
¼ u 2 u 0 ¼
dx
du dx
u2
(differenziert wurde nach der Kettenregel, da y von u und u wiederum von x abhängt)
Vollständige Substitution:
x y 0 þ y ¼ x y2
y ¼ u1 ¼
)
x
1
u0
, y0 ¼
u
u2
u0
1
1
u2
þ
¼ x
u
u2
u2
)
xu0 þ u ¼ x:
Diese lineare Dgl 1. Ordnung lösen wir durch „Variation der Konstanten‘‘. Zunächst wird die zugehörige homogene
Dgl durch „Trennung der Variablen‘‘ gelöst:
du
du
du
dx
xu0 þ u ¼ 0 ) xu0 ¼ x
¼ u ð 1Þ ) x
¼ u )
¼
)
dx
dx
u
x
ð
ð
du
dx
¼
) ln j u j ¼ ln j x j þ ln j C j ) ln j u j ¼ ln j C x j ) j u j ¼ j C x j )
u
x
u ¼ Cx ¼ K x
ðmit K ¼ CÞ
Rechenregeln: R1, R5 und R6
356
G Gewöhnliche Differentialgleichungen
„Variation der Konstanten‘‘ ðK ! K ðxÞÞ führt zu dem folgenden Lösungsansatz für die inhomogene Dgl (Ableitung
nach der Produktregel):
u ¼ K ðxÞ x ;
u 0 ¼ K 0 ðxÞ x þ 1 K ðxÞ ¼ K 0 ðxÞ x þ K ðxÞ
Einsetzen von u und u 0 in die inhomogene Dgl, Bestimmen der noch unbekannten Faktorfunktion K ðxÞ:
xu0 þ u ¼ x
)
x ½ K 0 ðxÞ x þ K ðxÞ þ K ðxÞ x ¼ x
x 2 K 0 ðxÞ x K ðxÞ þ x K ðxÞ ¼ x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
K ðxÞ ¼
K 0 ðxÞ d x ¼
ð
)
)
x 2 K 0 ðxÞ ¼ x : ð x 2 Þ
)
K 0 ðxÞ ¼
1
x
1
d x ¼ ln j x j þ K *
x
Allgemeine Lösung der inhomogenen Dgl: u ¼ K ðxÞ x ¼ ðln j x j þ K *Þ x
Durch Rücksubstitution erhalten wir schließlich die Lösung der Bernoulli-Dgl. Sie lautet:
y ¼
1
1
1
¼
¼
u
ðln j x j þ K *Þ x
x ln j x j þ K * x
Spezielle (partikuläre) Lösung für den Anfangswert y ð1Þ ¼ 0,2:
y ð1Þ ¼ 0,2
Lösung: y ¼
G18
1
)
1 ln j 1 j þ K * 1
1
ðln j x j þ 5Þ x
¼
¼
1
1
¼
¼ 0,2
0 þ K*
K*
)
K* ¼ 5
1
x ln j x j þ 5 x
y 0 þ y ¼ ðcos x sin xÞ y 2
Durch die Substitution u ¼ y 1 2 ¼ y 1 lässt sich diese Bernoulli-Dgl ðTyp C mit g ðxÞ ¼ 1, h ðxÞ ¼ cos x sin x
und n ¼ 2Þ in eine lineare Dgl verwandeln:
u ¼ y1 ;
y ¼ u1 ;
y0 ¼
dy
dy du
u0
¼ u 2 u 0 ¼
¼
dx
du dx
u2
(differenziert wurde mit Hilfe der Kettenregel, da y von u und u wiederum von x abhängt)
Vollständige Substitution:
y ¼ u1 ¼
y 0 þ y ¼ ðcos x sin xÞ y 2
1
u0
, y0 ¼
u
u2
)
u 0 þ u ¼ cos x sin x ð 1Þ
u0
1
1
þ
u2
¼ ðcos x sin xÞ
u
u2
u2
)
u 0 u ¼ cos x þ sin x
)
)
u 0 u ¼ sin x cos x
Diese lineare Dgl mit konstanten Koeffizienten lösen wir nach der Methode „Aufsuchen einer partikulären Lösung‘‘.
Zunächst wird die zugehörige homogene Dgl u 0 u ¼ 0 durch den Exponentialansatz u 0 ¼ C e l x gelöst:
u0 ¼ C e lx ;
u 00 ¼ l C e l x ;
u 00 u 0 ¼ l C e l x C e l x ¼ C e l x ðl 1Þ ¼ 0
|fflfflfflffl{zfflfflfflffl}
6¼ 0
Damit ist u 0 ¼ C e x die allgemeine Lösung der homogenen Dgl.
)
l ¼ 1
1 Differentialgleichungen 1. Ordnung
357
Partikuläre Lösung der inhomogenen Dgl
Aus der Tabelle (FS: Kapitel X.2.4.4 bzw. Bd. 2: Kapitel IV.2.6) entnehmen wir den folgenden Lösungsansatz für eine
partikuläre Lösung u P :
w ¼ 1
Störglied g ðxÞ ¼ sin x cos x
!
u P ¼ C 1 sin x þ C 2 cos x
Mit diesem Ansatz und der zugehörigen Ableitung gehen wir in die inhomogene Dgl ein:
u P ¼ C 1 sin x þ C 2 cos x ;
u 0P ¼ C 1 cos x C 2 sin x
u 0 u ¼ C 1 cos x C 2 sin x C 1 sin x C 2 cos x ¼ sin x cos x
Wir ordnen die Glieder und vergleichen dann die Sinus- bzw. Kosinusterme beider Seiten. Dieser Koeffizientenvergleich
liefert zwei leicht lösbare Gleichungen für die beiden Unbekannten C1 und C2 :
ð C 1 C 2 Þ sin x þ ðC 1 C 2 Þ cos x ¼ 1 sin x 1 cos x
ðIÞ
C1 C2 ¼
ðIIÞ
1
)
C1 C2 ¼ 1
2 C2 ¼ 0
þ
)
C 2 ¼ 0;
ðIIÞ
)
C1 ¼ 1 þ C2 ¼ 1 þ 0 ¼ 1
Somit gilt: u P ¼ 1 sin x þ 0 cos x ¼ sin x
Die allgemeine Lösung der inhomogenen linearen Dgl lautet damit: u ¼ u 0 þ u P ¼ C e x sin x
Durch Rücksubstitution erhalten wir schließlich die gesuchte Lösung der Bernoulli-Dgl:
y ¼
G19
1
1
¼
x
u
C e sin x
xyy0 ¼ 4x2 þ y2
Diese Dgl ist vom Typ B, denn sie lässt sich in der Form
y0 ¼
4 x2 þ y2
y2
y
4x2
4x
x
¼ 4
þ
þ
¼
þ
¼
x
y
y
xy
xy
xy
1
y
y
y
¼ 4
þ
x
x
x
darstellen ðx=y ist der Kehrwert von y=xÞ. Die Substitution
u ¼
y
;
x
y ¼ xu
)
y0 ¼ 1 u þ u0 x ¼ u þ xu0
ðAbleitung mit der Produktregel Þ
führt dann zu einer Dgl, die sich durch „Trennung der Variablen‘‘ lösen lässt:
1
y
y
4
) u þ x u 0 ¼ 4 u1 þ u ¼
þu )
þ
y0 ¼ 4
x
x
u
xu0 ¼ x
du
4
¼
dx
u
)
u du ¼
4
dx
x
ð
)
ð
u du ¼ 4
1
dx
x
xu0 ¼
4
u
)
)
1 2
1 2
u ¼ 4 ðln j x j þ ln j C j Þ )
u ¼ 4 ln j C x j 2 ) u 2 ¼ 8 ln j C x j
2
2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u ¼ 8 ln j C x j ¼ 2 2 ln j C x j
ðRechenregel : R1Þ
Durch Rücksubstitution erhalten wir schließlich die allgemeine Lösung der Dgl:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y ¼ x u ¼ 2 x 2 ln j C x j
)
358
G Gewöhnliche Differentialgleichungen
G20
y 0 ¼ 2 ð2 x þ y þ 1Þ 1
Diese Dgl ist vom Typ A. Mit der Substitution
u0 ¼ 2 þ y0 þ 0 ¼ 2 þ y0
u ¼ 2x þ y þ 1;
y0 ¼ u0 2
)
erhalten wir eine Dgl für die Variable u , die durch „Trennung der Variablen‘‘ lösbar ist:
y 0 ¼ 2 ð2 x þ y þ 1Þ 1
u0 ¼
)
u 0 2 ¼ 2 u1 ¼
2 ðu þ 1Þ
du
2 þ 2u
¼
¼
u
dx
u
)
2
u
)
u du
¼ 2 dx
uþ1
)
2
2 þ 2u
þ2 ¼
)
u
u
ð
ð
u du
¼ 2 dx )
uþ1
|fflfflfflfflffl{zfflfflfflfflffl}
u0 ¼
Integral 4 mit a ¼ b ¼ 1
u ln j u þ 1 j ¼ 2 x þ C
Durch Rücksubstitution erhalten wir die allgemeine Lösung in impliziter Form:
2 x þ y þ 1 ln j 2 x þ y þ 2 j ¼ 2 x þ C
G21
)
y ln j 2 x þ y þ 2 j ¼ C 1 ¼ K
ðK ¼ C 1Þ
x 2 y 0 ¼ y 2 x y ; Anfangswert : y ð 1Þ ¼ 1
Dividiert man die Dgl gliedweise durch x2 , so erhält man:
2
y2
xy
y2
y
y
y
0
¼
2 ¼
y ¼
2
2
x
x
x
x
x
x
Diese Dgl ist also vom Typ B. Wir lösen sie durch die Substitution
u ¼
y
;
x
y ¼ xu;
y0 ¼ 1 u þ u0 x ¼ u þ xu0
schrittweise wie folgt („Trennung der Variablen‘‘):
2
y
y
0
) u þ x u 0 ¼ u2 u
y ¼
x
x
du
dx
¼
2
x
u 2u
ð
)
du
¼
2
u 2u
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
ð
dx
x
)
)
(Ableitung mit der Produktregel Þ
xu0 ¼ x
du
¼ u2 2 u
dx
)
u 2
1
¼ ln j x j þ ln j C j ¼ ln j C x j
ln
2
u
Integral 63 mit a ¼ 1 , b ¼ 2 , c ¼ 0 ; D ¼ 4 < 0
u 2
¼ 2 ln j C x j ¼ ln j C x j 2 ¼ ln ðC xÞ 2
ln
u
(Rechenregeln: R1 und R3). Entlogarithmierung liefert (Rechenregeln: R5 und R6):
u 2
u2
2
¼ ðC xÞ 2 ¼ C 2 x 2 ¼ K x 2
)
ðmit K ¼ C 2 Þ
u ¼ ðC xÞ
u
u 2 ¼ K x2 u
)
u K x2 u ¼ 2
)
ð1 K x 2 Þ u ¼ 2
)
u ¼
2
1 K x2
)
2
)
1 Differentialgleichungen 1. Ordnung
359
Durch Rücksubstitution erhalten wir schließlich die allgemeine Lösung:
y ¼ xu ¼ x
2
2x
¼
2
1 Kx
1 K x2
Spezielle Lösung für den Anfangswert y ð 1Þ ¼ 1:
2
¼ 1 ð1 KÞ
¼
2
1K
1 K ð 1Þ
2 ð 1Þ
ð1 þ x 2 Þ y y 0 ¼ x ð1 þ y 2 Þ;
G22
)
2 ¼ 1 K
)
K ¼ 3
)
y ¼
2x
1 3x2
Anfangswert: y ð1Þ ¼ 3
Lösen Sie diese Dgl mit Hilfe der Substitution u ¼ 1 þ y 2 .
Mit der vorgeschlagenen Substitution gelingt die Integration der Dgl durch „Trennung der Variablen‘‘:
u ¼ 1 þ y2 ;
u0 ¼ 2yy0
ð1 þ x 2 Þ y y 0 ¼ x ð1 þ y 2 Þ
ð1 þ x 2 Þ
du
¼ 2xu
dx
)
ðKettenregel; denn y ist eine Funktion von x Þ
)
ð1 þ x 2 Þ
du
2x dx
¼
u
1 þ x2
)
yy0 ¼
1 0
u ¼ x u 2 ) ð1 þ x 2 Þ u 0 ¼ 2 x u
2
ð
ð
du
x dx
¼ 2
)
)
u
1 þ x2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
1 0
u
2
)
Integral 32 mit a 2 ¼ 1
ln j u j ¼ 2
1
ln ð1 þ x 2 Þ þ ln j C j ¼ ln ð1 þ x 2 Þ þ ln j C j ¼ ln j C ð1 þ x 2 Þ j
2
(Rechenregel: R1). Entlogarithmierung liefert (Rechenregeln: R5 und R6):
j u j ¼ j C ð1 þ x 2 Þ j
)
u ¼ C ð1 þ x 2 Þ ¼ K ð1 þ x 2 Þ
ðmit K ¼ CÞ
Rücksubstitution führt schließlich zur allgemeinen Lösung:
u ¼ K ð1 þ x 2 Þ ¼ 1 þ y 2
)
y 2 ¼ K ð1 þ x 2 Þ 1
)
Spezielle Lösung für den Anfangswert y ð1Þ ¼ 3:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K ð1 þ 1Þ 1 ¼ 3 )
2 K 1 ¼ 3 quadrieren
y ¼
y ¼
)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
K ð1 þ x 2 Þ 1
2K 1 ¼ 9
)
K ¼ 5
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5 ð1 þ x 2 Þ 1 ¼ 5 þ 5 x 2 1 ¼ 4 þ 5 x 2 ¼ 5 x 2 þ 4
Anmerkung: Wegen y ð1Þ ¼ 3 < 0 ist das negative Vorzeichen in der allgemeinen Lösung zu nehmen.
G23
y0 þ 4y ¼ 2
pffiffiffi
y
oder
y 0 þ 4 y ¼ 2 y 1=2
Mit der Substitution u ¼ y 1 1=2 ¼ y 1=2 ¼
h ðxÞ ¼ 2 und n ¼ 1=2Þ in eine lineare Dgl:
u ¼
pffiffiffi
y;
y ¼ u2 ;
y0 ¼
pffiffiffi
y überführen wir diese Bernoulli-Dgl ðTyp C mit g ðxÞ ¼ 4,
dy
dy du
¼
¼ 2u u0
dx
du dx
360
G Gewöhnliche Differentialgleichungen
Die Ableitung wurde mit der Kettenregel gebildet, da y von u und u wiederum von x abhängt. Die vollständige
Substitution lautet also:
pffiffiffi
y ¼ u2 ;
y ¼ u; y0 ¼ 2uu0
Wir erhalten mit dieser Substitution folgende lineare Dgl:
pffiffiffi
y 0 þ 4 y ¼ 2 y ) 2 u u 0 þ 4 u2 ¼ 2 u j : 2 u
)
u0 þ 2u ¼ 1:
Diese Dgl lösen wir durch „Variation der Konstanten‘‘. Die benötigte Lösung der zugehörigen homogenen Dgl
u 0 þ 2 u ¼ 0 erhalten wir am einfachsten mit dem Exponentialansatz u ¼ K e l x und der Ableitung
u 0 ¼ l K e lx :
u0 þ 2u ¼ 0
)
l K e l x þ 2 K e l x ¼ K e l x ðl þ 2Þ ¼ 0
|fflfflfflffl{zfflfflfflffl}
6¼ 0
)
lþ2 ¼ 0
)
l ¼ 2
Somit ist u ¼ K e 2 x die Lösung der homogenen linearen Dgl.
„Variation der Konstanten‘‘ führt zu dem folgenden Lösungsansatz für die inhomogene lineare Dgl ðK ! K ðxÞÞ:
u ¼ K ðxÞ e 2 x ;
u 0 ¼ K 0 ðxÞ e 2 x 2 K ðxÞ e 2 x
ðProdukt- und Kettenregel Þ
Diese Ausdrücke werden in die inhomogene Dgl eingesetzt und daraus dann die unbekannte Faktorfunktion K ðxÞ
bestimmt:
0
0
2x
2x
2x
0
2x
u þ 2 u ¼ 1 ) K ðxÞ e
2 K ðxÞ e
þ 2 K ðxÞ e
¼ 1 e 2 x
¼ 1 ) K ðxÞ e
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
K 0 ðxÞ ¼ e 2 x
)
K ðxÞ ¼
K 0 ðxÞ d x ¼
ð
e 2x d x ¼
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
1
e 2x þ C
2
Integral 312 mit a ¼ 2
G24
y0
¼
2
x
y ¼
;
x
y
1
e 2x þ C
2
1
1
þ C e 2x ¼ C e 2x þ
2
2
1 2
2
2x
þ
Rücksubstitution liefert dann die gesuchte Lösung der Bernoulli-Dgl: y ¼ u ¼ C e
2
Somit gilt: u ¼ K ðxÞ e
2x
e 2x ¼
Anfangswert : y ð 1Þ ¼ 2
Es handelt sich um eine Bernoulli-Dgl:
2
x
2
0
1
y
y ¼
¼ xy
mit g ðxÞ ¼ ; h ðxÞ ¼ x und n ¼ 1
x
y
x
Durch die Substitution u ¼ y 1 n ¼ y 1 ð 1Þ ¼ y 2 lässt sich diese Dgl in eine lineare Dgl überführen:
u ¼ y2 ;
u0 ¼
du
du dy
¼
¼ 2yy0
dx
dy dx
(da u eine Funktion von y ist und y wiederum eine Funktion von x, muss die Ableitung von u nach x mit der
Kettenregel gebildet werden). Wir multiplizieren die Bernoulli-Dgl beidseitig mit 2 y und führen dann die Substitution
wie folgt durch (2 y y 0 ¼ u 0 , y 2 ¼ u):
2yy0
4 2
y ¼ 2x
x
)
u0
4
u ¼ 2x
x
1 Differentialgleichungen 1. Ordnung
361
Diese lineare Dgl soll durch „Variation der Konstanten‘‘ gelöst werden. Dafür benötigen wir zunächst die Lösung der
zugehörigen homogenen Dgl, die wir durch „Trennung der Variablen‘‘ erhalten:
4
du
4
du
4
dx
u ¼ 0 ) u0 ¼
¼
u )
¼
dx ¼ 4
)
x
dx
x
u
x
x
ð
ð
du
dx
¼ 4
) ln j u j ¼ 4 ln j x j þ ln j C j ¼ ln j x j 4 þ ln j C j ¼ ln x 4 þ ln j C j ¼ ln j C x 4 j
u
x
u0
(Rechenregeln: R3 und R1). Entlogarithmieren liefert dann (Rechenregeln: R5 und R6):
juj ¼ jCx4 j
)
u ¼ Cx4 ¼ K x4
ðmit K ¼ C Þ
Hieraus erhalten wir durch „Variation der Konstanten‘‘ den folgenden Lösungsansatz für die inhomogene lineare Dgl
ðK ! K ðxÞÞ:
u ¼ K ðxÞ x 4 ;
u 0 ¼ K 0 ðxÞ x 4 þ 4 x 3 K ðxÞ
ðAbleitung mit der Produktregel Þ
Einsetzen dieser Ausdrücke in die inhomogene Dgl führt zu einer leicht lösbaren Dgl 1. Ordnung für die noch unbekannte Faktorfunktion K ðxÞ:
u0
4
u ¼ 2x
x
)
4
K ðxÞ x 4 ¼ 2 x )
x
) K 0 ðxÞ x 4 ¼ 2 x : x 4 )
K 0 ðxÞ x 4 þ 4 x 3 K ðxÞ
K 0 ðxÞ x 4 þ 4 x 3 K ðxÞ 4 x 3 K ðxÞ ¼ 2 x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
x 2
K ðxÞ ¼ K 0 ðxÞ d x ¼ 2 x 3 d x ¼ 2
þ K1 ¼ x 2 þ K1
2
K 0 ðxÞ ¼ 2 x 3
Damit gilt:
u ¼ K ðxÞ x 4 ¼ ð x 2 þ K 1 Þ x 4 ¼ x 2 þ K 1 x 4 ¼ K 1 x 4 x 2
Rücksubstitution liefert dann die gesuchte Lösung der Bernoulli-Dgl (zunächst in der impliziten Form):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y2 ¼ u ¼ K1 x 4 x2 ) y ¼ K1 x 4 x2
Lösung für den Anfangswert y ð 1Þ ¼ 2 (Einsetzen in die implizite Lösung):
K1 1 1 ¼ K1 1 ¼ 4
y ¼ þ
)
K1 ¼ 5
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5x 4 x2
Anmerkungen: Wegen y ð 1Þ ¼ 2 > 0 ist das positive Vorzeichen der allgemeinen Lösung zu nehmen.
Die Dgl ist auch mit Hilfe der Substitution u ¼ y=x lösbar.
1.3 Lineare Differentialgleichungen
Alle Differentialgleichungen in diesem Abschnitt lassen sich nach der Methode „Variation einer Konstanten‘‘ lösen.
Lehrbuch: Band 2, Kapitel IV.2.5
Formelsammlung: Kapitel X.2.4.3.1
G25
y0 þ
y
¼ ex
x þ1
)
362
G Gewöhnliche Differentialgleichungen
Homogene Dgl (Lösung durch „Trennung der Variablen‘‘)
y
¼ 0
x þ1
y0 þ
ð
dy
¼
y
y0 ¼
)
)
dy
dx
¼
y
x þ1
)
C
ln j y j ¼ ln j x þ 1 j þ ln j C j ¼ ln j C j ln j x þ 1 j ¼ ln
x þ 1
ð
dx
x þ1
|fflfflfflfflffl{zfflfflfflfflffl}
dy
y
¼
dx
x þ1
)
Integral 2 mit a ¼ b ¼ 1
(Rechenregel: R2). Wir entlogarithmieren (Rechenregeln: R5 und R6):
C
) y ¼ C ¼ K
j y j ¼
ðmit K ¼ C Þ
x þ 1
x þ1
x þ1
Variation der Konstanten: K ! K (x)
Der Lösungsansatz y ¼
0
y ¼
K ðxÞ
wird mit der zugehörigen Ableitung (Quotientenregel anwenden)
x þ1
K 0 ðxÞ ðx þ 1Þ 1 K ðxÞ
ðx þ 1Þ 2
¼
K 0 ðxÞ ð x þ 1 Þ
ðx þ 1Þ2
K ðxÞ
ðx þ 1Þ 2
¼
K 0 ðxÞ
x þ1
K ðxÞ
ðx þ 1Þ 2
in die inhomogene Dgl eingesetzt und die (noch unbekannte) Funktion K ðxÞ bestimmt:
K 0 ðxÞ
K ðxÞ
K ðxÞ
K 0 ðxÞ
y
¼
¼ e x )
¼ e x ðx þ 1Þ
þ
y0 þ
x þ1
x þ1
x þ1
ðx þ 1Þ 2
ðx þ 1Þ 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K 0 ðxÞ ¼ ðx þ 1Þ e x
ð
K ðxÞ ¼
)
ð
0
K ðxÞ d x ¼
)
ðx þ 1Þ e
x
ð
dx ¼
x e
x
ð
dx þ
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
e x d x ¼
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
Integral 313 mit a ¼ 1
Integral 312 mit a ¼ 1
¼ ð x 1Þ e x e x þ C ¼ ð x 1 1Þ e x þ C ¼ ðx þ 2Þ e x þ C
Die allgemeine Lösung der inhomogenen Dgl lautet somit: y ¼
G26
y 0 þ 4 x y ¼ 4 x e2x
K ðxÞ
x þ1
¼
ðx þ 2Þ e x þ C
x þ1
2
Wir lösen zunächst die zugehörige homogene Dgl y 0 þ 4 x y ¼ 0 durch „Trennung der Variablen‘‘:
y0 þ 4xy ¼ 0
)
y0 ¼ 4xy
)
dy
¼ 4xy
dx
)
dy
¼ 4x dx
y
)
ð
y
dy
2
¼ ð 4 xÞ d x ) ln j y j ¼ 2 x þ ln j C j ) ln j y j ln j C j ¼ ln ¼ 2 x 2
y
C
y
y
2
2
2
¼ e 2x2 )
¼ e 2x
) y ¼ C e 2x ¼ K e 2x
ðmit K ¼ C 2 Þ
C
C
ð
Rechenregeln: R2, R5 und R6
)
1 Differentialgleichungen 1. Ordnung
363
Variation der Konstanten
Wir ersetzen die Konstante K durch die (noch unbekannte) Funktion K ðxÞ und gehen mit dem Lösungsansatz
2
y ¼ K ðxÞ e 2 x in die inhomogene Dgl, wobei wir noch die Ableitung des Lösungsansatzes benötigen (Produktregel, Ableitung des rechten Faktors mit der Kettenregel):
y ¼ K ðxÞ e 2 x ¼ u v
|ffl{zffl} |fflffl{zfflffl}
u
v
2
)
y 0 ¼ u 0 v þ v 0 u ¼ K 0 ðxÞ e 2 x 4 x e 2 x K ðxÞ
2
2
)
y 0 þ 4 x y ¼ K 0 ðxÞ e 2 x 4 x K ðxÞ e 2 x þ 4 x K ðxÞ e 2 x ¼ 4 x e 2 x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
0
2 x2
2 x2
0
0
¼ 4x e
) K ðxÞ ¼ 4 x ) K ðxÞ ¼ K ðxÞ d x ¼ 4 x d x ¼ 2 x 2 þ C
K ðxÞ e
2
2
2
2
Die allgemeine Lösung der inhomogenen linearen Dgl lautet somit:
y ¼ K ðxÞ e 2 x ¼ ð2 x 2 þ C Þ e 2 x
2
G27
y0
1
x2 þ x þ 1
y ¼
;
x
x
2
Anfangswert : y ð1Þ ¼ 3
Homogene Dgl (Lösung durch „Trennung der Variablen‘‘)
1
y
y ¼ 0
x
0
)
dy
1
¼
y ¼
y
dx
x
0
)
ln j y j ¼ ln j x j þ ln j C j ¼ ln j C x j
dy
dx
¼
y
x
)
ð dy
y
ð
¼
dx
x
)
(Rechenregel: R1)
Durch Entlogarithmierung gewinnen wir die Lösung der homogenen Dgl (Rechenregeln: R5 und R6):
jyj ¼ jCxj
)
y ¼ Cx ¼ K x
Variation der Konstanten: K ! K (x)
ðmit K ¼ C Þ
(Konstante K durch Funktion K ðxÞ ersetzen)
Mit dem Lösungsansatz y ¼ K ðxÞ x und der mit Hilfe der Produktregel gewonnenen Ableitung
y 0 ¼ K 0 ðxÞ x þ 1 K ðxÞ ¼ K 0 ðxÞ x þ K ðxÞ
gehen wir in die inhomogene Dgl ein und bestimmen die noch unbekannte Faktorfunktion K ðxÞ:
1
1
x2 þ x þ 1
y ¼ K 0 ðxÞ x þ K ðxÞ
K ðxÞ x ¼ K 0 ðxÞ x þ K ðxÞ K ðxÞ ¼
x
x
x
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
0
x 2 þ x þ 1
x2 þ x þ 1
1
1
: x ) K 0 ðxÞ ¼
K 0 ðxÞ x ¼
¼ 1þ
)
þ
x
x
x2
x2
ð
ð
1
1
1
1þ
K ðxÞ ¼ K 0 ðxÞ d x ¼
þ
þC
d x ¼ x þ ln j x j
x
x
x2
y0
)
Die allgemeine Lösung der inhomogenen Dgl lautet somit:
1
þ C x ¼ x 2 þ x ln j x j 1 þ C x ¼ x 2 þ C x þ x ln j x j 1
y ¼ K ðxÞ x ¼ x þ ln j x j
x
Spezielle Lösung für den Anfangswert y ð1Þ ¼ 3:
y ð1Þ ¼ 3
)
1 þ C þ 1 ln 1 1 ¼ 3
|{z}
0
)
C ¼ 3
)
y ¼ x 2 3 x þ x ln j x j 1
364
G Gewöhnliche Differentialgleichungen
G28
y 0 sin x y cos x ¼ 4 sin 4 x
Die Lösung der zugehörigen homogenen Dgl erhalten wir durch „Trennung der Variablen‘‘:
y 0 sin x y cos x ¼ 0
ð
dy
¼
y
)
y 0 sin x ¼
dy
sin x ¼ y cos x
dx
dy
cos x
¼
d x ¼ cot x d x
y
sin x
)
ð
cot x d x
)
ln j y j ¼ ln j sin x j þ ln j C j ¼ ln j C sin x j
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
Integral 293 mit a ¼ 1
(cos x=sin x ¼ cot x ; Rechenregel: R1). Entlogarithmierung liefert (Rechenregeln: R5 und R6):
j y j ¼ j C sin x j
)
y ¼ C sin x ¼ K sin x
Variation der Konstanten: K ! K (x)
ðmit K ¼ C Þ
(Konstante K durch Funktion K ðxÞ ersetzen)
Wir setzen den Lösungsansatz y ¼ K ðxÞ sin x und die mit Hilfe der Produktregel bestimmte Ableitung
y 0 ¼ K 0 ðxÞ sin x þ cos x K ðxÞ
in die inhomogene Dgl ein und bestimmen die noch unbekannte Faktorfunktion K ðxÞ:
y 0 sin x y cos x ¼ ½ K 0 ðxÞ sin x þ cos x K ðxÞ sin x K ðxÞ sin x cos x ¼ 4 sin 4 x
K 0 ðxÞ sin 2 x þ K ðxÞ sin x cos x K ðxÞ sin x cos x ¼ 4 sin 4 x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K 0 ðxÞ sin 2 x ¼ 4 sin 4 x : sin 2 x ) K 0 ðxÞ ¼ 4 sin 2 x )
ð
K ðxÞ ¼
K 0 ðxÞ d x ¼ 4
ð
sin 2 x d x ¼ 4
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
sin ð2 xÞ
x
2
4
)
)
þ C ¼ 2 x sin ð2 xÞ þ C
Integral 205 mit a ¼ 1
Die allgemeine Lösung der inhomogenen Dgl lautet somit: y ¼ K ðxÞ sin x ¼ ð2 x sin ð2 xÞ þ CÞ sin x
Stromkreis mit einem zeitabhängigen ohmschen Widerstand
G29
di
þ ðcos tÞ i ¼ 2 cos t ;
dt
Anfangswert : i ð0Þ ¼ 0
Bestimmen Sie den zeitlichen Verlauf der Stromstärke i ¼ i ðtÞ .
Wir lösen zunächst die zugehörige homogene Dgl durch „Trennung der Variablen‘‘:
di
di
di
þ ðcos tÞ i ¼ 0 )
¼ ðcos tÞ i )
¼ cos t d t )
dt
dt
i
ð
ð
i
di
¼ cos t d t ) ln j i j ¼ sin t þ ln j C j ) ln j i j ln j C j ¼ ln ¼ sin t
i
C
i
¼ e sin t ) i ¼ e sin t ) i ¼ C e sin t ¼ K e sin t
ðmit K ¼ CÞ
C
C
Rechenregeln: R2, R5 und R6
)
1 Differentialgleichungen 1. Ordnung
365
Variation der Konstanten: K ! K (t)
Wir ersetzen die Konstante K durch die noch unbekannte Funktion K ðtÞ und gehen mit dem Lösungsansatz
i ¼ K ðtÞ e sin t und deren Ableitung in die inhomogene Dgl ein (die Ableitung erhält man mit Hilfe von Produktund Kettenregel ):
i ¼ K ðtÞ e sin t ;
di
¼ K_ ðtÞ e sin t cos t e sin t K ðtÞ
dt
di
þ ðcos tÞ i ¼ K_ ðtÞ e sin t cos t e sin t K ðtÞ þ cos t K ðtÞ e sin t ¼ 2 cos t
dt
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K_ ðtÞ e sin t ¼ 2 cos t esin t ) K_ ðtÞ ¼ 2 cos t e sin t )
ð
K ðtÞ ¼
K_ ðtÞ d t ¼ 2
)
ð
cos t e sin t d t
du
du
¼ cos t ; d t ¼
wie folgt:
dt
cos t
ð
ð
du
d t ¼ 2 cos t e u
¼ 2 e u d u ¼ 2 e u þ K * ¼ 2 e sin t þ K *
cos t
Dieses Integral lösen wir mit der Substitution u ¼ sin t ;
ð
K ðtÞ ¼ 2
cos t e sin t
Die allgemeine Lösung der inhomogenen Dgl lautet damit:
i ¼ K ðtÞ e sin t ¼ ð2 e sin t þ K *Þ e sin t ¼ 2 þ K * e sin t ;
t 0
Der Stromkreis ist zu Beginn ðt ¼ 0Þ stromlos. Aus diesem Anfangswert bestimmen wir die Integrationskonstante K * :
i ð0Þ ¼ 0
)
2 þ K * e sin 0 ¼ 2 þ K * e 0 ¼ 2 þ K * 1 ¼ 2 þ K * ¼ 0
Damit erhalten wir den folgenden zeitlichen Verlauf
für die Stromstärke i (siehe Bild G-6):
i = 2 1 – e– sin t
2
t 0
1
(Periodische Funktion mit der Periode 2 p. Im Periodeninter-
2
vall von 0 bis 2 p gilt:
–1
Maximum zur Zeit t ¼ p=2 ,
–2
Minimum zur Zeit t ¼ 3 p=2)
–3
4
8
Bild G-6
y 0 ðtanh xÞ y ¼ 2 cosh 2 x ;
Anfangswert : y ð0Þ ¼ 10
Wir lösen zunächst die zugehörige homogene Dgl durch „Trennung der Variablen‘‘:
y 0 ðtanh xÞ y ¼ 0
ð
dy
¼
y
)
y0 ¼
dy
¼ ðtanh xÞ y
dx
)
dy
¼ tanh x d x
y
ð
tanh x d x
)
ln j y j ¼ ln ðcosh xÞ þ ln j C j ¼ ln j C cosh x j
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
Integral 387 mit a ¼ 1
(Rechenregel: R1). Wir entlogarithmieren und erhalten (Rechenregeln: R5 und R6):
j y j ¼ j C cosh x j
)
K * ¼ 2
i
i ¼ i ðtÞ ¼ 2 2 e sin t ¼ 2 ð1 e sin t Þ ;
G30
)
y ¼ C cosh x ¼ K cosh x
ðmit K ¼ C Þ
)
14
18
t
366
G Gewöhnliche Differentialgleichungen
Variation der Konstanten: K ! K (x)
(Konstante K durch Funktion K ðxÞ ersetzen)
Den Lösungsansatz y ¼ K ðxÞ cosh x und die mit der Produktregel gewonnene Ableitung
y 0 ¼ K 0 ðxÞ cosh x þ sinh x K ðxÞ ¼ K 0 ðxÞ cosh x þ K ðxÞ sinh x
setzen wir in die inhomogene Dgl ein und bestimmen die noch unbekannte Faktorfunktion K ðxÞ wie folgt (unter
Verwendung der Beziehung tanh x ¼ sinh x=cosh xÞ:
y 0 ðtanh xÞ y ¼ K 0 ðxÞ cosh x þ K ðxÞ sinh x tanh x K ðxÞ cosh x ¼ 2 cosh 2 x
K 0 ðxÞ cosh x þ K ðxÞ sinh x K ðxÞ
sinh x
cosh x ¼ 2 cosh 2 x
cosh x
)
)
K 0 ðxÞ cosh x þ K ðxÞ sinh x K ðxÞ sinh x ¼ 2 cosh 2 x ) K 0 ðxÞ cosh x ¼ 2 cosh 2 x )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
2
2 cosh x
0
0
¼ 2 cosh x ) K ðxÞ ¼ K ðxÞ d x ¼ 2 cosh x d x ¼ 2 sinh x þ C
K ðxÞ ¼
cosh x
Allgemeine Lösung der inhomogenen Dgl
y ¼ K ðxÞ cosh x ¼ ð2 sinh x þ CÞ cosh x ¼ 2 sinh x cosh x þ C cosh x ¼ sinh ð2 xÞ þ C cosh x
(unter Verwendung der Formel 2 sinh x cosh ¼ sinh ð2 xÞ ! FS: Kapitel III.11.3.3)
Spezielle Lösung für den Anfangswert y ð0Þ ¼ 10:
y ð0Þ ¼ 10
)
sinh 0 þ C cosh 0 ¼ 0 þ C 1 ¼ C ¼ 10
)
C ¼ 10
Lösung: y ¼ sinh ð2 xÞ þ 10 cosh x
G31
y0 þ
2x
1 6x2
y ¼
1 þ x2
1 þ x2
Lösung der zugehörigen homogenen Dgl durch „Trennung der Variablen‘‘:
dy
dy
2x
2x
2x
¼
¼
y ¼ 0 ) y0 ¼
y )
dx
2
2
dx
y
1þx
1þx
1 þ x2
ð
ð
dy
x
1
¼ 2
ln ð1 þ x 2 Þ þ ln j C j )
d x ) ln j y j ¼ 2
2
y
2
1þx
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
y0 þ
)
Integral 32 mit a 2 ¼ 1
C
ln j y j ¼ ln ð1 þ x Þ þ ln j C j ¼ ln j C j ln ð1 þ x Þ ¼ ln
1 þ x2
2
2
(Rechenregel: R2). Entlogarithmierung führt dann zur Lösung der homogenen Dgl (Rechenregeln: R5 und R6):
C
K
) y ¼ C
jyj ¼
¼
ðmit K ¼ C Þ
2
2
1þx
1þx
1 þ x2
Variation der Konstanten: K ! K (x)
Den Lösungsansatz y ¼
y0 ¼
K ðxÞ
1 þ x2
(Konstante K durch Funktion K ðxÞ ersetzen)
und die mit Hilfe der Quotientenregel erhaltene zugehörige Ableitung
K 0 ðxÞ ð1 þ x 2 Þ 2 x K ðxÞ
ð1 þ x 2 Þ 2
¼
K 0 ðxÞ ð 1 þ x 2 Þ
ð1 þ x 2 Þ2
2x K ðxÞ
ð1 þ x 2 Þ 2
¼
K 0 ðxÞ
1 þ x2
2 x K ðxÞ
ð1 þ x 2 Þ 2
1 Differentialgleichungen 1. Ordnung
367
setzen wir in die inhomogene Dgl ein und bestimmen daraus die noch unbekannte Funktion K ðxÞ:
y0 þ
2x
1 þ x2
K 0 ðxÞ
1 þ x2
y ¼
K 0 ðxÞ
1 þ x2
2 x K ðxÞ
þ
2 x K ðxÞ
ð1 þ x 2 Þ 2
2 x K ðxÞ
¼
þ
2x
1 þ x2
1 6x2
K ðxÞ
1 þ x2
)
1 6x2
¼
K 0 ðxÞ
1 þ x2
¼
)
1 6 x 2
2
ð1 þ x Þ
2
1þx
1 þ x2
1 þ x2
ð1 þ x 2 Þ 2
ð1 þ x 2 Þ 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
0
2
0
K ðxÞ ¼ 1 6 x
) K ðxÞ ¼ K ðxÞ d x ¼ ð1 6 x 2 Þ d x ¼ x 2 x 3 þ C
)
Damit erhalten wir die folgende allgemeine Lösung der inhomogenen Dgl:
y ¼
K ðxÞ
x 2x3 þ C
¼
1 þ x2
1 þ x2
1.4 Lineare Differentialgleichungen mit konstanten Koeffizienten
Die homogene lineare Differentialgleichung wird durch einen Exponentialansatz gelöst, die inhomogene lineare Differentialgleichung entweder durch „Variation der Konstanten‘‘ oder durch „Aufsuchen einer partikulären Lösung‘‘.
Lehrbuch: Band 2, Kapitel IV.2.6
Formelsammlung: Kapitel X.2.4.4
Tabelle mit Lösungsansätzen für eine partikuläre Lösung: Band 2, Kapitel IV.2.6 (Tabelle 1) und Formelsammlung,
Kapitel X.2.4.4
G32
y0 þ y ¼
ex
;
1 þ x2
Anfangswert : y ð0Þ ¼ 2
Lösen Sie dieses Anfangswertproblem durch „Variation der Konstanten“.
Allgemeine Lösung der zugehörigen homogenen Dgl y 0 þ y ¼ 0
(Ansatz : y ¼ K e l x Þ:
y ¼ K e x
Variation der Konstanten: K ! K (x)
Lösungsansatz für die inhomogene Dgl:
y ¼ K ðxÞ e x ;
y 0 ¼ K 0 ðxÞ e x K ðxÞ e x
ðProdukt- und KettenregelÞ
e x
e x
y 0 þ y ¼ K 0 ðxÞ e x K ðxÞ e x þ K ðxÞ e x ¼
) K 0 ðxÞ e x ¼
1 þ x2
1 þ x2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
1
1
) K ðxÞ ¼ K 0 ðxÞ d x ¼
d x ¼ arctan x þ C
K 0 ðxÞ ¼
1 þ x2
1 þ x2
Allgemeine Lösung der inhomogenen Dgl:
y ¼ K ðxÞ e x ¼ ðarctan x þ CÞ e x
Partikuläre Lösung für den Anfangswert y ð0Þ ¼ 2:
y ð0Þ ¼ 2
)
ðarctan 0 þ CÞ e 0 ¼ ð0 þ C Þ 1 ¼ C ¼ 2
Lösung: y ¼ ðarctan x þ 2Þ e x
)
C ¼ 2
)
368
G Gewöhnliche Differentialgleichungen
y 0 þ 3 y ¼ e x þ 2 cos ð2 xÞ
Lösen Sie diese Dgl durch „Variation der Konstanten“.
G33
Allgemeine Lösung der zugehörigen homogenen Dgl y 0 þ 3 y ¼ 0
(Ansatz : y ¼ K e l x Þ :
y ¼ K e3x
Variation der Konstanten: K ! K (x)
Lösungsansatz mit der zugehörigen 1. Ableitung:
y ¼ K ðxÞ e 3 x ;
y 0 ¼ K 0 ðxÞ e 3 x 3 K ðxÞ e 3 x
ðProdukt- und Kettenregel Þ
Einsetzen in die inhomogene Dgl, unbekannte Faktorfunktion K ðxÞ bestimmen:
y 0 þ 3 y ¼ K 0 ðxÞ e 3 x 3 K ðxÞ e 3 x þ 3 K ðxÞ e 3 x ¼ e x þ 2 cos ð2 xÞ )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K 0 ðxÞ e 3 x ¼ e x þ 2 cos ð2 xÞ e 3 x ) K 0 ðxÞ ¼ e 4 x þ 2 e 3 x cos ð2 xÞ )
ð
ð
ð
ð
K ðxÞ ¼ K 0 ðxÞ d x ¼ ½ e 4 x þ 2 e 3 x cos ð2 xÞ d x ¼ e 4 x d x þ 2 e 3 x cos ð2 xÞ d x ¼
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 312 mit a ¼ 4
¼
Integral 324 mit a ¼ 3, b ¼ 2
1
2
e 4x þ
e 3 x ½ 3 cos ð2 xÞ þ 2 sin ð2 xÞ þ C
4
13
Allgemeine Lösung der inhomogenen Dgl:
1
2
3x
4x
3x
¼
y ¼ K ðxÞ e
e þ
e ½ 3 cos ð2 xÞ þ 2 sin ð2 xÞ þ C e 3 x ¼
4
13
¼
G34
1
2
ex þ
½ 3 cos ð2 xÞ þ 2 sin ð2 xÞ þ C e 3 x
4
13
y 0 þ 5 y ¼ cos x e 5 x ;
Anfangswert: y ðp=2Þ ¼ 0
Lösen Sie diese Anfangswertaufgabe durch „Variation der Konstanten“.
Allgemeine Lösung der zugehörigen homogenen Dgl y 0 þ 5 y ¼ 0
(Ansatz : y ¼ K e l x Þ:
y ¼ K e5x
Variation der Konstanten: K ! K (x)
Lösungsansatz mit der zugehörigen 1. Ableitung:
y ¼ K ðxÞ e 5 x ;
y 0 ¼ K 0 ðxÞ e 5 x 5 K ðxÞ e 5 x
ðProdukt- und Kettenregel Þ
Einsetzen in die inhomogene Dgl, unbekannte Faktorfunktion K ðxÞ bestimmen:
y 0 þ 5 y ¼ K 0 ðxÞ e 5 x 5 K ðxÞ e 5 x þ 5 K ðxÞ e 5 x ¼ cos x e 5 x )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
K 0 ðxÞ e 5 x ¼ cos x e 5 x ) K 0 ðxÞ ¼ cos x ) K ðxÞ ¼ K 0 ðxÞ d x ¼ cos x d x ¼ sin x þ C
Allgemeine Lösung der inhomogenen Dgl:
y ¼ K ðxÞ e 5 x ¼ ðsin x þ CÞ e 5 x
1 Differentialgleichungen 1. Ordnung
369
Spezielle Lösung für den Anfangswert y ðp=2Þ ¼ 0:
ðsin ðp=2Þ þ CÞ e 5 p=2 ¼ ð1 þ CÞ e 5 p=2 ¼ 0
|fflfflffl{zfflfflffl}
6¼ 0
Lösung: y ¼ ðsin x 1Þ e 5 x
y ðp=2Þ ¼ 0
G35
)
)
1þC ¼ 0
)
C ¼ 1
y 0 4 y ¼ e 4 x þ cos ð2 xÞ
Bestimmen Sie die allgemeine Lösung dieser Dgl durch „Aufsuchen einer partikulären Lösung“.
Die allgemeine Lösung y der inhomogenen Dgl wird aus der Lösung y 0 der zugehörigen homogenen Dgl und einer
partikulären Lösung y P der inhomogenen Dgl aufgebaut: y ¼ y 0 þ y P
Lösung der zugehörigen homogenen Dgl y 0 4 y ¼ 0
(Ansatz y 0 ¼ K e l x Þ:
y0 ¼ K e 4x
Partikuläre Lösung der inhomogenen Dgl
Aus der Tabelle entnehmen wir für die beiden Störglieder e4 x und cos ð2 xÞ die folgenden Lösungsansätze für eine
partikuläre Lösung y P :
Störglied g 1 ðxÞ ¼ e 4 x
a ¼ 4; b ¼ 4
Störglied g 2 ðxÞ ¼ cos ð2 xÞ
b ¼ a ¼ 4
w ¼ 2
!
! yP1 ¼ C1 x e 4x
ðNr: 7; Fall b ¼ aÞ
y P 2 ¼ C 2 sin ð2 xÞ þ C 3 cos ð2 xÞ
ðNr: 6Þ
Damit erhalten wir den folgenden Lösungsansatz (¼ Summe der Einzelansätze):
y P ¼ y P 1 þ y P 2 ¼ C 1 x e 4 x þ C 2 sin ð2 xÞ þ C 3 cos ð2 xÞ
Wenn dieser Ansatz stimmt (davon gehen wir natürlich aus), dann müssen sich die noch unbekannten Konstanten C1 ,
C2 und C3 eindeutig bestimmen lassen. Wir gehen daher mit diesem Ansatz und der zugehörigen Ableitung
y 0P ¼ C 1 e 4 x þ 4 C 1 x e 4 x þ 2 C 2 cos ð2 xÞ 2 C 3 sin ð2 xÞ
(Produkt- und Kettenregel ) in die inhomogene Dgl ein, ordnen die Glieder und fassen zusammen:
y 0 4 y ¼ C 1 e 4 x þ 4 C 1 x e 4 x þ 2 C 2 cos ð2 xÞ 2 C 3 sin ð2 xÞ
4 ½ C 1 x e 4 x þ C 2 sin ð2 xÞ þ C 3 cos ð2 xÞ ¼
¼ C 1 e 4 x þ 4 C 1 x e 4 x þ 2 C 2 cos ð2 xÞ 2 C 3 sin ð2 xÞ
4 C 1 x e 4 x 4 C 2 sin ð2 xÞ 4 C 3 cos ð2 xÞ ¼
¼ C 1 e 4 x þ ð2 C 2 4 C 3 Þ cos ð2 xÞ þ ð 4 C 2 2 C 3 Þ sin ð2 xÞ ¼ e 4 x þ cos ð2 xÞ
Aus der verbliebenen Gleichung
C 1 e 4 x þ ð2 C 2 4 C 3 Þ cos ð2 xÞ þ ð 4 C 2 2 C 3 Þ sin ð2 xÞ ¼ 1 e 4 x þ 1 cos ð2 xÞ þ 0 sin ð2 xÞ
(wir haben auf der rechten Seite den identisch verschwindenden Summand 0 sin ð2 xÞ 0 addiert) erhalten wir
durch Koeffizientenvergleich 3 Gleichungen für die 3 Unbekannten (wir vergleichen der Reihe nach die Koeffizienten
von e 4 x , cos ð2 xÞ und sin ð2 xÞ auf beiden Seiten):
C1 ¼ 1
ðIÞ
ðIIÞ
2 C2 4 C3 ¼ 1
ðIIIÞ
4 C2 2 C3 ¼ 0
ðIIÞ
)
2 C 2 4 C 3 ¼ 2 C 2 4 ð 2 C 2 Þ ¼ 2 C 2 þ 8 C 2 ¼ 10 C 2 ¼ 1
ðIIIÞ
)
C 3 ¼ 2 C 2 ¼ 2 0,1 ¼ 0,2
)
2 C3 ¼ 4 C2
)
C3 ¼ 2 C2
ðEinsetzen in (II)Þ
)
C 2 ¼ 0,1
370
G Gewöhnliche Differentialgleichungen
Die Konstanten besitzen somit folgende Werte: C 1 ¼ 1, C 2 ¼ 0,1 und C 3 ¼ 0,2. Die partikuläre Lösung y P
lautet also:
y P ¼ x e 4 x þ 0,1 sin ð2 xÞ 0,2 cos ð2 xÞ
Gesamtlösung (allgemeine Lösung der inhomogenen Dgl):
y ¼ y 0 þ y P ¼ K e 4 x þ x e 4 x þ 0,1 sin ð2 xÞ 0,2 cos ð2 xÞ ¼
¼ ðx þ KÞ e 4 x þ 0,1 sin ð2 xÞ 0,2 cos ð2 xÞ
Sinkgeschwindigkeit eines Körpers in einer zähen Flüssigkeit
Die Sinkgeschwindigkeit v einer Stahlkugel in einer
zähen Flüssigkeit genügt der folgenden Dgl (ohne
Auftrieb, siehe Bild G-7):
Kugel
m v_ þ kv ¼ m g
G36
v
m: Masse der Kugel
k : Reibungsfaktor ð k > 0Þ
g: Erdbeschleunigung
–kv
mg
Bild G-7
Bestimmen Sie das Geschwindigkeit-Zeit-Gesetz v ¼ v ðtÞ für die Anfangsgeschwindigkeit v ð0Þ ¼ 0
durch „Variation der Konstanten“. Welche Endgeschwindigkeit v E wird erreicht?
Wir dividieren die Dgl zunächst durch die Masse m und führen die Abkürzung a ¼ k=m ein:
m v_ þ k v ¼ m g
)
v_ þ a v ¼ g
ða ¼ k=mÞ
Die zugehörige homogene Dgl v_ þ a v ¼ 0 besitzt die Lösung v ¼ K e a t (dies ist das Ergebnis aus dem Exponentialansatz v ¼ K e l t ).
Variation der Konstanten: K ! K (t)
Lösungsansatz für die inhomogene Dgl mit der benötigten 1. Ableitung (Produkt- und Kettenregel ):
v_ ¼ K_ ðtÞ e a t a e a t K ðtÞ ¼ K_ ðtÞ e a t a K ðtÞ e a t
v ¼ K ðtÞ e a t ;
Einsetzen in die inhomogene Dgl führt zu einer einfachen Dgl für K ðtÞ, die wir durch direkte (unbestimmte) Integration leicht lösen können:
at
at
at
at
_
_
v_ þ a v ¼ g ) K ðtÞ e
a K ðtÞ e
þ a K ðtÞ e
¼ g e a t )
¼ K ðtÞ e
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
1
g
K_ ðtÞ ¼ g e a t ) K ðtÞ ¼ K_ ðtÞ d t ¼ g e a t d t ¼ g
e at þ C ¼
e at þ C
a
a
|fflfflfflfflffl{zfflfflfflfflffl}
Integral 312 mit a ¼ a
Allgemeine Lösung der inhomogenen Dgl:
v ¼ K ðtÞ e a t ¼
g
e at þ C
a
e at ¼
g
þ C e at ;
a
t 0
Die Bewegung der Kugel beginnt aus der Ruhe heraus. Aus diesem Anfangswert bestimmen wir die noch unbekannte
Konstante C:
v ð0Þ ¼ 0
)
g
g
g
þ C e0 ¼
þC 1 ¼
þC ¼ 0
a
a
a
)
C ¼
g
a
1 Differentialgleichungen 1. Ordnung
371
Damit ergibt sich der folgende zeitliche Verlauf der Sinkgeschwindigkeit (unter Berücksichtigung von a ¼ k=m):
k
g
g
g
mg
v ¼ v ðtÞ ¼
e at ¼
ð1 e a t Þ ¼
1 em t ; t 0
a
a
a
k
Im Laufe der Zeit (d. h. für t ! 1Þ nähert sich die Geschwindigkeit ihrem (konstanten) Endwert:
k
k
mg
mg
mg
mg
t
t
¼
¼
v E ¼ lim v ðtÞ ¼ lim
1e m
lim 1 e m
1 ¼
k
k
k
k
t!1
t!1
t!1
(die streng monoton fallende Exponentialfunktion strebt für t ! 1 asymptotisch gegen null).
Bild G-8 zeigt den zeitlichen Verlauf der Sinkgeschwindigkeit v
(„Sättigungsfunktion‘‘).
v
mg
k
k
v=
–
t
mg
1–e m
k
Bild G-8
t
Abkühlungsgesetz nach Newton
G37
Ein Körper mit der Anfangstemperatur T ðt ¼ 0Þ ¼ T0 wird durch vorbei strömende Luft der konstanten Temperatur TL < T0 gekühlt. Die Temperatur T ¼ T ðtÞ des Körpers genügt dabei der Dgl
dT
þ a T ¼ a TL
dt
ða > 0 : KonstanteÞ
Bestimmen Sie den Temperaturverlauf T ¼ T ðtÞ durch „Variation der Konstanten“.
Welche Endtemperatur TE erreicht der Körper?
Die zugehörige homogene Dgl T_ þ a T ¼ 0 wird durch den Exponentialansatz T ¼ C e l t gelöst:
T ¼ C e lt ;
T_ ¼ C l e l t
T_ þ a T ¼ 0 ) C l e l t þ a C e l t ¼ 0 ) C e l t ðl þ aÞ ¼ 0 ) l þ a ¼ 0 ) l ¼ a
|fflfflfflffl{zfflfflfflffl}
6¼ 0
Somit ist T ¼ C e a t die allgemeine Lösung der homogenen Dgl.
Variation der Konstanten: C ! C (t)
Lösungsansatz für die allgemeine Lösung der inhomogenen Dgl mit der zugehörigen aus Produkt- und Kettenregel
gewonnenen 1. Ableitung:
T ¼ C ðtÞ e a t ;
T_ ¼ C_ ðtÞ e a t a e a t C ðtÞ ¼ C_ ðtÞ e a t a C ðtÞ e a t
Einsetzen in die inhomogene Dgl, Faktorfunktion C ðtÞ durch direkte Integration bestimmen:
T_ þ a T ¼ a TL
)
C_ ðtÞ e a t a C ðtÞ e a t þ a C ðtÞ e a t ¼ a TL
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
at
_
C ðtÞ e
¼ a TL e a t
)
C_ ðtÞ ¼ a TL e a t
)
)
372
G Gewöhnliche Differentialgleichungen
ð
C ðtÞ ¼
ð
C_ ðtÞ d t ¼ a TL
e a t d t ¼ a TL
|fflfflfflfflffl{zfflfflfflfflffl}
1
e a t þ K ¼ TL e a t þ K
a
Integral 312
Somit gilt: T ¼ C ðtÞ e a t ¼ ðTL e a t þ KÞ e a t ¼ TL þ K e a t ;
t 0
Den Wert der Integrationskonstanten K ermitteln wir aus der Anfangstemperatur T ð0Þ ¼ T0 :
T ð0Þ ¼ T0
)
TL þ K e 0 ¼ TL þ K 1 ¼ TL þ K ¼ T0
)
K ¼ T0 TL
Die Temperatur des Körpers klingt mit der Zeit wie folgt exponentiell ab:
T ¼ T ðtÞ ¼ TL þ ðT0 TL Þ e a t ;
t 0
Die Endtemperatur, auf die der Körper im Laufe der Zeit abkühlt, erhalten wir für t ! 1:
TE ¼ lim T ðtÞ ¼ lim ðTL þ ðT0 TL Þ e a t Þ ¼ TL
t!1
t!1
at
(e
strebt für t ! 1 gegen null). Der Abkühlungsprozess
ist also beendet, wenn der Körper die Lufttemperatur TL erreicht hat.
T
T0
T = TL + (T0 – TL ) · e – at
Bild G-9 zeigt den zeitlichen Verlauf der Temperatur
(„Abklingfunktion‘‘).
TL
Bild G-9
t
G38
y 0 þ y ¼ 4 e x sin ð2 xÞ
Lösen Sie diese Dgl nach der Methode „Aufsuchen einer partikulären Lösung“.
Die gesuchte allgemeine Lösung y lässt sich darstellen als Summe aus der Lösung y0 der zugehörigen homogenen
Dgl und einer partikulären Lösung y P der inhomogenen Dgl: y ¼ y 0 þ y P
Die Lösung der zugehörigen homogenen Dgl y 0 þ y ¼ 0 lautet (Ansatz y 0 ¼ K e l x Þ:
y 0 ¼ K e x.
Partikuläre Lösung der inhomogenen Dgl
Wir versuchen einen Lösungsansatz in Form eines Produktes aus zwei Faktoren, die sich aus den Ansätzen der beiden
„Störfaktoren‘‘ e x und sin ð2 xÞ ergeben (der konstante Faktor 4 im Störglied hat keinen Einfluss auf den Lösungsansatz). Aus der Tabelle entnehmen wir folgende Ansätze:
Störfaktor g 1 ðxÞ ¼ e x
a ¼ 1
b ¼ 1
Störfaktor g 2 ðxÞ ¼ sin ð2 xÞ
!
w ¼ 2
yP1 ¼ C1 e x
!
ðNr: 8; Fall b 6¼ aÞ
y P 2 ¼ C 2 sin ð2 xÞ þ C 3 cos ð2 xÞ
Damit erhalten wir für die partikuläre Lösung y P (versuchsweise) den Lösungsansatz
y P ¼ y P 1 y P 2 ¼ C 1 e x ½ C 2 sin ð2 xÞ þ C 3 cos ð2 xÞ
den wir noch wie folgt vereinfachen können (nur noch 2 statt 3 Parameter):
y P ¼ e x ½ C 1 C 2 sin ð2 xÞ þ C 1 C 3 cos ð2 xÞ ¼ e x ½ A sin ð2 xÞ þ B cos ð2 xÞ
|fflffl{zfflffl}
|fflffl{zfflffl}
A
B
ðNr: 5Þ
1 Differentialgleichungen 1. Ordnung
373
Mit diesem Ansatz und der mit Hilfe der Produkt- und Kettenregel erhaltenen 1. Ableitung
y 0P ¼ e x ½ A sin ð2 xÞ þ B cos ð2 xÞ þ ½ 2 A cos ð2 xÞ 2 B sin ð2 xÞ e x ¼
¼ e x ½ A sin ð2 xÞ þ B cos ð2 xÞ þ 2 A cos ð2 xÞ 2 B sin ð2 xÞ
gehen wir in die inhomogene Dgl ein, kürzen den gemeinsamen Faktor 2 e x heraus und ordnen die Glieder:
y 0 þ y ¼ e x ½ A sin ð2 xÞ þ B cos ð2 xÞ þ 2 A cos ð2 xÞ 2 B sin ð2 xÞ þ
þ e x ½ A sin ð2 xÞ þ B cos ð2 xÞ ¼
¼ e x ½ A sin ð2 xÞ þ B cos ð2 xÞ þ 2 A cos ð2 xÞ 2 B sin ð2 xÞ þ A sin ð2 xÞ þ B cos ð2 xÞ ¼
¼ e x ½ 2 A sin ð2 xÞ þ 2 B cos ð2 xÞ þ 2 A cos ð2 xÞ 2 B sin ð2 xÞ ¼
¼ 2 e x ½ A sin ð2 xÞ þ B cos ð2 xÞ þ A cos ð2 xÞ B sin ð2 xÞ ¼ 4 e x sin ð2 xÞ
A sin ð2 xÞ þ B cos ð2 xÞ þ A cos ð2 xÞ B sin ð2 xÞ ¼ 2 sin ð2 xÞ
)
)
ðA BÞ sin ð2 xÞ þ ðA þ BÞ cos ð2 xÞ ¼ 2 sin ð2 xÞ þ 0 cos ð2 xÞ
(mathematischer „Trick‘‘: wir addieren auf der rechten Seite 0 cos ð2 xÞ 0). Der Koeffizientenvergleich für die
Sinus- bzw. Kosinusterme auf beiden Seiten führt zu 2 Gleichungen für die Unbekannten A und B:
)
ðIÞ
AB ¼ 2
þ ) 2 A ¼ 2 ) A ¼ 1 ; ðIIÞ ) A þ B ¼ 1 þ B ¼ 0 ) B ¼ 1
AþB ¼ 0
ðIIÞ
Die partikuläre Lösung lautet damit:
y P ¼ e x ½ sin ð2 xÞ cos ð2 xÞ
Die inhomogene Dgl besitzt demnach die folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ K e x þ e x ½ sin ð2 xÞ cos ð2 xÞ
Geschwindigkeit-Zeit-Gesetz einer konstant beschleunigten Masse bei geschwindigkeitsproportionaler Reibung
G39
Bestimmen Sie das Geschwindigkeit-Zeit-Gesetz v ¼ v ðtÞ einer Bewegung, die durch die Dgl
v_ þ a v ¼ b beschrieben wird (a > 0 , b > 0: Konstanten). Wie lautet die spezielle Lösung, wenn
die Bewegung zur Zeit t ¼ 0 aus der Ruhe heraus beginnt?
Verwenden Sie die Lösungsmethode „Variation der Konstanten“.
Allgemeine Lösung der zugehörigen homogenen Dgl v_ þ a v ¼ 0
(Ansatz v 0 ¼ K e l t Þ:
Variation der Konstanten: K ! K (t)
Lösungsansatz mit der benötigten 1. Ableitung (Produkt- und Kettenregel):
v ¼ K ðtÞ e a t ;
v_ ¼ K_ ðtÞ e a t a K ðtÞ e a t
Einsetzen in die inhomogene Dgl, Faktorfunktion K ðtÞ bestimmen:
v_ þ a v ¼ K_ ðtÞ e a t a K ðtÞ e a t þ a K ðtÞ e a t ¼ b )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K_ ðtÞ e a t ¼ b e a t ) K_ ðtÞ ¼ b e a t )
ð
ð
1
b
K ðtÞ ¼ K_ ðtÞ d t ¼ b e a t d t ¼ b
e at þ C ¼
e at þ C
a
a
|fflfflfflfflffl{zfflfflfflfflffl}
Integral 312
v0 ¼ K e at
374
G Gewöhnliche Differentialgleichungen
Damit erhalten wir die folgende allgemeine Lösung der inhomogenen Dgl:
b
b
v ¼ K ðtÞ e a t ¼
e at þ C e at ¼
þ C e at
a
a
Zu Beginn, d. h. zur Zeit t ¼ 0 ist v ¼ 0. Aus diesem Anfangswert lässt sich die Integrationskonstante C wie
folgt berechnen:
v ð0Þ ¼ 0
)
b
b
b
þ C e0 ¼
þC 1 ¼
þC ¼ 0
a
a
a
Das Geschwindigkeit-Zeit-Gesetz lautet damit wie folgt
(siehe Bild G-10):
v ¼
)
C ¼
v
b
a
b
b
b
e at ¼
ð1 e a t Þ
a
a
a
(für t 0)
v=
Endgeschwindigkeit ðt ! 1Þ:
v E ¼ lim
t!1
b
a
b
(1 – e – at )
a
Bild G-10
b
b
ð1 e a t Þ ¼
a
a
t
Wechselstromkreis mit einem ohmschen Widerstand und einer Induktivität (RL-Kreis)
G40
Ein Stromkreis enthält den ohmschen Widerstand R ¼ 6 W und die Induktivität L ¼ 2 H . Durch die
angelegte Wechselspannung u ðtÞ ¼ 20 V sin ð1 s 1 tÞ wird ein zeitabhängiger Strom i ¼ i ðtÞ
erzeugt, der der folgenden Dgl genügt:
L
di
þ R i ¼ u ðtÞ;
dt
Anfangswert : i ð0Þ ¼ 0
Bestimmen Sie den zeitlichen Verlauf der Stromstärke i nach der Methode „Aufsuchen einer partikulären
Lösung“. Wie lautet die sog. „stationäre“ Lösung nach Ablauf einer gewissen „Einschwingphase“?
Die Stromstärke i genügt der folgenden inhomogenen linearen Dgl 1. Ordnung mit konstanten Koeffizienten (ohne
Einheiten):
2
di
þ 6 i ¼ 20 sin t
dt
oder
di
þ 3 i ¼ 10 sin t
dt
Wir lösen sie nach der Methode „Aufsuchen einer partikulären Lösung‘‘.
Zugehörige homogene Dgl:
di
þ 3i ¼ 0
dt
)
i0 ¼ K e 3t
(Lösungsansatz : i 0 ¼ K e l t Þ
Partikuläre Lösung der inhomogenen Dgl
Aus der Tabelle entnehmen wir für das sinusförmige Störglied den folgenden Lösungsansatz (Nr. 5 mit w ¼ 1):
i P ¼ C 1 sin t þ C 2 cos t
Mit diesem Ansatz und der Ableitung
d iP
¼ C 1 cos t C 2 sin t
dt
gehen wir in die inhomogene Dgl ein und erhalten:
di
þ 3 i ¼ C 1 cos t C 2 sin t þ 3 ðC 1 sin t þ C 2 cos tÞ ¼
dt
¼ C 1 cos t C 2 sin t þ 3 C 1 sin t þ 3 C 2 cos t ¼ 10 sin t
1 Differentialgleichungen 1. Ordnung
375
Diese Gleichung ordnen wir wie folgt, wobei wir auf der rechten Seite 0 cos t 0 addieren:
ð3 C 1 C 2 Þ sin t þ ðC 1 þ 3 C 2 Þ cos t ¼ 10 sin t þ 0 cos t
Durch Koeffizientenvergleich (wir vergleichen auf beiden Seiten jeweils die Sinus- und Kosinusglieder) erhalten wir
zwei Gleichungen mit den Unbekannten C 1 und C 2 :
ðIÞ
ðIIÞ
3 C1
C 2 ¼ 10
C1 þ 3 C2 ¼ 0
)
C1 ¼ 3 C2
ðEinsetzen in (I)Þ
ðIÞ
)
3 C 1 C 2 ¼ 3 ð 3 C 2 Þ C 2 ¼ 9 C 2 C 2 ¼ 10 C 2 ¼ 10
ðIIÞ
)
C 1 ¼ 3 C 2 ¼ 3 ð 1Þ ¼ 3
)
C2 ¼ 1
Partikuläre Lösung: i P ¼ 3 sin t cos t
Im R L-Kreis fließt also der folgende (zeitabhängige) Strom:
i ¼ i 0 þ i P ¼ K e 3 t þ 3 sin t cos t ;
t 0
Aus dem Anfangswert i ð0Þ ¼ 0 berechnen wir noch die Integrationskonstante K:
i ð0Þ ¼ 0
)
K e 0 þ 3 sin 0 cos 0 ¼ K 1 þ 3 0 1 ¼ K 1 ¼ 0
i ¼ e 3 t þ 3 sin t cos t ;
)
K ¼ 1
t 0
Im Laufe der Zeit verschwindet die streng monoton fallende Exponentialfunktion und wir erhalten die folgende
„stationäre“ Lösung (sog. erzwungene Schwingung, siehe Bild G-11):
i stationär ¼ 3 sin t cos t
i/A
4
2
Bild G-11
–1
–2
2
5
10
15
20
t/s
–4
G41
y 0 þ 2 y ¼ x 3 e2x þ x
Bestimmen Sie die allgemeine Lösung „durch Variation der Konstanten“.
Allgemeine Lösung der zugehörigen homogenen Dgl y 0 þ 2 y ¼ 0:
y ¼ K e 2x
(Ansatz : y ¼ K e l x Þ
Variation der Konstanten: K ! K (x)
Lösungsansatz mit der zugehörigen 1. Ableitung:
y ¼ K ðxÞ e 2 x ;
y 0 ¼ K 0 ðxÞ e 2 x 2 K ðxÞ e 2 x
ðProdukt- und Kettenregel Þ
Einsetzen in die inhomogene Dgl, unbekannte Faktorfunktion K ðxÞ bestimmen:
y 0 þ 2 y ¼ K 0 ðxÞ e 2 x 2 K ðxÞ e 2 x þ 2 K ðxÞ e 2 x ¼ x 3 e 2 x þ x )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K 0 ðxÞ e 2 x ¼ x 3 e 2 x þ x e 2 x ) K 0 ðxÞ ¼ ðx 3 e 2 x þ xÞ e 2 x ¼ x 3 e 4 x þ x e 2 x
)
376
G Gewöhnliche Differentialgleichungen
ð
K ðxÞ ¼
K 0 ðxÞ d x ¼
ð
ð
ðx 3 e 4 x þ x e 2 x Þ d x ¼
ð
x 3 e 4x d x þ
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Integral 315 mit n ¼ 3, a ¼ 4
x e 2x d x ¼
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ 2
ð
x 3 e4x
3
2x 1
x 2 e4x d x þ
e2x ¼
¼
4
4
4
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 314 mit a ¼ 4
x 3 e 4x
3 16 x 2 8 x þ 2
2x 1
e 4x þ
e 2x þ C ¼
4
4
64
4
1 3
3 1 2
1
1
1
¼
x
x
x þ
e 4x þ
ð2 x 1Þ e 2 x þ C ¼
4
4 4
8
32
4
1 3
3 2
3
3
1
¼
x
x þ
x
e 4x þ
ð2 x 1Þ e 2 x þ C
4
16
32
128
4
¼
Allgemeine Lösung der inhomogenen Dgl:
1 3
3 2
3
3
1
2x
4x
2x
y ¼ K ðxÞ e
¼
x
x þ
x
e þ
ð2 x 1Þ e þ C e 2 x ¼
4
16
32
128
4
1 3
3 2
3
3
1
x
x þ
x
e 2x þ
ð2 x 1Þ þ C e 2 x
¼
4
16
32
128
4
Bewegung einer Masse unter dem Einfluss einer periodischen Kraft und einer geschwindigkeitsproportionalen Reibungskraft
Die Bewegung einer Masse wird durch die Dgl v_ þ 2v ¼ sin ð2 tÞ beschrieben.
G42
a) Wie lautet das Geschwindigkeit-Zeit-Gesetz v ¼ v ðtÞ, wenn der Körper zur Zeit t ¼ 0 aus der
Ruhe heraus startet?
b) Bestimmen Sie ferner das Weg-Zeit-Gesetz s ¼ s ðtÞ für die Anfangswegmarke s ð0Þ ¼ 3=4.
Verwenden Sie die Lösungsmethode „Variation der Konstanten“.
a) Allgemeine Lösung der zugehörigen homogenen Dgl v_ þ 2 v ¼ 0:
v ¼ K e 2t
(Ansatz : v ¼ K e l t Þ
Variation der Konstanten: K ! K (t)
Lösungsansatz mit der zugehörigen 1. Ableitung:
v ¼ K ðtÞ e 2 t ;
v_ ¼ K_ ðtÞ e 2 t 2 K ðtÞ e 2 t
ðProdukt- und Kettenregel Þ
Einsetzen in die inhomogene Dgl, unbekannte Faktorfunktion K ðtÞ bestimmen:
v_ þ 2 v ¼ K_ ðtÞ e 2 t 2 K ðtÞ e 2 t þ 2 K ðtÞ e 2 t ¼ sin ð2 tÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K_ ðtÞ e 2 t ¼ sin ð2 tÞ e 2 t ) K_ ðtÞ ¼ sin ð2 tÞ e 2 t )
ð
K ðtÞ ¼
K_ ðtÞ d t ¼
ð
sin ð2 tÞ e 2 t d t ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
e 2t
8
)
½ 2 sin ð2 tÞ 2 cos ð2 tÞ þ C ¼
Integral 322 mit a ¼ b ¼ 2
¼
e2t
1
e 2 t ½ sin ð2 tÞ cos ð2 tÞ þ C
2 ½ sin ð2 tÞ cos ð2 tÞ þ C ¼
4
8
1 Differentialgleichungen 1. Ordnung
377
Allgemeine Lösung der inhomogenen Dgl:
1
v ¼ K ðtÞ e 2 t ¼
e 2 t ½ sin ð2 tÞ cos ð2 tÞ þ C e 2 t ¼
4
¼
1
1
e 2 t e 2 t ½ sin ð2 tÞ cos ð2 tÞ þ C e 2 t ¼
4 |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
4
0
e ¼ 1
½ sin ð2 tÞ cos ð2 tÞ þ C e 2 t
Aus der Anfangsgeschwindigkeit v ð0Þ ¼ 0 bestimmen wir die Integrationskonstante C:
v ð0Þ ¼ 0
)
1
1
1
ðsin 0 cos 0Þ þ C e 0 ¼
ð0 1Þ þ C 1 ¼
þC ¼ 0
4
4
4
)
C ¼
1
4
Das Geschwindigkeit-Zeit-Gesetz lautet demnach wie folgt (Bild G-12):
v ¼
1
4
½ sin ð2 tÞ cos ð2 tÞ þ
1
1
e 2t ¼
4
4
½ sin ð2 tÞ cos ð2 tÞ þ e 2 t ; t 0
b) Die Geschwindigkeit v ist die 1. Ableitung des Weges s nach der Zeit t, d. h. v ¼ s_ . Daher gilt:
ð
ð
ð
1
s ¼ s_ d t ¼ v d t ¼
½ sin ð2 tÞ cos ð2 tÞ þ e 2 t d t ¼
4
1
¼
4
1
1
1
cos ð2 tÞ
sin ð2 tÞ
e 2t
2
2
2
þK ¼
1
8
½ cos ð2 tÞ þ sin ð2 tÞ þ e 2 t þ K
(Integrale der Reihe nach: 204 mit a ¼ 2, 228 mit a ¼ 2 und 312 mit a ¼ 2)
3
bestimmen wir die Integrationskonstante K:
4
1
1
1
3
ðcos 0 þ sin 0 þ e 0 Þ þ K ¼
ð1 þ 0 þ 1Þ þ K ¼
þK ¼
8
8
4
4
Aus der Anfangswegmarke s ð0Þ ¼
)
K ¼ 1
Damit erhalten wir das folgende Weg-Zeit-Gesetz (Bild G-13):
s ¼
1
8
½ cos ð2 tÞ þ sin ð2 tÞ þ e 2 t þ 1 ; t 0
v
s
0,4
1,2
0,2
0,75
1
2
3
4
5
6
7
t
0,4
– 0,2
– 0,4
1
Bild G-12
G43
y0 þ 4y ¼
2
3
4
5
6
7
Bild G-13
x þ6
e4x
x 2
Bestimmen Sie die allgemeine Lösung durch „Variation der Konstanten“.
Allgemeine Lösung der zugehörigen homogenen Dgl y 0 þ 4 y ¼ 0:
y ¼ K e 4x
(Ansatz : y ¼ K e l x Þ
t
378
G Gewöhnliche Differentialgleichungen
Variation der Konstanten: K ! K (x)
Lösungsansatz mit der zugehörigen 1. Ableitung:
y ¼ K ðxÞ e 4 x ;
y 0 ¼ K 0 ðxÞ e 4 x 4 K ðxÞ e 4 x
ðProdukt- und Kettenregel Þ
Wir setzen diese Ausdrücke in die inhomogene Dgl ein und erhalten eine einfache Dgl 1. Ordnung für die noch unbekannte Faktorfunktion K ðxÞ, die durch unbestimmte Integration lösbar ist:
x þ6
y 0 þ 4 y ¼ K 0 ðxÞ e 4 x 4 K ðxÞ e 4 x þ 4 K ðxÞ e 4 x ¼ K 0 ðxÞ e 4 x ¼
e 4x
x
2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
ð
x
þ
6
x þ6
) K ðxÞ ¼ K 0 ðxÞ d x ¼
d x ¼ x þ 8 ln j x 2 j þ C
K 0 ðxÞ ¼
x 2
x 2
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
)
Integral 20 mit a ¼ 1, b ¼ 6, p ¼ 1, q ¼ 2 ; D ¼ 8
Die allgemeine Lösung der inhomogenen Dgl lautet damit wie folgt:
y ¼ K ðxÞ e 4 x ¼ ðx þ 8 ln j x 2 j þ C Þ e 4 x
Ausgangssignal eines D T 1 -Regelkreisgliedes
Das zeitabhängige Ausgangssignal v ¼ v ðtÞ eines D T 1 -Regelkreisgliedes genüge der folgenden Dgl:
G44
0,2 v_ þ v ¼ cos t 1,24 sin t ;
t 0
Lösen Sie diese Dgl durch „Variation der Konstanten“ und bestimmen Sie die sog. „stationäre“ Lösung,
die sich nach einer gewissen „Einschwingphase“ einstellt.
Die zugehörige homogene Dgl 0,2 v_ þ v ¼ 0 oder v_ þ 5 v ¼ 0 hat die Lösung v 0 ¼ K e 5 t . Durch
„Variation der Konstanten‘‘ bestimmen wir die allgemeine Lösung der inhomogenen Dgl. Der Lösungsansatz
v ¼ K ðtÞ e 5 t enthält die noch unbekannte Faktorfunktion K ðtÞ, die wir so bestimmen müssen, dass der Lösungsansatz mitsamt seiner Ableitung
v_ ¼ K_ ðtÞ e 5 t 5 K ðtÞ e 5 t
ðProdukt- und Kettenregel Þ
die inhomogene Dgl erfüllt. Dies führt zu der folgenden einfachen Dgl für K ðtÞ, die durch unbestimmte Integration
leicht lösbar ist:
0,2 v_ þ v ¼ 0,2 ½ ðK_ ðtÞ e 5 t 5 K ðtÞ e 5 t Þ þ K ðtÞ e 5 t ¼
¼ 0,2 K_ ðtÞ e 5 t K ðtÞ e 5 t þ K ðtÞ e 5 t ¼ cos t 1,24 sin t )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K_ ðtÞ ¼ 5 ðcos t 1,24 sin tÞ e 5 t
0,2 K_ ðtÞ e 5 t ¼ cos t 1,24 sin t 5 e 5 t )
ð
K ðtÞ ¼
K_ ðtÞ d t ¼ 5
¼ 5
ð
ð
ðcos t 1,24 sin tÞ e 5 t d t ¼ 5
)
ð
cos t e 5 t d t 6,2
sin t e 5 t d t ¼
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 324
mit a ¼ 5, b ¼ 1
Integral 322
mit a ¼ 5, b ¼ 1
1
1
e 5 t ð5 cos t þ sin tÞ 6,2
e 5 t ð5 sin t cos tÞ þ C ¼
26
26
¼
1
e 5 t ð25 cos t þ 5 sin t 31 sin t þ 6,2 cos tÞ þ C ¼
26
¼
1
e 5 t ð31,2 cos t 26 sin tÞ þ C ¼ e 5 t ð1,2 cos t sin tÞ þ C
26
1 Differentialgleichungen 1. Ordnung
379
Damit erhalten wir das folgende Ausgangssignal (allgemeine Lösung der inhomogenen Dgl):
v ¼ K ðtÞ e 5 t ¼ ½ e 5 t ð1,2 cos t sin tÞ þ C e 5 t ¼ 1,2 cos t sin t þ C e 5 t ;
t 0
Der exponentielle Anteil im Ausgangssignal verschwindet im Laufe der Zeit (es handelt sich um eine streng monoton
fallende Funktion) und es verbleibt die sog. „stationäre“ Lösung (erzwungene Schwingung, siehe Bild G-14):
v stationär ¼ 1,2 cos t sin t
v
v = 1,2 · cos t – sin t
2
1,2
Bild G-14
2
4
6
8
10
12
14
t
–1
–2
1.5 Exakte Differentialgleichungen
Eine Differentialgleichung 1. Ordnung vom Typ
g ðx; yÞ d x þ h ðx; yÞ d y ¼ 0
mit
@g
@h
¼
@y
@x
(sog. „Integrabilitätsbedingung“)
heißt exakt oder vollständig. Die linke Seite dieser Gleichung ist dann das totale oder vollständige Differential einer
Funktion u ¼ u ðx; yÞ . Somit ist u x ¼ g ðx; yÞ und u y ¼ h ðx; yÞ. Die Lösung der exakten Differentialgleichung
lautet in impliziter Form:
ð
ð
ð
@g
g ðx; yÞ d x þ
h ðx; yÞ
d x d y ¼ const: ¼ C
(„Lösungsformel“)
@y
Die Lösung lässt sich auch aus den Gleichungen u x ¼ g ðx; yÞ und u y ¼ h ðx; yÞ durch unbestimmte Integration
bestimmen.
Lehrbuch: Band 2, Kapitel IV.2.4
Formelsammlung: Kapitel X.2.3
G45
ð1 x 2 e y Þ y 0 ¼ 2 x e y
Zeigen Sie, dass diese Dgl exakt ist und bestimmen Sie mit der „Lösungsformel“ die allgemeine Lösung.
Kontrollieren Sie das Ergebnis.
Wir bringen die Dgl zunächst auf die spezielle Form g ðx; yÞ d x þ h ðx; yÞ d y ¼ 0:
dy
2 x e y ¼ 0 d x )
ð1 x 2 e y Þ
2 x e y d x þ ð1 x 2 e y Þ d y ¼ 0
dx
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
g ðx; yÞ
h ðx; yÞ
Sie ist exakt, da die Integrabilitätsbedingung erfüllt ist:
@g
@
ð 2 x e y Þ ¼ 2 x e y
¼
@y
@y
9
>
>
>
=
>
>
@h
@
>
¼
ð1 x 2 e y Þ ¼ 0 2 x e y ¼ 2 x e y ;
@x
@x
)
@g
@h
¼ 2x ey
¼
@x
@y
380
G Gewöhnliche Differentialgleichungen
Lösung der exakten Dgl in impliziter Form (! FS: Kapitel X.2.3):
ð
ð
ð
@g
g ðx; yÞ d x þ
h ðx; yÞ
d x d y ¼ const: ¼ C
@y
ð
ð
ð
y
2
y
y
ð 2 x e Þ d x þ
ð1 x e Þ þ 2 x e d x d y ¼
ð
¼ ey
Lösung:
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
x2 ey
ð
2x dx þ
ð1 x 2 e y þ x 2 e y Þ d y ¼ e y x 2 þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ð
1 d y ¼ x 2 e y þ y ¼ const: ¼ C
x2 ey þ y ¼ C
Kontrolle: Das totale Differential der impliziten Lösung u ðx; yÞ ¼ x 2 e y þ y ¼ C führt auf die vorliegende Dgl:
du ¼
@u
@u
dx þ
d y ¼ 2 x e y d x þ ð x 2 e y þ 1Þ d y ¼ 2 x e y d x þ ð1 x 2 e y Þ d y ¼ 0
@x
@y
ð3 x 2 sin y y 2 sin xÞ d x þ ðx 3 cos y þ 2 y cos x þ 3 y 2 Þ d y ¼ 0
G46
Welche allgemeine Lösung besitzt diese exakte Dgl („Lösungsformel“ verwenden)?
Die vorliegende Dgl ist exakt, da die Faktoren
g ðx; yÞ ¼ 3 x 2 sin y y 2 sin x
und h ðx; yÞ ¼ x 3 cos y þ 2 y cos x þ 3 y 2
die Integrabilitätsbedingung erfüllen:
@g
@
¼
ð3 x 2 sin y y 2 sin x Þ ¼ 3 x 2 cos y 2 y sin x
@y
@y
9
>
>
>
=
>
>
@h
@
>
¼
ðx 3 cos y þ 2 y cos x þ 3 y 2 Þ ¼ 3 x 2 cos y 2 y sin x ;
@x
@x
)
@g
@h
¼
@y
@x
Wir bestimmen die allgemeine Lösung dieser Dgl in impliziter Form:
ð
ð
ð
ð
ð
@g
g ðx; yÞ d x þ
h ðx; yÞ
d x d y ¼ g ðx; yÞ d x þ ðh ðx; yÞ I Þ d y ¼ const: ¼ C
@y
|fflfflfflffl{zfflfflfflffl}
I
Mit
ð
ð
@g
I ¼
d x ¼ ð3 x 2 cos y 2 y sin xÞ d x ¼ x 3 cos y þ 2 y cos x
@y
folgt (die Integrationskonstante darf hier weggelassen werden):
ð
ð
g ðx; yÞ d x þ ðh ðx; yÞ I Þ d y ¼
ð
¼
ð
ð3 x 2 sin y y 2 sin xÞ d x þ
ð
¼
ð
ð3 x sin y y sin xÞ d x þ
2
2
Lösung (in impliziter Form):
ðx 3 cos y þ 2 y cos x þ 3 y 2 x 3 cos y 2 y cos xÞ d y ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3 y2
3 y 2 d y ¼ x 3 sin y þ y 2 cos x þ y 3 ¼ const: ¼ C
x 3 sin y þ y 2 cos x þ y 3 ¼ C
1 Differentialgleichungen 1. Ordnung
381
ð2 x e y Þ d x þ ð4 y þ 1 þ x e y Þ d y ¼ 0
G47
Zeigen Sie zunächst, dass diese Dgl exakt ist. Durch Integration der (dann bereits bekannten) partiellen
Ableitungen u x und u y bestimmen Sie die Lösung u ðx; yÞ ¼ const: der Dgl. Kontrollieren Sie das
Ergebnis.
Die Dgl ist exakt, da die Integrabilitätsbedingung erfüllt ist. Denn mit
g ðx; yÞ ¼ 2 x e y
und h ðx; yÞ ¼ 4 y þ 1 þ x e y
folgt (unter Verwendung der Kettenregel ):
9
>
>
>
>
=
@g
@
ð2 x e y Þ ¼ 0 þ e y ¼ e y
¼
@y
@y
@h
@
¼
ð4 y þ 1 þ x e y Þ ¼ 0 þ 0 þ 1 e y ¼ e y
@x
@x
>
>
>
>
;
)
@g @h
¼ e y
¼
@x
@y
Der Ausdruck auf der linken Seite der Dgl ist daher das totale oder vollständige Differential einer (noch unbekannten)
Funktion u ðx; yÞ und die Lösung der Dgl ist dann (in impliziter Form) u ðx; yÞ ¼ const: ¼ C . Wir könnten bei der
Lösung wie bei den bisherigen Aufgaben verfahren, wollen hier aber auf die sog. „Lösungsformel“ verzichten und
einen anderen Lösungsweg einschlagen. Da wir das totale Differential von u ðx; yÞ bereits kennen, sind die partiellen
Ableitungen 1. Ordnung dieser Funktion bekannt. Es gilt nämlich:
ux ¼
@u
¼ g ðx; yÞ ¼ 2 x e y
@x
und u y ¼
@u
¼ h ðx; yÞ ¼ 4 y þ 1 þ x e y
@y
Mit Hilfe dieser Ableitungen lässt sich die Funktion u ðx; yÞ wie folgt bestimmen:
ð
ð
y
ux ¼ 2x e
) u ¼ u x d x ¼ ð2 x e y Þ d x ¼ x 2 x e y þ K ð yÞ
Die bei der unbestimmten Integration auftretende Integrationskonstante kann dabei noch von der zweiten Variablen y
abhängen, da dieser Term beim partiellen Differenzieren nach x bekanntlich verschwindet (er enthält ja nur y, nicht
aber x ). Damit ist die Funktion u ðx; yÞ bis auf den Summand K ð yÞ bestimmt.
Jetzt differenzieren wir diese Funktion unter Verwendung der Kettenregel partiell nach y und vergleichen das Ergebnis
mit der bereits bekannten partiellen Ableitung u y ¼ h ðx; yÞ:
uy ¼
@
½ x 2 x e y þ K ð yÞ ¼ 0 þ x e y þ K 0 ð yÞ ¼ 4 y þ 1 þ x e y
@y
Durch Integration (nach y) erhalten wir schließlich:
ð
ð
K ðyÞ ¼ K 0 ð yÞ d y ¼ ð4 y þ 1Þ d y ¼ 2 y 2 þ y þ K 1
)
K 0 ð yÞ ¼ 4 y þ 1
ðmit K 1 2 RÞ
Die gesuchte Funktion lautet somit:
u ¼ u ðx; yÞ ¼ x 2 x e y þ K ð yÞ ¼ x 2 x e y þ 2 y 2 þ y þ K 1
Ihr totales Differential entspricht (wie man leicht nachrechnet) genau der linken Seite der vorliegenden Dgl. Damit
erhalten wir die folgende allgemeine Lösung (in impliziter Form):
x 2 x e y þ 2 y 2 þ y ¼ const: ¼ C
(die Konstante K 1 ist in C aufgegangen).
Kontrolle: Das totale Differential der impliziten Lösungsfunktion u ðx; yÞ ¼ x 2 x e y þ 2 y 2 þ y ¼ C führt
auf die vorliegende Dgl:
du ¼
@u
@u
dx þ
d y ¼ ð2 x 1 e y Þ d x þ ð x ð e y Þ þ 4 y þ 1Þ d y ¼
@x
@y
¼ ð2 x e y Þ d x þ ð4 y þ 1 þ x e y Þ d y
382
G Gewöhnliche Differentialgleichungen
ð3 x 2 þ y 2 þ 2 a xÞ d x þ 2 ðx aÞ y d y ¼ 0
G48
Mit
ðmit a > 0Þ
Lösen Sie diese exakte Dgl durch Integration der bereits bekannten partiellen Ableitungen u x und
u y der (noch unbekannten) Lösungsfunktion u ðx; yÞ ¼ const: der Dgl.
g ðx; yÞ ¼ 3 x 2 þ y 2 þ 2 a x
@g
¼ 0 þ 2y þ 0 ¼ 2y;
@y
und
h ðx; yÞ ¼ 2 ðx aÞ y
@h
¼ 2 ð1 0Þ y ¼ 2 y
@x
folgt:
)
@g
@h
¼
¼ 2y
@x
@y
Die Dgl ist also exakt. Wir lösen sie nach der selben Methode wie in der vorherigen Aufgabe. Die linke Seite der Dgl
ist das totale Differential einer (noch unbekannten) Funktion u ðx; yÞ, deren partielle Ableitungen 1. Ordnung aber
bekannt sind. Es gilt:
u x ¼ g ðx; yÞ ¼ 3 x 2 þ y 2 þ 2 a x
u y ¼ h ðx; yÞ ¼ 2 ðx aÞ y
und
Wenn wir u y nach y integrieren und dabei beachten, dass die Integrationskonstante noch von der anderen Variablen
(hier also x) abhängen kann, erhalten wir die gesuchte Funktion u ¼ u ðx; yÞ:
ð
ð
ð
u ¼ u y d y ¼ 2 ðx aÞ y d y ¼ ðx aÞ 2 y d y ¼ ðx aÞ y 2 þ K ðxÞ
Differenzieren wir jetzt u partiell nach x, so erhalten wir die bereits bekannte Ableitung u x ¼ g ðx; yÞ. Dies führt
zu einer einfachen Dgl für den noch unbekannten Summand K ðxÞ, die sich leicht lösen lässt:
ux ¼
@
@x
ðx aÞ y 2 þ K ðxÞ
K 0 ðxÞ ¼ 3 x 2 þ 2 a x
¼ ð1 0Þ y 2 þ K 0 ðxÞ ¼ y 2 þ K 0 ðxÞ ¼ g ðx; yÞ ¼ 3 x 2 þ y 2 þ 2 a x
ð
)
K ðxÞ ¼
K 0 ðxÞ d x ¼
)
ð
ð3 x 2 þ 2 a xÞ d x ¼ x 3 þ a x 2 þ K 1
Damit gilt: u ¼ u ðx; yÞ ¼ ðx aÞ y 2 þ K ðxÞ ¼ ðx aÞ y 2 þ x 3 þ a x 2 þ K 1
Die allgemeine Lösung der exakten Dgl lautet also:
u ðx; yÞ ¼ const:
)
x 3 þ a x 2 þ ðx aÞ y 2 ¼ const: ¼ C
(die Konstante K 1 ist in C aufgegangen)
ðx 2 y 2 þ x 3 Þ d x þ
G49
2 3
x y þ y3
3
dy ¼ 0;
Anfangswert : y ð1Þ ¼ 2
Lösen Sie diese exakte Dgl (Nachweis führen) durch Integration der bekannten partiellen Ableitungen
der (noch unbekannten) allgemeinen Lösung.
Wir zeigen zunächst, dass diese Dgl exakt ist. Mit
g ðx; yÞ ¼ x 2 y 2 þ x 3
und h ðx; yÞ ¼
2 3
x y þ y3
3
folgt nämlich:
@g
@
¼
ðx 2 y 2 þ x 3 Þ ¼ x 2 2 y þ 0 ¼ 2 x 2 y
@y
@y
@h
@
¼
@x
@x
2 3
x y þ y3
3
9
>
>
>
>
=
>
>
2
>
;
¼
3 x2 y þ 0 ¼ 2x2 y >
3
)
@g
@h
¼
¼ 2x2 y
@y
@x
1 Differentialgleichungen 1. Ordnung
383
Die Integrabilitätsbedingung ist also erfüllt, die linke Seite der exakten Dgl ist somit das totale Differential einer (noch
unbekannten) Funktion u ¼ u ðx; yÞ, deren partielle Ableitungen 1. Ordnung jedoch bereits bekannt sind. Es gilt:
ux ¼
@u
¼ g ðx; yÞ ¼ x 2 y 2 þ x 3
@x
und
uy ¼
@u
2 3
¼ h ðx; yÞ ¼
x y þ y3
@y
3
Wir integrieren ux nach x, beachten dabei, dass die auftretende Integrationskonstante noch von der anderen Variablen
(hier also y) abhängen kann und erhalten:
ð
ð
1 3 2
1 4
u ¼ u x d x ¼ ðx 2 y 2 þ x 3 Þ d x ¼
x y þ
x þ K ð yÞ
3
4
Um K ð yÞ zu bestimmen, differenzieren wir die Funktion u partiell nach y und erhalten die bereits bekannte partielle Ableitung u y ¼ h ðx; yÞ. Durch Vergleich folgt dann:
@
1 3 2
1 4
1 3
2 3
uy ¼
x y þ
x þ K ðyÞ ¼
x 2 y þ 0 þ K 0 ð yÞ ¼
x y þ K 0 ð yÞ ¼
@y 3
4
3
3
2 3
x y þ y3
3
¼ h ðx; yÞ ¼
)
K 0 ð yÞ ¼ y 3
ð
)
K ð yÞ ¼
K 0 ð yÞ d y ¼
ð
y3 d y ¼
1 4
y
4
(die Integrationskonstante dürfen wir an dieser Stelle weglassen). Damit gilt:
u ¼ u ðx; yÞ ¼
1 3 2
1 4
1 3 2
1 4
1 4
1 4
1 4
1 3 2
x y þ
x þ K ð yÞ ¼
x y þ
x þ
y ¼
x þ
y þ
x y
3
4
3
4
4
4
4
3
Allgemeine Lösung der exakten Dgl in impliziter Form:
u ðx; yÞ ¼ const:
)
1 4
1 4
1 3 2
x þ
y þ
x y ¼ const: 12
4
4
3
)
3 x 4 þ 3 y 4 þ 4 x 3 y 2 ¼ const: ¼ C
Spezielle Lösung für den Anfangswert y ð1Þ ¼ 2 (in impliziter Form):
y ð1Þ ¼ 2
)
3 1 þ 3 16 þ 4 1 4 ¼ 3 þ 48 þ 16 ¼ 67 ¼ C
)
C ¼ 67
Spezielle Lösung: 3 x 4 þ 3 y 4 þ 4 x 3 y 2 ¼ 67
4x2 y2
G50
x2
dx þ
2y
dy ¼ 0
x
Zeigen Sie, dass diese Dgl exakt ist und bestimmen Sie anschließend mit der „Lösungsformel“ die
allgemeine Lösung der Dgl. Wie lautet die Lösungskurve durch den Punkt P ¼ ð2; 2Þ? Welcher Art
sind die Lösungskurven?
Wir formen die Dgl zunächst wie folgt um:
!
y2
4
d x þ 2 y x 1 d y ¼ ð4 y 2 x 2 Þ d x þ 2 y x 1 d y ¼ 0
x2
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|fflfflffl{zfflfflffl}
g ðx; yÞ
h ðx; yÞ
Sie ist exakt, da die Integrabilitätsbedingung erfüllt ist:
@g
@
¼
ð4 y 2 x 2 Þ ¼ 0 2 y x 2 ¼ 2 y x 2
@y
@y
@h
@
¼
ð2 y x 1 Þ ¼ 2 y ð x 2 Þ ¼ 2 y x 2
@x
@x
9
>
>
>
>
=
>
>
>
>
;
)
@g
@h
¼
¼ 2 y x2
@y
@x
384
G Gewöhnliche Differentialgleichungen
Wir ermitteln jetzt die allgemeine Lösung der Dgl in der impliziten Form (! „Lösungsformel“):
ð
ð
ð
@g
g ðx; yÞ d x þ
h ðx; yÞ
d x d y ¼ const: ¼ C
@y
ð
ð4 y x
2
2
ð
Þ dx þ
2yx
1
ð
ð 2 y x
2
ð
Þ dx dy ¼
ð4 y x
2
2
ð
ð2 y x 1 2 y x 1 Þ d y ¼
Þ dx þ
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
2 y x1
ð
¼
ð4 y 2 x 2 Þ d x þ
4 x2 þ y2
¼ C*
x
)
ð
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
0 d y ¼ 4 x þ y2 x1 þ K ¼ 4 x þ
4 x2 þ y2 ¼ C * x
oder
y2
4 x2 þ y2
þK ¼
þK ¼ C
x
x
y2 þ 4 x2 C * x ¼ 0
)
ðmit C * ¼ C KÞ
Allgemeine Lösung der Dgl: y 2 þ 4 x 2 C * x ¼ 0
Es handelt sich um längs der x-Achse verschobene Ellipsen. Durch quadratische Ergänzung erhält man:
1 *
2
2
2
2
2
*
*
C x þ y 2 ¼ 4 ðx 2 2 C 1 xÞ þ y 2 ¼ 0
y þ 4x C x ¼ 4x C x þ y ¼ 4 x
4
|fflffl{zfflffl}
2 C1
2
2
2
2
2
2
2
4 ðx 2 C 1 x þ C 1 Þ þ y ¼ 4 C 1 ) 4 ðx C 1 Þ þ y ¼ 4 C 1 : 4 C 12 )
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
)
2: Binom : ðx C 1 Þ 2
ðx C 1 Þ 2
C 12
þ
y2
4 C 12
¼ 1
ðGleichung einer längs der x-Achse verschobenen EllipseÞ
Mittelpunkt: M ¼ ðC 1 ; 0Þ; Halbachsen: a ¼ j C 1 j, b ¼ 2 j C 1 j ¼ 2 a
Spezielle Lösung durch den Punkt P ¼ ð2; 2Þ:
y ð2Þ ¼ 2
4 þ 4 4 2 C * ¼ 20 2 C * ¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Lösung: y 2 þ 4 x 2 10 x ¼ 0 oder y ¼ 10 x 4 x 2
G51
)
)
2 C * ¼ 20
)
C * ¼ 10
ð0 x 2,5Þ
Zeigen Sie: Die nichtexakte Dgl ðx 2 yÞ d x þ x d y ¼ 0 lässt sich durch einen integrierenden Faktor
l ¼ l ðxÞ in eine exakte Dgl überführen. Bestimmen Sie diesen nur von x abhängigen Faktor und
integrieren Sie anschließend die (dann exakte) Dgl mit Hilfe der „Lösungsformel“.
Nach der (gliedweisen) Multiplikation der Dgl mit dem noch unbekannten integrierenden Faktor l ¼ l ðxÞ soll die
dann vorliegende Dgl
mit
g ðx; yÞ ¼ l ðx 2 yÞ
h ðx; yÞ ¼ l x
und
f
l ðx 2 yÞ d x þ l x d y ¼ 0
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
g ðx; yÞ
h ðx; yÞ
exakt sein. Die Koeffizientenfunktionen g ðx; yÞ und h ðx; yÞ müssen also die Integrabilitätsbedingung erfüllen:
@g
@
¼
½lðx2 y Þ ¼ lð0 1Þ ¼ l
@y
@y
@h
@
¼
ðl xÞ ¼ l 0 x þ 1 l ¼ x l 0 þ l
@x
@x
9
>
>
>
>
=
>
>
>
;
ðProduktregel Þ >
@g
@h
¼
@y
@x
)
l ¼ xl0 þ l
1 Differentialgleichungen 1. Ordnung
385
Diese Dgl 1. Ordnung für den integrierenden Faktor l ¼ l ðxÞ lässt sich leicht durch „Trennung der Variablen‘‘ wie
folgt lösen:
l ¼ xl0 þ l
ð
dl
¼ 2
l
ð
xl0 ¼ 2l
)
dx
x
)
x
dl
¼ 2l
dx
dl
2 dx
dx
¼
¼ 2
l
x
x
)
)
C
ln j l j ¼ 2 ln j x j þ ln j C j ¼ ln x þ ln j C j ¼ ln j C j ln x ¼ ln
x2
)
2
2
(Rechenregeln: R3 und R2). Durch Entlogarithmierung folgt (Rechenregeln: R5 und R6):
C
C
K
j l j ¼ ) l ¼
¼
¼ K x 2
ðmit K ¼ CÞ
x2
x2
x2
ber die Konstante K können wir frei verfügen. Wir wählen zweckmäßigerweise K ¼ 1. Der integrierende Faktor
lautet also l ¼ x 2 . Die vorgegebene Dgl geht damit über in die exakte Dgl
x 2 ðx 2 yÞ d x þ x 2 x d y ¼ 0
oder
ð1 x 2 yÞ d x þ x 1 d y ¼ 0
Wir bestimmen jetzt ihre allgemeine Lösung nach der bekannten „Lösungsformel“
ð
ð
ð
@g
d x d y ¼ const: ¼ C 1
g ðx; yÞ d x þ
h ðx; yÞ
@y
Mit
g ðx; yÞ ¼ 1 x 2 y ¼ 1 y x 2 ;
h ðx; yÞ ¼ x 1
und
@g
@
¼
ð1 y x 2 Þ ¼ 0 x 2 ¼ x 2
@y
@y
folgt daraus:
ð
ð
ð
ð
ð
2
1
2
2
ð1 y x Þ d x þ
x
þ x
d x d y ¼ ð1 y x Þ d x þ ðx 1 x 1 Þ d y ¼
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
0
x1
ð
ð
¼ ð1 y x 2 Þ d x þ 0 d y ¼ x y ð x 1 Þ þ K 1 ¼ x þ y x 1 þ K 1 ¼ const: ¼ C 1
Die gesuchte Lösung lautet somit:
x þ y x1 ¼ C1 K1 ¼ C *
)
x þ
y
¼ C*
x
)
x2 þ y ¼ C *x
)
y ¼ C *x x2
(mit C * ¼ C 1 K 1 Þ
In Bild G-15 sind einige Lösungskurven dargestellt (nach unten geöffnete Parabeln gleicher ffnung, gezeichnet für die
Parameterwerte C * ¼ 1; 3; 5 und 7; die Nullstellen liegen bei x 1 ¼ 0 und x 2 ¼ C *Þ.
y
12
8
4
Bild G-15
–2
1
3
5
7
x
–4
–8
1 3 57
1
3
5
7
386
G Gewöhnliche Differentialgleichungen
4 x d x þ ð2 x 2 e y Þ d y ¼ 0
G52
Die vorliegende Dgl ist nicht exakt, lässt sich jedoch durch einen nur von y abhängigen integrierenden
Faktor l ¼ l ð yÞ in eine exakte Dgl verwandeln. Bestimmen Sie diesen Faktor und integrieren Sie
anschließend die (dann exakte) Dgl.
Durch Multiplikation mit dem noch unbekannten integrierenden Faktor l ¼ l ð yÞ wird die Dgl exakt, d. h. die Koeffizientenfunktionen g ðx; yÞ und h ðx; yÞ der „neuen‘‘ (exakten) Dgl
4 x l d x þ ð2 x 2 e y Þ l d y ¼ 0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
|{z}
g ðx; yÞ
h ðx; yÞ
müssen die Integrabilitätsbedingung
@g
@
¼
ð4 x lÞ ¼ 4 x l 0
@y
@y
mit
g ðx; yÞ ¼ 4 x l und h ðx; yÞ ¼ ð2 x 2 e y Þ l
@g
@h
¼
erfüllen:
@y
@x
9
>
>
>
>
=
>
>
>
@h
@
;
¼
ð2 x 2 e y Þ l ¼ ð 4 x 0Þ l ¼ 4 x l >
@x
@x
)
4x l0 ¼ 4x l
)
l0 ¼ l
dl
mit l 0 ¼
dy
Diese einfache Dgl 1. Ordnung für l ¼ l ð yÞ lösen wir durch „Trennung der Variablen‘‘:
dl
dl
¼ l )
¼ 1 dy )
dy
l
ð
ð
dl
¼ 1 d y ) ln j l j ¼ y þ ln j C j
l
l0 ¼
)
ln j l j ln j C j ¼ y
)
l
ln ¼ y
C
(Rechenregel: R2). Entlogarithmieren liefert dann (Rechenregeln: R5 und R6):
l
¼ e y ) l ¼ e y ) l ¼ C e y ¼ K ey
ðmit K ¼ CÞ
C
C
Wir dürfen über die Konstante K frei verfügen und setzen K ¼ 1. Integrierender Faktor ist also l ¼ e y , die Dgl
4 x e y d x þ ð2 x 2 e y Þ e y d y ¼ 4 x e y d x þ ð2 x 2 e y 1Þ d y ¼ 0
ist exakt. Wir lösen sie mit der bekannten „Lösungsformel“:
ð
ð
ð
@g
g ðx; yÞ d x þ
h ðx; yÞ
d x d y ¼ const: ¼ C 1
@y
Mit
g ðx; yÞ ¼ 4 x e y ;
h ðx; yÞ ¼ 2 x 2 e y 1
und
@g
@
¼
ð4 x eyÞ ¼ 4 x e y
@y
@y
wird daraus:
ð
ð
ð
ð
ð
4x ey dx þ
2 x 2 e y 1 4 x e y d x d y ¼ 4 x e y d x þ ð2 x 2 e y 1 2 x 2 e y Þ d y ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
1
2x2 ey
ð
ð
y
¼ 4 x e d x þ ð 1Þ d y ¼ 2 x 2 e y y þ K 1 ¼ const: ¼ C 1
Lösung der exakten Dgl (in impliziter Form):
2 x2 e y y ¼ C1 K1 ¼ C *
ðmit C * ¼ C 1 K 1 Þ
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
387
2 Lineare Differentialgleichungen 2. Ordnung
mit konstanten Koeffizienten
Die homogene lineare Dgl wird durch einen Exponentialansatz gelöst, die inhomogene lineare Dgl durch „Aufsuchen
einer partikulären Lösung“.
Lehrbuch: Band 2, Kapitel IV.3 und IV.4
Formelsammlung: Kapitel X.3.2 und X.4
Tabelle mit Lösungsansätzen für eine partikuläre Lösung: Band 2, Kapitel IV.3.4 (Tabelle 2) und Formelsammlung,
Kapitel X.3.2.3
2.1 Homogene lineare Differentialgleichungen
G53
Lösen Sie die folgende Randwertaufgabe: y 00 þ p 2 y ¼ 0; Randwerte: y ð0Þ ¼ 1 ; y ð3=2Þ ¼ 5
Mit dem Ansatz y ¼ e l x , y 0 ¼ l e l x , y 00 ¼ l 2 e l x gehen wir in die Dgl ein und lösen die charakteristische
Gleichung:
y 00 þ p 2 y ¼ l 2 e l x þ p 2 e l x ¼ ðl 2 þ p 2 Þ e l x ¼ 0
|{z}
6¼ 0
)
l2 þ p2 ¼ 0
)
l 1=2 ¼ p j
Allgemeine Lösung der Dgl: y ¼ C 1 sin ðp xÞ þ C 2 cos ðp xÞ
Bestimmung der Integrationskonstanten aus den beiden Randbedingungen:
y ð0Þ ¼ 1
)
C 1 sin 0 þ C 2 cos 0 ¼ C 1 0 þ C 2 1 ¼ C 2 ¼ 1
y ð3=2Þ ¼ 5
)
C 1 sin ð3 p=2Þ þ C 2 cos ð3 p=2Þ ¼ C 1 ð 1Þ þ C 2 0 ¼ C 1 ¼ 5
)
C1 ¼ 5
Lösung der Randwertaufgabe:
G54
)
C2 ¼ 1
y ¼ 5 sin ðp xÞ þ 1 cos ðp xÞ ¼ 5 sin ðp xÞ þ cos ðp xÞ
y 00 þ 16 y 0 þ 100 y ¼ 0 ;
Anfangswerte: y ð0Þ ¼ 2 ;
y 0 ð0Þ ¼ 8
Mit dem Lösungsansatz y ¼ e l x und den zugehörigen Ableitungen y 0 ¼ l e l x und y 00 ¼ l 2 e l x erhalten wir
die folgende charakteristische Gleichung mit konjugiert komplexen Lösungen:
y 00 þ 16 y 0 þ 100 y ¼ l 2 e l x þ 16 l e l x þ 100 e l x ¼ ðl 2 þ 16 l þ 100Þ e l x ¼ 0
|{z}
6¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
64 100 ¼ 8 36 ¼ 8 6 j
l 2 þ 16 l þ 100 ¼ 0 ) l 1=2 ¼ 8
Die allgemeine Lösung der Dgl lautet damit:
y ¼ e 8 x ½ C 1 sin ð6 xÞ þ C 2 cos ð6 xÞ
)
388
G Gewöhnliche Differentialgleichungen
Die Parameter (Integrationskonstanten) C1 und C2 werden aus den Anfangswerten bestimmt :
y ð0Þ ¼ 2
)
e 0 ½ C 1 sin 0 þ C 2 cos 0 ¼ 1 ½ C 1 0 þ C 2 1 ¼ C 2 ¼ 2
)
C2 ¼ 2
y 0 ¼ 8 e 8 x ½ C 1 sin ð6 xÞ þ C 2 cos ð6 xÞ þ ½ 6 C 1 cos ð6 xÞ 6 C 2 sin ð6 xÞ e 8 x ¼
¼ e 8 x ½ 8 C 1 sin ð6 xÞ 8 C 2 cos ð6 xÞ þ 6 C 1 cos ð6 xÞ 6 C 2 sin ð6 xÞ
(unter Verwendung der Produktregel in Verbindung mit der Kettenregel )
y 0 ð0Þ ¼ 8
Spezielle Lösung:
)
e 0 ½ 8 C 1 sin 0 8 C 2 cos 0 þ 6 C 1 cos 0 6 C 2 sin 0 ¼ 8
)
1 ½ 8 C1 0 8 C2 1 þ 6 C1 1 6 C2 0 ¼ 8 C2 þ 6 C1 ¼ 8
)
6 C 1 ¼ 8 þ 8 C 2 ¼ 8 þ 8 2 ¼ 24
)
6 C 1 ¼ 24
)
C1 ¼ 4
y ¼ e 8 x ½ 4 sin ð6 xÞ þ 2 cos ð6 xÞ
Aperiodischer Grenzfall
Die Lösungen der Schwingungsgleichung
x€ þ 2 a x_ þ 0;25 x ¼ 0 mit
G55
a > 0
hängen noch vom Parameter a ab.
a) Wie muss a gewählt werden, damit der aperiodische Grenzfall eintritt?
b) Wie lautet die Lösung der Schwingungsgleichung im aperiodischen Grenzfall für die Anfangswerte
x ð0Þ ¼ 2 und v ð0Þ ¼ x_ ð0Þ ¼ 2?
x ¼ x ðtÞ: Weg-Zeit-Gesetz; v ¼ x_ ðtÞ: Geschwindigkeit-Zeit-Gesetz
a) Der aperiodische Grenzfall tritt (definitionsgemäß) genau dann ein, wenn die charakteristische Gleichung der Dgl
eine doppelte reelle Lösung besitzt. Mit dem Exponentialansatz x ¼ e l t ; x_ ¼ l e l t und x€ ¼ l 2 e l t erhält
man (unter Berücksichtigung von a > 0):
x€ þ 2 a x_ þ 0;25 x ¼ l 2 e l t þ 2 a l e l t þ 0;25 e l t ¼ ðl 2 þ 2 a l þ 0;25Þ e l t ¼ 0 )
|{z}
6¼ 0
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
l 2 þ 2 a l þ 0;25 ¼ 0 ) l 1=2 ¼ a a 2 0;25 ) a 2 ¼ 0;25 ) a ¼ 0;5
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
0
Der aperiodische Grenzfall tritt also für den Parameterwert a ¼ 0;5 ein, die charakteristische Gleichung hat dann
die Doppellösung l 1=2 ¼ a ¼ 0;5.
b) Die allgemeine Lösung der Dgl x€ þ x_ þ 0;25 x ¼ 0 lautet also im aperiodischen Grenzfall:
x ¼ ðC 1 t þ C 2 Þ e 0;5 t
Für die Bestimmung der Konstanten C1 und C2 aus den Anfangswerten benötigen wir noch die 1. Ableitung des
Weges x nach der Zeit t . Die Produktregel in Verbindung mit der Kettenregel liefert:
x_ ¼ C 1 e 0;5 t 0,5 e 0;5 t ðC 1 t þ C 2 Þ ¼ ðC 1 0;5 C 1 t 0;5 C 2 Þ e 0;5 t
Aus den Anfangswerten erhalten wir wie folgt die Parameter C 1 und C 2 :
x ð0Þ ¼ 2
)
ðC 1 0 þ C 2 Þ e 0 ¼ C 2 1 ¼ C 2 ¼ 2
v ð0Þ ¼ x_ ð0Þ ¼ 2
)
C2 ¼ 2
)
ðC 1 0,5 C 1 0 0,5 C 2 Þ e 0 ¼ ðC 1 0,5 C 2 Þ 1 ¼ C 1 0,5 C 2 ¼ 2
)
C 1 0,5 2 ¼ C 1 1 ¼ 2
)
C1 ¼ 1
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
Spezielle Lösung der Schwingungsgleichung
x ¼ ð t þ 2Þ e
0;5 t
389
x
; t 0
2
Bild G-16 zeigt den zeitlichen Verlauf
der aperiodischen Bewegung.
1
x = ( – t + 2) · e – 0,5 t
Bild G-16
2
8
t
– 0,5
Knickung eines Stabes nach Euler
Stäbe, die in axialer Richtung durch Druckkräfte belastet werden, zeigen bereits vor berschreiten der
Materialfestigkeit ein seitliches Ausbiegen (sog. Knickung). Das Verhalten eines beidseitig gelenkig
gelagerten Stabes der Länge l, der durch eine Druckkraft F axial belastet wird, lässt sich durch die
sog. Biegegleichung
y 00 þ
G56
F
y ¼ 0
EI
mit
y ð0Þ ¼ y ðlÞ ¼ 0
beschreiben (E I : konstante Biegesteifigkeit; y ¼ y ðxÞ: Biegelinie; Bild G-17).
Bestimmen Sie die sog. Eulerschen Knickkräfte, bei der die Zerstörung des Stabes infolge seitlichen
Ausknickens einsetzt.
Hinweis: Untersuchen Sie, unter welcher Voraussetzung die Biegegleichung nichttriviale Lösungen besitzt.
Stab
A
F
x
y
B
l
F
x
Biegelinie y (x )
y
Bild G-17
Wir bringen die Dgl zunächst in die folgende Gestalt:
y 00 þ
F
y ¼ 0
EI
)
y 00 þ w 2 y ¼ 0
F
mit w 2 ¼
EI
Mit dem bekannten Lösungsansatz y ¼ e l x , y 0 ¼ l e l x und y 00 ¼ l 2 e l x folgt dann:
y 00 þ w 2 y ¼ l 2 e l x þ w 2 e l x ¼ ðl 2 þ w 2 Þ e l x ¼ 0
|{z}
6¼ 0
)
l2 þ w2 ¼ 0
)
l 1=2 ¼ j w
Die allgemeine Lösung der Dgl lautet damit: y ¼ C 1 sin ðw xÞ þ C 2 cos ðw xÞ
Die beiden Randbedingungen führen zu den folgenden Gleichungen für die noch unbekannten Integrationskonstanten
C1 und C2 :
y ð0Þ ¼ 0
)
C 1 sin 0 þ C 2 cos 0 ¼ C 1 0 þ C 2 1 ¼ C 2 ¼ 0
)
C2 ¼ 0
y ð‘Þ ¼ 0
)
C 1 sin ðw lÞ þ C 2 cos ðw lÞ ¼ C 1 sin ðw lÞ þ 0 cos ðw lÞ ¼ C 1 sin ðw lÞ ¼ 0
|{z}
0
C1 muss von Null verschieden sein, andernfalls wäre y 0 (kein Knicken des Stabes). Wegen C 1 6¼ 0 muss demnach der Faktor sin ðw lÞ verschwinden. Diese Bedingung liefert uns die gesuchten Eigenwerte und Knickkräfte:
390
G Gewöhnliche Differentialgleichungen
sin ðw lÞ ¼ 0
)
wl ¼ k p
)
w ¼ k
p
l
ðk ¼ 1; 2; 3; . . .Þ
(wegen w > 0 kommen für k nur positive Werte in Frage)
w2 ¼
F
p2
¼ k2 2
EI
l
)
F ¼ k2
p2EI
l2
ðk ¼ 1; 2; 3; . . .Þ
Für k ¼ 1 erhalten wir den kleinsten Eigenwert w ¼ p = l. Die zugehörige Eigenfunktion
y ¼ C 1 sin
p
x ;
l
0 x l
ist in Bild G-18 dargestellt (die Konstante C 1 6¼ 0 bleibt
unbestimmt).
y
y = C1 · sin
π
x
l
C1
Bild G-18
0
l
x
Radialbewegung einer Masse auf einer rotierenden Scheibe
Bild G-19 zeigt eine mit konstanter Winkelgeschwindigkeit w rotierende Zylinderscheibe vom
Radius R, auf der sich eine Masse m reibungsfrei nach außen bewegt. Das Weg-Zeit-Gesetz r ¼ r ðtÞ
genügt dabei der Dgl
v
r€ w 2 r ¼ 0
Schiene
Wie lautet die Lösung dieser Dgl für die Anfangswerte
1
m
r ð0Þ ¼ 1 und v ð0Þ ¼ r_ ð0Þ ¼ 0?
M
v ¼ v ðtÞ ¼ r_ ðtÞ: Geschwindigkeit-Zeit-Gesetz
r
G57
v
R
rotierende
Zylinderscheibe
Bild G-19
Wir lösen diese homogene Dgl mit dem Exponentialansatz r ¼ e l t , r_ ¼ l e l t , r€ ¼ l 2 e l t :
r€ w 2 r ¼ l 2 e l t w 2 e l t ¼ ðl 2 w 2 Þ e l t ¼ 0
|{z}
6¼ 0
)
l2 w2 ¼ 0
)
l 1=2 ¼ w
Die allgemeine Lösung und ihre 1. Ableitung lauten damit:
r ¼ C1 e wt þ C2 e wt ;
r_ ¼ w C 1 e w t w C 2 e w t
ðKettenregel Þ
Aus den beiden Anfangsbedingungen lassen sich die Integrationskonstanten C1 und C2 wie folgt berechnen:
)
ðIÞ
C1 e0 þ C2 e0 ¼ C1 1 þ C2 1 ¼ C1 þ C2 ¼ 1
r_ ð0Þ ¼ 0
)
ðIIÞ
w C 1 e 0 w C 2 e 0 ¼ w C 1 1 w C 2 1 ¼ w ðC 1 C 2 Þ ¼ 0
f
r ð0Þ ¼ 1
C1 C2 ¼ 0
)
C1 ¼ C2
ðIÞ
)
C1 þ C2 ¼ C1 þ C1 ¼ 2 C1 ¼ 1
ðIIÞ
)
C2 ¼ C1 ¼
1
2
)
)
6¼ 0
ðin Gleichung ðIÞ einsetzenÞ
C1 ¼
1
2
ðin Gleichung ðIIÞ einsetzenÞ
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
391
Weg-Zeit-Gesetz der Masse m in der Führungsschiene (Bild G-20):
r
1
1
1
r ¼
e wt þ
e wt ¼
ðe w t þ e w t Þ ¼ cosh ðw tÞ
2
2
2
Zur Erinnerung: cosh x ¼
R
1 x
ðe þ e x Þ ! FS: Kapitel III.11.1.
2
1
Zum Zeitpunkt t ¼ t befindet sich die Masse am Scheibenrand.
r = cosh (v t )
Bild G-20
t
t
2.2 Inhomogene lineare Differentialgleichungen
G58
y 00 þ 4 y 0 þ 5 y ¼ 5 x 2 32 x þ 5
1. Schritt: Wir lösen die zugehörige homogene Dgl y 00 þ 4 y 0 þ 5 y ¼ 0 durch den Exponentialansatz y ¼ e l x
mit y 0 ¼ l e l x und y 00 ¼ l 2 e l x :
y 00 þ 4 y 0 þ 5 y ¼ l 2 e l x þ 4 l e l x þ 5 e l x ¼ ðl 2 þ 4 l þ 5Þ e l x ¼ 0
|{z}
6¼ 0
pffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
l 2 þ 4 l þ 5 ¼ 0 ) l 1=2 ¼ 2 4 5 ¼ 2 1 ¼ 2 j
)
Die allgemeine Lösung der homogenen Dgl lautet damit:
y 0 ¼ e 2 x ðC 1 sin x þ C 2 cos xÞ
2. Schritt: Aus der Tabelle entnehmen wir für das Störglied g ðxÞ ¼ 5 x 2 32 x þ 5 wegen b ¼ 5 6¼ 0 den
folgenden Ansatz für eine partikuläre Lösung der inhomogenen Dgl (Störglied vom Typ Nr. 1 mit n ¼ 2):
yP ¼ A x 2 þ B x þ C
mit den Ableitungen
y 0P ¼ 2 A x þ B
und
y 00P ¼ 2 A
Einsetzen in die inhomogene Dgl, ordnen nach fallenden Potenzen und ein Koeffizientenvergleich führen zu einem
gestaffelten linearen Gleichungssystem für die noch unbekannten Parameter A, B und C im Lösungsansatz, das sich
schrittweise von oben nach unten lösen lässt:
y 00 þ 4 y 0 þ 5 y ¼ 5 x 2 32 x þ 5
)
2 A þ 4 ð2 A x þ BÞ þ 5 ðA x 2 þ B x þ CÞ ¼ 5 x 2 32 x þ 5
)
2 A þ 8 A x þ 4 B þ 5 A x 2 þ 5 B x þ 5 C ¼ 5 A x 2 þ ð8 A þ 5 BÞ x þ ð2 A þ 4 B þ 5 CÞ ¼ 5 x 2 32 x þ 5
ðIÞ
5A ¼ 5
ðIIÞ
8 A þ 5 B ¼ 32
ðIIIÞ
2A þ 4B þ 5C ¼ 5
Partikuläre Lösung:
)
A ¼ 1
)
ðin die Gleichungen ðIIÞ und ðIIIÞ einsetzenÞ
5 B ¼ 32 8 A ¼ 32 8 1 ¼ 40
)
B ¼ 8
)
5 C ¼ 5 2 A 4 B ¼ 5 2 1 4 ð 8Þ ¼ 5 2 þ 32 ¼ 35
)
5 C ¼ 35
)
C ¼ 7
yP ¼ x 2 8 x þ 7
3. Schritt: Die allgemeine Lösung der inhomogenen linearen Dgl lautet damit:
y ¼ y 0 þ y P ¼ e 2 x ðC 1 sin x þ C 2 cos xÞ þ x 2 8 x þ 7
392
G Gewöhnliche Differentialgleichungen
G59
y 00 þ a 2 y ¼ 2 a sin ða xÞ
ða > 0Þ
1. Schritt: Wir lösen zunächst die zugehörige homogene Dgl y 00 þ a 2 y ¼ 0 mit dem Exponentialansatz y ¼ e l x ,
y 0 ¼ l e l x , y 00 ¼ l 2 e l x :
y 00 þ a 2 y ¼ l 2 e l x þ a 2 e l x ¼ ðl 2 þ a 2 Þ e l x ¼ 0
|{z}
6¼ 0
)
l2 þ a2 ¼ 0
)
l 1=2 ¼ j a
Die allgemeine Lösung der homogenen Dgl lautet demnach:
y 0 ¼ C 1 sin ða xÞ þ C 2 cos ða xÞ
2. Schritt: Störfunktion g ðxÞ ¼ 2 a sin ða xÞ (Störfunktion vom Typ Nr. 4 mit b ¼ a)
Da j b ¼ j a eine Lösung der charakteristischen Gleichung l 2 þ a 2 ¼ 0 ist (siehe 1. Schritt), entnehmen wir der
Tabelle den folgenden Ansatz für eine partikuläre Lösung der inhomogenen Dgl:
y P ¼ x ½ A sin ða xÞ þ B cos ða xÞ
Die benötigten Ableitungen y 0P und y 00P erhalten wir jeweils mit der Produktregel in Verbindung mit der Kettenregel:
y 0P ¼ 1 ½ A sin ða xÞ þ B cos ða xÞ þ ½ a A cos ða xÞ a B sin ða xÞ x ¼
¼ A sin ða xÞ þ B cos ða xÞ þ a x ½ A cos ða xÞ B sin ða xÞ
y 00P ¼ a A cos ða xÞ a B sin ða xÞ þ a ½ A cos ða xÞ B sin ða xÞ þ
þ ½ a A sin ða xÞ a B cos ða xÞ a x ¼
¼ a ½ A cos ða xÞ B sin ða xÞ þ a ½ A cos ða xÞ B sin ða xÞ
a 2 x ½ A sin ða xÞ þ B cos ða xÞ ¼
¼ 2 a ½ A cos ða xÞ B sin ða xÞ a 2 x ½ A sin ða xÞ þ B cos ða xÞ
Einsetzen in die inhomogene Dgl und ordnen der Glieder führt zu:
y 00 þ a 2 y ¼ 2 a sin ða xÞ
)
2 a ½ A cos ða xÞ B sin ða xÞ a 2 x ½ A sin ða xÞ þ B cos ða xÞ þ
þ a 2 x ½ A sin ða xÞ þ B cos ða xÞ ¼ 2 a sin ða xÞ
)
(die grau unterlegten Summanden heben sich auf)
2 a ½ A cos ða xÞ B sin ða xÞ ¼ 2 a sin ða xÞ : 2 a
)
A cos ða xÞ B sin ða xÞ ¼ sin ða xÞ ¼ 0 cos ða xÞ þ 1 sin ða xÞ
Wir haben noch auf der rechten Seite die fehlende Kosinusfunktion mit dem Faktor 0 ergänzt (0 cos ða xÞ 0).
Durch Koeffizientenvergleich erhalten wir zwei Gleichungen für die unbekannten Koeffizienten A und B (verglichen
werden jeweils die Kosinus- bzw. Sinusglieder der beiden Seiten):
ðIÞ
A ¼ 0;
ðIIÞ
B ¼ 1
)
Partikuläre Lösung der inhomogenen Dgl:
B ¼ 1
y P ¼ x ½ 0 sin ða xÞ 1 cos ða xÞ ¼ x cos ða xÞ
3. Schritt: Damit besitzt die inhomogene lineare Dgl folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ C 1 sin ða xÞ þ C 2 cos ða xÞ x cos ða xÞ ¼ C 1 sin ða xÞ þ ðC 2 xÞ cos ða xÞ
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
G60
393
y 00 þ 2 y 0 3 y ¼ 4 e x þ 6 x 10
1. Schritt: Wir lösen die zugehörige homogene Dgl y 00 þ 2 y 0 3 y ¼ 0 mit dem Exponentialansatz y ¼ e l x ,
y 0 ¼ l e l x , y 00 ¼ l 2 e l x :
y 00 þ 2 y 0 3 y ¼ l 2 e l x þ 2 l e l x 3 e l x ¼ ðl 2 þ 2 l 3Þ e l x ¼ 0 : e l x )
l2 þ 2l 3 ¼ 0
)
l 1=2 ¼ 1
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 3 ¼ 1 4 ¼ 1 2
)
l1 ¼ 1 ;
l2 ¼ 3
Die allgemeine Lösung der homogenen Dgl lautet somit:
y0 ¼ C1 e 1x þ C2 e 3x ¼ C1 e x þ C2 e 3x
2. Schritt: Für die Summanden g 1 ðxÞ ¼ 4 e x und g 2 ðxÞ ¼ 6 x 10 der Störfunktion g ðxÞ ¼ g 1 ðxÞ þ g 2 ðxÞ ¼
4 e x þ 6 x 10 entnehmen wir aus der Tabelle folgende Ansätze für eine partikuläre Lösung y P :
Störglied
c ¼ 1
!
g 1 ðxÞ ¼ 4 e x
yP1 ¼ A x e x
(Störglied vom Typ Nr. 2)
Begründung: c ¼ 1 ist eine einfache Lösung der charakteristischen Gleichung l 2 þ 2 l 3 ¼ 0 (1. Schritt).
Störglied
g 2 ðxÞ ¼ 6 x 10
b ¼ 3 6¼ 0
! y
P2
¼ Bx þ C
(Störglied vom Typ Nr. 1 mit n ¼ 1Þ
Der Lösungsansatz y P ist dann die Summe der beiden Teilansätze y P 1 und y P 2 :
yP ¼ yP1 þ yP2 ¼ A x e x þ B x þ C
Mit diesem Ansatz und den durch gliedweises Differenzieren unter Verwendung der Produktregel (1. Summand) gewonnenen Ableitungen
y 0P ¼ A e x þ e x A x þ B ¼ A e x þ A x e x þ B
y 00P ¼ A e x þ A e x þ e x A x ¼ 2 A e x þ A x e x
gehen wir in die inhomogene Dgl ein, ordnen die Glieder und erhalten:
y 00 þ 2 y 0 3 y ¼ 4 e x þ 6 x 10
)
2 A e x þ A x e x þ 2 ðA e x þ A x e x þ BÞ 3 ðA x e x þ B x þ CÞ ¼ 4 e x þ 6 x 10
)
2 A e x þ A x e x þ 2 A e x þ 2 A x e x þ 2 B 3 A x e x 3 B x 3 C ¼ 4 e x þ 6 x 10
ð2 A þ 2 AÞ e x þ ðA þ 2 A 3 AÞ x e x 3 B x þ 2 B 3 C ¼ 4 e x þ 6 x 10
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
4A
0
)
)
4 A e x 3 B x þ ð2 B 3 CÞ ¼ 4 e x þ 6 x 10
Durch Koeffizientenvergleich folgt (wir vergleichen dabei auf beiden Seiten der Reihe nach die Koeffizienten von e x ,
x und die absoluten Glieder):
ðIÞ
4A ¼ 4
ðIIÞ
3B ¼ 6
ðIIIÞ
2 B 3 C ¼ 10
Partikuläre Lösung:
)
A ¼ 1
)
B ¼ 2
)
(in Gleichung (III) einsetzen)
3 C ¼ 10 2 B ¼ 10 2 ð 2Þ ¼ 10 þ 4 ¼ 6
)
yP ¼ x e x 2 x þ 2
3. Schritt: Die allgemeine Lösung der inhomogenen Dgl lautet damit:
y ¼ y 0 þ y P ¼ C 1 e x þ C 2 e 3 x þ x e x 2 x þ 2 ¼ ðx þ C 1 Þ e x þ C 2 e 3 x 2 x þ 2
C ¼ 2
394
G Gewöhnliche Differentialgleichungen
G61
y 00 y 0 6 y ¼ 12 cosh ð3 xÞ
1. Schritt: Wir lösen zunächst die zugehörige homogene Dgl in der bekannten Weise mit dem Exponentialansatz
y ¼ e l x , y 0 ¼ l e l x und y 00 ¼ l 2 e l x :
y 00 y 0 6 y ¼ l 2 e l x l e l x 6 e l x ¼ ðl 2 l 6Þ e l x ¼ 0 )
|{z}
6¼ 0
rffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffi
1
1
1
25
1
5
l 2 l 6 ¼ 0 ) l 1=2 ¼
þ6 ¼
¼
) l1 ¼ 3 ;
2
4
2
4
2
2
l2 ¼ 2
Allgemeine Lösung der homogenen Dgl: y 0 ¼ C 1 e 3 x þ C 2 e 2 x
2. Schritt: Störglied g ðxÞ ¼ 12 cosh ð3 xÞ
In unserer Tabelle suchen wir vergebens ein Störglied von diesem Typ. Wir können aber die Hyperbelfunktion mit
Hilfe der Definitionsformel auf Exponentialfunktionen zurückführen (! FS: Kap. III.11.1):
g ðxÞ ¼ 12 cosh ð3 xÞ ¼ 12
1
ðe 3 x þ e 3 x Þ ¼ 6 e 3 x þ 6 e 3 x
2
Für die Einzelstörglieder entnehmen wir der Tabelle die folgenden Ansätze für eine partikuläre Lösung:
Störglied
g 1 ðxÞ ¼ 6 e 3 x
Störglied
g 2 ðxÞ ¼ 6 e 3 x
c ¼ 3
!
yP1 ¼ A x e 3x
c ¼ 3
!
yP2 ¼ B e 3x
(Störglied vom Typ Nr. 2)
(Störglied vom Typ Nr. 2)
Begründung: c ¼ 3 ist eine einfache Lösung, c ¼ 3 dagegen keine Lösung der charakteristischen Gleichung
l 2 l 6 ¼ 0, siehe 1. Schritt.
Damit erhalten wir folgenden Lösungsansatz für die partikuläre Lösung y P (Summe der beiden Einzelansätze):
yP ¼ yP1 þ yP2 ¼ A x e 3x þ B e 3x
Mit Hilfe der Produkt- und Kettenregel bilden wir noch die benötigten Ableitungen:
y 0P ¼ A e 3 x þ 3 e 3 x A x 3 B e 3 x ¼ A e 3 x þ 3 A x e 3 x 3 B e 3 x
y 00P ¼ 3 A e 3 x þ 3 A e 3 x þ 3 e 3 x 3 A x þ 9 B e 3 x ¼ 6 A e 3 x þ 9 A x e 3 x þ 9 B e 3 x
Die inhomogene Dgl geht dann über in:
y 00 y 0 6 y ¼ 6 e 3 x þ 6 e 3 x
)
6 A e 3 x þ 9 A x e 3 x þ 9 B e 3 x ðA e 3 x þ 3 A x e 3 x 3 B e 3 x Þ 6 ðA x e 3 x þ B e 3 x Þ ¼
¼ 6 e 3x þ 6 e 3x
)
6 A e 3x þ 9 A x e 3x þ 9 B e 3x A e 3x 3 A x e 3x þ 3 B e 3x 6 A x e 3x 6 B e 3x ¼
¼ 6 e 3x þ 6 e 3x
)
ð6 A AÞ e 3 x þ ð9 A 3 A 6 AÞ x e 3 x þ ð9 B þ 3 B 6 BÞ e 3 x ¼ 6 e 3 x þ 6 e 3 x
|fflfflfflffl{zfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
5A
0
6B
5 A e 3x þ 6 B e 3x ¼ 6 e 3x þ 6 e 3x
)
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
395
Koeffizientenvergleich (Vergleich der Glieder e3 x bzw. e 3 x auf beiden Seiten):
ðIÞ
5A ¼ 6
)
A ¼ 1,2
ðIIÞ
6B ¼ 6
)
B ¼ 1
y P ¼ 1,2 x e 3 x þ 1 e 3 x ¼ 1,2 x e 3 x þ e 3 x
Partikuläre Lösung der inhomogenen Dgl:
3. Schritt: Die inhomogene Dgl besitzt damit die folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ C 1 e 3 x þ C 2 e 2 x þ 1,2 x e 3 x þ e 3 x ¼ ðC 1 þ 1,2 xÞ e 3 x þ C 2 e 2 x þ e 3 x
G62
y 00 þ 2 y 0 þ 2 y ¼ 2 ;
Randbedingungen: y ð0Þ þ y 0 ðpÞ ¼ 0 ;
y ðpÞ ¼ 1
Lösen Sie diese Randwertaufgabe.
1. Schritt: Integration der zugehörigen homogenen Dgl y 00 þ 2 y 0 þ 2 y ¼ 0
Der Exponentialansatz y ¼ e l x mit y 0 ¼ l e l x und y 00 ¼ l 2 e l x führt zu der folgenden charakteristischen
Gleichung:
y 00 þ 2 y 0 þ 2 y ¼ l 2 e l x þ 2 l e l x þ 2 e l x ¼ ðl 2 þ 2 l þ 2Þ e l x ¼ 0
|{z}
6¼ 0
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
l 2 þ 2 l þ 2 ¼ 0 ) l 1=2 ¼ 1 1 2 ¼ 1
1 ¼ 1 j
)
Die allgemeine Lösung der homogenen Dgl lautet daher:
y 0 ¼ e x ðC 1 sin x þ C 2 cos xÞ
2. Schritt: Aus der Tabelle entnehmen wir für das konstante Störglied g ðxÞ ¼ 2 den Ansatz y P ¼ const: ¼ A für
eine partikuläre Lösung (das Störglied ist vom Typ Nr. 1 mit n ¼ 0).
Mit den Ableitungen y 0P ¼ 0 und y 00P ¼ 0 erhalten wir dann beim Einsetzen in die inhomogene Dgl eine Bestimmungsgleichung für die noch unbekannte Konstante A:
y 00 þ 2 y 0 þ 2 y ¼ 2
)
0 þ 2 0 þ 2A ¼ 2A ¼ 2
)
A ¼ 1
Somit ist y P ¼ 1 die gesuchte partikuläre Lösung der inhomogenen Dgl.
3. Schritt: Die allgemeine Lösung der inhomogenen Dgl lautet somit:
y ¼ y 0 þ y P ¼ e x ðC 1 sin x þ C 2 cos xÞ þ 1
4. Schritt: Aus den beiden Randbedingungen bestimmen wir die Konstanten C 1 und C 2 . Dabei benötigen wir noch
die 1. Ableitung der allgemeinen Lösung (Produktregel in Verbindung mit der Kettenregel ):
y 0 ¼ e x ðC 1 sin x þ C 2 cos xÞ þ ðC 1 cos x C 2 sin xÞ e x þ 0 ¼
¼ e x ðC 1 sin x þ C 2 cos x C 1 cos x þ C 2 sin xÞ
Wir berechnen zunächst die in den Randbedingungen auftretenden Werte y ð0Þ, y ðpÞ und y 0 ðpÞ:
y ð0Þ ¼ e 0 ðC 1 sin 0 þ C 2 cos 0Þ þ 1 ¼ 1 ðC 1 0 þ C 2 1Þ þ 1 ¼ C 2 þ 1
y ðpÞ ¼ e p ðC 1 sin p þ C 2 cos pÞ þ 1 ¼ e p ðC 1 0 þ C 2 ð 1ÞÞ þ 1 ¼ e p C 2 þ 1
y 0 ðpÞ ¼ e p ðC 1 sin p þ C 2 cos p C 1 cos p þ C 2 sin pÞ ¼
¼ e p ðC 1 0 þ C 2 ð 1Þ C 1 ð 1Þ þ C 2 0Þ ¼ e p ð C 2 þ C 1 Þ ¼ e p ðC 2 C 1 Þ
396
G Gewöhnliche Differentialgleichungen
Aus den Randbedingungen folgt dann:
y ð0Þ þ y 0 ðpÞ ¼ 0
y ðpÞ ¼ 1
ðIÞ
)
ðIIÞ
)
ðIÞ
C 2 þ 1 þ e p ðC 2 C 1 Þ ¼ 0
e p C2 þ 1 ¼ 1
)
ep C2 ¼ 0
0 þ 1 þ e p ð0 C 1 Þ ¼ 1 e p C 1 ¼ 0
)
)
)
C2 ¼ 0
e p C 1 ¼ 1
(in (I) einsetzen)
)
C1 ¼ e p
Damit erhalten wir die folgende Lösung für diese Randwertaufgabe:
y ¼ e x ½ e p sin x þ 0 cos x þ 1 ¼ e x e p sin x þ 1 ¼ e p x sin x þ 1
G63
Lösen Sie die folgende Anfangswertaufgabe:
y 00 þ y ¼ 2 cos x þ x
mit
y ðpÞ ¼ 2 p
und
y 0 ðpÞ ¼ p
1. Schritt: Die zugehörige homogene Dgl y 00 þ y ¼ 0 führt mit dem bekannten Exponentialansatz y ¼ e l x auf die
folgende charakteristische Gleichung ð y 0 ¼ l e l x , y 00 ¼ l 2 e l x Þ:
y 00 þ y ¼ l 2 e l x þ e l x ¼ ðl 2 þ 1Þ e l x ¼ 0
|{z}
6¼ 0
l2 þ 1 ¼ 0
)
)
l 1=2 ¼ 1 j ¼ j
Allgemeine Lösung der homogenen Dgl: y 0 ¼ C 1 sin x þ C 2 cos x
2. Schritt: Störglied
g ðxÞ ¼ 2 cos x þ x ¼ g 1 ðxÞ þ g 2 ðxÞ
g 1 ðxÞ ¼ 2 cos x
mit
und
g 2 ðxÞ ¼ x
Aus der Tabelle entnehmen wir die folgenden Ansätze für die partikulären Lösungen der einzelnen Störglieder:
Störglied
g 1 ðxÞ ¼ 2 cos x
b ¼ 1
!
y P 1 ¼ x ðA sin x þ B cos xÞ
ðStörglied vom Typ Nr. 4Þ
Begründung: j b ¼ j 1 ¼ j ist eine Lösung der charakteristischen Gleichung l 2 þ 1 ¼ 0, siehe 1. Schritt.
Störglied
g 2 ðxÞ ¼ x
b ¼ 1 6¼ 0
!
yP2 ¼ C x þ D
ðStörglied vom Typ Nr. 1 mit n ¼ 1Þ
Ansatz y P für das Störglied g ðxÞ ¼ g 1 ðxÞ þ g 2 ðxÞ ¼ 2 cos x þ x :
y P ¼ y P 1 þ y P 2 ¼ x ðA sin x þ B cos xÞ þ C x þ D
ðSumme der EinzelansätzeÞ
Mit diesem Ansatz und den mit Hilfe der Produktregel erhaltenen Ableitungen
y 0P ¼ 1 ðA sin x þ B cos xÞ þ ðA cos x B sin xÞ x þ C þ 0 ¼
¼ A sin x þ B cos x þ x ðA cos x B sin xÞ þ C
y 00P ¼ A cos x B sin x þ 1 ðA cos x B sin xÞ þ ð A sin x B cos xÞ x þ 0 ¼
¼ A cos x B sin x þ A cos x B sin x x ðA sin x þ B cos xÞ ¼
¼ 2 A cos x 2 B sin x x ðA sin x þ B cos xÞ
gehen wir in die inhomogene Dgl, ordnen die Glieder und erhalten durch einen Koeffizientenvergleich vier einfache
Gleichungen für die vier Unbekannten A, B, C und D:
y 00 þ y ¼ 2 cos x þ x
)
2 A cos x 2 B sin x x ðA sin x þ B cos xÞ þ x ðA sin x þ B cos xÞ þ C x þ D ¼ 2 cos x þ x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
2 A cos x 2 B sin x þ C x þ D ¼ 2 cos x þ 0 sin x þ x þ 0
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
397
Vor dem Koeffizientenvergleich haben wir auf der rechten Seite die noch fehlenden Glieder ergänzt (Sinusglied
0 sin x 0 und absolutes Glied 0, sie verändern nichts):
2A ¼ 2;
2B ¼ 0;
Partikuläre Lösung:
C ¼ 1;
D ¼ 0
)
A ¼ 1;
B ¼ 0;
C ¼ 1;
D ¼ 0
y P ¼ x ð1 sin x þ 0 cos xÞ þ 1 x þ 0 ¼ x sin x þ x
3. Schritt: Die inhomogene Dgl besitzt damit die folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ C 1 sin x þ C 2 cos x þ x sin x þ x
4. Schritt: Aus den Anfangswerten berechnen wir die noch unbekannten Koeffizienten C 1 und C 2 :
y ðpÞ ¼ 2 p
)
C 1 sin p þ C 2 cos p þ p sin p þ p ¼ C 2 þ p ¼ 2 p
|ffl{zffl}
|fflffl{zfflffl}
|ffl{zffl}
0
1
0
)
C2 ¼ p
y 0 ¼ C 1 cos x C 2 sin x þ 1 sin x þ ðcos xÞ x þ 1 ¼
¼ C 1 cos x C 2 sin x þ sin x þ x cos x þ 1
y 0 ðpÞ ¼ p
)
)
C 1 cos p C 2 sin p þ sin p þ p cos p þ 1 ¼ C 1 p þ 1 ¼ p
|fflffl{zfflffl}
|ffl{zffl} |ffl{zffl}
|fflffl{zfflffl}
1
0
0
1
C1 ¼ 1 þ 2 p ) C1 ¼ 1 2 p
Die gesuchte spezielle Lösung lautet damit:
y ¼ ð1 2 pÞ sin x p cos x þ x sin x þ x
Anregung eines Feder-Masse-Schwingers durch eine exponentiell abklingende äußere Kraft
G64
Ein schwingungsfähiges Feder-Masse-System mit der Masse m und der Federkonstanten c unterliege
der zeitabhängigen äußeren Kraft F ðtÞ ¼ F 0 e a t mit a > 0. Lösen Sie die Schwingungsgleichung
m x€ þ c x ¼ F 0 e a t
ðmit c > 0 und F 0 > 0Þ
für die Anfangswerte x ð0Þ ¼ 0 und v ð0Þ ¼ x_ ð0Þ ¼ 0. Wie lautet die „stationäre“ Lösung?
x ¼ x ðtÞ: Weg-Zeit-Gesetz; v ¼ v ðtÞ ¼ x_ ðtÞ: Geschwindigkeit-Zeit-Gesetz.
Wir bringen die Dgl zunächst auf eine etwas übersichtlichere Gestalt:
x€ þ
c
F0
e at
x ¼
m
m
oder
x€ þ w 2 x ¼ K 0 e a t
w2 ¼
c
m
und
K0 ¼
F0
m
1. Schritt: Die zugehörige homogene Dgl x€ þ w 2 x ¼ 0 wird durch den Exponentialansatz x ¼ e l t gelöst:
x ¼ e lt ;
x_ ¼ l e l t ;
x€ ¼ l 2 e l t
x€ þ w 2 x ¼ l 2 e l t þ w 2 e l t ¼ ðl 2 þ w 2 Þ e l t ¼ 0
|{z}
6¼ 0
)
l2 þ w2 ¼ 0
)
l 1=2 ¼ j w
Damit ist x 0 ¼ C 1 sin ðw tÞ þ C 2 cos ðw tÞ die allgemeine Lösung der homogenen Dgl.
2. Schritt: Den zur Störfunktion g ðtÞ ¼ K 0 e a t gehörenden Lösungsansatz für eine partikuläre Lösung x P der
inhomogenen Dgl entnehmen wir der Tabelle (das Störglied ist vom Typ Nr. 4; a ist keine Lösung der charakteristischen Gleichung, siehe 1. Schritt). Er lautet: x P ¼ A e a t . Mit diesem Ansatz und den Ableitungen
x_ P ¼ a A e a t und x€P ¼ a 2 A e a t gehen wir jetzt in die inhomogene Dgl und bestimmen den noch unbekannten Parameter A:
398
G Gewöhnliche Differentialgleichungen
x€ þ w 2 x ¼ K 0 e a t
)
a 2 A e a t þ w 2 A e a t ¼ K 0 e a t : e a t
Partikuläre Lösung:
xP ¼
K0
a2
þ w2
)
A ða 2 þ w 2 Þ ¼ K 0
)
A ¼
K0
a2
þ w2
e at
3. Schritt: Die allgemeine Lösung der Dgl lautet damit:
K0
x ¼ x 0 þ x P ¼ C 1 sin ðw tÞ þ C 2 cos ðw tÞ þ
a2
þ w2
e at ;
t 0
4. Schritt: Die Parameter C 1 und C 2 werden wie folgt aus den Anfangswerten bestimmt:
x ð0Þ ¼ 0
)
C 1 sin 0 þ C 2 cos 0 þ
)
C2 þ
K0
a2
þ
w2
¼ 0
K0
a2
)
C2 ¼
x_ ¼ w C 1 cos ðw tÞ w C 2 sin ðw tÞ a
x_ ð0Þ ¼ 0
)
Lösung:
x ¼
¼
K0
a2
þ
w2
¼ 0
e at
þ w2
K0
a2
)
þ w2
1 ¼ 0
þ w2
K0
a2
K0
a2
K0
a2
þ w2
w C 1 cos 0 w C 2 sin 0 a
w C1 a
e0 ¼ C1 0 þ C2 1 þ
K0
a2
¼ w C1 1 w C2 0 a
)
þ
w2
þ w2
ðSummen- und Kettenregel Þ
e0 ¼
1 ¼ 0
w C1 ¼ a
K0
a2
þ
w2
)
C1 ¼
K0
a
2
w a þ w2
K0
K0
K0
a
sin ðw tÞ
cos ðw tÞ þ
e at ¼
2
2
2
2
2
w a þw
a þw
a þ w2
K0
a2 þ w2
a
sin ðw tÞ cos ðw tÞ þ e a t ;
w
t 0
„Stationäre‘‘ Lösung: Im Laufe der Zeit (d. h. für t ! 1) spielt der Summand e a t keine nennenswerte Rolle
mehr und darf daher vernachlässigt werden ðe a t geht wegen a > 0 asymptotisch gegen null):
x stationär ¼
G65
K0
a2 þ w2
a
sin ðw tÞ cos ðw tÞ
w
¼
K0
w ða 2 þ w 2 Þ
ða sin ðw tÞ w cos ðw tÞÞ
Lösen Sie die folgende Schwingungsgleichung:
x€ þ x ¼ 10 ðcos t sin tÞ ;
Anfangswerte: x ð0Þ ¼ 1 ;
x_ ð0Þ ¼ 5
1. Schritt: Wir lösen zunächst die zugehörige homogene Dgl x€ þ x ¼ 0.
Lösungsansatz: x ¼ e l t , x_ ¼ l e l t , x€ ¼ l 2 e l t
x€ þ x ¼ l 2 e l t þ e l t ¼ ðl 2 þ 1Þ e l t ¼ 0
|{z}
6¼ 0
Allgemeine Lösung der homogenen Dgl:
)
l2 þ 1 ¼ 0
x 0 ¼ C 1 sin t þ C 2 cos t
)
l2 ¼ 1
)
l 1=2 ¼ j
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
399
Störglied g ðtÞ ¼ 10 ðcos t sin tÞ
2. Schritt:
Aus der Tabelle entnehmen wir den folgenden Lösungsansatz für eine partikuläre Lösung (das Störglied ist vom Typ
Nr. 4 mit b ¼ 1; j b ¼ j 1 ¼ j ist eine Lösung der charakteristischen Gleichung l 2 þ 1 ¼ 0; siehe 1. Schritt):
x P ¼ t ð A sin t þ B cos tÞ
Mit der Produktregel bilden wir die benötigten Ableitungen 1. und 2. Ordnung:
x_ P ¼ 1 ð A sin t þ B cos tÞ þ ð A cos t B sin tÞ t ¼ A sin t þ B cos t þ t ð A cos t B sin tÞ
x€P ¼ A cos t B sin t þ 1 ð A cos t B sin tÞ þ ð A sin t B cos tÞ t ¼
¼ A cos t B sin t þ A cos t B sin t t ð A sin t þ B cos tÞ ¼
¼ 2 A cos t 2 B sin t t ð A sin t þ B cos tÞ
Wir setzen diese Ausdrücke in die inhomogene Dgl ein:
x€ þ x ¼ 10 ðcos t sin tÞ
)
2 A cos t 2 B sin t t ð A sin t þ B cos tÞ þ t ð A sin t þ B cos tÞ ¼ 10 ðcos t sin tÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
2 A cos t 2 B sin t ¼ 10 cos t 10 sin t
)
Koeffizientenvergleich liefert dann (Vergleich der Kosinus- bzw. Sinusglieder auf beiden Seiten):
2 A ¼ 10 ;
Partikuläre Lösung:
2 B ¼ 10
)
A ¼ 5;
B ¼ 5
x P ¼ t ð5 sin t þ 5 cos tÞ ¼ 5 t ðsin t þ cos tÞ
3. Schritt: Die allgemeine Lösung der Schwingungsgleichung lautet damit:
x ¼ x 0 þ x P ¼ C 1 sin t þ C 2 cos t þ 5 t ðsin t þ cos tÞ ;
t 0
4. Schritt: Aus den Anfangsbedingungen berechnen wir die Parameter C 1 und C 2 :
x ð0Þ ¼ 1
)
C 1 sin 0 þ C 2 cos 0 þ 0 ¼ C 1 0 þ C 2 1 ¼ C 2 ¼ 1
)
C2 ¼ 1
x_ ¼ C 1 cos t C 2 sin t þ 5 ðsin t þ cos tÞ þ 5 t ðcos t sin tÞ
(Ableitung des letzten Summanden nach der Produktregel )
x_ ð0Þ ¼ 5
Lösung:
)
C 1 cos 0 C 2 sin 0 þ 5 ðsin 0 þ cos 0Þ þ 0 ¼ C 1 1 C 2 0 þ 5 ð0 þ 1Þ ¼ 5
)
C1 þ 5 ¼ 5
)
C1 ¼ 0
x ¼ 0 sin t þ 1 cos t þ 5 t ðsin t þ cos tÞ ¼ cos t þ 5 t ðsin t þ cos tÞ ;
Der zeitliche Verlauf der Schwingung ist in Bild G-21 dargestellt.
x
x = cos t + 5 t (sin t + cos t )
100
60
20
– 20
– 60
– 100
Bild G-21
2
6
10
14
18
t
t 0
400
G Gewöhnliche Differentialgleichungen
Elektrische Schwingung in einem L C-Stromkreis (Resonanzfall)
In einem L C-Stromkreis mit der Induktivität L und der Kapazität C genügt die Ladung q der Dgl
L q€ þ
G66
q
¼ u
C
Dabei ist u ¼ u ðtÞ die von außen angelegte Spannung. Bestimmen Sie den zeitlichen Verlauf der
Kondensatorladung q ¼ q ðtÞ, wenn die Wechselspannung
1
w 0 ¼ pffiffiffiffiffiffiffi
LC
angelegt wird. Der Kondensator soll zu Beginn, d. h. zur Zeit t ¼ 0 die Ladung q ð0Þ ¼ q 0 haben,
der Stromkreis zur gleichen Zeit stromlos sein.
u ¼ u 0 cos ðw 0 tÞ
mit
Hinweis: Die Stromstärke i ¼ i ðtÞ ist die 1. Ableitung der Ladung q ¼ q ðtÞ nach der Zeit t .
Wir bringen die Dgl zunächst auf folgende Gestalt:
1
u
q ¼
q€ þ
LC
L
oder
q€ þ
w 20
u0
q ¼
cos ðw 0 tÞ
L
mit
w 20
1
¼
LC
1. Schritt: Integration der zugehörigen homogenen Dgl q€ þ w 20 q ¼ 0
Lösungsansatz: q ¼ e l t , q_ ¼ l e l t , q€ ¼ l 2 e l t
q€ þ w 20 q ¼ l 2 e l t þ w 20 e l t ¼ ðl 2 þ w 20 Þ e l t ¼ 0
|{z}
6¼ 0
Lösung der homogenen Dgl:
)
l 2 þ w 20 ¼ 0
)
l 1=2 ¼ w 0 j
q h ¼ C 1 sin ðw 0 tÞ þ C 2 cos ðw 0 tÞ
u0
cos ðw 0 tÞ
L
Aus der Tabelle erhalten wir für die partikuläre Lösung q P der inhomogenen Dgl den folgenden Lösungsansatz (das
Störglied ist vom Typ Nr. 4 mit b ¼ w 0 ; j b ¼ j w 0 ¼ w 0 j ist eine Lösung der charakteristischen Gleichung
l 2 þ w 20 ¼ 0, siehe 1. SchrittÞ:
2. Schritt:
Störglied g ðtÞ ¼
q P ¼ t ½ A sin ðw 0 tÞ þ B cos ðw 0 tÞ
Mit der Produkt- und Kettenregel bilden wir die benötigten ersten beiden Ableitungen:
q_ P ¼ 1 ½ A sin ðw 0 tÞ þ B cos ðw 0 tÞ þ ½ w 0 A cos ðw 0 tÞ w 0 B sin ðw 0 tÞ t ¼
¼ A sin ðw 0 tÞ þ B cos ðw 0 tÞ þ t ½ w 0 A cos ðw 0 tÞ w 0 B sin ðw 0 tÞ
q€ P ¼ w 0 A cos ðw 0 tÞ w 0 B sin ðw 0 tÞ þ 1 ½ w 0 A cos ðw 0 tÞ w 0 B sin ðw 0 tÞ þ
þ ½ w 20 A sin ðw 0 tÞ w 20 B cos ðw 0 tÞ t ¼
¼ w 0 A cos ðw 0 tÞ w 0 B sin ðw 0 tÞ þ w 0 A cos ðw 0 tÞ w 0 B sin ðw 0 tÞ
w 20 t ½ A sin ðw 0 tÞ þ B cos ðw 0 tÞ ¼
¼ 2 w 0 A cos ðw 0 tÞ 2 w 0 B sin ðw 0 tÞ w 20 t ½ A sin ðw 0 tÞ þ B cos ðw 0 tÞ
Einsetzen in die inhomogene Dgl:
q€ þ w 20 q ¼
u0
cos ðw 0 tÞ
L
)
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
401
2 w 0 A cos ðw 0 tÞ 2 w 0 B sin ðw 0 tÞ w 20 t ½ A sin ðw 0 tÞ þ B cos ðw 0 tÞ þ
u0
cos ðw 0 tÞ
L
þ w 20 t ½ A sin ðw 0 tÞ þ B cos ðw 0 tÞ ¼
)
(die grau unterlegten Summanden heben sich auf)
u0
cos ðw 0 tÞ þ 0 sin ðw 0 tÞ
2 w 0 A cos ðw 0 tÞ 2 w 0 B sin ðw 0 tÞ ¼
L
ðmathematischer „Trick‘‘: wir haben die rechte Seite um das fehlende Sinusglied ergänzt: 0 sin ðw 0 tÞ 0Þ. Koeffizientenvergleich liefert zwei Gleichungen für die Unbekannten A und B, aus der sich diese bestimmen lassen:
u0
u0
2 w0 A ¼
; 2 w0 B ¼ 0 ) A ¼
; B ¼ 0
L
2 w0 L
u0
u0
Partikuläre Lösung: q P ¼ t
sin ðw 0 tÞ þ 0 cos ðw 0 tÞ ¼
t sin ðw 0 tÞ
2 w0 L
2 w0 L
3. Schritt: Die allgemeine Lösung der inhomogenen Dgl lautet damit:
u0
q ¼ q h þ q P ¼ C 1 sin ðw 0 tÞ þ C 2 cos ðw 0 tÞ þ
t sin ðw 0 tÞ ;
2 w0 L
t 0
4. Schritt: Aus den Anfangsbedingungen lassen sich die noch unbekannten Konstanten C 1 und C 2 wie folgt bestimmen:
q ð0Þ ¼ q 0
)
C 1 sin 0 þ C 2 cos 0 þ 0 ¼ C 1 0 þ C 2 1 ¼ C 2 ¼ q 0
q_ ¼ w 0 C 1 cos ðw 0 tÞ w 0 C 2 sin ðw 0 tÞ þ
¼ w 0 C 1 cos ðw 0 tÞ w 0 C 2 sin ðw 0 tÞ þ
)
C2 ¼ q0
u0
½ 1 sin ðw 0 tÞ t w 0 cos ðw 0 tÞ ¼
2 w0 L
u0
½ sin ðw 0 tÞ w 0 t cos ðw 0 tÞ
2 w0 L
(Ableitung durch gliedweises Differenzieren unter Verwendung von Ketten- und Produktregel )
Der Stromkreis ist zu Beginn stromlos, d. h. i ð0Þ ¼ 0. Daraus folgt dann:
u0
ðsin 0 0Þ ¼ 0
i ð0Þ ¼ q_ ð0Þ ¼ 0 ) w 0 C 1 cos 0 w 0 C 2 sin 0 þ
2 w0 L
)
w0 C1 1 w0 C2 0 þ
Lösung: q ¼ 0 sin ðw 0 tÞ þ q 0 cos ðw 0 tÞ þ
¼ q 0 cos ðw 0 tÞ þ
u0
0 ¼ w0 C1 ¼ 0
2 w0 L
)
C1 ¼ 0
u0
t sin ðw 0 tÞ ¼
2 w0 L
u0
t sin ðw 0 tÞ ;
2 w0 L
t 0
Bild G-22 zeigt den zeitlichen Verlauf der Kondensatorladung.
q
q0
Bild G-22
t
Erzwungene mechanische Schwingung
G67
Lösen Sie das folgende Schwingungsproblem:
x€ þ 6 x_ þ 8 x ¼ cos ð3 tÞ 18 sin ð3 tÞ
mit
x ð0Þ ¼ 2
und
x_ ð0Þ ¼ 0
Wie lautet die sog. „stationäre“ Lösung, die sich nach Ablauf der „Einschwingphase“ einstellt?
402
G Gewöhnliche Differentialgleichungen
1. Schritt: Integration der zugehörigen homogenen Dgl x€ þ 6 x_ þ 8 x ¼ 0 :
Lösungsansatz: x ¼ e l t , x_ ¼ l e l t , x€ ¼ l 2 e l t
x€ þ 6 x_ þ 8 x ¼ l e
2
l2 þ 6l þ 8 ¼ 0
)
Lösung der homogenen Dgl:
2. Schritt:
lt
þ 6l e
lt
þ8e
l 1=2 ¼ 3
¼ ðl þ 6 l þ 8Þ e
lt
2
lt
¼ 0 : e l t
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
9 8 ¼ 3 1 ¼ 3 1
)
)
l1 ¼ 2 ;
l2 ¼ 4
x0 ¼ C1 e 2t þ C2 e 4t
Störglied g ðtÞ ¼ cos ð3 tÞ 18 sin ð3 tÞ
Lösungsansatz für eine partikuläre Lösung x P der inhomogenen Dgl mit 1. und 2. Ableitung (Kettenregel):
x P ¼ A sin ð3 tÞ þ B cos ð3 tÞ ;
x_ P ¼ 3 A cos ð3 tÞ 3 B sin ð3 tÞ ;
x€P ¼ 9 A sin ð3 tÞ 9 B cos ð3 tÞ
Begründung: Das Störglied ist vom Typ Nr. 4 mit b ¼ 3; j b ¼ j 3 ¼ 3 j ist keine Lösung der charakteristischen
Gleichung l 2 þ 6 l þ 8 ¼ 0, siehe 1. Schritt.
Einsetzen in die inhomogene Dgl:
x€ þ 6 x_ þ 8 x ¼ cos ð3 tÞ 18 sin ð3 tÞ
)
9 A sin ð3 tÞ 9 B cos ð3 tÞ þ 6 ½ 3 A cos ð3 tÞ 3 B sin ð3 tÞ þ 8 ½ A sin ð3 tÞ þ B cos ð3 tÞ ¼
9 A sin ð3 tÞ 9 B cos ð3 tÞ þ 18 A cos ð3 tÞ 18 B sin ð3 tÞ þ 8 A sin ð3 tÞ þ 8 B cos ð3 tÞ ¼
ð 9 B þ 18 A þ 8 BÞ cos ð3 tÞ þ ð 9 A 18 B þ 8 AÞ sin ð3 tÞ ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
18 A B
A 18 B
ð18 A BÞ cos ð3 tÞ þ ð A 18 BÞ sin ð3 tÞ ¼ cos ð3 tÞ 18 sin ð3 tÞ
Koeffizientenvergleich der Kosinus- bzw. Sinusglieder beider Seiten führt zu den folgenden Gleichungen:
ðIÞ 18 A B ¼ 1
)
B ¼ 18 A 1
ðIIÞ A 18 B ¼ 18
)
A 18 ð18 A þ 1Þ ¼ A 324 A 18 ¼ 325 A 18 ¼ 18
)
325 A ¼ 0
)
A ¼ 0
B ¼ 18 A þ 1 ¼ 18 0 þ 1 ¼ 1
)
B ¼ 1
ðIÞ
)
Partikuläre Lösung:
)
B ¼ 18 A þ 1
ðEinsetzen in (II)Þ
ðEinsetzen in (I)Þ
x P ¼ 0 sin ð3 tÞ þ 1 cos ð3 tÞ ¼ cos ð3 tÞ
3. Schritt: Die allgemeine Lösung der inhomogenen Dgl lautet somit:
x ¼ x 0 þ x P ¼ C 1 e 2 t þ C 2 e 4 t þ cos ð3 tÞ ;
t 0
4. Schritt: Aus den Anfangswerten bestimmen wir die (noch unbekannten) Parameter C 1 und C 2 :
x ð0Þ ¼ 2
)
C 1 e 0 þ C 2 e 0 þ cos 0 ¼ C 1 1 þ C 2 1 þ 1 ¼ 2 ) ðI *Þ C 1 þ C 2 ¼ 3
x_ ¼ 2 C 1 e 2 t 4 C 2 e 4 t 3 sin ð3 tÞ
x_ ð0Þ ¼ 0
ðI *Þ
)
ðII *Þ )
ðKettenregelÞ
)
2 C 1 e 0 4 C 2 e 0 3 sin 0 ¼ 2 C 1 1 4 C 2 1 0 ¼ 0
)
2 C1 4 C2 ¼ 0
)
2 C1 ¼ 4 C2
C1 þ C2 ¼ 2 C2 þ C2 ¼ C2 ¼ 3
C1 ¼ 2 C2 ¼ 2 3 ¼ 6
)
)
ðII *Þ C 1 ¼ 2 C 2
C2 ¼ 3
ðEinsetzen in (I *)Þ
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
Spezielle Lösung:
403
x ¼ 6 e 2 t þ 3 e 4 t þ cos ð3 tÞ, t 0
5. Schritt: Stationäre Lösung nach einer gewissen Einschwingphase (d. h. für t 0; siehe Bild G-23):
x stationär ¼ cos ð3 tÞ
Begründung: Die beiden streng monoton fallenden Exponentialfunktionen in der (speziellen) Lösung spielen dann
keine nennenswerte Rolle mehr (sie streben asymptotisch gegen null) und dürfen daher vernachlässigt
werden.
x
x = cos (3 t )
1
Bild G-23
1
2
3
4
5
6
7
t
–1
Erzwungene Schwingung in einem mechanischen Schwingkreis
Bestimmen Sie die allgemeine Lösung der folgenden Schwingungsgleichung:
G68
x€ þ 16 x_ þ 64 x ¼ 79 cos t þ 47 sin t
Wie lautet die „stationäre“ Lösung dieser Dgl, dargestellt als phasenverschobene Sinusschwingung in
der Form xstationär ¼ C sin ðw t þ jÞ ðmit C > 0 und 0 j < 2 pÞ ?
1. Schritt: Integration der zugehörigen homogenen Dgl x€ þ 16 x_ þ 64 x ¼ 0
Lösungsansatz: x ¼ e l t , x_ ¼ l e l t , x€ ¼ l 2 e l t
x€ þ 16 x_ þ 64 x ¼ l e
2
l 2 þ 16 l þ 64 ¼ 0
lt
)
þ 16 l e
l 1=2
þ 64 e ¼ ðl þ 16 l þ 64Þ e
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ 8 64 64 ¼ 8 0 ¼ 8
lt
lt
2
lt
¼ 0 : e l t
)
Lösung der homogenen Dgl: x 0 ¼ ðC 1 t þ C 2 Þ e 8 t
2. Schritt: Störfunktion g ðtÞ ¼ 79 cos t þ 47 sin t
Aus der Tabelle entnommener Lösungsansatz für eine partikuläre Lösung x P der inhomogenen Dgl (mit 1. und
2. Ableitung):
x P ¼ A sin t þ B cos t ;
x_ P ¼ A cos t B sin t ;
x€P ¼ A sin t B cos t
Begründung: Das Störglied ist vom Typ Nr. 4 mit b ¼ 1; j b ¼ j 1 ¼ j ist keine Lösung der charakteristischen
Gleichung l 2 þ 16 l þ 64 ¼ 0, siehe 1. Schritt.
Einsetzen in die inhomogene Dgl und ordnen der Glieder:
x€ þ 16 x_ þ 64 x ¼ 79 cos t þ 47 sin t
)
A sin t B cos t þ 16 ð A cos t B sin tÞ þ 64 ð A sin t þ B cos tÞ ¼ 79 cos t þ 47 sin t
A sin t B cos t þ 16 A cos t 16 B sin t þ 64 A sin t þ 64 B cos t ¼ 79 cos t þ 47 sin t
ð B þ 16 A þ 64 BÞ cos t þ ð A 16 B þ 64 AÞ sin t ¼ 79 cos t þ 47 sin t
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
16 A þ 63 B
63 A 16 B
ð16 A þ 63 BÞ cos t þ ð63 A 16 BÞ sin t ¼ 79 cos t þ 47 sin t
404
G Gewöhnliche Differentialgleichungen
Koeffizientenvergleich (verglichen werden die Kosinus- bzw. Sinusglieder beider Seiten) liefert zwei einfache Gleichungen für die Unbekannten A und B:
)
)
ðIÞ 16 A þ 63 B ¼ 79 j 16
ðI *Þ
256 A þ 1008 B ¼ 1264
)
þ
ðIIÞ 63 A 16 B ¼ 47 j 63
ðII *Þ 3969 A 1008 B ¼ 2961
¼ 4225
4225 A
ðIÞ )
16 A þ 63 B ¼ 16 1 þ 63 B ¼ 16 þ 63 B ¼ 79
Partikuläre Lösung der inhomogenen Dgl:
)
)
A ¼ 1
63 B ¼ 79 16 ¼ 63
)
B ¼ 1
x P ¼ 1 sin t þ 1 cos t ¼ sin t þ cos t
3. Schritt: Die allgemeine Lösung der Schwingungsgleichung lautet damit:
x ¼ x 0 þ x P ¼ ðC 1 t þ C 2 Þ e 8 t þ sin t þ cos t ;
t 0
4. Schritt: Nach einer gewissen „Einschwingphase‘‘ (d. h. nach genügend langer Zeit t ) ist der 1. Summand in der
allgemeinen Lösung bedeutungslos und darf daher vernachlässigt werden ðe 8 t ! 0 für t ! 1Þ. Die stationäre
Lösung lautet daher (siehe Bild G-24):
+ cos
x stationär ¼ sin t þ cos t
x = sin t + cos t
x
1
1 · cos t
2
6
10
14
1
C
t
f
1
+ sin
1 · sin t
–1
Bild G-25
Bild G-24
Die erzwungene Schwingung lässt sich anhand des Zeigerdiagramms auch als phasenverschobene Sinusschwingung mit
pffiffiffi
der Amplitude C ¼ 2 und dem Nullphasenwinkel j ¼ 45 ¼
b p=4 darstellen (Bild G-25):
x stationär ¼ sin t þ cos t ¼ C sin ðt þ jÞ
C 2 ¼ 1 2 þ 1 2 ¼ 2 ðSatz des PythagorasÞ
Lösung:
x stationär ¼
)
pffiffiffi
2 sin ðt þ p=4Þ
C ¼
pffiffiffi
2;
tan j ¼
1
¼ 1
1
)
j ¼ arctan 1 ¼ p=4
Freie bzw. erzwungene Schwingung in einem mechanischen Schwingkreis
Gegeben ist ein schwingungsfähiges Feder-Masse-System mit den folgenden Kenndaten:
Masse: m ¼ 2 kg; Reibungsfaktor (Dämpferkonstante): b ¼ 10 kg/s; Federkonstante: c ¼ 12 N/m
G69
Die Lage der schwingenden Masse wird durch die zeitabhängige Koordinate x ¼ x ðtÞ beschrieben.
a) Wie lautet die spezielle Lösung x 0 ðtÞ für die Anfangswerte x 0 ð0Þ ¼ 0 m und x_ 0 ð0Þ ¼ 1 m /s.
b) Das System wird jetzt durch die äußere Kraft
F ðtÞ ¼ 50 sin t þ 10 cos t
(t in Sekunden, F in Newton)
zu erzwungenen Schwingungen erregt. Wie lautet die allgemeine Lösung der Schwingungsgleichung? Welche „stationäre“ Schwingung stellt sich nach Ablauf der sog. „Einschwingphase“ ein?
Stellen Sie diese (erzwungene) Schwingung in der phasenverschobenen Sinusform dar.
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
405
a) Die Schwingungsgleichung lautet (ohne Einheiten):
m x€ þ b x_ þ c x ¼ 0
)
2 x€ þ 10 x_ þ 12 x ¼ 0
oder
x€ þ 5 x_ þ 6 x ¼ 0
Lösungsansatz: x ¼ e l t , x_ ¼ l e l t , x€ ¼ l 2 e l t
x€ þ 5 x_ þ 6 x ¼ l 2 e l t þ 5 l e l t þ 6 e l t ¼ ðl 2 þ 5 l þ 6Þ e l t ¼ 0 ) l 2 þ 5 l þ 6 ¼ 0 )
|{z}
6¼ 0
rffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5
25
5
1
5
1
¼
l 1=2 ¼
6 ¼
) l1 ¼ 2 ; l2 ¼ 3
2
4
2
4
2
2
Die Lösung der homogenen Dgl beschreibt eine aperiodische Schwingung:
x0 ¼ C1 e 2t þ C2 e 3t ;
t 0
Die Parameter C 1 und C 2 bestimmen wir aus den Anfangsbedingungen wie folgt:
x 0 ð0Þ ¼ 0
)
ðIÞ C 1 e 0 þ C 2 e 0 ¼ C 1 1 þ C 2 1 ¼ C 1 þ C 2 ¼ 0
x_ 0 ¼ 2 C 1 e 2 t 3 C 2 e 3 t
x_ 0 ð0Þ ¼ 1
)
ðIIÞ
)
C1 ¼ C2
ðKettenregel Þ
2 C1 e 0 3 C2 e 0 ¼ 2 C1 1 3 C2 1 ¼ 2 C1 3 C2 ¼ 1
Aus Gleichung (I) folgt C 1 ¼ C 2 . Diesen Ausdruck setzen wir jetzt in Gleichung (II) ein und erhalten:
ðIIÞ )
2 C 1 3 C 2 ¼ 2 ð C 2 Þ 3 C 2 ¼ 2 C 2 3 C 2 ¼ C 2 ¼ 1
ðIÞ
C 1 ¼ C 2 ¼ ð 1Þ ¼ 1
)
Die spezielle Lösung lautet somit:
x0 ¼ e
2t
e
3t
;
)
C2 ¼ 1
x
t 0
0,15
x = e – 2t – e – 3t
Verlauf dieser aperiodischen Schwingung:
siehe Bild G-26
0,10
0,05
Bild G-26
0,5
1
1,5
2
t
b) Durch die äußere Kraft F ðtÞ ¼ 50 sin t þ 10 cos t wird das System zu erzwungenen Schwingungen erregt.
Die Schwingungsgleichung lautet jetzt:
2 x€ þ 10 x_ þ 12 x ¼ 50 sin t þ 10 cos t
oder
x€ þ 5 x_ þ 6 x ¼ 25 sin t þ 5 cos t
Lösungsansatz für eine partikuläre Lösung der inhomogenen Dgl (das Störglied ist vom Typ Nr. 4 mit b ¼ 1;
j b ¼ j 1 ¼ j ist keine Lösung der charakteristischen Gleichung l 2 þ 5 l þ 6 ¼ 0, siehe Teil a)):
x P ¼ A sin t þ B cos t ;
x_ P ¼ A cos t B sin t ;
x€P ¼ A sin t B cos t
Einsetzen in die inhomogene Dgl:
x€ þ 5 x_ þ 6 x ¼ 25 sin t þ 5 cos t
)
A sin t B cos t þ 5 ðA cos t B sin tÞ þ 6 ðA sin t þ B cos tÞ ¼ 25 sin t þ 5 cos t )
A sin t B cos t þ 5 A cos t 5 B sin t þ 6 A sin t þ 6 B cos t ¼ 25 sin t þ 5 cos t )
ð A 5 B þ 6 AÞ sin t þ ð B þ 5 A þ 6 BÞ cos t ¼ 25 sin t þ 5 cos t
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
5A 5B
5 A þ 5B
ð5 A 5 BÞ sin t þ ð5 A þ 5 BÞ cos t ¼ 25 sin t þ 5 cos t
)
406
G Gewöhnliche Differentialgleichungen
Koeffizientenvergleich (Sinus- und Kosinusglieder beiderseits vergleichen) führt zu zwei Gleichungen mit den beiden
Unbekannten A und B:
)
ðIÞ
5 A 5 B ¼ 25
þ
ðIIÞ 5 A þ 5 B ¼
5
¼ 20
10 A
ðIIÞ
)
)
A ¼ 2
ðEinsetzen in Gleichung ðIIÞÞ
5 A þ 5 B ¼ 5 ð 2Þ þ 5 B ¼ 10 þ 5 B ¼ 5
Die partikuläre Lösung lautet damit:
)
5 B ¼ 5 þ 10 ¼ 15
)
B ¼ 3
x P ¼ 2 sin t þ 3 cos t
Die allgemeine Lösung der inhomogenen Schwingungsgleichung erhalten wir, indem wir zur allgemeinen Lösung
x 0 der zugehörigen homogenen Dgl (siehe Teil a)) diese partikuläre Lösung addieren:
x ¼ x 0 þ x P ¼ C 1 e 2 t þ C 2 e 3 t 2 sin t þ 3 cos t ;
t 0
Die stationäre Lösung ist mit der partikulären Lösung x P identisch, da x 0 wegen der streng monoton fallenden
Exponentialfunktionen im Laufe der Zeit (d. h. für t ! 1) verschwindet:
x stationär ¼ x P ¼ 2 sin t þ 3 cos t ¼ K sin ðt þ jÞ
Amplitude K und Nullphasenwinkel j dieser erzwungenen Schwingung
lassen sich aus dem Zeigerdiagramm leicht berechnen (siehe Bild G-27):
pffiffiffiffiffi
K 2 ¼ 2 2 þ 3 2 ¼ 13 ðPythagorasÞ ) K ¼ 13 ¼ 3,606
3
3
) a ¼ arctan
¼ 56,31
tan a ¼
2
2
j ¼ 180 a ¼ 180 56,31
¼ 123,69
¼
b 2,159
+ cos
K · sin (t + f)
K
3
3 · cos t
2
a
– 2 · sin t
f
+ sin
Bild G-27
Stationäre Lösung:
x stationär ¼ 2 sin t þ 3 cos t ¼ 3,606 sin ðt þ 2,159Þ
Erzwungene Schwingung eines mechanischen Systems
G70
Lösen Sie die folgende Dgl einer erzwungenen Schwingung:
x€ þ 8 x_ þ 52 x ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
Geben Sie eine physikalische Deutung der sog. „stationären“ Lösung dieser Schwingungsgleichung.
1. Schritt: Zugehörige homogene Dgl x€ þ 8 x_ þ 52 x ¼ 0
Lösungsansatz: x ¼ e l t , x_ ¼ l e l t , x€ ¼ l 2 e l t
x€ þ 8 x_ þ 52 x ¼ l 2 e l t þ 8 l e l t þ 52 e l t ¼ ðl 2 þ 8 l þ 52Þ e l t ¼ 0 : e l t
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffi
36 ¼ 4 6 j
l 2 þ 8 l þ 52 ¼ 0 ) l 1=2 ¼ 4 16 52 ¼ 4
)
Lösung der homogenen Dgl (es handelt sich um eine gedämpfte Schwingung):
x 0 ¼ e 4 t ½ C 1 sin ð6 tÞ þ C 2 cos ð6 tÞ ;
2. Schritt:
t 0
Störfunktion g ðtÞ ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
Lösungsansatz für eine partikuläre Lösung der inhomogenen Dgl (aus der Tabelle entnommen) mit den benötigten
Ableitungen (unter Verwendung der Kettenregel ):
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
x P ¼ A sin ð10 tÞ þ B cos ð10 tÞ ;
407
x_ P ¼ 10 A cos ð10 tÞ 10 B sin ð10 tÞ ;
x€P ¼ 100 A sin ð10 tÞ 100 B cos ð10 tÞ
Begründung: Die Störfunktion ist vom Typ Nr. 4 mit b ¼ 10; j b ¼ j 10 ¼ 10 j ist keine Lösung der charakteristischen
Gleichung l 2 þ 8 l þ 52 ¼ 0, siehe 1. Schritt.
Einsetzen in die inhomogene Dgl, ordnen der Glieder:
x€ þ 8 x_ þ 52 x ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
)
100 A sin ð10 tÞ 100 B cos ð10 tÞ þ 8 ½ 10 A cos ð10 tÞ 10 B sin ð10 tÞ þ
)
þ 52 ½ A sin ð10 tÞ þ B cos ð10 tÞ ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
100 A sin ð10 tÞ 100 B cos ð10 tÞ þ 80 A cos ð10 tÞ 80 B sin ð10 tÞ þ
þ 52 A sin ð10 tÞ þ 52 B cos ð10 tÞ ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
)
ð 100 A 80 B þ 52 AÞ sin ð10 tÞ þ ð 100 B þ 80 A þ 52 BÞ cos ð10 tÞ ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
48 A 80 B
80 A 48 B
ð 48 A 80 BÞ sin ð10 tÞ þ ð80 A 48 BÞ cos ð10 tÞ ¼ 48 sin ð10 tÞ þ 464 cos ð10 tÞ
Koeffizientenvergleich der Sinus- bzw. Kosinusglieder auf beiden Seiten:
)
)
ðIÞ 48 A 80 B ¼ 48 j ð 3Þ
ðI*Þ
144 A þ 240 B ¼ 144
þ
)
ðIIÞ
80 A 48 B ¼ 464 j 5
ðIIÞ*Þ 400 A 240 B ¼ 2320
544 A
ðIÞ )
48 A 80 B ¼ 48 4 80 B ¼ 192 80 B ¼ 48
Partikuläre Lösung:
)
¼ 2176
)
A ¼ 4
80 B ¼ 240
)
B ¼ 3
x P ¼ 4 sin ð10 tÞ 3 cos ð10 tÞ
3. Schritt: Die allgemeine Lösung der Schwingungsgleichung lautet damit:
x ¼ x 0 þ x P ¼ e 4 t ½ C 1 sin ð6 tÞ þ C 2 cos ð6 tÞ þ 4 sin ð10 tÞ 3 cos ð10 tÞ ;
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
gedämpfte Schwingung
t 0
ungedämpfte Schwingung
(berlagerung aus einer gedämpften und einer ungedämpften Schwingung)
4. Schritt: Im Laufe der Zeit verschwindet die gedämpfte Schwingung (e 4 t ! 0 für t ! 1), das System
schwingt dann harmonisch mit der Kreisfrequenz w ¼ 10 des Erregers (sog. erzwungene Schwingung). Diese stationäre Lösung (identisch mit der partikulären Lösung)
x stationär ¼ 4 sin ð10 tÞ 3 cos ð10 tÞ
bringen wir noch mit Hilfe des Zeigerdiagramms auf die Sinusform x stationär ¼ K sin ð10 t þ jÞ (siehe Bild G-28):
K 2 ¼ 4 2 þ 3 2 ¼ 25 )
3
a ¼ arctan
¼ 36,87
4
Satz des Pythagoras:
tan a ¼
3
4
)
j ¼ 360 a ¼ 360 36,87
Stationäre Lösung:
¼ 323,13
K ¼ 5
+ cos
f
4 · sin (10 t )
a
¼
b 5,640
x stationär ¼ 4 sin ð10 tÞ 3 cos ð10 tÞ ¼
¼ 5 sin ð10 t þ 5,640Þ
Die stationäre Lösung ist eine ungedämpfte Schwingung mit der Amplitude
K ¼ 5, der Kreisfrequenz w ¼ 10 und dem Nullphasenwinkel j ¼ 5,640.
+ sin
4
K
3
– 3 · cos (10 t )
K · sin (10 t + f)
Bild G-28
408
G Gewöhnliche Differentialgleichungen
Elektrische Schwingung in einem Reihenschwingkreis ( R L C-Kreis; Bild G-29)
Der in Bild G-29 dargestellte Reihenschwingkreis enthält den ohmschen Widerstand R ¼ 20 W, eine
Spule mit der Induktivität L ¼ 1 H und einen Kondensator mit der Kapazität C ¼ 0,005 F. Beim
Anlegen der Wechselspannung u ðtÞ ¼ 200 V cos ð20 s 1 t Þ entsteht eine elektrische Schwingung.
G71
Bestimmen Sie den zeitlichen Verlauf der Kondensatorladung q ¼ q ðtÞ für die Anfangsbedingungen q ð0Þ ¼ 0 und q_ ð0Þ ¼ i ð0Þ ¼ 0 ðder Kondensator ist also zur Zeit t ¼ 0 ladungsfrei, der
Schwingkreis stromlos; i ¼ i ðtÞ: StromstärkeÞ.
R
L
i (t )
C
q (t )
u (t )
Hinweis: Die Kondensatorladung genügt der folgenden Dgl 2. Ordnung:
L q€ þ R q_ þ
Bild G-29
q
¼ u ðtÞ
C
Mit den angegebenen Werten erhalten wir die folgende Dgl (Schwingungsgleichung) für die Kondensatorladung q
(ohne Einheiten):
q
1 q€ þ 20 q_ þ
¼ 200 cos ð20 tÞ oder q€ þ 20 q_ þ 200 q ¼ 200 cos ð20 tÞ
0,005
Wir lösen sie schrittweise wie folgt:
1. Schritt: Integration der zugehörigen homogenen Dgl q€ þ 20 q_ þ 200 q ¼ 0
Lösungsansatz: q ¼ e l t , q_ ¼ l e l t , q€ ¼ l 2 e l t
q€ þ 20 q_ þ 200 q ¼ l 2 e l t þ 20 l e l t þ 200 e l t ¼ ðl 2 þ 20 l þ 200Þ e l t ¼ 0 : e l t
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
l 2 þ 20 l þ 200 ¼ 0 ) l 1=2 ¼ 10 100 200 ¼ 10
100 ¼ 10 10 j
)
Lösung der homogenen Dgl (gedämpfte elektrische Schwingung):
q 0 ¼ e 10 t ½ C 1 sin ð10 tÞ þ C 2 cos ð10 tÞ ;
t 0
2. Schritt: Störglied g ðtÞ ¼ 200 cos ð20 tÞ
Den Lösungsansatz für eine partikuläre Lösung q P der inhomogenen Dgl entnehmen wir der Tabelle (das Störglied
ist vom Typ Nr. 4 mit b ¼ 20 ; j b ¼ j 20 ¼ 20 j ist keine Lösung der charakteristischen Gleichung
l 2 þ 20 l þ 200 ¼ 0; siehe 1. SchrittÞ. Er lautet (mit den benötigten Ableitungen):
q P ¼ A sin ð20 tÞ þ B cos ð20 tÞ ;
q_ P ¼ 20 A cos ð20 tÞ 20 B sin ð20 tÞ ;
q€ P ¼ 400 A sin ð20 tÞ 400 B cos ð20 tÞ
Einsetzen in die inhomogene Dgl, ordnen der Glieder:
q€ þ 20 q_ þ 200 q ¼ 200 cos ð20 tÞ
)
400 A sin ð20 tÞ 400 B cos ð20 tÞ þ 20 ½ 20 A cos ð20 tÞ 20 B sin ð20 tÞ þ
þ 200 ½ A sin ð20 tÞ þ B cos ð20 tÞ ¼ 200 cos ð20 tÞ
400 A sin ð20 tÞ 400 B cos ð20 tÞ þ 400 A cos ð20 tÞ 400 B sin ð20 tÞ þ
þ 200 A sin ð20 tÞ þ 200 B cos ð20 tÞ ¼ 200 cos ð20 tÞ
ð 400 A 400 B þ 200 AÞ sin ð20 tÞ þ ð 400 B þ 400 A þ 200 BÞ cos ð20 tÞ ¼ 200 cos ð20 tÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
200 A 400 B
400 A 200 B
ð 200 A 400 BÞ sin ð20 tÞ þ ð400 A 200 BÞ cos ð20 tÞ ¼ 0 sin ð20 tÞ þ 200 cos ð20 tÞ
2 Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
409
Koeffizientenvergleich der Sinus- und Kosinusglieder beiderseits (der Vollständigkeit halber wurde die rechte Seite um
den fehlenden Sinusterm 0 sin ð20 tÞ 0 ergänzt) führt zu zwei Gleichungen für die unbekannten Koeffizienten A
und B:
ðIÞ
ðIIÞ
ðIÞ
200 A 400 B ¼
0
400 A 200 B ¼ 200
)
ðIIÞ )
)
200 A ¼ 400 B
j : 200
)
qP ¼
Partikuläre Lösung:
A ¼ 2B
2A B ¼ 1
A ¼ 2 B ¼ 2 ð2 A 1Þ ¼ 4 A þ 2
B ¼ 2A 1 ¼ 2
)
)
)
B ¼ 2A 1
5A ¼ 2
)
A ¼
ðEinsetzen in ðIÞÞ
2
5
ðEinsetzen in ðIIÞÞ
2
4
1
1 ¼
1 ¼
5
5
5
2
1
sin ð20 tÞ
cos ð20 tÞ
5
5
3. Schritt: Die allgemeine Lösung der inhomogenen Dgl lautet damit:
2
1
sin ð20 tÞ
cos ð20 tÞ ;
5
5
q ¼ q 0 þ q P ¼ e 10 t ½ C 1 sin ð10 tÞ þ C 2 cos ð10 tÞ þ
t 0
4. Schritt: Aus den Anfangswerten bestimmen wir die noch unbekannten Parameter C 1 und C 2
q ð0Þ ¼ 0
)
e 0 ðC 1 sin 0 þ C 2 cos 0Þ þ
)
1 ðC 1 0 þ C 2 1Þ þ
2
1
sin 0
cos 0 ¼ 0
5
5
2
1
1
0
1 ¼ C2
¼ 0
5
5
5
)
C2 ¼
1
5
q_ ¼ 10 e 10 t ½ C 1 sin ð10 tÞ þ C 2 cos ð10 tÞ þ ½ 10 C 1 cos ð10 tÞ 10 C 2 sin ð10 tÞ e 10 t þ
þ 8 cos ð20 tÞ þ 4 sin ð20 tÞ
(Ableitung mit Hilfe der Produkt- und Kettenregel)
q_ ð0Þ ¼ 0
)
10 e 0 ðC 1 sin 0 þ C 2 cos 0Þ þ ð10 C 1 cos 0 10 C 2 sin 0Þ e 0 þ
þ 8 cos 0 þ 4 sin 0 ¼ 0
)
10 1 ðC 1 0 þ C 2 1Þ þ ð10 C 1 1 10 C 2 0Þ 1 þ 8 1 þ 4 0 ¼ 0
10 C 2 þ 10 C 1 þ 8 ¼ 0
)
10 C 1 ¼ 10 C 2 8
)
)
1
6
3
8 ¼ 2 8 ¼ 6 ) C1 ¼
¼
5
10
5
3
1
2
1
Lösung: q ¼ e 10 t
sin ð10 tÞ þ
cos ð10 tÞ þ
sin ð20 tÞ
cos ð20 tÞ ;
5
5
5
5
10 C 1 ¼ 10
Physikalische Deutung: Wir erhalten eine
berlagerung aus einer gedämpften Schwingung
(Lösung der homogenen Dgl) und einer ungedämpften Schwingung ( partikuläre Lösung der inhomogenen Dgl). Nach einer gewissen „Einschwingphase‘‘ verschwindet die gedämpfte
Schwingung (1. Summand) und es verbleibt eine
ungedämpfte (elektrische) Schwingung mit der
Kreisfrequenz w ¼ 20 s 1 der äußeren Erregung, beschrieben durch die folgende Gleichung
(siehe Bild G-30):
q stationär ¼
2
1
sin ð20 tÞ
cos ð20 tÞ
5
5
t 0
q
q = 2 · sin (20 t ) – 1 · cos (20 t )
5
5
0,5
0,25
0,1
– 0,2
– 0,5
Bild G-30
0,4
0,7
t
410
G Gewöhnliche Differentialgleichungen
3 Integration von Differentialgleichungen 2. Ordnung
durch Substitution
Alle Differentialgleichungen in diesem Abschnitt lassen sich mit Hilfe einer geeigneten Substitution auf solche 1. Ordnung zurückführen.
Formelsammlung: Kapitel X.3.1
Lösen Sie die Anfangswertaufgabe
G72
x y 00 ln x ¼ y 0
mit
y ðeÞ ¼ 1
y 0 ðeÞ ¼ 2
und
mit Hilfe einer geeigneten Substitution.
Mit Hilfe der Substitution u ¼ y 0 , u 0 ¼ y 00 erhalten wir eine durch „Trennung der Variablen‘‘ leicht lösbare Dgl
1. Ordnung:
du
ln x ¼ u )
x y 00 ln x ¼ y 0 ) x u 0 ln x ¼ u ) x
dx
ð
ð
du
dx
) ln j u j ¼ ln j ln x j þ ln j C j ¼ ln j C ln x j
¼
u
x ln x
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
du
dx
¼
u
x ln x
)
Integral 343
(Rechenregel: R1). Durch Entlogarithmierung folgt (Rechenregeln: R5 und R6):
j u j ¼ j C ln x j
)
u ¼ C ln x ¼ K 1 ln x
ðmit K 1 ¼ CÞ
Rücksubstitution und Integration führen schließlich zur allgemeinen Lösung:
ð
ð
0
0
y ¼ u ¼ K 1 ln x ) y ¼ y d x ¼ K 1 ln x d x ¼ K 1 x ðln x 1Þ þ K 2
|fflfflfflfflffl{zfflfflfflfflffl}
Integral 332
Aus den Anfangswerten lassen sich die Parameter (Integrationskonstanten) K 1 und K 2 wie folgt berechnen:
y ðeÞ ¼ 1
)
K 1 e ðln e 1Þ þ K 2 ¼ K 1 e ð1 1Þ þ K 2 ¼ 0 þ K 2 ¼ 1
y 0 ðeÞ ¼ 2
)
K 1 ln e ¼ K 1 1 ¼ K 1 ¼ 2
Lösung:
)
)
K2 ¼ 1
K1 ¼ 2
y ¼ 2 x ðln x 1Þ þ 1
Differentialgleichung der Kettenlinie
G73
y
Die in Bild G-31 skizzierte Kettenlinie mit symmetrischer
Aufhängung genügt der nichtlinearen Dgl 2. Ordnung
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a y 00 ¼ 1 þ ð y 0 Þ 2
a
Kettenlinie
mit den Anfangsbedingungen
y ð0Þ ¼ a
und
y 0 ð0Þ ¼ 0 :
Lösen Sie diese Dgl durch eine geeignete Substitution.
x
Bild G-31
3 Integration von Differentialgleichungen 2. Ordnung durch Substitution
411
Die Substitution u ¼ y 0 , u 0 ¼ y 00 führt auf eine (nichtlineare) Dgl 1. Ordnung, die
blen‘‘ leicht lösen können:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
du
a y 00 ¼ 1 þ ð y 0 Þ 2 ) a u 0 ¼ 1 þ u 2 ) a
¼ 1 þ u2
dx
ð
ð
du
1
du
1
dx )
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ a 1 d x ) arsinh u ¼
a
1 þ u2
1 þ u2
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
wir durch „Trennung der Varia-
)
x
þ C1
a
Integral 123 mit a 2 ¼ 1
Wir lösen diese Gleichung nach u auf (zur Erinnerung: die sinh-Funktion ist die Umkehrfunktion der arsinh-Funktion):
x
þ C1
u ¼ sinh
a
Rücksubstitution und eine sich anschließende Integration führen dann zunächst zu:
ð
ð
x
x
0
0
y ¼ u ¼ sinh
) y ¼ y d x ¼ sinh
þ C1
þ C1 d x
a
a
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
t
Dieses Integral führen wir durch eine lineare Substitution auf ein Grundintegral zurück:
x
dt
1
þ C1 ;
¼
; dx ¼ a dt
a
dx
a
ð
ð
ð
x
y ¼ sinh
þ C 1 d x ¼ sinh t a d t ¼ a sinh t d t ¼
a
x
¼ a cosh t þ C 2 ¼ a cosh
þ C1 þ C2
a
t ¼
(nach erfolgter Rücksubstitution). Die Gleichung der Kettenlinie lautet also:
x
y ¼ a cosh
þ C1 þ C2
a
Die noch unbekannten Parameter C 1 und C 2 bestimmen wir aus den Anfangsbedingungen. Die dabei benötigte
Ableitung der Kettenlinie erhalten wir mit Hilfe der Kettenregel (Substitution: t ¼ x=a þ C 1 Þ:
x
1
x
y 0 ¼ a sinh
þ C1
þ C1
¼ sinh
a
a
a
y ð0Þ ¼ a
)
ðIÞ
a cosh ð0 þ C 1 Þ þ C 2 ¼ a cosh C 1 þ C 2 ¼ a
y 0 ð0Þ ¼ 0
)
ðIIÞ
sinh ð0 þ C 1 Þ ¼ sinh C 1 ¼ 0
ðIÞ
Lösung:
G74
)
)
C 1 ¼ arsinh 0 ¼ 0
a cosh C 1 þ C 2 ¼ a cosh 0 þ C 2 ¼ a 1 þ C 2 ¼ a þ C 2 ¼ a
y ¼ a cosh
ðEinsetzen in ðIÞÞ
)
C2 ¼ 0
x
a
Lösen Sie die folgende Randwertaufgabe mit Hilfe einer geeigneten Substitution:
y 00 þ
2y0
¼ 0;
x
Randwerte: y ð0,5Þ ¼ 2 ;
y ð1Þ ¼ 2
Diese homogene lineare Dgl 2. Ordnung lässt sich mit der Substitution u ¼ y 0 , u 0 ¼ y 00 in eine lineare Dgl
1. Ordnung überführen, die wir durch „Trennung der Variablen‘‘ lösen:
412
G Gewöhnliche Differentialgleichungen
y 00 þ
ð
2y0
¼ 0
x
du
¼ 2
u
ð
)
u0 þ
2u
¼ 0
x
du
2u
¼
dx
x
dx
x
)
ln j u j ¼ 2 ln j x j þ ln j C j ¼ ln x 2 þ ln j C j ¼ ln j C x 2 j
u0 ¼
)
)
du
dx
¼ 2
u
x
)
(Rechenregeln: R3 und R1). Entlogarithmieren liefert dann (Rechenregeln: R5 und R6):
j u j ¼ j C x 2 j
u ¼ C x 2 ¼ K1 x 2
)
ðmit K 1 ¼ CÞ
Rücksubstitution und unbestimmte Integration führen zur allgemeinen Lösung:
ð
ð
K1
x 1
y 0 ¼ u ¼ K1 x 2 ) y ¼ y 0 d x ¼ K1 x 2 d x ¼ K1
þ K2 ¼
þ K2
1
x
Aus den Randwerten bestimmen wir die (noch unbekannten) Parameter K 1 und K 2 :
y ð0,5Þ ¼ 2
)
ðIÞ
K1
þ K2 ¼ 2 K1 þ K2 ¼ 2
0,5
y ð1Þ ¼ 2
)
ðIIÞ
K1
þ K2 ¼ K1 þ K2 ¼ 2
1
ðIÞ
2 K1 þ K2 ¼ 2
ðIIÞ
K1 þ K2 ¼
K1
ðIIÞ
)
2
¼ 4
)
)
K1 ¼ 4
ðEinsetzen in ðIIÞÞ
K1 þ K2 ¼ 4 þ K2 ¼ 2
Die gesuchte spezielle Lösung lautet damit:
)
y ¼
K2 ¼ 2 þ 4 ¼ 6
4
þ6
x
Weg-Zeit-Gesetz einer beschleunigten Masse unter Berücksichtigung der Reibung
Das Weg-Zeit-Gesetz x ¼ x ðtÞ einer Masse m, die durch eine konstante Kraft F 0 beschleunigt wird,
G75
genügt bei Berücksichtigung der Reibung der folgenden Dgl 2. Ordnung:
m x€ þ b x_ ¼ F 0
ðb x_ : Reibungskraft;
b > 0: ReibungsfaktorÞ
Lösen Sie diese Dgl mit Hilfe einer geeigneten Substitution, wenn zu Beginn der Bewegung ðt ¼ 0Þ
folgende Bedingungen vorliegen: x ð0Þ ¼ 0 und x_ ð0Þ ¼ 0.
Hinweis: x_ ist die Geschwindigkeit, x€ die Beschleunigung der Masse.
Mit der Substitution u ¼ x_ , u_ ¼ x€ wird diese Dgl 2. Ordnung in eine inhomogene lineare Dgl 1. Ordnung mit
konstanten Koeffizienten übergeführt, die wir durch „Variation der Konstanten‘‘ lösen können:
m x€ þ b x_ ¼ F 0
)
m u_ þ b u ¼ F 0
oder
u_ þ a u ¼ K 0
ðmit a ¼ b=m und K 0 ¼ F 0 =mÞ
Zunächst lösen wir die zugehörige homogene Dgl durch „Trennung der Variablen‘‘:
u_ þ a u ¼ 0
ð
du
¼ a
u
)
u_ ¼
ð
1 dt
du
¼ au
dt
)
)
du
¼ a dt
u
ln j u j ¼ a t þ ln j C j
)
u
ln j u j ln j C j ¼ ln ¼ a t
C
(Rechenregel: R2). Entlogarithmierung führt schließlich zu (Rechenregeln: R5 und R6):
u
u
¼ e at ) u ¼ C e at ¼ K e at
ðmit K ¼ CÞ
¼ e at )
C
C
3 Integration von Differentialgleichungen 2. Ordnung durch Substitution
413
Damit lautet der Lösungsansatz für die inhomogene Dgl wie folgt ð„Variation der Konstanten‘‘: K ! K ðtÞÞ:
u ¼ K ðtÞ e a t ;
u_ ¼ K_ ðtÞ e a t þ e a t ð aÞ K ðtÞ ¼ K_ ðtÞ e a t a K ðtÞ e a t
(Ableitung mit der Produkt- und Kettenregel ) Einsetzen dieser Ausdrücke in die inhomogene Dgl liefert eine einfache
Dgl 1. Ordnung für die noch unbekannte Faktorfunktion K ðtÞ, die wir durch elementare Integration lösen können:
u_ þ a u ¼ K 0
)
K_ ðtÞ e a t a K ðtÞ e a t þ a K ðtÞ e a t ¼ K 0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
K_ ðtÞ e a t ¼ K 0 e a t
ð
K ðtÞ ¼
K_ ðtÞ d t ¼ K 0
K_ ðtÞ ¼ K 0 e a t
)
ð
e at d t ¼ K0
|fflfflfflfflffl{zfflfflfflfflffl}
)
)
K0
e at
þ C1 ¼
e at þ C1
a
a
Integral 312 mit a ¼ a
Die allgemeine Lösung lautet damit:
K0
K0
at
at
u ¼ K ðtÞ e
¼
e þ C1 e at ¼
þ C1 e at
a
a
Aus u ¼ x_ erhalten wir schließlich durch unbestimmte Integration die allgemeine Lösung der ursprünglichen Dgl
2. Ordnung:
ð
ð
ð
K0
K0
K0
C1
e at
x ¼ x_ d t ¼ u d t ¼
þ C1 e at d t ¼
t þ C1
þ C2 ¼
t
e at þ C2
a
a
a
a
a
|ffl{zffl}
Integral 312 mit a ¼ a
Allgemeine Lösung der inhomogenen Dgl:
x ¼
K0
C1
t
eat þ C2 ;
a
a
t 0
Die noch unbekannten Konstanten C 1 und C 2 bestimmen wir aus den Anfangswerten (die benötigte Ableitung x_ ist
bereits bekannt: x_ ¼ u ; siehe weiter oben):
x ð0Þ ¼ 0
x_ ¼ u ¼
x_ ð0Þ ¼ 0
)
ðIÞ
0
C1
C1
C1
e0 þ C2 ¼
1 þ C2 ¼
þ C2 ¼ 0
a
a
a
)
C2 ¼
C1
a
K0
þ C1 e at
a
)
ðIIÞ
K0
K0
K0
þ C1 e0 ¼
þ C1 1 ¼
þ C1 ¼ 0
a
a
a
)
C1 ¼
K0
a
(Einsetzen in Gleichung (I))
ðIÞ )
C2 ¼
C1
K0
¼
a
a2
Lösung (Weg-Zeit-Gesetz):
x ¼
K0
K0
K0
K0
t þ
e at
¼
ða t þ e a t 1Þ ;
2
2
a
a
a
a2
Im Laufe der Zeit verschwindet die streng monoton fallende
Exponentialfunktion e a t und das Weg-Zeit-Gesetz geht über
in das lineare Gesetz
x ¼
K0
a2
t 0
x
x = x (t )
ða t 1Þ
Asymptotischer
Verlauf für t >> 1
ðf ür t 1Þ
Bild G-32 zeigt das exakte Weg-Zeit-Gesetz und den linearen
asymptotischen Verlauf für t 1.
1/a
Bild G-32
t
414
G Gewöhnliche Differentialgleichungen
4 Lineare Differentialgleichungen 3. und höherer Ordnung
mit konstanten Koeffizienten
Die homogene lineare Dgl wird durch einen Exponentialansatz gelöst, die inhomogene lineare Dgl durch „Aufsuchen
einer partikulären Lösung“.
Lehrbuch: Band 2, Kapitel IV.5
Formelsammlung: Kapitel X.5
Tabelle mit Lösungsansätzen für eine partikuläre Lösung: Band 2, Kapitel IV.5.3 (Tabelle 3) und Formelsammlung,
Kapitel X.5.3 (Tabelle)
4.1 Homogene lineare Differentialgleichungen
G76
y 000 3 y 00 þ 3 y 0 y ¼ 0
Der Lösungsansatz
y ¼ e lx
mit
y 0 ¼ l e l x , y 00 ¼ l 2 e l x
und
y 000 ¼ l 3 e l x
führt zu der folgenden charakteristischen Gleichung:
y 000 3 y 00 þ 3 y 0 y ¼ l 3 e l x 3 l 2 e l x þ 3 l e l x e l x ¼
¼ ðl 3 3 l 2 þ 3 l 1Þ e l x ¼ 0
|{z}
6¼ 0
)
l3 3l2 þ 3l 1 ¼ 0
Durch Probieren findet man die Lösung l 1 ¼ 1, mit dem Horner-Schema wie folgt die restlichen Lösungen:
1
3
3
1
1
2
1
2
1
0
l1 ¼ 1
1
)
l 2 2 l þ 1 ¼ ðl 1Þ 2 ¼ 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
)
l 2=3 ¼ 1
2. Binom
Somit gilt l 1=2=3 ¼ 1 und die allgemeine Lösung der Dgl lautet daher: y ¼ ðC 1 þ C 2 x þ C 3 x 2 Þ e x
G77
y 000 2 y 00 þ 4 y 0 8 y ¼ 0 ;
Lösungsansatz: y ¼ e l x ,
y 0 ¼ l e lx,
Anfangswerte: y ð0Þ ¼ 0 ;
y 0 ð0Þ ¼ 12 ;
y 00 ð0Þ ¼ 40
y 00 ¼ l 2 e l x , y 000 ¼ l 3 e l x
Charakteristische Gleichung:
y 000 2 y 00 þ 4 y 0 8 y ¼ l 3 e l x 2 l 2 e l x þ 4 l e l x 8 e l x ¼
¼ ðl 3 2 l 2 þ 4 l 8Þ e l x ¼ 0
|{z}
6¼ 0
)
l3 2l2 þ 4l 8 ¼ 0
4 Lineare Differentialgleichungen 3. und höherer Ordnung mit konstanten Koeffizienten
415
Durch Probieren findet man die Lösung l 1 ¼ 2, mit Hilfe des Horner-Schemas die weiteren Lösungen:
1
2
4
8
2
0
8
0
4
0
l1 ¼ 2
1
)
l2 þ 4 ¼ 0
)
l2 ¼ 4
)
l 2=3 ¼ 2 j
Die allgemeine Lösung der Dgl lautet damit wie folgt:
y ¼ C 1 e 2 x þ C 2 sin ð2 xÞ þ C 3 cos ð2 xÞ
Die Integrationskonstanten C 1 , C 2 und C 3 bestimmen wir wie folgt aus den Anfangsbedingungen:
y ð0Þ ¼ 0
)
C 1 e 0 þ C 2 sin 0 þ C 3 cos 0 ¼ C 1 1 þ C 2 0 þ C 3 1 ¼ 0
)
ðIÞ
C1 þ C3 ¼ 0
y 0 ¼ 2 C 1 e 2 x þ 2 C 2 cos ð2 xÞ 2 C 3 sin ð2 xÞ
y 00 ¼ 4 C 1 e 2 x 4 C 2 sin ð2 xÞ 4 C 3 cos ð2 xÞ
(Ableitungen unter Verwendung der Kettenregel, Substitution jeweils u ¼ 2 x)
y 0 ð0Þ ¼ 12
)
2 C 1 e 0 þ 2 C 2 cos 0 2 C 3 sin 0 ¼ 2 C 1 1 þ 2 C 2 1 2 C 3 0 ¼ 12
ðIIÞ 2 C 1 þ 2 C 2 ¼ 12 : 2 oder C 1 þ C 2 ¼ 6
)
y 00 ð0Þ ¼ 40
)
)
4 C 1 e 0 4 C 2 sin 0 4 C 3 cos 0 ¼ 4 C 1 1 4 C 2 0 4 C 3 1 ¼ 40
ðIIIÞ 4 C 1 4 C 3 ¼ 40 : 4 oder C 1 C 3 ¼ 10
ðIÞ
C1 þ C3 ¼ 0
ðIIIÞ
C 1 C 3 ¼ 10
2 C1
¼ 10
)
þ
)
C1 ¼ 5
ðEinsetzen in ðIÞ und ðIIÞÞ
ðIÞ
)
C1 þ C3 ¼ 5 þ C3 ¼ 0
)
C3 ¼ 5
ðIIÞ
)
C1 þ C2 ¼ 5 þ C2 ¼ 6
)
C2 ¼ 6 5 ¼ 1
Partikuläre Lösung: y ¼ 5 e 2 x þ 1 sin ð2 xÞ 5 cos ð2 xÞ ¼ 5 e 2 x þ sin ð2 xÞ 5 cos ð2 xÞ
G78
y ð4Þ þ 5 y 000 þ 3 y 00 9 y 0 ¼ 0
Lösungsansatz: y ¼ e l x ,
y 0 ¼ l e lx,
y 00 ¼ l 2 e l x , y 000 ¼ l 3 e l x , y ð4Þ ¼ l 4 e l x
Charakteristische Gleichung:
y ð4Þ þ 5 y 000 þ 3 y 00 9 y 0 ¼ l 4 e l x þ 5 l 3 e l x þ 3 l 2 e l x 9 l e l x ¼
¼ ðl 4 þ 5 l 3 þ 3 l 2 9 lÞ e l x ¼ 0
|{z}
6¼ 0
)
l 4 þ 5 l 3 þ 3 l 2 9 l ¼ l ðl 3 þ 5 l 2 þ 3 l 9Þ ¼ 0
Eine Lösung ist l 1 ¼ 0, die restlichen erhält man aus der kubischen Gleichung l 3 þ 5 l 2 þ 3 l 9 ¼ 0. Durch
Probieren findet man eine weitere Lösung bei l 2 ¼ 1, mit dem Horner-Schema die restlichen:
416
G Gewöhnliche Differentialgleichungen
1
l2 ¼ 1
1
5
3
9
1
6
9
6
9
0
)
l 2 þ 6 l þ 9 ¼ ðl þ 3Þ 2 ¼ 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
)
l 3=4 ¼ 3
1. Binom
Damit lautet die allgemeine Lösung der Dgl wie folgt: y ¼ C 1 þ C 2 e x þ ðC 3 þ C 4 xÞ e 3 x
G79
y ð4Þ 16 y ¼ 0 ;
Lösungsansatz: y ¼ e l x ,
Anfangswerte: y ð0Þ ¼ 0 ;
y 0 ¼ l e lx,
y 0 ð0Þ ¼ 0 ;
y 00 ð0Þ ¼ 0 ;
y 000 ð0Þ ¼ 32
y 00 ¼ l 2 e l x , y 000 ¼ l 3 e l x , y ð4Þ ¼ l 4 e l x
Charakteristische Gleichung:
y ð4Þ 16 y ¼ l 4 e l x 16 e l x ¼ ðl 4 16Þ e l x ¼ 0
|{z}
6¼ 0
)
l 4 16 ¼ 0
)
l 4 ¼ 16
Diese einfache biquadratische Gleichung wird durch die Substitution u ¼ l 2 gelöst:
l
4
¼ 16
)
u
2
¼ 16
)
u 1=2 ¼ 4
l 2 ¼ u1 ¼ 4
)
l 1=2 ¼ 2
l 2 ¼ u2 ¼ 4
)
l 3=4 ¼ 2 j
Damit besitzt die Dgl die folgende allgemeine Lösung:
y ¼ C 1 e 2 x þ C 2 e 2 x þ C 3 sin ð2 xÞ þ C 4 cos ð2 xÞ
Aus den Anfangswerten bestimmen wir die noch unbekannten Parameter C 1 , C 2 , C 3 und C 4 . Die dabei benötigten
Ableitungen erhält man durch gliedweise Differentiation in Verbindung mit der Kettenregel (Substitutionen: t ¼ 2 x
bzw. t ¼ 2 x):
y 0 ¼ 2 C 1 e 2 x 2 C 2 e 2 x þ 2 C 3 cos ð2 xÞ 2 C 4 sin ð2 xÞ
y 00 ¼ 4 C 1 e 2 x þ 4 C 2 e 2 x 4 C 3 sin ð2 xÞ 4 C 4 cos ð2 xÞ
y 000 ¼ 8 C 1 e 2 x 8 C 2 e 2 x 8 C 3 cos ð2 xÞ þ 8 C 4 sin ð2 xÞ
y ð0Þ ¼ 0
y 0 ð0Þ ¼ 0
y 00 ð0Þ ¼ 0
y 000 ð0Þ ¼ 32
)
C 1 e 0 þ C 2 e 0 þ C 3 sin 0 þ C 4 cos 0 ¼ C 1 1 þ C 2 1 þ C 3 0 þ C 4 1 ¼ 0
)
ðIÞ
C1 þ C2 þ C4 ¼ 0
)
2 C 1 e 0 2 C 2 e 0 þ 2 C 3 cos 0 2 C 4 sin 0 ¼
)
ðIIÞ
)
4 C 1 e 0 þ 4 C 2 e 0 4 C 3 sin 0 4 C 4 cos 0 ¼
¼ 2 C 1 1 2 C 2 1 þ 2 C 3 1 2 C 4 0 ¼ 2 C 1 2 C 2 þ 2 C 3 ¼ 0 : 2
C1 C2 þ C3 ¼ 0
¼ 4 C 1 1 þ 4 C 2 1 4 C 3 0 4 C 4 1 ¼ 4 C 1 þ 4 C 2 4 C 4 ¼ 0 : 4
C1 þ C2 C4 ¼ 0
)
ðIIIÞ
)
8 C 1 e 0 8 C 2 e 0 8 C 3 cos 0 þ 8 C 4 sin 0 ¼
)
ðIVÞ
¼ 8 C 1 1 8 C 2 1 8 C 3 1 þ 8 C 4 0 ¼ 8 C 1 8 C 2 8 C 3 ¼ 32 : 8
C1 C2 C3 ¼ 4
4 Lineare Differentialgleichungen 3. und höherer Ordnung mit konstanten Koeffizienten
ðIÞ
C1 þ C2 þ C4 ¼ 0
ðIIIÞ
C1 þ C2 C4 ¼ 0
)
2 C4 ¼ 0
)
417
ðIIÞ
C1 C2 þ C3 ¼ 0
ðIVÞ
C1 C2 C3 ¼ 4
)
2 C3 ¼ 4
C4 ¼ 0
)
C3 ¼ 2
Diese Werte (C 3 ¼ 2 und C 4 ¼ 0) setzen wir in die Gleichungen (I) und (II) ein und addieren dann beide
Gleichungen:
)
ðIÞ C 1 þ C 2 þ 0 ¼ 0
þ
ðIIÞ C 1 C 2 2 ¼ 0
2 ¼ 0
2 C1
ðIÞ
)
2 C1 ¼ 2
)
C1 ¼ 1
ðEinsetzen in (I)Þ
C1 þ C2 þ C4 ¼ 1 þ C2 þ 0 ¼ 1 þ C2 ¼ 0
)
)
C2 ¼ 1
Damit ergibt sich folgende spezielle Lösung (C 1 ¼ 1 , C 2 ¼ 1 , C 3 ¼ 2 ; C 4 ¼ 0):
y ¼ 1 e 2 x 1 e 2 x 2 sin ð2 xÞ þ 0 cos ð2 xÞ ¼ e 2 x e 2 x 2 sin ð2 xÞ ¼
¼ 2
1
ðe 2 x e 2 x Þ 2 sin ð2 xÞ ¼ 2 sinh ð2 xÞ 2 sin ð2 xÞ ¼ 2 ½ sinh ð2 xÞ sin ð2 xÞ
2
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
sinh ð2 xÞ ! FS: Kapitel III.11.1
G80
y ð5Þ 2 y ð4Þ þ 10 y 000 18 y 00 þ 9 y 0 ¼ 0
y ¼ e l x , y 0 ¼ l e l x , y 00 ¼ l 2 e l x , y 000 ¼ l 3 e l x , y ð4Þ ¼ l 4 e l x , y ð5Þ ¼ l 5 e l x
Lösungsansatz:
Charakteristische Gleichung:
y ð5Þ 2 y ð4Þ þ 10 y 000 18 y 00 þ 9 y 0 ¼ l 5 e l x 2 l 4 e l x þ 10 l 3 e l x 18 l 2 e l x þ 9 l e l x ¼
¼ ðl 5 2 l 4 þ 10 l 3 18 l 2 þ 9 lÞ e l x ¼ 0
l 2 l þ 10 l 18 l þ 9 l ¼ 0
5
4
3
)
)
2
l ¼ 0
l ðl 4 2 l 3 þ 10 l 2 18 l þ 9Þ ¼ 0
)
l1 ¼ 0
l 4 2 l 3 þ 10 l 2 18 l þ 9 ¼ 0
Durch Probieren finden wir für die Gleichung 4. Grades eine Lösung bei l 2 ¼ 1 und für die durch Abspaltung des
zugehörigen Linearfaktors entstehende kubische Gleichung ebenfalls die Lösung l 3 ¼ 1. Wir verwenden das HornerSchema:
2
10
1
1
1
1
9
1
1
9
9
1
0
9
0
9
0
1
l2 ¼ 1
l3 ¼ 1
1
18
9
9 9
9
0
)
l3 l2 þ 9 l 9 ¼ 0
)
l2 þ 9 ¼ 0
)
( l 3 ¼ 1 ist eine Lösung )
l2 ¼ 9
)
l 4=5 ¼ 3 j
Damit besitzt die charakteristische Gleichung folgende Lösungen: l 1 ¼ 0, l 2=3 ¼ 1 und l 4=5 ¼ 3 j. Dies führt
zu der folgenden allgemeinen Lösung der Dgl:
y ¼ C 1 þ ðC 2 þ C 3 xÞ e x þ C 4 sin ð3 xÞ þ C 5 cos ð3 xÞ
418
G Gewöhnliche Differentialgleichungen
4.2 Inhomogene lineare Differentialgleichungen
G81
y 000 þ y 00 ¼ 6 x þ e x
1. Schritt: Wir lösen zunächst die zugehörige homogene Dgl y 000 þ y 00 ¼ 0 in der bekannten Weise durch den Exponentialansatz:
y ¼ e lx ;
y 0 ¼ l e lx ;
y 00 ¼ l 2 e l x ;
y 000 ¼ l 3 e l x
y 000 þ y 00 ¼ l 3 e l x þ l 2 e l x ¼ ðl 3 þ l 2 Þ e l x ¼ 0
|{z}
6¼ 0
l 2 ðl þ 1Þ ¼ 0
l2 ¼ 0
)
l 1=2 ¼ 0
lþ1 ¼ 0
)
l3 ¼ 1
)
l3 þ l2 ¼ 0
)
Lösung der homogenen Dgl: y 0 ¼ C 1 þ C 2 x þ C 3 e x
2. Schritt: Störfunktion
g ðxÞ ¼ 6 x þ e x ¼ g 1 ðxÞ þ g 2 ðxÞ
mit
g 1 ðxÞ ¼ 6 x
g 2 ðxÞ ¼ e x
und
Aus der Tabelle entnehmen wir für die einzelnen Störglieder folgende Lösungsansätze für eine partikuläre Lösung y P :
a0 ¼ a1 ¼ 0
!
Störglied g 1 ðxÞ ¼ 6 x
y P 1 ¼ x 2 ðA x þ BÞ ¼ A x 3 þ B x 2
c ¼ 1
!
Störglied g 2 ðxÞ ¼ e x
yP2 ¼ C x e x
ðStörglied: Typ Nr. 1Þ
ðStörglied vom Typ Nr. 2; r ¼ 1Þ
Begründung: c ¼ 1 ist eine einfache Lösung der charakteristischen Gleichung l 3 þ l 2 ¼ 0, siehe 1. Schritt.
Lösungsansatz y P (¼ Summe der Teilansätze) mit den benötigten Ableitungen 1. bis 3. Ordnung (unter Verwendung
der Produkt- und Kettenregel ):
yP ¼ y P1 þ y P2 ¼ A x 3 þ B x 2 þ C x e x ;
y 0P ¼ 3 A x 2 þ 2 B x þ C e x C x e x
y 00P ¼ 6 A x þ 2 B C e x C e x þ C x e x ¼ 6 A x þ 2 B 2 C e x þ C x e x
x
y 000
þ C e x C x e x ¼ 6 A þ 3 C e x C x e x
P ¼ 6A þ 2C e
Einsetzen in die inhomogene Dgl
y 000 þ y 00 ¼ 6 x þ e x :
6 A þ 3 C e x C x e x þ 6 A x þ 2 B 2 C e x þ C x e x ¼ 6 x þ e x
ð6 A þ 2 BÞ þ 6 A x þ ð3 C 2 CÞ e x þ ð C þ C Þ x e x ¼ 6 x þ e x
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
C
0
ð6 A þ 2 BÞ þ 6 A x þ C e x ¼ 0 þ 6 x þ e x
)
)
ðauf der rechten Seite wurde die Zahl 0 addiertÞ
Wir vergleichen auf beiden Seiten der Reihe nach die absoluten Glieder, die linearen Glieder und die Exponentialglieder (Koeffizientenvergleich):
6A þ 2B ¼ 0;
Partikuläre Lösung:
6A ¼ 6;
C ¼ 1
)
A ¼ 1;
B ¼ 3A ¼ 3 1 ¼ 3;
yP ¼ 1 x3 3 x2 þ 1 x ex ¼ x3 3 x2 þ x ex
3. Schritt: Die inhomogene Dgl besitzt damit die folgende allgemeine Lösung:
y ¼ y0 þ yP ¼ C1 þ C2 x þ C3 e x þ x 3 3 x 2 þ x e x ¼
¼ C 1 þ C 2 x 3 x 2 þ x 3 þ ðC 3 þ xÞ e x
C ¼ 1
4 Lineare Differentialgleichungen 3. und höherer Ordnung mit konstanten Koeffizienten
G82
419
y 000 þ y 0 ¼ 3 x 2
1. Schritt: Integration der zugehörigen homogenen Dgl y 000 þ y 0 ¼ 0 durch den Exponentialansatz y ¼ e l x mit
y 0 ¼ l e lx ;
y 00 ¼ l 2 e l x ;
y 000 ¼ l 3 e l x :
y 000 þ y 0 ¼ l 3 e l x þ l e l x ¼ ðl 3 þ lÞ e l x ¼ 0
|{z}
)
l 3 þ l ¼ l ðl 2 þ 1Þ ¼ 0
l ¼ 0
l2 þ 1 ¼ 0
6¼ 0
Die charakteristische Gleichung hat somit die Lösungen l 1 ¼ 0 und l 2=3 ¼ j .
Allgemeine Lösung der homogenen Dgl: y 0 ¼ C 1 þ C 2 sin x þ C 3 cos x
2. Schritt: Störfunktion g ðxÞ ¼ 3 x 2
Lösungsansatz für eine partikuläre Lösung (aus der Tabelle entnommen; das Störglied ist vom Typ Nr. 1 (a 0 ¼ 0,
a 1 6¼ 0, somit k ¼ 1, n ¼ 2) mit allen benötigten Ableitungen:
y P ¼ x ðA x 2 þ B x þ CÞ ¼ A x 3 þ B x 2 þ C x
y 0P ¼ 3 A x 2 þ 2 B x þ C ;
y 00P ¼ 6 A x þ 2 B ;
y 000
P ¼ 6A
Einsetzen in die inhomogene Dgl und ordnen der Glieder nach fallenden Potenzen:
y 000 þ y 0 ¼ 6 A þ 3 A x 2 þ 2 B x þ C ¼ 3 x 2
)
3 A x 2 þ 2 B x þ ð6 A þ CÞ ¼ 3 x 2 þ 0 x þ 0
Auf der rechten Seite wurden das fehlende lineare und absolute Glied „ergänzt‘‘ ð0 x ¼ 0Þ. Koeffizientenvergleich
entsprechender Potenzen auf beiden Seiten dieser Gleichung führt dann zu:
3A ¼ 3;
2B ¼ 0;
Partikuläre Lösung:
6A þ C ¼ 0
)
A ¼ 1;
B ¼ 0;
C ¼ 6A ¼ 6 1 ¼ 6
yP ¼ 1 x3 þ 0 x2 6 x ¼ x 3 6 x
3. Schritt: Die gesuchte allgemeine Lösung der inhomogenen Dgl lautet somit:
y ¼ y 0 þ y P ¼ C 1 þ C 2 sin x þ C 3 cos x þ x 3 6 x
G83
y 000 11 y 00 þ 35 y 0 25 y ¼ 32 e x
Anfangswerte: y ð0Þ ¼ 1 ;
y 0 ð0Þ ¼ 5 ;
y 00 ð0Þ ¼ 25
1. Schritt: Integration der zugehörigen homogenen Dgl y 000 11 y 00 þ 35 y 0 25 y ¼ 0 durch den Exponentialansatz
y ¼ e lx
mit y 0 ¼ l e l x ;
y 00 ¼ l 2 e l x
und
y 000 ¼ l 3 e l x :
y 000 11 y 00 þ 35 y 0 25 y ¼ l 3 e l x 11 l 2 e l x þ 35 l e l x 25 e l x ¼
¼ ðl 3 11 l 2 þ 35 l 25Þ e l x ¼ 0
|{z}
6¼ 0
)
l 3 11 l 2 þ 35 l 25 ¼ 0
Durch Probieren findet man die Lösung l 1 ¼ 1, mit Hilfe des Horner-Schemas erhalten wir die restlichen Lösungen
der charakteristischen Gleichung:
420
G Gewöhnliche Differentialgleichungen
11
1
l1 ¼ 1
35 25
1 10
10
1
25
25
)
0
l 2 10 l þ 25 ¼ ðl 5Þ 2 ¼ 0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
)
l 2=3 ¼ 5
2. Binom
Lösung der homogenen Dgl:
2. Schritt:
y 0 ¼ C 1 e x þ ðC 2 þ C 3 xÞ e 5 x
Störfunktion g ðxÞ ¼ 32 e x (Störfunktion vom Typ Nr. 2 mit c ¼ 1Þ
Da c ¼ 1 eine einfache Lösung der charakteristischen Gleichung ist, lautet der aus der Tabelle entnommene Lösungsansatz für eine partikuläre Lösung y P wie folgt (mit den benötigten Ableitungen, die wir unter Verwendung der Produktregel erhalten):
yP ¼ A x e x ;
y 0P ¼ A e x þ A x e x ;
y 00P ¼ A e x þ A e x þ A x e x ¼ 2 A e x þ A x e x
x
x
x
x
x
y 000
P ¼ 2A e þ A e þ Ax e ¼ 3A e þ Ax e
Einsetzen in die inhomogene Dgl und dann den gemeinsamen Faktor e x 6¼ 0 kürzen:
y 000 11 y 00 þ 35 y 0 25 y ¼ 32 e x
)
3 A e x þ A x e x 11 ð2 A e x þ A x e x Þ þ 35 ðA e x þ A x e x Þ 25 A x e x ¼ 32 e x
3 A þ A x 11 ð2 A þ A xÞ þ 35 ðA þ A xÞ 25 A x ¼ 32
)
3 A þ A x 22 A 11 A x þ 35 A þ 35 A x 25 A x ¼ 32
)
Partikuläre Lösung der inhomogenen Dgl:
16 A ¼ 32
)
)
A ¼ 2
yP ¼ 2 x e x
3. Schritt: Die inhomogene Dgl besitzt somit die folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ C 1 e x þ ðC 2 þ C 3 xÞ e 5 x þ 2 x e x ¼ ðC 1 þ 2 xÞ e x þ ðC 2 þ C 3 xÞ e 5 x
4. Schritt: Aus den Anfangswerten bestimmen wir die noch unbekannten Parameter C 1, C 2 und C 3 . Die dabei
benötigten Ableitungen lauten (Produktregel in Verbindung mit der Kettenregel):
y 0 ¼ 2 e x þ e x ðC 1 þ 2 xÞ þ C 3 e 5 x þ 5 e 5 x ðC 2 þ C 3 xÞ ¼
¼ ð2 þ C 1 þ 2 xÞ e x þ ð5 C 2 þ C 3 þ 5 C 3 xÞ e 5 x
y 00 ¼ 2 e x þ e x ðC 1 þ 2 þ 2 xÞ þ 5 C 3 e 5 x þ 5 e 5 x ð5 C 2 þ C 3 þ 5 C 3 xÞ ¼
¼ ðC 1 þ 4 þ 2 xÞ e x þ ð25 C 2 þ 10 C 3 þ 25 C 3 xÞ e 5 x
y ð0Þ ¼ 1
y 0 ð0Þ ¼ 5
)
C1 e0 þ C2 e0 ¼ C1 1 þ C2 1 ¼ 1
)
(I)
)
ð2 þ C 1 Þ e 0 þ ð5 C 2 þ C 3 Þ e 0 ¼ ð2 þ C 1 Þ 1 þ ð5 C 2 þ C 3 Þ 1 ¼
C1 þ C2 ¼ 1
)
C2 ¼ 1 C1
¼ 2 þ C1 þ 5 C2 þ C3 ¼ 5
y 00 ð0Þ ¼ 25
C1 þ 5 C2 þ C3 ¼ 3
)
(II)
)
ðC 1 þ 4Þ e 0 þ ð25 C 2 þ 10 C 3 Þ e 0 ¼ ðC 1 þ 4Þ 1 þ ð25 C 2 þ 10 C 3 Þ 1 ¼
¼ C 1 þ 4 þ 25 C 2 þ 10 C 3 ¼ 25
)
(III)
C 1 þ 25 C 2 þ 10 C 3 ¼ 21
4 Lineare Differentialgleichungen 3. und höherer Ordnung mit konstanten Koeffizienten
421
C 3 eliminieren (Gleichung (II) mit 10 multiplizieren, dann Gleichung (III) subtrahieren):
ðIIÞ
C1 þ 5 C2 þ
C 3 ¼ 3 j 10
)
10 C 1 þ 50 C 2 þ 10 C 3 ¼ 30
ðIIIÞ
C 1 þ 25 C 2 þ 10 C 3 ¼ 21
9 C 1 þ 25 C 2
¼ 9
)
(Gleichung (I) , d. h. C 2 ¼ 1 C 1 einsetzen)
9 C 1 þ 25 ð1 C 1 Þ ¼ 9 C1 þ 25 25 C 1 ¼ 9
)
16 C 1 ¼ 16
(I)
)
C 2 ¼ 1 C1 ¼ 1 1 ¼ 0
(II)
)
C1 þ 5 C2 þ C3 ¼ 1 þ 5 0 þ C3 ¼ 1 þ C3 ¼ 3
)
)
C1 ¼ 1
C3 ¼ 3 1 ¼ 2
Lösung: y ¼ ð1 þ 2 xÞ e x þ ð0 þ 2 xÞ e 5 x ¼ ð1 þ 2 xÞ e x þ 2 x e 5 x
Lösen Sie die folgende Anfangswertaufgabe:
G84
y ð4Þ þ y 00 ¼ 36 sin ð2 xÞ
Anfangswerte: y ð0Þ ¼ 1 ;
y 0 ð0Þ ¼ 5 ;
y 00 ð0Þ ¼ 0 ;
y 000 ð0Þ ¼ 26
1. Schritt: Integration der zugehörigen homogenen Dgl y ð4Þ þ y 00 ¼ 0 durch den Exponentialansatz
y ¼ e lx
mit y 0 ¼ l e l x ;
y 00 ¼ l 2 e l x ;
y 000 ¼ l 3 e l x
y ð4Þ þ y 00 ¼ l 4 e l x þ l 2 e l x ¼ ðl 4 þ l 2 Þ e l x ¼ 0
l þl
4
2
¼ l ðl þ 1Þ ¼ 0
2
2
Allgemeine Lösung der homogenen Dgl:
2. Schritt:
)
l2 ¼ 0
)
l 1=2 ¼ 0
l2 þ 1 ¼ 0
)
l2 ¼ 1
und
y ð4Þ ¼ l 4 e l x :
l4 þ l2 ¼ 0
)
(da e x 6¼ 0)
l 3=4 ¼ j
y 0 ¼ C 1 þ C 2 x þ C 3 sin x þ C 4 cos x
Störglied g ðxÞ ¼ 36 sin ð2 xÞ (Störglied vom Typ Nr. 4 mit b ¼ 2Þ
Da j b ¼ j 2 ¼ 2 j keine Lösung der charakteristischen Gleichung l 4 þ l 2 ¼ 0 ist (siehe 1. Schritt), lautet der aus
der Tabelle entnommene Lösungsansatz für eine partikuläre Lösung y P der inhomogenen Dgl wie folgt (mit den
benötigten Ableitungen des Ansatzes unter Verwendung der Kettenregel, Substitution: u ¼ 2 x):
y P ¼ A sin ð2 xÞ þ B cos ð2 xÞ
y 0P ¼ 2 A cos ð2 xÞ 2 B sin ð2 xÞ ;
y 000
P ¼ 8 A cos ð2 xÞ þ 8 B sin ð2 xÞ ;
y 00P ¼ 4 A sin ð2 xÞ 4 B cos ð2 xÞ
yð4Þ
¼ 16 A sin ð2 xÞ þ 16 B cos ð2 xÞ
P
Einsetzen in die inhomogene Dgl, ordnen der Glieder und ein Koeffizientenvergleich liefern zwei Gleichungen für die
noch unbekannten Parameter A und B:
y ð4Þ þ y 00 ¼ 16 A sin ð2 xÞ þ 16 B cos ð2 xÞ 4 A sin ð2 xÞ 4 B cos ð2 xÞ ¼ 36 sin ð2 xÞ
12 A sin ð2 xÞ þ 12 B cos ð2 xÞ ¼ 36 sin ð2 xÞ þ 0 cos ð2 xÞ
)
(auf der rechten Seite wurde der identisch verscwindene Term 0 cos ð2 xÞ ergänzt)
12 A ¼ 36 ;
12 B ¼ 0
)
A ¼ 3;
Partikuläre Lösung der inhomogenen Dgl:
B ¼ 0
y P ¼ 3 sin ð2 xÞ þ 0 cos ð2 xÞ ¼ 3 sin ð2 xÞ
)
422
G Gewöhnliche Differentialgleichungen
3. Schritt: Die allgemeine Lösung der inhomogenen Dgl lautet damit:
y ¼ y 0 þ y P ¼ C 1 þ C 2 x þ C 3 sin x þ C 4 cos x þ 3 sin ð2 xÞ
4. Schritt: Aus den Anfangsbedingungen ermitteln wir die noch unbekannten Werte der vier Integrationskonstanten.
Die dabei benötigten Ableitungen lauten (unter Verwendung der Kettenregel, Substitution: u ¼ 2 x):
y 0 ¼ C 2 þ C 3 cos x C 4 sin x þ 6 cos ð2 xÞ ;
y 00 ¼ C 3 sin x C 4 cos x 12 sin ð2 xÞ ;
y 000 ¼ C 3 cos x þ C 4 sin x 24 cos ð2 xÞ
y ð0Þ ¼ 1
) C 1 þ C 2 0 þ C 3 sin 0 þ C 4 cos 0 þ 3 sin 0 ¼ C 1 þ C 3 0 þ C 4 1 þ 3 0 ¼ 1
)
y 0 ð0Þ ¼ 5 )
)
y 00 ð0Þ ¼ 0
y 000 ð0Þ ¼ 26
ðIÞ
C1 þ C4 ¼ 1
C 2 þ C 3 cos 0 C 4 sin 0 þ 6 cos 0 ¼ C 2 þ C 3 1 C 4 0 þ 6 1 ¼ 5
ðIIÞ
C2 þ C3 þ 6 ¼ 5
)
C 3 sin 0 C 4 cos 0 12 sin 0 ¼ C 3 0 C 4 1 12 0 ¼ 0
)
ðIIIÞ
)
C 3 cos 0 þ C 4 sin 0 24 cos 0 ¼ C 3 1 þ C 4 0 24 1 ¼ 26
)
ðIVÞ
C4 ¼ 0
oder
)
C2 þ C3 ¼ 1
C4 ¼ 0
C 3 24 ¼ 26
)
C 3 ¼ 26 þ 24 ¼ 2
)
C3 ¼ 2
Somit ist C 3 ¼ 2 und C 4 ¼ 0. Die restlichen Unbekannten erhalten wir aus den Gleichungen (I) und (II):
ðIÞ
C1 þ C4 ¼ C1 þ 0 ¼ 1
)
C1 ¼ 1
ðIIÞ
C2 þ C3 ¼ C2 þ 2 ¼ 1
)
C2 ¼ 1 2 ¼ 3
Somit gilt: C 1 ¼ 1,
Spezielle Lösung:
G85
C 2 ¼ 3, C 3 ¼ 2 und C 4 ¼ 0.
y ¼ 1 3 x þ 2 sin x þ 0 cos x þ 3 sin ð2 xÞ ¼ 1 3 x þ 2 sin x þ 3 sin ð2 xÞ
y ð4Þ 6 y 000 þ 9 y 00 þ 4 y 0 12 y ¼ 8 e x
1. Schritt: Integration der zugehörigen homogenen Dgl y ð4Þ 6 y 000 þ 9 y 00 þ 4 y 0 12 y ¼ 0 durch den Exponentialansatz y ¼ e l x mit y 0 ¼ l e l x ; y 00 ¼ l 2 e l x ; y 000 ¼ l 3 e l x und y ð4Þ ¼ l 4 e l x :
y ð4Þ 6 y 000 þ 9 y 00 þ 4 y 0 12 y ¼ l 4 e l x 6 l 3 e l x þ 9 l 2 e l x þ 4 l e l x 12 e l x ¼
¼ ðl 4 6 l 3 þ 9 l 2 þ 4 l 12Þ e l x ¼ 0
)
l 4 6 l 3 þ 9 l 2 þ 4 l 12 ¼ 0
Die charakteristische Gleichung vom Grade 4 besitzt eine Lösung bei l 1 ¼ 2 (durch Probieren gefunden). Mit dem
Horner-Schema erhalten wir das 1. reduzierte Polynom vom Grade 3:
4 Lineare Differentialgleichungen 3. und höherer Ordnung mit konstanten Koeffizienten
1
6
9
4
12
2
8
2
12
4
1
6
0
l1 ¼ 2
1
)
423
l3 4 l2 þ l þ 6 ¼ 0
Auch diese Gleichung 3. Grades hat eine Lösung bei l 2 ¼ 2. Das Horner-Schema liefert dann eine quadratische
Gleichung für die restlichen Lösungen:
1
4
1
6
2
4
6
2
3
0
l2 ¼ 2
1
)
l2 2l 3 ¼ 0
)
l3 ¼ 1;
)
l 3=4 ¼ 1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1þ 3 ¼ 1
2
l4 ¼ 3
Die charakteristische Gleichung hat somit die Lösungen l 1=2 ¼ 2, l 3 ¼ 1 und l 4 ¼ 3. Daraus ergibt sich die
folgende allgemeine Lösung der homogenen Dgl:
y 0 ¼ ðC 1 þ C 2 xÞ e 2 x þ C 3 e x þ C 4 e 3 x
2. Schritt:
Störfunktion g ðxÞ ¼ 8 e x (vom Typ Nr. 2 mit c ¼ 1Þ
Aus der Tabelle entnehmen wir den folgenden Ansatz für eine partikuläre Lösung y P der inhomogenen Dgl (c ¼ 1
ist keine Lösung der charakteristischen Gleichung, siehe 1. Schritt):
yP ¼ A e x
mit
ð4Þ
x
y 0P ¼ y 00P ¼ y 000
P ¼ yP ¼ A e
Einsetzen in die inhomogene Dgl und kürzen durch e x :
y ð4Þ 6 y 000 þ 9 y 00 þ 4 y 0 12 y ¼ A e x 6 A e x þ 9 A e x þ 4 A e x 12 A e x ¼ 8 e x
4 A e x ¼ 8 e x : e x ) 4 A ¼ 8 ) A ¼ 2
Partikuläre Lösung der inhomogenen Dgl:
)
yP ¼ 2 e x
3. Schritt: Wir erhalten damit für die inhomogene Dgl folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ ðC 1 þ C 2 xÞ e 2 x þ C 3 e x þ C 4 e 3 x 2 e x ¼
¼ C 3 e x 2 e x þ ðC 1 þ C 2 xÞ e 2 x þ C 4 e 3 x
G86
y ð5Þ y ð4Þ þ 4 y 000 4 y 00 ¼ 12 x þ 4
1. Schritt: Integration der zugehörigen homogenen Dgl y ð5Þ y ð4Þ þ 4 y 000 4 y 00 ¼ 0 durch den Exponentialansatz
y ¼ e l x mit y 0 ¼ l e l x ; y 00 ¼ l 2 e l x ; y 000 ¼ l 3 e l x ;
y ð4Þ ¼ l 4 e l x und y ð5Þ ¼ l 5 e l x :
y ð5Þ y ð4Þ þ 4 y 000 4 y 00 ¼ l 5 e l x l 4 e l x þ 4 l 3 e l x 4 l 2 e l x ¼
¼ ðl 5 l 4 þ 4 l 3 4 l 2 Þ e l x ¼ 0
|{z}
6¼ 0
l5 l4 þ 4l3 4l2 ¼ 0
)
l 2 ðl 3 l 2 þ 4 l 4Þ ¼ 0
)
l 2 ¼ 0 ) l 1=2 ¼ 0
l3 l2 þ 4l 4 ¼ 0
Für die kubische Gleichung l 3 l 2 þ 4 l 4 ¼ 0 findet man durch Probieren die Lösung l 3 ¼ 1. Mit Hilfe
des Horner-Schemas lassen sich die restlichen Lösungen leicht bestimmen:
424
G Gewöhnliche Differentialgleichungen
1
1
4
4
1
0
4
0
4
0
l3 ¼ 1
1
)
l2 þ 4 ¼ 0
)
l2 ¼ 4
)
l 4=5 ¼ 2 j
Die Lösungen der charakteristischen Gleichung lauten also: l 1=2 ¼ 0, l 3 ¼ 1 und l 4=5 ¼ 2 j. Damit besitzt
die homogene Dgl die folgende allgemeine Lösung:
y 0 ¼ C 1 þ C 2 x þ C 3 e x þ C 4 sin ð2 xÞ þ C 5 cos ð2 xÞ
2. Schritt: Störglied g ðxÞ ¼ 12 x þ 4 (Störglied vom Typ Nr. 1)
Wegen a 0 ¼ a 1 ¼ 0, a 2 6¼ 0 liefert die Tabelle den folgenden Lösungsansatz für eine partikuläre Lösung y P der
inhomogenen Dgl (mit allen benötigten Ableitungen):
y P ¼ x 2 ðA x þ BÞ ¼ A x 3 þ B x 2
y 0P ¼ 3 A x 2 þ 2 B x ;
y 00P ¼ 6 A x þ 2 B ;
y 000
P ¼ 6A;
y ð4Þ
¼ 0;
P
y ð5Þ
¼ 0
P
Einsetzen in die inhomogene Dgl, die Glieder dann nach fallenden Potenzen ordnen:
y ð5Þ y ð4Þ þ 4 y 000 4 y 00 ¼ 0 0 þ 4 6 A 4 ð6 A x þ 2 BÞ ¼ 12 x þ 4
)
24 A 24 A x 8 B ¼ 24 A x þ ð24 A 8 BÞ ¼ 12 x þ 4
Wir vergleichen beiderseits die linearen und die absoluten Glieder und erhalten zwei einfache Gleichungen für die
noch unbekannten Parameter A und B:
ðIÞ
ðIIÞ
24 A ¼ 12
)
24 A 8 B ¼ 4
A ¼ 0,5
)
(Einsetzen in (II))
8 B ¼ 4 24 A ¼ 4 24 ð 0,5Þ ¼ 4 þ 12 ¼ 16
Partikuläre Lösung der inhomogenen Dgl:
)
B ¼ 2
y P ¼ 0,5 x 3 2 x 2
3. Schritt: Die inhomogene Dgl besitzt damit die folgende allgemeine Lösung:
y ¼ y 0 þ y P ¼ C 1 þ C 2 x þ C 3 e x þ C 4 sin ð2 xÞ þ C 5 cos ð2 xÞ 0,5 x 3 2 x 2 ¼
¼ C 1 þ C 2 x 2 x 2 0,5 x 3 þ C 3 e x þ C 4 sin ð2 xÞ þ C 5 cos ð2 xÞ
5 Lösung linearer Anfangswertprobleme
mit Hilfe der Laplace-Transformation
Lösungsweg: Das Anfangswertproblem wird zunächst in den Bildbereich transformiert (Laplace-Transformation), die
erhaltene algebraische Gleichung dann nach der Bildfunktion aufgelöst. Durch Rücktransformation mit Hilfe der Laplace-Transformationstabelle erhält man aus der Bildfunktion die gesuchte Originalfunktion, d. h. die spezielle Lösung
der Differentialgleichung.
5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation
425
5.1 Lineare Differentialgleichungen 1. Ordnung
mit konstanten Koeffizienten
Lehrbuch: Band 2, Kapitel VI.5.1.2
Formelsammlung: Kapitel XIII.5.2
Tabelle spezieller Laplace-Transformationen: Band 2, Kapitel VI.4.2 und Formelsammlung, Kapitel XIII.6
In den Lösungen wird die jeweilige Nummer der Laplace-Transformation mit den entsprechenden Parameterwerten
angegeben (z. B. Nr. 6 mit a ¼ 1Þ:
G87
y 0 þ y ¼ t et ;
Anfangswert: y ð0Þ ¼ 2
Die Dgl wird durch die Laplace-Transformation in die folgende algebraische Gleichung übergeführt (Transformation
in den Bildbereich; Y ðsÞ ¼ l fy ðtÞg) :
1
½ s Y ðsÞ y ð0Þ þ Y ðsÞ ¼ lft e t g ¼
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|ffl{zffl}
ðs þ 1Þ 2
Nr. 6 mit a ¼ 1
2
Diese Gleichung lösen wir nach der Bildfunktion Y ðsÞ auf:
s Y ðsÞ 2 þ Y ðsÞ ¼ ðs þ 1Þ Y ðsÞ 2 ¼
Y ðsÞ ¼
1
ðs þ 1Þ
3
þ
2
sþ1
1
ðs þ 1Þ
2
)
ðs þ 1Þ Y ðsÞ ¼
1
ðs þ 1Þ 2
þ2
)
Die Rücktransformation in den Originalbereich liefert die gesuchte Lösung:
(
)
(
)
1
2
1
1
1
1
1
¼
þ 2 l1
y ðtÞ ¼ l fY ðsÞg ¼ l
þ
¼ l
sþ1
sþ1
ðs þ 1Þ 3
ðs þ 1Þ 3
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
¼
G88
1 2
t e t þ 2 e t ¼
2
y 0 þ 4 y ¼ 10 cos t ;
1 2
t þ 2 e t ;
2
Nr. 13 mit a ¼ 1
Nr. 3 mit a ¼ 1
t 0
Anfangswert: y ð0Þ ¼ p
Wir transformieren die Dgl zunächst in den Bildbereich (Laplace-Transformation; Y ðsÞ ¼ l fy ðtÞg) :
s
½ s Y ðsÞ y ð0Þ þ 4 Y ðsÞ ¼ l f10 cos tg ¼ 10 l fcos tg ¼ 10
2
s þ1
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|ffl{zffl}
p
Nr. 25 mit a ¼ 1
Diese algebraische Gleichung lösen wir jetzt nach der Bildfunktion Y ðsÞ auf:
s
)
s Y ðsÞ p þ 4 Y ðsÞ ¼ ðs þ 4Þ Y ðsÞ p ¼ 10
2
s þ1
s
s
p
þ p ) Y ðsÞ ¼ 10
þ
ðs þ 4Þ Y ðsÞ ¼ 10
sþ4
s2 þ 1
ðs þ 4Þ ðs 2 þ 1Þ
Rücktransformation in den Originalbereich (inverse Laplace-Transformation):
(
)
s
p
1
1
y ðtÞ ¼ l fY ðsÞg ¼ l
þ
10
¼
sþ4
ðs þ 4Þ ðs 2 þ 1Þ
(
)
(
)
s
1
s
þ p l 1
þ p e 4t ¼
¼ 10 l 1
¼ 10 l 1
sþ4
ðs þ 4Þ ðs 2 þ 1Þ
ðs þ 4Þ ðs 2 þ 1Þ
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Nr. 3 mit a ¼ 4
F ðsÞ
426
G Gewöhnliche Differentialgleichungen
¼ 10 l 1 fF ðsÞg þ p e 4 t
s
Die Rücktransformation der Bildfunktion F ðsÞ ¼
erfolgt mit dem Faltungssatz (Band 2: Kapitel
ðs þ 4Þ ðs 2 þ 1Þ
VI.2.7 bzw. FS: Kapitel XIII.2.7):
F ðsÞ ¼
s
ðs þ 4Þ
ðs 2
¼
þ 1Þ
1
s
¼ F 1 ðsÞ F 2 ðsÞ
s þ 4 s2 þ 1
|fflffl{zfflffl} |fflfflffl{zfflfflffl}
F 1 ðsÞ F 2 ðsÞ
Aus der Transformationstabelle entnehmen wir die Originalfunktionen f 1 ðtÞ und f 2 ðtÞ zu F 1 ðsÞ und F 2 ðsÞ:
1
s
¼ cos t
f 1 ðtÞ ¼ l 1 fF 1 ðsÞg ¼ l 1
¼ e 4 t ; f 2 ðtÞ ¼ l 1 fF 2 ðsÞg ¼ l 1
sþ4
s2 þ 1
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Nr. 3 mit a ¼ 4
Nr. 25 mit a ¼ 1
Die Originalfunktion zu F ðsÞ ¼ F 1 ðsÞ F 2 ðsÞ ist dann das Faltungsprodukt f 1 ðtÞ * f 2 ðtÞ der Originalfunktionen
f 1 ðtÞ und f 2 ðtÞ:
ðt
f 1 ðtÞ * f 2 ðtÞ ¼
ðt
f 1 ðuÞ f 2 ðt uÞ d u ¼
0
0
ðt
cos u e
¼
ðt
f 2 ðuÞ f 1 ðt uÞ d u ¼
4tþ4u
0
ðt
du ¼
0
cos u e 4 ðt uÞ d u ¼
cos u e
4t
e
4u
du ¼ e
0
4t
ðt
cos u e 4 u d u ¼ e 4 t I
0
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
I
Die Auswertung des Integrals I erfolgt mit der Integraltafel der Formelsammlung (Integral 324 mit a ¼ 4, b ¼ 1):
ðt
I ¼
cos u e 4 u d u ¼
e 4u
ð4 cos u þ 1 sin uÞ
16 þ 1
0
t
¼
0
1
17
e 4 u ð4 cos u þ sin uÞ
t
0
¼
¼
1
1
½ e 4 t ð4 cos t þ sin tÞ e 0 ð4 cos 0 þ sin 0Þ ¼
½ e 4 t ð4 cos t þ sin tÞ 1 ð4 1 þ 0Þ ¼
17
17
¼
1
½ ð4 cos t þ sin tÞ e 4 t 4
17
Somit gilt:
f 1 ðtÞ * f 2 ðtÞ ¼ e 4 t I ¼ e 4 t
1
1
½ ð4 cos t þ sin tÞ e 4 t 4 ¼
½ 4 cos t þ sin t 4 e 4 t
17
17
l 1 fF ðsÞg ¼ l 1 fF 1 ðsÞ F 2 ðsÞg ¼ l 1
¼
1
s
2
sþ4 s þ1
¼ f 1 ðtÞ * f 2 ðtÞ ¼
1
ð4 cos t þ sin t 4 e 4 t Þ
17
Die Lösung der Anfangswertaufgabe lautet damit wie folgt:
10
ð4 cos t þ sin t 4 e 4 t Þ þ p e 4 t ¼
17
10
40
ð4 cos t þ sin tÞ þ p
e 4t ; t 0
¼
17
17
y ðtÞ ¼ 10 l 1 fF ðsÞg þ p e 4 t ¼
5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation
427
R L-Stromkreis mit linear ansteigender äußerer Spannung
Der in Bild G-33 skizzierte Stromkreis enthält einen ohmschen Widerstand R und eine Induktivität L .
Die von außen angelegte Spannung u ¼ k t steigt mit der Zeit t linear an ðk > 0Þ. Bestimmen Sie
den zeitlichen Verlauf der Stromstärke i ¼ i ðtÞ unter der Voraussetzung, dass der R L-Stromkreis im
Einschaltzeitpunkt t ¼ 0 stromlos ist.
G89
R
Anleitung: Aus der Maschenregel erhält man für die
Stromstärke i ¼ i ðtÞ die folgende Dgl 1. Ordnung:
L
i (t )
di
L
þ Ri ¼ u
dt
u (t )
Bild G-33
Wir transformieren die geringfügig umgestellte Dgl wie folgt in den Bildbereich ðdie Laplace-Transformierte der gesuchten Lösung i ¼ i ðtÞ bezeichnen wir mit I ðsÞ; Anfangswert: i ð0Þ ¼ 0Þ:
di
R
u
k
þ
i ¼
¼
t
dt
L
L
L
oder
di
þ ai ¼ bt
dt
ðmit a ¼ R=L und
b ¼ k=LÞ
1
½ s I ðsÞ i ð0Þ þ a I ðsÞ ¼ l fb tg ¼ b l ftg ¼ b
s2
|{z}
|ffl{zffl}
Nr. 4
0
Diese algebraische Gleichung lösen wir nach der Bildfunktion I ðsÞ auf:
s I ðsÞ þ a I ðsÞ ¼ ðs þ aÞ I ðsÞ ¼ b
1
s2
)
I ðsÞ ¼ b
1
ðs þ aÞ s 2
Rücktransformation aus dem Bildbereich in den Originalbereich (inverse Laplace-Transformation) führt zur gesuchten
Lösung der Anfangswertaufgabe:
(
)
(
)
1
1
e at þ a t 1
1
1
1
i ðtÞ ¼ l fI ðsÞg ¼ l
b
¼
¼ bl
¼ b
a2
ðs þ aÞ s 2
ðs þ aÞ s 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Nr. 11 mit a ¼ a
k
¼
L
e
R
t
L
þ
R
t 1
L
R2
L2
¼
k L2
LR2
R
R
R
kL
R
t
t
t 1 ¼
t 1 ;
e L þ
e L þ
L
L
R2
t 0
Da im Laufe der Zeit (d. h. für t 1) der erste Summand in der Klammer verschwindet (streng monoton fallende
Exponentialfunktion), erhält man für große Zeiten einen linearen Zusammenhang zwischen der Stromstärke i und der
Zeit t (Bild G-34):
i
kL
R2
R
k
L
t 1 ¼
t
;
L
R
R
t 1
i
i = i (t )
L /R
Bild G-34
Asymptotischer
Verlauf für t >> 1
t
428
G Gewöhnliche Differentialgleichungen
Sinkgeschwindigkeit eines Körpers in einer zähen Flüssigkeit
Die Sinkgeschwindigkeit v einer Stahlkugel in einer
zähen Flüssigkeit genügt der folgenden Dgl (ohne
Auftrieb, siehe Bild G-35):
Kugel
–kv
v
mg
m v_ þ k v ¼ m g
m: Masse der Kugel
G90
Bild G-35
k : Reibungsfaktor ð k > 0Þ
g: Erdbeschleunigung
Wie lautet das Geschwindigkeit-Zeit-Gesetz v ¼ v ðtÞ bei einer Anfangsgeschwindigkeit v ð0Þ ¼ v 0 ?
Welche Endgeschwindigkeit v E wird erreicht?
Hinweis: Siehe hierzu auch Aufgabe G 36, in der diese Dgl durch „Variation der Konstanten“ gelöst
wurde.
Wir stellen die Dgl zunächst geringfügig um und transformieren sie anschließend mit Hilfe der Laplace-Transformation
in den Bildbereich ðdie Bildfunktion von v ¼ v ðtÞ bezeichnen wir mit V ðsÞÞ:
v_ þ
k
v ¼ g
m
oder
v_ þ a v ¼ g
ðmit a ¼ k=mÞ
1
½ s V ðsÞ v ð0Þ þ a V ðsÞ ¼ s V ðsÞ v 0 þ a V ðsÞ ¼ l fgg ¼ g l f1g ¼ g
s
|{z}
|fflffl{zfflffl}
v0
Nr. 2
Diese algebraische Gleichung lösen wir nach der Bildfunktion V ðsÞ auf:
s V ðsÞ v 0 þ a V ðsÞ ¼ ðs þ aÞ V ðsÞ v 0 ¼ g
V ðsÞ ¼ g
1
s
)
ðs þ aÞ V ðsÞ ¼ g
1
þ v0
s
)
1
1
þ v0
sþa
s ðs þ aÞ
Rücktransformation in den Originalbereich (inverse Laplace-Transformation) liefert das Geschwindigkeit-Zeit-Gesetz
für t 0:
1
1
1
1
þ v0
¼
g
v ðtÞ ¼ l fV ðsÞg ¼ l
sþa
s ðs þ aÞ
1
1
e at 1
þ v0 l 1
¼ g
þ v0 e at ¼
sþa
a
s ðs þ aÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
¼ g l 1
Nr. 5 mit a ¼ a
¼
Nr. 3 mit a ¼ a
g
ðe a t 1Þ þ v 0 e a t ¼
a
v0
g
a
e at þ
g
¼
a
v0
mg
k
Die (konstante) Endgeschwindigkeit v E erhalten wir für den Grenzübergang t ! 1:
k
mg
mg
mg
mg
emt þ
¼ 0þ
¼
; t 0
v E ¼ lim v ðtÞ ¼ lim
v0
k
k
k
k
t!1
t!1
|ffl{zffl}
! 0
(die streng monoton fallende Exponentialfunktion verschwindet für t ! 1)
k
emt þ
mg
k
5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation
429
Bild G-36 zeigt den zeitlichen Verlauf der Sinkgeschwindigkeit v („Sättigungsfunktion“).
v
mg
k
v = v0 –
k
– t
mg
mg
·e m +
k
k
v0
Bild G-36
t
D T 1 -Regelkreisglied
Das Verhalten eines sog. D T 1 -Regelkreisgliedes der Regelungstechnik lässt sich durch die lineare Dgl
T v_ þ v ¼ K u_
G91
beschreiben. Dabei bedeuten:
T; K :
positive Konstanten
u ¼ u ðtÞ: Eingangssignal
v ¼ v ðtÞ: Ausgangssignal
Bestimmen Sie unter Verwendung des Faltungssatzes das zeitabhängige Ausgangssignal v ¼ v ðtÞ für
das periodische Eingangssignal u ¼ u ðtÞ ¼ E sin ðw tÞ und den Anfangswert v ð0Þ ¼ 0 .
Mit u_ ¼ E w cos ðw tÞ (Kettenregel) lautet die Dgl für das Ausgangssignal v ¼ v ðtÞ wie folgt:
T v_ þ v ¼ K u_ ¼ K E w cos ðw tÞ
oder
v_ þ a v ¼ b cos ðw tÞ
ðmit a ¼ 1=T und b ¼ ðK E wÞ=T Þ
Wir transformieren die Dgl mit Hilfe der Laplace-Transformation in den Bildbereich ðdie Laplace-Transformierte der
gesuchten Lösung v ¼ v ðtÞ bezeichnen wir mit V ðsÞÞ:
½ s V ðsÞ v ð0Þ þ a V ðsÞ ¼ s V ðsÞ þ a V ðsÞ ¼
|{z}
0
s
¼ l f b cos ðw tÞg ¼ b l fcos ðw tÞg ¼ b
2
s þ w2
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Nr. 25 mit a ¼ w
Diese algebraische Gleichung wird nach der Bildfunktion V ðsÞ aufgelöst:
s V ðsÞ þ a V ðsÞ ¼ ðs þ aÞ V ðsÞ ¼ b
s
s2 þ w2
)
V ðsÞ ¼ b
s
ðs 2 þ w 2 Þ ðs þ aÞ
Bei der Rücktransformation verwenden wir den Faltungssatz:
(
)
s
s
1
1
1
v ðtÞ ¼ l fV ðsÞg ¼ l
b
¼
¼ b l 1
s2 þ w2 s þ a
ðs 2 þ w 2 Þ ðs þ aÞ
|fflfflfflfflffl{zfflfflfflfflffl} |fflffl{zfflffl}
F 1 ðsÞ
F 2 ðsÞ
¼ b l 1 fF 1 ðsÞ F 2 ðsÞg ¼ b ð f 1 ðtÞ * f 2 ðtÞÞ
430
G Gewöhnliche Differentialgleichungen
Dabei ist f 1 ðtÞ * f 2 ðtÞ das Faltungsprodukt der noch unbekannten Originalfunktionen f 1 ðtÞ und f 2 ðtÞ der Faktorfunktionen F 1 ðsÞ und F 2 ðsÞ. Durch Rücktransformation aus dem Bild- in den Originalbereich erhalten wir:
s
1
¼ cos ðw tÞ ; f 2 ðtÞ ¼ l 1 fF 2 ðsÞg ¼ l 1
f 1 ðtÞ ¼ l 1 fF 1 ðsÞg ¼ l 1
¼ e at
sþa
s2 þ w2
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Nr. 25 mit a ¼ w
Nr. 3 mit a ¼ a
Wir ermitteln jetzt das Faltungsprodukt:
ðt
f 1 ðtÞ * f 2 ðtÞ ¼
ðt
f 1 ðuÞ f 2 ðt uÞ d u ¼
0
ðt
¼
cos ðw uÞ e
a ðt uÞ
ðt
cos ðw uÞ e a t þ a u d u ¼
du ¼
0
0
cos ðw uÞ e a t e a u d u ¼ e a t
0
ðt
cos ðw uÞ e a u d u ¼ e a t I
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
I
Auswertung des Integrals I mit Hilfe der Integraltafel der Formelsammlung (Integral 324 mit a ¼ a und b ¼ w):
ðt
I ¼
cos ðw uÞ e
du ¼
au
0
e au
½ a cos ðw uÞ þ w sin ðw uÞ
a2 þ w2
t
t
¼
0
¼
1
a2 þ w2
e a u a cos ðw uÞ þ w sin ðw uÞ
¼
1
a2 þ w2
¼
1
a2 þ w2
e a t a cos ðw tÞ þ w sin ðw tÞ e 0 ða cos 0 þ w sin 0Þ
|{z}
|ffl{zffl}
1
1
0
e a t ða cos ðw tÞ þ w sin ðw tÞÞ a
¼
¼
f
0
Damit gilt für das Faltungsprodukt:
f 1 ðtÞ * f 2 ðtÞ ¼ e a t I ¼ e a t
¼
1
a2 þ w2
1
½ e a t ða cos ðw tÞ þ w sin ðw tÞÞ a ¼
a2 þ w2
a cos ðw tÞ þ w sin ðw tÞ a e a t
Die Lösung der Dgl lautet daher wie folgt:
v ðtÞ ¼ b ð f 1 ðtÞ * f 2 ðtÞÞ ¼
¼
T
¼
¼
KEw
1
þ w2
T2
K EwT
1
þ w2
T2
T2
KEw
1 þ ðw T Þ 2
a2
b
þ w2
a cos ðw tÞ þ w sin ðw tÞ a e a t
1
1
cos ðw tÞ þ w sin ðw tÞ
e t=T
T
T
¼
1
1
cos ðw tÞ þ w sin ðw tÞ
e t=T
T
T
cos ðw tÞ þ w T sin ðw tÞ e t = T ;
¼
¼
t 0
Umformungen: Bruch vor der Klammer mit T erweitern, dann T bzw. T 2 in die Klammern multiplizieren.
5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation
431
5.2 Lineare Differentialgleichungen 2. Ordnung
mit konstanten Koeffizienten
Lehrbuch: Band 2, Kapitel VI.5.1.3
Formelsammlung: Kapitel XIII.5.3
Tabelle spezieller Laplace-Transformationen: Band 2, Kapitel VI.4.2 und Formelsammlung, Kapitel XIII.6
In den Lösungen wird die jeweilige Nummer der Laplace-Transformation mit den entsprechenden Parameterwerten
angegeben (z. B. Nr. 6 mit a ¼ 1Þ.
G92
Lösen Sie die folgende Schwingungsgleichung mit Hilfe der Laplace-Transformation:
x€ þ 2 x_ þ 5 x ¼ 0 ; Anfangswerte: x ð0Þ ¼ 10 ;
x_ ð0Þ ¼ 0
Wir transformieren die Dgl in den Bildbereich:
s 2 X ðsÞ s x ð0Þ x_ ð0Þ þ 2 s X ðsÞ x ð0Þ þ 5 X ðsÞ ¼ l f0g ¼ 0
|ffl{zffl}
|ffl{zffl} |ffl{zffl}
10
0
10
Diese algebraische Gleichung lösen wir nach der Bildfunktion X ðsÞ ¼ l fx ðtÞg auf:
s 2 X ðsÞ 10 s þ 2 s X ðsÞ 20 þ 5 X ðsÞ ¼ 0
ðs 2 þ 2 s þ 5Þ X ðsÞ ¼ 10 s þ 20 ¼ 10 ðs þ 2Þ
)
)
X ðsÞ ¼ 10
s2
sþ2
þ 2s þ 5
Vor der Rücktransformation müssen wir diese echt gebrochenrationale Funktion so zerlegen, dass wir die Glieder in
der Transformationstabelle finden (quadratische Ergänzung im Nenner):
sþ2
sþ2
ðs þ 1Þ þ 1
¼ 10
¼
¼ 10
2
þ 2s þ 5
ðs þ 2 s þ 1Þ þ 4
ðs þ 1Þ 2 þ 2 2
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
ðs þ 1Þ 2
!
sþ1
1
þ
ðs þ 1Þ 2 þ 2 2
ðs þ 1Þ 2 þ 2 2
X ðsÞ ¼ 10
s2
¼ 10
Rücktransformation in den Originalbereich führt jetzt zur gesuchten Lösung (inverse Laplace-Transformation):
(
!)
sþ1
1
1
1
x ðtÞ ¼ l fX ðsÞg ¼ l
10
þ
¼
ðs þ 1Þ 2 þ 2 2
ðs þ 1Þ 2 þ 2 2
(
¼ 10
l
1
sþ1
)
ðs þ 1Þ 2 þ 2 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Nr. 29 mit a ¼ 2, b ¼ 1
¼ 10
e t cos ð2 tÞ þ
(
þl
1
1
)!
ðs þ 1Þ 2 þ 2 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
¼
Nr. 28 mit a ¼ 2, b ¼ 1
e t sin ð2 tÞ
¼ 5 e t ½ 2 cos ð2 tÞ þ sin ð2 tÞ ;
2
t 0
432
G Gewöhnliche Differentialgleichungen
Der zeitliche Verlauf dieser gedämpften Schwingung ist in Bild G-37 dargestellt.
x
10
x = 5 · e – t · [ 2 · cos (2 t ) + sin (2 t ) ]
5
1
Bild G-37
1
2
3
t
–2
Stoßdämpferproblem
Ein schwingungsfähiges (gedämpftes) Feder-Masse-System mit der Masse m ¼ 50 kg, der Federkonstanten c ¼ 10 200 N/m und der Dämpferkonstanten b ¼ 2000 kg/s wird zur Zeit t ¼ 0 s aus
der Gleichgewichtslage heraus mit der Geschwindigkeit v 0 ¼ 2,8 m/s angestoßen. Untersuchen Sie
die Bewegung der Masse mit Hilfe der Schwingungsgleichung
G93
m x€ þ b x_ þ c x ¼ 0
und skizzieren Sie den zeitlichen Verlauf der Ortskoordinate x ¼ x ðtÞ .
Wir erhalten die folgende Schwingungsgleichung (ohne Einheiten):
50 x€ þ 2000 x_ þ 10 200 x ¼ 0
oder
x€ þ 40 x_ þ 204 x ¼ 0
Transformation in den Bildraum ðmit X ðsÞ bezeichnen wir die Laplace-Transformierte der gesuchten Lösung
x ¼ x ðtÞ; Anfangswerte: x ð0Þ ¼ 0; x_ ð0Þ ¼ v 0 ¼ 2; 8):
s 2 X ðsÞ s x ð0Þ x_ ð0Þ þ 40 s X ðsÞ x ð0Þ þ 204 X ðsÞ ¼ l f0g ¼ 0
|ffl{zffl}
|ffl{zffl} |ffl{zffl}
0
2,8
0
Wir lösen diese Gleichung nach X ðsÞ auf:
s 2 X ðsÞ 2,8 þ 40 s X ðsÞ þ 204 X ðsÞ ¼ 0
X ðsÞ ¼
)
ðs 2 þ 40 s þ 204Þ X ðsÞ ¼ 2,8
)
2,8
2,8
2,8
¼ 2
¼
s 2 þ 40 s þ 204
ðs þ 40 s þ 400Þ 196
ðs þ 20Þ 2 14 2
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1. Binom
Umformung des Nenners (Quadratische Ergänzung zu einem Binom):
s 2 þ 40 s þ 204 ¼ s 2 þ 40 s þ 20 2 20 2 þ 204 ¼ ðs 2 þ 40 s þ 400Þ 196 ¼ ðs þ 20Þ 2 14 2
Durch Rücktransformation in den Originalbereich erhalten wir das gesuchte Weg-Zeit-Gesetz (inverse Laplace-Transformation):
(
)
(
)
2,8
1
1
1
1
x ðtÞ ¼ l fX ðsÞg ¼ l
¼
¼ 2,8 l
ðs þ 20Þ 2 14 2
ðs þ 20Þ 2 14 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Nr. 32 mit a ¼ 14, b ¼ 20
¼ 2,8
e
20 t
sinh ð14 tÞ
¼ 0,2 e 20 t sinh ð14 tÞ ;
14
t 0
5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation
433
Es handelt sich (infolge der starken Dämpfung) um eine sog. aperiodische Schwingung, deren zeitlicher Verlauf in
Bild G-38 dargestellt ist.
x
0,6
x = 0,2 · e – 20 t · sinh (14 t )
0,4
0,2
Bild G-38
0,1
0,3
0,5
t
Erzwungene mechanische Schwingung
G94
Lösen Sie das folgende Schwingungsproblem:
x€ þ 25 x ¼ 2 sin ð2 tÞ ;
Anfangswerte:
x_ ð0Þ ¼ 1
x ð0Þ ¼ 0 ;
Transformation in den Bildbereich:
2
4
s 2 X ðsÞ s x ð0Þ x_ ð0Þ þ 25 X ðsÞ ¼ l f2 sin ð2 tÞg ¼ 2 l fsin ð2 tÞg ¼ 2
¼
|ffl{zffl} |ffl{zffl}
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
s2 þ 4
s2 þ 4
Nr. 24 mit a ¼ 2
0
1
Wir lösen diese algebraische Gleichung nach der Bildfunktion X ðsÞ ¼ l fx ðtÞg auf:
s 2 X ðsÞ 1 þ 25 X ðsÞ ¼
ðs 2 þ 25Þ X ðsÞ ¼
s2
4
s2 þ 4
4
þ1
þ4
)
)
ðs 2 þ 25Þ X ðsÞ 1 ¼
X ðsÞ ¼
4
ðs 2 þ 4Þ ðs 2 þ 25Þ
þ
4
s2 þ 4
s2
)
1
þ 25
Rücktransformation in den Originalbereich liefert das gesuchte Weg-Zeit-Gesetz:
(
)
4
1
1
1
x ðtÞ ¼ l fX ðsÞg ¼ l
¼
þ
s 2 þ 25
ðs 2 þ 4Þ ðs 2 þ 25Þ
(
)
1
¼ 4l
¼
þl
s 2 þ 25
ðs 2 þ 4Þ ðs 2 þ 25Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
1
1
Nr. 43 mit a ¼ 2, b ¼ 5
¼ 4
¼
2 sin ð5 tÞ 5 sin ð2 tÞ
10 ð4 25Þ
Nr. 24 mit a ¼ 5
þ
sin ð5 tÞ
5
¼
1
2 sin ð5 tÞ 5 sin ð2 tÞ þ
sin ð5 tÞ ¼
5
2
105
4
2
1
sin ð5 tÞ þ
sin ð2 tÞ þ
sin ð5 tÞ ¼
105
21
5
1
4
2
sin ð5 tÞ þ
sin ð2 tÞ ¼
5
105
21
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
21 4
17
¼
105
105
¼
17
2
sin ð5 tÞ þ
sin ð2 tÞ ;
105
21
t 0
434
G Gewöhnliche Differentialgleichungen
LRC-Stromkreis
Ein Stromkreis enthält die Induktivität L ¼ 1 H, den ohmschen Widerstand R ¼ 80 W und eine
Kapazität von C ¼ 400 mF ¼ 4 10 4 F. Er wird durch die Gleichspannung u ¼ 100 V gespeist.
Bestimmen Sie den zeitlichen Verlauf der Kondensatorladung q ¼ q ðtÞ, die der Dgl
G95
L q€ þ R q_ þ
q
¼ u
C
mit den Anfangswerten q ð0Þ ¼ 0 und i ðtÞ ¼ q_ ð0Þ ¼ 0 genügt.
i ¼ i ðtÞ ¼ q_ ðtÞ: Stromstärke (zeitliche Ableitung der Ladung)
Einheiten: t in s; i in A; q in As
Die Dgl für die Ladung q ¼ q ðtÞ lautet wie folgt (ohne Einheiten):
1 q€ þ 80 q_ þ
1
q ¼ 100
4 10 4
q€ þ 80 q_ þ 2500 q ¼ 100
oder
Wir transformieren sie in den Bildbereich (Laplace-Transformation):
100
s 2 Q ðsÞ s q ð0Þ q_ ð0Þ þ 80 s Q ðsÞ q ð0Þ þ 2500 Q ðsÞ ¼ l f100g ¼ 100 l f1g ¼
s
|ffl{zffl} |ffl{zffl}
|ffl{zffl}
|fflfflffl{zfflfflffl}
0
0
0
Nr. 2
Diese algebraische Gleichung lösen wir nach der Bildfunktion Q ðsÞ ¼ l fq ðtÞg auf:
s 2 Q ðsÞ þ 80 s Q ðsÞ þ 2500 Q ðsÞ ¼
Q ðsÞ ¼
100
s
)
ðs 2 þ 80 s þ 2500Þ Q ðsÞ ¼
100
s
)
100
s ðs 2 þ 80 s þ 2500Þ
Vor der Rücksubstitution zerlegen wir die echt gebrochenrationale Bildfunktion Q ðsÞ in Partialbrüche. Da der Faktor
s 2 þ 80 s þ 2500 auf konjugiert komplexe Nennernullstellen führt, erhalten wir für die Partialbruchzerlegung den
folgenden Ansatz (siehe FS: Kapitel V.3.3.1):
100
s ðs 2
þ 80 s þ 2500Þ
¼
A
Bs þ C
þ
s
s 2 þ 80 s þ 2500
Wir bringen alle Brüche der rechten Seite auf den Hauptnenner s ðs 2 þ 80 s þ 2500Þ und erhalten durch Vergleich
beider Seiten die folgende Gleichung:
100
s ðs 2 þ 80 s þ 2500Þ
¼
A ðs 2 þ 80 s þ 2500Þ þ ðB s þ CÞ s
s ðs 2 þ 80 s þ 2500Þ
)
100 ¼ A ðs 2 þ 80 s þ 2500Þ þ ðB s þ CÞ s ¼ A s 2 þ 80 A s þ 2500 A þ B s 2 þ C s ¼
¼ ðA þ BÞ s 2 þ ð80 A þ CÞ s þ 2500 A
Wir vertauschen beide Seiten und ergänzen dann auf der rechten Seite die noch fehlenden Glieder 0 s 2 und 0 s:
ðA þ BÞ s 2 þ ð80 A þ CÞ s þ 2500 A ¼ 0 s 2 þ 0 s þ 100
Durch Koeffizientenvergleich folgt (das LGS lösen wir von unten nach oben):
ðIÞ
AþB ¼ 0
)
B ¼ A ¼ 0,04
ðIIÞ
80 A þ C ¼ 0
)
C ¼ 80 A ¼ 80 0,04 ¼ 3,2
ðIIIÞ
2500 A ¼ 100
)
A ¼ 0,04
5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation
435
Wir haben dieses gestaffelte lineare Gleichungssystem schrittweise von unten nach oben gelöst. Damit gilt:
100
Q ðsÞ ¼
¼
0,04
0,04 s 3,2
0,04
s þ 80
¼
¼
þ
0,04
2
s
s
s þ 80 s þ 2500
s 2 þ 80 s þ 2500
s ðs 2 þ 80 s þ 2500Þ
1
s þ 80
¼ 0,04
2
s
s þ 80 s þ 2500
Damit wir bei der Rücktransformation die Glieder in der Transformationstabelle finden, bringen wir den 2. Bruch in
der Klammer auf die folgende Gestalt (quadratische Ergänzung im Nenner, anschließend den Bruch in zwei Teilbrüche
aufspalten):
ðs þ 40Þ þ 40
s þ 80
ðs þ 40Þ þ 40
¼
¼
¼
s 2 þ 80 s þ 2500
ðs 2 þ 80 s þ 1600Þ þ 900
ðs 2 þ 80 s þ 1600Þ þ 2500 1600
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
1. Binom: ðs þ 40Þ 2 30 2
¼
ðs þ 40Þ þ 40
2
ðs þ 40Þ þ
30 2
¼
s þ 40
2
ðs þ 40Þ þ
30 2
þ
40
ðs þ 40Þ 2 þ 30 2
Damit gilt:
Q ðsÞ ¼ 0,04
1
s þ 80
s
s 2 þ 80 s þ 2500
¼ 0,04
1
s þ 40
40
2
s
2
ðs þ 40Þ þ 30
ðs þ 40Þ 2 þ 30 2
!
Durch Rücktransformation erhalten wir die folgende Abhängigkeit der Ladung q von der Zeit t:
(
!)
1
s þ 40
40
1
1
q ðtÞ ¼ l fQ ðsÞg ¼ l
0,04
¼
s
ðs þ 40Þ 2 þ 30 2
ðs þ 40Þ 2 þ 30 2
¼ 0,04
(
)
(
)!
1
s þ 40
1
1
1
l
l
40 l
¼
s
ðs þ 40Þ 2 þ 30 2
ðs þ 40Þ 2 þ 30 2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
Nr. 2
¼ 0,04
¼ 0,04
1e
40 t
Nr. 29 mit a ¼ 30, b ¼ 40
Nr. 28 mit a ¼ 30, b ¼ 40
!
e 40 t sin ð30 tÞ
¼
cos ð30 tÞ 40
30
40
4
sin ð30 tÞ
¼ 0,04 0,04 e 40 t cos ð30 tÞ þ
sin ð30 tÞ
1 e 40 t cos ð30 tÞ þ
30
3
Die Kondensatorladung strebt im Laufe der Zeit (d. h. für t ! 1) gegen den konstanten Wert q E ¼ 0,04 As:
4
q E ¼ lim q ðtÞ ¼ lim 0,04 0,04 e 40 t cos ð30 tÞ þ
sin ð30 tÞ
¼ 0,04
3
t!1
t!1
Bild G-39 zeigt den zeitlichen Verlauf der Ladung q.
q
0,04
0,03
0,02
0,01
Bild G-39
0,02
0,06
0,10
0,14
0,18
t
436
H Komplexe Zahlen und Funktionen
Hinweise für das gesamte Kapitel
(1)
Die Darstellung einer komplexen Zahl z erfolgt entweder in der kartesischen Form oder in einer der beiden
Polarformen (Exponentialform oder trigonometrische Form):
Kartesische Form: z ¼ x þ j y
(mit x; y 2 R)
jj
Polarformen: z ¼ r e ¼ r ðcos j þ j sin jÞ
(mit r 0 und 0 j < 2 p)
Die Angabe des Winkels (Argumentes) von z erfolgt in der Regel als Hauptwert im Intervall 0 j < 2 p
(Drehung im mathematisch positiven Sinn, d. h. im Gegenuhrzeigersinn). In der Technik wird als Winkel häufig
der kleinstmögliche Drehwinkel angegeben, die Hauptwerte liegen dann im Intervall p < j p . Die Winkel
können auch im Gradmaß angegeben werden.
1
¼ j
j3 ¼ j ,
j4 ¼ 1 ;
Wir erinnern: j 2 ¼ 1 ,
j
Die zu z konjugiert komplexe Zahl kennzeichnen wir duch das Symbol z* .
(2)
(3)
1 Komplexe Rechnung
1.1 Grundrechenarten
Lehrbuch: Band 1, Kapitel VII.1 und 2.1
Formelsammlung: Kapitel VIII.1 und 2
Die nachfolgenden komplexen Zahlen sind sowohl in der Exponentialform z ¼ r e j j als auch in der
trigonometrischen Form z ¼ r ðcos j þ j sin jÞ mit r 0 und 0 j < 2 p darzustellen. Wie
lauten die zugehörigen konjugiert komplexen Zahlen in der Polarform und der kartesischen Darstellungsform?
H1
a) z ¼ 3 11 j
c) z ¼ ð2 jÞ * ð5 jÞ 2
b) z ¼ 4,5 1,8 j
Grundsätzlich sind zwei verschiedene Lösungswege möglich:
1. Die in der Polarform, d. h. in der trigonometrischen bzw. Exponentialform verwendeten Polarkoordinaten r und j
lassen sich rein geometrisch aus einer Lageskizze mit Hilfe eines rechtwinkligen Dreiecks bestimmen (siehe hierzu
als Musterbeispiel die Lösung der Teilaufgabe a)).
2. Die Polarkoordinaten r und j können auch mit den aus dem Lehrbuch (Band 1) und der Formelsammlung
bekannten „ Lösungsformeln “ berechnet werden:
r ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 þ y2 ,
tan j ¼
y
x
)
j ¼ arctan
y
x
þK
(! FS : Kap. VIII.1.3.2)
Dabei ist K eine von der Lage der komplexen Zahl z ¼ x þ j y in der Gaußschen Zahlenebene abhängige Konstante. Bei Beschränkung auf den Hauptwertbereich 0 j < 2 p (entspricht einer vollen Drehung im Gegenuhrzeigersinn) gilt dann: K ¼ 0 im 1. Quadrant, K ¼ p im 2. und 3. Quadrant und K ¼ 2 p im 4. Quadrant.
Bei der Lösung der Aufgaben werden wir im Regelfall den zuletzt beschriebenen Lösungsweg einschlagen.
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_8
1 Komplexe Rechnung
437
a) z ¼ 3 11 j ¼ r e j j ¼ r ðcos j þ j sin jÞ
(4. Quadrant, siehe Bild H-1)
1. Lösungsweg („geometrische Lösung“)
Aus dem rechtwinkligen Dreieck (in der Lageskizze dick umrandet) berechnen wir die Hypotenuse r und den
„ Hilfswinkel “ a und daraus dann den gesuchten Hauptwert des Winkels j:
Satz des Pythagoras:
Im ( z )
r 2 ¼ 3 2 þ 11 2 ¼ 9 þ 121 ¼ 130
pffiffiffiffiffiffiffiffi
r ¼ 130 ¼ 11,402
)
3
3
a
Re ( z )
Hilfswinkel a:
tan a ¼
11
3
)
a ¼ arctan
11
¼ 74,74
3
r
11
Polarwinkel j:
j ¼ 360 a ¼ 360 74,74
¼ 285,26 ¼
b 4,9786
– 11
(im Bogenmaß)
Ergebnis: z ¼ 3 11 j ¼ 11,402 e j 4,9786 ¼
z = 3 – 11 j
Bild H-1
¼ 11,402 ðcos 4,9786 þ j sin 4,9786Þ
Die konjugiert komplexe Zahl lautet:
z* ¼ ð3 11 jÞ* ¼ 3 þ 11 j ¼ 11,402 e j ð 4,9786Þ ¼ 11,402 e j ð 4,9786 þ 2 pÞ ¼ 11,402 e j 1,3046 ¼
¼ 11,402 ðcos 1,3046 þ j sin 1,3046Þ
(Hauptwert des Winkels: j ¼ 4,9786 þ 2 p ¼ 1,3046 ¼
b 74,74 )
2. Lösungsweg (Verwendung der „ Lösungsformeln “)
Die komplexe Zahl z ¼ 3 11 j liegt im 4. Quadrant (siehe Bild H-1).
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ 3 2 þ ð 11Þ 2 ¼ 9 þ 121 ¼ 130 ¼ 11,402
11
11
j ¼ arctan
þ 2 p ¼ arctan
þ 2 p ¼ 4,9786 ¼
b 285,26
3
3
ðim GradmaßÞ
z ¼ 3 11 j ¼ 11,402 e j 4,9786 ¼ 11,402 ðcos 4,9786 þ j sin 4,9786Þ
z* ¼ ð3 11 jÞ* ¼ 3 þ 11 j ¼ 11,402 e j ð 4,9786Þ ¼ 11,402 e j ð 4,9786 þ 2 pÞ ¼ 11,402 e j 1,3046 ¼
¼ 11,402 ðcos 1,3046 þ j sin 1,3046Þ
(3. Quadrant)
b) z ¼ 4,5 1,8 j ¼ r e j j ¼ r ðcos j þ j sin jÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
r ¼ ð 4,5Þ 2 þ ð 1,8Þ 2 ¼ 20,25 þ 3,24 ¼ 23,49 ¼ 4,847
1,8
þ p ¼ arctan 0,4 þ p ¼ 0,3805 þ p ¼ 3,5221 ¼
b 201,80
j ¼ arctan
4,5
z ¼ 4,5 1,8 j ¼ 4,847 e j 3,5221 ¼ 4,847 ðcos 3,5221 þ j sin 3,5221Þ
ðim GradmaßÞ
438
H Komplexe Zahlen und Funktionen
Die konjugiert komplexe Zahl lautet:
z* ¼ ð 4,5 1,8 jÞ* ¼ 4,5 þ 1,8 j ¼ 4,847 e j ð 3,5221Þ ¼ 4,847 e j ð 3,5221 þ 2 pÞ ¼ 4,847 e j 2,7611 ¼
¼ 4,847 ðcos 2,7611 þ j sin 2,7611Þ
(Hauptwert des Winkels: j ¼ 3,5221 þ 2 p ¼ 2,7611 ¼
b 158,20 )
c) Wir bringen z zunächst in die kartesische Form:
z ¼ ð2 jÞ * ð5 jÞ 2 ¼ ð2 þ jÞ ð25 10 j þ j 2 Þ ¼ 2 þ j ð25 10 j 1Þ ¼
¼ 2 þ j ð24 10 jÞ ¼ 2 þ j 24 þ 10 j ¼ 22 þ 11 j
ð2: QuadrantÞ
Umrechnung in die Polarform z ¼ r e j j ¼ r ðcos j þ j sin jÞ:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ ð 22Þ 2 þ 11 2 ¼ 484 þ 121 ¼ 605 ¼ 24,597
11
j ¼ arctan
þ p ¼ arctan ð 0,5Þ þ p ¼ 0,4636 þ p ¼ 2,6779 ¼
b 153,43
22
z ¼ 22 þ 11 j ¼ 24,597 e j 2,6779 ¼ 24,597 ðcos 2,6779 þ j sin 2,6779Þ
Konjugiert komplexe Zahl:
z* ¼ ð 22 þ 11 jÞ* ¼ 22 11 j ¼ 24,597 e j ð 2,6779Þ ¼ 24,597 e j ð 2,6779 þ 2 pÞ ¼
¼ 24,597 e j 3,6053 ¼ 24,597 ðcos 3,6053 þ j sin 3,6053Þ
(Hauptwert des Winkels: j ¼ 2,6779 þ 2 p ¼ 3,6053 ¼
b 206,57 )
H2
Die nachfolgenden komplexen Zahlen sind in der kartesischen Form z ¼ x þ j y dazustellen. Wie lautet
die jeweilige konjugiert komplexe Zahl (in kartesischer Darstellung)?
a) z ¼ 6 e j 2,5
b) z ¼ 10 ½cos ð 225 Þ þ j sin ð 225 Þ
c) z ¼ 4 ½ cos ð 40 Þ þ j sin ð 40 Þ þ 2 e j 30 3 þ 1,5 j
Lösungsweg: Schrittweise Umformung nach dem folgenden Schema:
Exponentialform
a) z
! trigonometrische Form
ausmultiplizieren
!
kartesische Form
¼ 6 e j 2,5 ¼ 6 ðcos 2,5 þ j sin 2,5Þ ¼ 6 cos 2,5 þ ð6 sin 2,5Þ j ¼ 4,807 þ 3,591 j
z * ¼ ð 4,807 þ 3,591 jÞ * ¼ 4,807 3,591 j
b) z
¼ 10 ½ cos ð 225 Þ þ j sin ð 225 Þ ¼ 10 cos ð 225 Þ þ ½ 10 sin ð 225 Þ j ¼ 7,071 þ 7,071 j
z* ¼ ð 7,071 þ 7,071 jÞ * ¼ 7,071 7,071 j
c) Die ersten beiden Summanden müssen zunächst in die kartesische Form gebracht werden, da die Addition komplexer
Zahlen nur in dieser Darstellungsform möglich ist:
z ¼ 4 ½ cos ð 40 Þ þ j sin ð 40 Þ þ 2 e j 30 3 þ 1,5 j ¼
¼ 4 cos ð40 Þ þ ½ 4 sin ð 40 Þ j þ 2 ðcos 30 þ j sin 30 Þ 3 þ 1,5 j ¼
¼ 3,064 2,571 j þ 2 cos 30 þ ð2 sin 30 Þ j 3 þ 1,5 j ¼
¼ 3,064 2,571 j þ 1,732 þ j 3 þ 1,5 j ¼ ð3,064 þ 1,732 3Þ þ ð 2,571 j þ j þ 1,5 jÞ ¼
¼ 1,796 0,071 j
z* ¼ ð1,796 0,071 jÞ * ¼ 1,796 þ 0,071 j
1 Komplexe Rechnung
439
Berechnen Sie mit den komplexen Zahlen
z1 ¼ 2 j ,
z2 ¼ 5 þ 2 j
und
z 3 ¼ 3 j
die folgenden Terme (Endergebnisse in der kartesischen Darstellungsform angeben):
H3
aÞ
bÞ
cÞ
z 3 ð2 z*2 3 z 1 Þ þ z*3 3 j z 1
z*1 þ 2 z 3 z 1 j z 2
2 ðz 2 z*3 Þ z 1
pffiffiffi
j z 1 j þ 2 j z 2 þ z*3 j þ z*1 z 2 18
j ðz 3 z 1 Þ * j j j ðz 1 z 2 Þ j
aÞ z 3 ð2 z*2 3 z 1 Þ þ z*3 3 j z 1 ¼ 3 j ½ 2 ð5 þ 2 jÞ * 3 ð2 jÞ þ ð 3 jÞ * 3 j ð2 jÞ ¼
¼ 3 j ½ 2 ð5 2 jÞ 6 þ 3 j þ 3 j 6 j þ 3 j 2 ¼
¼ 3 j ð10 4 j 6 þ 3 jÞ 3 j 3 ¼ 3 j ð4 jÞ 3 j 3 ¼
¼ 12 j þ 3 j 2 3 j 3 ¼ 15 j 3 3 ¼ 6 15 j
b) Der besseren bersicht wegen bringen wir zunächst in getrennter Rechnung Zähler und Nenner jeweils in die
kartesische Form.
Zähler:
z*1 þ 2 z 3 z 1 j z 2 ¼ ð2 jÞ * þ 2 ð 3 jÞ ð2 jÞ j ð5 þ 2 jÞ ¼
¼ 2 þ j 6 j ð2 jÞ 5 j 2 j 2 ¼ 2 þ j 12 j þ 6 j 2 5 j þ 2 ¼
¼ 2 þ j 12 j 6 5 j þ 2 ¼ ð2 6 þ 2Þ þ ð j 12 j 5 jÞ ¼
¼ 2 16 j ¼ 2 ð1 þ 8 jÞ
Nenner:
2 ðz 2 z*3 Þ z 1 ¼ 2 ½ 5 þ 2 j ð 3 jÞ * ð2 jÞ ¼ 2 ð5 þ 2 j 3 jÞ ð2 jÞ ¼ 2 ð5 jÞ ð2 jÞ ¼
¼ 2 ð10 5 j 2 j þ j 2 Þ ¼ 2 ð10 7 j 1Þ ¼ 2 ð9 7 jÞ
Berechnung des Bruches (dieser wird zunächst mit dem konjugiert komplexen Nenner, also der komplexen Zahl
9 þ 7 j erweitert; Faktor 2 vorher kürzen):
z*1 þ 2 z 3 z 1 j z 2
2 ð 1 8 jÞ
1 8j
ð 1 8 jÞ ð9 þ 7 jÞ
¼
¼
¼
¼
9 7j
ð9 7 jÞ ð9 þ 7 jÞ
2 ð9 7 jÞ
2 ðz 2 z*3 Þ z 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða bÞ ða þ bÞ ¼ a 2 b 2
¼
mit a ¼ 9; b ¼ 7 j
9 7 j 72 j 56 j 2
9 79 j þ 56
47 79 j
47
79
¼
¼
j ¼
¼
81 þ 49
130
130
130
81 49 j 2
¼ 0,362 0,608 j
c) Wir bringen zunächst (in getrennter Rechnung) alle Summanden im Zähler und Nenner des Bruches in die kartesische Form.
Summanden des Zählers
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
j z 1 j ¼ j 2 j j ¼ 2 2 þ ð 1Þ 2 ¼ 4 þ 1 ¼ 5
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 j z 2 þ z*3 j ¼ 2 j ð5 þ 2 jÞ þ ð 3 jÞ * j ¼ 2 j 5 þ 2 j þ 3 j j ¼ 2 j 5 þ 5 j j ¼ 2 5 2 þ 5 2 ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi pffiffiffiffiffi
pffiffiffiffiffiffiffiffi
¼ 2 25 þ 25 ¼ 2 50 ¼ 2 50 ¼ 100 ¼ 10
z*1 z 2 ¼ ð2 jÞ * ð5 þ 2 jÞ ¼ ð2 þ jÞ ð5 þ 2 jÞ ¼ 10 þ 4 j þ 5 j þ 2 j 2 ¼ 10 þ 9 j 2 ¼ 8 þ 9 j
440
H Komplexe Zahlen und Funktionen
Summanden des Nenners
j ðz 3 z 1 Þ * j ¼ j z 3 z 1 j ¼ j 3 j ð2 jÞ j ¼ j 3 j 2 þ j j ¼ j 2 2 j j ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ ð 2Þ 2 þ ð 2Þ 2 ¼ 4 þ 4 ¼ 8 ¼ 2 2
(unter Berücksichtigung von j z* j ¼ j z j )
j j ðz 1 z 2 Þ j ¼ j j j j z 1 z 2 j ¼ 1 j ð2 jÞ ð5 þ 2 jÞ j ¼ j 2 j 5 2 j j ¼ j 3 3 j j ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ ð 3Þ 2 þ ð 3Þ 2 ¼ 9 þ 9 ¼ 18 ¼ 3 2
Berechnung des Bruches
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
5 þ 10 þ 8 þ 9 j 18
5 þ 9j
j z 1 j þ 2 j z 2 þ z*3 j þ z*1 z 2 18
ð 5 þ 9 jÞ ð 2Þ
pffiffiffi
pffiffiffi
pffiffiffi ¼
pffiffiffi
pffiffiffi
¼
¼
¼
j ðz 3 z 1 Þ * j j j ðz 1 z 2 Þ j
2 23 2
2
ð 2Þ ð 2Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl
ffl}
pffiffiffi
Bruch mit 2 erweitert
pffiffiffi pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffiffiffi
5 2 9 2j
10 9 2 j
1 pffiffiffiffiffi
9 pffiffiffi
¼
¼
10
2 j ¼ 1,581 6,364 j
¼
2
2
2
2
Berechnen Sie mit den komplexen Zahlen
z1 ¼
H4
2þj
,
1 2j
die folgenden Ausdrücke:
pffiffiffi
a) z 1 þ 5 z 2 3 z*3
z 2 ¼ 2 e j p=3
b)
und
z 3 ¼ 4 ðcos 30 þ j sin 30 Þ
z*1 z 3
0,5 z 2
a) Addition und Subtraktion lassen sich bekanntlich nur in der kartesischen Darstellungsform durchführen. Wir müssen
daher die gegebenen Zahlen zunächst in diese Form bringen.
Umformungen: z 1 zunächst mit dem konjugiert komplexen Nenner, d. h. der komplexen Zahl 1 þ 2 j erweitern.
Die komplexe Zahl z 2 in die trigonometrische Form bringen, dann ausmultiplizieren. Die komplexe Zahl z 3 ausmultiplizieren.
z1 ¼
2þj
ð2 þ jÞ ð1 þ 2 jÞ
2 þ 4 j þ j þ 2 j2
2 þ 5j 2
5j
¼
¼
¼
¼
¼ j
1 2 j ð1 2 jÞ ð1 þ 2 jÞ
1þ4
5
1 4 j2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða bÞ ða þ bÞ ¼ a 2 b 2
z 2 ¼ 2 e j p=3 ¼ 2 ½ cos ð p=3Þ þ j sin ð p=3Þ ¼ 2 cos ð p=3Þ þ ½ 2 sin ð p=3Þ j ¼ 1
pffiffiffi
z 3 ¼ 4 ðcos 30 þ j sin 30 Þ ¼ 4 cos 30 þ ð4 sin 30 Þ j ¼ 2 3 þ 2 j
pffiffiffi
3j
Somit erhalten wir:
pffiffiffi
pffiffiffi
pffiffiffi pffiffiffi
pffiffiffi
pffiffiffi pffiffiffi
z 1 þ 5 z 2 3 z*3 ¼ j þ 5 ð1 3 jÞ 3 ð2 3 þ 2 jÞ * ¼ j þ 5 5 3 j 3 ð2 3 2 jÞ ¼
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
¼ j þ 5 5 3 j 6 þ 2 3 j ¼ ð5 6Þ þ ðj 5 3 j þ 2 3 jÞ ¼
pffiffiffi
pffiffiffi
¼ 1 þ ðj 3 3 jÞ ¼ 1 ð3 3 1Þ j ¼ 1 4,196 j
b) Die Berechnung des Bruches soll hier in der für Multiplikation und Division bequemeren Exponentialform erfolgen.
Umformungen: Die komplexen Zahlen z 1 und z 3 zunächst in die Exponentialform bringen, wobei wir das Ergebnis z 1 ¼ j aus Teilaufgabe a) berücksichtigen.
z1 ¼
2þj
¼ j ¼ 1 e j p=2 ,
1 2j
z 3 ¼ 4 ðcos 30 þ j sin 30 Þ ¼ 4 e j 30 ¼ 4 e j p=6
1 Komplexe Rechnung
441
z*1 z 3
ð1 e j p=2 Þ * ð4 e j p=6 Þ
4 e j p=2 e j p=6
¼
¼ 4 e j p=2 e j p=6 e j p=3 ¼
¼
0,5 z 2
e j p=3
0,5 ð2 e j p=3 Þ
¼ 4 e j ð 2 þ 6 þ 3 Þ ¼ 4 e j
p
p
p
3pþpþ2p
6
¼ 4 e j0 ¼ 4 e0 ¼ 4 1 ¼ 4
Alternative: Berechnung in kartesischer Form, wobei die Zahlen z 2 und z 3 zunächst in dieser Form dargestellt
werden müssen. Der Bruch wird dann mit z*2 erweitert, Zähler und Nenner anschließend ausmultipliziert.
Stellen sie die Summe
H5
z ¼ z 1 þ z 2 þ z 3 ¼ 2 e j 1,25 p þ 0,2 ð1 3 jÞ 3 þ
2j
3 þ 4j
in der kartesischen und exponentiellen Form dar.
Wir müssen zunächst die drei Summanden z 1 , z 2 und z 3 in die kartesische Form bringen, da Additionen nur in dieser
Form durchführbar sind:
z 1 ¼ 2 e j 1,25 p ¼ 2 ½ cos ð 1,25 pÞ þ j sin ð 1,25 pÞ ¼ 2 cos ð 1,25 pÞ þ ½ 2 sin ð 1,25 pÞ j ¼
pffiffiffi
pffiffiffi
¼ 2 þ 2j
z 2 ¼ 0,2 ð1 3 jÞ 3 ¼ 0,2 ð1 3 3 1 2 3 j þ 3 1 ð3 jÞ 2 ð3 jÞ 3 Þ ¼ 0,2 ð1 9 j þ 27 j 2 27 j 3 Þ ¼
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
Binom : ða bÞ3 ¼ a 3 3 a 2 b þ 3 a b 2 b 3
¼ 0,2 ð1 9 j 27 þ 27 jÞ ¼ 0,2 ð 26 þ 18 jÞ ¼ 5,2 þ 3,6 j
z3 ¼
2j
ð2 jÞ ð3 4 jÞ
6 8 j 3 j þ 4 j2
6 11 j 4
2 11 j
2
11
¼
¼
¼
j ¼
¼
¼
2
3 þ 4j
ð3 þ 4 jÞ ð3 4 jÞ
9 þ 16
25
25
25
9 16 j
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða þ bÞ ða bÞ ¼ a 2 b 2
¼ 0,08 0,44 j
Umformung: Die komplexe Zahl z 3 wurde zunächst mit dem konjugiert komplexen Nenner, d. h. der komplexen
Zahl 3 4 j erweitert.
Summenwert in kartesischer Form
pffiffiffi
pffiffiffi
z ¼ z 1 þ z 2 þ z 3 ¼ ð 2 þ 2 jÞ þ ð 5,2 þ 3,6 jÞ þ ð0,08 0,44 jÞ ¼
pffiffiffi
pffiffiffi
¼ ð 2 5,2 þ 0,08Þ þ ð 2 þ 3,6 0,44Þ j ¼ 6,534 þ 4,574 j
Summenwert in der Exponentialform
z ¼ 6,534 þ 4,574 j ¼ r e j j
ð2: QuadrantÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ ð 6,534Þ 2 þ 4,574 2 ¼ 63,6146 ¼ 7,976
4,574
þ p ¼ arctan ð 0,7000Þ þ p ¼ 0,6107 þ p ¼ 2,5308 ¼
b 145,01
j ¼ arctan
6,534
Ergebnis:
z ¼ 6,534 þ 4,574 j ¼ 7,976 e j 2,5308
442
H Komplexe Zahlen und Funktionen
1.2 Potenzen, Wurzeln, Logarithmen
Lehrbuch: Band 1, Kapitel VII.2.2 bis 2.4
Formelsammlung: Kapitel VIII.3 bis 5
Berechnen Sie die folgenden Potenzen mit Hilfe der Formel von Moivre. Die Ergebnisse sind in der kartesischen und exponentiellen Darstellungsform anzugeben (Winkel als Hauptwert im Intervall 0 j < 2 p).
pffiffiffi
pffiffiffi
a) ð1 2 jÞ 3
b) ð2 e j p=4 Þ 6
c) ½ 2 ðcos 30 þ j sin 30 Þ 8
H6
Die Basiszahlen der Potenzen müssen gegebenenfalls zunächst in die Exponentialform gebracht werden (betrifft die
Teilaufgaben a) und c), dann nach Moivre potenzieren: z n ¼ ðr e j j Þ n ¼ r n e j n j .
pffiffiffi
z ¼ 1 2 j ¼ r e jj
(z liegt im 4. Quadrant)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
pffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ j z j ¼ 1 2 þ ð 2Þ 2 ¼ 1 þ 2 ¼ 3
pffiffiffi
pffiffiffi
2
j ¼ arg ðzÞ ¼ arctan
þ 2 p ¼ arctan ð 2Þ þ 2 p ¼ 0,9553 þ 2 p ¼ 5,3279
1
pffiffiffi
pffiffiffi
Somit: z ¼ 1 2 j ¼ 3 e j 5,3279
a) Basis:
Berechnung der Potenz z 3 nach der Formel von Moivre:
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
z 3 ¼ ð1 2 jÞ 3 ¼ ð 3 e j 5,3279 Þ 3 ¼ ð 3Þ 3 e j ð3 5,3279Þ ¼ 3 3 e j 15,9837 ¼
pffiffiffi
pffiffiffi
pffiffiffi
¼ 3 3 e j ð15,9837 4 pÞ ¼ 3 3 e j 3,4173 ¼ 3 3 ðcos 3,4173 þ j sin 3,4173Þ ¼
pffiffiffi
pffiffiffi
¼ 3 3 cos 3,4173 þ ð3 3 sin 3,4173Þ j ¼ 5,000 1,415 j
(der Winkel liegt zunächst außerhalb des Hauptwertbereiches und muss um zwei volle Umdrehungen zurückgedreht
werden ) Hauptwert ¼ 15,9837 2 2 p ¼ 15,9837 4 p ¼ 3,4173)
pffiffiffi
pffiffiffi
Ergebnis: ð1 2 jÞ 3 ¼ 5,000 1,415 j ¼ 3 3 e j 3,4173 ¼ 5,196 e j 3,4173
b) Basis:
z ¼ 2 e j p=4 (z liegt bereits in der Exponentialform vor)
Berechnung der Potenz z 6 nach der Formel von Moivre:
z 6 ¼ ð2 e j p=4 Þ 6 ¼ 2 6 e j ð6 p=4Þ ¼ 64 e j 6 p=4 ¼ 64 e j 3 p=2 ¼ 64 e j ð 3 p=2 þ 2 pÞ ¼ 64 e j p=2 ¼
¼ 64 ½ cos ðp=2Þ þ j sin ðp=2Þ ¼ 64 ð0 þ j 1Þ ¼ 64 j
(Hauptwert des Winkels ¼ 3 p=2 þ 2 p ¼ p=2)
Ergebnis:
c) Basis:
ð2 e j p=4 Þ 6 ¼ 64 j ¼ 64 e j p=2
z ¼
pffiffiffi
pffiffiffi
2 ðcos 30 þ j sin 30 Þ ¼ 2 e j 30
Berechnung der Potenz z 8 nach der Formel von Moivre:
pffiffiffi
pffiffiffi
z 8 ¼ ð 2 e j 30 Þ 8 ¼ ð 2Þ 8 e j ð8 30 Þ ¼ 16 e j 240 ¼ 16 ðcos 240 þ j sin 240 Þ ¼
¼ 16 cos 240 þ ð16 sin 240 Þ j ¼ 8 13,856 j
pffiffiffi
Ergebnis: ½ 2 ðcos 30 þ j sin 30 8 ¼ 8 13,856 j ¼ 16 e j 240
1 Komplexe Rechnung
443
Berechnen Sie die Potenz
H7
3þj 4
1j
a) mit Hilfe der Binomischen Formel,
b) mit Hilfe der Formel von Moivre.
Das Ergebnis soll in der kartesischen Form angegeben werden.
a) Wir bringen die Basis z ¼
3þj
zunächst in die kartesische Form (Bruch mit dem konjugiert komplexen Nenner,
1j
d. h. der komplexen Zahl 1 þ j erweitern):
z ¼
3þj
ð3 þ jÞ ð1 þ jÞ
3 þ 3 j þ j þ j2
3 þ 4j 1
2 þ 4j
2
4
¼
¼
¼ þ
j ¼ 1 þ 2j
¼
¼
2
1j
ð1 jÞ ð1 þ jÞ
1þ1
2
2
2
1j
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða bÞ ða þ bÞ ¼ a 2 b 2
Die Binomische Formel ða þ bÞ 4 ¼ a 4 þ 4 a 3 b þ 6 a 2 b 2 þ 4 a b 3 þ b 4 mit a ¼ 1 und b ¼ 2 j liefert das
gesuchte Ergebnis:
3þj 4
4
z ¼
¼ ð1 þ 2 jÞ 4 ¼ 1 4 þ 4 1 3 2 j þ 6 1 2 ð2 jÞ 2 þ 4 1 ð2 jÞ 3 þ ð2 jÞ 4 ¼
1j
¼ 1 þ 8 j þ 24 j 2 þ 32 j 3 þ 16 j 4 ¼ 1 þ 8 j 24 32 j þ 16 ¼ 7 24 j
b) Wir bringen die Basis z ¼
3þj
¼ 1 þ 2 j in die Exponentialform:
1j
3þj
¼ 1 þ 2 j ¼ r e jj
ð1: QuadrantÞ
1j
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ j z j ¼ 12 þ 22 ¼ 1 þ 4 ¼ 5
2
¼ arctan 2 ¼ 1,1071
j ¼ arg ðzÞ ¼ arctan
1
pffiffiffi
3þj
¼ 1 þ 2 j ¼ 5 e j 1,1071
Somit: z ¼
1j
z ¼
Die Formel von Moivre liefert dann das gesuchte Ergebnis:
4
pffiffiffi
pffiffiffi 4 j ð4 1,1071Þ
3þj 4
4
j 1,1071
¼
5e
¼
5 e
¼ 25 e j 4,4284 ¼
z ¼
1j
¼ 25 ðcos 4,4284 þ j sin 4,4284Þ ¼ 25 cos 4,4284 þ ð25 sin 4,4284Þ j ¼
¼ 7,005 23,999 j
Anmerkung:
fehlern.
7 24 j
Die geringfügige Abweichung vom Ergebnis aus der (exakten) Rechnung in a) beruht auf Rundungs-
Einer Formelsammlung entnehmen wir die folgenden trigonometrischen Formeln:
H8
cos ð4 jÞ ¼ 8 cos 4 j 8 cos 2 j þ 1
sin ð4 jÞ ¼ 4 sin j cos j ð2 cos 2 j 1Þ
Leiten Sie diese Beziehungen aus der Formel von Moivre und unter Verwendung der Binomischen Formel
her.
444
H Komplexe Zahlen und Funktionen
½ r ðcos j þ j sin jÞ n ¼ r n ½ cos ðn jÞ þ j sin ðn jÞ
Formel von Moivre:
Wir setzen r ¼ 1 und n ¼ 4 und erhalten die folgende Gleichung (seitenvertauscht):
cos ð4 jÞ þ j sin ð4 jÞ ¼ ðcos j þ j sin jÞ 4
ð*Þ
Die rechte Seite entwickeln wir nach der Binomischen Formel für ða þ bÞ 4 :
ðcos j þ j sin j Þ 4 ¼ ða þ bÞ 4 ¼ a 4 þ 4 a 3 b þ 6 a 2 b 2 þ 4 a b 3 þ b 4 ¼
|fflfflfflffl{zfflfflfflffl}
|fflffl{zfflffl}
a
b
4
¼ ðcos jÞ þ 4 ðcos jÞ 3 ðj sin jÞ þ 6 ðcos jÞ 2 ðj sin jÞ 2 þ 4 ðcos jÞ ðj sin jÞ 3 þ ðj sin jÞ 4 ¼
¼ cos 4 j þ j ð4 cos 3 j sin jÞ þ j 2 ð6 cos 2 j sin 2 jÞ þ j 3 ð4 cos j sin 3 jÞ þ j 4 ðsin 4 jÞ ¼
¼ cos 4 j þ j ð4 cos 3 j sin jÞ 6 cos 2 j sin 2 j j ð4 cos j sin 3 jÞ þ sin 4 j ¼
¼ ðcos 4 j 6 cos 2 j sin 2 j þ sin 4 jÞ þ j ð4 cos 3 j sin j 4 cos j sin 3 jÞ
Dieser komplexe Ausdruck ist gleich der komplexen Zahl cos ð4 jÞ þ j sin ð4 jÞ (linke Seite der Gleichung (*)).
Durch Vergleich der Real- bzw. Imaginiärteile erhalten wir folgende Beziehungen:
cos ð4 jÞ ¼ cos 4 j 6 cos 2 j sin 2 j þ sin 4 j
sin ð4 jÞ ¼ 4 cos 3 j sin j 4 cos j sin 3 j
Mit Hilfe des „ trigonometrischen Pythagoras “ sin 2 j þ cos 2 j ¼ 1 lassen sich diese Formeln auf die in der Aufgabenstellung angegebene Form bringen:
cos ð4 jÞ ¼ cos 4 j 6 cos 2 j sin 2 j þ sin 4 j ¼ cos 4 j sin 2 j ð6 cos 2 j sin 2 j Þ ¼
|fflffl{zfflffl}
|fflffl{zfflffl}
1 cos 2 j
1 cos 2 j
¼ cos 4 j ð1 cos 2 jÞ ð6 cos 2 j 1 þ cos 2 jÞ ¼ cos 4 j ð1 cos 2 jÞ ð7 cos 2 j 1Þ ¼
¼ cos 4 j ð7 cos 2 j 1 7 cos 4 j þ cos 2 jÞ ¼ cos 4 j ð8 cos 2 j 1 7 cos 4 jÞ ¼
¼ cos 4 j 8 cos 2 j þ 1 þ 7 cos 4 j ¼ 8 cos 4 j 8 cos 2 j þ 1
sin ð4 jÞ ¼ 4 cos 3 j sin j 4 cos j sin 3 j ¼ 4 cos j sin j ðcos 2 j sin 2 j Þ ¼
|fflffl{zfflffl}
1 cos 2 j
¼ 4 cos j sin j ðcos 2 j 1 þ cos 2 jÞ ¼ 4 cos j sin j ð2 cos 2 j 1Þ
H9
Bestimmen Sie die folgenden Wurzeln in exponentieller und kartesischer Darstellungsform. Deuten Sie die
Ergebnisse geometrisch (Skizze anfertigen).
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi ffi
4
3
a)
2 2 3j
b)
8 e j p=4
Zur Erinnerung: Im Komplexen ist eine Wurzel immer mehrdeutig (Anzahl der verschiedenen Werte ¼ Wurzelexponent).
Der Radikand der Wurzel muss zunächst in die Exponentialform gebracht werden.
pffiffiffi
a) Radikand: a ¼ 2 2 3 j ¼ a 0 e j ða þ k 2 pÞ
(4. Quadrant; k 2 Z)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 0 ¼ j a j ¼ 2 2 þ ð 2 3Þ 2 ¼ 4 þ 12 ¼ 16 ¼ 4
pffiffiffi
pffiffiffi
2 3
p
1
6
5
þ 2 p ¼ arctan ð 3Þ þ 2 p ¼
þ 2p ¼ p þ
p ¼
p
a ¼ arg ðaÞ ¼ arctan
2
3
3
3
3
pffiffiffi
Somit: a ¼ 2 2 3 j ¼ 4 e j ð5 p=3 þ k 2 pÞ
1 Komplexe Rechnung
Wir setzen z ¼
445
ffiffiffi
p
4
a und erhalten daraus durch Potenzieren die Gleichung z 4 ¼ a . Mit dem Ansatz z ¼ r e j j
und a ¼ 4 e j ð5 p=3 þ k 2 pÞ folgt dann unter Verwendung der Formel von Moivre:
z4 ¼ a
)
ðr e j j Þ 4 ¼ r 4 e j ð4 jÞ ¼ 4 e j ð5 p=3 þ k 2 pÞ
Durch Vergleich der Beträge bzw. Winkel beiderseits erhalten wir zwei Bestimmungsgleichungen für die Unbekannten r und j:
r4 ¼ 4
)
r ¼
pffiffiffi
2;
4j ¼
5
p þ k 2p
3
jk ¼
)
5
p
5p þ k 6p
p þk
¼
12
2
12
ðmit k 2 ZÞ. Für den Winkel ergeben sich genau vier Hauptwerte (für k ¼ 0, 1, 2, 3):
j0 ¼
5
p ¼
b 75 ,
12
j1 ¼
11
p ¼
b 165 ,
12
j2 ¼
17
p ¼
b 255 ,
12
j3 ¼
23
p ¼
b 345
12
Die restlichen k-Werte führen zu Winkeln, die sich von einem der vier Hauptwerte um ein ganzzahliges Vielfaches
von 2 p unterscheiden. Diese sog. Nebenwerte liefern keine neuen Ergebnisse. So erhalten wir z. B. für k ¼ 4 den
Winkel
j4 ¼
5
p
5
p þ4
¼
p þ 2 p ¼ j0 þ 2 p
12
2
12
5
p genau um 2 p , d. h. um eine volle Umdrehung in der Zahlenebene unterscheidet.
12
Es gibt somit genau vier verschiedene Lösungen (Wurzeln). Sie lauten der Reihe nach:
pffiffiffi
pffiffiffi
z 0 ¼ 2 e j 75 ¼ 2 ðcos 75 þ j sin 75 Þ ¼ 0,366 þ 1,366 j
pffiffiffi
pffiffiffi
z 1 ¼ 2 e j 165 ¼ 2 ðcos 165 þ j sin 165 Þ ¼ 1,366 þ 0,366 j
pffiffiffi
pffiffiffi
z 2 ¼ 2 e j 255 ¼ 2 ðcos 255 þ j sin 255 Þ ¼ 0,366 1,366 j
pffiffiffi
pffiffiffi
z 3 ¼ 2 e j 345 ¼ 2 ðcos 345 þ j sin 345 Þ ¼ 1,366 0,366 j
der sich vom Winkel j 0 ¼
Geometrische Deutung in der Gaußschen Zahlenebene
(Bild H-2)
Im ( z )
z0
Die Bildpunkte der vier Wurzeln z 0 , z 1 , z 2 , z 3
liegenpauf
ffiffiffi dem Mittelpunktskreis mit dem Radius
R ¼ 2 und bilden die Ecken eines Quadrates
(der Winkel zwischen zwei benachbarten Bildpunkten beträgt jeweils 90 (rechter Winkel)).
2
z1
2
75°
Die Zeiger z 0 und z 2 bzw. z 1 und z 3 sind jeweils entgegengerichtet:
2
z 2 ¼ z 0 ¼ ð0,366 þ 1,366 jÞ ¼ 0,366 1,366 j
2
z 3 ¼ z 1 ¼ ð 1,366 þ 0,366 jÞ ¼ 1,366 0,366 j
b) Radikand:
a ¼ 8 e j p=4 ¼ 8 e j ðp=4 þ k 2 pÞ
Lösungsweg wie in Teilaufgabe a):
pffiffiffi
z ¼ 3 a ) z3 ¼ a
mit
z3 ¼ a
)
ðk 2 ZÞ
z ¼ r e jj
Bild H-2
z2
a ¼ 8 e j ðp=4 þ k 2 pÞ
und
ðr e j j Þ 3 ¼ r 3 e j ð3 jÞ ¼ 8 e j ðp=4 þ k 2 pÞ
Vergleich der Beträge bzw. Winkel beiderseits:
r3 ¼ 8
)
r ¼
p
ffiffiffi
3
8 ¼ 2;
3j ¼
p
þ k 2p
4
)
jk ¼
p
2
þk
p
12
3
ðk 2 ZÞ
Re ( z )
z3
446
H Komplexe Zahlen und Funktionen
Für k ¼ 0, 1, 2 erhält man die Winkelhauptwerte aus dem Intervall 0 j < 2 p , alle übrigen k-Werte liefern
nur Nebenwerte (d. h. Winkel, die sich von den Hauptwerten um ganzzahlige Vielfache von 2 p unterscheiden):
j 0 ¼ p=12 ¼
b 15 ,
j 1 ¼ 9=12 p ¼ 3=4 p ¼
b 135 ,
j 2 ¼ 17=12 p ¼
b 255
Es gibt somit genau drei verschiedene Lösungen (Wurzeln). Sie lauten:
z 0 ¼ 2 e j 15
¼ 2 ðcos 15 þ j sin 15 Þ ¼ 1,932 þ 0,518 j
z 1 ¼ 2 e j 135 ¼ 2 ðcos 135 þ j sin 135 Þ ¼ 1,414 þ 1,414 j
z 2 ¼ 2 e j 255 ¼ 2 ðcos 255 þ j sin 255 Þ ¼ 0,518 1,932 j
Geometrische Deutung in der Gaußschen Zahlenebene (Bild H-3)
Die Bildpunkte der drei Wurzeln z 0 , z 1 , z 2 liegen
auf dem Mittelpunktskreis mit dem Radius R ¼ 2
und bilden die Eckpunkte eines gleichseitigen Dreiecks (der Winkel zwischen zwei benachbarten Bildpunkten beträgt jeweils 120 ). Die Zeiger z 1 und
z 2 erhält man durch Drehung des Zeigers z 0 um
120 bzw. 240 im Gegenuhrzeigersinn.
Im ( z )
z1
2
120°
Bild H-3
z0
2
120° 120°
15°
Re ( z )
2
z2
H10
Berechnen Sie den natürlichen Logarithmus der folgenden komplexen Zahlen:
pffiffiffi
c) z ¼ ð4 3 jÞ 6
a) z ¼ 3 þ j
b) z ¼ 3 e j p=5
Geben Sie den jeweiligen Hauptwert an.
Zur Erinnerung: Der Logarithmus einer komplexen Zahl ist – im Gegensatz zum Logarithmus einer positiven reellen
Zahl – stets unendlich vieldeutig. Die Werte unterscheiden sich dabei im Imaginärteil um ganzzahlige Vielfache von 2 p.
Die komplexe Zahl muss zunächst in die Exponentialform gebracht werden und wird dann logarithmiert unter Verwendung der folgenden (bekannten) Rechenregeln:
ln ða bÞ ¼ ln a þ ln b ,
ln a n ¼ n ln a
und
ln e n ¼ n
ðmit a > 0 ; b > 0Þ
pffiffiffi
a) z ¼ 3 þ j ¼ r e j ðj þ k 2 pÞ
(2. Quadrant; k 2 ZÞ
ffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ j z j ¼ ð 3Þ 2 þ 1 2 ¼ 3 þ 1 ¼ 4 ¼ 2
1
1
p
1
6
5
pffiffiffi þ p ¼ arctan pffiffiffi þ p ¼
þp ¼
p þ
p ¼
p
j ¼ arg ðzÞ ¼ arctan
6
6
6
6
3
3
pffiffiffi
Somit: z ¼ 3 þ j ¼ 2 e j ð5 p=6 þ k 2 pÞ
Logarithmieren unter Verwendung der bekannten Rechenregeln:
ln z ¼ ln 2 e
j ð5 p=6 þ k 2 pÞ
Hauptwert ( k == 0):
¼ ln 2 þ ln e
Ln z ¼ 0,6931 þ
j ð5 p=6 þ k 2 pÞ
¼ 0,6931 þ j
5
p j ¼ 0,6931 þ 2,6180 j
6
5
p þ k 2p
6
ðk 2 ZÞ
1 Komplexe Rechnung
447
b) z ¼ 3 e j p=5 ¼ 3 e j ðp=5 þ k 2 pÞ
(k 2 ZÞ
Logarithmieren unter Verwendung der bekannten Rechenregeln:
ln z ¼ ln 3 e j ðp=5 þ k 2 pÞ
Hauptwert ( k == 0):
¼ ln 3 þ ln e j ðp=5 þ k 2 p Þ ¼ 1,0986 þ j
Ln z ¼ 1,0986 þ
p
þ k 2p
5
ðk 2 ZÞ
p
j ¼ 1,0986 þ 0,6283 j
5
c) ln z ¼ ln ð4 3 jÞ 6 ¼ 6 ln ð4 3 jÞ ¼ 6 ln a
|fflfflfflfflffl{zfflfflfflfflffl}
a
Die komplexe Zahl a ¼ 4 3 j wird in die Exponentialform gebracht:
a ¼ 4 3 j ¼ r e j ðj þ k 2 pÞ
ð4: Quadrant; k 2 ZÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ j a j ¼ 4 2 þ ð 3Þ 2 ¼ 16 þ 9 ¼ 25 ¼ 5
3
j ¼ arg ðaÞ ¼ arctan
þ 2 p ¼ arctan ð 0,75Þ þ 2 p ¼ 0,6435 þ 2 p ¼ 5,6397
4
Somit:
a ¼ 4 3 j ¼ 5 e j ð5,6397 þ k 2 pÞ
Logarithmieren unter Verwendung der bekannten Rechenregeln:
ln z ¼ 6 ln a ¼ 6 ln 5 e j ð5,6397 þ k 2 pÞ
¼ 6 ½ ln 5 þ ln e j ð5,6397 þ k 2 pÞ ¼
¼ 6 ½ ln 5 þ j ð5,6397 þ k 2 pÞ ¼ 6 ln 5 þ j 6 ð5,6397 þ k 2 pÞ ¼
¼ 9,6566 þ ð33,8382 þ k 12 pÞ j
Hauptwert ( k == 0):
ðk 2 ZÞ
Ln z ¼ 9,6566 þ 33,8382 j
1.3 Algebraische Gleichungen, Polynomnullstellen
Lehrbuch: Band 1, Kapitel VII.2.3
Formelsammlung: Kapitel VIII.4
H11
Bestimmen Sie sämtliche Lösungen der folgenden Gleichungen:
pffiffiffi
b) z 3 ¼ 4 5 j
a) z 2 ¼ ð 3 þ jÞ 3
Zunächst muss die rechte Seite der jeweiligen Gleichung in die Exponentialform gebracht werden.
pffiffiffi
(2. Quadrant)
a) z 2 ¼ a 3 mit a ¼ 3 þ j ¼ a 0 e j a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
a 0 ¼ j a j ¼ ð 3Þ 2 þ 1 2 ¼ 3 þ 1 ¼ 4 ¼ 2
1
1
p
5
pffiffiffi þ p ¼ arctan pffiffiffi þ p ¼
a ¼ arg ðaÞ ¼ arctan
þp ¼
p
6
6
3
3
pffiffiffi
Somit: a ¼ 3 þ j ¼ 2 e j 5 p=6
448
H Komplexe Zahlen und Funktionen
Die Potenz a 3 berechnen wir mit der Formel von Moivre:
pffiffiffi
a 3 ¼ ð 3 þ jÞ 3 ¼ ð2 e j 5 p=6 Þ 3 ¼ 2 3 e j ð3 5 p=6Þ ¼ 8 e j 5 p=2 ¼ 8 e j ð5 p=2 2 pÞ ¼
¼ 8 e j p=2 ¼ 8 e j ðp=2 þ k 2 pÞ
(Hauptwert des Winkels:
! Nebenwerte).
ðk 2 ZÞ
5 p=2 2 p ¼ p=2; dieser Winkel ist bis auf ganzzahlige Vielfache von 2 p bestimmt
Mit dem Ansatz z ¼ r e j j geht die Gleichung z 2 ¼ a 3 dann über in:
ðr e j j Þ 2 ¼ r 2 e j ð2 jÞ ¼ 8 e j ðp=2 þ k 2 pÞ
Vergleich von Betrag bzw. Winkel beiderseits:
pffiffiffi
pffiffiffi
r2 ¼ 8 ) r ¼ 8 ¼ 2 2
2j ¼
p
þ k 2p
2
)
jk ¼
p
þk p
4
ðk 2 ZÞ
Für den Winkel gibt es zwei Hauptwerte (für k ¼ 0, 1):
j0 ¼
p
¼
b 45 ,
4
j1 ¼
5
p ¼
b 225
4
Die restlichen Winkel unterscheiden sich von j 0 bzw. j 1 um ganzzahlige Vielfache von 2 p (Nebenwerte) und
liefern keine weiteren Lösungen.
pffiffiffi
Lösungen der Gleichung z 2 ¼ ð 3 þ jÞ 3 :
pffiffiffi
pffiffiffi
z 0 ¼ 2 2 e j p=4 ¼ 2 2 ½ cos ðp=4Þ þ j sin ðp=4Þ ¼ 2 þ 2 j
pffiffiffi
pffiffiffi
z 1 ¼ 2 2 e j 5 p=4 ¼ 2 2 ½ cos ð5 p=4Þ þ j sin ð5 p=4Þ ¼ 2 2 j
Anmerkung: z 1 ¼ z 0 ¼ ð2 þ 2 jÞ ¼ 2 2 j
b) z 3 ¼ a
a ¼ 4 5 j ¼ a0 e ja
(4. Quadrant)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 0 ¼ j a j ¼ 4 2 þ ð 5 Þ 2 ¼ 16 þ 25 ¼ 41
5
a ¼ arg ðaÞ ¼ arctan
þ 2 p ¼ arctan ð 1,25Þ þ 2 p ¼ 0,8961 þ 2 p ¼ 5,3871
4
pffiffiffiffiffi
pffiffiffiffiffi
ðk 2 ZÞ
Somit: a ¼ 4 5 j ¼ 41 e j 5,3871 ¼ 41 e j ð5,3871 þ k 2 pÞ
mit
(Hauptwert des Winkels a: 5,3871; Nebenwerte: 5,3871 þ k 2 p
mit
k 2 Z).
Mit dem Ansatz z ¼ r e j j und unter Verwendung der Formel von Moivre geht die Gleichung z 3 ¼ a dann über
in:
pffiffiffiffiffi
ðr e j j Þ 3 ¼ r 3 e j ð3 jÞ ¼ 41 e j ð5,3871 þ k 2 pÞ
Vergleich von Betrag bzw. Winkel beiderseits:
qffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
3 pffiffiffiffiffi
3
r ¼ 41 ) r ¼
41 ¼ 1,857
3 j ¼ 5,3871 þ k 2 p
)
j k ¼ 1,7957 þ k
2
p
3
ðk 2 ZÞ
Hauptwerte des Winkels j (für k ¼ 0, 1, 2):
j 0 ¼ 1,7957 ¼
b 102,89 ,
j 1 ¼ 3,8901 ¼
b 222,89 ,
j 2 ¼ 5,9845 ¼
b 342,89
Die restlichen Winkel sind Nebenwerte und führen zu keinen weiteren Lösungen.
1 Komplexe Rechnung
449
Lösungen der Gleichung z 3 ¼ 4 5 j:
z 0 ¼ 1,857 e j 1,7957 ¼ 1,857 ðcos 1,7957 þ j sin 1,7957Þ ¼ 0,414 þ 1,810 j
z 1 ¼ 1,857 e j 3,8901 ¼ 1,857 ðcos 3,8901 þ j sin 3,8901Þ ¼ 1,361 1,264 j
z 2 ¼ 1,857 e j 5,9845 ¼ 1,857 ðcos 5,9845 þ j sin 5,9845Þ ¼ 1,775 0,546 j
Lösen Sie die algebraische Gleichung
z 4 þ 4 z 2 þ 16 ¼ 0
H12
mit Hilfe einer geeigneten Substitution. Wie lassen sich die Lösungen in der Gaußschen Zahlenebene
geometrisch deuten?
Diese Gleichung 4. Grades ist biquadratisch (sie enthält nur gerade Potenzen von z) und lässt sich daher durch die
Substitution u ¼ z 2 in eine quadratische Gleichung überführen, die wir nach der p,q-Formel lösen:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
u 2 þ 4 u þ 16 ¼ 0 ) u 1=2 ¼ 2 4 16 ¼ 2 12 ¼ 2 12 j
Die insgesamt vier Lösungen der Ausgangsgleichung erhalten wir dann wie folgt durch Rücksubstitution:
z2 ¼ u1 ¼ 2 þ
pffiffiffiffiffi
12 j
Die rechte Seite wird in die Exponentialform gebracht:
pffiffiffiffiffi
a ¼ u 1 ¼ 2 þ 12 j ¼ a 0 e j ða þ k 2 pÞ
ð2: Quadrant; k 2 ZÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
pffiffiffiffiffi
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 0 ¼ j a j ¼ ð 2Þ 2 þ ð 12Þ 2 ¼ 4 þ 12 ¼ 16 ¼ 4
pffiffiffi
pffiffiffiffiffi
pffiffiffi
12
2 3
p
2
þ p ¼ arctan
þ p ¼ arctan ð 3Þ þ p ¼
a ¼ arg ðaÞ ¼ arctan
þp ¼
p
2
3
3
2
pffiffiffiffiffi
Somit: a ¼ 2 þ 12 j ¼ 4 e j ð2 p=3 þ k 2 pÞ
Wir lösen die Gleichung z 2 ¼ a mit dem Ansatz z ¼ r e j j unter Verwendung der Formel von Moivre:
z2 ¼ a
)
ðr e j j Þ 2 ¼ r 2 e j ð2 jÞ ¼ 4 e j ð2 p=3 þ k 2 pÞ
Vergleich von Betrag und Winkel beiderseits:
pffiffiffi
r2 ¼ 4 ) r ¼ 4 ¼ 2
2j ¼
2
p þ k 2p
3
)
jk ¼
p
þk p
3
ðk 2 ZÞ
Hauptwerte des Winkels j (für k ¼ 0, 1):
j0 ¼
p
¼
b 60 ,
3
j1 ¼
4
p ¼
b 240
3
Für alle übrigen Werte des Laufindex k erhalten wir Nebenwerte, d. h. Winkel, die sich von j 0 bzw. j 1 um
ganzzahlige Vielfache von 2 p unterscheiden und somit zu keinen neuen Lösungen führen.
pffiffiffiffiffi
Lösungen der Gleichung z 2 ¼ 2 þ 12 j:
pffiffiffi
z 0 ¼ 2 e j 60 ¼ 2 ðcos 60 þ j sin 60 Þ ¼ 1 þ 3 j
pffiffiffi
z 1 ¼ 2 e j 240 ¼ 2 ðcos 240 þ j sin 240 Þ ¼ 1 3 j
450
H Komplexe Zahlen und Funktionen
z2 ¼ u2 ¼ 2
pffiffiffiffiffi
12 j
Die Lösungen dieser Gleichung lassen sich auf gleiche Weise bestimmen. Einfacher ist hier der folgende Lösungsweg.
Da die biquadratische Ausgangsgleichung ausschließlich reelle Koeffizienten besitzt, treten komplexe Lösungen immer
paarweise als Paare konjugiert komplexer Zahlen auf. Mit den bereits bestimmten Lösungen z 0 und z 1 sind daher
auch z*0 und z*1 Lösungen der biquadratischen Gleichung:
pffiffiffi
pffiffiffi
Gesamtlösung: z 0 ¼ 1 þ 3 j, z 1 ¼ 1 3 j,
pffiffiffi
pffiffiffi
z 2 ¼ z*0 ¼ 1 3 j, z 3 ¼ z*1 ¼ 1 þ 3 j
Geometrische Deutung in der Gaußschen Zahlenebene (Bild H-4)
Die Bildpunkte der vier Lösungen liegen auf dem
Mittelpunktkreis mit dem Radius R ¼ 2 und bilden
die Ecken eines achsenparallelen Rechtecks.
Im ( z )
z3
Die Zeiger z 0 und z 1 bzw. z 2 und z 3 sind jeweils
entgegengerichtet:
pffiffiffi
pffiffiffi
z 1 ¼ z 0 ¼ ð1 þ 3 jÞ ¼ 1 3 j
pffiffiffi
pffiffiffi
z 3 ¼ z 2 ¼ ð1 3 jÞ ¼ 1 þ 3 j
2
–1
z1
H13
2
Bild H-4
Re ( z )
1
2
f ðzÞ ¼ 2 z 3 þ 4 z 2 þ 42 z 116
z0
3
2
– 3
z2
(z : komplexe Variable)
Bestimmen Sie sämtliche Nullstellen dieser Polynomfunktion. Wie lautet die Produktdarstellung?
Das Polynom ist vom Grade n ¼ 3 (ungerade), sämtliche Koeffizienten sind reell. Daher gibt es (mindestens) eine
reelle Nullstelle. Durch Probieren finden wir diese bei z 1 ¼ 2. Mit dem Horner-Schema reduzieren wir das Polynom
(Abspalten des Linearfaktors z 2) und berechnen die noch fehlenden beiden Nullstellen aus dem 1. reduzierten
Polynom:
2
z1 ¼ 2
2
4
42
116
4
16
116
8
58
0
) 1. reduziertes Polynom: 2 z 2 þ 8 z þ 58
Restliche Nullstellen (Nullstellen des 1. reduzierten Polynoms):
2 z 2 þ 8 z þ 58 ¼ 0 j : 2 ) z 2 þ 4 z þ 29 ¼ 0 )
pffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
z 2=3 ¼ 2 4 29 ¼ 2 25 ¼ 2 25 j ¼ 2 5 j
Nullstellen:
z1 ¼ 2 ,
Produktform:
z2 ¼ 2 þ 5 j ,
z3 ¼ 2 5 j
f ðzÞ ¼ 2 ðz 2Þ ½ z ð 2 þ 5 jÞ ½ z ð 2 5 jÞ ¼ 2 ðz 2Þ ðz þ 2 5 jÞ ðz þ 2 þ 5 jÞ
Von der algebraischen Gleichung 4. Grades
H14
z 4 4 z 3 2 z 2 þ 12 z 16 ¼ 0
ðz : unbekannte komplexe ZahlÞ
ist eine der insgesamt vier Lösungen bekannt: z 1 ¼ 1 þ j (führen Sie den Nachweis). Wo liegen die
übrigen Lösungen?
1 Komplexe Rechnung
451
Wir zeigen zunächst, dass z 1 ¼ 1 þ j eine Lösung der Gleichung ist (Einsetzen des Wertes in die Gleichung):
ð1 þ jÞ 4 4 ð1 þ jÞ 3 2 ð1 þ jÞ 2 þ 12 ð1 þ jÞ 16 ¼
¼ ð1 þ jÞ 2 ð1 þ jÞ 2 4 ð1 þ jÞ 2 ð1 þ jÞ 2 ð1 þ jÞ 2 þ 12 þ 12 j 16 ¼
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflffl{zfflfflfflfflffl}
"
"
"
"
ð1 þ jÞ 2 ¼ 1 þ 2 j þ j 2 ¼ 1 þ 2 j 1 ¼ 2 j
¼ 2 j 2 j 4 ð2 jÞ ð1 þ jÞ 2 2 j 4 þ 12 j ¼ 4 j 2 8 j 8 j 2 4 j 4 þ 12 j ¼ 4 þ 8 4 ¼ 0
Mit z 1 ¼ 1 þ j ist auch die konjugiert komplexe Zahl z 2 ¼ z*1 ¼ 1 j eine Lösung der Gleichung, da sämtliche
Koeffizienten der Gleichung reell sind und damit komplexe Lösungen nur paarweise auftreten können (als Paare konjugiert komplexer Zahlen). Die zu den Lösungen z 1 ¼ 1 þ j und z 2 ¼ 1 j gehörigen Linearfaktoren fassen wir zu
einem quadratischen Polynom zusammen und spalten dieses dann durch Polynomdivision vom Ausgangspolynom (linke
Seite der algebraischen Gleichung) ab:
ðz z 1 Þ ðz z 2 Þ ¼ ½ z ð1 þ jÞ ½ z ð1 jÞ ¼ ½ ðz 1Þ j ½ ðz 1Þ þ j ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða bÞ ða þ bÞ ¼ a 2 b 2 mit a ¼ z 1; b ¼ j
¼ ðz 1Þ 2 j 2 ¼ z 2 2 z þ 1 þ 1 ¼ z 2 2 z þ 2
Polynomdivision: ðz 4 4 z 3 2 z 2 þ 12 z 16Þ : ðz 2 2 z þ 2Þ ¼ z 2 2 z 8
ðz 4 2 z 3 þ 2 z 2 Þ
2 z 3 4 z 2 þ 12 z 16
ð 2 z 3 þ 4 z 2 4 zÞ
8 z 2 þ 16 z 16
ð 8 z 2 þ 16 z 16Þ
0
Restliche Lösungen (Nullstellen des Restpolynoms z 2 2 z 8):
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
z 2 2 z 8 ¼ 0 ) z 3=4 ¼ 1 1 þ 8 ¼ 1 9 ¼ 1 3
Gesamtlösung:
H15
z 1 ¼ 1 þ j,
z 2 ¼ 1 j,
z 3 ¼ 4,
)
z3 ¼ 4 ,
z4 ¼ 2
z4 ¼ 2
Die Polynomfunktion f ðzÞ ¼ z 4 þ 6 z 3 þ 10 z 2 2 z 15 besitzt an der Stelle z 1 ¼ 2 j
eine komplexe Nullstelle. Wo liegen die restlichen Nullstellen? Wie lautet die Zerlegung des Polynoms
in Linearfaktoren?
Da das Polynom 4. Grades ausschließlich reelle Koeffizienten hat, treten komplexe Nullstellen immer paarweise auf
(als Paare konjugiert komplexer Zahlen). Mit der bekannten komplexen Nullstelle z 1 ¼ 2 j ist daher auch
z 2 ¼ z*1 ¼ 2 þ j eine (komplexe) Nullstelle des Polynoms. Die beiden zugehörigen Linearfaktoren fassen wir zu
einem quadratischen Faktor (Polynom 2. Grades) wie fogt zusammen:
ðz z 1 Þ ðz z 2 Þ ¼ ½ z ð 2 jÞ ½ z ð 2 þ jÞ ¼ ½ ðz þ 2Þ þ j ½ ðz þ 2Þ j ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða þ bÞ ða bÞ ¼ a 2 b 2 mit a ¼ z þ 2; b ¼ j
¼ ðz þ 2Þ 2 j 2 ¼ z 2 þ 4 z þ 4 þ 1 ¼ z 2 þ 4 z þ 5
452
H Komplexe Zahlen und Funktionen
Diesen quadratischen Faktor spalten wir nun durch Polynomdivision vom Ausgangspolynom ab:
ðz 4 þ 6 z 3 þ 10 z 2 2 z 15Þ : ðz 2 þ 4 z þ 5Þ ¼ z 2 þ 2 z 3
ðz 4 þ 4 z 3 þ 5 z 2 Þ
2 z 3 þ 5 z 2 2 z 15
ð2 z 3 þ 8 z 2 þ 10 zÞ
3 z 2 12 z 15
ð 3 z 2 12 z 15Þ
0
Restliche Nullstellen (Nullstellen des Restpolynoms z 2 þ 2 z 3Þ:
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
z 2 þ 2 z 3 ¼ 0 ) z 3=4 ¼ 1 1 þ 3 ¼ 1 4 ¼ 1 2
Polynomnullstellen:
z 1 ¼ 2 j,
)
z 3 ¼ 1,
z4 ¼ 3
z 2 ¼ 2 þ j, z 3 ¼ 1, z 4 ¼ 3
Zerlegung des Polynoms in Linearfaktoren (Produktform):
f ðzÞ ¼ ½ z ð 2 jÞ ½ z ð 2 þ jÞ ðz 1Þ ðz þ 3Þ ¼ ðz 1Þ ðz þ 3Þ ðz þ 2 þ jÞ ðz þ 2 jÞ
f ðzÞ ¼ z 5 3 z 4 þ 7 z 3 11 z 2 þ 12 z 6
H16
(z: komplexe Variable)
Diese Polynomfunktion 5. Grades besitzt im komplexen Bereich genau fünf Nullstellen, eine davon
liegt bei z 1 ¼ 1 j, eine weitere im Rellen (sie ist positiv und ganzzahlig). Bestimmen Sie die noch
fehlenden Nullstellen. Wie lautet die Produktform der Polynomfunktion?
Da sämtliche Polynomkoeffizienten reell sind, treten komplexe Nullstellen immer als Paare konjugiert komplexer Zahlen
auf. Mit der bekannten komplexen Nullstelle z 1 ¼ 1 j ist daher auch z 2 ¼ z*1 ¼ 1 þ j eine (komplexe) Polynomnullstelle. Durch Probieren findet man die reelle Nullstelle bei z 3 ¼ 1 (Kriterium: die Summe aller Polynomkoeffizienten verschwindet). Die Linearfaktoren der inzwischen bekannten drei Nullstellen fassen wir jetzt zu einem Polynom
3. Grades zusammen und spalten dieses anschließend durch Polynomdivision vom Ausgangspolynom ab:
ðz z 1 Þ ðz z 2 Þ ðz z 3 Þ ¼ ½ z ð1 jÞ ½ z ð1 þ jÞ ðz 1Þ ¼ ½ðz 1Þ þ j ½ðz 1Þ j ðz 1Þ ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða þ bÞ ða bÞ ¼ a 2 b 2 mit a ¼ z 1; b ¼ j
¼ ½ ðz 1Þ 2 j 2 ðz 1Þ ¼ ðz 2 2 z þ 1 þ 1Þ ðz 1Þ ¼ ðz 2 2 z þ 2Þ ðz 1Þ ¼
¼ z3 z2 2 z2 þ 2 z þ 2 z 2 ¼ z3 3 z2 þ 4 z 2
Polynomdivision: ðz 5 3 z 4 þ 7 z 3 11 z 2 þ 12 z 6Þ : ðz 3 3 z 2 þ 4 z 2Þ ¼ z 2 þ 3
ðz 5 3 z 4 þ 4 z 3 2 z 2 Þ
3 z 3 9 z 2 þ 12 z 6
ð3 z 3 9 z 2 þ 12 z 6Þ
0
2 Anwendungen
453
Restliche Nullstellen (Nullstellen des Restpolynoms z 2 þ 3):
pffiffiffiffiffiffiffi
pffiffiffi
z 2 þ 3 ¼ 0 ) z 2 ¼ 3 ) z 4=5 ¼ 3 ¼ 3 j
pffiffiffi
Polynomnullstellen: z 1 ¼ 1 j ; z 2 ¼ 1 þ j ; z 3 ¼ 1 ; z 4 ¼ 3 j ;
Produktform:
pffiffiffi
z5 ¼ 3 j
pffiffiffi
pffiffiffi
f ðzÞ ¼ ½ z ð1 jÞ ½ z ð1 þ jÞ ðz 1Þ ðz 3 jÞ ðz þ 3 jÞ ¼
pffiffiffi
pffiffiffi
¼ ðz 1Þ ðz 3 jÞ ðz þ 3 jÞ ðz 1 þ jÞ ðz 1 jÞ
2 Anwendungen
In diesem Abschnitt finden Sie anwendungsorientierte Aufgaben zu den folgenden Themen:
Superposition gleichfrequenter Schwingungen (mechanische Schwingungen, Wechselströme)
Lissajous-Figuren
Komplexer Widerstand und Leitwert eines elektrischen Schaltkreises
Wirk-, Blind- und Scheinwiderstand
Ortskurven komplexwertiger Funktionen, Inversion von Ortskurven
Netzwerkfunktionen, Widerstands- und Leitwertortskurven elektrischer Schaltkreise
2.1 berlagerung von Schwingungen
Lehrbuch: Band 1, Kapitel VII.3.1
Formelsammlung: Kapitel VIII.8
Superposition gleichfrequenter mechanischer Schwingungen
Die gleichfrequenten mechanischen Schwingungen mit den Gleichungen
H17
y 1 ¼ 4 cm cos ðw t p=4Þ
und y 2 ¼ 3 cm sin ðw t p=6Þ
kommen ungestört zur berlagerung und ergeben eine resultierende Sinusschwingung
y ¼ y 1 þ y 2 ¼ A sin ðw t þ jÞ
mit A > 0 und 0 j < 2 p (t 0 s; Kreisfrequenz w ¼ 5 s 1 ). Bestimmen Sie die Schwingungsamplitude A und den Nullphasenwinkel j mit komplexer Rechnung.
Zunächst bringen wir die Kosinusschwingung y 1 auf die Sinusform (der Winkel vergrößert sich dabei um p=2):
y 1 ¼ 4 cm cos ðw t p=4Þ ¼ 4 cm sin ðw t p=4 þ p=2Þ ¼ 4 cm sin ðw t þ p=4Þ
Darstellung der beiden sinusförmigen Einzelschwingungen in komplexer Form:
y 1 ¼ 4 cm sin ðw t þ p=4Þ
! y 1 ¼ 4 cm e j p=4 e j w t ¼ A 1 e j w t
y 2 ¼ 3 cm sin ðw t p=6Þ
! y 2 ¼ 3 cm e j p=6 e j w t ¼ A 2 e j w t
Darstellung der resultierenden Sinusschwingung in komplexer Form:
y ¼ y 1 þ y 2 ¼ A sin ðw t þ jÞ
!
y ¼ y 1 þ y 2 ¼ A 1 e j w t þ A 2 e j w t ¼ ðA 1 þ A 2 Þ e j w t ¼ A e j w t
454
H Komplexe Zahlen und Funktionen
Die komplexen Amplituden A 1 ¼ 4 cm e j p=4 und A 2 ¼ 3 cm e j p=6 der Einzelschwingungen addieren sich zur
komplexen Amplitude A der resultierenden Schwingung (Bild H-5):
A ¼ A 1 þ A 2 ¼ 4 cm e j p=4 þ 3 cm e j p=6 ¼
¼ 4 cm ½ cos ðp=4Þ þ j sin ðp=4Þ þ 3 cm ½ cos ð p=6Þ þ j sin ð p=6Þ ¼
¼ 2,828 cm þ j 2,828 cm þ 2,598 cm j 1,5 cm ¼ ð5,426 þ 1,328 jÞ cm
Im ( z )
=
4
cm
A1
A = A1 + A2
1
A
A
45°
f
30°
A
2
=3
Bild H-5 Komplexe Addition der Einzelamplituden
nach der Parallelogrammregel
Re ( z )
cm
A2
Die (reelle) Amplitude A der resultierenden Sinusschwingung ist der Betrag von A, der Nullphasenwinkel j der
Winkel von A . Aus dem Zeigerdiagramm erhalten wir dann (Bild H-6):
Satz des Pythagoras:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
A ¼ j A j ¼ 5,426 2 þ 1,328 2 cm ¼ 5,586 cm
Im ( z )
A
1,328
A
tan j ¼
1,328 cm
¼ 0,2447
5,426 cm
)
f
5,426
j ¼ arctan 0,2447 ¼ 0,2400 ¼
b 13,75
1,328
5,426
Re ( z )
Bild H-6
Komplexe Schwingungsamplitude A in der Exponentialform:
A ¼ ð5,426 þ 1,328 jÞ cm ¼ A e j j ¼ 5,586 cm e j 0,2400
Resultierende Schwingung in komplexer Darstellung
y ¼ A e j w t ¼ 5,586 cm e j 0,2400 e j 5 s
1
t
1
¼ 5,586 cm e j ð5 s
t þ 0,2400Þ
¼
¼ 5,586 cm ½ cos ð5 s 1 t þ 0,2400Þ þ j sin ð5 s 1 t þ 0,2400Þ
Resultierende Schwingung in der (reellen) Sinusform (Imaginärteil von y)
y ¼ y 1 þ y 2 ¼ Im ðyÞ ¼ 5,586 cm sin ð5 s 1 t þ 0,2400Þ
berlagerung gleichfrequenter Wechselströme
H18
Zeigen Sie: Drei gleichfrequente sinusförmige Wechselströme mit den Scheitelwerten i 0 und den Nullphasenwinkeln j 1 ¼ 0 , j 2 ¼ 120 und j 3 ¼ 240 löschen sich bei ungestörter berlagerung
gegenseitig aus (Kreisfrequenz: w > 0Þ:
a) Rechnerische Lösung in komplexer Form.
b) Zeichnerische Lösung im Zeigerdiagramm.
2 Anwendungen
455
a) Wir stellen die sinusförmigen Wechselströme in der komplexen Form dar (Nullphasenwinkel im Bogenmaß):
i 1 ¼ i 0 sin ðw tÞ
!
i 1 ¼ i 0 e j w t ¼ i^1 e j w t
i 2 ¼ i 0 sin ðw t þ 2 p=3Þ
!
i 2 ¼ i 0 e j 2 p=3 e j w t ¼ ^
i2 e j w t
i 3 ¼ i 0 sin ðw t þ 4 p=3Þ
!
i 3 ¼ i 0 e j 4 p=3 e j w t ¼ i^3 e j w t
Sie haben der Reihe nach die folgenden komplexen Scheitelwerte:
^
i 1 ¼ i 0 ðreellÞ ,
^i 2 ¼ i 0 e j 2 p=3 ,
^
i 3 ¼ i 0 e j 4 p=3
Ihre Summe ist der komplexe Scheitelwert ^i des resultierenden Wechselstroms i ¼ ^
i e jwt :
^
i 2 þ ^i 3 ¼ i 0 þ i 0 e j 2 p=3 þ i 0 e j 4 p=3 ¼ i 0 ð1 þ e j 2 p=3 þ e j 4 p=3 Þ
i ¼ ^
i1 þ ^
Der in der Klammer stehende Ausdruck verschwindet (wir „entwickeln“ den 2. und 3. Summand jeweils mit Hilfe
der Formel von Euler: e j j ¼ cos j þ j sin j):
1 þ e j 2 p=3 þ e j 4 p=3 ¼ 1 þ cos ð2 p=3Þ þ j sin ð2 p=3Þ þ cos ð4 p=3Þ þ j sin ð4 p=3Þ ¼
¼ 1 0,5 þ
1 pffiffiffi
1 pffiffiffi
3 j 0,5
3 j ¼ 0 þ 0j ¼ 0
2
2
Somit ist auch ^i ¼ 0 und i ¼ 0. Die drei gleichfrequenten Wechselströme löschen sich – wie behauptet – aus.
b) Die Stromzeiger i 2 und i 3 liegen im Zeigerdiagramm spiegelsymmetrisch zur reellen Achse (konjugiert komplexe
Größen: i 3 ¼ i *2 ; siehe auch Bild H-7, linkes Teilbild). Wir fassen sie nach der Parallelogrammregel zu einem
resultierenden Zeiger i 2, 3 zusammen. Dieser Zeiger fällt in die negativ-reelle Achse, er hat die gleiche Länge i 0
wie die Zeiger der drei Einzelströme und ist somit dem Stromzeiger i 1 entgegen gerichtet:
i 2, 3 ¼ i 2 þ i 3 ¼ i 1
)
i1 þ i2 þ i3 ¼ 0
)
Die drei Wechselströme löschen sich aus:
Im ( z )
i2
i2
i0
i0
120°
i 2,3
120°
i0
120°
i0
60°
60°
i1
Re ( z )
i 2,3
Parallelen
i0
60°
i0
60°
i0
i1
30°
i0
i3
Bild H-7
i0
i3
Ungestörte berlagerung gleichfrequenter Wechselströme
Warum hat der Zeiger i 2, 3 die gleiche Länge i 0 wie die Zeiger i 1, i 2 und i 3 ? Das Parallelogramm aus den
Zeigern i 2 und i 3 ist ein Rhombus (eine Raute), alle vier Seiten haben die gleiche Länge i 0 : Die reelle Achse
zerlegt den Rhombus in zwei kongruente Dreiecke. Wir betrachten das obere Dreieck etwas genauer (Bild H-7,
rechtes Teilbild) und bestimmen die Innenwinkel des Dreiecks aus den bekannten Eigenschaften. Ergebnis: Die drei
Innenwinkel betragen jeweils 60 , das Dreieck ist daher gleichseitig. Somit hat der resultierende Zeiger i 2, 3 die
gleiche Länge wie die Zeiger i 2 und i 3 :
j i 2, 3 j ¼ j i 2 j ¼ j i 3 j ¼ i 0
456
H Komplexe Zahlen und Funktionen
Periodische Bahnkurve eines Massenpunktes (Lissajous-Figur)
Ein Massenpunkt bewege sich in der x,y-Ebene auf einer periodischen (geschlossenen) Bahn mit den
Parametergleichungen
x ¼ x ðtÞ ¼ cos t
H19
und y ¼ y ðtÞ ¼ sin ð2 tÞ
(x, y: zeitabhängige Lagekoordinaten; t 0: Zeitparameter).
Beschreiben Sie diese Bahn durch eine komplexwertige Funktion der reellen Variablen t (Zeitparameter).
Wie lautet die Gleichung der Bahnkurve (Ortskurve) in kartesischen Koordinaten? Skizzieren Sie die
Kurve unter Verwendung einer Wertetabelle.
Hinweis: Die Bahnkurve entsteht durch ungestörte berlagerung zweier aufeinander senkrecht stehender harmonischer Schwingungen, deren (Kreis-)Frequenzen im rationalen Verhältnis 1 : 2 stehen (sog.
Lissajous-Figur).
Wir deuten die periodischen Bewegungen (harmonischen Schwingungen) in x- und y-Richtung als Real- und Imaginärteil der komplexwertigen Funktion
z ðtÞ ¼ x ðtÞ þ j y ðtÞ ¼ cos t þ j sin ð2 tÞ
ðmit t 0Þ
Die geschlossene Bahnkurve (Ortskurve) wird dabei bereits im Periodenintervall 0 t 2 p durchlaufen. Sie lässt
sich auch wie folgt in kartesischen Koordinaten ausdrücken:
y ¼ sin ð2 tÞ ¼ 2 cos t sin t
j quadrieren
y 2 ¼ 4 cos 2 t sin 2 t ¼ 4 cos 2 t ð1 cos 2 t Þ ¼ 4 x 2 ð1 x 2 Þ
|fflffl{zfflffl}
|fflffl{zfflffl}
|fflffl{zfflffl}
1 cos 2 t
x2
ð 1 x 1Þ
x2
Umformung: Trigonometrische Formeln sin ð2 tÞ ¼ 2 sin t cos t und sin 2 t þ cos 2 t ¼ 1 verwenden; x ¼ cos t
(1. Parametergleichung).
Wegen der ausschließlich geraden Potenzen von x und y ist die Bahnkurve (Ortskurve) sowohl zur x- als auch zur yAchse (d. h. zur reellen und imaginären Achse) spiegelsymmetrisch. Bei der Erstellung der Wertetabelle können wir uns
daher auf den 1. Quadranten beschränken. Die Funktionsgleichung lautet dort:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0 x 1
y ¼ 4 x 2 ð1 x 2 Þ ¼ 2 x 1 x 2 ,
Wir wählen die Schrittweise D x ¼ 0,1. Bild H-8 zeigt den Verlauf der geschlossenen Bahnkurve.
Wertetabelle
x
y
y
0
0
0,1
0,20
0,8
0,2
0,39
0,6
0,3
0,57
0,4
0,4
0,73
0,5
0,87
0,6
0,96
0,7
1,00
0,8
0,96
0,9
0,78
1
0
1
Startpunkt (t = 0)
0,2
– 0,8
–1
– 0,4
– 0,6
0,4
– 0,2
– 0,2
– 0,6
– 0,8
–1
Bild H-8
0,2
0,8
0,6
1
x
2 Anwendungen
457
2.2 Komplexe Widerstände und Leitwerte
Lehrbuch: Band 1, Kapitel VII.3.2
Z 1 ¼ ð20 þ 10 jÞ W
Z2
Z 2 ¼ ð10 þ 0 jÞ W ¼ 10 W
Z1
Z 3 ¼ ð5 10 jÞ W
Z 4 ¼ ð15 þ 20 jÞ W
H20
Z3
Z4
Bild H-9
a) Bestimmen Sie zunächst formelmäßig den komplexen Gesamtwiderstand Z der in Bild H-9 dargestellten Schaltung mit den vier komplexen Einzelwiderständen Z 1 bis Z 4 .
b) Berechnen Sie dann mit den vorgegebenen Werten der Einzelwiderstände den komplexen Gesamtwiderstand sowie den Wirk-, Blind- und Scheinwiderstand der Schaltung.
c) Wie groß ist der komplexe Leitwert Y des Schaltkreises?
a) Wir fassen die komplexen Einzelwiderstände Schritt für Schritt zum komplexen Gesamtwiderstand Z zusammen
(Bild H10).
Z2
Z2
Z1
Z1
Z3
Z1
Bild H-10
Z4
Z5
Z6
Z
Schrittweise Zusammenfassung der vier Einzelwiderstände zum Gesamtwiderstand Z
1. Schritt: Die Widerstände Z 3 und Z 4 sind in Reihe geschaltet, sie addieren sich daher zum Ersatzwiderstand
Z5 ¼ Z3 þ Z4.
2. Schritt: Die Widerstände Z 2 und Z 5 sind parallel geschaltet, es addieren sich daher ihre Leitwerte (Kehrwerte der Widerstände) zum Leitwert des Ersatzwiderstandes Z 6 :
1
1
1
1
1
Z þ Z3 þ Z4
¼
þ
¼
þ
¼ 2
Z6
Z2
Z5
Z2
Z3 þ Z4
Z 2 ðZ 3 þ Z 4 Þ
Durch Kehrwertbildung folgt:
Z6 ¼
ðHauptnenner : Z 2 ðZ 3 þ Z 4 ÞÞ
Z 2 ðZ 3 þ Z 4 Þ
Z2 þ Z3 þ Z4
3. Schritt: Die Widerstände Z 1 und Z 6 sind in Reihe geschaltet und addieren sich zum gesuchten (komplexen)
Gesamtwiderstand Z des Schaltkreises:
Z ¼ Z1 þ Z6 ¼ Z1 þ
Z 2 ðZ 3 þ Z 4 Þ
Z2 þ Z3 þ Z4
458
H Komplexe Zahlen und Funktionen
b) Einsetzen der vorgegebenen Werte (Zwischenrechnung ohne Einheiten):
Z ¼ Z1 þ
Z 2 ðZ 3 þ Z 4 Þ
10 ð5 10 j þ 15 þ 20 jÞ
10 ð20 þ 10 jÞ
¼ 20 þ 10 j þ
¼ 20 þ 10 j þ
¼
10 þ 5 10 j þ 15 þ 20 j
30 þ 10 j
Z2 þ Z3 þ Z4
¼ 20 þ 10 j þ
10 ð20 þ 10 jÞ
20 þ 10 j
¼ 20 þ 10 j þ
¼ 20 þ 10 j þ
10 ð3 þ jÞ
3þj
ðder Bruch wurde erweitert mit 3 jÞ
¼ 20 þ 10 j þ
¼ 20 þ 10 j þ
60 20 j þ 30 j 10 j 2
32
j
2
ð20 þ 10 jÞ ð3 jÞ
ð3 þ jÞ ð3 jÞ
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
¼
3: Binom : ða þ bÞ ða bÞ ¼ a 2 b 2 mit a ¼ 3; b ¼ j
¼ 20 þ 10 j þ
60 þ 10 j þ 10
70 þ 10 j
¼ 20 þ 10 j þ
¼
9þ1
10
70
10
þ
j ¼ 20 þ 10 j þ 7 þ j ¼ 27 þ 11 j
10
10
Komplexer Gesamtwiderstand in kartesischer Darstellung:
ðin WÞ
Z ¼ ð27 þ 11 jÞ W
Komplexer Gesamtwiderstand in exponentieller Darstellung: Z ¼ ð27 þ 11 jÞ W ¼ Z e j j
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Z ¼ j Z j ¼ 27 2 þ 11 2 W ¼ 729 þ 121 W ¼ 850 W ¼ 29,155 W
11 W
j ¼ arg ðZÞ ¼ arctan
¼ arctan 0,4074 ¼ 0,3869 ¼
b 22,17
27 W
(1. Quadrant)
Z ¼ ð27 þ 11 jÞ W ¼ 29,155 W e j 0,3869
Somit:
Der Wirkwiderstand R ist der Realteil, der Blindwiderstand X der Imaginärteil, der Scheinwiderstand Z der
Betrag des komplexen Gesamtwiderstandes Z :
Wirkwiderstand:
R ¼ Re ðZÞ ¼ 27 W
Blindwiderstand:
X ¼ Im ðZÞ ¼ 11 W
Scheinwiderstand:
Z ¼ j Z j ¼ 29,155 W
c) Der komplexe Leitwert Y ist der Kehrwert des komplexen Gesamtwiderstandes Z :
Y ¼
1
1
¼
¼ 0,0343 S e j 0,3869 ¼ 0,0343 ½ cos ð 0,3869Þ þ j sin ð 0,3869Þ S ¼
29,155 W e j 0,3869
Z
¼ ð0,0318 0,0129 jÞ S
ðS ¼ 1=W : SiemensÞ
Komplexer Widerstand und Leitwert eines RLC-Schaltkreises
L
Ohmscher Widerstand:
C
H21
Induktivität:
Kapazität:
R ¼ 100 W
L ¼ 0,5 H
C ¼ 2 10 5 F
R
Bild H-11 RLC - Schaltkreis
Welchen komplexen Widerstand und Leitwert besitzt der in Bild H-11 skizzierte Wechselstromkreis bei
einer Kreisfrequenz von w ¼ 100 s 1 ?
2 Anwendungen
459
Da eine Parallelschaltung vorliegt, addieren sich die Leitwerte der drei Schaltelemente R, C und L zum komplexen
Leitwert Y des Schaltkreises (Zwischenrechnung ohne Einheiten):
1
1
1
1
1
1
Y ¼
þ jwC j
¼
þ j wC
¼
þ j 100 2 10 5
¼
R
wL
R
wL
100
100 0,5
¼ 0,01 þ j ð2 10 3 2 10 2 Þ ¼ 0,01 þ j ð0,002 0,02Þ ¼ 0,01 0,018 j
ðin S ¼ SiemensÞ
Der komplexe Widerstand Z des Schaltkreises ist der Kehrwert des komplexen Leitwertes Y (in der Einheit
Ohm ¼ W):
1
1
0,01 þ 0,018 j
0,01 þ 0,018 j
¼
¼
¼
¼
Y
0,01 0,018 j
ð0,01 0,018 jÞ ð0,01 þ 0,018 j Þ
0,01 2 0,018 2 j 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Z ¼
3: Binom : ða bÞ ða þ bÞ ¼ a 2 b 2 mit a ¼ 0;01 und b ¼ 0;018 j
¼
0,01 þ 0,018 j
0,01 þ 0,018 j
0,01
0,018
¼
¼
þ
j ¼ 23,58 þ 42,45 j
0,0001 þ 0,000 324
0,000 424
0,000 424
0,000 424
Umformung:
erweitert.
Ergebnis:
ðin WÞ
Der Bruch wurde mit dem konjugiert komplexen Nenner, d. h. der komplexen Zahl 0,01 þ 0,018 j
Z ¼ ð23,58 þ 42,45 jÞ W;
Y ¼ ð0,01 0,018 jÞ S
Komplexer Widerstand, Wirk-, Blind- und Scheinwiderstand eines Wechselstromkreises
R
L
Ohmscher Widerstand: R ¼ 50 W
C1
C2
H22
Induktivität:
L ¼ 2H
Kapazitäten:
C 1 ¼ C 2 ¼ C ¼ 5 10 5 F
Bild H-12
a) Bestimmen Sie formelmäßig den komplexen Widerstand Z des in Bild H-12 skizzierten Wechselstromkreises in Abhängigkeit von der Kreisfrequenz w der angelegten Wechselspannung.
b) Wie groß sind Wirk-, Blind- und Scheinwiderstand für die angegebenen Werte der Schaltelemente
R, L, C 1 und C 2 bei einer Kreisfrequenz von w ¼ 200 s 1 ?
a) Die komplexen Widerstände der insgesamt vier Schaltelemente fassen wir wie folgt schrittweise zum komplexen
Gesamtwiderstand Z des Wechselstromkreises zusammen (Bild H-13):
R
L
C2
R
C1
C2
Z1
R
Z2
Bild H-13
Z
Schrittweise Zusammenfassung der vier Einzelwiderstände zum komplexen Gesamtwiderstand Z
460
H Komplexe Zahlen und Funktionen
1. Schritt: Induktivität L und Kapazität C 1 ¼ C sind in Reihe geschaltet, ihre komplexen Wechselstromwiderstände addieren sich somit zum Ersatzwiderstand Z 1 :
1
1
1
w2 L C 1
¼ j wL
¼ j
Z1 ¼ jwL j
¼ jwL j
w C1
wC
wC
wC
2. Schritt: Kapazität C 2 ¼ C und Ersatzwiderstand Z 1 sind parallel geschaltet, daher addieren sich ihre Leitwerte zum Leitwert des Ersatzwiderstandes Z 2 (dieser ersetzt C 2 und Z 1 ):
1
1
1
1
wC
wC
¼
þ j w C2 ¼
þ jwC ¼
þ jwC ¼ j 2
þ jwC ¼
j w2 L C 1
w LC 1
Z2
Z1
Z1
1
1 þ w2 L C 1
w C ðw 2 L C 2Þ
þ
1
¼
j
w
C
¼
j
¼ jwC
w2 L C 1
w2 L C 1
w2 L C 1
Durch Kehrwertbildung erhalten wir für den Ersatzwiderstand Z 2 den folgenden Ausdruck:
w2 L C 1
1
w2 L C 1
w2 L C 1
1
Z2 ¼
¼ j
¼
¼ j
j w C ðw 2 L C 2Þ
j w C ðw 2 L C 2Þ
w C ðw 2 L C 2Þ
j
3. Schritt: Die Widerstände R und Z 2 sind in Reihe geschaltet und addieren sich zum gesuchten komplexen
Gesamtwiderstand Z :
Z ¼ Z ðwÞ ¼ R þ Z 2 ¼ R j
w2 L C 1
w C ðw 2 L C 2Þ
b) Einsetzen der vorgegebenen Werte (Zwischenrechnung ohne Einheiten):
Z ¼ 50 j
¼ 50 j
200 2 2 5 10 5 1
4 10 4 10 10 5 1
¼
50
j
¼
200 5 10 5 ð200 2 2 5 10 5 2Þ
10 3 10 5 ð4 10 4 10 10 5 2Þ
4 10 1
41
100 3
¼ 50 j 2
¼ 50 j
¼ 50 150 j
10 2 ð4 10 2Þ
10 ð4 2Þ
2
Komplexer Gesamtwiderstand:
ðin WÞ
Z ¼ ð50 150 jÞ W
Der Wirkwiderstand ist der Realteil, der Blindwiderstand der Imaginärteil und der Scheinwiderstand der Betrag des
komplexen Gesamtwiderstandes Z :
Wirkwiderstand:
Re ðZÞ ¼ 50 W
Im ðZÞ ¼ 150 W
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Scheinwiderstand: Z ¼ j Z j ¼ 50 2 þ ð 150Þ 2 W ¼ 2500 þ 22 500 W ¼ 25 000 W ¼ 158,11 W
Blindwiderstand:
2.3 Ortkurven, Netzwerkfunktionen, Widerstands- und
Leitwertortskurven elektrischer Schaltkreise
Lehrbuch: Band 1, Kapitel VII.4
Formelsammlung: Kapitel VIII.6
Bestimmen und skizzieren Sie die Ortskurven der folgenden komplexwertigen Funktionen einer reellen
Variablen t :
H23
a) z ðtÞ ¼ z 1 þ t ðz 2 z 1 Þ
1
þj
b) z ðtÞ ¼ 2 þ
t
c) z ðtÞ ¼ z 0 þ a e j t
ðz 1 6¼ z 2 ;
1 < t < 1Þ
ðt > 0Þ
ða > 0 ;
z0 ¼ x0 þ j y0 ;
0 t 2 pÞ
2 Anwendungen
461
a) Die lineare Funktion beschreibt eine Gerade
durch die Bildpunkte von z 1 und z 2 , die zu
den Parameterwerten t ¼ 0 und t ¼ 1 gehören (siehe Bild H-14):
Im ( z )
t
t =1
t =0
z ðt ¼ 0Þ ¼ z 1 þ 0 ðz 2 z 1 Þ ¼ z 1
z2
z (t )
z1
z ðt ¼ 1Þ ¼ z 1 þ 1 ðz 2 z 1 Þ ¼
¼ z1 þ z2 z1 ¼ z2
Bild H-14
Re ( z )
b) Wir führen den „ Hilfsparameter “ l ¼ 1=t ein. Die Funktion z ðtÞ geht dann über in die folgende linear von l
abhängige Funktion:
z ðlÞ ¼ ð2 þ lÞ þ j
ðmit l > 0Þ
Der Imaginärteil hat den konstanten Wert Im ðzÞ ¼ 1 , während der Realteil Re ðzÞ ¼ 2 þ l im Intervall l > 0
alle Werte von 2 (ausschließlich) bis 1 durchläuft. Die zugehörige Ortskurve ist eine Halbgerade, sie verläuft vom
Bildpunkt der komplexen Zahl z 0 ¼ 2 þ j ausgehend parallel zur reellen Achse, wie in Bild H-15 dargestellt.
Im ( z )
t =∞
t
t
1
z (t )
z (t )
Bild H-15
2
Re ( z )
c) Wir formen die Funktionsgleichung zunächst geringfügig um und bilden dann beiderseits den Betrag:
z ¼ z0 þ a e jt
)
z z0 ¼ a e jt
)
j z z 0 j ¼ j a e j t j ¼ a j e j t j ¼ a ¼ const:
|ffl{zffl}
1
Geometrische Deutung: Alle Bildpunkte der Funktion z ¼ z ðtÞ haben vom Bildpunkt der komplexen Zahl
z 0 ¼ x 0 þ j y 0 den gleichen Abstand d ¼ j z z 0 j ¼ a und liegen somit auf einem Kreis mit dem Mittelpunkt
M ¼ ðx 0 ; y 0 Þ und dem Radius R ¼ a (siehe Bild H-16).
Kreisgleichung
y
j z z 0 j ¼ j ðx þ j yÞ ðx 0 þ j y 0 Þ j ¼
¼ j x þ j y x0 j y0 j ¼
¼ j ðx x 0 Þ þ j ðy y 0 Þ j ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ ðx x 0 Þ 2 þ ðy y 0 Þ 2 ¼ a j quadrieren
2
2
Somit : ðx x 0 Þ þ ðy y 0 Þ ¼ a
z ðtÞ ¼ 5 ð1 þ e j t Þ,
H24
2
M
y0
a
z0
Bild H-16
x0
x
0 t p
a) Welche Ortskurve beschreibt diese komplexwertige Funktion der reellen Variablen t ?
b) Bestimmen und skizzieren Sie die durch Inversion entstandene Ortskurve (ohne Anwendung der bekannten Inversionsregeln).
462
H Komplexe Zahlen und Funktionen
a) Wir zeigen zunächst, dass die Bildpunkte von z ¼ z ðtÞ auf einem Kreis liegen:
z ¼ 5 ð1 þ e j t Þ ¼ 5 þ 5 e j t
)
z 5 ¼ 5 e jt
)
j z 5 j ¼ j 5 e jt j ¼ 5 j e jt j ¼ 5
|ffl{zffl}
1
Jeder Bildpunkt hat somit vom Bildpunkt der reellen Zahl z 0 ¼ 5 den gleichen Abstand d ¼ j z 5 j ¼ 5. Die
Bildpunkte liegen daher auf einem Kreis mit dem Mittelpunkt M ¼ ð5; 0Þ und dem Radius R ¼ 5 , allerdings
mit der folgenden Einschränkung. Aus
z ðtÞ ¼ 5 ð1 þ e j t Þ ¼ 5 ð1 þ cos t þ j sin tÞ ¼ 5 ð1 þ cos tÞ þ j ð5 sin tÞ
folgt, dass der Imaginärteil von z ðtÞ im Definitionsintervall 0 t p stets größer oder gleich null ist:
Im ðz ðtÞÞ ¼ 5 sin t 0
(bekanntlich gilt im Intervall 0 t p , d. h. im 1. und 2. Quadrant stets sin t 0). Die Kreispunkte unterhalb
der reellen Achse scheiden damit aus, die gesuchte Ortskurve ist der in Bild H-17 skizzierte Halbkreis.
Im ( z )
t = π/2
t
z (t )
z (t )
t =π
t =0
Bild H-17
5
10
Re ( z )
b) Durch Inversion erhalten wir aus z ðtÞ die folgende Funktion:
w ðtÞ ¼
1
1
0,2
0,2 ½ ð1 þ cos tÞ j sin t
¼
¼
¼
¼
j
t
z ðtÞ
5 ð1 þ e Þ
ð1 þ cos tÞ þ j sin t
½ ð1 þ cos tÞ þ j sin t ½ ð1 þ cos tÞ j sin t
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða þ bÞ ða bÞ ¼ a 2 b 2 mit a ¼ 1 þ cos t ; b ¼ j sin t
¼
0,2 ½ ð1 þ cos tÞ j sin t
ð1 þ cos tÞ 2 j 2 sin 2 t
¼
0,2 ð1 þ cos tÞ j ð0,2 sin tÞ
0,2 ð1 þ cos tÞ j ð0,2 sin tÞ
¼
¼
2 þ 2 cos t
1 þ 2 cos t þ cos 2 t þ sin 2 t
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1
¼
0,2 ð1 þ cos tÞ
0,2 ð1 þ cos tÞ j ð0,2 sin tÞ
0,2 sin t
0,1 sin t
j
¼
¼ 0,1 j
2 ð1 þ cos tÞ
2
ð1
þ
cos
tÞ
1 þ cos t
2 ð1 þ cos tÞ
ð0 t < pÞ
Umformungen: Der Bruch wurde zunächst mit dem konjugiert komplexen Nenner, d. h. der komplexen Zahl
ð1 þ cos tÞ j sin t erweitert. Ferner gilt: cos 2 t þ sin 2 t ¼ 1 (trigonometrischer Pythagoras).
Der Realteil der Funktion w ðtÞ hat den konstanten Wert
Re ðw ðtÞÞ ¼ 0,1. Der Imaginärteil dagegen durchläuft im Intervall 0 t < p alle Werte von 0 bis 1 . Die Ortskurve
von w ðtÞ ist daher eine Halbgerade parallel zur imaginären
Achse (siehe Bild H-18).
Im ( w )
t =0
Re ( w )
0,1
w (t )
t
w (t )
t
Bild H-18
2 Anwendungen
463
Bestimmen und skizzieren Sie die Ortskurve der komplexwertigen Funktion
H25
z ðtÞ ¼
1
,
1 þ jt
1 < t < 1
unter Verwendung der Inversionsregeln.
Hinweis: Untersuchen Sie zunächst den Nenner w ðtÞ ¼ 1 þ j t .
Der Nenner w ðtÞ ¼ 1 þ j t beschreibt im Intervall 1 < t < 1 eine zur imaginären Achse im Abstand 1 parallel
verlaufende Gerade (siehe Bild H-19). Die Funktion z ðtÞ geht dann aus w ðtÞ durch Inversion hervor: z ðtÞ ¼ 1=w ðtÞ.
Nach der 2. Inversionsregel beschreibt dann z ðtÞ einen durch den Nullpunkt gehenden Kreis, dessen genaue Lage wir
wie folgt bestimmen. Der Schnittpunkt der Parallelen w ðtÞ ¼ 1 þ j t mit der reellen Achse (er gehört zum Parameterwert t ¼ 0) hat von allen Punkten der Parallelen den kleinsten Abstand vom Nullpunkt und geht somit bei der Inversion in den Bildpunkt mit dem größten Abstand vom Nullpunkt über:
j w j min ¼ w ðt ¼ 0Þ ¼ 1
Inversion
!
j z j max ¼ z ðt ¼ 0Þ ¼
1
¼ 1
j w j min
Damit besitzt der gesuchte Kreis den Durchmesser 2 R ¼ j z jmax ¼ 1 und den Radius R ¼ 0,5. Der Mittelpunkt
des Kreises liegt auf der reellen Achse und fällt in den Punkt M ¼ ð0,5; 0) (siehe Bild H-20).
Im ( w )
Im ( w )
Im ( z )
t
z (t )
t
w (t )
t =0
1
t
w (t )
w (t )
t = 0 Re ( z )
M
Re ( w )
0,5
1
z (t )
Bild H-19
Bild H-20
t
Re ( w )
w (t )
t
Netzwerkfunktionen einer RL - Reihenschaltung
R
L
Bild H-21
H26
Die in Bild H-21 skizzierte Reihenschaltung enthält einen variablen ohmschen Widerstand R mit
0 R R 0 und eine Spule mit der konstanten Induktivität L, deren ohmscher Widerstand vernachlässigbar ist. Bestimmen Sie die folgenden Netzwerkfunktionen (bei konstanter Kreisfrequenz w der
angelegten Wechselspannung):
a) Komplexer Gesamtwiderstand
Z ¼ Z ðRÞ;
b) Komplexer Leitwert
Y ¼ Y ðRÞ.
Skizzieren Sie die Widerstands- und Leitwertortskurve.
a) R und L sind in Reihe geschaltet, ihre (komplexen) Wechselstromwiderstände addieren sich daher zum komplexen
Gesamtwiderstand:
Z ¼ Z ðRÞ ¼ R þ j w L
ð0 R R 0 Þ
Der Imaginärteil Im ðZÞ ¼ w L ist dabei unabhängig von der Variablen R, während der Realteil Re ðZÞ ¼ R alle
Werte von 0 bis R 0 durchläuft. Die Widerstandsortskurve ist daher Teil einer zur reellen Achse im Abstand
d ¼ w L parallel verlaufenden Geraden (Bild H-22).
464
H Komplexe Zahlen und Funktionen
Widerstandsortskurve Z (R )
Im ( Z )
R
R=0
R = R0
R
vL
Z (R )
Bild H-22
R0
Re ( Z )
b) Der komplexe Leitwert Y ist der Kehrwert des komplexen Widerstandes Z :
Y ¼ Y ðRÞ ¼
1
1
R jwL
R jwL
R jwL
¼ 2
¼
¼
¼
¼ 2
Z ðRÞ
R þ jwL
ð R þ j w LÞ ðR j w L Þ
R þ w2 L2
R j2 w2 L2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom : ða þ bÞ ða bÞ ¼ a 2 b 2 mit a ¼ R; b ¼ j w L
¼
R
wL
j 2
R2 þ w2 L2
R þ w2 L2
ð0 R R 0 Þ
Umformung: Der Bruch wird mit dem konjugiert komplexen Nenner, d. h. der komplexen Zahl R j w L erweitert.
Da die Widerstandsortskurve Z ðRÞ Teil einer Geraden ist, die nicht durch den Nullpunkt geht (siehe Bild H-22),
ist die durch Inversion entstandene Leitwertortskurve Y ðRÞ nach der 2. Inversionsregel Teil eines Kreises, der
durch den Nullpunkt verläuft. Die Lage dieses Kreises bestimmen wir wie folgt. Der zu R ¼ 0 gehörige Punkt auf
der Widerstandsortskurve Z ðRÞ hat von allen Punkten dieser Kurve den kleinsten Abstand vom Nullpunkt (siehe
Bild H-22):
j Z j min ¼ j Z ðR ¼ 0Þ j ¼ j j w L j ¼ j j j j w L j ¼ 1 ðw LÞ ¼ w L
Der entsprechende Punkt auf der Leitwertortskurve Y ðRÞ hat dann den größten Abstand aller Punkte dieser Kurve
vom Nullpunkt:
j Y j max ¼
1
1
¼
j Z j min
wL
Dies ist zugleich der Wert des Kreisdurchmessers, also gilt: 2 R ¼ 1=ðw LÞ. Der Mittelpunkt des Kreises liegt auf
der imaginären Achse bei 1=ð2 w LÞ, der Radius beträgt r ¼ 1=ð2 w LÞ. Der Verlauf der Leitwertortskurve
Y ¼ Y ðRÞ ist in Bild H-23 dargestellt (durchgezogene Kurve).
Im ( Z )
Im ( Y )
Widerstandsortskurve Z (R )
R
R=0
R = R0
R
Z (R )
Re ( Y )
R = R0
Y (R )
–
R
1
2 vL
Leitwertortskurve Y (R )
R
R=0
R0
Re ( Z )
Bild H-23
2 Anwendungen
465
Widerstands- und Leitwertortskurve eines Parallelschwingkreises
H27
Der in Bild H-24 dargestellte Parallelschwingkreis enthält einen ohmschen Widerstand R , eine Induktivität L und eine Kapazität C.
L
R
Bild H-24
Parallelschwingkreis
C
a) Bestimmen Sie die Abhängigkeit des komplexen Gesamtwiderstandes
Z von der Kreisfrequenz w
pffiffiffiffiffiffiffi
der angelegten Wechselspannung (0 w < w 0 ¼ 1= L C Þ und skizzieren Sie die zugehörige
Widerstandsortskurve.
b) Durch Inversion soll aus der Widerstandsortskurve Z ðwÞ die Leitwertortskurve Y ðwÞ ermittelt werden.
c) Wie groß sind Wirk-, Blind- und Scheinwiderstand für R ¼ 200 W, L ¼ 10 H und C ¼ 10 5 F
bei einer Kreisfrequenz von w ¼ 50 s 1 ?
a) Die parallel geschalteten Elemente L und C ersetzen wir im 1. Schritt durch den Ersatzwiderstand Z 1 (siehe
Bild H-25).
L
R
R
Z
Z1
C
Bild H-25
Schrittweise Zusammenfassung der Einzelwiderstände zum komplexen Gesamtwiderstand Z
Es addieren sich dabei die Leitwerte von C und L zum Leitwert Y 1 der Parallelschaltung:
1
1
ðw CÞ ðw LÞ 1
w2 L C 1
Y1 ¼ jwC j
¼ j wC
¼ j
¼ j
wL
wL
wL
wL
Der Ersatzwiderstand Z 1 ist der Kehrwert des Leitwertes Y 1 :
1
1
wL
wL
wL
¼ j 2
¼ j
Z1 ¼
¼ 2
j w LC 1
w LC 1
1 w2 L C
Y1
1
¼ j
j
Die Größe L C lässt sich noch wie folgt durch w 0 ausdrücken (siehe Aufgabenstellung, Teil a)):
pffiffiffiffiffiffiffi
1
1
1
quadrieren ) L C ¼ 2
w 0 ¼ pffiffiffiffiffiffiffi )
LC ¼
w0
w0
LC
Der Ersatzwiderstand Z 1 kann dann auch nach der folgenden Formel berechnet werden:
Z1 ¼ j
wL
wL
wL
w L w 20
w 20 L w
¼
j
¼
j
¼
j
¼
j
1 w2 L C
w 20 w 2
w 20 w 2
w2
w 20 w 2
|{z}
1 2
2
w0
w0
1=w 2
0
Im nächsten Schritt addieren wir die in Reihe geschalteten Widerstände R und Z 1 und erhalten den gesuchten
komplexen Gesamtwiderstand Z des Parallelschwingkreises in Abhängigkeit von der Kreisfrequenz w:
Z ðwÞ ¼ R þ Z 1 ¼ R þ j
wL
w 20 L w
¼
R
þ
j
1 w2 L C
w 20 w 2
ð0 w < w 0 Þ
466
H Komplexe Zahlen und Funktionen
Bestimmung der Widerstandsortskurve
Der Realteil von Z ðwÞ ist frequenzunabhängig, er hat den konstanten Wert Re ðZ ðwÞÞ ¼ R . Der Imaginärteil
dagegen hängt von der Kreisfrequenz w ab und durchläuft im Intervall 0 w < w 0 alle Werte von 0 bis 1.
Die Widerstandsortskurve ist daher eine zur imaginären Achse im Abstand d ¼ R parallele Halbgerade (Bild H-26).
Im ( Z )
v → v0
Z (v )
v
Widerstandsortskurve Z (v )
v=0
R
Bild H-26
Widerstandsortskurve
Re ( Z )
b) Durch Inversion der Widerstandortskurve Z ðwÞ erhalten wir die Leitwertortskurve Y ðwÞ . Aus der Halbgeraden
wird dabei nach der 2. Inversionsregel ein durch den Nullpunkt gehender Halbkreis, dessen genaue Lage sich wie
folgt bestimmen lässt. Der zu w ¼ 0 gehörige Punkt auf der Halbgeraden (Schnittpunkt mit der reellen Achse) hat
vom Nullpunkt den kleinsten Abstand. Er geht bei der Inversion über in den Punkt auf der Leitwertortskurve mit
dem größten Abstand vom Nullpunkt:
j Z j min ¼ j Z ðw ¼ 0Þ j ¼ R
Inversion
!
j Y j max ¼
1
1
¼
j Z j min
R
Dieser (auf der reellen Achse liegende) Punkt hat also den Abstand 1=R vom Nullpunkt. Der Durchmesser des
Kreises (bzw. Halbkreises) beträgt daher d ¼ 1=R , der Radius ist somit r ¼ 1=ð2 RÞ . Der Mittelpunkt liegt auf
der reellen Achse bei M ¼ ð1=ð2 RÞ; 0Þ. Bild H-27 zeigt den genauen Verlauf der halbkreisförmigen Leitwertortskurve (durchgezogene Kurve).
Im ( Z )
Im ( Y )
v → v0
Widerstandsortskurve Z (v )
Z (v )
M
v = v0
1/ (2R )
Y (R )
v → v0
v
v=0
v=0
1/R R
Re ( Y )
Re ( Z )
v
Leitwertortskurve Y (v )
Bild H-27 Widerstands- und Leitwertortskurve
c) Wir berechnen zunächst den komplexen Gesamtwiderstand Z (Zwischenrechnung ohne Einheiten):
Z ¼ Rþj
wL
50 10
500
¼ 200 þ j
¼ 200 þ j
¼
1 w2 L C
1 50 2 10 10 5
1 5 2 10 2 10 10 5
¼ 200 þ j
500
500
500
¼ 200 þ j
¼ 200 þ j
¼ 200 þ 666,67 j
2
1 25 10
1 0,25
0,75
ðin WÞ
Der Wirkwiderstand ist der Realteil, der Blindwiderstand der Imaginärteil, der Scheinwiderstand der Betrag von Z :
Wirkwiderstand:
Re ðZÞ ¼ 200 W
Im ðZÞ ¼ 666,67 W
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Scheinwiderstand: Z ¼ j Z j ¼ 200 2 þ 666,67 2 W ¼ 484 448,89 W ¼ 696,02 W
Blindwiderstand:
467
I Vektorrechnung
1 Vektoroperationen
In diesem Abschnitt finden Sie Aufgaben zu folgenden Themen:
Darstellung von Vektoren (Vektorkoordinaten oder skalare Vektorkomponenten, Betrag, Richtungswinkel)
Grundrechenoperationen mit Vektoren (Addition und Subtraktion, Multiplikation mit einem Skalar)
Skalar- und Vektorprodukt, gemischtes oder Spatprodukt
Lehrbuch: Band 1, Kapitel II.1 bis 3
Formelsammlung: Kapitel II.1 bis 3
I1
0 1
1
0
0 1
5
1
2
B C
C
B C ~ B
c ¼ @ 0 A . Berechnen Sie die skalaren
Gegeben sind die Vektoren ~
a ¼ @ 5 A , b ¼ @ 5 A und ~
1
8
3
Komponenten (Vektorkoordinaten) sowie die Beträge und Richungswinkel der folgenden Vektoren:
aÞ ~
s ¼ 5~
a 3 b~ þ 2~
c þ 3 ð2 ~
a~
cÞ
bÞ ~
s ¼ 3 b~ þ 4 ð ~
a~
cÞ ~
a ð~
a b~ Þ ð2~
cþ~
aÞ~
c
aÞ
~
s ¼ 5~
a 3 b~ þ 2~
c þ 3 ð2 ~
a~
c Þ ¼ 5~
a 3 b~ 6~
c þ 6~
a 3~
c ¼ 11 ~
a 3 b~ 9~
c ¼
0
1
0
1
0 1
0 1
0
1
0 1
0
1
20
3
45
2
5
22
1
B
C
B
C
B C
B C
B
C
B C
B
C
B
C
B
B C
B C
B
C
B
C
C
0C
¼ 11 B
A ¼ @ 40 A
@ 5 A 3 @ 5 A 9 @ 0 A ¼ @ 55 A þ @ 15 A þ @
0
9
1
33
24
3
8
Betrag: j~
sj ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
ð 20Þ 2 þ 40 2 þ 0 2 ¼ 2000 ¼ 44,72
Berechnung der drei Richtungswinkel a, b und g
cos a ¼
cos b ¼
20
¼ pffiffiffiffiffiffiffiffiffiffi ¼ 0,4472
j~
sj
2000
sx
sy
40
¼ pffiffiffiffiffiffiffiffiffiffi ¼ 0,8944
j~
sj
2000
)
a ¼ arccos ð 0,4472Þ ¼ 116,57
)
b ¼ arccos 0,8944 ¼ 26,57
Der Vektor ~
s liegt wegen s z ¼ 0 in der x, y-Ebene. Daher ist g ¼ 90
(rechter Winkel mit der z-Achse).
Richtungswinkel: a ¼ 116,57 , b ¼ 26,57 , g ¼ 90
b) Wir berechnen zunächst die Skalarprodukte ~
a~
c und ð ~
a b~Þ ð2~
cþ~
a Þ:
0 1 0 1
2
5
B C B C
~
a ~
c ¼ @ 5 A @ 0 A ¼ 10 þ 0 þ 3 ¼ 13
3
1
0
1
0
1
0 1
3
1
2
B
C
B
C
B C
~
a b~ ¼ @ 5 A @ 5 A ¼ @ 0 A ;
5
8
3
0 1
0 1
0 1
0 1
0 1
12
2
10
2
5
B C
B C
B C
B C
B C
2~
cþ~
a ¼ 2@0A þ @5A ¼ @ 0A þ @5A ¼ @ 5A
5
3
2
3
1
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_9
468
I Vektorrechnung
0
B
ð~
a b~Þ ð2~
cþ~
aÞ ¼ @
3
1
0
12
1
C B C
0 A @ 5 A ¼ 36 þ 0 25 ¼ 11
5
5
~
s ¼ 3 b~ þ 4 ð ~
a~
cÞ ~
a ð~
a b~Þ ð2~
cþ~
aÞ ~
c ¼ 3 b~ þ 52 ~
a
|fflfflfflffl{zfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
13
11
1
1
0
0
0 1
1
0 1
0
104
3
5
2
1
C
C
B
B
B C
C
B C
B
¼ 3 @ 5 A þ 52 @ 5 A 11 @ 0 A ¼ @ 15 A þ @ 260 A þ
Betrag: j~
sj ¼
24
1
3
8
11~
c ¼
0
B
@
156
55
1
0
52
1
C
C
B
0 A ¼ @ 245 A
121
11
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
52 2 þ 245 2 þ 121 2 ¼ 77 370 ¼ 278,15
Berechnung der drei Richtungswinkel a, b und g
cos a ¼
cos b ¼
cos g ¼
sx
52
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 0,1869
77 370
)
a ¼ arccos 0,1869 ¼ 79,23
245
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 0,8808
77 370
)
b ¼ arccos 0,8808 ¼ 28,26
121
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 0,4350
j~
sj
77 370
)
g ¼ arccos 0,4350 ¼ 64,21
j~
sj
sy
j~
sj
sz
Richtungswinkel: a ¼ 79,23 , b ¼ 28,26 , g ¼ 64,21
I2
Ein Vektor ~
a hat den Betrag j ~
a j ¼ 3 und die Vektorkoordinaten a x ¼ 2, a y ¼ 2 und a z < 0.
Berechnen Sie die fehlende Vektorkoordinate a z sowie die drei Richtungswinkel.
Wir bestimmen zunächst die Vektorkomponente a z unter Beachtung von a z < 0 :
j~
a j 2 ¼ a 2x þ a 2y þ a 2z
)
a 2z ¼ j ~
a j 2 a 2x a 2y ¼ 3 2 ð 2Þ 2 2 2 ¼ 1
)
pffiffiffi
az ¼ 1 ¼ 1
Berechnung der drei Richtungswinkel a, b und g
cos a ¼
ax
j~
aj
ay
¼
2
2
¼
3
3
2
¼
cos b ¼
3
j~
aj
)
a ¼ arccos
2
¼ 131,81
3
2
b ¼ arccos
¼ 48,19
3
1
1
¼
cos g ¼
¼
3
3
j~
aj
az
)
)
1
g ¼ arccos
¼ 109,47
3
Richtungswinkel: a ¼ 131,81 , b ¼ 48,19 , g ¼ 109,47
I3
Von einem Vektor ~
a sind folgende Eigenschaften bekannt:
j~
a j ¼ 10;
Richtungswinkel : a ¼ g ¼ 60 ; b > 90
Bestimmen Sie den noch fehlenden Richtungswinkel b sowie die drei Vektorkoordinaten a x , a y und a z .
1 Vektoroperationen
469
Wir berechnen zunächst den noch fehlenden Richtungswinkel b (wegen 90
cos 2 a þ cos 2 b þ cos 2 g ¼ 1
< b < 180
ist cos b < 0):
)
cos 2 b ¼ 1 cos 2 a cos 2 g ¼ 1 cos 2 60 cos 2 60
pffiffiffiffiffiffi
pffiffiffiffiffiffi
cos b ¼ 0,5 ) b ¼ arccos ð 0,5 Þ ¼ 135
¼ 1 0,25 0,25 ¼ 0,5
)
Berechnung der Vektorkoordinaten a x , a y und a z (a x = a z , da a = g)
a j cos a ¼ 10 cos 60
ax ¼ j~
¼ 5;
ay ¼ j~
a j cos b ¼ 10 cos 135
¼ 7,071
Vektorkoordinaten: a x ¼ 5; a y ¼ 7,071; a z ¼ 5
0 1
1
B C
~
a ¼ @5A;
2
I4
0
2
1
B
C
b~ ¼ @ 14 A ;
1
0 1
u
B C
~
c ¼ @1A
v
Bestimmen Sie die Parameter u und v so, dass der Vektor ~
c sowohl zu ~
a als auch zu b~ orthogonal
ist und zwar unter ausschließlicher Verwendung von
a) Skalarprodukten, b) Vektorprodukten.
a) Die Skalarprodukte ~
a~
c und b~ ~
c müssen jeweils verschwinden. Dies führt zu zwei Gleichungen mit den beiden
Unbekannten u und v:
0
1 0 1
0 1 0 1
u
2
u
1
B
C
B
C
B C B C
~
c ¼ @ 14 A @ 1 A ¼ 2 u þ 14 þ v ¼ 0
a~
c ¼ @ 5 A @ 1 A ¼ u þ 5 þ 2 v ¼ 0 ; b~ ~
v
1
v
2
ðIÞ
u þ 5 þ 2v ¼ 0
)
ðIIÞ
2 u þ 14 þ v ¼ 0
u ¼ 2v 5
Gleichung (I) nach u auflösen, den gefundenen Ausdruck dann in Gleichung (II) einsetzen:
ðIIÞ )
ðIÞ
2 u þ 14 þ v ¼ 2 ð 2 v 5Þ þ 14 þ v ¼ 4 v þ 10 þ 14 þ v ¼ 5 v þ 24 ¼ 0
)
5 v ¼ 24
)
v ¼ 4,8
ðEinsetzen in Gleichung (I)Þ
)
u ¼ 2 v 5 ¼ 2 ð 4,8Þ 5 ¼ 9,6 5 ¼ 4,6
Lösung: u ¼ 4,6; v ¼ 4,8
b) Das Vektorprodukt aus ~
a und b~ ist ein Vektor, der sowohl auf ~
a als auch auf b~ senkrecht steht. Der gesuchte
Vektor ~
c ist daher zum Vektor ~
a b~ entweder parallel oder antiparallel, d. h. ~
c und ~
a b~ sind kollineare
Vektoren (sie liegen in einer gemeinsamen Linie). Somit muss der Vektor ~
c ein Vielfaches von ~
a b~ sein:
~
ð
Þ
~
c ¼ l ~
a b . Diese Vektorgleichung führt dann zu drei Gleichungen für die drei Unbekannten l, u und v:
0
1
0 1
0
1
0
1
1
2
5 28
23
B
C
B C
B
C
B
C
~
a b~ ¼ @ 5 A @ 14 A ¼ @ 4 1 A ¼ @ 5 A
2
~
c ¼ l ð~
a b~ Þ
1
)
14 þ 10
24
1
0
1
0
0 1
23 l
23
u
C
B
C
B
B C
@1A ¼ l@ 5A ¼ @ 5lA
24 l
24
v
)
8
>
< ðIÞ u ¼ 23 l
ðIIÞ 1 ¼ 5 l
>
:
ðIIIÞ v ¼ 24 l
470
I Vektorrechnung
Aus Gleichung (II) folgt zunächst l ¼ 1=5 (die Vektoren ~
c und ~
a b~ sind somit antiparallel), aus den
beiden restlichen Gleichungen erhalten wir
1
1
u ¼ 23 l ¼ 23
¼ 4,6 und v ¼ 24 l ¼ 24
¼ 4,8
5
5
Lösung: u ¼ 4,6; v ¼ 4,8
(in bereinstimmung mit der Lösung aus Teil a))
C2
Beweisen Sie mit Hilfe der Vektorrechnung den Satz des Thales:
I5
„Jeder Peripheriewinkel über einem Kreisdurchmesser AB ist
ein rechter Winkel (Bild I-1)“.
R: Kreisradius
M : Kreismittelpunkt
C4
Bild I-1
A
Anhand von Bild I-2 führen wir folgende Bezeichnungen ein:
!
!
AM ¼ MB ¼ ~
a;
M
B
C
!
MC ¼ b~
v
j~
a j ¼ j b~j ¼ R
!
AC ¼ ~
u;
C3
C1
u
!
BC ¼ ~
v
b
Bild I-2
A
a
M
a
B
Wir müssen zeigen, dass der Winkel | ACB ein rechter Winkel ist. Dies ist genau dann der Fall, wenn die Vektoren
~
u und ~
v orthogonal sind, d. h. das Skalarprodukt aus ~
u und ~
v verschwindet. Zunächst drücken wir ~
u und ~
v durch
die gleichlangen „Hilfsvektoren“ ~
a und b~ wie folgt aus:
~
u ¼~
a þ b~ und ~
aþ~
v ¼ b~;
d: h: ~
v ¼ b~ ~
a
Damit erhalten wir für das Skalarprodukt aus ~
u und ~
v (unter Verwendung des Distributiv- und Kommutativgesetzes
für Skalarprodukte):
~
u~
v ¼
~
a þ b~ ð b~ ~
aÞ ¼ ~
a b~ ~
a~
a þ b~ b~ b~ ~
a ¼
2
2
¼~
a b~ j ~
a j 2 þ j b~j ~
a b~ ¼ j ~
a j 2 þ j b~j ¼ R 2 þ R 2 ¼ 0
Folgerung: Die Vektoren ~
u und ~
v stehen aufeinander senkrecht, der Winkel | ACB ist ein rechter. Damit ist der
Satz von Thales bewiesen.
I6
0 1
2
B C
Bilden Sie mit den Vektoren ~
a ¼ @1A;
5
(Skalar-, Vektor- bzw. Spatprodukte):
~
a b~;
ð~
a~
c Þ ð~
aþ~
c Þ;
0
B
b~ ¼ @
b~ ~
c;
1
1
C
3A
1
0 1
4
B C
und ~
c ¼ @ 5 A die folgenden Produkte
1
~
a þ b~ ð ~
c b~ Þ ;
c Þ b~ ¼ ½ ~
a~
c b~
ð~
a~
Zunächst bilden wir die benötigten Summen und Differenzen, dann die Produkte (Skalarprodukt, Vektorprodukt bzw.
Spatprodukt):
0 1
0 1
0 1
0
1
0 1
0 1
4
6
2
1
1
2
B C
B C
B C
B
C
B C
B C
B C
C
B C
B
C
C
B C
~
aþ~
c ¼ B
aþb ¼ B
@1A þ @5A ¼ @6A
@1A þ @ 3A ¼ @4A; ~
1
5
6
1
5
6
1 Vektoroperationen
471
0
1
0 1
0 1
2
4
2
B
C
B C
B C
B
C
C
B C
~
a~
c ¼ B
@1A @5A ¼ @4A;
4
5
1
0 1
0
1
0 1
4
1
5
B C
B
C
B C
C
B
C
B C
~
c b~ ¼ B
@5A @ 3A ¼ @2A
1
1
0
0 1 0
1
2
1
B C B
C
C B
C
~
a b~ ¼ B
@1A @ 3A ¼ 2 þ 3 þ 5 ¼ 6
5
1
0
1
0 1
6
B
C B C
C B C
ð~
a~
c Þ ð~
aþ~
cÞ ¼ B
@ 4 A @ 6 A ¼ 12 24 þ 24 ¼ 12
4
6
2
Das Skalarprodukt ð ~
a~
c Þ ð~
aþ~
c Þ lässt sich auch mit Hilfe des Distributiv- und Kommutativgesetzes
a Þ:
berechnen ð ~
a~
c ¼~
c~
0 1 0 1 0 1
4
2
2
B C B C B C
C B C B C
ð~
a~
c Þ ð~
aþ~
cÞ ¼ ~
a~
aþ~
a~
c~
c~
a ~
c~
c ¼~
a~
a~
c~
c ¼B
@1A @1A @5A
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
1
5
5
0
wie folgt
0 1
4
B C
B5C ¼
@ A
1
¼ ð4 þ 1 þ 25Þ ð16 þ 25 þ 1Þ ¼ 30 42 ¼ 12
0
B
b~ ~
c ¼ B
@
1
0 1
0
1
0
1
4
3 5
2
C
B C
B
C
B
C
B C
B
C
B
3C
5C
A @5A ¼ @ 4 þ 1A ¼ @
A
1
1
5 12
17
1
0 1
0
1
0
1
0 1
5
0 12
12
1
B C
B
C
B
C
B C
C
B C
B
C
B
C
~
a þ b~ ð ~
c b~ Þ ¼ B
@ 4 A @ 2 A ¼ @ 30 0 A ¼ @ 30 A
0
2 20
18
6
a~
c Þ b~ ¼ ½ ~
a~
c b~ auf zwei verschiedene Arten
Berechnung des Spatproduktes ð ~
1. Lösungsweg: Erst das Vektorprodukt ~
a~
c bilden, dann diesen Vektor skalar mit dem Vektor b~ multiplizieren:
0 1
0 1
0
1
0
1
2
4
1 25
24
B C
B C
B
C
B
C
C
B C
B
C
B
C
~
a~
c ¼ B
@ 1 A @ 5 A ¼ @ 20 2 A ¼ @ 18 A
5
1
10 4
6
0
B
ð~
a~
c Þ b~ ¼ B
@
24
1
0
C B
B
18 C
A@
6
1
1
C
3C
A ¼ 24 þ 54 þ 6 ¼ 84
1
2. Lösungsweg: Spatprodukt ð ~
a~
c Þ b~ ¼ ½ ~
a~
c b~ in der Determinantenform darstellen, Determinante dann
nach der Regel von Sarrus berechnen:
2 4 1 2 4
3 1 5 )
1 5
5 1
1 5 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
ð~
a~
c Þ b~ ¼ ½ ~
a~
c b~
ð~
a~
c Þ b~ ¼ 10 þ 60 1 þ 25 6 4 ¼ 84
472
I Vektorrechnung
Zeigen Sie, dass die drei Kräfte
0
0 1
0 1
1
5
30
10
B
B C
B C
C
~
~
~
F 1 ¼ @ 20 A N ; F 2 ¼ @ 0 A N und F 3 ¼ @ 10 A N
10
60
10
I7
~r (Kraftkomponenten, Betrag und
in einer Ebene liegen. Berechnen Sie ferner die resultierende Kraft F
Richtungswinkel).
Die drei Kräfte liegen genau dann in einer Ebene, wenn das aus ihnen gebildete Spatprodukt
det (Rechnung ohne Einheiten):
5 30 10
5 ð 1Þ
~
~
~
F 1 F 2 F 3 ¼ 20 0 10 ¼ 5 ð 4Þ
10 60 10
5 2
~2 F
~3
~1 F
F
verschwin-
1 1 1
10 1
30 0 10 1 ¼ 5 30 10 4 0 1 ¼ 1500 D
2 2 1
30 2 10 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D
30 1
Umformung: Die Spalten haben der Reihe nach die gemeinsamen Faktoren 5, 30 und 10 (grau unterlegt), die wir
bekanntlich vor die Determinante ziehen dürfen.
Determinantenberechnung
1 1 1 1
4 0 1 4
2 2 1 2
Somit gilt:
~2 F
~3
~1 F
F
nach der Regel von Sarrus:
1
0
)
D ¼ 0þ280þ2þ4 ¼ 0
2
¼ 1500 D ¼ 1500 0 ¼ 0
) Die drei Kräfte liegen in einer Ebene.
Alternative Lösung: Jede der 3 Kräfte muss als Linearkombination der beiden übrigen Kräfte darstellbar sein, z. B.
~3 ¼ l 1 F
~1 þ l 2 F
~2 . Dies führt zu einem eindeutig lösbaren linearen Gleichungssystem mit 3 Gleichungen und
F
2 Unbekannten (l 1 und l 2 ).
~r und ihrer Richtungswinkel a,
Berechnung der resultierenden Kraft F
0
1
0 1
0 1
5
30
10
B
C
B C
B C
~r ¼ F
~1 þ F
~2 þ F
~3 ¼ B 20 C N þ B 0 C N þ B 10 C N ¼
F
@
A
@ A
@ A
10
60
10
b und g
0
1
35
B
C
B 10 C N
@
A
80
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
F
~r ¼ F r ¼ 35 2 þ ð 10Þ 2 þ 80 2 N ¼ 7725 N ¼ 87,89 N
cos a ¼
Fx
35 N
¼ 0,3982
¼ pffiffiffiffiffiffiffiffiffiffi
Fr
7725 N
)
a ¼ arccos 0,3982 ¼ 66,53
cos b ¼
Fy
10 N
¼ pffiffiffiffiffiffiffiffiffiffi
¼ 0,1138
Fr
7725 N
)
b ¼ arccos ð 0,1138Þ ¼ 96,53
cos g ¼
Fz
80 N
¼ 0,9102
¼ pffiffiffiffiffiffiffiffiffiffi
Fr
7725 N
)
g ¼ arccos 0,9102 ¼ 24,47
Ergebnis: F r ¼ 87,89 N, a ¼ 66,53 , b ¼ 96,53 , g ¼ 24,47
)
8
F x ¼ 35 N
>
>
<
F y ¼ 10 N
>
>
:
F z ¼ 80 N
1 Vektoroperationen
473
pffiffiffiffiffi
~ vom Betrage F ¼ 100 14 N soll senkrecht auf einer Ebene E mit den RichtungsEine Kraft F
0 1
1
0
2
1
B C
C
B
~
vektoren ~
a ¼ @ 1 A und b ¼ @ 1 A stehen. Bestimmen Sie die (skalaren) Komponenten F x , F y
I8
1
1
und F z dieser Kraft. Wie viele Lösungen gibt es?
~ verläuft parallel oder antiparallel zum Normalenvektor ~
Der gesuchte Kraftvektor F
n der Ebene E (~
n steht bekanntlich senkrecht auf der Ebene). Ein solcher Normalenvektor ist das Vektorprodukt der Richtungsvektoren ~
a und b~,
das wir anschließend noch normieren, um einen Einheitsvektor ~
e gleicher Richtung zu erhalten:
1
0
0 1
1
1
0
0
2
1 1
2
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
C
B
B C
C
C
B
B
2
2 þ 32 ¼
C B 1 C ¼ B 2 1 C ¼ B 1 C ; j~
~
n
j
¼
ð
2Þ
14
þ
1
n ¼~
a b~ ¼ B
1
A
@
@ A
A
A
@
@
1
1
0
~
e ¼
1
1 B
~
n ¼ pffiffiffiffiffi B
@
j~
nj
14
2
1þ2
3
1
C
1C
A
3
~ hat entweder die gleiche Richtung wie der Einheitsvektor ~
Der gesuchte Kraftvektor F
e oder die Gegenrichtung,
pffiffiffiffiffi
seine Länge ist bekannt und beträgt F ¼ 100 14 N. Es gibt daher zwei Lösungen, die wie folgt lauten:
0
1
0
1
0
1
2
2
200
pffiffiffiffiffi
C
B
C
B
C
1 B
C
B
C
B
C
~¼ F~
F
e ¼ 100 14 pffiffiffiffiffi B
@ 1 A N ¼ 100 @ 1 A N ¼ @ 100 A N
14
3
3
300
Kraftkomponenten: F x ¼ 200 N, F y ¼ 100 N, F z ¼ 300 N bzw. F x ¼ 200 N, F y ¼ 100 N, F z ¼ 300 N
D
Berechnen Sie die Oberfläche O eines regulären Tetraeders
mit der Seitenlänge a (Bild I-3).
I9
C
A
Bild I-3
A
B
Das reguläre Tetraeder besteht aus vier kongruenten (deckungsgleichen) gleichseitigen Dreiecken mit der Seitenlänge a
(siehe Bild I-3). Es genügt daher, die Grundfläche A zu berechnen, die wir (wie in Bild I-4 dargestellt) in die x, y!
!
Ebene legen. Wir bestimmen zunächst die Seitenvektoren AB und AC , mit deren Hilfe dann der Flächeninhalt A
der Grundfläche berechnet werden kann (über das Vektorprodukt der beiden Seitenvektoren):
0
0
1
1
0 1
0
1
a=2
1
1
y
AM
B
C
B pffiffiffi
C
B C !
B pffiffiffi C
a
!
C
C
B
C
B
C
B
C
AB ¼ a B
@ 0 A; AC ¼ @ MC A ¼ @ 3 a=2 A ¼ 2 @ 3 A
60°
0
0
0
0
AM ¼ a=2;
MC ¼ a sin 60
a
1 pffiffiffi
3a
¼
2
a
h
M
60°
Bild I-4
A
a
„Bodenfläche“
60°
B
x
474
I Vektorrechnung
!
!
Vektorprodukt aus AB und AC und Flächeninhalt A der Grundfläche
0 1
1
B C
a
!
!
C
AB AC ¼ a B
@0A 2
0
0
1
1
2
B pffiffiffi C
B 3C ¼ a
@
A
2
0
0 1
1
B C
B0C
@ A
0
0 1
0
C
1 pffiffiffi 2 B
1 pffiffiffi 2
3a B
3a ~
¼
¼
ez
0C
@
A
2
2
1
0
1
1
2
B pffiffiffi C
B 3C ¼ a
@
A
2
0
0
00
0
1
0
1
2 B
C
B
C
B 0 0C ¼ a B 0C ¼
@
A
@
A
2
pffiffiffi
pffiffiffi
30
3
0
0 11
0
B CC
B
Bmit ~
CC
ez ¼ B
@0AA
@
1
!
!
Die gesuchte Grundfläche A entspricht der halben Fläche des Parallelogramms, das von den Vektoren A B und A C
aufgespannt wird. Die Parallelogrammfläche ist der Betrag des Vektorproduktes dieser Vektoren. Daher gilt:
1 !
1 1 pffiffiffi 2
1 pffiffiffi 2
!
ez j ¼
AB AC ¼
3 a j~
3a
2
2 2
4
|{z}
1
pffiffiffi 2
Gesamtoberfläche des Tetraeders: O ¼ 4 A ¼ 3 a
A ¼
0
I 10
0
1
0 1
1
B C
b~ ¼ @ 1 A
0
B
C
und
Zeigen Sie die lineare Unabhängigkeit der drei Vektoren ~
a ¼ @ 1 A,
1
0
1
0
1
2
1
C
B
C
B
~
r ¼ @ 1 A als Linearkombination dieser Vektoren dar.
c ¼ @ 0 A und stellen Sie den Vektor ~
1
1
Wie lauten die skalaren Vektorkomponenten von ~
r?
Die drei Vektoren ~
a, b~ und ~
c sind genau dann linear unabhängig, wenn das aus ihnen gebildete Spatprodukt
~
½~
a b~
c von null verschieden ist (wir verwenden hier die Determinantenschreibweise des Spatproduktes):
0 1 1 0 1
a b~~
c ¼ 0 þ 0 þ 0 1 0 1 ¼ 2 6¼ 0
0 1 1 ) ½~
1 1
1 0
1 1 0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
½~
a b~~
c
Die Vektoren ~
a, b~ und ~
c sind somit linear unabhängig, der vierte Vektor ~
r muss daher in der Form
0
1
0 1
0
1
0
1
2
0
1
1
B
B
B C
B
C
C
C
B 1 C ¼ l1 B 1 C þ l2 B 1 C þ l3 B 0 C
~
r ¼ l1 ~
a þ l 2 b~ þ l 3 ~
c
oder
@
A
@ A
@
A
@
A
1
1
0
1
darstellbar sein. Dies führt zu dem folgenden linearen Gleichungssystem für l1 , l2 und l3 :
0
1
0
1
0
1
0
0 1
1
l2
l2 l3
2
l3
0
B
C
B
C
B
C
B
B C
C
B 1 C ¼ B l1 C þ B l2 C þ B 0 C ¼ B l1 þ l2 C
@
A
@
A
@
A
@
A
@ A
l1
0
l1 þ l3
1
l3
1 Vektoroperationen
475
Komponentenweise geschrieben (und seitenvertauscht):
9
ðIÞ
l2 l3 ¼ 2 >
=
Wir addieren die 3 Gleichungen und erhalten:
)
ðIIÞ
l1 þ l2
¼ 1
>
2
l2 ¼ 2 ) l2 ¼ 1
;
ðIIIÞ l 1 þ
l3 ¼ 1
Die übrigen Werte erhalten wir aus den Gleichungen (I) und (II), wenn wir dort l 2 ¼ 1 setzen:
ðIÞ )
1 l3 ¼ 2
)
l 3 ¼ 1;
ðIIÞ )
l1 þ 1 ¼ 1
)
l1 ¼ 2
r besitzt die folgende Darstellung:
Somit ist l 1 ¼ 2, l 2 ¼ 1, l 3 ¼ 1 und der Vektor ~
0
1
0
1
0 1
0
1
0
1
0 1
0
1
2
0
1
1
0
1
1
B
C
B
C
B C
B
C
B
C
B C
B
C
B
C
C
B C
B
C
B
C
B C
B
C
~
r ¼ 2~
a þ 1 b~ 1~
c ¼ 2 B
@ 1A þ @1A @ 0A ¼ @2A þ @1A þ @ 0A ¼ @1A
1
1
0
1
2
0
1
Skalare Vektorkomponenten von ~
r : r x ¼ 2, r y ¼ 1, r z ¼ 1
I 11
Stellen Sie fest, ob die Vektoren ~
a , b~ und ~
c linear unabhängig oder linear abhängig sind:
0 1
0 1
0
1
0 1
0
1
0
1
2
1
2
5
1
13
B C
B C
B
C
B C
B
C
B
C
aÞ ~
a ¼ @ 1 A ; b~ ¼ @ 4 A ; ~
c ¼ @ 4A
bÞ ~
a ¼ @ 1 A ; b~ ¼ @ 0 A ; ~
c ¼ @ 2A
5
1
1
1
5
13
Die drei Vektoren ~
a , b~, ~
c sind genau dann linear unabhängig, wenn das aus ihnen gebildete Spatprodukt ½ ~
a b~~
c
nicht verschwindet (Berechnung der Determinante nach der Regel von Sarrus):
2 1 2 2 1
(
½~
a b~ ~
c ¼ 8 þ 20 2 þ 40 8 1 ¼ 57 6¼ 0 )
aÞ 1 4
4 1 4 )
linear unabhängige Vektoren
5 1
1 5 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
½~
a b~~
c
5 1 13 5 1
bÞ 1
0 2 1
0
1
5
13 1
5
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
½~
a b~~
c
I 12
(
)
½~
a b~ ~
c ¼ 0 þ 2 65 0 þ 50 þ 13 ¼ 0
)
linear abhängige Vektoren
0 1
0
1
0 1
1
4
11
B C ~ B
C
B C
Sind die Vektoren ~
a ¼ @ 5 A , b ¼ @ 0 A und ~
c ¼ @ 15 A komplanar?
3
3
3
Die drei Vektoren ~
a , b~, ~
c sind komplanar, wenn ihr Spatprodukt ½ ~
a b~~
c verschwindet (Berechnung der Determinante nach der Regel von Sarrus) :
1 4 11 1 4
(
½~
c ¼ 0 180 þ 165 0 45 þ 60 ¼ 0 )
a b~ ~
0 15 5
0 )
5
Die Vektoren sind daher komplanar:
3
3
3 3
3
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
½~
a b~ ~
c
476
I Vektorrechnung
I 13
0 1
1
B C
~1 ¼ B 2 C N;
F
@ A
5
0
B
~2 ¼ B
F
@
2
1
C
0C
A N;
3
0 1
5
B C
~3 ¼ B 2 C N
F
@ A
0
a) Zeigen Sie die lineare Unabhängigkeit dieser drei Kraftvektoren.
~res (Angabe der Kraftkomponenten, des Betrages und der Richb) Wie lautet die resultierende Kraft F
tungswinkel)?
a) Die drei Kraftvektoren sind linear unabhängig, da das aus ihnen gebildete Spatprodukt nicht verschwindet (Rechnung erfolgt ohne Einheiten; Berechnung der Determinante nach der Regel von Sarrus):
1 2 5 1 2
~2 F
~3 ¼ 0 20 þ 30 0 6 0 ¼ 4 6¼ 0
~1 F
0 2 2
0 )
F
2
5
3 0 5
3
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
~2 F
~3
~1 F
F
b) Die resultierende Kraft lautet wie folgt:
0 1
0
1
0 1
0
0 1
1
4
12þ5
5
2
1
B C
B
C
B C
B
B C
C
C
B
B
C
C
B
B
B
C
C
~res ¼ F
~1 þ F
~2 þ F
~3 ¼ 2 N þ
F
@ A
@ 0A N þ @2A N ¼ @2 þ 0 þ 2A N ¼ @4A N
8
5þ3þ0
0
3
5
~res j ¼
Betrag: j F
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
4 2 þ 4 2 þ 8 2 N ¼ 96 N ¼ 9,80 N
Berechnung der drei Richtungswinkel a, b und g (a = b wegen F x = F y )
cos a ¼
Fx
4N
¼ pffiffiffiffiffi
¼ 0,4082
~
j F res j
96 N
)
a ¼ arccos 0,4082 ¼ 65,91
cos g ¼
Fz
8N
¼ pffiffiffiffiffi
¼ 0,8165
~res j
jF
96 N
)
g ¼ arccos 0,8165 ¼ 35,26
Richtungswinkel: a ¼ b ¼ 65,91 , g ¼ 35,26
0
I 14
1
1
B
C
~1 ¼ B 2 C N;
F
@
A
1
0 1
2
B C
~2 ¼ B 0 C N;
F
@ A
5
0
1
1
B
C
~3 ¼ B 6 C N;
F
@
A
7
0
6
1
B C
~4 ¼ B 4 C N
F
@ A
18
Zeigen Sie, dass diese Kräfte in einer Ebene liegen.
~1 , F
~2 und F
~3 verschwindet und diese Kräfte damit in einer Ebene
Wir zeigen zunächst, dass das Spatprodukt aus F
liegen (Rechnung in der Determinantenschreibweise ohne Einheiten; Determinantenberechnung nach der Regel von
Sarrus):
1 2 1 1 2
~1 F
~2 F
~3 ¼ 0 12 þ 10 0 þ 30 28 ¼ 0
F
2 0 6 2 0 )
1 5 7 1 5
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
~1 F
~2 F
~3
F
1 Vektoroperationen
477
~1 und F
~2 aufgespannt, die somit als RichDiese Ebene wird z. B. durch die linear unabhängigen Kraftvektoren F
~
~
tungsvektoren der Ebene dienen können. F1 und F2 sind linear unabhängig und damit nichtkollinear (d. h. weder
parallel noch antiparallel), da ihr Vektorprodukt nicht verschwindet (ohne Einheiten):
0 1
0
0
0
1
1
1
0 1
2
10 0
1
10
0
B C
B
B
B
C
C
C
B C
B
C
B C
~
~2 ¼ B 2 C B 0 C ¼ B
~1 F
2 5C
F
@
@ A
@
A
A ¼ @ 3 A 6¼ @ 0 A ¼ 0
5
0þ4
4
1
0
~4 liegt dann ebenfalls in dieser Ebene, wenn das Spatprodukt der drei
Der noch verbliebene vierte Kraftvektor F
~
~
~
Kräfte F1 , F2 und F4 verschwindet. Dies ist hier der Fall:
1 2
6 1 2
~1 F
~2 F
~4 ¼ 0 þ 8 60 0 20 þ 72 ¼ 0
F
4 2 0 )
2 0
1 5 18 1 5
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
~1 F
~2 F
~4
F
Folgerung: Alle vier Kräfte liegen in einer gemeinsamen Ebene.
Ein homogenes Magnetfeld mit der Flussdichte
~j ¼ B 0 verläuft parallel zur z-Achse eines
B ¼ jB
räumlichen kartesischen Koordinatensystems. In diesem Feld wird ein metallischer Leiter mit der konstanten Geschwindigkeit v ¼ j ~
v j ¼ v 0 in Richtung der
Raumdiagonale eines achsenparallelen Würfels bewegt
(Bild I-5). Die dabei im Leiter induzierte elektrische
~ ist nach dem Induktionsgesetz das VekFeldstärke E
torprodukt aus dem Geschwindigkeitsvektor ~
v und
~ der magnetischen Flussdichte.
dem Vektor B
I 15
a) Bestimmen Sie die Komponenten und den Betrag
~.
des Feldstärkevektors E
z
B
1
Raumdiagonale
v
Leiter
1
y
1
x
Würfel der
Kantenlänge a = 1
Bild I-5
b) Unter welchem Winkel j gegenüber dem Magnetfeld bewegt sich der Leiter?
a) Es gilt:
0 1
0
B C
B C
~
B ¼ @ 0 A ¼ B0 @ 0 A
1
B0
0
~¼ ~
~ mit
E
vB
0
1
e
und ~
v ¼ v0~
Dabei ist ~
e der Einheitsvektor in Richtung der Raumdiagonale des Würfels. Wegen der Symmetrie müssen die drei
Vektorkoordinaten von ~
e übereinstimmen:
0 1
c
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
pffiffiffi
B C
e j ¼ c 2 þ c 2 þ c 2 ¼ c 3 ¼ 1 ) c ¼ 1= 3
e ¼ @ c A mit j~
ex ¼ ey ¼ ez ¼ c ) ~
c
1
pffiffiffi
0 1
0 1
1= 3
1
1
B pffiffiffi C
v0 B C
1 B C
C
B
~
v ¼ v0~
e ¼ @ 1= 3 A ¼ pffiffiffi @ 1 A und ~
e ¼ pffiffiffi @ 1 A
pffiffiffi
3
3
1
1
1= 3
0
478
I Vektorrechnung
Damit erhalten wir den folgenden elektrischen Feldstärkevektor:
0 1
1
1
0 1
0 1
0
0
0 1
0
1
1
10
1
0
v0 B C
v
B
v
B
v
B
0 0 B C
0 0 B
0 0 B
B C
C
C
C
~¼ ~
~ ¼ pffiffiffi @ 1 A B 0 B
E
vB
@ 0 A ¼ pffiffiffi @ 1 A @ 0 A ¼ pffiffiffi @ 0 1 A ¼ pffiffiffi @ 1 A
3
3
3
3
1
1
1
00
0
1
Skalare Komponenten der elektrischen Feldstärke:
v0 B0
E x ¼ pffiffiffi ;
3
v0 B0
E y ¼ E x ¼ pffiffiffi ;
3
Ez ¼ 0
Betrag der elektrischen Feldstärke:
v0 B0
~j ¼ p
E ¼ jE
ffiffiffi
3
rffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
v
B
2
0
0
2
1 2 þ ð 1Þ þ 0 2 ¼ pffiffiffi
2 ¼
v0 B0
3
3
~ eingeschlossene Winkel. Wir erhalten ihn über
b) der gesuchte Winkel j ist der von den Vektoren ~
v bzw. ~
e und B
das skalare Produkt dieser Vektoren:
~ ¼ j~
~j cos j ¼ 1 B 0 cos j ¼ B 0 cos j
~
eB
ej jB
)
0 1
0 1
0 1 0 1
1
0
0
1
B C
C
B0 B C B C
B0
B0
1 B
B
C
B
B
C
B
C
~
e B ¼ pffiffiffi @ 1 A B 0 @ 0 A ¼ pffiffiffi @ 1 A @ 0 C
B 0 cos j ¼ ~
A ¼ pffiffiffi ð0 þ 0 þ 1Þ ¼ pffiffiffi
3
3
3
3
1
1
1
1
B0
I 16
B0
cos j ¼ pffiffiffi
3
)
1
cos j ¼ pffiffiffi
3
)
j ¼ arccos
1
pffiffiffi
3
)
!
¼ 54,74
Eine Ladung q bewegt sich mit der Geschwindigkeit ~
v durch ein elektromagnetisches Feld mit
~ und der magnetischen Flussdichte B
~ und erfährt dort die Kraft
der elektrischen Feldstärke E
~
~
~
ð
Þ
F ¼ qE þ q ~
v B . Bestimmen Sie für
0
1
0
1
0
1
0
100
2
C V
C Vs
B
C m
~¼ B
~¼ B
E
v ¼ @ vy A
; B
@ 300 A
@ 1 A 2 und ~
m
s
m
300
vz
1
die Geschwindigkeitskomponenten v y und v z so, dass die Bewegung kräftefrei erfolgt.
~¼~
Aus der Bedingung F
0 erhalten wir folgende Vektorgleichung
~ ¼ qE
~ þ q ð~
~Þ ¼ ~
~ þ ð~
~Þ ¼
F
vB
0 : q ) E
vB
1 0
0
1
1 0
1
0
vy vz
2
0
100
C B
B
C
C B
C
B
B v y C B 1 C ¼ B 2 v z þ 100 C ¼ B 300 C
A @
@
A
A @
A
@
100 2 v y
1
300
vz
(Rechnung ohne Einheiten):
~
0
~Þ ¼ E
~ )
oder ð~
vB
1
1 0
0
vy vz
0
C
C B
B
C
C B
) B
@ 2 v z þ 100 A ¼ @ 300 A
100 2 v y
300
Komponentenweise Schreibweise führt zu einem leicht lösbaren linearen Gleichungssystem mit drei Gleichungen für
die beiden unbekannten Geschwindigkeitskomponenten v y und v z :
ðIÞ
vy vz ¼ 0
)
vz ¼ vy
ðIIÞ
2 v z þ 100 ¼ 300
)
2 v z ¼ 200
ðIIIÞ 100 2 v y ¼ 300
)
2 v y ¼ 200
)
)
v z ¼ 100
v y ¼ 100
Lösung: v x ¼ 100 m=s ðbereits vorgegebenÞ, v y ¼ 100 m=s, v z ¼ 100 m=s
2 Anwendungen
I 17
479
Eine Ladung q, die sich mit der Geschwindigkeit ~
v durch ein homogenes Magnetfeld mit der magne~
~ ¼ q ð~
~Þ .
tischen Flussdichte B bewegt, erfährt dort die sog. „Lorentzkraft“ F
vB
a) Wann erfolgt die Bewegung kräftefrei?
b) Zeigen Sie: Das Magnetfeld verrichtet an der Ladung keine Arbeit.
~ ¼ q ð~
~Þ ¼ ~
~ verschwinden muss. Dies ist
a) Aus F
vB
0 folgt wegen q 6¼ 0, dass das Vektorprodukt ~
vB
~ kollinear sind, d. h. entweder parallel oder antiparbekanntlich genau dann der Fall, wenn die Vektoren ~
v und B
allel verlaufen.
Folgerung: Die Ladung q bewegt sich kräftefrei, wenn sie in Richtung des Feldes oder in der Gegenrichtung in
~ sind parallel bzw. antiparallel, siehe Bild I-6).
das Magnetfeld eintritt (die Vektoren ~
v und B
Bild I-6
b) Die Bahnkurve der Ladung q im Magnetfeld lässt sich durch einen zeitabhängigen Ortsvektor ~
r ¼~
r ðtÞ beschreiben. Die nderung des Ortsvektors in dem kleinen Zeitintervall d t beträgt dann d ~
r ¼~
v d t (Bild I-7). Die auf
die Ladung bei dieser Verschiebung um d ~
r einwirkende Lorentzkraft verrichtet dabei definitionsgemäß die folgende
~ und dem Verschiebungsvektor d ~
Arbeit d W (die Arbeit d W ist das Skalarprodukt aus dem Kraftvektor F
r ):
~ d~
~Þ ~
dW ¼ F
r ¼ q ð~
vB
v dt ¼
Nullpunkt
~Þ q d t ¼ ½ ~
~ q d t ¼ 0
¼~
v ð~
vB
v~
vB
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
~
½~
v~
v B
0
v
dr = v dt
r
Bild I-7
q
Ein Spatprodukt mit zwei gleichen Vektoren verschwindet bekanntlich. Dies aber bedeutet, dass das Magnetfeld
keine Arbeit an der Ladung verrichtet und zwar unabhängig von der Geschwindigkeit ~
v der Ladung.
2 Anwendungen
In diesem Abschnitt finden Sie ausschließlich anwendungsorientierte Aufgaben zu folgenden Themen:
Geraden (vektorielle Parameterdarstellung, Richtungsvektor, Abstand Punkt-Gerade, Abstand paralleler Geraden, windschiefe Geraden, Schnittpunkt und Schnittwinkel von Geraden)
Ebenen (vektorielle Parameterdarstellung, Koordinatendarstellung, Richtungsvektoren, Normalenvektor, Abstand Punkt-Ebene, Abstand Gerade-Ebene, Abstand paralleler Ebenen, Schnittpunkt und Schnittwinkel mit
einer Geraden, Schnittgerade und Schnittwinkel mit einer Ebene)
Arbeit einer Kraft an Massen und elektrischen Ladungen in Kraftfeldern
Geschwindigkeits- und Beschleunigungsvektor von Massen und elektrischen Ladungen
Lehrbuch: Band 1, Kapitel II.4
Formelsammlung: Kapitel II.4
480
I Vektorrechnung
I 18
Wie lautet die Vektorgleichung der Geraden g durch den Punkt P 1 ¼ ð1; 5; 10Þ parallel zum Vektor
1
0
2
C
B
~
a ¼ @ 1 A ? Welche Punkte gehören zu den Parameterwerten l ¼ 3, l ¼ 5 und l ¼ 10?
2
Bestimmen Sie ferner alle auf der Geraden g gelegenen Punkte, die von P1 den Abstand d ¼ 6
haben.
Ansatz der Geradengleichung in der Punkt-Richtungs-Form mit dem
tungsvektor der Geraden):
0 1
0
1
0 1
1
2
1
B C
B
C
B C
C
B
C
B C
a ¼ B
g: ~
r ðlÞ ¼ ~
r1 þ l~
@ 5A þ l @1A ¼ @ 5A þ
10
2
10
Parameter l 2 R (der Vektor ~
a ist der Rich0
2l
1
0
1 þ 2l
1
B
C
B
C
BlC ¼ B 5 lC
@
A
@
A
2l
10 þ 2 l
Ortsvektoren für die Parameterwerte l ¼ 3, l ¼ 5 und l ¼ 10:
0 1
1
0
1
0
1
0
11
1 þ 10
5
16
B C
C
B
C
B
C
B
B C
C
C
B
C
~
r ðl ¼ 5Þ ¼ B
r ðl ¼ 3Þ ¼ B
@ 5 5 A ¼ @ 0 A;
@ 5 þ 3A ¼ @ 8A; ~
20
10 þ 10
4
10 6
0
1 þ 20
0
1
21
1
B
C
C
B
B
C
C
~
r ðl ¼ 10Þ ¼ B
@ 5 10 A ¼ @ 5 A
30
10 þ 20
Koordinaten der zugehörigen Punkte: ð 5; 8; 4Þ, ð11; 0; 20Þ, ð21; 5; 30Þ
Aus Bild I-8 entnehmen wir, dass es genau zwei Punkte Q 1
und Q 2 auf der Geraden g gibt, die vom Punkt P 1 den
Abstand d ¼ 6 haben. Daher gilt:
!
!
P Q ¼ P
¼ j l~
aj ¼ d ¼ 6
1
1
1 Q2
j l~
a j ¼ j l j j~
a j ¼ jlj
Q2
P1
Q1
g
d=6
d=6
Bild I-8
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 2 þ ð 1Þ 2 þ 2 2 ¼ j l j 3 ¼ 6
)
jlj ¼ 2
)
l 1=2 ¼ 2
Zur Erinnerung: Die Betragsgleichung j x j ¼ c > 0 hat zwei Lösungen x 1=2 ¼ c.
Wir bestimmen noch die Ortsvektoren
0
1
B
~
r ðl 1 ¼ 2Þ ¼ B
r ðQ 1 Þ ¼ ~
@ 5
10
der zugehörigen Punkte:
1
0
1
0
1
0 1
þ4
5
14
3
C
B
C
B
C
B C
C
B
C
B C
2C
r ðl 2 ¼ 2Þ ¼ B
r ðQ 2 Þ ¼ ~
A ¼ @ 3A; ~
@ 5 þ 2A ¼ @ 7A
þ4
10 4
6
14
Koordinaten der zugehörigen Punkte: Q 1 ¼ ð5; 3; 14Þ, Q 2 ¼ ð 3; 7; 6Þ
I 19
Stellen Sie fest, ob die drei Punkte in einer Geraden liegen und bestimmen Sie gegebenenfalls die
Vektorgleichung der Geraden.
a)
P 1 ¼ ð3; 3; 5Þ, P 2 ¼ ð1; 2; 4Þ, P 3 ¼ ð 5; 17; 1Þ
b) A ¼ ð2; 1; 0Þ, B ¼ ð3; 4; 2Þ, C ¼ ð 1; 1; 2Þ
2 Anwendungen
481
Drei Punkte P1 , P2 und P3 liegen genau dann in einer Geraden,
!
!
wenn die Vektoren P 1 P 2 und P 1 P 3 kollinear sind und somit das
Vektorprodukt dieser Vektoren verschwindet (Bild I-9).
Gerade
P3
P2
P 1P 2
P1
P 1P 3
Bild I-9
0
a)
13
1
0
2
1
C
B
C
B
!
C
B
C
P1 P2 ¼ B
@2 3A ¼ @5A;
1
45
0
5 3
1
0
8
1
C
B
C
B
!
C
B
C
P1 P3 ¼ B
@ 17 3 A ¼ @ 20 A
4
15
0 1
0
B
C
B C
B
C
B
C
!
!
~
B
C
B C
B
C
C
P1 P2 P1 P3 ¼ B
@ 5 A @ 20 A ¼ @ 8 8 A ¼ @ 0 A ¼ 0
40 40
0
4
1
0
2
0
1
8
1
0
20 20
1
Die Vektoren sind demnach kollinear, somit liegen die drei Punkte in einer Geraden. Zum gleichen Ergebnis kommt
!
!
man, wenn man erkannt hat, dass der Vektor P 1 P 3 genau das Vierfache des Vektors P 1 P 2 ist:
0
0
1
1
0
1
2
4 ð 2Þ
8
B
B
C
C
B
C
!
!
!
!
B
B
C
C
C
P1 P3 ¼ B
@ 20 A ¼ @ 4 ð 5Þ A ¼ 4 @ 5 A ¼ 4 P 1 P 2 ) P 1 P 2 und P 1 P 3 sind kollinear
1
4 ð 1Þ
4
|fflfflffl{zfflfflffl}
!
P1 P2
Geradengleichung in der Parameterform (Zwei-Punkte-Form)
0 1
0
1
0 1
0
1
0
1
3
13
3
2
3 2l
B C
B
C
B C
B
C
B
C
C
B
C
B C
B
C
B
C
~
r ðlÞ ¼ ~
r 1 þ l ð~
r2 ~
r 1Þ ¼ B
@3A þ l@2 3A ¼ @3A þ l@5A ¼ @3 5lA
5
45
5
1
5 l
!
!
b) Wir prüfen, ob die Vektoren AB und AC kollinear sind, d. h. in einer Geraden liegen:
1
0
1
0
0 1
1
0
3
1 2
1
32
C
B
C
B
B C
C
B
!
!
C
B
C
B
B C
C
AB ¼ B
@ 4 1 A ¼ @ 3 A ; AC ¼ @ 1 1 A ¼ @ 0 A
2
20
2
20
0
1
0 1
0 1
0
1
0
1
60
3
1
0
6
B
C
B C
B C
B
C
B
C
!
!
B
C
C
B C
~
B
C
B
C
AB AC ¼ B
@ 3 A @ 0 A ¼ @ 6 2 A ¼ @ 8 A 6¼ @ 0 A ¼ 0
2
2
0þ9
9
0
Die Vektoren sind nichtkollinear, d. h. die Punkte A, B und C liegen nicht in einer (gemeinsamen) Geraden.
I 20
Von einer Geraden g ist der Punkt P 1 ¼ ð2; 2; 1Þ und der Richtungsvektor ~
a mit den skalaren
Vektorkomponenten a x ¼ 1, a y ¼ 2 und a z ¼ 5 bekannt. Welchen Abstand besitzt der Punkt
A ¼ ð5; 10; 3Þ bzw. B ¼ ð 1; 8; 14Þ von dieser Geraden?
482
I Vektorrechnung
Gleichung der Geraden in der Punkt-Richtungs-Form
0 1
0
1
2
1
B C
B
C
C
B
C
g: ~
r ðlÞ ¼ ~
r 1 þ l~
a ¼ B
@2A þ l@2A ¼
1
5
0 1
0
1
0
1
2
l
2þ l
B C
B
C
B
C
B2C þ B2lC ¼ B2 2lC
@ A
@
A
@
A
1
5l
1 þ 5l
ðl 2 RÞ
Abstand d des Punktes A von der
0
1
1
B
C
~
a ð~
rA ~
r 1Þ ¼ @ 2 A
Geraden g (! FS: Kap. II.4.2.3)
0
1
0
1
0 1
0
1
0
1
52
1
3
4 40
44
B
C
B
C
B C
B
C
B
C
@ 10 2 A ¼ @ 2 A @ 8 A ¼ @ 15 2 A ¼ @ 13 A
5
31
5
2
8þ 6
14
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
r 1 Þ j ¼ ð 44Þ 2 þ 13 2 þ 14 2 ¼ 2301 ; j ~
j~
a ð~
rA ~
a j ¼ 1 2 þ ð 2Þ 2 þ 5 2 ¼ 30
d ¼
j~
a ð~
rA ~
r 1Þ j
j~
aj
pffiffiffiffiffiffiffiffiffiffi
2301
¼ pffiffiffiffiffi ¼ 8,758
30
Abstand d des Punktes B von der
0
1
1
B
C
~
a ð~
rB ~
r 1Þ ¼ @ 2 A
5
r 1Þ j ¼ j ~
0 j ¼ 0;
j~
a ð~
rB ~
Geraden g
0
1
0
1
0
1
0
1
0 1
1 2
1
3
30 30
0
B
C
B
C
B
C
B
C
B C
8 2A ¼ @ 2A @
6 A ¼ @ 15 þ 15 A ¼ @ 0 A ¼ ~
0
@
14 1
5
15
6 6
0
j~
aj ¼
pffiffiffiffiffi
30
)
d ¼
j~
a ð~
rB ~
r 1Þ j
j~
aj
0
¼ pffiffiffiffiffi ¼ 0
30
Der Punkt B liegt somit auf der Geraden.
I 21
0 1
1
B C
Gegeben sind zwei Geraden g1 und g2 mit dem gemeinsamen Richtungsvektor ~
a ¼ @ 3 A. Die Gerade
g1 enthält den Punkt P 1 ¼ ð5; 2; 3Þ, die Gerade g2 den Punkt P 2 ¼ ð1; 1; 8Þ.
2
Welchen Abstand haben diese Geraden voneinander?
Bestimmen Sie ferner einen Normalenvektor der von den Geraden g 1 und g 2 aufgespannten Ebene E .
Für die Berechnung des Abstandes
und ~
a (! FS: Kap. II.4.2.4):
0 1
1
B C
B
~
r 1Þ ¼ @ 3 C
a ð~
r2 ~
A
2
j~
a ð~
r2 ~
r 1Þ j ¼
d ¼
0
1
1
0
1
0
0 1
21
15 þ 6
4
1
B
C
C
B
B
C
B C
C
B
B 1 2 C ¼ B 3 C B 3 C ¼ B 8 5 C ¼ B 13 C
@
A
A
@
@
A
@ A
A
@
9
3 þ 12
5
2
83
0
15
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
21 2 þ ð 13Þ 2 þ 9 2 ¼ 691 ;
j~
a ð~
r2 ~
r 1Þ j
j~
aj
d der parallelen Geraden benötigen wir die Beträge der Vektoren ~
a ð~
r2 ~
r 1Þ
j~
aj ¼
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 þ 3 2 þ 2 2 ¼ 14
pffiffiffiffiffiffiffiffi
691
¼ pffiffiffiffiffi ¼ 7,025
14
Bestimmung eines Normalenvektors ~
n der Ebene E
Die Ebene E enthält beide Geraden und somit den Richtungsvektor ~
a sowie die Punkte P 1 und P 2 und somit den
!
!
n ist dann das Vektorprodukt aus ~
a und P 1 P 2 (bereits weiter oben
Vektor P 1 P 2 . Der gesuchte Normalenvektor ~
berechnet):
0
1
21
B
C
!
C
~
a ð~
r2 ~
n ¼~
a P1 P2 ¼ ~
r 1Þ ¼ B
@ 13 A
9
2 Anwendungen
I 22
483
Zeigen Sie, dass die Geraden g 1 und g 2 mit den Parameterdarstellungen
0 1
0
1
0
0 1
1
2
1
1
4
B C
B
C
B
B C
C
~
r1 þ l1 ~
r2 þ l2 ~
a 1 ¼ @ 1 A þ l 1 @ 3 A und ~
a2 ¼ @ 5 A þ l2 @ 0 A
r ðl 1 Þ ¼ ~
r ðl 2 Þ ¼ ~
3
1
4
3
windschief sind und berechnen Sie ihren Abstand.
a 2 ð~
a 2 6¼ ~
0 und ½ ~
a1 ~
r2 ~
r 1 Þ 6¼ 0 erfüllt sind (! FS:
Die Geraden sind windschief, wenn die Bedingungen ~
a1 ~
Kap. II.4.2.5):
0
1
0 1
0
1
0
1
0 1
1
4
9 0
9
0
B
C
B C
B
C
B
C
B C
C
B C
B
C
B
C
B C
~
~
a2 ¼ B
a1 ~
@ 3 A @ 0 A ¼ @ 16 3 A ¼ @ 13 A 6¼ @ 0 A ¼ 0
4
3
0 þ 12
12
0
1 4 ð 1 2Þ
1 4 3
r2 ~
r 1Þ ¼ 3 0
ð5 1Þ ¼ 3 0
a 2 ð~
4
½~
a1 ~
4 3
4 3 2
ð1 3Þ
Determinantenberechnung nach der Regel von Sarrus:
1 4 3 1 4
a1 ~
4 3 0 ) ½~
a 2 ð~
r2 ~
r 1 Þ ¼ 0 þ 64 þ 27 0 12 24 ¼ 55 6¼ 0
3 0
4 3 2 4 3
Die Geraden g1 und g2 sind also windschief. Ihr Abstand d beträgt (! FS: Kap. II.4.2.5):
d ¼
I 23
j ½~
a1 ~
r2 ~
r 1Þ j
a 2 ð~
j~
a1 ~
a2 j
55
55
¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffi ¼ 2,771
394
ð 9Þ 2 þ 13 2 þ 12 2
Zeigen Sie, dass sich die Geraden g1 und g2 schneiden und berechnen Sie den Schnittpunkt S und
den Schnittwinkel j.
0 1
0 1
5
1
B C
B C
B C
C
r ðl 1 Þ ¼ ~
r1 þ l1 ~
a1 ¼ B
g 1: ~
@ 1 A þ l1 @ 1 A
4
4
0 1
0 1
5
0
B C
B C
C
B C
r ðl 2 Þ ¼ ~
r2 þ l2 ~
a2 ¼ B
g 2: ~
@ 4 A þ l2 @ 3 A
6
2
a 2 6¼ ~
0 und
Die beiden Geraden schneiden sich genau dann in einem Punkt S, wenn die Bedingungen ~
a1 ~
½~
a1 ~
a 2 ð~
r2 ~
r 1 Þ ¼ 0 erfüllt sind (! FS: Kap. II.4.2.6):
1
1
0
0
0 1
0 1
10
1
0
2 12
C
C
B
B
B C
B C
C
C
B
C
B
B C
~
a1 ~
a2 ¼ B
@ 1 A @ 3 A ¼ @ 0 2 A ¼ @ 2 A 6¼
3
3 0
4
2
0 1
0
B C
B0C ¼ ~
0
@ A
0
484
I Vektorrechnung
1
a 2 ð~
½~
a1 ~
r2 ~
r 1Þ ¼ 1
4
0 ð5 5Þ
3 ð4 1Þ
2 ð6 4Þ
1
¼ 1
4
¼ 0
2 2
""
0
3
identische Spalten
0
3
)
Determinante ¼ 0
Die Geraden kommen also zum Schnitt.
Berechnung des Schnittpunktes S ¼ ðx S ; y S ; z S Þ
Der Schnittpunkt S liegt sowohl auf g1 als auch auf g2 . Somit gilt für den zugehörigen Ortsvektor ~
rS die folgende
Bedingung:
0 1
0 1
0 1
0 1
5
1
0
5
B C
B C
B C
B C
B C
B C
B C
C
~
a1 ¼ ~
a2 ) B
r1 þ l1 ~
r2 þ l2 ~
rS ¼ ~
@ 1 A þ l1 @ 1 A ¼ @ 4 A þ l2 @ 3 A
6
4
2
4
Wir formen diese Vektorgleichung noch geringfügig um:
0 1
0 1 0 1 0 1 0 1
1
0
5
5
0
B C
B C B C B C B C
B C B C B C B C
C
l1 B
@ 1 A l2 @ 3 A ¼ @ 4 A @ 1 A ¼ @ 3 A
4
2
4
6
2
0
)
1
0
1
0
1
0 1
0
B
C B
C B
C B C
B l1 C þ B 3 l2 C ¼ B l1 3 l2 C ¼ B 3 C
@
A @
A @
A @ A
4 l1
2 l2
4 l1 2 l2
2
l1
0
l1
Die Komponentenschreibweise führt zu einem leicht lösbaren gestaffelten linearen Gleichungssystem mit den beiden
unbekannten Parametern l1 und l2 :
ðIÞ
l1 ¼ 0
)
ðIIÞ
l1 3 l2 ¼ 3
)
ðIIIÞ 4 l 1 2 l 2 ¼ 2
)
l1 ¼ 0
ðEinsetzen in ðIIÞ bzw: ðIIIÞÞ
)
0 3 l2 ¼ 3
) l2 ¼ 1
0 2 l2 ¼ 2
Der Ortsvektor des Schnittpunktes S lautet demnach (berechnet aus der Gleichung der Geraden g1 für l 1 ¼ 0):
0 1
0 1
0 1
5
1
5
B C
B C
B C
C
B C
B C
r1 þ l1 ~
a1 ¼ B
~
rS ¼ ~
@1A þ 0 @1A ¼ @1A
4
4
4
)
S ¼ ð5; 1; 4Þ
Kontrolle (Berechnung des Ortsvektors ~
r S aus der Gleichung der zweiten Geraden g 2 für l 2 ¼ 1):
0 1
0 1
0 1
0 1
0
1
0 1
5
0
5
0
50
5
B C
B C
B C
B C
B
C
B C
C
B C
B C
B C
B
C
B C
~
rS ¼ ~
a2 ¼ B
r2 þ l2 ~
@4A 1 @3A ¼ @4A @3A ¼ @4 3A ¼ @1A
6
2
6
2
62
4
Berechnung des Schnittwinkels j
a2 . Wir erhalDefinitionsgemäß ist der Schnittwinkel j der Winkel zwischen den beiden Richtungsvektoren ~
a1 und ~
ten ihn über das Skalarprodukt dieser Vektoren:
~
a1 ~
a2 ¼ j~
a1 j j~
a 2 j cos j
)
cos j ¼
0 1 0 1
1
0
B C B C
C B C
~
a2 ¼ B
a1 ~
@ 1 A @ 3 A ¼ 0 þ 3 þ 8 ¼ 11
4
2
~
a2
a1 ~
j~
a1 j j~
a2 j
2 Anwendungen
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
1 2 þ 1 2 þ 4 2 ¼ 18 ;
j~
a1 j ¼
cos j ¼
I 24
485
~
a2
a1 ~
j~
a1 j j~
a2 j
j~
a2 j ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
0 2 þ 3 2 þ 2 2 ¼ 13
11
¼ pffiffiffiffiffi pffiffiffiffiffi ¼ 0,7191
18 13
)
j ¼ arccos 0,7191 ¼ 44,02
Welcher der drei Punkte A, B und C liegen auf der in der vektoriellen Parameterform vorliegenden
Geraden g?
0
1
0 1
0
1
1 2l
2
1
B
C
B C
B
C
B
C
C
B
C
ðmit l 2 RÞ
a ¼ B
g: ~
r ðlÞ ¼ ~
r1 þ l~
@2A þ l @ 1A ¼ @2 þ lA
4 þ 2l
4
2
A ¼ ð4; 1; 2Þ ;
B ¼ ð7; 1; 2Þ ;
C ¼ ð 15; 10; 20Þ
Es gibt verschiedene Möglichkeiten festzustellen, ob ein Punkt P auf einer Geraden g liegt oder nicht. Der Punkt
!
A ¼ ð4; 1; 2Þ beispielsweise liegt genau dann auf g , wenn die Vektoren P 1 A und ~
a kollinear sind (in einer Linie
!
!
~
a und somit P 1 A ~
a ¼ 0 ist (siehe Bild I-10). Dies ist hier nicht der Fall:
liegen), d. h. P 1 A ¼ l ~
0
41
0
1
3
1
A
B
C
B
C
!
B
C
C
P1 A ¼ B
@1 2A ¼ @1A
2
24
0
3
1
0
B
C
B
!
C
B
P1 A ~
a ¼ B
@1A @
2
2
1
0
C
B
B
1C
A ¼ @
2
2 þ 2
a
1
C
4 6C
A ¼
0
A
P1
P1
32
Bild I-10
0 1
0
B C
B
C
B C
~
C
¼ B
@ 2 A 6¼ @ 0 A ¼ 0
0
1
0
g
1
Der Punkt A liegt somit nicht auf der Geraden g.
Bei den Punkten B und C wollen wir einen anderen Lösungsweg einschlagen. Wenn B auf der Geraden g liegt,
dann gehört zu B ein eindeutiger Parameterwert l der Geradengleichung. Wir erhalten ein lineares Gleichungssystem
mit drei Gleichungen für den noch unbekannten Parameter l:
9
8
0
1
0
1
1 2l
ðIÞ 1 2 l ¼ 7 >
7
>
>
>
=
<
B
C
B
C
B
C
B
C
~
) l ¼ 3
ðIIÞ 2 þ l ¼ 1
r1 þ l~
a ) @1A ¼ @2 þ lA )
rB ¼ ~
>
>
>
>
;
:
ðIIIÞ 4 þ 2 l ¼ 2
4 þ 2l
2
Alle drei Gleichungen liefern den selben Wert l ¼ 3, d. h. der Punkt B liegt auf der Geraden g.
Ebenso gehen wir beim Punkt C vor:
0
1
0
1
15
1 2l
B
C
B
C
C
B
C
~
rC ¼ ~
r1 þ l~
a ) B
@ 10 A ¼ @ 2 þ l A
20
4 þ 2l
)
8
9
ðIÞ 1 2 l ¼ 15 >
>
>
>
<
=
ðIIÞ 2 þ l ¼ 10
>
>
>
>
:
;
ðIIIÞ 4 þ 2 l ¼ 20
Auch Punkt C liegt auf der Geraden g.
Ergebnis: Die Punkte B und C liegen auf der Geraden g, Punkt A dagegen nicht.
)
l ¼ 8
486
I Vektorrechnung
Gegeben ist eine Gerade g mit der folgenden vektoriellen Parameterdarstellung (alle Koordinaten in der
Einheit m ¼ Meter):
0 1
0 1
0
1
4
1
4þ l
B C
B C
B
C
C
B C
B
C
g: ~
r ðlÞ ¼ ~
r1 þ l~
a ¼ B
ðmit l 2 RÞ
@1A þ l @2A ¼ @1 þ 2lA
I 25
2
2þ
1
l
~ mit den Kraftkomponenten F x ¼ 8 N, F y ¼ 2 N
Eine Masse wird durch die konstante Kraft F
und F z ¼ 10 N längs dieser Geraden vom Punkt A aus nach B verschoben. Diese Punkte sind
durch die Parameterwerte l ¼ 2 (Punkt A ) und l ¼ 10 (Punkt B ) festgelegt. Welche Arbeit W
wird dabei an der Masse verrichtet? Wie groß ist der Winkel j zwischen der Kraft und dem Verschiebungsvektor?
!
Der Verschiebungsvektor ~
s ¼ AB lässt sich aus den Ortsvektoren der Punkte A und B wie folgt bestimmen (siehe
Bild I-11; alle Vektorkoordinaten in m):
1
0 1
0
6
4þ2
B
C
B C
B
g
F
C ¼ B5C
~
r ðAÞ ¼ ~
r ðl ¼ 2Þ ¼ B
1
þ
4
A
@ A
@
4
2þ2
0
A
1
0
1
4 þ 10
14
B C
B
C
B C
C
~
r ðBÞ ¼ ~
r ðl ¼ 10Þ ¼ B
@ 1 þ 20 A ¼ @ 21 A
12
2 þ 10
0
s
Bild I-11
0 1
6
B C
B C
!
B C
C
~
s ¼ AB ¼ ~
r ðBÞ ~
r ðAÞ ¼ B
@ 21 A @ 5 A ¼
12
4
14
f
1
0
14 6
1
0
8
1
B C
B
C
B 21 5 C ¼ B 16 C
@ A
@
A
8
12 4
~ bei der Verschiebung der Masse von A nach B verrichtete Arbeit W ist (definitionsgemäß) das
Die von der Kraft F
Skalarprodukt aus dem Kraft- und dem Verschiebungsvektor:
0
8
1
0
8
1
0
8
1
0
8
1
B
C
B C
B
C B C
C
B C
B
C B C
~~
W ¼ F
s ¼ B
@ 2 A N @ 16 A m ¼ @ 2 A @ 16 A Nm ¼ ð64 32 þ 80Þ Nm ¼ 112 Nm
10
8
10
8
~ und ~
Auch die Winkelberechnung erfolgt über dieses Skalarprodukt, wobei wir noch die Beträge der Vektoren F
s
benötigen:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
~j ¼ 8 2 þ ð 2Þ 2 þ 10 2 N ¼ 168 N ; j~
s j ¼ 8 2 þ 16 2 þ 8 2 m ¼ 384 m
jF
~~
~j j~
F
s ¼ W ¼ jF
s j cos j
)
cos j ¼
W
112 N m
¼ pffiffiffiffiffiffiffiffi
¼ 0,4410
pffiffiffiffiffiffiffiffi
~j j~
jF
sj
168 N 384 m
)
j ¼ arccos 0,4410 ¼ 63,83
Ergebnis: Arbeit W ¼ 112 N m; Winkel zwischen dem Kraft- und dem Verschiebungsvektor: j ¼ 63,83
2 Anwendungen
I 26
487
~ wird eine Ladung q längs einer
In einem homogenen elektrischen Feld mit dem Feldstärkevektor E
Geraden g vom Punkt A aus nach B verschoben. Berechnen Sie die dabei vom Feld verrichtete
Arbeit W sowie den Winkel j zwischen dem Kraft- und dem Verschiebungsvektor.
1
0
1
0
5
1 þ 2l
C V
B
C
B
9
C
B
C
~
g: ~
r ðlÞ ¼ B
As
@ 1 þ l A ðin m ; l 2 RÞ ; E ¼ @ 2 A m ; q ¼ 10
1
1 þ 2l
Ortsvektoren von A und B: ~
r ðAÞ ¼ ~
r ðl ¼ 2Þ; ~
r ðBÞ ¼ ~
r ðl ¼ 3Þ
Wir bestimmen zunächst die Ortsvektoren der Punkte A und B und
!
~
s ¼ AB (Bild I-12):
1 0
0
1
3
14
C B
B
C
C B
C
~
r ðAÞ ¼ ~
r ðl ¼ 2Þ ¼ B
@ 1 2 A ¼ @ 1 A ðin mÞ
3
14
0
1 0 1
1þ6
7
B
C B C
C B C
~
r ðBÞ ¼ ~
r ðl ¼ 3Þ ¼ B
@ 1 þ 3 A ¼ @ 4 A ðin mÞ
1þ6
7
1
1
0
0 1
0
7þ3
3
7
C
C
B
B C
B
!
C
C
B
C
B
~
s ¼ AB ¼ ~
r ðBÞ ~
r ðAÞ ¼ B
@4A @1A ¼ @4 þ 1A ¼
7þ3
3
7
daraus den benötigten Verschiebungsvektor
E
B
g
A
f
s
Bild I-12
0
10
1
B C
B 5C
@ A
10
ðin mÞ
Die auf die Ladung q ¼ 10 9 As im elektrischen Feld einwirkende Kraft beträgt:
1
1
1
0
0
0
5
5
5
C
C
C
B
B
B
~ ¼ qE
~ ¼ 10 9 As B 2 C V ¼ 10 9 B 2 C V A s ¼ 10 9 B 2 C N
F
A m
A
A m
@
@
@
1
1
1
Umrechnung der Einheiten: 1 V A s ¼ 1 W s ¼ 1 N m
)
1
VAs
¼ 1N
m
Die vom elektrischen Feld an der Ladung verrichtete Arbeit W erhält
Kraft- und Verschiebungsvektor:
0 1
0
1
0
1
10
5
5
B C
B
C
B
C
9 B
B C
C
C
~~
W ¼ F
s ¼ 10 9 B
@ 2 A N @ 5 A m ¼ 10
@2A
10
1
1
man definitionsgemäß als Skalarprodukt aus
0
10
1
B C
B 5C Nm ¼
@ A
10
¼ 10 9 ð50 10 þ 10Þ N m ¼ 50 10 9 N m ¼ 5 10 8 N m
Den Winkel j zwischen dem Kraft- und dem Verschiebungsvektor erhalten wir aus dem Skalarprodukt dieser Vektoren wie folgt:
~~
~j j~
F
s ¼ W ¼ jF
s j cos j
)
cos j ¼
W
~j j~
jF
sj
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
F
~ ¼ 5 2 þ ð 2Þ 2 þ 1 2 10 9 N ¼ 30 10 9 N;
cos j ¼
j~
sj ¼
W
5 10 8 N m
10
¼ pffiffiffiffiffi
¼ pffiffiffiffiffi ¼ 0,6086
9
~j j~
jF
sj
30 10
N 15 m
3 30
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
10 2 þ 5 2 þ 10 2 m ¼ 225 m ¼ 15 m
)
j ¼ arccos 0,6086 ¼ 52,51
Ergebnis: Arbeit W ¼ 5 10 8 N m; Winkel zwischen dem Kraft- und dem Verschiebungsvektor: j ¼ 52,51
488
I Vektorrechnung
I 27
Die Drehachse eines starren Körpers liegt in der Geraden g mit der vektoriellen Parameterdarstellung
0 1
0
1
1
1
B C
B
C
C
B
C
~
a ¼ B
r ðlÞ ¼ ~
r1 þ l~
ðalle Koordinaten in cm ; l 2 RÞ
@0A þ l@1A
1
1
~j ¼ w ¼
Der Körper rotiert um diese Achse mit der (konstanten) Winkelgeschwindigkeit j w
pffiffiffi
1
v des Körperpunktes Q ¼ ð2; 1; 2Þ cm.
¼ 10 3 s . Bestimmen Sie den Geschwindigkeitsvektor ~
~~
Anleitung: Es gilt ~
v ¼ w
r . Dabei ist ~
r der Ortsvektor von Q, von einem beliebigen Punkt der
~ der Vektor der Kreisfrequenz (~
Drehachse aus gemessen und w
w liegt in der Drehachse).
Wir führen gemäß Bild I-13 die folgenden Bezeichnungen ein:
g:
Drehachse (Gerade)
P0 :
Bezugspunkt auf der Drehachse (siehe weiter unten)
~
r0 :
Ortsvektor von P0
~
rQ :
Ortsvektor von Q
O:
Nullpunkt des räumlichen Koordinatensystems
g
starrer Körper
v
P0
r
r0
Q
rQ
g
Bild I-13
O
Den auf der Drehachse g liegenden Bezugspunkt P0 legen wir (willkürlich) durch den Parameterwert l ¼ 0 fest
(sie können auch einen anderen Bezugspunkt wählen). Sein Ortsvektor lautet damit:
0 1
0
1
0 1
0 1
0 1
1
1
1
0
1
B C
B
C
B C
B C
B C
C
B C
B
C
B C
B C
~
r ðl ¼ 0Þ ¼ B
r0 ¼ ~
ðin cmÞ
@0A þ 0@1A ¼ @0A þ @0A ¼ @0A
1
1
1
0
1
!
Wir bestimmen aus Bild I-13 den benötigten Verbindungsvektor ~
r ¼ P 0 Q:
1
0
0 1
0 1
0 1
1
2
1
21
C
B
B C
B C
B C
C
C
B
B C
B C
~
ðin cmÞ
r0 þ ~
r ¼~
rQ ) ~
r ¼~
rQ ~
r0 ¼ B
@1A @0A ¼ @1 0A ¼ @1A
21
1
2
1
pffiffiffi 1
~ vom Betrag w ¼ 10 3 s
Der Kreisfrequenzvektor w
liegt in der Drehachse und ist somit zum Richtungsvektor ~
a
der Geraden g parallel. Durch Normierung von ~
a erhalten wir den benötigten Einheitsvektor ~
e gleicher Richtung:
1
1
0
0
1
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
q
pffiffiffi
C
C
B
1
1 B
~
~
e ¼
und j ~
a j ¼ 1 2 þ ð 1Þ 2 þ 1 2 ¼ 3 ) ~
1C
a mit ~
a ¼ B
1C
e ¼ pffiffiffi B
A
A
@
@
j~
aj
3
1
1
Für den Bahngeschwindigkeitsvektor ~
v des Punktes Q auf dem starren Körper folgt dann unter Berücksichtigung
~ ¼ w~
von w
e:
~~
~
v ¼ w
r ¼ w~
e~
r ¼ w ð~
e~
rÞ )
0 1
1
0
1
0
1
1
0
0
1
1 1
2
20
1
pffiffiffi
B C
C cm
B
C cm
B
C cm
C
B
1 B
1
B C
C
B
C
B
C
~
v ¼ 10 3 pffiffiffi B
¼ 10 B
0C
@ 1 1 A s ¼ 10 @ 0 A s ¼ @
@ 1 A @ 1 A cm s
A s
3
1
1þ1
2
20
1
(Man beachte die Einheiten: w in s 1 , ~
r in cm, ~
e ist dimensionslos
)
~
v in cm=s)
2 Anwendungen
489
Komponenten des Geschwindigkeitsvektors ~
v:
v x ¼ 20 cm=s;
v y ¼ 0 cm=s;
v z ¼ 20 cm=s
Betrag der Geschwindigkeit:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
pffiffiffi
j~
v j ¼ ð 20Þ 2 þ 0 2 þ 20 2 cm=s ¼ 800 cm=s ¼ 20 2 cm=s ¼ 28,28 cm=s
I 28
Elektronen bewegen sich, wenn sie schräg in ein homogenes
Magnetfeld eintreten, auf einer schraubenlinienförmigen Bahn
mit dem zeitabhängigen Ortsvektor
0
1
R cos ðw tÞ
B
C
C
~
r ðtÞ ¼ B
@ R sin ðw tÞ A
ct
z
Richtung des
Magnetfeldes
r (t )
(w > 0: Kreisfrequenz; R: Radius; c > 0; siehe hierzu
Bild I-14).
Bestimmen Sie den Geschwindigkeitsvektor ~
v und den
Beschleunigungsvektor ~
a sowie deren Beträge.
R
y
x
Bild I-14
Die Geschwindigkeit ~
v ist die 1. Ableitung, die Beschleunigung ~
a die 2. Ableitung des Ortsvektors ~
r ¼~
r ðtÞ nach
der Zeit t, wobei komponentenweise zu differenzieren ist. Wir erhalten mit Hilfe der Kettenregel (Substitution:
u ¼ w t) und unter Verwendung des „trigonometrischen Pythagoras“ :
Geschwindigkeitsvektor v ¼ v ðtÞ
0
R cos ðw tÞ
0
1
B
C
d
d B
B R sin ðw tÞ C ¼ B
~
~
v ¼~
r ðtÞ ¼
r_ ðtÞ ¼
@
@
A
dt
dt
ct
R w sin ðw tÞ
1
C
R w cos ðw tÞ C
A
c
v2 ¼ j~
v j 2 ¼ ð R w sin ðw tÞÞ 2 þ ðR w cos ðw tÞÞ 2 þ c 2 ¼
¼ R 2 w 2 sin 2 ðw tÞ þ R 2 w 2 cos 2 ðw tÞ þ c 2 ¼
¼ R 2 w 2 ½ sin 2 ðw tÞ þ cos 2 ðw tÞ þ c 2 ¼ R 2 w 2 þ c 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
v ¼ j~
v j ¼ R 2 w 2 þ c 2 ¼ const:
Beschleunigungsvektor ~
a ¼ ~
a ðtÞ
0
d
d B
B
~
~
a ¼~
v ¼
r€ ¼ ~
v_ ¼
dt
dt @
R w sin ðw tÞ
1
0
R w 2 cos ðw tÞ
1
0
cos ðw tÞ
1
C
C
C
B
B
2B
2
C
C
B
R w cos ðw tÞ C
A ¼ @ R w sin ðw tÞ A ¼ R w @ sin ðw tÞ A
c
0
0
a2 ¼ j~
a j 2 ¼ ð R w 2 Þ 2 ðcos 2 ðw tÞ þ sin 2 ðw tÞ þ 0 2 Þ ¼ R 2 w 4
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
)
a ¼ j~
a j ¼ R w 2 ¼ const:
Folgerung: Die Elektronen bewegen sich in dem Magnetfeld auf schraubenlinienförmigen Bahnen mit (dem Betrage
nach) konstanter Geschwindigkeit und konstanter Beschleunigung.
490
I Vektorrechnung
Von einer Geraden g sind der Punkt P1 und der Richtungsvektor ~
a bekannt, von einer Ebene E der
Punkt P0 und der Normalenvektor ~
n:
0 1
0
1
2
2
B C
B
C
C
C
Gerade g : P 1 ¼ ð5; 1; 5Þ ; ~
a ¼ B
n ¼ B
@ 1 A ; Ebene E : P 0 ¼ ð1; 1; 8Þ ; ~
@ 0A
I 29
4
1
Zeigen Sie, dass Gerade und Ebene parallel verlaufen und berechnen Sie ihren Abstand.
Gerade g und Ebene E sind genau dann parallel, wenn das Skalarprodukt aus dem Normalenvektor ~
n der Ebene
und dem Richtungsvektor ~
a der Geraden verschwindet:
1 0 1
0
2
2
C B C
B
C B C
~
n~
a ¼ B
@ 0A @1A ¼ 4 þ 0 þ 4 ¼ 0 ) E k g
4
1
Abstand d zwischen g und E ( ! FS: Kap. II.4.3.5)
0
1 0
1
0
1 0
1
2
51
2
4
B
C B
C
B
C B
C
C B
C
B
C B
C
~
n ð~
r1 ~
r 0Þ ¼ B
@ 0 A @ 1 1 A ¼ @ 0 A @ 0 A ¼ 8 þ 0 3 ¼ 11
1
58
1
3
j~
nj ¼
d ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
ð 2Þ 2 þ 0 2 þ 1 2 ¼ 5
j~
n ð~
r1 ~
r 0Þ j
j~
nj
¼
j 11 j
11
pffiffiffi ¼ pffiffiffi ¼ 4,919
5
5
0 1
0
1
2
1
B C
B
C
Zeigen Sie zunächst, dass die Vektoren ~
a ¼ @ 0 A und b~ ¼ @ 1 A nichtkollinear sind und somit
3
1
I 30
zusammen mit dem Punkt P 1 ¼ ð2; 1; 3Þ in eindeutiger Weise eine Ebene E festlegen.
a) Wie lautet die Parameterdarstellung dieser Ebene?
b) Geben Sie die Koordinatendarstellung der Ebene an.
c) Welche Punkte der Ebene E gehören zu den Parameterwertepaaren
ðl; mÞ ¼ ð 3; 4Þ?
ðl; mÞ ¼ ð1; 2Þ
und
Die Vektoren ~
a und b~ sind nichtkollinear, wenn ihr Vektorprodukt nicht verschwindet. Dies ist hier der Fall:
0 1
1
1
0
0
0
1
0 1
0
03
3
1
2
B C
C
B
C
B
C
B
B C
~
B C
C
C
B
C
B
C
B
~
a b~ ¼ B
@ 0 A @ 1 A ¼ @ 3 2 A ¼ @ 5 A 6¼ @ 0 A ¼ 0
0
20
2
1
3
Die Vektoren ~
a und b~ können daher als Richtungsvektoren der Ebene E dienen, das Vektorprodukt selbst ist ein
Normalenvektor der Ebene: ~
n ¼~
a b~.
2 Anwendungen
491
a) Parameterdarstellung der Ebene E (Punkt-Richtungs-Form; l 2 R und m 2 R)
0
1
0 1
0
1
0
1
2
2
1
2 þ 2l m
B
C
B C
B
C
B
C
C
B C
B
C
B
C
~
a þ m b~ ¼ B
r ðl; mÞ ¼ r 1 þ l ~
@ 1A þ l @0A þ m @ 1A ¼ @ 1 þ m
A
3
3
1
3 þ 3l þ m
b) Koordinatendarstellung der Ebene E
0
~
a b~Þ ð~
r ~
r 1Þ ¼ 0
n ð~
r ~
r 1 Þ ¼ ð~
)
3
1
0
x 2
1
B
C B
C
B5C By 1C ¼ 0
@
A @
A
2
zþ3
)
3 ðx 2Þ 5 ð y 1Þ þ 2 ðz þ 3Þ ¼ 3 x þ 6 5 y þ 5 þ 2 z þ 6 ¼ 0
)
3 x 5 y þ 2 z þ 17 ¼ 0
c) Ortsvektoren für die Parameterwertepaare ðl; mÞ ¼ ð1; 2Þ und ðl; mÞ ¼ ð 3; 4Þ:
0
1
0 1
0
1
0
1
2þ22
2
264
8
B
C
B C
B
C
B
C
C ¼ B3C; ~
C ¼ B 5C
~
r ðl ¼ 1; m ¼ 2Þ ¼ B
r ðl ¼ 3; m ¼ 4Þ ¼ B
A
@ 1þ2
A
@ A
@ 1þ4
A
@
3 þ 3 þ 2
2
3 9 þ 4
8
Koordinaten der zugehörigen Punkte: ð2; 3; 2Þ, ð 8; 5; 8Þ
Zeigen Sie: Die drei Punkte P 1 ¼ ð5; 1; 1Þ, P 2 ¼ ð 2; 0; 3Þ und P 3 ¼ ð1; 6; 3Þ liegen in
einer Ebene E.
I 31
a) Wie lautet die Gleichung dieser Ebene in der vektoriellen Parameterform?
b) Bestimmen Sie die Koordinatendarstellung der Ebene.
c) Welche Koordinaten besitzen die in der Ebene E gelegenen Punkte, die zu den Parameterwertepaaren ðl; mÞ ¼ ð 1; 3Þ und ðl; mÞ ¼ ð2; 2Þ gehören?
r 1 und b~ ¼ ~
r3 ~
r 1 , gebildet aus
Wir zeigen zunächst mit Hilfe des Vektorproduktes, dass die Vektoren ~
a ¼~
r2 ~
den Ortsvektoren der drei Punkte P 1 , P 2 und P 3 , nichtkollinear sind und damit als Richtungsvektoren der Ebene E
geeignet sind (siehe hierzu auch Bild I-15):
0
0
1
1
0
1
Ebene E
2
5
7
B
B
C
C
B
C
B
C
C
B
C
~
a ¼~
r2 ~
r1 ¼ B
P3
@ 0A @ 1A ¼ @1A
3
1
4
b
0 1
0
1
0
1
1
4
5
B C
B
C
B
C
B
C
C
B
C
r1 ¼ B
b~ ¼ ~
r3 ~
@6A @ 1A ¼ @ 5A
3
1
4
0
7
1
0
B
B
C
B
C
~
a b~ ¼ B
@1A @
4
1
0
4 20
a
P1
P2
Bild I-15
r1
1
0
0 1
0
B
C
B
C
B C
C
B
C
B
~
B C
C
5C
A ¼ @ 16 þ 28 A ¼ @ 12 A 6¼ @ 0 A ¼ 0
39
35 4
4
0
4
r3
24
1
r2
O
492
I Vektorrechnung
Wegen ~
a b~ 6¼ ~
0 sind die Vektoren ~
a und b~ nichtkollinear. Das Vektorprodukt steht dabei bekanntlich senkrecht
~
auf der von ~
a und b aufgespannten Ebene und ist somit ein Normalenvektor dieser Ebene: ~
n ¼ ~
a b~.
a) Parameterdarstellung der Ebene E (Drei-Punkte-Form)
0
B
~
r2 ~
r 1 Þ þ m ð~
r3 ~
r 1Þ ¼ ~
r1 þ l~
a þ m b~ ¼ B
r ðl; mÞ ¼ ~
r 1 þ l ð~
@
0
B
¼ B
@
5
1
0
7l
1
0
C
C
B
B
C
B
B
1C
A þ @ lA þ @
1
4l
4m
0
1
5
0
1
7
1
0
B
C
C
B
B
C
B
1C
A þ l @1A þ m @
4
1
5 7l 4m
4
1
C
5C
A ¼
4
1
B
C
C
B
C
5mC
A ¼ @ 1 l þ 5mA
1 þ 4l þ 4m
4m
ðmit l 2 R und m 2 RÞ
b) Koordinatendarstellung der Ebene E
0
~
a b~ Þ ð~
r ~
r 1Þ ¼ 0
n ð~
r ~
r 1Þ ¼ ð ~
)
B
B
@
24
1
0
x 5
1
C
C B
C
B
12 C
A @y 1A ¼ 0
39
zþ1
)
24 ðx 5Þ þ 12 ð y 1Þ 39 ðz þ 1Þ ¼ 24 x þ 120 þ 12 y 12 39 z 39 ¼ 0
24 x þ 12 y 39 z þ 69 ¼ 0 j : ð 3Þ
B
B
~
r ðl ¼ 2; m ¼ 2Þ ¼ @
8 x 4 y þ 13 z 23 ¼ 0
ðl; mÞ ¼ ð 1; 3Þ und ðl; mÞ ¼ ð2; 2Þ:
1
0 1
12
0
C
B C
B C
15 C
A ¼ @ 17 A
12
7
c) Ortsvektoren für die Parameterwertepaare
0
5þ7
B
~
r ðl ¼ 1; m ¼ 3Þ ¼ B
@ 1þ1þ
1 4 þ
0
)
)
5 14 þ 8
1
0
1
1
C
B
C
B
C
1 2 10 C
A ¼ @ 11 A
1
1 þ 8 8
Koordinaten der zugehörigen Punkte: ð0; 17; 7Þ, ð 1; 11; 1Þ.
I 32
Bestimmen Sie die Gleichung der durch den Punkt P 1 ¼ ð5; 1; 5Þ gehenden Ebene E mit dem
0
1
1
B
C
Normalenvektor ~
n ¼ @ 2A:
1
Koordinatendarstellung der Ebene E
0
1 0
1
x 5
1
B
C B
C
C B
C
~
n ð~
r ~
r 1Þ ¼ 0 ) B
@ 2 A @ y 1 A ¼ 1 ðx 5Þ þ 2 ð y 1Þ 1 ðz 5Þ ¼ 0
1
z5
x þ 5 þ 2y 2 z þ 5 ¼ 0
)
Gleichung der Ebene: x 2 y þ z 8 ¼ 0
x þ 2y z þ 8 ¼ 0
oder
)
x 2y þ z 8 ¼ 0
2 Anwendungen
493
Der Normalenvektor ~
n einer Ebene E hat die Richtungswinkel a ¼ 120 , b ¼ 60 und g > 90 .
Wie lautet die Koordinatendarstellung dieser Ebene, die noch den Punkt P 1 ¼ ð8; 6; 8Þ enthält?
I 33
Wir müssen zunächst den Normalenvektor ~
n der Ebene bestimmen. Da seine Länge (sein Betrag) keine Rolle spielt
(solange j ~
n j 6¼ 0 ist), wählen wir j ~
n j ¼ 1 (Einheitsvektor). Der noch unbekannte Richtungswinkel g lässt sich
aus der Beziehung
cos 2 a þ cos 2 b þ cos 2 g ¼ 1
unter Beachtung der Vorgabe 90
< g < 180
und damit cos g < 0 (2. Quadrant) wie folgt bestimmen:
cos 2 g ¼ 1 cos 2 a cos 2 b ¼ 1 cos 2 120 cos 2 60 ¼ 1 ð 0,5Þ 2 0,5 2 ¼
pffiffiffiffiffiffi
pffiffiffiffiffiffi
¼ 1 0,25 0,25 ¼ 0,5 ) cos g ¼ 0,5 ) g ¼ arccos ð 0,5 Þ ¼ 135
Damit ergeben sich für den Normalenvektor ~
n folgende Vektorkomponenten:
9
0
1
0,5
nx ¼ j~
n j cos a ¼ 1 cos 120 ¼ 0,5
>
=
B
C
) ~
n ¼ @ 0,5 A
ny ¼ j~
n j cos b ¼ 1 cos 60 ¼ 0,5
>
;
0,707
n j cos g ¼ 1 cos 135 ¼ 0,707
nz ¼ j~
Koordinatendarstellung der Ebene E
0
1 0
1
0,5
x 8
B
C B
C
~
n ð~
r ~
r 1 Þ ¼ 0 ) @ 0,5 A @ y 6 A ¼ 0
0,707
z8
)
0,5 ðx 8Þ þ 0,5 ð y 6Þ 0,707 ðz 8Þ ¼ 0,5 x þ 4 þ 0,5 y 3 0,707 z þ 5,656 ¼ 0 )
0,5 x þ 0,5 y 0,707 z þ 6,656 ¼ 0 j ð 2Þ
)
x y þ 1,414 z 13,312 ¼ 0
Gleichung der Ebene: x y þ 1,414 z 13,312 ¼ 0
Eine Ebene E mit dem Normalenvektor ~
n enthält den Punkt P1 . Welchen Abstand besitzen die
Punkte A und B von dieser Ebene?
0
1
1
B
C
C
Ebene E : ~
n ¼ B
@ 1 A ; P 1 ¼ ð5; 1; 3Þ ; A ¼ ð10; 3; 8Þ ; B ¼ ð0; 2; 11Þ
1
I 34
Welche Höhenkoordinate z muss der Punkt P ¼ ð2; 4; zÞ haben, damit er in der Ebene E liegt?
Abstand d des Punktes A von der Ebene E ( ! FS: Kap. II.4.3.4):
1 0 1
1
0
1 0
0
5
1
10 5
1
C B C
C
B
C B
B
C B C
C
B
C B
~
n ð~
rA ~
r 1Þ ¼ B
@1A @ 3 þ 1A ¼ @1A @4A ¼ 5 4 þ 5 ¼ 6
5
1
83
1
j~
nj ¼
d ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
1 2 þ ð 1Þ 2 þ 1 2 ¼ 3
j~
n ð~
rA ~
r 1Þ j
j~
nj
pffiffiffi
pffiffiffi
pffiffiffi
6
6 3
6 3
¼ 2 3 ¼ 3,464
¼ pffiffiffi ¼ pffiffiffi pffiffiffi ¼
3
3
3 3
494
I Vektorrechnung
Abstand d des Punktes B von der Ebene E
0
1 0
1
0
1 0
1
1
05
1
5
B
C B
C
B
C B
C
C B
C
B
C B
C
~
r 1Þ ¼ B
n ð~
rB ~
@ 1 A @ 2 þ 1 A ¼ @ 1 A @ 3 A ¼ 5 3 þ 8 ¼ 0;
1
11 3
1
8
d ¼
j~
n ð~
rB ~
r 1Þ j
j~
nj
0
¼ pffiffiffi ¼ 0
3
)
j~
nj ¼
pffiffiffi
3
Punkt B liegt in der Ebene E :
Koordinatendarstellung der Ebene E
1
1 0
0
x 5
1
C
C B
B
~
n ð~
r ~
r 1Þ ¼ 0 ) @ 1 A @ y þ 1 A ¼ 0
z3
1
1 ðx 5Þ 1 ð y þ 1Þ þ 1 ðz 3Þ ¼ 0
Höhenkoordinate z des Punktes P ¼ ð2; 4; zÞ:
)
)
x 5y1þz3 ¼ 0
)
x yþz ¼ 9
z ¼ 9x þy ¼ 924 ¼ 3
Zeigen Sie, dass sich Gerade g und Ebene E schneiden und bestimmen Sie die Koordinaten des
I 35
Schnittpunktes S sowie den Schnittwinkel j.
0 1
0 1
2
4
B C
B C
B C
C
a ¼ B
g: ~
r ðlÞ ¼ ~
r1 þ l~
@1A þ l@1A;
5
2
0
B
E: ~
n ð~
r ~
r 0Þ ¼ B
@
1
1
0
x 1
1
C
C B
C
B
2C
A @y 1A ¼ 0
z0
1
Gerade g und Ebene E schneiden sich genau dann in einem Punkt S , wenn das skalare Produkt aus dem Normalenvektor ~
n der Ebene und dem Richtungsvektor ~
a der Geraden nicht verschwindet. Dies ist hier der Fall:
1 0 1
0
2
1
C B C
B
C B C
~
n~
a ¼ B
@ 2 A @ 1 A ¼ 2 þ 2 þ 5 ¼ 5 6¼ 0
5
1
Der Schnittpunkt S mit dem Ortsvektor ~
rS liegt sowohl auf g als auch in E. Daher gilt:
~
rS ¼ ~
r ðl S Þ ¼ ~
r1 þ lS ~
a
und
~
r 0Þ ¼ 0
n ð~
rS ~
In die zweite Gleichung setzen wir für ~
rS den Ausdruck ~
r1 þ lS ~
a ein und erhalten unter Verwendung des Distributivgesetzes für Skalarprodukte:
~
r 0Þ ¼ ~
n ð~
r1 þ lS ~
n ð½~
r1 ~
r0 þ lS ~
r 0 Þ þ l S ð~
n~
aÞ ¼ 0
a~
r 0Þ ¼ ~
aÞ ¼ ~
n ð~
r1 ~
n ð~
rS ~
Diese Gleichung lösen wir nach dem noch unbekannten Parameter lS auf:
n~
aÞ ¼ ~
n ð~
r1 ~
r 0Þ ¼ ~
n ð~
r0 ~
r 1Þ
l S ð~
)
lS ¼
~
r 1Þ
n ð~
r0 ~
~
n~
a
Berechnung des Parameters l S
1
1 0
1
0
1 0
0
3
1
14
1
C
C B
C
B
C B
B
C
C B
C
B
C B
~
n ð~
r0 ~
r 1Þ ¼ B
@ 2A @1 1A ¼ @ 2A @ 0A ¼ 3 þ 0 2 ¼ 1;
2
1
02
1
lS ¼
~
n ð~
r0 ~
r 1Þ
~
n~
a
¼
1
5
~
n~
a ¼ 5 ðs: obenÞ
2 Anwendungen
495
Ortsvektor ~
r S des Schnittpunktes S
Aus der Gleichung der Geraden g erhalten wir für l S ¼ 1=5:
0 1
0 1
4
2
B C
B C
1
1
C
B C
~
~
r ðl S ¼ 1=5Þ ¼ ~
r1 þ
a ¼ B
rS ¼ ~
@1A þ 5 @1A ¼
5
2
5
0 1
4
B C
B1C þ
@ A
2
0
0,4
1
0
4,4
1
B
C
B
C
B 0,2 C ¼ B 1,2 C
@
A
@
A
1
3
Schnittpunkt: S ¼ ð4,4; 1,2; 3Þ
Berechnung des Schnittwinkels j (! FS: Kap. II.4.3.7)
Wir benötigen noch die Beträge der Vektoren ~
n und ~
a:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffi
j~
n j ¼ ð 1Þ 2 þ 2 2 þ 1 2 ¼ 6 ; j ~
a j ¼ 2 2 þ 1 2 þ 5 2 ¼ 30 ;
!
!
j~
n~
aj
5
j ¼ arcsin
¼ arcsin 0,3727 ¼ 21,88
¼ arcsin pffiffiffi pffiffiffiffiffi
j~
n j j~
aj
6 30
~
n~
a ¼ 5 ðs. obenÞ
Schnittwinkel: j ¼ 21,88
Zeigen Sie, dass die Ebenen E 1 und E 2 parallel verlaufen und berechnen Sie ihren Abstand (von
jeder Ebene ist jeweils ein Punkt und der Normalenvektor bekannt):
1
1
0
0
1
3
C
C
B
B
C
C
Ebene E 1 : P 1 ¼ ð5; 10; 2Þ ; ~
n1 ¼ B
n2 ¼ B
@ 1 A ; Ebene E 2 : P 2 ¼ ð1; 5; 6Þ ; ~
@ 3A
1
3
I 36
Die Ebenen E 1 und E 2 sind genau dann parallel, wenn ihre Normalenvektoren ~
n1 und ~
n2 kollinear sind, d. h. in
einer gemeinsamen Linie (Geraden) liegen. Dies ist der Fall, da ~
n2 ein Vielfaches von ~
n1 ist:
0
1
0
1
3
1
B
C
B
C
C
B
C
~
n2 ¼ B
n1 ) E1 k E2
@ 3 A ¼ 3 @ 1 A ¼ 3~
3
1
|fflfflffl{zfflfflffl}
~
n1
Abstand d der beiden Ebenen ( ! FS: Kap. II.4.3.6)
0
1
1
1 0
0
1 5
1
1
B
C
C
C B
B
B
C
C
C B
r2 ~
r 1Þ ¼ B
~
n 1 ð~
@ 1 A @ 5 10 A ¼ @ 1 A
1
j~
n1 j ¼
d ¼
6 2
1
0
j~
n1 j
j3j
3
¼ pffiffiffi ¼ pffiffiffi ¼
3
3
pffiffiffi pffiffiffi
3 3
pffiffiffi
3
¼
1
C
B
B5C ¼ 4 þ 5 4 ¼ 3
A
@
4
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
1 2 þ ð 1Þ 2 þ ð 1Þ 2 ¼ 3
j~
n 1 ð~
r2 ~
r 1Þ j
4
pffiffiffi
3
496
I Vektorrechnung
Von zwei Ebenen E 1 und E 2 sind jeweils ein Punkt und ein Normalenvektor gegeben:
0
1
1
B
C
C
Ebene E 1 : P 1 ¼ ð1; 4; 5Þ ; ~
n1 ¼ B
@ 1 A ; Ebene E 2 : P 2 ¼ ð 2; 5; 5Þ ;
0
I 37
0 1
2
B C
C
~
n2 ¼ B
@3A
1
Zeigen Sie, dass sich die Ebenen längs einer Geraden g schneiden und bestimmen Sie die Gleichung
der Schnittgeraden und den Schnittwinkel j der beiden Ebenen.
n1 und ~
n2
Die Ebenen E 1 und E 2 schneiden sich genau dann längs einer Geraden g , wenn ihre Normalenvektoren ~
nichtkollinear sind, d. h. weder parallel noch antiparallel verlaufen und somit ~
n1 ~
n 2 6¼ ~
0 gilt. Dies ist hier der
Fall:
0 1
0
1
0
1
0 1
0
1
0
1
1 0
2
1
B C
B
C
B
C
B C
B
C
~
B C
B
C
B
C
B C
C
~
n1 ~
n2 ¼ B
@ 1 A @ 3 A ¼ @ 0 1 A ¼ @ 1 A 6¼ @ 0 A ¼ 0
0
5
3þ2
1
0
Ansatz für die Schnittgerade g in der Punkt-Richtungs-Form:
0
1
1
B
C
C
~
r ðlÞ ¼ ~
r0 þ l~
a mit ~
a ¼ ~
n1 ~
n2 ¼ B
@ 1 A und l 2 R
5
Denn der zunächst noch unbekannte Richtungsvektor ~
a der Schnittgeraden ist sowohl zu ~
n1 als auch zu ~
n2 orthon 2 darstellbar. ~
r0 ist dabei der Ortsvektor eines (zunächst beliebigen)
gonal und somit als Vektorprodukt ~
a ¼ ~
n1 ~
noch unbekannten Punktes P 0 ¼ ðx 0 ; y 0 ; z 0 Þ der Schnittgeraden g. Dieser Punkt liegt somit in beiden Ebenen und
lässt sich daher aus den Gleichungen
r0 ~
r 1Þ ¼ 0
~
n 1 ð~
und
~
n 2 ð~
r0 ~
r 2Þ ¼ 0
wie folgt berechnen:
0
r0 ~
r 1Þ ¼ 0
ðIÞ ~
n 1 ð~
)
1
1
0
x0 1
1
B
C
C B
B 1 C B y0 4 C ¼ 0
A
@
A @
0
z0 5
)
1 ðx 0 1Þ 1 ð y 0 4Þ þ 0 ðz 0 5Þ ¼ x 0 1 y 0 þ 4 ¼ 0
ðIIÞ ~
n 2 ð~
r0 ~
r 2Þ ¼ 0
)
1
0 1 0
x0 þ 2
2
C
B C B
@ 3 A @ y0 5 A ¼ 0
1
z0 5
)
x0 y0 þ 3 ¼ 0
)
2 ðx 0 þ 2Þ þ 3 ðy 0 5Þ þ 1 ðz 0 5Þ ¼ 2 x 0 þ 4 þ 3 y 0 15 þ z 0 5 ¼ 0
)
2 x 0 þ 3 y 0 þ z 0 16 ¼ 0
Gleichung (I) nach y 0 auflösen ( y 0 ¼ x 0 þ 3), den gefundenen Ausdruck in Gleichung (II) einsetzen:
ðIIÞ )
2 x 0 þ 3 ðx 0 þ 3Þ þ z 0 16 ¼ 2 x 0 þ 3 x 0 þ 9 þ z 0 16 ¼ 5 x 0 þ z 0 7 ¼ 0
Diese Gleichung ist nur lösbar, wenn wir für x 0 oder z 0 einen Wert vorgeben. Wir wählen z 0 ¼ 2. Daraus ergeben
sich folgende Werte für die restlichen Koordinaten:
ðIIÞ )
5 x0 þ z0 7 ¼ 5 x0 þ 2 7 ¼ 5 x0 5 ¼ 0
ðIÞ
x0 y0 þ 3 ¼ 1 y0 þ 3 ¼ 4 y0 ¼ 0
)
)
)
5 x0 ¼ 5
y0 ¼ 4
)
)
x0 ¼ 1
y0 ¼ 4
2 Anwendungen
497
Damit ist P 0 ¼ ð1; 4; 2Þ der gesuchte Punkt auf der Schnittgeraden g, deren Gleichung wie folgt lautet:
0 1
0
1
0
1
1
1l
1
B C
B
C
B
C
C
B
C
~
a ¼ B
r ðlÞ ¼ ~
r0 þ l~
ðmit l 2 RÞ
@4A þ l@1A ¼ @ 4 l A
5
2
2 þ 5l
Berechnung des Schnittwinkels j der beiden Ebenen (! FS: Kap. II.4.3.8)
Definitionsgemäß ist der Schnittwinkel j der Ebenen E 1 und E 2 der Winkel zwischen den beiden Normalenvekton2 . Wir erhalten ihn über das Skalarprodukt dieser Vektoren:
ren ~
n1 und ~
~
n1 ~
n2 ¼ j~
n1 j j~
n 2 j cos j
)
~
n2
n1 ~
cos j ¼
j~
n1 j j~
n2 j
0 1
1
2
B
C B C
C B C
~
n1 ~
n2 ¼ B
@1A @3A ¼ 2 3 þ 0 ¼ 1
0
1
0
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
1 2 þ ð 1Þ 2 þ 0 2 ¼ 2 ;
j~
n1 j ¼
cos j ¼
j~
n2 j ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
2 2 þ 3 2 þ 1 2 ¼ 14
~
n2
n1 ~
1
¼ pffiffiffi pffiffiffiffiffi ¼ 0,1890
j~
n1 j j~
n2 j
2 14
)
j ¼ arccos ð 0,1890Þ ¼ 100,89
Schnittwinkel: j ¼ 100,89
I 38
Eine Ebene
E
0 1
2
B C
steht senkrecht auf dem Vektor ~
n ¼ @1A
1
und enthält ferner den Punkt
P 1 ¼ ð2; 1; 5Þ. Welchen Abstand d hat der Punkt Q ¼ ð1; 2; 2Þ von dieser Ebene?
Bestimmen Sie die Gleichung der durch Q gehenden Parallelebene E *.
Abstand d des Punktes Q von der Ebene E (! FS: Kap. II.4.3.4)
1
0 1 0
1
0 1 0
1
2
12
2
C
B C B
C
B C B
C
B C B
C
C B
~
n ð~
rQ ~
r 1Þ ¼ B
@1A @ 2 þ 1A ¼ @1A @ 3A ¼ 2 þ 3 7 ¼ 6
7
1
2 5
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
j~
n j ¼ 22 þ 12 þ 12 ¼ 6 ;
d ¼
j~
n ð~
rQ ~
r 1Þ j
j~
nj
j6j
6
¼ pffiffiffi ¼ pffiffiffi ¼
6
6
pffiffiffi pffiffiffi
6 6
pffiffiffi
6
¼
pffiffiffi
6 ¼ 2,449
Parallelebene E * durch den Punkt Q
Da die Ebenen E und E * parallel verlaufen, gilt dies auch für die zugehörigen Normalenvektoren ~
n und ~
n *, d. h.
der Normalenvektor ~
n von E ist auch ein Normalenvektor der Parallelebene E *. Diese enthält ferner den Punkt Q.
Die Gleichung der gesuchten Ebene E * lautet damit in der Koordinatendarstellung wie folgt (mit ~
n* ¼ ~
n ):
1
0 1 0
x 1
2
C
B C B
C
C B
~
n ð~
r ~
r QÞ ¼ 0 ) B
n * ð~
r ~
r QÞ ¼ ~
@1A @y 2A ¼ 0 )
zþ2
1
2 ðx 1Þ þ 1 ð y 2Þ þ 1 ðz þ 2Þ ¼ 2 x 2 þ y 2 þ z þ 2 ¼ 2 x þ y þ z 2 ¼ 0
Gleichung der Parallelebene E * : 2 x þ y þ z 2 ¼ 0
498
I Vektorrechnung
I 39
Eine Ebene E enthält die Gerade g mit der Parameterdarstellung
0 1
0
1
1
2
B C
B
C
C
B
C
~
a ¼ B
r ðlÞ ¼ ~
r1 þ l~
ðmit l 2 RÞ
@2A þ l @1A
1
5
sowie den Punkt Q ¼ ð1; 4; 3Þ. Bestimmen Sie die Gleichung dieser Ebene
a) in der Parameterdarstellung,
b) in der Koordinatendarstellung.
Die Ebene E enthält den Richtungsvektor ~
a der Geraden g sowie die Punkte P1 ¼ ð1; 2; 1Þ und Q ¼ ð1; 4; 3Þ
!
~
(Bild I-16). Wenn die Vektoren ~
a und b ¼ P 1 Q nichtkollinear sind (d. h. nicht in einer Linie liegen), können sie als
Richtungsvektoren dieser Ebene verwendet werden. Ihr Vektorprodukt ~
a b~ ist dann ein Normalenvektor der Ebene.
Wegen
0 1
1
0
1
0
0
1 0 1
1
0
1 0
0
12
2 10
0
2
11
2
B C
C
B
C
B
B
C B C
C
B
C B
!
B C
C
B
C
B
B
C B C
C
C B
~
a b~ ¼ ~
a P1 Q ¼ B
@ 1 A @ 4 2 A ¼ @ 1 A @ 2 A ¼ @ 0 4 A ¼ @ 4 A 6¼ @ 0 A
0
4
4 0
2
5
31
5
sind ~
a und b~ nichtkollineare Vektoren und ~
n ¼ ~
a b~ daher ein Normalenvektor der gesuchten Ebene.
a) Parameterdarstellung der Ebene E (Punkt-Richtungs-Form)
0 1
0
1
0 1
1
2
0
B C
B
C
B C
C
B
C
B C
~
a þ m b~ ¼ B
r ðl; mÞ ¼ ~
r1 þ l~
@2A þ l @1A þ m @2A
1
5
2
g
a
~
a b~Þ ð~
r ~
r 1Þ ¼ 0
n ð~
r ~
r 1 Þ ¼ ð~
b
P1
ðmit l 2 R und m 2 RÞ
Q
r1
g
b) Koordinatendarstellung der Ebene E
0
)
12
1
0
x 1
O
1
C
B
C B
B 4C By 2C ¼ 0
A
@
A @
z1
4
)
Bild I-16
)
12 ðx 1Þ 4 ð y 2Þ þ 4 ðz 1Þ ¼ 12 x þ 12 4 y þ 8 þ 4 z 4 ¼ 0
12 x 4 y þ 4 z þ 16 ¼ 0 j : ð 4Þ
Ebene E
)
3x þ y z 4 ¼ 0
Gleichung der Ebene E: 3 x þ y z 4 ¼ 0
I 40
Von zwei Ebenen E 1 und E 2 sind jeweils ein Punkt und ein Normalenvektor gegeben:
0
0 1
1
1
1
B
B C
C
C
C
n1 ¼ B
n2 ¼ B
Ebene E 1 : P 1 ¼ ð1; 5; 3Þ ; ~
@1A
@ 2 A ; Ebene E 2 : P 2 ¼ ð2; 1; 1Þ ; ~
2
1
Bestimmen Sie diejenige Ebene E, die den Punkt Q ¼ ð2; 4; 6Þ enthält und sowohl auf E 1 als
auch auf E 2 senkrecht steht.
2 Anwendungen
499
Gleichungen der Ebenen E1 und E2 (Koordinatendarstellung)
0 1 0
1
1
x 1
B C B
C
C B
C
E1 : ~
n 1 ð~
r ~
r 1Þ ¼ 0 ) B
@2A @y 5A ¼ 0 )
1
zþ3
1 ðx 1Þ þ 2 ð y 5Þ þ 1 ðz þ 3Þ ¼ x 1 þ 2 y 10 þ z þ 3 ¼ 0
0
n 2 ð~
r ~
r 2Þ ¼ 0
E2 : ~
)
1
1
0
x 2
)
x þ 2y þ z 8 ¼ 0
1
C
C B
B
B1C By þ 1C ¼ 0
A
A @
@
z1
2
)
1 ðx 2Þ 1 ð y þ 1Þ þ 2 ðz 1Þ ¼ x 2 y 1 þ 2 z 2 ¼ 0
)
x y þ 2z 5 ¼ 0
Gleichung der Ebene E senkrecht zu E 1 und E 2 (Koordinatendarstellung)
Die gesuchte Ebene E steht sowohl auf E 1 als auch auf E 2 senkrecht, somit muss der (noch unbekannte) Normalenvektor ~
n der Ebene E sowohl auf ~
n 1 als auch ~
n 2 senkrecht stehen. Ein solcher Vektor ist das Vektorprodukt aus
~
n 1 und ~
n2:
1
1
0
1
0
0
0 1
5
4þ1
1
1
C
C
B
C
B
B
B C
C
C
B
C
B
C
B
~
n2 ¼ B
n ¼~
n1 ~
@2A @1A ¼ @ 1 2A ¼ @1A
3
1 2
2
1
Ferner enthält die Ebene E den Punkt Q ¼ ð2; 4; 6Þ. Ihre Gleichung lautet daher wie folgt (Koordinatendarstellung):
0
1
0
1
5
x 2
B
C
B
C
C
B
C
~
n ð~
r ~
r QÞ ¼ 0 ) B
@1A @y 4A ¼ 0 )
3
z6
5 ðx 2Þ 1 ðy 4Þ 3 ðz 6Þ ¼ 5 x 10 y þ 4 3 z þ 18 ¼ 0
)
5 x y 3 z þ 12 ¼ 0
Gleichung der Ebene E: 5 x y 3 z þ 12 ¼ 0
I 41
0 1
1
B C
Gegeben sind zwei parallele Geraden g1 und g2 mit dem gemeinsamen Richtungsvektor ~
a ¼ @ 2 A.
g1 verläuft durch den Punkt P 1 ¼ ð4; 1; 2Þ, g2 durch den Punkt P 2 ¼ ð 1; 2; 2Þ.
4
a) Berechnen Sie den Abstand d der Geraden.
b) Bestimmen Sie die Ebene E, die beide Geraden enthält (Parameter- und Koordinatendarstellung).
Die Gleichungen der beiden parallelen Geraden lauten in der Parameterdarstellung (Punkt-Richtungs-Form) wie folgt:
0
0 1
1
1
4
B
B C
C
ðmit l 1 2 RÞ
g1 : ~
r ðl 1 Þ ¼ ~
r1 þ l1 ~
a ¼ @ 1 A þ l1 @ 2 A
2
4
0 1
1
1
1
g2 : ~
a ¼ @ 2 A þ l2 @ 2 A
r ðl 2 Þ ¼ ~
r2 þ l2 ~
2
4
0
ðmit l 2 2 RÞ
a) Abstand d der parallelen Geraden (! FS: Kap. II.4.2.4)
1
1
0
1
0
0
1
0 1
0
0 1
4
8 4
5
1
1 4
1
C
C
B
C
B
B
C
B C
B
B C
C
C
B
C
B
B
C
B C
C
B
~
a ð~
r2 ~
r 1Þ ¼ B
@ 2 A @ 2 1 A ¼ @ 2 A @ 1 A ¼ @ 20 4 A ¼ @ 24 A
11
1 þ 10
4
4
2þ2
4
500
I Vektorrechnung
j~
a ð~
r2 ~
r 1Þ j ¼
d ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
4 2 þ ð 24Þ 2 þ 11 2 ¼ 713 ;
j~
a ð~
r2 ~
r 1Þ j
j~
aj
j~
aj ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
1 2 þ 2 2 þ 4 2 ¼ 21
pffiffiffiffiffiffiffiffi
713
¼ pffiffiffiffiffi ¼ 5,827
21
b) Gleichung der Ebene E
Die gesuchte Ebene E enthält den Richtungsvektor ~
a der parallelen Geraden, die Punkte P1 und P2 und damit
!
r2 ~
auch den Verbindungsvektor b~ ¼ P 1 P 2 ¼ ~
r 1 dieser Punkte (siehe hierzu Bild I-17). Die Vektoren ~
a und b~
sind nichtkollinear, da ihr Vektorprodukt ~
a b~ nicht verschwindet, wie wir bereits unter a) gezeigt haben:
!
~
a ð~
r2 ~
a b~ ¼ ~
a P1 P2 ¼ ~
r 1Þ ¼
1
0
1
0
0 1
4
5
1
C
B
C
B
B C
C
B
C
B
C
¼ B
@ 2 A @ 1 A ¼ @ 24 A 6¼
11
4
4
g2
g1
0 1
0
B C
B0C
@ A
0
a
a
b
P1
Bild I-17
P2
Ebene E
g2
g1
Daher können diese Vektoren als Richtungsvektoren der gesuchten Ebene E verwendet werden. Das Vektorprodukt
~
a b~ selbst ist ein Normalenvektor der Ebene, d. h. ~
n ¼~
a b~. Die Gleichung der Ebene E lautet damit wie folgt:
In der Parameterdarstellung (Punkt-Richtungs-Form)
0
1
0 1
0
1
4
1
5
B
C
B C
B
C
C
B C
B
C
~
r ðl; mÞ ¼ ~
r1 þ l~
a þ m b~ ¼ B
@ 1A þ l @2A þ m @ 1A
2
4
4
In der Koordinatendarstellung
~
a b~ Þ ð~
r ~
r 1Þ ¼ 0
n ð~
r ~
r 1Þ ¼ ð ~
0
)
4
1
0
ðmit l 2 R und m 2 RÞ
x 4
1
C
C B
B
@ 24 A @ y 1 A ¼ 0
zþ2
11
)
4 ðx 4Þ 24 ðy 1Þ þ 11 ðz þ 2Þ ¼ 4 x 16 24 y þ 24 þ 11 z þ 22 ¼ 0
)
4 x 24 y þ 11 z þ 30 ¼ 0
I 42
Eine Masse wird auf der Ebene E mit der Parameterdarstellung
0
1
0 1
0
1
1
1
1
B
C
B C
B
C
C
B C
B
C
~
r ðl; mÞ ¼ B
ðin der Einheit m ; l 2 R ; m 2 RÞ
@ 2A þ l @0A þ m @ 1A
1
1
0
~ ¼ ð10 NÞ ~
durch die Kraft F
e x þ ð20 NÞ ~
e y þ ð3 NÞ ~
e z geradlinig von P 1 ðl ¼ 0; m ¼ 1Þ nach
P 2 ðl ¼ 1; m ¼ 2Þ verschoben.
Berechnen Sie die dabei an der Masse verrichtete Arbeit W sowie den Winkel j zwischen dem Kraftund dem Verschiebungsvektor.
2 Anwendungen
501
!
Wir bestimmen zunächst den Verschiebungsvektor ~
s ¼ P 1 P 2 der Masse (Bild I-18). Dazu benötigen wir die Koordinaten bzw. den Ortsvektor der beiden Punkte (alle Koordinaten in der Einheit m):
0
1
0 1
0
1 0
1 0 1 0
1 0
1
1
1
0
1
1
2
B
C
B C
B
C B
C B C B
C B
C
C
B C
B
C B
C B C B
C B
C
~
r ðP 1 Þ ¼ ~
r ðl ¼ 0; m ¼ 1Þ ¼ B
@ 2 A þ 0 @ 0 A 1@ 1 A ¼ @ 2 A þ @ 0 A þ @ 1 A ¼ @ 1 A
1
1
0
1
0
0
1
0
1
0 1
0
1
0
1
0 1
0
1
0 1
1
1
1
1
2
0
B
C
B C
B
C
B
C
B C
B
C
B C
C
B C
B
C
B
C
B C
B
C
B C
~
r ðP 2 Þ ¼ ~
r ðl ¼ 1; m ¼ 2Þ ¼ B
@ 2A þ 1@0A þ 2@ 1A ¼ @ 2A þ @0A þ @ 2A ¼ @4A
1
1
0
1
1
0
0
1
1
0
1
0
1
0 1
2
2
0
C
B
B
C
B C
!
B
C
B
C
C
~
s ¼ P1 P2 ¼ ~
r ðP 2 Þ ~
r ðP 1 Þ ¼ B
@4A @ 1A ¼ @ 3A
1
1
0
F
Ebene E
P2
f
s
P1
Bild I-18
~
Die von der Kraft an der Masse verrichtete Arbeit W ist definitionsgemäß das Skalarprodukt aus dem Kraftvektor F
und dem Verschiebungsvektor ~
s:
0 1
0
1
0 1 0
1
10
2
10
2
B C
B
C
B C B
C
C
B
C
B C B
C
~~
W ¼ F
s ¼ B
@ 20 A N @ 3 A m ¼ @ 20 A @ 3 A N m ¼ ð 20 þ 60 þ 3Þ N m ¼ 43 N m
3
1
3
1
Den Winkel j zwischen dem Kraft- und dem Verschiebungsvektor erhalten wir ebenfalls über das Skalarprodukt
~~
F
s:
~~
~j j~
F
s ¼ W ¼ jF
s j cos j
~j ¼
jF
cos j ¼
W
~j j~
jF
sj
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
j~
s j ¼ ð 2Þ 2 þ 3 2 þ 1 2 m ¼ 14 m
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
10 2 þ 20 2 þ 3 2 N ¼ 509 N ;
cos j ¼
Ergebnis:
)
W
43 N m
¼ pffiffiffiffiffiffiffiffi
¼ 0,5094
pffiffiffiffiffi
~j j~
jF
sj
509 N 14 m
)
j ¼ arccos 0,5094 ¼ 59,38
W ¼ 43 N m; j ¼ 59,38
Eine Ebene E enthält die Punkte P 1 ¼ ð2; 1; 3Þ, P 2 ¼ ð3; 0; 2Þ und P 3 ¼ ð2; 2; 1Þ (alle Ko~ mit der z-Komponente F z ¼ 2 N an.
ordinaten in der Einheit m). In P 1 greift eine Kraft F
I 43
a) Bestimmen Sie die noch unbekannten Kraftkomponenten F x und F y so, dass der Kraftvektor senkrecht auf der Ebene steht.
!
b) Wie lautet der Momentenvektor M der Kraft bezüglich des Punktes Q ¼ ð5; 1; 2Þ m?
!
Anleitung: M ist das Vektorprodukt aus dem Verbindungsvektor ~
r von Q nach P 1 und dem Kraft~.
vektor F
502
I Vektorrechnung
!
!
a) Die in der Ebene E liegenden Vektoren ~
a ¼ P 1 P 2 und b~ ¼ P 1 P 3 sind linear unabhängig und können daher
als Richtungsvektoren dieser Ebene angesehen werden. Ihr Vektorprodukt ist daher ein Normalenvektor ~
n der
Ebene E (Bild I-19; alle Zwischenrechnungen ohne Einheiten):
0
1
0
1
0
1
0 1
Ebene E
F
32
1
22
0
P3
!
!
B
C
B
C
B
C
B C
~
a ¼ P 1 P 2 ¼ @ 0 1 A ¼ @ 1 A;
b~ ¼ P 1 P 3 ¼ @ 2 1 A ¼ @ 1 A
2þ3
1
0
1
0
0 1
9
4 5
0
C
B
C
B
B C
C
B
~
n ¼~
a b~ ¼ @ 1 A @ 1 A ¼ @ 0 4 A ¼ @ 4 A
1
10
4
5
0
1
b
1þ3
5
1
4
Bild I-19
a
P1
P2
Nullpunkt
~ senkrecht auf der Ebene E stehen soll, müssen F
~ und ~
~ ist
Da der Kraftvektor F
n kollineare Vektoren sein ( F
~
~
~
entweder parallel oder antiparallel zu ~
n ). Es gilt also F ¼ l ~
n und somit F ~
n ¼ 0 (mit l 2 R). Aus der
letzten Bedingung erhalten wir drei leicht lösbare Gleichungen für die noch unbekannten Kraftkomponenten
F x und F y :
0
1
0
0 1
0
1
1
Fy 8
Fx
0
9
B
B
C
B
C
C
B
C
~ ~
F
n ¼~
0 ) @ F y A @ 4 A ¼ @ 18 F x A ¼ @ 0 A )
2
ðIÞ
Fy 8 ¼ 0
ðIIÞ
18 F x ¼ 0
ðIIIÞ
4 Fx þ 9 Fy ¼ 0
)
1
4 F x þ 9 F y
0
Fy ¼ 8
)
F x ¼ 18
)
4 18 þ 9 8 ¼ 72 þ 72 ¼ 0
(diese Gleichung ist also erf üllt)
Die Kraftkomponenten lauten somit: F x ¼ 18 N, F y ¼ 8 N, F z ¼ 2 N
~ ¼ l~
Anmerkung: Sie können die Kraftkomponenten auch aus der Bedingung F
n bestimmen. Sie führt auf drei
Gleichungen mit den noch unbekannten Kraftkomponenten F x und F y und dem Parameter l :
9
8
1
1 0
0
1
0
9l
9
Fx
>
=
< Fx ¼ 9 l >
C
C B
B
C
B
~ ¼ l~
Fy ¼ 4 l
F
n ) @ Fy A ¼ l @ 4 A ¼ @ 4 l A )
>
>
;
:
l
1
2
2 ¼ l
Aus der unteren Gleichung folgt l ¼ 2 und somit aus den beiden oberen Gleichungen
F x ¼ 9 ð 2Þ ¼ 18 und
F y ¼ 4 ð 2Þ ¼ 8
(jeweils in N).
!
b) Mit Hilfe von Bild I-20 erhalten wir für das Moment M der
~ bezüglich des Punktes Q die
in P 1 angreifenden Kraft F
folgende Darstellung:
!
~
r ¼ Q P1 ¼ ~
r ðQÞ
r ðP 1 Þ ~
0
1
0
1
2
5
B
C
B
C
C
B
C
¼B
@ 1A @ 1A ¼
3
2
¼
0
B
B
@
3
1
C
0C
A
M =r ×F
F
Bild I-20
(in m)
Q
1
1
0
1
0
1
0
1
0
1
3
18
0þ8
8
1
!
C
B
C
B
C
B
C
B
C
~¼ B
r F
M ¼~
@ 0 A @ 8 A ¼ @ 18 6 A ¼ @ 24 A ¼ 8 @ 3 A
1
2
24 0
24
3
r
0
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
j M j ¼ 8 1 2 þ ð 3Þ 2 þ ð 3Þ 2 N m ¼ 8 19 N m ¼ 34,87 N m
!
(in N m
P1
503
J Lineare Algebra
Hinweise für das gesamte Kapitel
(1)
(2)
(3)
(4)
Für die Matrizenmultiplikation verwenden wir das Falk-Schema (! Band 2: Kapitel I.2.6.3 und Formelsammlung: Kapitel VII.1.3.3).
Die Berechnung dreireihiger Determinanten erfolgt nach der Regel von Sarrus (! Band 2: Kapitel I.3.3.1 und
Formelsammlung: Kapitel VII.2.2).
Die Streichung von Zeilen bzw. Spalten in einer Determinante oder Matrix wird durch Grauunterlegung der
betreffenden Zeilen bzw. Spalten gekennzeichnet.
Die Vorzeichenbestimmung der algebraischen Komplemente erfolgt meist mit der sog. „Schachbrettregel“
(! Band 2: Kapitel I.3.3.2 und Formelsammlung: Kapitel VII.2.3.2).
1 Matrizen und Determinanten
1.1 Rechenoperationen mit Matrizen
Lehrbuch: Band 2, Kapitel I.2.3 und 2.6
Formelsammlung: Kapitel VII.1.3
J1
Berechnen Sie mit den ð2; 3Þ-Matrizen
3 5 2
2 1
2
A ¼
; B ¼
und
1 4 0
5 8 1
C ¼
1
1
2
5
2
0
die folgenden Ausdrücke:
a) 3 A þ 2 B 5 C
b) 2 ðA 2 BÞ 3 ðB T A T Þ T 2 C
a) Zunächst werden die Matrizen A , B und C der Reihe nach elementweise mit den Skalaren 3, 2 und 5 multipliziert, anschließend die gleichstelligen Elemente addiert bzw. subtrahiert:
!
!
!
1 1 2
2 1
2
3 5 2
¼
5
þ2
3A þ 2B 5C ¼ 3
5 2 0
5 8 1
1 4 0
¼
9 15 6
3 12 0
!
þ
4
2
4
10 16
2
!
þ
5
5 10
25 10
© Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2020
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_10
0
!
¼
8
12
22
0
38 2
!
504
J Lineare Algebra
b) Summen und Differenzen werden gliedweise transponiert, zweimaliges Transponieren führt wieder zur Ausgangsmatrix, alle Matrizen sind dann vom Typ ð2; 3Þ:
2 ðA 2 BÞ 3 ðB T A T Þ T 2 C ¼ 2 A 4 B 3 ðB AÞ 2 C ¼ 2 A 4 B 3 B þ 3 A 2 C ¼
!
!
!
3 5 2
2 1
2
1 1 2
¼ 5A 7B 2C ¼ 5
7
2
¼
1 4 0
5 8 1
5 2 0
!
!
!
!
15 25 10
14
7 14
2 2 4
1
20 8
¼
þ
þ
¼
5 20
0
35 56
7
10 4
0
40 32
7
0
1
0
9 3
B
C
6 2 A und B ¼ @ 1
2
3 1
0
6
B
Zeigen Sie am Beispiel der 3-reihigen Matrizen A ¼ @ 4
2
J2
1
1 2
C
0
3 A,
3
0
dass die Matrizenmultiplikation nichtkommutativ ist, d. h. A B 6¼ B A gilt.
Wir berechnen beide Matrizenprodukte nach dem Falk-Schema:
B
A
6 9 3
4 6 2
2 3 1
0
1 2
1
0
3
2 3
0
15
10
5
3
2
1
39
26
13
A
B
0
1
2
1 2
0
3
3
0
6 9 3
4 6 2
2 3 1
0
0
0
AB
0
0
0
0
0
0
BA
Es ist A B 6¼ 0 , aber B A ¼ 0 und somit A B 6¼ B A.
0
J3
1
B
A ¼ @0
4
0
2
1
1
1
C
3A;
1
0
1
B
B ¼ @ 2
0
1
1 1
C
2 1A;
3 0
1
3 1
C
B
C ¼ @0 2A
1 5
0
Zeigen Sie am Beispiel dieser Matrizen die Gültigkeit der folgenden Rechenregeln (sofern alle Summen
und Produkte existieren):
a) ðA þ BÞ C ¼ A C þ B C
b) ðA BÞ C ¼ A ðB CÞ
a) Wir bilden zunächst die Summe A þ B (gleichstellige Elemente
dann die Produkte ðA þ BÞ C , A C und B C:
0
1
0
1
0
1 0 1
1
1 1
0 1
B
C
B
C
B
B
C
B
AþB ¼ B
3C
@0 2
A þ @ 2 2 1A ¼ @2 0
4 1
1
0
3 0
4 4
c) ðA BÞ T ¼ B T A T
werden addiert) und mit Hilfe des Falk-Schemas
0
1
C
4C
A
1
1 Matrizen und Determinanten
3
0
1
C
0
2
4
AþB
1
0
4
505
0
4
1
1
2
5
C
0 2
10 22
13 17
A
1
3
1
1 0
0 2
4 1
ðA þ BÞ C
3
0
1
1
2
5
2 4
3 19
13 11
B
1
2
0
C
3
0
1
1
2
5
1 1
2 1
3 0
2
7
0
6
3
6
AC
Wir bilden die Summe A C þ B C:
0
1
0
2 4
2
B
C
B
A C þ B C ¼ @ 3 19 A þ @ 7
13 11
0
BC
0
1
1
6
0 2
B
C
C
3 A ¼ @ 10 22 A
6
13 17
Ein Vergleich zeigt: ðA þ BÞ C ¼ A C þ B C.
b) Wir bilden zunächst unter Verwendung des Falk-Schemas das Matrizenprodukt A B , daraus dann ðA BÞ C
und schließlich A ðB CÞ , wobei das Produkt B C bereits aus a) bekannt ist:
A
1
0
4
0
2
1
B
1
1 1
2 2 1
0
3 0
1
3
1
1 2 1
4
5 2
2
5 5
C
AB
1
4
2
2 1
5 2
5 5
AB
3
0
1
1
2
5
2 0
14 24
1 33
2
7
0
BC
A
1 0 1
0 2
3
4 1
1
ðA BÞ C
6
3
6
2 0
14 24
1 33
A ðB CÞ
Ein Vergleich der Matrizenprodukte ðA BÞ C und A ðB CÞ zeigt: ðA BÞ C ¼ A ðB CÞ.
c) Das Matrizenprodukt A
miteinander vertauschen):
0
1 2
B
AB ¼ @ 4
5
2
5
B ist bereits aus b) bekannt, wir müssen es noch transponieren (Zeilen und Spalten
1
1
C
2A
5
0
ðA BÞ T
)
Jetzt transponieren wir die Matrizen A und B
0
0
1
1
1 0 1
B
B
C
T
A ¼ @0 2
3A ) A ¼ @ 0
1
4 1
1
A
BT
1
1
1
T
2 0
2 3
1 0
1
0
1
0
2
3
1
B
¼ @2
1
1
4 2
C
5
5A
2
5
und bilden dann das Matrizenprodukt B T A T :
0
1
1
0
0 4
1
1 1
1
B
C
C
B
T
2 1 A; B ¼ @ 2 2 1 A ) B ¼ @ 1
3 1
0
3 0
1
4
1
1
1 4 2
2 5
5
1 2
5
BT AT
Ein Vergleich der Matrizenprodukte ðA BÞ T und B T A T zeigt: ðA BÞ T ¼ B T A T .
1
2 0
C
2 3A
1 0
506
J Lineare Algebra
0
1
2
4 1
B
C
0
3 A und B ¼ @ 1
0
2
1
0
1
B
Gegeben sind die 3-reihigen Matrizen A ¼ @ 2
1
1
1
1
C
2 1 A.
1
0
a) Berechnen Sie mit dem Falk-Schema die folgenden Produkte:
J4
A B, B A, A2 ¼ A A, B2 ¼ B B
b) Berechnen Sie die folgenden Produkte auf zwei verschiedene Arten:
ðA þ BÞ 2 ¼ ðA þ BÞ ðA þ BÞ ;
ðA BÞ 2 ¼ ðA BÞ ðA BÞ ;
ðA þ BÞ ðA BÞ
Sind die bekannten Binomischen Formeln auf Matrizen anwendbar?
a) Mit dem Falk-Schema erhalten wir:
A
B
2
1
0
1
2
1
1
1
0
A
1
2
1
1 4 1
2 0
3
1 2
1
6
4
4
8
5
6
3
2
1
2 1
1
1 2 1
0 1
0
5
4
2
B
AB
4 1
0
3
2
1
10
2
0
2
4
3
BA
Erwartungsgemäß ist A B 6¼ B A (die Matrizenmultiplikation ist nicht kommutativ).
A
A
1
2
1
4 1
0
3
2
1
1
2
1
4 1
0
3
2
1
8
2
5 14
6
6
10
1
6
B
B
2 1
1
1 2 1
0 1
0
2 1
1
1 2 1
0 1
0
5 5
1
4 4 1
1 2 1
A A ¼ A2
B B ¼ B2
b) Die Matrizenprodukte (Potenzen) ðA þ B Þ 2 , ðA BÞ 2 und ðA þ BÞ ðA BÞ dürfen wir nicht nach den
Binomischen Formeln berechnen, da die Matrizenmultiplikation eine nichtkommutative Rechenoperation ist:
ðA BÞ 2 6¼ A 2 2 A B þ B 2
und ðA þ BÞ ðA BÞ 6¼ A 2 B 2
Vielmehr gilt:
ðA BÞ 2 ¼ ðA BÞ ðA BÞ ¼ A 2 A B B A þ B 2
ðA þ BÞ ðA BÞ ¼ A 2 A B þ B A B 2
Am einfachsten erhält man diese Produkte, in dem man zunächst die Matrizen A þ B bzw. A B bildet und
dann mit dem Falk-Schema die gesuchten Produkte berechnet:
0
0
1
1
0
1
1 4 1
3 5 0
2 1
1
B
B
C
B
C
C
B
B
C
C
AþB ¼ B
3C
@2 0
A þ @1 2 1A ¼ @3 2 2A
1 2
1
1 3 1
0 1
0
1
0
1
0
1
0
1
3 2
1 4 1
2 1
1
C
B
C
B
C
B
4A
A B ¼ @2 0
3A @1 2 1A ¼ @ 1 2
1
1
1
1 2
1
0 1
0
1 Matrizen und Determinanten
507
Berechnung der Matrizenprodukte (A B) 2
AþB
AþB
3
3
1
5
2
3
0
2
1
3
3
1
24
17
13
5
2
3
0
2
1
AB
25 10
25 6
14 7
AB
1
1
1
3
2
1
1
1
1
2
4
1
3 2
2
4
1
1
2 11 12
1
11 6
1
2
3
ðA þ BÞ2
ðA BÞ2
Kontrollrechnung:
ðA þ BÞ 2 ¼ ðA þ BÞ ðA
0
1
0
8 2 10
6
B
C
B
B
C
B
¼ @ 5 14 1 A þ @ 4
6 6 6
4
þ BÞ ¼ A 2
1
8 3
C
5
2C
Aþ
6 1
þ A B þ B A þ B2 ¼
0
1
0
1
0
5 10 2
5 5
1
24
B
B4 2 4C
CþB
B4 4 1C
C ¼ B
B 17
@
A
@
A
@
2 0 3
1 2 1
13
ðA BÞ 2 ¼ ðA BÞ ðA
0
1
0
8 2 10
6
B
C
B
C
B
¼ B
@ 5 14 1 A @ 4
6 6 6
4
BÞ ¼ A 2
1
8 3
C
5
2C
A
6 1
A B B A þ B2 ¼
0
1
0
1
5 10 2
5 5
1
B
B4 2 4C
CþB
B4 4 1C
C ¼
@
A
@
A
2 0 3
1 2 1
0
2
B
B1
@
1
25 10
1
25
C
6C
A
14
7
11
12
2
3
1
C
11 6 C
A
Berechnung des Matrizenproduktes (A + B) (A – B)
AB
AþB
3
3
1
5
2
3
0
2
1
1
3 2
1 2
4
1
1
1
2 1
1
7
3 2
In dem Produkt ðA þ BÞ ðA BÞ dürfen die Faktoren nicht
vertauscht werden:
ðA þ BÞ ðA BÞ ¼ A 2 A B þ B A B 2
14
4
11
ðA BÞ ðA þ BÞ ¼ A 2 þ A B B A B 2
ðA þ BÞ ðA BÞ 6¼ ðA BÞ ðA þ BÞ
ðA þ BÞ ðA BÞ
Kontrollrechnung:
ðA þ BÞ
0
8
B
B
¼ @5
6
ðA BÞ ¼ A 2
1
0
2 10
6
C
B
C
B
14 1 A @ 4
6 6
4
A B þ B A B2 ¼
1
0
1
0
8 3
5 10 2
5
C
B
C
B
C
B
C
B
5
2A þ @4 2 4A @4
6 1
2 0 3
1
0
Gegeben sind folgende Matrizen: A ð3;2Þ
J5
1
B
¼ @2
1
5
4
2
1
1
0
2
C
B
B
1C
A ¼ @1
1
3
1
3
2
C
0 A , B ð2; 2Þ ¼
3
4
1
2
1
7
2
14
1
C
4C
A
11
, C ð2; 3Þ ¼
a) Bilden Sie alle möglichen Produkte X Y mit zwei Faktoren.
b) Bilden Sie alle möglichen Produkte X Y Z mit drei verschiedenen Faktoren.
2
6
0 1
1
3
508
J Lineare Algebra
a) Die Produktbildung mit zwei Faktoren ist nur möglich, wenn die beiden Faktoren die folgende Bedingung erfüllen:
Spaltenzahl des linken Faktors ¼ Zeilenzahl des rechten Faktors
Damit ergeben sich folgende Produkte
(sie sind jeweils angekreuzt):
Að3, 2Þ
Bð2, 2Þ
Cð2, 3Þ
Að3, 2Þ
Bð2, 2Þ
rechter Faktor
Cð2, 3Þ
" linker Faktor
Berechnung der Matrizenprodukte A B , A C , B B ¼ B 2 , B C und C A nach dem Falk-Schema:
2
3
B
1
2
1
A
1
2
C
11 5
4
2
14 7
3
0
4
A
1
2
1
3
0
4
2
6
20 3
8
4 0 2
26 4 11
AB
2
3
B
1
2
B
2
3
B
2
3
1
2
1
2
7
0
0
7
AC
0
1
1
3
10
1
6 2
1
9
2
6
C
0 1
1
3
BB
1
2
1
A
C
2 0 1
6 1
3
BC
3
0
4
1 2
11 30
CA
b) Die möglichen Matrizenprodukte mit drei verschiedenen Faktoren entnehmen Sie der folgenden Tabelle:
Að3, 2Þ
Bð2, 2Þ
Cð2, 3Þ
ðA BÞð3, 2Þ ðA CÞð3, 3Þ ðB CÞð2, 3Þ ðC AÞð2, 2Þ
rechter Faktor
Að3, 2Þ
Bð2, 2Þ
Cð2, 3Þ
ðA BÞð3, 2Þ
ðA CÞð3, 3Þ
ðB CÞð2, 3Þ
ðC AÞð2, 2Þ
" linker Faktor
Berechnung der möglichen Produkte A ðB CÞ , B ðC AÞ , C ðA BÞ , ðA BÞ C , ðB CÞ A und
ðC AÞ B nach dem Falk-Schema:
BC
A
1
2
1
3
0
4
10
1
6 2
1
9
8 5 26
20
2
2
14 7 35
A ðB CÞ
CA
B
2
3
1
2
1
11
2
30
13
34
19 54
B ðC AÞ
1 Matrizen und Determinanten
11 5
4
2
14 7
AB
C
2
6
0
1
509
1
8
3 112
C
11 5
4
2
14 7
AB
3
49
C ðA BÞ
BC
10
1
6 2
1
9
0 1
1
3
8 5 26
20
2
2
14 7 35
ðA BÞ C
1
2
1
A
2
6
3
0
4
13
34
19 54
CA
B
2
3
1
2
1 2
11 30
8
112
3
49
ðB CÞ A
ðC AÞ B
Da für Matrizenprodukte das Assoziativgesetz gilt, ist erwartungsgemäß
A ðB CÞ ¼ ðA BÞ C ;
B ðC AÞ ¼ ðB CÞ A und C ðA BÞ ¼ ðC AÞ B :
Bilden Sie aus den 2-reihigen Matrizen (in diesem Zusammenhang auch als Untermatrizen bezeichnet)
2 1
1 4
1 2
1 3
0 0
P ¼
; Q ¼
; R ¼
; S ¼
und 0 ¼
1 3
2 1
2
3
5 8
0 0
die 4-reihigen Blockmatrizen
!
P 0
A ¼
und B ¼
0 Q
J6
R
0
0
S
!
und zeigen Sie, dass für das Matrizenprodukt A B folgende Beziehung gilt:
!
PR
0
AB ¼
0
QS
Die Blockmatrizen A und B enthalten
0
2 1 0
!
B1 3 0
P 0
B
¼ B
A ¼
@0 0 1
0 Q
0 0 2
jeweils vier Zeilen und Spalten. Sie lauten:
1
0
0
1 2 0
!
C
B
R
0
0C
3 0
B2
¼ B
C; B ¼
@0
4A
0 1
0 S
1
0
0 5
1
0
0C
C
C
3A
8
Wir berechnen zunächst das Matrizenprodukt A B unter Verwendung des Falk-Schemas:
A
2
1
0
0
1
3
0
0
0
0
1
2
B
1 2
2
3
0
0
0
0
0
0
4
1
4 1 0
0
7
7 0
0
0
0 21 35
0
0 7 14
0
0
1
5
AB
0
0
3
8
1
4 1
0 0
B7
7
0 0C
C
B
AB ¼ B
C
@0
0 21 35 A
0
0
7 14
0
)
510
J Lineare Algebra
Ferner benötigen wir noch die Matrizenprodukte P R und Q S (ebenfalls nach dem Falk-Schema berechnet):
P
2
1
R
1 2
2
3
1
3
4 1
7
7
S
1
2
Q
4
1
PR
1
5
3
8
21 35
7 14
QS
Die aus diesen Produkten gebildete 4-reihige Blockmatrix lautet somit:
1
0
4 1
0 0
!
B7
PR
0
7
0 0C
C
B
¼ B
C ¼ AB
@0
0 21 35 A
0
QS
0
0
7 14
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
AB
Sie stimmt (wie behauptet) mit dem Matrizenprodukt A B überein.
J7
a
c
b
d
Bestimmen Sie alle 2-reihigen Matrizen vom Typ X ¼
1 0
A ¼
sich kommutativ verhält ðA X ¼ X AÞ .
1 1
, deren Matrizenprodukt mit der Matrix
Wir berechnen zunächst die benötigten Matrizenprodukte A X und X A:
a
ða þ 0Þ
ðb þ 0Þ
a b
1 0
¼
¼
AX ¼
ðc aÞ
ð a þ cÞ ð b þ dÞ
c d
1 1
XA ¼
a b
c d
1
1
0
1
¼
ða bÞ
ðc dÞ
ð0 þ bÞ
ð0 þ dÞ
¼
ða bÞ
ðc dÞ
b
d
b
ðd bÞ
Somit müssen die noch unbekannten Elemente a, b, c und d die folgende Matrizengleichung erfüllen:
a
b
ða bÞ b
A X ¼ X A oder
¼
ðc aÞ ðd bÞ
ðc dÞ d
Durch Vergleich entsprechender Elemente auf beiden Seiten dieser Gleichung erhält man vier Gleichungen mit folgender Lösung:
9
ðIÞ
a ¼ a b ) b ¼ 0 ; a ¼ beliebig
>
>
>
>
>
=
ðIIÞ b ¼ b ) b ¼ beliebig
) a ¼ d ¼ beliebig ; b ¼ 0 ; c ¼ beliebig
ðIIIÞ c a ¼ c d ) d ¼ a ; c ¼ beliebig >
>
>
>
>
;
ðIVÞ d b ¼ d ) b ¼ 0 ; d ¼ beliebig
a 0
Lösung: X ¼
mit a 2 R ; c 2 R
c a
Kontrollrechnung:
AX ¼
XA ¼
1
1
a
c
0
a
0
1
a
c
0
a
1
1
0
1
¼
¼
a
ð a þ cÞ
a
ðc aÞ
0
a
0
a
¼
a
0
ðc aÞ a
9
>
>
>
>
=
>
>
>
>
;
)
AX ¼ XA
1 Matrizen und Determinanten
511
1.2 Determinanten
Lehrbuch: Band 2, Kapitel I.3
Formelsammlung: Kapitel VII.2
J8
Begründen Sie, warum die folgenden Determinanten verschwinden:
2 1
2 1
2 0
4 5
1
1
3 5 8
1
aÞ 0 3 0 bÞ 2
1 10 cÞ
1 5
1
0
1
6 12
4 0
30
1 6 6
0
4 3
4
dÞ 20 15 20
2
4
2
a) Die Determinante enthält den Nullvektor (3. Spalte).
b) Die Determinante enthält zwei proportionale Spalten (die 3. Spalte ist das 5-fache der 1. Spalte).
c) Die 4. Zeile ist die Summe der ersten beiden Zeilen und somit eine Linearkombination dieser Zeilen.
d) Die Determinante enthält zwei gleiche Spalten (1. und 3. Spalte).
J9
Entwickeln Sie die folgenden 3-reihigen Determinanten nach einer möglichst günstigen Zeile oder Spalte:
2
1 x x 2
1 0
aÞ D ¼ 5 4 2
bÞ D ¼ 1 y y 2
1
1 z z2
3 1
a) Wir entwickeln die 3-reihige Determinante nach den Elementen der 1. Zeile, da a 13 ¼ 0 ist (Alternative: Entwicklung nach der 3. Spalte):
D ¼ a 11 A 11 þ a 12 A 12 þ a 13 A 13 ¼ 2 A 11 þ 1 A 12 þ 0 A 13 ¼ 2 A 11 þ A 12
Berechnung der algebraischen Komplemente A 11 und A 12 (Vorzeichen nach der Schachbrettregel):
A 11 ¼ þ D 11
1 0
2
4 2
¼ 4 6 ¼ 10
¼ þ 5 4 2 ¼
3 1
1
3 1
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
D 11
A 12 ¼ D 12
1 0
2
5 2
¼ ð 5 2Þ ¼ 7
¼ 5 4 2 ¼
1
1
1
3 1
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
D 12
Somit gilt:
D ¼ 2 A 11 þ A 12 ¼ 2 ð 10Þ þ 7 ¼ 20 þ 7 ¼ 13
b) Wir entwickeln diese Determinante zweckmäßigerweise nach den Elementen der 1. Spalte (alle Elemente sind
gleich 1):
D ¼ a 11 A 11 þ a 21 A 21 þ a 31 A 31 ¼ 1 A 11 þ 1 A 21 þ 1 A 31 ¼ A 11 þ A 21 þ A 31
512
J Lineare Algebra
Berechnung der algebraischen Komplemente A 11 ,
minanten D 11 , D 21 und D 31 :
1 x x2
A 11 ¼ ð 1Þ 1 þ 1 D 11 ¼ þ 1 y y 2 ¼
1 z z2
A 21 ¼ ð 1Þ
2þ1
D 21
A 31 ¼ ð 1Þ 3 þ 1 D 31
A 21 und A 31 aus den entsprechenden zweireihigen Unterdeter
y
z
y 2
¼ y z2 z y2
z2
1 x x2
x
2
¼ 1 y y ¼
z
1 z z2
x 2
¼ ðx z 2 z x 2 Þ ¼ x z 2 þ z x 2
z2
1 x x2
x x2
2
¼ x y2 y x2
¼ þ 1 y y ¼
y y2
1 z z2
Damit besitzt die Determinante D den folgenden Wert:
D ¼ A 11 þ A 21 þ A 31 ¼ y z 2 z y 2 x z 2 þ z x 2 þ x y 2 y x 2 ¼ x 2 ðz yÞ þ y 2 ðx zÞ þ z 2 ðy xÞ
J10
Entwickeln Sie die folgenden 4-reihigen Determinanten nach einer günstigen Zeile oder Spalte und
berechnen Sie die dabei anfallenden 3-reihigen Determinanten nach der Regel von Sarrus:
0
1 3 0
2 1 4
4
1
10 4 3
2
0 1 0
aÞ D ¼
bÞ D ¼
0
0 2 1 4
4 0 2
1
1
0 5 0
0 3 2
a) Besonders günstig für die Laplace-Entwicklung ist die 3. Zeile, da diese zwei Nullen enthält ða 31 ¼ a 33 ¼ 0Þ:
D ¼ a 31 A 31 þ a 32 A 32 þ a 33 A 33 þ a 34 A 34 ¼ 0 A 31 þ 4 A 32 þ 0 A 33 2 A 34 ¼ 4 A 32 2 A 34
Berechnung der algebraischen Komplemente A32 und A34 nach der Regel von Sarrus:
2 1 4
0
0
2 4
10 4 3
2
A 32 ¼ ð 1Þ 3 þ 2 D 32 ¼
2 ¼ 112
¼ 10 3
0
4 0 2
1 3 2
1
0 3 2
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
D 32 ¼ 112
2 4
0 2 4
10 3
10 3 ) D 32 ¼ 12 þ 8 þ 0 0 þ 12 þ 80 ¼ 112
2
1 3 2 1 3
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D 32
A 34 ¼ ð 1Þ 3 þ 4 D 34
2 1 4
0
10 4 3
2
¼
0
4 0 2
1
0 3 2
2 1 4
¼ 10 4 3 ¼ 67
1
0 3
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
D 34 ¼ 67
1 Matrizen und Determinanten
2 1 4 2 1
10 4 3 10 4
1
0 3 1
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D 34
513
)
D 34 ¼ 24 3 þ 0 þ 16 þ 0 þ 30 ¼ 67
D ¼ 4 A 32 2 A 34 ¼ 4 ð 112Þ 2 ð 67Þ ¼ 448 þ 134 ¼ 314
Somit gilt:
b) Die 4. Spalte enthält drei Nullen ða 14 ¼ a 24 ¼ a 44 ¼ 0Þ, daher entwickeln wir die Determinante nach den Elementen dieser Spalte:
f
f
f
f
D ¼ a 14 A 14 þ a 24 A 24 þ a 34 A 34 þ a 44 A 44 ¼ 4 A 34
0
0
4
0
Berechnung des algebraischen Komplements A34 nach der Regel von Sarrus (Vorzeichenbestimmung nach der
Schachbrettregel):
1 3 0
4
4 1 3
1
0
1
0
¼ 1 0 1 ¼ ð 4Þ ¼ 4
A 34 ¼ D 34 ¼
0 2 1 4
1 0 5
1
0 5 0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
D 34 ¼ 4
4 1 3 4 1
1 0 1 1 0 ) D 34 ¼ 0 þ 1 þ 0 0 0 5 ¼ 4
1 0 5 1 0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
D 34
Somit: D ¼ 4 A 34 ¼ 4 4 ¼ 16
J11
Zeigen Sie durch elementare Umformungen, dass die Determinanten der folgenden Matrizen verschwinden:
1
0
1
0
2
5 18 1
1 3 1
B 4 3
5
6C
C
B
C
B
bÞ B ¼ B
aÞ A ¼ @ 1 1 1 A
C
@6
3 9
3A
2 18 8
0
2
5
0
Die vorgenommenen Umformungen in den Zeilen und Spalten der Determinante werden jeweils in der entsprechenden
Zeile bzw. Spalte angeschrieben (Z: Zeile).
1 3 1
1 3 1
1 3 1
aÞ det A ¼ 1 1 1 þ Z 1 ¼ 0 4 2
¼ 0 4 2 ¼ 0
2 18 8 2 Z
0 12 6 3 Z
0 0 0
Nullvektor
1
2
Die Determinante enthält in der 3. Zeile nur Nullen und hat daher den Wert null: det A ¼ 0.
Anmerkung: Bereits nach dem 1. Schritt enthält die Determinante zwei proportionale Zeilen (die 3. Zeile ist das
3-fache der 2. Zeile) und hat daher den Wert null. Wenn Sie dies erkannt haben, können Sie hier bereits abbrechen.
2
2
5
18 1
5 18 1
4 3
0 13 31
5
6 2 Z 1
8
bÞ det B ¼
¼
6
0
3 9
3 þ 3 Z1
18
45
0
Proportionale Zeilen
0
0
2
5
0
2
5
0
Die 3. Zeile ist das 9-fache der 4. Zeile, die Determinante hat daher den Wert det B ¼ 0.
514
J Lineare Algebra
J12
D ¼
1
0
0
2
0
2 1
1 1 0
¼ ?
4
0 4
3 5 1
Berechnen Sie diese Determinante durch Laplace-Entwicklung
a) nach der günstigsten Zeile,
b) nach der günstigsten Spalte.
a) Günstig sind die Zeilen 2 und 3, da sie beide zwei Nullen enthalten. Wir entscheiden uns für die 2. Zeile
ða 21 ¼ a 24 ¼ 0Þ:
D ¼ a 21 A 21 þ a 22 A 22 þ a 23 A 23 þ a 24 A 24 ¼ 0 A 21 þ 1 A 22 1 A 23 þ 0 A 24 ¼ A 22 A 23
Berechnung der algebraischen Komplemente A 22 und A 23 aus den entsprechenden 3-reihigen Unterdeterminanten
D 22 und D 23 nach der Regel von Sarrus (Vorzeichenbestimmung nach der Schachbrettregel):
0
2 1
1
2 1
1
0
1 1 0
¼ 0
A 22 ¼ þ D 22 ¼
0 4 ¼ 36
0
4
0
4
2 5 1
2 3 5 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D 22 ¼ 36
1
2
2 1 1
0
0 ) D 22 ¼ 0 þ 16 þ 0 0 þ 20 0 ¼ 36
0 4 0
2 5 1 2 5
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D 22
0
2 1
1
0 1
1
0
1
1
0
¼ 0
A 23 ¼ D 23 ¼
4 4 ¼ 8
0
4
0 4
2 3 1
2 3 5 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D 23 ¼ 8
0 1 1
1
0
4 4 0
2 3 1 2
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D 23
0
4
3
)
D 23 ¼ 4 þ 0 þ 0 8 þ 12 0 ¼ 8
Somit gilt:
D ¼ A 22 A 23 ¼ 36 ð 8Þ ¼ 36 þ 8 ¼ 44
b) Die 1. Spalte enthält die meisten Nullen ða 21 ¼ a 31 ¼ 0Þ, also entwickeln wir die Determinante nach den Elementen dieser Spalte:
D ¼ a 11 A 11 þ a 21 A 21 þ a 31 A 31 þ a 41 A 41 ¼ 1 A 11 þ 0 A 21 þ 0 A 31 þ 2 A 41 ¼ A 11 þ 2 A 41
Berechnung der algebraischen Komplemente A 11 und A 41 aus den entsprechenden 3-reihigen Unterdeterminanten
D 11 und D 41 nach der Regel von Sarrus (Vorzeichenbestimmung nach der Schachbrettregel ):
0
2 1
1
1 1 0
0
1 1 0
¼ 4
A 11 ¼ þ D 11 ¼
0 4 ¼ 36
0
4
0
4
3 5 1
2 3 5 1
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D 11 ¼ 36
1 Matrizen und Determinanten
1 1 0 1
4
0 4 4
3 5 1 3
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D 11
A 41 ¼ D 41 ¼
515
1
0
5
1
0
0
2
2 1 0
2
0
1 1 0 1 1
4
0 4 4
0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D 41
)
D 11 ¼ 0 þ 12 þ 0 0 þ 20 þ 4 ¼ 36
0
2 1
2 1
0
1 1 0
¼ 1 1 0 ¼ ð 4Þ ¼ 4
4
0 4
4
0 4
3 5 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D 41 ¼ 4
)
D 41 ¼ 0 þ 0 þ 0 þ 4 0 8 ¼ 4
Somit besitzt die Determinante den folgenden Wert (in bereinstimmung mit dem Ergebnis aus a)):
D ¼ A 11 þ 2 A 41 ¼ 36 þ 2 4 ¼ 36 þ 8 ¼ 44
J13
Berechnen Sie die Determinante
4 2 1
D ¼ det A ¼ 2 1 0
1 0 5
a) nach der Regel von Sarrus,
b) durch Laplace-Entwicklung nach der günstigsten Zeile oder Spalte,
c) durch Umformung auf Dreiecksform mit Hilfe elementarer Zeilenumformungen.
a) Determinantenberechnung nach Sarrus:
4 2 1 4 2
2 1 0 2 1 ) D ¼ 20 þ 0 þ 0 1 0 þ 20 ¼ 39
1 0 5 1 0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D
b) Besonders günstig für die Entwicklung der Determinante ist die zweite oder dritte Zeile bzw. die zweite oder dritte
Spalte. Wir entscheiden uns für die dritte Zeile:
D ¼ a 31 A 31 þ a 32 A 32 þ a 33 A 33 ¼ 1 A 31 þ 0 A 32 þ 5 A 33 ¼ A 31 þ 5 A 33
Berechnung der algebraischen Komplemente A31 und A33 aus den entsprechenden Unterdeterminanten D31 und
D33 (Vorzeichenbestimmung nach der Schachbrettregel ):
4 2 1
2 1
¼ 0 1 ¼ 1
A 31 ¼ þ D 31 ¼ 2 1 0 ¼
1 0
1 0 5
|fflfflfflffl{zfflfflfflffl}
D 31
4 2 1
4 2
¼ 4þ4 ¼ 8
A 33 ¼ þ D 33 ¼ 2 1 0 ¼
2 1
1 0 5
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
D 33
516
J Lineare Algebra
Somit gilt:
D ¼ A 31 þ 5 A 33 ¼ 1 þ 5 8 ¼ 1 þ 40 ¼ 39
c) Wir vertauschen zunächst die Zeilen 1 und 3 miteinander, wobei sich das Vorzeichen der Determinante ändert. Die
weiteren Zeilenumformungen sind jeweils angeschrieben:
5
5
1 0 5
1 0
1 0
4 2 1
10
¼ 0 1
10 ¼
D ¼ 2 1 0 ¼ 2 1 0 þ 2 Z 1 ¼ 0 1
4 2 1 4Z
0 2 19 2 Z
0 0 39
1 0 5
1
2
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
¼ ½ 1 1 ð 39Þ ¼ 39
J14
obere Dreiecksmatrix
ðProdukt der DiagonalelementeÞ
0
l1
Welche Lösungen besitzt die Gleichung 1
l1
2
0
2
1
1l
¼ 0?
Wir berechnen zunächst die 3-reihige Determinante D nach der Regel von Sarrus:
0
0
2 l 1
l1
1
1
l
1 )
l
1
1
2
2
0
0
1l
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D
D ¼ ðl 1Þ 2 ð1 lÞ þ 0 þ 0 þ 4 ðl 1Þ 0 0 ¼ ðl 1Þ 2 ð1 lÞ þ 4 ðl 1Þ
Die sich daraus ergebende kubische Gleichung lösen wir durch Ausklammern des gemeinsamen Faktors l 1 wie
folgt:
ðl 1Þ 2 ð1 lÞ þ 4 ðl 1Þ ¼ ðl 1Þ 3 þ 4 ðl 1Þ ¼ 0 )
|fflfflfflffl{zfflfflfflffl}
ðl 1Þ
l 1 ¼ 0 ) l1 ¼ 1
ðl 1Þ 3 4 ðl 1Þ ¼ ðl 1Þ ½ ðl 1Þ 2 4 ¼ 0
ðl 1Þ 2 4 ¼ 0 )
ðl 1Þ 2 4 ¼ 0
Lösung:
J15
)
ðl 1Þ 2 ¼ 4
)
l 1 ¼ 2 ) l ¼ 1 2
)
l2 ¼ 3 ;
l3 ¼ 1
l 1 ¼ 1, l 2 ¼ 3, l 3 ¼ 1
1
4
2 3
2 8 4 6
D ¼
7
5
1 0
1
0
5 1
¼ ?
Vereinfachen Sie diese Determinante durch elementare Umformungen in den Spalten so lange, bis Sie
eine Determinante erhalten, die in einer Zeile nur noch ein von Null verschiedenes Element enthält und
entwickeln Sie anschließend nach Laplace (Berechnung der anfallenden 3-reihigen Determinante nach
der Regel von Sarrus).
1 Matrizen und Determinanten
517
f
f
f
f
Wir nehmen folgende Umformungen in den Spalten der Determinante vor: von der vierten Spalte subtrahieren wir die
erste Spalte, von der dritten Spalte das 5-fache der ersten Spalte. Dann enthält die Determinante in der letzten (grau
unterlegten) Zeile nur noch ein von Null verschiedenes Element: a 41 ¼ 1, a 42 ¼ a 43 ¼ a 44 ¼ 0. Die Entwicklung
der Determinante nach den Elementen dieser Zeile führt dann auf eine dreireihige Determinante, die wir nach der
Regel von Sarrus leicht berechnen können (S 1 : i-te Spalte).
4
2 3
4
7
4
1
1
2 8 4 6
2 8 14
4
¼
¼ a 41 A 41 þ a 42 A 42 þ a 43 A 43 þ a 44 A 44 ¼ A 41
D ¼
7
7
5
1 0
5 34 7
1
0
0
0
1
1
0
0
0
0
5 1
" "
5 S1 S1
Berechnung des algebraischen Komplements A 41 aus der Unterdeterminante D 41 nach Sarrus:
4
7
4
1
7
4
4
2 8 14
4
¼ 8 14
A 41 ¼ ð 1Þ 4 þ 1 D 41 ¼ D 41 ¼
4 ¼ 2052
7
5
34
7
5 34 7
1
0
0
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D 41 ¼ 2052
4
7
7
4 4
8 14
4 8 14 ) D 41 ¼ 392 þ 140 þ 1088 þ 280 þ 544 392 ¼ 2052
5 34 7 5 34
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D 41
Ergebnis: D ¼ A 41 ¼ D 41 ¼ 2052
J16
1 1
Zeigen Sie, dass die Gleichung x x 1
y y
1
und P 2 ¼ ðx 2 ; y 2 Þ darstellt.
¼ 0 eine Gerade durch die Punkte P 1 ¼ ðx 1 ; y 1 Þ
1
x2
y2
Wir berechnen zunächst die 3-reihige Determinante nach der Regel von Sarrus:
1 1 1 1 1
x x1 x2 x x1 ) D ¼ x1 y2 þ x2 y þ x y1 x1 y x2 y1 x y2
y y
y2 y y1
1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D
Aus D ¼ 0 erhalten wir die folgende lineare Gleichung mit den Koordinaten x und y:
x1 y2 þ x2 y þ x y1 x1 y x2 y1 x y2 ¼ 0
ðx 2 x 1 Þ y þ ðy 1 y 2 Þ x þ x 1 y 2 x 2 y 1 ¼ 0
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
a
b
c
)
)
ay þ bx þ c ¼ 0
Diese Gleichung ist die Funktionsgleichung einer linearen Funktion in impliziter Form und repräsentiert bekanntlich
eine Gerade. Beide Punkte liegen auf der Geraden, da beim Einsetzen der Koordinaten von P 1 bzw. P 2 in die
Determinante der Ausgangsgleichung zwei gleiche Spalten entstehen und die Determinante somit jeweils verschwindet:
1 1 1
1 1 1
P 1 ¼ ðx 1 ; y 1 Þ ) x 1 x 1 x 2 ¼ 0 ;
P 2 ¼ ðx 2 ; y 2 Þ ) x 2 x 1 x 2 ¼ 0
y
y
y1 y2
y1 y2
1
2
"
"
" "
identische Spalten
identische Spalten
518
J Lineare Algebra
J17
Wie ändert sich der Determinantenwert einer n-reihigen Matrix A, wenn man diese Matrix mit dem
Skalar l multipliziert?
Die Multiplikation einer Matrix A mit einem Skalar l erfolgt bekanntlich elementweise, d. h. jedes Matrixelement
wird mit l multipliziert:
0
0
1
1
a 11 a 12 a 1 n
l a 11 l a 12 l a 1 n
B
B
C
C
B a 21 a 22 a 2 n C
B l a 21 l a 22 l a 2 n C
B
B
C
C
lA ¼ lB .
¼ B .
.. C
.. C
B ..
B
C
.
. A
. C
@
@ .
A
an1
an2
l an1
ann
l an2
l ann
Damit besitzt die Determinante der Matrix l A die folgende Gestalt:
l a 11
l a 21
det ðl AÞ ¼ .
.
.
la
n1
l a 12
l a 22
l an2
l a 1n
l a2n
..
.
l ann
In der Determinante von l A enthält somit jede der n Zeilen (Spalten) den gemeinsamen Faktor l. Bekanntlich
darf ein allen Elementen einer Zeile (Spalte) gemeinsamer Faktor vor die Determinante gezogen werden. Wir können
daher aus jeder der n Zeilen (Spalten) den gemeinsamen Faktor l vorziehen. Der Faktor l tritt daher genau n-mal
vor der Determinante auf:
l a 11 l a 12 l a 1 n
a 11 a 12 a 1 n
l a 21 l a 22 l a 2 n
a 21 a 22 a 2 n
n
det ðl AÞ ¼ .
.. ¼ l l l ..
.. ¼ l det A
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} .
..
.
.
la
a
n-mal
l an2 l ann
an2 ann
n1
n1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A
Folgerung: Wird eine n-reihige Matrix A mit dem Skalar l multipliziert, so multipliziert sich ihre Determinante
mit l n , d. h. es gilt:
det ðl AÞ ¼ l n det A
P
zffl}|ffl{
a b
Bc d
B
B
Zeigen Sie: Für die Determinante der 4-reihigen Blockmatrix A ¼ B
B
@ 0 0
det A ¼ ðdet PÞ ðdet QÞ
0 0
0
J18
Zahlenbeispiel für die folgenden Untermatrizen:
4 2
2 3
:
und Q ¼
P ¼
1 3
1 5
Berechnen Sie den Wert der Determinante det A.
1
0
C
0C
C
C gilt:
C
a bA
g d
|ffl{zffl}
Q
0
0
1 Matrizen und Determinanten
519
Berechnung der algebraischen Komplemente A 11
D 12 nach der Regel von Sarrus:
a b
c d
1þ1
A 11 ¼ ð 1Þ
D 11 ¼ D 11 ¼
0 0
0 0
d 0 0 d
0 a b 0
0 g d 0
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
D 11
0
a
g
)
f
f
f
f
Wir entwickeln die Determinante der Blockmatrix A nach dem Elementen der 1. Zeile:
a b 0 0
c d 0 0
det A ¼
¼ a 11 A 11 þ a 12 A 12 þ a 13 A 13 þ a 14 A 14 ¼ a A 11 þ b A 12
0 0 a b
a
b
0
0
0 0 g d
und A 12 aus den entsprechenden Unterdeterminanten D 11 und
d 0 0
¼ 0 a b ¼ d ða d b gÞ
a b
0 g d
g d
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
D 11 ¼ d ða d b gÞ
0
0
0
0
D 11 ¼ d a d þ 0 þ 0 0 d b g 0 ¼ d a d d b g ¼ d ða d b gÞ
A 12 ¼ ð 1Þ 1 þ 2 D 12 ¼ D 12
¼
a b
c d
0 0
0 0
0 0
c 0 0
0 0
¼ 0 a b ¼ c ða d b gÞ
a b
0 g d
g d
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
D 12 ¼ c ða d b gÞ
c 0 0 c
0 a b 0
0 g d 0
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
D 12
0
a
g
)
D 12 ¼ c a d þ 0 þ 0 0 c b g 0 ¼ c a d c b g ¼ c ða d b gÞ
Damit erhalten wir:
det A ¼ a A 11 þ b A 12 ¼ a d ða d b gÞ b c ða d b gÞ ¼ ða d b cÞ ða d b gÞ ¼ ðdet PÞ ðdet QÞ
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det P
det Q
Die beiden Faktoren dieses Produktes sind aber genau die Determinanten der Untermatrizen P und Q:
a b
a b
¼ ad bg
¼ a d b c ; det Q ¼
det P ¼
g d
c d
Zahlenbeispiel:
P
zfflffl}|fflffl{
2 3
B
B1 5
B
det A ¼ B
B
@0 0
0 0
0
0
0
1
0
C
0C
2
C
C ¼ ðdet PÞ ðdet QÞ ¼
C
1
2A
4
1 3
|fflffl{zfflffl}
Q
3 4
5 1
2
¼ ð10 3Þ ð12 2Þ ¼ 7 10 ¼ 70
3
520
J Lineare Algebra
J19
Gegeben sind die 3-reihigen Matrizen
0
1
0
1
1 2 0
1
1 1
B
C
B
C
A ¼ @ 1 5 3 A und B ¼ @ 0 5 3 A :
1 0 2
4
1 2
a) Berechnen Sie die Determinante des Matrizenproduktes A B auf zwei verschiedene Arten.
b) Welchen Wert besitzt die Determinante des Produktes B A?
a) Wir verwenden das Multiplikationstheorem für n-reihige Matrizen: det ðA BÞ ¼ ðdet AÞ ðdet BÞ .
1. Lösungsweg
Wir bilden zunächst das Matrizenprodukt A B nach dem Falk-Schema, dann die Determinante des Produktes
unter Verwendung der Regel von Sarrus:
B
A
1
1
1
2
5
0
0
3
2
1
1
0 5
4
1
1
3
2
1 9 7
11 23 20
9
3 5
AB
)
7 1 9
1 9
11 23 20 11 23
9
3
5 9
3
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
det ðA BÞ
det ðA BÞ ¼ 115 1620 þ 231 þ 1449 60 þ 495 ¼ 380
2. Lösungsweg
Wir berechnen die Determinanten von A und B nach der Regel von Sarrus und multiplizieren diese:
1 2 0
1 2
1 5 3 1 5 ) det A ¼ 10 þ 6 þ 0 0 0 þ 4 ¼ 20
1 0 2
1 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
det A
1
1
1 1 1
0 5 3 0 5
4
1
1 2 4
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
det B
)
det B ¼ 10 þ 12 þ 0 þ 20 3 0 ¼ 19
det ðA BÞ ¼ ðdet AÞ ðdet BÞ ¼ 20 19 ¼ 380
b) Aus dem Multiplikationstheorem für Determinanten folgt:
det ðB AÞ ¼ ðdet BÞ ðdet AÞ ¼ 19 20 ¼ 380
Somit ist det ðB AÞ ¼ det ðA BÞ, obwohl die Matrizenprodukte B A und A B verschieden sind.
J20
Zeige: Für eine n-reihige Diagonalmatrix A mit den Diagonalelementen a 11 ; a 22 ; a 33 ; . . . ; a nn gilt:
det A ¼ a 11 a 22 a 33 a nn
1 Matrizen und Determinanten
521
Wir entwickeln die n-reihige Diagonaldeterminante det A zunächst nach den Elementen der 1. Zeile, wobei nur das
Diagonalelement a 11 einen Beitrag liefert (die übrigen Elemente sind alle gleich null). Die Entwicklung führt zu
einer ðn 1Þ-reihigen Diagonaldeterminante mit den Diagonalelementen a 22 ; a 33 ; . . . ; a n n . Diese Determinante
entwickeln wir wieder nach den Elementen der 1. Zeile (nur das 1. Element a22 liefert einen Beitrag, die übrigen
Elemente sind wieder alle gleich Null).
Die Entwicklung führt dann auf eine ðn 2Þ-reihige Diagonaldeterminante mit den Diagonalelementen a 33 ; a 44 ;
. . . ; a n n . Dieses Verfahren setzen wir fort, bis wir auf die 1-reihige Determinante mit dem (einzigen) Element a n n
stoßen. Somit gilt:
det A ¼
a 11
0
0
0
0
a 22
0
0
0
0
a 33
0
0
..
.
0
..
.
0
..
.
a 44
..
.
0
0
0
0
¼ a 11 a 22
a 33
0
0 a 44
..
..
.
.
0
0
0
a 22
0
0
0
¼ a 11 0
0
.
..
..
.
0
ann
0
0
a 33
0
0
..
.
a 44
..
.
0
0
0
a 44
0
¼ a a a
..
11
22
33
.
..
.
0
ann
0
0
0 ¼
..
.
a
nn
0
.. ¼ ¼
.
ann
¼ a 11 a 22 a 33 a n 1; n 1 j a n n j ¼ a 11 a 22 a 33 a n n
|fflffl{zfflffl}
ann
Anmerkung: j a n n j ist die 1-reihige Determinante mit dem einzigen Element a n n (nicht zu verwechseln mit dem
Betrag von a n n ).
Der in Bild J-1 dargestellte elastische Balken der Länge l ¼ 2 a ist am linken Ende fest eingespannt
und trägt in der angegebenen Weise zwei gleiche Punktmassen m 1 ¼ m 2 ¼ m. Infolge seiner Elastizität ist er zu Biegeschwingungen fähig. Die Kreisfrequenzen w > 0 dieser sog. Eigenschwingungen
lassen sich aus der Determinantengleichung
5 2
ða w 2 Þ
w
3EI
2
¼ 0
mit
a
¼
5
m l3
w 2 ða 8 w 2 Þ
2
bestimmen (E I : Biegesteifigkeit des Balkens). Berechnen Sie diese Eigenkreisfrequenzen.
J21
A
Balken
m1
m2
C
B
a
a
Bild J-1
A; B:
Umkehrpunkte der
Biegeschwingung
C:
Gleichgewichtslage
des Balkens
522
J Lineare Algebra
Die Determinantengleichung führt zu einer biquadratischen Gleichung, die wir mit der Substitution u ¼ w 2 lösen:
5 2
w
ða w 2 Þ
25 4
2
w ¼ 0 )
¼ ða w 2 Þ ða 8 w 2 Þ
5 2
4
w
ða 8 w 2 Þ
2
4
25 4
7 4
a2 8 a w2 a w2 þ 8 w 4
w ¼
w 9 a w2 þ a2 ¼ 0
)
4
4
7
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
ð32 25Þ w 4 = 4 ¼ 7 w 4 = 4
36
4 2
36
4 2
a w2 þ
a ¼ 0 ) ðSubstitution : u ¼ w 2 Þ u 2
au þ
a ¼ 0 )
7
7
7
7
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
18
324 2
4 2
18
324 a 2 28 a 2
18
296 a 2
¼
¼
¼
a
a
a ¼
a
a
49
49
7
49
7
7
7
pffiffiffiffiffiffiffiffi
296 a
18
¼ 2,5714 a 2,4578 a ) u 1 ¼ 5,0292 a ; u 2 ¼ 0,1136 a
a
¼
7
7
w4
u 1=2
Rücksubstitution unter Beachtung der Bedingung w > 0 führt zu den folgenden Lösungen:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
w 2 ¼ u 1 ¼ 5,0292 a ) w 1 ¼ 5,0292 a ¼ 2,243 a
w 2 ¼ u 2 ¼ 0,1136 a
J22
)
w2 ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
0,1136 a ¼ 0,337 a
Berechnen Sie die Determinante der 5-reihigen Matrix
0
1
1 1 0 2 0
B 2
0 1 1 4C
B
C
A ¼ B
1 0 3 1C
B 0
C
B
C
@2
1 0 0 0A
2
0 1 2 2
a) durch Laplace-Entwicklung nach günstigen Zeilen oder Spalten (auf 3-reihige Determinanten zurückführen, die dann nach der Regel von Sarrus berechnet werden),
b) indem Sie die Matrix zunächst mit Hilfe elementarer Zeilenumformungen auf Diagonalgestalt bringen und dann die Determinante der Diagonalmatrix berechnen.
a) Besonders günstig sind die 3. Spalte und die 4. Zeile, die beide jeweils drei Nullen enthalten. Wir entscheiden uns
für die 4. Zeile. Die Entwicklung der Determinante nach Laplace enthält dann nur zwei von null verschiedene
Glieder:
f
f
f
2
f
f
det A ¼ a 41 A 41 þ a 42 A 42 þ a 43 A 43 þ a 44 A 44 þ a 45 A 45 ¼ 2 A 41 þ A 42 ¼
1
0
0
0
¼ 2 ð 1Þ 4 þ 1 D 41 þ ð 1Þ 4 þ 2 D 42 ¼ 2 ð 1Þ D 41 þ 1 D 42 ¼ 2 D 41 þ D 42
Die 4-reihigen Unterdeterminanten lauten:
D 41
1
2
¼ 0
2
2
1 0 2 0
1 0 2 0
0 1 1 4
0 1 1 4
1 0 3 1 ¼
;
1 0 3 1
1 0 0 0
0 1 2 2
0 1 2 2
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
det B
D 42
1 1 0 2 0
1 0 2 0
2
0 1 1 4
2 1 1 4
¼ 0
1 0 3 1 ¼
0 0 3 1
2
1
0
0
0
2 1 2 2
2
0 1 2 2
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
det C
1 Matrizen und Determinanten
523
Die Determinanten D 41 ¼ det B und D 42 ¼ det C entwickeln wir jeweils nach den Elementen der 1. Zeile, die
daraus resultierenden 3-reihigen Unterdeterminanten werden dann nach der Regel von Sarrus berechnet:
Entwicklung der Determinante D 41 = det B
B 11 ¼ ð 1Þ 1 þ 1
1 1 4 1
0 3 1 0
1 2 2 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
B 11
2
0
1
0
1
)
0
4
1
2
0
1 1 4
¼ 0 3 1 ¼ 7
1 2 2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
B 11 ¼ 7
B 11 ¼ 6 þ 1 þ 0 12 2 0 ¼ 7
1
0
1
0
1
0
1
2
1
3
2
f
0
1
0
1
0
1
3
2
B 13 ¼ ð 1Þ 1 þ 3
0 1 4 0
1 0 1 1
0 1 2 0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
B 13
f
1
f
f
det B ¼ b 11 B 11 þ b 12 B12 þ b 13 B 13 þ b 14 B 14 ¼ B 11 þ 2 B 13
0
1
0
1
)
2
1
3
2
0
4
1
2
0 1 4
¼ 1 0 1 ¼ 2
0 1 2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
B 13 ¼ 2
B 13 ¼ 0 þ 0 þ 4 0 0 2 ¼ 2
Somit gilt:
D 41 ¼ det B ¼ B 11 þ 2 B 13 ¼ ð 7Þ þ 2 2 ¼ 7 þ 4 ¼ 11
Entwicklung der Determinante D42 = det C
f
0
2
1
C 11 ¼ ð 1Þ 1 þ 1
1
2
0
2
0
1
0
1
Diese Determinante ist identisch
1 0
2 1
1þ3
C 13 ¼ ð 1Þ
0 0
2 1
2
1
3
2
0
4
1
2
f
f
f
det C ¼ c 11 C 11 þ c 12 C 12 þ c 13 C 13 þ c 14 C 14 ¼ C 11 þ 2 C 13
0
1 1 4
¼ 0 3 1 ¼ 7
1 2 2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
C 11 ¼ 7
mit der bereits berechneten Determinante B11 : C 11 ¼ B 11 ¼ 7.
2 0
2 1 4
1 4
¼ 0 0 1 ¼ 0
3 1
2 1 2
2 2
" "
proportionale Spalten (die 1. Spalte ist das 2-fache der 2. Spalte)
Zur Erinnerung: Eine Determinante mit zwei proportionalen Zeilen (oder Spalten) verschwindet.
524
J Lineare Algebra
Somit gilt:
D 42 ¼ det C ¼ C 11 þ 2 C 13 ¼ 7 þ 2 0 ¼ 7
Für die Ausgangsdeterminante det A erhalten wir damit den folgenden Wert:
det A ¼ 2 D 41 þ D 42 ¼ 2 11 7 ¼ 22 7 ¼ 15
b) Die durchgeführten Umformungen in den Zeilen der Matrix A sind jeweils angeschrieben:
0
1 1
0
2
0
1
1
1
0
3
1
0
0
0
1
2
B
B 2
B
A ¼ B
B 0
B
B2
@
2
0
1 1
0
1
0
0
1
1
þ Z3
1 2
0
5
1
0
C
4 C þ Z4
C
1C
C
C
0C
A
2 þ Z4
C
3 C Z5
C
0
3 1C
C
C
0
4 0C
A þ Z3
1 1 1
B
0
B0
B
B0
1
B
B
B0 1
@
0
0
0
2
0
1
1
0
0
1
0
2
1
1
1
1
0
3
1
0
0
1
1
2
5
1
B
C
B0 0 0 1 2C
C
B
) B
3 1C
C
B0 1 0
C
B
B0 0 0
7 1C
A
@
0 0 1 1 1
0
1
0
0
5
0
1
1
C
4 C Z3
C
1C
C
C
0C
A þ 2 Z1
2 Z3
0
1
3
1
C
B
3 1C
B0 1 0
B
C
B0 0 1 1 1C
B
C
B
C
B0 0 0 1 2C
@
A
0 0 0
7 1 þ 7 Z4
B
B 0
B
B 0
B
B
B2
@
0
)
0
1
1
0
2
)
0
5
1
1
C
B
3 1C
B0 1 0
B
C
C
) B
B0 0 0 1 2C
B
C
B0 0 1 1 1C
@
A
0 0 0
7 1
4
5
)
1
B
C
3
1C
B0 1 0
B
C
) B
1C
B0 0 1 1
C
B
C
B0 0 0 1
2C
@
A
0 0 0
0 15
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
6
Obere Dreiecksmatrix
Umformungen
1
Zur 2. und 5. Zeile addieren wir die 4. Zeile.
2
Von der 2. und 5. Zeile wird die 3. Zeile subtrahiert, zur 4. Zeile das 2-fache der 1. Zeile addiert.
3
Zur 1. und 4. Zeile wird die 3. Zeile addiert, von der 2. Zeile die 5. Zeile subtrahiert.
4
Wir vertauschen jeweils die 2. Zeile mit der 3. Zeile und die 4. Zeile mit der 5. Zeile.
5
Vertauschen der Zeilen 3 und 4.
6
Zur 5. Zeile wird das 7-fache der 4. Zeile addiert. Wir erhalten eine obere Dreiecksmatrix.
Berechnung der Determinante det A
Die vorgenommenen Zeilenumformungen in der Matrix A bewirken keine nderung des Determinantenwertes.
Mit einer Ausnahme: Beim Vertauschen zweier Zeilen ändert die Determinante ihr Vorzeichen. Insgesamt wurden
drei Vertauschungen vorgenommen (Operationen 4 und 5 ), so dass sich die Determinante mit
ð 1Þ ð 1Þ ð 1Þ ¼ 1 multipliziert. Somit gilt:
det A ¼ 1 ½ ð1Þ ð1Þ ð1Þ ð 1Þ ð15Þ ¼ 15
(für Dreiecksmatrizen gilt bekanntlich: det A ¼ Produkt der Diagonalelemente).
1 Matrizen und Determinanten
525
1.3 Spezielle Matrizen
Lehrbuch: Band 2, Kapitel I.2.4, 3 und 6
Formelsammlung: Kapitel VII.1.2, 1.4, 1.5 und 4
J23
Welche der nachfolgenden 3-reihigen Matrizen sind regulär, welche
(Nachweis über Determinanten)
0
0
1
0
1
1 0 0
a 1
1 4 2
B
B
C
B
C
A ¼ @0 1 2A; B ¼ @0 2 4A; C ¼ @1 0
2 1 1
0 3 6
2 1
singulär?
1
9
C
aA
1
ðmit a 2 RÞ
Eine n-reihige Matrix A ist regulär, wenn ihre Determinante nicht verschwindet, anderenfalls ist sie singulär. Die
Berechnung der hier vorliegenden 3-reihigen Determinanten erfolgt nach der Regel von Sarrus.
1 4 2 1
0 1 2 0
2 1 1 2
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det A
1 0 0 1
0 2 4 0
0 3 6 0
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det B
a 1 9 a
1 0 a 1
2 1 1 2
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det C
4
1
1
)
det A ¼ 1 þ 16 þ 0 4 2 0 ¼ 11 6¼ 0
)
0
2
3
)
det B ¼ 12 þ 0 þ 0 0 12 0 ¼ 0
B ist singulär
1
0
1
)
det C ¼ 0 þ 2 a þ 9 0 a 2 1 ¼ a 2 þ 2 a þ 8
) a 2 þ 2 a þ 8 ¼ 0 ð 1Þ
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ 1 1þ8 ¼ 1 9 ¼ 13 )
det C ¼ 0
)
a 1=2
a1 ¼ 4 ;
)
a2 2 a 8 ¼ 0
A ist regulär
)
a2 ¼ 2
Für a ¼ 4 bzw. a ¼ 2 ist die Matrix C demnach singulär, für alle übrigen reellen Werte von a regulär.
J24
Bestimmen Sie mit Hilfe elementarer Umformungen in den Zeilen bzw. Spalten der Matrix den Rang r
dieser Matrix und entscheiden Sie dann, ob die Matrix regulär oder singulär ist.
1
0
1
0
1
0
2
1
0 1
1
4
6
2
1
2
B1
2 2 0C
C
B
C
B
C
B
cÞ A ¼ B
bÞ A ¼ @ 2
5 3A
aÞ A ¼ @ 1
2 2A
C
@0
2
4 1A
8 7 21
2 2 1
0 2 16 4
Eine n-reihige Matrix A ist genau dann regulär, wenn ihr Rang r gleich n ist, anderenfalls ist sie singulär. Durch
elementare Zeilenumformungen bringen wir die Matrix A auf die „Trapezform“ A* und bestimmen den jeweiligen
Rang (er ist gleich der Anzahl der nichtverschwindenden Zeilen).
526
J Lineare Algebra
0
aÞ
2
B
A ¼ B
@1
2
0
1
2
B
B0 3
@
0 6
1
2
1
0
C
2 2C
A
2 1
2
1
3
0
2 Z2
1
1
4
6
C
B
A ¼ @2
5 3 A þ 2 Z1
8 7 21 8 Z 1
bÞ
r ¼ Rg ðAÞ ¼ Rg ðA*Þ ¼ 2 ;
0
cÞ
2
1
0 1
0
1
2 2
B
B0 1
B
B
B0
2
@
0
0
0
C
8 2C
C
C
4 1C
A þ 2 Z2
20
J25
r ¼ n ¼ 3
)
A ist regulär
1
1
4
6
C
B
) @0
13
9A
0 39 27 þ 3 Z 2
)
0
r < n ¼ 3
1
B
B2
B
B
B0
@
0
)
0
n ¼ 4
2
2
1
0
0
)
0
)
2
0
0
0
)
0
C
8 2C
C
C
20 5 C
A
r < n ¼ 4
1
B
) @0
0
1
1
20 5
0
)
Z3
)
1
4 6
C
13 9 A ¼ A*
Nullzeile
0 0
A ist singulär
C
1C
C 2 Z1
C
4 1C
A
20 5
2 2
1
B
B0 1
B
B
B0
0
@
5
r ¼ Rg ðAÞ ¼ Rg ðA*Þ ¼ 3 ;
1
0
0
)
2 Z1
C
6C
A ¼ A*
)
1
1
)
0 9
n ¼ 3
B
C
B1
2 2 0C
B
C
C
A ¼ B
B0
2
4 1C
@
A
0 2 16 4 þ Z 3
1
3
n ¼ 3
0
1
C
2C
A 2 Z1
2 2
1
B
B0
@
0
)
r ¼ Rg ðAÞ ¼ Rg ðA*Þ ¼ 3 ;
2
2
B
B2
1
@
2 2
)
C
6C
A
1
1
2
2
B
B0
B
B
B0
@
0
2
0
2
0
0
B
B 0 1
B
B
B0
0
@
1
C
4 1C
C þ Z3
C
4 1C
A
20 5
3
1
0
2
0
)
1
C
8 2C
C
C ¼ A*
20 5 C
A
0 0
Nullzeile
A ist singulär
Zeigen Sie, dass die Matrix A regulär ist und bestimmen Sie ihre Inverse A 1 mit Hilfe von Unterdeterminanten von D ¼ det A:
0
0
1
1
a 0 0
2 1 1
B
B
C
C
aÞ A ¼ @ 0 b 0 A ðmit a; b; c 6¼ 0Þ
bÞ A ¼ @ 3
4
1A
0 0 c
1 2
0
Kontrollieren Sie das Ergebnis.
Wir zeigen zunächst, dass det A 6¼ 0 ist und A somit eine reguläre und invertierbare Matrix ist. Die Berechnung
der inversen Matrix A erfolgt dann mit Hilfe der algebraischen Komplemente über die entsprechenden Unterdeterminanten (Vorzeichenbestimmung nach der Schachbrettregel ! FS: Kap. VII.2.3.2).
Die Ergebnisse werden kontrolliert durch den Nachweis der Beziehung A A 1 ¼ A 1 A ¼ E .
a 0 0
aÞ
det A ¼ 0 b 0 ¼ a b c 6¼ 0 ) A ist regulär
0 0 c
(A ist eine Diagonalmatrix, die Determinante von A somit gleich dem Produkt der Diagonalelemente!)
1 Matrizen und Determinanten
Berechnung der
ði; k ¼ 1; 2; 3Þ
a
D 11 ¼ 0
0
D 13
D 22
D 31
D 33
527
algebraischen Komplemente A i k aus den entsprechenden 2-reihigen Unterdeterminanten D i k
der Determinante D ¼ det A:
0 0
a 0 0
b 0
0 0
b 0 ¼
¼ b c 0 ¼ b c ; D 12 ¼ 0 b 0 ¼ 0 c ¼ 0 0 ¼ 0 ;
0
c
0 0 c
0 c
a 0 0
0 b
¼ 0 0 ¼ 0;
¼ 0 b 0 ¼
0 0
0 0 c
D 21
a 0 0
a 0
¼ ac 0 ¼ ac;
¼ 0 b 0 ¼
0 c
0 0 c
a 0 0
0 0
¼ 0 b 0 ¼
b 0
0 0 c
D 23
¼ 0 0 ¼ 0;
D 32
a
¼ 0
0
0
¼
0
0
¼ 0 0 ¼ 0;
c
a 0 0
a
¼ 0 b 0 ¼
0
0 0 c
0
¼ 0 0 ¼ 0;
0
a
¼
0
0
¼ 0 0 ¼ 0;
0
0
b
0
0
0
c
a 0
¼ 0 b
0 0
0
0
c
a 0 0
a 0
¼ ab 0 ¼ ab
¼ 0 b 0 ¼
0
b
0 0 c
A 11 ¼ þ D 11 ¼ b c ; A 22 ¼ þ D 22 ¼ a c ; A 33 ¼ þ D 33 ¼ a b ; alle übrigen algebraischen Komplemente verschwinden.
Inverse Matrix A1
0
A 1
A11
1 B
¼
A
@ 12
det A
A13
A21
A22
A23
1
0
bc
A31
1 B
C
A32 A ¼
@ 0
abc
0
A33
0
ac
0
1
0
0
1=a
C
B
0 A ¼ @ 0
ab
0
0
1=b
0
1
0
C
0 A
1=c
Kontrolle: Nachweis der Beziehung A A 1 ¼ A 1 A ¼ E mit dem Falk-Schema.
A
1=a
0
0
a 0 0
0 b 0
0 0 c
1
0
0
1
A
0
0
1=b 0
0
1=c
0
1
0
0
0
1
A
A A 1 ¼ E
1
1=a
0
0
0
1=b
0
A
a
0
0
0
b
0
0
0
c
0
0
1=c
1
0
0
0
1
0
0
0
1
A 1 A ¼ E
Somit gilt: A A 1 ¼ A 1 A ¼ E .
bÞ
2 1 1
2 1
3
4
1
3
4
1 2
0 1 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A ¼ D
) det A ¼ D ¼ 0 þ 1 þ 6 4 þ 4 0 ¼ 7 6¼ 0 ) A ist regulär
528
J Lineare Algebra
Berechnung der algebraischen Komplemente A i k aus den entsprechenden 2-reihigen Unterdeterminanten D i k
ði; k ¼ 1; 2; 3Þ:
2 1 1
4 1
¼ 0þ2 ¼ 2
D 11 ¼ 3
4
1 ¼
) A 11 ¼ þ D 11 ¼ 2
2 0
1 2
0
D 12
D 13
D 21
D 22
D 23
D 31
D 32
D 33
2 1 1
3
¼ 3
4
1 ¼
1
1 2
0
1
¼ 0þ1 ¼ 1
0
)
A 12 ¼ D 12 ¼ 1
2 1 1
3
¼ 3
4
1 ¼
1
1 2
0
4
¼ 6 þ 4 ¼ 2
2
)
A 13 ¼ þ D 13 ¼ 2
2 1 1
1
¼ 3
4
1 ¼
2
1 2
0
1
¼ 0 2 ¼ 2
0
)
A 21 ¼ D 21 ¼ 2
2 1 1
2
¼ 3
4
1 ¼
1
1 2
0
1
¼ 0 1 ¼ 1
0
)
A 22 ¼ þ D 22 ¼ 1
2 1 1
2
¼ 3
4
1 ¼
1
1 2
0
1
¼ 4 1 ¼ 5
2
)
A 23 ¼ D 23 ¼ 5
2 1 1
1 1
¼ 1 þ 4 ¼ 3
¼ 3
4
1 ¼
4
1
1 2
0
)
A 31 ¼ þ D 31 ¼ 3
2 1 1
2 1
¼ 2þ3 ¼ 5
¼ 3
4
1 ¼
3
1
1 2
0
)
A 32 ¼ D 32 ¼ 5
2 1 1
2 1
¼ 8 þ 3 ¼ 11
¼ 3
4
1 ¼
3
4
1 2
0
)
A 33 ¼ þ D 33 ¼ 11
1
1
0
A31
2
2
3
1B
1
C
C
Inverse Matrix : A 1
B
A32 A ¼
@1 1 5A ¼
7
7
2
5 11
A33
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
B
1
1
Kontrolle: Nachweis der Beziehung A A 1 ¼ A 1 A ¼ E und damit
ðA BÞ ¼
ðB AÞ ¼ E
7
7
bzw. A B ¼ B A ¼ 7 E .
0
A21
A22
A23
A11
1 B
¼
@ A12
det A
A13
B
A
2
3
1
1 1
4
1
2
0
2
2
3
1 1 5
2
5 11
7
0
0
0
7
0
AB
0
0
7
0
)
7
B
A B ¼ @0
0
0
7
0
1
0
1
0
1 0 0
C
B
C
0 A ¼ 7@ 0 1 0 A ¼ 7 E
7
0 0 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
E
1 Matrizen und Determinanten
2 1 1
3
4
1
1 2
0
A
B
529
2
2
3
1 1 5
2
5 11
7
0
0
0
7
0
0
)
0
0
7
7
B
B A ¼ @0
0
0
7
0
1
0
1
1 0 0
0
B
C
C
0 A ¼ 7@ 0 1 0 A ¼ 7 E
7
0 0 1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
E
BA
Somit gilt:
A B ¼ B A ¼ 7E
0
1
B
Die Matrix B ¼ @ 2
0
J26
und
A A 1 ¼ A 1 A ¼ E.
1
3
C
1 A ist die Inverse einer (noch unbekannten) Matrix A . Bestimmen Sie
9
0
1
2
diese nach dem Gauß-Jordan-Verfahren (mit Kontrollrechnung).
Es gilt B ¼ A 1 und somit A ¼ ðA 1 Þ 1 ¼ B 1 . Die gesuchte inverse Matrix von B bestimmen wir nach dem
Gauß-Jordan-Verfahren wie folgt (! FS: Kap. VII.1.5.2.2):
0
ðB j EÞ
0
1 0
B
@0 1
0 0
0
1
1
1 0
3 1 0 0
1 0
3 1 0 0
B
C
B
C
¼ @2 1
1 0 1 0 A 2 Z 1 ) @ 0 1 5 2 1 0 A
)
0 2 9 0 0 1
0 2 9
0 0 1 2 Z2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflffl{zfflfflfflfflffl}
B
E
1
1
0
3 1
0 0 3 Z3
1 0 0 11
6 3
C
C
B
5 2
1 0 A þ 5 Z 3 ) @ 0 1 0 18 9
5 A ¼ ðE j B 1 Þ
4 2 1
1
0 0 1
4 2
1
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
E
B 1
Damit gilt:
1
11
6 3
C
B
¼ @ 18 9
5 A und
4 2
1
0
A ¼ B 1
0
A 1
1
B
¼ B ¼ @2
0
1
0
3
C
1
1A
2 9
Kontrolle: Wir zeigen, dass A A 1 ¼ A 1 A ¼ E ist.
1
A
A
11
6 3
18 9
5
4 2
1
1
2
0
0
3
1
1
2 9
1
0
0
0
1
0
A
0
0
1
A 1
A A 1 ¼ E
0
Somit gilt: A A 1 ¼ A 1
1
B
A ¼ @0
0
1
2
0
0
3
1
1
2 9
11
6 3
18 9
5
4 2
1
1
0
0
0
1
0
0
0
1
A 1 A ¼ E
0
1
0
1
0
C
0 A ¼ E.
1
530
J Lineare Algebra
J27
Zeigen Sie zunächst mit Hilfe von Determinanten, dass die Matrix A regulär und somit invertierbar
ist und berechnen Sie dann nach dem Gauß-Jordan-Verfahren die inverse Matrix A 1 :
1
0
0
1
1 0
1 0
1 1 2
B1 1
0 1C
C
B
B
C
aÞ A ¼ @ 2 4
1 A bÞ A ¼ B
C
@ 2 2
1 1A
0 1
0
0 1 1 0
Kontrollieren Sie das Ergebnis.
a) Berechnung der 3-reihigen Determinante det A nach der Regel von Sarrus:
1 1 2 1 1
2 4
1 2 4 ) det A ¼ 0 þ 0 4 0 1 0 ¼ 5 6¼ 0
0 1
0 0 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
det A
)
A ist regulär
Berechnung der inversen Matrix A 1 nach Gauß-Jordan (! FS: Kap. VII.1.5.2.2)
1
0
1
0
1 1 2 1 0 0 Z 3
1 1 2 1 0 0
C
B
B
C
5 2 1 0 A Z 3
ðA j EÞ ¼ @ 2 4
1 0 1 0 A 2 Z 1 ) @ 0 2
0 1
0 0 0 1
0 1
00 0 1
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflfflffl{zfflfflfflffl}
A
E
0
1
0
1
1 0 2 1 0 1
1 0 2 1 0 1
B
C
B
C
5 2 1 1 A
) @0 1
0 0 0
1A
)
@0 1
0 1
0 0 0
1
0 1
5 2 1 1 Z2
0
1
B
@0
0
0
0 2 1
1
0 0
0
5 2
1 0 0
B
@0 1 0
0 0 1
|fflfflfflffl{zfflfflfflffl}
E
1
0 1
C
0
1A
1 2 : 5
0
)
1 0 2
1
B
0
0
@0 1
0 0
1 2=5
1
0 1
þ 2 Z3
C
0
1 A
1=5 2=5
1
1=5 2=5 9=5
C
0
0
1 A ¼ ðE j A 1 Þ
2=5 1=5 2=5
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A 1
Somit lautet die Inverse der Matrix A wie folgt:
0
1
1
0
0
1=5 2=5 9=5
1=5 2=5 9=5
1
1 B
B
C
C
B
1
0
0
5=5 A ¼
¼ @
0
0
1 A ¼ @
A
@ 0
5
2=5 1=5 2=5
2=5 1=5 2=5
2
1
2 9
C
0
5A
1 2
Kontrolle: Nachweis der Beziehung A A 1 ¼ A 1 A ¼ E mit dem Falk-Schema.
A 1
A
1 1 2
2 4
1
0 1
0
1=5 2=5 9=5
0
0
1
2=5 1=5 2=5
1
0
0
0
1
0
0
0
1
A A 1 ¼ E
A
A 1
1=5 2=5 9=5
0
0
1
2=5 1=5 2=5
1 1 2
2 4
1
0 1
0
1
0
0
0
1
0
0
0
1
A 1 A ¼ E
)
)
1 Matrizen und Determinanten
531
0
Somit gilt: A A 1 ¼ A 1
1
A ¼ @0
0
0
1
0
1
0
0 A ¼ E.
1
b) Wir entwickeln die 4-reihige Determinante D ¼ det A nach den Elementen der 1. Zeile und erhalten zwei 3-reihige
Determinanten, die dann nach der Regel von Sarrus berechnet werden:
f
f
f
f
D ¼ det A ¼ a 11 A 11 þ a 12 A 12 þ a 13 A 13 þ a 14 A 14 ¼ A 11 þ A 13
1
0
1
0
Die algebraischen Komplemente A11 und A13 erhalten wir aus den entsprechenden 3-reihigen Unterdeterminanten
D11 und D13 unter Beachtung der Vorzeichenregel (Schachbrettregel ! FS: Kap. VII.2.3.2):
1 0
1 0
1
0 1
1 1
0 1
¼ 2
A 11 ¼ þ D 11 ¼
1 1 ¼ 2
2 2
1 1
1 1 0
0 1 1 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D 11 ¼ 2
1
0 1 1
0
2
1 1 2
1 ) D 11 ¼ 0 þ 0 2 1 þ 1 0 ¼ 2
1 1 0 1 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D11
1 0
1 0
1 1 1
1 1
0 1
¼ 2 2 1 ¼ 3
A 13 ¼ þ D 13 ¼
2 2
1 1
0 1 0
0 1 1 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D 13 ¼ 3
1 1 1 1 1
2 2 1
2 2 ) D 13 ¼ 0 þ 0 þ 2 0 þ 1 0 ¼ 3
0 1 0
0 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D13
Somit gilt:
D ¼ det A ¼ A 11 þ A 13 ¼ 2 þ 3 ¼ 1 6¼ 0
)
A ist regulär und invertierbar:
Berechnung der inversen Matrix A 1 nach Gauß-Jordan (! FS: Kap. VII.1.5.2.2)
0
1 0
1 0
B1 1
0 1
B
ðA j EÞ ¼ B
@ 2 2
1 1
0 1 1 0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
A
1
1 0 0 0
0 1 0 0C
C þ Z1
C
0 0 1 0 A 2 Z1
0 0 0 1
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
E
1
1 0
1
0 1
0 0 0
B0 1
1
1 1
1 0 0C
C
B
C
B
@ 0 0 3 1 4 2 1 0 A 2 Z4
0 0 2 1 1 1 0 1
0
1 0
1 0 1
B0 1
1 1 1
B
B
@0 2 1 1 2
0 1 1 0 0
0
)
0
1
B0
B
) B
@0
0
0
1
0
1
1
1
0
1
1
0 2 1
0
1
1
1
2
0
1 1
0
1
0
0
0
0
1
0
1
0
0C
C
C
0 A 2 Z2
1 Z2
1
0
0 Z3
0
0C
C Z3
C
1 2A
0
1 þ 2 Z3
)
)
532
J Lineare Algebra
1 0 0 1 3
B0 1 0
0 3
B
B
@0 0 1
1 2
0 0 0
1 5
0
0
Inverse Matrix: A 1
1
1 0 0 0 2 1
1 1
B 0 1 0 0 3
1 1
2C
B
C
) B
C ¼ ðE j A 1 Þ
@0 0 1 0 3
A
1
1
1
0 0 0 1 5 1
2 3
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
E
A 1
0
1
0 1
2 þ Z4
1 1
2C
C
C
0
1 2 A Z4
1
2 3
1
2 1
1 1
B 3
1 1
2C
B
C
¼ B
C
@ 3
1 1
1A
5 1
2 3
Kontrolle: Nachweis der Beziehung A A 1 ¼ A 1 A ¼ E mit dem Falk-Schema.
A 1
A
1
1
2
0
0
1 0
1
0 1
2
1 1
1 1 0
2 1
1 1
3
1 1
2
3
1 1
1
5 1
2 3
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
A 1
A
1
1
2
0
2 1
1 1
3
1 1
2
3
1 1
1
5 1
2 3
1
0
0
0
A A 1 ¼ E
0
1 0
1
0 1
2
1 1
1 1 0
0
1
0
0
0
0
1
0
0
0
0
1
A 1 A ¼ E
Somit gilt: A A 1 ¼ A 1 A ¼ E .
J28
Lösen Sie die Matrizengleichungen A X ¼ B und Y A ¼ B durch Invertierung der Matrix A
nach dem Gauß-Jordan-Verfahren:
2 5
1 4
A ¼
; B ¼
1 3
2 3
Die Matrix A ist regulär und daher invertierbar, da ihre Determinante nicht verschwindet:
2 5
¼ 6 5 ¼ 1 6¼ 0 ) A ist regulär:
det A ¼
1 3
Mit dem Gauß-Jordan-Verfahren berechnen wir die zugehörige inverse Matrix A 1 (! FS: Kap. VII.1.5.2.2):
2 5 1 0
1 3 0 1
1
3 0
1 þ 3 Z2
ðA j EÞ ¼
)
)
)
1 30 1
2 5 1 0 2 Z1
0 1 1 2
|{z} |{z}
A
E
1 0 3 5
3 5
1
0 3 5
1
1
)
¼
ðE
j
A
Þ
)
A
¼
0 1 1
2
1
2
0 1 1 2 ð 1Þ
|{z} |fflfflfflfflffl{zfflfflfflfflffl}
E
A 1
Lösung der Gleichung A X = B
Wir multiplizieren die Gleichung von links mit A 1 (alle Matrizenprodukte sind vorhanden):
AX ¼ B
)
A 1 A X ¼ A 1 B
|fflfflfflfflffl{zfflfflfflfflffl}
E
)
E X ¼ A 1 B
|fflffl{zfflffl}
X
)
X ¼ A 1 B
1 Matrizen und Determinanten
533
Berechnung des Matrizenproduktes A 1 B mit dem Falk-Schema:
1
2
B
3 5
1
2
A 1
4
3
Lösung: X ¼ A 1 B ¼
7 3
3
2
7
3
3
2
A 1 B
Lösung der Gleichung Y A = B
Diese Gleichung wird von rechts mit A 1 multipliziert (alle Multiplikationen sind durchführbar):
YA ¼ B
)
Y A A 1 ¼ B A 1
|fflfflfflfflffl{zfflfflfflfflffl}
E
)
Y E ¼ B A 1
|fflffl{zfflffl}
Y
)
Y ¼ B A 1
Das Matrizenprodukt B A 1 berechnen wir mit dem Falk-Schema:
A 1
B
1
2
4
3
3 5
1
2
1
3
3
4
Lösung: Y ¼ B A
1
¼
1
3
3
4
B A 1
J29
Bestimmen Sie die Lösung X der Matrizengleichung A X ¼ B mit Hilfe der inversen Matrix A 1
(Berechnung nach dem Gauß-Jordan-Verfahren). Warum ist die Gleichung Y A ¼ B nicht lösbar?
2 1
2
5 8
A ¼
; B ¼
3
2
4 9 14
Wir zeigen zunächst, dass die 2-reihige Matrix A regulär und somit invertierbar ist:
2 1
¼ 4 þ 3 ¼ 1 6¼ 0 ) A ist regulär:
det A ¼
3
2
Die inverse Matrix A 1 berechnen wir nach dem Gauß-Jordan-Verfahren (! FS: Kap. VII.1.5.2.2):
1 1 1 1
1
1 1
1 þ Z2
2 1 1 0 þ Z 2
)
)
ðA j EÞ ¼
3 2 0 1 3 Z1
0 1 3 2
3
20 1
|fflfflfflfflffl{zfflfflfflfflffl} |{z}
A
E
1
0
0 1
2 1
3 2 ð 1Þ
)
1 0 2 1
¼ ðE j A 1 Þ
0 1 3
2
|{z} |fflfflfflfflffl{zfflfflfflfflffl}
E
A 1
)
A
1
¼
2
3
1
2
)
Die Matrizengleichung A X ¼ B lösen wir, indem wir beide Seiten von links mit A 1 multiplizieren (alle auftretenden Matrizenprodukte sind vorhanden):
A 1 A X ¼ A 1 B
|fflfflfflfflffl{zfflfflfflfflffl}
E
)
E X ¼ A 1 B
|fflffl{zfflffl}
X
)
X ¼ A 1 B
534
J Lineare Algebra
Berechnung des Matrizenproduktes A 1 B mit dem Falk-Schema:
B
A 1
2 1
3
2
2
4
5 8
9 14
0 1
2 3
2
4
Lösung: X ¼ A
1
B ¼
0
2
1
3
2
4
A1 B
Die Gleichung Y A ¼ B ist dagegen nicht lösbar. Um diese Gleichung nach Y aufzulösen, müssten wir zunächst
beide Seiten von rechts mit A 1 multiplizieren:
YA ¼ B
)
Y A A 1 ¼ Y E ¼ Y ¼ B A 1
|fflfflfflfflffl{zfflfflfflfflffl}
E
Das Matrizenprodukt B A 1 existiert nicht, da B vom Typ ð2; 3Þ, A 1 aber vom Typ ð2; 2Þ ist (Spaltenzahl
von B 6¼ Zeilenzahl von A1 ; 3 6¼ 2).
Lösen Sie die Matrizengleichung
0
10 1 0 1
0 1 1
x1
7
B
CB C B C
@ 1 0 3 A@ x2 A ¼ @ 14 A oder A X ¼ B
4 1 2
8
x3
|fflfflfflfflfflffl{zfflfflfflfflfflffl} |{z}
|{z}
A
X
B
durch Invertierung der Koeffizientenmatrix A nach dem Verfahren von Gauß-Jordan (mit Probe).
J30
Die 3-reihige Koeffizientenmatrix A ist regulär und somit invertierbar, da ihre Determinante nicht verschwindet
(Berechnung nach der Regel von Sarrus):
0 1 1 0 1
1 0 3 1 0 ) det A ¼ 0 þ 12 þ 1 0 0 2 ¼ 11 6¼ 0
4 1 2 4 1
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det A
Mit dem Gauß-Jordan-Verfahren berechnen wir die für die Lösung benötigte inverse Matrix A 1
Kap. VII.1.5.2.2):
0
0
1
1
1 0 3 0 1 0
0 1 1 1 0 0
B
B
C
C
) @ 0 1 1 1 0 0 A
)
ðA j EÞ ¼ @ 1 0 3 0 1 0 A
4 1 2 0 0 1
4 1 2 0 0 1 4 Z1
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflffl{zfflfflfflffl}
A
E
1
0
0
1
1 0
3 0
1 0
1 0
3 0
1 0
C
B
B
C
1 1
0 0A
)
) @0 1
1 1
0 0A
@0 1
0 1 10 0 4 1 Z 2
0 0 11 1 4 1 : ð 11Þ
0
1
B
@0
0
0
1
0
3
1
1
1
1
0
0
3 Z3
C
1
0
0
A
Z3
1=11 4=11 1=11
0
)
(! FS:
1
1 0 0 3=11 1=11
3=11
B
C
1=11 A ¼ ðE j A 1 Þ
@ 0 1 0 10=11 4=11
0 0 1 1=11
4=11 1=11
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
E
A 1
1 Matrizen und Determinanten
535
Somit gilt:
0
A 1
0
1
1
3=11 1=11
3=11
3 1
3
1 B
1
B
C
C
¼ @ 10=11 4=11
1=11 A ¼
1A¼
C
@ 10 4
11
11
1=11
4=11 1=11
1
4 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
C
Die Matrizengleichung A X ¼ B multiplizieren wir von links mit A 1 und erhalten:
AX ¼ B
)
A 1 A X ¼ A 1 B
|fflfflfflfflffl{zfflfflfflfflffl}
E
)
E X ¼ A 1 B
|fflffl{zfflffl}
X
)
X ¼ A 1 B ¼
1
ðC BÞ
11
Berechnung des Matrizenproduktes C B nach dem Falk-Schema:
B
C
3 1
3
10 4
1
1
4 1
7
14
8
11
22
55
0
1
0
1
11
1
1
1 @
22 A ¼ @ 2 A
Lösung: X ¼
ðC BÞ ¼
11
11
55
5
CB
Kontrolle durch Einsetzen in die Gleichung A X ¼ B:
A
0
1
4
1
0
1
X
1
2
5
1
3
2
7
14
8
0
)
1
7
A X ¼ @ 14 A ¼ B
8
AX
J31
Prüfen Sie, ob die Spaltenvektoren der folgenden Matrizen linear abhängig oder linear unabhängig
sind:
0
1
0
1
3 1
4
4
4 2
B4 3
6C
B
C
B
C
aÞ A ¼ @ 4 2
4 A bÞ A ¼ B
C
@0
4 3A
2
4
4
2
3
4
a) Wir zeigen, dass die aus den drei Spaltenvektoren a 1 , a 2 und a 3 gebildete 3-reihige Matrix A ¼ ða 1 a 2 a 3 Þ
regulär ist und die Vektoren somit linear unabhängig sind:
4
(
4
4
4 2
det A ¼ 32 32 32 þ 8 64 64 ¼ 216 6¼ 0 )
4 2
4 2 )
4
A ist regulär:
2
4
4
4 2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A
536
J Lineare Algebra
b) Die drei Spaltenvektoren a 1 , a 2 und a 3 aus dem R 4 sind genau dann linear unabhängig, wenn die aus ihnen
gebildete Matrix A ¼ ða 1 a 2 a 3 Þ vom Typ ð4; 3Þ den Rang r ¼ n ¼ 3 besitzt:
1
0
3 1
4
B4 3
6C
C
B
A ¼ ða 1 a 2 a 3 Þ ¼ B
Rg ðAÞ ¼ r 3
C;
@0
4 3A
2
3
4
Diese Matrix hat den Rang r ¼ 3, wenn es mindestens eine von null verschiedene 3-reihige Unterdeterminante
gibt. Die durch Streichen der 4. Zeile erhaltene Unterdeterminante D4 erfüllt diese Bedingung (Berechnung nach
der Regel von Sarrus):
4 3 1
3 1
4 3
6 4 3 ) D 4 ¼ 27 þ 0 þ 64 0 72 12 ¼ 7 6¼ 0
0
4 3 0
4
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D4
Damit gilt r ¼ 3, die drei Spaltenvektoren sind also linear unabhängig.
J32
Bestimmen Sie den Rang der nachfolgenden Matrizen unter ausschließlicher Verwendung von Unterdeterminanten:
1
0
0
1
0
1
5
1
6
2 1 1
1 1 1
1
C
B1 2
2C
B
B
C
B
C
aÞ A ¼ @ 1 1 2 A bÞ B ¼ B
cÞ C ¼ @ 2 2 3 1 A
C
@1
2 1A
2 1 2
0 0 1 3
0
3
3
Die Berechnung der anfallenden 3-reihigen Determinanten erfolgt nach der Regel von Sarrus.
a) Die 3-reihige Determinante von A ist von null verschieden, die Matrix A ist daher regulär und besitzt den Rang
r ¼ 3:
2 1 1 2 1
1 1 2 1 1 ) det A ¼ 4 þ 4 þ 1 2 4 2 ¼ 1 ¼
6 0 ) r ¼ Rg ðAÞ ¼ 3
2 1 2 2 1
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det A
b) Die Matrix B vom Typ ð4; 3Þ hat den Rang r ¼ 3, da es eine 3-reihige von null verschiedene Unterdeterminante D 1 gibt (wir streichen in B die 1. Zeile):
2 1 2
1 2
1
2 1 1
2 ) D 1 ¼ 6 þ 0 þ 6 0 þ 3 þ 6 ¼ 21 6¼ 0 ) r ¼ Rg ðBÞ ¼ 3
0
3
3 0
3
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D1
c) Zunächst gilt: r 3. Der Rang von C ist r ¼ 3, wenn es wenigstens eine von null verschiedene 3-reihige
Unterdeterminante gibt (wir streichen in C der Reihe nach die 1., 2., 3. bzw. 4. Spalte):
1
1 1 1
1 1
1 1
D 1 ¼ D 2 ¼ 2 3 1 ; 2 3 1 2 3 ) D 1 ¼ D 2 ¼ 9 þ 0 þ 2 0 þ 1 þ 6 ¼ 0
0 1 3
0 1 3 0 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D1 ¼ D2
1
1 1
1 1 1
D 3 ¼ 2 2 1 ¼ 0 ; D 4 ¼ 2 2 3 ¼ 0
0 0 3
0 0 1
" "
" "
identische Spalten
identische Spalten
1 Matrizen und Determinanten
537
Alle vier 3-reihigen Unterdeterminanten verschwinden somit. Daher ist r < 3 , d. h. r 2 . Es gibt aber
eine 2-reihige Unterdeterminante mit einem von null verschiedenen Wert (wir streichen in C die 1. und 2. Spalte
sowie die 3. Zeile), nämlich:
1
1
3 1 ¼ 1 3 ¼ 4 6¼ 0 ) r ¼ Rg ðCÞ ¼ 2
Bestimmen Sie den Matrizenrang mittels elementarer Umformungen in den Zeilen bzw. Spalten:
1
0
0
1
0
1
1 2
3
2
1
3 4
1 1
0
0 1 3
B 1
B4 5 5 1 4
4
9 10 C
5C
C
B
B
C
B
C
aÞ A ¼ @ 1
0 2 A bÞ B ¼ B
C cÞ B
C
@ 1 2 7 8 A
@0
3 3
3 2 1A
3 2 0
1
4 1
0
6 14 9 10 7
7
J33
a) Die Matrix A wird mit Hilfe elementarer
Rang von A ist dann gleich der Anzahl r
0
0
1
0 1 3
1
B
B
C
B
B
C
A ¼@ 1
0 2A ) @ 0
3 2 0
3
Umformungen in den Zeilen oder Spalten auf Trapezform gebracht. Der
der nichtverschwindenden Zeilen: Rg ðAÞ ¼ r .
1
0
1
0
1
0 2
1
0 2
1
0 2
C
B
C
B
C
C
C
1 3C
) B
) B
A
@0 1 3A
@0 1 3A
Nullzeile
2 0 þ 3 Z1
0 2 6 2 Z2
0
0 0
Somit gilt: Rg ðAÞ ¼ 2
1
1 2
3
2
B1
4
9 10 C
C þ Z1
B
B ¼ B
C
@ 1 2 7 8 A þ Z1
1
4 1
0 Z1
0
bÞ
0
1 2
3
B0
2
12
B
B
@0
0
20
0
0 40
0
cÞ
1
3
B4
5
B
B
@0
3
6 14
0
1
B0
B
B
@0
0
1
2
12 C
C
C
18 A
38 þ 2 Z 3
1
1 2
3
2
B0
2 12 12 C
C
B
C
B
@ 0 4 4 6 A þ 2 Z2
0
6 4 2 3 Z2
0
)
1
1 2 3
2
B0
2 12 12 C
C
B
C
B
@0
0 20 18 A
0
0 0 2
)
0
)
1
4
1 1
0
5 1 4
5C
C 4 Z1
C
3
3 2 1A
9 10 7
7 6 Z1
1
0 1
1
4
3
5 0 5 11 17 C
C þ 5 Z3
C
1 2
3
3
3A
7 1 16 15 32 þ 7 Z 3
1
1
0 1 1 4
3
B0 1 2 3 3
3C
C
B
C
B
@0
0 10 10 4 2 A
0
0 15 5 6 11 1,5 Z 3
0
)
)
Rg ðBÞ ¼ 4
1
3
4
1
B 0 17 11 5
B
B
@0
3
3
3
0 32 15 16
1
1
0
0
5C
C
C
2 1A
1
7
1
1
0
1 1 4
3
B0
0 10 10 4 2 C
C
B
C
B
@0 1
2 3 3
3A
0
0 15
5 6 11
)
ðSpalten vertauschenÞ
0
)
1
1
0
1
1 4
3
B0 1
2
3 3
3C
C
B
C
B
@0
0 10
10 4 2 A
0
0
0 10 0 8
)
0
0
)
)
Rang : r ¼ 4
538
J Lineare Algebra
Zeigen Sie, dass die folgenden Matrizen orthogonal sind:
0
0
1
1
sin a cos a 0
1 B
B
C
aÞ A ¼ @ cos a
sin a 0 A bÞ A ¼
@2
3
2
0
0
1
J34
1
2 2
C
1
2A
2 1
Wie lautet die jeweilige inverse Matrix A 1 ?
Eine n-reihige Matrix A ist orthogonal, wenn sie die Bedingung A A T ¼ E erfüllt. Für eine orthogonale Matrix A
gilt stets A 1 ¼ A T , d. h. die inverse Matrix A 1 ist die Transponierte von A .
a) Wir zeigen mit Hilfe des Falk-Schemas, dass die Matrix A die Eigenschaft A A T ¼ E besitzt:
A
A
sin a
cos a
0
cos a
sin a
0
0
0
1
ðsin 2 a þ cos 2 aÞ
ðcos a sin a sin a cos aÞ
0
ðsin a cos a cos a sin aÞ
ðcos 2 a þ sin 2 aÞ
0
0
0
1
T
sin a cos a 0
cos a
sin a 0
0
0
1
A AT
Unter Verwendung des „trigonometrischen Pythagoras“ sin 2 a þ cos 2 a ¼ 1 erhalten wir:
1
0
0
1
ðsin 2 a þ cos 2 aÞ
ðsin a cos a cos a sin aÞ 0
C
B
B
T
B
2
AA ¼ B
0C
ðcos 2 a þ sin aÞ
A ¼ @0
@ ðcos a sin a sin a cos aÞ
0
0
0
1
)
0
0
1
C
0C
A ¼ E
0
1
Die Matrix A ist somit orthogonal:
0
Inverse Matrix: A 1 ¼ A T
0
bÞ
A AT ¼
A AT ¼
1
1 B
B2
3 @
2
1
sin a cos a 0
B
C
¼ @ cos a sin a 0 A
0
0
1
2 2
1
2
0
1
1
2
2
1
0
1
2 2
1 0
1
2
2
1
C 1 B
C
C B
C
1B
B
B
C
B
C
2C
1
2C
A 3 @ 2 1 2A ¼ 9 @2
A@ 2 1 2 A
1
2 2 1
2 2 1
2 2 1
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
B
BT
1
ðB B T Þ
9
Berechnung des Matrizenproduktes B B T nach dem Falk-Schema:
B
B
1
2
2
T
2 2
1
2
2 1
1
2
2
9
0
0
2
2
1 2
2 1
0
9
0
B BT
0
0
9
0
9
0
0
1
1
1 B
B0 9 0C
C ¼
ðB B T Þ ¼
A
9
9 @
0 0 9
0
1
1 0 0
B
C
B
¼ @0 1 0C
A ¼ E ) A ist orthogonal:
0 0 1
A AT ¼
1
1 Matrizen und Determinanten
539
0
Inverse Matrix: A 1 ¼ A T
1
1 B
¼
@ 2
3
2
1
2
2
C
1 2A
2 1
Welche der nachstehenden Matrizen sind symmetrisch, welche schiefsymmetrisch?
1
0
1
0
1
0
0
2 3
0 1
3
2
3 6
C
B
C
B
C
B
1 8A;
0 4A; C ¼ @2
A ¼ @3 1 5A; B ¼ @ 1
3 8 0
3
4
0
6
5 4
J35
1
1
2 2
1 B
C
D ¼
1 2A;
@ 2
3
2 2 1
0
0
0
B 1
B
F ¼ B
@ 5
8
1
0
3
0
1
5 8
3 0C
C
C
0 4A
4 0
Bei einer symmetrischen Matrix sind die Elemente spiegelsymmetrisch zur Hauptdiagonalen angeordnet. Symmetrisch
sind daher die folgenden Matrizen:
0
2
B
A ¼ @3
6
1
3 6
C
1 5 A ¼ AT ;
5 4
0
1
1 B
D ¼
@ 2
3
2
1
2 2
C
1 2 A ¼ DT
2 1
Bei einer schiefsymmetrischen Matrix verschwinden sämtliche Diagonalelemente und spiegelsymmetrisch zur Hauptdiagonalen liegende Elemente unterscheiden sich nur im Vorzeichen. Schiefsymmetrisch sind daher:
0
1
0
1
0 1 5
8
0 1
3
B 1
0
3
0C
B
B
C
C
B ¼ @ 1
0 4 A ¼ BT ; F ¼ B
C ¼ FT
@ 5 3
0
4A
3
4
0
8
0 4
0
Die Matrix C ist weder symmetrisch noch schiefsymmetrisch (bei einer schiefsymmetrischen Matrix müssen alle
Diagonalelemente verschwinden, was hier nicht der Fall ist).
J36
Stellen Sie fest, ob die komplexe Matrix A hermitesch oder schiefhermitesch ist. Zerlegen Sie die
Matrix in einen Realteil B und einen Imaginärteil C . Welchen Wert besitzt die Determinante von A?
0
1
0
1
2
1 j 5 þ 2j
2j
1 þ j 2 þ 5j
B
C
B
C
aÞ A ¼ @ 1 þ j
0
3 þ jA
bÞ A ¼ @ 1 þ j
0
1 þ 3jA
5 2j 3 j
8
2 þ 5j 1 þ 3j
8j
a) Für eine hermitesche Matrix A gilt die Bedingung A ¼ A ¼ ðA *Þ T , die hier erfüllt ist:
0
1
0
1
2
1 j 5 þ 2j
2
1 þ j 5 2j
1
B
C
B
C 2
A ¼ @1 þ j
0
3 þ jA ) A* ¼ @1 j
0
3 jA )
5 2j 3 j
8
5 þ 2j 3 þ j
8
0
ðA *Þ T
1
2
1 j 5 þ 2j
B
C
¼ A ¼ @1 þ j
0
3 þ jA ¼ A
5 2j 3 j
8
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
540
J Lineare Algebra
Durchgeführte Operationen:
1
Konjugation: Die Matrixelemente werden durch die konjugiert komplexen Elemente ersetzt.
2
Transponieren: Zeilen und Spalten werden miteinander vertauscht (Spiegelung der Elemente an der Hauptdiagonalen).
Zerlegung der hermiteschen Matrix A in einen symmetrischen Realteil B und einen schiefsymmetrischen Imaginärteil C:
1
0
1
0
1
0
0 j 2j
2 1 5
2
1 j 5 þ 2j
C
B
C
B
C
B
j
0
jA ¼
A ¼ @1 þ j
0
3 þ jA ¼ @1 0 3A þ @
2j j
0
5 3 8
5 2j 3 j
8
1
0
1
0
0 1
2
2 1 5
C
B
C
B
0
1A ¼ B þ j C
¼ @ 1 0 3 A þ j@ 1
2 1
0
5 3 8
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
B
C
(symmetrisch)
(schiefsymmetrisch)
Berechnung der Determinante det A nach der Regel von Sarrus ð j 2 ¼ 1 beachtenÞ:
2
1j
1 j 5 þ 2 j
2
1þ j
0
0
3 þ j 1 þ j
5 2j 3 j
5 2j 3 j
8
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A
det A ¼ 0 þ ð1 jÞ ð3 þ jÞ ð5 2 jÞ þ ð5 þ 2 jÞ ð1 þ jÞ ð3 jÞ
0 ð3 jÞ ð3 þ jÞ 2 8 ð1 þ jÞ ð1 jÞ ¼
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
3. Binom
¼ ð3 þ j 3 j þ 1Þ ð5 2 jÞ þ ð5 þ 5 j þ 2 j 2Þ ð3 jÞ ð9 þ 1Þ 2 8 ð1 þ 1Þ ¼
¼ ð4 2 jÞ ð5 2 jÞ þ ð3 þ 7 jÞ ð3 jÞ 20 16 ¼
¼ 20 8 j 10 j 4 þ 9 3 j þ 21 j þ 7 36 ¼
¼ ð20 4 þ 9 þ 7 36Þ þ ð 8 j 10 j 3 j þ 21 jÞ ¼ 4 þ 0 j ¼ 4
b) Für eine schiefhermitesche Matrix A gilt die Bedingung A ¼ A ¼ ðA *Þ T , die hier erfüllt ist:
0
2j
B
A ¼ @ 1þ j
2 þ 5j
1 þ j
0
1 þ 3j
0
ðA *Þ T
2j
B
¼ A ¼ @1 j
2 5j
1
2 þ 5j
C
1 þ 3jA
8j
1 j
0
1 3j
0
1
)
2j
B
A* ¼ @ 1 j
2 5j
1 j
0
1 3j
1
2 5j
C
1 3jA
8j
2
)
1
0
1
2 5j
2j
1 þ j 2 þ 5j
C
B
C
1 3jA ¼ @ 1 þ j
0
1 þ 3jA ¼ A
8j
2 þ 5j 1 þ 3j
8j
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
Durchgeführte Operationen:
1
Konjugation: Die Matrixelemente werden durch die konjugiert komplexen Elemente ersetzt.
2
Transponieren: Zeilen und Spalten werden miteinander vertauscht (Spiegelung der Elemente an der Hauptdiagonalen).
Somit gilt A ¼ A und damit A ¼ A , d. h. A ist schiefhermitesch.
1 Matrizen und Determinanten
541
Zerlegung der schiefhermiteschen Matrix A in einen schiefsymmetrischen Realteil
Imaginärteil C:
0
0
1
0
1
2j j
0 1 2
2j
1 þ j 2 þ 5j
B
B
C
B
C
B
B
C
B
C
0
0 1A þ @ j
A ¼ @ 1þ j
0
1 þ 3jA ¼ @ 1
5j 3j
2 1 0
2 þ 5j 1 þ 3j
8j
0
B
¼B
@
0 1
2
1
0
2
1
5
B und einen symmetrischen
5j
1
C
3jC
A ¼
8j
1
C
B
C
B
C
1C
Aþ j @1 0 3A ¼ B þ j C
2 1
0
5 3 8
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
0
Realteil B
(schiefsymmetrisch)
Imaginärteil C
(symmetrisch)
Berechnung der Determinante det A nach der Regel von Sarrus ð j 2 ¼ 1 beachtenÞ:
2j
1 þ j
2j
1 þ j 2 þ 5 j
1þ j
0
0
1 þ 3j 1 þ j
2 þ 5j 1 þ 3j
8j 2 þ 5j 1 þ 3j
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A
det A ¼ 0 þ ð 1 þ jÞ ð1 þ 3 jÞ ð 2 þ 5 jÞ þ ð2 þ 5 jÞ ð1 þ jÞ ð 1 þ 3 jÞ
0 ð 1 þ 3 jÞ ð1 þ 3 jÞ 2 j 8 j ð1 þ jÞ ð 1 þ jÞ ¼
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
3. Binom
¼ ð 1 3 j þ j 3Þ ð 2 þ 5 jÞ þ ð2 þ 2 j þ 5 j 5Þ ð 1 þ 3 jÞ
ð 1 9Þ 2 j 8 j ð 1 1Þ ¼
¼ ð 4 2 jÞ ð 2 þ 5 jÞ þ ð 3 þ 7 jÞ ð 1 þ 3 jÞ þ 20 j þ 16 j ¼
¼ 8 20 j þ 4 j þ 10 þ 3 9 j 7 j 21 þ 36 j ¼
¼ ð8 þ 10 þ 3 21Þ þ ð 20 j þ 4 j 9 j 7 j þ 36 jÞ ¼ 0 þ 4 j ¼ 4 j
1
Zeigen Sie, dass die komplexe Matrix A ¼ pffiffiffi
3
J37
1j
1
j
1 þ j
unitär ist und berechnen Sie
ihre Determinante und die inverse Matrix A 1 .
a) Eine Matrix A ist unitär, wenn sie die Bedingung A A ¼ E erfüllt. Zunächst bilden wir die konjugiert transponierte Matrix A ¼ ðA *Þ T :
!
!
1
2
1j
j
1þj
j
1
1
A ¼ pffiffiffi
) A * ¼ pffiffiffi
)
1
1 þ j
1
1 j
3
3
ðA *Þ
T
1
¼ A ¼ pffiffiffi
3
1þj
j
1
!
1 j
Durchgeführte Operationen:
1
Konjugation: Die Matrixelemente werden durch ihre konjugiert komplexen Elemente ersetzt.
2
Transponieren: Spiegelung der Matrixelemente an der Hauptdiagonalen.
542
J Lineare Algebra
Berechnung des Matrizenproduktes A A
!
1j
j
1
1
A A ¼ pffiffiffi
pffiffiffi
1
1 þ j
3
3
1
¼
3
!
1j
j
1
1 þ j
1þj
1 j
j
1þj
!
1
1 j
j
!
1
¼
1
¼
3
b 11
b 12
b 21
b 22
!
Wir berechnen jetzt die Matrixelemente b 11 , b 12 , b 21 und b 22 unter Berücksichtigung der Beziehung j 2 ¼ 1:
b 11 ¼ ð1 j Þ ð1 þ j Þ þ ð jÞ j ¼ 1 j 2 j 2 ¼ 1 þ 1 þ 1 ¼ 3
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
b 12 ¼ ð1 j Þ 1 þ ð jÞ ð 1 j Þ ¼ 1 j þ j þ j 2 ¼ 1 1 ¼ 0
b 21 ¼ 1 ð1 þ j Þ þ ð 1 þ j Þ j ¼ 1 þ j j þ j 2 ¼ 1 1 ¼ 0
b 22 ¼ 1 1 þ ð 1 þ j Þ ð 1 j Þ ¼ 1 þ 1 þ j j j 2 ¼ 1 þ 1 þ 1 ¼ 3
Somit gilt:
AA ¼
1
3
b11
b21
b12
b22
¼
1
3
3
0
0
3
¼
1 0
¼ E
0 1
|fflfflfflffl{zfflfflfflffl}
E
Die Matrix A ist also unitär.
1
1
bÞ det A ¼ pffiffiffi pffiffiffi
3
3
¼
1j
1
1
1
½ ð1 j Þ ð 1 þ j Þ þ j ¼ ð 1 þ j þ j j 2 þ j Þ ¼
¼
3
3
1 þ j
j
1
1
ð 1 þ j þ j þ 1 þ jÞ ¼
3j ¼ j
3
3
)
j det A j ¼ j j j ¼ 1
c) Für eine unitäre Matrix A gilt stets A 1 ¼ A und somit:
1þj
1
1
A 1 ¼ A ¼ pffiffiffi
j
1 j
3
J38
Ist die komplexe Matrix A ¼
cos a
j sin a
j sin a
cos a
unitär?
Welchen Wert besitzt die Determinante von A, wie lautet die inverse Matrix A 1 ?
Die Matrix A ist unitär, wenn sie die Bedingung A A ¼ E erfüllt. Wir berechnen daher zunächst die konjugiert
transponierte Matrix A ¼ ðA *Þ T :
!
!
1
2
cos a
j sin a
cos a j sin a
*
A ¼
) A ¼
)
j sin a
cos a
j sin a
cos a
!
cos a
j sin a
T
*
ðA Þ ¼ A ¼
j sin a
cos a
1 Matrizen und Determinanten
543
Durchgeführte Operationen:
1
Konjugation: Die Matrixelemente werden durch ihre konjugiert komplexen Elemente ersetzt.
2
Transponieren: Spiegelung der Matrixelemente an der Hauptdiagonalen.
Wir bilden jetzt das Matrizenprodukt A A:
!
cos a
j sin a
AA ¼
j sin a
cos a
¼
¼
cos a
j sin a
j sin a
cos a
!
¼
ðcos 2 a j 2 sin 2 aÞ
ð j sin a cos a þ j sin a cos aÞ
ðj sin a cos a j sin a cos aÞ
ð j 2 sin 2 a þ cos 2 aÞ
!
ðcos 2 a þ sin 2 aÞ
0
0
ðsin 2 a þ cos 2 aÞ
¼
1
0
0
1
!
¼
!
¼ E
(unter Beachtung von j 2 ¼ 1 und der trigonometrischen Beziehung sin 2 a þ cos 2 a ¼ 1)
Aus A A ¼ E folgt, dass A eine unitäre Matrix ist.
¼ cos 2 a þ j 2 sin 2 a ¼ cos 2 a sin 2 a ¼
1
f
Berechnung der Determinante det A
cos a
j sin a
det A ¼
j sin a
cos a
¼ ðcos 2 a þ sin 2 aÞ ¼ 1
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
)
j det A j ¼ 1
Inverse Matrix A 1
Für eine unitäre Matrix gilt bekanntlich stets A 1 ¼ A . Somit ist
cos a
j sin a
1
¼ A ¼
A
j sin a
cos a
Für die hier vorliegende unitäre Matrix A gilt sogar A 1 ¼ A ¼ A.
a) Zeigen Sie: Eine quadratische Matrix A lässt sich stets als Summe der Matrizen
B ¼
J39
1
ðA þ A T Þ
2
und
C ¼
1
ðA A T Þ
2
darstellen, wobei B eine symmetrische und C eine schiefsymmetrische Matrix ist (Nachweis führen).
1
0
1 0 4
C
B
b) Zerlegen Sie die 3-reihige Matrix A ¼ @ 2 4 6 A auf diese Weise in einen symmetrischen
2 2 8
Anteil B und einen schiefsymmetrischen Anteil C .
c) Bilden Sie aus diesen Anteilen je eine hermitesche Matrix H und eine schiefhermitesche Matrix S .
a) Wir zeigen zunächst, dass A die Summe aus B und C ist:
BþC ¼
1
1
1
1 T
1
1 T
ðA þ A T Þ þ
ðA A T Þ ¼
Aþ
A þ
A
A ¼ A
2
2
2
2
2
2
544
J Lineare Algebra
Wir müssen ferner zeigen, dass B T ¼ B und C T ¼ C gilt (dann ist B symmetrisch und C schiefsymmetrisch):
B ¼
C ¼
1
ðA þ A T Þ
2
1
ðA A T Þ
2
1
1
ðA þ A T Þ T ¼
2
2
)
BT ¼
)
BT ¼ B
)
CT ¼
)
A T þ ðA T Þ T
|fflffl{zfflffl}
A
B ist symmetrisch:
1
1
ðA T þ AÞ ¼
ðA þ A T Þ ¼ B
2
2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
B
¼
1
1
1
ðA A T Þ T ¼
A T ðA T Þ T ¼
ðA T AÞ ¼
2
2
2
|fflffl{zfflffl}
A
1
¼ ðA A T Þ ¼ C ) C T ¼ C ) C ist schiefsymmetrisch
2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
C
b) Zerlegung der Matrix A in eine Summe aus einer symmetrischen und einer schiefsymmetrischen Matrix:
0
A þ AT
1
0
1 0 4
1
B
C
B
¼ @ 2 4 6A þ @0
2 2 8
4
0
2
1
1 B
B ¼
ðA þ A T Þ ¼
@2
2
2
2
0
1
1
1 0 4
B
C
B
¼ @ 2 4 6A @0
4
2 2 8
0
A AT
2
8
8
0
1
1
@
C ¼
ðA A T Þ ¼
2
2
0
A ¼ BþC
)
1
B
@ 2
2
2
4
6
1
0
2
2
C
B
2A ¼ @2
8
2
1
0
2
1
C
B
8A ¼ @1
16
1
2
4
6
1
2
C
8A
16
1
1
C
4A
8
1
4
4
0
1
1
0 2 6
2
B
C
C
0 4A
2A ¼ @ 2
6 4 0
8
1
0
0 2 6
0
A
@
2
0 4 ¼
1
6 4 0
3
0
4
2
2
8
8
1
1 3
0 2A
2 0
0
1
0
1
1
0 1
3
4
1 1 1
B
C
B
C
C
0
2A
6A ¼ @1 4 4A þ @ 1
3 2
0
8
1 4 8
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
symmetrisch
schiefsymmetrisch
c) Eine komplexe Matrix H mit einem symmetrischen Realteil und einem schiefsymmetrischen Imaginärteil ist stets
hermitesch. Somit ist die folgende Matrix hermitesch:
0
1
B
H ¼ B þ j C ¼ @1
1
1
4
4
1
0
1
0
1
0 1 3
1
C
B
C
B
4A þ j @ 1
0 2A ¼ @1 þ j
8
3 2 0
1 3j
1 j
4
4 2j
1
1 þ 3j
C
4 þ 2jA
8
Eine komplexe Matrix S mit einem schiefsymmetrischen Realteil und einem symmetrischen Imaginärteil ist immer
schiefhermitesch. Die folgende Matrix besitzt daher diese Eigenschaft:
1
0
0 1 3
1
C
B
B
S ¼ CþjB ¼ @ 1
0 2A þ j @1
3 2 0
1
0
1
4
4
0
1
j
1
B
C
4A ¼ @ 1 þ j
3 þ j
8
1 þ j
4j
2 þ 4j
1
3þ j
C
2 þ 4jA
8j
2 Lineare Gleichungssysteme
545
2 Lineare Gleichungssysteme
Wir verwenden die Abkürzung LGS für lineares Gleichungssystem.
Lehrbuch: Band 2, Kapitel I.5
Formelsammlung: Kapitel VII.3
Lösen Sie die folgenden homogenen quadratischen linearen Gleichungssysteme mit Hilfe elementarer
Umformungen in den Zeilen der Koeffizientenmatrix (Gaußscher Algorithmus):
0
10 1
0 1
3 x 1 þ 4 x 2 2 x3 ¼ 0
3
1 1
u
0
B
CB C
B C
aÞ 4 x 1 þ 5 x 2 x 3 ¼ 0
bÞ @ 1
2
3A @ vA ¼ @0A
5 3 7
w
0
x 1 x 2 þ x3 ¼ 0
J40
10 1
0 1
0
1 3 5
4
x1
C
C
B
B2 3 4
C
B
2 C B x2 C
B
B0C
cÞ B
CB C ¼ B C
@ 3 2 1 2 A @ x3 A
@0A
1 4 7
6
x4
0
0
Ein homogenes lineares ( n; n)-System A x ¼ 0 ist stets lösbar. Ist die Koeffizientenmatrix A regulär, d. h.
det A 6¼ 0, gibt es genau eine Lösung, nämlich die sog. triviale Lösung x ¼ 0 (alle Unbekannten haben den Wert
null). Bei einer singulären Koeffizientenmatrix A dagegen gibt es unendlich viele Lösungen mit n r Parametern,
wobei r der Rang von A ist.
a) Die Koeffizientenmatrix A ist regulär, da det A 6¼ 0 ist:
4 2 3
4
3
4
4
5
1
5 ) det A ¼ 15 4 þ 8 þ 10 3 16 ¼ 10 6¼ 0
1 1
1 1 1
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
det A
Das LGS ist daher nur trivial lösbar: x 1 ¼ x 2 ¼ x 3 ¼ 0 :
b) Die Koeffizientenmatrix A ist singulär, da det A ¼ 0 ist:
3
1 1
3
1
1
1
2
3
2 ) det A ¼ 42 þ 15 3 þ 10 þ 27 7 ¼ 0
5 3 7
5 3
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A
Es gibt also nichttriviale Lösungen. Wir bringen die Koeffizientenmatrix A mit Hilfe elementarer Zeilenumformungen auf Trapezform und lösen dann das gestaffelte LGS von unten nach oben:
0
3
1 1
1
þ 3 Z2
0
0
7
8
1
B
B
C
C
C
A ¼ B
2
3C
) B
@1
@1 2 3A
A
5 3 7 þ 5 Z2
0 7 8
0
1
0
1
1 2 3
1 2 3
B
B
C
B 0 7 8C
C
B
) @ 0 7 8C
@
A
A ¼ A*
0 7 8 Z2
0 0 0
Nullzeile
r ¼ Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ;
)
Anzahl der Unbekannten: n ¼ 3 ; r < n
546
J Lineare Algebra
Es gibt also wegen r < n ¼ 3 unendlich viele Lösungen mit n r ¼ 3 2 ¼ 1 Parameter, die wir aus dem
gestaffelten LGS A * x ¼ 0 wie folgt berechnen (wir wählen w ¼ l mit l 2 R als Parameter und lösen zunächst die untere Gleichung):
ðIÞ
u þ 2v þ 3w ¼ 0
ðIIÞ
7v þ 8w ¼ 0
Lösung:
u ¼
)
)
u
7v þ 8l ¼ 0
5
8
l, v ¼
l, w ¼ l
7
7
16
l þ 3l ¼ 0
7
)
)
7v ¼ 8 l
5
5
l ¼ 0 ) u ¼
l
7
7
8
v ¼
l ðEinsetzen in ðIÞÞ
7
u þ
)
(mit l 2 R als Parameter)
Kontrolle: Wir setzen die gefundenen (vom Parameter l abhängenden) Werte der drei Unbekannten in die Ausgangsgleichungen ein und zeigen, dass diese erfüllt sind:
15
8
7
l
ll ¼
ll ¼ ll ¼ 0
7
7
7
ðI*Þ
3u þ v w ¼
ðII*Þ
u þ 2v þ 3w ¼
ðIII*Þ
5u 3v 7w ¼
5
16
21
l
l þ 3l ¼
l þ 3l ¼ 3l þ 3l ¼ 0
7
7
7
25
24
49
lþ
l 7l ¼
l 7l ¼ 7l 7l ¼ 0
7
7
7
c) Wir bringen die Koeffizientenmatrix A zunächst auf Trapezform:
0
0
1
1
1 3 5
4
1
3 5
4
B
B
C
C
B2 3 4
B0 3
2C
6 6C
B
B
C 2 Z1
C: 3
C
C
A ¼ B
) B
B3 2 1 2C 3Z
B 0 7 14 14 C : ð 7Þ
1
@
@
A
A
1 4 7
6 Z1
0
1 2
2
0
1
3
5
4
1
B
C
B0 1
2 2C
B
C
B
C
B0
C þZ
1
2
2
2
@
A
0
1 2
2 þ Z2
r ¼ Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ;
0
)
1
3
B
B 0 1
B
B
B 0
0
@
0
0
5
4
)
1
C
2 2 C
C
C
0
0 C
A
0
0
¼ A*
Nullzeilen
Anzahl der Unbekannten: n ¼ 4 ; r < n
Es gibt also unendlich viele Lösungen mit n r ¼ 4 2 ¼ 2 unabhängigen Parametern, die wir aus dem gestaffelten LGS mit der Koeffizientenmatrix A * wie folgt bestimmen:
ðIÞ
x1 þ 3 x2 5 x3 þ 4 x4 ¼ 0
ðIIÞ
x2 þ 2 x3 2 x4 ¼ 0
Wir wählen x 3 ¼ l und x 4 ¼ m als Parameter und lösen Gleichung (II) nach x 2 auf:
ðIIÞ
)
x2 þ 2 l 2 m ¼ 0
)
x2 ¼ 2 l 2 m
In Gleichung (I) setzen wir für x 2 , x3 und x4 die gefundenen (parameterabhängigen) Werte ein und lösen nach
x 1 auf:
ðIÞ
)
x 1 þ 3 ð2 l 2 mÞ 5 l þ 4 m ¼ x 1 þ 6 l 6 m 5 l þ 4 m ¼ x 1 þ l 2 m ¼ 0
)
x1 ¼ l þ 2 m
Lösung:
x1 ¼ l þ 2 m, x2 ¼ 2 l 2 m, x3 ¼ l, x4 ¼ m
(mit den Parametern l 2 R und m 2 R)
Kontrolle (Probe): Wir zeigen, dass die gefundene Lösung jede der vier Ausgangsgleichungen erfüllt:
ðI*Þ
x 1 þ 3 x 2 5 x 3 þ 4 x 4 ¼ l þ 2 m þ 3 ð2 l 2 mÞ 5 l þ 4 m ¼
¼ l þ 2 m þ 6 l 6 m 5 l þ 4 m ¼ ð l þ 6 l 5 lÞ þ ð2 m 6 m þ 4 mÞ ¼ 0 þ 0 ¼ 0
2 Lineare Gleichungssysteme
ðII*Þ
547
2 x 1 þ 3 x 2 4 x 3 þ 2 x 4 ¼ 2 ð l þ 2 mÞ þ 3 ð2 l 2 mÞ 4 l þ 2 m ¼
¼ 2 l þ 4 m þ 6 l 6 m 4 l þ 2 m ¼ ð 2 l þ 6 l 4 lÞ þ ð4 m 6 m þ 2 mÞ ¼ 0 þ 0 ¼ 0
ðIII*Þ
3 x 1 þ 2 x 2 x 3 2 x 4 ¼ 3 ð l þ 2 mÞ þ 2 ð2 l 2 mÞ l 2 m ¼
¼ 3 l þ 6 m þ 4 l 4 m l 2 m ¼ ð 3 l þ 4 l lÞ þ ð6 m 4 m 2 mÞ ¼ 0 þ 0 ¼ 0
ðIV*Þ
x 1 þ 4 x 2 7 x 3 þ 6 x 4 ¼ l þ 2 m þ 4 ð2 l 2 mÞ 7 l þ 6 m ¼
¼ l þ 2 m þ 8 l 8 m 7 l þ 6 m ¼ ð l þ 8 l 7 lÞ þ ð2 m 8 m þ 6 mÞ ¼ 0 þ 0 ¼ 0
Lösen Sie die folgenden homogenen linearen ðm; nÞ-Systeme (mit m 6¼ n):
0 1
1 x1
0
0 1
u þ 3v
4 10 2 2 B C
0
2 u 18 v
C B x2 C
B
B C
bÞ
aÞ @ 2
3 1 5A B C ¼ @0A
@ x3 A
6u þ 2v
2 7 0
2
0
3u þ
v
x4
0 1
1 x1
0
0 1
1 2 1 0 4 B C
0
B 2 8 10 2 6 C B x 2 C
B0C
CB C
B
B C
cÞ B
C B x3 C ¼ B C
@3 0
@0A
9 1 3A B C
@ x4 A
5 6
3 2 10
0
x5
J41
þ 2w ¼ 0
þ w ¼ 0
þ 3w ¼ 0
þ 5w ¼ 0
Ein homogenes lineares (m; n)-System A x ¼ 0 ist stets lösbar. Die Lösungsmenge hängt noch vom Rang r der
Koeffizientenmatrix A ab, wobei gilt:
r ¼ n
) genau eine Lösung x ¼ 0 (sog. „triviale‘‘ Lösung, alle Unbekannten haben den Wert null )
r < n
) unendlich viele Lösungen mit n r voneinander unabhängigen Parametern
a) Durch elementare Zeilenumformungen bringen wir die Koeffizientenmatrix A auf Trapezform:
0
1
4 10 2 2 : 2
A ¼ @2
3 1 5A
2 7 0
2
0
1
2
5 1 1
) @2
3 1 5 A þ Z1
2 7 0
2 Z1
2
@
)
0
0
1
5
1 1
8
2 6A : 2
12 1
3
)
0
1
2
5
1 1
@0
4
1 3A
0 12 1
3 þ 3 Z2
1
2 5 1 1
@0 4 1 3A ¼ A*
0 0 2 6
0
r ¼ Rg ðAÞ ¼ Rg ðA *Þ ¼ 3 ;
0
)
Anzahl der Unbekannten: n ¼ 4 ; r < n
Es gibt unendlich viele Lösungen mit genau einem Parameter, da n r ¼ 4 3 ¼ 1 ist (wir wählen x 4 ¼ l
mit l 2 R als Parameter). Das gestaffelte LGS A * x ¼ 0 lautet wie folgt (wir lösen es sukzessive von unten
nach oben):
2 x1 þ 5 x2 þ x3 x4 ¼ 0
)
ðIIÞ
4 x2 þ x3 3 x4 ¼ 0
)
4 x2 þ 3 l 3 l ¼ 4 x2 ¼ 0
ðIIIÞ
2 x3 6 x4 ¼ 0
2 x3 6 l ¼ 0
f
ðIÞ
)
2 x1 þ 0 þ 3 l l ¼ 2 x1 þ 2 l ¼ 0
)
)
x2 ¼ 0
x3 ¼ 3 l
l
Lösung:
x 1 ¼ l, x 2 ¼ 0, x 3 ¼ 3 l, x 4 ¼ l (mit dem Parameter l 2 R)
)
x1 ¼ l
548
J Lineare Algebra
Kontrolle (Einsetzen der gefundenen parameterabhängigen Werte in die drei Ausgangsgleichungen):
ðI*Þ
4 x 1 þ 10 x 2 þ 2 x 3 2 x 4 ¼ 4 l þ 0 þ 6 l 2 l ¼ 0
ðII*Þ
2 x1 þ 3 x2 þ x3 5 x4 ¼ 2 l þ 0 þ 3 l 5 l ¼ 0
ðIII*Þ
2 x1 7 x2 þ 2 x4 ¼ 2 l 0 þ 2 l ¼ 0
b) In der Matrizendarstellung lautet dieses homogene (4; 3)-System wie folgt:
0 1
1
0
0
1
3 2 0 1
u
B0C
B 2 18 1 C
B C
CB C
B
C @ v A ¼ B C oder A x ¼ 0
B
@0A
@6
2 3A
w
0
3
1 5
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
|{z}
A
x
0
Wir bringen die Koeffizientenmatrix A zunächst auf Trapezform (mit Hilfe elementarer Umformungen in den
Zeilen):
0
1
0
1
0
1
1
3 2
1
3
2
1
3
2
B 2 18 1 C 2 Z
B 0 24 3 C : 3
B0 8 1C
B
C
B
C
B
C
1
A ¼ B
) B
)
) B
C
C
C
@6
@0
@0
2 3 A 6 Z1
20 15 A : 5
4
3A
3
1 5 3 Z1
0 8 1
0 8 1
1
1
3
2
B0
4
3C
C
B
C
B
@0 8 1A
0 8 1 Z3
1
1
3
2
B0
4
3C
C
B
C
B
@ 0 8 1 A þ 2 Z2
0
0
0
0
0
)
r ¼ Rg ðAÞ ¼ Rg ðA *Þ ¼ 3 ;
0
1
B0
B
B
@0
0
)
1
2
3C
C
C ¼ A*
5A
0
Nullzeile
3
4
0
0
Anzahl der Unbekannten: n ¼ 3 ; r ¼ n
Das homogene LGS ist wegen r ¼ n ¼ 3 nur trivial lösbar, d. h. u ¼ v ¼ w ¼ 0 .
Lösung:
u ¼ 0, v ¼ 0, w ¼ 0
c) Mit Hilfe elementarer Zeilenumformungen bringen wir die Koeffizientenmatrix A zunächst auf Trapezform:
0
1
2 1
0
B
B 2 8 10 2
B
A ¼ B
B3 0
9 1
@
0
1
B
B0
B
B
B0
@
5
6
2
1
2
4
6
1
2
0
4
1
0
C
6C
C 2 Z1
C
3C
A 3 Z1
10
2 1
4 1 5
0
4
1
0
)
)
1
2 1
1
0
0
4
1
4
2 1
0
0
0
0
)
1
)
2 6
0
4
0
1
B
B0 2 4 1 1C
C
B
C
B
C
B0 0
0 2 6C
@
A
0
0
B
C
B0
4 8 2 2C
B
C: 2
B
C
B 0 6 12 1 9 C
@
A
0 4
8 2 10 : 2
0
0
2 1
1
B
B0 2 4 1 1C
C
B
C
B
C
B0 0
0 4 12 C
@
A 2 Z4
þ Z2
1
B
B0 2 4 1 1C
C
B
C
B
C
B0 0
0 0
0C
@
A
0 0
0 2 6
)
5 Z1
C
1 1C
C
C
12 1 9 C
A þ 3 Z2
0 2
0
3
4
0
Spalten vertauschen
)
1
2
0 1
4
1
B
B 0 2 1 4 1 C
C
B
C
B
C¼ A *
B0 0 2
0 6 C
@
A
0 0 0
0
0
Nullzeile
2 Lineare Gleichungssysteme
549
Anmerkung: Am Schluss wurden die Spalten 3 und 4 miteinander vertauscht. Auch diese Operation ist eine äquivalente Umformung, da sie lediglich eine Umstellung der Unbekannten bedeutet, hier also die Unbekannten x 3 und
x 4 miteinander vertauscht.
r ¼ Rg ðAÞ ¼ Rg ðA *Þ ¼ 3 ;
Anzahl der Unbekannten: n ¼ 5 ; r < n
Es gibt somit unendlich viele Lösungen mit n r ¼ 5 3 ¼ 2 voneinander unabhängigen Parametern. Wir
lösen jetzt das erhaltene gestaffelte System A * x * ¼ 0 von unten nach oben (Parameter sind x 3 ¼ l und
x 5 ¼ m mit l 2 R und m 2 R):
ðIÞ
ðIIÞ
ðIIIÞ
Lösung:
x1 þ 2 x2 x3 þ 4 x5 ¼ 0
2 x2 þ x4 4 x3 x5 ¼ 0
2 x4 6 x5 ¼ 0
)
)
x 1 þ 2 ð2 l mÞ l þ 4 m ¼ x 1 þ 4 l 2 m l þ 4 m ¼ 0
)
x1 þ 3 l þ 2 m ¼ 0
)
2 x2 þ 3 m 4 l m ¼ 2 x2 þ 2 m 4 l ¼ 0
)
x2 ¼ 2 l m
2 x4 6 m ¼ 0
)
)
x1 ¼ 3 l 2 m
x4 ¼ 3 m
x 1 ¼ 3 l 2 m , x 2 ¼ 2 l m , x 3 ¼ l , x 4 ¼ 3 m , x 5 ¼ m (mit l 2 R und m 2 R)
Kontrolle (Einsetzen der gefundenen parameterabhängigen Werte in die Ausgangsgleichungen):
ðI*Þ
x 1 þ 2 x 2 x 3 þ 4 x 5 ¼ 3 l 2 m þ 2 ð2 l mÞ l þ 4 m ¼
¼ 3 l 2 m þ 4 l 2 m l þ 4 m ¼ ð 3 l þ 4 l lÞ þ ð 2 m 2 m þ 4 mÞ ¼
¼ 0þ0 ¼ 0
ðII*Þ
2 x 1 þ 8 x 2 10 x 3 þ 2 x 4 þ 6 x 5 ¼ 2 ð 3 l 2 mÞ þ 8 ð2 l mÞ 10 l þ 6 m þ 6 m ¼
¼ 6 l 4 m þ 16 l 8 m 10 l þ 6 m þ 6 m ¼
¼ ð 6 l þ 16 l 10 lÞ þ ð 4 m 8 m þ 6 m þ 6 mÞ ¼ 0 þ 0 ¼ 0
ðIII*Þ
3 x 1 þ 9 x 3 þ x 4 þ 3 x 5 ¼ 3 ð 3 l 2 mÞ þ 9 l þ 3 m þ 3 m ¼
¼ 9 l 6 m þ 9 l þ 3 m þ 3 m ¼ ð 9 l þ 9 lÞ þ ð 6 m þ 3 m þ 3 mÞ ¼ 0 þ 0 ¼ 0
ðIV*Þ 5 x 1 þ 6 x 2 þ 3 x 3 þ 2 x 4 þ 10 x 5 ¼ 5 ð 3 l 2 mÞ þ 6 ð2 l mÞ þ 3 l þ 6 m þ 10 m ¼
¼ 15 l 10 m þ 12 l 6 m þ 3 l þ 6 m þ 10 m ¼
¼ ð 15 l þ 12 l þ 3 lÞ þ ð 10 m 6 m þ 6 m þ 10 mÞ ¼ 0 þ 0 ¼ 0
J42
Lösen Sie die folgenden inhomogenen quadratischen
schen Regel:
0
x þ 10 y þ 5 z ¼ 3
2
B
aÞ
3x 6y 2z ¼ 2
bÞ @ 3
8 x þ 14 y þ 4 z ¼ 6
1
a) Das LGS lautet in der Matrizendarstellung wie folgt:
1
0
10 1
0
3
x
1 10
5
C
B
CB C
B
@ 3 6 2 A@ y A ¼ @ 2 A
6
z
8 14
4
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
linearen Gleichungssysteme mit Hilfe der Cramer-
3
5
4
10 1
0 1
1
1
x1
CB C
B C
2 A @ x2 A ¼ @ 3 A
12
5
x3
550
J Lineare Algebra
Wir berechnen zunächst die benötigten 3-reihigen Determinanten D ¼ det A , D 1 , D 2 und D 3 nach der Regel
von Sarrus:
1 10
5 1 10
3 6 2
3 6 ) D ¼ 24 þ 160 þ 210 240 28 120 ¼ 6
8 14
4 8 14
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D ¼ det A
„Hilfsdeterminanten“ D 1 , D 2 und D 3 (in
vektor der rechten Seite des LGS ersetzt):
5
3 10
3 10
2 6 2 2 6 ) D1
6 14
4
6 14
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D1
1
3
5 1
3
3 2 2
3
2 ) D2
8
6
4 8
6
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D2
3 1 10
1 10
3 6 2
3 6 ) D3
8 14
6 8 14
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D3
D werden der Reihe nach die 1., 2. und 3. Spalte durch den Spalten-
¼ 72 120 140 þ 180 þ 84 þ 80 ¼ 12
¼ 8 þ 48 þ 90 80 12 36 ¼ 18
¼ 36 þ 160 þ 126 144 28 180 ¼ 30
Die Cramersche Regel liefert die folgende Lösung:
x ¼
Lösung:
D1
12
¼
¼ 2;
D
6
y ¼
D2
18
¼
¼ 3;
D
6
z ¼
D3
30
¼
¼ 5
D
6
x ¼ 2, y ¼ 3, z ¼ 5
b) Die Berechnung der Determinante D ¼ det A und der „Hilfsdeterminanten“ D 1 , D 2 und D 3 erfolgt jeweils
nach der Regel von Sarrus:
2 3 1 2 3
3 5 2 3 5 ) D ¼ 50 6 12 þ 5 þ 16 þ 45 ¼ 2
1 4 5 1 4
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
D ¼ det A
Hilfsdeterminanten D 1 ,
1 3 1 1
3 5 2 3
12 4 5 12
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
D1
2 1 1 2 1
3 3 2 3 3
1 12 5 1 12
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
D2
D 2 und D 3 :
3
5
4
)
)
D 1 ¼ 25 72 12 þ 60 þ 8 þ 45 ¼ 4
D 2 ¼ 30 þ 2 þ 36 3 48 15 ¼ 2
2 Lineare Gleichungssysteme
1 2 3
2 3
3 5
3 3 5
1 4 12 1 4
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
D3
551
)
D 3 ¼ 120 9 12 þ 5 þ 24 þ 108 ¼ 4
Die Cramersche Regel führt zu der folgenden Lösung:
x1 ¼
Lösung:
J43
D1
4
¼ 2;
¼
2
D
x2 ¼
D2
2
¼ 1;
¼
2
D
x3 ¼
D3
4
¼ 2
¼
2
D
x 1 ¼ 2, x 2 ¼ 1, x 3 ¼ 2
Bestimmen Sie die Lösungen der folgenden quadratischen linearen Gleichungssysteme durch elementare Zeilenumformungen in der erweiterten Koeffizientenmatrix:
10 1
0
0 1
0 1
10 1
0
1 2
3 1
x1
1
2
x
1 1
1
C Bx C
B 3
B 3C
0
2
1
CB 2C
B
B C
B C
CB C
B
bÞ B
aÞ @ 3
15 9 A @ y A ¼ @ 6 A
CB C ¼ B C
@ 4
@ 1A
2 1
3 A @ x3 A
6
z
3 18 11
2
6 2 2
16
x4
0
10 1
0 1
5 0 1
x
2
B C
B
CB C
cÞ @ 2 1 1 A @ y A ¼ @ 1 A
1 3 2
z
1
Ein inhomogenes lineares (n; n)-System A x ¼ c ist nur lösbar, wenn der Rang der erweiterten Koeffizientenmatrix
ðA j cÞ mit dem Rang der Koeffizientenmatrix A übereinstimmt: Rg ðA j cÞ ¼ Rg ðAÞ ¼ r . Für r ¼ n gibt es
eine eindeutige Lösung (die Koeffizientenmatrix A ist dann regulär, d. h. det A 6¼ 0). Gilt jedoch r < n, so gibt
es unendlich viele Lösungen mit n r voneinander unabhängigen Parametern.
Das inhomogene lineare (n; n)-System A x ¼ c wird mit Hilfe elementarer Zeilenumformungen auf Trapezform gebracht. Im Falle der Lösbarkeit ðRg ðA j cÞ ¼ Rg ðAÞ ¼ rÞ wird das dann vorliegende gestaffelte System A * x ¼ c *
schrittweise von unten nach oben gelöst.
f
f
a) Wir bringen die erweiterte Koeffizientenmatrix ðA j cÞ zunächst mit Hilfe elementarer Zeilenumformungen auf
Trapezform:
0
1
0
1
1
1
1 2
1 1
1 2
C
B
C
B
ðA j cÞ ¼ @ 3
15 9 6 A 3 Z 1 ) @ 0
18 12 0 A : 6 )
þ 3 Z1
3 18 11 6
0 21
14 12
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
A
c
0
0
1
1
1 1
1 2
1 1
1 2
B
B
C
C
3 2 0 A
) @0
3 2 0 A ¼ ðA * j c *Þ
@0
0 21 14 12 þ 7 Z 2
0
0
0 12
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
A*
c*
Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ðA* enthält eine Nullzeile; grau unterlegtÞ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 3
f
Wegen Rg ðAÞ 6¼ Rg ðA j cÞ ist das inhomogene LGS nicht lösbar.
0
0
1
1 2
3 1
1 2
3 1 1
B 3
B
C
6 7
4
0
2
1 3 C 3 Z1
B
B0
) B
bÞ
ðA j cÞ ¼ B
C
@ 4
@ 0 10 13
7
2 1
3 1 A 4 Z 1
0
2
4 4
2
6 2 2 16 þ 2 Z 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
c
1
1
0C 3Z
C
4
C
3 A 5 Z4
18
)
552
J Lineare Algebra
0
1 2
3 1
B
B0
0 19 16
B
B
0
0 33 27
@
0
2
4 4
1
1
54 C
C
C
93 A : 3
18 : 2
1
1 2
3 1
1
B0
9C
1
2 2
C
B
C
B
@0
0 11
9 31 A 19
0
0 19 16 54 ð 11Þ
0
)
1
1 2
3 1
1
B0
1
2 2
9C
C
B
C
B
@0
0 209
171 589 A
0
0
209 176 594 þ Z 3
Rg ðAÞ ¼ Rg ðA *Þ ¼ 4 ;
1
1
9C
C
C ¼ ðA * j c *Þ
589 A
5
|fflffl{zfflffl}
c*
0
0
)
1 2
3 1
B0
1
2 2
B
B
@0
0 209 171
0
0
0 5
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A*
Rg ðA j cÞ ¼ Rg ðA * j c * Þ ¼ 4 ;
)
Anzahl der Unbekannten: n ¼ 4
Somit gilt Rg ðAÞ ¼ Rg ðA j cÞ ¼ r ¼ 4, das inhomogene LGS ist daher lösbar und zwar eindeutig, da
r ¼ n ¼ 4 ist.
Wir lösen jetzt das gestaffelte System A * x ¼ c * schrittweise von unten nach oben:
ðIÞ
x1 2 x2 þ 3 x3 x4 ¼ 1
)
ðIIÞ
x2 þ 2 x3 2 x4 ¼ 9
x2 þ 4 þ 2 ¼ x2 þ 6 ¼ 9
ðIIIÞ
209 x 3 þ 171 x 4 ¼ 589
ðIVÞ
5 x4 ¼ 5
1
B
@0
0
x2 ¼ 3
)
209 x 3 ¼ 418
)
x3 ¼ 2
x4 ¼ 1
1
2 5 Z3
C
1 A 2 Z3
1
0
)
0
B
@0
1
15
9
5
3
3 2
1
3 : ð 3Þ
1C
A
1
)
c
0
1
3 2 1
C
5
3 1 A
5 3 1 þ Z2
)
1
3 2
B
3
@0 5
0
0
0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
A*
1
1
1C
A ¼ ðA * j c *Þ
0
Nullzeile
f
5 0 1
B
ðA j cÞ ¼ @ 2 1 1
1 3 2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
A
0
209 x 3 171 ¼ 589
x1 ¼ 0
x1 ¼ 0, x2 ¼ 3, x3 ¼ 2, x4 ¼ 1
0
c*
A * und ðA * j c *Þ enthalten jeweils eine Nullzeile )
Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 2 ;
Anzahl der Unbekannten: n ¼ 3
Somit ist das inhomogene LGS lösbar, da Rg ðAÞ ¼ Rg ðA j cÞ ¼ r ¼ 2 gilt. Die Lösungsmenge enthält wegen
n r ¼ 3 2 ¼ 1 genau einen Parameter.
Wir lösen das gestaffelte System A * x ¼ c * schrittweise wie folgt von unten nach oben (als Parameter wählen wir
z ¼ l mit l 2 R):
ðIÞ
ðIIÞ
x þ 3y 2z ¼ 1
5y þ 3 z ¼ 1
f
cÞ
)
)
)
f
Lösung:
)
)
x1 6 þ 6 þ 1 ¼ x1 þ 1 ¼ 1
)
x þ
3
9
3
1
3
ð3 l þ 1Þ 2 l ¼ x þ
lþ
2l ¼ x
lþ
¼ 1
5
5
5
5
5
1
2
1
lþ
¼
ðl þ 2Þ
5
5
5
)
x ¼
)
5y þ 3l ¼ 1
)
5y ¼ 1 3l
)
l
Lösung:
x ¼
1
ðl þ 2Þ ,
5
y ¼
1
ð3 l þ 1Þ ,
5
z ¼ l
(mit dem Parameter l 2 R)
y ¼
1
ð3 l þ 1Þ
5
2 Lineare Gleichungssysteme
553
Kontrolle (Einsetzen der gefundenen parameterabhängigen Werte in die drei Ausgangsgleichungen):
5
ðl þ 2Þ l ¼ ðl þ 2Þ l ¼ l þ 2 l ¼ 2
5
ðI*Þ
5x z ¼
ðII*Þ
2x þ y z ¼
¼
ðIII*Þ
2
1
2
4
3
1
ðl þ 2Þ þ
ð3 l þ 1Þ l ¼
lþ
þ
lþ
l ¼
5
5
5
5
5
5
5
5
llþ
¼ llþ1 ¼ 1
5
5
x þ 3y 2z ¼
¼
1
3
1
2
9
3
ðl þ 2Þ þ
ð3 l þ 1Þ 2 l ¼
lþ
þ
lþ
2l ¼
5
5
5
5
5
5
10
5
l 2l þ
¼ 2l 2l þ 1 ¼ 1
5
5
0 1
10 1
1
x
1 1 1
B C
CB C
B
Die Lösungen des linearen Gleichungssystems @ a 1 2 A @ y A ¼ @ 2 A hängen noch vom
3
z
2 2 a
Wert des reellen Parameters a ab.
0
J44
Wann gibt es
a) eine eindeutige Lösung,
b) unendlich viele Lösungen,
c) keine Lösungen?
a) Es gibt genau dann eine Lösung, wenn die Koeffizientendeterminante von null verschieden ist. Wir berechnen daher
zunächst die Determinante nach der Regel von Sarrus:
1 1
1 1 1
a 1 2 a 1 ) det A ¼ a 4 2 a þ 2 4 þ a 2 ¼ a 2 a 6
2 2 a 2 2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
det A
Die „Nullstellen“ der Determinante müssen ausgeschlossen werden:
rffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
1
1
25
1
5
2
det A ¼ 0 ) a a 6 ¼ 0 ) a 1=2 ¼
¼
þ6 ¼
2
4
2
4
2
2
)
a 1 ¼ 3; a 2 ¼ 2
Mit Ausnahme der Werte a 1 ¼ 3 und a 2 ¼ 2 ist das LGS stets eindeutig lösbar.
b) Wir zeigen jetzt, dass es für den Parameterwert a ¼ 3 unendlich viele Lösungen gibt. Zu diesem Zweck bringen
wir die erweiterte Koeffizientenmatrix (mit a ¼ 3) durch elementare Zeilenumformungen auf Trapezform:
1
1
C
2 A þ 3 Z1
3 þ2Z
1
0
)
1
B
@0
0
1
4
4
1
5
5
1
1
C
5A
5 Z
2
c
0
)
1 1 1
B
@0 4 5
0 0 0
|fflfflfflffl{zfflfflfflffl}
A*
1
1
C
5 A ¼ ðA * j c *Þ
0
Nullzeile
f
1 1 1
B
ðA j cÞ ¼ @ 3 1 2
2 2 3
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
A
f
0
c*
A * und ðA * j c *Þ enthalten jeweils eine Nullzeile )
Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 2 ;
Anzahl der Unbekannten: n ¼ 3
Koeffizientenmatrix A und erweiterte Koeffizientenmatrix ðA j cÞ haben den gleichen Rang r ¼ 2. Das LGS ist
daher lösbar, es gibt wegen r < n ¼ 3 unendlich viele Lösungen, die noch von einem Parameter abhängen (Anzahl
der Parameter: n r ¼ 3 2 ¼ 1).
554
J Lineare Algebra
ist. Die erweiterte Koeffizientenmatrix (mit a ¼ 2)
1
0
0
0
1
1
1 1
1
C
B
0A
) @0 1 0
5 þ4Z
0
0 0
2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
A*
1
1
C
0 A ¼ ðA * j c *Þ
5
f
f
c) Wir zeigen jetzt, dass das LGS für a ¼ 2 nicht lösbar
wird wieder auf Trapezform gebracht:
0
0
1
1 1
1 1
1
1
C
B
B
ðA j cÞ ¼ @ 2 1
2 2 A 2 Z1 ) @ 0 1
2 2 2 3 þ 2 Z1
0
4
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
A
c
c*
A * enthält eine Nullzeile (grau unterlegt) und besitzt somit den Rang Rg ðA *Þ ¼ 2, die erweiterte Koeffizientenmatrix ðA * j c *Þ dagegen enthält keine Nullzeile und hat somit den Rang Rg ðA * j c *Þ ¼ 3 . Somit gilt:
Rg ðAÞ ¼ Rg ðA *Þ ¼ 2
und Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 3
)
Rg ðAÞ 6¼ Rg ðA j cÞ
Das LGS ist daher nicht lösbar.
f
f
J45
Lösen Sie das inhomogene lineare Gleichungssystem
0
10 1
0 1
1 0
1
x
3
B
CB C
B C
2 A @ y A ¼ @ 0 A oder A x ¼ B
@1 3
2 1 1
z
11
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
A
x
B
durch Invertierung der Koeffizientenmatrix A nach dem Gauß-Jordan-Verfahren.
Wir zeigen zunächst, dass die Determinante der 3-reihigen Koeffizientenmatrix A nicht verschwindet und A somit
regulär und daher invertierbar ist (Berechnung der Determinante nach Sarrus):
1
1 0
1 0
1 3
2 1 3 ) det A ¼ 3 þ 0 1 6 2 0 ¼ 12 6¼ 0
2 1 1
2 1
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
det A
Die inverse Matrix A 1 berechnen
0
1 0
1
B
ðA j EÞ ¼ @ 1 3
2
2 1 1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
A
0
1
B
@0
0
0
0
1
0 12
1 3
1 0 0
B
@0 1 0
0 0 1
|fflfflfflfflffl{zfflfflfflfflffl}
E
wir nach dem Gauß-Jordan-Verfahren (! FS: Kap. VII.1.5.2.2):
1
0
1
1 0 0
1 0
1 1 0 0
C
B
C
0 1 0 A þ Z1
) @0 3
3 1 1 0 A 3 Z 3 )
0 0 1 2 Z1
0 1 32 0 1
|fflfflfflfflffl{zfflfflfflfflffl}
E
1
0
1 0
7 1 3C
A : 12
2 0
1
0
)
1
B
@0
0
0
1
1 3
0
1
1
3=12
5=12 1=12
C
3=12
3=12
3=12 A ¼ ðE j A 1 Þ
7=12
1=12 3=12
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A1
1
Z3
1
0
0
C
2
0
1 A þ 3 Z3
7=12 1=12 3=12
)
2 Lineare Gleichungssysteme
555
Die inverse Matrix A 1 lautet somit:
0
0
1
1
5=12 1=12
3=12
5 1
3
1 B
1
B
C
C
A 1 ¼ @ 3=12
3=12
3=12 A ¼
3
3A ¼
C
@3
12
12
7=12
1=12 3=12
7
1 3
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
C
Das inhomogene LGS A x ¼ B lösen wir mit Hilfe der inversen Matrix A 1 wie folgt (beide Seiten werden von
links mit A 1 multipliziert):
Ax ¼ B
)
A 1 A x ¼ A 1 B
|fflfflffl{zfflfflffl}
E
E x ¼ A 1 B
|{z}
x
)
)
x ¼ A 1 B ¼
1
ðC BÞ
12
Berechnung des Matrizenproduktes C B mit dem Falk-Schema:
3
0
11
B
C
5 1
3
3
7
1
3
3
3
0
1
1 B
Lösungsvektor: x ¼
ðC BÞ ¼
@
12
12
48
24
12
Lösung:
1
0
1
48
4
C
B
C
24 A ¼ @ 2 A
12
1
x ¼ 4, y ¼ 2, z ¼ 1
CB
Bestimmen Sie unter Verwendung des Gaußschen Algorithmus in „elementarer Form“ (! Band 1:
Kap. I.5.2) die Gleichung der Parabel, die durch die drei Punkte P 1 ¼ ð1; 8Þ, P 2 ¼ ð2; 12Þ
und P 3 ¼ ð 1; 18Þ geht.
J46
In den Lösungsansatz y ¼ a x 2 þ b x þ c setzen wir der Reihe nach die Koordinaten der drei Punkte P 1 , P 2 und
P 3 ein und erhalten ein inhomogenes LGS mit drei Gleichungen und den drei unbekannten Koeffizienten a, b und c:
P 1 ¼ ð1; 8Þ
)
aþ
bþc ¼ 8
P 2 ¼ ð2; 12Þ
)
4 a þ 2 b þ c ¼ 12
P 3 ¼ ð 1; 18Þ
)
a
b þ c ¼ 18
Wir lösen das Gleichungssystem mit Hilfe des Gaußschen Algorithmus („elementares“ Rechenschema ! Bd. 1:
Kap. I.5.2):
a
b
c
1
1
1
8
5
4 E1
4
4
2
4
1
4
12
32
5
20
E1
1
1
1
1
1
1
18
8
17
5
2
3
20
15
2
0
10
12
E1
ci
si
ci : Absolutglied
si : Zeilensumme
Die grau unterlegten Zeilen
bilden das gestaffelte System.
556
J Lineare Algebra
Wir können an dieser Stelle abbrechen, da in der letzten Zeile nur noch eine Unbekannte auftritt. Das gestaffelte System
besteht dann aus der Gleichung E 1 und den letzten beiden Gleichungen des Rechenschemas und wird schrittweise von
unten nach oben gelöst:
ðIÞ
aþ
bþ
c ¼ 8
ðIIÞ
2b 3c ¼
ðIIIÞ
2b
Lösung:
)
20
)
10 3 c ¼ 20
¼ 10
)
b ¼ 5
a ¼ 3, b ¼ 5, c ¼ 10;
J47
a þ 5 10 ¼ 8
)
)
a 5 ¼ 8
3 c ¼ 30
)
)
a ¼ 3
c ¼ 10
Parabelgleichung: y ¼ 3 x 2 þ 5 x 10
Lösen Sie das lineare Gleichungssystem
0
10 1
0 1
1
5
2
u
4
B
CB C
B C
1 1A @ v A ¼ @0A
@1
2 3 2
w
7
a) nach der Cramerschen Regel,
b) mit Hilfe des Gaußschen Algorithmus (Zeilenumformungen in der erweiterten Koeffizientenmatrix),
c) durch Invertierung der Koeffizientenmatrix nach dem Gauß-Jordan-Verfahren.
a) Wir berechnen zunächst die benötigte Determinante D ¼ det A sowie die „Hilfsdeterminanten“ D 1 , D 2 und D 3
(jeweils nach der Regel von Sarrus):
5
2
1
5
1
1
1 1 1
1 ) D ¼ 2 10 þ 6 4 3 10 ¼ 23
2 3 2
2 3
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D ¼ det A
Hilfsdeterminanten D 1 , D 2 und D 3 :
5
2 4
5
4
0
0
1
1
1 ) D 1 ¼ 8 35 þ 0 14 12 0 ¼ 69
7 3 2 7 3
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D1
2
1 4
1 4
1 0 1 1 0 ) D 2 ¼ 0 8 14 0 þ 7 8 ¼ 23
2 7 2
2 7
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D2
5 4
1
5
1
1
1 0 1
1 ) D 3 ¼ 7 þ 0 þ 12 8 0 þ 35 ¼ 46
2 3 7
2 3
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
D3
Die Cramersche Regel liefert damit folgende Werte für die drei Unbekannten u, v und w:
u ¼
Lösung:
D1
69
¼ 3;
¼
23
D
v ¼
D2
23
¼ 1;
¼
23
D
u ¼ 3, v ¼ 1, w ¼ 2
w ¼
D3
46
¼ 2
¼
23
D
2 Lineare Gleichungssysteme
557
f
f
b) Wir bringen die erweiterte Koeffizientenmatrix ðA j cÞ mit Hilfe elementarer Zeilenumformungen in die Trapezform:
0
0
1
1
1
5
2 4
1
5
2 4
C
B
B
C
ðA j cÞ ¼ @ 1
1 1 0 A þ Z 1
) @0
6
1 4 A 13 )
2 3 2 7 2 Z1
0 13 6 1 6
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
A
c
0
0
0
1
1
1
1 5 2 4
1
5
2 4
1 5
2 4
C
B
B
B
C
C
) @ 0 6 1 4 A ¼ ðA * j c *Þ
78
13 52 A
) @ 0 78
13 52 A : 13
@0
0 0 1 2
0 78 36 6 þ Z 2
0 0 23 46 : ð 23Þ
|fflfflfflffl{zfflfflfflffl}
A*
c*
Rg ðAÞ ¼ Rg ðA *Þ ¼ 3 ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 3 ;
Anzahl der Unbekannten: n ¼ 3
Somit gilt Rg ðAÞ ¼ Rg ðA j cÞ ¼ r ¼ 3, das LGS ist daher lösbar und zwar wegen r ¼ n ¼ 3 eindeutig. Die
Lösung berechnen wir aus dem gestaffelten System A * x ¼ c * schrittweise von unten nach oben:
ðIÞ
u þ 5v þ 2w ¼ 4
6v þ
ðIIÞ
ðIIIÞ
Lösung:
w ¼ 4
)
uþ54 ¼ uþ1 ¼ 4
)
6v 2 ¼ 4
)
6v ¼ 6
)
u ¼ 3
)
v ¼ 1
w ¼ 2
u ¼ 3, v ¼ 1, w ¼ 2
c) Aus dem Lösungsteil a) ist bekannt, dass A wegen det A ¼ 23 6¼ 0 regulär ist und somit eine Inverse A 1
besitzt, die wir jetzt mit dem Gauß-Jordan-Verfahren berechnen wollen (! FS: Kap. VII.1.5.2.2):
0
0
1
1
1
5
2 1 0 0
1
5
2 1 0 0
B
B
C
C
) @0
6
1 1 1 0 A
)
ðA j EÞ ¼ @ 1
1 1 0 1 0 A þ Z 1
0 13 6 2 0 1 þ 2 Z 2
2 3 2 0 0 1 2 Z1
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflffl{zfflfflfflffl}
A
E
0
1
5
B
6
@0
0 1
0
2
1
4
1
1
0
0
1
2
1
0 þ 5 Z3
C
0 A þ 6 Z3
1
1 0 18
1
10
B
4
0
2
@0 1
0 0
1 1=23 13=23
1
1
0 18 1 10 5
C
B
0 23 1 13 6 A : ð 23Þ
@0
0 1 4 0 2 1 ð 1Þ
0
)
1
þ 18 Z 3
5
C
1 A 4 Z3
6=23
)
1
1 0 0 5=23
4=23
7=23
C
B
6=23
1=23 A ¼ ðE j A 1 Þ
@ 0 1 0 4=23
0 0 1 1=23 13=23 6=23
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
E
A 1
0
Die inverse Matrix A 1 lautet damit:
1
1
0
0
5 4
7
5=23
4=23
7=23
1 B
1
C
C
B
6
1A ¼
B
A 1 ¼ @ 4=23
6=23
1=23 A ¼
@ 4
23
23
1=23 13=23 6=23
1 13 6
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
B
)
558
J Lineare Algebra
Wir lösen jetzt die Matrizengleichung A x ¼ c nach dem unbekannten Vektor x auf, indem wir beide Seiten der
Gleichung von links mit A 1 multiplizieren:
Ax ¼ c
A 1 A x ¼ A 1 c
|fflfflffl{zfflfflffl}
E
)
E x ¼ A 1 c
|{z}
x
)
)
x ¼ A 1 c ¼
1
ðB cÞ
23
Berechnung des Matrizenproduktes B c nach dem Falk-Schema:
B
5
4
1
c
4
0
7
4
7
6
1
13 6
69
23
46
Lösungsvektor:
Lösung:
0
1
1 @
x ¼
ðB cÞ ¼
23
23
0
1
1
3
69
23 A ¼ @ 1 A
2
46
u ¼ 3, v ¼ 1, w ¼ 2
Bc
Eine viereckige Netzmasche enthält die ohmschen Widerstände R 1 ¼ 1 W, R 2 ¼ 2 W, R 3 ¼ 5 W
und R 4 ¼ 2 W sowie eine Spannungsquelle mit der Quellspannung U q ¼ 19 V (Bild J-2).
IA
R1
I1
ID
I1
A
D
I4
Uq
I2
R2
J48
R4
I4
I2
B
IB
C
I3
R3
I3
Bild J-2
IC
Die in den Knotenpunkten A und B zufließenden Ströme betragen I A ¼ 2 A und I B ¼ 1 A, der
im Knotenpunkt C abfließende Strom I C ¼ 1 A. Berechnen Sie mit Hilfe des Gaußschen Algorithmus die vier Zweigströme I 1 , I 2 , I 3 und I 4 aus dem folgenden linearen Gleichungssystem:
1
0
0
10 1
IA
1
1
0
0
I1
B I C
B 0
B C
1
1
0 C
B C
B
C B I2 C
B
B
CB C ¼ B
C
@ 0
@ IC A
0
1
1 A @ I3 A
Uq
R 1 R2
R3
R4
I3
Mit den vorgegebenen Werten erhalten wir das folgende quadratische LGS (ohne Einheiten; die noch unbekannten
Ströme sind dann in der Einheit Ampère anzugeben):
10 1
0
1
0
1 1
0
0
I1
2
B 0 1 1
B1C
B C
0C
C B I2 C
B
C
B
CB C ¼ B
B
C oder A I ¼ c
@ 0 0
@ 1A
1 1 A @ I3 A
1 2
5
2
19
I4
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
|ffl{zffl}
A
I
c
2 Lineare Gleichungssysteme
559
Trapezform:
1
1
0
3
0
0
1
0
1 1
5
2
1
2
1C
C
C
1A
21 3 Z
2
)
f
Wir bringen zunächst die erweiterte Koeffizientenmatrix ðA j cÞ auf
0
0
1
1 1
0
0 2
1
1C
B0
B 0 1 1
0
C
B
B
ðA j cÞ ¼ B
) B
C
@0
@ 0 0
1 1 1 A
1 2
5
2 19 þ Z 1
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
c
1 1
0
0
B0 1 1
0
B
B
@0 0
1 1
0 0
8
2
1
2
1C
C
C
1A
24 8 Z
3
0
)
1 1
0
0
B0 1 1
0
B
B
@0 0
1 1
0 0
0 10
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
A*
1
2
1C
C
C ¼ ðA * j c *Þ
1A
16
f
0
c*
Es gibt keine Nullzeilen, daher ist Rg ðAÞ ¼ Rg ðA j cÞ ¼ r ¼ 4 und das LGS mit n ¼ 4 Unbekannten ist (aus
physikalischer Sicht erwartungsgemäß) eindeutig lösbar ðr ¼ n ¼ 4Þ. Die Lösung erhalten wir aus dem gestaffelten
System A * I ¼ c * (schrittweise von unten nach oben gelöst):
ðIÞ
I1 þ I2
ðIIÞ
¼
I 1 þ 1,6 ¼ 2
)
I 1 ¼ 0,4
¼ 1
)
I 2 2,6 ¼ 1
)
I 2 ¼ 1,6
¼
1
)
I 3 1,6 ¼ 1
)
I 3 ¼ 2,6
10 I 4 ¼ 16
)
I 4 ¼ 1,6
I3 I4
ðIVÞ
I 1 ¼ 0,4 A;
0
J49
)
I2 I3
ðIIIÞ
Lösung:
2
I 2 ¼ 1,6 A;
1
B
@ 0
2
I 3 ¼ 2,6 A;
I 4 ¼ 1,6 A
0 1
10 1
0
x1
l
1
B C
CB C
2
1 A @ x2 A ¼ @ 1 A
2
x3
1l
3
Für welche Werte des reellen Parameters l besitzt das inhomogene lineare Gleichungssystem genau
eine Lösung?
Das inhomogene LGS A x ¼ c besitzt genau dann eine eindeutige Lösung, wenn det A 6¼ 0 gilt. Wir berechnen die
3-reihige Determinante nach der Regel von Sarrus:
l
1 1
l
1
0
2
1
0
2
2 1l
3
2 1l
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det A
det A ¼ 6 2 l þ 0 þ 4 ð1 lÞ 0 ¼ 2 2 l 1 þ l ¼ 3 l
Aus der Bedingung det A ¼ 3 l 6¼ 0 folgt l 6¼ 3 . Das LGS besitzt somit genau eine Lösung, wenn der
Parameter l von 3 verschieden ist.
560
J Lineare Algebra
Der in Bild J-3 skizzierte Balken der Länge 2 a mit loser Einspannung am linken Ende und schrägem
Loslager am rechten Ende wird in der Balkenmitte durch eine schräg unter dem Winkel a > 0 angreifende konstante Kraft F belastet.
F
Balken
a
45°
a
a
FB
F · sin a
F · cos a
J50
MA
Balken
FA
F B · sin 45°
Bild J-3
F B · cos 45°
Die beiden Lagerkräfte F A und F B sowie das Moment M A genügen dabei dem folgenden linearen
Gleichungssystem:
0
1
pffiffiffi
0
1
2
2 0 0 FA 1
2 F sin a
p
ffiffi
ffi
B
C
B 0 a 2 1 C @ F A ¼ @ a F sin a A
B
@
A
pffiffiffi
2 F cos a
M
A
0
2 0
Bestimmen Sie mit Hilfe der Cramerschen Regel die unbekannten Kräfte und Momente in Abhängigkeit vom Winkel a .
Hinweis: Die anfallenden 3-reihigen Determinanten sollen nach dem Laplaceschen Entwicklungssatz
berechnet werden.
Für die Berechnung der drei Unbekannten F A , F B und M A benötigen wir die Determinante D ¼ det A der Koeffizientenmatrix A sowie die aus D gewonnenen „Hilfsdeterminanten“ D 1 , D 2 und D 3 (in D wird der Reihe nach
die erste, zweite bzw. dritte Spalte durch den Spaltenvektor c der rechten Seite des LGS ersetzt). Wir berechnen diese
Determinanten jeweils nach Laplace durch Entwicklung nach möglichst günstigen Zeilen bzw. Spalten.
Koeffizientendeterminante D =
pffiffiffi
2
2
pffiffiffi
D ¼ det A ¼ 0 a 2
pffiffiffi
0
2
D ¼ a 11 A 11 ¼ a 11
pffiffiffi
2
2
pffiffiffi
¼ 2 0 a 2
pffiffiffi
0
2
Hilfsdeterminante D 1
2 F sin a
D 1 ¼ a F sin a
2 F cos a
det A
0
1
0
Entwicklung nach den Elementen der 1: Spalte;
wobei nur das Element a 11 ¼ 2 einen Beitrag leistet:
ð 1Þ 1 þ 1 D 11 ¼ a 11 D 11 ¼
pffiffiffi
0
a 2 1
pffiffiffi
pffiffiffi
¼ 2 ð0 2 Þ ¼ 2 2
1 ¼ 2 pffiffiffi
2 0
0
pffiffiffi
2
pffiffiffi
a 2
pffiffiffi
2
0
1
0
Entwicklung nach den Elementen der 3: Spalte;
wobei nur das Element a 23 ¼ 1 einen Beitrag leistet:
2 Lineare Gleichungssysteme
561
¼ a 23 ð 1Þ 2 þ 3 D 23 ¼ a 23 D 23 ¼
pffiffiffi
2 F sin a
2 0
pffiffiffi
2 F sin a
2
pffiffiffi
a F sin a a 2 1 ¼
pffiffiffi ¼
2 F cos a
2
pffiffiffi
2 F cos a
2 0
pffiffiffi
pffiffiffi
pffiffiffi
¼ ð2 2 F sin a 2 2 F cos aÞ ¼ 2 2 F ðcos a sin aÞ
D 1 ¼ a 23 A 23
¼ 1
Hilfsdeterminante
2
D2 ¼ 0
0
D2
2 F sin a
a F sin a
2 F cos a
0
1
0
Entwicklung nach den Elementen der 1. Spalte
(nur das Element a 11 ¼ 2 liefert einen Beitrag) :
D 2 ¼ a 11 A 11 ¼ a 11 ð 1Þ 1 þ 1 D 11 ¼ a 11 D 11 ¼
2 2 F sin a 0
a F sin a
¼ 2 0 a F sin a 1 ¼ 2
2 F cos a
0 2 F cos a 0
Hilfsdeterminante D 3
pffiffiffi
2
2
p
ffiffiffi
D3 ¼ 0 a 2
pffiffiffi
0
2
2 F sin a
a F sin a
2 F cos a
1
¼ 2 ð0 2 F cos aÞ ¼ 4 F cos a
0
Entwicklung nach den Elementen der 1. Spalte
(nur das Element a 11 ¼ 2 liefert einen Beitrag) :
D 3 ¼ a 11 A 11 ¼ a 11 ð 1Þ 1 þ 1 D 11 ¼ a 11 D 11 ¼
pffiffiffi
2
pffiffiffi
2 2 F sin a
a 2 a F sin a
pffiffiffi
¼ 2 0 a 2 a F sin a ¼ 2 pffiffiffi
¼
2 2 F cos a
pffiffiffi
0
2 2 F cos a
pffiffiffi
pffiffiffi
pffiffiffi
¼ 2 ð2 2 a F cos a 2 a F sin aÞ ¼ 2 2 a F ð2 cos a sin aÞ
Berechnung der drei Unbekannten nach der Cramerschen Regel
pffiffiffi
D1
2 2 F ðcos a sin aÞ
¼ F ðcos a sin aÞ ¼ F ðsin a cos aÞ
¼
FA ¼
pffiffiffi
D
2 2
FB
MA
Lösung:
D2
4 F cos a
2 F cos a
¼
¼
¼
¼
pffiffiffi
pffiffiffi
D
2 2
2
2
D3
¼
¼
D
pffiffiffi pffiffiffi
pffiffiffi
2 2 F cos a
¼ 2 F cos a
pffiffiffi
2
pffiffiffi
2 a F ð2 cos a sin aÞ
¼ a F ð2 cos a sin aÞ ¼ a F ðsin a 2 cos aÞ
pffiffiffi
2 2
F A ¼ F ðsin a cos aÞ,
FB ¼
pffiffiffi
2 F cos a,
M A ¼ a F ðsin a 2 cos aÞ
562
J Lineare Algebra
J51
Jedem Punkt P ¼ ðx 1 ; x 2 ; x 3 Þ des 3-dimensionalen Raumes wird durch die Gleichung y ¼ A x in
eindeutiger Weise ein Bildpunkt Q ¼ ð y 1 ; y 2 ; y 3 Þ zugeordnet. Dabei ist x der Ortsvektor von P
und y der Ortsvektor des Bildpunktes Q und A die Abbildungsmatrix dieser linearen Abbildung.
Bestimmen Sie die sog. Fixpunkte der Abbildung, d. h. diejenigen Punkte, die in sich selbst abgebildet
0
1
4
1
0
werden ( y ¼ x) für die Abbildungsmatrix A ¼ @ 0
3
1A.
3 3 1
Aus y ¼ A x und y ¼ x erhalten wir das folgende homogene LGS für den Ortsvektor x des Fixpunktes:
Ax ¼ x
)
A x x ¼ A x E x ¼ ðA EÞ x ¼ 0 ) B x ¼ 0
|fflfflffl{zfflfflffl}
B
(E: 3-reihige Einheitsmatrix; 0: Nullvektor des 3-dimensionalen Raumes). Die Koeffizientenmatrix
1
0
1
0
1
0
3
1
0
1 0 0
4
1
0
C
B
C
B
C
B
2
1A
B ¼ A E ¼ @0
3
1A @0 1 0A ¼ @0
3 3 2
0 0 1
3 3 1
bringen wir durch elementare Zeilenumformungen auf Trapezform:
0
1
0
1
3
1
0
3
1
0
B
C
B
C
B ¼ @0
2
1A
) @0
2
1A
3 3 2 Z1
0 4 2 þ 2 Z2
0
)
3
B
@0
0
1
2
0
1
0
C
1A¼ B*
Nullzeile
0
Die Koeffizientenmatrix B bzw. B * besitzt den Rang r ¼ 2, das homogene LGS mit n ¼ 3 Unbekannten hat
somit unendlich viele Lösungen (Anzahl der Parameter: n r ¼ 3 2 ¼ 1). Wir lösen jetzt das gestaffelte System
B * x ¼ 0 von unten nach oben (als Parameter wählen wir x 2 ¼ l mit l 2 R):
1
l
3
3 x1 þ x2 ¼ 0
)
3 x1 þ l ¼ 0
)
x1 ¼
ðIIÞ
2 x2 þ x3 ¼ 0
)
2 l þ x3 ¼ 0
)
x3 ¼ 2 l
f
ðIÞ
l
Lösung:
x1 ¼
1
l, x 2 ¼ l, x 3 ¼ 2 l
3
(mit l 2 R)
Damit gibt es unendlich viele Fixpunkte mit den Koordinaten x 1 ¼ l=3, x 2 ¼ l und x 3 ¼ 2 l (mit l 2 R).
Diese Punkte gehen bei der Abbildung in sich selbst über.
Lösen Sie die folgenden linearen Gleichungssysteme durch elementare Umformungen in den Zeilen der
erweiterten Koeffizientenmatrix (Gaußscher Algorithmus):
0
J52
1
B
aÞ @ 7
2
cÞ
1
5
C
11 A
3
x
y
!
0 1
2
B C
¼ @7A
4
1 5 1 9
6 6 9 15
!
1
x1
Bx C
B 2C
B C ¼
@ x3 A
x4
u
2u
bÞ
6u
3u
0
1
21
!
þ 3v þ 2w
18 v þ w
þ 2v þ 3w
þ
v þ 5w
¼ 19
¼ 85
¼
1
¼ 16
2 Lineare Gleichungssysteme
563
Ein inhomogenes lineares ðm; nÞ-System A x ¼ c ist nur lösbar, wenn der Rang der Koeffizientenmatrix A mit dem
Rang der erweiterten Koeffizientenmatrix ðA j cÞ übereinstimmt: Rg ðAÞ ¼ Rg ðA j cÞ ¼ r . Im Falle der Lösbarkeit
hängt die Lösungsmenge noch wie folgt vom Rang r ab:
r ¼ n
)
genau eine Lösung
r < n
)
unendlich viele Lösungen mit n r voneinander unabhängigen Parametern
f
a) Wir bringen die erweiterte Koeffizientenmatrix ðA j cÞ mit Hilfe elementarer Zeilenumformungen auf Trapezform:
0
0
0
1
1
1
1
5 2
1
5 2
1
5 2
C
B
B
B
C
C
ðA j cÞ ¼ @ 7 11 7 A 7 Z 1 ) @ 0 24 7 A
) @ 0 24 7 A þ 24 Z 3 )
2 Z1
2 3 4
0 13 0 : ð 13Þ
0
1 0
|fflfflffl{zfflfflffl}
A
c
1
B
@0
0
5
0
1
0
1
2
7C
A
0
)
1 5
B
@0 1
0 0
|ffl{zffl}
A*
1
2
0C
A ¼ ðA * j c *Þ
7
f
0
c*
A * enthält eine Nullzeile (grau unterlegt), ðA * j c *Þ dagegen keine! Daraus folgt:
Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 3
Somit ist Rg ðAÞ 6¼ Rg ðA j cÞ, das inhomogene LGS ist daher nicht lösbar.
b) Die erweiterte Koeffizientenmatrix ðA j cÞ wird zunächst durch elementare Zeilenumformungen auf Trapezform
gebracht:
0
0
1
1
1
3 2 19
1
3
2
19
B 2 18 1 85 C 2 Z
B 0 24 3 123 C : ð 3Þ
C
C
1
B
B
ðA j cÞ ¼ B
)
) B
C
C
@6
@0
2 3
1 A þ 6 Z1
20 15 115 A : 5
3
1 5 16 3 Z 1
0 8 1 41
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl} |{z}
A
c
1
3
2
B0
8
1
B
B
@0
4
3
0 8 1
1
19
41 C
C
C
23 A 0,5 Z 2
41 þ Z
2
0
1 3 2
B0 8 1
B
)B
@ 0 0 2,5
0 0 0
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
A*
1
19
41 C
C
C ¼ ðA * j c *Þ
2,5 A
0
Nullzeile
f
0
c*
A * und ðA * j c *Þ enthalten jeweils eine Nullzeile (grau unterlegt). Es gilt:
Rg ðAÞ ¼ Rg ðA *Þ ¼ 3 ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 3 ;
Anzahl der Unbekannten: n ¼ 3
Somit ist Rg ðAÞ ¼ Rg ðA j cÞ ¼ r ¼ 3 und wegen r ¼ n ¼ 3 gibt es genau eine Lösung, die sich aus dem
gestaffelten System A * x ¼ c * leicht berechnen lässt (von unten nach oben):
ðIÞ
ðIIÞ
ðIIIÞ
Lösung:
u þ 3 v þ 2 w ¼ 19
)
u þ 15 þ 2 ¼ u þ 17 ¼ 19
w ¼ 41
)
8 v þ 1 ¼ 41
2,5 w ¼ 2,5
)
w ¼ 1
8v þ
u ¼ 2, v ¼ 5, w ¼ 1
)
8 v ¼ 40
)
)
u ¼ 2
v ¼ 5
564
J Lineare Algebra
f
c) Zunächst wird die erweiterte Koeffizientenmatrix ðA j cÞ durch elementare Umformungen in den Zeilen in die
Trapezform gebracht:
!
!
1 5 1 9 1
1 5 1 9 1
ðA j cÞ ¼
)
)
6 6 9 15 21 : 3
2 2 3
5 7 þ 2 Z1
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
A
c
!
1
5 1
9 1
¼ ðA * j c *Þ
0 12 5 13 9
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A*
c*
Rg ðAÞ ¼ Rg ðA *Þ ¼ 2 ;
Rg ðA j cÞ ¼ Rg ðA * j c *Þ ¼ 2 ;
Anzahl der Unbekannten: n ¼ 4
Das inhomogene LGS ist lösbar, da Rg ðAÞ ¼ Rg ðA j cÞ ¼ r ¼ 2 ist. Es gibt aber wegen r < n unendlich
viele Lösungen mit n r ¼ 4 2 ¼ 2 Parametern. Wir lösen jetzt das gestaffelte System A * x ¼ c * schrittweise von unten nach oben und wählen dabei x 3 und x 4 als Parameter ðx 3 ¼ l, x 4 ¼ m mit l; m 2 R):
5
ðIÞ x 1 þ 5 x 2 x 3 9 x 4 ¼ 1 ) x 1 þ
ð5 l þ 13 m 9Þ l 9 m ¼ 1 )
12
x1 þ
25
65
45
12
108
12
lþ
m
l
m ¼
12
12
12
12
12
12
x1 ¼
Lösung:
f
12 x 2 5 x 3 13 x 4 ¼ 9
x2 ¼
l
m
1
ð5 l þ 13 m 9Þ
12
x1 ¼
x1 þ
13
43
45
12
l
m
¼
12
12
12
12
)
13
43
33
1
lþ
mþ
¼
ð 13 l þ 43 m þ 33Þ
12
12
12
12
f
ðIIÞ
)
)
12 x 2 5 l 13 m ¼ 9
)
12 x 2 ¼ 5 l þ 13 m 9
)
ðEinsetzen in Gleichung (I)Þ
1
1
ð 13 l þ 43 m þ 33Þ ; x 2 ¼
ð5 l þ 13 m 9Þ; x 3 ¼ l ; x 4 ¼ m
12
12
(mit l; m 2 R)
Kontrolle (Einsetzen der gefundenen von zwei unabhängigen Parametern abhängigen Werte in die beiden Ausgangsgleichungen):
1
5
ð 13 l þ 43 m þ 33Þ þ
ð5 l þ 13 m 9Þ l 9 m ¼
ðI*Þ x 1 þ 5 x 2 x 3 9 x 4 ¼
12
12
13
43
33
25
65
45
lþ
mþ
þ
lþ
m
l 9m ¼
12
12
12
12
12
12
13
25
43
65
33
45
lþ
ll þ
mþ
m 9m þ
¼
¼
12
12
12
12
12
12
12
108
12
ll þ
m 9m
¼ ðl lÞ þ ð9 m 9 mÞ 1 ¼ 0 þ 0 1 ¼ 1
¼
12
12
12
¼
ðII*Þ 6 x 1 þ 6 x 2 9 x 3 þ 15 x 4 ¼
¼
6
6
ð 13 l þ 43 m þ 33Þ þ
ð5 l þ 13 m 9Þ 9 l þ 15 m ¼
12
12
1
1
ð 13 l þ 43 m þ 33Þ þ
ð5 l þ 13 m 9Þ 9 l þ 15 m ¼
2
2
13
43
33
5
13
9
l
m
þ
lþ
m 9 l þ 15 m ¼
2
2
2
2
2
2
13
5
43
13
33
9
¼
lþ
l 9l þ
mþ
m þ 15 m þ
¼
2
2
2
2
2
2
18
30
42
l 9l þ
m þ 15 m
¼ ð9 l 9 lÞ þ ð 15 m þ 15 mÞ 21 ¼ 21
¼
2
2
2
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
¼
0
0
2 Lineare Gleichungssysteme
J53
565
Der in Bild J-4 skizzierte verzweigte Stromkreis mit den Ohmschen Widerständen R 1 ¼ 5 W,
R 2 ¼ 10 W und R 3 ¼ 20 W wird durch eine Gleichspannungsquelle mit der Quellenspannung
U q ¼ 70 V gespeist. Die noch unbekannten Zweigströme I1 , I2 und I3 genügen dem folgenden
linearen Gleichungssystem:
R3
I3
0
10 1
0
1
0
I1
1
1
1
B
C
B
C
0 A @ I2 A ¼ @ Uq A
@ R1 R2
II
Uq
R3
I3
0
R2
t =0
Berechnen Sie diese Ströme mit Hilfe der Cramerschen Regel.
I2
S
R2
Uq
I
I1
R1
Bild J-4
f
f
Einsetzen der vorgegebenen Werte für die Teilwiderstände und die Spannung führen zu dem folgenden inhomogenen
LGS (wir rechnen zunächst ohne Einheiten, die Teilströme sind dann in der Einheit Ampère anzugeben):
1
0
10 1
0
1
1 1
0
I1
C
B
CB C
B
0 A @ I2 A ¼ @ 70 A oder A I ¼ c
@ 5 10
0
10 20
70
I3
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
I
c
Für die Cramersche Regel benötigen wir die Determinante D ¼ det A sowie die drei „Hilfsdeterminanten“ D 1 , D 2
und D 3 (in D wird der Reihe die 1., 2. bzw. 3. Spalte durch den Spaltenvektor c ersetzt):
1
1 1 1
1
5 10
5 10
0
) D ¼ 200 þ 0 þ 50 0 0 þ 100 ¼ 350
0
10 20
0
10
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D ¼ det A
0
1 1
0
1
70 10
70 10
0
70
10 20
70
10
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D1
1
0
0 1 1
5 70
5 70
0
0
0
70
70 20
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D2
1
1
1
0 1
5 10 70 5 10
0
0
10
10
70
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D3
)
D 1 ¼ 0 þ 0 þ 700 700 0 þ 1400 ¼ 1400
)
D 2 ¼ 1400 þ 0 þ 350 0 0 0 ¼ 1750
)
D 3 ¼ 700 þ 0 þ 0 0 700 þ 350 ¼ 350
566
J Lineare Algebra
Damit erhalten wir folgende Werte für die drei Teilströme I 1 , I 2 und I 3 (in Ampère):
I1 ¼
Lösung:
D1
1400
¼
¼ 4;
D
350
I 1 ¼ 4 A,
I2 ¼
I 2 ¼ 5 A,
D2
1750
¼
¼ 5;
D
350
I3 ¼
D3
350
¼
¼ 1
D
350
I3 ¼ 1 A
Das in Bild J-5 skizzierte Rollensystem enthält in symmetrischer Anordnung drei gleiche Massen
m 1 ¼ m 2 ¼ m 3 ¼ m, die durch ein über Rollen führendes Seil miteinander verbunden sind. Die
noch unbekannten Beschleunigungen a1 , a2 und a3 dieser Massen sowie die im Seil wirkende konstante Seilkraft FS lassen sich mit Hilfe des Gaußschen Algorithmus aus dem linearen Gleichungssystem
1
10 1
0
0
a1
mg
m 0 1
C
B
CB C
B
@ 0 m 4 A @ a3 A ¼ @ m g A
0
1 2 0
FS
J54
berechnen (wegen der Symmetrie gilt a 1 ¼ a 2 ).
Welchen Wert besitzen diese Größen?
Anmerkung: Rolle und Seil werden als masselos
angenommen, Reibungskräfte vernachlässigt (g: Erdbeschleunigung).
m
m
m1
m2
a
m
Bild J-5
Wir bringen
0
m
B
B0
@
1
0
zunächst
0 1
m 4
2 0
die erweiterte Koeffizientenmatrix durch elementare Zeilenumformungen auf Trapezform:
1
0
1
1 2 0 0
mg
C
B
C
C
) B
)
mgA
@ 0 m 4 mgA
0
m 0 1 m g m Z1
1
2
0 0
C
m
4 m g A
2 m 1 m g þ 2 Z2
1
B
@0
0
m3
0
)
1
B
@0
0
1
2 0 0
C
m 4 m g A
0 9 3mg
Da es keine Nullzeilen gibt, haben Koeffizientenmatrix und erweiterte Koeffizientenmatrix den gleichen Rang r ¼ 3 .
Das quadratische LGS mit n ¼ 3 Unbekannten ist somit wegen r ¼ n ¼ 3 eindeutig lösbar. Die Lösung erhalten
wir wie folgt aus dem gestaffelten System (von unten nach oben gelöst):
a1 þ 2 a3
ðIÞ
ðIIÞ
m a 3 þ 4 FS ¼ m g
ðIIIÞ
Lösung:
¼ 0
a1 ¼ a2 ¼
9 FS ¼ 3 m g
2
g,
3
a3 ¼
2
g ¼ 0
3
)
a1
)
m a3 þ
)
FS ¼
1
mg
3
1
g,
3
FS ¼
1
mg
3
)
4
mg ¼ mg
3
a1 ¼
)
2
g
3
m a3 ¼
1
mg
3
)
a3 ¼
1
g
3
Physikalische Deutung: Die beiden äußeren Massen bewegen sich nach unten, die mittlere Masse mit halb so großer
Beschleunigung nach oben.
3 Eigenwertprobleme
567
3 Eigenwertprobleme
Lehrbuch: Band 2, Kapitel I.7
Formelsammlung: Kapitel VII.5
J55
Bestimmen Sie die Eigenwerte und Eigenvektoren der folgenden 2-reihigen Matrizen:
1 0
1 0,5
aÞ A ¼
bÞ B ¼
8 2
2 1
Berechnen Sie ferner aus den Eigenwerten Spur und Determinante der Matrix (mit Kontrollrechnung).
a) Das Eigenwertproblem lautet:
ðA l EÞ x ¼ 0
1l
8
oder
0
2l
!
x1
x2
!
0
0
¼
!
Berechnung der Eigenwerte aus der charakteristischen Gleichung det ðA l EÞ ¼ 0:
0
1l
¼ ð1 lÞ ð2 lÞ 0 ¼ ð1 lÞ ð2 lÞ ¼ 0
det ðA l EÞ ¼
8
2l
l1 ¼ 1 ;
)
l2 ¼ 2
Wir berechnen jetzt die zugehörigen (normierten) Eigenvektoren.
l1 ¼ 1
ðA 1 EÞ x ¼ 0
oder
0
8
0
1
!
!
x1
x2
0
0
¼
!
Die Koeffizientenmatrix dieses homogenen LGS enthält eine Nullzeile (grau unterlegt) und besitzt daher den Rang
r ¼ 1. Es gibt somit wegen n r ¼ 2 1 ¼ 1 unendlich viele Lösungen mit einem Parameter. Das gestaffelte
LGS besteht aus einer Gleichung mit den beiden Unbekannten x 1 und x 2 , von denen wir eine frei wählen dürfen
(wir entscheiden uns für x 1 und setzen x 1 ¼ a mit a 6¼ 0):
8 x1 þ x2 ¼ 0
)
8 a þ x2 ¼ 0
)
x2 ¼ 8 a
Somit gilt x 1 ¼ a und x 2 ¼ 8 a. Diesen Eigenvektor normieren wir (für a > 0):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
a
1
x1 ¼
¼ a
) j x1 j ¼ j a j
1 2 þ ð 8Þ 2 ¼ j a j 65 ¼ 1
8a
8
1
1
Normierter Eigenvektor zum Eigenwert l 1 ¼ 1: ~
x 1 ¼ pffiffiffiffiffi
8
65
l2 ¼ 2
ðA 2 EÞ x ¼ 0
oder
1
8
0
0
!
x1
x2
!
¼
0
0
!
oder
)
1
a ¼ pffiffiffiffiffi
65
x1 þ 0 x2 ¼ 0
8 x1 þ 0 x2 ¼ 0
Dieses homogene LGS lässt sich auf die erste Gleichung reduzieren (die beiden Gleichungen sind proportional), in
der die Unbekannte x 2 jeden reellen Wert annehmen kann ð0 x 2 ¼ 0 für x 2 2 RÞ. Damit erhalten wir folgende vom Parameter x 2 ¼ b abhängige Lösung:
x1 þ 0 x2 ¼ 0
)
x1 þ 0 b ¼ 0
|ffl{zffl}
0
)
x1 ¼ 0 ;
x 2 ¼ b ðmit b 6¼ 0Þ
568
J Lineare Algebra
Normierung des Eigenvektors (für b > 0):
!
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0
0
02 þ 12 ¼ j b j ¼ 1
¼ b
) j x2 j ¼ j b j
x2 ¼
b
1
0
Normierter Eigenvektor zum Eigenwert l 2 ¼ 2: ~
x2 ¼
1
)
b ¼ 1
Die Eigenvektoren x 1 und x 2 sind linear unabhängig, da die Determinante der aus ihnen gebildeten Matrix nicht
verschwindet:
a
0
6 0 ðda a 6¼ 0 und b 6¼ 0Þ
8a b ¼ ab 0 ¼ ab ¼
Spur und Determinante der Matrix A
Die Spur ist die Summe, die Determinante das Produkt der Eigenwerte:
Sp ðAÞ ¼ l 1 þ l 2 ¼ 1 þ 2 ¼ 3 ;
det A ¼ l 1 l 2 ¼ 1 2 ¼ 2 ;
Kontrolle : Sp ðAÞ ¼ a 11 þ a 22 ¼ 1 þ 2 ¼ 3
1 0
¼ 20 ¼ 2
Kontrolle : det A ¼
8 2
b) Das Eigenwertproblem lautet:
ðB l EÞ x ¼ 0
1l
0,5
2
1l
oder
!
x1
x2
!
0
0
¼
!
Berechnung der Eigenwerte aus der charakteristischen Gleichung det ðB l EÞ ¼ 0:
0,5
1l
¼ ð1 lÞ 2 þ 1 ¼ 1 2 l þ l 2 þ 1 ¼ l 2 2 l þ 2 ¼ 0
det ðB l EÞ ¼
2
1l
pffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
1 ¼ 1j
l 1=2 ¼ 1 1 2 ¼ 1
Berechnung der zugehörigen Eigenvektoren
l1 ¼ 1 þ j
ðB ð1 þ jÞ EÞ x ¼ 0
oder
j
2
0,5
j
!
x1
x2
!
¼
0
0
)
!
Dieses homogene LGS besteht aus zwei proportionalen Gleichungen (multipliziert man die erste Gleichung mit
2 j, so erhält man die zweite Gleichung):
ðIÞ
j x 1 þ 0,5 x 2 ¼ 0 j ð 2 jÞ
)
2 j2 x1 j x2 ¼ 2 x1 j x2 ¼ 0
ðidentisch mit ðIIÞÞ
ðIIÞ 2 x 1 j x 2 ¼ 0
Das System lässt sich daher auf Gleichung (II) reduzieren, in der wir über x 1 oder x 2 frei verfügen dürfen (wir
wählen x 2 als Parameter und setzen x 2 ¼ 2 a mit a 6¼ 0):
ðIIÞ 2 x 1 j x 2 ¼ 0
)
2 x1 j 2 a ¼ 0
)
x1 ¼ j a
Der Eigenvektor x 1 mit den Komponenten x 1 ¼ j a und x 2 ¼ 2 a wird noch normiert
der Normierungsbedingung: x 1 x *1 ¼ 1 erhalten wir mit
x1 ¼
ja
2a
¼ a
j
2
und x *1 ¼ a
(für a > 0). Aus
j
2
das folgende Ergebnis:
x 1 x *1 ¼ a
j
2
j
a
¼ a 2 ð j 2 þ 2 2 Þ ¼ a 2 ð1 þ 4Þ ¼ 5 a 2 ¼ 1
2
)
1
a ¼ pffiffiffi
5
3 Eigenwertprobleme
569
Normierter Eigenvektor zum Eigenwert l 1 ¼ 1 þ j:
l2 ¼ 1 j
ðB ð1 jÞ EÞ x ¼ 0 oder
1
~
x 1 ¼ pffiffiffi
5
j 0,5
2 j
!
j
2
x1
x2
!
¼
0
0
!
Wiederum erhalten wir zwei proportionale Gleichungen:
ðIÞ
j x 1 þ 0,5 x 2 ¼ 0 j 2 j
ðIIÞ 2 x 1 þ
)
2 j2 x1 þ j x2 ¼ 2 x1 þ j x2 ¼ 0
ðidentisch mit ðIIÞÞ
j x2 ¼ 0
Das LGS lässt sich daher auf Gleichung (II) reduzieren, wobei wir über eine der beiden Unbekannten frei verfügen
dürfen. Wir entscheiden uns für x 2 und setzen x 2 ¼ 2 b mit b 6¼ 0:
ðIIÞ 2 x 1 þ j x 2 ¼ 0
)
2 x1 þ j 2 b ¼ 0
)
x1 ¼ j b
Der Eigenvektor x 2 mit den Komponenten x 1 ¼ j b und x 2 ¼ 2 b soll noch normiert werden (für b > 0):
x 2 x *2 ¼
jb
2b
jb
2b
j
j
j
j
2
¼
¼ b
b
¼ b
2
2
2
2
1
b ¼ pffiffiffi
! 5
j
1
~
x 2 ¼ pffiffiffi
2
5
¼ b 2 ðj 2 þ 2 2 Þ ¼ b 2 ð1 þ 4Þ ¼ 5 b 2 ¼ 1
Normierter Eigenvektor zum Eigenwert l 2 ¼ 1 j:
)
Die (parameterabhängigen) Eigenvektoren x 1 und x 2 sind linear unabhängig, denn die Determinante der aus
ihnen gebildeten Matrix ist stets von null verschieden:
ja jb
ðda a 6¼ 0 und b 6¼ 0Þ
2 a 2 b ¼ j 2 a b j 2 a b ¼ j 4 a b 6¼ 0
Spur und Determinante der Matrix B
Die Spur ist die Summe, die Determinante das Produkt der Eigenwerte:
Sp ðBÞ ¼ l 1 þ l 2 ¼ ð1 þ jÞ þ ð1 jÞ ¼ 1 þ j þ 1 j ¼ 2
det B ¼ l 1 l 2 ¼ ð1 þ jÞ ð1 jÞ ¼ 1 j 2 ¼ 1 þ 1 ¼ 2
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
Kontrolle : Sp ðBÞ ¼ b 11 þ b 22 ¼ 1 þ 1 ¼ 2;
J56
1
det B ¼
2
0,5
¼ 1þ1 ¼ 2
1
Die Spiegelung eines Punktes P ¼ ðx 1 ; x 2 Þ an der (vertikalen) x 2 -Achse führt zum Bildpunkt
1 0
Q ¼ ð y 1 ; y 2 Þ und lässt sich durch die Abbildungsmatrix A ¼
beschreiben. Es gilt:
0 1
!
!
!
1 0
x1
y1
¼
oder y ¼ A x
0 1
y2
x2
x und y sind dabei die Ortsvektoren von P und Q . Bestimmen Sie diejenigen Punkte, deren Ortsvektoren bei der Abbildung in ein Vielfaches von sich selbst übergehen, d. h. für die y ¼ l x mit
l 6¼ 0 gilt.
Hinweis: Die Lösung dieser Aufgabe führt auf ein Eigenwertproblem. Versuchen Sie eine geometrische
Deutung der Eigenwerte und ihrer zugehörigen Eigenvektoren.
570
J Lineare Algebra
Die gesuchten Ortsvektoren x müssen die Bedingungen y ¼ A x und y ¼ l x erfüllen (mit l 2 R). Dies führt
zu dem Eigenwertproblem
Ax ¼ lx
)
A x l x ¼ A x l E x ¼ ðA l EÞ x ¼ 0
(E: 2-reihige Einheitsmatrix). Die Komponenten x 1 und x 2 der Ortsvektoren x genügen somit dem folgenden
homogenen LGS:
!
!
!
1 l
0
x1
0
ðA l EÞ x ¼ 0 oder
¼
0
1l
0
x2
Die Eigenwerte sind die Lösungen der charakteristischen Gleichung det ðA l EÞ ¼ 0:
0
1 l
¼ ð 1 lÞ ð1 lÞ 0 ¼ ð 1 lÞ ð1 lÞ ¼ 0
det ðA l EÞ ¼
0
1l
l1 ¼ 1 ;
)
l2 ¼ 1
Berechnung der zugehörigen Eigenvektoren
l1 ¼ 1
ðA þ 1 EÞ x ¼ 0
0
0
oder
0
2
!
x1
x2
!
¼
0
0
!
Dieses homogene LGS wird wie folgt gelöst (unendlich viele Lösungen):
0 x1 þ 0 x2 ¼ 0
) x1 ¼ a ; x2 ¼ 0
ðmit dem reellen Parameter a 6¼ 0Þ
0 x1 þ 2 x2 ¼ 0
1
a
¼ a e x (mit a 6¼ 0)
¼ a
Eigenvektor x 1 zum Eigenwert l 1 ¼ 1: x 1 ¼
0
0
l2 ¼ 1
ðA 1 EÞ x ¼ 0
oder
2
0
0
0
!
x1
x2
!
¼
0
0
!
Wir lösen dieses homogene LGS wie folgt (unendlich viele Lösungen):
2 x1 þ 0 x2 ¼ 0
ðmit dem reellen Parameter b 6¼ 0Þ
) x2 ¼ b ; x1 ¼ 0
0 x1 þ 0 x2 ¼ 0
0
0
¼ b e y (mit b 6¼ 0)
Eigenvektor x 2 zum Eigenwert l 2 ¼ 1: x 2 ¼
¼ b
1
b
Geometrische Deutung
1. Die zum Eigenwert l 1 ¼ 1 gehörenden Eigenvektoren x 1 ¼ a e x beschreiben die Ortsvektoren der auf der
(horizontalen) x 1 -Achse gelegenen Punkte P ¼ ða; 0Þ, die bei der Spiegelung an der vertikalen Achse (x 2 -Achse)
in ihr Spiegelbild Q ¼ ð a; 0Þ übergehen (Richtungsumkehr des Ortsvektors, siehe Bild J-6).
2. Die zum Eigenwert l 2 ¼ 1 gehörenden Eigenvektoren x 2 ¼ b e y beschreiben die Ortsvektoren der auf der
(vertikalen) x 2 -Achse gelegenen Punkte P ¼ ð0; bÞ, deren Lage sich bei der Spiegelung an der vertikalen Achse
(x 2 -Achse) nicht verändert (der Ortsvektor bleibt erhalten, siehe Bild J-7).
x2
x2
b
Spiegelachse
Q = (– a ; 0)
–a
Spiegelachse
P = (a ; 0)
a
P = Q = (0; b)
Bild J-6
x1
Bild J-7
x1
3 Eigenwertprobleme
J57
571
Berechnen Sie jeweils
(mit Kontrolle):
0
a
B
aÞ A ¼ @ b
0
die Eigenwerte der Matrix A und daraus Spur und Determinante der Matrix
1
b 0
C
a bA
b a
0
1
3 2 1
B
C
bÞ A ¼ @ 2 6 2 A
0 0
2
a) Die Eigenwerte der Matrix A sind die Lösungen der charakteristischen Gleichung det ðA l EÞ ¼ 0 (die Berechnung der 3-reihigen Determinanten erfolgt nach der Regel von Sarrus):
a l
b
b
0 a l
b
b
a
l )
a
l
b
0
0
b
b
al
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det ðA l EÞ
det ðA l EÞ ¼ ða lÞ 3 þ 0 þ 0 0 b 2 ða lÞ b 2 ða lÞ ¼ ða lÞ 3 2 b 2 ða lÞ ¼
¼ ða lÞ ½ ða lÞ 2 2 b 2
det ðA l EÞ ¼ 0
)
ða lÞ 2 2 b 2 ¼ 0
Eigenwerte:
l 1 ¼ a,
ða lÞ ða lÞ 2 2 b 2
¼ 0
al ¼ 0
)
l1 ¼ a
ða lÞ 2 2 b 2 ¼ 0
ða lÞ 2 ¼ 2 b 2 ) a l ¼
pffiffiffi
pffiffiffi
l 2 ¼ a þ 2 b, l 3 ¼ a 2 b
)
pffiffiffi
2b
)
)
l 2=3 ¼ a
pffiffiffi
2b
Spur und Determinante der Matrix A
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 ¼ a þ ða þ
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
2 bÞ þ ða 2 bÞ ¼ a þ a þ 2 b þ a 2 b ¼ 3 a
Kontrolle: Sp ðAÞ ¼ a 11 þ a 22 þ a 33 ¼ a þ a þ a ¼ 3 a
pffiffiffi
pffiffiffi
det A ¼ l 1 l 2 l 3 ¼ a ða þ 2 bÞ ða 2 bÞ ¼ a ða 2 2 b 2 Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom: ða þ bÞ ða bÞ ¼ a 2 b 2 mit a ¼ a; b ¼
Kontrolle (Regel
a b 0 a
b a b b
0 b a 0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
det A
pffiffiffi
2b
von Sarrus):
b
a
b
)
det A ¼ a 3 þ 0 þ 0 0 a b 2 a b 2 ¼ a 3 2 a b 2 ¼ a ða 2 2 b 2 Þ
b) Berechnung der Eigenwerte aus der charakteristischen Gleichung det ðA l EÞ ¼ 0:
2
2
1 3 l
3l
2
2
6l )
6l
2
0
0
0
0
2l
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det ðA l EÞ
det ðA l EÞ ¼ ð3 lÞ ð6 lÞ ð2 lÞ þ 0 þ 0 0 0 4 ð2 lÞ ¼
¼ ð3 lÞ ð6 lÞ ð2 lÞ 4 ð2 lÞ ¼ ð2 lÞ ½ ð3 lÞ ð6 lÞ 4 ¼
¼ ð2 lÞ ð18 3 l 6 l þ l 2 4Þ ¼ ð2 lÞ ðl 2 9 l þ 14Þ
572
J Lineare Algebra
det ðA l E Þ ¼ 0
l 9 l þ 14 ¼ 0
2
l2 ¼ 7 ;
)
)
2l ¼ 0
ð2 lÞ ðl 2 9 l þ 14Þ ¼ 0
l 2=3
9
¼
2
)
l1 ¼ 2
l 9 l þ 14 ¼ 0
2
)
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffi
81
9
81 56
9
25
9
5
14 ¼
¼
¼
4
2
4
2
4
2
2
)
l3 ¼ 2
Eigenwerte (neu nummeriert):
l 1=2 ¼ 2,
l3 ¼ 7
Spur und Determinante der Matrix A
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 ¼ 2 þ 2 þ 7 ¼ 11
Kontrolle: Sp ðAÞ ¼ a 11 þ a 22 þ a 33 ¼ 3 þ 6 þ 2 ¼ 11
det A ¼ l 1 l 2 l 3 ¼ 2 2 7 ¼ 28
Kontrolle (Regel von Sarrus):
3 2 1 3 2
2 6 2 2 6 ) det A ¼ 36 þ 0 þ 0 0 0 8 ¼ 28
0 0
2 0 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
det A
Normalschwingungen eines linearen Moleküls vom Typ X Y2
Ein lineares symmetrisches 3-atomiges Molekül vom Typ X Y 2 wie CO 2 oder NO 2 kann modellmäßig als ein System aus drei linear angeordneten Massenpunkten verstanden werden, die durch elastische Federn gekoppelt sind (Bild J-8).
Bild J-8
Y
J58
X
Y
Ein solches System ist zu harmonischen Schwingungen fähig, wobei in dieser Aufgabe nur die längs
der Systemachse (Molekülachse) möglichen sog. Normalschwingungen untersucht werden sollen. Unter
einer Normalschwingung eines Systems gekoppelter Massenpunkte versteht man einen Bewegungsablauf, bei dem alle Massen (Atome) mit der gleichen Kreisfrequenz w um ihre Gleichgewichtslagen
schwingen. Die Schwingungen unterscheiden sich lediglich in den Phasenwinkeln und den Amplituden
und lassen sich mathematisch durch ein System aus drei gekoppelten linearen Differentialgleichungen
2. Ordnung mit konstanten Koeffizienten beschreiben. Die weitere Behandlung führt schließlich auf das
folgende Eigenwertproblem:
1
0
0 1
w 2a
0
w 2a
A
B
C
B C
2
2
B
C
ðK l EÞ x ¼ 0 mit K ¼ @ 0
w a w a A und x ¼ @ B A
2
C
w
w2
2 w2
b
b
b
Dabei sind A und B die Schwingungsamplituden der beiden äußeren Massen (Atome Y ) und C die
Amplitude der Zentralmasse (Atom X ). Die in der Koeffizientematrix K auftretenden Größen w 2a
und w 2b sind Konstanten, die von den Massen und der Federkonstanten der beiden Kopplungsfedern
abhängen.
Bestimmen Sie zunächst die Eigenwerte
l der Matrix K und daraus die Kreisfrequenzen w der Norpffiffiffi
malschwingungen, wobei w ¼ l gilt und nur positive Werte physikalisch sinnvoll sind (warum?).
Wie lauten die zugehörigen Eigenvektoren (Schwingungsamplituden)?
3 Eigenwertprobleme
573
Die Eigenwerte und damit auch die Eigenkreisfrequenzen werden aus der charakteristischen Gleichung
2
wa l
0
w 2a
det ðK l EÞ ¼
0
w 2a l
w 2a ¼ 0
2
2
w2
w
2w l
b
b
b
bestimmt. Zunächst müssen wir die Determinante berechnen (Regel von Sarrus):
2
wa l
0
w 2a w 2a l
0
0
w 2a l )
0
w 2a l
w 2a
w2
w 2b
2 w 2b l w 2b
w 2b
b
det ðK l EÞ ¼ ðw 2a lÞ 2 ð2 w 2b lÞ þ 0 þ 0 w 2a w 2b ðw 2a lÞ w 2a w 2b ðw 2a lÞ 0 ¼
¼ ðw 2a lÞ 2 ð2 w 2b lÞ 2 w 2a w 2b ðw 2a lÞ ¼
¼ ðw 2a lÞ ½ ðw 2a lÞ ð2 w 2b lÞ 2 w 2a w 2b ¼
¼ ðw 2a lÞ ð2 w 2a w 2b w 2a l 2 w 2b l þ l 2 2 w 2a w 2b Þ ¼
¼ ðw 2a lÞ ðl 2 w 2a l 2 w 2b lÞ ¼ ðw 2a lÞ ðl w 2a 2 w 2b Þ l
Damit erhalten wir folgende Eigenwerte:
det ðK l EÞ ¼ 0
l 1 ¼ w 2a ;
)
ðw 2a lÞ ðl w 2a 2 w 2b Þ l ¼ 0
l 2 ¼ w 2a þ 2 w 2b ;
)
l3 ¼ 0
ðdie 3 Faktoren werden der Reihe nach gleich null gesetztÞ
pffiffiffi
Daraus ergeben sich die folgenden Kreisfrequenzen für die Normalschwingungen ðw ¼ l > 0Þ:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffi
pffiffiffiffiffi
pffiffiffiffiffi
w 1 ¼ l 1 ¼ w 2a ¼ w a ; w 2 ¼ l 2 ¼ w 2a þ 2 w 2b
(l 3 ¼ 0 führt zu w 3 ¼ 0 und scheidet somit aus, physikalische Interpretation dieses Sonderfalls am Ende dieser
Aufgabe.)
Berechnung der Eigenvektoren (Schwingungsamplituden)
0
0
0
B
2
2
B
l1 ¼ w a
) ðK w a EÞ x ¼ 0 oder @ 0
0
2
w b w 2b
E
Die Koeffizientenmatrix B ¼ K
umformungen auf Trapezform:
0
0
0
w 2a
B
B ¼ @ 0
0
w 2a
w 2a
w 2b
0
B
@
w 2b
w 2b
w 2b
0
0
0
0
2 w 2b
2 w 2b
1
1
0 1
A
0
C
B C
B C
C
2
wa A @ BA ¼ @0A
C
0
2w2 w2
b
a
dieses homogenen LGS bringen wir zunächst mit Hilfe elementarer Zeilen1
0
C
A
B
@
)
w 2a
w 2b
w 2b
0
0
0
0
2 w 2b w 2a
w 2a
w 2a
1
C
A
Z2
)
Z2
0
: ð w 2b Þ
C
w 2a A : ð w 2a Þ
0
10
w 2a
)
1
1 1 2
@0 0
1A ¼ B*
0 0
0
Nullzeile
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Es gibt somit wegen r < n ¼ 3 unendlich viele Lösungen, die noch von einem Parameter abhängen. Das gestaffelte
System B * x ¼ 0 liefert dann die folgenden Lösungen (als Parameter wählen wir B ¼ a mit a 6¼ 0):
574
J Lineare Algebra
ðIÞ
A þ B 2C ¼ 0
ðIIÞ
)
Aþa0 ¼ 0
)
A ¼ a
C ¼ 0
ðin die obere Gleichung ðIÞ einsetzenÞ
0
1
0
1
1
a
Eigenvektoren zum Eigenwert l 1 ¼ w 2a : x 1 ¼ @ a A ¼ a @ 1 A
0
0
0
2 w 2b
B
l 2 ¼ w 2a þ 2 w 2b ) ðK ðw 2a þ 2 w 2b Þ EÞ x ¼ 0 oder B
@ 0
w 2b
Die Koeffizientenmatrix B ¼ K ðw 2a þ 2 w 2b Þ E
umformungen auf Trapezform:
0
1
2 w 2b
0
w 2a 2 Z 3
B
C
)
0
2 w 2b w 2a A
@
w 2b
w 2b
w 2a
0
0
0
0
B
@ 0
2 w 2b
w 2b
w 2b
0
1
C
w 2a A
)
w 2a
10
0 1
1
0
A
C
2CB BC ¼ B0C
wa A@ A
@ A
2
0
C
w
w 2a
0
2 w 2b
w 2b
a
dieses homogenen LGS bringen wir mit Hilfe elementarer Zeilen0
0
2 w 2b
w 2a
0
w 2b
2 w 2b
w 2b
w 2a
w 2a
w 2b
w 2a
B
@
w 2b
B
@ 0
(mit a 6¼ 0)
C
A
þ Z2
)
ð 1Þ
1
C
w 2a A ¼ B *
2 w 2b
0
1
0
0
Nullzeile
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Es gibt wiederum unendlich viele Lösungen, die noch von einem Parameter abhängen. Sie werden wie folgt aus dem
gestaffelten System B * x ¼ 0 bestimmt (als Parameter wählen wir die Unbekannte B und setzen B ¼ b mit
b 6¼ 0; zunächst die untere Gleichung (II) lösen):
!
2
2
w
b
ðIÞ w 2b A þ w 2b B þ w 2a C ¼ 0 ) w 2b A þ w 2b b þ w 2a
b ¼ w 2b A þ w 2b b 2 w 2b b ¼ 0
w 2a
) w 2b A w 2b b ¼ 0 ) w 2b A ¼ w 2b b
ðIIÞ
2 w 2b B w 2a C ¼ 0 ) 2 w 2b b w 2a C ¼ 0 ) w 2a C ¼ 2 w 2b b ) C ¼
0
Eigenvektoren zum Eigenwert l 2 ¼ w 2a þ 2 w 2b :
)
ðK 0 EÞ x ¼ K x ¼ 0 oder
1
b
B
x2 ¼ @
0
C
B
A ¼ b@
b
1
1
1
2 w 2b
w 2a
b
C
A ðmit b 6¼ 0Þ
2 w 2b =w 2a
10 1
0 1
w 2a
0
A
C
2 C B BC ¼ B0C
wa A @ A
@ A
2
0
C
2w
ð2 w 2b =w 2a Þ b
0
l3 ¼ 0
) A ¼ b
B
B
@
w 2a
0
0
w 2a
w 2b
w 2b
b
Bevor wir dieses homogene LGS lösen, bringen wir die Koeffizientenmatrix K 0 E ¼ K auf Trapezform:
0
B
B
K ¼ B
@
w 2a
0
0
w 2a
w 2b
0
1
0 1
w 2b
1
B
B0 1 1C
C
@
A
0 1 1 Z2
1
: w 2a
C
C
2
w 2a C
A : wa
2 w 2b : ð w 2b Þ
w 2a
0
)
1
0 1
1
B
B0 1 1C
C
@
A
1 1 2 Z1
)
0
)
1
1 0 1
B
C
@ 0 1 1 A¼ K *
0 0
0
Nullzeile
Rg ðKÞ ¼ Rg ðK *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten: n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
3 Eigenwertprobleme
575
Wir lösen jetzt das gestaffelte System K * x ¼ 0 von unten nach oben, wobei wir die Unbekannte C als Parameter
wählen (C ¼ g mit g 6¼ 0):
AC ¼ 0
)
Ag ¼ 0
)
BC ¼ 0
)
Bg ¼ 0
)
A ¼ g
B ¼ g
ðin die obere Gleichung einsetzenÞ
0 1
0 1
1
g
@
@
A
(mit g ¼
6 0)
Die zugehörigen Eigenvektoren lauten somit: x 3 ¼ g ¼ g 1 A
1
g
Physikalische Deutung der Ergebnisse
1. Normalschwingung mit der Kreisfrequenz w 1 = w a
Die Zentralmasse X ist in Ruhe, die beiden äußeren Massen schwingen mit gleicher Amplitude in Gegenphase
(Bild J-9).
bzw.
Y
X
Y
Bild J-9
Y
2. Normalschwingung mit der Kreisfrequenz w 2 ¼
X
Y
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
w 2a þ 2 w 2b
Die beiden äußeren Massen schwingen mit gleicher Amplitude in Phase, die Zentralmasse X mit einer i. a. anderen
Amplitude in Gegenphase (Bild J-10).
bzw.
Y
X
Y
Bild J-10
Y
X
Y
3. Translationsbewegung
0 1
1
Der Eigenvektor x 3 ¼ g @ 1 A zum Eigenwert l 3 ¼ 0 und damit zur Kreisfrequenz w 3 ¼ 0 beschreibt keine
1
Schwingung (sonst müsste w > 0 sein), sondern eine Translation, bei der sich alle drei Massen in gleicher Richtung in gleicher Weise bewegen (Bild J-11).
Bild J-11
Y
X
Y
1
2
0 0
0
B0
2 0
0C
C
B
A ¼ B
C
@1 2 0 1A
2 4 1
0
0
J59
Welche Eigenwerte besitzt diese Matrix? Berechnen Sie ferner det A und Sp ðAÞ .
Die gesuchten Eigenwerte der Matrix A sind die Lösungen der charakteristischen Gleichung det ðA l EÞ ¼ 0.
Die 4-reihige Determinante entwickeln wir zunächst nach den Elementen der 1. Zeile, wobei nur das 1. Element einen
Beitrag liefert (die übrigen Elemente sind alle gleich null; gleichwertige Alternativen: Entwicklung nach der 2. Zeile
oder der 3. oder 4. Spalte):
576
J Lineare Algebra
0
2l
0
2l
det ðA l EÞ ¼
2
1
2
4
0
0
0
¼ a 11 A 11 ¼ a 11 ð 1Þ 1 þ 1 D 11 ¼ a 11 D 11 ¼
l 1
1 l
0
2l
0
¼ ð2 lÞ
1
2
0
2l
2l
0
0
¼ ð2 lÞ 2
2
l 1
4
4
1 l
0
0
0
l 1
1 l
0
Die verbliebene 3-reihige Determinante entwickeln wir wiederum nach der 1. Zeile (auch hier gilt: nur das 1. Element
liefert einen Beitrag) und erhalten schließlich:
0
0
2l
l 1
2
¼ ð2 lÞ 2 ðl 2 þ 1Þ
det ðA l EÞ ¼ ð2 lÞ ð2 lÞ 2
l 1 ¼ ð2 lÞ
1
l
4
1 l
det ðA l EÞ ¼ 0
Eigenwerte:
l 1=2 ¼ 2,
)
2
ð2 lÞ ðl þ 1Þ ¼ 0
2
ð2 lÞ 2 ¼ 0
)
l 1=2 ¼ 2
l2 þ 1
)
l2 ¼ 1
¼ 0
)
l 3=4 ¼ j
l 3=4 ¼ j
Determinante und Spur von A
det A ¼ l 1 l 2 l 3 l 4 ¼ 2 2 j ð jÞ ¼ 4 j 2 ¼ 4 ð 1Þ ¼ 4
ð j 2 ¼ 1Þ
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 þ l 4 ¼ 2 þ 2 þ j j ¼ 4
J60
Berechnen Sie die Eigenwerte und (auf möglichst einfache Art) die Determinante und Spur der Matrix A
(mit Kontrollrechnung):
0
1
0
1
a 1 0
1 0 0
B
C
B
C
bÞ A ¼ @ 1 a 2 A
aÞ A ¼ @ 2 3 0 A
0 2 a
0 1 2
a) Die Eigenwerte der Matrix A werden aus der charakteristischen Gleichung
0
0
1l
det ðA l EÞ ¼ 2
3l
0 ¼ 0
0
1
2l
ermittelt. Determinantenberechnung nach der Regel von Sarrus:
0
0 1 l
0
1l
2
2
3
l
0
3
l )
0
1
2l
0
1
det ðA l EÞ ¼ ð1 lÞ ð3 lÞ ð2 lÞ þ 0 þ 0 0 0 0 ¼ ð1 lÞ ð3 lÞ ð2 lÞ
det ðA l EÞ ¼ 0
Eigenwerte:
l 1 ¼ 1,
)
ð1 lÞ ð3 lÞ ð2 lÞ ¼ 0
l 2 ¼ 2,
l3 ¼ 3
)
l1 ¼ 1 ;
l2 ¼ 2 ;
l3 ¼ 3
3 Eigenwertprobleme
577
Determinante und Spur der Matrix A
det A ¼ l 1 l 2 l 3 ¼ 1 2 3 ¼ 6;
Kontrollrechnung
1
det A ¼ 2
0
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 ¼ 1 þ 2 þ 3 ¼ 6
(A ist eine Dreiecksmatrix):
0 0
3 0 ¼ a 11 a 22 a 33 ¼ 1 3 2 ¼ 6;
1 2
Sp ðAÞ ¼ a 11 þ a 22 þ a 33 ¼ 1 þ 3 þ 2 ¼ 6
b) Berechnung der Eigenwerte aus der charakteristischen Gleichung
1
0
al
det ðA l EÞ ¼ 1
al
2 ¼ 0
0
2
al
Determinantenberechnung nach der Regel von Sarrus:
1
0 a l
1
al
1
1
a
l
2
a
l )
0
2
al
0
2
det ðA l EÞ ¼ ða lÞ 3 þ 0 þ 0 0 4 ða lÞ ða lÞ ¼ ða lÞ 3 5 ða lÞ
det ðA l EÞ ¼ 0 ) ða lÞ 3 5 ða lÞ ¼ ða lÞ ða lÞ 2 5
¼ 0
al ¼ 0
ða lÞ 2 5 ¼ 0
Aus der oberen Gleichung folgt l 1 ¼ a, die untere Gleichung liefert zwei weitere Lösungen:
pffiffiffi
pffiffiffi
ða lÞ 2 5 ¼ 0 ) ða lÞ 2 ¼ 5 ) a l ¼ 5 ) l 2=3 ¼ a 5
pffiffiffi
pffiffiffi
Eigenwerte: l 1 ¼ a, l 2 ¼ a þ 5 , l 3 ¼ a 5
Determinante und Spur der Matrix A
pffiffiffi
pffiffiffi
det A ¼ l 1 l 2 l 3 ¼ a ða þ 5 Þ ða 5 Þ ¼ a ða 2 5Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 ¼ a þ ða þ
Kontrollrechnung:
a 1 0 a
1 a 2 1
0 2 a 0
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det A
1
a
2
)
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
5 Þ þ ða 5 Þ ¼ a þ a þ 5 þ a 5 ¼ 3 a
det A ¼ a 3 þ 0 þ 0 0 4 a a ¼ a 3 5 a ¼ a ða 2 5Þ
Sp ðAÞ ¼ a 11 þ a 22 þ a 33 ¼ a þ a þ a ¼ 3 a
0
J61
3 5
B
Gegeben ist die 3-reihige Matrix A ¼ @ 1 3
0 2
a) sämtliche Eigenwerte,
b) Spur und Determinante sowie
c) die Eigenvektoren dieser Matrix.
d) Sind die Eigenvektoren der Matrix A linear
1
0
C
2 A . Bestimmen Sie
3
unabhängig?
578
J Lineare Algebra
a) Berechnung der Eigenwerte der Matrix A
Die gesuchten Eigenwerte der Matrix A sind die Lösungen der charakteristischen Gleichung
5
0
3l
det ðA l EÞ ¼ 1
3l
2 ¼ 0
0
2
3l
Berechnung der Determinante nach der Regel von Sarrus:
5
0 3 l
5
3l
1
3l
2 1
3l )
0
2
3l 0
2
det ðA l EÞ ¼ ð3 lÞ 3 þ 0 þ 0 0 4 ð3 lÞ 5 ð3 lÞ ¼ ð3 lÞ 3 9 ð3 lÞ ¼
¼ ð3 lÞ ð3 lÞ 2 9
det ðA l EÞ ¼ 0
)
ð3 lÞ ð3 lÞ 2 9
¼ 0
ð3 lÞ 2 9 ¼ 0 ) ð3 lÞ 2 ¼ 9 ) 3 l ¼
Eigenwerte:
l 1 ¼ 3,
l 2 ¼ 6,
3l ¼ 0
)
l1 ¼ 3
2
ð3 lÞ 9 ¼ 0
3 ) l 2=3 ¼ 3 3
)
l2 ¼ 6 ;
l3 ¼ 0
l3 ¼ 0
b) Spur und Determinante der Matrix A
Die Spur ist die Summe, die Determinante das Produkt der Eigenwerte:
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 ¼ 3 þ 6 þ 0 ¼ 9;
det A ¼ l 1 l 2 l 3 ¼ 3 6 0 ¼ 0
Kontrollrechnung (Determinantenberechnung nach Sarrus):
Sp ðAÞ ¼ a 11 þ a 22 þ a 33 ¼ 3 þ 3 þ 3 ¼ 9
3 5 0 3
1 3 2 1
0 2 3 0
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
det A
5
3
2
)
det A ¼ 27 þ 0 þ 0 0 12 15 ¼ 0
c) Berechnung der Eigenvektoren der Matrix A
Die Berechnung der Eigenvektoren erfolgt aus der Gleichung ðA l EÞ x ¼ 0:
Eigenvektoren zum Eigenwert l 1 = 3
0
l1 ¼ 3
)
ðA 3 EÞ x ¼ 0 oder
0
B
@1
0
5
0
2
0 1
10 1
0
0
x1
B C
CB C
2 A @ x2 A ¼ @ 0 A
x3
0
0
Die Koeffizientenmatrix B ¼ A 3 E dieses homogenen LGS bringen
zunächst auf Trapezform („Gaußscher Algorithmus“):
0
1
0
1
0
0 5 0 2,5 Z 3
0 0 0
1 0
B
C
B
C
B
B ¼ @1 0 2A
) @1 0 2A
) @0 0
0 2 0
0 2 0
0 2
wir durch elementare Zeilenumformungen
1
2
C
0A
0
0
)
1
B
@0
0
1
0 2
C
2 0 A¼ B *
Nullzeile
0 0
3 Eigenwertprobleme
579
Die Matrix B hat also den Rang r ¼ Rg ðBÞ ¼ Rg ðB *Þ ¼ 2, die Anzahl der Unbekannten beträgt n ¼ 3. Es
gibt daher wegen r < n ¼ 3 unendlich viele Lösungen mit einem Parameter (n r ¼ 3 2 ¼ 1), die sich
aus dem gestaffelten System B * x ¼ 0 leicht berechnen lassen (gewählter Parameter: x 3 ¼ a mit a 6¼ 0; zunächst die untere Gleichung lösen):
ðIÞ
x1 þ 2 x3 ¼ 0
)
ðIIÞ
2 x2 ¼ 0
x2 ¼ 0
)
x1 þ 2 a ¼ 0
)
x1 ¼ 2 a
ðin die obere Gleichung einsetzenÞ
0
1
0
1
2a
2
Eigenvektoren zum Eigenwert l 1 ¼ 3: x 1 ¼ @ 0 A ¼ a @ 0 A
a
1
(mit a 6¼ 0)
Eigenvektoren zum Eigenwert l 2 = 6
0
l2 ¼ 6
)
B
@
ðA 6 EÞ x ¼ 0 oder
0 1
0
B C
CB C
1 3
2 A @ x2 A ¼ @ 0 A
0
0
2 3
x3
3
5
0
10
x1
1
Die Koeffizientenmatrix B ¼ A 6 E wird zunächst auf Trapezform gebracht, das dann vorliegende gestaffelte
System von unten nach oben gelöst:
0
0
0
1
1
1
3
5
0 þ 3 Z2
0 4
6
1 3
2
B
B
B
C
C
C
B ¼ @ 1 3
2A
) @1 3
2A
) @0 4
6 A þ 2 Z3 )
0
2 3
0
2 3
0
2 3
0
1 3
B
@0
0
2
1
0
C
0A
0
)
2 3
1
3
2
0
0
1
C
2 3 A¼ B *
B
@0
0
Nullzeile
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Lösung des gestaffelten Systems B * x ¼ 0 (gewählter Parameter: x 3 ¼ b mit b 6¼ 0):
ðIÞ
x1 3 x2 þ 2 x3 ¼ 0
)
x 1 3 1,5 b þ 2 b ¼ x 1 2,5 b ¼ 0
)
2 x2 3 x3 ¼ 0
)
2 x2 3 b ¼ 0
x 2 ¼ 1,5 b ðEinsetzen in ðIÞÞ
ðIIÞ
)
2 x2 ¼ 3 b
0
Eigenvektor zum Eigenwert l 2 ¼ 6:
x2
1
0
1
2,5 b
2,5
¼ @ 1,5 b A ¼ b @ 1,5 A
b
1
)
x 1 ¼ 2,5 b
(mit b 6¼ 0)
Eigenvektoren zum Eigenwert l 3 = 0
0
l3 ¼ 0
)
ðA 0 EÞ x ¼ A x ¼ 0
oder
3
B
@1
0
5
3
2
10 1
0 1
0
0
x1
B C
CB C
2 A @ x2 A ¼ @ 0 A
0
x3
3
Die Koeffizientenmatrix A wird zunächst auf Trapezform gebracht, das dann vorliegende gestaffelte System von
unten nach oben gelöst:
0
3
B
A ¼ @1
0
0
1
B
@0
0
3
0
2
5
3
2
1
2
C
0A
3
1
0 3 Z2
C
2A
3
0
)
1
B
@0
0
0
)
3
2
0
0
B
@1
0
1
4 6
C
3
2A
2
3
1
1
3
2
C
B
@ 0 4 6 A þ 2 Z3
0
2
3
0
)
)
1
2
C
3 A¼ A *
Nullzeile
0
Rg ðAÞ ¼ Rg ðA *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
580
J Lineare Algebra
Lösung des gestaffelten Systems A * x ¼ 0 (gewählter Parameter: x 3 ¼ g mit g 6¼ 0):
ðIÞ
ðIIÞ
x1 þ 3 x2 þ 2 x3 ¼ 0
)
x 1 4,5 g þ 2 g ¼ x 1 2,5 g ¼ 0
2 x2 þ 3 x3 ¼ 0
)
2 x2 þ 3 g ¼ 0
)
x 2 ¼ 1,5 g
x 1 ¼ 2,5 g
ðin Gleichung ðIÞ einsetzenÞ
0
Eigenvektor zum Eigenwert l 3 ¼ 0:
1
0
1
2,5 g
2,5
x 3 ¼ @ 1,5 g A ¼ g @ 1,5 A
g
1
)
(mit g 6¼ 0)
d) Die aus den drei Eigenvektoren x 1 , x 2 und x 3 gebildete Matrix ist regulär, da ihre Determinante einen von null
verschiedenen Wert besitzt:
2 a 2,5 b
2,5 g
2,5
2 2,5
0
1,5 b 1,5 g ¼ a b g 0 1,5 1,5 ¼ 13,5 a b g 6¼ 0
ðda a 6¼ 0; b 6¼ 0; g 6¼ 0Þ
a
1 1
b
g
1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D ¼ 13,5
(die drei Spalten haben der Reihe nach den gemeinsamen Faktor a, b bzw. g, den wir vor die Determinante
ziehen dürfen). Die Determinante D wurde dabei wie folgt nach der Regel von Sarrus berechnet:
2,5 2 2,5
2 2,5
0 1,5 1,5 0 1,5 ) D ¼ 3 3,75 þ 0 3,75 3 0 ¼ 13,5 6¼ 0
1 1
1 1 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
D
Folgerung: Die Eigenvektoren sind linear unabhängig.
J62
Bestimmen Sie auf möglichst einfache Art Eigenwerte, Determinante und
1
0
4
0 0 0
0
1
0
1 0 0
5
B0 2 0 0C
C
B
A ¼ B
C; B ¼ @2 5 0A; C ¼ @ 0
@0
0 5 0A
3 1 4
0
0
0 0 2
Spur der folgenden Matrizen:
1
1 3
2
5A
0
7
A ist eine Diagonalmatrix, B und C sind Dreiecksmatrizen. Die gesuchten Eigenwerte dieser Matrizen sind daher
mit den Hauptdiagonalelementen identisch. Die Spur ist stets die Summe, die Determinante stets das Produkt der
Eigenwerte. Somit gilt:
Matrix A
Eigenwerte : l 1 ¼ 4, l 2 ¼ 2, l 3 ¼ 5, l 4 ¼ 2
Sp ðAÞ ¼ l 1 þ l 2 þ l 3 þ l 4 ¼ 4 2 þ 5 þ 2 ¼ 9
det A ¼ l 1 l 2 l 3 l 4 ¼ 4 ð 2Þ 5 2 ¼ 80
Matrix B
Eigenwerte : l 1 ¼ 1, l 2 ¼ 5, l 3 ¼ 4
Sp ðBÞ ¼ l 1 þ l 2 þ l 3 ¼ 1 þ 5 þ 4 ¼ 10;
Matrix C
det B ¼ l 1 l 2 l 3 ¼ 1 5 4 ¼ 20
Eigenwerte : l 1 ¼ 5, l 2 ¼ 2, l 3 ¼ 7
Sp ðCÞ ¼ l 1 þ l 2 þ l 3 ¼ 5 þ 2 þ 7 ¼ 4;
det C ¼ l 1 l 2 l 3 ¼ ð 5Þ 2 7 ¼ 70
3 Eigenwertprobleme
581
Berechnen Sie die Eigenwerte und Eigenvektoren der 3-reihigen symmetrischen Matrix
0
1
1 2 2
A ¼ @2 1
2A:
2
2 1
J63
Bestimmen Sie ein System aus drei orthogonalen Eigenvektoren.
Berechnung der Eigenwerte der Matrix A
Die Eigenwerte sind die Lösungen der charakteristischen Gleichung det ðA l EÞ ¼ 0. Wir berechnen zunächst die
Determinante nach der Regel von Sarrus:
1 l
2
2 1 l
2
2
2
1
l
2
1
l )
2
2
1 l
2
2
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det ðA l EÞ
det ðA l EÞ ¼ ð 1 lÞ 3 þ 8 þ 8 4 ð 1 lÞ 4 ð 1 lÞ 4 ð 1 lÞ ¼
¼ ð 1 lÞ 3 12 ð 1 lÞ þ 16
det ðA l EÞ ¼ 0
)
ð 1 lÞ 3 12 ð 1 lÞ þ 16 ¼
¼ 1 3 l 3 l 2 l 3 þ 12 þ 12 l þ 16 ¼ l 3 3 l 2 þ 9 l þ 27 ¼ 0
Durch Probieren findet man die Lösung l 1 ¼ 3, mit Hilfe des Horner-Schemas die beiden (falls überhaupt vorhanden) restlichen Lösungen (Nullstellen des 1. reduzierten Polynoms):
1
3
l1 ¼ 3
1
l 1 ¼ 3,
Eigenwerte:
9
27
3
18 27
6
9
0
)
l2 6 l 9 ¼ 0
)
l 2=3 ¼ 3
)
l 2 þ 6 l þ 9 ¼ ðl þ 3Þ 2 ¼ 0
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
1. Binom
l 2=3 ¼ 3
Eigenvektoren der Matrix A
0 1
10 1
4 2 2
0
x1
B
B C
CB C
2 A @ x2 A ¼ @ 0 A
@2 4
x3
2
2 4
0
0
l1 ¼ 3
)
ðA 3 EÞ x ¼ 0 oder
Wir bringen die Koeffizientenmatrix B ¼ A
gen auf Trapezform (Gaußscher Algorithmus):
0
1
4 2 2 2 Z2
B
C
B ¼ @2 4
2A
)
2 4 Z2
1
0
0
6 6 : 6
C
B
2 A : ð 2Þ
@2 4
3 E dieses homogenen LGS mit Hilfe elementarer Zeilenumformun0
B
@2 4
2
0
0
0
6 6
0
0
)
C
2A
6 6
1
0
1
)
Z1
1 2 1
C
B
@ 0 1 1A¼ B*
0
0
0
Nullzeile
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
582
J Lineare Algebra
Das homogene LGS ist somit lösbar, die Lösungsmenge hängt aber wegen r < n von einem Parameter ab. Wir lösen jetzt
das gestaffelte System B * x ¼ 0 (gewählter Parameter: x 3 ¼ a mit a 6¼ 0; zunächst die untere Gleichung lösen):
ðIÞ
x1 þ 2 x2 x3 ¼ 0
)
x2 x3 ¼ 0
)
x1 þ 2 a a ¼ x1 þ a ¼ 0
)
x1 ¼ a
x2 a ¼ 0 ) x2 ¼ a
ðin die obere Gleichung einsetzenÞ
0
1
0
1
1
a
(mit a 6¼ 0)
Eigenvektoren zum Eigenwert l 1 ¼ 3: x 1 ¼ @ a A ¼ a @ 1 A
1
a
0 1
10 1
0
0
x1
2 2 2
B C
CB C
B
l 2=3 ¼ 3
) ðA þ 3 EÞ x ¼ 0 oder @ 2
2
2 A @ x2 A ¼ @ 0 A
0
x3
2
2
2
ðIIÞ
Die Koeffizientenmatrix B ¼ A þ 3 E wird auf Trapezform gebracht:
0
2 2
B ¼ @2
2
2
2
1
2
2 A þ Z1
2 þ Z1
0
2
@0
0
)
1
2 2
0
0A
0
0
¼ B*
2 Nullzeilen
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 1 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 1 ¼ 2
Die Lösungsmenge enthält zwei voneinander unabhängige Parameter. Wir lösen jetzt das gestaffelte System B * x ¼ 0
(es besteht aus einer Gleichung mit drei Unbekannten; gewählte Parameter: x 2 ¼ b und x 3 ¼ g mit b 6¼ 0,
g 6¼ 0):
2 x1 2 x2 2 x3 ¼ 0
)
2 x1 2 b 2 g ¼ 0
2 x1 ¼ 2 b þ 2 g
)
x1 ¼ b þ g
0
Eigenvektoren zum Eigenwert l 2 = 3 ¼ 3:
1
bþg
x ¼ @ b A
g
)
(mit b 6¼ 0 , g 6¼ 0)
Sie sind wie folgt als Linearkombination zweier linear unabhängiger Eigenvektoren x 2 und x 3 darstellbar:
0
1
0 1 0 1
0 1
0 1
bþg
b
g
1
1
B
C
B C B C
B C
B C
x ¼ @ b A ¼ @bAþ@ 0A ¼ b@1A þ g@0A ¼ x2 þ x3
g
0
g
0
1
|{z}
|{z}
x2
x3
Die Eigenvektoren x 2 und x 3 bilden zusammen mit dem zum Eigenwert l 1 ¼ 3 gehörenden Eigenvektor x 1 ein
System linear unabhängiger Vektoren (Kontrolle: Determinante der 3 Eigenvektoren ist ungleich null).
System aus drei orthogonalen Eigenvektoren
Bei einer symmetrischen Matrix gilt: Die zu verschiedenen Eigenwerten gehörenden Eigenvektoren sind orthogonal.
Damit sind x 1 und x 2 bzw. x 1 und x 3 orthogonale Eigenvektoren, und zwar unabhängig vom Wert der reellen
Parameter a, b und g. Wir wählen die (speziellen) orthogonalen Vektoren ~
x 1 mit a ¼ 1 und ~
x 2 mit b ¼ 1,
deren Skalarprodukt verschwindet:
0
1 0 1
1
1
B
C B C
~
x1 ~
x2 ¼ @ 1 A @ 1 A ¼ 1 þ 1 þ 0 ¼ 0
1
0
~ 1 als auch zu ~x 2
Der dritte noch fehlende Eigenvektor x 3 gehört zum Eigenwert l 2=3 ¼ 3 und muss sowohl zu x
0
1
bþg
B
C
orthogonal sein. Er ist in der Form ~x 3 ¼ @ b A darstellbar. Wir bestimmen die noch unbekannten Parameter b
g
und g so, dass die genannten Orthogonalitätsbedingungen erfüllt sind (die skalaren Produkte von ~
x 3 mit den Eigenvektoren ~
x 1 bzw. ~x 2 müssen verschwinden):
3 Eigenwertprobleme
583
0
1 0
1
1
bþg
B
C B
C
~ 3 ¼ @ 1 A @ b A ¼ 1 ð b þ gÞ þ b þ g ¼ b g þ b þ g ¼ 0
~1 x
x
1
g
Diese Bedingung ist also unabhängig von den Parameterwerten stets erfüllt.
0 1 0
1
bþg
1
B C B
C
~
x2 ~
x 3 ¼ @ 1 A @ b A ¼ 1 ð b þ gÞ þ b ¼ b þ g þ b ¼ 2 b þ g ¼ 0
g
0
Wir setzen b ¼ 1 und erhalten g ¼ 2 b ¼ 2. Der Eigenvektor ~
x 3 besitzt damit der Reihe nach die (skalaren)
Komponenten b þ g ¼ 1 2 ¼ 1, b ¼ 1 und g ¼ 2. Das gesuchte System aus drei orthogonalen Eigenvektoren lautet somit wie folgt:
0
1
0 1
0
1
1
1
1
B
C
B C
B
C
~
x 1 ¼ @ 1 A ; ~x 2 ¼ @ 1 A ; ~x 3 ¼ @ 1 A
1
0
2
Kontrolle (über Skalarproduktbildung):
0
1 0 1
1
1
B
C
B
C
B
B
C
~
x1 ~
x2 ¼ @ 1A @1C
A ¼ 1 þ 1 þ 0 ¼ 0;
0
1
0 1
1
C
B
B
~
x2 ~
x3 ¼ @ 1 C
A
0
0
B
B
@
1
0
B
~
x1 ~
x3 ¼ B
@
1
1
0
C B
B
1C
A@
1
1
1
C
1C
A ¼ 1þ12 ¼ 0
2
1
C
1C
A ¼ 1 þ 1 þ 0 ¼ 0
2
Bestimmen Sie die Eigenwerte und Eigenvektoren der 3-reihigen symmetrischen Matrix
0
1
0 1 0
A ¼ @ 1 0 1 A und zeigen Sie, dass die drei (zu verschiedenen Eigenwerten gehörenden) Eigen0 1 0
J64
vektoren ein orthogonales System bilden, d. h. paarweise aufeinander senkrecht stehen.
Berechnung der Eigenwerte der Matrix A
Die Lösungen der charakteristischen Gleichung det ðA l EÞ ¼ 0 liefern die Eigenwerte (Berechnung der 3-reihigen Determinante nach Sarrus):
l
1
0 l
1
1 l
1 l ) det ðA l EÞ ¼ l 3 þ 0 þ 0 0 þ l þ l ¼ l 3 þ 2 l
1
0
1 l 0
1
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det ðA l EÞ
pffiffiffi
det ðA l EÞ ¼ 0 ) l 3 þ 2 l ¼ l ð l 2 þ 2Þ ¼ 0 ) l 1 ¼ 0 ; l 2=3 ¼ 2
pffiffiffi
pffiffiffi
Eigenwerte: l 1 ¼ 0, l 2 ¼ 2 , l 3 ¼ 2
Berechnung der zugehörigen Eigenvektoren
0
l1 ¼ 0
)
ðA 0 EÞ x ¼ A x ¼ 0
oder
0
B
@1
0
1
0
1
0 1
10 1
0
x1
0
B C
CB C
1 A @ x2 A ¼ @ 0 A
0
x3
0
584
J Lineare Algebra
Die Koeffizientenmatrix A bringen wir zunächst mit Hilfe elementarer Umformungen in den Zeilen auf Trapezform
und lösen dann das gestaffelte System schrittweise von unten nach oben:
0
1
0
1
0
1
0 1 0
0 1 0
1 0 1
B
C
B
C
B
C
A ¼ @1 0 1A
) @1 0 1A
) @0 1 0A ¼ A*
Nullzeile
0 1 0 Z1
0 0 0
0 0 0
Rg ðAÞ ¼ Rg ðA *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Gestaffeltes System A * x ¼ 0 (gewählter Parameter: x 3 ¼ a mit a ¼
6 0):
ðIÞ
x1 þ x3 ¼ 0
)
x1 þ a ¼ 0
x2 ¼ 0
)
x2 ¼ 0
ðIIÞ
)
x1 ¼ a
0
1
1
1
a
x1 ¼ @ 0 A ¼ a @ 0 A
1
a
0
Zum Eigenwert l 1 ¼ 0 gehörende Eigenvektoren:
0
pffiffiffi
l2 ¼ 2
pffiffiffi
ðA 2 EÞ x ¼ 0 oder
)
pffiffiffi
2
1
pffiffiffi
B
@
1 2
0
1
(mit a 6¼ 0)
0 1
10 1
0
x1
0
B C
CB C
¼
0A
x
@
A
A
@
1
2
pffiffiffi
0
x3
2
pffiffiffi
Koeffizientenmatrix B ¼ A 2 E auf Trapezform bringen, dann das gestaffelte System schrittweise von unten
nach oben lösen:
1
0
1
0 pffiffiffi
pffiffiffi
1 2
1
2
1
0
C pffiffiffi
B pffiffiffi
C
B
pffiffiffi
B ¼ B
) B
1
0 C
1 2
1 C
A þ 2 Z1 )
@ 2
A
@
pffiffiffi
pffiffiffi
0
1 2
0
1 2
0
pffiffiffi
1 2
B
B0
@
0
1
1
1
1
pffiffiffi C
2C
A
pffiffiffi
2 þ Z2
0
)
1
B
B0
@
0
pffiffiffi
2
1
0
1
1
pffiffiffi C
*
2C
A¼ B
Nullzeile
0
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Gestaffeltes System B * x ¼ 0 (zunächst die untere Gleichung lösen; gewählter Parameter: x 3 ¼ b mit b 6¼ 0):
pffiffiffi
pffiffiffi pffiffiffi
ðIÞ x 1 2 x 2 þ
x3 ¼ 0 ) x1 2 2 b þ b ¼ x1 2 b þ b ¼ x1 b ¼ 0 ) x1 ¼ b
pffiffiffi
pffiffiffi
pffiffiffi
ðIIÞ
x 2 þ 2 x 3 ¼ 0 ) x 2 þ 2 b ¼ 0 ) x 2 ¼ 2 b ðin ðIÞ einsetzenÞ
pffiffiffi
Zum Eigenwert l 2 ¼ 2 gehörende Eigenvektoren:
1
0
1
0
1
b
B pffiffiffi C
B pffiffiffi C
ðmit b 6¼ 0Þ
x2 ¼ @ 2 b A ¼ b @ 2 A
b
l3 ¼
pffiffiffi
2
)
1
ðA þ
pffiffiffi
2 EÞ x ¼ 0
oder
pffiffiffi
Die Koeffizientenmatrix B ¼ A þ 2 E bringen
System schrittweise von unten nach oben:
0 pffiffiffi
1
0
1
2 1
0
pffiffiffi
B
C
B pffiffiffi
B ¼ @ 1
) @ 2
2 1 A
pffiffiffi
0
0
1
2
0 pffiffiffi
2
B
@ 1
0
0 1
10 1
0
x1
1
0
pffiffiffi
B C
CB C
2 1 A @ x2 A ¼ @ 0 A
pffiffiffi
0
x3
1
2
wir zunächst auf Trapezform, anschließend lösen wir das gestaffelte
1
pffiffiffi
2 1
C pffiffiffi
1
0 A 2 Z1
pffiffiffi
1
2
)
3 Eigenwertprobleme
0
1
B
@0
0
pffiffiffi
2
1
1
585
1
1
pffiffiffi C
2A
pffiffiffi
2 þ Z2
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ;
0
)
1
B
@0
0
1
pffiffiffi
2
1
pffiffiffi C
1 2A ¼ B*
Nullzeile
0
0
Anzahl der Unbekannten: n ¼ 3 ;
Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Gestaffeltes System B * x ¼ 0 (gewählter Parameter: x 3 ¼ g mit g 6¼ 0):
pffiffiffi
pffiffiffi
pffiffiffi
ðIÞ x 1 þ 2 x 2 þ
x 3 ¼ 0 ) x 1 þ 2 ð 2 gÞ þ g ¼ x 1 2 g þ g ¼ x 1 g ¼ 0 ) x 1 ¼ g
pffiffiffi
pffiffiffi
pffiffiffi
ðIIÞ
x2 2 x3 ¼ 0 ) x2 2 g ¼ 0 ) x2 ¼ 2 g
ðin ðIÞ einsetzenÞ
0
1
0
1
1
g
pffiffiffi
pffiffiffi
pffiffiffi
ðmit g 6¼ 0Þ
Eigenvektoren zum Eigenwert l 3 ¼ 2 : x 3 ¼ @ 2 g A ¼ g @ 2 A
1
g
Wir zeigen jetzt mit Hilfe des Skalarproduktes, dass die drei Eigenvektoren x 1 , x 2 und x 3 orthogonal sind (die
Bedingungen lauten: x i x k ¼ 0 für i 6¼ k ; i; k ¼ 1; 2; 3):
1
0
0
1 0
0
1
1
1
1
1
1
B pffiffiffi C
B
C B pffiffiffi C
B
C
x 1 x 2 ¼ a @ 0 A b @ 2 A ¼ a b @ 0 A @ 2 A ¼ a b ð 1 þ 0 þ 1Þ ¼ 0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1
1
1
1
0
0
1
0
1 0
1
1
1
1
1
1
p
ffiffi
ffi
p
ffiffi
ffi
B
C B
B
C
B
C
C
x 1 x 3 ¼ a @ 0 A g @ 2 A ¼ a g @ 0 A @ 2 A ¼ a g ð 1 þ 0 þ 1Þ ¼ 0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1
1
1
1
0
0
0
1 0
1
0
1
1
1
1
1
1
B pffiffiffi C B pffiffiffi C
B pffiffiffi C
B pffiffiffi C
x 2 x 3 ¼ b @ 2 A g @ 2 A ¼ b g @ 2 A @ 2 A ¼ b g ð1 2 þ 1Þ ¼ 0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
1
1
1
0
pffiffiffi
Alternative: Zeigen, dass det ðx 1 x 2 x 3 Þ 6¼ 0 ist (Lösung: det ðx 1 x 2 x 3 Þ ¼ 4 2 a b g 6¼ 0)
0
0
J65
1
B
Gegeben ist die Matrix A ¼ @ 3
3
2
2
3
1
0 1
1
3
C
B C
2 A und der Spaltenvektor x 1 ¼ @ 5 A .
4
8
a) Zeigen Sie: Der Vektor x 1 ist ein Eigenvektor der Matrix A . Wie lautet der zugehörige Eigenwert ?
b) Bestimmen Sie die restlichen Eigenwerte und Eigenvektoren.
a) Wenn der Vektor x 1 ein Eigenvektor der Matrix A ist, dann muss das Matrizenprodukt aus A und x 1 ein (noch
unbekanntes) Vielfaches des Vektors x 1 sein, d. h. die Gleichung A x 1 ¼ l x 1 muss eine eindeutige Lösung für l
ergeben:
0
10 1
0
1
0 1
0 1
0
1
1 2 1
3
3 þ 10 þ 8
21
3
3l
B
CB C
B
C
B C
B
C
B C
A x 1 ¼ @ 3 2 2 A @ 5 A ¼ @ 9 þ 10 þ 16 A ¼ @ 35 A ; l x 1 ¼ l @ 5 A ¼ @ 5 l A
3 3 4
8
9 þ 15 þ 32
56
8
8l
0
1
1
3l
21
B
C
B C
@ 35 A ¼ @ 5 l A
8l
56
0
A x1 ¼ l x1
)
)
9
8
>
=
< 3 l ¼ 21 >
5 l ¼ 35
>
>
: 8 l ¼ 56 ;
)
l ¼ 7
Die drei Gleichungen mit der Unbekannten l führen jeweils zum gleichen Ergebnis l ¼ 7 . Somit ist der Vektor x 1
ein Eigenvektor der Matrix A zum Eigenwert l 1 ¼ 7 .
586
J Lineare Algebra
b) Die Eigenwerte der Matrix A sind die Lösungen der charakteristischen Gleichung
2
1
1l
det ðA l EÞ ¼ 3
2l
2 ¼ 0
3
3
4l
Die Berechnung der 3-reihigen Determinante nach Sarrus führt auf eine Gleichung 3. Grades für l:
2
2
1 1 l
1l
3
3
2
l )
2
l
2
3
3
3
3
4l
det ðA l EÞ ¼ ð1 lÞ ð2 lÞ ð4 lÞ þ 12 þ 9 3 ð2 lÞ 6 ð1 lÞ 6 ð4 lÞ ¼
¼ ð2 l 2 l þ l 2 Þ ð4 lÞ þ 21 6 þ 3 l 6 þ 6 l 24 þ 6 l ¼
¼ ð2 3 l þ l 2 Þ ð4 lÞ þ ð3 l þ 6 l þ 6 lÞ þ ð21 6 6 24Þ ¼
¼ 8 2 l 12 l þ 3 l 2 þ 4 l 2 l 3 þ 15 l 15 ¼
¼ l 3 þ ð3 l 2 þ 4 l 2 Þ þ ð 2 l 12 l þ 15 lÞ þ ð8 15Þ ¼ l 3 þ 7l 2 þ l 7
Somit gilt:
det ðA l EÞ ¼ 0
)
l3 þ 7 l2 þ l 7 ¼ 0
Eine Lösung haben wir bereits in Teil a) bestimmt: l 1 ¼ 7. Die restlichen Lösungen erhalten wir aus dem
1. reduzierten Polynom mit Hilfe des Horner-Schemas (Abspalten des Linearfaktors l 7):
1
l1 ¼ 7
7
1
7
7
0
7
0
1
0
1
)
l2 þ 1 ¼ 0
)
l2 ¼ 1
)
l 2=3 ¼ 1
Somit gibt es genau drei verschiedene Eigenwerte: l 1 ¼ 7, l 2 ¼ 1, l 3 ¼ 1. Wir bestimmen jetzt die noch
fehlenden Eigenvektoren zu den Eigenwerten l 2=3 ¼ 1 .
Eigenvektoren zum Eigenwert l 2 = 1
0
l2 ¼ 1
)
ðA 1 EÞ x ¼ 0 oder
0
B
@3
3
2
1
3
0 1
10 1
0
x1
1
B C
CB C
2 A @ x2 A ¼ @ 0 A
0
x3
3
Wir bringen dieses homogene LGS zunächst auf Trapezform:
0
0
B
B3
@
3
2
1
1
1
C
2C
A
3
3
0
)
Z2
0
B
B3
@
0
2
1
0
1
1
C
2C
A
2
1
0
B
B3
@
0
)
Z1
2
1
0
1
1
C
2C
A
0
0
)
3
B
B0
@
0
1
2
1
2
C
1C
A
0
0
Nullzeile
Der Rang der Koeffizientenmatrix ist r ¼ 2 (die Matrix enthält eine Nullzeile). Es gibt somit wegen r < n
unendlich viele Lösungen, die noch von einem Parameter abhängen ðn r ¼ 3 2 ¼ 1Þ. Das gestaffelte System wird wie folgt gelöst (wir wählen x 2 als Parameter, setzen also x 2 ¼ a mit a 6¼ 0):
ðIÞ
ðIIÞ
3 x1 þ x2 þ 2 x3 ¼ 0
2 x2 þ
x3 ¼ 0
)
3 x1 þ a 4 a ¼ 3 x1 3 a ¼ 0
)
2 a þ x3 ¼ 0
)
x3 ¼ 2 a
Zum Eigenwert l 2 ¼ 1 gehören damit folgende Eigenvektoren:
0
1
0
1
a
1
B
C
B
C
x2 ¼ @ a A ¼ a @ 1 A
ðmit a 6¼ 0Þ
2a
2
)
3 x1 ¼ 3 a
)
x1 ¼ a
ðin Gleichung ðIÞ einsetzenÞ
3 Eigenwertprobleme
587
Eigenvektoren zum Eigenwert l 3 = – 1
0
l3 ¼ 1
)
ðA þ 1 EÞ x ¼ 0 oder
Dieses homogene LGS bringen wir
0
0
1
2
2 2 1
B
C
B
B3 3 2C
) B
@
A
@3
3 3 5 Z2
0
2
B
@3
3
2
3
3
10 1
0 1
1
0
x1
B C
CB C
2 A @ x2 A ¼ @ 0 A
x3
5
0
zunächst mit Hilfe elementarer Zeilenumformungen
0
1
1
2 2 1
2 1
B
C
C
B
C
3 2C
)
A 1,5 Z 1 ) @ 0 0 0,5 A
2 Z2
0 0 1
0 3 : 3
auf Trapezform:
0
1
2 2 1
B
B 0 0 0,5 C
C
@
A
0 0 0
Nullzeile
Rang der Matrix: r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Lösung des gestaffelten Systems (zunächst die untere Gleichung lösen, gewählter Parameter: x 2 ¼ b mit b 6¼ 0):
ðIÞ
2 x1 þ 2 x2 þ x3 ¼ 0
)
2 x1 þ 2 b þ 0 ¼ 2 x1 þ 2 b ¼ 0
0,5 x 3 ¼ 0
)
x3 ¼ 0
ðIIÞ
)
2 x1 ¼ 2 b
)
x1 ¼ b
ðin ðIÞ einsetzenÞ
Zum Eigenwert l 3 ¼ 1 gehören somit folgende Eigenvektoren:
1
0
1
0
1
b
C
B
C
B
ðmit b 6¼ 0Þ
x3 ¼ @ b A ¼ b @ 1 A
0
0
0
J66
1
@
Wie lauten die Eigenwerte und Eigenvektoren der hermiteschen Matrix A ¼
0
2j
Zeigen Sie die lineare Unabhängigkeit der Eigenvektoren.
1
0 2j
0
0 A?
0
4
Berechnung der Eigenwerte der Matrix A
Die Eigenwerte sind die Lösungen der charakteristischen Gleichung det ðA l EÞ ¼ 0 (die 3-reihige Determinante
berechnen wir nach Sarrus):
1 l
0
2 j 1 l
0
0
0
l
0
l )
2j
0 4l
2j
0
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
det ðA l EÞ
det ðA l EÞ ¼ ð1 lÞ ð lÞ ð4 lÞ þ 0 þ 0 4 j 2 l 0 0 ¼ l ð1 lÞ ð4 lÞ þ 4 l ¼
¼ l ð1 lÞ ð4 lÞ 4
det ðA l EÞ ¼ 0
Eigenwerte:
l 1=2 ¼ 0,
)
¼ l ð4 l 4 l þ l 2 4Þ ¼ l ðl 2 5 lÞ
l ðl 2 5 lÞ ¼ l 2 ðl 5Þ ¼ 0
)
l 1=2 ¼ 0 ;
l3 ¼ 5
Berechnung der zugehörigen Eigenvektoren
0
l 1=2 ¼ 0
)
ðA 0 EÞ x ¼ A x ¼ 0
oder
1
B
@0
2j
10 1
0 1
0 2j
0
x1
CB C
B C
0
0 A @ x2 A ¼ @ 0 A
x3
0
4
0
l3 ¼ 5
588
J Lineare Algebra
Wir bringen zunächst die Koeffizientenmatrix A 0 E ¼ A durch elementare Zeilenumformungen auf Trapezform:
0
1
A ¼ @0
2j
1
0 2j
0
0A
2 j Z1
0
4
0
)
1
1 0 2j
@0 0
0A
0 0
0
¼ A*
2 Nullzeilen
Rg ðAÞ ¼ Rg ðA *Þ ¼ r ¼ 1 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 1 ¼ 2
Wir lösen das gestaffelte System A * x ¼ 0, das aus einer einzigen Gleichung besteht und dessen Lösungsmenge zwei
unabhängige Parameter enthält (wir wählen x 2 ¼ a und x 3 ¼ b mit a 6¼ 0, b 6¼ 0):
x1 2 j x3 ¼ 0
)
x1 2 j b ¼ 0
)
x1 ¼ 2 j b ¼ 2 b j
Damit erhalten wir die folgenden von zwei Parametern a und b abhängenden Eigenvektoren zum (doppelten) Eigenwert l 1=2 ¼ 0:
0
1
2bj
x ¼ @ a A
ðmit a ¼
6 0 ; b 6¼ 0Þ
b
Wir können diesen Eigenvektor auch wie folgt als Linearkombination zweier linear unabhängiger Eigenvektoren x 1
und x 2 darstellen, die nur von a bzw. b abhängen:
0
1
0 1
0
1
0 1 0 1
2bj
0
2bj
0
2j
B
C
B C
B
C
B C B C
x ¼ @ a A ¼ @ a A þ @ 0 A ¼ a @ 1 Aþ b @ 0 A ¼ a x 1 þ b x 2
b
0
b
0
1
|{z}
|ffl{zffl}
x1
x2
0
l3 ¼ 5
)
ðA 5 EÞ x ¼ 0 oder
4
B
@ 0
2j
0
5
0
0 1
10 1
0
x1
2j
B C
CB C
0 A @ x2 A ¼ @ 0 A
0
x3
1
Die Koeffizientenmatrix B ¼ A 5 E bringen wir zunächst auf Trapezform und lösen dann das gestaffelte System:
0
0
1
1
0
1
4
0 2j : 2
2
0 j
2
0 j
B
B
C
C
B
C
B ¼ @ 0 5
0A
) @ 0 5
0 A¼ B *
) @ 0 5
0A
Nullzeile
2j
0 1
0
0
0
2j
0 1 þ j Z1
Rg ðBÞ ¼ Rg ðB *Þ ¼ r ¼ 2 ; Anzahl der Unbekannten : n ¼ 3 ; Anzahl der Parameter : n r ¼ 3 2 ¼ 1
Wir lösen das gestaffelte System B * x ¼ 0 (gewählter Parameter ist x 3 ¼ 2 g mit g 6¼ 0):
ðIÞ
2 x1 j x3 ¼ 0
ðIIÞ
5 x2 ¼ 0
)
)
2 x1 j 2 g ¼ 0
)
2 x 1 ¼ j 2g
)
x1 ¼ j g
x2 ¼ 0
0
Eigenvektoren zum Eigenwert l 3 ¼ 5:
1
0
1
jg
j
x3 ¼ @ 0 A ¼ g @ 0 A
2g
2
ðmit g 6¼ 0Þ
Die drei Eigenvektoren x 1 , x 2 und x 3 (mit g ¼ 1) sind linear unabhängig, da die aus ihnen gebildete Determinante von null verschieden ist (Determinantenberechnung durch Entwicklung nach den Elementen der 2. Zeile, wobei nur das Element a 21 ¼ 1 einen Beitrag leistet):
0 2j
det ðx 1 x 2 x 3 Þ ¼ 1 0
0 1
2j
¼
1
j
0
2þ1
0 ¼ a 21 A 21 ¼ a 21 ð 1Þ
D 21 ¼ 1 ð 1Þ 1
0
2
j
¼ ð4 j þ jÞ ¼ 5 j 6¼ 0
2
2j
0
1
j
0 ¼
2
3 Eigenwertprobleme
589
1
2
Bestimmen Sie die Eigenwerte und Eigenvektoren der symmetrischen Matrix A ¼
.
2 2
x 2 gebildete Matrix
Zeigen Sie dann, dass die mit den normierten Eigenvektoren ~
x 1 und ~
T ¼ ð~x 1 ~x 2 Þ die Matrix A auf Diagonalgestalt transformiert:
J67
T1 A T ¼ D
ðD : DiagonalmatrixÞ
Welche Bedeutung haben die Diagonalelemente dieser Diagonalmatrix?
Das Eigenwertproblem lautet:
ðA l EÞ x ¼ 0
oder
1l
2
2
2 l
!
x1
x2
!
¼
0
0
!
Die Eigenwerte berechnen wir aus der charakteristischen Gleichung det ðA l EÞ ¼ 0:
2
1l
¼ ð1 lÞ ð 2 lÞ 4 ¼
det ðA l EÞ ¼
2
2 l
¼ 2 l þ 2 l þ l2 4 ¼ l2 þ l 6 ¼ 0
l 1=2
1
¼
2
rffiffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffi
1
1
25
1
5
þ6 ¼
¼
4
2
4
2
2
)
)
l1 ¼ 2 ;
l2 ¼ 3
Berechnung der zugehörigen Eigenvektoren
l1 ¼ 2
)
1
2
ðA 2 EÞ x ¼ 0 oder
2
4
!
x1
x2
!
0
0
¼
!
Dieses homogene LGS reduziert sich auf eine Gleichung (wir wählen die erste Gleichung), da die beiden Gleichungen
proportional sind:
ðIÞ
ðIIÞ
x 1 þ 2 x 2 ¼ 0 j ð 2Þ
)
2 x1 4 x2 ¼ 0
ðidentisch mit Gleichung (II)Þ
2 x1 4 x2 ¼ 0
Wir dürfen daher über eine der beiden Unbekannten frei verfügen und wählen x 2 als Parameter (x 2 ¼ a mit a 6¼ 0):
ðIIÞ
)
2 x1 4 a ¼ 0
)
2 x 1 ¼ 4a
)
x1 ¼ 2 a
Der Eigenvektor x 1 mit den Komponenten x 1 ¼ 2 a und x 2 ¼ a
x 1 x 1 ¼ 1; a > 0):
2a
2a
x1 x1 ¼
¼ 4 a2 þ a2 ¼ 5 a2 ¼ 1 )
a
a
pffiffiffi !
2= 5
Normierter Eigenvektor zum Eigenwert l 1 ¼ 2: ~
x1 ¼
¼
pffiffiffi
1= 5
l2 ¼ 3
)
ðA þ 3 EÞ x ¼ 0 oder
4
2
2
1
!
x1
x2
!
¼
0
0
wird noch normiert (Normierungsbedingung:
a2 ¼
1
pffiffiffi
5
1
5
)
1
a ¼ pffiffiffi
5
2
1
!
Wiederum erhalten wir zwei proportionale Gleichungen (die erste Gleichung ist das 2-fache der zweiten Gleichung):
ðIÞ 4 x 1 þ 2 x 2 ¼ 0 j : 2
) 2 x1 þ x2 ¼ 0
ðIIÞ 2 x 1 þ x 2 ¼ 0
590
J Lineare Algebra
Da die verbliebene Gleichung noch beide Unbekannte enthält, können wir x 1 oder x 2 frei wählen. Wir entscheiden
uns für den Parameter x 1 ¼ b mit b 6¼ 0:
2 x1 þ x2 ¼ 0
)
2 b þ x2 ¼ 0
)
x2 ¼ 2 b
Den Eigenvektor x 2 mit den Komponenten x 1 ¼ b und x 2 ¼ 2 b müssen wir noch normieren ( b > 0):
b
b
1
1
¼ b2 þ 4 b2 ¼ 5 b2 ¼ 1 ) b2 ¼
) b ¼ pffiffiffi
x2 x2 ¼
5
2b
2b
5
pffiffiffi !
1
1= 5
1
Normierter Eigenvektor zum Eigenwert l 2 ¼ 3: ~
x2 ¼
¼ pffiffiffi
pffiffiffi
2
2= 5
5
Transformation der Matrix A auf Diagonalgestalt
~ 2 bilden wir die Transformationsmatrix T und deren Inverse T 1 :
Mit den beiden normierten Eigenvektoren ~x 1 und x
! 1
pffiffiffi
pffiffiffi !
pffiffiffi
2
1
2= 5
1= 5
1
1
1
1
¼ pffiffiffi B ; T
¼ pffiffiffi
¼ pffiffiffi B
¼ 5 B1
T ¼ ð~
x 1 ~x 2 Þ ¼
pffiffiffi
pffiffiffi
1= 5 2= 5
5 1 2
5
5
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
B
Die Matrix B invertieren wir nach dem Gauß-Jordan-Verfahren (! FS: Kap. VII.1.5.2.2):
!
!
2
1 1 0
1 2 0 1
1 2
)
)
ðB j EÞ ¼
1 2 0 1
2
1 1 0 2 Z1
0
5
|fflfflffl{zfflfflffl} |ffl{zffl}
B
E
!
!
1 2 0
1
1 0 2=5
1=5
þ 2 Z2
)
¼ ðE j B 1 Þ
0
1 1=5 2=5
0 1 1=5 2=5
|ffl{zffl} |fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
E
B1
0
1
1
2
!
: 5
)
Somit gilt:
T
1
pffiffiffi
pffiffiffi 2=5
¼ 5 B1 ¼ 5
1=5
1=5
2=5
pffiffiffi
2
5
¼
5
1
1
2
1
¼ pffiffiffi
5
2
1
1
¼ pffiffiffi B
1 2
5
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
B
Wir transformieren die Matrix A mit Hilfe der Transformationsmatrix T und ihrer Inversen T 1 wie folgt auf
Diagonalgestalt:
1
1
1
1
A ! D ¼ T 1 A T ¼ pffiffiffi B A pffiffiffi B ¼
ðB A BÞ ¼
ðB AÞ B
5
5
5
5
Die Matrizenprodukte B A und ðB AÞ B berechnen wir mit dem Falk-Schema:
A
B
2
1
1 2
1
2
4
3
2
2
2
6
BA
4
3
B
2
1
1
2
2
6
10
0
0
15
BA
ðB AÞ B
Damit erhalten wir:
D ¼ T
1
1
1
ðB AÞ B ¼
AT ¼
5
5
10
0
0 15
¼
2
0
0
3
Die Transformation führt in der Tat auf eine Diagonalmatrix, deren Diagonalelemente die Eigenwerte der Matrix A
sind (l 1 ¼ 2 und l 2 ¼ 3).
591
K Wahrscheinlichkeitsrechnung
und mathematische Statistik
1 Wahrscheinlichkeit von Ereignissen
Lehrbuch: Band 3, Kapitel II.1, 2 und 3
Formelsammlung: Kapitel XV.1, 2 und 3
Einer Lieferung von 30 elektronischen Bauteilen (darunter befinden sich unbekannterweise 2 defekte Teile)
wird eine Stichprobe vom Umfang n ¼ 3 entnommen. Bestimmen Sie die Wahrscheinlichkeit dafür, dass
K1
die Stichprobe
a) ausschließlich einwandfreie Teile,
b) mindestens 1 defektes Teil enthält.
Wir betrachten die folgenden Ereignisse:
A i : Die i-te Ziehung liefert ein einwandfreies Bauteil (i ¼ 1, 2, 3)
a) Das Ereignis A 1 \ A 2 \ A 3 beschreibt dann die (nacheinander erfolgte) Ziehung dreier einwandfreier Bauteile.
Nach dem Multiplikationssatz (! FS: Kap. XV.3.5) gilt dann für die Wahrscheinlichkeit dieses Ereignisses:
P 0 ¼ P ðA 1 \ A 2 \ A 3 Þ ¼ P ðA 1 Þ P ðA 2 j A 1 Þ P ðA 3 j A 1 \ A 2 Þ ¼
28 27 26
¼ 0,8069
30 29 28
80,7 %
Berechnung der Wahrscheinlichkeiten P ðA 1 Þ, P ðA 2 j A 1 Þ und P ðA 3 j A 1 \ A 2 Þ
Die Ziehung eines Bauteils erfolgt rein zufällig und ist für alle Bauteile gleichwahrscheinlich (es handelt sich um
ein Laplace-Experiment ! FS: Kap. XV.3.3). P ðA 2 j A 1 Þ und P ðA 3 j A 1 \ A 2 Þ sind dabei bedingte Wahrscheinlichkeiten (! FS: Kap. XV.3.4).
1. Ziehung: 30 Teile, darunter 28 einwandfreie Teile; gezogen wird ein einwandfreies Teil (Ereignis A 1 Þ
) P ðA 1 Þ ¼ 28=30
2. Ziehung: Das Ereignis A 1 ist eingetreten (Ziehung eines einwandfreien Teils), unter den verbliebenen 29 Teilen
befinden sich damit 27 einwandfreie Teile; gezogen wird wiederum ein einwandfreies Teil (Ereignis A 2 Þ
) P ðA 2 j A 1 Þ ¼ 27=29
3. Ziehung: Die Ereignisse A 1 und A 2 und somit das Ereignis A 1 \ A 2 sind eingetreten (zweimalige Ziehung
eines einwandfreien Teils); unter den verbliebenen 28 Teilen befinden sich 26 einwandfreie Teile; gezogen wird
wiederum ein einwandfreies Teil (Ereignis A 3 Þ ) P ðA 3 j A 1 \ A 2 Þ ¼ 26=28
b) P (mindestens 1 defektes Teil) ¼ 1 P 0 ¼ 1 0,8069 ¼ 0,1931
19,3 %
©
Springer Fachmedien Wiesbaden
ein Teil von
Springer Nature 2020
Papula/Klausurentrainer
2019 GmbH,
3B2
O:/Springer/Papula_Klausurentrainer_2019/3d/36vi011d.3d
L. Papula, Mathematik für Ingenieure und Naturwissenschaftler – Klausur- und Übungsaufgaben,
https://doi.org/10.1007/978-3-658-30271-9_11
Bearb.: DP
592
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Schwimmwettbewerb
Die Gewinnchancen der vier Teilnehmer (A, B, C und D) eines Schwimmwettbewerbs verhalten sich auf-
K2
grund der gezeigten Trainingsleistungen wie 4 : 2 : 3 : 1. Wie groß sind dann die Wahrscheinlichkeiten für
folgende Ereignisse?
a) A gewinnt,
b) D gewinnt,
c) A oder C gewinnt (wobei ein sog. „totes“ Rennen, d. h. gleicher Zieleinlauf ausgeschlossen wird).
Die Gewinnchancen der Teilnehmer beschreiben wir durch die Wahrscheinlichkeiten P ðAÞ, P ðBÞ, P ðCÞ und P ðDÞ.
Wir setzen (willkürlich) P ðDÞ ¼ p und damit P ðAÞ ¼ 4 p, P ðBÞ ¼ 2 p, P ðCÞ ¼ 3 p. Da einer der vier Teilnehmer gewinnt (sog. sicheres Ereignis), gilt:
P ðAÞ þ P ðBÞ þ P ðCÞ þ P ðDÞ ¼ 4 p þ 2 p þ 3 p þ p ¼ 10 p ¼ 1
)
p ¼ 0,1
a) A gewinnt: P ðAÞ ¼ 4 p ¼ 4 0,1 ¼ 0,4 ¼
b 40 %
b) D gewinnt: P ðDÞ ¼ p ¼ 0,1 ¼
b 10 %
c) A oder C gewinnt, beschrieben durch das Ereignis A [ C , wobei sich die Ereignisse A und C gegenseitig ausschließen (ein „totes“ Rennen wurde ausgeschlossen). Aus dem Additionssatz für sich gegenseitig ausschließende
Ereignisse folgen dann (! FS: Kap. XV.3.2):
P ðA [ CÞ ¼ P ðAÞ þ P ðCÞ ¼ 4 p þ 3 p ¼ 7 p ¼ 7 0,1 ¼ 0,7 ¼
b 70 %
Zwei Sportschützen treffen die Zielscheibe mit einer Wahrscheinlichkeit von 20 % (Schütze Nr. 1) bzw.
K3
40 % (Schütze Nr. 2), wie man aus den Trainingsleistungen schließen kann.
a) Wie groß ist die Wahrscheinlichkeit, dass die Scheibe getroffen wird, wenn beide gleichzeitig schießen?
b) Mit welcher Wahrscheinlichkeit trifft nur einer der beiden Schützen?
Wir betrachten die folgenden Ereignisse:
A: 1. Schütze trifft;
B: 2. Schütze trifft
a) Die Scheibe wird getroffen, wenn das Ereignis A [ B eintritt (entweder trifft der 1. Schütze oder der 2. Schütze
oder beide). Dann gilt nach dem Additionssatz für beliebige Ereignisse (! FS: Kap. XV.3.2):
P ðA [ BÞ ¼ P ðAÞ þ P ðBÞ P ðA \ BÞ
Die Wahrscheinlichkeiten für die Ereignisse A und B sind bereits bekannt: P ðAÞ ¼ 0,2 und P ðBÞ ¼ 0,4. Die
Wahrscheinlichkeit für das Ereignis A \ B (beide Schützen treffen gleichzeitig) erhalten wir aus dem Multiplikationssatz für stochastisch unabhängige Ereignisse (! FS: Kap. XV.3.6):
P ðA \ BÞ ¼ P ðAÞ P ðBÞ ¼ 0,2 0,4 ¼ 0,08
(das Ergebnis des einen Schützen hat keinen Einfluss auf das Ergebnis des anderen Schützen). Die Scheibe wird
somit mit der folgenden Wahrscheinlichkeit getroffen:
P ðA [ BÞ ¼ P ðAÞ þ P ðBÞ P ðA \ BÞ ¼ 0,2 þ 0,4 0,08 ¼ 0,52 ¼
b 52 %
b) Uns interessiert das folgende Ereignis:
C: Nur einer der beiden Schützen trifft
D. h. entweder trifft der 1. Schütze und der 2. Schütze trifft nicht (Ereignis ðA \ BÞ oder umgekehrt der 2. Schütze
trifft und der 1. Schütze trifft nicht (Ereignis ðB \ AÞ1) ). Somit lässt sich das Ereignis C wie folgt beschreiben:
1Þ
A ist das zu A komplementäre Ereignis (der 1. Schütze trifft nicht). Analog B: Zu B komplementäre Ereignis (der 2. Schütze trifft nicht).
1 Wahrscheinlichkeit von Ereignissen
593
C ¼ ðA \ BÞ [ ðB \ AÞ
Die Wahrscheinlichkeit, dass nur einer der beiden Schützen trifft, beträgt dann nach dem Additionssatz (die Ereignisse A \ B und B \ A schließen sich gegenseitig aus):
P ðCÞ ¼ P ðA \ BÞ þ P ðB \ AÞ ¼ P ðAÞ P ðBÞ þ P ðBÞ P ðAÞ ¼ 0,2 0,6 þ 0,4 0,8 ¼
¼ 0,12 þ 0,32 ¼ 0,44 ¼
b 44 %
P ðAÞ ¼ 1 P ðAÞ ¼ 1 0,2 ¼ 0,8 ;
P ðBÞ ¼ 1 P ðBÞ ¼ 1 0,4 ¼ 0,6
Windhundrennen
An einem Windhundrennen nehmen vier Hunde (A, B, C und D) teil und zwar der Reihe nach mit den
Gewinnchancen 10 %, 20 %, 20 % und 50 %. Es finden zwei Rennen unter jeweils gleichen Bedingungen
K4
statt. Mit Hilfe des Ereignisbaumes (Baumdiagramms) sollen die Wahrscheinlichkeiten folgender Ereignisse (Rennergebnisse) bestimmt werden:
a) Windhund A gewinnt das 1. und Windhund B das 2. Rennen;
b) Windhund D gewinnt beide Rennen;
c) Windhund B gewinnt das 1. und Windhund C das 2. Rennen oder umgekehrt.
In beiden Rennen gelten für die Wahrscheinlichkeiten, das Rennen zu gewinnen:
P ðAÞ ¼ 0,1; P ðBÞ ¼ P ðCÞ ¼ 0,2; P ðDÞ ¼ 0,5.
Ereignisbaum (Baumdiagramm; siehe Bild K-1)
1. Rennen
D
0,
0,5
D
5
0,2
O
Eingezeichnet sind nur die interessierenden Pfade
mit den entsprechenden Wahrscheinlichkeiten
(Zwischen- und Endergebnisse; O: „Wurzel“
des Baumes = Ausgangspunkt), Der Ausgang
des 1. Rennens hat dabei keinen Einfluss auf
das 2. Rennen (es handelt sich hierbei um
stochastisch unabhängige Ereignisse).
2. Rennen
C
0,2
B
0,2
0,1
B
0,2
C
0,2
A
B
Bild K-1 Ereignisbaum
Mit Hilfe der Pfadregeln (! FS: Kap. XV.3.7) erhalten wir die gesuchten Wahrscheinlichkeiten. Sie betragen:
a) P ðO A BÞ ¼ P ðAÞ P ðBÞ ¼ 0,1 0,2 ¼ 0,02 ¼
b 2%
b) P ðO D DÞ ¼ P ðDÞ P ðDÞ ¼ 0,5 0,5 ¼ 0,25 ¼
b 25 %
c) P ðO B C [ O C BÞ ¼ P ðO B CÞ þ P ðO C BÞ ¼ P ðBÞ P ðCÞ þ P ðCÞ P ðBÞ ¼ 2 P ðBÞ P ðCÞ ¼
¼ 2 0,2 0,2 ¼ 0,08 ¼
b 8%
594
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Eine Warenlieferung besteht aus 200 ohmschen Widerständen, die in einem Werk auf drei verschiedenen
Maschinen M 1 , M 2 und M 3 hergestellt wurden, wobei gilt:
K5
Maschine
M1
M2
M3
produzierte Stückzahl
(in der Lieferung)
60
100
40
Ausschussanteil p i
(i ¼ 1, 2, 3)
2%
3%
1%
Der Lieferung wird rein zufällig ein Widerstand entnommen und auf seine Funktionsfähigkeit überprüft
(intakt oder defekt).
a) Wie groß ist die Wahrscheinlichkeit, dass dieser Widerstand defekt ist?
b) Sollte der entnommene Widerstand defekt sein, mit welcher Wahrscheinlichkeit wurde er dann auf der
Maschine M 1 produziert?
Wir interessieren uns also für die folgenden Ereignisse:
A i : Der entnommene Widerstand wurde auf der Maschine M i produziert (i ¼ 1, 2, 3)
D: Der entnommene Widerstand ist defekt
Die Wahrscheinlichkeiten der Ereignisse A i betragen dabei:
P ðA 1 Þ ¼
60
¼ 0,3 ;
200
P ðA 2 Þ ¼
100
¼ 0,5 ;
200
P ðA 3 Þ ¼
40
¼ 0,2
200
Die gesuchten Lösungen (Wahrscheinlichkeiten) erhalten wir mit Hilfe des Baumdiagramms (Ereignisbaum; siehe Bild
K-2).
Drei Pfade führen vom Ausgangspunkt O („Wurzel“
des Baumes) über die Zwischenstationen A 1 bzw. A 2
bzw. A 3 nach D. Die Pfadregeln liefern dann die
gesuchten Wahrscheinlichkeiten (! FS: Kap. XV.3.7).
A3
0,
O
0,
2
0,5
0,
A2
3
01
0,03
0,
D
02
A1
Bild K-2 Baumdiagramm
a) P ðO A 1 DÞ ¼ P ðA 1 Þ P ðD j A 1 Þ ¼ P ðA 1 Þ p 1 ¼ 0,3 0,02 ¼ 0,006
P ðO A 2 DÞ ¼ P ðA 2 Þ P ðD j A 2 Þ ¼ P ðA 2 Þ p 2 ¼ 0,5 0,03 ¼ 0,015
P ðO A 3 DÞ ¼ P ðA 3 Þ P ðD j A 3 Þ ¼ P ðA 3 Þ p 3 ¼ 0,2 0,01 ¼ 0,002
Anmerkung: Die bedingten Wahrscheinlichkeiten P ðD j A i Þ sind die vorgegebenen Ausschussanteile, d. h.
P ðD j A i Þ ¼ p i (i ¼ 1, 2, 3).
1 Wahrscheinlichkeit von Ereignissen
595
Die gesuchte totale Wahrscheinlichkeit des Ereignisses D beträgt damit:
P ðDÞ ¼ P ðO A 1 DÞ þ P ðO A 2 DÞ þ P ðO A 3 DÞ ¼ 0,006 þ 0,015 þ 0,002 ¼ 0,023 ¼
b 2,3 %
b) Die Formel von Bayes liefert dann (! FS: Kap. XV.3.7) die gesuchte Wahrscheinlichkeit dafür, dass der entnommene Widerstand defekt ist und auf der Maschine M 1 produziert wurde:
P ðA 1 j DÞ ¼
P ðO A 1 DÞ
PðDÞ
¼
0,006
0,023
¼ 0,2609 ¼
b 26,09 %
Anmerkung: Es gibt genau einen „günstigen“ Pfad, nämlich O A 1 D, siehe Baumdiagramm (Bild K-2).
Autorennen (Formel 1)
Aufgrund der Ergebnisse aus den Vorjahren wird erwartet, dass zwei bestimmte Rennwagen W 1 und W 2
bei künftigen Rennen das Ziel mit einer Wahrscheinlichkeit von 80 % bzw. 90 % erreichen und zwar unabhängig voneinander. Bestimmen Sie die Wahrscheinlichkeiten für folgende (zukünftige) Ereignisse (Renn-
K6
ergebnisse):
a) Beide Wagen erreichen das Ziel;
b) Beide Wagen fallen aus;
c) Genau einer der beiden Wagen erreicht das Ziel;
d) Mindestens einer der beiden Wagen erreicht das Ziel.
Wir betrachten die folgenden Ereignisse:
A i : Wagen W i erreicht das Ziel (i ¼ 1, 2)
A i : Wagen W i fällt aus (i ¼ 1, 2)
Diese Ereignisse haben folgende Wahrscheinlichkeiten (A i ist das zu A i komplementäre Ereignis):
P ðA 1 Þ ¼ 0,8 ;
P ðA 1 Þ ¼ 0,2 ;
P ðA 2 Þ ¼ 0,9 ;
P ðA 2 Þ ¼ 0,1
Wir lösen die gestellte Aufgabe mit Hilfe des Additions- und Multiplikationssatzes für (stochastisch) unabhängige
Ereignisse (! FS: Kap. XV.3.2 und 3.6).
a) Ereignis ðA 1 \ A 2 Þ: Beide Wagen erreichen das Ziel.
P ðA 1 \ A 2 Þ ¼ P ðA 1 Þ P ðA 2 Þ ¼ 0,8 0,9 ¼ 0,72 ¼
b 72 %
b) Ereignis ðA 1 \ A 2 Þ: Beide Wagen fallen aus.
P ðA 1 \ A 2 Þ ¼ P ðA 1 Þ P ðA 2 Þ ¼ 0,2 0,1 ¼ 0,02 ¼
b 2%
c) Ereignis C ¼ ðA 1 \ A 2 Þ [ ðA 1 \ A 2 Þ: Entweder erreicht W 1 das Ziel und W 2 fällt aus (Ereignis A 1 \ A 2 )
oder W 1 fällt aus und W 2 erreicht das Ziel (Ereignis A 1 \ A 2 ).
P ðCÞ ¼ P ðA 1 \ A 2 Þ [ ðA 1 \ A 2 Þ ¼ P ðA 1 \ A 2 Þ þ P ðA 1 \ A 2 Þ ¼
¼ P ðA 1 Þ P ðA 2 Þ þ P ðA 1 Þ P ðA 2 Þ ¼ 0,8 0,1 þ 0,2 0,9 ¼ 0,08 þ 0,18 ¼ 0,26 ¼
b 26 %
Anmerkung: Die Ereignisse A 1 \ A 2 und A 1 \ A 2 schließen sich gegenseitig aus.
596
K Wahrscheinlichkeitsrechnung und mathematische Statistik
d) Ereignis ðA 1 [ A 2 Þ: Entweder erreicht W 1 das Ziel und W 2 fällt aus oder umgekehrt W 2 erreicht das Ziel
und W 1 fällt aus oder beide Wagen erreichen das Ziel. Mit dem Additionssatz für beliebige Ereignisse (! FS:
Kap. XV.3.2) erhalten wir dann:
P ðA 1 [ A 2 Þ ¼ P ðA 1 Þ þ P ðA 2 Þ P ðA 1 \ A 2 Þ ¼ P ðA 1 Þ þ P ðA 2 Þ P ðA 1 Þ P ðA 2 Þ ¼
¼ 0,8 þ 0,9 0,8 0,9 ¼ 1,7 0,72 ¼ 0,98 ¼
b 98 %
Ein Bogenschütze trifft mit einer Wahrscheinlichkeit von p ¼ 0,3 ins „Schwarze“ (¼ Zentrum der Zielscheibe). Bestimmen Sie bei drei abgegebenen Schüssen die Wahrscheinlichkeiten der folgenden Ereignisse (Resultate):
K7
a) 3 Treffer;
b) 2 Treffer;
c) mindestens 2 Treffer.
d) Wie oft muss er mindestens schießen, um mit einer Wahrscheinlichkeit von 90 % wenigstens einmal zu
treffen?
Wir betrachten die Ereignisse
T : Treffer und T : Fehlschuss
mit den Wahrscheinlichkeiten P ðTÞ ¼ p ¼ 0,3 und P ðTÞ ¼ 1 P ðTÞ ¼ 1 0,3 ¼ 0,7. Das Ergebnis eines
Versuches (Treffer oder Fehlschuss) ist dabei unabhängig vom Ergebnis des vorangegangenen Schussversuches
(stochastisch unabhängige Ereignisse).
a) Der Multiplikationssatz (! FS: Kap. XV.3.2) liefert für das Ereignis T T T (¼ 3 Treffer):
P ð3 TrefferÞ ¼ P ðT T TÞ ¼ P ðTÞ P ðTÞ P ðTÞ ¼ 0,3 0,3 0,3 ¼ 0,3 3 ¼ 0,027 ¼
b 2,7 %
b) Drei mögliche Ereignisse (Fehlschuss beim 1. bzw. 2. bzw. 3. Versuch): T T T, T T T, T T T.
P ð2 TrefferÞ ¼ P ðT T TÞ þ P ðT T TÞ þ P ðT T TÞ ¼ 0,7 0,3 0,3 þ 0,3 0,7 0,3 þ 0,3 0,3 0,7 ¼
¼ 3 ð0,7 0,3 2 Þ ¼ 0,189 ¼
b 18,9 %
c) P ðmindestens 2 TrefferÞ ¼ P ð2 TrefferÞ þ P ð3 TrefferÞ ¼ 0,189 þ 0,027 ¼ 0,216 ¼
b 21,6 %
(unter Berücksichtigung der Ergebnisse aus a) und b))
d) Der Bogenschütze muss mindestens n Schüsse abgeben, um die Scheibe wenigstens einmal mit einer Wahrscheinlichkeit von 90 % zu treffen (n ist dabei zunächst noch unbekannt). Mit p ðiÞ bezeichnen wir die Wahrscheinlichkeit, dass der Schütze die Scheibe erstmals beim i-ten Schuss trifft (i ¼ 1, 2, . . . , n; alle vorangegangenen
Schüsse sind Fehlschüsse). Dabei gilt:
p ð1Þ ¼ 0,3 ;
... ;
p ð2Þ ¼ 0,7 0,3 ¼ 0,3 0,7 1 ;
p ð3Þ ¼ 0,7 0,7 0,3 ¼ 0,3 0,7 2 ;
p ðnÞ ¼ 0,7 0,7 . . . 0,7 0,3 ¼ 0,3 0,7 n 1
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
ðn 1Þ-mal
Die ganzzahlige Unbekannte n genügt dann der folgenden Bedingung:
p ð1Þ þ p ð2Þ þ p ð3Þ þ . . . þ p ðnÞ ¼ 0,3 þ 0,3 0,7 1 þ 0,3 0,7 2 þ . . . þ 0,3 0,7 n 1 ¼
0,7 n 1
0,3 ð0,7 n 1Þ
¼
¼ 1 0,7 n ¼ 0,9
¼ 0,3 ð1 þ 0,7 1 þ 0,7 2 þ . . . þ 0,7 n 1 Þ ¼ 0,3
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0,7 1
0,3
geometrische Reihe (! FS: Kap. I.3.3)
0,7 n ¼ 0,1 j ln
)
ln 0,7 n ¼ ln 0,1
)
n ln 0,7 ¼ ln 0,1
)
n ¼
ln 0,1
ln 0,7
¼ 6,4557
)
1 Wahrscheinlichkeit von Ereignissen
597
Da n ganzzahlig sein muss (n ¼ Anzahl der abgegebenen Schüsse), lautet die Lösung n ¼ 7. D. h. der Schütze
muss mindestens 7 Schüsse abgeben, um mit einer Wahrscheinlichkeit von 90 % wenigstens einmal die Scheibe zu
treffen.
Für die Montage eines Elektrogerätes werden u. a. drei verschiedene ohmsche Widerstände R 1 , R 2 und
K8
R 3 und zwei verschiedene Kapazitäten (Kondensatoren) C 1 und C 2 benötigt, die alle aus Serienproduktionen mit Ausschusswahrscheinlichkeiten von 5 % (bei den Widerständen) und 3 % (bei den Kondensatoren) stammen. Wie groß ist die Wahrscheinlichkeit, dass mindestens 1 defektes Bauteil eingebaut wird und
das Gerät damit nicht funktionsfähig (d. h. defekt) ist?
Wir betrachten die folgenden stochastisch unabhängigen Ereignisse:
A i : Einwandfreier Widerstand R i (i ¼ 1, 2, 3)
B k : Einwandfreier Kondensator mit der Kapazität C k (k ¼ 1, 2)
Zunächst bestimmen wir die Wahrscheinlichkeit für das Eintreten des Ereignisses
C ¼ A1 \ A2 \ A3 \ B1 \ B2
(das Elektrogerät enthält nur einwandfreie Bauteile). Der Multiplikationssatz für stochastisch unabhängige Ereignisse
(! FS: Kap. XV.3.6) liefert dann mit P ðA i Þ ¼ 1 0,05 ¼ 0,95 und P ðB k Þ ¼ 1 0,03 ¼ 0,97 das folgende
Ergebnis:
P ðCÞ ¼ P ðA 1 \ A 2 \ A 3 \ B 1 \ B 2 Þ ¼ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ P ðB 1 Þ P ðB 2 Þ ¼
¼ 0,95 0,95 0,95 0,97 0,97 ¼ 0,95 3 0,97 2 ¼ 0,8067
Dann gilt für das zu C komplementäre Ereignis C (das Elektrogerät enthält mindestens 1 defektes Bauteil und ist
damit nicht funktionsfähig):
P ðCÞ ¼ 1 P ðCÞ ¼ 1 0,8067 ¼ 0,1933 ¼
b 19,33 %
Fertigungsstraße mit drei Stationen
Eine Fertigungsstraße mit drei Stationen S 1 , S 2 und S 3 , die unabhängig voneinander ausfallen können,
wird in regelmäßigen zeitlichen Abständen gewartet, d. h. auf ihre Funktionsfähigkeit überprüft.
Den Ereignissen
A i : Station S i funktioniert einwandfrei (i ¼ 1, 2, 3)
K9
können dabei aufgrund langjähriger Erfahrungen die folgenden Wahrscheinlichkeitswerte zugeordnet werden: P ðA 1 Þ ¼ 0,97; P ðA 2 Þ ¼ 0,93; P ðA 3 Þ ¼ 0,95. Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
a) B k : Genau k der 3 Stationen funktionieren einwandfrei (k ¼ 0, 1, 2, 3)
Hinweis: k ¼ 0 bedeutet, dass keine Station funktioniert!
b) C : Mindestens eine Station funktioniert!
Die zu A i komplementären Ereignisse
A i : Station S i funktioniert nicht einwandfrei (i ¼ 1, 2, 3)
besitzen dann folgende Wahrscheinlichkeiten:
598
K Wahrscheinlichkeitsrechnung und mathematische Statistik
P ðA 1 Þ ¼ 1 P ðA 1 Þ ¼ 1 0,97 ¼ 0,03 ;
P ðA 2 Þ ¼ 1 P ðA 2 Þ ¼ 1 0,93 ¼ 0,07 ;
P ðA 3 Þ ¼ 1 P ðA 3 Þ ¼ 1 0,95 ¼ 0,05
Die Berechnung der gesuchten Wahrscheinlichkeiten erfolgt mit dem Additions- und Multiplikationssatz für stochastisch unabhängige Ereignisse (! FS: Kap. XV.3.2 und 3.6; die Stationen arbeiten unabhängig voneinander).
a)
k ¼ 0
Ereignis B 0 ¼ A 1 \ A 2 \ A 3 : Keine der 3 Stationen funktioniert.
P 0 ¼ P ðB 0 Þ ¼ P ðA 1 \ A 2 \ A 3 Þ ¼ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ ¼ 0,03 0,07 0,05 ¼
¼ 0,000 105
0,01 %
Dieses Ereignis (alle 3 Stationen fallen aus) ist also sehr unwahrscheinlich!
k ¼ 1
Ereignis B 1 ¼ ðA 1 \ A 2 \ A 3 Þ [ ðA 1 \ A 2 \ A 3 Þ [ ðA 1 \ A 2 \ A 3 Þ: Nur eine Station funktioniert (entweder funktioniert S 1 oder S 2 oder S 3 ; die beiden übrigen Stationen dagegen fallen aus).
P 1 ¼ P ðB 1 Þ ¼ P ðA 1 \ A 2 \ A 3 Þ þ P ðA 1 \ A 2 \ A 3 Þ þ P ðA 1 \ A 2 \ A 3 Þ ¼
¼ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ þ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ þ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ ¼
¼ 0,97 0,07 0,05 þ 0,03 0,93 0,05 þ 0,03 0,07 0,95 ¼
¼ 0,003 395 þ 0,001 395 þ 0,001 995 ¼ 0,006 785
k ¼ 2
0,68 %
Ereignis B 2 ¼ ðA 1 \ A 2 \ A 3 Þ [ ðA 1 \ A 2 \ A 3 Þ [ ðA 1 \ A 2 \ A 3 Þ: Nur 2 Stationen funktionieren (entweder fällt S 1 aus oder S 2 oder S 3 ; die beiden übrigen Stationen dagegen funktionieren).
P 2 ¼ P ðB 2 Þ ¼ P ðA 1 \ A 2 \ A 3 Þ þ P ðA 1 \ A 2 \ A 3 Þ þ P ðA 1 \ A 2 \ A 3 Þ ¼
¼ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ þ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ þ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ ¼
¼ 0,03 0,93 0,95 þ 0,97 0,07 0,95 þ 0,97 0,93 0,05 ¼
¼ 0,026 505 þ 0,064 505 þ 0,045 105 ¼ 0,136 115
k ¼ 3
13,61 %
Ereignis B 3 ¼ A 1 \ A 2 \ A 3 : Alle Stationen funktionieren.
P 3 ¼ P ðB 3 Þ ¼ P ðA 1 \ A 2 \ A 3 Þ ¼ P ðA 1 Þ P ðA 2 Þ P ðA 3 Þ ¼
¼ 0,97 0,93 0,95 ¼ 0,856 995
85,70 %
Kontrolle der Rechnung:
P 0 þ P 1 þ P 2 þ P 3 ¼ 0,000 105 þ 0,006 785 þ 0,136 115 þ 0,856 995 ¼ 1
b) P ðCÞ ¼ 1 P 0 ¼ 1 0,000 105 ¼ 0,999 895
100 %
Man kann davon ausgehen, dass stets mindestens eine Station funktioniert.
2 Wahrscheinlichkeitsverteilungen einer Zufallsvariablen
Lehrbuch: Band 3, Kapitel II.4
Formelsammlung: Kapitel XV.4
Integraltafel: Formelsammlung, Anhang Teil A („gelbe Seiten“)
Hinweis: In den Lösungen wird die jeweilige Nummer des Integrals mit den entsprechenden Parameterwerten angegeben (z. B. Integral 313 mit a ¼ 2).
2 Wahrscheinlichkeitsverteilungen einer Zufallsvariablen
599
Ein homogener Würfel wird dreimal geworfen. Bestimmen Sie die Verteilung der diskreten Zufallsvariablen
K10
X ¼ Anzahl der Würfe mit der Augenzahl 1 oder 6
a) Zeichnen Sie das zugehörige Stabdiagramm sowie den Verlauf der Verteilungsfunktion F ðxÞ.
b) Berechnen Sie den Mittelwert m (Erwartungswert) sowie die Varianz s 2 der Zufallsvariablen X.
a) Ereignis A: Wurf der Augenzahl 1 oder 6
Komplementäres Ereignis B ¼ A: Wurf der Augenzahl 2, 3, 4 oder 5
Alle Augenzahlen sind gleichwahrscheinlich mit der Wahrscheinlichkeit p ¼ 1=6 (Laplace-Experiment, ! FS:
Kap. XV.3.3).
Die Ereignisse A und B besitzen dann die Wahrscheinlichkeiten P ðAÞ ¼ 2=6 ¼ 1=3 und P ðBÞ ¼ 4=6 ¼ 2=3.
Bei 3 Würfen sind genau 8 verschiedene Ergebnisse (Elementarereignisse) möglich: AAA, BAA, ABA, AAB, ABB,
BAB, BBA, BBB. Die Zufallsvariable X kann die Werte 0, 1, 2, 3 annehmen. Der Multiplikations- und Additionssatz liefert dann die folgenden Wahrscheinlichkeitswerte (! FS: Kap. XV.3.2 und 3.6):
X ¼ 0
Elementarereignis: BBB (B bei jedem der 3 Würfe)
P ðX ¼ 0Þ ¼ P ðBBBÞ ¼ P ðBÞ P ðBÞ P ðBÞ ¼
X ¼ 1
2 2 2
8
¼
3 3 3
27
3 Elementarereignisse: ABB, BAB, BBA (A beim 1. bzw. 2. bzw. 3. Wurf)
P ðX ¼ 1Þ ¼ P ðABBÞ þ P ðBABÞ þ P ðBBAÞ ¼ 3 P ðABBÞ ¼ 3 P ðAÞ P ðBÞ P ðBÞ ¼
¼ 3
1 2 2
12
¼
3 3 3
27
(die Elementarereignisse unterscheiden sich lediglich in der Reihenfolge der Faktoren und sind daher gleichwahrscheinlich; jeweils einmal A und zweimal B).
X ¼ 2
3 Elementarereignisse: BAA, ABA, AAB (B beim 1. bzw. 2. bzw. 3. Wurf)
P ðX ¼ 2Þ ¼ P ðBAAÞ þ P ðABAÞ þ P ðAABÞ ¼ 3 P ðBAAÞ ¼ 3 P ðBÞ P ðAÞ P ðAÞ ¼
¼ 3
2 1 1
6
¼
3 3 3
27
(die Elementarereignisse unterscheiden sich lediglich in der Reihenfolge der Faktoren und sind daher gleichwahrscheinlich; jeweils einmal B und zweimal A).
X ¼ 3
Elementarereignis: AAA (A bei jedem der 3 Würfe)
P ðX ¼ 3Þ ¼ P ðAAAÞ ¼ P ðAÞ P ðAÞ P ðAÞ ¼
1 1 1
1
¼
3 3 3
27
Verteilungstabelle ð f ðxÞ ¼ P ðX ¼ xÞ: WahrscheinlichkeitsfunktionÞ
xi
0
1
2
f ðx i Þ
8=27
12=27
6=27
F ðx i Þ
8=27
20=27
26=27
3
1=27
27=27 ¼ 1
600
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Stabdiagramm (Bild K-3) und Verteilungsfunktion (Treppenfunktion, Bild K-4)
F (x)
f (x)
1
26/27
12/27
20/27
8/27
6/27
8/27
1/27
Bild K-4
Bild K-3
0
1
b) m ¼ E ðXÞ ¼
2
4
X
3
x
x i f ðx i Þ ¼ 0
i¼1
s 2 ¼ Var ðXÞ ¼
4
X
0
2
3
x
8
12
6
1
0 þ 12 þ 12 þ 3
27
þ1
þ2
þ3
¼
¼
¼ 1
27
27
27
27
27
27
ðx i mÞ 2 f ðx i Þ ¼ ð0 1Þ 2
i¼1
¼ 1
1
8
12
6
1
þ ð1 1Þ 2
þ ð2 1Þ 2
þ ð3 1Þ 2
¼
27
27
27
27
8
12
6
1
8þ0þ6þ4
18
2
þ0
þ1
þ4
¼
¼
¼
27
27
27
27
27
27
3
Ein Sportschütze trifft eine kreisförmige Zielscheibe vom Radius R ¼ 6 cm mit einer Wahrscheinlichkeit von 60 %. Die Scheibe wurde durch zwei konzentrische Kreise mit den Radien r 1 ¼ 2 cm
und r 2 ¼ 4 cm in drei kreisringförmige Bereiche unterteilt (Bild K-5).
Bereich (I):
R
0 r r1
Bereich (II): r 1 r r 2
r2
Bereich (III): r 2 r R
r1
K11
Bild K-5 Zielscheibe
Trifft der Schütze die Scheibe, so erhält er in Abhängigkeit vom getroffenen Bereich die folgenden
Punkte (bei einem Fehlschuss gibt es keinen Punkt):
Getroffener Bereich
(I)
(II)
(III)
außerhalb (Fehlschuss)
Punkte
10
6
2
0
Bestimmen Sie die Wahrscheinlichkeitsfunktion f ðxÞ.
Welche Punktzahl kann man bei einem abgegebenen Schuss im Mittel erwarten?
2 Wahrscheinlichkeitsverteilungen einer Zufallsvariablen
601
Zufallsvariable: X ¼ erreichte Punktzahl (X ¼ 0, 2, 6, 10)
Der Schütze trifft die Scheibe mit der Wahrscheinlichkeit P ðScheibeÞ ¼ 0,6 ¼ 3=5. Für die Vergabe der Punkte ist
jedoch zu berücksichtigen, dass die Treffwahrscheinlichkeit von Bereich zu Bereich verschieden ist. Ein sinnvoller
Multiplikator, der die Lage des Bereiches auf der Scheibe angemessen berücksichtigt, ist das Verhältnis der Fläche des
Bereiches zur Gesamtfläche der Scheibe. Somit erhalten wir die folgenden Treffwahrscheinlichkeiten für die einzelnen
Bereiche:
X ¼ 10
Treffer im Bereich (I)
Ringfläche ðIÞ
P ðX ¼ 10Þ ¼ f ð10Þ ¼
¼
X ¼ 6
43
36 5
¼
12
3 12 5
¼
Ringfläche ðIIÞ
1
35
p R2
3
¼
5
ð2 cmÞ 2
ð6 cmÞ
2
3
5
¼
4 cm 2
36 cm 2
3
¼
5
1
¼
15
P ðScheibeÞ ¼
Scheibenfläche
ð16 4Þ cm 2
3
36 cm 2
¼
5
12 3
36 5
¼
p ðr 22 r 12 Þ
p
R2
3
¼
ð4 cmÞ 2 ð2 cmÞ 2
5
ð6 cmÞ
2
3
¼
5
1
5
Treffer im Bereich (III)
P ðX ¼ 2Þ ¼ f ð2Þ ¼
¼
X ¼ 0
¼
p r 12
Treffer im Bereich (II)
P ðX ¼ 6Þ ¼ f ð6Þ ¼
X ¼ 2
Scheibenfläche
P ðScheibeÞ ¼
Ringfläche ðIIIÞ
Scheibenfläche
ð36 16Þ cm 2
36 cm 2
3
¼
5
P ðScheibeÞ ¼
20 3
36 5
¼
p ðR 2 r 22 Þ
p R2
453
43 3 5
¼
3
5
¼
ð6 cmÞ 2 ð4 cmÞ 2
ð6 cmÞ
2
3
¼
5
1
3
Scheibe verfehlt (Fehlschuss)
P ðX ¼ 0Þ ¼ f ð0Þ ¼ 1 P ðScheibeÞ ¼ 1
3
5
0
2
f ðx i Þ ¼
2
5
f ðxÞ ¼ P ðX ¼ xÞ
Verteilungstabelle
xi
¼
¼
5
2
6
1
15
3
¼
6
5
1
15
5
¼
10
3
1
15
15
Der Erwartungswert (Mittelwert) der Zufallsvariablen X, d. h. die mittlere Punktzahl beträgt damit:
E ðXÞ ¼
4
X
i¼1
x i f ðx i Þ ¼ 0
6
5
3
1
0 þ 10 þ 18 þ 10
38
þ2
þ6
þ 10
¼
¼
¼ 2,53
15
15
15
15
15
15
Die stetige Zufallsvariable X genüge einer Exponentialverteilung mit der Wahrscheinlichkeitsdichte-
K12
funktion f ðxÞ ¼ l e lx für x 0 (im übrigen Bereich verschwindet f ðxÞ; l > 0). Welchen
1 2
Erwartungswert besitzt die von X abhängige Funktion (Zufallsvariable) Z ¼ g ðXÞ ¼ X
?
l
602
K Wahrscheinlichkeitsrechnung und mathematische Statistik
"
E ðZÞ ¼ E
X
1
ð
¼ l
0
¼
1
l
1
2#
1
ð
¼
l
1
ð
g ðxÞ f ðxÞ d x ¼
1
1
x
2
l
0
l elx d x ¼
1
ð 2 2
2x
1
l x 2lx þ 1
2
lx
x
dx ¼ l
elx d x ¼
þ 2 e
l
l
l2
0
1
ð
ðl 2 x 2 2 l x þ 1Þ e l x d x
0
Aufspalten des Integrals in 3 Teilintegrale liefert dann (! Integrale 312, 313 und 314, jeweils mit a ¼ l):
E ðZÞ ¼
¼
¼
1
"
1
ð
l
l
1
2
lx
1
ð
dx 2l
0
"
l
l
1
x e
2
l
0
Integral 314
Integral 313
l3
1
l
dx þ
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
e
lx
2l
ðl 2 x 2 þ 2 l x þ 2Þ e l x
2
l
#
1
ð
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
!
l2 x2 þ 2 l x þ 2
2
x e
lx
e
lx
dx
¼
0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
Integral 312
lx 1
l2
e
lx
ð l x 1Þ e l x
1
l
1
l
#1
e
lx
¼
0
elx
1
¼
0
1
1
2 2
lx
lx
lx
ðl x þ 2 l x þ 2Þ e
þ 2 ð l x 1Þ e
þe
¼
¼
l
l
0
1
¼
¼
1
l2
1
l
2
ðl 2 x 2 þ 2 l x þ 2 2 l x 2 þ 1Þ e l x
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
0
ðl x þ 1Þ e
2
2
lx
1
¼
0
1
l
2
ð0 1Þ ¼
1
¼
0
1
l2
Hinweis: lim P ðxÞ e l x ¼ 0 für ein beliebiges Polynom P ðxÞ und l > 0; hier ist P ðxÞ ¼ l 2 x 2 þ 1.
x!1
Anmerkung: Der Erwartungswert E ðZÞ ¼ 1=l 2 ist die Varianz der Zufallsvariablen X!
f (x)
a
Gegeben ist die in Bild K-6 skizzierte symmetrische Drei-
K13
ecksverteilung einer stetigen Zufallsvariablen X. Berechnen
Sie den Mittelwert m und die Varianz s 2 dieser Verteilung
unter Berücksichtigung der Spiegelsymmetrie.
–1
Bild K-6
1
x
2 Wahrscheinlichkeitsverteilungen einer Zufallsvariablen
603
Zunächst bestimmen wir den Parameter a durch Normierung der noch unbekannten Dichtefunktion f ðxÞ:
ð1
f ðxÞ d x ¼ 2
a
¼ a ¼ 1
2
1
Das Integral entspricht
und die Dichtefunktion
8
1
>
>
<
f ðxÞ ¼
>
>
:
1þ
dem Flächeninhalt A ¼ a des grau unterlegten gleichschenkligen Dreiecks. Somit ist a ¼ 1
f ðxÞ kann (abschnittsweise) durch die folgenden Geradengleichungen beschrieben werden:
9
x
0 x 1>
>
=
f ür
¼ 1 jxj; 1 x 1
>
>
;
x
1 x 0
(für j x j > 1 gilt f ðxÞ ¼ 0Þ; j x j ¼ x für x 0 und j x j ¼ x für x 0)
Berechnung des Mittelwertes (Erwartungswertes) m ¼ E ðXÞ
1
ð
m ¼ E ðXÞ ¼
ð1
x f ðxÞ d x ¼
x ð1 j x j Þ d x ¼ 0
1
1
Begründung: Eine (direkte) Berechnung des Integrals ist überflüssig. Denn f ðxÞ besitzt das Symmetriezentrum
x 0 ¼ 0 (gerade Funktion, spiegelsymmetrisch zur y-Achse). Für eine solche Funktion gilt bekanntlich E ðXÞ ¼ x 0 ,
hier also E ðXÞ ¼ 0 (! FS: Kap. XV.4.3). Ohne diese Kenntnisse müssen Sie das Integral zunächst in zwei Teilintegrale zerlegen und diese dann berechnen:
ð1
ð0
ð0
x ð1 þ xÞ d x þ
m ¼
1
¼
¼
x ð1 xÞ d x ¼
ðx þ x Þ d x þ
1
0
1 2
1 3
x þ
x
2
3
ð1
0
1 2
1 3
x
x
2
3
þ
1
ðx x 2 Þ d x ¼
2
0
1
¼
0
1
1
1
1
0þ0
þ
þ
0þ0 ¼
2
3
2
3
1
1
1
1
þ
þ
¼ 0
2
3
2
3
Berechnung der Varianz s 2 ¼ Var ðXÞ
h
s ¼ Var ðXÞ ¼ E ðX mÞ
2
2
i
h
¼ E ðX 0Þ
2
i
1
ð
¼ E ðX Þ ¼
ð1
x f ðxÞ d x ¼
2
1
ð1
¼ 2
ð1
x ð1 j x j Þ d x ¼ 2
0
¼ 2
1
1
0þ0
3
4
0
¼ 2
ðx 2 x 3 Þ d x ¼ 2
2
1
1
3
4
|fflfflffl{zfflfflffl}
1=12
0
¼ 2
1
ð1
x ð1 xÞ d x ¼ 2
2
x 2 ð1 j x j Þ d x ¼
2
1 3
1 4
x
x
3
4
1
¼
0
1
1
¼
12
6
Dabei haben wir die Integration auf das Intervall 0 x 1 beschränken können, da beide Faktoren des Integranden
x 2 ð1 j x j Þ und somit auch der Integrand selbst gerade Funktionen sind und ferner die Integrationsgrenzen spiegelsymmetrisch zum Nullpunkt liegen (daher der Faktor 2 vor dem Integral; j x j ¼ x für x 0).
604
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Lebensdauer eines elektronischen Bauelementes
Die „Lebensdauer“ T eines speziellen elektronischen Bauelementes ist eine stetige Zufallsvariable mit
der von der Zeit t abhängigen Verteilungsfunktion
K14
F ðtÞ ¼ 1 ð1 þ c tÞ e c t
Welche durchschnittliche Lebensdauer
c ¼ 0,001 h
1
ðc > 0 ; t in Stunden ¼ hÞ
T
hat ein solches Element für den Parameterwert
?
Die für die Berechnung der durchschnittlichen Lebensdauer benötigte Wahrscheinlichkeitsdichtefunktion f ðtÞ ist die
1. Ableitung der Verteilungsfunktion F ðtÞ. Mit der Produkt- und Kettenregel erhalten wir:
F ðtÞ ¼ 1 ð1 þ c tÞ e c t ¼ 1 u v mit
u ¼ 1 þ c t , v ¼ ect
und u 0 ¼ c , v 0 ¼ c e c t
F 0 ðtÞ ¼ f ðtÞ ¼ 0 ðu 0 v þ v 0 uÞ ¼ u 0 v v 0 u ¼ c e c t þ c e c t ð1 þ c tÞ ¼
¼ ð c þ c þ c 2 tÞ e c t ¼ c 2 t e c t
T ist dann der Erwartungswert der Zufallsvariablen T :
1
ð
T ¼ E ðTÞ ¼
1
ð
t f ðtÞ d t ¼ c
2
1
t2 ect d t ¼ c2
c2 t 2 þ 2 c t þ 2
ect
c3
0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1
¼
0
Integral 314 mit a ¼ c
1
¼
c
c t þ 2ct þ 2 e
2 2
ct
1
¼
0
1
2
2
ð0 2Þ ¼
¼
¼ 2000 h
c
c
0,001 h 1
Hinweis: Für jede Polynomfunktion P ðtÞ und c > 0 gilt lim P ðtÞ e c t ¼ 0; hier ist P ðtÞ ¼ c 2 t 2 þ 2 c t þ 2.
t!1
Fazit: Die durchschnittliche Lebensdauer eines Bauelementes beträgt 2000 Stunden.
Mit einem homogenen Würfel wird solange gewürfelt, bis erstmals eine gerade Augenzahl (Elementarereignis g) oder insgesamt dreimal eine ungerade Augenzahl (Elementarereignis u) erscheint (Ereignis A).
K15
a) Bestimmen Sie mit Hilfe des Ereignisbaumes die Verteilung der diskreten Zufallsvariablen
X ¼ Anzahl der Würfe bis zum Eintreten des Ereignisses A
b) Wie viele Würfe sind im Mittel nötig, bis das beschriebene Ereignis eintritt?
a) Die Elementarereignisse g (gerade Augenzahl) und u (ungerade Augenzahl) sind gleichwahrscheinlich (jeweils 3
von 6 möglichen Ergebnissen). Daher gilt für die zugehörigen Wahrscheinlichkeiten p ðgÞ ¼ p ðuÞ ¼ 3=6 ¼ 1=2.
2 Wahrscheinlichkeitsverteilungen einer Zufallsvariablen
605
Ereignisbaum (Baumdiagramm; Bild K-7)
2. Wurf
1. Wurf
3. Wurf
O: „Wurzel“ des Baumes (Ausgangspunkt)
g
1/2
O
g
1/2
1/2
u
1/2
1/2
g
u
1/2
u
Bild K-7 Ereignisbaum
Mögliche Werte der Zufallsvariablen X : 1, 2, 3
1
2
X ¼ 1
Im 1. Wurf g: P ðX ¼ 1Þ ¼ P ðO gÞ ¼ p ðgÞ ¼
X ¼ 2
Zunächst u, dann g: P ðX ¼ 2Þ ¼ P ðO u gÞ ¼ p ðuÞ p ðgÞ ¼
X ¼ 3
Zunächst zweimal u, dann im 3. Wurf g bzw. u:
1 1
1
¼
2 2
4
P ðX ¼ 3Þ ¼ P ðO u u gÞ þ P ðO u u uÞ ¼ p ðuÞ p ðuÞ p ðgÞ þ p ðuÞ p ðuÞ p ðuÞ ¼
¼
1 1 1
1 1 1
1
1
1
þ
¼
þ
¼
2 2 2
2 2 2
8
8
4
Wahrscheinlichkeitsfunktion f ðxÞ ¼ P ðX ¼ xÞ
Verteilungstabelle
xi
1
2
3
f ðx i Þ
1=2 ¼ 2=4
1=4
1=4
b) Erwartungswert der Zufallsvariablen X (mittlere Anzahl von Würfen bis zum Eintreten des Ereignisses A):
E ðXÞ ¼
3
X
x i f ðx i Þ ¼ 1
i¼1
2
1
1
2
2
3
7
þ2
þ3
¼
þ
þ
¼
4
4
4
4
4
4
4
Fazit: Im Mittel benötigen wir also zwei Würfe bis zum Eintreten des Ereignisses A.
Ein Schütze trifft die Zielscheibe mit einer hohen Wahrscheinlichkeit von p ¼ 90 %.
a) Wie lautet die Wahrscheinlichkeitsfunktion f ðxÞ ¼ P ðX ¼ xÞ für die diskrete Zufallsvariable
K16
X ¼ Anzahl der abgegebenen Schüsse bis zum ersten Treffer?
b) Wie groß ist die Wahrscheinlichkeit, die Scheibe bei insgesamt vier abgegebenen Schüssen zu treffen?
606
K Wahrscheinlichkeitsrechnung und mathematische Statistik
a) Der Schütze trifft erstmals beim x-ten Schuss (vorher also x 1 Fehlschüsse, jeweils mit der Wahrscheinlichkeit
1 p ¼ 1 0,9 ¼ 0,1). Mit dem Multiplikationssatz für stochastisch unabhängige Ereignisse (! FS: Kap.
XV.3.6; die abgegebenen Schüsse beeinflussen sich nicht gegenseitig) erhalten wir die folgende Wahrscheinlichkeitsfunktion:
f ðxÞ ¼ P ðX ¼ xÞ ¼ ð0,1 0,1 . . . 0,1Þ 0,9 ¼ 0,1 x 1 0,9
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
(X 1) Fehlschüsse
ðx ¼ 1, 2, 3, . . .Þ
1 Treffer
b) Treffer beim 1. oder 2. oder 3. oder spätestens beim 4. Schuss (die Wahrscheinlichkeiten addieren sich nach dem
Additionssatz ! FS: Kap. XV.3.2):
P ¼ f ð1Þ þ f ð2Þ þ f ð3Þ þ f ð4Þ ¼ 0,1 0 0,9 þ 0,1 1 0,9 þ 0,1 2 0,9 þ 0,1 3 0,9 ¼
¼ ð0,1 0 þ 0,1 1 þ 0,1 2 þ 0,1 3 Þ 0,9 ¼ ð1 þ 0,1 þ 0,01 þ 0,001Þ 0,9 ¼ 1,111 0,9 ¼ 0,9999
1
Folgerung: Wegen P ¼ 0,9999
1 können wir davon ausgehen, dass der Schütze bei jeweils vier abgegebenen
Schüssen fast immer die Scheibe mindestens einmal trifft!
Qualitätskontrolle bei einer Warenanlieferung
Einer Lieferung von 20 baugleichen elektronischen Elementen (unter denen sich 2 defekte befinden)
wird zwecks Qualitätskontrolle eine Stichprobe vom Umfang k ¼ 3 entnommen.
a) Wie viele Stichproben sind möglich?
K17
b) Bestimmen Sie die Verteilung der diskreten Zufallsvariablen
X ¼ Anzahl der defekten Elemente in einer Stichprobe
c) Mit welcher Wahrscheinlichkeit enthält eine Stichprobe höchstens 1 defektes Element?
Hinweis: Verwenden Sie bei der Lösung dieser Aufgabe die Hilfsmittel der Kombinatorik (! FS:
Kap. XV.1).
a) Aus n ¼ 20 Elementen werden rein zufällig und ohne Zurücklegen (wie bei einer Stichprobe allgemein üblich)
k ¼ 3 Elemente entnommen. Es handelt sich hier also um Kombinationen 3. Ordnung ohne Wiederholung, da die
Reihenfolge der Ziehung keine Rolle spielt und jedes der 20 Elemente höchstens einmal gezogen werden kann.
Somit gibt es
20
20 19 18
C ð20 ; 3Þ ¼
¼
¼ 1140
3
123
verschiedene Möglichkeiten (Stichproben vom Umfang k ¼ 3).
b) Wertebereich der Zufallsvariablen X : 0, 1, 2 (in der Stichprobe können sich höchstens 2 defekte Elemente befinden). In der Lieferung befinden sich 18 einwandfreie und 2 defekte Elemente.
X ¼ 0
Die Stichprobe enthält nur einwandfreie Elemente.
Die 3 einwandfreien Elemente stammen aus den insgesamt 18 einwandfreien Elementen der Lieferung. Die Anzahl
der möglichen Stichproben mit ausschließlich einwandfreien Elementen beträgt dann
18 17 16
18
¼ 816
C ð18 ; 3Þ ¼
¼
3
123
2 Wahrscheinlichkeitsverteilungen einer Zufallsvariablen
607
Die Wahrscheinlichkeit für eine solche Stichprobe ist daher
P ðX ¼ 0Þ ¼ f ð0Þ ¼
816
¼ 0,716 ¼
b 71,6 %
1140
(816 der insgesamt möglichen 1140 Stichproben enthalten nur einwandfreie Elemente)
X ¼ 1
Die Stichprobe enthält 1 defektes und 2 einwandfreie Elemente (Bild K-8):
18 x
2x
defekt
einwandfrei
Bild K-8
1 defektes Element aus 2 defekten Elementen ! Kombination 1. Ordnung ohne Wiederholung
2 einwandfreie Elemente aus 18 einwandfreien Elementen ! Kombinationen 2. Ordnung ohne Wiederholung
Somit gibt es
C ð2 ; 1Þ C ð18 ; 2Þ ¼
2
18
2 18 17
¼
¼ 18 17 ¼ 306
1
2
1
1 2
mögliche Stichproben mit 1 defekten und 2 einwandfreien Elementen. Die zugehörige Wahrscheinlichkeit beträgt
P ðX ¼ 1Þ ¼ f ð1Þ ¼
X ¼ 2
306
¼ 0,268 ¼
b 26,8 %
1140
Die Stichprobe enthält 2 defekte und 1 einwandfreies Element.
2 defekte Elemente aus insgesamt 2 defekten Elementen ! Kombinationen 2. Ordnung ohne Wiederholung
1 einwandfreies Element aus insgesamt 18 einwandfreien Elementen ! Kombinationen 1. Ordnung ohne Wiederholung
Somit gibt es
C ð2 ; 2Þ C ð18 ; 1Þ ¼
2
18
2 1 18
¼
¼ 1 18 ¼ 18
2
1
1 2
1
mögliche Stichproben mit 2 defekten und 1 einwandfreien Element. Die Wahrscheinlichkeit für eine solche Stichprobe beträgt dann
P ðX ¼ 2Þ ¼ f ð2Þ ¼
18
¼ 0,016 ¼
b 1,6 %
1140
Verteilung ð f ðxÞ ¼ P ðX ¼ xÞ: Wahrscheinlichkeitsfunktion der Zufallsvariablen X Þ
xi
0
1
2
f ðx i Þ
816
1140
306
1140
18
1140
Kontrolle: f ð0Þ þ f ð1Þ þ f ð2Þ ¼
816 þ 306 þ 18
1140
¼
¼ 1
1140
1140
608
K Wahrscheinlichkeitsrechnung und mathematische Statistik
c) P ðX 1Þ ¼ P ðX ¼ 0Þ þ P ðX ¼ 1Þ ¼ f ð0Þ þ f ð1Þ ¼
816 þ 306
1122
¼
¼ 0,984
1140
1140
Mit der hohen Wahrscheinlichkeit von 98,4 % befindet sich in einer Stichprobe vom Umfang k ¼ 3 höchstens
1 defektes Element.
3 Spezielle Wahrscheinlichkeitsverteilungen
Wir erinnern: Liegt eine Gaußsche Normalverteilung mit den Parametern m (Mittelwert) und s (Standardabweichung) vor, so wird diese mit Hilfe der linearen Transformation U ¼ ðX mÞ=s zunächst auf die Standardnormalverteilung (m ¼ 0; s ¼ 1) mit der Verteilungsfunktion F ðuÞ zurückgeführt.
Tabelle der Verteilungsfunktion F ðuÞ der Standardnormalverteilung: Band 3 (Tabelle 1 im Anhang, Teil A) und
Formelsammlung (Tabelle 1 im Anhang, Teil B)
3.1 Diskrete Wahrscheinlichkeitsverteilungen
Lehrbuch: Band 3, Kapitel II.6.1 bis 6.3
Formelsammlung: Kapitel XV.5
K18
Die Abgabe von Schrauben aus einer Serienproduktion mit einem Ausschussanteil von 4 % erfolgt in
Packungen mit jeweils 100 Stück. Wie groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte
Packung 5 unbrauchbare Schrauben enthält?
Zufallsvariable: X ¼ Anzahl der unbrauchbaren Schrauben in einer Packung
X ist binomialverteilt mit den Parametern n ¼ 100 (Anzahl Schrauben in einer Packung) und p ¼ 0,04 (Ausschussanteil). Die Wahrscheinlichkeitsfunktion dieser Zufallsvariablen lautet damit wie folgt (mit q ¼ 1 p ¼
1 0,04 ¼ 0,96):
n
100
0,04 x 0,96 100 x
ðx ¼ 0, 1, 2, . . . , 100Þ
f ðxÞ ¼ P ðX ¼ xÞ ¼
px qnx ¼
x
x
Für die gesuchte Wahrscheinlichkeit f ð5Þ ¼ P ðX ¼ 5Þ erhalten wir dann:
100
100 99 98 97 96
0,04 5 0,96 95 ¼ 0,1595
P ðX ¼ 5Þ ¼
0,04 5 0,96 100 5 ¼
5
12345
Wir können daher erwarten, dass rund 16 % aller Packungen 5 unbrauchbare Schrauben enthalten.
Eine Baugruppe besteht aus 12 gleichartigen Elementen, die unabhängig voneinander in einem bestimmten Zeitintervall mit der für jedes Element gleichen Wahrscheinlichkeit von 5 % ausfallen können.
Mit welcher Wahrscheinlichkeit fallen
K19
a) genau 3 Elemente aus,
b) mindestens 10 der 12 Elemente nicht aus?
c) Die Baugruppe fällt komplett aus, wenn auch nur 1 Element ausfällt. Bestimmen Sie die Ausfallwahrscheinlichkeit der Baugruppe.
3 Spezielle Wahrscheinlichkeitsverteilungen
609
Zufallsvariable: X ¼ Anzahl der im Zeitintervall ausgefallenen Elemente
X ist binomialverteilt mit den Parametern n ¼ 12 (Anzahl der Elemente der Baugruppe) und p ¼ 0,05 (Ausfallwahrscheinlichkeit eines Elementes). Die Wahrscheinlichkeitsfunktion dieser Zufallsvariablen lautet somit (mit
q ¼ 1 p ¼ 1 0,05 ¼ 0,95):
n
12
x
nx
f ðxÞ ¼ P ðX ¼ xÞ ¼
p q
0,05 x 0,95 12 x
¼
ðx ¼ 0, 1, 2, . . . , 12Þ
x
x
a)
b)
X ¼ 3
Es fallen genau 3 Elemente aus:
12
12 11 10
P ðX ¼ 3Þ ¼
0,05 3 0,95 12 3 ¼
0,05 3 0,95 9 ¼ 0,0173
3
123
X 2
Es fallen höchstens 2 Elemente aus, d. h. entweder kein oder 1 oder 2 Elemente:
P ðX 2Þ ¼ P ðX ¼ 0Þ þ P ðX ¼ 1Þ þ P ðX ¼ 2Þ ¼
12
12
12
0
12 0
1
12 1
þ
0,05 0,95
þ
0,05 2 0,95 12 2 ¼
¼
0,05 0,95
1
2
0
¼ 1 1 0,95 12 þ 12 0,05 0,95 11 þ
12 11
0,05 2 0,95 10 ¼
12
¼ 0,5404 þ 0,3413 þ 0,0988 ¼ 0,9805
Folgerung: Mit der hohen Wahrscheinlichkeit von rund 98 % fallen höchstens 2 Elemente aus.
c)
X 1
Mindestens 1 Element fällt aus (es können bis zu 12 Elemente ausfallen):
12
P ðX 1Þ ¼ 1 P ðX ¼ 0Þ ¼ 1
0,05 0 0,95 12 ¼ 1 0,5404 ¼ 0,4596
0
Die Ausfallwahrscheinlichkeit der Baugruppe beträgt in diesem Fall rund 46 %.
Ein Bogenschütze trifft die Zielscheibe mit einer Wahrscheinlichkeit von 70 %. Er gibt 10 Schüsse ab.
K20
Wie groß ist die Wahrscheinlichkeit, die Scheibe
a) genau 2-mal,
b) mindestens 2-mal,
c) keinmal zu treffen?
d) Wie viele Treffer sind bei 10 abgegebenen Schüssen im Mittel zu erwarten?
Zufallsvariable: X ¼ Anzahl der Treffer bei 10 abgegebenen Schüssen
X ist binomialverteilt mit den Parametern n ¼ 10 (Anzahl der abgegebenen Schüsse) und p ¼ 0,7 (Treffwahrscheinlichkeit). Die Wahrscheinlichkeitsfunktion dieser Zufallsvariablen lautet dann wie folgt (mit q ¼ 1 p ¼
1 0,7 ¼ 0,3):
n
10
0,7 x 0,3 10 x
ðx ¼ 0, 1, 2, . . . , 10Þ
f ðxÞ ¼ P ðX ¼ xÞ ¼
px qnx ¼
x
x
a)
X ¼ 2
Genau 2 Treffer:
10 9
10
0,7 2 0,3 8 ¼ 0,00145
P ðX ¼ 2Þ ¼
0,7 2 0,3 10 2 ¼
2
12
b)
X 2
0,15 %
Mindestens 2 Treffer:
P ðX 2Þ ¼ 1 P ðX ¼ 0Þ P ðX ¼ 1Þ ¼ 1
10
10
0,7 0 0,3 10 0
0,7 1 0,3 10 1 ¼
0
1
¼ 1 1 1 0,3 10 10 0,7 0,3 9 ¼ 1 0,000 006 0,000 138 ¼ 0,999 856
1
610
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Wir können davon ausgehen, dass der Bogenschütze bei jeweils 10 abgegebenen Schüssen (fast immer) mindestens
2-mal die Scheibe trifft!
c)
X ¼ 0
Kein Treffer:
10
P ðX ¼ 0Þ ¼
0,7 0 0,3 10 0 ¼ 1 1 0,3 10 ¼ 0,000 006 ¼
b 0,0006 %
0
Folgerung: 10 Fehlschüsse sind (fast) unmöglich!
d) Erwartungswert (Mittelwert): m ¼ n p ¼ 10 0,7 ¼ 7
Im Mittel trifft der Schütze bei 10 abgegebenen Schüssen 7-mal.
Kartenspiel „Skat“
K21
Beim Skat (3 Spieler, 32 Karten) erhält jeder Spieler 10 Karten, die restlichen 2 Karten bleiben verdeckt. Mit welcher Wahrscheinlichkeit erhält ein Spieler
a) alle 4 „Asse“, b) kein „Ass“?
Zufallsvariable: X ¼ Anzahl der „Asse“ eines Spielers
X ist hypergeometrisch verteilt mit den folgenden Parametern: N ¼ 32 (Anzahl der Karten); M ¼ 4 (Anzahl der
„Asse“); n ¼ 10 (Anzahl der Karten eines Spielers). Die Wahrscheinlichkeitsfunktion der diskreten Zufallsvariablen
X lautet damit wie folgt:
M
N M
4
32 4
x
nx
x
10 x
¼
ðx ¼ 0; 1; 2; 3; 4Þ
f ðxÞ ¼ P ðX ¼ xÞ ¼
N
32
n
10
a)
X ¼ 4
Ein Spieler erhält alle 4 „Asse“:
28 !
28 !
28 !
28
4
32 4
1
4
10 4
6
6 ! ð28 6Þ !
ð6 !Þ ð22 !Þ
6!
28 ! 10 !
¼
¼
¼
P ðX ¼ 4Þ ¼
¼
¼ ¼
6 ! 32 !
32 !
32 !
32 !
32
32
10
10
10 ! ð32 10Þ !
ð10 !Þ ð22 !Þ
10 !
¼
ð28 !Þ ð10 !Þ
ð6 !Þ ð32 !Þ
¼
ð28 !Þ ð6 !Þ 7 8 9 10
ð6 !Þ ð28 !Þ 29 30 31 32
Umformungen: 10 ! ¼ ð6 !Þ 7 8 9 10 ;
¼
7 8 9 10
29 30 31 32
¼ 0,0058
32 ! ¼ ð28 !Þ 29 30 31 32
Fazit: Die Chance, dass ein Spieler alle 4 „Asse“ erhält, ist also sehr gering (die Wahrscheinlichkeit beträgt rund
0,6 %).
b)
X ¼ 0
Ein Spieler erhält kein „Ass“:
28 !
28 !
4
32 4
28
1
10
0
10 0
18 !
ð10 !Þ ð28 10Þ !
28 ! 22 !
P ðX ¼ 0Þ ¼
¼
¼
¼
¼ ¼
18 ! 32 !
32 !
32 !
32
32
10
10
ð10 !Þ ð32 10Þ !
22 !
¼
ð28 !Þ ð22 !Þ
ð18 !Þ ð32 !Þ
¼
ð28 !Þ ð18 !Þ 19 20 21 22
ð18 !Þ ð28 !Þ 29 30 31 32
Umformungen: 22 ! ¼ ð18 !Þ 19 20 21 22 ;
¼
19 20 21 22
29 30 31 32
¼ 0,2034
32 ! ¼ ð28 !Þ 29 30 31 32
Fazit: Die Wahrscheinlichkeit, dass ein Spieler kein „Ass“ erhält, beträgt rund 20,3 %.
3 Spezielle Wahrscheinlichkeitsverteilungen
611
Qualitätskontrolle bei Warenanlieferung
Eine Kiste mit 100 gleichartigen Artikeln wird bei der Warenanlieferung einer Qualitätskontrolle unter-
K22
worfen. Dabei werden der Kiste (rein zufällig und ohne Zurücklegen) 5 Artikel entnommen. Die Ware
wird nur angenommen, wenn diese Stichprobe höchstens einen defekten Artikel enthält. Wie groß ist
die Wahrscheinlichkeit der Annahme, wenn sich in der Kiste genau 4 defekte Artikel befinden?
Zufallsvariable: X ¼ Anzahl der defekten Artikel in der Stichprobe vom Umfang n ¼ 5
X ist hypergeometrisch verteilt mit den folgenden Parametern: N ¼ 100 (Anzahl der Artikel in der Kiste); M ¼ 4
(Anzahl der defekten Artikel in der Kiste); n ¼ 5 (Umfang der entnommenen Stichprobe). Damit erhalten wir die
folgende Wahrscheinlichkeitsfunktion der diskreten Zufallsvariablen X:
f ðxÞ ¼ P ðX ¼ xÞ ¼
M
x
N M
nx
N
n
4
100 4
x
5x
¼
100
5
ðx ¼ 0; 1; 2; 3; 4Þ
Die Kiste wird nur angenommen, wenn die Stichprobe entweder keinen oder genau einen defekten Artikel enthält. Die
Annahmewahrscheinlichkeit beträgt dann:
P ðAnnahmeÞ ¼ P ðX ¼ 0Þ þ P ðX ¼ 1Þ ¼
96
96
4
100 4
4
100 4
1
þ4
5
4
0
50
1
51
¼
¼
þ
¼
100
100
100
5
5
5
96 !
¼
ð5 !Þ ð96 5Þ !
þ4
96 !
ð4 !Þ ð96 4Þ !
100 !
ð5 !Þ ð100 5Þ !
¼
96 !
4 96 !
þ
ð5 !Þ ð91 !Þ
ð4 !Þ ð92 !Þ
100 !
ð5 !Þ ð95 !Þ
¼
Z
N
Zähler (Z) und Nenner (N) des Bruches werden noch wie folgt umgeformt:
Z ¼
¼
96 !
4 96 !
ð96 !Þ 92
4 ð96 !Þ 5
92 ð96 !Þ þ 20 ð96 !Þ
þ
¼
þ
¼
¼
ð5 !Þ ð91 !Þ
ð4 !Þ ð92 !Þ
ð5 !Þ ð91 !Þ 92
ð5 !Þ ð92 !Þ
ð4 !Þ 5 ð92 !Þ
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
92 !
5!
ð92 þ 20Þ ð96 !Þ
ð5 !Þ ð92 !Þ
¼
112 ð96 !Þ
ð5 !Þ ð92 !Þ
¼
112 ð92 !Þ 93 94 95 96
ð5 !Þ ð92 !Þ
¼
112 93 94 95 96
5!
Umformungen: Brüche auf den Hauptnenner ð5 !Þ ð92 !Þ bringen, d. h. den 1. Bruch mit 92 und den 2. Bruch mit 5
erweitern ! gemeinsamen Faktor 96 ! im Zähler ausklammern und dann zerlegen; 96 ! ¼ ð92 !Þ 93 94 95 96
! Faktor 92 ! kürzen.
N ¼
ð95 !Þ 96 97 98 99 100
100 !
96 97 98 99 100
¼
¼
ð5 !Þ ð95 !Þ
5!
ð5 !Þ ð95 !Þ
Umformungen: 100 ! zerlegen ! 100 ! ¼ ð95 !Þ 96 97 98 99 100 ! gemeinsamen Faktor 95 ! kürzen.
612
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Damit erhalten wir:
112 93 94 95 96
P ðAnnahmeÞ ¼
Z
112 93 94 95
5!
¼
¼ 0,9984
¼
N
97 98 99 100
96 97 98 99 100
5!
Die Wahrscheinlichkeit, dass die Ware (Kiste) angenommen wird, ist also sehr hoch (sie beträgt rund 99,8 %).
Unter 50 Packungen mit je 100 Schrauben (so lautet die Aufschrift) befinden sich 3 unvollständige
Packungen (sie enthalten also weniger Schrauben als angegeben).
K23
a) Wie groß ist die Wahrscheinlichkeit, dass ein Kunde beim Kauf von 5 Packungen 2 unvollständige
Packungen erhält?
b) Mit welcher Wahrscheinlichkeit erhält ein Kunde beim Kauf von einer Packung eine vollständige
Packung?
Zufallsvariable: X ¼ Anzahl der unvollständigen Packungen beim Kauf von n Packungen
X ist hypergeometrisch verteilt mit den folgenden Parametern: N ¼ 50 (Anzahl der Packungen); M ¼ 3 (Anzahl
der unvollständigen Packungen unter den 50 Packungen); n : Anzahl der gekauften Packungen; n ¼ 5 in Teilaufgabe
a) bzw. n ¼ 1 in b). Die Wahrscheinlichkeitsfunktion der diskreten Zufallsvariablen X lautet damit wie folgt:
f ðxÞ ¼ P ðX ¼ xÞ ¼
M
x
N M
nx
N
n
3
50 3
x
nx
¼
50
n
ðx ¼ 0; 1; 2; . . . nÞ
a) n ¼ 5 (5 gekaufte Packungen)
X ¼ 2
2 unvollständige Packungen:
3 2 47 46 45
3
50 3
3
47
2
52
2
3
3 45
123
1 2
¼
¼
¼
P ðX ¼ 2Þ ¼
¼
50 49 48
50
50
50 49 48 47 46
5
5
45
123 45
¼
3 45
50 49 48
20
¼
3 45 20
¼ 0,0230
50 49 48
2,3 %
b) n ¼ 1 (1 gekaufte Packung)
X ¼ 0
1 vollständige, d. h. keine unvollständige Packung:
3
50 3
3
47
0
10
0
1
1 47
¼ 0,94
P ðX ¼ 0Þ ¼ P ðvollständigÞ ¼
¼
¼
50
50
50
1
1
Die Wahrscheinlichkeit, dass die eine gekaufte Packung vollständig ist, beträgt 94 %.
3 Spezielle Wahrscheinlichkeitsverteilungen
613
Emission von a-Teilchen (radioaktive Substanz)
Bei der Emission von a-Teilchen einer bestimmten radioaktiven Substanz werden mit einem Zählrohr
K24
in einer Stunde genau 1620 a-Teilchen registriert. Welche Wahrscheinlichkeit besteht, dass in einem 10Sekunden-Intervall
a) genau 2, b) mehr als 2 a-Teilchen emittiert werden?
Zufallsvariable: X ¼ Anzahl der in einem 10-Sekunden-Intervall emittierten a-Teilchen
X genügt einer Poisson-Verteilung mit dem noch unbekannten Parameter (Mittelwert) m, den wir wie folgt bestimmen
(1 h ¼ 3600 s; h: Stunden; s: Sekunden):
Mittlere Anzahl emittierter a-Teilchen pro Sekunde:
1620
¼ 0,45
3600
Im 10-Sekunden-Intervall werden somit im Mittel m ¼ 10 0,45 ¼ 4,5 a-Teilchen emittiert. Die Wahrscheinlichkeitsfunktion der diskreten Zufallsvariable X lautet damit wie folgt:
f ðxÞ ¼ P ðX ¼ xÞ ¼
a)
X ¼ 2
X > 2
ðx ¼ 0; 1; 2; . . . Þ
Genau 2 emittierte a-Teilchen:
P ðX ¼ 2Þ ¼
b)
mx
4,5 x
em ¼
e 4,5
x!
x!
4,5 2
e 4,5 ¼ 0,1125 ¼
b 11,25 %
2!
Mehr als 2 emittierte a-Teilchen:
P ðX > 2Þ ¼ 1 P ðX 2Þ ¼ 1 P ðX ¼ 0Þ P ðX ¼ 1Þ P ðX ¼ 2Þ ¼
4,5 0
4,5 1
4,5 2
4,5 0
4,5 1
4,5 2
4,5
4,5
4,5
e
e
e
þ
þ
e 4,5 ¼
¼ 1
¼ 1
0!
1!
2!
0!
1!
2!
¼ 1 ð1 þ 4,5 þ 10,125Þ e 4,5 ¼ 1 15,625 e 4,5 ¼ 0,8264 ¼
b 82,64 %
„Endloskabel“ (Kabelrolle)
Ein „Endloskabel“ (Kabelrolle) ist fehlerbehaftet, auf je 100 m Kabellänge kommen durchschnittlich
2 fehlerhafte Stellen. Das Kabel wird in Stücke von je 10 m Länge zerschnitten. Die diskrete Zufalls-
K25
variable
X ¼ Anzahl der fehlerhaften Stellen in einem Teilstück der Länge 10 m
genügt einer Poisson-Verteilung mit dem noch unbekannten Parameter (Mittelwert) m. Wie groß ist die
Wahrscheinlichkeit, dass ein beliebiges 10 m langes Teilstück fehlerhaft ist, d. h. mindestens eine fehlerhafte Stelle besitzt?
Wir bestimmen zunächst den Parameter m der Verteilung (Dreisatz!):
100 m Kabellänge ! 2 Fehler
10 m Kabellänge ! x Fehler
)
)
x
2
¼
10 m
100 m
)
x ¼
2
2
10 ¼
¼ 0,2
100
10
Wir setzen m ¼ x ¼ 0,2 und erhalten damit die folgende Wahrscheinlichkeitsfunktion der diskreten Zufallsvariablen X:
f ðxÞ ¼ P ðX ¼ xÞ ¼
mx
0,2 x
em ¼
e 0,2
x!
x!
ðx ¼ 0; 1; 2; . . . Þ
614
K Wahrscheinlichkeitsrechnung und mathematische Statistik
X 1
Mindestens eine fehlerhafte Stelle:
P ðfehlerhaftÞ ¼ P ðX 1Þ ¼ 1 P ðX < 1Þ ¼ 1 P ðX ¼ 0Þ ¼ 1
¼ 1 e 0,2 ¼ 0,1813
0,2 0
1
e 0,2 ¼
e 0,2 ¼ 1
1
0!
18,1 %
3.2 Stetige Wahrscheinlichkeitsverteilungen
Lehrbuch: Band 3, Kapitel II.6.4 und 6.5
Formelsammlung: Kapitel XV.6
„Lebensdauer“ einer Energiesparlampe
Die „Lebensdauer“ T einer Energiesparlampe kann als eine exponentialverteilte stetige Zufallsvariable
angesehen werden. Nach Angaben des Herstellers beträgt die mittlere Lebensdauer m ¼ 10 000 Stun-
K26
den (h). Bestimmen Sie die Wahrscheinlichkeit folgender Ereignisse:
a) Die Lampe brennt in den ersten 1000 Betriebsstunden durch;
b) Die Lampe brennt zwischen der 5000. und 6000. Stunde durch;
c) Die Lampe brennt mindestens 12 000 Stunden.
Die Verteilungsfunktion der stetigen Zufallsvariablen T (in diesem Zusammenhang auch als Ausfallswahrscheinlichkeit
bezeichnet) mit dem Parameter l ¼ 1=m ¼ 1=10 000 ¼ 0,0001 lautet wie folgt (l in h 1 ):
F ðtÞ ¼ P ðT tÞ ¼ 1 e l t ¼ 1 e 0,0001 t
a)
T 1000
ðt 0 ; t in hÞ
Maximale Lebensdauer von 1000 Stunden:
P ðT 1000Þ ¼ F ð1000Þ ¼ 1 e 0,0001 1000 ¼ 1 e 0,1 ¼ 0,0952
b)
5000 T 6000
9,5 %
Lebensdauer zwischen 5000 und 6000 Stunden:
P ð5000 T 6000Þ ¼ F ð6000Þ F ð5000Þ ¼ ð1 e 0,0001 6000 Þ ð1 e 0,0001 5000 Þ ¼
¼ ð1 e 0,6 Þ ð1 e 0,5 Þ ¼ 1 e 0,6 1 þ e 0,5 ¼ e 0,6 þ e 0,5 ¼
¼ 0,5488 þ 0,6065 ¼ 0,0577
c)
T 12 000
5,8 %
Die Lebensdauer beträgt mindestens 12 000 Stunden:
P ðT 12 000Þ ¼ 1 P ðT < 12 000Þ ¼ 1 F ð12 000Þ ¼ 1 ð1 e 0,0001 12 000 Þ ¼ 1 ð1 e 1,2 Þ ¼
30,1 %
¼ 1 1 þ e 1,2 ¼ e 1,2 ¼ 0,3012
Wartungsdauer einer Maschine
Die Wartungsdauer T einer bestimmten Maschine ist eine nahezu exponentialverteilte stetige Zufalls-
K27
variable mit einer mittleren Wartungsdauer von m ¼ 5 Stunden (h). Wie groß ist die Wahrscheinlichkeit, dass die Wartung
a) höchstens 3 Stunden, b) zwischen 3 und 5 Stunden beträgt,
c) länger als 6 Stunden dauert?
3 Spezielle Wahrscheinlichkeitsverteilungen
615
Die Verteilungsfunktion der Zufallsvariablen T mit dem Parameter l ¼ 1=m ¼ 1=5 ¼ 0,2 (in h 1 ) lautet wie folgt:
F ðtÞ ¼ P ðT tÞ ¼ 1 e l t ¼ 1 e 0,2 t
a)
T 3
Die Wartungszeit beträgt höchstens 3 Stunden:
P ðT 3Þ ¼ F ð3Þ ¼ 1 e 0,6 ¼ 0,4512
b)
ðt 0 ; t in hÞ
3 T 5
45,1 %
Die Wartungszeit liegt zwischen 3 und 5 Stunden:
P ð3 T 5Þ ¼ F ð5Þ F ð3Þ ¼ ð1 e 1 Þ ð1 e 0,6 Þ ¼ e 1 þ e 0,6 ¼ 0,1809
c)
T > 6
18,1 %
Die Wartung dauert länger als 6 Stunden:
P ðT > 6Þ ¼ 1 P ðT 6Þ ¼ 1 F ð6Þ ¼ 1 ð1 e 1,2 Þ ¼ e 1,2 ¼ 0,3012
30,1 %
Funktionsdauer (Lebensdauer) eines elektronischen Bauelementes
Die Funktionsdauer („Lebensdauer“) T eines speziellen elektronischen Bauelementes ist eine exponentialverteilte stetige Zufallsvariable mit einer mittleren Lebensdauer von m ¼ 20 000 Betriebsstunden.
K28
Mit welcher Wahrscheinlichkeit fällt ein solches Element
a) in den ersten 2000 Betriebsstunden,
b) zwischen der 5000. und 8000. Betriebsstunde,
c) nach über 25 000 Betriebsstunden aus?
Die Verteilungsfunktion der Zufallsvariablen T mit dem Parameter l ¼ 1=m ¼ 1=20 000 ¼ 0,00005 (in h 1 ) lautet
wie folgt (h: Stunde):
F ðtÞ ¼ P ðT tÞ ¼ 1 e l t ¼ 1 e 0,00005 t
a)
T 2000
Ausfall in den ersten 2000 Betriebsstunden:
P ðT 2000Þ ¼ F ð2000Þ ¼ 1 e 0,1 ¼ 0,0952
b)
ðt 0 ; t in hÞ
5000 T 8000
9,5 %
Ausfall zwischen der 5000. und 8000. Betriebsstunde:
P ð5000 T 8000Þ ¼ F ð8000Þ F ð5000Þ ¼ ð1 e 0,4 Þ ð1 e 0,25 Þ ¼
¼ 1 e 0,4 1 þ e 0,25 ¼ e 0,4 þ e 0,25 ¼ 0,1085
c)
T > 25 000
10,9 %
Ausfall nach über 25 000 Betriebsstunden:
P ðT > 25 000Þ ¼ 1 P ðT 25 000Þ ¼ 1 ð1 e 1,25 Þ ¼ e 1,25 ¼ 0,2865
28,7 %
Spannungsschwankungen in einem elektrischen Netz
In einem elektrischen Netz treten zufallsbedingte Spannungsschwankungen auf. Die als normalverteilt
K29
angesehene Zufallsvariable
X ¼ elektrische Spannung (in Volt (V))
besitze den Mittelwert m ¼ 230 V und die Standardabweichung s ¼ 10 V. Ein an das Netz angeschlossenes Gerät kann bei einer Spannung unter 210 V nicht mehr betrieben werden. Wie groß ist die
Wahrscheinlichkeit, dass das Gerät sich wegen zu geringer Spannung abschaltet?
616
K Wahrscheinlichkeitsrechnung und mathematische Statistik
X < 210
Das Gerät ist außer Betrieb:
bergang von der Zufallsvariablen X zur standardnormalverteilten Zufallsvariablen U ¼
X m
X 230
¼
:
s
10
210 230
¼ P ðU < 2Þ ¼ F ð 2Þ ¼ 1 F ð2Þ ¼ 1 0,9772 ¼
P ðX < 210Þ ¼ P U <
10
¼ 0,0228
2,3 %
ðaus Tab: 1Þ
Zylindrische Bohrung in einem Werkstück
Ein Werkstück aus Edelstahl soll eine zylindrische Bohrung mit einem Solldurchmesser von m ¼ 80 mm
erhalten. Die Toleranzgrenzen liegen dabei zwischen x u ¼ 79,91 mm und x o ¼ 80,06 mm. Der Bohrautomat wird so eingestellt, dass der Durchmesser X der Bohrungen eine normalverteilte Zufallsvariable
mit dem Mittelwert (¼ Sollwert) m ¼ 80 mm und der Standardabweichung s ¼ 0,03 mm ist. Ein
K30
Werkstück gilt dann als Ausschuss, wenn der Durchmesser größer als x o ausfällt. Eine Nachbesserung
(Nachbohrung) soll erfolgen, wenn der Durchmesser kleiner als x u ist. Wie groß ist die Wahrscheinlichkeit dafür, dass eine Bohrung
a) qualitätsgerecht ausfällt, der Durchmesser also innerhalb des Toleranzbereiches liegt,
b) nachgebessert werden muss?
c) Mit welcher Wahrscheinlichkeit wird Ausschussware produziert?
Bild K-9 zeigt den Toleranzbereich für den Durchmesser X der Bohrung:
Toleranzbereich
Sollwert
x u = 79,91
μ = 80
x o = 80,06
x/mm
Bild K-9 Toleranzbereich
x < xu
nachbohren
qualitätsgerecht
x > xo
Ausschussware
bergang von der Zufallsvariablen X zur standardnormalverteilten Zufallsvariablen U ¼
a)
X m
X 80
¼
s
0,03
xu X xo
Der Durchmesser liegt im Toleranzbereich (Bild K-9):
79,91 80
80,06 80
¼ P ð 3 U 2Þ ¼
U
P ðx u X x o Þ ¼ P ð79,91 X 80,06Þ ¼ P
0,03
0,03
¼ F ð2Þ F ð 3Þ ¼ F ð2Þ 1 F ð3Þ ¼ F ð2Þ 1 þ F ð3Þ ¼ F ð2Þ þ F ð3Þ 1 ¼
¼ 0,9772 þ 0,9987 1 ¼ 0,9759
97,6 %
Folgerung: Mit einer hohen Wahrscheinlichkeit von rund 97,6 % sind die Bohrungen qualitätsgerecht, liegen also
im vorgegebenen Toleranzbereich.
3 Spezielle Wahrscheinlichkeitsverteilungen
b)
617
X < xu
Der Durchmesser fällt zu klein aus (Nachbohrung):
79,91 80
P ðX < x u Þ ¼ P ðX < 79,91Þ ¼ P U <
¼ P ðU < 3Þ ¼ F ð 3Þ ¼ 1 F ð3Þ ¼
0,03
¼ 1 0,9987 ¼ 0,0013 ¼
b 0,13 %
Folgerung: Eine Nachbohrung wird äußerst selten nötig sein!
c)
X > xo
Der Durchmesser fällt zu groß aus (Ausschussware):
80,06 80
P ðX > x o Þ ¼ P ðX > 80,06Þ ¼ P U >
¼ P ðU > 2Þ ¼ 1 P ðU 2Þ ¼ 1 F ð2Þ ¼
0,03
¼ 1 0,9772 ¼ 0,0228
2,3 %
Bei einer Serienproduktion beträgt der Ausschussanteil rund 2,3 %.
Serienmäßige Herstellung elektrischer Widerstände
K31
In einem Werk werden serienmäßig elektrische (ohmsche) Widerstände mit einem Sollwert von
m ¼ 200 W hergestellt. Aufgrund langjähriger Erfahrung kann man dabei von einer Standardabweichung
von s ¼ 1 W ausgehen.
a) Wie groß ist der Ausschussanteil, wenn der Widerstand höchstens um 1 % vom Sollwert abweichen
darf bei vorausgesetzter Normalverteilung?
b) Wie viele Widerstände in einer Lieferung von n ¼ 500 Widerständen aus dieser Serienproduktion
erfüllen im Mittel die Qualitätsforderung (maximal 1 % Abweichung vom Sollwert) somit nicht?
Zufallsvariable: X ¼ ohmscher Widerstand (in Ohm (W))
X ist nach Voraussetzung normalverteilt mit dem Mittelwert (Sollwert) m ¼ 200 W und der Standardabweichung
s ¼ 1 W.
a) Maximale Abweichung vom Sollwert m ¼ 200 W: 1 %, d. h. 2 W
Wir berechnen zunächst die Wahrscheinlichkeit dafür, dass der produzierte ohmsche Widerstand X zwischen 198 W
und 202 W, d. h. im Toleranzbereich liegt.
bergang von X zur standardnormalverteilten Zufallsvariable U ¼
X m
X 200
¼
¼ X 200 :
s
1
P ðToleranzbereichÞ ¼ P ð198 X 202Þ ¼ P ð198 200 U 202 200Þ ¼ P ð 2 U 2Þ ¼
¼ F ð2Þ F ð 2Þ ¼ F ð2Þ 1 F ð2Þ ¼ F ð2Þ 1 þ F ð2Þ ¼ 2 F ð2Þ 1 ¼
¼ 2 0,9772 1 ¼ 0,9544
Ausschussanteil: P ¼ 1 P ðToleranzbereichÞ ¼ 1 0,9544 ¼ 0,0456
4,6 %
b) Anzahl fehlerhafter Widerstände (Ausschussanteil) in der Lieferung:
n P ¼ 500 0,0456 ¼ 22,8
23
Folgerung: Eine Lieferung von 500 Widerständen wird im Mittel 23 fehlerhafte Widerstände enthalten.
618
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Vollautomatische Abfüllanlage in einem Weingut
In einem Weingut wird auf einer vollautomatischen Abfüllanlage eine große Menge Weißwein in Literflaschen abgefüllt. Nach den Angaben des Herstellers ist die Anlage so eingestellt, dass das Abfüllvolumen
K32
X als eine normalverteilte Zufallsvariable mit dem Sollwert (Mittelwert) m ¼ 1 Liter ¼ 1000 cm 3 und
der Standardabweichung s ¼ 20 cm 3 angesehen werden kann.
a) Mit welcher Wahrscheinlichkeit enthält eine Flasche weniger als 960 cm 3 ?
b) Wie groß ist die Wahrscheinlichkeit, dass das Abfüllvolumen X um maximal 1 % (nach unten bzw.
oben) vom Sollwert abweicht?
bergang von der Zufallsvariablen X zur standardnormalverteilten Zufallsvariablen U ¼
a)
X m
X 1000
¼
:
s
20
X < 960
Die Füllmenge ist kleiner als 960 cm 3 :
960 1000
¼ P ðU < 2Þ ¼ F ð 2Þ ¼ 1 F ð2Þ ¼ 1 0,9772Þ ¼
P ðX < 960Þ ¼ P U <
20
¼ 0,0228
2,3 %
Folgerung: Rund 2,3 % der Literflaschen enthalten weniger als 960 cm 3 Wein.
b) Maximale Abweichung vom Sollwert: 1 %, d. h. 10 cm 3 .
Das Abfüllvolumen X liegt dann zwischen 990 cm 3 und 1010 cm 3 .
990 1000
1010 1000
P ð990 X 1010Þ ¼ P
U
¼ P ð 0,5 U 0,5Þ ¼
20
20
¼ F ð0,5Þ F ð 0,5Þ ¼ F ð0,5Þ 1 F ð0,5Þ ¼ F ð0,5Þ 1 þ F ð0,5Þ ¼
¼ 2 F ð0,5Þ 1 ¼ 2 0,6915 1 ¼ 0,383 ¼
b 38,3 %
Rund 38,3 % aller Flaschen enthalten entweder zu viel oder zu wenig Wein (maximale Abweichung vom Sollwert
m ¼ 1000 cm 3 : 10 cm 3 ).
3.3 Approximationen diskreter Wahrscheinlichkeitsverteilungen
Hinweise
(1)
(2)
Die Approximationen sind nur unter bestimmten Voraussetzungen zulässig (Faustregeln beachten).
Bei der Approximation einer diskreten Wahrscheinlichkeitsverteilung durch die Gaußsche Normalverteilung ist
die sog. „Stetigkeitskorrektur“ zu berücksichtigen (! Lehrbuch: Band 3, Kapitel II.6.6).
Lehrbuch: Band 3, Kapitel II.6.6 und 6.7 (Tabelle)
Formelsammlung: Kapitel XV.5.4 (Tabelle)
Ein Massenartikel wird mit einem Ausschussanteil von 1 % produziert und in Packungen mit jeweils
100 Stück in den Verkauf gebracht. Der Käufer einer Packung hat ein Reklamationsrecht, wenn sich in
K33
der Packung mehr als 2 defekte Artikel befinden. Wie groß ist die Wahrscheinlichkeit, dass der Kunde
reklamieren muss,
a) unter Verwendung der Binomialverteilung,
b) in der Näherung durch die Poisson-Verteilung?
3 Spezielle Wahrscheinlichkeitsverteilungen
619
a) Zufallsvariable: X ¼ Anzahl der defekten Artikel in einer Packung
X ist binomialverteilt mit den Parametern n ¼ 100 (Anzahl der Artikel in einer Packung), p ¼ 0,01 (Ausschussanteil) und q ¼ 1 p ¼ 1 0,01 ¼ 0,99. Die Wahrscheinlichkeitsfunktion dieser diskreten Zufallsvariablen lautet somit wie folgt:
n
100
x
nx
f ðxÞ ¼ P ðX ¼ xÞ ¼
p q
¼
0,01 x 0,99 100 x
x
x
ðx ¼ 0; 1; . . . ; 100Þ
Reklamationsrecht besteht, falls X > 2 ist:
P ðX > 2Þ ¼ 1 P ðX 2Þ ¼ 1 P ðX ¼ 0Þ P ðX ¼ 1Þ P ðX ¼ 2Þ ¼
100
100
100
0
100 0
1
100 1
0,01 0,99
0,01 2 0,99 100 2 ¼
¼ 1
0,01 0,99
1
2
0
¼ 1 1 1 0,99 100 100 0,01 0,99 99
100 99
0,01 2 0,99 98 ¼
12
¼ 1 0,3660 0,3697 0,1849 ¼ 0,0794 ¼
b 7,94 %
b) Die Faustregel für eine Approximation der Binomialverteilung durch die Poisson-Verteilung ist erfüllt (Faustregel:
n p 10 und n 1500 p ! FS: Kap. XV.5.4):
n p ¼ 100 0,01 ¼ 1 < 10 ;
n ¼ 100 > 1500 p ¼ 1500 0,01 ¼ 15
Die Wahrscheinlichkeitsfunktion der Poisson-Verteilung mit dem Parameter (Mittelwert) m ¼ n p ¼ 100 0,01 ¼ 1
lautet damit wie folgt:
f ðxÞ ¼ P ðX ¼ xÞ ¼
mx
1x
1
e1
em ¼
e1 ¼
x!
x!
x!
ðx ¼ 0; 1; . . . ; 100Þ
Reklamationsrecht besteht, wenn X > 2 ist:
P ðX > 2Þ ¼ 1 P ðX 2Þ ¼ 1 P ðX ¼ 0Þ P ðX ¼ 1Þ P ðX ¼ 2Þ ¼
1
1
1
1
1
1
1
1
1
¼ 1
e
e
e
þ
þ
e1 ¼
¼ 1
0!
1!
2!
0!
1!
2!
1
e 1 ¼ 1 2,5 e 1 ¼ 0,0803 ¼
¼ 1 1þ1þ
b 8,03 %
2
Kernreaktor mit 1200 Brennelementen
An die Brennelemente eines Kernreaktors werden extrem hohe Qualitätsanforderungen gestellt. In einem
K34
konkreten Fall beträgt die Wahrscheinlichkeit, dass ein Brennelement diesen Anforderungen nicht genügt, p ¼ 10 5 . Wie groß ist dann die Wahrscheinlichkeit, dass alle 1200 Brennelemente des Reaktors die vorgeschriebenen Qualitätsbedingungen erfüllen?
a) Exakte Rechnung, b) Näherungsrechnung mit der Poisson-Verteilung.
Zufallsvariable: X ¼ Anzahl der Brennelemente, die den Anforderungen nicht genügen
a) X ist binomialverteilt mit den Parametern n ¼ 1200 (Anzahl der Brennelemente im Reaktor), p ¼ 10 5 ¼
0,00001 (Ausfallwahrscheinlichkeit für ein Brennelement) und q ¼ 1 p ¼ 1 10 5 ¼ 0,99999. Die Wahrscheinlichkeitsfunktion der Zufallsvariablen X lautet damit wie folgt:
1200
n
x
nx
f ðxÞ ¼ P ðX ¼ xÞ ¼
p q
¼
0,00001 x 0,99999 1200 x
x
x
ðx ¼ 0; 1; . . . ; 1200Þ
620
K Wahrscheinlichkeitsrechnung und mathematische Statistik
X ¼ 0
Alle Brennelemente erfüllen die Qualitätsanforderungen:
1200
P ðX ¼ 0Þ ¼
0,00001 0 0,99999 1200 0 ¼ 1 1 0,99999 1200 ¼ 0,9881
0
Rund 98,8 % der Brennelemente erfüllen die hohen Qualitätsanforderungen.
b) Die Faustregel für die Approximation der Binomialverteilung durch die Poisson-Verteilung ist erfüllt (Faustregel:
n p 10 und n 1500 p ! FS: Kap. XV.5.4):
n p ¼ 1200 10 5 ¼ 0,012 < 10 ;
n ¼ 1200 > 1500 p ¼ 1500 10 5 ¼ 0,015
Die Wahrscheinlichkeitsfunktion der Poisson-Verteilung mit dem Parameter m ¼ n p ¼ 1200 10 5 ¼ 0,012
lautet damit wie folgt:
f ðxÞ ¼ P ðX ¼ xÞ ¼
X ¼ 0
mx
0,012 x
em ¼
e 0,012
x!
x!
ðx ¼ 0; 1; . . . ; 1200Þ
Alle Brennelemente genügen den Qualitätsanforderungen:
P ðX ¼ 0Þ ¼
0,012 0
1
e 0,012 ¼ e 0,012 ¼ 0,9881
e 0,012 ¼
1
0!
98,8 %
Die Näherungsrechnung mit der Poisson-Verteilung führt zum gleichen Ergebnis wie die exakte Rechnung mit der
Binomialverteilung!
Ampelschaltung
Eine Landstraße ist wegen Bauarbeiten auf einer bestimmten Teilstrecke nur einspurig befahrbar (d. h.
es gibt nur eine gemeinsame Fahrbahn für beide Richtungen). Die Verkehrsregelung erfolgt dabei durch
eine Ampelschaltung. Aufgrund der (schlechten) Erfahrungen muss man davon ausgehen, dass ca. 5 %
K35
der Autofahrer versuchen werden, die Ampel innerhalb der ersten 3 Sekunden der „Rotphase“ noch
schnell zu passieren.
a) Wie groß ist die Wahrscheinlichkeit, dass von 20 Fahrern mehr als einer die Ampel bei Rot passiert? Wie groß ist die mittlere Anzahl dieser Verkehrssünder?
b) Mit welcher Wahrscheinlichkeit verhalten sich höchstens 3 von 100 Fahrern verbotswidrig? Zu welchem Ergebnis führt eine Näherungsrechnung mit der Poisson-Verteilung?
Zufallsvariable: X ¼ Anzahl der Verkehrssünder („Rot-Sünder“)
a) X ist binomialverteilt mit den Parametern n ¼ 20 (Anzahl der Autofahrer), p ¼ 0,05 (Anteil an Verkehrssündern) und q ¼ 1 p ¼ 1 0,05 ¼ 0,95. Die Wahrscheinlichkeitsfunktion dieser Zufallsvariablen lautet damit
wie folgt:
n
20
x
nx
f ðxÞ ¼ P ðX ¼ xÞ ¼
p q
¼
0,05 x 0,95 20 x
ðx ¼ 0; 1; . . . ; 20Þ
x
x
X > 1
Mehr als 1 Verkehrssünder unter den 20 Fahrern:
P ðX > 1Þ ¼ 1 P ðX 1Þ ¼ 1 P ðX ¼ 0Þ P ðX ¼ 1Þ ¼
20
20
0,05 1 0,95 20 1 ¼
¼ 1
0,05 0 0,95 20 0
1
0
¼ 1 1 1 0,95 20 20 0,05 0,95 19 ¼ 1 0,3585 0,3774 ¼ 0,2641
Mittlere Anzahl an Verkehrssündern: m ¼ n p ¼ 20 0,05 ¼ 1
26,4 %
3 Spezielle Wahrscheinlichkeitsverteilungen
b)
X 3
621
Höchstens 3 Verkehrssünder unter 100 Fahrern:
Exakte Rechnung: X ist binomialverteilt mit den Parametern n ¼ 100, p ¼ 0,05 und q ¼ 1 0,05 ¼ 0,95.
Die Wahrscheinlichkeitsfunktion dieser Zufallsvariablen lautet daher:
100
n
x
nx
0,05 x 0,95 100 x
f ðxÞ ¼ P ðX ¼ xÞ ¼
p q
¼
ðx ¼ 0; 1; . . . ; 100Þ
x
x
Die Wahrscheinlichkeit dafür, dass sich höchstens 3 von 100 Fahrern verkehrswidrig verhalten, beträgt dann:
P ðX 3Þ ¼ P ðX ¼ 0Þ þ P ðX ¼ 1Þ þ P ðX ¼ 2Þ þ P ðX ¼ 3Þ ¼
100
100
100
100
0
100
1
99
2
98
¼
0,05 0,95
þ
0,05 0,95 þ
0,05 0,95 þ
0,05 3 0,95 97 ¼
0
1
2
3
¼ 1 1 0,95 100 þ 100 0,05 0,95 99 þ
100 99
100 99 98
0,05 2 0,95 98 þ
0,05 3 0,95 97 ¼
12
123
¼ 0,00592 þ 0,03116 þ 0,08118 þ 0,13958 ¼ 0,25784
25,8 %
Näherungsrechnung: Die Approximation durch die Poisson-Verteilung ist erlaubt, da die Faustregel für diese
Näherung erfüllt ist (Faustregel: n p 10 und n 1500 p ! FS: Kap. XV.5.4):
n p ¼ 100 0,05 ¼ 5 < 10 ;
n ¼ 100 > 1500 p ¼ 1500 0,05 ¼ 75
Die Wahrscheinlichkeitsfunktion der Poisson-Verteilung mit dem Parameter (Mittelwert) m ¼ n p ¼ 100 0,05 ¼ 5
lautet damit wie folgt:
f ðxÞ ¼ P ðX ¼ xÞ ¼
X 3
mx
5x
em ¼
e5
x!
x!
ðx ¼ 0; 1; . . . ; 100Þ
Höchstens 3 Verkehrssünder unter 100 Fahrern:
P ðX 3Þ ¼ P ðX ¼ 0Þ þ P ðX ¼ 1Þ þ P ðX ¼ 2Þ þ P ðX ¼ 3Þ ¼
50
51
52
53
þ
þ
þ
0!
1!
2!
3!
e 5 ¼
¼ ð1 þ 5 þ 12,5 þ 20,8333Þ e 5 ¼ 0,2650 ¼
b 26,5 %
Dieser Näherungswert ist in guter bereinstimmung mit dem exakten Wert von 25,8 %.
Telefon-Hotline
Eine Hotline (1820 Uhr) erreichen in diesem Zeitraum durchschnittlich 100 Anrufe (wie man aus
langjähriger Erfahrung weiß). Wie groß ist die Wahrscheinlichkeit, dass
K36
a) mehr als 100 Anrufe eingehen,
b) zwischen 60 und 80 Anrufe eingehen,
c) weniger als 50 Anrufe erfolgen?
Lösen Sie diese Aufgabe näherungsweise mit Hilfe der Normalverteilung!
Zufallsvariable: X ¼ Anzahl der eingehenden Anrufe (zwischen 18 und 20 Uhr)
X ist poissonverteilt mit dem Parameter (Mittelwert) m ¼ 100, kann aber in diesem speziellen Fall durch die rechnerisch
pffiffiffiwesentlich
pffiffiffiffiffiffiffiffi bequemere Normalverteilung mit dem Mittelwert m ¼ 100 und der Standardabweichung
s ¼ m ¼ 100 ¼ 10 ersetzt werden (die Faustregel m > 10 für diese Approximation ist erfüllt ! FS:
Kap. XV.5.4).
622
K Wahrscheinlichkeitsrechnung und mathematische Statistik
bergang von der Zufallsvariablen X zur standardnormalverteilten Zufallsvariable U ¼
X m
X 100
¼
:
s
10
(F ðxÞ: Verteilungsfunktion der Normalverteilung; F ðuÞ: Verteilungsfunktion der Standardnormalverteilung)
Bei der Approximation ist die Stetigkeitskorrektur zu berücksichtigen, bei der die Grenzen um jeweils 0,5 nach außen
hin verschoben werden!
a)
X > 100
Mehr als 100 Anrufe:
P ðX > 100Þ ¼ 1 P ðX 100Þ ¼ 1 F ð100 þ 0,5 Þ ¼ 1 F ð100,5Þ ¼ 1 F
|{z}
100,5 100
10
¼
Stetigkeitskorrektur
¼ 1 F ð0,05Þ ¼ 1 0,5199 ¼ 0,4801
b)
60 X 80
48 %
Zwischen 60 und 80 Anrufe:
P ð60 X 80Þ ¼ F ð80 þ 0,5Þ F ð60 0,5Þ ¼ F ð80,5Þ F ð59,5Þ ¼
"
"
Stetigkeitskorrektur
80,5 100
59,5 100
F
¼ F ð 1,95Þ F ð 4,05Þ ¼
10
10
¼ 1 F ð1,95Þ 1 F ð4,05Þ ¼ 1 F ð1,95Þ 1 þ F ð4,05Þ ¼
¼ F
¼ F ð4,05Þ F ð1,95Þ ¼ 1 0,9744 ¼ 0,0256
c)
X < 50
2,6 %
Weniger als 50 Anrufe (höchstens 49 Anrufe):
P ðX < 50Þ ¼ P ðX 49Þ ¼ F ð49 þ 0,5 Þ ¼ F ð49,5Þ ¼ F
|{z}
49,5 100
10
¼ F ð 5,05Þ ¼
Stetigkeitskorrektur
¼ 1 F ð0,05Þ ¼ 1 1 ¼ 0
Wir folgern: Dieses Ereignis (weniger als 50 Anrufe) ist höchst unwahrscheinlich!
Klausur mit Multiple-Choice-Aufgaben
Eine Klausur besteht aus 50 Multiple-Choice-Aufgaben. Pro Aufgabe sind dabei 4 verschiedene Antworten (Lösungen) vorgegeben, darunter genau 1 richtige. Die Klausur gilt als bestanden, wenn min-
K37
destens 20 Aufgaben richtig gelöst (angekreuzt) werden. Ein Student konnte sich (krankheitsbedingt)
kaum vorbereiten und versucht nun, die Klausur durch zufälliges Ankreuzen der richtigen Antworten zu
bestehen. Wie beurteilen Sie seine Chancen, d. h. mit welcher Wahrscheinlichkeit wird er die Klausur
bestehen?
Hinweis: Lösen Sie diese Aufgabe (näherungsweise) mit Hilfe der Normalverteilung.
Zufallsvariable: X ¼ Anzahl der richtig gelösten Aufgaben (richtigen Antworten)
X ist binomialverteilt mit den Parametern n ¼ 50 (Anzahl der Aufgaben), p ¼ 1=4 ¼ 0,25 (1 von 4 Antworten ist
richtig) und q ¼ 1 p ¼ 1 0,25 ¼ 0,75. Der extrem hohe Rechenaufwand wird vermieden, wenn man die Binomialverteilung näherungsweise durch die rechnerisch wesentlich bequemere Normalverteilung ersetzt (die Faustregel
für diese Approximation ist hier erfüllt: n p q ¼ 50 0,25 0,75 ¼ 9,375 > 9 ! FS: Kap. XV.5.4).
4 Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen
623
Näherungsrechnung mit der Normalverteilung mit dem Mittelwert m ¼ n p ¼ 50 0,25 ¼ 12,5 und der Standardpffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
abweichung s ¼ n p q ¼ 9,375 unter Berücksichtigung der Stetigkeitskorrektur:
X 20
Mindestens 20 richtige Antworten (Lösungen):
bergang von der Zufallsvariablen X zur standardnormalverteilten Zufallsvariablen U ¼
P ðX 20Þ ¼ 1 P ðX 19Þ ¼ 1 F ð19 þ 0,5 Þ ¼ 1 F ð19,5Þ ¼ 1 F
|{z}
X m
X 12,5
¼ pffiffiffiffiffiffiffiffiffiffiffi :
s
9,375
!
19,5 12,5
¼
pffiffiffiffiffiffiffiffiffiffiffi
9,375
Stetigkeitskorrektur
¼ 1 F ð2,286Þ ¼ 1 0,9889 ¼ 0,0111
1,1 %
Folgerung: Die Chance, die Klausur zu bestehen, ist sehr gering!
4 Wahrscheinlichkeitsverteilungen von mehreren
Zufallsvariablen
Lehrbuch: Band 3, Kapitel II.7
Formelsammlung: Kapitel XV.7
Die diskreten und stochastisch unabhängigen Zufallsvariablen X und Y genügen den folgenden Verteilungen (Wahrscheinlichkeitsfunktionen):
K38
xi
0
2
5
yi
0
1
3
7
f 1 ðx i Þ
0,3
0,5
0,2
f 2 ðy i Þ
0,2
0,3
0,2
0,3
a) Bestimmen Sie den Mittelwert und die Varianz der beiden Verteilungen (Randverteilungen).
b) Wie lautet die Wahrscheinlichkeitsfunktion f ðx ; yÞ der gemeinsamen Verteilung?
a) E ðXÞ ¼ m x ¼
3
X
x i f 1 ðx i Þ ¼ 0 0,3 þ 2 0,5 þ 5 0,2 ¼ 0 þ 1 þ 1 ¼ 2
i¼1
Var ðXÞ ¼ s 2x ¼ E ðX 2 Þ m 2x ¼
3
X
i¼1
x i2 f 1 ðx i Þ m 2x ¼ ð0 2 0,3 þ 2 2 0,5 þ 5 2 0,2Þ 2 2 ¼
¼ ð0 þ 2 þ 5Þ 4 ¼ 7 4 ¼ 3
E ðYÞ ¼ m y ¼
4
X
y i f 2 ðy i Þ ¼ 0 0,2 þ 1 0,3 þ 3 0,2 þ 7 0,3 ¼ 0 þ 0,3 þ 0,6 þ 2,1 ¼ 3
i¼1
Var ðYÞ ¼ s 2y ¼ E ðY 2 Þ m 2y ¼
4
X
i¼1
y 2i f 2 ðy i Þ m 2y ¼ ð0 2 0,2 þ 1 2 0,3 þ 3 2 0,2 þ 7 2 0,3Þ 3 2 ¼
¼ ð0 þ 0,3 þ 1,8 þ 14,7Þ 9 ¼ 16,8 9 ¼ 7,8
624
K Wahrscheinlichkeitsrechnung und mathematische Statistik
a) X und Y sind nach Voraussetzung stochastisch unabhängig. Somit gilt: f ðx ; yÞ ¼ f 1 ðxÞ f 2 ðyÞ. Wir erhalten
die folgende Verteilungstabelle:
Y
0
1
3
7
0
0,06
0,09
0,06
0,09
0,30
2
0,10
0,15
0,10
0,15
0,50
5
0,04
0,06
0,04
0,06
0,20
0,20
0,30
0,20
0,30
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
X
f 1 ðxÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
f 2 ðyÞ
Berechnung der Funktionswerte am Beispiel f ð2 ; 3Þ:
f ð2 ; 3Þ ¼ f 1 ð2Þ f 2 ð3Þ ¼ 0,5 0,2 ¼ 0,10
ðin der Tabelle grau unterlegtÞ
Lagervorrat an Bauteilen
Ein spezielles Bauteil eines Gerätes hat eine mittlere „Lebensdauer“ von m ¼ 30 h bei einer Standard-
K39
abweichung von s ¼ 2 h (h: Stunde; die Art der Verteilung ist nicht bekannt). Fällt das Bauteil aus,
so wird es durch ein gleichartiges aus dem Lager ersetzt. Reicht ein Vorrat von n ¼ 100 Bauteilen
(für 1 Jahr) aus, wenn das Gerät im Jahr insgesamt 2950 h einwandfrei arbeiten soll?
Die diskreten und stochastisch unabhängigen Zufallsvariablen
X i ¼ Lebensdauer des i-ten Bauteils aus dem Lagervorrat (i ¼ 1, 2, . . . , 100)
besitzen alle den gleichen Mittelwert m i ¼ m ¼ 30 h und die gleiche Standardabweichung s i ¼ s ¼ 2 h. Dann ist
die Zufallsvariable
Z ¼
100
X
X i ¼ Gesamtlebensdauer aller 100 Bauteile aus dem Lager
i¼1
annähernd normalverteilt mit den folgenden Kennwerten (die Mittelwerte und Varianzen der Zufallsvariablen X i
addieren sich jeweils):
mz ¼
100
X
m i ¼ 100 m ¼ 100 30 h ¼ 3000 h
i¼1
s 2z ¼
100
X
i¼1
s 2i ¼ 100 s 2 ¼ 100 ð2 hÞ 2 ¼ 400 h 2
)
s z ¼ 20 h
Die Faustregel n > 30 für diese Näherung ist erfüllt, keine der n ¼ 100 Zufallsvariablen dominiert (! FS: Kap.
XV.7.2.3).
Die Wahrscheinlichkeit, dass ein Vorrat von 100 Bauteilen für 1 Jahr ausreicht, beträgt dann:
2950 3000
P ðZ 2950Þ ¼ 1 P ðZ < 2950Þ ¼ 1 P U <
¼ 1 P ðU < 2,5Þ ¼
20
¼ 1 F ð 2,5Þ ¼ 1 1 F ð2,5Þ ¼ 1 1 þ F ð2,5Þ ¼ F ð2,5Þ ¼ 0,9938
4 Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen
625
Hinweis: bergang von der normalverteilten Zufallsvariablen Z zur standardnormalverteilten Zufallsvariablen
U ¼
Z mz
Z 3000
; F ðuÞ ist die Verteilungsfunktion der Standardnormalverteilung.
¼
20
sz
Fazit: Mit der hohen Wahrscheinlichkeit von fast 99,4 % wird der Vorrat von 100 Bauteilen (Ersatzteilen) für 1 Jahr
ausreichen.
Eine Urne enthält 2 weiße und 2 schwarze Kugeln. Nacheinander werden 2 Kugeln zufällig entnommen
ohne Zurücklegen. Bestimmen Sie die gemeinsame Verteilung der beiden Zufallsvariablen
K40
X; Y ¼ Farbe der gezogenen Kugel bei der 1. bzw. 2. Ziehung
mit Hilfe des Ereignisbaums. Warum sind die beiden Variablen stochastisch abhängig? Wie lauten die
zugehörigen Randverteilungen der gemeinsamen Verteilung?
Baumdiagramm (Ereignisbaum; siehe Bild K-10)
1. Ziehung
Vereinbarung: Die Zufallsvariablen X und Y
besitzen den Wert 0, wenn eine weiße Kugel
gezogen wurde und den Wert 1 bei Ziehung
einer schwarzen Kugel.
2. Ziehung
1/3
1/2
1/2
2/3
2/3
1/3
Bild K-10 Baumdiagramm
1. Ziehung: In der Urne befinden sich gleichviele weiße und schwarze Kugeln (jeweils 2 Kugeln). Die Ziehung einer
weißen bzw. schwarzen Kugel erfolgt somit in beiden Fällen mit der gleichen Wahrscheinlichkeit p ¼ 2=4 ¼ 1=2
(2 aus 4).
2. Ziehung: Das Ergebnis der 2. Ziehung hängt dagegen wesentlich davon ab, ob zunächst eine weiße oder eine
schwarze Kugel gezogen wurde. Im 1. Fall befinden sich vor der 2. Ziehung 1 weiße und 2 schwarze Kugeln in der
Urne, im 2. Fall ist es genau umgekehrt. Die Zufallsvariablen X und Y sind daher stochastisch abhängig.
Aus dem Baumdiagramm (Ereignisbaum; siehe Bild K-10) entnehmen wir mit Hilfe der Pfadregeln (! FS: Kap.
XV.3.7) die folgenden Werte der Wahrscheinlichkeitsfunktion f ðx ; yÞ der gemeinsamen Verteilung:
Pð
Þ ¼ f ð0 ; 0Þ ¼
1 1
1
¼
;
2 3
6
Pð
Þ ¼ f ð0 ; 1Þ ¼
1 2
2
¼
;
2 3
6
Pð
Þ ¼ f ð1 ; 0Þ ¼
1 2
2
¼
;
2 3
6
Pð
Þ ¼ f ð1 ; 1Þ ¼
1 1
1
¼
2 3
6
626
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Verteilungstabelle (Wahrscheinlichkeitsfunktion f ðx ; yÞ der gemeinsamen Verteilung)
Y
0
1
0
1=6
2=6
1=2
1
2=6
1=6
1=2
1=2
1=2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
X
f 1 ðxÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
f 2 ðyÞ
Randverteilungen Wahrscheinlichkeitsfunktion f 1 ðxÞ und f 2 ðyÞ
xi
0
1
yi
0
1
f 1 ðx i Þ
1=2
1=2
f 2 ðy i Þ
1=2
1=2
Produktionsdauer eines elektronischen Gerätes
Die Herstellung eines elektronischen Gerätes erfolgt in 10 voneinander unabhängigen Arbeitsgängen.
Die stetigen Zufallsvariablen
T i ¼ Dauer des i-ten Arbeitsganges (in Stunden (h); i ¼ 1, 2, . . . , 10)
sind dabei alle gleichverteilt im Zeitintervall 1 h t 3 h und stochastisch unabhängig (jeder Ar-
K41
beitsgang dauert also zwischen 1 und 3 Stunden).
a) Bestimmen Sie zunächst den Mittelwert m i und die Standardabweichung s i der Zufallsvariablen
T i.
b) Die Gesamtproduktionsdauer wird durch die Zufallsvariable T ¼
10
X
T i beschrieben. Welchen Er-
i¼1
wartungswert (Mittelwert) und welche Varianz besitzt diese Zufallsvariable?
a) Die Zufallsvariablen T 1 bis T 10 besitzen alle dieselbe Gleichverteilung. Wir setzen X ¼ T i und bestimmen der
Reihe nach die Wahrscheinlichkeitsdichtefunktion f ðxÞ, den Mittelwert m und die Varianz s 2 dieser Zufallsvariablen.
Wahrscheinlichkeitsdichtefunktion f ðxÞ (siehe Bild K-11)
Normierung der Dichtefunktion:
f (x)
ð3
Symmetrieachse
f ðxÞ d x ¼ 2 H ¼ 1
H
)
H ¼
1
2
1
H
(Fläche des grau unterlegten Rechtecks)
H
1
3
x
x0 = 2
Bild K-11 Wahrscheinlichkeitsdichtefunktion
Somit gilt: f ðxÞ ¼ H ¼
1
für 1 x 3
2
4 Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen
627
Mittelwert: Das Symmetriezentrum der Gleichverteilung liegt bei x 0 ¼ 2. Daher ist m ¼ x 0 ¼ 2 (! FS: Kap.
XV.4.3, Anmerkung 5).
1
ð
Varianz : s ¼ Var ðXÞ ¼ E ðX Þ m ¼
2
2
ð3
x f ðxÞ d x m ¼
2
2
2
1
1 3 3
1
x 1 4 ¼
¼
6
6
1 2
x d x 22 ¼
2
1 3
x
6
1
3
4 ¼
1
1
13
13 12
1
27 1 4 ¼
26 4 ¼
4 ¼
¼
6
3
3
3
Für alle T i ¼ X gilt daher: m i ¼ m ¼ 2 h und s 2i ¼ s 2 ¼
1 2
h .
3
b) Die Zufallsvariable T (¼ Summe aller T i ) besitzt damit den Mittelwert
E ðTÞ ¼ m T ¼
10
X
m i ¼ 10 m ¼ 10 2 h ¼ 20 h
i¼1
und die Varianz (! FS: Kap. XV.7.2.3)
Var ðTÞ ¼ s 2T ¼
10
X
i¼1
s 2i ¼ 10 s 2 ¼ 10
1 2
10 2
h ¼
h
3
3
Gesamtwiderstand einer Reihenschaltung von ohmschen Widerständen
Die Einzelwiderstände R 1 bis R 4 einer Reihenschaltung (siehe Bild K-12) können als stochastisch
unabhängige und normalverteilte Zufallsgrößen mit den folgenden Mittelwerten und Standardabweichungen aufgefasst werden (alle Werte in Ohm (W)):
K42
i
1
2
3
4
mi
100
150
70
si
2
3
80
pffiffiffi
3
100 V
150 V
80 V
70 V
R1
R2
R3
R4
3
Bild K-12 Reihenschaltung von Widerständen
a) Berechnen Sie den Mittelwert m und die Standardabweichung s des Gesamtwiderstandes
4
X
R ¼
R i der Schaltung.
i¼1
b) Bestimmen Sie die Grenzen des zum Mittelwert m symmetrischen Intervalls, in dem der Gesamtwiderstand R mit einer Wahrscheinlichkeit von 90 % vermutet wird.
a) Die Mittelwerte und Varianzen addieren sich jeweils (! FS: Kap. XV.7.2.1):
m ¼
4
X
m i ¼ ð100 þ 150 þ 80 þ 70Þ W ¼ 400 W
i¼1
s2 ¼
4
X
i¼1
pffiffiffi
s 2i ¼ ð2 2 þ 3 2 þ_ ð 3 Þ 2 þ 3 2 Þ W 2 ¼ ð4 þ 9 þ 3 þ 9Þ W 2 ¼ 25 W 2
)
b) Die normalverteilte Zufallsvariable R liegt mit einer Wahrscheinlichkeit von 90 % im Intervall
j R m j ¼ j R 400 j c, d. h. es gilt P ð j R 400 j cÞ ¼ 0,90
ðsiehe Bild K-13Þ
s ¼ 5W
628
K Wahrscheinlichkeitsrechnung und mathematische Statistik
c
c
Bild K-13
400 – c
400
400 + c
R/V
Bestimmung der Schranke c
Rm
R 400
¼
.
bergang von der Zufallsvariablen R zur standardnormalverteilten Zufallsvariablen U ¼
s
5
Aus dieser Transformationsgleichung folgt j R 400 j ¼ 5 j U j und somit:
c
c
P ð j R 400 j cÞ ¼ P ð5 j U j cÞ ¼ P j U j
¼ 2F
1 ¼ 0,90 )
5
5
c
c
c
2F
¼ 1,90 ) F
¼ 0,95 )
¼ u 0,95 ¼ 1,645 ) c ¼ 8,225
ðaus Tab: 2Þ
5
5
5
Lösung: j R 400 j c ¼ 8,225
,
391,775 W R 408,225 W
5 Häufigkeitsverteilungen und Kennwerte
einer Stichprobe
Lehrbuch: Band 3, Kapitel III.1 und 2
Formelsammlung: Kapitel XVI.1 und 2
Leistung baugleicher Pumpen
Für die Leistung X baugleicher Pumpen ergab eine Stichprobe vom Umfang n ¼ 5 folgende Urliste
K43
(alle Werte in Liter pro Minute (l=min)):
20,4 ;
21,2 ;
21,0 ;
20,8 ;
21,6
Bestimmen Sie den Mittelwert x, die Varianz s 2 und die Standardabweichung s dieser Stichprobe.
x ¼
5
1 X
1
105 ¼ 21
xi ¼
5 i¼1
5
i
xi
x i2
1
20,4
416,16
2
21,2
449,44
3
21,0
441,00
1
s ¼
51
4
20,8
432,64
¼ 0,2
5
P
21,6
466,56
105,0
2205,80
2
s ¼
"
5
X
i¼1
#
x i2
5x
2
1
¼
4
ðin l=minÞ
2205,80 5 21
ðin ðl=minÞ 2 Þ
pffiffiffiffiffi
pffiffiffiffiffiffi
s 2 ¼ 0,2 ¼ 0,4472
0,45
ðin l=minÞ
2
¼
5 Häufigkeitsverteilungen und Kennwerte einer Stichprobe
629
Der Tagesproduktion von ohmschen Widerständen mit einem Sollwert von 100 W wurde eine Stichprobe vom Umfang n ¼ 20 mit der folgenden Häufigkeitsverteilung entnommen (alle Werte in Ohm (W);
n i : absolute Klassenhäufigkeit; k ¼ 5 KlassenÞ:
K44
i
1
2
3
4
5
xi
98
99
100
101
102
ni
1
3
12
2
2
Bestimmen Sie die Häufigkeitsfunktion f ðxÞ mit dem zugehörigen Stabdiagramm, die Verteilungsfunktion F ðxÞ, den Mittelwert x und die Standardabweichung s der Stichprobe.
Verteilung ( f ðx i Þ ¼ n i =20) und Stabdiagramm, Bild K-14
f (x)
i
1
2
3
4
5
xi
98
99
100
101
102
ni
1
3
12
2
2
f ðx i Þ
0,05
0,15
0,60
0,10
0,10
F ðx i Þ
0,05
0,20
0,80
0,90
1
0,60
0,50
0,40
0,30
0,20
Berechnung der Kennwerte (Maßzahlen) x, s 2 und s
0,15
i
xi
f ðx i Þ
x i f ðx i Þ
1
98
0,05
4,90
480,20
2
99
0,15
14,85
1 470,15
3
100
0,60
60,00
6 000,00
4
101
0,10
10,10
1 020,10
5
P
102
0,10
10,20
1 040,40
100,05
10 010,85
1
x ¼
5
X
x i f ðx i Þ ¼ 100,05
x i2 f ðx i Þ
0,10
0,05
98
99
100 101 102
Bild K-14 Stabdiagramm
ðin WÞ
i¼1
20
s2 ¼
20 1
s ¼
"
5
X
i¼1
#
x i2
f ðx i Þ x
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s 2 ¼ 0,8921 ¼ 0,9445
2
20
¼
19
0,945
10 010,85 100,05
ðin WÞ
2
¼ 0,8921
ðin W 2 Þ
x/V
630
K Wahrscheinlichkeitsrechnung und mathematische Statistik
„Lebensdauer“ eines elektronischen Bauteils
Der Serienproduktion eines bestimmten elektronischen Bauteils wurde eine Stichprobe vom Umfang
n ¼ 40 entnommen. Dabei wurde die „Lebensdauer“ X dieser Elemente bestimmt und die Messwerte
wie folgt in k ¼ 5 Klassen gleicher Breite D x ¼ 20 eingeteilt (alle Werte in Stunden (h); n i : absolute Klassenhäufigkeit):
X
K45
1. Klasse
2. Klasse
3. Klasse
4. Klasse
5. Klasse
500520
520540
540560
560580
580600
4
8
18
6
4
ni
a) Bestimmen Sie die Häufigkeitsfunktion mit dem zugehörigen Histogramm sowie die Verteilungsfunktion der Stichprobenverteilung.
b) Berechnen Sie den Mittelwert sowie die Varianz und die Standardabweichung der Stichprobe.
a) x~i : Klassenmitte; f ð~
x i Þ ¼ n i =40: Häufigkeitsfunktion; F ð~
x i Þ: Verteilungsfunktion (i ¼ 1, 2, . . . , 5)
Klasse i
1
2
3
4
5
x~ i
510
530
550
570
590
ni
4
8
18
6
4
f ð~
x iÞ
0,10
0,20
0,45
0,15
0,10
F ð~
x iÞ
0,10
0,30
0,75
0,90
1
f(x)
0,45
0,40
0,30
0,20
0,15
0,10
Histogramm: Bild K-15
510
500
530
550
570
590
600
x/h
Bild K-15 Histogramm
b)
i
x~ i
f ð~
x iÞ
x~ i f ð~
x iÞ
x~ 2i f ð~
x iÞ
5
X
x ¼
x~ i f ð~
x i Þ ¼ 549
1
510
0,10
51
26 010
i¼1
2
530
0,20
106
56 180
3
550
0,45
247,5
136 125
40
s ¼
40 1
4
570
0,15
85,5
48 735
5
P
590
0,10
59
34 810
549
301 860
1
2
¼
s ¼
40
39
"
5
X
i¼1
ðin hÞ
#
x~ 2i
f ð~
x iÞ x
2
¼
301 860 549 2 ¼ 470,769
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s 2 ¼ 470,769 ¼ 21,697
21,70
ðin h 2 Þ
ðin hÞ
5 Häufigkeitsverteilungen und Kennwerte einer Stichprobe
631
Benzinverbrauch eines PKW
Der Benzinverbrauch X eines neuen PKW-Modells wurde anhand von n ¼ 25 zufällig ausgewählten
Testfahrzeugen näher untersucht und ergab Verbrauchswerte zwischen 7 und 9,4 Liter pro 100 km Fahrstrecke (l=100 km), die wie folgt in k ¼ 5 Klassen gleicher Breite D ¼ 0,5 gruppiert wurden (alle
Werte in l=100 km; n i : absolute Häufigkeit der i-ten Klasse):
K46
Klasse Nr. i
1
2
3
4
5
x
7 x < 7,5
7,5 x < 8
8 x < 8,5
8,5 x < 9
9 x < 9,5
ni
2
4
12
6
1
Bestimmen Sie die folgenden Eigenschaften und Kennwerte (Maßzahlen) der gruppierten Stichprobe:
Häufigkeits- und Verteilungsfunktion, Mittelwert, Varianz und Standardabweichung der Stichprobe.
x~i : Klassenmitte; f ð~
x i Þ ¼ n i =25 bzw. F ð~
x i Þ: Häufigkeits- bzw. Verteilungsfunktion der gruppierten Stichprobe
(i ¼ 1, 2, . . . , 5)
Klasse i
1
2
3
4
5
x~i
7,25
7,75
8,25
8,75
9,25
ni
2
4
6
1
f ð~
x iÞ
0,08
0,16
0,48
0,24
0,04
F ð~
x iÞ
0,08
0,24
0,72
0,96
1
12
Histogramm: Siehe Bild K-16
f(x)
0,48
0,40
0,32
0,24
0,16
0,08
7,25
7,75
Bild K-16 Histogramm
8,25
8,75
9,25
x (in l/100 km)
632
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Berechnung der Kennwerte (Maßzahlen) x, s 2 und s
Klasse i
x~ i
f ð~
x iÞ
x~i f ð~
x iÞ
x~i2 f ð~
x iÞ
1
7,25
0,08
0,58
4,2050
2
7,75
0,16
1,24
9,6100
3
8,25
0,48
3,96
32,6700
4
8,75
0,24
2,10
18,3750
5
P
9,25
0,04
0,37
3,4225
1
8,25
68,2825
x ¼
5
X
x i Þ ¼ 8,25
x~ i f ð~
ðin l=100 kmÞ
i¼1
25
s ¼
25 1
"
2
s ¼
5
X
i¼1
#
x~ 2i
f ð~
x iÞ x
¼
2
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s 2 ¼ 0,2292 ¼ 0,4787
0,48
25
24
¼ 0,2292
68,2825 8,25 2
ðin ðl=100 kmÞ 2 Þ
ðin l=100 kmÞ
Vollautomatische Abfüllanlage einer Weinkellerei
In einer Weinkellerei wurden auf einer vollautomatischen Abfüllanlage über 10 000 Literflaschen mit
Weißwein gefüllt. Eine nach der Füllung gezogene Stichprobe vom Umfang n ¼ 50 ergab dabei (vermutlich aufgrund einer falschen Einstellung des Automaten) Fehlmengen bis zu 40 cm 3 pro Flasche mit
der folgenden Häufigkeitsverteilung (Zufallsvariable: X ¼ Fehlmenge in einer Literflasche in cm 3 ;
k ¼ 4 Klassen):
K47
Klasse i
1
2
3
4
Fehlmenge X (in cm 3 )
010
1020
2030
3040
Anzahl der Flaschen
6
20
16
8
a) Ermitteln Sie die Häufigkeitsfunktion mit dem zugehörigen Stabdiagramm sowie die Verteilungsfunktion der gruppierten Stichprobe.
b) Berechnen Sie die Kennwerte (Maßzahlen) x, s 2 und s der Stichprobe.
a) x~i : Klassenmitte; f ð~
x i Þ ¼ n i =50: Häufigkeitsfunktion der Stichprobe;
F ð~
x i Þ: Verteilungsfunktion der Stichprobe (i ¼ 1, 2, 3, 4)
Klasse i
1
2
3
4
x~i
5
15
25
35
ni
6
20
16
8
f ð~
x iÞ
0,12
0,40
0,32
0,16
F ð~
x iÞ
0,12
0,52
0,84
1
6 Parameterschätzungen
633
Stabdiagramm: siehe Bild K-17
~
f (x)
0,40
0,32
0,16
0,12
0,04
Bild K-17 Stabdiagramm
5
b) x ¼
4
X
15
25
35
~
x/cm 3
x i Þ ¼ 5 0,12 þ 15 0,40 þ 25 0,32 þ 35 0,16 ¼ 20,20
x~ i f ð~
ðin cm 3 Þ
i¼1
50
s ¼
50 1
2
50
¼
49
s ¼
"
4
X
i¼1
#
x~ 2i
f ð~
x iÞ x
¼
2
50
49
5 2 0,12 þ 15 2 0,40 þ 25 2 0,32 þ 35 2 0,16 20,20 2
50
3 þ 90 þ 200 þ 196 408,04 ¼
80,96 ¼ 82,6122
49
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s 2 ¼ 82,6122 ¼ 9,0891
9,09
¼
ðin cm 6 Þ
ðin cm 3 Þ
6 Parameterschätzungen
Voraussetzung für eine Parameterschätzung: Der Typ der Wahrscheinlichkeitsverteilung ist bekannt, die Parameter jedoch noch unbekannt und müssen daher geschätzt werden (z. B. Normalverteilung, deren Mittelwert m und Standardabweichung s noch unbekannt sind).
6.1 Punktschätzungen
Bei einer Punktschätzung werden die unbekannten Parameter einer vom Typ her bekannten Verteilung geschätzt.
Lehrbuch: Band 3, Kapitel III.3.2 und 3.3
Formelsammlung: Kapitel XVI.3.2
Brenndauer einer Leuchtstoffröhre
Die Brenndauer T einer speziellen Leuchtstoffröhre genüge einer Verteilung mit der zeitabhängigen
Dichtefunktion
K48
f ðt; lÞ ¼ 2 l t e l t ;
2
t 0
(für t < 0 ist f ðt; lÞ ¼ 0Þ. Bestimmen Sie für den noch unbekannten Parameter l unter Verwendung der vorgegebenen Stichprobe t 1 ; t 2 ; . . . ; t n einen Schätzwert l^ nach der Maximum-LikelihoodMethode.
634
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Aufstellen der Likelihood-Funktion:
L ¼ L ðlÞ ¼ f ðt 1 ; lÞ f ðt 2 ; lÞ . . . f ðt n ; lÞ ¼ ð2 l t 1 e l t 1 Þ ð2 l t 2 e l t 2 Þ . . . ð2 l t n e l t n Þ ¼
2
2
2
¼ ð2 lÞ n ðt 1 t 2 . . . t n Þ e l ðt 1 þ t 2 þ ... þ t n Þ ¼ ð2 lÞ n a e l b ¼ ð2 lÞ n a e b l
2
2
2
(mit den Abkürzungen a ¼ t 1 t 2 . . . t n und b ¼ t 12 þ t 22 þ . . . þ t n2 ; der Faktor 2 l tritt dabei n-mal auf)
Rechenregel: e m 1 e m 2 . . . e m n ¼ e m 1 þ m 2 þ ... þ m n
Wir verwenden die logarithmierte Form der Likelihood-Funktion:
L * ¼ ln L ðlÞ ¼ ln ð2 lÞ n a e b l ¼ ln ð2 lÞ n þ ln a þ ln e b l ¼ n ln ð2 lÞ þ ln a b l
Rechenregeln: ln ðu v wÞ ¼ ln u þ ln v þ ln w ;
ln u n ¼ n ln u ;
ln e m ¼ m
Ableitungen 1. und 2. Ordnung von L * nach l bilden (Kettenregel):
dL*
1
n
¼ n
2 þ0b ¼
b;
dl
2l
l
d2 L*
n
n
¼ 2 0 ¼ 2 < 0
2
dl
l
l
Maximum von L * und somit auch von L bestimmen:
dL*
¼ 0
dl
n
b ¼ 0
l
)
)
n
¼ b
l
)
l ¼
n
b
Da die 2. Ableitung stets negativ ist, ist auch die hinreichende Bedingung für ein Maximum erfüllt. Somit ist
n
n
¼
l^ ¼
2
2
b
t 1 þ t 2 þ . . . þ t n2
der gesuchte Schätzwert für den unbekannten Parameter l.
Lebensdauer eines elektrischen Gerätes
Die „Lebensdauer“ T eines bestimmten elektrischen Gerätes genügt einer speziellen Weibull-Verteilung
mit der Dichtefunktion
K49
f ðt; aÞ ¼
1
1=3
a t 2=3 e a t ;
3
t 0
(für t < 0 gilt f ðt; aÞ ¼ 0Þ. Mit Hilfe der Maximum-Likelihood-Methode bestimme man einen
^ für den noch unbekannten Parameter a > 0 auf der Basis einer vorgegebenen StichSchätzwert a
probe t 1 ; t 2 ; . . . ; t n .
Aufstellen der Likelihood-Funktion, die anschließend logarithmiert wird:
L ¼ L ðaÞ ¼ f ðt 1 ; aÞ f ðt 2 ; aÞ . . . f ðt n ; aÞ ¼
1=3
1=3
1=3
1
1
1
2=3
2=3
a t1
a t2
a t n 2=3 e a t n
e a t1
e a t2
¼
...
¼
3
3
3
¼
¼
1
a
3
1
a
3
n
2=3
ðt 1
n
2=3
t2
c eba
1=3
. . . t n 2=3 Þ e a ðt 1
1=3
1=3
þ t 2 þ ... þ t n Þ
Þ ¼
n
1
a c eab ¼
3
6 Parameterschätzungen
635
2=3
2=3
(mit dedn Abkürzungen c ¼ t 1
t2
. . . t n 2=3 und b ¼ t 1
1=3
1=3
þ t2
þ . . . þ t n1=3 ; der Faktor
dabei n-mal auf)
1
a tritt
3
Rechenregeln: e m 1 e m 2 . . . e m n ¼ e m 1 þ m 2 þ ... þ m n
Logarithmieren (Rechenregeln: ln ðu v wÞ ¼ ln u þ ln v þ ln w; ln u n ¼ n ln u; ln e m ¼ m):
n
n
1
1
1
ba
ba
*
¼ ln
a c e
a þ ln c þ ln e
a þ ln c b a
¼ n ln
L ¼ ln L ðaÞ ¼ ln
3
3
3
Wir bilden die benötigten Ableitungen 1. und 2. Ordnung von L * nach a:
dL*
1
¼ n
da
1
d2 L*
n
n
¼ 2 0 ¼ 2 < 0
2
da
a
a
1
n
þ0b ¼
b;
3
a
a
3
Die 1. Ableitung muss bei einem Maximum notwendigerweise verschwinden:
dL*
¼ 0
da
n
b ¼ 0
a
)
)
n
¼ b
a
)
a ¼
n
b
Die 2. Ableitung ist stets negativ, somit ist auch die hinreichende Bedingung für ein Maximum erfüllt. Damit ist
^ ¼
a
n
n
¼
1=3
1=3
1=3
b
t1 þ t2 þ . . . þ tn
der gesuchte Schätzwert des Parameters a.
Radioaktiver Zerfall
Eine radioaktive Substanz emittiert regellos a-Teilchen, wobei die diskrete Zufallsvariable
X ¼ Anzahl der in einem bestimmten Zeitintervall emittierten a-Teilchen
in guter Näherung einer Poisson-Verteilung mit der Dichtefunktion
f ðxÞ ¼
mx
em
x!
ðx ¼ 0, 1, 2, . . .Þ
genügt. In einem Experiment wurde in n ¼ 100 aufeinander folgenden Zeitintervallen gleicher Länge
K50
D t ¼ 10 s jeweils die Anzahl x i der emittierten a-Teilchen registriert (s: Sekunde). Das Messprotokoll hatte das folgende Aussehen (n i : Anzahl der Zeitintervalle mit x i emittierten a-Teilchen;
i ¼ 1, 2, . . . , 6):
i
1
2
3
4
5
6
xi
0
1
2
3
4
5
ni
2
14
22
35
23
4
Bestimmen Sie aus dieser Stichprobe einen Schätzwert m^ für den noch unbekannten Parameter m in
der Dichtefunktion.
Der gesuchte Schätzwert m^ ist der Mittelwert x der Stichprobe:
m
m^ ¼ x ¼
¼
6
X
1
1
ð2 0 þ 14 1 þ 22 2 þ 35 3 þ 23 4 þ 4 5Þ ¼
ni xi ¼
100 i ¼ 1
100
1
1
ð0 þ 14 þ 44 þ 105 þ 92 þ 20Þ ¼
275 ¼ 2,75
100
100
636
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Die stetige Zufallsvariable
T ¼ „Lebensdauer“ eines elektronischen Bauelementes
K51
kann als exponentialverteilt mit dem (noch unbekannten) Parameter l angesehen werden. Bestimmen
Sie anhand der folgenden Stichprobe vom Umfang n ¼ 10 einen Schätzwert l^ für den Parameter l
(Stichprobe: Lebensdauer von 10 willkürlich entnommenen Bauelementen in der Einheit Stunde (h)):
i
t i =h
1
2
3
4
5
6
7
8
9
10
450
430
505
490
450
470
495
470
465
425
Wie lautet die Dichtefunktion dieser Exponentialverteilung?
Der gesuchte Schätzwert l^ des Parameters l ist der Kehrwert des Stichprobenmittelwertes t (! FS: Kap. XVI.3.2.4):
t ¼
¼
10
1 X
1
ð450 þ 430 þ 505 þ 490 þ 450 þ 470 þ 495 þ 470 þ 465 þ 425Þ h ¼
ti ¼
10 i ¼ 1
10
1
4 650 h ¼ 465 h
10
1
1
Schätzwert: l^ ¼
¼
¼ 0,002 151 h 1
t
465 h
Dichtefunktion: f ðtÞ ¼ l e l t ¼ 0,002 151 e 0,002 151 t
ðt 0 ; t in hÞ
Qualitätskontrolle
K52
Aufgrund langjähriger Erfahrung kann man bei der Serienproduktion eines bestimmten Massenartikels
von einem Ausschussanteil von höchstens 2 % ausgehen. Zwecks Qualitätskontrolle wird der Tagesproduktion eine Stichprobe vom Umfang n ¼ 120 entnommen, in der sich genau k ¼ 2 defekte Artikel
befanden. Welchen Schätzwert p^ für den unbekannten Ausschussanteil p liefert diese Stichprobe?
Schätzwert für den Ausschussanteil p (! FS: Kap. XVI.3.2.3): p^ ¼
k
2
1
¼
¼
n
120
60
1,67 %
Fazit: Die Stichprobe ergibt für den Parameter p (Ausschussanteil) einen Wert unterhalb von 2 % und bestätigt damit
den aus der langjährigen Erfahrung gewonnenen Wert.
Serienmäßige Produktion von ohmschen Widerständen
Die stetige Zufallsvariable
R ¼ Ohmscher Widerstand
K53
ist normalverteilt mit den noch unbekannten Parametern m (¼ Mittelwert) und s (¼ Standardabweichung). Welche Schätzwerte für diese Parameter liefert die folgende Stichprobe (Messung von n ¼ 8
Widerständen aus einer Tagesproduktion, alle Werte in der Einheit Ohm (W)):
i
1
2
3
4
5
6
7
8
Ri
98,2
99,5
98,8
100,5
101,2
99,7
99,0
97,5
6 Parameterschätzungen
637
Wir bestimmen zunächst den Mittelwert R und die Varianz s 2 bzw. Standardabweichung s der Stichprobe:
R ¼
¼
s2 ¼
8
1 X
1
ð98,2 þ 99,5 þ 98,8 þ 100,5 þ 101,2 þ 99,7 þ 99,0 þ 97,5Þ W ¼
Ri ¼
8 i¼1
8
1
794,4 W ¼ 99,3 W
8
8
X
1
1 h
ðR i RÞ 2 ¼
ð98,2 99,3Þ 2 þ ð99,5 99,3Þ 2 þ ð98,8 99,3Þ 2 þ
8 1 i¼1
7
i
þ ð100,5 99,3Þ 2 þ ð101,2 99,3Þ 2 þ ð99,7 99,3Þ 2 þ ð99,0 99,3Þ 2 þ ð97,5 99,3Þ 2 W 2 ¼
i
1 h 2
1,1 þ 0,2 2 þ 0,5 2 þ 1,2 2 þ 1,9 2 þ 0,4 2 þ 0,3 2 þ 1,8 2 W 2 ¼
7
i
1 h
1
¼
1,21 þ 0,04 þ 0,25 þ 1,44 þ 3,61 þ 0,16 þ 0,09 þ 3,24 W 2 ¼
10,04 W 2 ¼ 1,4343 W 2
7
7
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
s ¼ s 2 ¼ 1,4343 W 2 ¼ 1,198 W
¼
Schätzwerte für die Parameter m und s (! FS: Kap. XVI.3.2.2):
m
m^ ¼ R ¼ 99,3 W ;
s
s^ ¼ s ¼ 1,198 W
1,20 W
6.2 Intervallschätzungen
Bei einer Intervallschätzung wird ein sog. Vertrauens- oder Konfidenzintervall konstruiert, in dem der unbekannte Parameter einer vom Typ her bekannten Verteilung mit einer vorgegebenen (großen) Wahrscheinlichkeit vermutet wird.
Lehrbuch: Band 3, Kapitel III.3.4
Formelsammlung: Kapitel XVI.3.3
Tabellen zur Wahrscheinlichkeitsrechnung und Statistik (Tabellen 2 bis 4):
Band 3 (Anhang, Teil A) und Formelsammlung (Anhang, Teil B)
Vollautomatische Abfüllanlage einer Weinkellerei
In einer Weinkellerei wird eine größere Menge Weißwein auf einer automatischen Abfüllanlage in Literflaschen gefüllt. Die Zufallsvariable
X ¼ Füllmenge einer Flasche (in l ¼ 1000 ml)
ist dabei eine normalverteilte Größe mit der Standardabweichung s ¼ 2 ml (ein aus langjähriger Erfah-
K54
rung gewonnener Wert). Zu Kontrollzwecken wurden n ¼ 80 gefüllte Flaschen wahllos entnommen und
ihre Abfüllmenge gemessen. Diese Stichprobe ergab eine mittlere Füllmenge von x ¼ 999,2 ml, d. h.
einen Wert knapp unterhalb des vorgegebenen Sollwertes m 0 ¼ 1 Liter ¼ 1000 ml. Muß die Abfüllanlage daher neu eingestellt werden?
Anleitung: Bestimmen Sie zunächst ein Vertrauensintervall für den wahren (aber unbekannten) Mittelwert m der Zufallsvariablen X auf dem Vertrauensniveau g ¼ 95 % und treffen Sie dann eine Entscheidung.
638
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Wir lösen die Aufgabe schrittweise wie folgt (! FS: Kap. XVI.3.3.2):
1. Schritt: Das Vertrauensniveau ist vorgegeben
(g ¼ 0,95).
0,95
2. Schritt: Berechnung der Konstanten c aus
der Bedingung P ð c U cÞ ¼ g ¼ 0,95
für die standardnormalverteilte Zufallsvariable
X m
U ¼
pffiffiffi (siehe Bild K-18):
s= n
0,025
0,025
–c
0
u
c
Bild K-18
P ð c U cÞ ¼ F ðcÞ F ð cÞ ¼ F ðcÞ 1 F ðcÞ
2 F ðcÞ ¼ 1,95
)
F ðcÞ ¼ 0,975
)
¼ 2 F ðcÞ 1 ¼ 0,95
c ¼ u 0,975 ¼ 1,960
)
ðaus Tab: 2Þ
3. Schritt: Der Mittelwert x der Stichprobe ist bereits bekannt: x ¼ 999,2 (in ml)
4. Schritt: Bestimmung des Vertrauensintervalls x k m x þ k für den Mittelwert m
s
2
Hilfsgröße k : k ¼ c pffiffiffi ¼ 1,960 pffiffiffiffiffi ¼ 0,44
n
80
Vertrauensintervall für den Mittelwert m (alle Werte in ml):
999,2 0,44 m 999,2 þ 0,44
,
998,76 m 999,64
Folgerung und Entscheidung: Der Sollwert m 0 ¼ 1000 ml liegt außerhalb des Vertrauensintervalls, d. h. die Füllmengen sind zu gering und die Abfüllanlage muss daher neu eingestellt werden.
Umfrage eines Automobilclubs zum Benzinverbrauch eines PKW
Die Umfrage eines Automobilclubs zum Benzinverbrauch eines bestimmten PKW-Modells ergab bei
n ¼ 35 Teilnehmern für die als normalverteilt angesehene Zufallsvariable
K55
X ¼ Benzinverbrauch im Stadtverkehr in Liter pro 100 km Fahrstrecke (l=100 km)
folgende Werte: Mittelwert x ¼ 7,62 l=100 km; Standardabweichung s ¼ 1,12 l=100 km.
Bestimmen Sie für den unbekannten Mittelwert m der Zufallsvariablen X ein Vertrauens- oder Konfidenzintervall auf dem Vertrauensniveau g ¼ 0,90.
Es handelt sich in diesem Beispiel um eine sog. umfangreiche Stichprobe, da die Faustregel n > 30 für eine solche
Stichprobe erfüllt ist: n ¼ 35 > 30 (! FS: Kap. XVI.3.3.3). Daher dürfen wir die Zufallsvariable X als normalverteilt mit dem noch unbekannten Mittelwert m und der bekannten Standardabweichung s
s ¼ 1,12 l=100 km betrachten. Das gesuchte Vertrauensintervall läßt sich dann (wie in der Formelsammlung in Kap. XVI.3.3.2 beschrieben)
schrittweise wie folgt bestimmen:
1. Schritt: Das Vertrauensniveau g ¼ 0,90 ist bereits vorgegeben.
2. Schritt: Berechnung der Konstanten c aus der Bedingung P ð c U cÞ ¼ g ¼ 0,90 für die standardnorX m
malverteilte Zufallsvariable U ¼
pffiffiffi (siehe Bild K-19):
s= n
6 Parameterschätzungen
639
P ð c U cÞ ¼ F ðcÞ F ð cÞ ¼
¼ F ðcÞ 1 F ðcÞ ¼ 2 F ðcÞ 1 ¼ 0,90
2 F ðcÞ ¼ 1,90
c ¼ u 0,95 ¼ 1,645
)
F ðcÞ ¼ 0,95
0,90
)
0,05
0,05
ðaus Tab: 2Þ
–c
0
c
u
Bild K-19
3. Schritt: Der Mittelwert x ist bereits bekannt:
x ¼ 7,62.
4. Schritt: Bestimmung des Vertrauensintervalls x k m x þ k für den Mittelwert m
s
s
1,12
Hilfsgröße k : k ¼ c pffiffiffi ¼ c pffiffiffi ¼ 1,645 pffiffiffiffiffi ¼ 0,311
n
n
35
Vertrauensintervall für den Mittelwert m (alle Werte in l=100 km):
7,62 0,311 m 7,62 þ 0,311
,
7,309 m 7,931
Die Serienproduktion von Bauteilen für elektronische Geräte erfolgt mit einem (noch unbekannten) Ausschussanteil p. Aus der laufenden Produktion wird eine Stichprobe vom Umnfang n ¼ 500 entnommen, wobei sich k ¼ 40 Bauteile als unbrauchbar (defekt) erweisen. Schätzen Sie den Parameter p
K56
der binomialverteilten Grundgesamtheit und konstruieren Sie ein Vertrauensintervall auf dem Vertrauensniveau g ¼ 95 %:
Hinweis: Zeigen Sie zunächst, dass es sich hier um eine sog. umfangreiche Stichprobe handelt (!
FS: Kap. XVI.3.3.6).
Schätzwert des Parameters p: p^ ¼
k
40
¼
¼ 0,08
n
500
Die Faustregel für eine sog. umfangreiche Stichprobe ist erfüllt:
D ¼ n p^ ð1 p^Þ ¼ 500 0,08 ð1 0,08Þ ¼ 36,8 > 9
Die Zufallsvariable
X ¼ Anzahl der defekten Bauteile in einer Stichprobe vom Umfang n ¼ 500
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ist daher nahezu normalverteilt mit den Parametern m ¼ n p (Mittelwert) und s ¼ n p ð1 pÞ (Standardabweichung). Das gesuchte Vertrauensintervall läßt sich damit schrittweise wie folgt bestimmen (! FS: Kap. XVI.3.3.6):
1. Schritt: Das Vertrauensniveau ist mit g ¼ 0,95 vorgegeben.
2. Schritt: Berechnung der Konstanten c aus der Bedingung P ð c U cÞ ¼ g ¼ 0,95 für die standardnorX m
n P^ n p
malverteilte Zufallsvariable U ¼
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi (siehe Bild K-20):
n p ð1 pÞ
s
640
K Wahrscheinlichkeitsrechnung und mathematische Statistik
P ð c U cÞ ¼ F ðcÞ F ð cÞ ¼
¼ F ðcÞ 1 F ðcÞ ¼ 2 F ðcÞ 1 ¼ 0,95
2 F ðcÞ ¼ 1,95
c ¼ u 0,975 ¼ 1,960
)
F ðcÞ ¼ 0,975
0,95
)
0,025
0,025
ðaus Tab: 2Þ
–c
3. Schritt: Der Schätzwert für p ist bereits
bekannt: p^ ¼ k=n ¼ 0,08 (siehe weiter oben).
0
u
c
Bild K-20
4. Schritt: Bestimmung des Vertrauensintervalls p^ k p p^ þ k für den Parameter p
Hilfsgröße k: k ¼
c pffiffiffiffi
1,960 pffiffiffiffiffiffiffiffiffi
36,8 ¼ 0,024
D ¼
n
500
Vertrauensintervall für den Ausschussanteil (Parameter) p: 0,08 0,024 p 0,08 þ 0,024
0,056 p 0,104 oder
5,6 % p 10,4 %
Geschwindigkeitskontrolle auf einer Autobahn
An einem bestimmten Messpunkt auf einer Autobahn wurde die Geschwindigkeit von n ¼ 500 vorbeifahrenden Autos gemessen. Dabei wurden k ¼ 80 Verstöße wegen zu hoher Geschwindigkeit regis-
K57
triert. Bestimmen Sie einen Schätzwert p^ sowie ein Vertrauens- oder Konfidenzintervall auf dem Vertrauensniveau g ¼ 95 % für den Anteil p an Fahrern, die mit zu hoher Geschwindigkeit gemessen
wurden (p ist der Parameter einer Binomialverteilung mit der Zufallsvariablen X ¼ Anzahl der Fahrer
mit zu hoher Geschwindigkeit).
Schätzwert für den Anteil p: p^ ¼
k
80
¼
¼ 0,16 ¼
b 16 %
n
500
Es handelt sich hier um eine sog. umfangreiche Stichprobe, da die Faustregel für eine solche Stichprobe erfüllt ist
(! FS: Kap. XVI.3.3.6):
D ¼ n p^ ð1 p^Þ ¼ 500 0,16 ð1 0,16Þ ¼ 67,2 > 9
Das gesuchte Vertrauensintervall für den Anteil p (Parameter einer Binomialverteilung) lässt sich dann in guter Näherung schrittweise wie folgt bestimmen (! FS: Kap. XVI.3.3.6):
1. Schritt: Das Vertrauensniveau g ¼ 0,95 ist
vorgegeben.
2. Schritt: Berechnung der Konstanten c aus
der Bedingung P ð c U cÞ ¼ g ¼ 0,95
für die standardnormalverteilte Zufallsvariable
n P^ n p
U ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi (siehe Bild K-21):
n p ð1 pÞ
0,95
0,025
0,025
–c
Bild K-21
0
c
u
6 Parameterschätzungen
641
P ð c U cÞ ¼ F ðcÞ F ð cÞ ¼ F ðcÞ 1 F ðcÞ
2 F ðcÞ ¼ 1,95
)
F ðcÞ ¼ 0,975
)
¼ 2 F ðcÞ 1 ¼ 0,95
c ¼ u 0,975 ¼ 1,960
)
ðaus Tab: 2Þ
3. Schritt: Der Schätzwert p^ wurde bereits berechnet: p^ ¼ 0,16.
4. Schritt: Bestimmung des Vertrauensintervalls p^ k p p^ þ k für den Anteil p (siehe weiter oben)
Hilfsgröße k: k ¼
c pffiffiffiffi
1,960 pffiffiffiffiffiffiffiffiffi
D ¼
67,2 ¼ 0,032
n
500
Vertrauensintervall für den Anteil p:
0,16 0,032 p 0,16 þ 0,032
0,128 p 0,192 bzw: 12,8 % p 19,2 %
Umfrage über das Fahrverhalten eines PKW
Sind Sie mit dem Fahrverhalten Ihres PKW zufrieden? So lautete die Umfrage eines Automobilclubs
K58
unter den Besitzern eines bestimmten Automodells, das zu den Marktführern gehört (also in großer
Stückzahl produziert wird). Unter den n ¼ 2000 befragten Personen waren k ¼ 48 unzufriedene
Personen. Bestimmen Sie für den unbekannten Anteilswert p (Anteil der unzufriedenen Fahrer des
Automodells) einen Schätzwert p^ sowie das Vertrauensintervall auf dem Vertrauensniveau g ¼ 95 %.
Schätzwert für den Parameter p: p^ ¼
k
48
¼
¼ 0,024
n
2000
2,4 % der befragten Personen sind somit unzufrieden!
Die Umfrage liefert eine sog. umfangreiche Stichprobe, da die Faustregel für eine solche Stichprobe erfüllt ist (! FS:
Kap. XVI.3.3.6):
D ¼ n p^ ð1 p^Þ ¼ 2000 0,024 ð1 0,024Þ ¼ 46,848 > 9
Das gesuchte Vertrauensintervall für den Anteilswert p lässt sich dann schrittweise wie folgt konstruieren.
0,95
1. Schritt: Das Vertrauensniveau g ¼ 0,95 ist vorgegeben.
2. Schritt: Berechnung der Konstanten c aus
der Bedingung P ð c U cÞ ¼ g ¼ 0,95
für die annähernd standardnormalverteilte
n P^ n p
Zufallsvariable U ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi (Bild K-22):
n p ð1 pÞ
0,025
0,025
–c
0
c
Bild K-22
P ð c U cÞ ¼ F ðcÞ F ð cÞ ¼ F ðcÞ 1 F ðcÞ
2 F ðcÞ ¼ 1,95
)
F ðcÞ ¼ 0,975
)
¼ 2 F ðcÞ 1 ¼ 0,95
c ¼ u 0,975 ¼ 1,960
ðaus Tab: 2Þ
3. Schritt: Der Schätzwert des Parameters p ist bereits bekannt: p^ ¼ 0,024 (siehe weiter oben).
4. Schritt: Konstruktion des Vertrauensintervalls p^ k p p^ þ k für den Parameter p (Anteilswert)
Hilfsgröße k: k ¼
c pffiffiffiffi
1,960 pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
46,848 ¼ 0,0067
D ¼
n
2000
u
642
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Vertrauensintervall für den Anteilswert (Parameter) p: 0,024 0,0067 p 0,024 þ 0,0067
0,0173 p 0,0307
1,73 % p 3,07 %
oder
Systolischer Blutdruck
Der systolische Blutdruck einer Person kann als eine normalverteilte Zufallsvariable X betrachtet werden. Die an n ¼ 8 Personen vorgenommenen Messungen ergaben dabei folgende Werte (in mm Hg):
K59
i
1
2
3
4
5
6
7
8
xi
124
128
119
121
130
128
125
129
Bestimmen Sie für die folgenden Parameter der Normalverteilung jeweils ein Vertrauens- oder Konfidenzintervall auf dem Vertrauensniveau g ¼ 90 %:
a) Mittelwert m,
b) Varianz s 2
a) Da sowohl m als auch s 2 unbekannt sind, lässt sich mit Hilfe der t-Verteilung wie folgt ein Vertrauensintervall
für den Mittelwert m bestimmen (! FS: Kap. XVI.3.3.3):
1. Schritt: Das Vertrauensniveau g ¼ 0,90
ist vorgegeben.
0,90
2. Schritt: Berechnung der Konstanten c aus
der Bedingung P ð c T cÞ ¼ g ¼ 0,90
X m
für die Zufallsvariable T ¼
pffiffiffi , die der
S= n
t-Verteilung mit f ¼ n 1 ¼ 8 1 ¼ 7
Freiheitsgraden genügt (siehe Bild K-23):
0,05
0,05
–c
)
F ðcÞ ¼ 0,95
t
c
Bild K-23
P ð c T cÞ ¼ F ðcÞ F ð cÞ ¼ F ðcÞ 1 F ðcÞ
2 F ðcÞ ¼ 1,90
0
)
¼ 2 F ðcÞ 1 ¼ 0,90
c ¼ t ð0,95; 7Þ ¼ 1,895
)
ðaus Tab: 4Þ
3. Schritt: Berechnung des Mittelwertes x und der Varianz s 2 bzw. der Standardabweichung s der Stichprobe
vom Umfang n ¼ 8.
x ¼
s2 ¼
8
1 X
1
1
xi ¼
ð124 þ 128 þ 119 þ 121 þ 130 þ 128 þ 125 þ 129Þ ¼
1004 ¼ 125,5
8 i¼1
8
8
8
X
1
1
ð124 125,5Þ 2 þ ð128 125,5Þ 2 þ ð119 125,5Þ 2 þ
ðx i xÞ 2 ¼
8 1 i¼1
7
þ ð121 125,5Þ 2 þ ð130 125,5Þ 2 þ ð128 125,5Þ 2 þ ð125 125,5Þ 2 þ ð129 125,5Þ 2 ¼
¼
1
1,5 2 þ 2,5 2 þ 6,5 2 þ 4,5 2 þ 4,5 2 þ 2,5 2 þ 0,5 2 þ 3,5 2 ¼
7
1
1
2,25 þ 6,25 þ 42,25 þ 20,25 þ 20,25 þ 6,25 þ 0,25 þ 12,25Þ ¼
110 ¼ 15,7143
7
7
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s ¼ s 2 ¼ 15,7143 ¼ 3,9641
¼
6 Parameterschätzungen
643
4. Schritt: Konstruktion des Vertrauensintervalls x k m x þ k für den Mittelwert m
s
3,9641
Hilfsgröße k: k ¼ c pffiffiffi ¼ 1,895 pffiffiffi ¼ 2,6559
n
8
2,66
Vertrauensintervall (alle Werte in mm Hg): 125,5 2,66 m 125,5 þ 2,66
,
122,84 m 128,16
b) Ein Vertrauensintervall für die unbekannte Varianz s 2 lässt sich wie folgt mit Hilfe der Chi-Quadrat-Verteilung
bestimmen:
1. Schritt: Das Vertrauensniveau g ¼ 0,90 ist vorgegeben.
2. Schritt: Berechnung der Konstanten c 1 und c 2 aus den Bedingungen
F ðc 1 Þ ¼
1
1
ð1 gÞ ¼
ð1 0,9Þ ¼ 0,05 und
2
2
für die Zufallsvariable Z ¼ ðn 1Þ
F ðc 2 Þ ¼
1
1
ð1 þ gÞ ¼
ð1 þ 0,90Þ ¼ 0,95
2
2
S2
, die einer Chi-Quadrat-Verteilung mit f ¼ n 1 ¼ 8 1 ¼ 7 Freis2
heitsgraden genügt (! FS: Kap. XVI.3.3.5 und Bild K-24):
0,90
F ðc 1 Þ ¼ 0,05
)
c 1 ¼ z ð0,05; 7Þ ¼ 2,17
0,05
0,05
ðaus Tab: 3 entnommenÞ
F ðc 2 Þ ¼ 0,95
)
c 2 ¼ z ð0,95; 7Þ ¼ 14,06
ðaus Tab: 3 entnommenÞ
0
c1
c2
z
Bild K-24
3. Schritt: Die Stichprobenvarianz s 2 ist bereits aus Teil a) bekannt: s 2 ¼ 15,7143.
4. Schritt: Konstruktion des Vertrauensintervalls k 1 s 2 k 2 für die Varianz s 2
Hilfsgrößen k 1 , k 2 :
k1 ¼
ðn 1Þ s 2
ð8 1Þ 15,7143
¼
¼ 7,82 ;
c2
14,06
Vertrauensintervall für die Varianz s 2 :
k2 ¼
ðn 1Þ s 2
ð8 1Þ 15,7143
¼
¼ 50,69
c1
2,17
7,82 s 2 50,69
Stillstandszeiten bei Maschinen
Bei Maschinen gibt es immer wieder sog. Stillstandszeiten, bedingt durch einen Ausfall (technischer
Defekt) und einer sich anschließenden zeitaufwendigen Reparatur. Wir beschreiben diese Zeiten durch
K60
eine stetige Zufallsvariable X, deren Verteilung jedoch zunächst unbekannt ist. Bei einem bestimmten
Maschinentyp erhielt man bei insgesamt n ¼ 100 Ausfällen folgende Werte für den Mittelwert x und
die Standardabweichung s der Stichprobe: x ¼ 1,5 h, s ¼ 0,8 h (h ¼ Stunde). Bestimmen Sie für
den Mittelwert m der Zufallsvariablen X ein Vertrauens- oder Konfidenzintervall auf dem Vertrauensniveau g ¼ 95 %.
644
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Es liegt hier eine sog. umfangreiche Stichprobe vor, da die Faustregel n > 30 für eine solche Stichprobe erfüllt ist:
n ¼ 100 > 30 (! FS: Kap. XVI.3.3.4). Daher dürfen wir die Zufallsvariable X als annähernd normalverteilt betrachten mit dem noch unbekannten Mittelwert m und der ebenfalls unbekannten Varianz s 2 . Die Konstruktion des
gesuchten Vertrauensintervalls erfolgt damit wie in der Formelsammlung ausführlich beschrieben mit Hilfe der t-Verteilung (! FS: Kap. XVI.3.3.3).
1. Schritt: Das Vertrauensniveau g ¼ 0,95
ist vorgegeben.
0,95
2. Schritt: Berechnung der Konstanten c aus
der Bedingung
0,025
0,025
P ð c T cÞ ¼ g ¼ 0,95
X m
pffiffiffi , die einer
S= n
t-Verteilung mit f ¼ n 1 ¼ 100 1 ¼ 99
Freiheitsgraden genügt (siehe Bild K-25):
–c
für die Zufallsvariable T ¼
)
F ðcÞ ¼ 0,975
c
t
Bild K-25
P ð c T cÞ ¼ F ðcÞ F ð cÞ ¼ F ðcÞ 1 F ðcÞ
2 F ðcÞ ¼ 1,95
0
)
¼ 2 F ðcÞ 1 ¼ 0,95
c ¼ t ð0,975; 99Þ ¼ 1,984
)
ðaus Tab: 4Þ
3. Schritt: Mittelwert x und Standardabweichung s der Stichprobe sind bekannt: x ¼ 1,5 h; s ¼ 0,8 h.
4. Schritt: Konstruktion des Vertrauensintervalls x k m x þ k für den Mittelwert m
s
0,8
Hilfsgröße k : k ¼ c pffiffiffi ¼ 1,984 pffiffiffiffiffiffiffiffi ¼ 0,16
n
100
Vertrauensintervall (alle Werte in h): 1,5 0,16 m 1,5 þ 0,16 oder
1,34 m 1,66
7 Parametertests
Ein Parametertest ist ein statistisches Prüfverfahren für die unbekannten Parameter einer vom Typ her bekannten Wahrscheinlichkeitsverteilung.
Lehrbuch: Band 3, Kapitel III.4
Formelsammlung: Kapitel XVI.4
Tabellen zur Wahrscheinlichkeitsrechnung und Statistik (Tabellen 2 bis 4):
Band 3 (Anhang, Teil A) und Formelsammlung (Anhang, Teil B)
Die Serienproduktion von Kondensatoren mit einer Kapazität von 100 mF (Sollwert) soll einer Qualitätskontrolle unterzogen werden. Die Kapazität X der Kondensatoren kann dabei als eine annähernd nor-
K61
malverteilte Zufallsvariable mit einer Standardabweichung von s ¼ 2 mF angesehen werden. Eine
Stichprobe von n ¼ 9 entnommenen Kondensatoren ergab eine mittlere Kapazität von x ¼ 97,5 mF.
Man teste mit einer Irrtumswahrscheinlichkeit von a ¼ 1 %, ob der vorgegebene Sollwert (Mittelwert)
m 0 ¼ 100 mF
eingehalten
wurde,
die
festgestellte
Abweichung
x ¼ 97,5 mF vom Sollwert m 0 ¼ 100 mF also zufallsbedingt ist.
des
Stichprobenmittelwertes
7 Parametertests
645
Zweiseitiger Test mit der Nullhypothese H 0 : m ¼ m 0 ¼ 100 und der Alternativhypothese H 1 : m 6¼ m 0 ¼ 100
(! FS: Kap. XVI.4.2.1):
1. Schritt: Die Irrtumswahrscheinlichkeit a ist vorgegeben (a ¼ 0,01).
2. Schritt: Berechnung des kritischen Wertes c
0,99
X m0
X 100
Testvariable: U ¼
pffiffiffi ¼
pffiffiffi ¼
2= 9
s= n
¼
X 100
2=3
¼
3
0,005
0,005
ðX 100Þ
2
–c
Berechnung des kritischen Wertes c aus der Bedingung
P ð c U cÞ H 0 ¼ 1 a ¼ 1 0,01 ¼ 0,99
0
u
c
Bild K-26
für die standardnormalverteilte Testvariable U (siehe
Bild K-26):
P ð c U cÞ H 0 ¼ F ðcÞ F ð cÞ ¼ F ðcÞ 1 F ðcÞ
2 F ðcÞ ¼ 1,99
)
F ðcÞ ¼ 0,995
)
¼ 2 F ðcÞ 1 ¼ 0,99
c ¼ u 0,995 ¼ 2,576
)
ðaus Tab: 2Þ
Annahmebereich (nichtkritischer Bereich): 2,576 u 2,576
3. Schritt: Berechnung des Testwertes u^
u^ ¼
3
3
3
ðx 100Þ ¼ ð97,5 100Þ ¼
ð 2,5Þ ¼ 3,75
2
2
2
4. Schritt (Testentscheidung): Der Testwert u^ ¼ 3,75 liegt außerhalb des Annahmebereiches, also im kritischen
Bereich. Die Nullhypothese H 0 muss daher abgelehnt, der Sollwert m 0 ¼ 100 mF neu eingestellt werden.
Benzinverbrauch eines PKW
Der Benzinverbrauch eines PKW lässt sich in guter Näherung durch eine normalverteilte Zufallsvariable X beschreiben (Angabe in Liter pro 100 km Fahrstrecke (l=100 km)). Ein Automobilhersteller gibt
für ein bestimmtes Modell einen mittleren Verbrauch von m 0 ¼ 7,5 l=100 km an. Diese Angabe wurde
K62
von einer Fachzeitschrift mit Hilfe einer Stichprobe überprüft und führte zu dem folgenden Ergebnis:
Bei n ¼ 25 Testfahrzeugen wurde ein mittlerer Benzinverbrauch von x ¼ 8,4 l=100 km ermittelt mit
einer (empirischen) Standardabweichung von s ¼ 2,1 h=100 km,
Prüfen Sie mit einem geeigneten einseitigen Test auf dem Signifikanzniveau a ¼ 5 %, ob die Angabe
des Herstellers noch länger aufrecht erhalten werden kann.
Einseitiger Test mit der Nullhypothese H 0 : m ¼ m 0 7,5 und der Alternativhypothese H 1 : m > m 0 ¼ 7,5 (Abgrenzung nach oben; ! FS: Kap. XVI.4.2.2).
1. Schritt: Das Signifikanzniveau a ¼ 0,05 ist vorgegeben.
2. Schritt: Da die Varianz s 2 unbekannt ist, lautet die Testvariable wie folgt:
T ¼
X m0
X 7,5
X 7,5
5 ðX 7,5Þ
¼
pffiffiffi ¼
pffiffiffiffiffi ¼
S= n
S= 25
S=5
S
646
K Wahrscheinlichkeitsrechnung und mathematische Statistik
T genügt dabei einer t-Verteilung mit f ¼ n 1 ¼ 25 1 ¼ 24 Freiheitsgraden. Die Berechnung des kritischen
Wertes (kritischen Grenze) c erfolgt aus der Bedingung P ðT > cÞ H 0 ¼ a ¼ 0,05 unter Verwendung der Tabelle 4
(siehe Bild K-27):
0,95
0,05
Bild K-27
0
c
t
Annahmebereich
P ðT > cÞ H 0 ¼ 1 P ðT cÞ H 0 ¼ 1 F ðcÞ ¼ 0,05
c ¼ t ð0,95; 24Þ ¼ 1,711
)
F ðcÞ ¼ 0,95
)
ðaus Tab: 4Þ
Annahmebereich (nichtkritischer Bereich): t 1,711
3. Schritt: Berechnung des Testwertes ^t
^t ¼
5 ðx 7,5Þ
5 ð8,4 7,5Þ
¼
¼ 2,143
s
2,1
4. Schritt (Testentscheidung): Der Testwert ^t ¼ 2,143 liegt im kritischen Bereich (d. h. außerhalb des Annahmebereiches). Die Nullhypothese wird daher abgelehnt, der tatsächliche mittlere Benzinverbrauch ist größer als vom Hersteller angegeben.
Auf einer Maschine werden Wellen von hoher Präzision in großer Stückzahl produziert. Als Genauigkeitsmaß dient dabei die Standardabweichung s des normalverteilten Wellendurchmessers X, die auf
den Sollwert s 0 ¼ 0,1 mm eingestellt wurde. Zu Kontrollzwecken (Qualitätsüberwachung) wurde der
laufenden Produktion eine Zufallsstichprobe vom Umfang n ¼ 15 entnommen. Die Auswertung ergab
K63
eine im Vergleich zum Sollwert s 0 ¼ 0,1 mm deutlich größere (empirische) Standardabweichung
von s ¼ 0,2 mm. Muss man die Maschine neu einstellen oder kann die beobachtete Abweichung als
zufallsbedingt betrachtet werden?
Anleitung: Führen Sie einen geeigneten einseitigen Test für die Varianz s 2 der Zufallsvariablen X
(Wellendurchmesser) auf dem Signifikanzniveau a ¼ 5 % durch. ndert sich die dann getroffene Entscheidung, wenn der Test auf der Basis a ¼ 1 % durchgeführt wird?
Wir testen die Nullhypothese H 0 : s 2 s 20 gegen die Alternativhypothese H 1 : s 2 > s 20 (einseitiger Test, Abgrenzung nach oben; ! FS: Kap. XVI.4.2.4):
Test auf dem Signifikanzniveau a ¼ 0,05
1. Schritt: Das Signifikanzniveau ist vorgegeben (a ¼ 0,05).
2. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches.
Testvariable ist die Zufallsvariable
Z ¼ ðn 1Þ
S2
S2
1400
¼
ð15
1Þ
¼
S2
2
2
mm 2
s0
ð0,1 mmÞ
7 Parametertests
647
0,95
Z genügt dabei einer Chi-Quadrat-Verteilung mit
f ¼ n 1 ¼ 15 1 ¼ 14
Freiheitsgraden.
Die kritische Grenze c wird aus der Bedingung
0,05
P ðZ cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95
wie folgt berechnet (siehe Bild K-28):
c
0
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 0,95
c ¼ z ð0,95; 14Þ ¼ 23,68
z
)
Annahmebereich
ðaus Tab: 3Þ
Bild K-28
Annahmebereich: z 23,68
3. Schritt: Berechnung des Testwertes ^z der Testvariablen Z
z ¼ ðn 1Þ
^
s2
1400
1400
1400
¼
s2 ¼
ð0,2 mmÞ 2 ¼
0,04 mm 2 ¼ 1400 0,04 ¼ 56
mm 2
mm 2
s 20
mm 2
4. Schritt (Testentscheidung): Der Testwert ^z ¼ 56 liegt außerhalb des Annahmebereiches, die Nullhypothese H 0
muss daher zugunsten der Alternativhypothese H 1 abgelehnt werden. Die Abweichung ist signifikant, d. h. nicht zufallsbedingt. Die Maschine muss daher neu eingestellt werden.
Test auf dem Signifikanzniveau a ¼ 0,01
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 1 a ¼ 1 0,01 ¼ 0,99
)
c ¼ z ð0,99; 14Þ ¼ 29,14
ðaus Tab: 3Þ
Annahmebereich (nichtkritischer Bereich): z 29,14
Testentscheidung: Der (unveränderte) Testwert z^ ¼ 56 liegt auch in diesem Fall außerhalb des Annahmebereiches,
d. h. die Entscheidung ist die gleiche wie im Fall a ¼ 5 % (H 0 wird abgelehnt).
Die serienmäßige Herstellung eines bestimmten elektronischen Bauelements erfolgt nach den Angaben
des Produzenten mit einem Ausschussanteil von höchstens p 0 ¼ 2 %. Bei Anlieferung einer größeren
K64
Menge an einen Kunden wurde eine Gütekontrolle in Form einer Stichprobe von n ¼ 625 entnommenen Elementen durchgeführt. Unter diesen befanden sich k ¼ 16 defekte Elemente. berprüfen Sie
die Angaben des Herstellers bezüglich des maximalen Ausschussanteils durch einen geeigneten einseitigen Test auf dem Signifikanzniveau a ¼ 1 %.
Die Bedingung n p 0 ð1 p 0 Þ > 9 für eine umfangreiche Stichprobe aus der binomialverteilten Grundgesamtheit ist
hier erfüllt (! FS: Kap. XVI.4.2.5):
n p 0 ð1 p 0 Þ ¼ 625 0,02 ð1 0,02Þ ¼ 625 0,02 0,98 ¼ 12,25 > 9
Wir testen die Nullhypothese H 0 : p p 0 ¼ 0,02 gegen die Alternativhypothese H 1 : p > p 0 ¼ 0,02 (einseitiger
Test, Abgrenzung nach oben).
1. Schritt: Das Signifikanzniveau a ¼ 0,01 ist vorgegeben.
2. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
648
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Die kritische Grenze c wird aus der Bedingung
P ðU > cÞ H 0 ¼ a ¼ 0,01 für die annähernd normalverteilte Zufallsvariable
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
U ¼
ðP^ p 0 Þ ¼
p 0 ð1 p 0 Þ
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
625
¼
ðP^ 0,02Þ ¼
0,02 ð1 0,02Þ
0,99
0,01
0
c
u
Annahmebereich
¼ 178,5714 ðP^ 0,02Þ
Bild K-29
unter Verwendung der Tabelle 2 wie folgt bestimmt
(siehe Bild K-29):
P ðU > cÞ H 0 ¼ 1 P ðU cÞ H 0 ¼ 1 F ðcÞ ¼ 0,01
c ¼ u 0,99 ¼ 2,326
)
F ðcÞ ¼ 0,99
)
ðaus Tab: 2Þ
Annahmebereich (nichtkritischer Bereich): u 2,326
3. Schritt: Wir bestimmen den Schätzwert p^ des Parameters p und den Testwert u^ der Testvariablen U:
p^ ¼
k
16
¼
¼ 0,0256 ¼
b 2,56 %
n
625
u^ ¼ 178,5714 ð^
p 0,02Þ ¼ 178,5714 ð0,0256 0,02Þ ¼ 178,5714 0,0056 ¼ 1
4. Schritt (Testentscheidung): Der Testwert u^ ¼ 1 liegt im Annahmebereich u 2,326. Die Angabe des Herstellers bezüglich eines maximalen Ausschussanteils von p 0 ¼ 2 % kann daher auf der Basis dieser Stichprobe nicht
widerlegt werden, die festgestellte Abweichung ist zufallsbedingt.
Vergleichsmessungen von ohmschen Widerständen
Für Messungen von ohmschen Widerständen stehen zwei verschiedene Messgeräte A
und B zur
Verfügung, die auf unterschiedlichen Messmethoden beruhen. Vergleichsmessungen (Parallelmessungen)
an fünf Widerständen ergaben das folgende Messprotokoll (alle Werte in Ohm (W)):
Messung Nr. i
1
2
3
4
5
xi
150,2
151,8
148,5
150,5
149,2
yi
148,2
150,2
148,0
149,9
147,9
K65
Die Stichprobenwerte (Messwerte) sind Realisierungen der normalverteilten Zufallsvariablen X und Y
(sie beschreiben die Messwerte der beiden Geräte). Testen Sie auf dem Signifikanzniveau a ¼ 1 %,
ob beide Geräte (Messmethoden) als gleichwertig betrachtet werden können oder ob die beobachteten
Abweichungen signifikant, d. h. nicht zufallsbedingt sind.
Die beiden Stichproben (Messreihen) sind abhängig (sog. verbundene Stichproben), zu jedem Messwert x i gehört
genau ein Messwert y i (mit i ¼ 1, 2, . . . , 5). Durch Differenzbildung z i ¼ x i y i erhalten wir dann die folgende
Stichprobe (Realisierungen der ebenfalls normalverteilten Zufallsvariablen Z ¼ X Y; alle Werte in W):
Messung Nr. i
1
2
3
4
5
zi ¼ xi yi
2,0
1,6
0,5
0,6
1,3
7 Parametertests
649
Die Messgeräte A und B werden als gleichwertig betrachtet, wenn diese Stichprobe aus einer normalverteilten
Grundgesamtheit mit dem Mittelwert m ¼ m 1 m 2 ¼ 0 stammt ( m 1 und m 2 sind die Mittelwerte der Zufallsvariablen X und Y). Wir testen daher die Nullhypothese H 0 : m ¼ m 0 ¼ 0 gegen die Alternativhypothese H 1 :
m 6¼ m 0 ¼ 0 wie folgt (! FS: Kap. XVI.4.2.3.1 und 4.2.2).
1. Schritt: Das Signifikanzniveau a ¼ 0,01 ist vorgegeben.
2. Schritt: Da die Varianz s 2 der Zufallsvariablen Z ¼ X Y unbekannt ist, müssen wir die Testvariable
T ¼
pffiffiffi Z
Z m0
Z 0
pffiffiffi ¼
pffiffiffi ¼ 5
S= n
S
S= 5
verwenden, die einer t-Verteilung mit f ¼ n 1 ¼ 5 1 ¼ 4 Freiheitsgraden genügt (! FS: Kap. XV.4.2.2). Den
kritischen Wert c bestimmen wir aus der Bedingung
P ð c T cÞ H 0 ¼ 1 a ¼ 1 0,01 ¼ 0,99
(siehe Bild K-30):
0,99
P ð c T cÞ H 0 ¼ F ðcÞ F ð cÞ ¼
¼ F ðcÞ 1 F ðcÞ ¼ 2 F ðcÞ 1 ¼ 0,99
2 F ðcÞ ¼ 1,99
)
F ðcÞ ¼ 0,995
c ¼ t ð0,995; 4Þ ¼ 4,604
ðaus Tab: 4Þ
0,005
0,005
)
–c
0
c
t
Annahmebereich
Annahmebereich (nichtkritischer Bereich):
4,604 t 4,604
Bild K-30
3. Schritt: Berechnung des Mittelwertes z, der Varianz s 2 und der Standardabweichung s der Stichprobe sowie des
Testwertes ^t der Testvariablen T
5
1 X
1
ð2,0 þ 1,6 þ 0,5 þ 0,6 þ 1,3Þ ¼ 1,2
z ¼
zi ¼
5 i¼1
5
s2 ¼
¼
5
X
1
ðz i zÞ 2 ¼
5 1 i¼1
i
1 h
ð2,0 1,2Þ 2 þ ð1,6 1,2Þ 2 þ ð0,5 1,2Þ 2 þ ð0,6 1,2Þ 2 þ ð1,3 1,2Þ 2 ¼
4
1
1
1
ð0,8 2 þ 0,4 2 þ 0,7 2 þ 0,6 2 þ 0,1 2 Þ ¼
ð0,64 þ 0,16 þ 0,49 þ 0,36 þ 0,01Þ ¼
1,66 ¼ 0,415
4
4
4
pffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
s ¼ s 2 ¼ 0,415 ¼ 0,6442
¼
Testwert: ^t ¼
pffiffiffi z
pffiffiffi
1,2
5
¼ 5
¼ 4,165
s
0,6442
4. Schritt (Testentscheidung): Der Testwert ^t ¼ 4,165 liegt im Annahmebereich. Die beobachtete Abweichung ist
zufallsbedingt und wir dürfen die beiden Messgeräte (bzw. Messmethoden) als gleichwertig betrachten.
K66
Ein elektronisches Bauelement wird in zwei Werken A und B in jeweils großer Stückzahl nach dem
gleichen Verfahren hergestellt. Es wird vermutet, dass die im Werk A produzierten Elemente eine
größere „Lebensdauer“ besitzen. Die Vermutung wird durch die folgende Stichprobenuntersuchung offenbar gestützt (die beiden Stichproben sind voneinander unabhängig; h ¼ Stunde):
Werk
Anzahl der untersuchten Elemente
Mittlere Lebensdauer
Standardabweichung
A
n 1 ¼ 100
x ¼ 2070 h
s 1 ¼ 160 h
B
n 2 ¼ 100
y ¼ 2000 h
s 2 ¼ 150 h
650
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Die beiden Zufallsvariablen X, Y (= Lebensdauer eines im Werk A bzw. B produzierten Elements)
dürfen dabei als normalverteilte Größen mit unbekannten Mittelwerten ( m 1 bzw. m 2 ) und unbekannten Varianzen (s 21 bzw. s 22 ) vorausgesetzt werden. Zeigen Sie: Ein einseitig durchgeführter Differenzentest für die Mittelwerte auf dem Signifikanzniveau a ¼ 1 % bestätigt die Vermutung m 1 > m 2 .
Hinweis: Beachten Sie, dass es sich hier um sog. umfangreiche Stichproben handelt.
Wir testen die Nullhypothese H 0 : m 1 m 2 gegen die Alternativhypothese H 1 : m 1 > m 2 . Die unbekannten Varianzen bzw. Standardabweichungen der Zufallsvariablen X und Y dürfen dabei näherungsweise ersetzt werden durch
die empirischen Werte, da die Faustregel für umfangreiche Stichproben (n 1 > 30 und n 2 > 30) erfüllt ist:
n 1 ¼ n 2 ¼ 100 > 30. Daher gilt näherungsweise
s1
s 1 ¼ 160 h
und
s2
s 2 ¼ 150 h
(Testverfahren ! FS: Kap. XVI.4.2.3.2)
1. Schritt: Das Signifikanzniveau ist vorgegeben (a ¼ 0,01).
2. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
X Y
mit der Standardabweichung
s
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
s 21
s 22
ð160 hÞ 2 þ ð150 hÞ 2
¼
þ
¼ 481 h ¼ 21,932 h
n1
n2
100
Testvariable ist die standardnormalverteilte Zufallsvariable U ¼
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s 21
s2
s ¼
þ 2
n1
n2
Die kritische Grenze c wird aus der Bedingung
0,99
P ðU cÞ H 0 ¼ 1 a ¼ 1 0,01 ¼ 0,99
berechnet (siehe Bild K-31):
0,01
P ðU cÞ H 0 ¼ F ðcÞ ¼ 0,99
c ¼ u 0,99 ¼ 2,326
)
0
ðaus Tab: 2Þ
c
u
Annahmebereich
Annahmebereich: u c ¼ 2,326
Bild K-31
3. Schritt: Berechnung des Testwertes u^ der Testvariablen U
u^ ¼
x y
ð2070 2000Þ h
70
¼
¼ 3,192
¼
s
21,932 h
21,932
4. Schritt (Testentscheidung): Der Testwert u^ ¼ 3,192 liegt außerhalb des Annahmebereiches u 2,326. Die
Nullhypothese H 0 wird daher zugunsten der Alternativhypothese H 1 abgelehnt. Die Stichprobenuntersuchung bestätigt also die Vermutung m 1 > m 2 , d. h. wir können davon ausgehen, dass die im Werk A produzierten Elemente eine
größere Lebensdauer besitzen.
7 Parametertests
651
Gleichwertigkeit zweier Pumpen
Die Gleichwertigkeit zweier Pumpen P1 und P 2 soll anhand einer Stichprobenuntersuchung nachgewiesen werden. Dabei wird vorausgesetzt, dass die beiden voneinander unabhängigen Zufallsvariablen
X; Y ¼ Fördervolumen pro Minute der Pumpe P1 bzw. P 2
normalverteilt sind mit den unbekannten Mittelwerten m 1 und m 2 und den ebenfalls unbekannten
(aber als gleich angenommenen) Varianzen s 21 und s 22 (s 21 ¼ s 22 ). Eine konkrete Stichprobenunter-
K67
suchung vom gleichen Umfang n 1 ¼ n 2 ¼ n ¼ 10 brachte das folgende Ergebnis (empirische Mittelwerte und Standardabweichungen):
Pumpe P1
x ¼ 70 l=min;
s 1 ¼ 4,1 l=min
Pumpe P 2
y ¼ 72 l=min;
s 2 ¼ 4,3 l=min
(l=min ¼ Liter pro Minute)
Testen Sie mit einer Irrtumswahrscheinlichkeit (Signifikanzzahl) von a ¼ 5 %, ob die Zufallsvariablen X und Y einer identischen Normalverteilung genügen ( m 1 ¼ m 2 ).
Zweiseitiger Test mit der Nullhypothese H 0 : m 1 ¼ m 2 und der Alternativhypothese H 1 : m 1 6¼ m 2 (! FS: Kap.
XVI.4.2.3.2)
1. Schritt: Das Signifikanzniveau ist vorgegeben (a ¼ 0,05).
2. Schritt: Bestimmung des kritischen Wertes und des Annahmebereiches
Die Testvariable lautet (Sonderfall n 1 ¼ n 2 ¼ n ¼ 10 beachten):
T ¼
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
s 21 þ s 22
ðX YÞ ¼
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
10
4,1 2 þ 4,3 2
ðX YÞ ¼ 0,5322 ðX YÞ
T genügt einer t-Verteilung mit f ¼ n 1 þ n 2 2 ¼ n þ n 2 ¼ 2 n 2 ¼ 20 2 ¼ 18 Freiheitsgraden. Der
kritische Wert c wird aus der Bedingung
P ð c T cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95
wie folgt berechnet (siehe Bild K-32):
0,95
P ð c T cÞ H 0 ¼ F ðcÞ F ð cÞ ¼
¼ F ðcÞ 1 F ðcÞ
¼ 2 F ðcÞ 1 ¼ 0,95
2 F ðcÞ ¼ 1,95
)
c ¼ t ð0,975; 18Þ ¼ 2,101
0,025
¼
)
F ðcÞ ¼ 0,975
ðaus Tab: 4Þ
0,025
–c
)
0
c
t
Annahmebereich
Bild K-32
Annahmebereich (nichtkritischer Bereich): 2,101 t 2,101
3. Schritt: Berechnung des Testwertes ^t der Testvariablen T
^t ¼ 0,5322 ðx yÞ ¼ 0,5322 ð70 72Þ ¼ 0,5322 ð 2Þ ¼ 1,0644
4. Schritt (Testentscheidung): Der Testwert ^t ¼ 1,0644 liegt im Annahmebereich, die Nullhypothese H 0 kann daher
nicht abgelehnt werden. Die beiden Pumpen dürfen somit bezüglich ihrer Leistung als gleichwertig angesehen werden.
652
K Wahrscheinlichkeitsrechnung und mathematische Statistik
8 Chi-Quadrat-Test
Der Chi-Quadrat-Test ist ein sog. Anpassungs- oder Verteilungstest: Einer Grundgesamtheit mit der unbekannten
Verteilungsfunktion F ðxÞ wird eine bekannte Verteilungsfunktion F 0 ðxÞ „angepasst“.
Lehrbuch: Band 3, Kapitel III.5.3
Formelsammlung: Kapitel XVI.5
Tabellen der Wahrscheinlichkeitsrechnung und Statistik (Tabellen 1 und 3):
Band 3 (Anhang, Teil A) und Formelsammlung (Anhang, Teil B)
Beim Würfeln mit einem homogenen Würfel erwarten wir eine Gleichverteilung der sechs möglichen
Augenzahlen (1, 2, . . . , 6) bei einer großen Anzahl von Würfen. Eine Stichprobe aus n ¼ 600 Würfen ergab für die Zufallsvariable
X ¼ Augenzahl des Würfels
K68
die folgende Verteilung:
Augenzahl i
n i ¼ Anzahl der Würfe
mit der Augenzahl i
1
2
3
4
5
6
108
101
95
99
94
103
Spricht diese Stichprobe für oder gegen eine Gleichverteilung? Treffen Sie eine Entscheidung mit Hilfe
des Chi-Quadrat-Tests auf dem Signifikanzniveau (Irrtumswahrscheinlichkeit) a ¼ 5 %.
Gleichverteilung bedeutet, dass jede der sechs Augenzahlen mit der gleichen Wahrscheinlichkeit p i ¼ p ðiÞ ¼ 1=6
auftritt (es handelt sich um ein Laplace-Experiment). Nullhypothese H 0 und Alternativhypothese H 1 des Chi-Quadrat-Tests lauten daher wie folgt:
H0 : pi ¼
1
;
6
H 1 : p i 6¼
1
6
ði ¼ 1, 2, . . . , 6Þ
1. Schritt: Die Klasseneinteilung ist vorgegeben; die k ¼ 6 Klassen entsprechen den 6 Augenzahlen (Spalte 1 der
nachfolgenden Tabelle). Die zugehörigen Besetzungszahlen (absoluten Häufigkeiten) n i sind ebenfalls bekannt und in
der 2. Spalte der Tabelle aufgeführt.
2. Schritt: Berechnung der theoretischen Besetzungszahlen (Klassenhäufigkeiten) n i*
Die Berechnung der theoretischen Besetzungszahlen ergibt die folgende Gleichverteilung (unter der Voraussetzung,
dass die Nullhypothese zutrifft):
i-te Klasse
n i* ¼ n p i ¼ 600
1
¼ 100
6
ðf ür i ¼ 1, 2, . . . , 6Þ
Die Werte für p i und n i* sind in der folgenden Tabelle zusammengestellt (Spalten 3 und 4):
8 Chi-Quadrat-Test
Klasse Nr. i
(Augenzahl i)
653
D n i ¼ n i n i*
ðD n i Þ 2
n i*
ni
pi
n i*
1
108
1=6
100
8
64=100
2
101
1=6
100
1
1=100
3
95
1=6
100
5
25=100
4
99
1=6
100
1
1=100
5
94
1=6
100
6
36=100
6
103
1=6
100
3
9=100
600
1
600
0
136=100
P
3. Schritt: Berechnung des Testwertes ^z der Testvariablen Z
Spalte 5 enthält die Abweichungen zwischen den beobachteten und den theoretischen Besetzungszahlen
(D n i ¼ n i n i*). Diese Werte werden quadriert und dann durch die jeweilige theoretische Besetzungszahl n i*
dividiert (siehe Spalte 6). Durch Aufsummieren erhält man schließlich den gesuchten Testwert ^
z der Testvariablen Z
(grau unterlegter Wert in der Tabelle):
z ¼
^
6
6
X
X
ðD n i Þ 2
ðn i n i*Þ 2
136
¼
¼
¼ 1,36
100
n i*
n i*
i¼1
i¼1
4. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
Die kritische Grenze c wird aus der Bedingung P ðZ cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95 für die Testvariable Z
berechnet, die einer Chi-Quadrat-Verteilung mit f ¼ k 1 ¼ 6 1 ¼ 5 Freiheitsgraden genügt (siehe Bild K-33):
0,95
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 0,95
c ¼ z ð0;95; 5Þ ¼ 11,07
)
ðaus Tab: 3Þ
Annahmebereich: z c ¼ 11,07
0,05
c
0
z
Annahmebereich
Bild K-33
5. Schritt (Testentscheidung): Der Testwert ^
z ¼ 1,36 liegt im Annahmebereich z 11,07. Die Nullhypothese
wird daher angenommen, d. h. nicht abgelehnt. Wir können somit von einer Gleichverteilung der Augenzahlen beim
Würfeln ausgehen, die Stichprobe spricht für einen einwandfreien homogenen, d. h. unverfälschten Würfel.
654
K Wahrscheinlichkeitsrechnung und mathematische Statistik
„Lebensdauer“ einer Batterie
Die „Lebensdauer“ einer speziellen Batterie lässt sich durch eine stetige Zufallsvariable T
beschrei-
ben, von der vermutet wird, dass sie einer Exponentialverteilung mit der Verteilungsfunktion
F 0 ðtÞ ¼ 1 e 0,001 t genügt ( t in Stunden (h); t > 0). Eine Stichprobenuntersuchung mit
n ¼ 100 wahllos herausgegriffenen Batterien aus der Serienproduktion führte zu dem folgenden Ergebnis (die 100 Messwerte der Lebensdauer T wurden dabei in k ¼ 6 Klassen mit den angegebenen
K69
Besetzungszahlen n i aufgeteilt; i ¼ 1, 2, . . . , 6):
1. Klasse
2. Klasse
3. Klasse
4. Klasse
5. Klasse
6. Klasse
29
18
10
13
15
15
ni
t i : Klassengrenze
0
400
800
1200
1600
2000
!
t/h
Prüfen Sie mit dem Chi-Quadrat-Test, ob die Annahme (Vermutung) einer Exponentialverteilung bei
einem gewählten Signifikanzniveau von a ¼ 5 % noch länger aufrechterhalten werden kann.
Nullhypothese H 0 : F ðtÞ ¼ F 0 ðtÞ ¼ 1 e 0,001 t
Alternativhypothese H 1 : F ðtÞ 6¼ F 0 ðtÞ
Der Chi-Quadrat-Test wird schrittweise wie folgt durchgeführt:
1. Schritt: Die Einteilung der Stichprobenwerte (Messwerte) in k ¼ 6 Klassen ist vorgegeben, die Besetzungszahlen
(beobachtete absolute Klassenhäufigkeiten) n i sind ebenfalls bekannt (Spalten 1 und 2 in der nachfolgenden Tabelle).
2. Schritt: Berechnung der Wahrscheinlichkeiten und hypothetischen Besetzungszahlen der Klassen
Berechnung der Wahrscheinlichkeit p i mit der als wahr angenommenen Verteilungsfunktion F 0 ðtÞ ¼ 1 e 0,001 t
( p i ist die Wahrscheinlichkeit, dass ein Messwert in die i-te Klasse fällt; i ¼ 1, 2, . . . , 6):
1: Klasse: 0 T < 400
p 1 ¼ P ð0 T < 400Þ ¼ F 0 ð400Þ F 0 ð0Þ ¼ ð1 e 0,4 Þ ð1 e 0 Þ ¼ 1 e 0,4 1 þ e 0 ¼
¼ e 0 e 0,4 ¼ 1 0,6703 ¼ 0,3297
2: Klasse: 400 T < 800
p 2 ¼ P ð400 T < 800Þ ¼ F 0 ð800Þ F 0 ð400Þ ¼ ð1 e 0,8 Þ ð1 e 0,4 Þ ¼
¼ 1 e 0,8 1 þ e 0,4 ¼ e 0,4 e 0,8 ¼ 0,6703 0,4493 ¼ 0,2210
3: Klasse: 800 T < 1200
p 3 ¼ P ð800 T < 1200Þ ¼ F 0 ð1200Þ F 0 ð800Þ ¼ ð1 e 1,2 Þ ð1 e 0,8 Þ ¼
¼ 1 e 1,2 1 þ e 0,8 ¼ e 0,8 e 1,2 ¼ 0,4493 0,3012 ¼ 0,1481
4: Klasse: 1200 T < 1600
p 4 ¼ P ð1200 T < 1600Þ ¼ F 0 ð1600Þ F 0 ð1200Þ ¼ ð1 e 1,6 Þ ð1 e 1,2 Þ ¼
¼ 1 e 1,6 1 þ e 1,2 ¼ e 1,2 e 1,6 ¼ 0,3012 0,2019 ¼ 0,0993
8 Chi-Quadrat-Test
655
5: Klasse: 1600 T < 2000
p 5 ¼ P ð1600 T < 2000Þ ¼ F 0 ð2000Þ F 0 ð1600Þ ¼ ð1 e 2 Þ ð1 e 1,6 Þ ¼
¼ 1 e 2 1 þ e 1,6 ¼ e 1,6 e 2 ¼ 0,2019 0,1353 ¼ 0,0666
6: Klasse: T 2000
p 6 ¼ P ðT 2000Þ ¼ 1 P ðT < 2000Þ ¼ 1 F 0 ð2000Þ ¼ 1 ð1 e 2 Þ ¼
¼ 1 1 þ e 2 ¼ e 2 ¼ 0,1353
Die Berechnung der hypothetischen Besetzungszahlen n i* erfolgt nach der Formel n i* ¼ n p i ¼ 100 p i . Die Werte
für p i und n i* sind in den Spalten 3 und 4 der folgenden Tabelle zusammengestellt:
ðD n i Þ 2
n i*
Klasse Nr. i
ni
pi
n i* ¼ 150 p i
D n i ¼ n i n i*
1
29
0,3297
32,97
3,97
0,4780
2
18
0,2210
22,10
4,10
0,7606
3
10
0,1481
14,81
4,81
1,5622
4
13
0,0993
9,93
3,07
0,9491
5
15
0,0666
6,66
8,34
10,4438
6
P
15
0,1353
13,53
1,47
0,1597
100
1
100
0
14,3534
3. Schritt: Berechnung des Testwertes ^z der Testvariablen Z
Zunächst werden die Abweichungen der beobachteten Besetzungszahlen von den hypothetischen Besetzungszahlen bestimmt (D n i ¼ n i n i* ; Spalte 5 der Tabelle). Dann werden diese Differenzen quadriert und durch die jeweilige
hypothetische Besetzungszahl n i* dividiert (Spalte 6). Durch Aufsummieren erhält man den gesuchten Testwert (in der
Tabelle grau unterlegt):
z ¼
^
6
6
X
X
ðD n i Þ 2
ðn i n i*Þ 2
¼
¼ 14,3534
n i*
n i*
i¼1
i¼1
4. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
Die kritische Grenze c wird aus der Bedingung P ðZ cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95 für die Testvariable Z
berechnet (Z genügt einer Chi-Quadrat-Verteilung mit f ¼ k 1 ¼ 6 1 ¼ 5 Freiheitsgraden; siehe Bild K-34):
0,95
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 0,95
c ¼ z ð0;95; 5Þ ¼ 11,07
)
0,05
ðaus Tab: 3Þ
Annahmebereich: z c ¼ 11,07
0
c
Annahmebereich
Bild K-34
z
656
K Wahrscheinlichkeitsrechnung und mathematische Statistik
5. Schritt (Testentscheidung): Der Testwert ^z ¼ 14,3534 liegt außerhalb des Annahmebereiches z 11,07, die
Nullhypothese H 0 muss daher verworfen werden. Wir können also davon ausgehen, dass die Lebensdauer T der
Batterien nicht exponentialverteilt ist.
Es wird vermutet, dass die diskrete Zufallsvariable X einer Poisson-Verteilung genügt. Zu welchem
Ergebnis führt ein auf dem Signifikanzniveau a ¼ 5 % durchgeführter Chi-Quadrat-Test, dem die
folgende Stichprobe vom Umfang n ¼ 150 zugrunde liegt?
K70
i
1
2
3
4
5
xi
0
1
2
3
4
ni
67
52
26
4
1
(n i : absolute Häufigkeit des Stichprobenwertes x i mit i ¼ 1, 2, . . . , 5)
Der Parameter (Mittelwert) m der Poisson-Verteilung ist noch unbekannt und muss daher aus der Stichprobe geschätzt
werden (Schätzwert ¼ Stichprobenmittelwert x):
x ¼
¼
5
X
1
1
1
ð67 0 þ 52 1 þ 26 2 þ 4 3 þ 1 4Þ ¼
ð0 þ 52 þ 52 þ 12 þ 4Þ ¼
ni xi ¼
150 i ¼ 1
150
150
120
¼ 0,8
150
Somit gilt m
x ¼ 0,8 und die Wahrscheinlichkeitsfunktion der vermuteten Poisson-Verteilung lautet damit:
f 0 ðxÞ ¼ P ðX ¼ xÞ ¼
mx
0,8 x
em ¼
e 0,8
x!
x!
ðx ¼ 0, 1, 2, . . .Þ
Wir testen die Nullhypothese H 0 : f ðxÞ ¼ f 0 ðxÞ gegen die Alternativhypothese H 1 : f ðxÞ 6¼ f 0 ðxÞ.
1. Schritt (Klasseneinteilung): Das Stichprobenmaterial muss zunächst (unter Beachtung der Regel, dass jede Klasse
mindestens 5 Stichprobenwerte enthalten sollte) in Klassen unterteilt werden. Sinnvollerweise bilden wir k ¼ 4 Klassen: X ¼ 0, X ¼ 1, X ¼ 2 und X 3 mit der Reihe nach 67, 52, 26 und 5 Messwerten (siehe Spalten 1 und 2
der nachfolgenden Tabelle, die schrittweise erweitert wird).
2. Schritt: Berechnung der Wahrscheinlichkeiten p i ¼ f 0 ðx i Þ und der theoretischen Besetzungszahlen (absoluten
Klassenhäufigkeiten) n i* ¼ n p i ¼ 150 p i (p i : Wahrscheinlichkeit, dass ein Stichprobenwert in die i-te Klasse fällt)
p 1 ¼ P ðX ¼ 0Þ ¼ f 0 ð0Þ ¼
0,8 0
e 0,8 ¼ 1 e 0,8 ¼ e 0,8 ¼ 0,4493
0!
p 2 ¼ P ðX ¼ 1Þ ¼ f 0 ð1Þ ¼
0,8 1
e 0,8 ¼ 0,8 e 0,8 ¼ 0,3595
1!
p 3 ¼ P ðX ¼ 2Þ ¼ f 0 ð2Þ ¼
0,8 2
0,64
e 0,8 ¼ 0,1438
e 0,8 ¼
2
2!
p 4 ¼ P ðX 3Þ ¼ 1 P ðX ¼ 0Þ P ðX ¼ 1Þ P ðX ¼ 2Þ ¼ 1 f 0 ð0Þ f 0 ð1Þ f 0 ð2Þ ¼
¼ 1 0,4493 0,3595 0,1438 ¼ 0,0474
Die Werte für p i und n i* ¼ 150 p i bilden die Spalten 3 und 4 der folgenden Tabelle:
8 Chi-Quadrat-Test
657
Klasse i
ni
pi
n i* ¼ 150 p i
D n i ¼ n i n i*
ðD n i Þ 2
n i*
1 (X ¼ 0)
67
0,4493
67,395
0,395
0,0023
2 (X ¼ 1)
52
0,3595
53,925
1,925
0,0687
3 (X ¼ 2)
26
0,1438
21,570
4,430
0,9098
4 (X 3)
P
5
0,0474
7,110
2,110
0,6262
150
1
150
0
1,6070
3. Schritt: Berechnung des Testwertes ^z der Testvariablen Z
Wir bestimmen zunächst die Abweichungen der beobachteten Besetzungszahlen von den theoretischen Besetzungszahlen (D n i ¼ n i n i*), quadrieren dann diese Werte und dividieren sie schließlich durch die entsprechende theoretische Besetzungszahl n i* (Spalten 5 und 6 der Tabelle). Durch Aufsummieren erhalten wir den gesuchten Testwert (in
der Tabelle grau unterlegt):
z ¼
^
4
4
X
X
ðD n i Þ 2
ðn i n i*Þ 2
¼
¼ 1,6070
n i*
n i*
i¼1
i¼1
4. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
Die kritische Grenze c bestimmen wir aus der Bedingung P ðZ cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95 (siehe Bild
K-35) für die einer Chi-Quadrat-Verteilung genügenden Testvariable Z wie folgt (Anzahl der Freiheitsgrade:
f ¼ ðk 1Þ r ¼ ð4 1Þ 1 ¼ 2; k ¼ 4 Klassen; r ¼ 1: Anzahl der zunächst unbekannten Parameter):
0,95
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 0,95
c ¼ z ð0;95; 2Þ ¼ 5,99
)
ðaus Tab: 3Þ
0,05
Annahmebereich: z c ¼ 5,99
c
0
z
Annahmebereich
Bild K-35
5. Schritt (Testentscheidung): Der Testwert ^z ¼ 1,6070 liegt im Annahmebereich z 5,99, die Nullhypothese
H 0 wird daher angenommen (d. h. nicht abgelehnt). Die Zufallsvariable X darf daher als poissonverteilt mit dem
Parameter m
0,8 angesehen werden.
Es wird vermutet, dass die Zufallsvariable X standardnormalverteilt ist. Eine Stichprobe vom Umfang
n ¼ 30 ergab folgende Verteilung bei einer Einteilung der Stichprobenwerte in k ¼ 4 Klassen:
K71
i-te Klasse
1. Klasse
1 < x 1
2. Klasse
1 < x 0
3. Klasse
0 < x 1
4. Klasse
1 < x < 1
ni
5
9
11
5
(n i : absolute Klassenhäufigkeit; i ¼ 1, 2, 3, 4)
Testen Sie mit einer Irrtumswahrscheinlichkeit (Signifikanzzahl) von a ¼ 5 %, ob diese Vermutung
durch die Stichprobe gestützt wird (Chi-Quadrat-Test verwenden).
658
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Chi-Quadrat-Test mit der Nullhypothese H 0 : F ðxÞ ¼ F ðxÞ („die Zufallsvariable X genügt der Standardnormalverteilung mit der Verteilungsfunktion F ðxÞ“) und der Alternativhypothese H 1 : F ðxÞ 6¼ F ðxÞ.
1. Schritt: Klasseneinteilung (bereits vorgegeben)
k ¼ 4 Klassen mit 5, 9, 11 und 5 Stichprobenwerten (Spalten 1 und 2 der nachfolgenden Tabelle).
2. Schritt: Theoretische Häufigkeitsverteilung
Wir berechnen mit der als wahr angenommenen Verteilungsfunktion F ðxÞ der Standardnormalverteilung (siehe Tabelle 1) die Wahrscheinlichkeiten für die vier Klassen:
1: Klasse
p 1 ¼ P ðX 1Þ ¼ F ð 1Þ ¼ 1 F ð1Þ ¼ 1 0,8413 ¼ 0,1587
2: Klasse
p 2 ¼ P ð 1 < X 0Þ ¼ F ð0Þ F ð 1Þ ¼ F ð0Þ 1 F ð1Þ
¼ F ð0Þ 1 þ F ð1Þ ¼
¼ F ð0Þ þ F ð1Þ 1 ¼ 0,5 þ 0,8413 1 ¼ 0,3413
3: Klasse
p 3 ¼ P ð0 < X 1Þ ¼ F ð1Þ F ð0Þ ¼ 0,8413 0,5 ¼ 0,3413
4: Klasse
p 4 ¼ P ðX > 1Þ ¼ 1 P ðX 1Þ ¼ 1 F ð1Þ ¼ 1 0,8413 ¼ 0,1587
Damit ergeben sich die folgenden Wahrscheinlichkeiten und hypothetischen Besetzungszahlen (absoluten Häufigkeiten)
n i* ¼ n p i ¼ 30 p i , zusammengestellt in der folgenden Tabelle (Spalten 3 und 4):
D n i ¼ n i n i*
ðD n i Þ 2
n i*
Klasse i
ni
pi
n i* ¼ 30 p i
1
5
0,1587
4,761
0,239
0,011 998
2
9
0,3413
10,239
1,239
0,149 929
3
11
0,3413
10,239
0,761
0,056 560
4
P
5
0,1587
4,761
0,239
0,011 998
0
0,230 485
30
1
30
3. Schritt: Berechnung des Testwertes ^z der Testvariablen Z
Spalte 5 der Tabelle enthält die Abweichungen zwischen den beobachteten und den hypothetischen (theoretischen)
Besetzungszahlen, Spalte 6 die quadrierten Abweichungen, dividiert durch die jeweilige hypothetische Besetzungszahl
z (in der Tabelle grau unterlegt):
n i*. Durch Aufsummieren dieser Werte erhält man den gesuchten Testwert ^
z ¼
^
4
4
X
X
ðD n i Þ 2
ðn i n i*Þ 2
¼
¼ 0,230 485
n i*
n i*
i¼1
i¼1
4. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
Die kritische Grenze c wird aus der Bedingung P ðZ cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95 für die einer ChiQuadrat-Verteilung mit f ¼ k 1 ¼ 4 1 ¼ 3 Freiheitsgraden genügenden Testvariable Z bestimmt (siehe
Bild K-36):
8 Chi-Quadrat-Test
659
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 0,95
c ¼ z ð0;95; 3Þ ¼ 7,81
0,95
)
ðaus Tab: 3Þ
Annahmebereich: z c ¼ 7,81
0,05
Bild K-36
c
0
z
Annahmebereich
5. Schritt (Testentscheidung): Der Testwert ^z ¼ 0,230 485
0,23 liegt im Annahmebereich z 7,81. Die Nullhypothese H 0 wird daher beibehalten (angenommen). Wir können somit davon ausgehen, dass die Stichprobenwerte
aus einer normalverteilten Grundgesamtheit stammen (wie vermutet).
Eine Stichprobenuntersuchung an n ¼ 50 Kondensatoren aus einer Serienproduktion soll darüber Aufschluss geben, ob das dabei untersuchte Merkmal
X ¼ Kapazität des Kondensators (in Mikrofarad (mF))
als eine normalverteilte Zufallsvariable mit den noch unbekannten Parametern m (Mittelwert) und s
(Standardabweichung) angesehen werden kann. Die 50 Messwerte lagen dabei zwischen 97 mF und
K72
102 mF und wurden wie folgt in k ¼ 5 Klassen gleicher Breite D x ¼ 1 mF aufgeteilt:
Klasse Nr. i
1
2
3
4
5
Klassenmitte x~ i (in mF)
97,5
98,5
99,5
100,5
101,5
Besetzungszahl n i
5
10
16
12
7
Prüfen Sie mit Hilfe des Chi-Quadrat-Tests auf dem Signifikanzniveau a ¼ 5 %, ob die Vermutung
einer normalverteilten Kapazität begründet ist.
Null- und Alternativhypothese des Tests lauten wie folgt:
x m
; H 1 : F ðxÞ 6¼ F 0 ðxÞ
H 0 : F ðxÞ ¼ F 0 ðxÞ ¼ F
s
Dabei ist F ðuÞ mit u ¼ ðx mÞ=s die Verteilungsfunktion der Standardnormalverteilung (siehe Tabelle 1). Zunächst aber müssen wir die noch unbekannten Parameter m (Mittelwert) und s (Standardabweichung) der als wahr
angenommenen Normalverteilung aus der Stichprobe schätzen (als Schätzwerte verwenden wir den Stichprobenmittelwert x und die Stichprobenstandardabweichung s ! FS: Kap. XVI.2.1):
5
1 X
1
n i x~ i ¼
ð5 97,5 þ 10 98,5 þ 16 99,5 þ 12 100,5 þ 7 101,5Þ ¼
50 i ¼ 1
50
x ¼
¼
1
1
ð487,5 þ 985 þ 1592 þ 1206 þ 710,5Þ ¼
4981 ¼ 99,62
50
50
s2 ¼
5
X
1
1
n i ð~
x i xÞ 2 ¼
5 ð97,5 99,62Þ 2 þ 10 ð98,5 99,62Þ 2 þ 16 ð99,5 99,62Þ 2 þ
50 1 i ¼ 1
49
¼
1
69,28 ¼ 1,413 878
49
)
1
ð22,472 þ 12,544 þ 0,2304 þ 9,2928 þ 24,7408Þ ¼
49
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
1,189
s ¼ s 2 ¼ 1,413 878
þ 12 ð100,5 99,62Þ 2 þ 7 ð101,5 99,62Þ 2
¼
x ¼ 99,62 ; s
s ¼ 1,189 (jeweils in mF)
x 99,62
Vermutete Verteilungsfunktion: F 0 ðxÞ ¼ F
1,189
Somit gilt näherungsweise: m
660
K Wahrscheinlichkeitsrechnung und mathematische Statistik
1. Schritt (Unterteilung in Klassen): Nach Vorgabe k ¼ 5 Klassen mit insgesamt n ¼ 50 Messwerten.
2. Schritt: Berechnung der Wahrscheinlichkeiten p i und der hypothetischen Besetzungszahlen n i* ¼ n p i ¼ 50 p i
der einzelnen Klassen. Die Berechnung der Wahrscheinlichkeiten p i erfolgt auf der Grundlage der folgenden Klasseneinteilung mit der Verteilungsfunktion der Standardnormalverteilung (Tabelle 1):
1. Klasse
2. Klasse
3. Klasse
4. Klasse
5. Klasse
X < 98
98 X < 99
99 X < 100
100 X < 101
X 101
1: Klasse
2: Klasse
98 99,62
¼ F ð 1,362Þ ¼ 1 F ð1,362Þ ¼
p 1 ¼ P ðX < 98Þ ¼ F 0 ð98Þ ¼ F
1,189
¼ 1 0,9134 ¼ 0,0866
99 99,62
98 99,62
p 2 ¼ P ð98 X < 99Þ ¼ F 0 ð99Þ F 0 ð98Þ ¼ F
F
¼
1,189
1,189
¼ F ð 0,521Þ F ð 1,362Þ ¼ ð1 F ð0,521Þ 1 F ð1,362Þ ¼
¼ F ð1,362Þ F ð0,521Þ ¼ 0,9134 0,6988 ¼ 0,2146
3: Klasse
100 99,62
99 99,62
F
¼
1,189
1,189
¼ F ð0,320Þ F ð 0,521Þ ¼ F ð0,320Þ ð1 F ð0,521Þ ¼ F ð0,320Þ þ F ð0,521Þ 1 ¼
p 3 ¼ P ð99 X < 100Þ ¼ F 0 ð100Þ F 0 ð99Þ ¼ F
¼ 0,6255 þ 0,6988 1 ¼ 0,3243
4: Klasse
101 99,62
100 99,62
F
¼
p 4 ¼ P ð100 X < 101Þ ¼ F 0 ð101Þ F 0 ð100Þ ¼ F
1,189
1,189
¼ F ð1,161Þ F ð 0,320Þ ¼ 0,8772 0,6255 ¼ 0,2517
5: Klasse
p 5 ¼ P ðX 101Þ ¼ 1 P ðX < 101Þ ¼ 1 F 0 ð101Þ ¼ 1 F
101 99,62
¼
1,189
¼ 1 F ð1,161Þ ¼ 1 0,8772 ¼ 0,1228
Die folgende Tabelle (die im nächsten Schritt noch um zwei weitere Spalten erweitert wird) enthält in der 3. Spalte die
berechneten Wahrscheinlichkeiten p i und in der 4. Spalte die hypothetischen Besetzungszahlen (absoluten Klassenhäufigkeiten) n i* ¼ n p i ¼ 50 p i :
Klasse Nr. i
ni
pi
n i* ¼ 50 p i
D n i ¼ n i n i*
ðD n i Þ 2
n i*
1
5
0,0866
4,33
0,67
0,1037
2
10
0,2146
10,73
0,73
0,0497
3
16
0,3243
16,215
0,215
0,0029
4
12
0,2517
12,585
0,585
0,0272
5
P
7
0,1228
6,14
0,86
0,1205
0
0,3040
50
1
50
9 Ausgleichskurven
661
3. Schritt: Berechnung des Testwertes ^z der Testvariablen Z
Wir ergänzen die Tabelle um zwei Spalten. Spalte 5 enthält die Abweichungen zwischen den beobachteten und den
theoretischen Besetzungszahlen (D n i ¼ n i n i*). Diese Werte werden quadriert und durch die jeweilige theoretische Besetzungszahl n i* dividiert (Spalte 6). Aufsummieren dieser Werte liefert den gesuchten Testwert (in der Tabelle
grau unterlegt):
z ¼
^
5
5
X
X
ðD n i Þ 2
ðn i n i*Þ 2
¼
¼ 0,3040
n i*
n i*
i¼1
i¼1
4. Schritt: Berechnung der kritischen Grenze und des Annahmebereiches
Die Berechnung der kritischen Grenze c erfolgt aus der Bedingung P ðZ cÞ H 0 ¼ 1 a ¼ 1 0,05 ¼ 0,95 (siehe
Bild K-37) für die Testvariable Z, die einer Chi-Quadrat-Verteilung mit f ¼ ðk 1Þ r ¼ ð5 1Þ 2 ¼ 2 Freiheitsgraden genügt (r ¼ 2: Anzahl der zunächst unbekannten Parameter, die erst geschätzt werden mussten):
0,95
P ðZ cÞ H 0 ¼ F ðcÞ ¼ 0,95
c ¼ z ð0;95; 2Þ ¼ 5,99
)
ðaus Tab: 3Þ
0,05
Annahmebereich: z c ¼ 5,99
0
c
z
Annahmebereich
Bild K-37
5. Schritt (Testentscheidung): Der Testwert ^z ¼ 0,3040 liegt im Annahmebereich z 5,99. Die Vermutung, dass
die Kapazität der Kondensatoren eine normalverteilte Zufallsgröße ist, wird damit bestätigt.
9 Ausgleichskurven
Lehrbuch: Band 3, Kapitel IV.5
Formelsammlung: Kapitel XI.5
Zusammenhang zwischen Leistung und Drehzahl bei einem Dieselmotor
Bei einem Dieselmotor besteht zwischen der Leistung Y und der Drehzahl X ein gewisser Zusammenhang. Dabei ist Y eine Zufallsvariable und X eine normale Variable. Zeigen Sie anhand der folgenden
Stichprobe (bestehend aus n ¼ 6 Messpunkten), dass zwischen den beiden Variablen ein nahezu linea-
K73
rer Zusammenhang besteht und bestimmen Sie dann die Ausgleichs- oder Regressionsgerade.
i
1
2
3
4
5
6
xi
1000
1400
1800
2200
2600
3000
(in Umdrehungen
pro Minute)
yi
12,5
18,3
24,6
30,5
36,0
42,2
(in PS)
Welche Motorleistung darf man bei 2500 Umdrehungen pro Minute erwarten?
662
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Alle benötigten „Hilfsgrößen“ (x i2 , y 2i , x i y i ) haben wir in der folgenden Tabelle zusammengestellt:
x i2 10 4
y 2i
x i y i 10 3
i
xi
yi
1
1 000
12,5
100
156,25
12,50
2
1 400
18,3
196
334,89
25,62
3
1 800
24,6
324
605,16
44,28
4
2 200
30,5
484
930,25
67,10
5
2 600
36,0
676
1 296,00
93,60
6
P
3 000
42,2
900
1 780,84
126,60
12 000
164,1
2 680
5 103,39
369,70
Berechnung der Mittelwerte x und y und des Korrelationskoeffizienten r
x ¼
6
6
1 X
1
1 X
1
12 000 ¼ 2000 ; y ¼
164,1 ¼ 27,35
xi ¼
yi ¼
6 i¼1
6
6 i¼1
6
6
X
xi yi 6 x y
369,70 10 3 6 2000 27,35
r ¼ vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
!
!
u 6
6
X
u X 2
4 6 2000 2 Þ ð5103,39 6 27,35 2
2
2
2
t
2
680
10
xi 6 x
yi 6 y
i¼1
i¼1
i¼1
ð369,70 6 2 27,35Þ 10 3
41,5 10 3
¼ sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ 0,999 865
2,8 615,255 10 3
26,80 6 4 10 6 615,255
Wegen r ¼ 0,999 865
1 besteht zwischen der Leistung Y und der Drehzahl X ein linearer Zusammenhang.
Bestimmung der Ausgleichs- oder Regressionsgeraden: Ansatz in der symmetrischen Form y y ¼ a ðx xÞ
6
X
Steigung : a ¼
xi yi 6 x y
i¼1
6
X
i¼1
¼
x i2 6 x 2
369,70 10 3 6 2000 27,35
2680 10 4 6 2000 2
y 27,35 ¼ 0,014 821 ðx 2000Þ ¼ 0,014 821 x 29,642
Erwartete Leistung bei x ¼ 2500 Umdrehungen pro Minute:
y ¼ 0,0148 2500 2,292 ¼ 34,708
34,7
ðin PSÞ
¼
41,5 10 3
¼ 0,014 821
2,8 10 6
)
y ¼ 0,0148 x 2,292
9 Ausgleichskurven
663
Barometrische Höhenformel
Zwischen dem Luftdruck p und der Höhe h (gegenüber dem Meeresniveau h ¼ 0 gemessen) besteht bekanntlich der folgende exponentielle Zusammenhang (sog. barometrische Höhenformel bei vorausgesetzter konstanter Lufttemperatur):
p ¼ p ðhÞ ¼ p 0 e c h
ðh in km ; p in barÞ
Bestimmen Sie aus den folgenden 5 Messpunkten durch lineare Regression Näherungswerte für die
K74
noch unbekannten Parameter p 0 und c > 0.
i
1
2
3
4
5
hi
0,5
1
1,5
2
2,5
(in km)
pi
0,961
0,880
0,845
0,795
0,744
(in bar)
Anleitung: Die Gleichung zunächst logarithmieren (halblogarithmische Form), dann die Ausgleichsoder Regressionsgerade bestimmen.
f
|{z}
y
f
ln p ¼ ln p 0 e c h ¼ ln p 0 þ ln e c h ¼ ln p 0 c h ¼ c h þ ln p 0 ¼ a x þ b
|ffl{zffl}
a x
Rechenregeln: ln ðu vÞ ¼ ln u þ ln v ;
Ansatz: y ¼ a x þ b
mit
b
ln e n ¼ n
y ¼ ln p; a ¼ c; h ¼ x
und
b ¼ ln p 0
Tabelle mit allen benötigten „Hilfsgrößen“ (y i ¼ ln p i , x i2 , y 2i , x i y i ) aufbauen:
i
xi ¼ hi
pi
y i ¼ ln p i
x i2
y 2i
xi yi
1
0,5
0,961
0,0398
0,25
0,001 584
0,0199
2
1
0,880
0,1278
1
0,016 333
0,1278
3
1,5
0,845
0,1684
2,25
0,028 359
0,2526
4
2
0,795
0,2294
4
0,052 624
0,4588
5
P
2,5
0,744
0,2957
6,25
0,087 438
0,7393
0,8611
13,75
0,186 338
1,5984
7,5
Berechnung der Mittelwerte x und y
x ¼
5
1 X
1
xi ¼
7,5 ¼ 1,5 ;
5 i¼1
5
y ¼
5
1 X
1
yi ¼
ð 0,8611Þ ¼ 0,1722
5 i¼1
5
Bestimmung der Ausgleichsgeraden: Ansatz in der symmetrischen Form y y ¼ a ðx xÞ
5
X
Steigung : a ¼
xi yi 5 x y
i¼1
5
X
i¼1
¼
x i2 5 x 2
1,5984 5 1,5 ð 0,1722Þ
13,75 5
1,5 2
y þ 0,1722 ¼ 0,1228 ðx 1,5Þ ¼ 0,1228 x þ 0,1842
¼
0,3069
¼ 0,1228
2,5
664
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Ausgleichsgerade: y ¼ a x þ b ¼ 0,1228 x þ 0,0120
Berechnung der gesuchten Parameter p 0 und c:
ln p 0 ¼ b ¼ 0,0120
p 0 ¼ e b ¼ e 0,0120 ¼ 1,012 ;
)
c ¼ a ¼ 0,1228
Barometrische Höhenformel: p ¼ p 0 e c h ¼ 1,012 e 0,1228 h
ðh in km ; p in barÞ
Zusammenhang zwischen Bremsweg und Geschwindigkeit bei einem Fahrzeug
Zwischen dem Bremsweg s und der Geschwindigkeit v eines bestimmten Automodells wird ein nahezu quadratischer Zusammenhang angenommen. Bestimmen Sie aus der folgenden Messreihe die Ausgleichsparabel s ¼ a v 2 þ b v þ c:
K75
Messung Nr. i
1
2
3
4
5
v i (in km=h)
50
70
80
100
120
s i (in m)
27
50
61
91
123
Welchen Bremsweg kann man bei einer Geschwindigkeit von v ¼ 75 km=h erwarten?
Wir erstellen die folgende Tabelle mit den benötigten „Hilfsgrößen“ v 2i , v 3i , v 4i , v 2i s i und v i s i :
i
vi
si
v 2i 10 2
v 3i 10 3
v 4i 10 4
v 2i s i 10 2
1
50
27
25
125
625
675
1 350
2
70
50
49
343
2 401
2 450
3 500
3
80
61
64
512
4 096
3 904
4 880
4
100
91
100
1 000
10 000
9 100
9 100
5
P
120
123
144
1 728
20 736
17 712
14 760
420
352
382
3 708
37 858
33 841
33 590
Die drei Normalgleichungen für die noch Unbekannten a, b und c lauten (! FS: Kap. XI.5.3):
ðIÞ
5
X
i¼1
!
v 4i
aþ
5
X
i¼1
!
v 3i
bþ
5
X
i¼1
!
v 2i
c ¼
5
X
v 2i s i
i¼1
ð37 858 10 4 Þ a þ ð3 708 10 3 Þ b þ ð382 10 2 Þ c ¼ 33 841 10 2
ðIIÞ
5
X
i¼1
!
aþ
v 3i
5
X
i¼1
!
v 2i
bþ
5
X
!
vi
c ¼
i¼1
5
X
vi si
i¼1
ð3 708 10 3 Þ a þ ð382 10 2 Þ b þ 420 c ¼ 33 590
ðIIIÞ
5
X
i¼1
!
v 2i
aþ
5
X
!
vi b þ n c ¼
i¼1
ð382 10 2 Þ a þ 420 b þ 5 c ¼ 352
5
X
i¼1
si
vi si
9 Ausgleichskurven
665
Diese Gleichungen dividieren wir noch der Reihe nach durch den jeweiligen Koeffizienten von c, d. h. durch
382 10 2 bzw. 420 bzw. 5:
ðIÞ
9 910,4712 a þ 97,0681 b þ c ¼ 88,5890
ðIIÞ 8 828,5714 a þ 90,9524 b þ c ¼ 79,9762
ðIIIÞ 7 640 a þ 84 b þ c ¼ 70,4
Jetzt eliminieren wir c durch geeignete Differenzbildung zweier Gleichungen:
ðI *Þ ¼ ðI IIÞ
1081,8998 a þ 6,1157 b ¼ 8,6128
ðII *Þ ¼ ðII IIIÞ
1188,5714 a þ 6,9524 b ¼ 9,5762
Beide Gleichungen dividieren wir durch den jeweiligen Koeffizienten von b und eliminieren dann b durch Differenzbildung:
ðI *Þ
176,9053 a þ b ¼ 1,4083
ðII *Þ
170,9584 a þ b ¼ 1,3774
5,9469 a
)
¼ 0,0309
)
a ¼ 0,005 196
ðI *Þ
)
b ¼ 1,4083 176,9053 a ¼ 1,4083 176,9053 0,005 196 ¼ 0,489 100
ðIIIÞ
)
c ¼ 70,4 7 640 a 84 b ¼ 70,4 7 640 0,005 196 84 0,489 100 ¼ 10,38184
Lösung (gerundet auf 4 Nachkommastellen): a ¼ 0,0052; b ¼ 0,4891; c ¼ 10,3818
s ¼ a v 2 þ b v þ c ¼ 0,0052 v 2 þ 0,4891 v 10,3818
ðs in m; v in km=hÞ
Bremsweg bei der Geschwindigkeit v ¼ 75 km=h:
v ¼ 0,0052 75 2 þ 0,4891 75 10,3818 ¼ 55,5507
ðin mÞ
55,6
Zusammenhang zwischen der Laufzeit und den Wartungskosten einer Maschine
Zwischen den Laufzeiten und den Wartungskosten einer speziellen Maschine besteht offenbar ein linearer Zusammenhang, wie man dem folgenden Messprotokoll für die vergangenen 6 Monate entnehmen
kann:
K76
i
1
2
3
4
5
6
t i (in h)
50
46
56
60
54
58
y i (in Euro)
35
34
37
39
36
38
(i ¼ 1: letzter Monat; i ¼ 2: vorletzter Monat usw.; t i , y i : Laufzeit bzw. Wartungskosten im i-ten
Monat; i ¼ 1, 2, . . . , 6)
Bestimmen Sie die Ausgleichs- oder Regressionsgerade y ¼ a t þ b.
666
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Die benötigten „Hilfsgrößen“ t i2 , y 2i und t i y i haben wir in der folgenden Tabelle zusammengestellt:
i
ti
yi
t i2
y 2i
ti yi
1
50
35
2 500
1 225
1 750
2
46
34
2 116
1 156
1 564
3
56
37
3 136
1 369
2 072
4
60
39
3 600
1 521
2 340
5
54
36
2 916
1 296
1 944
6
P
58
38
3 364
1 444
2 204
324
219
17 632
8 011
11 874
Berechnung der Mittelwerte t und y und des Korrelationskoeffizienten r
t ¼
6
1 X
1
324 ¼ 54 ;
ti ¼
6 i¼1
6
6
X
y ¼
6
1 X
1
219 ¼ 36,5
yi ¼
6 i¼1
6
ti yi 6 t y
11 874 6 54 36,5
r ¼ vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
!
!
u 6
6
X
u X 2
17 632 6 54 2 Þ ð8 011 6 36,5 2
t
ti 6 t2
y 2i 6 y 2
i¼1
i¼1
i¼1
48
48
¼ 0,9839
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
136 17,5
48,785 244
Folgerung: Die Messpunkte liegen wegen r ¼ 0,9839
daher gerechtfertigt.
1 nahezu auf einer Geraden, die lineare Regression ist
Regressionsgerade: Ansatz in der symmetrischen Form y y ¼ a ðt tÞ
6
X
Steigung : a ¼
ti yi 6 t y
i¼1
6
X
i¼1
¼
t i2 6 t 2
11 874 6 54 36,5
17 632 6 54 2
¼
48
¼ 0,3529
136
y 36,5 ¼ 0,3529 ðt 54Þ ¼ 0,3529 t 19,0566
)
y ¼ 0,3529 t þ 17,4434
Monatliche Absatzzahlen eines PKW (Trendkurve)
Ein vor 6 Monaten neu auf den Markt gebrachtes PKW-Modell wurde im 1. Monat 810-mal verkauft,
im soeben zu Ende gegangenen 6. Monat jedoch nur noch 260-mal. Die folgende Tabelle enthält die
K77
stark rückläufigen monatlichen Absatzzahlen der letzten 6 Monate:
i
1
2
3
4
5
6
xi
1
2
3
4
5
6
ni
810
645
506
402
320
260
9 Ausgleichskurven
667
x i : i-ter Verkaufsmonat, gezählt vom Verkaufsbeginn an (i ¼ 1, 2, . . . , 6)
n i : Absatz im i-ten Verkaufsmonat
Als Ausgleichskurve (Trendkurve) wähle man die exponentiell abnehmende Funktion n ¼ K c x mit
K > 0 und 0 < c < 1.
a) Bestimmen Sie mit Hilfe der linearen Regression Näherungswerte für die noch unbekannten Kurvenparameter K und c.
b) Welche monatlichen Absatzzahlen sind in den auf das vergangene Halbjahr folgenden 3 Monaten zu
erwarten, wenn sich der Trend der rückläufigen Verkaufszahlen in der unter a) bestimmten Weise
fortsetzt?
Die Funktionsgleichung wird zunächst logarithmiert:
ln n ¼ ln ðK c x Þ ¼ ln K þ ln c x ¼ ln K þ x ln c ¼ ðln cÞ x þ ln K ¼ a x þ b
|{z}
|fflffl{zfflffl}
|{z}
y
a
b
Rechenregeln: ln ðu vÞ ¼ ln u þ ln v;
ln a m ¼ m ln a
Linearer Ansatz für die Regression: y ¼ a x þ b mit y ¼ ln n, a ¼ ln c, b ¼ ln K
Die folgende Tabelle enthält die benötigten „Hilfsgrößen“ y i ¼ ln n i , x i2 und x i y i :
i
xi
ni
y i ¼ ln n i
x i2
1
1
810
6,6970
1
6,6970
2
2
645
6,4693
4
12,9386
3
3
506
6,2265
9
18,6795
4
4
402
5,9965
16
23,9860
5
5
320
5,7683
25
28,8415
6
P
6
260
5,5607
36
33,3642
36,7183
91
124,5068
21
xi yi
Berechnung der Mittelwerte x und y
x ¼
6
1 X
1
21 ¼ 3,5 ;
xi ¼
6 i¼1
6
y ¼
6
1 X
1
36,7183 ¼ 6,1197
yi ¼
6 i¼1
6
Regressionsgerade: Ansatz in der symmetrischen Form y y ¼ a ðx xÞ
6
X
Steigung: a ¼
xi yi 6 x y
i¼1
6
X
i¼1
¼
x i2 6 x 2
124,5068 6 3,5 6,1197
91 6
3,5 2
¼
y 6,1197 ¼ 0,2290 ðx 3,5Þ ¼ 0,2290 x þ 0,8015
4,0069
¼ 0,2290
17,5
)
y ¼ 0,2290 x þ 6,9212
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflffl{zfflfflffl}
a
b
668
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Berechnung der Kurvenparameter c und K
ln c ¼ a
)
c ¼ e a ¼ e 0,2290 ¼ 0,7953 ;
ln K ¼ b
)
K ¼ e b ¼ e 6;9212 ¼ 1013,54
Trendkurve: n ¼ K c x ¼ 1013,54 0,7953 x
b) n ðx ¼ 7Þ
204 ;
n ðx ¼ 8Þ
n ðx ¼ 9Þ
162 ;
129
Entladung eines Kondensators
Durch die Gleichung u ¼ u ðtÞ ¼ u 0 e k t wird die zeitliche Entladung eines Kondensators mit der
Kapazität C über einen ohmschen Widerstand R beschrieben (u: Kondensatorspannung; t: Zeit; u 0 :
Spannung zu Beginn der Entladung, d. h. zum Zeitpunkt t ¼ 0; k ¼ 1=RC). Bestimmen Sie aus den
folgenden 5 Messwerten die noch unbekannten Parameter u 0 und k:
K78
i
1
2
3
4
5
ti
5
10
20
30
50
ui
39,0
30,5
18,2
11,1
in Sekunden (s)
4,2
in Volt (V)
Anleitung: Die Gleichung zunächst durch Logarithmieren auf die halblogarithmische Form bringen,
dann eine lineare Regression durchführen.
|{z}
f
ln u ¼ ln u 0 e k t ¼ ln u 0 þ ln e k t ¼ ln u 0 k t ¼ k t þ ln u 0 ¼ a t þ b
|fflffl{zfflffl}
y
a
b
Rechenregeln: ln ðv wÞ ¼ ln v þ ln w ;
ln e m ¼ m
Ansatz für die Ausgleichsgerade: y ¼ a t þ b
y ¼ ln u; a ¼ k
mit
und b ¼ ln u 0
Tabelle erstellen mit den benötigten „Hilfsgrößen“ y i ¼ ln u i , t i2 und t i y i :
i
ti
ui
y i ¼ ln u i
t i2
ti yi
1
5
39,0
3,663 562
25
18.317 81
2
10
30,5
3,417 727
100
34,177 27
3
20
18,2
2,901 422
400
58,028 44
4
30
11,1
2,406 945
900
72,208 35
5
P
50
4,2
1,435 085
2 500
71,754 25
13,824 741
3 925
254,486 12
115
Berechnung der Mittelwerte t und y
t ¼
5
1 X
1
ti ¼
115 ¼ 23 ;
5 i¼1
5
y ¼
5
1 X
1
yi ¼
13,824 741 ¼ 2,764 948
5 i¼1
5
9 Ausgleichskurven
669
Regressionsgerade: Ansatz in der symmetrischen Form y y ¼ a ðt tÞ
5
X
a ¼
ti yi 5 t y
i¼1
5
X
i¼1
¼
254,486 12 5 23 2,764 948
3 925 5
t i2 5 t 2
23 2
¼
63,4829
¼ 0,049 596
1280
y 2,764 948 ¼ 0,049 596 ðt 23Þ ¼ 0,049 596 t þ 1,140 708
)
y ¼ 0,049 596 t þ 3,905 656
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
a
b
Berechnung der Kurvenparameter u 0 und k
ln u 0 ¼ b
u 0 ¼ e b ¼ e 3,905 656 ¼ 49,682 661
)
k ¼ a ¼ ð 0,049 596Þ ¼ 0,049 596
49,68
0,0496
Lösung: u ¼ u ðtÞ ¼ u 0 e k t ¼ 49,68 e 0,0496 t
ðt in s ; u in VÞ
Welche Potenzfunktion v ¼ v ðuÞ ¼ K u n mit den noch unbekannten Parametern K > 0 und
K79
n > 0 passt sich den folgenden 4 Messpunkten „optimal“ an:
Anleitung: Näherungsweise
i
1
2
3
4
ui
1
3
4
5
vi
3,4
55,1
111,3
193,8
Berechnung der gesuchten
Kurvenparameter mit Hilfe
der linearen Regression.
Wir bringen die Funktionsgleichung durch Logarithmieren auf die folgende (doppellogarithmische) Form:
f
ln v ¼ ln ðK u n Þ ¼ ln K þ ln u n ¼ ln K þ n ln u ¼ b þ a x ¼ a x þ b
|{z}
|{z}
|{z}
y
b
a
x
Linearer Ansatz: y ¼ a x þ b mit y ¼ ln v, x ¼ ln u, a ¼ n und b ¼ ln K
Die folgende Tabelle enthält alle benötigten „Hilfsgrößen“ (x i ¼ ln u i , y i ¼ ln v i , x i2 und x i y i ):
x i ¼ ln u i
i
ui
1
1
0
2
3
3
4
P
vi
y i ¼ ln v i
x i2
xi yi
3,4
1,223 775
0
0
1,098 612
55,1
4,009 150
1,206 948
4,404 500
4
1,386 294
111,3
4,712 229
1,921 811
6,532 535
5
1,609 438
193,8
5,266 827
2,590 291
8,476 632
15,211 981
5,719 050
19,413 667
4,094 344
Berechnung der Mittelwerte x und y
x ¼
4
1 X
1
4,094 344 ¼ 1,023 586 ;
xi ¼
4 i¼1
4
y ¼
4
1 X
1
15,211 981 ¼ 3,802 995
yi ¼
4 i¼1
4
670
K Wahrscheinlichkeitsrechnung und mathematische Statistik
Ansatz der Ausgleichsgeraden (in symmetrischer Form): y y ¼ a ðx xÞ
4
X
a ¼
xi yi 4 x y
i¼1
4
X
i¼1
¼
x i2 4 x 2
19,413 667 4 1,023 586 3,802 995
5,719 050 4
1,023 586 2
¼
3,842 897
¼ 2,514 760
1,528 137
y 3,802 995 ¼ 2,514 760 ðx 1,023 586Þ ¼ 2,514 760 x 2,574 073
)
y ¼ 2,514 760 x þ 1,228 922
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
a
b
Berechnung der gesuchten Kurvenparameter K und n
ln K ¼ b
)
K ¼ e b ¼ e 1,228 922 ¼ 3,417 543
Lösung (Ausgleichskurve): v ¼ K u n ¼ 3,418 u 2,5148
3,418 ;
n ¼ a ¼ 2,514 760
2,5148