подготовка к
С. И. Колесникова
ДОМАШНИЙ РЕПЕТИТОР
МАТЕМАТИКА
ИНТЕНСИВНЫЙ КУРС ПОДГОТОВКИ
К ЕДИНОМУ ГОСУДАРСТВЕННОМУ ЭКЗАМЕНУ
Допущено
ФИПИ
Отработка
навыков
быстрого
решения
20 вариантов
с ответами

pi
НИ»
П 0 Д Г 1
о т о в к а ^Н^Я^^ЯВ
да»
ш
m
С. И. Колесникова
ДОМАШНИЙ РЕПЕТИТОР
интенсивный курс подготовки
К ЕДИНОМУ ГОСУДАРаВЕННОМУ ЭКЗАМЕНУ
Допущено ФИПИ к использованию
в образовательных учреждениях
Российской Федерации
в качестве учебного пособия для подготовки
к итоговой аттестации и ЕГЭ по математике
6-е издание
МОСКВА
АЙРИС ПРЕСС
2008

УДК 373.167.1:51
ББК 22.1я727
К60
Серийное оформление А. М. Драгового
Колесникова, С. И.
К60 Математика. Интенсивный курс подготовки к Единому
государственному экзамену / С. И. Колесникова. — 6-е изд. —
М.: Айрис-пресс, 2008. — 304 с. — (Домашний репетитор:
Подготовка к ЕГЭ).
ISBN 978-5-8112-3165-2
Книга адресована прежде всего выпускникам, сдающим ЕГЭ,
традиционные выпускные или вступительные экзамены, а также
учителям и учащимся, начиная с 8 класса, руководителям факультативов.
В пособии собраны эффективные (не всегда стандартные) методы
решения наиболее «проблемных» уравнений и неравенств алгебры, в
нем содержится 20 тренировочных вариантов ЕГЭ, часть задач для
которых взята из вступительных экзаменов в МГУ и МФТИ.
Приведены решения многих заданий, в том числе полностью двух
вариантов, даны ответы на все задания.
Автор книги несколько десятилетий преподает математику в МФТИ,
обладает большим опытом работы со старшеклассниками, преподает в
заочной физико-математической школе МФТИ, более десяти лет
работает в школе № 463 г. Москвы, является соросовским учителем.
Часть заданий, включенных в пособие, выходят за рамки
школьной программы по математике и превышают уровень сложности ЕГЭ,
о реальном уровне сложности которого можно судить по имеющимся в
пособии демонстрационным вариантам ЕГЭ 2006-2007 гг.
ББК 22.1я727
УДК 373.167.1:51
© ООО «Издательство
ISBN 978-5-8112-3165-2 ^^ «АЙРИС-пресс», 2004

Предисловие к пятому изданию
С момента выхода первого издания прошло больше трех
лет. Автор продолжает активную работу в пропаганде
эффективных и быстрых методов решений, основанных на
равносильности преобразований. За это время произошли изменения и
в методической литературе — равносильные преобразования
встречаются все чаще. В частности, знакомство с материалами
КИМов показывает, что авторы все чаще используют
равносильные преобразования, не изучаемые в большинстве школ, и
оформляют решения с их помощью (иногда употребляя значок Ф=Ф,
иногда записывая этот факт словами). За это время вышла
вторая книга автора, в которой большое количество сложных задач
этой книги решены.
Несколько изменилась и структура экзамена — поэтому и
мы изменили структуру вариантов в соответствии с ЕГЭ-2007:
уменьшено количество заданий серии А, увеличено количество
заданий серии В, добавлено задание по стереометрии в серию С.
Вместе с изменением структуры усложнились последние
задания серии В и усложнились задания серии С. Наши варианты
не совпадают с вариантами ЕГЭ какого-либо года. Это
сделано намеренно — ведь нельзя серьезно подготовиться к
экзамену следующего года, прорешав даже все варианты
предыдущего. Наши задания серии А и В не всегда соответствуют уровню
трудности настоящего ЕГЭ этих серий. Это тоже сделано
намеренно т. к. наша книга — домашний репетитор. Поэтому, чтобы
и сильному школьнику не было бы скучно привыкать к новому
типу оформления ответов, в серии А встречаются трудные
задания. Трудные задания серии В тоже полезны тем, что заведомо
имеют хорошие ответы — поэтому школьнику не придется
забираться в дебри вычислений, а можно сосредоточиться на
обдумывании самого решения. Одни и те же задачи могут оказаться
сложными для большинства, но обычными и интересными для
Детей с олимпиадным типом мышления. Мы хотели, чтобы все
нашли для себя задачи для тренировки. Трудно предугадать, ка-
3

кие задания будут в следующем году — это во многом зависит
от «команды», составляющей их.
Проведение ЕГЭ во всей стране предполагается начать с
2009 г. Известно, что Московская область подключается к
повсеместному проведению ЕГЭ уже в 2008 г. Для тех регионов,
где ЕГЭ еще не было, интересно узнать, какие варианты были в
прошлых годах. Поэтому перед нашими вариантами мы решили
опубликовать демонстрационные варианты 2006 и 2007 г. В нем
присутствует в несколько измененном виде, по крайней мере,
три задачи вступительного экзамена на различные
факультеты МГУ (две из них были последними в вариантах МГУ), одна
задача из МФТИ (тоже последняя в варианте МФТИ). Это еще
раз говорит о том, что наш подход к подбору вариантов оказался
верен: разнообразие идей хватит на многие будущие ЕГЭ. Ведь
идеи заданий серии С не повторяются.
Исправлены замеченные к этому времени ошибки и
опечатки.
Автор выражает благодарность директору ФЗФТШ при
МФТИ Чугуновой Т. А., доценту ГУ-ВШЭ Шагину В. А. и
научному редактору Черноруцкому В. В. за внимательное и
серьезное прочтение книги, за удивительно точное понимание точки
зрения автора и, конечно, за их ценные советы и замечания.

От автора
Дорогие выпускники! Всем вам предстоит сдавать
выпускной экзамен на аттестат зрелости. Многим из вас придется
сдавать вступительные экзамены в вузы. Некоторые из вас будут
сдавать два этих экзамена одновременно — в виде Единого
государственного экзамена — ЕГЭ. С каждым годом число
выпускников, принимающих участие в сдаче ЕГЭ, увеличивается.
Известно, что вступительные экзамены в вузы имеют
значительные различия в содержании проверяемого учебного
материала. Это естественно, потому что в разных вузах в процессе
обучения требуется разный объем знаний, например, по
математике. ЕГЭ проводится, в частности, для того, чтобы уравнять
шансы всех абитуриентов при поступлении в любой вуз.
Опыт проведения ЕГЭ говорит о том, что
предварительное знакомство школьников со структурой ЕГЭ, содержанием
и требованиями, которые предъявляются к оформлению
решений и ответов, очень помогает при выполнении самого экзамена.
Именно такую помощь и призвана оказать эта книга.
Трудность вступительных экзаменов в вузы для
подавляющего большинства абитуриентов состоит в следующем.
1. Программа 10-11 классов очень сильно отличается от
программы вступительных экзаменов: в школе в течение двух
последних лет изучают элементы математического анализа,
который школьники зачастую плохо осваивают. Материал
изучается при полном отсутствии понятия предела. Поэтому
школьник вынужден зазубривать все о производных, касательных,
экстремумах, интегралах и т. д. Учителя вынуждены много
времени уделять технике дифференцирования. В связи с этим
времени на освоение тригонометрии, показательных и, особенно,
логарифмических функций остается в обрез. Задач на эти темы
решается мало, а уж повышенной трудности тем более. Поэтому
школьники, собирающиеся поступать в вузы, начинают
игнорировать элементы математического анализа и серьезно берутся
5

за алгебру и геометрию. Вытянуть на равных то и другое очень
трудно.
2. К этому времени совершенно забыта планиметрия.
3. Время, отведенное на повторение, опять уходит на
экстремумы, критические точки и вычисление площадей с
помощью интегралов, потому что это часто бывает на выпускных
экзаменах. Мало времени уделяется повторению элементарных
формул и решению уравнений тригонометрии. Нет времени и на
тождественные преобразования алгебраических или
тригонометрических выражений.
4. В школе дети практически не видят задач с параметрами.
5. Корни уравнений чаще всего являются рациональными
Лг 1 ± л/5
числами. Увидев на вступительном, что sini = —~—,
школьник забывает сравнить полученные числа с 1.
При подготовке к ЕГЭ у выпускника появляются новые
трудности. Главное отличие ЕГЭ от выпускного экзамена по
математике состоит в том, что при подготовке к сдаче ЕГЭ
придется, как к вступительному экзамену, повторить весь материал,
изучаемый в течение 7-11 классов. ЕГЭ-2007 предлагает
выпускнику сразу 26 задач на 4 часа. При этом школьнику
предлагается самому выбирать задания, с которыми он может справиться.
Но ведь это уже очень трудная задача для учащегося, который
привык стараться справиться с тем, что задано учителем. Кроме
того, ни одно домашнее задание не содержало такого количества
задач. Разве что репетиторы столько задают при подготовке в
престижные вузы!
Вопрос. Может ли успевающий в школе учащийся получить
3 или даже 2?
Ответ, Да. Ведь при решении задач серии А ученик
может получить верный ответ, но, по невнимательности или из-за
волнения, долго искать нужный пункт, теряя при этом время,
или просто случайно написать не тот, который имел в виду. При
решении задач серии В по тем же причинам можно записать не
тот ответ при абсолютно верно решенном задании.
6

Вопрос. Помогает ли наличие вариантов ответов в серии А
при решении задач этой серии?
Ответ. Да. Потому что если задача, по-вашему, решена и
вы нашли свой ответ среди предложенных только в одном
пункте, то с хорошим настроением можно продолжать работать. Это
несмотря на то, что 100%-й уверенности, что ваш ответ верен,
нет, так как ответы записаны с учетом типичных ошибок,
допускаемых школьниками при решении данного задания (может
быть, именно эту ошибку вы и допустили!). Если же, наоборот,
вашего ответа нет среди предложенных или ваш ответ
встречается в нескольких пунктах, то надо собраться и делать задачу
заново.
Вопрос. Стоит ли заглядывать в задачи серии С, не
справившись с серией В?
Ответ. Стоит. Среди задач серии В могут быть более
трудные именно для вас задачи (например, планиметрия,
стереометрия, задачи с параметрами, нестандартные уравнения,
решаемые только графически), чем некоторые задачи серии С.
Вопрос. Есть ли особенности при решении серии В?
Ответ. Да, конечно. Во-первых, теперь нет никаких
ответов. Во-вторых, при правильном решении нельзя ошибаться
в арифметике или просто сделать описку при решении, так как
никто вашего решения не увидит, а ошибка в арифметике сводит
на нет все ваши усилия — задача не засчитывается.
Вопрос. Чем отличаются задачи серии С от задач серии В?
Ответ. Во-первых, задачи могут быть несколько сложнее,
чем в серии В. Но главное — их надо оформить так, как
оформляют «медальные» работы.
Вопрос. Как получить хорошую отметку?
Ответ. Во-первых, к ЕГЭ дадо готовиться по предмету, а
во-вторых, психологически. Это связано с тем, что задания ЕГЭ
могут быть сформулированы в непривычной для учащегося
форме и, кроме того, большинство школьников должно смириться
с тем, что все задачи они не решат в отведенное время.
Сконцентрироваться надо на понятных для вас задачах, решать их
7

спокойно и до конца, независимо от того, в какой серии они
находятся.
О структуре и целях данного пособия
Книга состоит из четырех частей.
Первая часть посвящена эффективным методам решения
некоторых основных типов задач алгебры и анализа. При
овладении этими методами школьник получит возможность не
просто научиться решать многие типичные задачи, но решать их
быстро, коротким способом, экономя экзаменационное время на
более сложные (нестандартные задания).
В основном, в первой части нашей книги обсуждаются
методы решения неравенств, позволяющие свести решения задач к
классическому (школьному) методу интервалов для
многочленов. Эта часть состоит их неравноценных параграфов.
В некоторых из них лишь напоминаются те или иные
основные свойства — это касается, например, свойств степеней. В
других — рассматриваются только те вопросы, которым в школе
уделяется мало внимания, — это, например, понятие обратных
тригонометрических функций, сложная экспонента и др.
Основное внимание уделяется методам решения
неравенств. Эти методы не относятся к стандартным школьным, но
позволяют многие неравенства решить быстро и красиво.
Обобщенный метод интервалов является универсальным для
решения неравенств, но он таит в себе неприятности: бывает трудно
найти «пробную» точку, при выяснении знака сложной функции
в «пробной» точке вычисления могут оказаться громоздкими, и
в результате арифметической ошибки знак может оказаться
неверным. В условиях вступительного экзамена на исправление
такой ситуации, если далее абитуриент почувствовал это,
времени нет.
Основную роль при решении всех наших задач будут играть
равносильные переходы, о которых в школьном учебнике очень
мало сведений. Однако иногда без них трудно обойтись, и тогда
в методической литературе робко проскальзывают слова: равно-
8

сильно, тождественное преобразование. Мы равносильные
переходы будем обозначать значком Ф=^. В книге приведено
довольно много условий равносильности.
Благодаря этим условиям, основные уравнения и
неравенства, содержащие модуль, мы будем решать, не раскрывая
модуль, т. е. не обращая внимания на знаки выражений, входящих
под знак модуля. Мы рассмотрим свойства логарифмов, которые
необходимы для решения задач, но отсутствуют в большинстве
учебников. Мы рассмотрим, наконец, функции, которые
называются сложной экспонентой у(х) = а(х)^х' и логарифмом с
переменным основанием у(х) = log^) f(x).
Отметим, что в первой части не разбираются методы
решения задач по геометрии, текстовых и логических задач. Это
связано с тем, что планиметрия и стереометрия требует
отдельной и серьезной подготовки. Главное, надо повторить все
формулы: ведь не известно, на какую тему дадут задачи. Они могут
быть простыми, но выбор способа решения и необходимых
формул требует времени. Среди заданий ЕГЭ таких относительно
мало по сравнению с заданиями по алгебре и
математическому анализу, к тому же задачи по геометрии не учитываются
при выставлении оценки за школьный курс алгебры. Тем не
менее, некоторые геометрические задачи решены в четвертой части
книги.
Текстовые задачи школьники начинают решать
практически с первого класса, но в это время не все к ним психологически
готовы, так как для некоторых обучение математике и логике
рассуждений дается по-разному, и страх перед такими задачами
остается надолго. Выпускники уже взрослые люди, и им нечего
бояться простых текстовых задач. Ну а сложные задачи или
задачи на сообразительность в заданиях ЕГЭ встречаются редко,
их, конечно, решат немногие, но они на них и рассчитаны.
Вторая часть содержит тренировочные варианты ЕГЭ, она
выполняет информационную задачу, так как, во-первых,, она
знакомит школьников со стилистикой заданий ЕГЭ, а во-вторых,
дает возможность подготовиться к традиционному (не тестово-
9

му) экзамену в вузы с повышенными требованиями по
математике, так как в основе части приведенных заданий лежат
задачи вступительных экзаменов в два престижных вуза страны —
МГУ и МФТИ. Уровень всех этих заданий, если включать
задания серии С, достаточен для подготовки в любой вуз. Такой
подход, как показало время, прошедшее с момента выхода
первого издания, оправдал себя — в 2005-2007 годах появились,
несколько изменившись, задачи вступительных экзаменов МГУ
и МФТИ.
Предлагаемые тренировочные варианты не соответствуют
точно структуре ЕГЭ в том смысле, что мы не стремились,
например, помещать задачи на конкретные темы именно под тем
же номером, как они встречались в ЕГЭ последних лет. Не
следили мы за количеством задач на конкретную тему или за
количеством тем, охваченных в варианте (не во всех вариантах,
например, есть текстовые задачи). Мы следили за тем, чтобы
совокупностью всех вариантов были охвачены все темы. В наших
вариантах, например, довольно много задач, содержащих явно
или неявно решение квадратных уравнений или неравенств,
потому что в школе эти темы проходят наиболее полно и подробно.
В трудных задачах с параметром очень часто решение сводится
именно к квадратному уравнению или неравенству. В высшей
школе тоже без этих знаний не обойтись.
Иногда задачи одного типа даны в разных формулировках.
Например, «вычислите без таблиц», или «упростите», или
«вычислите значение выражения» и т. д. Это сделано по той
причине, что выпускник может встретиться с любой из этих
формулировок.
При подготовке тренировочных вариантов разные
авторы отдают предпочтение тем или другим типам задач, готовят
основной вариант, а затем несколько аналогичных.
Составители утверждают, что задания для ЕГЭ составляются в расчете
на ограниченное число формул, которые должны быть прочно
усвоены. Но выбор этих формул очень зависит от пристрастий
составляющих, точно так же, как задания вступительных экза-
10

менов различных вузов или задания выпускных экзаменов
разных городов отличаются друг от друга (что естественно, так как
требования по математике к будущим программистам или,
например, ветеринарам разные).
Наше пособие отличается от тех, в которых даются
рекомендации по подготовке к ЕГЭ. В данной работе приведено 20
тренировочных вариантов, включая демонстрационные
варианты 2006 и 2007 гг., среди которых нет основного варианта. Не
все задания различных тренировочных вариантов аналогичны.
В варианты включены самые разные задачи, чаще всего
встречающиеся на выпускных или вступительных экзаменах. Они
отличаются большим разнообразием идей и необходимостью
применять очень разные методы решений. Это должно помочь
каждому учащемуся подготовиться к любому варианту ЕГЭ, к
вступительным экзаменам в любой вуз страны на любой факультет
и одновременно оценить самостоятельно уровень своей
подготовки.
В третьей части книги приводятся решения всех
заданий двух вариантов и разобраны некоторые задания из других
вариантов. Решения задач оформлены с равносильными
переходами, с которыми не все привыкли работать, но не спешите
отложить эти решения в сторону. Внимательно всмотритесь в
написанное и, сначала не обращая внимания на значок *Ф=^,
прочитайте решение, потом постарайтесь, если хотите, решить по-
своему. Переход от одного соотношения к равносильному связан,
как правило, с некоторыми преобразованиями заданных
выражений или вычислениями (например, квадратных выражений).
Эти преобразования видны, если внимательно сравнить
исходное и равносильное соотношение. Мы приводим решения задач
и для того, чтобы было видно, как иногда они красивы или
громоздки, иногда очень просты или, наоборот, сложны. Некоторые
задачи можно решать несколькими способами. Если есть время,
можно не заботиться о выборе способа решения, но если время
в дефиците, то придется выбирать оптимальный способ.
11

Четвертая часть содержит ответы на все задания всех
вариантов.
Книга адресована прежде всего, конечно, выпускникам, но
может оказаться также полезной для работы в классах с
углубленным изучением математики начиная с 8 класса, когда дети
впервые всерьез начинают работать с модулем, и просто для тех
школьников, которые хотят научиться решать задачи наиболее
простыми способами. Она может служить прекрасным
дополнением к обычному школьному учебнику, а также сможет помочь
в проведении факультативных занятий.
Для тех, кто хочет глубже заниматься математикой или
просто познакомиться с требованиями мехмата МГУ или
физтеха, надо особенно обратить внимание на задания серии С. Кто-то
их решать будет самостоятельно и проверять свои силы,
оценивая свою возможность поступления в престижные вузы (с
повышенными требованиями по математике), для других это будет
очень трудно — тогда разберите наши решения, они многому
смогут научить. Задания серии С настоящего ЕГЭ, думается,
будут, в основном, проще многих предложенных.
Желаем всем удачи!

РАЗДЕЛ ПЕРВЫЙ
ЭФФЕКТИВНЫЕ МЕТОДЫ РЕШЕНИЯ
ОСНОВНЫХ ТИПОВ ЗАДАЧ
АЛГЕБРЫ И АНАЛИЗА
В этом разделе книги мы остановимся на самых «больных»
моментах алгебры и начал анализа. Внимание будет уделено
практическим навыкам решения задач. Методы, изложенные
ниже, позволят, при их успешном освоении, не только правильно
решать многие типичные задачи, но и решать их быстро, что
очень важно для тех, кто хочет получить высокий итоговый балл
на Едином государственном экзамене.
Понятие равносильности уравнений
и неравенств
При решении неравенств и уравнений фундаментальное
значение имеет понятие равносильности, и в нашей работе это
будет играть большую роль.
Два неравенства
h (х) > 9\ (х) и /2 (х) > д2 (х)
или два уравнения
h (х) = 9i (х) и /2 (х) = 32 (х)
называются равносильными на множестве X, если каждое
решение первого неравенства (уравнения), принадлежащее
множеству X, является решением второго и, наоборот, каждое
решение второго, принадлежащее X, является решением первого;
13

или ни одно из неравенств (уравнений) на X не имеет
решений. Таким образом, неравенства (или уравнения) называются
равносильными на X, если множества решений этих
неравенств (уравнений) совпадают. Отсюда следует, что, вместо
того чтобы решать данное неравенство (уравнение), можно
решать любое другое, равносильное данному. Замену одного
неравенства (уравнения) другим, равносильным данному на X,
называют равносильным переходом на X, Равносильный переход
обозначают двойной стрелкой 4=^. Если уравнение f(x) = О
равносильно уравнению д(х) = 0, то это мы будем обозначать
так: f(x) = О <==> д(х) — 0. Если же все решения уравнения
f(x) = 0 являются решениями уравнения д(х) = 0, то
уравнение д(х) = 0 является следствием f(x) = 0. В этом случае
будем пользоваться значком =>: f(x) = 0 =>■ д(х) = 0. Например,
х — 1=>х = (х — I)2.
Примеры.
1. х2 < 1 4=> |х| < 1.
2. у/х2 — 4 = 1-х2 4=> у sin2 х — 2 = 0, т. к. ни то, ни другое
уравнение не имеет решений.
Отметим основные операции, приводящие к равносильным
соотношениям.
1. Если функции /(ж), з(ж)? h(x), определены на множестве
X, то на X
f{x) < д(х) <=> f{x) + h(x) < д{х) + h{x),
fix) = д(х) «=> fix) + h(x) = g(x) + h(x).
2. Если h(x) > 0 на X, то на X
fix) < g(x) ^=> fix)hix) < g(x)h(x),
т.е. при умножении неравенства на положительную функцию
знак неравенства не меняется.
3. Если hix) ф 0 на X, то на X
f{x) = д(х) ^ f(x)h(x) = g(x)h(x).
14

4. Если h(x) < О на X, то на X
f(x) < д(х) <=> f{x)h{x) > g{x)h{x),
т.е. при умножении неравенства на отрицательную функцию
знак неравенства меняется на противоположный.
5. Если f(x) ^ 0, д(х) ^ 0 на X, то на X
f(x)<g(x)*=>f2(x)<g2(x),
fix) < g(x) » S4x) ^ <?>),
т.е. если обе части неравенства или уравнения
неотрицательны, то возведение в квадрат (или любую четную степень) обеих
частей неравенства или уравнения приводит к равносильному
неравенству или уравнению соответственно.
Если левая и правая части неравенства имеют разные
знаки, то нельзя возводить неравенство в квадрат, т. к. возведение
в квадрат может привести как к истинному неравенству, так и
к ложному: -4 < 5 и 16 < 25; -7 < 5, но 49 > 25.
Если же f(x) и д(х) имеют разные знаки, то из
уравнения f(x) = д(х) следует уравнение f2n(x) = д2п(х), но оно не
равносильно заданному, т. к. содержит еще решение уравнения
f(x) = — д(х). Именно поэтому при возведении в четную степень,
чаще всего в квадрат, могут появляться посторонние корни.
Тогда нужна проверка.
Пример: Решите уравнение
Решение:
При возведении в квадрат могли появиться посторонние
корни, поэтому после нахождения корней необходима проверка. В
данном случае проверка показывает, что х = 0 — посторонний
корень, и1
Ответ: 3.
I означает конец решения.
15

Замечание: Этот же пример можно решить и без проверки,
если использовать равносильные переходы.
Решение:
В книге мы будем использовать следующие обозначения и
термины.
N — множество всех натуральных чисел.
Z — множество всех целых чисел.
Q — множество всех рациональных чисел.
Ш — множество всех действительных чисел.
Рп(х) — аохп + а\хп~1 + ... + ап — многочлен степени п,
« = » — это знак тождественных преобразований, т. е.
таких преобразований, которые верны при всех значениях
входящих в преобразуемые выражения букв и переменных. Например,
(х + а)2 = х2 + 2ах + а2, но aloga ь и Ъ не равны друг другу
тождественно, т. к. выражение Ь имеет смысл для любого
действительного числа Ь, a alogab имеет смысл лишь при а > О, а ф 1,
Ь > 0. Этот значок будем иногда употреблять, когда придется
упрощать какое-то выражение с помощью нескольких
последовательных преобразований, чтобы не спутать с уравнениями.
Промежуток. Под конечным или бесконечным
промежутком понимается одно из знакомых множеств действительных
чисел, которые обозначаются как (—оо;+оо), (—оо;а), (а;+оо),
(-оо; а], [а; +оо), (а; 6), [а; 6), (а; Ь], [а; 6], а < 6, а, b E R
ОДЗ (область допустимых значений) уравнения,
неравенства, системы или совокупности неравенств (уравнений)
называется множество, являющееся пересечением областей
определения всех функций, входящих в эти уравнения, неравенства,
системы или совокупности неравенств (уравнений). Если не
оговорено что-то специально, то под множеством X, на котором
производятся равносильные преобразования, всегда будет
подразумеваться ОДЗ.
16

Иногда будем использовать знак
равносильность в ОДЗ.
од;
, который обозначает
Степень с рациональным показателем
Уравнение вида
хп = а, п е N
Начертим эскизы графиков функции у = хп для четных и
нечетных п (рис. 1, 2).
У
\ у
\\
—хо О
/у=>
хо х
Рис. 1
Рис. 2
Из графиков видно, что прямая у = const ф 0 либб совсем
не пересекает график функции у = ж2п, либо пересекает график
в двух различных точках.
Видно также, что прямая у = const пересекает график
функции у = х2п~1 в единственной точке.
Рассмотрим функции у = х2п и у = х2п~1 только при х ^ О
(части графиков отмечены жирными линиями).
Теперь видим, что уравнение хп = а, п Е N имеет
единственное неотрицательное решение хо для любого
неотрицательного числа а и любого натурального числа п. Это решение
обозначается хо = л/а и называется арифметическим корнем
из числа а (запоминаем, что арифметический корень
определяется только для неотрицательного числа!). В математической
17

литературе, если не оговорено, четно п или нечетно, под ^/а
понимается именно арифметический корень.
Второе, отрицательное, решение уравнения х2п = а равно
(—xq) и обозначается (— >/а), п £ N.
Для отрицательных а уравнение х2п = а не имеет решений.
Уравнение х2п~1 = а, как видно из графика, имеет
единственное решение при любом действительном а. Это решение
называется корнем нечетной степени из числа а и
обозначается 2п~у/а. Для неотрицательных а значение 2п~у/а совпадает с
арифметическим корнем.
Итак,
х2п = а *=> х = ± Va, а ^ 0, п е N.
х2п~х = а Ф=* ж = 2п"Уа, oEl, n e N.
Число вида Щ, где п — произвольное натуральное число,
а т — произвольное целое число, называется рациональным
числом. Множество всех рациональных чисел обозначается
буквой Q.
Теперь для любого положительного числа а, любого
натурального числа п, п ^ 2 и любого целого числа т определяется
степень с рациональным показателем
аИ = \/а™, а > 0, п £ N, n ^ 2, m G Z.
Если дробь ^ > 0, то рациональная степень определяется
для неотрицательных а.
Графики функций у = 2^/ж и у = 2п+^/ж, n G N,
представлены на рис. 3 и 4.
По определению, а0 = 1 для любого действительного а ф 0.
Выражение 0° не определено.
В частности,
I ,-
an = -^a, a ^ 0, n G N, n ^ 2.
I
Спрашивается, верно ли, что $"ж = #з? Нет, неверно, т.к.
левая часть определена при любых #, а правая часть определена
только при х ^ 0.
18

О
y=
У\
у=
Рис.3
Рис. 4
Верно ли, что у/х = ж 2? Да, это верно!
Напомним свойства степеней с рациональным показателем.
Для любых положительных чисел а, Ь и любых
рациональных чисел р, q выполнены равенства
аРа? = ар+<1:
На первый взгляд, задания из части 1 билетов Единого
государственного экзамена на упрощение степенных выражений
являются стандартными. Однако это не совсем так.
Первая сложность состоит в том, что введенный в 9 классе
у/а определен по-разному для четных и нечетных п. Отсюда, в
частности, следует, что в общем случае у/а • у/а ф а. Тождество
у/а • у/а = а имеет место только для а ^ 0, a v? • у/а = а для
любого а G Ш.
В 10-11 классах в средней школе этот факт практически не
используется.
Вторая сложность состоит в том, что степень с нецелым
рациональным показателем определена только для
положительных чисел (с добавлением 0 при положительном показателе).
Здесь наиболее пытливые, но не очень внимательные,
учащиеся моментально запутываются, почему, например, у/а = а2, a
Находить значения буквенных выражений при заданных
значениях входящих в них букв можно по-разному.
19

1. Учащийся, который хорошо владеет формулами
сокращенного умножения и увидел, как их применение изменит
заданное выражение, может сначала упростить буквенное выражение,
а затем подставить туда заданные числа.
2. Иногда можно сначала упростить заданное выражение
при помощи введения вспомогательной переменной, а потом
подставить числа.
3. Иногда можно сразу в заданное выражение подставить
числа. Это особенно удобно, если заданы такие числа, что
хотя бы некоторые входящие в выражение корни извлекаются
нацело.
Поэтому естественно, что с преобразованиями числовых
выражений, содержащих корни, которые встречаются в
дальнейшем постоянно, учащиеся справляются намного успешнее, чем
с преобразованиями выражений, содержащих буквы.
/ I \
I а 2 — 4 1
/ I \ I
Пример: Упростите выражение I а 2 — 4 1 + 8а 2.
Решение:
2 I I I
+8а2 =а-8а2+16 + 8а2 =а + 16, а ^ 0.
Условие а ^ 0 приписано потому, что слагаемые, несущие
информацию об ОДЗ всего выражения, в результате
преобразований сократились. ■
Ответ: а + 16 при а ^ 0.
Ограничения, возникающие при преобразовании буквенных
выражений, особенно важны при решении уравнений.
2 1
Пример: Решите уравнение ——:-у— = — 2.
#"12
Решение: Грамотные учащиеся сразу скажут, что
уравнение не имеет решений, т. к. левая часть положительная при
любых х е ОДЗ.
20

Те же, кто сначала преобразует, не обращая внимания на
ОДЗ, получат готовый неверный «ответ» х = —2. ■
Ответ: Нет решений.
Еще труднее работать с арифметическими корнями.
Пример: Упростите выражение ~= • у 5.
Решение:
Ь = V V ь) V V6/ Ь =
а г-г /г V а
ab>0.
Здесь лучше сразу подставить, если будут даны числа.
Ответ: |6| - 1, аЬ > 0.
Пример: Упростите выражение h 2.
Vx2 + 2^ + 4
Решение: В отличие от предыдущих примеров, заданное
выражение определено при любых(!) ж. Произведем
преобразования:
+ 2= , J-X ,Л/- . ,+2=^5-2 + 2 =
Здесь х может быть любым, и нельзя вести преобразования,
считая, что у/х = #з ? т. к. это неверно. ■
Ответ:
Пример: Найдите значение выражения
s + У i
2 II 2 ^ '
hj/3
если а: = 8, у = 25.
21

Решение: Первый способ. Упростим сначала данное
выражение, т. к. в знаменателе просматривается неполный квадрат
разности:
/I 1\ / 2 11 i\
г U3 Н-2/3 J lxs -хзуз +y3j x
112* 2111
+2/3 Ж3 -хЗуЗ +уЗ
I
Следовательно, значение выражения при х — 8 равно 2.
Второй способ. Подставим заданные числа в выражение:
8 + 25
^ 2
4-2^25+^(25)2 4-2^25+^(25)2
Заметим, что если вычислять 252 = 625, то выкладки могут
усложниться.
Выбирайте тот способ, которым вы решите задачу
быстрее. ■
Ответ: 2.
2 ^
Пример: Решите неравенство ^-j жЗ + Ах ^ 0.
жз -4
Решение:
-4
;'-4)(^+4) i (х>о,
4=*a:€[0;43)U(43;+oo),
Ответ: х 6 [0; 64) U (64; +оо).
22

Пример (МГУ, 1978, мехмат): Упростите выражение
12л/5-29 -
Решение:
29 =
- 20 - 9
2л/5)2 =
- З)2 - 3 - 2\/5 = 2>/5 - 3 - 3 - 2\/б = -6.
Ответ: —6.
Пример: Упростите выражение v^P • у/а2№ — \/аъЪ&.
Решение:
= 6 • ^ • И ~ av^o
Ответ: vcfi • Ь • (\ab\ — ab).
Рациональные уравнения
и неравенства
Квадратные уравнения. Уравнения,
сводящиеся к квадратным
Самой главной темой математики, которую изучают в
школе подробно и до конца, является тема «Квадратные уравнения
и неравенства».
23

Большинство школьников владеет формулами решений
квадратного уравнения, но не все правильно решают их.
Уравнения часто решаются неверно, если коэффициенты приводят
к громоздким выкладкам. Поэтому, когда коэффициент при х
число четное, полезной оказывается следующая формула для
корней квадратного уравнения ах2 + Ъх + с = О, а ф 0:
Пример: Решите уравнение 144ж2 + 24ж — 287 = 0.
Решение:
144а:2 + 24ж - 287 = 0 «=*>
_ -12 ± у/144 -Ц44 -287 _ -1 ± у/Ш
^=*х~ 144 12
Если же пользоваться обычной формулой, то надо уметь
рационально вычислять дискриминант уравнения с четным
коэффициентом при х. В данном случае D = 24 • 24 + 4 • 144 • 287 =
= 12 • 12(4 + 4 • 287) = 122 • 22 > 288 = 242 -122 • 2, тогда
-12 ± 24 ■ 12>/2 = -1 ± 12л/2
Ж 2-12-12 12
Если в этом примере все квадраты и произведения вычислять, то
ответ или не получится вовсе, или получится очень не скоро. ■
Ответ: -^±л/2.
Уравнение можно считать решенным, если удается найти
замену переменных, которая сведет заданное уравнение к
квадратному.
Пример: Решите уравнение (х2 — I)2 — 7 \х2 — l| — 18 = 0.
24

Решение:
_ i|2 _ 7 |х2 - 1| - 18 = 0
\х2 - l| = 9 <=> х2 = 10 <=> х = ±л/Ш.
Ответ: ±л/Ш.
Пример: Решите уравнение 2^~1 + 2 • 21~^ -3 = 0.
Решение:
-1 + 2 . г1"^ -3 = 0 <^=Ф 2^~1 + —£ 3 = 0
2Vi-i
+ 2 = 0
^lv_i = o'^
Ответ: 1; 4.
Пример (МГУ, 1999, биофак): Решите уравнение
8cos6z- 12sin3a; = 3.
Pemewwe:
16sin23x + 12sin3rc - 5 = 0
lo
8
п€
Ответ: а; = . arcsin
25

Пример (МГУ, 1981, ф-т почв.): Решите уравнение
2(lg:c)2 + (1 - у/2) \g(x2) = 2л/2.
Решение: ОДЗ: х > 0. Поэтому lg х2 = 2 lg x и
2(lga;)2 + (1 - \/2)lg(a;2) =
\gx=
Ответ: 10"1,
Уравнения вида
Рп(ж) = о, п ^ 3 и сводящиеся к ним
Одним из способов решения уравнений высших степеней
является разложение на множители многочлена, стоящего в
левой части уравнения. Этот способ основан на применении
теоремы Безу: если число а является корнем многочлена Рп(х), то
этот многочлен можно представить в виде
Это значит, что если известен один корень уравнения
степени п, то с помощью теоремы Безу задачу можно свести к
решению уравнения степени п— 1, т. е., как говорят, понизить степень
уравнения. Если Рп(х) можно представить в виде (x—a)kQn-k(x)
и число х = а не является корнем многочлена Qn-i(^)5 TO
говорят, что а является корнем многочлена Рп(х) кратности к.
Как найти хотя бы один корень? Его приходится
«угадывать».
Чтобы понять, как угадывать, приведем без доказательства
теорему и ее следствия.
26

Теорема 1. Пусть несократимая дробь -, р £ Z, q Е N,
является корнем уравнения а^хп + а\хп~1 + ... + ап-\х + ап = О
с целыми коэффициентами. Тогда число р является делителем
свободного члена an, a q — делителем ао — коэффициента при
старшей степени х.
Следствие 1. Любой целый корень уравнения с
целыми коэффициентами является делителем его свободного члена.
Следствие 2. Если коэффициент при старшей степени
уравнения с целыми коэффициентами равен 1, то все
рациональные корни уравнения, если они существуют, являются целыми
числами.
Если удалось угадать корень а, то найти частное от
деления на (х — а) можно, по крайней мере, тремя способами:
делением под углом; по схеме Горнера; последовательным выделением
слагаемых, имеющих множитель (х — а).
Пример: Решите уравнение ж3 — 2х + 1 = 0.
Решение: Замечаем, что х = 1 является корнем уравнения.
Выделим множитель (х — 1) при помощи деления углом.
X3
X3
+ 0
—
■х2-
X2
х2-
х2-
1хЛ
2х
X
—х-
—х-
-1
rl
X
X2
-1
+ Х-1
Тогда
{х-1)(х2
X =;
-\±у/Ь
Ответ: 1,
27

Пример: Решите уравнение
з
(х + 1)2 - 6(х + 1) + 16л/аГ+1 -8 = 0.
Решение: Пусть у/х + 1 = £, £ ^ 0. Замечаем, что при такой
замене переменных ОДЗ квадратного корня выполняется
автоматически, т. к. х +1 = £2, и подкоренное выражение
неотрицательно при любом t. Исходное уравнение примет вид:
t3 - 6i2 + Ш - 16 = 0 «=» (t - 2)(t2 - At + 8) = 0 <=>
<=> t = 2 =»- \/жП = 2 «=Ф д: = 3. р
Ответ: 3.
Квадратные неравенства.
Метод интервалов для рациональных
функций
В школе, независимо от профиля, все изучают следующие
методы решений неравенств:
а) решение линейных неравенств;
б) решение квадратичных неравенств;
в) метод интервалов для многочленов и рациональных функций.
Многие школьники после изучения метода интервалов и
квадратичные неравенства решают этим методом.
В классах с математическим профилем изучается
обобщенный метод интервалов, который можно применять для
произвольных непрерывных функций или их частного. В нашей
работе мы его применять не будем.
Исследование квадратного трехчлена, наравне с решением
квадратного уравнения, является основной темой в школьной
программе по неравенствам.
Что необходимо знать о квадратном трехчлене?
28

1. Уметь строить эскиз графика любого конкретного
квадратного трехчлена
у(х) = ах2 + Ьх + с, а ф 0.
Для построения эскиза можно использовать разные подходы.
а) Если у квадратного трехчлена есть корни, то надо уметь их
найти. Зная, что вершина находится посередине между корнями,
уметь найти координаты вершины. Затем построить параболу по
трем найденным точкам.
б) Можно сразу воспользоваться соответствующими формулами
ру
У = ^^= —ц, D = Ь2 - 4ос и построить
2а ^ц
эскиз графика (направление ветвей определяется знаком
числа а). При необходимости, можно найти корни.
Полезно уметь приводить квадратный трехчлен к
каноническому виду с помощью выделения полного квадрата. Это
умение может пригодиться и при решении других задач. Произведем
тождественные преобразования
A
Отсюда сразу будет видно, как расположена наша парабола по
сравнению с классической параболой у = х2. Кроме того, хорошо
видно, какова роль дискриминанта.
2. Знать, без построения эскиза, что у квадратного
трехчлена с положительным коэффициентом при квадрате переменной
всегда есть минимальное значение, а у квадратного трехчлена
с отрицательным коэффициентом при переменной всегда есть
максимальное значение. Эти значения равны значению
квадратного трехчлена в вершине.
29

3. Уметь находить максимальное и минимальное значение
квадратного трехчлена на заданном отрезке или другом
заданном промежутке.
Это проще всего сделать, имея эскиз графика. Например,
на рисунке 5 а), б), в) видны наибольшие и наименьшие значения
квадратных трехчленов на отрезке [а; 6].
У
х
Важнейшим методом решения неравенств является метод
интервалов.
В 9 классе изучается метод интервалов прежде всего для
многочленов. Он основан на том, что двучлен (х — а)
положителен при х > а и отрицателен при х < а, т. е. меняет знак при
переходе через точку а.
Заметим, что
1) двучлен (х — а) в нечетной степени ведет себя так же,
как (х — а),
2) двучлен (х — а) в четной степени ведет себя по-другому:
он не меняет знак при переходе через точку о.
3) квадратный трехчлен, имеющий положительный
коэффициент при х2 и отрицательный дискриминант, всегда
положителен и может быть опущен при решении любого неравенства.
4) при переходе через точку а может изменить знак только
множитель (# —а)*, выражение (х — Ъ)п,Ъф а при переходе через
а знак не меняет.
30

Пример: Для функции
f(x) = (х - 1)2(х + 1,5)3(:г - 2){х + 2)4{х - 5)7
решить неравенства a) f(x) > О, б) f(x) < О, в) f(x) ^ О,
г) /(*) ^ О.
Решение: Для решения строгого неравенства наносим на
числовую ось нули функции кружочками (дырками).
Теперь расставим знаки (рис. 6). Замечаем, что при
больших х (х > 5) все множители положительны. При переходе через
точку х = 5 функция меняет знак, т. к. (х — 5) входит в
нечетной, седьмой, степени. По этой же причине при переходе через
х = 2 функция опять меняет знак, а вот при переходе через
точку х = 1 функция не меняет знак, т. к. (х — 1) входит в четной,
второй, степени, и т. д.
-2 -1,5 12 5 х
Рис.6
1. Теперь отметим «прямоугольниками» решение
неравенства а) (рис. 7) и записываем ответ: а) х £ (—1,5; 1) U (1;2) U
U(5;+oo).
A +-J,
-2 -1,5 12 5 х
Рис.7
2. Теперь отметим «прямоугольниками» решение
неравенства б) (рис. 8) и записываем ответ: а) х Е (—оо; —2)и(—2; —1,5)U
и(2;5).
-А - Д + о + J, - 3, + .
-2 -1,5 12 5 х
Рис. 8
31

3. Вспоминаем, что, по определению,
/(*) ^ 0 « 0) — Г/(Ж) = °'
0).
Для решения нестрогих неравенств наносим нули функции на
числовую ось точками. Затем расставляем знаки в промежутках
(рис. 9).
-2 -1,5
1 2
Рис. 9
4. При этом промежутки интересующего нас знака
замыкаются и к ним добавляются остальные нули функции (рис. 10).
-2 -1,5
. + I
1 2
Рис. 10
5. Теперь с рисунка 10 «снимаем» ответ: в) х £ {—2} U
U[-l,5;2]U[5;+oo).
6. Отмечаем решение неравенства (рис. 11) и записываем
ответ: г) х G (—сю; 1,5] U {1} U [2; 5]. ■
-2 -1,5
1 2
Рис. 11
Ответ: а) х G (-1,5; 1) U (1; 2) U (5; +оо), б) х € (-оо; -2) L
U (-2;-1,5) U (2; 5), в) х б {-2} U [-1,5; 2] U [5;+оо), г) х С
€(-«>; 1,5] U {1} U [2; 5].
Метод интервалов легко распространяется на рациональ
ные функции.
32

Рациональной называется функция, которая может быть
представлена в виде частного двух многочленов, т.е. в виде
Р(х)
Неравенства называются рациональными, если их правые и
левые части являются рациональными функциями.
Рациональные неравенства чаще всего решаются сравнением с нулем, т. е.
Р(х)
решаются неравенства вида > 0 ( < 0). Заметим, что дробь
Q[x)
положительна (отрицательна) тогда и только тогда, когда
числитель и знаменатель имеют одинаковые (противоположные)
знаки, поэтому метод интервалов применяется к дроби точно
так же, как и к многочленам — именно поэтому нули
знаменателя можно не отмечать в ОДЗ дроби при решении строгого
неравенства. Итак,
Щ > 0 (< 0) <=> P(x)Q(x) > 0 (< 0).
Нестрогое неравенство подразумевает, что решается или
Р(х)
уравнение . . = 0, которое равносильно смешанной системе
Q{x)
Р{х) = 0, ,
п( \ -и п 'где неравенств0 н© решается, а только после нахо-
ждения корней уравнения проверяется), или стросое
неравенство P(x)Q{x) > 0 ( < 0). Итак,
Р(х)
(х) — О
> О « 0)
P(x)Q(x) > 0 (< 0).
Иррациональные уравнения
Иррациональным называется уравнение, в котором
переменные входят под знаком корня (радикала).
33
2 Зяи ОА1

Пример: Решите уравнение
Решение:
(1)
Теперь заменим разность v^rr — 2 —
уравнения (1)). Получим уравнение
~^\ на v^3# — 8 (в силу
-8 = 2 - х.
(2)
Заметим, что это, вообще говоря, уже не равносильный
переход! Это уравнение является лишь следствием заданного
уравнения: если х = хо — корень уравнения (1), то х = хо будет
корнем и нового уравнения, но если если х — х\ — корень
нового уравнения, то это не значит, что х = х\ является корнем
уравнения (1), потому что в новом уравнении нет связи между
сомножителями, заданной исходным уравнением (1).
Решим получившееся уравнение:
(2)
- 2)(х - 4)(3ж - 8) = -(х - 2)3
(х - З)2 = О
Проверка (т. к. в одном месте не было равносильности!)
показывает, что х = 2 является единственным корнем уравнения. ■
Ответ: 2.
При решении любых уравнений, где есть хотя бы один
неравносильный переход, надо делать проверку!
34

Уравнения вида
Рассмотрим уравнение \ffjx) = д(х). ОДЗ уравнения:
/(*) > 0.
В ОДЗ левая часть уравнения всегда неотрицательна —
поэтому решение может существовать только тогда, когда д(х) ^ 0.
В этом случае обе части уравнения неотрицательны, и
возведение в квадрат дает равносильное уравнение. Мы получаем, что
9(*) > 0, (3)
Обратим внимание на то, что при этом ОДЗ выполняется
автоматически, и его можно не писать, а условие д(х) ^ 0
необходимо проверять.
Это очень важное условие равносильности. Во-первых, оно
освобождает учащегося от необходимости исследовать, а после
нахождения решений и проверять условие f(x) ^ 0 —
неотрицательности подкоренного выражения.
Во-вторых, акцентирует внимание на проверке условия
д(х) ^ 0 — неотрицательности правой части. Ведь после
возведения в квадрат на самом деле решается уравнение y/f(x) =
= =Ь?(ж), т. е. решаются сразу два уравнения (но на разных
промежутках числовой оси!):
1. у//(х) = д(х) — там, где д(х) ^ 0 и
2. >Jf{x) = -д{х) — там, где д(х) < 0.
Между тем многие, по школьной привычке находить ОДЗ,
поступают при решении таких уравнений ровно наоборот:
а) проверяют, после нахождения решений, условие f(x) ^ 0
(которое автоматически выполнено), делают при этом
арифметические ошибки и получают неверный результат;
б) игноририруют условие д(х) ^0 — и опять ответ может
оказаться неверным.
Наше условие равносильности особенно полезно при
решении тригонометрических уравнений, в которых нахождение ОДЗ
35

связано с решением тригонометрических неравенств, что гораздо
сложнее, чем решение тригонометрических уравнений.
Проверку в тригонометрических уравнениях даже условия д(х) ^ О не
всегда просто сделать.
Пример: Решите уравнение л/2ж3 — Ъх2 — 8х + 2 = у/2(х—1).
Решение: Воспользуемся (3):
\/2х* - Ьх2 - 8х + 2 = у/2(х - 1)
х - 1 ^ 0,
2ж3 - Ъх2 - 8х + 2 = 2х2 -Ах+ 2.
{
х(2х2 - 7а; - 4) = 0 ^ |ж = 0, х = 4, х = -±
Обратите внимание на то, что нет необходимости
проверять, и тем более находить ОДЗ — условие f(x) ^ 0. Заметим,
что в этом примере неравенство f(x) ^0 вообще трудно
исследовать. При таком способе решения ОДЗ уравнения (возведение в
квадрат) всегда выполняется автоматически, а вот посторонние
корни появляются, но они отсекаются условием х — 1 > 0. ■
Ответ: 4.
В общем случае при возведении в квадрат лишние корни
могут появиться, а могут и не появиться.
Пример: Решите уравнение \j2x2 — 8х + 9 = х — 1.
Решение:
\(x'-i)(x-i) =
x2 - 6x + 8 = 0. ^ 1 (x - 2)(x -4) = 0*^
la; = 4.
Ответ: 2; 4.
36

В этом примере не оказалось лишних корней.
Рассмотрим теперь самый простой вариант уравнения
y/f{x) = д(х) — уравнение
л/ах + Ь = сх + d. (4)
Такие уравнения можно решать различными способами.
Приведем некоторые из них.
1. Уравнение такого вида можно решать с помощью замены
переменных, положив t = л/ах + Ь, t^O. Тогда
ax -f 0 =
а
Уравнение (4) в новых переменных примет вид
_ c(t2 -b) 2
и задача сводится к нахождению неотрицательных решений
квадратного уравнения ct2—at—bc+ad = 0, что под силу любому
школьнику.
2. Часто школьники решают уравнение (4), возводя обе
части в квадрат. Получается квадратное уравнение
ах + Ъ = (сх + d)2. (5)
Но это уравнение, вообще говоря, не равносильно заданному
уравнению, т.к. заданное уравнение имеет решение лишь при
условии сх + d ^ 0. Поэтому после нахождения решения
уравнения (5) необходимо подставить найденные решения в заданное
уравнение (4) или проверить условие сх + d ^ 0.
Итак,
сх + d ^ 0,
ах + Ь= (cx + d)2.
При решении уравнений вида y/fjx) = g(x) школьники
прежде всего «честно» находят ОДЗ: д(х) ^ 0, но совершенно не
37

обращают внимания на то, что уравнение имеет решение только
для д(х) > 0, и получают «лишние» корни.
Покажем на простейшем уравнении у/ахЛ-Ъ = сх + d
важность условия д(х) ^ 0 и причину появления «лишних» корней.
Начертим эскизы левой и правой частей (рис. 12).
у-схЛ-d,
с>0
= cx+d
Рис. 12
Рис. 13
Сразу ясно, откуда берутся «лишние» корни: это
пересечение графика у = д(х) с графиком у = —yjf(x).
В данном случае хорошо видно, что это пересечение прямой
у = сх + d с полупараболой у = —у/ах + Ь, а > О, Ь > 0 (рис. 13)
Но «лишние» корни могут и не появиться — рис. 13.
Уравнения вида
Пусть задано уравнение y/fjx) = л/д(х). Его ОДЗ:
№ > о,
д(х) > о.
В ОДЗ обе части неотрицательны, и возведение в квадрат
дает равносильное уравнение /(аг) = д(х). Поэтому
y/gjx) ^ f(x) = g(x) в ОДЗ

или
/(*) ^ О
(ж) = д(х),
а;) ^ 0.
При таком способе решения достаточно проверить
неотрицательность одной из функций — можно выбрать более простую.
Пример: Решите уравнение
\/4я3 + 9х2 - Ах + 2 = \/ж2 - Зх + 4.
Решение: Воспользуемся (6), выбрав проверку знака более
простой функции — д{х). Видим, что д(х) = х2 — Зх + 4 > 0 для
всех действительных чисел. Поэтому
9z2 - 4ж + 2 = Vx2 - Zx + 4
«=* 4z3 + 9ж2 - 4ж + 2 = х2 - Зж + 4 4=*>
с3 + 8ж2 - х - 2 = 0 <=> 4х2(х + 2) - (ж + 2) = О
Ответ: -2, |, -|.
Иррациональные неравенства
Иррациональными называют неравенства, в которых
переменные входят под знаком корня. Так как корень четной
степени существует только у неотрицательных чисел, то при решении
неравенств, содержащих такое выражение, прежде всего удобно
найти ОДЗ.
39

Неравенства вида
у/ах
Неравенства вида
л/ах + Ь ^ сх + d (7)
или
у/ах Л- b ^ cx + d (8)
можно решать по-разному.
Первый способ. Можно решать с помощью замены
переменных, положив t = у/ах + Ь, t ^ 0. Тогда
ах + b =
и неравенство, (7), например, в новых переменных примет вид
_ c{t2-b)
a +
ct2 — at + ad — be
и задача о нахождении решения иррационального неравенства
(7) сводится к нахождению неотрицательных решений
квадратного неравенства
ct2 — at + ad — be ^ n
a ^u'
Второй способ. В отличие от уравнения, возводить в
квадрат обе части неравенства можно только тогда, когда обе части
его неотрицательны. Поэтому неравенства (7) или (8) решаются
в зависимости от знака < или ^ по-разному.
1. Из неравенства (7) следует, что cx+d ^ 0 в ОДЗ. Поэтому
после возведения в квадрат обеих частей получим равносильное
в ОДЗ квадратное неравенство ах + b ^ (сх + d)2. Осталось
приписать ОДЗ: cx + d^0.
40

Итак,
2. Неравенство с другим знаком решается сложнее.
Придется рассмотреть два случая.
а) Если cx + d < О, то неравенство выполнено для всех х из ОДЗ:
ах + Ъ ^ 0.
б) Если сх + d ^ 0, то в ОДЗ обе части неотрицательны.
Возводим их в квадрат и получаем равносильное в ОДЗ неравенство
ax + b^ (cx + d)2. Из последнего неравенства следует, что в этом
случае ОДЗ выполнено автоматически. Поэтому
сх + d < 0,
ах + b > 0;
сх + d ^ 0,
Ь^ (cx + d)2.
Третий способ. В тестовых заданиях, где ответ
целочисленный, иногда удается решить уравнение или неравенство
практически устно, если прикинуть эскиз графика правой и
левой частей уравнения или неравенства. Тогда окажется, что
неравенства (7) и (8) могут быть решены с помощью решения
единственного уравнения. При таком способе решения
необходимо только найти точки пересечения графиков функций,
стоящих справа и слева в неравенстве. В зависимости от знаков а, 6,
с, d и знаков неравенства <, >, ^, ^ получатся сплошные или
пунктирные промежутки, такие, как на рисунках 14-18.
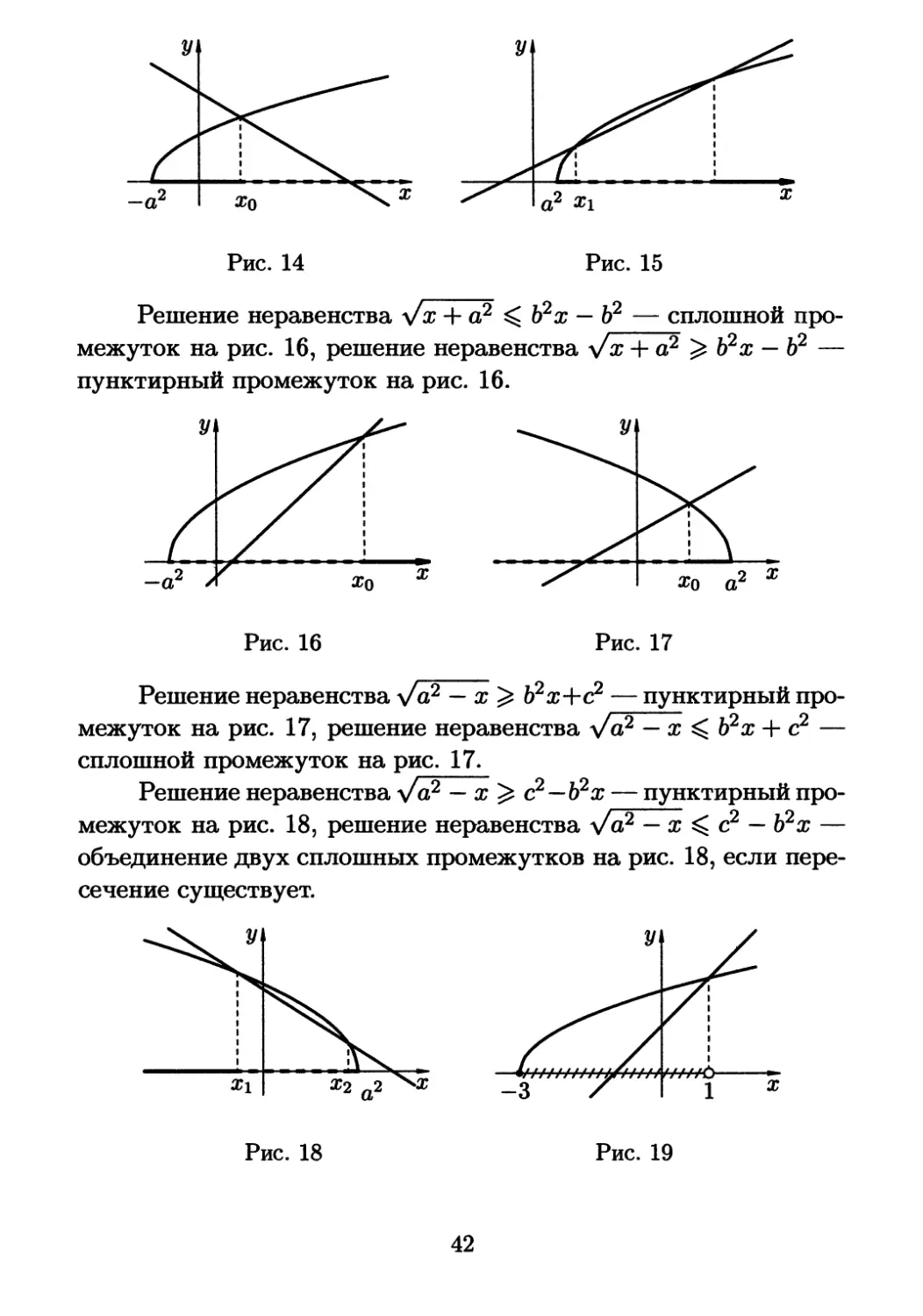
Решение неравенства у/х + а2 < с2 — Ь2х — сплошной
промежуток на рис. 14, решение неравенства у/х + а2 ^ с2 — Ь2х —
пунктирный промежуток на рис. 14.
Решение неравенства у/х — а2 < Ь2х + с2 — объединение
двух сплошных промежутков на рис. 15, решение неравенства
Vx — а2 ^ Ь2х + <? — цунктирный промежуток на рис. 15, если
пересечение есть.
41

a2 xx
Рис. 14
Рис. 15
Решение неравенства у/х + а2 ^ Ь2х — Ь2 — сплошной
промежуток на рис. 16, решение неравенства
пунктирный промежуток на рис. 16.
У
Ь2х — Ъ2 —
—а
х0
х0
г.2 X
Рис. 16
Рис. 17
Решение неравенства л/а2 — х ^ Ь2х+с2 — пунктирный
промежуток на рис. 17, решение неравенства Vа2 — х ^ Ь2х + с2 —
сплошной промежуток на рис. 17.
Решение неравенства у/о,2
межуток на рис. 18, решение неравенства у/а2 — х ^ с2 — Ъ2х —
c2—b2x — пунктирный про-
X
объединение двух сплошных промежутков на рис. 18, если
пересечение существует.
У\ У\
Рис. 19
42

Пример (МГУ, 1998, химфак): Решите неравенство
у/х + Ъ > х + 1.
Решение: Это неравенство можно решить любым из
вышеизложенных способов. Мы решим его графически. Построим
графики функций у = л/х + 3, у = х + 1 (рис. 19), посмотрим, где
первый график расположен выше второго. Для нахождения
решения останется решить только уравнение у/х + 3 = х + 1 (и не
надо рассматривать случаи разных знаков для х + 1).
x + 3 = x2 + 2x + l
x> -1,
Теперь можно получить решение неравенства: х Е [—3; 1). ■
Ответ: [-3; 1).
Кстати, как видно, решение этого уравнения можно было
получить и устно, в момент построения графиков. Графики
особенно удобно использовать, если, например, необходимо найти
количество решений в задачах с параметром или без него.
Неравенства вида
у/
ах2
Сначала квадратный трехчлен у = ах2 + Ьх + с приводится
к каноническому виду y(t) = et2 + f.
В зависимости от коэффициентов все сведется к
неравенствам вида (где коэффициенты а, 6, с, d уже другие, вообще
говоря, числа):
V а2 — х2 ^ сх + d или у а2 — х2 ^ сх + rf,
V а2 + х2 ^ сх + d или у/а2 + х2 ^ сх + d,
\Jx2 — a2 ^cx + d или \Jx2 — а2 ^ cx + d.
43

Левые и правые части неравенств легко можно построить
и для их решения достаточно решить только соответствующие
уравнения.
1. у/а2 - х2 ^cx + d (рис. 20).
Рис. 20
2. у/а2 - х2 ^cx + d (рис. 21).
3. у/а2 + х2 ^ сх + d (рис. 22).
У
Рис. 21
Рис. 22
4. у/х2 - a2 ^cx + d (рис. 23, 24).
Графики особенно удобно использовать, если, например,
необходимо найти количество решений в задачах с параметром
или без него.
Пример: Решите неравенства
а) у/х2 + 2х - 3 ^| + 1,
б) у/х2 + 2х - 3 ^? + 1.
44

Рис. 23
Рис. 24
Решение: Начертим эскизы правой и левой частей (рис. 25).
Видно, что для решения обоих неравенств достаточно найти
Рис. 25
45

Найдем их.
4
При наличии такого эскиза отпадает необходимость срав-
* * о -12-4V69
нивать между собой числа —3 и т-= , т.к. ясно, что
хх < -3. 15
Ответ получаем сразу для двух неравенств.
а) \/ж2 + 2х - 3 ^f + 1
-12-
«=» ж € -оо;
15J U [16
б) \/х2 + 2х - 3 < | + 1
-12-4у/б9
15 -3\и[^ 15 J-
л , / —12 - 4л/б91 ,, Г—12 -Ь 4л/б9 , \
Ответ: а) 1-оо; ^ и 15 5+00)'
Г-12-4х/69 If -12 + 4л/69]
[ is ;-3J U ^1; ^ j.
Неравенства вида
При решении этого неравенства, как выясняется,
школьники очень часто ошибаются. Воспользуемся определением не-
46

строгого неравенства (для определенности будем рассматривать
один знак, например, ^):
= о,
(т) — О
Ко
■«=*■
Г/И > 0,
\д(х) > 0.
Пример: Решите неравенство
л/6 — ж — ж2
Решение: ОДЗ: 6 - ж - ж2 ^ О <=>■ ж G [-3; 2]. Далее,
х = -3,
х = 2,
б — х — х2
х2-\
*"~ Гжб(-3;2), —
Дж2 -КО
<*=> ж € {-3} U (-1; 1) U {2} . ■
Ответ: {-3} U (-1; 1) U {2}.
Замечание: Школьники часто забывают записать в ответ
точки ж = —3 и ж = 2.
Неравенства вида
S) >«)*(*)
Для решения неравенств обязательно придется найти ОДЗ:
f{x) ^ 0.
Рассмотрим разность y/f(x) — #(ж). Квадратный корень,
если он существует, т.е. если х G ОДЗ, принимает
неотрицательные значения. Поэтому,
47

а) если д(х) < О, то разность положительна в ОДЗ и
неравенство y/f(x) > д(х) выполнено в ОДЗ, а неравенство y/JJx) <
< д(х) не имеет решений;
б) если же д(х) ^ 0, то знак разности может быть любым, но
сумма y/f{x)+g(x) ^ 0 (неотрицательна), и умножение разности
на эту сумму не меняет знака разности, т. к.
- д(х)) (
д(х)) = /(*) - 92(х)
в ОДЗ. Поэтому, если д(х) ^ 0, то
у/1Щ-д(х) < 0 (> 0) &f(x) -92{х) < О (> 0).
Правило 1. Если д(х) ^ 0, то знак разности
совпадает со знаком разности f(x) — g2(x) в ОДЗ.
Этот же результат получаем, если учтем, что обе части
неравенств неотрицательны и возведение в квадрат приводит к
равносильным в ОДЗ неравенствам f(x) > д2(х) и f(x) < д2{х)
соответственно. Отсюда следуют условия равносильности
ff(x)>g{x)
(д(х) < 0,
\f(x) > 0;
fg(x) > 0,
l\f(x) > дЧ
д(х) > о,
fix) > 0,
Пример (МФТИ, 1983): Решите неравенство
48

Решение: ОДЗ:
х2 - 6ж == х(х - 6) > О Ф=> ж G (-оо; 0] U [6; +оо).
Далее,
/8 + 2а; > 0,
гх > -4,
Учтем ОДЗ и получим, что х Е (-2; 0] U [6; +оо). I
Ответ: (-2;0] U [б;+оо).
Пример (МФТИ, 1983): Решите неравенство
2-Зх <
Решение: 1 способ. Найдем сначала ОДЗ.
4 + 9х - 9х2 ^ 0 <^>> 9х2 - 9х - 4 < 0
Теперь рассмотрим два случая.
Если 2 — Зх < 0 («Ф=> ж > ^ 1, тогда неравенство выполнено
вОДЗ,Т.е.Жб(|;|].
Бели 2 - Зж ^ 0 Г ^=^> ж ^ | J, тогда
2 - Зж < у/4: + 9х - 9х2 <=)> (2 - Зж)2 < 4 + 9ж - 9ж2 «=>■
49

2 /21
Учитывая то, что х < ~, получаем в этом случае х Е (0; ^ .
Объединяя рассмотренные два случая, получаем х £ (0; «г .
2 способ — графический. Построим эскизы правой и левой
частей (рис. 26). Выделим полный квадрат под корнем в правой
части неравенства:
Рис. 26
Сразу видно решение неравенства же (О; f •
Ответ: х € ((); |].
Неравенство вида
ОДЗ неравенства:
о,
[9(х) > 0.
В ОДЗ обе части неравенства неотрицательны, и возведение
в квадрат приводит к равносильному неравенству f(x) ^ д(х)..
50

Из этого неравенства видно, что не обязательно решать
неравенство д(х) ^ 0, а достаточно только решить f(x) ^ 0. Поэтому
\
f(x)
о,
(9)
или
Отсюда, в частности, вытекает полезное следствие:
Правило 2. Знак разности y/f(x) — у/д{х) совпадает со
знаком разности f(x) — д(х) в ОДЗ.
Пример: Решите неравенство у/2х + 1 ^ \/ж3 — 4а:2 + х + 5.
Решение: Воспользуемся (9):
/2х + 1
+ х + 5
2# + 1 < ж3 - Ах2 + х + 5,
2х + 1 > 0.
-1 -0,5
1
Рис. 27
Неравенства решили методом интервалов — рис. 27.
Ответ: [-i; ll U [4; +оо).
51

Более сложные неравенства
Т. к. при д(х) ^ 0 знак разности y/fjx) — д(х) совпадает
со знаком разности f(x) — д2(х) в ОДЗ, то получаются условия
равносильности:
• если д(х) ^ 0, то
0)
< О О 0);
если ^(ж) < 0,
Или, объединив оба условия, получим, что
д(х) < О,
h(x)>0(<0),
д{х) > О,
/(ж)-<,2Ы
h(x)
Так как знак разности y/f{x) — \/g{x) совпадает со знаком
разности f(x) — g(x) в ОДЗ, то
Пример (МФТИ, 1997): Решите неравенство
26 - Зж + Ух2 - 2ж - 24 _1
ж-10
Решение: ОДЗ. ж2 - 2ж - 24 ^ 0 <^> ж € (-оо; -4] U [6; +оо).
Теперь решаем неравенство в ОДЗ:
26 - Зж + Ух2 - 2ж - 24 ^. . Ух2 - 2ж - 24 - 2(ж - 8)
ж -10 < <J=* ж^Тб
52

1. Если х — 8 < 0, то числитель положителен в ОДЗ, а
знаменатель отрицательный, и неравенство верно, т. е.
хе (-oo;-4]U[6;8).
2. Если х — 8 ^ 0, то воспользуемся тем, что в ОДЗ знак
разности y/f(x) — д(х) совпадает со знаком f(x) — д2(х). Тогда
/ж2^2ж - 24 - 2(х -8) х2 - 2х - 24 - 4(ж - 8)2
v / <о — v ;
ж - 10
-Зге2 + 62* - 280 _ 3 (а? - f) (х - 14)
ж-10 " х-10
Учитывая ОДЗ и условие х ^ 8, получаем, что
se[8;10)U(14;+oo).
Суммируя результаты 1 и 2, получаем ответ. ■
Ответ: (-оо; -4] U [6; 10) U (14; +оо).
Уравнения, содержащие модуль
Уравнения вида
\f(x)\ =
Такие уравнения можно решать двумя способами.
Первый способ — он применяется в том случае, когда
Функция f(x) проще, чем д(х).
Там, где f(x) > 0, выполнено равенство |/(х)| = f(x) и
Уравнение примет вид f(x) = д(х); там, где f(x) < 0, выполнено
Равенство \f(x)\ = —f(x) и уравнение примет вид —f(x) = д{х).
И, наоборот, если f(x) ^0 и f(x) = д(х), то \f(x)\ = д(х), а
/(ж) < 0 и —f(x) = д{х), то опять |/(ж)| = д{х)> или
53

(х) < О,
Ц/И = -s(z).
При этом не надо решать неравенства, а надо только
подставить в них полученные решения соответствующих уравнений
Можно поступить и так: решить совокупность уравнений
"/(я?) = д(х),
я) = -50*0,
а затем просто сделать проверку.
Пример: Решите уравнение \х — 7| = ж3 — 15ж2 + ж + 7.
- 7| = ж3 -
ж + 7
ж - 7 ^ О,
х - 7 = ж3 - 15ж2 + ж + 7;
ж - 7 < О,
ж - 7 = -ж3 + 15ж2 - ж - 7
ж3 - 15ж2 + 14 = 0;
7,
ж3 - 15ж2 + 2х = 0
(ж-1)(ж2-14ж-14) = 0;
ж< 7,
Дж(ж2-15ж + 2) = 0
(ж - 1)(ж - (7 + \/63))(ж - (7 - УбЗ)) = 0;
ж < 7,
15-л/2Г^\ _п
ж ^ ) "и
54

"ж = 7 + \/63;
х = 0,
15-V2I7
X =
Ответ: 0; 7 + v/бЗ;
15 ~
Второй способ — он применяется обычно, если функция
д(х) проще, чем /(ж).
Заметим, что уравнение \f(x)\ = g(x) не имеет решений,
если д(х) < 0. Если же д(х) ^ 0, то там, где f(x) ^ 0, уравнение
имеет вид f(x) = д(х), а там, где f(x) < 0, уравнение имеет вид
—f{x) = д(х). Отсюда следует , что
!/(*)! =
гд(х) > 0,
\f(x) = g(x);
\f(x) = -д(х
Пример: Решите уравнение |бж3 — 2х2 + 4ж — 331 = 10ж —35.
Решение: Этот пример проще решать вторым способом, т. к.
гораздо проще проверить для корней условие д(х) ^ 0, чем
условие f(x) ^ 0.
Итак, если 10ж — 35 ^ 0, то
- 2х2 + 4ж - 331 = 10ж - 35
[бя3 - 2х2 + Ах - 33 = 10s - 35,
- 2х2 + Ах - 33 = -Юя + 35
Гбж3 - 2х2 - 6ж + 2 = 0,
[бж3 - 2ж2 + 14а: - 68 = 0.
Первое уравнение легко разлагается на множители
группировкой, а во втором угадывается корень х = 2, и получается
равносильная совокупность
"2(Зж-1)(ж2-1) = 0,
(х-2)(3х2 + 5ж + 17) =0.
х = 2.
55

Учитывая, что 10ж — 35 ^ О, получаем ответ.
Ответ: Нет решений (0).
Уравнения вида
!/(*)! = 1<К*)1
Так как обе части уравнения неотрицательны, то
/2(х) - д2(х) = (/(я) - g(x))(f(x) + д(х)) = О
[f(x) = -g(x).
И мы получаем следующее условие равносильности
(т\ __ п(т\ — о
/ \ , ^f гг,\ Л
Оно удобно тем, что никак не связано со знаками f(x
и д(х).
Пример: Решите уравнение
\хь - 6х2 + 9х - б| = \х5 - 2а;3 +
Решение:
\хь - 6а;2 + 9а; - б| = |а:5 - 2а;3 + 6а;2 -
"2ж5 - 2ж3 - Ах = О,
2ж3 - 12а;2 + 22а; - 12 = 0.
2а;(а;4 - а;2 - 2) = 0,
2(а;-1)(а;2-5а; + 6)=0.
х{х2 - 2)(х2 + 1) = 0,
- 13а; + б|.
(х = 0,
\х = ±л/2;
(х = 1,
\х = 2,
[х = 3.
56

И мы получаем ответ. ■
Ответ: 0, ±л/2, 1, 2, 3.
Уравнение вида
\ах + Ь\ = сх + d
При решении уравнений вида \ах + Ь\ = cx+d удобно
прикинуть эскизы правой и левой частей. Эскиз для уравнения может
дать ответ на вопрос о количестве решений уравнения (рис. 28).
Рис. 28
Рис. 29
Пример: Сколько решений имеет уравнение \х + 1| = Щ + а
в зависимости от параметра а?
Решение: Начертим сначала эскиз графика функции у(х) =
= |ж + 1| (рис. 29).
Прямые у = ^ + а, в зависимости от а, параллельно
перемещаются вдоль оси ординат, проходя через точку (0;а), и
Решение видно. Осталось определить а, при котором «первая»
пРямая пересечет «угол» в вершине: эта прямая проходит через
(—1;0)=Ф>а=х. Поэтому получаем ответ. ■
Ответ: Нет решений при а < ^; одно решение при а = ^>;
1
решения при а > -^.
57

Неравенства, содержащие модуль
В этом параграфе рассматриваются неравенства,
содержащие переменную под знаком абсолютной величины (под знаком
модуля).
Во многих случаях для решения таких неравенств
целесообразно разбить числовую ось на промежутки так, чтобы
функции, стоящие под знаком модуля, на каждом из промежутков
сохраняли знак, т. е. были или положительными, или
отрицательными. Тогда на каждом таком промежутке неравенство можно
записать без модуля. В таком случае говорят, что мы раскрыли
модуль.
Простейшие неравенства
Простейшими неравенствами, содержащими модуль,
являются неравенства вида \ах + b\ ^cx + dn \ах + Ь\ ^ сх + d, а Ф 0.
Полезно уметь строить эскиз графика функции у — \ах 4- Ь\.
Для этого сначала строим график прямой у = ах + Ь (это умеют
все — см. рис. 30).
Затем отражаем «отрицательную» (пунктирная тонкая
полупрямая) часть прямой относительно оси абсцисс (жирная
пунктирная полупрямая) и получаем нужный график — «угол»
с вершиной в точке хо = — g, правый луч которого образует с
осью абсцисс угол а, для которого tga = \а\ (рис. 31).
При решении неравенств вида
\ах + Ь\ < сх + d и \ах + b\^ cx + d
удобно прикинуть эскизы правых и левых частей.
Тогда вместо решения неравенств достаточно только найти
точки пересечения жх, #2, если такие есть, «угла» у = \ах + Ь\ с
58

>""**= Л
Рис. 30
Рис. 31
прямой у = сх + d, т. е. решить только одно уравнение \ах + Ь\ =
= еж + d, а затем для неравенства записать ответ в зависимости
от знака неравенства.
Рис. 32
Таким образом,
\ax + b\ < cx + d «<=> x E [хц x2] — (рис. 32);
\ax + b\^ ex + d <£=>• x G (—00; x\] U [x2\ +00).
«Угол» может пересекаться с прямой только в одной точке,
тогда (рис. 33)
\ах + Ь\ < сх + d <=> х G [х\] +оо);
\ах + b\^ cx + d <=$> х G (—оо; х{\.
59

у — схЛ-d
Рис. 33
Рис. 34
«Угол» может и вовсе не пересекаться с прямой, тогда
(рис. 34)
\ах + b\ ^cx + d
\ах + Ь\ ^ сх + d
0;
Для неравенств вида \f(x)\ < g(x), \f{x)\ > g(x), \f(x)\ <
< \д(х)\ мы приведем сейчас такие условия равносильности, при
использовании которых знаки функций f(x) и д(х) не имеют
никакого значения.
Неравенства вида
\f(x)\<g(x)
Пусть в некоторой точке а выполнено неравенство \J{x)\ <
< д(х), тогда д(а) > 0 и |/(а)| < д(а).
Тогда выполнены неравенства — д(а) < f(a) < д(а) и на
числовой оси имеет место ситуация, изображенная на рисунке 35.
1 м д
-(W////////V//////////D-
9(а)
Рис. 35
И, наоборот, пусть в некоторой точке о выполнены
неравенства —д(а) < f(a) < д(а).
60

Тогда, во-первых, — д(а) < д(а) -Ф=Ф- д(а) > 0, а, во-вторых,
|/(а)| < д(а). Следовательно, имеет место условие
равносильности
д(х) <£=» -д(х) < f(x) < д(х)
(f(x) < д(х),
\f(x) > ~д(х).
(10)
Пример: Решите неравенство |ж — а| + |ж — 2|-+-а — 4 ^0 при
всех а.
Решение:
\х - а\ + \х - 2\ + а - 4 < 0 <=> \х - а\ < 4 - а - \х - 2| «=>
• — In -4- 4
х — 2 ^ 4 — ж,
ж — 2 ^ х — 4;
а — 1.
а-1 3 х
Рис. 36
Из рисунка 36 видно, что решением будет промежуток
[а — 1; 3]. Итак, решений при а > 3 нет, а при a G (—оо; 3] имеем
а-1<ж<3. ■
Ответ: я? € [о — 1; 3] при а Е (—оо; 3]; нет решений при a G
6(3;+оо).
Неравенства вида
\f(x)\>g(x)
Пусть дано неравенство \f(x)\ > g(x). Тогда,
если д(х) < 0, то неравенство выполнено, т. к. модуль
принимает неотрицательные значения и всегда больше любого
отрицательного числа;
61

если д(х) ^ 0, то выполнена совокупность неравенств
\f(x) > д(х),
[f(x) < -д(х)
и на числовой оси имеет место ситуация, изображенная на
рисунке 37.
На)
-д(а) 0 д(а) х
Рис. 37
И, наоборот, пусть в некоторой точке х — а имеет место
совокупность неравенств
\f(a)>g(a),
\f (a) < -д{а).
Тогда,
• если д(а) < О, то неравенство |/(а)| > д(а) выполнено,
• если д(а) ^ 0, то имеет место ситуация рис. 37 и выполнено
неравенство \f(a)\ > д(а).
Следовательно, имеем равносильные соотношения
f(x) > д(х),
f(x) < -д(х).
Пример (МГУ, 1983, биофак): Решите неравенство
8 + 6- |3-л/яг + 5| >х.
Решение: Воспользуемся условием (11). Тогда
I > х - 8
8 + 6 • |3 - л/ж + 5| > х <=> 6 - |3 — у/х
Г18 - бл/я + 5 > х - 8,
(И)
< 26 - х,
> 10 +ж.
62

-5
У\
х
-1
/ -5
Рис. 38
Рис. 39
Решим неравенства графически. Для первого неравенства
находим х* (рис. 38).
Решение неравенства «снимаем» с рисунка. Для х* имеем:
(х* < об
бл^Тб = 26 - а* « [^ + ;8() = 2б2 _ 52ж, + (я#)2 <=>
Ф=^ ж* = 44 - 12л/10.
Решение первого неравенства совокупности х G [—5; 44 — 12л/Ш).
Для решения второго неравенства находим х\ и х2 из
уравнения
= 10 + а; 4=^ Збж + 180 = 100 + 20ж + х2
Ж1 = -4,
ж2 = 20.
Теперь решение второго неравенства «снимаем» с рисунка 39:
же (-4;20).
Так как 44 — 12л/Ш < 20, то решением совокупности будет
же [-5;20). ■
Ответ: [-5; 20).
Пример (МГУ, 2000 , ВМК): Решите неравенство
Решение:
2 1 О I
63

\х2
Ъх- 18| - х2 < -
X
I\x2 + Ъх - 18| > x2 - x + 18,
\X ~h 0Ж — 18 ^ X ~\~ X — 18
'x2 + Ъх - 18 ^ x2 - ж + 18,
ж2 + 5ж - 18 < -x2 + x - 18;
я2 + 5я - 18 < х2 + х - 18,
х2 + Ъх - 18 > -ж2 - ж + 18
"Об,
ф; + 2К0;
[{
Ответ: (-оо; -6] U [-2; 0] U [6; +оо).
-6.
Неравенства вида
|/(g)| < \д(х)\
Рассмотрим разность |/(ж)| — |^(х)|. Она может быть любого
знака, но сумма \f{x)\ + \g{x)\ всегда неотрицательна, и
умножение разности на эту сумму не изменит знака разности, т. е.:
Правило 3. Знак разности модулей \f(x)\ — \д(х)|
совпадает со знаком произведения (/(#) + g(x))(f(x) — д{х)).
Действительно,
(\f(x)\ - \д(х)\) (|/(*)| + \д(х)\) = (|/(х)|2 - \д(х)\2) =
= (f2(x) - д2(х)) = (f(x) - g(x))(f(x) + д(х)).
Отсюда, в частности, следует, такое
64

Правило 4. Если д(х) ^ 0, то знак разности \f(x)\—g(x)
совпадает со знаком произведения (f(x)—g(x))(f(x)+g(x)).
Итак, имеем еще одно условие равносильности
|/(х)| < \д(х)\ *=* (f(x) - g(x))(f(x) + g(x)) < 0. (12)
Условия равносильности имеют тот же вид для нестрогих
неравенств.
Пример (МГУ, 1998, ф-т почвоведения): Решите
неравенство
2
Решение:
1 о |ж + 1|
Мы воспользуемся тем, что знак разности \х + 1| — 1 совпадает
со знаком произведения (ж+ 1 + 1) (ж+ 1 — 1) и аналогично для
разности |ж + 1| — 2
(х + 1 + 1)(ж + 1 - 1)(ж + 1 + 2)(х + 1-2)
\х = -1,
[х{х + 2)(ж + 3)(ж - 1) < 0. ^^
ж € (-3;-2) U {-1} U (0; 1).
Ответ: (-3; -2) U {-1} U (0; 1).
65
Зак243

Показательные и логарифмические
уравнения
Введение. Основные свойства логарифма
В школьном курсе для любого положительного числа а
т
определяется число а п , где т — целое число, an — натураль-
т
ное число. Если -^ > 0, то а п определено и для а = 0.
Затем для любого положительного числа а вводится
понятие аж, где х — любое действительное число.
Если х > 0, то 0х = 0. Заметим, что 0° не определено.
Если а = 1, то Iх = 1 для любого х.
Принимается без доказательства, что для любых
положительных чисел а и b и любых действительных чисел х и у
справедливы свойства:
ах-ау = ах+2/; Щ: = а*"2';
ау
(ах)у = аху; ах-Ъх = {аЪ)х;
(13)
Так как при а > 0 для любого действительного числа х
определено число аж, то можно рассматривать функцию у = аж,
определенную на всей действительной оси.
Если а > 0, а ф 1, то функция ах отлична от постоянной.
Ее называют показательной функцией с основанием а.
Если о > 1, то функция ах — монотонно возрастает на 1R;
если 0 < а < 1, то функция ах монотонно убывает на R
Область значений показательной функции — множество
R+ всех положительных чисел (рис. 40-41).
Отсюда и из монотонности (любая горизонтальная прямая
у = N, N > 0 пересекает график функции у = ах,а>0, а ф\
ровно один раз) следует, что если а > 0, а ф 1, то для любого
положительного числа N существует единственное число Ь,
такое, что аь = N. Это число называется логарифмом числа N по
66

0
1
i
. «>0 / \у = а*,
Ь х 1
0<а<1
sr
1 0
У
X
Рис. 40
Рис. 41
основанию а и обозначается Ъ = loga iV. Из определения следует
равенство
aloga JV = Nt
Это равенство называется основным логарифмическим
тождеством. Но по сути, тождеством оно не является, так как оно
верно не для всех значений а и N. Оно верно только для N > 0,
а > 0, а ф 1. Эти значения называются ОДЗ выражения loga N.
Из определения следует, что основанием логарифма может
бьщъ любое положительное число, не равное единице, а
логарифмы существуют только у положительных чисел.
В школьном курсе математики показывается, что если а >
>0, a^l,M>0, iV>0, a — любое действительное число, то
верны формулы:
loga MN = loga M + loga N;
loga =
loga Ma = a loga M.
Если, к тому же, Ь > 0, b ф 1, то
(14)
(15)
(16)
(17)
Последняя формула позволяет переходить от логарифма по
основанию о к логарифму по основанию Ь. Она называется
формулой перехода к новому основанию.
67

Свойства (14)—(17) при вышеописанных условиях (М > О,
N > 0) являются тождествами и читаются как справа налево,
так и слева направо.
Заметим, однако, что левые и правые части равенств в (14)
и (15) имеют разные области определения: левая часть
определена при MN > 0, а правая — при М > 0, N > 0. Это надо
учитывать при решении задач: MN > 0 не только тогда, когда
М > 0, N > 0, но и тогда, когда М < 0, N < 0. Учтем, что
MN = (_J\fr)(_JV), и для -М > 0, -N > 0 (в силу (13))
loga((-M)(-i\0) = loga(-M) + loga(-iV).
Теперь запишем более общие формулы.
Если MN > 0, то
loga(MiV)=loga|M|
Если М ф 0, N Ф 0, то
loga|M|+loga|iV| =
Аналогично показывается, что если MN > 0, то
logoM = logo|M|-loga|JV|.
Если М Ф 0, N Ф 0, то
logo|M|-loga|JV| =
Если М ф 0, то для любого натурального п
logaM2n = 2nloga|M|.
Все свойства читаются в обе стороны (т. е. являются
тождествами) при выполнении приведенных для каждого из них условий.
Учитывая все свойства показательной функции и
определение логарифма, можно построить эскизы графиков — рис. 42-43.
68

У
0
I
l/=loga
X,
a>\
X
= logax, 0<a<l
Рис. 42 Рис. 43
Отметим некоторые наиболее употребляемые частные
свойства:
1) loga 1 = 0, a > 0, а ф 1, т. е. логарифм числа 1 при любом
допустимом основании равен 0;
2) loga ах = #, а > 0, а ф 1. Это свойство часто применяют в
«обратном» порядке — чтобы выразить заданное число Ь через
логарифм по основанию а, а именно, Ъ = loga аь.
Пример (МГУ, 1998, биофак): Вычислите
если logdс = v5.
Решение: Так как logd с = \/5, то d > 0, d ф 1, с > 0, и все
корни можно заменить рациональными степенями.
Чтобы вычислить значение данного выражения, перейдем
к новому основанию, равному d. Используем также формулы
(14)-(16). Тогда
log
С4/3
Ответ:
20л/5-3
3(20 +
4+|logdc
20\/5-3
3(20 + 6л/5)'
69

Принято логарифм числа х по основанию 10 обозначать
lga;, а логарифм числа х по основанию е обозначать 1пх.
Логарифмирование и потенцирование
При решении показательных и логарифмических
уравнений особенно часто используются два преобразования:
потенцирование и логарифмирование. Эти преобразования не являются
равносильными переходами.
Логарифмированием уравнения f(x) = д(х) по основанию
а (а > 0, а ф 1) называется переход от уравнения f(x) = д(х)
к уравнению loga/(#) = \ogag(x). При этом область
существования (ОДЗ) уравнения сужается, т. к. логарифмы существуют
только у положительных чисел.
Например,
х = — 1, но lga;3 = lgz <=$■ х = 1.
Уравнения я;3 = х и lga:3 = \gx не равносильны, т. к. имеют
разные множества решений.
Потенцированием называется переход от уравнения
к уравнению f(x) = g(x). При этом область определения
расширяется, т. к. второе уравнение может существовать при любых
/(ж), д(х), а первое — только при положительных.
Поэтому запишем и запомним: если f(x) = д(х) и f(x) > 0
или д(х) > 0, то
. (18)
Из равенства функций и положительности одной из них следует
положительность другой, поэтому проверяем условие
положительности только той функции, для которой это сделать проще.
70

Если loga f(x) = logag(x), то
f(x) > 0, g(x) > 0 и f(x) = g(x). (19)
Итак, из (18) и (19) следует условие равносильности
При решении логарифмического уравнения удобно пользоваться
той системой, в которой неравенство проще проверить.
Показательные уравнения
Из монотонности показательной функции следует, что
ах = ау ^=> х = у.
Из свойств показательной функции следует, что если а > 0,
а ф 1, то простейшее показательное уравнение ах = Ь при
Ь ^ 0 не имеет решения, а при Ъ > 0 имеет единственный
корень ж = loga Ь.
Для успешного решения большинства учебных примеров
решающим является умение преобразовать исходное уравнение
к более простому.
При этом необходимо знать решения следующих основных
уравнений (а > 0, а ф 1, Ь(х) > 0):
1. аЛ*> = cflW <=* f(x) = д(х).
2. аЛ*> = Ь{х) «=* /(я?) = loga Ь(х).
3. g{a>f(x^) = 0. Это уравнение заменой переменных а^х^ = f
сводится к уравнению g(t) =0 (где ^(t) чаще всего будет
многочленом 2-й или 3-й степени), у которого отыскиваются
положительные корни, а затем решаются уравнения типа 2.
4. Для любых а > 0, Ъ > 0, с > 0, с ^ 1, h > 0, d > 0:
a . b'W = h • d5(a:) «=* logc a + f(x) logc 6 = logc h + g(x) logc d.
71

Уравнения, в которых основанием являются числа 1 или О,
не относятся к показательным, потому что функции Iх и 0х, по
определению, не называются показательными. Можно отметить,
что имеют место соотношения:
lf& = Ъ(х)
Ь{х) =
Выражение 0° в математике не определено.
Пример: Решите уравнение 8Х-13-4Х.3Х--2Х-9Х + 13-З3х = 0.
Решение: Уравнение является однородным 3 степени
относительно 2х и 3х. Оно сводится к уравнению с одним
переменным, если его разделить на 23х или 33х. Удобнее делить на
23х, чтобы новое уравнение содержало показательную функцию
с основанием, большим 1.
8х - 13 - 4х • 3х - 2х • 9х + 13 • 33х = 0
26х - 13 • 22х • 3х - 2х • 32х + 13
= 0
Пусть ( ^ J = £, t > 0, тогда последнее уравнение примет вид
1 - Ш - t2 + Ш3 = 0. Решаем его:
1 - 13* -12 + 13i3 = (1 - *2)(1 - 13*) = 0
t —
13'
Теперь с учетом условия * > 0, возвращаемся к переменной х:
Ответ: 0, — Iog3 13.
2
I
Пример: Решите уравнение 500 • 8х = 8 • 5 я.
72

Решение:
500 • 8х = 8 • Ъх «=*> 53 • 22 • 23* = 23 • 55 <=> 231"1 = 5*~3
-1)log52 = |-3 «=>• Зж2log5 2-a:(log5 2-3)-l = 0
log52-3±(log52
~ 61og52
Ответ: ^, — Iog25.
Пример: Решите уравнение щ + ^ = 5.
а О
Решение: Это уравнение удается решить, используя то, что
левая часть уравнения является строго убывающей функцией,
которая любое положительное значение принимает только один
раз. Подбором убеждаемся, что х = — 1. ■
Ответ: —1.
Логарифмические уравнения
Традиционно логарифмические уравнения вызывают
затруднения у многих школьников. Во-первых, потому, что у
логарифма есть область определения. Во-вторых, подлогарифми-
ческие выражения могут быть любыми положительными
функциями, и надо помнить, что последующие преобразования могут
быть неравносильными (например, возведение в квадрат) и
потеря или приобретение корней в промежуточных выкладках уже
не связано с ОДЗ логарифмов.
Поэтому при решении простых логарифмических
уравнений лучше пользоваться равносильными преобразованиями. В
противном случае надо записать ОДЗ уравнения, но не надо
находить его (решить все неравенства, связанные с ОДЗ, бывает
намного труднее, чем решить само уравнение, а иногда и просто
невозможно). После нахождения корней необходимо в этом
случае сделать проверку. Если корень не принадлежит ОДЗ, то он
73

не может быть решением. Если же корень принадлежит ОДЗ, то
надо подставить его в уравнение.
Основными типами логарифмических уравнений являются
следующие уравнения
0(loge/(aO) = O.
Второе уравнение сводится соответствующей заменой
переменных к одному или нескольким уравнениям первого вида.
Пример: Решите уравнение Iog4(#2) + Iog2(a; + 5) = 2.
Решение: ОДЗ:
гг, / ОДЗ ^
Теперь решаем уравнение (знак <=$- используется для
обозначения «равносильности с учетом ОДЗ»):
Iog4(2r) + Iog2(a; + 5) = 2 ч=> log2 х2 + 2Iog2(# + 5) = 4
Шх2(х + 5)2 = 16 «=>► {x2 + 5x- 4)(x2 + bx + 4) = 0.
Решаем уравнение и, учитывая ОДЗ, получаем, что
Л , . -5 + л/ЗТ
Ответ: — 1, -4, ^—.
Пример: Решите уравнение
log2(2\/a; + 5 + 5) + Iog0j5(-a; - 0,5)
Решение:
a: + 5 + 5) + Iog0j5(-x - 0,5) =
74

+ 5 + 5) - Iog2(-x - 0,5) =
Vz + 5 + 5) = Iog2(-2n: - 1)
5 = -2x - 1 4=> 2\/ж + 5 = -2x - 6
(мы воспользовались тем, что 2у/х + 5 + 5 > 0 в ОДЗ)
5 = х2 + 6х + 9 ^^ \ж2 + 5ж + 4 = 0
-5 ± 3 «=^ ж = -4.
Ответ: —4.
Замечание: Обратите внимание на то, что посторонний
корень ж = — 1 входит в ОДЗ уравнения, но не является решением,
т. к. не является решением промежуточного уравнения.
Пример (МГУ, 1999, мехмат): Решите уравнение
|log3(2z + 5)| = log3(l -\х + 2|) + log3(l + \х + 2|).
Решение: Так как |log3(2rr + 5)| ^ 0, а
log3(l - \х + 2|) + log3(l + \х + 2|) = log3(l - (х + 2)2) ^ 0,
то равенство |log3(2x + 5)| = Iog3(l - \х + 2|) + Iog3(l + \x + 2|)
имеет место тогда и только тогда, когда
Iog3(l-(a; + 2)2)=0
Ответ: —2.
Метод интервалов для логарифмических
и показательных неравенств
В курсе математического анализа для 10 класса
доказывается теорема:
75

Теорема 2. Если f(x) непрерывна на отрезке [а;Ь] и не
обращается в 0 на открытом промежутке (а, Ь), то f(x) имеет
один и тот же знак во всех внутренних точках отрезка [а; Ь].
Это и есть основание для обобщенного метода интервалов
для непрерывной функции: найти нули f(x) и определить
знаки f(x) на промежутках между соседними нулями, вычислив
значения в «пробных» точках. Однако иногда «пробную» точку
выбрать трудно, иногда при выяснении знака функции в
«пробной» точке вычисления могут оказаться громоздкими, и из-за
арифметической ошибки результат окажется неверным. Кроме
того, очень часто школьники вообще не проверяют знаки, а
расставляют их по аналогии с тем, как это делается для
рациональной функции, не задумываясь о том, действительно ли данная
функция меняет знак при переходе через «ноль».
Мы выведем такие условия равносильности, которые часто
за один шаг сведут решение самых распространенных
показательных и логарифмических неравенств к решению
рациональных неравенств.
Показательные неравенства
Рассмотрим неравенство а^х^ > а9^.
Пусть f(x) и д(х) — непрерывные функции на некотором
промежутке X, а > 0. Тогда а^х\ а9^ — тоже непрерывны на
X, и к неравенству а^х^ > а9^ применим метод интервалов.
Его решение зависит от того, является ли число а большим или
меньшим 1.
• Если а > 1, то f(x) > д(х) и (а - 1)(/(ж) - д{х)) > 0.
• Если 0 < а < 1, то f(x) < д(х) и опять (а — 1)(/(ж) — д(х)) >
Верно и обратное: если (а — 1)(/(ж) — д(х)) > 0, то
при а > 1 имеем f(x) > д(х) и а^х^ > а9^]
если 0 < а < 1, то f(x) < д(х) и опять а^х^ > ад(х\
76

Таким образом, мы вывели условие равносильности
9(х)
- д(х)) > 0.
Теперь рассмотрим нестрогое неравенство а^х)
а > 0. Тогда
(20)
, где
(а -
(о -
= 0,
< 0
Итак, для любого а > 0 верно, что
/() () (а -
При рассмотрении неравенства а
произведения в (20), и мы получаем
_ / 4N
0.
х^ < а9^ меняется знак
Правило 5. Знак разности а^х^ —а9^ совпадает со
знаком произведения (а — 1)(/(ж) — д(х)).
При конкретном а неравенство а^х^ > ад^х\ конечно, может
быть решено стандартным способом, и объем выкладок тот же.
Но здесь есть некоторое преимущество — не надо задумываться
над тем, какое а: больше оно или меньше 1.
Кроме того, из правила 5 следует, что для любой функции
h(x) имеет место еще одно условие равносильности:
А это условие может очень облегчить решение неравенств такого
типа.
Пример: Решите неравенство
-4- х — 2
(3*-1)(2ж2-16)
0. '
77

Решение: Так как, в силу правила 5, знак разности (3х — 3°)
совпадает со знаком произведения (3 — 1) (х — 0), знак разности
(2х — 24) совпадает со знаком произведения (2 — 1)(х2 — 4), то
(3х - 1)(2х2 - 16) х(х2-4)
ж <Е (0; 1] U (2; +оо).
Ответ: (0; 1] U (2;+00).
Пример (МГУ, 1976, мехмат): Решите неравенство
7 > 2
9* _2 ^ Зж- Г
Решение: Запишем цепочку равносильностей, в которой
третий переход осуществлен в силу правила 5:
2 • 32х - 7 • 3х + 3 ^
3*-1 (9*-2)(Зх-1) ^
(ж - 1) (х - log3 i)
U
4
Логарифмические неравенства
Неравенство вида
logq/(a:)>0«0)
Рассмотрим неравенство loga f(x) > 0 (< 0), где а —
заданное положительное число, отличное от 1. ОДЗ: f(x) > 0.
78

Если а > 1, то \ogaf(x) > 0(< 0) тогда и только тогда,
когда f(x) > 1 (< 1), т. е. (а - 1)(/(я?) - 1) > 0 (< 0).
Если 0 < а < 1, то loga f(x) > 0 (< 0) тогда и только тогда,
когда f(x) < 1 (> 1), т. е. опять (а - 1)(/(ж) - 1) < 0 (> 0).
И, наоборот, если (а — l)(f(x) — 1) > 0 (< 0), то
при а > 1 имеем f(x) > 1 (< 1), а тогда loga /(#) > 0 (< 0);
при 0 < а < 1 имеем f(x) < 1 (> 1), а тогда loga/(:z) > 0
(<0).
Следовательно, имеет место условие равносильности
logo f{x) > 0 (< 0) Ш [а - 1)(/(х) - 1) > 0 (< 0). (21)
Можно записать полное условие равносильности,
включающее ОДЗ:
log. /(«) > 0 (< 0) ♦* {{« >°.(а;) _ ц > 0 (< 0) (22)
Условия равносильности (21) и (22) верны (для обоих
знаков) и для нестрогого неравенства
logo f{x) > 0 Ш (а - l)(/(s) - 1) > 0.
Полное (с учетом ОДЗ) условие равносильности для нестрогого
неравенства имеет вид
i*/W < о(> о)«-» {/« > *w _ ц < 0(> 0)
Пример: Решите неравенство log i (x — 4) > 0.
з
Решение: Воспользуемся (22):
>-4>0,
log I (x -4)
з
Ответ: (4; 5).
79
{
х>4,
х < 5

Преимущество использования условий равносильности по
сравнению с обычным способом решения даже таких
простейших неравенств состоит в том, что мы не думаем о том, большим
или меньшим единицы является основание. Кроме того, нет
необходимости писать фразы о той или другой монотонности. Это
особенно важно при решении тестов ЕГЭ, когда время для их
решения ограничено. Из (21) следует
Правило 6. Знак loga/(rr) совпадает со знаком
произведения (а - 1)(/(ж) ~ 1) в ОДЗ.
Пример: Решите неравенство
logil2^-60x + 77
2
X2 - ЪХ + 6
\2х2 60ж •+■ 77
Решение: В силу правила 6, знак log^ -т со-
2 4
впадает со знаком произведения
- 60* + 77
Поэтому
jQ 12х2 - 60ж + 77
_ ^ s (_ 1) ^-60*+ 73)
х2 - 5* + 6 х2 - Ъх + 6
30-л/24
Решаем неравенство методом интервалов. Строим рисунок 44 и
с него снимается ответ. ■
80

2 is -Ve is + x/6 3 x
6 6
Рис. 44
Для сравнения попробуйте решить это неравенство
обычным способом.
Неравенство вида
Рассмотрим неравенство logaf(x) > logag(x), где а > О,
аф\. ОДЗ определяется системой
/(*) > О,
д(х) > 0.
• Если а > 1, то \ogaf(x) > logag(x) тогда и только тогда,
когда f(x) > д(х), т.е. (а — l)(f(x) — д{х)) > 0.
• Если 0 < а < 1, то logaf(x) > logag(x) тогда и только
тогда, когда f(x) < д(х), т. е. опять (а — l)(f(x) — д(х)) > 0.
И, наоборот. Если (а — l)(f(x) — д{х)) > 0, то
• при а > 1 имеем f(x) > д(х), а тогда loga f(x) > loga g{x).
• при 0 < а < 1 имеем /(#) < #(#), а тогда опять loga f(x) >
>logag(x).
Мы получили условие равносильности
loga f(x) > (<) loga 9(х) Ш(а- !)(/(*) - д(х)) > 0 (< 0). (23)
Можно записать полное условие равносильности,
включающее ОДЗ.
)
(24)
81

Правило 7. Знак разности loga / (а;)—loga g(x) совпадает
со знаком произведения (а — 1)(/(х) — д(х)) в ОДЗ.
При решении простейших логарифмических неравенств,
конечно, можно не использовать (21) и (23). Однако (21) и (23)
дают возможность просто справиться с неравенствами, решение
которых обычным способом потребует гораздо больше
вычислений.
Например, теперь можно очень просто решить неравенство
вида
(0(Q
Воспользовавшись правилом 7, немедленно получаем, что
loga /(at(~*)Oga 9{х) > °(< 0) & {а" 1){ф)'9{х))
Условия равносильности (23) и (24) верны (для обоих
знаков) и для нестрогого неравенства
loga f(x) > lOgoд(х) Ш(а- 1)(/(аг) - д(х)) > О
или
(
{
f(x)>0,
9(х) > О,
-!)(/(*)-$(*))< 0.
Более сложные неравенства
/(s)(Iogogi(x) - loga9г{х)) ^ п
Рассмотрим неравенство "— , .—= > 0,
Iog3(x)
g63()
где а > 0, а Ф 1, 6 > 0, Ь Ф 1. ОДЗ выражений, входящих в
неравенство, определяется системой gi(x) > 0, г = 1, 2, 3.
82

Решение рассматриваемого неравенства определяется
знаками множителей. Воспользуемся тем, что в ОДЗ знак разности
loga д\{х)—loga д2{х) совпадает (в силу правила 7) со знаком
произведения (a — l)(gi(x) — 92(х)), & знак logb g$(х) совпадает в ОДЗ
со знаком (Ъ — 1)(дз(х) — 1) в силу (23). Поэтому
одз f(x)(a-l){gi(x)-g2{x))
Замечательно то, что мы освобождаемся от всех
логарифмов за один шаг!
Пример: Решите неравенство
16(3ж2 - Зх + 7) - lg(6 + х - х2)
(10х-7)(10х-3) " "
Решение: Найдем ОДЗ:
-х +х + б > 0, ^ х G ^ Q ^ и ^ Q ^ и ^ ^
ж ^= и,7,
Воспользуемся правилом 7 в РДЗ:
lg(3x2 - Зх + 7) - Ig(6 + х - х2) одз
(10ж-7)(10ж-3) "^"^
ОГО Зж2 - Зж + 7 + х2 - х - 6 _ (2ж - I)2
Теперь с учетом ОДЗ получаем ответ (рис. 45).
(){}()
83

2
-2 JL I JL 3 5
10 2 10
Рис. 45
Пример (МГУ, 1974, геогр. ф-т): Решите неравенство
lQg3 (g + g) ^ Q
Решение: Найдем ОДЗ:
Теперь воспользуемся (23) для числителя и знаменателя:
знак log3 (х + ^ 1 совпадает со знаком произведения
(3 - 1) (х + | - l) ,
а знак
log7 (х2 - 2х + ^
совпадает со знаком произведения
Поэтому в ОДЗ имеем
log7 (ж2 - 2х + i) ж2 - 2ж - А
<0
х-\
84

L
1
I 1
\ 4
+ i
1
5
Рис.
1
1 ]
5 '
46
.
|
9
4
i
+
[
X
1
9 X
4
Рис. 47
Решая неравенство классическим методом интервалов (рис. 46),
получаем, что х £ ( —оо> —j ) U ( f5 f )•
Учтем ОДЗ (рис. 47) и получим ответ. ■
Ответ- M--±W±-±W2-^
Ответ. ^ 5, 4jUU'4jUU'4j'
Сложная экспонента и логарифм
с переменным основанием
Особняком стоят уравнения и неравенства, которые нельзя
отнести ни к показательным, ни к логарифмическим. Они
содержат функции вида log^) f(x) и (a(x))f(x\
Рассмотрим выражение у(х) = а(х)^х\ Что это за
функция, какова ее область определения? Что можно сказать о ее
непрерывности или дифференцируемости там, где непрерывны
и дифференцируемы функции а(х) и /(ж)?
1. Если а(х) = const = oo, f(x) ф const, то а$ —
показательная функция, где t = f{x). Она определена при ао > 0.
2. Если а(х) Ф const, f(x) = const = /о, то Ф — степенная
функция, где t = a(x). Ее область определения зависит от /о:
• если /о — натуральное число, то t может принимать любые
значения;
• если /о — отрицательное целое число, то * ф 0;
• если /о не целое число, то t > 0, при этом, если /о > 0, то
t>0.
85

Мы видим, что при а > О определены обе функции —
степенная и показательная — для любых t.
По определению, полагают (для любого с > О, с ф 1,
а(х) > 0):
a(x)f(x>) = с/(ж)logc а(ж).
Эту функцию называют сложной экспонентной, и областью
определения сложной экспоненты является множество X, на
котором а(х) > 0, а сама функция принимает только положительные
значения. Эта функция не является уже ни показательной, ни
степенной (она, например, уже не является, вообще говоря,
монотонной функцией).
Из определения теперь четко следует, что сложная
экспонента является непрерывной функцией там, где непрерывны
а(х) и /(ж), и дифференцируемой там, где дифференцируемы
а(х) и /(ж). Ясно также, по каким правилам дифференцируется
сложная экспонента. Можно строить график.
Построим, например, график функции у(х) = хх. Найдем
сначала ОДЗ: х > 0 •<=> х Е (0; +оо). Отсюда следует, что
прежде всего надо найти два предела.
lim хх = lim e*ln* = e^xlax = e° = 1.
ж-»+0
lim xx = lim exlnx = ex-++°° = +00.
x—>-foo
Найдем производную:
y'(x) = (exlnx)f = exlnx (1пж + х,• £) = ж*(1пя + 1).
Теперь найдем критические точки:
у'(х) = 0 4=* \пх = -1 4=> х = i =* ymin (i) = (I) e •
График функции изображен на рис. 48.
Рассмотрим уравнение
86

Рис. 48
Его ОДЗ: а(х) > 0. Воспользуемся определением сложной
экспоненты а(ж)^1) = lQ/W1»^*), а(ж)9(х) = 10»(*) &«<*), тогда
10/(*)ige(x) =
ж) = g(x)lga(x)
= 0
\а(х) = 1,
Следовательно,
Запишем полное условие равносильности
[а(х) = 1,
(а(х) > О,
l\f(x)=g(x).
Замечание: Мы не решаем уравнение (—2)х =
что показательная функция не определена при а =
—8, потому
—2.
87

Однако мы решаем уравнение (—2)п = —8, где заранее
известно, что п — число целое (а операция возведения в целую
степень отлична от операции возведения в рациональную
степень).
Рассмотрим уравнение вида
Его ОДЗ: а(х) > 0.
1. Если д(х) ^ 0, то уравнение не имеет решений, т. к.
сложная экспонента принимает положительные значения.
2. Если д(х) > 0, то
= д(х)
f(x)\ga(x)=lgg(x),
т.е.
а(х)№ = д(х) &f(x)]ga{x) = lgg(x).
И опять равносильное уравнение домучается формальным
логарифмированием заданного уравнения.
Пример: Решите уравнение хх = х~2~3х.
Решение: Воспользуемся определением сложной
экспоненты:
(х2 + Зх + 2) \gx = 0 <=> (х + 2){х + 1) lga: = 0
х = -2,
Корни — 1, —2 не входят в ОДЗ, а потому не являются ре-
шениямц уравнения. Это, несмотря на то что (—I)1 = (—I)1,
(—2)4 = (—2)4, но здесь х имеет право быть рациональным, и мы
88

4
получаем противоречие в том, что ( — tj ) 7^(^"^)1 (левая часть
не определена, а правая часть существует!). ■
Ответ: {1}.
Замечание: Корни —1, —2 не входят в ОДЗ, а потому не
являются решениями уравнения. Нельзя не согласиться с тем,
что эти числа действительно обращают уравнение в тождество:
(—I)1 = (—I)1, (—2)4 = (—2)4. В школьных учебниках нет ни
единого слова о свойствах такой функции. Алгоритма
нахождения отрицательных корней в подобных примерах не существует.
Искать такие корни не надо. В некоторых регионах заставляют
обязательно подставлять а(х) = 0, а что касается
отрицательных а(х), то в некоторых наказывают за их отсутствие, в других,
наоборот, за присутствие. Но если школьник нашел хотя бы
некоторые из них, то, видимо, не стоит считать это ошибкой. В
аналогичных заданиях ЕГЭ сразу указывается, что надо найти
положительные решения — поэтому путаницы не возникает.
Пример (МГУ, 1966, геол. ф-т): Решите уравнение
x(\og3x)z-3\og3x _ 3-3
Решение: Прологарифмируем обе части уравнения по
основанию 3:
(\oglx - 31og3a;)log3S = (8 - 4)
х = 9,
Ответ: 9; ^.
Пример (МГУ, 1999, ф-т психологии): Решите уравнение
Решение: Воспользуемся в ОДЗ основным
логарифмическим тождеством х = 2log2aJ:
89

_ 5 . 2loS7x _ 4 = о >—^ 2log7 4 log2 x + 5 • 2log7 x — 4 = 0
2i оIog7X
°g7 *iog72 + 5 . 2i°g7* _ 4 = (2log7X)2 + 5 • 2log7x -4 = 0
Ответ: 7iog2(V5T-5)-ie
Логарифмы с переменным основанием
Рассмотрим выражение у(х) = loga/a.\ /(ж). По
определению, для любого с > 0, с ф 1 полагают
т.е. log^.) f(x) — это частное двух логарифмов, и областью
определения является множество X, на котором
f{x) > 0, а(х) > О, а(х) ф 1.
Теперь ясно, что у(х) = loga(x) f(x) непрерывна и
дифференцируема там, где непрерывны и дифференцируемы функции а (х)
и f(x).
Построим, например, график функции у = logx#. Эта
функция не равна 1 тождественно, ее ОДЗ задается системой
х >0,
хф1.
В ОДЗ log^ х = 1, и график функции у = logx x имеет вид,
изображенный на рис. 49.
Рассмотрим уравнение
х) f(x) = 9(х)-
90

о
1
Рис. 49
ОДЗ рассматриваемого уравнения задается системой
га(х) >0,
а(х) ф 1,
J(x)>0.
Воспользуемся определением (25), где в качестве с берется
число 10, и получим в ОДЗ
\ga(x)
т.е.
= д(х) <=> lgf(x) = g(x)lga(x) «=* f(x) = а
Ux) f{x) = 9(x) ШПх) = a{x)°W.
(26)
И опять равносильное соотношение получается формальным
потенцированием, хотя и по «переменному» основанию.
Рассмотрим уравнение
Его ОДЗ задается системой
'а{х) > 0,
а(х) ф 1,
f(x) > 0,
д{х) > 0.
Воспользуемся определением (25) и получим в ОДЗ:
= lgg(x)
91

Итак,
loga(x) f(x) = loga(x) g(x) <t=> f(x) = g(x).
Можно записать полное условие равносильности
logo(x) /0*0 =
9(x)
a(x) > 0,
a(x) ф 1,
[f(x)>0
f(x) = g(x),
a{x) > 0,
a(x) ф 1,
[g(x) > 0.
(27)
Рекомендация. При решении уравнения
f{x) = loga(x) з(ж)
можно использовать различные подходы.
1. Можно сначала решить уравнение f(x) = g(x), затем
отобрать корни. Для этого достаточно проверить условия в одной из
систем (27), той, в которую входит более простое (для проверки)
подлогарифмическое выражение.
2. Можно решить уравнение f(x) = д(х) и не
пользоваться условиями равносильности (27), а вместо этого затем
сделать проверку, подставив найденные корни в заданное уравнение
Выбор способа зависит от сложности входящих в уравнение
выражений.
Пример (МФТИ, 1972): Решите уравнение
tog(i_*)(3 - х) = log(3_x)(l - х).
Решение: ОДЗ задается системой:
fl-s>0,
3 - х > О,
92

В ОДЗ имеем
-,)(3-*) =
- •) -1. Г» - - * - ••
- я?) = -1 3 - а = т
1-х
Учитывая ОДЗ, получаем, что х = 2 — д/2.
Ответ: 2-лД.
Показательные неравенства
с переменным основанием
Рассмотрим неравенство
где а(ж), /(ж), 0(х) — непрерывные функции на -X"; ОДЗ:
а(х) > 0.
Воспользуемся определением сложной экспоненты, взяв в
качестве с число е (можно взять любое другое допустимое
число).
Неравенство a(x)f№ > a(x)9^ принимает вид
ef(x)\na(x) > ед(х)\па(х)
и, используя (20), получим равносильное неравенство
а, используя (21), найдем окончательное условие
равносильности
(а(х) - 1)(/(а?) - д(х)) > 0.
93

Можно записать полное условие равносильности для строгого
неравенства
(28)
- д(х)) >0. '
Отсюда следует
Правило 8. Знак разности а(х)^х^ — а(х)д^ совпадает
со знаком произведения (а(х) — l)(f(x) — д{х)) в ОДЗ.
Преимущество этого правила состоит в том, что если а (ж),
/(я), д(х) — рациональные функции, то за один шаг мы перешли
к классическому варианту метода интервалов.
Замечание: Для нестрогих неравенств имеет место
следующее условие равносильности
Пример: Решите неравенство
(56 - х - ж2)*3"2*2 > (56 - х - х2)2хЧ5х.
Решение: ОДЗ:
56 - х - х2 > 0 «=^ х2 + х - 56 < 0 Ф=> х е (-8; 7).
В ОДЗ, в силу (29), имеем:
(56 - х - ж2)*3"2*2 > (56 - гс - х2)2хЧ5х *^
(55 - х - х2)(х3 - 2х2 - 2х2 - 5х) > 0
-1 - л/22Т
( -\
\х—
Решаем неравенство методом интервалов, затем наносим на ту
же ось ОДЗ (рис. 50).
С рисунка «снимаем» ответ. ■
U[-l;0IU [б,
94

-8 ~l-
-1 О
Рис. 50
Пример (МГУ, 2001, мехмат): Решите неравенство
{2х + 0,09 • 2~х) 2х ^ (2х + 0,09 • 2~х) i - *.
Решение: Воспользуемся (28):
(2х + 0,09 • 2"х)S ^ (21 + 0,09 • 2~х) i -'
1 ' ^(ar-l)
(ox 1_\ (<)х 9_\ (~ _ 1^
х(х - 1)
Последняя равносильность — в силу (20).
Рис. 51
С рисунка 51 «снимаем» ответ. ■
Ответ: [log2 ^; log2 ^] U (в; ±] U (1; +оо).
95

Неравенства для логарифмов
с переменным основанием
Рассмотрим неравенство log^) f(x) > 0. ОДЗ левой части
определяется системой
\а{х) > 0,
а(х) ф 1,
_ х) >0.
По определению,
\, а(х) > 0, а(х) ф 1, f(x) > 0.
В силу правила 7, знаки lg/(x), lga(rr) совпадают со
знаками разностей f(x) — l и а(х) — 1 соответственно. Поэтому знак
lg/Q*Q f(x) - 1
т—тт совпадает со знаком частного —т-т или со знаком
*&а\х) а\х) L
произведения (а(х) — l)(f(x) — 1).
Поэтому и в этом случае получаем
Правило 9. Знак функции loga(x) f(x) совпадает со
знаком произведения (а(х) — l)(f(x) — 1) в ОДЗ.
Имеет место условие равносильности
log.(x) /(*) > 0 (< 0) Щ (а(х) - 1)(/(х) - 1) > 0 (< 0). (30)
Можно записать полное условие равносильности,
включающее ОДЗ:
'а(х) > 0,
0(<0)^{f(x)>0, (31)
Для нестрогого неравенства условие выглядит по-другому:
(а{х) > 0,
/S > 0,
96

Пример (МГУ, 1966, химфак): Решите неравенство
\х~* 2'
Решение: ОДЗ:
х + | > О,
0
I 2ж - 3 * U
Воспользуемся (26) в ОДЗ:
(ж + |) (х - 5 - 2х + 3)(ж - 5 + 2х - 3) _
(2ж - З)2
(ж + |)(ж + 2)(За;-8)
>0
(2х - З)2
Учтём ОДЗ и получим, что х € (-|; -2) U (-|; |) U (|; |).
Рассмотрим неравенство log^) /(ж) > loga(a.) з(ж)? гДе а(ж)?
/(ж), д(х) непрерывные функции и о(ж) > 0, а(х) ф 1.
По определению, loga(ic) /(ж) - loga(ic) 5(ж) = Щ/^~^9^ и,
в силу правила 7 и (21), справедливо
Правило 10. Знак разности log^) f(x) — loga(x) g(x)
совпадает со знаком произведения (а(х) — l)(f(x) — g(x)) в
ОДЗ.
97
4 Зах 243

Из этого правила следует, что
W /(*) < (>) bga(iE) д(х) Ш (а(х) - l)(f(x)-g(x)) > 0 (< 0).
Заметим, что из (30) автоматически следует, что а(х) ф 1,
поэтому при решении строгих неравенств условие а(х) ф 1 в ОДЗ
можно опустить и так записать полное условие равносильности,
включающее ОДЗ:
(а(х) > 0,
fix) > 0,
д(х) > 0,
/0*0 < loge(x) g(x)
При решении нестрогих неравенств условия
равносильности примут вид
а(х) > О,
а(х) ф 1,
Дх)>0,
и
logo(x) /(«)
ogo(a:)
'о(ж) > 0,
о(ж) # 1,
/(«) > 0,
5(ж) > 0,
Преимущество и красота приведенных условий равносильности
состоит в том, что мы за один шаг освободились от
логарифмов и переменных оснований, и теперь, если основание
логарифма и подлогарифмическое выражение являются рациональными
функциями, можно воспользоваться классическим методом
интервалов.
98

Заметим, что все условия равносильности формально
точно такие же, как и для логарифмов с постоянным основанием, а
потому легко запоминаются. Но, как показывает практика,
полными условиями равносильности не всегда удобно пользоваться.
Это происходит, если входящие в условия равносильности
неравенства громоздки. Тогда удобно отделить нахождение ОДЗ от
решения основного неравенства, как мы иногда и будем делать.
Пример (МГУ, 1985, ВМиК): Решите неравенство
Решение: Найдем ОДЗ:
1-
1-
-3
-3
42ж2-
х -
5
6
N
N
-i
Ф
Ф
4|:
0
о,
1,
t\ +
>1
\х\
X -
1:
<
5
" 6
>С
1
3'
t*
ф
1, ^^
7-л/7
42
0.
1 Е \U' 42 )U\ 42 ' Зу '
Видим, что х < ^ в ОДЗ. Для исходного неравенства тогда
получаем:
:ж2-14|а;| + 1)
-3|i|) Vх 6/
log(i-3|x|) (б ~ Х)
99

[в силу (30) и (26)]
1 - 3|х| - 1) (42ж2 - 14|ж|
- | + х)
42ж2-14|ж| + ж + ±
ж+|
ж^О,
42ж2 - 13ж + | ^ О;
ж<0,
42ж2 + 15ж + ±
хЕ
L 13-vHTl
0;
х<0,
84 J
. [13 + >/Ш I
U[ 84 ;+OOJ'
-15-л/197
84
84
Теперь, анализируя рис. 52 и рис. 53, получаем окончательный
ответ. ■
ж>0:
0 13-л/Ш 7-\/7 7+л/7 13+л/Ш I
84 42 42 84 3
Рис.52
х<0:
-15-\/197 -I
84 3
-7-У? -I
42 6
Рис. 53
-7+\/7 -
42
84
Ответ- ( 1-
Ответ. ^ 3,
U
U
) 84 J
U
84
. 1Л
'3/
100

Пример (МФТИ, 1996): Решите неравенство
°g|z+2|(4~x — 1) < log|x+2|(2~~x + 1) + log|a.+2|(2~x~1 + !)•
Решение: Находим ОДЗ:
О, [хф-%
> 0, <=> < х < О,
1 I /г -4- 9 -L •
4~ж - 1 > 0, <=> < х < 0, 4=>
±1
ж G (-оо; -3) U (-3; -2) U (-2; -1) U (-1; 0)
В ОДЗ имеем цепочку равносильностей
log|I+2|(4-x -1) - 1ощх+2\(2~х +1) - Ъоцг+цр-*-1 +1) < О
tog|«+2|(2-x " 1) " logix^^"1-1 + 1) < 0
(в силу (30))
(\х + 2| - 1) (2~х -l-2
(в силу (12) на стр. 65)
(ж + 2 + 1)(ж + 2 - 1)(2~х - 4) < 0
(в силу правила 5 на стр. 77)
(х + 3)(ж + 1)(х + 2) > 0 <=» х Е (-3; -2) U (-1; +оо).
Учитьшая ОДЗ, получаем ответ.
Ответ:. (-3;-2) U (-1;0).
bge(«) /(ж) - loga(l) g(x)
Рассмотрим неравенство т-т-т ^ 0 (^ 0).
Л(аг)
Воспользовавшись (30), получаем, что в ОДЗ
101

Щ
h(x) " ^
Пример (МГУ, 1990, геол. ф-т): Решите неравенство
Решение: ОДЗ:
Тогда
log9 х6 " logx 3
71og3x + 2
одз
ОДЗ
Учитывая ОДЗ, получаем, что х G I 0; —^ I U fl; v^9 .
Ответ: же (о; -^zl U (l; Щ.
102

Пример (МФТИ, 1990): Решите неравенство
log9 х + 4
1 + logg X
Решение: ОДЗ:
4106,3-1.
se(o;±)u(±;l)u(l;+oo).
Далее,
;4io&3-i
< 4108,31 «|<r
logg Ж Х logg Ж + 1 logg X
_ 21og|o; + 31og9a;^2 <Q _^ (log9 x + 2)(log9a; - \)
log9 a;(log9 x + 1) ^ log9 a:(log9 а; + 1)
_ (log9 x - log9 ^) (log9 x - log9 3) ^
log9 ж (log9 ж - log9 |)
Ответ: [i; I) и (1;3].
Пример (МФТИ, 1996): Решите неравенство
bg|3*-3|(25* - 9х) < log|3:B_3|(5a: + F) + к^-з^1-1 + З*"1).
Решение: ОДЗ: (j? "J f®'<=>xE (0; 1)U(1; +00). Тогда
^о — о ^> U
-aiCS1 + З1) + log^e-1 + З1"1)
(|3а? - 3| - ^(б1 - 3х - б*"1 - 3х-1) < О
103

(|3х - 3| - 1) (J • Ъх - |
(в силу (12) на стр. 65 и правила 8 на стр. 94)
(Зх - 4)(3* - 2)
I)-1 - (§)°)
< 0
И теперь с рисунка 54 «снимаем» ответ.
Рис, 54
Ответ:(0;|)и(1;|).
Сформулируем, в заключение, условия равносильности,
которые немедленно следуют из предыдущих условий
равносильности и которыми мы неоднократно пользовались.
Так как, в силу правила 8, знак разности
совпадает со знаком произведения (а(х) — 1)(/(ж) — д(х)) в ОДЗ,
то
Или полное условие равносильности
h(x)
104

fa(x) >0,
)
h(x)
Так как, в силу (30), знак разности loga(x) f(x) -loga(a.) g(x)
совпадает со знаком произведения {а(х) — l)(f(x) — д(х)) в ОДЗ,
то
logo(x) /(*) - logB(x)g(a;)
или полное условие равносильности
'а(ж) > 0,
/(гг) > 0,
д{х) > 0,
h(x)
Для нестрогого неравенства условие другое —
я (ж)
'а(ж) > 0,
(я) ^ 1,
(«) > 0,
105

Тригонометрия
Функции у = sin ж, у = cos ж, у = tgrc, у = ctgrr называются
основными тригонометрическими функциями. По определению
синусом (соответственно, косинусом) угла а называется
ордината (соответственно, абсцисса) точки М на тригонометрическом
круге (рис. 55), получающейся поворотом вектора ОМо(1;0) на
угол а радиан вокруг начала координат.
Рис. 55
Тангенсом угла а называется отношение
отношение называется котангенсом:
sin a
обратное
sina
cosa
Из определения вытекает, что tga • ctga = 1 при a ^ ^? n E Z.
Функции у = sin х ставит в соответствие любому
действительному числу х значение синуса угла поворота на х
радиан. Аналогично определяются остальные тригонометрические
функции действительного аргумента.
106

функций
Полезно запомнить таблицу значений тригонометрических
щий углов в 30° (или ~ радиан), 45° (j рад.) и 60° (~ рад.).
а ^\
0° (0)
30° (|)
450 (!)
60° (|)
90° (|)
sin a
0
1
2
1
л/2"
л/3
2
1
cos а
1
л/3
2
1
1
2
0
tga
0
1
л/3
1
л/3
ctga
—
л/3
1
1
л/3
0
Функции sin(#), tg(x) и ctg(x) являются нечетными, а
функция cos (х) — четная, т. е. для всех допустимых значений х
выполнены равенства
cos(—х) = cos ж, sin(—х) = — shirr,
tg(-z) = - tg ж, ctg(-sc) = - ctg x.
Функция у = f(x) называется периодической на X, если
существует такое отличное от нуля число Т, для которого
выполнены два условия:
1. Если х е х, то х + т е х, х - т е х.
2. Для любого х е X => f(x + Т) = f(x) = f(x - Г).
Если функция имеет период Т, то любое число вида пТ,
п € Z — тоже период. Поэтому, говоря о периоде функции,
часто имеют в виду наименьший положительный период, если
таковой существует. Из школьного курса известно, что функции
у = sin ж, у = cos ж имеют наименьший положительный
период Т = 2тг, а функции у = tgrr, у = ctg ж имеют наименьший
положительный период Г = тг. Отсюда следует, что
sin(a; + 2тгп) = sin ж, cos(rc + 2тгп) = cos #,
107

tg(# + тгп) = tg ж, ctg(x + тгп) = ctg x
для всех допустимых значений х и для всех п Е Z.
Области определения tg ж и ctg ж не совпадают с 1R, но явля-
ются «периодичными» с периодом тг. Например, областью
определения tg ж является объединение бесконечного множества
интервалов вида ( — тг + тгп; тг + тгп), п Е Z, т. е.
п=+оо
= U
-§ + *»;§
Это множество симметрично относительно 0. Мы это множество
привыкли обозначать просто (—тт + тгп; ^ + тгп], п Е Z.
Но не все периодические функции имеют наименьший
положительный период. Например, у(х) = sin2 ж + cos2 ж является
суммой двух функций, каждая из которых имеет наименьший
положительный период тг, но сумма у(ж) такого периода не
имеет, т. к. у = sin2 ж + cos2 ж = 1, и ее периодом является любое
положительное действительное число (наименьшего нет).
Для успешного решения задач надо знать простейшие
формулы приведения:
sin ( 77 ± х) = cos ж; cos ( ~ — ж) = втж;
V2 J \2 J (32)
cos (тг + х) =-sma;;
| - ж^ = ctg ж; tg ^| + ж^ = - ctg ж;
ctgff-ж) =^ж; ctg(f+ ж) =-^ж.
Более сложные, но полезные формулы приведения:
втж, к = 2n, n E Z;
sm(TT& + х) = (—l)fc sin ж =
cos(ttA: + х) = (—1)* cos ж =
— sm ж, к = 2п + 1, n GZ;
cos ж, к = 2n, n E Z;
- cos ж, к = 2п + 1, пе Z.
108

Очень часто приходится работать с различными
формулами, связанными с cos 2х:
a;- I = l-2sin2x, (33)
1 + cos 2х = 2 cos2 х\ 1 - cos 2x = 2 sin2 я, (34)
(35)
Полезно помнить формулы преобразования произведения
синусов и косинусов в сумму:
sin a cos 6=4 (sin(a + b) + sin(a — Ь));
sin a sin Ь = ^(cos(a — b) — cos(a + 6));
cos a cos 6 = 7Г (cos(a + 6) + cos(a — b)).
Обратные тригонометрические функции
Основные тригонометрические функции являются
периодическими. Всякая периодическая функция принимает каждое
свое значение бесконечно много раз, т. к. f(x) = f(x + fcT), для
любого х € -X", к € Z — поэтому периодическая функция не
может осуществлять взаимно однозначного соответствия, а, значит,
не имеет обратной.
Рассмотрим не всю синусоиду, а только ее часть —
функцию у = sinx, D(y) = — ~; ~ (рис. 56). Любая прямая у = а,
a G [—1; 1] пересекает график этой функции в единственной
точке, абсцисса которой и обозначается arcsina.
Функция у = sin ж, D(y) = — т^тП возрастает, т.е.
строго монотонна на области определения, поэтому имеет обратную
(рис. 57):
х = arcsiny, jD(arcsiny) = [-1; 1], jE(arcsiny) = ^~; |j .
109

2/ = arcsina;
1 x
Рис. 56
Рис. 57
Обычно независимая переменная обозначается буквой ж, а
зависимая — буквой у. Поэтому в этих обозначениях можно
записать
ina;) = —77; \ •
у = arcsinx, D(axcsmx) = [—1; 1],
Аналогично определяются функции:
у = arccos ж, J9(arccos х) = [—1; 1], J5(arccos х) = [0; тг];
у = axctg х, D(axctg ж) = R, #(arctg x) = (-1; |) ;
у = arcctg ж, JD(arcctg rr) = М, £?(arcctg х) = (0; 7г),
графики которых представлены на рис. 58-60.
Полезно помнить следующие важные соотношения: так как
arcsina € ~^; ~ , то cos(arcsina) ^ 0, откуда
cos(arcsina) = у 1 — sin2(arcsina) = yl — a2;
а так как arccos a G [О;тг], то sin(arccosa) ^ 0, откуда
sin(arccosa) = \1\ — sin2 (arcsina) = у 1 — a2;
sin(2 arcsina) = 2sin(arcsina) • cos(arcsina) = 2a\/l — a2.
110

1 x
Рис. 58
У
2/ = arctg ж
"it"
"2
Пример: Найдите значение выражения 2vT3cos ( arctg ^ J.
Решение: Многих учащихся задача ставит в тупик.
Заметим, что все «арки» (значения обратных тригонометрических
функций) от положительных чисел — это углы, лежащие в
первой четверти, т. е. острые углы. Поэтому их можно найти в пря-
моугольном треугольнике. Например, а = arctg ^ — это «угол»
о
111

в треугольнике, тангенс которого равен ~, т. е. противолежащий
катет относится к прилежащему как 2:3. Вот и построим
треугольник с катетами 2 и 3 (рис. 61).
По теореме Пифагора находим гипотенузу. Теперь можно
находить значение любой тригонометрической функции этого
арктангенса: cosarctg ~ т= -~- => 2 \/ТЗ cosarctg ^ = 6. ■
6 л/13 6
Ответ: 6.
Рис. 61
Рис. 62
Пример: Найдите: a) tg ( arcsin = J, б) tg (2 arcsin ^J.
Решение: По заданному арксинусу рисуем прямоугольные
треугольники (рис. 62, 63) и находим значения нужных
тригонометрических функций.
=J = —
(arcsin =J =
*)tg(
6)" tg (2 arcsin £) =
Ответ: а)
4л/з'
2 tg (arcsin |)
1 — tg2 (arcsin |)
; 6) 4V5.
2-4=
При вычислении значений тригонометрических функций
для отрицательных или тупых углов полезны формулы:
arcsin(—а) = — arcsin а; arctg(-a) = — arctga;
arccos(-a) = тг — arccosa; arcctg(—а) = тг — arcctga.
Отсюда следуют и более сложные соотношения:
tg(arcsin(—a)) = — tg(arcsina);
tg(arccos(—a)) = tg(?r — arccosa) = — tg(arccosa);
(36)
112

cos(arctg(—a)) = cos(—arctga) = cos(arctga).
Пример: Вычислите tg f arccos (— «r) ) •
Решение: Воспользовавшись формулой (36), получим
tg (arccos ( —^)) = tg Г тг — arccos ^ J = — tg arccos ^ = —2>/2
(рис. 64). ■
Ответ: -2л/2.
л/5
Рис. 63
2л/2
Рис. 64
Как найти arcsin(sina)? График arcsinsinrc имеет вид,
изображенный на рис. 65.
Рис. 65
Надо запомнить, что если х € — ~; тИ, то arcsin(sino;) = х.
Поэтому при нахождении arcsin(sina) прежде всего из числа а
надо выделить целое число периодов синуса (а это сделать
проще всего) так, чтобы оставшаяся разность а — 2тгА? принадлежала
отрезку [0;2тг].
113

Тогда из графика видно, что если угол (а — 2тгк)
принадлежит первой четверти, то arcsinsina = (a — 2тг&); если
угол (а — 2пк) принадлежит второй или третьей четверти, то
arcsinsina = 7г —(а — 2тгк) = тг(2& + 1) — а; если угол (а — 2тгк) при
надлежит четвертой четверти, то arcsinsina = (a — 2тгк) — 2тг =
= a - 2тг{к + 1).
Если не помнить график, то можно это найти на
тригонометрическом круге (рис. 66).
Рис. 66
1. Если разность а — 2жк попадет в первую четверть — угол
АОВ, то arcsin(sina) = arcsin(sin(a — 2nk)) = a — 2тгА;, при этом
О < а - 2пк < | и
arcsinsina = a — 2тг&.
2. Если a — 2тгА; попадет во вторую четверть — угол АОС,
то надо перейти к углу АОВ, т. к. их синусы равны, но угол АОВ
лежит в первой четверти, при этом
ZAOC = тг - ZAOB
ZAOB = тг -
= тг - (а - 2тгЛг).
Поэтому arcsin(sina) = arcsin(sin(a — 2тгЛ)) = тг — (а — 2тг&) при
этом 0 ^ 2тгк + тг — а < ^, т. е.
arcsin(sina) = 2тг/г + тг — а.
114

3. Если разность а — 2тгк попадает в третью четверть —
угол АОМ, то надо перейти к отрицательному углу АОЕ =
= тг — (а — 2тг&), т. к. их синусы равны, при этом
arcsin(sina) = arcsin(sin(a —2тг&)) = arcsin(sin(7r — (а — 2тгк))) =
= тг — (а — 2тгк) = 2тгк + тг — а,
| тг-а<0, т.е.
arcsin(sina) = 2тгк + тг — а. (37)
Видно, что во второй и третьей четвертях формулы одинаковы.
4. Если разность а — 2тг& попала в четвертую четверть —
угол АОЕ, то надо опять перейти к отрицательному углу АОЕ =
= —(2тг — (а — 2тг&)). Поэтому
arcsin(sina) = arcsin(sin(a —
= arcsin(sin(-(2Tr - (а - 2тгЛ)))) = -(2тг - (а - 2тгк)) =
= а-2тг(А; + 1),
-| <а-2тг(А; + 1) < 0, т.е.
arcsin(sina) = а - 2тг(А; + 1). (38)
Пример: Найдите arcsin(sin(2003,5Tr)).
Решение: Выделим целое число периодов 2тг и получим
2003,5тг = 1001 • 2тг + Щ-. По формуле (37) или (38) (т.к. угол
2003,5 — 2тг • 1001 на границе четвертей) имеем
arcsin(sin(2003,5Tr)) = 2003,5тг - 2тг(1001 + 1) = ~. ■
Ответ: -f.
Пример: Найдите arcsin(sinl7).
115

Решение: Замечаем, что тг < 17 — 27г - 2 < 4г, т.е. угол
(17 — 2тг • 2) принадлежит 3-й четверти, тогда по формуле (37)
arcsin(sin 17) = 2тг • 2 + тг - 17 = 5тг - 17. ■
Ответ: 5тг - 17.
Как найти arccos(coso)? График функции у = arccoscosx
имеет вид, изображенный на рис. 67.
У
тг
Рис. 67
Запомним, что если а Е [О;тг], то arccos(cosa) = a.
Если а не принадлежит этому промежутку, то прежде всего
надо выделить целое число 2тг, представить заданное число в
виде а — 2тг&, где О < а — 2тгк < 2тг. Тогда,
1. Если О ^ а — 2кк ^ тг — угол принадлежит первой или
второй четверти, то
arccos(cosa) = а — 2тг&.
2. А для третьей и четвертой четвертей выполнено
arccos(cosa) = 2тг - (a - 2тгк) = 2тг(А; + 1) - а. (39)
Это же можно увидеть и на тригонометрическом круге.
Пример: Найдите arccos(cos35,4).
Решение: Так как
35,4 = 2тг . 5 + (35,4 - Ютг) и тг < (35,4 - Ютг) < ^,
116

то, применяя формулу (39), в которой к = 5, получаем
arccos(cos 35,4) = 12тг — 35,4.
Ответ: 12тг - 35,4.
Зтг
Пример: Найдите arccos(cos24).
Решение: Действуем аналогично: 24 = 2тг • 3 + (24 — бтг),
—^ < (24—бтг) < 2тг и по формуле (39), в которой к = 3, получаем
arccos(cos 24) = 87Г — 24. ■
Ответ: 8тг - 24.
Как найти arctg(tga)?
Если а Е (-|; |), то arctg(tga) = о.
2/1
М
Рис. 68
Если а £ (— ~; ~ j, то надо выделить целое число периодов
7г так, чтобы 0 < а — тг& ^ тг.
Таким образом, получаем, что если 0 ^ a — тгА; < ^ — угол
в первой четверти (угол АО В на рис. 68), то
arctg(tga) = а — тгАг;
• — угол во второй че
рис. 68), то надо перейти к отрицательному углу АОМ, который
а если 77 ^ a — тгА; ^ тг — угол во второй четверти (угол АОС на
117

равен — (тг—(а—тгк)) = а—тг(А;+1), при этом —~ ^ а—тг(&+1) ^ О,
и
arctg(tga) = а - тг(к + 1). (40)
Пример: Найдите arctg(tgl8).
Решение: Так как 18 = бтг + (18 - 5тг) и ~ < (18 - 5тг) < тг.
Применяя формулу (40), в которой к = 2, получаем
arctg(tg 18) = 18 - бтг. ■
Ответ: 18 — бтг.
Как найти arctg(ctga)? Если a Е (О;тг), то arctg(ctga) = a.
Если а £ (О;тг), то выделим целое число периодов тг так, чтобы
0 ^ а — тгк ^ тг, тогда для 0 < а — пк < тг получаем
arctg(ctga) = а — тг&,
Пример: Найдите arctg(ctg23).
Решение: Так как 23 = 7тг + (23 - 7тг) и 0 < 23 - 7тг < тг, то
arctg(ctg23) = 23 - 7тг. ■
Ответ: 23 - 7тг.
Основные виды тригонометрических
уравнений и способы их решения
Решения простейших уравнений:
sin ж = а <=> х = (—l)n arcsina + тгп, п € Z, \а\ < 1.
cos х = о <£=> х = ± arccos а + 2тгп, п G Z, |а| ^ 1.
tg ж = а Ф=> ж = arctg а + тгп, п е Z, oGt
ctg x = а Ф=> х = arcctg а + тгп, п € Z, а G R
Самый распространенный метод решения
тригонометрических уравнений — это разложение на множители.
118

1. Уравнение вида о sin 2ж+Ь cos х = 0 или a sin 2х + b sin x =
= 0 разложением на множители сводится к двум элементарным
уравнениям. Например,
[cos х = О,
asin2x + Ьсовж = 0 4=> cos ж(2а sin ж + 6) = О <$=М • Ь
2. Уравнения вида
a cos 2x + frsinж + с = 0 или a cos 2ж + bcos ж + с = О
приводятся к квадратным уравнениям относительно sin ж или
cos ж соответственно:
a cos 2ж + 6 cos ж = с <Ф=> a(2 cos2 ж — 1) + Ь cos ж = с
<*=> 2acos2 ж + 6cosж — (а + с) = 0.
8И1ж = с <=> а(1 — 2 sin2 я) +6 sin я = с <=>
2а sin2 ж — bsinz + (с — а) = 0.
Пример (МГУ, 1995, ф-т почв.): Найти все значения
параметра а, при которых уравнение cos 2у + 4a cos у + 2а2 + 1 = 0 не
имеет решений.
Решение:
cos2y + 4а cos у + 2а2 + 1 = 0
2- l + 4acosy + 2a2 + l = 0
2(cos у + а)2 = 0 <*=> cos у = -а.
Очевидно, что уравнение не имеет решений, если \а\ > 1. ■
Ответ: (-оо; -1) U (1; +оо).
3. Уравнение вида a cos2 ж+bsin2 x + csm2x = 0 (abc ^0) —
однородное относительно cos ж, sin ж:
a cos2 ж + bsin2 ж + сзт2ж = 0
119

асов2х + bsin2rr + 2csin#cosa; = 0
b • tg2 x + 2c • tgx + a = 0.
4. Уравнение вида a cos2 x+b sin2 rr+c sin ж cos x — d сводится
к однородному:
acos2 a: + bsin2a; + csinxcosrr = d
о i • 9 • i/9 • 9 \ Ъф-CL
a cos # + о sin ж + с sin ж cos x = a(cos ж + sin x) *—v
(b - d) tg2 ж + с • tgz + (a - d) = 0.
5. Уравнение вида sin ж + cos x = ас помощью формул
приведения сэодится к элементарному уравнению. Воспользуемся
одной из формул (32):
sinz + cosrr = a 4=» sina; + sin (^ — x) = a <=$►
Ф=^ л/2 cos Гж - j j = a.
6. Уравнение вида sinarr + cosbx = 0 с помощью формул
приведения сводится к двум элементарным уравнениям:
sinaa; + cos bx = 0 <=> sin ax + sin ( ^ — bxj = 0
Пример: Решите уравнение sin7# — cos 19# = 0.
Решение:
sin 7х — cos 19# = 0 <=> sin 7х — sin ( «• — 19# 1=0 <=>
2 sin (13ж — т ) cos (т "~ 6ж J =0
V 4/ V4 /
120

sin ^13ж - |J = О,
-т — 6х) =0.
ктг тг , ктг
7. Уравнение вида a sin ax + b cos аж — 0, ab ф 0 сводится к
элементарному уравцению относительно tg ax или ctg ax:
asina# + ftcosax = 0 <=$> atgax + 6 = 0.
Пример: Решите уравнение 4 sin За; — 7 cos За; = 0.
Решение:
7
4 sin За; - 7 cos За; = 0 <=> tg3x = jr
х = |
| + for) .
Ответ: ^arctg-j + ^-, keZ.
о 4 о
Пример (МГУ, 2001, ф-т почв.): Решите уравнение
2 + cos 2a; = 4 cos x.
Решение: Уравнение 2+cos 2a; = 4 cos2 x может быть решено
разными способами.
Первый способ — используем формулу (34):
2 + cos 2а; = 4 cos2 х <=$• 1 + 2 cos2 х = 4 cos2 х ^=> cos2 х = ^ <=3>
л*
Л I Ч \
cos х = ±-^= <=$> х = ± arccos
у/2 тг
т. к. arccos -^- = j, arccos
/ \/5\ Зтг
( —=- I = ^-.
121

Второй способ — понизим степень уравнения, используя
формулу (35):
2 + cos2z = 4cos2 x «=> 2 + cos2a; = 2(1 + cos2rr)
cos 2x = 0 <==> 2х = %
х = f +
4
ke
Если отметить множества решений из первого и второго
способов на тригонометрическом круге, то увидим, что они
совпадают, хотя и записываются разными формулами (рис. 69)!
Рис. 69
Третий способ — воспользуемся основным
тригонометрическим тождеством:
2 + cos2х = 4cos2 х <==>
2 (sin2 x + cos2 x) + cos2 x - sin2 x = 4 cos2 x <=>
sin2 x - cos2 x = 0 4=^ cos 2ж = 0. ■
Ответ: | + ^, fc G Z.
8. Уравнения вида F(sin2a;, (sin rr±cos х)) = 0 приводятся к
уравнению с одним неизвестным с помощью замены переменных
t = sina; dh cos ж.
122

Действительно, заметим, что
(sin а; — cos ж)2 = 1 — sin 2х <Ф=> sm2# = 1 — (sin x — cos ж)2.
Поэтому удобно ввести замену переменных
t = sin ж — cos ж =Ф- F(sin2x,sina; — cos x) = F(l — £2,£) = О,
т. е. получили уравнение с одной переменной.
Для другого знака
(sin х + cos x)2 = 1 + sin 2x -Ф=Ф* sin 2x = (sin x + cos x)2 — 1.
Поэтому, сделав замену переменных t = sin a; + cos ж, получим
F(sin 2ж, sin х + cos х) = F(t2 - 1, t) = 0.
Пример: Решите уравнение sin х+cos х = cos 2х (1 — 2 sin 2ж).
Решение: Сначала воспользуемся формулой (33):
sin х + cos ж = cos 2ж(1 — 2 sin 2x)
(cosrr + sinrr)(l — (cos ж — sin#)(l — 2sin2a;)) = 0
[cos ж -fsina: = 0,
[l — (cos x — sina;)(l — 2sin2#) = 0.
Для первого уравнения этой совокупности имеем
tg# = -I <=^> х = -j + тгп, neZ.
Для решения второго уравнения совокупности сделаем
замену переменных:
t = cosa; — sinx=>t=l — sin2a; =Ф- sin2a; = 1 — t
и второе уравнение примет вид
1 — *(1 — 2(1 - t2)) = О Ф=Ф -2<3 +1 + 1 = 0 <==>
(t - l)(2t2 + It + 1) = 0 <$=> t = 1.
123

Возвращаясь к исходной неизвестной, получаем
cos х — sin x: = 1 <Ф=>
sin Г~ - ам — sinx = 2cos ~ sin (j - # j = 1
д: = 2тгА;, fc € Z (n — четное),
x = -| + 2тгА;, fe € Z (n — нечетное). "
Ответ: -| + тгп, -| + 2тгп, 2тгп, n G Z.
Прежде чем появится уравнение того или иного типа,
приходится воспользоваться или формулами тригонометрии, или
группировкой слагаемых.
Применяя формулы тригонометрии, всегда надо помнить,
что не все формулы тригонометрии являются тождествами.
Формула
не является тождеством, как формулы для синусов и косинусов,
т. к. левая часть определена для cos(a + b) ф 0, а правая для
cos(a + b) ф 0, cos афО, cos ЬфО.
Чтобы не пользоваться неравносильными переходами для
тангенсов и котангенсов, лучше переходить сразу к синусам и
косинусам.
9. Отбор корней в тригонометрических уравнениях.
Пример (МФТИ, 1984): Решите уравнение
\/6sina;cos2a; = у/—7sin2a;.
Решение: При решении иррациональных уравнений,
содержащих тригонометрические функции, особенно важно помнить,
что при решении уравнений ОДЗ пишем, но не находим. Ведь
решить тригонометрическое неравенство гораздо сложнее, чем
124

уравнение! В данном примере на поиск ОДЗ,,,задаваемой
системой
Jsin2# ^ О,
\sinxcos2a: ^ О,
уйдет зря много времени. На самом деле после нахождения
решений надо проверить или отобрать корни, используя при этом
более удобные неравенства. Отбор корней при решении
тригонометрических уравнений играет большую роль. Поэтому делать
это надо грамотно. Итак,
Г 6 sin # cos 2х = —7 sin 2#,
л/б sinx cos 2x = л/—7sin2rr <£=>• < Fsin2a; < 0,
[ [sina:cos2^ ^ 0.
Решим уравнение из этой системы:
• - 3) = 0 «=Ф
1 \х = тгп, п G Z,
cos а; = ^, 4=> 1
^ о \х = ±arccos ^ + 2тгп, п € Z.
L
Теперь надо отобрать корни. Очевидно, что х = тгп, п 6 Z —
решение, т. к. при этом sin 2x = 0.
Из более простого неравенства совокупности sin2# ^ 0
(<$=^ 2 sin х cos rr < 0) в системе следует, что если cos ж = i > 0,
то sin ж < 0. Поэтому имеем
I COSX= ^, 1 , о
3 <ф=ф- х = — arccos £ + 2тгп, п
Отсюда следует окончательный ответ. ■
Ответ: тгп, — arccos ~ + 2тгп, п 6 Z.
Пример: Решите уравнение V7 — cos x — 6 cos 2ж = 4 sin ж.
125

Решение: Запишем условие равносильности для
иррационального уравнения (3):
у/7 — cos x — 6 cos 2x = 4 sin x
fsinx ^ 0,
\7 — cos ж — 6 cos 2ж = 16 sin2 ж
Jsinx ^ 0,
\7 - cos x - 6(2 cos2 x - 1) = 16(1 - cos2 ж)
{sinrr ^ 0
[cosx = l,
— 3
l^cosa; — —g
\x = 2тгА;,
"^ [ж = arccos (~|) + 2nk. "
Ответ: 27rfc, arccos (~т) + 2тгк, к E Z.
«Школьная» проверка неотрицательности подкоренного
выражения здесь совсем ни к чему, т. к. подкоренное выражение
равно квадрату правой части уравнения и автоматически
всегда остается неотрицательным. А вот следить за знаком правой
части при найденном решении уравнения обязательно.
10. Универсальная подстановка t = tg Щ приводит
уравнение F(siu ж, cos x) = 0 к алгебраическому уравнению
относительно £.
Заметим, что 1 + tg2 ^ = —~—. Тогда если cos ~ ф 0, то
cosrr - cos2 ^ - sin2 ^ - cos2 ^ (l - te-2 £\ - 1~tg 2
cosz - cos 2 sin 2 - cos ^1 tg J -
2J - ! + tg2 i
Поэтому уравнение примет вид
126

Универсальная подстановка «работает», если cos^ Ф 0.
Поэтому надо обязательно проверить для данного уравнения, не
являются ли те ж, для которых cos Щ = 0, решениями уравнения.
Универсальной подстановкой пользуются в случаях
крайней необходимости, так как она приводит, как правило, к
алгебраическому уравнению высокой степени.
11. Уравнения вида a sin х+Ъ cos х = с, аЪ ф 0 можно решать
методом введения вспомогательного угла.
Рассмотрим выражение
у(х) =
= * /„2 _i_ ia .
Заметим, что
(-«-V+M-V-i.
sinx H—, .^ cosx j .
Поэтому точки с координатами
в которых сочетание знаков произвольно, принадлежат
единичной окружности (всего восемь точек), и каждая пара координат
может быть принята за косинус и синус соответствующего угла.
Можно полагать, например,
= cos a, , " тл = sin a.
л/а2 + Ь2 Va2 + Ь2
Тогда заданное выражение у (ж) = a sin х + Ъ cos x принимает вид
у (х) = у/а2 + Ъ2 (cos a sin ж + sin a cos ж) = у^^2 + Ь2 sin(a + #).
Уравнение a sin ж + Ъ cos ж = с примет простейший вид
sin(a + х) = — с
127

Но это же уравнение можно решать и с помощью
универсальной подстановки — оно сводится к однородному после
замены с на (sin2 ^ +cos2 ~j. Однако в некоторых случаях без
введения вспомогательного угла обойтись трудно.
Пример: Найдите наименьшее и наибольшее значения
выражения —3 cos х — 4 sin x.
Решение: Выражение
— 4sina: = —5 (~
si
можно преобразовать несколькими способами.
Положим, например, •=■ = sin а, -=■ = cos а, тогда
о о
— 5 ( ~ cos х + ц sin х J = —5(sin a cos x + cos a sin x) =
= —5sin fa + arcsin ^ J .
Теперь ясно, что выражение принимает все значения из отрезка
[-5;5].И
Ответ: —5 и 5.
12. Нестандартные уравнения. Некоторые уравнения или
неравенства, особенно тригонометрические или смешанные (в
которых, кроме тригонометрических, присутствуют логарифмы
или функции «другого» типа), решаются рассмотрением области
значений входящих выражений. Тогда нередко оказывается, что
решение уравнения (неравенства) возможно только в «крайних»
случаях. К сожалению, общих рекомендаций здесь дать нельзя.
Рассмотрим пример.
Пример: Решите уравнение cos Ъх + cos Зх = 2.
Решение: Левая часть уравнения принимает значение 2,
только если оба слагаемых равны единице одновременно:
128

г , о о fcos5a; = 1,
cos Ъх + cos Зх = 2 <*=*► < о /
[cos3x = 1
cos (3L|2E* J = i <=> fc = 5n
Ответ: 2тгп, n G Z.
Пример: Решите уравнение sin8 x — cos5 x = 1.
Решение:
sin8 ж — cos5 or = 1 4=> sin8 x — cos5 ж = sin2 x + cos2 x <=$>
sin2 ar(l — sin6 x) + cos2 ж(1 + cos3 x) = 0
• 2 /1 • б \ л
sir x(l - sir rr) = 0,
m + cos<5x) = 0
sin2a; = 0,
шьж = 1,
х = 77 + тг^г, n G Z.
Ответ: тг(2п + 1), x = f + тгп, n G Z.
Аналогично решаются уравнения sinm+2 x + cosn+2 x = 1 и
sinm+2 a? — cosn+2 ж = 1 при любых n, m G N.
Пример (МГУ, 1991, химфак): Решите уравнение
16 cos4 f + 6 sin2 f = 3 cos ~ + 12 cos2 f cos 3x.
4 4 2 4
129
5 Зак 243

Решение:
16 cos4 7 + 6 sin2 j = 3 cos ~ + 12 cos2 j cos 3a;
16cos4 7 + 6 - 6cos2 7 = 6cos2 7 - 3 + 12cos2 7 cos3a;
4 4 4 4
2
+ 12cos2 |(1 - cos За;) = 0 4=>
f cos2 £ = 3
<=^COS 4 4'
[cos 3a; = 1.
-i
Из первого уравнения вытекает, что cos тт = т>5 откуда
а подставив это во второе уравнение, получаем
cos (з (±^ + 4тгп)) = cos(±2tt + 12тгп) = 1.
Значит, ответ найден. ■
Ответ: ±Щ- + 4тгп, п G Z.
о
Пример: Решите уравнение
(sin | + 3 cos 14aA =18-2 cos 2x.
Решение: Так как (sin~ + 3cos 14a;j ^ 16, а 18 — 2cos2a;
^ 16, то
f sin | + 3 cos 14arJ =18-2 cos 2a;
{
sin§ + 3cosl4a; =
18 — 2 cos 2a; = 16
f [sin f = cos 14a; = 1,
< sinf = co
1 L 2
[cos2a; = 1.
130

Если sin jr = 1 <Ф=Ф- х = тг + 4тгп, то условия cos 14a: = 1 и
cos2# = 1 выполнены. Если sin— = — 1 <=> х = —тг + 4тгп, то
условие cos Ых = — 1 не выполняется. Значит, ответ найден. ■
Ответ: тг(1 + 4n), n e Z.
Пример: Решите уравнение
1 + In (l + y/{x-7)(U-xf) = cos^"1 тгж, fcEN.
Решение: В общем виде, если дано уравнение
1 + loga(l + f2(x)) = cos2*1"1 irx при a > 1,
то из неравенств 1 < l+loga(l + /2(#)) = cos2*1"1 тгж ^ 1 вытекает
равносильная система
170*0 = о,
I COSTTX = 1.
В нашем случае получаем
Ответ: 14.
Элементы математического анализа
Область определения функции
Любая функция у = f(x) имеет область определения,
которая обозначается D(y) или D(f).
Такие элементарные функции, как Рп(х), 2п~у/х, sin ж, cos я,
жп, п G N, определены на всей числовой оси.
Другие элементарные функции имеют меньшую область
определения.
131

1. Дробь определена там, где знаменатель не равен нулю.
2. Корень четной степени существует только из
неотрицательных чисел. Например, D(y/x) : х ^ 0 <==$- х Е [0; 4-оо).
3. Степень при произвольном действительном нецелом
а определена для положительных чисел. Например, D(xa):
х>0 <=> х е (0; +оо). Если же а > 0, то D(xa) = [0; +оо).
4. Логарифмы существуют только у положительных чисел.
Например, если дана функция у = lgx2, то D(y) : х ^0 Ч=> х G
е (-oo;0)U(0;+oo).
Видно, что область определения функций из п.п. 1-4
определяется неравенством для аргумента.
Большинство функций, с которыми приходится работать,
являются сложными функциями. Чтобы найти их область
определения, необходимо решить некоторые неравенства.
Пример: Найти область определения функции
1
(х2-Зх+1)\ ""3
Решение: Область D(y) определяется как решение
неравенства
-в)
> 0 <^> З2 > 31°S4(x2-3x+l)
х2 - Зх + 1 > 0,
х2 - Зя + К 16
г f 3-л/5\ ,,
е (-оо;-т-) и
)
^ /3-\/69 Зи
Ответ: (i=jM; Ц^) и
132

Множество значений функции
У любой функции у = f(x) есть множество значений,
которое обозначается Е(у) или E(f).
Как найти множество значений? Проще всего это сделать,
если построить эскиз графика заданной функции. А это проще
всего сделать, если уметь строить графики элементарных
функций и их композиций (сложных функций).
Пример: Найдите множество значений функции у = sinx,
хь U' з г
Решение: Функция не является монотонной на заданном
промежутке. Можно, например, просмотреть множество
значений на тригонометрическом круге. Видно (рис. 70), что при
изменении х от j до ~ синус изменяется от
нении х от 77 до 4т- синус изменяется от 1 до ~г" > %г- Отсюда
следует, что синус принимает все значения от -^- до 1, т. е.
до 1, а при изме-
V2
Ответ
#■]•
Рис. 70
133

Пример: Найдите множество значений функции
y = logi{6-x-x2).
2
Решение: В задачах, если это возможно, лучше перейти к
основанию, большему 1 (с ним работать проще):
у = log 1 (6 -х -z2) = -\og2{6-x-x2) = -Iog2(6,25-(z + 0,5)2).
2
Квадратный трехчлен
принимает все значения из промежутка ( — оо; -~ . Логарифмы
существуют только у положительных чисел, поэтому аргумент
логарифма принимает все значения из промежутка (О; =£• ,
тогда log2 I -т— (х + -р: 1 1 принимает все значения из
промежутка f —оо; log2-^Ч. Отсюда следует, что у = ^^(6 — х — х2)
принимает все значения из промежутка — log2 -~;+ooJ, т.е.
#(</)= [-1ов2б|;+оо).Я
Ответ: —log26j;+cx)J.
До сих пор на вступительных экзаменах в МГУ задач на
нахождение Е(у) практически не встречалось. В 2003 году такое
задание появилось. А в билетах ЕГЭ подобные задачи
присутствуют в каждом варианте!
Пример (МГУ, 2003, ф-т фундаментальной медицины):
Найдите множество значений функции
/|s + 2| + |z-4|\
У = log(6+4i-2a;2) I 3 ) '
134

Решение: Найдем сначала область определения D(y):
4х-2ж2>0,
Из найденной области определения следует, что
ж + 2 > О и я - 4 < О,
поэтому \х + 2| + \х — 4| = х 4- 2 — х + 4 = 6, тогда
U2 и
Поэтому в области определения
/U + 2I -f \х — 41 \
У(х) = log(6+4x-2x2) f д J =
log2
~ Iog2(6 + 4х - 2х2) ~ Iog2(8 - 2(ж - I)2)'
Квадратный трехчлен /(ж) = 8 — 2(х — I)2 принимает все
значения из промежутка (—оо; 8], логарифм log2 /(ж) существует
для всех значений f(x) € (0; 8]. Но логарифм стоит в
знаменателе — поэтому необходимо промежуток разбить на два, исключив
значение /(ж) = 1. Итак,
0 < 8 - 2(х - I)2 < 1,
К 8 - 2(ж - I)2 < 8
-оо < log2(8 - 2(х - I)2) < 0, Г-°о < У(х) < О,
О < log2(8 - 2{х - I)2) < log2 8 = 3 [| ^ у(х) < +оо.
[с
Поэтому Е(у) = (-оо;0) U [|; +оо).
Ответ: (-оо;0) U [|;+оо).
135

Основные понятия математического анализа
в курсе средней школы
Перечислим основные понятия математического анализа,
изучаемые в школе.
1. Непрерывность функции в точке.
2. Непрерывность функции на промежутке.
3. Производная функции в точке.
4. Геометрический и физический смысл производной
функции в точке.
5. Критические точки функции (точки, в которых
производная не существует или равна нулю).
6. Экстремум функции. Наименьшее и наибольшее
значение функции на промежутке.
7. Первообразная функции.
8. Определенный интеграл. Вычисление площади
криволинейной трапеции.
Все это изучается на первом курсе любого технического
вуза, и усваивают эту дисциплину далеко не все студенты.
Вспомним, что введение элементов математического
анализа в программу средней школы автор этого проекта академик
Андрей Николаевич Колмогоров перед первым выпускным
экзаменом по новой программе весной 1978 г. объяснял тем, что
выпускники, которые больше никогда не встретятся с математикой,
должны иметь представление о том, что, например, скорость
движущихся объектов не всегда постоянна, что тела в
природе, не являющиеся шарами, пирамидами и другими известными
фигурами, тоже имеют объем, и его можно посчитать с
помощью интеграла и т.д. И, конечно, этим ученикам совершенно
ни к чему знать «первообразную для функции f(x) = ех + —
на промежутке (0; +оо), график которой проходит через точку с
координатами (1; 1)». А что такое для них число е? Выпускники,
поступившие в вуз, все это будут изучать с самого начала!
136

Повторить здесь этот материал содержательно даже
вкратце нет возможности. Поэтому напомним лишь некоторые
основные понятия.
Непрерывность в точке — локальное свойство, оно
определяется поведением функции в точке и некоторой ее окрестности.
По определению, функция называется непрерывной на
промежутке или объединении промежутков, если она непрерывна в
каждой точке в отдельности. Все изучаемые в школе функции
являются непрерывными в области определения. К таким
относятся, например: линейная функция у = кх + Ь, х Е (—оо; +оо);
квадратичная функция у — ах2 + Ьх + с, х £ (—оо; +оо); у — 2у/х,
п е N, х е [0;+оо); у = 2п~^/х, п е N, х G (-оо;+оо);
у = sinx, у = cos ж, х £ (—оо;+оо); показательная функция
у = ах, х Е (—оо;+оо); логарифмическая функция у = loga#,
х Е (0; +оо); любой многочлен от вышеприведенных функций на
соответствующем промежутке.
Во всех этих случаях рассмотренные промежутки
являются областями определения функций. Непрерывность
элементарных функций доказывается непосредственно, а непрерывность
для многочленов следует из теорем о непрерывности суммы и
произведения непрерывных функций.
Более сложной является теорема о непрерывности
частного:
Теорема 3. Если f(x) и д(х) непрерывны в точке хо и
если знаменатель в точке xq не обращается в ноль, т. е. д(хо) ф 0,
то частное , ч непрерывно в точке xq.
Отсюда следует непрерывность в области определения
многих известных функций, области определения которых
являются уже не промежутками, а объединениями промежутков. Это
прежде всего у = tg ж, определенная там, где cos х ф 0, т. е.
U (~f+ **;§ + **), k€
к=—оо
137

в школе это объединение обозначают просто
рациональная функция у (х) = п , где числитель и знамена-»
тель — многочлены и Qm(x) ф 0, и т. д.
Часто в качестве примера разрывной функции приводят
функцию у = ~. Но в области определения она непрерывна!
Дело в том, что у = — не определена в точке х = 0, она определена
в проколотой окрестности точки х = 0 и, по определению, х = О
является точкой разрыва этой функции. При этом оказывается,
что при любом доопределении в точке х = 0 функция (на рис. 71
функция доопределена в точке 0 значением а) будет разрывна в
нуле!
Рис. 71
Свойство убывания или возрастания функции на
множестве не является локальным, т. к. здесь сравниваются между
собой значения функции в двух произвольных точках множества.
Отсюда, в частности, следует, что для функции у — —
неправильно написать, что она убывает на множестве
(-oo;0)U(0;+oo),
138

т. к. у(2) = ^ > у(—1) = —1. Можно записать так: функция у = —
убывает на каждом из множеств (—оо; 0), (0; +оо) в отдельности
(отдельно! — не на объединении!).
Производная функции и ее вычисление
Таблица производных элементарных функций.
/'(*)
Л*)
жа
«ж0"1
е*
ех
sin ж
cos ж
ах
ах1па
cos ж
— sin ж
In ж
1
ж
tgs
1
COS2 Ж
logos
1
ж1па
ctga;
1
sin2 ж
Самым сложным в дифференцировании, конечно,
является дифференцирование сложной функции. Напомним, что если
сложная функция задана формулой у = f(g(x)) (обозначим:
д(Х) =и=>у = /(tt)), ТО у'(х) = fu • tfx.
Пример: Найдите у'(—1) для функции у(х) = л/1 — Зж.
Решение: Заметим, что у(ж) = у/1 — Зж — сложная
функция: у(яг) = f(g(x)), где /(г) = V^5 ^ = д(х) = 1 - Зят. Поэтому
Ответ: — ^.
Пример: Найти производную функции у(х) = sin(3 — 2ж).
Решение: Данная функция у(х) = sin(3 — 2х) — сложная
функция: у(х) = f{g(x)), где f(z) = sin2:, г = д(х) = 3 - 2ж.
Поэтому
j/(a:) = /'(
(-2) = -2cos(3 - 2х).
Ответ: f'(x) = -2cos(3 - 2х).
139

Пример: Найдите производные функций:
а) у(ж) = %/5-ж;
б) у{х) = вт(ж3 - За;2);
в) у(ж) = ec«(7*-i);
г) у(х) = (е(4-5*>2)2 - cos (e(4"5a!)2).
Решение:
а) /М = л/^j и(х) = 5 - # =Ф-
=> у(ж) = f(u(x)) = у/и(х) = л/5 — а; =>
Му'(х) = --^
2v5
у v — ж
б) /(«) = sin«, «(ж) = ж3 - Зж2 =Ф-
=Ф- у(ж) = /(и(ж)) = зт«(ж) = вт(ж3 - Зж2) =*>
yi = /и • и'х = cos «• (Зж2 - 6ж) = (Зж2 - 6ж) соз(ж3 - Зж2)
у'(ж) = (Зж2 - 6ж) сов(ж3 - Зж2)
в) /(и) = еи, u(v) = cost), «(ж) = 7ж — 1 =*►
=» у(ж) = /(и(ю(аг))) = еи("(ж)> = е00"^*"1) =»
=*■ j4"= /«•<•< = еи • (- sin«) • 7 = -7eC0S(7x-V ■ зт(7ж -1)
у'(ж) = -Те008^"1) • яп(7ж - 1)
г) f(u) = и2 - cos и, и(и) = е", «(ж) = (4 - 5ж)2 = (5ж - 4)2 =*>
=» u(v(x)) = е" = е(4"5а;)2 =J>
=» у(ж) = f(u(v(x))) = и2 («(ж)) - cos «(«(ж)) =
= (е(5-4)2)2 _ cose(5*-4)' ^ у; = ^ . и; . ,; =
= 2и • е" • 2(5ж - 4) • 5 - (-sin« • е" ■ 2(5ж - 4) • 5) =
= (2и + sinu) • е" • (5ж - 4) • 10 <=Ф
у'(ж) = 10 (2е^-4)2 + sine(5*-4>2) (5ж - 4) • е^"4)2.
140

Геометрический смысл производной функции
в точке
Учащиеся легко строят прямые по двум точкам, гораздо
реже они пользуются геометрическим смыслом коэффициентов
уравнения прямой (и это правильно, т. к. первое верно в любой
системе координат, а второе имеет смысл в декартовой, хотя они
этого и не знают). И это несмотря на то, что в обыденной жизни
и прикладных науках чаще всего говорят о прямых,
наклоненных к плоскостям (полу, стенке и т. д.) или прямым под данным
углом.
У\
А
У
/Ч
а
Рис. 72
Напомним, что геометрический смысл к в уравнении у =
= кх + 6, к Ф 0 состоит в том, что к = tg а,- т. е. к — это тангенс
угла, который образует прямая у = кх + Ь, к ф 0 с
положительным направлением оси ж, т.е. с положительной полуосью
абсцисс. На рис. 72 а) к > О (угол а — острый), а на рис. 726)
к < О (угол а — тупой). Обратим внимание на то, что углом
между прямой и полуосью является и угол /3, tg /3 = tg(—(тг — а)) =
= — tg(vr — а) = tg а, /3 — отрицательный угол. Число к в
уравнении у = кх + Ь, к ф 0 называется угловым коэффициентом
прямой.
Не будем углубляться в то, что такое касательная.
Запишем уравнение касательной к графику функции у = f(x) в
точке с абсциссой xq: у = f'(xo)(x — xq) + f(xo) или в другом виде
у = f'(xo)x + (/(#o) "~ f'(%o)%o)- Видим, что в роли А;
выступает f'(xo). Отсюда сразу следует, что /;(хо) — это тангенс угла
141

наклона касательной в точке xq к положительной полуоси, или
угловой коэффициент касательной.
Зная это, можно решить обратную задачу: определив на
графике угол наклона касательной к графику функции в точке
жо5 сразу выписываем производную этой функции в точке xq.
Пример: На рисунке 73 изображен график функции у =
= f(x) и касательная к нему в точке с абсциссой х = 2.
Определить значение у'(2).
V
\
\
У
2
0
1
/
J
f
2
/
W
у
А
/\
X
Рис. 73
Решение: Из рисунка видно, что у'(2) = 2.
Возрастание и убывание функции
на промежутке. Экстремумы функций
Теорема 4. Если функция f(x) непрерывна на
промежутке 1У а производная f'(x) ^ 0 (неотрицательна) или /'(#) ^ О
(неположительна) внутри J, причем производная обращается в
ноль лишь в конечном числе точек, то функция возрастает
(соответственно убывает) на всем промежутке /.
Пример: Найдите промежутки убывания и возрастания
функции у = ж4 — ж3.
Решение: Найдем производную заданной функции
142

Теперь найдем критические точки:
Нанесем знаки производной на числовую ось (рис. 74):
— — |
• • »
О з я
4
Рис. 74
Видно, что на f —сю; ^J, т.е. внутри промежутка ( — оо; j ,
производная неотрицательна, обращается в 0 лишь в одной
точке х = 0. Отсюда следует, что функция убывает на f — оо; 4 . На
( ^; +ooj производная положительна — значит, функция
возрастает на промежутке ~; +оо ]. ■
Зачем изучаются производные в школе? Прежде всего для
исследования экстремумов и построения графиков.
О п р е д е л е н и е 1. Точка х = а называется точкой
максимума (минимума) для функции у = /(ж), если найдется
такая окрестность точки а, что для всех ж, принадлежащих этой
окрестности, выполнено неравенство /(а) ^ f(x) {f(a) ^ /(#))•
Говорят еще, что это точка локального максимума
(минимума), т. к. определяется поведением функции лишь в некоторой
окрестности точки х = а.
Точки, в которых функция имеет максимум или минимум,
называются точками экстремума.
Если в некоторой окрестности точки х = а выполнено
строгое неравенство для всех ж, не совпадающих с а, то имеем
строгий максимум (минимум); если неравенство нестрогое, то
максимум (минимум) нестрогий.
143

Теорема 5 (Ферма). Если у функции у = f(x) в
точке х = а существует производная и имеет место экстремум, то
/'(«) = о.
Такая точка часто называется стационарной.
Определение 2. Точка, в которой производная равна
нулю или не существует, называется критической точкой.
Поэтому стационарная точка — частный случай
критической.
Эти точки играют большую роль в приложениях
математики. Дело в том, что если производная в точке а существует
и не равна 0, например, /'(а) > 0, то существует такая
окрестность точки а, что для всех точек х из этой окрестности,
находящихся слева от а, выполнено неравенство f(x) < /(а), а для
всех ж, находящихся справа от точки а, выполнено неравенство
f(x) > f(a). Если же производная в точке равна нулю или не
существует, то ничего нельзя сказать о знаке разности f(x) — f(a)
справа и слева от точки а без дополнительного исследования.
Это особенно хорошо видно на двух классических примерах.
1. Производная функции у = х2 равна 0 в точке х = 0. Из
графика (рис. 75) сразу видно, что в начале координат имеем
минимум.
fy=;
У
х
Рис. 75
Рис. 76
2. Производная функции у = ж3 тоже равна 0 в точке х = 0.
Но из графика (рис. 76) этой функции сразу видно, что в нача-
144

ле координат никакого экстремума нет — функция продолжает
возрастать.
Исследования поведения функций в окрестностях
критических точек — центральный вопрос многих прикладных разделов
математики.
Теорема 6 (достаточные условия экстремума). Если
функция f(x) непрерывна в точке а?о, имеет производную в
проколотой окрестности точки хо1, справа и слева от точки
производная имеет разные знаки, то xq — точка экстремума. Причем,
если слева fr(x) < О, справа f'(x) > О, то xq — точка
минимума; если же слева ff{x) > О, справа ff(x) < О, то #о — точка
максимума.
Если же при переходе через точку хо производная не
меняет знак, то экстремума нет.
Классический пример — функция у = ж3. Для нее имеем
у1 = Зх2 и у* = О <=> х = 0. Но по обе стороны от точки х =
= 0 производная имеет один и тот же знак — экстремума нет. На
всем промежутке (—оо; +оо) производная неотрицательна,
функция монотонно возрастает.
Пример: Сколько экстремумов имеет функция, график
которой представлен на рис. 77?
Рис. 77
окрестность точки хо без самой точки
145

Решение: Функция имеет на отрезке [—3; 2] два экстремума
максимум в точке х = — 2 и минимум в точке х = 0. Заметим
при этом, что в точке х = — 2 выполнены достаточные условия
экстремума, а в точке х = 0 не выполнены, т. к. функция в этой
точке разрывна.
Кажется, что точке х = 2 производная равна 0 и там
максимум. На самом деле это не так, потому что, по определению
экстремум определяется во внутренней точке, принадлежащей
области определения функции, т.е. в такой точке, некоторая
окрестность которой лежит внутри области определения. У
точки х = 2 только левая часть окрестности принадлежит области
определения. Функция принимает в этой точке наибольшее на
отрезке значение. ■
Наибольшее и наименьшее значение функции на
промежутке — не простые понятия. Это, как говорят, глобальное, а не
локальное свойство функции, т. к. оно определяется поведением
функции на всем промежутке. Наибольшее и наименьшее
значение функции на промежутке могут и не существовать.
Например, функция
1, при х = 0,
у(х) = #, при х Е (0;2),
1, при х = 2
не имеет ни наибольшего значения, ни наименьшего значения на
отрезке [0; 2] — рис. 78.
2 х
Рис. 78
Если же функция непрерывна на отрезке [а, Ь], то она всегда
имеет наибольшее и наименьшее значение на этом отрезке.
146

Зачем нужны графики? Не все уравнения, даже
алгебраические, можно решить аналитически, а иногда и вовсе не нужны
корни уравнения, а важно знать, сколько их.
Пример: Сколько корней имеет уравнение 7#4+4#3 = а при
каждом значении параметра а?
Решение: Построим эскиз графика левой части уравнения
у(х) = 7х4 + 4#3 = xs (7х + 4) (рис. 79), найдя предварительно
lim (7ж4 + 4ж3) = lim х4 (7 + $) = +оо,
Рис. 79
Рис. 80
Из эскиза видно, что горизонтальные прямые или не
пересекают график, или пересекают график в одной или нескольких
точках (перегиб в точке 0 рисовать, конечно, не обязательно, и
он не влияет на решение). Для решения задачи необходимо знать
минимальное значение функции.
Для этого найдем производную данной функции:
f'{x) = 28я3 + 12ж2 = 28я2 (х + |) .
Теперь найдем критические точки, т. е. точки, в которых
производная равна нулю:
Расставим знаки производной, применив метод
интервалов. Из рисунка 80 видно, что производная меняет знак (с
147

о
— на +) только при переходе через х = — = , значит, в этой
точке имеем единственный экстремум — локальный минимум
(3\ 27
— =1 = —з* В точке х = О производная равна 0, но
при переходе через нее не меняет знак — в этой точке
экстремума нет! Отсюда следует, что количество решений уравнения
7х4 + 4х3 = а равно
О, при а <-
27
1, при а = -ш,
97
2, при а > -;§.
27
Ответ: Нет решений при а < — ^То 5 одно решение при а =
27 27
= ~343; два Решения ПРИ а > ~
Пример (МФТИ, 1982): В точках А и В параболы у =
= ж2 — Зх + 1 проведены касательные, угловой коэффициент
одной из касательных равен 1. Парабола у = Ах2 + ах + 1 (а > 0)
также касается каждой из этих прямых. Найдите значение
параметра и расстояние между точками Аи В.
Решение: Для первой параболы у'{хо) = 2жо — 3, и
уравнение касательной имеет вид у = (2#о — 3)(ж — xq) + х% — Зжо + 1
где хо — абсцисса точки касания.
Для одной из касательных у' = 1, тогда
2ж0 - 3 = 1 «=Ф ж0 = 2,
поэтому точка А (рис. 81) имеет координаты А(2; —1) и
уравнение этой касательной примет вид у = х — 3. Эта прямая, па
условию, является касательной и для второй параболы, т. е.
имеет с ней единственную точку пересечения, не лежащую на оси
параболы. Поэтому дискриминант уравнения
4х2 + ах + 1 = х - 3 <==> 4х2 + х(а - 1) + 4 = 0
148

Рис. 81
равен нулю, т. е. (а — I)2 — 64 = 0, откуда или а = 9, или а = —7.
Последнее значение меньше нуля и потому не подходит по
условию задачи, значит, а = 9.
Найдем теперь абсциссы точек, касательные в которых для
первой параболы являются касательными и для второй
параболы. Для этого напишем уравнение (условие принадлежности)
9х + 1 =
х\-
означающее, что точка с абсциссой х\ принадлежит и
касательной, и второй параболе. Уравнение равносильно уравнению
4х2 + 2ж(6 — х\) + х\ = 0, и оно должно иметь одно решение
(условие касания), поэтому, из равенства нулю дискриминанта,
имеем
36 - 12^1 + х\ - Ах\ = 0 <=> хг - 2 ± 4.
Итак, первая точка имеет координаты х = 2, у = — 1 (это точка
А, мы ее уже нашли), вторая точка, точка В, имеет координаты
х = —6, у = 55. Расстояние между ними равно
= 40л/2.
Ответ: 9; 40\/2.
149

Неопределенный интеграл.
Площадь криволинейной трапеции
Таблица первообразных для элементарных функций
F(x)
ха
ха+\
а + 1
cos ж
sin ж
sin ж
1
COS2 Ж
tga;
1
sin2 ж
ctgx
ех
ех
ах
ах
In а
1
Ж
In
х\
Нахождение неопределенного интеграла, или множества
всех первообразных, — операция, обратная
дифференцированию. Поэтому всегда проверяйте свой ответ, находя его
производную. Приведем несколько примеров интегралов от сложных
функций.
(4 —rr)2+1 о ,
2. I sin(5a; + 2) dx = -| cos(5o: + 2) + С.
3.
4. f{x4 - Зх2 + 7х - 11) dx =z 3d - 3 • ^ + 7 • ^ - Пж + С.
5. / sin 5ж • cos Зж dx = „ (sin 8# + sin 2x) dx =
= ~т~ cos 8ж — ~ cos 2ж + С.
16 4
7.
8.
+ 1
Площадь фигуры, ограниченной кривыми у = fi{x) и у =
= /2(#) (рис. 82), где /i(x) ^ /2(#)> и прямыми а; = о и ж = 6,
вычисляется по формуле S = / (/i (ж) — /2(ж)) da:.
150

~
Рис. 83
Пример: Найдите площадь фигуры, ограниченной кривыми
у = х2 и у = 2х — х2.
Решение: Найдем прежде всего точки пересечения
заданных кривых у = х2 и у = 2х — х2:
х2 = 2х- х2
2х2 - 2х = О
Теперь построим эскизы данных кривых (рис. 83) и
вычислим площадь.
S =
'=1-2 = 1
о 3 3'
Ответ: ^

РАЗДЕЛ ВТОРОЙ
ОБРАЗЦЫ ТРЕНИРОВОЧНЫХ
ВАРИАНТОВ ЕГЭ
Структура ЕГЭ (Единого
государственного экзамена)
по математике
Для выполнения ЕГЭ в 2007 году отводится 4
астрономических часа, (240 минут, т. е. примерно 6 школьных уроков). Работа
состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1-А10, В1-ВЗ)
обязательного уровня по материалу курса «Алгебра и начала анализа»
10-11 классов. К каждому заданию А1-А10 приведены 4
варианта ответа, из которых только один верный. При выполнении
этих заданий надо указать номер верного ответа. К заданиям
В1-ВЗ надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4-В11, С1,
С2) по материалу курса <<Алгебра и начала анализа» 10-11
классов, а также различных разделов курсов алгебры и геометрии
основной и средней школы. К заданиям В4-В11 надо дать
краткий ответ, к заданиям С1 и С2 — записать решение.
Часть 3 содержит 3 самых сложных задания, два —
алгебраических (СЗ, С5) и одно — геометрическое (С4). При их
выполнении надо записать обоснованное решение.
За выполнение работы выставляются две оценки:
аттестационная отметка и тестовый балл. Аттестационная отметка за
усвоение курса алгебры и начал анализа 10-11 классов выста-
152

вляется по пятибалльной шкале. При ее выставлении не
учитывается выполнение четырех заданий (В9, BIO, B11, С4).
Тестовый балл выставляется по 100-балльной шкале на
основе первичных баллов, полученных за выполнение всех
заданий работы.
При выполнении заданий А1-А10 в бланке ответов № 1
под номером выполняемого задания поставьте знак «х» в
клеточку, номер которой соответствует номеру выбранного вами
ответа.
Образец заполнения приведен на рис. 84.
указан ответ №2 на задание А5
DDDDDDDD,
Q п D D S D D D
□ а □ а □ п d а<
.'DDDDDDDD
1 * D D D □ D □ D tf
f з d a d a d о □ □
I * d d a a a a a qJ
Рис. 84
К каждому заданию дано 4 варианта ответов, среди
которых только один верный.
Вот как формулируется задание в первой части.
Пример: А5 Укажите решение неравенства Iog2(£ + 3) ^ 1.
1) (-оо;-1] 2) (-3;-1] 3) [-3;-1] 4) (-оо;-2]
153

Решение:
Первый ответ неверен, т. к. забыто ОДЗ логарифма:
х + 3 > 0.
Второй ответ верен.
Третий ответ неверен, т. к. ОДЗ указано неправильно.
Четвертый ответ написан «учеником», имеющим весьма
смутное представление о логарифмах. ■
Ответ: 2).
Решение не сдается и никем не проверяется, только
ставится крестик.
Ответом к заданиям В1-В11 будет некоторое целое число
или число, записанное в виде десятичной дроби. Это число надо
будет записать в бланк ответов № 1 справа от номера задания,
начиная с первой клеточки. Каждую цифру, знак минус отри-
цательного числа или запятую в записи десятичной дроби надо
писать в отдельной клеточке строго по образцу из верхней
части бланка. Единицы измерений писать не надо.
Пример заполнения бланка дан на рис. 85.
Это задания (В1-В11) по материалу курса «Алгебра и
начала анализа» 10-11 классов, а также различных разделов курса
алгебры и геометрии основной и средней школы.
Пример: В1 Найдите наибольшее значение функции
у- 24
У ~ х3 + 2х
на промежутке [2; 12].
Решение: Знаменатель дроби возрастает на заданном
промежутке, значит, дробь убывает. Следовательно, наибольшее
154

Результаты выппг*
Рис. 85
значение — это значение дроби на левом конце промежутка, т. е.
- 24 _ 9 _
Унаиб ~~ 23 + 22
Ответ: 2.
Замечание: Многие школьники, однако, будут решать эту
задачу с помощью дифференцирования и запутаются.
Решение не сдается и никем не проверяется, только число 2
записывается в соответствующую клеточку — рис. 85.
Для записи ответов на задания С1 и С2 используйте бланк
ответов № 2. Запишите сначала номер выполняемого задания, а
затем решение.
Для записи ответов на задания (СЗ-С5) используйте бланк
ответов № 2. Запишите сначала номер выполняемого задания, а
затем обоснованное решение.
Часть 3 содержит 3 самых сложных задания. При их
выполнении требуется записать полное решение. За выполнение
каждого задания этой серии в зависимости от полноты и
правильности представленного решения выставляется от 0 до 4
баллов. Для оценки этих заданий составителями разрабатываются
критерии оценки каждой конкретной задачи.
Приведем примеры нашего оформления решений двух
заданий ЕГЭ-2003.
155

Пример (ЕГЭ-2003, С1): Решите уравнение
Решение: Воспользуемся тождественными
преобразованиями логарифмов в ОДЗ и решим получившееся иррациональное
уравнение.
х = 2 (log2 ^ + | log2ж)
=> 0.0 + log2 x = -2 + log2 x
-2 + log2 x ^ 0,
10 + log2 x = 4 - 41og2 x + log2 x.
'б±7 *=Mog2z = 6<=>x = 26.
Ответ: 64.
Можно решение оформить по-другому.
Решение: Известно, что переход к новому допустимому
основанию является равносильной операцией. Поэтому
log* 2 =
кроме того, в ОДЗ верно, что
Уравнение примет вид ^/10 + log2 х = — 2 + log2 x. Введем новую
переменную t = log2 a:, t ф 0, и решим получившееся уравнение.
156

t = 6 <=> log2 x = 6 <=> ж = 64. ■
Ответ: 64. ■
Замечание: В обоих случаях использовались равносильные
в ОДЗ операции.
И ни в одном из этих решений не надо находить
«школьное» ОДЗ: 10 + -—^—т ^ 0. Оно не работает, потому что в обоих
случаях выполняется автоматически, т. к. подкоренное
выражение приравнивается квадрату правой части. Отбор корней
происходит за счет выполнения необходимого условия
существования решения иррационального уравнения — неотрицательности
правой части: —2 + log2 x ^ 0.
Пример (ЕГЭ-2003, С4): Из области определения функции
(5ж + 2\
аа-а* + 2 \
взяли все целые положительные числа и сложили их. Найдите
все положительные значения а, при которых такая сумма будет
больше 9, но меньше 13.
Решение: Заметим, что целые положительные числа — это
натуральные числа. Логарифмы существуют только у
положительных чисел, поэтому все #, принадлежащие ОДЗ,
удовлетворяют неравенству
5ж + 2
Для решения неравенства воспользуемся условием
равносильности (20) или правилом 5
Га>0,
»{
157

Итак, при a = 5 в решение неравенства входит бесконечно много
натуральных чисел, значит, а = 5 не является решением задачи
Теперь рассмотрим вторую систему, где а > 0, а ф 5.
Неравенство
>0
X "t" «)
довольно громоздкое, поэтому рассмотрим два случая отдельно
Рассмотрим сначала а, для которых (а —1)(а —5) > 0. Тогда
_ / 2(а-1)\ _ / 2(а-1)\
(а - 1)(а - 5) т ^—- > ° ^=> ^—Г^ > 0.
v A ; (ж + 2) ж + 2
Неравенство выполнено вне корневого промежутка, который со
держит бесконечное множество натуральных чисел независимо
от того, какие значения может принимать выражение
( 2(«-1)\
v «-5 ;•
Потому решений задачи в этом случае нет.
Рассмотрим теперь о, для которых (а — 1) (а — 5) < 0. Тогда
/ 2(g-l)\ / 2(fl-ir
— \ п с I *Ь I _ с
(ж+ 2) ^^" л: + 2
В этом случае неравенство выполнено внутри корневого
промежутка — это отмечено на рис. 86 а) и б), в зависимости от того
/ 2(а-1)\
что больше, —2 или I ^— I.
V а~5 /
158

б
~^a-5 a-5
Рис. 86
Видно, что в случае б) решений задачи тоже нет, т. к.
решение вообще не содержит натуральных чисел независимо от того,
/ 2(а-1)\
какие значения может принимать выражение I =— I.
V а~ь )
( 2(а-1)\
Остается единственный вариант: I —2; =— I.
V а~~5 /
Замечаем, что 9<1 + 2 + 3 + 4<13, а1 + 2 + 3 + 4 + 5>13.
Поэтому для существования решения задачи необходимо и
достаточно, чтобы в промежуток вошли числа 1, 2, 3, 4, но не вошло
число 5, т. е. выполнялись неравенства:
a-5
Теперь можно записать ответ. ■
(]
Оценивание результатов ЕГЭ
Каждая задача серий А и В оценивается в 1 балл, серии
С — до 4 баллов. Итак, можно набрать от 0 до 41 баллов. Но это
так называемые первичные или «сырые» баллы. Пересчет
оценки в 100-бальную шкалу проходит по специальной процедуре
после статистической обработки работ всех экзаменующихся, то
есть набранный вами балл будет зависеть и от результатов
других школьников, сдающих ЕГЭ в данном году. Приблизительно,
конечно, вы можете достаточно точно оценить свой конечный
балл. Для этого надо прикинуть набранные первичные баллы и
Умножить это число на -т(г.
159

Особенности заданий в ЕГЭ
Задания серии А и серии В проверяются только
компьютером. Компьютерная проверка предъявляет дополнительные
требования к школьнику: ему не только надо решить уравнение
или неравенство, но выполнить еще какое-нибудь
дополнительное задание, чтобы ответ легко проверялся компьютером. Это
или надо указать тот промежуток из предложенных в ответе,
которому принадлежат корни уравнения, или найти сумму корней,
или найти наименьший или наибольший корень. Для учащихся
это требует времени и, главное, внимания (при его непростом
состоянии!).
При выполнении большинства заданий А с годами все реже
удается угадать верный ответ. Чаще всего необходимо провести
некоторые преобразования, а потом и арифметические
вычисления, которые кажутся простыми, но для школьников, впервые
пишущих такую большую работу, это совсем не так. Затем
надо сравнить полученный ответ с предложенными и, если ответ
совпал с одним из них, отметить в «бланке ответов» номер
выбранного ответа. Здесь школьника поджидает первая ловушка,
совпавший ответ может оказаться неверным, т. к. предложенные
варианты часто записаны с учетом типичных ошибок,
допускаемых школьниками при решении данного задания (может быть,
именно эта ошибка и допущена!).
Первая часть, серия А, в 2003 г. состояла из 16 заданий
(А1-А16), содержащих, как утверждают составители, задачи
по обязательному для школ любого профиля материалу курса
«Алгебра и начала анализа» 10-11 классов.
На взгляд автора, это не совсем так. В 2003 году за
решение менее 5 задач первой части ставилась оценка 2 (таких среди
решавших оказалось 87000). На наш взгляд, это не удивительно.
Попробуем понять, почему так много двоек. Задания 1, 2, 4, 5
из ЕГЭ-2003 относятся к основной школе, и с ними троечникам
справиться не просто, потому что они сдали экзамен в 9 классе
и решили, что больше изученное не понадобится.
Например, типичными заданиями были такие:
160

А1. Представьте выражение
23,5 а 2~^
~1
в виде степени с основанием 2.
А2. Вычислите \/Ъ • 162.
А4. Упростите выражение
cosz a — sin^ a
A5. Укажите множество решений неравенства
М < п
Эти задания могут быть классическими заданиями
выпускного экзамена за 9 класс. Почему же они могут вызвать
затруднения?
А2: В XXI веке, когда и двоечники справляются с
компьютерами в тысячу раз лучше, чем академики математики, мало
кто в 11 классе вычисляет \/& •162 в уме или тем более
разложением на множители. Для этого есть калькуляторы, считают они.
А4: Здесь в одном примере две самые употребляемые
математиками формулы, но столь же плохо запоминаемые
школьниками. Узнать сразу и синус, и косинус двойного угла троечнику
тоже трудно, но в этом нет необходимости, считает он: на это
есть справочники,
А5: Метод интервалов изучался в 9 классе, и троечники
его забыли. Кроме того, в А5 есть ловушка, в которую
попадаются многие: здесь нельзя автоматически поставить знак + при
больших ж, это просто неверно. Всегда целесообразно привести
дробь к каноническому виду — чтобы во всех скобках слагаемые
были расположены в порядке убывания степеней с
положительным коэффициентом при старшей степени. При приведении к
такому виду возможно изменение знака неравенства на
противоположный. В нашем случае
(2-ж)(4х + 3) ^"^ (я._2)(я: + |) " '
и теперь ошибиться трудно.
161
6 Зак.243

Задания по материалу 11 класса.
A3. Вычислите 0,231og<>>25.
Решение этого задания требует не только знания
школьной формулы loga#a = alogarr, но и умения применить ее в
«обратном» порядке, что, как известно любому учителю, уже
троечнику не под силу.
Особенностью ЕГЭ является также и необычность
постановки некоторых по сути обычных школьных задач.
Пример (ЕГЭ-2002, А5): Укажите промежуток, которому
принадлежат все корни уравнения у/х2 — 5 = 2.
1)(-3; 0) 3)[-3;3]
2)(0;3] 4)(-3;3)
Решение: Естественно, аккуратный школьник начнет
искать ОДЗ: х2 — 5 ^ 0 <$=> х2 ^ 5. Аккуратный ученик — это
тот ученик, который делает так, как его учили в школе. А все
дети знают, что квадратный корень существует только из
неотрицательных чисел, но далеко не все знают, что при решении
такого уравнения после возведения в квадрат получается
равносильное уравнение и ОДЗ выполняется автоматически. Поэтому
при решении этого уравнения не надо искать ОДЗ.
При этом аккуратный, но слабый ученик найдет ОДЗ
неверно, написав, что х ^ л/5. Затем он формально решит
уравнение, получит правильный ответ (т. к. лишние корни не
приобретаются), забудет про ОДЗ и укажет верный ответ. Как можно
судить о его знаниях? А если, наоборот, учащийся все сделал
верно, но, по невнимательности или из-за неважного зрения,
отметил не тот номер?
Решить неравенство х2 ^ 5 не самая простая задача для
обычного школьника: он гораздо быстрее решит сложное
квадратное уравнение!
Если же ученик аккуратный, но более сильный, то он
правильно найдет ОДЗ, т. е. правильно найдет те промежутки,
которым принадлежат корни: х Е (—оо; —\/5] U [\/5; +оо). Но ничего
похожего нет в предложенных ответах. Многие при этом
растеряются.
162

Тогда сильный ученик сделает то, чего составители явно
не просят, — он найдет корни уравнения! Он решит уравнение
у/х2 — 5 = 2 <=$► х2 — 9 <=$> х = ±3. Вот теперь сильный ученик
найдет среди предложенных правильный ответ 3). ■
Если учащийся заранее познакомится с такой постановкой
задачи, то он не будет тратить время зря.
Дорогие школьники, даже при выполнении задания серии
А старайтесь быть собранными: не спешите, пишите аккуратно
и четко, несмотря на то что эти вычисления вы не будете
сдавать; вспоминая формулы, которые вы собираетесь применить,
запишите сначала их на бумагу, присмотритесь к ним, вспомните
какие-то ассоциации, связанные с ними, и, когда будете
уверены в правильности формулы, применяйте ее. Особое внимание
уделите правильности вычислений. Госпожа арифметика очень
капризна! (Это в полной мере испытано автором при
формировании ответов на предлагаемые варианты.)
Задачи серии В требуют от учащихся еще больше. Здесь
надо не только знать, но и думать. Задания второй части не
очень трудные, но они требуют от учащихся твердых навыков
при решении стандартных задач, умения быстро свести не
совсем стандартную задачу к стандартной.
Пример: Найти все целочисленные решения уравнения
Решение: Если стандартно раскрывать модуль, то на это
уйдет время. Проще быстро решить два квадратных уравнения
(а без этого не обойтись при любом способе решения!):
х2 + За; = 2х + 2
и
х2 + Зх = -2х - 2
Очень легко проверяется условие х + 1 ^ 0.
Ответ: 1.
163

Работа в вузах показывает, что хуже всего студенты
знают формулы тригонометрии и потому не владеют умением
производить тригонометрические преобразования. А ведь именно
школьная тригонометрия больше всего применяется в вузовской
математике. При решении заданий по тригонометрии есть
опасность не найти свой правильный ответ среди предлагающихся.
Пример: Решите уравнение
Решение:
Первый способ.
sinz + 2cos# = 1 <=з> 2sin | cos | + 2 (cos2 | - sin2 |) =
= sin2 | + cos2 ! Ф=* 3tg2 ! - 2tg | - 1 = 0
2 3
| = | + тгп, n € Z,
§ = - arctg ? + тгп, n €
Ответ: \ + 2тгп, -2 arctg \ + 2тгп, n G Z.
L «5
Второй способ.
sinrr + 2 cos x = 1 «Ф=^ л/б ( Ц= sinrr H—— cos дг I =
\л/5 у/5 J
V5
х = - arccos -~= + (-1)Л arcsin -~= + тгп, п Е
л/5 v5
Ответ: — arccos -==. + (—l)n arcsin -*= + тгп, п Е Z.
л/5 л/5
164

Третий способ.
sinx + 2 cos x = 1 =$► (sin# + 2 cos x)2 = 1 <=$>
sin2 ж + 4 sin x cos rr + 4 cos2 a: = 1
4=> 3cos2# + 4sinrrcoso; = 0 <=> cosx (т + tgar) =
[cos x = 0, \x = ~ + тгп, n E Z,
tgx = -j [a: = - arctg | + тгп, n G Z.
Но отсюда ответ не следует, т. к. при возведении в квадрат
получилось неравносильное уравнение, и поэтому придется
отбирать корни. Если х = ~ 4- тгп, то
sin (77 + тгп) +2cos (77 + тгп) = (—1)п,
поэтому п может быть только четным.
о
Если tga; = — ~, то или
sinx=f, cosx = — f,
5 о
о о
sin а;+ 2 cos ж = ~ — f = —1,
т. е. решений нет, или
3 8
sinx + 2 cos a; = —f + f = 1
о о
и ж = - arcsin | + 2тгА;, А; Е Z. ■
о
Ответ: ~ + 2тгА;, - arcsin | + 2тгАг, fc € Z.
4 О
Из этого примера видно, что ответы могут получаться в
разных формах. Думается, что, во-первых, далеко не все
школьники с этим сталкивались, а, во-вторых, не всегда
составляющим удается сделать так, чтобы ответ можно было бы записать
в единственной форме.
165

Что делать школьнику? Ответ: Не известно. Просто,
наверное, такие задания не стоит помещать в серию А! В
тренировочных вариантах они могут встречаться, чтобы школьники
научились решать элементарные тригонометрические уравнения.
Все примеры были приведены для того, чтобы понять, что
к ЕГЭ надо готовиться.
Ниже предлагается 20 тренировочных вариантов ЕГЭ.
Сначала приводится демонстрационный вариант 2007 г. Уровень и
стилистика следующих шести вариантов (с 1 по 6) вполне
соответствуют уровню и стилистике реальных вариантов ЕГЭ 2003-
2007 гг. Следующие варианты (с 7 по 19) более сложные. Эти
тренировочные варианты не рассчитаны на то, чтобы выполнить
их в короткий промежуток времени. Два варианта (1-й и 12-й)
решены полностью, из остальных вариантов задачи решены
выборочно.
Демонстрационный вариант 2007 г.
А1 Найдите значение выражения 46р • 4~4р при р = -т.
1) 1 2) 2 3) 32 4) 4
А2 Упростите выражение
1) 1,2 2) 5-^р 3) 2,4 4) ^2
A3 Найдите значение выражения Iog4(64c), если log4 с = —Зг5
1) -6,5 2) -0,5 3) -10,5 4) -67,5
А4 На одном из чертежей, представленных на рисунке 87,
изображен график нечетной функции. Укажите этот чертеж.
166

1)
3)
■—
— -—
1
/
/
/....
0
У
(
\
i
/
1
/
!
1
!
* • • • •
•
\
/^
^ '
0
У
*—
X :
X :
Рис. 87
А5 Найдите производную функции у = (х — 3) cos #.
1) у' = cos х + (х — 3) sin ж 3) у; = cos х — (ж — 3) sin a;
2) у1 = (# — 3) sinx — cos ж 4) $/ = — sina:
А6 Укажите множество значений функции у = 2х + 5.
1) (5; +оо) 2) (0; +оо) 3) (-оо; +оо) 4) (7; +оо)
А7 На рисунке 88 изображены графики функций у = f(x) и
у = д(ж), заданных на промежутке [—3; 6]. Укажите множе-
167

ство всех значений х, для которых выполняется неравен!
ство f(x) ^ д(х).
)[;]
2)[-3;-2]U[4;6]
)[;
4) [^2;4]
/
\
У
1
li
1
\
о
^
\
У =
с
/(*)
>
к
!\
► :
Х\
* :
Рис. 88
А8 Найдите область определения функции f(x) =
l)[0;3)U(3;+oo)
2)[0;+оо)
3) [0;81)U(81;+co)
4)(-oq;81)U(81;+oo)
А9 Решите неравенство logi_ (7х — 21) > logi_(6«).
2 2
1) (-оо; 21) 2) (3; 21) 3) (3; +оо) 4) (21; +оо)
А10 Решите уравнение 2cos утх) —1 = 0.
l)±| + 8n, n€Z 1) ±| + 4n, n€Z
2) | + 8n, n € Z 1) | + 4п, п € Z
В1 Решите уравнение 7 • 5logsI = ж + 21.
168

В 2 Найдите значение выражения 5 sin(4r+o»)+cos ( ~ + а), если
sin a = 0,5.
83 Решите уравнение х2у/х — 1 — Ау/х — 1 =*= 0.
(Если уравнение имеет более одного корня, то в ответе
запишите сумму всех его корней).
84 Найдите значение выражения 2х — у, бели (х\ у) является
решением системы уравнений
у ,
2Х+1 - Зу = 43.
В5 Функция у = f(x) определена на промежутке (—4; 5). На
рисунке 89 изображен график ее производной. Найдите
число касательных к графику функции у = /(ж), которые
наклонены под углом в 45° к положительному направлению
оси абсцисс.
' -\ 1
: : \ ': :
i -: : V :0
: у\ : : : ":
/ :\! : J: :
/1 \ '/ Я-
/: ! I : : :
к ; - • ; ; ;
Рис. 89
В6 Найдите значение выражения
у/х - 2\/х- 1 + ух

В7 Найдите наименьший корень уравнения
88 Периодическая функция у = f(x) определена для всех
действительных чисел. Её период равен 2 и /(1) = 5. Найдите
значение выражения 3/(7) — 4/(—3).
89 Денежный вклад в банк за год увеличивается на 11%.
Вкладчик внес в банк 7000 рублей. В конце первого года он
решил увеличить сумму вклада и продлить срок действия
договора еще на год, чтобы в конце второго года иметь на
счету не менее 10000 рублей. Какую наименьшую сумму
необходимо дополнительно положить на счет по окончании
первого года, чтобы при той же процентной ставке (11%)
реализовать этот план? (Ответ округлите до целых.)
810 В правильной четырехугольной призме ABCD A\B\C\D\
высота равна 8, а сторона основания равна 6\/2. Найдите
расстояние от вершины А до плоскости A\BD.
811 Дан ромб ABCD с острым углом В. Площадь ромба
равна 320, а синус угла В равен 0,8. Высота СН пересекает
диагональ BD в точке К. Найдите длину отрезка СК.
С1 Найдите значение функции
в точке максимума.
С2 Решите уравнение sin2# • tgrr + 1 = 3sinx.
СЗ Найдите все значения #, которые удовлетворяют
неравенству (2а—1)х2 < (а+1)х+3а при любом значении параметра
а, принадлежащем промежутку (1;2).
170

С4 Дана правильная треугольная пирамида со стороной
основания, равной 2\/7. Центр основания пирамиды является
вершиной конуса, окружность основания которого
вписана в боковую грань пирамиды. Найдите радиус основания
конуса.
С5 Найдите количество всех решений системы уравнений
'у(1-х)2 + хг = 0,
±2— = 51og32(0,125y2)-7.
Демонстрационный вариант 2006 г.
А1 Вычислите: v^48 • 27.
1) 36 2) 18 3) 6 4) 12
2 4
А2 Представьте в виде степени выражение 5з • 5з.
1)259 2)59 3)252 4)52
A3 Найдите значение выражения ^ • 2log210.
1) 10 2) 5 3) log210 4) 20
А4 Укажите множество значений функции, график которой
изображен на рисунке 90.
1)[-3;7) 3)[-4;3]
2) [-3; -2] U [2; 5] 4) [-4; -1) U (-1; 3]
А5 Найдите область определения функции
f(x) = 1оё0)5(2ж - х2).
1)(0;2) 3)[0;2]
2) (-оо; 0) U (2;+оо) 4) (-оо; 0] U [2; +оо)
171

-3 -
4 5
-1
\
-3
-4
Рис. 90
А6 Укажите наибольшее значение функции у = 1 — cos За:.
1) 1 2) 2 3) 0 4) 4 I
А 7 На рисунке 91 изображены графики функций у = f(x) и у =
= д{х), заданных на промежутке [—3; 6]. Укажите те
значения ж, для которых выполняется неравенство f(x) ^ д(х).
l)[-3;-l]U[l;6] 3)[-3;-2]U[2;6]
2) [-1; 1] 4) [-2; 2]
\
\
\
»
г
\
_\
У
1
0
\
1
1
/
v =
—. . . :"
/(х)
У-.9(*
У
» :
X:
Рис. 91
172

А8 Решите уравнение sin3:r = ^.
1) (-1)" • I + f n, n e z з) (-1)" • £ + f n, n e
У О Хо О
2) ±£ + ^Ln, n G Z 4) ±f + ^n,i.6Z
/1 \Зж-7
А9 Решите неравенство f ^ J > 0,04.
1) (-оо; 3) 2) (-оо; |) 3) (3; +оо) 4) (-оо; -|
А10 Укажите абсциссу точки графика функции
f(x) = 5 + Ах - ж2,
в которой угловой коэффициент касательной равен нулю.
1) 0 2) 2 3) -2 4) 5
3sin(| + a) n
В1 Найдите значение выражения — ; г-, если а = -—-.
2cos(7r-a) 4
82 Решите уравнение у/2х + 37 = а: + 1.
83 Решите уравнение Iog16(5a: + 8) — log16 3 = log1>6 7.
B4 Вычислите
B5 Функция у = /(ж) определена на промежутке (—3;7). На
рисунке 92 изображен график ее производной. Найдите
точку жо? в которой функция у = f(x) принимает наибольшее
значение.
86 Найдите наибольшее значение функции у = 2,7 • е3*2-*3"4
на отрезке [1;3].
87 Решите уравнение 0,2ж+1 = у/ЗЬ + 5х. В ответе запишите
корень уравнения или сумму корней, если их несколько.
173

:
: о
/
/
\
. .1.
Г
0
У
\
\
1
ч
У
v....
\
\
1
\
)
\
\
7
(
1
Рис. 92
88 Нечетная функция у = f(x) определена на всей числовой
прямой. Для всякого неотрицательного значения перемей^
ной х значение этой функции совпадает со значением
функции д(х) = х(2х + 1)(х — 2)(х — 3). Сколько корней имеет
уравнение f(x) =0?
89 По пенсионному вкладу банк выплачивает 10% годовых. Цо
истечении каждого года эти проценты капитализируются,
т. е. начисленная сумма присоединяется к вкладу. На
данный вид вклада был открыт счёт в 50 000 рублей, который
не пополнялся и с которого не снимали деньги в течение
3 лет. Какой доход был получен по истечении этого срока?
810 Основанием прямой призмы ABCDA\B\C\D\ является
прямоугольник ABCD, стороны которого равны 6л/5 и
12\/5. Высота призмы равна 8. Секущая плоскость
проходит через вершину D\ и середины ребер AD и CD. Найдите
косинус угла между плоскостью основания и плоскостью
сечения.
811 Трапеция ABCD вписана в окружность. Найдите среднюю
линию трапеции, если ее большее основание AD равно
синус угла ВАС равен ;г, синус угла ABD равен ^.
174

С1 Решите уравнение 4 cos x ctg x + 4 ctg x + sin a: = 0.
С2 При каких значениях х соответственные значения функций
f(x) = log2 х и д(х) = Iog2(3 — ж) будут отличаться меньше,
чем на 1?
СЗ Для монтажа оборудования необходима подставка объёмом
1296 дм3 в форме прямоугольного параллелепипеда.
Квадратное основание подставки будет вмонтировано в пол, а её
задняя стенка — в стену цеха. Для соединения подставки
по рёбрам, не вмонтированным в пол или стену,
используется сварка. Определите размеры подставки, при которых
общая длина сварочного шва будет наименьшей.
С4 Основанием пирамиды FABC является треугольник ABC,
в котором /.ABC = 90°, АВ = 3, ВС = 4. Ребро AF
перпендикулярно плоскости ABC и равно 4. Отрезки AM
и AL являются соответственно высотами треугольников
AFB и AFC. Найдите объем пирамиды AMLC.
С5 Шесть чисел образуют возрастающую арифметическую
прогрессию. Первый, второй и четвертый члены этой
прогрессии являются решениями неравенства
а остальные не являются решениями этого неравенства.
Найдите множество всех возможных значений первого
члена таких прогрессий.
Вариант 1
А1 Вычислите у/(2 + \/Е)2 - ^(2 - у/5)2.
1) 2л/5 2) 4 3) -2>/5 4) -4
175

А2 Вычислите 21о^43.
1)3 2)4 3)л/3 4)2
A3 Найдите область определения функции у(х) = * •= .
у О X
1)[1;5) -3)[1;5]
2) (-оо; 1] U (5; +оо) 4) [б; +оо)
А4 Укажите промежуток, которому принадлежит наименьшее
целое число, являющееся решением неравенства
1)[0;2] 2) [4; 8) 3)[1;3] 4) (-оо;2]
А5 На рисунке 93 представлены графики функций у = у/5 — х
11 —- Т
и у = —?—. Укажите промежуток, йа котором выполнено
неравенство у 5 — х > —=—.
1)[1;5] 3)(-oo;-4]U[l;+oo)
2)(-4;1) 4) (-4; 5)
А6 Решите неравенство Iog2(a; + 7) < 2.
1) (-7; 2] 2) [-3; 0) 3) (-7; -3] 4) (-оо; -3]
А7 Найдите производную функции у(х) = cos 2x + Ах в точке
х- £
х- 4.
1)2 2)4 3)-6 4)5
А8 На рисунке 94 представлен криволинейный треугольник,
ограниченный графиком функции у = f(x) и прямыми у =
= 1 и х = 2. Его площадь равна 7. Чему равен
2
1)3 2)7 3)9 4)5
176

—4
Рис. 93
Рис. 94
А9 На рисунке 95 представлены кривые, описываемые
формулами у(х) = 2у/х — 1, у(х) = 2у/х +1, у(х) = 2\/1 — ее и
у(#) = 2л/—х — 1. Под каким номером нарисован график
функции у(х) ;= 2\/а: + 1?
1) 1 2) 2 3) 3 4) 4
Рис. 96
А10 На рисунке 96 представлен график зависимости
координаты х в зависимости от времени для автобуса при движении
из А и обратно. Сколько времени при этом автобус
находился в движении?
1) 7 2) 5 3) 4 4) 14
177

ВХ Найдите 20 cos (а — /3), если выполняются равенства:
:osa + cos/3 = 0,3; siim-f-3in/? = —1,1.
[МГУ, 2000, ф-т почв.]
В2 Найдите решение уравнения (в градусах)
л/5 sin х + cos 2х + 2 cos x = 0,
принадлежащее промежутку [0°;360°].
7Г
2
ВЗ Вычислите определенный интеграл / 2 sin 2ж ete.
84 Решите уравнение Iog3(3:r — 8) = 2 — ж (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
85 Найдите длину промежутка, являющегося решением
неравенства у/х + 3 > х + 1.
86 Найдите длину промежутка, являющегося решением нера-
, -40ж2
87 Найдите корень (или сумму всех корней, если их
несколько) уравнения 52х = 115 • 5х"1 + 50.
88 Найдите корень (или наибольший корень, если их
несколько) уравнения lg(x2 — х — 2) = lg(2 — х).
89 Первый член арифметической прогрессии в два раза
больше первого члена геометрической прогрессии и в пять раз
больше второго члена геометрической прогрессии.
Четвертый член арифметической прогрессии составляет 50% от
178

второго члена арифметической прогрессии. Найдите
первый член арифметической прогрессии, если известно, что
второй ее член больше третьего члена геометрической
прогрессии на 36. [МГУ, 1995, ф-т почв]
810 Через сторону основания правильной треугольной
пирамиды и центр вписанного в нее шара проведена плоскость.
Боковое ребро пирамиды в 3,5 раза больше стороны
основания. Найдите отношения объемов частей пирамиды
(большей к меньшей), на которые делит ее данная плоскость.
811 Диагонали равнобедренной трапеции перпендикулярны.
Найдите высоту трапеции, если ее площадь равна 25. [МГУ,
1995, химфак]
С1 Найдите сумму всех различных действительных решений
уравнения ж4 + 5х3 + Ах2 — Ъх + 1 = 0.
С2 Решите неравенство
' i* JL ""*"" **X *""~
2х + 2
СЗ Решите неравенство 3<х+2)2 + т~ < З*2"3 + 92х+2. [МГУ, 1999,
мехмат]
С4 Основанием пирамиды FABC является треугольник ABC,
в котором ZABC = 90°, АВ = 3, ВС = 4. Ребро AF
перпендикулярно плоскости ABC и равно 4. Отрезки AM
и AL являются соответственно высотами треугольников
AFB и AFC. Найдите объем пирамиды AMLC.
С5 Укажите, при каких значениях параметра а уравнение
25х - (а - 1)5* + 2а + 3 = 0
имеет единственное решение.
179

Вариант 2
А1 Вычислите —
(л/7 — л/3)
1) -2 3) -2v/21
2) 10 - 2\/21 4) 5
A2 Вычислите 7log«9.
1)9 2)3 3)7 4)49
A3 Найдите область определения функции у(х) = аЦ .
у I X
1)[-2;7) 3)(-оо;+оо)
2) (-оо;-1] U (7;+оо) 4) (-оо; 7) U (7;+оо)
А4 Найдите множество значений функции у(х) = у 10 — 2х2.
1)[0;3] 3)[0;+оо)
2)[0;10] 4)[-log210;log210]
А5 Укажите промежуток, которому принадлежит наименьшее
натуральное число, являющееся решением неравенства
2-Зж ^ к
1)(-2;-1) 2)(-1;2) 3) (3;4) 4) (4; 5)
А6 На рисунке 97 представлены графики функций у = \Jx + 3
и у = х — 3. Укажите промежуток, на котором выполнено
неравенство у/х + 3 > х — 3.
1)[-3;3] 2)[3;6] 3)[-3;6] 4)[6;+оо)
А7 Решите неравенство logi^ (x + 4) > —3.
1) (-4; +оо) 2) [4; +оо) 3) (-4; 4] 4) (-4; -2]
180

А8 На рисунке 98 представлен криволинейный треугольник,
ограниченный графиком функции у = f(x) и прямыми
у = 2, х = 3. Известно, что
о
ff(x)dx = 9.
Чему равна площадь заштрихованной фигуры?
1) 3 2) 12 3) 9 4) 6
х
Рис. 98
Рис. 99
А9 График зависимости координаты х в зависимости от от
времени для движения путника представлен на рис. 99.
Сколько раз останавливался путник на отдых при движении из
пункта А в пункт В?
1)1 2)2 3)3 4)4
181

AlO Какое утверждение относительно треугольника со
сторонами 5, 9, 15 верно?
1) Треугольник остроугольный.
2) Треугольник тупоугольный.
3) Треугольник прямоугольный.
4) Такого треугольника не существует.
81 Сколько решений уравнения sin2 х = -т принадлежит
отрезку [—2тг; 2тг]?
82 Найдите длину промежутка, являющегося решением нера-
х2 - Зх - 4
венства
х + 1
83 Найдите наибольшее целочисленное решение неравенства
log3(13-4*)>2.
е3
84 Вычислите определенный интеграл / -~.
1
85 Найдите наименьшее целочисленное решение неравенства
Ух2 + Ъх - 84
86 Пусть (#; у) — то решение системы уравнений
х + 2у = 6,
Зх2 -ху + 4у2 = 48,
у которого х и у — целые числа^Найдите сумму этих х и у.
87 Сколько решений, удовлетворяющих условию 0 ^ тг ^ ~^,
имеет уравнение sin2a: = sin (|г — х) ?
88 Найдите корень (или сумму всех корней, если их
несколько) уравнения Iog5(x + 1) + Iog5(o: + 5) = 1.
182

В9 Имеется 40 литров 0,5% раствора и 50 литров 2% раствора
уксусной кислоты. Сколько литров первого раствора нужно
добавить во второй раствор, чтобы получился 1,5% раствор
уксусной кислоты? [МГУ, 2000, филфак]
810 Радиус сферы, описанной около правильной
четырехугольной пирамиды, в 3 раза больше высоты пирамиды. Найдите
квадрат отношения площади боковой поверхности
пирамиды к площади ее основания.
811 В выпуклом шестиугольнике ABCDEF все внутренние
углы при вершинах равны. Известно, что АВ = 3, ВС = 4,
CD = 5, EF = 1. Найдите сумму DE и AF. [МГУ, 2001,
химфак]
С1 Найдите сумму всех целочисленных решений неравенства
х2 — Ъх — 4
G2 Решите неравенство (2 + лД)х + 2 < 3(2 - л/3)х. [МГУ, 1997,
химфак]
СЗ Решите систему уравнений
= 3.
[МФТИ, 2002]
С4 Около прямой четырехугольной призмы ABCDA\B\C\D\
описан цилиндр. Основание призмы — прямоугольник
ABCD, диагонали которого образуют угол AOD, равный
60 градусам, а расстояние между боковым ребром АА\
призмы и скрещивающейся с ним диагональю BD осцова-
ния равно 1 + л/3. Найдите площадь боковой поверхности
призмы, если объем цилиндра равен 120тг. [ЕГЭ, 2003]
183

С5 Найдите все а, при которых уравнение
Iog3(a? + л/5-а) + log i (а - 2 - х) = log9 4
з
имеет решение. [МФТИ, 2001]
Вариант 3
А1 Вычислите у (л/3 - 2)2 +
X) 2л/3 2)4 3)0 4)2л/3-2
I i
А2 Вычислите log15 —~ log15 2 г .
7-33-55
1) -1 2) 0 3) 1 4) 2
ж — 4
A3 Найдите область определения функции у(ж) = lg -x .
* Z — х
l)(-oo;2)U(4;+oo) 3) (2; 4)
2) (-4;-2) 4)(0;+оо)
А4 Найдите множество значений функции у(х) = 2х — ж2 — j.
1)[0;1] 2)(-ос;1] 3) [J;+oq) 4) (-|; J]
А5 Укажите промежуток, которому принадлежит цаиболыдее
целре число, являющееся решением неравенства _ 1 ^ 2"
-°°;з] 3)[i;+0°)
А6 Укажите промежуток, которому принадлежат все корни
уравнения 4х + 2х — 2 = 0.
1) [р; 1] 2) (-оо; -i] 3) [I; +oo) 4) (2; 3]
184

А 7 Решите неравенство Iog2(4 — у/х) < 1.
1)(-оо;-16) 2)(4;+оо) 3) [2; 4) 4) [4; 16)
А8 Площадь заштрихованной части криволинейной трапеции,
ограниченной кривой у = f(x) и прямыми у = 0, х = О,
х = 3, представленными на рисунке 100, равна 10. Чему
равен / /(ж) dxi
о
1) 13 2) 7
У\
y=f(x)
01 3
Рис. 100
3)4
4)16
X
Рис. 101
А9 На рисунке 101 представлен график функции у = ах.
Укажите а.
1)2 2)i 3)3 4)±
А1О Сколько точек максимума на отрезке АВ у функции,
график которой представлен на рисунке 102?
1) 4 2) 3 3) 2 4) 1
В1 Найдите корень (или сумму всех корней, если их
несколько) уравнения
log2 х + Iog2(s + 1) = 1.
185

в х
Рис. 102
Рис. 103
82 Функция определена на (а; 6). График ее производной
представлен на рисунке 103. Сколько точек минимума имеет
заданная функция на (а; Ь)?
83 Решите уравнение
/Зтг + 1 \ /37Г--1 \ л
cos 1 —~—х 1 • cos ( —~—х 1 = 1
(если уравнение имеет более одного корня, то в ответе
запишите сумму всех корней).
2
84 Вычислите определенный интеграл / Зх2 dx.
1
85 Найдите наименьшее натуральное число, являющееся ре?
шением неравенства 2|гс+1|>ж + 4.
86 Найдите наибольшее целочисленное решение неравенства
\/6 + х - х2
х-х2
В7 Найдите наибольшее целое число, которое является реше-
2х2 - Их + 15 ^ Л
нием неравенства ^с—а ^ "'
186

88 Сколько пар целых чисел являются решениями системы
уравнений?
Г х + 2у = 6,
Зх2 -ху + Ау2 = 48
89 Сколько решений уравнения cos7# — \/3sin7a: = — \/2
принадлежит промежутку (0,4тг; ^)?
810 В конус с радиусом основания 4 и высотой 4л/3 вписана
треугольная призма, у которой все ребра равны. Найдите
объем призмы. [ЕГЭ, 2001]
811 Две стороны треугольника имеют длины 6 и 10, причем
угол между ними острый. Площадь этого треугольника
равна 18. Найдите квадрат третьей стороны. [МГУ, 2000,
биофак]
С1 Решите неравенство
\х5 - 6ж2 + 9х - б| ^ хь - 2xs + 6х2 - 13х + 6.
С2 Решите неравенство у/х2 + Ах + 3 < 1 + у/х2 — 2х + 2.
[МФТИ, 2001]
СЗ Пусть /(ж) — периодическая функция с периодом 8, такая,
что f(x) = 8х — х2 при х G [0; 8]. Решите уравнение
[МГУ, 2000, ф-т почв ]
С4 В правильной треугольной пирамиде, сторона основания
которой равна Ь, а боковое ребро равно 26, через середину
бокового ребра, перпендикулярно к нему проведена
плоскость. Найдите площадь образовавшегося сечения.
187

С5 Найдите все значения параметра а, при каждом из
которых неравенство х2 + 2 \х — а\ ^ а2 справедливо для всех
действительных х. [МГУ, 1993]
Вариант 4
2)4
А1 Вычислите
1) 14
A2 Вычислите 25-4 2 .
1) 25 2) 5
3)28
3)1
4)0,2
A3 Найдите область определения функции Iog2(2 — у/х).
1)(4;+оо) 2)[0;4) 3) (-оо;4) 4) (2; 4)
А4 Найдите множество значений функции у(х) = sin4#.
1)[-1;4] 2) [-4; 4] 3) [-1; 1] 4)[0;1]
А5 На рисунке 104 представлены графики функций у = \/ж + 3
и у = х — 3. Укажите промежуток, на котором выполненй
неравенство у/х + 3 < х — 3.
1)[-3;6] 2) [6; +оо) 3) [3;6] 4) [3;+оо)
188

А6 Найдите cos 2z, если sin2 x = j.
1)1
2)0,5
з
4) -0,5
A7 Известно, что / f(x) dx = 12. Найдите площадь заштрихо-
o
ванной части криволинейной трапеции, ограниченной
кривой у = f(x) и прямыми у = 0, х = 0, х = 3, изображенной
на рисунке 105.
3) 12 4) 6
1)9
2)15
У\
Рис. 105
Рис. 106
А8 На рисунке 106 представлен график функции у = logarr.
Укажите а.
1) ± 2) 10 3) 1 4) 2
А9 На рисунке 107 представлен график функции у = f{x).
Укажите абсциссу той точки максимума функции, в
которой производная не существует.
1) -2 2) 0 3) 4 4) 1
А10 Какое утверждение относительно треугольника со
сторонами 6, 7, 10 верно?
1) Треугольник остроугольный.
2) Треугольник тупоугольный.
3) Треугольник прямоугольный.
4) Такого треугольника не существует.
189

-2
О
Рис. 107
81 Укажите наибольшее значение функции у(х) = 5"
82 Пусть f(x) — периодическая функция с периодом Т = \/2.
Найдите значение 3/(л/8), если известно, что
4 = 0 и /2(-л/2) + 3/(л/§) + ^ = 0.
[МГУ, 1996, геогр. ф-т]
83 Вычислите площадь фигуры, ограниченную линиями у =
= ±, у = 0, х = 1, х = е2.
84 Найдите наименьшее целочисленное решение неравенства
2 < х
2~V^T3 ^
85 Найдите наименьшее целочисленное решение неравенства
В6 Найдите наибольшее целочисленное решение неравенства
В7 Пусть (ж, у) — то решение системы уравнений
ГЗ- 2* + у = 13,
\22х+1 + Зу = 35,
190

у которого хиу являются целыми числами. Найдите сумму
х + у для этого решения.
88 Найдите наибольшее целочисленное решение неравенства
11 ■ З*"1 - 31 > 5
4 9х -11 -3х-1 -5 "
89 Найдите сумму квадратов всех корней уравнения
4*2 + 2х2 - 6 = 0.
810 Боковые ребра пирамиды наклонены к плоскости
основания под углом, равном arccos^. В основании пирамиды
является квадрат со стороной 6л/2. Найдите объем
пирамиды. [ЕГЭ, 2002]
811 Через центр окружности, вписанной в треугольник ABC,
провели прямую MN параллельно основанию АВ (М
лежит на ВС, N лежит на АС). Найдите длину отрезка MN,
если известны периметр р = 14 четырехугольника ABMN
и длина основания АВ = 6. [МГУ, 2000, филфак]
С1 При каких значениях х соответственные значения функций
f{x) = log2 х и д(х) = Iog2(3 - х)
будут отличаться меньше, чем на 1?
С2 Определите, что больше: А = arccos (—«) " *оё81 (07) или
В = sin ^ • tg3 (-^f) • Ctg ~t. [МГУ, 1999, ф-т почв ]
191

СЗ Решите неравенство | \х2 - 8х + 2| - х2| ^ 2х + 2. [МГУ, 2000,
ВМиК]
С4 В правильной четырехугольной усеченной пирамиде
ABCDA'B'C'D* проведено два сечения АА'С'С и ABC'D*.
Первое сечение имеет площадь 5i, второе — площадь S2-
Найдите площадь сечения, проходящего через середину
высоты, параллельно основаниям.
С5 Найдите все значения параметра а, при которых уравнение
(а + 3 — \х + 2|)(а + х2 + 4ж)ч = 0 имеет ровно три корня.
[МФТИ, 2002]
Вариант 5
А1 Вычислите
1) 2 2) 0 3) 1 4) -1
logo 8
А2 Вычислите ■?=.
log2\/2
1)2 2)4 3)6 4)8
A3 Найдите область определения функции
аг)= /logi(*-2).
2
2)(2;3) 3) (2;3] 4)[3;+оо)
А4 Найдите множество значений функции у(х) = 2x~2s'n x.
1)[-1;1] 2) [0,5; 2] 3) [2;3] 4) (0,5; 2)
192

А5 Укажите промежуток, которому принадлежит наименьшее
натуральное число, являющееся решением неравенства
1 /о
2)[0,5;3] 3) [3;4]
4) (0,5; 2)
А6 На рисунке 108 представлены графики функций у = у/х + 2
и у = л/16 — х. Укажите множество решений неравенства
л/х + 2 ^ у/16 - х.
1) (-оо; -2] 2) [7; +оо) 3) [-2; 7] 4) [7; 16]
У\
А7 Укажите промежуток, которому принадлежат все корни
уравнения 4Ж — 5 • 2х + 4 = О
1)[-1;1] 2)[0;3] 3) [3;4] 4) (0,5; 2)
А8 Известно, что площадь криволинейной трапеции,
ограниченной кривой у = fi(x) и прямыми у = 0, х = 1, х = 3,
изображенными на рисунке 109, равна 14, а
о
Jf2(x)dx = 4.
Чему равна площадь заштрихованной части?
1) 18 2) 10 3) 6 4) 12
7 Зак 243
193

Рис. 109
-1 0
Рис. 110
А9 На рисунке 110 представлены кривые, описываемые
формулами у(х) = 2у/х — 1, у(х) = 2у/х +1, у(х) = 2у/\ — х
и у(х) = 2у/—х — 1. Под каким номером нарисован график
функции у(х) = 2у/—х — 1?
1) 1 2) 2 3) 3 4) 4
А10 Какое утверждение относительно треугольника со
сторонами 5, 6, 10 верно?
1) Треугольник остроугольный.
2) Треугольник тупоугольный.
3) Треугольник прямоугольный.
4) Такого треугольника не существует
81 Упростите выражение tg2rr-ctg(70°— #)+tg2#-ctg(20°— x) —
- ctg(20° - х) - ctg(70° - ж), если cos 2х ф 0. [МГУ, 1972, биофак]
82 Найдите наибольшее значение функции у(х) = Зж4 — 4ж3 на
отрезке [—1;2].
83 Решите уравнение л/8х2 — 7 = Зх — 4 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
194

В4 Найдите наименьшее целочисленное решение неравенства
В5 Найдите наименьшее целое число #, для которого
выполнено неравенство
у/(х-5){х + Ъ)
x - 4) - 1 " "•
В6 Найдите сумму квадратов всех целых чисел, являющихся
решением неравенства
87 Пусть (ж; у) является решением системы уравнений
х - у = 6,
я3 - у3 = 126.
Найдите сумму х + у для того решения, у которого \х\ > \у\.
88 Тангенс угла наклона касательной к параболе
у = х2 + Зах - 7
в точке с абсциссой х = 4 равен — 1. Найдите а.
89 Торговая база закупила у изготовителя партию альбомов
и поставила ее магазину по оптовой цене, которая на 30%
больше цены изготовителя. Магазин установил розничную
цену на альбом на 20% выше оптовой. При распродаже в
конце сезона магазин снизил розничную цену на альбом на
10%. На сколько рублей больше заплатил покупатель по
сравнению с ценой изготовителя, если на распродаже он
приобрел альбом за 70,2 р.? [ЕГЭ, 2005]
195

BIO Дана треугольная пирамида, длины ребер которой равны
15, 9, 9, 12, 12, 3. Найдите радиус описанной вокруг
пирамиды сферы. [МГУ, 1999, геогр. ф-т]
В11 Пусть М — точка пересечения диагоналей выпуклого
четырехугольника ABCD, в котором стороны АВ, AD и ВС
равны между собой. Найдите угол CMD (в градусах), если
известно, что DM = МС, а угол CAB не равен углу DBA.
[МГУ, 1998, ф-т почв.]
С1 Решите неравенство
lQ/v.3 От^ К*г Л- 1 I <? т^ 9т^ т -4- 1
\ОХ — LX — ОХ Т^ 1 ^ X — LJj — Хт 1.
С2 Решите систему уравнений
log20n/)-log4a:y = 2,
8х -у = 1.
[МГУ, 2000, мехмат]
СЗ Решите систему неравенств
Ъх2 + 2ху + 3 < 0,
у2 + 6у + 18ж ^ 0.
[МФТИ, 2001]
С4 В основании тетраэдра ABCD лежит прямоугольный
треугольник ABC с прямым углом С. Ребро AD
перпендикулярно плоскости ABC, AD = ВС = 3, АС = 4. Найдите
радиус вписанной в тетраэдр сферы.
С5 Найдите все значения параметра а, при которых уравнение
имеет ровно два корня. [МФТИ, 2002]
196

Вариант 6
А1 Упростите выражение
[МГУ, 1996, ф-т почв.]
1) -2 2) -26 3) 14 4) 18
А2 Не пользуясь калькулятором, сравните числа а = log3 75 и
b = log2 22. [МГУ, 1972, эконом, ф-т]
1) а > Ь 3) а = Ъ
2) Ъ > а 4) нельзя определить
A3 Найдите область определения функции
Зж
3)(-оо;+оо)
2)(-oo;l]U[2;+oo) 4)[1;2]
А4 Найдите множество значений функции у(х) = 2~'Х1.
1) (0; 1] 2)[-^;у/Щ 3)(-оо;+оо] 4)[1;2]
А5 Укажите промежуток, содержащий все корни уравнения
Ъу/х = Зх - 12.
1)[3;7] 2) [5; 10] S)[-l;8] 4) [13; 15]
А6 Укажите промежутки, в которых функция, представленная
на рис. 111, принимает положительные значения.
l)(-2;-l)U(2;4] 3) [-2; -1] U [2; 4]
2)(-3;4) 4) (-2; 4)
А7 Укажите промежуток, которому принадлежат все корни
уравнения 4х - 21+х -8 = 0.
1)[3;7] 2) [5; 10] 3)[-1;8] 4) [13; 15]
197

Г"*
Рис. Ill
Рис. 112
А8 На рисунке 112 представлен график функции у = /(ж).
Укажите промежуток, которому принадлежит наименьшее
значение функции у = \ogi f(x).
2
1)[-3;0] 2) [5; 10] 3) [-2;8] 4) [1;3]
А9 Множеством значений функции у — —х2 + 2х + Ъ являетсй
промежуток (—оо;3]. Укажите промежуток, которому
принадлежит значение Ь.
1)[-3;0] 2)[-2;1] 3) [5; 10] 4)[1;3]
А10 Какое утверждение верно по отношению к корням
уравнения у/х + 4 = 3(ж + 1)?
1) Уравнение имеет два корня одного знака (оба корня или
положительны, или оба корня отрицательны).
2) Уравнение имеет только один корень, и он отрицателен.
3) Уравнение имеет два корня разных знаков.
4) Уравнение имеет только один корень, и он положителен.
В1 Решите уравнение log2 ^Ц 1- log2 ^ 1 = 1 (если уравне-
0 X ~г 1
ние имеет более одного корня, то в ответе запишите сумму
всех корней).
198

82 Укажите наибольшее значение функции
cos х + 3 sin x
у(х) = 2 x/io .
83 Решите уравнение log2 х + 2 log^ 2 = 3 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
84 Найдите производную функции у(х) = у/х ^ в точке
х1
85 Вычислите площадь фигуры, ограниченной линиями
у = 2у/х, у = 15-х, у = 0.
86 Найдите наименьшее целочисленное решение неравенства
у/х2 - 16
87 Найдите наименьшее целое число, принадлежащее
множеству решений неравенства 4 • 9х — 5 • 3Z+1 —4^0.
88 Найдите корень (или сумму всех корней, если их
несколько) уравнения
- 5)2 - 4 = 1оёл/з(ж - 1).
В9 Сколько общих точек у графика функции у = \ 4гг
о
и касательной, проведенной к этому графику через точку
(0; 18)?
199

BIO Найдите объем правильной треугольной пирамиды, высота
которой равна 2л/3, а все плоские углы при вершине
прямые. [ЕГЭ, 2003]
В11 В равнобедренном треугольнике ABC (AB = ВС)
проведены высота АН и медиана AM. Найдите cos /.BACy если
отношение площади треугольника АМН к площади
треугольника ABC равно 0,42.
С1 Решите неравенство Iog(5a;-4x2)(4~x) > 0-
С2 Решите уравнение Vf4x — х2 + у/Ах — х2 — 3 = 3 + \/2х — х2.
[МГУ, 2001, химфак]
СЗ Решите неравенство \х2 + 7х + 10| + \х + 7| < х2 + 8х + 21.
[МГУ, 1998, биофак]
С4 В треугольной пирамиде SABC боковая грань SBC
образует с плоскостью основания ABC двугранный угол, равный
~. Треугольники SBC и ABC — равнобедренные с общим
основанием ВС = а. Высота пирамиды равна h. Центр
шара, описанного около пирамиды, лежит в плоскости
основания. Найдите радиус описанного шара.
С5 Найдите все ж, при которых хотя бы одно из двух
выражений А(х) = \х - 3| (\х — 5| — |ж — 3|) -бжи В(х) =
= \х\ (\х\ — \х — 8|) + 24 неположительно, и при этом его
модуль не меньше модуля другого. [МГУ, 1999, мехмат]
Вариант 7
_ 5(л/27-л/5)
Вычислите - -.
1) 5 2) 20л/3 3) 60 4) 15
200

i 3/To"
A2 Упростите выражение , если b ф 0.
л/о4
1) Ь3 2) Ьз 3) ^Ь 4) 6
A3 Найдите sin2x, если (sin ж + cos х) = ~.
1)| 2)2 8)-2 4)-|
А4 Укажите промежуток, внутри которого лежат все решения
(ж + 2)2(3-ж) п
неравенства j^ < 0.
1)(-5;-1) 2)(-оо;-3) 3) [-3;4] 4)[2;5]
А5 Найдите множество значений функции у(х) = Iog2(l — х2).
1)(-оо;+оо) 2)[-1;+оо) 3)[0;+оо) 4) (-оо;0]
А6 Какое утверждение верно по отношению к корням
уравнения у/7 -х = 4(ж + 1)?
1) Уравнение имеет два корня одного знака (оба корня или
положительны, или оба корня отрицательны).
2) Уравнение имеет два корня разных знаков.
3) Уравнение имеет только один корень, и он положителен.
4) Уравнение имеет только один корень, и он отрицателен.
А7 Укажите множество значений функции, график которой
представлен на рис. ИЗ.
l)[-4;4] 3)[0;l]U(2;4]
2)[0;4] 4) [-1; 1]
А8 Решите неравенство З4"* — 3 > 0.
1)(-оо;3) 2)(-2;1) 3)(-оо;1) 4) (-2;+оо)
А9 Решите неравенство logi (х + 2) > —1.
з
1)(-<х>;1) 2)(-2;1) 3) (1;+оо) 4) (-2;+оо)
201

У
4
2cf
/
-1Т i *
Рис. 113
А10 Найдите первообразную для функции
f(x) = х3 + 6х2 - 15ж + 48,
проходящую через точку (0;0).
1) Зх2 + Ylx 3) х4 + 6ж3 - 15ж2 + 48ж2
4)4 + 2*3-
81 Найдите наибольшее значение функции 2 cos 2x — 4 sin x + 4.
82 Найдите производную функции у(х) = 3(х — I)2 +1 в точке
ж = 2.
83 Укажите длину промежутка, в котором определена
функция у(х) = л/16 — х2.
84 Найдите длину промежутка, на котором выполнено
неравенство у/х + 2 ^ 2а; — 11.
85 Укажите решение (или сумму решений, если их несколько)
уравнения
log2(a;-l)+log2(z + 2)=2.
В6 Вычислите tg2 (arcsin ^ j.
202

В7 Найдите решение (или сумму решений, если их несколько)
уравнения
x/cos тгж — 1 = (х — 1)(х — 2).
88 Укажите абсциссу точки, в которой прямая у = — х + 5
касается кривой у = 4^/1 — х.
89 Сумма третьего и пятого членов арифметической
прогрессии равна 8. Найдите сумму первых семи членов этой
прогрессии. [МГУ, 1993, ИСАА]
810 Основание прямой призмы АВСА\В\С\ — треугольник
ABC, в котором АС = 90°, ВС = 6, АС = 8. Угол между
плоскостями ABC и АВС\ равен 45°. Найдите площадь
боковой поверхности призмы. [ЕГЭ, 2004]
811 На боковой стороне ВС равнобедренного треугольника
ABC как на диаметре построена окружность,
пересекающая основание этого треугольника в точке D. Найдите
квадрат расстояния от вершины А до центра окружности, если
AD = л/3, а угол ABC равен 120°. [МГУ,1993, ИСАА]
С1 Найдите максимальную длину промежутка, на котором
выполнено неравенство 3 \х — 2| + \Ъх — 4| ^ 10.
С2 Найдите все значения параметра а, при каждом из которых
неравенство х "~ _^ "~ < 0 выполнено для всех х Е [1;2].
[МГУ, 1974, ф-т почв.]
СЗ Найдите сумму всех целых чисел, являющихся решениями
неравенства
л/56 -х-х2 -х-7 /Л
203

С4 Определите высоту правильной треугольной пирамиды,
сторона основания которой равна а, а двугранный угол
между боковыми гранями равен а.
С5 Решите неравенство
Iog5(s2 - Ах - II)2 - lognpE2 - 4а; - II)3
2 - Ъх - Ъх2 '
[МГУ, 1979, эконом, ф-т]
Вариант 8
А1 Вычислите
1) 112л/5 2) 7 3) 35 4) 28л/5
А2 Упростите выражение
если d > 0.
l)rf~5 2)d-x 3)d 4)d2
A3 Найдите sin2a:, если (sin a; — cosx) = —f.
D| 2)1 3)-| 4)-|
A4 Укажите промежуток, внутри которого лежат все решения
неравенства
(* + б)а(2-*)
1)[-6;4] 2) [-4; 5] 3) [2; 6] 4) [-8; 2]
204

А5 Решите уравнение sin(37r — 7х) = —4.
±|f + 2п&, n € Z
A6 Найдите множество значений функции
у (х) =2
2
1)(-оо;+оо) 2) [-2; 2) 3)[0;+оо) 4) (~оо;0]
А7 Укажите промежуток, которому принадлежит абсцисса
точки, в которой прямая у = Зх — ^ касается кривой
1)[3;6] 2)[-1;0,5] 3) [-4;0] 4) (0,5; 2]
А8 Укажите множество значений функции, график которой
представлен на рис. 114.
l)[-4;4] 3)[0;l]U(2;4]
2)[0;4] 4)[-1;3]
I
А9 Решите неравенство 4* ^ 4.
4) (-oo;0)U(0;+oo)
A10 Найдите первообразную для функции у/4х — 1,
проходящую через точку f j; О].
1 1 з) 2 -1
4 \/4а: — 1
В1 Укажите длину промежутка, в котором выполнено
неравенство 4х2 € 1.
205

-4
Рис. 114
82 Найдите наименьшее значение функции 4 cos 2ж+8 cos х—11.
83 Найдите решение (или сумму решений, если их несколько)
уравнения
В4 Сколько решений имеет уравнение
bx- Ах2 - 2х* = 2х + 1 ?
85 Вычислите площадь фигуры, ограниченной линиями
у = х2 - 2х + 2 и у = 2 + 4ж — я2.
86 Найдите решение (или сумму решений, если их несколько)
уравнения
В7 Вычислите cos2 f arcsin -j- j.
206

В8 Найдите решение (или сумму решений, если их несколько)
уравнения
(z + l)2+21og2(2-z)=4.
В9 Число 128 разделили на четыре части так, что первая часть
относится ко второй части как 2:3, вторая к третьей —
как 3 : 5, а третья к четвертой — как 5:6. Найдите третью
часть. [МГУ, 1993, ф-т почв.]
810 Высота правильной четырехугольной пирамиды равна 2.
Перпендикуляр, опущенный из центра шара, описанного
около пирамиды, на ее боковую грань, образует с высотой
о
угол, равный arcctg ^. Определите объем пирамиды,
о
811 Окружность, центр которой лежит на гипотенузе АВ
прямоугольного треугольника ABC, касается катетов АС и
ВС соответственно р точках Е nD. Найдите величину угла
ABC (в градусах), если известно, что АЕ = 1, BD = 3.
[МГУ, 1993, ИСАА]
С1 Решите неравенство
Ах + 15 -Ах2 ^п
у/Ах + 15 + 2х
[МГУ, 1995, мехмат]
С2 Найти все значения параметра а, при каждом из которых
уравнение
{х2 — 6 |яг| — а)2 + 12(д;2 - б \х\ - а) + 37 = cos Ц&-
имеет ровно два корня. [МГУ, 1995, биофак и ф-т
фундаментальной медицины]
СЗ Решите неравенство 3 J^ + 4°X > Зж - 10. [МФТИ,
1999]
207

С4 Площадь поверхности сферы, вписанной в конус, равна
ЮОтг. Длина окружности, по которой сфера касается
поверхности конуса, равна бтг. Найдите радиус основания
конуса. [ЕГЭ, 2001]
С5 Решите неравенство logx(20a; + Зх2 - хг) > 3. [МГУ, 1992,
филфак]
Вариант 9
2(л/3 - л/7)
А1 Вычислите —
1)2 2) л/7 + л/3 3)-1 4)-±
А2 Упростите выражение j , если а > 0.
3 31
1) а 2)а5 3)ою 4) а2
(\ 10 /о
? — 5a;J = = .
1) (-!)*!агапп^М+ 2^, fc€Z
2) (-1)* arccos ^=f^ + ^, А; е Z
1U О
A4 Укажите длину промежутка, в котором определена
функция у(х) = л/1 — ж2-
1) 1 2) 2 3) 3 4) 4
208

А5 Найдите множество значений функции у(х) — logi_(4 — х2).
1)(-2;2) 2)[-2;+оо) 3)[0;2) 4) (-оо;2]
А6 Решите неравенство
4 • 9х - 5 • Зх+1 - 4 > 0.
[МГУ, 1996, ИСАА]
I)[log38;+oo)
2)[log34;+oo)
3)[-log34;log34]
4)[-log32;log38]
A7 Какое утверждение верно по отношению к корням
уравнения 5л/7 -я = 13 - xl
1) Уравнение имеет два корня одного знака (оба корня или
положительны, или оба корня отрицательны).
2) Уравнение имеет два корня разных знаков.
3) Уравнение имеет только один корень, и он положителен.
4) Уравнение имеет только один корень, и он отрицателен.
А8 Укажите множество значений функции, график которой
представлен на рис. 115.
1)[-1;3] 2)[0;2] 3) [-1;2] 4) (-1;2]
Рис. 115
А9 Вычислите sin I arccos [ -^-
209

А10 Найдите первообразную на промежутке (0; +оо) для
функции
f(x) = х~ъ + 6х2 - 15х~г + 48,
проходящую через точку (1;0).
1) -ЗяГ4 + 12ж + 15аГ2 - 24
2) х~2 + 6х- 15яГ2 + 48ж - 40
3) -0,5ar2 + 2х3 - 15 In ж + 48я - 49,5
4) -ЗяТ2 + Зж - 15 In x + А8х - 48
В1 Вычислите
82 Укажите абсциссу точки, в которой прямая у = — 4х + 5
касается кривой у = —.
ж4
83 Найдите разность между наибольшим и наименьшим
целочисленными решениями неравенства 2\/х + 5 > х + 2.
84 Решите уравнение л/2ж2 — 9ж + 11 = 3 — х (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
85 Найдите решение (или сумму решений, если их несколько)
уравнения л/sin
л/si
— 1 = х2 — 1.
В6 Найдите целочисленное решение (или сумму решений, если
их несколько) уравнения
\х2 -Зх\ =2х-А.
87 Укажите решение (или сумму решений, если их несколько)
уравнения
log3(a?-l)-logi(a; + 5) = 3.
з
88 Найдите sin2rr, если (sinx + cos ж) = -г.
210

В9 В городе Н в течение 2 лет наблюдается рост жителей. Во
втором году процент роста жителей города Н увеличился
на 1 по сравнению с процентом роста числа жителей в
первом году. Найдите процент роста числа жителей в первом
году, если известно, что он на 5,2 меньше, чем процент
роста населения за два года.
810 Все 8 граней выпуклого многогранника — правильные
треугольники (октаэдр). В него вписана сфера. Определите
радиус сферы, если площадь поверхности октаэдра равна
12л/3.
811 В прямоугольном треугольнике ABC точки D и Е лежат
соответственно на катетах ВС и АС так, что CD = СЕ = 1.
Точка О есть точка пересечения отрезков AD и BE.
Площадь треугольника BOD больше площади треугольника
АОЕ на 0,5. Кроме того, AD = л/Ш. Найти длину
гипотенузы АВ. [МГУ, 1995, химфак]
С1 Найдите все значения параметра а, при каждом из которых
уравнение
asin3x+ у/Щ - a) cos За; = 2а - 3
имеет ровно три решения на отрезке [—7г; тг]. [МИФИ]
С2 Найдите все значения параметра а, при каждом из которых
уравнение
- 48ах + 24а2 - 19| = \8х2 - Шх + 8а2 - 15|
имеет четыре различных решения. Найдите эти решения.
СЗ Решите неравенство
13 - Зх + Ух2 -х-6
Ъ-х
[МФТИ, 1997]
211

С4 Около прямой шестиугольной призмы описан цилиндр.
Площадь боковой поверхности цилиндра равна 16тг-\/3-
Расстояние между осью цилиндра и диагональю боковой грани
призмы равно 2-\/3. Найдите объем призмы. [ЕГЭ, 2003]
С5 Решите неравенство
log»-»» ( 14 ) > L
16 V /
[МГУ, 1966, химфак]
Вариант 10
(■*■-
А1 Вычислите —
з
1)1 2)2 3)4л/3 4)|
8
|
_1
А2 Упростите выражение с''Я— , если с > 0.
vc4
1) tyc 2) 1 3) с5 4) с
A3 Укажите промежуток, внутри которого лежат все решения
(ar-3)a(s-2) ^n
неравенства -j-= < 0.
1) [-8; 4] 2) [3; +оо) 3) [-10; 2] 4) (-оо; -7)
А4 Сколько раз функция, представленная на рис. 116, меняет
знак?
1) 1 2) 2 3) 3 4) 4
212

Рис. 116
А5 Какое утверждение верно по отношению к корням
уравнения 3\/10 - х = 12 - х?
1) Уравнение имеет два корня одного знака (оба корня или
положительны, или оба корня отрицательны).
2) Уравнение имеет два корня разных знаков.
3) Уравнение имеет только один корень, и он положителен.
4) Уравнение имеет только один корень, и он отрицателен.
А6 Найдите первообразную для функции f(x) = 6х2 —15#—#3,
проходящую через точку (1;0).
l)12:z-15-iaf з
6
2) 2х3 - 7,5я2 - 0,
3) 2xs - 7,5s2 - 0,75*3
6,25
x-l
А7 Решите неравенство 4х +
1) (-1; 1]
1.
з) (-оо;-1)
А8 Найдите множество значений функции у(х) = logi (1 — а;2).
2
1) (-ос; +оо) 2) [-1; +оо) 3) [0; +оо) 4) (-оо; 0]
А9 Укажите множество значений функции, график которой
представлен на рис. 117.
1) [-1; 2] 2) [0; 4] 3) [0; 2] U (3; 4] 4) [2; 3]
213

У
4
3
2
-1 0
7
■г-
2 х
Рис. 117
А10 Укажите промежуток, внутри которого лежат все решения
I
неравенства 2 ж ^ 2.
В1 Найдите 3tg —~—, если выполняются равенства:
cos a + cos/3 = 0,3; sin a + sin /3 = —1,1.
[МГУ, 2000, ф-т почв ]
B2 Укажите абсциссу точки, в которой прямая у = х + 'б
касается кривой у = Ау/х — 1.
83 Укажите решение (или сумму решений, если их несколько)
уравнения л/8х2 + 9х + 2 = 2х + 1.
84 Укажите максимальную длину промежутка, в котором вы-
полнено неравенство 2х ^16.
85 Найдите наименьшее значение функции
2 cos 2ж +12 cos ж+ 10.
86 Сколько целочисленных решений имеет неравенство
|Т2 _ 9| < -, _ ?
214

87 Найдите длину отрезка, являющегося решением
неравенства
л/28-ж - у/х + 1 < л/ж+ 6.
88 Найдите корень (или сумму корней, если их несколько)
уравнения
В9 Найдите sin2#, если (sinx — cos ж) = — ~.
810 Найдите двугранный угол (в градусах) при основании
правильной четырехугольной пирамиды, если плоскость,
проведенная через сторону основания, делит этот угол
пополам, а боковую поверхность пирамиды на две равновеликие
части.
811 Вершины В, С, D четырехугольника ABCD расположены
на окружности с центром О, которая пересекает сторону
АВ в точке F, а сторону AD — в точке Е. Известно, что
угол BAD равен 85°, длина хорды EF равна длине
хорды FB, и длины хорд ВС, CD, ED равны между собой.
Найдите угол АВО (в градусах).
С1 Решите неравенство |ж3 -Ь # — 3 —5 ^ ж3 — х + 8.
(с- f/c\
1, если logrf с = \/5. [МГУ, 1998,
биофак]
СЗ Решите неравенство
^~6 > 2х "" 10'
[МФТИ, 1999]
ОЛЬ

С4 Через центр сферы проведено сечение. Точка F выбрана на
сфере, а точки А, .В, С, D — последовательно на
окружности сечения так, что объем пирамиды FABCD
наибольший. Найдите синус угла между прямой AM и плоскостью
BFD, если М — середина ребра FB. [ЕГЭ, 2005]
С5 Решите неравенство
[МФТИ, 1990]
Вариант 11
Al
A2
Упростите
l)af
Упростите
■п 47
выражение
2)1
выражение
2ч 47
2) 35
2
аз
3)
v *
3)
если а
5
>45
329
>0.
*
4)
4)
5
аЗ
47
7, /К
A3 Сравните число А = log2v/2 4 • (log9 Зл/3)2 и число
[МГУ, 1973, ф-т почв.]
1) В > А 3)А = В
2) А > В 4) нельзя определить
216

А4 Решите уравнение cos f ^ + 5х) = -т-.
2) (-l)n+1 arcsin || + тгп, n G
3) (_l)«+i . I arcsin ^ + 22», n G Z
4) (-1)" • | arcsin ^ + 22» ? n 6 z
A5 Укажите промежуток, внутри которого находятся все ре-
(х-1)2(х-2) ^п
шения неравенства = ^ 0.
1)[0;2) 2) (-оо;-2] 3) [-2; 8) 4)[2;+оо)
А6 Найдите область определения функции у = «/А — (h) ■
1)[0;+оо) 2) (-оо;-2] 3) [-2;+оо) 4)[2;+оо)
А7 Найдите множество значений функции у = 3sina\
1) (-оо; +оо) 2) [|; з] 3) [-3; 3] 4) (0; +оо)
А8 Найдите у'(—1) для функции у(х) = \/1 — За;.
1)| 2)"| 8)J 4)-I
А9 Найдите множество значений функции f(x) = 16 — ^ на
отрезке [—1;2].
1)[0;7] 2) [7; 16] 3)[-1;16] 4) [-1;7]
А10 Решите неравенство 22х — 2х — 2 < 0.
1)(-оо;1) 3)(-1;2)
4)(-oo;-2)U(l;+oo)
217

В1 Укажите значение выражения
(y/2a-Vb V2a +
если а > О, Ь > О, 2а - b ф О. [МГУ, 1998, ф-т почв ]
В2 Вычислите площадь фигуры, ограниченную линиями
У=^ У = 0 Х = Ь Х =
83 Найдите наибольшее значение функции /(ж) = 2а;2 — ж4 на
отрезке [—2; 2].
84 Найдите наибольшее целочисленное решение неравенства
1 < А
85 Вычислите ctg2 ( arccos ~ J.
2
86 Вычислите определенный интеграл / 3(х — I)2 dx.
1
87 При каких значениях параметра а система уравнений
(ах — 4у = а + 1,
\2x+(a + G)y = a + 3
не имеет решений? [МГУ, 1970, биофак]
88 Решите уравнение л/х + 1у/х + 6 = 6 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
218

1
В9 Решите уравнение 5ж5 == ж+ 4 (если уравнение имеет более
одного корня, то в ответе запишите сумму всех корней).
810 Плоское сечение SAB, проходящее через вершину S
прямого кругового конуса, имеет площадь 42. Точки А и В,
лежащие на окружности основания конуса, делят ее длину
в отношении 1:5. Найдите ^-^—, где V — объем конуса,
о
если угол SAB равен arccos —р=. [МГУ, 1996, биофак]
v58
811 В ромбе ABCD из вершины D на сторону ВС опущен
перпендикуляр DK. Найдите квадрат стороны ромба, если
АС = 2л/б, АК = л/14. [МФТИ, 1992]
С1 Найдите наименьшее целое число, которое является
решением неравенства
С2 Решите уравнение \l\ogx \/2x-log4 х = — 1. [МГУ, 2003, биофак]
СЗ При каких значениях параметра а неравенство
, fsinx — \/3cosa; — а — 4\ Л
log -2а -13 *—е — > 0
5 \ ° /
выполняется для любых значений #? [МГУ, 1996, ИСАА]
С4 Дан куб ABCDAiBiCiDi, где ААЪ ВВЪ ССЪ DDX —
боковые ребра. В каком отношении делит ребро В\С\
точка Е, которая принадлежит плоскости, проходящей через
вершину А и центры граней A\B\C\D\ и В\С\СВ1
С5 Найти все значения параметра а, при каждом из которых
сумма длин интервалов, составляющих решение
неравенства
х2 + (2а2 + 2)х - а2 + 4а - 6
х2 + (а2 + 5а - Ъ)х - а2 + 4а - 6
не меньше 1. [МГУ, 1999, мехмат]
219

Вариант 12
А1 Упростите выражение
г) Ж 2)^ 3)5 4)1
А2 Найдите область определения функции
>м = \Щ-
1) (-оо; 5) U (5; +оо) 3) (-оо; -5)
2) (-оо; +оо) 4) (5; +оо)
A3 Пусть
и
Найдите область определения функции g(f(x)).
1)ж#-1;2
2)(0;+оо)
»>(*АМ)
4) (-оо; -4 - л/21) U (-1; -4 + >/§!)
А4 Найдите множество значений функции у = 21 -1.
1) (-оо; +оо) 2) [1; +оо) 3) (i; +oo) 4) [i; +oo)
А5 Укажите, является ли функция у = In ——^ четной, нечет-
ной или функцией общего вида.
1) Четная. 3) Функция общего вида.
2) Нечетная. 4) Нельзя определить.
220

Аб Напишите уравнение касательной к графику функции
f(x) = х3 в точке с абсциссой х = 2.
1) у = 12ж - 16 3) у = Зж - 16
2) у = 12я - 6 4) у = Zx - 4
А7 Сколько экстремумов имеет функция, график которой
представлен на рис. 118?
1) 2 2) 1 3) 3 4) 4
В
Рис. 118
А8 Найдите множество всех первообразных для функции
f(x) = х2 — 3sin4#.
l)2z2-12sin4s
2) ^p-
4) у
A9 Какое утверждение верно по отношению к корням
уравнения Ь\/х + 5 = х + 11?
1) Уравнение имеет два корня одного знака (оба корня или
положительны, или оба корня отрицательны).
2) Уравнение имеет два корня разных знаков.
3) Уравнение имеет только один корень, и он положителен.
4) Уравнение имеет только один корень, и он отрицателен.
221

А10 Решите неравенство |5 — 7х\ < 2.
4) (0; 1)
В1 Вычислите значение выражения
sin||.cosZ|_cos||.sinI|.
В2 Вычислите значение выражения
(1 5 1 1\2 / 1 5 ! ±\2
а~бЬб +аЗЬз 1 + I а~б6б -азбз )
2а + 4а2
а2 -
если а > 0, Ь > 0, а - Ь ф 0. [МГУ, 1970, геолог ф-т]
1
ВЗ Вычислите определенный интеграл / Щг.
J хг
В4 Функция у = f(x) определена на промежутке (—6; 4).
График ее производной изображен на рисунке 119. Сколько
точек максимума на промежутке (—6; 4) имеет эта функция?
Рис. 119
В5 Найдите наибольшее значение функции 2 cos 2x—Yl sin x—6.
222

86 Найдите сумму целых чисел, не являющихся решением
неравенства (х2 + Зх + 1)(х2 + Зх - 3) ^ 5.
87 Пусть точка движется прямолинейно по оси Ож, где
координата х меняется по закону x(t) = Ы2 — 4t + 1 (см). В
какой момент времени (в секундах) скорость станет равной
26 (см/с)?
88 Числа а и b таковы, что система уравнений
\а2х — ау = 1 — а,
€ + (3 - 2b)y = 3 + a
имеет единственное решение х — 1, у — 1. Найдите число а.
В9 Найдите утроенную сумму корней уравнения
810 Основанием пирамиды SABC является прямоугольный
треугольник ABC {С — вершина прямого угла). Все
боковые грани пирамиды наклонены к ее основанию под
одинаковым углом, равным arcsin y~. Найдите площадь
боковой поверхности пирамиды, если 50 — высота пирамиды,
АО = 1, ВО = 3\/2. [МГУ, 1998, биофак]
811 Биссектрисы внутренних углов треугольника продолжены
до пересечения с описанной около треугольника
окружностью в точках, отличных от вершин исходного
треугольника. В результате попарного соединения этих точек
получился новый треугольник. Известно, что углы исходного
треугольника равны 30°, 60° и 90°. Найдите (t + 1)2, где t —
отношение площади исходного треугольника к площади
нового треугольника. [МГУ, 2000, ф-т почв.]
С1 Решите неравенство
223

С2 Решите неравенство Iog2# • Wlogx (hV%) ^ 1- [МГУ, 1970,
эконом ф-т]
СЗ Решите систему уравнений
I у/У + Vх + У = У - Зж - 6.
[МФТИ, 2003]
С4 Радиус основания прямого кругового конуса равен Д,
высота равна Н. В конус вписан цилиндр (т. е. одно основание
цилиндра лежит на основании конуса, а другое лежит на
боковой поверхности конуса). Какое наибольшее значение
может иметь боковая поверхность цилиндра?
С5 Решите уравнение Зх2 + Ьху + 2у2 = 7 в целых числах. [МГУ,
2001, ф-т почв]
Вариант 13
т. ^ logo 24 logo 192
А1 Вычислите без помощи таблиц — —. [МГУ, 1971,
log96 2 log12 2
ф-т психологии]
1) 2 2) 4 3) 3 4) у/2
х
А2 Решите неравенство 1— > 0.
Х
)(;) )(;)
2) (3;+оо) 4) (l;2)U(3;+oo)
A3 Найдите сумму квадратов всех целых чисел, являющихся
решениями неравенства —£&•— ^ 1.
хг + 2
1)3 2)2 3)4 4)5
224

А4 Укажите наибольшее значение функции
y = l-2sin|
на отрезке [0; 2тг].
1) 2 2) 1 3) 3 4) 4
А 5 Найдите сумму решений уравнения
\/cos2 тгх — 1 = (х — 1)(х — 2).
1) 2 2) 1 3) 3 4) 2п, п в Z
А6 Укажите промежуток, внутри которого лежат бее решения
неравенства
(^()
1) [4; 6] 2) [5; 7] 3) [-6; 5] 4) (-оо; Т5]
А7 На рисунке 120 представлены графики функций
у = д/ж + 5 и у = ах + Ь.
Запишите уравнение прямой, для которой решением
неравенства
у/х + 5 ^ аж + Ь
является отрезок [—1;4].
А8 Укажите промежуток, внутри которого находятся все
решения неравенства
225
8 Зак 243

-5-1 О
Рис. 120
А9 Решите уравнение
cos 2х = 2(cos х + sin x).
[МГУ, 1995, химфак]
1) нет решений 3) — j +
2) тгп, ~ + тгп, п е Z 4) -21
А10 Укажите промежуток, которому принадлежат все решения
неравенства 7Ж - 2Х+2 < 5 - 7х"1 - 2х'1.
1) (0; 8) 2) (-оо; 2) 3) (3; +оо) 4) (-3; 3)
В1 Вычислите значение выражения
2Ь~1 а"1 - л
х -Ц; р-,
za + о
'2Ь~2+26""1
если а > О, Ь > 0.
В2 Сколько целочисленных решений имеет неравенство
ВЗ Вычислите площадь фигуры, ограниченной линиями
у = у/х- 1, у = 0, ж = 9.
226

В4 Найдите сумму положительных решений уравнения
xx4i =
85 Решите уравнение log2 х + Iog2(# + 1) = 1 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
86 Найдите максимальную длину промежутка, в котором
выполнено неравенство у/х + 5 < 7 — х.
87 Найдите наименьшее целое число, принадлежащее
множеству решений неравенства 4 • 9х — 5 • Зх+1 — 4^0.
88 Упростите выражение
1OgI 2 А 1
5 * ^
[МГУ, 1973, географ ф-т]
В9. Третий член геометрической прогрессии равен (—10), а его
квадрат в сумме с седьмым членом дает утроенный пятый
член. Найдите первый член прогрессии.
810 Высота основания правильной треугольной пирамиды
равна 9, боковые грани наклонены к плоскости основания под
углом 30°. Найдите площадь боковой поверхности
пирамиды. [ЕГЭ, 2001]
811 Диагонали равнобедренной трапеции перпендикулярны.
Найдите площадь трапеции, если ее средняя линия равна 5.
[МГУ, 1995, химфак]
1х3|-|5а;|
С1 Решите уравнение , = 0. [МГУ, 1995,
у/2х2 - 4ж - 1 - Ы + 2
мехмат
227

С2 Решите неравенство
1
л/ж2 + 2ж-8 -4 2|я? — 3| — 5"
[МФТИ, 2003]
СЗ Найдите все значения параметра Ь, при каждом из которых
для любого значения а неравенство
(х - а - 2Ь)2 + (у - За - Ь)2 < |
имеет хотя бы одно целочисленное решение (х, у). [МГУ, 2003,
филолог, ф-т]
С4 Дана правильная призма АВСА\В\С\, где AAi, ВВ\ и
CCi — боковые ребра. Сфера, центр которой лежит на
ребре AAi, пересекает ребро А\С\ в точке М и касается
плоскости основания ABC и плоскости СВВ\. Известно, что
АВ = 12, А\М : МС\ = 3:1. Найдите площадь боковой
поверхности призмы.
С5 Найдите все значения параметра а, при каждом из которых
уравнение cos4 х — (а + 2) cos2 х — (а + 3) =0 имеет решение.
[МГУ, ВМиК, 1970]
Вариант 14
А1 Упростите выражение
если ж > 0, у > 0, я - Зу ^ 0. [МГУ, 1998, ф-т почв ]
228

А2 Сравните числа
A=2logil"3FJ+2 и B =
2l3FJ
[МГУ, 1998, ф-т психологии]
1) А > В 3) А < В
2) А = В 4) нельзя определить
а2 г-
A3 Вычислите loga62 ^~, если log6 a = V2. [МГУ, 1982, физфак]
l з)1 4)2
2
А4 Найдите область определения функции
1) (-оо; 4) U (4;+оо) 3) (4;+оо)
2)[1;4) 4) (-со; 1] U (4;+оо)
А5 Найдите множество значений функции
sin22x-x2-l.
1) (0; +оо) 2) [1; +оо) 3) [3; +оо] 4) (-1; 0]
А6 Найдите множество первообразных для функции
у(х) = х — sin х.
2
1) 1 - cosx + С 3) у - cosz + С
2
) C )2 С
А7 Укажите промежуток, которому принадлежат все решения
уравнения
log5(-2x) ^2
1) [0; 1] 2) [1; 2] 3) [-±; l] 4) [-0,8; -0,4]
229

А8 Укажите промежуток, которому принадлежат все решения
уравнения у/Зх + 2 = 2х — 4.
1)[2;3] 2) [4; 5] 3) [6; 7] 4) [3;4]
А9 Решите неравенство log2 ж2 < 2.
1)(-2;0) 3)[-2;0)U(0;2]
2)(0;2]U{-2} 4) [-2; 2]
А10 Решите неравенство — log2 ^ ^ 2.
1)(1;2)U(2;3] * 3) (0; 1) U (1; 2]
В1 Для функции у(х) = ж3 + Зх2 + Зх — 112 найдите точки, в
которых у'(х) = 0.
82 Вычислите определенный интеграл / sin(a; + тг) da;.
—7Г
83 Найдите площадь фигуры, ограниченной кривой у = 6х —
— Зх2 и прямой у = 6х — 12.
84 Найдите наименьшее значение функции
В5 Найдите сумму квадратов всех целочисленных решений
неравенства
л/6 + х - х2 > у/6 + х-х2
2х + 5 ^ х + 4
В6 Найдите наибольшее целочисленное решение неравенства
4
230

В7 Найдите значение параметра а (или сумму значений, если
их несколько), при каждом из которых система уравнений
х2 + у2 = 2 + а,
имеет два решения.
В8 Найдите сумму квадратов всех корней уравнения
1-я:11 1-х9
/г
1 - х9 1-х
В9 Числа а, 6, с, d являются последовательными членами
геометрической прогрессии. Известно, что а + d = 10, ad = 7.
Найдите Ь3 + с3. [МГУ, 1996, ВМиК]
810 Боковые ребра пирамиды наклонены к плоскости
основания под углом, равном 45°. Стороны основания равны 10,
6, 8. Найдите объем пирамиды. [ЕГЭ, 2002]
811 В трапеции ABCD заданы углы /.BAD = 90°, /ADC =
= 30°. Окружность, цейтр которой лежит на отрезке AD,
касается прямых AJ5, ВС, CD. Найдите площадь трапеции,
если известно, что радиус окружности равен 4v 6 + \/3.
[МФТИ, 1982]
С1 Решите уравнения \х2 — Зх| = 2х — 4.
С2 Решите неравенство ^ [МФТИ,
2 - у/х2 - Зж у/х2 -2х + 4
2001]
СЗ Количество членов клуба любителей цветов возрастает
ежегодно в геометрической прогрессии и за 6 лет
увеличилось на 19285 человек. Найдите первоначальную
численность членов клуба. [МГУ, 2003, ф-т фундаментальной медицины]
231

С4 В правильной треугольной пирамиде SABC плоскость,
проходящая через сторону АС основания и
перпендикулярная ребру SB, отсекает пирамиду DABC, объем которой
в полтора раза меньше объема пирамиды SABC.
Найдите площадь боковой поверхности пирамиды SABC, если
С'5 Найдите все значения а, при которых система уравнений
flog2(3 - х + у) + 3 = Iog2(25 - 6х + 7у),
\у + 2 = {х - 2а)2 + а + 2х
имеет ровно два решения. [МФТИ, 2002]
Вариант 15
А1 Упростите выражение v^-27 • л/2 + \/8 + 5л/-8 • \/4.
1) 8 2) 20 + лД 3) -20 4) -20 - л/2
А2 Упростите выражение _ CQS а • tg2 ^, если sin а ф 0.
1)1 2) tg4 f 3)ctga 4) sin a
A3 Найдите cosfa + тП, если известно, что sin a = — ~, а
tga > 0. [МГУ, 1996, ф-т почв]
,ч 4-3^3 9ч \/3 „xV3 л Зл/3-4
Х) 2) 3) 4J
9 л
А4 Найдите область определения функции
1)[2;3] 2)[1;2] 3)[6;7] 4) [3;4]
232

А5 Найдите наименьшее значение функции у(х) — —х2 — 2х на
отрезке [—2; 2].
1) 1 2) 0 3) -8 4) -3
А6 Найдите производную функции у(х) = 4х3 — j в точке с
абсциссой х = 0,5.
1) -1 2) 7 3) 3,25 4) 2,75
А7 Решите уравнение 2 cos2 х + 3 sin х = 0. [МГУ, 1972, геол. ф-т]
1) ±| + 2тгп, n G Z 3) (-l)n+11 + тгп, п Е Z
2) (-1)п+1| + 2тгп, n G Z 4) (-1)"+1| + тгп, п € Z
А8 Укажите промежуток, которому принадлежат все корни
уравнения
17 lS
1-Х15 Х13-1"
1) [0; 1] 2)[-1;0] 3)[1;2] 4) [-0,5; 1]
о о
А9 Решите неравенство ——=г- < 5. [МГУ, 2000, биофак]
1) (-оо; -2) U (-2; +оо) 3) (4; +оо)
2) (-оо; -2) U [-1; +оо) 4) (-оо; 1] U (4; +оо)
А10 Решите неравенство :—Ц-г > -—Ц^. [МГУ, 2001, химфак]
\х — 2\ \х + 2\
1) (-оо;-2) U (2;+оо) 3) (0; 2) U (2;+оо)
2)[1;4) 4)(-oo;l]U(4;+oo)
В1 Найдите сумму квадратов всех натуральных чисел,
являющихся решениями неравенства
В2 Вычислите площадь фигуры, ограниченную линиями у
= 3(яг - I)2, у = 0, х = 2.
233

83 Решите уравнение 2л/х + 5 = х + 2 (если уравнение имеет
более одного корня, то в ответе запишите сумму всех
корней).
84 Решите уравнение х2 + 1 + \х — 1| = 2 |#| (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
85 Решите уравнение 52х = 115 - 5х"1 + 50 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
86 Найдите сумму целочисленных решений неравенства
(ж + 2)(я-3) ^0
х{х — 5) ^
87 Найдите сумму целочисленных решений неравенства
л/35 + 2х - х2 ^п
88 Упростите выражение л/|40л/2 — 57| - \/40л/2 + 57. [МГУ,
1978, мехмат]
89 Найдите сумму первых двадцати членов арифметической
прогрессии, если известно, что сумма третьего, седьмого,
четырнадцатого и восемнадцатого ее членов равна 10. [МГУ,
1988, ВМиК]
ВЮ Концы отрезка АК лежат на окружностях двух оснований
цилиндра. Секущая плоскость проходит через точку А и
ось цилиндра. Угол между прямой АК и плоскостью
основания цилиндра равен 30°, АК =16, площадь боковой
поверхности цилиндра равна 80тг. Найдите периметр осевого
сечения цилиндра. [ЕГЭ, 2005]
234

В11 Окружность, построенная на стороне AD
параллелограмма ABCD как на диаметре, проходит через середину
диагонали АС и пересекает сторону АВ в точке М. Найдите
отношение 44т, если АС = WD. [МФТИ, 1983]
С1 Найдите сумму квадратов всех корней уравнения
{х - 7)2 - \х - 7| = 30.
С2 Решите неравенство
1оё,ж_2|(9ж - 4х) < log|x_2,(3* + 2*) + log|x_2|(3—2 + 2Ж).
[МФТИ, 1996]
СЗ Решите неравенство ^ [МФТИ,
2 - у/х2 + Зх у/х2 + 4х + 7
2001]
С4 В прямой круговой конус вписано два шара так, что
шары касаются друг друга, каждый из них касается боковой
поверхности конуса, центры шаров лежат на оси конуса,
нижний (больший) шар касается основания конуса.
Найдите объем конуса, если радиус верхнего шара равен а,
нижнего — Ь.
С5 Найдите все значения параметра а, при каждом из
которых уравнение у/х — 8 = —ах + За + 2 имеет единственное
решение. [МФТИ, 2000]
Вариант 16
iii i
А1 Упростите выражение 1252 + 8з -52 - 5 • 492.
1)7л/5-35 2)4-л/5 3) 35 - 7л/5 4)11
235

А2 Сравните числа
И д =
[МГУ, 1994, биофак]
l)p>q 3)p = q
2) q > р 4) нельзя определить
A3 Найти без таблиц tg2a, если sina=jH0^a<^. [МГУ,
1972, филфак]
2) 7
А4 Найдите область определения функции f(x) = д/f •
у О — X
1)1-5; 5) 3)(5;+оо)
2)(-oo;5)U(5;+oo) 4) (-оо;5]
А5 Решите уравнение 2 + cos 2x = 4 cos2 x. [МГУ, 2001, ф-т почв.]
A6 Решите неравенство ж2 ^ 9.
1)[3;+оо) 3)(-оо;3]
2)[-3;3] 4) (-оо;-3] U [3;+оо)
А7 Решите неравенство Iog2(a; + 3) < 1.
1)[2;15] 2) [-1; 1] 3)(-3;-1] 4)[-2;1]
О О
А8 Решите неравенство —*-= + 2 < *.. [МГУ, 2001, ф-т наук
X Z J т 4
о материалах]
l)(-3;0)U(0;2) 3) (-4;-1) U (-1;2)
2) (-4; -1) U (2; 12) 4) (-оо; -4) U (2; +оо)
236

А9 Решите неравенство 2х > \х\ + 1. [МГУ, 1994, химфак]
1) [5; 15) 2) (-ос; 5) 3) (1; +оо) 4) (-оо; 5]
А10 Решите неравенство 2Х~1 > (т^)Х- [МГУ, 1980, физфак]
1) [5; 15) 2) (-оо; 5) 3) (1; +оо) 4) (0; +оо)
В1 Вычислите значение выражения
82 Вычислите площадь фигуры, ограниченной линиями у =
= 4 ~ 3, у = 0, х = ±
X **
83 Пусть у = у(х) — уравнение касательной к окружности
х2 + у2 = 25 в точке (—3; —4). Найдите абсциссу точки
пересечения этой прямой с прямой у = — 1.
84 Решите уравнение у/х + 1 — у/2х — 12 = 1 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
85 Решите уравнение log2 ^Ц Ь log2 —7-7 = 1 (если уравне-
О X "Т 1
ние имеет более одного корня, то в ответе запишите сумму
всех корней).
86 Найдите наименьшее целочисленное решение неравенства
В7 Найдите сумму квадратов целочисленных решений
неравенства
(ж2 - Их + 30) Iog2(z - 3) < 0.
237

88 Упростите выражение
((^3 - ^7)2 + 7) • ((^3 + л/27)2 - 7) .
[МГУ, 1996, ф-т почв.]
89 Найдите #, если известно, что числа — 1, х + 2, sin(arcsinar),
взятые в указанном порядке, образуют геометрическую
прогрессию. [МГУ, 1995, ИСАА]
32
810 Шар, объем которого равен -«-тг, вписан в конус. Найдите
о
высоту конуса, если радиус основания равен 2\/3. [ЕГЭ, 2001]
811 В остроугольном треугольнике ABC проведены
биссектриса AD и медиана BE. Точки М и N являются
ортогональными проекциями на сторону АВ точек DnE
соответственно, причем
АМ_ = 9 AN = 2
MB V NB 3'
AD2
Найдите отношение . [МФТИ, 1985]
BE
С1 Найдите все ж, при каждом из которых функция у(х) =
= 6 cos2 х+6 sin ж — 2 принимает наибольшее значение. [МГУ,
1982, ВМиК]
С2 Решите неравенство
л/-х2 + 2х + 8
СЗ Найдите наибольшее значение функции
f(x) = arctg(-\/3cos8a?) + arcctg(sin3a;)
и все ж, при которых оно достигается. [МИФИ]
238

С4 В правильной четырехугольной пирамиде SABCD
плоскость, проведенная через сторону AD основания
перпендикулярно к грани BSC, делит эту грань на две части,
одинаковые по площади. Найдите площадь полной поверхности
пирамиды, если AD = а.
С5 Найдите все значения параметра а, при каждом из которых
расстояние между корнями уравнения
ах2 + (2а + 2)х + (а + 3) = О
больше 1. [МГУ, 2001, социолог ф-т]
Вариант 17
А1 Упростите выражение \/а2№ • y/a2b2 — \/a5b6.
1) 0 3) 2ab2 - #a2
2) b • \№(\ab\ - ab) 4) J . b ■ (|a6| - ab)
A2 Сравните числа
(5400)--1 и g =
[МГУ, 1998, ф-т псих ]
l)q>p 3)g<p
2) р = q 4) нельзя определить
A3 Решите уравнение cos Зх + sin x sin 2x = 0. [МГУ, 2000, химфак]
1) -J-, | + y,n,AeZ 3) 7гп, -j + "2", n, A; G Z
2) 1 + тгп, | + ^, n,fcGZ 4)| + тгп, | + тгАг, n,fcGZ
А4 Вычислите loga /g —~=, если loga Ь = л/7. [МГУ, 1982, физфак]
/7 + 2
\/7 + 2 2 + \/7
239

А5 Найдите Зл/IOcos ^, если известно, что
tgo=| и тг<а<2тг.
1) 6уД 2) -3 3) 3
1а. — х
А 6 Найдите область определения функции f(x) = 4 /—
у X
1)[-1; 4] 3)(-l;4]
2) (-po; -1] U [4; +oo] 4) (-00; -1) U [4; +00)
A7 Решите неравенство
3) (-оо; -1) U [1; +оо)
4) [0; 1]
А8 Решите уравнение 5 + cos 2х = 6 cos x.
1) тгп, п е Z 3) 2тгп, п е Z
2) | + 2тгп, n E Z 4) тг(2п + 1), п G Z
А9 Укажите промежуток, которому принадлежат все корни
уравнения log^^ 3 = 2.
1) [—7; 1 — voj 3) (1 + vo; 5J
2)[0;3] 4)[3;5]
А10 Найдите все значения параметра а, для каждого из
которых все числа хну, удовлетворяющие системе уравнений
х + у = а,
От 01 *Х
AJj у О
удовлетворяют также церавенству х > у. [МГУ, 1977, физфак]
1) (-оо; -6) 2) (6; +oq) 3) (-6; 6) 4) (-оо; 6)
240

81 Найдите 2/' (я) для функции у(х) = (4ж — 1)sin(4x2 — 2х).
82 Вычислите значение выражения
83 Вычислите площадь фигуры, ограниченной линиями у =
= 27rcos7r#, у = 0, ж = 0, х = j!r.
84 Решите уравнение log2 # + 2 log,,. 2 = 3 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
85 Найдите сумму квадратов всех корней уравнения
7 - х = 3\/5 - х.
В6 Найдите наибольшее целое число, не являющееся
решением неравенства -—-—- > г—^—-.
|а?1| |я? + 1|
87 Решите уравнение х2 — 6ж + 5 = — Ъу/х — 3 (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
88 Найдите наименьшее целочисленное решение неравенства
В9 Сумма третьего и пятого членов арифметической
прогрессии равна 8. Найдите сумму первых семи членов этой
прогрессии, [МГУ, 1993, ИСАА]
241
9 Зак 243

BIO Основание прямой призмы BCDB\C\D\ — треугольник
BCD, в котором BD = DC, ВС = 4л/7. На ребре DDX
отмечена точка А так, что DA : D\A = 2:5. Угол между
плоскостями BCD и ABC равен 45°. Найдите расстояние
между прямыми CD ъВ\С\, если АВ = 6. [ЕГЭ, 2005]
В11 Диагонали BD, АС выпуклого четырехугольника ABCD
перпендикулярны, пересекаются в точке О, АО = ^, ОС =
= 3. Точка N лежит на стороне АВ, причем ^г= = ^
Треугольник DNC равносторонний. Найдите 5л/3, где S —
площадь треугольника DNC. [МФТИ, 1988]
С1 Решите уравнение
|5я? — 3| — |7я? — 4| =2ж-1.
[МГУ, 1996, геогр ф-т]
С2 Решите уравнение
л/ж2 + 4ху + Зу2 + 9 + (4я2 + Ъху - 6у2)2 = 0.
[МГУ, 2001, ф-т наук о материалах]
СЗ Найдите все значения а, при каждом из которых оба
числа 2 cos a + 9 и 2 cos 2a + 4 cos a + 4 являются решениями
неравенства
2 - log2 [Ж - 5[ ^Q
С4 Основанием пирамиды FABC является треугольник ABC,
в котором /.АСВ = 90°, тангенс угла ВАС равен 4. Ребро
AF перпендикулярно плоскости ABC. Отрезки AM и AL
являются соответственно высотами треугольников AFB и -
AFC. Найдите отношение объема пирамиды AMLB к
объему пирамиды AMLC.
242

С5 Найдите все значения параметра а, при каждом из которых
решением неравенства
ахА + ж3 + (2а + За3)ж2 + 2х + 6а3 > О
является ограниченный промежуток. [МГУ, 2001, ф-т
психологии!
Вариант 18
А1 Упростите выражение л/а^ • у/—а3 + avcfi.
1)0 2)а(а-|а|) 3) 2а 4) 2 |af
А2 Вычислите loga v^6, если log6 a = л/13.
xv 2л/13 + 1 2) 2л/13-1 3. 2\/1з + 1 4) ЗлДЗ +
3 Зл/13 + 1 Зл/13-1
A3 Задано четыре функции 1) у = х sin х + ж3; 2) у = cos ж — х\
3) у = cos #— |ж|; 4) у = л/ж2 — х. Укажите четную функцию.
1) 1 2) 2 3) 3 4 4
А4 Решите уравнение
2 sin ^~ • cos т^ = sin ж.
[МГУ, 2002, химфак]
1) j,n6Z 2) тгп, n G Z 3) у, n G Z 4) 2тгп, n G Z
А5 Вычислите cos 2a, если sin a = ^. [МГУ, 1980, ВМиК]
7 Q 7 7
1^ 18 2^ П 3^ "~9 4^ 9
А6 Найдите производную функции у (х) = 4 cos 2а? — sin4x в
точке с абсциссой х = j.
1) 4 2) -1 3) -12 4) -4
243

А7 Найдите область определения функции у(х) = * -г .
у 4 X
1) (-оо; 1] U (4;+оо) 3) [1;4)
2)[1;4] 4)(-oo;l]U[4;+oo)
А8 Упростите выражение у^|12\/5 — 29| - л/12л/5 + 29. [МГУ,
1978, мехмат]
1) 1 2) б 3) -6 4) -10
А9 Какое утверждение верно по отношению к корням
уравнения Ьу/—х — 1 = —2х ?
1) Уравнение имеет два корня одного знака (оба корня или
положительны, или оба корня отрицательны).
2) Уравнение имеет только один корень, и он отрицателен.
3) Уравнение имеет два корня разных знаков.
4) Уравнение имеет только один корень, и он положителен.
А10 Решите неравенство 5* - Зх+1 > 2(5Х"Х - Зж~2). [МГУ, 1982,
физфак]
1) (-оо; 1] U (4;+оо) 3) [1;4)
2)(3;+оо) 4)(-oo;l]U[4;+oo]
В1 Вычислите значение выражения
о 7у/Зу/а-7л/Е\/Ъ За-56
6л/15аб'
если а > О, Ь > 0, За - 56 ф 0.
е2
82 Вычислите определенный интеграл / -~.
1
83 Сколько корней имеет уравнение 27ж3 — 9х2 — ЗОх — 8 = 0?
В4 Решите уравнение у/хг + х2 — х — 6 = х (если уравнение
имеет более одного корня, то в ответе запишите сумму всех
корней).
244

85 Решите уравнение 2^ — 21 ^ = 1 (если уравнение имеет
более одного корня, то в ответе запишите сумму всех
корней).
86 Найдите максимальную длину отрезка, на котором
выполнено неравенство
у/21 -х -
87 Найдите наименьшее целое число #, для которого
выполнено неравенство
log|(s - 7) - 3Iog2(s - 7) + 2 > 0.
88 Найдите длину промежутка, который является решением
неравенства 2|# + 1|^ж + 4.
89 Даны арифметическая и геометрическая прогрессии.
Сумма их первых членов равна (—3), сумма третьих членов
равна 1, а сумма пятых членов равна 5. Найдите разность
арифметической прогрессии. [МГУ, 1997, мехмат]
810 Дан куб ABCDA\B\C\D\. Через точки J5, D и середину
ребра Т)\С\ проведена секущая плоскость. Найдите площадь
полной поверхности куба, если площадь сечения равна 144.
[ЕГЭ, 2003]
811 Через вершины А, В и С трапеции ABCD (AD || ВС)
проведена окружность. Известно, что окружность касается
прямой CD, а ее центр лежит на диагонали АС.
Найдите 5\/3, где S — площадь трапеции ABCD, если ВС = 2,
AD = 8. [МФТИ, 1995]
С1 Решите уравнение y/T+s'mx + cos а; = 0. [МГУ, 1974, мехмат]
С2 Решите неравенство
|43х _ 24*+2 . 3*+1 + 20 • 12х - Зж| ^ 8 • 6х • (8х"1 + 6х).
[МГУ, 2002, химфак]
245

СЗ Решите систему уравнений
\у/аГ+~у + 2х + у = 16.
[МФТИ, 2002]
С4 Площадь боковой поверхности правильной треугольной
пирамиды со стороной основания а в 5 раз больше площади
основания. Найдите объем конуса, вписанного в эту
пирамиду. [МГУ, 1997, ф-т почв.]
С5 Решите уравнение
Ъх - 2 \х - 2| = Зл/Зя + 18 - 2 |л/Зя + 18 - 2|.
[МГУ, 2001, мехмат]

РАЗДЕЛ ТРЕТИЙ
РЕШЕНИЯ
Решение варианта 1
А1 Решение: Вспомним, что л/а? = |ж|, поэтому у(2 — л/5)2 =
= л/5-2, и получаем ^/(2 + л/5)2 - ^/(2 - л/5)2 = 4. ■
Ответ: 2)1.
А2 Решение: Воспользуемся формулой перехода к новому ос-
log6iV
нованию logfl N = , основным логарифмическим тожде-
logfe a
ством N = aloga N и формулой а = loga aa. Тогда
log2 3
2^43 = 2"~2 = 2log2^ = л/3. ■
Ответ: 3).
A3 Решение: Корень четной степени определен для
неотрицательных значений подкоренного выражения, поэтому заданная
х — 1
функция определена, если -= ^ 0. Решать такое неравенство
О X
удобнее, если расположить все многочлены в порядке убывания
степеней, т. е. рассматривать неравенство
ж—5
0.
1 Ответ в этой задаче, конечно, 4, но здесь и далее мы указываем номер
правильного ответа, как это требуется в заданиях ЕГЭ
247

Тогда при больших х дробь всегда (или любой многочлен)
принимает положительные значения.
Решаем методом интервалов. «Снимаем» ответ с
рисунка 121: хе [1;5).
1 5 х
Рис. 121
Но грамотный школьник запишет ответ сразу, используя
тот факт, что
х-1
5 — х
и то, что квадратный трехчлен отрицателен между его
корнями. ■
Отэет: 1).
А4 Решение: Решим данное в| условии неравенство:
Ь~ >0
\ х2-х +
Наименьшим натуральным числом, удовлетворяющим
неравенству, является число 4, которое содержится в промежутке
[4;8).и
Ответ: 2).
А5 Решение: Из рисунка 93 сразу видно, что решением
является интервал (—4; 1). ■
Ответ: 2).
А6 Решение: log2(a;+7) < 2 <=> \Х * 1 J °' <=> х б (-7; -3]. ■
[X -р ( ^ 4.
Ответ: 3).
248

А7 Решение; Найдем сначала производную, а затем подставим
заданную точку. Получаем,
у'(х) = -sin2x - 2 + 4 =Ф у' (|) = -2sin§ + 4 = 2- ■
Ответ: 1).
А8 Решение: Известно, что площадь криволинейной трапеции,
ограниченной графиком функции у = f(x) и прямыми у = О,
2
ж = 0, а; = 2, равна / f(x)dx и состоит из заштрихованного
о
криволинейного треугольника и прямоугольника (рис. 94). По
условию, площадь заштрихованной части равна 7, площадь пря-
2
моугольника равна 2, следовательно, / f(x) dx = 9. ■
о
Ответ: 3).
А9 Решение: Функция у(х) = 2\/# + 1 определена для ж ^ — 1
и у(—1) = 0. Следовательно, это график под номером 3. ■
Ответ: 3).
А10 Решение: Из рисунка 96 видно, что автобус стоял 2 часа (с
2 до 4 часов), поэтому он двигался 5 часов. 9
Ответ: 2).
В1 Решение: Найдем из заданных соотношений cos (а — /3):
Г cos a + cos /3 = 0,3, Г cos2 qt + 2 cos a cos ft + cos2 /3 = 0,09,
\sina +sin/3 = —1,1 \sin2a + 2sinasin/3 + sin2/3 = 1,21.
Сложим уравнения и получим:
2 + 2 cos(a - /3) = 1,3 4=> cos(a - /3) = -0,35,
откуда 20cos(a - /3) = -0,35 • 20 = -7.
Ответ: —7.
249

В2 Решение: Представим исходное уравнение в виде
л/5 sin х + cos 2х = — 2 cos ж
и воспользуемся условием равносильности (3) на стр. 35:
у/Ь sin х + cos 2x = —2 cos x
, ^ fcosz ^0,
\5sina; + (I — 2 sin2 ж) = 4(1 — sin2 ж).
fcosz^O, (cosz^O,
\2 sin2 ж + 5 sinx — 3 = 0. | sinx = ~
x = ~^ + 2тгп, , n € Z.
Заданному промежутку принадлежит единственный корень х =
= 150°. ■
Ответ: 150.
83 Решение: Применим формулу Ньютона-Лейбница:
7Г
2 £
/ 2sin2a?cte = -cos2a: 2= -(-1 - 1) = 2. ■
J lo
о
Ответ: 2.
84 Решение: Воспользуемся тем, что 2 — х = log3 32~x. Тогда
1оёз(3* - 8) = 2 - х «=>. log3(3x - 8) = log3 3
2"1
3х - 8 = З2 • ^
О
(ОДЗ логарифма выполнено автоматически)
(Зж)3 ~8-Заг-9 =
Уравнение Зж = — 1 решений не имеет.
Ответ: 2.
250

В5 Решение: Стандартный способ.
Рассматриваем 2 случая знака правой части:
1х + 3 > х + 1
х2 + 2х
-3<х<-1, Г,.6г_з._1
в + 2)(* -1) < о ^ж е I-i; 1)
Длина промежутка равна 4.
Графический способ.
Грамотный школьник прикинет эскизы правой и левой
частей.
У
Рис. 122
Из рисунка 122 сразу видно решение: х Е [—3; жо), где хо —
решение уравнения
1х + 3 = х + 1
+ 3 = х1 + 2х + 1
Это решение можно и угадать — корень извлекается нацело при
Ответ: 4.
251

В6 Решение: Решим неравенство:
»3x+i
34«»-3x+i
4х2 - Зх + ± ^ 40ж2 <^=* (ж + ±) (ж - i) < 0
Длина промежутка, являющегося решением, равна у~ + ^ = т-
Ответ: 0,25.
87 Решение:
Ъ2х = 115 • б*"1 + 50 *=> (5х)2 - 23(5Ж) + 50 = 0
О — ZO,
5х = -2.
Показательная функция принимает только положительные
значения, поэтому уравнение 5х = —2 не имеет решений.
Таким образом, сумма всех корней уравнения равна 2. ■
Ответ: 2.
88 Решение:
~2 — От — 4 — 9 — т
Второй корень, х = 3, квадратного уравнения
я2 - ж - 6 = 0
не является решением заданного логарифмического уравнения,
т. к. не удовлетворяет условию 2 — х > 0, т. е. не принадлежит
ОДЗ уравнения. Единственный корень х = — 2 является
наибольшим. ■
Ответ: —2.
252

В9 Решение: Формализуем условия задачи. Пусть ап —
арифметическая прогрессия с разностью d, Ьп — геометрическая
прогрессия со знаменателем q. Тогда
bi 5'
= 0,5ai,
a2-36 =
f O£
Подставляем значения для Ь\ и q в четвертое уравнение и
решаем его совместно с третьим:
{0,5ai = —2,5d, ai 2
^ •"у)» д^ — -—- — 36 == oTr"ai )>•
а\ 4- a — 36 = 0,5ai • ^ 5 25
=> ai = 50. ■
Ответ: 50.
BIO Решение: Пусть SABC — данная пирамида, ABC —
правильный треугольник в ее основании. Пусть плоскость
проведена через сторону АС и центр вписанного шара О. Плоскость
пересекает ребро SB в точке D (рис. 123). Так как О — центр
вписанного шара, то плоскость ADC делит двугранный угол при
стороне АС пополам. Каждая точка этой плоскости
равноудалена от граней ASC и ABC. В частности, точка D
равноудалена от граней ASC и ABC. Поэтому высоты пирамид ADCS и
ADCB одинаковы. Значит, их объемы относятся как площади
оснований AS С и ABC. Эти основания имеют общую сторону,
следовательно, их площади относятся как высоты SH и ВН
треугольников ASC и ABC, опущенные на их общую сторону АС.
Найдем это отношение. Пусть длина стороны основания
равна а, тогда длина бокового ребра, по условию, равна 3,5а.
Высоты находятся из соответствующих равнобедрюнных
треугольников ASC и ABC, и мы получаем, что
253

vA
= 4.
Ответ: 4.
3,5a
Рис. 123
Bll Решение: Пусть дана трапеция ABCD (рис. 124), О —
точка пересечения диагоцалей. Так так трапеция равнобедренная,
то треугольник ВОС равнобедренный, а так как угол ВОС —
прямой (по условию), то /.ВСО = 45°. Проведем высоту MN
через точку О. Тогда она делит утол ВОС пополам. Поэтому
ZNBO = ZBON = ZNOC = ZNCO = 45°. Отсюда BN =
= NC = N0. Аналогично, AM = МО.
Площадь равна
25 =
AD + BC
MN = {МО + MN) • MN = MN2,
откуда MJV = 5.
Ответ: 5.
254

С1 Решение: Заметим, что х = 0 не является решением
уравнения, поэтому
х* + 5х3 + 4ж2 - 5ж + 1 = О
х2 (х2 + 5ж + 4 - | + -L J =
О
ж-±--2
х х - z,
х2 + 2х - 1 = О,
= -1 ± V2,
-3±л/13
о: =
Сумма всех четырех решений равна —5. ■
Ответ: —5.
С2 Решение: Сначала найдем ОДЗ: х2 + х + 1
Теперь воспользуемся правилом 3 на стр. 64:
х
х + 1 - 2х - 1
( уж2 + х + 1 — 2х -
.2 j. /,. j_ 1 0-г 1
>0
2) х
- 2х - г) > 0
(-4s - 3) > 0 «=Ф ж € (-оо; -|) .
X
Ответ: (-оо;-0,75).
СЗ Решение: Преобразуем сначала выражения, стоящие в
правой и левой частях неравенства, а потом воспользуемся
правилом 5 на стр. 77:
!=► З*2 • 34х • 81 + 4 - Сг - 81
255

81
*(3*2 - 1) - 5!_ZlA = 81(3x2 - 1)(34*
<=> x2{4x + 7) < 0 4=> x e (-oo;
Ответ: (-оо; -1,75] U {0}.
7?) ^ 0
U {0} .
C4 Решение: Первый способ.
F
1. Объем пирамиды AMLC вычислим по формуле
Vamlc = -nScLMK
о
где /i — высота пирамиды (рис. 125). По условию FA X ABC.
Значит, FA ± ВС. Но АВ ± ВС, следовательно, ВС _L ABF и
поэтому AM -L ВС. Значит, AM — высота пирамиды AMLC,
опущенная на плоскость грани CLM, т.е. h = AM. Из
прямоугольного треугольника ABF:
h _ ABAF _ 3-4 _ 12
BF ~~ 5 "" 5 "
256

2. Треугольники CLM и CFM имеют общую высоту,
проведенную из вершины М. Поэтому
Sclm = CL_
Scfm CF'
Аналогично, CFM __ _^М.# Следовательно,
&CFB &"
Sclm ^
Scfb CFBF'
Отсюда Sclm = %'™ ' Scfb>
3. Отрезки CF и СХ, BF и FM найдем соответственно из
прямоугольных треугольников ACF и AFB. Имеем
V41
BF = y/AB2 + AF2 = 5, FM =
4. Поскольку jBC -L ABF, to jBC JL BF. Поэтому площадь
треугольника CFB найдем по формуле
Scfb = ^2БС = 10.
Вычислим площадь основания пирамиды AMLC:
_CLFM л ^А 16 1 1 in - 160
- CF5F ^CFB " V4 5 ^/iT 5 1U "" 41 '
а искомый объем VAMlc = \'1[Г'Т = Ж'
Второй способ.
1. Объем пирамиды AMLC вычислцм по формуле
Уamlc = -^Salc^m,
где км — расстояние от вершины М до плоскости FAC (см.
рис. 126). Так как FA ± АС и AL ± FC, то
257

в
Рис. 126
лр . \г* on
и AL = ^ - ^ = ~7=- Следовательно,
400 25
л/5Г
ALLC 250
= 2 = 1Г'
2. Проведем высоту кв прямоугольного треугольника ABC,
кв JL АС. Так как AF J_ Л5С, то /i£ -L AF. По признаку
перпендикулярности прямой и плоскости /i# J_ FAC. Поэтому к в —
расстояние от вершины В до плоскости FAC.
3. Вычислим кв-
h = Aff ■ ВС = 12
в АС 5 '
Перпендикуляры ВХ и МР, опущенные на плоскость FAC из
точек В и М, параллельны между собой и лежат в плоскости,
содержащей прямую BF. Поэтому треугольники FBK и FMP
подобны. Отсюда
BF BK kB
MF МР км'
Поэтому км = "Е"
258

4. Из прямоугольного треугольника FAB:
= 5 и AM =
5 "
Из прямоугольного треугольника FAM:
10 1 fi
Следовательно, км = ¥• • ^к и
о о • о
v =1 12-16 250 = 4 ■ 16 - 2 = 128 _
AMLC 3 " 125 41 41 41 '
Ответ: Щ.
41
С5 Решение: Пусть 5х = £, t > 0, тогда уравнение примет вид
£2 — (а — l)t + 2а + 3 = 0. Задача сводится к нахождению таких
значений параметра а, при которых квадратное уравнение имеет
одно положительное решение.
Это имеет место, во-первых, если уравнение имеет
единственное решение и оно положительно, т. е.
D = а2 - 10а - 11 = (а - 11)(а + 1) = 0 Р ^
и £ > 0. В нашем случае при этом t = —^—? и решение
положительно, если а = 11.
Во-вторых, одно положительное решение будет и тогда,
когда дискриминант положителен, но решения разных знаков. Это
имеет место, если
D>0, /o6(-po;-l)U(ll;+oo)
Если D > 0, но 2а + 3 = 0, то * = -|.
259

Из этих условий следует, что о€ (— оо; — ^ 1.
Ответ: (-оо; -1,5) U {11}.
Решение варианта 12
А1 Решение:
= 250 + 2 л/5 = 28
г, 5^ ' 9 5-
Ответ: 1).
А2 Решение: Функция определена при всех #, кроме х = 5.
Такой ответ дан под первым номером. ■
Ответ: 1).
A3 Решение: Выпишем, для наглядности, сложную функцию
\ 5 — 8lgж — lg2 ж
) = ^П
Теперь видно, что область определения D(y) задается системой
х > 0, fx > 0,
Такой ответ дан под третьим номером. ■
Ответ: 3).
А4 Решение: Данная функция имеет вид
?/ — 2Х*~1 — i . 2°°2 — i - 2Z
y_z -2 ~~2'
где z = х2. Функция z = х2 принимает все значения,
принадлежащие промежутку [0;+оо). Непрерывная функция 2Z на
260

[0; +оо) принимает все значения, принадлежащие промежутку
2
[1;+оо). Отсюда следует, что ~ • 2Z принимает все значения из
промежутка [0,5; +оо). ■
Ответ: 4).
4 ~—
4 ~— пг
А5 Решение: Функция у(х) = In ——-г является нечетной, т. к.
Х
Ответ: 2).
А6 Решение: Уравнение касательной к кривой у = f(x) в точке
с абсциссой х = хо имеет вид:
В данном случае f(x) = Зж2, х0 = 2, /'(2) = 12, /(2) = 8 и
уравнение искомой касательной имеет вид
у = 12(ж - 2) + 8 = 12ж - 16. ■
Ответ: 1).
А7 Решение: На графике 118 две критические точки, но один
локальный максимум. ■
Ответ: 2).
А8 Решение:
такой ответ дан под третьим номером. Ответ желательно
проверить дифференцированием:
( Цг + jcos4rc 1 = х2 — 3sin4o;.
И вообще, правильный ответ можно найти, взяв производные от
предложенных вариантов. ■
Ответ: 3).
261

А9 Решение: Задачи такого типа легко решаются
построением графиков левой и правой частей. Получаются рисунки типа
рис. 93. Кроме того, задачу можно решить и аналитически:
Ъу/х + 5 = х 4-
Ответ: 2).
А10 Решение:
|5 — 7х\ <
Ответ: 1).
В1 Решение:
Ответ: —0,5.
В2 Решение: Учтем, что
Так как
3 при a ^ 0.
/1й I 1\2 / „I 5 1 1
( сГббб +азЬз 1 +(а б6б-аЗбз
(3/ Г 3/7 f\ / 3/~9 i З/То , ЗГ~Г\ СХ — Ь
va"1 — v Ь"1) ( у а1 + у о2 + уаЬ\
/ _1 5 2 2\
2 fa зЬз +азЬз 1
262

2a
1 1
2a?+ 2ab 2b2 + 2ab - 2a? - 2ab
b-a
b-a
b-a
= 2(a
то
ВЗ
исходное
Ответ:
выражение
2.
Решение:
Ответ:
2.
1
1
3
равно 2.
г
г
3
В4 Решение: Максимум функции будет в тех точках, где
производная равна нулю и меняет знак с «+» на «—», т.е. надо
найти все точки, в которых график производной пересекает ось
сверху вниз. На рисунке 127 эти точки отмечены.
Рис. 127
Ответ: 3.
263

В5 Решение: Преобразуем заданное выражение:
2cos2z- 12sinz-6 = 2(l -2sin2£) - 12sinx-6 =
|) +5.
(Q\ 2
t + ~ J +5 убывает на
отрезке [-1; 1], а поэтому /max(*) = /(-1) = 4.
Ответ: 4.
B6 Решение:
(х2+Зр+1){х2+Зх-3) ^ 5 <=> (x2+Zx)2-2(x2+3x)-8 ^ О
((х2 + Зх) - 4) ((я2 + Зх) + 2) ^ О ^=Ф
(х + 4)(х - 1){х + 2)(х + 1) ^ 0.
Решая неравенство методом интервалов, получаем, что
х € (-оо; -4] U [-2; -1] U [1; +оо).
В рещрние не входят два целых числа: — 3 и 0. ■
Ответ: -3.
87 Решение: Скорость v(t) — это производная от координаты,
т. е. в нашем случае v(t) = x'(t) = 10* — 4. По условию v(i) = 26,
т. е. 10* - 4 = 26, откуда t = 3 (с), ■
Ответ: 3.
88 Решение: Найдем а, при которых пара х = 1, у = 1 является
решением системы:
(а2-а = 1-а, /о = ±1 Гв = 1, 6 =-1;
\Ь + 3 - 26 = 3 + о \Ь = -а [а = -1, Ъ = 1.
Теперь выясним, сколько решений имеет система при этих а, Ь.
264

Рассмотрим случай а = 1, Ь = — 1:
-x + Ъу — 4 *
Рассмотрим случай а = —1,6 = 1:< , _ «' — эта систе-
ма имеет бесконечно много решений.
Поэтому а = 1, Ь = —1. ■
Ответ: 1.
В9 Решение: Преобразуем уравнение:
_ 8 = 2 . 8*2+з <*=» АгхЧх - 8 - 2 •
. 2з*2+х -8 = 0 4=» 23а;2+х = 4
Зх2 + х - 2 = 0 Ф=> (Зж - 2)(х + 1) = 0.
Корнями уравнения являются числа — 1 и ^, их утроенная сумма
равна —1. ■
Ответ: — 1.
В10 Решение: Так как грани равнонаклонены к основанию, то
вершина пирамиды проектируется в центр вписанной в
основание окружности (докажите!). Ее центр, точка О лежит на
пересечении биссектрис треугольника ABC (рис. 1286)). В этом
треугольнике отрезки AN и AM равны, как касательные,
проведенные из одной точки к окружности, аналогично, ВК = ВМ.
Пусть г — радиус вписанной в основание окружности, р —
полупериметр основания. Тогда АВ = AN + В К и
p=
Обозначим ZCAO = /.ВАО = а. Тогда
ZOBM = 90° ^ 2а = 45° - а.
265

а б
Рис. 128
Вычислим /.АОВ:
/.АОВ - /АОМ + /MOB = (90° - а)+(90° - (45° - а))= 135°.
По теореме косинусов для треугольника АОВ имеем
АВ2 = 1 + (3\/2)2 - 2 • 1 • Зл/2 • cos 135° = 25 <=> АВ = 5;
а так как для площади треугольника АОВ выполнено равенство
Saob - \ ■ 1 • 3\/2 • sin 135° = \ ■ АВ ■ МО «=h | = |МО,
О
то мы нашли г = МО = f — радиус вписанной окружности.
5
Так как по условию sin(/.SMO) = тг, то из треугольника
SMO имеем (рис, 128 а)):
МО = SMcosZSMO «=► ! = SM • 4/1 -
Теперь найдем искомую площадь
25
169
Ответ: 3,64.
266

В11 Решение: Пусть ABC — исходный треугольник.
Обозначим угол, равный 30°, буквой Л, угол в 60° — буквой U, угол в
90° — буквой С. Полученный по продолжениям биссектрис
треугольник обозначим LNM (рис. 129). По свойству биссектрисы
и правилам вычисления вписанных углов имеем:
Z.M = ZLMC+ZNMC = ZLAC+ZNBC =
/Б) = 45°.
м
Рис. 129
Аналогичнр рассуждая, получаем: Z.L = 75°, ZN = 60°. Йо
теореме синусов, длина стороны вписанного треугольника равна
произведению диаметра окружности на синус противолежащего
угла. Отсюда следует:
Sabc = \ • АВ • ВС • sinZJB = | • 2JRsin30° • 2i*sin90° • sin60°,
Slmn = \ • 2R sin 75° - 2^sin45° • sin 60°.
Теперь вычисляем t:
£ Sabc
Slmn
Отсюда (t +
Ответ:
3.
sin 30°
sin 75°
•sin 90°
•sin 45°
■
§ (cos 30°
l
2
-cos 120°)
V3 + i
267

С1 Решение: Решаем неравенство:
VX - ft — (х > О,
О
xe{0}U(l;7).
Ответ: {0}U(l;7).
С2 Решение: Найдем ОДЗ, используя правила 1 на стр. 48 и 9
на стр. 96:
Г#>0, хф 1,
Перейдем во всех логарифмах к основанию 2:
log2 х
ж • л
log2a;
log2 ж
Решим леравенство в каждом промежутке ОДЗ отдельно:
1. х Е (0; 1) =r> log2 х < 0 и неравенство выполнено.
2. Если х G [4;+оо), то Iog2# ) 2и неравенство можно
возводить в квадрат:
a: - 2) < 2
(log2* - (1 - л/3)) (log2x- (1 + л/3)) < 0 £3
268

(log2 x - log2 21+л/5) < 0 <^> [x -
(воспользовались правилом 7 на стр. 82).
Окончательный ответ получаем, объединяя оба случая.
Ответ: (O;1)U [4;]
СЗ Решение: Пусть у/х + у = и ^ 0, х = v => у = и2 — v, тогда
исходная система уравнений примет вид (х ф 0):
Зх2 — х — у — 2ху/х + у = 0,
л/у + л/я + у = у - Зж - 6
= (v _ t*)(3v + и) = О,
= w2 - 4v - 6.
Решением первого уравнения является и = v или м = — 3v.
Теперь решим второе уравнение для каждого из этих случаев
отдельно.
1. В случае и = v получаем:
и = 6,
и2 -Ьи-6 = 0
Так как и ^ 0, то вторая пара не является решением. Переходя
к старым переменным, получаем х = 6, у = 30.
2. В случае и = —3v второе уравнение примет вид:
\/9v2 - v - 3v = 9v2 - Av - 6
9v2 - Av) -
9v2 - Av - 9 = 0
Av = 3-
v =
v =
9
\/85
Г 2 - л/85 29 - \/85
* = —9—•» = —у—;
[гх = — 3v < 0 (решений нет).
269

Объединяя оба случая, получаем окончательный ответ.
С4 Решение: Пусть равнобедренный треугольник AS В
является осевым сечением конуса (рис. 130), О — середина основания.
Тогда SO = Я, О А = R. Прямоугольник MNKL является
осевым сечением вписанного цилиндра. Пусть ОМ = х — радиус
цилиндра, MN = h — его высота.
Из подобия треугольников AMN и AOS имеем -~ = —^~^?
откуда h = %(R — %)• Площадь боковой поверхности цилиндра
вычисляется по формуле
S6oK = S(x) = 2irxh =
2тгЯ
x(R-x)
и является (как функция радиуса х) квадратным трехчленом,
точка максимума которюго находится посередине между корня-
ми, т. е. в точке х = -у. Для этой точки получаем максимальное
значение площади
R
2тгЯ (R
wHR
Ответ: |
270

С5 Решение: Разложим левую часть на линейные множители:
Зх2 + Ъху + 2у2 = 7 <=> (х + у)(3х + 2у) '= 7.
Так как 7 число простое, то оно равно произведению двух целых
чисел в четырех случаях:
= -1,
' U = 5,
аг = 13,
у = -20.
Ответ: (-5; 4), (5;-4), (-13; 20), (13;-20).
Решение избранных задач
из других вариантов
Вариант 2
В1 Решение: Функция у = sin2 x — четная, потому достаточно
найти число решений на отрезке [0; 2тг]. Итак,
cos2x = —-у
х = ±-^ + тгп, п Е Z.
Отметив эти корни на тригонометрическом круге (рис. 131),
видим, что на отрезке [0; 2тг] цаходится 4 нуля, значит, йа заданном
отрезке находится 8 корней. ■
Ответ: 8.
271

Рис. 131
Замечание: Можно было воспользоваться тем, что у =
— sin2 х имеет период, равный тг. А так как на [О;тг] исходное
уравнение цмеет 2 корня, то сразу получаем ответ.
В2 Решение: Решаем неравенство:
х2 - Зх - 4
В силу правила 4 на стр. 65, знак разности \х — 4| — 2 совпадает
со'знаком произведения (х — 4 + 2}(х — 4 — 2), поэтому получаем
неравенство (х — 2)(х — 6) ^ 0. Решением является отрезок [2; 6],
длина которого 4. ■
Ответ: 4.
В7 Решение:
sin 2х = sin ( ~ — # J «Ф=>> 2 sin ж cos х = cos ж <Ф=Ф>
cos х = 0, Гж == т> + я^э
> >w I 1 ^ >w I Z _ 4
| 8ШХ = t: iP ^ V~~l) "2" "Г 7ГУ1, 71 E ^j
L Z L и
%_ f 7Г 2t Q7T 37Г1 ^- Ггч Зтг I
=^ 16'2' 6 ' 2 Xе- L ? 2 J'
Их можно явно не находить, а лишь отметить на тригонометри-
ческрм круге (см. рис. 132) — их четыре. ■
Ответ: 4.
272

Рис. 132
В9 Решение: Добавим т литров первого раствора во второй.
Тогда в нем будет (50+т) -0,015 литров кислоты, из них т-0,005
литров из первого раствора, 50 • 0,02 литров второго. Итак,
получаем, что (50 + т)1,5 = 50 • 2 + т • 0,5 <=> т = 50 • 0,5. ■
Ответ: 25.
В10 Решение: Пусть дана пирамида SABCD (рис. 133). Пусть
высота пирамиды SE равна Л, тогда радиус ОС описанной сфе-
10 Зак 243
273

ры равен ЗЛ. Обозначим апофему боковой грани SH. Товда
искомая величина равна
(2CDSH)2
CD2
\SOch)
CD2 '
Из треугольника ОСЕ получаем СЕ2 = ОС2-ОЕ2 = 9/i2-4h2 =
= 5Л2, из треугольника СЕН вычисляем СН2 = \СЕ2 = \У? и
7
из треугольника
14
5 7
получаем 5Я2 = h2 + ^h2 = ~Л2. Теперь
=
CD2 (2СЯ)2
Ответ: 1,4.
В11 Решение: В шестиугольнике все углы равны, значит,
каждый угол равен ^ = -^ и поэтому каждый смежный
угол равен ■=-. Отсюда вытекает, что треугольники (см. рис. 134)
о
KLM, ALBj CMD и EKF — равносторонние, следовательно,
1 + FA + 3 = 3 + 4 + 5 = 5 + DE + 1, откуда FA = 8, DE = 6 и
их сумма равна 14. ■
Ответ: 14.
К 1
274

С1 Решение: ОДЗ неравенства х Ф — 1. Как и при решении
задачи В2, воспользуемся правилом 4 на стр. 65:
1^2 - 5ж - 4| - 2 [д; Ч- Ц ^ ^ ^дз
^ U Ч»
Х + 1
\х + 1\
(ж2 - Ъх - 4 + 2х + 2)(х2 - Ъх - 4 - 2х - 2) < О
(ж2 - Ъх - 2){х2 - 7ж - 6) < О «=* (х - —
и
Первый промежуток целых чисел не содержит, а во второй
промежуток входят целые числа 4, 5, 6, 7. Их сумма равна 22. ■
Ответ: 22.
С2 Решение: Заметим, что (2 + л/3)(2 — л/3) = 1. Обозначим
(2 + л/3)х через t. Решаем исходное неравенство, учитывая, что
t>0:
t + 2 < | 4=> t2 + 2t - 3 ее (t + 3)(* - 1) < 0 => t < 1
Ответ: (~оо;0).
СЗ Решение: Введем новые переменные и = л/\1х — у, и ^ 0;
t; = д/у — ж, г; ^ 0. Тогда
- у = п2, одз Гж = 0,1(г/2 + v2),
- х = v2 <==^ \у = 0,1(1Ь2 + г^2),
и, кроме того, 6у — 26ж = — 2(11х — у) + 4(у — х) = —2гх2 + 4v2.
Теперь в новых переменных система принимает вид
275

_ 5 = о ^^ v =
Ответ: (0,5; 1,5).
Вариант 3
ВЗ Решение: Используем формулу преобразования
произведения косинусов в сумму:
cos ( 7ГJ" х) • cos ( ЖГ х) = 1 4=> совЗтга; 4-cosx = 2
f cos Зга = 1,
\cosa: = 1.
Решением второго уравнения системы является х = 2тгп, п Е Z.
Подставив его в первое уравнение, получаем, что cos67r2n = 1.
Так как тг — иррациональное число, то это возможно только при
п = 0. ■
Ответ: 0.
В7 Решение: Воспользуемся правилом 5 на стр. 77:
2(х - 3) (х - |)
2х-
х - log2 б
Проведем сравнение чисел | и log2 6:
log2 36 > log2 32 ^=^> 2 log2 6 > 5 «=» log2 6 > |.
276

Теперь решим неравенство методом интервалов и получим, что
z<E(-oo;2,5)U(log26;3).
Следовательно, наибольшим целочисленным решением
является х = 2. ■
Ответ: 2.
С1 Решение: Применяем условие равносильности (11) со
стр. 62:
\хъ - 6а:2 + 9х - 6| ^ хь - 2а:3 + 6а:2 - Ш + 6 <=>
Га:5 - баг2 + 9х - 6 ^ ж5 - 2ж3 + бгг2 - 13ж + 6,
| - бж2 + 9гг - 6 ^ -о:5 + 2я3 - 6ж2 + 13а: - б
я5 - я3 - 2а: < 0.
[х2 + 1)(х - л/2)(ж + уД) < О
Гхе[1;2]и[3;+оо),
|х€(-оо;-\/2]и[0;л/2].
х € (-оо; -л/2] U [0; 2] U [3; +оо).
Ответ: (-оо; -у/Ц U [0; 2] U [3; +оо).
С2 Решение: Найдем сначгша ОДЗ:
(V + 4х + 3 ^ 0, (х € (-со; -3] U [-1; +оо),
\аг2 - 2х + 2 > 0 \х е К
<J=^> а; € (-оо; -3] U [-1; +оо).
Так как обе части неотрицательны в ОДЗ, то
\/a:2 + 4а: + 3 < 1 + \/а:2 - 2а: + 2
^1 а:2 + 4х + 3 < 3 + а:2 - 2а: + 2д/ж2 -2х
277

yjx2 - 2:r + 2 > 3rr
i
о,
х2 - 2х + 2 > 9х2
хе 0;
8 ' 8
Учитывая ОДЗ, получаем ответ. ■
Ответ: (-оо; -3] U -1; ~~ \
СЗ Решение: В силу периодичности /(ж), во-первых,
достаточно найти решения уравнения на любом отрезке длины 8, во-
вторых, f(2x + 16) = /(2rr), поэтому
f(2x + 16) + 23 =
23 =
Посмотрим, при каких п аргумент /(2ж+п-8) принадлежит
промежутку, в котором формулой определена /(ж), т.е.
О < 2х < 8 - 8п,
16 > 2х > -8п
Рассмотрим каждый случай.
При п = 1 имеем 0 < ж < О
уравнение не имеет решений.
При п = 0 получаем
Гп<1,
ж = 0, тогда /(0) = 0, и
О < 2х < 8
О < ж ^ 4 =Ф /(2ж) = 8 • 2х - (2ж)2
==» 16ж - 4х2 + 23 = 40ж - Ъх2 ■■
При п = — 1 получаем
О < 2х - 8 ^ 8 ^=» 4 < х < 8
/(2ж) = /(2ж - 8) = 8(2ж - 8) - (2х - 8)2
16ж - 64 - 4х2 + 32s - 64 + 23 = 40ж - 5ж2
278

х2 + 8х - 105 = 0 =» х = 7.
В силу периодичности, решениями будут числа 1 + 8п,
7 + 8m, n, m e Z. ■
Ответ: 1 + 8п, 7 + 8m, n, m G Z.
С5 Решение: Воспользуемся условием равносильности (11) на
стр. 62:
2 [2(# — а) ^ а2 — #2
2
-х2 <=> \п) [^ 2 2
[2( ) ^а
) [^ 2 2
и теперь видно, что решение задачи зависит от взаимного
расположения точек а, —а — 2, —а + 2.
1. Пусть а ^ 0. Тогда можно нанести на числовую ось
точки а, —а, —а — 2 и решение первого неравенства совокупности
увидеть на рисунке 135: х G (—оо; —а — 2] U [а; +оо).
-а-2 о
////////А 1 1 *5^
-а 0 х
Рис. 135
Решение второго неравенства зависит от расположения
точки х = —а + 2 относительно точки х = а. Это или
ж Е (-оо; -а + 2] U [а; +оо) или х G (-оо; а] U [-а + 2; +оо).
Теперь ясно, что только во втором случае решением
совокупности может быть вся числовая ось — для этого необходимо и
достаточно, чтобы
-а+ 2 ^ а 4=> а ^ 1.
Итак, а€ [0;1].
2. Пусть а < 0, тогда решение второго неравенства можно
увидеть на рисунке 136: х G (—оо; a] U [—а + 2; +оо).
279

а -a+2
О -а х
Рис. 136
При этом решением первого неравенства будет либо
множество (—оо; —а — 2] U [а; +оо), либо (—оо; о] U [—а — 2; +ос).
Видно, чтобы решением совокупности неравенств была вся числовая
ось, необходимо и достаточно выполнение условия:
-а-2 ^ а<=>а > -1.
Получаем, что a Е [—1;0).
Объединяя оба случая, получаем окончательный ответ. ■
Заметим, что совокупность неравенств легко можно решить
графически в плоскости (ж; а).
Ответ: [—1;1].
Вариант 4
В2 Решение: В силу периодичности, /(0) = /(fc\/2), к Е Z.
Следовательно,
/(0) = /(2ч/2) = /(V8) = /(-л/2) = /(6л/2) = /(л/72).
Поэтому
/(0) = -|.
Поэтому 3/(\/8) = -4.
Ответ: —4.
280

В8 Решение:
11 • 3х-1 - 31 > 5 ^^
4 • 9х - 11 ■ 3х-1 - 5 ""
20 • (3х)2 - f • 3х - 25 - ^ • 3х + 31
4(3Х)2 - Ц- • 3х - 5
12 • (З1)2 - 11 • Зж - 15 (З1 - |) (3х + |
1 5
3х - 3 gs з
х€ (-оо; log3 i] U [log3 |; log3
и наибольшим целым решением является число 0, т. к.
1 > log3 | > 0 > log3 |.
Ответ: 0.
С2 Решение:
7г + |) ' *S3 (f - Зтг) ctg (тг
- _1.
" 2
Так как -| < -|, то Л < В. ■
Ответ: 5 (второе число больше).
281

СЗ Решение:
\w-
- х2
\х2 - 8х + 2| - х2
2,
-ж2 < -2ж-
ж2-8ж + 2| ^ж2 + 2ж +
2 - 8ж + 2 > ж2 + 2х + 2,
ж2 - 8ж + 2 < -ж2 - 2х - 2;
ж2 - 8ж + 2 > -ж2 + 2ж 4- 2
жб[1;2];
Г > 2
Г^ 3'
Дж€ (-oo;0]U[5;+oo)
ж € (-оо; 0] U [1; 2] U [5; +оо).
Ответ: (-оо; 0] U [1; 2] U [5; +оо).
С4 Решение: Пусть сторона нижнего основания равна а,
верхнего — 6, высота пирамиды — /г, высота трапеции AD'C'B
равна h\. Тогда
искомая площадь равна S = ( ^— J . Найдем связь между h и
h\. Для этого прюведем сечение EGFK, перпендикулярное
основаниям (рис. 137). Четырехугольник EGFK — равнобедренная
трапеция, FM = h — ее высота.
Из треугольника EFM получаем
+h2 =
2_(а + Ь)2
282

Ответ: ^5| - 0,5 • Sjf.
C5 Решение:
:^
Совокупность уравнений проще всего решить графически в
плоскости (ж, а). На рис. 138 видно, что имеется ровно три решения
при a = -3 и о = 4. ■
Ответ: —3; 4.

Вариант 5
В1 Решение: Проведем тождественные преобразования,
используя формулы
sin(a ± /3) = sin a cos /3 ± cos a sin /3
и cos f ~ — aj = sin a:
tg 2ж • ctg(70° - or)+tg 2a; • ctg(20° - a?) - ctg(20° - ж) • ctg(70° - ж) =
cos(70° - ж) cos(20° - ж)
+
_ /co
~ tg " Vsi
cos(20° - ж) со8(70°-ж) _ Sjn2x sin(70° - x + 20° - ж)
sin(20° - ж) ' sin(70° - ж) "~ сов2ж ' sin(70° - ж) sin(20° - ж)
соз2ж
= ^
sin(20° - ж) sin(70° - ж) cos 2ж ' sin(70° - ж) sin(20° - ж)
\ (sin 2ж + cos 50°) sin 2x-\ (sin 2ж + cos (90° - 40°))
sin(70° - ж) sin(20° - ж) sin(70° - ж) sin(20° - ж)
|(sin2a; - sin40°) _ sin(a? - 20°) соз(ж + 20°)
"" sin(70° - ж) sin(20° - ж) "~ sin(70° - ж) sin(20° - ж)
sin(a; - 20°) сов(ж + 20° + 70° - 70°)
= -1.
sin(70° - ж) sin(20° - ж)
_ - sin(20° - x) sin(70° - ж)
"" sin(70° - ж) sin(20° - ж)
Ответ: — 1.
Cl Решение: Воспользуемся условием равносильности (10) со
стр. 61:
|3ж3 - 2ж2 - 5ж + 1| < ж3 - 2х2 - х + 1
f Зж3 - 2ж2 - Ъх + 1 < х3 - 2х2 - х + 1,
I Зж3 - 2х2 - Ъх + 1 ^ -ж3 + 2х2 + х - ]
284

xG (-оо;-л/2]и[0;л/2],
Ответ:
C2 Решение: Найдем сначала ОДЗ: {х > 0, 4ж ^ 1> У > 0}.
Далее,
Uog2(xy) • log4a:y = 2,
\8x - у = 1
2/ = 4
J(log2 у - 2)(log2 x + log2 у + 2) = 0, ^ J | _ i.
™"" 4'
Если ху = -т, то а; = QO и оба значения не входят в ОДЗ. Если
же у = 4, то х = ^. ■
о
Ответ
о
: (|;4).
СЗ Решение: Заметим, что во втором неравенстве легко
выделяется полный квадрат. Тогда
Зх2 + 2ху + 3 < 0, (Зх2 + 2ху + 3 < О,
О \(у + З)2 - 9 + 18ж ^ О
Зж2 + 2х(у + 3 - 3) + 3 < О,
285

Зх2 + 2х{у + 3) - 6х + 3 ^ О,
(у + З)2 - 9 + 18х < О.
Теперь очевидно, что, если сложить утроенное первое
неравенство со вторым, то избавимся одновременно от свободного и
линейного относительно х членов. Получим
= (Зх + у)2 + 6(3х + у) + 9 = (Зх + у + З)2 < 0 <=>
<=> (Зх + у + З)2 = 0 «=* 3(3ж2 + 2ху + 3) + у2 + 6у + 18ж = 0.
Таким образом, заключаем, что система неравенств
равносильна системе уравнений, так как сумма неположительных чисел
равна 0 тогда и только тогда, когда оба равны 0. Решаем
систему
\
у = -За; - 3,
х2 + 2х - 1 = 0
х = -1 ± л/2,
у = тЗл/2.
Ответ: (-1 =F \/2;
Вариант 6
В8 Решение: В этом уравнении присутствует «ловушка»:
нельзя Iog3(a; — 5)2 заменить на 21og3(x — 5), потому что в ОДЗ
разность х — 5 может быть как положительной, так и
отрицательной. Итак,
Iog3(* - 5)2 - log3 81 = log3(x - I)2
\(х - 5)2 = 81(я? - I)2 ^ \(4 - 8я?)(10я: - 14) = 0
286

х = 1,4. ■
Ответ: 1,4.
Замечание: Если избавляться от квадрата х — 5, то надо
воспользоваться формулой Iog3(# — 5)2 = 21og3 |ж — 5| и далее
решать уравнение |гг — 5| = 9(о; — 1) при условии х > 1.
С2 Решение: В ОДЗ обе части неотрицательны, и
стандартный метод возведения в квадрат обеих частей приведет к
равносильному, но еще более громоздкому уравнению. Пойдем другим
путем. Преобразуем квадратные трехчлены в подкоренных
выражениях и учтем, что у/а2 — Ъ2 ^ |а|. Тогда
у/Ах -х2 + у/Ах - х2 - 3 = 3 + л/2х - х2
А-{х- 2)2 + y/l - {х - 2)2 = 3 + л/2я? - х2.
Теперь замечаем, что при всех х верно:
у/А - (х - 2)2 ^ 2; ^1 - (я? - 2)2 < 1; 3 + д/2я - ж2 ^ 3,
причем, равенство имеет место тогда и только тогда, когда все
выражения принимают свои «крайние» значения, т. е.
х - х2 + л/4ж - х2 - 3 = 3 +
f
1 - (х - 2)2 = 1, «=► х = 2
кж(2-ж) = 0
Ответ: 2.
СЗ Решение: Пользуемся условием (10) со стр. 61:
\х2 + 7х + 10| < х2 + 8х + 21 - \х + 7|
fa;2 + 7а; + 10 < х2 + 8х + 21 - \х + 7|,
[х2 + 7х + 10 ^ -а;2 - 8а; - 21 + |а; + 7|
287

\х + 7| < 2х2
Т> —ж — 11,
+ 7 < 2ж2 + 15а; + 31,
7 $* -2х2 - 15х - 31
31
<11,
(х + 4) (я? + 3) ^ О,
х2 + 8х + 19 ^ О
ж G [-9; -4] U [-3; +оо)
Ответ: [-9; -4] U [-3; +оо).
С5 Решение: Условие задачи можно записать в виде
совокупности неравенств
\А\ > \В\,
(в^о,
Х\в\ > I
\А\
{
\В\ < -А;
{:
JB < -А,
\В>А;
(А ^ -В,
[А + В^О;
В^О
Осталось решить полученное неравенство:
А + В < 0.
\х - 3| (|ж - 5| - \х - 3|) -6х + \х\ (\х\ - \х - 8|) +24 < 0
|ж2-8ж+15| < |ж2-8ж|-15
X -*- оЖ + 10 ^ Ж — оХ\ — 1о,
ж2 - 8ж + 15 ^ 15 - |ж2 - 8ж|
|ж2 - 8ж| > 8х - ж2
I
{
288

Ответ: [3;5].
х2
8ж$
ж2 — 8х ^
х2 - 8х ^
х2 - 8х $
о>
:ж(ж
0^:
;-х2
ъ 8х-
1х2 -
30,
-8)5
0
8х +
+ 8х
х2,
8х,
5
30,
-30;
Вариант 11
В1О Решение: Пусть О — центр основания конуса, R — радиус
его основания, тогда 50 — его высота. Из условия следует, что
ОСЛО
/.АО В — д = 60°, значит, треугольник АО В —
равносторонний ий = ОВ = АВ, В треугольнике SAB имеем:
АВ = 2-AS cos /A = 2 AS
\/58
Тогда по формуле площади
откуда R2 = 72. Из 5ЛО имеем
со2 - 4 ^?2 /?2 - 58 . 79 - 79 - 79 . 58 ~" 36
bU - ЛЬ - К - g2 72 72 - 72 36
и теперь можем вычислить искомый объем:
= 44,
V = | • тгД2 • 50 = i • тг • 72 • \/44 = 487гл/1Т.
Отсюда следует, что
Ответ: 528.
= 528.
289

В11 Решение: Обозначим угол DC А буквой а (рис. 139), длину
стороны ромба буквой а. Тогда из треугольника DOC имеем
СО = a cos a = Vo,
//7
следовательно, cos a = -^-. Теперь из прямоугольного
треугольника DKC получаем
KD = asin2a = a-2sinacosa = 2a-^--Wl - -~ = 2>/б- Q ■
Наконец, из прямоугольного треугольника ADK по
теореме Пифагора имеем
= KD2 + а2
14 = 4 • 6 • ^^ + а2
а4 + 10а2 - 144 = 0 Ф=4> а2 = 8
Ответ: 8.
С2 Решение:
у l
^. \/2ж • log4 rr = -
1<_> flog4a;<0,
\logj. л/2х • log| x = 1
290

{log2a:<0, ,
Hog22# /1ок9я\ <*=> <, о
log2x V 2 /
frr < 1,
i log2 ж =
-1±л/53
~l-\/33
= 2 2"
-1-\/33
Ответ: 2 2
Здесь трудно делать проверку, поэтому уметь делать
равносильные переходы полезно.
СЗ Решение: Сначала преобразуем выражение sin a; — \/3cosa;
методом введения вспомогательного угла
sina; —
= 2 ( ^sinx ^-cosx I = 2sin (x— ~J .
Теперь решим неравенство:
(2sin (ж — |) — а — 4^
5
-2а - 13 ^ ,
> О
2 sin
in (х - |) - а - 4 > 5;
a
-а-4 < 5
-9,
9 + а
2 '
a + 4
< sin ж - £
9 + а
291

Так как синус изменяется от —1 до 1, то, чтобы неравенство
выполнялось для всех #, необходимо и достаточно, чтобы
выполнялись неравенства
а
2
9 + а
Га < -11,
[а е (-7;-6,5).
Ответ: (-оо; -11) U (-7; -6,5).
С5 Решение: Дискриминанты числителя и знаменателя очень
громоздкие многочлены четвертой степени (от а), поэтому
проанализируем графики числителя и знаменателя.
Пусть f(x) — числитель, д(х) — знаменатель. Обе эти
функции являются квадратными трехчленами, их графики —
параболами.
f(x)
Задача сводится к неравенству < 0, т. е. к нахожде-
нию промежутков, в которых введенные функции имеют разные
знаки. Видно, что ветви обеих парабол направлены вверх и
/(0) = 5(0) = -(а2 - Аа + 6) = -(о - 2)2 - 2 < 0,
т. е. параболы пересекаются при ж = 0и имеют по два различных
корня. По теореме Виета для корней xi, X2 уравнения f(x) = 0
имеем
f xi + х2 = -2(а2 + 1) < 0,
2
Отсюда следует, что f(x) = 0 имеет корни разных знаков,
причем отрицательный корень больше по модулю.
292

По теореме Виета для корней #з, #4 уравнения д(х) = О
имеем
_ /Л2 , с~ гч_ /. л/45-5'
+ #4 = —(а2 + 5а
— 5) = — ( а —
т. е. корни д(х) = 0 имеют разные знаки (знак их суммы не
определен).
Парабола может быть по разному расположена
относительно параболы (рис. 140а), б)).
v\ fix) 9(x)
у\ящ1т
Рис. 140
Разность / — д имеет вид f(x) — д(х) = х(а2 — 5а + 7). А так
как а2 — 5а + 7 > 0 для любого а, то знак разности f(x) — д(х)
совпадает со знаком х. Поэтому параболы расположены так, как
показано на рис 140 а).
Точки решения неравенства являются объединением
промежутков (&1,£з) U (#2?#4)? сумма длин которых равна
Хз—Хг+Х4 — Х2 = (#3 + #4) - (#1 + #2) =
= -а2 - 5а + 5 + 2а2 + 2 = а2 - 5а + 7.
Так как по условию это число не меньше 1, то
а2 - 5а + 6 ^ 0 4=Ф а G (-оо; 2] U [3; +оо). ■
Ответ: (-сю; 2] U [3; +оо).

РАЗДЕЛ ЧЕТВЕРТЫЙ
ОТВЕТЫ
Ответы на задачи А1-А10
Номер
варианта
Демо2007
Демо2006
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Номер вопроса
А1
2
3
2
4
2
3
4
3
4
3
3
2
3
1
3
3
4
1
2
2
А2
3
4
3
2
1
3
3
2
3
2
1
2
2
1
2
3
1
2
3
1
A3
2
2
1
4
3
2
3
4
2
3
1
1
2
3
4
2
4
1
2
3
А4
4
3
2
1
2
3
2
1
3
1
2
2
3
4
3
2
2
2
2
3
А5
3
1
2
2
3
2
2
2
4
4
2
1
3
2
3
4
3
1
2
4
Аб
1
2
3
3
1
4
4
1
4
1
2
2
3
1
3
2
2
4
3
4
А7
4
2
1
3
4
1
2
3
3
2
2
1
2
2
3
3
3
3
1
3
А8
3
3
3
1
1
4
2
1
1
1
4
3
2
3
4
4
2
3
3
3
А9
2
1
3
2
4
3
1
4
2
3
1
3
3
2
3
3
2
3
2
1
А10
1
2
2
4
2
2
2
2
4
2
3
2
1
1
2
3
3
4
4
2
294

Ответы на задачи В1-В11
Вариант Демо2007: 1. 3,5; 2. -3; 3. 3; 4. 17; 5. 3; 6. 2; 7. -10;
8. -5; 9. 1239; 10. 4,8; 11. 10.
Вариант Демо2006: 1. -1,5; 2. 6; 3. 2,6; 4. 0,2; 5. 1; 6. 2,7;
7. -2; 8. 5; 9. 16550; 10. 0,6; 11. 12.
Вариант 1: 1. -7; 2. 150; 3. 2; 4. 2; 5. 4; 6. 0,25; 7. 2; 8. -2;
9. 50; 10. 4; 11. 5.
Вариант 2: 1. 8; 2. 4; 3. 0; 4. 3; 5. -12; 6. 5; 7. 4; 8. 0; 9. 25;
10. 1,4; 11. 14.
Вариант 3: 1. 3; 2. 2; 3. 0; 4. 7; 5. 3; 6. 3; 7. 2; 8. 1; 9. 3;
10. 18; 11. 40.
Вариант 4: 1. 5; 2. -4; 3. 2; 4. -3; 5. 6; 6. 2; 7. 3; 8. 0; 9. 2;
10. 192; 11. 4.
Вариант 5: 1. -1; 2. 16; 3. 23; 4. -1; 5. 5; 6. 5; 7. 4; 8. -3;
9. 20,2; 10. 7,5; 11. 120.
Вариант 6: 1. 1; 2. 2; 3. 6; 4. 129; 5. 54; 6. 4; 7. 2; 8. 1,4; 9. 2;
10. 36; 11. 0,2.
Вариант 7: 1. 7; 2. 6; 3. 8; 4. 9; 5. 2; 6. 0,125; 7. 2; 8. -3; 9. 28;
10. 115,2; 11. 7.
Вариант 8: 1. 1; 2. -17; 3. 2; 4. 2; 5. 9; в. 2; 7. 0,8125; 8. -2;
9. 40; 10. 3,84; 11. 30.
Вариант 9: 1. -1; 2. 1; 3. 9; 4. 3; 5. 1; 6. 4; 7. 4; 8. 0,5625; 9. 4;
10. 1; 11. 5.
Вариант 10: 1. -11; 2. 5; 3. -0,25; 4. 4; 5. 0; 6. 1; 7. 25; 8. 1;
9. -0,5625; 10. 45; 11. 75.
Вариант 11: 1. 4; 2. 6; 3. 1; 4. 2; 5. 0,125; 6. 1; 7. -4; 8. 3; 9. 1;
10. 528; 11. 8.
Вариант 12: 1. -0,5; 2. 2; 3. 2; 4. 3; 5. 4; 6. -3; 7. 3; 8. 1;
9. -1; 10. 3,64; 11. 3.
Вариант 13: 1. 2; 2. 4; 3. 12; 4. 5; 5. 1; 6. 9; 7. 2; 8. 6; 9. -2;
10. 54; 11. 25.
Вариант 14: 1. -1; 2. 2; 3. 32; 4. 3; 5. 14; 6. 0; 7. 5; 8. 1; 9. 70;
10. 40; 11. 264.
Вариант 15: 1. 14; 2. 1; 3. 4; 4. 1; 5. 2; 6. 4; 7. 20; 8. -10;
9. 50; 10. 36; 11. 0,8.
295

Вариант 16: 1. 13; 2. 4; 3. -7; 4. 8; 5. 1; 6. 3; 7. 77; 8. 47;
9. -1; 10. 6; 11. 2.
Вариант 17: 1. 2; 2. 1; 3. 1; 4. 6; 5. 17; 6. 1; 7. 4; 8. 5; 9. 28;
10. 7; 11. 13.
Вариант 18: 1. 7; 2. 2; 3. 3; 4. 2; 5. 1; 6. 25; 7. 8; 8. 4; 9. 3;
10. 768; 11. 30.
Ответы на задачи С1-С5
Вариант Демо2007: 1. 2; 2. (-1)" • | + тгп, n € Z; 3. (-1; 2];
4. 1; 5. 2.
Вариант Демо2006: 1. ± (тг - arccos |) + 2тгп, п € Z; 2. (1; 2);
3. 12 дм, 12 дм и 9 дм; 4. ^; 5. (2; 2,5).
Вариант 1: 1. -5; 2. (-оо; -0,75); 3. (-оо; -1,75] U {0}; 4. Щ-;
5. (-оо;-1,5) U {11}.
Вариант 2: 1. 22; 2. (-оо;0); 3. (0,5; 1,5); 4. 120л/3;
5.
Вариант 3: 1. (-оо; -у/Щ U [0; 2] U [3; +оо);
2. (-оо; -3] U |-1; ~*+о ); 3. 1 + 8п, 7 + 8m, n, m e Z;
^[]
Вариант 4: 1. (1; 2); 2. В; 3. (-оо; 0] U [1; 2] U [5; +оо);
4. ^/5| - 0,5 • S'f; 5. -3; 4.
Вариант 5: 1. Го; ^Ц^]; 2. (|;4); 3. (-1 - л/2;Зл/2),
(-1 + ^;-Зл/2);4. |;5. (-оо;-3)и|^2"7|и(4;+оо).
Вариант 6: 1. (и; ±) U (l; |); 2. 2; 3. [-9; -4] U [-3; +оо);
4. ^л/а4 + 64/i4; 5. [3;5].
Вариант 7: 1. 2,5; 2. (0,5; 1); 3. 25; 4. a
5. (-оо; -2) U (-2; 2 - л/15) U [6; +оо).
296

Вариант 8: 1. [-^;-|) U (-§;§]; 2. -3; 9;
3. [0;|]и{^}и(4;5];4. 15; 5. (1;4].
1 /Л 7
Вариант 9: 1. 1; 2. а € К, xit2 = а ± 4, ^3,4 = а ± —т—;
3. (-оо; -2] U [3; 5) U (7; +оо); 4. 144; 5. (-3; 1) U (3; 4).
Вариант 10: 1. [-#5; 8]; 2. 20^~3 ■ 3. [0;4] U {5} U (6; 7,5];
60 + 18v 5
4. У|; 5. (-оо;-0,5) U (I,5;log23).
-1-у/33
Вариант 11: 1. 1; 2. 2 2 ; 3. (-оо; -11) U (-7; -6,5);
4.2:1; 5. (-со; 2] U [3;+оо).
Вариант 12: 1. {0} 11(1; 7); 2. (0; 1) U [4;21+v^]; 3. (6; 30),
(/S; 2!z_v/8Fj. 4. inRH; 5. (-5;4), (5;-4), (-13;20),
(13; -20).
Вариант 13: 1. -л/5; 2. (-6; -4) U
U (^; 5 + л/б); 3. Ь ф |, п € Z; 4. 324ч/3; 5. [-3; -2].
Вариант 14: 1. 4, Х +2 ; 2. (-оо; -1) U {0} U (4; +оо);
3.1856; 4. ^^;5. (-1;3).
Вариант 15: 1. 170; 2. (0; 1) U (2; 3);
3. (-оо; -4) U {-3} U (1; +оо); 4. ^ ; 5. {-0,1} U [0; 0,4].
оа(о — а)
Вариант 16: 1. (-1)п| + тгп, п е Z; 2. [-2; 2 - \/2) U
4. а2(1 + \/4 + 2\/2); 5. (-2 - 2\/2";0) U (0;-2 + 2\/2).
Вариант 17: 1. f-oo;|l; 2. (6;-3), (-6;3); 3. ±| + 2тгп,

Вариант 18: 1. -~ + 2тгп; тг(2га + 1),пЕ Z; 2. (-оо;0] U
U flog4 4;log4 7l U [log4 12;+ooV 3. (-4; 20); 4. ^^; 5. 6.
298

Содержание
Предисловие к новому изданию 3
От автора 5
РАЗДЕЛ ПЕРВЫЙ
ЭФФЕКТИВНЫЕ МЕТОДЫ РЕШЕНИЯ ОСНОВНЫХ ТИПОВ
ЗАДАЧ АЛГЕБРЫ И АНАЛИЗА
Понятие равносильности уравнений и неравенств 13
Степень с рациональным показателем 17
Уравнение вида хп = а, п £ N 17
Рациональные уравнения и неравенства 23
Квадратные уравнения.
Уравнения, сводящиеся к квадратным 23
Уравнения вида Рп(х) = 0, n ^ 3 и сводящиеся к ним .... 26
Квадратные неравенства.
Метод интервалов для рациональных функций 28
Иррациональные уравнения 33
Уравнения вида y/f(x) = д(х) 35
Уравнения вида \/f(x) = \/д{х) 38
Иррациональные неравенства 39
Неравенства вида у/ах + Ь ^ (^) схЛ- d 40
Неравенства вида у/ах2 + Ъх + с ^ (^) dx + / 43
Неравенства вида —т-г— ^ 0 (или ^0) 46
Неравенства вида \/f{x) > (<) д(х) 47
Неравенство вида y/f(x) ^ \/д(х) 50
Более сложные неравенства 52
Уравнения, содержащие модуль 53
Уравнения вида |/(#)| = д(х) 53
Уравнения вида \f(x)\ = \д(х)\ 56
Уравнение вида \ах + Ь\ = сх + d 57
Неравенства, содержащие модуль 58
Простейшие неравенства 58
Неравенства вида |/(х)| < д(х) 60
Неравенства вида \f(x)\ > д(х) 61
299

Неравенства вида \f(x)\ < \g(x)\ 64
Показательные и логарифмические уравнения 66
Введение. Основные свойства логарифма 66
Логарифмирование и потенцирование 70
Показательные уравнения 71
Логарифмические уравнения 73
Метод интервалов для логарифмических
и показательных неравенств 75
Показательные неравенства 76
Логарифмические неравенства 78
Неравенство вида loga/(x) > 0 (< 0) 78
Неравенство вида logaf(x) > loga^(a:) 81
Более сложные неравенства 82
Сложная экспонента и логарифм с переменным основанием 85
Логарифмы с переменным основанием 90
Показательные неравенства с переменным основанием 93
Неравенства для логарифмов с переменным основанием ... 96
Тригонометрия 106
Обратные тригонометрические функции 109
Основные виды тригонометрических уравнений
и способы их решения 118
Элементы математического анализа 131
Область определения функции 131
Множество значений функции 133
Основные понятия математического анализа
в курсе средней школы 136
Производная функции и ее вычисление 139
Геометрический смысл производной функции в точке 141
Возрастание и убывание функции на промежутке,
Экстремумы функций 142
Неопределенный интеграл.
Площадь криволинейной трапеции 150
РАЗДЕЛ ВТОРОЙ
ОБРАЗЦЫ ТРЕНИРОВОЧНЫХ ВАРИАНТОВ ЕГЭ
Структура ЕГЭ (Единого государственного экзамена)
по математике 152
300

Демонстрационный вариант 2007 г. * 166
Демонстрационный вариант 2006 г. 171
Вариант 1 175
Вариант 2 180
Вариант 3 184
Вариант 4 188
Вариант 5 192
Вариант 6 197
Вариант 7 200
Вариант 8 204
Вариант 9 208
Вариант 10 212
Вариант 11 216
Вариант 12 220
Вариант 13 224
Вариант 14 228
Вариант 15 232
Вариант 16 235
Вариант 17 239
Вариант 18 243
РАЗДЕЛ ТРЕТИЙ
РЕШЕНИЯ
Решение варианта 1 247
Решение варианта 12 260
Решение избранных задач из других вариантов 271
РАЗДЕЛ ЧЕТВЕРТЫЙ
ОТВЕТЫ 294

По вопросам оптовых закупок обращаться:
тел./факс: (495) 785-15-30, e-mail: trade@airis.ru
Адрес: Москва, пр. Мира, 104
Наш сайт: www.airis.ru
Вы можете приобрести наши книги с II00 до 1730,
кроме субботы, воскресенья, в киоске по адресу:
пр. Мира, д. 104, 4 этаж, тел. (495) 785-15-30
Адрес редакции: 129626, Москва, а/я 66
Издательство «АЙРИС-пресс» приглашает к сотрудничеству
авторов образовательной и развивающей литературы.
По всем вопросам обращаться
по тел.: (495) 785-15-33, e-mail: editor@airis.ru
Учебное пособие
Колесникова Софья Ильинична
МАТЕМАТИКА
Интенсивный курс подготовки
к Единому государственному экзамену
Ведущий редактор В В Черноруцкий
Художественный редактор А М Драговой
Иллюстрации Н Г Рысьева
Оформление А М Драговой
Иллюстрации на обложку М К Антошин
Макет, техническое редактирование С С Коломеец
Компьютерная верстка Е Г Иванов
Корректор 3 А Тихонова
Подписано в печать 14 02 08 Формат 60x88/16
Печать офсетная Печ л 19 Уел -печ л 17,1
Тираж 12 000 экз Заказ № 243
ООО «Издательство «АЙРИС-пресс»
113184, Москва, ул Б Полянка, д 50, стр 3
ОАО «Альянс «Югполиграфиздат», ПК «Офсет»
400001, г Волгоград, ул КИМ, дб