Текст
лсноз
ЕННАЯ
УПРУГИЕ
ЧАСТЕЙ
ЮЛЕБАНИЯ
АМОЛЕТА
/Д'-'.•. . ( —
ЛЕНИНГРАДСКАЯ
ЛЕНИНГРАДСКАЯ КРАСНОЗНАМЕННАЯ
ВОЕННО-ВОЗДУШНАЯ ИНЖЕНЕРНАЯ АКАДЕМИЯ
Е. П. ГРОССМАН и Я. Г. ПАНОВКО
6ДХ
r\
ж
IV * напечатано
КЗ i должно быть
(
f Ц !
напечатано
. 31 должно быть
4^ j
напечатано
V У /
должно быть
напечатано
t - b.< % должно быть
напечатано
должно быть
i > напечатано
u t
должно быть
1
*‘710 напечатано
должно быть
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ И ИСКАЖЕНИЯ
страница 93, 9 строка снизу
^тах * 0,05—0,06 сек~х
^тах ~ 0,65—0,75 сек-1
страница 163, 11 строка снизу, формула (27.3)
х-[-х0= у (1 — соф)
b
х-}-х0= у ('— cos-ф)
страница 163, 12 строка снизу, формула (27.4)
1 (x)=2V Aoctg-^
[
A) ctg S
1
стоаница 175, 3 строка сверху, формула (29.7)
Q2=-£[PJn (-t + 6) + P>,co(7 + 6)]-’ -
Qs= - Е [Pxj sin ( у. + 6) 4- Ру. cos ( т
страница 175, 14 строка '
[PJn (у + 6)4-Р. -
sin(yf-'-s'
страница 17₽
ДАНИЕ ЛКВВИА
Ленинград — 1947
стра
A sin
п
ОТ АВТОРОВ
Настоящая книга рассчитана на слушателей Военно-воздуш ных
инженерных академий и студентов авиационных институток», но
может оказаться полезной и более широкому кругу читателей,—
работникам заводов, исследовательских институтов и т. п.
При составлении книги была широко использована новейшая
литература. Ряд мест заимствован из „Курса вибраций ( частей
самолета* Е. П. Гроссмана, изданного в 1940 году. Деопросы
влияния сжимаемости на критическую скорость флатт/ра в ос-
новном тексте не отражены. Кратко этих вопросов авторы
коснулись в приложении (стр. 257). /
Параграфы 3 — 6 и 21—39 написаны Е. П. Гроссмадом, параг-
рафы 1—2, 7 — 20, 40 — 42 — Я- Г. Пановко. /
Авторы с благодарностью отмечают большую шрмощь, ока-
занную им при подготовке рукописи к печати I адъюнктом
ЛКВВИА тов. Л. М. Слонимским, а также внимаю Ь и заботу,
проявленные при издании настоящей книги тсхншДским редак-
тором М. И. Юрченко. /
Е. П. Гроссман Я. Г. Пановко
доктор техн, наук, инженер-майор,
лауреат Сталинской' премии. проф., д-р техн. наук.
( X
Технический редактор М. И. Юрченко
Подписано к печати 19.3.47. Печатных листов 16.25. Авт. листов 18,6. В 1 печ.
листе 46400 зн. Бумага 64x92. Заказ № 119/1565. Г29009
Тнпо-адтография ЛКВВИА
(3)
гри-
ВВЕДЕНИЕ
А. Общие замечания
(от-
ует?
чай.
За время эксплоатации самолет подвергается воздействию
различного рода сил. Силы эти могут действовать на самолет
либо изменяясь во времени сравнительно медленно (аэродинами-
ческая нагрузка при маневрах, или почти не меняющаяся сила
веса), либо изменяясь во времени весьма быстро (удар шасси
при посадке, удар предкрылка при выпуске, периодические знако-
переменные силы, возникающие при работе винтомоторной
группы и меняющиеся с большой частотой). Конструктор дол-
жен обеспечить прочность и надежность конструкции в експло-
атации под действием любых нагрузок, могущих встретиться
в течение срока службы самолета. Задачи действия медленно
меняющихся (практически постоянных) сил относятся к кругу
вопросов статической прочности-, действие же ударных и быст-
ро меняющихся знакопеременных нагрузок составляет круг вопро-
сов динамической прочности. Особенную остроту приобрели еба-
лроблемы динамической прочности за последние годы, в связи мно-
го значительным ростом скорости полета и мощности винтомо- /дут
торной группы. ТОЯ-
В настоящей книге рассматривается только та часть вовро- тиво
сов динамической прочности самолета, которая связана с появле- всех
лием в конструкции упругих колебаний; вопросы ударных наг- огда
рузок, как составляющие особую область, мы в рассмотрение
йе включаем. и с,
Существует ряд причин, приводящих к появлению колебаний иная
в конструкции самолета. В первую очередь источником колеба- про-
ний являются мотор и винт. Переменные усилия, связанные с ра- [сно,
ботой винтомоторной группы, всегда приводят к появлению ко- для
лебаний; интенсивность последних зависит не только от вели- иент
чины усилий, но и от массы и жесткости самой колеблющейся оха-
коиструкции. Поэтому одновременно с задачами уменьшения ве- ется
личины импульсов винтомоторной группы и изоляции конструк- (ЭМИ
ции от влияния этих импульсов, возникает задача рациональ-
ного выбора параметров самой конструкции. Следует всегда ном-
нить, что прочность конструкции при вибрационных нагрузках шли-
3
не обусловливается ее прочностью при постоянных (статических);
нагрузках. Иногда из двух однотипных конструкций лучше про-
тивостоит вибрациям та, которая менее прочна при постоянных
нагрузках. Это связано с тем, что размахи колебаний обусловле-
ны не только жесткостными, но и массовыми характеристиками
конструкции.
Статические нагрузки опасны только в тех случаях, когда
они могут повести к разрушению. Колебания, даже не угрожая не-
посредственно прочности конструкции, весьма неприятны, так
как могут оказаться серьезной помехой для нормальной экспло-
атации самолета. В результате колебаний могут возникнуть по-
дергивания ручки управления, дрожание приборов на доске пи-
лота, появляются неприятные ощущения у экипажа. Другое от-
личие вибрационных нагрузок от статических заключается в том.
что их разрушающее действие на конструкцию может сказаться
не сразу. Иногда требуется весьма большое число (измеряемое
сотнями тысяч и миллионами) циклов изменения нагрузки для
того, чтобы вызвать разрушение конструкции. При этом сама по
себе максимальная величина периодически действующей наг-
рузки, при действии ее статическим образом, не вызвала бы раз-
рушения. Это явление носит название усталости конструкции.
Таким образом, если действие статической силы на конструк-
цию полностью определяется величиной силы, то эффект дина-
мической нагрузки зависит также и от длительности ее дейст-
вия. С явлением усталости необходимо считаться особенно в тех
частях самолета, которые более всего подвержены длительному
действию знакопеременной нагрузки (подмоторные рамы, лопасти
винта).
Наряду с колебаниями самолета, вызванными работой винто-
моторной группы, на самолете иногда наблюдаются колебания,
происходящие от аэродинамических причин. Возникновение их
может быть связано с плохой обтекаемостью передней части
самолета. Наличие плохо обтекаемых надстроек на крыле или
плохого сочленения крыла с фюзеляжем приводит к вихреобра-
зовапиям. Срывающиеся вихри создают в области хвостового-
оперения пульсирующий поток, бьющий по хвостовому опере-
нию и вызывающий его тряску. Эта тряска обычно бывает ' осо-
бенно интенсивна на больших углах атаки, когда усиливается
срыв, и наблюдается она, главным образом, на соответствующих
режимах полета: на некоторых фигурах, при взлете, посадке.
Колебания этого типа носят название .баффтинг".
До сих пор речь шла о колебаниях, вызываемых периодичес-
кими усилиями, как бы извне прилагаемыми к упругой конструк-
ций, и независящими от свойств системы. Источником этих уси-
лий являются либо мотор пли винт, либо вихри, срывающиеся
с передних частей самолета. Но на самолете могут наблюдаться
также вибрации, возникающие без каких-либо внешних периоди-
ческих усилий. В этом случае деформации конструкции при ко-
4
лебаниях сами вызывают такие дополнительные аэродинамичес-
кие силы, которые в свою очередь увеличивают деформации.
Колебания этого типа наступают при некоторой вполне опре-
деленной скорости полета и имеют часто настолько интенсивный
характер, что приводят к разрушению самолета. Описываемый
вид колебаний носит название вибраций типа „флаттер*. Ско-
рость полета, при которой возникает флаттер, называется крити-
ческой скоростью флаттера. Флаттер является самой резкой,
и самой опасной формой колебаний самолета и возможность его
наступления всегда должна быть предотвращена конструктив-
ными мероприятиями.
Соответственно вышеизложенному, все содержание настоя-
щей книги разделено на две части: в первой части рассматри-
ваются колебания, возникающие вследствие работы винто-мо-
торной группы, во-второй—колебания, вызываемые аэродинами-
ческими причинами.
Основным назначением книги является изложение теории
указанных вопросов; экспериментального исследования колебаний
авторы касаются лишь вскользь.
Рассчитывая на читателя, имеющего некоторую подготовку
в области упругих колебаний, авторы, стремясь к цельности из-
ложения, все же сочли полезным кратко напомнить основные
положения общей теории колебаний.
Б. Элементы общей теории малых колебаний упругих
систем
а) Системы с одной степенью свободы
Свободные колебания. Рассмотрим в качестве типичного при-
мера груз, укрепленный на невесомой упругой консоли (фиг. 1)
и прогибающий ее своим
весом так, что прямоли-
нейная исходная ось /
изгибается в положение
11. Колебания такой си-
стемы можно вызвать, на-
пример, ударом. Тогда
груз начнет колебаться
Фиг, 1. Типичный пример колебаний упру-
гой системы с одной степенью свободы.
Положение II соответствует состоянию
упругого равновесия системы.
внешних сил
около положения стати-
ческого равновесия (ко-
торое на чертеже обоз-
начено цифрой II) между
положениями Ilia и 1116.
Если после первоначального удара никаких
к грузу не прикладывать и считать, что энергия системы не рас-
сеивается, то отклонение груза от положения равновесия будет
происходить по закону, изображенному на фиг. 2, где по оси
абсцисс отложено время, а по оси ординат—величина отклоне-
ния груза от положения равновесия. Такие колебания, по приз-
наку отсутствия внешних усилий после первоначального возму-
щения (толчка), называются свободными (или собственными).
Промежуток времени Т между двумя последовательными про-
хождениями груза через положение равновесия в одном и том
же направлении называется периодом колебаний системы.
Оказывается, что период колебаний совершенно не зависит
от того, каким образом система была приведена в состояние
колебаний (т. с. от характеристики исходного толчка), и опреде-
ляется исключительно свойствами самой системы. Поэтому
период Т называется собственным периодом системы. Число
колебаний и, совершаемое системой h единицу времени (1 сек.),
называется собственной частотой колебаний.
Между частотой и периодом существует очевидная простая
т- * 1
связь: 1 — — .
п
Выясним количественное значение величины и в зависимости от
свойств системы;- для этого составим уравнение движения груза,
предполагая колебания малыми. На колеблющийся груз в про-
цессе колебаний действует только сила упругости балки, которая
пропорциональна отклонению груза у1), но направлена всегда
в другую сторону. Обозначив коэфициент пропорциональности
через с (величина этого коэфнциента вычисляется с помощью
приемов строительной механики и будет пояснена ниже), можем
записать, что сила упругости балки равна— су. По принципу
Даламбера сумма этой силы и силы инерции равна нулю:
где Л1 — масса груза. Обозначив:
<>
можно записать уравнение в виде:
(2)
’) Отсчет перемещений у будем вести от положений статического равно-
весия (кривая II на фиг. 1).
2) В это уравнение не включен ни вес груза, ни уравновешивающая его
сила упругости балки, развивающаяся при статическом изгибе о г положения,
I до положения If; Сумма этих постоянных величин равна нулю.
6
Решение этого уравнения:
у = Д sin(p£ + а)
(3)
выражает так называемое гармоническое колебание и иллюстри-
ровано на Фиг' 2^
Из (3) видно, что в мгновения и t\ + ~ величина у (от-
клонение груза)
что величина
имеет одно и то же значение. Отсюда следует,
является собственным периодом колебании,
Фиг. 2. График свободных (собственных) ко-
лебаний при отсутствии сил затухания (рас-
сеяние энергии отсутствует).
частотой.
определяемым при уче-
те (1) формулой:
г=2'}/т- (4>
Как видно, величи-
на р в 2« раз более
собственной частоты,
т. е. представляет со-
бой число колебаний
в 2п сек. Очень часто
имеют дело именно с
величиной р, а не с ча-
стотой п, и называют р
собственной круговой
Чрезвычайно важно, что величины Т и р для малых колеба-
ний совершенно не зависят от начальных условий (определяю-
щих постоянные А и а1), т. е. колебания данного груза будут
происходить с одним и тем же периодом, независимо от обстоя-
тельств возникновения колебаний и их размахов. Это справедливо
не только для частного случая консольной балки, по и для всех
случаев колебаний точечной массы на упругой связи, когда
колебания описываются одним уравнением типа (3).
Разъясним подробнее значение коэфициепта жесткости с,
входящего в формулу (1). По определению сила, вызывающая
прогиб балки у, равна су, следовательно сила, вызывающая про-
гиб, равный единице, и есть коэфициент жесткости с. Ясно,
что чем более жестка балка, тем большая сила необходима для
создания прогиба, равного единице—тем больше коэфициент
жесткости с. Очевидно, что жесткость балки может быть оха-
рактеризована также величиной прогиба /, который развивается
П0Д действием веса груза Mg (фиг. 1). Связь между величинами
О Величина А представляет собой наибольшее отклонение груза, когдй
изогнутая ось балки достигает крайнего положения IU. А называется ампли-
*удои колебаний. Величина а называется начальной фазой.
•с и f очень проста. Если сила Mg способна вызвать прогиб f,
то Mg-cf-, следовательно с =
Mg „ ...
-у—. Подставляя это в (1), полу-
чим:
(5)
В этом виде формула очень удобна для приложений, так как
для определения круговой частоты нужно знать только величину
статического прогиба f, вызываемого собственным весом груза.
Из (5) ясно, что гибкая система(когд? величина f велика) будет
обладать малой собственной частотой, а жесткая система (когда
величина f мала)—большой собственной частотой.
Мы видим, что когда па колеблющийся груз действуют только
силы упругости, колебания, раз возникнув, будут продолжаться
сколь угодно долго с постоянной амплитудой. Это находится
в связи со сделанным выше замечанием о том, что энергия, со-
общенная системе начальным толчком, не рассеивается. Чтобы
убедиться в этом, умножим уравнение (2)na^rff и проинтегри-
руем по времени. Будем иметь:
1 n.(dyV , 1 , .
4 „с/— const; (6)
2 \dt I 2 •
Первый член этого выражения представляет собой кинети-
ческую энергию, а второй—потенциальную (по абсолютной ве-
личине равную работе упругих сил). Таким образом соотноше-
ние (6) выражает собой закон сохранения энергии: полная энер-
гия системы, равная сумме кинетической и потенциальной энер-
гии во все время движения сохраняет постоянное значение. Дви-
жение происходит таким образом, что кинетическая энергия
системы непрерывно трансформируется в потенциальную и об-
ратно, причем их сумма сохраняет постоянную величину.
В моменты времени, соответствующие максимальному откло-
нению груза от положения равновесия, кинетическая энергия
системы равна нулю, а потенциальная имеет максимальное зна-
чение. Точно также, при прохождении груза через положение
равновесия, кинетическая энергия будет иметь максимальное
значение, а потенциальная энергия будет равна нулю. В силу
закона сохранения энергии максимальные значения кинетической
и потенциальной энергии равны друг другу (и равны той энергии,
которая сообщена системе первоначальным толчком).
Затухающие колебания. Из опыта известно, что если какую-
либо реальную упругую систему привести в колебательное дви-
жение и затем предоставить самой себе, то колебания в конце
концов затухнут (фиг. 3). Это объясняется тем, что во всякой
8
реальной конструкции при колебаниях неизбежно развивается
некоторое внутренее трение как в узлах и в сочленениях, так и
в самом материале. На преодоление трения постепенно расхо-
дуется исходная энергия. " ’ ---- -
толчком, постепенно
затухают.
Для нас будет пред-
ставлять основной
интерес " Л
случаи,
и колебания, вызванные однократным
Фиг. 3. График затухающих колебаний.
Если силы затухания пропорциональны
скорости движения, то амплитуды убы-
вают в геометрической прогресии.
тот частый
когда силы
трения можно считать
пропорциональными
скорости движения си-
стемы- Анализ показы-
вает, что в этом ’ слу-
чае уменьшение разма-
хов происходит по за-
кону убывающей гео-
метрической прогрес-
сии, т. е. отношение
двух последователь-
ных максимальных отклонений уп и yn+i остается постоянным.-
Логарифм отношения :_Vn+i называется декрементом затухания;
он характеризует способность системы к быстрому затуханию
и не зависит от величины первоначального толчка, вызвавшего
колебания.
Фиг. 4. Влияние величины декремента затуха-
ния на колебания: Я-случай большого декре-
мента (быстрое затухание); В—случай малого
декремента (медленное затухание).
От величины этого толчка не зависит и период колебания
Л> который и в этом случае остается неизменным во все время
колебательного процесса. Величина периода затухающего коле-
бания всегда больше периода соответствующего колебания Г
(т- е. периода, вычисляемого без учета сил внутреннего трения),
хотя это различие обычно незначительно. Поэтому, если две
системы отличаются только интенсивностью рассеяния энерпш
(т. е. величинами развивающихся при колебаниях сил внутрен-
него трения), но совпадают во всем остальном, то колебания
будут происходить со значительной разницей в быстроте зату-
хания (фиг. 4) »при относительно малом различии периодов
(для придания большей ясности,
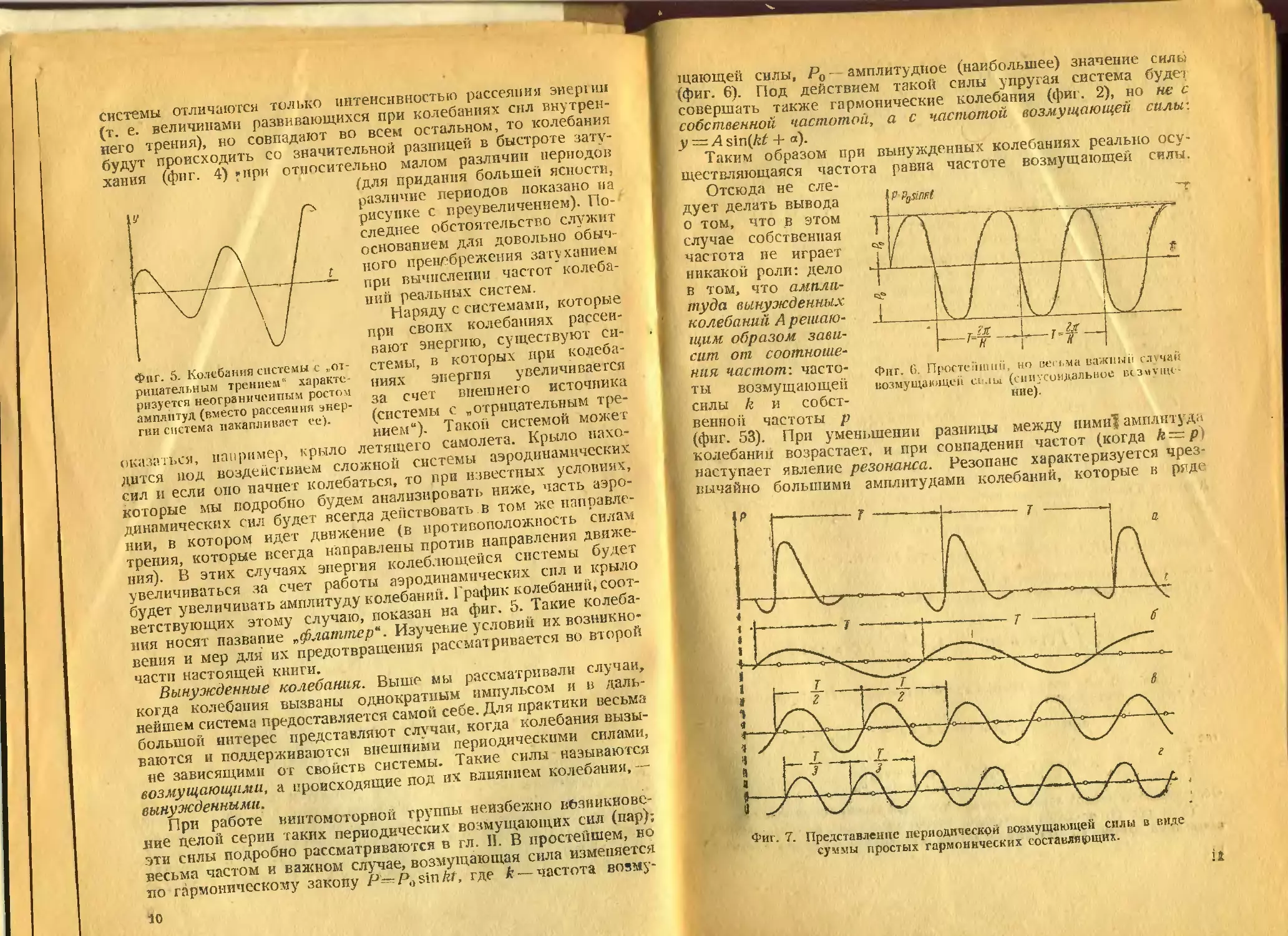
Фпг. 5. Колебания системы с „от-
рицательным трением" характе-
ризуется неограниченным ростом
амплитуд (вместо рассеяния энер-
гии система накапливает ее).
различие периодов показано на
рисунке с преувеличением). По-
следнее обстоятельство служит
основанием для довольно обыч-
ного пренебрежения затуханием
при вычислении частот колеба-
нип реальных систем.
Наряду с системами, которые
при своих колебаниях рассеи-
вают энергию, существуют си-
стемы, в которых при колеба-
ниях энергия увеличивается
за счет внешнего источника
(системы с „отрицательным тре-
нием"). Такой системой может
Крыло нахо-
оказаться,
например,
крыло летящего самолета.
дится под воздействием сложной системы аэродинамических
сил и если оно начнет колебаться, то ври известных условиях,
которые мы подробно будем анализировать ниже, часть аэро-
динамических сил будет всегда действовать в том же направле-
нии, в котором идет движение (в противоположность силам
трения, которые всегда направлены против направления движе-
ния). В этих случаях энергия колеблющейся системы будет
увеличиваться за счет работы аэродинамических сил и крыло
будет увеличивать амплитуду колебаний. График колебаний, соот-
ветствующих этому случаю, показан на фиг. 5. Такие колеба-
ния носят название „флаттер*. Изучение условий их возникно-
вения и мер для их предотвращения рассматривается во второй
части настоящей книги.
Вынужденные колебания. Выше мы рассматривали случаи,
когда колебания вызваны однократным импульсом и в даль-
нейшем система предоставляется самой себе. Для практики весьма
большой интерес представляют случаи, когда колебания вызы-
ваются п поддерживаются внешними периодическими силами,
не зависящими от свойств системы. Такие силы называются
возмущающими, а происходящие под их влиянием колебания, —
вынужденными.
При работе винтомоторной группы неизбежно возникнове-
ние целон серии таких периодических возмущающих сил (пар);
эти силы подробно рассматриваются в гл. П. В простейшем, но
весьма частом и важном случае, возмущающая сила изменяется
по гармоническому закону Р— Р,} sin kt, где k — частота возму-
10
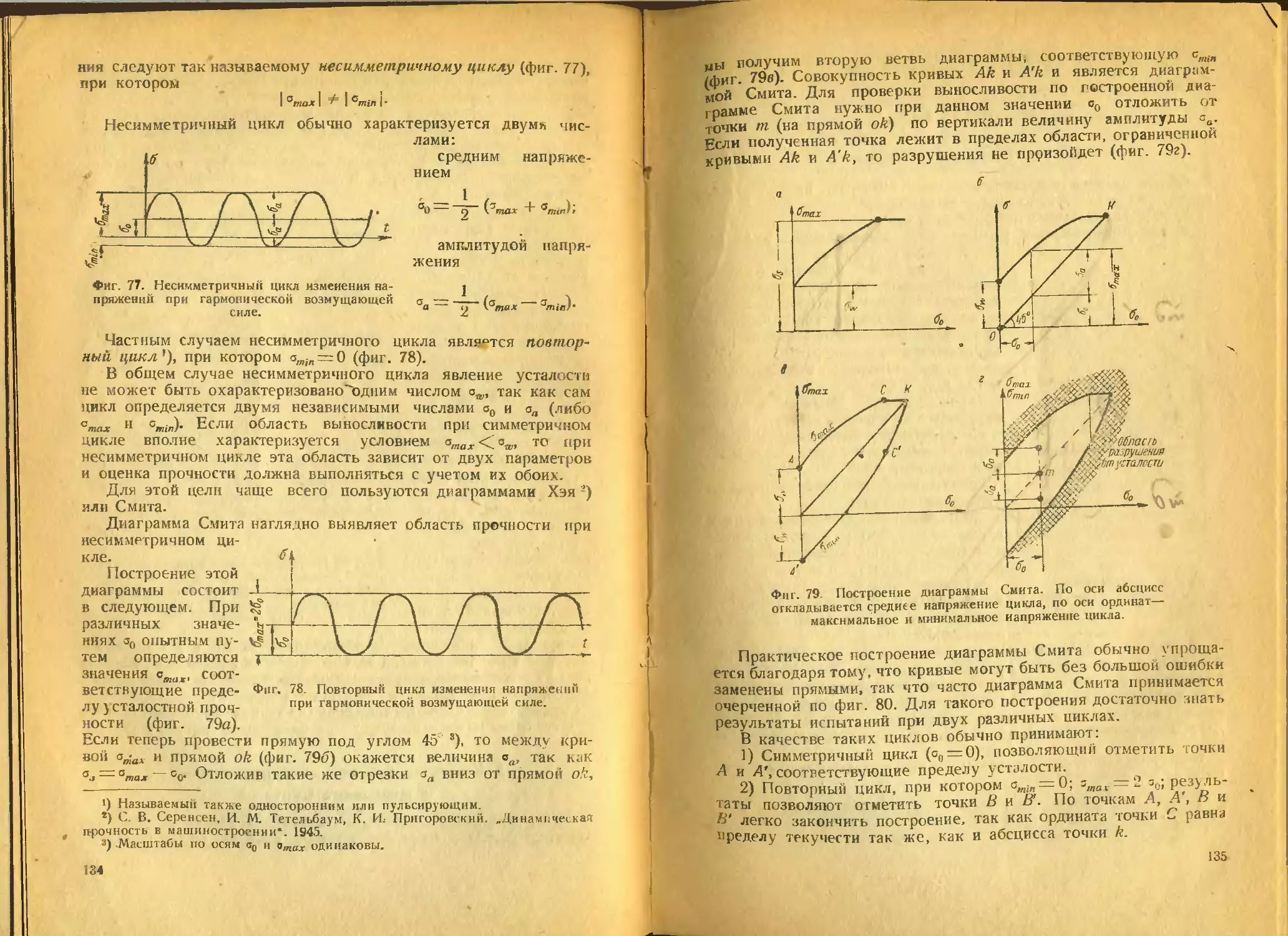
щающей силы, Ро- амплитудное (наибольшее) значение силы
(фиг. 6). Под действием такой силы упругая система будет
совершать также гармонические колебания (фиг. 2), но не с
собственной частотой, а с частотой возмущающей силы-.
у — A sin(A£ + а).
Таким образом при вынужденных колебаниях реально осу-
ществляющаяся частота
Отсюда не сле-
дует делать вывода
равна
PPgSlnnt
частоте
возмущающей силы.
о том, что в этом
случае собственная
частота не играет
никакой роли: дело
в том, что ампли-
туда вынужденных
колебаний А решаю-
щим образом зави-
сит от соотноше-
Фиг. (>. Простеiiitiiiii, но весьма важны!! случай
возмущающей силы (синусоидальное всзчуще-
ние).
ния частот-, часто-
ты возмущающей
силы k и собсг-
венной частоты р
(фиг. 53). При уменьшении разницы между ними! амплитуда
колебании возрастает, и при совпадении частот (когда k~ р
наступает явление резонанса. Резонанс характеризуется чрез-
вычайно большими амплитудами колебаний, которые в ряде
Фиг. 7. Представление периодической возмущающей силы в виде
суммы простых гармонических составляющих.
случаев далеко выходят за рамки допустимых по условиям
прочности. Поэтому одной из наиболее серьезных задач, ко-
торые стоят перед инженером, имеющим дело с периодиче-
скими возмущениями, является устранение возможностей резо-
нанса; эти вопросы рассматриваются подробно в первой части
настоящей книги.
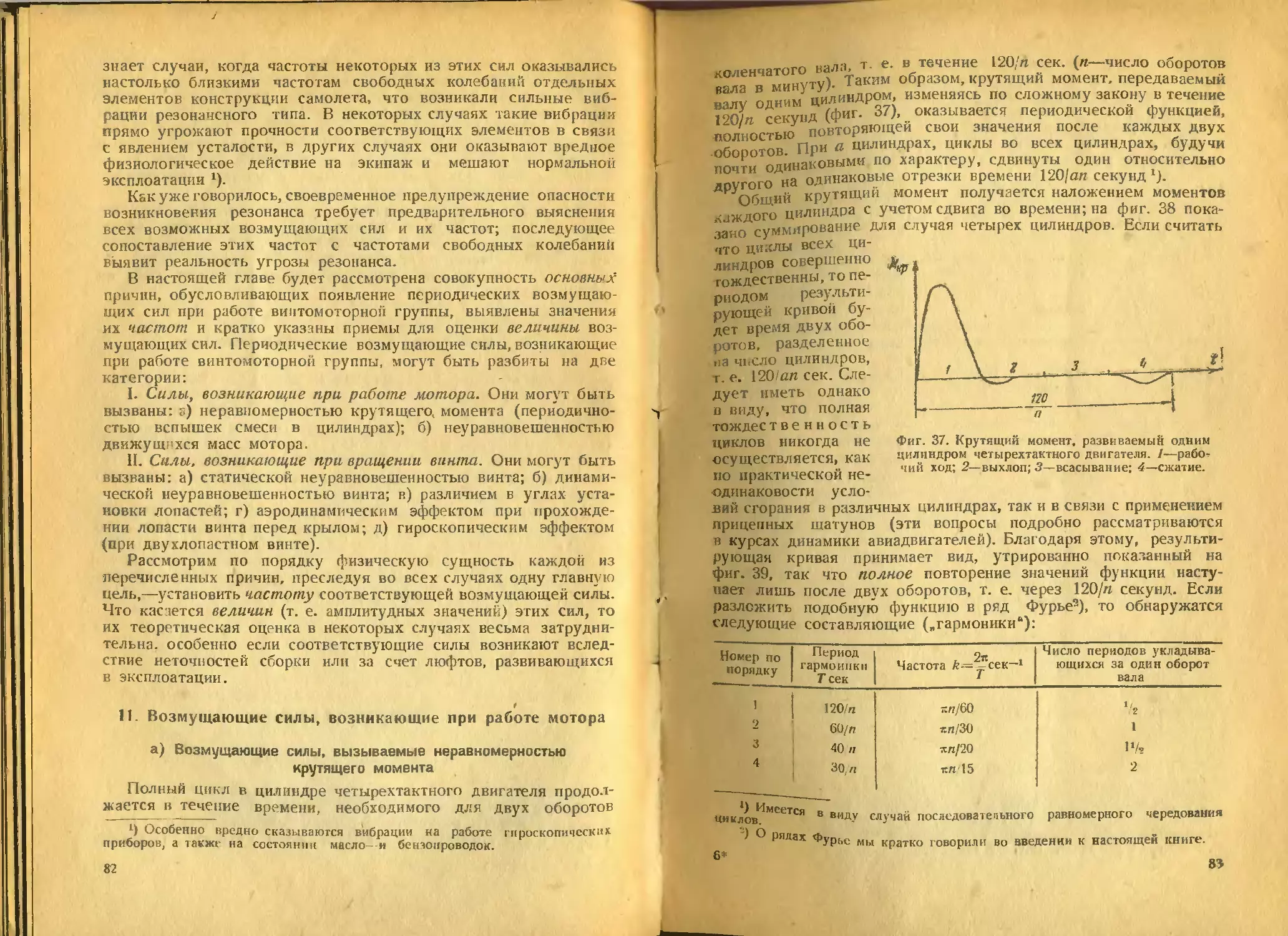
Часто бывает, чго возмущающая сила (пара) носит периоди-
ческий характер, но не является гармонической функцией вре-
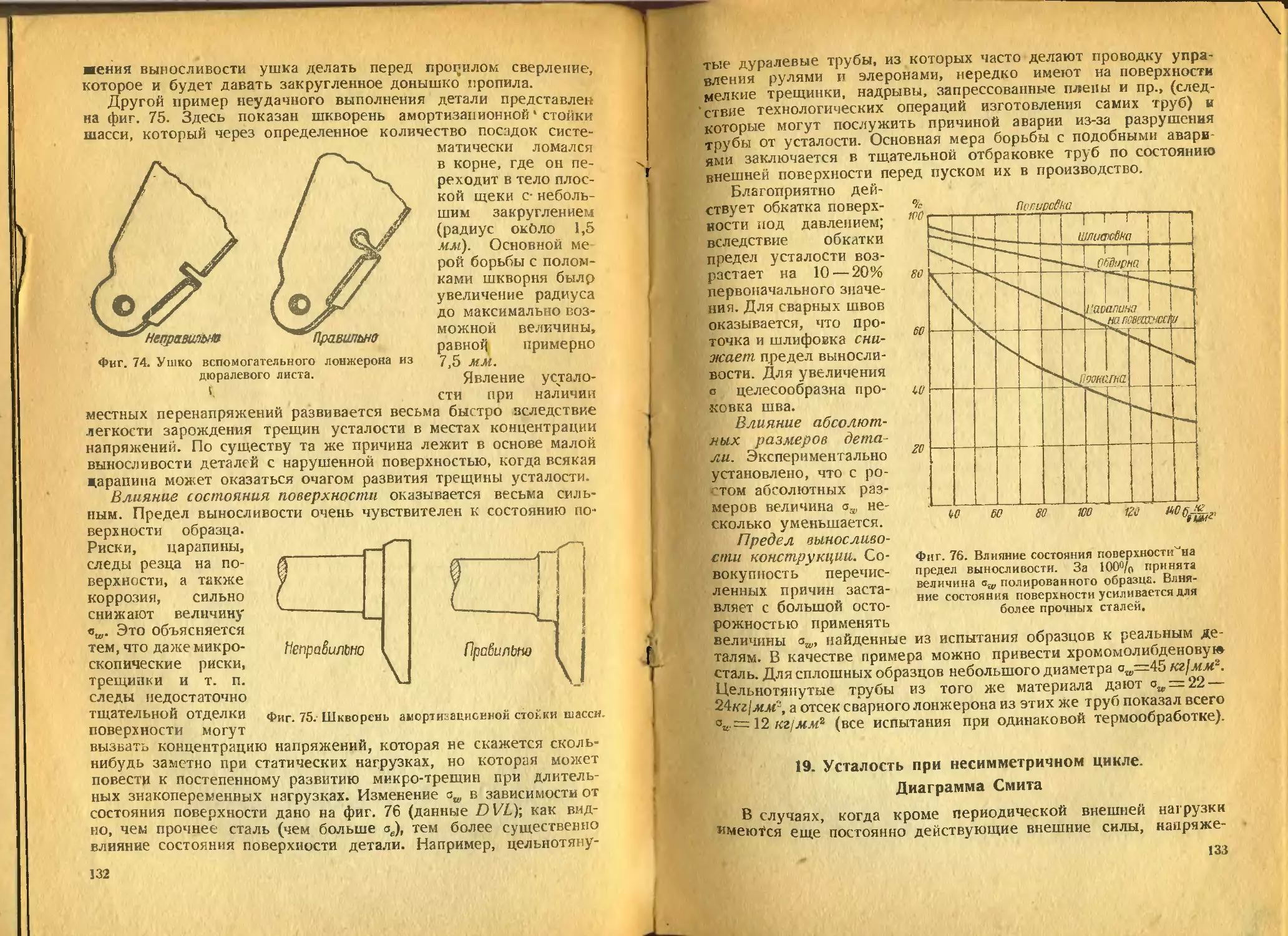
мени (см. например, фиг. 7а, где показано изменение крутящего
момента в одноцилиндровом четырехтактном двигателе); в этих
случаях такую силу раскладывают в ряд Фурье, удерживая
для дальнейшего анализа лишь несколько первых наиболее
значительных слагаемых. Каждое из слагаемых представляет
собой простую гармонику того типа, который показан на фиг. 6.
На фиг. 76, 7 в и 7 г иллюстрировано разложение силы, данной
на фиг. 7 а- здесь показаны только три „низшие" гармоники —
дальнейшие слагаемые образуются по тому же принципу. Перио-
ды составляющих гармоник равны соответственно Т, 1/2 Т, 1)‘s Г...,
а частоты k, 2k, ЗА.... Амплитуды отдельных гармоник зависят
от вида исходной функции и вычисляются по формулам опре-
деления коэфициентов ряда Фурье.
Сделаем несколько поясняющих замечаний для читателя, незнакомого с
рядами Фурье. Периодическую функцию (т. е. функцию полностью повторя-
ющую свое изменение через равные интервалы аргумента), как, например,
функцию, показанную на фиг. 7 а, всегда можно представить в виде беско-
нечного ряда (формально математические ограничения, называемые условиями
Дирихле, в наших задачах нас практически не стеснят; именно поэтому мы гово-
рим „всегда", хотя это и не вполне математически строго);
/ (/) = г?! sin kt 4- а2 sir, 7.kt -f- аз sin 3kt 4- • • • • -J- b0 -J- bx cos kt 4- b2 cos Ikt +
~bs cos 3kt... .(а), где k > T—период функции (т. e. тот интервал аргу-
мента, после которого функция начинает вновь повторять своп значения).
Коэфициенты ряда определяются помощью интегрирования
т Т
k Г k г
ип — ~] f (t) sin nktdt', bn — ~] f(t)cosnktdf.
О О
Часто члены ряда с одинаковыми аргументами ап sin nkt 4- bn cos nkt удоб-
но соединить в один член:
а„ sin nkt 4- bn cos nkt = An sin {nkt 4- оя),
где
<?„-arctgL*.
К
Обратной подстановкой легко убедиться, что такая замена всегда законна.
Тогда ряд (а) окажется состоящим только из синусов, но с различными
начальными фазами tf„. Тем самым всякая периодическая функция оказыва-
12
ется замененной суммой чистых гармонических слагай иых: это чрезвычайно
удобно в большом числе практических вопросов. Именно такое разложение
по синусам можно видеть на фиг. 7. При вычислении коэфициентов ап и Ь„
часто приходится пользоваться численным интегрированием, для которого
разработаны’ специальные вычислительные схемы (см. Ден-Гартог „Теория
колебаний*, 1942, стр. .’9—35).
Замена периодической функции рядом Фурье носит название гарменичес
кого анализа. Важно обратить внимание, что частоты слагаемых ряда возрастают
в весьма простой закономерности: k, 2k, 3k, где k — „основная* частота (т. е.
2it „ ,
k = ^,где Т—период разлагаемой функции).
так просты, и ряде случаев, даже пос
Фиг. 3. Системы с двумя степенями свободы.
б) Системы с несколькими степенями свободы
Во всех рассмотренных выше случаях колебательное движе-
ние вполне описывается одной функцией у =f(t). Однако ре-
альные задачи не всегда
ле упрощений и схема-
тизаций явления, движе-
ние системы может быть
полностью определено
лишь несколькими функ-
циями. соответственно
числу независимых коор-
динат, определяющих по-
ложение системы в про-
цессе колебаний. Так,
невесомая балка, пока-
занная на фиг. 8 а, обла-
дает двумя степенями
свободы (ее колебания
определяются двумя
функциями yt = и уъ~1?. <0* Плоский Г - образный стер-
жень, показанный на фиг. 8 б, также обладает двумя степенями
свободы (за обобщенные координаты можно принять переме-
щения груза в вертикальном и горизонтальном направлениях).
Практически важная задача о колебаниях мотоустановки как
жесткого тела на упругой невесомой мотораме, сводится к рас-
смотрению системы с шестью степенями свободы [за обобщен-
ные координаты могут быть приняты три линейных перемеще-
ния центра тяжести вдоль осей X, Y, Z и три поворота вокруг
этих осей (фиг. 11)].
_ Свободные колебания. Оказывается, что системы такого типа
обладают несколькими собственными частотами, поймем число
собственных частот равно числу степеней свободы системы.
Если систему, имеющую п степеней свободы вывести из состо
яния статического равновесия, то возникнут колебания, причем
Аля каждой из обобщенных координату окажется:
13
Фиг. 9. Формы собственных колебаний
системы с двумя степенями свободы.
к=^П
У1 = У Aik sin {Pkt + «J- (7)
K=I
Другими словами, колебание будет как бы состоять из п про-
стых гармонических колебаний, каждое из которых обладает
своей частотой pk. Как и для системы с одной степенью сво-
боды, амплитуды отдельных составляющих колебаний Aik зави-
сят от начальных условий; при различном характере выведения
системы из состояния рав-
новесия соотношения меж-
ду амплитудами отдельных
слагаемых будут также раз-
личны.
Иногда искусственным
подбором начальных усло-
вий можно обратить в нуль
все амплитуды, кроме од-
ной, т. е. вызвать однотон-
ные колебания с одной ча-
стотой по уравнению (3).
Так, например, если систе-
му, показанную на фиг. 8 а
и имеющую две степени
свободы, вывести из равно
весия двумя одновременны-
ми и симметричными им-
пульсами (фиг. 9 а), то ко-
лебания системы будут про-
стыми гармоническими, т. е.
каждая масса будет изги-
баться между положениями
а и b (фиг. 9 а) с некото-
рой частотой pt. Если ту
же систему вывести из по-
ложения равновесия иным
способом—двумя обратно-
симметричными импульсами (фиг. 9 в), то колебания будут так-
же простыми, гармоническими, но с частотой ра. Если, наконец,
систему привести в состояние колебаний каким-либо случайный
образом, не совпадающим ни с фиг. 9 а, ни с фиг. 9 в, то коле-
бания каждого груза будут определяться суммой двух слагаемых;
у,==Аи sin(Pjt 1- aL) + vAKsin(p./ 4- as); (г —1,2),
причем роль каждого слагаемого в общей сумме зависит от на-
чальных условий.
Можно сказать, что каждой из частот системы с п степеням»
свободы соответствует своя форма колебания, причем таких
14
форм столько же, сколько и частот, т. е. в конечном счете,
сколько степеней свободы. Эти формы колебаний зависят исклю-
чительно от свойств системы и так же, как и частоты, называ-
ются собственными. Как правило, высшим частотам соответ-
ствуют более сложные формы.
Вынужденные колебания. Если на систему с п степенями
свободы и собственными частотами р1г ра,... рп действует гар-
моническая сила то колебания происходят с частотой k
возмущающей силы, а размахи зависят от близости частоты k к
собственным частотам р. На фиг. 10 дана типичная кривая для
такого случая. По оси абсцисс отложена частота возмущающей
Фпг. 10. Влияние частоты возмущающей силы на ампли-
туду вынужденных колебаний в системе с тремя степенями
свободы.
силы k\ а по оси ординат — амплитуды колебаний. При k~pt,
k.=zp,... имеют место резонансные колебания.
Следует обратить внимание, что резонанс с высшими частота-
ми как правило менее опасен; нафиг. 10 видно, что амплитуды
резонансных колебаний убывают по мере перемещения вправо
по графику, т. е. по мере повышения частот. Если на систему
с п степенями свободы действует периодическая сила, гармони-
ки которой имеют частоты k{, kt, k3... (см. фиг. 7), то резонанс
наступает при совпадении хотя бы одной из собственных частот
Pi, рг... рп с одной из частот возмущающей силы klt
в) Системы с непрерывным распределением масс
О возможностях точного решения. Системы, рассмотренные
в предыдущих параграфах обладают конечным числом степеней
свободы вследствие того, что массы сосредоточены в нескольких
15
точках. В некоторых реальных случаях такая схематизация окат
зывается недопустимой и следует считаться с непрерывным
распределением массы-, в этих случаях юг одна функция у
ни несколько функций уЛ yz—fz(t),.... yn=fn(t), не могут
вполне описать движения.
Так, например, колебания консоли, показанной на фиг. 1, при
непрерывном распределении массы балки описываются бесконеч-
ным числом выражений yt—fi(t), так как необходимо иметь
такую функцию для каждой точки балки; иными словами, для
полного описания движения нужно иметь функцию двух пере-
менных у = у(х, t), которая обычно представляется г. виде:
y(x,0=S /«(х) sin (Р/+ «/)> гДе функции ft (х) зависят только
/=1
от х. Каждое из слагаемых /,i(x)sin(p/ + af) представляет собой
простое (однотонное) колебание, для которого функция /фх) вы-
ражает форму, т. е. уравнение упругой оси для мгновения,
когда отклонение максимально. Каждой из частот рг соответст-
вует своя форма fa (х), причем более высоким частотам отве-
чают и более сложные (т. е. с большим числом точек перегиба
максимумов и минимумов) формы.
Подобная характеристика явления относится не только к из-
гибным колебаниям, но вообще ко всем системам, обладающим
непрерывным распределением масс.
Такие системы могут быть названы системами с бесконечным
числом степеней свободы: им свойственно бесконечно большое
число как собственных частот pv ps,...., таки собственных форм.
Вычисление этих частот оказывается обычно весьма сложным
и без дополнительных упрощений удается лишь в отдельных ча-
стных случаях, например, в случае колебаний изгиба стержней
постоянного сечения; к этому случаю сводится задача о колеба-
ниях проводки управления на самолете (рассмотрена в п. 8). Как
правило же, приходится облегчать решение путем некоторых
упрощений.
Метод Рэлея. Такое упрощение решения задачи дает предло-
женный Рэлеем приближенный метод, обеспечивающий достаточ-
ную точность результатов. Этот метод широко использован ниже
(колебания лопасти винта и колебания крыла). Идея метода со-
стоит в том, что для определения низшей частоты мы наперед
задаемся подходящей (по условиям задачи) собственной формой
колебания и затем используем условие постоянства суммы кине-
тической и потенциальной энергии (вводимое здесь пренебреже-
ние внутренним трением для определения частот несущест-
венно). Проследим применение этого метода на простейшей за-
даче о колебаниях консоли при непрерывном распределении
масс.
Положим, что нами разыскивается низшая частота рг кото-
рой соответствует собственная форма А\(л'). Последней необхо-
16
димо задаться, стремясь наиболее просто удовлетворить гранич-
ным условиям; можно принять, например,
А;(х) = ал2^ — |-), (8)
что удовлетворяет граничным условиям:
Прогиб Угол поворота Момент Поперечная сила
при х=0 при X / ^(О^О X'i (0) = 0 EJX/' (/) = 0 [EJXEV W = o
Как видно ниже, величина а, входящая в (8), при опреде-
лении частоты роли не играет. Колебания, соответствующие рас-
сматриваемой форме, будут описываться уравнением:
Ji (х, t) = (х) sin (pj + «J.
Скорость в точке с абсциссой х будет:
%- - ЛА'1(*) • cos(p/ + aj;
Кинетическая энергия элемента балки, выделенного двумя бес-
конечно близкими сечениями:
1 /дм 1
2'( ~dt) d"' ~ 2 Р1'Х1‘ COsS ^plt + т dx’
где dm — т (л) dx—масса выделенного элемента; т(х)—интен-
сивность распределения массы вдоль балки.
Кинетическая энергия всей балки:
I
т (л) Хх-(х) dx.
о
Потенциальная энергия всей балки:
i I I
EJdx = sin2(pj£ + у Хг"® (x)EJdx,
- и о
где M — EJ —изгибающий момент, EJ— изгибная жесткость
балки.
' Гроссман и Пановко. i j
РЕ COS2 + ЯГ
Из условия постоянства суммы Т + U, следует:
^(7+U) = 0.
Вычисляя:
I
4т (Т + 1Г) = — ~ P1S sin 2 (P1t + aj ( m (z) X^ (x) dx +
cZr J
b
/
4- —pi sin 2(р/ + аг) I X/ '® (x) EJdx.
£
4)
немедленно находим:
1 ' '
P2 — f A'/'2 (x) EJ (x) dx : I'm (x) X2 (x) dx.
о 0
Тот же результат мог Сыть получен и прямым приравниванием
1 f*
значений максимальной кинетической энергии j-p? / m(х)Х^х)(1х
о
/
1 Z»
и максимальной потенциальной энергии у I EJX1"s(x)dx.
О
Если известно распределение жесткостей EJ(х) и массы /?/.(х)
то задача сводится к обычному интегрированию, так как функ-
цией Х/х) мы задались заранее. Положим, что в нашем случае
EJ— const, m— const, а Х^х) принято в соответствии с (7).
Тогда получится:
f 1 Х\2
p2—EJ Г 4а3(/•— x)sdx :m f aixi[l —
о о
(так как X" (х) ~ 2а (I — х)).
Фактически интегрируя, найдем:
что незначительно отличается от точного значения низшей ча-
стоты
18
Подчеркнем, что формула (Р) справедлива для любых изги-
б -> ых стержней при любых граничных условиях-, важно, что
"помощью этой формулы можно определить частоту для стерж-
’ перемецной жесткости и переменного распределения масс,
Н Если система помимо изгиба испытывает при колебаниях
также кручение, растяжение и т. д., то все рассуждения остаются
ч силе- разумеется, однако, что выражения Т и U получают при
чтом соответствующие дополнительные слагаемые.
результаты применения метода Рэлея могут быть улучшены
последовательными приближениями, которыми уточняется не
только значение частоты, но—что не менее важно для приложе-
ний—уточняется форма колебаний (которая в исходном этапе
выкладок может довольно сильно отличаться от истинной}. Ме-
тод последовательных приближений подробно рассмотрен ниже.
Часть 1 СОБСТВЕННЫЕ КОЛЕБАНИЯ ЧАСТЕЙ
САМОЛЕТА ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ, ВОЗНИКАЮЩИЕ
ПРИ РАБОТЕ МОТОРА
ГЛАВА I
Собс1венные колебания частей самолета
1. Вводные замечания
Расчет кол*’баний желательно завершить вычислением дина-
нап.?1жений, чтобы получить возможность сделать за-
-е ЧеСоответст1'Ующие °ченки прочности. Такое вычисление тре-
бует исследов;1НИЯ вынУжДенных колебаний системы. Однако для
того необхо'1,,мь1 полные сведения о частотах и амплитудах
КГИ1М1/НТЯ1ЛПТИХ сил- Как будет видно ниже, амплитуды некото-
количествен-
напряжении
даже невоз-
анализа вы-
возмущающих u...“
пых из возму|цающих сил ие поддаются надежной
и й оценке и ПОЭТОМУ вычисление динамических
оказывается в таких слУчаях затруднительным, и
можным-^стд^дрт нередко отказаться от полного
* ННЬ1Х К(>лебаний, обращаясь к способу более простому,
и^тАи не вп',лне исчерпывающему вопрос. Этот способ требует
х°тя и we жесткостных и массовых данных рассчитывае-
мой системы лишь частот возмущающих сил; он носит обычно
азвание па*гчета иа резонанс" и состоит из следующих этапов:
а) установлен*16 частот возмущающих сил А,; б) установление
частот собст1‘енных колебаний р/, в) сопоставление частот k.:
„ .. nr,nnAt,Ka Достаточности разницы между ними (достаточ-
ного удалена»1 частот k‘ от ?он резонанса).
Расчет на резонанс освобождает от необходимости уточнять
величины во:*мУщаю1Дих сил и обычно выполняется без учета
затухан*,я’ поскольку последние обычно незначительно
влияют на в<’личины А1); благодаря этому, он приобрел значи-
j. „ “^7|Юмнить. что влияние затухания на амплитуды колебаний зна-
' Лсобе|1Н0 в(*лизп резонансного режима).
чительно t совпадение частот не всегда указывает на непосредственную
замети , ч )жнь! случаи когда и при совпадении собственной частоты
опасность, (ущающей СИЛЬ11 амплитуды колебания будут все же ничтожны,
с частотой з совпадении собственной частоты тяги проводки управления,
Например, р высоть) с числом оборотов мотора, колебания тяги могут быть
идущей к ру л1Ь1, так как энергия импульсов от мотора рассеивается, пока
почти неощу до тяги в этих случаях необходима опытная проверка коле-
имнульс доидет на земле)
баний (гонкой М к
20
г
тельное распространение, несмотря на некоторую неполноту по-
лучаемых с его помощью результатов.
J Для некоторых частей самолета практикой выработаны
вполне определенные рекомендации относительно минимально
допустимого различия между и д; эти рекомендации придают
расчету на резонанс достаточную определенность и будут даны
ниже в надлежащих местах. Настоящая глава посвящена опре-
делению собственных частот мотоустановок, крыла, лопасти винта,
проводки управления и трубопроводов, питающих мотор-
Здесь же заметим, что предварительное вычисление собствен-
ных частот и собственных форм колебаний оказывает большую
юмощь и для полного расчета вынужденных колебаний (кото-
рый рассматривается в 3-й главе) и для определения критичес-
кой скорости флаттера (рассматриваемого во П части). Соответ-
ственно этому, на содержание следующих параграфов настоящей
главы следует смотреть и как на главнейшую часть расчета на
резонанс *), и как на вспомогательную (но весьма существенную)
часть расчета на флаттер и полного расчета вынужденных коле-
баний.
2. Собственные частоты мотоустановок
Будем считать: 1) мотор и детали мотоустановки, связанные
картером, представляют собой жесткое целое тело; 2) моторама
обладает идеальной упругостью и совершенно лишена массы
(практически масса моторамы пренебрежимо мала по сравнению
массой мотора); 3) узлы крепления моторамы абсолютно несме-
щаемы (или масса самолета бесконечно велика)г).
В этих предположениях мотоустановка представляет собой
колебательную систему с шестью степенями свободы, соответст-
венно числу независимых координат, определяющих ее движение.
В качестве координат примем:
% — перемещения центра тяжести вдоль осей X, У, Z;
• ’•Зв» % — углы поворота колеблющейся массы вокруг тех же
осей. 5
Оси X, У, Z направим согласно фиг. 11, совместив начало
; положением, занимаемым центром тяжести мотоустановки при
отсутствии колебаний.
Обозначим через перемещение (либо линейное, либо угло-
3ю ' в направлении %, вызванное единичной силой (парой), дей-
ТпУ*ощей в направлении тд. Так, например, о26 представляет собой
паи? вопрос о частотах возмущающих сил рассматривается в следующей
уг
,.Ьупагп:сет влияния конечной массы самолета см. в статье К. A. Browne,
Vol. 44 ^иЛ₽СП5‘оп ~а method of aircraft engine mountiug" (S. A. E. May 1939
обычно nJ S' Фиг- 12). Как оказывается, изменение частот за счет этого влияния
не превосходит 10%.
21
линейное перемещение центра тяжести в направлении оси У при
действии единичной пары вокруг оси Z; является угловым,
перемещением мотоустановки вокруг оси Z при действии еди-
ничной силы в направлении оси У. Как известно, для малых пе-
ремещений упругих систем по теореме Максвелла °ik — 8/г1 *).
Для полного перемещения по направлению т]£, вызванного силой
(парой) Рй=1, действующей в направлении можно сразу за-
писать:
''а = Pk^ik>
Фиг. 11. Расчетная схема к анализу колебаний процесс описываете
шестью функциями т(.(0-
так как перемещение т)г, вызванное силой Рк, в Р,г раз больше,
чем соответствующее единичное перемещение (вычисляемое при
Р* = О-
При нескольких силах (парах) Рк, действующих в различных
направлениях, полное перемещение будет:
«=б
'rii — k^‘k’
«=1
(2.1)
Возможность простого наложения эффектов, вызываемых
отдельными силами (парами) вытекает из оговоренной выше
идеальной упругости моторамы и малости рассматриваемых коле-
баний.
1) См. напр. И. М. Рабинович .Курс строительной механики стержневых
систем*, ч. 2. 1938.
22
При свободных колебаниях на мотораму действуют силы
инерции мотоустановки:
. /Игц, — — 7И\3 —вдоль осей X, Y, Z,
и инерционные пары:
— Ц''и> — Л; —вокруг осей X, Y, Z.
•>
Здесь М—-величина колеблющейся массы; 4> /5, 1е—главные
центральные моменты инерции колеблющейся массы относи-
тельно осей X, Y, Z (индексы 4, 5, 6 выбраны в соответствии
с индексами соответствующих угловых перемещений т;4, rt., 7(й).
Если в (2.1) в качестве внешних сил ввести силы инерции
и инерционные пары, то полная величина перемещения по t-му
направлению будет:
tji =— AhAi — М — М r.,oi3 — 4 7]48i4 — /s т;гД.3 — /с -/)c8j6,
пли, в развернутом виде:
— — М М т)2о12 /1'1 т]3о13 4 тц814 4 t]5615 /с т1Со16,
Т|2 — М T|j821 /14 Т|3032 /14 Т|.(823 4 TQ4<j24 4 т)5с2- 4 t]6o2g,
^3 — At АЛ Т)аО32 — М /4 Т|4С34 — 4 Tjjtj.jj. 4 7](.63U1(2.2)
Гц= — Х1 rh841 — Л4 t;2o4., — /14 т)3843 — 4 TUo44 — 4 — 4 rIcS4G;
Vi = — АЛ tj/Lj — /14 т12о-2 — /14 7|38-3 — Ц 7|4о54 — /5 т|6о;6 — 4 t]g6-g;
т)с = — /14 -г(1ос1 — /14 т128,.2 — Л1 — Д т]4864 — 4 Tj-Sy- — 4 7|Г8вс ’).
Полученная система однородных диференциальных уравне-
ний имеет частное решение вида:
vif = 7(/ sin (pt 4- а), (2.3 )
где 7(i—амплитуда перемещения т1Ь р— круговая частота колеба-
ния; а—начальная фаза. Подставляя (2.3) в (2.2), получим систе-
му уравнений, определяющих амплитуды:
t]j — /14 т), /?58и + /Ит;,р-812 + Л4т)зр'-813 + 4т)4р2614 +
+ Л%Р2515 +
Ъ = М 7],p3821 + AAf]2p2^2 + /14 7)3р2823 ф- 4TU/’2Bi4 +
_________ +4,v.p2S2o +
) Запись уравнений колебаний в форме (2.2) через единичные перемеще-
ИсгаиовИтСя в последнее время наиболее распространенной (см. особенно
• *->ернштейн. „Основы динамики сооружений". 1941).
23
rt3 = M vtpso3l + Л4^зР2333 + Afvi3pa633 4- /4 д4/’25з< +
+ 4 + вчерне; <2-4)
А = Л1 р-’О41 + М + ЛЬ]3 РЧ.П + 4 +
+ 4АЛ.+ W2V.
А = ЛЪ^о-л + м^2р28.2 + ЛЙзРЧз + ЛАрЧч +
+ 4 wAc + 4 ър2^
А = Al 'liP^ei + Л^зРАэ + Л1 %Гй6з + л -fuP^M +
+ 4^бР3°65 + 4 71бР1 2,4б-
Система алгебраических уравнений (2.4) однородна. Для того,
чтобы все vji одновременно не обращались в нуль1), необходимо,
чтобы равнялся нулю детерминант, составленный из коэфициен-
тов при т]г:
ГА Л1-1 ; рА. М; Р%Л1; р-’оиЛ; р’А54‘. P^IS le
р3»,. М; рЧ,,Л1-1- РА../И; р’Й,4/4; Р2й43/б; Р2Ч I.
Р’А, />'А, /И; р’ом Л1 -1; р3831 /4; р2й,в р~^зо 4
P=stl м-. р3о4, Л1; р\3М; р2внЛ-1; р28154; 4
P\i М; р\2 Л1; р %, М; р !й. 4 /4; Р3ой Л,—1; pAo 4
РА, РАа'И; p^/W; p=o61/4; рЧз4; =0 Ie 1 (2.5)
Развернув детерминант, мы получаем характеристическое
уравнение, определяющее частоту колебании:
B^pvl + Blf,p10+В8р« + Ввр6+В4р1 + В.,р* + Во = О, (2.6)
имеющее шесть корней р2, р2. р2, р3~, р-'\ рс\ Как доказыва-
ется в общей теории линейных колебаний, все эти корни веще-
ственны и положительны, так что для всех частот рг получа-
ются вещественные ответы. Каждой частоте отвечает своя
форма колебаний, т. е. вполне определенное соотношение между
амплитудами т;г. На выяснении этих форм мы здесь не останав-
ливаемся; отметим, однако, что обычно каждая форма характе-
ризуется преимущественно колебаниями в каком-либо одном
направлении—вдоль оси Z, или вокруг оси X и т. д., причем
эти колебания в общем случае сопровождаются также незначи-
тельными колебаниями в других направлениях.
Таким образом для определения собственных частот p-t необ-
ходимо: 1) вычисление единичных перемещений 2iJ6; 2) состав-
ление детерминанта (2.5) и его развертывание в характеристи-
1) Для всякой^ однородной системы существует тривиальное решение
TqI—ij3=v]3=i)I =/]-,= q(i= 0, обозначающее отсутствие колебании.
24
ческое уравнение (2.6); 3) решение характеристического урав-
нения (2.6).
В общем случае эта задача оказывается весьма громоздкой
Оздако для обычных мотоустановок плоскость XOY с большой
степенью точности может считаться плоскостью симметрии. При
этом многие из перемещений 81Д оказываются равными нулю,
что влечет распадение детерминанта (2.5) на два независимых
детерминанта третьего порядка.
Действительно, если XOY является плоскостью симметрии, то
сп ты и пары, действующие в этой плоскости, не вызывают пере-
мещений вдоль оси Z и вокруг осей X и Y. Следовательно от
сил и пар Pt (вдоль оси А), Р3 (вдоль оси Г) и Рв (вокруг оси Z)
н возникает перемещений в направлениях тд3 (вдоль оси Z)
j (вокруг оси А'), т|5 (вокруг оси У); мы можем записать поэтому;
о31 — 0; о33 = 0; о3в = 0;
°41 = 0; ?>42~ 0; 84б~0;
°5i~—0; —0; — 0.
По теореме Максвелла будет также:
0; t>33 — 0; 8ез — 0;
о14 = 0; ^ — О; £в4 = 0;
Si-> =0; йг5 = 0; з65 = о.
Три этом система (2.4) распадается на дгзе раздельные системы
T)t = + ^т,гР3^1’ + Aj'W’ Gi6
= ЛЬ] ,р30.,, + 7Ит12р20г, +/67)6рзг26
Tie = AlTjjp'-e,, +A?T]2p2ofi2 + l^r.p^c
(2-7)
Т|3 = 7Ит)3р2о33 + Лт)4/>2% +
Vi = ^VsP^is+^iViP^u + kViP^a
ч6 = м^33+7лрЧ4+/й^6рзг55
и вместо громоздкого и трудного для развертывания детерми-
нанта (2.5), мы получаем два детерминанта третьего порядка:
Мр^-Г, МрЪ„; 1ер^1в
Мр2821; Л4р282,~1; l6p2^2s
7Ир28б1; /Лс—1
Мр~833 1; /tp~83i; 75р2835
/Л-1; 4ра845
МЛ; Цр2^;
(2.9)
(2.Ю)
25
Вместо одного характеристического уравнения шестой степени
(2.6) получается два характеристических уравнения:
Сср6 + С^ + С2р" + Со = О (2.11)
О6рв+Р^+Е>^+О0 = 0, (2.12)
каждое из которых, будучи третьей степени относительно р3*
дает три значения частоты.
Решениям уравнения (2.11) соответствуют колебания мото-
установки в плоскости XOY-, решениям уравнения (2.12) соот-
ветствуют боковые колебания мотоустановки, при которых все
точки колеблющейся массы перемещаются только перпендику-
лярно плоскости XOY.
Фактическое вычисление частот требует предварительного
знания единичных перемещений Их определение чрезвы-
чайно упрощается тем обстоятельством, что все необходимые
выкладки выполняются в статическом расчете моторамы.
Как известно из курса строительной механики, наиболее
удобным средством определения является формула Мора1),
которая для рамных систем имеет вид (при обычном в этих
случаях пренебрежении деформациями, вызванными продольными
и поперечными силами):
5,.= V у /»*+У (2.13)
ООО
и для ферм:
г»= (2Л4>
Здесь обозначено:
Mb Mk—изгибающие моменты в сечениях элементов рамы в пер-
вой главной плоскости, вызываемые соответственно действием
сил Pj = 1 и Pk = 1;
Mt, Mk—то же во второй главной плоскости;
—крутящие моменты в сечениях, вызываемые ми
же силами Р,—1 и Рй=1;
TV,- ,Nk~-продольные усилия в стержнях, вызываемые силами
Р, —1 и Pk— 1.
EJt—жесткость изгиба в первой главной плоскости.
EJ.,—жесткость изгиба во второй главной плоскости.
GJKp— жесткость кручения.
Сложившаяся в настоящее время методика расчета прочности
моторам содержит в качестве первого этапа раздельное выясне-
>) См. папр. И, М. Рабинович. Курс строительной механики стержневых
систем. Ч. 2. 1938.
26
ние внутренних усилий (N, М, М ,М“Р) от единичных внешних
сил, действующих по направлениям оси X, оси Y, оси Z у
также от единичной внешней парывокруг оси X. Эти „элемен-
тарные" внутренние усилия (N, М, М МКР} служат основой для
определения усилий от
действительных нагрузок
в расчетных случаях Аму,
Мму, Иму и т. д. Именно
эти самые элементарные
внутренние усилия и дол-
жны быть использованы для
вычисления нужных нам ве-
личин по формулам (2.13)
и (2.14)'). Поскольку все
необходимые операции яс-
ны, мы на них не останав-
ливаемся. ™,фиг- 12- СлУчай двух’плоскостей сим-
Дальнейшее упрощение метрпи. Сила Р} вызывает перемеще-
получается В тех случаях,^ ние только в своем направлении,
когда плоскость XOZ так-
же является плоскостью симметрии моторамы и центр тяжести
мотоустановки лежит в этой плоскости при этом достигается,
дальнейшее разделение колебаний—как продольных (в плоскости
XOY), так и боковых. Действительно, в этом случае:
Фиг. 13. Случай двух Гплоско-
стсй симметрии. Пара Р4 вы-
зывает только поворот мото-
установки вокруг оси X.
а) сила Pi не вызывает пере-
мещений по направлениям т)2 (вдоль
оси Y) и 7]fi (вокруг оси Z) (фиг. 12)
б) пара Pt не вызывает переме-
щений по направлениям тй (вдоль
оси Z) и т,5 (вокруг оси У) (фиг. 13).
Благодаря этому обращается в
нуль еще восемь перемещений
о91 = ols — oG1 — o1G—о;!1 =
= S48=S54 = 345=0.
Вместо двух систем (2.7) и (2.8)
образуется уже четыре независи-
мых системы уравнений;
г^Мгцр^ц, (2.15)
J) При этом потребуется лишь дополнительное рассмотрение действия
единичных пар вокруг осей Y п Z, которое в статическом расчете не де-
лается ввиду отсутствия соответствующих расчетных случаев в .Норма
прочности-. '
27
1
1!2 = АЬ12р-о22 + /вт1вр-о2в
Г|6 — Л1 'fisP“'J62 4" A: rieP G6C
Tl3 = Mrl3p4tt + I^P%t:,
Ъ, =М'Ч1Р*ЪМ + 1Г^Р ’О;.,-,
тц — 1лР~°и
Частоты определяются из уравнений:
Л4р2оп—1=0,
! IRp4i6
I Mp3S62; /вр2ч 6—1
А1р%-1; /вр“А3 | = ()
Mp~oi3; A/Al-r,— 1
(2.16)
(2.17)
(2.18)
(2-19)
(2.20)
(2.21)
(2.22)
/j’-S44—1=0.
Эти уравнения, будучи первой или второй степени относи-
тельно р2, дают возможность весьма просто вычислить весь спектр
собственных частот. Из (2.15)—(2.18) видно, что колебания будут
иметь следующие формы: 1) колебание, соответствующее коорди-
нате Tjj вдоль оси X (в чистом виде); 2) колебания, соответ-
ствующие координатам tj, и -д,-вдоль оси Y и вокруг оси Z
(связанные колебания); 3) колебания, соответствующие коорди-
натам т|3 и дь—вдоль оси Z и вокруг оси Y (связанные коле-
бания); 4) колебание, соответствующее координате ^—вокруг
оси Z (в чистом виде).
Раздельность колебаний представляет значительные преиму-
щества не только вычислительного характера. Дело в том, что
лри раздельных колебаниях возможно изменять отдельные
собственные частоты (в целях устранения возможности резонанса)
без изменения других частот. При связанных же колебаниях
изменение одной из частот влечет немедленное изменение других,
так что, выводя одну частоту из опасной зоны резонанса, можно
невольно другие частоты ввести в близость с частотами возму-
щающих сил.
При раздельных колебаниях удается менять только избран-
ные частоты, оставляя другие неизмененными. Такая возможность
весьма желательна, но вполне осуществима только при оконча-
тельном разделении колебаний, которые частично связаны даже
при двух плоскостях симметрии мотоустановки. Для полного
.разделения необходимо, чтобы последние побочные перемещения
2S
236 = о- и о., - oe2 также обратились в нуль1 2). Хотя в обычных
конструкциях это не достигается (несколько лет назад были?
предложены специальные, так называемые, „динамические под-
веси“ обеспечивающие полную независимость колебаний; об
этих подвесках, примененных в опытном самолетостроении Аме-
рики будет сказано в п. 15, посвященном амортизаторам мотоуста-
новок) заметим, что и при обычной подвеске для грубой оценки
собственных частот допустимо положить, что все побочные
перемещения SjA. G/А’) равны нулю (включая о3. и %(i). Тогда
для собственных часто! из (2.19)—(2.22) следуют простые фор-
мулы:
л=|/'^3; *=1,2,3.]
I 'П r‘ii 1
______ } (2.23>
/’< —*I -у1,- ; i = 4.5,6. I
I /",7 I
Bbinje мы не упоминали о влиянии гироскопического момента
винта на частоты колебаний мотоустановки, гем самым отож-
дествляя явление собственных колебаний мотоустановки при
остановленном винте, с явлением, имеющим место при вращении
винта. Однако для современных винтов и мотоустановок это
пренебрежение не особенно существенно -).
Отметим в заключение, что по современным требованиям
собственные частоты должны быть меньше 900 кол./мин.
(р<94 сек ’); это вызывает необходимость настолько большой
гибкости установки, которая не может быть достигнута без
устройства дополнительных амортизаторов. Об этом сказано под-
робно в п/ 1,5.
3. Собственные колебания кручения крыла
(консольная схема)
Настоящий параграф посвящается определению собственных
частот и форм колебаний крыла. Надобность в этом определении
вытекает не из необходимости расчета на резонанс, как это было
в предыдущем параграфе (резонанс крыла представляет собой
неопасное явление, ввиду большой интенсивности рассеяния энер-
гии), а из соображений последующего расчета на флаттер.
Дело в том, что нужные для такого расчета величины аэро-
динамических сил, возникающих при колебаниях, тесным обра-
зом связаны с формами колебаний. Однако, независимо от ко-
нечных целей, вопрос о собственных колебаниях крыла рассмат-
1 Побочными перемещениями, как принято в строительной механике
«ы называем перемещения f>jk (гфй).
2) См. цитированную выше работу К. A. Browne.
29
ривается именно здесь, как близко примыкающий по содержанию
к другим параграфам настоящей! главы.
Уравнения задачи. Будем считать, что фюзеляж служит
абсолютно жесткой и несменяемой заделкой, и крыло может быть
схематизировано в виде консольной балки (фиг. 14), деформации
которой подчиняются обычным зависимостям сопротивления мате-
риалов.
В настоящем параграфе мы ограничимся рассмотрением такого
случая, когда центр тяжести в каждом сечении крыла совпадает
с центром жесткости. Если этого ограничения не ввести, то коле-
бания будут обязательно совместными, т. е. будут иметь место
Фиг. 14. Схема крыла к составлению урав-
нения крутильных колебаний.
не только закручивания
сечений около оси жест-
кости, но также и изгиб
крыла.
. Пусть 0—угол закру-
чивания какого-либо се-
чения крыла. Он изме-
няется вдоль размаха
крыла и, кроме того, при
колебаниях меняется в
каждом сечении крыла со
временем. Поэтому 0 есть
функция двух перемен-
ных z и t (ось Z на-
правлена вдоль оси жесткости крыла—см. фиг. 14).
Рассмотрим отсек крыла между двумя соседними сечениями
тп и и составим условие равновесия этого отсека, прира-
внивая нулю сумму моментов инерционных и упругих сил отно-
сительно оси жесткости. Упругие крутящие моменты, действую-
щие на рассматриваемый элемент крыла, будут:
в сечении тп: —GJKp-^- ,
в соседнем сечении т.п.: GJ, п-т- + -<-| GJ..n \dz,
р dz dz \ р dz
гдз GJKp—жесткость крыла на кручение в рассматриваемом
сечении. Предполагая, что центр тяжести в каждом сечении крыла
совпадает с осью жесткости, легко написать также выражение
момента инерционных сил, действующих на элемент mnmji^:
mdt? '
где погонный полярный момент инерции массы крыла отно-
сительно оси жесткости, и, следовательно, J„,dz момент инерции
массы рассматриваемого элемента.
30
ГТ оавняв НУЛЮ СУММУ всех моментов, получим уравнение
крутильных колебаний крыла:
д ( <56 \ . <536 _
— "X ' I GJKn —S— I "тп л —- 0- (3.1)
dz у Kpdz т dt- 4 '
Пля полного определения задачи к этому уравнению необхо-
о добавить граничные и начальные условия.
ДИМра личные условия. Так как в корневом сечении крыла
закручивания равен нулю, а на свободном конце должен
ыть равен нулю крутящий момент, то
6 = 0 при 2 — 0
GJkp dz ~° ПрИ Z = l
(3.2)
Начальные условия заключаются в распределении углов
кручения и угловых скоростей по размаху крыла в начальный
момент движения. Следовательно для того, чтобы до конца опре-
делить все характеристики движения, нужно задать и и
как функции z при t =0. Эти функции для наших целей неважны,
так как мы не будем определять полностью колебательное дви-
жение крыла, а ограничимся только onpedeAenueM собственных
частот и собственных форм, независящих от начальных усло-
вий. Всюду в дальнейшем, занимаясь собственными частотами и
формами, мы также не будем интересоваться начальными усло-
виями.
Вообще говоря, CJKp и Jm являются функциями z (изменяются
по размаху крыла). Уравнение (3.1) может быть точно проинте-
грировано только при некоторых частных видах зависимости GJKp
и Jm от 2. В общем же случае его интеграция возможна лишь
приближенными методами.
Будем искать частное решение уравнения (3.1) в виде произве-
дения двух функций, из которых одна зависит только от времени,
а другая только от координаты 2:
O(2,o = ?(z)-^(0- (з.з)
После подстановки этого выражения в уравнение (3.1) неремен-
нЫе в нем разделяются и мы получаем:
(GJKp '?) __ Я и (3.4)
Лп ? я
---"----------
Ч Здесь и всюду далее штрихами мы будем обозначать днференцирование
По координате г, а точками,—дпференцирование по временя t.
31
Так как слева стоит функция только z. а справа функция
только t, то каждое из отношений может быть только постоян-
ной величиной. Обозначая эту постоянную через — р2, получим
из (34) для определения <p(z) и q(t) уравнения:
q + p*q = 0, (3.5)
?')' + р3-4 ? = 0- (з 6)
Как видно из введения, уравнения типа (3.5) определяют
гармоническое колебание с круговой частотой р и периодомТ——?-
В дальнейшем для краткости условимся, вместо „круговая
частота", писать просто „частота".
Обратимся к уравнению (3.6), определяющему форму коле-
баний (закон изменения углов кручения по размаху крыла). Это
уравнение второго порядка и поэтому имеет два линейно-незави-
симых частных интеграла, которые обозначим <р (z) и <р (z). Тогда
уравнение (6) удовлетворяется функцией
? (z) = TWj <? (z) + Л13 <р (z), (3.7)
где Aft и — постоянные интеграции. Функция o(z) должна
удовлетворять граничным условиям, которые получим из (3.2),
подставляя туда выражение (3.3). Следовательно должно быть:
»=° при. з=0) ,(3 8)
= 0 при z — l |
Подставляя сюда значение ®(д) из (3.7), придем к следующей
системе уравнений для определения постоянных интегрирования
Л/j и ЛТ2;
Х?(0) + М>«(0) = 0 I
! (39>
^^(0 + ^40= о)
Эта система однородных уравнений может иметь отличные от
нуля решения тогда, когда ее определитель равен нулю; это
приводит к следующему условию:
? (0)-<?'(/) ~ ? (0) ?'(0 - °- (З.Ю)
Так как <р и —интегралы у равнения (3.6), коэфициенты
которого зависят от р, то и сами функции и <р будут зависеть
ог р. Поэтому уравнение (3.10) .можно рассматривать как
условие для определения частоты р. Это уравнение называется
уравнением частоты или характеристическим уравнением.
32
Таким образом уравнение (3.6) может иметь интеграл, удо-
влетворяющий граничным условиям не всегда, а только при
некоторых частных значениях параметра р, входящего в это
уравнение (именно только при значениях р, являющихся корнями
характеристического уравнения п). Так как р есть частота коле-
баний, то это означает, что колебания могут происходить лишь
с определенными частотами. Для каждого значения частоты,
определенного из уравнения (3.10), существует интеграл уравне-
ния (3.6), удовлетворяющий граничным условиям.
Этот интеграл определяет соответствующую данной частоте
форму колебаний.
Характеристическое уравнение имеет ряд корней рл, р2, . .
Соответственно каждому значению частоты, находим отноше-
ние постоянных Л41 :/И2 из любого уравнения системы (3.9) и
затем, подставляя найденное значение р в выражение и о, на-
ходим по формуле (3.7) соответствующую данной собственной
частоте р = р„ собственную функцию <? = ?„(£). Интегрируя
уравнение (3.5) при р — рп, найдем также соответствующее дан-
ному рп выражение функции q~qn (£) 2). Таким образом каждой
собственной частоте р — рп будет соответствовать свое выра-
жение функции угла закручивания крыла = (г)^п(0 и общее
решение будет найдено как сумма:
(3.77)
Первое слагаемое <?1(г) (£) называется основным тоном ко-
лебания, слагаемое «^(z)^^)—вторым тоном, ?3(г)^3(О,—третьим
тоном и т. д. Все слагаемые, кроме первого, называются также
обертонами (высшими тонами). Соответственно говорят об ос-
новной (низшей) частоте и высших частотах р2, р3 . . . , а
также об основной форме (z) и высших формах (z), ®з С2)» •
Однако, чтобы фактически выполнить все указанные операции,
нужно знать частные интегралы с и если жесткость балки и
момент инерции изменяются вдоль ее длины, то найти эти част-
ные интегралы обычно трудно. В этом случае для определения
частоты колебаний применяются различные приближенные спосо-
бы, среди которых заслуженной популярностью пользуется ме-
тод Рэлея.
Метод Рэлея. Как отмечалось в введении, существо ме-
тода заключается в том, что заранее делается определенное пред-
положение относительно формы колебания балки (крыла) и час-
тоту находят из рассмотрения энергии колеблющейся системы.
’) При всех других значениях р уравнение (3.6) имеет только тривиаль-
ное решение a (z) == 0.
2) Постоянные интеграции могут быть при этом найдены нз начальных
условий.
3 Гроссмен и Пановк'
33
В самом деле, предположим, что функция формы колебания <» (-)
известна. Тогда, поскольку угол закручивания ищется в виде (3.4):
е(г,о = т(*)т (3-12)
движение будет полностью определено, если будет найдена функ-
ция времени q (t). Для получения соотношения, определяющего
эту функцию, составим выражение кинетической и потенциаль-
ной энергии колеблющейся балки (крыла) для произвольного мо-
мента времени.
Потенциальная энергия определяется известной формулой со-
противления материалов для энергии закрученной балки:
/ I
U==^f GJKp^dz = ^ J GJKp<?*dz. (3-13)
о о
Кинетическая энергия системы
1 „ 1
г=4[ J^'idz= i /J^dz- (3 l4)
о 0
Воспользуемся законом сохранения энергии:
Т+ U = const.
Диференцируя это выражение по времени, получим уравнение,
определяющее
г1 г1
q I Jm^dz + q I GJKp<f'2dz = 0. (3.15)
о о
Легко видеть, что если ввести обозначение:
I 1
Р2 = f GJKp^dz-. fjm<?dz, (3.16)
о о
то уравнение (3.15) совпадает с уравнением (3.5), которое рас-
сматривалось выше. Мы видели, что это уравнение определяет
функцию q(t), изменяющуюся по гармоническому закону с кру-
говой частотой р. Таким образом формула (3.16) определяет
частоту колебаний. Если бы было известно точное значение
функции формы <p(z), то выражение (3.16) определяло бы точ-
ное значение частоты р. Задавая функцию <p(z) приближенно,
мы получаем из (3.16) и приближенное значение частоты. Обыч-
но, если задать функцию <p(z) так, чтобы она удовлетворяла
граничным условиям задачи (3.8), то значение частоты по фор-
34
муле (3.16) довольно близко совпадает с точным значением, да-
же если выбранная функция формы и не очень близка к дейст-
вительной.
Метод Рэлея дает возможность определить только час-
тоту колебаний, но не форму их. Кроме того, точность опре-
деления частоты зависит от более или менее удачного выбора
функции <f(z), а для такого выбора достаточных критериев не
дается. Поэтому метод Рэлея обычно применяют в сочетании
с методом последовательных приближений; с помощью послед-
него можно сколь угодно близко подойти как к точному зна-
чению частоты, так и к точному выражению формы колебаний.
Метод последовательных приближений. Для определения
функции 9 (z) необходимо проинтегрировать диференциальное
уравнение (3.6) при граничных условиях (3.8).
Прежде всего подчеркнем, что диференциальным уравнением
и граничными условиями функция 9 (z) определяется только с
точностью до постоянного множителя. В самом деле, если функ-
ция у (z) удовлетворяет диференциальному уравнению (3.6) и
граничным условиям (3.8), то функция Д<х>(г), где. — произ-
вольное постоянное число, будет также удовлетворять указан-
ному уравнению и граничным условиям.
Умножение функции <?(z) на произвольный множитель А не
отразится на величине частоты, так как числитель и знаменатель
в формуле Рэлея (3.16) приобретут одинаковый множитель, ко-
торый может быть сокращен.
Правом сокращать (или умножать) функцию <p(z) на любой
постоянный множитель мы в дальнейшем воспользуемся. Пере-
несем в уравнении (3.6) последний член в правую часть и проин-
тегрируем уравнение в пределах от z до I. Разделив результат
на GJKP, получим:
Z
<P'(z) = - V— [ Jm^(z)dz.
UKPfJ
Пределы выбраны таким образом, чтобы удовлетворить вто-
рому из граничных условий. Интегрируем последнее выражение
в пределах от нуля до z [нижний предел выбран равным нулю
для того, чтобы удовлетворить первому из условий (3.8)[:
г z
<p(z)~pt -Л_ J Jm(?{z)dz^
О I
Пользуясь (3.17), можно определить функцию у (z) следующим
образом. В качестве исходного нулевого приближения задаемся
какой-либо функцией <р(°) (z) и вычисляем соответствующее значе-
з*
35
ние частоты р(°) по формуле (3.16). Для получения следующего
(первого) приближения подставляем выражения <р (®)(z) и р(°) в пра-
вую часть формулы (3.17). Выполнив указанные действия1), най-
дем первое приближение для функции ® (z), которое обозначим
через <p(l)(z).
Для получения второго приближения подставляем в
(3.16) и находим соответствующее значение частоты pl1). Затем
значения срС1) (z) и />(’) подставляем в правую часть формулы (3.17)
и находим второе приближение ®(2) (z). Этот процесс продолжаем
до тех пор, пока функции ^(z), полученные при двух последо-
вательных приближениях, практически не совпадут. Обычно для
этого бывает достаточно двух-трех приближений.
Весь процесс можно упростить, если воспользоваться сделан-
ным выше замечанием, что функцию <p(z) мы вправе сокращать
на любой постоянный множитель. Будем сокращать функции,
получаемые в каждом из последовательных приближений, на
множитель р2 (это величина постоянная, т. е. не зависит от z).
Тогда вместо (3.17) для получения л-го приближения из п—1-го
будем иметь следующую формулу:
Z Z
®(")(z) = С ~~ Г Jm ®(n-1)(z) dz'. (3«18)
() кр г
Таким образом отпадает необходимость в каждом приближе-
нии определять частоту. Только после того, как процесс оконча-
тельно сошелся, р определяется по формуле (3.16).
Для удобства сравнения между собой функций, получающих-
ся в различных приближениях, следует умножать их на такой
множитель, чтобы получать на конце крыла (при z — l) одно и
то же значение (обычно принимают <р (/) = 1). В качестве исход-
ного приближения для функции можно задаться, например, функ-
цией первого тона колебания крыла постоянного сечения:
<р(°) (z) = sin .
В общей теории доказывается, что независимо от удачности
выбора исходной функции, описанный процесс является сходящим-
ся к истинной функции ®(z), выражающей собственную форму
первого тона колебаний."
Для вычисления форм и частот обертонов приходится выпол-
нять несколько более громоздкие выкладки. Прежде чем давать
схему этих выкладок, остановимся на так называемом условии
ортогональности:
*) Например, числовым методом, разделив полукрыло на 10 — 20 участ-
ков.
36
Jm(?t'fjdZ — G, (319>
0
справедливом для двух любых различных собственных форм г-ого
иу-ого тонов.
Для доказательства вернемся к уравнению (З.о), которое долж-
но быть удовлетворено как функцией ®;, так и функцией »/):
(04₽?9'+а94,%=о
(04 р ?/)'+/’/ 4 ъ=о-
Умножим первое тождество на ®у, а второе на и, вычтя одно
из другого, проинтегрируем результат в интервале О, Z:
Г1 С
/ [(ОЛр?/)' Ъ - %] dz + (р/ —рр) J Jm ъъ dz—Q
6 •>
Первый интеграл непосредственно поддается интегрированию и
дает:
04/?;^ —?»?/)•
Это выражение равно пулю в силу граничных условий (3.8); а так
как pt^Pj, то из последнего равенства и вытекает условие орто-
гональности (3.19). Физический смысл условия (3.19) состоит в
равенстве кинетической энергии суммарного движения
I
± У 4(^^+^ъ)3^
о
сумме кинетических энергий обоих движений
I I
У J" J"
О О
Условие (3.19) необходимо иметь в виду при вычислении обер-
тонов крутильных колебаний, хотя само вычисление базируется
на том же уравнении (3.18); последнее, разумеется, справедливо
для функции любого тона. Процесс последовательных прибли-
жений для определения форм обертонов колебаний строится так,
чтобы удовлетворить условию ортогональности в каждом при-
ближении.
Следует, помнить, что ф. и у . представляет собой ие t-oe и у-ое прибли-
жение, а истинные значения функций г-ого и у-ого тонов.
37
Поясним вычисление функции второго тона. В качестве ис-
ходного приближения принимаем: »
?2(0) = Лв(?(0) + Св!Р1),
где <?(°) — произвольная функция, за которую можно, например,
принять ту же функцию <?(°) — sin которой мы задавались в
качестве исходной при определении функции первого тона;
Ti ~ функция первого тона, которая должна быть обязательно
найдена заранее;
Со — постоянная, определяемая из условия ортогональности (3.19):
/ /
I dz=f + Со Til dz = О,
о о
откуда получается:
l 1
Со = - J Jm <р(°) dz : J* Jm (¥1)3 dz (3.20)
о о
Ло — постоянная, назначаемая с таким расчетом, чтобы при z = /:
функция <р2(°) принимала значение, равное единице.
После определения у2(с) следует подставить ее в правую часть
основного уравнения (3.18) и найти затем интегрированием функцию
?2е)(г).
Первым приближением будет функция
?,(*)(«)=л, (?2w+c1?1),
где находится из условия ортогональности, подобно (3.20) в ви-
де:
I I
Ci~ f Jm<f^idz: J Jm('fi)2dz
и о
At — вычисляется как и выше из условия ср2С)(/) = 1.
Подобным же образом строится второе приближение. В пра-
вую часть (3.18) подставляется %(’) и после интегрирования на-
ходится функция ч>20; затем образуется выражение
?2(2)(г) = Л2(^0 + С2Ф1),
где С2 — определяется из условия ортогональности, а Л8 из усло-
вия <р2(2)(/)= 1.
Это’т процесс продолжается до достаточно близкого совпаде-
ния функций <?2(”)(<г) и <p2(n-1)(z), после чего из (3.16) находится
частота второго тона.
38
4 Собственные колебания изгиба крыла (консольная схема)
Как и выЩе> будем схематизировать крыло как консольную
бачку жестко заделанную в фюзеляже. Для получения уравне-
ни колебательного движения такой балки воспользуемся изве-
стным диференциальным уравнением упругой линии стержня,
нагр женного распределенной нагрузкой интенсивности s;
d3 { г. , д3у \
-д-Д EJ =5,
dz-1 dz3 )
где EJ — жесткость балки (крыла) на изгиб и у—у (z,/) —про-
гиб балки. В случае крыла под у будем понимать прогиб оси
жесткости крыла.
При свободных колебаниях крыло нагружено лишь силами
инерции, и под 5 следует понимать интенсивность их распреде-
ления по длине крыла. Обозначим через т погонную массу кры-
л d3v ,
ла; тогда будем иметь х =— т и уравнение упругой ли-
нии примет следующий вид:
^('£/^Л + т^=0. (4.1)
dz3\ dz3 J dt2 4 '
Для полного определения задачи к этому уравнению необходи-
мо добавить граничные и начальные условия.
Граничные условия:
при г —0, в силу абсолютной жесткости заделки:
, = 0; -& = 0.
J dz
при г — I, на свободном конце, исчезают изгибающий момент и
поперечная сила:
И^=0; (4 9)
dz2 ’ dz\ dz2) I4-2/
где I— расстояние от корня до конца крыла.
В дальнейшем, как и выше, начальные условия нам будут
не нужны. Для решения уравнения (4.1) могут быть применены
те же’ методы, которые использованы выше в случае крутиль-
ных колебаний. Будем искать частное решение уравнения (4.1)
в виде произведения двух функций, из которых одна зависит
только от z, а другая—только от времени f:
y=/(z).^(0. (4.3)
Подставляем это в уравнение (4.1) и разделяем в нем перемен-
ные:
(EJfT _ q
mf ~ q ' ( >
39
Так как слева стоит функция только z, а справа—функция толь-
ко Л и они равны друг другу при любом значении z и t, то
каждая часть полученного выражения должна быть равна посто-
янной величине. Эту постоянную обозначим через—р2.
Приравнивая каждую часть уравнения (4.4) постоянной — р~,
получим два уравнения для определения функций /(г) и q(t):
q+p*q = O-, (4.5)
(EJf")" - p*mf=O. (4.6)
Граничные условия для функции /(г) (предполагая, что
жесткость изгиба на конце крыла не обращается в нуль):
При г = 0 ввиду абсолютной жесткости заделки должно быть
/ = 0;/' = 0; (4.7)
при z~l обращается в нуль изгибающий момент и попереч-
ная сила; поэтому должно быть
/" = 0; [£//"]' = 0.
Уравнение (4.5) совпадает с уравнением (3.5), отсюда ясно,
что изучаемое движение является гармоническим колебанием
q (t) — A sin (pt + a),
где p — круговая частота колебаний.
Так же, как и в задаче о крутильных колебаниях, уравнение
(4.6), определяющее функцию формы колебаний f(z), имеет ре-
шение, удовлетворяющей граничным условиям только при не-
которых определенных значениях параметра р, которые являют-
ся собственными значениями параметра для диференциального
уравнения (4.6).
Метод Рэлея. Обычно при расчете изгибных колебаний
крыла переменного сечения пользуются методом последователь-
ных приближений. Прежде чем его излагать, покажем как можно
определить частоту колебаний, если известна их форма, т. е.
если известен закон распределения амплитуд колебаний по раз-
маху крыла, характеризуемый функцией/. Поступим, как и при
анализе колебаний кручения.
Потенциальная энергия изгиба определяется известной фор-
мулой сопротивления материалов
40
Диференцируя
определяющее
Обозначая
[
Кинетическая энергия колеблющейся балки.
т y3dz — J'mf dz.
о о
Из закона сохранения энергии следует:
Т + U— const.
это выражение па времени, найдем уравнение,
?(*):
I I
"q [ mf2 dz У q J EJf'3 dz = 0.
« 0
z z
p2 = f' EJf,3dz: I'rnfdz, (4.8)
о 0
получим q + p3q = 0, как и в задаче о кручении; следовательно
р является круговой частотой колебаний. За приближенное зна
чение f(z) часто принимают функцию первой формы колебаний
балки (крыла) постоянного сечения (приводим ее без вывода)1)
ch 1,875 ----cos 1,875 ) - 0,734( sh 1,875-?--
I / / \ I
— ch 1,875 -?-) . (4.9)
Дальнейшие уточнения частоты и формы делаются методом по-
следовательных приближений.
Метод последовательных приближений. Перепишем уравне-
ние (4.6) в виде:
(EJf)''=p3mf. (4.10)
Задавшись функцией f—f^(z), например, по ф-ле (4.9), вы-
числяем по формуле (4.8) соответствующее значение р = pw- За-
тем подставляем вместо f(z) и р в правую часть (4.10) (г) и
Интегрируя после этого полученное выражение два раза,
найдем:
। 9 EJf' = [р(°)|2 f j' mf!>)(z)dzdz. (4.11)
/ i
Пределы интегрирования выбраны таким образом, чтобы удовле-
творить граничным условиям (4.7). Обе части выражения (4.11)
’) См. напр. Е. П. Гроссман. Курс вибраций частей самолета. 1940.
41
делим на EJ, после чег.о результат опять дважды интегрируем^
снова выбирая пределы интегрирования в соответствии с усло-
виями (4.7):
Z Z . Z Z
f(z) = [p(°)F f / f т/(°) (z) dz*. (4.12)
0 0 I I
Найденное таким образом значение функции f (z), мы обозна-
чим через/(9 (z); это и есть значение искомого интеграла в первом
ириближении. Для получения следующего приближения повторя-
ем весь процесс, приняв за исходную функцию/ б) (z). В резуль-
тате мы найдем функцию /(2)(z) (второе приближение). Берем
эту функцию за исходную, опять повторяем весь процесс и т. д.
до тех пор, пока два последовательные приближения не дадут
достаточно близких значений для функций f(n— 1) и /("). Обычно,
как и в задаче кручения, для этого оказывается достаточным
двух-трех приближений.
Расчет значительно облегчается, если, как и выше, принять
во внимание, что вследствие однородности уравнения мы можем
сокращать функцию f (z) на любое постоянное число.
Функции, получаемые в каждом из последовательных прибли-
жений, будем сокращать на множитель р2. Тогда вместо (4.12) для
получения очередного n-го приближения из п— 1-го мы будем
иметь:
Z Z . Z Z
(г) = f Ш J /dz *. (4.13)
О у ’l I
Лишь после окончательного определения функции f (г), на-
ходим частоту по формуле (4.8).
Для сравнения функций, полученных в различных приближе-
ниях, их принято нормировать таким образом, чтобы значения
У<л) (/) на конце крыла (для z = Z) были одинаковы во всех при-
ближениях.
5. Собственные совместные колебания крыла
(консольная схема)
а) Характер движения и основные уравнения
Выше были рассмотрены чисто крутильные и чисто изгибные
колебания крыла в пустоте. Однако в действительности такие
колебания могли бы существовать только в том случае, если
бы центр тяжести и центр жесткости в каждом сечении крыла
совпадали. Если это условие не соблюдено (как оно всегда и
бывает), то колебания крыла будут обязательно совместными,
т. е. крыло будет испытывать одновременно и деформации изги-
42
центр жесткости все время
крыла в направлении оси
ба, и деформации кручения. Чисто изгибных и чисто крутиль-
ных коле*бапий у крыла не бывает, хотя совместные колебании
протекают обычно, таким образом, что как по форме, так и по
частоте мало отличаются от чисто изгибных и чисто крутиль-
ных Поэтому часто не производят расчета совместных колеба- .
ний крыла, а характеристики (частоту и форму), полученные из
расчета чисто изгибных и чисто крутильных колебаний, прини-
мают за характеристики действительного колебательного движения
крыла.
Рассмотрим колеблющееся в пустоте крыло, центр тяжести
которого С находится на расстоянии о от центра жесткости
(фиг. 15)- Пусть ХО Y— неподвижная система координат, выбран-
ная таким образом, что ось OY проходит через центр жесткости
сечения Е и по направлению совпадает с направлением изгибной
деформации крыла. При движении
остается на оси О Y, (жесткость
ОХ предполагается бесконечно
большой).
Покажем, что, даже если на-
чальный импульс, вызвавший дви-
жение, был чисто изгибающим,
или чисто крутящим, колебания
крыла все равно будут совместны-
ми. Пусть, например, мы изогнули
крыло вниз и затем предоставили его
самому себе. Исходное отклонение
предположено вниз, чтобы, во избе-
жание путаницы в знаках, ускоре-
ние с самого начала было положи-
тельным. Под действием сил упру-
гости элементы крыла начнут дви-
Фиг. 15. Начальный изгиб
крыла вызывает кручение.
гаться к своему положению равновесия с ускорением
у — прогиб крыла. При этом равнодействующая всех
ции элементарного отсека крыла будет:
dz.
сил инер-
(5.1)
Здесь т — погонная масса крыла в рассматриваемом сечении и
mdz—общая масса отсека. Знак минус обозначает, что сила Pt на-
правлена против ускорения, т. е. вниз, как это и показано на фиг. 15.
Силы инерции, вызванные изгибным движением, сводятся не толь-
ко к силеРр действующей вдоль оси О/ и приложенной в центре
тяжести, но также к моменту относительно центра жесткости:
= та dz, (5.2)
43
где = — абсцисса центра тяжести. Знак момента взят противополож-
ным знаку силы инерции, так как отрицательная сила при положи-
тельном значении а вызывает положительный момент (по ходу часо-
вой стрелки).
Поскольку момент относительно оси жесткости отличен от
нуля, неизбежно возникает кручение крыла; если центр тяжести
крыла совпадает с его осью жесткости (с —0), то момент 7И, от
сил инерции также обращается в нуль и, следовательно, лишь у
крыла с совмещенными осями жесткости и центров тяжести
возможны чисто изгибные колебания. У крыла с несовмещен-
ными осями чисто изгибные колебания невозможны, — они обяза-
тельно перейдут в совместные.
Точно так же, если линия центров тяжести и ось жесткости
крыла не совпадают, невозможны и чисто крутильные колеба-
ния крыла: они также неизбежно перейдут в совместные. В са-
мом деле предположим, что
*пг. 16. Начальное кручение крыла
вызывает изгиб.
мы закрутили крыло на не-
который угол и предоста
вили его самому себе (фиг.
16). При этом возникнут
крутильные колебания, про-
исходящие с угловым уско-
<?26
рением где поп ре жнем у
6 — угол закручивания кры-
ла. Тогда каждой матери-
альной точке сечения кры-
ла будет соответствовать
линейное ускорение ,
(где — расстояние от точки т, до оси жесткости) и, следова-
тельно, появится сила инерции — mici Знак минус обозна-
чает, что эта сила направлена против ускорения, т. е. вверх, как
это и показано на фиг. 16.
Эти силы направлены по нормали к радиусу—вектору точки
и для весьма тонкого- крыла с малой кривизной близки
к вертикальным. Для элементарного отсека момент этих сил
относительно оси жесткости получим, если умножим каждую
силу на соответствующее плечо 8 и затем произведем суммирова-
ние по всем точкам отсека:
М'~ J" дГ dZ'
(5-3)
где Jm — погонный массовый момент инерции крыла относительно
оси жесткости в рассматриваемом сечении.
«54
Однако силы инерции, действующие на различные точки
рассматриваемого отсека крыла, имеют также равнодействующую,
слагающая которой по оси ОУ и вызовет изгибные колебания
крыла. Слагающая по оси ОУ силы инерции mt of , дей-
ствующей в точке Мт-, есть с точностью до малых высших по-
рядк в Суммируя элементарные силы по всем точкам
отсека, получим:
о V <?20 ,
Р,= У т-.х-. -575- = тс ~ dz.
“ _> ‘ dt- дО
(5-4),
Рели ось жесткости совпадает с центром тяжести, то с —О,
р _-о и изгибные колебания крыла не возникнут.
2 Отметим, что все силы и моменты Pit Р2, Л1г и являются
периодическими функциями времени, так как при колебательном
движении ускорение (которому пропорциональны эти силы и
моменты) изменяется периодически. Таким образом ясно, что
вследствие несовпадения центра тяжести и жесткости сечений
крыла изгибные и крутильные колебания связаны между собой,
и один вид колебаний неизбежно вызовет другой.
Обратимся теперь к составлению и решению уравнений дви-
жения. Как и выше будем исходить из обычных уравнений:
для изгиба
д3/' д2у\
—J EJ-r-t = s
егд dz* ]
и для кручения
d_
dz
(5.5)
Здесь s— погонная нагрузка и p—погонный крутящий момент ’).
При вибрациях крыло нагружено лишь силами инерции, и под
s следует понимать сумму погонных сил инерции, а под р—
сумму их моментов относительно оси жесткости. Выше в (5.1)—
(5.4) мы нашли выражения сил инерции, действующих на отсек
-------------- : л.З
Вторая формула получается следующим образом. Из сопротивления ма-
териала известно, что крутящий момент в любом сечении балки:
Mhp—GJkp
Но крутящий момент в любом сечении крыла г1 создается действием сил
находящихся на всей части крыла от сечения z = Zi до конца z = /. Если р—
погонный крутящий момент, то
I
Mkp=J'vdz .
Z
Днференцируя это выражение по г, приходим ко второй формуле (5.5).
45
крыла dz и их моментов. Чтобы получить погонные значения
сил и моментов, делим соответствующие выражения на ширину
отсека dz. Таким образом, при совместных колебаниях на крыло
действуют следующие погонные инерционные силы и моменты
(погонные значения будем обозначать той же буквой, как и
значения для элементарного отсека, но с чертой сверху):
Сила инерции, возникающая вследствие изгибных колебаний
крыла *
Р,=-т
dt2
сила инерции, возникающая вследствие колебаний кручения крыла
ft2
момент си.
чрции от изгибных колебаний
“лл ^У
момент сил инерции от крутильных колебаний
Следовательно:
д2у д2Ь
s=~mdF +пиж
д‘у , дг0
Подставляя эти значения в (5.5), получаем систему уравнений
движения при совместных колебаниях крыла в пустоте:
d2
dz2
д
dz
d2y (?26
+ —0
32У , , О
“+ Jm “775 — 0
dt2 т dt2
(5.6)
Заметим, что уравнения (5.5) справедливы также и для кры-
ла, колеблющегося в потоке воздуха. В последнем случае только
следует учесть, что в s и р входят, кроме инерционных, также
и аэродинамические силы и моменты. z
Система уравнений движения (5.6) в случае с = 0 распадается
на два независимых уравнения, которые были изучены выше:
уравнение чисто изгибных и уравнение чисто крутильных колебаний.
46
Как и выше, граничные условия для у и 0 будут:
при 2 = 0: j/ = 0; ^ = 0; 0 = 0;
_/. ^ = 0-— 1е7-У-\ = 0- -- = 0.
при z — I. дгг ’dz\ Эг2/ ’ dz
(5.7)
Уравнения (5.6) вместе с граничными условиями (5.7) служат
для определения прогиба у и угла кручения 0 при совместных
колебаниях крыла в пустоте*). Проинтегрировав эту систему,
можно определить как формы колебательного движения, так и
частоты.
б) Метод Рэлея
Как и в предыдущих случаях воспользуемся для определения
частот методом Рэлея.
Для подсчета кинетической энергии колебли 'ося крыла
рассмотрим перемеще-
ния произвольного се-
чения крыла. Как вид-
но из фиг. 17 (коорди-
натная система как на
фиг. 16), перемещение
центра тяжести вдоль
оси ОУ составляется из
двух частей: первая
представляет собой
перемещение центра
жесткости у, а вто-
рая — дополнительное
перемещение <Л, воз-
Фиг. 17. Перемещение центра тяжести сече-
ния составляется из двух частей.
никающее вследствие
весов падения центров
тяжести и жесткости.
Воспользуемся теоре-
мой Кенига о полной кинетической энергии.
Кинетическая энергия поступательного движения элементар
ного отсека:
йТу~-^т\у — aftfdz, (5.8)
тяжеСТ°Я1Цее в скобках выражение является скоростью центра
,’и Вдоль оси OY. Кинетическая энергия вращения элемен-
тарного отсека:
мнтересующихЬИЫХ Условиях мы не упомянули, как о несущественных для
нас характеристик (частот и форм).
47
ЛТъ raj2)ij2 dz-
(5.9)
Стоящее в скобках выражение представляет собой величину
ногонного массового момента инерции относительно центра
тяжести. Это выражение непосредственно следует из извест-
ной формулы механики J1 = 70 + /no2, где Jo—момент инерции
относительно центра тяжести, —момент инерции относительно
точки, отстоящей на расстоянии о от центра тяжести; в данном
случае J1 = Jm. Складывая (5.8) и (5.9), найдем суммарную кине-
тическую энергию по теореме Кенига:
dT=~[m(y — а 6)2 + (4-"1°2) •
Раскрывая скобки, получим общую кинетическую энергию эле-
ментарного отсека:
d Т= ~ my2dz+ ~ Jm& dz—jncyhdz.
(5.10)
Чтобы получить полную кинетическую энергию всего крыла,
необходимо просуммировать кинетическую энергию отдельных
отсеков:
(5.11)
Потенциальная энергия крыла слагается из потенциальной энер-
гии изгиба и потенциальной энергии кручения:
" I I
f EJy'!2dz-i- / GJkp№dz
о о
(5.12)
Отметим, что найденные нами выражения потенциальной и
кинетической энергии, как ясно из самого способа их получе-
ния, не зависят от того, колеблется ли крыло в пустоте или
в потоке воздуха. Они остаются справедливыми и в последнем
случае, и мы ими будем пользоваться также в дальнейшем при
изучении колебаний крыла в потоке воздуха.
Как обычно ищем решение в виде:
y(z,t) — q[tYf(z)-, b(z,t) = r(t)<?(z). (5.13)
48
Подставляя эго в уравнения (5.11)—(5.12), найдем:
/'= ^(Cn'^+c.^-j-c^qr
U= -{а^ + а.^
(5.14)
где обозначено:
/
С1; '= / nt/adg;
О
/
с3,= бг=-./>М*;
о
I
aa—fEJf"*dz-,
о
i
а*,= f'GJkp^dz-,
о
(5.15)
1
Сц~ f Jm^dZ .
о
Функции / и », определяющие форму колебаний, будем
считать известными. Тогда движение будет полностью опреде-
лено, если будут определены q и г, как функции времени. Для
их определения воспользуемся уравнениями Лагранжа:
d /дТ\ dT dU
4 ’
dt \дг ) dr dr ' ’
Фактически, выполняя дифференцирование, мы придем к двум
уравнениям:
ги7+с1г/-+• wnf — °; (5.16>
са1^ + с22г 4-h2.z =0.
Система уравнений (5.16) представляет собою систему линейных
диференциальных уравнений с достоянными коэфнцнентами,
частное решение этой системы
q .4 sin(pt-ha); r=x Bsin(/?/ + a). (5.17)
Подставляя это в (5 16), получаем систему алгебраических урав-
нений для определения амплитуд Д и й:
Д(/г1Г р*сХ1)+В( р^с^—О )
A В(а.,., — рас.3.,) О j
(5.18)
’) См. напр. Лонцянский Л. Г. и Лурье А. И. Kvpc чеоретнческой мехамк-
“» ч П.
4
Фрссман н Панидк!
40
Так как эта система однородна, то она имеет отличные от
нуля решения1 только тогда, когда определитель ее равен нулю.
Приравнивая определитель системы нулю, получаем характери-
стическое уравнение, определяющее параметр р;
AjA—CrfA + Ь\ = 0. (5.19)
где
At--^*11^22. --Н1^52 Т --^'11^22* (5.20)
Согласно (5.17) q и г определяются уравнениями, выражающими
гармоническое колебание с круговой частотой р и амплитудами
соответственно А и В.
Если бы функции формы /(г) , <р(г) были точно известны, то
из (5.15) можно было бы вычислить точные значения коэфициен-
тов Яц,... сп,... и из уравнения (5.19) найти точные значения
частот совместных колебаний. Обычно частоты совместных ко-
лебаний определяют приближенно следующим образом.
Прежде всего рассчитывают часто изгибные и чисто крутиль-
ные колебания рассматриваемого крыла и определяют их форму,
как это было показано выше. Найденные таким образом функции
считаются мало отличающимися от функции формы совместных
колебаний и принимаются за основу при определении частоты,
т. е. они используются при вычислении коэфициентов (а.15), после
чего находятся из (5.Г9) частоты/?! и р8.
Уравнение (5.19) дает два значения частоты совместных ко-
лебаний. Можно показать, что одно из этих значений всегда
несколько меньше частоты чисто изгибных колебаний, а другое
несколько больше частоты чисто крутильных колебаний ’). Соот-
ветственно и формы колебаний мало разнятся: при частоте pt—
от формы чисто изгибных колебаний и при частоте р2—от формы
чисто крутильных колебаний. Это значит, что при частоте pt
амплитуда изгибных колебаний велика, а при частоте р2 мала,
по сравнению с амплитудой крутильных колебаний-
Особенно это ясно при экспериментальных исследованиях
вибрирующего крыла: при частоте рх на глаз невозможно заме-
тить кручения, даже при весьма значительной амплитуде изгиб-
ных колебаний. При частоте р2 почти незаметно изгиба и в то
же время крутильные колебания происходят весьма интенсивно.
Но все же следует всегда помнить, что термины „изгибные11 и
„крутильные" колебания являются условными, так как в дей-
ствительности колебания всегда совместны. В дальнейшем
колебания с частотой рл мы будем называть совместными изгиб-
ными колебаниями, а колебания с частотой р2—совместными
крутильными колебаниями. Следовательно, совместные изгибные
колебания—это совместные колебания с преобладанием ампли-
туды изгибных колебаний, а совместные крутильные колебания—
1) См. Гроссман Е. П. Курс вибраций частей самолета, 1940.
50.
это совместные колебания с преобладанием амплитуды крутиль-
ных колебаний.
Метод последовательных приближений, подробно изложенный
выше применительно к чисто крутильным и чисто изгибиым ко-
лебанием, может быть распространен и для расчета совмест-
ных колебаний. Однако практически пользоваться им приходится,
весьма редко и потому мы его не излагаем, отсылая интересую-
щихся к специальной литературе ’).
6. Собственные колебания самолета
(свободно плавающая схема)
а) Формы колебаний крыла
В предыдущих параграфах мы схематизировали крыло, как
консольную балку. Такое представление было бы вполне точным,
только в том случае, если бы фюзеляж обладал бесконечно,
большой массой и потому не принимал бы участия в колебаниях
крыла. В действительности колебания крыла, передаваясь фюзе-
ляжу, вызывают также и его колебания.
Рассмотрим колебания крыла с учетом конечности массы фю-
зеляжа, причем будем считать крыло свободно плавающим
в пространстве, а фюзеляж бесконечно узким. Из анализа коле-
баний такого крыла в пустоте мы получим некоторые общие свой-
ства движения, которые в значительной мере сохраняют свою
силу и для реального самолета в условиях полета. В настоящем
параграфе мы ограничимся рассмотрением изгибных колебаний.
Условие равновесия сил для отсека dz свободно плавающего
крыла будет то же, как и для консольного крыла. Поэтому^
уравнение движения (4.1) сохраняется без изменения:
EJ + /п^8 = 0. . (6.1)
dzl dtf v
Граничные условия заключаются в том, что изгибающий мо-
мент и перерезывающая сила на концах крыла должны обра-
щаться в нуль, т. е. при z = + / Должно быть:
У" (О =У" (-1) = [EJ/']' -L - [EJy^Yi = 0. (6.2)
В сечении z = 0 крыло несет на себе массу.фюзеляжа Мф, ко-
торую будем считать сосредоточенной в этом сечении. По-
этому в отличие от предыдущего в этом сечении должны вы-
полняться следующие условия сопряжения:
') Труды ЦАГИ. Вып. 472. 1940. А. И. Комай. Совместные колебания крыли
с сосредоточенными грузами.
1. Равенство прогибов сечения z~Л) при подходе тс нему
справа и слева:
У (О + ) —_v(0—). ’) (6.31
2. Равенство углов наклона касательной к линии изгиба
в том же сечении при подходе к нему справа и слева:
У(О+)=У(О-). (6.4)
3‘. Равенство изгибающие моментов в том же сечении:
у'(О + )'~у'(0 —). (6.5)
4. Условие, выражающее действие силы инерции фюзеляжа:
[W'l'o + -1 = — м#у(О) (6.6)
(разность поперечных сил правее и левее сечения z = 0 равна
силе инерции фюзеляжа).
Как н всюду выше ищем решение (6.1) в виде:
y = V(0-/(z). (6.7)
Подставляя это в основное уравнение (6.1) и разделяя пере*
менные, получим, как и ранее:
q+p1q = Q (6.8)
(EJfT p’mf—O. (6.9)
Уравнение (6.8), неоднократно рассматривавшееся ламп выше,
иеносредственно показывает, что q (t) есть гармоническая функ-
ция времени с круговой частотой р. Уравнение (6.9) вместе
с граничными условиями и условиями сопряжения определяет
функцию формы колебания /(г).
Подставляя выражение (6.7) в граничные условия и условия
сопряжения и заменяя в последнем нз них значение q на—р'*ц,
в соответствии с (6.8), получим:
Г (0=/"( 0=0; (£7/'Эг' = (£#"У-г = 0;
Л 0+ ) = /(0-); /’<0 + )=/'(() - ); /"(0 +) = /"(0-);
(£7/")'о г = (EJf (O)Jy,
(6.10)
Прежде всего отметим, что система уравнений (6.9) — (6.10)
имеет следующие очевидные решения:
1) р = 0; f=Ct-,
1) Аргументы 0-(- и 0— соотвегствуют среднему сечению при тгриГмижеинм
к нему отрава и слева.
52
2) р = 0 f =
(6.11)
г^с С}. С„ произвольные постоянные. Эти решения дают парал-
лельное перемещение и поворот в пространстве всей системы,
как твердого тела (фиг. 18). Такое решение должно естественно
существовать, поскольку рассматриваемая нами система сво
б'одна в пространстве и, следовательно, кроме упругих дефор
маний может так же пере-
мещаться в пространстве,
как твердое тело.
Для определения форм
более высоких тонов коле-
баний воспользуемся свой-
ством ортогональности соб-
ственных функций (оно ана-
логично тому, которым мы
уже пользовались выше при
определении обертонов кру-
ти 1ьных колебаний).
Будем обозначать через
Д (г) -функцию i-ro и че-
рез fj(zi—функцию /-го то-
на колебания. Согласно (6.9)
имеем;
(EJji’’} —P'tnfi-,
Умножаем первое из этих
равнений на /7, втооое на
f\, затем вычитаем одно из
ио длине крыла. Будем иметь-
Фиг. Две простейшие (.нулевые*)
формы колебаний свободно плавающего
крыла.
другого п результат пнтегрируем-
1-/
([fAEJf,")" fAEJf/yjdz-^-p/) (6.12)
— i
Первый интеграл можно преобразовать интегрированием но
> 'тям; раскроем квадратные скобки и рассмотрим сначала пер-
кып член:
0— -(-/
I fAEJf-r'dz= f f} (JMfl'Y dz + f
—l 0+-
= f (£7Л71о- IfAEJtЛ7 -i~ {f'jEJfi'%- + +
+ f EJfA'f/'dz.
ST
положение равновесия. Для выполнения условия (6.17) также
необходимо, чтобы функция f(z) обратилась по крайней мере
один раз в нуль на интервале O.Z. Так как. кроме того, при анти-
симметричных колебаниях /(0)—О, то в этом случае функция/(?)
будет иметь вид, показанный на фиг. 20.
В порядке возрастания частот эти формы располагаются
следующим образом: наименьшая отличная о г нуля частота
соответствует симметричной, форме, обладающей наименьшим чис-
лом узлов при деформациях крыла^2 узла. фиг. 19а). Следующим
обертоном является антисимметричная форма колебаний с тремя
узлами (фиг. 20а), затем иду г симметричная форма с четырьмя уз-
лами (фиг. 196), антисимметричная с пятью узлами (фиг. 206) и т. д.
Рассмотрим, как изменяется характер колебаний при измене-
нии массы фюзеляжа. Антисимметричные колебания не зави-
сят от Это объясняется гем, что масса фюзеляжа нами
Фиг 21 Форма котеблний крыла относительно мало зависит от массы
фюзеляжа.
сосредоточена в том сечении в котором находится узел анти-
симметричных колебаний и следовательно при таких колебаниях
инерционных сил не развивает. Амплитуда колебаний массы
фюзеляжа при симметричных колебаниях будет тем меньше,
чем больше .масса фюзеляжа по отношению к массе крыла. Чтобы
убедиться в этом, рассмотрим, например, форму колебаний,
изображенную на фиг. 19а.
На фиг. 21 показаны значения функции /(д) для некоторого кры-
ли при различных значениях отношения М,р: /И„., f mdz -
O’J
—масса всего крыла). Как видно' вид функции f(z} весьут мало
меняется при различных значениях Мф. Во всяком случае это
изменение весьма мало скажется на величине второго слагае-
мого в условии (6.16). Следовательно, при различных значениях
доджио мало меняться и первое слагаемое в этом выраже-
нии. А это означает, что при увеличении МА должна умень-
шаться величина /(0), г. е. амплитуда колебании массы фюзе-
ляжа
При бесконечно большой массе фюзеляжа сечение г —Оста-
новится неподвижным и каждое полукрыло ведет себя как кон-
с"ль. колебания которой были изучены выше.
Расчеты показывают, что с увеличением частота и форма
колебаний свободного крыла приближается к соответствующим
величинам для консольного крыла весьма быстро, так что при
практически встречающихся соотношениях массы фюзеляжа
в крыла вполне допустимо делать расчет симметричных изгиб-
ных колебаний крыла, схематизируя его как консольную балку.
Практически гак всегда и поступают 1). Однако, расчет крыла,
т:ах консольной балки (или, как принято выражаться, „по кон-
сольной схеме"), не выявляет антисимметричных форм колебания,
которые в некоторых случаях являются весьма существенными.
Насколько важны эти
формы, становится
особенно ясным, если
рассмотреть колеба-
ть. крыла в связи с
колебанием элеронов.
Правый и левый
Фш. 22. Невозможная форма антисимме-
тричных колебаний свободно плавающего
крыла.
элероны связаны меж-
ду собой через про-
водку. Поэтому, если
в проводке не проис-
ходил деформаций,
го при отклонении правого элерона вниз, левый будет откло-
няться вверх и обратно. Таким образом, при колебаниях эле-
ронов, когда проводка работает как механизм, правый и левый
концы крыла получают импульсы противоположного знака.
Естественно, что такие импульсы вызовут антисимметричные
олебапия крыла, когда правый и левый концы крыла дви-
гаются в противоположные стороны. При этом форма колебании
м жет быть только типа, изображенного на фиг. £0, так как мы
установили, что только эти формы антисимметричных колеба-
ний удовтетворяюг условиям динамического равновесия. Поэтому,
например, невозможны колебания формы, показанной на фиг. 22,
тек, как при такой форме не выполняется условие (6.15), т. е.
Остается неуравновешенный момент инерционных сил вокруг
продольной оси самолет:.
Забегая несколько вперед, укажем, что существуют весьма
•опасные Для само дета формы совместных изгибно-элеронших
колебаний в полете. Как уже ясно из сказанного, такие формы
Могут быть двух типов:
1) Симметричные колебания, неизбежно сопровождающиеся уп-
ругими деформациями проводки управления элеронами, когда пра-
') За исключением особых схем самолетов, например, типа „летающее
Ггрыло". См. работу Л. С. Попова „О влиянии фюзепяжа и хвостового опе-
фения на колебания самолета", Труды НАГИ № 343. 1940.
5?
вый и левый элероны в каждый момент времени отклоняются:
в одну и ту же сторону. При этом ручка управления отклоне-
ний не испытывает. Расчет формы колебаний крыла при этом
можно производить по консольной схеме.
2) Антисимметричные колебания, когда проводка работает
как жесткий механизм, правый и левый элероны отклоняют
в разные стороны. Ручка управления колеблется, следуя за дви-
жением элеронов. Расчет формы долебапия крыла в этом слу-
чае следует производить по уравнениям (6.9) — (6.10).
6) Расчет антисимметричных изгибных колебаний крыла
Расчет, как и в предыдущем параграфе, ведется методом по-
следовательных приближений, который сводится к тому, что вс
второй член уравнения (6.9) вставляется наперед заданная фупк
ция/(д), затем производится интегрирование полученного урав-
нения и находится следующее приближение. При выполнении
интегрирования учитываются все условия (6.3) — (6.6), которым
должна удовлетворять функция. В данном случае расчет облег-
чается тем, что мы сразу ищем только антисимметричное ре-
шение у(г)=—/(— z). Поэтому все вычисления ведутся
в интервале 0.../, а решение на интервале—/...0 найдется из
условия /(— г) = —f(z).
Пусть /я-1 (г) — значение функции /(г) в п—1-ом приближении
и ри-i — значение частоты в том же приближении. Подставляем
это значение в последний член уравнения (6.9) и интегрируем
результат. Получим:
г
(EJf'Y — — j mfn idz + A.
i
В силу второго из условий (6.10) постоянная интегрирования
обращается в нуль и мы имеем:
(EJfJ- - 4'%-» (г), (6.18)
где
Z
Ч<' ’„1 (Z) — J mfa~idz.
i
Интегрируем (6.18) еще раз и, принимая во внимание первое
из условий (6.10), найдем:
EJf” ~ р2^ (л), (6.19)
где
z
’^•л (z)
1
5в
Делим обе части (6.19) на EJ и результат дважды интегрм
руем.
Будем иметь:
и + Вп .^ + (6.20)
где обозначено:
4*3)^ (г) - f ; Т’%_! (z) = / W3»^, dz.
о L'-J о
Постоянная интегрирования Cn—1 обращается в нуль в силу
чистой антисимметрии колебаний. Постоянная Вп—1 определится
из условия динамического равновесия (6.17):
/ /
Вп—\ ~ —J'm’F‘%—1 z dz : j' mz2 dz. (6.21)
о о
Так как все уравнения задачи однородны, то они определя-
ют функцию f (z) только с точностью до постоянного множителя
Чтобы исключить неопределенность в выборе этого множителе,
принято функцию/(г) нормировать умножением на такой постоя»
ный множитель, чтобы на конце крыла /(/)=1. Это приводит
к условию, определяющему рп—]:
L ~ Вп-\ I ' (6,г2)
Таким образом, метод последовательных приближений в «ан
ном случае сводится к следующему:
1- Задаемся какой-либо функцией ’F0) в качестве исходной
^например, можно принять W’4)——-^. Выбранную функцию
нулевого приближения 'И4* подставляем в формулы (6.21)—(БЛ2)
и определяем Во и р02.
Вычисляем функцию первого приближения /г по форму
J,e (6.20), имея в виду, что Со = 0.
V ( ' ф^рСлеД°вательным интегрированием вычисляем функции
Вновь вычисляем В и р2 по формулам (6.21)—(6.22) и
полое значение функции f по формуле (6.20).
о. Вычисления по п. 3 и 4 повторяем до тех нор, «ока
д а слеДУющие друг за другом приближения не совпадут.
5й
•Фйг. 23. При антисимметричных ко-
лебаниях крыла оперение также
вовлекается в колебательный про-
цесс.
в) Спектр частот и форм колебаний самолета
Выше было показано, что крутильные колебания крыла неиз-
бежно порождают изгибные и обратно. При симметричных изгиб-
ных колебания^ крыла (фиг. 19) среднее сечение совершает по
стуиательное движение, при антисимметричных (фиг. 20) оно
поворачивается вокруг продольной оси самолета. Так как в дей-
ствительности фюзеляж не является абсолютно жестким, то эти
движения должны породить упругие колебания фюзеляжа, в
нервом случае — изгибные, вр втором — крутильные. Таким о€>-
пазом в действительности изгибные колебания крыла всегда со-
провождаются колебаниями фюзеляжа. Ясно, что справедливым
бут;ет и обратное: если роз-
х никнут колебания фюзеляжа,
\ го неизбежно появятся и ко-
, у лебания крыла. Точно также
связаны колебания фюзеляжа
и оперения. Самолет пред-
ставляет собой единую упру-
гую систему и все его части
совершают колебания сов-
местно.
Возможные формы колеба-
ний можно установить опять-
таки с помощью условий ди-
намического равновесия. Если
рассматривать самолет как си-
стему, свободно плавающую в
пространстве, то силы инерции
а их моменты относительно любых осей должны сами собой
уравновешиваться. Отсюда получается шесть устовий равнове-
им: три условия равновесия сил инерции по трем взаимно нер
пендикулярным направлениям и три условия равенства нулю мо-
ментов сил инерции вокруг трех взаимно перпендикулярных осей.
Было показано, что если схематизировать самолет, как сво-
бодно плавающую балку с жестким грузом посередине, то крыло
не может иметь формы колебаний, изображенной на фиг. 22,
к как при зтом окажется неуравновешенным момент сил инер-
ции вокруг продольной оси. Однако, если принять во внимание
упругость фюзеляжа и оперения, то весьма похожая форма ко-
лебаний крыла окажется уже возможной; она неизбежно бу-
дет сопровождаться скручиванием фюзеляжа таким образрм,
”то момент сил инерции крыла вокруг продольной оси будет
уравновешиваться моментом от инерционных сил оперения (схе-
матически это показано на фиг. 23).
Так как масса крыла и особенно его момент инерции относи-
гелыю оси фюзеляжа во много раз превосходит соответствующие
величины для оперения, то для равновесия моментов инерцион-
•*л»
имх сил необходимо, чтобы амплитуда колебаний оперении в,
много раз превосходила амплитуду колебаний крыла. Так оно
в действительности и происходит. При возникновении колебании
формы, показанной на фиг. 23, основной деформацией является
скручивание задней части фюзеляжа, деформации же крыла ни-
чтожно малы по сравнению с деформациями фюзеляжа. Поэтому
колебания этого типа условно называют крутильными колебани-
ями фюзеляжа, хотя в действительности эго есть только одна
ш возможных форм (один из гонов) колебаний целого самолета.
Б данном случае поступают
так же, как и ПРИ колебаниях
крыла, ’ которые условно раз-
бивают на изгибные и крутиль-
ные, хотя в действительности
они всегда являются совмест-
ными изгибяо-крутндьн Ым и.
Рассматривая свободней пла-
вающее крыло, мы убедились,
что для него возможен ряд
различных форм колебаний
(фиг. 19 и 20). Естественно,
что для самолета возможные
Фиг. 24. Изгибные колебании крыла;
относительно гибкий фюзеляж.
формы колебаний значительно
многообразнее.
Рассмотрим основные формы колебаний
Фиг 25. Изгибные колебания крыла; относи-
тельно жесткий фюзеляж.
двухмоторного са-
молета’). Еще раз
подчеркиваем, чт«
самолет представ-
ляет собой единую
упругую систему к
ноэтому, хотя все-
колебания являются
совместными, дли
удобства анализа
Принято различи гь
отдельно колебания
крыла (изгибные ‘ и
крутильные), коле-
бания фюзеляжа, ко
лебання оперения к
т. д., подразумевая
каждый раз основной вид деформации, соответствующий данной
частот е.
1. Форма колебаний самолета при изгибных колебаниях кры-
ла в случае, когда частота крыла меньше частоты фюзеляжа.
‘) Резник А. Л. и Смрчек А. В „Исследование частот и форм собствен-
мых колебаний самолета" (рукопись). Влияние упругой подгески мотора см. в-
работе М. В. Келдыша и Я _М. Наркомовского „Колебания крыла с улруго-
мрикрепленяым мотором". Труды ЦАГИ № 535. 1941.
схематически показана на фиг. 24. Если бы фюзеляж был абсо-;
лютно жестким, то при колебаниях крыла он следовал бы за
средней частью последнего. То же самое, как видно из рисунка,
происходит и в случае упругого фюзеляжа при условии, что его
собственная частота больше частоты крыла; одндко, вследствие
деформации фюзеляжа перемещения его конца оказываются
больше перемещений в
месте сопряжения фюзе
ляжа с крылом.
2. Если частота фюзе-
ляжа. меньше частоты
крыла, то форма колеба-,
ний самолета при изгиб-
ных колебаниях крыла
будет такой, как изобра-
.жеио на фиг. 25. На фю-
зеляже появляется узел.
3. Форма колебаний
Фиг 26. Изгибные колебания фюзеляжа; самолета При изгибных
относительно гибкое крыло. колебаниях фюзеляжа,
для случая, когда часто-
та фюзеляжа больше частоты крыла, показана иа фиг. 26,
а когда она меньше частоты крыла — па фиг. 27. Объяснение
появления этих форм вполне аналогично объяснению форм
форм
Фиг. 27. Изгибные колебания фюзеляжа; относительно
жесткое крыло.
(
поме-
фиг. 24 и 25. В данном случае фюзеляж и крыло как бы
нялись местами.
Во всех вышерассмотренных случаях деформации стабилиза-
тора бывают очень малы, поэтому на фиг. 24-27 мы нигде не
отметили деформации стабилизатора, хотя в действительности,
они, конечно, имеют место. Отклонения концов стабилизатора
направлены всегда в сторону движения хвостовой части фюзе-
62
ляяса, что> является следствием большой частоты стабилизатора
но сравнению с фюзеляжем.
4. Колебание изгиба крыла второго Тона. Форма колебаний
крыл'1 показана на фиг. 20а. Эти колебания сопровождаются
скручиванием фюзеляжа.
5. Колебания кручения фюзеляжа‘ могут быть двух форм:
а) если частота изгиба крыла пер-
вого тона больше частоты круче-
ния фюзеляжа, то фюзеляж скру-
чивается приблизительно так же,
как свободная балка с двумя со-
средоточенными грузами на концах.
Только за счет собственной упру-
гости крыла, горизонтального и
। артикального оперения, последние
будут, кроме поворота, претерпе-
на Ь изгиб (фиг. 28); б) если Ча- фцр. 28. Крутильные колебания
СТОТа изгиба крыла первого тона фюзеляжа; относительно жесткое
меньше частоты кручения, то фор- крыло,
ма колебаний самолета при кру-
тильных колебаниях фюзеляжа будет иметь вид, показанный на
фиг. 29. Возникновение этой формы объясняется тем, что соб-
ственная частота колебаний изгиба крыла первого тона меньше
частоты, с которой колеблется самолет, т. е. меньше частоты
кручения фюзеляжа (или, что то же, частоты поворота корне-
вых сечений крыла).
Как уже указывалось, для равенства моментов необходимо,
чтобы поворот сечения фюзеляжа у крыла был значительно
меньше, чем поворот сечения фю-
зеляжа возле Оперения. Поэто-
му колебания форм, изображен-
ных на фиг. 28, происходят
так, что узел колебаний фюзеля-
жа лежит вблизи крыла. Други-
ми словами, хвостовая часть фю-
зеляжа колеблется почти так,
как если бы она была консоль-^
ной балкой, заделанной в абсо-
лютно жестком и неподвижном
крыле.
Мы не будем подробно описывать возможных форм колеба-
НИЙ горизонтального и вертикального оперений. Укажем лишь,
чт° Их частоты обычно бывают значительно выше соответству-
ющих частот крыла.
Рассмотренных форм колебаний, в диапазоне частот
° 2500 кол/мин. лежат также собственные частоты органов
влиюВ^еНИР (РУлей н элеронов). Существенный интерес предста-
1 слеДующне формы колебаний органов управления: а) ай-
63
тнснмметричные колебания элеронов, koi ia правый и тевый
элероны движутся в разные стороны; б) симметричные колеба-
ния элеронов, когда правый н левый элероны, за счет деформа-
ции проводки, движутся одновременно в одну и ту же сторону;
в) симметричные колебания руля высоты.
Руль высоты колеблется, как твердое тело, упруго закрепленное
на оси (упругость создается проводкой); г) антисимметричные
колебания руля высоты происходящие вследствие скручивания
лонжерона руля. Правая и левая половины руля высоты закру-
чиваются в разные стороны, \причем углы закручивания нараста-
ют от оси самолета к концам оперения; д) колебания руля на-
-мравления, когда последний колеблется как твердое тело, упру-
го закрепленное иа осн.
Таким образом самолету присущ ряд собственных частот и
соответствующих форм колебаний. В начале этой главы указы-
валось, что при вибрациях в потоке воздуха важную роль играет
форма колебаний. В гл. 7 выяснится, какие из этих форм могут
переходить во флаттер, т. е. могут перейти в колебание с нара-
стающей амплитудой при наличии аэродинамических сил. Именно
в этих целях в п. 5-6 были рассмотрены способы вычисления
собственных частот и соответствующих форм колебаний.
7. Собственные колебания лопасти винта
а) Общие положения расчета
Лопасть может оыть схематизирована в виде жестко закре-
пленной консоли переменного сечения, имеющей естественную
закрутку. Обычно, однако, закручениостью пренебршают, пола-
гая при анализе что лопасть представляет собой стержень с
неизменным направлением главных осей инерции сечений ио всей
своей длине; за угол установки лопасти принимается угол уста-
новки на радиусе 0,75 R. Кроме того, обычно пренебрегают
несовпадением центров тяжести сечений с центрами жесткости;
благодаря этому, для лопастей становятся возможны ии
раздельные колебания изгиба и кручения.
Специфической особенностью задами о собственных колебаниях
лопасти виита является наличие центробежных сил, существенно
влияющих на частоты; кроме того, в последнее время колебания
первого тона изгиба лопасти рассматриваются часто с учетом
упругого кручения вала.
Практически оказывается достаточным рассмотрение следую-
щих главнейших форм колебаний: 1) колебания изгиба в нлос
кости наименьшей жесткости (первый тон и второй тон); 2) ко-
лебания изгиба в плоскости наибольшей жесткости (первый тон)—
только для металлических лопастей: 3) колебания кручения — толь-
ко для деревянных лопастей.
44
Собственные колебания кручения металлических лопастей, так
же как и колебания изгиба в плоскости наибольшей жесткости
деревянных лопастей, характеризуются настолько высокими зна-
чениями частот, что опасность резонанса оказывается' практиче-
ски нереальной и указанные формы лишены практического ин-
тереса.
При вычислении частот и форм собственных колебаний можно
пренебречь рассеянием энергии, которое на самом деле неизбеж-
но вследствие действия как сил внутреннего трения, так н аэро-
динамических сил [).
б) Колебания изгиба лопасти
Для определения формы основного тона воспользуемся най-
денным 1ыше выражением (4.12), которое даст решение задачи
о колебаниях изгиба без учета эффектов скручивания вала н
центробежных сил. Ниже мы покажем способы внесения соответ-
ствующих поправок на указанные влияния.
При этом пренебрежении справедливость (4.12) в нашем случае
не вызывает сомнений, так как указанное выражение по самому
с\ ществу вывода верно не только для крыла, по и вообще для
всякой консольной балки, совершающей чисто изгибпые колеба-
ния, в частности и для лопасти винта.
Для лопасти (4.12) можно записать в виде:
7г’ ’I
(7|)
со г г
здесь аргументом служит относительный радиус г r:R, >де
г—радиус текущего сечения (ось Or считается равномерно вра-
щающейся вместе с винтом); R— радиус лопасти, EJ—жест-
кость изгиба (при анализе колебаний в плоскости наименьшей
жесткости EJ~EJmin и при анализе колебаний в плоскости
наибольшей жесткости EJ~EJmilx}, — плотность материала
винта, р=. F (г) —площадь сечения лопасти.
Погонная масса т, стоящая под знаком интегрирования в вы-
ражении (4.12), заменена здесь произведением pmF. Величина рт
оставлена иод знаком интеграла, так как для деревянных лопа-
стей опа является функцией относительного радиуса.
*) Влияние аэродинамических сил на собственные частоты колебаний лопа-
ет» было исследовано П. М. Ризом. Труды ЦАРИ. № 242. 1S35. Приложение 1.
II. М. Ризу принадлежит большое число теоретических н экспериментальных
исследований, касающихся вибраций воздушного винта. Изложение этих
ионросов в настоящей книге основано в значительной мере па работах ука-
танного автора.
5 Гроссман и Пановко.
65
Использование основной зависимости (7.1) производится точ-
но тем же способом, как это было выше описано для крыла
ь п. 5. После того, как форма колебания / (г) уточнена последо-
вательными приближениями (в качестве исходного приближения
можно грубо принять — можно определить частоту по
формуле Рэлея (4.8), которая в нашем случае принимает вид:
1 1
р2 = J EJf^dT-.f p„Ftfdr~ (7.2)
о 6
Для второго тона изгибных колебаний следует воспользо-
ваться теми же зависимостями (7.1) и (7.2), требуя одновремен-
ного удовлетворения условию ортогональности собственных
функций;
f = (7-3)’
О
w
Здесь/j — функция основного тона и f., — функция второго то-
на. Вывод совершенно аналогичен выводу условия ортогональ-
ности для задачи колебаний изгиба крыла, который дай выше
в п. 6 [формула (6.13)[.
Поступаем далее, как и в п. 3. Принимая в качестве исход-
ного приближения подходящую функцию, например
/3(о)==7* + с072,
находим Со из условия ортогональности (7.3), после чего под
ставляем /ДО) в (7.1) и после интегрирования приходим к функции
/2‘. Далее строим функцию первого приближения
/Д^/ДО + С^. (7.4)
которая надлежащим выбором может быть сделана
ортогональной функции Д; с этой целью подставим (7.4) в (7.3)
и определим С,. Получив/ДО, вновь используем (7.1) и т. д. Этот
процесс продолжается до практической сходимости^ Таким путем
мы установим форму колебания /2, а затем из (7.2) найдем ча-
стоту второго тона изгибных колебаний.
в) Учет влияния скручиваемое™ вала на изгибные
колебания лопасти
Обратимся теперь к оценке влияния скручиваемости вала, ко-
торое, как отмечалось выше, ощутимо лишь для основного то-
на колебаний. Рассмотрим систему, состоящую из приведенной
66
массы вращающихся и поступательно движущихся частей мо-
тора, массы винта и соединяющего их вала; массой вала мы
будем пренебрегать (фиг. 30).
Пусть Jb —полярный массовый момент инерции винта,
j ________то же для маховой массы мотора,
б'л_угол поворота втулки винта при крутильных колеба-
ниях вала ’),
Фиг. 30. Расчетная схе-
ма системы винт—мо-
тор.
б _угол поворота приведенной маховой массы мотора,
при крутильных колебаниях вала 1),
k-—число лопастей винта.
Крутильную жесткость вала обозначим через с (с. — предста-
вляет собой крутящий момент, способный вызвать угол за-
кручивания вала, равный единице;
из теории сопротивления материалов
известно, что с — . где I—длина
вала). Описанная система представляет
собой простейшую схематизацию дей-
ствительной конструкции; правила при-
ведения движущихся частей мотора
к эквивалентной маховой массе, так же
как и способы вычисления приведенной
длины вала даются в курсах конструк-
ции авиадвигателей и мы на этих вопро-
сах не останавливаемся, считая, что ве-
личины Jm и с известны2).
Кинетическая энергия колебаний такой системы будет:
1 kR Г
Т=2 Jm^d2+ ~2~J + v')dr-
О
(7.5)
Здесь первый член выражает кинетическую энергию маховой
массы частей мотора, а второй — кинетическую энергию всех k
лопастей винта. Через ut и vt мы обозначили упругие переме-
щения сечения лопасти в направлениях наименьшей и наибольшей
жесткости сечения.
Потенциальная энергия системы:
1
£/ = | с (EJ^+EJ^d? (7.6)
о
i) Углы н $т/ отсчитываются от равномерно вращающегося радиуса
«ктора Or и являются малыми величинами, добавляющимися к углу поворота
гсей вращающейся системы и/, где «> — средняя угловая скорость вращения вала.
*) См. напр. Ден-Гартог. Теория колебаний. 1942, § 40.
67
также состоит из слагаемого, соответствующего закручиванию
вала, и слагаемого, соответствующего изгибу лопастей 1).
Примем как и всюду выше:
lit = и (г) q (f)\ Г',= v (г) q (7); 'Jw = 0ь (г) q (f):
Составив cvmmv T + U и воспользовавшись условием -уДТ , Е)~
at
= 0, найдем:
Фиг. 31. Полные перемещения и н v соста-
вляются из двух частей; а) чисто изгибные
перемещения и,А?, и vuv (при нескручнвае-
мом вале), б) перемещения и и и, вызывае-
мые поворотом втулки винта на угол 0.
Перемещение за
счет поборете
бтцпни бинта
Ч [ 4V + kR J ?mF («й +
О
+ <7*)dr] +q [< (% —
1
-4,,^ + kR ] (e/ji"* +
0
+ £J..t’"2) .-o.
Мы уже неоднократно
встречались выше с по-
добными уравнениями; из
самой записи видно, что
4(f) = A sin(pf ; а).
причем частота определяется дробью:
с (6й - 0,„)2 + kR I (EJtu"* + EJqo"*) dr
и (7.7)
i
4 V + kR J p„;F(«3 + t'3) dr
Сравнивая полученную формулу с (7.2), мы видим, что й
числитель и знаменатель приобрели дополнительные слагаемые
за счет скручиваемости вала. Кроме тою, перемещения и п v
обусловлены не только изгибом лопасти, но и поворотом втулки
винта на угол 06. В самом деле, благодаря этому повороту сече-
ние на радиусе г смещается в плоскости вращения на вели-
чину Ььг- раскладывая смещение на составляющие в направле-
1) Первое слагаемое получается с помощью известной из сопротивления
материалов формулы потенциальной энергии скручиваемого вала ту .<s;;рг
где — угол закручивания нала, равный в нашем случае разности углов
0^—6^, а —крутящий момент, равный произведению коэфициента жестко-
сти с на угол закручивания. Второе слагаемое вряд ли нуждается в пояснениях.
б«
ииях главных осей жесткости сечения (фиг. 316), получим, что
общие перемещения сечения и и v составляются из двух частей
и = и„„~OftrshiS; v -- vuJlrrcos -i, (7.8)
где и.йзг и vUM— смещения, обусловленные упругими деформаци-
ями лопасти при изгибе (фиг. 31<т), 5 — угол установки сечения.*
Таким образом даже при бесконечном .значении большей жест-
кости (£73 = < ) смещение v не обращается в нуль, хотя в этом
случае пИЛ, = 0.
Подставляя (7.8) в (7.7), найдем, пренебрегая изгибом в на-
правлении наибольшей жесткости (т. е. полагая 0); i
1
kR^EJ^'^dr
(7-9)
и
sin + kR I ^FiR^dr
о
Для фактического использования этой формулы необходимо
знагь величины 06 и 6т, что требует некоторых дополнительных
зависимостей, к составлению которых мы и переходим.
На маховую массу частей мотора при колебаниях действует
только момент от скручиваемого вала с(6,, — 0от); уравнение
движения маховой массы будет;
с(6«-М ЛХ = 0 (7.10а)
Для винта аналогично получим
c(°w— + ^cosfJ)rr/r = 0. (7.106)
о
Здесь второй член выражает собой сбщий момент сил инерции,
развивающихся благодаря изгибу лопастей и кручению вала. Под-
ставляя в (7.10) полученные выше выражения:
nl~itsin(pf + a); *щ = vs\n(pt + а); 0w = % bi п (pt + a);
6,„/ = fJmsin(p^+a),
р‘йдем после сокращения на sin (/>/ + %):
с(^-ост)+4Л = о, (7.11)
с — 6,„) + kp2Rl J* p,„F(w sin fl + v shift) rdr—0 (7.12)
0
69
Принимая во внимание (7.8) и полагая — 0, найдем вмест -
(7.12):
1 1
с + kP2f? I РтГиизг sin $rdr — Ap* 2/?3 *06 f ?mFr2dr = 0.
О О
Содержащееся в последнем члене выражение /г/?3 fpmFr2dr прет-
ставляет собой полярный массовый момент инерции винта; по-
этому уравнение (7.12) получает вид:
1
с (% — 6т) - -МьР2 = - kps/F J pmFuuJ siП '}dr (7.13)
0
Можно рассматривать уравнения (7.11) и (7.13) как условия,
определяющие 0Ь и 0вг, если считать величину р2 и функцию ашг
известными.
Решение этих уравнений дает достаточную точность, если при
нять за частоту р и за функцию иияг результаты, получаемые без
учета скручиваемости вала (см. предыдущий пункт). После решения
уравнений можно по формуле (7.9) найти исправленное значение
частоты. Таким образом определение собственной частоты основ-
ного тона колебаний *), с учетом скручиваемости вала, состоит из
следующих операций: 1) определение формы колебаний основ-
ного тона без учета скручиваемости вала с помощью последо-
вательных приближений по уравнению (7.1); 2) вычисление час-
тоты колебаний основного тона без учета скручиваемости вала
по формуле (7.2); 3) вычисление величин 0$ и Ът по уравне-
ниям (7.11) и <7.13); 4) вычисление частоты основного тона
с учетом скручиваемости вала по формуле (7.9).
Указанная последовательность действий приводит к достаточно
точным результатам в тех случаях, когда влияние скручиваемо-
сти вала относительно невелико, т. е. когда деформации кручения
вала малы сравнительно с деформациями изгиба лопасти; если
это условие не выполняется, приходится строить более сложную
схему последовательных приближений, на которой мы здесь не
останавливаемся 2).
г) Учет влияния центробежных сил на частоты изгибных
колебаний лопасти
При колебаниях изгиба лопасти центробежные силы совер-
шают некоторую работу, гак как вследствие изгибных деформа-
ций каждое сечение лопасти несколько перемещается в направле-
’) Для остальных тонов влияние скручиваемости вала несущественно.
2) Изложенный выше прием приближенного учета скручиваемости вала пред-
ложен в ЦАГИ П. М. Ризом н А. И. Пожалостииым. См. также Деи-Гартог.
Теория колебаний. 1942. стр. 320-321.
•70
лии действия указанных сил (радиуса вращения). Этот эффект
оказывается всегда достаточно ощутительным (в особенности,
для обертонов) и во всех случаях подлежит обязательному учету.
Рассмотрим показанную на фиг. 32 схему изгиба лопасти. На
рисунке принято: О—центр втулки винта, ОХ—ось вращения
винта, гОп — подвижная система координат, вращающаяся вместе
с лопастью, Or—направление недеформироваиной сси лопасти,
0—угол между направлением изгиба лопасти и осью вращения ОХ.
Пусть А — положение центра тяжести текущего сечения лопас-
ти в процессе колебаний. Проекции точки А на плоскости гОХ
и гОп обозначены соответственно через Аг и As, проекция на
ось Or—через А:(, проекция на ось ОХ — через Д4. Через Ав
Фиг. Л?. Схема изгиба лопасги к определению работы
центробежной силы. Координатная система гОп pan
номерно вращается вокруг оси ОА.
обозначено положение центра тяжести сечения до деформации.
Перемещение, на котором совершает работу центробежная сила,
действующая в сечении А, следует измерять в направлении ее
действия, т. е. вдоль перпендикуляра, опущенного из точки .4
на ось вращения ОХ\ этот перпендикуляр показан на рисунке
отрезком АА4. Величина указанного перемещения может быть
вычислена как разность между расстоянием точки .4 от осп ОХ
после деформации (ДД4) и расстоянием той же точки от оси
ОХ до деформации (ОД0).
Расстояние точки А от оси ОХ, т. е. длина отрезка АА4 мо-
жет быть найдена из прямоугольного треугольника AA4A4:
___ II -
АА4— 1 r- + UfSin^ = r I 14-A-Sins?
(чак как катет А1А4 = С)А3 = г, а катет ДА4 = ДД, sin 3 = u4 sin 0).
71
До деформации центр тяжести рассматриваемого сечения
лежал на оси Or на расстоянии 0.4 р которое равно длине кри-
вой 0.4. поскольку при изгибных колебаниях длина оси лопасти
,пе меняется ’).
Таким образом можно записать:
5 ч .V Г
ОАа = ОА=$ ds — Г V~dr- + du/ = j | dr.
0 0 0
Теперь мы получаем искомое перемещение сечения в направле-
нии действия центробежной силы:
________г _____________
— / и2 С
; = ДД4— СМ„=г | lf-^sin’3 М l+и/’с/г.
и
Вторые члены под обоими ра дикалами весьма малы сравнительно
с единицей. В таких случаях можно с точностью до малых выс-
ших порядков принимать:
У нас будг'т:
г
г- г ( 1 *“ 2г- sin’ ,3) (г + 4 У 2-/г) ’
о
Или окончательно:
•з 1 г*
? = ^3 sin“ 3 - у I “/2dr.
и
Центробежная сила, развиваемая массой элементарного отсека лопа-
сти dP—'i„Fa^rd', где ?mFdr -масса отсека. Работа этой силы при
изгибе лопасти: idP—^^F^rdr. Полная работа всех элементар-
ных центробежных сил по всем отсекам лопастей:**
*) Последнее замечание не обозначает пренебрежения деформацией растя-
жения под тенствием центробежной силы;однако ага деформация остается
все время неизменной н дчя нашей операции (сравнение двух длин np.t из-
гибе) может не рассматриваться.
72
Потенциальная энергия систем возрастает на величину пос-
леднего выражения, но взятого обратным знаком, и вместо
{7.6) составит, после перехода к размерному радиусу.
1
Далее поступим как и в предьг '1ем п) нкте составим сумму
кинетической ') и потенциальной ,неРгии и приравняем нулю
производную этой суммы В резу/аге получим обычное урав-
нение гармонических колебаний, 8агем выражение для частоты
(выкладки опущены):
р^=р-^- (7Л4)
Здесь р? определяется без учета /#ствия центрооежпых сил —
по ф-ле (7.4), а второе слагаемое ?ыРажает влияние вращения,
возрастающее пропорционально кы’РатУ угловой скорости. Ко-
эфиццент ; имеет значение:
kf\‘ | 4ll31'1 2dr — R г>т^иизг~ S*H-? dr
ti ' О ‘ (7.15)
1
+ -W 2УгД [ dr + kR J r^Fll^dr
д «
Длч обертонов тремя первыми суземыми знаменателя можно
пренебречь, принимая = = —,е' не считаться со скручива-
В обычных случаях величина ,’эфициеша *,• для основного
тона несколько больше единицы, р быстро возрастает для сле-
дующих топов. Коэфициеит р, выч:-1Яенньв* Моррисом для нес-
кольких низших тонов изгибных Ki -оании лопасти постоянного
сечения, имеет значения3 *):
= 1,17;
7.34; и = 20,6; Тз —66,6; тс_ 99,6.
Заметим, между прочим, что рЛ^тат вычисления по фор-
муле (7.14) дает для основного ток несколько завышенные зна-
n v... случае не отличается, конечно,
с Вел™ТИЧеСКаЯ 'НСрГ"Я СИСТемЫ,!”а)енн6й в предыдущем пункте.
ТлоиДм КтН№ИЧ DKOV\Hepr,^HrM Victy. Dec. 1936. Vol. 42. № ЗЗи.
-) Journal of the Royal \eronantical ib J
CrP- 10H6.
73
чения частоты, соответственно общему свойству, присущему ме-
тоду Рэлея. Используя теорему Саусвелла, дающую всегда
заниженные значения частоты, Ден-Гартог получил формулу
(7 14) с коэфициентом т = 1 для основного тона1).
Удобство формулы (7.14) состоит в том, что частоту р мож-
но достоверно определить из эксперимента с невращающим с я
винтом, а затем ввести теоретическую поправку на центробеж
ный эффект2); такой путь обеспечит весьма высокую точность
результатов.
д) Колебания кручения лопасти
Как было сказано в начале параграфа, допущение о совпаде-
нии центров тяжести и жесткости дало возможность рассматри-
вать изгиб, независимо от кручения; это же самое позволяет
здесь анализировать кручение лопасти, независимо от изгиба.
Колебания кручения консоли переменного сечения были рас-
смотрены выше применительно к крылу. Выведенная там фор-
мула (3 17) целиком приложима и к нашей задаче кручения лопа-
сти; эту формулу мы перепишем в виде:
Г J
(Н = рЧ? Г I Jp'f dr*, (7-16>
J иЛр J
О г
где Jp — погонный полярный массовый момент инерции лопасти.
На использовании этой формулы мы не останавливаемся, по-
скольку соответствующие разъяснения даны выше. Точно также,
за отсутствием места, мы не останавливаемся на учете центробеж-
ного эффекта. Повторяем, что вычисление частоты крутильных
колебаний (и то только первого тона) необходимо лишь для
деревянных винтов.
В заключение отметим, что если вычисленные частоты отли-
чаются от частот возмущающих сил меньше, чем на 10—12 сек.,
опасность больших вибраций становится вполне реальной; для
исключения этой опасности считают, что частоты должны раз-
ниться не менее чем на 15-20 сек.-1
8. Собственные колебания тяг проводки управления
Для проводки управления, как и для некоторых других ча-
стей самолета, следует считаться с возможностью разонанса, ко-
торый может наступить при совпадении хотя бы одной из частот
возмущения с одной из частот собственных колебаний. Решаю-
I) Ден-Гартог. Теория колебаний. 1942. стр. 317-318.
’) Труды НАГИ № 242. 1935 П. М. Риз. Резонансный метод определения
собственных частот вибрации лопастей воздушных винтов.
74
щую роль в проверке этой возможности играет, однако, не тео-
ретический расчет, а эксперимент. Дело в том, что в конструк -
ции происходит весьма интенсивное рассеяние энергии на пути
от источника вибраций (винтомоторной группы) до отдельны;;,
тяг проводки; благодаря этому, даже при совпадении часто t
колебания могут быть совершенно незаметными, так как ам-
плитуды реально доходящих до тяги сил оказываются ничтожно-
малыми. Мы говорим «могут быть", потому что в конце концов
решение зависит о г фактического рассеяния энергии, которое
может быть оценено лишь опытным путем.
Экспериментальная проверка возможности разонанса состоит
в наблюдениях за изгибными колебаниями отдельных тяг на а -
личных режимах работы мотора. При обнаружении резонансных
колебаний необходимо изменение конструктивных параметров,
вот именно здесь, для разумного вмешательства в характеристи
ки конструкции, необходимо твердое знание влияния отдельных
параметров, которое может быть получено лишь после соответст-
вующего теоретического изучения.
Такое теоретическое изучение оказывается в данном случае
относительно несложным, поскольку каждая тяга представляет
собой стержень постоянного поперечного сечения с достаточно
ясными граничными условиями. Благодаря этим обстоятельствам
возможно определение собственных частот колебаний отдельных,
тяг с помощью строгой теории, относящейся к малым изгибным
колебаниям стержней постоянного сечения.
Рассуждая, как и при выводе формулы (4.1), получим ди(>е-
ренциальное уравнение колебаний в виде:
д3
дхг
д'!у
здесь EJ—жесткость изгиба тяги, у — линейное перемещена
при изгибе, х— абсцисса сечения, т—погонная масса.
Так как для тяг EJ— const, то
д4У .
dxi EJ dt*
(8.1>
Этому уравнению можно удовлетворить, полагая:
y=/(x)sin(/tf + ?).
(8.2;
где /(х) зависит только от абсциссы х и определяет фирму
изгиба стержня.
Подставляя (8.2) в (8.1), мы обратим диференциальное уря<п
йие в частных производных (8.1) в обыкновенное уравнение-
;1V—л3/=0,
EJg J
где погонная масса т заменена выражением
Г-г
—- (F—площадь
g
сечеаия, 7 — плотность материала, «—ускорение силы тяжести).
Интеграл этого уравнения:
f — Л si п а. х + В cos а х- - Csh а х + D ch о х,
(8.3)
1де. A,B,C,D— постоянные интегрирования,
а — 1 f р‘* . (8.4)
Г EJs
Пользуясь граничными условиями, можно не только- выяснить
постоянные А,В,С и /Э‘)> но, — исходя из условия существова-
ния решения — величин} а.
Зная а, можно будет с помощью (8.4) найти частоту р, что и
явится результатом решения задачи.
Покажем эти операции на простейшем случае шарнирного
опирания стержня.
На шарнирном конце должно быть:
7=0; /" = 0.
(8.5)
Первое условие выражает отсутствие линейного перемещения
опорною сечения, второе, отсутствие момента.
Из (8.3) следует:
f" — а-- [ — A siп а .г — В cos а х + С sh а л + D ch а ,у]. (8.6)
Используем (8.5) дважды—для х = 0 и x—L
При л: = 0 из (8.3) следует:
’ B + D= 0;
л,ч (8.6) следуе г
— B+D — 0-,
отследи сразу получаем, что
fi = D=().
При х — 1 из (8.3) следует.
Д sin а /4-Csh al = 0;
из (8.6) следует
— A Sin а I + С sh а I = 0.
Отсюда получаем: ' •
A sin.al = 0;
С sh я I — 0:
(а)
(б)
Из уравнения (б) следует либо С- 0, либо а=0 (напомним,
что при вещественном аргументе, неравном нулю, гиперболичес-
кий синус, — в отличие от круювого, — в нуль никогда не обра-
•} Говоря точнее—три независимых соотношения между ними.
ГС
щается). Однако, тривиальном) решению <х — 0 соответствует
отсутствие колебании1)» так что нам нужно продолжить поиски
др\ гил решении, полагая я Ф 0.
Так как предположение /1=0 также приводит к случаю отсут-
ствия колебаний, чтобы удовлетворить (а) следует принять
sin «7 = 0, что и является характеристическим уравнением нашей
задачи. Решением этого уравнения служит: а 7 п~(п — 1,2 . . )»
Отсюда получаем формулу для частоты:
<8'7>
Подставляя сюда последовательно н —1,2, . . найдем значения
соответствующих частот pt, р.,, . . При этом каждому значению
р, согласно (8.3) будет соответствовать своя форма колебаний
sin в; х; общее решение задачи составится из суммы реше-
нии вида (8.2):
У—^ft sjn (A ^4-aJ.
Как показывают экспериментальные исследования, для тяг про-
водки управления практическое значение имеет обычно только
первая (основная) частота:
(8.8)
Вычисление по формуле (8.8) с пересчетом на число колебаний
, ’ 60 А
в минуту (т. е. после умножения р на величину у-) для дюра-
ралевых труб приводит к следующим результатам.
Число собственных колебаний в минуту свободно опертых
ралевых труб (основной тон):
• Сечение .им Длина с и
100 150 200
20 16 2060 1310 741
30 26 4500 2040 1150
• 40 3G 6230 2760 1560
50 46 7850 •3490 1970
0 В (8.3) все члены обращаются в нуль.
77
Совершенно аналогичным путем можно получить уравнения
типа (8.7) для определения частот и в других случаях заделки
концов; во всех случаях эти характеристические уравнения
оказываются трансцендентными, т. е. определяют бесконечное
число корней и соответственно собственных частот.
Опуская соответствующие выкладки, дадим сводку результа-
тов для некоторых иных случаев закрепления однопролетного
стержня1)?
Род закрепления Характерно и- ческое ур-ние Корни характеристического уравнения
для х — 0 для х = 1
(a0t (я /)3 (а/)„ (л >2)
Конец свободен Конец свободен Cll а/ COS а 1 =1 4,730 7,853 2»_+Ln 2
Конец свободен Конец th al—tg а/ =- 0 3,9.7 7,068 4л +1
оперт 4
Конец заделан Конец оперт th al—tg al — 0 3,927 7,068 4л + 1 я 4
конец заделан Конец заделан ch al COS al — 1 4,730 7,853 2л 4-1 Г> л.
Конец заделан Конец свободен Chai COS a/= —] 1,875 4,694 2п —1 я 2
По приведенным значениям al и формуле (8.4) могут быть
вычислены частоты р.
Реальные тяги н.т качалках всегда могут быть схематизированы
в виде шарнирно опертого стержня так что для них дейстри
тельна формула (8.7); тяги на роликовых направляющих могут
составлять довольно сложные неразрезные систрмы, определе-
ние частот для которых громоздко, хотя и не отличается с прин-
ципиальной стороны от только что изложенного пути.
В рамках настоящего курса нет ни надобности, ни возможно-
сти рассматривать большое число случаев; мы ограничимся
лишь несколькими типовыми случаями, приводя окончательные
результаты 2).
На фиг. 33 показана проводка с роликовыми направляющими,
причем различные тяги подвешены различным образом. Во всех
случаях формула круговой частоты колебаний приводится к виду:
*) См. А. Н. Крылов, Вибрация судов", стр. 356.
а) Заимствованы из работы И. В. Ананьева .Расчет на резонанс проводки
управления самолетом* (Труды ЦАГИ № 537. 1941). Там же см. ряд других
случаев опирания тяг.
78
т. к что число колебаний в минуту составит
p-9,55a^/'-EJS_
F у ъ
Значения отвлеченного
al в только что рас-
смотренных случаях),
зависит от условий
подвески тяги.
Тяга № 1 может
коэфициента at (равного произведению
Фиг. 33. Проводка управления в роликовых на
правляющих.
быть схематизирована
в виде балки с шар-
нирными концами при
жестком опирании одного конца и упругом опирании другого.
Величины dj в зависимости от отношения 1Х'.1 и параметра:
сТ
С'~ EJ ’
где с—коэфициент жесткости правой опоры (т. е. левого конца
тя; и № 2 на фиг. 33) даны на фиг. 34.
Фиг. 34. Случай тяги с упругим опиранием одного конца
и шарнирно неподвижным опиранием другого.
Тяга № 2 схематизируется в виде балки с двумя консолями,
на концах которых имеются сосредоточенные массы (равные
половинам масс примыкающих тяг № 1 и № 3). Величины о,
даны на фиг. 35 для случаев равных концевых масс в зависи-
мости от параметра:
С,—
(z=z1+lz2)
и отношения Zt: Z.
ml ’
79
Гяга № 3 рассчитывается по формуле (8.8).
Г яга Лг 4 может быть рассматриваема как двухпролетная
неразрезная балка; величины alt вычисленные при пренебрежении
Фиг. 35. Случай двухконсольлой тяги.
консолями, даны на фиг. 36 в зависимости от отношения /,: I,
где /„—длина левого пролета, /--общая длина обоих пролетов.
Фиг. 36. Случай двухпролетной неразрезпон тяги.
Как видно из (8.5), с возрастанием длины частота р быстро
падает. Что касается величины то ее УД^бнее предога-
/ Ее 2J
вить в виде гу/ , где г ~ | —полярный радиус инер-
ции сечения (равный для тонкостенных труб среднему радиусу
80
сечения.) Из последней формулы видно, что значение радикала
не изменится при изменении толщины стенки, т. е. частота р
не зависит от толщины, стенки-, при увеличении диаметра
трубы частота р пропорционально увеличивается. Это обстоя-
тельство надлежит иметь в виду при всякого рода конструктив-
ных переделках, помня, однако, что такие переделки в одном
участке немедленно отражаются на частотах соседних тяг и
должны производиться осмотрительно, с учетом возможности
появления резонанса в других участках.
При проверке тяг на резонанс следует, избегая резонанса
с двумя низшими частотами возмущения, требовать отли-
чия числа собственных колебаний тяги в минуту от экспло-
атационного числа оборотов вала по крайней мере на
300 кол1мин, а от удвоенного числа оборотов вала на
j- 400 кол!мин.
9. Собственные колебания трубопроводов
Питающие мотор трубопроводы находятся всегда в услови-
ях непосредственной близости к источникам возмущающих сил, по-
являющихся при работе мотора; именно поэтому опасность резо-
нанса трубопроводов не может быть сглажена значительным
рассеянием энергии. Необходимость достаточного различия между
собственными частотами и частотами возмущения заставляет предъ-
являть весьма строгие требования к вибрационным характери-
стикам трубопроводов.
По современным требованиям, собственные частоты колебаний
трубопроводов не должны находиться в пределах SCO—SOOO
ьол!мин. Эти частоты надежно могут быть определены лишь
экспериментом; для прикидочного расчета они могут быть вычи-
слены в зависимости от свободной длины и способов подвески
по тем же графикам, что и для проводки управления.
ГЛАВА 2
Возмущающие силы, передаваемые самолету
винтомоторной группой
10. Вводные замечания
Одним из основных источников, вызывающих вибрации на
^амолете, является винтомоторная группа. При работе мотора
вРаЩении винта возникают периодические возмущающие силы,
р даваемые конструкции самолета через мотораму. Практика
6 U'OCCIMH и ПвИОВКО о.
знает случаи, когда частоты некоторых из этих сил оказывались
настолько близкими частотам свободных колебаний отдельных
элементов конструкции самолета, что возникали сильные виб-
рации резонансного типа. В некоторых случаях такие вибрации
прямо угрожают прочности соответствующих элементов в связи
с явлением усталости, в других случаях они оказывают вредное
физиологическое действие на экипаж и мешают нормальной
эксплоатации х).
Как уже говорилось, своевременное предупреждение опасности
возникновения резонанса требует предварительного выяснения
всех возможных возмущающих сил и их частот; последующее
сопоставление этих частот с частотами свободных колебаний
выявит реальность угрозы резонанса.
В настоящей главе будет рассмотрена совокупность основных
причин, обусловливающих появление периодических возмущаю-
щих сил при работе винтомоторной группы, выявлены значения
их частот и кратко указаны приемы для оценки величины воз-
мущающих сил. Периодические возмущающие силы, возникающие
при работе винтомоторной группы, могут быть разбиты на две
категории:
I. Силы, возникающие при работе мотора. Они могут быть
вызваны: з) неравномерностью крутящего, момента (периодично-
стью вспышек смеси в цилиндрах); б) неуравновешенностью
движупшхся масс мотора.
II. Силы, возникающие при вращении винта. Они могут быть
вызваны: а) статической неуравновешенностью винта; б) динами-
ческой неуравновешенностью винта; в) различием в углах уста-
новки лопастей; г) аэродинамическим эффектом при прохожде-
нии лопасти винта перед крылом; д) гироскопическим эффектом
(при двухлопастном винте).
Рассмотрим по порядку физическую сущность каждой из
перечисленных причин, преследуя во всех случаях одну главную
цель,—установить частоту соответствующей возмущающей силы.
Что касается величин (т. е. амплитудных значений) этих сил, то
их теоретическая оценка в некоторых случаях весьма затрудни-
тельна. особенно если соответствующие силы возникают вслед-
ствие неточностей сборки или за счет люфтов, развивающихся
в эксплоатации.
11. Возмущающие силы, возникающие при работе мотора
а) Возмущающие силы, вызываемые неравномерн стыв
крутящего момента
Полный цикл в цилиндре четырехтактного двигателя продол-
жается в течение времени, необходимого для двух оборотов
Особенно вредно сказываются вибрации на работе гироскопических
приборов, а такж< на состоянии масло—и бензопроводов.
82
„пленчатого «ала, т. е. в течение 120,'л сек. (п—число оборотов
тля в минуту)- Таким образом, крутящий момент, передаваемый
«tiv одним цилиндром, изменяясь по сложному закону в течение
120/ секунд (фиг- 37), оказывается периодической функцией,
полностью повторяющей свои значения после каждых двух
обопотов При а цилиндрах, циклы во всех цилиндрах, будучи
почти одинаковыми по характеру, сдвинуты один относительно
лоугого на одинаковые отрезки времени 120/ал секунд *).
ДР Общий крутящий момент получается наложением моментов
каждого цилиндра с учетом сдвига во времени; на фиг. 38 пока-
зано суммирование для случая четырех цилиндров. Если считать
что циклы всех ци
линдров совершенно
тождественны, то пе-
риодом результи-
рующей кривой бу-
дет время двух обо-
ротов, разделенное
на число цилиндров,
т. е. 1201 ап сек. Сле-
дует иметь однако
в виду, что полная
Фиг. 37. Крутящий момент, развиваемый одним
цилиндром четырехтактного двигателя. 1—рабо-
чий ход; 2— выхлоп; 3— всасывание; 4—сжатие.
тождес твенность
циклов никогда не
осуществляется, как
по практической не-
одинаковости усло-
вий сгорания в различных цилиндрах, так и в связи с применением
прицепных шатунов (эти вопросы подробно рассматриваются
в курсах динамики авиадвигателей). Благодаря этому, результи-
рующая кривая принимает вид, утрированно показанный на
фиг. 39, так что полное повторение значений функции насту-
пает лишь после двух оборотов, т. е. через 120/тг секунд. Если
разложить подобную функцию в ряд Фурье3), то обнаружатся
следующие составляющие („гармоники”):
Номер по порядку Период гармоники Т сек ,, , 2л , Частота А’ =- сек—1 Число периодов укладыва- ющихся за один оборот вала
1 120/и ки/60 *'2
2 60/л жл/30 1
3 40 п хл/20 1‘/2
4 '3Q,n ил 15 2
ловИМЕеТСя 8 ВИДУ случай последовательного равномерного чередования
) О рядах Фурьс мы кратко ГОВОрили во введении к настоящей книге.
6*
85
Фиг. '28. Крутящий момент, развиваемый
четырехцклиндровым двигателем; при со-
вершенном подобии циклов суммарный
момент имеет период 30/и сек.
Соответственно числам последнего столбца (числу периодов
за один оборот) эти гармоники называют обычно половинной,
первой, полуторной, двойной и т. д., или говорят о ПОЛОВИННОМ,,
первом и т. д. порядке гармоники.
Среди дальнейших гармоник особенно большие амплитуды
обычно имеет составляющая, успевающая а раз уложиться за
два оборота вала, т. е. а/2 раз за один оборот вала(для 9 цилин-
дрового двигателя эта
гармоника имеет порядок
4*/2, для 13 цилиндро-
вого—порядок 61/2 и т. д.).
Эта „основная" соста-
вляющая будет одновре-
менно и самой „млад-
шей" составляющей, если
циклы всех цилиндров
одинаковы (фиг. 38). В
этом случае будут иметь
место гармоники, лишь
начиная с с/2 порядка
(т. е. а/2, а, 3/2 а...).
Следует помнить, что
с изменением скорости
вращения вала, конечно,
изменяется и круговая
частота возмущения, од-
нако порядок гармоники
остается постоянным.
так как число периодов
за один оборот неиз-
менно.
Что касается амплиту
дных значений соответ-
ствующих гармоник, ""О-
они определяются опыт-
ным путем с последую-
щим гармоническим ана
лизом (т. е. разложением
в ряд Фурье) экспери-
ментальной кривой *). Крутящий момент передается, с одной
стороны, винту и совершает полезную работу его вращения.
*) См. например результаты испытаний 9 и 13-цилиндровых звезд
образных двигателей в статье G. Р. Bentley „Vibration of radial aircraft engine-,
(Journal of the aeronautical sciences. May 1939. Vol. 6. № 7 p. 283). Так, Д if
исследованного 9- цилиндрового двигателя амплитуда гармоники порядка 41/-
оказалась примерно в пять раз большей, чем амплитуды других гармоник.
Типичные значения гармонических составляющих см. например В. А. Гэплии,
„Колебания в машинах*. 1944, стр. 88.
81
л с другой стороны,—в виде реактивного воздействия мотораме.
Тем самым неравномерность крутящего момента и оказывается
источником вибраций мотоустановки.
(время двух оборотив вала)
Фиг. 39. При неполной тождественности циклов, пе-
риодом крутящего момента служит время двух оборо-
тов вала.
4
5) Возмущающие силы, вызываемые неуравновешенностью масс,
связанных с вращением коленчатого вала
Как известно, стремление к полному уравновешиванию вала
и связанных с ним частей, полным успехом не увенчивается;
кроме того всегда неизбежны некоторые
ния и зазоры сборки, так что центры
тяжести вращающихся частей оказыва-
ются несколько смещенными от оси
вращения. Развивающиеся в эксплоата-
ции люфты способствуют увеличению
этих эксцентриситетов. Благодаря это-
му появляются центробежные силы, ком-
поненты которых носят ясно выраженный
периодический характер. Для уяснения
вопроса рассмотрим простейшую схему,
данную на фиг. 40.
11ри эксцентриситете г центробеж-
ная сила будет Р = Л1а>гг, где ш-—угло-
вая скорость вращения вала, М—масса
неуравновешенных частей.
Вертикальная составляющая силы Р
рсть Pe= Рcos а горизонтальная со-
ставляющая Pr = Psin<D£. Как видно
из самой записи, обе составляющие явля-
неточности изготовле-
Фиг. 40. Появление перио-
дических возмущающих сил
вследствие эксцентрисите-
та вращающихся масс.
•отся периодическими функциями времени, имеющими одну и ту
круговую частоту <и= сек-1 и одинаковый период
п сек.; эти силы дают гармонику первого порядка, так
претерпевают один цикл изменения за один оборот вала.
ш =
85
Указанные силы передаются на мотораму, образуя также момент
вокруг осей. Y и Z, проходящих через центр тяжести мотора.
Кроме инерционных сил, развивающихся согласно схеме, покат
заниой на фиг. 40, при работе мотора появляются инерционные
силы иного происхождения,—силы, связанные с возвратно-посту-
пательным движением поршня. Характер этих сил требует пред-
варительного рас-
смотрения кинема
тики шатунно-кри
вошипного механиз-
ма (фиг. 41ц).
Определим по-
ложение поршня. в
функции угла <•>/-
если пренебречь раз-
ницей в длинах АС
и ВС, то перемеще-
ние х поршня рав
но отрезку DB — г
Фиг. 41. Схема к определению инерционных сил, О COS«>£)> где Г
возникающих при возвратно-поступательном дви- радиус кривошипа,
женин поршня. Внесем теперь по-
правку на разность
длин АС и ВС, которая составляет /(1 —cos?), где I - длина
шатуна.
Следовательно:
л = г(1—cosw/) + Z(l cos?);
угол ? может быть выражен через «>£, так как
АВ — I sin ? = г sin u>Z.
Отсюда следует:
COS ? = 1 _ sin3 v>t.
г
При малом отношении можно принять:
га
cos ? — 1 — - sin2 ц> t.
А так как
sin2oZ = ~(l cos2<o0>
то
cos ? = 1 - (1 - cos 2о> 0-
Окончательно получаем:
№
х = г(1 —COSW^) + -тт(1 —
cos 2u> t).
Дважды диференцируя, найдем ускорение поршня:
X — Г ш3 (cos wt + — COS 2otf).
Сила инерции поршня будет:
—Мпх ——М„гшг (cos + -у cos 2w t),
(М„— приведенная масса поршня).
Эта сила инерции через шатун и кривошип передается корен-
ным подшипникам вала и далее на мотораму. В самой записи
этой силы отчетливо обозначаются периодические слагаемые
с частотами «> и 2ш *). Частота возмущения ш нами уже отмечалась
выше; здесь отметим наличие возмущающей силы с частотой
, _ 2тг/1 ~п .
к = 2'"^ 30 = 15
т. е. гармонику второго порядка (два цикла изменения за один
оборот вала).
Разложение силы Млх на направление АС и Y показано на
фиг. 416.
Усилие в шатуне направлено вдоль прямой АС, составляющей
с осью X угол ®; вследствие инерционной силы Мпх в шатуне
Мпх „ч
развивается усилие ---). Составляющая, направленная вдоль
оси Y, имеет значение:
714- х . .. .
—5- - sin в = х TgO
cos <s
и действует на стенки цилиндра (через палец С и тело поршня),
благодаря усилию М,х tg<p вокруг оси двигателя О развивается
момент:
OCM„xtgv.
*) Слагаемые с более высокими частотами, получающиеся при полном
разложении cos sp, имеют пренебрежимо малые амплитуды.
0 Кроме основных усилий, возникающих о г давления газов в камере
сгорания.
Заменяя здесь
ОС — OB + BC — r cos wt + I cos <p -21'
№
Sr cos lot 4- /[1 —(1— cos 2<u/)];
Г
х = го>2 (cos wt 4- -j- cos 2 ад);
sin© . ,, 1 . „ .
tg® = Tri-----sin <? (1 + -9 sin8<p)=
у 1 — sin-? z
Г Г*"
— у sin (14- -gp sin2 wt);
получим для инерционного момента:
/ f 3/* \
М„г2<*>* sin wtl------1- cos wt 4- -7ГГ cos 2wt),
" \ 21 21 /
г
где по малости опущены члены, содержащие -у в степени выше
первой
Пользуясь тригонометрическими соотношениями:
sin <i>£ • cos 2&t — "2" I s’n 3<“£ — s*n "rt j i
sin vit. • cos <ot =4j- sin 2<ot,
найдем для инерционного момента:
2
—sin шг 4- sin 2<ot + 2^ sin Зш/
Для нас важно выявление новой третьей гармоники возмущения
(член sln3«>£ в последнем выражении).
Таким образом мы Здесь отметим наличие возмущающей пары
с частотой:
, _ 3wz
A>_3oj— 30 — 10
сек~*,
т. е. гармонику третьего порядка (три
оборот вала). Здесь мы рассмотрели
цикла изменения за один
силы инерции, развиваю-
8 8
тпиеся при работе только» одного цилиндра. При нескольких
цилиндрах явление разумеется усложняется, подобно тому как
мы это видели выше, разбирая действие газового давления. Не
«даваясь в подробности отметим, что и при этом усложнении
выявленные нами частоты остаются действительными.
12 Возмущающие си-лы, возникающие при вращении
винта
а) Возмущающие силы, вызываемые статической
' неуравновешенностью винта
Статическая неуравновешенность винта, состоящая в смещении
ею центра тяжести относИтельно оси вращения, вызывает появ-
ление центробежной силы с компонентами:
рв —- р cos <о/; Рг —Р sin wt
(см фиг 40) где «Г—угловая скорость вращения вала винта.
При наличии редуктора, она отличается от_угловой скорости
вращения коленчатого вала ш и составляет: = где с—коэ-
фициент редукции.
Таким образом, рассматриваемые
возмущающие силы имеют частоту.
k = w- Есек-1-
OV
Подобно вышеизлоя<е11НОМУ’ Эти
силы, имея один цикл изменения за
один оборот винта, дают первую гар-
монику винта.
Фиг. 42. Динамическая не-
уравновешенность винта.
силы образуют в этом
б) Возмущающие силы, вызываемые
динамической неуравновешенностью
винта
Динамическая неуравновешенность
винта состоит в том, что центры тя-
жести отдельных лопастей не лежат
в одной плоскости вращения. Разви-
вающиеся при вращении инерционные
случае пару (см фиг 42, *Де изображена схема, относящаяся к
Двухлопастному винту). Эта пара, будучи неизменной по вели-
чине (при данной установке лопастей и фиксированном числе,
оборотов), изгибает вал попеременно в разные стороны; за по-
ловину оборота винта лопасти меняются местами и изгиб вала
89
по ходу часовой стрелки (фиг. 42а) сменяется изгибом против
хода часовой стрелки (фиг. 426). Периодом изменения этой
возмущающей пары является время одного оборота вала виита
60
—г- сек., а частотой величина:
л?
, 2кя, т.п . ,
*=60t = -30 EceK~-
i
Как и в предыдущем случае, это возмущение дает первую гармо-
нику винта.
Легко сообразить, что формула для k остается справедливой
при любом числе лопастей. Величина возмущающей пары про
порциснальна плечу пары центробежных сил и квадрату угло-
вой скорости вращения.
в) Возмущающие силы, вызываемые различием в углах
установки лопастей
Непосредственным результатом такого различия оказывается
неодинаковость сил тяги, развиваемых лопастями (фиг. 43), а
следовательно, воз-
никновение изгибаю-
щей пары того же
типа, как и в преды-
дущем случае дина
мической неуравно-
вешенности. Плос-
Фиг. 43. Эффект различия в углах установки ло- кость действия изги-
пастей. бающей пары вра-
щается вокруг оси
вала со скоростью вращения винта, так что частотой рассматри-
ваемого возмущения будет
, «га , .
* = 30 ' сек“ •
(первая гармоника винта). Интенсивность этого возмущения опре-
деляется различием в углах установки лопастей.
г) Возмущающие силы, вызываемые аэродинамическим эффектом
прохождения лопасти винта перед крылом
При прохождении лопасти винта непосредственно перед крылом,
тяга этой лопасти несколько возрастает относительно своего
среднего значения. Такое возрастание тяги обусловлено тем, что
струя от винта перед крылом частично подтормаживается и
появляется добавочное давление на лопасть со стороны крыла
90
Для двухлопастного винта это изменение происходит одю-
временно и приблизительно на одинаковую величину у обоих
лопастей, в связи с чем будет пульсировать общая тяга. Период
. 30
этой пульсации равен половине времени оборота винта -у сек.
(вторая гармоника винта), а частота:
, 2тг/г т.п , _.
*=30Е = Т5ЕсеК 4
Для трехлопастного винта изменение тяги происходят
у отдельных лопастей неодновременно (фиг. 44).
Фиг. 44. При прохождении лопасти перед крылом появ-
ляется дополнительная тяга.
Общая сила тяги будет меняться в мгновения прохода одной
из лопастей перед крылом, т. е. через интервалы времени, необ-
ходимые для поворота винта на 60э (на Че окружности): [I
1 60 10
- —v = —г сек.
6 п? «Н
(шесть циклов изменения за один оборот винта—шестая гармоника
винта).
Частота изменения общей силы тяги будет:
, 2ки кп „
k = сек
1U о
Кроме того, при этом развивается в плоскости’ крыла изгиба
ющий момент, действующий попеременно в разные стороны
(фиг. 45). Полный цикл изменения момента происходит за время
поворота винта на 1it окружности:
(третья гармоника винта).
91
Частота изменения момента:
, П'1 Г
*=-Ioec“_
При четырехлопастном винте изгибающий момент можно
считать отсутствующим (полагая, что влияние крыла одинаково
Фиг. 45. Появление дополнительного момента в пло-
скости XOZ.
проходе снизу вверх).
при проходе лопасти сверху вниз и при
Пульсация общей силы тяги происходит с периодом, равным вре-
мени 1/4 оборота винта:
_ 1 60
Т — —-------г- сек.
4 тк.
{четвертая гармоника винта) с соответствующей частотой:
Фиг. 46. Схема к опре-
делению поворотного
ускорения при слож-
, 2л 2лп „ .
А = =Ч5-'сек-
д) Возмущающие силы, возникающие вследст-
вие гироскопического эффекта винта
Пусть материальная точка М (фиг. 46)
вращается в плоскости YOZ с угловой ско-
ростью <о. Положим, что сама плоскость YOZ
вращается вокруг оси Z, с угловой скоростью
2. Как известно, при этом возникает пово
ротное ускорение (в направлении, перпенди-
кулярном плоскости вращения YOZ), равное
яом движении матери-
альной точки.
по теореме Кориолиса величине 2 2o>z, где
х — расстояние точки от оси Y. Рассмотрим
элемент лопасти винта при кабрировании са
молета, полагая оси направленными согласно фиг. 47. Обоз-
начив угловую скорость вращения винта ш, угловую скорость
92-
самолета при кабрировании £2 *), найдем, что сила инерции рас
сматриваемого элемента, соответствующая установленной величине
ускорения, составляет 2Qu2$dm, где dm — масса элемента.
Момент силы инерции
элемента относительно оси
К равен 2 2 caz1 * dm. Момент
всех элементарных сил инер-
ции (гироскопический мо-
мент):
И" 2 ,Г~г ^т~2 &05
м
где jy — момент инерции
винта относительно оси У'.
Для трех- и четырехло-
пастных винтов величина
Jy не меняется при враще-
нии винта_^) (фиг. 48, 49),
поэтому -------
является
винта 3).
и
Фиг.
осей
47. Расположение координатные
самолета к определению гироско-
пических сил.
гироскопического момента
установленное значение
постоянной величиной, неменяющейся при поворотах
Фиг. 48. Гироскопический момент трехлопастного вин-
та не зависит ст угла поворота лопастей.
Иначе обстоит дело с двухлопастным винтом. В мгновения,
когда винт становится вдоль поперечной оси самолета (фиг. 50<z),
величина Jy оказывается наибольшей; наибольшего значения
достигает и гироскопический момент. При повороте винта на 90°
*) &тах ~ 0,05—0,06 сек-1.
Ч 113 теории моментов инерции известно, что, если относительно двух глав-
ных осей моменты инерции одинаковы, то все другие оси также являются
главными и момент инерции вообще не зависит от направления оси.
3) Следует помнить, что гироскопический момент, соответствующий одной
лопасти таких винтов, меняется во времени вместе с изменением Jy отдель-
ной лопасти; это обстоятельство будет учтено при расчете самого винта, ко-
торый в целом не сообщает самолету периодических возмущений, но испы-
тывает их своими частями.
93
величина Jy падает почти до нуля (фиг. 500, так что и гироскопи-
ческий момент становится весьма малым. Таким образом, при
вращении винта гироскопический момент периодически изменя-
Фиг. 49. Гироскопический момент четырехлопастиого
винта не зависит от угла поворота лопастей.
ется по величине, совершая полный цикл изменения за время по-
, I 60 30
лопины оборота, т. е. за —г — > сек., и вызывает появ-
г 2 лЕ лЕ
ленме второй гармоники винта.
Фиг. 50. Гироскопический момент двухлопастного вин-
та изменяется весьма сильно при повороте винта.
Частота рассматриваемого возмущения:
, 2wit т.п t .
‘=зоЕ = ТбЕсек-
Для X - образных четырехлопастных винтов (нашедших при-
менение на некоторых иностранных самолетах) гироскопический
момент также будет периодической функцией времени.
<И
13. Сводка результатов
Нчми установлен спектр возмущающих сил, развивающихся
пн паботе винтомоторной группы. Не повторяя одинаковых ча-
стот- приведем здесь окончательную сводку полученного.
Значения круговых частот (сек—').
Двухлопастный винт Трехлопастный винт Четырехлопастный винт
От мо- тора От винта От мо- тора От винта От мо- тора От винта
Низшая частота КП 60 кп 60' —5 кп 60 —
Обертон КП 30 кп 30 3 кп 30 кп 30 5 кп 30' ял 30*
* кп 20 — кп "20* — кп 20 —
« кп тг -п6 15 е кп 15 КП 15 е кп 15 кп 15 -
кп 12 —- кп 12 — кп 12 ——
» кп 10 — кп 10 кп 10 5 кп "10 —
»» КП 7 60 — 60 — 7-"” 1 60 —
* Т.П 215 — кп 2 15 —- т.п 2 Тб 2-Я" 2 15
кп 320 — кп 3 20 — кп 3 20' —t
» »» К.П 60 а кп т КП 60' й — кп 60 а —
Здесь обозначено: п—число оборотов вала мотора в минуту, tj—коэфициент
редукции, а—число цилиндров.
Приведенной сводке может быть придана большая нагляд-
ность, если от круговых частот перейти к порядкам соответствую-
щих гармоник.
Порядок гармоник, возникающих при вращении, вала двига-
теля {т. е. число циклов изменения возмущающей силы (мо-
мента) за один оборот вала мотора): ’/т; 1; l‘/s; 2: —%-.
95
Фиг. 51. График частот возмущающих
сил. Частоты линейно растут с ростом
числа оборотов.
Порядок гармоник, возникающих при вращении винта
(число циклов изменения за один оборот вала винта):
а) двухлопастный винт: 1; 2; 6;
б) трехлопастный винт: 1; 2; 3;
в) четырехлоластный винт: 1; 2; 4.
Выше подчеркивалось, что с изменением скорости вра-
щения вала (или винта) линейно изменяется и круговая частота
возмущения каждой гармоники. Для последующего анализа
частот возмущения весьма удобно графическое представление
этого изменения. На фиг. 51 дан такой примерный график для
двигателя с трехлопастиым
винтом при коэфициенте
7 п
редукпии —х).
По оси абсцисс отло-
жены числа оборотов вала
двигателя, а по оси ординат
числа изменений соответст-
вующих возмущающих сил
за одну минуту (для того,
чтобы получить круговые
частоты, нужно было бы
эти последние разделить из
60 и умножить на 2я).
Если на этот график
нанести также кривые изме
нения собственных частот,
то точками пересечения
кривых обоих семейств бу-
дут определены резонанс-
ные режимы. Это сделано
на фиг. 52 для случая ло-
пасти винта, когда собст-
венные частоты согласно
(7.14) также зависят от
угловой скорости вращения.
В заключение настоящего параграфа отметим, что не все
из перечисленных возмущающих сил создают реальную опасность
значительных колебаний; некоторые из этих сил настолько не-
велики по своим амплитудным значениям, что их эффект даже
в неблагоприятных условиях ничтожен благодаря парирующему
влиянию сил внутреннего трения. Наибольшую опасность обычно
представляют следующие гармоники* 2):
!) Заимствован из статьи: W. В. Bergen „Experimental investigation in aln -
raft dynamics* (Journal of the aeronautical sciences. Oct. 1943. Vol. 10. № 8. p.
233-248).
2) E. S. Taylor and K- A. Browne „Vibration isolation of aircraft power plants".
(Proceedings of the fifth international congress for applied mechanics. 1939. p. 656 >.
96
от мотора от винта
Силы вдоль оси Л'............. нет, нет;
Силы вдоль осей YnZ........... 2; нет;
Момент вокруг оси X............1; а/2; нет;
Моменты вокруг осей YnZ. . . 2; 1;’6 (b—число
Фиг. 52. Точки пересечения кривых двух се-
мейств (k и р) определяют резонансные режимы.
Эти гармоники указаны жирным шрифтом в проведенной выше
сводке.
ГЛАВА 3
Вынужденные колебания частей самолета,
возникающие вследствие работы винтомоторной
группы
14. Вынужденные колебания мотоустановок
Периодические возмущающие силы, подробно рассмотрен-
ные в предыдущей главе, в первую очередь вызывают коле-
бания моторамы. Размахи этих вынужденных колебаний зависят,
С одной стороны, от величин и частот возмущающих сил, с дру-
Гроссман и Пановко 07
гой стороны—от свойств самой колебательной системы, т. е. от
собственных частот plt р.,,.... Эти размахи становятся особенно
значительными при близости частоты возмущения k какой-либо
собственной частоте pt. При полном совпадении (А~р) насту-
пает явление резонанса, когда колебания приобретают наиболь-
шие размахи (при отсутствии рассеяния энергии резонанс харак-
теризуется неограниченным нарастанием амплитуды колебаний).
Следует однако иметь в виду, что и при удалении от ре-
зонансного режима возможны опасные вибрации, если возму-
щающие силы достаточно велики по своему амплитудному зна-
чению.
Полный расчет вынужденных колебании всякой системы,
в частности моторамы, состоит из следующих элементов:
а) установление частот и амплитудных значений всех гармо-
ник возмущающих сил;
б) составаение и решение уравнений колебаний;
в) вычисление динамических напряжений;
г) оценка прочности рассчитываемой части с учетом явления
усталости материала.
Такой расчет является вполне исчерпывающим, но требует
надежного количественного определения возмущающих сил; это
определение выполняется обычно экспериментальным путем.
Среди множества возмущающих причин, о которых шла речь
в главе второй, одной из наиболее важных является неравномерность
крутящего момента во времени, иллюстрированная на фиг. 381).
Эго возмущение содержит в качестве составляющих гармоники
типа:
М; = М° sin 7г/
где величины /г,- даны в таблице в конце предыдущей главы и
М-' — наибольшее (амплитудное) значение рассматриваемой гар-
моники.
Рассмотрим вынужденные колебания -мотоустановки, вызы-
ваемые действием какой-либо составляющей действие дру-
гих гармонических составляющих крутящего момента (так же,
как и действие прочих возмущающих сил) может быть проана-
лизировано совершенно аналогичным образом 2).
Л1отоустановка схематизируется нами точно так же, как и
при анализе собственных колебаний в п. 4.
Для того, чтобы привести нашу запись в соответствие с обо-
значениями п. 2 будем писать вместо выражение P4sin kt
(см. фиг. И).
7 Для действительных конструкций колебания кр>тящего момента получа-
ются опытным путем.
-) Действия частных гармоник ввиду линейности системы независимы И
могут быть просто сложены.
98
место уравнений (2.2), относящихся к собственным колеба-
ниям мотоустановки, мы будем иметь:
-| TWtjjSj!-Л1'/(а®12' Л>71б°16 Л)71б®16 + VJ14 Sltl kt
у(Ит)2О33 Л ^4624 " A^G^G + ^\°2451П kt
rJg = — Л^т)1°з1 — 4Т)4Ь34 •^з’*Зь°з-5 Af'lc'A, + ^Vjm sin kt
vj4 = — ЛН]1°41 M'f]soi3 ЛаАй A'lc^c + 'Лз sin Af
Tj- -— /ИТНО51 ^^2°б2 ’^Чз^бЗ 4Т14°54 А^з^бб •Ав’^С^йв + ^4°64 Sifi kt
r|C = -— ^4э°са ^‘ri3rja3 Zs^i^er '^orti'JGi + ^°gi s'11
(14.1)
что отличается от (2.2) свободными членами P48j4sinA(, выражаю-
щими перемещения от действия пары P4sinA£. Как и в п. 2. мы
для упрощения анализа пренебрегаем силами затухания, т. е. рас-
сеянием энергии при колебаниях;такой анализ позволит выявить
многое существенное в явлении вынужденных колебаний и при-
ведет к существенным ошибкам в амплитудах лишь вблизи резо-
нанса. Учет сил затухания будет дан ниже для более простого
случая.
Частным решением системы служит;
гн — т,-sin AZ'. (14.2)
Подставляя эго в (14.1), получим систему уравнений, опреде-
ляющих шесть амплитуд г^:
V1=•*)! М A28j! + М 7j2A224 2 + 7Ит)3 з+J4iq4AsSj 44-J5v)5A28j 5+Л4е£8Ч в+Л3и
^2=^tZWoil+/zf7j2A3o22 + /WT)3A2o2.!+/4T;)A28244-J3iri5A3o.35+Jg-zi6A?o26+P4o24
43=7]1Л4А2о31 + Л17]2А3оУ2 4-.М713А2Оз3+/47]4А2гз4+Уб-г]5А3Оз5+/ст^А2гзе+Р4о34
т14 - гиМА3о41 , Л171зА3о424-/И7]3А2г4з+/4г)4А2о444-/бг;зА2845+/б^б^2й4б+Лй44
т13='П1‘?14А3о51 + ЛЬр>2о33 + /14т)3 t2o63+J4-z]4A3o51+J5r;3A2S55-|-J(.7]cA2o6i;+P4oS4:
*.’«= -*1iMA2o6 । + /Wv#862 + ^;.А2осз+/4т]4А2о64+Л-^А!8б5+/в^иА2гб0
Для полноты решения следовало бы добавить к (14.2) еще решение одно-
родной системы (2.2): опуская эту добавку мы тем самым пренебрегаем коле-
баниями мотоустановки с частотами р..
Такое пренебрежение вполне целесообразно, так как этим исключаются
колебания, быстро затухающие с течением времени. Считая, что реше-
нием служит (14.2), Мы рассматриваем лишь так называемую стационарную
часть вынужденных колебаний, т. е. колебательный режим, который устано-
вится после затухания неучтенной нами части (практически для такого за-
тухания достаточно нескольких секунд). Несколько подробнее об этом сказано
ниже в п. 15 б.
' 4 JG4
(14.3)
7*
99
Из полученных шести уравнений могут быть однозначно най-
дены все шесть амплитуд т^; после этого можно перейти и к со-
ответствующим напряжениям в элементах моторамы.
Остановимся подробнее на случае, когда мотоустановка сим-
метрична относительно плоскостей XOY и XOZ. Как указыва-
лось в п. 4, при этом в нуль обращаются все побочные переме-
щения 8,* (/./-£), кроме 8,-=863 и 8г6 = 8С2.
В связи с этим свободный член сохранится только в четвер-
том уравнении (14.3); решением системы (14.3) будет:
ст
т], = 7]3 = т]3= т|5 = = 0; — - J J ' (14.4
Здесь т(4ст представляет собой то статическое перемещение,
которое было бы вызвано парой Р4 при ее статическом дей-
ствии:
Следовательно, в этом случае будут отсутствовать какие бы
то ни было колебания, кроме чистых поворотов вокруг оси А".
Из (14.4) видно, что если k приближается к величине J j-v—,
то амплитуда колебания iq4 стремится тк бесконечности. Так как
- - представляет собой частоту р4 собственных колебаний
(см. 2.22), то рассматриваемый случай резонанса имеет место при
совладении частот k и р4.
При можно записать: т]4 = |j.7]4ct, (14.5)
1 1 .. .
где и. = -т---=-------------г,---динамический коэфициент.
1 ^4^44^ 1
р?
Из (14.5) следует, что эффект действия пары Р4 sinA£ врраз более
соответствующего статического эффекта. Соответственно этому,
амплитудные значения напряжений в элементах моторамы от
P4sinAf определяются выражением:
(И.б)
где сС1 —напряжения, вычисляемые в предположении статичес-
кого действия пары Р4.
Величина динамического коэфициента отчетливо характери-
зует динамичность явления, показывая во сколько раз переме-
щения и напряжения превосходят соответственные величины,
вычисляемые в предположении статического действия нагрузки.
Величина динамического коэфициента у зависит только от со-
отношения частот k:pit устремляясь в бесконечность при резо-
нансе (Л=р4). Следует, однако, помнить, что все выкладки сде-
ланы в предположении отсутствия рассеяния энергии, тогда как
100
самом деле некоторое рассеяние всегда неизбежно. При учете
ит затухания для р. получается более сложное выражение:
_________1______
И ~ П & V .
1 Vw) +тт'
(14-7)
ского коэфициента р. при раз-
личных коэфициентах затухания.
где й—коэфициент, характеризующий затуханиег). Благодаря
этому кривая динамического коэфициента оказывается практически
всегда ограниченной (фиг. 53).
Для уменьшения вибра-
ций необходимо нарушить
совпадение частот (6=р4),
изменяя жесткость конструк-
ции, т. е. величину собст-
венной частоты р. Рассмотре-
ние кривых на фиг. 53 пока-
зывает, что всегда выгоднее
удаляться от резонансного ре-
жима вправо, т. е. пользовать-
ся уменьшением собственной
частоты р. При этом динами
ческий коэфициент может быть
сделан сколь угодно малым.
Выражение динамического коэ-
фициента является вполне об-
щим и годится для любой упру-
гой системы с одной степенью
свободы.
15. Приемы уменьшения вибраций и амортизаторы
мотоустановок
а) Способы уменьшения вибраций
Вредное влияние импульсов, возникающих при работе винто-
моторной группы, может быть уменьшено различными принци-
пиально независимыми способами, из которых укажем главнейшие:
Уменьшением величины, возмущающих сил. К такому умень-
шению всемерно стремятся при конструировании, производстве
и сборке винтомоторной группы, однако, и после всех баланси-
ровок остаются возмущающие силы (например, силы, возникаю-
щие при движении шатунов), что вызывает необходимость обра-
щения к следующим способам.
Введением демпфирующих устройств—гасителей колебаний,
способных поглощать (рассеивать) значительную часть энергии
источника вибраций и тем Сильно понижать размахи последних.
1) Подробности и вывод формулы (14.7) см. ниже на стр. 103-107.
101
Из полученных шести уравнений могут быть однозначно най-
дены все шесть амплитуд после этого можно перейти и к со-
ответствующим напряжениям в элементах моторамы.
Остановимся подробнее на случае, когда мотоустановка сим-
метрична относительно плоскостей XOY и XOZ. Как указыва-
лось в п. 4, при этом в нуль обращаются все побочные переме-
щения кроме 8S,( = 8B3 и 826 = 862.
В связи с этим свободный член сохранится только в четвер-
том уравнении (14.3); решением системы (14.3) будет:
~ ст
7j, — vj, — 7]3= т;5 — т;6 = 0; т(4 = ~ ।_J k2$ti ’ G4-4
Здесь 'Z]4CI представляет собой то статическое перемещение,
которое было бы вызвано парой Р± при ее статическом дей-
ствии: т;/1 = Р4о44,
Следовательно, в этом случае будут отсутствовать какие бы
то ни было колебания, кроме чистых поворотов вокруг оси А.
Из (14.4) видно, что если k приближается к величине у~,
то амплитуда колебания т(4 стремится к бесконечности. Так как
f - представляет собой частоту р4 собственных колебаний
(см. 2.22), то рассматриваемый случай резонанса имеет место при
совладении частот k и р4.
При k-фрь можно записать: 7]4 = pi]4CT, (14.5)
где р — -j---- - 2 =-------—- — динамический коэфициент.
J. J ч
м 2
Из (14.5) следует, что эффект действия пары Р4 sin kt врраз более
соответствующего статического эффекта. Соответственно этому,
амплитудные значения напряжений в элементах моторамы от
P4sinA/ определяются выражением:
зв = о"р, О4-6)
где с" —напряжения, вычисляемые в предположении статичес-
кого действия пары Р±.
Величина динамического коэфициента отчетливо характери-
зует динамичность явления, показывая во сколько раз переме-
щения и напряжения превосходят соответственные величины,
вычисляемые в предположении статического действия нагрузки.
Величина динамического коэфициента р зависит только от со-
отношения частот k-.pit устремляясь в бесконечность при резо-
нансе (А=р4). Следует, однако, помнить, что все выкладки сде-
ланы в предположении отсутствия рассеяния энергии, тогда как
100 \
На самом деле некоторое рассеяние всегда неизбежно. При учете
сит затухания для р. получается более сложное выражение:
/ / k* у , ww
V Pi) + Pi*
(14-7)
где Л—коэфициент, характеризующий затуханиеJ). Благодаря
этому кривая динамического коэфициента оказывается практически
всегда ограниченной (фиг. 53).
Для уменьшения вибра-
ций необходимо нарушить
совпадение частот (k=pi'),
изменяя жесткость конструк-
ции, т. е. величину собст-
венной частоты р. Рассмотре-
ние кривых на фиг. 53 пока-
зывает, что всегда выгоднее
удаляться от резонансного ре-
жима вправо, т. е. пользовать-
ся уменьшением собственной
частоты р. При этом динами-
ческий коэфициент может быть
сделан сколь угодно малым.
Выражение динамического коэ-
фициента является вполне об-
щим и годится для любой упру-
гой системы с одной степенью
свободы.
Фиг. 53. Изменение динамиче-
ского коэфициента р при раз-
личных коэфициеитах затухания.
15. Приемы уменьшения вибраций и амортизаторы
мотоустановок
а) Способы уменьшения вибраций
Вредное влияние импульсов, возникающих при работе винто-
моторной группы, может быть уменьшено различными принци-
пиально независимыми способами, из которых укажем главнейшие:
Уменьшением величины возмущающих сил. К такому умень-
шению всемерно стремятся при конструировании, производстве
и сборке винтомоторной группы, однако, и после всех баланси-
ровок остаются возмущающие силы (например, силы, возникаю-
щие при движении шатунов), что вызывает необходимость обра-
щения к следующим способам.
Введением демпфирующих устройств—гасителей колебаний,
способных поглощать (рассеивать) значительную часть энергии
источника вибраций и тем сильно понижать размахи последних.
1) Подробности и вывод формулы (14.7) см. ниже на стр. 103-107.
101
Нередко большое поглощение энергии колебаний обеспечивается
естественными свойствами конструкции, что освобождает от не-
обходимости включения специальных демпферов.'Так, части са-
молета, достаточно удаленные от мотора, практически могут не
резонировать даже при совпадении их собственной частоты с ча-
стотой возмущающей силы; это объясняется тем, что путь про-
хождения возмущающих сил лежит через длинный ряд элемен-
тов конструкции, причем каждый из них (а в особенности их
сочленения) является в известной мере поглотителем, и энергия
источника практически рассеивается по пути.
Следует иметь в виду, что при достаточно низких собствен-
ных частотах, затухание может играть отрицательную роль. Это
утверждение, которое на первый взгляд звучит парадоксом, будет
разъяснено ниже.
Созданием значительного различия между частотами возму-
щения k и частотами собственных колебаний р. При этом,
как указывалось в предыдущем параграфе, динамический коэфи-
циент может быть сделан весьма малым'), так что динамический эф-
фект действия силы Р sin kt может оказаться много меныиим,
чем эффект, вызываемый силой при ее статическом приложении
(см. фиг. 53). Уменьшение собственных частот р достигается
смягчением связен, наложенных на колеблющуюся массу. Ради-
кальные результаты дает применение специальных гибких вклю-
чений-амортизаторов, сильно снижающих значение /?-(хотя бы
для некоторых наиболее опасных форм колебаний).
Величина сил, передающихся мотораме (и далее—конструкции
самолета) оказывается вследствие амортизации меньшей, чем
величина возмущающих сил источника колебаний. Тем самылб
мотор, как важный источник периодических импульсов, ока-
зывается как бы изолированным от конструкции самолета.
„В ряде случаев после постановки на эластичную подвеску мо-
тора или моторной рамы, вибрации частей самолета практически
исчезали и самолеты с точки зрения эксплоатации становились
неузнаваемыми" 2).
На этом же принципе основана изоляция приборных досок,
бензобаков и маслобаков: введение амортизаторов обеспечивает
резкое падение собственной частоты, а вместе с этим и- динами-
ческого коэфициента. Благодаря этому, эффект возмущающих
сил, передающихся указанным частям, оказывается сильно сгла-
женным. Благотворное уменьшение собственных частот дости-
гается не только введением специальных амортизаторов; простое
изменение жесткости самой конструкции дает принципиально
') Выражение р, строго справедливое для системы с одной степенью сво-
боды при гармоническом возмущении, отражает принципиальные закономер-
ности, действительные и для большего числа степеней свободы.
-) См. А. В. Чесалов—„Опыт борьбы с вибрациями на самолете", стр. 37
Труды ЦАГИ № 494, 1940.
102
то же самое. Этим пользуются, например, для устранения опас-
ных вибраций тяг управления, изменяя их жесткость изгиба J).
Своеобразным средством изменения динамической структуры
системы является применение так называемых динамических
демпферов; последние представляют собой дополнительные
упруго подвешенные массы небольшой величины, резко мепяю-
щи_ частотные характеристики основной системы.
б) Роль рассеяния энергии (сил затухания)
I Особо следует остановиться на роли затухания при работе
амортизаторов. На первый взгляд может показаться, что при
всех обстоятельствах затухание уменьшает динамический эффект,
вызываемый периодическими возмущающими силами; на самом
деле это не всегда так.
Для анализа указанного
влияния рассмотрим про-
стейший случай, в котором,
однако, можно будет отчет-
ливо выявить все существен-
ное (фиг. 54).
Положим, что масса М
подвешена на упругих амор-
тизаторах (рессорах) и мо-
жет колебаться только по
вертикали; будем считать,
что при колебаниях возни-
кает не только реакция
упругих связей (пропорцио-
нальная перемещению'), но
и сила затухания, пропор-
циональная скорости. Эта
пикает в тех же связях, что
Фиг. 54 Принципиальная схема систе-
мы с одной степенью свободы при на-
личии упругих связей и вязкого погло-
тителя энергии.
сила в реальных условиях воз-
и сила упругая, ибо действитель-
как свойствами упругости,
ные связи одновременно обладают
так и свойствами вязкого сопротивления. Для ясности в схеме,
показанной на фиг. 54, упругие связи а показаны отдельно от
связи, воспроизводящей вязкое поглощение энергии Ь. Схема
фиг. 54 отображает конструкцию моторамы; масса М играет
') Амортизация приборных досок необходима в связи с резким сокраще-
нием сроков службы гироскопических приборов при больших вибрациях.
Опыты показали, что вибрации с амплитудой большей 0.5 мм сокращают
срок службы этих приборов в 10 раз. Для устранения чрезмерных вибрации
круговая частота приборной доски не должна превосходить 65—70 сек-1 (См.
Кербер Б. Л.—„Амортизация приборных” досок на самолетах" Технические
заметки ЦАГИ № 49, 1935).
Новая конструкция амортизатора для самолетного оборудования описана
в ‘ Рудах НИСО № 7, 1045 г. (Ю. И. Иорнш—„Равночастотные амортизаторы
виорацпй для самолетного оборудования*).
103
роль массы мотора, основание представляет конструкцию само-
лета, а пружина—упругую мотораму с амортизаторами.
Если рассматривать свободные колебания такой системы, то
благодаря действию сил вязкого сопротивления эти колебания,
будучи вызваны каким-либо начальным толчком, с течением
времени будут затухать, как это было показано выше на фиг. 3.
Рассмотрим теперь вынужденные колебания этой системы. Пусть
на массу М действует возмущающая сила PosinA£. Записывая
уравнение равновесия сил, мы в согласии с принципом Далам-
бера, получим:
Ро sin kt — ay — су— Му = 0.
Здесь первый член левой части,—внешняя возмущающая сила,
второй,—сила затухания, пропорциональная скорости у, третий,—
сила упругости сжатых рессор, пропорциональная перемещении»
у, и последний,—сила инерции. Перепишем это уравнение в виде:
2hy 4- ръу — sin kt, (15.1)
Полное решение уравнения состоит из двух частей:
1) Решения соответствующего однородного уравнения (т. е.
при отсутствии правой части):
У1 = e~ht{Clsin Vp'^hH+C^osVp^nFtY (15.2)
2) Частного решения уравнения (15.1), которое может быть
записано в виде:
°5”
ЧЧМ + ~^
Здесь р = 1/ — частота собственных колебаний, вычисля-
г М
емая при пренебрежении затуханием, а <р определяется из ф-лы:
. 2.Ш
р* — F •
г
Такщ! образом у=у1 + у2, причем постоянные интеграции
Q и С2 выясняются из начальных условии.- Как видно, с тече-
нием времени слагаемое yt будет быстро затухать вследствие
убывания величины e~htJ стоящей в качестве множителя; по про-
шествии некоторого (для реальных конструкций весьма незначи-
тельного) времени, сохранится лишь колебание, выражаемое вто-
104
рым слагаемым и называемое стационарной частью вынужден-
ных колебаний *).
В этом решении необходимо отметить следующее: а) колеба-
ния носят гармонический незатухающий характер; б) частотой
колебаний является величина k, т. е. частота изменения возму-
щающей силы Р-, в) перемещения „отстают" по времени от силы;
это отставание характеризуется сдвигом фазы <р, зависящим от
коэфициента затухания h (при отсутствии затухания Л=0
и вместе с этим ср — 0), так что в мгновения, когда сила дости-
гает максимума (Ртах — ро при sin££ = l) перемещение оказы-
вается не наибольшим [ибо при этом sin (kt— 1J; г) при
совпадении частот k—p перемещения оказываются ограничен-
ными; д) амплитуда колебания имеет значение:
где yzm~= Ро: с (перемещение, вызываемое статически действую-
щей силой Ро).
Обозначив теперь
И ~ , Л Л, Щ2 4^” ’
Iх V ру + pi
можно записать:
Утах=№ст-
Из формулы для динамического коэфициента следует, что
с возрастанием коэфициента затухания h, величина р. умень-
шается, а в месте с ней уменьшается и амплитуда колебаний.
Однако, остается открытым чрезвычайно существенный вопрос
о силе, передающейся основанию, т. е. конструкции самолета
будет ли и она убывать с ростом величины Л? Дело в том, что
эта сила пропорциональна не только перемещению у, но и ско-
рости у, образуясь из двух частей:
N = су + «у,
как это и было принято при составлении уравнения (15'1).
Развернув выражения:
су = сутах sin (kt — <р) = Мр*усту- sin (kt — <р),
ay~akymax cos (kt — <f>) = 2Mhkycmy- cos (kt — <f>),
’) По этим соображениям мы и ограничились анализом стационарной
части вынужденных колебании мотоустановки в п. 14, принимая решение си-
стемы (14.1) в виде (14.2).
1«5
получае1
N ~ Мр*\>уст
'2kh
sin {kt — <?)+ -~г cos (kt — <?) .
(15.4)
Преобразуем разность, стоящую в скобках, по формуле:
a sin а + b cos a — ]/a2 + b3 sin (а + р),
х b
где pr-arctg —.
В напем случае:
sin(/?t- ?) + ~^cos(Atf—?)=]/1 + ^~?- sin(/tf — © + ₽),
к , %kh
прич£« ₽= aic 1g -р-.
Отсюда видно, что максимальное значение скобки в (15.4) со-
ставляе"-
(15.5)
’ Р4
Выражение, стоящее перед скобкой, может быть также пре-
образовано:
Мр-\>уст = <yycm — рР0. (15.6)
Учи'ывая (15.5) и (15.6), получим для максимального значения
силы А, передающейся основанию;
л’ 1Z< 4k? № „
h max — I1 У 14 Pq-
Из ?того выражения видно, что сила, передающаяся основа-
нию, больше силы Ро не в р. раз, а в ;» у 1 4-— раз. Это
выражение, называемое коэфициентом передачи силы, обозна-
чим через р-п
, 4k2/i3
1 4-
4kW
!X1 = !x V 1 + —^T-
Ау- <)И>
р4
Это'г коэфициент показывает, во сколько раз сила, передаю-
щаяся основанию, больше силы Ро, действующей на массу 7W.
Коэфициент [h при отсутствии затухания (Л = 0) совпадает с коэ-
106
Фиг. 55. Изменение коэфициен-
та передачи силы p.t при раз-
личных коэфицпентах затуха-
ния. Правее точки гп затухать
оказывается вредным.
фициентом динамичнее™ а (фиг. 53), но при /г у- 0 оказывается
отличным от [>-.
Интересно проследить изменение коэфициента передачи силы
v в зависимости от отношения k:p при различных значениях А-
Это изменение показано на фиг. 55, где по оси абсцисс отло-
жены отношения частот /?:/>, а по оси ординат величины рц-
каждой кривой отвечает определенное значение коэфициента
затухания.
Существенно, что все кривые проходят через одну и ту же
точку т, абсцисса которой равна у 2, а ордината- единице. Дей-
ствительно, если k:p~y2, то величина коэфициента стано-
вится независящей от коэфици-
ента затухания, так как в (15.7)
числитель становится равным
знаменателю; для_ соотношения
частот к : р =]/ 2 величина зату-
хания, как видно, вообще не бу-
дет играть никакой роли. При
меньши'х отношениях k:p (левее
точки т) затухание играет поло-
жительную роль, так как с ро-
стом величины h происходит
уменьшение коэфициента При
больших отношениях k: р (пра-
вее точки т) затухание оказы-
вает отрицательное влияние, ибо
с ростом А кривые проходят все
выше и выше, определяя все
большие величины иР
Так как устройством амор-
тизаторов достигается сильное
смягчение подвески, когда /г ока-
зывается значительно больше р,
то практически амортизаторы
обеспечивают работу моторамы
в области, расположенной правее точки т, т. е. в условиях, когда
затухание невыгодно. Это обстоятельство следует иметь в виду
при конструировании амортизаторов. Одновременно необходимо
помнить, что при работе амортизаторов в области резонанса
(что может иметь место на малых оборотах двигателя) затуха-
ние играет исключительно полезную роль; поэтому стремле-
ние к понижению вязкого сопротивления не должно быть чрез-
мерным.
в) Роль нелинейности амортизаторов
В заключение следует остановиться на ограничении чрезмер-
ной податливости (гибкости) амортизаторов. Хотя смягчение под-
107
вески может сильно уменьшить вибрации, однако в полете при
перегрузках такое смягчение приведет к возрастанию переме-
щения мотора относительно конструкции самолета. По совре-
менным требованиям возможные перемещения мотора не должны
превышать 3 мм по любому направлению и в любых условиях
полета,—в противном случае возникает опасность нарушения
нормальной работы системы питания двигателя.
Поэтому вне пределов обычных вибраций амортизирующая
система должна быть достаточно жесткой. В связи с этим же-
лательно, чтобы при малых перемещениях мотора (т. е. на ре-
жимах вибраций) жесткость амортизации была возможно мень-
ллей, и в то же время резко возрастала для больших пере-
мещений (при статической
перегрузке). В свете ска-
занного становится понят-
ным, почему стремятся
иметь нелинейную диа-
грамму работы амортиза-
тора, по типу фиг. 56 г).
В рабочем диапазоне ab,
соответствующем дейст-
вию нормально возникаю-
щих возмущающих сил,
хороший амортизатор до-
статочно мягок 3) и тем
самым обеспечивает низ-
кие значения соответ-
Фиг. 56. Целесообразная характеристика
работы амортизатора.
ствующих частот. Вне
этого диапазона он обладает гораздо большей жесткостью
и препятствует развитию чрезмерно больших перемещений.
Следует помнить, что при вынужденных колебаниях вне интер-
вала ab, все наши уравнения теряют свою силу. Не углубляясь
в вопросы работы нелинейных систем, заметим только что даже
при отсутствии затухания, амплитуды колебаний нелинейных
-систем всегда ограничены * 3).
Таким образом, основными принципами конструирования мото-
рамы и подбора амортизации являются:
1) Частоты собственных колебаний мотоустановки должны
исключать возможность резонанса в эксплоата'ционном диа-
пазоне и величины р должны быть меньше частот k-t
') R. С. Roche „Engine smoothness and protection through shear rubber moun-
tings (S. A. E. July 1942 vol. 50 . № 7. p. 317).
-) Напомним, что крутизна наклона кривой пропорциональна жесткости
амортизатора.
3) Изложение прикладной стороны вопроса см. Ден-Гартог „Теория коле-
баний," 1942, стр. 413—418, § 72.
1С8
основных возмущающих сил (см. п. 13) по крайней мере
в у2 раз1 2).
2) Формы колебаний моторамы должны быть по возможности
разделены.
3) Вязкое сопротивление не должно быть чрезмерным.
4) Характеристика амортизатора должна быть нелинейной,
создающей возможную мягкость при малых, и возможно боль-
шую жесткость, при больших перемещениях мотора.
Все сказанное поможет уяснить принципиальные основания
устройства амортизаторов.
г) Амортизаторы мотоустановок
Для всех современных мощных моторов применение амор-
тизирующей подвески признается совершенно обязательным.
Простые резиновые или текстолитовые прокладки, приме-
няемые при установке рядных моторов, по существу являются
амортизаторами, хотя и весьма несовершенными. Дело в том,
что при работе на сжатие резина оказывается довольно жесткой
и для эффективности амортизации такие прокладки нужно делать
слишком толстыми. Тот же недостаток присущ и простым рези-
новым втулкам, при установке звездообразных моторов. В связи
с этим, во всех новейших конструкциях амортизаторов аморти-
зирующий материал (нм, обычно, служит резина), работает не
на сжатие, а на сдвиг 3). Отдельные типы упругих подвесок отли-
чаются как конструктивными особенностями, так и местом располо-
жения амортизаторов.
По месту расположения можно выделить четыре основных?
типа:
1) амортизаторы расположены в узлах крепления мотора к
мотораме,
2) амортизаторы расположены в узлах крепления моторамы
к конструкции самолета,
3) амортизаторы установлены одновременно по п. п. 1и2,
4) амортизаторы включены в конструкции самих стержней
моторамы.
Расположение первого типа обладает тем достоинством, что
при этом сама моторама в значительной мере изолируется от
возмущающих сил, возникающих в моторе, а амортизаторы оказы-
ваются менее нагруженными. Кроме того, центр жесткости мо-
тоустановки приближается к центру ее тяжести, так что величи-
ны о32 и о26, выражающие связанность колебаний, оказываются
относительно небольшими; колебания становятся близкими
О Чтобы коэфициенты р и Hi были меньше единицы; иногда ставится
условие fi, 0,5, что потребует еще большего различия частот.
2) Модуль сдвига резины в 4—7 раза меньше модуля нормальной упругости;
коэфициент затухания приблизительно одинаков при сдвиге и при сжатии.
к раздельным, разброс частот уменьшается и облегчается упра-
ление ими (см. п. 4). Иногда конструктивно более удачным
оказывается решение по п. 2 или 3.
На фиг. 57 схематически показано устройство по типу 4, при-
мененное на самоле-
Фиг. 57. Схема амортизатора включенного в стер-
жне моторамы.
работающие на сдвиг в одном направлении,
, 2) амортизаторы, работающие на сдиг в двух направлениях.
Характерным представителем первого типа является аморти-
затор фирмы Lord *). На фиг. 58 показана установка амортиза-
торов на кольце моторамы самолета В-25, а на фиг. 59—кон-
струкция амортизатора. Амортизатор состоит из двух стальных
втулок—внутренней и наружной; к наружной жестко крепится
мотор, внутренняя
втулка жестко кре-
пится к кольцу мо-
торамы. Между
втулками находится
слой вулканизиро-
ванной резины, проч-
но соединенной с ме-
таллом. Резина рабо-
тает на сдвиг только
вдоль осн втулки;
в поперечном ц^пра-
вленпи резина рабо-
тает на сжатие и
амортизатор оказы-
вается относительно
значительно более
жестким.
Как видно из
фиг. 58, ось каждо-
го амортизатора пер-
пендикулярна радиу-
су опорного кольца
в соответствующем
те Ju-52; резина про-
чно связана со стен-
ками труб вулкани-
зацией.
По своей конст-
рукции современ-
ные амортизаторы
могут быть разделе-
ны нд две группы:
1) амортизаторы,
Фиг. 58. Установка амортизаторов Lord (мо-
то}'становка самолета В-25).
месте. При такой установке амортизаторы
i) Применяется на самолетах В-25, Бостон и др.
110
Серага Крепления
К матчраме
РезинпСая шайБа-
ограничит
Фиг. 59. Схема амортизатора Lord.
Наружная вгул/v
крепления мот ера
ЧИайРа
рграниеит.
Внутренне
втуттна
обладают наименьшей жесткостью в направлении касательной
к кольцу, благодаря чему они оказываются вполне эффективными
при крутильных колебаниях мотоустановки и радикально умень-
шают вибрации, связанные с не-
равномерностью крутящего мо-
мента.
Представителями второго ти-
па могут служить амортизаторы
т1Динафлекс“ и отечественные
амортизаторы типа ЦАГИ. Амор-
тизатор лДинафлекс“ состоит из
трех металлических пластинок,
между которыми проложено два
слоя вулканизированной резины.
Мотор жестко крепится к вну-
тренней пластинке; наружные
пластинки крепятся к мотораме
(фиг. 60). Число амортизаторов
обычно соответствует числу то-
чек крепления мотора к кольцу
Амортизаторы рассматриваемого
[(фиг. 61).
жесткость
подмоторнои рамы
типа имеют малую
Фиг. 60. Схема амортизатора „Динафлекс".
при деформациях в плоскости кольца, а потому успешно изоли-
руют колебания в направлениях осей Y и Z, а также крутиль-
ные колебания вокруг оси X.
ш
Кенструкция амортизаторов типа ЦАГИ схематически пока-
зана, на фиг. 621).
Несмотря на большую сложность амортизаторов „Динафлекс"
и ЦАГИ, они эффективнее чем амортизаторы Lord, так как спо-
собны смягчать влияние более обширной группы возмущающих
причин (не только момент вокруг оси X, но и силы в направле-
ниях осей Y и Z).
В связи с отмеченной выше необходимостью нелинейности
амортизаторов, всегда предусматривается устройство ограничи-
Фнг. 61. Установка амортизатора „Динафлекс" на коль-
це моторамы.
телей (см. фиг. 57, 59, 60, 62), благодаря которым при больших
перемещениях жесткость резко возрастает.
Особняком стоят амортизаторы, названные американцами „ди-
намическими подвесками". Эти подвески, разработанные фирмой
Lord, предназначены не только для амортизации, но и для раз-
деления колебаний; с их помощью достигается обращение в нуль
побочных перемещений 835 и 826.
9 Подробное описание см. Н. П. Серебрянский — „Амортизаторы типа
ЦАГИ под звездообразные и рядные моторы". Технические отчеты ЦАГИ
№ 7, 1942.
112
Ров ,ч
ВнуТреННМ
IL’CW’jU
^Болтине»
нцймотери
Раиновое юмцо Зотюлншп.
жесткости
Конструкция динамической подвески была впервые предложена
проф. Тэйлором ’) и в первоначальном варианте представляет
собой серию амортизаторов „Дина-
флекс", повернутых из плоскости
кольца так, что взаимно пер-
пендикулярные направления главных
упругих осей (/, //, III) каждого из
амортизаторов занимают положение
согласно фиг. 63. Направления I для
всех амортизаторов пересекаются в
одной точке на оси А'. (
При этом можно так подобрать
угол Й, что побочные перемещения
?;(5 = 86:1 и о2й = S63 также обратятся
в нуль и все колебания окажутся
раздельными 2 3).
При таком типе подвески ампли-
туды колебаний могут быть умень-
шены, примерно, вдвое (см. фиг.
64 ;,У
Численные значения жесткостей
амортизаторов, необходимые для вы-
числения частот, определяются экспе-
риментально по трем главным упру-
гим направлениям, условным линеа-
ризированием кривых „сила—дефор-
мация" в области малых перемеще-
ний 4 * * * 8).
Фиг, 62. Схема амортизатора
типа ЦАГИ.
!) См. Journal of the aeronautical sciences. Dec. 1938 r.
-) Определение указанного значения 0 см. А. А. Белоус,—„Вибрации мою-
сстановок с жесткими и эластичными креплениями звездообразного мотора'*
(Труды ЦАГИ № 499. 1940).
3) См. упомянутую выше статью К. A. Browne (S.A.E. 1939, стр. 187,
фиг. 6).
*) Материалы по расчету амортизаторов см. также;
И. В. Ананьев и др,- „Расчет на резонанс мотоустановок на эластичной
подвеске" (Т. В. Ф. № 4, 1941).
И. В. Ананьев и др.—„Эластичная подвеска моторных установок”
(Т. В. Ф. № 1, 1942).
И. В. Ананьев и Н. П. Серебряиский —„Упругие характеристики мотор
ных рам и амортизаторов иностранных самолетов и частоты их мотоустановок"
(Г. В. Ф. № 5-6, 1942).
Н. П. Серебряиский „Амортизаторы типа НАГИ** (Технические отчеты
ЦАГИ № 7, 1942).
И. В. Ананьев и др. „Рекомендации по расчету вибраций винтомоторных
установок и примерные конструкции амортизаторов". (Технические отчеты
ЦАГИ № 60, 1946 г.).
Вопросы расчета и подбора т. н. динамического демпфера (дополнитель-
ной массы, упруго подвешенной к мотору) см. И. В. Ананьев—„Расчет дина-
мического демпфера**. Технические отчеты ЦАГИ № 46, 1945 г.
8 Гроссман и Пановко.
113
16. Динамические напряжения в лопасти винта
а) Общие замечания
Рассмотренные в предыдущей главе возмущающие силы,
могут вызывать значительные динамические напряжения в лопа-
Фиг. 63. Направления главных осей жесткости аморти-
заторов при „динамической подвеске* не совпадают
с направлениями осей XYZ
сти винта даже при большой разнице между собственными часто-
тами лопасти и частотами этих сил. Не все из возмущающих сил
могут быть надежно оценены количественно. Это вынуждает нас
ограничиться учетом лишь наиболее достоверных влияний; к вычи-
сленным таким способом динамическим напряжениям вводится
поправочный коэфициент на влияния неучтенных возмущений.
Вряд ли нужно пояснять, что подобная постановка задачи
не способна обеспечить вполне надежных результатов, но
114
позволяет все же выяснить примерный порядок динамических
напряжений.
Из возмущающих сил подчиняются относительно достовер-
ному определению лишь две категории сил:
Периодические тангенциальные силы инерции, возникающие
‘"[ скорости вращения винта относи-
Фиг. 65. Тангенциальная сила инерции,
возникающая вследствие переменности уг-
ловой скорости.
вследствие колебаний угловой
тельно_ среднего значе-
ния переменность
угловой скорости харак-
теризуется угловым уско-
рением тесно связан-
ным с неравномерностью
крутящего моментаЛЛрак-
, Ju)
тически функция мо-
жет быть получена обра-
боткой опытных торсио-
грамм, снимаемых при
испытаниях двигателя; оставляя в стороне этот вопрос как отно-
сящейся к курсу динамики авиадвигателей, мы будем считать
здесь периодическую функцию известной. Элемент лопасти
развивает тангенциальную силу инерции:
Фиг. 66. Гироскопическая сила, развивае-
мая элементом лопасти.
dT = ^dt ^.(16.1)
(см. фиг. 65), где обоз-
начения как и в п. 7;
dto
величина г пред-
ставляет собой ли-
нейное ускорение, а
pmFdr—массу элемента.
Периодические ги-
роскопические силы,
возникающие при эволюциях самолета, вследствие появления
угловой скорости вращения самолета, вокруг поперечной оси Z
(фиг. 66); для элементарного отсека лопасти:
dG = 22<в $mFzdr,
здесь 2— угловая скорость вращения самолета вокруг оси Z,
22<ог — ускорение (см. п. 12), ?mFdr— масса элемента лопасти.
8* Ц5
Так как z — г cos orf, то
dG~2Qoip,„Fr cos mt dr. (16.2)
Влияние сил dT и dG приближенно может быть вычислено
в предположении их статического действия; при этом, конечно,
остаются неучтенными вторичные инерционные силы, развива-
ющиеся вследствие колебаний лопасти. Иными словами, при
вычислении, сил dT n dG лопасть считается обладающей массой;
однако влияние этих сил определяется в предположении, что
лопасть лишена массы (или бесконечно жестка). Такое решение
задачи ’) заманчиво по своей сравнительной простоте, но может
дать хорошие результаты только при достаточной жесткости
лопасти; в этом рлучае амплитуда колебаний,—а следовательно,
силы инерции, развивающиеся вследствие этих колебаний,—
невелики.
Оказывается, что подобное решение дает приемлемую точ-
ность только для гироскопических сил: влияние тангенциальных
сил инерции должно быть оценено с учетом колебаний. В сле-
дующих двух пунктах исследуются напряжения от обоих ука-
занных причин, причем колебания считаются происходящими
только в направлении наименьшей жесткости.
б) Напряжения, возникающие от действия гироскопических сил
Поскольку мы намерены учитывать действие гироскопических
сил статически, будем рассматривать максимальное значение
гироскопической силы dG\ из формулы (16.2) получим:
Фиг. 67. Ось наименьшей жесткости сечения соста-
вляет с плоскостью вращения угол о.
Пусть в сечении, определяемом координатой гр ось наимень-
шей жесткости составляет угол у с плоскостью вращения винта
J) См. работу А. И. Пожалостина «Расчет воздушных винтов на усталость
(Труды НАГИ № 436, 1939 г.).
116
\
/фиг. 67). Момент относительно этой оси, вызываемый элемен-
тарной гироскопической силой dGmax:
cIMq = (г — r^dG = 22cos ср (г—г±) dr.
Момент от всех сил dG действующих на лопасть от сечения гх
до конца лопасти:
R
Mq = 22 w cos <р J p„Fr(r — rj) dr.
G
Преобразуем интеграл по частям:
R Г г 1/? ,R г
f (г — r^dr = (г — гi) J pFrdr — J f pmFrdr\
i\ R Q rj R
Квадратная скобка после подстановки пределов обращается
в нуль и мы получаем для изгибающего момейтд:
R R _ 11
Mq- = 22 <о cos ср J l‘p Frdr* = 22 ш /?’ cos <Р j’ f pmFrdr2.., (16.4)
П r r\ 7
Деля этот момент на минимальный момент сопротивления сечения,
найдем напряжение изгиба от действия гироскопических сил:
22 <о R" cos ср ’ * _
°G (ri) = W~n J J ?mFrdr2 (16-5)
G г
Угловая скорость самолета 2, прямым образом связанная с ма-
невренностью самолета, задается в официальных руководствах.
в) Действие колебаний угловой скорости вращения
Рассмотрим изгибные колебания лопасти вращающегося винта,
загруженной силами dT, определяемыми ф-лой (16.1).
Изгибаемая лопасть, вследствие растяжения центробежными
силами находится в условиях продольно-поперечного изгиба.
Как известно из курса сопротивления материалов, в случаях
продольно-поперечного изгиба теорема Ш ведлера-Журавского :
г//И_ п
~dr — Ч
117
становится неверной (М — изгибающий момент, Q—поперечная
сила, г—текущая координата сечения).
Учет растягивающего усилия при рассмотрении равновесия
элемента стержня (лопасти) приводит к выражению:
dr dr
{N—растягивающее усилие, и—упругий прогиб текущего сече-
ния), заменяющему запись теоремы Шведлера-Журавского.
Диференцируя последнее соотношение один раз, получим:
{EJu")"— s + {Nu')',
так как M — EJu" и Q'=s (s—погонная интенсивность поперечной
нагрузки).
В нашем случае это основное уравнение принимает вид:
{EJu")" = —?mFu + Si + s2 + {Nu')', (16.6)
где pmF— погонная масса; —[>mFu —погонная сила инерции, раз-
вивающаяся при упругих колебаниях лопасти; Sj—погонная попе-
речная нагрузка, создаваемая силами dT (формула 16.1); s2—
погонная поперечная нагрузка, создаваемая центробежными
силами.
Обратимся к силам dT. Изгиб в направлении наименьшей
жесткости будет вызывать только составляющая dTsin tp. Погон-
ную величину этой силы мы обозначили через sp, она получается
делением выражения drsincp на величину dr:
dT . d<o .
Положим, что угловая скорость вращения винта, имея своим
средним значением величину ш0, разложена в ряд Фурье, т. е.
изменяется по закону:
= w0+ toj sin (•/,£ + Yj) + ш2 sin (v/+t2)+ ....,
здесь <un <i>2_.—амплитудные значения гармоник; v3..—частоты
гармоник; у2,..—начальные фазы.
При этом
~ cos (vxZ + 71) + <o3v3 cos (V+y2)+ ...
118
Таким образом, внешняя погонная возмущающая сила S! опре-
делится функцией:
*'1 = PmFr sin ? 5 ®л v« COS { >nt + T„).
п = 1
(16-7)
Необходимо подчеркнуть, что в отличие от рассмотренных
выше задач здесь речь идет о возмущающих силах, непрерывно
распределенных вдоль консольной лопасти, т. е. лд является
функцией не только времени t, но и координаты сечения г. Это
обстоятельство потребует от нас ниже применения особого
метода решения—разложения вынужденных колебаний по соб-
ственным функциям.
Рассмотрим теперь поперечную нагрузку, создаваемую дей-
ствием центробежных сил. Для упрощения решения будем счи-
тать, что центробежные силы могут вычисляться по средней
угловой скорости 1»0. Как показывают сравнительные расчеты,
такое упрощение не вносит в результат серьезной погрешности.
Элементарный отсек лопасти длиной dr развивает элементар-
ную центробежную силу:
cZC = р„, F <о0а г dr,
Фиг. 68. Схема к определению поперечной
нагрузки от центробежной силы элемента ло-
пасти dC
которая также дает проекцию на направление упругого переме-
щения и.
Для выяснения этой
приведенной выше
фиг. 31. На рисунке
Д — центр тяжести
рассматриваемого
отсека после де-
формации, ОХ —
ось вращения винта,
гОп—подвижная си-
стема координат,
вращающаяся вмес-
те с лопастью с по-
стоянной угловой
скоростью w0, Or—
направление неде-
формированной оси
лопасти, а — угол
между направле-
нием изгиба лопасти
и осью вращения
ОХ. Д1 и Д2—проек-
ции точки А на плоскости гОХ и пОХ; Д3 и А4 — проекции точ-
ки А на оси Or и ОХ.
проекции рассмотрим фиг. 68, подобную
119
Таким образом, отрезок АА3 представляет собой перемещение
и, а центробежная сила dC действует вдоль прямой АА4, прохо-
дящей через центр тяжести вращающегося элемента и ось вра-
щения ОХ. Мы ищем проекцию dC на направление AA.t. Разло-
жим dC на компоненты вдоль направлений ААХ и АА2. Сразу
отметим, что второй компонент не дает проекции на направле-
ние AAS.
Компонент dC вдоль АА^.
dC- sin₽ = dC- — <йпа. (16.8)
/ г
Проектируя его на направление А43, получим, что проекция dC
на направление изгиба составляет
dC-11 sin a-sin а = рЛ /чоо2 U sinsadr. (16.9)
Относя ее к единице длины (т. е. деля на dr), мы получим:
s2 = РдаЛоо2» sin2 а; (16-10)
с учетом (16-7) и (16-10) основное уравнение (16-6) запишется в
виде:
со
(£'Jtt")''+pOTFd—(ЛГм'У—р„Ло03йsin2 a —pmFr sin aVw„v„cos (v/ + f„).
П—1
так как <p = a.
Полученное нами диференциальное уравнение линейно; это
дает право искать решение его как сумму решений от действия
каждого слагаемого правой части (заданной функции г и I).
Заменив также 7V=woaS, где
R
S= p^Frdr, (16.11)
Г
мы будем искать теперь решение уравнения:
(EJu!')"+pmFil — w02 (Sи')' — Fa>02« sin2 a =
= Pm Fr w„ v„ sin a cos (yrt + ?„) (16.1?)
с тем, чтобы затем суммировать результаты таких решений соот-
ветственно различным правым-частям.
120
Сразу заметим, что уравнение (16.12) удовлетворяется подста-
новкой;
«=/(r)cos(V+f„) (16.13)
и переходит в обыкновенное диференциальное уравнение;
(EJf'T _ рт F^f «02 (s/')' pm FmcVsin2 а =
= Pm^/'%v«sina. (16.14)
Выражение (16.13) показывает, что лопасть совершает гармо-
нические колебания, частота которых есть частота v„ возмуще-
ния. Нам остается найти функцию формы /(г), которая предста-
вляет собой уравнение изогнутой оси в мгновения, когда дефор-
мация лопасти максимальна, т. е. когда cos(v^+yn)=: 1. Для оп-
ределения f$r) и служит уравнение (16-14).
Б\дем искать выражение /(г) в виде:
СО
/('') = £c/i(''), (16.15)
/=1
где f-, (г) функции собственных форм, которые мы считаем из-
вестными: с, коэфициенты, определение которых и составляет
задачу дальнейшего.
Не останавливаясь на доказательстве, отметим, что данное
(16.15) разложение формы вынужденных колебаний по собст-
венным функциям всегда возможно и является сходящимся. Ра-
зумеется, что такое разложение будет эффективным, если соб-
ственные функции /Дг) уже фактически найдены; мы предполо-
жим, что собственные функции /;(г), так же, как и собственные
частоты р^ определены (например, приемами, указанными в п. 7).
Временно отвлечемся от нашей задачи и рассмотрим в общем
виде свободные колебания лопасти в поле центробежных сил;
для этого нужно в (16.12) положить правую часть равной нулю.
Ч стное решение такого однородного уравнения будет иметь
вид:
Пг=/, COS (/>/ + £;),
где ft—собственная функция и p-t — собственная частота. Если под-
ставить это в (16.12) без правой части, получится:
- Рт Fp^fi - (Sf’S - Рга F^*ft sin2 a = 0.
Записывая такие уравнения для всех функций fti и умножая далее
каждое из уравнений на сг, получим, после суммирования всех
левых и правых частей:
со
(EJfT - -Pm^/sin2» = 0.
2=1
121
Вернемся к уравнению (16.14). Сравнивая его левую часть с
только что записанным выражением, можно вместо (16.14) запи-
сать:
М оо
= Pm^'^^sina, (16.16)
t=i t=t
где коэфициенты q все еще пока остаются неизвестными. С целью
их определения воспользуемся условием ортогональности собст-
венных функций:
R
[>mFfifkdr — Q приг^/г (16.17)
е
[см. ф-лу (7.3)]. Умножим обе части (16.16) на и проинтегриру-
ем их в пределах 0... R. При, учете (16.17) получится:
?mFf?dr-v^Ci
отсюда и находим для коэфициентов разложения (16.15):
Таким образом для решения (16.12) окончательно будет:
со
« = (Xci/tjcos(v^+Tn).
'i=l
(16.19)
В этой сумме обычно достаточно удержать всего два слагаемых.
Определив перемещения и в функции расстояния г и времени t,
мы без труда найдем и напряжения при изгибных колебаниях.
Для этого составим выражение изгибающего момента EJu," и
разделим его на момент сопротивления сечения Wmin.
В мгновения, когда напряжения в сечении достигают макси-
мума, будет:
Wmin’ ’ (16.20)
z=1
122
Теперь следует вспомнить, что решение (16.18) относится лишь
к одной гармонике разложения (16.7). Обычно учитывают все
существенные гармоники и поэтому для напряжения получается:
oz=Z2a/«cos(v^+Tn)- (16.21)
Для Оценки развивающихся динамических напряжений рассма-
тривают ряд сечений лопасти (г = г1; г = г% и т. д.) и для каж-
дого сечения строят график изменения напряжений с в функции
времени по (16.21). Это требует предварительного вычисления
с, по (16.18) и затем по (16.20).
Интервал, в течение которого исследуется изменение напря-
жений, должен быть принят равным времени двух оборотов ва-
ла. После построения таких графиков можно выявить максималь-
ное напряжение в каждом сечении и затем построить сводный
график таких максимальных напряжений в функции г для суж-
дения о прочности винта.
Следует иметь в виду, что изло-
женная выше методика, основан-
ная на учете изменения угловой
скорости о, не учитывает влияния
других возмущающих сил; поэтому
принято полученные здесь напряже-
ния увеличивать умножением их
на коэфициент, больший единицы,
чтобы косвенно учесть прочие воз-
мущения. После этого могут быть
добавлены напряжения, определяе-
мые формулой (16.5).
Подчеркнем, что для оценки запаса прочности простое сум-
мирование динамических напряжений со статическими (от изги-
ба аэродинамическими силами, от центробежных сил) недопусти-
мо. Подробнее об этом будет сказано в следующей главе.
В заключение необходимо отметить, что вращение лопасти служит при-
чиной ие только изменения ее собственной частоты колебаний (соответствен
но дополнительному слагаемому в ф-ле (7.14), но может также изме-
нить частоту возмущения, передающегося лопасти.
Положим, например, что центр втулки винта совершает горизонтальные
колебания по закону х = х031пхЛ вызванные неуравновешенностью двига-
теля, а винт вращается с угловой скоростью о> (фиг.69)1).
Указанное гармоническое перемещение центра втулки разложим на направ-
ления АО' (вдоль оси лопасти) и АО (поперек лопасти). Первый компонент
перемещения не повлияет на изгиб лопасти, тогда как второй очевидно будет
служить поперечным возмущением изгибных колебаний лопасти.
’) Результаты не изменятся, если вместо горизонтальных колебаний
центра втулки рассматривать вертикальные колебания.
Фиг. 69. Преобразование
частоты возмущения вслед-
ствие вращения винта
123
Это возмущение, согласно фиг. 69, определяется функцией
х sin = х0 sin kt sin шТ
«I no известной тригонометрической формуле может быть представтеио в
виде:
2 cos (k t — -у cos (k -] w) t
Таким образом, частотой фактического возмущения уже не будет частота ко-
лебаний центра втулки А; в данной случае возмущение окажется обладающим
двумя частотами k — ши Это и менение частоты возмущения, вызван-
ное вращением винта, необходимо иметь в виду при графическом определе-
нии резонансных точек, подобном данному на фиг. 516.
Полное изучение этого вопроса возможно при совместном рассмотреин i
•изгибных колебаний винта и крутильных колебаний коленчатого вала; этот
вопрос мы здесь не рассматриваем.
ГЛАВА IV
Усталость частей самолета
17. Явление усталости и предел выносливости
Многочисленные вибрационные явления, сопровождающие
конструкцию самолета в течение всего срока ее службы, тре-
буют самого пристального внимания к поведению материалов при
переменной нагрузке. Повторно переменная нагрузка вызывает
разрушение при напряжениях не только меньших предела проч-
ности1), но часто даже меньших предела текучести. Это явле-
ние, получившее наименование усталости материалов, наблю-
далось во всех областях техники и часто служило причиной раз-
личных поломок и аварий. С явлением усталости необходимо
серьезно считаться и в самолетостроении ввиду обилия всякого
рода переменных нагрузок; известны случаи преждевременного
разрушения отдельных частей самолета, происшедшие именно
вследствие недостаточной усталостной стойкости (выносливости)
этих частей. Этот круг вопросов здесь в полном объеме не рас-
сматривается; для достижения основных целей настоящей книги
мы полагаем возможным изложить только основные понятия.
Процесс усталостного разрушения состоит вкратце в следу-
ющем. При действии переменных напряжений в наиболее нагру-
женной зоне возникает трещина („трещина усталости"), посте-
пенно проникающая вглубь детали. Этот процесс стимулируется
концентрацией напряжений, которая неизбежна у краев трещины.
По мере развития трещины усталости, поперечное сечеиие осла-
') Или, как часто говорят, временного сопротивления.
1’24
бляется все сильнее и, наконец, когда сопротивление уцелев
шей части оказывается недостаточным, — наступает окончатель-
ное разрушение. Поверхность излома имеет две зоны: наружную
гладкую, притертую и внутреннюю—грубозернистую. Первая со-
ответствует трещине усталости, края которой при переменных
деформациях то сближаются и нажимают друг на -друга, то рас-
ходятся. Вторая зона соответствует той части сечения, которая
сохранилась до последнего момента, предшествовавшего полному
разрушению.
При гармонической возмущающей силе напряжения s в сече-
ниях работающей части также будут следовать гармоническому
закону; если кроме указанной силы деталь'не испытывает посто-
янно действующей нагрузки, то напряжения изменяются по так
называемому симметричному циклу (фиг. 70), т. е. от нуля в обе
стороны на одинаковую величину.
Огромный опытный материал, накопленный к настоящему вре-
менн, свидетельствует, что
амплитудой цикла (т. е. ве-
личиной максимального на-
пряжения owejt) и числом
циклов изменения нагрузки,
которые может выдержать
при этом работающая де-
таль без разрушения1 2). Эту
связь устанавливают сле-
дующим путем. Заготов-
ляют достаточное количе-
ство совершенно одинако-
всегда существует связь между
ння напряжения при гармонической
возмущающей силе.
вых по форме и размерам
образцов из обследуемого материала, приспособленных к испы-
танию на определенной испытательной машине3). Машина дол-
жна позволять вести испытание при различных величинах нагру
зок на образец.
Для первого образца за величину атах выбирают величину,
несколько меньшую предела прочности, и доводят образец
до разрушения путем большого числа циклов изменения нагрузки,
фиксируя это число. Затем испытывают последующие образцы,
уменьшая каждый раз величину °тчх- и определяя число циклов,
потребовавшееся для разрушения образца. Естественно, что
чем ниже величина °тах, тем больше циклов нагружения
способен выдержать образец до разрушения. Уменьшая для
каждого последующего образца величину °тах, можно дойтй,
1) Следует заметить, что частота нагружения (или, иными словами, ско
рость изменения внешней нагрузки) на эту связь практически не влияет.
2) Существует много различных типов машин для испытания на усталость
(для испытания на изгиб, на кручение, на растяжение—сжатие, для комбини-
рованного нагружения).
125
наконец, до образца, который вовсе не сломается, сколько бы
практически не продолжать испытание.
Связь между числом циклов, необходимых для доведения
материалов до разрушения, и напряжением атал можно просле-
дить по результатам следующего типичного испытания (мягкая
сталь):
№№ образцов 1 2 з 4 5 6 7 8 1
в кг/мм2 max 1 35,7 26.6 22,1 21,6 21.1 20,7 202 20,0
N миллионов 0,05 0,16 0,48 0,88 1,26 1,68 2,63 „ (без 10,00 раз. i РУШ)
Результаты испытания образцов нанесены на фиг. 71 в виде
точек, через которые проведена плавная
кривая, показывающая
изменение числа ци-
клов нагруженир,
необходимых для
разрушения образца,
с изменением вели-
чины наибольшего
напряжения
Кривая эта носит на-
звание кривой вы-
носливости мате-
риала или кривой
Велера (по имени
одного из первых
исследователей яв-
ления). Как видно
Фиг. 71. Результаты экспериментального ис-
следования выносливости (кривая выносли-
вости).
кривая Велера, вначале, при высоких значениях стах, круто спа-
дает вниз, т. е. требуется сравнительно большое снижение
напряжения атах, чтобы получить заметное увеличение числа
циклов нагружения до разрушения. Из дальнейшего течения
кривой видно, что все меньшим напряжением атах будут
отвечать все большие изменения в числах циклов нагруже-
ний и, в конце концов, кривая Велера выйдет на направле-
ние, параллельное горизонтальной оси на высоте cw от начала
координат (равной во взятом случае 20 кг/л/лб2), которая и пред-
ставляет собой предел выносливости исследуемого мате-
риала. Таким образом, на графике предел выносливости предста-
вляет собой напряжение, определяемое горизонталью, к которой
стремится кривая выносливости. Различные материалы имеют
различные по виду кривые выносливости: одни из них имеют
более крутое падение и более быстрый выход на горизонталь,
другие, наоборот, очень плавно и постепенно спадают и долго
126
Фиг. 72. Две типичных формы кривых выно-
сливости.
не выходят на горизонталь. Примеры таких характерных кривых
показаны на фиг. 72, где кривая / дает крутое падение и быст-
рый выход на горизонталь при Nwl, а кривая // дает плавное
падение и выход на горизонталь при относительно большом Л7да2.
Соответственные пределы выносливости будут и ода2. Число
циклов нагружения Nw, при котором кривая выносливости выхо-
лит на горизонталь, является очень важной характеристикой
материала и определяет необходимую длительность испытания
образцов на выносливость.
Итак, максимальное напряжение симметричного цикла
при котором любое число циклов изменения нагрузки не вызы-
вает разрушения, называется пределом выносливости1). Многим
частям современных самолетов за весь срок своей службы при-
ходится претерпеть десятки миллионов циклов изменения нагруз-
ки. Существование
у материалов преде-
ла выносливости
дает возможность
создания безусловно
прочных частей, тре-
буя, чтобы Срасч <
Разумеется, это тре-
бование должно
предъявляться лишь
к таким деталям, для
которых пульсирую-
щая знакоперемен-
ная нагрузка являет-
l. осно-вной.
Выяснение вели-
чины для сталей
облегчается тем обстоятельством, что уже при 4—5 миллионах цик-
лов кривая выносливости весьма близка к своей асимптоте(см. кри-
вую I на фиг. 72). Для цветных металлов кривая достаточно близко
подходит к пределу выносливости лишь при 30—40 миллионах цик-
лов и носит характер кривой II на фиг. 72. Принято определяться
на базе ограниченного, твердо установленного, числа циклов. Это
число принимается равным 10 миллионам для стали и 100 мил-
лионам для цветных металлов. С помощью изложенной выше
методики находят то предельное максимальное напряжение omz2jr,
при котором не происходит разрушения в течение 10 миллионов
циклов (для стали). Это напряжение принимается за предел вы-
носливости. Разумеется, что zmax для последних двух образцов
'Разрушившегося при 10’ и неразрушившегося при AZ = 107)
не должщд сильно отличаться (см. стах для образцов №№ 7 и 8
япм '\,^Н°ГЛа термин .предел выносливости* заменяют менее удачным термн-
”предея усталости*
127
в таблице, приведенной выше (стр. 126), где'за о можно принять
20 кг) мм2).
Необходимо иметь в виду, что величина в некоторой ме-
ре зависит от характера изменения напряжений в течение од-
ного цикла. Обычно исследуется наиболее важный случай сип}
соидального изменения а (фиг. 70); из других случаев большой
практический интерес представляет приложение нагрузки не в
виде гармонической непрерывной силы, а в виде кратковремен-
ных периодических ударных импульсов. В этом случае характе-
ристикой выносливости может служить предельная величина
импульса, которая не разрушает данного образца при практи-
чески любом числе импульсов, либо число ударов заданной ве-
личины, необходимое для разрушения образца ’).
Все сказанное о явлении усталости и о пределе выносливости
относится как к случаю растяжения—сжатия, так и к случаям
изгиба среза, кручения. Простой связи между пределами выно-
сливости в этих случаях пе существует. Экспериментальный
материал позволяет считать установленными лишь сугубо ориен-
тировочные зависимости:
. Предел усталости при растяжении — сжатии
• = (0,75 ±0,25) а~;
Предел выносливости при срезе
Г‘ = (0,58 ±0,05)
Предел выносливости при кручении
t№ = (0,58 ±0,12) ато,
где а,,,— предел выносливости при изгибе.
Точно также не существует простой связи между пределом
выносливости и важнейшей характеристикой сопротивления ста-
тической нагрузке—пределом прочности (ав).
Дробь k — aw:ae, показывающая отношение динамической
прочности материала к его статической прочности (образно ваз
ванная Гафом отношением полезного действия), колеблете
в весьма широких пределах.
Для дюралюминия коэфициент k находится в пределах 0,2о
0,32.
1) Подробнее об этом см. Н. И. Давиденков „Динамические испытания .
таллов', 1936. Подобные испытания производятся для исследования уда!
прочности шасси (копровые испытания).
128
Для отечественных авиационных сталей данные о пределах
выносливости и коэфициентах k сведены в таблицу д):
Марка Изделие кг °б мм* кг Vo2 k Примечание
30 ХГСА Листы 170 50 0,29 Закалка в масле
Прутки 170 60 0,35 при температу-
30 ХМА Листы 160 45 0,28 ре 890°Ц и отпуск при
Прутки 160 65 0,41 200° Ц
В нижеследующей таблице даны те же сведения, касающиеся
древесины:
Материал кг °е ммг кг ^млГ2 k
Сосна 8,3 2,8 0,34
Береза 11,9 3,1 0,26
Дуб 11,7 4,1 0,35
Ясень 13,0 2,8 0,21
Авиационная фанера ®) 12—18 3,0 — 4,5 0,25
18. Влияние конструктивных, технологических
и эксплоатационных факторов на предел
выносливости
Влияние частоты нагружения. К настоящему времени твер-
до установлено, что в практически интересном диапазоне 100—5000
никлов в минуту, предел выносливости не зависит от частоты
нагружения; это позволяет определять предел выносливости при
любой частоте указанного интервала (в зависимости от обору-
дования) и считать его действительным для всех других, прак-
тически возможных частот.
Влияние предварительного наклепа выяснено для углеро-
дистой стали. Оказывается, что предварительный наклеп бла-
ялг 11 {^атеРиал по хромансилю см. Н. И. Марин и М. В. Серов. .Выносли-
’ * Тр'нЛР°мансиль ЗОХГСА". Технические отчеты ЦАГИ. № 65. 1946 г.
Км То ^ietz. Н. Crinsfeld .Behavior of plywood under repeated stresses"
«ехннческий перевод ЦАГИ № 86, 1944). 9
9 Гроссман и Пановко. 129
гопрнятно отзывается hj величине повышая ее весьма ощути-
тельно. В следующей таблице даются числа, полученные при
испытании стали с 0,24% углерода:
Характеристика наклепа %
Ненаклеианный образец . . • Предварительное растяжение: 23 100
до предела текучести 24 104
до 10°о удлинения 30 131
до 20% . Предварительное сжатие: 34 148
до предела текучести 26 113
до 10% укорочен ня 29 12G
до 20% , . ’ • * 32 139
Влияние предварительного -знакопеременного перенапряже-
ния. Допустим, что Деталь некоторое время (даже относитель-
но непродолжительное) работала при переменном напряжении
большем предела выносливости. Возникает вопрос: изме-
нится ли величина предела выносливости, если его затем опреде-
лять для такой ранее перенапряженной детали? Оказывается,
что даже относительно непродолжительное знакопеременное пере-
напряжение сильно снижает предел выносливости. В следующей
таблице даются результаты испытания стали с = 22 кг!мм‘,
при 100 000 циклов предварительного перенапряжения:
Величина перенапряжения ’тел кг; мм- Обнаруженный после перенапряжения предел усталости:
a' w кг! мм-
22 22 100
24 18 82
26 16 73
27 16 73
Если принять во внимание, что при работе мотора для 100000
циклов требуется менее одного часа, то станет ясной недопусти-
мость даже кратковременного вибрационного перенапряжения *).
1) См. также Бахарев В. М. „Об утомляемости стали при повторных пе-
регрузках" (Труды ЦИАМ № 91, 1945).
130
Влияние формы детали. Установлено, что концентрация на-
пряжений, даже неопасная при статических нагрузках, играет
пагубную роль при знакопеременном нагружении. Следует счи-
тать особо существенным, чтобы детали, подвергаемые повторным
нагрузкам, выполнялись без резких изменений формы с возмож-
но более плавными очертаниями. Надлежит избегать всякого
рода заточек или выполнять их с малой кривизной.
Приведем ряд примеров, иллюстрирующих нерациональную
и рациональную форму переходов1).
Очень часто встречающаяся в практике ошибка иллюстриро-
вана на фиг. 73, изображающей обычный болт. Слева показан болт,
выполненный совершенно неправильно, если он нагружается
многократно переменной осевой нагрузкой. Переход от тела
болта к головке, выполненный почти без закругления, дает очень
высокую концентрацию напряжений, которая часто приводит к
отрыву головки. Другое опасное место — выход резьбы на цилин-
дрическое тело болта.
Фиг. 73. При отсутствии плавных переходов неизбежна кон-
центрация напряжений, сильно понижающая выносливость
детали.
Концентрацию напряжений в этом месте можно понизить, вводя
заточку с соответствующим радиусом закругления, отделяющую
нарезку от цилиндрического тела болта. Справа на фиг. 73 по-
казан болт с меньшей концентрацией напряжений и потому бо-
лее прочный при переменных осевых нагрузках.
На фиг. 74 представлено ушко вспомогательного лонжерона
крыла одного из. самолетов. Ушко выполнено из дюралевого
листа. На нижней кромке ушка сделана отбортовка, отделяющаяся
от самого ушка пропилом. Слева показано у шко в том виде,
как оно было поставлено на самолет. При испытании целого
крыла на выносливость слабейшим местом оказалось именно это
ушко, которое разрушилось по месту пробила, сделанного но-
жовкой и имевшего резко очерченное с острыми углами доныш-
ко; между тем в общей схеме крыла, нагруженного на изгиб,
эта деталь была второстепенной. Более правильным для повы-
1) Примеры заимствованы из книги Е. П. Гроссмана, М. В. Келдыша и
Н И Марина „Вибрации на самолете". 1942 г.
9*
131
мения выносливости ушка делать перед пропилом сверление,
которое и будет давать закругленное донышко пропила.
Другой пример неудачного выполнения детали представлен
на фиг. 75. Здесь показан шкворень амортизационной ‘ стойки
шасси, который через определенное количество посадок систе-
Фиг. 74. Ушко вспомогательного лонжерона из
дюралевого листа.
V
магически ломался
в корне, где он пе-
реходит в тело плос-
кой щеки с- неболь-
шим закруглением
(радиус окбло 1,5
мм). Основной ме
рой борьбы с полом-
ками шкворня былр
увеличение радиуса
до максимально воз-
можной величины,
равной примерно
7,5 мм.
Явление устало-
сти при наличии
местных перенапряжений развивается весьма быстро вследствие
легкости зарождения трещин усталости в местах концентрации
напряжении. По существу та же причина лежит в основе малой
выносливости деталей с нарушенной поверхностью, когда всякая
царапина может оказаться очагом развития трещины усталости.
Влияние состояния поверхности оказывается весьма силь-
ным. Предел выносливости очень чувствителен к состоянию по-
верхности образца.
Риски, царапины,
следы резца на по-
верхности, а также
коррозия, сильно
снижают величину
Это объясняется
тем, что даже микро-
скопические риски,
трещинки и т. п.
следы недостаточно
тщательной отделки Фиг. 75. Шкворень амортизационной стойки шасси,
поверхности могут
вызвать концентрацию напряжений, которая не скажется сколь-
нибудь заметно при статических нагрузках, но которая может
повести к постепенному развитию микро-трещин при длитель-
ных знакопеременных нагрузках. Изменение ow в зависимости от
состояния поверхности дано на фиг. 76 (данные DVL)-, как вид-
но, чем прочнее сталь (чем больше ае), тем более существенно
влияние состояния поверхности детали. Например, цельнотяну-
132
тые дуралевые трубы, из которых часто делают проводку упра-
вления рулями и элеронами, нередко имеют на поверхности
мелкие трещинки, надрывы, запрессованные плены и пр., (след-
ствие технологических операций изготовления самих труб) и
которые могут послужить причиной аварии из-за разрушения
трубы от усталости. Основная мера борьбы с подобными авари-
ями заключается в тщательной отбраковке труб по состоянию
внешней поверхности перед пуском их в производство.
Благоприятно дей-
ствует обкатка поверх-
ности под давлением;
вследствие обкатки
предел усталости воз-
растает на 10 — 20%
первоначального значе-
ния. Для сварных швов
оказывается, что про-
точка и шлифовка сни-
жает предел выносли-
вости. Для увеличения
с целесообразна про-
ковка шва.
Влияние абсолют-
ных размеров дета-
ли. Экспериментально
установлено, что с ро-
стом абсолютных раз-
меров величина аа, не-
сколько уменьшается.
Предел выносливо-
сти конструкции. Со-
вокупность перечис-
ленных причин заста-
вляет с большой осто-
рожностью применять
величины найденные
Фиг. 76. Влияние состояния поверхности^на
предел выносливости. За 1ОО°/о принята
величина полированного образца. Влия-
ние состояния поверхности усиливается для
более прочных сталей.
из испытания образцов к реальным де-
талям. В качестве примера можно привести хромомолибденовую
сталь. Для сплошных образцов небольшого диаметра ow=45 кг)мм3.
Цельнотянутые трубы из того же материала дают % = 22—
24кг/мм2, а отсек сварного лонжерона из этих же груб показал всего
.= 12 кг!мм2 (все испытания при одинаковой термообработке).
19. Усталость при несимметричном цикле.
Диаграмма Смита
В случаях, когда кроме периодической внешней нагрузки
имеются еще постоянно действующие внешние силы, напряже-
133
ния следуют так называемому несимметричному циклу (фиг. 77),
при котором
I атах I | атщ | •
Несимметричный цикл обычно характеризуется двумя чис-
лами:
средним напряже-
нием
1 .
°0 — 9
амплитудой напря-
жения
Фиг. 77. Несимметричный цикл изменения на-
пряжений при гармонической возмущающей
силе.
аа 2 (атах
Частным случаем несимметричного цикла является повтор-
ный цикл1 *), при котором а,Л(П = 0 (фиг. 78).
В общем случае несимметричного цикла явление усталости
не может быть охарактеризовано"одпим числом cw, так как сам
цикл определяется двумя независимыми числами с0 и <за (либо
стах н Если область выносливости при симметричном
цикле вполне характеризуется условием ^,nax<i^w, то ПРИ
несимметричном цикле эта область зависит от двух параметров
и оценка прочности должна выполняться с учетом их обоих.
Для этой цели чаще всего пользуются диаграммами Хэя -)
или Смита.
Диаграмма Смита наглядно выявляет область прочности при
несимметричном ци-
кле.
Построение этой
диаграммы состоит
в следующем. При
различных значе-
ниях а0 опытным пу-
тем определяются
значения cmux, соот-
ветствующие преде-
лу у сталостной проч-
ности (фиг. 79а).
Если теперь провести прямую под углом 45 3), то между кри-
вой и прямой ой (фиг. 796) окажется величина аа, так как
о, = — с0. Отложив такие же отрезки ая вниз от прямой ой,
Фиг. 78. Повторный цикл изменения напряжений
при гармонической возмущающей силе.
’) Называемый также односторонним или пульсирующим.
4) С. В. Серенсен, И. М. Тетельбаум, К. И.- Прнгоровский. „Динамическая
прочность в машиностроении". 1945.
3) .Масштабы по осям а0 и отах одинаковы.
184
мы получим вторую ветвь диаграммы, соответствующую cmin
(фиг. 79в). Совокупность кривых Ak и А'/г и является диаграм-
мой Смита. Для проверки выносливости по построенной диа-
грамме Смита нужно при данном значении с0 отложить от
точки т (на прямой ok) по вертикали величину амплитуды
Если полученная точка лежит в пределах области, ограниченной
кривыми Ak и A'k, то разрушения не произойдет (фиг. 79г).
Фиг. 79. Построение диаграммы Смита. По оси абсцисс
откладывается среднее напряжение цикла, по оси ординат—
максимальное и минимальное напряжение цикла.
Практическое построение диаграммы Смита обычно упроща-
ется благодаря тому, что кривые могут быть без большой ошибки
заменены прямыми, так что часто диаграмма Смита принимается
очерченной по фиг. 80. Для такого построения достаточно знать
результаты испытаний при двух различных циклах.
В качестве таких циклов обычно принимают:
1) Симметричный цикл (со = О), позволяющий отметить точки
А и Д', соответствующие пределу усталости.
2) Повторный цикл, при котором аот;я = 0; з/ЛО1. = 2 з0; резуль-
таты позволяют отметить точки В и Д'. По точкам А, А', В и
В' легко закончить построение, так как ордината точки С равна
пределу текучести так же, как и абсцисса точки k.
135
При отсутствии оборудования, позволяющего осуществить
повторный цикл J), точки В и В' намечаются приближенно, прини-
мая, что:
сПтах= 1,2-? 1,5 2).
20. Усталость частей самолета
Среди случаев разрушения частей самолета, происходящих
вследствие усталости, наиболее характерны:
1) разрушение металлических винтов;
2) разрушение частей
Фиг. 80. Упрощенная диа-
грамма Смита может быть
построена по точкам А, В и С.
моторам (как сварных швов и узлов,
так и самих стержней);
3) разрушение капотов (обычно
начиналось вблизи замков крепления,
вследствие трещин технологического
и эксплоатационного происхождения
при числе циклов изменения нагруз-
ки, значительно меньшем 10е, т. е. при
явно недостаточной выносливости,
логда оягдх (3И/),
4) разрушение бензобаков, либо
нарушение их герметичности;
5) разрушение выхлопных коллек-
торов (особенно в местах, ослаблен-
ных сваркой);
6) поломки кронштейнов крепле-
ния элеронных тяг;
7) поломки кронштейнов, крепящих
грузы балансиров к рулям и элеро-
нам (были случаи заклинения элеро-
нов вследствие этих поломок).
Перечисленные части требуют осо-
бо тщательного обеспечения вынос-
ливости при конструировании и экс-
плоатации.
В борьбе с разрушением от усталости существенную роль
играет как теоретический расчет, так и эксперимент. Расчет поз-
воляет еще в процессе проектирования предотвратить значитель
ные амплитуды колебаний. Эксперимент, состоящий в испыта-
ниях выносливости отдельных элементов и целых агрегатов,
дает возможность проверить на натуре в какой мере оправ да-
!) Обычные конструкции испытательных машин предназначены для испы-
тания по симметричному циклу.
*) Одннг теоретически нашел, что в случае растяжения чвтах —
(см. И. А. Одинг «Усталость металлов и задачи машиностроения". 1941 г.,
стр. 79).
136
дись принятые в процессе проектирования меры; если вследствие
неточности расчетных методов или неучтенных обстоятельств,
в эксперименте обнаружится опасный вибрационный режим,
грозящий усталостным разрушением, то последующие измене-
ния конструкции делаются в увязке с положениями теории,
которая дает определенные указания — в какую сторону должно
быть произведено изменение параметров конструкции.
Решающее слово в этой области все же принадлежит экспе-
рименту. Это объясняется в первую очередь тем, что экспери-
ментальные величины пределов выносливости определяются обыч-
но лишь на специальных образцах и для какого-либо определен-
ного вида нагрузки (растяжение-сжатие или кручение и т. д.).
Эти данные, как уже отмечалось, лишь весьма приблизительно
можно относить к реальной детали, работающей в сложной конст-
рукции, особенно если она претерпевает сложное нагружение
(изгиб с кручением и т. п.). Кроме того, на величине предела
выносливости детали весьма сильно отражается технология ее
изготовления, тщательность обработки и т. д. Поэтому за пос-
леднее время принято агрегаты самолета, подвергающиеся осо-
бенно сильному действию знакопеременных нагрузок специаль-
но испытывать на выносливость в целом виде. В особо ответст-
венных случаях таким испытаниям подвергают целый самолет.
Эти испытания производятся в соответствии со специальными
\ казаниями, которыми устанавливается сколько циклов реального
нагружения должен выдержать агрегат (самолет). Мероприятия
по необходимому увеличению выносливости обычно легко наме-
чаются на основе такого эксперимента, т. к. они сразу подсказы-
ваются местом и характером поломки.
Обязательной экспериментальной проверке выносливости под-
вергаются новые конструкции моторам, винтов и бензобаков.
Принцип, который кладется в основу экспериментального
исследования, сводится к следующему. В условиях реальной
эксплоатацин (в полете) снимается вибрационный режим, на
котором работает конструкция (частоты, формы колебаний, ам-
плитуды). Затем эти условия воспроизводятся для изолирован-
ной конструкции в лабораторных условиях; этот режим иод
держивается в течение ряда часов, необходимых для выполне-
ния 10 миллионов циклов изменения нагрузки. Если конструкция
выдерживает такое испытание, то она считается достаточно вы
носливой.
Часть II. КОЛЕБАНИЯ КРЫЛА И ОПЕРЕНИЯ,
ВОЗНИКАЮЩИЕ ОТ АЭРОДИНАМИЧЕСКИХ ПРИЧИН
ГЛАВА 5
Общий метод определения критической скорости
флаттера
21. Явление флаттера
В первой главе были изучены колебания крыла в пустоте.
Было показано, что если не учитывать трения в кбчструкцпи,
то энергия вибрирующей системы остается постоянной, колеба-
ния будут гармоническим;, и раз начавшись, будут продолжа-
ться вечно. За счет несовпадения линий центров тяжести и осп
жесткости крыла, между колебаниями изгиба и кручения крыла
существует связь такого рода, что один вид движения неизбе-
жно порождает другой. Это означает, что при колебаниях энер-
гия изгиба трансформируется в энергию кручения и обратно,
однако, общее количество энергии в системе не изменяется.
Каргина будет иной, если колебания крыла происходят в
потоке воздуха. При этом развиваются аэродинамические си-
лы, которые могут как поддерживать колебания, так и проти-
водействовать им. В первом случае будут происходить колеба-
ния с нарастающей амплитудой, во втором — колебания буду!
затухающими. Колебания, возрастающие -за счет энергии по-
тока, носят название колебаний типа „флаттер" *). Они весьма
опасны, так как вследствие интенсивного увеличения амплитуды
колебаний конструкция обычно быстро разрушается * 2). Покажем
на простом примере возможность возникновения флаттера. Пред-
положим, что крыло изогнулось вследствие какой-либо случай-
ной причины (резкое движение элеронами, воздушная яма и т. и.).
Некоторое сечение крыла при изгибе из положения равнове-
сия ОХ (фиг. 81л) перейдет в положение 1. После прекращения
действия изгибающего импульса, крыло, под действием силы
!) Flutter (англ.) — махать (крыльями).
2) Случаи флаттера наблюдались еще во время войны 1914—1918 гг. Пер-
вая попытка теоретического исследования флаттера быта предпринята Блази-
усом в 1918 году (см. Kiissner „Angenblicklicher F.ntwiklungsstaiid der Frage des
Flugzeugelflatters“. Luftfahrtforschung 1935. B. 12. № 6. s. 193—209). У нас с явпе
нием флаттера впервые столкнулись в 1935 году; к этому же времени отно-
сится начало теоретической и экспериментальной разработки проблемы флат-
тера в ЦАГИ.
138
упругости, начнет двигаться к своему положению равновесия
Это движение будет ускоренным и потому возникнут <_илы
инерции. Момент всех сил инерции, действующих на элемен-
тарный отсек крыла между сечениями z и z+dz, будет
Ми — тъ dz,
от3
где mdz — масса отсека, а — расстояние между центром i я “ле-
сти и центром жесткости.
Фиг. 81о. Механизм появления возбуждающей силы при нзгибнс-
крутильных колебаниях. При движении крыла вниз (I—V) за счет
закручивания появляется аэродинамическая сила, действующа.»
также вниз. При движении крыла вверх (VI—fX) появляется аэро*
динамическая сила, действующая также вверх.
Этот момент вызовет кручение крыла. При этом существен
но отметить в какую сторону будет закручиваться крыло. В
положениях
равновесия.
/—III крыло движется ускоренно к положению
т. е. ускорениенаправлено вниз. Сила инерции,
приложенная в центре тяжести, направлена против ускорения
(вверх) и ее момент Ми перекрутит крыло в сторону отрица-
тельных углов атаки. После того, как крыло перешло по
1Ж»
инерции положение равновесия, знак ускорения переменится,
следовательно, переменится и знак крутящего момента — крыло
будет раскручиваться (положения III—V). Достигнув крайнего
положения (V), крыло под действием сил упругости вновь начнет
двигаться к положению равновесия (V—VU), ускорение будет
направлено вверх и, следовательно, крыло закрутится в сторону
•полежительных углов атаки. В положениях VII— IX знак уско-
рения переменится и крыло будет раскручиваться.
Существенно подчеркнуть, что при движении вниз угол ата-
ки крыла уменьшится за счет кручения, а при движении вверх
— увеличится. Вследствие изменения угла атаки изменится и
.подъемная сила, действующая на крыло. Дополнительная
подъемная сила, которая получается за счет закручивания
крыла, будет направлена вниз при движении крыла вниз (по-
ложения 1—V) и будет направлена вверх при движении крыла
вверх (положения V— IX). Таким образом, эта подъемная сила
усиливает деформацию изгиба, так как направлена всегда в ту
же сторону, куда направлено изгибное движение крыла. Увели-
чение же изгибных колебаний вызывает увеличение ускорения
<Ру
и гем самым — крутящего момента Ми, что вызовет увели-
чение кручения крыла, а следовательно, и дальнейшее увеличе-
ние подъемной силы. Получается, что колебания изгиба вызывают
такого рода силы, которые стремятся дальше увеличить дефор-
мацию, а это в свою очередь увеличивает силы и т. д., до тех
лор, пока не произойдет поломка крыла.
Схематически сказанное можно представить следующим обра-
зом :
340
Таким образом при колебаниях в потоке воздуха появляют-
ся силы, стремящиеся эти колебания увеличить. Здесь были
рассмотрены далеко не все силы и моменты, действующие на
крыло во время колебаний в потоке воздуха. Ниже будет да»
более полный анализ явления флаттера, здесь же мы хотели
только показать, что флаттер возможен и указать на качествен-
ную природу порождающих его причин.
После сказанного может возникнуть вопрос: если при любой
случайной деформации вниз всегда возникают силы, вызываю-
щие колебания с нарастающей амплитудой, то почему же вооб-
ще не происходит разрушения у каждого самолета?
Объясняется это тем, что наряду с возбуждающими силами,
при колебаниях в потоке воздуха всегда имеются и демпфирую-
щие силы. Например, демпфирующей является аэродинамическая
сила, зависящая от скорости изгибных колебаний. Мы видели,
что при движении вниз (фиг. 81, положения I—V), крыло пере-
кручивается таким образом, что угол атаки его уменьшается и вслед-
ствие этого возникает дополнительная подъемная сила, действую-
щая в сторону движения. Но угол атаки будет изменяться не
только за счет перекручивания крыла, а также и вследствие
появления добавочной вертикальной скорости воздуха, равной
Фиг.81tf. Изменение угла атаки за счет ско-
рости изгибных колебаний.
по абсолютной величине скорости изгибных колебаний.
Если крыло изгибается со скоростью у, то аэродинамически
это эквивалентно тому, как будто воздух обтекает крыло со ско-
ростью—у. Складывая эту скорость со скоростью набегающего
основного потока (фиг. 816), убеждаемся, что угол атаки изменя
ется на величину
4,=_А
При движении крыла вверх угол атаки уменьшается, а нри
Движении вннз, —увеличивается. В связи с изменением угла атаки
появится дополнительная подъемная сила, которая направлена
вверх при движении крыла вниз и направлена вниз при движе-
нии крыла вверх. Эта подъемная сила, в отличие от подъемной
силы, возникающей за счет кручения крыла, всегда направлена
против движения, т.е. стремится гасить (демпфировать) колебания,
141
Более детальный аналгз показывает, что наряду с указанны^
ми имеются и другие возбуждающие и демпфирующие силы
и моменты (например, появляющиеся за счет угловой скорости
крутильных колебаний). Все эти силы, как и вообще силы аэро-
динамической природы, зависят от скорости набегающего на кры-
ло потока воздуха. Обычно при малых скоростях возбуждаю-
щи воздействия -бывают меньше, чем демпфирующие и потому
возникающие колебания затухают. Но с ростом скорости возбуж-
дающие воздействия растут быстрее, чем демпфирующие и, начи-
ная с некоторой скорости VKp начинают их превосходить (см.
ниже фиг. 112). При скоростях больших VKp случайно возника-
ющие колебания не затухают. Скорость полета VKf> носит наз-
вание критической скорости флаттера.
Опыт показывает, что при достижении критической скорости
амплитуда колебаний весьма быстро нарастает и происходит раз-
рушение конструкции !). Поэтому, еще в процессе проектирова-
ния необходимо обеспечить такое значение VKp, которое
превосходит максимально достижимую скорость данного
самолета. Для этого, очевидно, необходимо ум^ть расче-
том определять критическую скорость конструкции, а такж
знать как она зависит от различных конструктивных пара-
метров. Решение этих двух вопросов и будет нашей ближай-
шей задачей.
Расчет на флаттер, т. е. определение критической скорости,
( пкняется тем обстоятельством, что каждый самолет имеет
щлъш ряд критических скоростей:. Мы показали, что изгибно-
крутильные колебания крыла в потоке воздуха могут происхо-
дить с нарастающей амплитудой. Но с нарастающей амплитудой
могут происходить не только из гиб но-крутильные, но и другие
виды совместных колебаний 2). Предположим, например, что кры-
ло является абсолютно жестким на кручение, но учтем, что на
крыле имеется элерон, могущий отклоняться относительно кры-
ла (за счет упругости проводки, люфтов и т. д.). Оказывается,
что в этом случае также возможны совместные колебания кры-
ла (изгибные) и элерона с нарастающей амплитудой- Флаттер
этой формы носит название изгибно-элеронного.
Критические скорости изгибно-крутильного и изгибно-элерон-
ноио флаттера естественно зависят от конструктивных параметров
и, как правило, различны. Кроме этих двух критических скоро-
стей, могут быть и другие: скорость крутильно-элеронного флат-
тера (отсутствует изгиб крыла, но имеет место закручивание
крыла п отклонение элерона) и скорость изгибно-крутидьно эле-
Именно поэтому исследование флаттера в полете чрезвычайно опасно и
в прямом виде почти никогда не применяется.
*) Ниже будет показано, что для возникновения флаттера совместность коле-
f-ьяий необходима.
142
ройного флаттера (когда крыло одновременно изгибается и за-
кручивается, а элерон отклоняется относительно крыла). Каж-
дому из этих типов колебаний соответствуют свои значения кри-
тических скоростей.
Хвостовое оперение; обладает еще большим количеством крити-
ческих скоростей, так как может испытывать больше различных
комбинаций деформации (изгиб и кручение стабилизатора, откло-
1 нения рулей — изгиб и кручение фюзеляжа и т. д.).
Таким образом различные части самолета могут иметь ряд
форм совместных колебаний; это число еще больше увеличива-
ется за счет обертонов. Каждая из этих форм совместных колеба-
ний может перейти во флаттер, и каждой из них соответстует
своя критическая скорость, причем практический интерес пред-
, ставляет только наименьшая из этих критических скоростей.
К сожалению, не существует способа, который давал бы воз-
можность заранее определить какая из критических скоростей
является наименьшей. Поэтому для каждой конструкции при-
ходится на основании качественных соображений и статистичес-
ких данных определять минимальное число расчетных случаев
| производить расчет на каждый из них. Более подробно о вы-
ре расчетных случаев будет сказано ниже.
Из изложенного вытекает следу ющий способ построения ра-
<четного метода.
Необходимо рассмотреть, как меняется характер колебаний
. зависимости от скорости, и найти такую скорость, при кото-
рой возникающие . колебания перестанут затухать. Нарастание
' или затухание колебаний характеризуется декрементом затухания
(см. введение, фиг. 4). Критическая скорость, — эго такая скорость,
при которой декремент затухания обращается в нуль: на мень-
шей скорости он отрицателен и колебания затухают (фиг. 3),
на большей—положителен и колебания происходят с нараста-
| ющеп амплитудой (фиг. 5). Если же декремент затухания равен
нулю, то колебания будут гармоническими—не нарастающими
| и не затухающими. Поэтому, можно сказать, что критическая
Г скорость это есть такая скорость полета, при которой воз-
I ложны гармонические колебания с постоянной амплитудой.
При всякой другой скорости колебания будут либо затухающими,
либо возрастающими.
Подчеркнем, что критическая скорость не зависит от началь-
ных условий, т. е. от величины начального импульса. Если ско-
рость полета превышает критическую, то как бы ни был мал
начальный импульс, колебания будут происходить с нарастающей
амплитудой. Определение критической скорости есть задача ди-
намической устойчивости: на скорости, меньшей критической,
1 конструкция крыла устойчива (т. е- если дать крылх малое
возмущение, то с течением времени последнее будет затухать
и конструкция вернется к положению равновесия), на скорости,
большей критической, конструкция крыла неустойчива (т. е.
143
если крыло испытывает малое возмущение, то с течением времени
это возмущение нарастает вплоть до поломки крыла).
В теории флаттера ограничиваются определением критической
скорости и изучением зависимости этой скорости от конструк-
тивных параметров. Поэтому теория флаттера строится на основе
теории малых колебаний. Хотя такая теория не сможет дать
ответа на ряд вопросов (вопрос о напряжениях, возникающих
в конструкции при флаттере, об изменении амплитуды колебаний
со временем и т. д.), но для целей практики она вполне доста-
точна, так как требуется чтобы флаттер не возник, а как он
будет протекать— безразлично.
Из всех характеристик флаттеру практический интерес пред-
ставляет только критическая скорость.
22. Колебания системы с двумя степенями свободы в потоке
воздуха
Обладая непрерывным распределением масс, самолет являете/
системой с бесконечным числом степеней свободы. Для получения
практически пригодных расчетных формул приходится при рас-
чете колебаний самолета вводить ряд упрощающих допущений,
смысл которых в конечном итоге сводится к тому, чтобы огра-
ничить число степеней свободы. Задание закона изменения про-
гибов и углов закручивания крыла вдоль размаха (п.п. 3-5) сводит
систему с бесконечным числом степеней свободы к системе
с двумя степенями свободы. Для определения положения любой
точки крыла в каждый момент времени достаточно установить,
как функции времени, всего два параметра: прогиб и угол кру-
чения на конце крыла. Если не удается свести число степеней
свободы к двум или, в крайнем случае, к трем, то расчет полу-
чается настолько громоздким, что практически пользоваться им
почти не представляется возможным. Прикладные методы анализа
колебаний самолета в потоке воздуха основаны на таких допу-
щениях, которые сводят число степеней свободы к двум, и в ред-
ких случаях — к трем.
Важно отметить, что основные принципиальные за-
кономерности одинаковы для всех случаев, будь то изгибно-кру-
тильные колебания крыла, или колебания руля высоты совме-
стно с фюзеляжем и т. д. Поэтому в настоящей главе мы раз-
виваем общий метод анализа колебаний произвольной системы
с двумя степенями свободы в потоке воздуха, имея в виду
в дальнейшем применить этот метод к изучению различных
форм колебаний крыла и оперения в полете.
Рассмотрим в самом общем виде какую-либо упругую систе-
му, положение которой в каждый момент времени определяется
двумя параметрами qr, q2 служащими обобщенными координа-
тами. Движение системы будет определено, если параметры qu 9*
144
будут известны как функции времени. Такими параметрами мо-
гут быть в нашем случае, например, величины прогиба и угла
закручивания конца крыла: если эти величины определены как
функции времени, то определено и все движение, так как
закон изменения прогибов и углов кручения по размаху счита-
ется наперед известным.
Мы будем рассматривать малые колебания, совершаемые си-
стемой, выведенной из положения равновесия какой-либо при
чиной и в дальнейшем движении иредоставленой самой себе.
Не нарушая общности, можно принять, что обобщенные ко-
ординаты отсчитываются от положения равновесия системы,
д. е. последнее характеризуется значениями т/1 = 93 = 0.
Поместим рассматриваемую систему в поток воздуха и иссле-
дуем ее малые колебания при наличии аэродинамических сил.
Для анализа движения воспользуемся уравнениями Лагранжа1):
— ди— О
М \ + ~
4./ д'£ \ __ £L + dJ£ —о ' ^22Л)
ilt\dq.,l dq, dq2~~ 1
Здесь Т кинетическая энергия системы, 67 — потенциальная
энергия, создаваемая силами упругости и. Q,, Q,— обобщенные
силы, которые определяются формулами:
К Q, = v(p„^ Р&Р,#}
Ц 11 ()q{ dq\ dqx J
. 1 / 1x6 (22-~>
Q.,^ У (Pti ~ ' Pri + P£i
dq., dq, dq.,)
rxi' Pyi> Рг1 — кем •*' ненты внешней Силы, действующей в г-ой
точке системы с координатами х,-, yt; zp, суммирование распри
<|раняется по всем точкам системы.
Внешними силами в рассма! рив. емой задаче являются аэро-
зин. мические силы [упругие силы учтены последними членами
•'квих частей уравнений (22.1)’, сл ^ивауельно Pxi, Pyi, Pzi есть
компоненты аэродинамической силы, действующей на i - ую точ-
ку системы.
Не нарушая общности, можно отсчет во х сил произво-
дить от положения равновесия (./j =7а —0)> т- е' иметь дело
•и»-, с приращениями сил от сложения равновесия.
*i Лойцянский Л. Г. и Л'рье A. If. ,Kvpc теоретической механики-, ч. II.
111 11 «Семан и Пановко. 145
Для того, чтобы воспользоваться уравнениями (22.1), необ-
ходимо найти выражения кинетической и потенциальной энергии,
а также обобщенных сил в функции обобщенных координат q^q*.
Определим в первую очередь обобщенные силы.
В выражения обобщенных сил (22.2) входят значения лроиз-
[дх, ду х
водных декартовых координат по обобщенным ,^-ит.д. )
Следовательно, необходимо выразить декартовы координаты
каждой точки системы xit yit z-t через обобщенные координаты:
^=^(71- ^г);
zi = zi(qv q3).
(22.3)
Разлагаем правую часть первого из выражений (22.3) в р^д
Маклорена:
I дх> \ , / dxA , 1
Д| X; ’ + I т ) *71 "р I ’ J I q~' + ~п~
1 1 \^i/o \д^!0 2
Здесь л0, декартова координата рассматриваемой точки систе-
мы в положении равновесия, т. е. значение х) при qr = q., = 0.
Индекс „0“ при производных показывает, что значения про-
изводных берутся в положении равновесия системы при qx = q3 — 0.
Аналогично записываются разложения для у, и z, в (22.3).
Ввиду малости обобщенных координат q2, q3 (колебания
считаются малыми!), в разложении (22.4) можно ограничиться
линейными членами:
(22.5;
...зависят только от геоме-
трических параметров рассматриваемой системы.
Переходим к рассмотрению структуры внешних аэродинами-
ческих сил Pxi, Pyi, Pzi. Как известно, аэродинамические силы
146
«висят от положения системы (например, если рассматри-
ваемая система есть крыло,— от его угла атаки) йог скоро-
стей движения системы, т. е. они зависят от qx, q„, q\, q*
разлагая РЛ1, Pyi, Psi в ряд по этим величинам и ограничиваясь
опять только линейными членами, получим:
P-ici — aliQi + a2i^2“b aii^l + а4/7з
Pyi = Mi + Мг + Mi + Pi/72
P^i = 7i/7i + Ws + 7a/7i + 74/7?
(22.6)
Коэфициенты a, p и у зависят от параметров системы и,
конечно, о г величины V, так как аэродинамические силы зави-
сят от скорости набегающего потока.
Если выражения (22.5) и (22.6) подставить в формулы (22.2)
и затем собрать все члены с qt, q>, qlt q2, то мы получим выра-
жение обобщенных сил в виде:
Q1 — Р1171 + Р127з + 8ц71 + 8127г |
Q, = -f- р2з7‘2 + + 8.227а *;
(22.7)
Здесь коэфициенты р и 8 — постоянные величины, зависящие от
параметров системы и скорости набегающего потока воздуха И.
Переходим к определению кинетической энергии системы:
Т~ "2 2 т'1 + У'3 + Zi^’ {22’8^
где /и,- — масса г-ой точки системы; xit у„ zt—компоненты
скорости движения по осям декартовой системы координат;
суммирование ведется по всем точкам системы. Чтобы получить
выражение кинетической энергии через обобщенные коорди-
наты, воспользуемся выражениями (22.5), устанавливающими за-
висимость декартовых координат от обобщенных.
Диференцируя эти выражения по времени, находим:
(dxi \ . / 0х.\ .
^ijo7i+
Лfyi\ - , (дуЛ .
Vi \ dqt J0^ + \ dqz)0<h'
(dz-, \ . ( dzi \ .
10*
147
Подставляем эти значения в (22.8), 'qz и g2!, gs2> найдем
Г — у fcw/ + 2c)8‘7lg2 + c=ag8,). <22-9)
Здесь величины cn, cf.2, c.J2 являются постоянными коэфицпен-
тами и выражаются через массы точек системы и ее геомет-
рические параметры.
Обратимся к потенциальной энергии системы (отсчитываемой
как сказано, от положения равновесия). Проекции перемещения
i-Oii точки на оси координат будут:
При этом компоненты упругой силы, действующей в /-ой
точке системы по осям координат:
Лр— -куДх,— л/)
Yi—~Kiy(yi—y^
~ Kjz (Zj ~j°),
где kIv, h'iy, i<i,~коэфициепты пропорциональности, характери-
зующие жесткость системы (эти коэфициепты могут быть ра -
ными для разных точек системы).
При перемещении системы из положения равновесия в поло-
жение, соответствующее рассматриваемому моменту времени,
упругие силы совершают работу;
. \ 3'
Я/з I Zi ~ z\ | • (22 10)
Нам необходимо получить выражение потенциальной энщ -
гии в функции обобщенных координат. Для этого подставляем
значения xt, yL, z-t по формулам (22.5) в выражение (22.10). Со-
бирая затем члены при одинаковых степенях qx и найдем
выражение потенциальной энергии, равной величине R с обр< -
иым знаком:
— R — чу ( «11713 - « п?22 •
148
Теперь-можно составить уравнения движения в форме (22.1).
Подставляя в уравнения (22.1) значения Q, Г, U по формулам
(22.7), (22.9), (22.11), получим:
------ *'11?1 + (аИ Р11) Ч\ + C\iQ‘Z r‘ll4'l + (t?t2 j
C»\Q\ ----------------------------------------------------- ^2lVl (/41 ?21) Vi 4" ^22Vl ^2aV’2 ”4 (^22 Pij) 91 ==
Во втором из уравнений в целях симметрии вместо с12 и с12 мы
пишем соответственно с21 и а21.
Повторим, что коэфициепты с зависят от величины и распре-
деления масс системы, коэфициепты а — от ее жесткостных
свойств, а коэфициенты р и 8 — от скорости набегающего по-
тока воздуха. Кроме того, все коэфициенты зависят от геомет-
рических параметров системы. При расчете на флаттер какой-
либо части самолета (крыла или оперения и т. д.) первым эта-
пом всегда служит нахождение выражений этих коэфициентов
для данной задачи; характер движения полностью определяется
этими коэфициентами.
Уравнения (22.12) представляют собою систему однородных
диференциальных уравнений, решения которой будем искать в
виде:
— Me^'t; q., — Ne> >. (22.13)
Подставляя эти выражения в (22.12) и затем сокращая на eKt,
получим систему линейных однородных алгебраических уравне-
ний относительно неизвестных М и N:
М (спК3 — 8И>. + аи— Рп) + iV(c12xa — 312>, + й12—|31а)=0
Л4 (02Лг~ ®2?- + а21-₽21) + N (С22^-~522Л + С22-₽и)=0-
(22.14)
Чтобы из (22.14) для М и N получались отличные от нуля ре-
шения, необходимо, чтобы равнялся нулю определитель, состав-
ленный из коэфициентов при М и №). В развернутом виде это
условие приобретает вид
+ 4- О.2 - D't -f- £ =0, (22. 15)
"Че коэфициенты имеют значения:
^1 С 11 Сло — С Jo ^21 5
В ''ll6!! ^22’'ll + ^13°21 ^21 Г'Г->
(а2з —Рва) + *Рп) cia(°2i Pai)
_ — C21 P12) + &11 .
2n(a22 —p22) —83»(an —Рп) + ''laV^i—P21) "L
4" ^21 (aia P12)’
~ (йц ---Pll)(az2--P22)---(a12 ?‘s) Pai)-
') К тому же, можно прнтти, если отношения д,-. получаемые
Того из[уравнений, приравнять друг к другу.
(22.16)
из кань
«49
Подчеркнем, что коэфициенты уравнения (22.15) зависят «.ак:
от параметров рассматриваемой системы, гак и о г скорости на-
бегающего на нее потока воздуха. х
Уравнение (22.15) служит для определения X и называется
характеристическим уравнением. Будучи четвертой степени,
оно имеет четыре корня л,, Х3, Х4 (мы будем рассматривать
только гот случай, когда все корни характеристического уравне-
ния' различны). Подставляя в уравнения (22.14) поочередно все
четыре значения, найдем соответствующие каждому из корней
значения М и 7V1). Общее решение, как известно, есть сумма
частных и потому решением (22.12) будет:
qx + 7W3eV 4- Л^ё'-ё, |
0» = ё + N^-ё + + N^eht. f ' 171‘
23. Анализ корней характеристического
уравнения
Характеристическое уравнение (22.15) может иметь действи-
тельные, комплексные или чисто мнимые корни. Рассмот-
рим, каково будет движение системы в каждом из этих случаев.
Допустим, что какой-либо из корней характеристического
уравнения, например Х„ — действителен. Соответствующий част-
ный интеграл системы (22.12) будет:
01 = Mte\t; 0.2 = Nxe>it.
Если >1>0. то 0! и 03 будут с увеличением времени монотонно
возрастать, если же Хх < 0, то qx и 0., с течением времени будут
монотонно убывать.
Следовательно, если среди корней характеристического урав-
нения хотя бы один действителен и положителен, то по край-
ней мере один из членов в выражениях (22.17) монотонно воз-
растает и, следовательно, с течением времени система сколь
угодно далеко -) уйдет от положения равновесия, причем движе-
ние будет апериодическим. Такое апериодическое движение, мо-
нотонно уводящее систему от положения равновесия, называют
дивергенцией. Если же действительный корень отрицателен,
то соответствующее этому корню движение осуществляется
гак, что система монотонно приближается к положению равно-
весия (фиг. 82).
') Точнее,— соотношение между М и N.
Выражение ,сколь угодно далеко” надлежит понимать условно, ибо речь-
все время идет о малых колебаниях. Практически указанное выря' елие обо-
значает удаление системы от статического уровня вплоть до поломки кон-
струкции.
150
Фиг 82. Апериодическое дви-
жение, соответствующее чисто
вещественному корню характе-
ристического уравнения а) зату-
хающее движение (><0); в) ди-
вергенция (л>0).
Допустим, что среди корней характеристического уравне-
ния имеется хотя бы один чисто мнимый i^ — ip, где р — дей-
ствительное число. Так как алгебраическое уравнение с действи
тельными коэфициентами всегда
имеет мнимые и комплексные
корни попарно сопряженными, то
среди корней характеристичес-
кого уравнения в этом случае
обязательно будет также суще-
ствовать корень А, = —ip.
Движение, соответствующее
корням Ах и А,, будет определять-
ся суммой частных интегралов
= Mxetpi + М.2е — ipt (и анало-
гично для с/2). Оба слагаемых
здесь комплексны.
Однако qx и </., являются опре-
деленными геометрическими ве-
личинами (линейными или угло-
выми перемещениями) и должны
быть вещественны. Это будет
только в том случае, если оба
члена в выражен! ь qx являются
сопряженными величинами. По-
скольку e‘pt и e — ‘pt — сопряжен-
ные величины, должны быть сопряженным также и с М.,;
если Aft имеет выражение A’j + ikn, то Af9 должно иметь выра-
жение /г, — Д,. Тогда,
пользуясь известными
формулами Эйлера
eipt = cos pt + i sin pt:
e — ipt~cos pt—i sin pt,
можно выражение <р
преобразовать к дей-
ствительной форме-
t
Фиг. 83. Чисто гармоническое колебание (мни-
мый корень характеристического уравнения).
<р — 2 cos pt —
— 2 sin pt.
Введем обозначения:
a -ZVkf+kJ-.tgfr—t? ; тогда 2^=acos₽; 2Z?j = asinfi и тля <р
можно окончательно записать:
<р = a cos (pt + f!).
lol
Отсюда видно, что в этом случае движение является гармони-
ческим колебанием.
График изменения qv в рассматриваемом случае' показан на
фиг. 83 (аналогично выглядит график <?.,).Таким образом, если среди
корней характеристического уравнения имеется чисго мнимый
корень к —ip, то соответ-
ствующее этому корню
движение представляет
собой гармоническое ко-
лебание с постоянной
амплитудой, причем р
есть круговая частота ко-
лебания.
Рассмотрим теперь слу-
чай, когда среди корней
характеристического
уравнения есть комплекс-
~ный короне кх + ip.
Характерней! ческое
уравнение будет иметь
также сопряженный ко-
рень K — v—ip. Движение, соответствующее этим корням, опре-
деляется суммой частных интегралов
4- M..e'il — е^ (Afteipt М.е — Ф').
Выражение, стоящее в скобках, можно преобразовать теми же
приемами как и в
предыдущем случае;
тогда будет:
qt = ас'** cos (pt -t p)
Фиг. 8-5. Затухание колебаний (v<0).
Отличие от пре-
дыдущего случая за-
ключается в том, что
теперь амплитуда ко-
лебаний равна ае^,
т. е- зависит gt вре
меня. Если v>0, то
амплитуда колеба-
ний с течением вре-
мени будет монотонно возрастать (фиг. 84), если же v<0, то ампли-
туда колебаний с течением времени будет монотонно убывать
(фиг. 85).
Таким образом, комплексным корням характеристического
уравнения соответствует колебательное движение, — затухающее,
если действительная часть корня отрицательна, и с нарастающей
амплитудой, если действительная часть корня положительна. Как
и в предыдущем случае, коэфициент мнимой части корня р
служит круговой частотой колебаний.
Резюмируя полученные результаты, мы . можем сказать, что
если среди корней характеристического уравнения имеется хотя
бы один, действительная часть которого положительна (незави-
симо от того будет равна нулю мнимая часть корня или нет),
то значение обобщенной координаты будет со временем неогра-
ниченно возрастать. Каковы бы ни были остальные корни характе-
ристического уравнения, в выражениях (22.17) по крайней мере
один член будет с течением времени неограниченно возрастать
и, следовательно, система будет неограниченно удаляться от
-положения равновесия.
Если же все корни характеристического уравнения имеют
отрицательную вещественную часть, то с течением времени си-
стема будет неограниченно приближаться к положению равнове-
сия.
Рассмотрим еще случай, когда один из корней характера
стического уравнения, например, равен нулю, а все остальные
корни (будь то комплексные, или действительные) имеют отри,
дательную вещественную часть.
Потставляя в (22.17) Кг=0, найдем:
qt — Л1х 4- М2с'^ 4- МйеЧ 4-
Поскольку к2, а3, z4 имеют отрицательные действительные
•части, последние три члена в этом выражении при возрастании
времени будут стремиться к нулю и qY будет стремиться к по-
стоянной величине Мх. Таким образом, в этом случае система
будет стремиться к некоторому фиксированному положению рав-
новесия, вообще говоря, отличному от первоначального поло-
жения в момент/— О,
Следовательно, если система, находящаяся в потоке возду
ха будет выведена из положения равновесия и в дальнейшем
предоставлена самой себе, то она будет стремиться к поло-
жению равновесия, тогда и только тогда, когда все корни
характеристического уравнения (22.151 будут иметь отрица-
тельные действительные части.
Так как коэфициенты характеристического уравнения
зависят, в частности, от скорости набегающего на систему по-
тока воздуха (для самолета — от скорости полета), то и
корни характеристического уравнения также зависят от скорости
потока.
Могут представиться следующие случаи:
1) При всех скоростях потока среди корней характеристичес-
кого уравнения существует по крайней мере один с положитель-
ной вещественной частью. В этом случае при всех скоростях
потока система ведет себя как неустойчивая, т. е. любое сколь
утоню малое начальное возмущение системы с течением
времени уведет ее сколь угодно далеко от положения рав
новесия.
2) При всех скоростях потока все корни характеристического
уравнения имеют отрицательные действительные части. В этом
случае при всех скоростях потока система будет устойчива,
т. е. после малых начальных возмущений с течением времени
система возвратится в положение равновесия.
3) Действительные части корней характеристического уравне-
ния, являющиеся функциями скорости набегающего потока, изме
няют свой знак при изменении скорости, т. е. при некоторых
значениях скорости потока хотя бы одна из этих частей поло-
жительна, при других — все отрицательны. В этом случае суще-
ствуют такие* диапазоны скоростей, при которых система устой-
чива, и такие диапазоны скоростей, — при которых она неустой-
чива. Значения скорости потока, при которых происходит изме-
нение знака действительной части какого-либо корня характери-
стического уравнения (система из устойчивой становится
неустойчивой или обратно), естественно назвать критическими ско
ростами системы.
Таким образом, неустойчивость системы может быть двух
видов; система может удаляться от положения равновесия моно-
тонно (апериодически) или могут происходить колебания с
нарастающей амплитудой. Первый вид движения, как было ска-
зано, носит название дивергенции, второй называется флаттером.
Найдем условия, при которых возможны дивергенция или
флаттер, другими словами, найдем условия неустойчивости си-
стемы. Как было выяснено, система устойчива тогда и только
тогда, когда характеристическое уравнение имеет все корни с от-
рицательной вещественной частью. Раус показал1), что для опре-
деления знака действительных частей корней характеристическо-
го уравнения нет необходимости .решать уравнение и находить
его корни. Он формулировал признаки, позволяющие прямо по
коэфициентам характеристического уравнения решить вопрос о
знаках действительных частей его корней. Признаки или условия
Рауса формулируются следующим образом: для того, чтобы вс»
корни уравнения четвертой степени (22.15) имели отрицательны»
действительные части, необходимо и достаточно, чтобы все его
коэфициенты Л,В,С,D.Е, а также величина R — BCD—B^E — D'Ar
были одного знака. Величина R носит название дискриминанта
Рауса.
Не останавливаясь на доказательстве, отметим, что в рассма-
триваемой задаче коэфициент .4 всегда положителен [Л есть дис-
криминант квадратичной формы (22-9), которая по смыслу всег-
да положительна). Следовательно, для устойчивости самолета,
») См., наир. Б. А. Сушкевич .Основы высшей алгебры".
154
колеблющегося в потоке воздуха, необходимо и достаточно вы
волнение условий:
/?>0; С>0; £> > 0; £>0; BCD - В2Е - ОгА>и. (23 1)
Конструкция каждого самолета должна быть такой, что-
бы эти условия выполнялись при всех реально возможных ско
ростях полета ; в противном случае, любое случайное возму
щение вызовет дивергенцию или флаттер конструкции, т. е. при
ведет к нарастанию амплитуды вплоть до разрушения. Расчет,
на флаттер или дивергенцию состоит в определении диапазона
скоростей полета, при которых выполняются все условия (23.1),
т. е. в определении безопасного диапазона скоростей полета. По-
лет самолета со скоростью, при которой хотя бы одно из усло-
вий (23.1) не выполняется, — недопустим.
Опытом эксплоатации самолетов установлено, что при очень
малой скорости движения (например, при начале разбега)
флаттер, ни дивергенция не возникают. Поэтому мы можем счи-
тать, что реальные самолетные конструкции осуществлены таким
образом, что при скорости движения, близкой к нулю, условия
(23.1) выполняются1). Докажем, что с увеличением скорости по
лета раньше других обращаются в нуль величины Е или R, нп ас
B,C,D. Другими словами, покажем, что наименьшая критическая
скорость определяется условиями
Е — 0 или R — 0. . (23.21
Допустим противное: пусть при очень малой скорости все усло-
вия (23.1) выполнены и при увеличении скорости первой обра-
тилась в нуль величина В. Но при этом будет /?=—D'A, что
меньше нуля. Следовательно, величина R обратилась в нуль уже
раньше. Точно также доказывается, что С и D не могут обра-
титься в нуль раньше R. Таким образом, при увеличении скоро-
сти раньше всего произойдет нарушение условий устойчивости
0(1 или /?>0. Критическая скорость, при которой система
из устойчивой превратится в неустойчивую, определяется од-
ним из у равнений (23.2). Уравнение Е—0 определяет критическую
скорость дивергенции; в самом деле, при Е ~ 0 характеристичен
кое уравнение (22 15) будет иметь корень Л = 0 Из трех осталь-
ных корней два будут комплексными и сопряженными, а третий
должен быть вещественным. Движение, соответствующее этому
последнему корню, является апериодическим.
1) Вычисление коэфициентов характеристического уравнения и проверка
условий (23.1) для реальных самолетных конструкций при V=0 показывает,
что и в этом случае возможно невыполнение условий (231). Этот ре-
зультат объясняется пренебрежением силами внутреннего демпфиро
яания конструкций и соответствует незатухающим гармоническим ше-
баииим крыла в пустоте.
155
Условия и /? = 0 можно получить и непосредственно
из характеристического уравнения (22.15), если искать условия,
при которых возможно движение с постоянной амплитудой. Как
лило показано, движение с постоянной амплитудой может со
ответствовать только чисто мнимому корню характеристического
уравнения. Найдем условие, при котором характеристическое
уравнение будет иметь чисто мнимый корень > ~ip- Подставляя
j.~ip в (22.15), получим для определения р уравнение-
Ар* — iBp* - Ср- + iDp + Е= О,
"которое может быть удовлетворено лишь если равны нулю дей-
ствительная и мнимая части по отдельности:
-V4—Ср +£ = 0 1 (23.3)
p^-D)=.O j
Рассмотрим случай дф О, что как было выяснено, соответствует
колебательному движению. В этом случае из второго уравнения
<23.3) находим:
(23.4)
п
Подставляя это.выражение в первое из уравнений (23.3) полу
чим условие:
BCD— B3E—D"A~0,
(23-5)
что совпадает с последним условием (23.1). Таким образом, усло-
вие А? — 0 есть условие существования чисто мнимого^ корпя ха
«оактеристического уравнения, т. е. условие существования iap
ионических колебаний.
Рассмотрим теперь случай р = 0. Соответствующее движение
носит апериодический характер (дивергенция). При р— 0 удовле-
творяется второе из уравнений (23.3), а чтобы удовлетворить
также и первому, необходимо, чтобы Е — 0, что совпадает с пер-
вым из уравнений (23.2). Как видно, и этим путем мы приходим
выводу, что первое из условий (23.2) определяет критическую
(корость дивергенции.
ак.чм образом, для любой части самолета (крыло или опере-
ние), движение которой может быть определено заданием двух
параметров, расчет на флаттер производится следующим образом ,
прежде всего в явном виде вычисляют коэфициенты уравнений
.(22.12) и затем коэфициенты (22,16). Эти коэфициенты окажутся
Д5С>
^висящими от скорости полета. Подставляя их в (23.5), можно-
1)ПРеделить кРитическУю скорость флаттера1).
Так же производится расчет критической скорости диверген-
ции, только вместо уравнения (23.5) решается уравнение £ = <).
В дальнейшем этим путем выведены расчетные формулы длт
расчета И31 ибно-крутильного флаттера крыла.
ГЛАВА 6
Аэродинамические воздействия, испытываемые
колеблющимся крылом
24. Вихревая пелена, образующаяся за крылом при
колебаниях
Для того, чтобы практически применить метод определения
критической скорости (гл. 5), необходимо у меть определи i ь аэро-
фит. йб. Вихревая система крыла при постоянном угле
атаки (вид сверку).
динамические силы, действующие на вибрирующую в потоке
воздуха систему. Решены л этой задачи мы и займемся в пер-
вую очередь.
Рассмотрим крыло, г а холящееся под опр^ селенным утлом
атаки в потоке идеальной жидкости. Такое крыло с аэро;3пна-
1) Если '. равнение (23.5) ;ц. i ы скорости комплексные .-на1 ния,
। значит,(чю колебания ( постоянной амплитудой невозможны, а гак к.;
они являются затухающими при малой скорости, то они б;, дут затух пЬщнм;\
и при любой другой скорости полета. Таким образом, комплексность корней
уравнения (23.5) показывает, что рассчитываемая система не нод эрл ' > :
; 1 .юру ни при какой скорости полета.
157
мической точки зрения эквивалентно вихревой системе1), со-
стоящей из присоединенных вихрей, расположенных вдоль крыла
и вихревых усов (свободных вихрей), уходящих вместе с пото-
ком в бесконечность (фиг. 86). Эквивалентность в данном слу-
Фиг. 87. Присоединенные вихри, возникающие при изме-
нении угла атаки крыла.
V
Фиг.‘ 88. Полная вихревая система крыла
(вид сверху).
чае следует понимать в том смысле, что указанная вихревая сис-
тема оказывает на поток то же действие и испытывает со сто-
роны потока те же силы, как и действительное крыло. Существо-
вание свободных вих-
рей обусловлено тем,
что циркуляция в иде-
альной жидкости не
может исчезать. Так
как циркуляция в ка-
ких-либо двух сече-
ниях, например, ab и cd
вообще говоря различ-
на, то это можно объ-
яснить только тем, что
с крыла между сече-
ниями ab и cd сбегает
вихрь, циркуляция ко-
торого в точности рав-
на уменьшению цир-
куляции от сечения
ab и cd.
Пусть теперь рас-
сматриваемое крыло
будет увеличивать
угол атаки. Как из-
возрастает подъемная
сила крыла, т. е. возрастает циркуляция присоединенных вих-
рей. Так как общая сумма циркуляции в идеальной жидкости
меняться не может, то наряду с добавлением положительной
вестно, при увеличении угла атаки
I) Б. Н. Юрьев .Экспериментальная аэродинамика*.
158
вркуляции,с крыла должен сбежать вихрь равной и противо-
положной по знаку циркуляции. При непрерывном увеличении
угла атаки из этих сбегающих с крыла вихрей образуется за
крылом вихревая пелена: общая сумма циркуляции вихрей вну-
три произвольного контура L (фиг. 87), охватывающего крыло и
вихревую пелену, остается неизменной и равной величине цир-
куляции на крыле до момента начала увеличения угла атаки.
Таким образом, при увеличении угла атаки наряду с вихревы-
ми усами, направленными по потоку, позади крыла возникают
также свободные вихри, располагающиеся параллельно размаху
(пунктир на фиг. 88). То° же происходит и при уменьше-
нии угла атаки, только с противоположным знаком возникаю-
щих вихрей. При колебаниях крыла, когда происходит периоди-
ческое увеличение и уменьшение угла атаки, позади крыла об-
разуется вихревая пелена, уносимая назад потоком, состоящая
из продольных и поперечных вихрей. Поскольку циркуляция на
крыле переменна во времени, с крыла все время сбегают вихри
различной циркуляции и поэтому циркуляция свободных вихрей
различна в разных точках вихревой пелены.
Чтобы определить аэродинамические силы, возникающие на
крыле, необходимо учесть индукцию вихревой пелены на присо-
единенные вихри. Задача эта чрезвычайно сложна и только
недавно М. В. Келдышу удалось получить ее решение.
Однако это решение оказалось весьма громоздким и совершенно
непригодным для практического применения. Расчет на флаттер
до настоящего времени производят на основе приближенных аэро-
динамических теорий, которые дают возможность сравнительно
просто определять аэродинамические силы, а тем самым и кри-
тическую скорость.
Грубо можно сказать, что эти теории основаны на пренебре-
жении, влиянием на крыло либо продольных, либо поперечных
вихрей, составляющих вихревую пелену. Рассмотрим несколько
подробнее основные черты этих теорий.
25. Нестационарная теория
Известно, что если рассматривать неподвижный профиль, обте-
каемый плоско параллельным потоком идеальной жидкости, то
никаких вихревых усов за крылом не будет. Как выше уже было
объяснено, вихревые усы обязаны своим возникновением изме-
нению циркуляции от одного сечения крыла к другому. В плоско
параллельном потоке все сечения имеют одинаковую цирку-
ляцию, а потому и не возникает продольных вихревых усов. Одно
из допущений, которое кладется в основу определения аэроди-
намических сил при флаттере сводится к предположению, что
каждое из сечений вибрирующего крыла работает независимо
от других сечений, как бы находясь в условиях плоско парал-
лельного потока. Таким образом, задача решается следующим
159
образом:рассматривается профиль в плоском потоке, двигающийся
с переменными поступательными скоростями и и v (в. проекциях
на оси координат) и с переменной угловой скоростью о> вокру
некоторого связанного с крылом центра вращения. При этол
учитывается, что циркуляция вокруг профиля меняется во врс
мени, и с крыла сбегает вихревая пелена (фиг. 87). При этих
условиях вычисляются действующие на профиль аэродинамиче-
ские силы. Полученные результаты затем переносятся на профиль,
составляющий элемент реального крыла конечного размаха, и на-
ходящийся в условиях неплоского потока.
Как показала экспериментальная проверка, эта теория,
которая может быть названа плоской нестационарной теорией,
приводит к неудовлетворительным результатам для | реальных
крыльев конечного размаха. Невидимому результаты, получен-
ные для плоского потока, нельзя непосредственно переносить на
профиль, работающий в системе крыла конечного размаха. Тем
не менее за границей до сих пор плоская нестационарная теория
весьма широко используется при расчете флаттера1)> хотя но
нашему мнению она п приветит к неудовлетворительным резуль-
татам. 1см. таблицу па стр. ]blj.
26. Стационарная теория
В СССР при расчетах флаттера пользуются приближенной
теорией,которая можетбытьназвана „стационарной теорией аэроди-
намических <ил“. Если в нестационарной теории пренебрегают
вихревыми усами, то в стационарной теории базируются на пре-
небрежении частью вихревой пелены, сходящей с крыла вследст-
вие изменения циркуляции во времени (фиг. 87), причем учиты-
вается конечность размаха.
Указанная гипотеза о структуре потока около вибрирующею
крыла носит название „гипотезы стационарности" и может быть
формулирована следующим образам: аэродинамические характери-
стики крыла в неустановившемся движении с переменной скоро-
стью V и угловой скоростью о) заменяются в каждый момент
времени характеристиками того же крыла, движущегося с постоян-
ными линейной и угловой скоростями V и о>; V и «о в каждый
момент времени равны скоростям действительного движения,
в этот момент, причем, наклон V к профилю также считается
постоянным и равным действительному наклону в рассматривае
мый момент времени.
*) Наибило- популярна'работа Теодорсена General Theory of aerodynamic
instability and lie mechanism of flutter (Rep: NACA 196. 1935); Кассиером и Ф:ц|
гадо разрабог пя графики дня определения критической скорости на основе
нестационарны! теории (см, Luftfalirtforsclning В 13. 19' . стр. 374-387). (
тлкле Дсн-Гартог. 'leopiu колебаний. 19*12. с,р. >77-384).
1С0
Следовательно, мы как бы снимаем непрерывный ряд момен-
тальных фотографий потока с движущимся крылом и вычисляем
гилы так, как если бы движение, соответствующее каждой фо-
тографии, продолжалось бесконечно долго; истинный поток око-
ло крыла в каждый момент времени заменяется установившимся.
Тогда циркуляция в каждом сечении крыла в каждый момент
времени будет неизменной ( но в различные моменты времени
она будет различной, так как скорости движения, соответствую-
щие каждому моменту времени, различны), и потому с крыла не
будут сходить поперечные вихри. При этих условйях оказывает-
ся нетрудным подсчитать аэродинамические силы, действующие
на крыло.
Экспериментальная проверка стационарной теории на весьма
обширном и разнообразном материале (как для крыла, так и для
оперения) показали, что эта теория дает вполне достаточную
для практического применения точность. В качестве примера
приведём результаты расчета нескольких крыльев (см. таблицу).
№№ (опыт) м.1сек vKP (расчет по плоской не- стационар- ной теории) м;сек (расчет по стационар- ной теории) М'Се.к
1 35,5 35 29,5
2 33 16 25,5
3 48 53 45
4 38 81,5 34,5
5 66 69 59,4
6 33 — 35 22 30
Особенный интерес представляют результаты по крыльям
№ № 1 — 5. Дело в том, что эти крылья являлись динамически
подобными моделями реальных самолетных крыльев, в то вре-
мя, как крыло № 6 — схематическая модель.
Модели называются динамически подобными, если они подобны реальным
конструкциям как по своим геометрическим, так и по упругим и инерцион-
ным свойствам. Такие модели дают возможность осуществить в аэродинами-
ческой трубе полное подобие явлению флаттера у натурального самолета и
наблюдать в трубе реальные режимы флаттера. Подчеркнем, что все законы
построения динамически подобных моделей как для крыла, так и для опере-
ния следуют из общей теории подобия и не опираются на какие-либо приб-
лиженные допущения. Поэтому результаты, полученные с помощью продувки
Динамически подобных моделей, могут быть пересчитаны на натуру путем
простого умножения на масштабный коэфициент. Эксперимент на дннами-
П Гроссман и Пановко.
161
чески подобных моделях особенно важен в случаях, когда расчет не дает
желаемой точности вследствие особенностей конструкций. Тогда всегда
можно уточнить результаты расчета путем продувки динамически подобной
модели (крыла пли оперения) в аэродинамической трубе.
В виду того, что в СССР реальные расчеты флаттера произ-
водятся исключительно на базе «стационарной теории, мы в даль-
нейшем ограничимся изложением только этой теории. Нестацио-
нарная теория нами излагаться не будет.
27. Аэродинамические силы, действующие на колеблющееся
крыло в плоско-параллельном потоке
Вычисление аэродинамических сил мы будем вначале произ-
водить для профиля в плоско-параллельном потоке, а затем
уже учтем поправки, вносимые конечностью удлинения.
Рассмотрим тон-
кий профиль MN
(фиг. 89), произволь-
ным образом дви-
жущийся в потоке
идеальной жидкости
и при этом деформи-
рующийся по про-
извольному закону
(примером деформи-
рующегося профиля
Фиг. 89. Схема тонкого деформирующегося про- может служить, на-
филя в потоке. пример, крыло, снаб-
женное элероном).
Пусть XOY—неподвижная в пространстве прямоугольная
система координат, ось ОХ которой ориентирована по скорости
основного потока. Уравнение профиля в этой системе координат
у=у(х/).
(27.1)
Пусть х0 — расстояние от передней кромки профиля до начала
координат, отсчитываемое вдоль оси X; b — хорда профиля. На
крыло набегает поток, обладающий вдали от крыла основной
скоростью IZ, направленной вдоль оси X. Около крыла частицы
набегающего потока обладают, кроме того, добавочными скоро-
стями: и—направленной по основной скорости потока и v—
перпендикулярной к ней. Эти скорости вызваны влиянием крыла
и малы по сравнению со скоростью V основного потока. Точно
также считается малой амплитуда отклонений профиля от оси X
(у мало по сравнению с хордой).
162
• Vv
и 1
Если бы профиль был неподвижным, то, вертикальная слага-
ющая скорости частицы жидкости около профиля была бы
. Но так как частица движется вместе с профилем
дх
ду
с вертикальной скоростью то общая вертикальная скорость
частицы равна
дУ
dt
V —
Ограничиваясь членами первого порядка малости, можем
записать:
дх dt
(27.2)
Введем новую переменную Ф, связанную с х зависимостью
х + х0 = -| — соф у (27.3)
При изменении х от—х0 до b — хс (от передней до задней кром-
ки, вдоль профиля), ф будет изменяться от 0 до к.
Заменим профиль непрерывной вихревой пеленой с напряже-
нием вихрей на элементе dx, равным -((x)dx. Функцию у (х) под-
берем из того условия, чтобы поток, создаваемый вихревой
пеленой, совпадал с действительным потоком около профиля.
Как и в стационарной теории тонких профилей 1) будем искать
у(х) в виде тригонометрического ряда:
Ф
T(x)==2I7 z10ctg-^- +
Ап inn б
(27.4)
Найдем вертикальную скорость, создаваемую вихревой пеленой,
и определим неизвестные коэфициенты А„, исходя из того усло-
вия, чтобы эта скорость совпадала со скоростью v действитель-
ного потока, т. е. чтобы поток, создаваемый вихрями, обтекал
профиль без срыва. Так как профиль предполагается мало отли-
чающимся от оси X, то при вычислении поля скоростей системы
вихрей у (х), заменяющих профиль, делается допущение, что
вихри расположены по оси X. Тогда скорость, индуцированная
вихрями в точке профиля с координатой х, будет
Ь—х0
Г l(x1)dx1
I 2т: (Xj—х)'
_______________ — *о
*) Глауэрт. .Теория крыльев и вннта“.
11*
163
Приравнивая эту скорость к вертикальной скорости действитель-
ного потока (уравнение 27.2), получаем условие, определяющее рас-
пределение циркуляции у(х):
й —х0
Г _ vdy ду
J 2тг (хх — л) дх -г dt ‘
—*0
в левую часть у(х1) из (27.4). и делая
Подставляя
затем замену переменного х на ф по уравнению (27.3), можно
вычислить интеграл, стоящий в левой части J).
V -Ло +
Апcos п ф
д\) ду
дх dt
(27.5)
Из этого соотношения легко определить коэфициенты Ап методом,
которым обычно определяются коэфициенты разложения какой-
либо функции в ряд Фурье. Умножаем поочередно обе стороны
последнего равенства на dty, созфг/ф, соз2фс/ф, ... и интегри-
руя результат в пределах от нуля до я, найдем:
L Г (дУ, LdZ
х J I/dz1
0
(27.6)
1 ду
Vdt
о
COS пфг/ф
Таким образом, коэфициенты Ап определены и, тем самым, опре-
делена циркуляция у(х). Дальше уже не представляет затруд-
нения, пользуясь теоремой Жуковского, определить силы, дей-
ствующие на крыло.
Подъемная сила, действующая на единицу длины крыла, будет:
Ь — х0
Р = J"?- 17-у (x)dx.
— хр
Подставляя сюда значение у (л) из (27.4) и заменяя, согласно
(27.3), переменную х через ф, после выполнения интегрирования
получим:
р=*Рь (дс + L Ai V L CjPd izs,
’) Подробное вычисление этого интеграла имеется в книге Глауэрта.
164
откуда
су = 2-Л40 + ^А
(27.7)
Аналогично вычисляется момент подъемной силы относительно
начала координат (напомним, что начало координат отстоит на
расстоянии х, от передней кромки);
b—Хо
М = —J”р 1А( (%) xdx = —р17Ьхок —
—хо
-1- pv^(a0 + ау-}та^
или
где
сга£=_^Л1-А2)ч (27.8)
Таким же образом могут быть вычислены и силы, действующие
на какую-либо часть крыла. Например, если крыло обладает эле-
роном, передняя кромка которого находится на расстоянии х*,
а шарнир на расстоянии хш от передней кромки крыла, то шар-
нирныи’момент может быть вычислен по формуле:
6 —х0
Мш == J*p Уу (х) (х — хш + х0) dx.
—х0+ х*
Мы, с целью изучения метода, в дальнейшем подробно остано-
вимся только на вычислении подъемной силы и момента крыла.
Для шарнирного момента метод вычисления остается тем же
и мы ограничимся только указанием окончательных результатов.
Полученные формулы пригодны при любом законе движения
профиля. Для получения аэродинамических характеристик в каж-
дом конкретном случае, когда известен закон движения, т. е.
известно уравнение (27.1), необходимо вычислить сначала коэ-
фициенты Ап по формулам (27.6), а затем подъемную силу и
момент по формулам (27.7) и (27.8).
Проделаем эти вычисления для случая крыла, совершающего
совместные изгибно-крутильные колебания.
Пусть MN (фиг. 90) — профиль крыла в статическом положе-
нии (до возникновения колебаний) в плоско-параллельном потоке.
165
Выберем начало координат в точке Е профиля, отстоящей на х0
от передней кромки (удобно за эту точку принять центр жест-
кости крыла), ось X направим по скорости основного потока и
•сь Y — перпендикулярно к ней. Вычислим аэродинамические
характеристики крыла, когда совершаемое движение слагается
из перемещения в направлении, перпендикулярном скорости по-
тока, и из вращения вокруг какой-либо точки, лежащей на про-
филе. Пусть MiEiN1— положение колеблющегося профиля в
какой-либо момент времени. Точка Е заняла положение Ev Рас-
стояние ЕЕг обозначим через Y и будем в дальнейшем назы-
вать прогибом крыла; угол поворота сечения вокруг точки Е,
Фиг. 90. Движение профиля в плоско-параллельном
потоке.
обозначим 0. Прогиб и угол закручивания крыла (т. е. его откло-
нения от положения равновесия) считаются малыми, точно так
же, как и ординаты профиля в статическом положении, которые
обозначим через уст. Составим для изучаемого движения урав-
нение (27.1).
Ординаты точет; профиля в произвольный момент времени можно'
с точностью до малых высших порядков выразить следующим
образом (см. фиг. 90):
„ У=Ует+У-х(Е (27.9)
ото и есть в развернутом виде для рассматриваемого случая урав-
нение (27.1), определяющее закон движения.
Для подстановки в формулы (27.6), находим:
_ е; — У—д-6. (27. Ю)
их dx dt ,
166
,-де точки над буквами, обозначают диференцировапие по вре-
мени.
Подставляем (27.10) в (27.6), затем заменяем х по формуле
(27.3). После интегрирования будет:
^о —^orm + ®+ 1/(2—хо)(*—
I Л1=д,„44.. ' . (27-41
7^2 — ^1ст>
где
Л,«, = -4 (27.12)
о о
есть значения коэфициентов циркуляции Ло, Л] . . . для про-
филя в статическом положении.
Подставляя найденные выражения коэфициентов в формулу
(27.7), получим:
с — с J. 2тг 0 + (— — G____________________- • У 1
су — Суст ' 44 b)V V ’
где
уст — I ^Ост
(27.13)
(27.14)
есть значение су для неколеблющегося профиля в статическом
положении.
Таким образом, окончательное выражение коэфициента подъ-
емной силы колеблющегося крыла в плоском потоке найдено.
Подъемная сила выражена непосредственно через параметры дви-
жения и если закон движения задан, т. е. заданы прогиб У и угол
поворота 0 в функции времени, то может быть подсчитана подъ-
емная сила для любого мгновения.
Обратимся к вычислению момента. Формула (27.8) состоит из
двух членов. Легко видеть, что. первый член есть стЕо — значе-
ние коэфициента момента относительно начала координат при
угле атаки, соответствующем нулевой подъемной силе. Поэтому
(27.8) можно переписать в виде
где
(27.15)
167
Пользуясь (27.11), находим
^тЕо — С'тЕо егп
(27.16)
Формулы (27.15) и (27. 16) вместе с выражением (27.13) полно-
стью определяют момент колеблющегося крыла в плоском потоке.
28. Учет влияния конечности размаха на
аэродинамические силы
Определим теперь, как изменятся полученные формулы при
Переходе от плоского потока к крылу конечного размаха. Как
Известно из аэродинамики', статическое значение коэфициента
подъемной силы (значение су для неподвижного профиля) в плос-
ком потоке всегда может быть представлено в виде
су ст 2тс (afm а0),
(28.1)
гДе аст—угол атаки хорды профиля и аи—угол атаки нулевой
Подъемной силы (угол атаки, при котором ^=0 х).
!) Выражение (28.1) может быть непосредственно получено из формулы
(27.14). Пусть (фиг. 91) MN—профиль крыла в статическом положении. XEY—
прямоугольная система координат, совпадающая с системой фиг. 90. Введем
в рассмотрение также систему координат X^Yy начало которой совпадает
с передней кромкой профиля и ось MXt направлена по его хорде. Угол
м^жду хордой профиля и скоростью V набегающего потока есть статический
^гол атаки ас/и, очевидно, равный углу между осями X и А',. Между углами
Наклона касательных в обеих системах координат имеем зависимость:
dy _
dx iZxj ~ ’
Определяем коэфициенты (27.12):
л к
. Г rdv I rdyx ,
= J = J dif-{-acm
0 0
2 pdy 2 / dyx
Ancm = ~Z / cos n ф rf'i = — / созпфт/ф.
0 0
Подставляя эти значения в (27.14), находим
су ст = 2л (Уст “о)>
1 / dy,
/ dxx a-cos-Wrf'b
0
Зависит только от формы профиля и не зависит от угла атаки его хорды.
аким образом справедливость формулы (28.1) доказана.
168
Введя выражение (28.1) в (27.13), мы убеждаемся, что фор-
мула для су сохранит такую же структуру, как и формула (28.1),
но только вместо а.ст будет стоять величина а, равная
ь , / 3 х0 \ b . 1 .
“ — аст + в + I 4 1 р/6 р? У.
(28.2)
Следовательно, если выражение (28.1) подставить в формулу
(27.13), то .получим
Су = 2к(а- «,). (28.3)
Сравнение этого выражения с (28.1) показывает, что величину
я можно рассматривать как мгновенное значение угла атаки при
колебаниях крыла. Так как выражение (28.3) имеет такую же
структуру, как и выражение (28.1) для статического значения су,
переход к конечному размаху можно совершить так же, как это
обычно делается в случае установившегося движения.^
При переходе к крылу конечного размаха, к геометрическому
углу атаки добавляется еще угол скоса Да, возникающий вслед-
ствие влияния вихревых усов, сходящих с крыла. Добавтяя
угол скоса в выражение (28.3), получаем для крыла конечного
размаха:
Су ~ 2~ (а — а0 — Да).
Это выражение представим в следующем виде:
163
Величина 2^ 11 —
\ де
------- есть, как известно, значение <->
« — % / до:
для крыла конечного размаха, так что
„ дсу / л
о=
(28.4)
Отношение -—— будет меняться по размаху крыла (так как
прогибы У и углы кручения 0, входящие в выражение а ме-
няются вдоль размаха). Поэтому, строго говоря, при колебаниях
дсу
величина -л- меняется от сечения к сечению вдоль раз-
оа
маха крыла. Однако приближенно эту величину заменяют сред-
ним значением и считают одинаковой для всех сечений крыла,
о дсу
За это среднее значение принимают значение , получаемое
при продувках в аэродинамической трубе, т. е. обычное стати-
ческое значение.
Подставляя в (28.4) значение а из (28.2), получаем окон-
чательное значение су для колеблющегося крыла конечного
размаха
+ ^-[ » + » - |г] • (28.5)
Остается еще перейти к конечному размаху в формуле (27.5)’
определяющей момент колеблющегося крыла. Как известно, вели-
чина с1пЕо не зависит от удлинения и одинакова как для про-
филя в плоском потоке, так и для крыла конечного размаха.
Это объясняется тем, что сгпЕо есть значение стЕ при г^=0,
а так как при угле атаки, при котором ^ = 0 около крыла нет
циркуляции, то следовательно нет и сходящих с крыла вихре-
вых усов, которые создавали бы угол скоса. Поэтому выражение
(27.16) при переходе к крылу конечного размаха остается без
изменения. Для того, чтобы получить значение момента крыла
конечного размаха при су, отличном от нуля, достаточно в фор-
мулу (27.15) подставить значение су для крыла конечного раз-
маха [т. е. из формулы (28.5)]. Тогда окончательно получим:
с р — с г _ ~J> 6 , дсу(хъ_____1 Vfl . 0___I у (28 6)
/n£ тЕ‘т 8 17 + аДу 4/1 \4 b]V I/ JV 1
Существенно отметить, что как подъемная сила, так и мо-
мент крыла являются линейными функциями параметров
движения, 0, 9, У. Это, конечно, верно постольку, поскольку
колебания предполагаются малыми.
170
Для расчета тел форм колебаний, в которых участвует эле-
рон, необходимо также знать величину шарнирного момента
колеблющегося элерона. Подъемная сила и момент крыла, снаб-
женного элероном будут, очевидно, также зависеть от угла
отклонения элерона р и скорости его вращения р. Не проводя
соответствующих выкладок, приведем лишь окончательные ре-
зультаты.
Коэфициент подъемной силы крыла, снабженного элероном,
имеет значение
»+(J - Яг ’+°*+- И • <28-7)
Коэфициент момента крыла, снабженного элероном:
СтЕ стЕСт g уО + 2/р + 2/ у 4 )
О р+Ср + Л/рр
(28.8)
Шарнирный момент колеблющегося элерона имеет значение
Mul = Multm-9W
[ + +23р + а4^р+ УфУ
(28.9)
Величины G, Н, I, J, Qi...,2-O являются функциями двух отно-
шений:
ь»к Ьэ г .
~j~— и , где Ьо к—расстояние от передней кромки до шарнира
элерона, характеризующее степень осевой компенсации, Ь3 -хорда
элерона и Ь—хорда крыла. Аналитические выражения этих функ-
ций довольно громоздки и существуют специальные таблицы,
в которых даны их числовые значения в зависимости от ука-
занных двух отношений х). Для наших целей достаточно заме-
тить, что эти коэфициенты зависят только от геометрических
параметров крыла и элерона и могут быть подсчитаны, как только
эти параметры заданы.
Результаты, полученные нами для крыла, легко могут быть-
перенесены и па колеблющееся оперение. Роль элерона в этом,
случае будет играть руль.
Таким образом могут быть определены аэродинамические
воздействия при колебаниях как для крыла, так и для оперения
Е. П. Гроссман—„Формулы и таблицы для определения аэродинами-
ческих коэфицпеитов крыла с элероном или хвостового оперения с рулями
при вибрациях".Технические отчеты ЦАГИ вып. Ш-4, 1940 г.
171
ГЛАВА 7
Изгибно-крутильный флаттер крыла *)
29. Определение критической скорости изгибно-
кругильного флаттера крыла
В 5-й главе был развит метод определения критической ско-
рости флаттера для общего случая системы с двумя степенями
свободы. Применим этот метод к определению критической
скорости крыла, совершающего в полете изгибно-крутильные
колебания.
Было показано, что критическая скорость определяется как
корень уравнения (23.5). Для того, чтобы определить из этого
уравнения критическую скорость, необходимо в явном виде вы-
числить коэфициенты А, В, С, D, Е по уравнениям (22.16), что
становится возможным лишь после предварительного вычисле-
ния коэфициентов а, с, 8, (3, входящих в уравнения (22.12). Для
получения этих коэфициентов повторим применительно к рас-
сматриваемому случаю составление уравнений (22.12).
Как и при рассмотрении собственных колебаний (п. 5) пред-
ставим прогиб и угол закручивания крыла в виде г).
У (*, t) =/ (г). qt (/); 0 (z,t) = <? (г). ?2(0. (29.1)
Многочисленные расчеты показали, что форма колебаний
крыла в потоке воздуха очень мало отличается от формы соб-.
ственных колебаний того же крыла в пустоте. Поэтому можно
считать, что функции f(z)u с (г) таковы же, как при изгиб-
ных и крутильных колебаниях крыла в пустоте. В п. 5 были
подробно изложены методы определения этих функций для
произвольного крыла; тем самым функции формы f(z) и «(г)
здесь можно считать известными. При этих условиях движение
крыла будет полностью определено, если будут найдены также
функции времени qx(t) и q,(f), принимаемые за обобщенные
координаты.
Уравнения (22.12) есть уравнения Лагранжа, составленные для
обобщенных координат <?!и Нам нужно вычистить коэфициенты
этих уравнений. Напомним, что согласно (22.9) коэфициенты
т12, c2i — есть коэфициенты квадратичной формы, определяющей
кинетическую энергию колеблющейся системы:
7^= + 2^12 qY q<i ~J~ c^q^)-
’) См. E. П. Гроссман, С. С. Кричевский, А. А. Бор ш—„К вопросу об устой-
чивости конструкции крыла в полете" (Тр'ды ЦАГИ № 202, 1935 г.) Е. П. Грос-
сман ..Перекручивание монопланного крыла" (Труды ЦАГИ № 253, 1936 г.).
Его же „Флаттер" (Труды ЦАГИ № 284, 1937 г.) Его же „О причинах флат-
тера" (Труды ЦАГИ .№ 350, 1938 г.)
Влияние колебании крыла в плоскости хорд несущественно и будет
считаться отсутствующим. .
172
Кинетическая энергия крыла, совершающего пзгибно-крутиль
ные колебания, была определена в главе 1 (п. 5); по формуле
(5.48) для крыла без сосредоточенных масс:
(29.2)
Коэфициенты яп, а)г, с21, входящие в уравнения (22.12), есть
коэфициенты квадратичной формы (22.11) определяющей потен-
циальную энергию колеблющегося крыла:
£/ = + 2c127i72 -f- a2,q^).
Сравнивая это с формулой (5.47) первой главы, выведенной для
потенциальной энергии при изгибно-крутильных колебаниях
крыла, находим, согласно (5.48):
и
= а
(29.31
Таким образом, для уравнений (22.12) остается еще опреде-
лить коэфициенты о и [3, — коэфициенты выражений обобщен-
ных сил (22.7). Повторим для нашей задачи вывод выражений,
обобщенных сил, исходя из формул (22.2):
р .дх*+р.&.
Xldq, y‘dq.
>
Zldq.
о ~^(р ^1 + р.-дУ1-
Ча~xidq2 yt dq2
dzt
'dq2
Напомним, что в этих выражениях Pxi, Pyi, Pzi компоненты
внешних (в нашем случае—аэродинамических) сил, действующих
173
s i-ой точке системы, с координатами х;, yit zt. Суммирование
распространяется по всем точкам системы.
Нам необходимо получить в развернутом виде для рассматри-
ваемого случая изгибно-крутильных колебаний крыла формулы
(22.7), т. е. выражения обобщенных сил через обобщенные ко-
ординаты qx и q2. Для этого выразим декартовы координаты то-
чек системы через обобщенные координаты и подставим резуль-
тат в формулы (22.2). Пусть MN— профиль крыла в положении
равновесия и положение того же профиля в какой-либо
момент времени при-колебаниях. Начало координат прямоуголь-
ной системы XEY выбираем в центре жесткости крыла Е и
ось ЕХ ориентируем по скорости набегающего потока V (фиг. 92).
Фиг. 92. Перемещения сечения крыла при колебаниях.
Произвольная точка профиля Ло заняла положение Л;. Обозначим
полярные координаты точки в положении равновесия через
с;; 7,. В рассматриваемый момент времени координаты точки
будут:
Х(. = of cos (Tl -f- 6); yz = У— ъ sin (у, -ф 0). (29.4)
Подставляя сюда значение прогиба У и угла закручивания 6
из (29.1), найдем связь между х,-, у,- и qlt q2>
с. cos (уг + <р^2); у,- —fq^ Gzsin (у, + «?.,). (29.5)
Подставляя эти значения в формулы (22.2) и учитывая, что
z-t не зависит от q± и д3, т. к. расстояние сечения от оси само-
лета не меняется (с точностью до малых второго порядка),
<21 = = — S [P^sin (у; ф- yqJ+'Pyi cos (у^)^. (29.6)
174
Выражение Qa удобнее записать, заменив величину cos (у, + <?#.,)
через б в соответствии с (29.1):
Q3 = - 2 [Рх1п(7 + о) + ^'э Г-НФ? (29-7)
В формулах (29.6) и (29.7) суммирование производят сначала
по всем точкам одного какбго-либо отсека крыла, а затем уже
по всем отсекам.
Начнем с величины QP Так как функция f меняется только
от сечения- к сечению (/ зависит только от z), то при суммиро-
вании по точкам одного элементарного отсека функцию/можно
вынести за знак суммы. Тогда под знаком суммы останется сумма
проекций на ось Y всех сил, действующих на отсек, т. е. проек-
ция на ось Y равнодействующей внешних сил, действующих на
отсек. Обозначим эту сумму dPy. Суммируя затем результат п«
всем отсекам крыла и помня, что f есть функция z, получаем:
1
Q^ffdPy- (29.8)
о
Аналогично можно преобразовать выражение Q2. Величина,
стоящая в квадратных скобках в формуле (29.7), есть проекция
силы с компонентами Pxi, Pyi, ^действующей в точке Д на нор-
маль к отрезку сг, соединяющему точку Д с осью жесткости
крыла (фиг. 92). Следовательно, выражение:
[Р, in (у + 0) Д Р..-С о j 4- i)| i,
•есть момент внешней силы, действующей в точке At относи-
тельно оси жесткости Е, но только взятый с обратным знаком,
так как положительное направление моментов нами выбрано
в сторону увеличения угла атаки (от положительной оси Y к по-
ложительной оси X). Суммируя далее момент по всем точкам
отсека, а. затем по всем отсекам крыла, находим:
1
Q2=f <fdME, (29.9)
0
тде dME— результирующий момент всех внешних сил, дей-
ствующих на рассматриваемый отсек крыла.
Внешними силами в рассматриваемой задаче являются силы
аэродинамические и поэтому:
dPy = ~ Cy?bV2dz-
dME=^-cm^V2dz
(29.10)
175
Значения су и стЕ были определены выше формулами (28.5)
и (28.6). Подставляя эти значения в (29.10), а затем результат
в (29.8) и (29.9), окончательно получим:
,Q1 = ^1а^2^8 ^12 ^2 — ^11 j . ?og J
Q2 = — b22 V2q2 — di2 Vq2 — d.2l Vq2 j ’
где обозначено:
Сравнивая (29.11) с формулами (29.7) 5-й главы, сразу находим
Зн = 0;
₽12 = -А2И2;
Р21 — 0;
$м=-ь22уе-
°11 —• d-ll И
°i2 = ~d12 V7;
°21 = ^21
' d2217.
(29.13)
Так как теперь найдены все коэфициенты уравнений (22.12),
не представляет труда найти критическую скорость. В главе 5
было показано, что для этого необходимо вычислить коэфициенты
А, В, С, D, Е [формулы (22.16)] и затем определить скорость
из уравнения (23.5). Выражения А, В, С, D, Е можно теперь
176
представить на основании (29.2), (29.3) и (29 .4)
виде:
А=Аг;
В~В^
c=cx+c2v2\
D = D\V+DaV3-,
E~E1 + EaV2.
Здесь постоянные А,, В{... £, не зависят
имеют следующие значения:
от скорости полета и
^11 ^11^22 ^12^21>
В^ ^ц^22 4“^ц^22 Пз^21 ^13^12»
Cj---Н1^22 4* ^11^22?
D1 d 11^22 ^11^2 J >
в следующем
(29.14)
(29.15)
f 1 —- flfj jfZo2 f
f>2 H1^2S ^12^21 4* ^11^92 ^12^21>
E) 2 ^11^22 ^12^21 >
E> —— ^u^22*
Составляем теперь уравнение (23.5), определяющее крити-
ческую скорость. Подставляя в него значения Av Вт.. .Е9 из
(29. 14), придем к уравнению:
LV4-]-MV2 + N = 0,
где
L=BiC2D.i— D22At;
A^=B1C2Di+B1C1D2-B12Ei-2D1D,A1->
L = B^Di—B2E —AsAv
(29.16)
(29.17)
Таким образом, схема определения критической скорости
изгибно-крутильного флаттера крыла сводится к следующему:
1) Прежде всего вычисляются функции f(z) и y(z), опреде-
ляющие форму колебаний. Эти функции находятся методом по-
следовательных приближений, изложенным в п. 5.
2) Вычисляются коэфициенты a, b,c, d по формулам (29.2),
(29.3) и (29.12).
3) Вычисляются коэфициенты АХ,...Е., по формулам (29. 15).
4) Вычисляются коэфициенты L, Л1, N по формулам (29. 17).
5) Находится критическая скорость решением уравнения
(29.16).
Уравнение (29.16) дает для критической скорости флат-
тера два значения. В главе 5 было показано, что каждый корень
этого уравнения дает такую скорость полета, которая разграни-
чивает область затухания колебаний от области нарастания коле-
12 Гроссман и Пановко. 177
бапий. Пусть корни уравнения (29.16) будут Ц и V.,, причем
V. % ]/,. Если самолет летит со скоростью V< Ц, то колебания
будут затухающими. Когда скорость полета достигнет величины
Vp колебания перестанут затухать и при большей скорости поле-
та вплоть до значения К будут происходить с нарастающей ампли-
тудой. Так как при скорости несколько меньшей 1/а колебания
нарастают, то при скорости большей V», они будут затухать.
Таким образом, уравнение (29.16) определяет следующие диа-
пазоны скоростей голета: ,
1) V Ц—возникающие в полете колебания крыла являются
затухающими;
2) Ц<С Ц— колебания происходят с нарастающей ампли-
тудой ;
3) V —колебания являются затухающими.
Таким образом, за критическую скорость флаттера должен
быть принят .меньший корень уравнения (29.16).
Область скоростей полета, при которых возможен изгибно-
крутильный флаттер крыла, лежит между меныиим и боль-
шим корнем уравнения (29.16). Если оба корня этого уравнения
комплексны, то, как было показано в главе 5, флаттер невозмо-
жен ни при какой скорости полета.
Большое количество опытов, а также анализ случаев флаттера,
имевших место в полете, позволяют утверждать, что изложен-
ный метод расчета дает критическую скорость с точностью вполне
достаточной для практических расчетов. Ошибка в расчетной
величине критической скорости по сравнению с действительной
лежит в пределах 15—18%. Такую точность следует признать
вполне удовлетворительной, особенно если принять во внимание,
что значения исходных параметров, необходимых для расчета
(жесткости крыла на изгиб и кручение, распределение масс и
моментов инерции и т. д.) обычно бывают известны не с боль-
шей точностью. Кроме того, во всех наблюдавшихся до сих пор
случаях, расчет всегда давал критическую скорость меньшую,
чем действительная (см. напр. таблицу в п. 26). Это обстоятель-
ство является весьма ценным, так как расчет обеспечивает до-
полнительный запас. Благодаря этому, коэфициент безопасности
по отношению к расчетной величине критической скорости мо-
жет быть принят сравнительно небольшим. В современных нор-
мах коэфициент безопасности по отношению к критической
скорости, вычисленной изложенным методом, принят равным
1,2. Это значит, что полеты самолета разрешаются до скорости
V%:1,2, где • VKp—расчетное значение критической скорости.
Все сказанное относится к критической скорости Ц, т. е. к
меньшему корню уравнения (29.16). Что касается большего
корня этого уравнения (то есть скорости полета, при которой
флаттер прекращается), то он расчетом определяется со значи-
тельно меньшей точностью. Это вполне понятно, если вспомнить,
178
что весь метод расчета базируется на теории малых колебаний
и поэтому он правильно отображает только те явления,
которые происходят в начале колебаний, когда амплитуды
еще малы. В дальнейшем амплитуды колебаний достигают
значительных величин и прекращение флаттера происходит
при условиях, когда теория малых колебаний становится
весьма неточной. Однако практически это не имеет значения,
так как интерес представляет только скорость, соответствующая
началу флаттера, поскольку полеты на более высоких скоростях
вызывают почти неизбежную аварию. К конструкции никогда не
предъявляют требования, чтобы она могла выдержать флаттер;
конструктор должен осуществить такую конструкцию, флаттер
которой не возникает ни при какой, возможной в эксплоатации,
скорости полета. Поэтому из всех характеристик флаттера
практический интерес представляет только одна — наимень-
шая критическая скорость.
Мы видели, что для определения критической скорости пред-
варительно необходимо произвести расчет собственных колебаний
и определить функции формы изгибных /(г) и крутильных <p(z)
колебаний. Но, как было показано в п.п. 5—6, крыло имеет бес-
численное множество возможных форм изгибных и крутильных
колебаний. Подставляя в наши формулы функции формы раз-
личных тонов колебаний, мы будем получать различные кри-
тические скорости, каждая из которых соответствует определен-
ному тону колебаний. Другими словами, флаттер различной
формы может возникать на различных скоростях полета.
Очевидно, практический интерес представляет только наи-
меньшая из этих критических скоростей. Однако до насто-
ящего времени не разработано способа, который давал бы воз-
можность заранее строго определить тон, критическая скорость
которого является наименьшей, и приходится базироваться на
статистике большого количества расчетов. Оказывается, если
на крыле нет сосредоточенных грузов, то наименьшая крити-
ческая скорость соответствует первому тону колебаний (функции
f(z) и <?(z) вычисляются для первого тона изгибных и крутиль-
ных колебаний). Иное дело, если на крыле имеются сосредото-
ченные грузы значительной величины, например, мотор. В этом
случае обычно оказывается, что наименьшую критическую ско-
рость дает сочетание изгиба первого и кручения второго тона.
Если грузы на крыле не очень велики, то наименьшую скорость
может дать как первый, так и второй тон колебаний кру-
чения, и в настоящее время нет способа заранее предсказать,
критическая скорость какого тона будет наименьшей. Поэтому
для крыла с сосредоточенными грузами (мотор, поплавки и т. д.)
обычно определяются обе критические скорости—для первого
и второго тона колебаний. Еще более сложен вопрос для много-
моторных самолетов. Здесь приходится исследовать несколько
первых тонов колебаний.
12 179
30. Анализ энергообмена между колеблющимся
крылом и потоком
Явление флаттера развивается по существу из-за того, что
приток энергии в систему превосходит расходование энергии.
В связи с этим значительный интерес представляет анализ
энергообмена между колеблющимся крылом и потоком; в про-
цессе этого анализа можно будет установить физическую кар-
тину возникновения флаттера и наметить принципиальные пути
предотвращения этой исключительно опасной формы колебаний.
а) Колебания крыла в пустоте
Рассмотрим прежде всего колеблющееся в пустоте крыло,
центр тяжести которого в каждом сечении находится на рас-
стоянии о от оси жесткости. Как было выяснено в гл. 1, колеба-
Фиг. S3. Энергообмен
крыла при колебаниях
в пустоте.
ния такого крыла будут обязательно совместными изгибно-кру-
тильными, независимо от того, был ли
первоначальный импульс чисто изгибаю-
щим, чисто крутящим или комбиниро-
ванным.
Один вид колебаний неизбежно вы-
зовет другой. Мы можем поэтому гово-
рить о наличии двух инерционных свя-
зей: инерционной связи изгиба на кру-
чение (инерционный периодический кру-
д2у
тящий момент тс ~^3, появляющийся
вследствие изгибных колебаний л вы-
зывающий колебания кручения) и инер-
ционной связи кручения на изгиб (перио-
дическая сила инерции тс , появля-
ющаяся вследствие колебаний кручения
и вызывающая колебания изгиба). Эти инерционные связи вызы-
вают переход энергии из движений изгиба в движения кручения
и обратно, не меняя запас энергии в колеблющейся системе
крыла.
Если бы затухания, вызванного гистерезисом конструкции,
не существовало, то колебания крыла в пустоте, раз начавшись,
продолжались вечно, так как запас энергии, сообщенный крылу
первоначальным импульсом, никуда исчезнуть не может.
В действительности же эта энергия будет расходоваться на
гистерезис, и колебания крыла в пустоте будут обязательно
затухающими.
Схематически энергообмен в колеблющейся системе крыла
можно представить диаграммой, показанной на фиг. 93. Запас
энергии, сообщенный крылу первоначальным импульсом, непре-
180
рывио перераспределяется между движениями изгиба и круче-
ния ввиду наличия инерционных связей, изображенных стрел-
ками: АВ—инерционная связь изгиба на кручение и CD—инер-
ционная связь кручения на изгиб. Стрелки О и О' показывают
рассеивание энергии колеблющейся системы на внутренний гисте-
резис.
б) Колебания крыла в неподвижной среде
Колебания крыла в неподвижной среде протекают так же,
как и в пустоте, и также будут затухающими. Затухание в этом
случае произойдет еще быстрее, так как энергия, сообщенная
Крылу первоначальным импульсом, будет затрачиваться не толь-
ко на внутренний гистерезис, но и на преодоление сопротивле-
ния среды.
Как выше было выяснено, причина появления инерционных
связей лежит в несовпадении центра тяжести и центра жест-
кости в каждом сечении крыла. Если оба эти центра совме-
стить (соответствует а=;0), то инерционные связи исчезнут.
В крыле с совмещенными осями тяжести и жесткости колеба-
ния изгиба и кручения разделяются. Такое крыло может со-
вершать как чисто изгибные (без кручения), так и чисто кру-
тильные (без изгиба) колебания.
в) Колебания крыла в потоке воздуха
Изгибно-крутильные колебания крыла, подвергнутого началь-
ной деформации изгиба.
Пусть крыло, у которого ось жесткости находится впереди
оси центров тяжести, находясь в потоке воздуха, подверглось
действию изгибающего импульса. Мы уже установили, что,
вследствие инерционных связей, дальнейшие колебания будут
изгибно-крутильными. Но если крыло находится в потоке воз-
духа, то, кроме инерционных, имеются еще и аэродинамические
связи.
Мы видели на стр. 141, что наличие скорости изгибных
колебаний вызовет изменение угла атаки на величину
л 1 дУ
Дк:-у' 'dt ’
Такое изменение в свою очередь изменит не только подъемную
силу, но и погонный аэродинамический момент МЕ относительно
оси жесткости на величину
да 2 да
ду V н
dt ' 9 2 Ь-
181
Этот момент будет периодическим, меняющим свой знак
вместе со знаком , и может вызывать крутильные колебания.
Крутильные колебания в данном случае черпают свою энергию
из набегающего потока, так как момент создается не за счет
энергии, накопленной колеблющейся системой вследствие началь-
ного импульса, а за счет энергии набегающего потока.
Итак, вследствие колебаний изгиба, появляется внешний
крутящий аэродинамический момент, периодически меняющий
свой знак и вызывающий крутильные колебания. Но как только
образовались крутильные колебания, появляется сила инерции
0*0 , .
тз (инерционная связь кручения на изгиб), вызывающая даль-
нейшее увеличение изгибных колебаний. Таким образом, часть
полученной от потока энергии через инерционную связь пере-
Фиг. 94. Первый цикл энерго-
обмена.
ходит из движения кручения в дви-
жение изгиба. Но увеличение изгиб-
ных колебаний вызывает увеличение
ду
и, как следствие, дальнейшее уве-
личение аэродинамического момента
УМе- Тем самым увеличиваются кру-
тильные, а через инерционную связь,
и изгибные колебания. Этот цикл
энергообмена, непрерывно продол-
жаясь, приводить к непрерывному
притоку энергии из потока, и если
количество притекающей энергии ста-
новится больше, чем ее расход (на
гистерезис, на преодоление вышеуказанных демпфирующих аэро-
динамических сил и т. д.), то возникают колебания с непрерывно
нарастающей амплитудой (флаттер).
Мы установили таким образом процесс, который приводит
к увеличению энергии в колеблющейся системе. Характер этого
процесса таков, что приток энергии в систему создает предпо-
сылки для дальнейшего притока энергии. Приток энергии возни-
кает благодаря наличию аэродинамической связи, которую мы
назовем аэродинамической связью изгиба на кручение (приток
энергии получается вследствие того, что движение изгиба поро-
ждает аэродинамический момент).
Найденную нами схему возможного возникновения флаттера
мы назовем первым циклом энергообмена. Схематически первый
цикл изображен на фиг. 94.
Изгибно-крутильные колебания крыла, подвергнутого началь-
ной деформации кручения. Пусть под влиянием начального
имульса возникли крутильные колебания. Вследствие колебаний
кручения происходит изменение подъемной силы за счет: 1) де-
182
формации кручения (что в аэродинамическом отношении эквива-
лентно изменению угла атаки) и 2) скорости крутильных колеба-
ний (как показывает анализ, изменение скорости крутильных
колебаний эквивалентно изменению угла атаки хорды крыла с
одновременным изменением кривизны его средней линии1). По-
лучающаяся за счет колебаний кручения подъемная сила будет,
очевидно, менять свой знак вместе с изменением знака О, т, е.
будет силой периодической. Эта сила вызывает изгибные коле-
бания крыла.
Здесь мы имеем дело с новой аэродинамической связью
кручения на изгиб. Благодаря колебаниям кручения набегающий
поток создает подъемную силу, которая вызывает колебания
изгиба, иначе юворя, колебания возникают за счет энергии
набегающего потока.
Но как только возникнут колеба-
ния изгиба, образуется инерционный
д’у /
момент тс (инерционная связь из-
Ьиба на кручение), который дальше
увеличивает колебания кручения, чем
опять создается предпосылка для даль-
нейшего притока энергии.
Здесь мы имеем второй цикл энер-
Рообмена, в котором есть звено (аэро-
динамическая связь кручения на изгиб),
создающее переход энергии из пото-
ка в колеблющуюся систему. Схема-
тически этот цикл представлен на
фиг. 95.
Третий цикл энергообмена. Рас-
сматривая колебания крыла без на-
бегающего потока, мы показали, что,
Фиг. 95. Второй цикл энер-
гообмена.
если в крыле совмещены оси тяжести и жесткости, то инерци-
онные связи между колебаниями изгиба и кручения отсутствуют.
Оба рассмотренные выше цикла энергообмена в этом случае ока-
зываются нарушенными. Значит ли это, что в данном случае не
существует такого процесса перехода энергии от потока к крылу,
который, раз начавшись, создавал бы предпосылки для даль-
нейшего перехода энергии? Оказывается, такой процесс все же
существует.
Пусть первоначально возникли колебания изгиба. За счет
скорости этих колебаний, как мы видели выше, образуется пе-
риодический аэродинамический крутящий момент, меняющий
свой знак вместе с : этот момент вызовет колебания круче-
dt
9 См. Е. П. Гроссман, С. С. Кричевский и А. А. Борин. К вопросу о потере
устойчивости конструкцией крыла в полете. Труды ЦАГИ выи. 202, 1935 г.
183
ния. Колебания кручения, как было показано, повлекут перио-
дическое изменение подъемной силы, вызывающее, в свою
очередь, колебания изгиба. Таким образом и при отсутствии
инерционных связей все же существует замкнутый цикл энер-
гообмена через две аэродинамические связи (третий цикл), при-
чем здесь переход энергии из по-
тока в крыло происходит в двух
звеньях, что схематически пока-
зано на фиг. 96. Следователь-
но совмещение осей центров тя-
жести и жесткости недоста-
точно для предотвращения воз-
можности флаттера.
Общий случай, уничтоже-
ние притока энергии. Обычно
крыло сконструировано таким
Знергия колебаний
изгиба
Энергия колебаний
кручения
Фиг. 96. Третий цикл энергооб- образом, что при его колебаниях
мена. имеются налицо все указанные
выше связи. Энергообмен со-
вершается при этом сразу через все четыре связи (т. е. все
три цикла имеют место одновременно), что представлено схе-
мой фиг. 97.
На этой схеме мы нанесли также 'стрелки, показывающие
расход энергии.
Три цикла энергообмена, рас-
смотренных выше, схематически
представлены контурами:
первый цикл—контуром АА^СА;
второй цикл—контуром DiDBBiDx\
третий цикл—контуром AArDxDA.
Хотя в крыле имеются налицо
все четыре связи, однако это еще
не значит, что флаттер обязательно
должен возникнуть. Из опыта из-
вестно, что вибрации с нарастаю-
щей амплитудой могут возникнуть
только при скорости набегающего
потока, превосходящей некоторую
Фиг. 97. Общий случай энерго-
обмена.
строго определенную для данного
крыла величину (критическую скорость). Чем объясняется
наличие этой скорости?
Мы видели, что наряду с притоком энергии происходит и
ее рассеивание. Количество притекающей и расходуемой энер-
гии зависит и от конструкции крыла (взаимного расположения
осей центров тяжести, жесткости и фокусов, величины жесткостей
изгиба и кручения, величины масс, моментов инерции и т. д.) и
184
от скорости набегающего потока. Для возникновения флат-
тера недостаточно только притока энергии благодаря свя-
зям, — необходимо еще чтобы и количество притекающей
энергии было больше количества расходуемой энергии. И вот
это-то обстоятельство имеет место только при некоторых
условиях.
Сами связи также необязательно вызывают приток энергии,—
они могут вызывать и дополнительный ее расход. Рассмотрим,
например, аэродинамическую связь кручения на изгиб.
Действие этой связи, как было указано, вызывает возникно-
вение дополнительной подъемной силы вследствие изменения
угла атаки крыла от кручения 1). Направление этой подъемной
силы может быть различным. Если крыло при движении вниз
- центр жесткости
• •• тяжести
Фиг. 98. Обращенное явление при перед-
нем положении центра тяжести
перекручивается на отрицательные углы атаки, а при движении
вверх—на положитель-
ные (фиг. 81), появляю-
щаяся подъемная сила
будет все время напра-
влена по направлению
движения изгиба и будет
его усиливать. Этот слу-
чай соответствует разоб-
ранному выше действию
аэродинамической связи
кручения на изгиб. Но
возможен и другой слу-
чай. Крыло может быть
сконструировано таким
образом, что при движе-
нии вниз оно перекручи-
вается в сторону положи-
тельных углов атаки, а
при движении вверх—в сторону отрицательных (фиг.98). Твгда
подъемная сила будет время противодействовать движений
изгиба. Рассмотрим, при каких условиях будет иметь место
первый случай, при каких второй.
Вначале рассмотрим крыло, у которого ось жесткости рас-
положена впереди центра тяжести. Выше указано, что в этом
случае подъемная сила будет направлена всегда по направлению
движения изгиба (фиг. 81).
Иначе происходит движение, если ось жесткости крыла рас-
положена позади его центра тяжести. При ускоренном движе-
нии такого крыла под действием упругих сил по направлению
к положению равновесия центр тяжести будет вследствие инерции
отставать от оси жесткости, и так как он находится перед осью
жесткости, то крыло будет закручиваться, как показано на
*) Для простоты мы опускаем здесь влияние на подъемную силу угловой
скорости колебаний.
185
фиг. 98. .В этом случае подъемная сила будет противодейство-
вать движению изгиба.
Итак, подъемная сила, получающаяся вследствие кручения
крыла от сил инерции, будет увеличивать колебания, если центр
тяжести расположен позади оси жесткости, и будет им противо-
действовать (демпфировать), если центр тяжести расположен
впереди оси жесткости.
Второй цикл энергообмена в последнем случае не будет
давать притока энергии, а будет дополнительно рассеивать ее.
Схематически это изображено на фиг. 99.
Покажем, что первый цикл энергообмена путем соответству-
ющей конструкции крыла также можно превратить в источник,
демпфирования колебаний.
Для этого достаточно поместить
ось жесткости впереди фокуса
крыла. В самом деле, пусть крыло
закручивается в сторону увеличе-
ния угла атаки. При увеличении
угла атаки приращение аэродина-
мического момента 6} дет положи-
тельным, т. е. будет действовать
в сторону дальнейшего увеличения
угла атаки, если ось жесткости
расположена за фокусом; прира-
щение момента будет отрицатель-
ным, если ось жесткости, к кото-
рой мы относим момент, будет рас-
положена впереди фоку са.
В первом случае момент будет
стремиться закрутить крыло даль-
ше в сторону увеличения угла ата-
ки (именно этот случай действия
Фиг. 99. Обращенный второй
цикл энергообмена.
аэродинамической связи изгиба на кручение мы и рассматривали
во всех предыдущих схемах); во втором случае момент будет
противодействовать движению. Очевидно, что при кручении
крыла в сторону отрицательных углов атаки картина будет та
же: если ось жесткости расположена за фокусом, аэродинамиче-
ский момент будет помогать кручению; если же она расположена
впереди фокуса, возникает аэродинамический момент, демпфи-
рующий движение кручения.
Схема первого цикла энергообмена в крыле с осью жестко-
сти, расположенной перед фокусом, показана на фиг 100.
Схема действия аэродинамической связи изгиба на кручение
в этом случае такова. При движении крыла вниз угол атаки’уве-
личивается, так что возникает аэродинамическим момент, стре-
мящийся уменьшить угол атаки, благодаря чему и сам момент
по абсолютной величине уменьшается. При движении крыла
вверх угол атаки уменьшается, но возникает аэродинамический
момент, стремящийся его увеличить. Таким образом момент,
1SS
возникающий в этом случае, создает предпосылки для своего
собственного уничтожения, в то время как при расположении
оси жесткости за фокусом действие аэродинамического момента
обратно: его действие создает
предпосылку дальнейшего ро-
ста.
На фиг. 101 изображена
схема энергообмена в крыле,
у которого действие обеих
аэродинамических связей об-
ращено, для чего, очевидно,
необходимо и достаточно по-
местить центр тяжести крыла
перед осью жесткости и ось
жесткости—перед осью фоку-
сов. Поскольку крыло, скон-
струированное таким образом,
не поглощает энергию из на-
бегающего потока воздуха, оно
не может быть подвержено фл
Мы не. будем останавливал
случаях, могущих представиться
Фиг. 101. Обращенный общий слу-
чай энергообмена.
крыла поместить центр тяжести
центр жесткости перед фокусом,
мических связей обращается, и
демпфирующие силы.
Однако указанное расположение осей чрезвычайно трудно
осуществить конструктивно. В современных конструкциях
крыльев они расположены как раз обратно: центр тяжести на-
ходится позади оси жесткости, а ось жесткости—позади фокуса.
(В среднем для крыльев обычной конструкции фокус находится,
на 25%, центр жесткости на 32-36% и центр тяжести на 44-50%
хорды от передней кромки).
Фиг. 100. Обращенный первый
цикл энергообмена.
ITT еру.
?я на многих промежуточных
при различных конструкциях
крыла, так как метод анализа
достаточно ясен, и читатель
легко может провести этот
анализ самостоятельно.
г) Меры предотвращения
изгибно-крутильного флат-
тера
Выше мы уже указали иде-
альную конструкцию крыла,
при которой флаттер стано-
вится невозможным: для этого
достаточно в каждом сечении
перед центром жесткости и
При этом действие аэродина-
поток создает дополнительные
18”
Для предотвращения флаттера достаточно не обращать
Сс'чзи, а нарушить замкнутость циклов энергообмена; тогда не-
возможен будет периодический процесс, при котором переход
энергии от потока к крылу создает предпосылки для дальнейшего
перехода этой энергии. Достаточно совместить все три цен-
тр* в каждом сечении крыла (тяжести, жесткости и фокусов)
в одной точке; тогда будут отсутствовать обе инерционные
связи, благодаря чему разрушатся первый и второй циклы энер-
гос4мева.
Рассмотрим, что произойдет при этом с аэродинамической
связью изгиба на кручение. Эта связь создается благодаря тому,
что при изгибных колебаниях происходит изменение угла атаки,
влекущее за собой изменение аэродинамического момента отно-
сительно оси жесткости. Но фокус кры-
Ряергия колебаний ।
изгиба
ла есть такая точка, момент относитель-
но которой не зависит от угла атаки, и
если ось жесткости совпадает с осью
фокусов крыла, то изменение угла ата-
ки не вызовет никакого изменения мо-
мента относительно оси жесткости. Сле-
довательно, в данном случае, аэродина-
мическая связь изгиба на кручение от-
Яритон сутствует, и замкнутость третьего цик-
энергии ла энергообмена также нарушается.
ла энергообмена также нарушается.
Диаграмма энергообмена крыла с тре-
мя совмещенными осями показана на
Энергия колебаний
вручения
ФнГ 102. Случай совмеще-
еи» центра тяжести с цен-
трем жесткости и фокусом.
фиг. 102. Движение кручения в данном
случае только рассеивает свою энергию
и потому непременно затухнет, — тем
самым оборвется аэродинамическая
связь кручения на изгиб, прекратится
приток энергии в движение изгиба, и
оно также затухнет.
Таким образом при совмещении трех
осей крыла в одной точке флаттер так-
же становится невозможным.
Указанные выше пути устранения флаттера основаны на воз-
можности создать такую конструкцию крыла, при которой пол-
ностью прекращается приток энергии по крайней мере в один
из видов движения. Возможен и другой путь устранения опас-
ности флаттера, основанный на количественном анализе энерго-
обмена. Для предотвращения флаттера нет необходимости пол-
ностью прекращать приток энергии в колеблющуюся систему,
достаточно, чтобы количество притекающей энергии было мень-
ше, чем ее рассеивание. В этом случае колебания также будут
затухающими. Кроме того, нет необходимости конструировать
крыло так, чтобы оно ни при каких условиях не было подвер-
жено флаттеру. Достаточно, чтобы флаттер становился возмож-
J.88
ным только при скоростях, значительно превосходящих макси-
мальную скорость самолета.
Количество притекающей и расходуемой при колебанияк
крыла энергии зависит от жесткостей изгиба и кручения крыла,
его масс, моментов инерции, формы крыла и т. д., а также от
скорости полета. Каковы должны быть эти факторы для преду-
преждения возникновения флаттера, мы увидим из дальнейше-
го количественного анализа явления. Укажем лишь, что уче1
расходуемой энергии позволяет сделать тот вывод, что возмож-
на конструкция крыла, у которого ось жесткости совмещена с
фокусом, а центр тяжести находится позади ее, и которое тем
не менее не подвержено флаттеру ни при каких скоростях. В
самом деле, у такого крыла приток энергии в движение кру-
чения получается только через инерционную связь изгиба на
кручение. Если центр тяжести находится на небольшом расстоя-
нии от оси жесткости, то этот приток энергии невелик и может
быть сделан меньше, чем ее расход, благодаря чему флаттер
станет невозможным.
31. Влияние конструктивных параметров на критическую
скорость изгибно-крутильного флаттера крыла
Изложенный выше метод определения критической скорвсти
позволяет определить скорость по заданным конструктивным
параметрам крыла. Однако, если по расчету оказалось, что кри-
тическая скорость крыла с/ишком низка, конструктор для ее
увеличения должен знать — какие параметры и в какую сторону
наиболее целесообразно изменять. Кроме того, нужно выяснись,
за какими параметрами в первую очередь должен следить кон-
структор в процессе проектирования, чтобы обеспечить безо-
пасность конструкции от флаттера.
Оказывается, что основными параметрами, которые может
менять конструктор для увеличения критической скорости, явля-
ются: жесткость конструкции, отношение GJKp :Jm („частотная
характеристика") и положение оси центров тяжести по размаху.
В первую очередь мы остановимся на влиянии этих основных
характеристик, а затем кратко укажем также и на влияние осталь-
ных конструктивных параметров (массы, формы крыла и т. д);
однако последние обычно не удается менять без капитально'
переделки конструкции.
а) Влияние жесткости крыла на критическую скорость
Можно доказать, что одновременное изменение в п раз же-
сткости крыла на изгиб и кручение влечет за собой изменение
критической скорости в раз.
Укажем, что эта теорема справедлива не только в отноше-
нии крыла, но и в отношении любой системы, подвержена >
189.
флаттеру (например, крыло с элероном, хвостовое оперение):
изменение всех жесткостей системы в п раз влечет за собой
изменение критической скорости в х/п раз. Однако, влияние
изгнбной жесткости EJ и крутильной жесткости GJKp неодина-
ково. Исследование физических причин возникновения изгиб-
но-крутилыюго флаттера показывает, что основную роль при
флаттере играет кручение. Поэтому всегда параметры., харак-
теризующие кручение, влияют на критическую скорость силь-
нее, чем параметры, характеризующие изгиб.
На фиг. 103 показана типичная кривая изменения критичес-
кой скорости в зависимости от жесткости крыла на кручение.
Исходным служило крыло, для которого Икр=155 м/сек. За-
тем жесткость кручения этого
крыла была изменена в т] раз
(одинаково по всему размаху),
а все остальные параметры кры-
ла (в том числе и жесткость
изгиба) сохранены. С достаточ-
ной точностью закон изменения
критической скорости в зави-
симости от изменения жесткости
кручения для данного крыла
можно представить формулой:
где —критическая скорость
исходного варианта крыла. Во-
обще, из большого числа расче-
тов было установлено, что кри-
тическая скорость изменяется почти точно пропорционально
корню квадратному из жесткости кручения. Следовательно,
если какое-либо крыло имеет критическую скорость v,.p и жест-
кость кручения крыла изменить одинаково по всему размаху
в раз, то критическая скорость измененного крыла будет:
<311)
Наиболее рациональной, с этой точки зрения, конструкцией
является кессонное крыло, как обладающее относительно боль-
шей крутильной жесткостью.
Следует подчеркнуть, что сказанное будет справедливо толь-
ко в том случае, если частота крутильных колебании крыла
значительно выше частоты изгибных колебаний, как практичес-
ки й бывает. Ниже будет подробно выяснен смысл этой ого-
ворки.
Формула (31.1) позволяет, с одной стороны, быстро прики-
нуть значение критической скорости, которое получается при
.390
изменении жесткости кручения крыла, а с другой стороны, опре-
делить величину необходимого изменения жесткости, чтобы по-
лучить заданную величину критической скорости.
Как уже говорилось, жесткость крыла на изгиб влияет
гораздо слабее жесткости кручения. На фиг. 104 показано что
происходит с критической скоростью крыла одного существую-
щего самолета, если жесткость изгиба меняется в Е раз. Любо-
пытно, что увеличение жесткости на изгиб ведет сначала даже
к уменьшению критической скорости; при некотором значении
жёсткости изгиба критическая скорость достигает минималь-
ного значения и только при дальнейшем увеличении жестко-
сти изгиба критическая скорость увеличивается. Выясним при-
чину этого явления.
Крыло имеет две собственные частоты колебания: частоту
изгибных колебаний и частоту крутильных колебаний, причем
частота колебаний изгиба
кручения. При увеличении
жесткости изгиба частота
изгибных колебании также
увеличивается и при доста-
точно большом значении EJ
может достигнуть частоты
крутильных колебаний. Ока-
зывается, критическая ско-
рость изгибно-крутильного
флаттера крыла, имеет ми-
нимум именно при совпа-
дении частот изгиба и кру-
чения1). Явление это носит
название внутреннего резо-
нанса. Следовательно, величина критической скорости зависит
не только от абсолютной величины жесткостей крыла на изгиб
и кручение (которые обусловливают определенные величины ча-
стот), ио также и от различия между частотами.
Из изложенного вытекает, что при конструировании нужно
следить, чтобы частоты различных форм колебания не были
очень близки. Особенно это касается хвостового оперения,
где возможно много различных форм колебания; об этом мы
скажем ниже.
Отметим, что это указание зафиксировано как обязательное
требование в нормах прочности США.
б) Частотная характеристика
Частотной характеристикой мы будем называть отношение
ОАр :Jm. Характер изменения этого отношения вдоль размаха
’) Точнее — при почти полном совпадении.
Фиг. 104. Влияние жесткости изгиба
на (реальный самолет).
191
крыла оказывает существенное влияние на величину критичес-
кой скорости. Это объясняется тем, что частотная характери-
стика в основном определяет вид функции кручения в (z), т. е.
характер распределения амплитуд крутильных колебаний по
длине крыла. Важно поэтому прежде всего заметить, как влия-
ет вид функции о (г) на величину критической скорости.
Как показывают расчеты, если
для двух крыльев функции
и ®2 имеют вид, показанный на
фиг. 105, то для соответствую-
щих критических скоростей ока-
жется I/2<V1. В большинстве
современных конструкций отно-
шение GJKp : Jm по размаху крыла
имеет характер, указанный на
фиг. 106а, т. е. понижается
к концу крыла. Это говорит о
том, что конец крыла относи-
тельно перетяжелен по сравне-
жесткость кручения к концу кры-
Фиг. 105. Две функции формы
крутильных колебаний.
Фиг. 106. Изменение частотной
характеристики по размаху: а—
обычное, б — желательное.
нию с корневой частью, т. е.
ла убывает быстрее, чем момент инерции.
Естественно, что при этом амплитуда колебаний конца будет
относительно велика, т. е. кривая ® будет иметь характер кри-
вой (фиг. 105) ипкак толь-
ко что говорилось,' критиче-
ская скорость поэтому будет
снижена.
Следует стремиться к то-
му, чтобы частотная характе-
ристика GJKp :Jm к концу кры-
ла не снижалась, а если воз-
можно, то даже увеличива-
лась (фиг. 1066). Если притом
на крыле нет участков с рез-
ким падением жесткости, то
вид функции ф будет прибли-
жаться К (фиг. 105).
Особо нужно подчеркнуть,
что из-за трудностей измене-
ния частотной характеристики
чиной GJKp:Jm (особенно на концевой части крыла) нужно тща-
тельно следить еще в4стадии проектирования.
готовой конструкции, за вели-
на
в) Положение осей центров тяжести, центров жесткости
и фокусов по размаху крыла
На основании качественных соображений было показано, что
критическая скорость существенным образом зависит от поло-
192
Фиг. 107. Влияние
расположения цен-
тров тяжести и
жесткости на VKp.
ження в крыле трех осей: фокусов, центров жесткости и центров
тяжести. Из этих трех осей сильнее всего влияет на величину
критической скорости положение оси центров тяжести.
На фиг. 107 показано изменение критической скорости одного
крыла в зависимости от положения оси центров тяжести г :Ь для
оазличных положений оси жесткости хй -,Ь (неизменных по всему
размаху). Здесь г и х„ расстояния от передней кромки до центра
тяжести и до центра жесткости. Из графиков можно сделать
следующий вывод; если центр тяжести крыла расположен не
дальше 50—55% хорды от передней кромки, то положение цент-
ра тяжести весьма сильно влияет на величину критической ско-
рости. Передвижение оси центра тяжести сечений крыла вперед
всего на 1 % хорды дает значительное
увеличение критической скорости. Так,
например, перемещение оси центров тя-
жести с 42 до 41% хорды увеличивает
критическую скорость на 11 лс/сек., т. е.
почти на 40 юи/час. Так как у совре-
менных крыльев центр тяжести располо-
жен ближе 50% хорды от передней кром-
ки, то в современной конструкции крыла
следует бороться за каждый процент
в положении центра тяжести с тем,
чтобы помещать центр тяжести как
можно ближе к передней кромке.
Положение центра тяжести является
тем параметром, вариацией которого чаще
всего увеличивают критическую скорость
на готовой конструкции, если критическая
скорость оказывается недостаточней. Для
этого загружают переднюю кромку крыла
и максимально облегчают заднюю (напри-
мер, изменяя вес элерона заменой метал-
лической обшивки на полотняную и т. и.).
Нет нужды изменять положение центра тяжести во всех сече
ниях крыла. Так как наибольшее влияние на флаттер всегда
оказывает конструкция конпевой части крыла, то переднюй»
кромку загружают вблизи конца крыла (вообще при конструи
ровании нужно особенно тщательно следить за положением
центра тяжести в концевой части крыла).
Обычно бывает достаточно очень небольшого дополнитель-
ного груза в передней кромке вблизи конца крыла, чтобы зна-
чительно увеличить критическую скорость. Так, для одного
крыла вессм .'.СО кг, удалось повысить критическую скорость
с 90 до 140 .м/сек. установкой грузов по 4 кг на правое и левое
полукрыло (всего 8 кг). Но возможны случаи, когда для полу
чения достаточной величины критической скорости требуется
довольно значительный вес.
13 Гроссман и Пановко
193
На фн1. 108 показана типичная кривая изменения критической
скорости в зависимости от положения центра тяжести. Если
ценному самолету соответствует точка В этой кривой, то малей
шее изменение в положении центра тяжести существенно отра-
зится на величине критической скорости. Если же расположение
центра тяжести в крыле соответствует точке Д, то небольшие
изменения его положения не смогут ощутительно повлиять на
«величину критической скорости; большинство современных кон
струкций соответствует первому случаю.
Очень распространено мнение, что на величину критической
(корости влияет не столько расстояние от центра тяжести до
Фиг. '08. Влияние положе-
ния центра тяжести на VKp
положения центра
жесткости на VKp
передней кромки г:Ь, сколько взаимное расположение осей
центров тяжести и жесткости. Как было показано в п. 30, это,
однако, неверно. На фиг. 109 показано изменение критической
скорости некоторого крыла, в зависимости от положения оси
жесткости при двух фиксированных положениях центра тяжести.
Мы видим, что при изменении положения оси жесткости крити-
ческая скорость меняется не очень сильно (тем более, ч то реаль-
но возможные значения : & = 0,23 4-0,40), несмотря на то, что
расстояние между осями жесткости и тяжести (з = г — %,) меня
ется очень значительно. Даже совмещение осей жесткости и
тяжести (точки кривых фиг. 109, для которых г = х<3) не дает
заметного изменения критической скорости, если положение оси
иентров тяжести относительно передней кромки крыла (г) фикси-
ровано. Между тем, при одном и том же положении оси жест-
'94
кости изменение г от г = 0,4 b до г = 0,5& изменяет критическую
скорость чуть ли не вдвое.
Тот же вывод можно сделать и из внимательного рассмотре-
ния фиг. 107. Из сказанного следует, что при конструирования
можно ие особенно заботится о положении в крыле оси жест-
кости.
Оказывается, что всегда можно подобрать в крыле взаимное
положение осей тяжести, жесткости и фокусов таким образом,
чтобы крыло не было подвержено флаттеру ни при каких ско
ростях.
Прежде всего рассмотрим случай крыла, у которого ось
жесткости крыла совмещена с осью фокусов крыла. Напомним,
что фокус находится на расстоянии 25°/0 хорды от носка про
филя и потому в рассматриваемом частном случае мы принимаем:
= (31.2)
Для рассматриваемого случая, согласно (29.12), будем иметь:
I
=0; d2l =0; =-P^f bsfdz. (31.3}
и
В силу этого по формулам (29.15) находим:
О2 = 0; £а = 0. (31.4)
Поэтому в формулах (29.17) получается:
L = 0; М = W = B^D^ — BliEt — D*At. (31.5)
и критическая скорость, вместо уравнения (29.16), определится
из уравнения:
MV2 + N=0,
>ткуда
Формула (31.6) позволяет определить положение линии центров
тяжести крыла, при котором критическая скорость перестает
существовать.
Так как при малых скоростях условия (23.1) должны выпол-
няться, то, принимая во внимание (29.14), сразу получаем:
«1>0, £>, >0, Дг>0.
13“
-л****®»
Таким образом, скорость, определяемая формулой’(31.6), может
существовать только в тем случае, когда С2<0, т. к. если
> 0» VKp будет мнимой величиной.
Таким образом, при
С,>0
(31.7)
крыло будет устойчиво ври всех скоростях.
Пользуясь (29.15), межьо загл.с<.ть (31.7) в развернутом виде
— ~4~ d \\d^> О,
т. к. согласно (31.3) £22 = сГ21 = 0.
Подставляя значения &13,csl,rf1P d2i из уравнений (29.2) и (29.12).
найдем:
Il ii
— р j'&f'pdz-J msfodz + ' р j bf2dz • у^Р JbWdz^O. (31.8)
0 0 0 0
Так как мы рассматриваем случай, когда ось жесткости сов-
падает с осью фокусов крыла (х0[Ь = */4), то:
Подставляя это, находим окончательное условие, которому дол-
жно удовлетворять положение 1иьии центров тяжести сечений
крыла, чтобы оно не могло Сыть подвержено флаттеру ни при
каких скоростях:
i I
bfydz § mbfadzJ bfydz +
о о
(31.9)
Если расстояние от центра тяжести до передней кромки
в долях хорды по всем сечениям крыла одинаково (г -Ь = const),
то это условие можно переписать в следующем виде:
/ i
J bpdz J b'^dz
r 1 к о_______________о________
ft 4 16Р I (
j* rnbfvdz J bfadz
и Q
(31.101
196
Предположим теперь, что положение линии центров тяжести
течений крыла удовлетворяет условиям (31.9j или (31.10), но ось
жесткости не совпадает с линией фокусов, а сдвинута назад.
Расчеты, произведенные для различных крыльев, показывают,
что если при xolb — i/i критическая скорость отсутствует, то
онт будет отсутствовать и при xjb'^1^. Следовательно (так как
реально не бывает), можно считать, что выполнение
условий (31 9) али (31.10) обеспечивает крыло от флаттера
на любых скоростях при всех реально встречающихся поло
жениях оси жесткости.
г) Влияние распределения, масс по хорде крыла
Разнесение масс по хорде крыла при фиксированной величине
самих масс и их центра тяжести, может быть охарактеризовано
радиусом инерции х = i .
у т
На фтг. 110 показано влияние
на критическую скорость радиуса
инерции некоторого крыла. Сред-
ние значения х для консольной ча-
сти крыла —26—30 % хорды. Из гра-
фика видно, что даже небольшие
изменения в величине радиуса инер-
ции (при фиксированном положе-
нии линии центров тяжести) могут
заметно изменить критическую ско-
рость. Увеличение масс также вле-
чет за собой уменьшение критиче-
ской скорости (хотя и в меньшей
степени). Поэтому можно было бы
рекомендовать максимально облег-
чать крыло, но и без того всегда
крыло бывает уже облегчено на-
столько, насколько это возможно.
Во всяком случае, учитывая влия-
Фиг. ПО. Влияние радиу-
са инерции на VKp.
ние массовых характеристик в целом, следует еще раз подчер-
кнуть необходимость размещения всех масс в крыле возможно
ближе к передней кромке и максимального облегчения элеронов
д) Влияние формы крыла в плане
Форма крылз в плане во многом уже предопределяет вели-
чину остальных конструктивных параметров крыла. Поэтому,
чтобы исследовать ее влияние на критическую скорость, необ-
ходимо задаться определенной зависимостью между формой
крыла в плане и его жесткостью, массой, расположением осей
Тяжести и жесткости и т. д. Можно приближенно считать, что
197
конструктивные параметры крыла связаны с его формой еле
•дующим образом: жесткости изгиба и кручения пропорциональ-
ны четвертой степени хорды; масса (погонная) пропорциональна
квадрату хорды; расстояние от оси жесткости до передней кром
ки, расстояние от центра тяжести до оси жесткости, а также
радиус инерции, — пропорциональны хорде.
При этих условиях для серии трапецевидных крыльев, отли-
чающихся только сужением Е (5 — отношение концевой хорды
к корневой), подсчитано:
Е 1 0,8 0,6 ОД | 0,2
VKP юо о/о 155% 203 о/0 254%^304%
Следовательно, из серии крыльев одинакового размаха *
площади наибольшую скорость обеспечивает крыло с ма.к^
симальным сужением.
Этот вывод и следовало ожидать: флаттер вызывается аэро-
динамическими силами, которые тем меньше, чем меньше хорда
крыла. Сужение крыла с сохранением площади и размаха ведет
к уменьшению А>рды, следовательно, и аэродинамических сил
па концевой части, т. е. именно там, где жесткость крыла наи
меньшая. Это естественно, влечет за собой увеличение крити-
ческой скорости.
Следует кроме того отметить, что сильно коническое крыло
может быть сделано относительно более жестким,чем крыло менее
суживающееся.
е) Изменение критической скорости с высотой полета
С высотой полета изменяется плотность воздуха р, а, следо
вательно, и критическая скорость. Выясним влияние высоты
иолета, чтобы установить обеспечит ли расчет критической ско
рости, проведенный для определенной высоты, безопасность по-
лета и на других высотах.
Чтобы получить условия пересчета критической скорости-,
с одной высоты на другую, обратимся к формулам (29.15).
Введем обозначения:
— си^22“С"— dtifin- (31.11)
Тогда согласно (29.15):
С.-С.+ С\.
(31.12)
W8
далее введем следующие обозначения:
L' = В£Я). - D. L" =
М‘ = fljG/D, + ВХС& — Вг*Е9 — 2DXD2A,; At” = BXC^DX (31.13}
Тогда согласно (29.17):
£ = £'+£"; Af = M'+M" (31.И)
Легко непосредственно убедиться в том, что £' пропорци-
онально р4; L" пропорционально р5; М' пропорционально р8:
714" пропорционально р4; N пропорционально ра. оэтому, если
вычислены значения L', L", Л1', Л1", М для какой-либо высоты
полета Н, которой соответствует значение плотности воздуха р,
затем по формулам (31.14) определены L, М, N и из уравнения
(29.16) найдена критическая скорость на этой высоте, то для:
получения критической скорости на высоте Н„ которой соог
ветствует плотность воздуха рь поступаем следующим образом
Умножаем L' на (pt:p)2: £*—на (р. :р)8; 714'—на р( :р; At"— на
(PiTp)2; N оставляем без изменения. Затем определяем L, М, N
по формулам (31.14) и критическую скорость на новой высоте
по ургвнению (29.16).
Если С"2 мало по сравнению с С'г (что обычно и бывает)
то можно считать, что:
V VJ’
где V—критическая скорость на высоте Н’, V, — критическая
скорость на высоте Нх, и а лежит в пределах 0,35—0,5.
Таким образом, с ростом высоты (и падением р) критике.-
кая скорость увеличивается.
ГЛАВА 8
Элеронные формы флаттера крыла1)
32. Явление изгибно-элеронного флаттера
Изгибно-крутильпый флаттер крыла встречается сравнительно
редко. Большинство случаев возникновения флаттера крыла в
полете порождалось несбалансироьаш ыми в весовом отношении
элеронами. Поясним вкратце сущность этого явления.
Ц Е. П. Гроссман, М В. Келдыш, Я. А1. Пархомовский. Вибрации «рыл*
е мереном (Труды ЦАГИ. К» 5с7. 1W7 г ). См. танке Е. П. Гроссман. Изгибно
элеронный флаттер Пруды ЦАГИ № 534, 1941 г.).
№
Выведем крыло из положения равновесия, отклонив конец его
вверх, и затем предоставим его самому себе. Крыло начнет со-
вершать колебательное движение. Последовательные положения
крыла и элерона показаны на фиг. Ill, причем, кручение крыла
считается отсутствующим. В начальный момент I крыло придет
в движение под действием <\<л упругости и станет приближать^
к своему положению равновесия III.
Если центр тяжести элерона находится позади оси вращения,
го вследствие инерции он будет отставать от движения крыла и
элерон отклонится так, как показано в положениях //и III. Пос-
ле того, как крыло по инерции перейдет положение равновесия,
упругие силы начнут действовать в обратную сторону, крыло
станет двигаться замедленно и центр тяжести элерона начнет до-
гонять в своем движении крыло (IV). Для простоты предположим,
что к моменту остановки крыла (V) элерон опять займет как раз
центральное положение. После того, как силы упругости оста;
повят крыло, оно начнет двигаться вверх (положения V—IX),
причем вначале элерон по инерции.отклонится вниз (VI и VII),
! п т tv v w я ®
Фиг. ill. Схема возникновения побуждающей силы при изгибных ко-
лебаниях крыла с элероном.
затем, когда крыло перейдет среднее положение и движение его
будет замедляться, элерон будет по инерции догонять крыло
(VII—IX). Далее опять ншнется движение вниз и т. д. Из ска-
занного ясно, что элерон будет отклоняться все время в сторо-
ну, прогивош ложную направлению движения самого крыла.
За счет отклонения элерона возникает дополнительная подъ-
емная сила, которая, очевидно, будет направлена вниз, если эле-
рон отклонен вверх, и направлена вверх, еслч элерон отклонен
вниз. Таким образом в рассматриваемом случае (когда центр
тяжести элерона находится позади его оси вращения) подъемная
сила, во знаке ощяя за счет отклонения элерона, будет всегда
направлена в ту же сторону, куда движется крыло. Эта подъ-
емная сила. б;дет стремиться дальше увеличивать колеба-
ния и. может вызвать флаттер.
Здесь возникает замкнутый цикл энергообмена между
системой крыло-элерон и потоком: возникшие изгибные колеба-
ния крыла вызывают инерционные силы, отклоняющие элерон, а
за счет отклонения элерона возникает аэродинамическая сила,
увеличивающая изгибные колебания. Когда увеличиваются из-
гибные колебания, увеличивается и отклонение элерона, вслед-
ствие чего, еще более увеличивается и сила, усиливающая коле-
300
бания. Таким образом в данном случае имеется непрерывный
процесс перехода энергии от потока к крылу такого характера,
при котором становится возможным флаттер. Разумеется, что,
наряду с рассмотренной возбуждающей силой, при изгибных
колебаниях крыла возникают также и демпфирующие силы. По-
этому для появления флаттера необходимо, чтобы возбуждение
превосходило демпфирование.
Силы воздействия воздуха на крыло зависят от скорости по-
лета. Чем больше скорость почета, тем больше будут и аэроди
иамические силы, кик демпфирую-
щие так й возбуждающие. При ма-
лых скоростях полета, когда аэро-
динамические силы относительно
невелики, большую роль играет
внутреннее трение и колебания,
возникшие в результате действия
какого-либо импульса, будут зату-
хающими.
С увеличением скорости воз-
буждающие силы растут быстрее
демпфирующих и, начиная с неко-
торой скорости работа, совершае-
мая возбуждающими силами, ста-
нет превышать работу, затрачивае-
мую системой на преодоление
демпфирующих воздействий. Начи-
Фиг. 11?. При V = Vxp работа
возбуждающих сил равна работе
демпфирующих сил.
ная с этой скорости полета амплитуда колебаний, возникших под
действием любого случайного импульс), будет возрастать, т. е.
возникнет флаттер. На фиг. 112 показано примерное изменение
работы возбуждающих и демпфирующих сил за один цикл коле
бания, с изменением скорости полета.
Может быть и такой случай, когда работа возбуждающих
сил при любой скорости полета меньше, чем работа демпфиру-
ющих сил. Например, если бы элерон был жестко закреплен к
крылу, то исчез бы источник возбуждающие сил и при колеба-
ниях возникла бы только демпфирующая сила колебаний самого
крыла. У такой система флаттер не мог бы возникнуть ни при
какой скорости полета; при всех скоростях колебания были бы
затухающими.
Мы видели, что э перон при движении крыла вниз отклоняется
вверх и обратно. Такое отклонние элерона поручается благо
даря тому, что центр тяжести элерона находится позади его оси
вращения и когда последняя движется ускоренно вместе с кры-
лом, центр тяжести по инерции отстает. Поэтому, для предот-
вращения возможности возникновения флаттера надо поместить
центр тяжести элерона впереди его оси вращения путем установки
специальных грузов (балансиров) в передней кромке элерона или
на специальных кронштейнах (фиг. 113). У такого крыла откло-
201
колебаний крыла, то элерон при флаттере будет вести себя так
же. как если бы груза не было вовсе. Вообще эффективность
балансирующего груза существенно зависит от того, в каком се-
пенни элерона этот 1руз помещается. Весьма распространено
мнение, что эффективность весовой балансировки целиком опре
деляется положением центра тяжести системы, груз-элерон.
Это было бы справедливо, если бы все сечения крыла двшались
одинаково. Положение центра тяжести само по себе не опре-
деляет поведения крыла с элероном при флаттере.
Обратимся к выводу количественного критерия, который
определяет степень балансированное™ элерона с учетом распре-
Фнг. 1>4. Схема изгибных колебаний крыла с элероном
деления амплитуд колебания по размаху крыла. Таким Крите
рием служит величина момента инерционных сил, развиваемых
элероном и балансиром при изгибных колебаниях крыла.
Рассмотрим крыло, совершающее изгибные колебания и по-
казанное в перспективе на фиг. 114. Пусть ось жесткости
крыла, совпадавшая в положении равновесия с осью Az, в рас-
сматриваемый момент времени занимает положение A'z'. Прогиб
крыла, как и выше обозначим У. Выделим элемент элерона, за-
ключенный между двумя соседними сечениями тп и т'п', йахо-
дящимися на расстоянии dz друг от друга. Масса этого элемента
dm — mdz где тэ—погонная масса элерона. При колебаниях
(У-У ,
разовьется сила инерции, соответствующая этой массе—dz.
Момент силы инерции вокруг оси вращения элерона 00’ будет
где °в—расстояние центра тяжести рассматриваемого
-.264
сечения элерона от его оси вращения (считаегся положительным,
если центр тяжести лежит позади оси вращения). Суммируя
моменты инерционных сил по всем сечениям элерона, найдем
общий момент инерционных сил Мо, вращающий элерон при
изгибных колебаниях крыла
(32.1)
(интегрирование распространяется на всю длину элерона).
Принимая, как и выше,
найдем:
Я J m^tfdz = c^,
zi
(32 2)
где через с1а обозначено
(32-3)
Допустим, чю на элероне нет никаких балансирующих гру-
зов и центр тяжести во всех сечениях элерона лежит позади
оси вращения (аэ>0). Функцию формы колебаний f(z) мы усло-
вились всегда нормировать так, чтобы на конце крыла было
/(/)=+ 1 (п. 5). Тогда почти на всем участке, занятом элероном,
будет /(z)>0. Следовательно в рассматриваемом случае, когда
центры тяжести сечений элерона находятся позади его оси вра-
щения, будет с13<0. Но как было показано выше, в этом слу-
чае элерон под влиянием инерционного момента Л1и отклоняется
таким образом, что появляется аэродинамическая сила, вызы-
вающая флаттер.
Чтобы флаттер не мог возникнуть, момент /Ии должен откло-
нять элерон в противоположную сторону, для чего знак момента
должен быть другим, т. е. должно быть с18>0. Из формулы
(32-3) видно, что этого можно достигнуть, например, балансируя
каждое из сечений элерона таким образом, чтобы центры тя-
жести всех сечений находились впереди оси вращения, т. е. для
всех z было бы аэ<0. Таким образом мы опять приходим к вы-
воду, уже полученному нами ранее из физических соображений:
если центры тяжести всех сечений элерона находятся
впереди его оси вращения, то элеронный флаттер невозможен.
21*5-
Рассмотрим теперь, как будет вести себя элерон, сбаланси-
-рованный при помощи сосредоточенных грузов (фиг. 115). Пусть
/И6—масса сосредоточенного груза и аб—расстояние его центра
тяжести от оси вращения элерона О, принятое положительным,
когда центр тяжести груза находится впереди оси вращения
элерона. Чтобы получить инерционный момент, вращающий эле-
рон при изгибных колебаниях крыла, в данном случае необхо-
димо к моменту от масс самого элерона, который определяется
формулой (32-2), добавить еще момент от инерционных сил гру-
за. Ускорение груза будет причем f(z6) есть
значение /(z) в сечении z = z6, в котором расположен груз.
Инерционная сила, развиваемая гру-
зом при колебаниях равна M6f(z,,)q
и момент этой силы относительно
оси вращения элерона
+M(fl6f(z6)'q.
Фнг. 115. Балансировка элеро-
на сосредоточенными грузами
Уже отсюда видно, что эффектив-
ность груза зависит от его место-
положения (координаты гб). Доба-
вляя этот момент к моменту (32-2)
самого элерона, получим значение
полного момента инерционных сил:
= (32-4)
где
с12 =— $mf,fdz+Mez6f (z6) (32-5)
zi
|нри нескольких грузах второе слагаемое должно быть принято
в виде E/U^j/^i)].
Для невозможности флаттера должно быть с12>0(т. е. инер-
ционный момент должен вращать элерон в ту сторону, как на
фиг. 113, а не в ту, как на фиг. 111). Минима 1ьно необходимая
масса балансирующего груза может быть определена из условия
ci9 — О и равна:
• Z2
J* tn^fdz
<32’6)
acJ (zd)
Эта величина гем меньше, чем больше /(гД т. е. чем боль-
ше Относительная амплитуда колебаний того сечения, в котором
1/06
—
установлен балансир. Поэтому балансиры рациональнее всего
располагать возможно ближе к внешнему концу элерона.
Часто степень весовой балансировки элерона определяют от-
ношением статического момента балансирующих грузов к ста-
тическому моменту элерона без грузов:
Е—- (32-7)
Г
J mB\„dz
выраженное в процентах и не отражающее положения балансира
но размаху. Тем самым за критерий, определяющий свойства
конструкции, принимается только положение центра тяжести
системы элерон-грузы. Конечно такой критерии не пригоден;
мы выше уже приводили пример, когда даже при 100%
балансировке [согласно критерию (32-7)[, элерон в отношении
флаттера будет вести себя как неуравновешенный. Из получен
ных нами формул, так и из физических соображений, с очевид-
ностью следует, что один и тот же груз, но помещенный в раз-
ных сечениях элерона, может оказать совершенно различное
действие, т. к. значения функции f(z) в разных сечениях могут
отличаться во много раз (см. фиг. 18—19). Между тем формула
при любом положении груза покажет одну и ту же степень
балайсировки. Из сказанного ясно, что определение степени
балансировки по формуле (12 -7), т. е. с помощью только ста-
тического момента, непригодно для суждения о свойствах
системы в отношении флаттера и распространенность этого
. способа до настоящего времени есть плод недоразумения.
За критерий весовой балансировки следует принять отноше-
’ ние
С1Я~~~С1Я
^*12
(32-8)
Здесь числитель с12—с13 согласно (32-3) и (32-5) есть инерцион-
ный момент балансирующих грузов, а знаменатель—абсолютное
значение инерционного момента самого элерона. Тогда 100%
балансировка будет означать, что инерционный момент от балан
сирующих грузов при колебаниях полностью гасит инерционный
момент от масс самого элерона. Легко видеть, что отношение
(32-8) имеет вполне реальный физический смысл: это есть инер
ционный момент от балансирующих грузов, вращающий элерон
при изгибных колебаниях крыла, выраженный в долях инерцион
ного момента от массы конструкции элерона. Если под степенью
балансировки понимать выражение (32-8), то можно утверждать,
что при 100% балансировке флаттер невозможен, В дальней-
S0?
шем всюду под степенью балансировки будем подразумевать
выражение (32-8)* 1).
Существенно отметить, что степень балансировки зависит от
функции f(z), т. е. от формы колебаний. Элерон, полностью
• балансированный по отношению к симметричной форме эле
ронного флаттера, может оказаться недобалансированным по
отношению к антисимметричной ферме и обратно.
Полная балансировка гарантирует крыло от возникновения
изгибно-элеронного флаттера 2). Однако это условие, являясь
достаточным для предотвращения флаттера, вовсе не является
необходимым. Весьма часто встречаются случаи, когда частичная
балансировка вполне достаточна для предотвращения возмож-
ности флаттера на всем летном диапазоне скоростей, или даже-
нри любой скорости воздушного потока. Нередко даже при пол-
ном отсутствии весовой балансировки элеронный флаттер все же
не будет иметь места. Однако для того, чтобы сказать, нуждае-
тся ли конкретнее крыло в балансировке и каков должен быть
процент балансировки,—необходимо произвести полный расчет
на флаттер, т. е. определить для данного крыла критическую
скорость элеронного флаттера. Из качественных соображений
дать ответы на поставленные вопросы не представляется возмож-
ным, поэтому в настоящее время для каждого самолета тре-
буется либо полная балансировка элеронов в указанном выше
смысле, либо расчет на флаттер и осуществление баланси-
ровки в соответствии с результатами расчета. При полной
балансировке элеронов расчет на флаттер лишен всякого смыс
ла, так как в результате расчета наверняка окажется, что действи-
тельной критической скорости не существует, т. е. колебания на
любой скорости будут затухающими.
Приведем примеры, иллюстрирующие указанные положения.
Были ^произведены расчеты элеронного флаттера для четырех
различных истребителей. В результате оказалось, что три из
этих четырех истребителей не нуждаются ни в какой весовой
балансировке элеронов. Между тем у двух из этих трех истре-
бителей элероны были полностью сбалансированы, так как
конструктор своевременно не произвел необходимых расчетов
на флаттер и потому, согласно существующих требований, выну-
жден был полностью уравновесить элероны. В результате про-
веденных расчетов балансировка была снята, что ощутительно
облегчило крылья.
Расчет четвертого истребителя показал, что он нуждается
в весовой балансировке элеронов, но и в данном случае, благо-
даря расчетам, удалось груз расположить рациональнее, чем
1) Оба определения степени балансировки (32.7) и (32.8) совпадают лишь,
если /(z) = const, когда все сечения крыла перемещаются при колебаниях оди-
наково; для реальных самолетных крыльев это не имеет места.
1) Напомним, что мы считаем элерон полностью аэродинамически
компенсированным.
208
это было сделано на заводе, и тем значительно облегчить эле-
рон. Расчеты этого истребителя показали, что и с полностью разба-
лансированными элеронами симметричный элеронный флаттер для
него невозможен ни при какой скорости полета. Но для предотвра-
щения антисимметричной формы флаттера была признана необхо-
димой весовая балансировка. На фиг. 116 показана кривая распре-
деления амплитуд [форма колебаний/(г) крыла истребителя при ан-
тисимметричном элеронном флаттере] и указано существовавшее
расположение балансирующих грузов на элероне. Как видно,
балансирующий груз был установлен в зоне небольших ампли-
туд и поэтому при колебаниях развивал сравнительно небольшие
инерционные силы. По расчету даже при этом невыгодном рас-
положении балансирующего груза для безопасности от флаттера
достаточен вес груза 1,25 кг, в то время как на самолете вес
фиг. 116. Практический пример весовой балан-
сировки.
и тогда для обеспечения безопасности по-
груза составлял 2,09
кг (при этом весе
центр тяжести эле-
рона находился на
оси вращения) на
каждый элерон.
Эффективн ость
балан сирующего
груза удалось еще
более повысить, пе-
реместив его в зону
больших амплитуд.
Груз был установлен
как это показано на
фиг. 116 (рекомен-
дованное положение)
летов оказался достаточен груз весом всего 0,5 кг.
Из изложенного можно сделать следующие выводы:
1. Следует рекомендовать всегда производить расчет элерон-
ного флаттера, так как этот расчет во многих случаях может
показать нецелесообразность весовой балансировки элеронов.
2. В тех случаях, когда критическая скорость недостаточна,
следует путем расчета подобрать наилучший способ предотвра-
щения флаттера (наряду с весовой балансировкой есть и другие
способы борьбы с флаттером, о чем будет сказано ниже). Расчет
дает возможность подобрать добавочные грузы минимального
веса.
Выше мы предположили, что элерон полностью аэродинами-
чески компенсирован. Как показывают специальные исследова-
ния /), полученные выводы мало изменятся, если это предполо-
жение отбросить.
’) См. Л. С. Попов «Влияние степени аэродинамической компенсации
элеронов на флаттер крыла* (Технические отчеты ЦАГИ J48. 1943).
14 Гроссман и Пановко. ®
Второе допущение, сделанное нами ради простоты анализа,
состояло в пренебрежении закручиванием крыла. Хотя в действи-
тельности изгибные колебания крыла неизбежно порождают
и крутильные колебания, но при элеронном флаттере зак-
ручивание крыла пренебрежимо мало и результаты, полученные
в предположении отсутствия кручения, прекрасно согласуются
с опытом. Поэтому при расчете всегда предполагается, что коле-
бания состоят только в изгибе крыла и отклонении элерона.
Эта форма флаттера носит название изгибно-элеронного флат-
тера. Всюду в дальнейшем мы будем рассматривать только эту
.•форму.
33. Определение критической скорости изгибно-элеронного
флаттера
Перейдем к выводу расчетных формул, позволяющих опреде-
лить критическую скорость изгибно-элеронного флаттера.
Как и для всякой системы с двумя степенями свободы, кри-
тическая скорость элеронного флаттера определяется уравне-
нием (23.5). Для составления этого уравнения в развернутом '
виде нужно в явном виде вычислить коэфициенты системы ура-
внений (22.12) и коэфициенты (22.16). С составления этих коэ-
фициентов для системы крыло-элерон мы и начнем.
Прогиб крыла, как обычно, представим в виде
У(и,0 = /(2).^(0. (33.1)
Угол отклонения элерона относительно крыла р одинаков
для всех сечений элерона, так как последний мы предполагаем
недеформирующимся и движущимся как твердое тело. Поэтому
р является только функцией времени и мы можем этот угол
принять за вторую обобщенную координату ^2(£), определяющую
вместе с ^(t) положение колеблющейся системы в каждый
момент времени
₽ = ^(0- (33.2)
Напомним, что си, с13, с22 есть коэфициенты квадратичной
формы (22.9), определяющей кинетическую энергию Т колеб-
лющейся системы через обобщенные координаты qx и q2.
Для получения выражений с1Ь с13, ci3 поступим так же,
как и выше, выразив кинетическую энергию через декартовы
координаты системы:
у 2 т* + у? + ^33
и заменив затем декартовы координаты точек системы через обоб-
щенные.
210
Рассмотрим какое-либо сечение крыла с элероном. Пусть
МША/(фиг. 117) это сечение в положении равновесия и M'LLTN'— то
же сечение во время колебаний. Отнесем рассматриваемое сече-
ние к прямоугольной системе координат АО У, ось ОУ которой
ориентирована в направлении изгиба крыла. В положении рав-
новесия элерон ШХ со-
ставляет угол р0 с напра-
влением оси X. При виб-
рациях элерон повернет-
ся на угол р вокруг оси
вращения ZZ/'и будет со-
ставлять с тем же напра-
влением угол р0+ р. Про-
извольная точка С-, на кры-
ле займет положение С/,
а произвольная точка на
элероне Eit отстоящая на
расстоянии с4 от оси вра-
щения Ш, займет поло-
жение Е'.
Координаты произ-
вольной точки С/, нахо-
дящейся на крыле:
xi — xicm
Vi — Vim+У
Zi zicm
(33.4)
Фиг. 117. Схема колебаний крыла с эле-
роном.
Координаты произвольной точки Е/, находящейся на элероне:
xi = xIU-)-oicos(p0+ р)
Уг^Лт+У-ММРи+Р)
— Zicm
(33 4)
Здесь обозначено: xiem, yicm, ziem—координаты точки Ct или Е
в положении равновесия; х ,—координата оси вращения элеро-
на, которая ост ается неизменной поскольку крыло совершает
только изгибные колебания в направлении оси У. Ось Z напра-
влена вдоль размаха крыла (перпендикулярно чертежу). Поскольку
колебания считаются малыми, мы пренебрегаем изменением рас-
стояния сечения от плоскости симметрии самолета за счет про-
гиба крыла и потому zl = zitm.
Фиференцируем выражения (33.4) по времени и подставляем
результаты в формулу (33.3), производя суммирование отдельна
по крылу и по элерону. Будем иметь;
4 2 т* +^2т'~cos ++•
к 3
14»
211
Подставляя сюда значения У и р по формулам (33.1) и (33.2)
и принимая cos(p0 + p)=l по малости углов р0 и р, получим:
Т— F У}™//3 (*i)+ V/raJVi) 1 —9i 92£т1с;/(^) +
k э э
+ 4^22Smi°i?- <33'5)
3
Индекс около знака суммы означает, что соответствующая
сумма распространяется на все точки системы крыла, а индекс
„э", что сумма берется по точкам элерона.
Произведем суммирование сперва по точкам одного элементар-
ного отсека, затем по всем отсекам крыла и элерона. Для
отсека первые три суммы будут:
y;/n,-/2 (zj + VmJ3 (z;) = mf'2 (z)dz-, Vm^f^z^ =m.csfdz,
• k Э Э
где m — интенсивность массы в рассматриваемом сечении (крыла
и элерона вместе) ; сэ — расстояние центра тяжести элерона от
оси вращения; тэ—интенсивность массы элерона в рассматрива-
емом сечении.
Последнюю сумму в выражении (33.5) можно вычислить сразу
для всего элерона. Очевидно ——-т. е. массовому мо-
э
менту инерции Элерона относительно его оси вращения.
Производя далее суммирование по всем отсекам крыла и эле-
рона, окончательно получим: У}т7/3(г;) + у^т^)=/mfdz; k э (33.6)
j mac:ifdz-, 3
9 3
где zv z3— координаты начала и конца элерона; I—полуразмах
крыла.
В силу соотношения (33.6) мы можем (33.5) переписать
в виде (22.9):
Т = ~(сп^ + 2с13 ум + с23 д3г\ (22.9)
212
причем через сп, с1а, с2а обозначено:
I z?
ca—^mfdz-, с22 — }тэ. (33.7)
О zi
Переходим к определению коэфициентов аи, а12, а32 квадра-
тичной формы (22.11), определяющей потенциальную энергию
колеблющейся системы.
В рассматриваемом случае упругие силы возникают, во-пер-
вых, вследствие изгиба крыла и, во-вторых, за счет деформации
проводки при отклонении элерона (в частном случае антисим-
метричных колебаний, когда проводка работает как механизм,
последняя сила может быть равна нулю). Будем предполагать,
что упругая сила проводки пропорциональна углу отклонения
элерона. Это означает, что при отклонении элерона на угол р,
возникнет упругий момент, стремящийся вернуть элерон в поло-
жение равновесия, и равный — /?р, где /?—коэфициент пропор-
циональности. Работа упругого момента—/?р при отклонении
элерона на урл р будет равна—-- Rfi2. Таким образом, потенци-
альная энергия рассматриваемой системы слагается из потенци-
альной энергии изгиба крыла и энергии, накопляющейся при
отклонении элерона (последняя равна работе упругого момента
с обратным знаком):
1
2 о 2
Подставляя сюда выражения У и р через обобщенные коорди-
наты [формулы (33.1) и (33.2)], получим:
1
и = ^ EJf'2dz + ±-R<rf. (33.8)
2 о 2
Сравнивая это выражение с (22.11), сразу находим:
/
an=4-J EJf'^dz', a„4 — R\ о1Я = 0. (33.9)
2 О
Из коэфициентов уравнений (22.12) остается еще определить
° и р— коэфициенты выражений обобщенных сил (22.7). Для
их получения удобнее всего, как мы это делали и при анализе
изгибно-крутильного флаттера крыла, полностью повторить
213
вывод выражений обобщенных сил, исходя из их общего выра-
жения:
Qi=2
Q,=v
р дх; ду; dzt\
xldqi + P*dqx + P^dq1 j
p ™i-+P ^+p dz‘
x‘dqs yidq2Xtdq2
(22.2)
Для получения выражений обобщенных с Ил через обобщен-
ные координаты qlt q2 выразим последние через xit yt, zh а за-
тем результат подставим в формулы (22.2).
Подставляя в (33.4) значения У и {3 по формулам (33.Г) и
(33.2), получим выражение декартовых координат через обоб-
щенные:
х- — х,-°
Для точек крыла Для точек элерона y^yf+fyi z, = = + cos(₽0+?B) У1 =J'i° +/?i — sin (Ро + zi — zi* . (33.10)
Подставляем эти значения в (22.2):
Q1= 2
Qo = -21PXi sin (Ро + ₽)+pyi COS (Ро + ₽)К
э
(33.11)
Индекс ,Л+э“ при первой сумме показывает, что суммирование
распространяется на точки как крыла, так и элерона.
Будем в формулах (33.11) производить суммирование, как
мы это всегда делаем, вначале по одному какому-либо элемен-
тарному отсеку крыла, а затем уже по всем отсекам. Начнем
с величины Qj.
Так как для всех точек элементарного отсека функция f
одинакова, то при суммировании по одному отсеку функцию f
можно вынести за знак суммы. Остающаяся сумма Pyi пред-
• #-|-э
ставляет собою проекцию равнодействующей внешних сил,
действующих на отсек dz, на ось Y. Эту проекцию обозначим
Pydz, где Ру—погонная подъемная сила крыла с элероном.
Суммируя затем результат по всем сечениям крыла и помня,
чго / есть функция z, получаем:
/
Q1 =Jpyf(z)dz. (33.12)
214
вращаемся к вычислению Q3. Легко видеть, что выражение,
Соченное в квадратные скобки в формуле (33.11), есть проек-
зак'1 силы с компонентами Pxi, Pyi на нормаль п к элеронч
111,51 117). Так как s, есть плечо этой проекции, относительно
(Фи1 ^ращения ИГ, то выражение, стоящее под знаком суммы,
оси ромеит этой силы вокруг оси вращения элерона. Суммирование
есТд1-орой формуле (33.11) распространяется на все точки эле-
в0 и следовательно Qa есть момент всех внешних (аэродина-
Сских) сил, действующих на элерон, относительно его оси
вращения, т. е. шарнирный момент элерона
?9
Q3 = ///<,,
*1
(33.13)
чр — шарнирный момент для элементарного отсека элерона.
гд р главе 6 были даны формулы, как для погонной подъемной
силН кРыла с элероном (28.7), так и для погонного шарнирного
MOMt>HTa ЭлеРопа (28.9). В этих формулах применительно к рас-
сма1’РиваелюмУ слУчаю следует положить 0 = 0, так как мы пред-
п‘ол.||-аем крыло не закручивающимся. Подставляя указанные
знацрния подъемной силы и шарнирного момента в (33.12) и
(33 1$» ОКОнчательпо получим:
Qi= — bXiV2 — dx2Vq2~ dxxVqx I
Q2 =—b22 V2q2— d22 Vq2 — d2X Vq2 I
(33.14)
обозначено:
1 de 22 Z2
= —9-^p ,fGbfdz-, bVi = pj <d.JPdz-,
г, zx
I 1 d
dxx~4y P J bf 2dz-, dxt = P SHb2fdz\
2 0 г,
1 «г г3
P J <IJPfdz-, tZ.22 = p/(2#<Z2.
Zl ZX )
(33.15)
Сравнивая выражения (33.14) с формулами (22.7), находим
₽п = 0;
о.
Pai -
^2=-^^;
j 9 d ] 212
831 = d2X 1/
Ьо3-- "^22 1
(33.16)
Теперь, когда нами найдены гее коэфициенты уравнений
(22 12), можно перейти к определению критической скорости; для
215
этого необходимо вычислить коэфициенты А, В, С, D, Е согласно
(22.16). Легко видеть, что выражения этих коэфициентов для
изгибно-элеронного флаттера совпадут с их выражениями для
изгибно-крутильного флаттера крыла [это объясняется тем, что
в обоих случаях a12 = pli = Pi2 = 0, а также тем, что [Э и 8 в обоих
случаях одинаково зависят от скорости полета, что видно из
сравнения формул (33.16) с формулами (29.13)]. Поэтому мы не
будем прозводить их вычисление, а сразу воспользуемся гото-
выми формулами (29.14), (29.17). Следует только помнить, что
значения коэфициентов а, с, b и d в обоих случаях различны.
Критическая скорость обеих форм элеронного флаттера
(симметричной и антисимметричной) определяется по одним и тем
же формулам. Все отличие заключается только в разном задании
функции формы колебания /. Если мы в формулы (33.7), (33.9)
и (33.15) подставим функцию формы симметричных колебаний,
то получим в результате расчета критическую скорость симмет-
ричной формы флаттера, если же подставим функцию формы
антисимметричных колебаний,—то получим критическую ско-
рость антисимметричного флаттера.
Таким образом, может быть намечена следующая схема опре-
деления критической скорости изгибно-элеронного флаттера.
1. Прежде всего производится расчет собственных колебаний
методом, изложенным в п. п. 5 — 6, и определяется функция формы
изгибных колебаний крыла /(г). В зависимости от расчетной
формы флаттера определяется функция симметричных или анти-
симметричных колебаний.
2. Вычисляются коэфициенты по формулам (33.7), (33.9)
3. Вычисляется критическая скорость по формулам (29.15)—
(29.17).
В расчет изгибно-элеронного флаттера входит величина я22, равная
согласно (33.9) коэфициенту упругости проводки элерона R. Последний
получается обычно из эксперимента; для этого удобно выразить R через час-
тоту собственных колебаний изолированного элерона. Уравнение этих коле-
баний:
*₽+Jm,₽=O. (33.17)
Здесь — есть, по определению величины R, упругий восстанавливающий
момент, возникающий при деформации проводки, a —момент инерцион-
ных сил колеблющегося элерона (обе величины берутся относительно оси вра-
щения элерона).
Уравнение (33.17) относится к тому же типу, что и уравнение (3),
рассмотренное во введении и неоднократно встречавшееся выше.
Из привычной теперь для нас записи следует, что величина
R
Iта
216
является круговой частотой свободных колебаний изолированного элерона
GOp,
Если заменить ра через число колебаний в минуту лэ = — • то выражение
/? может быть записано в виде:
/ 2п \« 2 ,
R—у 60 ) Пэ ~*та (33.18)
Тем самым коэфициент, характеризующий жесткость проводки управле-
ния, выражен через число собственных колебаний элерона; это число как при
симметричных, так и при антисимметричных колебаниях может быть экспери-
ментально определено при частотных испытаниях самолета.
Сделаем некоторые замечания относительно возможных в прак-
тике иных расчетных случаев. Изложенный метод легко распро-
странить на случай, когда на крыле имеется сосредоточенный
груз (например, мотор). В этом случае к кинетической энергии
колеблющейся системы следует добавить кинетическую энергию
сосредоточенного груза:
где ЛГ—масса груза, находящегося на крыле и zM—координата
его. отсчитываемая вдоль размаха от оси симметрии самолета.
Прибавляя полученное выражение кинетической энергии к (22.9),
мы видим, что все отличие от крыла без груза будет заключаться
в коэфициенте который вместо значения, определяемого
формулой (32.7), примет значение:
I
о
Само собой разумеется что функция f должна быть в этом
случае вычислена с учетом груза М.
Если имеется груз на элероне, то к кинетической энергии
следует еще добавить энергию этого груза. В этом случае;
I
cil=\mfzdz+M6f1(z6)
д
ctS = —J тД/й!г + /Ибаб/(го-)
*1
йоц = д,ПЭ 4" TUjjOg
(33.19)
где Мб — масса балансира; z6—расстояние его от оси вращения
элерона, считаемое положительным, если балансир находится
217
впереди оси; f{zc}—значение функции / в сечении, в котором
находится балансир. Величина массы балансира Мб бывает ничтожно
мала по сравнению с массой крыла и потому нет необходимости
учитывать ее при расчете формы колебаний. Поэтому как для
элерона с балансиром, так и для элерона без балансира при-
нимают одну и ту же функцию формы f (г). По этой же причине
может быть пренебрежен и второй член в выражении сп.
34. Меры предотвращения изгибно-элеронного флаттера
а) Весовая балансировка элерона
Коэфициент С12 оказывает весьма сильное влияние на крити-
ческую скорость. Иногда небольшое изменение этого коэфици-
ента ведет к значительному изменению критической скорости.
Фиг. 118. Влияние коэфициента с13 на
критическую скорость. При ;с12|<]сои|
флаттер невозможен.
Это станет вполне понят-
ным, если заметить, что
физически этот коэфици-
ент представляет собой
инерционный момент,
влияние которого было
выше показано в связи
с выводом формулы (32.8).
Поэтому, для подбора не-
обходимой величины ба-
лансирующего груза по-
ступают следующим об-
разом: вычисляется кри-
тическая скорость при не-
скольких значениях коэ
фициента с12 и строится
график критической ско-
рости по коэфициенту с12
(диапазон изменения с12
выбирается от нуля до
ющего элерону без балансирующих
значения с12 соответству-
грузов). По этому графику
определяется значение с12, при котором критическая скорость
становится мнимой (флаттер становйтся невозможным ни при
какой скорости полета) или достигает желаемой величины. За-
тем по второй формуле (33.19) подбираются такие массы балан-
сира, его плечо и место установки, чтобы коэфициент с12 достиг
нужной величины.
На фиг. 118 показан типичный график критической скорости
изгибно-элеронного флаттера в функции коэфициента с12. Если, на-
пример с12 имеет значение с1а*, то биквадратное уравнение (29.16) —
будет иметь два корня. По мере стремления с12 к нулю оба корня
сближаются, пока не сольются в одно значение при Cj2o. При
218
дальнейшем уменьшении с13 критическая скорость будет иметь
мнимые значения. Как и в случае изгибно-крутильного флаттера
крыла меньший корень уравнения (29.16) определяет скорость
полета, при которой возникает флаттер, а верхний — скорость
полета, при которой флаттер прекращается. Область скоростей
полета, при которых будут иметь место незатухающие колебания
крыла с элероном лежит между обоими корнями. Практический
интерес, конечно, представляет только нижний корень, так как
уже он представляет собою верхнюю границу допустимых при
эксплоатации самолета скоростей прлета. Обычно критические
скорости изгибно-элеронного флаттера (если они действитель-
ны') бывают довольно невелики и для обеспечения безопасности
приходится прибегать к балансировке, которую осуществляют
так, чтобы коэфициент для балансированного элерона был по
абсолютной величине меньше сГ1°. В этом случае безопасность
обеспечивается при любых скоростях полета.
Изложенный способ определения необходимой степени весовой
балансировки неточен, так как при изменении параметров ба-
лансира (массы и плеча) меняется не только коэфициент с13, но
и с22 в (33.19). Однако ошибка, получаемая при таком способе
невелика и, что особенно важно, она идет вх сторону безопас-
ности, т. е. при указанном способе несколько завышается пот-
ребная масса балансира. Объясняется это тем, что с увеличением
мометна инерции элерона, т. е. с увеличением коэфициента c.,.s
критическая скорость увеличивается. Иногда это обстоятельство
даже используют Для того, чтобы обеспечить безопасность поле-
тов, увеличивая критическую скорость не путем балансировки
элерона, а путем увеличения его момента инерции. Поскольку
в указанном выше способе подбора потребной массы балансира
пренебрегается увеличением коэфициента ст при балансировке
элерона, постольку критическая скорость в этом способе несколько
занижается. Разумеется, что после построения диаграммы (фиг. 118)
можно уточнить результаты расчета, учтя изменение коэфици-
ента саз для выбранных массы и плеча балансира.
б) Увеличение инерции вращения элерона (инерционное демпфирование’)
Как мы только что сказали, в некоторых случаях имеет
смысл увеличивать критическую скорость не путем весовой ба-
лансировки элерона, а путем увеличения его момента инерции
(говоря точнее, путем увеличения инерции деталей, соединенных
с элероном). Одним из расчетных случаев элеронного флаттера
является антисимметричный элеронный флаттер, при котором
проводка движется как механизм; в этом случае к кинетической
энергии системы элерон-крыло следует добавить кинетическую
См. Я. М. Пархамовскнй. «Инерционные демпферы как-средство повыше-
ния критической скорости флаттера' (Труды ЦАГИ № 542. 1941).
энергию проводки. Подсчитать эту кинетическую энергию не
представляет труда. Проводка состоит из поступательно движу-
щихся частей (тяг) и вращательно движущихся частей (качалки,
ручка управления). Пусть при отклонении элерона на угол р тяги
переместятся на расстояния х1( %s, . . . х„, качалки и ручка
повернутся на углы ах, а2, . . . ат. Очевидно все перемещения
будут пропорциональны углу отклонения элерона, т. е.
(7=1,2. . . л; / = 0,1,2,. . т),
где k, т(—коэфициенты пропорциональности. Диференцируя эти
соотношения по времени, получим поступательные скорости тяг
и угловые скорости качалок и ручки
%г = А(р; ay = Tj7p.
Определяем кинетическую энергию проводки:
. (34.1)
т
«где через k обозначена величина ])
k = \jniiki2_ + Jrnj'tf-
п т
(34'.2)
Величина k носит название коэфициента инерции проводки и
зависит от массы поступательно движущихся частей, моментов
инерции вращательно движущихся частей и кинематических со-
отношений в проводке. Он имеет размерность момента инерции.
Суммируя выражение (34.1) с (33.5), найдем, что в данном слу-
чае изменится только коэфициент с22, который вместо (33.7) будет
иметь значение
---1тэ + k .
Если на элероне есть еще балансирующий груз, жестко скреп-
ленный с элероном, то в соответствии с (33.19) коэфициент с5,
будет иметь значение
С22 ~^тЭ + k + Мб-<3бг. (34.3)
Таким образом, для случая антисимметричного элеронного
флаттера с недеформирующейся проводкой (т. е. при /? = 0),
1) При подсчете величины k в формулу (34.1) следует вводить только по-
ловину момента инерции ручки, так как весь расчет ведется для полукрыла
с одним элероном.
220
коэфициент с32 увеличивается за счет инерции проводки. Иногд;
для увеличения критической скорости в этом случае вмест,
весовой балансировки прибегают к искусственному увеличении
инерции проводки путем установки специальных грузов на ручке
управления или баранке штурвала.
Еще чаще в проводку вблизи элерона включают специальные
груз, кинематически связанный с элероном. При анализе флат-
тера следует принять во внимание кинетическую энергию,
ваемую таким грузом. Пусть,’
например, внутри крыла по-
мещен груз, вращающийся в
плоскости крыла вокруг вер-
тикальной оси СС'(фиг. 119) и
кинематически связанный с
элероном таким образом, что
при отклонении элерона на
угол р около оси ОО', груз
отклоняется на угол —
передаточное число) около оси
СС. Пусть М — масса груза,
I — его пл^чо и J„ — его мо-
мент инерции, относительно
оси СС, равный Mt1.
Определим кинетическую
энергию, развиваемую грузом
элерон. Для этого, как обычно, найдем декартовы координ
груза в функции обобщенных координат и затем определим
Фиг. 119. Схема инерционного демп-
фера. Ось СС' вертикальна
при колебаниях системы крыло
нетичёскую энергию:
Т=^М(х* + jr + z2).
(зз.;
Пусть при колебаниях отсек крыла с грузом переместите
из положения 1 в положение II (фиг. 120). Ось вращения эл(
рона из положения GO переместилась в положение О'О' и эле
рон повернулся вокруг нее на угол р. Ось вращения груза и
положения СС переместилась в положение СС и груз повер
нулся вокруг нее на угол Прогиб крыла в сечении, в коте
ром расположен груз, будет
У—
где zt — расстояние от оси самолета до сечения крыла, в
ром расположён груз..
Координаты груза в рассматриваемый момент времени,
видно, имеют значения:
X = Хе — ZcOS Tjp
Уг~ У,
z = zc 4- Z sin т|р,
где хс ^ — координаты шарнира балансира;
Диференцируем эти выражения по времени и подставляем
результат в (33.3); заменяя затем = У=У1}(?е), найдем,
1 '= т W2 (*<)] + J- HVk?-
Фиг. 120. Колебания крыла с инерционным демпфером.
Прибавляя это значение к кинетической энергии системы
крыло—элерон (33.5), найдем, что коэфициенты и с22 в данном
случае принимают значения
/
cii — f tnf^dz 4- Al/3^)
о
С22 = Лиэ +
(34.4)
Коэфициент останется без изменения, т. е. груз, включен-
ный в систему по схеме фиг. 119 не меняет степень баланси-
ровки.
Изменение коэфициента можно не учитывать, так как
масса груза пренебрежимо мала по сравнению с массой крыла.
В данном случае увеличение коэфициента можно произво-
дить не только за счет массы груза и его плеча, но и за счет
передаточного числа тр Это весьма существенно, так как за
счет увеличения т, удается иногда значительно снизить потреб-
ный вес груза.
Приспособления, которые увеличивают коэфициент с22, назы-
ваются инерционными демпферами, — они создают такой же эффект,
как и увеличение момента инерции элерона;важно заметить, что
они не меняют при этом степени весовой балансировки.
Инерционные демпферы выгодны только тогда, когда
j дается осуществить большие передаточные числа tj, т. е. когда
амплитуда колебаний демпфера значительно больше амплитуды
колебаний элерона. Тогда демпфер при сравнительно небольшой
массе развивает значительные инерционные силы. Выше было
указано, что для предотвращения антисимметричной формы эле-
ронного флаттера при R — 0 можно установить груз на ручке
управления. По существу такой груз может служить Инерцион-
ным демпфером.
Величина ТИ/2^2 в (34.4) характеризует эффективность демп-
фера; как видно она пропорциональна квадрату передаточного
числа.
Следует сказать, что инерционный демпфер в весовом отно-
шении не выдерживает сравнения с балансирами. Однако инер-
ционное демпфирование >может оказаться более удобным по со-
ображениям конструктивно-компоновочного характера (удобство
размещения).
с
и
в) Кинематическая балансировка (весовая балансировка в сочетании
с инерционным демпфированием 1)
Наиболее выгодным будет такая связь балансирующего груза
элероном, когда он соединяет в себе свойства балансира
инерционного демпфе-
ра. Достичь этого можно,
соединяя кинематически
груз с элероном так же,
как на фиг. 119, но делая
Фнг. 121. Кинематический балансир является
комбинацией инерционного демпфера и весо-
вого балансира.
ось вращения груза не
вертикальной, а горизон-
тальной, чтобы груз вра-
щался в той же плоско-
сти, что и элерон. Такая
схема включения показана на фиг. 121. При изгибных колеба
*) См. статью Я. М. Пархомовского и Л. С. Попова „О влиянии инерции
Управления на вибрации самолета" (Техника воздушного флота.
№ 7, 1940).
223
пиях крыла такой груз, оставаясь инерционным демпфером,
создает эффект обычного балансира. В этом случае можно
также использовать большое передаточное число и поместить
груз в зоне наиболее выгодных амплитуд для создания наи-
больших инерционных сил.
Для определения эффективности включения груза по схеме
фиг. 121, поступим как и в предыдущем случае—-определим
изменение коэфициентов сп, с12, с22, вызванное наличием груза.
Кинетическую энергию, развиваемую грузом при колебаниях,
определим опять по формуле (33.3). Пусть сечение крыла, в ко-
тором расположен груз, переместилось из положения 1 в поло-
жение 2 (фиг. 122). Передаточное число опять обозначим т(.
Фиг, 122. Колебания крыла с кинематическим балансиром.
Если координаты шарнира балансира О в положении равно-
весия 1 обозначим хе, уе, zc, то координаты груза в рассматри-
ваемый момент времени будут:
х — хе — I cos 7$,
У —Ус + У + / cos т;р,
Z,— лг.
Диференцируем эти выражения по времени и результат
подставляем в формулу (33.3). Заменяя затем р = y~Qifizc)>
получим:
L [Mf* (гс)] № 'fl
Прибавляя это значение к кинетической энергии системы
крыло-элерон (33.5), найдем, что коэфициенты с в рассматривае-
мом случае принимают значения:
224
I Zg
C11 — f mf2dz + Af/2(ze) C12=—J m^fdz + Ml^f(zc)
0 Zj
СМ —^тЭ + М12~ф
(34.5)
Изменением коэфициента cIt за счет массы груза можно пре-
небречь по тем же причинам, как и в предыдущем случае. Сле-
довательно груз, соединенный с элероном по схеме фиг. 121
изменяет одновременно как коэфициент саз, (давая тот же эф-
фект как увеличение момента инерции элерона), так и коэфициент
с12, т. е. изменяет степень весовой балансировки. Такие приспо-
собления, соединяющие эффект инерционного демпфера и ве-
сового балансира и соединенные с элероном кинематически,
носят название кинематических балансиров. Они могут ока-
заться значительно выгоднее обычных весовых балансиров, если
передаточное число осуществить достаточно большим. Так
как эффективность кинематического балансира Определяется не
только его весом и плечом, но и передаточным числом, то за
счет увеличения последнего можно добиться значительного сни-
жения потребного веса балансирующего груза. Увеличение пере-
даточного числа по существу означает увеличение амплитуд
колебаний груза по отношенью к амплитуде колебаний элерона,
а это, в свою очередь, ведет к увеличению инерционных сил
балансирующего груза, которые в конце концов и определяют
эффект элерона при колебаниях. Благодаря кинематической связи
между элероном и грузом, последний можно поместить в зону
больших значений /(г,), что, как следует из второй формулы
(34.5), также увеличит его интенсивность.
Обычно в крыле сравнительно редко удается осуществить
большое передаточное число, так как габариты крыла ограничи-
вают возможный угол отклонения груза. Поэтому применение
кинематических балансиров в крыле сравнительно редко. Забе-
гая несколую вперед, укажем, что наиболее рационально упо-
треблять/кинематические балансиры для предотвращения
флатте/с оперения, соединяя их с рулем высоты. Об этом
еще будет сказано в главе 9.
г) Энергетическое демпфирование
Упомянем еще об одном способе борьбы с флаттером, кото-
рый подробно исследовался рядом авторов (в частности М.В. Кел-
дышем й Я- М. Пархомовским) как теоретически, так и экспери-
ментальноЛМы имеем в виду так называемые энергетические
демпферы. Идея их заключается в том, что между элероном
и крылом вводится устройство, оказыв;ющее вязкое сопротивле-
ние отклонению элерона и тем самым при вибрациях поглощаю-
щее энергию колеблющейся системы. Две возможные принципи-
15 Гроссман и Пановко. 225
V
альные схемы энергетических демпферов показаны на фиг. 123.
Демпфер представляет, собой наполненный жидкостью цилиндр,
соединенный с крылом; внутри цилиндра В поступательно дви-
жется поршень А или вращается лопатка, которые кинематически
связаны с элероном. В поршне (лопатке) имеются отверстия для пе-
ретекания жидкости с одной стороны поршня (лопагки)на другую.
При проталкивании жидкости через отверстия возникает дополни-
тельное сопротивление. Сила сопротивления поршня (лопатки)
будет тем больше, чем больше скорость движения элерона.
Когда летчик для управления самолетом движет ручку управле-
Фиг. 123. Энергетические демпферы.
ния, отклоняя эле-
рон, угловая ско-
рость последнего
сравнительно неве-
лика и сопротивле-
ние жидкости весь-
ма слабо. Но при
упругих колебаниях,
частота которых со-
ставляет несколько
сотен колебаний в
минуту, угловая ско-
рость вращения эле-
рона, а следователь-
но и скорость дви-
жения поршня (лопатки) очень велика. Сила сопротивления
жидкости становится настолько большой, что не дает развиться
колебаниям.
Преимущество энергетического демпфера по сравнению с обыч-
ными противофлаттерными средствами (балансировка, инерцион-
ные демпферы) заключается в его малом весе (всего 1 — 2 кг).
Но он обладает и весьма существенными недостатками. Демпфер
по существу представляет собою сложный прибор со специаль-
ным терморегулятором (чтобы при различных температурах сила
сопротивления оставалась неизменной), сложный в изготовлении
и в эксплоатации. Этими недостатками объясняется, почему
энергетические демпферы до сих пор не получили широкого
распространения.
д) Влияние упругости проводки
Мы подробно исследовали как сказываются на критической
скорости силы инерции, развиваемые элероном и связанными
с ним грузами. Исследуем теперь влияние сил упругости про-
водки которое характеризуется коэфициентом упругости про-
водки, или частотой собственных колебаний элерона пэ (32.8.)
Удобнее анализировать влияние отношения частот
226
где пи—собственная частота изгибных колебаний крыла, опреде-
ляемая согласно п. п. 5 —6.
При рассмотрении симметричной формы элерона флаттера
под к следует понимать отношения частоты симметричных коле-
баний элерона к частоте симметричных колебаний крыла, а при
рассмотрении антисимметричной формы под х следует понимать
отношение частот антисимметричных колебаний элерона и крыла.
Типичный график критической скорости в зависимости от к
показан на фиг. 124а. При увеличении х от нуля критическая
скорость уменьшается, достигает минимума обычно вблизи значе-
ния х = 1 и затем увеличивается, пока кривая при некотором
значении х = х * не завернется. Верхняя ветвь кривой, как мы
уже знаем, дает скорость прекращения флаттера.
Уменьшение критической скорости при приближении к значе-
нию х=1 вызвано, как уже говорилось в главе 7, внутренним
резонансом, так как величина х —1 означает па=па, т. е. совпа-
дение частот колебаний элерона и крыла. Значение х* обычно
лежит д^зольно близко к 1 (порядка х=1,2—1,5). При часто-
тах элр^она, соответствующих значениям х>х®, флаттер невоз-
можен ни при какой скорости полета.
В сравнительно редких случаях график зависимости крити-
ческой скорости от отношения частот элерона и крыла имеет
вид, показанный на фиг. 1245. До xSZl характер графика такой
же, как на фиг. 124а, но затем критическая скорость монотонно
увеличивается с ростом х, однако кривая нигде не заворачи-
15»
227
вается. 1). В этом случае критическая скорость существует при
любом значении х и возникает лишь вопрос о ее величине.
Интересно рассмотреть изменение критической скорости эле-
ронного флаттера в функции отношения частот элерона и крыла,
при различной степени весовой балансировки. Последняя, как
было указано, характеризуется коэфициентом В (32.8). Нафиг. 125
Фиг. 125. Влияние отношения частот и весовой балансировки на кри-
тическую скорость.
показан типичный график, характеризующий это влияние. Участки
кривых, соответствующих х<0 не имеют физического смысла и
построены лишь для наглядности.
При увеличении степени весовой балансировки больший и
меньший корень уравнения, определяющего критическую ско-
рость, сближаются между собой, пока кривая VKp в функции •/
не будет вытеснена в отрицательную область значений х(фиг. 125
для 5=100%). Так как реально всегда х>0.то это означает,'
что критическая скорость перестает существовать, т. е. на лю-
бой скорости полета колебания затухающие.
Расчет на флаттер обычно производится до постройки само-
лета, когда частота собственных колебаний элерона еше не
известна, так как пв определяется опытным путем на готовом
самолете. Поэтому при расчете полностью строятся кривые VKP
в функции х. После определения пэ, определяется х и на постро-
енной диаграмме отмечается точка, соответствующая этому /..
Тем самым окончательно определяется критическая скорость
рассчитываемого самолета.
!) Критическая скорость определяется из биквадратного уравнения
ди-рм P4-JV=0
График Г\рВ функции х имеет вид фиг. 124л если £>0, и вид фиг. 1240, если
/.<0. Зависит это от конструктивных параметров элерона.
228
Построение кривой VKP по к необходимо еще и по другой
личине. Допустим, что для исследуемого самолета х несколько
больше, но очень близко к х* (фиг. 126). Расчет для этого х
дает мнимое значение критической скорости. Однако действи-
тельная кривая VKp по х несколько отличается, естественно, от
расчетной, и самолет может попасть в зону флаттера, причем крити-
ческая скорость может оказаться весьма низкой. Следовательно ну-
жно иметь некоторый коэфициент безопасности не только по отно-
шению к величине критической скорости, но и по отношению к вели-
чине х. Необходимо полностью строить кривую VKp по х с целью убе-
диться, что значение х для самолета достаточно превышает х®
и диапазон между дей-
ствительным х и х® не мо-
жет перекрываться воз-
можной погрешностью
расчета или погрешно-
стью в определении ис-
ходных параметров кры-
ла и элерона (массы, же-
сткость изгиба и т. д.).
То же самое относится
и к потребной степени
весовой балансировки
(фиг. 118); значение с12для
самолета не должно быть
слишком близким к с°12.
Следует всегда помнить,
что критическая ско-
рость при очень неболь-
шом изменении пара-
метра, может резко из-
Фиг. 126. Малая ошибка в определении х
может вызвать большую ошибку в опре-
делении VKpam.
мениться. Например, при
переходе через значение
с('1а критическая скорость
из мнимой становится
сразу действительной, и возможно, небольшой. Запас по отно-
шению к таким параметрам как степень весовой балансировки и
отношение частот элерона и крыла, для самолетов с мнимой
критической скоростью столь же обязателен, как и запас по
отношению к величине критической скорости для самолетов с
действительным значением последней.
Все сказанное выше относительно влияния параметров эле-
рона на критическую скорость флаттера крыла справедливо для
аэродинамически неперекомпенсированных элеронов. При значи-
тельной аэродинамической лерекомпенсации приведенные соотно-
шения будут другими; так как обычно перекомпенсация элеро-
нов не допускается, то этот случай не представляет практичес-
кого интереса. Иногда, правда, при серво-компепсации ставят
229
серво-компенсатор только на одном из элеронов. Тогда может
оказаться, что хотя суммарный шарнирный момент обоих элеро-
нов действует в сторону, противоположную отклонению ручки,
но элерон, на котором установлен серво-компенсатор, — переком-
пенсирован. В связи с опасностью флаттера это крайне нежела-
тельно, так как перекомпенсация элерона может повести к
значительному снижению критической скорости.
ГЛАВА 9
Флаттер хвостового оперения ')
35. Формы флаттера оперения
В п. п. 5 — 6 было показано, что любые колебания самолета
являются совместными. В частности колебания оперения или фю-
зеляжа неизбежно сопровождаются колебаниями крыла. Однако,
ввиду сравнительной малости этих колебаний крыла, часто при-
нимают, что при колебаниях оперения крыло является не-
подвижным, а фюзеляж схематизируется как упругая кон-
сольная балка, несущая на конце сосредоточенный груз (опе-
рение). Следует указать, что если схематизация крыла при из-
гибно-крутильном флаттере в виде консольной балки дает боль-
шую точность, то такая же схематизация фюзеляжа дает зна-
чительно меньшую точность (особенно для одномоторных само-
летов). Это обстоятельство вызывает необходимость построения
такой схемы расчета оперения, которая базируется на рас-
смотрении самолета, как свободно плавающей упругой системы.
Ошибки консольной схемы все же не столь велики, чтобы
признать базирующийся на ней метод расчета полностью неудовле-
творительным. Во всяком случае качественный анализ, базирую-
щийся на такой схеме, дает правильные результаты. Для простоты
римем в своем изложении именно консольную схему. Дальней-
шим упрощением является предположение о независимости ви-
браций горизонтального и вертикального оперения. Примем,
что при вибрациях горизонтального оперения вертикальное ве-
дет себя как абсолютно жесткая сосредоточенная масса; так же
ведет себя горизонтальное при вибрациях вертикального. Такое
предположение вводится для уменьшения числа степеней сво-
боды и достаточно хорошо согласуется с наблюдениями.
1) В настоящей главе особенное внимание уделяется вопросам балансировки,
т. е. условиям, исключающим возможность флаттера. Для определения крити-
ческой скорости читатель должен будет обратиться к специальной литературе
(Е. П. Гроссман „Флаттер хвостового оперения". Труды ЦАГИ № 501, 1940 г.).
230
Оперения современных самолетов осуществляются таким об-
разом, что при флаттере можно считать стабилизатор и киль
недеформирующимися, ввиду их относительно большой жесткости
(частоты собственных колебаний стабилизатора и киля обычно
бывают в 2-4 раза больше частот собственных колебаний фю-
зеляжа). Руль поворота также можно считать абсолютно-
твердым телом. Руль высоты, ввиду его большого удлинения,
имеет сравнительно небольшую жесткость при кручении; поэ-
тому при колебаниях следует учесть возможность скручива-
ния руля высоты.
Таким образом, считаются возможными следующие упругие
и жесткие перемещения: изгиб фюзеляжа, кручение фюзеляжа,
Фиг. 127. Форма колебаний при изгибно-рулевом флат-
тере горизонтального оперения.
скручивание руля высоты (когда правая и левая половины руля
высоты движутся в разные стороны), отклонения рулен как це-
лого. В соответствии с этим легко наметить расчетные случаи:
1) Флаттер вертикального оперения. Допустим,
что произошло отклонение руля поворота. Очевидно, при этом
направленная вбок аэродинамическая сила создает также момент
около продольной оси самолета. Сама сила вызовет изгиб фюзе-
ляжа вбок (в горизонтальной плоскости), а ее момент вызовет
кручение фюзеляжа. Таким образом, флаттер вертикального опе-
рения должен рассматриваться с учетом трех степеней свободы:
изгиб фюзеляжа, кручение фюзеляжа, отклонения руля.
2) Флаттер горизонтального оперения. Допустим,
что произошло отклонение руля высоты. Дополнительная аэро-
динамическая сила вызовет симметричный изгиб фюзеляжа в
вертикальной плоскости без скручивания. Таким образом возмож-
ны колебания горизонтального оперения с двумя степенями
свободы: изгиб фюзеляжа, отклонение руля высоты.
231
Допустим, что произошло скручивание руля высоты. Возни-
кающие при этом аэродинамические силы, вследствие симметрии,
создадут чистую пару вокруг оси фюзеляжа и вызовут скручи-
вание фюзеляжа без его изгиба. Таким образом возможен также
и другой вид колебаний фюзеляжа с двумя степенями свободы:
скручивание руля высоты, кручение фюзеляжа.
Итак, возможны следующие формы колебаний хвостового
оперения:
1) флаттер вертикального оперения (три степени свободы:
изгиб и кручение фюзеляжа, отклонение руля направления);
2) изгибно-рулевой флаттер горизонтального оперения (две
степени свободы: изгиб фюзеляжа, отклонение руля глубины,
как твердого тела — фиг. 127);
Фиг. 128. Форма колебаний при крутильно-рулевом флатте-
ре горизонтального оперения.
3) крутильно-рулевой флаттер горизонтального оперения [(две
степени свободы:кручение фюзеляжа, скручивание руля высоты —
(фиг. 128)].
Исследование этих форм флаттера является обязательным для
каждого опытного самолета. Кроме того, для каждого самолета
проверяется законность пренебрежения деформациями стабили-
затора и киля, что делается путем сравнения опытных значений
частот собственных колебаний различных агрегатов оперения (ста-
билизатора, фюзеляжа, киля, рулей). Частоты стабилизатора и
киля должны быть значительно выше частот фюзеляжа.
Если бы оказалось, что они близки, потребовался бы расчет еще на так,
называемые безрулевые формы флаттера хвостового оперения:
1) симметричный безрулевой флаттер, когда происходит симметричный изгиб
и кручение стабилизатора и изгиб фюзеляжа;
2) антисимметричный безрулевой флаттер, когда происходит антисимметрич-
ный изгиб и кручение стабилизатора, и кручение фюзеляжа.
232
При безрулевых формах флаттера рули считаются неподвижными относи-
тельно стабилизатора и рассматриваются как части конструкции последнего.
рассмотрим теперь каждую из форм флаттера по отдельности.
36. Флаттер вертикального оперения
Как было показано, при анализе флаттера вертикального
оперения необходимо учитывать не менее трех степеней свобо-
ды (изгиб фюзеляжа в горизонтальной плоскости, кручение его
и отклонения руля направления). Расчет на флаттер для системы
с тремя степенями свободы весьма громоздок ’) и поэтому расчет
флаттера вертикального оперения производится лишь в редких
случаях. Обычно конструктор предпочитает /Зез расчета осуще-
ствить мероприятия, обес-
печивающие безопасность
самолета от возникнове-
ния флаттера, хотя бы
проведение таких меро-
приятий и требовало не-
которого излишнего веса.
Большей частью про-
изводится полная ба- Г
лансировка руля напра-
вления, хотя если про- (
извести расчет, то мо- 1
жет оказаться, что доста-
точно частичной балан
Сировки, или даже ПО- Фиг. 129. К анализу флаттера вертикаль-
следняя вообще не нужна. него оперения.
Рассмотрим, как должна
осуществляться весовая балансировка руля направления.
Рули производят такое же действие на колеблющееся опере-
ние, как элерон на колеблющееся крыло (см. главу 8). Целью
весовой балансировки рулей является создание инерционного
момента, стремящегося повернуть руль в сторону, противопо-
ложную той, куда стремится повернуть его инерционный момент
от масс конструкции руля. Определим, каковы должны быть
параметры балансирующего груза (масса, плечо, место установ-
ки), чтобы полностью парализовать инерционный момент кон-
струкции руля; прежде всего подсчитаем величину этого момента.
Пусть (фиг. 129) Сг — произвольная точка руля направления,
в которой сосредоточена масса тг Расстояние этой точки от оси
вращения руля АА' обозначим л'( и от оси фюзеляжа ОСУ—у,.
>) Е. П. Гроссман — .Расчет критической скорости флаттера вертикального
оперения* (Техннч. отчеты ЦАГИ № 12, 1942 г.).
233
При колебаниях фюзеляж закручивается около оси ОО' и
изгибается в горизонтальной плоскости. Ввиду малости хорды
вертикального оперения по сравнению с общей длиной фюзеля-
жа, можно считать что на участке, занятом вертикальным опе-
рением, угол закручивания и прогиб фюзеляжа одинаковы во
всех точках. Обозначим через Z(t)—боковой прогиб оси ОО' в
зоне оперения и через 6(£)— угол закручивания фюзеляжа вок-
руг этой оси; очевидно, что для точки Сг:
zt = Z + у fl.
Вследствие движения фюзеляжа разовьется боковая сила
инерции, равная для точки Сг:
d?z.
=~mi(z+y^
Эта сила создает момент, стремящийся повернуть руль вок-
руг его оси вращения АА':
— ttii(Z +yib')xi.
Суммируя моменты инерционных сил по всему рулю, най-
дем:
ми = — S mi (Z +У1«) xi = — z S mixi~e S Wr
Очевидно, V m. xt = Mp cp, где Mp — масса руля (без балансиру-
ющего груза) и а — расстояние его центра тяжести от оси вра-
щения; 2j т^у^ Jmxy — центробежный массовый момент инер-
ции руля относительно осей ОО' и АА'. Поэтому, окончательно
— Мр Яр Z ^тху ® •
Чтобы парализовать действие этого инерционного момента и
не допустить отклонения руля (а еще лучше—вызвать отклоне-
ние руля в сторону, противоположную той, куда его стремится
повернуть момент 7ИЙ), поместим впереди оси вращения на рас-
стоянии £ груз М (фиг. 129). Расстояние груза от оси фюзеляжа
ОО' пусть будет tj. Рассуждая, как и в предыдущем случае, най-
дем, что при вибрациях фюзеляжа груз разовьет силу инерции
— -M(Z + t1G)> направленную в ту же сторону, куда и сила инер-
ции в точке С;. Момент этой силы инерции относительно оси
вращения АА' будет иметь другой знак, чем (так как М и
Сг находятся по разные стороны оси вращения) и составляет:
М5 — М (Z-j-y 6): = Mi Z+Mi tq 0.
234
Общий момент, вращающий руль при колебаниях фюзеляжа*
будет
Ми + Мб = (М? - Z 4- (М т] - Jmxj)b.
Чтобы руль при отклонениях (под действием инерционного
момента) не создавал аэродинамической силы, усиливающей ко-
лебания фюзеляжа, необходимо:
Мо + Мб>0
Очевидно это будет выполнено, если инерционный момент ба-
лансира перевешивает инерционный момент от массы руля:
(36.1)
Первое из этих условий носит название условия статической
балансировки и сводится к требованию, чтобы статический мо-
мент балансирующего груза был больше или равен статическому
моменту массы руля, т. е. чтобы центр тяжести системы руль-
балансир находился на оси вращения или впереди ее. При ра-
венстве статических моментов, когда центр тяжести руля с гру-
зом находится на оси вращения, руль не будет отклоняться за
счет инерционных сил при перемещениях, параллельных оси АА"
(без поворота около оси ОО'). Однако при этом может возник-
нуть вращающий инерционный момент за счет кручения фюзеля-
жа [например, если балансирующий груз расположен очень близ-
ко к оси ОО’ или даже на ней (tq = 0)[. Чтобы парализовать
этот момент, необходимо выполнение второго из условий (36.1).
Оба условия (36.1) вместе носят название условий динами-
ческой балансировки. Таким образом и в данном случае так же>
как и при колебаниях крыла с элероном, положение центра тя-
жести само по себе еще не определяет свойств системы в смыс-
ле возможности флаттера. Существенную роль играет также и.
положение балансирующего груза по размаху, определяемое ве-
личиной 7j. В частности, если сбалансировать каждое сечение
руля, параллельное ОО', в отдельности так, чтобы центр тяжести
каждого сечения руля вместе с грузом находился на оси враще-
ния АА', то оба условия (36.1) будут удовлетворены. Если цент-
ры тяжести различных сечений находятся на одинаковом расстоя-
нии от его оси вращения, то для выполнения условий динами-
ческой балансировки достаточно поместить груз в сечении, где
расположен общий центр тяжести всего руля (или еще дальше
от оси ОО') и подобрать этот груз так, чтобы центр тяжести
системы руль-балансир находился на оси вращения АА'.
Весьма заманчиво установить балансир в таком месте, чтобы
его можно было спрятать в фюзеляже. Очевидно этого можно
достигнуть, только установив балансир вблизи оси ОО’. Однако
235
такой балансир при кручении фюзеляжа почти бездействует, так
как, находясь слишком близко к оси вращения, где амплитуда
колебаний невелика, создает очень малые инерционные силы.
С целью получения минимально допустимой величины балан-
сирующего груза, массу его обычно подбирают из условия ста-
тической балансировки, так, чтобы было
= (36.2)
Задаваясь плечом ?, находят необходимую массу балансирую-
щего груза:
М = Мр^ .
Подставляя это значение 7И во второе из условий (36.1), опре-
деляют нужное расстояние груза от оси фюзеляжа
> м^р- (36.3)
Вообще, при подборе балансира одну из величин М или 5
можно задавать по произволу, тогда вторая определится из усло-
вия (36.2), а расстояние балансира от оси фюзеляжа из условия
<36.3).
Иногда имеет смысл устанавливать не один, а несколько
балансирующих грузов, например, если на руле имеется роговая
аэродинамическая компенсация и желательно часть балансирую-
щего груза установить в роге.
Если'/Ир/И.,,...М„ массы, ?j,c2, — плечи балансирующих
грузов, т]1,т]2,... т]„ —- расстояния этих грузов от оси фюзеляжа, то
вместо (36.1) должно быть:
М1£1 + М2£а+ .. . + Mnzn 'Mp яр |
/и, *1 ,!1+м, ъ ъ +...+7jn > Jmxy / • (36Л)
Указанные выше условия балансировки получены в предполо-
жении, что руль является абсолютно жестким телом. Если руль
сам может деформироваться, то этих условий может оказаться
недостаточно, а потому все рули следует делать по возможности
жесткими.
Опыт показывает, что выполнение условий динамической ба-
лансировки является достаточной гарантией невозможности флат-
тера’), и для самолетов с динамически сбалансированным рулем
поворота расчета на флаттер вертикального оперения обычно
не производят.
’) Т. е. неучтенное нами изменение шарнирного момента не в состоянии
создать условия флаттера.
236
37 Изгибно-рулевой флаттер горизонтального оперения
Расчет изгибно-рулевого флаттера является обязательным для
каждого самолета. Однако и в этом случае можно указать усло-
вия балансировки, соблюдение которых обычно бывает достаточ-
ным для предотвращения изгибно-рулевой формы флаттера. Как
и для крыла с элероном (или для руля направления), эти условия,
получаются из требования, чтобы инерционные силы, создаваемые
балансирующим грузом при колебаниях фюзеляжа были доста-
точны для уравновешивания инерционных сил от масс самого
руля.
Поясним, каким образом руль высоты может поддерживать
колебания фюзеляжа. Пусть, вследствие какого-либо случайного
импульса, фюзеляж изогнулся (фиг. 130, положение /). Предо-
Фнг. 130. К анализу изгибно-рулевого флаттера.
ставленный затем самому себе фюзеляж будет ускоренно двигать-
ся к положению равновесия (III). Если центр тяжести рул
высоты находится позади его оси вращения, то руль при
этом будет по инерции отставать и отклонится вверх. После пе-
рехода через положение равновесия III, фюзеляж под действием
сил упругости будет двигаться замедленно, в то время как центр
тяжестй руля стремясь по инерции сохранить приобретенную
скорость, будет нагонять в своем движении стабилизатор (поло-
жения IV и V). Следовательно, при движении фюзеляжа вниз,
руль оказывается отклоненным вверх. Точно также при движе-
нии стабилизатора вверх—руль будет отклоняться вниз. За счет
отклонения.руля возникнет дополнительная подъемная сила, ко-
торая будет все время направлена в ту же сторону, куда движег-
*) См. также Е. П. Гроссман и А. М. Ершов .Упрощенный метод опреде-
ления скорости нзгибно-рулевого флаттера"(Технич.отчеты ЦАГИ №3, 1941г)
237
«ся фюзеляж, и будет стремиться усилить колебания послед-
ив?».
Чтобы сделать флаттер невозможным (мы пока не учитываем
изменения аэродинамического шарнирного момента руля при ко-
лебаниях фюзеляжа), нужно потребовать, чтобы при движении
вниз руль относительно стабилизатора отклонялся также вниз и
при движении стабилизатора вверх—руль отклонялся также
вверх, т. е. противоположно тому, как показано на фиг. 130. С
первого взгляда кажется, что для этого достаточно потребовать,
чтобы центр тяжести руля находился впереди его оси вращения.
Однако в действительности дело обстоит несколько сложнее, так
как необходимо учесть^еще силы инерции, возникающие вслед-
Фиг. 131. К определению момента инерционных сил при изгибных колебаниях
фюзеляжа.
ствие поворота стабилизатора на угол 6. Этот поворот создает
неравномерность амплитуды колебания вдоль хорды опере-
ния и потому одна и та же масса, но расположенная в разных
местах, создает разные силы инерции.
Чтобы получить количественный критерий потребной весовой
балансировки, определим момент инерционных сил, вращающий
руль при изгибных колебаниях фюзеляжа. Этот момент и необ-
ходимо компенсировать моментом сил инерции от балансирующих
грузов.
Пусть (фиг. 131) I—фюзеляж с оперением в положении рав-
новесия. Вследствие изгиба фюзеляжа, оперение займет положе-
ние II. Обозначим через I расчетную длину фюзеляжа (за конец
фюзеляжа условно принимается сечение, происходящее посре-
дине между узлами крепления стабилизатора к фюзеляжу), рш—
расстояние от конца фюзеляжа до оси вращения руля высоты,
у—прогиб фюзеляжа в произвольном сечении (у — есть функция
координаты х, измеряемой вдоль фюзеляжа, и времени t), У— про-
238
гиб конца фюзеляжа, 6 — угол поворота концевого сечения фю-
зеляжа; величины У и 6 зависят только от t.
Пусть при колебаниях произвольная точка Сг руля, находя-
щаяся на расстоянии ог от его оси вращения и в которой сосре-
доточена масса mit займет положение С\. Если yt— прогиб точки
С |как видно из фиг. 131, У+(рст + с)0], то соответствующая
сила инерции будет:
Ри-= — = — mi [У+(Р«+Ог)Н
Момент этой силы относительно оси вращения руля, очевид-
но, равен—и считается отрицательным, так как положи-
тельное направление как и везде выбрано по ходу часовой стрел-
ки (Ра вращает руль против хода часовой стрелки). Общий мо-
мент инерционных сил:
AfB == — £ puai = S mi°i I (Pm + °i) = m'pz'p (.м'рс'р?ш +
+ZJ&. . (37.1)
Так как ^miai = Mpcp и Emp(’= J'mp, где Мр—масса конструк-
ции всего руля, zp—расстояние его центра тяжести от оси
вращения, J’mp—момент инерции массы руля относительно его
оси вращения.
Между прогибом конца фюзеляжа У и углом поворота
концевого сечения 6 существует связь. Прогиб произвольного
сечения фюзеляжа для определенного тона колебания предста-
вим, как обычно, в виде
У = Ф(*к(0>
где х — абсцисса текущей точки оси фюзеляжа, ф(х) — функция,
определяющая форму колебания. Тогда, очевидно, для конца
фюзеляжа:
y=6(/)^(Z); 6 = ф'(^(0-
Подставляя эти значения в формулу (37.1), будет иметь:
7Ил = ^(ОФ(/Х°12. (37.2)
где
+ (MpvpPm+J\p)^ • (З7.з)
Чтобы определить отношение ф' (/):ф(0> необходимо точно рас-
считать форму колебаний фюзеляжа; однако, статистика расче-
тов по ряду самолетов позволяет приближенно принять:
Ф'(О = )ф(Л,
239
где А = 1,9 для сухопутных самолетов и Х = 2,2 для летающих
лодок.
Таким образом, коэфициент с12° можно вычислять по при-
ближенной формуле:
=Мр’о‘ + + J'inp) |. (37.4)
Пусть впереди оси вращения руля на расстоянии 5 помещен
груз, масса которого М (фиг. 131). При колебаниях фюзеляжа
этот груз разовьет силу инерции Рб, направленную в ту же
сторону, куда и сила Ри:
Рб=-Л![У+(р(„-е)0|.
Однако момент этой силы:
Мб = + Р6Ч = - М [У + (рш-5)’б |
стремится повернуть руль в сторону, противоположную моменту
Л1Ц. Рассуждая, как и при вычислении момента Ми, найдем
^6 = 9 (ОФ (W12>
где
Лс1г = —М - (Мря — J) у,
J = /ИВ2 — момент инерции груза М.
Полный инерционный момент, развивающийся при колеба-
ниях фюзеляжа, будет:
Ми + 7Иб = ?(ЭД(/)с13,
где
= ^12° + Ас 12 = + (Л^'ср'— МВ) р(И + (J'mp + J)
^.(37.5)
Условием того, что инерционный момент от балансирующего
груза перевешивает инерционный момент от массы самого руля,
будет
о. (37.6)
При соблюдении этого условия инерционные силы будут
стремиться повернуть руль таким образом, чтобы создавалась
аэродинамическая сила, демпфирующая колебания: при движе-
нии стабилизатора вниз руль также отклонится вниз, а при дви-
жении стабилизатора вверх и руль отклонится вверх.
Обозначим Мр— массу руля вместе с балансиром и ар—
расстояние центра тяжести системы руль-балансир от оси враще-
240
я руля. Пусть также Jmp — момент инерции системы руль-
Галансир.
Тогда:
Мр = Мр + М; Мрар=Мр'ср—ЛИ; Jmp=J'mp + J
и силу (37.5) мы можем условие (37.6) записать в виде
Мр°р + {МРОР?Ш + Jnlp)j < 0. (37.7)
Как показывает опыт, если инерционный момент руля урав-
новешен, то как и в случае флаттера вертикального оперения
изменения шарнирного момента при колебаниях фюзеляжа не-
достаточно, чтобы вызвать флаттер. Поэтому при соблюдении
условия (37.7) можно считать оперение безопасным в смысле
возникновения изгибно-рулевоп формы флаттера.
Следует, однако, подчеркнуть, что выполнить условие (37.7)
довольно тяжело. Оно требует, чтобы было Мр°р < 0 или ар<0,
т. е. центр тяжести руля (вместе с балансиром) должен лежать
впереди оси вращения. Если под полной балансировкой, как
обычно, понимать помещение центра тяжести на оси вращения,
то условие (37.7) требует, чтобы руль был перебалансирован.
Необходимость перебалансировки руля объясняется поворотом
стабилизатора при изгибе фюзеляжа (угол & на фиг. 131.) Бла-
годаря такому повороту амплитуда колебаний массы, поме-
щенной впереди оси вращения руля меньше, чем амплитуда
колебаний массы, помещенной на таком же расстоянии позади
оси вращения руля. Тем самым при одинаковой величине мас-
сы и одинаковом плече, масса, помещенная впереди оси враще-
ния, будет развивать меньшую силу инерции, чем масса, поме-
щенная позади этой оси. А так как балансир на фиг. 131.
помещен впереди оси вращения, то чтобы компенсировать силы
инерции масс, находящихся позади оси вращения, оказалось
необходимым, чтобы его статический момент был больше стати-
ческого момента этих масс. Если бы стабилизатор перемещался
параллельно самому себе, для полного уравновешивания сил инер-
ции было бы достаточно совмещения центра тяжести системы
руль-балансир с осью вращения.
Из сказанного ясно, что при изгибно-рулевом флаттере, так
же как и при элеронном флаттере, выгодно помещать баланси-
рующий груз в зону больших амплитуд, чтобы он создавал
большие инерционные силы.
Как и при элеронном флаттере можно достигнуть больших
амплитуд колебаний груза, соединяя его с рулем кинематически
и добиваясь большого передаточного числа, т. е. требуя, чтобы
угол отклонения груза был больше угла отклонения руля.
Гроссман и Пановко. 241
Одним из наиболее 'удачных решений является разме-
щение груза в обтекателе фюзеляжа (фиг. 132). При этом груз
попадает в зону наибольших амплитуд ф ляжа; кроме того,
за счет соотношения плеч можно добиться передаточного числа,
большею единицы. Читатель сам не затруднится составить вы-
ражения коэфициента Дс);1 для рассматриваемого случая; мы же
ограничимся приведением окончательного ре ультата:
Фиг 132. Баланснрукмций груз следует пс-.-ещать в зону
больших колебаний фюзеляжа.
г.
где^ = --—передаточное число. Остальные величины показаны
на фиг. 132. Условие (37.6) запишется так
лт/о/+(Л4ро;Р,,+/тр)у-ж(1 -I
В данном случае можно достигнуть yi лдения массы балан-
сира М путем увеличения передаточного числа Кроме того
мы достигаем уменьшения массы балансире’, помещая его воз-
можно дальше назад, где амплитуды колей ня наибольшие.
Как и кинематические балансиры для тронов, кинематиче-
ские балансиры руля высоты можно вк. вдчать в систему про-
водки управления. На фиг. 133 приведен пример такого балан-
сира, осуществленного на одном самоЛ' ге и оказавшегося
весьма рациональным. Следует также помнить, что влияние ба-
242
а существенно зависит от амплитуды его колебаний при
'1аНибе фюзеляжа. Поэтому балансиры, располагаемые вблизи
кабин ы пилота, мало эффективны, хотя бы они и уравновешивали
статический момент
руля. Считается, что
на критическую ско-
рость флаттера балан-
сиры, находящиеся
вблизи ручки управле-
ния, вообще не влияют,
так как амплитуда их
колебаний при вибра-
циях фюзеляжа нич-
тожна по сравнению с
амплитудой колебаний
горизонтального опе-
рения и потому раз-
виваемые ими при ко-
лебаниях инерционные
силы ничтожно малы
по сравнению с инер-
ционными силами от
массы руля.
иСЬ РраЩёНУЯ P~u
Фиг. 133. Кинематический балансир руля
высоты.
ось вращения
балансира.
Этим обстоятельством пользуются для улучшения пилотажных свойств ма-
шины. Дело в том, что перебалансировка руля весьма неприятно отражается
на пилотажных качествах самолета. Пилот начинает испытывать необычные
Фиг. 134. Ухудшение пилотажных свойств вследствие перебалансировки. При
перегрузках груз стремится увеличить отклонение руля.
ощущения на ручке, так как балансир слишком разгружает руль. Так, напри-
мер. может оказаться, что при выводе из пикирования, когда пилот хочет
взять ручку на себя, он, вместо того, чтобы преодолеть некоторое усилие, бу-
дет вынужден сдерживать ручку, которая под действием балансира сама будет
стремиться двигаться к положению „на себя". Причина этого кроется в центро-
бежной силе, которая будет развиваться балансиром при выводе из пикирования
(фиг. 134). Обратные усилия на ручке при перебалансировке появляются не
16» 243
только при выводе из пикирования, но и в горизонтальном полете. Однако
особенно неприятно сказывается на устойчивости и управляемости влияние
балансира при фигурных полетах, когда действие'его усиливается под влиянием
перегрузки.
Чтобы избежать ухудшения пилотажных свойств вследствие перебаланси-
ровки, руль разбалансируют с помощью груза, установленного на ручке
пилота (фиг. 135). Такой груз, называемый контрбалаисиром, создает статнчес-
Фиг. 135. Контрбалапсир парирует вредное влияние перебалансировки
кий момент, направленный обратно статическому моменту от балансирующего
груза и парирует вредное влияние перебалансировки. Существенно отметить
что перегрузка действует одинаково как на балансир, так и на контрбалансир,
и потому эффект перебалансировки уничтожается во всех случаях полета. На
свойства же конструкции в отношении флаттера оперения контрбатансир
Фиг. 136. Установка амортизационного троса для борьбы с вредным влиянием
перебалансировки.
сколько-нибудь заметно не сказывается, так как он расположен в зоне ни-
чтожно малых амплитуд.
Иногда употребляется другой способ борьбы с вредным влиянием пере-
балансировки — установка амортизационного троса (или пружины), крепящейся
одним концом к неподвижной точке на фюзеляже н другим — к проводке та-
ким образом, чтобы натяжение троса уменьшало действие балансирующего
груза (фиг. 136); такая схема имеет существенный недостаток: при криволи-
нейном полете перегрузка увеличивает действие балансирующего груза, в то
244
как сила натяжения амортизатора остается постоянной. Поэтому на
₽1? '1жах при выводах из пикирования и т. д., все явления, связанные с пере-
'анснрОВКОЙ все же наблюдаются. Дать же настолько сильное натяжение
й отизатору. чтобы он и при перегрузках компенсировал перебалансировку,
Я । ,1 так как при сильном натяжении амортизатор будет мешать управле-
н1 в горизонтальном полете.
Итак мы получили условие, достаточное для предотвращения
(Ьчаттера. Однако это условие требует перебалансировки руля
высоты, что ухудшает пилотажные качества самолета и, в свою
очередь, требует установки контрбалансиров. Все это ведет к
увеличению веса самолета и усложняет производство. В то же
время, найденное выше условие безопасности от флаттера,
являясь достаточным, вовсе не является необходимым.
Вполне возможно, что критическая скорость флаттера окажется
достаточно большой и в том случае, когда условие (37.6) не
выполнено. Однако убедиться в этом можно только проведя
расчет критической скорости. Поэтому такой расчет произво-
дится для каждого самолета и необходимая степень балансировки
устанавливается расчетом.
Гак как метод определения критической скорости изгибно-рулевого флат-
1 .па строится так же. как и метол расчета изгнбно-крутильного или изгибно-
эдеринного флаттера (г. е. на основе результатов главы 7), мы на этом воп-
росе останавливаться не будем, отсылая интересующихся к специальной лите-
ра ’е !). Укажем лишь, что поскольку влияние руля высоты при флаттере
горизонтального оперения во всем подобно влиянию элерона при фчаттере
крыта, расчетные случаи выбираются так же, как и для изгибно-элеронного
флит.ера. Так же Строится кривая зависимости'критической скорости от от-
ношения частот колебаний руля и фюзеляжа, ход которой совершенно похож
на ход кривой VKp изгибно-элеронного флатт ера по отношению частот элерона
и ыла (фиг. 124). Изменение вида этой кривой в зависимости от степени
весе ай балансировки происходит совершенно так же, как изменение вида
Соответствующей кривой при изгибио-элеронном флаттере.
На критическую скорость изгибно-рулевого флаттера оказывает суще-
ствепноё влияние величина момента инерции руля. При увеличении момента
инерции руля критическая скорость растет точно так же, как критическая
ч орость изгибно-элеронного флаттера при увеличении момента инерции
элерона.
38. Крутильно-рулевой флаттер горизонтального
оперения
опе^аССМ01 рение крутильно-рулевого флаттера горизонтального
рения начием также с выявления достаточных условий для
° "Редупреждения.
П. Гроссман „Флаттер хвостового оперения" (Труды ЦАГИ, вып. 501. 1940)
245
Пусть фюзеляж совершает крутильные колебания вокруг оси
ОО'. Рассмотрим движение в какой-либо момент времени и пусть
угловое ускорение движения в этот момент будет а (фиг. 137)1).
Тогда точкам С, и С,, расположенным симметрично относительно
оси ОО' на расстояниях+ г, от нее, будут соответствовать ли-
нейные ускорения +г2а, направленные в противоположные сто-
роны. Если /и2 — масса, сосредоточенная в каждой из точек Q
и С2, то соответствующая сила инерции будет + /nz2 а. Силы инер-
ции в точках Cj и Са, очевидно, будут равны и действовать в проти-
Фиг. 137. При крутильно-рулевом флаттере сущест-
венно распределение масс по размаху оперения.
воположные стороны, создавая пару вокруг оси 00'. Эти силы
будут также закручивать руль вокруг его оси вращения АА'
причем кручение правой и левой половин руля будет происхо-
дить в разные стороны.
Благодаря тому, что правая и левая половины руля жестко
связаны между собой, сечение руля, находящееся на оси самолета
закручиваться не будет, но чем ближе к концу руля, тем более
будет нарастать уголкручения. Другими словами, каждая половина
руля закручивается так же, как если бы она была консольной
балкой, защемленной в сечении, находящемся в плоскости сим-
метрии самолета. Если бы руль был абсолютно жестким, то
флаттер был бы невозможен (при отсутствии закручивания руля
неоткуда было бы взяться аэродинамическим силам, поддержш
вающим колебания фюзеляжа).
!) См. Я. М. Пархомовский. „Крутильно-рулевой флаттер хвостового опе-
рения* (Труды ЦАГИ № 524, 1940).
246
Из сказанного 'ледует, что нельзя получить условий отсут-
твия крутильно-рулевого флаттера тай» как это было сделано
тая изгибно-рулевсчо флаттера. Тогда рУлв рассматривался как
вердое тело и налгчие момента сил инерции неизбежно вызывало
отклонение руля. Кроме того,—что особенно важно,—поскольку
пуль рассматривался как твердое тело, безРазлично было в каком
сечении руля был приложен крутящий,момепт инерционных сил—
при одинаковой величине этого момеНта возникал одинаковый
угол отклонения руля, а следовательно и одинаковая аэродина-
мическая сила. В рассматриваемом же случае (когда руль яв-
ляется упругой балкой, закрепленной в среднем сечении) сущест-
венно, где приложен момент инерционЯых си-Л> угол закручива-
ния может быть разным даже при одиг<аков°й величине крутя-
щего инерционного момента,—в зависиМ0СТИ ст координаты се-
чения, в котором сн приложен. Поэт<)МУ в рассматриваемом
случае условие отсутствия флаттера мы Должны сформулировать
несколько иначе.
При закручивании руля силы инер»1ИИ производят некото-
рую работу; обратимся к ее определений?-
Пусть масса элементарного отсека fflpdz, где тр — погонная
масса руля; соответствующая этой масс*’ сила инерции будет,—
mpzrJ.dz.
Момент этой силы инерции относитеЛьно осн АА':
— mpza.xpdz, (38.1)
где хр—расстояние центра тяжести отс^<<а от оси
Пусть при колебаниях руля его сеченРя> закручиваясь, повора-
чиваются на углы р, причем р зависит как от времени t, так
и от координаты сечения г1); тогда раб°та этого момента за
время Сбудет:
дЭ
где dt — приращение угла поворота р за время dt.
Полагая как всегда
₽=?(/)<?(,?),
найдем для работы элементарного момеИта сил инерции:
mpz a xpq <f> dzdt. *
Ч При учете углов отклонения сечения 3 слеАОва^° принять для
силы инерции отсека более точное выражение ™PZ а eiz—mpfixpdz. второй
член которого учитывает добавочное ускорение появляющееся вследствие по-
воротов сечения вокруг осн АА'. Однако, второй члеи значительно меньше
первого и может быть опущен.
247
Полная работа всех элементарных моментов за время dt на
полуразмахе руля:
dR= —
aq dt,
где z,- полуразмах руля. В силу симметрии, для всего руля
будет:
dR = a qc\3dt,
где обозначено:
•н
с°13 = —2 ^nipX^zdz.
о
(38 2)
Допустим, что на расстояниях т( от оси ОО' (справа и слева
от нее), на расстоянии с впереди оси вращения руля, помещены
балансирующие грузы, общая масса которых равна М. Работа
сил инерции грузов может быть подсчитана только что приме-
ненным способом и приведена к виду:
d R6~ aq\c 13dt,
где
Дс13 = 2Мт^(т]).
Здесь ср (т|)--значение функции с (г) в сечении z — rlt в кото-
ром помещен балансирующий груз.
Общая работа сил инерции системы груз-балансир за время
dt очевидно имеет значение aqc13dt, где
с13 = 2/14 ?7|ср (0 2 J nipx^zdz. (38 3
За условие безопасности от флаттера можно принять требова-
ние, чтобы работа сил инерции балансира превосходила работу
сил инерции самого руля 1):
с13>0. (38.4)
В случае установки одного балансира на каждой половине
коэфициент с13 вычисляется по формуле (38.3). Если груз уста
навлнвается в передней кромке и распределяется вдоль размаха,
коэфициент с13 можно определять по формуле (38-2), считая
массу батансира составной частью конструкции руля.
') Это же требование может быть выставлено и в рассмотренных ранее
случаях изгпбно-рулевого или элеронного флаттера, но оно приведет к тем же
условиям балансировки, как и найденные нами. Это объясняется тем, что
в указанных случаях руль (элерон) рассматривался как твердое тело, что со
ответствует ъ = const.
248
В обоих случаях предварительно необходимо определить
,уцкцию формы 9 (г), что делается методом последовательных
приближений, описанным в главе 1 (п. 5). Руль при этом схемати-
зируется как консольная балка. Если балансир является сосре-
доточенным грузом, то и функцию 9 (г) нужно определять по
схеме балки, несущей сосредоточенный груз.
Величина потребного для руля высоты балансировочного
груза и его плечо обычно определяются расчетом изгибно-руле-
вого флаттера или из условия (37.6). Поэтому условие (38.3)
используется только для определения места расстановки грузов
вдоль размаха оперения.
В предыдущем параграфе был указан ряд возможных
схем кинематических балансиров, связанных с проводкой
управления. Такие балансиры прячутся внутрь фюзеляжа. Усло-
вие же (38.4) требует определенного отдаления балансирующих
грузов от оси фюзеляжа и потому не дает возможности прятать
балансирующие грузы в фюзеляж. К счастью это условие, как
и условие (37.6), являясь достаточным т), не является в то же
время необходимым. В большинстве случаев полный расчет кри-
тической скорости3) показывает, что выполнять это условие необя-
зательно. Поэтому всегда выполняется расчет критической ско-
рости крутильно-рулевого флаттера. Если этот расчет показы-
вает, что условие (38.4) нет необходимости выполнять, то можно
прятать балансирующие грузы внутрь фюзеляжа. В противном
случае приходится мириться с разнесением грузов вдоль размаха
оперения.
Условие (37.6) носит название условия статической баланси-
ровки руля высоты, а условие (38.4)—условия динамической ба-
лансировки. Оба условия являются достаточными для обеспече-
ния безопасности флаттера, но в полной мере применяются
только в тех случаях, когда почему-либо не делается расчета
критической скорости. Они приводят к слишком жестким тре-
бованиям и потому обычно степень балансировки определяется
не этими условиями, а расчетом.
При расчете изгибно-рулевого флаттера всегда строится
график критической скорости в зависимости от степени стати-
ческой балансировки руля, а при расчете кругильно-рулево! о
флаттера строится график критической скорости в зависимости
от степени динамической балансировки руля [подобно тому, как
при расчете элеронного флаттера строится график критической
скорости в зависимости от степени балансировки элерона,—
(см. гл. 8)].
1) Более подробный анализ показывает, что условие (38.4) является доста-
точным, если частота антисимметричных крутильных колебании руля высоты
больше частоты кручения фюзеляжа. Практически это всегда имеет место.
si См. Я. М. Пархомовскпй „Крутильно-рулевой флаттер хвостового опе-
рения" (Труды ЦАГИ, вып. 524/ Там же содержится подробный анализ влия
нпя конструктивных параметров.
249
итческой J балансировки верти-
jtjo возможности более жест-
изгибно-рулевого флаттера
помощью кинематического
управления, или, еще лучше,
1) Осуществление полной динам
?:альцого оперения.
2 Осуществление руля высоты
.им iSa КруЧение.
Предотвращение возможности
п\ rext статической балансировки с.
ia.iancnpa, включенного в проводку
.оедиценного непосредственно с ру.т
ГЛАВА 10
Баффтинг
40. Явление баф»^тинга
г частей самолета, вызванные
Ьац)фТингом называют колебания <ogTeKaHHtl передних частей
потокам воздуха, завихренным при колебания оперения или
самолета1) (обычно имеются в виДл
хвостовой части фюзеляжа). . как не ВПОлне регулярные
Бившие баффтинг воспринимается одергивания управления и
удары п0 оперению, вызывающие Иногда эги удары бывают
Ездра1^ивания конструкции самолета.^яоактера с частотой порядка
почти правильного периодического % случаях они не имеют ясно
1—5 Колебаний в секунду; в другие
вьфаж енного периода.
юность баффтанга; а —малый
Ф».г . 140. Влияние угла атаки па B03mC^)W; б—большой угол атаки
J'TO-V атаки—вихри проходят ниже онере переН11е.
вихри попадают на
, , . гЯ является колебательный
Физической причиной баффтинг ующегОся за телом при
характер аэродинамического следа, о Кармана это свойство
его об>екании; с точки зрения те’одически срываются дис-
следа ^объясняется тем, что с тела п 1 п с закоиом Био-Савара
кретны е вихри, которые в соответс ,гей за этим телом. Такое
индуци руют периодическое поле скор быть вызвано отдель-
период мческое вмхреобразование мо инструкции самолета: пая-
ными п дохо обтекаемыми частями 1
iffet (англ.) — тряска.
252
стройками на крыле или фюзеляже, мотоустановками на крыле
всасывающими патрубками или выхлопами, фонарем или стрел-
ковой башней. Кроме того, с верхней поверхности крыла на
больших углах атаки всегда наблюдается срыв вихрей (особенно
при планировании, спиралях с убранным газом, на посадке или
взлете, при выполнении фигур высшего пилотажа). Влияние .1ла
атаки на направление следа можно видеть на фиг. 140.
Явление баффтинга приобретает особенную сил} в тел
чаях, когда оно вызвано срывом потока с крыла, так как в
этом случае вблизи оперения проходят вихри большой интеп
сивности. Наиболее опасным баффтинг оказывается при близости
периода ударов к собственным периодам оперения или ф. >зе-
ляжа, так как при резонансе размахи колебаний прогрессивно
возрастают. Однако и при отсутствии резонанса удары могу г
быть достаточно большими, чтобы угрожать прочности конструк-
ции.
Попадание оперения в область завихренного потока, наряду
с баффтингом связано с уменьшением эффективности рулей, и
оперения, что в свою очередь втечет за собой падение устой-
чивости на больших углах атаки.
*
41. Возможности количественной оценки параметров
возмущающих сил
Из отмеченного выше колебательного характера стета выте-
кает, чго у оперения индуцируются переменные во времени вер-
кальные скорости, следствием которых являются периодические
возмущающие силы, действующие на оперение. В пастояще-
параграфе будет дана оценка частоты этих сил для случая,
когда причиной баффтинга является срыв потока в крыле.
Частота действующих на оперение возмущающих сил есть
частота срыва вихрей; последняя, не подчиняясь теоретическому
определению может быть найдена опытным путем по испытанию
модели. Пересчет на истинные размеры производится с помог”
числа Струхаля:
(41.1)
Опытным путем найдено, что число Струхаля для различных
самолетов лежит в довольно узких пределах:
57 = 0,14-0,16.
В формуле (41.1) /го— частота впхреобразования (число сорвав-
шихся вихрей в секунду); V—скорость потока; С —линейный
размер обтекаемого тела, взятый перпендикулярно направлению
потока. Для крыла:
25J
С — b sin a,
где b — хорда, a — угол атаки.
Таким образом, для крыла:
ko —0,15-7—
tfsina
и соответственно круговая частота:
k == 2к/го
V
bsina '
(41-2)
Аналитическое определение верхнего значения величины воз-
мущающих сил возможно теоретическим путем *); дело в том,
что наибольшая величина подъемной силы оперения зависит от
свойств самого оперения или, говоря определеннее, от его кри-
тического угла атаки. Принимая, что гипотеза стационарности
справедлива и для быстрого колебательного процесса, можно
для максимального значения погонной интенсивности возмущаю-
щей силы принять:
{-£) (41-3)
\ /го
где Лаго — наибольшее приращение угла атаки оперения, при
котором еще возможно увеличение подъемной силы, равное раз-
ности o-kp—«; а — угол атаки оперения при отсутствии колеба-
ний; Ьги — текущее” значение хорды оперения.
Очевидно, что выражение (41.3) дает результат во всяком случае
не меньший истинного значения погонной подъемной силы, так
как дает верхнюю границу последней. Однако при таком рас-
чете остается открытым вопрос о значении вводимого преувели-
чения; в огромном большинстве случаев это преувеличение
оказывается настолько значительным, что вычисление теряет
всякую достоверность. Поэтому обычно расчет на 'баффтинг
не производится. Если во время полетов у самолета обчару
жено явление баффтинга, то борьба с ним ведется опытным
путем. Обыкновенно прежде всего снимается в полете (с пс
мощью наклеиваемых па крыло и фюзеляж ленточек) спект;
обтекания и обнаруживается место и причина срыва внх
рей, вызывающих тряску оперения. Эта причина устраняете
путем улучшения обтекания соответствующего места.
Такой путь борьбы с баффтингом может успешно приме
няться благодаря тому, что баффтинг в отличие от флат-
0 См. Абдрашитов Г. Г. „К вопросу о баффтннге хвостового оперения™
(Труды ЦАГИ № 494, 1939).
254
мера, не вызывает быстрой полочки конструкции. Полеты на
самолете, у которого имеется баффтинг, как правило, не грозят
непосредственной опасностью.
42. Меры борьбы с баффтингом
Борьба с баффтингом должна вестись конструктивным путем.
При компоновке самолета обязательно заботятся о том, чтобы
оперение самолета не попадало в область срыва крыла. При
правильном расположении оперения устраняются наиболее непри-
ятные виды баффтинга, вызванные срывом потока с централь-
ной части крыла. При этом следует добиваться устранения бафф-
тинга не только выносом оперения из области сорванного
потока, но и уменьшением срыва. Величина области срыва
зависит в большой степени от удачности выполнения мест
сочленения крыла и фюзеляжа и сочленения крыла с мотогон-
долами на двухмоторных самолетах. Неудачное сочленение
приводит к преждевременному появлению срыва. Одной из
форм борьбы со срывом в сочленениях является постановка
зализов.
Во всех случаях борьбу с баффтингом ведут за счет улуч-
шения обтекания, а не за счет увеличения жесткости деформи-
рующихся частей самолета. Уже при проектировании стараются
-сделать так, чтобы не было срывов, попадающих на оперение.
Наличие вредных срывов может быть обнаружено при продув-
ках модели самолета в трубе. Однако картина срыва на модели
не всегда точно соответствует картине срыва на самолете и,
кроме того, на самолете могут появиться добавочные надстройки,
не предусмотренные на модели. Это приводит, в ряде случаев,
к необходимости устранения срыва на уже построенном само-
лете. Следует отметить, что баффтинг может быть вызван и
в эксплоатации самолета появлением добавочных надстроек,
связанны^, например, с перевооружением самолета или подвес-
кой к самолету бомб.
После того, как установлены причины баффтинга. т. е. вы-
явлены места, нарушающие плавное обтекание передней части
самолета, следует найти конструктивные мероприятия по устра-
нению срыва или, если это не удается, следует добиться того, что-
бы оперение не оказалось в зоне сорванного потока.
Ввиду того, что причины, вызывающие срыв потока, могут быть весьма
разнообразны, нельзя дать точных указаний по устранению баффтинга и
приходится, руководствуясь вышесказанными общими соображениями, в каж-
дом отдельном случае находить наиболее удачные конструктивные меропри-
ятия по устранению баффтинга. Чтобы дать представление о тех мероприя-
тиях, которыми пользуются, мы приведем описание характерного случая
устранения баффтинга на конкретном самолете 1) в процессе летных испытаний.
*) А. В. Чесалов .Опыт борьбы с вибрациями на самолетах". (Труды
ЦАГИ вып. 494, 1940 г.).
255
(
1
z
>
г
i\
с
п
н
<1
21
На самолете ЦАГИ-7, представляющем собой моноплан с низкораспсю-
женным крылом, наблюдались явления баффтиига при планировании н спира-
лях с убранным газом (при 300-400 об/мин) на скоростях, начиная с 140-150 км час.
и ниже. При планировании на скорости 120км)час удары были столь сильны ли
что полет становился невозможным из-за опасности поломки оперения. В мог р.’
ном полете никаких колебаний оперения не наблюдалось и самолет вел сс5д
вполне нормально. Бывали случаи, когда на планировании баффтинг приводил
к поломке киля самолета.
Для выявления источника срыва потока с крыла был снят спектр обте-
кания крыла и капотов моторов с помощью ленточек. При помощи спектра
было установлено, что при прикрытии газа на планировании иа ско-
ростях 150 км час и меньше начинается срыв у задней кромки крыла
между мотоустановками и фюзеляжем. Область срыва увеличивалась с увели-
чением угла атаки и па скорости 115—120 км)час охватывала всю центр; ;ь-
ную часть крыла.
Полеты показали, что сейчас же вслед за появлением срыва на крыт
начинается раскачивание оперения. При помощи длинных лент, наклеенных.
на крыло, было обнаружено, чгб стр} и
воздуха, сходящие с крыла на больших
. скоростях, проходят ниже стабп.тизато-
ра, а при переходе на большие уг..
атаки попадают на стабилизатор (см.
I IF 1*1 • фиг. 140). Таким образом, было уст
| новлено, что вибрации оперения вы-
• о зываются ударами вихрей, срывающич-
Фиг. 141. Закрылки затягивают ,
срыв и отводят направление следа ся с центроплана.
вниз. Для устранения баффтиига надо
было ликвидировать преждевременный срыв потока с крыла. Испытания
установили, что мелкие надстройки на поверхности крыла практически не
влияли на начало срыва. Из ряда мер по устранению баффтиига, испробован-
ных в процессе летных испытаний, наиболее эффективной оказалась noci
новка закрылков.
При наличии закрылков (или щитков) путь сходящих с крыла вихрей
оказывается отклоненным книзу и обычно минует оперение (фиг. 141).
Из приведенных примеров видно, что конструктивные меры,
борьбы с баффтингом естественно разделить на три группы:
1. Ликвидация причин, создающих баффтинг (предотвращение,
либо уменьшение срывов).
2. Вынесение оперения из аэродинамической тени крыла,
обычно, путем отклонения тени вниз установкой закрылков.
3. Изменение частот собственных колебаний хвостовой части.
Какие из этих мероприятий являются наиболее эффективными
нужно отдельно решать для каждого конкретного' случая.
Первая группа мер сводится к улучшению обтекания: поста-
новка зализов, предкрылков, закрылков и т. д. Особенно необ-
ходимо устройство зализов в месте стыкования центроплана с
фюзеляжем. Меры второй группы могут настолько отвести опе-
256
рение от сбегающих вихрей, что будут индуцированы лишь
весьма незначительные возмущения. Это достигается внесением
горизонтального оперения возможно выше; или отклонением вниз
аэродинамического следа, при этом на летных углах атаки завих-
ренный след проходит много ниже оперения.
Третья группа мероприятий является обычной! при борьбе
с любыми вынужденными колебаниями. Некоторую помощь при
проектировании может оказать предварительное сопоставление
частоты срыва с частотой собственных колебаний оперения; это
сопоставление возможно с помощью ф-лы (41.1) и способов,
развитых в п. 6.
ПРИЛОЖЕНИЕ
Замечания о влиянии сжимаемости на критическую скорость флаттера
Изложенная выше теория флаттера не учитывает влияния сжимаемости воз-
духа на величину критической скорости. Между тем известно, что сжимае-
мость воздуха при околозвуковых скоростях существенно влияет на величины
аэродинамических сил и на закон их распределения по профилю, а следова-
тельно, она должна повлиять и на величину критической скорости.
В настоящее время сделаны лишь первые шаги в исследовании этого воп-
роса, главным образом, экспериментального характера. Теории, позволяющей
расчетом определить критическую скорость флаттера в области околозвуковых
скоростей, не существует.
Полученные до сего времени результаты сводятся к следующему:
I. Сжимаемость не оказывает существенного влияния на критическую ско-
рость флаттера до чисел Маха порядка 0,6.
2. В диапазоне чисел Маха 0,6 — 0,75 влияние сжимаемости сказывается в
уменьшении критической скорости по сравнению со значением, определен-
ным без учета сжимаемости. Это уменьшение тем сильнее, чем больше число
Маха и для Ма = 0,75 доходит до 30 процентов и более.
3. Влияние сжимаемости при числах Маха больших 0,75 — 0,80 достоверно
не выяснено. Не исключена возможность, что при Ма>0,75 — 0,80 уменьше-
ние критической скорости за счет сжимаемости будет уже не столь большим,
— а может быть его и вообще не будет.
4. Влияние сжимаемости на флаттер органов управления (элеронов, рулей)
совершенно не исследовано.
Ввиду отсутствия метода расчета, учитывающего влияние сжимаемости при
больших числах Маха, практические расчеты приходится производить без
учета влияния сжимаемости, и для высокоскоростных самолетов следует поль-
зоваться увеличенным коэфициентом безопасности.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
М В Г' ВОПРОСУ о баффтинге хвостового оперения. Труды
Ананьев И. В. Расчет на резонанс проводки управления самолетом.
Труды ЦАГИ № 537. 1941.
плптН?.Ньев И- В- Расчет динамического демпфера. Технические отчеты
ЦА1 И № 46. 1915.
по А н а н ь е в И. В., Панкратов А. И., Тимофеев П. Г. Рекомендации
„,,„раСчету вибрации винтомоторных установок и примерные конструкции
амортизаторов. Технические отчеты ЦАГИ № 60. 1946.
Труды3ЦИАм' 91^ 194*^ Утомляемости стали при повторных перегрузках.
k-npn^fJ!,°yc А А' ^чбрацин мотоустановок с жесткими и эластичными
I лениями звездообразного мотора. Труды ЦАГИ № 499. 1940.
. 257
Г р о с с м а и Е. П., К р и ч е в с к и й С. С., Нории А. А. К вопросу об
устойчивости конструкции крыла в полете. Труды ЦАГИ № 202. 1935.
Гроссман Е. П. Перекручивание монопланного крыла. Труды ЦАГИ
№ 253. 1936.
Гроссман Е. П. Флаттер. Труды ЦАГИ № 284 1937.
Гроссман Е. П., Келдыш М. В., Пархомовский Я. М. Вибра-
ции крыла с элероном. Труды ЦАГИ № 337. 1937.
Гроссман Е. П. О причинах флаттера. Труды ЦАГИ № 350. 1938
Гроссман Е. П. Флаттер хвостового оперения. Труды ЦАГИ№ 501.1940.
Гроссман Е. П. Курс вибраций частей самолета. 1940. -
Гроссман Е. П. Изгибно-элеропный флаттер. Труды ЦАГИ № 534 1941.
Гроссман Е. П. и Ершов А. М. Упрощенный метод определения ско-
рости изгибно-рулевого флаттера. Технические отчеты ЦАГИ № 3. 1941.
Гроссман Е. П. Расчет критической скорости флаттера вертикального
оперения. Технические отчеты ЦАГИ № 12. 1942.
Гроссман Е. П., Келдыш М. В., Марин Н. И. Вибрации на само-
лете. 1942.
Ден-Гарт о г. Теория колебаний. 1912.
Житомирский Ф. Е., Житомирский В К. О вибрациях моторной
I руппы в полете. Труды ЛИИ (ЦИАМ. № 15) 118. 1916.
Иориш Ю. И. Равночастотные амортизаторы вибраций для самолетного
оборудования. Труды НИСО № 7. 194о.
Келдыш М. В. и П а р х о м о в с к и й Я. М. Колебания крыла с упруго
прикрепленным мотором. Труды ЦАГИ № 535. 1941.
Кома й А. И. Совместные колебания крыла с сосредоточенными грузами.
Труды ЦАГИ № 472. 1940.
Кербер Б. Л. Амортизация приборных досок на самолетах. Технические
заметки ЦАГИ № 49. 1935.
Л о й ц я п с к и и Л. Г. и Л у р ь е А. И. Курс теоретической механики. 1939
Мар ин Н. И, и С е р о в М. В. Выносливость стали хромансиль ЗОХГСА
Технические отчеты ЦАГИ № 65. 1946.
Одинг И. А. Усталость металлов и задачи машиностроения. 1941.
П а р х о м о в с к и й Я. М Крутильно-рулевой флаттер хвостового оперения.
Труды ЦАГИ № 524. 1940.
Пожал ост ин А. И. Расчет воздушного винта на усталость. Труды
ЦАГИ № 436. 1939.
Попов Л. С. О влиянии фюзеляжа и хвостового оперения на колебания
самолета. Труды ЦАГИ № 343. 1940.
По п о в Л. С. Влияние степени аэродинамической компенсации элеронов
на флаттер крыла. Техни геские отчеты ЦАГИ № 8. 1943.
П р и г о р о в с к и й Н. И, Серенсен С. В.Тетельбаум И. М. Дина-
мическая прочность металлов. 1945.
Рабинович И. М. Курс строительной механики стержневых систем. 1938.
Риз 11. М. Резонансный метод определения собственных частот вибрации
лопастей воздушных винтов. Труды ЦАГИ № 242. 1935.
Р п з П. М. Флаттер крыла с учетом колебаний в плоскости наибольшей
жесткости. Труды ЦАГИ № 340. 1937.
РизП. М. Флаттер воздушного винта. Труды ЦАГИ № 391. 1939.
Серебря некий Н.П. Амортизаторы типа ЦАГИ под звездообразные
и рядные моторы Технические отчеты ЦАГИ № 7. 1942.
Т э п л и н. Колебания в машинах. 1941.
Чесалов А. В. Опыт борьбы с вибрациями на самолете. Труды ЦАГИ
№ 491. 1940.
Юрьев Б. Н. Экспериментальная аэродинамика 1936.
Журнал „Техника Воздушного Флота".
Proceedings of the fifth international congress for applied mechanics, 1939.
Иностранные журналы: Journal of the aeronautical sciences, Journal of the
koyal Aeronautical society, S. A. E. Journal, Aircraft Engineering, NACA (repori
№ 496), Luftfabrtforschung, Aero-Digest.
ОГЛАВЛЕНИЕ
Введение
Стр.
А. Общие замечания................................• . . . 3
Б. Элементы общей теории малых колебаний упругих систем. . . 5
ЧАСТЬ I.' СОБСТВЕННЫЕ КОЛЕБАНИЯ ЧАСТЕЙ САМОЛЕТА.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ, ВОЗНИКАЮЩИЕ ПРИ РАБОТЕ
МОТОРА
Глава I. Собственные колебания частей самолета
1. Вводные замечания......................................... 20
2. Собственные частоты мотоустановок......................... 21
3. Собственные колебания кручения крыла (консольная схема). . 29
4. Собственные колебания изгиба крыла (консольная схема) . . 39
5. Собственные совместные колебания изгиба крыла (консоль-
ная схема)............................................... 42
6. Собственные колебания самолета (свободно плавающая схема). 51
7. Собственные колебания лопасти винта....................... 64
8. Собственные колебания тяг проводки управления............. 74
9. Собственные колебания трубопроводов....................... 81
Глава 2. Возмущающие силы, передаваемые самолету
винтомоторной группой
10. Вводные замечания........................................ 81
11. Возмущающие силы, возникающие при работе мотора... 82
12. Возмущающие силы, возникающие при вращении винта. ... 89 •
1, 3. Сводка результатов............................. . 95
Глава 3. Вынужденные колебания частей самолета,
возникающие вследствие работы винтомоторной группы
14. Вынужденные колебания мотоустановок..................... 97-
15. Приемы уменьшения вибраций и амортизаторы мотоустаповок. 101
16. Динамические напряжения в лопасти винта................ 114
Глава 4. Усталость частей самолета
17. Явление усталости и предел выносливости................ 124
18. Влияние конструктивных, технологических н зксплоага-
цнонных факторов на предел выносливости................. 129
,19. Усталость при несимметричном цикле. Диаграмма Смита. . . 133
20. Усталость частей самолета.. ................. 13(5
ЧАСТЬ II. КОЛЕБАНИЯ КРЫЛА И ОПЕРЕНИЯ, ВОЗНИКАЮЩИЕ
ОТ АЭРОДИНАМИЧЕСКИХ ПРИЧИН
Глава 5. Общий метод определения критической скорости
флаттера
21. Явление флаттера........................................ 138
22. Колебания системы с двумя степенями свободы в потоке воз-
духа....................................................... 144
23. Анализ корней характеристическою уравнения............. 150
Глава 6. Аэродинамические воздействия, испытываемые
колеблющимся крылом
21. Вихревая пелена, образующаяся за крылом при колебаниях. . 15?"
25. Нестационарная теория............................... 159
26. Стационарная теория................................. 160
27. Аэродинамические силы, действующие на крыло в плоско-па-
раллельном потоке....................................... 162
28. Учет влияния конечности размаха на аэродинамические силы. 168
Глава 7. Изгибно-крутильный флаттер крыла
29. Определение критической скорости изгнбпо-крутильного флат-
тера крыла................................................. 172
30. Анализ энергообмена между колеблющимся крылом и потоком. 180
31. Влияние конструктивных параметров на критическую скорость
изгпбно-крутильного флаттера................................ 189
Глава 8. Элеронные формы флаттера крыла
32. Явление изгибно-элеронного флаттера........................ 199
33. Определение критической скорости изгибно-элеронного фтат-
тера........................................................ 210
31. Меры предотвращения изгибно-элеронного флаттера. ... 218
Глава 9. Флаттер хвостового оперения
35. Формы флаттера оперения..................... . .. . 230
36. Флаттер вертикального оперения............................ 233
37. Изгибпо-рулевой флаттер горизонтального оперения. • . . . . 237
38. Крутплыто-рулевоп флаттер горизонтального оперения. 245
39, Рекомендации............................................... 251
Глава 10. Баффтинг
40. Явление баффтинга............................. ........ 252
41, Возможности количественной оценки параметров возмущаю-
щих сил....................,........................... ... 253
4'2. Меры борьбы с баффтингом.................................. 255
Приложение. Замечания о влиянии сжимаемости па критическую
скорость флаттера ... 257
Литература ... .............. . . ............. . 257
А. 1
3