Автор: Поливанов К.М.
Теги: электротехника физика энергетика издательство энергия линейные цепи электромеханические системы
Год: 1965
Текст
&О«Й]
К. М. ПОЛИВАНОВ
.
:ть ПЕРВАЯ
7iiji
№лЛ
ЬЖ^К ,-
.
^^Ив®
?«wWw
KBolvaW
"
основь
-V >.' '.. :'.. : .> . . \ ;.. \ -
‘ ЭЛЕКТР
4
ваейо
fcfis
йЭЙлуЙ
Й'Ж
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ
ЭЛЕКТРОТЕХНИКИ
В ТРЕХ ЧАСТЯХ
Часть первая
ИЗДАТЕЛЬСТВО «Э'Н Е Р Г И Я»
МОСКВА
1965
ЛЕНИНГРАД
к. м. ПОЛИВАНОВ
ЛИНЕЙНЫЕ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
С СОСРЕДОТОЧЕННЫМИ
ПОСТОЯННЫМИ
ИЗДАТЕЛЬСТВО «Э Н Е Р Г И Я»
МОСКВА 1965 ЛЕНИНГРАД
УДК 621.3.01
П 50
Посвящается шестидесятилетию
Московского ордена Ленина
энергетического института
В книге рассматриваются элементы теории
линейных цепей с сосредоточенными постоянны-
ми. Уделено внимание цепям с полупроводниками
и электромеханическим системам. Значительное
место в книге занимает рассмотрение переходных
процессов в линейных электрических цепях.
Книга предназначена для студентов электро-
технических специальностей втузов.
ПРЕДИСЛОВИЕ
Публикуемый курс написан чле-
нами кафедры Теоретических основ
электротехники Московского ордена
Ленина энергетического института.
В первой части (Книги рассмат-
ривается- теория линейных цепей
с сосредоточенными постоянными
в установившемся и переходном ре-
жимах, составляющая первую часть
курса Теоретических основ электро-
техники. Во второй части книги из-
лагается теория нелинейных цепей
и цепей с распределенными постоян-
ными; в ней же рассматривается
теория фильтров и четырехполюс-
ников. Третья часть книги посвяще-
на теории электромагнитного поля.
Содержание книги и уровень из-
ложения соответствуют программе
курса, утвержденной для электро-
технических и радиотехнических
специальностей Министерством
высшего и среднего специального
образования СССР. Следует, однако,
иметь в виду, что из-за существен-
ного различия интересов разных
электротехнических факультетов
(например, электроника и электро-
энергетика) отдельные разделы
курса Н4 разных факультетах про-
ходятся с неодинаковой подроб-
ностью.
При изложении многих вопросов
теории особенное внимание обра-
щалось на то, чтобы научить при-
менению их к анализу конкретных
задач; при этом авторы стремились
по возможности разъяснить их об-
щее значение и связь с различными
областями электротехники.
В начале первого раздела книги,
так же как и в последующих гла-
вах, кратко излагаются некоторые
общие положения физики, однако
такое изложение должно рассматри-
ваться только как напоминание
важнейших представлений и зако-
нов, ранее изучавшихся в курсе фи-
зики. Сказанное относится и к не-
которым математическим выводам,
включенным в текст книги.
В написании первой части книги
принимали участие сотрудники^ ка-
федры Теоретических основ элек-
тротехники Московского ордена
Ленина энергетического института
доценты Н. М. Бурдак (гл. 2 и гл. 9),
В. Н. Кудин (гл. 2) и Л. П. Собо-
лева (гл-. 2). В обсуждении руко-
писи участвовали и другие сотруд-
ники той же кафедры; их замеча-
ния по возможности приняты во
внимание. В подготовке рукописи
к печати автору оказали большую
помощью Н. П. Преображенская,
А. А. Брауде, Е. И. Калугин и дру-
гие товарищи по кафедре—автор
выражает им искреннюю благодар-
ность. Автор благодарит также
своих рецензентов — их замечания
были очень полезны и во /многом
учтены. Автор не может обойти бла-
годарностью редактора книги доц.
Б. Я. Жуховицкого, который пред-
ложил несколько редакционных ва-
риантов, непосредственно включен-
ных в книгу (влияние размыкания
и замыкания ветви, некоторые вы-
воды в теории резонанса).
СОДЕРЖАНИЕ
Предисловие......................... 5
Введение........................... 13
Электротехника (13). Теорети-
ческие основы электротехники
(14). Электрические цепи (15).
Характеристика основных задач,
стоящих в области теории це-
пей (15). Классы цепей (16)
Раздел I
/ ЦЕПЬ ПОСТОЯННОГО ТОКА
Глава первая. Основные физи-
ческие представления и законы
1-1. Потенциальное электрическое
поле.............................. 17
1-2. Емкость. Конденсатор .... 19
1-3. Электрический ток..........20
Закон сохранения количества
электричества (21)
1-4. Преобразование энергии в цепи
электрического тока..........21
Энергия электрического поля
конденсатора (21). Рассеяние
электрической энергии в про-
водниках (22). Мощность элек-
трического тока (22)
1-5. Электродвижущая сила .... 22
Работа сторонних сил в элек-
трической цепи (23)
1-6. Закон Ома. Линейные и нели-
нейные элементы................ 24
1-7. Закон Джоуля—Ленца .... 26
1-8. Напряжение на выходных за-
жимах источника. Обобщенный
закон Ома...................... 26
Источник э. д. с. как идеаль-
ный источник напряжения (26).
Фиксированность положитель-
ных направлений; их обозначе-
ние (27).
1-9. Законы Кирхгофа............ 27
Первый закон Кирхгофа (27).
Второй закон Кирхгофа (28)
1-10. Магнитное поле ....... 29
Сторонняя напряженность поля,
возникающая при движении в
магнитном поле (30). Измери-
тельные приборы, основанные на
взаимодействии тока и магнит-
ного поля (30). Единица тока
ампер — основная единица -абсо-
лютной практической системы и
системы СИ (30)
1-11. Электромагнитные машины в
электрической цепи.............. 32
Возникновение э. д. с. в про-
стейшем генераторе (32). Элек-
трический двигатель [(32). Элек-
трические машины (33). 1-12.
Закон электромагнитной индук-
ции (34)
Глава вторая. Цепь постоян-
ного тока................... . . 34
2-1. Простейшие электрические це-
пи ......* ................ 34
Последовательное соединение
(34) . Параллельное соединение
(35) . Условие отбора макси-
мальной мощности (35). Цепь
с двумя источниками э. д. с.
(36) . Роль выбора положитель-
ных направлений (36). Потенци- •
альная диаграмма (37). Простая
последовательно-параллельная
цепь (37). Цепь с параллельно-
последовательными ветвями (39).
Метод пропорциональных вели-
чин (39). Сложные цепи (40)
2-2. Источники питания в электри-
ческой цепи..................... 40
Простейшие источники питания
(40). Внешняя характеристика
6
•источников (41). Эквивалент-
ность двух типов источников пи-
тания (41). Идеальные источ-
ники (41). Определение эквива-
лентных значений Э и по
вольт-амперной характеристике
-(42). Регулируемые источники
(42). Источники тока (43). Термо-
электронный генератор с прямым
преобразованием тепловой энер-
гии в электрическую (44)
2-3. Применение законов Кирхгофа 45
Система уравнений Кирхгофа
(45). Решение системы уравне-
ний Кирхгофа для цепи с источ-
никами э. д. с. (46). Система
уравнений цепи, содержащей
источники тока (46). Решение
системы уравнений цепи, содер-
жащей источники э. д. с. и
тока (47). Число независимых
узловых уравнений [доказатель-
ство равенства (2-46)] (47).
Число независимых контурных
уравнений [доказательство ра-
венства (2-48)] (48). О незави-
симых уравнениях при наличии
источников тока (48)
2-4. Принцип суперпозиции (нало-
жения) ...................... 48
Обобщение понятия проводимо-
сти (50). Суперпозиция источ-
ников тока (50)
2-5. Принцип компенсации..........51
2-6. Принцип линейности ..... 52
2-7. Эквивалентные источники. Ак-
тивный двухполюсник...........54
Определение внутреннего сопро-
тивления эквивалентного источ-
ника (rt-) при расчетах (55)
2-8. Системы уравнений для кон-
турных токов и узловых потен-
циалов ..................... 57
Метод контурных токов (57). Ме-
тод узловых потенциалов (60).
Система уравнений, в правой
части которых стоят приведен-
ные узловые токи (61). Систе-
ма уравнений с приведенными
узловыми токами, решенная от-
носительно потенциалов (62).
Выбор между системами урав-
нений (63)
2-9. Принцип взаимности..........64
2-10. Преобразование электрических
* ‘ цепей .................... 65
Преобразование треугольника
в трехлучевую звезду (65). Об-
щий случай преобразования мно-
голучевой звезды в многоуголь-
ник (67). Уравнения активного
многополюсника (68)
2-11. Влияние изменения парамет-
ров цепи....................... 68
Подключение дополнительной
ветви (69). Отключение ветви
(70). Теорема вариации (71)
2-12. Цепь с двумя внешними вет-
вями (четырехполюсник) 73
Уравнения четырехполюсника -
(73)
. 2-13. Методы расчета и анализа
электрических цепей................ 74
1. Методы частичного анализа
(74). 2. Расчеты по Кирхгофо-
вым уравнениям (75). 3. Пре-
образование (75). 4. Примене-
ние теории четырехполюсников
(75). 5. Метод пропорциональ-
ных величин и его развитие
(76). 6. Суперпозиция эквива-
лентных источников (77). 7. Ме-
тод определяющих токов (78).
8. Расчетные столы, модели
и цифровые машины (79)
Раздел II
ЦЕПЬ ПЕРЕМЕННОГО ТОКА
(установившийся режим)
Глава третья. Введение в тео-
рию переменных токов .... 81
3-1. Общая характеристика цепей
переменного тока................... 81
Усложнения, обусловленные
переменностью тока (81). Пе-
риодические и непериодические
переменные величины (81). При-
чины распространенности пере-
менного тока (83). Частота
переменного тока (85). Источ-
ники переменного тока (85).
Машинный генератор перемен-
ного тока (86). Переменный
ток в микрофонной цепи (86)
3-2. Переменный ток в цепи г, С 87
Процесс заряда и разряда кон-
денсатора (87). Цепь г, С (89)
Рассеивание энергии в сопротив-
лении г (90)
7
3-3. Действующее (среднее квадра-
тичное) значение периодических .
величин........................ 9@
3-4. Собственная индуктивность
в цепи изменяющегося тока . . 911
Самоиндукция (91). Индуктив-
ность в электрической цепи
(92). Энергия магнитного поля
индуктивности (93). Закон Лен-
ца (93)
3-5. Переменный ток в цепи г, L 94
3-6. Переменный ток в цепи С9 г, L.
Резонанс................... 95
3-7. Законы Кирхгофа для развет-
вленной цепи переменного тока 99
3-8. Измерения в цепи переменного
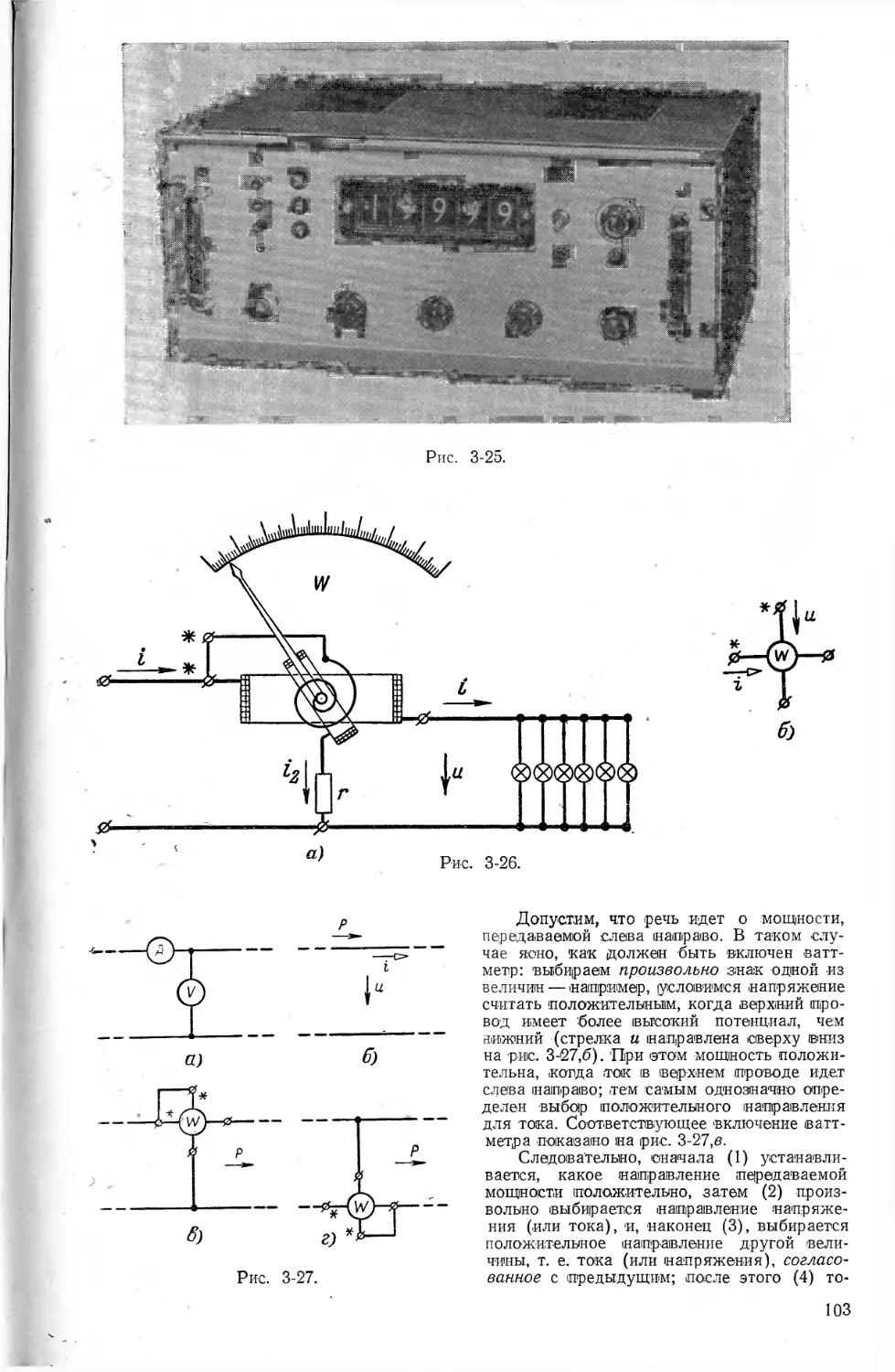
тока.......................101
Вольт- и амперметры (101).
Ваттметр (102). Включение ватт-
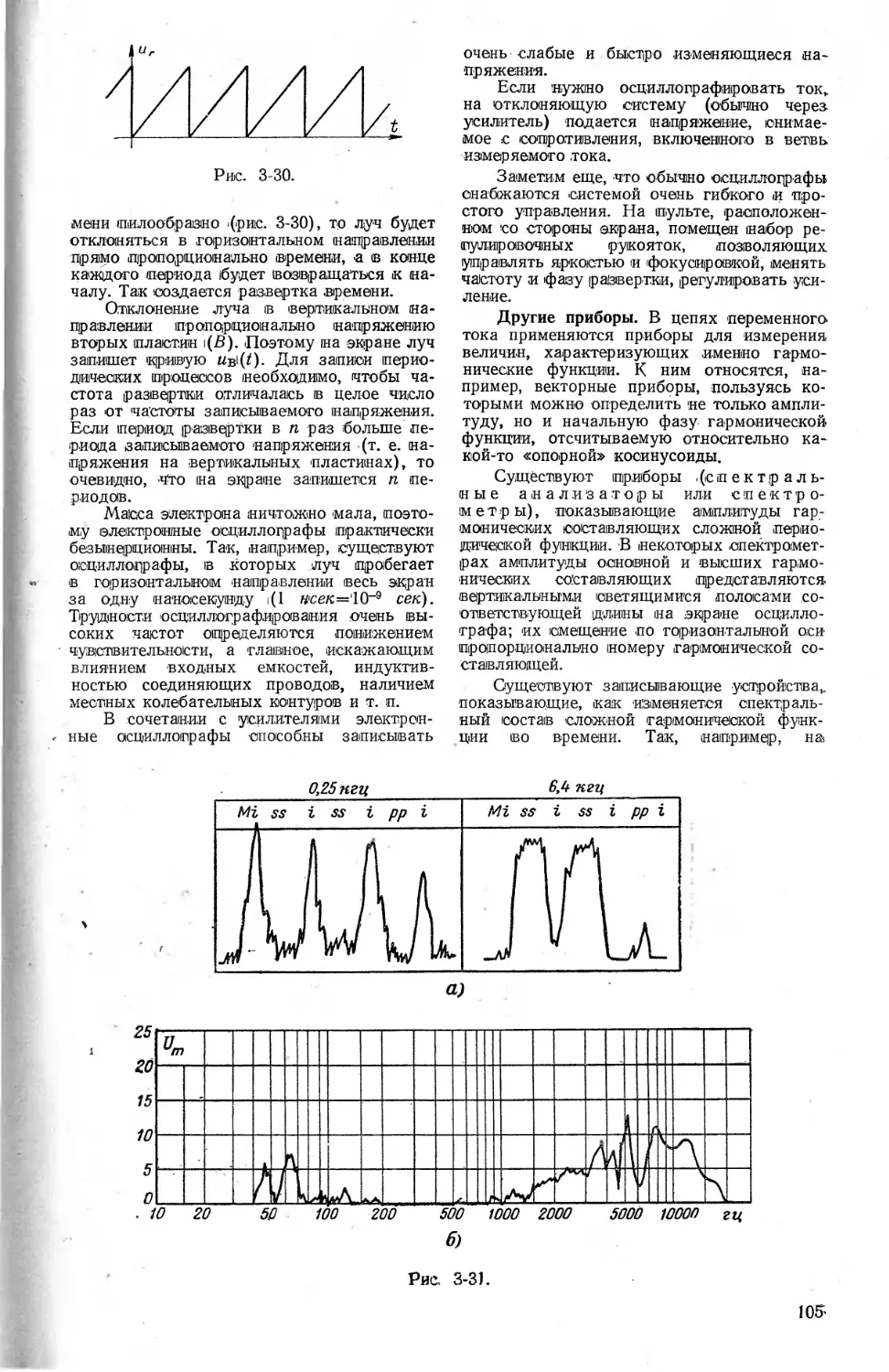
метра (102). Осциллографы (104).
Другие приборы (105)
Глава четвертая. Математи-
ческие операции с простыми
гармоническими функциями . . 106
4-1. Геометрический метод .... 106
4-2. Комплексный (символический)
метод..............................108
Обоснование метода (108). Сло-
жение гармонических функций
(109). Комплексная плоскость
(110). Комплексные амплитуды
и комплексные действующие зна-
чения (111). Дифференцирование
гармонических функций (111).
Комплексное сопротивление цепи
г, L (112). Интегрирование гар-
моническихфункций (113). Комп-
лексное сопротивление цепи г,
С (ИЗ). Соответствие комплекс-
ных и дифференциальных уравне-
ний (ИЗ). Нелинейные опера-
ции с комплексами (115). Раз-
личие комплексов типа 1 и Z
(116). Дополнительное замеча-
ние о комплексном методе (116)
4-3. Уравнения прямой и окруж-
ности на комплексной пло-
скости ..........................117
Прямая (117). Окружность (117).
Определение точки W на окруж-
ности по заданному £ (119)
Г л а ва пятая. Основные положе-
ния теории линейных цепей
переменного тока, содержащих
г, L, С............................120
8
5-1. Уравнения электрической цепи
в комплексной форме .... 120
Законы Кирхгофа (120). Сопро-
тивление (120). Проводимость
(121).
5-2. Мощность в цепи переменного
тока.............•...............125
Полная мощность (125). Компен-
сация фазового сдвига (126).
Реактивная мощность (126).
Комплексная мощность (127). По-
лучаемая и отдаваемая мощность
(127). Баланс мощности (128).
Активные и реактивные состав-
ляющие токов и напряжений (131)
5-3. Передача энергии в цепи пере-
менного тока- ...................132
Условие передачи максималь-
ной мощности (133). Влияние
на входное сопротивление при-
емника дополнительных реак-
тивных ветвей (134). Цепи,
предназначенные для передачи
энергии (135). Падение и поте-
ря напряжения (136). Цепь
с двумя источниками (138).
Синхронные машины в цепи пере-
менного тока (139). Дополни-
тельные замечания (141). Парал-
лельные линии с различными со-
противлениями (142). Выбор се-
чения проводов по допустимому
току (142)
5-4. Потенциальная диаграмма на
комплексной плоскости (топо-
графическая диаграмма) ... 143
Построение (143). Анализ элек-
трических цепей по их топогра-
фическим диаграммам (144). Мо-
сты (146). Простейший фазовра-
щатель (146)
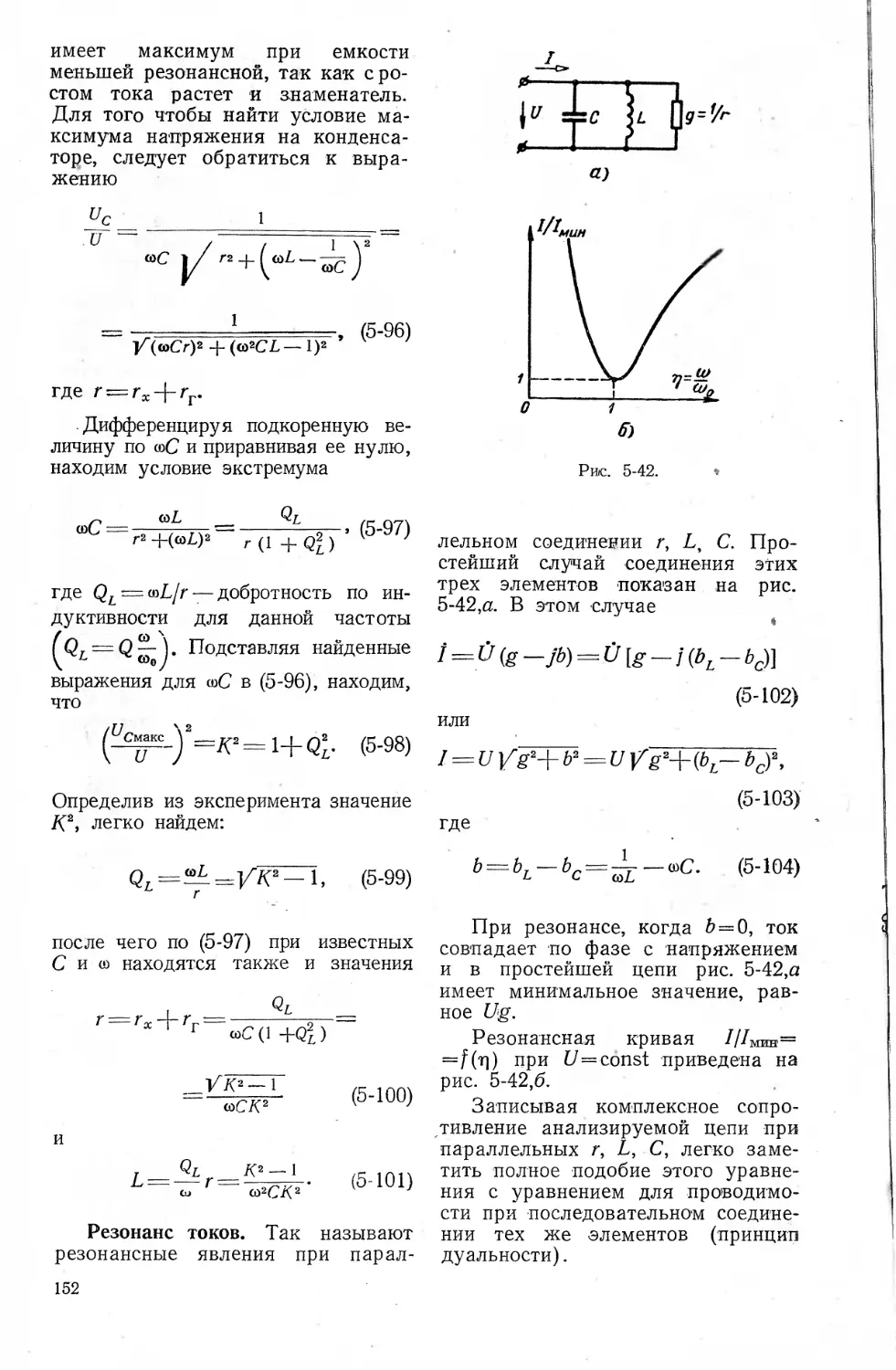
5-5. Анализ резонансных эффектов 147
Резонанс напряжений (147). Ре-
зонансные измерения (150). Ку-
измерения Гиг (151). Резонанс
токов (152). Эквивалентные па-
раллельные ветви и общая до-
бротность резонансного контура
(154). Резонанс в сложных кон-
турах (155)
5-6. Частотные характеристики . . 155
Двухполюсники (155). Частот-
ные характеристики реактив! ых
двухполюсников (158). Четырех-
полюсники (159). Частотные ха-
рактеристики реальных эле мен-
тов электрической цепи (160).
Сопротивление (160). Емкость
(162). Индуктивность (166). Ре-
зонанс в цепи с параметрами
г, L, С, зависящими от частоты
(170). Заключительные замеча-
ния (171)
Глава шестая. Цепь перемен-
ного тока с взаимной индук-
тивностью . . •...............171
6-1. Взаимная индукция........171
Основные определения (171).
Взаимная индукция в электриче-
ской цепи (173). Энергия маг-
нитного поля двух индуктивно
связанных ветвей (174). Коэф-
фициент магнитной связи (174).
Согласование положительных
направлений тока и разметка
концов индуктивных элементов
(175). Способы разметки концов
(177). Цепь с несколькими ин-
дуктивными элементами (178).
Положительные и отрицатель-
ные взаимные индуктивности
(178)
6-2. Индуктивно связанные цепи 180
Уравнения электрической цепи
с взаимной индуктивностью
(180). Число независимых Кирх-
гофэвых уравнений (180). Две
параллельные индуктивно свя-
занные ветви (180). Две после-
довательные индуктивно связан-
ные ветви (181). Топографиче-
ская потенциальная диаграмма
(181). Передача мощности и по-
казания ваттметров в цепи с
взаимной индукцией (182). За-
ключительные замечания (183)
6-3. Трансформатор в линейном
режиме...................• . . 184
Основные уравнения, их анализ
(185). Входное сопротивление
трансформатора (186). Магнитное
состояние сердечника; связь по-
тока с токами и напряжениями
обмоток (187). Коэффициент
трансформации (188). Идеальный
трансформатор (189). Эквива-
лентная цепь с устраненными
индуктивными связями (189).
Наиболее важные схемы замеще-
ния трансформаторов (189).
Определение параметров схемы
замещения по данным опыта
(192). Трасформатор как согла-
сующий элемент (192)
Глава седьмая. Цепь перемен-
ного тока с триодами в линей-
ном режиме.......................193
7-1. Некоторые обобщающие заме-
чания о многополюсных эле-
ментах .................... . . 193
Условия квазилинейности (194).
Нарушение принципа взаимно-
сти (195). Триоды при гармони-
ческих напряжениях (195)
7-2. Электронно-вакуумный триод
как линейный элемент элек-
трической цепи.................196
Схемы замещения триода (197)
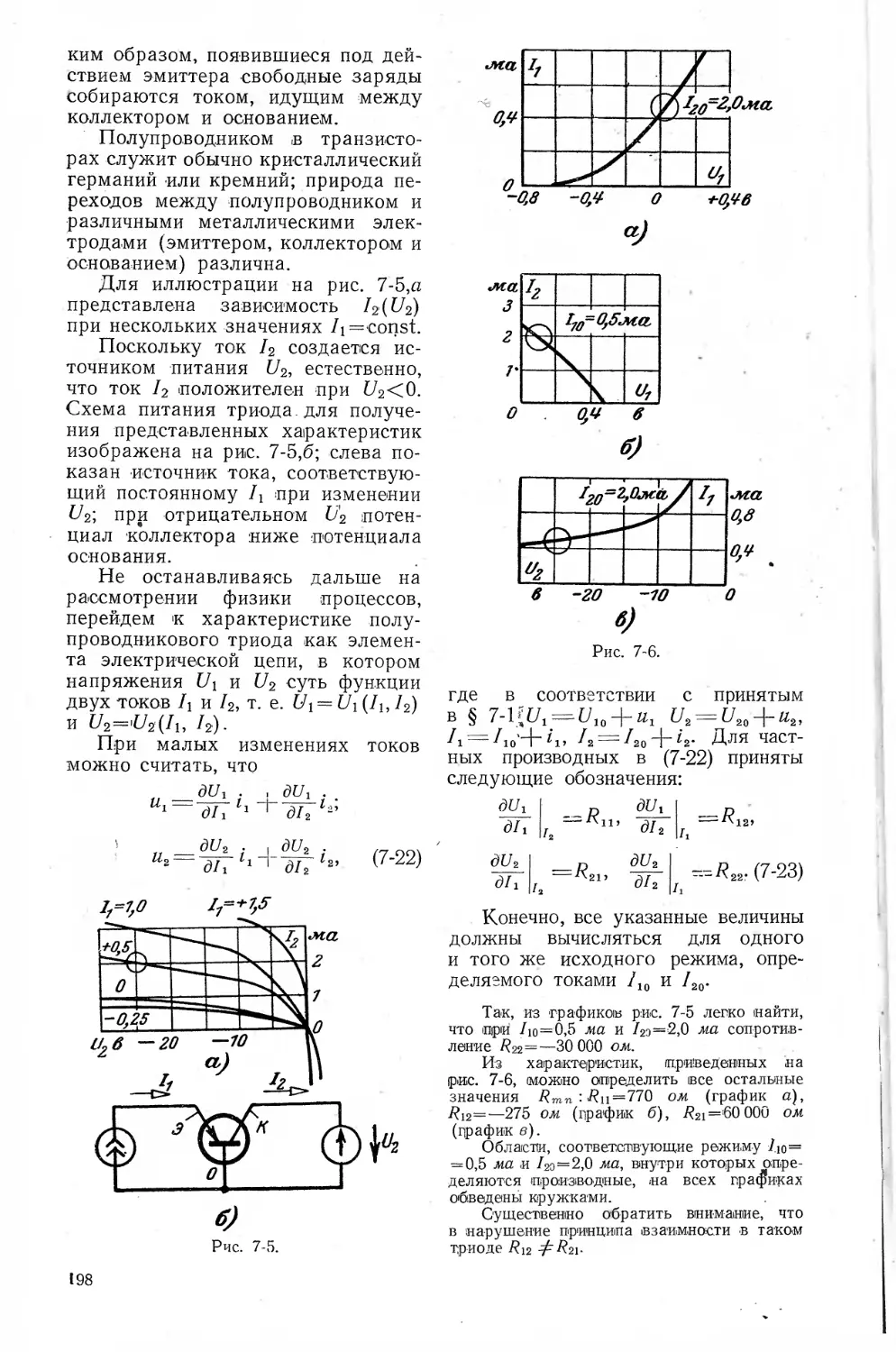
7-3. Полупроводниковый триод как
линейный элемент электриче-
ской цепи......................197
Уравнения транзистора и его
схемы замещения (199)
7-4. Простейшие цепи с триодами 200
Усилительный каскад (201). Внут-
реннее сопротивление эквива-
лентного генератора (202). Ка-
тодный повторитель (202). Триод-
ные генераторы гармонических
колебаний (203). Цепи с обрат-
ной связью (204). Интегрирую-
щие, и дифференцирующие кон-
туры (205)
Глава восьмая. Трехфазная
цепь.............•...........206
8-1. Трехфазный генератор .... 208
Фазный множитель трехфазной
системы (209). Соединение об-
моток генератора в звезду
(209). Соединение обмоток ге-
нератора в треугольник (210)
8-2. Симметричная трехфазная цепь 211
Звезда-—звезда (211). Звезда—
треугольник (212). Треугольник—
треугольник (213). Эквивалент-
ность различных соединений
(214)
8-3. Мощность трёхфазной симмет-
ричной цепи.....................214
Измерение мощности (215)
8-4. Передача энергии по трехфаз-
ной линии в симметричном ре-
жиме ...........................217
Сравнение к. п. д. трехфазной
и однофазной линии (217). Рас-
9
чет на одну фазу (218). Расчет
линии с учетом емкости (219)
8-5. Индуктивность трехфазной ли-
нии. Индуктивность на фазу 219
8-6. Трехфазные трансформаторы 221
8-7. Вращающееся магнитное поле.
Асинхронный и синхронный
двигатели ...»..............222
Принцип работы асинхронного
двигателя (224). Принцип рабо-
ты синхронного двигателя (225)
8-8. Несимметричная трехфазная
цепь при статической нагрузке 226
Звезда — звезда (227). Цепь
для определения последователь-
ности фаз (228). Однополюсное
замыкание на землю (228). Сме-
шанный соединения (229)
8-9. Симметричные составляющие
несимметричной трехфазной
цепи . . . ................• . . 230
Разложение несимметричной си-
стемы векторов на. три симмет-
ричные (230). Физическое разли-
чие сопротивления симметричной
цепи для составляющих разных
последовательностей (231). Со-
противление для токов нулевой
последовательности (231). Со-
противления прямой и обратной
последовательностей (233).
Мощность, выраженная через
симметричные составляющие
(233). Расчет цепи с несиммет-
ричными параметрами (234).
Общий .случай несимметричной
системы (236)
Гл ава девятая. Несинусои-
дальные токи в электрической
цепи............................236
9-1. Сложные гармонические токи х
в линейной цепи.............236
9-2. Расчет цепей при сложных гар-
монических токах............239
Основные методы расчета (239).
Сглаживание пульсирующего на-
пряжения (240). Искажение мо-
дулированного колебания в ре-
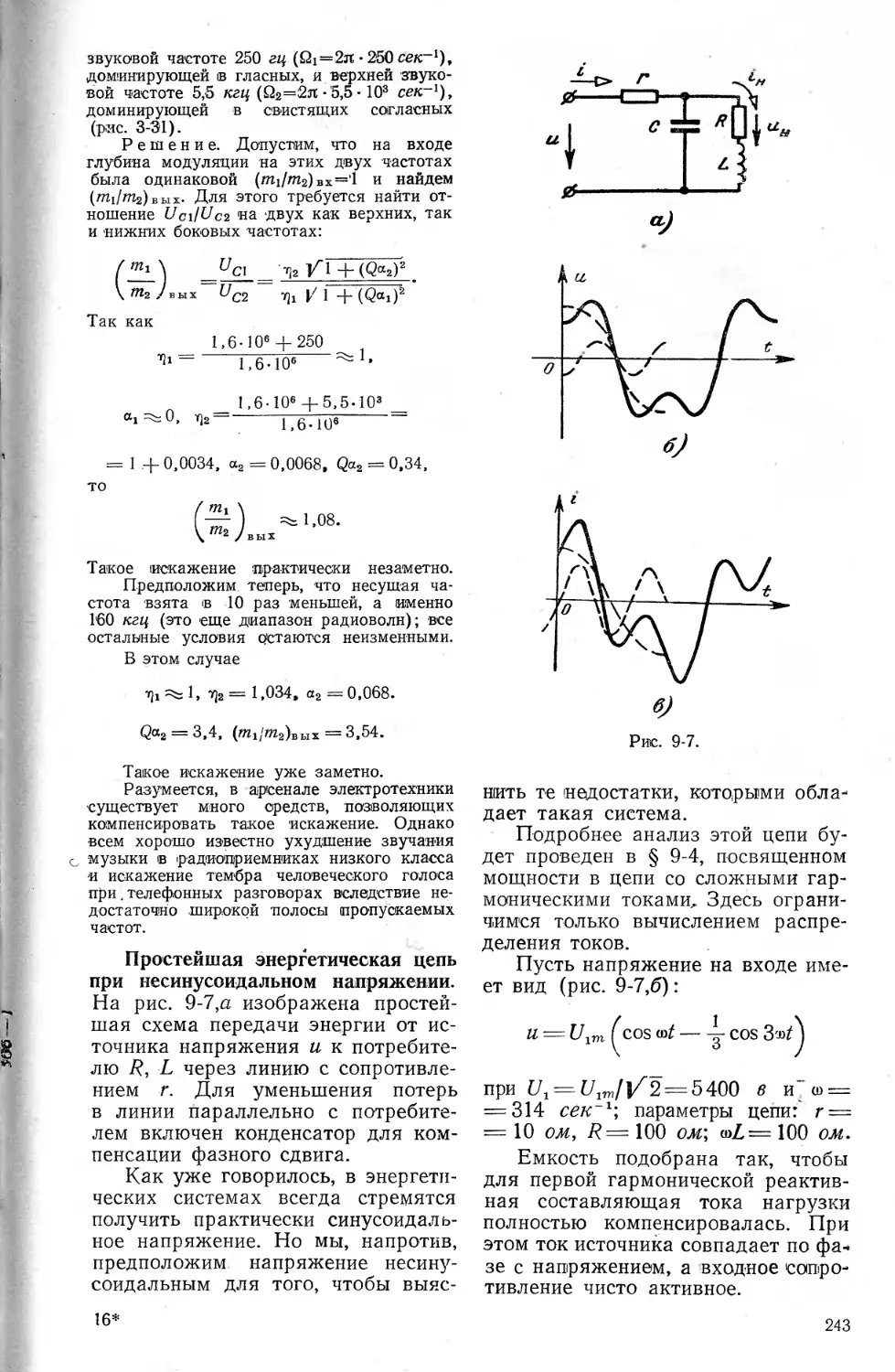
зонансном контуре (242). Про-
стейшая энергетическая цепь при
несинусоидальном напряжении
(243)
9-3. Действующее значение и дру-
гие характеристики сложных
гармонических величин .... 244
Различного вида средние (245).
Коэффициенты, характеризующие
форму (246). Измерения при на-
личии разных гармонических (247)
9-4. Мощность....................248
9-5. Высшие гармонические в трех-
фазных системах..............250
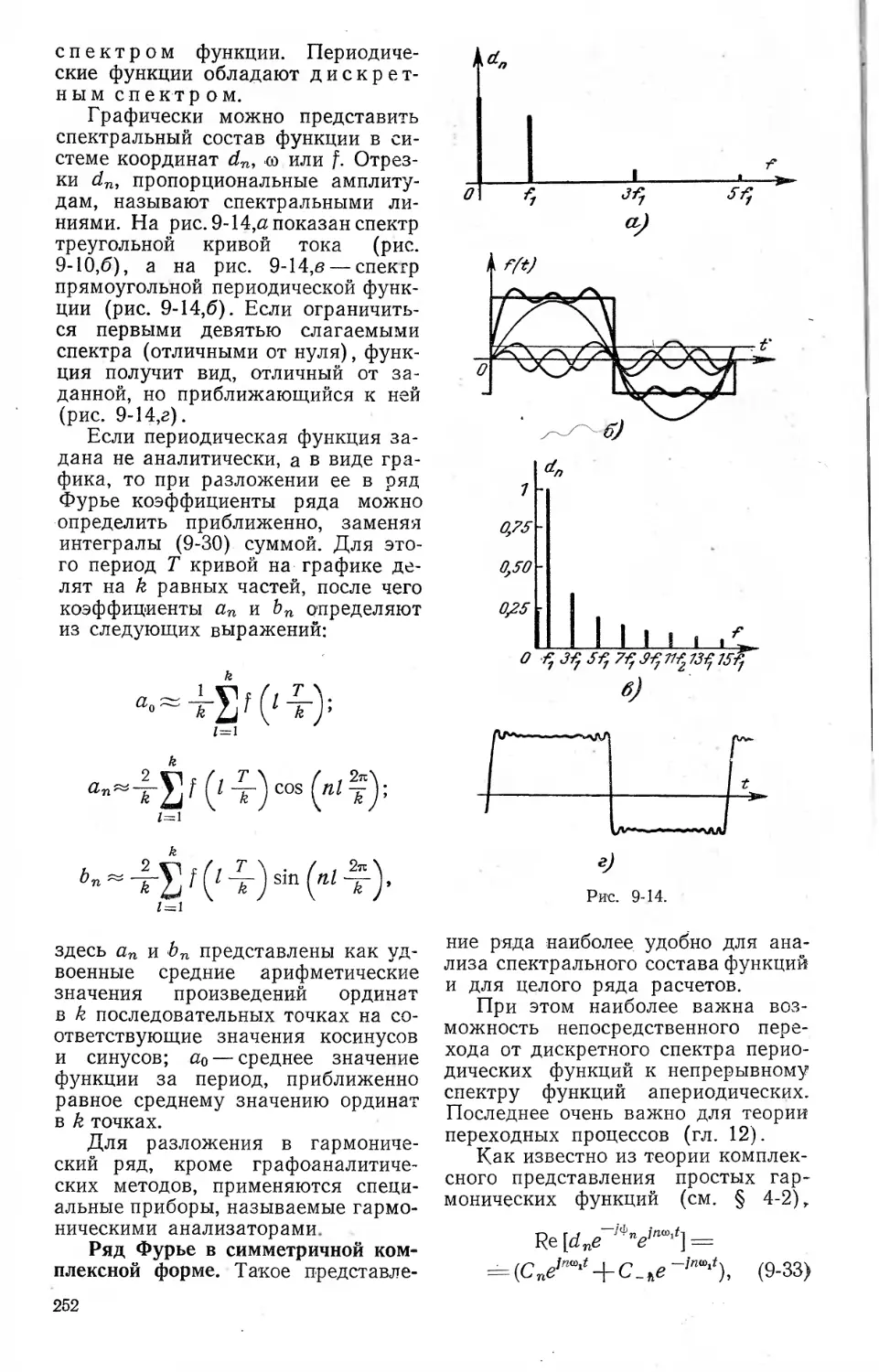
9-6. Разложение периодических
функций на гармонические со-
ставляющие ..................251
Ряд Фурье в симметричной комп-
лексной форме (252). Спектраль-
ное представление функций (253)
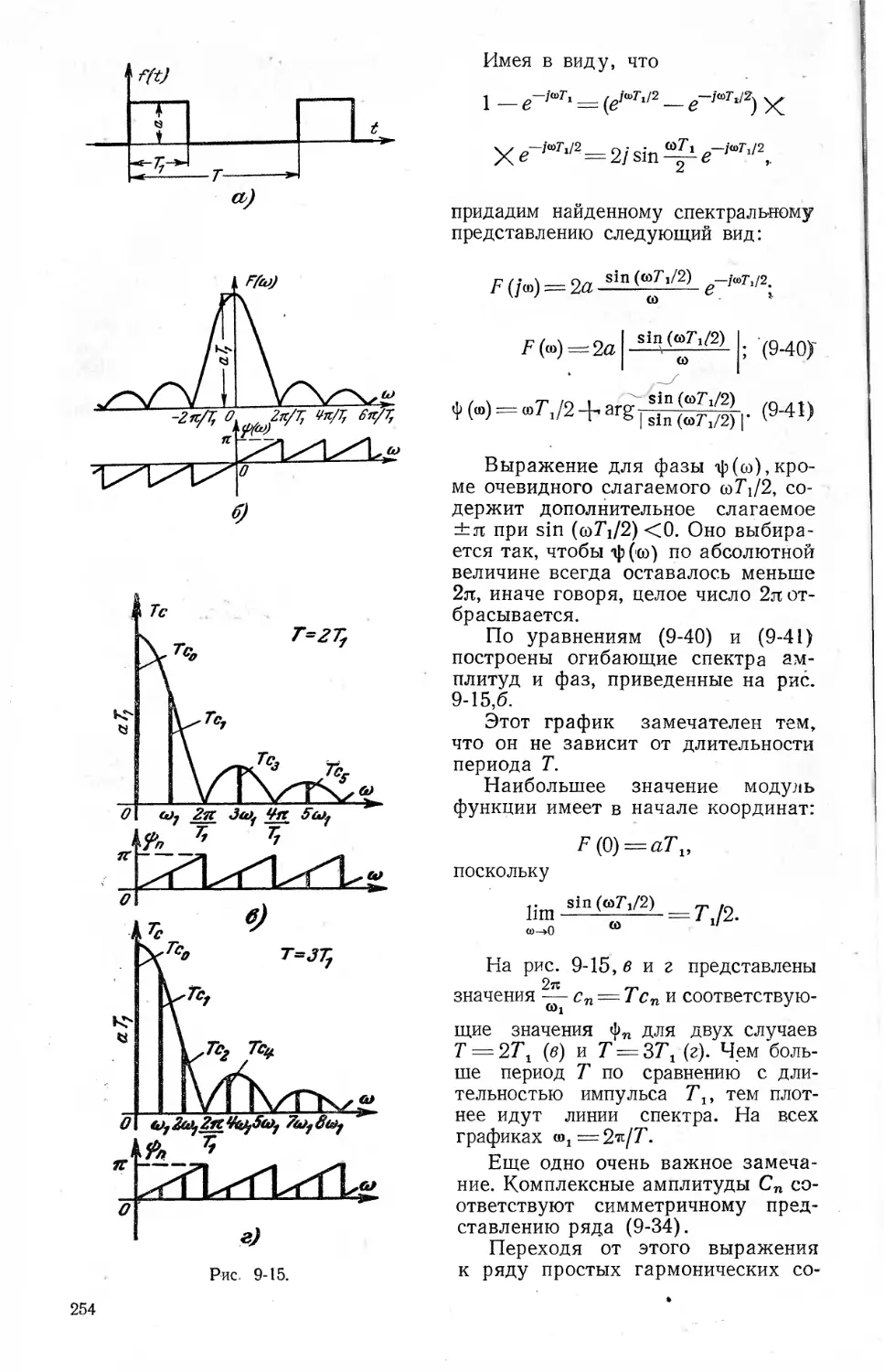
9-7. Спектральное представление
некоторых функций............255
Раздел III
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В ЛИНЕЙНЫХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ
постоянными
Вводные замечания (257)
Глава десятая. Основные поло-
жения теории переходных про-
цессов. Их расчет путем непо-
средственного интегрирования
уравнений (классический ме-
тод) .........................259
10-1. Дифференциальные уравнения;
определение начальных усло-
вий (законы коммутации);
свободный и принужденный
режимы.....................259
10-2. Источник постоянного на-
пряжения в цепи г, С . . . . 260
10-3. Источник постоянного напря-
жения в цепи L, г..........262
10-4. Источник изменяющегося на-
пряжения в цепи г, С . . - . 264
Напряжение линейно возрастает
(264). Передача сигнала через
разделительный конденсатор
(265). Импульс напряжения (265).
Включение цепи к источнику
периодического напряжения (266)
10-5. Источник изменяющегося на-
пряжения в цепи Ц г . . . . 267
Включение источника гармониче-
ского напряжения (267). Переход
от одного установившегося ре-
жима к другому (коммутация)
(267). Импульс напряжения (268)
10-6. Контур Lt г, С............269
Уравнения для свободных со-
ставляющих (269). Энергетиче-
ские соотношения при свободном
$
10
режиме (271). Аналогия с коле-
баниями механической системы
'(271). Колебательный разряд кон-
денсатора (272). Апериодический
разряд (273). Включение контура
L, rt С к источнику гармониче-
ского напряжения (274). Включе-
ние контура L, г, С к постоян-
ному напряжению (274). Свобод-
ный режим -в контуре £, г, С
при ненулевых нач-альных усло-
виях iL (— 0) ф 0 и ис (— 0) ф 0
(275). Граничный режим (275)
10-7. Общий случай расчета развет-
вленной электрической цепи 275
Система дифференциальных
уравнений и ее решение (275).
Составление характеристическо-
го уравнения (278). Метод глав-
ного определителя цепи (278).
Метод входного сопротивления
(279). Включение источников на-
пряжения и источников тока
(279). Определение действитель-
ных токов и напряжений в мо-
мент включения (280). Примени-
мость всех методов расчета,
основанных на линейности цепи
(280). Характер переходного
процесса и корни характеристи-
ческого уравнения (282). Отри-
цательное сопротивление в це-
пях с обратной связью (282)
10-8. Переходные процессы в про-
стейших электромеханических
и электротермических систе-
мах . ...........................284
£0-9. Процесс в цепи при воздей-
ствии произвольно изменяю-
щегося напряжения .... 285
Интеграл Дюамеля (285). Выра-
жение заданной функции и (t)
через дифференциальное уравне-
ние (287)
10-10. Переходные процессы при
„некорректных“ начальных
условиях.........................288
Ранее формулированные законы
коммутации имеют ограниченную
применимость (288). Закон сохра-
нения заряда (289). Цепь с кон-
денсаторами (289). Преобразова-
ние энергии (290). Цепь с индук-
тивностями (291). Закон сохране-
ния магнитного потокосцепления
(294). Энергетические преобразо-
вания в цепи £, г (294). Анало-
гия цепи г, С с источником на-
пряжения и цепи L, г с источни-
ком тока (295). Разрыв ветви,
содержащей индуктивность (296).
Пример из механики (296)
10-11. Функция Хевисайда 1 и
функция Дирака 5......297
Глава одиннадцатая. Расчет
переходных процессов опера-
торным методом.............300
11-1. Операторный метод......301
11-2. Изображение простейших
функций.................302
Изображение ^-функции (303).
Изображение простой производ-
ной (df/dt) (303). Определенный
интеграл (304). Изображение
степеней t (304). Изображение
экспоненты (304). Определение
значений функции f (+0) и f (оо)
по ее изображению (304)
11-3. Решение дифференциальных
уравнений операторнььм мето-
дом ............................305
Взаимная однозначность ориги-
налов и их изображений (306).
Заключительные замечания (306)
11-4. Таблица изображений F (р)
и соответствующих оригина-
лов f (t).......................307
Показатели экспонент и корни
знаменателя Изображений (307).
Гиперболические и круговые
функции (307). Другие формулы
(309)
11-5. Расчет переходных процессов
при нулевых начальных усло-
виях ...........................310
Нулевые начальные условия для
уравнений, Содержащих инте-
гралы (311). Простейшие элект-
ромеханические системы (312).
Обратная задача (313)
11-6. Операторные сопротивления
и передаточные функции . . . 314
11-7. Переходные процессы при не-
нулевых начальных условиях 319
1. Прямые аналитические мето-
ды (319). Уравнения с простыми
(необобщенными) производными
(319). Уравнения с обобщенными
производными при ненулевых на-
чальных условиях (321). 2. Me-
ll
тод эквивалентных источников
(324). Двухполюсник, эквива-
лентный емкости с ненулевым
начальным напряжением (324).
Двухполюсник, эквивалентный
индуктивности с ненулевым на-
чальным током (324). 3. Метод
суперпозиции (326)
11-8. Цепь с гармоническими источ-
никами . . . . •................329
Метод суперпозиции (330)
11-9. Формула разложения Хеви-
сайда ..........................331
Формула Хевисайда для источ-
ников гармонических возмуще-
ний (333). Определение началь-
ного и установившегося значе-
ния f (t) по ее операторному
представлению F (р) в случае
гармонических источников (333)
11-10. Дальнейшее расширение опе-
раторного метода. Свертка 333
Глава двенадцатая. Инте-
гральные преобразования Фурье
и Лапласа..........................335
12-1. Переходные процессы и спект-
ральные (частотные) пред-
ставления .......................335
12-2. Спектры апериодических функ-
ций. Интегральные преобра-
зования Фурье ....... 336
12-3. Определение спектра функции
Хевисайда 1 (/) ...... . 337
12-4. Связь спектрального пред-
ставления апериодических
функций с операторным изо-
бражением ........................338
Обратное преобразование Фурье
(339)
12-5. Значение спектральных ха-
' рактеристик. Приближенные
методы определения переход-
ных процессов..................339
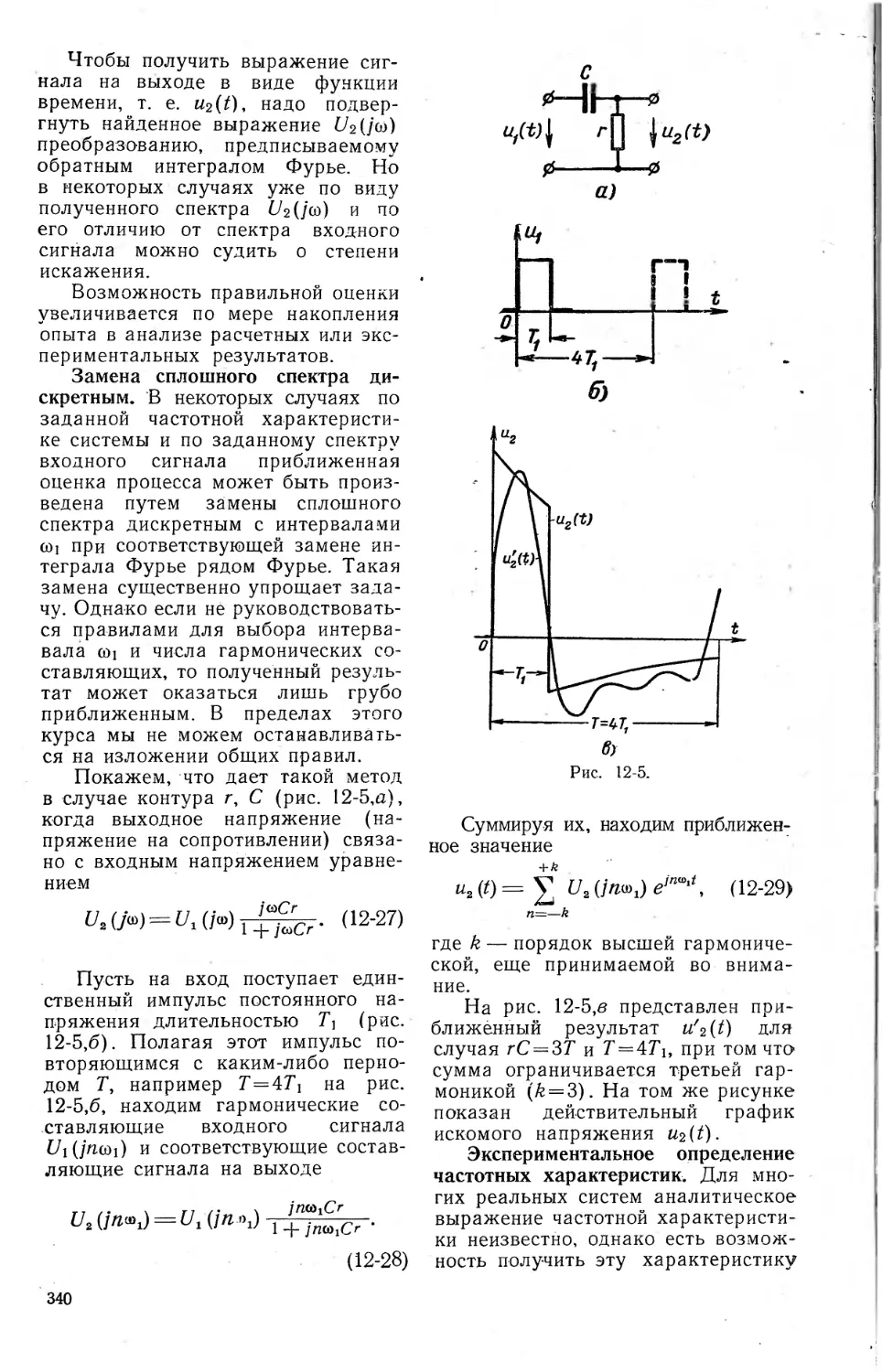
Замена сплошного спектра ди-
скретным (340). Эксперименталь-
ное определение частотных ха-
рактеристик (340). Методы тра-
пеций (341). Метод простой тра-
пеции (342). Метод логарифми-
ческой трапеции (342)
12-6. Интегральные преобразова-
ния Лапласа....................343
Глава тринадцатая. Пере-
ходные и установившиеся ре-
жимы при воздействии серии
возмущений.......................344
13-1. Реакция на эшелон возмуще-
ний ...........................344
13-2. Реакция на эшелон коротких
возмущений.................• . 347
13-3. Периодические режимы в це-
пи, определяемые методом
расчета реакции на эшелон
возмущений.....................349
13-4. Реакция на эшелон возмуще-
ний, модулированных по амп-
литуде ........................350
13-5. Режим в цепи при периодиче-
ски повторяющихся ступен-
чатых изменениях ее пара-
метров ...................353
Физическое изменение реактивных па-
раметров (355)
Литература.........................359
ВВЕДЕНИЕ
Электротехника. Развитие элек-
тротехники и ее широкое проникно-
вение во все области жизни совре-
менного общества (промышлен-
ность, транспорт, связь, медицина,
быт) объясняются тем, что средст-
вами электротехники успешно ре-
шаются задачи преобразования и
передачи энергии, а также преобра-
зования и передачи сигналов или
информации Г
На гидро- и тепловых станциях
огромная энергия больших рек и
топлива преобразуется в электриче-
скую энергию, передаваемую на
многие сотни километров, где она
преобразуется в механическую энер-
гию, приводя в действие и большие
станки, и маленькие двигатели раз-
нообразных автоматов; электриче-
ская энергия преобразуется и в теп-
ловую энергию, расплавляя металл
в больших печах и накаливая нить
ламп электрического освещения.
Широкое применение находят и дру-
1 Существуют устройства, в которых
электромагнитные процессы играют другую
роль. Например, в электрохимических уст-
ройствах иногда существенно только коли-
чество протекшего электричества । (электро-
лиз), при этом энергетические соотношения
сами по себе несущественны; в телевизион-
ных трубках устанавливаются постоянные
магниты с целью создания заданного по-
стоянного поля, только фокусирующего луч.
Можно привести и другие примеры из об-
ласти электротехнологии >(магнитные и элек-
трические сепараторы), электротерапии и
т. д. В большинстве случаев такие устрой-
ства могут быть отнесены к классу уст-
ройств управления. Если этому слову при-
давать более широкое значение, то можно
отнести к классу устройств управления и си-
стемы преобразования и передачи как энер-
гии, так и сигналов. Однако такой широкий
объем понятия «управление» в значитель-
ной мере лишает его конкретности.
<
гие преобразования электрической
энергии (лампы газового разряда,
электролиз, зарядка аккумуляторов
и т. п.). В настоящее время в каче-
стве важнейшей задачи современ-
ной энергетики стоит принципиаль-
но разрешенная задача преобразо-
вания тепловой энергии в электриче-
скую без промежуточного механи-
ческого звена (без вращающихся
машин).
Уже первые опыты по электриче-
ской передаче энергии (в России
Ф. А. Пироцкий— 1874 г., в Герма-
нии и во Франции Депре— 1882,
1883 гг.) обратили на себя всеоб-
щее внимание. Маркс и Энгельс
придавали большое значение рабо-
там Депре, отмечая важные со-
циальные последствия, к которым
приведет решение задачи о переда-
че энергии на большие расстояния.
Не меньшую роль играет элек-
тротехника при решении задач пе-
редачи сигналов и хранения инфор-
мации (телеграф, радио, магнитная
запись), а также в преобразовании
сигналов и информации: звук чело-
веческой речи преобразуется в элек-
тромагнитные колебания (телефон
й радио); изображение видимой
картины после сложных электриче-
ских преобразований появляется на
экране телевизионного приемника;
заданная математическая функция
представляется в форме изменяю-
щегося во времени тока и простыми
элементами электрической цепи ин-
тегрируется или дифференцируется;
вычислительные машины с огром-
ной скоростью выполняют любые
математические операции, в том
числе и решение сложных уравне-
ний.
13
По существу дела, на преобразо-
вании сигналов основаны и разно-
образные электрические измерения,
применяемые как в научных иссле-
дованиях (биология, астрономия
и др.), так и в промышленности, где
электрическими методами часто из-
меряются неэлектрические величи-
ны, характеризующие механические,
тепловые и химические процессы;
такие измерения лежат в основе
контроля и автоматизации промыш-
ленных установок. Исключительную
роль играет электротехника и в про-
ведении современных физических
экспериментов.
Значение электротехники и элек-
трификации, т. е. широкого проник-
новения электротехники во все
области жизни современного об-
щества, были высоко оценены
В. И. Лениным. Электрификация
Советского Союза неразрывно свя-
зана с именем В. И. Ленина. Фор-*
мула Ленина «Коммунизм — это
есть Советская власть плюс элек-
трификация всей страны» дает ключ
к пониманию задач, которые
стоят перед электрификацией нашей
Родины. Исчерпывающая характе-
ристика этих задач дана Лениным
на III съезде комсомола в 1920 г.:
«Мы знаем, что коммунистиче-
ского общества нельзя построить,
если не возродить промышленности
и земледелия, причем надо возро-
дить их не по-старому. Надо возро-
дить их на современной, по послец-
нему слову науки построенной осно-
ве. Вы знаете, что этой основой яв-
ляется электричество, что только
когда произойдет электрификация
всей страны, всех отраслей промыш-
ленности и земледелия, когда вы
эту задачу осв'оите, только тогда вы
для себя сможете построить то ком-
мунистическое общество, которого
не сможет построить старое поколе-
ние. Перед вами стоит задача хозяй-
ственного возрождения всей страны,
реорганизация, восстановление и
земледелия, и промышленности на
современной технической основе,
которая покоится на современной
науке, технике, на электричестве.
Вы прекрасно понимаете, что
к электрификации неграмотные люди
не подойдут и мало тут одной про-
стой грамотности. Здесь недостаточ-
но понимать, что такое электричест-
во: надо знать, как технически при-
ложить его и к промышленности, и
к земледелию, и к отдельным отрас-
лям промышленности и земледелия.
Надо научиться этому самим, надо
научить этому все подрастающее
трудящееся поколение» Ч
Теоретические основы электро-
техники. Теоретические основы элек-
тротехники заложены физикой (уче-
ние об электричестве и магнетизме)
и математикой (методы описания и
анализа электромагнитных явле-
ний) . Наряду с этим развитие элек-
тротехники привело к ряду новых
физических понятий, новых форму-
лировок физических законов, к раз-
витию специальных математических
методов, связанных с анализом и
описанием типичных явлений, про-
текающих именно в электротехниче-
ских устройствах.
Общий объем всех научных по-
ложений, образующих основы со-
временной электротехники, чрезвы-
чайно велик. Поэтому в учебном
курсе могут быть рассмотрены лишь
основные, наиболее общие и сравни-
тельно простые вопросы.
Содержание Теоретических основ^
электротехники (ТОЭ), как фунда-
ментальной учебной дисциплины,
высшей школы, готовящей инжене-
ров-электриков, было определено»
у нас главным образом курсами
лекций и учебниками акад.
В. Ф. Миткевича и член-’корр..
К. А. Круга — основателей и руко-
водителей кафедр теоретических
основ электротехники в Ленинград-
ском политехническом институте
(В. Ф. Миткевич) и ’в Московском
энергетическом институте
(К. А. Круг).
В курсе Теоретических основ
электротехники можно выделить две
тесно связанные между собой обла-
сти— это теория электрических це-
пей и теория электромагнитного*
поля. Несмотря на. их близость, эти
две области существенно отличают-
ся как постановкой технических за-
дач, так и применяемыми методами
1 В. И. Ленин, Собрание сочинений,,
т. 31, стр. 264.
14
математического анализа; напри-
мер, обыкновенные дифференциаль-
ные уравнения—-основной аппарат
теории электрических цепей, тогда
как в теории поля основной матема-
тический аппарат — дифференциаль-
ные уравнения в частных производ-
ных.
Электрические цепи. Рассмат-
ривая электротехнические установки
или электромагнитные устройства,
говорят об электрических цепях,
когда можно отчетливо выделить
ветви с определенным током в каж-
дой из них, а напряжение на каж-
дой ветви можно определить как
разность потенциалов между ее
концами. В простейшем случае вет-
ви — это изолированные провода,
соединяющие между собой какие-
либо узлы или полюсы цепи; они
легко могут быть выделены в обыч-
ной электротехнической установке.
Существуют, однако, такие элек-
тротехнические устройства, в кото-
рых невозможно выделить ветви и
узлы, в которых вообще не имеет
смысла говорить о напряжении меж-
ду какими-либо точками. Например,
помещая в переменное электромаг-
нитное поле какое-либо металличе-
ское тело, его можно сильно на-
греть (если нужно, до плавления)
возбуждаемыми в нем вихревыми
токами; воздействуя переменным
магнитным полем на струю жидко-
го металла, можно управлять его
течением (электромагнитные насо-
сы) ; в этих случаях говорить о вет-
вях тока или о разности потенциа-
лов между какими-либо точками
металла бессмысленно.
Характеристика основных задач,
стоящих в области теории цепей.
Можно выделить три основные груп-
пы задач теории цепей:
1. Расчеты и анализ цепей, т. е.
определение связи между токами,
напряжениями, параметрами задан-
ной цепи и теми величинами, кото-
рые определяют работу рассматри-
ваемой установки. В энергетических
системах — это величина передавае-
мой энергии, к. п. д., падение и по-
теря напряжения, величина токов
короткого замыкания (способных
оказывать разрушительное дейст-
вие, если их вовремя не. отключить),
усилия между проводами и т. п.
В измерительной технике расчету
подлежит связь между измеряемой
величиной и показанием прибора
при данных параметрах измеритель-
ной цепи. В автоматике и системах
передачи информации рассчиты-
вается зависимость между сигналом
на входе, т. е. в одной части цепи, и
сигналом на выходе, т. е. в прием-
ном или управляемом устройстве;
при этом существенным предметом
анализа могут быть искажения в си-
стемах'передачи (в канале связи),
инерционность передающих или
преобразующих звеньев цепи и т. п.
Все подобные расчеты, по суще-
ству дела, основаны на очень не-
большом числе простых законов, из-
вестных из курса физики (закон
Ома, закон Джоуля — Ленца, два
закона Кирхгофа и т. п.). Однако
умение систематически применять
эти законы для составления уравне-
ний цепи, владение методами их ре-
шения даются только в результате
тренировки и отчетливого понима-
ния свойств электрических цепей.
К этой группе задач могут быть
отнесены и общие математические
методы описания цепей (геометрия
и топология цепей, матрицы и тен-
зоры), а также методы решения и
анализа систем уравнений электри-
ческой цепи.
2. Принцип работы и общие
свойства важнейших и наиболее
распространенных электротехниче-
ских устройств и элементов элек-
трической цепи. Рассмотрение прин-
ципов работы многих электротехни-
ческих устройств и многих явлений
в электрических цепях в значитель-
ной мере относится к физике (об-
щая теория колебаний, резонансов,
процессы в вакуумных и полупро-
водниковых приборах, даже прин-
ципы работы основных преобразо-
вателей энергии — генераторов и
трансформаторов). Однако, когда
речь идет о работе этих устройств
в электротехнических системах и об
анализе процессов в электрических
цепях, изучение соответствующих
вопросов теории наполняется своим
чисто электротехническим содержа-
нием. Например: вопрос о согласо-
вании приемника с источником пи-
15
тания для получения максимальной
мощности; расчеты цепей с триода-
ми; теория частотных характери-
стик, связанная, в частности, с рабо-
той фильтров, пропускающих (или
задерживающих) только определен-
ные гармонические составляющие
тока; теория резонанса, в частности,
связанная в электроэнергетике с чи-
сто экономической задачей компен-
сации cos<p, и другие подобные во-
просы относятся именно к электро-
технике.
Много примеров анализа рабо-
ты электромагнитных элементов,
имеющих чисто электротехническое
содержание, можно привести из об-
ласти нелинейных устройств (цепи
со стальными сердечниками и полу-
проводниковыми элементами и т. п.).
Так, задачи стабилизации (напря-
жения или тока), умножения и де-
ления частоты, усиления сигнала
и т. п. целиком принадлежат элек-
тротехнике. Часто физические прин-
ципы, на которых основываются по-
добные устройства, ire столь суще-
ственны и не столь сложны, как
принципы- их технического примене-
ния и теория эффектов, очень важ-
ных с точки зрения электротехники.
Теория отдельных электротехни-
ческих устройств и важнейших эле-
ментов электрических цепей часто
развивается в самостоятельные тех-
нические дисциплины (теория транс-
форматоров, теория колебаний, тео-
рия фильтров, теория усилителей и
цепей с обратной связью и т. п.).
Однако в теорию цепей безусловно
входят принципиальные основы рас-
сматриваемых электротехнических
устройств, а также их работы как
элементов электрической цепи
(трансформаторы в электрической
цепи, условия возникновения неза-
тухающих колебаний, генерация
гармоник и т. п.).
3. Синтез электрических цепей.
Задачи синтеза заключаются в раз-
работке методов такого выбора схе-
мы соединений элементов цепей и
такого подбора параметров этих
элементов, чтобы полученная цепь
обладала заданными характеристи-
ками. В предлагаемом курсе теории
цепей вопросы синтеза затрагивают-
ся очень мало. Впрочем, даже такой
простой вопрос, как выбор парамет-
ров треугольника, эквивалентного
заданной звезде, по существу дела
относится к задаче синтеза.
Классы цепей. Электрические
цепи могут содержать линейные или
нелинейные параметры (т. е. сопро-
тивления, емкости, индуктивности,
независящие или зависящие от про-
текающих токов и приложенных на-
пряжений). По этому признаку раз-
личают линейные и нелинейные
цепи.
Кроме того, существенно разли-
чаются цепи с сосредоточенными
параметрами и цепи с распределен-
ными параметрами. К первым отно-
сятся цепи, в' которых сопротивле-
ния, емкости и индуктивности могут
рассматриваться как сосредоточен-
ные в ветвях, соединяющих узлы.
При этом ток может изменяться
только при переходе через узел (пе-
реход к другой ветви).
Ко вторым относятся цепи, в ко-
торых ток и напряжение непрерыв-
но изменяются вдоль проводов
вследствие непрерывного ответвле-
ния тока через проводимость или
емкость, распределенные вдоль про-
вода, обладающего и непрерывно
распределенными продольным со-
противлением и индуктивностью.
Простейший пример цепи с распре-
деленными параметрами представ-
ляет собой длинная двухпроводная
линия постоянного тока, в которой
ток непрерывно переходит с одного
провода на другой (ток утечки) че-
рез поперечную проводимость и вме-
сте с тем в проводах происходит не-
прерывное падение напряжения из-
за продольного сопротивления про-
водов.
В первой книге по теории цепей
рассматриваются только линейные
цепи с сосредоточенными постоян-
ными.
Нелинейным цепям, цепям с рас-
пределенными параметрами, а так-
же общей теории четырехполюсни-
ков и фильтров, изучение которых
тесно связано с теорией длинных ли-
ний, посвящена вторая книга курса
теоретических основ электротех-
ники.
РАЗДЕЛ I
ЦЕПЬ ПОСТОЯННОГО ТОКА
ГЛАВА ПЕРВАЯ
ОСНОВНЫЕ ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ
И ЗАКОНЫ
1-1. ПОТЕНЦИАЛЬНОЕ
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Электрические заряды одного
знака взаимно отталкиваются, заря-
ды противоположного знака притя-
гиваются в соответствии с зако-
ном Кулона:
f = JL£i£i (М)
' е0 4тсг2 ’ ' '
где f — сила отталкивания;
?2 — взаимодействующие заряды;
г — расстояние между заряда-
ми;
е0 — электрическая постоянная,
зависящая от выбора систе-
мы единиц; в системе единиц
СИ1 80 = 8,855-10-12 ф/м.
Формула (1-'1) записана для не-
поляризуемой среды — вакуума и
практически воздуха.
Рассмотрим два изолированных
металлических тела (электроды),
например параллельные пластины,
которым сообщены равные заряды
противоположного знака (рис. 1-1).
Эти заряды в основном распреде-
ляются на внутренних сторонах
пластин в силу того же закона Ку-
лона (заряды противоположного
знака притягиваются). До тех пор
пока силы, действующие на заря-
ды, меньше некоторой предельной
величины, они остаются связанными
с металлическими телами и не могут
1 ОИ — .система интернациональная.
В этой (системе метр (л*), килограмм (кг),
секунда {сек) и ампер (а) — основные еди-
ницы. Таким образом, для всех электротех-
нических 'величин она совпадает с известной
системой МКС-А.
перейти в разделяющий их изолиру-
ющий слой, например воздух, стек-
ло, вакуум.
Если между электродами имеют-
ся заряженные частицы, способные
свободно перемещаться, то они бу-
дут двигаться под действием Куло-
новых сил: положительно заряжен-
Г- П
Рис. 1-1.
ные частицы — к отрицательному
электроду (катоду), отрицательно
заряженные —к положительному
(аноду).
Возникновение сил, действую-
щих на заряженные частицы, объяс-
няют существованием электри-
ческого поля.
Интенсивность (сила) электриче-
ского поля характеризуется векто-
ром напряженности поля Е.
Сила f, испытываемая в электри-
ческом поле заряженной частицей,
равна произведению ее заряда q и
напряженности поля Е:
f=7E. (1-2)
Замечательное свойство электри-
ческого поля, в котором все силы,
действующие на заряды, определя-
ются законом Кулона, заключается
в том, что работа, совершаемая си-
лами поля при переносе заряда q
из одной точки (1) в другую (2), за-
висит не от пути, по которому этот
2 К- М. Поливанов
17
перенос совершался, а только от по-
ложения начальной и конечной то-
чек.
Сказанное позволяет все точки та-
кого поля характеризовать скаляр-
ной величиной — потенциалом
ф. При этом разность потенциалов
между двумя точками ф1—ф2 опре-
деляют по работе, которую способ-
ны совершить силы поля при пере-
носе заряда из первой точки во вто-
рую *:
Л=^(ф1—ф2). (1-3)
В системе единиц СЙ сила изме-
ряется в ньютонах (я), работа —
в джоулях (дж), потенциалы —
в вольтах (в).
Поверхности, нормальные к на-
пряженности поля Е, обладают оди-
наковым потенциалом, так как при
любом перемещении, нормальном
к действующей силе f=^Е, не совер-
шается работы.
В условиях статики (отсутст-
вие упорядоченного движения заря-
дов) металлические электроды об-
ладают постоянными потенциалами.
Рис. 1-2.
В противном случае внутри провод-
ника заряды перемещались бы в на-
правлении поля.
На рис. 1-2 схематически пока-
зано распределение поверхностей
равного потенциала между плоски- * 1
1 Из сочетания определений (1-2) и (1-3)
следует, что
А = С fdl = ? f Edl,
1—2 1—2
или
т. е. разность потенциалов между двумя
любыми точками 1 и 2 равна линейному
интегралу от напряженности поля, взятому
вдоль любой линии /, соединяющей точки
1 и 2.
ми электродами; в се-
чении плоскостью чер-
тежа они представля<
ются линиями. На том
же рисунке пунктиром
показаны линии элек-
трического поля. В лю- Рис. 1-3.
бой точке вектор на-
пряженности поля направлен по ка-
сательной к этим линиям.
Сила, действующая на движущуюся
заряженную частицу, совершает работу.
В простейшем случае движения частицы
в вакууме совершаемая работа переходит
в кинетическую энергию частицы.
<В электронной лампе (рис. 1-3) из на-
каленного катода вылетают электроны
с некоторой начальной скоростью vq. Они
увлекаются силами электрического поля
к положительному аноду. Приобретаемая
электронами, движущимися со скоростью и,
энергия
2
ту2 mvQ
~2~ ' "г-= <7(?н^?а)
отдается аноду при ударе об него и пере-
ходит в тепловую энергию (часть энергии
может перейти в излучение, возникающее
при ударе). В такой системе анод может
сильно разогреваться.
Заметим, что в последней формуле
Фк—Фа<0, но одновременно и #<0 (заряд
электрона отрицателен), поэтому произведе-
ние этих величин положительно '(см. конец
§2-2).
В потенциальном (Кулоновом)
поле разность потенциалов между
любыми точками можно отождест-
вить с напряжением между
ними:
^12 = Ф1—ф2. (1-4)
Два индекса около буквы и, обо-
значающей напряжение, повторяют
индексы потенциалов — первый
уменьшаемого, второй вычитаемого.
Физическое определение было
дано только для разности потенци-
алов. Из этого факта следует, что
к величинам всех потенциалов мот
жет быть добавлена любая одина-
ковая произвольная постоянная, так
как при этом разность потенциалов
не изменяется. Другими словами,
любая точка поля может быть при-
нята за начало отсчета потен-
циалов, т. е. ее потенциал может
быть произвольно принят равным
нулю.
18
1-2. ЕМКОСТЬ. КОНДЕНСАТОР
Разность потенциалов между
электродами, несущими заряды +q
и —q, при любой конфигурации
электродов прямо пропорциональна
их заряду:
Ф1—:ф2~^12 = ti—kq.
Это утверждение согласуется с за-
коном Кулона: сила, испытываемая
«пробным» зарядом, расположен-
ным между электродами, должна
быть пропорциональна заряду элек-
тродов q\ следовательно, и работа,
совершаемая при перемещении за-
ряда, т. е. разность потенциалов,
пропорциональна заряду электро-
дов.
Приведенная формула, перепи-
санная в несколько иной форме,
служит определением очень важной
в электротехнике величины, называ-
емой электрической емкостью систе-
мы из двух электродов (буквенное
обозначение С):
Емкость двух разноименно за-
ряжаемых электродов (при отсут-
ствии влияния других заряженных
тел) равна отношению заряда к раз-
ности их потенциалов. Единицей ем-
кости служит фарада (ф), т. е. ку-
лон на вольт.
Система двух изолированных
электродов, предназначенная для
образования определенной емкости,
называется конденсатором.
Для получения большой емкости
стремятся уменьшить расстояние
между электродами и увеличить их
поверхность.
Емкость конденсатора из двух.
параллельных пластин (плоского
конденсатора) вычисляется по фор-
муле
Рис. 1-4.
bu-uiiiuil
О 5 10мм
Рис. 1-5.
где s — площадь каждой из пла-
стин;
d — расстояние между ними;
8 — диэлектрическая проницае-
мость изолирующего слоя (см. табл.„
стр. 80);
8о — электрическая постоянная..
Емкость двух параллельных,
воздушных проводов (в ф!км\'.
C=[36-106ln(d/r)]-1; (1-6б>
обозначения понятны из рис.
Емкость коаксиального кабеля;
длиной I:
С = 2л8о8//1п (J?/r), (1 -6в)
где 8 — диэлектрическая- проницае-
мость изоляции кабеля; остальные
обозначения понятны из рис. 1-4,6.
Емкость технических конденсато-
ров достигает десятков и сотен ми-
крофарад (1 жкф=10-6 ф). В тех-
нике высоких частот приходится
19*
считаться и с гораздо меньшими ем-
костями, измеряемыми в пикофара-
дах (1 ft$=10~12 ф).
Внешний вид различных конден-
саторов показан на рис. 1-5 (кон-
денсаторы емкостью 10~9 ф для
установок высокого напряжения и
радиотехнические конденсаторы
емкостью в десятки пикофарад).
Соединим электроды конденса-
тора каким-либо проводником г
(рис. 1-6), т. е. таким телом, внутри
которого может происходить более
или менее свободное перемещение
зарядов под действием сил электри-
ческого поля. Если конденсатор за-
ряжен, то в проводнике под дейст-
вием Кулоновых сил положительные
заряды будут стремиться перейти
к отрицательному электроду, а от-
рицательные — к положительному,
т. е. возникает упорядоченное дви-
жение зарядов (электрический ток),
в результате чего конденсатор раз-
ряжается (заряды на каждом из его
электродов уменьшаются по абсо-
лютной величине). Процесс будет
происходить до тех пор, пока конден-
сатор не разрядится полностью.
1-3. ЭЛЕКТРИЧЕСКИЙ ТОК
Мерой упорядоченного движения
электрических зарядов, т. е. элек-
трического тока, служит коли-
чество электричества (заряд), про-
ходящее в единицу времени через
заданную поверхность s (через по-
перечное сечение провода, рис. 1-7):
i=dq!dt. (1-7)
Эту величину называют силой тока,
интенсивностью тока или просто то-
ком.
Говоря о переходе заряда dq че-
рез поверхность s, нужно уточнить
направление этого перехода, т. е.
сказать, имеется ли в виду переход
через поверхность слева направо
(положительное направление) или
справа налево (отрицательное на-
правление) .
Это условие определяет и поло-
жительное направление то-
ка. Пусть, например, на рис. 1-7
имеется в виду переход заряда сле-
ва направо через сечение проводни-
ка s; в этом случае и положитель-
ное направление тока — это направ-
ление слева направо.
Как ток, так и количество элек-
тричества, прошедшее через поверх-
ность s, всегда понимаются в алге-
браическом смысле: и ток, и заряд
могут быть как положительными,
так и отрицательными. Однако мож-
но говорить об их отрицательных
значениях только после того, как
выбрано положительное направле-
ние перехода через поверхность s.
Надо еще заметить, что переход
через поверхность s положительного
заряда q'=\q\, скажем, слева на-
право эквивалентен переходу через
поверхность такого же отрицатель-
ного заряда q"=—|#| справа нале-
во (рис. 1-7). Если движение по-
ложительного заряда 7х>0 вдоль
проводника со скоростью г/>0 со-
ответствует положительному току
/>0, то и движение отрицательного
заряда q"<0 в противоположном
направлении со скоростью v"<0
также соответствует положительно-
му току. Результирующий ток про-
порционален сумме.
q'v'+q"v"
(произведение q"v" положительно,
когда и qf' и v" отрицательны).
Что же касается заряда внутри
проводника q, то он определяется
алгебраической суммой
Поэтому ток может быть отличен от
нуля, тогда как общий заряд ра-
вен нулю.
2D
Закон сохранения количества
электричества. Изменение количест-
ва электричества внутри любой обла-
сти, ограниченной замкнутой по-
верхностью, всегда равно количест-
ву электричества, прошедшему че-
рез эту поверхность. Заряд нигде
не возникает и не уничтожается,—
происходит только перемещение за-
рядов.
Появление положительного заря-
да +!7 в какой-либо области может
происходить и за счет удаления от-
рицательного заряда —q (до этого
заряды компенсировались). Анало-
гично заряд может стать равным ну-
лю за счет внесения в ту же об-
ласть такого же заряда противопо-
ложного знака. И в том, и в другом
случае переносимый заряд проходит
через поверхность, ограничивающую
рассматриваемую область.
Применяя сказанное к разряду
конденсатора, приходим к выводу,
что уменьшение заряда на положи-
тельном электроде (рис. 1-8) всег-
Рис. 1-8.
да равно заряду, переносимому то-
ком через поверхность иначе го-
воря,
—dq = idt. (1-8)
Имея в виду, что q=ucC, находим,
что ток разряда конденсатора (при
неизменной емкости) равен:
•__ dq_________г
dt ~ U dt ’
(1-9)
где ис = qpi—ф2 — напряжение на
конденсаторе.
На остальных участках цепи
рис. 1-8, где накопления или умень-
шения заряда *не происходит, коли-
чество электричества, входящее че-
рез какую-нибудь часть любой за-
мкнутой поверхности, равно количе-
ству электричества, выходящему че-
рез другую часть этой же поверх-
ности. Применяя сказанное & по-
верхности s2 рис. 1-8, находим, что
входящий в нее ток i равен выходя-
щему. Это значит, что через любое
поперечное сечение ветви, соединя-
ющей два узла электрической цепи,
проходит одинаковый ток.
По существу дела, на всех про-
водах электрической цепи могут на-
капливаться заряды, но благодаря
относительно малой поверхности
проводов и относительно большому
расстоянию между ними эти заря-
ды малы, и очень часто при расче-
тах ими пренебрегают.
При всех расчетах, проводимых
в этой книге, нужно принимать во>
внимание заряды, распределенные
на проводах, только в том случае,
когда специально оговаривается на-
личие емкости или когда в цепи со-
держатся конденсаторы. Во всех
случаях при изображении цепи на
схеме наличие емкости изображает-
ся соответствующим знаком.
1-4. ПРЕОБРАЗОВАНИЕ ЭНЕРГИИ
В ЦЕПИ ЭЛЕКТРИЧЕСКОГО ТОКА
Энергия электрического поля
койденсатора. До начала разряда
конденсатора между его электрода-
ми существовало поле. К концу
разряда (#=0, Ис = 0) поле распа-
лось. По работе, совершенной Ку-
лоновыми силами в процессе раз-
ряда конденсатора, можно судить
о величине энергии поля заряженно-
го конденсатора.
Когда при напряжении на кон-
денсаторе ис с его положительного
электрода на отрицательный пере-
носится заряд dq, Кулоновы силы
совершают работу:
dA — Ucdq. (1-10)
Но при переносе заряда dq (в про-
цессе разряда) происходит умень-
шение напряжения:
С duc — —dq.
Подставляя выражение для dq
в выражение элементарной работы,
находим, что
dA ——исС duc
(еще раз обратим внимание на
смысл знака минус: работа, со-
вершаемая силами поля при пере-
носе заряда, положительна, когда
21
происходит разряд конденсатора, и
d«c<0 при ис>0).
Интегрируя последнее выраже-
ние от ‘ начала разряда, когда
до конца разряда, когда
^0 = 0, найдем полную работу, со-
вершенную силами поля:
«С=° о
я Г UpC
Л = — I исС duc=--^-- — W^
ис—ис
(1-11)
По предположению, эта работа
равна всей энергии поля IF3, сущест-
вовавшей в заряженном конденса-
торе.
Рассеяние электрической энергии
в проводниках. Заряды, движущиеся
внутри обычного (несовершенного)
проводника под действием сил элек-
трического поля, встречают на сво-
ем пути ряд препятствий, при столк-
новении с которыми они отдают ве-
ществу проводника кинетическую
энергию, приобретенную на пути от
одного препятствия к другому. При
этом они движутся в среднем с по-
стоянной, сравнительно небольшой
скоростью.
Подобное явление хорошо знако-
мо из макроскопической механики:
любое тело, встречающее сопротив-
ление своему движению, при дейст-
вии постоянной силы приобретает
в конце концов постоянную ско-
рость, при которой приложенная си-
ла «расходуется» на преодоление
трения и уже не создает ускорения.
Работа сил при этом переходит в те-
пло, выделяющееся при трении.
Точно так же работа, совершае-
мая силами поля, переходит в те-
пловую энергию (закон Джоуля —
Ленца). Частицы проводника приоб-
ретают дополнительную кинетиче-
скую энергию, которую им отдают
при торможении электрические за-
ряды, движущиеся под действием
сил электрического полях.
В рассмотренном выше процессе
разряда конденсатора через несо-
вершенный проводник вся запасен-
ная в нем энергия электрического
поля переходит в тепловую. Если бы
разряд конденсатора происходил че-
рез вакуумную лампу, внутри кото-
рой электроны, испускаемые като-
дом, могут свободно перемещаться
(см. рис. 1-3), то вся энергия поля
все равно превращалась бы в теп-
ло. Процесс преобразования энер-
гии происходил бы так: свободно
летящие в вакууме электроны уско-
ряются при переходе к более высо-
кому потенциалу, при ударе об анод
они отдают ему приобретенную ки-
нетическую энергию, анод нагре-
вается.
Мощность электрического тока.
Когда по ветви при разности потен-
циалов и проходит ток i=dqldt,
в ней за время dt силами поля со-
вершается элементарная работа:
dA = udq. (1-12)
Следовательно, мощность, харак-
теризующая приток энергии к этой
ветви, равна:
p = dAldt=ui. (1-13)
Если ветвь представляет собой
несовершенный проводник (обыч-
ные провода), то эта мощность рас-
сеивается в ветви.
1-5. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
В потенциальном (Кулоновом)
поле заряды всегда стремятся дви-
гаться от точек более высокого по-
тенциала к точкам более низкого по-
тенциала, в результате чего все по-
тенциалы выравниваются, все заря-
ды разного знака взаимно компен-
сируются и все электрические эф-
фекты исчезают. Поэтому необходи-
мо существование каких-то процес-
сов, в которых отрицательные заря-
ды удаляются от положительных во-
преки закону Кулона. Без этого
нельзя было бы наблюдать ни Ку-
лоново притяжение разноименных
зарядов (их надо было разделить),
ни разряд конденсатора (конденса-
тор надо было зарядить).
Силы, стремящиеся разделить
разноименные заряды, противодей-
ствуя силам Кулона, называют сто-
ронними (по отношению к силам
Кулона) или некул о новы ми.
Наличие сторонних сил совер-
шенно необходимо для работы элек-
тротехнических устройств. Без сто-
ронних сил электротехника не могла
бы существовать, так же как не су-
ществовало ’ бы ни рек, ни водопа-
дов, если бы движение воды проис-
ходило только под действием сил
земного тяготения (в направлении
от более высокого уровня к более
низкому). Но под влиянием солнеч-
ных лучей вода испаряется; мощные
потоки ее молекул подымаются
(сторонними силами) вверх, преодо-
левая силу земного притяжения.
Опускаясь в виде дождя и снега,
огромные количества воды оказыва-
ются уже на более высоком уровне,
чем те поверхности, с которых про-
исходило испарение.
Участие сторонних сил в пере-
распределении зарядов или в их
движении по электрической цепи мо-
жет оцениваться работой, которую
способны совершить эти силы при
переносе единичного заряда через
область действия сторонних сил.
Эта величина называется элек-
тродвижущей силой (э. д. с.)
и обозначается Э:
э. д. с. = Э=Хст/9, (1-14)
где АСт работа сторонних сил.
Область действия сторонних сил
в электрической цепи обыкновенно
может быть строго локализована —
она заключена внутри генераторов
(источников питания): гальваниче-
ских элементов, аккумуляторов,
электромагнитных машин и тому по-
добных устройств. При изображе-
нии электрических цепей область
действия сторонних сил изображает-
ся кружком, внутри которого может
ставиться стрелка, показывающая
направление, в котором сторонние
силы стремятся перемещать поло-
жительный заряд (левая часть
рис. 1-9).
Соединим генератор, имеющий
известную э. д. с., и конденсатор по-
средством проводов, как это пока-
зано на рис. 1-9.
Конденсатор зарядится, так как
сторонние силы источника будут ле-
Рис. 1-10.
реносить положительный заряд
с нижнего электрода на верхний,
преодолевая действие Кулоновых
сил и сил трения в соединительных
проводах. Перенос зарядов происхо-
дит до тех пор, пока разность по-
тенциалов на конденсаторе ис не до-
стигнет значения, равного э. д. с. ис-
точника Э, Если бы разность потен-
циалов ис была больше Э, то для
переноса заряда q надо было бы
производить работу quc, на что ис-
точник уже не способен, так как по
определению он способен произво-
дить работу АСт, равную q3.
Из рассмотренного вытекает оп-
ределение электродвижущей силы
источника — она равна напряжению
(разности потенциалов) на его за-
жимах при отсутствии тока в источ-
нике, Другими словами, э. д. с. ис-
точника равна напряжению холосто-
го хода (/=0) на его зажимах.
Работа сторонних сил в электри-
ческой цепи. Рассмотрим электриче-
скую цепь, представленную на
рис. 1-10, в которой конденсатор мо-
жет разряжаться через замыкаю-
щий его проводник (правая часть
рисунка). В такой цепи пойдет ток L
В правой части цепи, подчиняясь
закону Кулона, положительные за-
ряды переходят от то.чек более вы-
сокого потенциала <pi к точкам бо-
лее низкого ф2 (нижний электрод),
но в левой части цепи-положитель-
ные заряды переносятся источником
сторонних сил . от нижнего электро-
да к верхнему. При установившемся
режиме наступит равновесие, при
котором конденсатор не разряжает-
ся и не заряжается, так как в каж-
дое мгновение заряды, стекающие
через правую ветвь, пополняются за-
рядами, подводимыми источником.
При этом ток источника равен току
в правой ветви. Подобный режим
в цепи может существовать до тех
пор, пока цепь тока не прервана,
23
а источник развивает неизменную
э. д. с.
В цепи рис. 1-10 устанавливают-
ся постоянные токи и потенциалы,
при этом наличие конденсатора и
величина его емкости перестают
оказывать влияние на процессы
в цепи.
Существенное отличие сторонних
сил от сил потенциального поля за-
ключается в том, что при переносе
заряда q по замкнутому контуру
(например, из точки 1 в точку Л
работа сторонних сил отлична от
нуля:
A^ = q3, (1-15)
где Э — э. д. с., действующая в рас-
сматриваемом контуре, а работа сил
потенциального поля при этом рав-
на нулю.
Сказанное может показаться не-
достаточно убедительным. Действи-
тельно, пусть источник э. д. с', за-
мкнут несовершенным проводником
(прямоугольник на рис. 1-11). В нем
Рис. 1-11.
происходит рассеяние энергии при
движении зарядов. Предположим,
что рассеяние энергии внутри источ-
ника настолько мало, что им мож-
но пренебречь (такие условия впол-
не осуществимы). При этом между
верхним и нижним концами несо-
вершенного проводника установится
разность потенциалов, практически
равная э. д. с. источника:
<Р1—ф2 = «12 = 5,
а в проводнике под действием Куло-
новых сил установится упорядочен-
ное движение зарядов (электриче-
ский ток i). Движущиеся заряды
преодолевают встречаемые препят-
ствия и нагревают несовершенный
проводник.
Разве работа совершается не си-
лами потенциального поля? Да, дей-
ствительно так. Но эта работа со-
вершается только на правом участ-
ке цепи. При дальнейшем движении
зарядов — а заряды непрерывно
движутся по замкнутому контуру —
они переносятся сторонними силами
от точек более низкого потенциала
(ф2) к точкам более высокого (<pt).
Но на левом участке цепи также
действуют силы потенциального по-
ля. И если на правом участке силы
потенциального поля, перенося за-
ряд 9, совершили работу
4пр= (<Р1—фг)<7,
то на левом—работа потенциальных
сил равна работе потенциальных
сил на правом участке и противо-
положна ей по знаку:
^лев— (ф2—Ф’1) 7-
В результате полная работа сил по-
тенциального поля равна нулю.
В то же время работа сторонних
сил равна:
Лст = 37= (ф1—ф2)д.
Именно эта работа, производимая
внутри генератора сторонними сила-
ми, и рассеивается, превращаясь
в тепло, при прохождении заряда че-
рез правый участок. Выражение
для работы совершаемой сторонни-
ми силами, вытекает из самого оп-
ределения э. д. с. (1-14) и является
общим.
При рассмотрении цепей элек-
трического тока часто оказывается
более удобным рассматривать мощ-
ность источника, т. е. работу, совер-
шаемую в единицу времени:
p-dA^dt.
Если учесть, что за время dt пе-
реносится заряд dq=idt и, следова-
тельно, за это время совершается
работа
dACT=9i dt,
то мощность можно выразить про-
изведением э. д. с. и тока:
P=3Z. (1-16)
1-6. ЗАКОН ОМА. ЛИНЕЙНЫЕ
И НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ
На основании многочисленных
экспериментов с металлическими
проволоками, различными по длине,
сечению и материалу, немецкий уче-
24
ный Г. С. Ом установил следующий
закон: разность потенциалов на
концах проводника —tp2 про-
порциональна току в проводнике;
при неизменности прочих физиче-
ских условий (температура провод-
ника, его растяжение и т. п.)
u—ir. (1-17)
Коэффициент пропорциональности г,
входящий в эту формулу, Ом на-
звал электрическим сопро-
тивлением.
В простейшем случае для одно-
родного проводника постоянного по-
перечного сечения, его сопротивле-
ние прямо пропорционально длине
I и обратно пропорционально сече-
нию s:
r=?lls. (1-18)
Коэффициент пропорционально-
сти р для проводников из разных
материалов различен; его называют
удельным сопротивлением
материала, из которого состоит про-
водник (см. табл. 1 и 2 на стр. 80).
Величину, обратную сопротивле-
нию, называют проводимостью:
§ = (1-19)
В последней формуле ст—у дель-
ная электрическая прово-
димость материала (электро-
проводность) .
• В системе СИ сопротивление из-
меряется в омах (ом), а проводи-
мость в сименсах (сим), причем
1 сим=1 ом~г; единицы, в которых
выражаются р и сг, определяются
самой структурой формул (1-18) и
(1-19).
Пользуясь понятием сопротивле-
ния, можно'так формулировать ос-
новное содержание закона Ома: со-
противление проводников не зави-
сит от проходящего по ним тока при
неизменности других физических
условий.
Все металлические проводники,
как правило, подчиняются закону
Ома в самом широком диапазоне
изменений тока. Напротив, полупро-
водники, электрическая дуга, разре-
женные газы (газоразрядные лам-
пы) не подчиняются закону Ома.
Однако определение сопротивления
г=иН и проводимости g=i/u приме-
нимо и в тех случаях, когда закон
Ома нарушается. Но в этих случаях
r=f(z) не может служить простым
параметром проводника, как в слу-
чае выполнения закона Ома.
Электрическая характеристика
w=f(z), называемая часто вольт-
.амперной характеристи-
кой, для проводников, подчиняю-
щихся закону Ома, выражается на-
клонной прямой линией (рис. 1-1)2).
Поэтому проводники, подчиняющие-
ся этому закону, а также цепи, со-
ставленные из таких проводников,
называют линейными.
На схемах электрических цепей
проводники, сопротивление которых
необходимо учитывать, изобража-
ются прямоугольником, ” как на
рис. 1-6—1-11.
На рис. 1-13 приведена нелиней-
ная характеристика проводника,
к которому закон Ома неприменим.
Чтобы снять такую характери-
стику, надо иметь источник, напря-
жение которого можно регулиро-
вать; значение тока и напряжения
определяется измерительными при-
борами (амперметром и вольтмет-
ром), включение которых показано
на рис. 1-14.
Важно подчеркнуть, что, говоря
о сопротивлении проводника или
о сопротивлении ветви электриче-
ской цепи, предполагают отсутст-
вие в этой ветви источников; други-
ми словами, имеют в виду, что раз-
ность потенциалов на концах про-
водника вызвана только протекани-
ем тока, а не сторонними силами,
действующими на заряды, или что
ток вызван только разностью потен-
циалов на концах проводника, а не
сторонними силами. Обе формули-
ровки равносильны.
Поскольку в сопротивлениях
происходит только рассеяние энер-
25
Рис. 1-14.
§3
гии, и они не могут служить источ-
никами питания; участки цепи, не
содержащие источников, называют-
ся пассивными элементами
цепи.
Характеристики рис. 1-12 и 1-13
называют вольт-амперными харак-
теристиками линейного и нелинейно-
го пассивных элементов.
В заключение хочется обратить внима-
ние на те трудности, с какими встречался
Ом при .выполнении своего исследования.
В его распоряжении имелась очень скудная
измерительная аппаратура и очень несовер-
шенные и неустойчивые источники питания.
Его работа «Математическая обработка
гальванической цепи», опубликованная
в 1827 г., была первой попыткой аналитиче-
ского описания процессов в электрической
цепи. В ней содержалась, правда в недоста-
точно общем и полном виде, формулиров-
ка законов, ставших впоследствии извест-
ными как законы Кирхгофа.
Применение закона Ома к практичен
ским расчетам и его широкая проверка
связаны с работами русских электротехни-
ков Ленца и Якоби, что специально отмеча-
лось в решении Английской Академии наук
(Королевского общества) о присуждении
премии Ому.
1-7. ЗАКОН ДЖОУЛЯ— ЛЕНЦА
Из ранее данного определения
мощности электрического тока и со-
вершаемой им работы (1-12) и
(М3)
p — iii, A — uq = ^ ui dt
легко получить известную формули-
ровку закона Джоуля — Ленца. Ес-
ли напряжение представить как
произведение /г, то получаем, что
p = i2r, А = С i2rdt. (1-20)
Эти формулы выражают мощность
и энергию, рассеиваемые в провод-
нике при протекании тока и превра-
щающиеся в тепло.
В этих формулах мощность вы-
ражается в ваттах (вт), а энергия
в ватт-секундах (вт-сек) или джоу-
лях (дж). Для выражения энергии
в калориях или мощности в кало-
риях за секунду следует .правые ча-
сти равенств (1-20) умножить на
коэффициент 0,24.
1-8. НАПРЯЖЕНИЕ НА ВЫХОДНЫХ
ЗАЖИМАХ ИСТОЧНИКА.
ОБОБЩЕННЫЙ ЗАКОН ОМА
Замкнем источник питания, об-
ладающий внутренним сопро-
тивлением г2-, ветвью с сопротив-
лением г (рис. 1-15).
В образовавшейся замкнутой це-
пи пойдет ток Л
Рж. 1-Г5.
Мощность, отдаваемая источни-
ком р = Э1, рассеивается (по закону
Джоуля — Ленца) во внутреннем и
внешнем сопротивлениях цепи:
Э/=й(г2+'г). (1-21)
После сокращения на i приходим
к очень важному выражению, содер-
жавшемуся и в исследованиях Ома:
5 = Z(r.+’r), (1-22)
По закону Ома, напряжение на
внешнем участке цепи равно напря-
жению на выходных зажимах источ-
ника:
иаЪ==1г.
Из сопоставления последнего
уравнения с предыдущим находим,
что
иаЪ-Э—ifi, (1-23)
т. е. напряжение на зажимах источ-
ника меньше его э. д. с. (Э) на ве-
личину внутреннего падения
напряжения (ir^.
Источник э. д. с. как идеальный
источник напряжения. Уравнение
(1-23) дает возможность предста-
вить источник питания с внутренним
сопротивлением г2 как два последо-
вательно включенных элемента:
идеальный источник — источник
26
э. д. с. или источник напряже-
ния, напряжение на зажимах кото-
рого т и b равно Э, и последова-
тельно включенное сопротивление
r-i (рис. 1-16). Очевидно, что при
Рис. 1-16.
этом напряжение между выходными
зажимами а и Ь выражается имен-
но формулой (1-23).
Действительно, потенциал точки
т выше потенциала точки b на ве-
личину э. д. с., а потенциал точки а
ниже потенциала точки т на вели-
чину падения потенциала (напряже-
ния) в сопротивлении определяе-
мого по закону Ома.
В дальнейшем следует всегда
считать источник идеальным, если
около его изображения не стоит
буква, обозначающая внутреннее со-
противление.
Формулу (1-23) можно приме-
нять к ветви, содержащей э. д. с, и
Рис. 1-17.
любое последовательно включенное
сопротивление г, величина которого
содержит и внутреннее сопротивле-
ние источника (рис. 1-17).
При этом
и^= фо, ф& — Э ir. (1 -24)
Эта формула выражает обоб-
щенный закон Ома. **
Фиксированность положительных
направлений; их обозначение. Равен-
ство (1-24) написано-в предположе-
нии совершенно определенного выбо-
ра положительных направлений то-
ка и э. д. с., а также определенной
последовательности уменьшаемого и
вычитаемого потенциалов (фа—фь)
при определении напряжения. Имея
в виду эту последовательность, го-
ворят, что напряжение «направле-
но» от уменьшаемого к вычитаемо-
му. Два индекса около буквы, обо-
значающей напряжение, ставятся
так, чтобы первый соответствовал
уменьшаемому.
Положительные направления мо-
гут быть выбраны произвольно, но
всегда должны быть строго фикси-
рованы. Заметим, что ответить на
вопрос «чему равно напряжение
между концами ветви, содержащей,
скажем, э. д. с. 100 в, сопротивление
2 ом при токе 5 аЪ> совершенно не-
возможно, если тем или иным спосо-
бом не указаны положительные на-
правления.
На рис. 1-17 приведены обозна-
чения положительных направлений
тока и э. д. с., не нуждающиеся в по-
яснениях; кроме того, стрелкой обо-
значено напряжение, определяемое
как разность потенциалов <ра—Ф&.
При этом стрелка направлена
от уменьшаемого к'вы читае-
мо му. Такое обозначение принято
на протяжении всешкниги.
Необходимо обратить внимание
на то, что направление сторонних
сил совпадает с направлением
стрелки, обозначающей э. д. с. (ес-
ли э. д. с. положительна), а направ-
ление напряженности потенциально-
го (Кулонова) поля совпадает с на-
правлением стрёлки, обозначающей
напряжение (если напряжение по-
ложительно) .
Стрелка напряжения должна
ставиться обязательно вне кружка,
обозначающего источник; стрелка
э. д. с. должна ставиться только
внутри кружка, обозначающего ис-
точник.
1-9. ЗАКОНЫ КИРХГОФА
Первый закон Кирхгофа — пря-
мое следствие закона сохранения ко-
личества электричества: сумма всех
токов, приходящих к узлу электри-
ческой цепи, равна сумме всех то-
ков, уходящих от этого узла. ч
27
Можно сказать короче: алгебра-
ическая сумма всех токов, сходя-
щихся к любому узлу цепи, равна
нулю:
2г=0. (1-25)
При невыполнении этого закона
на узле накапливался бы электри-
ческий заряд.
В применении к узлу, изобра-
женному на рис. 1-18, первый закон
Кирхгофа формулируется равенст-
вом
И + Z2—Z3 = 0.
Второй закон Кирхгофа: для лю-
бого замкнутого контура электри-
ческой цепи алгебраическая сумма
всех э. д. с. равна алгебраической
сумме всех падений потенциала:
2Э=2г. (1-26)
Со знаком плюс берутся все
э. д. с. и все произведения Zr, для
которых направления э. д. с. и токов
совпадают с выбранным направле-
нием обхода контура. В противном
случае соответствующие слагаемые
берутся со знаком минус перед бук-
венным обозначением слагаемого.
Как во всей алгебре, обозначаемые
буквами величины могут оказаться
как положительными, так и отрица-
тельными.
Для внешнего контура цепи
рис. 1-19
31—Э2=-/1Г1—гУз—^2-
Формулированный здесь второй
закон Кирхгофа представляет собой
прямое следствие того факта, что
напряжение между любыми узлами
электрической цепи может быть
представлено как разность потен-
циалов. Например:
12 ~ ф 1 ф'2 и ^23 — ф'2---------фз >
^12 + ^23 = Ф1----фЗ = ^13-
РИС. 1-18.
Обобщая, можно
сказать, что сумма на-
пряжений любого чис-
ла последовательно
примыкающих один к
другому участков рав-
на разности потенциа-
Рис. 1-19.
лов между началом первого участка
и концом последнего:
^12 + ^§з+ ••• ~VUmn — 'ф1—ф'п.
Но если все рассматриваемые уча-
стки образуют замкнутый контур, то
последняя точка совпадает с первой.
В таком случае фп = ф1 и вся сумма
обращается тождественно в нуль.
При этом необходимо, чтобы при
обходе по замкнутому контуру на-
пряжение на каждом из участков
контура определялось или как убы-
вание потенциала (ф!—ф2, затем
Ф2—Фз и т. д.) или же как возраста-
ние потенциала (ф2—фь фз—ф2>
ф'4—фз и т. д.).
Если участок цепи содержит ис-
точник э. д. с. и сопротивление, то
повышение потенциала на этом уча-
стке выражается как разность меж-
ду э. д. с. и падением потенциала
в сопротивлении Э—ir в том случае,
если э. д. с. и ток направлены по
принятому обходу контура. Напри-
мер, для первой ветви, цепи
рис. 1-19
Uac = ’фа—фс “ *51—ЦГ 1.
В этой ветви потенциал возраста-
ет на величину Эц и убывает на ве-
личину
При ином направлении тока и
э. д. с. перед соответствующим сла-
гаемым знак следует изменить. Так,
для третьей ветви возрастание по-
тенциала (при обходе слева напра-
во)
Uba = фь—фа = hr 3-
Из того, что сумма всех напря-
жений и=Э—ir замкнутого контура
равна нулю, непосредственно и сле-
дует приведенная в начале парагра-
фа формулировка второго закона
Кирхгофа.
В формуле второго закона сум-
мы 23 и 2Zr могут распространять-
28
ся и на часть контура, обход по ко-
торому обрывается в точке а и во-
зобновляется в точке Ъ. В этом слу-
чае к правой части добавляется раз-
ность потенциалов между этими точ-
ками:
2Э=2/г+'иаЬ, (1-27)
при этом все э. д. с. Э и токи i бе-
рутся со знаком плюс, если они со-
впадают с направлением обхода кон-
тура.
Если применить последнюю фор-
мулу к внешнему контуру рис. 1-19,
совершая обход по часовой стрелке,
обрывая обход по контуру в точке а
и возобновляя обход по контуру
в точке Ь, то найдем, что
Э1 —Э2 — /1’Г 1 —igf2 + ^ab •
ЫО. МАГНИТНОЕ ПОЛЕ
В проводнике с током могут про-
исходить различные физические
процессы (напрев проводника, пере-
пое металла в растворе металличе-
ских солей и др.). Все эти явления
зависят от свойств проводящей сре-
ды. Существует, однако, явление,
всегда однозначно связанное имен-
но с самим током. Это — сопровож-
дающее ток магнитное поле.
В отсутствие других токов или
намагниченных тел магнитное поле
проводника с током зависит только
от пространственного расположения
проводника с током и всегда про-
порционально току.
Существование магнитного поля
легко обнаружить хотя бы по его
действию на компасную стрелку
(рис. 1-20).
Но самое важное в характери-
стике магнитного поля — это то, что
оно возникает вследствие движения
зарядов и обнаруживается по си-
лам, действующим на движущиеся
заряды, а следовательно, и на про-
водники с током.
Магнитное поле в каждой точке
пространства в количественном от-
ношении исчерпывающим образом
характеризуется вектором магнит-
ной индукции В, который мож-
но называть также интенсивностью
магнитного поля. Компасная стрел-
ка ориентируется именно по направ-
лению этого вектора.
Сила, испытываемая в магнит-
ном поле прямолинейным отрезком
I провода, несущего ток I, равна
F=iBl, (1-28)
если провод расположен перпенди-
кулярно вектору индукции
(рис. 1-21,а). При этом направление
силы F связано с направлениями
отрезка 1 (направление 1 принима-
ется совпадающим с направлением
тока) и вектора В, как связаны
между собой координатные оси г, х,
у (рис. 1-21,а).
Рассматривая F, I и В как век-
торы, формулу (1-28) можно запи-
сать в виде векторного произведе-
ния:
F=ilXB. (1-29)
Сила, испытываемая зарядом,
движущимся в магнитном поле,
в векторной форме выражается ра-
венством
f=gvXB, (1-ЗЭ)
где q — заряд, v — его скорость.
В соответствии с этой формулой
движущийся заряд испытывает си-
лу (а значит, и ускорение) только
в направлении, нормальном скоро-
сти. Поэтому если скорость движе-
ния заряда не имеет составляющей,
параллельной вектору В (эта со-
ставляющая скорости не изменяется
под действием магнитного поля), то
в однородном магнитном поле тра-
ектория свободного движущегося
заряда—окружность. На рис. 1-21,6
и в схематически показано движе-
ние положительного и отрицатель-
ного зарядов в магнитном поле.
29
Сторонняя напряженность поля
возникающая при движении в маг-
нитном поле. Сопоставляя выраже-
ния (1-2) и (1-30), можно говорить
о том, что на движущиеся заряды
действует стороннее поле с напря-
женностью
ECT==vXB. (1-31)
Взаимодействие магнитного по-
ля и тока определяет работу огром-
ного числа электротехнических
устройств, к ним относятся практи-
чески почти все электрические ма-
шины (двигатели, машинные гене-
раторы и др.), электромагниты, ре-
ле и приборы для измерения тока,
напряжения и мощности.
Измерительные приборы, основанные на
взаимодействии тока и магнитного поля.
На рис. 1-22 изображены типичные устрой-
ства измерительной техники:
а) узкая проволочная петля (л) с при-
клеенным к ней зеркальцем (з), располо-
жена между полюсами магнита (л*). Когда
по петле проходит ток, она слегка повора-
чивается магнитными силами, и по откло-
нению светового луча, падающего на зер-
кальце, .судят о величине тока. Вследствие
малой инерционности петли, пользуясь та-
ким устройством (магнитоэлектрический
осциллограф), можно фотографировать на
подвижной пленке кривую изменяющегося
тока /=/(/);
б) рамка, обмотанная проводом, по ко-
торому проходит измеряемый постоянный
ток, расположена между полюсами магнита
(магнитоэлектрический прибор).
Повороту рамки противодействует пру-
жинка. Отклонение стрелки, связанной
с рамкой, прямо пропорционально току i.
При известном сопротивлении проводов
прибора г можно определять и постоянное
напряжение w=n. Когда прибор служит для
измерения именно напряжения, в его цепь
обычно вводят достаточно большое доба-
вочное сопротивление;
в) в электродинамическом приборе вра-
щающий момент, действующий на подвиж-
ную рамку с током, определяется магнит-
ным полем другого тока в неподвижной
рамке. В этом случае момент .пропорциона-
лен произведению двух токов. Таким же
будет и отклонение, если жесткость пружи-
ны постоянна. Электродинамический прибор
может служить для измерения мощности,
т. е. применяться в качестве ваттметра, ес-
ли один из измеряемых токов (обычно ток
в подвижной рамке) пропорционален на-
пряжению и\ рамка, подключаемая к зажи-
мам с напряжением и, соединяется, как
правило, последовательно с добавочным
сопротивлением, расположенным внутри
прибора. При изменении направления одно-
го из токов изменяется знак вращающего
момента. Поэтому три включении ваттмет-
ра надо со всей тщательностью следить за
порядком присоединения его зажимов к
цепи.
Единица тока ампер — основная едини-
ца абсолютной практической системы и си-
стемы СИ. По силе взаимодействия между
-проводами при заданном их пространствен-
ном расположении можно с большой' точ-
ностью определить величину проходящего
по ним тока. Единица силы ньютон (н)
определяется по известным основным еди-
ницам длины (метр), массы (килограмм) и
времени (секунда). Поэтому, условившись
о форме записи основных уравнений элек-
тродинамики и принятых значениях посто-
янных, входящих в эти уравнения, можно
однозначно определить единицу тока — ам-
пер (а) в конструируемой системе единиц.
Так, в случае д!вух длинных параллель-
ных проводов с током i на 1 лс их длины
действует сила (рис. 1-23)
Г^М/(2ла), (1-32)
где а — расстояние между дров одами.
Магнитной постоянной go при этом припи-
сывается точное числовое’значение 4л* 10-7;
размерность этой постоянной, как ;следует
из формулы (1-32), кг • м • а~2 • сект2, т. е.
go=4л • 10-7 кг • м/а2 • сек2. (1 -33)
После определения единицы тока (в до-
полнение к метру, килограмму и секунде)
единицы всех остальных электрических и
магнитных величин определяются уже как
производные. Так, единица заряда кулон—
30
Рис. 1-22.
это ампер-секунда, вольт — это джоуль
в секунду, деленный на ампер, и т. д. Заме-
тим, что джоуль — единица энергии, равная
107 'Эргов, определяется по трем основным
единицам [(.метру, килограмму, секунде)
аналогично определению эрга в системе
сгс.
В электротехнике в большинстве слу-
чаев удобнее размерность различных вели-
чин выражать не через основные единицы
(мерр, килограмм, секунда, ампер), а через
наиболее подходящие электрические едини-
цы, хотя бы они и не были основными. Так,
магнитную постоянную в системе СИ удоб-
но выражать следующим образом:
Цо =’4л • 10~7 в > сек)а • м=4тс • 10~7 гн/м1.
(1-34)
При этом, конечно,
1 в * сек!а • кг • м/а? • сек2.
1 гн — сокращенное обозначение еди-
ницы индуктивности генри (см. § 3-4).
В этом легко убедиться, обращаясь
к выражению кинетической энергии тс2/2.
Ее единица — джоуль — может быть выра-
жена как 1 кг • m2Jсек2 или 1 в • а • сек.
Рис. 1-23.
31
1-11. ЭЛЕКТРОМАГНИТНЫЕ
МАШИНЫ В ЭЛЕКТРИЧЕСКОЙ
ЦЕПИ
Возникновение э. д. с. в простей-
шем генераторе. Рассмотрим провод
длиною I, движущийся со скоростью
v между полюсами магнита (на
рис. 1-24 показан только нижний по-
люс). -При этом 1, v и В |взаи.мно-
перпендикулярны.
В проводнике содержатся как
положительные, так и отрицатель-
ные заряды (в равном количестве,
если проводник не заряжен). Заря-
ды внутри проводника могут пере-
мещаться. При движении проводни-
ка в магнитном поле на них дейст-
вуют силы стороннего электрическо-
го поля (1-31). В результате в дви-
жущемся проводе произойдет раз-
деление зарядов: конец провода,
обращенный к нам (рис. 1-24), ока-
жется заряженным положительно,
а противоположный конец — отри-
цательно. Эти заряды создадут Ку-
лоново поле (Ек), направленное
навстречу стороннему (Ест). Когда
поля станут равными (по абсолют-
ной величине), движение зарядов
прекратится, так как напряженность
суммарного поля
Е=£ст—Ек=0. (1-35)
Однако между концами провода
теперь установится разность потен-
циалов, обусловленная Кулоновым
потенциальным полем:
Uab = фа ф'Ь == Е^1 — Е3, (1-36)
где Э — э. д. с., наводимая в прово-
де при его движении в маг-
нитном поле.
Рис. 1-24.
Если движущийся проводник
замкнуть посредством соединитель-
ных проводов на сопротивление г,
в образовавшемся контуре пойдет
ток
где г0 — сопротивление самого дви-
жущегося провода.
Разность потенциалов на его
концах теперь уменьшится. Действи-
тельно, по закону Ома для внешнего
участка цепи
Uab — ir,
или, учитывая предыдущее равен-
ство,
иаЬ=Э—ir^ir.
Пока цепь была разомкнута,
в проводе не было тока, и его дви-
жение не тормозилось магнитным
полем. Когда в проводе установит-
ся ток z, его движению будет про-
тиводействовать сила
F=iBil. (1-38)
Той же величине должна рав-
няться -внешняя сила. Умножая ее
на скорость, найдем расходуемую
механическую мощность
РМех = Fv = IB lv (1-39)
или
Р мех = (1 -40 )
где Э — э. д. с., наводимая в про-
воднике при его движении
в магнитное поле;
3=Ec^l=vBl.
Механическая мощность преоб-
разуется в тепло, выделяемое во
всей цепи по закону Джоуля —
Ленца:
Р=/2Г() + /2Л (Ь41)
Последнее слагаемое равно
мощности, отдаваемой во внешнюю
часть цепи.
Рассмотренная примитивная мо-
дель работает как генератор.
Электрический двигатель. Если
от внешнего генератора (Г) через
провод той же модели (рис. 1-24)
пропустить ток i противоположного
направления (рис. 1-25), то на про-,
вод будет действовать сила
. F=iBl,
32
Рис. 1-25.
совпадающая с направлением ско-
рости V.
Это значит, что движущийся
провод теперь может совершать ме-
ханическую работу, отдаваемую
внешней системе. Рассматриваемая
модель двигателя может, например,
подымать груз, вес которого F
(рис. 1-25). Мощность двигателя
Рмех=Fv=iBlv = id, (1 -42)
где Э — э. д. с. наводимая в движу-
щемся проводе.
Мощность, подводимая от внеш-
него источника электрической энер-
гии, т. е. от генератора, включен-
ного к узлам ab,
P=uabi. (1-43)
Но теперь
иаЬ=Э+1г, (1-44)
так как ток направлен навстречу
э. д. с. Следовательно, поступающая
от внешнего источника электриче-
ская мощность
провода, для того чтобы э. д. с. по
отношению к внешней цепи сохра-
няла неизменное направление при
движении под полюсом N и полю-
сом S.
Однако основные особенности
электрической машины как части
электрической цепи, как ее элемен-
та, легко (понять из рассмотренной
модели.
Машина всегда может быть
представлена как сопротивление /%•
и последовательно включенный
источник с э. д. с. Э.
Рассматривая машину как гене-
ратор, следует считать э. д. с.
совпадающей по направлению с то-
ком (рис. 1-26). В этом случае че-
рез зажимы ab во внешнюю часть
цепи поступает мощность
Р = Uabi = — РГг. (1-46)
Рассматривая машину как дви-
гатель, ее э. д. с. следует считать
направленной навстречу току
(рис. 1-27,а). В этом случае через
узлы ab из внешней части цепи по-
ступает мощность
Р = ад = /Эдв + г^. (1-47)
Часть этой мощности (/Эдв) преоб-
разуется в механическую, часть
(^г) — в тепло в обмотке машины.
P=3i+i2\r0 (1-45)
частично расходуется на совершае-
мую электрическим двигателем ра-
боту (Рмех=Э1), а частично рассеи-
вается в тепло в сопротивлении
провода 12т0.
Электрические машины. В реаль-
ных электрических машинах движет-
ся целая система проводов, причем
поступательное движение заменено
вращательным. В машинах постоян-
ного тока, кроме того, производится
еще и периодическое переключение
(коммутация) на коллекторе, к ко-
торому присоединены движущиеся
3 к. М. Поливанов
33
Рис. 1-28.
} }3=~d$/dt
Двигатель в электрической
цепи может быть представлен по-
средством только сопротивлений
(рис. 1-27,6). При этом мощность,
рассеиваемая в эквивалентном со-
противлении гэ, должна быть равна
механической мощности двигателя:
Р=/Эдв=/%. (1-48)
Преобразование электрической
мощности в механическую в такой
эквивалентной схеме представляет-
ся как необратимое рассеяние.
1-12. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ
ИНДУКЦИИ
От рассмотренного случая воз-
никновения э. д. с. в движущемся
проводе можно прийти к самой об-
щей формулировке закона электро-
магнитной индукции: в контуре,
охватывающем изменяющийся маг-
нитный поток, наводится электро-
движущая сила, равная скорости
убывания магнитного потока Ф,
сцепленного с данным контуром:
3=—d^!dt. (1-49)
При этом предполагается, что
положительное направление э. д. с.
согласуется правоходовой системой
с положительным направлением
магнитного потока (рис. 1-28), т. е.
потока вектора магнитной индукции
Ф= jBdS. (1-50)
Эта формула полностью приме-
нима и для провода (рис. 1-24).
Из приведенной формулировки
отчетливо виден смысл измерения
потока Ф в вольт-секундах (в-сек),
а индукции В в вольт-секундах на
1 м2 (в • сек/м2).
В системе СИ этим единицам
присвоены следующие наименова-
ния:
1 в*сек=\ вебер (вб),
1 в- сек/м2=1 тесла (тл).
Полезно помнить, что 1 вебер=
= 108 максвеллов (мкс) и 1 тесла =
= 104 гаусс (гс), где максвелл и
гаусс — единицы магнитного потока
и магнитной индукции в симметрич-
ной системе СГС (система Гаусса).
ГЛАВА ВТОРАЯ
ЦЕПЬ ПОСТОЯННОГО ТОКА
2-1. ПРОСТЕЙШИЕ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Применение законов Ома, Кирх-
гофа и Джоуля — Ленца к простей-
шим цепям не представляет сколь-
ко-нибудь существенных трудностей.
Однако уменье найти распределе-
ние токов и потенциалов при после-
довательном и параллельном со-
единениях, а также при простых
параллельно-последовательных со-
единениях должно быть усвоено
настолько же хорошо, как, скажем,
таблица умножения или азбука.
В этой главе рассматриваются
цепи постоянного тока, т. е. цепи,
в которых ток, напряжение и э. д. с.
в пределах рассматриваемого вре-
мени остаются постоянными и обо-
значаются большими (прописными)
буквами.
Последовательное соединение»
При последовательном соединении
источника э. д. с. и двух сопротивле-
ний (рис. 2-1) по ним проходит оди-
наковый ток
/=Э/(п + г2). (2-1)
Мощность, выделяемая во вто-
ром сопротивлении,
92
= (2'2>
При ряде последовательно соеди-
ненных сопротивлений все они мо-
34
гут быть заменены одним эквива-
лентным:
^э=^1 + /*2+^3+ • • • (2-3)
Отношение между током I и общим
напряжением /7=3 при этом не из-
меняется.
Параллельное соединение. На-
пряжение на всех параллельных
ветвях одинаково. Если оно извест-
но, то для каждой ветви ток опре-
деляется по закону Ома:
(2-4)
где §П=1/Лг— проводимость вет-
ви п.
Общий ток (первый закон Кирх-
гофа) равен сумме токов всех вет-
вей:
1~Ц + /2+ ... = U(§1<+§2 + ...).
При параллельном соединении
все ветви можно заменить одной
эквивалентной с проводимостью
ga=gi'+g2+ • • • (2-5)
При этом связь между общим током
I и напряжением U окажется та-
кой же, как в исходной цепи:
I=Ug„ (2-6)
В случае двух параллельных вет-
вей (рис. 2-2)
I=U (§г4-§2)
или
(£1 + £2) *
Очевидно, что при этом
Мощность, выделяемая во второй
ветви,
Р2 = UI2 = U2g2= (g/+^ ^2-
(2-8)
Сравнивая цепи рис. 2-1 и 2-2,
можно сказать, что для таких цепей
Рис. 2-2.
во всех основных уравнениях со-
ответственно аналогичны Э, г, I и
Д §, <7.
Когда две ветви с сопротивле-
ниями Г1 = 1/§1 и г2=1/§2 заменяют-
ся одной эквивалентной >Гэ=1/§э,
то в случае параллельного соедине-
ния ветвей
г э
Г1Г2
+ Га’
(2-9)
а в случае последовательного со-
единения
Формулы (2-9) и (2-10) —прямое
следствие (2-3) и (2-5). Их полезно
запомнить.
Условие отбора максимальной
мощности. Для ряда технических
устройств ставится условие от-
бора максимальной мощности из
заданной цепи подключаемой к ней
ветвью. Эта мощность, конечно, за-
висит от сопротивления самой под-
ключаемой ветви.
В случае цепи рис. 2-1 зависи-
мость мощности, рассеиваемой в со-
противлении ,г2, от сопротивления
ветви выражается уравнением (2-2).
При Г2=0 (короткое замыкание,
когда t/2 = 0) и г2-»оо (холостой ход,
когда / = 0) Р2=0.
• При /*2=П мощность
Р2~ Р2 макс* (2-11)
Это легко найти обычными ме-
тодами (дифференцируя Р2 по г2. и
приравнивая производную нулю).
Получаемая при этом мощность
макс — Э2/(4г2) (2-112)
составляет половину мощности, от-
даваемой источником
Ри=Э/=Э2/(2г2). (2-13)
Соблюдение этого условия очень
важно в том случае, когда от источ-
ника поступает слабый сигнал и
желательно получить наибольшую
мощность в приемном устрой-
стве (г2).
Напротив, это условие не-
приемлемо для регулярной работы
устройств, предназначенных для
передачи энергии, так как половина
з*
35
Рис. 2-3.
энергии источника рассеивается, не
дойдя до потребителя, т. е. до вет-
ви г2 (к. п. д. передачи равен 50%).
В энергетических устройствах най-
денное соотношение важно с совсем
другой точки зрения. Когда в линии
произошло короткое замыкание,
цепь должна быть выключена. Ма-
ксимальная мощность выделяется
в выключателе, когда сопротивле-
ние между его контактами г2 ока-
жется равным Эта мощность мо-
жет быть чрезвычайно велика, по-
этому процесс выключения (разры-
ва цепи) должен заканчиваться
возможно быстро.
Аналогично, для цепи с источни-
ком заданного тока /=const (рис.
2-2) мощность, отбираемая -второй
ветвью (при gi = const), максималь-
на при
, g2=gi. (2-14)
Величина этой мощности
гмакс = —(2-15)
Цепь с двумя источниками э. д. с.
В неразветвленной цепи с двумя
последовательно включенными ис-
точниками (рис. 2-3) их э. д/с. ал-
гебраически складываются, а ток
в цепи находится делением этой
суммы э. д. с. на сумму всех сопро-
тивлений. Направление тока в та-
кой цепи совпадает с направлением
большей, из э. д. с. Для схемы
рис. 2-3
Г1 + Ъ + г3 ’
(246)
при этом />0, если Э\>Э2.
Если Гр—внутреннее сопротив-
ление первого источника, то напря-
жение на его выходных зажимах,
т. е. разность потенциалов между
точками а и с.
U ас— 1
(247)
(уравнение, предполагающее режим
генератора); при этом
/=(Э!-иас)/п. (248)
Пусть г2 — внутреннее сопротив-
ление второго источника; напряже-
ние на его выходе £ДС определяется
иначе, так как для него положи-
тельные направления тока и э. д. с.
противоположны:
Ubc— Э2 + 1г 2
(249)
(уравнение, предполагающее ре-
жим двигателя или заряжаемого
аккумулятора); при этом
/=(t7&c-32)/r2. (2-20)
Роль выбора положительных на-
правлений. Несмотря на простоту
формул типа (2-17)—42-20), выра-
жающих обобщенный закон Ома, их
применение в конкретных случаях
часто сопряжено с недоразумениями
-Рис. 2-4.
36
в выборе знаков. Это происходит
вследствие того, что положитель-
ные направления э. д. с. и тока мо-
гут совпадать, а могут быть направ-
лены и противоположно; кроме того,
напряжение между выходными за-
жимами, равное разности их потен-
циалов, также можно определять
по-разному:
U = U ас = фо—фс
или
/V=(7ca = (pc—фа* (2-21)
Для правильного выбора знаков
следует помнить, что: 1) ток в со-
противлении всегда направлен от
более высокого потенциала к более
низкому, т. е. потенциал падает по
направлению тока; 2) э. д. с., на-
правленная от точки с к точке а, по-
вышает потенциал последней на
величину Э; 3) напряжение JJ=Vac
положительно, когда потенциал точ-
ки а выше, чем потенциал точки с.
При обозначении напряжения
(разности потенциалов) на схемах
посредством стрелки она ставится
так, чтобы ее начало было
обращено к уменьшаемому, а ко-
нец (острие) — к вычитаемому
(см. рис. 2-3); L
Для -тренировки, очень полезно .написать
уравнения типа U=3+Ir и I=}(U—Э)/г
для шести случаев с различными сочетания-
ми выбранных .положительных направлений,
изображенных на рис. 2-4, правильно вы-
брав знаки перед всеми слагаемыми (отве-
ты приведены в конце параграфа).
Возможность путаницы со знаками воз-
растает еще из-за того, что любая из вели-
чин /, U, Э (а в некоторых случаях даже
я г) .может быть как положительной, так и
отрицательной.
Так, для уравнения (2-19), если, напри-
мер, t/=l/bC=84 в, а Э—'Э2=—16 в и г—
=г2=Ю ом, то /=10 а.
Эти затруднения совершенно подобны
затруднению при вычислении разности
3—(—2); тем не менее полезно найти токи
для случаев, показанных на рис. 2-4, при
следующих данных:
1)3=12 в, £7=15 в, г= 10 ом,
2) Э——4 в, U='—16 в, r=il0 ом,
3) Э=—4 в, £7=16 в, г=10 ом.
Ответы для схем рис. 2-4,а и е при этих
данных приведены в конце параграфа.
1 Иногда в литературе принимается
прямо противоположное правило для стрел-
ки, указывающей разность потенциалов, и
для порядка индексов в формулах типа
(2-21).
Потенциальная диаграмма. Для
правильного понимания того, как
изменяется потенциал вдоль элек-
трической цепи, полезно построить
график, на котором по одной оси
(по вертикали) откладываются зна-
чения потенциала, а по другой по-
следовательно располагаются точки
цепи, лежащие на выбранном кон-
туре. При этом расстояние между
точками целесообразно брать про-
порциональным сопротивлению вет-»
ви (если оно известно), соединяю-
щей соседние точки. Для цепи
рис. 2-3 при положительных значе-
ниях э. д. с. и тока и при Э\><Э2
распределение потенциала в цепи
изображено на рис. 2-5,а. Само со-
бой разумеется, что при обходе по
замкнутому контуру, т. е. вернув-
шись в исходную точку, мы должны
вернуться к прежнему значению
потенциала. Потенциальная диа-
грамма рис. 2-5 построена начиная
с точки с и закончена на точке с.
Потенциал этой точки произвольно
принят за начало отсчета.
На рис. 2-5,6 построена диаграм-
ма для той же цепи рис. 2-3 при
отрицательном значении э. д. с. Э2.
Простая последовательно-парал-
лельная цепь. Ненамного сложнее
37
расчет цепи рис. 2-6. Заменяя па-
раллельные ветви эквивалентным
сопротивлением
/'э=>/'2Гз/(г2+/'з), . (2-22)
Рис. 2-7.
находим общий ток
Л=-[7/(Г1+гэ) (2-23)
и напряжение на двух параллель-
ных ветвях
^2=Лгэ, (2-24)
после чего легко находим токи
^2—^2/г2» /з=*^2/гз- (2-25)
Подставляя в последние форму-
лы U2 из (2-24), а затем Л и r0
из (2-23) и (2-22), можно придать
выражениям для всех токов более
законченный вид:
К = Ц = иг^>, (2-26)
Л = 17(г2 + г3)/р,
где р — сумма всех различных пар-
ных произведений из сопротивлений
трех ветвей:
P = /'Z2,++ (2-27)
Найденный результат можно
формулировать словами: в простой
последовательно-параллельной цели
ток в одной из параллельных вет-
вей равен э. д. с. источника, умнэ-
женной на сопротивление другой
параллельной ветви и деленной
на р — на сумму всех различных
парных произведений трех сопро-
тивлений цепи.
Эта общая формулировка при-
годна для токов /2 и /3, а ток /1
равен их сумме.
Из формул (2-26) отчетлйво
видно и соотношение между токами:
Соотношения (2-26) — (2-28)
часто встречаются при расчетах
цепей. Их полезно запомнить и не
прибегать к повторному выводу.
Приведем несколько примеров
применения этих формул. Особое
внимание следует обратить на тре-
тий пример, приводящий к практи-
чески важному методу измерения.
Пример 2-1. Для измерения больших
токов параллельно амперметру включена
шунтирующая ветвь, сопротивление кото-
рой гш мало. Требуется найти сопротивле-
ние гш> если ток в амперметре должен быть
равен 5 а при токе в н ©разветвленной цепи
/=100 а. Сопротивление амперметра г=
=0,800 ом.
Р е ш е в и е. Пользуясь формулой
(2-28), легко находим, что
Г ттт
5 = ЮО -—। n -Q или = 0,0421 ом.
Г III T" 0,0
Пример 2-2. Требуется измерить сопро-
тивление проволочного реостата гх, поль-
зуясь показаниями вольтметра и ампермет-
ра (рис. 2-7).
Казалось бы, можно считать, основы-
ваясь на законе Ома, что
Гх— U vJIА-
Однако эта формула дает достаточно точ-
ный результат только при условии, что со-
противление вольтметра очень велико или
сопротивление амперметра очень мало (по
сравнению с гх); если же сопротивление ам-
перметра ненамного /меньше измеряемого
или сопротивление вольтметра ненамного
больше измеряемого, то в результате изме-
рения можно допустить существенную не-
точность.
Какую из схем включения приборов
(рис. 2-7) следует предпочесть в случаях:
1) г а=0,200 ом, = 1000 ом, гх=4 ом;
2) сопротивления амперметра и вольтметра
такие же, как в предыдущем случае, но
гх —400 ом; 3) гА = 1,00 ом, гv = 50,0 ом,
гх=(Ю,0 ом?
Предлагается самостоятельно найти
(для каких-либо из приведенных данных)
погрешность при разных схемах измерения:
где r'x=UvHA.
. Пример 2-3. Пользуясь формулами
(2-26) и законом Ома, требуется показать.
Рис. 2-6.
что независимо от величины сопротивлений
fv, г а. и .истинное значение гх выражает-
ся равенством
rx= UV<JI АЬ
оде UV2—показание вольтметра при втором
положении переключателя П .на рис. 2-8
I а\ — показание амперметра при первом
положении того же переключателя. Предпо-
лагается, что напряжение источника U—
='const.
Цепь с параллельно-последова-
тельными ветвями. Сложную элек-
трическую цепь нередко можно
представить в виде ряда последова-
тельно и параллельно соединенных
сопротивлений. Пусть, например,
несколько сосредоточенных нагру-
зок (гнЬ гн2, ...) присоединены
к одной линии, сопротивление от-
дельных участков которой глЬ
ГЛ2, • • • (рис. 2-9).
В случае двухпроводной линии,
когда весь ток, идущий по одному
проводу, возвращается по другому,
сопротивление любого из ее участ-
ков (например, .гЛ1) складывается
из сопротивлений прямого и обрат-
ного провода (скажем, и
Сл1/2) и может быть представлено
включенным в один провод. От та-
кой перестановки сопротивлений
полное падение потенциала на
участке линии не изменяется.
Рассматривая схему рис. 2-9,
легко увидеть, что ветвь с сопро-
тивлением Гн4+^л4 (последняя на-
грузка с последним отрезком ли-
нии) параллельна ветви с сопротив-
лением гнз (нагрузка на предпослед-
нем участке). Эти две ветви можно
заменить одной эквивалентной, ко-
торая оказывается включенной по-
следовательно с сопротивлением глз
(предпоследний участок линии).
Таким путем можно «свернуть»
всю цепь, приводя ее к простейшей.
Для такой цепи легко найти ток
источника (/л1). После этого мож-
но найти и напряжение на первой
нагрузке
= 3 W Л1,
затем ее ток
='Undrhi,
а затем ток во втором участке
линии
^л2 = ^л1 Лн1-
Продолжая, можно найти все токи
и напряжения в цепи.
Метод пропорциональных вели-
чин. Проведение расчета значительно
упрощается, когда он может бьиь
проведен в числах при заданном на-
пряжении вначале (£7=3) и при
заданных сопротивлениях всех вет-
вей.
В этом случае расчет следует
начинать с конца, произвольно за-
давшись током в последней нагруз-
ке, скажем,
IН4 = 1 а.
Вычислив напряжение в месте
присоединения предыдущей на-
грузки
^ДнЗ = ^н4 ('Гн4 + '^л4) ,
найдем ее ток:
^нз нЗ-
После этого вычисляем ток на пре-
дыдущем участке линии:
Лп:3 = Лнз + Лн4
и напряжение на ветви
U'pZ ~ t7ZH3 + У sitf лЗ-
Продолжая расчет по тому же
пути, найдем, наконец, напряжение
в начале U', соответствующее про-
извольно выбранному значению
тока в конце Гна-
Рж. 2-8.
Рис. 2-9.
39
a
Рис. 2-10.
На рис.’ 2-10 изображена цепь,
ветви которой соединены как в мо-
сте Уитстона. Среди всех ее шести
ветвей не существует ни параллель-
но, ни последовательно соединен-
ных.
Интересно показать, что к такой
схеме сводится цепь (рис. 2-11), со-
держащая два работающих двига-
теля (Э2, г2 и Э4, г4), питаемых по
кольцевой кабельной линии от од-
ного источника (Э6, г6).
Если на самом деле напряжение
в начале и=Э в tj раз больше, т. е.
UIU'^ (2-29)
то в действительности и все токи
в т] раз больше найденных при рас-
чете:
/н4=='П^,н4> ЛтЗ — Ц^нЗ, ••• (2-30)
Аналогично и для напряжений
^н4“Ц^н4, £/нЗ =/П^нЗ» ••• (2-31)
Сказанное следует из того, что
все напряжения и токи пропорцио-
нальны току в конце, как это видно
из приведенных расчетов.
Описанный метод называют м е-
годом пропорциональных
величин или методом по-
добия.
Сложные цепи. Далеко не во всех
цепях соединения ветвей могут быть
представлены как параллельные или
последовательные. К таким цепям
методы, изложенные в этом пара-
графе, уже неприменимы.
Для схем рис. 2-4:
а) и^'—Э+Ir; 1^(и+Э)/г;
б) и~Э+1г; 1=(и—Э)/г;
в) U—'9—Ir\ 1^(Э—и)1г\
г) U=^—(34-Zr); /==_<( tf+3)/г;
д) 11=.'—(Э4-/г); /=_Д£7+Э)/г;
е) и=Э+1г;
При цифровых данных 1), 2) и 3;
(стр. 37) для схем рис. 2-4,а и е токи
(в амперах) соответственно равны:
а) 23 \ —2; 1,2
е) 0,3; —1,2; 2,0.
2-2. ИСТОЧНИКИ ПИТАНИЯ
В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Простейшие источники питания.
В простейшем случае источник пи-
тания (источник энергии, генератор)
можно представить содержащим
или источник заданного на-
пряжения (или э. д. с. Э)
с последовательно включенным со-
противлением Гг, ИЛИ ИСТОЧНИК
заданного тока J с парал-
лельно включенной ветвью, обла-
дающей Проводимостью £г=1/.Гг
Оба типа источников показаны на
рис. 2-12,6? и б. На рис. 2-12,в пред-
ставлено общее обозначение источ-
ника как активного двухполюс-
ника Ч
Положительные направления
тока / и напряжения U на внешние
полюсах (зажимах) источника вы-
бирают так (рис. 2-12), чтобы их
произведение выражало мощность.
1 Двухполюсником называют цепь, об
ладающую двумя [внешними полюсами (уз-
лами или зажимами). Двухполюсник на'зы
вают активным, когда внутри него ;содер
жатся источники, способные Отдавать энеп
гию во внешнюю цепь.
40
отдаваемую источником во внеш-
нюю часть цепи:
P=UI. (2-32)
Эта мощность получается за
счет преобразования какой-либо
энергии, подводимой к источнику.
Отдаваемая во внешнюю часть
цепи мощность может быть отри-
цательной, если в цепи присутству-
ет другой источник питания, напри-
мер с большей э. д. с. При этом
внутри активного элемента может
происходить обратное преобразова-
ние поступающей извне электриче-
ской энергии (например, машина
работает двигателем, аккумулятор
заряжается).
Внешняя характеристика источ-
ников. При постоянстве параметров
источника (3 = const, J = const, r$ =
=const) их вольт-амперная ха-
рактеристика представляет
прямую линию:
U==A+IB, (2-33)
где А и В — постоянные коэффи-
циенты.
Действительно, для источника
первого типа
(2-34)
а для источника второго типа
I=J-Ugu (2-35)
где Ugi — ток, ответвляющийся че-
рез параллельную ветвь с проводи-
мостью gi. Остальная часть (/) все-
го тока источника J проходит во
внешнюю часть цепи (первый закон
Кирхгофа). Решая последнее ра-
венство относительно напряжения
U=Jn—Irt=А+В1, (2-36)
приходим к выражению, аналогич-
ному (2-33) и (2-34).
Внешняя хар ак-
г теристика источни-
*=* ка питания (так назы-
вают его вольт-ампер-
& ную характеристику)
полностью определяет
его свойства с точки
зрения внешней части
цепи.
Следовательно, два
источника можно счи-
тать эквивалентными
при тождественности их внешних
характеристик.
Эквивалентность двух типов
источников питания. Из уравнений
(2-33) — (2-36) очевидно, что два
типа источника эквивалентны при
r.:=l/gi, (2-37)
Поэтому любой линейный источ-
ник питания (активный двухполюс-
ник) всегда может быть представ-
лен или последовательно включен-
ными источником э. д. с. Э и сопро-
тивлением ir$, или параллельно
включенными источником тока / и
проводимостью gi.
Во многих расчетах оказывается
целесообразным заменять источник
одного типа эквивалентным ему
источником другого типа.
Идеальные источники. Полагая
в источнике первого типа г$ = 0, на-
ходим, что напряжение U на его
выходных полюсах не зависит от
нагрузки (от тока, т. е. от сопротив-
ления внешней цепи); его внешняя
характеристика выражается гори-
зонтальной прямой. Такой идеаль-
ный источник и называют источни-
ком заданного напряжения. В ре-*
альном генераторе при наличии вну-
треннего сопротивления к этому
условию можно приблизиться соот-
ветствующим регулированием его
э. д. с.
Полагая в источнике второго
типа gi = 0, находим, что ток /, про-
ходящий через внешние полюсы, не
зависит от нагрузки (от сопротивле-
ния внешней цепи, от напряжения);
его внешняя характеристика выра-
жается вертикальной прямой.
Такой идеальный источник назы-
вают источником заданного тока
или просто источником тока.
В реальных генераторах к этому
условию можно приблизиться соот-
4Ь
еетствующим регулированием от-
даваемого тока.
Важно заметить, что мощность,
которую можно получить от иде-
альных источников, ничем не огра-
ничивается. Поэтому такие источни-
ки часто называют источниками
бесконечной мощности.
Максимальная мощность, кото-
рую можно получить от источников
с внутренним сопротивлением г*,
равна U2x / (4гили /2 г*/4, где Ux—
напряжение холостого хода, /к —
ток короткого замыкания, как это
непосредственно следует из формул
(2-12) и (2-15).
Определение эквивалентных зна-
чений Э и по вольт-амперной
характеристике. У многих реальных
генёраторов внешняя характеристи-
ка приближается к линейной, хотя
часто и не на всем интервале токов
от нуля до короткого замыкания
(рис. 2-13).
Однако, если в условиях реаль-
ной работы генератора значение
токов лежит в пределах линейного
участка характеристики, то такой
генератор можно заменить эквива-
лентным линейным.
Запишем для линейного участка
характеристики уравнение
U=A+B1.
Из его сопоставления с уравне-
нием простейшего генератора
следует, что в пределах линейного
участка характеристики
А = Э и В== — г{. (2-38)
При этом очевидно, что постоян-
ное слагаемое А равно напряжению
холостого хода (когда 7=0):
А=}их = Э. (2-39)
Постоянный коэффициент В ра-
вен отношению А к току короткого
замыкания (когда t/=0), взятому
с обратным знаком, т. е.
В — ё/х//к— fy- (2-40)
Таким образом, из двух данных
опыта или расчета (холостого хода
и короткого замыкания) определя-
ются параметры эквивалентного
источника или константы вольт-ам-
перной характеристики А и В.
Так как определению подлежат
два неизвестных параметра—А и
В или Э и полностью характери-
зующие активный двухполюсник, то
всегда достаточно знать значения
U и I для каких-либо двух режи-
мов, скажем, U', Г и U", Г', при
двух значениях нагрузки. Эти два
режима могут и не совпадать с ре-
жимами короткого замыкания или
холостого хода. Более того, часто
именно эти два крайних режима
практически неосуществимы. Так,
в энергетических устройствах ток
короткого замыкания чрезвычайно
велик и может быть опасен для
целости установки (если он не будет
быстро отключен), а некоторые
цепи не могут нормально работать
при разомкнутой внешней ветви или
в них чрезмерно возрастает напря-
жение холостого хода. Кроме того,
часто именно вблизи этих крайних
точек (холостого хода и короткого
замыкания) реальная цепь теряет
свойства линейности (см. рис. 2-13,
а также ниже, пример 2-4).
Регулируемые источники. Как
уже говорилось, внешняя характе-
ристика генератора иногда опреде-
ляется специально предусмотрен-
ным регулированием тока или
э. д. с.
И в этом случае, если характери-
стика остается линейной, генератор
42
может быть представлен простей-
шей эквивалентной цепью.
Когда потребитель, скажем, лам-
пы электрического освещения, под-
ключается к генератору через линию
с заметным сопротивлением (гл),
в ней происходит заметное падение
напряжения (/гл)- Однако крайне
желательно, чтобы при увеличении
нагрузки напряжение на лампах
(U—1гл) по возможности не умень-
шалось, конечно, до тех пор, пока
нагрузка не превзойдет нормально
допустимую. Для этого нужно, что-
бы с ростом тока возрастала э. д. с.
Э генератора, как показано на
рис. 2-14; такая характеристика лег-
ко осуществляется в машинных ге-
нераторах (смешанное возбужде-
ние). Допустим, что э. д. с. генера-
тора линейно возрастает с током
Э=Д + К/. (2-41)
В этом случае внешняя характери-
стика генератора остается линей-
ной:
U= Э—lTi=А+В1, (2-42)
где В = К—-Гг>0, если К>гг.
Активный двухполюсник с такой
характеристикой можно представить
как последовательно соединенные
источник с постоянной э. д. с. Э=А
и отрицательнее сопротивление =
==—B=Ti—К. На самом деле, ра-
зумеется, внутреннее сопротивление
генератора положительно (гг->0).
Источники тока. В электротехни-
ческой практике встречаются источ-
ники питания, в которых тем или
иным способом поддерживается
определенная величина тока. На-
пример, характеристика источника
питания для подогрева катода элек-
тронных ламп имеет вид, представ-
ленный на рис. 2-13,6. В таком
источнике ток практически остается
постоянным: I=J, если напряжение
на его зажимах остается в преде-
лах Ui<U<U2. Такой источник
питания целесообразно представ-
лять (конечно, в пределах £/]<[/<
<С/2) как источник заданного тока.
В обычной электрической цепи,
когда путем урегулирования поддер-
живается определенное значение
тока, отдаваемого генератором,
соответствующий источник питания
можно также считать источником
тока.
Можно привести примеры и фи-
зических условий, приводящих к ре-
жиму цепи с источником тока. Са-
мым простым служит цепь с элек-
тронной лампой, в которой ток
ограничивается количеством элек-
тронов, испускаемых катодом за
1 сек (ток насыщения электронной
лампы).
Характеристику с резко падаю-
щим напряжением (рис. 2-13,/?)
стремятся получить при конструиро-
вании генераторов, часто работаю-
щих в режиме, близком к коротко-
му замыканию (сварочные генера-
торы). И в этом случае на отдель-
ных участках характеристику мож-
но представить прямой линией.
Во всех случаях при резко па-
дающей линейной характеристике,
т. е. когда ток мало изменяется при
больших изменениях напряжения,
целесообразно источник питания
представлять как источник тока J
с параллельно включенным сопро-
тивлением Гг- Внешняя характери-
стика такого источника линейна.
Пример 2-4. Источник питания, к за-
жимам которого а и b может подключаться
нагрузка /(рис. 2-15,а} содержит небольшое
сопротивление г=0,1 ом, включенное парал-
лельно /выходным зажимам, и генератор
с большим внутренним сопротивлением
J?r; э. д. с. генератора Эг регулируется экс-
периментатором так, чтобы отдаваемый им
ток J оставался неизменно равным 50 ма.
Таким способом этот генератор превраща-
ется в истопник заданного тока 7=50 ма,
к которому параллельно подключено сопро-
- тивление г.
Найти Э и гi эквивалентного генерато-
ра (рис. 2-15,6).
Решение. Из условия эквивалентной
замены источника тока /источником э.. д. с.
находим: &
3=Zr=5 мв, г^=г=0,1 ом.
Технический смысл описанного устрой-
ства состоит в том, что генератор с боль-
шим внутренним сопротивлением 7?г превра-
43
Рис. 2-15.
гцается в эквивалентный источник э. д. с.
с малым внутренним сопротивлением г<.
Пример 2-5. Источник питания содер-
жит устройство, -стабилизирующее ток.
Вольт-амперная характеристика источника
в широких пределах изменения напряжения
может считаться линейной. При двух режи-
мах работы цепи, лежащих в пределах ли-
нейности, найдены следующие значения то-
ка и напряжения источника:
7z=il0 ма, Z7,=il0 в и Г'~\\ ма, U"=5 в.
Требуется определить параметры двух
эквивалентных схем, которыми можно пред-
ставить данный источник.
Решение. Пользуясь уравнениями
линейной характеристики (2-34)—*(2-36) по
заданным координатам двух точек (10 в,
10 ма и 5 в, 14 ма) находим для первой
схемы 3=60 в, Гг=5 ком, а для второй схе-
мы /===12 ма, ri—Б ком.
Термоэлектронный генератор с прямым
преобразованием тепловой энергии в элек-
трическую. Рассмотрим, в заключение это-
го параграфа принцип работы источника,
в котором тепловая энергия непосредствен-
но превращается в электрическую. Он во
многом подобен известным преобразовате-
лям с термо-э. д. с., но отличается тем, что
в нем очень отчетливо видно действие сто-
ронних и Кулоновых сил на движущиеся
заряды.
Внешняя вольт-амперная характеристи-
ка обычной электронной вакуумной лампы
с накаленным катодом, т. е. зависимость
анодного тока от анодного напряжения'
(рис. 2-16), замечательна, между прочим,
тем, что она не проходит через начало ко-
ординат 0. Это значит, что в цепи электрон-
ной лампы проходит ток при равенстве ну-
лю напряжения между ее внешними полю-
сами (короткое замыкание, при котором
ка=0). Этот ток остается конечным (хотя
бы и очень малым) и при отрицательном
анодном напряжении (ма<0), противодей-
ствующему току. Ток обращается в нуль
только тогда, когда напряжение иа достиг-
нет значения — Uo. Последний режим полу-
чается, например, при размыкании внешней
цепи (холостой ход, z=0).
Конечно, электронные лампы не пред-
назначены для работы в режимах wa<0,
однако нас сейчас интересует именно уча-
сток характеристики— 170<«а<0, так как
при этом лампа работает как генератор, не-
посредственно преобразующий .тепловую
энергию в электрическую. Действительно,
замкнем лампу ветвью с сопротивлением г
(рис. 2-17,а); по нему пойдет ток, величину
которого легко определить из совместного
решения нелинейного уравнения, выражаю-
щего характеристику лампы,
wa =/•(/)
и уравнения внешней цепи (закон Ома)
wa=—
Графическое решение (точка пересече-
ния двух линий) представлено на рис. 2-17,6.
Очевидно, что при таком режиме во
внешней цепи выделяется мощность
p=z2r,
т. е. лампа работает как генератор.
Откуда же берется энергия? Все дело
в том, что электроны, покидая накаленный
катод, имеют начальную скорость vq, отлич-
ную от нуля и, следовательно, обладают ки-
нетической энергией Двигаясь к ано-
ду, они тормозятся силами Кулакова поля
dv
m — <?ЕК = — <?ЕК , (2-43>
где е — заряд электрона, m — его .масса.
'Пролетая в межэлектродном простран-
стве, они отдают электрическому полю энер-
гию, пропорциональную пройденной разно-
сти потенциалов.
Таким образом, силы инерции уравно-
вешивают силы Кулонова поля. По прин-
ципу Даламбера мы можем написать, что
dv
F = gEK — ш = 0. (2-44>
Но по определению напряженность по-
ля равна силе, действующей на заряд, де-
ленной на величину заряда; поэтому по-
следнее равенство можно представить в та-
ком виде:
Е = ЕК+ЕСТ = О, (2-45>
44
m dv
где второе слагаемое представ-
ляет собой стороннюю /напряженность поля,
обусловленную силами инерции.
Вычислим работу при перемещении за-
ряда по замкнутому контуру, работу, со-
вершаемую силами, действующими на за-
ряд, и отнесенную к единице заряда. Оче-
видно, что вычисление этой работы равно-
сильно вычислению интеграла от напряжен-
ности поля Ек4-Ест (т. е. от силы, действу-
ющей на заряд и деленной на величину за-
ряда) по тому же ‘контуру. Но этот инте-
грал равен нулю для 1межэлектрод1ного про-
странства [уравнения ’(2-43) и (2-44) спра-
ведливы для’ свободного движения заряда
в вакууме], а для внешней цепи интеграл
равен, по 'закону Ома, произведению ir. Та-
ким образом, мы определили э. д. с., дей-
ствующую в контуре,
3=ir
<и нашли ’ ее физическое происхождение:
электроны движутся против сил поля за
счет расходования своей кинетической
энергии.
Остается рассмотреть еще одно звено •
в процессе преобразования энергии. Когда
электроны испускаются накаленным като-
дом, т. е. когда его покидают наиболее бы-
стрые частицы, катод охлаждается; это яв-
ление подобно охлаждению жидкости при
испарении.
Коэффициент полезного действия ва-
куумной лампы, работающей как генера-
тор, очень мал; очень, мала и мощность, ко-
торую от нее можно получить. Однако ве-
личина к. п. д. и мощность могут быть зна-
чительно повышены 1 при заполнении лампы
разреженными инертными газами и при
специальном изготовлении электродов. На
рис. 2-18 приведена внешняя характеристи-
ка одного из таких генераторов. На участ-
ке m—п генератор может быть представлен
в виде источника, содержащего э. д. с. Э=
— 1,85 в и внутреннее, сопротивление г$ =
=0,63 ом.
1 При никель-бариево1М керамическом
катоде с температурой, близкой к 1 000° С,
при заполнении криптоном ю давлением
0,2 тор и при покрытии анода полупроводя-
щим слоем цезиевых соединений к. п. д. до-
стигает 8,6%, *а 1в отдельных экземплярах
изготовленных ламп даже 20%.
2-3. ПРИМЕНЕНИЕ ЗАКОНОВ
КИРХГОФА
Практически все методы расче-
та, цепей прямо или косвенно осно-
вываются на применении законов
Кирхгофа. Пользуясь ими, можно
найти распределение токов и потен-
циалов в сколь угодно сложной цепи
при достаточном числе исходных
данных. Например, можно найти
токи всех ветвей, если известны все
сопротивления и э. д. с. всех источ-
ников.
Применение законов Кирхгофа
очень важно для проверки правиль-
ности найденного распределения то-
ков и потенциалов (независимо от
того, как это распределение было
найдено — путем расчета или путем
измерений). Подчеркнем, что про-
верить, удовлетворяет ли предпола-
гаемое решение известной системе
уравнений, несравненно проще, чем
решить эту систему.
Однако едва ли не самое заме-
чательное из всего, что дают законы
Кирхгофа, заключается в возмож-
ности, отнюдь не решая систему
уравнений, установить некоторые
общие свойства линейных электри-
ческих цепей, обычно называемые
принципами (принцип суперпози-
ции, линейности).
Система уравнений Кирхгофа.
Рассмотрим сначала цепь, содержа-
щую только источники э. д. с. (на-
пряжения) . Пусть число ветвей дан-
ной цепи равно В, а число узлов,
служащих границами ветвей, рав-
но У. В таком случае число неза-
висимых уравнений, составляемых
по первому закону,
К1 = У—1, (2-46)’
т. е. на единицу меньше числа
узлов 1.
Эти уравнения будем называть
узловыми, так как каждое из них
составляется для токов, сходящихся
к одному из узлов; для узла
SZn=O. (2-47)
В эти уравнения входят токи с оди-
наковы^ знаком (перед буквенным
1 Доказательство выражений (2-46) и
(2-48) приведено в конце параграфа.
45
обозначением тока), если они оди-
наково ориентированы относительно
рассматриваемого узла. Противопо-
ложно ориентированные токи берут-
ся с противоположным знаком.
Узловое уравнение для послед-
него узла оказывается всегда пря-
мым следствием остальных (У—1)
уравнений.
По второму закону Кирхгофа
можно составить еще К2 независи-
мых уравнений: 9
К2=В—К^В + 1—У. (2-48)
Эти уравнения составляются для
замкнутых контуров
=• S/nrn, (2-49)
(для контура) (для контура)
поэтому будем их называть кон-
турными.
В контурные уравнения с одина-
ковым знаком перед буквенными
обозначениями Эп и 1п входят э. д. с.
и токи, одинаково ориентированные
относительно произвольно выбран-
ного направления обхода по кон-
туру.
Независимость контурных урав-
нений очевидна, если в каждый
контур входит по крайней мере одна
новая ветвь, не входившая в осталь-
ные контуры1.
Полная система независимых
уравнений равна числу ветвей В,
Таким образом, если для всех
ветвей известны сопротивления и
э. д. с., то из системы уравнений
можно найти В неизвестных токов
всех В ветвей.
Решение системы уравнений воз-
можно и в том случае, когда те или
иные э. д. с. (или сопротивления)
неизвестны. При этом, однако, необ-
ходимо, чтобы были заданы токи
некоторых ветвей, так как общее
число неизвестных не должно пре-
восходить В.
Пример 2-6. На рис. 2-19 представлена
цепь, содержащая четыре узла и шесть вет-
вей. Требуется составить систему уравне-
ний Кирхгофа.
Решение. Для этой цепи по первому
1 Это условие всегда достаточно^ но не
необходимо.
Р*ис. 2-19.
закону Кирхгофа .можно составить
= У—1=3 независимых узловых уравнения:
Ц—Ц—Is=0 (узел А);
Л—h—(узел Б);
^з+Д—Л=0 (узел Д).
Легко убедиться, что уравнение для четвер-
того узла (Г) —следствие первых трех.
'По второму закону Кирхгофа необходи-
мо составить К2=В + 1—4=3 независимых
контурных уравнения. Например, для кон-
туров, указанных на рис. 2-19:
•^6 = Лг6 + ЛГ1 + 12Г2'\
‘^6 = ^6гб + Дгз + Лг4‘,
5-----------1зг3-
Решение системы уравнений
Кирхгофа для цепи с источниками
э. д. с. Для цепи, содержащей толь-
ко источники э. д. с., решение си-
стемы уравнений относительно то-
ков всегда имеет такой вид:
Л := Ч~ *^2^12 Ч- *5з^1з 4“ • • •>
Л *^1^21 4“ 32g22 Ч~ Э3£23 ~|- . •
Л =Z ^1§31 ^2^32 Ч~ ^зёзз Ч" • • •’
(2-50)
где все коэффициенты gkp не зави-
сят от токов, если цепь линейна,
т. е. если не зависят от токов сопро-
тивления всех ветвей цепи, входя-
щие в контурные уравнения множи-
телями при токах.
Система уравнений цепи, содер-
жащей источники тока. В этом слу-
чае число независимых ,узловых и
контурных уравнений определяется
прежними выражениями (2-46) и
(2-48), однако в последнем выра-
жении в число ветвей В не должны
46
Рис. 2-20.
входить ветви, содержащие источ-
ники тока. Эти ветви не должны
входить и в контурные уравнения.
Пример 2-7. Составить систему урав-
нений для цепи «рис. 2-20.
Решение. Цепь содержит пять не-
известных токов и пять ветвей (не считая
ветвь с источником тока). Для нее можно
составить три узловых уравнения (число уз-
лов равно четырем) и два контурных:
A+Zs=J
Z i-15 12 = 0
Z3+Z5—Ц=0
(узел А);
(узел 5);
(узел В);
Z^ 1 + Z2^2—^4r4—Ar3 = 0;
ZjiTj -р Zgf5-13Г3 = 0.
Решение системы уравнений цепи,
содержащей источники э. д. с. и
тока. В самом общем случае, когда
цепь содержит как источники тока,
так и источники э. д. с., решение
системы уравнений относительно
токов ветвей (не содержащих источ-
ников тока) всегда имеет вид:
/ г =э^1± 4~ 32g 12 +... +
И- 4“ •Zm^iTn 4" • • * ’ «
Л = *5^21 4~ ^2^22 4^ • • -4“
4- 1^21 + ЛтЛ 2 -т 4- • • * ’
..........................)
(2-51)
где все коэффициенты gkp и hkn не
зависят от токов и напряжений.
Пример 2-8. При питании потребителя
с сопротивлением Гз=2 ом от двух источни-
ков питания Э1 и Э2 регулируется э. д. с.
так, что ток первого источника Ц под-
держивается постоянным и равным 2а
(рис. 2-21). При этом первый источник дол-
жен рассматриваться как источник тока
Zi=Zi = 2 а. Э. д. с. второго источника
Э2—10 в, сопротивления: /т=3 ом, г2=4 ом.
Требуется найти токи Z2 и Z3.
Рис. 2-21.
Решение. По первому закону Кирх-
гофа можно составить только одно уравне-
ние (У—il = l):
Л—h—h- (а)
По второму закону также можно соста-
вить только одно уравнение (К2=В+1—
—У=.1):
=Z2r2+Z3r3. (б )
Подставляя ток 73 из’ (а) в (б) и решая от-
носительно тока Z2, получаем:
Z2 = S2_g~’ — <Z 1 “д' = 1 а. (в)
Подставляя найденное Z2 в (а), нахо-
дим, что
1 2
/3 = Z2 + Ji = Э2 "б- + /1 ~з“ = 3zz. (г)
Сопоставляя последние два уравнения
с (2-51), находим коэффициенты: ^22=
= 7б CUM, Л21 = — !/з, £32=7б сим,
Число независимых узловых уравнений
[доказательство равенства (2-46)].
Пусть например, цепь содержит четы-
ре узла, каждый из которых соединен
с каждым другим одной ветвью (рис. 2-22,а).
Уравнения для этих узлов имеют вид:
Zi2+Zi3+Zi4=0;
Z2i+Z234-Z24=0;
^31+^32+^34=0;
Z4i+Z42+Z4s=0,
где Imn — ток ветви, соединяющей узлы m
и п, направленный от узла m к узлу п.
Взяв сумму первых трех уравнений и
замечая, что
/12+^21=0, Zi3+/31=0, . . . ,
Рис.
2-22.
47
зайдем, что сумма
^14+^24+^34=0
содержит токи, сходящиеся к четвертому
узлу. Эта сумма отличается только знаком
всех слагающих от уравнения для послед-
него узла, которое, таким образом, оказы-
вается следствием всех предыдущих.
Независимость первых трех уравнений
очевидна, так как в каждое из них входит
ио крайней мере один новый ток (ток /т4
ветви, соединяющий данный узел т с по-
следним) .
Если бы .между двумя узлами, напри-
мер 1 и 2, содержалось несколько ветвей
с токами /z,i2, . . . , то соответственно
в оба первые уравнения вошли бы /'12+
+^,,12+ . • • и /'21+/,,2’1 + . • . и ход дока-
зательства не изменился бы, так как
/,12 + ^/21 = 0, • • •
Проведенное доказательство легко рас-
пространить и на цепь, содержащую любое
число узлов У=п.
Число независимых контурных уравне-
ний [доказательство равенства (2-48)]. В лю-
бой цепи, имеющей У узлов, можно выде-
лить такие ветви, что они соединят между
собой все узлы, не образуя ни одного за-
мкнутого контура. Проще всего это сделать,
соединяя одной ветвью узлы 1 и 2, затем
другой ветвью узлы 2 и 5, затем 3 и 4
’и т. д. до последнего узла п=У. Такое со-
единение показано на рис. 2-22,6 для ранее
рассмотренной цепи с четырьмя узлами.
Очевидно, что таких ветвей окажется
всегда на 1 меньше числа узлов. Все эти
ветви включены последовательно, и цепь не
замкнута, поскольку мы остановились на
последнем узле, не соединив- его с первым.
Так как все узлы соединены между собой,
то присоединение любой новой ветви уже
приведет к образованию контура. Ветви, ко-
торые можно включить, не создавая конту-
ров, называют ветвями дерева, а образо-
ванную ими структуру называют дере-
вом.
По самому определению, всякая новая
ветвь, добавленная к дереву, уже образует
контур (иначе такая ветвь принадлежала
бы к числу ветвей дерева). Такие замыкаю-
щие ветви называют мостами. Ветви-мосты
на рис. 2-22,6 показаны пунктиром
Число ветвей-мостов М равно разности
между числом всех ветвей В и числом вет-
вей, вошедших в дерево (У—1):
М=В— (У— 1).
Для каждого контура, образованного
после присоединения одной ветви моста,
можно составить уравнение по второму за-
1 Заметим, что, добавляя к дереву один
моют, можно разорвать образовавшийся
контур, выбросив одну ветвь ранее постро-
енного дерева. Получится новое дерево, т. е.
цепь без замкнутых контуров. Однако чис-
ло ветвей любого нового дерева останется
прежним, так как после каждого присоеди-
нения одной ветви моста нужно выбрасы-
вать именно одну ветвь дерева.
кону Кирхгофа. При этом каждое из таких
уравнений безусловно независимо от дру-
гих:, поскольку в каждое из них входит но-
вое неизвестное — ток в ветви, добавление
которой образует замкнутый контур.
•Следовательно, число независимых кон-
турных уравнений равно М, т. е. именно
В—|(У—1)-, что и требовалось доказать.
Контуры, для которых составляются
уравнения Кирхгофа, могут отличаться от
простейших контуров, содержащих только
один мост. Это очевидно хотя бы из того,
что, складывая два независимых уравнения
между собой, получаем новое уравнение,
которое в сочетании или с первым, или со
вторым также образует два независимых
уравнения. Конечно, общее число независи-
мых уравнений остается прежним.
П р и м е ч а н -и е. Неразветвленную
цепь следует рассматривать как цепь, со-
держащую одну ветвь v(B=--l), у которой
два ограничивающих ее узла сливаются в
один -(У='1). При этом и. к такой цепи* при-
менимы приведенные формулировки^ К\ =
= У— и К2=В+1—У=-1.
Действительно, для такой цепи можно
составить только одно контурное уравне-
ние.
Заметим еще, что сказанное полностью
соответствует такому определению: узлом
называют каждую из двух гра-
ниц ветви; при этом один и тот
же узел может служить грани-
цей нескольких ветвей.
О независимых уравнениях при нали-
чии источников тока. Присоединение источ-
ника тока к электрической цепи можно рас-
у сматривать как добавление новой ветви, ток
которой, однако, известен: 1=1. Определе-
нию подлежат токи остальных В ветвей
(в число которых не входят ветви с источ-
никами тока). Для цепи, образованной эти-
ми В ветвями, сохраняет силу доказатель-
ство о числе независимых контурных урав-
нений.
Что касается числа, независимых узло-
вых уравнений, то приведенный вывод пол-
ностью применим и к тому случаю, когда
среди рассматриваемых токов, притекаю-
щих к узлу, содержатся токи источников
тока.
Конечно, наличие источников тока пря-
мо изменяет узловые уравнения, а косвен-
но влияет и на контурные, поскольку под
действием источников тока изменяются и
токи ветвей.
2-4. ПРИНЦИП СУПЕРПОЗИЦИИ
(НАЛОЖЕНИЯ)
Названный принцип супер-
позиции, или наложения, непосред-
ственно следует из решения системы
уравнений Кирхгофа: ток в любой
ветви равен сумме токов, обуслов-
ленных в отдельности каждым ис-
точником, действующим в отсутст-
вие остальных.
48
гЭтот принцип называют также3
п р и нципом неза в и с им о г о
д.е й-с т в и я.
Действительно, решение системы
уравнений Кирхгофа . для - линейной
цепи, содержащей только источники
э. д. с., имеет вид [см. (2-50)]:
Л — ^1^11 + + *93^ia-j- • • •;
/2--- ^1^21 4“ ^2§22 “F" *^3^23 “F * * ’ ’
3 *^1^31 ~Ь *5'2^32 “Г —1~ • • • ,
(2-52)
где все коэффициенты gkp не зави-
сят от токов. Поэтому ток в любой
ветви можно представить как сум-
му токов, протекающих в ней под
действием только одного первого
источника, затем только одного
второго источника и т. д.:
/'2=5ig21, (2-53)
^1=*Э2§'12, I"2==92g22, ...
Действительные токи равны сумме
всех найденных слагаемых:
/1=Л+/,,1 + ..., (2-54)
/2 —1'2 + ^/?2 + • • •
Рис. 2-23.
Сопоставляя решение с уравнениями
(2-52) можем записать, что
4 3
gsi — сим и ^32— 20 сим»
При действии только одного из
источников, э. д. с. всех остальных
источников предполагается равной
нулю. Идеальные источники э. д. с.
при этом просто заменяются корот-
ким замыканием между точками их
включения. Однако, если источники
питания содержат внутренние со-
противления, эти сопротивления
должны оставаться включенными
в цепь.
Пример 2-9. Найти ток /3 в цепи рис.
2-23,а .при г 1='3 ом, г2=4 ом, г3=2 ом как
сумму тока /'3 при действии^ одного источ-
ника 3j = 12 в (при этом Э2=0) и тока /"3
при действии одного второго источника Э2—
= 10 в (при этом 31=0).
Решение. Рассчитывая ток для каж-
дого из двух режимов (рис. 2-23,6 и в) по
формуле для простой последовательно-па-
раллельной цепи (2-26), находим:
4 3
Zj = /'3 -р /"3 = 31 pg -г-Э2 2g = Зя. (а)
Точно так же можно определить и ток
11 как сумму токов 1'1 и Г\ (обратить вни-
мание на знаки!):
р _ Э А р, _ Э А
1 1 — 1 26 ’ 1 1---“Аб ‘
Действительный ток
Л=Л+/,,1=2 а. (б)
Заметим в заключение, что обычно в
энергетической системе и и г2 (сопротивле-
ния проводов линии и самих источников),
как правило, много меньше, чем сопротив-
ление нагрузки г3. Поэтому, производя вы-
числения по формуле (б), мы встретимся
с разностью двух больших чисел, подсчи-
танных приближенно. А это может привести
к существенным неточностям.
В .этом случае, прежде чем вычислять
отдельные слагаемые в (б), необходимо за-
кончить все алгебраические преобразования.
Принцип суперпозиции можно
применять и в более общей форме,
полагая для первого режима одни
значения всех э. д. с. Э\, Э\, ...,
4 К- М. Поливанов
49
а для другого — другие Э'\, Э"2,...
Если цри этом 9'i+9'\=9p, Э'2+
+Э"2^Э2, ..., то действительные
токи
Л = /,1+/,,1, /2==^72 + ^Г,,2, • • •>
где штрихами (') и (") обозначены
токи этих двух режимов.
Обобщение понятия проводимо-
сти. Коэффициенты при э. д. с.
в уравнениях (2-52) имеют размер-
ность проводимости. Коэффициенты
с одинаковыми индексами (£ц, g22)
носят название собственных
или входных проводимостей.
Их физический смысл очевиден, они
численно равны току ветви при дей-
ствии единственной э. д. с. в 1 в,
включенной в эту самую ветвь
(рис. 2-24).
Рис. 2-24.
Обратную величину входной
проводимости называют входным
сопротивлением ветви
Пвх= 1/£и- (2-55)
Для неразветвленной цепи вход-
ная проводимость (сопротивление)
совпадает с элементарным понятием
проводимости (сопротивления).
Коэффициенты с разными индек-
сами (gi2, £1з, £21 .. •) называют
передаточными (или относи-
тельными, или взаимными) про-
водимостями. Их физический смысл
также легко понять: передаточная
проводимость ветви 1 относительно
ветви 2 (т. е. £21) равна току в вет-
ви 2 при действии единственной
э. д. с. 31 = 1 в. Для пояснения обоб-
щенного понятия проводимости на
рис. 2-24 показаны две ветви любой
сложной цепи, содержащей единст-
венную э. д. с. 31.
Из приведенного определения ко-
эффициентов gmn в сочетании
с принципом суперпозиции возмож-
но и такое их определение: возра-
стание тока в ветви 2 (или 1) при
возрастании э. д. с. Зх в ветви 1 рав-
но проводимости £21 (или £цД ум-
ноженной на приращение э. д. с. Зь
Сказанное равносильно и тако-
му определению:
дЭх S21’ d3i sii, •••,
J^=gmn, (2-56>
вытекающему из основных уравне-
ний (2-52).
Суперпозиция источников тока.
Если цепь содержит, кроме источни-
ков э. д. с. (3^), также источники
тока (Jz), решение системы урав-
нений Кирхгофа имеет вид:
I 1 ^1ё и + ^£12 + • • • +
^Jbhcb-\~ • * ’ ’
Л = *51£21 + ‘Э2£22 + • • • +
| *^cJ^2CL + J~|~“ • • • ,
1
. (2-57)
I
В линейной системе коэффици-
енты Ли, hxb также не зависят от
токов. Поэтому из системы (2-57)
непосредственно следует принцип
суперпозиции для источников тока.
Положим для простоты, что в цепи
существуют только источники тока
(суперпозиция источников э. д. с.
уже рассматривалась), и что систе-
ма уравнений имеет вид:
Д — ДЛю ДЛ1& Д-• • •; 1
/2 =- Jahza -ф- -ф...; / (2-58)
Из последней системы видно, что
ток в любой ветви равен сумме то-
ков, протекающих в этой ветви под
действием только одного первого
источника, затем только одного вто-
рого источника и т. д.:
I 1 — Jafilay I 2 — $а^2а, • • •,
Z''i=‘Mi&, r'2=-hh2b. ... (2-59)
Действительные токи равны:
71 = /,1+/,,1+ ...,
/2=/,2+/,,2+ ... (2-60)
При действии только одного из
источников ток всех остальных
50
предполагается равным нулю. От-
сутствие тока в ветви источника
равносильно разрыву этой ветви.
Коэффициенты hmn имеют раз-
мерность отвлеченного числа и на-
зываются передаточными ко-
эффициентами.
2-5. ПРИНЦИП КОМПЕНСАЦИИ
В любой электрической цепи
ветвь (или часть ветви) с током Iv
и сопротивлением гъ можно заме-
нить источником с встречной э. д. с.
(рис, 2-25):
В -у—1 -у/* X)-
(2-61)
При такой замене распределение то-
ков во всей цепи остается прежним.
Действительно, влияние выде-
ленной ветви rv на всю остальную
цепь определяется только разностью
потенциалов между ее концами:
U ab~ = 9V. (2-62)
Сказанное непосредственно сле-
дует из уравнений Кирхгофа. Выде-
лим слагаемое Ivrv в уравнениях, со-
ставленных для контуров, проходя-
щих через эту ветвь,
S3 = 2Zr+Vv (2-63)
и перенесем это слагаемое в левую
часть:
2Э—Izrv=^Ir.
Из последнего уравнения ясно,
что слагаемое Ivrv можно рассма-
тривать как э. д. с. и записывать со-
ответствующие контурные уравне-
ния в такой форме:
S3—9v=?Jr. (2-64)
В правой части этих уравнений,
т. е. в сумме произведений /г, уже
не содержится сопротивления rv.
При такой замене все параметры
остальной части цепи не изменились,
также не изменилась и запись узло-
вых уравнений. А это значит, что си-
стема уравнений Кирхгофа после за-
мены (.2-63) на (2-64) эквивалентна
прежней. Ее решение приводит
к прежним значениям токов, хотя
они теперь и выражаются иначе:
• • • + ।
Jah ia + b^ib + • • • + |
12 = *5^21 + ^2g22 + .... + I
~\~JahZa 4" Jbh^b 4“ ’ * ‘ |
I'D = *51^1 + d2gV2 4“ |
Jahva 4~ Ibhvb 4-... 4“ 9vgvv. j
(2-65)
Среди других токов ветвей
в найденном решении содержится
и ток Iv,
Необходимо обратить внимание
на то, что все коэффициенты и
h^h в этих выражениях определяют-
ся конфигурацией цепи и сопротив-
лениями всех ветвей, и что сопро-
тивление rv принимается равным ну-
лю—оно отсутствует в правой час-
ти уравнений (2-64), входя в скры-
том виде в значение э. д. с. 9V.
В любой электрической цепи
ветвь с током Iv можно заменить ис-
точником тока (рис. 2-26):
I1v* (2-оо)
При такой замене распределение
токов во всей цепи остается преж-
ним, что опять же следует из систе-
мы уравнений Кирхгофа.
Действительно, узловые уравне-
ния сохраняют прежний вид, с той
только разницей, что для узлов, со-
единенных с ветвью v, слагаемое Ц
рассматривается как заданный ток
источника Jv Контурные уравнения
теперь составляются иначе. В них
уже не входит ветв ь и (а следо-
вательно, и сопротивление этой
ветви rv). Они составляются для
цепи, в которой ветвь с как бы ра-
зомкнута. Однако число контурных
уравнений остается достаточным,
^тобы совместно с узловыми урав-
Рис. 2-25.
Рис, 2-25.
51
нениями образовать систему, одно-
значно определяющую токи всех ос-
тальных ветвей.
Решение этой системы приводит
к прежним значениям токов осталь-
ных ветвей, хотя они теперь и вы-
ражаются иначе:
Ц ?— 4~ 12 + • • • + I
4~ 4“ ЛА& 4~ • • • 4~ |
/2 — А&214” Э2§22-\- • • •+ }
+ jа^2а ~\~ Ъ^2Ь 4“ • • • 4~ |
I
' (2-67)
Как ясно из самого составления
уравнений Кирхгофа, значения коэф-
фициентов gmn и hki не зависят от
сопротивления ветви v; они соответ-
ствуют цепи с разомкнутой ветвью
v, т. е. цепи, в которой rv = oo.
Возможность замены любой вет-
ви электрической цепи источником
э. д. с. или тока называют принци-
пом компенсации.
Такое название объясняется возмож-
ностью -следующей формулировки.
Изменение сопротивления -ветви v от
значения rv до нуля (короткое замыкание)
компенсируется источником встречной
э. д. с. изменение сопротивления
ветви v от rv до бесконечности (разрыв вет-
ви). компенсируется источником тока Jv —
=Д. Слово «компенсируется» обозначает,
что при этом все токи и напряжения в це-
пи остаются прежними..
Следует обратить внимание на то, что
в случае изменения параметров цепи, приво-
дящем к изменению тока Iv и напряжения
Ivrv, изменяются также ток или э. Д; с..
эквивалентного источника.
Сопоставляя выражения для тока Z3
в примерах 2-8 и 2-9, полезно убедиться
в различии коэффициента при Э2 до и пос-
ле замены Ц эквивалентным током источ-
ника (уравнение г примера 2-8 и уравнение
а примера 2-9).
2-6. ПРИНЦИП ЛИНЕЙНОСТИ
Если в электрической цепи оста-
ются неизменными э. д. с. всех ис-
точников и сопротивления всех вет-
вей, кроме параметров одной ветви
v, то на основании изложенного
в предыдущем параграфе изменение
всех токов определяется только из-
менением эквивалентной э. д. с. Эъ:
А *^1^и 4~~ *^2^12 4“ • • • 4~ ।
Л = 3^214- s2g22 4~ • • • ~Ь 3vg2V\ «
V--^igvi "Т” 32gv2 4- . . . *7“ dvgw J
(2-68)
В этой системе все коэффициен-
ты gmn остаются постоянными так
же как и значения всех э. д. с, кро-
ме э. д. с., 9V. Поэтому уравнения
(2-68) можно записать в такой
форме:
А = сьг + giv9Vi
I2 = cl2 4- g2rd^-> ► (2-69)
7 v — 4~
где все коэффициенты amt gmv по-
стоянны.
Исключая из уравнений (2-69) пе-
ременную 3V, найдем, что
А ---&1V 4” ^IvAj
А ---~ | ^2V^Vi
а также
Л “ ^12+^12^2.
} (2-70)
(2-71)
Последние уравнения показыва-
ют, что изменение всех токов связа-
но между собой простыми линейны-
ми уравнениями, если это измене-
ние токов вызвано изменением па-
раметров (сопротивления или
э. д. с.) только одной ветви (v) рас-
сматриваемой цепи.
Уравнения (2-69) позволяют
формулировать тот же принцип ли-
нейности и для любых напряжений,
например,
Uac=l+fnlv. (2-72)
Действительно, рассматривая
ветви, связывающие между собой
какие-либо узлы, скажем, а и с на
схеме рис. 2-27, найдем:
^ас = А^б + А^7-
Но каждый из токов (в том числе
и токи A, h) можно представить
формулой (2-70), откуда при посто-
янных Гб и П получается формула
(2-72).
Выразив по той же формуле
(2-70) какие-либо два напряжения,
1 В том числе и коэффициенты, содер-
жащие индекс v.
62
например Ui и Um, из этих двух
уравнений можно исключить пере-
менное Iv и найти зависимость меж-
ду двумя напряжениями, которая
опять же оказывается линейной:
Ui=s+tUm, (2-73)
Принцип линейности имеет ис-
ключительное значение для анализа
и расчета электрических цепей. Осо-
Рис. 2-27.
бенно важно подчеркнуть тот факт,
что все коэффициенты в уравнениях
линейной зависимости могут быть
определены как из расчета, так и из
опыта. Для этого достаточно знать
значения соответствующих перемен-
ных (/ или U) для каких-либо двух
режимов цепи. Часто наиболее удоб-
ными оказываются режимы холо-
стого хода (7^=0) и короткого за-
мыкания (СД=О).
Значения токов 1т и напряжений
Ui для этих двух режимов принято
обозначать, добавляя индекс «х»
(холостой ход) или «к» (короткое
замыкание).
Пример 2-10. При включении двигате-
ля в одном из цехо-в завода 1пока'зание
вольтметра на (распределительном щите па-
дает с 550 до 490 в (пока двигатель непо-
движен). При нормальной работе двигате-
ля ток, потребляемый им, составляет 140 а,
а напряжение, показываемое вольтметром,
540 в.
Требуется определить ток, потребляе-
мый двигателем при его запуске.
Решение. Задачу решим, пользуясь
уравнением
1=1+mU,
Из решения этих уравнений находим,
что 1=7 700 и т=—14.
Поэтому искомый ток при запуске дви-
гателя
7=7 700—<14-490=840 а.
Пример 2-11. Сигнал поступает к при-
емнику от источника напряжения через ка-
кую-то сложную линейную цепь (линия свя-
зи, боковые ответвления, утечка через изо-
ляцию и т. л.), все параметры которой, оста-
ются постоянными. На рис. 2-28 источник
сигнала изображен как источник э. д. с. Эс,
вся -передающая цепь представлена прямо-
угольником, приемник показан ветвью с со-
противлением rv.
Рис. 2-28.
Из опытов найдено, что при холостом
ходе (rv = oo, 7„=0) напряжение между точ-
ками присоединения приемника Г/г)Х=1,5 в.
При коротком замыкании (г«=0, П«=,0)
ток в ветви приемника 7^к=25 ма.
Требуется найти сопротивление прием-
ника rv, при котором получаемая им мощ*
ность .максимальна.
Р е ш е н -и е. По уравнению линейной
цепи
Uv='a+blv
и двум опытным данным находим [7vx=a=
=4,5 в и 0=1,54-7» 0,025. откуда Ь =—60 ом.
Мощность в приемнике
7\ ='UVIV=alv 4- bPv.
Максимум Pv определим, приравнивая
нулю производную
д Р
= ct -}~ 2Z»7V = 0.
Для этого условия:
7v=—a/(26) =0,0125 а\
а 1
Uv = cl — b ------2" а = 0,75 в.
Искомое сопротивление
гd = 'UvJIv = 60 ом.
При таком сопротивлении мощность
Pv~Pv макс = 9,4 МвТ.
Заметим, что уравнение линейности не
противоречит уравнению, связывающему
Uv и Iv по закону Ома:
где 7 — ток двигателя, a U— показание
вольтметра. Значения коэффициентов I и т
определим по данным для двух режимов:
0=Z4-m550;
140=Z4-m540.
U v — I vC v-
Однако из последнего уравнения нельзя
найти ни ток короткого замыкания 0=
=7ГК • 0, ни напряжение холостого хода
Пг?х=0-оо, ни тем более решить поставлен-
ную задачу.
53
2-7. ЭКВИВАЛЕНТНЫЕ
источники.
АКТИВНЫЙ ДВУХПОЛЮСНИК
Уравнение линейной зависимости
применимо и в том случае, когда
рассматриваются ток I и напряже-
ние U той самой единственной вет-
ви, в которой изменяется сопротив-
ление:
U=A + BI или I=K+NU. (2-74)
Эта ветвь с сопротивлением rv=r
показана на рис. 2-29,а; все источни-
ки и остальные ветви, имеющие по-
стоянные параметры, заключены
внутри прямоугольника А.
Очевидно, что (2-74) выражают
внешнюю характеристику линейного
активного двухполюсника
(А на рис. 2-29,а). Она не отличает-
ся от характеристики простейших
линейных источников, изображен-
ных на рис. 2-29,6 и в и подробно
рассмотренных в § 2-2.
Зная параметры А и В (или К
и N) линейной характеристики
(2-74), легко определить параметры
простейшего генератора (г$ и Э или
/), имеющего тождественную харак-
теристику:
П=— В = —1/7V, Э = их=А,
(2-75)
Такой генератор эквивалентен
цепи, рассматриваемой в качестве
активного двухполюсника, и, следо-
вательно, зависимость тока нагруз-
ки I от сопротивления внешней вет-
ви г выражается простой формулой
(рис. 2-29,6) :
Аналогичной формулой выража-
ется напряжение на выходе в зави-
симости от проводимости внешней
ветви g=A!r (рис. 2-29,в):
/к К
ё + ёг ё — М'
(2-77)
Полагая в (2-76) г=0, найдем
ток короткого замыкания
1^их/ц. (2-78)
Аналогично, полагая в (2-77)
Я=0, найдем напряжение холостого
хода
U^I^Igi. (2-79)
Каждая из этих формул приво-
дит к тому, что
ri^lgi=Uxm. (2-80)
Заметим, что выражения, представ лен-
ные в правой части равенства (2-76), мож-
но получить и не обращаясь к представле-
нию о какой бы то ни было замене цепи
эквивалентным генератором. Действительно,
первое из уравнений (2-74) содержит два
неизвестных: U и I. Но эти же неизвестные
связаны .между собой еще одним уравнени-
ем (в простейшем случае -законом Ома):
U=Ir.
(2-81)
Подставляя (2-81) в (2-74) находим, что
U=Ir=A+BI. (2-82)
Решая это уравнение относительно то-
ка, получаем (2-76). Аналогично подста-
новка
I=Ug (2-83)
в левую часть второго из уравнений (2-74)
приводит к уравнению (2-77). Однако изо-
бражение (Двухполюсника конкретной схе-
мой эквивалентного генератора более на-
глядно.
Представление сложной цепи.
с неизменными параметрами в виде
активного двухполюсника часто по-
зволяет упростить аналитический
расчет цепи. К тому же (а это очень
существенно) параметры, полностью
определяющие внешнюю характери-
стику линейного двухполюсника, мо-
гут быть определены по данным
опыта: зная значения £/', Г и U", I"
для. каких-либо двух режимов на-
грузки, можно всегда определить
два параметра (две константы)
каждого из уравнений (2-74).
54
Пример 2-12. Между проводами элек-
трической сети при отключенной нагрузке
(/=0) напряжение равно 640 в. После
включения нагрузки, через которую пошел
ток 50 а, напряжение уменьшилось до зна-
чения 620 в.
Требуется: 1) найти схему замещения
сети, рассматриваемой как простой источ-
ник питания; 2) определить ожидаемую ве-
личину тока 1П;ри коротком замыкании про-
водов (в рассматриваемой точке сети).
Решение. Ищем параметры уравне-
ния (2-74). Из опыта холостого хода нахо-
дим А =640 в. Подставляя- это значение
в уравнение (2-74) при значениях U и I
второго режима, находим, что
620=640+505,
откуда В =—0,4 ом.
Следовательно, эквивалентная схема
может быть представлена источником
•с э. д. с. Э=А=640 в и внутренним сопро-
тивлением Г г——В = 0,4 ом.
Ожидаемый ток короткого замыкания
(если не нарушится линейность)
Э 640
1к~ г{ 0,4 = 1 600 а'
Пример 2-13. В цепи, показанной на
рис. 2-21, два параллельно включенных ис-
точника питают общую нагрузку (г3). Пер-
вый генератор отрегулирован так, что отда-
ваемый им ток равен 40 а. Э. д. с. второго
генератора 660 а, его внутреннее сопротив-
ление Г2='1 ом. Требуется определить зави-
симость напряжения U на нагрузке от ее
сопротивления, которое может изменяться
от 2 до 20 ом.
Для выполнения расчета предлагается
заменить оба источника питания одним ис-
точником тока J (рис. 2-30).
Решение. Для того чтобы прийти
к схеме рис. 2-30, заменим второй источник
эквивалентным источником тока J2=32lr2=
=660 а с параллельно включенным сопро-
тивлением r$=ir2’. Складывая токи, прите-
кающие к узлу а, найдем общий ток экви-
валентного источника:
J=J2+7j=700 а.
В этом случае напряжение между уз-
лами а и b
При изменении г3 ют 2 до 20 ом напря-
жение U изменяется (как нелинейная функ-
ция г3) от 467 до 667 в.
b
Рис. 2-30.
Определение внутреннего сопро-
тивления эквивалентного источника
(fi) при расчетах. При расчетах
значение обычно проще .опреде-
лять не как отношение UJ1K, а как
входное .сопротивление двухполюс-
ника
Гг = Гвх (2-84)
•при равенстве нулю э. д. с. Э и то-
ков J всех внутренних источников.
Для этого нужно замкнуть нако-
ротко зажимы источников напряже-
ния, сохраняя, конечно, последова-
тельно включенные внутренние со-
противления; разорвать ветви, со-
держащие источники тока, сохра-
няя параллельно включенные вну-
тренние сопротивления. Действи-
тельно, этим осуществляется усло-
вие 3=0 и /=0.
Равенство (2-84) непосредственно сле-
дует из эквивалентной замены активного
двухполюсника эквивалентным генерато-
ром. Действительно, после замены напря-
жения на нагрузке 1г (рис. 2-29,я), эквива-
лентной встречной э. д. с. 3V—Ir (принцип
компенсации), можно рассматривать дейст-
вительный ток I как суперпозицию тока Г
при действии только всех внутренних ис-
точников, заключенных внутри активного
двухполюсника, и тока I" при действии
только одной внешней э. д. с. 3V. Очевидно,
что этот последний ток равен произведению
3vgvv, аде 1/^®=|Гвх — входное сопротив-
ление двухполюсника при отсутствии вну-
тренних источников. Обращаясь к эквива-
лентному генератору (рис. 2-29,6) и опре-
деляя внешний ток I также по принципу
суперпозиции, найдем, что при действии
только внешней э. д. с. 3V—Ir искомый ток
Г равен произведению. 3vgi. Из сказанного
непосредственно следует доказываемое ра-
венство (2-84). Оно получается также из
общего анализа уравнений, составленных
по законам Кирхгофа, и сопоставления их
с уравнением эквивалентного генератора.
Пример 2-14. Требуется найти ток /5
в диагонали моста Уитстона, питаемого от
источника тока J (рис. 2-31,а).
Решение. Искомый ток можно выра-
зить из уравнения (2-76)
Л = '^х/(^*5 + гг), (а)
где Ux — напряжение между узлами Б и В
при холостом ходе (когда диагональ ра-
зомкнута) , а г г — входное сопротивление
цепи между узлами Б и В при токе источ-
ника /=0.
При разомкнутой диагонали (рис.
2-31,6)
= U'EBx = I з — I i*r 1*
Входящие в это равенство токи легко
находятся по формуле для распределения
55
Рис. 2-31.
заданного тока J между параллельными
ветвями (2-28)
I —JГ-^— Г —1 г— -
1 зх—J R 9 11х—J 7^ ’
где 7?=г1+г2-гА*з+^4.
При этом после простых сокращений
находим:
их=J\(r2r3—Г!Г4) /R. (б)
Заметим, что £7х=0 при r2r3=rxr4 (условие
урав'НО1вешен;ности моста). При этом ток
в диагонали равен нулю.
Входное сопротивление между узлами
Б и В при разомкнутой .ветви питания (J=
=0) легко найти как сопротивление двух
параллельных ветвей (рис. 2-31,в). Сопро-
тивление одной ветви Г1+гз> а другой г2+
+г4. При этом
Гвх = Гг=;(П+Г3) (r2+r4)IR. (в)
Подставляя (б) и (в) в (а), находим:
^+(п+г3)(г2 + г4)-
Пример 2-15. Ставится та же задача,
что в предыдущем примере,, только мост
Уитстона .питается источником заданного
напряжения U=3 = UAr (рис. 2-32,я).
Решение. Как и в предыдущем при-
мере, ток можно выразить уравнением
s~ rs+ri'
(а)
Однако теперь напряжение холостого
хода Ux между узлами Б, В (рис. 2-32,6);
равно:
U U
Ux ~ иБВ* - г3 + г4 г 8 ~ гг + г2 Г1 -
Гг^—Г]Г4
{Гi + г2) (<з + rj
(б)
Заметим, что условие равновесия моста
(Пх = 0) в этом случае тождественно с усло-
вием, найденным в предыдущем примере.
Входное сопротивление между узлами
Б и 73 ищется теперь при П=0, т. е. для
•схемы рис. 2-32,в: две параллельные ветви
с сопротивлениями гх и г2 теперь включены
последовательно с двумя другими парал-
лельными ветвями с сопротивлениями
г3 и г4.
Поэтому
_ Г1Г* I ГзГ4
Гвх-Гг-Г1+Г2-Г-Г8+Г4
(в>
__________Рз___________
(Г1 + r2) (rs + г4) ’
б)
56
где Рз- — сумма всех «различных ироизведе-
иий, содержащих три: сомножителя из че-
тырех сопротивлений й, г2, Лз, й, Д. е
Рз =Г1Г2Гз+ПГ2Г4+Г1ГзГ4 + Г2^зГ4.
Подставляя (б) и (в) ib (а), находим:
. TJ . йй —nr4___________
5 U Рз + (й + + й) Г5 •
В заключение заметим, что тео-
рию активного двухполюсника,
представленного источником э. д. с.
и внутренним сопротивлением, на-
зывают теорем ой Тевенена, а
теорию активного двухполюсника,
представленного источником тока и
внутренним сопротивлением, — тео-
ремой Нортона (по и-мени уче-
ных, впервые доказавших общую
применимость соответствующих эк-
вивалентных схем).
2-8. СИСТЕМЫ УРАВНЕНИЙ
ДЛЯ КОНТУРНЫХ токов
И УЗЛОВЫХ ПОТЕНЦИАЛОВ
Число уравнений для расчета
распределения токов и напряжений
в электрической цепи может быть
уменьшено, если составлять их толь-
ко по одному из законов Кирхгофа,
т. е. только для контуров или толь-
ко для узлов.
Само собой разумеется, эти
уравнения должны составляться
так, чтобы обеспечивалось выполне-
ние другого закона. Два метода со-
ставления таких уравнений были
предложены Максвеллом (§ 280 и
§ 282 b его Трактата об электриче-
стве и магнетизме, 1873); один из
них называют методом контурных
токов, другой — методом узловых
потенциалов.
Метод контурных токов5 Ток в лю-
бой ветви электрической цепи всег-
да можно представить составлен-
ным из нескольких токов, каждый
из которых замыкается по своему
контуру, оставаясь вдоль него неиз-
менным. Такие составляющие дей-
ствительных токов называют кон-
турными. Ток в любой ветви, при-
надлежащей только одному конту-
ру, .совпадает с контурным. Ток
в ветви, принадлежащей сразу двум
или нескольким контурам, равен
алгебраической сумме соответству-
ющих контурных токов. Контурные
токи, проходя через узел, остаются
непрерывными, следовательно, пер-
вый закон Кирхгофа при таком
представлении токов выполняется
автоматически. Поэтому уравнения
с контурными токами составляются
только по второму закону Кирхго-
фа>При этом контуры, для которых
получаются независимые уравнения,
выбираются так же, как при состав-
лении уравнений. Кирхгофа. Числе
таких независимых уравнений, рав-
ное числу независимых контурных
токов, опр ед ел яется фор мулой
К2=В + 1— У (2-85)
(В — число ветвей, У — число уз-
лов, см. § 2-3).
На рис. 2-33 показана простая
цепь с двумя контурными токами
Л и /2- Токи в ветвях а п b равны
контурным токам
/а=Л, Ib=I2.
Ток в ветви с равен сумме токов,
двух других ветвей; он равен и
сумме контурных токов, проходя-
щих через эту ветвь, общую для
двух контуров:
/с = Л+^2-
По второму закону Кирхгофа^
для первого контура цепи (рис. 2-33)*
1аГ аТ~ 1СГс~^а
ИЛИ
К (/'а + ^с) +^2^с==5а—Эс,
или, введя новые обозначения,
+^2^i2=«5i, (2-86,а У
где гц = га+'гс— сумма сопротивле-
ний- всех ветвей, образующих пер-
вый контур;
Рис. 2-33.
5Г
?\2=гс — сопротивление ветви,
общей для первого и второго кон-
туров;
Э1=Эа—Эс—алгебраическая сум-
ма всех э. д. с., содержащихся
в первом контуре; со знаком минус
берется э. д. с., действующая на-
встречу контурному току рассмат-
риваемого контура.
Аналогично для второго конту-
ра (рис. 2-33)
/141 Л~ 12^, (2-86,6)
где
41 = 4, 42 =4+4, Э2 = ЭЪ— Эс.
По самому определению (сопро-
тивление ветви, общей для двух кон-
туров)
41 = 42. (2-87)
Рассмотрим еще пример цепи,
содержащей три контура (рис. 2-34).
Записывая для нее контурные урав-
нения, получим:
(2-88)
В первом слагаемом первого урав-
нения
rn=re+rc+rf,
так как первый контурный ток про-
ходит по ветвям е, с, f. Что же ка-
сается второго слагаемого /24г, то
оно должно -быть равно падению
потенциала .в ветви, общей для кон-
туров 1^2, вызванному током вто-
рого контура. Но направления кон-
турных токов в этой ветви противо-
положны, поэтому
/242=--hre и 42 = —ге.
По тем же соображениям
4з=—4-
В этом же уравнении
Э] —Эе.
Для большей ясности составим урав-
нение для того же контура 1, выражая па-
дение потенциала в каждой из ветвей как
произведение тока ветви на сопротивление
ветви:
7е^е *4“ 7с^с Ifff === Эе*
Выразив токи ветвей через контурные
токи
4 = 4-4, 4 = 4, 4 = 4—7Ъ
получим:
(/1 - 4) ге + 1ггс - (73 — 7J г, = Эе
или
71 (4 + 4 + 4) — 44 — I3rf = Эе*
Из сопоставления последнего уравне-
ния с первым уравнением системы (2-88),
приходим к только что указанным значе-
ниям Гц, г12 И г13.
Из аналогичных рассуждений для вто-
рого и третьего уравнения системы (2-88):
41 — 42 - -ге,
4з = 42 = * d>
41 = 4з=“4>
Э3 =— 3d*
4s = 4+ 4 +4»
Э2 = 3d — Эе\
rzz=-ra*\-rd-Yrit
Обобщая полученные результа-
ты и называя все коэффициенты
при токах сопротивлениями, заме-
тим, что в системе уравнений для
контурных токов сопротивления
с одинаковыми индексами рав-
ны сумме сопротивлений во всех
ветвях одноименного (т) контура;
все сопротивления rmn с разными
индексами (т^п) равны сопротив-
лению ветвей, общих для контуров
m и п, взятому со знаком минус, ес-
ли токи контуров типе общей
ветви направлены противоположно.
По самому определению очевид-
но, что всегда
Gnn = 4m- . (2-89)
На основании сказанного систе-
ма уравнений для любой цепи,
яге содержащей источников тока, со-
ставляется по единому шаблону:
Эта система может быть сокращен-
но представлена равенств-ом
ПТП~ Эп-
При такой 'записи предполагает-
ся, что производится суммирование
?по одноименным индексам, т. е. что
тп' тлп
и каждому из значений п соответ-
ствует отдельное уравнение.
Решение системы (2-90) также
легко представить в общем виде:
Л “f~ *^2^12 • • • 5 ]
A = 51g’2i + *52g,22 + .. .; | (2-91)
пли в сокращенной записи /п =
--^rngnm*
Все коэффициенты gnm в послед-
ней системе представляются через
определитель D уравнений (2-90) и
соответствующие алгебраические до-
полнения Апт:
gls=^, gzl=^,...,
gnm = ^. (2-92)
Очень важно обратить взимание,
что в системе (2-91)
gmn~ gnm* (2-93)
Это следует из симметрии коэф-
фициентов гтп==гпт в исходной си-
стеме (2-90), которая приводит к ра-
венству алгебраических дополнений
Атп ~Апт.
Система уравнений (2-91) имеет
внешнее сходство с аналогичной си-
стемой уравнений для токов ветвей,
найденной из -решения уравнений
Кирхгофа (2-50) и (2-52). Ее су-
щественное отличие заключается
в том, что в системе (2-91) все токи
1п — это контурные токи, а Эт —
это контурные э. д. с. Поэтому в об-
щем случае коэффициенты gmn, ко-
торые могут быть названы контур-
ными проводимостями, отличаются
от соответствующих коэффициентов
gmn при э. д. с. ветвей в выражени-
ях для токов ветвей. Эти коэффици-
енты тождественно совпадают в тех
случаях, когда контурные токи со-
впадают с токами ветвей, а контур-
ные э. д. с. совпадают с э. д. с. вет-
вей.
Например, при выборе контуров,
показанном на рис. 2-35, контурные
э. д. с. 31, Э2 и контурные токи Л,
/2 совпадают с э. д. с. и токами в
ветвях генераторов. В этом случае
коэффициенты £ц, £12 = g21, g22
в уравнении (2-91) совпадают с
входными и передаточными прово-
димостями ветвей 1 и 2.
Все предыдущие выводы относи-
лись к цепям, не содержащим ис-
точников тока. Однако это ограни-
чение несущественно, поскольку лю-
бой источник тока может быть за-
менен эквивалентным источником
э. д. с., как было показано в преды-
дущем параграфе.
Влияние источников тока может
быть учтено и непосредственно при
составлении контурных уравнений.
Для этого ток источника Ja, присо-
единенного к каким-либо двум уз-
лам, предполагается проходящим
через любые ветви, соединяющие
эти узлы. К слагающим уравнения
для любого контура т добавляются
слагающие вида Цгта, где гтп—-
сопротивление -ветви, по которой
проходит ток Ja и которая принад-
лежит контуру т\ сопротивление
берется со знаком минус, если кон-
турный ТОК И ТОК Jа В ЭТОЙ ВОТВИ
направлены противоположно.
59
ra rb
Рис. 2-36.
Рассмотрим цепь рис. 2-36 с ис-
точником тока в правой ветви. Для
цепи достаточно составить два кон-
турных уравнения, поскольку, опре-
деляя число уравнений по формуле
(2-85), не следует считать ветви с
источником тока (§ 2-3).
Составляя эти уравнения, нуж-
но учитывать падение потенциала,
вызванное током /а:
соответствующим выражением всех
токов через разности потенциалов
и э. д. с.
Пусть в ветви (рис. 2-37), соеди-
няющие узлы I и m, Iim— ток, иду-
щий от узла I к узлу т, Эгт—э. д. с.,
включенная в ту же ветвь и направ-
ленная от / к т, а % — сопротивле-
ние ветви. В таком случае разность
Рис. 2-37.
потенциалов между узлами I и т
запишется так:
^1^*11 '"“Н а?ха —
Л^21 ] -^2^22 “Н 2а ------------
(2-94)
Если предполагать, что ток
проходит по ветви гп, то гХа=0, так
как ток Ja не проходит через ветви
первого контура, а г2а=гп, так как
ток Ja проходит по ветви гп второго
контура и совпадает ,по направле-
нию с током второго контура.
Заметим, что можно было бы
предполагать иной путь для тока
Ja, например через ветви гь и гт.
В этом случае в формуле (2-94) сле-
дует полагать:
И Г2а = —(Гд+М-
В обоих случаях значения коэф-
фициентов при контурных токах
определяются согласно с общим
правилом:
П1 = Га + Гт, Г12=Г21=—г™,
^22 — rm + ^&+^ п-
Доказательство возможности разложе-
ния токов ветвей на контурные токи легко
шолучить из анализа цепи, •приведенного
в § 2-3 для вывода числа независимых
уравнений. Контурные токи могут быть
отождествлены с токами в ветвях-мостах,
при этом токи всех остальных ветвей цепи,
образующих дерево, оказываются выражен-
ными через токи в мостах, т. е. через кон-
турные токи.
Метод узловых потенциалов. Сле-
дуя названному -методу, достаточно
составить только узловые уравне-
ния для токов. Выполнение второго
закона Кирхгофа 'Обеспечивается
ф? фт— (2-95)
Выражая из этого уравнения ток,
можно быть уверенным в том, что
второй закон Кирхгофа автоматиче-
ски выполняется. Из (2-95) нахо-
дим, что
/ы=:(ф1 фт“Ь^/тп) (2-96)
где gzm=l/nm-
В принятой системе обозначений
HO
= (2-97}
Перейдем теперь к составлению
узловых уравнений, полагая извест*
ними сопротивления (или проводи-
мости) всех ветвей цепи с п узлами*
а также все 9im источников э. д. с.
и все Jh источников тока.
Если к узлу 1 извне (от источни- <
ка тока) притекает ток Д, то по
первому закону Кирхгофа для пер-
вого узла
/12 + 71з +’... — Jь
Аналогично для узла 2
/21 + /23 + • • • +72тг —72
и т. д.
Раскрывая выражение для каж-
дого- из токов по (2-96), получим
для первого узла:
(ф1--ф2 + Э12) gi2 +’ (ф'1—фз + 51з) £13 +
+ ... + (ф:1—фп4‘51п)§,1п:=71.
(2-98)
60
Группируя .множители при неиз-
вестных потенциалах, произвольно
полагая потенциал последнего узла
л равным нулю (фп=0) и перенося
все известные величины в правую
часть, придадим такой вид уравне-
нию для первого узла:
ф1£11--ф'2^12-фзЯ13 — - •. —
Ф??—ig^i(n—i)==7 1- (2-99)
В этом выражении для сокраще-
ния записи введены следующие
обозначения:
gl\ ==S’12 + g'13 + • • +gln
— сумма проводимостей всех вет-
вей, сходящихся к первому узлу;
j^/l+^lg^ + ^sigis-p ... +
-r^nigin
(здесь изменены знаки перед всеми
э. д. с. одновременно с изменением
их индексов!). Последняя сумма
имеет очень простой смысл: это
полный ток, притекающий к узлу 1
от действительных и эквивалентных
источников тока; последние полу-
чаются после замены источников
э. д. с. в ветвях, сходящихся к узлу /,
параллельно включенными источни-
ками тока (рис. 2-38). Величину 7]
можно назвать приведенным значе-
нием узлового тока.
Уравнения, аналогичные (2-99),
можно составить и для остальных
узлов, кроме последнего узла, для
которого соответствующее уравне-
ние оказывается следствием осталь-
ных.
Система уравнений, в правой ча-
сти которых стоят приведенные узло -
Рис. 2-38.
вые токи. Легко представить всю
систему, содержащую
= 1
(У=п— полное число узлов) неза-
висимых уравнений и столько же
неизвестных потенциалов:
^2 ——
fn-igi (n-i)
— — ?з§23 ‘
Tn- 1S2 (п-1) 2’
91£(?2-1)1 92^(72-1)2 ••’“Ь
4“ 9‘П- 1g (П- 1) (П - 1) JП-!• )
(2-100)
Полученная система уравнений
для узловых потенциалов (как и си-
стема уравнений для контурных то-
ков) записывается независимо от
вида заданной цели, влияющей
только на значение коэффициентов
gmi и на значение свободных членов
7 77г-
В системе (2-100) все коэффи-
циенты gmi==gi?n при 1^=т равны
проводимости ветви, соединяющей
узлы т и /; все коэффициенты gmrn
с одинаковыми индексами . равны
сумме проводимостей всех ветвей,
сходящихся к узлу т:
gmm ~ gml ”Ь gm2 “F • • •
(2-101)
Каждый приведенный ток
Jrn, = IЭ\mgm\ ЧгЭ2тёт2~Ь - - • +
“Н ^n'mgmn (2-102)
равен току действительных и экви-
валентных источников тока, подво-
дящих ток к узлу т. Полезно за-
помнить, что для узла т ток экви-
валентного источника положителен,
когда э. д. с. в соответствующей
ветви направлена к узлу т.
Во всех приведенных выводах
предполагалось, что узлы I и т со-
единены одной ветвью. Если на са-
мом деле между этими узлами со-
держится несколько параллельных
ветвей с проводимостями g'im,
g"im,..., то очевидно, что проводи-
мость эквивалентной ветви
glm — g lm~\~g Zm~F - • -
61
Если каждая из этих ветвей содер-
жит свой источник э. д. с. 9'im,
9"im,..., то ток эквивалентного ис-
точника тока для параллельных
ветвей (ток, входящий извне
в узел т)
J 1т, —Э img im~i~ 9 img"lm + . - .
Заметим, что при этом не изме-
няются приведенные ранее форму-
лировки: gmm — сумма проводимо-
стей всех ветвей, сходящихся к уз-
лу m, Jm — ток всех действительных
и эквивалентных источников тока,
входящий в узел т.
Система уравнений с приведенны-
ми узловыми токами, решенная от-
носительно потенциалов. Решение си-
стемы уравнений (2-100) относи-
тельно потенциалов приводит к но-
вой системе:
(2-103)
Zl^ll + *^2^12 “4“ • • •
“4“ 1)^1 (n-1)>
<р2 = 11^21 "4” Za^22 + • • • "4“
+ ^(п-1)^2 (гг- i)>
Значения коэффициентов ам на-
ходятся обычными методами реше-
ния системы линейных уравнений.
В новой системе
аш=аы (2-104)
в силу того, что в исходной системе
'(2-100), по определению gki=gik-
Потенцй'ал последнего узла пра-
вей нулю (фп = 0) по исходному
предположению. Этот узел называ-
ют базисным. Очевидно, что по-
тенциалы остальных узлов могут
быть представлены как напряжения
относительно базисного узла:
ф1 — UIn? ф2 — U2т • • -
Очень часто вместо индекса п ба-
зисному узлу приписывают индекс 0.
Применение системы уравнений
для узловых потенциалов особенно
эффективно, когда ' число ветвей
увеличивается за счет ряда парал-
лельных соединений. Так, в случае
цепи с двумя узлами
(рис. 2-39,а) напряжение между уз-
лами определяется из одного урав-
нения. Для цепи, изображенной на
рис. 2-39,а, выбирая ф2=0, получим
по (2-99):
qpiS=9 ig! +9zg2+93g3+94g4,
где
S=gll=gl +g2+gz + g4,
откуда
^12 = Ф1= (9igi~[-92g2~[~9^g^ +
+94g4)/S, (2-105>
Разумеется, что э. д. с. любого
из источников может’ 'быть равной
нулю; при этом в числителе выпа-
дает соответствующее слагающее^
однако в сумму S входит проводи-
мость и этой ветви.
Только что найденное выраже-
ние (2-105) можно применить к ре-
шению такой часто встречающейся
задачи: к узлам с заданными потен-
циалами фа, фь, ... подключены вет-
ви, сходящиеся к общему узлу 0;,
требуется найти токи в ветвях, про-
водимости которых известны. Такая
цепь показана на рис. 2-39,6, она
называется .звездой, а ее вет-
ви — лучами звезды.
Сопоставляя цепи, изображен-
ные на рис. 2-39,а и 2-39,6, легко
убедиться в том, что, заменяя в фор-
муле (2-105) 91, Э2, ..на потен-
циалы ф|а, фь, .. и соответственно
Рис. 2-39.
d
&
gi, g2, •. на ga, gb, ..., найдем по-
тенциал точки 0:
ср __ ~Ь Ус^с (2-106)
Зная потенциалы всех узлов и
определив потенциал средней точки,
легко найти ток в любой ветви:
1а “(фа—фо) ga\
Д=(фь—фоШ, ...
Такой метод расчета в электро-
технике встречается очень часто.
Выбор между системами уравне-
ний. При расчете цепей по уравне-
ниям Кирхгофа всегда следует за-
писывать их или как уравнения для
контурных токов, или как уравне-
ния для узловых потенциалов. Из
этих двух систем естественно выби-
рать ту, которая для данной цепи
приводит к меньшему числу урав-
нений.
Пример 2-16. Цепь, изображенная на
.рис. 2-40,<2, имеет гири параллельные ветви
с э. д. с. 31=43 в, 32=10 в,‘33=8 в и про-
водимостями £1 = 0,2 CUM, £2 = 0,1 CUM, £з =
=0,2 сим. Остальная часть цепи показана
в виде прямоугольника.
Требуется заменить три параллельные
ветви одной ветвью с э. д. с. Зэ и проводи-
мостью £э (рис. 2-40,6).
Решение. Рассматривая три парал-
лельные ветви относительно точек 1 и 2 как
активный двухполюсник, -можем заменить
его эквивалентным генератором с э. д. с. Зэ,
равной напряжению хблостого хода Ui2x
(когда остальная часть цепи отсоединена),
и внутренним сопротивлением, равным вход-
ному сопротивлению двухполюсника гвх.
При холостом ходе напряжение между
узлами / и 2 найдем по формуле для цепи
с двумя узлами (2-105):-
о тт 31£1 4“ За£а — З3£3
= = + й + ---4- в-
Проводимость
ёэ = -— =gi + gt +йз = 0.5 сим.
г вх
Пример 2-17. Цепь, схематически изо-
браженная на рис. 2-41, изображает кольце-
вую линию передачи. Сопротивление прово-
дов линии на трех участках соответственно
равно 1/£а, Ч/£ь, 1/£с. Три потребителя £ь
£2, £з присоединены в трех точках этого
кольца.
Питание линии производится двумя ге-
нераторами, у одного из которых регули-
руется ток 7Г=Л, а у другого напряжение
иг=и3.
Требуется найти ток потребителя £2.
Решение. Цепь имеет четыре узла и
семь ветвей (не считая ветви с источником
тока). Поэтому, казалось бы, нужно соста-
вить или
К1=У— 1=з
— уравнения для узловых потенциалов, или
К=В + 1— 4=4
— уравнения для контурных токов.
На самом деле число уравнений и той и
другой системы на одно меньше, поскольку
потенциал узла 3 уже известен (он равен
напряжению генератора), а также можно
считать известным и ток ветви 3 (он ра-
вен U3g3).
При этом все равно необходимое число
уравнений меньше в первой системе.
Перенося -сразу в правую часть слагае-
мое с известным потенциалом фз=^з» при-
ходим к уравнениям?
— ЫГ12 = <рз£1з + А;
-- <Plg21 + ^2^22 = <?з£23»
в которых £11 = £1 + £ъ + gc, g22 = g2 +
+ ^с4"^> &21 = £12 ~ go giz—gb» £23==
Рис. 2-40.
63
Решая систему, найдем:
US (£13^21 + £2з£11) + Д^21
Ср 2 —г 9
£11£2 2 £12
а затем и ток
1ъ — ¥.2£2.
CL)
2-9. ПРИНЦИП ВЗАИМНОСТИ
В наиболее общей форме прин-
цип взаимности для двух внешних
ветвей любой разветвленной линей-
ной пассивной цепи (рис. 2-42) мо-
жет быть формулирован так. Обоз-
начим одним и двумя штрихами то-
ки и напряжения при двух разных
режимах во внешних ветвях (все
параметры пассивной цепи, заклю-
ченной внутри прямоугольника, оста-
ются неизменными). В таком слу-
чае всегда выполняется следующее
равенство:
= I\U\+T'2U'2. (2-107)
В частном случае переноса ис-
точника напряжения из первой вет-
ви (рис. 2-43,а) во вторую (рис.
2-43,6), при коротком замыкании
другой ветви, из уравнения (2-107)
получаем:
о+г2э=-/,,1э+о
или
If2=I'\. (2-108)
Интересно обратить внимание на
то, что из уравнения (2-107) нельзя
сделать никаких заключений относи-
тельно токов /71 и /"2.
Частный случай выражаемый
равенством (2-108), непосредствен-
но вытекает из уравнений для кон-
турных токов. Полагая Г\ и кон-
турными токами, из уравнений (2-91)
находим:
Л = Э^21 и I"i = 3gl2i (2-109)
так как в первом случае Э1=Э и
ВТОрОМ Э2 = Э. |ПрИ ЭТОМ g21=gl2)
как было показано (2-93).
6)
Рис. 2-43.
В другом частном случае, когда
из первой ветви во вторую (рис.
2-44,а, б) переносится источник то-
ка, а другая ветвь остается разомк-
нутой, из уравнения (2-107) нахо-
дим, что
JU'\-hO=0+JU/i
или
Uf\ = U\. (2-110)
Заметим, что при этом из принципа
взаимности ничего нельзя заклю-
чить о напряжениях (7/ и U„2-
Равенство (2-110) может быть
получено из системы уравнений для
узловых потенциалов (2-103), в ко-
торых ^12=^21 (2-104).
Из анализа двух систем уравне-
ний, записанных для двух режимов,^
после достаточно длинных алгебраи-
ческих преобразований может быть
выведена и общая формулировка
(2-107). Однако ее вывод значитель-
но проще получается методами тео-
рии поля.
1'=О
а)
т"=п
б)
Рис. 2-44.
Рис. 2-42.
-64
•Передаточные проводимости gim
и передаточные коэффициенты (со-
противления) aik в силу изложенно-
го часто называют взаимными.
2-10. ПРЕОБРАЗОВАНИЕ
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
В предыдущих параграфах уже
неоднократно применялось преобра-
зование электрических цепей в це-
лях их упрощения: замена парал-
лельных ветвей одним эквивалент-
ным сопротивлением, замена раз-
ветвленной активной цепи эквива-
лентным генератором и др. Во всех
этих случаях один двухполюсник
заменялся другим, эквивалентным
ему в электрическом отношении.
Для упрощения расчета и анали-
за электрических цепей иногда це-
лесообразно прибегать к преобра-
зованию участков цепи, связанных
с остальной цепью в трех и более
точках (трехполюсники и многопо-
люсники) .
Их преобразование заключается
в замене данного многополюсника
другим многополюсником, эквива-
лентным в электрическом отноше-
нии, но содержащим иную схему
внутренних соединений.
Эквивалентность двух многопо-
люсников означает,’ что потенциалы
соответствующих полюсов ^одного
(ф1, ф2, . . .) И другого (фч, JP2, . . .)
соответственно равны (ф1=фь ф2 =
=ф2, -. •) при любом режиме, т. _е.
при любых значениях токов (Л = 7ь
/2=/2, .. •), притекающих извне к по-
люсам одного (/i, /2, . • •) и другого
(71, /2, . . •) многополюсников.
Попутно -заметим, что это условие не
выполняется три замещении участка цепи
по принципу компенсации источником на-
пряжения или тока; э. д. с. или ток такого
источника зависит от режима цепи.
Рис. 2-45.
Преобразование треугольника в
трехлучевую звезду. В практике рас-
чета электрических цепей широкое
распространение получили прямое и
обратное преобразования пассив-
ного треугольника в пас-
сивную трехлучевую звез-
ду*
На рис. 2-45 показано соедине-
ние трех ветвей в треугольник (а)
и в звезду (б); такие трехполюсни-
ки называют также П- и Т-схемами
(рис. 2-46, а и б) по сходству с эти-
ми буквами при соответствующем
графическом изображении. При
этом, конечно, предполагается, что
средняя (общая) точка звезды 0 не
соединена с внешней цепью, так как
иначе звезду следовало бы считать
цепью с четырьмя полюсами.
Определим соотношения между
сопротивлениями ветвей треуголь-
ника и звезды, при которых трехпо-
люсники эквивалентны.
Запишем для треугольника и
звезды уравнения, связывающие по-
тенциалы их узлов с токами, прите-
кающими к узлам. Пусть для звез-
ды
Ф'1 = бХц/] + &12/2;
ф2 = #21/1 + #22^ 2,
а для треугольника
<Pi=ai гД+ &12/2;
ф2 —^21/1+^22^2-
Потенциал третьего полюса
принят равным нулю.
Очевидно, что условие эквива-
лентности рассматриваемых трехпо-
люсников определяется тремя урав-
нениями:
#11 = ^11, #12 = &12, #22 = &22 (2-111)
5 К. М. Поливанов
65
(коэффициенты 021 = 012 и 021 = 012,
как было показано в § 2-8).
При подборе эквивалентного
трехполюсника мы имеем возмож-
ность выбирать нужные значения
трех сопротивлений. Поэтому следу-
ет предполагать, что задача разре-
шима — значения трех сопротивле-
ний должны удовлетворять такому
же числу условий (2-111).
Для определения коэффициентов
012 и 012 приравняем нулю ток 71
и вычислим потенциал первого по-
люса (рис. 2-47) при заданном то-
ке /2-
При этом для звезды (рис.
2-47,6)
(Р1=72Гз, (2-112)
и, следовательно,
012 = ^з- (2-113)
Для треугольника (рис. 2-47,0)
'Ф1=*з1Лзл (2-114)
где 713 — часть тока /2, которую лег-
ко вычислить, учитывая, что ток Z2
распределяется по двум параллель-
ным ветвям:
/ — / (0-
13 2 12 4~ Г23 4“ Г31 *
Подставив (2-115) в (2-114), найдем,
что
(2-116)
~~ _____ ________31г23________
12 Г12 + Г23 + Г31
а)
Приравнивая и а12, находим одно
из условий эквивалентности:
г3 =----. (2
^*12 4" ^23 4“ Г31
Это условие позволяет опреде-
лить одно из сопротивлений луча
звезды по трем заданным сопротив*
лениям ветвей (сторон) треуголь*
ника.
Связь сопротивлений двух дру-
гих лучей звезды и сопротивлений
сторон эквивалентного треугольни-
ка можно найти, приравнивая меж-
ду собой остальные коэффициенты.
Однако значительно проще восполь-
зоваться принципом симметрии. И у
звезды, и у треугольника все ветви
расположены симметрично относи-
тельно внешних полюсов; следова-
тельно, формулы для вычисления
сопротивлений двух других лучей
звезды должны иметь такую же
структуру, как и (2-117). Поэтому
выражения для всех сопротивлений
звезды можно получить из (2-117)
круговой заменой индексов:
П = rx^!R, г2=Г23П2//?,
^*з=^з1^2з/7?, (2-118)
где 7? = Г12 4-:Г2з4-Гз1. г
При таких сопротивлениях звез-
ды она эквивалентна заданному
треугольнику.
Полезно самостоятельно убе-
диться, что при указанных значени-
ях сопротивлений выполняется и
условие 0ц = 01Г, условие 022=022 по-
лучается путем замены индексов 1
на 2 и 2 на 1.
Решив систему (2-118) относи-
тельно сопротивлений сторон тре-
угольника, получим их значения,
обеспечивающие эквивалентность
треугольника звезде с заданными с
сопротивлениями лучей гь г2, гз:
r12 = G + ra + ^; ]
г3
rss = rs + r3 + -^-: } (2-119)
К тому же результату легко прийти, за-
писывая уравнения для токов, 'выраженных
через потенциалы. При этом удобно вос-
пользоваться формулой (2-106) для потен-
циала нулевой точки звезды.
66
Выразив все сопротивления че-
рез проводимости, последним фор-
мулам можно придать более сим-
метричный вид:
g\2^g\g2lS, gzs = g2g3>IS,
g3i=gsgi/S, (2-120)
где +1£2+£з.
В частном случае одинаковых
сопротивлений всех лучей звезды и
всех сторон треугольника
Рис. 2-49.
ГД = 3гх-
(2-121)
Выведенные условия эквивалент-
ности легко применить и тогда,
когда в ветвях звезды или треуголь-
ника содержатся источники э. д. с.
Но в этом случае необходимо пред-
варительно -отнести источники во
внешнюю часть цепи; при этом для
треугольника источники э. д. с. сле-
дует заменить эквивалентными ис-
точниками тока.
Преобразование треугольника
в звезду или наоборот часто упро-
щает расчетную схему. Так, напри-
мер, цепь с четырьмя узлами, пред-
ставленная на рис. 2-48,а, содержит
Рис. 2-48.
сопротивления ri2, г23, /31, соединен-
ные в треугольник. После их заме-
ны эквивалентной звездой (2-48,6)
цепь значительно упрощается, пре-
вращаясь в цепь с двумя узлами.
Общий случай преобразования
многолучевой звезды в многоуголь-
ник. Такое преобразование всегда воз-
можно, если-к общему узлу звезды не при-
текает внешний ток.
Составляя уравнения для
чах звезды (рис. 2-49,а)
токов в лу-
11 = (<Р1 — ?о) £1»
/2= (<р2 — 0o)g2
и выражая потенциал общей точки по фор-
муле (2-106)
?0 — (?1£1 + ?2^2 + • • •)/$,
где 5 = gt + g2 + • • • — сумма проводи-
мостей всех лучей звезды, найдем, что
/> = yigi (1 — gi/S) — yzgigtJSj—
— тз^3/5—. -
/2 —--¥1^2^1/5и4- <р2&2 (1 -^г/5) -
— Тз^з/S —.. .;
Записывая аналогичные уравнения для
многоугольника (рис. 2-49,6)
Л=ф1£11--ф2^12--фз£13- • * •*»
Ц——Ф1^21 + ф2^22-ф3^23- • • •;
(см. § 2-8) и сопоставляя две системы урав-
нений, находим, -что:
gi2-gig2/S, £1з=£1£з/<$;
£11 = £12 + £1з + - . - + gln~
=£1‘(£2+£з+. . .+£п)/«$* (2-122J
Таким образом получаем самое общее
выражение для проводимости любой ветви
многоугольника, связывающей узлы k и /:
gki-gkgilS, (2-123)
где gk и gi — проводимости лучей звезды,
отходящих от узлов k и Z, a S — сумма про-
водимостей всех лучей звезды.
5*
67
Рис. 2-50.
Многоугольник и звезда, для которых
проводимости ветвей связаны уравнением
(2-123), эквивалентны.
Рассмотренное преобразование равно-
сильно просто исключению одного неизвест-
ного (><ро) к исходной системе уравнений или
исключению из схемы одного узла.
Заметим, что обратное преобразование
многоугольника в звезду в общем случае
невозможно, так как в формуле (2-123) тре-
буются определенные соотношения между
проводимостями ветвей многоугольника:
£12/gl3 — gdgz
и
g2 п /gs п — §2/§3'
В произвольном многоугольнике эти усло-
вия могут и не выполняться.
Для трехлучевой звезды и треугольни-
ка однозначно выполнимы как прямое, так
и обратное 1преобр аз окания.
Уравнения активного многополюсника.
Когда внутри многополюсника содержатся
источники ((не вынесенные наружу в виде
токов эквивалентных источников), ранее
приведенная система уравнений 1
(2-124)
I
1 Выражения (2-124) и (2-125) и сле-
дующие представляют собой сокращенную
запись системы уравнений.
должна быть дополнена свободными члена-
ми в правой части:
+ (2-125)
I
Соответственно и решение последней
системы уравнений относительно потенциа-
лов будет содержать свободные члены:
= + dt. (2-126)
k
Смысл свободных членов (2-125) и
(2-126) легко понять:
ck=h (2-127)
при равенстве нулю всех потенциалов
(<Pz=O при любом /),
di-^i (2-128)
при равенстве нулю всех внешних токов
(Д = 0 при любом k}. Сказанное поясняется
рис. 2-50.
И в случае активных многополюсников
может быть решена задача об условии их
эквивалентности и о преобразовании звезды
в многоугольник. Однако эта задача проще
решается путем вынесения источников во
внешнюю цепь и, если нужно, их обратного
введения в преобразованный пассивный
многополюсник.
Все коэффициенты — bhi, aiki Ck и di —
могут быть определены или из опыта пу-
тем надлежащего числа измерений, или рас-
четным путем, если известны все параметры
цепи
2-11. ВЛИЯНИЕ ИЗМЕНЕНИЯ
ПАРАМЕТРОВ ЦЕПИ
При анализе и расчете цепей ча-
сто требуется определить, как изме-
няются токи и напряжения в цепи
при том или ином изменении ее па-
раметров. Например, спрашивается,
какой дополнительный ток пойдет
в одной ветви при подключении до-
полнительной ветви между какими-
либо двумя узлами цепи—в част-
ности, при их коротком замыкании;
как изменится ток в одной ветви при
изменении сопротивления в- другой
ветви — в частности, при разрыве
какой-либо ветви с известным то-
ком?
Для того чтобы ответить на эти
вопросы, необходимо знать харак-
терные параметры цепи, однако при
этом нет необходимости произво-
дить полный расчет цепи, к тому
же многие из характерных парамет-
ров могут быть найдены эксперт
ментально.
68
Подключение дополнительной вет-
ви. Пусть требуется найти прираще-
ние тока б/j в ветви 1 при подклю-
чении к точкам а и b дополнитель-
ной ветви v -с сопротивлением rv
(рис. 2-51,а). Режим цепи до под-
ключения будем считать известным;
в частности, известны ток 1\ и на-
пряжение U'v между точками а и b
(рис. 2-51,6).
Для определения приращения
тока 6Д применим метод наложе-
ния. Включим в ветвь v два допол-
нительных источника э. д. с. 9V=>
=9v=U'v (рис. 2-52,а). При этом
токи во всех ветвях те же, что и
в цепи рис. 2-51,а, так как э. д. с.
9V и 9'v направлены навстречу.
При действии всех источников,
кроме э. д. с. 9V (рис. 2-52,6), токи
во всех ветвях будут такими же,
как в цепи рис. 2-51,6, и по условию
задачи они нам известны. Эквива-
лентность цепей рис. 2-51,6 и 2-52,6
объясняется тем, что напряжение
между точками а и b обеих цепей
одинаково и равно U'v.
Очевидно, что при действии по*
следнего источника с э. д. с. 9V ток
в ветви 1 должен быть как раз ра-
вен 611 (рис. 2-52,в).
Таким образом, для определения
приращения тока бД в ветви 1 (как
и в любой другой ветви) достаточно
рассчитать цепь рис. 2-52,в. Если
найдена взаимная проводимость giv
ветвей 1 и и, то можно сразу запи-
сать для ветви I:
6li=giv9v=givU/v; (2-1*29)
для ветви v:
61 v— gw^
(2-130)
Последнее выражение совпадает
с ранее полученным (2-76). Дей-
ствительно, напряжение U'v — это
напряжение холостого хода Ux для
ветви v; приращение тока 6Iv рав-
но току Iv после подключения ветви
(Л=0), а
где гВх — входное сопротивление це-
пи относительно точек а и b до за-
мыкания рубильника (рис. 2-51,6),
которую можно рассматривать как
активный двухполюсник.
При коротком замыкании точек
а и b проводимости giv и gw нужно
определять, считая г^ = 0.
Пример 2-18. к узлам а и b цепи рис.
2-53,а 'подключается ветвь с сопротивлением
гг=4 ом.
Требуется найти ток 1\ после замыка-
ния (рубильника. Параметры цепи: ri=4cw,
г2—2 ом, г3=4 ом, 3=8 в, 7=2,5 а. Режим
цепи'до замыкания подключаемой ветви из-
вестен: /'1=^1,30 a, U'ab = U'v==2fi9 в (эти
данные легко определить, составив одно
контурное ур авнение).
69
Рис. 2-53.
а)
Решение. Для определения прираще-
ния тока 6Л составим схему с одним источ-
ником э. д. с. Эv =2,80 в (рис. 2-53,6). При-
ращение тока [см. (2-26)].
где р — Г®А‘з+'Гз(П+г2) + (rl+^2)rv-
Вычисляя, находим: 671=0,175 а. Поэтому
71=71'+6Л=1,475а.
Пример 2-19. Для измерения внутрен-
него сопротивления источника его включают
в мост Уитстона (рис. 2-54). Мост может
быть уравновешен, т. е. можно подобрать
такие значения сопротивлений, что ток
в гальванометре обратится в нуль. Однако
это условие не позволяет определить сопро-
тивление гх, если не известны значения
э. д. с. Эх и Эб1.
Рис. 2-54.
Но можно поступить так (метод Маи-
са): сопротивления четырех плеч моста под-
бирают такими, что замыкание и размыка-
ние рубильника 1в ветви питания (рис. 2-54)
не изменяет ток, идущий через гальвано-
метр (6). При этом Г1<г4=г2гз.
Требуется обосновать этот метод, поль-
зуясь выводами, изложенными в этом пара-
графе. Решение приведено в конце пара-
графа.
1 При равновесии
Пг4 —г2г3
Г2 (г3 + Q) *
причем в г! входит неизвестное гх (см.
рис. 2-54).
Отключение ветви. Пусть требует-
ся найти приращение тока 6Л в вет-
ви 1 при разрыве ветви v (рис.
2-55,а). Режим цепи до разрыва
считаем известным; в частности, из-
вестны токи Г\ и I'v (рис. 2-55,6).
Для определения приращения
тока 6Л спять применим метод на-
ложения. Включим в ветвь v два до-
полнительных источника тока Jv=
(рис. 2-56,а). Токи во всех
ветвях цепи рис. 2-56,а те же, что и
в цепи рис. 2-55,а, так как токи Jv
и J'v направлены навстречу.
я/
6)
70
При действии всех источни-
ков, кроме источника тока Jv
(рис. 2-56,6), токи во всех вет-
вях такие же, как в цепи рис. 2-55,6,
«1 по условию задачи они нам из-
вестны. Очевидно, что при действии
одного источника тока Jv в ветви 1
проходит ток sd/i (рис. 2-56,в).
Таким образом, для определе-
ния приращения тока в вет-
ви 1 (или в любой другой вет-
ви) достаточно рассчитать цепь
рис. 2-56,в. Если известен пе-
редаточный коэффициент hiv для ис-
точника тока в ветви v и тока в вет-
ви 1, то
v—hivlfv (2-131)
Теорема вариации. Нетрудно най-
ти изменение тока 6Ц при произ-
вольном изменении сопротивления
drv в ветви v.
Пусть токи в ветвях 1 и v равны
/'1 и I'v (рис. 2-57,8) при 6Л)=0,
в при заданном значении 6rv соот-
ветственно равны (рис. 2-57,6):
Л=.Л + бЛ, Ц=1'МЦ. (2-132)
Заметим, что 6/х и dlv следует
понимать как приращения в алгеб-
раическом смысле. Так, например,
очевидно, что
Х<° при 6rv>0.
Напряжение иаЪ (рис. 2-57,6)
можно заменить (принцип компен-
сации) эквивалентным источником
Рис. 2-57.
э. д. с. 9V, включенным между теми
же точками а и Ъ (рис. 2-57,в):
9 и — U ofc ==
ИЛИ /
9v=\(I'v+'67v)6rv. (2-133)
При этом дополнительные сла-
гающие тока б/i и dlv легко выра-
жаются через э. д. с. дополнитель-
ного источника (9V) и соответствую-
щие проводимости:
6/i (2-134)
6/^=—gw9v (2-135)
В последнем равенстве справа
поставлен знак минус, так как по-
ложительные направления 9V и то-
ка dlv прямо противоположны.
Подставляя 9V из (2-133) в
(2-135), находим, что
dlv=—g™ (7%+’6/^) drv. (2-136)
Решая последнее равенство от-
носительно dlv, получаем искомое
выражение для приращения тока
в ветви v в зависимости от прира-
щения сопротивления в ветви vi
(2-137)
1 “Г gv.V0' V
Как видно из равенств (2-134) и
(2-135),
5/1 = —(2-138)
&®®
Поэтому из (2-137) и (2-138) нахо-
дим выражение для приращения тока
в ветви 1 в зависимости от
щения сопротивления в ветви
s г _. I'vglifirу
1 1 -f- §vv^rv
Формулы (2-137) и (2-139) вы-
ражают теорему вариации.
Следует "обратить внимание на то,
что в правой части этих формул 7ZV,
giv и gw — параметры, не завися-
щие от drv (вычислены при 6rv=0).
В ряде случаев они могут быть
определены непосредственно из со-
поставления этих формул с резуль-
татами эксперимента или расчета.
Изменение сопротивления ветви
можно рассматривать и как под-
подключение или отключение ру-
бильника, параллельного части со-
прира-
v:
(2-139)
71
противления ветви (бг^), т. е. ре-
шить задачу включением дополни-
тельного источника э. д. -с. или тока.
Пример 2-20. Требуется найти зависи-
мость тока I5 IB диагонали моста Уитстона
от изменения сопротивления 'brv «в его пер-
вой ветви (рис. 2-58,а). При — 0 мост
уравновешен. При этом r1=r2=r3=r4=rs=r,
что соответствует наибольшей 'чувствитель-
ности моста. Питание моста стабилизирова-
но по току Ig=J.
Решение. По теореме вариации
, 5.7
ZS-d/s- 1+^Гф.
Ток в первой ветви * при уравновешенном
режиме находится очень просто:
/'„ = -тр J .
Значения gw и gw следует определять
для цепи (рис. 2-58,6), в которой источник
э. д. с. включен (на место бг« навстречу то-
ку /г, а ветвь с источникам тока разомкну-
та (/=0). Однако gw проще определить
как отношение тока в ветви 1 (при 6rv=0)
к э. д. с. Э5, включенной в диагональ
(рис. 2-58,в), т. е. найти gvb—gw- При этом
ветви Г1Ч-Г3 и Гз+^4 оказываются включен-
ными параллельно, а последовательно с ни-
ми включена ветвь г5. В случае симметрич-
ного моста сопротивление каждой из па-
раллельных ветвей 2г, а сопротивление, эк-
вивалентное двум параллельным ветвям,
равно г; общее входное сопротивление для
источника Э5 равно 2г; в ветвь 1 попадает
половина общего тока. Таким образом,
gv5-g5v=—1/(4г)
(знак минус соответствует положительным
направлениям токов и э. д. с. схемы
рис: 2-58,6, повторенным на рис. 2-58,в).
Значение gw можно определить как
входную проводимость при включении ис-
точника питания в ветвь 1 (рис. 2-58,6).
Однако проще ((особенно (при неуравнове-
шенном мосте) исходить из того, что
blvlbh=—gwlgw как это следует из
(2-138).
Значения blv и б/5 очень просто найти
для случая drv = oo, т. е. когда ветвь 1 ра-
зомкнута (рис. 2-58,г). В этом случае 6Л,=
=—1'ъ и бД=/5. Ток источника распреде-
ляется по параллельным ветвям г5+г2 и г4
обратно пропорционально их сопротивле-
ниям, следовательно
т —___j------£1___
5 Г2 + ^4+ ГЪ
При равных плечах /5=—J/3.
Зная g5v, находим, что
3
gw— gw gr •
Подставляя найденные параметры в фор-
мулу для д/5, находим ответ:
г _ _ J
----J 8/. + з§г„-
Знак минус показывает, что при увели-
чении сопротивления в плече 1 ток идет
в направлении, противоположном указанно-
му стрелкой на рис. 2-58,а.
Если сопротивление ’ плеча 1 уменьша-
ется (становится меньше и), величину бг^,
следует считать отрицательной.
Пример 2-21. Требуется решить задачуу
отличающуюся от рассмотренной в преды-
дущем примере только тем, что источник
питания |(ри;с. 2-58,а) стабилизирован по на-
пряжению. Сравнив выражения, найденное
выше для тока /5 и получающееся в этом
примере, определить, в каких пределах
изменения бгг зависимость между /5 и бг^
можно считать линейной с точноетью при-
близительно до 1%.
72
Решение. Расчет отличается от из-
ложенного в примере 2-20 только тем, что
при определении gV5 и gvv отсутствие ис-
точника питания (сМ) представляется ко-
ротким замыканием между узлами А и Г
(рис. 2-58,а). В итоге получается выражение
. _ U$rv
15-----r(8r+5Sr®) *
Зависимость между /5 и 6rv можио счи-
тать с точностью до 1% ‘линейной до тех
пор, пока знаменатель изменяется не боль-
ше, чем на 1 %; поэтому предельное измене-
ние 6гv выражается при питании от источ-
ника тока формулой
3 | Sr® | 0,01-8г или [ Sr® | 0,0267г,
а при питаний от источника напряжения —
формулой
5 | Sr® | 0,01 -8г или | Sr® | 0,0160г.
Решение примера 2-19. При раз-
мыкании и замыкании ветви с источником
питания изменение тока в ветви гальвано-
метра (G) пропорционально взаимной про-
водимости этих ветвей, как это следует из
формулы i(2-129). Но при уравновешенном
мосте (г1(Т4=‘Г2^з) и одном источнике пита-
ния Эб ток в гальванометре отсутствует,
т. е. gG6=0.
2-12. ЦЕЛЬ С ДВУМЯ ВНЕШНИМИ
ВЕТВЯМИ (ЧЕТЫРЕХПОЛЮСНИК)
При анализе цепей мы уже не
раз приходили к рассмотрению цепи
с двумя внешними ветвями. Рас-
смотрим теперь общий случай такой
цепи. Введем обозначения для то-
ков и напряжений внешних ветвей,
показанные на рис. 2-59. Такую
цепь, имеющую четыре внешних за-
жима, называют также четырех-
полюсником. При его анализе
предполагается, что ток /2» выходя-
щий из верхнего правого полюса,
входит в нижний правый полюс;
точно так же ток /1, входящий
в верхний левый полюс, выходит че-
рез нижний левый полюс, т. е. цепь
рис. 2-59 рассматривается именно
как цепь с двумя внешними ветвя-
ми. Такой четырехполюсник назы-
вают р е г у л я р н Ы M;
Рис. 2-59.
При отсутствии источников пита-
ния внутри четырехполюсника его
называют пассивным. В даль-
нейшем (если не делается особых
оговорок) четы|рехполюсниками на-
зываются именно пассивные регу-
лярные четырехполюсники.
В электротехнической практике
анализ цепей в огромном числе слу-
чаев сводится именно к анализу че-
тырехполюсников.
Уравнения четырехполюсника.
Представляя, что напряжения -СД и
U2 обусловлены соответствующими
источниками э. д. с. 9i = Ui и Э2=
= С/2, находим, что по принципу су-
перпозиции
h — Ulgn--Uzgl2, --U2g22*
(2-140)
Знак минус поставлен перед t/2, так
как при положительном Э2= U2
ток /2 отрицателен; gi2 (положитель-
но, если при положительном 9i~Ui
положителен и ток /2. Знакам урав-
нения (2-140) соответствуют поло-
жительны^ значения всех gmn в про-
стейших Т и /7-схемах, которые
можно рассматривать как четырех-
полюсники (рис. 2-60,а и б).
Для анализа четырехполюсни-
ков уравнения (2-140) удобно ре-
шить относительно входного тока/i
и входного напряжения Z7i, выра-
женных через ток и напряжение на
выходе:
U^AU. + BI^ |
i1=cu2 + di2. j
(2-141)
6)
Рис. 2-60.
73
Очевидно, что для четырехпо-
люсника -с неизменными параметра-
ми (gn, gi2, g22 постоянны) все ко-
эффициенты четырехполюсника Л,
В, С и D постоянны.
Для любой заданной цепи из
расчета или из опыта легко опреде-
лить значения этих коэффициентов,
рассматривая режимы холостого хо-
да и короткого замыкания.
При холостом ходе в конце
U^—AU^
так как /2—0; следовательно,
Л=7/1х/£72х,
При коротком замыкании в конце
^1к==-2Дк> IlR — BIzib
так как £/2=0; следовательно,
В —U1К//2к, D = I 1кД2к«
Производя опыт короткого за-
мыкания, во многих случаях необ-
ходимо уменьшать входное напря-
жение до величины £ЛК, при кото-
рой токи короткого замыкания ска-
зываются не слишком большими.
Иногда (выбирают оба режима так,
чтобы значения и /2к оставались
равными U2 и I2 в нормальном ре-
жиме работы четырехполюсника.
Между четырьмя коэффициента-
ми Л, В, С, D существует уравнение
связи
AD—ВС=1. (2-142)
Его можно вывести из уравнений
(2-141), применяя к ним принцип
взаимности, а также из уравнений
(2-140), в которых по принципу
ВЗаиМНОСТИ gl2 = gr21.
Уравнение (2-142) показывает,
•что четырехполюсники характери-
зуются всего тремя независимыми
параметрами, а четвертый (любой
из Л, В, С, £>) может быть опреде-
лен из уравнения (2-142). Также
тремя независимыми сопротивле-
ниями характеризуются и цепи,
изображенные на рис. 2-60 (Т- и
П-образные схемы или звезда
и треугольник). Поэтому всегда
:в расчетах четырехполюсник с за-
данными параметрами можно заме-
нить эквивалентной Т- или 77-схе-
мой (речь идет, конечно, как и во
всем этом параграфе, о регулярном
четырехполюснике, т. е. о цепи
с двумя внешними ветвями).
Это важно также в лаборатор-
ной практике и в моделировании
электрических цепей.
2-13. МЕТОДЫ РАСЧЕТА
И АНАЛИЗА ЭЛЕКТРИЧЕСКИХ
ЦЕПЕЙ
В предыдущих параграфах этой
главы при изложении элементов
теории линейных электрических це-
пей уже обращалось внимание на
применение теоретических выводов
к расчету и анализу процессов
в электрических цепях.
Однако проводившиеся в тексте
указания нуждаются «в систематиза-
ции, некотором развитии и обобще-
нии, чему и посвящается этот за-
ключительный параграф первой
главы. По необходимости в нем
рассматриваются только линейные
цепи постоянного тока, но многие
выводы и рекомендации без сущест-
венных изменений могут быть при-
менены к линейным цепям при пе-
ременном токе и в переходном ре-
жиме.
1. Методы частичного анализа.
Так можно назвать практически
очень важную труппу приемов ана-
лиза, основанных на эксперимен-
тальном или расчетном определении
только нескольких характерных па-
раметров цепи. Знание их позволяет
судить о режиме и работе цепи без
детального расчета токов и напря-
жений всех ее ветвей.
Этим приемам уделялось боль-
шое внимание во всем предыдущем
тексте: замена всей цепи активным
двухполюсником, свойства которого
характеризуются двумя данными
опыта или расчета (короткое замы-
кание и холостой ход); определение
влияния изменений одного из пара-
метров цепи (короткое замыкание,
разрыв ветви, изменение одного из
сопротивлений brv) на ток или на-
пряжение в какой-либо другой ин-
тересующей нас ветви и т. п.
Эти методы часто могут сущест-
венно упростить расчеты, к тому же
они очень важны для руководства
при экспериментировании и для вы-
74
вод ов из данных, полученных
в опыте.
2. Расчеты по Кирхгофовым
уравнениям. Эти расчеты дают воз-
можность наиболее полного сужде-
ния о всей цепи. При этом практи-
чески всегда уравнение следует за-
писывать или для контурных токов,
или для узловых потенциалов (в за-
висимости от того, какая из систем
•оказывается более простой для дан-
ной конкретной задачи).
Полученную систему уравнений
(если она состоит -больше чем из
трех уравнений) следует решать,
пользуясь приемами, тщательно
разработанными в вычислительных
методах линейной алгебры.
Выбор метода диктуется наи-
меньшим количеством числовых
операций и простотой контроля про-
межуточных числовых результатов.
Заметим, что метод последователь-
ного исключения неизвестных (ме-
тод Гаусса) приводит заведомо
к .меньшему числу операций, чем
метод определителей; последний мо-
жет 'быть рекомендован лишь как
метод анализа уравнений, а не как
метод их числового решения. Осо-
бенно следует рекомендовать про-
верку промежуточных результатов
(пользуясь, например, методом кон-
трольных сумм), так как это избав-
ляет при ошибке в начале расчета
от большого числа бесполезных вы-
числений.
При большом числе уравнений
следует: 1) решать систему уравне-
ний, разбивая -ее на части (см. пп. 3,
4, 5 и в особенности пп. 6 и 7); этот
метод следует рекомендовать, если
даже число уравнений в системе
равно всего четырем и даже трем;
2) применять специальные приемы
приближенных вычислений или
3) обращаться к моделям и вычи-
слительным машинам (см. и. 8).
3. Преобразование. Метод пре-
образования в ряде случаев очень
удобен благодаря наглядности всех
проводимых промежуточных дейст-
вий. Так,, преобразование звезды
(или треугольника) в треугольник
(или звезду) позволяет упростить
рассматриваемую цепь и каждый
этап преобразований изображать
графически. То же самое относит-
ся и к случаю разбивки сложной
цепи на несколько соединяемых
между со-бой двух, трех- или четы-
рехполюсников.
Такое преобразование схем соот-
ветствует разбивке заданной систе-
мы уравнений на две (или несколь-
ко) подсистем, каждая из которых
решается в отдельности, а потом
(при соединении многополюсников
между собой) производится согла-
сование таких решений, как будет
показано в следующем п. 4.
Заметим, что даже в тех случа-
ях, когда преобразование, скажем,
треугольник—звезда, не приводит к
уменьшению числа числовых опера-
ций, этот метод часто привлекает
инженеров своей наглядностью.
4. Применение теории четырех-
полюсников. Пусть, например, в це-
пи рис. 2-61,а нужно найти на-
пряжение U2 при заданном напря-
жении -Ui. Цепь содержит пять уз-
лов и восемь ветвей. В общем слу-
чае ее расчет очень громоздок. Рас-
чет упрощается, если разбить цепь
на два четырехполюсника (рис.
2-61,6 и 2-61,в), для каждого из ко-
торых очень просто вычислить ко-
эффициенты Д7, В', С', D' (четырех-
полюсник б) и Д77, В77, С", D" (че-
тырехполюсник в).
Ограничимся здесь частным слу-
чаем, когда /2=0. Запишем для этих
четырехполюсников первые уравне-
ния:
U\=A'U'2+BT2
и
U'\=A"U"2+B"I"2.
Они должны совместно решаться
• при условиях (рис. 2-61,й)
/2=/72+/772=о,
= = U'2=U"2=U2.
Принимая во внимание эти усло-
вия, деля уравнение для U'\ на В',
а уравнение для на В", и скла-
дывая их, найдем, что
Следовательно,
75
Рис. 2-61.
Тем самым задача решена,
остается только .рассчитать и под-
ставить значения коэффициентов А',
А", В', В".
Множитель при Ux в последнем
уравнении, очевидно, равен 1/А,
где А — коэффициент результирую-
щего четырехполюсника (рис.
2-61,а)
Аналогично могут быть опреде-
лены и другие коэффициенты экви-
валентного четырехполюсника, по-
сле чего цепь рис. 2-61,а может
быть рассчитана при любых С/2> А
по уравнениям (2-141).
Подобное решение, совершенно
ясное по общему ходу и требующее
отдельного вычисления коэффициен-
тов по очень простым формулам,
несоизмеримо проще прямого реше-
ния системы четырех контурных или
узловых уравнений, не говоря уже
о решении системы, состоящей из
восьми уравнений Кирхгофа.
5. Метод пропорциональных ве-
личин и его развитие. Применяя ме-
тод пропорциональных величин к
сложной последовательно-парал-
лельной цепи (§ 2-1), мы, по суще-
ству дела, решали одну часть урав-
нений цепи независимо от другой, а
1 Для частного случая г'а = г'ъ =
== 2г"с = Rlt г"а == г"ъ = 2r'c = R2 (обозна-
чения рис. 2-61,а) имеем
t72 = f7i(l + ₽2)/(l + 4g + P),
где р =
затем согласовывали напряжение
в начале U и значение £7', найден-
ное из расчета остальной части це-
пи при произвольно выбранном зна-
чении тока в конце (/')•
Аналогичный метод может быть
применен и к некоторым более
сложным задачам. Ограничимся од-
ним примером. Расчет цепи часто
значительно упрощается, если пре-
небрегать внутренним сопротивле-
нием источника, полагая, что на
входе рассматриваемой цепи напря-
жение известно: ивх=Э (см, при-
меры 2-15 и 2-21).
Пусть при этом найдены токи In
и напряжения Z7n.
Если источник питания содержит
внутреннее сопротивление (г<), на-
пряжение на его зажимах, т. е. на
входе рассматриваемой цепи
(рис. 2-62),
Usx = 9-/ri = 9-^-ri,
г ВХ
где ток источника представлен че-
рез входное сопротивление питае-
мой им цепи. Из этого уравнения и
рис. 2-62 следует, что
где
^вх = 5г],
Ц—ГвхЖх + Гг).
В силу линейности цепи все дей-
ствительные токи In и напряжения
Un в т] раз отличаются от найден-
ных из расчета, производившегося
76
без учета внутреннего сопротивле-
ния источника:
In
6. Суперпозиция эквивалентных
источников. Этот метод часто ока-
зывается очень эффективным. Нач-
нем с рассмотрения конкретного
случая. Пусть расчету подлежит
цепь рис. 2-63,62 с четырьмя узлами
и шестью ветвями. Для ее расчета
нужно решать систему трех узловых
или контурных уравнений.
Расчет значительно упрощается,
если заменить токи каких-либо двух
ветвей токами эквивалентных ис-
точников, например
и /5 = ^5.
Все токи и напряжения в дейст-
вительной цепи можно найти пу-
тем суперпозиции соответствующих
значений, найденных при действии
только одного первого источника
рис. 2-63,6 (ветвь второго источни-
ка разомкнута) и при действии од-
ного второго источника рис. 2-63,в
(ветвь первого разомкнута). Подле-
жащие расчету схемы оказываются
элементарно простыми. )
При действии только источника
Л (рис. 2-63,6)
U ВБ = ' U Б В =
*1^ (G “Г" ^4) 0*1 Н“* Г3)/R ===: А^55 ’
и *^5 0*2^3 zr::z А 7*56 >
где ^ = г1 + г2 + г3 + г4-
При действии только источника
J6 (рис. 2-63, в)
U := 0*2^з ' ? 1^4)/== *Л^6 5’
и"АГ = Л (и + G) 0*3 + = Л^бб •
Нетрудно увидеть, что r56=r6S
в соответствии с принципом взаим-
ности. По принципу суперпозиции
в действительной цепи
[7 4-J7" —
Ы5 ЬВ « ЬВ
----J Г - I.. J г
‘V 55 1 J6'65’
u.r = U’„+U"„ =
-- - "Т- 'A^rr •
5 5о 1 6 bb
Если произвольно выбранные то-
ки источников совпадают с дейст-
вительными, то одновременно эти
напряжения по закону Ома пред-
ставляются равенствами
TJ — Г г . Т] _____________ Ъ _____ Т г
БВ ‘'б'б’ АГ--------------*^6 */б,б
Подставляя эти условия в выра-
жения, полученные путем суперпо-
зиции, получаем после элементарных
преобразований систему двух урав-
нений:
Эб = —15^56 Н-1б(^6б+^б) j
О = —15 (Г55 + / 5) +16^65-
Из их решения находим:
7б=‘Эб (/"5 + ^55) /В,
где D——г25б+ (Гбб+^б) (гее+^б) —
определитель системы коэффициен-
тов при /5 и Jq,
В последних формулах принято
во .внимание, что ^56=^65.
Совершенно аналогично можно
любые два напряжения в заданной
цепи представить в виде предпола-
гаемых источников э. д. с.,^скажем
31 и Э2. Токи ветвей с этими источ-
никами /1 и h легко найти путем
суперпозиции. В этом случае расчет
цепи упрощается, поскольку при
Рис. 2-63.
77
31=0 (или Э2=0) соответствующие
узлы объединяются. Найденные та-
ким путем токи (выраженные через
31 и 32) должны быть согласованы
по уравнениям для действительных
токов и напряжений.
С точки зрения теории линейных
уравнений этот метод представляет
собой решение системы уравнений
по частям с последующим согласо-
ванием найденных решений. При
надлежащем .выборе эквивалентных
источников он очень упрощает рас-
четы. К тому же уравнения состав-
ляются для простых цепей первого
и второго режима часто по хорошо
известным шаблонам (например,
две параллельные ветви на схемах
рис. 2-63,6 и в) и легко проверя-
ются.
В более сложных цепях может
оказаться целесообразным вводить
три эквивалентных источника. При
этом, конечно, получаются и три
уравнения связи, из которых долж-
ны ‘Определяться три тока источни-
ков (или три э. д. с.).
7. Метод определяющих токов.
Этот метод, разработанный Н. Г.
Максимовичем, -часто оказывается
наиболее эффективным, особенно
в случае расчета сложных цепей.
Сущность метода состоит в сле-
дующем.
В сложной электрической цепи
часто можно выбрать несколько
ветвей N так, чтобы токи во всех
остальных ветвях -определялись че-
рез токи этих ветвей из последова-
тельно составляемых простейших
уравнений для узлов или контуров.
Токи в этих выбранных ветвях и на-
зывают определяющими.
При надлежащем выборе опре-
деляющих токов каждый новый не-
известный ток находится из одного
единственного уравнения, содержа-
щего, кроме искомого, только опре-
деляющие токи и ранее уже найден-
ные неизвестные. Таким путем токи
во всех ветвях оказываются выра-
женными только через определяю-
щие токи.
Для цепи с числом ветвей В
можно составить столько же (В)
независимых уравнений по законном
Кирхгофа. Пусть N — число опреде-
ляющих токов. В таком случае для
определения всех остальных токов
потребуется
К=В—N
уравнений. Следовательно, неис-
пользованным остается именно
столько уравнений'
B—K=N,
сколько в цепи определяющих то-
ков.
Составляя уравнения для №
оставшихся неиспользованными
узлов и контуров, получим систему
из N уравнений, достаточную для
отыскания значений N определяю-
щих токов.
Применим изложенный метод к
конкретной цепи, например к толь-
ко что рассмотренному мосту рис.
2-63,я.
Рекомендуемые вспомогательные
обозначения и представление ре-
зультатов в таблице станут понятны
из примера.
На рис. 2-64 показана рассчиты-
ваемая цепь; кружком обведены то-
ки, принятые в качестве определяю*
щих. Индексы сопротивлений совпа*
дают с индексами токов. Узлы обо*
значены большими буквами, а кон*
туры — цифрами. Выразим все токи
через определяющие Ц и 1q:
По уравнению для узла А
h=h—
по уравнению для контура /
h— (Дгз—hr 1)/Гб.
Эти равенства и дальнейшие вы-
ражения для токов собраны в таб-
лицу, где обозначены контуры и уз-
Рис. 2-64.
78
лы, для которых пишется соответст-
вующее уравнение; решение каждо-
го уравнения представлено в той же
таблице. Затем каждое из решений
приводится к виду
1п~ Сп 4“^тг-^1 4“ Мб.
Значения сп, ап и Ьп представ-
лены в той же таблице, где допу-
скается для краткости выражение
этих коэффициентов через ранее
найденные; например, написано,
что
Я2=1— а$,
где я5 =— (п4-Гз)Лб, как видно из
предыдущей строки таблицы.
В приведенной таблице
06 =—(а3гз4-щг4)/г6;
Ь6=—’(ЬзГз + Ь^/гв,
значения аз, а4, ..., &з, Ь4 содер-
жатся в предыдущих строках той
же таблицы.
При расчете изложенным мето-
дом в качестве определяющих вели-
чин могут быть .взяты не только то-
ки ветвей, но и напряжения или по-
тенциалы узлов; принципиально
можно принимать в качестве опре-
деляющих величин и контурные то-
ки, выражая потом остальные кон-
турные токи через определяющие
Определяющие величины — токи ветвей Л и Z6
Ток Узел • Кон- тур Уравнение Коэффициенты в уравнении In==Cn + anIj- + Ьп!* Числовой результат
п Сп ап Ь„
/» А — 3 0 —1 1
/8 — 1 Лн)/г8 5 0 (Г 1+ГзУГ5 r3frb
1г Б — Л=Л — /« 2 0 1—#5 -Ьз
ц В — ^4 — Гз 4 0 Ь3 4*
I' / — 3 -^6 ~ ( Iзгз —/л+ЭбУг б 6 + Э^/гй W з 4 Г6 •—^3Г3 ^4^4 г.
/1 — 2 ^1 = ( 2 “~^бгб + Эб)/Г1 1 Э^/Гг — д2г2 Г1 —ЬзГг — г, Г1
После того как определены вы-
ражения для всех токов, подводит-
ся черта и составляются уравнения
для узлов и контуров, не использо-
ванных в предыдущих четырех
строках. Речь идет, конечно, только
о тех узлах и контурах, для которых
возможно составление независимых
уравнений (бессмысленно , состав-
лять уравнение для узла Г, так как
оно оказалось бы следствием пре-
дыдущих) .
Эти добавочные уравнения ре-
шаются относительно определяю-
щих токов.
Полученная в итоге система
уравнений:
1ъ—Эъ1гь+аъ11 +'&б^б5
Ii — del/'i + aili + bile
позволяет найти значения опреде-
ляющих токов.
(само собой разумеется, что при
этом бессмысленно применять урав-
нения для узлов).
8. Расчетные столы, модели и
цифровые машины. Если расчет
не требует особой точности и вмес-
те с тем достаточно сложен, то,
безусловно, следует обращаться
к составлению модели цепи: под-
бирая требуемые значения элемен-
тов цепи (источников питания и со-
противлений) и включая измери-
тельные приборы, легко найти инте-
ресующие значения напряжений и
токов.
При этом можно все напряже-
ния и токи в модели пропорцио-
нально увеличивать или уменьшать-
по сравнению с их значениями в дей-
ствительной цепи. Очевидно, что
уменьшение токов и напряжений
в т раз приводит к уменьшению
79s
мощностей в m2 раз. Выбор мас-
штабного множителя т определяет-
ся условиями задачи.
Широкое распространение полу-
чили так называемые расчетные
столы, в которых заранее подготов-
лен большой набор регулируемых
сопротивлений и источников, а так-
же аппаратура для осуществления
нужных измерений и соединений.
Следует заметить, что, пользу-
ясь расчетными столами и моделя-
ми, часто оказывается очень важ-
ным иметь в виду общие свойства
линейных цепей, особенно когда ис-
следуются различные режимы рабо-
ты цепи.
Точность измерительных прибо-
ров, регулируемых сопротивлений и
источников на хорошо изготовлен-
ных столах и моделях имеет тот же
порядок, что и точность хорошей
счетной линейки.
В тех редких случаях, когда при
расчете сложных цепей требуется
повышенная точность, следует об-
ращаться к расчетам на быстродей-
ствующих цифровых машинах, уже
получивших достаточное распро-
странение.
Таблица 1
Основные характеристики проводниковых материалов при 20° С
Название Плотность, Температура Удельное электрическое Температурный коэффи-
материала г]см? плавления, °C сопоотивление, ом-ммР/м циент сопротивления, 1/°С
Алюминий 2,7 657—669 0,0263—0,0288 0,00403—0,00429
Вольфрам 19,3—20,0 3 370—3 400 0,053—0,055 0,0040—0,0050
Латунь 8,4—8,7 900—960 0,0310—0,0790 0,0020
Медь 8,71—8,89 1 083 0,01752—0,01820 0,0040
Никель 8,8—8,9 1 452 0,0703—0,0790 0,0060
Сталь 7,8 1 400—1 530 0,103—0,137 0,0057—0,0062
Серебро 10,5 960,5 0,0160—0,0162 0,0034—0,0036
Чугун 7,2—7,6 1 200 0,501—0,40 0,0009—0,0010
Константан 8,7—8,9 1 260—1 275 0,45—0,52 5-Ю-6
Манганин 8,14—8,4 920—960 0,42—0,50 (3—6)-10-5
Нихром 8—8,4 1 380—1 530 1,02—1,36 (0,08—0,17). 10-3
Фехраль 7,2—7,4 1 450—1 480 1,1—1,25 0,05-10-3
Таблица 2
Основные характеристики диэлектриков при 20° С
Название Удельное сопротивление е при частоте tg & при частоте Электриче- ская проч- ность, кв/мм
объем- ное, Ьм-м поверхностное, ом, при относи- тельной влаж- ности 100 гц 100 Мгц 1 кгц 1 Мгц 3*Ю3 Мгц
60% 90%
Бакелит 109 1012 1010 4,9 3,7 0,03 0,04 24
Бумага 1010 ю11 10’ 3,7 — 0,009 .— _— 16
Вода 5-103 — — —— 77 Большой 0,03 0,15 —.
Кварц 10п 1010 106 3,8 3,8 0,001 0,005 0,0001 8
Плексиглас 1014 1016 Ю16 3,4 2,6 0,06 0,006 40
Полихлорвинил — — — 3,2 2,8 0,01 — 0,006 32
Полистирол — 1021 — 2,55 2,52 0,0005 — 0,0025 24
Слюда 5-Ю11 1010 1018 5,4 5,4 0,002 —. >0,0003 10 до 100
Стекло пирекс 10’2 — 1011 5,6 4,9 0,01 —. 0,01 14
Трансформа- торное масло 1011 — — 2,24 2,18 <0,001 0,0005 — 12
РАЗДЕЛ II
ЦЕПЬ ПЕРЕМЕННОГО ТОКА
(установившийся режим)
ГЛАВА ТРЕТЬЯ
ВВЕДЕНИЕ В ТЕОРИЮ ПЕРЕМЕННЫХ ТОКОВ
3-1. ОБЩАЯ ХАРАКТЕРИСТИКА
ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
Усложнения, обусловленные пе-
ременностью тока !. Процессы в элек-
трической цепи значительно услож-
няются, когда величины, характери-
зующие ее состояние, — ток, напря-
жение и т. п.,—изменяются во вре-
мени. Так, при переменном напря-
жении ис на конденсаторе его заряд
q=ucC
также изменяется.^При этом в вет-
ви с конденсатором (рис. 3-1, см.
Рис. 3-1.
также § 1-3) проходит ток, подво-
дящий заряды ±q к его электро-
дам:
i=dq[dt=Cduddt. (3-1)
При переменном токе сопровож-
дающее его магнитное поле (см.
§§ 1-10, 1-11) также изменяется во
времени. Но изменяющееся магнит-
ное поле в соответствии с законом
электромагнитной индукции (закон
Фарадея) наводит в электрической
цепи э. д4 с.
э=— dW/dt, (3-2)
1 Заметим сразу же, что, говоря о «пере-
менном токе, обычно имеют «в «виду приме-
нимость сказанного и к другим переменным
величинам, характеризующим ’электриче-
скую цепь, т. е. к напряжению, заряду, маг-
нитному потоку и др.
где Т — магнитный поток, сцеплен-
ный с рассматриваемым контуром,
т. е. с контуром, для которого опре-
деляется э. д. с.; в простейшем слу-
чае одинакового потока Ф, сцеплен-
ного с каждым из w витков контура
(рис. 3-2), потокосцепление
ЧГ=^Ф. (3-3)
Периодические и непериодические
переменные величины. В этом разде-
ле, говоря о переменном токе, мы
ограничимся рассмотрением перио-
дически изменяющихся величин,
определяемых условием
при Г—const. (3-4)
Эта формула" говорит о том, что
весь цикл изменений рассматривае-
мой величины повторяется через ин-
тервал времени Т, называемый п е-
р иодом, как это иллюстрирует
рис. 3-3.
Величина, обратная периоду, на-
зывается частотой:
f—д. (3-5)
Частота измеряется в герцах (гц).
Периоду Т=0,02 сек соответствует
частота f=50 гц — стандартная
6 К, М. Поливанов
81
lf(t)
t
Рис. 3-3.
частота в электроэнергетических
системах; .периоду Т=1 мксек=
=10“6 сек соответствует частота
f = 1 Мгц (.мегагерц) =406- гц.
Простейшие периодические
функции — это простые гармониче-
ские колебания, т. е. косинусоидаль-
но (или синусоидально) изменяю-
щиеся величины (рис. 3-4):
ся амплитудами и фазами гармони-
ческих составляющих различных ча-
стот. Такие функции будут рассмот-
рены в последней главе этого раз-
дела.
Сумма простых гармонических
функций одинаковой частоты всегда
может -быть представлена как одна
простая гармоническая функция
той же частоты, амплитуда и фаза
которой определяются хотя бы пу-
тем прямых тригонометрических
преобразований (icm. также гл. 4):
F™icos(coi/+ai) +Fm2cos(-co-/+a2) =
—cFmcos(G)»/+ia),
где
f (0 = Fm cos (erf + а) =
Fm------(FmiCOS j— J"fTjgCOS
= Fm sin + а (3-6)
+ (Fmi sin a, -|- Fm2 sin a2)2 ,
где f (t) — мгновенное значе-
ние;
Fm — амплитуда;
со — угловая (круговая,
циклическая) ч а-
стота;
+ « + —фаза, вы-
ражаемая в радианах или
градусах, минутах и се-
кундах;
а; а+ ”2-начальная фаза.
В первых главах этого раздела
рассматриваются только простейшие
периодические функции, которые мы
будем называть простыми гармони-
ческими.
Любая периодическая функция
может быть представлена как сум-
ма ряда простых гармонических
функций (образующих ее спектр):
fit) =FmiCOs(W+ai) +
+Fm2cos(co2/+a2) + ... (3-7)
(см. например, рис. 9-1), имеющих
кратные частоты moi = nco.2= ..
где т, и,... — целые числа.
Спектральный состав сложной
периодической функции определяет-
tga =
Fml sin at + Fm2 sin a2
Fml cos cci+F™2 cos a2
(3-8)
Наряду с периодическими в элек-
трических цепях часто приходится
иметь дело с переменными величи-
нами, обусловленными воздействием
непериодических или апериодиче-
ских возмущений — например, вклю-
чение постоянного напряжения в
цепь с сопротивлением и емкостью
г, С (рис. 3-5,а) или воздействий
одиночного импульса или серии не-
периодических импульсов в цепи г, L
(рис. 3-5,6). Апериодические про-
цессы в линейных цепях, вызы-
ваемые включением и выключе-
нием источников питания иди из-
менением режимов цепи, называют
переходными процессами.
Они подробно рассматриваются в
разделе III; там же рассмотрена
Рис. 3-4.
82
и реакция цепи на импуль-
сы.
При включении источ-
ника с периодическим на-
пряжением в цепи тоже не
сразу устанавливается пе-
риодический режим, как это
показано на рис. 3-5,в для
тока в цепи г, L. Лишь че-
рез некоторое время ток
становится периодическим Ч
В линейных цепях при
гармоническом напряжении
источников с течением вре-
мени всегда устанавливают-
ся гармонические токи и на-
пряжения, имеющие часто-
ту напряжения источников
питания; в частности, по-
стоянный ток устанавли-
вается при постоянном на-
пряжении источников, для
которых можно считать
со = 0. Такой режим и
называют установив-
шимся.
Апериодические состав-
ляющие возникают только
вслед за изменением режи-
ма цепи и обычно быстро
затухают.
Причины распространен-
ности переменного тока. При-
менение Переменных токов,
усложняя протекающие про-
цессы, представляет и но-
вые возможности для ра-
боты электрических цепей.
Так, наведение э. д. с. из-
меняющимся магнитным по-
током, сопровождающим
переменный ток, позволило
сконструировать наиболее
простые электрические ма-
шины— генераторы и дви-
гатели.
В электроэнергетике широчай-
шее распространение получил имен-
но переменный ток благодаря воз-
можности легко преобразовывать
напряжение, при котором передает-
ся электрическая энергия по ли:
ниям передачи переменного тока.
Это преобразование происходит
в тр ансформ атор ах, отличающихся
простотой, надежностью и высоким
1 Об индуктивности (L) в электриче-
ской цепи см. § 3-4, 3-5.
в)
Рис. 3-5.
коэффициентом полезного дей-
ствия.
На рис. 3-6 схематически изо-
бражен изобретенный Яблочковым.
(1876 г.) трансформатор. В нем
связь между левой и правой частя-
ми цепи осуществляется общим маг-
нитным потоком Ф, замыкающимся
в стальном сердечнике. Этот поток
охватывает первичную (слева) и
вторичную (справа) обмотки, поме-
щенные на сердечник.
6*
83'
Рис. 3-6.
Изменяющийся поток наводит в
каждой из обмоток э. д. с., пропор-
циональную числу ее витков,
э1=—widCbldt, э2=—w2d&ldt.
(3-9)
Отношение этих э. д. с. равно отно-
шению числа витков о-бмоток.
Напряжение на зажимах транс-
форматора практически равно на-
водимой э. д. с. (^1=31, ^2=32), а
мощность, рассеиваемая (теряемая)
•в трансформаторе, очень мала; она
;может составлять доли процента от
мощности, передаваемой через
трансформатор. В таком случае
можно считать, что для нормально
работающего трансформатора про-
изведение тока и напряжения на
входе равно такому же произведе-
нию на выходе. Другими словами,
если напряжение на выходе транс-
форматора повышается, скажем, в
100 раз, то во столько же раз умень-
шается ток.
Простота устройства трансфор-
маторов и малость теряемой в них
энергии позволяют в процессе пере-
дачи энергии несколько раз изме-
нять напряжение. Так, например,
типичной можно считать такую си-
стему (рис. 3-7): генератор (Г) вы-
рабатывает энергию при одном на-
пряжении 1, скажем, 11 кв, которое
значительно повышается первым
трансформатором (Тр1), например,
до 110 кв; при этом высоком напря-
жении энергия передается по длин-
ной, линии и поступает во второй
трансформатор (Тр'2) после чего
энергия распределяется по город-
ской кабельной сети при сниженном
напряжении, подходящем для раз-
ветвленной кабельной сети (напри-
мер, 6,6 Кв); наконец, после треть-
1 Здесь названы напряжения вУ"2 раз
меньше соответствующих амплитуд (см. ни-
же § 3-3).
11 кв
110 кв
Рис. 3-7.
его трансформатора (ТрЗ) энергия
поступает к потребителю при низ-
ком напряжении (например, 220 в.)
При рассмотренном соотношении
напряжений ток в линии передачи
оказывается почти в 500 «раз мень-
ше тока, поступающего к потреби-
телю электроэнергии, а потери в
проводах пропорциональны квадра-
ту тока (закон Джоуля—Ленца).
Из этого примера видно экономиче-
ское значение трансформаторов.
Конечно, в приведенной схеме
очень упрощены черты действитель-
ной электроэнергетической системы:
в ней не показаны возможные мно-
гочисленные разветвления, связи
с несколькими генераторами и т. п.
На самом деле количество транс-*
формаций часто бывает значитель-
но больше трех, а наивысшее напря-
жение длинных линий может прево-
сходить 500 кв. В современных си-
стемах, имеющих, вероятно, боль-
шое -будущее, встречаются и взаим-
ные преобразования переменного и
постоянного тока.
Однако не только соображения
энергетики определили развитие и
распространение техники перемен-
ных токов.
Необходимость передачи гармо-
нических токов во многих случаях
связана с природой поставленной
задачи. Так, при разговоре по те-
лефону (Бел, Г876 г.) под действи-
ем звукового давления в цепи мик-
рофона возникают гармонические
токи, спектральный состав которых
подобен спектральному составу зву-
ка. Для того чтобы похожий звук
возник в приемном телефонном ап-
парате, по соединяющим проводам
должен проходить ток с таким же
(подобным) спектральным соста-
вом.
Значение телефонной едязи и
ее широкое распространение оче-
видны; по мере ее развития возни-
кало множество вопросов по теории,
переменных токов, ставились совер-
84
шенно новые электротехнические
задачи.
Новое и значительное развитие
техники переменных токов в суще-
ственно новом направлении было
обусловлено открытием и развити-
ем радиотехники (возбуждение и
прием электромагнитных волн —
Герц 1888 г.; радиопередача — По-
пов, 1895 г.).
Один из способов получения ра-
диоволн заключается в возбужде-
нии переменных токов очень высо-
кой частоты в электрической цепи,
соединенной с передающей антен-
ной. Волны, падающие на приемную
антенну, возбуждают токи в цепи
приемного устройства. Радиотехни-
ческие' цепи, часто бывают очень
сложны и содержат много линейных
и нелинейных элементов; их анализ
и расчет проводятся методами тео-
рии цепей.
Частота переменного тока. В энер-
гетических системах СССР и Евро-
пы принята стандартная частота
/=50 гц, о=2л/=314 се/с-1.
В США принята частота
f=60 гц, со-=2 л/=376 сек-1.
Более низкие частоты применяются
-сравнительно редко. Интересно от-
метить, что тепловая инерция ламп
накаливания позволяет применять
частоту приблизительно до 25 гц
(при более низкой частоте становит-
ся заметной пульсация света).
Для исследования на моделях
применяют инфранизкие частоты в
доли герца. Диапазон звуковых ча-
стот лежит приблизительно от 20az{
до 20 кгц. В радиотехнике диапазон
обычных приемников охватывает
частоты от 150 кгц до 12 Мгц.
В сверхвысокочастотной (с. в. ч.)
технике применяются частоты, из-
меряемые тысячами мегагерц (ги-
гагерцы) . Развитие с. в. ч. техники
началось с радиолокации -в годы
Великой Отечественной войны. В
дальнейшем эти частоты стали ши-
роко применяться для различных
видов связи и в технике физических
наблюдений и эксперимента. Так,
радиоастрономия, в которой прибо-
ры высокой чувствительности вос-
принимают и анализируют радио-
волны, испускаемые и поглощаемые
различными астрономическими объ-
ектами, в настоящее время произво-
дит переворот в нашем изучении
космических объектов.
Развитие электронной техники,
в особенности устройств молекуляр-
ной электроники, в которых посту-
пающие радиосигналы взаимодейст-
вуют со световым потоком, привело
к тому, что частоты с. в. ч. диапа-
зона сомкнулись с частотами тепло-
вого и даже видимого излучения.
Источники переменного тока. Ге-
нерирование переменного тока про-
мышленной частоты обычно про-
изводится вращающимися машин-
ными генераторами, часто образую-
щими один агрегат с турбинами
(турбогенераторы). Схематическое
описание такого генератора приво-
дится ниже. Для получения высоких
частот в основном применяются ге-
нераторы с электронными лампами
или полупроводниковыми триодами;
принцип работы такого генератора
излагается в § 7-4. Электронные и
полупроводниковые генер аторы
применяются и для получения очень
низких частот. Изучение устройств
с. в. ч. техники и с. в. ч. генераторов
выходит за рамки теории цепей.
О них вкратце будет сказано в
третьей части книги (Теория элек-
тромагнитного поля). Отметим, од-
нако, что ряд понятий и теорехМ об-
щей теории цепей находит примене-
ние и в технике с. в. ч.
Во многих случаях генерирова-
ние гармонически изменяющихся
электрических и магнитных величин
происходит в самих источниках сиг-
нала, подлежащего приему (микро-
фон, астрономические объекты и др.).
Существует очень много источни-
ков таких электромагнитных коле-
баний, которые рассматриваются
только как помехи для приема дру-
гих сигналов: помехи радиоприему
и связи, возникающие при атмо-
сферных разрядах (гроза), при ра-
боте электрического зажигания в
автомобильных двигателях, при
искрении щеток электрических дви-
гателей и т. п. В этих случаях зада-
ча электротехники состоит в защите
85
.от помех или в их подавлении (спе-
циальные контуры, содержащие со-
противление и емкость и подключае-
мые ^параллельно свечам электриче-
ского зажигания в автомобильном
двигателе, электрические фильтры и
др.).
Машинный генератор переменного то-
ка. Генератор состоит из неподвижного
статора и вращающегося ротора. Обычно
на роторе располагаются электромагниты
(рис. 3-8). -Их обмотка, называемая обмот-
Рис. 3-8.
кой возбуждения, питается через кольца и
щетки от источника постоянного тока. В .па-
зах статора, собранного ив тонких стальных
листов <(0,35—0,5 мм), находятся проводни-
ки обмотки статора. Они соединены друг
с другом последовательно то с переднюй, то
с задней стороны статора (эти соединения
показаны соответственно оплошными и
пунктирными линиями).
Э. д. с., наводимая в одном проводе об-
мотки статора,
9i = Blv, (3-10)
где В — радиальная составляющая магнит-
ной индукции поля, движущегося относи-
тельно провода;
I — активная длина провода,
v — скорость перемещения магнитного
поля относительно провода.
Закон изменения э. д. с. определяется
изменением значения индукции В непосред-
ственно под проводом, поскольку I и v
постоянны.
Для получения синусоидальной э. д. с.,
к чему обычно стремятся, нужно, чтобы рас-
пределение магнитной индукции по окруж-
ности статора было близко к синусоидаль-
ному.
За один оборот ротора происходит р
полных периодов изменения э. д. с., где
Р — число пар полюсов. Если ротор делает
п оборотов в минуту, то получается рп пе-
риодов в минуту и, следовательно, частота
r-SF- о-11»
Для получения частоты f=50 гц генераторы
с одной парой полюсов должны делать
3 000 об]мин, с двумя парами полюсов —
1 500 об!мин, и т. д. Для обеспечения меха-
нической прочности при таких больших ско-
ростях вращения роторы выполняют без вы-
ступающих полюсов.
В генераторах крупных тепловых и ги-
дростанций амплитуды тока достигают де-
сятков тысяч ампер.
Высокочастотные .машинные генераторы
по конструкции отличаются от рассмотрен-
ных. Они изготовляются для частот, дости-
гающих 8—10 кгц, и применяются наряду
с ламповыми генераторами в электротерми-
ческих установках. Переменные токи более
высоких частот получают исключительно от
электронных -(ламповых) или полупроводни-
ковых генераторов.
Переменный ток в микрофонной цепи.
В одном из распространенных типов микро-
фона (упрощенная схема показана на
рис. 3-9,а) между металлическими электро-
дами а, b находится угольный порошок,
благодаря которому сопротивление между
электродами зависит ют избыточного давле-
ния р на электрод а (мембрана); в первом
приближении можно считать, что
Га&=Г0(1—
где rQ и k — постоянные.
Последовательно с микрофоном через
провода телефонной линии включен репро-
дуктор звука — телефон. Он состоит из фер-
Рис. 3-9.
86
ромапнитной мемб-равы, притягиваемой по-
стоянным магнитом \(N—S), (на который на-
несена обмотка. Ток в обмотке усиливает
магнитную индукцию В, которую можно
представить уравнением
В=Bq (1 + ci),
где Во и с — постоянные.
Сила, действующая на мем>брану, про-
порциональна квадрату индукции:
F тВ2 — тВ2 [1 + 2d + (с/)2]
тВ% + 2тсВц1.
Приближенное равенство составлено для
условия
<(ci)2<l,
которое обязательно должно выполняться
при передаче телефонного разговора.
При включении в телефонную цепь ис-
точника с постоянным напряжением U ток
в цепи
U U 7
Ro
Здесь Во — постоянная составляющая со-
противления всей цепи, а ур — относитель-
ное (уменьшение сопротивления, обусловлен-
ное звуковым давлением р. Приближенное
равенство справедливо при |ур|<^1.
Допустим, что состав звука, восприни-
маемого !микрофоном, характеризуется дву-
мя гармониками переменного давления
(рис. 3-9,6): 44
р=Рт1 sin со/—Р m2 Sin 2со/.
В таком случае ток
« 5= (1 +уРт1 sin at — '(Рт! sin 2at) =
= /о +1 ml sin at — Im2 sin 2<oZ
содержит переменные составляющие, про-
порциональные звуковому давлению у ми-
крофона, а следовательно, те же составляю-
щие содержит сила F, действующая на мем-
брану репродуктора. Так работает телефон.
В приближенном расчете, приведенном
здесь, не учтены ни влияние э. д. с., наво-
с димОй переменным магнитным потоком, ни
токи, ответвляющиеся на зарядку емкости
между проводами. Кроме того, при делении
и возведении в квадрат отброшены слагае-
мые, пропорциональные высшим степеням р
и i. Их наличие приводит к появлению но-
вых гармонических составляющих, иска-
жающих тембр передаваемого звука. Дей-
ствительно, пользуясь простыми тригономе-
трическими преобразованиями, легко найти,
что
12 — Zo+j2 Uml + + 2Г</mi sin at —
I mil m2 COS (fit —• 2/o^7n2 sin 2(ft —•
1 2
2 m\ COS 2co/ Irad m2 ^OS 3(ot —
~T7m2cos4“t
т. e. что квадрат тока содержит гармони-
ческие составляющие с частотами Зсои 4 со.
При этом искажается спектральный состав
передаваемого сигнала.
3-2. ПЕРЕМЕННЫЙ ТОК
В ЦЕПИ г, С
Процесс заряда и разряда кон-
денсатора. Когда источник перемен-
ного напряжения и замкнут на кон-
денсатор С-(рис. 3-10,а), в его цепи
идет переменный ток i.
Представим себе, например, не-
нагр уженную (рис. 3-10,6) кабель-
ную сеть, присоединенную к генерато-
ру переменного напряжения. Между
изолированными друг от друга про-
водами сети образуется электриче-
ское поле, а на проводах появляют-
ся избыточные заряды: положитель-
ный +q на проводе более высокого
потенциала и отрицательный —q на
проводе более низкого потенциала.
При этом заряд равен произведе-
нию емкости и напряжения:
q=ucC=uC. (3-12)
- Изменение заряда -сопровождается
током
i=dq^dt = C duc/dt =
— Cdufdt. (3-13)
Полагая напряжение заданным
«=[7w=cosco^ (3-14)
и выполняя дифференцирование, на-
ходим ток
i — — CwUrn sin (ot =
cosf 4----у Y (3-15)
\ z J
87
Рис. 3-10.
Ток, выражаемый гармонической
функцией той же частоты, что и на-
пряжение, имеет амплитуду
1т — С (jylJт (3-16)
и опережает напряжение по фазе на
угол л/2.
Заметим, что эта формулировка
применима независимо от значения
начальной фазы напряжения на
конденсаторе.
В случае разветвленной кабель-
ной сети емкостный ток может быть
довольно большим. Например, при
емкости кабельной сети С=10“5 ф
(общая протяженность кабельной
сети ~25 кж), напряжении Um=
=9,5 кв и частоте f=50 гц ампли-
туда тока /т=29,8 а.
На рис. 3-10,в показаны графики
•мгновенных значений тока и напря-
жения. При этом положительные
значения напряжения, согласно с
обозначением на рис. 3-10,а, соот-
ветствуют интервалу времени, в те-
чение которого потенциал верхнего
электрода выше, чем потенциал
нижнего. Положительные значения
тока согласно с обозначением на
рис. 3-10,а соответствуют притека-
нию положительного заряда к верх-
нему электроду.
Простые соображения о связи
функции и ее производной делают
понятным то обстоятельство, что ток
равен нулю при экстремальных зна-
чениях напряжения и достигает экс-
тремальных значений (±/т) в мо-
менты, когда напряжение хотя и
равно нулю, но изменяется с наи-
большей скоростью.
Энергия поля заряженного кон-
денсатора
и2С qu q2
= (347)
Изменение энергии поля сопря-
жено -с обменом энергией между ге-
нератором и заряжаемым кабелем.
Мощность, отдаваемая генератором
в каждый момент времени, равна
произведению тока и напряжения:
p = ui. (*3-18)
Подставляя в эту формулу выраже-
ние для тока из (3-15) и сопостав-
ляя результат с выражением (3-17)
легко увидеть, что мощность равна
скорости нарастания энергии поляг
dw3 d fCu2\ п du 1ПХ
^T) = uC~dt- (3-19>
Пользуясь любым из приведенных
выражений мощности, найдем, что
она пульсирует с двойной частотой:
p — ui = — U2 Се) cos cot sin cot=
л тп
и2 с
~-------- co sin 2<оЛ (3-20)
Очевидно, что рассматриваемая
мощность, т. е. мощность, отдавае-
мая генератором, отрицательна в те
моменты, когда напряжение на кон-
денсаторе убывает по абсолютной
величине. В течение соответствую-
щего интервала времени конденса-
тор разряжается, отдавая свою
энергию генератору. Мощность, от-
даваемая генератором, положитель-
на, когда напряжение на конденса-
торе возрастает по абсолютной ве-
личине. В течение соответствующе-
го интервала конденсатор заряжает-
ся, увеличение энергии его поля
88
происходит за счет мощности, по-
ступающей от генератора.
-Графики энергии и мощности
представлены на рис. 3-10,г. Следу-
ет обратить внимание и на то об-
стоятельство, что мощность положи-
тельна, когда ток и напряжение
имеют одинаковые знаки, и отрица-
тельна, когда знаки противополож-
ны, и обращается в нуль, когда рав-
ны нулю или ток или напряжение.
По прошествии периода энергия
конденсатора принимает прежнее
значение, поэтому очевидно, что
•средняя мощность, отдавае-
мая генератором за целый период,
равна нулю:
1 т
P=-~^pdt=0. (3-21)
0
Здесь, в соответствии о общепри-
нятым в теории переменных токов,
средняя (за период) мощность обо-
значена большой буквой Р. Конеч-
но, равенство нулю средней мощно-
сти непосредственно -следует из ее
представления в виде синусоиды.
Цепь г, С. Рассмотрим теперь
цепь, содержащую сопротивление,
включенное последовательно с кон-
денсатором (рис. 3-1-1,а). Такое
включение очень часто применяет-
ся в цепях с электронными лампа-
ми: конденсатор С, изолируя две ча-
сти цепи по постоянному напряже-
нию, позволяет передавать сигналы
из одной части цепи в другую.
Для иллюстрации на рис. 3-11,6 показан
усилитель сипн-алов с 'двумя электронными
лампами Лх и Л2. При подаче переменного
напряжения на сетку ci первой лампы на ее
аноде «1 появляется переменное напряже-
ние Одновременно на аноде существует
и постоянная составляющая напряжения,
обычно' значительно превосходящая пере-
менную. Это постоянное напряжение полу-
чается от -источника питания, присоединен-
ного к узлам Л, О. Для того чтобы пере-
дать на сетку с2 второй лампы только пере-
менную слагающую напряжения, между
анодом ai первой лампы Л^ и сеткой с2
лампы Л2 включается конденсатор С. При
этом между сеткой и катодом лампы Л2
включается дополнительное сопротивле-
ние г. Переменный ток /, проходя через
сопротивление г, создает на нем напря-
жение uT=‘ir, которое и представляет собой
переменную слагающую напряжения на сет-
ке второй лампы. Для того чтобы найти
связь между переменными напряжениями
Wi и иг, надо рассчитать цепь С, г, обведен-
ную пунктиром на рис. 3-11,6 и соответст-
вующую схеме рис. 3-11,а.
Допустим, что переменное напряже-
ние на конденсаторе
UC=UCm^ соЛ (3-22)
В таком случае в рассматриваемой
цепи проходит ток
i-CdUc
dt
=CwUCmsm (<^ + ~2
— C<aUCtn COS wt = Im COS wt. (3-23)
Зная ток, легко найти напряже-
ние на сопротивлении г непосред-
ственно по закону Ома:
ur=ri=rlm cos at. (3-24)
Напряжение на входе цепи г, С
u = Umcos (wt-[-<?) = иг-\-ис —
= Imr COS wt sin wt =
- Imr cos wt -|- cos
(3-25)
В последнем слагаемом ампли-
туда напряжения на конденсаторе
выражена через амплитуду тока
(3-16).
(®* ~ y) •
89
Путем прямых тригонометриче-
ских преобразований (3-8) можно
найти, что
Um —lm j/r2 4- —
(3-26)
(3-27)
Пусть, например, С=/10-9 ф, г=
='Г04 ом, <о=’1,2-5 • 105 сект1 (частота
/=20 кгц). В таком случае при
входном сигнале с амплитудой
Um — 1 мв в цепи пойдет ток с ам-
плитудой
Г -- [J I ( г2 I 1 у/2 —
= 0,785- 1СГ7я,
напряжение на сопротивлении г бу-
дет иметь амплитуду Urm=Imr=
— 0,785 мв, а напряжение на емко-
сти— t/Cm=-Zm/coC=-0,980 мв.
Арифметическая сумма ампли-
туд напряжений на двух последо-
вательно включенных элементах це-
пи г и С оказывается больше ам-
плитуды общего напряжения:
U rmA~ U1 >76 MB'^>lU— 1 мв.
Это совершенно естественно, так
как в каждый момент складывают-
ся не амплитуды, а мгновенные зна-
чения, для которых по исходному
предположению выполняется урав-
нение (3-25), справедливое во всех
случаях, когда напряжение на эле-
ментах цепи может определяться
как соответствующая разность по-
тенциалов.
Определив для приведенного при-
мера значение начальной фазы об-
щего напряжения <р = —Sl^O7, по-
лезно построить график мгновенных
значений всех трех напряжений
в соответствии с уравнением (3-25).
На этом же примере отчетливо
видна роль высокой частоты. Если
бы напряжение на входе цепи име-
ло частоту 50 гц, то амплитуда на-
пряжения на сопротивлении Urm=
= Imr составляла бы ничтожную до-
лю амплитуды входного напряже-
ния.
Рассеивание энергии в сопротив-
лении г. Когда переменный ток про-
ходит через сопротивление г, в нем
рассеивается мощность, определяе-
мая в каждое мгновение законом
Джоуля — Ленца
р == uri = i2r.
(3-28)
Средняя за период мощность
равна среднему значению квадрата
тока (/2), умноженному на сопро-
тивление г:
т
Р = ^ j prdt=i2r.
6
(3-29)
Но квадрат тока всегда положи-
тельная величина, поэтому и сред-
нее значение квадрата i2 также по-
ложительно.
Сравнивая энергетические соот-
ношения при заряде конденсатора
и при переменном токе в сопротив-
лении, следует обратить внимание
на следующее. В первом случае
происходят обратимые преобразова-
ния, т. е. энергия, сообщенная кон-
денсатору при повышении напряже-
ния, отдается им при снижении на-
пряжения. Во втором случае проис-
ходит необратимое рассеяние энер-
гии — преобразование электромаг-
нитной энергии в тепловую.
Для простого гармонического
тока
p — I2 г cos2 со/ =
= г ~ (1+ COS (3-30)
Но среднее значение гармониче-
ской функции cos2cln£ за период рав-
но нулю, поэтому средняя мощность
(3-31)
3-3. ДЕЙСТВУЮЩЕЕ (СРЕДНЕЕ
КВАДРАТИЧНОЕ) ЗНАЧЕНИЕ
ПЕРИОДИЧЕСКИХ ВЕЛИЧИН
Корень квадратный из среднего
значения квадрата называют сред-
ним квадратичным. Среднее квадра-
тичное значение'тока
90
i2dt
(3-32)
среднее квадратичное значение на-
пряжения
и т. п.
. Как видно из (3-29) и (3-31), для
простых гармонических функций сред-
нее квадратичное значение равно
амплитуде, деленной на у/ 2 :
, и =-^. (3-34)
У2 ' '
Средние квадратичные в теории
переменных токов принято обозначать
большими (прописными) буквами без
дополнительных индексов, как это
видно из приведенных выше формул.
Таким образом, вместо (3-31)
можно писать:
Р = 12г.
(3-35)
Среднее квадратичное называют
действующим или э ф ф е к т и в-
н ы м значением. Это наименование
объясняется тем, что во всех случа-
ях, когда производимое действие
пропорционально квадрату мгновен-
ных значений, как в случае закона
Джоуля — Ленца,г оно в среднем
пропорционально квадрату дей-
ствующего значения.
Например, сила взаимодействия
проводников с током i пропорцио-
нальна квадрату тока, сила элек-
тростатического взаимодействия
двух заряженных электродов про-
порциональна квадрату напряже-
ния. Поэтому в среднем эти силы
пропорциональны квадрату дей-
ствующего значения.
Постоянный ток /, проходя по
сопротивлению г, производит такое
же действие, как простой гармони-;
ческий ток с амплитудой
3-4. СОБСТВЕННАЯ ИНДУКТИВНОСТЬ
В ЦЕПИ ИЗМЕНЯЮЩЕГОСЯ ТОКА
Самоиндукция. Электрический ток обя-
зательно сопровождается магнитным полем
(§ 1-ГО). Для тороида •(кольцевого сердеч-
ника) с равномерно наложенной обмоткой
(рис. 3-12) напряженность .магнитного поля
в сердечнике (:по закону полного тока)
равна:
H=dNll,
где / — средняя длина линий магнитного по-
ля, i — ток в обмотке, N — число витков об-
мотки.
Рис. 3-12.
Магнитная индукция зависит от прони-
цаемости ц сердечника и равна:
где Цо=4л; • 10~7 в • сек!а • м — магнитная по-
стоянная системы единиц СИ.
Магнитный поток, -сцепленный с каж-
дым витком обмотки, равен Ф—Bs, где s —
сечение сердечника. Таким образом,
При изменении тока изменяется и магнит-
ный поток. При 'Этом в обмотке наводится
э. д. с. Это явление называется самоиндук-
цией ^собственный ток цепи сам наводит в
ней э. д. с.). Если магнитная проницаемость
постоянна (|i=const), то во всей обмотке,
содержащей N витков, наводится э. д. с.
N2s di
э = — NdQ/dt = — цц0 —I—
Коэффициент пропорциональности меж-
ду ©. д. с. и производной от тока называют
коэффициентом• самоиндукции
или собственной индуктивно-
стью. Принятое обозначение собственной
индуктивности —L.
Для тороида
s
L= pp-oAf2 —р.
Индуктивность в системе СИ измеряется
в генри '(1 гн='1 в*сек/а). Пользуясь этой
единицей, можно писать: • 10-7 гн!м.
Например, тороид с параметрами N=-
=400, Z=:12,5 см, s=!l см2, 1 000 обла-
дает собственной индуктивностью L —
=0,16 гн.
91
Рис. 3-13.
э
ЭаЬ~ dt
Рис. 3-14.
Индуктивность двухпроводной воздуш-
ной линии (рис. 3-13,а)
Т 1 1 а
L==l-_in--
индуктивность коаксиального кабеля (рис.
3-13,6).
т 1 Jiii Г2
L ~ 12л 1п г.
(обозначения понятны из рис. 3-13).
В электрическом контуре типа мн ого-
витковой катушки магнитное поле далеко
не всегда можно представить .в .виде пото-
ка Ф, сцепленного с каждым из витков.
Магнитный поток, сцепленный с одним вит-
ком, может отличаться от потока, сцеплен-
ного с другим (так, на рис. 3-14 видно, что
поток, пронизывающий крайние витки, мень-
ше потока, пронизывающего средние вит-
ки). В этом случае и э. д. с., наводимая
в разных витках, различна. Чтобы найти
э. д. с., наводимую во всей катушке, надо
просуммировать э. д. с., наводимую во всех
витках. Для этого вводится понятие маг-
нитного потокосцепления:-
Ф=2Фй, (3-36)
где Фа—лоток, сцепленный с одним k-м
витком, а сумма распространяется на все
витки.
Очевидно, что вся наводимая э. д. С-
(закон Фарадея)
6?Ф
3 = -^г- (3-37>
Потокосцепление пропорционально току:
Ф = Li. (3-38>
Сопоставляя (3-37) и (3-38), приходим к та-
кому выражению закона Фарадея:
di
a=-L~dt‘ (3-39>
Индуктивность в электрической
цепи. При схематическом изображе-
нии электрической цепи индуктив-
ность -представляется витками ка-*
тушки (рис. 3-15,а). При этом пред-
полагается, что область простран-
ства, в которой существует непотен-
циальное поле (индуктированная
сторонняя напряженность электри-
ческого поля), локализована внутри
катушки, обозначенной буквой Ц
как ранее внутри источников пита-
ния. Вне индуктивности, т. е. между
точками ее присоединения к цепи,
поле остается потенциальным. Об-
Рис. 3-15.
92
ращаясь к примеру тороида, пред-
ставим себе, что юн заключен в ко-
робку и что наружу выведены толь-
ко два конца его обмотки; при этом
поле вне коробки потенциально.
Очень важно понимать смысл
знака минус в формулировках зако-
на Фарадея (3-37) и i(3-39). Этот
знак говорит о том, что э. д. с. от-
рицательна при возрастании потока,
т. е. э<0 при (№1dt>-0 или dildt^Q.
Но сказанное имеет определенный
смысл только при фиксированных
положительных направлениях э, i,
V или Ф.
В законе Фарадея (3-37) поток
считается положительным, когда он
«связан с направлением обхода по
контуру правилом правоходового
винта (рис. 3-Г5,б); при этом поло-
жительное направление э. д. с. сов-
ладает с направлением обхода по
контуру (рис. 3-15,в).
Аналогично согласуются поло-
жительные направления тока и
э. д. с.; они совпадают с направле-
нием обхода контура.
Как правило, при всех расчетах
электрической цепи напряжение на
зажимах ветви, содержащей индук-
тивность, принимают равным э. д. с.,
взятой со знаком минус:
и = — э, (3-40)
как это видно из рис. 3-15,в. По-
следнее равенство соответствует
Определению напряжения как раз-
ности потенциалов
«=’фа—'Ф'ь,
при том, что в качестве уменьшае-
мого берется потенциал узла, в ко-
торый ток входит извне .(узел а),
и в качестве вычитаемого — потен-
циал узла, через который ток выхо-
дит (узел &).
Применяя (3-40) к выражениям
(3-37) й (3-39), можно записать за-
кон Фарадея уравнениями
. u=dW/dt\
u=Ldi/dt. (3-41)
Разность потенциалов (входное
напряжение) на зажимах ветви, со-
держащей индуктивность L и сопро-
тивление г (рис. 3-15,г), выражает-
ся равенством
u = Uab = tr — s = ir (3-42)
При постоянном токе наличие
индуктивности в электрической це-
пи не оказывает никакого влияния
(г di г\\
на процессы в цепи =
Энергия магнитного поля индук-
тивности. Магнитное’ поле, как и по-
ле электрическое, всегда обладает
энергией.
Найдем выражение энергии маг-
нитного поля при прохождении то-
ка i по ветви с индуктивностью L.
Если ветвь г, L (рис. 3-15,г) со-
единена с каким-то источником пи-
тания, то поступающая в нее мощ-
ность
Мощность, выражаемая первым
слагаемым (£2г), рассеивается в со-
противлении, преобразуясь в тепло.
Второе слагаемое, обусловленное
присутствием индуктивности,
__ . j di_ d f Li2\
PL=tL~dt —~dt J
может выражать собой только ско-
рость возрастания энергии, запасае-
мой в цепи, вследствие содержащей-
ся в ней индуктивности. Эту энер-
гию естественно отождествлять с
энергией магнитного поля индук-
тивного элемента цепи. Из послед-
него равенства следует, что эта
энергия
и>м = £-Д (З-44)
Закон Ленца. Выведенное здесь
выражение энергии индуктивности
(3-44) позволяет понять смысл за-
кона Ленца в применении к цепи,
содержащей индуктивность L: э. д. с.,
наводимая в индуктивности, всегда
стремится противодействовать про-
исходящему изменению тока [см.
(3-42)].
Действительно, при увеличении
тока (независимо от его знака) энер-
гия магнитного поля возрастает, и,
93
следовательно, для увеличения тока
должна быть подведена энергия.
Напротив при уменьшении тока
энергия, запасенная в индуктивно-
сти, уменьшается. Она должна быть
отдана индуктивностью в остальную
часть цепи, т. е. индуктивность ра-
ботает как генератор, поддержи-
вающий протекание тока в прежнем
н ацр а в леням. В ьфажение (3-44)
аналогично выражению кинетиче-
u / mv2 \
скои энергии I- , поэтому реак-
ция индуктивности на изменение то-
ка совершенно подобна реакции
инертного тела на изменение ско-
рости его движения.
3-5. ПЕРЕМЕННЫЙ ТОК
В ЦЕПИ г, L
Рассмотрим двухпроводную воз-
душную ЛИНИЮ (рис. 3-116) длиной /,
обладающую сопротивлением г0 и
индуктивностью Lo на единицу дли-
ны (можно рекомендовать само-
стоятельно подсчитать для подобной
линии ее параметры г0 и Lo, задав-
шись сечением проводов и расстоя-
нием между ними).
Пусть в конце линия коротко-
замкнута, а в начале соединена
с генератором.
Если по линии идет ток
iz=zI'm COS COi/,
то напряжение генератора по (3-42)
и = ir -|- L == Imr cos сп/ 4-
4-/mLcD cos f со/ 4“ у
= /wr cos со/ — ImL^ sin со/, (3-45)
Где г=г$1, L-=LqI.
Применяя тригонометрические
преобразования (3-8) для разности
i
Рис. 3-16.
двух простых гармонических функ-
ций, найдем, что напряжение гене-
ратора
U=Um COS (й>/ + ф)
имеет амплитуду
ит = /т Kr2 +W (3-46)
и опережает по фазе ток на угол
? = arctg^. (347)
Например, при параметрах це-
пи— rG = 0,5 ом)км, Lo=i2,04 мгн/км
и /=10 км, амплитуде напряжения
генератора £7?п=9,35 кв и частоте
/==50 гц амплитуда тока [из форму-
лы (3-46)] Ln =1,М ка. При этом
ток отстает по фазе на угол
ф^52°эо'.
Мощность. Мощность, отдаваемая
генератором ,в цепь, может быть
найдена как произведение напряже-
ния и тока
p — ui = Um COS (со/ 4- ф)/ж COS со/ =
=4 tcos ?+cos
(3-48)
Это мгновенная мощность
р(/).
Как видно из последней части
написанного равенства, она содер-
жит постоянную слагающую, кото-
рая и равна средней мощности:
Р — ImUrr. cos COS ср. (3-49)
Эта формула, разумеется, при-
менима ко всем случаям мощности
в цепи с напряжением и током,
сдвинутым по фазе на угол ф1.
Пульсирующая мощность двой-
ной частоты, пропорциональная
cos (2со/ + ф), в среднем равна ну-
лю. Ее существование объясняется
и тем, что рассеиваемая в сопро-
тивлении мощность непостоянна
(i2r), и тем, что энергия магнитного
/г *2 \
поля! L -у ) непрерывно изменяется.
1 Предлагается самостоятельно примет
нить вывод, аналогичный (3-48)—(3-49),
к цепи г, С.
94
К выражению (3-48) можно
прийти также из чисто энергетиче-
ских соображений. Действительно,
по (3-43)
<м°)
При i = Im cos простые преобра-
зования правой части (3-50) приводят
к равенству (3-48) или аналогичному:
р=4 о + c°s 2®о—
1 9
— = (3-51)
При такой записи второе слагае-
мое выражает мощность, обуслов-
ленную изменением энергии магнит-
ного поля. Имея в виду (3-45),
(3-46) и (3-8), легко найти, что
—5^772 'COS ф,
/шСоТ/ — 5^772 sin ср, (3-52)
после чего можно отождествить
(3-48) и (3-51).
На рис. 3-17 изображены графи-
ки тока, напряжения, мгновенной
мощности, ее двух составляющих,
значение мощности (Р) и
значение энергии магнитно-
а также энергии магнитного поля.
Пунктирными линиями (показаны
среднее
среднее
го поля
— __( Li2\_LIz
—\~2~J ~2~* (3-0 3)
Анализируя приведенные графи-
ки, следует обратить внимание на
•следующие их особенности:
1) мгновенное значение мощно-
сти обращается в нуль и когда ра-
вен нулю ток, и когда равно нулю
напряжение. Но хотя мощность, от-
даваемая генератором, в последнем
случае (zz=*O, f=#0) и равна нулю,
мощность, выделяемая в сопротив-
лении (рг=72г), не равна нулю. Она
получается в этот момент только за
счет убыли энергии магнитного по-
ля; при этом мощность pL отрица-
тельна и равна по абсолютной ве-
личине положительному значению
мощности рг’,
2) среднее значение всей мощно-
сти равно среднему значению мощ-
ности, выделяемой в сопротивлении,
так как среднее значение мощности
pL равно нулю;
3) поступающая от генератора
мощность отрицательна (р<0) в те
моменты времени, когда мощность,
отдаваемая изменяющимся магнит-
ным полем (т. е. — pL), превосхо-
дит мощность, рассеиваемую в со-
противлении (рг).
3-6. ПЕРЕМЕННЫЙ ТОК В ЦЕПИ г,
С,£. РЕЗОНАНС
Наиболее интересны особенности
цепи переменного тока, содержащей
как индуктивность, так и емкость,
поскольку система Л, С образует ко-
лебательный контур.
Действительно, если замкнем за-
ряженный конденсатор с напряже-
нием С7|0 на индуктивную катушку
(рис. 3-18), то он начнет разряжать-
ся, отдавая запасенную в нем энер-
гию w3=Cu2c/2.
В цепи возникает ток
i=—С duddt (3-54)
(при выбранных на рис. 3-18 на-
правлениях ток положителен, когда
конденсатор разряжается). Энер-
95
Рис. 3-18.
гия электрического поля конденса-*’
тора переходит в энергию магнитно-
го поля катушки w^ = i2LI<2.
Когда конденсатор полностью
разрядится («с=0), вся существо-
вавшая .в нем энергия перейдет
в энергию магнитного поля. В
этот момент (ис — 0) ток в ин-
дуктивности достигает наиболь-
шего значения. В следующие мо-
менты времени ток будет поддер-
живаться «силами инерции» (закон
Ленца) и начнет перезаряжать
конденсатор. Ток прекратится лишь
в тот момент, когда вся энер-
гия вновь перейдет в энергию поля
противоположно заряженного кон-
денсатора ис ——U-q. Конденсатор
опять начнет разряжаться, создавая
ток противоположного направления.
Но энергия поля не зависит от зна-
ков ис и i, поэтому весь процесс
(с другими знаками) повторится.
Перейдем к аналитическому рас-
смотрению процесса. В любой мо-
мент напряжение на конденсаторе
ис должно быть равно напряжению
н а индуктивности ис==L di/dt;
поэтому, выражая ток по (3-54),
приходим к уравнению
_ d2u~
Uc-~LC^- (3-55)
Этому уравнению удовлетворяет
гармоническая функция
uc—U® cos со«о/, (3-56)
ний контура определяется равен-
ством
или «>0 = 1//LC. (3-57)
Эти колебания с необходимостью
будут затухать из-за того, что в ре-
альной цепи существует сопротив-
ление г, которое не учитывалось
в проведенном расчете. В этом со-
противлении происходит необрати-
мее -рассеяние энергии, и, следова*
тельно, энергия колеблющейся си-
стемы С, L постепенно убывает. При
высоких частотах необходимо учи-
тывать и возможное излучение энер-
гии (радиоволны).
Рассмотрим теперь цепь, содер-
жащую С, L, г (последовательный
контур) и подключенную к источни-
ку гармонического напряжения
(рис. 3-19), частота которого со. сов-
падает с частотой соо собственных
колебаний контура L, С (резо-
нанс). При этом в элементах L, С
установятся колебания, в точности
подобные рассмотренным, а рассея-
ние энергии в сопротивлении «по-
крывается» мощностью, подводимой
от источника питания.
При частоте, совпадающей с ча-
стотой собственных колебаний
(со-2£С=1 или со£= 1/со-С), напряже-
ния на емкости и на индуктивности
в любой момент времени компенси-
руют друг друга, поэтому все на-
пряжение источника приходится на
сопротивление, т. е. и=иг. Это не-
трудно показать из общего уравне-
ния цепи
И == U q ~р UL -р Нт — “р —р -•
(3-58)
В цепи рис. 3-19 ток
dun
(З-59)
где Uq — напряжение на конденса-
торе в начальный момент,
так как по условию ^с (О) =
Подставляя (3-56) в (3-55), по-
лучаем:
it/o cos coo t—’LC^oUv cos coo t,
откуда видно, что круговая частота
собственных гармонических колеба-
Рис. 3-19.
96
так как при выбранных на рис. 3-19
направлениях положительный ток
заряжает конденсатор, увеличивая
его напряжение.
Выражая все переменные вели-
чины в правой части =(3-58) через
напряжение на конденсаторе, при-
ходим к уравнению
, r . d2ur dur
u^uc + LC^+rC^-. (3-60)
Предполагая, что напряжение
на емкости простое гармоническое
«c=^cmcos,co/, и выполняя диффе-
ренцирование, находим, что
&L==—LCc02'[/Cm(COS to/,
Ur = —Г to C,/7’cmSin со/. (3-61)
Следовательно, напряжение источ-
ника равно сумме трех напряжений:
t/mCOS(to/+₽) = UCm(l —
—LCw2) cos co'/—UcrnT co. C sin co/.
(3-62)
При резонансе, когда rzb + ^c = O,
т. e. когда 1—LC o^=O, напряжение
источника равно напряжению на со-
противлении:
и=иг=—Ucmr со. С sin со/, (3-63)
и, следовательно, амплитуда напря-
жения на конденсаторе UCm и ам-
плитуда напряжения источника свя-
заны соотношением
ч ' Um—Ucm^ayC. (3-64)
Это значит, что амплитуда на-
пряжения на конденсаторе может
б&ть больше и даже много больше,
чем амплитуда напряжения источ-
ника, когда г to С меньше единицы.
Отношение UcmlUm показывает,
насколько можно увеличить входное
•напряжение, пользуясь эффектом
резонанса. Поэтому этим отношени-
ем характеризуют качество или
добротность контура. Из про-
веденных расчетов видно, что при
резонансе добротность контура г,
'L, С .
Q = (3-65)
Um ru>C г г v 1
Постепенное раскачивание коле-
бательной системы до больших ам-
плитуд при том, что раскачивающее
усилие действует в такт с периодом
собственных колебаний (резонанс),
каждому знакомо хотя бы из опыта
раскачивания качелей. Сначала под
действием слабого усилия система
отклоняется от равновесия очень
мало, но при повторении усилий
(в такт с периодом собственных ко-
лебаний) система постепенно раска-
чивается. Именно на таком накоп-
лении действия слабых сил и осно-
вано раскачивание резонансной си-
стемы.
На рис. 3-20,а показано, как по-
степенно нарастают колебания в
контуре г, Z, С при добротности
Q = 500, если в момент /==0 вклю-
чается источник с напряжением
и=—sin со /.
Уже в конце второго периода
максимальное напряжение на кон-
денсаторе превосходит приблизи-
тельно в 6 раз амплитуду напряже-
ния источника, тогда как в устано-
вившемся режиме при полной рас-
качке контура амплитуда напряже-
ния на конденсаторе превосходит
амплитуду источника в 500 раз.
На рис. 3-20,6 для того же кон-
тура .показано отношение макси-
мального напряжения на конденса-
торе ис макс -К его амплитуде UCm при
Рис. 3-20.
7 К. М. Поливанов.
97
установившемся режиме в функции
времени, протекшего с момента
включения генератора. Как видно
из графика, через 100 периодов это
отношение составляет приблизи-
тельно 0,45; через 500 периодов это
отношение уже близко к единице
(около 0,96).
В процессе ра-скачивания конту-
ра энергия, поступающая от источ-
ника за каждый период, частично
рассеивается в сопротивлении, а ча-
стично идет на увеличение энергии
колеблющейся системы (энергия
магнитного поля индуктивности
аналогична кинетической энергии
при колебаниях механической систе-
мы; энергия электрического поля
конденсатора аналогична потенци-
альной энергии в механических си-
стемах). Когда колебания переста-
ют нарастать, т. е. достигается уста-
новившийся режим, то в случае ре-
зонанса вся мощность источника
p = ui в каждый момент времени
равна мощности, рассеиваемой в со-
противлении uri=i2r\ это объясняет-
ся тем, что общая энергия двух эле-
ментов Л и С остается постоян-
ной:
wQ 4- = ис С/2 i2L/2 — const.
(3-66)
В этом можно убедиться прямой
подстановкой мгновенных значений
ис и i в (3-66), принимая во вни-
мание, что
cos2 со/+ sin2 со</=4.
В хорошем резонансном контуре,
обладающем добротностью, равной
500, входной сигнал с амплитудой
0,1 мкв способен раскачать систему,
настроенную в резонанс, и создать
на конденсаторе напряжение 50ждв.
Напряжение такой величины уже
легко может быть усилено электрон-
ными лампами, тогда как напряже-
ние в 0,1 мкв оказалось бы потерян-
ным в ши-роком спектре различных
помех и собственных шумов лампы.
Существенно заметить, что благода-
ря резонансному контуру усиливает-
ся именно сигнал, имеющий строго
определенную частоту.
В контурах с высокой доброт-
ностью Q малое отступление от ре-
зонансной частоты на т)%! приводит
к уменьшению амплитуды напряже-
ния на [конденсаторе в 2Qt]/100 раза,
разумеется, при той же амплитуде
на входе. При доб-ротности, равной
500, отступление от резонансной ча-
стоты на 1 %': приводит к уменьше-
нию амплитуды в 10 раз.
Пример 3-1. В контуре с индуктивно-
стью L—5,0 мкгн, емкостью С=2 000 пф и
сопротивлением г=0,1 ом сигнал на (Входе:
имеет амплитуду .1 мкв и частоту со =
='1О7 сек-1. Найти амплитуды тока ib цепи
1т и напряжения на индуктивности
при заданной частоте и при частоте, сни-
женной на 0,5%.
Р е ш е нп е. -При заданных условиях
со2АС='1 все напряжение приходится на со-
противление, и, [следовательно, ток имеет
амплитуду
/m='^m/r=10 мка.
При этом амплитуда напряжения на индук-
тивности
ULm = a)LIm=5Q0 мкв и Q=500.
Пои изменении частоты на 0,5% нужно
исходить из общего уравнения цепи:
U—UСт1-(1—(02АС) COS со/—reoCt/emSin со/.
6 Пои заданной расстройке 0,5% частота
со = 107(1—0,005) сек-1, и, следов ательно,
1 —co2LC=0,01—0,0052 ~ 0,01,
тогда как гсоС=0,002.
В итоге приходим к уравнению
а = Um cos’(co/ + f) =
= UCm [0,01 cos со/ —10,002 sin со/],
откуда z
V (0,01)2 + (0,002)2
Амплитуда напряжения на индуктивности
ULm & Ст ~ 100 мкв, амплитуда тока
1т 2 мка.
Приближенность проведенных вычис-
лений очевидна. Однако такая точность до-
статочна для выявления особенностей ре-
зонансного контура.
В технике с. в. ч. резонаторы
(которые условно можно представить
подобными А, С контуру) имеют зна-
чительно более высокую доброт-
ность, достигающую десятков тысяч.
Резонанс в энергетических си-
стемах также играет очень сущест-
венную роль. Если в энергетических
•системах высокого напряжения об-
разуется колебательный контур, по-
добный рассмотренному, возникаю-
щее в нем увеличение напряжения
(резонансные перенапряжения) спо-
98
собно привести к разрушающим эф-
фектам. Но .в энергетических систе-
мах существуют и другого рода ре-
зонансы, играющие важную и 'при-
том положительную роль.
Представим себе, что линия с со-
противлением г питает «потребитель
с индуктивной нагрузкой (гн, А).
В этом случае, как было показано
в § 3-5, энергия, запасаемая в ин-
дуктивности, попеременно то полу-
чается от генератора, то возвра-
щается ему; но такой переброс энер-
гии связан с большими «транспорт-
ными расходами», так как в сопро-
тивлении проводов линии при пере-
броске через нее энергии происхо-
дят процессы необратимого тепло-
вого рассеяния. Если же параллель-
но с индуктивной нагрузкой вклю-
чить конденсатор соответствующей
«емкости, он может служить тем ре-
зервуаром, с которым происходит
обмен энергией, то отдаваемой, то
получаемой индуктивностью. При
этом пульсирующая энергия не про-
ходит через линию передачи и не
создает в ней излишних потерь.
Включение конденсатора уменьшает
общий ток, передаваемый по линии
при заданной мощности потреби-
теля.
Подобная.система будет подверг-
нута анализу в гл. б после того, как
будут изложены более совершенные
методы расчета.
3-7. ЗАКОННЫ КИРХГОФА
ДЛЯ РАЗВЕТВЛЕННОЙ ЦЕПИ
ПЕРЕМЕННОГО ТОКА
Как было показано, напряжение
на любом из элементов цепи г, L, С
может быть представлено как раз-
ность потенциалов. Поэтому напря-
жение между любыми точками це-
пи, составленной из таких элемен-
тов, также может быть представле-
но как .разность потенциалов. А это
и есть условие применимости второ-
го закона Кирхгофа.
Так, например, в цепи рис. 3-21
Цг “ Uad = Uab
Ubd~ Ubc + Ucd,
ГДе Umn = фттг фп •
В этих равенствах имеются в ви-
ду мгновенные значения потенциа-
7*
лов и напряжений. Для каждой вет-
ви в отдельности, например для
ветви а, b (рис. 3-21), напряжение
может быть представлено как
сумма:
Uab ~Ur-\- Ul 4“ Uq.
При ЭТОМ
di . diip
ur=^ir, ul = L-^- , 1=С-^-
или
= -Б С i dt.
с J
Рассматривая только установив-
шийся режим при простых гармони-
ческих токах, мы нашли, что им со-
ответствуют простые гармонические
напряжения той же частоты. При
этом дифференцирование и интегри-
рование приводят только к измене-
нию начальной фазы на +л/2 (диф-
ф ер енциров ание; см., н апр им ер,
(3-45)] или на —л/2 [интегрирова-
ние; ом., например, (3-25)] с одно-
временным умножением или делени-
ем амплитуды на со.
Сказанное справедливо только
при постоянстве параметров цепи г,
L, С.
Действительно, при переменном г про-
изведение
uT=r.(t)I
m icos (со/4-а)
уже не будет выражаться простой гармони-
ческой функцией. Более'того, при диффе-
ренцировании потокосцепления 4r=Lf, если
бы индуктивность была функцией времени,
напряжение представлялось бы равенством
сШ____т di i ,dL
uL==~di' — L dt +х dt ‘
Точно так же при зависимости С от време-
ни ток заряда емкости выражался бы ра-
венством
r daC dC
~dF==C~dT +uCdT
d
Рис. 3-21.
'Изменение параметров цепи может
быть обусловлено какой-либо- внешней при-
чиной (ем. гл. 13). В нелинейных цепях при
переменном токе эти параметры переменны
в силу того, что они зависят от тока или
напряжения.
Только при этом в системе в целом
закон сохранения количества элек-
тричества не будет нарушен:
Для анализа и расчета развет-
вленной цепи к ней в дополнение
ко второму закону должен быть
применен первый закон Кирхгофа.
Можно ли его применять к цепи
переменного тока? Каким условиям
при этом должна удовлетворять
.цепь?
Первый закон Кирхгофа — это
закон сохранения количества элек-
тричества, формулированный на
языке теории цепей: алгебраическая
сумма токов всех ветвей, сходящих-
ся к общему узлу, равна скорости
изменения заряда узла. В условиях
постоянного напряжения заряды на
узлах не могут возрастать или убы-
вать, так как при изменении заряда
изменялся бы потенциал узла. При
переменном напряжении заряд узла
может изменяться, если этот узел
обладает некоторой емкостью.
Допустим, что заряд узла 1
(рис. 3-22), приносимый токами ia,
ib и fc, возрастает. Тогда в -соответ-
ствии с законом сохранения заряда
^ = ia + ib+ie- (3-67)
Если заряд какого-то узла 1 воз-
растает, то со всей необходимостью
заряд каких-то других узлов, ска-
жем, узлов 2 и 5, должен убывать
так, чтобы
Но в таком случае между узла-
ми 1, 2 и /, 3 существуют емкости
С12 и С13, которые можно предста-
вить в виде конденсаторов, вклю-
ченных между соответствующими
узлами (рис. 3-22). При этом заряд
первого узла распределяется меж-
ду электродами двух конденсаторов,
присоединенных к узлу /:
— ^2+93-
Равный по величине, но противо-
положный по знаку заряд узлов 2 и
3 (—92 и —q^) появляется на дру-
гих электродах этих же конденсато-
ров Cj2 и С13.
^Следовательно, заряд первого
узла можно представить равенст-
вом
91= 92 + 93 = ^12^12 +
+ C*i3Wi3.
(3-68)
Вернемся к составлению уравне-
ния по первому закону Кирхгофа *
для узла 1 (рис. 3-22). В случае
переменного напряжения, кроме -
ветвей а, &, с, нужно принять во
внимание еще две ветви, сходя-
щиеся к узлу /,— это ветви с кон-
денсаторами С12 и С13. По этим вет-
вям от узла 1 уходят токи
j du 12 • du 13
+12 — ° 12 и +13 —
Следовательно, применяя закон
сохранения заряда (3-67) к узлу /,
находим, что
ia + ib + ic =
du12 г du 13
12
Таким .образом, мы пришли
к первому закону Кирхгофа: сумма
токов, приходящих к узлу, равна
сумме токов, уходящих от узла.
100
1
3
Этот закон сохраняет силу, если
учитываются токи, заряжающие ем-
кости, представленные в виде кон-
денсаторов. Законы Кирхгофа при-
менимы к мгновенным значениям
токов и напряжений цепи перемен-
* ного тока, если в ней могут быть
выделены ветви (участки цепи с
одинаковым током на >всем участке)
и узлы, напряжение между которы-
ми можно определять как разность
потенциалов. При этом изменение
зарядов на узлах должно рассма-
триваться как изменение зарядов на
конденсаторах, соединяющих меж-
ду собой различные узлы.
Этим условиям удовлетворяют
не все электротехнические устройст-
ва. Им не удовлетворяют и цепи,
называемые цепями с распределен-
ными постоянными, например про-
стая линия электропередачи, вдоль
которой непрерывно распределены
индуктивность и сопротивление,
а ме^кду проводами непрерывно
распределены емкость и. проводи-
мость изоляции (рис. 3-23,а).
В первом приближении (при не
слишком большой длине, при не
очень высокой частоте, а также при
сравнительно малой проводимости
между проводами) такую линию
с достаточной точностью можно за-
менить цепью с сосредоточенными
постоянными (рис. 3-23,6), разде-
ляя йсд) линию с продольной индук-
тивностью и сопротивлением на две
равные части и включая в середине
линии всю емкость и всю попереч-
ную проводимость. Цепи с распреде-
ленными постоянными в этой части
книги не рассматриваются (их тео-
рия излагается во второй части
книги),
3-8. ИЗМЕРЕНИЯ В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
Вольт- и амперметры. Наибольшее рас-
пространение, ззо всяком случае на промыш-
ленных частотах, имеют стрелочные ампер-
метры, вольтметры и ваттметры. В большин-
стве случаев они градуируются в действую-
щих значениях.
•Приборы, основанные на механическом
взаимодействии проводников с током -(элек-
тродинамические, рис. 1-22,в) или двух 'за-
ряженных электродов (электростатические,
рис. 3-24,а), реагируют на среднее значение
силы, которое в этих приборах пропорцио-
нально среднему значению квадрата изме-
ряемой величины тока или напряжения. Эти
приборы, независимо от закона изменения
измеряемой величины, показывают ее дей-
ствующее значение.
Приборы, основанные на тепловом дей-
ствии тока (тепловые), также показывают
действующее значение. На рис. 3-24,6 схе-
матически показана тонкая проволока, на-
греваемая током Z; при ее удлинении, обу-
словленном нагревом, пружинка оттягивает
нить, охватывающую ось, на которой укреп-
лена стрелка.
Широкое распространение имеют элек-
тромагнитные приборы (рис. 3-24,б), наибо-
лее простые по устройству. Они основаны
на втягивании ферромагнитного сердечника
в катушку с током; при этом сила не зави-
сит от направления тока. Однако их точ-
ность невелика.
Приборы, показания которых зависят
от направления тока, т. е. приборы типа
магнитоэлектрических, могут применяться
для измерения переменных токов только
вместе с выпрямляющим элементом (де-
тектором), благодаря которому в измери-
тельной цепи проходит ток одного направ-
ления.
Интересно отметить, что в практике по-
следних лет находят все большее примене-
ние измерительные приборы с прямым циф-
ровым отсчетом (рис. 3-25). Цифры появля-
ются в результате.работы достаточно слож-
ного и точного электронного преобразова-
теля входной (величины.
Показанный на рис. 3-25 вольтметр ан-
глийской фирмы ДМ имеет точность поряд-
ка 0,01% и чувствительность 10 мкв на еди-
ницу.
101
Рис. 3-24.
Цифры на приборе (19999) юоответст-
вуют (Предельному значению измеряемого
напряжения.
Ваттметр. В качестве ваттметров обыч-
но применяются электродинамические при-
боры.
Схематически устройство электродина-
мического ваттметра показано на рис.
3-26,а. Неподвижная обмотка с током i соз-
дает магнитное поле, индукция которого В
пропорциональна току; подвижная обмот-
ка, связанная механически с указателем, ис-
пытывает вращающий момент т, -пропор-
циональный индукции В и току i2 в самой
подвижной обмотке: m—kiBi2, где k\ — ко-
э фф ициент пр оп орцио н а л ьн ости.
Но индукция В пропорциональна току Z,
а ток i2=ujr, где г — большое сопротивле-,
ние, включенное в цепь подвижной обмотки,
а и — напряжение, подведенное к внешним
зажимам. Поэтому
m=kiu.
Очевидно, что знак момента зависит от
направления токов i и i2. Когда токи совпа-
дают с положительными направлениями,
указанными на схеме, момент положителен,
т. е. стрелка поворачивается вправо. Ее по-
вороту противодействует пружинка.
При переменном токе в силу инерцион-
ности системы ее отклонение пропорцио-
нально среднему значению момента. Для
тока
l — ImCOS tot
и напряжения
u='Um cos ф)
среднее значение момента равно:
M^m=kiu—kIU'cos ф.
Таким образом, в случае простых гар-
монических функций ваттметр показывает
произведение действующих значений тока,
напряжения и (косинуса угла сдвига по фа-
зе (cos ф).
Необходимо заметить, что при выводе
предполагалось вполне определенное поло-
жительное направление для тока и напря-
жения: ток положителен, когда он входит
в токовый зажим, обозначенный знаком +
или * (рис. 3-26); напряжение положи-
тельно, когда на зажимах напряжения бо-
лее высоким потенциалом обладает зажим,
обозначенный знаком + или *. Если поме-
нять порядок включения зажимов тока или
напряжения, изменится знак среднего мо-
мента; изменение порядка на обеих парйх
зажимов не приводит к изменению знака.
В схемах включения ваттметр часто
изображается, как показано на рис. 3-26,6.
Включение ваттметра. Несмотря на
простоту всего изложенного, вопрос о пра-
вильном включении ваттметра часто оказы-
вается неясным. (Представим себе, что ста-
вится задача измерить мощность, переда-
ваемую по двухпроводной линии (рис. 3-27).
Как нужно включить ваттметр? Ведь на ли-
нии нет никаких знаков положительных на-
правлений, а включенные в цепь ампер-
метр и вольтметр (рис. 3-27,а) показывают
действующие значения; к тому же на самом
деле и ток и напряжение дважды за период
изменяют направление (100 раз в секунду
в обычной энергетической сети при частоте
/=50 гц).
Но это несущественно. Надо получить
определенный ответ на другой вопрос. Тре-
буется измерить мощность, передаваемую
по этой линий слева направо .(генератор сле-
ва, потребитель оправа) или справа налево
(генератор справа, потребитель слева).
102
Рис. 3-25.
Р
Jky&ymwM.' что речь идет о мощности,
передаваемой слева направо. В таком слу-
чае ясно, как должен быть включен -ватт-
метр: выбираем произвольно знак одной из
величин — например, условимся напряжение
считать положительным, когда верхний про-
вод имеет более высокий потенциал, чем
нижний (стрелка и направлена сверху вниз
на рис. 3-27,6). При ©том мощность положи-
тельна, когда ток в верхнем проводе идет
слева направо; тем самым однозначно опре-
делен выбор положительного направления
для тока. Соответствующее включение ватт-
метра показано на рис. 3-27,в.
Следовательно, сначала (1) устанавли-
вается, какое направление передаваемой
мощности положительно, затем (2) произ-
вольно выбирается направление напряже-
ния (или тока), и, наконец (3), выбирается
положительное направление другой вели-
чины, т. е. тока (или напряжения), согласо-
ванное с предыдущим; после этого (4) то-
103
Рис. 3-28.
©одам, -соединяющим две -части цепи. Следо-
вательно, мощность, получаемая потребите-
лями:
первым РП1 = Рг — Р3 = 250 кет;
вторым РП2 = Р3 + Р2 = 750 кет.
Если ‘бы показание третьего (ваттметра
было отрицательно, например Рз=—250 квз\
то из тех же формул (следовало бы, что
ковые зажимы (ваттметра (включаются в рас-
сечку провода так, чтобы положительный
ток входил в зажим, обозначенный тем же
знаком, 'что и .зажим напряжения, присоеди-
няемый к проводу, потенциал которого вы-
ше при положительном значении напряже-
ния.
•Нетрудно убедиться, что .включение
ваттметра, показанное на рис. 3-27,г, также
соответствует измерению мощности, переда-
ваемой слева направо.
Но встречаются такие условия работы
линии, когда на каждой из ее сторон содер-
жатся и генераторы и потребители (рис.
3-28). В этом случае показания ваттметра
могут быть как положительными, так и от-
рицательными. Положительные показания
соответствуют передаче (мощности в одном
направлении, отрицательные говорят о том,
что мощность передается в направлении,
противоположном тому, которое условно
принято за положительное.
Пример 3-2. В цепи рис. 3-28 два по-
требителя энергии /71 и П2 питаются от двух
генераторов 7\ и Г2. В цепь включены три
ваттметра; их показания: Pi =='500 кет, Р2—
=500 кет, Рз=(250 кет. Чему patena мощ-
ность, получаемая первым и вторым потре-
бителями?
Решение. Ваттметры Pi и Р2 пока-
зывают мощность, отдаваемую каждым из
генераторов. Ваттметр Р3 показывает мощ-
ность, передаваемую слева направо по про-
РП1 = Рг — Р$ — 750 к епт,
РП2 = рз 4- р2 = 250 кет.
Осциллографы. Можно увидеть весь
ход изменений переменного тока во време-
ни, применяя осциллограф.
Магнитоэлектрический осциллограф был
кратко описан в § 1-10 (рис. 1-22,а). .
При увеличении (скорости колебаний
петли влияние инерционности механической
системы возрастает. Поэтому при высоких
частотах применяют* только электронные
осциллографы.
В специальной вакуумной трубке элек-
троны, испускаемые катодом .(рис. 3-29)„
разгоняются сильным электрическим полем
анода, фокусируются полем дополнительных
электродов и образуют электронный луч»—
тонкий пучок летящих электронов. При
отсутствии других 'сил электронный луч по-
падает -в центр экрана, светящегося в точ-
ках падения луча. Но на пути луча имеют-
ся две пары отклоняющих пластин. Напря-
жение, приложенное к первой паре пластин
(Г)/ вызывает горизонтальное отклонение
луча, ‘ (напряжение на второй паре (В) —
вертикальное. Отклонение луча пропорцио-
нально напряжению на пластинах. Направ-
ление отклонения определяется знаком на-
пряжения (электроны притягиваются к по-
ложительной пластине).
Если' к горизонтальным пластинам при-
ложить напряжение, изменяющееся во вое-
Рис. 3-29.
104
Рис. 3-30.
имени пилообразно -(-рис. 3-30), то луч будет
отклоняться в горизонтальном направлений
прямо пропорционально времени, -а в конце
каждого периода будет возвращаться к на-
чалу. Так создается развертка времени.
Отклонение луча в вертикальном на-
правлении пропорционально напряжению
вторых пластин i(B). Поэтому на экране луч
запишет кривую Для записи перио-
дических процессов необходимо, чтобы ча-
стота развертки отличалась в целое число
раз от частоты записываемого напряжения.
Если период развертки в п раз больше пе-
риода записываемого напряжения (т. е. на-
пряжения на вертикальных пластинах), то
очевидно, -что на экране запишется п пе-
риодов.
Масса электрона ничтожно -мала, поэто-
му электронные осциллографы практически
безынерционны. Так, например, существуют
осциллографы, в которых луч пробегает
в горизонтальном направлении весь экран
за одну наносекунду ,(1 //|сек=,10-9 сек).
Трудности осциллографирования очень вы-
соких частот определяются понижением
чувствительности, а -главное, искажающим
влиянием входных емкостей, индуктив-
ностью соединяющих проводов, наличием
местных колебательных контуров и т. п.
В сочетании с усилителями электрон-
ные осциллографы способны записывать
очень слабые и быстро изменяющиеся на-
пряжения.
Если нужно осциллографировать токг
на отклоняющую систему (обычно через
усилитель) подается напряжение, снимае-
мое с сопротивления, включенного в ветвь
измеряемого тока.
Заметим еще, что обычно осциллографы
снабжаются системой очень гибкого «и про-
стого управления. На пульте, расположен-
ном со стороны экрана, помещен набор ре-
гулировочных рукояток, позволяющих
управлять яркостью и фокусировкой, менять
частоту и фазу развертки, регулировать уси-
ление.
Другие приборы. В цепях -переменного
тока применяются приборы для измерения
величин, характеризующих именно гармо-
нические функции. К ним относятся, на-
пример, векторные приборы, пользуясь ко-
торыми можно определить не только ампли-
туду, но и начальную фазу гармонической
функции, отсчитываемую относительно ка-
кой-то «опорной» косинусоиды.
Существуют приборы .(с п е к т р а л ь-
ные анализаторы или спектро-
метры), показывающие амплитуды гар-
монических составляющих сложной перио-
дической функции. В некоторых спектромет-
рах амплитуды основной и высших гармо-
нических составляющих представляются
вертикальными светящимися полосами .со-
ответствующей длины на экране осцилло-
графа; их смещение по горизонтальной оси
пропорционально номеру гармонической со-
ставляющей.
Существуют записывающие устройства
показывающие, как изменяется спектраль-
ный состав сложной гармонической функ-
ции во времени. Так, например, на
Рис< 3-31.
105'
рис. 3-31,а1 показано, как на выходе ми-
крофона изменяются амплитуды двух гар-
монических составляющих (имеющих часто-
ты 250 гц и 6,4 кгц), когда произносится
слово Миссисипи. Как видно из рис. 3-31,а,
на частоте 250 гц наибольшие амплитуды
соответствуют звуку «и» (/), тогда как на
частоте 6,4 кгц наибольшие амплитуды
соответствуют звуку «с» (SS). Спектраль-
ный состав звука «с>> в том же слове
Миссисипи представлен отдельно на
1 Воспроизведены результаты записи,
произведенной датской фирмой Брюэль и
Кьеэр.
рис. 3-31,6, где по горизонтальной оси
отложены частоты в логарифмическом мас-
штабе, а по вертикальной — амплитуды со-
ответствующих гармонических.
Электрический анализ спектрального
состава звуков исключительно важен при
обучении правильному произношению на
иностранных языках, а также для оценки
качества телефонной и радиопередачи,
звукозаписи, акустики аудиторий и кон-
цертных валов и т/ п.
•Некоторые принципиальные вопросы из-
мерений на переменном токе рассматри-
ваются ниже, при анализе цепей переменно-
го тока.
ГЛАВА ЧЕТВЕРТАЯ
МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ С ПРОСТЫМИ
ГАРМОНИЧЕСКИМИ ФУНКЦИЯМИ
При расчетах линейных цепей
приходится многократно выполнять
операции сложения и вычитания,
дифференцирования и интегрирова-
ния простых гармонических функ-
ций, умножаемых на те или иные
постоянные величины.
В простейшем случае, когда ис-
ходные функции имеют одинаковую
частоту, в результате всех перечис-
ленных линейных операций
получается гармоническая функция
той же частоты. Следовательно,
подлежат определению только ам-
плитуды и начальные фазы этих
функций.
Сложение двух гармонических
функций можно производить, поль-
зуясь аналитическими формулами
преобразования тригонометрических
функций (3-8). Однако геометриче-
ское толкование таких преобразова-
ний приводит всегда к большей на-
глядности, простоте вывода различ-
ных соотношений и в значительной
мере предупреждает возможность
ошибок.
Еще большие возможности пред-
ставляет комплексный метод, кото-
рый будет рассмотрен вслед за
геометрическим.
4-1. ГЕОМЕТРИЧЕСКИЙ МЕТОД
Вектор А на плоскости можно
определить его длиной А и углом о,
на который он повернут-относительно
оси, выбранной в качестве начала
отсчета углов (рис. 4-1). Положи-
тельным значениям угла соответст-
вует поворот против часовой стрел-
ки. При этом удобно пользоваться
таким обозначением вектора
А=ААо, (4-1)
где А и сг — его полярные координа-
ты, называемые также модулем
и аргументом.
В печати векторы представляют-
ся полужирным шрифтом; в -руксь
писном тексте рекомендуется соот-
ветствующие буквы подчеркивать,
ставить над буквами стрелку (Л)
или даже просто черту (Л),
как это сделано на рис. 4-1—4-4
и др. Если аргумент является ли-
нейной функцией времени
ст ='а + со/,
(4-2)
то проекция вектора на ось, от ко-
торой отсчитываются углы, равна
мгновенному значению гармониче-
ской функции:
а=А cos (со/+а). (4-3)
На этом основан известный
способ построения косинусоиды
о
Рис. 4-1.
106
(или синусоиды) по проекциям вра-
щающегося вектора (рис. 4-2,а).
Вместо вращения вектора (его
поборота на угол со/) можно вра-
щать в противоположную сторону
ось, на которую проектируется не-
подвижный вектор Л Ze; такая ось
называется осью времени
(рис. 4-2,6).
На основании всего сказанного
понятно, что вектор А может быть
назван изображением гармониче-
ской функции а. При известной ча-
стоте со вектор A=4Ztt содержит
всю необходимую информацию: его
модуль определяет амплитуду, ар-
гумент— начальную фазу.
Сложение мгновенных, значений
гармонических функций можно за-
менить сложением изображающих
векторов. Для доказательства
рассмотрим плоскость (рис. 4-3,а),
на которой лежат три вектора: А=
—AZa, B = BZ|3 и вектор С, рав-
ный их сумме,
C=A+B = CZy. (4-4)
Проекция вектора суммы всегда
равна алгебраической сумме проек-
ций слагающих векторов, поскольку
складываемые векторы образуют
замкнутый треугольник. Поэтому,
проектируя векторы на ось времени
(рис. 4-3,6), находим, что
a+b=A cos (cof+a) +
+'Bcos (со^+р) =
= c=Ccos (со/+у), (4-5)
причем
A cos а + В cos В = С cos у:1
- I (4-6
Asin”a-j-Bsinp = Csinу. J
Каждого из уравнений (4-6) в от-
дельности недостаточно для опреде-
ления двух неизвестных С и у по
известным А, В, а, р.
107
Решая совместно уравнения (4-6)
относительно у и С, находим, что
, ___ A sin а + В sin з
® ‘ A cos а + В cos f ’
= tir-j-uL при i = /т cos г = 5 ом, L =
= 20,7 мгн, со = 314~1 сек.
Найти значения и у из построен-
ной в масштабе векторной диаграммы для
тока 7™= 1,14 ка (см. § 3-5).
Решение представлено на рис. 4-4.
С — У (A cos a -j- В cos Р)2 -f- {A sin a -j- В sin р)2. (4-7)
Эти равенства имеют очевидное
геометрическое толкование (рис.
4-3).
Важно заметить, что первое из
уравнений (4-7) не дает однознач-
ного решения для у, так как tgy=
=tg (у+л).
-Дополнительные сведения о зна-
чении угла у дает знак одной из
ортогональных проекций вектора С,
выражаемых формулами (4-6): по-
ложительному значению С cos у со-
ответствуют углы у, заключенные
в первом или четвертом квадран-
тах; отрицательному С cos у—углы
у в третьем или втором квадрантах.
Геометрическое построение век-
торов, изображающих гармониче-
ские функции, а также их суммиро-
вание называют векторными
диаграммами. Такие -диаграм-
мы наглядно иллюстрируют ход ре-
шения. При точном построении
можно непосредственно из диаграм-
мы определить искомые амплитуды
и фазы. Приближенное построение
при аналитическом решении служит
надежным контролем и позволяет
легко определить квадрант, в кото-
ром лежат определяемые векторы.
Пример 4-1. Построить векторную
<> (^1
диаграмму для уравнения и = ir + Ь - =
Пример 4-2. Построить векторную
диаграмму для уравнения г
u — ir + L+ -g- I i dt = ur+ uL + ezc.
полагая i = /m cos co/, Im = 1 a» r = 1 ом»
а>Ь=20 ом, 1/coC = 22 ом.
Найти значения U и <p из диаграммы
построенной в‘ масштабе.
Решение представлено на рис. 4-5.
4-2. КОМПЛЕКСНЫЙ
(СИМВОЛИЧЕСКИЙ) МЕТОД
Изложенный путь геометриче-
ских решений часто оказывается
чрезмерно трудоемким, но, главное,
пользуясь им, трудно записывать
уравнения цепи в общем виде и ана-
лизировать их. Поэтому среди
электротехников получил всеобщее
распространение комплексный
или символический метод,
предложенный и '.подробно разрабо-
танный американским электротехни-
ком Чарльзом Штейнметцом.
Обоснование метода. Для обо-
снования метода1 обратимся к из-
вестному представлению косинуса
через полусумму экспонент с мни-
мым показателем
а = Ат cos (<»/ -f- а)=
где / = •/—1.
Чтобы упростить запись г после-
дующих выводов, введем такие обо-
значения и наименования:
комплексная амплитуда
Ат=Ате1а = Ат (cos а + j'sin а); (4-9)
1 См. также дополнительные замечания
в конце этого параграфа.
108
комплексная гармониче-
ская функция
Ат [cos (со/ —|— ос) —[—
+ / sin (<»t 4~ а)], (4-10)
9 Сопряженные им величины, т. е.
отличающиеся только знаком при /,
обозначаются поставленной звездоч-
кой:
Ат = Ame~J‘“— Ат (cos а — j sin а);
а* = Ате~№ = Ат [cos (totа) —
—/sin (tot + а)]. (4-11)
В формулах (4-9)—(4-11) переход
от показательной формы к двучлен-
ной тригонометрической произведен
по известной формуле Эйлера
= cos у + / sin у.
Пользуясь введенными обозначе-
ниями, можно выражение гармони-
ческой функции (4-8) записать в та-
ком виде: •
а — Ат cos (tot -ф- а) =
=1(а + а*) =
= j- (Amefaf +Ame~imt) (4-12)
или проще: {
а = Ат cos (<at -f- а) = Re а =
= ReA„e;“', (4-13)
где Re — знак, указывающий на то,
что 'берется только вещественная
часть комплекса (первые буквы
французского слова «рээль»— ве-
щественный) .
Выражения (4-8) и (4-12) мож-
но назвать полным комплексным
Представлением гармонической
функции или тождественным ком-
плексным представлением, а комп-
лексы а-и А„г могут быть названы
комплексными изображе-
ниями (символами) гармониче-
ской функции, переход к которой
осуществляется по формулам (4-12),
(4-13). Комплексная амплитуда Ат
достаточно полно изображает функ-
цию только в тех случаях, когда
известна частота (со=2л/). При
этом гармоническую функцию нель-
зя приравнивать ее комплексному
изображению, а можно говорить
только о их соответствии, обозначая
его каким-нибудь знаком, отлич-
ным от знака равенства; например,
можно писать, что
а а или а Ат*
Пример 4-3. Комплексное изображе-
н-
ные напряжения Um — \We , частота
f — 50 гц. Требуется найти соответствую-
щую функцию времени, а также мгновен-
ное значение напряжения в моменты вре-
мени t = 0, / = Т/4.
Решение. По определению и =
= 100 cos . При Z = 0 имеем
л Т
и (0) = 100 cos — 70,7 в, при
2тс Т те
когда <ot = ~T---
f Т \ Зте
и ( ~4~ )= ЮО cos —
70,7 в.
Сложение гармонических функ-
ций. Пусть требуется найти сумму с
двух гармонических функций.
Воспользуемся для выполнения
этой операции формулой (4-13):
а b = Re а -|- Re b = с — Re с;
(4-14)
здесь а, b и с — комплексные изо-
бражения соответствующих гармони-
ческих функций и их суммы.
Но сумма вещественных частей
двух комплексов всегда равна ве-
щественной части суммы самих
комплексов.
Поэтому
a + & = Re(a+^j, (4-15)
или, в случае одинаковой частоты
слагаемых,
a + ^^Re^ + B»)^]. (4-16)
109
Сопоставляя (4-16) и (4-14), на-
ходим, что
c^Cmeiat —(Ат + Вт) eimt
или Ст — (4-17)
т. е. комплексная амплитуда суммы
двух простых гармонических функ-
ций одинаковой частоты равна сум-
ме комплексных амплитуд слагае-
мых; таким образом, операцию
сложения мгновенных значений
можно заменить операцией сложе-
ния изображающих комплексов.
Комплексная плоскость. Любой
комплексной величине Лт, Вт од-
нозначно соответствует точка на
плоскости (рис. 4-6), если по од-
ной из двух ортогональных коор-
динатных осей отсчитывается его
вещественная часть, а по другой
мнимая. При этом комплекс на
плоскости представляется векто-
ром, проведенным из начала коор-
динат в эту точку:
Ат = А'т -ф- jA"m=Am (cos а-ф-/ sin а),
(4-18)
а его вещественная и мнимая части
отождествляются с координатами
по двум осям.
Тот- же комплекс может быть
представлен и в полярных коорди-
натах:
Ат = Ате1а = Ат/_а, (4-19)
где Ат — длина вектора (модуль
комплекса), а — угол поворота век-
тора относительно оси веществен-
ных величин (аргумент).
При сложении двух комплексов
всегда целесообразно переходить
к алгебраической форме
Ат = А'т -\-jA"m, Вт = Brm-\-jBrrт
и складывать отдельно веществен-
ные и отдельно мнимые составляю-
щие
— (А'т-{- В'т) -ф- / (А"т -ф- В"т).
(4-20)
Таким образом, операция сло-
жения гармонических функций при
пользовании комплексным методом
практически не отличается от опе-
раций геометрического метода
(рис. 4-7), причем из формул (4-18)
и (4-20) непосредственно следуют
ранее выведенные формулы (4-7) и
(3-8).
•При пользовании комплексным
методом рекомендуется строить век-
торные диаграммы, которые отли-
чаются от ранее рассмотренных
только тем, что одна из координат-
ных осей рассматривается как ось
мнимых величин.
Заметим, что в пределах опера-
ций сложения преимущество-комп-
лексного метода по сравнению
с геометрическим ничтожно. Его
можно увидеть лишь в том, что
множитель j—v^ —1 служит удоб-
ным знаком для отличия двух со-
ставляющих.
Вся сила этого метода обнару-
живается при рассмотрении более
сложных операций, описываемых
дифференциальными уравнениями.
Прежде чем перейти к их рассмот-
рению, рекомендуется решить не-
сколько примеров на сложение
комплексных величин и построение
соответствующих диаграмм и гар-
монических функций. При этом на-
стойчиво рекомендуется пользовать-
ПО
ся счетной линейкой для перехода
от полярной (показательной) фор-
мы к двучленной (алгебраической).
Пример 4-4. В цепи последовательно
включенных г, L (рис. 3-15,г) при токе
i — Im cos cat общее напряжение представ-
ляется равенством (3-42)
। j
U=lr+L4t
или*
и = Um COS (со/ + у) = г!т COS со/ +
+ (&LIm cos ( со/ +
Полагая 1т — 20 а, г — 10 ом, &L—20 ом,
записать в комплексной форме /т, Um,
Umr, Um[- (последние два комплекса соот-
ветствуют напряжениям на г и на L); по-
строить векторную диаграмму.
Решение. В соответствии с уравне-
нием для мгновенных значений находим,
что
im = 20 а, йтг = 200 в, UmL —
400 тс/2 = /400 в, Um = 200+/400=
= 448 Д 63°30' в.
Векторная диаграмма представлена на
рис. 4-8,а.
Пример 4-5. В цепи последовательно
включенных г, С (рис. 3-11,а) при токе
f=/mcosco/ общее напряжение представ-
ляется равенством (3-25)
и — Ur + Uc = rim COS со/ +
Полагая г = 1 000 ом, 1/соС = 700 ом, 1т=
== 1 ма, записать в комплексной форме 1тг
Um, Umr, UmC (последние два комплекса
соответствуют напряжениям на г и на С);
построить векторную диаграмму.
Решение. В соответствии с уравне-
нием для мгновенных значений находим,
что
I т '— 1 MCI, Uт г —* т.Г'’— J 0’I в,
Um = 1 — /0,7 = 1,21 /2—35° в.
Векторная диаграмма представлена на
рис. 4-8,6'.
Примечание к примерам. Сме-
щение по фазе на + тс/2, соответствующее
умножению на е , представляется
7t
+ /
умножением на + j, так как е — + Д
При этом умножение на — j равно-
сильно делению на /, так как 1//= — /,
поскольку /2 = — 1.
Комплексные амплитуды и комп-
лексные действующие значения. В
большинстве расчетов токи и напря-
жения характеризуются действую-
щими значениями, поэтому обычно
их комплексное представление так-
же выражается не в амплитудных^
а в действующих значениях. При
этом комплексное действующее
значение определяется как комп-
лексная амплитуда, деленная на
/2:
и = ит/]/~2 , 7 = /т/]/2 И т. п.
(4-21)
Их обозначение отличается от
комплексных амплитуд только тем,,
что опускается индекс т.
Векторные диаграммы для дей-
ствующих значений отличаются от
диаграмм для комплексных ампли-_
туд масштабным множителем }/"2.
Дифференцирование гармони-
ческих функций. При дифферен-
цировании гармонической функции
ее изображение умножается на ju.
Другими словами, если комплекс-
ная величина А изображает диф-
ф ер енциру ему ю г а р-мони ч е скую
функцию, то производная этой функ-
ции изображается комплексом /соД.
Заметим еще раз, что умножение
на / равносильно увеличению аргу-
мента (или повороту вектора) на
1П
угол зт/2. Сказанное можно пред-
ставить следующими формулами:
а —Ат cos (о>£ 4“ а) Ат — Ameh;
— ®Ат cos^co/ + а+ £ j^J®Am = Вт.
(4-22)
• Формулированное правило непо-
средственно следует из дифферен-
цирования полного комплексного
представления гармонической функ-
ции (4-12) или (4-8):
= £ (Amef(Ot+Ame~^) _
dt dt 2
__—JtoXg /toZ) .
(4-23)
2
В правой части формулы множи-
тель при e/toZ, т. е. комплексная ам-
плитуда, теперь равен faAm = Bm.
Рассмотрим цепь г, L (рис. 3-15,г),
.для которой напряжение представ-
.ляется следующей суммой:
zr-|-L^- = zz. (4-24)
Положим, что в цепи идет ток
i ;— Iтп COS (со/ —Ос) IYfiC* =— j
здесь, разумеется, i и 1т взаимно
соответствуют.
Заменяя дифференцирование
умножением на /со и применяя пра-
вило сложения, находим для комп-
лекса, изображающего напряжение
и, следующую формулу:
ит = ите* = (г + /ш£) 1т. (4-25)
Комплексное сопротивление
цепи г, L, Первый комплексный
множитель в правой части (4-25)
называют комплексным со-
противлением цепи г, L. Его
обозначают буквой Z, представляя
в показательной или двучленной
форме:
Z = zeJ<? = z / <р = г ]®L =
= гЦ-/х£, (4-26)
где z — | Z | = У г2 -[- (о>£)2 ; <р =
= arctg—>0; xl=zmL— индук-
тивное сопротивление.
Пользуясь комплексным сопротив-
лением, равенство (4-25) можно за-
писать в таком виде:
Um = ZIm. (4-27)
Это значит, что в цепи переменного
тока напряжение равно произведению
тока и сопротивления, если все ве-
личины выражать в комплексной
форме. Раскрывая в деталях все опе-
рации с комплексами в (4-27), пи-
шем, что
7==z Um / Р Z / ф * 7 т / CL =
= г/т/а-|-<р.
В произведении двух комплексов
аргументы складываются, что осо-
бенно отчетливо видно при пользова-
нии показательной формой записи
= £/(<p+a). Следовательно, р, т.,е.
начальная фаза напряжения Um
в (4-27), равна сумме аргумента (ср)
комплексного сопротивления Z и на-
чальной фазы (а) тока /т:
р = <р4-а. (4-28)
При этом амплитуда напряжения
равна амплитуде тока, умноженной
на модуль сопротивления:
Um=zlm. (4-29)
Равенства (4-27) и (4-29) после
деления обеих частей на /2 при-
менимы и к комплексному изображе-
нию действующих значений:
U = Zl\U = zI. (4-30)
При этом Z имеет прежнее зна-
чение, так же как и фазовые соот-
ношения (4-28).
Пример 4-6. В цепи г, L (рис. 3-15, г)
проходит ток, изображаемый комплексом
/ = 2ДЧ5° а.
Параметры цепи: г = 4 ом, L = 1 мгн af=
= 500 гц.
Требуется найти амплитуду и началь-
ную фазу напряжения.
112
Решение. Прежде всего ишем комп-
лексное сопротивление:
Z = 4+/2л-500-0,001 =5,082/38°10' ом.
После чего находим £/ = Z/ = (7</₽’
где
СТ = Zz = 2-5,08 10,2 в
пряжение при положительных на-
правлениях, указанных на схеме,
выражается равенством u=ir+uCi
где
Представляя все члены уравне-
ния
и
Р = ?4-а = 83°10'.
(4-32)
Если 1 — 2 а — действующее значение
тока, то соответственно амплитуды 1т =
= 2/1 = 2,28 a, Um= 10,2/2 = 14,4 в.
Диаграмма на комплексной плоскости
для данных этого примера отличается от
диаграммы рис. 4-8,а тем, что ток 1 имеет
начальную фазу, отличную от нуля (век-
тор должен быть повернут на угол
+ 45°).
Интегрирование гармонических
функций. При интегрировании гар-
монической функции ее изображе-
ние делится на ]ы. Другими слова-
ми, если комплексная величина А
изображает интегрируемую функ-
цию, то ее интеграл изображается
комплексом А Цы.
Заметим еще раз, что деление
на j равносильно изменению аргу-
мента (или повороту вектора) на
угол —л/2.
Сказанное можно представить
формулами:
При этом существенно заметить,
что мы рассматриваем только гар-
моническую составляющую, полу-
ченную в результате интегрирова-
ния, т. е. рассматриваем установив-
шиеся режим и отбрасываем посто-
янную составляющую, если даже
она отлична от'нуля.
Формулированное правило легко
вывести, производя интегрирование
полного комплексного представле-
ния гармонических функций (4-12)
илц (4-8).
Пусть, например, необходимо
найти напряжение на зажимах це-
пи г, С (рис. 3-11,а). Искомое на-
их комплексными изображениями, на-
ходим, что
1<*С \ 1 /соС j
(4-33)
Комплексное сопротивление це-
пи г, С. Множитель при комплекс-
ном токе (4-33) можно назвать ком-
плексным сопротивлением цепи г, С:
~ , 1 .1
Z — Г + —тг—Г — / —F =
1 усоС J <оС
(4-34)
где
= г — jxc = ze}c?,
1
<»С ~
<p = arctg—2—<0,
хс=1/(оС — емкостное сопро-
тивление; причем так же, как в цепи
Г, Zz, ПрИ I тп Iгп & те
угол р = <р-ра- Знак минус в выра-
жении для <р определяется тем, что
теперь мнимая составляющая отри-
цательна:
1 _ • 1
усоС соС’
Соответствие комплексных й диф-
ференциальных уравнений. На осно-
вании изложенных правил можно
составить комплексные алгебраиче-
ские уравнения, соответствующие
любому линейному дифференциаль-
ному уравнению электрической це-
пи или системе таких уравнений, за-
писанных по законам Кирхгофа для
гармонических функций. Заметим
еще раз, что при этом имеется вви-
ду установившийся режим, в кото-
ром все токи и напряжения пред-
ставляются гармоническими функ-
8 К. М. Поливанов
113
днями. Так, например, уравнению
цепи с последовательно включен-
ными С, L, г (рис. 3-19)
, т at ,
и = tlc -4-L +г£
или
ц==± fz^ + L^- + ri (4-35)
соответствует алгебраическое ком-
плексное уравнение
бг = (т^с+/в)£+г)/- (4'36)
Для полного описания процессов
в простой последовательно-парал-
лельной цепи на рис. 4-9 можно со-
ставить два уравнения по второму
закону Кирхгофа
° = f — r3i3 — Ls
и одно уравнение .по первому закону
^1 = i2 —j— /3.
Этим уравнениям соответствуют
комплексные алгебраические урав-
нения
O=(r,+/«,L1)/,+ 7-^/,;
1 = /
2 1 J 2 ~ 1 3‘
Таким образом, решение систе-
мы дифференциальных уравнений
сводится к решению системы алге-
браических уравнений.
В этом и заключается главная
особенность комплексного (симво-
Рис. 4-9.
лического) ” метода, обеспечившая
ему широчайшее распространение.
Рассмотрим системы комплекс-
ных алгебраических уравнений для
цепи рис. 4-9. Допустим, что общее
напряжение (7, частота со и все па-
раметры цепи (Г1, Гз, С, Li, L3) из-
вестны и требуется определить токи
Л, Л, 73. В этом случае из трех ал-
гебраических уравнений системы
надлежит последовательно исклю-
чить два неизвестных, после чего
останется одно уравнение с одним
неизвестным.
Но решение системы комплекс-
ных уравнений электрической цепи
приводится к уже известным шаб-
лонам (трафаретам), найденным
в теории цепей постоянного тока.
Действительно, обозначая комп-
лексное сопротивление каждой вет-
ви буквой Z с соответствующим ин-
дексом, запишем систему уравнений
в таком виде:
+ 0 = /2Z2-/3Z3;
4 = 4 + 4;
здесь
Zs = r8+>L8,
z —___!_
2 — /«С ’
Последняя система уравнений от-
личается от соответствующей си-
стемы для цепи постоянного тока
только заменой всех сопротивлений
(гп) на комплексные сопротивле-
ния (Zn) и представлением всех,
токов и напряжений в комплексной
форме. Поэтому вместо прямого
решения этой системы уравнений
можно воспользоваться уже извест-
ным решением для токов в простой
последовательно-параллельной це-
пи (см. § 2-й):
4 = #у, (4-37)
где С = Z±Z2 -ф- Z2Z3 -ф- Z3Z r
Конечно, все вычисления теперь
носят совсем другой характер, а ре-
зультат выражен комплексом, оп-"
ределяющим амплитуду и фаз} ис-
комого тока.
114
Пример 4-7. Пусть в цепи на рис. 4-9
гг = 2 ом, г2=4 ом, ыЦ — Ьом, u>Ls =
— 20 ом, - 1/соС — 50 ом, U — 100 в.
Требуется найти все токи..
Решение. Ток /2 можно найти, при-
меняя формулу (4-37). Покажем весь ход
необходимых вычислений. Найдем прежде
всего $. Для этого выразим сначала все Z
в показательной (или полярной) форме:
Zi-=2 + /5 = 5,38 /.68° 10';
Z2 = —j50 = 50/.—90 °;
Z3 — 4 + /20 = 20,4/, 78°40'.
Затем найдем все парные произведения,
выраженные, в полярной форме1:
5,38-50 /68°10' — 90° +
+ 50-20,4 / —90° + 78°40' +
+ 20,4-5,38 Z78°40' + 68° 10' =
= 969 Д— 21 °50' + 1 020 L—11°20' +
+ 110/.146°50'.
Для того чтобы выполнить сложение,
следует вновь каждое из слагаемых пред-
ставить в двучленной форме:
£ = (249 — /100) + (1 000 — /200) —
— (92 — /60) = 1 157 — /240 =
= 1 180 21— 11°40' ом*.
Результат вновь выражен в комплекс-
ной форме, наиболее удобной для деления.
Зная С и Z3, легко находим, что
} -рА-юр. 20,4Z78°40'
Ji —и ? — iWj 18011°40'
(
= 1,73 90°20'^= /1,73 а.
Аналогично находится третий ток:
. Z2
/3 = U =0,86 —/4,15.
Первый ток равен их сумме
/1=/2+ /3 = 0,86 — /2,42 =
= 2,57/—70°30' а.
Нелинейные операции с комплек-
сами. Простейший пример нелиней-
ной операции, которая встречается
1 Переход от двучленной формы к по-
лярной* и обратно настойчиво рекомендует-
ся произ1водить, пользуясь логарифмической
линейной.
при анализе линейных цепей, — это
произведение двух гармонических
функций. Действительно, мощность
в цепи переменного тока опреде-
ляется произведением напряжения
и тока:
p — iu, (4-38)
где в общем случае
z=/wcos (ш/+а), и= t7mcos (со/+р).
Можно ли выразить эту опера-
цию, пользуясь комплексами? Да,
но только при условии тождествен-
ного представления гармонических
функций через комплексы [см. урав-
нения (4-8) и (4-12)].
/=+н-Г*);
(4-39)
и = (it —//*) э
где u=Umei?eimt; со-
пряженные им величины —
Подставив (4-39) в (4-38) и про-
изведя последовательно все требуе-
мые операции (умножение)., получим,
что
р=itt=-L (Z-f- 7*) (и +?=) =
=-Г К1 м + z*«*) + (Z*M + ««*)]•
(4-40)
Рассмотрим теперь, что представ-
ляют собой отдельные слагаемые
внутри квадратных скобок. Первое
из них
iu = U^e^e^\
второе представляет сопряженную
величину первого. Поэтому четверть
их суммы
4 о * +*«*)=
| ^/(avb₽ + 2<oZ) j е—/(a+p+2<tf)
= 4 cos (а + Р
выражает гармоническую функцию
двойной частоты.
8*
115
Третье слагаемое в (4-40) равно
постоянной величине1 *:
«7*— [7. / —т] г
и, I, - кУ т-и ,
четвертое представляет сопряженную
величину третьего. Поэтому четверть
их суммы
*4" JJnJ т
U mJ т) —•
UmJ т
2 “
2
—~2 UnJт cos (3 а) —
^j-ReOm/m=ReU/.
В итоге находим, что мгновенное
значение мощности
р=4 и™1™ [c°s (р—а)+
4“ cos (2^ + а + Р)] (4-41)
содержит слагаемое, выражаемое
гармонической функцией двойной ча-
стоты, и постоянное слагаемое, рав-
ное средней мощности
Р----“гГ UnJга COS (Р Gt) —-
= UI cos (Р — a) = Ret/Z (4-42)
Конечно, к тому же результату
нетрудно прийти из прямого триго-
нометрического преобразования
cos х cos у =
=у [cos (Л — у) + cos (х + у)}.
Однако при более сложных не-
линейных выражениях, в особенно-
сти содержащих слагаемые разных
частот, указанный метод операций
с тождественным (полным) . комп-
лексным представлением гармони-
ческих функций имеет существен-
ные ' преимущества. Основное из
1-: Произведение множителей и
равно единице. - *
этих преимуществ заключается в
возможности выполнения аналитиче-
ских выводов без законченных три-
гонометрических преобразований
в промежуточных выражениях.
Различие комплексов типа / и Z.
Как очевидно из самого определения, ком-
плексы, изображающие гармонически изме-
няющиеся величины / 7(0, U •••
отличны от комплексов типа Z.
Первым 1 = lJa, U ==Ue^ ,... соответ-
ствуют гармонические функции времени
i =Im cos (со/ 4- а), и =Um cos (со/ + g), •••
имеющие амплитуды Im, Um, ... и началь-
ные фазы а, р, ... ~
Комплексы второго типа, такие как
Z = ze1®, имеют иной смысл: они вводятся
как множители, устанавливающие- связь
между двумя изображениями гармониче-
ских функций. Модуль z такого комплекса
равен отношению между амплитудами двух
гармонических функций
п т Um
= ИЛИ Z = -r-----,
7П
а его аргумент (р показывает «разницу меж-
ду начальными фазами этих ’ гармонических
-функций Р и а, гг. е.
Ф=Р—а.
Комплексы iBToipio.ro типа могут «быть назва-
ны комплексными операторами. Само собой-
очевидно, что их можно изображать на ком-
плексной плоскости, однако на этой плюско-
сти они имеют иной смысл и не изображают
синусоидально изменяющихся величин.
Для отличия о г изображения гармони-
ческих функций их не рекомендуется обо-
значать с точкой над буквой. Комплексные
операторы обычно оставляют без особого
знака. Если нужно специально подчеркнуть
комплексный характер .величины, обозначае-
мой какой-либо буквой, над ней ставят осо-
бые знаки, например, /\ или <.
Вполне правомерна и другая точка зре-
ния, .согласно которой комплексы типа I и
U тоже представляют собой операторы при
комплексном изображении простой гармо-
нической функции С этой точки зре-
ния комплексы типа /, U так же, как и
комплексы типа Z, (следует обозначать оди-
наково. Тогда можно рекомендовать знак ~
для комплексных функций времени й— •
= Ue}' + а остальные комплексные
величины оставлять без дополнительных
знаков, как это принято в радиотехнике и
электродинамике ((или ставить над буквой
знак Z); точка над буквой-при этом сохра-
няется как знак дифференцирования по
времени, как это принято в физике и меха-
нике.
. • •
Дополнительное замечание о
комплексном методе. Мы определя-
116
ли гармоническую функцию как ве-
щественную часть комплекса:
а = Re (Ате]<й*) = Ат cos (со/ Д- а).
(4-43)
Однако в электротехнике не ме-
нее распространено определение
гармонической функции как мнимой
части того же комплексного изоб-
ражения:
а=Im (A— Ат sin (arf Д- а).
(4-44)
В этом случае при изображении
на комплексной плоскости в каче-
стве мгновенного значения .рассмат-
ривается проекция не на веществен-
ную, а на мнимую ось.
Все приведенные выше выводы
при этом сохраняют свою силу.
Лишь в конечном результате пере-
ход к мгновенным значениям про-
изводится по формуле (4-44), а не
пр: (4-430.
4-3. УРАВНЕНИЯ ПРЯМОЙ
И ОКРУЖНОСТИ НА КОМПЛЕКСНОЙ
плоскости
При анализе цепей переменного
тока бывает важно знать, как изме-
няются модуль и аргумент комп-
лексов тока /, напряжения U или
входного сопротивления ZBX и т. п.
в зависимости от изменения какого-
либо из параметров цепи, например
г, Z или со. Часто оказывается воз-
можным найти закономерности в ви-
де кривых, по которым на комплекс-
ной плоскости перемещается конец
рассматриваемого вектора. Поэто-
му важно знать, какими уравнения-
ми выражаются простейшие кривые
на комплексной плоскости.
Наибольшее практическое значе-
ние имеют прямая и окружность на
комплексной плоскости W~u+ju.
Прямая. В самом общем случае
на комплексной плоскости прямая
выражается линейной функцией
W—A+xB, (4-45)
где х — вещественная переменная,
А = a Z >а, В = b Z. р — постоянные
комплексы, модули которых а и Ъ.
Эта прямая образует угол р
с осью вещественных величин
(рис. 4-10,а). Важные частные слу-
чаи: при Л = 0 прямая проходит че-
рез начало координат (рис. 4-10,6);
при B—jb прямая параллельна оси
мнимых величин (рис. 4-10,в); при
В = Ь прямая параллельна оси ве-
щественных величин (рис. 4-10,г).
Окружность. Обратная величи-
на линейной функции
представляет уравнение окружно-
сти, проходящей через начало ко-
ординат.
Иными словами, окружность
представляет собой геометрическое
место обратных величин вектора,
скользящего по прямой. Поэтому
окружность, проходящую через на-
чало координат, называют инвер-
сией (обращением) прямой.
Для доказательства того, что
равенство (4-46) есть уравнение
окружности, разделим его числи-
тель и знаменатель на А, после че-
го равенство (4-46) примет вид:
117
t
где 5 = л
b
X— — вещественная
переменная; С —1/ А—с / — а — по-
стоянный комплекс; 6 = [5 — а — по-
стоянный угол.
Из (4-47) следует, что
W (1 4- fe/s) = W + =
— const.
(4-48)
Изобразив графически это равен-
ство (рис. 4-11,а), получим тре-
угольник, одна сторона которого
вектор W, другая — вектор %Welb,
повернутый относительно W на
угол 6, третья сторона С = const.
Таким образом, мы получим тре-
угольник с постоянным основанием
С и постоянным углом при верши-
не (б—const). Геометрическое ме*
сто вершин такого треугольника —
окружность, что известно из курса
геометрии. Другими словами, гео-
метрическое место концов вектора
W— окружность, если в уравнении
(4-47) единственная переменная —
вещественное число g. Эта окруж-
ность проходит через начало коор-
динат, поскольку IF=0 при g = oo.
Важно заметить, что угол< при
вершине (б = const) становится ут-
лом между касательной к окруж-
ности в конце вектора С и продол-
жением этого вектора, когда век-
тор W, скользя по окружности, сов-
падет с вектором С (рис. 4-11,а).
Простой метод построения
окружности по уравнению (4-47)
состоит в следующем. На комплекс-
ной плоскости откладываем вектор
С (рис. 4-11,6). Через его конец
проводим прямую, образующую
угол б с продолжением вектора С;
эта прямая — касательная к иско-
мой окружности в конце вектора С.
Восставляя перпендикуляр к хорде
С из ее середины и перпендикуляр
р к касательной в конце вектора С,
находим точку пересечения этих
перпендикуляров (точка О' на
рис. 4-11,6). Как известно из геомет-
рии, эта точка есть центр окруж-
ности. Следовательно, искомая
окружность найдена; известен ее
центр О7 и две точки (начало и ко-
нец вектора С). Нетрудно вычис-
лить и ее диаметр 2р =*|C/sin б).
Окружность -можно построить, найдя
любые се грри точки. В том случае, когда
задано уравнение прямой Л+хВ~ инверсией
которой является окружность [уравнение
(4-46)], достаточно найти три точки, «обрат-
ные» трем точкам, лежащим на -заданной
прямой.
Пусть эти точки на прямой определяют-
ся векторами
Л42=т2/р2, M3 = m3/fx3,
в таком случае обратные им точки (инвер-
сия точек) определяются комплексами
Г1=
Точки, определяемые комплексами IFi, W2,
по условию лежат на окружности.
В общем случае окружность
может и не проходить через нача-
ло координат. Для этого достаточ-
но сместить ранее найденную
окружность на какую-либо задан-
ную величину 157О, т. е. к выраже-
нию (4-47) следует прибавить по-
стоянную слагающую IF0.
118
В результате, приходим к уравне-
нению окружности в самом общем
виде:
i:' <449)
Построение такой окружности от-
личается от уже рассмотренного
только определением хорды С. Как
очевидно из (4-49),
где —значение вектора W при
1 = 0, оно равно IFO-|-C; 1^|^=0о —
значение того же вектора при В=оо,
т. е. IF6.
.Предоставляем доказать -само-
стоятельно, что уравнение, обрат-
ное (4-49), вновь оказывается урав-
нением окружности. Это значит, что
инверсией окружности, не проходя-
щей через начало координат, ока-
зывается опять окружность.
Определение точки W на окруж-
ности по заданному g. Чтобы охва-
тить все геометрические построе-
ния, встречающиеся в дальнейшем
тексте, покажем, как найти точки на
окружности W, которые соответст-
вуют заданным значениям перемен-
ного g.
Заметим прежде всего, что в тре-
угольнике 123 (рис. 4-12) по са-
мому построению отношение сторон
> (_
23/12 = 1.
Этим отношением однако неудобно
пользоваться, поскольку в нем и
Рис. 4-12.
числитель и знаменатель перемен-
ные. Очевидно, что для определе-
ния I было бы удобно найти тре-
угольник, подобный треугольнику
123, в котором сторона, соответст-
вующая 12, была бы постоянной.
Такой треугольник легко построить.
Проведем из произвольной точ-
ки О" (рис. 4-12), лежащей на хор-
де С или на ее продолжении, пря-
мую линию, повернутую на угол —б
относительно С. Продолжая сторо-
ну 12 до пересечения с этой прямой
в точке 3', получим треугольник
1 О"3', подобный треугольнику 123.
Действительно, у этих треугольни-
ков один угол общий (при вершине
/), а другой (при вершинах 2 и О")
по построению одинаков и равен
л—б. Следовательно, отношение от-
резков
о*з'1Ю”=е.
Таким образом, прямая, прохо-
дящая через точки О", 3' может
служить шкалой для <g. Последним
отношением определяется и мас-
штаб этой шкалы: g=’l, когда
длина отрезка О"3', отсчитывае-
мая от точки О", .равна длине от-
резка 10".
На основании изложенного по-
ставленная задача решается так:
после того, как построены окруж-
ность и линия g (рис. 4-12), нужно
соединить прямой точку заданного
g с точкой 1 (конец вектора Wq)-,
точка пересечения этой прямой
с окружностью и определяет поло-
жение вектора W на окружности
при заданном g. Точка 3 соответст-
вует g=0; точка 1 соответствует
g=oo, так как линия g параллельна
касательной к окружности в точке
1; дуга 123 соответствует положи-
тельным значениям g, остальная
часть окружности соответствует от-
рицательным g.
Заметим в заключение, что все
построения рис. 4-11. и 4-12 выпол-
нены для положительных б. Во-
многих электротехнических зада-
чах б оказывается отрицательной
величиной. При этом все построе-
ние проводится тем же методом, но
поворот на угол |б| производится
по часовой стрелке, так как б=—|б|.
119
ГЛАВА ПЯТАЯ
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ЛИНЕЙНЫХ
ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩИХ л L, С
5-1. УРАВНЕНИЯ
ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
В КОМПЛЕКСНОЙ ФОРМЕ
Законы Кирхгофа. Методы ана-
лиза и расчета цепей переменного
тока с постоянными параметрами
г, L, С основываются на примени-
мости законов Кирхгофа к мгновен-
ным значениям токов и напряже-
ний, а следовательно, и на примени-
мости этих законов для установив-
шегося режима и простых гармони-
ческих токов при записи этих зако-
нов в комплексной форме.
Условия применимости законов
Кирхгофа определяются, во-первых,
возможностью представлять напря-
жение между рассматриваемыми
точками цепи как разность их по-
тенциалов и, во-вторых, равенст-
вом нулю суммы мгновенных значе-
ний всех токов, притекающих к лю-
бому из рассматриваемых узлов.
Более подробный анализ этих ус-
ловий может быть проведен только
на основании теории электромаг-
нитного поля. Во всем последую-
щем изложении считается, что эти
условия выполняются во всех рас-
сматриваемых цепях.
Сказанное приводит к выводу
о применимости к линейным цепям
переменного тока всех методов рас-
чета и всех теорем теории цепей
постоянного тока. Конечно, при
этом появляется много особенно-
стей, вытекающих из применения
комплексных уравнений.
Так, например, говоря о равен-
стве двух напряжений или двух
комплексных сопротивлений, необ-
ходимо иметь в виду как равенство
модулей, так и равенство аргумен-
тов; режим цепи определяется не
только величинами напряжений и
токов источников питания, но так-
же их фазами и частотой и т. п.
В теории переменных токов возни-
кает и ряд совершенно новых по-
нятий.
Сопротивление. Комплексное со-
противление любой ветви и любого
120
пассивного двухполюсника в об-
щем случае состоит из веществен-
ной и мнимой составляющих:
Z=r+/x.
(5-1)
При этом, разумеется,
U = 1Z, (5-2)
где V и 1 —'комплексные напряже-
ние и ток на входе двухполюсника.
Комплексное сопротивление Z
может быть представлено через мо-
дуль (абсолютную величину) и ар-
гумент:
Z = z / или Z=ze^ (5-3)
при г = ]/г2-|-л2 и tg<p = y
или
9=argZ.
Пусть 1 — и U = JJв
таком случае
17 = /z/a + 9,
где модуль напряжения
U=Iz,
а начальная фаза
(5-4)
(5-5)
, Модуль комплексного сопротив-
ления называют также полным
сопротивлением. Веществен-
ную часть комплексного сопротив-
ления, т. е. г, называют просто со-
противлением или активным со-
противлением (но это активное
сопротивление пассивной цепи!);
мнимую часть, т. е. х, называют р е-
активным сопротивлением.
Реактивное сопротивление ин-
дуктивности положительно:
ZL — jx — J(oL = ~jxL, х — х^> 0.
(5-6)
Реактивное сопротивление емко-
сти отрицательно:
]х Jac “ 1 <ЬС “ !хс>
х = — хс < 0.
(5-7)
Комплексное сопротивление по-
следовательно включенных г, Z, С
Z — г jx —г j (<*>L
= г + / (хд — Хс). (5-8)
В этом случае реактивное сопротив-
ление1 может быть и положительным
и отрицательным
мер, сопротивление Z ветви с по-
следовательно включенными г, Л, С
(рис. 5-1,а) при изменении частоты
характеризуется на комплексной
плоскости прямой линией, парал-
лельной мнимой оси (рис. 5-1,6).
Эквивалентное сопротивление Z9
двух параллельных ветвей с сопро-
тивлениями Z] и Z2 равно:
z==-z7Tt=r- + '-t- <5'10*
Оно также состоит из. вещественной
гэ и мнимой xQ 'составляющих; в об-
щем виде их выражение через со-
ставляющие Zi и Z2 представляет-
ся довольно громоздкой алгебраи-
ческой формулой
х — —xL хс,
(Г1 + jXi) (г2 + jx2)
Г1 + f 2 + j (Х1 + Х2)
0 при со2или xL^>xc
0 при 0)2 Тг ИЛИ XL < хо
Реактивное сопротивление х рав-
но нулю при резонансе, когда
ф = ш0
1
уLC’
(5-9)
при более низкой частоте оно отри-
цательно, при более высокой—по-
ложительно.
Сопротивление Z можно изобра-
жать графически на комплексной
плоскости. Последнее особенно удоб-
но, когда ищется характер изме-
нения Z при изменении того или
иного параметра цепи. Так, напри-
Рис. 5-1.
= (^2 + + г2 (*1 + +
/ [0*1^2 ,Г2-^1) (/* 1 “Ь g)
— — хгх2) (хН-х,)]: В,
где £ = (г1 + г2)2+(х1 + х2)2.
Это выражение получается после
умножения и знаменателя и числи-
теля на величину, сопряженную
знаменателю. При этом гэ>0 неза-
висимо от знаков Xi и х2.
Проводимость. Величину, обрат-
ную комплексному сопротивлению
Z, (называют комплексной про-
водимостью
ИЛИ
У=у — (5-12)
где
И
, ь
<p = arctgy.
Модуль (абсолютную величину)
проводимости, т. е. у называют
полной проводимостью; g и b на-
зывают активной и реактив-
121
ной проводимостями. При парал-
лельном соединении \г и L
ь J г * /соЛ ’
откуда
g=:llrf b=\l(dL — bLf
где bL=\l<nL — индуктивная прово-
димость.
При параллельном соединении г
и С (рис. 5-2,а)
Y = g-ib^+_L_^hC,
откуда
g = Y> Ь = — (оС = — Ьс>
где Ьс — (оС — емкостная проводи-
мость.
При параллельном соединении г,
L, С
Y = g — jb = — -\—!_I—-_
ё J г 1 ja>L‘ 1/JaC ’
откуда
g=~, b=~—^C = b.-~br
r coL L С»
Как и в цепях постоянного тока,
при параллельных ветвях склады-
ваются их проводимости, т. е. эк-
вивалентная проводимость двух па-
раллельных ветвей
Y9—Y1-\-Y2 (5-13)
равна сумме их комплексных про-
водимостей. Само собой разумеется,
что при этом в общем случае мо-
дуль суммы (r/э) не равен сумме
модулей (У1 + г/2).
Рис. 5-2.
Из самого определения проводи-
мости следует, что
1 = UY и I = Uy. (5-14)
Представляя Z как сумму r+jx,
из (5-11>) находим, что
у = 1 _ г —/X
г + ]Х г2 + X2 ’
откуда в соответствии с (5-12)
g
г
Г2 -]_Х2 ’
(5-15)
Из последней формулы очевидно,
что: 1) £>0 при г>0, 2) б>0
при х J>0, в частности при x = xL=
= &L и 3) b<^0 цр1ГЛ<0, в част-
ности при х — — хе =—1/(оС).
В литературе часто принимается
иной выбор знака в формуле реак-
тивной проводимости
Y=^g + ib.
Во всем последующем тексте мы
будем считать, что знак реактивной
проводимости определяется выраже-
нием (5-12).
Проводимости также можно изо-
бражать на комплексной плоскости.
Геометрическое место концов векто-
ра У представляет кривую, обрат-
ную кривой Z. Поэтому проводи-
мость ветви с последовательно
включенными г, Ц С выражается
вектором, описывающим окруж-
ность при co=var (рис. 5-1,в, где
₽=-&).
Если геометрическое место кон-
цов вектора У—прямая (рис. 5-2,6),
как в случае параллельно включен-
ных г, С и переменной частоты со
(рис. 5-2,а и б) или переменного г
(рис. 5-6,а и б), то геометрическое
место концов вектора Z— окруж-
ность (рис. 5-2,в и 5-3,в).
В заключение этого параграфа
приведем примеры простых расче-
тов цепей переменного тока, пока-
зывающих сходство и различие ме-
тодов расчета цепей переменного и
постоянного токов. Более сложные
примеры приводятся после рассмот-
122
рения мощности в цепи переменного
тока и теории топографических диа-
грамм. 9 -
Пример 5-1. Две параллельные ветви
с )соп|рот.и1в лениями Zi=3—/4 ом, Z2=44-
+/ 3 ом (подключены .к источнику (перемен-
ного напряжения (рис. 5-4,а). Требуется
вычислить (проводимости каждой из ветвей
и^ сложив их, найти общую проводимость;
Найти показания трех амперметров,
если вольтметр (показывает 100 в и если
известно, что все включенные приборы по-
казывают действующие значения.
•Построить векторную диаграмму токов.
Решение. Вычисляя обратную вели-
чину сопротивлений, находим:
1 3 + /4
Pi = 2 — j4~ 25 ~ 0,12 +
!1 4 — J3
Y2 - 4ууз = -25^ = 0,16—>0,12 сим.
Общая проводимость
У = Y1 У2 — 0,28 /0,04 сим.
Модули проводимостей
Ух~= 0,20 сим', #2 = 0,20 сим*,
у — 0,282 сим.
Соответственно показания амперметров
11 = Uух = 20 и ; 12== Uу2 = 20 и;
Л = |Л + А1 = ^# = 28,2 а.
Векторная диаграмма токов представ-
лена на рис. 5-4,0 в предположении, что
V = U; при этом l2 = UY2i 1Z — UY.
Пример 5-2. Последовательно вклю-
чены два сопротивления, из которых пер-
вое чисто активное, а второе содержит
индуктивность и сопротивление (рис. 5-5,а).
Приборы, включенные в цепь, показывают
действующие значения:
I = 2а; Ux — 20 в; U2 = 36 в; (7 = 50 в.
а)
Рис. 5-4.
Построив векторную диаграмму, опре-
делить активную и реактивную составляю-
щие второго сопротивления Z2 = ^ + 7Х2-
Решение. Для напряжений, пред-
ставленных в комплексной форме, должен
выполняться второй закон Кирхгофа
й1 + и2 = и9
причем напряжение Uх должно совпадать
по фазе с током а напряжение U2
должно опережать 1. Этим условиям при
заданных модулях удовлетворяет единст-
венный треугольник векторов на комплекс-
ной плоскости. Построение такого треуголь-
ника легко осуществить, пользуясь цирку-
лем (рис. 5-5,0). Проведя по направлению
1 вектор Ux из его начала и конца, радиу-
сами U и (72 засекают дуги; точка пересе-
чения этих дуг и определяет положение
векторов U и 02.
123
Разумеется, что для Ut u19 U2 выби-
рается одинаковый масштаб.
Из построенной диаграммы легко найти
cos ^>2 и sin ^2, а также угол <р2 == 57°20'.
Модуль искомого сопротивления изве-
стен из показания приборов
z2 = U2/I = 18 ом.
Для данного примера
Z2 = z2 (cos <р2 + j sin <p2) = Ю + /15 ом.
Тот же результат, конечно, можно найти и
чисто аналитически.
Из равенств
Та = I Ui = 1гй
U = I У (ri + Гг)2 + -*2
следует, что
х2 =’1^/^ j — = 15 ом.
Преимущество наглядности остается за
графическим методом.
Пример 5-3. В примере 2-3 (гл. 2) бы-
ло указано, что можно устранить влияние
собственных 1со1п|роти1влений приборов при
измерении сопротивления методом вольт-
метра и амперметра.
На рис. 5-6 приведена подобная схема
в’ применении к измерению на переменном
токе (ZA и Zv —сопротивления ампермет-
ра и вольтметра). Доказать, что в этом
случае
2х=П2/Л,.
где zx—•-модуль измеряемого сопротив-
ления;1
U2, Ц—показания приборов при вто-
ром i(I72) и первом (Л) положе-
ниях. переключателя.
Решение. К простой' последователь-
но-параллельной цепи при пользовании ком-
плексами применима формула
Л = UZ^t
где £=Zi Z2+Z2Z3 -f- ZzZx — сумм а п арных
произведений из сопротивлений всех ветвей
(Zi — последовательная ветвь, Z2 и Z3—
параллельные ветви).
Рис. 5-7.
Но ток в (сопротивлении (Zx) при вто-
ром положении переключателя ((рис 5-6)
равен току в амперметре (ZA) при первом
положении переключателя, поскольку
в обоих случаях токи определяются (в одной
из параллельных ветвей три условии, что-
другая параллельная ветвь в обоих случаях
одна и та же (Zv).
Следовательно, напряжение, измеренное
при втором положении,
U2—I\ZX.
Тем самым требуемое положение показано.
Пример 5-4. Найти отношение комп-
лексов напряжений на выходе и на входе
А ==:= U ВЫхД/ вх
для цепи, изображенной на рис. 5-7, при»
С'=2С и J?z=JR/2, пользуясь формулой, вы-
веденной для двойного Т-образного четы-
рехполюсника в цепи постоянного тока
(рис. «2-61, § 2-13, п. 4),
i+p2
С^вых/Г/вх = ! I 4g J о2 ♦
Решение. Переходя к комплексам^
подставляя R вместо Ri и Z2=l/(/(oC) вме-
сто Т?2, находим, что |3=/(оС7? и получаемz
U в ы х 1 — а2
/7ВХ “ 1 — «2 + у4а’
где а = (&CR.
Пример 5-5. Найти входное сопротив-
ление двухполюсников, изображенных на
рис. 5-8, взяв (следующие данные:
для рис. 5-8,я: для рис. 5-8,6:
X] х2 г Xi х2 г
—1 400 1 200 1 200 750 —852 1 200
— 200 —1 200 1200 —396 634 100
Анализируя алгебраическое выражение
для Гвх и приведенные здесь параметры,
легко увидеть, что входное сопротив-
ление всех двухполюсников одинаково
а)
Рис. 5-8.
124
а) б)
Рис. 5-9.
ное сопротивление задано с такой щсе боль-
шой точностью (~ 0,2%) • В противном слу-
чае следует принимать ^=200 ком и X—
= 10 ком.
5-2. МОЩНОСТЬ В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
-2вх=Гвх+р:вх = 600—,/800 ом. Из этого вид-
но, что при наличном активном сопротив-
лении г можно изменять эквивалентное
(входное) активное сопротивление (гВх),
подбирая добавочные реактивные сопротив-
ления. Практическое значение такого пре-
образования анализируется в § 5-3.
Пример 5-6. При частоте f =50 гц
входное * сопротивление двухполюсника
ZB х=г+jx=0,5004- / 10,0 ком. Можно ли
представить этот-двухполюсник (рис. 5-9,а)
состоящим из двух параллельных вет-
вей— одной чисто активной и другой чисто
реактивной, как показано на рис. 5-9,6?
Если 1М0ЖН0, то определить сопротивления
R и X ©тих двух ветвей.
Решение. ‘Входная проводимость за-
данного двухполюсника
Y______L =_____L_ _ : *
вх Zbx r2+x2 J Г2 X2 *
Входная проводимость двух параллельных
ветвей, сопротивления которых R и X,
Увх — = g —jb,
х Очевидно, что всегда можно выбрать
такие .значения R и X, чтобы в двух напи-
санных выражениях оказывались равными
как вещественные, так и мнимые части:
1 _ Г 1 _ X
£ R г2 + Л2 и Ь== ~Х г2 + х2 *
t
Следовательно, заданный. двухполюсник
можно представить состоящим из двух па-
раллельных ветвей — одной, содержащей
только активное сопротивление
Г2_^д;2
R = —~— = 200,5 ком,
и другой,, содержащей только реактивное
сопротивление
Понятия мгновенной мощности
p=ui (5-16)
и средней мощности
Р=р (5-17)
не требуют дополнительных разъяс-
нений. Как уже было показано,
(4-42) при простом гармоническом
токе .
Р = UI cos <р = Re £7/, (5-18)
где ф=|р—«а— сдвиг по фазе меж-
ду напряжением и током, или фазо-'
вый угол, на который ток отстает
от напряжения, при этом coscp на-
зывают коэффициентом мощности.
Для анализа цепей очень важны
и другие понятия, относящиеся
к мощности — это так называемая
полная (кажущаяся), реактивная и
комплексная мощности.
Полная мощность. Полная мощ-
ность определяется как произведе-
ние действующих значений тока и
напряжения:
S=>UI. (5-19)
Представим себе генератор пере-
менного тока /, связанный кабель-
ной линией с потребителем П
(рис. 5-10).
Предельное напряжение, допу-
скаемое для генератора и кабельной
линии, определяется уровнем их
изоляции; из соображений электри-
ческой прочности системы подъем
напряжения выше, номинального
/7Н недопустим. Предельный ток
в системе ограничивается номиналь-
ным значением
тока /ы из-за нагре-
= 10,025 ком,.
В этом случае как X, так
и х положительны, т. е. эти эле-
менты — индуктивности. Заме-,
тим, что числа, стоящие на чет-
вертом месте после первой зна-
чащей цифры,с имеют смысл
лишь в том случае, когда вход-
125
ва обмоток генератора и жил кабе-
ля. Оба эти ограничения устанавли-
ваются отдельно для тока и отдель-
но для напряжения и, конечно, не
зависят от фазового сдвига между
ними. Произведение номинальных
(допустимых) значений напряжения
и тока определяет номинальную
(допустимую) кажущуюся мощ-
ность
SH = t/HZs. (5-20)
Какая же действительная,
т. е. средняя мощность может пере-
даваться такой системой? Это зави-
сит от фазового сдвига между на-
пряжением и током, который опре-
деляется характером нагрузки. Так,
при индуктивном характере нагруз-
ки ток потребителя отстает от на-
пряжения по фазе на угол <р2- В та-
ком случае потребляемая мощность
не должна превосходить
Л =UHJH2cos(f2 = SH2cos<?2. (5-21)
Пусть, например, (номинальные значе-
ния тока и напряжения в конце линии:
Z7h2=1-1,5 кв, /н2=200 а и :cos ср2=0,8.
В таком случае потребляемая мощность
не должна превосходить
Р2=2,3- 106 -0,8=1,84 Мет.
При более низком cos ср2 допу-
стимое значение потребляемой мощ-
ности Р2 также снижается, посколь-
ку допустимая кажущаяся мощ-
ность остается неизменной.
Компенсация фазового сдвига.
Включим параллельно с потребите-
лем конденсатор такой емкости, что-
бы сдвиг по фазе между напряже-
нием и током в конце кабеля рав-
нялся нулю, т. е. коэффициент мощ-
ности С08ф2л=1. Тогда по линии
можно передать мощность, равную
полной
Л = 5ц2 Щ И С08<Р2л=1.
При этом ток в конце линии /2л
не превосходит номинального, хотя
ток самого потребителя 12 -может
быть больше чем .номинальный.
Сказанное поясняется векторной,
диаграммой (рис..5-11), из которой
очевидно, что в рассматриваемых
условиях ток в конденсаторной
ветви
/2С = 12 sin ?2,
а ток в конце линии
Лл=Л c°s ?2-
Поскольку /2С= ^2СоС, то для любых
заданных конкретных условий мож-
но найти требуемую емкость, кон-
денсатора.
Полагая, 'Что ток <в конце линии /2Л ра-
вен допустимому номинальному, находим
для приведенных выше числовых данных
h = Лл/cos — 250 а.
В таком случае 72С=/2 sin cp2=150 а_
При номинальном напряжении в конце ли-
нии для частоты 50 гц находим:
he 150
С “ Й7Г = 314-11 500 “ 4 ’5
Реактивная мощность. Эта вели-
чина определяется как произведе-
ние действующих значений напряже-
ния и тока, умноженных на синус
угла сдвига по фазе между ними:
Q = U1 sin <f> = S^sin <р. (5-22)
Напомним, что по условию ф— это
угол, на который напряжение опе-
режает ток.
Поскольку напряжение UL=j(nLI
и sin <р = sin ~ = 1, то реактивная
мощность, потребляемая индуктив-
ностью,
LI2
Q^QL = ULI = ^LI2 = m-~^. (5-23)
Поскольку ток I = j(x>CUc опере-
жает напряжение на тс/2 и sin <р =
= sin (— гс/2) = — 1, то реактивная
мощность, потребляемая емкостью,
Q = —Qc = -UcI^ — ^CU2 =
cu2m
2
(5-24)
126
Оба выражения (5-23) и (5-24)
имеют определенный физический
смысл: они равны максимальней
энергии поля соответствующего
элемента, умноженной на круговую
частоту. Таким образом, Q равно
максим альной мгновенной мощно-
сти, потребляемой соответствую-
щим реактивным элементам Ч
Различие знака реактивной мощ-
ности также имеет физический
смысл, который отчетливо виден
лишь в простейшем случае последо-
вательно (или параллельно) вклю-
ченных L й С. В обоих случаях мо-
мент потребления максимальной
мощности одним из элементов сов-
падает с моментом отдачи макси-
мальной мощности другим; пульса-
ции мощности в L и С сдвинуты по
фазе на угол д.
Приведенный выше пример ком-
пенсации фазового сдвига основан
именно на компенсации реактивной
мощности индуктивной нагрузки
реактивной мощностью параллельно
включенного конденсатора.
Вопрос о том, какую из двух
реактивных мощностей считать по-
ложительной, решается совершенно
условно. Например, в Америке при-
няты иные (но тоже противополож-
ные) знаки для Q.
Из приведенного определения
слёдует, что полная (кажущаяся)
мощность равна корню квадратно-
му из суммы квадратов Р и Q:
S = /^2 + Q2
ИЛИ '
Q = zt/S2 —Р2. (5-25)
В некоторых случаях последнее
определение может считаться более
общим.
Комплексная мощность. Эта ве-
личина определяется как произве-
1 Wja = i2L/2 = -% LI^ cos2 v)t;
dw™ rr2 . ,
p = sln tot COS tot ~
1 2
— — ~2 sin 2cof;
1 r 9
— 2 toLIm.
дение комплекса напряжения и со-
пряженного комплекса тока
S = Ul = P + jQ. (5-26)
Ее вещественная часть равна сред-
ней мощности (активной), а мнимая —
реактивной. Это легко псказать, рас-
крывая произведение комплексов.
Пусть U =='U и / = при
этом
S = Uf=U^-I K = UI
(5-27)
где ф=р—а — фазовый угол, на ко-
торый ток отстает от напряжения.
Естественно, что мгновенная и
средняя мощности измеряются
в ваттах (ет) или в соответствую-
щих кратных (кет, Мет) и доль-
ных (мет, мкет и т. д.) единицах,
а другие виды мощностей измеря-
ются в условных единицах: кажу-
щаяся мощность — IB вольт-амперах
(еа), реактивная ib вольт-амперах
реактивных (еар) или в соответст-
вующих кратных (кеа, Меа, кеар,
Меар),
Поскольку загруженность линий
передачи и генераторов определяет-
ся не только активной, но и полной
мощностью,- в энергосистемах учи-
тывают не только количество дей-
ствительно полученной энергии
(кет • ч или Мет • ч)
< t
= ^Pdt, (5-28)
о
но и загруженность реактивной
мощностью, которую определяют
как «реактивную энергию»
t
Wv=\Qdt, (5-29)
выражаемую в реактивных кило-
вольт-ампер-часах или реактивных
мегавольт-ампер-часах (кеар • ч,
Меар - ч).
Получаемая и отдаваемая мощ-
ность. В случае любого двухполюс-
ника можно говорить о той мощно-
сти, которая извне поступает к нему,
т. е. потребляется двухполюсником.
127
Но можно говорить и ю мощно-
сти, которая отдается этим двухпо-
люсником во внешнюю цепь
(см. §3-8).
В обоих случаях мощность опре-
деляется одинаковыми формулами
р = и1, S — Ul = P-\-jQ
или
р — Q = VI sin <р.
Однако согласованность положи-
тельных направлений тока и напря-
жения в этих двух случаях раз-
лична.
При определении отдаваемой
мощности следует считать положи-
тельным ток, идущий во внешнюю
цепь из положительного полюса,
т. е. из полюса, потенциал которого
выше при положительном напряже-
нии (рис. 5-12,а). При определении
поступающей извне мощности сле-
дует считать положительным ток,
входящий извне в положительный
полюс (рис. 5-12,6).
Из сказанного следует, что для
любого двухполюсника можно
иметь в виду как отдаваемую им
Ротд, так и получаемую рПол мощно-
сти, причем всегда
Рот Д pTLOSL*
Сказанное относится к мгновен-
ной, комплексной, активной и реак-
тивной мощностям. Что касается
кажущейся мощности, то по опреде-
лению она всегда выражается поло-
жительным числом.
Знак реактивной мощности за-
висит не только от того, получае-
мая эта мощность или отдаваемая,
но и от того, положительна (индук-
тивность) или отрицательна (ем-
кость) эта реактивная мощность.
Рис. 5-1-2.
а — отдаваемая мощность p=ui, получае-
мая мощность р——ui\ б-— получаемая
мощность p=ui, отдаваемая мощность
p=^ui.
Рис. 5-13.
Так, например, о двухполюсни-
ке, потребляющем отрицательную
реактивную мощность, можно ска-
зать, что он отдает (генерирует)
положительную реактивную мощ-
ность.
Пример 5-7. В цепи, образованной
двумя двухполюсниками, положительные
направления тока и напряжения выбраны,
как показано на рис. 5-13. Требуется найти
комплексную мощность, отдаваемую пер-
вым двухполюсником и получаемую вто-
рым, для следующих данных:
А) и = 100 4-у 100 в, I = 40 —/20 а\
Б) и = 100 + /100. в,. 1 = 20 —/60 а.
Кроме того, нужно определить, какой
из двухполюсников можно (Считать пассив-
ным, и определить характер его реактивно-
го сопротивления -(емкостный при х<0,
индуктивный при х>0*).
Решение. В -случае А мощность, отда-
ваемая первым ДВУХПОЛЮСНИКОМ,
$отд1 — UI — 2 000 4“ /6 000 ва.
Второй двухполюсник получает ту же’мощ-
ность (Sno л2 = S0T д1) . Первый ДВуХПОЛЮС-
ник содержит генератор, второй двухполюс-
ник можно считать пассивным; его сопро-
тивление
Z2 = U/i = 3,16,/72015' ом
носит индуктивный характер (<р>0).
В случае Б мощность, отдаваемая пер-
вым двухполюсником,
So тд 1 — U I = — 4 000 4~ /8 000 в и,
т. е. фактически мощность отдается вторым
двухполюсником.
Первый двухполюсник можно считать
пассивным, его сопротивление
Z, = и/(— 1) = 2,24/— 63°257 ом
носит емкостный характер.
Реактивная мощность, получаемая пер-
вым двухполюсником, отрицательна. Можно
сказать и по-другому:- он отдает положи-
тельную реактивную мощность.
Баланс мощности. Из закона со-
хранения энергии следует, что в лю:
бой цепи вся - мощность,- поступаю-
щая в цепь, в любой момент равна
128
всей мощности, потребляемой це-
пью, если речь идет о мгновенных
значениях мощности (р). Из этого
следует, что вся средняя мощность,
поступающая в цепь от различных
источников (генераторов), также
равна всей средней потребляемой
мощности.
Такому же балансу удовлетво-
ряет и реактивная мощность: сумма
всей реактивной мощности, отда-
ваемой в цепь отдельными ее эле-
ментами, равна сумме всей реактив-
ной мощности, потребляемой осталь-
ными элементами цепи.
Это (равенство, не вытекающее непо-
средственно из закона 1С0Х|ранения энергии,
можно доказать следующим путем.. Соста-
вим систему уравнений по пердюму закону
Кирхгофа для токов всех узлов цепи, обо-
значив индексом тп ток, идущий от узла т
к узлу п:
712 + 713 + / 14+ ••• = О»
/21 + /23 + •••
Заменяя все токи их сопряженными
значениями и умножая каждое из равенств
на потенциал соответствующего узла, при-
ходим к системе
* . * . * .
/12<р1 + /1з?1 + /14? i+ ••• = 0;
* . * * .
Л1?2 + ^23?2 + / 24?2 + ••• =0;
Складывая все эти равенства и принимая
во внимание, что 1тП = —1пт, получаем
уравнение
/12 (?i — ?г) 4“ /13 (?i— ¥з) + ••• = 0, (5-30)
в котором каждое из слагаемых равно мощ-
ности, потребляемой соответствующей
ветвью 12, 13, ...:
«• . . * . * .
S12 — 112 (?1 - ?г) = /12^12» S13=/ 13(713,...,
где
?1 -- ?2 — /12^12 - 312J
Комплексную мощность, потреб-
ляемую в ветви с сопротивлением
Z, можно представить формулой,
аналогичной формуле Джоуля —
Ленца:
s=L7*=/z/*=/2z.
Поэтому баланс комплексных мощ-
ностей можно представить и равен-
ством
S37=S72Z,
(5-32)
если положительное направление
тока в любом источнике принимает-
ся совпадающим с направлением
его э. д. с.
В машинах переменного тока
. *
произведение Э1 может иметь отри-
цательную вещественную часть. Это
значит, что такая машина работает
как двигатель, а не как генератор.
Если заранее известно, что какая-
либо машина работает как двига-
тель, можно изменить для нее вы-
бор положительного направления
тока. Для такой машины произве-
. *
дение Э1 выражает потребляемую
ею мощность. При этом в формуле
(5-32) соответствующее слагаемое
должно быть перенесено в правую
часть.
Подробнее вопрос о машинах
в цепи переменного тока рассмат-
ривается в § 5-3.
Рассмотрим теперь решение од-
ной частной задачи, основанное
на балансе мощности.
Измерение больших индуктивно-
стей иногда производят, применяя
такой метод: параллельно с индук-
тивной ветвью, сопротивление кото-
рой
Z=r+]xL,
подключают конденсатор (рис.
5-14) такой емкости, чтобы общий
i/13 — /13^13 "Э13,...,
если э. д. с. Этп направлена- от узла т
к узлу п.
Уравнение (5-30) выражает баланс
комплексных (мощностей всех ветвей цепи,
а следовательно, и баланс реактивных мощ-
ностей:
Vsmn = 0, £ Qran = о. (5-31)
Рис. 5-14.
9 К- М.' Поливанов
129
ток источника оставался по величи-
не неизменным при включении и от-
ключении индуктивной, ветви. Зная
величину емкости, удовлетворяю-
щей этому условию, можно одно-
значно определить индуктивность,
если известна частота напряжения
источника; результат не зависит от
активного сопротивления индуктив-
ной ветви.
В осуществимости такого режима мож-
но убедиться, исходя из уравнений {мощно-
сти. Полная мощность при «включенной и
отключенной индуктивной ветви по условию
одинакова, следовательно,
S2==P2 + (q£_qc)2 = q2c.
В этом равенстве квадрат полной мощности
в первом режиме представлен как сумма
квадрата активной мощности и квадрата
алгебраической суммы реактивных мощно-
стей, а во втором режиме как квадрат
только реактивной мощности, потребляе-
мой конденсаторной ветвью.
Раскрывая скобки и сокращая Q2C, по-
лучаем равенство
P2 + Q2_2QtQc=0< (а)
в котором
U2r U2xT
Р =-------9-’ Qr =-------Г
г2 + X2L l г2 + XZL
и
Qc= U2!xc.
После подстановки этих выражений
в равенство (а) и сокращения на
[U2/(r2+x2L)Y, приходим к уравнению
(б)
Казалось бы, в последнем уравнении
можно сократить одинаковый множитель,
стоящий в круглых скобках, т. е. разделить
обе части равенства на 1—2хъ]хс. Но после
такого сокращения мы .приходим к равен-
ству
гг=_х2,
которое противоречит предположению о том,
что и г и xL — вещественные числа.
Однако уравнение (б) имеет еще одно
решение
2Хт
лс
(В)
при котором сокращать общий множитель
в уравнении (б) нельзя (деление на 0 ли-
шено математического смысла). Это един-
ственное решение, при котором в обоих ре-
жимах полная мощность одинакова. Заме-
чательно, что оно не зависит от величины
активной мощности, т. е. от сопротивле-
ния г.
Из решения (в) следует, что
1
.= 2xl или Ь = 2СЧ^-
Пусть, например, при питании от сети
со=314 сек-1 требуемые условия дости-
гаются, когда емкость равна 0,517 мкф.
В таком случае индуктивность составляет
9,8 ен.
В технике большие .индуктивности
обычно получаются только при наличии
ферромагнитного сердечника, как, напри-
мер, в трансформаторах. При этом индук-
тивность нелинейна, т. е. она зависит от
приложенного напряжения. Поэтому произ-
водить подобные измерения можно только
при напряжении, близком к рабочему.
Приведенный здесь вывод, ко-
нечно, не единственный. Исходное
условие неизменности кажущейся
мощности равносильно условию не-
изменности модуля общего тока..
Очень наглядным является доказа-
тельство, основанное на построении
круговой диаграммы.
Требуется доказать, что в цепи
на рис. 5-14 общий ток I остается
постоянным по модулю незави-
симо от величины сопротивления
(т. е. при r=var), если
Предполагается, конечно, что
напряжение на входе U остается не-
изменным.
Доказательство. Ток в индуктив-
ной ветви
1 = —й-
L г + /coL ‘
При r = var вектор IL описывает
окружность. Действительно, деля
в формуле для 1L и числитель и зна-
менатель на /соА, приходим к урав-
нению
j =——С_______
L i + ez-"/2’
где С = t7//(oL = const, В= Гг —
= var. d
Но это и есть ранее выведенное
уравнение окружности (4-47). Эта
130
окружность построена на рис. 5-15,а.
Ее диаметр (точка г — 0) равен
а положение центра О'
окружности определяется вектором
U^L.
Добавив к току IL постоянную
величину тока в емкостной ветви
получим выражение для общего тока
'=4+4.
Но добавление Л = const смещает
г G
всю окружность lL на постоянную
величину, как это было показано при
выводе формулы (4-49). Если смеще-
ние 1С = jwCU равно — U/2jaL
то центр окружности О' переносится
в начало координат (рис. 5-15,6).
При этом величина общего тока
1= 111 при любом г остается неиз-
менной и равной радиусу окруж-
ности.
Это и требовалось доказать.
Активные и реактивные состав-
ляющие токов и напряжений. Исходя
из выражения для комплексной
мощности
S = UI — 57 cos <р 4" /57 sin?,
часто вводят понятия активной
/а и реактивной /р состав-
ляющих тока, определяя их ра-
венствами
/a = /cos<? и Zp = Z sin ?. (5-33)
Это значит, что комплекс тока I
разлагается на две составляющие, из
которых одна /а совпадает по фазе
с напряжением U, а другая /р орто-
гональна напряжению U.
Сказанное равносильно тому, что
пассивный двухполюсник представ-
ляется схемой замещения с двумя
параллельными активной и реактив-
ной ветвями (рис. 5-16,а). Для та-
кой цепи
YBX = -L=g-jb,
поэтому
i=UY=U(g-jb)^i&+iv,
где ...
iv=—Ujb.
При этом
/a=f/g, =
что соответствует определению
(5-33).
Рис. 5-16.
9*
131
Пользуясь понятием активной и
реактивной составляющих тока,
можно записать комплексную мощ-
ность в таком виде
S = P + jQ = UI* + jUIp.
Представляя реактивную состав-
ляющую тока как алгебраическую
величину, получаем, что реактивная
мощность
Q==U2b = IpU.
Действительно,
* * * *
. • /^Uy = U{g + jb)i
поэтому
S^ul=u*(g + jb).
Пример 5-8. Напряжение и ток заданы
комплексами:
A) U = 100 4- /100 в, 1=5 + /5 а;
Б) U = 50 /100 в, 1 = /10 а.
Требуется найти активную и реактивную
составляющие тока в случаях А и Б.
Решение. В случае А ток совпадает
по фазе с напряжением; следовательно,
/а = / =7,07 а\ /р=0.
В случае Б напряжение отстает от тока
на угол 26°30', т. е. в этом случае и =
s= — 26°30'. При этом
== 8,92 а\ 7Р = — 4,46 а.
Легко убедится, что
S = UI = 1 000 — /500 = U (7а4- //р) =
= 112(8,92-/4,46).
Из проведенных вычислений вид-
но, что разложение тока на актив-
ную и реактивную составляющие
совершенно отлично.от разложения
на вещественную и мнимую части.
Эти разложения совпадают только
при чисто вещественном значении
напряжения U=U.
Аналогично вводятся понятия
активной и реактивной со-
ставляющих напряжения (рис.
5-16,6), когда двухполюсник или
ветвь представляется двумя после-
довательно соединенными элемен-
тами (активным и реактивным)
ZBX = -y=r + /x:
U& = U cos <Р, Up — U sin <р
или
U^ = lr Up = Ijx.
>(5-34)
При этом комплекс мощности
S = IU^+]IUp.
Смысл введения таких составляю-
щих очевиден. Иногда возникает
вопрос, а какой смысл имеет произ-
ведение активных (или реактивных)
составляющих тока и напряжения,
т. е. laU* (или /pf/p). Можно дать
ясный ответ — никакого.
5-3. ПЕРЕДАЧА ЭНЕРГИИ
В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Требования, предъявляемые к си-
стемам, в которых происходит пере-
дача энергии переменным током,
существенно различны для систем,
служащих для передачи сигнала, и
для систем энергетических. В пер-
вых обычно от заданного источника
сигнала стремятся получить макси-
мально возможную мощность, не
считаясь с коэффициентом полезно-
го действия (к. п. д.). Кроме того,
при анализе таких систем часто ста-
вится вопрос об их частотных ха-
рактеристиках, если частота сигнала
может изменяться или передавае-
мый сигнал содержит гармониче-
ские составляющие с разными ча-
стотами (этот вопрос подробнее
анализируется в гл. 9).
В энергетических системах, на-
против, очень существен вопрос
о к. п. д. и совершенно несуществен
вопрос о влиянии частоты на
условия передачи энергии, так как
в энергетических системах частота
поддерживается практически неиз-
менной. При анализе энергетиче-
ских систем часто ставится вопрос
о том, как изменяется напряжение
у потребителя при изменении на-
грузки, поскольку в большинстве
случаев допустимое для потребите-
ля изменение напряжения ограни-
132
чивается несколькими процентами
(лампы электрического освещения,
двигатели).
Некоторые основные вопросы,
относящиеся к системам передачи
таких двух типов, анализируются
в этом параграфе.
Условие передачи максимальной
мощности. Система передачи энер-
гии по двухпроводной линии может
рассматриваться как передача энер-
гии от активного двухполюсника
к пассивному (рис. 5-17,а). При
этом активный двухполюсник может
быть представлен как некоторый
эквивалентный генератор с э. д. с.
Э и заданным внутренним сопротив-
лением Zi = R+jX, а пассивный
двухполюсник—-как ветвь с сопро-
тивлением Zn==r+jx (рис. 5-17,6).
Мощность, отбираемая приемни-
ком (или потребителем), по закону
Джоуля—Ленца равна:
Р=Рг, (5-35)
где
/ = =- =. (5-36)
В системах передачи сигнала
ставится вопрос о том, каким дол-
жно быть сопротивление приемника
(Zjf) при заданных параметрах ис-
точника (3 = const, Zi = const) для
того,/чтобы в приемник поступала
максимально возможная активная
мощность, т. е. ищутся значения г
И X, При которых Р = Р макс-
Из выражений (5-35) и (5-36)
очевидно, что при постоянном г
мощность возрастает с ростом тока
и что она максимальна при
(5-37)
а)
Рис. 5-18.
При этом мы приходим к выра*
жению мощности
известному из теории цепей постов
явного тока (§ 2-1), где было пока*
зано, ЧТО Р = Рмакс при
r=R. (5-39)
Два найденных условия в ком-
плексной форме представляются
одним равенством
Zn = 4 (5-40)
При этом значение максимальной
мощности, получаемой приемником,
Рмакс=^. (5-41)
Такая же мощность рассеивает-
ся в сопротивлении источника (так
как г=/?) и, следовательно, к. п. д,
системы составляет 50%. Конечно,
такой низкий к. п. д. совершенно не
приемлем для энергетических линий
передачи. В них, как правило, г
много больше R.
Источники сигнала часто обла-*
дают большим внутренним актив-
ным сопротивлением, а иногда и
большим реактивным сопротивле*
нием, например
Zi = 600+/800 ojw,
при этом для получения максималь*
ной мощности сопротивление при*
емника должно быть равным
Zn = 600 —/800 ом.
т. е. в простейшем случае иметь с®*
противление, равное 600 ом. вклю*
ченное последовательно с конден-
сатором (отрицательное реактивное
сопротивление).
Такая цепь изображена на
рис. 5-18 в предположении, что со*
133
противление источника содержит
последовательно включенные сопро-
тивление R и индуктивность L~
=Х/со.
В цепи на рис. 5-17 приемник от-
бирает максимальную мощность
только при определенной частоте;
если частота изменится, нарушатся
и требуемые условия. Так, напри-
мер, для приведенных числовых
данных при увеличении частоты
в 2 раза
Zi + Zn = 1 200 + j (1 600 — 400) =
= 1200 +/1200 ом.
При этом мощность будет состав-
лять лишь половину максимально
возможной при данной э. д. с. сиг-
нала.
Влияние на входное сопротивле-
ние приемника дополнительных ре-
активных ветвей. В тех случаях, ко-
да активное сопротивление прием-
ника г по физическим или конструк-
тивным соображениям нельзя сде-
лать равным активному сопротив-
лению источника R, существует
много разных способов, все же
удовлетворяющих условию отбора
максимальной мощности (5-40).
Покажем здесь, что требуемое
условие может быть достигнуто, ес-
ли ввести в приемник, в дополне-
ние к заданной ветви с сопротивле-
нием г, еще дополнительные реак-
тивные ветви, как это изображено
на рис. 5-8.
Очевидно, что при этом условию
(5-40) должно удовлетворять вход-
ное сопротивление получившегося
нового двухполюсника
== в*х + +вх === R — ]Х.
(5-42)
Активная составляющая входного
сопротивления гвх, конечно, может
существенно отличаться от задан-
ного сопротивления приемника г.
При этом Гвх может быть и мень-
ше и больше, чем г, в зависимости
от выбранной схемы (рис. 5-8,а
или б) и от параметров двух реак-
тивных элементов (х1 и х2) 1.
1 Результаты вычисления ZBx подобных
двухполюсников приведены в примере 5-5.
Равенство (5-42) содержит два
уравнения rBX=R и хвх=—X. По-
этому есть основание предполагать,
что оно может быть удовлетво-
рено надлежащим выбором двух
переменных X] и х2, разумеется, при
условии, что решение этих уравне-
ний приводит к вещественным, по-
ложительным или отрицательным,
значениям хх и х2.
В ветви х > 0 должна быть вклю-
чена индуктивность (jx = j(f)L),
в ветви х<<0 должна быть вклю-
/. 1 . 1 \
чена емкость ( ix=
I J 1(£>С (оС j
Очевидно, что требуемое усло-
вие, достигнутое для одной частоты,
при изменении частоты может на-
рушиться.
Предполагая - заданными значе-
ния R, X и г, находим требуемые
значения Xi и х2 для двух схем
включения на рис. 5-8.
В случае схемы на рис. 5-8,а
входное сопротивление
/вх
--^ВХ + М'вх----/+
jx2r
г + jx2
Х2Г2
Г2 +
г2+ х|*
Приравнивая его вещественную часть
заданному сопротивлению источника
находим, что
Х^Г
г* + xf
R,
(5-43)
(5-44)
^ВХ---:
— R ’
Искомое решение существует толь-
ко в случае r>R. При этом в ветвь
2 может быть включена или индук-
тивность (х2>0, если перед корнем
выбирается знак « + »), или ем-
кость (х2<0, если перед корнем
выбирается знак «—»i).
Приравнивая мнимую часть вход-
ного сопротивления хвх реактивно-
му сопротивлению источника с из-
мененным знаком, т. е. —X, полу-
чаем, что
134
После подстановки найденных соот-
ношений для л2 и простых преобра-
зований [целесообразно воспользо-
ваться равенством (5-43)] находим:
A = —-/?)). (5-45)
В этой формуле верхний знак пе-
ред корнем соответствует выбору
положительного знака для х2. За-
метим, что получается вещест-
венным (положительным или отри-
цательным) только при том же ус-
ловии r>R.
Аналогично выводятся формулы
для схемы рис. 5-8,6.
Пример 5-9. Дано Zi=R + jX=
= 600+/800 ом и г=1200 ом. Требуется
подобрать реактивные сопротивления, кото-
рые должны (быть -включены по .схеме на
рис. 5-8,а для согласования приемника
с источником.
Р е .ш е н и е. По (выведенным формулам
jc2=±1200 ом и Xi=—(800±600) ом.
Первое значение Xi =—1 400 ом соответ-
ствует индуктивности в ветви 2 (х2=
= 1 200 ом)\ второе xY=—200 ом соответ-
ствует емкости в ветви 2 (х2=—1 200 ом).
Подро:бнее найденное решение рассмат-
ривается в следующем параграфе в связи
«с построением топографических диаграмм
для полученных схем.
Цепи, предназначенные для пе-
редачи энергии. В простейшем слу-
чае такая цепь содержит источник
питания Ui, соединенный с потреби-
телем Zn ’посредством линии 7Л
(рис. 5-19). Сопротивление источ-
ника считаем входящим в сопро-
тивление линии (2Л).
Если заданы напряжение источ-
ника а также сопротивления
2Л и Zn, то легко найти общий ток
цепи
l=O1/(Za + Zr) (5-46)
H напряжение потребителя
U^lZ^U.Z^Z^Z^ (5-47)
При этом потребляемая мощ-
ность
S2 = i?27=P2+/Q2. (5-48)
Мощность, отдаваемая источни-
ком,
s,== р.+1Q.=S2 4-
(5-49)
Коэффициент полезного действия
рассматриваемой цепи
(S’60»
Пользуясь теми же формулами,
можно определить режим цепи и
в том случае, когда известны дру-
гие исходные данные, например
U2, Zл.
При этом из формулы (5-48)
следует, что ток
/ = sA=^-(5.51)
и2 и2
а напряжение в начале по (5-46)
и (5-47)
^ = ^ + /4-!. (5-52)
Ток зависит не только от актив-
ной, но и от реактивной мощности
потребителя, иначе говоря, от его
коэффициента мощности (cos ф2) •
Модуль тока при этом можно вы-
разить так:
Подставляя это выражение ,тр^
ка в (5-50), получаем формулу,
очень удобную для расчета к. п. д.
простейшей передачи:
Т=; .у-к- -- (5-54)
cos2 у2
Из этой формулы видно, что
к. п. д. возрастает с ростом напря-
жения у потребителя и с ростом
соэф2; можно сказать точнее, что
к. п. д. возрастает с ростом актив-
ной составляющей напряжения
в конце линии, т. е. Н2а=U2cos ф2.
Если Н2а=const, но растет пере-
даваемая мощность, то для сохра-
нения того же к. п. д. необходимо
уменьшить активное сопротивление
линии. Формула (5-54) показыва-
ет, как важно повышать напряже-
135
ние линий передачи энергии для
достижения большого к. п. д. Уве-
личив напряжение в 17,5 раза
(•скажем, от 6,3 кв до ПО кв), мож-
но увеличить в 10 раз сопротивле-
ние линии и в 30 раз увеличить пе-
редаваемую мощность при том же
к. п. д.
Пример 5-10. Напряжение у потреби-
теля U2— 6,3 кв; потребляемая (мощность
Р2—6 Мет; сопротивление линии £л =
=0,4+/ 0,8 ом.
Требуется найти к. «п.‘ д. и напряжение
в начале линии для следующих значений
фазового угла ф2:
1) cos ф2=0,6, sin ф2=0,8 (индуктивная
нагрузка, ф2=53о10/); 2) cosiT2=l, 8Шф2=
=0; 3) -со&ф2=0,8; sin ф2=—0,6 .(емкостная
яафузка, ф2=—36о50').
Решение. Значение к. н. д. подсчи-
тывается по формуле (5-54). Результаты
приведены ib таблице.
Однако с точки зрения потребите-
ля важно знать прежде всего мо-
дуль напряжения U2 в конце ли-
нии при данных параметрах систе-
мы и заданном напряжении {Д.
Другими словами, важно знать
разность модулей напряжения в на-
чале и в конце линии
^U = Ui^U2, (5-56)
называемую потерей напря-
жения.
В общем случае модуль разно-
сти (модуль падения напряжения)
не равен разности модулей.
Положим U2 = U2, т. е. чисто
вещественным, и <р2>0. В таком
COS сра 7а> а /р, а I, а Ulf кв ч
1 0,6 0,857 952 1 270 -* 1 587 * 7,70 1°50'
2 1 0,943 952 0 952 6,70 6° 10*
3 0,8 0,916 952 —715 1 190 6,20 9э40'
случае / = /а -f- /р =7 а — /7Р
(рис. 5-16,а) и
^71 = С72“-|~/2д = С72-{-
Условиями задачи задана неизменная
активная мощность P2=S2'.cos ф2, поэтому
реактивную мощность Q2—S2 sin ф2 можно
определять по формуле
<?2=Р2 tg ф2-
В этих условиях формуле (5-51) можно
придать такой вид:
. Р*
I =~ (1— J tg?2).
U2
Полагая U2=U2, находим для наших дан-
НЫХ, что ток
i =Ia — jIp=Q52(l — j tg <?2)
и напряжение в начале линии
Ui = U2
Подсчитанные значения приведены в таб-
лице.
Падение и потеря напряжения.
По закону Ома, зная ток / и ком-
плексное сопротивление линии, лег-
ко нДйти падение напряжения
в ней:
Uz = iZn. . (5-55)
4" (^а — // р) (гл + рсл) —
-- 4“ АГЛ 4“ 4“
4“ / (Iа-^л Iргл)« (5-57)
Определяя модуль как корень квад-
ратный из суммы квадратов веще-
ственной и мнимой части, нахо-
дим:
t/i « и2 /агл -j-1р-^л (5-58)
с погрешностью менее 1 % при
/ Iа-Л^л I рЛи
\ U2 -J- / а^л /р-^л
0,02.
(5-59)
Последнее условие, как правило,
выполняется во всех энергетиче-
ских системах, в которых боль-
шие падения напряжения не допу-
стимы.
Следовательно, в указанных
условиях можно считать, что
Д[/ = С/,-С/2^/аГл + /Рл:л. (5-60)
136
Из этой формулы видно, что
потеря напряжения в значитель-
ной мере зависит от сдвига по фа-
зе между напряжением и током
в конце линии. При отрицательном
реактивном токе (емкостная на-
грузка) и положительном реактив-
ном сопротивлении линии (индук-
тивное сопротивление) потеря на-
пряжения может оказаться даже
отрицательной.
Аналитически выведенная фор-
мула (5-60) имеет простое геоме-
трическое толкование. Как видно
из векторных диаграмм на рис.
5-20, формула (5-58) соответствует
предположению о возможности
•приравнять модуль напряжения U\
его проекции на линию вектора U29
т. е. принять Ur ~ Ос; на тех же
диаграммах ab = /2гл cos <р2 = /агл
и be = I2xn sin <р2 = 7рхл.
Пример 5-11. Подсчитать по формуле
(5-60) потерю напряжения для цепи преды-
дущего примера при 'заданных там значе-
ниях <р2; «сопю.ст-а1вйть полученный результат
с разностью модулей Ui—U2. Значения /а и
/р, а также модулей lh приведены в табли-
це предыдущего примера.
Решение. Пользуясь формулой (5-60),
находим для трех значений <р2‘
1) £Л~6,3+0,952-0,4+1,27-0,8=7,70 кв;
2) Ui «6,3+0,952 * 0,4=6,68 кв;
3) 3+0,952-0,4—0,715.0,8=6,11 кв.
Лишь в последнем случае формула
(5-60) приводит к ошибке, превосходя-
щей 1%.
Изложенное показывает, что в
заданной линии при заданной на-
грузке в конце можно в известных
Рис. 5-20.
пределах регулировать потерю на-
пряжения реактивной мощностью.
Поэтому при расчете даже про-
стейших цепей, передающих энер-
гию, задача может быть поставле-
на так:
Заданы: 1) сопротивление линии
7Л, 2) активная мощность в конце
₽2, 3) напряжение как в конце U2>
так и в начале линии Ui (речь
идет, конечно, о модулях напря-
жений) ;
ищется реактивная мощность Q2,
при которой может быть осуще-
ствлен требуемый режим, разумеет-
ся, если он вообще осуществим Ч
Расчет можно вести по прибли-
женной формуле
она получается из (5-60) после
умножения обеих частей равенст-
ва на U2. Из полученной формулы
следует, что
W2~ Лл
— Л-^-. (5-61)
Л. л
Применимость приближенного вы-
ражения (5-61) легко проверить,
подставляя найденное значение Q2
и заданное Р,2 в формулу (5-59)
после умножения и числителя и
знаменателя внутри скобок на U2.
Приближенный, расчет дает погреш-
ность порядка 1 % при
Р чх л — Q?x л \2
^2 4~ л “НЗз-я’л j
(5-62)
Если последнее условие не выполняется,
следует обратиться к (5-57); умножая обе
части последнего равенства на U2i находим,
что
UiU2 — РуЗг^Р л 4“ Qa-^л -f- j (РчХл О^л.)
или
(U1U2)1 2 — (Р24~ Р2Гя. 4~ @2-Ял)2 4~
4- (Рг-^л — 0,2гл)2.
1 Когда режим неосуществим, Q2 в ре-
зультате решения может оказаться содер-
жащим мнимую часть, скажем, Q2 = Qf2 4~
4" В таком случае S2 == Р2 4- /Q2 =
— Р2 — Q"24~ IQ's- Это значит, что по-
требляемая мощность должна быть умень-
шена на величину Q"2.
0
137
Решая последнее равенство относительно
Q2, находим, что
* Л л.
ое
_ Ц%хл
-4- х%
гл ‘ Лл
Из этого аналитического решения (вид-
ны условия осуществимости заданного ре-
'жи.ма: подкоренное выражение должно
'-быть положительным.
Пример ’ 5-12. Задано /л=Гл+/хл =
= 6+/6 ом; Р2=0,500 Мет; Ui — 6,3 кв,
£4=5,5 кв. Определить Q2 и. /2*
Решение. По формуле (5-61) Q2 =
(6,3 —5,5)5,5 6
---0’5"б"==0’-232 Мвар.
6
Подставляя найденное -значение Q2 в левую
^асть (5-62), находим ее равной 0,00217.
Следовательно, решение дается с по-
грешностью, меньшей 1%.
Искомый ток при U2 = U2
12 =91 —/42,2 а.
Цепь с двумя источниками.
В энергетических системах пита-
ние сети часто производится не-
сколькими источниками. Рассмот-
рим простейший случай (рис. 5-21),
•когда потребитель Zn соединен с
двумя источниками, имеющими
э. д. с. Эх и Э2, линией с сопротив-
лениями Z<jIi=Zji2==ZjI. В эти со-
противления входят и внутренние
сопротивления источников. Режим
такой системы определяется не
только величинами э. д. с., но и
•сдвигом фаз между э. д. с. Э1иЭ2.
Активная и реактивная состав-
ляющие мощности, которую гене-
рирует каждый из источников, мо-
гут быть как положительными, так
и отрицательными. Если источник
ютдает отрицательную активную
мощность, это значит, что он по-
требляет положительную актив-
Рис. 5-21.
ную мощность, например, работая
как двигатель. Генерирование по-
ложительной реактивной мощности
равносильно потреблению отрица-
тельной реактивной мощности. По-
этому источник, отдающий реак-
тивную мощность Q>0, равноси-
лен конденсатору, потребляющему
отрицательную Q<0 реактивную
мощность.
Для цепи на рис. 5-21 при Zi4i = ^Л2=^=
=2Л можно составить систему уравнений;
/1Z11 + /2Zi2 = «91*,
/iZ2i 4~ /2Z22 = Э2,
где
Zu — Z22 =j= Zji -J- Zn,
Z12 = Z21 = Zn*
Решая систему, находим, что
. 3\Z22—32Zi2 .
71 = D ’
. 32Zu — 3-lZ2x
D ’
где
D = Z11Z22 — ^12*
Ток потребителя
^п = А+А»
его напряжение
П = 7 nZn*
ИскомьТе мощности: отдаваемые генерато-
рами
Si=3i/i, $2 — Э212,
получаемая потребителем
Sn — U id п
и теряемая (потребляемая) в линиях
При этом должен выполняться баланс мощ-
ностей
Si + S2 = Sjii + 8Л2 + Sn.
Уравнения цепи переменного
тока с двумя источниками питания
показывают существенное отличие
цепи переменного тока при нали-
чии реактивных элементов от ана-
логичной цепи постоянного тока.
В последней увеличение э. д. с. од-
138
ного из источников влияет только
на долю отдаваемой им мощности.
Если э. д. с. источника постоянного
тока становится меньше напряже-
ния холостого хода на полюсах це-
пи, к которым присоединяется ис-
точник, отдаваемая им мощность
становится отрицательной, т. е. ис-
точник становится потребителем
(двигатель, заряжаемый аккуму-
лятор).
В цепи переменного тока уве-
личение э. д. с. одного из источ-
ников питания необязательно при-
водит к увеличению отдаваемой им
мощности. Оно может привести
только к генерированию реактив-
ной мощности. Очень существенное
влияние на величину отдаваемой
мощности оказывает фазовый угол
э. д. с.
Синхронные машины в цепи перемен-
ного тока. Электрическая машина, схема-
тически рассмотренная в гл. 3 (<рис. 3-8),
относится к очень (важному виду с и н-
х р о н н ы х машин. Такие машины назы-
вают синхронными (согласованными во
времени), потому что при работе-на общую
сеть они должны вращаться с одинаковой
скоростью, поскольку частота э. д. с. таких
машин прямо пропорциональна скорости их
вращения. Если 'бы э. д. с. машины не со-
впадала по частоте с напряжением сети,
она была бы не способна уравновешивать
внешнее напряжение. Такая машина, вы-
шедшая из синхронизма, должна быть авто-
матически выключена. Синхронная машина
в (зависимости ют соотношения между ее
э. д. с. и напряжением, подводимым от
внешнего источника |(о.т сети), может рабо-
тать как генератор., отдавая мощность
в сеть, к которой она присоединена, или как
двигатель, потребляя мощность из сети.
Рассмотрим мощную сеть переменного
тока ((провода линии передачи, рассчитан-
ной на большую мощность, шины электро-
станции,’ питаемые рядом мощных генера-
торов и г. п.), в которой присоединяемая
нагрузка не способна изменить ни величину
напряжения U, ни его фазу, ни тем более
частоту. Такую сеть можно представить
идеальным источником напряжения U
(рис. 5-22). Слева к нему подключена на-
грузка Zn, потребляющая постоянную мощ-
ность, поскольку по условию [7=const.
Предположим, что к такой сети
присоединяется еще синхронная ма-
шина (с. м.), сидящая на одном валу
с первичным двигателем п. дв.), как
это показано на рис. 5-22 справа.
Внутреннее сопротивление машины
примем чисто реактивным (/х). Из
ранее проведенного анализа очевид-
но, что мощность, отдаваемая син-
' хронной машиной, зависит от соотно-
шения между модулями и фазами
э. д. с. этой машины м напряжением иде-
ального источника I/.
Если активная мощность, отдаваемая
синхронной машиной, положительна, то
часть мощности потребитель Zri получает
именно от этой машины; если же активная
мощность, отдаваемая синхронной маши-
ной, отрицательна, то она работает как дви-
гатель, получая мощность от идеального
источника. ,
Первичный двигатель по условию дол-
жен вращаться с постоянной скоростью, со-
гласованной с частотой сети. Для синхрон-
ной машины с одной парой полюсов
(рис. 5-22) скорость вращения машины оз,
выраженная в радианах в секунду, равна
угловой частоте напряжения.
Роторы, вращающиеся со скоростью со и
наводящие э. д. с. в обмотках машин, схе-
матически показаны на рис. 5-22, причем по-
казано возможное относительное смещение
роторов одной и другой машины. При их
относительном смещении на угол у на такой
же угол смещается фаза э. д. с. Э относи-
тельно напряжения U.
Амплитуда (модуль) э. д. с. синхронной
машины может регулироваться током воз-
буждения, создающим магнитное поле вра-
щающегося ротора. Цепь возбуждения на
рис. 5-22 не показана.
Если вращающий механический момент
М первичного двигателя действует в на-
правлении вращения (Л4>0), то он стремит-
ся ускорить вращение связанной с ним син-
хронной машины. Однако усилие первично-
го двигателя приведет лишь к тому, что
ротор машины, вращаясь синхронно с ро-
тором идеального генератора, будет опере-
жать его на некоторый постоянный угол.
Величина этого угла у зависит от прило-
женного момента: чем больше момент М,
тем больше угол опережения. Такая связь
между Л1 и у существует до тех пор, пока
моменту М, стремящемуся увеличить угол
у, способен противодействовать момент син-
хронизирующих сил. Противодействующий
синхронизирующий момент обусловлен
взаимодействием магнитного поля статора,
по обмотке которого идет ток, и магнитного
поля ротора. Это взаимодействие равно-
сильно существованию как бы упругой овя-
зи между роторами синхронных машин.
Для того чтобы понять поведение син-
хронных машин в электрической цепи, мож-
но не рассматривать подробнее устройство
машин; достаточно знать, что синхронизи-
рующий момент стремится уменьшить угол
между роторами машин, работающих на
общую сеть. С увеличением угла у противо-
действующий синхронизирующий момент
возрастает до известного предельного зна-
Н
п.дв.
Рис. 5-22.
139
чен'ия угла у (три очень большом по абсо-
лютной величине моменте М угол у может
превзойти предельное значение и машины
выйдут из синхронизма).
При отрицательном моменте первичного
двигателя 2И<0 он стремится затормозить
вращающуюся синхронную машину. Одна-
ко вследствие существования синхронизи-
рующего момента действие отрицательного
момента М приведет только к отрицательно-
му смещению ротора синхронной машины
на угол у<0 и к отставанию по фазе э. д. с.
этой машины на такой же угол у относи-
тельно напряжения U.
Вернемся к электрической цепи рис. 5-22.
Ток синхронной машины
f Э ---- U
I =—7-— (0-63)
(положительные направления тока I и
э. д. с. машины Э выбраны согласно). Мощ-
ность, отдаваемая машиной в сеть (мощ-
ность, передаваемая справа налево через
зажимы а, Ъ)
S = P + = UI.
При рассмотрении энергетического ба-
ланса в системе на рис. 5-22 нео;бходимо
еще учесть (мощность, поступающую в син-
хронную .машину от первичного двигателя,
РдВ = Л4со. (5-64)
Поскольку в самой синхронной машине
не происходит самозарождения (энергии и
поскольку мы пренебрегли активным сопро-
тивлением ее электрической цепи, а- также
не учитываем рассеяния энергии из-за тре-
ния, то активная мощность, отдаваемая
в сеть синхронной машиной, должна рав-
няться мощности, отдаваемой первичным
двигателем,
Р = (5-65)
Перейдем теперь к самому важному,
т. е. рассмотрим энергетические соотноше-
ния в электрической цепи на рис. 5-22 в раз-
ных режимах работы.
1. Машина работает вхолостую 214 = 0.
При этом синхронизирующие силы приво-
дят к совпадению по фазе (синфазность)
напряжения идеального источника U и
э. д. с. Э.
Рис. 5-23.
«9
Падение напряжения в реактивном со-
противлении машины =(/х) равно Э—й=
=jxl. Так как сопротивление машины чи-
сто реактивное, ток смещен по фазе на
угол зт/2 относительно разности U—Э.
На рис. 5-23 представлены соответст-
вующие векторные диаграммы при х>0 (ин-
дуктивное сопротивление) для случаен
U>9 и UO. Мощность, отдаваемая в сеть
синхронной машиной,
s = Р + iQ = UI = и Л- / ♦ (5-66>
/Л.
б)
Рис. 5-24.
Поскольку фазы Э и U совпадают, то
й(э — иу = и(Э—и)
и вся мощность, отдаваемая машиной^,
чисто реактивная
.UQ-U)
ь J х
(5-67>
Активная мощность Р=0, что следует из^
уравнений (5-64) и i(5-65).
Если 3>U, машина отдает в сеть поло-
жительную реактивную мощность или, что-
равносильно, потребляет отрицательную ре-
активную мощность. Такая «перевозбужден-
ная» (Э>и) синхронная машина равно-
сильна конденсатору, присоединенному к за-
жимам a, Ь, поскольку именно конденсатор
потребляет отрицательную реактивную*
мощность. Если Э<и, то машина отдает'
отрицательную реактивную мощность илш
потребляет положительную.
2. Момент первичного двигателя поло-
жителен _214>О, э. д. с. опережает напряже-
ние U на угол у.
В этом случае мощность, поступающая *
от первичного двигателя (5-64) и активная
мощность, отдаваемая синхронной, машиной
в сеть, положительны.
Разлагая э. д. с. Э на две составляю-
щие, из которых первая Эг совпадает по*
фазе с напряжением [7, а вторая Э" опере-
жает напряжение на угол эт/2 (рис. 5-24,а),,
т. е. полагая •
.9 = Э' + 3",
140
находим по формуле (5-66):
__ Ц (Э-Uy . ЩЭ'-Ц) ,
X 1 х "*
/
। UЭ” . U (Э cos у — £7)
х х *"
, (ZSsinY
+ —F~±'==^Q + Р* (5~68)
Следовательно, синхронная машина рабо-
тает как генератор и отдает во внешнюю
цепь активную мощность, пропорциональ-
ную синусу угла опережения.
В соответствии с законом сохранения
энергии по формулам (5-64), (5-65) полу-
чаем, что
U3 sin y
---- —'-=М(>) = Р. (5-69)
Эта формула приводит к очень интересному
результату о предельной мощности, больше
которой принципиально нельзя получить от
данной синхронной -машины, так как
sin у*С1.
Разумеется, теория синхронных машин
•не так проста, Однако из приведенного ана-
лиза видно, что к синхронной машине нель-
зя прикладывать любой момент, не выводя
-ее из синхронизма, что предельная мощ-
ность возрастает с ростом Э и U и убывает
с ростом х; ото сопротивление как бы ос-
лабляет синхронную связь.
3. Первичный двигатель создает отри-
цательный момент Л4<0 (тормозящий мо-
мент). Такой режим получается в том слу-
чае, когда синхронная машина работает
как электрический двигатель, приводящий
во вращение станки или другие рабочие
машины, стремящиеся затормозить синхрон-
ную машину. Они бы и затормозили ее, ес-
ли бы противодействующий синхронизирую-
щий момент был недостаточен.
В рассматриваемом режиме угол у от-
рицателен |(рис. 5-24,6), соответственно от-
рицательна и активная мощность, отдавае-
мая синхронной машиной в сеть в соответ-
ствии с уравнениями (5-68) и (5-69). В ос-
тальном анализ подобен предыдущему.
Все изложенное показывает следующее
замечательное свойство синхронных машин:
в них можно отдельно регулировать э. д. с.
и мощность; последняя регулируется толь-
ко моментом первичного двигателя (т. е. от-
даваемой им мощностью РдВ, которая мо-
жет быть как положительной, так и отри-
цательной) .
Весь анализ проводился в предположе-
нии, что реактивное сопротивление машины
положительно, т. е. х>0. Естественно дол-
жен возникнуть вопрос, как изменятся по-
лученные результаты, если сопротивление
х<0; такие условия можно осуществить,
включая, например, конденсатор последова-
тельно с синхронной машиной.
Обращаясь к формулам '(5-68) и
(5-69), мы придем к странному, казалось
,бы, результату, во всяком случае нуждаю-
щемуся в анализе: при отрицательном х ак-
Рис. 5-25.
тивная мощность отрица-
тельна, при положительном
у<л. Вместе с тем мы пред-
полагали, что приложен по-
ложительный момент Л4>0,
стремящийся повернуть ро-
тор на положительный угол
и сообщающий машине по-
ложительную мощность.
Не значит ли это, что
отдаваемая машиной мощ-
ность отрицательна? Не зна-
чит ли это, что из внешней
сети поступает положитель-
ная мощность, действующая
на машину в направлении,
совпадающем с вращающим
моментом? Именно так. При
этом ротор машины, отклонившись на малый
угол у, не будет вращаться синхронно. Такое
положение неустойчиво. Ротор повернется
еще на угол л, так что в итоге э. д. с. Э маши-
ны будет сдвинута по фазе на угол л+у
относительно напряжения U. Так как
8ш(л-Ьу)=—sin у, то выражение для ак-
тивной мощности окажется -положительным
(х<0). При дальнейшем увеличении угла
машина будет отдавать в сеть большую
мощность, а для этого требуется, -чтобы воз-
рос и момент М. -Значит положение ротора,
отклонившегося на угол л+у, устойчиво.
Соответствующая векторная диаграмма
•изображена рис. 5-25.
Дополнительные замечания.
Продольная компенсация.
Выше было показано, какую боль-
шую роль в регулировании режима
работы энергетических систем иг-
рает реактивная мощность. При
этом рассматривались дополни-
тельные источники (или потреби-
тели) реактивной мощности, вклю-
чаемые параллельно основной на-
грузке, т. е. между проводами ли-
/ 7
Рис. 5-26.
нии. В линиях очень высокого на-
пряжения (240—500 кв) иногда
выгоднее применять последова-
тельную (продольную) компенса-
цию, когда весь ток линии прохо-
дит через конденсатор. При этом
напряжение, приходящееся на кон-
денсатор, может оказаться меньше,
чем напряжение на конденсаторе
при его поперечном включении
(пунктир на рис. 5-26).
Эквивалентный генера-
тор. Расчет распределения токов,
141
напряжений и мощностей в слож-
ных энергетических системах, осо-
бенно в системах, содержащих
длинные линии, много сложнее,
чем расчеты приведенных выше
простых примеров.
Однако с точки зрения потре^
бителя, присоединяемого к сети
сложной энергосистемы, эта сеть
может быть заменена эквивалент-
ным -генератором с эквивалентной
э. д. с. и эквивалентным внутрен-
шим сопротивлением, после чего
цепь приводится к виду, изобра-
женному на рис. 5-19.
К такой цепи применимы все
изложенные выше расчеты, кроме
расчета к. п. д., так как дополни-
тельные потери, вносимые во всю
систему подключаемым потреби-
телем, м-огут не совпадать с поте-
рями в цепи эквивалентного гене-
ратора (в цепи постоянного тока
' они совпадают).
Определение параметров экви-
валентного генератора для цепи
переменного тока осложняется тем,
что надо знать как вещественную,
так и мнимую части £э, а легко
бывает, как правило, измерить
лишь действующие значения тока и
напряжения и фазовый угол пере-
менной нагрузки. Указанные вели-
чины могут быть измерены прибо-
рами, включение которых показа-
но на рис. 5-27. Там же показан
эквивалентный генератор с внут-
ренним сопротивлением Z3=ir3+
+/хэ; э. д. с. этого генератора Ээ
равна напряжению холостого хо-
да t7x.
Если измерения тока произво-
дятся при двух известных значени-
ях нагрузки, то из совместного ре-
шения уравнений для тока цепи
Рис. 5-27.
Рис. 5-28.
можно найти две неизвестные ве-
личины гэ и xQ. Однако точность та-
кого решения часто теряется при
вычислении арифметической раз-
ности сравнительно близких вели-
чин.
Параллельные линии с различ-
ными сопротивлениями. На практи-
ке встречаются случаи, когда на-
грузка соединена с источником
двумя параллельными линиями с
различными сопротивлениями 7Л1
и Ил2, как прказано на рис. 5-28,
где сопротивления, линии показаны
сосредоточенными в одном прово-
де, а обратный провод представлен
общим для двух линий и не содер-
жащим сопротивления.
Ток нагрузки I распределяется
по двум' линиям, обратно пропор-
ционально их сопротивлениям
Г __Т ^Л2 . Г __ j 2Л1
1 2л1 -4“-^Л2 ’ 2 2л1~Ь-^Л2-
Если при этом отношение активных
и реактивных сопротивлений в двух
линиях различно, т. е. х^1т^Ф
то сумма модулей двух
токов Л+/2 может быть больше,
чем модуль общего тока.
Если, например, общий ток на-
грузки составляет 100 а и подво-
дится к потребителю параллельно
проложенными кабельной линией
2л1=.г и воздушной 2л2=(1+/)г,
то в кабельной линии пойдет ток
63,3 а, а в воздушной 44,8 а; сумма
этих значений 108,1 а, т. е. боль-
ше 100 а.
Выбор сечения проводов по до-
пустимому току. В случае коротких
линий, соединяющих источник с
нагрузкой, часто потеря напряже-
ния в них оказывается очень малой
из-за небольшой длины линий; по
той же причине мощность, теряе-
мая в них, может быть очень ма-
лой по сравнению с передаваемой.
142
Однако мощность, поглощаемая в
линии на единицу длины, может
оказаться недопустимо большой с
точки зрения перегрева проводов.
В этих случаях нижний предел
сечения проводов (кабеля или воз-
душной линии) определяется то-
ком. Он не должен превосходить
установленного нормами макси-
мального значения, зависящего от
сечения проводов, их типа и усло-
вий охлаждения. Иногда выбор се-
чения проводов определяется и
возможным значением тока корот-
кого замыкания, при котором соот-
ветствующий участок линии дол-
жен быть автоматически отключен,
так как он может быть опасным
из-за возможного перегрева прово-
дов.
5-4. ПОТЕНЦИАЛЬНАЯ ДИАГРАММА
НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
(ТОПОГРАФИЧЕСКАЯ ДИАГРАММА)
Построение. Потенциал каждой
точки цепи а, Ь,с,... переменного то-'
ка определяется комплексной вели-
чиной фа, фй, фс ...; поэтому распре-
деление потенциалов в цепи можно
представить на комплексной плос-
кости, сопоставляя точки цепи с
определенными* точками на плоско-
сти. При таком построении (рис.
5-29) разность потенциалов между
двумя произвольными точками це-
пи а и & может быть представлена
вектором, соединяющим точки а и
Ь на плоскости. В соответствии с
обычными правилами вектор
^аЬ = ?а—(5-70)
направлен от точки b к точке а,
как и показано на рис. 5-29.
Векторная диаграмма, при ко-
торой каждой точке цепи соответ-
ствует определенная точка на пло-
скости, носит название топогра-
фической.
Проведем построение топографи-
ческой диаграммы для простей-
шей цепи рис. 5-30, а; нагруз-
ка гн=20 ом подключена к сети
через индуктивную катушку, об-
ладающую сопротивлением Z=5 +
+/35 ом, которое на схеме пред-
ставлено как последовательно
включенные г=5 ом и = =
= 35 ом', ток в цепи 7=5,0 а. По-
строим векторную диаграмму для
такой цепи, соблюдая принцип то-
пографичности.
Приняв равным нулю потенциал
цепи в точке О, найдем, что потен-
циал. точки с выше, чем потенциал
точки О на величину
(ток идет от „более высокого" по-
тенциала к „более низкому").
Выбрав направление тока 1 (на-
пример, по вещественной оси), [от-
кладываем по его направлению
в выбранном масштабе вектор 1гн =
= Uco из начала координат (<р0 = 0).
Длина отрезка /гн в нашем случае
соответствует 100 в. Конец вектора
/гн изображает потенциал <рс точки
цепи с (рис. 5-30,0:
Потенциал следующей точки b
выше потенциала точки с на вели-
чину IjaL. Действительно, для при-
143
нятого положительного направления
тока (от b к с)
УЬ Тс '== iZftQ
или
Т&1=3 ?с 4“ 12Ъе.
Для цепи рис. 5-30,а
=?с + Л’35.
Это значит, что из точки с нужно
провести отрезок, повернутый на
угол эт/2 относительно вектора то-
ка (т. е. вектор //35). В нашем слу-
чае 7=5,0 а, поэтому отрезок cb
должен соответствовать в выбран-
ном уже масштабе напряжению
175 в. Конец этого отрезка изобра-
жает потенциал точки цепи, обозна-
ченной буквой Ь.
Аналогично из точки b отклады-
ваем отрезок, соответствующий про-
изведению 1гаЬ = Ъ1 и находим на
плоскости положение точки а, опре-
деляющее потенциал <ра точки а
цепи.
Напряжение источника, опреде-
ляемое как разность потенциалов
точек а и О, т. е.
на топографической диаграмме изо-
бражается вектором, проведенным
из точки О в точку а. Измеряя этот
отрезок, находим, что в выбранном
масштабе он соответствует напря-
жению 214 в. Значит, ток в цепи бу-
дет равен 5 а при напряжении ис-
точника 214 в.
Часто задача ставится иначе.
Известны напряжение источника и
параметры цепи, а ток должен быть
определен.
В этом случае следовало бы за-
даться произвольным значением то-
ка, построить всю ^HairpaiMMyiH опре-
делить, какое при выбранном токе
получается напряжение.
Из отношения действительного
напряжения Ua0 к найденному из
диаграммы U'a0, т. е. из отношения
Ъ = (5-71)
легко заключить, что в действитель-
ности ток I отличается от произ-
вольно выбранного U . коэффициен-
том т], т. е.
1 = ^1'. (5-72)
В отличие от подобного метода
расчета (метода пропорциональных
величин), изложенного в гл. 2, те-
. перь коэффициент ц—комплексное
число. Это значит, что действитель-
ный ток отличается от произвольно
выбранного не только по модулю,
но и по фазе.
Все построение топографической
диаграммы производится очень про-
сто, следует только запомнить, что
всегда
Ут ‘ Уп--Iтп^тп) (5-73)
и, следовательно,
Ут---Уп ^тп^тпч (^"74)
если для тока в ветви с сопротив-
лением выбрано положитель-
ное направление от точки т к точ-
ке п.
Вторая особенность чисто фор-
мальная, однако на нее следует об-
ратить внимание. Мы условились
на схемах, изображающих цепь,
обозначать напряжение
^тп Ут, Уп
стрелкой, направленной от точки т
к точке тг, тогда как на топографи-
ческой диаграмме вектор (7тгг про-
водится от точки п к точке т. Срав-
ните, например, направление .стрелок,
изображающих напряжения Uа0 и Uс0
на схеме рис. 5-30,а, и направление
векторов, изображающих те же на-
пряжения на топографической диа-
грамме рис. 5-ЗОД.
Заметим, что в -литературе существует
и 'Другой способ построения топографиче-
ских -диаграмм, отличающийся направле-
нием стрелок, точно так же как существует
и другой способ обозначения положитель-
ных направлений на схемах.
Анализ электрических цепей по
их топографическим диаграммам.
Построим топографическую диа-
грамму для цепи, в которой для
получения максимальной мощно-
сти у потребителя включены допол-
144
нительные реактивные элементы
(§ 5-3). Сама цепь и построенная
для нее диаграмма показаны на
рис. 5-31. Построение выполнено
для следующих данных: /?+/Х=
= 600+/800 ом, %! =—1 400 ом,
х2 = +1 200 ом, r= 1 200 ом [см.
первый вариант решения в приме-
ре 5-5, § 5-1, а также формулы
(5-42) —(5-45) § 5-3].
Для построения диаграммы
произвольно задаемся током /н=
= 1 а и принимаем потенциал точ-
^йи О равным нулю.
В таком случае потенциал' точ-
ки а определяется как прсизведе-
ние /нг:
1200 в.
Для того чтобы вести дальней-
шее построение, т. е. определить
потенциал точки 6, нужно найти ток
1 = 1* Д-Д. Но ток /2 отстает по
фазе от напряжения Ua0 = <?a на
угол й/2 и численно равен току /н
(так как х2 = г = 1 200 ом). Скла-
дывая токи /н и /2, находим на диа-
грамме вектор тока в цепи источ-
ника /. Величина этого тока I =
= |/2 а. Но = Z/Х, следо-
вательно,
?6 =<Ра + //Х1.
Это значит, что мы придем в точ-
ку с потенциалом <рь, проводя из точ-
ки а вектор длиною bq; он от-
стает на угол тс/2 относительно
тока /, так как <С 0 (емкость).
В vконце этого вектора, численно
равного ]/*2 • 1 400 = 1 980 в, ставим
точку Ь.
Найдем теперь потенциал точки с:
ic^ib+ijX-
Для этого из точки b откладываем
вектор IjX, опережающий по фазе
ток I на угол тг/2, так как X > 0.
Длина этого вектора /2 - 800 =
= 1 130 в- Точка с при заданных
f параметрах попадает на линию тока 1,
проведенную из начала координат.
Наконец, ищем точку с потен-
циалом
Вектор IR совпадает с направлением
вектора тока /. Его длина |/2 -600=
= 850 в. Но точка с лежит на линии
вектора тока I. Следовательно, и
точка d лежит на той же линии.
Это значит, что напряжение UdQ =
= U (вектор, проведенный из точки
О в точку d) совпадает F по фазе
с током источника /, что и требо-
валось условиями отбора максимальной
мощности.
Пользуясь построенной диаграм-
мой, интересно продолжить анализ
этих условий.
Входное активное сопротивление
двухполюсника, включенного между
точками ЬО, равно R, тогда как фак-
тически единственное активное со-
противление, содержащееся в одной
из его ветвей г R (в нашем случае
г=2/?).
Активная мощность, рассеиваемая
в двухполюснике, может быть выра-
жена и как I2R, и как /^г. Очевид-
но, что эти выражения совпадают
только в том случае, когда
72//2н = г//?. (5-75)
Иначе говоря, если активное сопро-
тивление ветви г больше входного
7?, то через сопротивление г должен
проходить меньший ток.
Из построенной диаграммы лег-
ко увидеть, что в рассматриваемом
случае, когда г=27?, проходящий
через сопротивление г ток /н именно
10 К- М. Поливанов
145
в ]/2 раз меньше тока Д входяще-
го в двухполюсник, что соответст-
вует формуле (5-75).
Полезно самостоятельно убе-
диться в том, что реактивная мощ-
ность, потребляемая двухполюсни-
ком, может быть определена и как
квадрат тока на входе, умножен-
ный на входное реактивное сопро-
тивление, т. е. 72%вх, и как сумма
произведений каждого из фактиче-
ски содержащихся в цепи реактив-
ных сопротивлений на квадрат со-
ответствующего тока:
А^ВХ ==: ^1*^1 2^2*
На рис. 5-32 построена топогра-
фическая диаграмма аналогичной
цепи при R ==600+/800 ом, г=
= 1 200 ом, Xi=—200 ом, х2 =
=—1 200 ом.
Рекомендуется самостоятельно
выполнить построение и провести
анализ, подобный проделанному.
Построение топографических
-диаграмм очень полезно при ана-
лизе мостовых и компенсационных
схем, схем, предназначенных для
поворота фазы, и т. п.
Мосты. Для измерения комплекс-
ных сопротивлений при переменном
токе широко применяются мо-
стовые схемы, подобные мосту
Уитстона, однако содержащие в че-
тырех плечах в общем случае че-
тыре комплексных сопротивления
(рис. 5-33). В уравновешенном
мосте обязательно должно выпол-
няться отношение
ZJZ^ZJZ» (5-76)
которое в отличие от мостов посто-
янного тока распадается на два
независимых условия
zjz2 = zzlz^ —?2 = ?3 — ?4, (5-77)
где — аргументы соответствую-
щих комплексных сопротивлений.
Наличие двух условий равнове-
сия соответствует поставленной за-
даче.
Если в результате измерения по>
трем известным комплексным со-
противлениям мы определяем чет-
вертое неизвестное Zx, то нам нуж-
но знать.'два параметра — его мо-
дуль и его аргумент.
Анализируя уравнения (5-77) для
тех или иных конкретных условий,
например
Z^ ==: Г5С /со£/х, И2 Г2 |
Z3=r3, Z^ = r^ или Z1 = rx^-j^LXT
Z2 = Z3 = r, Z^ = r^-\-\jj^C^ ‘
легко найти условия равновесия
моста, а также ответить на вопро-
сы: можно ли в общем случае до-
биться равновесия, изменяя только1
одно из трех сопротивлений, или
необходимо иметь возможность ре-
гулировать по крайней мере два из
них? Нарушается ли равновесие,
установленное при определенной
частоте, если частота изменится?
Простейший фазовращатель.
Пользуясь топографической диа-
граммой, очень просто понять, что»
в цепи рис. 5-34 напряжение
^аЬ = ?а —
остается неизменным по величине,,
но изменяется по фазе, если .изме-
няется г, L или со.
. .146
Рис. 5-34.
Действительно, потенциал точ-
ки а
где l = ^L{r.
Это значит, что вектор фа пере-
мещается по окружности, диамет-
ром которой служит вектор общего
напряжения.
Топографические диаграммы
находят широкое применение в раз-
нообразных областях, в частности
они широко применяются в теории
многофазных цепей (гл. 8).
5-5. АНАЛИЗ РЕЗОНАНСНЫХ
ЭФФЕКТОВ
Резонанс напряжений. Так назы-
вают резонанс при последователь-
ном соединении L, г. С (рис.
5-35,а)Ток в таком контуре
/ = г+)(Л-лс> =7^7 <S-79)
ИЛИ
1 = z = .. = — = =,(5-80)
]/ Г2 _|_ Х2 |/ Г2 + _ Хсу
где x = xl-xc=^L —
При резонансной частоте
®0=-2= (5-81)
0 V LC
ток становится максимальным
/макс =4 <5-82>
и совпадает по фазе с напряжение
ем на входе контура, так как реак-
тивное сопротивление х=0. Ска-
занное иллюстрируется векторными
диаграммами рис. 5-35,6.
Как видно из (5-81), к условиям
резонанса можно всегда прийти,
либо изменяя частоту напряжения
источника (со), либо изменяя реак-
тивные параметры контура (L
или С).
Зависимости /, UL или Uc от со,
L или С называют резонансными
кривыми (или резонансными хараю-
теристиками). Наибольшей обще
ностью обладают резонансные крие
вые, построенные в функции отное
сительной частоты
= со/а)0 = со , (5-83)
при заданной добротности кон-
тура
Q = %L/r = — VLjCjr, (5-84)
как параметре, определяющим ход
резонансной кривой.
Величину У L/C называет х а р а к-
т еристич еским сопротивле-
нием контура.
Чтобы получить выражение обоб-
щенной резонансной кривой тока,
Рис. 6-35.
10*
147
введем переменную 7) и параметр Q
в формулу (5-80):
где знак относится к значению
т]2, а знак „—“ к значению Та-
ким образом,
(5-85)
Как видно из полученного выра-
жения и кривых рис. 5-36, построен-
ных для различных Q, форма резо-
нансной кривой—ее острота—зависит
от добротности контура.
Очень важной характеристикой
резонансного контура служит так
называемая ширина резонанс-
ной кривой А?} или полоса про-
пускания контура, определяемая
как разность частот т2 и тд, при ко-
торых ток в /2 раз меньше макси-
мального (рис. 5-37), а значит, пол-
ное сопротивление контура в У 2 раз
больше, чем минимальное гмин=.г
при резонансе.
Значения и находим из
(5-85), принимая т. е.
из уравнения
ИЛИ
1 ——— Q CQi ,2 1/^11»2),
О ол 0,8 1,2 1,6 2,0
Рис. 5-36.
11 11
^2 у,---/J ^1 Q -
(5-86)
Складывая эти выражения, полу-
чаем:
Т|2 + ^ -*^±^- = 0,
i2 1 11
откуда
^2=1 или % —, (5-87)
т. е. резонансная частота равна
геометрическому среднему гранич-
ных частот полосы пропускания.
Заметим, что резонансную ча-
стоту соо можно определить из экс-
перимента как частоту, при кото-
рой ток достигает максимума. Од-
нако значительно точнее из опыта
можно найти две частоты coi и 02
(П1 и Лз), вблизи которых ток из-
меняется очень резко. Резонансная
частота находится как их геоме-
трическое среднее.
Вычитая второе из равенств
(5-86) из первого, получаем:
^2—^1
| ~ _ 2
зд Q
или
Т]2 —1)1 = Д-n=(5-88)
Следовательно, ширина резонанс-
ной кривой равна обратной вели-
чине добротности контура, и по ре-
зонансной характеристике всегда
можно определить добротность.
148
Напряжения на индуктивности
и емкости
^=“=7ST₽tW;(5-89)
Uc='i:
-----= .= (5-90)
<оС V^*2 + (°>£ — 1/<оС)2
или, вводя относительную частоту
и учитывая (5-85),
UyQ
/l+Q2(^-l/4)2
UyQ
Vе 1 -|-Q2a2 ’
(5-91)
1
7]C00C
_________UQ_________
j/T-J- Q2 (7]—1Л])2
7 UQ
7} Y1 +Q2a2 ’
(5-92)
где а=т]—1/t]—параметр, характе-
ризующий расстройку контура1.
Резонансные кривые f/b=f(co) и
(со) показаны на рис. 5-38.
Первая достигает максимума (ес-
ли Q>l/j/*2) при более высокой
частоте, чем резонансная [со — в
числителе 5-89)], вторая—.при бо-
лее низкой [со — в знаменателе
(5-90)].
Значение соответствующих ча-
стот можно найти путем обычного
определения максимума:
_____ 1 _____________ 1
^L~~ Y1 + 1/4Q2 ’ Y1 — 1/4Q2‘
(5-93)
Здесь и т]с — значения относи-
тельных частот, при которых дости-
гают максимума соответственно UL
и Uc.
Максимальные значения этих на-
пряжений одинаковы:
иг = Un = - (5-94)
£макс Смаке _1/4Q2 ' 7
Предоставим читателю самосто-
ятельно вывести последние форму*
лы, ограничившись таким замена*
нием: максимум Uc и UL, выража*
емый формулами (5-93) и (5-94),
проще всего искать, определяя ми*
нимум квадрата обратной величи*
ны в зависимости от т]2.
Выражения (5-93) и (5-94) по-
казывают, что при добротности Q,
превышающей 5, с погрешностью
порядка 1% можно считать макси-
мумы Uс и UL равными QU при
резонансной частоте (т]о= 1)-
Выражения (5-91) и (5-92) очень удоб-
ны для определения уменьшения Uc и UL
при расстройке контуров высокой доброт-
ности. Из этих выражений при (Qa)2^>J
непосредственно следует, что
1
£4 макс
ис , 1_______________i
С макс ^'yiQ-lal
(5-95)
при
₽z==h_l|«l.
Пример 5-13. В контуре очень высокой
добротности Q=500 отступление от резо-
нансной частоты составляет 0,5%, т. е.
(3 = |т)—1|—0,005.
Требуется найти, насколько напряжение
на емкости меньше максимального значения,
достигаемого три резонансе.
Решение. Для заданных цифр по
формуле (5-95)
макс [5
1 Расстройку контура часто характе-
ризуют величиной
со2 — со?
t ___--------------
? (О2
/ “о
= а/У) = — а.
' 1 со
т. е. при очень малой расстройке напряже-
ние уменьшается в 5 раз.
Характер зависимости напряжения на
конденсаторе от частоты определяется до-
бротностью контура. При нулевой частоте
(постоянный ток) все напряжение источни-
149
ка ложится на конденсатор при любых г,
При возрастании частоты напряжение
на конденсаторе может (рис. 5-39):
1) сразу увеличиваться dUcldv^_£^,
2) оставаться сначала неизменным
dUc/dv^_^ = 0 или 3) уменьшаться
dUc/d^<G.
При большой частоте напряжение на
конденсаторе во всех случаях уменьшается,
поскольку сопротивление конденсатора 1/соС
стремится к нулю.
Обращаясь к формуле (5-92), нетрудно
определить, при каких значениях Q зависи-
мость ^с|(л) будет иметь характер первого,
второго или третьего типа.
Для простоты математических опера-
ций вместо производной от Uс по ч будем
искать (производную от квадрата знаменате-
ля в выражении (5-92) по квадрату отно-
сительной частоты, т. е.
д
^.[Ч2 (1 + Q2a2)] = 1 + 2 0)2 - I)'Q2.
При т] = 0 эта производная равна 1 —2Q2.
Очевидно, что при Q — 1/V'2 или г —
L
= у %~с~ производная равна нулю, т. е.
с ростом частоты напряжение на конденса-
торе вначале остается постоянным; при
Q>l/|/'2 знаменатель уменьшается с уве-
личением частоты, иначе говоря, напряже-
ние возрастает; при Q < 1/У2* знаменатель
растет с увеличением частоты и, значит,
напряжение уменьшается.
Заметим, что проведенный здесь ана-
лиз и, !в частности, уравнения вида (5-88) —
(5-92) применимы к исследованию резонанс-
ных систем, эквивалентных контуру г, L,
С, в которых, однако, колебания энергии и
ее рассеяние могут быть обусловлены ины-
ми физическими процессами.
Резонансные измерения. Ряд ме-
тодов измерений на высокой часто-
те основывается на проведенном
здесь анализе простой резонансной
системы. Измеряя ток в контуре
или рассеиваемую в нем мощность
и меняя частоту генератора, мож-
но определить частоты coi и со2 (или
т]1 и Т)2),. а следовательно, доброт-
ность и резонансную частоту кон-
тура. Повторим, что вблизи частот
и т]2 происходит быстрое изме-
нение тока с частотой, что облегча-
ет точное определение .этих частот.
Если в исследуемом контуре г,
L, С, кроме того, известен один из
параметров (обычно С), то на ос-
новании резонансных измерений
можно определить и дваv других па-
раметра (г и L).
Пример 5-14. Величина тока в резо-
нансном контуре при частотах fi = 99,5 кгц
и /2=100,5 кгц меньше максимального зна-
чения в У2 раз.
Емкость конденсатора С=0,01 мкф. Тре-
буется определить сопротивление контура и
его индуктивность.
Решение. Резонансная частота кон-
тура
<x>g = 04 = (2тс)2 1010 гц2,
следовательно,
_I— = 0,253 мгн.
^ос (
Добротность контура
^=_^о__ = 100>
7 Г й>2 — COi ’
следовательно, ,
(02 -СО1
г = (<о2-Ю1)£= ^^-=0.713 ом.
Последовательный контур, как
уже было отмечено, можно настра-
ивать в резонанс изменением ем-
кости или индуктивности.
При такой настройке положе-
ния Uьмакс ИЛИ U смак с НеСКОЛЬКО
смещаются из-за того, что в выра-
жения (5-89) и (5-90) входят из-
меняющиеся множители L или С.
На рис. 5-40,а показано, как из-
меняются /, Uc, UL при L=var, а
на рис. 5-40,6 — при C=var; осталь-
ные параметры постоянны.
Все кривые построены по уравнениям
(5-85), (5-89) и (5-90), приведенным к виду,
удобному для расчетов. В обоих случаях
ток удобно вычислять по формуле
____/макс____
= V 1 + Q2(₽—I)2’
(О/'О Y f r Y
где при L = var Q=~y~9 % = L/Lq, a —
индуктивность, при которой в контуре воз-
150
яикает резонанс; при С = var Q~—-р— ,
$ = Со/С, а Со — емкость, при которой в
контуре возникает резонанс.
Напряжение на изменяющемся элементе
и__________________
’ Л +<Э2(₽-1)2’
где U9 — U т при L — var и Uv — Uc при
«С = Var.
Напряжение на постоянном элементе
цепи прямо пропорционально току. Из (вы-
ражения для Uv легко обычными (методами
найти значение Р, при котором UV = U «макс*
Для этого целесообразно, предварительно
разделив числитель и знаменатель на р,
найти минимум подкоренного «выражения.
Он наступает при
1+Q2
- Q2 ’
т. е. в случае L = var
1 +Q2
L ~ макс ПРИ Ь = Lo qz 9
а в случае С = var
Q2
== Uс макс при С — Со j _|-Q2 •
Как видно из полученных формул, сме-
щение максимумов Uv и I (меньше 1% при
<Q>10, если в качестве переменного рассма-
тривать р.
Заметное смещение наблюдается только
при малых добротностях, как, например, по-
казано на рис. 5-40,а и б, где Q=2, и сам
эффект резонанса, естественно, слабо выра-
жен.
Ку-измерения L и г. Теория ре-
зонанса лежит в основе широко
распространенного прибора — ку-
метра, пользуясь которым можно
определять добротность (Q), индук-
тивность, емкость и сопротивление
на высоких частотах.
Прибор содержит точно калиб-
рованный переменный конденсатор,
параллельно которому включен
электронный вольтметр, практиче-
ски не влияющий на режим конту-
ра. Схема куметра изображена на
рис. 5-41,а, где L и гх — измеряе-
мые индуктивность и сопротивле-
ние, a Z — внутреннее сопротивле-
ние генератора, обычно большое.
Регулировка генератора произво-
дится так, чтобы в его цепи проте-
кал определенный ток /г, измеря-
емый амперметром. При этом гене-
ратор работает как источник тока
с параллельным сопротивлением
гг. Это сопротивление точно из-
вестно и мало.
Напряжение (э. д. с.) и вну-
треннее сопротивление эквивалент-
ного генератора (рис. 5-41,6) 17э=
= /ггг и г* —гг.
Изменяя емкость при фиксиро-
ванной частоте, можно прийти к
условию резонанса (/Макс)- Одна-
ко измеряемое напряжение на кон-
денсаторе
Рис. 5-41.
151
имеет максимум при емкости
меньшей резонансной, так как сро-
стом тока растет и знаменатель.
Для того чтобы найти условие ма-
ксимума напряжения на конденса-
торе, следует обратиться к выра-
жению
1
_—=======, (5-96)
|/-(C0Cr)2+(G)2CL— I)2
а)
где г — гх + гг
- Дифференцируя подкоренную ве-
личину по соС и приравнивая ее нулю,
находим условие экстремума
Рис. 5-42.
t (5-97)
r2+(G>L)2 r(l+Q2) k }
где Ql — <nL/r — добротность по ин-
дуктивности для данной частоты
Подставляя найденные
выражения для адС в (5-96), находим,
что
/Г7 \2
= Q2. (5.98)
Определив из эксперимента значение
Д’2, легко найдем:
Ql = =УК2 — 1, (5-99)
после чего по (5-97) при известных
С и о находятся также и значения
г = гх -4- гг =--------?—=
Г <оС(1 +Q1)
1
<оС№
(5-100)
№ —1
со2СЛ2
(5-101)
Резонанс токов. Так называют
резонансные явления при парал-
лельном соединении г, Л, С. Про-
стейший случай соединения этих
трех элементов показан на рис.
5-42,а, В этом случае
4
/ : U (g —jb) = U[g — j (bL — 6C)]
(5-102)
или
z = и УУ+ b* = U yg2+(bL- bcy
(5-103)
где
= = (5-104)
При резонансе, когда 6 = 0, ток
совпадает по фазе с напряжением
и в простейшей цепи рис. 5-42,а
имеет минимальное значение, рав-
ное Ug.
Резонансная кривая ///мин=
=/(1]) при (7=const приведена на
рис. 5-42,6.
Записывая комплексное сопро-
тивление анализируемой цепи при
параллельных г, L, С, легко заме-
тить полное подобие этого уравне-
ния с уравнением для проводимо-
сти при последовательном соедине-
нии тех же элементов (принцип
дуальности).
152
При последовательном
соединении (рис. 5-35, а)
Y=g-Jb =
=_______1_______
r + j(wL-^
бмакс — 1/^мин — 1//*J
При параллельном
соединении (рис. 5-42,а)
Z = г + jx =
1
/ 1 X ’
8 + 1 (®С~
1 — * 1 ‘
''макс — п • о t
умин &
У __ 1 —]Qa _ Z
£макс 1 +Q2a2 Гмакс
1 со 1
В обоих случаях: соо =
При параллельном соединении
ветвей, содержащих и реактивные
и активные сопротивления, анализ
резонансных явлений усложняется.
Такая цепь получается, например
(рис. 5-43,а), при параллельном сое-
динении реальной индуктивной /вет-
ви (L, гь) /и реального конденсатора
(С и gc, соединенные параллельно).
Подробнее схемы замещения рас-
сматриваются в § 5-6. В такой цепи
условие минимума общего тока
может не совпадать с условием ра-
венства нулю реактивной слагаю-
щей входной проводимости.
Из сказанного вытекает необхо-
димость уточнить значение, припи-
сываемое слову резонанс.
Условимся называть ре-
зонансом такой режим цепи,,
когда реактивная составляющая
входной проводимости (а следова-
тельно, и входного сопротивления)
равна нулю.
В простейшей последовательной
цепи С, г, L этому условию соот-
ветствует и максимум тока, а в
простейшей параллельной цепи
С, г, L — минимум тока.
Иначе обстоит дело в более
сложных цепях. Так, в цепи рис.
5-43,а, если изменяется только ча-
стота, резонанс наступает при ча-
стоте
2 1 г2
---•------------
О lc L*
(в этой формуле и всех последую-
щих r=rL).
При этой частоте, как нетрудно
убедиться, реактивная составляю-
щая входной проводимости равна
нулю.
Минимальное значение общего
тока достигается при другой, не-
сколько более высокой частоте
СО-
МИН
LC
—r2!L\
В справедливости сказанного легко
убедиться, обратившись к выражению вход-
ной проводимости для цепи рис. 5-43,а
/ .
Увх = —/&вх = г2 _|_((o£)2 "т
+gc — i<* +
153
квадрат модуля этой проводимости
2 / Г у
Увх Г2 (со£)2 ** &СJ Г
. / L V 9 ,9
0)2 у2 (g>£)2 J ^ВХ "Ь ^ВК*
Когда модуль проводимости минима-
9
лен, производная по частоте от г/вх долж-
на быть равна нулю.
Заметим, что при отыскании соМЕН,
<, 2
при которой г/вх—минимум, могут встре-
титься очень громоздкие выражения. Они
значительно упрощаются при дифференци-
ровании по С = г2 + (<oL)2. При [этом
следует считать со2 = (£ — r2)/L2, а г, L, С,
g — постоянными. Найдя значение 5, соот-
ветствующее минимуму, легко перейти к
соответствующей частоте а>мин.
Эквивалентные параллельные
ветви и общая добротность резо-
нансного контура. При рассмотре-
нии ветви rLiL в цепи рис. 5-43,а
иногда бывает полезно заменить
эту ветвь двумя эквивалентными
параллельными ветвями — чисто
•активной и чисто реактивной. Про-
водимость индуктивной ветви
Y = 1 — 1 — ~/<oL
~ Z rL + juL
(5-105)
Определяя ее добротность отно-
шением
QL=a)L/r£, (5-106)
можно выражение (5-105) записать в
таком виде
1 1 Ql
z 'i.V + Ql') «L(1+QD
«отождествляя первое слагаемое с
проводимостью эквивалентной чи-
сто активной ветви, а второе — с
проводимостью эквивалентной чи-
сто реактивной ветви, содержащей
только индуктивность Ld (рис.
5-43,6).
При этом
_ 1 1
ga^Ra ~ r£(l+Q2) ’
(5-107)
Следует обратить внимание,
что чем выше добротность индук-
тивной ветви, тем меньше эквива-
лентная проводимость. Таким об-
разом, малое последовательное
сопротивление гь заменяется боль-
шим параллельным /?э. Напротив,
индуктивность Lq в параллельной
схеме замещения при большой
добротности практически равна
индуктивности в заданной ветви с
последовательными rL и L.
Из сопоставления (5-106) и
(5-107) легко увидеть, что
= ^LfrL =
(5-108)
Заменяя параллельные ветви с
чисто активными проводимостями
gc и gQ одной ветвью с проводи*
мостью
g=gc+g^ (5-109)
придем к цепи, изображенной на
рис. 5-43,в.
При резонансе в такой цепи (не
отличающейся от цепи рис. 5-42)
входная реактивная проводимость
должна быть равна нулю, следо-
вательно, при to = too
"c=i-
В таком случае добротность
рассматриваемого контура при ре-
зонансе (to = too)
<2=^=^’ <5-ш>
где g — полная (эквивалентная)
проводимость.
Общая добротность Q контура
при резонансе связана с добротно-
стями индуктивной и емкостной
ветвей простым равенством:
<5-ч2)
где (см. рис. 5-43,а)
Qc^^C/gc> QL = *LlrL. (5-113)
Это нетрудно доказать. По (5-109)
и (5-111)
(5-114)
154
Но при резонансной частоте ==
= j»L3. Тем самым равенство (5-112)
доказано.
Можно; доказать, что равенство
(5-112) обладает большой общно-
стью: оно применимо и к парал-
лельному , и к последовательному
соединению элементов C,gc и Цгь,
справедливо и в том случае, когда
у краденсатора имеется не только
параллельная проводимость gc, нои
последовательное сопротивление
Гс и т. п.
Резонанс в сложных контурах.
Если двухполюсник содержит боль-
ше чем два реактивных элемента
(например, рис. 5-44), его входное
сопротивление может иметь не од-
но, а несколько экстремальных
значений при изменении частоты
или сопротивления одного из реак-'
тивных элементов.
Так, в случае цепи на рис. 5-44
возможен резонанс токов при
<оЛ2—'1/соС. При этом входная про-
водимость равна нулю, что соот-
ветствует принятой идеализации
для параллельных ветвей — в них
отсутствуют активные элементы.
Входцая проводимость становится
максимальной, когда
-----—i— = 0
или
<*L2
ыСЬ2 — 1'
Последнее условие выполняется при
11 -f- L>2 -tr_ 1
частоте & = - , при этом Y
В сложных цепях условие экс-
тремальности входной проводимо-
сти по модулю может не совпадать
с равенством нулю реактивной со-
ставляющей этой проводимости,
как это было показано для цепи
на рис. 5-43,а.
Рис. 5-44.
Ри-с 5-45.
Но и в сложных цепях целесо-
образно определять условия резо-
нанса по равенству нулю мнимой
составляющей входного сопротив-
ления или входной проводимости
двухполюсника.
Однако можно определять резо-
нанс и по условию экстремального
значения модуля входной проводи-
мости. Наконец, при малых актив-
ных потерях можно определять
резонансные частоты как частоты
собственных колебаний рассматри-
ваемого сложного контура при ра-
венстве нулю активных слагающих
(последовательных сопротивлений и
параллельных проводимостей).
При малых активных слагаю-
щих может отчетливо наблюдаться
несколько резонансных частот, каж-
дая из которых приблизительно
удовлетворяет всем трем указанным
выше определениям.
В некоторых случаях при боль-
ших активных слагающих типичные
явления резонанса вообще исчеза-
ют. Так, например, в цепи на
рис. 5-45 (параллельный контур),
если rx=r2 = VL/C, то при любой ча-
стоте входная проводимость остается
чисто активной и равной у/C/L, т. е.
условия резонанса сохраняются при
любой частоте.
Сказанное проще всего доказы-
вается построением круговой диа-
граммы для токов каждой из вет-
вей.
5-6. ЧАСТОТНЫЕ
ХАРАКТЕРИСТИКИ
Двухполюсники. Наиболее полное
суждение о линейном двухполюсни-
ке, т. е. о его реакции на любое при-
ложенное напряжение, можно полу-
чить из его частотной характери-
стики.
В случае двухполюсников, говоря
о частотной характеристике, имеют
в виду зависимость от частоты веще-
155
ственной и мнимой части его вход-
ной проводимости или входного со-
противления:
у(/о>) = g (о)) — ]'Ь (<о) = у / — <р, |
Z (/о>)=г (<в)4-/х(®) ==£,/<?. j
(5-115)
Зная частотную характеристику,
можно определить ток и тогда,
когда приложенное напряжение со-
держит несколько гармонических
составляющих (см. гл. 9); по ча-
стотной характеристике можно
определить и ток в переходном ре-
жиме (см. гл. 12).
• Интересно заметить, что в случае
пассивного линейного двухполюс-
ника существует определенная за-
висимость между частотными ха-
рактеристиками вещественной и
мнимой части комплексной прово-
димости или между частотными
характеристиками ее модуля и аргу-
мента. Не останавливаясь на теории
этой связи между характеристика-
ми, укажем только, что в общем
случае значение одной составляю-
щей при любой заданной частоте
(01 можно определить, только зная
всю частотную зависимость второй
составляющей от со = 0 до <о = оо.
При этом необходимо сделать
следующие оговорки: 1) иногда та-
кое определение возможно только
с точностью до постоянной величи-
ны, не зависящей от- частоты, 2) не-
обходимо, чтобы как вещественная,
так и мнимая часть функции оста-
вались конечными при (о —+оо.
Поэтому, например, в случае
последовательно соединенных г, L
можно говорить о связи частотных
характеристик g(co) и Ъ (со) или
у (со) и ф(со), так как все эти вели-
чины остаются конечными при
со —оо. Напротив, х(со) и z(co)
в этом случае стремятся к беско-
нечности, поэтому к этим величинам
неприменимо правило о взаимной
связи частотных характеристик ве-
щественной и мнимой частей.
На основании обязательного су-
ществования определенной связи
между частотными характеристика-
ми иногда оказывается возможным
обнаружить ошибочность экспери-
ментальных данных.
Заметим, например, что при по-
стоянстве модуля z(co) обязательно
постоянство аргумента <р(<о), как в
случае двухполюсника, состоящего
из двух параллельных ветвей R-A-j^L
и ПРИ R2=L[C (см.
рис. 5-45): его входное сопротивление
Z (ja) = R = const при ср = 0 = const.
Если известны составляющие
комплекса только для одной часто-
ты — скажем, известна проводи-
мость У (/(01), то значение соответ-
ствующего комплекса при другой
частоте У (/(о2) можно определить
только в том случае, когда цепь со-
держит не больше одного неизвест-
ного реактивного и одного неизвест-
ного активного элемента и когда
известна схема их соединения.
Так, например, зная, что Y (/X) =
= £ (<°i) — № (ш1) = °’4 — /0,2 сим„
можно утверждать, что в случае сое-
динения по схемам а или б, пока-
занным на рис. 5-46, при частоте 2^:
в схеме а
У (/2^) = 0,4 — /0,1 сим\
Рис. 5-46.
в схеме б
У (у2«)1)=0,25—/0,25 сим.
Если же соединение
выполнено по схеме в
рис. 5-46, то определить
У (/2(01) по единственно
известному значению
У (/(01) невозможно. Дей-
ствительно значение
У(/2(0.1) в случае цепей а
и б рис. 5-46 можно най-
ти, поскольку два парамет-
156
ра Г1, Li или/2, ^2 легко определяют-
ся по заданному У(/<01) при извест-
ном (01. Но цепь в рис. 5-46 содержит
три неизвестных параметра, и двух
чисел ^((01) и 6(coi) недостаточно
для определения трех неизвестных.
Также при наличии двух неизве-
стных реактивных элементов
(рис. 5-46,г и д), хотя бы г и было
задртю, по входной проводимости
при одной частоте невозможно
определить входную проводимость
при другой.
Из этих простых примеров вид-
но, что чем сложнее цепь, тем боль-
шее число точек характеристики
У (/со) необходимо знать для опре-
деления У (/со) при любой другой
частоте.
Из анализа тех же примеров
легко прийти к такому важному
заключению: при заданной схеме
соединений невозможно осущест-
вить двухполюсник с произвольно
выбранной характеристикой. Так,
в случае цепи рис. 5-46,в и заданной
У(jcoi) можно потребовать, чтобы
при увеличении частоты, скажем,
вдвое, определенным образом изме-
нилась или вещественная (g*), или
мнимая (&) часть входной прово-
димости; изменение второй состав-
ляющей однозначно определяется
заданным изменением первой.
Пример 5-15. В цепи на рис. 5-46,в
пр1и частоте coj (входная (проводимость
У(/Ю1) =0,4—j 0,2 сим.
Чему равна -.мнимая часть «входной про-
водимости при удвоении частоты, если при
этом- вещественная часть оказалась равной
g (2coi ) = 0,352 сим.
Решение. При решении поставленной
задачи проще от числовых значений прово-
димости переходить к числовым значениям
сопротивления. Даже при этом мы придем
к системе, уравнений, содержащей четыре
неизвестных и, г %, х—Лсоь 6(2 <0i), входя-
щих как в первой, так и в высших степенях
Г2 Г
Г2Х2 t . Г2Л
г^+х* +J г^ + хг
ность 6(2 при заданной схеме соедине-
ний и заданных g((0i), g(2(0i), b(coi). Для
этого следует решить более простую зада-
чу, т. е. определить проводимости по за-
данным сопротивлениям.
Для расчета примем, что ri=d ом, г2=
=2 ом и х~2 ом при о=й)ь При этих пара-
метрах удовлетворяются поставленные в
задаче условия.
В -результате простых вычислений на-
ходим, что для этих данных Ь(2<01) =
=0,108 сим.
Частотные характеристики двух-
полюсников могут быть найдены
экспериментально. Они более пол-
но определяют свойства двухполюс-
ников, чем расчет по известной схе-
ме цепи и заданным параметрам,
поскольку iT, С, L в ряде случаев
сами зависят от частоты, особенно
в области высоких частот. Кроме
того, рисуя себе схему соединения
элементов цепи, мы часто упрощаем
ее, не принимая во внимание в дей-
ствительности существующих малых
емкостей, индуктивностей, сопро-
тивлении.
Если известна частотная харак-
теристика двухполюсника, то для
всех расчетов цепи, -содержащей
этот двухполюсник, уже не нужно
знать схему соединения различных
элементов внутри двухполюсника
и параметры этих элементов.
Более того, частотная характе-
ристика двухполюсника может быть
вполне определенной и может быть
представлена в терминах теории це-
пей У(/со) =g(co)—/&(со) и в том
случае, когда внутри двухполюс-
ника протекают процессы преобра-
зования электромагнитной энергии,
выходящие за рамки представлений
об электрической цепи и ее элемен-
тах.
Так, например, генератор уль-
тразвуковых колебаний (рис. 5-47)
преобразовывает поступающую на
вход электромагнитную энергию
в энергию механических колебаний
ультразвуковой частоты, распро-
страняющихся, например, в воде.
Эти колебания служат для опреде-
g — jb g2 + b2 '
^Можно 'избежать сложных вычислений
и в то же время понять содержание постав-
ленной задачи — однозначную определен-
0-4- Ультразвук
ж _
Рис. 5-47.
157
ления глубины (эхолот), для связи
с подводными лодками, для очистки
металлических предметов, погру-
женных в воду, и т. п. Мощность
таких колебаний может быть очень
большой. С точки зрения электриче-
ской цепи, питающей преобразова-
тель, он представляется двухполюс-
ником с вполне определенной ча-
стотной характеристикой У (/со); эта
характеристика может носить от-
четливо выраженный резонансный
характер. Знание такой характери-
стики очень важно для согласова-
ния источника питания с двухпо-
люсником, служащим нагрузкой,
несмотря на то что активные и
реактивные составляющие входной
проводимости преобразователя в ос-
новном определяются механически-
ми свойствами колеблющейся систе-
мы, а совсем не параметрами г,
С, L,
Точно так же антенна, излучаю-
щая радиоволны, для питающего ее
кабеля представляется как двухпо-
люсник.
При параллельном соединении
двухполюсников (рис. 5-48,а) скла-
дываются их проводимости. Поэто-
му характеристика двухполюсника,
получившегося после таких соеди-
нений, У (/со) равна сумме характе-
ристик каждого из двухполюсников,
соединенных параллельно,
(5-116)
При последовательном соедине-
нии (рис. 5-48,6) складываются со-
противления; общее входное сопро-
тивление
2 (/со) = А (/со) Z2 (/со). (5-117)
Если при этом для отдельных
двухполюсников заданы характери-
Рис. 5-49.
стики проводимостей, следует пере-
ходить к обратным величинам:
z(w=m>=M%- (И18>
Частотные характеристики реак-
тивных двухполюсников. При кон-
струировании цепи из реактивных
элементов для выявления особенно-
стей частотной характеристики по-
лучившегося двухполюсника мож-
но в первом приближении прене-
бречь неизбежно существующими
малыми активными составляю-
щими.
На рис. 5-49 показана цепь с по-
следовательно-параллельными со-
единениями L, С. На рис. 5-50 пока-
заны частотные характеристики
отдельных элементов, ветвей ab и
cd, а также входного сопротивления-
двухполюсника.
На рис. 5-50,а показаны частот-
ные характеристики индуктивностей
х2=’со^2 и х3 = со£3, на рис. 5-50,6 —
емкостей х4=—1/соС4 и х$——
Для каждой из ветвей аЬ и cd ха-
рактеристика сопротивления полу-
чается путем алгебраического сло-
жения характеристик сопротивления
последовательно соединенных эле-
ментов (рис. 5-48,в):
хаЪ — -^2 4" ’
d = *3 4~ •
Рис. 5-48.
Чтобы найти входную проводи-
мость двух параллельных ветвей,
нужно перейти к проводимостям
каждой из них (рис. 5-50,г и д) и
сложить их (рис. 5-50,е-)
и и \ к 1 I 1
ь — ьаъ 4" bed—~ 4“ у. . *
-л ао с а
Частотная характеристика, вход-
ного сопротивления всего двухпо- ;
‘158
люсника (рис. 5-50, и) находится
сложением характеристик сопротив-
ления ^ух параллельных ветвей
х=1/& (рис. 5-50,ж) и сопротив-
ления последовательно включенной
индуктивности (рис. 5-50,з)
хъ^ = х1-\-х.
В двух ветвях, -содержащих по-
следовательно соединенные L и С,
наблюдается резонанс напряжений
(рис. 5-50,в) при разных частотах
со7! и со7з. При параллельном соеди-
нении этих ветвей наблюдается еще
резонанс токов при частоте ©2, когда
суммарная проводимость равна ну-
лю (рис. 5-50,3 и ж). Последова-
тельно включенная индуктивность
(Л1 на рис. 5-49) смещает частоты
резонанса напряжений (coi и соз
вместо cozi и g/з) , не меняя частоту
резонанса токов со2 (рис. 5-50,и) *.
* Все построения рис. 5-50 (соответст-
вуют. принятому здесь знаку -перед jb, ука-
занному в (5-12). При широко распростра-
ненном пробив опо ложном условии относи-
тельно знака jb на рис. 5-50 изменится знак
соответствующих составляющих.
Четырехполюсники. В электро-
технике часто имеет смысл выделять
промежуточное звено цепи, соеди-
няющее два узла (два полюса) од-
ной части цепи с двумя узлами
(с двумя полюсами) другой части
цепи, например источник и прием-
ник сигнала или источник и прием-
ник энергии. Как и в цепи постоян-
ного тока (§ 2-12), такое промежу-
точное звено всегда может быть
представлено четырехполюсником
(рис. 5-51).
Если цепь состоит из любых пас-
сивных линейных элементов, то на-
пряжение и ток на входе (С\ =(7ВХ,
/1 = /вх) связаны с напряжением и
током на выходе (U2 = UBblx, /2 —
= /вых) уравнениями
U^AU^Bi^ 1
Л = СС72-}-Р/2, J
(5-119)
где Л, В, С и D — коэффициенты
четырехполюсника.
В случае, четырехполюсника,
159
Рис. 5-51.
замкнутого на пассивный двухпо-
люсник— приемник, имеем:
u2=i2z2,
где Z2 — входное сопротивление
приемника.
Коэ ффициенты ч еты р ехпо л ю с-
ника Л, В, С, D в общем случае
комплексные величины, зависящие
от частоты. Между ними существует
определенная связь AD—ВС=\.
Поэтому^ частотная характеристика
трех коэффициентов четырехполюс-
ника исчерпывающим образом ха-
рактеризует его свойства.
Теории 'четырехполюсника в цепях пере-
менного тока будет посвящен специальный
раздел второй части книги.
Ограничимся здесь напоминанием о том,
что в предыдущих параграфах было рассмо-
трено несколько четырехполюсников дри хо-
лостом ходе (/2=0). Так, например, фазо-
вращатель |(рис. 5-34,а) может быть пред-
ставлен как четырехполюсник (рис. 5-52).
Легко найти, что для такого четырехполюс-
ника
Л = —2,/2«,
где а = arctg сот: при z — L/r.
Как в уравнениях четырехполюсника,
так и во всех уравнениях линейных цепей,
связывающих токи и напряжения разных
ветвей посредством передаточных сопро-
тивлений и проводимостей
Ui = lnZin (jco),
/n==^zKnz(7co), (5-120)
передаточных коэффициентов
U2 = (AAi (/co), 12 = 1гН21 (» (5-121)
Рис. 5-52.
или коэффициентов линейных зависимостей
U2 = K + UiN, U2 = W + f2B (5-122)
и т. п., все линейные множители Z, У, Л, Н,
В, N и постоянные К, IF в общем случае—
комплексные величины зависящие от ча-
стоты
Zin (/*>) = г1п (со) + jxin (со),
Д (усо) = Ki (со) + JK2 (со.) и т. д.
Существенно обратить .внимание, что
последнее из уравнений (5-122) выражает
внешнюю характеристику активного двух-
полюсника, т. е. эквивалентного генератора
с э. д. ю. 3=W и с внутренним сопротивле-
нием Zi=—В:
U2 = Э---12Z г J
при изменении частоты может изменяться
как Э, так и Zi.
В общем случае частотные характери-
стики вещественной и -мнимой частей всех
этих множителей не могут быть связаны
между собой простыми соотношениями,
справедливыми для вещественной и мнимой
частотных характеристик -.пассивного двух-
полюсника.
Так, если в случае двухполюсника по-
лучаем z (до) = const ТОЛЬКО При ф=const,
то в случае четырехполюсника возможна
зависимость от частоты, выражаемая урав-
нениями |(5-119), когда |4(jGj)|«const при
а=/(со) const.
Частотные характеристики реаль-
ных элементов электрической цепи.
Во всех предыдущих расчетах мы
считали, что в любой цепи можно
отчетливо выделить ветви, в которых
содержатся сопротивления, индук-*
тивности и-емкости, что любой двух-
полюсник можно представить себе
состоящим из различно соединенных
активных и реактивных элементов.
Однако реально осуществить эле-
мент цепи, обладающий только со-
противлением, только емкостью или
только индуктивностью, можно лишь
с той или иной степенью приближе-
ния.
Сопротивление. В случае обыкно-
венного проволочного реостата
(рис. 5-53,а) даже при низкой ча-
стоте может оказаться заметной
индуктивность, обусловленная маг-
нитным потоком. Для уменьшения
магнитного потока применяют би-
филярную обмотку (рис. 5-53,6);
в этом случае магнитный поток,
сцепленный с контуром, очень мал;
так как в соседних проводах токи
направлены противоположно. Одна-
160
Рис. о-53.
ко при такой намотке проволоки
становится более заметной емкость
между проводами особенно из-за
того, что вход и выход проволочного
сопротивления расположены рядом,
тогда как именно здесь между про-
водами- существует наибольшее на-
пряжение. '
При высоких частотах избегают
применять и бифилярную обмотку.
Типы высокочастотных проволочных
сопротивлений, в которых наименее
заметны индуктивность и емкость,
показаны на рис. 5-53,в;.
Для уменьшения общей длины
проволоки Тюименяются специаль-
ные металлические сплавы с боль-
шим удельным сопротивлением. При
этом выбирают сплавы, сопротивле-
ние которых по возможности мало
зависит от температуры.
В технике высоких частот (в ра-
диотехнике) наилучшими оказыва-
ются непроволочные сопротивления
из специальных составов (углероди-
стые- массы, полупроводящая кера-
мика и т. п.); их малые размеры
при больщом сопротивлении и от-"
сутст’вии сравнительно сильного
магнитного поля (неизбежно появ-
ляющегося на поверхности проволок
малого сечения) приводит к тому,
что такие сопротивления в ряде слу-
чаев могут считаться практически
не обладающими индуктивностью.
Но, помимо влияния индуктив-
ности и емкости, обусловленного
11 к. М. 'Поливанов
электромагнитным полем между
проводами, само сопротивление
проводов зависит от частоты. На-
пример, сопротивление, измеренное
на постоянном токе (иногда его
называют омическим или омовским
сопротивлением), может существен-
но отличаться от активного сопро-
тивления, определяемого при пере-
менном токе. Здесь большую роль
может играть поверхностный
эффект (скин-эффект). Перемен-
ный ток распределяется «неравно-
мерно по сечению проводника. Его
внутренние области оказываются
экранированными наружными про-
водящими слоями, и быстро изме-
няющееся электромагнитное поле
не успевает полностью проникнуть
внутрь.
В результате напряженность
электрического поля на поверхно-
сти оказывается больше, чем на-
пряженность электрического поля
внутри, соответственно большей
оказывается и плотность тока.
Чем выше частота, тем на мень-
шую глубину проникает поле. Так,
в медных проводах электрическое
поле и плотность тока уменьшаются
приблизительно в 3 раза (по срав-
нению с поверхностью): на глубине
1 см • при f = 50 гц, на глубине
0,1 мм при f=0,5 Мгц, на глубине
0,01 мм при частоте 50 Мгц; назван-
ная глубина (условная глубина
проникновения) обратно пропор-
циональна корню из частоты.
Поэтому в установках высокой
частоты основную роль играет по-
верхностный слой проводов.
Зависимость активного сопро-
тивления проводов от частоты рас-
считывается методами теории поля,
которая рассматривается в третьей
части книги. Из приведенных дан-
ных видно, однако, что изменение
активного сопротивления из-за по-
верхностного эффекта на промыш-
ленной частоте (50 гц) заметно
только в пооводах очень большого
сечения.
'Как бы ни были сложны про-
цессы в проводниках (влияние на-
водимой в них э. д. с. распределен-
ным магнитным полем, замыкание
тока через емкостные связи и т. п.),
частотная характеристика входного
161
сопротивления (или проводимости)
оказывается исчерпывающей ха-
рактеристикой рассматриваемого
элемента.
На рис., 5-54 приведена рассчи-
танная частотная характеристика
двухполюсника, представляющего
собой постоянное чисто активное
сопротивление при низкой частоте
(при 800 гц увеличение актив-
ной составляющей входного сопро-
тивления меньше 1%)- Однако при
расчете принято во внимание суще-
ствование индуктивности, включен-
ной последовательно с сопротивле-
нием г, причем г и L зависят от
частоты. Главное влияние на ча-
стотную характеристику в области
высоких частот оказывает емкость,
существующая между проводами
на входе двухполюсника. Парамет-
ры рассчитанной цепи таковы, что
при частоте 800 гц активное сопро-
тивление очень мало отличается от
соцротивления при постоянном токе,
а реактивная составляющая дости-
гает уже 3% от активного сопро-
тивления. Но при значительном по-
вышении частоты (при f=120 кгц)
активное сопротивление достигает
наибольшего значения, возрастая
почти в 1,5 раза, а реактивное со-
противление обращается в нуль
вблизи гвх=‘ГВх.макс- -При еще более
высоких частотах реактивная со-
ставляющая входного сопротивле-
ния отрицательна, т. е. значитель-
ная часть тока проходит через
емкостные связи между зажимами.
Приведенная характеристика
отражает типичные черты, хотя и
в несколько преувеличенном виде,,
обычных активных сопротивлений,
если, конечно, это не сопротивления,
специально рассчитанные на работу
при высокой частоте.
Заметим в заключение, что в тех
случаях, когда активное сопротив-
ление меняется с частотой, эквива-
лентная схема обязательно содер-
жит и реактивное сопротивление,
зависящее от частоты.
Емкость. Обычные конденсаторы
представляют собой специально
сконструированные элементы с от-
носительно большой поверхностью
электродов 5 и сравнительно малым?
расстоянием между ними d (т. е~
при d2 < 5). Воздушные конденса-
торы (имеющие воздушную изоля-
цию между электродами) только
при очень высоких частотах отлича-
ются от идеальных из-за необходи-
мости учитывать индуктивность
соединяющих проводов.
Воздушный конденсатор пере-
менной емкости схематически изо-
бражен на рис. 5-55. Емкость воз-
душных конденсаторов, невелика
(десятки пикофарад). Конденса-
торы больших емкостей (единицы
микрофарад), как правило, состоят
из металлической фольги, разделен-
ной тонким слоем изоляции. Широ-
ко применяются также электролити-
ческие конденсаторы, в которых
изолирующая ' прослойка между
металлическим электродом и элек-
тролитом образуется очень тонкой
электролитически осажденной плен-
кой. Их емкости бывают очень ве*
Рис. 5-55.
162
лики (десятки и сотни ми-
крофарад). При работе в
цепи переменного тока к
ним дополнительно должно
быть приложено постоян-
ное напряжение для того,
чтобы не разрушить изо-
лирующий слой.
В технике высоких ча-
стот применяются керами-
ческие конденсаторы (еди-
ницы и десятки пикофа-
рад). В них электроды раз-
делены диэлектриком, рас-
считанным на высокую ча-
стоту^-И^азмеры радиотех-
нических конденсаторов часто
очень малы, их объем порядка де-
сятков кубических миллиметров,
в печатных схемах емкостная связь
между контурами может осущест-
вляться тем, что печатаемые метал-
лические полюсы, служащие прово-
дами, находят одна на другую на
длине порядка нескольких санти-
метров, при промежуточной изоля-
ции в виде тончайшей пленки. Кон-
денсаторы, применяемые в технике
высоких'напряжений, имеют разме-
ры в несколько метров (рис. 1-5).
Небольшая активная составляю-
щая входной проводимости конден-
саторов в ряде случаев совершенно
несущественна, например, когда
они применяются в энергетических
системах для компенсации фазового
сдвига'. Напротив, конденсаторы,
применяемые в резонансных конту-
рах, должны обладать очень боль-
шой добротностью, поэтому актив-
ная проводимость, составляющая
всего сотую долю реактивной, уже
снижает их качество.
В реальных конденсаторах . фа-
зовый угол между напряжением и
током обычно отличается от л/2 на
небольшую величину б, как это по-
казано на рис. 5-56. На рис. 5-56,6
схематически изображен конденса-
тор, электроды которого разделены
неидеальным диэлектриком (штри-
ховка); в этом диэлектрике и про-
исходит необратимое рассеяние
электромагнитной энергии; такой
конденсатор потребляет активную
мощность.
Ток /, смещенный по фазе отно-
сительно напряжения U на . угол,
Рис. 5-56.
меньший тс/2, можно разложить на
две составляющие (рис. 5-56,а): ак-
тивную /а (она в фазе с напряжением)
и реактивную /р (она ортогональна
напряжению). В эквивалентной элект-
рической цепи эти две составляющие
можно представить как токи в па-
раллельных ветвях, из которых одна—•
идеальный конденсатор Спар, дру-
гая—чисто активное сопротивление
/?=1/G.
Можно произвести и другое разло-
жение на составляющие (рис. 5-56,в),
а именно полное напряжение U пред-
ставить как сумму активной состав-
ляющей напряжения t/a (она в фазе
с полным током /) и реактивной со-
ставляющей (она ортогональна
току /). В эквивалентной электриче-
ской цепи эти составляющие можно
представить как напряжения на двух
последовательно включенных эле-
ментах, ‘ из которых один — чисто
активное’ сопротивление г, а другой—
идеальный конденсатор Спос-
Параллельная и последовательная
схемы замещения эквивалентны дей-
ствительной цепи с реальным конден-
сатором; в обеих схемах токи I и
напряжения U одинаковы, так же
•как и фазовый угол между ними
nJ2 — S.
В параллельной схеме замещения
(рис. 5-56,а)
поэтому
Zp WCnap юСдарА
(5-123)
и*
163
и добротность конденсатора
Qc = ^=»CEap/?. (5-124)
Далее, имея в виду, что /a = /sin6
и /p=/cos6, находим
шСпар -—
I Ъ
— COS о =
I 1
V1 + tg2 а
G=T=4=4sin8==
_ / tg 8
“ и -|Л1 _|_tg23
(5-125)
В последовательной схеме заме-
щения (рис. 5-56 л)
следовательно,
tgS^^^ojCnocr (5-126)
и добротность конденсатора
= ----i (5-127)
'С tg о (9G лос Г
Далее, поскольку Ua = U siti 8 и Uv—
=£7 cos 8, находим
r I I
=-^Vi+tg28;
J/ tg 8
/ / j -j. tg2 a '
Из сопоставления (5-125) и (5-128)
следует, что
^пос == С пар (1 1g2 8),
tg2S (5-129)
- • Г R l-|-tg28 •
При tg-6<.0,l, т. e. Qc>l10, что спра-
ведливо для всех реальных конден-
саторов, можно считать с погреш-
ностью, меньшей 1%, что
Спос Ci;ap, г = R tg2 5. (5-130)
Л 64
Добротность реальных конденсато-
ров обычно составляет тысячи и де-
сятки тысяч.
Активная мощность, потребляе-
мая реальным конденсатором (рас-
сеиваемая в нем),
P=^Ula = UJ = UIsm^ (5-131)
ее часто выражают более удобными
для пользования формулами, вводя
реактивные составляющие тока
/а=/р tg б или напряжения U&=
= f/p tg б,
P = (7/ptg8 = C72(DCnaptg8 (5-132)
или
P=£7p/tg 8 = tg 8. (5-133)
tub пос
Как указывалось выше, при за-
данных параметрах и частоте обе
схемы замещения (параллельная и
последовательная) «• эквивалентны
заданному реальному конденса-
тору. Однако частотные ха-
рактеристики этих двух схем
•существенно различны. В па-
раллельной схеме при постоян-
ных R И Спар с ростом частоты tg б
уменьшается (добротность возра-
стает); в последовательной схеме
при постоянных г и Снос с ростом
частоты tg б увеличивается (доброт-
ность падает).
Легко представить себе реаль-
ный конденсатор, соответствующий
параллельной схеме, — это конден-
сатор неизменной емкости С=Спар,
в котором активная составляющая
тока обусловлена только несовер-
шенством его изоляции. Если про-
водимость изоляции не зависит от
частоты, то естественно, что доброт-
ность такого конденсатора увеличи-
вается с ростом частоты, так как
в этом случае реактивная проводи-
мость возрастает ('&='СоСпар).
Также легко себе представить
реальный конденсатор, соответст-
вующий последовательной схеме, —
это конденсатор неизменной емко-'
сти С=='СЛос с идеальной изоляцией,
включенный в цепь через провода,
обладающие постоянным сопротив-
лением г. Очевидно, что доброт-
ность такого конденсатора должна
уменьшаться с ростом частоты, так
как в этом случае емкостное сопро-
тивление конденсатора уменьшается
(*С = 1/coCiioc) •
В силу сказанного в некоторых
случаях есть основания для выбора
между эквивалентными схемами за-
мещения.
Потери в конденсаторе с реаль-
ным диэлектриком в основном
обусловлены процессами поляриза-
ции диэлектрика, находящегося
в переменном поле, их называют
диэлектрическими потерями; по
своей^физической сущности они
отлЦчны от джоулевых потерь (йг).
Теория поляризации диэлектри-
ков и происходящего в них тепло-
вого рассеяния энергии электро-
магнитного поля составляет пред-
мет теории поля (третья часть кни-
ги) или специальных дисциплин.
Однако в пределах теории цепей
можно объяснить основной эффект,
приводящий к диэлектрическим по-
терям.
Заряд на электродах конденсатора «про-
порционален приложенному напряжению.
Если пространство между электродами за-
полнено поляризуемым диэлектриком (е> 1),
этот заряд в несколько раз -(в 8 раз) боль-
ше, чем в отсутствие диэлектрика. Но поля-
ризация диэлектрика происходит не мгно-
венно вслед за появлением напряжения. По-
ляризация запаздывает по времени. Поэто-
му, когда к электродам приложено гармо-
нически изменяющееся напряжение t7, за-
ряд на электродах Q также изменяется по
гармоническому закону, но отстает по фазе
от напряжения. Это отставание и характе-
ризуется углом б (рис. 5-57):
Q = (JCe~il. (5-134)
Уже много раз говори л ось, что ток
в ветви, содержащей конденсатор, равен
производной от заряда на электродах; по-
этому в нашем случае ток
I = jwQ = (7jcoCe-/8 (5-135)
опережает по фазе напряжение именно на
л/2—б.
Основываясь на выражениях (5-134) и
(5-135), можно ввести понятие комплексной
емкости:
С = Се~‘ъ = С — jC". (5-136)
Применяя формулы, выведенные для
проводимости и сопротивления идеального
конденсатора, к случаю конденсатора с по-
терями, получаем, что
Y = g — jb = усоС = соС" + /соС' (5-137)
и
1 V\
Z = (5-138) L
j(aC
Этими формулами удоб- у
но пользоваться в тех слу- '—«Л
чаях, когда запаздывание
заряда относительно наир я- рИ(С
жения представлено в виде
явной функции от частоты.
Так, например, в первом приближении мож-
но представить запаздывание заряда отно-
сительно напряжения формулой
(S-1S9)
которая выводится в теории поляризации
диэлектриков.
Из последнего выражения следует, что
комплексная емкость
1
б* = 6*0 J
-c-T+^F“c'-ic" I5-14”
Постоянная т, входящая в приведенные
формулы, называется временем релаксации
диэлектрика и составляет обычно величину
порядка долей миллисекунды или даже
микросекунды; Со — емкость конденсатора
при со=О.
В том случае, когда комплексная ем-
кость изменяется по закону (5-140), ее ком-
плексное сопротивление в точности соответ-
ствует последовательной схеме замещения
с постоянными Спо с -и г. Действительно,
при этом
_____I _ 1 + /мт _
— jaC
-i+isr.- <М41>
тогда как
~ Сд2-С + /со
У = = Со о + jbc. (5-142)
Мощность, рассеиваемую в конденсато-
ре, проще всего представить формулой Р=
= U2G. Подставляя в нее выражение для ак-
тивной проводимости ив (5-142), получаем:
со2т
Р = IPCo ( .
Частотные характеристики С (/со) и
У (/со), определяемые формулами (5-140) и
(5-142), а также график мощности Р(со)
•представлены на рис. 5-5'8.
* При сот=1 наибольшее значение прини-
мают Ьс и С"; при этом
Р=Р(1)=С2Со/2т.
165
О 1 2
С дальнейшим (ростом частоты мощ-
ность 'возрастает, стремясь в пределен удво-
енному значению, т. е. ж 2P(i).
Существованием достаточно больших
диэлектрических потерь в полях высокой
частоты пользуются для технологического
нагрева диэлектриков (напрев резины,
пластмасс и даже стекла). В тех случаях,
когда диэлектрические потери обусловлены
именно рассмотренным здесь релаксацион-
ным законом запаздывания поляризации,
выбирают частоту, при которой сот> 1 (для
названных (материалов применяют частоты
/=,Ю—30 Мгц при т порядка 10“7 сек).
Мы ограничились здесь рассмотрением
конденсаторов с линейным диэлектриком,
когда можно считать, что заряд пропорцио-
нален напряжению. Нелинейные эффекты,
обусловленные диэлектриком, составляют
предмет теории нелинейных цепей.
Индуктивность. Когда в электри-
ческую цепь нужно ввести опреде-
ленную индуктивность, ее осущест-
вляют в виде многовитковой катуш-
ки. Для увеличения индуктивности
применяют катушки с ферромагнит-
ными сердечниками.
Воздушные катушки (без ферро-
магнитных сердечников), кроме
индуктивности, обладают некоторым
активным сопротивлением. При вы-
сокой частоте начинает сказываться
и межвитковая емкость, поэтому
при радиочастотах стремятся укла-
дывать витки так, чтобы крайние
Рис. 5-59.
витки были расположены возможно
дальше друг от друга, например
в случае двухслойной обмотки по-
следовательность витков соответст-
вует изображенной на рис. 5-59,а.
Катушки с большим числом витков
при высоких частотах (мегагерцы)
вообще не применяются.
Кроме простейших случаев (то-
роидальной катушки, однослойной
длинной катушки и кольцевого про-
водника), индуктивность, рассчиты-
вается по эмпирическим формулам.
Так, в случае очень распространен-
ного типа катушки, показанной на
рис. 5-59,6, индуктивность опреде-
ляют по формуле.
т____ 0,32а2п2 in-6
Ь ~6а + 9Ь + 10с ‘
гн,
где а, b и с — размеры катушки
в сантиметрах, п— число витков.
Эта формула дает достаточно
точный результат, если все слагае-
мые в знаменателе одного порядка.
Влияние . межвитковой емкости
в первом приближении может быть
представлено некоторым конденса-
тором Cd, включенным параллельно
с индуктивностью (рис. 5-60). Зна-
чения L и Cd могут быть определе-
ны из таких двух опытов. Парал-
лельно к индуктивности подклю-
чается градуированный конденсатор
переменной ёмкости, и при двух
разных частотах coi и <о2 находятся
значения Сх и С2, при которых ре-
Рис. 5-60.
166
жим контура близок к резонансу
токов. При этом
(С, + Cd); L (С2 + С<0
(1>1 со2
и, следовательно,
1 1 =L(C1_C2)
или
£= с 1 с (—2--------Н (5-143)
С1—с2 I (°2 /
После того как найдено L, зна-
чение Cd определяется по одной из
исходных формул.
В небольших катушках с индук-
тивностью порядка десятой доли
миллигенри емкость Q очень мала
(порядка нескольких пикофарад).
Поэтому эта емкость становится
заметной лишь при частотах, пре-
вышающих /сотни килогерц.
Схема индуктивной катушки
с параллельно включенной емко-
стью применима в ограниченном
диапазоне частот. В самом общем
случае для суждения о свойствах
катушки нужно знать всю ее частот-
ную характеристику, которую мож-
но снять, пользуясь куметром
(§ 5-5).
Ферромагнитные сердеч-
н и к и способны существенно изме-
нить свойства индуктивных кату-
шек. Прежде всего наличие ферро-
магнитного сердечника способно во
много раз (в сотни, тысячи и даже
в сотни тысяч раз) увеличить ‘ин-
дуктивность. Кроме того, индуктив-
ность таких катушек становится
нелинейной: их потокосцепление
W — сложная функция тока в об-
мотке. Эффекты, вызванные нели-
нейностью, составляют предмет
теории нелинейных цепей и в этой
части книги не рассматриваются.
Ограничимся анализом катушек
о ферромагнитными сердечниками,
работающих в линейном режиме
или в режиме, близком к линей-
ному, когда можно считать, что
потокосцепление пропорционально
току. Однако обычно это утвержде-
ние справедливо только с дополни-
Рию. 5-61.
тельной оговоркой: при гармониче-
ском изменении тока / в обмотке
потокосцепление Т также изменяет-
ся по гармоническому закону, но
с некоторым отставанием по фазе
(рис. 5-61):
W=^lLe~ib. (5-144)
В результате напряжение на катушке
и = /шф = jvLe-^i (5-145)
опережает ток на угол л/2 — б.
С точки зрения теории цепей
угол б в случае индуктивности при-
водит к таким же эффектам, как
угол б в случае конденсаторов.
Физические основания, приводя-
щие к запаздыванию потокосцепле-
ния Ф* относительно намагничиваю-
щего тока /, также имеют много
общего с процессами в диэлектри-
ке: поляризация ферромагнитного
сердечника (его намагничение) про-
исходит не мгновенно вслед за по-
явлением тока; для того чтобы
поляризация достигла установивше-
гося значения, соответствующего
току в обмотке, требуется некото-
рое время; это время, как правило,
очень мало (миллисекунды или да-
же микросекунды), но при быстром
изменении намагничивающего то-
ка I сказанное приводит к вполне
заметному, хотя бы и малому запа-
здыванию по фазе потокосцепления
Ф* на угол б.
В металлических ферромагнит-
ных сердечниках существует и дру-
гой процесс, приводящий к отста-
ванию изменений потока от измене-
ний тока: по закону Ленца всякое
изменение магнитного потока наво-
дит э. д. с., стремящуюся вызвать
ток, препятствующий изменению по-
тока.
167
Представим себе металлический
сердечник (рис. 5-62), охватывае-
мый обмоткой, один виток которой
показан на схематическом рисунке.
При указанном направлении тока i
в сердечнике существует поток Ф,
направление которого показано
стрелкой. Если ток в обмотке умень-
шается, в металлическом сердечни-
ке наводится ток, препятствующий
изменению потока и направленный
так, чтрбы поддерживать поток
в прежнем направлении.
Возникающие в металлических
сердечниках токи называют вих-
ревыми, они, конечно, отличаются
от токов в электрических цепях, где
токи ограничены своими ветвями.
шается, так же как уменьшается
поток, проходящий по одной пла-
стине. Чем выше частота, тем тонь-
ше делают пластины (от 0,50 —
0,35 мм при f = 50 гц и до несколь-
ких микрон при частотах порядка
сотен килогерц). При радиочасто-
тах применяют сердечники, со-
ставленные из тонкого ферромаг-
нитного порошка, спрессованного
с изолирующей массой.
Другой путь к уменьшению
влияния вихревых токов — увели-
чение удельного электрического со-
противления ферромагнетиков. Уве-
личенным удельным сопротивлени-
ем (по сравнению с обычной
сталью) обладают и листовые элек-
тротехнические стали, применяе-
мые для трансформаторов и ма-
шин переменного тока.
Существуют и неметаллические
ферромагнетики — ферриты, удель-
ное сопротивление которых близко
к удельному сопротивлению полу-
проводников и изоляторов. В этих
материалах практически отсутст-
вуют вихревые токи, однако и в
ферритах наблюдается запаздыва-
ние намагничения, причем чем
Рис.
Приведенное элементарное рас-
смотрение реакции вихревых токов
позволяет понять почему, изготов-
ляя ферромагнитные сердечники
для устройств переменного тока, их
не делают сплошными, а составля-
ют из ряда тонких пластин, изоли-
рованных одна от другой. В тонких
пластинах затруднено протекание
вихревых токов, так как длины
контуров токов остаются большими,
а сечение для тока резко умень-
5-63.
больше их магнитная проницае-
мость, тем сильнее сказывается
этот эффект.
Процессы намагничения ферро-
магнетиков, возникновения в них
вихревых токов и происходящего
при этом теплового рассеяния
энергии электромагнитного поля
составляют предмет теории поля
(третья часть книги) - или специ-
альных дисциплин. Ограничившись
сделанными замечаниями, перей-
168
дем к анализу следствий из век-
торной диаграммы индуктивной
катушки с ферромагнитным сер-
дечником (рис. 5-61).
Векторная диаграмма напряже-
ния и тока индуктивной катушки
с ферромагнитным сердечником
изображена на рис. 5-63,6. Под
диаграммой б показано схематиче-
ское изображение такой катушки..
На рис. 5-63, а представлена
векторная диаграмма с разложе-
нием тока на активную и реактив-
ную составляющие; там же пока-
зана эквивалентная схема, содер-
жащая две параллельные ветви:
чисто активную 7?, по которой про-
ходит активная составляющая то-
ка, и чисто реактивную £Лар, по ко-
торой проходит реактивная состав-
ляющая тока.
На рис. 5-63.,в представлена
векторная диаграмма, в которой
напряжение разложено на актив-
ную И' реактивную составляющие,
а также эквивалентная схема с по-
следовательными Г И Lnoc.
Все построения рис. 5-63 совер-
шенно аналогичны построениям
рис. 5-56. Также аналогично фор-
мулам (5-123) — (5-133), выведен
ным для конденсатора с потерями,
выводятся и расчетные формулы
для индуктивности с потерями.
В параллельной схеме замеще-
ния (рис. 5-61,8)
В последовательной схеме заме-
щения (рис. 5-63,8)
— 1 /фАпо с л ^а — If >
tg 8 = £7a/[7p = r
1 ____w-^iioc
^L— tg“F r~
f»Lroc — UV[I = U cos 8/7 =
U 1
1 ’ V1 +tg*a ’
r = Ua/I = Usin8// = 4 7 tg5 T•
1 1 1 pH+tgaa
Добротность реальных катушек
обычно составляет несколько де-
сятков или сотен. Она может быть
значительно увеличена при глубо-
ком охлаждении катушек или да-
же при достижении состояния
сверхпроводимости их проводов,
что в настоящее время технически
вполне осуществимо.
Из сопоставления выражений
для параметров параллельной и
последовательной эквивалентных
схем находим, что
7>пар — Дтос (1 1g2
tg2&
1 + tg2 3 ’
(5-146)
При tgo<0,l, т. е. Ql>10
с погрешностью, меньшей . 1%.
АЛар.~АЛос> f ~7?tg28. (5-147)
tg 8 — /а//р — шТпарС;
Q = J_______L_.
tg а — ®rnapG >
“t-пар = U/I-p = Uj! COS, 8 ==
= 7-У1 +tg2 8;
R^±=U!I& = UH sin 8 =
_ г/ V i + tg2 s
i tgd
Активная мощность, выраженная
через реактивные слагающие и tg 5,
P = {//ptg8 = ^tg8 (5-148)
ИЛИ
р = u^l tg 8 = АвАЛ0С tg 8. (5-149)
Интересно обратить внимание
на соответствие формул для после-
довательной схемы индуктивности
и параллельной схемы конденса-
тора при перемене мест для I и U.
Это одно из проявлений принципа
дуальности.
16S
Все, что было сказано о частот-
ных характеристиках параллель-
ной и последовательной эквива-
лентных схем для конденсатора,
содержащего, диэлектрик с потеря-
ми, применимо и к случаю индук-
тивности с ферромагнитным сер-
дечником.
<В случае сердечника с запаздывающей
магнитной поляризацией иногда наиболее
•близкий к опыту результат можно полу-
чить, представляя 1индуктивность комплекс-
ной величиной с зависимостью от частоты,
подобной ранее рассмотренной для конден-
сатора >(5440),
= (5.150)
При этом в последовательной схе^ме
замещения
~ (О2Т 4- /СО
Z — r + Iх ” ~ Lo j (сох)2 (5-151)
и, следовательно,
со2т
Г = 1 4-(<От)2’
Лп0° 1 4-(сот)г’ (5-152)
т. е. как г, так и L изменяются с часто-
той.
Напротив, в параллельной схеме заме-
щения
y = (5.153)
и, следовательно,
G=TT; <5-154)
т. е. при рассматриваемой зависимости
комплексной индуктивности от частоты в
параллельной схеме замещения остаются
постоянными как £пар —£0, так и G —
= *c/L0.
Очевидно, что в обеих схемах
tg § = 1 /Ql — сот. (5-155)
Резонанс в цепи с параметрами
г, А, С, зависящими от частоты.
В таких цепях также можно гово-
рить о резонансе в последователь-
ном и в параллельном контурах.
Однако зависимость основных па-
раметров от частоты существенно
изменяет основные соотношения,
характерные для цепей с постоян-
ными параметрами. Все эти осо-
бенности легко выводятся из ана-
лиза уравнений, >в которые непо-
средственно вводятся заданные
частотные характеристики.
Отметим прежде всего принци-
пиальную неприменимость в этом
случае некоторых формул, выве-
денных для зависимости токов и
напряжений от частоты; так, на-
пример, неприменимо определение
резонансной частоты и добротно-
сти по ширине резонансной кривой
(§ 5-5). Напротив, сохраняя часто-
ту фиксированной и меняя, ска-
жем, известную емкость С, мож-
но по ранее выведенным формулам
определить по измеренному значе-
нию UcI'IJcmxkc как добротность, так
и индуктивность контура с L (ja)).
Производя подобные измерения
куметром для разных частот мож-
но определить зависимость Q и L
или г и L от частоты. Аналогич-
ные измерения возможны и для
конденсатора с потерями С (/со).
Пример 5-16. В цепи .последовательно
включены конденсатор без потерь С и ин-
дуктивность, • частотная характеристика ко-
торой
L = L° 1 + Joi '
Требуется: /
1) найгги три заданной частоте <0i зна-
чение емкости С, при которой напряжение
на конденсаторе максимально; показать,
что в соответствии с формулами (5-98) и
(5-155)
и С макс —~9
— -----=]/ 14-Q£, где Ql= 1/gk,
2) определив емкость С, соответствую-
щую Uс макс anqpiH заданной частоте он, най-
ти частоту со2, при которой мнимая состав-
ляющая входной проводимости равна нулю.
Расчет выполнить для следующих дан-
ных:
<ог = тс4 05 сек-1, £о = 1,ОО мгн при двух
значениях т: а) т = 3,540“6 сек, б) т =
= 10“6 сек.
Решение. Определяя Uc/U по фор-
муле
U
VС — Z ja>C
при
Z = /<оС + 1 + /от ’
находим, что
С? _ 1 /________1 + (ц>?)2____
U V (1 — <О2£оС)2 + (<от)2 ’ W
170
Коода изменяется только С, условие .макси-
мума Uс очевидно
1 — (h2LqC = 0. (г)
Следовательно, емкость при заданной
частоте coj имеет значение С = —?— =
= 0,01013 мкф, не зависящее от *с.
Из выражения (в) при условии (г) на-
ходим отношение
макс - ' 1
(J = У 1 + ((0^)2 ’
которое (получается равным: а) 1,35, б) 3,33.
Чтобы ответить на второй вопрос, сле-
дует обратиться к выражению (б) и поло-
жить в нем мнимую часть равной нулю при
найденном значении С. Это приводит к урав-
нению для искомой частоты со2’
ИЛИ
1_____ (02^0
W2C 1 (to2T)2
1 --COjT2
Из -этого равенства следует, что при
т==3,5«10—6 сек не существует частоты,
при -которой Z=ir; иначе говоря, реактив-
ное сопротивление -емкости С всегда больше
реактивного сопротивления индуктивности
из-за 'быстрого падения L.
При т=10~6 сек (условие б) такая ча-
стота существует: со2—1,05(О1.-
Заключительные замечания. Рас-
сматривая частотные характери-
стики реальных элементов, мы
представляли их в виде двухполюс-
ников, содержащих небольшое чи-
сло постоянных г, L, С. Во многих
случаях такое представление хоро-
шо согласуется с характеристикой
реального двухполюсника в из-
вестном диапазоне частот. Однако
во всех случаях такое представле-
ние можно считать лишь прибли-
женной заменой функции К(/со) ко-
нечным рядом членов. Характери-
стики У (/со) иногда представляют-
ся трансцендентными функциями
(например, th у/Разлагая та-
кую функцию в степенной ряд,
можно ограничиться несколькими
первыми членами и найти электри-
ческую цепь с конечным числом г,
L, С, обладающую частотной харак-
теристикой, соответствующей этим
членам ряда, конечно, в некотором
ограниченном диапазоне.
В общем случае составление
схемы соединений элементов г, L,
С и -определение параметров этих
элементов с тем, чтобы получив-
шаяся цепь (двухполюсник или
четырехполюсник) обладала за-
данной частотной характеристи-
кой, представляется основной про-
блемой синтеза электрических це-
пей.
ГЛАВА ШЕСТАЯ
ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ВЗАИМНОЙ
ИНДУКТИВНОСТЬЮ
В предыдущей главе были до-
статочно подробно развиты основ-
ные положения теории переменных
токов. При этом однако рассма-
тривались цепи, содержащие толь-
ко элементы г, L и С, что позво-
лило несколько упростить изложе-
ние. В этой главе будут рассмотре-
ны -цепи, содержащие, помимо эле-
ментов г, L, С, также индуктивные
связи между ветвями или конту-
рами.
Распространение всех ранее вы-
веденных положений теории наце-
пи с взаимной индуктивностью
требует очень незначительных до-
полнений. Однако благодаря ин-
дуктивной связи между контурами
переменного тока возможны
устройства, обладающие сущест-
венными особенностями. К числу
таких устройств относятся прежде
всего трансформаторы. Теории
трансформаторов как элементов
электрической цепи посвящен
§ 6-3.
6-1. ВЗАИМНАЯ ИНДУКЦИЯ
Основные определения. При до-
статочной близости двух контуров
какой-либо электрической цепи
магнитное поле тока одного из них
может распространяться на об-
171
a)
Рис. 6-1.
ласть расположения второго (рис.
6-1). В результате, когда ток про-
ходит только по первому контуру
(/1=?4=0, z2='O), второй контур ока-
жется сцеплен с магнитным пото-
ком, пропорциональным первому
току (рис. 6-1,а):
Т21 = 7И2Л. (6-1)
Поток, сцепленный с первым
контуром Тп, при этом равен про-
изведению первого тока на собст-
венную индуктивность Lp
= (6-2)
Аналогично, когда ток сущест-
вует только во втором контуре, с
первым контуром сцеплен поток
W12 = A412z2, - (6-3)
собственное . потокосцепление вто-
рого контура
W22 = L2z2. (6-4)
Когда изменяется только ток в
первом контуре, во втором контуре
наводится э. д. с.
= <«-5>
Точно так же при изменении тока
только во втором контуре в первом:
контуре наводится э. д. с.
<6~6>
Это явление называют в з а-
имной индукцией, а коэф-
фициенты пропорциональности
М12, ТИ21 называют коэффициента-
ми взаимной индукции или в з а-
И !М Н Ы М И И H Д у К Т1И в н о с т я-
м и. Взаимная индуктивность М9
как и собственная индуктивность^
измеряется в генри (гн).
При гармонических токах ра-
венства (6-5), (6-6) можно запи-
сать в комплексной форме:
Э2 = —./(оМзХ; Эг =— /о)7И12/2.
(6-7>
Представим себе, что на торо-
идальный (кольцевой) сердечник
(рис. 6-1,6), кроме первой обмотки
с числом витков М, намотана вто-
рая обмотка с числом витков TV2.
В таком случае под влиянием толь-
ко тока /1 первой обмотки с каж-
дым витком второй обмотки ока-
жется сцепленным магнитный поток
где ц — магнитная проницаемость
сердечника; I — средняя длина
магнитной линии в сердечнике; s—
поперечное сечение сердечника,
линейные размеры которого много-
меньше I.
Полное потокосцепление второй,
обмотки при этом равно:
v₽-21 = г\. (б-9>
Множитель при 1\ и представ-*
ляет собой взаимную индуктив-
ность
Mzl=w^s. (6-10}
Так как взаимная индуктивность за-»
висит от произведения чисел вит-*
ков, то
172
Взаимная индуктивность двух
параллельных двухпроводных воз-
душных линий (рис. 6-1,а) длиной
I равна:
Л1 = /^Мп —, (6-11)
2тс <213 я24 4 7
где атп—-расстояние между про-
водами т и п; ан — расстояние
между первым и четвертым прово-
дом; £24 — между вторым и чет-
вертым и т. д.
Из выражения (6-11) видно,
что 2И12=7И21=Л1, так как замена
индексов 1, 2 на индексы 3, 4, а
3, 4 на 1, 2 не меняет результата.
В том случае, когда ток прохо-
дит как в первом, так и во втором
контуре (ветви, обмотке, катушке),
полное потокосцепление представ-
ляется алгебраической суммой по-
токосцепления, обусловленного
•собственной и взаимной индуктив-
ностями (рис. 6-1)
«•1==Ti1 + T12 = L1z1 + ^12/2;
(6-12)
^2, + ^ = ^ + ^;
здесь Ti и Т2 — полное потоко-
сцепление первого и соответствен-
но второго контура.
Формулы (6-12) написаны в
предположении,- что потокосцепле-
ние каждого из контуров при поло-
жительном токе в нем увеличивает-
ся под влиянием положительного
тока другого контура (рис. 6-1,£).
Сказанное налагает определенное
требование на согласованный вы-
бор положительных направлений
токов. Если выбранные положи-
тельные направления противоречат
этому требованию, коэффициенты
взаимной индукции в формулах
(6-12) должны считаться отрица-
тельными.
Взаимная индукция в электриче-
ской цепи. Как уже не раз говори-
лось, электротехническую систему
можно представлять как электриче-
скую цепь в тех случаях, когда на-
пряжение между ее узлами равно
разности между их потенциалами.
Поэтому в цепях с взаимной ин-
дукцией *мы должны считать, что
процесс наведения э. д. с. не на-
рушает указанных условий, оста-
Рис. 6-2.
ваясь локализованным в отдель-
ных ветвях; при этом наводимая
э. д. с. может быть представлена
как источник э. д. с., включенный
в соответствующую ветвь *. Так, на-
пример, для индуктивно связан-
ных ветвей рис. 6-2,£ входное
напряжение может быть выраже-
но равенствами:
— 4G 1
I г dii । я ж di2 9
' dt dt >
(6-13)
при этом принято представление
потокосцепления формулами (6-12).
На рис. 6-2,6 наводимые в ветвях
э. д. с. самоиндукции и взаимоин-
дукции представлены в виде соот-
ветствующих источников.
Если бы положительные направ-
ления э. д. с. источников были со-
гласованы с положительным на-
правлением тока (обратно показан-
ному на, рис. 6-2,6), то и в выра-
жениях соответствующих э. д. с.
1 Существуют цепи, содержащие такие
узлы, к которым явсе сказанное (выше непо-
средственно неП|р1И!мен1И1МО. В подобных слу-
чаях из рассмотрения должно исключаться
напряжение между такими узлами. ’
173
следовало изменить знак, полагая
э. д. с. самоиндукции и взаимоин-
дукции равными
т di -п д di
~L~dF и
Энергия магнитного поля двух
индуктивно связанных ветвей. Энер-
гию поля токов /1 и i2 двух индук-
тивно связанных ветвей найдем,
определив энергию, полученную от
источников питания при том, что
вначале fi=iZ2 = 0.
Пусть сначала источник питания
включен только в первую ветвь при
условии, что вторая ветвь остается
разомкнутой (Z2=0). В таком слу-
чае при возрастании тока ц от нуля
до h в течение времени tx первый
источник должен отдать энергию
ti Л
Л = f Ч G dt + j i Л -§- dt. (6-14)
б 0
Вычитая из Xi энергию, рассеи-
ваемую в сопротивлении (первое
слагаемое), находим, что первый
источник отдал магнитному полю
энергию
^=,£^/2. (6-15)
Пусть в момент новый источ-
ник включается во вторую ветвь, и
к моменту t2 ток в ней возрастает
ОТ нуля ДО 1Г*2. Если при ЭТОМ ТОК /1
остается постоянным, то источник
второй ветви должен отдать маг-
нитному полю энергию
w2=Jz2£2^-^ = L2z|/2.
tl
Однако в первой ветви наводит-
ся э. д. с. 9i=M12di2[dt при нараста-
нии тока /2; для того чтобы ток в
первой ветви оставался постоянным
(ii = const), первый источник дол-
жен создавать напряжение
«i = iZi + zW12
уравновешивающее не только паде-
ние потенциала в сопротивлении
(6'Г1), но и наводимую в первой вет-
ви э. д. с. Поэтому энергия, отда-
ваемая первым источником магнит-
ному полю за время нарастания
второго тока, выражается равен-
ством
t3
wlt == J i^dt — f z, t\ dt —
i, f,
i, j MI2 ^dt = i1i2Mli. (6-16}
В итоге полная энергия магнит-
ного поля при токах и /2 в двух
индуктивно связанных ветвях
W = Y +4 +г'1ЦИ12’ (6-17}
Повторяя совершенно тот же
ход рассуждений, но сначала вклю-
чая источник питания во вторую
ветвь, а затем в первую, находим,
что
W = 2~ Л*1 + +Z1Z2^21- (6-18)
Разница >в формулах (6-17) и (6-18)
лишь в том, что одна содержит ко-
эффициент 7И1.2 (равный потокосцеп-
лению первого элемента при еди-
ничном токе во втором), а другая—
коэффициент М21 (равный потоке-
сцеплению второго элемента ппд
единичном токе в первом). Но кю-
нечное состояние цепи в обоих слу-
чаях одинаково: при «и и 12 в систе-
ме существует магнитное поле, од^
позначно определяемое для задан-
ной конфигурации проводов. Ска-
занное позволяет заключить о ра-
венстве взаимных индуктивностей
М12 = М21. (6-19)
Коэффициент магнитной связи.
Как было показано, энергия двух
индуктивно связанных ветвей (эле-
ментов)
w = Т (i* Ц + z22 L2 + 2^М). (6-20)
Очевидно, что это выражение
остается положительным при любом
соотношении между токами 12=хЦ.
В предельном случае энергия w мо-
жет обратиться в нуль.
174
Найдем значение х (оно может
быть как положительным, так и от-
рицательным), при котором энергия
системы минимальна. Подставляя
в (6-20) xii вместо z*2, находим, что
2w = F (х) = i j (Lj -|- x2L2'+ 2х7И).
Дифференцируя F(x) по х и при-
равнивая производную нулю, нахо-
дим, что
2х£>2 + 27И = О
или
х = — М/Ь2.
Соответствующее минимальное
значение энергии
1 .2 (т М2 \
—-уЧ 27J-
Очевидно, что при любых значе-
ниях Li, L2, М минимальная энер-
гия не может быть меньше нуля и,
следовательно, М2 «С т. е. вза-
имная индуктивность по модулю
всегда меньше или в пределе рав-
на корню квадратному из произве-
дения индуктивностей.
Отношение
й = (6-21)
называют коэффициентом
магнитной связи двух эле-
ментов, он всегда меньше едини-
цы, а в пределе равен единице.
В случае тороида с двумя рав-
номерно ‘распределенными обмотка-
ми, содержащими и N2 витков,
можно считать
Л =>оР^1 Ц = р.0Н^2 SH- (6-22)
При этом, как было найдено,
М = 1 = VLrL2 и k = 1.
(6-23)
Напротив, когда вторичная об-
мотка намотана лишь на части то-
роида (рис. 6-1,6), ее индуктив-
ность Ь2 больше, чем выражаемая
формулой (6-22), так как часть по-
тока второй обмотки проходит по
воздуху (в дополнение к потоку,
проходящему в сердечнике); эта
часть потока не полностью сцепле-
на с витками первой обмотки (&<1)..
Согласование положительных на-
правлений тока и разметка концов
индуктивных элементов. Как для
составления уравнений Кирхгофа
необходимо фиксировать направле-
ния токов и э. д. с., выбираемые в;
качестве положительных, так и не-
обходимо разметить концы ветвей:
или содержащихся индуктивных:
элементов Мкп для определения*
знака складываемых потокосцепле-
ний и наводимых э. д. с.
Обычно один из концов каждого*
индуктивного элемента принимают
за начало, ставя около соответству-
ющего полюса (зажима) тот или
иной знак, чаще всего звездочку-
или точку. При этом потокосцепле-
ние каждого из элементов выра-
жается равенствами:
(6-24>
если токи ii и i2 одинаково ориенти-
рованы относительно отмеченных
зажимов соответствующих индук-
тивных элементов (рис. 6-35а).
Если же токи в двух ветвях раз-
лично ориентированы относительна
отмеченных зажимов индуктивных
элементов (рис. 6-3,6), то потоко-
сцепление каждого из этих элемен-
тов выражается равенствами:
1 — *2^; j
T2 = z2L2 — i.M.I
т. е. в них слагаемые iM входят со-
знаком минус.
В выражениях (6-24) и (6-25) в.
качестве положительного потоко-
сцепления принимается потокосцеп-
ление, создаваемое положительным
током рассматриваемого элемента.
Сказанное очевидно из того, что<
inLn ^0 при /п>0, поскольку всег-
да 0.
Иначе обстоит дело со слагае-
мыми в которых величина М
должна рассматриваться в общем
случае как алгебраическая.
Если разметка зажимов выпол-
нена так, что потокосцепление пер-
175.
вого элемента Wi возрастает под
влиянием положительного тока f2,
то взаимная индуктивность 7И>0.
В противном случае Л4<0.
Если в одном из элементов из-
менить положения знака «начало»
(перенести звездочку на другой за-
жим), то величина М изменит знак.
Однако и в последнем случае все
пр авил а относительно согл асов а-
ния положительных направлений
токов в индуктивных элементах со-
храняют силу.
На .рис. 6-3 'показано несколько схем
индуктивно связанных элементов с различ-
но ориентированными токами; определите
самостоятельно, «в каких схемах положи-
тельные токи согласованы и в каких не со-
гласованы. Иначе 'говоря, в каких схемах
потокосцепление определяется по формулам
(6-24) и в каких по формулам (6-25).
Электродвижущая сила, наводи-
мая в каждом элементе, равна про-
изводной со знаком минус от соот-
ветствующего потокосцепления.
Так, при согласованности положи-
тельных направлений для токов Zi
и Z2 (рис. 6-3,а) в соответствии
с формулой (6-24)
' п ____А_________т dii । д л di2 I
Э1 dt L1 dt ‘ М dt I
__ d^2_г di2 । х/г dii
2~~ ~dr~"L'2~dr 1 m~dt-
(6-26)
Напротив, когда положительные
направления токов не согласованы
(рис. 6-3 Д), тогда в соответствии
с формулой (6-25)
__ т Idir
dt L1 dt ~~
di
~dt
_ d^2___j di2
~Э2 ~dT ~ ~di~ “
dt
(6-27)
Заметим еще, что во всех случа-
ях положительное направление
э. д. с. ориентировано по току, про-
ходящему в самом индуктивном
элементе. Поэтому, считая напря-
жение на индуктивности, обуслов-
ленное самоиндукцией, равным
г dix
UL\ — ~dF ’
находим, что напряжение на том же
элементе при согласованных направ-
лениях токов [см. также рис. 6-2
и формулы (6-13)]
= + (6-28)
а при несогласованных
= (6-29)
t CLL U/ Ъ
Все выведенные соотношения
для токов и напряжений справедли-
вы, разумеется, и для гармониче-
ских переменных; при этом все опе-
рации можно производить с ком-
плексами, заменяя операцию диф-
ференцирования множителем /со.
Так, вместо (6-28) и (6-29) для
гармонических токов .можно писать
О, = hLj, (6-30)
(знак « + » при согласованном и
«—» при несогласованном направ-
лении токов).
В выражениях (6-24) — (6-30)
знаки перед слагаемыми, пропорци-
ональными М9 выбираются в соот-
ветствии с ориентацией токов отно-
сительно фиксированной разметки
концов. Что же касается самой ве-
Рис. 6-3.
176
личины взаимной индуктивности
Л4, она в общем случае представля-
ет собой алгебраическую величину.
При разметке концов всегда стре-
мятся к тому, чтобы величина М
была положительна. Это, однако,
в некоторых случаях физически не-
возможно. Такие случаи разбира-
ются в конце этого параграфа.
Способы разметки концов. 1. Если про-
странственное расположение обмоток и на-
правление магнитных потоков, создаваемых
каждым из токов, известны, одинаковым
знаком «начало» должны быть отмечены за-
жимы (полюсы) обмоток, в которые долж-
ны -входить токи |с тем, чтобы каждый из
них увеличивал поток, сцепленный с другой
обмоткой; при этом Л4>0.
На рис. 6-4 схематически показаны две
обмотки, нанесенные на общий цилиндриче-
ский каркас, и направление потоков Ф1 и
Ф2, обусловленных токами ц и Z2.
Проиввольно поставив знак * у верх-
него зажима верхней обмотки, мы должны
такой же знак поставить и у верхнего зажи-
ма нижней обмотки.
Рис. 6-4.
2. Если картина поля и расположение
обмоток неизвестны, можно выбрать одно-
именные зажимы «начало» или «конец»
.двух элементов, пользуясь измерительными
приборами.
На рис. 6-5 показано включение гальва-
нометра в цепь катушки с зажимами а, Ь.
Направление тока через гальванометр, при
котором отклонение гальванометра положи-
тельно, известно; оно показано стрелкой на
рис. 6-5. К другой обмотке подключается
источник, как показано на этом же рис. 6-5.
Один из зажимов этой обмотки произволь-
но обозначается знаком «начало» .(звездоч-
ка на рис. 6-5).
Непосредственно вслед за включением
источника стрелка гальванометра кратко-
временно отклоняется либо в положитель-
ную, либо в отрицательную сторону. По на-
правлению этого отклонения можно опре-
Рис. 6-6.
делить, какой из зажимов а или Ъ следует
отметить знаком «начало»: при положитель-
ном отклонении гальванометра за начало
следует считать зажим а. При такой раз-
метке Л4>0.
3. На рис. 6-6 показано включение двух
вольтметров при питании первого индуктив-
ного элемента от источника переменного
тока. Один из его зажимов произвольно обо-
значен звездочкой [(начало).
Для того чтобы второй вольтметр пока-
зывал определенное напряжение, зажимы
индуктивных элементов (d и Ь) соединены
в общий узел. Из сравнения показаний двух
вольтметров можно определить, какой из
зажимов а или Ъ следует обозначить звез-
дочкой, полагая 2И>0.
Действительно,
йI — <рс — = A 4" Г1)
и
Uab = Ча -- ?Ъ = ± 1
« + », если начало — это зажим а\ и «—»,
если начало — это зажим Ь.
Сл едо в ательно,
£/2 = ?с - = Л [и + №. + Л4)],
где перед М стоит знак «—», когда нача-
ло— это зажим 'а, и «+», когда начало —
это зажим Ь.
Таким образом, если t/2<t/i, звездоч-
кой следует обозначить зажим а\ если же
^2>’^ь то зажим Ь.
4. На рис. 6-7 показаны два индуктив-
ных элемента, включенных последователь-
но. Однако в случае индуктивной связи
между элементами могут быть два разных
вида последовательных включений: со-
гласное |(в обоих элементах ток одинако-
во ориентирован относительно звездочек) и
встречное .(в одном элементе ток вхо-
дит через звездочку, в другом ток выходит
через звездочку).
Рис. 6-5.
12 К. М. Поливанов
177
При «соглаоном включении
U1 = Ц (Г1 + jcoL, + >А1) +
+ /1 (г2 + j^Lz + jaM) =
ментов можно представить равен-
ствами:
= г’1Мп + 4-^12 + ^И18 + • •.;
^2 = г’1^21 + + г2^2з + • • ’ >
= A [ri 4~ r2 + /<° (А4“ А 4“ (6-31)
^3 4-^31 Ч~ ^2^32 —Н ^33 "4“ • • • у
При 1Встреч1НО1М включении
(71 == A [ri + г2 4” J® (А4~А—27И)]. (6-32)
Полагая 7И>0 и сравнивая -отношение на-
пряжения к току .при одном и другом -вклю-
чениях, «можно юр азу определить, какое из
них согласное, а какое встречное:
После этого легко расставить звездочки
у зажимов .двух элементов.
Пример 6-1. В цепи рис. 6-8 в некото-
рый момент времени ток и=40 а, скорость
его возрастания diildt=\\ ООО а!сек. В ин-
дуктивно связанном элементе ток i2=50 а,
скорость его возрастания di2ldt=—800 а!сек.
Параметры цепи: и = 10 ом, jLi=40 мгн, М—
=50 мгн.
Требуется найти напряжение
^аЬ =
Решение. Искомое напряжение
. r dii ,. di2
Uab — llrl dt dt *
Последнее слагаемое взято co знаком ми-
нус, поскольку токи i\ и i2 ориентированы
различно относительно звездочек у элемен-
тов.
Подставляя числовые значения, нахо-
дим иаъ = 100+40+40=480 в. Напряжение,
обусловленное взаимной индукцией, положи-
тельно, так как производная di2ldt отрица-
тельна. ~
Цепь с несколькими индуктив-
ными элементами. Все сказанное об
индуктивной связи двух элементов
легко распространить на -случай
трех и более элементов. Так, пото-
косцепление каждого из этих эле-
если все токи z2, z3, ... одинаково
ориентированы относительно звез-
дочек соответствующих индуктив-
ных элементов.
В последних равенствах коэффи-
циенты -с одинаковыми индексами—
индуктивности соответствующих
элементов, т. е. Л1П = Л1, А122=£2
и т. д., а коэффициенты с двумя
разными индексами — взаимные ин-
дуктивности между соответствую-
щей парой элементов. При этом к
любому из них применимо ранее
найденное доказательство о равен-
стве Л112 и Л421, поэтому всегда
--^пт- (6-33)
Положительные и отрицатель-
ные взаимные индуктивности. Вза-
имные индуктивности ТИ12, 7И23,
и т. д. в общем случае могут быть
как положительными, так и отри-
цательными; в соответствии -с пра-
вилами алгебры это проявляется
только при подстановке соответст-
вующих числовых значений, напри-
мер ТИ12=—0,14 мгн.
В случае всего двух индуктив-
ных элементов Lx и L2, связь между
которыми/ выражается одной вза-
имной 'индуктивностью, р азметка
концов дзвездочки) всегда делает-
ся так, чтобы коэффициент М имел
положительное значение. Впрочем,
и в случае всего двух контуров, свя-
занных регулируемой взаимной ин-
дуктивностью, коэффициент М в ре-
зультате регулирования может при-
нимать как положительное, так и
отрицательное значение. Например,
в устройстве, называемом варио-
метром, две обмотки располагаются
на общей оси и одна из них может
поворачиваться относительно дру-
гой (вид сверху на такой вариометр
показан на рис. 6-9). Если при а=О
взаимная индуктивность равна 7И0„
то при повороте на 180° она стано-
вится равной —Мо. Заметим, что и
178
в этом случае разметка концов ос-
тается необходимой.
При нескольких индуктивных
связях, например при связи трех
элементов L2, характеризуе-
мых коэффициентами М2з, Л431,
целесообразно полагать, что при за-
данной разметке концов каждого
элемента значения коэффициентов
могут иметь как положитель-
ные, так и отрицательные значения.
Это диктуется прежде всего тем,
что в ряде случаев невозможно так
разметить концы всех элементов,
Рис. 6-9.
чтобы все значения Мы были поло-
жительны1.
На рис. 6-10 полусхематически
изображены три большие катушки,
расположенные одна рядом с дру-
гой; реакторы, применяемые в энер-
гетических системах, часто имеют
примерно такое же расположение.
На рисунке показаны направления
потоков -Ф1, Ф2, Фз, принимаемые
положительными для каждой из
катушек. Именно так направлен по-
ток в каждом из реакторов, когда
магнитное поле создается собствен-
ным положительным током реакто-
ра. На том же рисунке показан по-
ток, пронизывающий витки второго
и третьего реакторов; когда этот по-
ток создается положительным то-
ком первого реактора, потоки Ф21
и Ф2 направлены противоположно,
1 Это всегда (возможно для любой- пары
индуктивных элементов. Но при этом, обо-
значая, например, концы Ц и L2 звездочка-
ми так, чтобы Л112 было больше 0, прихо-
дится концы iLj и lL3 для М1з и концы L2 и
Аз для ТИ23 размечать иначе i(ставя, напри-
мер знаки А или 0 для одноименных кон-
цов второй и третьей пары). Это крайне
неудобно.
Рис. 6-10.
так же противоположно направлены
потоки Фз1 и Фз-
Считая за начало каждой обмот*
ки ее верхний конец (звездочки на
рис. 6-10), напишем выражения для
потокосцеплений всех трех реакто-
ров:
Ч?*1 = i1L1 -j- i2M12 4" 1з>
^*2 -- 4-^21 4“ ^2^2 4" ^3-^23»
3 == 4“ ^2^32 "Т" 4^3 > .
(6-34)
где 7И12 = Л421, 7И13 = /И31, ТИ23 =
^32*
В этом случае все взаимные ин-*
дуктивности отрицательны. Заме-
тим, что нет способа разметки кон-
цов этих трех катушек одним зна-
ком «начало» (звездочкой), при ко-
тором все три коэффициента Мм
были бы положительны.
Напряжение на первом реакторе
при коротком замыкании всех ниж-
них концов (рис. 6-11)
^ао = 117ю (Л — ^1з) +
+ /2>(7И12-Л413), (6-35)
что непосредственно следует из
(6-34); здесь в соответствии с пер-
вым законом Кирхгофа
4=-(А+4)-
В равенстве (6-35), однако, коэффи-
циенты Мтп отрицательны.
Рис. 6-11.
12*
179
Напряжение между узлами а, Ь
определяется как разность Ua0—0Ъй.
Поэтому для большей отчетливости
выпишем сначала выражение для
Ubo — (-^2 — ^2з)~Ь
+Л>(^12-ти23). (6-36)
Искомое напряжение найдем как
разность. (6-35) и (6-36)
иаЬ = / J® (Lx + М3 - Ж12 - 2И18) +
+ Л703 (^12 + ^23 — 7И13—Д*)-
Пример 6-2. Вычислить напряжение
Uao в схеме -на spine. 6-11 ;атр»и следующих
данных: Ai=4,0 мгн, М\г=—0,10 мгн., Mi2—
=—0,20 мгн, 71=1 000 a, I2— \ 000Z—120° а,
со=314 сек-1.
Решение. При этих данных
#ао=/314[4+О,1 +<(—0,2+0,1) Z—120°]=
=/ 314(4,1—0,1 (—0,5—/ 0,867)]=
=—27,2+/ 1 300 в.
6-2. ИНДУКТИВНО СВЯЗАННЫЕ
ЦЕПИ
Уравнения электрической цепи
с взаимной индуктивностью. Нали-
чие индуктивных связей в цепи пе-
ременного тока приводит к появле-
нию дополнительных э. д. с. взаим-
ной индукции, которые должны
быть учтены при составлении урав-
нений по второму закону Кирхгофа.
По существу единственная труд-
ность сводится к необходимости:
1) правильно выбрать знак перед
слагаемыми и 2) учесть все
э. д. с. от всех других индуктивно
связанных с контуром элементов.
Так, например, на рис. 6-12 пока-
заны в виде трех источников все
индуктированные э. д. с. в первой
ветви цепи на рис. 6-11.
Рис. 6-13.
«7
Число независимых Кирхгофовых урав-
нений. Представим себе две цепи, электри-
чески не связанные (между собой, т. е. две
цепи, между которыми отсутствуют связи
через проводимость и емкость :(рис. 6-13).
Составляя для каждой из них систему
уравнений по первому и второму законам
Кирхгофа, можно руководствоваться ранее
выведенными правилами о числе независи-
мых уравнений. Однако получившаяся си-
стема уравнений должна решаться совмест-
но, если между этими цепями существуют
индуктивные связи, поскольку в контурные
уравнения одной цепи входят (слагаемые
(7©ТИ7), содержащие токи другой цепи:
Для каждой из цепей ч!исло независи-
мых уравнений, составляемых по первому
закону Кирхгофа
д-1 = у, — 1, к.\ = У2 — 1, (6-37)
и по второму
д-i^Bx + l —Ух, К” = В2 + 1—У2.
(6-38)
В ©тих выражениях индексы I и II-обо-
значают первый и соответственно второй за-
коны, а индексы 1 и 2 цеп^, к которой от-
носится соответствующее число. Следова-
тельно, для обеих цепей
К1 = У—Н; К^^В+Н—У, (6-39)
где У — полное число узлов; В—полное
число ветвей; Н — число электрически не-
связанных контуров.
Выражения i(6-i39)’ применимы к любому
числу электрически "не связанных цепей.
В (случае одной цепи 77=1; в случае двух
цепей (рис. 6-13) 77=2. При этом следует
помнить, что мы - условились одноконтур-
ную цепь считать содержащей один узел.
Так, в случае двух одноконтурных це-
пей (рис. 6-13,6) К1=2—2=0 и К11 =2+2*—
—2=2, т. е. полная система уравнений со-
стоит из двух уравнений, составленных по
второму закону Кирхгофа.
В случае 77 электрически не связанных
цепей в каждой из них потенциал одного из
узлов может быть принят равным произ-
вольно выбранному значению.
Две параллельные индуктивно
связанные ветви. В этом простей-
шем случае (рис. 6-14) для опреде-
Рис. 6-12.
180
ления трех токов /, Д, 12 можно
составить три независимых уравнения
/=Л+4;
[7 = /jZn
U = / 1/со7И -1-12Z22,
(6-40)
где и Z22=Z2+/(dL2.
Последние два уравнения из си-
стемы (6-40) отличаются от урав-
нений для параллельных ветвей без
индуктивных связей тем, что в каж-
дое из них входят два тока.
Решая полученную систему, на-
ходим, что
Т __ fj (^22--faM) .
1 1 £2 ’
7 fj(Zn—> j&M) ~
2 2 £2 »
7 _ TJ (^11 ~Н^22 —2/соЛ4)
— £2
)
где
^z^-^му.
(6-41)
Входное сопротивление двух па-
раллельных ветвей
7 __ Z11Z22 + (<О/И)2 /£ JQ\
Zbx —Z11+Z22_2/^ • ^Z)
При отсутствии индуктивной
связи между ветвями эта формула
превращается в ранее известную.
На рис. 6-14 показано согласное
включение индуктивно связанных
ветвей, такому включению 'соответ-
ствуют и выведенные здесь форму-
лы. При встречном включении (если
одна из звездочек стоит у нижнего
зажима индуктивного элемента) во
всех формулах следует изменить
знак перед М (конечно, знак М2 не
меняется).
Рис. 6-15.
При встречном включении реак-
тивная составляющая входного со-*
противления уменьшается, вследст-
вие того что потоки, обусловленные
двумя токами, направлены встреч-
но. На рис. 6-15 схематически пока-»
заны витки двух индуктивно свя-
занных элементов при согласном
(а) и встречном (б) включениях.
Если обмотки этих элементов рав-
номерно намотаны на общий коль-
цевой сердечник, то магнитный по-
ток, общий для обеих обмоток, при
встречном включении
g,
где Ni, N2— числа витков этих эле-
ментов.
Встречно направленные токи
уменьшают магнитное поле.
Две последовательные индуктив-*
но связанные ветви. В этом случае
также следует различать согласное
и встречное включение [см. рис.
6-7 и формулы (6-31), (6-32)].
Топографическая потенциальная
диаграмма. После того как система
уравнений решена (или только
предполагается решенной), очень
полезно построение топовр афичес-
кой диаграммы, наглядно показы-
вающей распределение потенциалов
в электрической цепи и фазовые со-
отношения между ними.
На рис. 6-16,а показаны цепь,
содержащая С, г, L\, и участок вто-
рой цепи, имеющей с первой цепью
только индуктивную связь. На рищ
6-16,6 показана топографическая
диаграмма, .построенная по задан-
ным токам /1 и 12 при известных па-
раметрах цепи.
Рис. 6-14.
181
Разность потенциалов между точ-
ками а и О определяется суммой
э. д. с. самоиндукции 9L — — ijwL
и взаимной индукции Эм=—1г]'ч>М:
^ао = fa ?о — — — Эм =
(11 и /2 одинаково ориентированы от-
носительно своих звездочек).
Оба слагаемых показаны на век-
торной диаграмме (рис. 6-16,6); пер-
вое и второе слагаемые представля-
ются векторами, повернутыми на углы
it/2 соответственно, относительно век-
торов I, и 1Л.
Потенциал точки b выше потен-
циала точки а на величину Цгг.
Потенциал точки с еще выше на ве-
личину IJjwC. Разность потенциалов
точек с и О равна напряжению
источника
= — ?0 =
—Л Q®!,+п +
На том же рис. 6-16,6 справа по-
каз ана топографическая диаграмма
для -напряжения на участке второго
контура:
= fd — fe = — Л/®АГ —1^LZ.
Передача мощности и показания
ваттметров в цепи с взаимной ин-
дукцией. В пределах потенциального
поля, т. е. там, где напряжение
представляется разностью потенци-
алов, мощность, передаваемая
вдоль проводов, всегда .может быть
представлена как произведение на-
пряжения на ток. Поэтому мощ-
ность, поступающая в какой-либо
двухполюсник,
p = ui.
соответствующее комплексное вы-
ражение этой мощности
S=UI*
Однако эта мощность- может от-
личаться от мощности, потребляе-
мой внутри двухполюсника; послед-
няя может частично поступать че-
рез магнитную связь из другой
электрической цепи, не входящей
в двухполюсник. Этот поток мощ-
ности не может быть представлен
как произведение ui. так как он
связан с непотенциальным электри-
ческим полем, существующим в об-
ласти переменного магнитного по-
ля. В силу сказанного этот поток
мощности не может быть учтен
обычными ваттметрами, показание
которых пропорционально среднему
значению произведения ui.
Для иллюстрации рассмотрим конкрет-
ную цепь, содержащую две индуктивно свя-
занные ветви с включенными в нее ваттме-
трами, и сопоставим их показания с мощ-
ностью, потребляемой в ветвях.
Цепь с двумя параллельными индуктив-
но связанными ветвями питается от источ-
ника переменного напряжения .(рис. 6-17,а).
Параметры цепи: Z7i='l 50-Ь/150 в, п—5ож,
г2 = 10 ом, cobj = 15 ом, ыЬ2—^?==0,
сьМ = 10 ом.
При этих данных по формулам (6-41)
легко найти значения токов Ц = 10 — /10 а,
/2 = 5 + /5 а, 1 = 15 — /5 л. Соответ-
ствующие векторы токов показаны на
рис. 6 -17, б.
182
Вся мощность, поступающая в цепь от
источника питания, учитывается ваттметром
W, она равна:
Р — Re (UI) = 1 500 вт.
По закону Джоуля—Ленца легко най-
ти мощность, рассеиваемую ib первой и вто-
рой ветвях:
Pi = /fn = 1 000 вт, Р2 = 1^г2 = 500 вт.
Как и должно быть, P=Pi+P2.
Вычислив показания -ваттметров, най-
дем, что показание ваттметра первой ветви
равно нулю:
PWi = Re (W*) = 0,
поскольку вектор напряжения и вектор пер-
вого тока ортогональны; показание ваттме-
тра второй ветви
= Re (^2) = 1 500 вт.
Если бы между ветвями не было индук-
тивной связи, показания ваттметров равня-
лись бы мощностям, потребляемым <в каж-
дой из ветвей.
В рассматриваемом случае -можно счи-
тать, что мощность Pw2, поступающая от
источника питания во вторую ветвь, частич-
но потребляется в ней (Р2=500 вт), а ча-
стично передается через .мапйитную связь
в первую ветвь (Pwz—P2—Pi).
Заключительные замечания. На
основании изложенного в этом па-
раграфе можно рассчитать любую
электрическую цепь с взаимной ин-
дукцией, построить ее топографиче-
скую диаграмму и произвести не-
обходимый анализ. Заметим, что
при составлении уравнений рассма-
триваемых цепей наиболее удобно
пользоваться методом контурных
токов; при этом в любое взаимное
сопротивление Zmn естественно вхо-
дит не только сопротивление ветви,
общей для контуров т и п, но и
комплексное сопротивление взаим-
ной индукции ]®Мтп. Таким обра-
зом, не изменяется даже внешний
вид уравнений. Наличие взаимных
индуктивностей не нарушает и
принцип взаимности, поскольку,
как было доказано, всегда Мтп =
~ Мпт'
Обратим внимание на то обстоя-
тельство, что, составив систему
уравнений цепи, можно всегда со-
ставить n-контурную цепь без ин-
дуктивных связей, подобрав ее па-
раметры так, чтобы все Zmn такой
цепи соответствовали коэффициен-
там Zmn заданной системы уравне-
ний. Замена цепи с индуктивными
связями цепью, не содержащей ин-
дуктивных связей, будет подробнее
рассмотрена в следующем парагра-
фе в 'применении к цепи с двумя
контурами.
Частотные характеристики в слу-
чае индуктивно связанных цепей и
наблюдаемые в них резонансные
эффекты отличаются главным обра-
зом тем, что индуктивная связь
приводит к лишним реактивным
слагаемым (]ыМтп). Во многих
случаях это равносильно лишним
реактивным элементам в цепи без
индуктивных связей.
Все сказанное в предыдущей
главе о частотных характеристи-
ках L можно отнести к частотной
зависимости параметра М: частот-
ная зависимость магнитной прони-
цаемости ферромагнитного сердеч-
ника приводит к комплексному зна-
чению если в индуктив-
ной связи между контурами уча-
ствуют ферромагнитные тела; при
высоких частотах становятся замет-
183
ними емкостные связи между кон-
турами, не обнаруживаемые при
низкой частоте и т. п.
Индуктивные связи часто созда-
ются умышленно для получения
нужных свойств цепи. Например,
очень удобно регулировать собст-
венную индуктивность контура,
плавно изменяя (хотя бы посредст-
вом (вариометра рис. 6-9) взаим-
ную индуктивность между его дву-
мя элементами; пользуясь взаим-
ной индуктивностью, легко осуще-
ствить (и регулировать) любой
фазовый сдвиг между одним из
напряжений и одним из токов
(например, угол л/2 между U и /1
в цепи на рис. 6-17,а)« Наиболее
важные свойства индуктивно свя-
занных цепей проявляются в устрой-
стве и применении трансформато-
ров, которым посвящен следующий
параграф.
Нельзя не отметить и нежела-
тельные эффекты, обусловленные
индуктивными связями. Например,
некоторая хотя бы и слабая индук-
тивная связь существует и между
контурами, отстоящими друг от
друга на довольно большие рас-
стояния; при этом влияние цепей
сильного тока, например энергети-
ческих систем, мощных высокоча-
стотных контуров и т. п., на цепи
слабого тока, например на теле-
фонные линии, на линии сигнализа-
ции, на цепи тонких измерительных
устройств и т. п., может быть край-
не нежелательным; -оно может при-
вести к серьезным помехам,
6-3. ТРАНСФОРМАТОР
В ЛИНЕЙНОМ РЕЖИМЕ
Трансформатор в простейшем
случае представляет собой два ин-
дуктивно связанных контура при
сильной связи между ними. Для
усиления связи контуры выполня-
ются обычно в виде обмоток, наде-
тых на общий ферромагнитный сер-
дечник (рис. 6-18,а). Впрочем, при
высоких частотах применяют и воз-
душные трансформаторы, т. е. не
содержащие ферромагнитных сер-
дечников. Электротехнический
смысл такого устройства заклю-
чается, во-первых', в возможности
трансформации напряжения: при
сильной связи между обмотками
почти одинаковый поток Ф прони-
зывает каждый из витков, поэтому
э. д. с., индуктируемые в обмотках,
пропорциональны числам витков;
во-вторых, в возможности изолиро-
вать в электрическом отношении
одну цепь от другой, сохраняя воз-
можность передачи энергии и сиг-
нала.
Ферромагнитный сердечник мо-
жет привести к нелинейной зависи-
мости между величиной потока
в сердечнике и полным намагничи-
вающим током всех обмоток, наде-
тых на сердечник. Вытекающие из
этого нелинейные эффекты рассма-
триваются во второй части книги.
Здесь мы ограничимся лишь анали-
зом трансформатора в линейном ре-
184
жиме, когда все потокосцепления
прямо пропорциональны токам и
могут быть выражены через собст-
венные и взаимные индуктивности,
величины которых не зависят от
тока.
Заметим, что в системах сигна-
лизации и связи, а также в изме-
рительных устройствах сердечники
трансформаторов по большей части
действительно находятся в линей-
ном режиме. Основные черты рабо-
чего режима энергетических транс-
форматоров также достаточно от-
четливо выявляются при расчетах,
предполагающих линейность.
Основные уравнения, их анализ.
Как в случае сильной, так и в слу-
чае слабой связи полная система
уравнений трансформатора в линей-
ном режиме представляется двумя
уравнениями для токов первого
(первичного) и второго (вторично-
го) контуров:
1 — IД212, ] (6-43)
й — i z —i z (
V/ 2 - 1^21 1 2^22* J
В уравнениях (6-43)
2ц --1 ‘ | 222--2 Н” /^^2>
^12 = ,
где л, г2 — активные сопротивле-
ния первой и второй
обмоток;
Li, L2—их индуктивности;
М — взаимная индуктив-
ность.
При записи этих уравнений по-
ложительные направления выбра-
ны так, как показано на рис. 6-18,а
и б. Именно так принято выбирать
положительные направления токов
в четырехполюснике. Заметим, что
такой несимметричный выбор поло-
жительных направлений можно
считать естественным в том случае,
когда рассматриваемая система
(четырехполюсник и, в частности,
трансформатор) служит звеном,
через которое энергия передается
из первичной цепи во вторичную.
При этом мощность, поступающая
на вход из первичной цепи,
St = р. +JQi = U1I1, (6-44)
а мощность, отдаваемая с выхода
во вторичную цепь,
S2 = P2-{-jQ2 = U2I2. (6-45)
На рис. 6-18,в показана вектор-
ная диаграмма трансформатора при
активной нагрузке U2 — I2rs. Сначала
построена диаграмма для вторичного
контура по второму уравнению (6-43),
которое можно переписать так:
Дг2 Ч~ =о
(все слагаемые перенесены в левую
часть, конечно, с изменением знака,
а О2 представлено как /2гн).
Направление тока /2 выбрано
произвольно, ток Л отстает на угол
л/2 от напряжения Л/со7И. Сама
величина /ЛсоТИ определяется как
сумма остальных известных слагае-
мых в соответствии с последним
уравнением. Векторная диаграмма
для первичного контура построена
по первому уравнению (6-43):
+AHi—i а/«>м
Обращаясь к системе уравнений
(6-43), легко найти выражение
внешней характеристики трансфор-
матора:
fj __fr j Z11Z22 — (/<оЛ4)2
2 -<-> 1 7 12 7 .
£ц £ц
(6-46)
В этом выражении первое слагаемое—
э. д. с. эквивалентного генератора,
а множитель при 12—эквивалентное
внутреннее сопротивление:
q _ jj ]<&М % rZnZ22 — (/с£>Л4)2
1 Z11 ’ 1 Zu
(6-47)
Соответствующая эквивалентная
цепь изображена на рис. 6-19.
Эквивалентная э. д. с. равна
вторичному напряжению трансфор-
матора в режиме холостого хода,
следовательно, по (6-43) она равна
первичному напряжению, умножен-
ному на отношение
JaM
Zu Г1 + jc&Li
185
Рис. 6-19.
Как правило, в трансформаторах
гг < соЛь Так, например, в боль-
шом трансформаторе энергетиче-
ской цепи п^0,02 ом и =
= 173 ом. Поэтому с большой сте-
пенью приближения можно счи-
тать, что
М
Zu Li
В трансформаторах с сильной маг-
нитной связью магнитный поток
в любом поперечном сечении ферро-
магнитного сердечника почти оди-
наков, и с каждым из витков как
первичной, так и вторичной обмо-
ток сцеплен почти одинаковый по-
ток Ф. В этих условиях можно
считать, что коэффициенты само-
индукции пропорциональны квадра-
там своих витков:
L2 = N22L0, (6-48)
а коэффициент взаимной индукции
пропорционален произведению чи-
сел витков NiN2 почти с тем же
самым коэффициентом пропорцио-
нальности
M^N^L^VL^. (6-49)
JB общем случае
М = к\ГЦГ2,
(6-50)
где /гкоэффициент связи.
В трансформаторах с тщатель-
но собранным сердечником из хоро-
вшего ферромагнитного материала
^коэффициент связи близок к еди-
нице (£ — 0,99). В этих условиях
М
N2
Ni
(6-51)
:и э. д. с. эквивалентного генерато-
ра, равная напряжению холостого
-хода (/2=0) вторичной обмотки, во
столько же раз больше первичного
напряжения, во сколько число вит-
ков вторичной обмотки больше, чем
первичной:
Э=,и2Х = й^. (6-52)
Перейдем к оценке внутреннего
сопротивления эквивалентного гене-
ратора. Полагая в выражении
(6-47) для Zi активные сопротивле-
ния очень малыми по сравнению
с реактивными и представляя М по
формуле (6-50), после самых про-
стых преобразований приходим
к следующему равенству:
Z, = = (1 - f).
(6-53)
В трансформаторах высокого
напряжения реактивное сопротив-
ление 0^2 очень велико; например,
в большом энергетическом транс-
форматоре с вторичным напряже-
нием 242 кв это сопротивление
порядка 40 ком, что совершенно
естественно: при малом сопротивле-
нии со<£2 как можно было бы под-
ключить обмотку трансформатора
под напряжение 242 кв? В ней про-
текал бы огромный ток.
Однако эквивалентное внутрен-
нее сопротивление сравнительно
невелико в силу того, что 1 — k2
очень малая величина \ для транс-
форматора, параметры которого
сейчас приводились, 1 —k20,0032
Следовательно 2*= 128 ом при
со£2=40 кам.
Входное сопротивление транс-
форматора. Входным сопротивле-
нием трансформатора называют от-
ношение напряжения Ui к току Л:
Оно зависит от сопротивления ZH,
на которое замкнута вторичная об-
мотка.
1 Разность 1—№ называют коэффи- .
циентом рассеяния
1186
Обращаясь к основным уравне-
ниям (6-43) и добавляя к ним равен-
ство U2 = jzZu, легко найти, что
Z j 1Z22 — Zj2 + ZhZj 1
=--------z.-lTZ------- <6’54)
Zh -р Z22
При обоснованных ранее допуще-
ниях
Z1X jwN2 Lo, Z22 ~ j<»N22 Lo,
^12 1N2-£'0^
И При условии, ЧТО -I ZH I < I Z221, при-
ходим к следующему приближенному
выражению входного сопротивле-
ния:
Zh (6‘55)
Таким образом, включение транс-
форматора преобразовывает сопротив-
ление нагрузки ZH.
Из формулы (6-54) можно опре-
делить входное сопротивление и в
режиме холостого хода (ZH -> сю),
и в режиме короткого замыкания
(ZH-^0).
Магнитное состояние сердечника;
связь потока с токами и напряже-
ниями обмоток. Резкое уменьшение
эквивалентного внутреннего сопро-
тивления по сравнению с индуктив-
ным сопротивлением обмотки легко
объяснить, рассматривая магнитные
процессы в сердечнике. Обращаясь
к рис. 6-18, мы видим, что токи /1
и /2 ориентированы различно отно-
сительно потока в сердечнике. По-
этому если первый ток (когда
Zi >0) стремится создать магнитный
поток в положительном направле-
нии (Ф>0), второй ток (когда
*2>0) стремится уменьшить этот по-
ток.
Сказанное, конечно, не зависит
от произвольного выбора положи-
тельных направлений токов и непо-
средственно следует из закона Лен-
ца.
Магнитное состояние заданного
сердечника определяется полным
током, сцепленным с замкнутым
контуром, проведенным внутри сер-
дечника (закон полного тока), т. е.
величиной, которую можно предста-
вить в комплексной форме равен-
ством
/^7^-7^. (6-56)
Полный ток называют намагничи-
вающей или магнитодвижу-
щей силой (н. с. или м. д. с.).
С другой стороны, магнитное со-
стояние сердечника определяется
его потоком Ф, который в линейном
режиме прямо пропорционален
полному току:
Ф = ZF = 2 (I1N1 — 72N2),
где — коэффициент пропорцио-
нальности.
Существование определенной за-
висимости между потоком и полным
током позволяет говорить, что за-
данному значению полного тока со-
ответствует определенный поток;
это приводит к обиходному выра-
жению «магнитный поток создается
током». Однако к таким словам
нельзя применять буквальное тол-
кование и всегда следует помнить,
что ток и магнитный поток (или
магнитное поле) —две стороны од-
ного явления, две взаимно связан-
ные интегральные характеристики
одного процесса.
Вспомним электрическую цепь.
В простейшем случае ветви г мож-
но сказать, что напряжение и — 1г
создается током; но можно сказать
иначе: ток i — ulr создается прило-
женным напряжением и. Выбор то-
го или иного выражения зависит
от того, что задано — ток или на-
пряжение.
Так же точно обстоит дело и
с магнитным сердечником трансфор-
матора. Если задан полный ток,
можно говорить, что он создает (им
обусловлен) магнитный поток; если
же задан магнитный поток, следует
говорить, что заданный поток обус-
ловливает протекание определенно-
го полного тока.
187
В трансформаторах очень часто
условиями работы задается именно
магнитный поток. Действительно,
пусть обмотка с числом витков
присоединяется к сети с напряже-
нием U\ при частоте со; вторичная
обмотка разомкнута. В таком слу-
чае, пренебрегая потерей напряже-
ния в активном сопротивлении пер-
вичной обмотки, находим, что
в каждом витке должна наводиться
э. д. с.
Эо = — /а)Фх = —
Все напряжение иг уравновеши-
вается э.'д. с., которая равна числу
битков Nj, помноженному на э. д. с.,
индуктируемую потоком в одном
витке. Таким образом, заданное на-
пряжение О19 число витков N1 и ча-
стота со однозначно определяют
именно магнитный поток
<6-57)
Ток, который при этом идет по
обмотке, находится из уравнения
связи между потоком и полным то-
ком. Этот ток можно назвать то-
ком холостого хода или на-
магничивающим током
(6-58)
Замкнем теперь вторичную об-
мотку на какое-либо сопротивление
нагрузки ZH. В ней пойдет ток
(рис. 6-19)
4=^ =-z^z ’ (6’59)
разность ампер-витков двух обмо-
ток. Поэтому из (6-58) и (6-56) сле-
дует, что
p^Njix = liNi — i2N2
или
л1лх+4^. (6-60)
Возникновение тока /2 во вторич-
ной обмотке увеличивает первичный
ток по сравнению с током холостого
хода на величину, пропорциональ-
ною вторичному току I2N2/Ni. Вто-
ричный ток как бы проходит через
первичную цепь, причем с соответ-
ствующим пересчетным множителем
N2/Ni-
В большинстве случаев особенно
для приближенных расчетов первым
слагаемым в правой части равенст-
ва (6-60) можно пренебречь 1 и счи-
тать, что
(6-61)
Таким образом, из анализа про-
цессов в трансформаторе мы нашли,
ЧТО [формула (6-52)],
При этом вся мощность,
поступающая на вход, равна мощ-
ности, отдаваемой нагрузке:
IN 1 /V 2
(6-62)
Коэффициент трансформации.
Во многих рассмотренных выше
уравнениях появляется отношение
где О2Х — напряжение холостого хода
на зажимах вторичной обмотки.
• В первом приближении можно
п о - nip еж н ему пренебречь п а дени ем
напряжения в сопротивлениях обмо-
ток и считать, что индуктируемая
э. д. с. практически не изменилась.
В таком случае не должен изменить-
ся и магнитный поток Ф = ФХ, а это
значит, что прежнее значение долж-
но сохраниться и у полного тока,
который теперь выражается как
1 Ток холостого хода в трансформато- t
pax с ферромагнитным сердечником не пре-
восходит 5—10% от тока 1г при нормаль-
ной нагрузке; в измерительных трансфор-
маторах он составляет еще меньшую долю.
К тому же, если вторичная цепь замкнута
на активное сопротивление, ток /2 практи-
чески совпадает по фазе с напряжением
U2*> а следовательно, и с напряжением
вместе с тем ток холостого хода /1х от-
стает от напряжения почти на л/2 как ток 3
в индуктивности (мы уже отмечали, что
Zn^/coLi). Поэтому с еще большим пра-
вом можно пользоваться приближенным
равенством (6-61).
188
чисел витков /V2/^=^2i. Это -отно-
шение очень близко к коэффициен-
ту трансформации
k^U^/U^k^N./N,,
Идеальный трансформатор. Со-
отношения
(6-63)
где вместе с вытекающи-
ми из них равенствами (6-62) спра-
ведливы для идеального тран-
сформатора; в схемах электри-
ческих цепей его изображают как
на рис. 6-20.
К. соотношениям идеального
трансформатора приводят предпо-
ложения:
^11-- /й)/^ —> СХ’, ^22---
И
vuu
т. е. что сопротивления обмоток
чисто реактивные и очень большие
(стремящиеся к оо), а коэффициент
связи стремится к 1.
Эквивалентная цепь с устранен-
ными индуктивными связями. Вернемся
к анализу L системы уравнений (6-43). Эти
уравнения "можно рассматривать какзурав-
нения цепи с двумя контурными токами Д
и /2; такая цепь 1 должна содержать по
крайней мере три независимых параметра
Za, Zb, Zc, чтобы контурные сопротивле-
ния (Zn, Z22) и взаимное сопротивление
(Z12) этой цепи совпадали с одноименными
величинами в системе (6-43).
Система уравнений для цепи рис. 6-21
имеет вид, тождественный с системой
(6-43) при
Zn = Za ~l~[Zc, Z22 = Zb + Zc,
Z12 = Z21 — Zc.
Рис. 6-20.
Рис. 6-21.
Полагая Zn, Zi2, Z22 заданными, из
последней системы легко найти требуемые
значения Za, Zb, Zc-
Za~ Zn — Z12 = ri + /со (Li — Л4);
Zb=Z22 — Z12 = ^2 4-/co (Lg—Al); (6-64)
Zc = Z12 = /coAf.
В -том случае, когда цепь ;рис. 6-21 /при-
нимается в качестве схемы замещения по-
высительного трансформатора (U2x/Ui —
==-£т>1) и Ц<М, первое продольное со-
противление Za содержит отрицательное
реактивное сопротивление co(Li—Al); иначе
говоря, в ©той ветви в .схеме замещения со-
держится конденсатор (рис. 6-22).
Аналогичным путем можно прийти
к эквивалентным цепям без индуктивных
связей и при других включениях индуктив-
но связанных ветвей йли контуров.
Наиболее важные схемы замеще-
ния трансформаторов. Наибольшее
практическое значение имеют схемы
замещения трансформаторов (экви-
валентные цепи), составленные для
приведенных значений токов
и напряжений
— UT2 — U2lm. (6-65)
В этих формулах т — коэффи-
циент приведения, выбирае-
мый так, чтобы приведенное вторич-
ное напряжение было близко к пер-
вичному; при этом сближаются и
значения первичного и вторичного
токов.
Заметим, что, не приводя вторич-
ные токи и напряжения, практиче-
ски невозможно построить общую
векторную диаграмму цепи при
больших отношениях чисел витков
вторичной и первичной обмоток.
Рис. 6-22.
189
Выбрав коэффициент приведения
для вторичных тока и напряжения,
мы с необходимостью приходим и
к определенному коэффициенту при-
ведения для сопротивлений. Если
для действительных токов и напря-
жений ВТОрИЧНОЙ ЦеПИ t?2 = ^H^2, то
для приведенных
U'2 = ZrJ'2, (6-66)
откуда
Z'H = ZH/m2. (6-67)
Для приведенных значений
(6-65), (6-67) мощность остается ин-
вариантной:
= U*/2, I2 Za = (I'tf Z’B. (6-68)
Т-образная симметричная схема
замещения. Запишем основные урав-
нения для действительной цепи
U — т 7 ____i 7 •
1-- 7 1^11 7 2^12>
и —17 17
2-- 7 1^12 7 2^22
и для цепи с приведенными значе-
ниями
^I1Zll — j\Z' 12;
й'2=1^12—i'2zr22. (6-69)
Подставив в последнюю систему
истинные значения токов и напря-
жений, умноженные на коэффициен-
ты приведения, и умножив второе
уравнение на т, получим следую-
щую систему:
--/ 1Z11 I ^YlZ 12,
и2 = — l2n?Zr22. (6-70)
Сопоставляя первую систему
с последней, находим, что они тож-
дественны при условии
mZr12 = Z12, m2Z'22 = Z22. (6-71)
Система (6-69) становится симмет-
ричной, если в ней принять
Z22 = ZX1. (6-72)
Это условие вместе с (6-71) одно-
значно определяет выбор коэффи-
циента приведения
(6-73)
Т Z11
Поскольку в трансформаторах
с сильной связью
/а>ЛГ| L„ и Z„ ж Lo,
то коэффициент приведения оказы-
вается близким к отношению чисел
витков вторичной и первичной обмо-
ток:
“ = / Й- = Е-=4- <W4>
Определив значение коэффици-
ента приведения, находим из (6-71), .
что
Z'12 = Z^2[m = Z12 У g-. (6-75)
Для выражения всех параметров
цепи удобно воспользоваться обоб-
щенным коэффициентом
связи двух контуров
7< = Z12//Z^. ' (6-76)
В том случае, когда все сопро-
тивления обмоток чисто реактивные,
обобщенный коэффициент связи сов-
падает с коэффициентом связи, ра-
нее введенным для двух индуктивно
связанных контуров.
Выражая в (6-75) Zi2 по форму-
ле (6-76), найдем, что
Z\2=Z^K.
Обратимся теперь к Т-образной
схеме (рис. 6-23) и найдем значение
ее сопротивлений Zra, Z'b, Z'c, при
которых она эквивалентна транс-
форматору с приведенными током и
н ап р яжен и ем. С истем а ура внений
для контурных токов цепи рис. 6-23:.
Рис. 6-23.
190
Сопоставляя эти уравнения с (6-69),
находим, что
-f-Z'c — Z1X, Z'C = Z'12,
Z'fc -j- Z'c = Zz22
или
Z^^c Z 12, Z'a = ZM — Z'12,
Z = Z 22 Z 12.
Принимая во внимание (6-77)
и (6-72), находим, что
Z7a = Z'b = Z11(l — Д'),
Z'c = Zn^ (6-78)
При этом эквивалентная цепь
представляется очень простой сим-
метричной схемой, показанной на
рис. 6-24; справа показана нагрузка
Z'H, присоединяемая ко вторичным
зажимам. В приведенной схеме дей-
ствительное значение сопротивления
нагрузки должно быть заменено
приведенным:
Z'H = ZH>2.
Расчет цепи по такой схеме замеще-
ния очень прост.
Входное сопротивление цепи
рис. 6-24 при коротком замыкании
на выходных зажимах
Z1K=Z11(l-№). (6-79)
Упрощенная эквивалентная схе-
ма легко может быть получена из
схемы рис. 6-24, если |,1—К\ < 1-
В этом случае можно просто пре-
небречь суйхествованием поперечной
ветви, т. е. пренебречь током холо-
стого хода, который замыкается че-
рез эту ветвь.
Такая схема показана на
рис. 6-25; интересно обратить вни-
мание, что в последней схеме при
коротком замыкании
Z1K = 2Z11(1 — К).
Этот результат может сначала
показаться противоречащим (6-79).
Но когда |Д| мало отличается от
единицы, выполняется приближен-
нее .равенство 1 — К2~2(1— К).
Г-образная схема замещения.
Аналогично предыдущим выводам
можно найти параметры эквива-
лентной Г-образной схемы (рис.
6-26). Сопоставляя уравнения (6-69)
с контурными уравнениями для це-
пи рис. 6-26 и принимая во внима-
ние уравнения (6-71), находим, что
цепь эквивалентна приведенному
трансформатору при условиях
ZM = Z'c, Z'12 = Z'c = Z12M
Zr
22
Но первые из этих равенств одно-
временно определяют и единствен-
но возможный в этом случае коэф-
фициент приведения
m^ZJZ^. (6-80)
Практически он мало отличается
от '.ранее принятого (6-73) для сим-
метричной Т-образной схемы, а по
Рис. 6-24.
Рис. 6-26.
191
модулю точно равен коэффициенту
трансформации Ч
Определение параметров схемы заме-
щения по данным опыта. Найденные выше
схемы замещения на рис. 6-24 «и рис. 6-26
замечательны тем, что их параметры легко
находятся по данным опыта.
Обычно известны следующие данные
опыта, характеризующие трансформатор.
1) Напряжение короткого за-
м-ык ап и я т]к <в процентах от номинально-
го. Пр.и таком напряжении проходит номи-
нальный ток 1во вторичной обмотке в усло-
виях короткого замыкания выходных зажи-
мов.
Следовательно, входное сопротивление
при коротком замыкании
6^1 но М • 1 00т)к
-------.
2) Потери при коротком з а-
м ы к а н и и. Они позволяют определить ак-
тивную составляющую сопротивления Z1K.
3) Ток холостого хода Чх в про-
центах от номинального.
Следовательно, входное сопротивление
при холостом ходе
ЕЛном
1Х / 1Н0М ’ 100^
4) Потери холостого хода. Они
позволяют определить активную составляю-
щую сопротивления Zix.
Пользуясь этими даины-ми, можно опре-
делить параметры эквивалентных схем
рис. 6-24 и 6-26, если, конечно, даны номи-
нальные напряжения на входе и выходе
Um ом, U2Hom и номинальная передаваемая
мощность
<S — UIHOM^ 1НОМ U2НО 2НО М •
В соответствии с ранее изложенным
в § 5-6 о характеристиках реальных индук-
тивностей сопротивление в схемах замеще-
ния трансформатора может представляться
двумя параллельно включенными ветвями—
чисто активной и чисто реактивной. При
этом сохраняются в силе все выведенные
формулы, однако в них коэффициенты М и
L следует считать комплексными.
Заметим, что при комплексных М и L
в схеме замещения для неприведенных зна-
1 Может показаться непонятным тот
факт, что исходной цепи с тремя независи-
мыми параметрами 2ц, Zi2, Z22 соответст-
вует эквивалентная цепь всего с двумя па-
раметрами Z'b, Z'c. в том, что исход-
ные данные определяют и третий параметр
эквивалентной цепи — коэффициент приве-
дения т.
Заметим, что и в случае эквивалентной
цепи рис. 6-24 мы отказались от возможно-
сти независимого определения всех трех Z
эт©й цепи, наложив требование симметрии.
Тем самым определился выбор коэффици-
ента приведения.
192 •
чений появляются не только отрицательные
реактивные, но и отрицательные активные
сопротивления.
Трансформатор как согласующий
элемент. Кроме электрического от-
деления одной части цепи от другой
и преобразования напряжений и то-
ков, при которых происходит пере-
дача энергии, трансформаторы име-
ют большое значение как согласую-
щие элементы.
При подключении приемника
с сопротивлением irH к источнику пи-
тания с заданной э. д. с. и заданным
внутренним сопротивлением Vi мак-
симальная передаваемая мощность
СООТВеТСТВуеТ УСЛОВИЮ Гг=1Гн.
Включение трансформатора меж-
ду источником и приемником пре-
образует сопротивление приемника
в эквивалентное приведенное г'н=-
= rH/;m2.
, Соответствующим подбором 4 от-
ношения Z11/Z22 можно получить ра-
венство = при котором ИСТОЧ-
НИК питания и приемник оказывают-
ся согласованными.
Пример 6-3. Построить векторную диа-
грамму трансформатора для «приведенных
значений вторичных тока и (напряжения
(рис. 6-24).
Параметры трансформатора Zu = Z'22=
= Г1/coLi, Zi2 = /coAl, 6^2ном/6^1но м
&2i известны.
Построение провести в общем виде,
полагая заданными вторичное напряжение
и потребляемую мощность U2=U2hom и
S2 ?= Р2 + jQ2 Для случаев: a) Q2 > 0;
б) Q2<0.
Решение. Произвольно выбирая на-
чало отсчета фаз, полагаем U2 = jU2, при
этом приведенное значение тока
* *
/'2 = I2m = mS2/U2 = wS2/(—/U2).
Построение диаграммы выполнено на
рис. 6-27, для случая а, где /1Х—ток
в сопротивлении KZu.
Пример 6-4. Определить параметры
симметричной Т-образной схемы замеще-
ния трансформатора (рис. 6-24), характери-
зуемого следующими данными:
Номинальные мощность и напряжения
«Shq м === 10 tCBCLy U 1но м ==: 6,3 Кв,
U2hom == 400 в\
напряжение и потери короткого замы-
кания (при Zi=Zihom)
U 1к ==:= 5,C>yoU1но м, Рк ;— 335 вТ71)
ток и потери холостого хода (при
= U 1ном)
/lx == 10% 11ном» Ps == 105 вт.
I
Рис. 6-27.
Решение. Полагая
Z1K~2Zn(il-A),
т. е. пренебрегая попереч1ной ветвью
(рис. 6-25) при расчете входного Сопротив-
ления при коротком замыкании, находим
его модуль по данному напряжению корот-
кого замыкания UiK:
^1к === 0»055(/1НОМ//1НОМ •= 218 ом,
ГДе 11ном == *$1но м/6^ 1ном = 1,58 CL.
Активную составляющую этого сопро-
тивления находим по даннььм потерям при
короткОхМ замыкании
Г1к = 7-)к//^ном= 133 ом.
Реактивная составляющая определяется
по формуле
х 1к ==: j/" 2iK — Г1К = 173 ом.
Следовательно,
’ Zii(l—2O = 66,5+ /86,5 ом.
По данному току холостого хода на-
ходим:
21Х = t7iHOM/(0,1/1ном) === 39,7 ком.
Зная потери холостого хода, находим, что
Пх = ^/(ОДЛном)2 = 4,18 ком.
По этим результатам вычисляем
xlx = |Л zfx—rfx = 39,5 ком.
Следовательно,
Zu = Zx = Гх + jxn = 4,18 + /39,5 ком.
Теперь легко найти К и. составить Т-образ-
ную схему по рис. 6-24.
Пример 6-5. Источник сигнала
э=Эт cos со/ имеет внутреннее сопротивле-
ние Zi=75+/100 ом. Приемник имеет ак-
тивное сопротивление гн=5 ом.
Для (увеличения мощности, передавае-
мой приемнику, последний подключается
к источнику через согласующий трансфор-
матор. Однако в нем при передаче мощно-
сти нужно ожидать рассеяния мощности по-
рядка 10% от передаваемой. Током холо-
стого хода, т. е. проводимостью поперечной
ветви в схеме замещения (рис. 6-23 и 6-24),
можно пренебречь. Реактивные слагающие
всех последовательно соединенных элемен-
тов компенсируются последовательно вклю-
ченным конденсатором.
Требуется определить коэффициент
трансформации согласующего трансформа-
тора.
Решение. В соответствии с условия-
ми расчету подлежит цепь, представленная
на рис. 6-25 и питаемая от источника с
э. д. с. э и внутренним сопротивлением Z*.
По условию активное сопротивление
.трансформатора г'а=г'ъ = 0,05 г'н, так как
в нем рассеивается 10% мощности, получае-
мой приемником.
Максимальная мощность, передаваемая
приемнику, соответствует условию:
1,1г'н = Г г
или
г'н = g/1,1 = 68 ом.
При этом коэффициент трансформации
=/и2 =гн/г'н, откуда 1/£2i—3,68.
Это понижающий трансформатор.
ГЛАВА СЕДЬМАЯ
ЦЕПЬ ПЕРЕМЕННОГО ТОКА
С ТРИОДАМИ В ЛИНЕЙНОМ РЕЖИМЕ
7-1. НЕКОТОРЫЕ ОБОБЩАЮЩИЕ
ЗАМЕЧАНИЯ О МНОГОПОЛЮСНЫХ
ЭЛЕМЕНТАХ
Элемент электрической цепи на-
зывают двухполюсником (диодом),
трехполюсником • (триодом), четы-
рехполюсником (тетродом), пятипо-
люсником (пентодом) и т. д. в за-
висимости от числа электродов, т. е.
полюсов или зажимов, через кото-
рые он может быть связан с осталь-
ной частью электрической цепи. По
сложившейся традиции названия,
поставленные в скобках, применя-
ют, как правило, только к элемен-
там с нелинейными характеристика-
13 К. М. Поливанов
193
ми (электронные лампы, транзисто-
ры и т. д.).
Распределение потенциалов
в триоде (рис. 7-1) полностью
определяется двумя напряжениями,
например,
«РЗ И = — (М)
В силу первого закона Кирхгофа
ток третьего электрода всегда равен
разности тока Zi, входящего в пер-
вый электрод, и тока /2, ’выходяще-
го из второго электрода. Поэтому
всегда достаточно знать токи двух
электродов, например Ц и /2. Все
четыре величины 7Л, t/2, Л, h и при-
нятые для них положительные на-
правления показаны на рис. 7-1.
Каждый из токов триода одно-
значно определяется двумя задан-
ными напряжениями:
Л = Л(£Л, f/2), /2 = Wn tu
(7-2)
Точно так же каждое из напря-
жений однозначно определяется
двумя заданными токами:
(Л, /2), С72 = С72(Д, /2).
(7-3)
Уравнения (7-2), (7-3) позволя-
ют утверждать, что существуют так-
же следующие функциональные за-
висимости:
и>-или„ /2), К=1Ли» Л)-
(7-4)
Можно напомнить, что формулы
(7-2) соответствуют задаче опреде-
ления токов, притекающих к узлам,
при заданном распределении потен-
циалов, тогда как выражения (7-3)
соответствуют задаче определения
потенциалов при заданных токах,
входящих в узлы; формулы (7-4)
соответствуют уравнениям линейно-
го четырехполюсника
иг = A U2 + В/2, Д = CU2 + РД.
Во всех приведенных формулах
большими буквами Д, Ui обознача-
ются токи и напряжения любого за-
данного режима. Обозначим теми
же буквами с индексом 0 значения
соответствующих величин при неко-
тором исходном режиме, например,.
7го— 72 (С710, t/20); ^720 = С72(/10, До..
и т. д.,
а малыми буквами — приращения
этих величин при отступлении от
исходного режима, так для ра-
венств (7-2) и (7-3) '
72 720 | z2 I2 (£710 { и1, U2j-\-u2}
JJ2 — t/20-|-w2 — U2 (/10 -j-До-|-Д)
(7-5}
Применяя к функциям от двух
переменных, например /2(t/b t/2)y
разложение в ряд Тейлора, получим
при введённых обозначениях, что
72 — 720 -{-z2 — Д(Р10, U2q)~}-
df2
dU~2
^2Ч~
I 1 p2Z2 -2 i o d2I2 j
2 j du2 wi + 2 dU^dW2 «1^2+
I
'du'i
2
(7-6)
В линейных системах все выс-
шие производные равны нулю — это
и есть определение линейности, по-
этому
2 /^7
г2 —~ «г ~г (7-7)
I /'-7 Q\
11 — U1 + dUT Ы2'
Условия квазилинейности. В слу-
чае нелинейных систем уравнения
(7-7) и (7-8) можно считать спра-
ведливыми только при малых зна-
чениях переменных составляющих
щ, и2 и т. д., когда в разложении
(7-6) можно пренебречь слагаемы-
ми в фигурных скобках, содержа-
щими вторые степени малых вели-
чин и\ и и2. Тем более можно пре-
небречь следующими членами ряда
194
Тейлора, не выписанными в форму-
ле 1 (7-6).
Системы, которые можно считать
линейными лишь при определенных
условиях, назьъвают «квазилинейны-
ми. При только что оговоренных ус-
ловиях малости щ и и2 триоды ква-
зилинейны.
Применяя равенства (7-7) и
(7-8) к нелинейным системам, необ-
ходимо иметь в виду, что .производ-
ные, оставаясь постоянными в пре-
делах малых изменений щ и и2. су-
щественно зависят от значения не-
зависимых переменных в исходном
режиме, т. е. от значений (7ю, U^.
Напомним, что с квазилинейны-
ми элементами цепи мы уже встре-
чались в § 2-2; там же было пока-
зано, что эквивалентная схема не-
линейного двухполюсника может
содержать источник питания и на
разных рабочих участках эквива-
лентные параметры различны.
Равенства, аналогичные (7-7),
можно написать и для уравнений
с другими величинами, принятыми
за независимые переменные. Так,
из уравнений (7-3) следует, что
Так, производные в равенствах
(7-9) 1
д1Л I
д1' к
дЦг
д12
dU2
д[2
I - Z?22 (7-11)
1л
могут быть названы входными и пе-
редаточными сопротивлениями
Нарушение принципа взаимно-
сти. В линейных цепях R2i = Ri2,
поэтому передаточные сопротивле-
ния в теории линейных цепей часто
называют взаимными. В нелиней-
ных цепях, хотя бы при очень ма-
лых изменениях тока, возможно на-
рушение этого равенства, т. е.
R2i=^=Ri2. Это значит, что в таких
цепях нарушается принцип взаим-
ности.
Триоды при гармонических на-
пряжениях. В тех случаях, когда
малые изменения носят характер
гармонических переменных, напри-
мер
u1 = Uim sinw^,
диг
д!г
диг
д12
_<Я/2 ;
~ дЦ 11
dU2
д12 129
(7-9)
они вызывают, конечно, и гармони-
ческие изменения тока или других
связанных с напряжением щ вели-
чин.
Так из уравнения (7-7) при
[72 = const, т. е. при и2=0, находим,
что
z*2 = ^7tL 'U1' (7-!2)
дУ2 | „
^2»
а из уравнений (7-4) следует, что
_ дЩ । dU•
“ ди2 "Т- дЦ
. __д!г । дЦ .
11 ~dU7U2'~df7lz'
(7-Ю)
Все изложенное соответствует
строго формальному применению
дифференциального исчисления к
уравнениям / электрической цепи.
В большинстве случаев каждой из
производных можно дать отчетли-
вое электротехническое толкование.
1 Предполагается, что дифференцируе-
мые функции «в .пределах рассматриваемых
изменений достаточно плавны, поэтому не
возникает редкого увеличения вторых про-
изводных.
При этом в некоторых случаях
ток i2, изменяясь по гармоническому
закону с той же частотой, что и
напряжение щ, может отличаться
от напряжения и\ по фазе. Это
обусловлено различным значением
dl2ldU\ в статическом и динамиче-
ском режимах.
Переходя к комплексам, равен-
ство (7-Г2) представим в таком ви-
де:
где обычно Yi2=‘g\2 заменяет произ-
водную, взятую на статической
1 Около производных в (7-11) внизу
прямой черты поставлено обозначение той
величины, которая остается постоянной при
дифференцировании — это вторая независи-
мая переменная в дифференцируемой функ-
ции.
13*
195
характеристике. Большей
частью можно «принимать значения
производных во *всех рассмотренных
уравнениях как производные от
статических характеристик, т. е. от
функций Zi (t7i, -С/а)» 72(£Л, ^2), спра-
ведливых для медленно изменяю-
щихся независимых переменных или
снятых при постоянных напряжени-
ях и токах. Фазовую поправку, если
она необходима, вводят, добавляя
к триоду реактивные и активные
связи.
7-2. ЭЛЕКТРОННО-ВАКУУМНЫЙ
ТРИОД КАК ЛИНЕЙНЫЙ ЭЛЕМЕНТ
ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
В электронно-вакуумном триоде
все три Электрода: накаленный ка-
тод (к), анод (а) и разделяющая
их сетка (с) расположены в колбе,
внутри которой создан высокий ва-
куум (рис. 7-2). Цепь электрическо-
го тока, служащая для разогрева
катода, на рис. 7-2 не показана. На-
гретый катод легко испускает элек-
троны (электронная эмиссия), кото-
рые устремляются кулоновскими си-
лами к положительному аноду. По-
ле, создаваемое сеткой, управляет
потоком электронов.
• Если потенциал сетки много ни-
же, чем потенциал катода, электро-
ны отталкиваются отрицательным
зарядом сетки и не могут попасть
на анод. Ток в анодной цепи отсут-
ствует. При повышении потенциала
сетки электроны получают возмож-
ность протекать сквозь отверстия
сетки и попасть нй анод. Для того
чтобы электроны не попадали на
сетку, ей сообщается постоянный
отрицательный потенциал (£7i<0),
при этом /1=0.
В соответствии с тем, что ток
в анодной цепи может проходить
внутри триода только от анода к ка-
тоду (навстречу потоку электро-
нов), общепринято рассматривать
не ток выходящий ив триода во
внешнюю цепь, а ток 7а =—/2
(рис. 7-2).
Ток в анодной цепи /а— функция
двух переменных UA и U2:
U2): (7-13)
Поэтому при малых изменениях
напряжения t7i=(t7iO+^i и U2=
= U2o + u2 можно считать, что
7а = Ao + z’a — 7ао -j- U± 4“
1 dU2
или
Z*a ~ дй\ U1 + OUT (7-14)
где /а, ^1, и2 — малые переменные
составляющие.
Выражение (7-44) и есть урав-
нение электронно-вакуумного трио-
да в квазилинейном режиме. Мы
ограничимся рассмотрением режи-
мов триода, при которых Л=0 и
уравнение (7-14) полностью описы-
вает работу триода. Входящие в не-
го частные производные имеют оп-
ределенные наименования:
называют крутизной анодного
тока; S — крутизна характеристики
7а(£Л) при U2 = const;
называют внутренним сопро-
тивлением триода.
Поскольку в электронном триоде
функция /а(<71, U2) нелинейная, зна-
чения рассматриваемых производ-
ных, т. е. крутизны и внутреннего
сопротивления, зависят от 'постоян-
ных составляющих анодного напря-
жения >и2о и сеточного напряжения
Uiq (сеточное смещение), которые
обеспечиваются специальными ис-
точниками в анодной и сеточной це-
пях (рис.-7-2).
Когда для того или иного триода
даются значения S и п, всегда ука-
зывается, какими должны быть при
ЭТОМ U20 и U10.
Обратимся к анализу уравнения
(7-14). Введя в него обозначения
(7-15) и (7-16)
ja==SWj +АИг> (7-17)
легко перейти к внешней характе-
ристике триода
й2 = — + zVb (7-18)
где
P = Sr< (7-19)
называют коэффициентом
усиления.
Схемы замещения триода.
Уравнение (7-18) замечательно и
своей простотой и тем, что ему со-
ответствует столь же простая схема
замещения, показанная на рис. 7-3,а,
где триод заменяется источником
эквивалентной э. д. с.
(7-20)
с последовательно включенным со-
противлением Ti, при этом положи-
тельное направление э. д. с. э сов-
падает с положительным направле-
нием тока za.
На рис. 7-3,6 показана эквива-
лентная цепь с источником тока
/=5^, (7-21)
параллельно которому включена
ветвь с сопротивлением
Основное значение рассматри-
ваемых триодов заключается в том,
что коэффициент ц может быть
больше и даже во много раз боль-
ше единицы, благодаря чему вход-
ное напряжение усиливается. После
того как найдено уравнение триода
в линейном режиме и выведено
правило его замены эквивалентной
цепью, легко рассчитать любую
цепь, содержащую триод.
7-3. ПОЛУПРОВОДНИКОВЫЙ ТРИОД
КАК ЛИНЕЙНЫЙ ЭЛЕМЕНТ
ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Процессы в полупроводниковых
триодах — транзисторах лишены та-
кой наглядности, как процессы
в электронной лампе.
Сущность работы полупро-
водникового триода — тран-
зистора (рис. 7-4) состоит в том,
что электрическая проводимость
между первым и вторым электрода-
ми, отделенными друг от друга по-
лупроводником, зависит от тока,
Рис. 7-4.
входящего в полупроводник через
третий электрод. Первый электрод
называют базой или основанием
(о), второй — коллектором (к),
а третий — эмиттером (э). Слова
эмиттер и коллектор соответствуют
следующему представлению о про-
цессе в полупроводнике. Большое
сопротивление между коллектором
и базой объясняется малым количе-
ством свободных зарядов в полу-
проводниковом переходе между эти-
ми электродами, т. е. зарядов, спо-
собных перемещаться под действи-
ем электрического поля между кол-
лектором и базой; появлению сво-
бодных зарядов в переходной обла-
сти коллектор — база способствует
ток, идущий между третьим элек-
тродом и базой и вызывающий
эмиссию (испускание) свободных
зарядов. Появляющиеся * свободные
заряды движутся под действием бо-
лее сильного поля между коллекто-
ром и базой, при этом, если коллек-
тор имеет отрицательный потенциал
относительно базы, к нему движут-
ся свободные положительные заря-
ды, а к базе — отрицательные; та-
Рис. 7-3.
197
ким образом, появившиеся под дей-
ствием эмиттера свободные заряды
собираются током, идущим между
коллектором и основанием.
Полупроводником <в транзисто-
рах служит обычно кристаллический
германий или кремний; природа пе-
реходов между полупроводником и
различными металлическими элек-
тродами (эмиттером, коллектором и
основанием) различна.
Для иллюстрации на рис. 7-5,6/
представлена зависимость /2( U2)
при нескольких значениях /i=const.
Поскольку ток 12 создается ис-
точником питания U2, естественно,
что ток 12 .положителен при (72<0.
Схема питания триода.для получе-
ния пр е дстав л ен н ых характер и-сти к
изображена на рис. 7-5,6; слева по-
казан источник тока, соответствую-
щий постоянному Ц при изменении
U2; при отрицательном U2 потен-
циал коллектора ниже потенциала
основания.
Не останавливаясь дальше на
рассмотрении физики процессов,
перейдем к характеристике полу-
проводникового триода как элемен-
та электрической цепи, в котором
напряжения U\ и U2 суть функции
двух токов Л и /2, т. е. /71 = (7b /2)
и t/2=i[72(/b /2).
При малых изменениях токов
можно считать, что
е)
Рис. 7-5.
где в соответствии с принятым
Л = Ло'+й> Л = Ло + г’2- &ля част-
ных производных в (7-22) приняты
следующие обозначения:
dUi | р dUi_\ _
d/1 |/2 dl2 |Zi -
dUz I _____р 6U2 ___Г) /у С)О\
dh |/2 — ^21’ д12 Л —
Конечно, все указанные величины
должны вычисляться для одного
и того же исходного режима, опре-
деляемого токами /10 и /20.
Так, из графиков рис. 7-5 легко найти,
что при /ю=0,5 ма и /2э=2,0 ма сопротив-
ление /?22=—30 000 ом.
Из характеристик, приведенных на
рис. 7-6, (можно определить псе остальные
значения 7?™™ :/?ц=770 ом (график а),
Т?12=—275 ом (график б), /?21=60 000 ом
(график в).
Области, соответствующие режиму 7.ю=
=0,5 ма и /2о=2,О ма, внутри которых опре-
деляются производные, на всех графиках
обведены кружками.
Существенно обратить внимание, что
в нарушение принципа взаимности -в таком
триоде Rw -#^2ь
198
Рис. 7-7.
Уравнения транзистора и его схе-
1иы замещения. Подставляя в (7-22 )
обозначения (7-23), приходим к си-
стеме линейных уравнений:
«1 — Rtlia + Я12гк; |
W2 ~ ^21ZS ^22ZK, 1
где /э — ij, iк — z2*
Этой системе уравнений соответ-
ствует эквивалентная электрическая
цепь (рис. 7-7) с параметрами
Лц ~R129 ^12> j
--Ri2 ^22> J
(7-25)
в чем легко убедиться, составляя
уравнение Кирхгофа для цепи
рис. 7-7.
Эта цепь содержит источник, эк-
вивалентная э. д. с. которого про-
порциональна току эмиттера:
э = гт1ь, (7-26)
ГГ =^?12 ~Ь ^2Г
На рис. 7-8 представлена цепь,
также эквивалентная триоду, по-
лучающаяся после замены источни-
ка э. д. с. i^pnc. 7-7) источником то-
ка
• . гг .
/ — /г
' к
(7-27)
После того как составлены урав-
нения (7-24) и соответствующие схе-
мы замещения рис. 7-7 и 7-8 с пара-
метрами,- определяемыми по форму-
лам (7-25) — (7-27), можно рассчи-
тать любую цепь, содержащую по-
лупроводниковые триоды (транзи-
сторы) . Само собой разумеется, что
все параметры транзистора R тп, т. е.
Rn, Rl2, ..или гт, т. е. гэ, гк, ..
должны быть известны и в цепь
должны быть включены постоянные
источники питания, обеспечивающие
требуемый режим (т. е. Ло, /20), для
которого заданы параметры триода.
Транзисторы могут быть по-раз-
ному включены в электрическую
цепь, для которой входные ток и на-
пряжение необязательно совпадают
с током эмиттера и с напряжением
эмиттер —база. Для любого спосо-
ба включения остаются применимы-
ми выведенные уравнения и найден-
ные эквивалентные цепи.
Пример 7-1. Транзистор включен в цепь
по схеме рис. 7-9,а (источники питания на
схеме не показаны).
Требуется найти напряжение на выхо-
де и2 при заданном напряжении на вхо-
де Ui, сопротивления Г\ — 100 ом, г2=Ю ком.
Напряжения имеют '.малые амплитуды,
так что триод находится -в линейном ре-
жиме.
В качестве параметров транзисторов
принять значения Rn, /?12, • •вычисленные
по графикам рис. 7-5 и 7-6.
Решен де. Пользуясь схемой заме-
щения рис. 7-7, приходим к цепи рис. 7-9,6
в которой гэ= 0,495 ком, г0 = 0,275 ком, гк =
= 29,7' ком, гг=59,7 ком.
Рис. 7-9.
199
Эти значения находятся по фор-мулам
(7-25) и (7-26).
Составим уравнения для двух конту-
ров эквивалентной цепи
*1Г 11 ~Ь *2** 12 == Ml* *1 (**21 - Гг) + *2 *22 = 0«
В (последнем равенстве э. д. ю. контура
должна стоять в правой части, но так как
значение э. д. с. равно йгг, естественно пере-
нести этот член в левую часть. В получен-
ной системе {уравнений
Гц == **1 + **э + **о = 0,870 ком]
г22 === **0 + гк + **2 = 40,0 ком]
г\2~г2\=—го ——0,275ком] г21—гг=—60ком.
Решая систему уравнений, находим, что
«2 = *2*2=32,8 Щ.
Здесь коэффициент 32,8 можно назвать
к о э ф ф и ц и е н т о м усиления по на-
пряжен и ю.
Пример 7-2. В отличие от предыдущего
примера рассмотрим цепь, в которой источ-
ник обладает большим внутренним сопро-
тивлением Г1 = 1,0 ком, а нагрузка имеет не-
большое сопротивление г2=0,1 ком.
Транзистор с параметрами из предыду-
щего примера включен по схеме рис. 7-10,а.
При таком включении общим для двух
контуров 'оказывается коллектор, а не осно-
вание (база).
Требуется найти напряжение на выходе
**2 = *2*2*
Решение. Можно воспользоваться
эквивалентной схемой замещения триода
(рис. 7-7). Однако теперь ток эмиттера
*э=—12, тогда как в предыдущем примере
/э=*ь Отличными будут теперь и контурные
сопр отив ления.
Уравнения для двух контуров цепи
рис. 7-10,6:
*1** 11 + *2 (**12 + *г) = >
*1**21 + *2 (**22 - **г) = 0,
где
Гц = Г1 Г о —}— Гк == 31 ком,
r12 = г21 = — гк = — 29,7 ком,
г22 = *"к -р гэ г2 = 30,3 ком,
г 12 —|— Гг = 30,0 ком,
г22 — *т — — 29,4 ком.
Из уравнений находим:
u2=i2r2= 1,145 иь
Интересно обратить внимание на то, что
при подключении нагрузки г2=0,1 ком
к источнику напряжения щ с внутренним
сопротивлением Г1=1,0 ком .(без транзисто-
ра) имели бы ц2=0,10 К тому же при
включении по схеме рис. 7-10 значительно
уменьшается внутреннее сопротивление экви-
валентного генератора.
7-4, ПРОСТЕЙШИЕ ЦЕПИ
С ТРИОДАМИ
Расчет любой цепи с триодами в .квази-
линейном режиме осуществляется обычны-
ми методами теории линейных цепей после
того, как найдены эквивалентные схемы за-
мещения триодов или уравнения эквива-
лентного линейного трехполюсника.
Схемы включения лриодов (а также
тетродов и пентодов) чрезвычайно разно-
образны и дают возможность получить
связь между сигналами на входе и выходе
цепи, соответствующую различным техниче-
ским требованиям.
•Самое важное свойство рассматривае-
мых триодов заключается в возможности
усиливать входной сигнал не только по на-
пряжению или току, но и по мощности,
которая на выходе триода может быть во
много раз больше, чем мощность на входе.
Мощность на входе в ряде случаев может
практически оставаться равной нулю при
конечной мощности на выходе. Это объяс-
няется тем, что источником отдаваемой
мощности служат постоянные источники пи-
тания триода (((источник анодного напряже-
ния в электронной лампе, источники по-
стоянных составляющих /э0 и /ко в транзи-
сторах); роль входного напряжения или
тока сводится к управлению этой мощ-
ностью и к ее преобразованию.
Мощность источника постоянного на-
пряжения при этом может преобразовы-
ваться в мощность, отдаваемую на перемен-
ном токе.
•В триоде с переменным напряжением
на входе и источниками питания постоянно-
го напряжения переменный ток возникает
вследствие изменения сопротивления цепи
подобно тому, как это происходит в микро--
фонной цепи. На рис. 7-11 изображены про-
стейшие четырехполюсники с постоянным
напряжением Z7=const или током /==const
на входе и переменными током и напряз^е-
. 200
Рис. 7-11.
нием на выходе. Переменный .ток возникает
вследствие изменений одного из сопротив-
лений i(r=var); если это сопротивление ме-
няется периодически, то и во вторичной
цепи проходит периодический ток не
содержащий постоянной составляющей.
Усилительный каскад. Допустим, что
усиливаемый сигнал представляется гармо-
ническим напряжением (7ВХ. Подавая сиг-
нал непосредственно на сетку лампы £7ВХ==
= Ui (рис. 742,а), .можно снимать усилен-
ное гармоническое напряжение Яых=^2
между анодом и' катодом лампы (точки 2
и 3 на рис. 7-12,а)\
Рис. 7-12.
На рис. 7-.12,<7 показано соответствую-
щее включение триода. Питание триода осу-
ществляется источником постоянного напря-
жения £/а, включенным между заземленным
катод ом и верхней точкой схемы. В цепи
источника последовательно с триодом
включено сопротивление Za. В цепи сетки
показан источник постоянного напряжения,
обеспечивающий отрицательное смещение
.сетки. Эквивалентная цепь показана на
рис. 7-12,6.
Потенциал точки 2 имеет не только
интересующую нас переменную составляю-
щую '(-(/г), ио также и значительную по-
стоянную составляющую. Поэтому при уси-
лении гармонического сигнала достаточно
высокой частоты между точкой 2 и прием-
ником '(сопротивление R) ставят или транс-
форматор или конденсатор, как это показа-
но на рис. 7-13,а и 6; при таком соедине-
нии в приемник не попадает постоянная
составляющая потенциала. На том же ри-
сунке показаны эквивалентные схемы. Со-
противление Za может быть выполнено в ви-
де большой индуктивности, юно может быть
и непосредственно первичной обмоткой
Рис. 7-13.
201
трансформатора. Трансформатор обычно мо-
жет быть заменен упрощенной эквивалент-
ной схемой, св которой нагрузка представ-
ляется приведенным сопротивлением.
На практике часто применяют несколь-
ко каскадов усиления, подавая выходное
напряжение первого каскада на вход вто-
рого. При этом можно получить систему
с очень большим усилением.
Трудно переоценить значение электрон-
ных усилителей в развитии всей современ-
ной техники. Без них не были бы.возмож-
ны ни радиотехника, ни космические полеты,
ни врачебная диагностика i(электрокардио-
граммы).
Ограничения, которые Bice же суще-
ствуют для восприятия очень слабых сигна-
лов, состоят не в трудности получить боль-
шой коэффициент усиления, а в том, что
очень слабые сигналы (порядка 0,1 мкв)
оказываются не отличимыми от неизбеж-
ных случайных колебаний напряжения, вы-
званных как внешними помехами, так и
собственным «шумом» триодов (тепловые
флуктуации). Собственный шум электронно-
вакуумных триодов меньше собственного
шума транзисторов.
Внутреннее сопротивление эквивалент-
ного генератора. До тех пор, пока триод
работает в линейном режиме, уравнение, вы-
ражающее его внешнюю характеристику,
всегда может быть приведено к виду•
[/выХ = (7-28)
которому соответствует простая схема
эквивалентного генератора, имеющего
э. д. с. Э = Л0[7вх и внутреннее или вы-
ходное сопротивление Zi (рис. 7-14).
Комплексный <(в общем случае) коэф-
фициент До называют коэффициентом уси-
ления по напряжению в режиме холостого
хода.
В триодах, включенных по схемам
рис. 7-13, обычно выходное сопротивление
очень велико.
Пример 7-3. Триод включен по схеме
рис. 7-13,6. Параметры триода: р=100, п =
= 66 ком. Параметры цепи У? —100 ком, С=
= 0,01 мкф, Za=7?a=100 ком.
Найти коэффициент усиления Ло при
холостом ходе и выходное сопротивле-
ние Zi для круговой частоты со = 5 000,
50 000 и 314 сект1.
Найти напряжение [/ВЫх при низшей и
высшей из указанных частот.
Решение. Обращаясь к эквивалент-
ной схеме рис. 7-13,6 и основываясь на
уравнении
Uв Ы X = AqU 1 / В ы "S.Z i ,
легко найти Ао, полагая /Вых = 0 (т. е.
R = оо); Zi можно найти как входное со-
противление цепи относительно точек при-
соединения сопротивления R при £71=0.
В нашем случае
р7?а _ 10 000
А° = ri +7?а 166
60,2
и не зависит от частоты.
Внутреннее сопротивление
Zj==/_+.j7< .7
j<&C Ra -|- Гi
104
= — j---+ 39,7 ком.
Реактивное -сопротивление при частоте
5 000 сект1 составляет всего -2 ком, а при
частоте 50 000 сект1 всего 0,2 ком, т. е. оно
мало по сравнению с активной составляю-
щей. ‘Однако для сигнала с частотой f=
=50 гц реактивное сопротивление возра-
стает до 31,8 ком.
Напряжение на приемнике (рис. 7-14)
найдем по формуле %
fr AqCi .
Uвых — | R — AU 1 •
Здесь коэффициент А указывает действи-
тельное усиление сигнала. Для частоты со =
= 50 000 сек-1 имеем 4/Вых = 43[71, для
промышленной частоты’ со = 314 сек-1 по-
лучим [7Вых — Стг 42 / 12°50'.
Катодный повторитель. Получая замет-
ное усиление напряжения даже в одном
каскаде, мы обычно подучаем столь боль-
шое выходное сопротивление, что практиче-
ски трудно воспользоваться достигнутым
усилением, если приемник .имеет значитель-
но меньшее входное сопротивление.
Так, в примере 7-3 мы получили замет-
ный коэффициент усиления при внутреннем
сопротивлении эквивалентного генератора
порядка 40 ком. Если потребитель имеет
в 100 раз меньшее сопротивление (400 ом),
напряжение на нем будет очень мало из-за
большого внутреннего падения напряжения.
Конечно, мы внаем ряд способов согла-
сования сопротивлений. Однако в большин-
стве случаев параметры согласующей цепи
должны изменяться с частотой, кроме того,
они всегда усложняют схему. Поэтому
очень большое значение имеет схема вклю-
чения триода, при которой хотя и не про-
исходит усиления по напряжению (выход-
ное напряжение только повторяет напряже-
ние, поданное на сетку), однако выходное
сопротивление может быть уменьшено на
несколько порядков.
Такая схема включения триода, называе-
мая катодным повторителем, показана на
рис. 7-15. В ней нагрузка присоединена па-
Рис. 7-14.
202
раллельно сопротивлению г между катодом
и землей-. Поэтому достоянная юсчставляю-
щая потенциала .на катоде невелика.
Уравнение, выражающее внешнюю ха-
рактеристику катодного повторителя, легко
получить из схемы замещения, изображен-
ной на рис. 7-15 внизу. Составляя такую
схему, необходимо особенно тщательно сле-
дить за знаками или положительными на-
правлениями: э. д. с. эквивалентного гене-
ратора = —t/вых) направлена от
анода к катоду, а положительным полюсом
для выходного напряжения считается катод,
поэтому на эквивалентной схеме замещения
э. д. с. направлена к положительному полю-
су выхода.
Вместо обращения к эквивалентной схе-
ме всегда можно непосредственно исходить
из уравнения триода, выражая входящие
в него токи и напряжения через токи и на-
пряжения других (ветвей электрической
цепи.
Так, в случае катодного повторителя
(рис. 7-15) можно исходить из уравнения
триода
is, = SU1 (7-29)
написанчэгэ для гармонических перемен
ных. При этом, как следует из схемы
включения,
1 - U в X - U ВЫХ,
, 1 ,
• г t/вых; Ч~ с вых = 0. (7-30)
Следует обратить особое внимание на по-
следнее равенство. Оно вытекает из того,
что источник анодного питания U& не со-
держит переменной составляющей.
OU-
Подставляя /а, Z/j и U2 из (7-30)
в (7-29), находим после решения относи-
тельно [7вых, что
t/ вых — вх Zi 1 вых j
ri ’ ri
1х И- 1 ~7 Iх -г 1
где
р, = Sri.
К тому же выражению приводит и рас-
чет по эквивалентной схеме.
Для данных примера 7-3 при г=4,5 ком
имеем Л0=О,‘87 -и Zi=690 ом.
Катодный повторитель часто ставится
как последнее звено усилителя, содержаще-
го один или несколько каскадов с анодным
выходом. При этом получается и большой
коэффициент усиления и возможность .при-
соединять к усилителю нагрузку с неболь-
шим сопротивлением.
Все показанные здесь методы расчета
применимы, конечно, и к цепям с полупро-
водниковыми триодами.
Триодные генераторы гармонических
колебаний. Как уже говорилось, триоды
способны преобразовывать энергию, посту-
пающую от источников постоянного напря-
жения ’.(или тока), в энергию, передаваемую
в цепь переменного тока. Следовательно,
они могут служить генераторами .перемен-
ного напряжения. При этом можно пере-
менное напряжение, поступающее на сетку,
получать как часть переменного напряже-
ния, возникающего на выходе, т. е. триод
может работать как генератор с самовоз-
буждением.
Частота генерируемого напряжения мо-
жет быть очень высокой. Полупроводнико-
вые триоды служат генераторами до частот
порядка 100 Мгц, электронно-вакуумные
триоды—до сверхвысоких частот 4 300 Мгц
(длина волны 7 см). Для генерирования бо-
лее высоких частот применяют электронио-
вакуумные устройства, уже отличающиеся
от простого .триода. Мощность больших
электронно-вакуумных триодов серийного
выпуска при частоте в несколько десятков
мегагерц -(генерируемая одним триодом) до-
стигает сотен киловатт. Мощные генератор-
ные триоды совсем не похожи на знакомые
всем электронные лампы радиоприемников.
Их размеры достигают по высоте 1,5 м.
Вследствие большой «мощности, рассеивае-
мой на аноде при падении на него потока
электронов, они имеют специальную систе-
му охлаждения. Анодное напряжение боль-
ших генераторных триодов достигает 10 кв,
ток накала — 300 а.
Рассмотрим простейший генератор с ко-
лебательным контуром в анодной цепи при
индуктивной связи с сеткой (рис. 7-16, на
котором источники питания не ‘показаны).
При -выбранной разметке зажимов (звез-
дочки на рис. 7-16) и выбранном направ-
лении тока I напряжение на сетке U\ =
= —Ij(£)M.
Рис. 7-15.
203
Рис. 7-16.
Составляя уравнения для контурных то-
ков I и /а, находим, что
/ ('+>£ +/У
+ 7а ;«С = 0:
1 (/<оС+;’“Л4(А) + 1а (/<оС
Система этих однородных уравнений
имеет решение, отличное от нулевого толь-
ко в том случае, когда определитель равен
нулю. Последнее условие приводит к двум
уравнениям (нулю равны как веществен-
ная, так и мнимая части определителя):
<О2 = ЮЦ1 + -^-), (7-31)
где
2 1
СО0— LC,
и
= СГгГ + L.
(7-32)
Найденное решение приводит к усло-
виям существования установившихся коле-
баний. Однако в пределах теории линейных
цепей из этих уравнений нельзя опреде-
лить амплитуды токов. Заметим только, что
если М меньше требуемой по условию (7-32)
величины, то генерация прекращается, если
же М больше, то колебания нарастают до
тех пор, пока коэффициент усиления не
уменьшится вследствие выхода из линейной
области.
На рис. 7-17 -показана схема без источ-
ников питания генератора на полупровод -
пиковом триоде с параллельным конту-
ром L, С в ветви основания (базы). Внизу
показана эквивалентная схема. В ней резо-
нансный контур представлен двумя парал-
лельными ветвями с чисто реактивной (jb)
и с чисто активной (g) проводимостью.
Цля этой цепи можно составить .урав-
нения:
1 к (^к + г) -[- /вгэ;
/ - t h i 8+Jb_ 1
7к-/э [l + 1+Mg + /7)) r3J.
После подстановки /к из второго
уравнения в первое получаем, что
/э
Гг—- гэ —
(г« + г> [1 + ! + r0 (g + jb) r’]} ~ °’
Очевидно, что при /э 7^0 должен быть
равен нулю множитель, стоящий в фигур-
ных скобках. Его мнимая часть обращается
в нуль только -при Ь—0. Следовательно, ве-
щественная часть обращается в нуль при
гт = rs + (гк + г)
Равенство нулю реактивной проводимо-
сти определяет частоту генерируемых коле-
баний.
Цепи с обратной связью. В рассмот-
ренных генераторах существенную роль
играли колебания в контурах г, L, С; эти
колебания оказывались незатухающими бла-
годаря тому, что рассеяние энергии, про-
исходящее в сопротивлении контура, ком-
пенсировалось энергией, подводимой от
источников питания триода. Характерным
для всех случаев при этом оказывалось су-
ществование обратной связи между выхо-
дом и входом. ’
Замечательно, что пр!и надлежащей
обратной связи триод может служить гене-
ратором даже при отсутствии в цепи коле-
бательного контур а.
Рассмотрим сначала некоторые общие
понятия, относящиеся к цепям с обратной
связью. Представим себе усилитель с за-
данным соотношением между напряжения-
ми на входе и выходе:
& вых = AU вх>
где A — комплексная величина, в общем
случае зависящая от частоты и от тока на
выходе. Такой усилитель изображен на схе-
мах (рис. 7-18,а) как четырехполюсник, вну-
три которого стоит знак > (заметим, кстати^
Рис. 7-17.
204
что он (связывает большую и меньшую вели-
чины 'Прямо противоположно принятому
в (математике; ©тот знак указывает направ-
ление, в котором производится усиление).
Снимая напряжение с выхода и подавая его
на вход пассивного четырехполюсника (К),
получаем на выходе последнего напря-
жение
UО. С == KUВЫХ,
оде К — опять же некоторый комплексный
коэффициент. Напряжение на выходе этого
четырехполюсника обозначено индексами
«о. с» ((обратная связь), так как оно будет
подано снова на вход усилителя (рис.
7-18,6).
Если при этом замкнуть накоротко
внешние входные зажимы (на левой сторо-
не рис. 7-18,6), то со всей необходимостью
придем к равенству
С7вх + U0,c =0.
Сопоставляя это равенство с двумя преды-
дущими, приходим к уравнению
U^ + KAU^ = 0.
Онэ может иметь решение, отличное от
нулевого (йъх =f= 0), только при КА = — 1.
В общем курсе теории линейных цепей
невозможно осветить сколько-нибудь полно
теорию цепей, содержащих обратную связь;
заметим только, что именно такие цепи
представляют наибольший интерес для си-
стем автоматического управления и регули-
рования. (Полная теория цепей с обратной
связью, так же как теория применения
триодов, обязательно требует знакомства
с нелинейной теорией цепей.
Интегрирующие и дифференцирующие
контуры. Ограничимся здесь анализом
простых случаев обратной связи, применяе-
мой в устройстве 'интегрирующих и диффе-
ренцирующих . контуров. Их рассмотрение
очень полезно для расширения представле-
ний о применении цепей переменного тока;
Рис. 7-19.
кроме того, методы их анализа типичны
для всех цепей,, содержащих обратную
связь.
Простейшие контуры г, С или г, L
(р1ис. 7-(19) могут применяться в качестве
интегрирующих или дифференцирующих.
Действительно, если в контуре г, С
(рис. 7-19,а) активное (сопротивление много
больше реактивного, то
г jaC’
поскольку при г^>1/соС
~~ г г
Но деление на /со комплекса, изобра-
жающего гармоническую функцию, и есть
не что (иное, как интегрирование.
Если, напротив, г<^1/<оС, то можно
считать, что ток
1 ^zUijaC.
В таком случае напряжение на сопро-
тивлении г
й г= ir-^zU ij^cr
может рассматриваться как величина, про-
порциональная производной от напряже-
ния 1/1, поскольку умножение комплекса на*
/•© соответствует дифференцированию гар-
монической функции.
Предоставляем читателю самостоятель-
ный анализ условий применения конту-
ра г, L в качестве дифференцирующего и
интегрирующего (рис. 7-19,6).
При условиях, приведенных выше, вы-
ходные напряжения очень малы по сравне-
нию с входными; к тому же на них может
сильно влиять ток, потребляемый приемни-
ком, напряжение на котором равно интегра-
лу или производной от входного напря-
жения.
Качество контуров, выполняющих ука-
занные математические операции, значи-
тельно улучшается, когда те же элементы
г, С, L включаются в цепь с обратной
связью, как показано на рис. 7-20. При этом
расширяется диапазон частот (особенно
в сторону низких частот), при которых оо-
Рис.. 7-18.
205
где
Рис. 7-20.
грешность остается еще незначительной.
Для цепи рис. 7-20 при условии, что
входное сопротивление усилителя очень ве-
лико, входной ток
1 . 1 + А 1
/1 = (^ВХ + 6 2) f = б 2 Д
ИЛ i
Очевидно, что контур можно рассмат-
ривать как интегрирующей при условии
/ 1 \
А < 1 + А .
Г72 = Жх
Предполагается, что А — большое
шественное число. Следовательно,
-ве-
= й2
1
~А
[1 + '“(1+Л>]
При этом необязательно к чему
приводило, условие г <о£.
Особенность составления уравнений
Кирхгофа для цепей с обратной связью за-
ключается, во-первых,, в наличии дополни-
тельной связи -между напряжениями на вхо-
де и на. выходе усилителя и, во-вторых,,
в необходимости различать входное напря-
жение цепи и входное напряжение усили-
теля.
Многие цепи с обратной связью анали-
зируются аналогично.
ГЛАВА ВОСЬМАЯ
ТРЕХФАЗНАЯ ЦЕПЬ
В электротехнике и особенно
в электроэнергетике распростране-
ны цепи с многофазными (главным
образом, трехфазными) генератора-
ми. В отличие от простых однофаз-
ных генераторов, имеющих два -вы-
ходных зажима или полюса, у мно-
гофазного генератора на выходе М
фазных полюсов; он может иметь
еще один нейтральный или нулевой
полюс /V, как показано на рис. 8-1,а.
Гармоническое напряжение меж-
ду любой парой полюсов многофаз-
ного генератора имеет одинаковую
частоту. Для простоты фазный по-
люс часто называют просто ф а-
з о й, а нейтральный полюс — ней-
тралью. В симметричном
многофазном генераторе между лю-
бой фазой (фазным полюсом) и
нейтралью напряжения одинаковы
по величине и последовательно от-
стают по фазе на одинаковый угол
а = 2я/7И (рис. 8-1,6):
иА=ив=ис = ...,
OA = UBa,UB = Oca.... (8-1)
где UA = UAN, UB = bBN,.. .,а =
— е1а. Комплекс а называют фаз-
ным множителем.
Между любой парой смежных
фазных полюсов, т. е. между Л и В,
В и С, ..., (М—1) и 7И, М и Д, на-
пряжения также одинаковы по ве-
личине и последовательно смещены
по фазе (рис. 8-1,в):
= (8-2>
2'ifi
Рис. 8-2.
ДОЙ
где
ubc^jb-Oc,...-
при этом1 * * * *
/Ш £>С 7 £>С GJ 7
Многофазный и, в частности,
трехфазный генератор всегда может
быть представлен в виде М незави-
симых однофазных генераторов с ф а з-
ными напряжениями UA ,UB,-..9
включенных между соответствую-
щими фазными полюсами и нейтралью
(рис. 8-2,а). На рис. 8-2,6 представ-
лена топографическая векторная диа-
грамма симметричного трехфазного
генератора и график мгновенных
значений фазных напряжений UA,
UB, Uc при UA = UB=UC=U$. Меж-
дуфазные или линейные напря-
жения UАВ=и' —U ,
— Uc,, .. имеют при этом также
одинаковую величину, в J/” 3 раз
большую фазной:
Они последовательно смеще-
ны по фазе друг относитель-
но друга на 120°. В этом
легко убедиться непосредст-
венно из топографической
векторной диаграммы или
аналитического вывода. На
рис. 8-2,в показаны векторы
и соответствующие мгновен-
ные значения междуфазных
напряжений. Заметим, что
векторная диаграмма рис.
8-2,в нетопографична.
Потребитель может быть
присоединен к любой паре
фазных полюсов, а также
между нейтралью и каж-
из фаз. Потребитель пред-
ставляет собой симметричную на-
грузку, если между нейтралью и
каждой из фаз включены ветви
с одинаковыми сопротивлениями
(Z' на -рис. 8-3); точно так же на-
грузка симметрична, когда между
каждой парой фазных полюсов
включены одинаковые ветви (Z" на
рис. 8-3). Цепи, содержащие много-
фазные генераторы, назььвают мно-
гофазными цепями.
Все основные звенья современ-
ных трехфазных цепей были разра-
ботаны М. О. Доливо-Доброволь-
ским (1862—1919 гг.). Изобретен-
ный им асинхронный трехфазный
двигатель (§ 8-7) оказался более
простым и надежным, чем электри-
ческие двигатели ;всех других типов.
Вероятно, это обстоятельство оказа-
ло решающее влияние на распрост-
ранение трехфазных систем. Впро-
чем, трехфазные системы обладают
и другими преимуществами: трех-
фазные цепи распределения энер-
гии экономичнее однофазных (§ 8-4);
мгновенная мощность, отдаваемая
трехфазными генераторами, при
1 Действительно, принимая во внима-
ние (8-1),
uBC=uB-uc^-irc(a-i),
откуда следует, что АВ~ Uвс:а, посколь-
ку CJB = Uca.
23‘7
симметричной нагрузке постоянна
(§ 8-3), тогда как мгновенная мощ-
ность однофазных генераторов
пульсирует; в случае трехфазной
цепи чрезвычайно просто создается
вращающееся .магнитное поле (эта
особенность, лежащая в основе ра-
боты асинхронных двигателей До-
ливо-Добровольского, приводит
к применению трехфазных цепей
в некоторых устройствах измери-
тельной техники и автоматики); при
выпрямлении переменного тока
в случае многофазных систем резко
уменьшается пульсация выпрямлен-
ного тока, поэтому в выпрямитель-
ной технике часто применяют не
только трехфазные источники пита-
ния, но даже шести-, а иногда и
двенадцатифазные.
Расчет симметричных многофаз-
ных цепей может быть всегда све-
ден к независимому расчету цепи
любого из однофазных генераторов
или, как говорят, к расчету одной
фазы. Несимметричные многофаз-
ные цепи приходится рассчитывать
как цепи с несколькими источника-
ми питания; в некоторых случаях
расчет таких цепей может быть при-
веден к суперпозиции нескольких
симметричных режимов (метод сим-
метричных составляющих, § 8-9).
Поскольку широкое распростра-
нение получили именно трехфазные
системы, в последующих парагра-
фах будет рассмотрен только этот
вид многофазных цепей.
8-1. ТРЕХФАЗНЫЙ ГЕНЕРАТОР
Машинный трехфазный генера-
тор отличается от обычного (одно-
фазного) генератора лишь тем, что
в нем имеется не одна, а три обмот-
ки. Они расположены на общем ста-
торе так, что наводимые в них
э. д. с. смещены по фазе одна отно-
сительно другой на 120°. На
рис. 8-4,а схематически показан та-
кой трехфазный генератор. Внутри
цилиндр ического ф ер р ом агн итн ого
статора вращается цилиндрический
ротор, создающий магнитное поле.
Его магнитный поток замыкается
через статор. С внутренней стороны
статора прорезаны пазы, и в них
заложены провода, в которых наво-
дятся э. д. с. при вращении ротора.
Провод, .заложенный в пазу J, вы-»
веден с задней стороны статора
к полюсу А; с передней стороны он
соединен с проводом, заложенным
в лазу 4; этот последний выведен
с задней стороны статора к полю-
су X.
В проводах 1 и 4 э. д. с. наво-
дятся в разных направлениях, но
при указанном соединении эти две
э. д. с. складываются; их сумма рав-
на фазной э. д. с. За, направленной
от полюса X к полюсу А. Действи-
тельно, при вращении ротора про-
тив часовой стрелки и при его рас-
положении, показанном на рис. 8-4,
э. д. с., наведенная в проводе /, на-
правлена от передней стороны -ста-
тора к задней; э. д. с. в проводе 4
направлена прямо противоположно;
сумма этих э. д. с. ЭА направлена
от X кА, как показано на рис. 8-4,6.
Очевидно, что э. д. с, ЭА максималь-
на в тот момент, когда провода 1
и 4 находятся непосредственно
в плоскости полюсов S — N. При
дальнейшем повороте ротора она
уменьшается. При надлежа-
щем (косинусоидальном)
распределении магнитного
поля ротора мгновенное зна-
чение э. д. с. в рассматри-
ваемой обмотке
э =3mcosco£, (8-3)
где о>= 2л/п — угловая ско-
рость вращения ротора,
а п—число оборотов рото-
ра в 1 сек.
Аналогично ‘ находится,
фазная э. д. с. Эв-, наводи/
208
мая в проводах 3 и 6Ч соединенных
с полюсами В и Y. Однако эти про-
вода смещены на 120° относитель-
но проводов 1 к 4. Поэтому после
перемещения ротора на 7з оборота
провод 3 окажется против полюса
S, а провод 6 .против полюса N.
В силу сказанного очевидно, что
э. д. с. Эв в проводах, выведенных
к полюсам BY, отстает по фазе от
э. д. с. ЭА на 7з периода или на
120°
aB = 3™cosM—120°). (8-4)
Аналогично находим, что
эс = Эт cos (pt — 240°) ==
= Эт cos (со/ + 120°). (8-5)
Электродвижущие силы трех об-
моток .генератора или его трех фаз
можно представить в комплексной
форме:
3=3, Эв=Эа~\ Эг = Эа,
А 7 а
(8-6)
где фазный множитель
1/120° =
= -0,5-НТЗ/2. (8-7)
В тех случаях, когда внутренним
падением напряжений в -обмотках
можно пренебречь, напряжения на
полюсах генератора равны его фаз-
ным э. д. с., т. е.
£Л=3., = ^с = ^с-
Фазный множитель трехфазной
системы. Умножение на а поворачи-
вает вектор на +420°; умножение
на а~х поворачивает вектор на
—-120° или, что то же самое, на
угол +240°. Вместе с тем поворот
на +240° выражается умножением
на а2:
а2=а -1 = 1 Z240° = 1 /—120° =
= — 0,5 —/У 3/2. (8-8)
Это соответствует очевидному ра-
венству a3=tl. Сказанное иллюстри-
Рис. 8-5.
рует рис. 8-5. Из приведенных фор-
мул вытекает и простое соотноше-
ние
. 1 + а + ^2 = 0. (8-9)
Конструкция действительных -генерато-
ров, конечно, 'много .сложней рассмотренной
принципиальной модели. В действительных
генераторах многовнтковая обмотка распре-
делена по всей внутренней поверхности ста-
тора, имеющего большое число пазов.
В .массивном роторе больших генерато-
ров та1кже вырезаны продольные пазы;
в них заложены провода, питаемые (через
угольные щетки, скользящие по кольцам)
от специальных генераторов постоянного
тока. Этот ток и создает магнитное поле
ротора. Расположение пазов в роторе,
а также определенный порядок последова-
тельности включаемых проводов обмотки
статора обеспечивают достаточное прибли-
жение наводимой э. д. с. к простой гармо-
нической.
Соединение обмоток генератора
в звезду. Объединяя концы всех
трех фазных обмоток, т. е. точки
X, У, Z, в общую точку — нейтраль,
получим трехфазный генератор, со-
единенный в звезду (рис. 8-2,а и
8-3).
К четырем зажимам получивше-
гося генератора может быть присо-
единено четыре провода: три фазных
(А, В, С) и один нейтральный
(7V).
Напряжение между фазными
проводами (линейное напряжение)
при этом в l/З раз больше фаз-
ного напряжения, т. е. напряжения
между любой из фаз и нейтралью.
Это легко показать, пользуясь фаз-
ным множителем. Действительно,
линейное напряжение U вс — UB —
— UC = U А(а2— а), поскольку
= и U —U а.
Следовательно, U вс = — %йА [см.
формулы (8-7) и (8-8)].
14 К- М. Поливанов
209
Полученное выражение показы-
вает, что линейное напряжение
между двумя фазными проводами,
например В, С, в ]/* 3 раз больше
фазного и отстает от фазного- на-
пряжения оставшейся (Л) фазы на
угол тс/2. Применяя эту формулиров-
ку к двум другим линейным напря-
жениям, находим, что ОСА — -—
^АВ = — iV^>Uc (Рис- 8'2)-
Те же три обмотки (рис. 8-4)
можно соединить в звезду иначе.
Объединяя в общую точку N' точки
Л, В, С, получим трехфазный гене-
ратор с четырьмя внешними зажи-
мами X, У, Z и N'. При этом точки
X, Y, Z можно назвать Л7, В7, С'.
Топографическая диаграмма, из ко-
торой легко найти все фазные и ли-
нейные напряжения, показана на
рис. 8-6. В этом случае все напря-
жения отличаются по знаку от со-
ответствующих напряжений ранее
рассмотренного соединения (рис.
8-2,6).
Соединение обмоток генератора
в треугольник. Соединяя последова-
тельно начало одной фазной обмот-
ки с концом предыдущей (рис.8-7,а),
получим замкнутый треугольник.
Такое соединение возможно в слу-
чае симметричной трехфазной си-
стемы, так как для нее сумма после-
довательно включенных э. д. с. рав-
на нулю (рис. 8-7,6):
^A + ^B + ^C = ^A(l + aZ + a) =
= 0, (8-10)
Генератор, соединенный в тре-
угольник, имеет на выходе только
три полюса Л, В, С. При этом ли-
нейные напряжения равны фазным
напряжениям генератора:
^АВ — ^А~^А' ^BC~^B~^B”
бСА=йс=эс,
Заметим, что как и в случае одно-
фазных генераторов, напряжение
равно э. д. с. только при отсутствии
нагрузки или при ничтожно малом
внутреннем сопротивлении генера-
тора.
Соединение обмоток в треуголь-
ник можно произвести и в иной по-
следовательности (рис. 8-8,а). При
этом линейные напряжения отлича-
ются по фазе от линейных напряже-
ний при ранее рассмотренном соеди-
нении. Соединения по рис. 8-7 иног-
да называют левым, а по рис. 8-8 —
правым треугольниками.
Пример 8-1. Два симметричных трех-
фазных генератора имеют обмотки, соеди-
ненные в правый и левый треугольники
(рис. 8-9). Во всем остальном генераторы
одинаковы.
Фазы С и Сг этих двух генераторов*,
соединены внешним проводом. Междуфаз-
ные напряжения каждого из генераторов
одинаковы. Вольтметры 1 и 2 показывают
220 в. Какое напряжение покажут вольт-
метры 5, 4^5, 6?
Решение. Нужно построить топо-
графическую диаграмму левого (А, В, С)
210
a'
Ток в нейтральном проводе 1N
по закону Кирхгофа равен сумме
трех фазных токов:
4-А.+4+4. (8-12)
Рис. 8-10.
Сопоставляя последние два выраже-
ния, находим, что при симметрии
ток в нейтральном проводе равен
нулю:
iN=:iA (14-д+^)=о,
поскольку 1+й + а2 = 0 [см. формулу
(8-9)]. Но если это так (т. е. Лу = 0),
то потенциалы точек N и N' совпа-
дают. Следовательно, полное фаз-
ное напряжение генератора подает-
ся на последовательно включенные
сопротивления Z$ и Z и по закону
Ома
/ - 1 •
А /ф+Z ’ /ф + Z ’
ь Лф -j- z
и правого (А7, В7, С7) треугольников, со-
вместив точки С и С7 (такая диаграмма
изображена на рис. 8-10, однако рекомен-
дуется построить ее самостоятельно, обра-
тившись к рисунку только для проверки).
Зная, что отрезки АВ и А7В7 соответ-
ствуют напряжению 220 в, легко найти
ответы:
1) 220 в; 2) 220 в; 3) 220 в; 4) 382 в;
5) 220 в; 6) 0.
8-2. СИММЕТРИЧНАЯ
ТРЕХФАЗНАЯ ЦЕПЬ
Звезда — звезда. Простейшее
соединение симметричной нагрузки
получим, включая одинаковые со-
противления Z между каждой фазой
и нейтралью. Два способа изобра-
жения такой цепи показаны на
рис. 8-11, где /ф—сопротивления
соединительных фазных проводов,
ZN — сопротивление нейтрального
провода.
Естественно предположить из
соображений симметрии, что токи
в фазных проводах (1Д, 1В, /с) оди-
наковы по величине и последова-
тельно смещены по фазе. на 120°,
т. е.
' JB=iAa'2’ ic—iAa- (8-н)
Таким образом, в симметричной
трехфазной системе нейтральный
провод оказывается лишним. Одна-
ко в случае нарушения симметрии
нагрузки (например, при отключе-
нии нагрузки в одной из фаз) на-
пряжения на отдельных фазах на-
грузки могут существенно отличать- .
Рис. 8-11.
14*
211
ся друг от друга по величине. На-
личие нейтрального провода в зна-
чительной мере предупреждает за-
висимость напряжения на одной фа-
зе от ’соотношения нагрузок во всех
трех фазах.
Топографическая векторная диа-
грамма рассмотренной цепи пред-
ставлена на рис. 8-12. Треугольни-
ки, гипотенуза которых соединяет
точки А и Д', В и В', С и С', пред-
ставляют падение напряжения
в фазных проводах:
&а ~~ U'A=iAZ^ 1а(гф + (8-14)
Как и в случае простой однофазной
цепи, потеря фазного напряжения
UА — U9А 1А(гф cos ? + хф sin <р),
(8-15)
где — фазный угол сопротивления
нагрузки (Z), он равен отставанию
по фазе фазного тока относительно
фазнэго напряжения. Векторы линей-
ных напряжении U АВ ,
^А’В" ^ВС’" НЭ ДИаГ-
рамме рис. 8-12 не по-
казаны. Очевидно, что
линейное напряжение
генератора UAB изобра-
жается вектором, сое-
диняющим точки В и Л
линейное напряжение по-
требителя UА,в, изобра-
жается вектором, соеди-
няющим точки Вг и Д',
и т. д.
Линейная потеря напряжения
и АВ — V А'В' ~ (ГФ cos ? +
4-Хф81П<р), (8-16)
как это следует из сопоставления
формулы (8-15) и топографической
диаграммы.
Звезда — треугольник. На рис.
8-13,62 показана цепь, в которой к ге-
нератору, соединенному :в звезду,
присоединен потребитель, соединен-
ный в треугольник.
Пренебрежем сначала сопротив-
лениями проводов. В таком случае
(2ф = 0) каждая из сторон треуголь-
ника окажется включенной на ли-
нейное (межфазное) напряжение,
которое по величине jb у/ 3 раз
больше фазного. Соответственно то-
ки в сторонах треугольника равны:
IАВ~ UАВ ВС = UВС
<8-14
В симметричной системе эти то-
ки последовательно смещены один
относительно другого на 120°
212
(рис. 8-13,6) и отстают на углы фот
своих фазных напряжений.
Токи в фазных проводах, или
линейные токи, легко найти по
первому закону Кирхгофа:
А= АВ СА ’ В~ 1ВС АВ ’
<8-18)
По абсолютной .величине линейные
токи :в раз больше токов в сто-
ронах треугольника. Линейные токи
совпадают с токами в фазах генера-
тора, соединенного в звезду.
От системы звезда — треугольник
легко перейти к системе звезда —
звезда, преобразовав треугольник
нагрузки в эквивалентную звезду.
В случае симметричного треуголь-
ника с ветвями ветви эквива-
лентной звезды /имеют сопро-
тивления, в 3 раза меньшие (см.
§2-10):
Если сопротивлениями Z# нель-
зя пренебречь, то их следует приба-
вить к сопротивлениям эквивалент-
ной звезды.
Все сказанное непосредственно
следует из векторных диаграмм
рис. 8-13 или может быть найдено
аналитически.
Пример 8-2. В цепи 8-13,я мощность,
получаемая потребителем, Р=30 кет -при
cos<p=0,8 (ф>0). Линейное напряжение
у потребителя UA'B> = ^B'C' = ^С'А'^
=380 в. Сопротивление каждого из соеди-
нительных проходов 7ф = 0Д+/0,2 ом.
Требуется найти:. 1) напряжение гене-
ратора; 2) мощность, теряемую в прово-
дах.
Р е ш е н и е. Мощность на одну фазу
потребителя S=10+/7,5 кеа. Следователь-
но, сопротивление сторон треугольника
2д=^л'в/8 = 11,5/:36о50'.
Сопротивление .ветвей эквивалентной
звезды Za = Za/3. Ток в фазном проводе
при = 380//3 = 219 в
iA=^'Ai\ = ^'AlZb- .
= 57,2/2— 36°50' а.
Фазное напряжение генератора
UA = U'a + 1А (ГФ cos У + sin ?)
= 219 + 57,2 (0,1-0,8+0,2-0,6) = 230 в.
Линейное (междуфазное) напряжение
генератора
Vab=V*Ua = 398s.
Мощность, теряемая в проводах,
ДР == 3/2 Гф = 980 вт.
Треугольник—треугольник. Пусть
теперь и генератор и потребителе
соединены в треугольник. Сопротив-
ление, проводов будем считать рав-
ным нулю, т. е. /ф==0 (,ри>с. 8-14).
В этом случае токи в треугольнике
потребителя находятся по задан-
ным линейным напряжениям.
Токи в ветвях генератора равны
токам в соответствующих парал-
лельно подключенных ветвях потре-
бителя: ток 1АВ равен току в ветви
э. д. с. ЭА, LBC — току в ветви с
э. д. с. Эв\ 1СА — току в ветви с
э. д. с. Эс.
Для доказательства следует обратиться
к контурным уравнениям. Цепь рис... 8-14
содержит три узла А, В> С и шесть вет-
вей, следовательно,, это цепь с четырьмя
независимыми контурами. Контурные токи
первых трех контуров — это токи ветвей
потребителя 1АВ, I^c^ca* Ток четвертого
контура /4 равен нулю при сколь угодно
малом, но все же конечном сопротивлении
ветвей генератора (Zr), разумеется, при
условии ЭА + 3Б + Эс = 0. Если же Zr =
= 0, этот четвертый ток может иметь про-
извольное значение.
А
* Рис. 8-14.
213
Система уравнений всех контуров:
(2+гг)+42г = Эл;
I вс (^ 4- ^г) 4" — Эв>
IСА (^ + Zp) + 1 — Эс\
( t АВ + IВС + ^СА ) =
= эА + эв + эс.
Складывая первые три уравнения и
вычитая из суммы последнее (или состав-
ляя уравнение для контура, образованного
треугольником потребителя), найдем, что
АВ + iЕС + Ica}Z “° ИЛИ +
+ /вс + ^СА == °-
В такОлМ случае при равенстве нулю сум-
мы всех э.д. с. из уравнения для четверто-
го контура следует, что I43Zr = 0 или
/4 — 0 при Zr ф О*
Эквивалентность различных со-
единений. Переходя от треугольника
к эквивалентной звезде или от звез-
ды к эквивалентному треугольнику,
можно свести любую симметричную
цепь к простому соединению звез-
да— звезда, обычно наиболее удоб-
ному для анализа; впрочем, можно
любое соединение представить и как
треугольник — треугольник.
Особенно удобно преобразование
треугольника в звезду в тех случа-
ях, когда между треугольником на-
грузки и генератором включены со-
противления проводов (2ф), кото-
рые непосредственно складываются
с сопротивлениями лучей звезды,
эквивалентной треугольнику.
Прежде чем переходить к даль-
нейшим обобщениям, целесообразно
подробнее рассмотреть вопрос
о мощности симметричной трехфаз-
ной цепи.
8-3. МОЩНОСТЬ ТРЕХФАЗНОЙ
СИММЕТРИЧНОЙ ЦЕПИ
В случае симметричной нагруз-
ки, соединенной в звезду, мощность
первой фазы
S/= СA1 A=UА1 ? + i Sin ?)’
(8-20)
а полная потребляемая мощность
в 3 раза больше
8 = Р-Н<Э = 35л=
= 3(7j4/^(cos'? + /sin<p). (8-21)
Это выражение определяет и актив-
ную, и реактивную мощности сим-
метричной трехфазной системы.
В случае звезды линейный- ток
/л равен фазн'Ому_/А; линейное на-
пряжение Usi в КЗ раз больше фаз-
ного UA. Поэтому полная мощность
(8-21) может быть выражена через
линейные токи и напряжения фор-
мулой
s = Р + /(?=]/ (cos <р + j sin у).
(8-22)
Важно заметить, что в этой форму-
ле ф — сдвиг по фазе между фазны-
ми напряжением и током:
К той же формуле (8-2:2) приводит
расчет мощности в случае нагрузки,
соединенной в симметричный тре-
угольник. В последнем случае для
стороны треугольника АВ
. *
S —U I —
АВ---АВ 1 АВ---
= Uab !ав (cos ? +1sin ?)’ (S * * 8"23)
где ф — сдвиг по фазе между на-
пряжением и током в сторонах тре-
угольника. Мощность, ‘ потребляе-
мая всем треугольником,
S = 384В = 3UAB 1 АВ <C0S f + / Sin %)’
(8-24)
В этом случае линейное напряже-
ние £7Л равно напряжению UAB,
а линейный ток /л в |Z3 раз боль-
ше тока 1АВ в любой из сторон тре-
угольника. Переходя в выражении
(8-24) к линейным напряжению и
току, приходим к прежней форму-
ле (8-22), в которой опять же ф —
сдвиг по фазе между напряжением
и током в фазных ветвях треуголь-
ника.
Мгновенное значение мощности
симметричной трехфазной системы
постоянно, как это легко найти,
складывая мгновенные мощности
всех трех фаз. Например, в случае
соединения звездЬй для фазы А
Ра = иА1А=иАГА\-^ Ч + C0S (2<в/+ ?)L
214
если иА= j/ 2Ua cos <nt и iA =
— ]/ 21A cos (atf — <p). Но в фазе В
напряжение и ток отстают на углы
2^/3 от напряжения и тока в фазе А:
ив—^ 2(7Bcos (orf — 2^/3);
zB=j/ 2/Bcos (ад/ — 2^/3 — <p);
следовательно, мгновенная мощность
этой фазы
рв= ^в^^ ? + cos
Аналогично для фазы С
с— lcos ? + cos (2(D^+^4~4^/3)].
Складывая мгновенные значения
-мощности .всех трех фаз симметрич-
ной системы, находим, что сумма их
переменных составляющих равна
нулю, поскольку
(здесь <х = 2со£-Нф). Обращение
в нуль этой суммы нам уже извест-
но, так как это сумма трех гармо-
нических составляющих одинаковой
амплитуды, последовательно сме-
щенных по фазе одна относительно
другой на 2л/3.
В симметричной системе (звезда)
I А= I В~ 1с=
Поэтому мгновенная мощность
Р = РА+ Рв+ Рс = 3~7^/л cos т- е-
равна средней или активной мощ-
ности:
р = Р = V 3/7л/л cos
Найденный результат замечателен тем,
что мощность, отбираемая от симметрич-
ного трехфазного генератора при симмет-
ричной нагрузке, постоянна; следователь-
но, постоянным оказывается и вращающий
момент на валу двигателя, соединенного
с ротором. В однофазном генераторе от-
даваемая мощность пульсирует. Конечно,
эти пульсации при 'большой инерционности
ротора и вала поглощаются в основном
пульсацией механических напряжений в мас-
сивной стальной системе ротор — вал, не
доходя до рабочих частей первичного дви-
гателя. Все же они представляют нежела-
тельное явление.
Мгновенная мощность, развиваемая ге-
нератором и передаваемая линией симмет-
ричной трехфазной системы, постоянна и
равна, средней -(активной) мощности. Это
значит, что при чисто реактивной нагрузке
мгновенное значение передаваемой мощно-
сти все время остается равным нулю.
Может показаться, что сказанное про-
тиворечит ранее приведенному анализу ре-
активной мощности. Это, однако, не так.
В самом деле, несмотря на равенство нулю
средней мощности, передаваемой по всей
трехфазной линии, в проводах идет ток,
вызывающий в них потери. Действительно,
передача энергии происходит в сущности по
двум двухпроводном линиям с одним об-
щим проводом (рйс. 8-115). По каждой из
этих двух линий происходит переброс энер-
гии между источником и потребителем да-
же в случае симметричной чисто реактив-
ной нагрузки: мощность, передаваемая по
каждой из этих линий, например по линиям
АВ и СВ, имеет мгновенные значения, от-
личные от нуля. При этом энергия, возвра-
щаемая источнику чю одной двухпроводной
линии трехфазной системы, равна в каждое
мгновение энергии, отбираемой через дру-
гую двухпроводную линию.
Измерение мощности. Трехфаз-
ную цепь с тремя проводами, со-
единяющими генератор с потребите-
лем, всегда можно рассматривать
как две двухпроводные линии, имею-
щие один общий провод, например
как линии АВ и СВ с общим про-
водом В (рис. 8-15). При этом в пер-
вой линии при напряжении UАВ =
= иА—UB идет ток 1А, а по вто-
рой линии при напряжении Uсв =
— Uc—UB идет ток 1С.
Рис. 8-15.
215
Мощность, передаваемая по пер-
вой линии,
= (8-25)
а мощность, передаваемая по второй
линии,
S> = UCBIC- (8-26)
Полная мощность, передаваемая по
трехпроводной линии,
S^Si + Ss. (8-27)
Из сказанного вытекает возмож-
ность измерять мощность, переда-
ваемую по трехпроводной линии
трехфазной системы, двумя ваттмет-
рами, каждый из которых измеряет
мощность, передаваемую по одной
из двух двухпроводных линий. Та-
кая схема включения ваттметров
(схема Арона) изображена на
рис. 8-15.
При выводе не делалось никаких
предположений о симметрии систе-
мы, следовательно, найденный ме-
тод измерения мощности двумя
ваттметрами применим как в слу-
чае симметричной, так и в случае
несимметричной трехфазной трех-
проводной системы.
Векторная диаграмма токов и
напряжений в .цепи рис. 8-15 для
симметричной системы представле-
на на рис. 8-16; более толстыми ли-
ниями изображены напряжение и
токи ваттметров. Ток 1а первого
ваттметра, отстает от фазного на-
пряжения иЛ на угол ф, опреде-
ляемый характером нагрузки. Ли-
нейное напряжение Uab, приложен-
ное к первому ваттметру, опережа-
ет фазное напряжение UA' на угол
30°. Поэтому сдвиг по фазе между
напряжением и током ваттметра
Рис. 8-16.
Wi составляет ф+30°. Напряжение
Uсв опережает ток 1С ваттметра
как видно из диаграммы, на фаз-
ный угол ф—30°. Поэтому показа-
ния ваттметров, включенных по схе-
ме рис. 8-15, в случае симметричной
цепи равны:
Рг = Re (UAB ТА) = £/л7л cos (30° + ?);
P2=Re (UCB *с)=и^ cos (30°-?).
При чисто активной нагрузке (ф=0)
показания обоих ваттметров одина-
ковы.
Полное значение передаваемой
(активной) мощности равно алгеб-
раической сумме показаний обоих
ваттметров. На практике часто два
ваттметра ставятся на общую ось.
Показания такого сдвоенного ватт-
метра непосредственно равны всей
(активной) мощности, передавае-
мой.по трехпроводной линии.
На основании последних выра-
жений легко вывести формулу, поз-
воляющую определить угол ф по по-
казаниям ваттметров:
tgy^j/З^-Т.^1.. (8-28)
' 2 Т
Из этой формулы непосредственно
можно определить реактивную мощ-
ность симметричной системы по по-
казаниям тех же двух ваттметров:
Q = Р tg <р =К~3(Л — PJ- (8-29)
Пример 8-3. В симметричной трехфаз-
ной системе линейные напряжения ил =
=10 кв и токи /л =200 а, фазный угол на-
грузки ф=30°. Найти передаваемую мощ-
ность и показания ваттметров, включенных
по схеме рис. 8-1'5.
Решение. Передаваемая мощность
Р = УЗ ил1л cos у> = 3 000 кет.
Показания ваттметров
Pi = U Л1 л. cos 60° = 1000 кет;
Ръ — Uni л cos 0 = 2 000 кет.
Пример 8-4. Определить фазный угол
нагрузки, активную, реактивную и полную»
мощность, если показания ваттметров.,
включенных по схеме рис. 8-15, Pi=0, Р2=
= 100 кет.
216 .
Решение. По формуле (8-28) нахо-
дим, что tg у ==^3 и у = 60°. В таком
случае реактивная мощность
Q = (Рх + Р2) tg у = 173 ква
или по формуле (8-29)
Q = j/З (Р2 — А) = 173 ква.
Полная (кажущаяся) мощность
S = />2 _|_ Q2 — 200 ква.
8-4. ПЕРЕДАЧА ЭНЕРГИИ
ПО ТРЕХФАЗНОИ ЛИНИИ
В СИММЕТРИЧНОМ РЕЖИМЕ
После анализа симметричной
трехфазной цепи можно перейти
к рассмотрению общего случая пе-
редачи энергии от трехфазного ис-
точника к трехфазному потребите-
лю по трехпроводной линии с про-
дольным сопротивлением 7ф в каж-
дом из фазных проводов (рис. 8-17).
Такое представление линии возмож-
но, во-первых, если линия симмет-
рична (см. ниже § 8-5) и, во-вторых,
если ее длина невелика и можно не
учитывать ток, ответвляющийся че-
рез емкость между проводами ли-
нии. •
При рассмотрении цепи рис. 8-17
с заданной мощностью S —P+/Q
(или Р и <р), которая должна быть
передана потребителю, требуется
найти к. п. д. и потерю напряжения
при передаче этой мощности при
заданном сопротивлении каждого
провода 7ф=1Гт+/хт й при выбран-
ном линейном напряжении.
При этом, естественно, могут
рассматриваться и вопросы о влия-
нии cos ф и его регулирования, о до-
пустимой нагрузке проводов задан-
ного сечения и т. п. Однако все эти
вопросы решаются так же, как и
в ранее рассмотренных однофазных
системах.
Для того чтобы найти мощность,
теряемую в проводах, а также поте-
Рис. 8-17.
рю напряжения, надо знать линей-
ный ток. Последний может быть оп-
ределен по заданной мощности и
линейному напряжению независимо
от того, соединен потребитель
в звезду или в треугольник:
р =/3/7/cos?, (8-30)
где U, 1 — линейные величины.
Потеря напряжения рассчиты-
вается по приближенной формуле
д^уод — (rT cosy-f-xT sin у). j qq .
(8-31)
Очевидно, что мощность, теряе-
мая (рассеиваемая) во всех прово-
дах, определяется по закону Джоу-
ля— Ленца:
ДР = 3/2гт. (8-32)
Выражая в последнем равенстве ток,
пользуясь формулой (8-30), потерю
мощности можно представить так:
др = —Р1_Гт. (8-33}
U2 cos2 у v 7
В итоге находим, что к. и. д. трех-
фазной линии
'”1т ~ р-{-др~ р ♦ (8-34}
1 + У2 COS2 у Гт
Сравнение к. п. д. трехфазной и одно-
фазной линии. Как было показано ранее,,
к. п. д. однофазной линии
1
vjo ="• р 9 (8-35)
1 +2[/а COS2? Г°
где г о — сопротивление каждого из прово-
дов двухпроводной линии, по которьш про-
ходит ток
/=_^.
Ucos у *
Сравнивая выражения (8-34) и (8-35),
можно подумать, что к. п. д. трехфазной,
линии выше. Однако, если исходить из-
предположения одинакового количества ме-
ди в двух- и трехпроводной лидиях, надо*
учесть, что сопротивление каждого из про-
водов однофазной линии в il,5 раза меньше
сопротивления каждого из проводов трех-
фазной линии:
2
г о = Tj. (8-37)
217
Рис. 8-18.
После подстановки этого значения
в (8-35) найдем, что
1
р • (8-38)
1 + 3 U2 cos2 у Гт
Теперь можно сопоставить выражения
(8-34) и (8-38). Экономическое ’Преимущест-
во по к. п. д. все же оказывается на сто-
роне трехфазной передачи, хотя оно и не-
велико. Пусть, например,
Р
Г 79 _ 9 f т 0,11 1 •
U2 cos2 у
В таком случае ’Т]т=0,9 -и т}0 = 0,872.
Проводя это сравнение, мы предпола-
гали, что линейные напряжения трех- и
-однофазной линии одинаковы. Этому усло-
вию соответствует, например, питание осве-
тительной сети однофазной и трехфазной
линией (рис. 8-48). Но в ряде случаев,
сравнивая линии, надо исходить из равен-
ства фазного напряжения трехфазной ли-
нии половине линейного напряжения одно-
фазной. Например, в линиях с заземленной
нейтральной точкой изоляция проводов от-
носительно земли находится именно под
таким напряжением (рис. 8-19). В этом слу-
чае к.п. д. однофазной и трехфазной линий
одинаковы. Наконец, можно сравнивать ли-
нии питания осветительной сети, имеющие
дополнительный нейтральный провод (рис.
8-20). В таких сетях сечение нейтрального
провода часто выбирают в 2 раза меньшим
сечения остальных проводов, так как при
равномерной (полной) нагрузке ток в нем
равен нулю. В нейтральном проводе про-
ходит ток только’ при неравномерной на-
грузке. Применяя к последнему случаю
формулы (8-34) и- (8-35), следует считать,
что сечение всей меди в трехфазной линии
делится на 3,5, а в однофазной — на 2,5.
При этом сопротивление рабочих проводов
2,5
г о = g 5 гт- (8-39)
После подстановки такого значения г0 в
(8-35) находим, что
‘По — 5 Р * (8-40)
1 + 3?5 (72 cos2 ¥ Гт
и если л] т=0,9, то т]0== 0,865. Очевидно, что
именно в сетях последнего типа преимуще-
ство трехфазных линий по к. п. д. наиболее
заметно, хотя тоже незначительно.
В заключение подчеркнем, что преиму-
щества одной системы перед другой опре-
деляются не только величиной к. п. д. Очень
большую роль играет стоимость монтажа и
(изоляции, стоимость трехфазного и одно-
фазного кабеля (размеры однофазного
двухпроводного кабеля оказываются боль-
ше при одном й том же количестве меди
из-за худшего геометрического заполнения,
если провода имеют круглое сечение) и -Де-
лый ряд других факторов. '
-Однако, решающую роль в распростра-
ненности трехфазных систем играют про-
стота и надежность трехфазных машин.
Расчет на одну фазу. В рассмат-
риваемой системе рис. ,8-17 всегда
можно представить, что как генера-
тор, так и потребитель соединены
в звезду, причем между 'нейтраль-
ными точками этих звезд t(N и -N')
разность потенциалов равна нулкТ.
Поэтому расчет можно вести для
одной фазы независимо от всех
остальных; другими словами, расче-
ту подлежит цепь рис. 8-21.
Покажем, как определить иЛ и
Z этой цепи по заданной мощности
S и заданному линейному напряже-
нию U' у потребителя.
Рис. 8-20.
218
Рис. 8-21.
Очевидно, что
U'A=U’//3,
А У 3 Ur cos <р
(8-41)
(8-42)
(8-43)
Значение cos<p в (8-42) должно быть
задано непосредственно или опреде-
ляется по заданной комплексной мощ-
ности S = Р Ц- jQ. Значение началь-
ного угла фазного напряжения U' А
выбирается произвольно, обычно его
принимают равным нулю, т. е. пола-
гают U'A = UrА. При %гом
/ = s/(|/3t/') = s/(3d'4); (8-44)
z=U'A/i = 3 (U'Ay/s=(U'y/s.
(8-45)
Пример 8-5. Линейное напряжение у
потребителя £/'=35 кв, потребляемая
мощность S = 40,0 + /10,0 Мва, сопротив-
ление одной фазы линии 2ф = 2,5-f-j5 ом.
Требуется найти Z, и' А, UA в схеме
рис. 8-21 и к. п. д. системы.
Решение. Непосредственно по фор-
муле (8-45) находим:
Z = 28,6 + /7,15 ом.
Далее находим ток по формуле (8-44)
7=682/—14° а, полагая U'A=U'A.
В таком случае
Ua^U'a+ /2ф=37,5+ /2,9 кв.
Потери мощности (на фазу) и к. п. д.
LP = 11 2Гф = 1,16 Мвт\ т] =
= Р/(/> + ЗДР) = 0,92.
Расчет линии с учетом емкости. В слу-
чае симметричных относительно, длинных
линий, <в особенности кабельных линий
с большой емкостью между проводами, рас-
чет удобно вести, также переходя к пара-
Рис. 8-22.
метрам, отнесенным к одной фазе. На
рис. 8-22 схематически показаны емкости
между всеми тремя проводами кабеля
(Са в, с, ССа), а также емкости каж-
дого из проводов относительно оболочки
(Саа, Свв, Ссс). Эти емкости называют
частичными. Для симметричной линии
и кабеля
Сав = Свс = Сса
и
Саа — Свв — Ссс- (8-46)
Межпроводные емкости (С а в, Св с,
С с а) образуют треугольник, а емкости
между проводами и оболочкой — звезду.
После преобразования симметричного тре-
угольника приходим к эквивалентной звез-
де емкостей {рис. 8-23)
Сф = Саа+ЗСав (8-47)
(именно ЗСав, так как
к эквивалентной звезде от
треугольника сопротивле-
ния лучей должны быть
уменьшены в 3 раза по
сравнению с сопротивле-
ниями сторон треугольни-
ка; но уменьшению сопро-
тивления соответствует
увеличение «емкости). При
расчете не слишком длин-
ных линий \ переходя
к расчету на фазу, можно
всю фазную емкость счи-
при переходе
симметричного
Рис. 8-23.
С
тать включенной в середине линии или счи-
тать, что половина емкости Сф включена в
начале и половина в конце.
8-5. ИНДУКТИВНОСТЬ
ТРЕХФАЗНОЙ ЛИНИИ.
ИНДУКТИВНОСТЬ НА ФАЗУ
В общем .случае существования
индуктивных связей в трехпровод-
ной линии целесообразно представ-
лять эту линию состоящей из двух
петель, имеющих один общий про-
вод (рис. 8-24).
При этом каждая из двух пе-
тель / и 2 обладает -своей собствен-
1 См. следующую часть книги, где рас-
сматриваются цепи с распре де ленными па-
раметрами.
219
Рис. . 8-24.
А0-
В 0-
С 0-
Рис. 8-25.
как это показано на рис. 8-25. В та-
кой цепи уже не содержится допол-
нительных индуктивных связей1.
В симметричной линии
ной индуктивностью L] и Ь2, а меж-
ду двумя петлями существует
взаимная индуктивность М = Ь12.
Пусть линия с проводами АВС
без сопротивления замкнута в кон-
це накоротко. Две петли проводов
АВ и СВ имеют общий провод В
(рис. 8-24). Очевидно, что напряже-
ние на входе петли 1
иА—йв^^Aixi+4 С8’48)
где Х1='СО-Л1, Х12~ СО-^12-
Аналогично выражается и на-
пряжение на входе петли 2:
JJC—UB=^Icjx2 + IAjx21, (8-49)
где
Х2 -- ^21--•^'12 - <®В12.
х. = xR = хг. (8-оЗ>
A D С. 4 '
Этим равенством и определяется,
симметрия линии. Если оно не вы-
полняется, то линия несимметрична...
Из сопоставления равенств
(8-52) и (8-53) вытекает важное и
сразу неочевидное для симметрич-
ных линий равенство
L= Lr= L2 = 2L12 = 2M. (8-54}
Собственная индуктивность любой*
петли из двух проводов вдвое боль-
ше взаимной индуктивности любой
пары двухпроводных петель, из ко-
торых можно себе представить
состоящей данную симметричную
трехпроводную линию.
Симметрия трехпроводной линии
достигается соответствующим сим-
метричным расположением прово-
дов. На рис. 8-26 показаны симмет-
В случае трехпроводной линии
А “Ь О’
(8-50)
поэтому, заменяя в (8-48) 1С через IА
и iB, а в (8-49) 1А через 1В и /с,
приходим к равенствам
^4 ^12)
(8-51)
& с ° в — 7с 1 (*^2_ -^12) fв
рии. 8-26.
1 Эквивалентная схема рис. 8-25 в лю-
бом случае позволяет найти связь между
напряжением на входе (UАВ> ивс, Uqa) и
токами 1 л, /с, 1 в =— (JaA-Jc)9 Одна-
ко в случае несимметричной системы по
схеме рис. 8-25 нельзя определить напря-
жение между каким-либо из входных по-
люсов (Л, В, С) и правым узлом, к кото-
рому: сходятся все три провода,-
Эти выражения замечательны тем,
что они -соответствуют цепи, в кото-
рой каждый из проводов А, В, С
содержит свое последовательно
включенное реактивное сопротивле-
ние
«Уд — Хт Х12,
•%в ^12,
(8-52)
с---X 2 X j 2 j
220
ричный трехфазный кабель с тремя
круглыми жилами, симметричная
трехпроводная линия (она симмет-
рична, если можно пренебречь раз-
личным .влиянием земли на прово-
да) и симметричный шинопровод,
рассчитанный на десятки тысяч ам-
пер, в нем определенным образом
изогнутые медные полосы (шины)
заключены в круглую оболочку.
На рис. 8-27 изображена несим-
метричная трехфазная воздушная
линия. Она может быть сделана
симметричной путем ^ перестановки
(транспозиции) проводов по схеме
рис. 8-28. На участке линии длиной
/о каждый из проводов последова-
тельно находится в трех различных
положениях относительно двух дру-
гих.
Аналогичные выводы могут быть
сделаны для трехфазной линии
с четвертым нейтральным проводом.
В линиях с заземленными нейтра-
лями таким проводом служит зем-
ля. В случае симметрии проводов
А, В, С относительно друг друга и
относительно четвертого провода N
совершенно аналогично предыдуще-
му приходим к равенствам:
& д — ^а 1 (х хм) 1хм>
UВ ~ IВ i Лм) Av
~ С I хм) iXM‘
Рис. 8-28.
А&
3 0-
С0-
N0-
Рис. 8-29.
В этих формулах Xm=WM, где
Ni — взаимная индуктивность лю-
бых двух петель, образованных
фазным и нейтральным проводами;
х — Хм==^ф — фазные сопротивления
проводов А, В, С; xN=xM— сопро-
тивление нейтрального провода
(рис. 8-29).
Обыкновенно влияние земли не-
значительно при отсутствии тока
в земле, т. е. когда /а+Лв+^с—О и
IN=Q. В таком случае сопротивле-
ние на фазу в проводах А, В, С мо-
жет быть рассчитано, как было из-
ложено ранее для трехпроводной
линии. Индуктивное сопротивление
xN нейтрального провода для тока,
идущего по земле, значительно боль-
ше; оно приблизительно соответст-
вует индуктивности петли, образо-
ванной фазным проводом (А, В или
С) и таким же проводом, лежащим
под землей на глубине приблизи-
тельно 1000 м .(при частоте 50 гц).
Заметим, что при этом наряду с ре-
активным сопротивлением появляет-
ся и активное сопротивление, обус-
ловленное рассеянием энергии при
протекании тока в земле.
Все приведенные здесь выводы
были сделаны в предположении от-
сутствия активного сопротивления
проводов и для режима закорочен-
ного конца линии. Очевидно, что
при любом режиме найденные зна-
чения реактивных сопротивлений
оказываются включенными соответ-
ственно в провода А, В, С, N.
8-6. ТРЕХФАЗНЫЕ
ТРАНСФОРМАТОРЫ
Напряжение трехфазных систем
можно преобразовать посредством
трех однофазных трансформаторов.
Их обмотки могут соединяться как
в треугольник, так и в звезду. Наи-
221
Рис. 8-30.
более частое соединение: треуголь-
ник на стороне низшего напряжения
и звезда на стороне высшего. Такое
включение трансформаторов пока-
зано на рис, 8-30. На рис. 8-30,а
схематически показаны сердечники
трансформаторов и надетые на них
обмотки, а на рис. 8-30,6 —схема
соединений. При этом начала и
концы обмоток .одной фазы обозна-
чают а, х и А, X, другой — Ь, у и
В, У, третьей — с, z н С, Z; строч-
ные буквы относятся к обмоткам
низшего напряжения, а прописные—
к обмоткам высшего. В зависимо-
сти от порядка соединения обмоток
получается то или иное расположе-
ние векторов фазных и линейных
напряжений. Для соединения по
схеме рис. 8-30,6 на рис. 8-30,в по-
казано расположение векторов.
Хотя однофазные трансформато-
ры и применяются в трехфазных си-
стемах (главным образом при очень
большой мощности и очень высоком
напряжении), более широко распро-
странены трехфазные трансформа-
торы. В простейшем случае такие
трансформаторы имеют три сердеч-
ника: по одному сердечнику на
каждую фазу (рис. 8-31, на котором
для упрощения вторичные обмотки
не показаны). Потоки в сердечниках
связаны с напряжениями соответ-
ствующих обмоток простыми ра-
венствами:
0Ьу=ФпФь-,
/1/ — /(£>лФс.
При составлении этих равенств
для наглядности индуктированные
э. д. с. приравнены напряжениям,
т. е. не учтены падения напряже-.
ния, обусловленные активными со-
противлениями обмоток, и весь по-
ток, сцепленный с обмоткой, пред-
ставлен как поток в сердечнике.
Если сумма напряжений трех об-
моток равна нулю:
U ах + ^Ъу + ^cz = 0, (8-56)
то равна нулю и сумма потоков трех
стержней:
Фа + Фь + Фс = 0. (8-57)
Это значит, что поток каждого из'
стержней замыкается через два дру-
гих стержня, например
Фа = — Ф& —Фе-
Условие (8-56) обязательно вы-
полняется при соединении обмоток
в треугольник. Оно выполняется
также при соединении обмоток
в звезду без нулевого провода.
Вторичные обмотки трехфазного *
трансформатора соединяются неза-
висимо от соединения первичных.
Более подробный анализ работы
трехфазных трансформаторов выхо-
дит за рамки курса теоретических
основ электротехники. Некоторые
особенности трехфазных трансфор-
маторов в несимметричном режиме
будут рассмотрены в § 8-9.
8-7. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ
ПОЛЕ. АСИНХРОННЫЙ
И СИНХРОННЫЙ ДВИГАТЕЛИ
Рассмотрим сначала три катуш-
ки (рис. 8-32,а), оси которых про-
ходят через общий центр (0) и по-
Рис. 8-31.
222
словленных всеми тремя катушка-
ми:
Вх=Вха+Вхъ+Вхс. (8-59)
Аналогично для составляющих по
оси у
Ву = Вуа + ВуЬ + Въс. (8-60)
Рис. 8-32.
Из геометрического расположения
катушек ясно, что
BXa==-kiai Вуа^=^09
ВхЪ — — &zbcos60°, ВуЪ =£/bCos30°,
Вхс =—Azccos60°, ВЬс=—Azccos30°-
В таком случае
Bx = k [zа — (ib + zc) cos 60°] =
з
= kia (1 Ц- cos 60°)—klm COS <о/
(8-61)
(здесь принято во внимание, что
zc = — *а)«
Ищем теперь вторую составляю-
щую вектора индукции
By = k(ib — ic) cos 30°.
Из векторной диаграммы токов,
(рис. 8-32 Д) видно, что
ib---k = j ]/3 I а
ИЛИ
1Ъ — ic = ]/з Im cos (<nt — 90°) =
вернуты одна относительно другой
на 120°. При этом через одну катуш-
ку а проходит ток фазы А
через другую b ток
фазы В ib=‘lmcos (со/—1!20°) и че-
рез третью с ток фазы С
/c=/m'Cos(:co!/+!1200). Каждая из ка-
тушек в центре создает свою со-
ставляющую магнитного поля, ин-
дукция .которого пр опорциюн а л ьн а
току
B=\ki (8-58)
и направлена по оси катушки (век-
торы Ва, Вь, Вс на рис. 8-32,а).
Проведем координатные оси х, у
так, чтобы ось х совпадала с осью
катушки а. Очевидно, что состав-
ляющая полного, вектора магнитной
индукции по оси х равна сумме со-
ответствующих составляющих, обу-
= V31т sin со/.
В таком случае
By — k 1/3 Im cos 30° sin со/ =
= -|- Ы™ sin co/. (8-62)
Выражения (8-61) и (8-62) показыва-
ют, что вектор магнитной индукции
остается постоянным по абсолютной
величине
B~klm (8-63)
и вращается в пространстве со ско-
ростью со. Сказанное иллюстрирует-
ся рис. 8-32,в
1 Вектор магнитной индукции
3
В = ехВх + еуВу = у klm (ех cos at +
+ еу sin &t).
223
Рис. 8-33.
Направление вращения поля из-
менится на противоположное, если,
сохр аняя геом етр ическое р а оно л о-
жение обмоток, изменить -фазы то-
ков в двух обмотках, например об-
мотку b питать током фазы С, а об-
мотку с питать током фазы В.
На рис. 8-33,а показаны в разре-
зе три катушки, оси которых также
сдвинуты друг относительно друга
на 120°, а сами катушки, как и в си-
стеме рис. 8-32, питаются трехфаз-
ным током. Очевидно, что и в этом
случае создается вращающееся по-
ле. Если витки трех катушек поме-
стить в пазах полого ферромагнит-
ного цилиндра (рис. 8-3,6), а во
внутреннюю область поместить ме-
таллический ферромагнитный ци-
линдр, то в получившейся системе
также будет существовать вращаю-
щееся магнитное поле, причем зна-
чительно усиленное благодаря тому,
что значительная часть пути магнит-
ного потока лежит в среде с боль-
шой магнитной проницаемостью.
Магнитное поле во внутреннем ци-
линдре и воздушном зазоре при
этом очень похоже на поле, созда-
ваемое полюсами магнита (N — S),
вращающегося со скоростью со
(рис. 8-34) L
Принцип работы асинхронного
двигателя. Рисунок 8-33,6 можно
считать схематическим изображени-
ем асинхронного двигателя;
внешнее неподвижное кольцо — ста-
тор, обмотки которого создают вра-
щающееся поле; внутренний ци-
линдр—ротор, увлекаемый вращаю- <
щимся полем. Асинхронный двига-
тель— это именно тот двигатель, о
простоте и надежности которого го-
ворилось в связи с распространением
трехфазных систем.
Вращая магнит (рис. 8-34), легко убе-
диться в том, что он «будет приводить во
(вращение находящийся в его иоле массив-
ный п-роводящий ротор '(цилиндр или диск).
Это знаменитый опыт французского физика
и астронома Араго (диск Араго). . *
Вращая магнит при неподвижном рото-
ре, можно заметить, -что массивный ротор
тормозит вращение магнитов: для преодо-
ления тормозящего действия надо прило-
жить к магнитам вращающий момент То
и, следовательно, отдавать системе мощ-
ность A)=7oG>. Этот факт объясняется тем,
что движущееся магнитное поле наводит
1 Радиальная составляющая вектора
магнитной индукции в воздушном зазоре
выражается уравнением
В = Bm cos (coZ — а),
где а — угловая координата, отсчитываемая
от горизонтальной оси. Поле рис. 8-34 со-
ответствует моменту времени /=0.
224
в проводнике э. д. с.-, *в нем возникают вих-
ревые токи и происходит рассеяние, энергии
по закону Джоуля — Ленца. С другой сто-
роны, возникновение тормозящего момента
объясняется взаимодействием наведенных
токов с полем магнитов. Само собой разу-
меется, что такой же момент То должен
быть приложен к ротору для того, чтобы
удержать его неподвижным. Вихревые то-
ки, их взаимодействие с полем магнитов,
а следовательно, и вращающий момент 7,
испытываемый ротором, зависят от скоро-
сти относительного движения поля • магни-
тов и ротора, т. е. от разности угловых ско-
ростей вращающегося магнитного поля
<оСт и ротора (Орот. Эту разность называют
скольжением
5 = СО ст—СОр от»
Если ротор вращается с такой же ско-
ростью, с какой вращаются магниты. i(s=0),
в роторе не возникает никаких токов, так
как магниты и ротор неподвижны друг от-
носительно друга..
На рис. 8-35 представлена зависимость
вращающего момента Т от величины отно-
сительного скольжения
(0с т СОрот
с = ----------
С0с т
При -СдСт = Const.
Точка (Т='О соответствует отсутствию
относительного движения (сдСт = <йрот); при
этом говорят, что ротор вращается синхрон-
но (одновременно) с полем. Очевидно, что
в этой .точке момент, испытываемый рото-
ром, равен нулю. Точка сг='1 соответствует
неподвижности ротора. При этом на ротор
действует момент 70. Опыт показывает, что
при некоторой относительной скорости (сгм)
момент, действующий на ротор, может
иметь максимальную величину 7маКс>7о-
Объяснение этого факта требует более под-
робного анализа происходящих процессов Е
Ограничимся некоторыми замечаниями
к характеристике рис. 8-35. Если внешний
момент (момент нагрузки 7Н) больше мо-
мента 7, обусловленного электромагнитны-
ми процессами при данной скорости <ор0т,
1 При большой относительной скорости
магнитное поле, в котором находится ро-
тор, изменяется так быстро, что оно не
успевает достаточно глубоко проникнуть
в массивный ротор. Это одно из проявле-
ний поверхностного эффекта, рассматривае-
мого в теории электромагнитного поля.
то скорость ротора начнет уменьшаться до
тех пор, пока момент 7 не достигнет зна-
чения 7Н. При этом установится динамиче-
ское равновесие (ускорение равно нулю).
Но это возможно только на участке ха-
рактеристики, где 7 возрастает с уменьше-
нием скорости i(ot о=0 до о=ом). Если
момент нагрузки превосходит 7макс, двига-
тель остановится.
Ко всему сказанному остается
добавить, что когда в асинхронном
двигателе (рис. 8-33,6) вращающе-
еся поле создается трехфазным то-
ком .в обмотке статора, мощность,
необходимая для вращения магнит-
ного поля, подводится от цепи трех-
фазного тока; для нее механическая
м ощность, отдав а ема я двигателем,
может быть представлена эквива-
лентной активной нагрузкой. Оче-
видно, что когда двигатель работа-
ет, его ротор должен .-вращаться со
скоростью, меньшей, чем скорость
вращающегося поля соСт- Ротор вра-
щается со скольжением или асин-
хронно (несинхронно, неодновре-
менно) .
. Кроме асинхронных двигателей со
•сплошным (массивным) ротором, широко
применяются двигатели, .ротор которых
-имеет обмотку. В проводах этой обмотки
наводится э. д. с. при скольжении ротора
относительно вращающегося поля статора.
Ток этой обмотки, взаимодействуя с маг-
нитным полем статора, создает вращающий
момент. В некоторых машинах обмотка
ротора выводится через контактные кольца
и может -быть замкнута на регулируемое
сопротивление; меняя это сопротивление,
можно изменять зависимость момента 7 от
скольжения.
Принцип работы синхронного
двигателя. Принципиальное отличие
синхронного двигателя от
систем, изображенных на рис. 8-33,6
и 8-34, заключается в устройстве ро-
тора. Ротор синхронной машины
представляет собой магнит со сво-
ими полюсами N— 5. Он может
быть выполнен как постоянный маг-
нит (в малых машинах) или как
электромагнит. В последнем случае
в ротор закладывается обмотка, пи-
таемая от источника постоянного то-
ка через контакты (щетки), сколь-
зящие по кольцам.
Для того чтобы объяснить ха-
рактер работы синхронного двига-
теля, представим вращающееся по-
ле как поле вращающихся полюсов
15 К. М. Поливанов
225
“) б)
Рис. 8-36.
магнита; ротор машины тоже мо-
жет быть представлен как магнит
(рис. 8-36,а). Когда ось поля внеш-
них мягнитов (поле статора) совпа-
дает с осью магнитного поля рото-
ра, последний не испытывает ника-
кого вращающего момента. Именно
так расположится ротор в непод-
вижной системе. Если же оси маг-
нитных полей не совпадают (повер-
нуты на угол у), то на ротор дейст-
вует вращающий момент; он стре-
мится привести оси к совпадению,
поворачивая ротор по кратчайшему
пути. Возникновение такого момента
очевидно из магнитного закона Ку-
лона (разноименные полюсы при-
тягиваются), а также из правила
Фарадея, примененного к картине
магнитного поля, схематически изо-
браженной на рис. 8-36,6. По прави-
лу линии поля стремятся сократить-
ся по длине (они представляют со-
бой как бы растянутые упругие ни-
ти).
Зависимость вращающего момента Т от
угла у представлена на рис. 8-37. Вид этой
зависимости определяется геометрией 'маши-
ны (формой полюсов, распределением об-
моток), однако для такой зависимости
всегда остается характерным изменение
знака момента при увеличении угла у на
половину периода (на л). Поэтому при
асинхронном вращении, когда относитель-
ное расположение осей '(угол у) изменяется
со скоростью (Ост— (Орот, средний момент,
действующий на ротор, равен нулю за каж-
дый полный оборот относительного распо-
ложения осей. Из сказанного следует, что
ротор, обладающий заметной инерцией,
останется неподвижным во внешнем вра-
щающемся поле. Если вращающееся поле
создается трехфазной обмоткой пятидесяти-
периодного тока (угловая скорость со =
—314 рад/сек), то сто раз в течение секун-
ды вращающий момент меняет направление
и ротор, не успевающий за полпериода
приобрести заметную скорость, останется
неподвижным.
Рис. 8-37.
Если ротор вращается синхронно
с внешним полем (с такой же скоростью)»
то угол у остается постоянным, постоянными
остается и вращающий момент Т. Так рабо-
тает синхронный двигатель. При возраста-
нии нагрузки |(до тех пор, пока ее момент
Тн<Тмакс) увеличивается угол у, но ротор
продолжает вращаться синхронно. Если же
момент нагрузки превзойдет ТмаКс, ротор
«выпадет из синхронизма» и машина оста-
новится.
Для запуска рассмотренного здесь син-
хронного двигателя необходимо предвари-
тельно раскрутить ротор до синхронной ско-
рости с углом у, близким к нулю (предва-
рительная синхронизация), раскручивание
ротора в асинхронном режиме производит-
ся такими же силами, как в асинхронном'
двигателе. Если в асинхронном режиме
скольжение невелико (небольшая нагрузка)»
то момент синхронных сил (рис. 8-37) мо-
жет за четверть периода сам довести ско-
рость, ротора до синхронной.
В том случае, когда внешнее вращаю-
щееся поле создается неподвижной трехфаз-
ной обмоткой статора, в ней наводится
э. д. с. магнитным полем вращающегося
ротора. При у=0 наведенная э. д. с. сдви-
нута по фазе относительно тока соответст-
вующей обмотки на угол зт/2. Когда поле
ротора отстает от поля статора на угол у
(рис. 8-36,6), появляется вращающий мо-
мент Т, действующий на ротор (режим дви-
гателя). При этом сдвиг по фазе между
приложенным внешним напряжением и то-
ком становится меньше чем л/2, т. е. из:
сети поступает активная мощность, соответ-
ствующая моменту Т, умноженному на ско-
рость вращения ротора со.
Эти соображения полностью соответ-
ствуют общему 'анализу синхронной маши-
ны как элемента электрической цепи (§ 5-3)..
Направление вращения синхронных, как
и асинхронных двигателей, зависит от по-
следовательности фаз, питающих обмотки?
статора.
8-8. НЕСИММЕТРИЧНАЯ
ТРЕХФАЗНАЯ ЦЕПЬ
ПРИ СТАТИЧЕСКОЙ НАГРУЗКЕ
Трехфазную цепь при несиммет-
ричной нагрузке и несимметричных
источниках можно рассматривать
просто как разветвленную цепь
с несколькими источниками пита-
ния, применяя к ее расчету общие
226
методы. Это утверждение неприме-
нимо к цепям с вращающимися ма-
шинамщ поскольку их эквивалент-
ное сопротивление зависит от степе-
ни несимметрии приложенного на-
пряжения. В некоторых случаях оно
неприменимо и к цепям с трехфаз-
ными трансформаторами. Подроб-
нее этот вопрос рассматривается
в следующем параграфе, посвящен-
ном специальным методам расчета
несимметричных трехфазных цепей.
Здесь мы ограничимся цепями со
статическими нагрузками (без вра-
щающихся машин) при заданных
напряжениях генератора (без учета
его внутренних сопротивлений). Рас-
смотрим несколько характерных
примеров несимметричных трехфаз-
ных систем.
Звезда — звезда. Такую ‘цепь
(рис. 8-38) при любых фазных на-
пряжениях UA, -UB, Uс и любых со-
противлениях в трех лучах звезды
ZA, ZB, Zc и в нейтральном проводе
ZN целесообразно рассчитывать как
цепь с двумя узлами, определяя
прежде всего смещение ней-
трали по формуле [см. (2-105),
§ 2-8] цепи с двумя узлами
tj ___&ауа+^вув + ^сус
ya + yb+Yc + Yn
Зная это напряжение, легко найти
все фазные токи. Например,
(8-65)
Пример 8-6. По кабельной ливни с фаз-
ным- сопротивлением 2ф=г$=0,051 ом («ка-
бель с сечением медных жил 35 мм2 при
длине ~il00 м) и с сопротивлением ней-
трального провода Z^=f№0,14 ом пи-
тается осветительная нагрузка, состоящая
из трех групп ламп ’мощностью по <10 кет
при напряжении 127 в, включенных между
фазой и нейтралью. Фазное напряжение на
’входе кабеля t/ф = 130 в.
Считая сопротивление каждой группы
не зависящим от напряжения и равным
гп = 1,61 ом, .найти фазное напряжение U'$
•на выходе кабеля: 1) при нормальной на-
грузке и 2) при отключении одной группы
ламп (нагрузка остается только в двух
фазах), как показано на рис. 8-39.
Решение. 1) При нормальной нагруз-
ке по ранее найденным формулам
U'$ = U$ — 1гф — ~ ~ гн = 126 в.
• ф ' н
2) При отключении одной фазы рас-
чету подлежит цепь рис. 8-39. Для нее
tf/V'TV— Vaya 2Ya+Yn
= 4,66-/8,10 в,
где
£/Л = [7Л = 13Э в. Ул=(2ф+гв)-’
Токи в фазах А и В:
1А = Фа - У а = 75,5/-3°40' а-,
1В = Фв - У А = 75.6Z-• 123°40' а.
При этом напряжение на включенных
группах ламп
= IдГн U'в IBKr =
К системе звезда — звезда без
нейтрального провода можно при*
менять тот же метод расчета, пола-
гая Ук = 0. Однако несколько проще
в этом случае исходить из заданных
227
15*
Рис. 8-40.
б)
Рис. 8-41.
линейных напряжений, представляя
их .в виде двух источников, вклю-
ченных между тремя фазными по-
люсами, например так, как показа-
но па рис. 8-40,а. Рассматривая та-
кую цепь как цепь с двумя узлами
А и N', находим напряжение между
узлами по формуле
fr &СА YC + ^ВА YB
Зная это напряжение, легко найти
на топографической диаграмме по-
ложение точки N' (-рис. 8-40,6).
Дальнейший путь расчета очевиден.
Цепь для определения последо-
вательности фаз. Присоединив к од-
ной фазе, которую условно
можно считать фазой А, чисто
реактивный элемент (конден-
сатор или .индуктивность), к
двум другим фазам включают
электрические лампы накали-
вания (рис. 8-41,а). Из-за не-
симметричного смещения точ-
ки N' одна из ламп окажется
горящей ярко, а другая туск-
ло.
Если в фазе А включен
конденсатор, то ярче горит
лампа в отстающей фазе
(в фазе В).
Действительно, по фор-
муле (8-66)
и = й_______s.__
N'A
где U = 0CA+UBA (рис.
8-41,0, g = l/r.
Выбирая g—wC, находим
ЧТ0 ^N'A = V (°’4 /°’2).
Для этих данных -построена
диаграмма -на рис. 8-41,6.
Напряжение на лампе *в фа-
зе С изображается отрезком
N'C, а на другой лампе—от-
резком N'B.
При индуктивности в
фазе А ярче горит лампа в
опережающей фазе (в фа-
зе С).
Однополюсное замыкание на
землю. Рассмотрим трехпровод-
ную линию электропередачи, в ко-
торой каждый из проводов обла-
дает емкостью С на землю, а ней-
траль N -источника .(обычно это нейтраль
вторичной обмотки трансформатора) может
быть соединена с землей через индуктивную
катушку :(рис. 8-4'2,а). Пусть в такой линии,
питаемой от симметричного трехфазнбго ис-
точника, происходит замыкание на землю
одного Из проводов, например фазы С, как
показано на схеме рис. 8-42,а.
Требуется определить ток в месте про-
исшедшего замыкания, равный току в фа-
зе С.
Для простоты расчета не учитывается
влияние остальных параметров цели; они
или не влияют на результат (емкость меж-
ду проводами, незначительное фазное со-
противление цроводов), пли осложняют рас-
чет (внутреннее сопротивление источника,
сопротивление в месте замыкания на землю
и др.).
Для большей четкости на рис. 8-42,6
228
изображена расчетная схема, из которой
ясно, что
Л? = а + в)’»
4 =
А - ^с) № + (йв_ йс) jvc
или
Л4 "Е Ав = ci^c •
поскольку в симметричном трехфазном
источнике
^л + ^в — йс.
Таким образом, искомый ток замыка-
ния на землю
Если нейтраль N не заземлена, первое сла-
гаемое ’в круглых скобках следует полагать
равным нулю i(/№=0).
‘-При надлежащем выборе значения ин-
дуктивности для заданной линии, а именно
при 1/соА—ЗсоС, ток однофазного ' замыка-
ния на землю равен нулю. Включение та-
кой индуктивности в нейтраль было пред-
ложено немецким инженером Петерсеном
(катушка Петерсена, предназначенная для
предупреждения образования электрической
дуги при замыкании одного из проводов на
землю).
Смешанные соединения. Когда
нагрузка соединена в треугольник
•и линейные напряжения известны,
ток в каждой ветви находится сра-
зу >по закону Ома. Сложнее обстоит
дело, когда между -полюсами ‘источ-
ника А, В, С с известными напря-
жениями и треугольником нагрузки
включены фазные сопротивления
линии (ZA, Zb, Zc на рис. 8-43,а).
В этом случае «рекомендуется преоб-
разовать треугольник (Zb Z2, Z3)
в эквивалентную звезду; сопротив-
ления в лучах такой звезды (ZZA,
Z7B, Z'c на рис. 8-43,6) оказываются
последовательно включенными с
фазными сопротивлениями линии, и
расчету подлежит уже знакомая
цепь.
Р-ис. 8-43.
Определив в такой цепи потен-
циал узлов Л', В7, С', легко найти
токи в ветвях треугольника.
Задача еще усложняется, если
к узлам Л', В', С7, кроме треуголь-
ника, присоединена звезда. В этом
случае рекомендуется: 1) звезду
преобразовать в треугольник; 2) сло-
жить параллельные ветви двух тре-
угольников; 3) преобразовать этот
•новый треугольник в звезду и прий-
ти к расчету цепи, показанной на
рис. 8-43,6.
Преобразовывая сначала тре-
угольник в звезду, мы пришли бы
к цепи с двумя звездами, подклю-
ченными к узлам Л', В7, С7, как это
показано на рис. 8-44. Важно обра-
тить внимание на то, что ветви та-
ких звезд нельзя рассматривать как
параллельные, поскольку потенциа-
лы их нейтралей N7 и N" могут быть
различны.
Если требуется рассчитать цепь
-рис. 8-44, то следует: 1) сначала
преобразовать каждую из звезд
в треугольник; 2) сложив парал-
лельные ветви двух треугольников,
прийти к одному эквивалентному
треугольнику; 3) преобразовать этот
эквивалентный треугольник в экви-
валентную звезду. После последней
операции приходим к расчету цепи
чо знакомой схеме (рис. 8-43,6).
Наглядность метода преобразова-
ний и его универсальность при рас-
четах несимметричных трехфазных
цепей делают понятным то обстоя-
тельство, что этот метод был раз-
работан и предложен американским
инженером Кеннели именно для ра-
счета трехфазных цепей. В дальней-
шем, как видно из гл. 2, этот ме-
тод получил широкое применение и
при анализе других сложных цепей.
229
Расчет сложных несимметричных
трехфазных цепей очень трудоемок.
В цепях энергетических систем
обычно приходится учитывать толь-
ко несимметрию, вызванную обры-
вом провода или коротким замыка-
нием в одной из точек цепи. При
этом для расчета сложных цепей
часто пользуются расчетными сто-
лами (моделями). Ряд особенностей
реакции реальных трехфазных це-
пей на несимметричные режимы за-
ставляет переходить к специально-
му методу расчета, понятие о кото-
ром дается в следующем парагра-
фе.
8-9. СИММЕТРИЧНЫЕ
СОСТАВЛЯЮЩИЕ НЕСИММЕТРИЧНОЙ
ТРЕХФАЗНОЙ ЦЕПИ
Разложение несимметричной си-
стемы векторов на три симметрич-
ные. Обозначим три комплекса (или
вектора), изображающих гармони-
чески изменяющиеся величины бук-
вами А, В, С. Три вектора образуют
симметричную систему прямой
последовательности, обозна-
чаемую индексом 1, когда
А1=^аВ1 = а2С1, иначе
в\а2А1У С^аА^ (8-67)
Л2 на фазный угол 2л/3, а вектор С2
отстает от вектора А,2 на такой же
угол 2л/3 (рис. 8-45,а в центре).
Очевидно, что для векторов, обра-
зующих систему обратной последо-
вательности,
Я2 = яЛ2, С2 = а2Л2. (8-68)
Три вектора могут образовать и
третью симметричную систему. Ее
называют системой нулевой (по-
следовательности и соответ-
ствующие векторы снабжают индек-
сом 0. Три вектора симметричной
системы нулевой последовательно-
сти равны друг другу (рис. 8-45,а
справа):
А0 = В0 = С0. (8-69)
Складывая одноименные векто-
ры трех разных последовательно-
стей, получаем несимметричную си-
стему (рис. 8-45,6):
Л = Ло -]- Л1 Л2;
в^в.+в^в,,
с=с0 -j- Ci 4“ С2.
Выразив составляющие всех ^сим-
метричных систем через соответст-
вующие векторы Ло, Ль Л2 по фор-
мулам (8-67) — (8-69), представим
только что написанную систему ра-
где а-—известный уже фазный мно-
венств в таком виде:
житель трехфазной системы (рис.
8-5). Три вектора прямой по-
следовательности изображены сле-
ва на рис. 8-45,а. Три вектора могут
образовать и другую симметричную
систему, называемую системой о б-
ратной последовательно-
Л — Ло 4~ Л14~ Л2;
В = Ао 4- cl2Аг —j— clA2\
с=Ло 4- ^Лх 4“ &2Л2.
(8-70)
Определитель этой системы уравне-
ний
с т и. Векторы обратной последовав
тельности обозначают индексом 2.
В системе обратной последователь-
ности вектор В2 опережает вектор
1 1 1
1 а2 а
1 а а2
=з(«—«2)=/зГз
Рис. 8-45.
230
отличен от нуля. Следовательно, эта
система всегда может быть решена
относительно Ао, Аг, А2 при задан-
ных А, В, С:
Л0 = (А + 5 + С)/3;
Аг = (А —[— аВ —|- я2С)/3;
Д — (Л + я2В + аС)/3.
(8-71)
Решение легко находится, если
иметь в .виду, что а3='1 и что
1 +а+а2=\0.
Таким образом, для любой за-
данной системы трех векторов А, В,
С можно найти составляющие пря-
мой, обратной и нулевой последова-
тельностей.
Пусть, например, фазные напря-
жения генератора, соединенного
в звезду, несимметричны и равны
IJA, Uв. >UC (рис. 8-46,а)..Такой ге-
нератор может быть представлен
в виде трех источников напряжения
в каждой фазе (рис. 8-46Д) при ус-
ловии, что
Рис. 8-46.
U в = aU2 [70;
(8-72)
и, следовательно,
’j, = fia+aOB + a‘L>c}/3-,
Л ..гЪ 7.
(8-73)
Пример 8-7. В системе рис. 8-46,а
<UA = 300 в, йв = — /200 в, йс = /200 в)
требуется найти симметричные составляю-
щие напряжения.
Решение. По формулам (8-73) на-
ходим:
Uo = 100 в, йг = 215 в, Сг2 = — 15 в.
Правильность найденного решения
можно проверить по формулам (8-72).
Физическое различие сопротивле-
ния симметричной цепи для состав-
ляющих разных последовательно-
стей. К расчету токов в цепи с не-
симметричным источником может
быть применен принцип суперпози-
ции в силу линейности всех пара-
метров. При этом расчет цепи с сим-
метричными параметрами сводится
к трем операциям: 1) при действии
симметричного источника прямой
последовательности находится сим-
метричный ток прямой последова-
тельности для фазы A —
2) определяется ток обратной после-
довательности для той же фазы А
I2 — U2jZ2; 3) определяется ток нуле-
вой последовательности 1Q — UJZQ.
После того как найдем все сим-
метричные составляющие токов,
легко находятся токи в фазах А,
В, С по формулам (8-70), применен-
ным к токам
(8-74)
Для выполнения указанного расчета
необходимо знать сопротивления на
фазу прямой. (Zi), обратной (Z2) и
нулевой (Zo) последовательностей.
В общем случае эти сопротивления
различны.
Сопротивление для токов нуле-
вой последовательности. В симмет-
ричной цепи, соединенной в звезду
231
Рис. 8-47.
о симметричной воздушной линии
или статической нагрузке. В этом
случае сопротивления проводов
одинаковы для токов всех трех
последовательностей. Совершенно
иначе обстоит дело, когда в цепь
включены трансформаторы или вра-
щающиеся машины.
На рис. 8-48,а представлены од-
нофазные трансформаторы в трех-
фазной цепи. Их первичные обмот-
ки соединены в звезду, нейтраль
которой соединена с нейтралью ге-
с нейтральным проводом при дейст-
вии источников нулевой последова-
тельности (рис. 8-47), токи во всех
фазных проводах одинаковы (/0),
а ток в нейтральном проводе /*№’
= 3/0. Поэтому, если сопротивление
каждой фазы Z$, а сопротивление
нейтрального провода ZN, то по
второму закону Кирхгофа
tre = /o^ + 3/0Z;v = /0Z0> (8-75)
откуда сопротивление на фазу для
токов нул ев ой п осл едо в а тел ьн ости
Zo^ + SZ^ (8-76)
Ток нулевой последовательности
может проходить в цепи только
при наличии нейтрального провода
или двух заземленных нейтралей
в начале и в конце линии. В по-
следнем случае Zo определяется
в основном сопротивлением систе-
мы провод — земля.
Понятие сопротивления на фазу
Zo для токов нулевой последователь-
ности не нуждается в дополнитель-
ном объяснении* когда речь идет
Рис. 8-48.
нератора.
Вторичные обмотки трансфор-
матора отключены от внешней
цепи (режим холостого хода). На
рис. 8-48, а вторичные обмотки
соединены в звезду, а на рис. 8-48,6—-
в треугольник. В остальном транс-
форматоры одинаковы. Оказывают
ли обмотки трансформаторов одина-
ковое сопротивление Zo для токов
нулевой последовательности в этих
двух случаях? Будут ли они отли-
чаться от сопротивления на фазу
для токов прямой последовательно-
сти? На эти вопросы нетрудно отве-
тить.
При соединении звезда — звезда
во вторичных обмотках ток отсут-
ствует и сопротивление в каждой
фазе очень велико: оно равно вход-
ному сопротивлению трансформато-
ра при холостом ходе Z0=Zix. При
этом во вторичных обмотках наво-
дится э. д. ю. Однако она не играет
никакой роли, поскольку вторичные
обмотки соединены звездой, а внеш-
няя цепь отключена.
Если же вторичные обмотки со-
единены треугольником, в них воз-
никает такой же ток, как
при их коротком замыка-
нии. Действительно, э. д. с.
нулевой последовательности
во всех трех обмотках оди-
накова по величине и по
фазе. В таком случае со-
противление на фазу оказы-
вается равным входному
сопротивлению трансформа-
тора при коротком замыка-
нии вторичной обмотки Zo=
=Z1K. Как было показано в
§ 6-3, у трансформатора Zix
превосходит Z1K в 100 раз и
даже больше.
232
В том случае, когда в трехфаз-
ной цепи применяется трехстержпе-
вой трансформатор |(рис. 8-31) с об-
мотками звезда — звезда, ZQ значи-
тельно .меньше, чем Zix, так как во
всех трех стержнях поток Фо -дол-
жен быть одинаковым и, следова-
тельно, он не может замыкаться це-
ликом через ферромагнитные сер-
дечники. Поэтому индуктивность об-
моток существенно уменьшается.
Сопротивления прямой и обрат-
ной последовательностей. В симмет-
ричных цепях без вращающихся ма-
шин сопротивления прямой и обрат-
ной последовательностей совпадают:
Zt = Z2 = Z^. (8-77)
Иначе обстоит дело при наличии
вращающихся машин.
Действительно, пусть в синхрон-
ной машине вращающееся поле соз-
дается токами прямой последова-
тельности и ротор вращается с той
же скоростью ко, что и поле. Э. >д. с.,
наводимая в обмотках статора вра-
щающимся ротором, принадлежит
также к системе прямой последова-
тельности. Следовательно, состав-
ляющие напряжения обратной по-
следовательности не уравновешива-
ются встречной э. д. с. вращающей-
ся синхронной машины. Напряже-
ния обратной последовательности
уравновешиваются лишь падением
напряжения в обмотках.
В случаях асинхронного двига-
теля, как уже говорилось, режим
определяется скоростью относитель-
ного вращения внешнего поля и ро-
тора. Пусть токи прямой последо-
вательности создают поле, вращаю-
щееся со скоростью icoi=’coct, в та-
ком случае токи обратной последо-
вательности создают поле, .вращаю-
щееся с такой же скоростью в про-
тивоположную сторону: <02=—<01 =
——«ст- Поэтому относительная ско-
рость для прямой последовательно-
сти Q] = сост—фрот, где (Орот — ско-
рость вращения ротора; для
обратной последовательности И2 =
=—(сост +’0)рот). Очевидно, что эк-
вивалентное входное сопротивление
симметричного асинхронного двига-
теля совершенно различно для то-
ков прямой и обратной последова-
тельностей.
Заметим еще, что поле обратной
последовательности создает вра-
щающий момент Т2, действующий
навстречу моменту Д поля прямой
п ос л е д ов ател ьн ости.
Если одна из фаз цепи, питаю-
щей двигатель, -оборвана, то напря-
жения прямой и обратной последо-
вательностей оказываются равными
(£Л =—(72). Если ротор асинхронно-
го двигателя неподвижен и к его
полюсам подведены только две фа-
зы, то он и остается неподвижным,
так как в этом случае относитель-
ные скорости поля прямой и обрат-
ной последовательностей одинаковы,
а следовательно, одинаковы и про-
тивоположно направленные момен-
ты Г1 = Т2.
Если же отключить одну фазу
у вращающегося асинхронного дви-
гателя, то при небольшой нагрузке
он будет продолжать вращаться,
так как момент прямой последова-
тельности оказывается больше
встречного момента (несмотря на
равенство напряжений прямой и об-
ратной последовательностей).
Мощность, выраженная че-
рез симметричные составляющие.
Пусть в цепи известны симметричные-
составляющие напряжения U2, Uo
и токи Д, Д, /0. Мощность, отда-
ваемая такой системой
s=uAL+uBfB+uc/Ci
равна сумме мощностей, отдаваемых
прямой обратной S2 = tZs/2!
• *
и нулевой S0 = c/0/0 последователь-
ностями в отсутствие других состав-
ляющих. Иначе, говоря, мощность
взаимодействия токов одной последо-
вательности и напряжений другой
последовательности равна нулю. Этим?
характеризуется ортогональность раз-
ложения на симметричные состав-
ляющие.
Утверждение, что
S = S1-|-S2-|-S0,
легко доказать. Например, для то-
ка нулевой и напряжения прямой
последовательностей
233.
= t7/o(l + ^ + a) = 0.
Аналогично для тока .прямой и на-
пряжения обратной последователь-
ностей и т. д.
Пример 8-8. К двигателю приложена
^несимметричная система напряжений, вели-
чины которых приведены в примере 8-7. Со-
противления прямой и обратной последова-
тельностей двигателя соответственно Zi =
=3,0+/3,0 ом и Z2=0,i15+/0,5 ом. Ней-
тральная точка двигателя изолирована. Тре-
буется найти токи в цепи, питающец дви-
гатель, и мощность, подводимую к двига-
телю.
Решение. Зная соответствующие на-
пряжения разных последовательностей из
примера 8-7, находим, что
/ — 45° а;
Л = £/2/Z2 = _ 30,0 Z. — 73°20' а.
/Мощность, отдаваемая двигателю,
S = 3 (i/iZ* + U2I2) =24,1 + /25 кет.
Расчет цепи с несимметричными
параметрами. Метод симметричных
•составляющих широко применяется
к расчету трехфазных цепей с сим-
метричными генераторами и несим-
метрией, вызванной короткими за-
мыканиями или обрывами проводов.
В этом случае удобно предполагать,
что несимметрия обусловлена вклю-
чением дополнительного эквива-
лентного несимметричного источни-
ка (генератора) при симметрии
jBcefi остальной цепи.
Различают два вида несиммет-
рии: продольную и поперечную. При
продольной несимметрии
•эквивалентный источник включает-
ся «в рассечку» трехфазной линии.
На рис. 8-49,а и б представлены два
случая продольной несимметрии,
когда один из проводов оборван
(а) и когда в одной из фаз сопро-
тивление нагрузки Zh замкнуто на-
коротко (б). Включенный в цепь
эквивалентный генератор несим-
метричен, а вся остальная цепь мо-
жет уже рассматриваться как сим-
метричная' На рис. 8-49,в показано,
что эквивалентный генератор содер-
жит последовательно включенные
источники напряжения прямой, об-
ратной и нулевой последовательно-
стей. Действительный генератор, пи-
тающий цепь, симметричен пря-
мой последовательности, его э. д. с.
(в фазе Д) равна Эр
Определив для симметричной це-
пи сопротивления прямой Zp обрат-
ной Z2 и нулевой Zo последователь-
ностей, составляем уравнения для
одной фазы всех трех последова-
тельностей:
0=t72+z2z2=t72+/2(z+zH);
o=£/0+/0z0=t7e+70(z+
+ ZH + 3ZAJ). I
(8-78)
В этих уравнениях э. д. с. генера-
тора отлична от нуля только для
прямой последовательности. Система
трех уравнений (8-78) содержит шесть
неизвестных (t7x, U2, Uo, /х, I2,
поэтому она должна быть дополнена
еще тремя уравнениями, которые оп-
ределяются по виду нарушения сим-
метрии.
В случае обрыва провода в фазе
А (рис. 8-49,8) одно из этих допол-
234
нительных уравнений очень легко
записать:
/л = Д + /а + 7о = 0 (8-79)
(обрыв в фазе А). Два других урав-
нения следуют из того, что напря-
жения эквивалентного генератора
в фазах В и С (рис. 8-49,в) равны
нулю (провода непосредственно сое-
диняют конец линии с нагрузкой,
рис. 8-49,а). Следовательно,
^1«2+у2«+^о=0;
^4 <2 4“ ^2<22 + ^0 = 0.
(8-80)
Три дополнительных уравнения сов-
После подстановки этих значений в
(8-78) получим простые выражения
для всех интересующих нас величин.
Так, в общем случае
IJ _i) __________
— ZjZa +Z2ZO +Z0Zt ’
а при Z1 = Z2
с^эдЖоТ^)-
В случае короткого замыкания
(рис. 8-49,6) основные уравнения
(8-78) имеют такой же вид. Изменя-
Рис. 8-50.
местно с тремя основными позволя-
ют определить искомые токи
-j—/0,
/—- 1yCL - j— /2^
/ —о/ — Г I /
1N--02 о--1 в 1 1 С 9
а также напряжение между концами
оборванного провода
[71+(72 + (7о=^,.
Несмотря на угрожающий вид по-
лученной системы уравнений (шесть
уравнений и шесть неизвестных),
она решается чрезвычайно просто.
Действительно,. из (8-80) легко най-
ти1, что Ub = U2 — U1. Также легко
найти из (8-79), что —/0 = /1Ц-/2<
1 Путем сложения и вычитаний урав-
нений.
ются только дополнительные урав-
нения, которые записываются так:
U,a + U2a2 + U. = 0 (8-81)
(короткое замыкание на сопротивле-
нии ZH в фазе С);
t/i 4- и2 4- uQ=(/i 4-12 4-1 q) zH
(8-82)
(напряжение эквивалентного гене-
ратора в фазе А равно падению на-
пряжения в сопротивлении ZH, че-
рез которое проходит ток фазы Л);
4- 4- и Q =
= (М24-М + Л)^н (8-83)
[то же, что (8-82), но только для фа-
зы В].
При поперечной несимметрии эк-
вивалентный генератор включает-
ся параллельно к трехфазной ли-
235
нии, как показано на рис. 8-50 при
однополюсном замыкании на зем-
лю. Для простоты в этом случае не
учтены сопротивления генераторов
в линии (к тому же их можно счи-
тать малыми по сравнению с сопро-
тивлением индуктивности, включен-
ной в нейтраль).
Можно показать, что напряже-
ние ' эквивалентного генератора
в этом случае имеет составляющую
нулевой последовательности, рав-
ную и противоположную по знаку
напряжению фазы, замкнувшейся
на землю, а также составляющую
прямой последовательности, совпа-
дающую с напряжением (э. д. с.)
источника.
При этом потенциалы точек А,
В, С в левой и правой схемах
рис. 8-50 оказываются одинаковы-
ми. Составляющие прямой последо-
вательности не создают тока нуле-
вой последовательности (в симмет-
ричной цепи). Поэтому весь ток
в нейтрали эквивалентного генера-
тора, равный току замыкания на
землю, обусловливается нулевой со-
ставляющей.
Для нулевой составляющей на-
пряжения эквивалентного генерато-
ра индуктивная катушка L и три
емкости С оказываются включенны-
ми параллельно. Поэтому приЗсоС =
=i1/g>L в цепи получается резонанс
токов и ток эквивалентного генера-
тора равен нулю, как показано
в § 8-8.
Общий случай несимметричной систе-
мы. Когда несимметричны источники и
параметры цепи, э. д. с. любой симметрич-
ной составляющей способна вызвать токи
всех трех составляющих. Уравнения такой
цепи имеют следующий вид:
Э1 == 1 iZii + /2Z12 + / ©Zi0;
Э2 == i 1Z21 + 12Z22 4“
Эь—i iZoi 4-1 2z02 4* Az00
или
/i = ByYii Э2У 12 4~ io;
/2 = ЭТУ21 4- ЭТУ22 4- ЭТУ20J
/0== Э-УУ01 4“ ЭТУ02 4~ ЭТУoo.
В этих выражениях Zmn и Утп— переда-
точные сопротивления и проводимости од-
ной из симметричных составляющих отно-
сительно другой.
ГЛАВА ДЕВЯТАЯ
НЕСИНУСОИДАЛЬНЫЕ ТОКИ
В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
9-1. СЛОЖНЫЕ ГАРМОНИЧЕСКИЕ
ТОКИ В ЛИНЕЙНОЙ ЦЕПИ
В электротехнике очень часто
приходится встречаться с перемен-
ным током (или напряжением), со-
стоящим из ряда простых гармони-
ческих (или гармонических состав-
ляющих), например:
/ — /0 4" Am cos (<о/ -|~ ах) -[-
4-/3m COS (3«rf + а3)
или
u=U0+U 1ТП cos(<o/4-p1) +
-f- Usm cos (2®£ p2).
На рис. 9-1 приведены графики
соответствующих функций при раз-
ных начальных фазах щ., аз» Pi, р-2-
На графике по горизонтальной
оси откладывается время в одина-
ковом масштабе для любой гармо-
нической, поэтому их аргументы
(в радианах, градусах или долях
периода) имеют разные масштабы:
отрезок, соответствующий л/2 (или
90°) для первой гармонической, для
n-й гармо!Н1Ической соответствует
уже пл/2 радиан (или п90°). За
этим надо строго следить при по-
строении, в особенности откладывая
начальную фазу (ai, ^2, .-pi, • •)•
Полезно самостоятельно построить гра-
фики функций с различными начальными
фазами, например график функции
f = Fim COS (<о/ + 30°) —
— F2m sin (3<Df 4-60°}
при
F эти — 0,25F irn,.
236
Амплитуды и начальные -фазы
различных гармонических состав-
ляющих определяют спектраль-
ный состав сложной гармониче-
ской функции. (При одинаковом
спектральном составе по амплиту-
дам, т. е. при совпадающих ампли-
тудах гармонических составляющих
одинаковой частоты, вид функций
может быть различен, если не сов-
падают значения их начальных фаз,
как это отчетливо видно из сопо-
ставления кривых рис. 9-1,а,б или
в, г.
В некоторых электротехнических
устройствах играет роль именно вид
кривой; однако часто существенным
оказывается только спектральный
состав по амплитудам. Так, напри-
мер, если давление воздуха, созда-
ваемое телефонной мембраной, из-
меняется во времени, как показано
на рис. 9-1,в или г (аналогично а
или б), звуковое ощущение остается
одинаковым.
Сложные гармонические функ-
ции могут быть как периодическими,
так и непериодическими. Они перио-
дичны в том случае (и только в том
случае), когда существует время Т,
кратное каждому из периодов гар-
монических составляющих.
Наименьшее возможное значение
Т (наименьшее общее кратное) и
является периодом сложной гармо-
нической функции. Например, для
суммы двух гармонических с пе-
риодами 1\ и Т2
T^lT^kT^ (9-1)
где I и k — наименьшие возможные
целые числа Ч
Любая сумма простых гармони-
ческих
f (0 = X Ап cos
п
при целых (или рациональных) п,
есть периодическая функция.
Замечательное свойство гармо-
нических функций заключается
в том, что любая периодическая
функция может быть представлена
как сумма конечного или бесконеч-
ного ряда простых гармонических
с-оста1вляющих с надлежащим обра-
зом подобранными амплитудами и
начальными фазами (ряд Фурье).
Разложение периодических функций
на гармонические составляющие
рассматривается в § 9-6 и 9-7.
1 По определению
f2 (f) = fz it + y2) = f 2 (f 4- kT2).
Следовательно, при условии (9-1)
f(i) = fi (0 + f2(<) = fi (t + +
+ f2 (t + kT2) = f(t+T).
237
Однако f (/) =Л1 cos (coiZ+ai) +
+Л2соз (-со^ + аг) оказывается не-
периодической, если отношение
(oi/co2 не выражается рациональным
числом (см. § 9-7).
Чаще всего сложный спектраль-
ный состав напряжений и токов
встречается при передаче сигналов
(информации) и при их преобразо-
ваниях. В обычных энергетических
системах, в особенности в трехфаз-
ных линиях передачи энергии, стре-
мятся поддерживать напряжение
строго синусоидальным, т. е. содер-
жащим единственную гармониче-
скую составляющую. При этом
существуют довольно строгие тре-
бования к допустимому содержа-
нию высших гармонических. ;В та-
ких системах высшие гармониче-
ские возникают главным образом
из-за нелинейных характеристик
многих реальных элементов элек-
тротехнических устройств; прежде
всего это относится к току в цепях
недогруженных трансформаторов.
Но, как и во всей электротех-
нике, в энергетических устройствах
находят шипокое применение ион-
ные или полупроводниковые (вен-
тильные) устройства, преобразую-
щие, например, переменный ток
в постоянный. Напряжение на вы-
ходе такого преобразователя наря-
ду с доминирующей постоянной
составляющей содержит и высшие
гармонические. На рис. 9-2,я пока-
зано напряжение, получающееся на
выходе шестифазного выпрямителя^
а на рис. 9-2,6 ив — напряжение
на выходе одно- и двухполупериод-
ных выпрямителей.
Чрезвычайная гибкость, просто-
та и безынерционность управленйя
электромагнитными процессами по-
средством электронно-ионных и по-
лупроводниковых приборов привели:
к применению их как в системах
связи и автоматики, так и в энер-
гетических устройствах. Например,,
можно «открывать» путь току
в различные моменты полупериода
(рис. 9-3,в), тем самым регулируя:
отбираемую от сети мощность.
В автоматике, ра-
диотехнике и связи, в
элементах математиче-
ских машин, выполня-
ющих сложные логиче-
ские функции, часто
бывает важным посы-
лать сигналы высокой
частоты (иногда очень
большой мощности) в.
течение опр ед ел енного
интервала времени* Гг
и повторять такие сиг-
налы через период Т
(отношение Г/Ti ха-
р актер изует скв аж-
ность сигн алов). • Для
этого специальный ге-
нератор посылает си-
стему периодически по-
238
вторяющихся прямоугольных им-
пульсов (рис. 9-3,6). Подавая по-
добные импульсы напряжения на
генератор высокой частоты, можно
заставить его работать в течение
действия импульса и бездейство-
вать в течение пауз (рис. 9-3,в).
Впрочем, прямоугольные импульсы
широко применяются и независимо
от их заполнения высокочастотны-
ми колебаниями.
Очень важный тип сложной гар-
монической функции представляют
собой гармонические колебания,
амплитуда которых модулирует-
ся (изменяется) по гармониче-
скому закону:
и = Uo (1 -}- т cos GO cos
при Q < о),
где т — глубина модуляции (как
правило, m<l); Q— частота моду-
ляции; со—основная или несущая
частота. Закон изменения амплиту-
ды модулированных колебаний
(огибающей) зависит от вида мо-
дулирующего сигнала. При простом
гармоническом модулирующем
сигнале [с(/) на рис. 9-4,а] и полу-
чается модулированное колебание
(9-3), представленное на рис. 9-4,6.
Колебания, показанные на рис.
9-3,в, также модулированы по
амплитуде, однако в них моду-
лирующий сигнал имеет прямо-
угольную форму (рис. 9-3,6). Кроме
простейшей амплитудной модуля-
ции, существуют и другие виды мо-
дуляции (см. § 9-7).
Модулированные колебания вы-
сокой частоты имеют исключитель-
ное значение, так как после их
выпрямления — детектирова-
ния воспроизводится именно мо-
дулирующий сигнал (рис. 9-4,а).
Вся радиосвязь и телевидение ос-
нованы на передаче модулирован-
ных высокочастотных колебаний..
•Интересно, что в случае про-
стейших колебаний, гармонически
модулированных по амплитуде
(9-3). очень легко найти все гармо-
ни веские составляющие. Действи-
тельно, применяя формулу
cos a cos 6 = ~ [cos (а Д- Ь) Ц-
-j-cos (а— #)],
приводим выражение (9-3) к следую-
щему виду:
и — Uo cos (ot 4- mU0 cos (<»— О) 14~
4—mU0 cos (<d 4- Q) t.
(9-4)
Таким образом, гармоническое
колебание с гармонически модули-
рованной амплитудой состоит из
трех простых гармонических состав-
ляющих с основной или несущей
частотой оз и с двумя боковыми
частотами со—Q и со+й.
Все изложенное показывает
важность анализа цепей со слож-
ными гармоническими токами или%
как принято говорить, цепей с не-
синусоидальными токами;
при этом, конечно, подразумева-
ются периодические токи при уста-
новившемся режиме.
Задача, которую мы ставим себе
в этой главе, заключается в изло-
жении методов расчета и анализа
линейных цепей со сложными гар-
моническими токами. Вопрос о воз-
никновении таких токов и о преоб-
разовании их формы будет рас-
смотрен в части книги, посвященной
нелинейным цепям.
9-2. РАСЧЕТ ЦЕПЕЙ
ПРИ СЛОЖНЫХ ГАРМОНИЧЕСКИХ
ТОКАХ
Основные методы расчета. Осно-
вываясь на принципе наложения
(суперпозиции), справедливом для
239
линейных цепей, можно вести ра-
счет для каждой гармонической
в отдельности и потом суммировать
результат.
Такой метод расчета имеет наи-
большее распространение в тех слу-
чаях, когда необходимо найти спек-
тральный состав реакции цепи на
сложное гармоническое возмущение.
В тех случаях, когда периодическое
возмущение содержит большое чи-
сло высших гармонических (сущест-
венно несинусоидальное возмуще-
ние) и когда при расчете и анализе
важно найти не только спектраль-
ный состав реакции, но и функцио-
нальную зависимость реакции от
времени, следует применять сущест-
венно отличные методы расчета, из-
ложенные в гл. 13.
В настоящей главе будут рас-
сматриваться решения, основанные
на принципе наложения.
Пусть известен спектральный со-
став напряжения, заданный в ком-
плексной форме:
U(jn^) = Un = UnZ}n9 (9-5)
т. е. даны амплитуды и начальные
фазы всех гармонических составля-
Складывая мгновенные значения
соответствующих гармонических
(представленных в комплексной
форме), можно найти искомое мгно-
венное значение тока
со
i С) = Л + Re у; /21пе~,п^, (9-7)
«=1
где 70 — постоянная составляющая
тока, соответствующая
п=0.
Спектральный состав тока, так
же как и характеризующая его кри-
вая i(t)r может существенно^ отли-
чаться от спектрального состава на-
пряжения и характеризующей его
кривой «(/), если линейное сопро-
тивление зависит от частоты Ч
Этот очень простой метод расче-
та иллюстрируем несколькими ха-
рактерными задачами.
Сглаживание пульсирующего на-
пряжения. Источник напряжения и
.содержит, кроме постоянной состав-
ляющей, ряд высших гармонических.
Нагрузка г соединена с источником
питания ('рис. 9-5,а) через последо-
вательно включенную индуктивность
для уменьшения колебаний тока на-
Рис. 9-5.
6)
ющих с частотами ncoi, или, проще
говоря, комплексные напряжения
каждой n-й гармоники.
Пусть рассматриваемое напря-
жение приложено к ветви с ком-
плексным сопротивлением, значение
которого известно для любой часто-
ты ПСОр
Z = Zn = /<fn.
В таком случае легко найти все гар-
монические составляющие тока
I71 171 / ^*71 ==‘ --
—фп» (9.5)
грузки. Действительно, индуктив-
ность, не оказывая никакого влия-
ния на постоянную составляющую
тока, представляет для высших гар-
1 По заданному спектральному соста-
ву (9“5) мгновенное значение напряжения
может быть представлено в форме ряда
Фурье
п=ос
и (О = Uq + У2 Un cos (nG^t + Р„).
п~\
В такой же форме может быть представ-
лено и мгновенное значение тока
л=оо
г (О = /0 + V1п cos (ncoif + а„).
п=1
240
конических сопротивление ргацЬ.
Для этой же цели параллельно с на-
грузкой включен конденсатор, через
который ответвляются высшие гар-
монические составляющие.
Индуктивность L и емкость С
в схеме рис. 9-5,а составляет Г-об-<
разный фильтр, задерживающий
высшие гармонические. Те же эле-
менты L и С можно включить и по
схеме симметричного Т-фильтра
(рис.. 9-5,6), где L1=£2='L/2.
Не ставя перед собой задачу
полного анализа работы таких филь-
тров (теории фильтров посвящены
специальные главы во второй части
книги), поставим следующие кон-
кретные вопросы:
а) во сколько раз уменьшится
процентное содержание высших гар-
монических в токе по сравнению
с напряжением при конкретных зна-
чениях г, L, С и ncoi?
б) при какой схеме соединений
Полагая Z2 = 0 и — находим
для цепи рис. 9-5,а
/ —и ________ 1____________
J п-,--------------------—
г у (1 — n2^LC)2 + п2<£>\ —
В обоих случаях для постоянной
составляющей
^о— г •
Пусть в напряжении источника со-
держатся гармонические составляю-
щие с частотами Зсо! и бсоь Их ам-
плитуды
[/3 = -{У0/723 и UQ=UofnQ.
Обозначим амплитуды тока соответ-
ствующих гармонических:
В таком случае из выведенных фор-
мул получаем для цепи рис. 9-5,6:
(рис. 9-5,а или 6) сглаживание пуль-
саций тока более эффективно?
Применяя обычные методы рас-
чета с комплексами к цепи рис.
9-5Д находим, что для n-й гармо-
нической (частота /гсох) ток в на-
грузке
U __________1----------->
п г (.1 — n^LiC) + /ИСО! (Li +
+L2—/22<of LxL2C)
ИЛИ
и для цепи рис. 9-5,а
, 1
Ц -------------------------------
Из последних формул легко уви-
деть, что устройства, подобные по-
казанным на рис. 9-5, будут сглажи-
вать пульсацию тока далеко не при
всех параметрах. Действительно,
при больших значениях сопротивле-
ния нагрузки г подкоренное выра-
жение может оказаться меньше еди-
ницы. Прежде всего это относится
/ + L2— n2(^LiL2C)2
(1 _ n2co2 L.C)2 + п2^--------------------------
Полагая L1 = L2 = L/2, находим для цепи рис. 9-5,6
16 К. М. Поливанов
241
к области частот, для которых пер-
вая скобка в подкоренном выраже-
нии приближается к нулю.
Сказанное легко объяснить из об-
щефизических соображений: при
большом сопротивлении г цепь об-
разует последовательный резонанс-
ный контур. При этом для некото-
рых частот амплитуда гармониче-
ской составляющей напряжения на
конденсаторе может во много раз
превосходить амплитуду соответст-
вующей гармонической составляю-
щей на входе.
Закончим анализ .рассматриваемой цепи
вычислением для конкретных параметров:
г =10 ом, coiL=15 ом, Ш1С=0,0300 сим
(L^SQmzh и С«-100мкф при 01=314 сект1).
В таком случае для гармонических со-
ставляющих в схеме рис. 9-5,а при п=3
/3=т3-0,183, при п=6 /б=^6 • 0,0570,
а в схеме рис. 9-5,6 при п=3 /3=т3-0,48,
При л=6 /б=тб • 0,0355.
При заданных параметрах схема рис.
9-5,6 оказывается менее эффективной для
третьей гармонической, ню более эффектив-
ной для шестой и более высоких гармони-
ческих.
Искажение модулированного ко-
лебания в резонансном контуре.
В радиотехнике, связи, автоматике
и .др. сигнал передается и восприни-
мается как огибающая модулирован-
ных гармонических колебаний. При
этом модулирующий сигнал может
также иметь сложный спектральный
состав, который и будет воспринят
после выпрямления (детектирова-
ния). Так, например, модулирован-
ное напряжение
Uo (1 + ш1 CQsQJ-Ymz cos fl2Z) cos
при высокой несущей частоте coi
(скажем, порядка 1 Мгц) модули-
руется на звуковой частоте Qi с од-
ной глубиной модуляции mb а на
звуковой частоте Q2 с другой глу-
биной модуляции т2.
Очень часто по одной и той же
кабельной линии (не говоря уже
о радиоволнах в эфире) передаются
сигналы на многих различных несу-
щих частотах. Для того чтобы вы-
брать из множества сигналов имен-
но тот, который нас интересует, про-
ще .Bicero .настроить приемное
устройство в резонанс с той несущей
частотой, которая передает интере-
сующую нас информацию. Такое
устройство в принципиальных чер-
тах показано на рис. 9-6. Напряже-
ние на выходе (т. е. напряжение на
конденсаторе цепи рис. 9-6) выра-
жается формулой (5-92), выведен-
ной при анализе резонансных явле-
ний:
с Wl + (Q“)2
где Q — добротность контура;
'<1 = <в/ш0;
1
а — 71---.
7]
При высокой добротности (Q =
= 200—500) сравнительно незначи-
тельное отступление от резонансной
частоты приводит к резкому относи-
тельному уменьшению напряжения
на выходе. Так, при Q = 500, 13 = 0,9,
а=—0,21 получаем Uc =5,30 U&
вместо 500 /70 при резонансе.
Но мы знаем, что при амплитуд-
ной модуляции с частотой Q появ-
ляются наряду с несущей частотой
coi колебания на боковых частотах
-i- mUo [cos (о) — Q) t cos (да -|- Q) £].
Как пройдут эти колебания через
остронастроенный колебательный
контур? Как изменится отношение
глубины модуляции на часто-
тах Qi и Й2 в выходном напряже-
нии? Если это отношение на входе и
выходе будет сильно отличаться, то
изменится спектральный состав оги-
бающей. Вместе с тем мы знаем,,
что, например, различные звуки че-
ловеческой речи характеризуются
именно разным спектральным соста-
вом. Искажение спектра огибающей,,
т. е. воспроизведенного после детек-
тирования сигнала, приведет и к ис-
кажению передаваемой речи.
Пример 9-1. Сравнить отношение
на входе и на выходе цепи .рис. 9-6 при до-
бротности контура Q = 500, несущей частоте
1,6 Мгц (со1 = 2л: • 1,6 • 106 сект1), нижней
242
звуковой частоте 250 гц (Qi==2ji • 250 сек-1),
доминирующей ов гласных, и верхней звуко-
вой частоте 5,5 кгц (Q2=2jt • 5,5 • 103 сек-1),
доминирующей в свистящих согласных
(рис. 3-31).
Решение. Допустим, что на входе
глубина модуляции на этих двух частотах
была одинаковой вх—1 и найдем
(mi/m2)Bbix. Для этого требуется найти от-
ношение Uc\IUc2 на двух как верхних, так
и нижних боковых частотах:
ЛМ У1 +(Q°»2)2
\ т2 Дых UC2 7)1 1 + (Q«i)2
Так как
1,6-Ю6 + 250
1,6-106
1,6-106 + 5,5-103
1,6-Ю6
= 1 + 0,0034, а2 = 0,0068» Qa2 = 0,34,
то
Такое искажение практически незаметно.
Предположим теперь, что несущая ча-
стота взята в 10 раз меньшей, а именно
160 кгц (это еще диапазон радиоволн); все
остальные условия остаются неизменными.
В этом случае
1, т]2 = 1,034, а2 — 0,068.
Рис. 9-7.
Q®2 — 3,4, (^1/Ш2)вых — 3,54.
Такое искажение уже заметно.
Разумеется, в арсенале электротехники
существует много средств, позволяющих
компенсировать такое искажение. Однако
всем хорошо известно ухудшение звучания
музыки в радиоприемниках низкого класса
и искажение тембра человеческого голоса
при t телефонных разговорах вследствие не-
достаточно широкой полосы пропускаемых
частот.
Простейшая энергетическая цепь
при несинусоидальном напряжении.
На рис. 9-7+ изображена простей-
шая схема передачи энергии от ис-
точника напряжения и к потребите-
лю R, L через линию с сопротивле-
нием г. Для уменьшения потерь
в линии параллельно с потребите-
лем включен конденсатор для ком-
пенсации фазного сдвига.
Как уже говорилось, в энергети-
ческих системах всегда стремятся
получить практически синусоидаль-
ное напряжение. Но мы, напротив,
предположим напряжение несину-
соидальным для того, чтобы выяс-
нить те недостатки, которыми обла-
дает такая система.
Подробнее анализ этой цепи бу-
дет проведен в § 9-4, посвященном
мощности в цепи со сложными гар-
моническими токами. Здесь ограни-
чимся только вычислением распре-
деления токов.
Пусть напряжение на входе име-
ет вид (рис. 9-7,6):
и = Uim (cos W---cos
k & J
при £/ = 1/^/1^2 = 5400 в h7<d =
= 314 сек~х\ параметры цепи7 г =
= 10 ом, R = 100 ом\ <»L = 100 ом.
Емкость подобрана так, чтобы
для первой гармонической реактив-
ная составляющая тока нагрузки
полностью компенсировалась. При
этом ток источника совпадает по фа-
зе с напряжением, а входное сопро-
тивление чисто активное.
16*
243
Запишем входное сопротивление
для первой гармонической:
R + j [g>L (1 — <&LC) — VCR*]
(1 — co2£C)2 + (шСТ?)2
Чтобы получить выражение входно-
го сопротивления для третьей гар-
монической, достаточно в получен-
ной формуле рядом с каждым со по-
ставить множитель 3:
23 = г +
R + / [3coL (1 — 9g>2ZZ?) — ЗсоСТ?2]
(1 — 9со2ЛС)2 + (ЗсоС/?)2
Очевидно, что входное сопротив-
ление для первой гармонической чи-
сто активное при
шЛ (1 — cd2LC) — «О?2 = О,
откуда
Я2 + (соЛ)2 •
При данных числовых значениях
<д^ = 25б сим и с°2^С=0,5.
В таком случае, произведя вычис-
ление, найдем, что
2^ = 210 ом, Z3=16b9—j83 ом,
< /, = ^-=25,7 а, /, = -
Ла 1 OZ# з
= —21Д/78э30' а.
График мгновенных .значений тока
построен на рис. 9-7,в.
Напряжение на параллельных
ветвях (нагрузка и конденсатор)
проще всего найти теперь как раз-
ность входного напряжения и паде-
ния напряжения в сопротивлении г,
9-3. ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ
И ДРУГИЕ ХАРАКТЕРИСТИКИ
СЛОЖНЫХ ГАРМОНИЧЕСКИХ
ВЕЛИЧИН
Действующее (эффективное)
значение мы уже определили как
средне квадратичное за период и до-
статочно подробно останавливались
на смысле такого определения. Оно
применимо к любой периодической
функции, в том числе и представ-
ляемой рядом гармонических со-
ставляющих.
Действующее значение функции
может быть определено путем непо-
средственного (аналитического или
графического) интегрирования квад-
рата мгновенных значений. Однако,
если известен спектральный состав
периодической функции, действую-
щее значение может быть определе-
но непосредственно по ряду ампли-
туд всех гармонических составляю-
щих.
Допустим, что периодическая
функция (напряжение, так и т.- д.)
f (0 = Рй + Рут cos (ю/ + aj +
4- F2m cos (2«>/ + a2) 4-...
. 4- Fkm cos {kwrt 4- afe) 4-... (9-8)
В таком случае ее среднее квад-
ратичное
=1/^4-^ + ^ + ..- + ^+---’
(9-9)
где
г? F 1т г; Fkm
F1=W’
— действующие значения соответст-
вующих гармонических.
Выражение (9-9) легко доказы-
вается. Квадрат функции (9-8) со-
держит сумму квадратов всех сла-
гающих ряда и сумму членов, содер-
жащих произведение простых гар-
монических с разными частотами:
fmn (t) = cos cos (шо/-ф- an)
при n^m.
(9-10)
Среди них содержатся и произведе-
ния, в которых т=0; результат ум-
ножения постоянного члена FQ на
любую гармоническую.
Но интеграл за период Т от про-
изведений типа (9-10) тождественно
244
обращается в нуль L Поэтому от-
личной от нуля оказывается только
сумма интегралов от квадратов про-
стых гармонических составляющих;
но каждый из интегралов равен
именно действующему значению со-
ответствующей гармонической.
Пример 9-2. Напряжение как функция
времени представляется равносторонним
треугольником (рис. 9-8). Найти его дейст-
вующее значение: ’1) прямым интегрирова-
нием; 2) применяя формулу (9-9) к извест-
ному разложению напряжения в гармониче-
ский ряд
Г-1-
U = Uм акс о
4 / . COS ScOj/ ,
JF (cos(Ojf Ч------&------4
и ограничиваясь двумя и тремя первыми
членами разложения.
Решение. Представляя функцию на
участке О <С t Tj2 уравнением и =
1
“^7максуу2^ и вычисляя интеграл от а* 2
только на интервале 0 — Т/2 (что можно
сделать из соображений симметрии), полу-
чаем:
U макс
Гз
0,577£7макс
По формуле разложения» ограничиваясь
двумя членами, находим:
0,575(7 макс»
что очень близко к истинному значению.
Учет третьего члена дает незначительную
поправку.
Точное суммирование членов бесконеч-
ного ряда, поскольку
96 ’
приводит, разумеется, к точной формуле.
Пример 9-3. Требуется найти действую-
щие значения напряжения и тока на входе
цепи рис. 9-7,а по данным, приведенным
в конце § 9-2.
f тпп (i) = чу cos
+ cos [(от — n) + Vnm].
Для каждого из слагаемых при m ф п
в одном периоде Т — 2^/0)! содержится
нескольких целых периодов.
Решение. На входе напряжение
и == Uim (cos coj/ —cos , поэтому
по формуле (9-9)
(7Bx = i7, j/ 1 +у=1/, 1,052 =
= l,052I7lm/J?2 = 5 700 в.
Ток i на входе определяется комплексами
/1 = 25,7 а, /3 = —21.22/78°30',
поэтому действующее значение входного
тока
I = 25,72 4- 21,22 = 33,3 а.
Различного вида средние. Еще
три средних значения часто пред-*
ставляют важную характеристику
периодических функций: арифмети*
ческое среднее за период, выражаю-
щее постоянную составляю-
щую
т
(9-11)
О
среднее по модулю
т
= 1/(01^ (9-12)
О
и, наконец, среднее максималь-
ное за половину периода
4+Г/2
— 2 С
/макс ^ср.макс i
(9-12')
Среднее за половину периода за-
висит от выбранного интервала, т. е.
от выбранного значения tx. По опре-
делению /1 выбирается так, чтобы
интеграл был максимальным Ч
г Пусть, например, f (/) — Um cos со/. Вы-
бирая /1=0, получаем интеграл равным ну-
лю. Полагая /1 = 1,5 зт/со, получаем макси-
мальное -значение интеграла, равное
2 (7 ттг /зт.
245'
Данное здесь определение при-
меняется к периодическим функци-
ям, когда они удовлетворяют следу-
ющим условиям симметрии:
ИЛИ
При этих условиях постоянная со-
ставляющая отсутствует. Для про-
стой гармонической функции
Fcp--4f“=:°’637/'’"’
где Fm — амплитуда, FCp — среднее
по модулю или среднее максималь-
ное, так как для простой гармони-
ческой эти средние совпадают.
Физический смысл среднего по
модулю поясним на примере измере-
ния переменного тока магнитоэлек-
трическим прибором, включенным
через выпрямляющую цепь, которая
показана на рис. 9-9,а. В каждом из
плеч моста включен вентильный ди-
од— элемент, свободно пропускаю-
щий ток одного направления и не
пропускающий ток противоположно-
го направления.
На рис. 9-9,6 показаны графики
тока f, поступающего на вход вы-
прямляющего моста, и тока iA, про-
ходящего по диагонали, в которую
включен амперметр. Показания ам-
перметра магнитоэлектрической си-
стемы пропорциональны среднему
значению проходящего тока вслед-
ствие инерционности системы и пря-
мой пропорциональности момента
току. Поэтому такой амперметр,
включенный по схеме рис. 9-9,а, по-
казывает именно среднее значение
тока по модулю.
Рис. 9-9.
Чтобы объяснить, зачем нужна
величина, которую мы здесь назва-
ли средней максимальной за поло-
вину периода, рассмотрим напряже-
ние, индуктируемое изменяющимся
потоком:
u(t) = dWjdt.
Как видно из (9-12'),
АФ —— U
макс— 2 v ср. макс
ИЛИ
Uср.макс =2/АТмакс,
где f=\/T — частота.
Коэффициенты, характеризующие
форму. Для характеристики формы
периодических кривых вводятся ко-
эффициенты амплитуды &а,
ф о р м ы <Аф и искажений £и. Ко-
эффициент амплитуды определяется
как отношение максимального зна-
чения к действующему:
(9-13)
для простой гармонической функ-
ции (для синусоиды) ^а = 1/2=1,41.
Коэффициент формы равен от-
ношению действующего значения
к среднему по модулю или к сред-
нему максимальному за половину
периода:
(9-14)
СР
для простой гармонической функции
(для синусоиды) &ф=1,11.
Коэффициент искажения опреде-
ляется как отношение действующего
значения основной гармонической
к полному действующему значению:
ka = ^-. (9-15)
В электроакустике вводится еще
коэффициент kf, называемый коэф-
фициентом гармоник (клирфакто-
ром). Он равен отношению действу-
ющего значения всех высших гар-
монических Fs к действующему зна-
чению основной гармонической:
где ^о—•
(9-16)
246
Заметим, что последние
два коэффициента можно
определить, зная спектраль-
ный состав только по ампли-
тудам. Для определения
остальных коэффициентов
требуется знание самой
функции, которую можно
построить по спектральному
-составу, если известны и
.амплитуды, и фазы каждой
гармонической.
Измерения при наличии
разных гармонических. По-
казания приборов разных
систем по-разному 'зависят
от формы кривой напряже-
ния и тока. Это всегда следует пропорционально
иметь в виду, когда измеряемые
величины могут иметь сложный
спектральный состав.
Представим себе, что в цепь тока
включены амперметры по четырем
схемам, изображенным на рис.
9-10,а. Через амперметр 1 проходит
весь ток Zi = f; через 2— только
положительная составляющая; че-
рез 3—ток Z3 = |^|; через 4 (он вклю-
чен через измерительный трансфор-
матор)— только переменная состав-
ляющая.
Допустим, что ток имеет форму
равностороннего треугольника (рис.
*9-10,6) при t>0 и /Макс =100 а или
форму равностороннего треугольни-
ка, но без постоянной составляющей
(рис. 9-10,в).
Что покажут амперметры, если
по принципу действия они показыва-
ют: А — действующее значение;
Б — среднее значение; В — макси-
мальное значение? Ответ представ-
лен в таблице.
Рис. 9-10.
максимальному
или среднему значению, но шкала
проградуирована в действующих
значениях при измерении простых
гармонических величин. Показания
этих приборов неправильны при
сложном гармоническом воздейст-
вии.
На основании измерений, резуль-
таты которых приведены в таблице,
можно определить коэффициенты
амплитуды и формы для кривых
рис. 9-10,6 и в (они одинаковы!):
у __/макс__ 100__50 ___ Z7T
— 5778“'2879"“ V °’
, I 57,8 28,9 2 . 1С-
50 ~ 25 — уз— I’15’
Чтобы найти коэффициент иска-
жения, необходимо выделить пер-
вую гармоническую.
Отдельные гармонические можно
выделить посредством резонансных
контуров, настроенных на опреде-
• Система амперметра Включение по схеме
1 1 2 3 4
А (действующее) Б (среднее) В (максимальное) 57,8/28,9 50/0 100/50 57,8/14,5 50/12,5 100/50 57,8/28,9 50/25 100/50 28,9/28,9 0/0 50/50
Над чертой указаны значения,
•соответствующие кривой тока б, под
чертой — соответствующие кривой
тока в (рис. 9-10).
Большое распространение имеют
«еще приборы, показание которых
ленные частоты. Схематически та-
кой простейший гармонический
анализатор изображен на рис.
9-11. В нем через индуктивность £0
проходит только постоянная состав-
ляющая; первая гармоническая
247
пройдет через следующую парал-
лельную ветвь, для которой
вторая гармоническая пройдет через
ветвь, для которой
Так как обычно все сопротивления плеч
моста одинаковы: Г1==Г2=Гз=Г4, то
1
kf Ut rt
И Т. Д.
Разделение гармонических про-
изводится тем точнее, чем выше до-
бротность каждого из резонансных
контуров и чем больше индуктивное
сопротивление ацЛо-
Рассмотрим в заключение мостовую
цепь (рис. 9-Г2), применяемую для измере-
ния коэффициента гармоник kf переменного
напряжения, не содержащего постоянной
составляющей.
Ветвь 1 настраивается емкостью С
в резонанс на основную частоту Oj. При
балансе моста, когда rilr2=r2lr^ напряже-
ние на диагонали моста UАБ = Ua (положе-
ние переключателя а) минимально, так как
для основной гармоники мост находится
в равновесии. Для высших гармоник сопро-
тивление ветви 1 столь значительно, что
практически напряжение Ua равно падению
напряжения от тока высших гармоник на
сопротивлении г4:
Во втором положении переключателя
(положение б) вольтметр измеряет падение
напряжения на сопротивлении г от тока
основной частоты:
причем величина г -подбирается перемеще-
нием движка потенциометра так, чтобы по-
казания вольтметра в первом (а) и вто-
ром (б) положении были одинаковы;
Ua = U6.
т. e. kf определяется по положению движка
на потенциометре ветви 2.
Для уменьшения погрешности в изме-
рении kf выбирают L и С так, чтобы до-
бротность ветви 1 была не меньше 10:
При этом сопротивление ветви 1 для выс-
ших гармонических гораздо больше, чел®
для основной.
9-4. МОЩНОСТЬ
Определение мощности, средней
за период,
т
P^^uidt. (9-17)
О
применимо к любым периодическим
функциям u(t) и i(t). Если напря-
жение и ток состоят из ряда гар-
монических, то под знаком интегра-
ла окажется сумма произведений
гармонических одной частоты вида
и nm COS (««>/ + Р„) I пт COS (fUOj + <ХП)
и сумма произведений гармонических
разных частот вида
U пт COS + pn) I km COS (kwj -]- ай)
При
248
Очевидно, что каждое из слага-
емых первого типа после интегриро-
вания окажется равным средней
мощности соответствующих гармо-
нических
рп = UnrrJnr. cos _ ап) =
--U Til 71 ц» (9“18)
Интеграл за целый период Т в про-
изведениях второго типа тождест-
венно обращается в нуль (см. также
§ 9-3). Таким образом, мы прихо-
дим к очень важному результату:
средняя мощность периодического
тока, состоящего из ряда простых
гармонических, равна сумме сред-
них мощностей всех гармонических:
Р = £ Рп—и010 + UJ1 cos ?х +
«=;0
+ UJ2 cos <р2 +... (9-19)
При этом постоянные составляющие
/0, Uo рассматриваются как гармо-
нические составляющие с нулевой
частотой.
По аналогии с понятиями, выве-
денными для цепи простого пере-
менного тока (т. е. содержащего
единственную гармоническую со-
ставляющую), среднюю мощность Р
называют активной и вводят поня-
тия реактивной мощности
Q = У Qn—sin ?! +
э Д sift ?2 4~ • • • (9-20)
и полной (кажущейся) мощности
S=UI=
(9-21)
Последняя определяется как произ-
ведение действующих значений на-
пряжения и тока. Из сопоставления
выражений (9-19), (9-20) и (9-21)
очевидно, что в общем случае
&^P*+Q?. (9_22)
Квадрат полной мощности ра-
вен сумме квадратов активной и
реактивной мощностей только в
случае, когда кривая тока i(t)
имеет такой же вид как кривая на-
пряжения u(t). Практически это
имеет место только в цепи с чисто
активным сопротивлением, одина-
ковым для всех гармонических
u{t)
В силу сказанного вводят еще
один вид мощности, характеризую-
щий различие ;в форме кривых тока
и напряжения, эту мощность назы-
вают мощностью искажения
Т = /S2 — Р2 — Q2. (9-23)
Заметим, что законы сохранения
применимы к активной и реактив-
ной 1 * * мощностям: сумма соответст-
вующих мощностей всех источников
равна сумме соответствующих мощ-
ностей всех потребителей. Этот за-
кон неприменим к мощности иска-
жения Т и так называемой полной
мощности S.
Из сопоставления выражений
для 5’и Р можно вывести понятие
коэффициента мощности, который
по аналогии с цепями простого гар-
монического тока обозначают как
cos 6:
’ Р = S cos 6 = UI cos 0. (9-24)
Последнему выражению соответ-
ствует представление сложных гар-
монических функций эквивалент-
ными простыми гармоническими
(эквивалентными синусоидами)
с действующими значениями U и I
и с фазовым сдвигом 0.
Если для таких эквивалентных
простых гармонических определить
эквивалентную реактивную мощ-
ность
Q3 = Ssin0, (9-25)
мы придем к еще одному понятию
мощности, которую можно назвать
эквивалент но й реактивной.
Из сопоставления (9-24), (9-25)
с (9-23) найдем, что
Q8 = + Q2 = /S2 — Р2. (9-26)
1 К реактивной мощности вакон сохра-
нения 'применим только в случае линейных
цепей.
249
Низкий коэффициент мощности
<cos 0, как и cos <р в цепях с простым
переменным током, характеризует
недоиспользование источников и ли-
ний передач и приводит к сущест-
венному понижению к. п. д.
В цепях со сложными гармони-
ческими токами полная компенса-
ция коэффициента мощности невоз-
можна, как это видно из анализа
депи рис. 9-7,а, проведенного
в § 9-2. Компенсация реактивной
мощности потребителя по первой
гармонической приводит к значи-
тельному реактивному току третьей
гармонической.
Пример 9-4. Определить • мощности на
«входе цепи Р, Q, S, Т и к. п. д. цепи рис.
"9-7,а. Сравнить с результатами, получен-
ными для той же цепи, но питаемой от се-
'ти, содержащей только основную гармони-
ческую составляющую. Параметры цепи:
.г=10 ом, Р=!100 ом, соЛ=100 ом,
^=200 ом,
и = 5 400 I cos 314 t—g-cos3-314M в.
Решение. По данным, вычисленным
-в конце § 9-2 и в примере 9-3, находим все
виды мощности на входе:
Р — Uili cos <pi + 17373 cos у3 = 146 кеш;
= C/171 sin 4- sin <р3 = — 37*4 кеар',
S — UI — 190 ква\ Т = 115 ква.
Зная действующее значение тока 7 и
-сопротивление линии г, находим к. п. д.
"передачи энергии
Р — 1Ч
7] =----р-----100 = 92,50/0.
В случае простого гармонического напря-
жения при той же отдаваемой мощности
Р — 146 кет имеем U = иг — 5 530 в, I —
= 71 = 26,3 а. При этом Q = 0, Т = 0 и
S = Р. Коэффициент полезного действия
Р— 72г
т) = —-р .100 — 95,5о/о.
В энергетических системах выс-
шие гармонические составляющие
.могут приводить и к другим неже-
лательным эффектам. Они увеличи-
вают коэффициент амплитуды, что
в установках высокого напряжения
ъюжетбыть существенным; часто по-
является опасность резонансов на
частотах высших гармонических;
высшие гармонические создают ме-
шающие влияния энергетических си-
стем на линии связи и сигнализации.
О некоторых особенностях высших
гармонических в трехфазных систе-
мах будет сказано в следующем
параграфе.
9-5. ВЫСШИЕ ГАРМОНИЧЕСКИЕ
В ТРЕХФАЗНЫХ СИСТЕМАХ
В симметричных трехфазных це-
пях токи и напряжения в любой из
фаз смещены на 7з периода основ-
ной гармонической относительно то-
ков и напряжений в других фазах.
Но 7з периода основной гармониче-
ской равна целому периоду третьей
гармонической. Поэтому третьи гар-
монические в трехфазных симмет-
ричных цепях оказываются совпада-
ющими (рис.\9-13). То же самое
можно сказать о всех гармониках,
кратных трем, и о постоянной со-
ставляющей (в симметричной систе-
ме). В общем случае для напряже-
ний п-х гармонических в фазах А,
В, С симметричной системы выпол-
няется соотношение
. 2и . 2 тс
. . ]п — . — jn —
UAn=UBn^ = Uc^ • (В 9-27)
Аналогично для токов
. 2тс . 2тс
1П-— . — Щ —
= = 'с.е . (9-28)
250
Из написанных формул очевид-
но, что гармонические, кратные
трем, образуют нулевую последова-
тельность; гармонические 2, 5, 8, 11
и т. д. образуют обратную последо-
вательность, в то время как 1, 4, 7
и т. д. образуют прямую последова-
тельность.
Сказанным объясняется особен-
ность поведения третьих гармониче-
ских (и кратных трем) в симмет-
ричных трехфазных системах: в ли-
нейном напряжении эти гармониче-
ские отсутствуют; в нейтральном
проводе течет утроенный ток этих
гармонических; при отсутствии ней-
трального провода напряжение меж-
ду нейтральными точками звезды
«определяется только этими гармони-
ческими; если в фазных э. д. с. со-
держатся третьи гармонические, то
при соединении обмоток генератора
в треугольник в них протекает гок
даже при отсутствии нагрузки
(в фазном напряжении, которое
в последнем случае совпадает с ли-
нейным, конечно, не может появить-
ся третьих гармонических, так как
в каждой из фазных обмоток э. д. с.
третьей гармоники полностью ком-
пенсируется падением напряжения).
Особенно резкое влияние на ли-
нии связи оказывают гармоники,
кратные трем, трехфазных линий
передачи . -с заземленными нейтра-
лями.
Токи этих гармонических как
токи нулевой последовательности
проходят по широкой петле (про-
води земля) и имеют повышенную
частоту, к тому же близкую к ча-
стотам спектра разговорной речи.
Пример 9-5. Известно, что в фазном
напряжении обмоток трансформатора со-
держатся первые и третьи гармонические
«составляющие. Система симметрична. При
«соединении обмоток в звезду найдено фаз-
ное напряжение, равное 131 кв, «и линейное
напряжение, равное 220 кв. Чему равно
фазное напряжение третьей гармонической?
Решение. Фазное напряжение U& =
= <41 +4з> а линейное U2 = (^ЗС/ф1)2.
Поэтому 317фз — 3{7ф — СУ®, откуда
^ФЗ=|/ кв'
9-6. РАЗЛОЖЕНИЕ
ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
НА ГАРМОНИЧЕСКИЕ
СОСТАВЛЯЮЩИЕ
По фундаментальной теореме
Фурье любая периодическая функ-
ция
f(O=f(/+n
может быть разложена на простые
гармонические составляющие, часто-
ты которых равны целым кратным
основной частоты:
f(O=ae+
“ЬУ* («п cos nw^t + bn sin (9-29)
n=l
где
2тг .
при этом все амплитудные коэффи-
циенты 6ZO, ^i,..., bi, b%,..., опре-
деляются по формулам Фурье —
Эйлера:
Т/2
«0=4-
—Т/2
Т/2
ап — ~г cos n^t dt\ (9-30)
—Т/2
Т/2
bn = -^- \ f (/) sin funj dt.
—Т/2
После элементарного преобразо-
вания
a.
n cos n^,t bn sin —
— dncosinw^— фп), (9-31)
где
a2^b2-= d2
n 1 n n
И
можно ряд (9-29) представить и в
такой форме:
оо
f (/) = da -j-V dn cos (ло>/ — ф„) =
n=l
co
= d0 + v Re {dne 1Фпеina>lt}, (9-32)
/г— 1
где d0 = a0.
Совокупность амплитуд dn и со-
ответствующих фаз фп называют
251
спектром функции. Периодиче-
ские функции обладают дискрет-
ным спектром.
Графически можно представить
спектральный состав функции в си-
стеме координат dn, -со или f, Отрез-
ки dn, пропорциональные амплиту-
дам, называют спектральными ли-
ниями. На рис. 9-14,а показан спектр
треугольной кривой тока (рис.
9-10,6), а на рис. 9-14,в — спекгр
прямоугольной периодической функ-
ции (рис. 9-14,6). Если ограничить-
ся первыми девятью слагаемыми
спектра (отличными от нуля), функ-
ция получит вид, отличный от за-
данной, но приближающийся к ней
(рис. 9-14,г).
Если периодическая функция за-
дана не аналитически, а в виде гра-
фика, то при разложении ее в ряд
Фурье коэффициенты ряда можно
определить приближенно, заменяя
интегралы (9-30) суммой. Для это-
го период Т кривой на графике де-
лят на k равных частей, после чего
коэффициенты ап и Ьп определяют
из следующих выражений:
здесь ап и Ьп представлены как уд-
военные средние арифметические
значения произведений ординат
в k последовательных точках на со-
ответствующие значения косинусов
и синусов; ао — среднее значение
функции за период, приближенно
равное среднему значению ординат
в k точках.
Для разложения в гармониче-
ский ряд, кроме графоаналитиче-
ских методов, применяются специ-
альные приборы, называемые гармо-
ническими анализаторами.
Ряд Фурье в симметричной ком-
плексной форме. Такое представле-
252
ние ряда наиболее удобно для ана-
лиза спектрального состава функций
и для целого ряда расчетов.
При этом наиболее важна воз-
можность непосредственного пере-
хода от дискретного спектра перио-
дических функций к непрерывному
спектру функций апериодических.
Последнее очень важно для теории
переходных процессов (гл. 12).
Как известно из теории комплек-
сного представления простых гар-
монических функций (см. § 4-2) г
Re[tZne~;'4/n<M]==
= (Cne/ra“,i + C_fte“/'2<”1<), (9-33)
где
п 1 . —/Фп
С тг- 2
И
C_n=Td^n,
Поэтому ряд (9-32) можно предста-
вить в таком виде:
f(0= У Cnein^. (9-34)
п——оо
Сопоставляя это выражение с ранее
записанными (9-29), (9-31) и (9-32),
находим, что при
Сп = 4г (ап ~jbn) = спе~1Фп, (9-35)
где
tg^n = bn/an
При /г = 0 C0 = aQi
Заметим еще, что
CLn~CL—пч Ьп = Ь—п,
как это видно из (9-35), поскольку
Фп = —ф—п
Применяя формулы Эйлера —
Фурье (9-30) к комплексу Сп, най-
дем, что
Т/2
сп = спеЧФ n = j f(t) e~inWlidt.
—Т/2
(9-36)
Последнее выражение позволяет
сразу определить и амплитуду, и фа-
зу гармонических составляющих.
Одно это выражение заменяет три
формулы (9-30), поскольку оно при
/г = 0 определяет непосредственно и
постоянную составляющую С0=^о.
Спектральный состав функции
можно характеризовать рядом Спи
фп. Существенно заметить, что при
этом Со=£о, но при п=#=0
cn=^dn. (9-37)
Спектральное представление
функций. Спектральный состав
функции f(/) можно характеризо-
вать не только дискретным рядом
комплексных амплитуд Сп, но и не-
прерывной спектральной функ-
цией
Г(у(») = ^(ф)е_/Ф(ю) =
Т/2
= J f(t)e~itt,tdt. (9-38)
—Т/2
Модуль спектральной функции,
т. е. /?(;со), представляет собой оги-
бающую спектральных амплитуд
|Сп| = сп, умноженных на Т=2зт/со1.
Аргумент спектральной функции,
т. е. —ф(со), представляет огибаю-
щую аргументов дискретного спект-
ра —фп*
Как видно из самих определений
(9-36) и (9-38),
Cn = ^F^)
9 (9-39)
При = И со1=—.
Обычно спектральную функцию
строят только для со^'0, так как
этим она полностью определяется,
поскольку
F(— co)=f (со), Сп — С-п
и
ф(а>)= — ф(— ш).
Спектр ал ьный состав полностью
определяет соответствующую функ-
цию времени, поэтому он может
быть назван ее спектральным
(или Фурье) представле-
нием.
Рассмотрим спектральное пред-
ставление периодической последова-
тельности импульсов f(/), определя-
емой в пределах периода Т равен-
ством
(а
10
при
при
0<*<Л
Вид этой функции изображен на
рис. 9- 15а
Выполняя интегрирование (9-38),
находим:’
+Т/2
F (]<»)= J f (t) e~‘atdt =
—Т/2
— e~ia>idt =a^ e~'wtdt =
о о
=Л(1— е'лТ1).
itn v 7
253
a)
Рис. 9-15.
Имея в виду, что
1 _ = _ е~
Xe-^^S/sin^e-^72,.
придадим найденному спектральному
представлению следующий вид:
F (jm) = 2а 51п<юЛ/2) е-/шЛ/2:
F(<»)=:2a| ; (9-40)'
^(.) = .7,/2 + argJHgg|>-|. (М1)
Выражение для фазы ф(со),кро-
ме очевидного слагаемого со7\/2, со-
держит дополнительное слагаемое
±л при sin (соЛ/2) <0. Оно выбира-
ется так, чтобы ф (со) по абсолютной
величине всегда оставалось меньше
2л, иначе говоря, целое число 2л от-
брасывается.
По уравнениям (9-40) и (9-41)
построены огибающие спектра ам-
плитуд и фаз, приведенные на рис.
9-15,6.
Этот график замечателен тем,
что он не зависит от длительности
периода Т.
Наибольшее значение модуль
функции имеет в начале координат:
F (Q) —аТ 19
поскольку
lim sin-(<o7’1-2)-=ri/2.
На рис. 9-15, в и г представлены
значения — сп = Тсп и соответствую-
щие значения для двух случаев
Т = <2Т1 {в) и Т = 37\ (г). Чем боль-
ше период Т по сравнению с дли-
тельностью импульса Т19 тем плот-
нее идут линии спектра. На всех
графиках о)1=2^/7п.
Еще одно очень важное замеча-
ние. Комплексные амплитуды Сп со-
ответствуют симметричному пред-
ставлению ряда (9-34).
Переходя от этого выражения
к ряду простых гармонических со-
254
ставляющих с частотами 0, юь 2&>i,
Зсо! и т. д., находим, что
f (0 = Со + У 2сп cos (nw.t — ф„) ==
72 = 1
= do + £ dnC0S ~ W'
n=l
Поэтому иногда в качестве спек-
тральной функции принимают
2F(/cd).
9-7. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ
НЕКОТОРЫХ ФУНКЦИЙ
Периодические функции, которые
могут быть изображены кривыми,
симметричными относительно оси
абсцисс, считая от начала первой и
второй половины периода (рис.
9-16), т. е.
f(t) — — f + ~2~j, представляются
рядом (9-32) нечетных гармонических
без постоянной составляющей
f (t) = d1 cos (ш/ — <]>,) +
-|- d3 cos (Зсо/ — ф3) + • • • (9-42)
Выпрямленное напряжение или ток
(рис. 9-2) содержит обязательно по-
стоянную составляющую и может
содержать четные гармонические.
Если —t) при соответ-
ствующем выборе начала отсчета
времени (рис. 9-17) ряд (9-29) не
содержит синусов
f (/) — #о cos +
4~ cos 2ю/ Ц- a3rcos Зо)^ + ... (9-43)
В электротехнике встречаются
несинусоидальные функции с перио-
дическими огибающими, которые
можно представить суммой некрат-
ных гармонических составляющих.
К таким функциям относятся бие-
ния и модулированные колебания.
Рис. 9-17.
Наиболее простым является бие-
ние, образованное суммой двух гар-
монических колебаний с равными?
амплитудами и с близкими частота-
ми:
f (^) = Д (cos cos (9-44)
После, преобразования суммы коси-
нусов
f (t) = 2 A cos 1 х
X COS
<01 -|- Cl>2
2
(9-45>
t
функцию можно рассматривать-
так, как будто у простого гармони-
ческого колебания с частотой <о =
= ——- амплитуда изменяется по-
о <01 ' ®2
косинусоиде с частотой £2 = —~:
/ (/) = 2A cos Clt cos W. (9-46)
Если отношение <o/Q— число не-
рациональное, то функция /(/) не-
периодическая, хотя и может быть
представлена суммой двух косину-
соид. Если отношение co/Q =2^4-1,
где k — целое число, то период бие-
ний Гб = л/Q равен периоду функции
f(£), что очевидно из следующего’
выражения:
Г(#+тс)=
= 2А cos (£1/ -|- тс) cos 4г j •
В широком смысле слова моду-
лированные колебания—это гармо-
нические колебания с переменной во
времени амплитудой (амплитудная
модуляция—AM), или с переменной
во времени частотой (частотная мо-
дуляция— ЧМ), или с переменной
во времени фазой (фазовая моду-
ляция— ФМ). В этой книге мы
ограничиваемся анализом только*
255
амплитудно модулированных коле-
баний (см. § 9-1).
В колебаниях, модулированных
по частоте, амплитуда остается по-
стоянной, а изменяется частота
f (t) — A cos (otf <р)
при о) = О)0 (/),
здесь оо и До) — постоянные.
При колебаниях, модулирован*
ных по фазе (ФМ),
f (0 = A cos></ + ? (0J.
Полагая
<р (0 ="Д®х](01,
можно свести частотную модуляцию
к фазовой.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ
С СОСРЕДОТОЧЕННЫМИ постоянными
ВВОДНЫЕ ЗАМЕЧАНИЯ
В предыдущих разделах курса
изучались электрические цепи в
установившемся режиме; который
практически всегда наступает после
достаточно длительного1 действия
источников с постоянным или пери-
одически изменяющимся напряже-
нием, если параметры цепи остают-
ся постоянными (или изменяются
периодически). Однако в инженер-
ной практике очень важны не толь-
ко установившиеся, но и переход-
ные режимы, наступающие после
тех или иных коммутаций (включе-
ние и выключение нагрузки или ис-
точников питания), а также после
изменения параметров цепи. В це-
пях с источниками апериодически
изменяющихся напряжений (токов)
иногда вообще нельзя говорить об
установившемся режиме.
Электротехнические устройства
часто находятся непрерывно в пере-
ходном режиме. Водитель троллей-
буса в сложных условиях управле-
ния городским транспортом включа-
ет двигатель и, не дав ему набрать
скорость установившегося режима,
вновь выключает его, затем, вклю-
чив двигатель, быстро переводит его
1 Слова недостаточно длительно» здесь
имеют условный смысл: длительно по
сравнению ю той или иной характерной для
рассматриваемой цепи величиной. Во мно-
гих случаях «длительно» может обозначать
ничтожные доли секунды. Понятие доста-
точной длительности станет ясным из даль-
нейшего анализа.
17 К. М. Поливанов
из одного режима в другой с тем,
чтобы получить достаточное, но не
чрезмерное ускорение. В телеграф-
ной линии быстро следуют один за
другим сигналы различной длитель-
ности; если на ее входе сигналу со-
ответствует практически мгновенно
возникающее постоянное напряже-
ние, а в интервалах между сигнала-
ми напряжение равно нулю, то па
выходе линии, т. е. 'в приемном
устройстве, сигналы расплываются,
размазываются (ток постепенно на-
растает и постепенно спадает) из-за
неизбежного переходного процес-
са — р астянутость этого процесса
определяет наименьшую допусти-
мую длительность сигналов и ин-
тервалов между ними.
В электрических цепях, содержа-
щих триоды, часто одну ее часть от-
деляют от другой конденсатором,
включенным последовательно с со-
противлением (рис. 10-5, а)\ При
этом напряжение, поступающее во
вторую часть цепи, снимается с со-*
противления. Это напряжение иг=
= ir повторяет без искажения сиг-
нал, поданный на вход, если за вре-
мя действия сигнала Т конденсатор
не успевает заметно зарядиться,
т
т. е. если Заметим, что
6
при этом на конденсаторе может су-
ществовать постоянная составляю-
257
щая напряжения t7Co=const, не
влияющая на передаваемый сигнал.
Для такого разделительного устрой-
ства рабочим режимом часто явля-
ется именно переходный.
Короткое замыкание в цепи энер-
гетических систем может привести
к серьезным повреждениям, если на-
длежащий участок автоматически
не отключается (рис. 10-33). Макси-
мально возможное значение тока
короткого замыкания должно быть
известно, инженерам-проектировщи-
кам; в простейшем случае для цепей
переменного тока оно определяется
нарастанием тока за первую поло-
вину периода после момента замы-
кания. Очевидно, что это именно пе-
реходный режим.
Электротехникам часто прихо-
дится иметь .дело с тепловыми
расчетами электротехнических
устройств, потому что при пере-
грузках угрожающим может ока-
заться перегрев кабеля, обмоток
машин, трансформаторов /и т. п.
В случае короткого замыкания или
кратковременной перегрузки их
тепловой режим должен рассчиты-
ваться как переходный; при этом
главную роль может играть тепло-
емкость системы, а не теплопровод-
ность между источником тепла и
охлаждающей средой, тогда как
в установившемся режиме темпера-
тура определяется теплопровод-
ностью (см. § ГО-8).
Очень существенно влияние пе-
реходных процессов в устройствах,
предназначенных для измерения бы-
стро изменяющихся величин. Ис-
ключительную роль играют переход-
ные процессы в импульсной техни-
ке, в системах автоматического
управления и в быстродействующих
элементах автоматики.
Вообще говоря, изучение пере-
ходных процессов несколько слож-
258
нее, чем изучение установившихся.
Во всяком случае для изучения пе-
реходных режимов необходимо от-
четливое знание теории электриче-
ских цепей при установившемся ре-
жиме. Это следует особенно подчер-
кнуть потому, что расчет переход-
ных процессов почти всегда требует
расчета той же системы при устано-
вившемся режиме.
При расчете переходных процес-
сов иногда оказывается необходи-
мым считаться и с конечной ско-
ростью распространения электро-
магнитных сигналов в"доль провесов,
соединяющих источник с приемни-
ком (нагрузкой). Подобные систе-
мы будут рассмотрены во второй ча-
сти книги, где изложена теория це-
пей с распределенными параметрами.
Здесь всегда будем предпола-
гать, что длительность распростра-
нения сигналов вдоль проводов нич-
тожно мала по сравнению с интер-
валами времени, в течение которых
происходит сколько-нибудь замет-
ное изменение рассматриваемых ве-
личин (например, токов или напря-
жений) Ч Такие цепи называют це-
пями с сосредоточенными парамет-
рами. Переходным процессам в ли-
нейных цепях с сосредоточенными
постоянными и посвящен последний
раздел этой части книги.
1 Однако мы будем часто предполагать,
что та или иная величина изменяется мгно-
венно. Наицример, включая -в цепь источник
постоянного напряжения, мы будем считать,
что включение происходит мгновенно и на-
пряжение на соответствующих полюсах це-
пи также мгновенно возрастает. На самом
деле, как бы быстро не происходила комму-
тация, она растянута во времени. Но во
многих случаях, 'правда не всегда, с этой
растянутостью можно не 'считаться и пере-
ходить к идеализированному представлению
о ’Мгновенном нарастании напряжения. До-
пуская такую идеализацию, мы тем не ме-
нее будем пренебрегать длительностью рас-
пространения электр о магнитного сигнала
вдоль проводов, если их протяженность не-
велика (скорость распространения в воз-
душных линиях 3 • 1010 см] сек и примерно
в 1,5—2 раза меньше в кабелях).
ГЛАВА ДЕСЯТАЯ
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ПЕРЕХОДНЫХ ПРОЦЕССОВ. ИХ РАСЧЕТ ПУТЕМ
НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ
УРАВНЕНИИ
(КЛАССИЧЕСКИЙ МЕТОД)
10-1. ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ; ОПРЕДЕЛЕНИЕ
НАЧАЛЬНЫХ УСЛОВИЙ
(ЗАКОНЫ КОММУТАЦИИ);
СВОБОДНЫЙ И ПРИНУЖДЕННЫЙ
РЕЖИМЫ
При расчете переходных процес-
сов следует исходить из основных
дифференциальных уравнений цепи,
отыскивая их полное решение, а не
ограничиваться частным решением,
справедливым только для устано-
вившегося режима. Так, например,
для цепи, содержащей последова-
тельно соединенные элементы L, г,
С, подключенные к источнику с на-
пряжением iz(Z), решению подлежит
уравнение
+/г+ <// = «(/). (10-1)
При разветвленных цепях прихо-
дится иметь дело с системой урав-
нений, составленных для контуров
и узлов в соответствии с законами
Кирхгофа (§ 10-7). Важно сразу за-
метить, что в случае линейных це-
пей все дифференциальные уравне-
ния цепи линейны.
Решение дифференциальных
уравнений должно производиться
при так или иначе заданных на-
чальных условиях. Исчерпывающая
полнота в задании начальных усло-
вий совершенно необходима для
однозначного решения дифферен-
циальных уравнений. Действитель-
но, в одной и той же цепи при
одинаковых переключениях, но при
разных начальных условиях про-
цессы могут протекать различно.
Пусть коммутация, т. е. измене-
ние в цепи, вызывающее период-
ный процесс, происходит мгновенно
в момент времени £=0. В таком
случае можно говорить о значении
той или иной величины f(t) в мо-
мент, непосредственно предшест-
вующий коммутации, f(—0), и
в момент, непосредственно следую-
17*
щий за коммутацией, f(+0). Для
того чтобы различать эти значения,
аргумент t -> 0 в первом случае
обозначается как —0, а во вто-
ром— как +0.
Часто такое обозначение излишне и
можно писать просто ДО), когда и без того
ясно, о чем идет речь,
В момент коммутации некоторые
величины могут изменяться скач-
ком, в этом случае
f(-O)^f(+O). (10-2)
Другие величины, напротив, мо-
гут изменяться только непрерывно,
для них обязательно
f(-0W( + 0). (10-3)
Если мощность обмена энергией
между отдельными элементами
цепи остается конечной (т. е. про-
изведение ui конечно), то непре-
рывно изменяются все те величины,
значения которых определяют энер-
гию, содержащуюся в элементах
цепи.
Так, энергия электрического поля
конденсатора постоянной емкости С
определяется только его напряже-
нием
Са2с
Подводимая к нему мощность
due
Сис~аГ = ис*-
при конечной
когда uci остается
dwQ
р=чг
Поэтому
мощности,
конечным, напряжение на конден-
саторе изменяется непрерывно
(ducl'dt конечно) и, следовательно,
ис{—0) = цс(4~0). (10-4)
Точно так же энергия магнит-
ного поля элемента цепи, обладаю-
щего индуктивностью L, опредег
ляется только током, проходящим
через индуктивность
25^
Поэтому при конечной
мощности
М-0)=*ь( + 0). (10-5)
Равенства (10-4) и (10-5) вы-
ражают законы коммутации
электрической цепи (конечной мощ-
ности), достаточные для определе-
ния всех необходимых начальных
условий по известным токам во
всех индуктивностях и по известным
напряжениям на всех емкостях, су-
ществовавшим к началу коммута-
ции.
Решение линейных дифферен-
циальных уравнений, например
(10-1), часто удобно представлять
в виде суммы двух функций (прин-
цип суперпозиции)
(Ю-6)
из которых первая функция удовле-
творяет однородному уравне-
нию (правая часть равна нулю)
1S-+ri'+4- j l'dt=°’ (10’7>
а вторая представляет собой любое
частное решение заданного урав-
нения
+ri”+4- (d'dt=и(10’8)
В силу линейности решаемого
уравнения, складывая (10-7) и
(10-8), при условии (10-6), прихо-
дим к (10-1).
Законам коммутации должно
удовлетворять только полное реше-
ние. Это необходимо сразу твердо
усвоить.
В уравнениях электрической
цепи правая часть обычно представ-
ляет напряжение источника или ток,
или, говоря обобщенно, внешнюю
возмущающую силу. Одно-
родное уравнение, например (10-7),
соответствует режиму цепи в отсут-
ствие внешнего возмущения, или
свободному режиму; поэтому токи и
напряжения, удовлетворяющие од-
нородному уравнению, называют
свободными.
Частное решение в случае по-
стоянной или периодической правой
части можно отождествлять с реше-
нием для установившегося режи-
ма. В общем случае это решение
называют решением для принуж-
денного режима, а соответствующие
токи и напряжения называют п р и-
нужденными.
Действительное (полное) реше-
ние представляется при этом сум-
мой свободного и принужденного
Z — ^св“Ь4гр, U — ^свН“^пр’ (10-9)
10-2. источник постоянного
НАПРЯЖЕНИЯ В ЦЕПИ г,
Пусть к источнику С ПОСТОЯННЫМ
напряжением U через сопротивле-
ние г присоединяется конденсатор С
(рис. 10-1). При -установившемся
режиме в такой цепи ток отсутст-
вует ф=0 (нет замкнутого проводя- k
щего контура)-, напряжение на кон-
денсаторе uc~U, его заряд q=CUy
запасенная энергия w3=C[/2/2
(энергия электрического поля).
Предположим, что к моменту
включения рубильника t = 0 конден-
сатор имел напряжение, отличное
от t/, например вовсе не был заря-
жен, и энергия его электрического
поля равнялась нулю. В таком слу--
чае должен существовать переход-
ный процесс, в течение которого от
источника передается энергия к кон-*
денсатору, а по проводам идет ток,
заряжающий конденсатор. Имея
в виду, что ток в цепи равен ско-
рости нарастания Заряда на элек-
тродах конденсатора i-=dqldt=
= Cduddt, и применяя закон Кирх-
гофа
ri-Vuc—'U,
легко составить дифференциальное
уравнение рассматриваемой цепи
diir U — иг
i = C-£-=-----
dt г
или
(10-10)
(10-11)\
dar ,
~~ 4- и = и,
at 1 с
где z = rC.
Рие. 10-1.
-260
Решение этого простого уравне-
ния можно считать известным:
ис — и'с + и”с — + (10"12)
В нем первое слагаемое и'с —
_ £
— Ае представляет собой реше-
ние однородного уравнения, т. е.
уравнения (10-11) при правой части,
равной нулю:
du!r ,
х-3г + и'с = 0 (10-13)
(уравнение свободного режима).
Второе слагаемое (гг,,с=<7) —
частное решение неоднородного
уравнения (10-11) или установив-
шееся (принужденное) значение.
Решение однородного уравнения
содержит постоянную интегрирова-
ния А. Ее значение невозможно
определить из уравнения (10-13),
правая часть которого равна нулю.
Действительно, это уравнение
остается справедливым при умно-
жении найденного решения и7 с на
любую постоянную величину. Таким
образом, основываясь только на
дифференциальном уравнении, нель-
зя найти решение, которое одно-
значно описывало бы исследуемый
процесс.
Обращаясь к полному решению
(10-12), легко увидеть, что оно од-
нозначно определяет установившее-
ся состояние ис=и при £ > т. Од-
нако при />0 и при /= +0 величина
uc(t) зависит от постоянной А. Так,
при /=+0 из (10-12) находим, что
ис( + 0)=А + и, (10-14)
Последнее уравнение имеет от-
четливый физический смысл: по-
стоянная А, а следовательно, и
процесс в цепи зависят от напряже-
ния на конденсаторе ис( + 0)^в на-
чальный момент.
,Но напряжение на конденсаторе,
как уже было сказано, не может
изменяться скачком ис (+0) =.
= Нс(—0). При этом условии из
(10-14) следует, что
A = zzc(_O) — U. (Ю-15)
Таким образом, для определе-
ния постоянной интегрирования до-
статочно знать напряжение на кон-
денсаторе перед коммутацией
ис(—0) —это и есть необходимое и
достаточное начальное условие для
полного решения дифференциаль-
ного уравнения цепи г, С.
Свободная составляющая напря-
жения на конденсаторе
и’с=Ае~^ (1Й6)
выражается экспонентой, скорость
уменьшения которой определяется
постоянной времени
х=гС, (10-17)
зависящей только от параметров
рассматриваемой цепи (т не зави-
сит от начальных условий и напря-
жения источника). Эта постоянная
имеет размерность времени, так как
показатель должен выражаться
числом, т. е. безразмерной величи-
ной (что и подтверждается при под-
становке единиц г и С, выраженных
через вольты, амперы и секунды).
Абсолютная величина свободной
составляющей уменьшается в е раз,
когда время t равно т.
Легко понять физический смысл
выражения постоянной х=гС: при
заданном токе напряжение на ем-
кости изменяется тем медленнее,
чем больше емкость, а при задан--
ной разности напряжения источни-
ка и напряжения на емкости в цепи
проходит тем меньший ток, чем
больше сопротивление. Например,
при емкости 30 мкф и сопротивле-
нии 10 Мом постоянная времени
т=300 сек\ это значит, что свобод-*
ная составляющая уменьшится в е
раз через 5 мин. Если же С=
= 0,01 мкф и г= 1 ом, то свободная
составляющая уменьшится в е раз
через 0,01 мксек.
Рассмотрим переходные про-
цессы в цепи г, С при различных на-
чальных условиях:
А) Незаряженный конденсатор
С подключается через сопротивле-
ние г к источнику постоянного на-
пряжения [/(нулевые началь-
ные условия). В этом случае
261
ис(—О)=ОГ следовательно, по
(10-15) A =—U и
uc = U(l~ e~i/x). (10-18)
Ток в цепи
U j I-
1^СЧГ=~е (10-19)
Б) To же, но конденсатор к мо-
менту включения был заряжен до
напряжения ис(—0)==t//2 (нену-
левые начальные условия).
В этом случае Л = —<U/2 и, следо-
вательно,
ur=u( 1—4-е“И-
В) То же, но конденсатор был
предварительно заряжен до напря-
жения, равного по абсолютной вели-
чине U, но знак заряда противопо-
ложен заряду при установившемся
режиме, т. е. ис(—0) =;—V. В этом
случае
uc = U(A—2e~t,x).
Хотя в последнем случае коли-
чество энергии электрического поля
в начальный момент и при устано-
вившемся режиме одинаково, в цепи
протекает переходный процесс, по-
скольку не согласованы знаки на-
пряжения на конденсаторе.
Для всех трех различных началь-
ных условий графики изменения
напряжения на. конденсаторе пока-
заны на рис. 10-2. На том же ри-
сунке пунктиром показаны графики
токов.
Г) Рассмотрим, наконец, случай,
когда С7=0, а ис(—0) ={.UQ>0. Это
случай разряда конденсатора. По
Рис. 10-2.
определению теперь может сущест-*
вовать только свободный режим,
при котором
иc = Uoe~t,x, i = -^=
GO’ r
= —^e~tlx. (10-20)
d
тора
Процесс поддерживается энер-
гией, ‘ запасенной в конденсаторе.
Легко составить баланс энергии:
скорость убывания энергии конд^нса-
~2~
должна быть равна
мощности, рассеиваемой в сопротив-
лении по закону Джоуля—Ленца,
d (Си2с\___. ^duc
dt \ 2 J UC"' dt —
и*
= -uci-=^ (Ю-21)
Найденные выражения для ис и i
согласуются с последним равенст-
вом, в чем можно убедиться прямой
подстановкой.
Ток в цепи г, С может изменять-
ся скачком (рис. 10-2), поскольку
цепь не содержит индуктивности.
Заметим, что на самом деле всякая
цепь содержит хотя бы очень малую
индуктивность. Ее влияние на про-
цесс в цепи г, С ничтожно при
больших т. Но при т порядка ми-
кросекунд и долей микросекунд ско-
рость изменений тока столь велика
в течение всего процесса, что индук-
тивностью, как правило, пренебре-
гать нельзя (см. § 10-6).
ю-з. источник постоянного
НАПРЯЖЕНИЯ В ЦЕПИ £, г
Рассмотрим включение источни-
ка постоянного напряжения U в цепь
последовательно соединенных эле-
ментов L, г (рис. 10-3). Запишем
уравнение цепи, неоднократно ветре-
Рис. 10-3.
262
чавшееся в теории переменных
Стоков:
L^-\-ri = U. (10-22)
С математической точки зрения
оно не отличается от уравнения
(10-11) и его решение можно счи-
тать известным:
z = + (10-23)
где x=ljr.
Здесь, как и в предыдущем при-
мере, одним и двумя штрихами от-
мечены решение однородного урав-
нения (свободный режим) и частное
решение или установившийся (при-
нужденный) режим. Свободная со-
ставляющая снова выражается экс-
понентой, как и в случае цепи г, С.
Постоянная времени теперь про-
порциональна L и обратно пропор-
циональна «г. Особенно отчетливо
физический смысл именно такого
значения постоянной времени мож-
но увидеть, когда в цепи существу-
ет только свободна^ составляющая
тока (см. конец этого параграфа).
Полное решение по-прежнему со-
держит постоянную А. Ее значение
определяется по начальному току
в индуктивности Ц + 0). Если в цепи
ток отсутствовал до момента вклю-
чения (нулевые начальные усло-
вия), то
Ц+0)=4 + Я=г(-0) = 0.
(10-24)
При этом из (10-23) находим, что
г=-^(1-е-?Л). (10-25)
Можно рекомендовать читателю
самостоятельно построить соответ-
ствующие графики тока и напряже-
ния на индуктивности* 1:
UL = L А = Ue~th. (SQ-26)
Ток в цепи начинается с нуля. По-
этому в начальный момент все на-
пряжение источника ложится на ин-
дуктивность.
1 В следующего выражении проведено
L 1
очевидное сокращение: —---— — 1.
Пример 10-1. На рис. 10-4,а представ-
лена схема цепи, в которой после размыка-
ния рубильника протекает переходный про-
цесс при ненулевых -начальных условиях.
Дано £71 = 16 в, U2—А в, Ri=R2=8 ом, ri =
=г2=2 ом, £=0Д гн. Требуется найти
ТОК 42.
Решение. Дифференциальное урав-
нение для тока 1*2 после размыкания ру-
бильника
di2 _
ri2 + L U2
(здесь г = r2 + Rz) имеет уже известное
решение:
/2 = V 2 Iй 2 = Ав х *4 ~ =
= 4-0,4;
здесь if2 — решение однородного уравнения
(или ток свободного режима), содержащее
постоянную интегрирования; i"2 — частное
решение, соответствующее новому устано-
вившемуся режиму.
•Если перед размыканием рубильника
в цепи существовал установившийся режим
(ста^рый), то в индуктивности к моменту
переключения проходил вполне определен-
ный ток (—0) =—2 а.
Это значение тока и служит началь-
ным условием. Сразу после коммутации
f2(+0) —0) =—2 а, поскольку ток в ин-
дуктивности не может изменяться скачком.
На основании сказанного находим,
что
U2
A==iL (—0)----^=—2,0 —0.4 = —2,4
и, следовательно, г2 = 0,4— 2,4^“100f при
t >0.
На рис. 10-4,6 показан график тока z2.
Если в цепи рис. 10-4,а второй
источник отсутствует (С/г=О), то
после отключения рубильника во
263
втором контуре остается только
свободный ток:'
^2 = z*2(0)^/T при 72 (0) — z2 (—0).
(10-27)
Ток поддерживается энергией,
'запасенной в индуктивности: ско-
рость убывания этой энергии долж-
на быть равна мощности, рассеивае-
мой в сопротивлении,
Чем больше Л, тем больше первона-
чальный запас энергии, но чем боль-
ше г, тем интенсивнее расходуется
запасенная энергия. Поэтому есте-
ственно, что увеличение сопротивле-
ния г ускоряет изменение тока,
а увеличение индуктивности L за-
медляет его; этому . и соответст-
вует выражение постоянной време-
ни x='Llr.
Сопоставьте полученный резуль-
тат и само уравнение (10-28) с ана-
логичным уравнением (10-21) для
разряда конденсатора (свободный
режим).
10-4. ИСТОЧНИК ИЗМЕНЯЮЩЕГОСЯ
НАПРЯЖЕНИЯ В ЦЕПИ г, С
В тех случаях, когда напряже-
ние включаемого источника u(t)
(рис. 10-1) непостоянное, но выра-
жается простыми функциями, для
которых легко найти соответствую-
щее частное решение, расчет пере-
ходного процесса ненамного услож-
няется.
Напряжение линейно возрастает.
Пусть напряжение источника изме-
няется по закону
z,x [0 при /<Г0;
и ft) = I г
\UQt/T при />0.
дящей функции, не руководствуясь
даже какими бы то ни было особы-
ми правилами. В нашем случае
естественно предположить, что
где К— const; затем надо выбрать
постоянную К так, чтобы она унич-
тожила постоянную, получаемую
в результате дифференцирования;
du"c Uo /
'c4z~ = x Т •
Очевидно, что этому требованию
удовлетворяет К — —
Таким путем частное решение
найдено:
Решение однородного уравнения
принципиально не зависит от вида
правой части; оно уже известно
£
итс=^Ае при т = гС.
Остается определить постоянную
интегрирования А.
Если конденсатор предваритель-
но не был заряжен (достаточное
начальное условие), то
ис (+0) = и’с (+0) 4- и"с (+0) =
= Д —t-^ = zzc(—0) = 0.
Окончательное решение принима-
ет вид:
ис~
— т ( 1 —
(10-29)
Для того чтобы найти напряже-
ние на конденсаторе, нужно для
уравнения, аналогичного (10-11),
аир
Ток в рассматриваемой цепи
_£
1=c> = c^(i-e
(10-30)
сначала найти частное решение и”с.
Заметим, что частное решение
можно искать путем подбора подхо-
После длительного включения
(когда т) в цепи установится
постоянный ток CU^T, а напряже-
264
ние на конденсаторе будет линейно
возрастать, отличаясь от напряже-
ния источника на постоянную вели-
чину падения напряжения в сопро-
тивлении г.
Передача сигнала через раздели-
тельный конденсатор. Как уже гово-
рилось, практический интерес пред-
ставляет анализ переходного про-
цесса в цепи г, С, на вход которой
поступает заданный сигнал, переда-
ваемый в следующую часть цепи
(например, на сетку электронного
триода, рис. 10-5,#) как напряжение
на сопротивлении. Пусть сигнал
продолжительностью Т подается в
форме постоянного напряжения
^вх=^о. Требуется определить на-
пряжение на сопротивлении и на
конденсаторе.
Решение задачи для интервала
времени 0<7<Т ничем не отли-
чается от рассмотренного в § 10-2.
Если к моменту /=0 конденсатор не
был заряжен, искомое напряжение
ur = ir — U^e х . (10-31)
Это напряжение меньше
го на величину напряжения
денсаторе
__ £
#c = t70(l — е “j-
входно-
на кон-
(10-32)
а)
Последнее очень мало при t/x <1
и напряжение на сопротивлении
близко к входному.
Такое же заключение можно сделать и
для линейно возрастающего напряжения
на входе. Из уравнения (10-30) видно, что
Разлагая экспоненту в ряд
и ограничиваясь первыми двумя слагаемы-
ми в круглых скобках (для 1), нахо-
дим, что
Напряжение на сопротивлении
полностью воспроизводит входной
сигнал лишь до тех пор, пока t < т.
Таким образом, оказывается, что
система r, С связи двух участков
цепи (рис. 10-5,#) принципиально
работает только в переходном ре-
жиме.
Рассмотрим теперь решение для
времени t>T, когда напряжение
сигнала (или напряжение источни-
ка) равно нулю, что равносильно
короткому замыканию входных за-
жимов.
При этом в цепи происходит
просто разряд конденсатора, имею-
щего напряжение ис(Т) к моменту
начала нового режима,
ис=ис(Т)е~в/г, (10-33)
где 6 = / — Т.
Напряжение на сопротивлении
иг——ис (обратите внимание на
выбор положительных направле-
ний) .
График напряжений #вх(0 и
показан на рис. 10-5,6.
При Tlx < 1 напряжение иг от-
личается незначительно от поданно-
го сигнала.
Импульс напряжения. После толь-
ко что проделанного анализа не-
трудно рассмотреть общий случай
воздействия импульса напря-
жения на цепь г, С.
В механике и физике интеграл
функции по времени называют ее
265
импульсом. Интеграл от входного
напряжения за время его действия
мы также должны называть им-
пульсом напряжения
т
; (10-34)
о
В цепях, постоянная времени х
которых велика по сравнению
с длительностью Т действовавшего
на нее возмущения, все процессы
при t>T определяются именно им-
пульсом этого возмущения.
Действительно, в цепи г, С за
время t < х=гС конденсатор не
успевает заметно зарядиться, и
практически все входное напряже-
ние и приходится на сопротивление.
При этом ток в цепи
(10-35)
Но в таком случае заряд на конден- .
саторе в конце зарядки
т т
q = ^idt=-L^udt = -^K, (Ю-36)
о о
а напряжение на конденсаторе
(10-37)
где К— импульс напряжения.
После окончания импульсного
воздействия конденсатор разряжается
и его напряжение
ис (9) = ис (Т) е~в,х = 4- е~61\ (10-38)
где 6 — t— Т.
При 6 > Т можно полагать 6
где t отсчитывается от начала дей-
ствия импульса.
Пример 10-2. На входе цепи цис. >10-5,а
постоянное напряжение сигнала -£/0—400 в
длится 7=100 мксек. Параметры контура:
С=0,4 мкф, г=50 ком и, следовательно,
т=2*10-2 сек^> Т. Показать, что рассмот-
ренное детальное решение, представленное
формулой (10-33), совпадает с решением,
представленным выражением 1(10-38).
Решение. Для данных условий
K—UqT и, следовательно, по ((10-38)
ac(0)=t/o-4e-e/\
Сопоставляя это выражение с (10-33), на-
ходим, что требуется доказать равенство
«C(7) = t/O7/T. Но по (10-32)
ис(П = Уо(1-^ГЛ).
Разлагая в ряд экспоненту и полагая
приходим к требуемому равенству.
В современной электротехнике
(автоматика, связь, электрические
измерения) применение кратковре-
менных воздействий на электриче-
ские системы получило настолько
широкое распространение, что часто
говорят об импульсной .тех-
н и к е. При этом импульсом назы-
вают и само кратковременно дейст-
вующее возмущение (что не совсем
строго), и его интеграл по времени
(т. е. в строгом смысле слова им-
пульс) .
Включение цепи к источнику
периодического напряжения. Реше-
ние можно вести по уже знакомому
трафарету: ищется частное решение
f"— это установившийся режим (оно
хорошо известно из теории пере-
менных токов); затем ищется реше-
ние для свободного режима
определяемое с точностью до про-
извольного множителя (постоянная
интегрирования); наконец, к пол-
ному решению приме-
няется начальное условие, позво-
ляющее определить постоянную,
оставшуюся не определенной.
В ряде случаев решение задачи
л^гко найти, применяя принцип на-
ложения (суперпозиции). Пусть, на-
пример, в момент £=0 в цепь вклю-
чается напряжение u=<Uq (1—cos art).
Требуется найти в такой цепи ток.
Заданное напряжение можно
разложить на два слагаемых
Ui = UQ и и2=—t/0cosco/. По прин-
ципу наложения можно отдельно
определить реакцию цепи на вклю-
чение только первого (щ) и только
второго (и2) напряжения. Реакция
на действительное напряжение в
силу линейности всех уравнений
равна сумме найденных функций
i— ii
При этом нельзя забывать, что
законы коммутации применяются
только к полному решению. Однако
в случае нулевых начальных уело-
266
вии можно считать, что и для каж-
дого отдельного решения начальные
условия остаются нулевыми.
10-5. ИСТОЧНИК ИЗМЕНЯЮЩЕГОСЯ
НАПРЯЖЕНИЯ В ЦЕПИ Ц г
Включение источника гармониче-
ского напряжения. Пусть генератор
переменного тока (источник сину-
соидальной э. д. с.)
u = Um sin (со/ -j- ф) (10-39)
включается в ветвь с последователь-
но включенными сопротивлением г
и индуктивностью L (рис. 10-3).
В выражении (10-39) начальная
фаза ф определяет напряжение
источника u=Umsin ф в момент
включения рубильника /=0.
Требуется найти ток переходно-
го режима.
Для решения дифференциально-
го уравнения цепи
+ = (10-40)
следуя общему методу, находим
сначала частное решение, т. е.
установившийся ток i", хорошо из-
вестное из теории переменных
токов:
irr = An sin (о/ ф — <р), (10-41)
где
, coL
im — —== <p = arctg —.
Затем записываем решение одно-
родного уравнения цепи г, L, содер-
жащее постоянную интегрирования,
I' — Ae~th.
Um
(10-42)
Значение постоянной А опреде-
ляем из начального условия для
тока в индуктивности. Поскольку
включаемая ветвь была j£a-
зомкнута, имеем нулевое на-
чальное условие
^(+0) = ^(+0) + i,z(+0) =
= iL (—0) = 0,
с л едовательно,
Л = —/msin(<b —?>). (10-43)
Рис. 10-6.
Искомое выражение для дейст-
вительного тока (полное решение)
i = Im [sin И + Ф — ?) —
— sin (<[> — ?) e~z/x], (10-44)
его график показан на рис. ГО-6.
В цепи с большой постоянной
времени т > Т (малое г и боль-
шое L) свободная составляющая
тока за пол периода Т/2 изменяется
ненамного, тогда как первое сла-
гаемое в квадратных скобках (i")
через полпериода изменяет знак.
Поэтому в наиболее неблагоприят-
ных условиях включения (при
ф=0) максимальное значение тока
*макс при переходном процессе мо-
жет почти в 2 раза превосходить
амплитуду тока /га установившегося
режима (при ср~зт/2).
Переход от одного установивше-
гося режима к другому (коммута-
ция). Любое изменение режима це-
пи, вызванное, например, каким-
либо переключением, также сопро-
вождается переходным процессом.
Рассмотрим цепь переменного тока
(рис. 10-7), в которой существовал
установившийся режим, а в момент
/=0 произошло короткое замыка-
Рис. 10-7.
267
ние между точками а и Ь. Устано-
вившийся р^жим в цепи существо-
вал при напряжении генератора
^=^mcbs(co/+ip), где фаза ф за-
дана для момента коммутации, и
сопротивлении цепи Z=-r1+/(oZq +
+гг+/(о^2- При этом ток в цепи
был равен:
I = ~ или i — Ira cos (at + ф — <p),
где
/TO = KF-^-, <p = argZ.
После коммутации в первой
(правой) части цепи должен уста-
новиться ток установившегося ре-
жима
I =...
1 Г1 + j^Li
или •
1 = Лт COS (<ot + ф — fo),
7 U
где /1т— ./—5--------
у 4 + (wii)2
~ Л.
cp^argZ^afctg —,
а ток во второй части цепи должен
упасть до нуля (f,,2=0).
Свободный ток (решение одно-
родного уравнения) для двух участ-
ков цепи выражается различно:
/\ = Are~tl4 и iT2 = A2e~t!\
где i;1 = L1/r1 и ^2 = Щг2.
Действительно, после замыка-
ния обе части цепи оказываются от-
деленными одна от другой и харак-
теризуются своими постоянными
времени. Кроме того, постоянные
интегрирования Ах и А2 также мо-
гут быть различны: начальное зна-
чение тока для обеих частей цепи
одинаково
ч(+о)=/2(+о)=« (-о)=
= ZTOcosCp —<р)
(ток в индуктивности Ц и в индук-
тивности L2 не изменяется скачком);
однако принужденные значения для
начального момента различны
i”i (+0) = Iim cos (ф — «pj,
/"2(+0) = 0.
Поэтому из уравнений
М+о)-Н"х(+о)=
= г'2(+0) + »"2(+0) = г(-0)
находим, что
А = cos (ф — ?) — Iim cos (ф — fO;
Л = /тСО8(ф — <f).
Окончательное выражение для
тока в месте короткого замыкания
(в ветви, замыкающей точки а и Ь):
/к.3 = П — *2 = Лт COS (G)Z-j- ф — <Р) 4-
+ Ae~*/Tl —
Импульс напряжения. Если
напряжение и отлично от нуля в те-
чение-интервала Т, малого по сравне-
нию с постоянной контура T = L/r,
то режим _в цепи при 1^> Т опре-
деляется только импульсом напря-
т
жения, т. е. величиной К = J и dt.
о
В самом деле, из основного уравне-
ния цепи (10-40) находим, что
di = -^-dt — ^idt-, (10-45)
т т
i(T) = ±-^udt------------(10-46)
о о
Но по теореме о среднем
т
if. 7
—-1 i dt = -—- ZCp.
Т 1 *Б
о
Этим слагаемым можно пренебречь
по сравнению с первым инте-
гралом, поскольку по предположе-
нию Tlx < 1.
Таким образом, можно считать,
что к концу действия приложенного
268
напряжения &(/), независимо от его
формы, ток в цепи
т
i(T)=-j-^udt —А (10-47)
о
Если входное напряжение при
t>T равно нулю, ток определяется
выражением
i (0) = А е~9,х, (1048)
где Q — t — T.
Можно рекомендовать само-
стоятельно решить подобную задачу
для прямоугольного импульса
(и=0 при /<0 и t>T; при
0<t<T) ^и сопоставить решение
с (10-48).
Интересно также рассмотреть
с новой точки зрения вопрос о ма-
ксимальном токе переходного режи-
ма при включении синусоидального
напряжения в цепь L, г, у которой
постоянная времени т много больше
периода Т переменного тока.
По формуле (10-47) максималь-
ное значение тока в конце импульса
соответствует максимальному зна-
чению импульса напряжения. Но
при заданных амплитуде и частоте
максимальное значение импульса
соответствует включению именно
синусоидального напряжения с ну-
левой начальной фазой (ф=0).
10-6. КОНТУР Л, г, с
Уравнения для свободных состав-
ляющих. Электрическая цепь, содер-
жащая три элемента L, «г, С, не-
сколько сложнее рассмотренных ра-
нее и описывается дифференциаль-
ным уравнением второго порядка.
Однако и к ней можно применить
изложенные методы расчету
Пусть последовательно соединен-
ные элементы L, г, С включаются
в цепь источника (рис. 10-8) с на-
Рйс. 110-8.
пряжением u(t). Составляя диффе-
ренциальное уравнение, целесооб-
разно в качестве неизвестного вы-
брать напряжение на конденсато-
ре ис, выражая через него ток
в рассматриваемой цепи
. _nd“c
1 lL — U dt ’
При этом уравнение контура (10-1)
запишется так:
du~ d2u^
ис + гС^+ЬС^ = и^ (Ю49)
[второе слагаемое в правой части —
это ri, а третье слагаемое —это
L (dildt)].
Полагая и (/) = 0, получаем урав-
нение для свободного режима (от-
сутствие источников питания):
du'n d2u'r
u’c + rC-df + LC-^f = Q, (10-50)
которому соответствует характери-
стическое уравнение
1 + гСу + 1Су2 = 0 (10-51)
с корнями
^•2== — 2Г — |/ (jr) =
= — adzji. (10-52)
Это значит, что свободное напря-
жение на конденсаторе выражается
суммой двух экспонент
И'с = ДеТ1< + £еЧ (10-53)
где А и В — постоянные интегриро-
вания.
Свободный ток в той же цепи
dar
ir = i'L — С —
= С(у14еь/ + т25^). (10-54)
Частное решение зависит от вида
функции
Постоянные интегрирования А и
В определяются из начальных усло-
вий, применяемых к действитель-
ным напряжениям и токам, т. е.
к сумме частного решения и реше-
ния однородного уравнения (свобод-
269
ный режим). При этом две постоян-
ные А и В,, определяются из двух
начальных условий в сочетании
с двумя законами коммутации:
энергия электрического поля в кон-
денсаторе Си1 2с]2 и энергия магнит-
ного поля в индуктивности Lz2/2 не
могут изменяться скачком при ко-
нечных токах и конечных напряже-
ниях в цепи.
Пусть непосредственно перед
коммутацией напряжение на кон-
денсаторе и ток в индуктивности
заданы и соответственно равны
ис{—0) и iL(—0).
В таком случае непрерывность
изменения этих величин приводит
к равенствам:
й'с(+0) + й%(+0) = ^(-0); |
W№(+0)4H>)> J
(10-55)
где и"с( + 0) и zv,b( + 0)—частные
решения для начального момента
времени непосредственно после ком-
мутации.
Заданными начальными значе-
ниями ис{—0) и iL(—0) при извест-
ном частном решении [^"с(+0) и
f'b(+0)] полностью определяются
значения свободных составляющих
напряжения на конденсаторе и тока
в индуктивности в начальный мо-
мент после коммутации, т. е. вели-
чины и'с( + 0) и ^ь(+0). Подстав-
ляя их в (10-53) и (10-54), состав-
ляем систему уравнений
^с(0) = Д + В
и
i'L (0) = С(у1Л-|-у25))
из которой определяются постоян-
ные интегрирования
Л=<Х^)[Сьа’<.(0)~С(<>№
В [CTXJ0) -.7(0)1.
Для сокращения записи здесь и
в дальнейшем мы пишем просто
а'с (0) и irL (0) вместо и!с (Д-0) и
/'с (4-0).
После подстановки значений А и
В в (10-53) и (10-54) и ряда не-
сложных алгебраических преобразо-
ваний1, получаем для свободных
значений напряжения на конденса-
торе и тока в индуктивности сле-
дующие выражения:
} i'L(0) eU_e!,t .
‘Ср. 2
1 L — Ср. 2 4-
(10-56)
Разумеется, что второе
ние можно получить из первого, так
как в рассматриваемом контуре ток
в индуктивности равен току, заря-
/ du/r\
жающему конденсатор К
Полусуммы и полуразности экспо-
нент, входящих в выражения (10-56),
удобно представить через гиперболи-
ческие функции2:
к'с = [и'с (°) [Ch + v sh +
। *'/, (°) Д at
4~ ср. J
, ( ч'г (0)
г L = | sh \>t 4~ i’L (0) X ;
X [ch vi — y- sh p/j |
(10-567 c
Следует обратить внимание, что
1/Срь и (подобно 1//(»С и /о)Л)
представляют своего рода сопротив-
ления и выражаются в омах.
В случ^
2 / г
а =(.21
2 1
1 LC
или
г<2]/"-^-> или Q>-|-
1 Имея в виду, что 71,2= — «iPs где
ji = Уа2 — 1/LC, и, следдватёльно,
72 — Yi = —- 2р., а 7^2 == а2 — р.2 = 1/LC.
2 Имея в виду, что
Д1’2* = — е at [ch p.f + sh p»/].
270
значение р. становится мнимым, а Кор-
ин Yi ,2 — сопряженно комплексными,
Ты=- а±/₽,' (10-57)
где
j₽ = p=//l/LC-a* и а=^-.
При этом гиперболические функ-
ции переходят в круговые ch /р/ =
= cos р/ и sh /р/ = / sin р/, а выра-
жения для свободных значений напря-
жения и тока принимают вид:
= {и'с (0) [cos pZ + -у- s^n +
J и'с(0) • D, .
^=^1 -₽£-Sln^ +
-f- f/(0) [^cos ---sin e~at-
(10-58)
Они описывают затухающие
гармонические колебания
с угловой частотой рис коэффи-
циентом затухания а.
При записи последних формул
иногда производят дополнительное
преобразование
cos р/ ± -р sin р/ =
1
cos (р^д=х),
где
Z = arctg-^.
Энергетические соотношения при
свободном режиме. Колебания в цепи
L, г, С уже рассматривались
(см. § 5-5), поэтому ограничимся
здесь анализом энергетических со-
отношений. Записав уравнение кон-
тура при отсутствии источника (сво-
бодный режим).
“c + ^ + i^- = 0.
умножив все его слагаемые на ток
dur *
/ — С___- > получим
dt ,
du~ fii
Сис-^- ++ LiW= °- (10‘59)
tj о df 1 dfz
Ho i ~dt=~2~~^^ поэтому уравнению
(10-59) можно придать такой вид:
I I d л
dt\ 2 J'1 Г * dt \ 2 J —u‘
(10-60)
В нем крайние члены представ-
ляют скорость возрастания энергии
электрического поля емкости и со-
ответственно энергии магнитного
поля индуктивности; эти члены мо-
гут быть как положительными
(энергия возрастает), так и отрица-
тельными (энергия убывает). Сред-
ний член уравнения (10-60) при
г>0 и z#=0 всегда положителен; он
выражает необратимый процесс
превращения энергии электромаг-
нитного поля в тепло (рассеяние
энергии колебательной системы).
Поэтому очевидно, что общая энер-
гия, запасенная в системе, может
только убывать
d ( Li* . C«c \ ..
-zr(4^-+—
Аналогия с колебаниями механической
системы. Колебания .в системе L, г, С по-
добны колебаниям в механической систе-
ме. «Пусть, например, тело с массой т удер-
живается в положении равновесия х=0
упругими* силами пружины (рис. 10-9,а).
В такой системе упругая энергия деформи-
рованной пружины
1
kx2
аналогична энергии поля емкости, а кине-
тическая энергия
аналогична магнитной энергии индуктивно-
сти, если считать координату х аналогич-
ной заряду «конденсатора, а скорость dxldt
аналогичной току.
В механических системах, часто с до-
статочно хорошим приближением, можно
Рис. 10-9.
271
силу трения полагать пропорциональной
скорости. Уравнение движения механиче-
ской системы при этом принимает вид, пол-
ностью аналогичный только что рассмотрен-
ному уравнению контура L, г, С:
d2x , dx .
m4F + P~dF+kx^
При малом сопротивлении системы,
т. е. при
0 < г < 2 -Д- или Q > v
F О £
в системе возникают затухающие
колебания, описываемые уравнения-
ми (10-58). В нашем случае [и'с(0) =
= U0 и г-/ь(0)=0] эти уравнения
имеют вид:
ис = Uo (cos + у sin ) e~at;
i = — sin $te . .
Рассмотрим процесс в цепи с опреде-
ленными параметрами. Пусть, например,;
L = l,0 мгн, С=ы0,10 мкф,
г = 20 ол<21/Г-у=200 ом, Ut'= 100 в.
В этом случае
г
а=—fv-=104 сек-1,
^ — Vlc
_ 02=9,95.10*
сек^1.
(сила инерции плюс сила трения плюс
сила упругой деформации равны внешней
силе).
Другую простую аналогию представ-
ляет механическая система крутильных ко-
лебаний (рис. .10-9,6). Тело, характеризуе-
мое моментом инерции J, повооачивается
вокруг оси против действия упругих сил
(пружина маятника ручных часов, нить под-
веса гальванометра и т. п.). Уравнение дви-
жения такой системы также аналогично
уравнению электрического колебательного
контура L, г, С.
Колебательный разряд конденса-
тора. Вернемся к рассмотрению ко-
лебаний в цепи L, ir, С при разряде
конденсатора (рис. 10-10,а), заря-
женного первоначально до напряже-
ния uc(0) = Uq. В этом случае
принужденный (установившийся)
ток отсутствует i"=Q , а в началь-
ный момент и общий ток равен ну-
лю. Следовательно,
Z(O) = f(O)=zL (— 0) = 0.
Свободное напряжение на кон-
денсаторе в начальный момент рав-
но исходному напряжению
т. к. принужденное (установившее-
ся) напряжение отсутствует.
ос/р = 0,1005.
Если время t Измерять в миллисекун-
дах, то
ис — 100 (cos 99,5f—|—0,1005 sin 99,5f) £-10*б;
i = — 1,005 sin 99,5Ze“10*#.
Период свободных гармонических ко-
лебаний в рассматриваемом контуре Т =
= 2л/Р = 63 мксек, а частота f=l/T =
= 15,45 кгц.
На рис. 10-1 ОД показаны графики
uc(t) и i(t). Пунктиром проведены
экспоненты, характеризующие убы-
вание амплитуд
За каждый период Т амплитуда
(и тока, и напряжения) убывает в
еаТ = е ₽ раз. Эту величину назы-
вают декрементом (убылью) колеба-
ний. Ее логарифм, т. е. на-
зывают логарифмическим де-
крементом.
Заметим еще следующее. В на-
чальный момент гармоническое из-
менение напряжения определяемое
множителем cos р/ + у sin р^ еще не
достигло своего максимума; однако
272
благодаря множителю е “ производ-
ная от произведения равна нулю при
£ = 0, что и требуется, так как при
t—Q производная от ис должна быть
равна нулю (ток в цепи отсутствует).
Апериодический разряд. Если
сопротивление в цепи относительно
велико, т. е.
г>2|/'-^- или Q<|.
то разряд конденсатора происходит
апериодически. В этом случае кор-
ни характеристического уравнения
(10-51) вещественны, и решение
можно представить формулами
(10-56). Начальные свободные зна-
чения напряжения и тока опреде-
ляются, как и в предыдущем
случае:
«'с(0) =Ua, i'L(0) = 0.
Поэтому (‘при • положительных
направлениях рис. 10-10,а):
(10-61)
вен нулю, поэтому и производная от
напряжения на конденсаторе равна
нулю; касательная к кривой ис
в точке t—0 горизонтальна;
2) экстремальное значение тока
имеет место в тот момент времени,
когда кривая ис проходит точку пе-
региба, т. е. когда вторая производ-
ная от ис проходит через нуль и
изменяет знак; 3) напряжение на
индуктивности (пропорциональное
второй производной от ис) изменяет
знак после прохождения тока через
экстремальное значение (так как
производная от I изменяет знак)—
сначала э. д. с. самоиндукции про-
тиводействует току разряда, а зач-
тем поддерживает его в соответст-
вии с законом Ленца.
Когда г 2 L/C, влияние ин-
дуктивности на процесс разряда
конденсатора сколько-нибудь за-
метно только в самом начале про-
цесса (при'Малых </); в дальнейшем
процесс разряда конденсатора опре-
деляется только постоянной време-
ни гС> 2 i/LC. В этом случае
корни (10-52) характеристического
уравнения можно представить в та-
ком видео-
графики напряжения ис и тока
i приведены на рис. 10-11. На том
же рисунке построены кривые на-
пряжений на индуктивности (—иь =
= —Ldi/dt) и на сопротивлении
(—цг=—п), в сумме равные напря-
жению на конденсаторе («с=
=—иь—ит}.
Обратим внимание на следую-
щее: 1) в начальный момент ток ра-
2L I/ г2С гС’
Эти корни совпадают с корнями
характеристических уравнений кон-
тура г, С (первый корень) и конту-
ра L, г (второй корень). Имея вви-
ду, что
найдем по (10-61) надряжение на
конденсаторе:
* Здесь применяется очень полезная
для приближенных расчетов формула
у 1 — 2ез=1 — е при е 1.
18 К. М. Поливанов
273
При условии г2 4 первым
слагаемым можно пренебречь и по-
лучить простое выражение для на-
пряжения разряда конденсатора на
сопротивление.
Предоставляем читателю само-
стоятельно показать, что тот же
путь приводит к такому выражению
тока:
При исходном условии г > 2 X
XVL/C коэффициент затухания пер-
вой экспоненты много больше коэф-
фициента второй r/L > 1/гС.
Это значит, что, хотя ток в на-
чальный момент и равен нулю, т. е.
i(0) = 0, он очень быстро принимает
значение
Г
такое же как при разряде конден-
сатора на сопротивление в отсутст-
вие индуктивности.
Включение контура £, г, С к ис-
точнику гармонического напряже-
ния. Для рассматриваемой цепи
(рис. 10-8) следует сначала опреде-
лить значения и"с и i" (частное ре-
шение или установившийся режим),
пользуясь известными методами
теории переменных токов. По най-
денным значениям для установив-
шегося режима легко находятся
свободные составляющие и'с(0) и
г'ь(О) из начальных условий (10-55).
В выражениях для действительных
напряжения на конденсаторе ис =
= и'с+и"с и тока свобод-
ные составляющие представляются
формулами (Т0-56) или (ДО-58).
Характер протекающего переход-
ного процесса зависит от парамет-
ров контура, частоты сети и фазы
гармонического напряжения в мо-
мент включения.
На рис. 10-12 показаны графики
переходного процесса в предположе-
нии нулевых начальных условий для
колебательного режима (r<22[^L/C)
при (верхний график), ш <2 Р
(средний график) и для случая резо-
нанса р « <о.
При большой добротности контура
1/* А
п &ql V с
—-— процесс нарастания
колебаний в резонансном контуре
происходит очень медленно, посколь-
ку затухание свободной составляю-
щей мало. Действительно, за' один
период показатель экспоненты (лога-
рифмический декремент) увеличи-
вается в аТ = 2^ у раз.
Обращаясь к (10-57), находим,
что
г _ 1 _ 1
/4(£со0)2 — г2 p/'4Q2—1 ЭД*
Таким образом, при добротности
100 получаем аТ=0,0314, т. е. за
один период амплитуда свободной
составляющей (а они гасят ампли-
туду колебаний установившегося
режима) уменьшается всего на 3%.
Включение контура Ь,г,Ск по-
стоянному напряжению. После всего
изложенного выше такую задачу
читатель может решить самостоя-
тельно.
274
Свободный режим в контуре £,
г, С при ненулевых начальных усло-
виях —0)=^=0 и 0)^0.
При отключении источника пе-
ременного тока от индуктивной вет-
ви с параллельно включенной ем-
костью (рис. 10-13) в начальный
момент ток в индуктивности и на-*
пряжение на емкости могут отли-
чаться от нуля.
Рис. 10-13.
После отключения в цепи су-
ществуют только свободные состав-
ляющие, для которых &'с(0) и ^ь(О)
равны соответственно ис(—0) и
iL(—0), т. е. значениям, действи-
тельно существовавшим в цепи не-
посредственно перед моментом ком-
мутации (отключения).Теперь в вы-
ражениях (10-56) или (10-58) от-
личны от нуля как rz'c(O), так
и /'ь(О).
Граничный режим. Выше анали-
зировались уравнения апериодиче-
ского режима (корни yi и различ-
ные и вещественные) и колебатель-
ного режима (корни yi и уг ком-
плексно сопряженные).
На границе этих двух режимов
при г=2j/A или Q = i/2 два
корня (10-52) характеристического
уравнения (10-51) совпадают (случай
кратных корней)
Yi.2= а= 2ZT ’
а2 — 7^ = 0.
Выражения (10-56) при этом стано-
вятся неопределенными.
Раскрывая неопределенность по
правилу Лопиталя (дифференцируя
по ц), получаем вместо (10-56) сле-
дующие выражения для свободных
значений тока и напряжения:
и!с = и'с (0) (1 + at) e~at +
i_^(0) te~at-
~г С
= te^+i^(0)(1— at)e~at-
10-7. ОБЩИЙ СЛУЧАЙ РАСЧЕТА
РАЗВЕТВЛЕННОЙ
ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Система дифференциальных урав-
нений и ее решение. Переходные
процессы в разветвленной электри-
ческой цепи описываются системой
дифференциальных уравнений. Эти
уравнения составляются для конту«
ров и узлов заданной цепи по зако-
нам Кирхгофа аналогично алгебраи-
ческим уравнениям для установив-
шегося режима.
Если система уравнений пол-
ностью описывает рассматриваемую
электрическую цепь (или другую
физическую систему), то, последова-
тельно исключая неизвестные, всег-
да можно прийти к одному уравне-
нию, содержащему одно неизвест-
ное. Исключаемые неизвестные мо-
гут встречаться и непосредственно
под знаком производной или ’ин-
теграла. Поэтому для исключения
может оказаться необходимым не
только умножение уравнений на те
или иные коэффициенты, но также
их дифференцирование или инте-
грирование; этим повышается поря-
док высшей производной в оконча-
тельном уравнении (с одним неиз-
вестным) по сравнению с порядком
высших производных в отдельных
уравнениях системы.
Полученное уравнение с одним
неизвестным линейно, поскольку ли-
нейны все исходные уравнения. Его
решение, как это делалось в случае
простейших цепей, можно предста-
вить в виде суммы частного реше-
ния uz/, I" (при постоянном или гар-
моническом напряжении источника
это установившийся режим) и ре-
шения и', i' системы однородных
уравнений (свободный режим).
18*
275
Последнее для линейных уравне-
ний всегда может быть представле-
но суммой экспонент, например
известных постоянных В2 ....
Очевидно, что в случае трех посто-
янных такая система для тока
(10-63) имеет вид:
i' ^B1ep,i+B2ep,f, J
(10-62)
i(0) = i" (O+B.-HV-Hk
где pi,2... — корни характеристиче-
ского уравнения, а Bi>2...—
постоянные интегрирования.
Число корней и число постоян-
ных равны порядку дифференциаль-
ного уравнения.
Решение имеет вид (10-62) при
отсутствии кратных корней (все pi,
р2... различны). В случае кратных
корней добавляются новые слагае-
мые вида Atke^ (в случае двух
равных корней 6=1). К решению
для кратных корней можно прийти
от общего решения путем предель-
ного перехода и раскрытия неопре-
деленностей, как было показано
в § 10-6.
Постоянные интегрирования
определяются из начальных усло-
вий, применяемых к полному реше-
нию. Необходимое число на-
чальных условий равно числу
определяемых постоянных (а следо-
вательно, и порядку дифференци-
ального уравнения).
Все постоянные, входящие в вы-
ражение искомой функции, напри-
мер тока
z = i" + V = i" + +
di |
I f=o
__di”
~~~dt
I + B1pl +
li=o
+ B2P2 -|- B3pz\
+ ^ЛГ+...,
(10-63)
можно найти, применяя следующий’
общий метод.
Для момента / = 0 из начальных
условий определяются значение то-
ка и такого числа его производных,
чтобы можно было составить столь-
ко уравнений, сколько имеется не-
Рис. 10-14.
d2i I
~d&\
d2i”
+ Bjpf -[- B2/?2 -j- B3pl.
(10-64)
Известно, что начальные условия
определяют только значения токов
в индуктивностях и напряжений на
емкостях. Однако, применяя законы
Кирхгофа к электрической^ цепи
с заданными начальными условиями
ыс(0) и гь(0), всегда можно выра-
зить и требуемые начальные значе-
ния определяемой функции, напри-
мер тока, и ее производных.
Пример 10-3. В цепи рис. 10-14 при по-
ложении 2 -рубильника существовал уста-
новившийся режим. Напряжение источника
постоянно /7=240 в. В момент. £=0 рубиль-
ник мгновенно переводится в положение /.
Требуется найти ток iL в ветви с индуктив-
ностью.
Параметры цепи: /?=И0 омк г=2 ом.
£=0,1 гн, С=4 00 мкф.
Решение. Составим систему уравне-
ний по законам Кирхгофа:
1l+1c=i;
dil,
Ri 4- riL + L
diT
^C = riL + L~dt'
(a)
В этой, системе, кроме трех неизвестных
токов (/, г’ь, ic), содержится ещё неизвест-
ное напряжение на конденсаторе (wc). По-
этому к системе (а) добавим уравнение,
связывающее между собой ис и i’c,
duc
lc= с dt '
Пусть ищется г*ь. Тогда исключаем сна-
чала «с, дифференцируя третье из уравне-
ний (а), предварительно умноженное на С.
Обратим внимание, что этим, уже повы-
шается порядок дифференциального урав-
нения (в нем появляется вторая производ-
ная от тока iL). Затем исключаем ток i,
подставляя его значение из первого урав-
276
нения системы во второе. В итоге прихо-
дим к двум уравнениям:
dl '
*L (^ + r) + — 0;
diL d*L В)
«с =Cr at +CL dt*
с двумя неизвестными II и «с-
Из этих уравнений легко исключить ic
подстановкой ic из второго уравнения
в первое; после чего приходим к одному
уравнению с одним неизвестным
dir
(R + г) iL + (CrR + L)
d2ir
+CLR^=0. (r)
Для решения однородного уравнения
(г) составляем характеристическое урав-
нение
(Я + '*) + (CrR +L)p + CLRp* = 0 (д)
и находим его корни: р\ ——136 сек-1, р2—
=—884 сек-1.
В рассматриваемых условиях сущест-
вует только свободный режим, при котором
искомый ток
iL = + Аер< (е)
Остается только определить постоянные
интегрирования Л1 и А2} следуя системе
уравнений (10-64):
(0) = Л1 + Лг>
&L
dt
—AiPi + А2р2*
(ж)
Одно из начальных условий ib(0) находим
сразу из расчета цепи до коммутации
U
“20 а- (3)
Второе начальное условие найдем из треть-
его уравнения цепи (а), в котором при
/=0 известно напряжение на емкости
Ur
7^+r 40 в* (и)
Таким образом, имея в виду (з) и (и), на-
ходим, что
diL I йс(°) г
dt |<=0~ L ~ L lL^ = ^-
Теперь, зная начальные условия, находим
постоянные интегрирования из уравнений
(ж): Л 1=23,64, Л2=—3,6 и, следовательно,
ток *
fL==23,64e“136* — 3,б£-884* а.
Включение разветвленной цепи
к источнику произвольно изменяю-
щегося напряжения можно рас-
сматривать, применяя только что
изложенные приемы; отличие за-
ключается лишь ® частном реше-
нии, которое, очевидно, зависит от
вида приложенного напряжения.
Корни хар актер истического
уравнения не меняются (поскольку
они находятся из свободного режи-
ма). Остается прежним и метод
определения постоянных. Хотя зна-
чение постоянных может оказаться
иным из-за иных начальных значе-
ний -свободных токов и напряжений.
Пример 10-4. Найти ток в индуктивной
ветви iL при включении цепи на рис. 10-14
к источнику гармонического напряжения
и— t/7ncos(o)/-bif)); 540 в, со=314 сек~\
'ф=40°.
Параметры цепи те же, что .в приме-
ре ‘10-3. Включение происходит в момент
f=0 (рубильник переводится из -положе-
ния 1 в положение 2).
Решение. Искомое решение
i ь—i' l + if,L
состоит из свободной составляющей
i'L = Л1в^ + А2ер**
и составляющей установившегося режи-
ма i"L.
•Составляющую установившегося режи-
ма находим, пользуясь комплексным мето-
дом
== U/[R 4- Г 4- /со! 4- jtoCR (г 4- /<oL)j
или производя вычисления
46°10'а
L /2
i"£= 16,95 cos (314/—46° 10') а.
•Корни характеристического уравнения
Pi и р2 цепи рис. 10-14 уже были най-
дены в примере 10-3. Остается определить
постоянные интегрирования Ai и А2 из си-
стемы уравнений, аналогичных (10-64):
zL(0) = f"L(0)4-A + A;
(к)
diL I di”L\
~dF |/=о=“ЗГ к=о+/?1Л +Р*А*>
где
i"L (0) = 16,95 cos (—46° 10'),
I = — 16,95-314 sin (—46°10').
dt |/=o
Первое начальное условие iL (0) — 0 зада-
diL\
но. Второе начальное условие I Q опять
277
находим, применяя уравнения Кирхгофа к
цепи на рис. 10-14 [третье из уравнений (а)
примера 10-3]. Нэ в условиях рассматри-
ваемой задачи ис (0) = 0 при t = 0а поэ-
тому
«с (°)
L
£-z£(0) = 0.
hf=O
Теперь из уравнений (к) определяем =
= — 19,0, А —7,26 и, следовательно,
iL = — 19,0е~136* + 7,26е ~884* +
Подставим в (10-65) составляю-
щие с показателем pi (в общем слу-
чае pk) N^p^, выполним
дифференциальные операции (вклю-
чая в них интегрирование) и сокра-
тим на еР**. Тогда получим:
+ гМг +Lp1M1 — Lp1N1 —
— r^=0;
+ 16,95 cos (314£ — 46° 10').
Как видно из примеров 10-3 и
10-4, исключение всех неизвестных
величин, кроме искомой, из системы
дифференциальных уравнений
Кирхгофа необходимо только для
получения характеристического
уравнения (д).
Составление характеристического
уравнения. В случае разветвленной
цепи задачу можно упростить, поль-
зуясь методами главного определи-
теля или входного сопротивления
(см. также гл. 11, § 11-6).
Метод главного определителя це-
пи. Рассмотрим, например, цепь на
рис. 10-14 после коммутации (ру-
бильник переведен в положение /),
составим уравнения для контурных
токов Zi и 72, равных токам в ветвях
i и ict
Ril + ri1 + L^-L^—
-Lp^-rM.+^N^
+ Lp1N1 + rN1 = 0
ИЛИ
(7?+г 4- P1L) М, - (r+P1L) N. = 0;
(10-67)
Стоящие в скобках величины
в выражении (10-67) отличаются от
комплексных сопротивлений конту-
ров (Zmrn) и общей ветви {Zmn)
только заменой /ко на рд. Так, для
первого контура (рис. 10-14) Zn =
=7?+г+/со£, для общей ветви Zi2==
=Z2i=r+j(0'L и т. д. Аналогично
для свободного режима
— rz2==0;
^~dt rZi+'cr J*2
+L^-+ri. = 0.
(10-65)
Каждый из контурных токов, как
ток iL в только что разобранных
примерах, представляется суммой
двух экспонент (в общем случае
суммой п экспонент):
i2 = Nieplt+NzePtt. )
(10-66)
При этом составляющие каждого из
токов, выраженные через экспонен-
циальные функции с одинаковыми
показателями, должны удовлетво-
рять системе уравнений (10-65) как
одно из частных решений.
Z11(Pi) = R+r + PiL
^12 (Р1) :== ^21 (Pl) =: Р 4“ PlL
И т. д.
Здесь Zwn(Pi) понятное обозначе-
ние. На основании сказанного при-
дадим выражениям (10-67) такой
вид:
2ц {pk) АГй-]“212 (рй) IVk=O; ) /|q
Z21(Pk)Mk+Z22(pk)Nk=oJ
Поскольку все сказанное в при-
менении к корню pi справедливо и
для другого корня р2, в последнем
выражении индекс 1 всюду заменен
обобщающим индексом k. В полу-
ченной системе однородных уравне-
ний можно считать М& и Nk неизве-
стными. Любое решение, отличное
От нулевого (Alfc=='JVfe=O), может су-
ществовать только при равенстве
278
нулю определителя системы, т. е.
при
Д(Рй) = Zis(A) =о>
z21(a)z22(a)
Таким образом, любой из корней
p=pk характеристического уравне-
ния обращает определитель Д(р)
в нуль. Значит, уравнение
Д(р)=0
можно рассматривать как характе-
ристическое.
Например, для цепи рис. 10-14
имеем:
Л(Р) =
R -|-r-\-pL — (г Ч~ pL)
~~ — (r+pL) гpL~^=.
= ^ + ^L+^i-+i = 0,
т. е. RrpC+Rp%LC+R+r+pL==O,
что совпадает с уравнением (д) при-
мера 10-3.
Метод входного сопротивления.
Характеристическое уравнение мож-
но получить, приравняв нулю вход-
ное сопротивление ZBX(p) цепи для
источника э. д. с., включенного в лю-
бую из ветвей.
Действительно, исключая из
уравнения типа (10-67/) все неизве-
стные, кроме Ж, получаем урав-
нение
Z{pk)Mk = 0,
допускающее решение Ж=^=0 толь-
ко при Z(pk) =0. Но Z(pk), т. е. мно-
житель при Ж, легко может быть
истолкован как входное сопротивле-
ние для источника э. д. с., включен-
ного в ветвь соответствующего
тока.
Для какого бы контурного тока
не решалась исходная система одно-
родных уравнений, она может иметь
решение, отличное от нуля (Ж¥=0,
Ж=^=0) только при Д(рь)=0. Иначе
говоря, только при выполнении по-
следнего условия выполнимы усло-
вия
ZBX 1 (Ph) = 0, ZBX 2 (Р/г) 0
и т. д.
Вернувшись к цепи на рис. 10-14
и записав ZBX(p)=0 для ветви
с первым (или вторым) контурным
током, легко увидеть, что получен-
ное уравнение имеет своим решени-
ем ранее найденные значения pi и
Таким образом, характеристиче-
ское уравнение можно, получить, со-
ставив комплексное входное сопро-
тивление для любой ветви, заменив
/со на р и приравняв полученную ве-
личину нулю.
Так как характеристическое урав-
нение цепи не зависит от вида и ме-
ста включения источников э. д. с.
в цепи, то оба метода составления
характеристического уравнения при-
годны для любых цепей с источни-
ками э. д. с. любого вида.
Характеристическое уравнение
составляется для цепи после комму-
тации.
Включение источников напряже-
ния и источников тока. До сих пор
во всех примерах переходных про-
цессов источники питания рассма-
тривались как источники напряже-
ния (э. д. с.).
Если заменить источник напря-
жения (рис. 10-15,(2) эквивалентным
&
е)
Рис. 10-15.
279
источником тока (рис. 10-15,6), то
ни самый процесс, вызванный той
или иной коммутацией, ни метод его
расчета не изменятся. Действитель-
но, установившийся (принужден-
ный) режим по условию эквивалент-
ности источников остается неизмен-
ным. Что же касается свободного
режима, который определяется од-
нородным уравнением, то по усло-
вию в этом уравнении отсутствуют
источники возмущения, т. е. источ-
ники питания, создающие заданный
установившийся или принужденный
режим.
Другими словами, в цепи, со-
ответствующей свободно!му режи-
му, э. д. с. источников и токи источ-
ников тока равны нулю. Но при ра-
венстве нулю э. д. с. ее источник за-
мыкается накоротко (остаются по-
следовательно включенные пассив-
ные элементы цепи), а при равенст-
ве нулю тока источника тока его
ветвь разрывается (остаются парал-
лельно включенные пассивные эле-
менты). Поэтому в цепи с эквива-
лентными источниками питания
(рис. 10-15,а и 6) свободному режи-
му соответствует в точности одна и
та же пассивная цепь (рис. 10-15,8).
Совершенно иначе обстоит дело,
если вместо источника напряжения
в ту же ветвь включается источник
тока (рис. 10-16,62 и б). Нетрудно
так подобрать значения Эи/, что-
бы в установившемся режиме рас-
пределения токов и напряжений
тождественно совпадали в обеих це-
пях при заданных параметрах Ч Од-
нако в переходном режиме после
включения источников питания
процессы в первом и во втором
случае существенно различны.
В этом легко убедиться, обра-
щаясь к схемам цепи в свободном
режиме: для цепи с источником
э. д. с. схема получается из условия.
Э=0 (рис. 10-16,в); для цепи с ис-
точником тока — из условия 7 = 0
(рис. 10-16,г). Очевидно, что раз-
личным схемам цепи соответствуют
и различные корни характеристиче-
ского уравнения.
Определение действительных то-
ков и напряжений в момент включе-
ния. В случае включения источника
в цепь с нулевыми начальными ус-
ловиями очень легко найти все дей-
ствительные токи и напряжения
в момент включения (/=0). Для
этого следует считать в момент /=0
разорванными все ветви, содержа-
щие индуктивность, поскольку по
условию Zl(0)=0, а все емкости ко-
роткозамкнутыми, поскольку по ус-
ловию &с(0)=0. Так, например,
в цепи на рис. 10-16,а в начальный
момент ток в ветви, содержащей
конденсатор, /с(0) =Э/г.
Применение этого простого пра-
вила часто оказывается очень полез-
ным, во-первых, потому, что иногда
бывает важно знать именно началь-
ные токи и напряжения, а во-вто-
рых, потому, что простое определе-
ние действительных токов и напря-
жений «в начальный момент может
оказаться полезным для определе-
ния постоянных, входящих в выра-
жение свободных составляющих
[см. (10-64) и примеры 10-3, 10-4].
Применимость всех методов рас-
чета, основанных на линейности це-
пи. При расчете переходных процес-
сов в электрической цепи в силу ее
линейности, а следовательно, и ли-
нейности всех дифференциальных
уравнений, можно применять все
методы решения, основанные на
принципе суперпозиции.
1 Если бы источник э. д. с. был заме-
нен эквивалентным источником тока, то
в результате такой замены распределение
токов в остальной цепи не менялось бы при
любых параметрах цепи.
280
Рис. 10-17.
В частности, применяются два приема,
основанные на суперпозиции (см. также
§ 2-1*1).
1. Пусть к цепи, содержащей источники
питания, подключается новая ветвь в ре-
зультате замыкания рубильника. На рис.
10-47,а показана цепь, в которой ищется
переходной процесс, вызванный замыканием
точек а и Ь; внутри прямоугольника нахо-
дится вся цепь со своими источниками (Л—
активный четырехполюсник или цепь с дву-
мя внешними ветвями); одна ее ветвь с ис-
комым током i вынесена за пределы пря-
моугольника. Вызванный такой коммута-
цией переходный процесс можно рассматри-
вать как наложение на старый режим до-
полнительного.
Искомый ток i можно представить как
сумму двух токов /Ст и /д. Первый из них
(старый) представляет собой ток в той же
цепи, остающейся в старом режиме
(рис. 10-17,6). Второй (дополнительный)
представляет собой ток, возникающий
в пассивной цепи, когда к точкам а и b
включается источник с э. д. с. э=и (рис.
10-17,в), т. е. создающий между этими точ-
ками напряжение, равное, но противопо-
ложно направленное напряжению и~иаЬ
цепи до коммутации (рис. 10-17,6).
В этом дополнительном режиме на-
чальные условия нулевые. Пассивная цепь,
заключенная внутри -прямоугольника П
(пассивный четырехполюсник), отличается
от действительной только тем, что в ней
э. д. с. всех источников равны нулю, так
же как равны нулю все токи источников
тока.
2. Пусть в заданной цепи происхо-
дит разрыв какой-либо ветви, показанный
на рис. 10-18,а как размыкание рубиль-
ника.
Вызванный такой коммутацией пере-
ходный процесс можно рассматривать как
наложение на старый режим (рис. 10-18,6)
дополнительного (рис. 10-18,в). В этом до-
полнительном режиме между точками раз-
рыва включается источник тока J. (Заме-
тим, что включение источника тока пред-
ставлено размыканием рубильника, парал-
лельного источнику тока.) Его ток ра-
вен и противоположно на-
правлен току /р, который
проходил бы через разор-
ванную ветвь, если бы она
оставалась замкнутой (рис.
10-118,6). При этом предпо-
лагается отсутствие всех дей-
ствительных источников пи-
тания. В этом дополнитель-
ном режиме начальные усло-
вия считаются нулевыми.
Пример 10-5. Для цепи
на рис. 10-19,а дано э=
“100 cosco/ в, coL=lO ом,
/?1=#2=10 ом, w =314 сел;-1;
размыкание происходит в мо-
мент /=0, когда в цепи уже
существует установившийся
режим.
Требуется определить-
ток и после отключения ру-
бильника, пользуясь изло-
женным методом.
Решение. Искомый ток до коммута-
ции /ют' и ток, существовавший в разры-
ваемой ветви, легко находим как токи уста-
новившегося режима:
ip =4,47 cos (со/—63° 25') а;
ii с т=4,47 cos (со/—63° 25') а.
Затем ищем дополнительный ток в ветви
с сопротивлением R\ при включении источ-
ника тока J=ip в цепь на рис. 10-19,6 (об-
ратите внимание на положительные направ-
ления!).
Этот ток имеет составляющую устано-
вившегося режима Г'1Д=3,16 cos (со/—18°25'>
и свободную составляющую
»'1Д = лхер^,
где
Р1= — Ri/L = — 314 сек-1.
Постоянную интегрирования Ai найдем
из начальных условий для дополнительного
режима. В начальный момент весь ток ис-
точника J=ip должен проходить через
ветвь так как в индуктивности в на-
чальный момент ток равен нулю по закону
коммутации. Следовательно,
Лд (0) = 7 (0) = Г,д (0) + :"1Д (0)
или
4,47 cos(—63°25') =3,16 cos(—18°25')
откуда
Л1=—1 а.
Действительный ток переходного ре-
жима в ветви Ri определим как сумму
старого тока в этой ветви Ист и дополни-
тельного тока, состоящего из двух состав-
ляющих Г1Д и /"1Д:
/1 == /1СТ + Г1д + =
= 4,47 cos (со/ — 63°25') — U~3J4‘ +
4-3,16 cos (со/ — 18°25').
Рис. 10-18.
284
Рис. 10-19.
Этот ток в первый момент (/=0) ра-
вен всему току источника э. д. с. э (;в его
ветви содержится индуктивность). Очень
быстро этот ток становится равным ново-
му установившемуся значению.
Характер переходного процесса
и корни характеристического уравне-
ния. Из всего предыдущего видно,
какую большую роль играют корни
характеристического уравнения, по-
скольку при переходном процессе
токи (и напряжения) содержат экс-
поненты
/св = Ateplt + А2ер‘* +... (10-68)
Если корни вещественны и отри-
цательны, например pi,2=—cc±ip<0,
то каждая из свободных составля-
ющих переходного процесса моно-
тонно затухает.
Если корни комплексны, напри-
мер pi,2=—ia±/p, в цепи возникают
колебания. Эти колебания затухают
при отрицательной вещественной
части корней Re(pi,2)=—*а<0.
Если вещественная часть хотя бы _
одного корня положительна, пере-
ходный процесс не затухает: состав-
ляющая eplt — e~~ate+^ при a<0,
т. е. при RefpJX), экспоненциально
возрастает. При а = 0ир5А0в цепи
устанавливаются незатухающие сину-
соидальные колебания, при а=р = О
в цепи без источников питания может
установиться постоянный ток (сверх-
проводящий контур).
Поскольку все коэффициенты
при р в характеристическом уравне-
нии вещественны, комплексные кор-
ни могут появляться только как
комплексно сопряженные пары.
На рис. 10-20 представлено пере-
мещение корней по комплексной
плоскости при уменьшении сопротив-
ления г в последовательном контуре
L, г, С. При r>2^L[C корни рг
и р2 различны и отрицательны (круж-
ки на вещественной оси £<0). При
г-^2УЦС корни рг и р2 сходятся
к одной точке. При дальнейшем
уменьшении г корни становятся сопря-
женно комплексными (треугольники
на пунктирной .кривой); при г — 0
корни лежат н'а мнимой оси. Нако-
нец, при r<fo вещественная часть
корней (г) положительна. Такая си-
стема оказывается неустойчивой: на-
чавшиеся в ней колебания хотя бы
с ничтожно малой амплитудой посте-
пенно возрастают, и это возрастание
ничем не ограничивается (до тех пор,
пока система остается линейной).
На рис. 10-21 схематически пока-
зано изменение свободной составля-
ющей в функции времени при раз-
личных значениях корней, соответст-
вующих этой составляющей.
Отрицательное сопротивление
в цепях с обратной связью. В обыч-
ных линейных цепях сопротивление,
как бы оно ни было мало, все же
больше нуля. Поэтому в линейных
цепях с постоянными параметрами
и без обратной связи вещественные
части всех корней всегда отрица-
тельны.
Однако в цепях, содержащих
управляемые сопротивления, напри-
мер в цепях с триодами, можно
установить обратную связь,
т. е. связь между управляющим на-
пряжением (напряжение на сетке
электронной лампы) и напряжением
282
Рис. 10-21.
на одном из элементов цепи лампы.
В результате обратной связи экви-
валентное сопротивление цепи мо-
жет обратиться в нуль и даже стать
отрицательным (см. также § 7-4).
Простейшая схема обратной
связи показана на рис. 10-22,я, где
напряжение на сетке ис связано че-
рез взаимную индуктивность с то-
ком в индуктивной ветви контура.
На рис. 10-22,6 показана эквива-
лентная схема лампы: э. д. с. экви-
валентного источника равна напря-
жению на сетке
diT
умноженному на коэффициент уси-
ления р (обратите внимание на зна-
ки « около индуктивно связанных
обмоток). В схеме замещения п —
внутреннее 'сопротивление лампы.
Система уравнений для рассма-
триваемой цепи (рис. 10-22,6) Ч
duc л
* ~ lL + 1С — 1'L + ~йГ ’
Г diL ,
uc L +
*diL л diL ,
-э =?М 4F = tri-YL rtL.
Исключив из этой системы все
неизвестные, кроме iL, придем к
уравнению
d'1'- \-с(г4
ric J dt'
1 В предыдущем <и в последующих
уравнениях следует различать ис (напря-
жение на сетке) и ис (напряжение на кон-
денсаторе) .
Сравнив его с известным уже урав-
нением колебательного контура L,
г, С, найдем, что этот контур обла-
дает эквивалентным сопротивле-
нием
Очевидно, что для заданного коэф-
фициента усиления р можно -всегда
подобрать такую индуктивную
связь М, чтобы гэ=0. Это требова-
ние выполняется при
рЛ4 = Л + гггС.
Заметим, что при большем М
эквивалентное сопротивление ста-
новится отрицательным; отрицате-
лен становится и коэффициент за-
тухания
Амплидута колебаний в такой
системе ограничивается только тем,
Рис. 10-22.
283
что коэффициент усиления ц умень-
шается с ростом амплитуды напря-
жения на сетке лампы и лампа уже
не может рассматриваться как ли-
нейный элемент цепи.
10-8. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В ПРОСТЕЙШИХ
ЭЛЕКТРОМЕХАНИЧЕСКИХ
И ЭЛЕКТРОТЕРМИЧЕСКИХ
СИСТЕМАХ
Все изложенное в этом разделе о пе-
реходных процессах можно отнести не
только к токам и напряжениям электриче-
ской цепи, но и к любым физическим вели-
чинам, если они входят в аналогичные
дифференциальные уравнения и если ана-
логично определяются их начальные, •зна-
чения, например, из выражения тех или
иных видов энергии (кинетической или
потенциальной в электромеханических си-
стемах, тепловой энергии в электротерми-
ческих системах и т. п.). С подобными за-
дачами очень часто приходится встречать-
ся в электротехнике, особенно когда меха-
нические силы, моменты или температура
определяются электрическими процессами
и в свою очередь влияют на процессы
в электрической^ цепи. В дальнейшем бу
дут приведены примеры расчета простей-
ших электромеханических систем (гл. 11,
примеры 11-6 и 11-7).
Здесь мы приведем только расчет про-
стейшего переходного процесса в электро-
термической системе, а именно нагрев ка-
беля при кратковременной перегрузке.
Пусть жилы кабеля при длительно
протекающем токе 7Н нагреваются до тем-
пературы 0н, здесь Он — допустимое превы-
шение температуры жил кабеля над темпе-
ратурой окружающей среды (например,
воды для подводного кабеля, почвы для
кабеля, проложенного в земле). Сопротив-
ление одной жилы кабеля на единицу его
длины равно г.
В этих условиях весь отвод тепла, вы-
деляемого в жилах, определяется тепло-
проводностью между жилой и окружаю-
щей средой. Из теплового закона
Ge9 = P (10-69)
(теплопроводность, умноженная на раз-
ность температур, равна отводимой мощ-
ности) по известным значениям 0Н, /н, г
легко найти значение теплопроводности:
Р !нг
(10-7°)
Но уравнение (10-69) применимо только
к установившемуся режиму (6 = const).
Если же температура жилы кабеля изме-
няется, то изменяется и тепловая энергия
жилы, равная произведению температуры 9
и теплоемкости Сб. При этом часть мощ-
ности идет на увеличение этой энергии:
^0 d9
dt ~~С6 dt
(10-71)
Поэтому при переменной температуре
уравнение (10-69) должно быть заменено
более общим
j J9
(10-72)
где первое слагаемое определяет тепло,,
отводимое через теплопроводность, л вто-
рое— тепло, поглощаемое нагреваемым
телом.
Решение уравнения (10-72) легко най-
ти при постоянном значении р=Ро: -
0=^-+Ле~«»,
Ge
где a = Gg/Cg находится из характеристи-
ческого уравнения. Первое слагаемое —
установившееся значение температуры (ча-
стное решение); второе — решение однород-
ного уравнения, оно содержит постоянную*
интегрирования, определяемую из .началь-
ных условий.
Если в начальный момент времени
(t = 0) температура жилы была известна
0 (0) — 60, то
Л = 0.-^-.
Подставляя найденное значение по-
стоянной А, находим решение:
0 = £*-(1—<?-<•»)+0ое-«*. (10-73>
При малой теплопроводности и большой
теплоемкости коэффициент а может быть
очень малым (большая постоянная време-
ни т=‘1/а). Поэтому -при большой, но крат-
ковременной перегрузке кабеля температу-
ра его жил может возрасти ненамного.
Пример 10-6. Медный трехжильный
кабель с номинальным напряжением 10 кв,
прокладываемый в воде, имеет сечение каж-
дой жилы S = 35 мм2, сопротивление одной
жилы г = 0.52 ом/км, допустимый ток /н—
180 а при 8Н = 45° С.
При коротком замыкании ток в кабеле
возрастает в 10 раз и отключается через
0,02 сек.
Требуется найти температуру жилы
при такой кратковременной перегрузке.
Решение. По формуле (10-70) нахо-
дим значение теплопроводности для каж-
дой из жил Gg = 3,74«10“3 emlcM'Zpad*
(обратите внимание на единицы измере-
ния).
Теплоемкость на 1 см жилы
Cg = CS^,
284
где с = 0,380 вт • сек! г • град — удельная
теплоемкость меди; 5—сечение жилы (см2),
равное объему меди (см3) на 1 см длины;
7 = 8,9 г!см? — плотность меди. Для ука-
занных данных Се==1,18 вт-сек!см-град.
При этом постоянная времени t=1/zz=
= C6/Gq==316 сек и а = 3,17« 10~3 сек-1.
При 10-кратном возрастании тока мощ-
ность, рассеиваемая в жилах, возрастает
в 100 раз. Поэтому, если при номинальном
токе температура 6Н —45°С, то при рас-
сматриваемой перегрузке в установившемся
режиме 0уст = 4 500° С. Подставляя най-
денные числовые значения в формулу
(10-73), получаем:
6 = 4 500 (1 — e~at) + 45e~at,
где 8о =45° С — превышение температуры
кабеля над температурой воды, окружаю-
щей кабель, достигнутое при длительной
но(рмальной нагрузке кабеля. Через -интер-
вал времени /1=0,02 сек -(когда ток корот-
кого замыкания будет выключен) показа-
тель степени приобретает значение аЛ=
=б,з- ю-5 < а.
'«Поэтому, разлагая экспоненту в сте-
пенный ряд, находим, что вызванное то-
ком короткого з-амыкания повышение тем-
пературы (по сравнению с температурой
нормального режима) составляет прибли-
зительно 0,28° С.
Из приведенного расчета видно, что
кабель устойчив к кратковременным пере-
грузкам. Достигаемая им температура
определяется «импульсом мощности», т. е.
всей энергией, выделяющейся в нем при
кратковременной перегрузке «(см. § 10-4).
«Нетрудно подсчитать допустимую пе-
регрузку по току 1т, на время в 1 сек, ис-
ходя, например, из допустимого увеличе-
ния температуры жил кабеля на 10° С. До-
пустимый ток /т~'8,3/н-
При больших сечениях устойчивость
к перегреву значительно увеличивается.
Приведенные в примере цифры носят >ил-
люстративный характер, так как в дейст-
вительности весь процесс сложнее.
10-9. ПРОЦЕСС В ЦЕПИ
ПРИ ВОЗДЕЙСТВИИ
ПРОИЗВОЛЬНО ИЗМЕНЯЮЩЕГОСЯ
НАПРЯЖЕНИЯ
Прямой метод решения подоб-
ных задач состоит в отыскании ча-
стного решения в соответствии с за-
данными э. д. с. или токами источ-
ников. Он уже был рассмотрен на
ряде примеров.
Перейдем к рассмотрению двух
других «методов, из которых первый
широко применяется.
Интеграл Дюамеля. Интеграль-
ное преобразование Дюамеля приме-
няется для отыскания реакции пас-
сивной системы при воздействии
возмущения, произвольно завися-
щего от времени, в тех случаях,
когда известна реакция системы
Д(/) на единичное возмущение, на-
пример, при включении пассивной
цепи к источнику единичного напря-
жения (рис. 10-23):
«(0 = 1 ° при (10-74)
I 1 при />0.
В общем случае реакцию Д(/)
называют переходной функ-
цией. Если, например, при вклю-
чении последовательно соединен-
н и
1 ---------
___________t
Tl
Рис. 10-23.
ных С и г к постоянному напряже-
нию (10-74) искомая реакция есть
ток, то переходная функция (10-19)
A(t) = ±e~tlrC-,
ее называют переходной про-
водимостью. Если в тех же
условиях искомая реакция — напря-
жение на конденсаторе, то переход-
ная функция (10-18)
X (/) = (!— e~t,rC);
ее называют передаточной пе-
реходной функцией.
Сущность излагаемого метода ос-
новывается на принципе суперпози-
ции, т. е. на возможности для лю-
бой линейной системы представить
реакцию на действительное возму-
щение u(t) как сумму реакций на
отдельные слагаемые этого возму-
щения.
Пусть, например, это возмуще-
ние можно представить как сумму
п слагаемых
«(0 = S«n(0. (Ю-75)
п
и пусть zn(</) есть реакция на от-
дельное слагаемое un(t}, В таком
случае полная искомая реакция
/(0=£М0-
п
(10-76)
285
Пусть заданное возмущение
представляется непрерывной функ-
цией u(t) при £>0 и равно нулю
при f<0, как показано на рис. 10-24.
Такую функцию можно приближен-
но представить рядом постоянных
слагаемых иП9 каждое из которых
добавляется к предыдущему в мо-
мент времени т. Сумма таких сту-
пенчатых функций в точности равна
u(\t)9 если полагать, что через каж-
дый малый интервал времени dx
добавляется слагаемое
, da
du
dt
dz
или
, da i
du—~^ dx,
если значение производной du/dt
в момент т обозначать как duldx.
Очевидно, что в этом случае
сумма (10-75) переходит в интеграл
t
U(t)=^^dz (10-77)
i=0
или
t
«(0 = и(0)+ (10-78)
i=0
если в начальный момент включает-
ся конечная ступень «(0), т. е.
функция &(/) претерпевает разрыв
в момент if—0.
Реакция в момент времени t>x,
обусловленная ступенью du, появив-
шейся в момент времени т, может
быть представлена выражением
di — dx, (10т79)
где аргументом переходной функ-
ции служит разность t—т, т. е. вре-
мя, отсчитываемое от момента по-
a(t)
явления соответствующей слагаемой
возмущения du.
Полная искомая реакция (10-76)
на заданное действительное возму-
щение и (it) представляется как ин-
теграл от (10-79) р
Z(/) = pe-^^/(10-80)
1=0
если u(t)—непрерывная функция,
равная нулю при /=0.
Если же в момент t=0 функция
и (it) сразу изменяется от 0 до зна-
чения и;(0), то наряду с бесконечно
малыми ступенями du на систему
действует постоянная слагаемая
и(0), включившаяся в момент 0.
При этом вместо (10-80) полная
реакция представляется выраже-
нием
t
i(t)=u(O)A.(t)+ ^A(t-^dx,
1=0
(10-81)
которое «и называют интегралом
Дюамеля.
Полученный вывод нетрудно
распространить и на случай, когда
заданная функция претерпевает
разрыв и в какой-либо иной точке,,
например, скачком спадает до нуля
в момент Т (рис. 10-25).
В этом случае для интервала
0 <КТ по-прежнему применима
формула (40-81). Но для t>T сле-
дует считать, что в момент t=T
к напряжению и(Ф) добавляется
еще одна конечная ступень.—и(Т),
а в дальнейшем никаких новых сту-
пеней du уже не появляется. Ска-
занное равносильно тому, что при
t>T в системе действуют постоян-
ные напряжения и(Т) и —и(Т).
Сумма этих двух слагаемых соот-
ветствует действительному равенст-
ву нулю общего напряжения.
286
Выражение для полной реакции
при t>T принимает вид:
т
— A(t)-\- С A(t — т)
т=0
у
~r~dz —
az
— u(T)A(t — T). (10-82)
Следует обратить внимание, что,
хотя верхний предел интеграла те-
перь остается постоянным т=Т,
сам интеграл есть фукция времени
t, поскольку последнее входит в ка-
честве параметра в подынтеграль-
ную функцию. Постоянство верхнего
предела можно объяснить и так:
при t>T функция гг(/)=ц(Т) =
=const и, следовательно, ее произ-
водная тождественно обращается
в нуль при t>T.
Рассмотрим еще функцию, претерпе-
вающую разрыв -в точке 7, но не обра-
щающуюся в зтой точке в нуль. Пусть, на-
цример (рис. 10-26), м=0 при /<0, и=щ,
при 0<t<T и и=и2 при t>T.
В таком случае для t>T
т
+ С rz'i('c)X(^ — т:) dz +
t=:0
+ 1«2 (П- «1(П1 Т) +
t
+ J u'z^z) A(t— z) dz. (10-83)
В этом выражении
Пример 10-7. В цепи 7 = 5 мгн, г =
= 0,2 ом действует напряжение, показан-
/ t \
ное на рис. 10-26, где к1==201 1 +*у ) в
и «2 = — 30г~100 d—T) в При 7 = o^oi сек.
Требуется найти ток при t > Т.
Р е щ е н и е. Для данной цепи пере-
ходная проводимость (10-25)
А (0 = 5(1 —
и
A (t — t) = 5 (1 — «-"‘е40’).
Подставляя заданные Mi, и2, А и Т
в формулу (10-83), получаем
/ = 100(1—г-40*)+
0,01
+ Г 104(1 — е-4»‘е40т) dt +
о
+ (—30 — 40) 5(1— ei0T e~iot) +
t
+ Г 1,5.104е“100т?°ог(1— e-№teiOx)dz =
o;oi
= Ю0е-10ое — 49,5е—400 а,
где 0 = t — Т.
Задачи, подобные приведенной
в этом примере, часто проще ре-
шать операторным методом (см.
гл. 11), суперпозируя решения для
отдельных функций. Применение
интеграла Дюамеля может ока-
заться полезным, когда функция
u(i) задана графиком, не имеющим
аналитического выражения. В этом
случае искомую реакцию /(£) для
момента t можно найти, пользуясь
формулой (10-81). При этом надо
продифференцировать графически
заданную кривую, умножить ее на
функцию A(t—т) при /=const и
выполнить графическое интегрирО'
вание. Такой ход вычислений, одна-
ко, достаточно трудоемок (см.
§ 12-6).
Выражение заданной функции «(/) че-
рез дифференциальное уравнение. Пусть
в уравнении цепи
л0/+ —a(t) (10-84)
функция u(t) удовлетворяет известному
дифференциальному уравнению
&оИ + 61-^+...=0. (10-85)
В таком случае, умножая первое уравне-
ние на Ьо
b^aQi -j- (О»
затем дифференцируя первое уравнение и
умножая его на Ь\
. dl J.!, ЛЧ _L —А ДЕ.
dt* + bl dt
и T. Д.,
Рис. 10-26.
287
^получаем систему уравнений, в правой ча-
сти которых последовательно стоят сла-
гаемые однородного дифференциального
уравнения для u(t), т. е. уравнения (10-85).
Складывая все полученные таким путем
^уравнения, приходим к однородному урав-
нению для искомой функции i(t):
di
+ (Ml + Mo) =
— b^u Ь^ b••• —0. (10-86)
При этом, конечно, порядок дифферен-
циального уравнения и число постоянных
интегрирования повышаются, а следова-
тельно, увеличивается и число необходи-
мых начальных условий. Дополнительные
начальные условия определяются данными
для u(t) и его производных в момент /=0.
Хотя в явной форме этот метод редко
применяется, он имеет принципиальное
значение, поскольку по существу именно
•к нему сводятся широко распространенные
/приемы операторного метода при произ-
вольной форме включаемого напряжения
(см. гл. 11).
10-10. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
ПРИ «НЕКОРРЕКТНЫХ»
НАЧАЛЬНЫХ УСЛОВИЯХ
Ранее формулированные законы
коммутации имеют ограниченную
/применимость. Часто без достаточ-
ного основания к числу некоррект-
но поставленных задач относят за-
дачи, в которых нарушаются основ-
ные законы коммутации:
ис{— 0) = йс(Д-0) (10-87)
(непрерывное изменение напряже-
ния на конденсаторе) и
iL(- 0)=Zx(4-0) (10-88)
-'(непрерывное изменение тока в ин-
дуктивности) .
Первый из этих законов нару-
шается при подключении конденса-
тора Ci, заряженного до- напряже-
ния иС\(—0), к конденсатору С2,
заряженному до другого напряже-
ния иС2(—0) (рис. 10-27).
Рис. 10-28.
Действительно, начальные усло-
вия по формуле (10-87) для двух
конденсаторов запишутся так:
( -Р) — «Р)’
(10-89)
( Р) = ^С2 (4“
Но сразу после коммутации напря-
жение на конденсаторах должно
быть одинаковым, т. е.
^i(+°) = ^2(+°)- (10“9°)
В общем случае при иС\ (—0)
=7^02 (—0) противоречие (10-89) и
(10-90) очевидно.
Точно так же нарушение перво-
го закона коммутации наблюдает-
ся при включении конденсатора или
группы конденсаторов непосредст-
венно к источнику заданного на-
пряжения (рис. 10-28 и 10-29).
Исключить это видимое наруше-
ние, казалось бы, бесспорного за-
кона можно, обращаясь к малым
параметрам, которыми пренебрегли
при постановке задачи. Действи-
тельно, провода, соединяющие пер-
вый и второй конденсаторы в схеме
на рис. 10-27, обладают хотя бы и
очень малым, но конечным сопро-
тивлением р (рис. 10-30,6), на ко-
торое и ляжет первоначальная раз-
ность начальных напряжений. Если
это сопротивление мало, в соедини-
тельном проводе пойдет большой
ток, в результате чего напряжения
на конденсаторах быстро сравняют-
ся. Кроме того, в контакте, замы-
кающем цепь, сопротивление сна-
чала было бесконечно велико и
лишь постепенно (хотя бы и очень
быстро) спадало до нуля (или до
тысячных долей ома). Можно учесть
и наличие хотя бы малой индуктив-
ности % (пусть даже порядка долей
микрогенри) в контуре, образован-
ном после замыкания рубильника.
288
Учитывая эти малые параметры,
можно «(корректно» поставить за-
дачу, в результате чего все началь-
ные условия в точности будут со-
ответствовать двум основным зако-
нам коммутации. Однако такое
стремление к корректности ради
корректности может без всякой не-
обходимости чрезвычайно услож-
нить не только решение, но и поста-
новку задачи. Например, от некор-
ректной схемы рис. 10-27 можно
прийти к совершенно корректной
схеме рис. 10-30,а или к упрощен-
ной, но тоже корректной схеме
рис. 10-30,6. Однако, если длитель-
ность всех процессов, обусловлен-
ных наличием дополнительных ма-
лых параметров, очень мала по
сравнению с постоянной времени
r(Ci + C2), то идеализация цепи,
представленная (схемой на рис. 10-27,
вполне правомочна.
Теперь относительно наруше-
ния закона коммутации ис(—0) =
—'^с(+0).
(При выводе этого закона (см.
начало главы) подчеркивалась ко-
нечная величина мощности (ш),
передаваемой от одного элемента
цепи к другому. .При конечном зна-
чении этой мощности энергия лю-
бого элемента не можёт изменяться
скачком (и2сС12 для конденсатора
и i2iJLI2 для индуктивности). Но
если сопротивление проводов, со-
единяющих конденсаторы Gi и С2,
стремитсячк нулю, то протекающий
19 К. М. Поливанов
ток стремится к бесконечности, по-
ка иС1^=иС2- Это значит, что к та-
кой цепи, так же как к цепям
рис. 10-128 и 10-29, закон коммута-
ции Uc(+0) —Uc(—0) неприменим.
Поэтому при рассмотрении той
или иной конкретной задачи сле-
дует исходить из более общих зако-
нов (например, закона сохранения
заряда) не зависящих от того,
остается ли мощность конечной.
При этом следует помнить, что ко-
нечное изменение заряда за беско-
нечно малое время коммутации мо-
жет происходить только на тех кон-
денсаторах, через которые в момент
коммутации кратковременно прохо-
дил бесконечно большой ток1.
Закон сохранения заряда. Для
двух параллельно включаемых кон-
денсаторов, имевших различные
напряжения, условие коммутации
может быть формулировано как
инвариантность их общего заряда:
ис\ (— 0) Cj + йС2 (— 0) С2 =
^zzc(+O)(C1 + C2), (10-91)
т. е. сумма зарядов, существовав-
ших на конденсаторах до коммута-
ции, равна их общему заряду после
коммутации, когда оба конденсато-
ра имеют одинаковое напряжение
(+ 0).
Цепь с конденсаторами; Прове-
дем анализ процесса в трех схемах
(рис. 10-27—10-29), обратив особое
внимание на происходящие в них
преобразования энергии.
Для переходного процесса в це-
пи на рис. 10-27 уравнение цепи
после коммутации имеет вид:
_ . dllr .
UQ~r (С1-]ГС2) +
Решение этого уравнения
uc = UQ-[~Ae~t/x, (10-92)
где т=г(С1 + С2), а А—постоянная
интегрирования.
Постоянную интегрирования
однако теперь нельзя определять
1 Ток, © сражаемый . {посредством д
функции (юм. следующий (параграф).
289
из предположения о неизменности
напряжения на конденсаторах; оно
неприменимо к нашей некоррект-
ной задаче. Но по закону сохране-
ния заряда первоначальный заряд
двух конденсаторов теперь распре-
делился между параллельными
конденсаторами с общей емкостью
Ci + C2, поэтому в начальный мо-
мент после коммутации
—^ci(+0)—^С2(+о) —
Uq\ ( 0) С\ -р ( 0) С2
Ci+C2
. (10-93)
Этому значению и равна сумма
Следовательно,
Д = «с(+0)-С7о
и окончательное решение:
zzc = t/0 + [«c(+0)-(70]^.
Ток источника по закону Ома
. ис (+ 0) Z/t
Преобразование энергии. Най-
денное из закона сохранения за-
ряда мгновенное изменение напря-
жения приводит к следующему за-
ключению относительно энергии.
До коммутации в конденсаторах
содержалась энергия
UCl(~~ °) С1 «с2("~°)С2
(10-94)
После коммутации энергия поля
обоих конденсаторов
/ I «с(+°)(^+С2) /1ПП^
а>(+0) =---------g------ (10-9о)
стала меньше первоначальной.
Но закон сохранения энергии
здесь, конечно, не нарушается. Раз-
ность начальной и конечной энер-
гий электрического поля
Lw = w (— 0) — w( + 0) (10-96)
в процессе коммутации преврати-
лась в тепло по закону Джоуля-
Ленца (если не учитывать электро-
магнитного излучения).
290
Путем несложных преобразова-
ний из (ПО-93) — (10-96) можно по-
лучить следующее выражение:
д» = [„с1(-о)-у-О)]‘?^_.
( (Ю-97)
Обращаясь к схеме рис. 10-30Д,
легко догадаться, что энергия могла
рассеяться в сопротивлении р. Если р
очень мало (р—>0), через это сопро-
тивление кратковременно проходит
очень большой ток (/->оо), поэтому
J i2pdt мбжет оставаться конечным
6
даже при очень малом интервале
времени (Д/^0).
Более подробно анализ проводится
в применении к схеме рис. 10-28.
В этой цепи после мгновенного беско-
нечно большого броска тока конден-
сатор заряжается до напряжения
источника uc = UQ. При этом энергия,
отданная источником,
/ t .
с* diis> q
wH = \uaidt = \U0C-£dt = U20C
о о
(10-98)
в 2 раза больше энергии, полученной
конденсатором (И? С/2). Следователь-
но, половина энергии, подведенной
от источника, рассеялась в сопротйв-
лении контакта.
Этот результат не зависит. от
того, какое сопротивление было
включено между источником напря-
жения и конденсатором, так как в
выражение мощности входит только
ток, равный С . Если к моменту
AZ процесс заряда можно считать
оконченным и ис = 170, то совершенно
несущественно, как изменялось зна-
чение производной в течение про-
цесса заряда.
На рис. 10-29 представлена схе-
ма двух конденсаторО(В с разной
емкостью и с различными сопротив-
лениями изоляции Г1 и г2. Сразу
после -включения источника бросок
тока заряжает последовательно
включенные конденсаторы, и, сле-
довательно, на каждом из них за-
ряд сразу после коммутации оди-
наков. При этом, как известно из
физики, напряжения на конденса-
торах обратно •пропорциональны их
емкостям:
“с, (+°)=£7«<лтг;
(+°) —;
(10-99)
иС1 иС2------Up
Если при этом через сопротив-
ления ri и г2 проходят разные токи,
то их разность ir\—iT2 приносит до-
полнительный заряд ко второму
конденсатору. С течением времени
этот дополнительный заряд приве-
дет к такому перераспределению
напряжения между конденсаторами,
при котором эти токи сравняются.
Только при этом условии наступит
установившийся режим и прекра-
тится дальнейшее перераспределе-
ние зарядов. Очевидно, что усло-
вию равенства токов через сопро-
тивление изоляции соответствует
распределение напряжения
— U ________г-1___.
ci и*Г1 + ге
(10-100)
UC2 & о
Из сказанного понятно, почему
работа емкостного делителя напря-
жения зависит от частоты и он не
годится при постоянном напряже-
нии (распределение по сопротивле-
ниям изоляции).
Рассмотрим некоторые количественные
соотношения, подтверждающие правомоч-
ность изложенного подхода.
Пусть в цепи рис. 10-29 Сг=
=8-10-9 0, C2=l - IO-9 ф, Г1 = 103 Мом,
г2—250 Мом. Мы полагали, что сопротив-
ление р, включенное последовательно с ис-
точником, равно нулю; на самом деле оно
существует и может составлять сотые доли
ома. В таком случае при включении к ис-
точнику 17о=‘Ю0 в ток хотя и достигнет
10 000 а, но останется конечным. Такой ток
способен зарядить наши конденсаторы зп
время порядка 10~10 сек, так как требуе-
мый заряд
Qo=^oCiC2/(Ci + C2)=!1,6-10-7 к.
К тому же результату мы придем,
оценивая постоянную времени цепи без
учета больших параллельных сопротивле-
ний (т. е. полагая ri=r2~oo); эта постоян-
ная времени т порядка «10“п сек.
Естественно, что мы пренебрегали пока
током через сопротивление, изоляции, ко-
торый не превосходит десятимиллионную»
долю ампера. Заряд, переносимый им за
время в несколько микросекунд, ничтожно-
мал. Но после того, как достигнуто на-
чальное распределение напряжений 1(4-0}
и wcsi(+9), разность токов через сопротив-
ления Мс1(4-О)/Г1—«с4+0)/г2~0,3 мка уже
способна сделать заряды двух конденса-
торов отличными от первоначального зна-
чения Qo за промежуток времени порядка
десятых долей секунд.
Цепь с индуктивностями. В це-
пях с индуктивностями нарушение
закона коммутации iL (—0) =
=1’ь(+0) происходит при разрыве
ветви, содержащей индуктивность
(рис. 10-31) или при последователь-
Рис. 10-31.
ном включении двух индуктивно-
стей, имевших разные токи перед
моментом коммутации (рис. 10-32).
Анализ цепи рис. 10-3il пред-
ставляется очень важным в теории
коммутационной аппаратуры, так
как отключение ветви с индуктив-
ностью, особенно при питании от
источников высокого напряжения,
представляет тяжелую техническую
задачу. Между контактами, разры-
вающими цепь, устанавливается ду-
га, горение которой поддерживается
не только напряжением источника,
но и высоким 'напряжением, возни-
кающим в индуктивности (Ldildt)
при быстром изменении тока. При
отключении индуктивности в цепи
переменного тока задача облегчает-
19*
291
Рис. 10-33.
ся тем, что 2 раза за период ток
должен проходить через нуль, а при
первом же нулевом токе дуга
гаснет. Она уже не загорится .вновь,
если достигнутое .расстояние между
.контактами достаточно велико (до-
статочная, электрическая прочность
промежутка).
Однако при отключении тока ко-
роткого замыкания в ^современной
аппаратуре стремятся прервать ток
значительно быстрее, чтобы он не
успел достигнуть максимального
значения, которое может оказаться
опасным для установки. Для иллю-
страции на рис. 10-33 приведена
схематизированная осциллограмма
процесса отключения тока коротко-
го замыкания современным выклю-
чателем -с устройством-для быстро-
го гашения дуги (дуга разбивается
рядом пластин, по которым она
скользит и которые служат для ин-
тенсивного охлаждения дуги). Ра-
бота выключателя начинается при
токе f, приблизительно ib 2 раза пре-
вышающем максимум номинального
тока; уже через четверть периода,
достигнув 83 ка, ток начинает спа-
дать. Если бы выключатель не сра-
ботал, ток нарастал бы по кривой,
изображенной пунктиром; егсГ<мак:
симальное значение составляло бы
260 ка.
На том же рис. 10-33 показан
график напряжения и на выключа-
теле, оно равно нулю до начала ра-
боты выключателя, а после отклю-
чения тока равно напряжению сети.
Не рассматривая процесс выключе-
ния тока в подробностях, ограни-
чимся выполнением двух простых
расчетов.
Во-первых, обращаясь к . ма-
лым параметрам, можно считать,
что параллельно с отключаемой ин-
дуктивной ветвью содержится хотя
бы незначительная емкость (пока-
занная пунктиром на рис. 10-31).
В таком случае, когда источник от-
ключается, ток ветви L, г замыкает-
ся через емкость С. Пренебрегая
энергией, потерянной в сопротивле-
ниях, легко оценить максимальное
напряжение, которое появится на
емкости, когда ток в индуктивности
обратится в нуль. Для этого сле-
дует приравнять энергию магнитно-
го поля, существовавшую в индук-
тивности в момент отключения, и
энергию электрического .поля (при
токе, равном нулю)
4максС/2=^£/2, (10-101)
где /р — разрываемый ток.
В такой цепи легко возникают
колебания; для их гашения и для
облегчения условий отключения
иногда вводят дополнительное со-
противление, шунтирующее индук-
тивную катушку.
Оценивая возможное напряже-
ние на отключаемой ветви по фор-
муле (10-101), мы получаем сильно
преувеличенное значение из-за то-
го, что не учтено поглощение энер-
гии в сопротивлении выключателя.
Другой приближенный расчет позво-
ляет очень просто оценить энергию, выде-
ляемую в выключателе, если пренебречь
существованием емкости С. Последнее мы
вправе сделать при малой величине этой
емкости, так как большое напряжение, ко-
торое на ней может появиться, вызовет-
электрический пробой между контактами,
в результате чего цепь окажется замкну-
той.
Допустим, что напряжение источника
(рис. 10-31) в процессе выключения остает-
ся постоянным и равным Uq. В таком слу-
чае напряжение, приходящееся на выклю-
чатель (если пренебречь малой емкостью С,
параллельной L, г),
f di \
= Zp (i) = U0—\L +ir\, (10-102)
где р(£)ь—переменное сопротивление
между контактами выключателя.
Мощность, выделяемая в выключателе,
Рв = Шв,
292
а энергия, выделившаяся в .нем за время
выключения А/,
ы
— — С di
= Uoi At — г2Гд/ _ [л — dt. (10-103)
о
Легко написать дифференциаль-
ное уравнение цепи для />0:
U0 = ir+Ld/t, (10-104)
где r = r1-j-rs и L — Д + Ц, и ре-
шить его
1 = ^ + Ае~(/\
В этом выражении i обозначает некоторое
промежуточное значение тока (по теореме
о среднем), которое во «всяком случае не
превосходит начальное значение /о-
'Интеграл, стоящий в правой части,
легко вычислить, так как
di 1
/ dt = idi = ~2 d (/2).
При этом очевидно, что
д/
С di t
J Ll dt dt —
Lt
"2"-^ J d (Z2)
0
поскольку в момент /=0 ток равен i0,
а в момент А/ (конец выключения) ток
равен нулю.
Если время At мало (Af-^O), первые
два -слагаемых в правой части выражения
(10JlO3) могут быть приняты малыми по
сравнению с интегралом, который равен
всей энергии, содержавшейся в индуктив-
ности. Следовательно, вся эта энергия
в процессе выключения рассеив-ается в вы-
ключателе независимо от того, как изме-
няется во времени его сопротивление.
На самом деле часть энергии может
рассеяться в выключателе, а другая часть
(обычно небольшая) перейти в энергию
поля конденсатора.
При отключении разветвленной цепи
ток -в выключателе может быть равен ну-
лю, хотя в отдельных контурах отключае-
мой цепи еще сохраняется ток и связан-
ные с ним запасы энергии.
Схема на рис. 10-32 (представ-
ляет большой интерес, поскольку
в подобном режиме работают мно-
гочисленные элементы контактных
релейных систем. После размыка-
ния контакта в этой схеме две ин-
дуктивные ветви с первоначально
различными токами /Д—0)^=/2(—0)
оказываются -включенными последо-
вательно. К концу коммутации в це-
пи установится одинаковый ток
/( + 0), как этого требует первый
закон Кирхгофа.
где x=Llr, а постоянная интегриро-
вания А определяется из начально-
го значения тока после коммутации
(/=+>0).,
А=Ц4-0)-^.
Остается определить начальное
значение тока, т. е. z( + 0). Однако
это надлежит сделать, не обраща-
ясь к ранее формулированному за-
кону коммутации (§ 1'0-1), который
теперь заведомо нарушается, по-
скольку
4(+0) = z2(+0) = z(+0),
а
(10-105)
Причина этого нарушения содер-
жится в предположении о быстром
(A/—+0) разрыве контакта. Дейст-
вительно при этом в дифференци-
альном уравнении, применимом
к процессу коммутации,
(10-106)
слагаемые diildt и di^dt неограни-
ченно возрастают. Но при этом не-
ограниченно возрастает и напряже-
ние на каждом из индуктивных эле-
/ т di \ л
ментов ( чем и обуслов-
лена возможность конечного изме-
нения энергии каждого из индук-
тивных элементов за бесконечно
малый промежуток At. Естественно,
что закон коммутации при этом не
выполняется; при его выводе пред-
полагалось, что для каждого эле-
мента цепи произведение ui остает-
ся конечным.
Значение общего тока i (-ф- 0) пос-
ле закончившейся коммутации можно
определить из анализа уравнения
293
(10-106). Действительно, по (10-106)
сумма должна оста-
CLL СИ,
ваться конечной, так как все осталь-
ные слагаемые, входящие в уравне-
ние, заведомо конечны.
Каждую из производных din/dt
можно представить как предел отно-
шения AinIAt при Д£->0. Но =
= /(+0)-Z1(-0) и Д/2 = /(+0)-
-4(-0).
В таком случае рассматриваемую
сумму можно представить выраже-
нием
j di\ । » diz lini *-Ь£2А^2
'dt “if® ДГ~
Эта сумма остается
Д^ -> 0 только при
LrAiх £2Д/2 = 0 или
(10-107)
конечной при
условии, что
(L14-L2)i(+0) =
= (_0) + £2z2(-0).
(10-108)
Закон сохранения магнитного по-
токосцепления. Последнее равенство
выражает очень важный закон со-
хранения магнитного потокосцепле-
ния.
Заметим, что при выполнении
закона коммутации iL (—0) = iL (+ 0)
выполняется также и закон сохра-
нения потокосцепления.
Из выражения (10-408) опреде-
ляется искомое значение тока сра-
зу после коммутации /(+0). К то-
му же результату можно прийти
интегрированием всех слагаемых
уравнения (10-106) в пределах
времени коммутации (от 0 до At)
с последующим выделением сла-
гаемых, стремящихся к нулю «при
Рис. 10-34.
At—>0, как это было сделано ранее
в уравнении (10-ЮЗ)1. \
На рис. 10-34 приведены графи-
ки токов £ и £ для схемы на
рис. 10-32 при (7о=24О в, Г1 = г2—
=40 ом, г3=40 ом, £•(—0) =5 а,
£(—0)=4 a, z-(oo) =%/(г1+1г2)=3 а.
Кривые на рис. 10-34,а построены
для Li=il60 мгн и £2=40 мгн, а на
рис. 10-34,6 для £1=40 мгн и £2=
= 160 мгн. Очевидно, что в обоих
случаях после коммутации постоян-
ная времени одинакова т=2,-5 мсек.
Однако, значения начального тока
(после коммутации) различны:
в первом случае Z(+0)=4,2 а
(рис. 10-34,а); во втором случае
/( + 0) = 1,8 а (рис. 10-34,6).
Энергетические преобразования в цепи
L,r. Из полученного решения легко найти
энергию Aw, выделяемую .в контакте при
размыкании цепи:
hw = w(— 0) — о)(+0), (10-109)
где по-прежнему эта энергия принимается
равной разности энергий в цепи до ком-
мутации
zh-o)/.!
w (—0) =-----2----
4(-0)£2
2
(10-110)
и посде коммутации
, 1П\ /2 * * * * * * * (+0) (£i + £2) п н
w (+0) =----------2---------• (10~111)
Подставляя н последнее равенство зна-
чение тока г(+0), найденное из закона
сохранения магнитного потокосцепления
(10-108) и производя простые алгебраиче-
ские преобразования, находим, что
Л — -------в) -*2 ("""в)]2 т г
Дда — 2(Li+L2) L1Lz' С °-112)
Интересно сравнить это ‘выражение
с (10-97).
1 Можно выбрать и такой путь. Допу-
стим, что в результате коммутации ветвь,
параллельная второй индуктивности, не пол-
ностью разрывается, а остается проводя-
щей, ню с очень большим сопротивлением R.
При этом получается задача с корректными
начальными условиями, хотя и значительно
более сложная. Решение будет содержать
две постоянные времени, существенно раз-
личные по порядку величин. За время, боль-
шое по сравнению с меньшей постоянной
времени, устанавливается режим, найден-
ный нами из условия сохранения магнитно-
го потокосцепления. В пределе можно -пола-
гать R —>оо и надлежащим образом рас-
крыть неопределенности.
294
Рассмотрим еще пример, пока-
зывающий необходимость учитывать
знаки токов и потокосцеплении.
Пусть цепь, содержащая две . па-
раллельные индуктивные ветви
(рис. 10-35,а), в которых до комму-
тации существовал установившийся
режим, отключается от источника
постоянного напряжения UQ.
После отключения в обеих вет-
вях протекает одинаковый ток, на-
правление которого в одной из вет-
вей обязательно противоположно
первоначальному. При этом урав-
нение -сохранения потокосцепления
следует записывать, учитывая поло-
жительное направление общего то-
ка после коммутации. Если это на-
правление принято совпадающим
с направлением тока в первой ветви
(|рис. 10-35,6), то при этом вместо
значения тока i2 (рис. 10-35, а)
в формулу для потокосцепления
следует (подставлять —i2.
i (+ 0) (Ц + L2) = i.L, -i2L2. (10-113)
Аналогично формулу i(10-112). для
энергии, ‘выделяемой ‘в выключателе,-в дан-
ном случае следует писать так:
д (Ч + ^г)2
hw== 2(L,+L2)
(10-114)
Если потокосцепления в двух
ветвях первоначально были одина-
ковы (jLi/i=’L2^), то после отклю-
чения ток в сохранившемся конту-
ре равен нулю.
aj
б)
Рис. 10-36.
Аналогия цепи г, С с источником
напряжения и цепи L, г с источни-
ком тока. Подключим две парал-
лельные индуктивные ветви к источ-
нику тока J (рис. 10-36). Это можно
представить как размыкание ветви,
параллельной с источником: когда
ветвь коротко замкнута, во внеш-
нюю цепь ток не идет, после ее раз-
мыкания весь ток источника J про-
ходит во внешнюю цепь. Если ком-
мутация происходит мгновенно, мы
вновь встречаемся с некорректной
задачей, так как в индуктивностях
Li и L2 ток должен возрасти мгно-
венно.
Найдем начальные значения то-
ков, в этих ветвях z'i(-FO) и ^( + 0).
Очевидно, что при быстром на-
растании токов напряжение каждой
из- ветвей можно считать обуслов-
ленным э. д. с. индукции:
“=£-в-'=Л-гг- <10-115>
Произведя интегрирование этого
равенства за время коммутации, най-
дем что
д/
Jl, ^’Л=дг\(+о) =
о
= jL2 J2 = L2i2 (+ 0). (10-116)
о
По закону Кирхгофа при разом-
кнутом рубильнике, т. е. после
включения источника тока,
7=/i(+0) + Z2(4-0), (10-117)
поэтому
и
Рис. 10-35.
295
Расчет переходного процесса
после окончания коммутации не
отличается от расчета корректных
задач. Особенность ‘ некорректной
задачи сводится к определению на-
чальных значений токов (токов
в конце коммутации)... .. .
Не рассматривая общий прин-
цип (принцип дуальности), по ко-
торому каждой цепи с источником
напряжения можно привести -в со-
ответствие цепь с источником тока,
обратим внимание на полную ана-
логию цепей на рис. 10-36 и
рис. 10-29, а также уравнений, ко-
торыми описываются протекающие
в них процессы. При этом анало-
гичными оказываются последова-
тельные С, г и параллельные L, г
соединения. Аналогично мы при-
ходим к некорректным условиям,
включая в параллель два конден-
сатора (с разными напряжениями)
или источник напряжения и конден-
сатор; в индуктивных цепях мы
приходим к тем же некорректным
условиям, последовательно включая
индуктивности (с разными токами)
или источник тока и индуктивность.
Разрыв ветви, содержащей ин-
дуктивность. Отключение коротко-
замкнутой ветви быстродействую-
щим выключателем (рис. 10-37)
представляет практически важный
случай, очень близкий к уже рас-
смотренным. Эту задачу предлагает-
ся разобрать самостоятельно. Нали-
чие в цепи генератора переменного,
а не постоянного тока несуществен-
но, так как процесс коммутации
(разрыва цепи) можно предпола-
гать протекающим очень быстро, и
для определения энергии, выделяе-
мой в выключателе, нужно знать
только значения токов к началу
процесса отключения.
Пример из механики. В заключение
полезно рассмотреть простую задачу тех-
Рис. 10-38.
нической механики, где появляются не-
корректные начальные условия.
Представим себе, что две части вяла,
первоначально вращавшиеся с разными
скоростями cot и <02, 'внезапно соединяются
муфтой, окажем, при сближении дисков
сцепления (рис. 10-38). При этом на ва-
лах насажены маховики с разными мо-
ментами инерции /1, /2-
•Очевидно, что в конце коммутации,
т. е. когда диски сцепления плотно соеди-
нены, обе части вала вращаются уже
с одинаковой скоростью со. Требуется опре-
делить эту скорость.
Казалось бы, можно исходить 'при ре-
шении задачи из закона сохранения энергии
®2 (/1 + Л) _ “l7* , “272
2 2 + 2
(10-119)
где слева — кинетическая энергия соеди-
ненной системы, вращающейся с общей
скоростью <о, а справа — сумма энергий,
которыми обладали раздельные части до
коммутации.
Такое решение однако неправильно.
При решении задачи следует исходить из
другого, также общего принципа, а имен-
но из закона сохранения момента количе-
ства движения
со (/1 7 2) == С01/ j —со2/2« (10-120)
В левой части этого равенства — импульс
момента (момент’ количества, движения)
системы »в целом после коммутации,
а в правой части — сумма импульсов мо-
ментов, которыми обладали раздельные
части до их сцепления |(до коммутации).
Противоречивость уравнений (10Л19) и
Д10-120) очевидна.
Бесспорная справедливость второго
уравнения видна из следующего: произ- .
водная от момента количества движения
равна действующему на систему вращаю-
щему моменту:
d /
(coilt) =
d
dt (®272) ==
(следствие второго закона Ньютона: ско-
рость изменения количества движения
d(mv)ldt равна силе f).
296
Но но условию задачи вращающие мо-
менты 7И1 и М2 равны и ‘противоположны,
так как в свободно вращающейся системе
.момент, вызывающий ускорение одного
маховика (Afi), может уравновешиваться
только моментом, вызывающим торможе-
ние другого (М2——7И1); сказанное оче-
видно из того, что в любой точке соприка-
сающихся дисков на каждый из них дей-
ствуют равные и противоположно направ-
ленные силы (fi——if на рис. 10-39). А это
значит, что
d rd
~dt ~~~di
или
dt (<°i/i + ^2/2) = 0.
Кажущееся противоречие между зако-
ном сохранения момента и энергии легко
разрешается: в балансе энергии, выражен-
Заметим, что при неподвижности од-
ного из маховиков (со2=О) и при равенст-
ве -моментов инерции Ji=J2=J в коммути-
рующем элементе теряется половина кине-
тической энергии вращающегося маховика.
Сходство результатов (10-1120) и (10-'122)
с соответствующими уравнениями электри-
ческой цепи легко увидеть. В случае пря-
мого соединения в параллель двух конден-
саторов закону сохранения моментов соот-
ветствует закон сохранения заряда, в слу-
чае прямого последовательного соединения
индуктивностей — закон сохранения пото-
косцепления. Из сочетания этих законов
с законом сохранения энергии находится
энергия, рассеиваемая при коммутации, по
формулам, совершенно -аналогичным фор-
муле (10-122): при параллельном соедине-
нии конденсаторов (10-97); при последова-
тельном включении индуктивностей (10-112).
В заключение отметим, что важ-
ность рассмотрения задач, совер-
шенно корректных и только условно
названных здесь задачами с некор-
ректными начальными условиями,
в советской научной литературе
впервые была отмечена проф.
С. И. Куреневым, исследования ко-
торого в этой области содержат су-
щественные и новые результаты, ча-
стично отраженные здесь.
ном уравнением (1IO-1119), необходимо учесть
энергию, рассеянную в муфте Aw (тепло-
та трения дисков при неполном сцеплении
или энергия нацрева <и остаточной дефор-
мации неупругого удара сцепляющихся де-
талей). В таком случае «в одной части ра-
венства должна стоять сумма кинетиче-
ской энергии всей системы после коммута-
ции и энергии, рассеянной в коммутирую-
щем элементе (в дисках сцепления),
в другой — по-прежнему сумма кинетиче-
ских энергий раздельных частей системы
до коммутации:
Дш+------2-----+~2~-
(10-121)
Это уравнение не только совместимо
с уравнением (U0-il20), выражающим за-
кон сохранения момента количества дви-
жения, но из двух уравнений .(110-120) и
(10-121) может быть найдена энергия,
с необходимостью рассеиваемая в муфте
при каждом сцеплении. Действительно, из
(10-120) находим, что
<01/1 -|- <02/2
Подставляя найденное значение - со в
(10-121), находим, что
= (<О1 — <о2)2 о(/А | /а) * (Ю-1£2)
10-11. ФУНКЦИЯ ХЕВИСАЙДА 1
И ФУНКЦИЯ ДИРАКА б
В теории лер входных процессов
часто лриходится
с функциями
иметь дело
о
<?(0
f(0={
при
при
(10-123)
т. е. равными нулю при f<0 и
отличными от нуля при / > 0.
Так, при расчете тока в цепи г,
С, включаемой к постоянному
напряжению Uo, мы писали урав-
нение
ri + ^-^idt = u, (10-124)
полагая, что и = 0, когда / < 0 и и =
= 170 при t > 0. Его решение i =
=— e~t,rC также относится только
Г
ко времени f >0 (до коммутации ток
равен нулю).
Для записи подобных условий
Хевисайд ввел функцию включения
/(/) = / 0 npiU<° (Ю-125)
( 1 при
297
графическое изображение которой
показано на рис. 10-40,я. Эту функ-
цию записывают в виде наклонной
цифры 1 и называют функцией
Хевисайда (а также единич-
ным скачком, единичной
функцией ит. п.). Пользуясь
Хевисайда и умение производить
с ней математические операции (на-
пример, взять производную от этой
функции) играют очень важную
роль. Особенно важна связь функ-
ции Хевисайда с функцией Дирака
д(0.
г~т~
7
J ♦ I
И а
0
Рис. 10-40.
этой функцией, вместо (10-123),
можно писать1.
f(0 = ?(Z)/(0, (10-126)
например,
u = U0-l(t)- i = J(t)^
Существенно заметить, что в мо-
мент t = Q функция принимает
все значения от 0 до 1; сказанное
можно представить, предполагая,
что вблизи t~0 функция f(t) моно-
тонно возрастает от 0 до 1 на интер-
вале е, стремящемся к нулю
(рис. 10-41, а).
Вместо l(t) можно просто пи-
сать /, имея в виду, что эта функ-
ция возрастает от 0 до 1 именно
при ;/==0. Если хотят отметить, что
включение происходит в момент
t=a, то пишут 1 (t—а): аргумент
функции становится положительным
при t>a (рис. 10-40,6). Функция,
имеющая значение 1 при КО и
равная 0 при £>0, выражается
функцией Хевисайда /(—t) с аргу-
ментом —it. В этом случае аргу-
мент функции положителен при
/<0 (рис. 10-40,в). Очевидно, что
1 (_•(/). (Ю-127)
Чаще всего вообще можно об-
ходиться без функции Хевисайда,
пользуясь записью типа (10-123)
или ограничиваясь словами о том,
что рассматривается состояние си-
стемы после коммутации, происхо-
дящей в момент /—0. Однако в ря-
де случаев анализ свойств функции
1 Порядок множителей .не играет роли,
т. е. 7(Дф(^) =1фД)-Д/),,1как это следует из
определения (10-125).
Функция Дирака или
дел ьта - функция (6-функция)
определяется тем, что она неогра-
ниченно возрастает, когда ее аргу-
мент обращается в нуль, рагна ну-
лю при любых иных значениях
аргумента, а ее интеграл равен
единице, если только нулевое зна-
чение аргумента лежит внутри пре-
делов интегрирования:
^2
J 8 (£) dt = 1 при < 0 и t2 > 0.
(10-128)
При любом неограниченном воз-
растании пределов (охватывающих
точку '/ = 0) интеграл остается рав-
ным единице.
Из сказанного легко увидеть
связи d-функции с функцией Хеви-
сайда
t
J 6 (t) dt = (10-129)
/1<0
Действительно, при отрицатель-
ном нижнем пределе t\ этот интег-
рал равен нулю при /<0 и равен
единице при />0, что и соответст-
вует определению /(/).
Сказанное позволяет определить
6-функцию как производную от
функции Хевисайда 2:
5(/) = ^/(0 = Г(0- (10-130)
2 Функции 1 и 6 не удовлетворяют тре-
бованию классической математики, «по кото-
рому функция должна иметь определенное
значение 'при каждом значении аргумента,
лежащем в рассматриваемых пределах. В си-
лу сказанного Дирак назвал подобные
функции несобственными. В общем случае
298
Рис. 10-41.
В электротехнике 6-функция ста-
ла широко (применяться в связи
с развитием импульсной техники и
получила название импульсной
(или импульсивной) функции пер-
вого порядка. Производную от
операции дифференцирования и интегриро-
вания таких функций требуют •дополнитель-
ного определения. Впрочем, для всех рас-
сматриваемых в этом курсе операций
с функциями 1 и б (вполне достаточно опре-
делений, данных в тексте. Не углубляясь
в анализ затронутых вопросов, приведем ци-
тату из квантовой механики Дирака ^Осно-
вы квантовой механики, изд. 2, ОНТИ
ГТТЛ, 1937, § 20), в которой -была введена
эта функция.
«Главная несобственная функция, с ко-
торой мы будем иметь дело,— это б-функ-
ция, определяемая следующим образом:
4-оо
Г S (х) dx = 1;
J (2)
—оо х
§ (х) = 0 при х ф 0. .
Для того чтобы составить себе наглядное
•представление о б(х) возьмем такую функ-
цию Вещественной переменной х, которая
исчезает повсюду, за исключением лишь то-
чек внутри некоторого маленького интерва-
ла длины е, окружающего точку х=0, и
которая настолько велика внутри этого ин-
тервала, что ее интеграл, распространенный
на этот интервал, равен 1. Точная форма
функции внутри этого интервала несущест-
венна, если только функция не меняется
там каким-либо особенно диким обра-
зом,— иными словами, если она, например,
всегда остается порядка в-1. Тогда в пре-
деле при е —> 0 эта функция перейдет
в б-функцию».
6-функции называют импульсной
функцией второго порядка.
На рис. 10-41,а, б, в схематиче-
ски представлена связь между им-
пульсными функциями нулевого
первого 6=7' и -второго 6'=/" по-
рядков.
Заметим, что изображенному на
рис. 10-41 переходу функции /0(£)
от 0 к 1 на интервале 8 можно при-
дать различные аналитические вы-
ражения, имеющие первую и вто-
рую производные, а затем полагать
е 0. После перехода к пределу
вид выбранного аналитического
приближения уже не играет роли.
Смысл 6-функции становится
совершенно ясным из рассмотре-
ния простейших электротехниче-
ских примеров. Рассматривая вклю-
чение цепи г, С .к постоянному на-
пряжению 74, т. е. при u(t) = 1 • t/0,
приходим и известным выраже-
ниям для тока и заряда:
t
q (t) = Сис (t) — С i (t) dt —
о
= l.CU0(i-e~t,y
Чем меньше сопротивление
цепи, тем большего значения до-
стигает ТОК /(/)макс==*( + 0) = Шл
тем скорее он спадает до нуля и
тем скорее заряд конденсатора,
т. е. интеграл от тока, достигает
предельного значения q(oo) =CUq.
При Г“*0 ток неограниченно
возрастает, но длится бесконечно
малое время, мгновенно заряжая
конденсатор; он выражается как
6-функция, умноженная на UqC,
т. е. ir^Q=CUG^ (рис. 10-42). Заряд
как интеграл от этой функции
мгновенно возрастает от нуля до
установившегося значения; он вы-
ражается как функция Хевисайда,
умноженная на UGC, т. е. qr-+o =
= CUO-1.
Рассмотрим еще цепь г, L
(рис. 10-43), в которой э. д. с. воз-
буждается разрывом индуктивно
связанного контура с током ii = /o.
Пользуясь функцией Хевисайда,
представим этот ток равенством
299
В таком случае уравнение., для
контура г, L принимает вид1:
ir+Z,g’ = M/o8(0- (Ю-131)
Если предполагать, что мы еще
не знаем как решаются дифферен-
циальные уравнения, содержащие
в правой части б-функцию, можно
эффициенты дифференциального
уравнения. Но решение уравнения
(10-.124) нам известно; поэтому ток
переходного процесса, описываемо-
го для цепи рис. 10-43 уравне-
ниями (40-131) и (10-132), выра-
жается равенством:
MI0 - L *
L е
при
i
Из всего изложенного здесь ста-
новится ясным, что к задачам с не-
корректными начальными условия-
Рис. 10-42.
Рис. 10-43.
предварительно взять интеграл от
обеих частей равенства. Произведя
интегрирование, придем к выраже-
нию
t
Li-\-r J idt = MlQl9 (10-132)
f<0
отличающемуся от уравнения
(10-124) только буквенными обо-
значениями: L вместо г, г вместо
1/C, М1Ц вместо u=UQ при £>0
(и н=0 при /<0).
Очевидно, что решение не мо-
жет зависеть от того, какими бук-
вами обозначаются постоянные ко-
1 Поскольку в контуре действует
э. д. с., равная
dit d
ми, рассмотренными в предыдущем
параграфе, мы приходим в слу-
чаях, когда одна из перем>енных но-
сит характер 6-функции; к этой
функции чаще всего приводит диф-
ференцирование ступенчато изме-
няющейся величины, т. е. диффе-
ренцирование Хевисайдовой функ-
ции.
Когда хотя бы одна из перемен-
ных имеет вид 6-функции, напри-
мер напряжение в цепи рис. 10-43
или ток -заряда конденсатора, ана-
лизируемый на предыдущей страни/
це, мощность кратковременно ста-
новится бесконечно большой, /что
приводит к необходимости отказать-
ся от законов коммутации, выведен-
ных в первом параграфе из предпо-
ложения, что мощность все время
остается конечной.
ГЛАВА ОДИННАДЦАТАЯ
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ
ОПЕРАТОРНЫМ МЕТОДОМ
Операторный метод, вве-
денный в электротехнику ан-
глийским инженером Хевисайдом
(1850—1925 гг.), существенно упро-
щает многие расчеты переходных
процессов. Значение этого метода
можно сравнить с значением ком-
плексного метода в теории пер'е-
менных токов. Введенный Хевисай-
дом оператор переходных процес-
зоо
сов р во многом сходен с операто-
ром /со в 'комплексном методе тео-
рии переменных токов.
В современной литературе об-
основание операторного метода час-
то видят в его отождествлении
с методом интегральных преобра-
зований Карсона или Лапласа.
Метод интегральных преобразо-
ваний -в применении к простым -за-
дачам теории линейных цепей с со-
средоточенными постоянными при-
водит более сложным путем к тем
же результатам и расчетным при-
емам, что и операторный метод Хе-
висайда Ч Существенное преимуще-
ство 'последнего — возможность
простого обоснования, не требую-
щего ни знания теории функций
комплексного переменного, ни об-
ращения к иным сколько-нибудь
сложным математическим выводам.
Кроме элементарного обоснова-
ния метода Хевисайда и составле-
ния таблицы взаимно соответствую-
щих операторных выражений F(p)
и функций времени /(/), в этой гла-
ве рассматриваются разнообразные
приложения метода.
Учащиеся, знакомые по -курсу
математики с операторным мето-
дом или с преобразованиями Лап-
ласа, могут непосредственно пере-
ходить к параграфам, посвящен-
ным приложению метода (§ Ы-5 и
следующие), а также «к рассмотре-
нию изложенных в этой главе при-
меров.
Сопоставлению метода Хевисай-
да с методом интегральных преоб-
разований Лапласа посвящена
гл. 12, где излагается также очень
важная теория интегральных пре-
образований Фурье.
11-1. ОПЕРАТОРНЫЙ МЕТОД
В простейшем случае переход-
ные процессы протекают после
включения цепи, которое происхо-
дит в момент времени, прйнимае-
1 Метод интегральных отреобр азов амий
в случае сложных «задач признается более
мощным и общим. Однако развитие «собст-
венно операторного 'метода (работы Мину-
синского и др.) приводит во всяком случае
к не менее общим и сильным методам ана-
лиза и расчета.
мый за начало отсчета (/=()). По-
этому прежде всего нас интересуют
функции, описывающие этот про-
цесс, определяемые для и рав-
ные нулю при /<0:
f(0=
(°
/<о,
или f (t) = l-V (t). (11-1)
Сущность операторного метода
в современном толковании, связан-
ном с идеями Ван-дер-Поля, за-
ключается в том, что функции f (/),
называемой оригиналом, со-
поставляется ее изображение
F(p), где р — некоторое перемен-
ное, отличное от t, а сама функция
f(i) определена при и непре-
рывна при t>0.
Соответствие оригиналов и изо-
бражений будем обозначать зна-
ком т. е.
f(t)~F(p) или f~F. (11-2)
Это соответствие должно быть
взаимно однозначным: любой функ-
ции. f соответствует единствен-
ное изображение F, любому изо-
бражению F соответствует един-
ственная функция /, т. е. оригинал
(ом. § L1-3).
В -силу того, что мы рассматри-
ваем линейные системы, конструи-
руемая система изображений долж-
на удовлетворять п ринцип у ли-
нейности, который можно фор-
мулировать так:
f=af1+bf2^F = aFi + bF2i (11-3)
если
fi~A й /2~F2,
а множители а и b — постоянные.
Из последней формулы очевид-
но, что умножению оригинала на
постоянную (величину, соответствует
умножение изображения на ту же
величину; сложению оригиналов со-
ответствует сложение изображений.
В общем случае математическим
операциям над оригиналами могут
соответствовать иные, но вполне
определенные операции над изо-
бражениями. Если в результате та-
ких операций Д превращается в f2,
301
a Fj в F2, to между результатами
должно сохраняться соответствие
fl-A, fz~F2.
Операторный метод введен для
решения дифференциальных урав-
нений, поэтому система изображе-
ний строится >с таким расчетом,
чтобы дифференциальные операции
заменялись более простыми алге-
браическими операциями над изо-
бражениями. В таком случае реше-
ние системы дифференциальных
уравнений для оригиналов заме-
няется решением алгебраических
уравнений для изображений!.
Поскольку дифференцирование
есть линейная операция
I = + ’ если f =
(Н-4)
соответствующая алгебраическая
операция с изображениями должна
быть также линейной.
Простейшая линейная опера-
ция — это умножение на р; она и
принята в операторном методе как
операция, соответствующая диффе-
ренцированию
ecjIK f^F. (11-5)
При этом предполагается, что
dfldt выражает обобщенную произ-
водную от функции /(/), опреде-
ленной для t>0, непрерывной при
/>0 и равной нулю при /<0
(рис. 11-1).
Обобщенная производ-
ная отличается от обычной или
простой производной тем, что диф-
ференцирование р а спр остр ан я ется
1 Полезно напомнить, что простейшие
случаи перехода от оригиналов к их изобра-
жениям с -соответствующей заменой опера-
ций всем хорошо известны. Так, -можно рас-
сматривать логарифмы чисел как их изобра-
жения /V^/=ln N, причем умножение ори-
гиналов заменяется сложением их изобра-
жен ий N=2^l=l\+l2-
По найденной сумме изображений I
находим оригинал N, равный произведению
оригиналов.
Более близкий пример — это изображе-
ние простых гармонических функций ком-
плексами. При этом дифференцированию
оригиналов соответствует умножение их изо-
бражений на до.
и на время t=0, когда функция
изменяется скачком от нуля до ко-
нечного значения f ( + 0).
Различие между этими двумя
п ро и зв о д н ым и -можно пр ед ст а в и т ь
формулой
zf=f<+°»8+(f) "Р" 'а-°.
(11-6)
в которой круглые скобки означа-
ют, что это простая производная,
а б есть дельта-функция (см.
§ 10-11). Простая и обобщенная
производные совпадают при t>0.
Формула (Г1-6) написана в
предположении, что f (/) =0 при
/<0, и, следовательно, скачок
функции определяется значением
f( + 0), что соответствует рис. П-11.
Обобщенная производная не от-
личается от простой в том случае,
когда f ( + 0) =0, т. е. функция изме-
няется плавно, иначе говоря,
остается непрерывной и в точке
t=0.
К формуле (11-6) легко
ставляя функцию по (H:l-il),
f(t) = lv(t).
Дифференцируя последнее выражение
(11-1) по правилу дифференцирования про-
изведения, находим, что
прийти, пред-
т. е. полагая
где
df dl dv
° ~dt~ + 1 ~dt
dv
dv
dt
dl
~dF=s-
11-2. ИЗОБРАЖЕНИЕ
ПРОСТЕЙШИХ ФУНКЦИЙ
Введя понятие соответствия
оригинала и его операторного изо-
бражения, мы формулировали
требование линейности (11-3), а
1 Некоторые дальнейшие обобщения
рассматриваются в § 11-7.
302
также условились в 'изображении
обобщенной производной (11-5).
Чтобы найти изображения кон-
кретно заданных функций, необхо-
димо еще выбрать вид изображе-
ния для какого-либо определенного
оригинала. Этим устанавливается
форма связи между изображения-
ми и оригиналами, распространяю-
щаяся на всю систему соответствий
в целом; устанавливается как бы
код перехода от f (\t) к F(p), после
чего вся система соответствий ока-
зывается взаимно однозначно опре-
деленной.
Простейшее соотношение вы-
брано в операторном методе Хеви-
сайда:
1~1 (Ы-7)
— единица изображается едини-
цей.
Однако по 'соображениям, кото-
рые излагаются в гл. 12, чаще при-
меняют соотношение, соответствую-
щее интегральному преобразова-
нию Лапласа:
1-V (11-8)
— единица изображается как еди-
ница, деленная на р.
Можно было бы поступить и так: оста-
вить неопределенным выражение для изо-
бражения /(£), записывая его в виде
В таком случае перед всеми формулами
F(p) следовало бы писать дополнительный
множитель 1(р), как это делал иногда сам
Хевисайд и некоторые авторы, развившие
его метод.
В этой книге автор вынужден
п р идержив аться систем ы Л апл аса,
так как именно ею пользуются
в специальных курсах, хотя -систе-
ма Хевисайда обладает рядом пре-
имуществ !.
1 Эту точку зрения разделяют многие.
Отметим здесь некоторые из преиму-
ществ системы Хевисайда.
1. Вся система может быть построена
путем элементарных рассуждений, тогда
как изображение 1 через 1/р требует до-
полнительных обоснований. Метод Хевисай-
да представляет мощное орудие для расче-
та переходных процессов, которым легко
пользоваться без каких-либо дальнейших
обобщений или обоснований. Их целесооб-
разно рассматривать позже.
Еще раз повторим, что изобра-
жаемая функция (оригинал) пред-
полагается равной нулю при /<0 и
совпадает с заданной f (t) только
при Это .значит, что 1 в левой
части (41-7) и (11-8) —по сущест-
ву функция Хевисайда 7(/).
Изображение 6-функции. Приме-
няя к (11-8) формулу (11-5), а так-
же имея в виду, что производная от
функции Хевисайда есть б-функция
(см. § 10-11), находим, что
g=S^l. (11-9)
Изображение простой производ-
ной (dj/dt). Применяя к выражению
(11-6) соотношение линейности
(11-3) и формулы (11-5), (11-9),
находим, что
(11-10)
Аналогично могут быть найдены и вы-
ражения для высших производных.
2. В системе Хевисайда размерности
(единицы измерения) оригиналов и изобра-
жений совпадают, что облегчает проверку
всех формул по принципу .размерной одно-
родности; многие формулы записываются
в более простой для запоминания и вычис-
лений форме, например изображение прос-
той производной по Хевисайду изображает-
ся формулой
/ df \
(“dTj^-H+O)],
тогда как по Лапласу
/ df \
Проще и определение значений ориги-
нала при /=0 по его -изображению: в си-
стеме Хевисайда /i(0) =^(оо) (см. конец
§ 11-2), тогда как в системе Лапласа
HOWP^P^oo-
Впрочем, между этими двумя система-
ми нет принципиальной разницы и нетрудно
привыкнуть к пользованию любой из них.
Заметим еще, что вместо формулы (П-7)
или (111-8) с равным правом можно было
бы написать, что 1^р~2 или 1~р^2
и т. п. При этом получились бы, конечно,
иные формулы соответствий.
Пользуясь таблицами формул, следует
всегда проверить, приводятся в ней изобра-
жения по Хевисайду Н(р) или по Лапласу
L(p). Как очевидно из сопоставления фор-
мул (11-7) и (1-1-8), они должны отличать-
ся множителем р:
7f(p)=pL(p).
303
Так,
/ dtf \
\Jdt^J ^P2F~Pf (+°)-Г'(+°). (Н-П)
Г» /'<+0)-(>Уа+о.
Последняя формула легко выводится
из предыдущей, если полагать
= С11’12)
и применить к y^Y формулу (111-10) для
изображения производной (dy/dt).
Определенный интеграл. Из пре-
дыдущего следует, что интегрирова-
нию оригинала в пределах от 0 до/
соответствует деление изображения
на р:
t
^fdt^j-F, если f^F. (11-13)
О
Действительно, полученная функ-
ция
t
x=^fdt^X (11-14)
6
равна нулю при /=0, т. е. х(+0)==
= 0,
Применяя к ее производной фор-
мулу (1'1-5), находим, что
£ = f^pX = F. (11-15)
Тем самым доказывается, что изо-
бражение интеграла X=F/p.
Изображение степеней t. Пусть
f=t~F, в таком случае
^=1~^=1/А
Из правой части последнего вы-
ражения находим, что
F=~^t- (11-16)
1/
Аналогично получаем, что
(1Ы7)
Г
Изображение экспоненты. Пусть
f — e~at^<,F, (11-18)
в таком случае по (11-10)
(1Ы9)
С другой стороны, выполняя диф-
ференцирование, находим, что1
I dt
~ — ae'at^ — aF. (11-20)
Левые части (11-19) и (11-20)
равны, поэтому должны быть равны
и .правые части (поскольку предпо-
лагается взаимная однозначность
оригиналов и изображений), т. е.
pF— 1 = — aF,
откуда находим, что
(11-2D
Определение значений функции
f (+0) и f(oo) по ее изображению.
Из рассмотрения изображений про-
стейших функций легко обнаружить
существование следующей простой
связи между /(/) и pF(p)\
1. Значение оригинала при
0 равно значению изображе-
ния, умноженному на р, при р-^оо:
f(+0) = [^(^co. (11-22)
2. Значение оригинала при t -> оо
равно значению изображения, умно-
женному на р, при ,р -> 0:
f(oo) = [pF(p)]^, (11-23)
если только f(t) имеет конечный
предел при t сю (в некоторых
случаях конечный предел должна
иметь лишь величина /(/)//). /
Справедливость формул (11-22)
и (11-23) легко проверить на соот-
ношениях (11-8), (11-9), (11-16),
(11-17), (1*1-21). Легко убедиться и
в необходимости сделанной оговор-
ки об условиях применимости фор-
мулы (11-23). Она явно неприме-
нима к (1:1-21) при а=—&<0:
f (со) = еь~ [pF (^0
1 Так как умножение оригинала на —а
равносильно умножению изображения на ту
же .величину в соответствии с принципом
линейности, а изображение экспоненты есть
Fno (11-18).
304
а также при; а = /ад
f(oo)=^-°V
О
О + /со’
О выводе формул (11-22) и (11-23)
будет сказано в гл. 42.
11-3. РЕШЕНИЕ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ОПЕРАТОРНЫМ МЕТОДОМ
Пусть требуется решить урав-
нение
+ = (П-24)
при заданном начальном условии
Н+о).
Пользуясь правилами изобра-
жения производных и полагая, что
в заданном уравнении все произ-
водные — это пр остые пр оизв од-
ные, составляем операторное урав-
нение, соответствующее заданно-
му дифференциальному уравнению
(И-24)
^[^-/(+0)] + ^Г = Ф, (11-25)
Решение. Дифференциальное урав-
нение цепи
t
ir + J i dt = «г,
о
t
J i dt = ис — напряжение на кон-
о
денсаторе.
Соответствующее операторное уравне-
ние
Zr+cF/==^(^’
где
откуда
а=\\[Сг.
где
Оригинал, отличающийся от найденно-
го выражения только постоянным множи-
телем, нам известен (11-21). Кроме того,
мы знаем, что af^aF, если f^F (11-3).
Поэтому находим, что искомая функция
времени
где
F~f и Ф~ф.
В уравнении (11-25) учтено на-
чальное условие, оно вошло в вы-
ражение первой производной. Ре-
1цая (11-25) относительно F, нахо-
дим, что
Ф + aJ (+ 0)
(11-26)
Чтобы найти искомую функцию
времени f(t), нужно знать ориги-
нал, -соответствующий найденному
выражению F(p).
Пример 11-1. Найти ток в цепи г, С
при включении источника постоянного на-
пряжения uv=Uq (рис. 14-2). До коммута-
ции конденсатор не был заряжен.
Рис. 11-2.
Пример 11-2. То же, что в предыду-
щем примере, но до коммутации конденса-
тор -был заряжен до напряжения Цс(0).
Решение. В отличие от предыдущего
•примера напряжение на конденсаторе пред-
ставляется, равенством
t
. 1 Г
Uq — ис (0) + -Q- \ i dt,
о
Поэтому дифференциальное уравнение цепи
имеет вид:
t
ir + ис (0)4—i dt' — Uo,
0
Операторное уравнение в этОхМ случае за-
писывается так
/r+V“c(0)+cF7
Следовательно, изображение искомого
тока
С70 — нс(0) 1
1 = г р + а ’
а искомая функция времени
17»-«с (°)
i = ———------e~at.
20 К. М- Поливанов
305
Аналогично составляются урав-
нения для изображений и в тех
случаях, когда даны дифференци-
альные уравнения высших поряд-
ков. Например, уравнению
соответствует операторное уравнение
а2 \p2F -/;/(+ 0)- f (+0)] +
+ a, [pF—f (+ 0)] + я0Г=Ф, (11-28)
[производные .в (11-27) здесь рас-
сматриваются как простые], откуда
определяется изображение F.
Взаимная однозначность ориги-
налов и их изображений. Следует об-
ратить внимание на то, что в выра-
жение как функции f, так и ее изо-
бражения F входят все необходи-
мые начальные условия; в данном
случае это /(+0) и f( + 0).
Таким образом, очевидно, что
вид функции F различен для урав-
нений, отличающихся коэффициен-
тами (бхо, ai ...), начальными усло-
виями или видом правой части ра-
венства (ф).
Тем самым доказана взаимная
однозначность оригиналов и их
изображений для функций /(/),
определяемых дифференциальными
уравнениями.
Действительно, пусть в правой части
дифференциального уравнения (>11-27)
<р(О=/ • При заданных коэффициентах
#о, 6Zi, а2 и при заданных начальных усло-
виях f(+0), f'(+0) существует единствен-
ная функция f(t), удовлетворяющая урав-
нению (11-27).
Но между изображением F этой функ-
ции, которое определяется из (М-28), и за-
данным дифференциальным уравнением
также существует однозначное соответствие.
Взаимная однозначность сохраняется
бесспорно и в том случае, когда в правой
части (11-27) стоит функция времени ср(/),
взаимно однозначно связанная со своим
изображением Ф(р). Это условие выпол-
няется во всяком случае тогда, когда сама
функция ф(/) может быть представлена как
решение какого-либо дифференциального
уравнения (см. § 10-9), имеющего в своей
правой части функцию вида Al(t). Такое
ограничение для cp(f) пока нас вполне удов-
летворяет. Однако можно показать, что та-
кое ограничение необязательно (см. §11-10).
Заключительные замеча-
ния. Здесь было показано, как перей-
ти от дифференциального уравнения
к операторному, учитывая все не-
обходимые начальные условия..
Однако,-чтобы от операторного (вы-
ражения F(p) перейти к искомому
оригиналу ?(/), необходимо знать
соответствия для различных функ-
ций, которые могут, .встретиться
в решении тех или инт-тх задача
С этой целью целесообразно зара-
нее составить таблицу -соответствий
f~F. -Следующий параграф и по-
священ составлению небольшой
таблицы, достаточной для реше-
ния очень многих задач. Широко*
распространены таблицы, содержа-
щие изображения сотен различных
функций. К этим таблицам и. сле-
дует обращаться при решении бо-
лее -сложных задач.
Обратим внимание еще на сле-
дующий практически необходимый
шаг в процессе решения задач при
помощи таблиц. В найденном вы-
ражении F(p) следует произвести
такие алгебраические преобразова-
ния, которые позволяют отождест-
вить это выражение с одним из;
имеющихся в таблице. Прежде 'все-
го сказанное относится к виду зна-
менателей. Во всех табличных фор-
мулах высшая степень знаменателя
стоит с коэффициентом единица у
поэтому, получив, скажем, выра-
жение
1 Fi (р)
р тр2 -[-пр + k ’
его следует привести к виду
1 Л (р)
т Р(Р2 + ^‘+^)’
где
r = njm, s = kjni.
Рекомендуется, конечно, выпол-
нить все обычные алгебраические
преобразования, упрощающие по-
лученное выражение. В некоторых
случаях целесообразно произво-
дить деление, приводя выражение
к виду правильной дроби относи-
тельно р.
306
11-4. ТАБЛИЦА ИЗОБРАЖЕНИИ F(p)
И СООТВЕТСТВУЮЩИХ
ОРИГИНАЛОВ f(t)
Первые пять формул табл. 11-1—
это уже найденные соотношения
(11-8), (1'1-9), (11-16), (11-17) и
(11-21).
Формулы 6 и 7 легко получают-
ся по принципу линейности: беря
разность 1 и 5, приходим к 6
1 -nt 1 1 а
1 g at ---------—.--------
Р Р+а Р^Р-Г^У
Аналогично беря разность форму-
лы 3, умноженной на а, и 6, прихо-
дим к 7.
Очевидно, что 6 и 7 можно так-
же получить из 5 и 6, интегрируя
оригиналы в пределах от 0 до t и
деля соответствующие изображе-
ния на р.
Применение того же приема
к разности e~at—e~bt и к разности
соответствующих изображений при-
водит после простых преобразова-
ний к формуле 9. В ней f (0) =0, по-
этому, интегрируя (или дифферен-
цируя) f(tf) и деля (или умножая)
на р, приходим к 8 (или 10).
Показатели экспонент и корни
знаменателя изображений. Если изо-
бражение имеет вид дроби
(11-29)
а изображаемая функция f(t) пред-
ставляется суммой/ экспонент, то
коэффициенты ши в показателях
этих экапоненхравны корням урав-
нения
// pFz (р) = 0.
Этб общее свойство вытекает из
следующего: сумма изображений
экспонент
+ + + Д-/— Д-
* ‘ 1 /?+ а 1
ч-в Аа+-и1-30)
1 р + & 1 р pfap) л 7
приводится к дроби, знаменатель
которой имеет вид:
pF2(p)=p(p+a) (p+b) ....
Следовательно, уравнение
pFi(p) =0
имеет корни ро=О, pi = —а, р%=
= —b ..., равные коэффициентам
при t в показателях экспонент;
Корень ро=О соответствует экс->
поненте *с нулевым показателем,
т. е. постоянной N,
Среди формул 8—10 таблицы
только -первая содержит корень
р = 0 и только соответствующая
f(t) содержит постоянную состав-
ляющую.
Гиперболические и круговые
функции. В формулах 8—10 табли-
цы —а и —b — это корни квадрат-
ного уравнения
(р+а) (р+Ь)=0.
Эти корни часто удобнее представ-
лять в такой форме:
Р1,2 = —^(Х±Ц,
где
Р1 = — а = — а-|-р,
/?2== —£= —а —р.
При этом произведение (р +а) X
Х(р + &) целесообразно записы-
вать в таком виде:
(Р + «) (/? + Ь) = (р + а)2 — р.2.
При таком представлении кор-
ней разность и -сумму двух экспо-
нент удобно выражать через гипер-*
болические функции:
е-^_е-ы=е^^_е-^= ,
== е~а/ 2 sh pt
Принимая во внимание, что
b—а=2ц, можно формуле 9 табли-
цы придать такой вид:
1 _
(р+а)(р + Ь) —
= -—i—~ — £-a/shpt
(р + «)2 —Р2 Р
Это формула 12 таблицы. Ан ало*
гично получены формулы 1'1-14.
20:
307
Таблица 11-1
F(P) / (0
1 Up 1
2 1 a
3 l//?2 t
4 n\fp^+ 1 tn
5 l/(p +a) e~at
6 alp (p + a) 1 —e~at
7 a^p* (p +a) at — (1 — e~at)
8 ?ъ~[р(р-\-а)(р + b)] ~1 1 г 1 1
ab [1 + a — b {be a ae
•9 P Fs a-b
10 P2 Fs
a—b ^ae a be f
И Л1 ={p[(j5 + a)2-p.2]}-’ i Г 1 (r»h -k — ch t./^ Л—a^l
a2_^cn p.r i sn pj \e |
12 P I'll y— ё~^ sh jxZ
13 Р2 Til _f a \ e (ch —— sh p^t J
14 (P2 + Pa) Fn e~at ch
15* /715 = {P((/’+«)2+P2]}-1 J Г 1 /лл<-.12/ —I— „ J D 4- А л I
a2 _j_ p I 1 1cos h* ‘ p sln j e J “mf1 sm л v)]
16* p Л у e~at sin p^=y Im e~
17* P2 Fa (cos₽? p singf^ ai— sinA Im(e"+
18* (P2 + P«) Ло e~at cos 0i = Re e~
19 ’ l:(P2 + f2) у sin 0f
20 p: (pa + 02) cos 0f
21 1 :fP (p+«)2] -^rll-(l +at)e-°t]
22 V t/7 (P + a)2] te~at
23 p2:\p (p+a)2] (1 — at)e~<4
1 j ( e~^i Г
24 Л4 = {р(/’ + <>)[(р + + “)2 + ₽2]}“’ (a2 + g2) a (a—a)2 +?2 |a2+p2 |J2a"~
fi2 _1_ a r0 _ a\ -i } a) cos g/ p sin PZ j e */<5 |
308
Продолжение табл. 11-1
f (t)
25 (И/?3 4“ Д^2 4“ Ср) ^2 4
^Lg)f°++pC [* ^~e “f(cos(tf +
+-a-g g sin + Ae~at cos pf +
26** pF — f (— 0)
df
dt
t
^<u
* В формулах 15—18 приняты следующие обозначения:
7 = а — /р = |т| е~А, sin X = р/|у|
7 = “ + J0, (р 4- а]2 4- ₽2 = (р 4- 'О (Р 4-
** См. § 11-7, формула (11-59).
Для комплексно сопряженных
корней
А = -а=-«+/р,
А = —6 = —а—/Р
достаточно подставить ц=/₽ -в
111-14, чтобы получить формулы
15—18 таблицы.
Обыкновенными тригонометри-
ческими преобразованиями и пере-
ходом к комплексам можно f(/)
в формулах 15—18 выразить в фор-
^М^-даогда более удобной для рас-
четов.
Полагая коэффициент затуха-
ния а равным нулю, приходим
к изображению круговых синуса и
косинуса.
Другие формулы. Путем предель-
ных переходов из ’ряда найденных
выражений легко прийти, к новым
интересным результатам.
Так, полагая Ь->а в формуле 8,
приходим к выражению, содержаще-
му неопределенность. Она легко
раскрывается по правилу Лопиталя:
^-b[be~at — ae~bt]
lim----д---------= — (1+а0 е~ at-
b~*a dtSa~b^
Зная этот результат, непосредст*
венно из формулы 8 таблицы при-
ходим к формуле 21. Дифференци-
руя оригинал и умножая изображе-
ние на р, приходим к формулам 22
и 23. Особенность этих трех фор-
мул в том, что их знаменатель
имеет кратные корни.
Аналогичным путем выводятся
выражения, знаменатель которых
содержит более высокие, степени р.
Очевидно, что в этом случае нужно
брать сумму изображения трех экс-
понент соответственно трем корням
знаменателя. В результате алге-
браических преобразований, подоб-
ных ранее рассмотренным, полу-
чается формула 24 для -случая
двух комплексно сопряженных кор-
ней pi,2=—и одного вещест-
венного корня рз = —о-
В конце таблицы повторены
важнейшие формулы, которыми ча-
сто приходится пользоваться при
переходе от дифференциальных
уравнений к операторным.
Полезно обратить внимание на
применимость формул (11-22),
(11-23) (при соответствующей ого-
ворке) ко всем формулам таблицы.
Изложенного в предыдущих па-
раграфах достаточно для решения
разнообразных задач электротехни-
ки. Они легко решаются на основе
результатов, представленных фор-
мулами таблицы 11-1.
309
Приводимые в следующих 'па-
раграфах примеры должны научить
пользоваться операторным мето-
дом
11-5. РАСЧЕТ ПЕРЕХОДНЫХ
ПРОЦЕССОВ ПРИ НУЛЕВЫХ
НАЧАЛЬНЫХ УСЛОВИЯХ
Пусть высшая производная в
рассматриваемом уравнении имеет
порядок п. Запись соответствующе-
го операторного уравнения чрезвы-
чайно упрощается, если при этом
все низшие производные, начиная
с (п—1)-й, в начальный момент
равны нулю:
/(n-i)(0) = f(n-2)(0)— ,. = о. (11-31)
Формулированные условия и назы-
вают н ул ев ы м и начальными
условиями. При этих условиях
любая производная порядка т
в операторном уравнении представ-
ляется просто множителем р в сте-
пени т:
y^PmF. (11-32)
Пример 11-3. Контур L, г, С (рис. 11-3)
подключается к источнику постоянного
напряжения «г_£/0. Напряжение на кон-
денсаторе ис и ток в индуктивности iL =
duc
= С в начальный момент равны нулю.
Требуется найти напряжение на кон-
денсаторе и ток в цепи.
Решение. Уравнение цепи
d2uc duc
LC~dtz~ + rC ~dT +ac = Ur
в операторной форме имеет вид:
(LCp* + rCp+ 1)UC = UV9
rwUc~Uc(p), Ur~Uv(p) — оператор-
ные изображения напряжений на емкости
и генераторе.
Следовательно,
U?
uc-(LCp2 + rCp + l) •
Для условий чхкла. корни
знаменателя комплексно сопряженные:
Р1.2------
/ 1 7 г \г
±J' |/ LC \2Г) “ ±
процесс имеет колебательный характер
и формулу для Uc удобно представить
в таком виде:
_ Ur 1
ис~ LC (р + »)2 + ₽2'
Ток легко найти как производную от ис\
duc
~dt
Этому соответствует простое умноже-
ние операторного выражения на р, по-
скольку по условию Й£(0)=0. Таким об-
разом, операторное выражение для тока
, Ur Р
1 - L (р+а)2 + р-
В выражения для Uc и I входит изо-
бражение напряжения на генераторе (7Г.
По условиям задачи происходит включение
на постоянное напряжение Ur=UQ, при
этом ur = — U„. s
Пользуясь формулами 15 и 16 табли-
цы, находим соответствующие оригиналы:
i = е at sin 0/
(здесь принято во внимание, что «2 + 02 ==
= 1/LC),
Пример 11-4. То же, что в примере
11-3, но требуется найти ток в цепи, если
напряжение генератора изменяется по за-
кону = 170 при t > 0.
Рис. 11-3.
Решение. В этом случае изображение
иг = Щг-±£ (формула 3 табл. 11-1).
* г
Изображение тока
, 1
l~TL' р [(р + а)* +
310
н оригинал (формула 15 табл. 11-1)
+ у sw)].
В этом случае 'в цепи с течением вре-
мени установится ‘постоянный ток, соответ-
ствующий линейно возрастающему напря-
жению на конденсаторе {ср. формулу 10-30
§ 10-4].
Очень полезно проверить все формулы
<по размерности (например, обратить внима-
ние на то, что в последней формуле раз-
мерность С/Т такая же, как размерность
реактивной проводимости (оС=2лС/Т).
Пример 11-5. В контуре L, г, С наво-
дится э. д. с., имеющая вид 6-функции; это
происходит в результате мгновенного раз-
рыва тока /о в индуктивно связанном кон-
туре (рис. 11-4). В этом случае роль напря-
жения иг играет индуктированная э. д. с.
din
иг = э = — М —[j
Ищется ток i и напряжение ис.
Решение. Искомые величины выра-
жаются формулами, выведенными в приме-
ре Ш-З, однако в них теперь
47Г=Ж.
В результате находим, что
Л4/о 1
Uc— LC (р + <х)2 + Р2’
т ст, М1° Р
l—pbUc— L ^р + а)2+^
Sb к табл. 11-1 (формулы 16
ем:
Г a "1 ,
cos p/ — y- sin $t e -
Важно обратить внимание на то, что
под воздействием напряжения, имеющего
вид '6-функции, ток в индуктивности мгно-
венно возрастает на конечную величину
i’ (+0^ =hMIL, а напряжение на конденсаторе
в начальный момент остается равным нулю
<ср. анализ цепи рис. 10-43, § 10-1.1).
Сказанное имеет простое физическое
содержание: ток изменяется скачком, бла-
годаря кратковременному действию беско-
нечно большой э. д. с. -(6-функция). Для
изменения скачком напряжения на конден-
саторе необходимо бесконечно большое зна-
чение тока; однако это условие в рассмат-
риваемом случае не может выполняться:
существование бесконечно большого тока
в индуктивности связано с бесконечным
значением энергии i(i2L/2), тогда как под
влиянием 6-функций становится бесконечно
большой только мощность и только на бес-
конечно малое время, так что сообщаемая
энергия остается конечной.
Нетрудно найти эту энергию1 * * * У
w = Af2/g/2L.
Нулевые начальные условия для
уравнений, содержащих интегралы.
Сказанное в начале этого парагра-
фа о нулевых начальных условиях
[формулы (11-31) и (11-32)] рас-
пространяется и на уравнения, со-
держащие интегралы, которые фор-
мально можно рассматривать как
производные отрицательного по-
рядка.
Возьмем, например, уравнение
для тока в цепи г, С, подключаемой
к источнику ит (рис. 1.1-2):
— ir 4- ~ J i dt. (11-33)
В этом случае высшая произ-
водная имеет нулевой порядок —
это сама функция £(/).
При этом имеют место нулевые
начальные условия, выражаемые
формулой (11-31), если значение
производной минус первого поряд-
ка, т. е. «порядка— 1» равно нулю
в момент t=0, т. е.
«c(0) = ±J< <й|м=о.
Это змачит, что конденсатор не
был заряжен к моменту коммута-
ции и, следовательно, интеграл
в (11-33) 'берется в пределах от 0
до t.
----ta-г
Рис. 11 -4.
1 Заметим, что при ее определении из
4-s
интеграла J iu dt при е —> 0 следует по-
—е
лагать
+е
У 1 б dt = -у1.
—е'
311
Сама функция i(t) в начальный
момент может отличаться от нуля
[f(+0)#=0], так как она представ-
ляет собой высшую из встречаю-
щихся производных п=0.
Отличие от нуля при выс-
шей производной не нарушает фор-
мулированные выше нулевые на-
чальные условия (il'1-31).
Простейшие электромеханические
системы. В электротехнике часто
приходится рассматривать -переход-
ные процессы в электромеханиче-
ских системах. При решении таких
задач также с успехом применяется
операторный метод. Особенность ре-
шения таких задач по существу де-
ла сводится только к составлению
исходных дифференцильных уравне-
ний, как это видно из приводимых
ниже примеров.
Пример 11-6. Рассмотрим переходный
процесс в магнитоэлектрическом осцилло-
графе, когда через петлю его вибратора
•проходит ток i=l Iq. Отклонение от поло-
жения равновесия петли с зеркальцем
(рис. 11-5) происходит под действием вра-
щающего момента N, обусловленного взаи-
модействием тока с постоянным магнитным
полем, в котором находится петля; этот
момент прямо пропорционален току N=ci.
Уравнение движения петли
dy d2y
N = ci = k-( + ?4F + J^r2,
где у — угол поворота петли. В этом ра-
венстве первое слагаемое обусловлено упру-
гими силами, второе — силами трения
(в первом приближении создаваемый ими
момент пропорционален угловой скорости
dyjdt), третье — инерцией системы (/ —
момент инерции петли).
При нулевых начальных условиях, т. е.
для системы, находившейся в состоянии
статического равновесия (у —0, dy/dt=ty,
можем написать, переходя к операторной
форме:
с! й/Р = (k + ?Р + J Р2)[Г,
где Г=Г(р)—операторное изображение ис-
комой функции времени у=у(О-
Рис.
11-5.
Рис. 11-6.
Решение этого уравнения:
J р (р + а) (р + Ь) ’
где
, Р ,
Pl.2 = —о, —b = —2j~ +
/" / Р \2 k
±|/ \2J J j ~ ~ “ ± Р-
И
ab-=k/Jt b — a = 2p.
Искомое отклонение зеркальца вибра-
тора по формуле 8 таблицы
с Г
b^~a<be~at
ае~ы)
Пример 11-7. Рассмотрим еще один
пример переходного процесса в простой
электромеханической системе. Ненагружен-
ный двигатель постоянного тока с незави-
симым возбуждением включается * к источ-
нику постоянного напряжения Z70 (рис. 11-'6).
Вращающий момент двигателя N прямо
пропорционален току N=mi и уравновеши-
вается моментом, обусловленным механиче-
ской инерцией. Последний равен моменту
инерции системы /, умноженному на угло-
вое ускорение d^ldt.
Таким образом, уравнение механиче-
ской системы:
d<&
N = mi — J —jj.
При вращении двигателя в нем разви-
вается встречная э. .д. с., пропорциональная
скорости вращения э=—kca. Поэтому
в уравнение электрической цепи Ц г допол-
нительно входит и скорость вращения:
di
Uo = ir + L
Из самых общих соображений коэффи-
циенты k и т должны быть тождественно
равны один другому. Это связано с прин-
ципом обратимости генератора и двигателя^
впервые установленным в исследованиях
Якоби и Ленца.
Равенство этих коэффициентов можно
доказать из следующих энергетических со-
312
отражений. Мощность, подводимая к си-
стеме,
di
р (0 — Uoi = i1 2r + Li + ki<£)
состоит .из трех слагаемых: первое слагае-
мое — это мощность, преобразуемая в тепло
по закону Джоуля — Ленца (i2r); второе
слагаемое равно скорости увеличения энер-
гии магнитного поля индуктивности
\d(Li2/2)/dt]- третье слагаемое может пред-
ставлять собой только механическую мощ-
ность двигателя, равную произведению мо-
мента N=mi и угловой скорости со, т. е.
kite =\N<& = imco.
Из последнего -выражения и следует
тождественное равенство наших -коэффици-
ентов &=т.
Вернемся к решению полученной систе-
мы уравнений.
При нулевых начальных условиях (f=0,
<d=^0) каждую из производных можно за-
менить символом р и перейти к оператор-
ным алгебраическим уравнениям
ml — JpQ;- U0/p—(г + pL) IkQ,
где 2 =S(p) co(O«
Решая совместно операторные уравне-
ния системы, найдем, что
Uo/P = (Г + pL) ~ pQ + kQ
и
Q___________и^т________
р [p2LJ + pJ г ф- km] ’
откуда, приводя последнее выражение
к табличной формуле 11, найдем, что при
t > О
<0(0 =
I
k и°
1 — ( ch pt + — sh
где
г Г km
a~2L~ и ^ = V а2~ТГ-
Аналогично, решая исходные уравнения
относительно тока, найдем, что
__ ________J________
p2LJ + pJr -j- km
Знаменатель в этом уравнении совпа-
дает с множителем при р в знаменателе
уравнения для Q. Следовательно, корни
Pi,2=—ct'±|i в решении для тока имеют
прежние значения. (Выражение для. тока
в функции времени можно найти по фор-
муле 12 таблицы:
1=де sh^-
'В рассматриваемом примере ток равен
нулю в начале -процесса (из-за наличия ин-
дуктивности в цепи) и при установившемся
режиме\ так как мы предположили иде-
альный холостой ход, не учитывая даже не-
избежных сил трения.
Из полученных выражений легко пока-
зать2, что разность подведенной от источ-
ника питания энергии
00
Ги = У0
6
и энергии, превратившейся в тепло,
W = r^i2 dt
о
равна кинетической энергии вращающегося
двигателя
^кин I/—оо —
со2 (оо)
2 ’
Последняя равна половине всей подведен-
ной энергии.
Заметим, что это утверждение, требуе-
мое законом сохранения энергии, оказы-
вается справедливым только при k=m.
Интересно обратить внимание на тог
что хотя механическая система и электри-
ческая цепь, рассматриваемые независимо
одна от другой, описываются дифференци-
альными уравнениями первого порядка, од-
нако при их совместном решении порядок,
уравнения повышается и в системе могут
возникнуть колебания. Физически это соот-
ветствует существованию двух накопителей
энергии Jco2/2 и Lf2/2. Так, при достаточно-
большой инерции J и малом сопротивле-
нии г ток в цепи может достичь, большой
величины; при его уменьшении появляется
добавочная э. д. с. самоиндукции, дейст-
вующая в том же направлении, что источ-
ник питания; в результате двигатель может
приобрести скорость, превосходящую ско-
рость при установившемся режиме.
Условие возникновения колебаний мате-
матически формулируется неравенством
**2<!4^2£//. При этом
Здесь речь идет, разумеется, не об уста-
новившихся колебаниях, а только о колеба-
ниях при подходе к установившемуся ре-
жиму.
Обратная задача. В заключение
этого параграфа рассмотрим реше-
ние такой задачи: известно напря-
жение (или ток, или скорость, или
любая иная величина) на выходе,
требуется определить, каким при
этом должно быть напряжение
(или другая (величина) на входе.
1 Заметим, что р* < а.
2 При интегрировании проще всего
переходить к экспонентам
e~at sh pt = у « Ч.
313.
Рис. 11-7.
на соответствующие операторные
изображения
u-+v(/>), 1-+1(р) (11-34)
и все множители /ш на р:
(11-35)
Сказанное непосредственно сле-
дует из аналогичного представления
производных и интегралов
(“-Зв)
Рис. 11-8.
Пример 11-8. При 'включен-ии ненагру-
женного трансформатора (цепы, L рис. 1*1-7)
требуется получить на вторичной обмотке
постоянное напряжение w2—7*Г70 (рис.
11-8,а). Найти напряжение на входе
Решение. Составляя уравнение
1 Ui (Р)
Ui(p)^-Ut = pM
находим, ‘что требуемое входное напряже-
ние
U1 О) — р Ua (М + М р')’
Следовательно, по формулам 1 и 3
таблицы входное напряжение должно изме-
няться во времени по закону (см. рис. 11-8,6)
/ L . г X
Wi (f) = + -до- tJ.
11-6. ОПЕРАТОРНЫЕ
СОПРОТИВЛЕНИЯ И ПЕРЕДАТОЧНЫЕ
ФУНКЦИИ
Из всего изложенного ранее и,
в частности, из примеров предыду-
щего параграфа видно, что при ну-
левых начальных условиях все
уравнения цепи, записанные в опе-
раторной форме, подобны уравне-
ниям цепи синусоидального тока,
записанным в комплексной форме.
Последние переходят в первые, если
в них заменить все комплексные
изображения переменных величин
Так, например, для цепи после-
довательно включенных L, г, С
(рис. 11-3)
уравнение для установившегося ре-
жима простого гармонического тока
(L7o) + r + ^/=6r (Ц-37)
аналогично уравнению переходного
процесса, написанному в операторной
форме (при нулевых начальных ус-
ловиях),
(^ + r+i)/=ar- С11’38)
Развивая эту аналогию, можно
ввести понятие операторного сопро-
тивления £(/?), аналогичного комп-
лексному сопротивлению Z(/a>):
Z(p) = Z(y<»)|/_/j. (11-39)
Так, в случае цепи Д г, С из
(11-37) и (11-38) находим, что
Z (/ш) = L/ю 4- г +
Z(p) = Lp + r + ±
Сказанное можно распространить
и на проводимости
Г(р) = У(/о>)|/и^, (11-40)
и на передаточные коэффициенты или
функции. Пусть, например,
Ua = H(J«>)Ub ИЛИ /o = S(/a>) 1Ъ,
(11-41)
314
© таком случае
Ua(p) = H(p)Ub(p)
шли
/a(p)^S(p)Ib(p}. (11-42)
В этом легко убедиться, имея
в виду, что в теории переменных
токов все преобразования и выво-
ды, приводящие, например, к
(11-41), основываются на примене-
нии к цепи двух законов Кирхгофа.
Уравнения цепи записываются в об-
щем случае в дифференциальной
«форме. Рассматривая установив-
шийся режим гармонических коле-
баний, эти уравнения переписывают
в комплексной форме по правилам
(11-36). При решении задач опера-
торным методом основываются на
тех же законах Кирхгофа, переходя
к операторной форме по правилам
(11-36). Естественно, что получен-
ные формулы переходят одна в дру-
гую в соответствии с (11-34) и
(11-35).
Эти простые результаты практи-
чески очень важны. Зная решение
для какой-либо цепи в комплексной
«форме, от него очень легко перейти
к расчету переходного процесса
{при нулевых начальных условиях);
кроме того, привычные операции и
навыки в решении задач комплекс-
ным методом непосредственно пере-
носятся на решение задач оператор-
ным методом.
В начальный момент (при нуле-
вых начальных условиях) токи во
всех индуктивностях и напряжения
на всех конденсаторах равны нулю.
•Сказанное равносильно утвержде-
нию, что в начальный момент (/=
= +0) проводимость всех индуктив-
ностей (1/Lp) равна нулю, так же
как равно нулю сопротивление всех
конденсаторов (1/Ср). Очевидно,
что этому правилу и соответствует
^формула (11-22), в которой с вре-
менем £—+0 сопоставляется зна-
чение р=оо.
Аналогично легко заключить,
что для источников постоянного
напряжения или тока в установив-
шемся режиме (/->оо) сопротив-
ление индуктивности Lp стремится
к нулю, так же как и проводимость
конденсатора Ср, Это простое со-
Рис. 11-9.
ображение приводит к выводу о том,,
что с временем /->оо сопоставляет-
ся значение р = 0 в соответствии
с формулой (11-23).
Из рассмотренной аналогии меж-
ду Z(/co) и Z(p) легко заключить,
что в цепи с гармоническими ис-
точниками, когда при t—*оо в цепи
существует установившийся режим
гармонических колебаний, т. ,е. от-
сутствует предел для токов и на-
пряжений, формула (11-23) непри-
менима. В этом случае устано-
вившемуся режиму (см. также
§ 11-9) соответствует сопротивление
Пример 11-9. Для цепи рис. 11-9
требуется найти ток в сопротивлении г2.
Решение. Пользуясь комплексным
методом, найдем, что
д=!)г________________________=
(У40)2 LCr 2+/<o(C’r1r2-|-L)+r1-|-r2
В таком случае
12 (/>) - Ur (/>) p2LCri+p (Cr1r2+£)+r1+r2-
Окончательное выражение зависит от ви-
да иг(/).
Пример 11-10. Найти изменение напря-
жения u2(t) при включении на вход двой-
ной Т-схемы (рис. 11-10,а) постоянного на-
пряжения Wi=I70.
Решение. Для этой цепи, широко
применяемой в радиотехнике, известно, что
при синусоидальном напряжении на вхо-
де Ui и разомкнутом выходе (см. при-
мер 6-4)
1 — а2
U 2 = 1 — аг + 4/1 ~
4уа
I — а2 -|- 4/а
где
а = ыгС.
315
Переписывая эту формулу так, чтобы
она имела вид явной функции от /со:
t72=£/i 1
__________4fCj(i)__________
1 + 4гС/со + (гС)2 (/со)2
Пример 11-11. Источник постоянного
тока Jo включается в цепь, содержащую
две параллельные ветви (рис. 11-1.1), со-
противления которых в операторной форме
Za—ra4-pL и Zd=rb+-g^.
Требуется найти напряжение на кон-
денсаторе.
Решение. Как- известно, токи в па-
раллельных ветвях распределяются обрат-
но пропорционально сопротивлениям, поэто-
му ток в ветви b
‘ь- р Za +iZb
Напряжение, создаваемое этим током на
конденсаторе,
1
ис = /ь Cj}
или после простых преобразований для
случая (га Ч- rb)2 < 4L/C
Т1 J 0___ra Н~ pL
Uc-CL р[(р+ «)*+№'9
где
г°+гь » 1/ 1
“ — 2L ’ LC~ '
Полученному выражению по формулам
15 и 16 таблицы соответствует
и заменяя /со на р, получаем в оператор-
ной форме:
1 Г 4rC р 1
= /Г U° [ 1 — 1 +4rCp+(rC)2psj ’
U>q — J Q?a \ 1
cos $t
1 — aCra .
---74---- sin
pOa
Производя простейшие алгебраические
преобразования, придадим последней фор-
муле вид, подобный формулам таблицы:
р
р2 + 4\р + Л2
_ 1 / р \
~ р и° V1 ~ 4 (р + “)2 —Р-2 ) ’
где Х= 1/0, а корни знаменателя
Pi,2 = — а±^ = — 2Л + У (2Л)2 — Л2 =
= — 2Х±'ргЗЛ.
Пользуясь таблицей, находим по фор-
мулам 1 и 12
На рис. 11-10,6 -представлен график на-
пряжения u2(t). Интересно заметить, что
независимо от значений г и С минимум на-
пряжения и2 представляет приблизительно
0,116 Uo. Чем больше г, С, тем позднее до-
стигается это минимальное значение (6 =
=0,755 гС).
Как видно из полученных формул,
в установившемся режиме напряжение на
конденсаторе оказывается равным Jora. Это
легко объяснить. В установившемся режи-
ем ток через ветвь с конденсатором не про-
ходит, а падение напряжения на индуктив-
ности равно нулю.
Из тех же формул видно, что в пере-
ходном режиме напряжение на конденсато-
ре может превосходить установившееся
значение. При м-а-лом затухании, когда
оно превосходит установившееся
значение приблизительно в У'ЩС раз.
Пример 11-12. Последовательно соеди-
нены два конденсатора, обладающие емко-
стями С], С2 и сопротивлениями изоляции
г2. Они подключаются к источнику постоян-
ного напряжения UQ (рис. 110-29). Требуется
Рис. 11-11
316
найти распределение напряжения на кон-
денсаторах.
Решение. Представив -сопротивление
каждого конденсатора в операторной форме
________1
£1,2 + *
найдем, что
1 Zi
Ui = Р и° z,+z2 ~
.J rZ £2 +• рС2
Р °£i + £2 + Р (Ci + С2)*
Этому выражению соответствует сле-
дующая функция времени для t > 0:
“-ц-[с, + с, ‘"‘ +
где
Si + §2 _ 1
а~ Сг + Сг’ ^1,2—Л1,2‘
Полученное равенство показывает, что
в начальный момент напряжение распреде-
ляется обратно пропорционально емкостям
(как в электростатике), а при установив-
шемся режиме — обратно пропорционально
проводимостям,. Рекомендуется построить
график изменения напряжения на конденса-
торах для следующих данных: Ci =8 • 10~9 ф,
C2=i2-I10“9 ф, £i=d.0“9 сим, £2=4- 10~9 сим\
при этом а=0,5 сек-1.
«Вначале Wi(( + 0) =O,i21/o; -при установив-
шемся режиме Mii(oo) =0,8 Uq.
Пример 111-13. Как уже отмечалось,
из-за ряда причин и прежде всего вслед-
ствие зависимости от частоты диэлектриче-
ской проницаемости и диэлектрических по-
терь, емкость конденсатора при различных
частотах различна и в общем случае долж-
на представляться комплексом, зависящим
от частоты (при этом мнимая часть емкости
соответствует наличию в ней рассеяния
энергии). Пусть, например, в -цепи перемен-
ного тока
/ т \
С = Со (1 + - J + /(от J
при
Со=1О—8 ф, т=99, т='10~6 сек.
Требуется найти ток в цепи такого кон-
денсатора, включаемого через сопротивле-
ние г =10 ом к источнику постоянного на-
пряжения U о.
Решение. Имея в виду известное
комплексное выражение для гармоническо-
го режима и сразу заменяя /со на р, нахо-
дим операторное выражение искомого тока
1 — р U° 1 Uo 1 + гСр
г+ рС
В этих формулах С=С(р), промежуточные
преобразования опущены.
Корни знаменателя pi,2——а*±р выра-
жаются через а и ц, имеющие следующие
значения для приведенных выше пара-
метров:
1
“= 2
l+w\ ,
----- —55 мксек-1'.
т /
-----г
|X = V а2--с^
= 55(1— 0,00165) мксек-1.
Обращаясь к табл. Ы-1, по формулам
12 и 13 находим:
i = 0, Шо (ch — 2,82 sh ^) е~55*.
Числовое значение а подставлено в предпо-
ложении, что время измеряется в микросе-
кундах. Хотя величина ц отличается от а
всего на 0,165%, в этой, формуле нельзя их
считать равными: если бы ц=а, то при
больших t (скажем, /=10 мсек)
ch р/ sh = -g- eat>
В таком случае мы нашли бы, что при
больших t в цепи устанавливается постоян-
ный ток —0,09.1 UG, что, разумеется, не
соответствует физике и получено от неуме-
ния обращаться с различными, но близкими
числами.
Большую наглядность и четкость отве-
та получим, пользуясь представлением тока
через две экспоненты с существенно разны-
ми показателями
— at —— (а — |л) и —bt =— (а+Р*)^
где а—0,0907 мксек-1 и Ь— 440 мксек-1.
Для этого следует обратиться к форму-
лам 9 и 10 таблицы. После подстановки
найденных числовых значений и простых
•преобразований получаем:
i = о, 1 и0 [0,090 е -110* + 0,909г - 0,0 m q}
здесь t—время в миллисекундах.
В начальный момент в цепи проходит
ток £(0) = £7о/г.
Пример 11-14. Аналогично предыдуще-
му примеру проводится расчет тока в цепи
с индуктивностью, величина которой зави-
сит от частоты. Пусть, например, нужно
определить ток при подключении последова-
тельной цепи г, L к постоянному напряже-
нию Uо, когда зависимость индуктивности
от частоты выражается уравнением
/ . т \
L = L° (1+ j j-
Решение. Очевидное выражение
для тока в операторной форме
Up
Г1
pt + 1 + т
Р2 + Р
1
CQrt
1
P и*
t
1
т
1 +1 + ръ
317
В следующих двух .примерах рас-
сматриваются цепи, содержащие
усилители. В них показывается, как
для решения поставленных задач
можно составлять уравнения Кирх-
гофа непосредственно в операторной
форме.
Пример 11-15. На рис. 11-12,а показан
дифференцирующий контур, в котором бла-
годаря обратной связи (сопротивление гс
в катодной цепи) резко уменьшается посто-
янная времени. На вход цепи подается на-
пряжение
«1 — т I т р2 •
Требуется найти напряжение на выходе и2
и определить, в какой мере ‘выполняется
ожидаемое дифференцирование u2^kdud,dt.
Решение. Переходя к схеме замеще-
ния (рис. Ы-42,6), находим, что
la (^?+^i+^c+ pL) = [X ([Ji -1аГс)
или г рТ/ х
1а = R + П + Гс (р. + 1)+Р^‘
Искомое напряжение
U2 = рМ1а
или после простых преобразований
тт pUi
Uz- L p + a ’
где
R + Гi Гс (P- + 1)
П. = -------z-----.
a)
Рис. 11-12.
Для заданного вида (t) имеем:
п г 1
р(р + а) -
и. Р-М „ .
Благодаря обратной связи величина а
достаточно велика, поэтому найденное зна-
чение практически пропорционально произ-
водной от &г(/), которая в данном случае
должна быть постоянной и равной Z70/^-
Так, например, при г^=4 ком, 7? ==0,5 ком^
гс=0,5 ком, Л =<10,0 мгн, ц=200 находим^
что а=.1,05 • 107 сек~1. Уже через 0,4 мксек.
экспоненциальная слагающая, обусловли-
вающая отступление от постоянной величи-
ны (пропорциональной производной), со-
ставляет всего 1,5%.
Огромная роль, которую здесь играет
обратная связь, становится понятной из то-
го, что при г.с=0, если индуктивность и со-
противление анодной цепи остаются преж-
ними, значение а становится много меньше,,
а именно а=4,05-105 сек~*. При этом по-
грешность превосходит 1,5% в интервале
времени до 10 мксек.
Пример 11-16. В цепи рис. Ш-13 содер-
жится идеальный усилитель, у которого*
входное сопротивление бесконечно вёлико,.
а напряжение на выходе и2 в точности про-
порционально напряжению на входе усили-
теля «ь
и2=— Kai.
Такая цепь применяется как интегрирую-
щий контур.
Требуется найти напряжение на выходе
u2(t), когда на вход подается постоянное
напряжение и=1 • Uo~ Udp.
Решение. Составляя уравнение цепй
и решая его совместно с уравнением уси-
лителя
= - KUt.
находим, что
К 1
----U, СГ(К+Г) 'р(р+ау
1
где а — Сг(/С + •
318
Искомая функция времени
= —tf0K(l—£-“*)•
Разлагая экспоненту в ряд, находим
К
u^^ — Uo t
с большой степенью точности, до тех пор
пока at^l. Так, для С = 0,1 мкф, г —
— 100 ком, К = 1 000 получаем at 0,01
для t 0,01/я — 0,01Сг (К + 1)=5= Ю сек.
11-7. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
ПРИ НЕНУЛЕВЫХ НАЧАЛЬНЫХ
УСЛОВИЯХ
В этом параграфе сначала рас-
сматриваются прямые аналитиче-
ские методы, основанные на учете
ненулевых начальных условий при
записи изображения производных и
интегралов. Затем рассматривают-
ся метод эквивалентных источни-
ков, при наличии которых дальней-
ший расчет системы ведется уже
для нулевых начальных условий, и
метод суперпозиции. Все эти мето-
ды получили широкое распростране-
ние, однако можно рекомендовать
преимущественно: 1) из прямых
аналитических методов — метод
уравнений с обобщенными произ-
водными и 2) метод суперпозиции.
1. ПРЯМЫЕ АНАЛИТИЧЕСКИЕ
МЕТОДЫ
Уравнения с простыми (необобщенны-
ми) производными. Первый из этих методов
основан на том, что все производные в диф-
ференциальных уравнениях рассматривают-
ся как простые производные. Соответствен-
но переход к изображениям производится
по формулам (1140) и (lil-lil):
(11-43)
-^p*F-pf (+0)-7(+0),
а второе слагаемое (определенный интег-
рал) равно изменению рассматриваемой ве-
личины х за время t, протекшее после ком-
мутации.
В силу сказанного переход от интегра-
ла к его изображению должен производить-
ся по формуле
х (Г) = f f dt -~F + у х (0). (11-45>
Пусть дано дифференциальное уравне-
ние, подлежащее решению, причем известны,
все необходимые начальные условия. В та-
ком случае, переходя к изображениям по*
формулам (Ы-43) и (11-45), получаем урав-
нение, которое и должно быть решено от-
носительно изображения искомой функции..
Искомая функция времени находится как
оригинал полученного изображения.
Все сказанное относится и к случаю*
решения не одного дифференциального
уравнения, а системы уравнений.
Рассмотрим, например, переходный,
процесс в контуре £, г, С, который отклю-
чается от генератора переменного тока-
(рис. 11-14). После коммутации в контуре'
уже не содержится источников питания,
однако в начальный момент в индуктивно-
сти контура мог существовать ток г’ь(—0),.
отличный от нуля, и на емкости могло быть-
некоторое напряжение ис'(—0). Величины
и знаки тока и напряжения зависят от их
фаз в момент отключения.
При fr(—0)-#0 и ад(—0) -#0 в конту-
ре запасена энергия и значит в нем будет
проходить ток, несмотря на отсутствие
внешних источников.
Решение получается наиболее простым,
если уравнение для контура рис. 1-L-14 за-
писать в таком виде:
П + J idt = Q. (11-46>
При указанных на рис. 11-14 положи-
тельных направлениях
t
—-^-^idt — ис(0). (11-47>
0
Подставляя это выражение интеграла
в (11-46), получаем уравнение
t
L—&+ri+ -q W dt — rzc(O) = O,
где dfldt, d2fjdt2 — простые, а не обобщен-
ные производные.
Встречающиеся в уравнениях интегра-
лы х= J f dt всегда следует считать выра-
жающими значение величины х в момент
времени t. При этом интеграл должен пред-
ставляться как сумма
t
x(0=x(0)+ ^fdt, (11-44)
о
где первое слагаемое равно значению х (ве-
личины, выражаемой интегралом) .непосред-
ственно после коммутации х(0)=х(+0),
319
ют которого легко перейти к изображениям
по формулам (11-43) и (11-45):
.£ [pl - i (+0)]+ rl I - j- ис (0) = 0.
(11-48)
Входящие в это уравнение начальные
условия легко находятся, так как по зако-
нам коммутации
Z(+0) = fb(~0), Wc(0) =«с(+0) =«с(—0).
Решая уравнение (11-48) относительно /,
находим, что
1
^•Л(-0) + -«с(-°)
/ =-------------------------- (11-49)
Lp + r +cF
Это уравнение имеет очень простое тол-
кование: в знаменателе стоит Z(p) контура,
следовательно, числитель выражает э. д. с.
эквивалентного генератора; она отлична
ют нуля благодаря энергии, запасенной
в индуктивности [при iL (—0) =/= 0] и в кон-
денсаторе [при ис (—0) ф 0].
Производя формальные преобразова-
ния, придаем изображению тока обычный
вид:
ЬСрЧт (— 0) + Срис (— 0)
'=——_— —.
lc\p2 + lp + lc)p
Этому выражению соответствует иско-
мая функция времени
i = tL(-0)
а
cos — у sin
e~ai
ur (— 0)
1—---------Sin pi e~at, (11 -50)
где а = r/2L и p = J/ — a2.
От найденного тока (11-49) можно
перейти к напряжению на конденсаторе
по формулам (11-47) и (11-45):
После подстановки I из (1’1-49) и про-
стых преобразований получим формулу, для
которой легко найти оригинал, пользуясь
табл. 11-1.
Искомое напряжение uc(t) можно
определить и по уравнению
di
uc=Ldi + ri’
подставив значение i из i (11-50). От по-
следнего выражения можно перейти и
к операторной форме, принимая во внима-
ние первую из формул (11-43):
Uc(p)==L[pI-i(+0)]^rI.
.Но уравнения для того же контура L,
г, С можно записать и в таком виде:
d2ur dtir
iC c + rCc+ 0; (11.52)
dt2 dt
dur
i = iL — — C—^- (11-53)
(положительные направления указаны на
рис. 11-14).
Переходя от (11-52) к изображениям
по формулам (11-43), получаем:
LC [p2Uc - рас (+ 0) - и'с (+ 0)] +
+ rC [pUc — ис (4- 0)] + Uc = 0. (11-54)
Теперь нужно определить начальные зна-
чения Wci(+0) и w'c(+0), входящие в по-
следнее равенство.
Поскольку напряжение на конденсаторе
не может изменяться скачком, находим, что
Пс'(+0) = ис(—0),
где ис(—0)—известное напряжение на
конденсаторе непосредственно перед ком-
мутацией (оно определяется предшествую-
щим режимом).
Что же касается производной от на-
пряжения на конденсаторе, то ее значение
после коммутации и'с(+0) никак не свя-
зано с ее значением до коммутации
и'с\—0)—эта величина может изменяться
скачком.
Искюм'ое начальное условие и'с(+0)
может быть найдено из уравнения (1'1-53),
справедливого для рассматриваемой цепи
после произведенной коммутации. Посколь-
ку ток в индуктивности не может изменять-
ся скачком, то
iL (- 0) = iL (+ 0) = - Си’с (+ 0). ) V
Следовательно,
и'с (“Ь 0) = — с7
тогда как до коммутации скорость возра-
стания напряжения на конденсаторе опре-
делялась током в ветви конденсатрра ic,
т. е.
Си' q ( 0) ( 0)»
и могла иметь совершенно иное значение.
Начальные условия для таких величин,
как и'с, называют зависимыми, так как они
не определяются непосредственно законами
коммутации, а связаны 'с ними промежуточ-
ными уравнениями. В случае и'с таким
Промежуточным уравнением послужило
(11-53).
Необходимость определять зависимые
начальные условия осложняет решение.
Придерживаясь следующей общей реко-
мендации, можно всегда избежать этих
осложнений: к операторным уравнениям
нужно переходить еще до совместного ре-
320
шения исходных дифференциальных урав-
нений.
Так, наир им ер, уравнение (11-52) полу-
чено из двух -исходных уравнений
di dur
LTt+ir = uc и i = -C —
содержащих неизвестные ис и i.
Записывая исходные уравнения в опе-
раторной форме
L[pl — Z (+ 0)] + Zr = 47с и
[ = _ С[рис~ ис(-|-0)],
мы не встретимся с зависим*ы*М|И начальны-
ми условиями. Исключая из .последних
двух уравнений Z, приходим к выражению
для Uc:
= LCр2ис (—0) +р \гСис (—0) —LiL (—0)]
(рис. 11-15,6), отличающуюся от •
предыдущей только тем, что ее зна-
чение в области отрицательных t
при >0 отлично от нуля; сказан-
ное можно записать так:
f (-0)^=0. (11-56)
Обобщенная производная в по-
следнем случае отличается от
(11-55) только множителем при
6-функции, так как теперь скачок,
происходящий при Z=0, равен
f(+O)-f(-O), а не f(+0).
В этом и заключается учет пред-
шествующего ненулевого состояния.
Следовательно, обобщенную произ-
водную при ненулевых начальных
условиях — обозначим ее [df/dt] —
можно записать так:
LCp + L Р + LC
также не содержащему .зависимых началь-
ных условий.
Уравнения с обобщенными про-
изводными при ненулевых началь-
ных условиях. Понятие обобщенной
производной было введено в § 11-1
в предположении, что дифференци-
руемая функция /(/) равна нулю
при /<0 и может скачком возра-
стать до значения if ( + 0), как это
было схематически показано на
рис. 11-1 и еще раз повторено на
рис. 11-15,а. Обобщенная производ-
ная (11-6) такой функции при /^0
Й = /(+О)«+(Й) (11-55)
f (- °)18+
+(%) при ^0. (11-57)
Она отличается от (11-55)
слагаемым f(—0)8, т. е.
df]_
dt] ~
d[
dt
H-W,
только
(11-58)
отличается от простой производной
(dffdt) наличием дополнительного
слагаемого, равного 6-функции, ум-
ноженной на f ( + 0), поскольку при
t — О функция изменялась скачком
именно на f (+0).
Рассмотрим теперь функцию
где [df/dt] — обобщенная производ-
ная для ненулевого предшествую-
щего значения функции f(—0) #=0
(ненулевые начальные условия),
df/dt— тоже обобщенная производ-
ная, но записанная в предположе-
нии, что 'f(Z)=O при /<0, т. е.
f(—о)=о.
Из сказанного следует, что изоб-
ражение такой производной выра-
жается формулой
(11-59)
поскольку б ~ 1 и по условию
df/dt ~ pF.
11 /-/у.) При t РО
При t<O '
f(-O)=O
a.)
При t<O
1 О
11 fft) При tPO
Рис. 11-15.
21 К. M. Поливанов
321
По существу дела введенное
• здесь обозначение излишне, так как
при f(—0) =0 значения обобщен-
ных производных совпадают. По-
этому в дальнейшем мы не будем
вводить особого обозначения для
обобщенной производной с учетом
предшествующего значения. По той
же причине формула (11-59) приве-
дена в табл. 11-1 без особого обоз-
начения для производной.
Выражения (11-57) и (11-58)
можно получить и строго аналити-
чески. Представим рассматривае-
мую функцию следующим равенст-
вом (рис. 11-15,6):
. f (t) = (1 - /) w (0 + Iv (t), (1 l-59a)
где w и v — непрерывные функции.
Оно показывает, что f (t) — w (t)
при t < 0 и f (/) = v (/) при t 0, по-
скольку 1 = 0 при t < 0 и 1 = 1 при
Дифференцируя 11-59а, находим,
что
df dl , iXdw । dl . y dv
Tt—7tw + (i~^dt+Ttv + 1^t
или для Z>0
(0) + Sn (0) + (11-596)
(поскольку 1 — 1 — 0 для t > 0).
Но в выражении (11-596) dv/dt
совпадает с простой производной
(df/dt), w(0) = f(— 0) и n(0) =
=7 (+0).
Таким образом, (11-596) совпада-
ет с (11-57).
Аналогично формуле (11-59) (можно
найти изображения и для высших обобщен-
ных производных, учитывающих предшест-
вующие ненулевые значения функции или
ее производных [f(—0)-^0, f'(—0)^0
и т. д.]. Например, легко получить, что
p2F_f'(_0)-^(-0), (11-60)
где 6'=d§!dt=d2l/dt2— импульсная функ-
ция второго порядка.
Однако в большинстве конкретных за-
дач не только не приходится пользоваться
высшими производными, но следует их из-
бегать для того, чтобы не получить ошибоч-
ных результатов; такого рода ошибки по-
лучаются из-за того, что, пользуясь пра-
вильной формулой (11-60), не учитывают
некоторые тонкости в определении входя-
щих в нее значений f'(—0) (зависимые
начальные условия).
В случае корректных задач оба
изложенных здесь метода тождест-
венно совпадают, поскольку в та-
ких задачах гь(—О)=/г( + 0) и
и с (—0) = Uc (+ 0).
Однако метод обобщенных про-
изводных с учетом предшествую-
щих состояний оказывается более
общим: например, он применим и
к «некорректным» задачам (при-
мер 11-17). Этот метод обладает и
таким преимуществом: пользуясь
им, нет надобности обращаться
к каким бы то ни было законам
коммутации, так как необходимые
начальные условия /f( + 0) автомати-
чески входят в решение по дан-
ным предшествующего состояния
f(—0), как это видно из примеров
11-17 и 11-18.
Пользуясь обоими методами,
следует помнить о рекомендации
переходить к операторным выраже-
ниям непосредственно от системы
исходных дифференциальных урав-
нений и решать систему уравнений
уже в операторной форме1.
Рассматривая, например, от-
ключение контура L, г, С от источ-
ника при замыкании рубильника
рис. 11-16, получаем контур, к ко-
торому применимо уравнение
d2u,~ , dun
LC + rC -\-uc — Q
при ненулевых начальных условиях.
Вместо определения начального
уравнения для производной duddt
как зависимого лучше обратиться
к’ двум исходным уравнениям, сра-
зу представляя их в операторной
форме:
i = C^^/=C[pl7c-uc(-0)l.
__________ (П-61)
1 В противном случае, т. е. при пере-
ходе от системы (дифференциальных урав-
нений с (несколькими неизвестными к одно-
му уравнению, происходит повышение по-
рядка дифференциального уравнения, а ори
переходе от высших производных к их опе-
раторному изображению встретится необ-
ходимость в определении зависимых началь-
ных условий.
322
т di i •
Ldi+rt=
=—uc^L [pl—i (— 0)] + r/= — Uc
(11-62)
Исключая из этих уравнений /,
находим:
__(Lp+r)Cuc(— 0) + Щ—0)
UC— LCp*+rCp+l
(11-63)
Из тех же исходных уравнений
можно найти /. Зная операторные
выражения, легко найти соответст-
вующие функции времени.
Пример 11-17. Конденсатор разря-
жался на ветвь г, L (рис. -11-17). В момент
параллельно был 'присоединен второй
заряжённый конденсатор С2. До коммута-
ции напряжения на конденсаторах были
различны и равны иСт(—0), иС2(—0), в ин-
дуктивности проходил ток lL(—0).
Требуется найти операторное выраже-
ние для общего напряжения на трех парал-
лельных ветвях Uс-
Решение. По двум законам Кирхго-
фа составляем очевидные уравнения
^С1Ч“/с2_Ь^Ь=0 или
Рис. 11-16.
Для сокращения записи в последнем
уравнении приняты следующие обозначе-
ния: Q (—0) == Ciuc it (—0) 4- С2«с2!(—0) — пер-
воначальный заряд двух конденсаторов; С
= Ci + C2. Применяя к этому выражению
формулу (dil-22) ис (+0) =pUc\ нахо-
дим начальное напряжение ис(+0) сразу
после коммутации:
М+0) —Q(—0)/С.
Этот результат имеет простой смысл:
весь заряд двух конденсаторов, деленный
на общую емкость двух параллельно вклю-
ченных конденсаторов, равен начальному
напряжению после коммутации.
Пример 11-18. Рассмотрим электриче-
ский двигатель примера 11-7, предполагая*
что он имел начальную скорость <о(—0) и
начальный ток f(—0) к моменту включения
напряжения UQ.
В таком случае два основных урав-
нения
dtj
Uc-L — + iLr.
Соответствующие операторные уравне-
CApUc-ncl (- 0)] +
+ с2 [р17с - «с2 (- 0)];+ IL = 0;
Uc = L[plL-iL(-Q)] + lLr.
ki <= J и Uo = ir L dj kca
переходят в операторные уравнения при
ненулевых начальных условиях:
kl — J [pS — со (— 0)]
и
j- Uо = Ir + L [pl - i (- 0)] + kQ.
Их совместное решение для 2 теперь
принимает такой вид:
UQk + LJp^ (— 0) + р [Lki (— 0) + /гео (— 0)]
Ьь — —— -----------------
р (р2Ы + prj 4- Л2)
Обратим внимание, что хотя после комму-
тации напряжения на конденсаторах одина-
ковы и в выражение первого закона Кирх-
гофа входят одинаковые для7 />0 произ-
водные duddt, однако напряжения конден-
саторов до коммутации были различны, по-
этому различны и обобщенные произ-
водные.
Исключая IL из полученных уравнений,
находим:
"с
Lp*Q (-0) -\-rpQ (-0) —pLiL (-0)
/ г 1 \
Применяя формулу (11-22), находим, как
и следовало ожидать из физических сооб-
ражений, что
«(+ о) =и₽)^=Д= <(— °>-
Поскольку в цепи действует источник
постоянного напряжения и переходные про₽
цессы затухают, можно найти установив-
шуюся скорость по (11-23)
“ (оо) = (р) |р==о = u»lk-
Очевидно, что как значение тока 0), так
и скорость со(—0) могут иметь как полб-7
21*
323
Рис. 11-17.
Рис. -11-18.
жительные, так ?и отрицательные значения.
Например, о>(—0)<0 и /(—0)<0, если про-
исходит реверсирование двигателя.
2.. МЕТОД ЭКВИВАЛЕНТНЫХ
ИСТОЧНИКОВ
Расчет цепи при ненулевых на-
чальных условиях можно заменить
расчетом цепи с нулевыми началь-
ными условиями, вводя в цепь до-
полнительные источники, наличие
которых эквивалентно заданным на-
чальным значениям токов и напря-
жений. Этот метод обладает боль-
шой наглядностью.
Двухполюсник, эквивалентный
емкости с ненулевым начальным на-
пряжением. Зависимость между то-
ком и напряжением такого конден-
сатора (рис. 11-18,а) выражается
уравнением
Uc = т j i dt -\-ис (0), (11-64)
о
где ^с(О) ~ис(—О1). —напряжение
на конденсаторе в момент t=Q. Та-
ким же уравнением выражается за-
висимость между напряжением и то-
ком двухполюсника, содержащего
последовательно включенный источ-
ник с постоянным напряжением
ис(—0) и конденсатор с начальным
напряжением иСд (—0), равным ну-
лю (рис. 11-18,6), где uCQ — напря-
жение на конденсаторе эквивалент-
ной схемы.
Следовательно, любой конденса-
тор, имевший начальное напряже-
ние, отличное от нуля, может быть
заменен таким же конденсатором
с нулевым начальным напряжением
Wc(0)=0 и последовательно с ним
включенным источником постоян-
ного напряжения ис(—0); напря-
жение такого источника в оператор-
ной форме равно ис(—®)/р*
Источник напряжения (рис.
11-18,6) по общему правилу мож-
но заменить эквивалентным источ-
ником тока /э (рис. 11-18,в). В опе-
раторной форме ток источника
/э = Срис (— 0)//7 = Сис (— 0),
(11-65)
ток источника в схеме рис. 11-18,6
равен напряжению источника в схе-
ме рис. 11-18,6 [т. е. ис(—0)/р], по-
множенному на проводимость ветви
рС.
Двухполюсник, эквивалентный ин-
дуктивности с ненулевым начальным
током. Для такой индуктивности
(рис. 11-19,62) зависимость тока от
напряжения выражается уравне-
нием
t
idt —[— i (0),
о
(11-66)
Рис. 11-19.
324
к которому приводит известное ра-
венство при этом /ь(0) =
dt
= Д(-0).
Очевидно, что таким же урав-
нением выражается зависимость
тока от напряжения для двухпо-
люсника (рис. 11-19,6), который со-
держит источник тока /(—0), вклю-
ченный параллельно с индуктив-
ностью, имеющей нулевой началь-
ный ток 4(—0) =0, здесь /э — ток
в индуктивности эквивалентной схе-
мы. Ток 1источ1н1ика в операторной
форме выражается как i(—0)/р, по-
скольку
z(-O)~Z(-O)/p.
Источник тока можно заменить
источником напряжения (рис.
11-19,в).
В операторной форме напряже-
ние эквивалентного источника
^8 = ^£1±г0> = £г-(_0), (Ц-67)
р
где pL — операторное сопротивле-
ние индуктивности.
Этот источник включен после-
довательно с индуктивностью L
(рис. 11-19,в), не имеющей уже соб-
ственного начального тока. Однако
ток в индуктивности может мгно-
венно возникнуть под действием
напряжения
U^uQ(ty^iL (— 0)Т8.
Заменяя в заданной цепи с не-
нулевыми начальными условиями
все заряженные конденсаторы и
индуктивности эквивалентными
двухполюсниками, приходим к це-
пи с нулевыми начальными усло-
виями, но с дополнительными экви-
валентными источниками.
Заметим в заключение, что связь
между напряжением и током для
сопротивления г выражается зако-
ном Ома u=ir независимо от тока
в предшествующие моменты. Поэто-
му не требуется никакой эквива-
лентной замены этого сопротивле-
ния.
Пример 11-19. В цепи -рис. 11-20,я зна-
чение тока источника внезапно изменилось
с 0.5 до 1,5 а. До этого момента в цепи
Рис. 1.1-20.
существовал установившийся режим. Пара-
метры цепи известны: С='10~8 ф, r=20 OMt
L=0,l гн.
Требуется найти напряжение на кон-
денсаторе и ток индуктивности в переход-
ном .режиме.
Решение. Начальные значения тока
в индуктивности и напряжения на 'конден-
саторе z‘l(—-О) =0,5 а, ис(—0) =0,5-20=10 в.
Составим для заданной цепи схему с по-
следовательно включенными эквивалентны-
ми источниками напряжения (рис. 11-20,6)
в операторной форме; на той же схеме Jo/p
операторное представление тока источника
тока /и=/о=‘1,5 а. По характеру задачи
удобно перейти к эквивалентным источни-
кам тока, включенным к узлам а, b парал-
лельных ветвей (рис. Ы -20,в) Общий ток
такого эквивалентного источника
/э = KIp — - у --- -—— + Сис (— 0).
Lp + r
Искомое напряжение на конденсаторе
Uc = Uab равно току эквивалентного источ-
ника, деленному на сумму проводимостей
двух параллельных ветвей:
иаъ — /э : ( Ср + f J,
325
или после простых алгебраических преобразований
иаь
1Ср^с (- 0) + р [- LiL (- 0) + гСис (- 0) + Uo] 4- г/0
/ r 1 \
P2 + Z7P+ZC ) Р
При записи довольно сложных формул
полезно убедиться в надлежащей размер-
ности всех членов, а также проверить на-
чальные и установившиеся значения. В дан-
ном случае выражения
Чаь (0) = pUab(p) 1^00 = ис (— 0);
' «аЬ (со) = pUab (р) 1^=0 = П0
соответствуют ожидаемым результатам.
Очень важно заметить, что изображе-
ние тока <в ветви, например в ветви L, г,
теперь нельзя найти простым делением
Иаъ (р) на Z (рУ— г + Lp, так как в цепи
рис. 11-20,6 ветвь L, г содержит эквива-
лентный источник, э. д. с. которого в опе-
раторной форме равна LiLi(—0). Поэтому
т __Uab+LiL(—0)
L- r + PL---------
Очевидно, что к тому же результату
приводит и запись изображений (с учетом
предшествующих значений) для дифферен-
циального уравнения ветви (рис. .11-20,а)
diT
riL = иаЪ.
Соответствующее уравнение для изо-
бражений
Цр^ — *£ (“~ ^)] + r?L “ ^аЪ
приводит к той же формуле для IL.
3. МЕТОД СУПЕРПОЗИЦИИ
Когда в электрической цепи (или
другой системе) протекает переход-
ный процесс, его всегда можно рас-
сматривать как процесс перехода
от некоторого старого состояния
к новому. Этот процесс всегда обу-
словлен включением новых источ-
ников или изменением параметров
цепи, например включением или от-
ключением новой ветви.
На рис. 11-21,а показана цепь,
в которой (при /<0) старый режим
определялся только одним источ-
ником Новый режим определяет-
ся появлением второго источника,
напряжение которого и2 равнялось
нулю в старом режиме (/СО).
В новом режиме (/>0) напряже-
ние этого второго источника изме-
няется по закону u2(t).
Результирующее состояние цепи
можно рассматривать как наложе-
ние на старый режим дополнитель-
ного возмущения, вызванного но-
вым источником. Это, дополнитель-
ное возмущение в силу линейности
не зависит от состояния цепи в ста-
ром режиме (принцип суперпози-
ции). Поэтому расчет процессов, вы-
званных появлением источника
u2(t), производится при нулевых
начальных условиях и, конечно, при
отсутствии первого источника (рис
11-21,6).
Чтобы найти действительный ре-
жим, нужно все найденные напря-
жения и токи (ZH, &н), вызванные
включением нового источника, ал-
гебраически сложить с напряже-
ниями и токами (гс, ис) старого ре-
жима, т. е. обусловленными дейст- '
вием одного источника щ.
Пример 11-20. В цепи .рис. 11-21,а, со
держащей источник постоянного напряже-
ния £Л=1 100 в, существовал установивший-
ся режим. В момент t—’O начинает дейст-
вовать второй источник также с постоян-
ным напряжением U2— 100 в. Требуется
найти напряжение на конденсаторе в пере-
ходном режиме. Дано, что L=0,1 гн, С=
=5<10“3 4 ф, Г1=100 ом, г2= 10 ом.
Решение. Под действием источника
П2 напряжение на конденсаторе изменяется
9
-Рис. 11-21.
326
s соответствии с операторным уравнением
для цепи рис. 11-21,6:
^ = ^2
У Ср
/2 (Р)
(в знаменателе стоит входное сопротивле-
ние всей цепи для генератора С2, а в чис-
лителе — сопротивление конденсатора).
После простых преобразований прида-
дим написанному выражению такой вид:
н J05 110+0,1р
Р (р+«? + ^
Рис. 11-23.
при а = 100 сек~\ р = 316 сек-1.
Соответствующая функция времени
«£ = 100(1— е~^ cos РО-
• Напряжение на конденсаторе в старом
режиме, т. е. когда в цепи существовал
только первый генератор, легко находится:
исс= 100 в.
Результирующее напряжение на конден-
саторе при t 0 оказывается равным:
== 100<?“at cos
(здесь взята разность и , так как в
двух расчетах приняты различные положи-
тельные направления для ис). График ис (t)
показан на рис. 11-22.
Рассмотрим теперь переходные
процессы, вызванные -включением
или отключением какой-либо ветви,
как показано, например, на рис.
11-23,я и 11-24,а. Такую коммутацию
всегда можно представить как вклю-
чение эквивалентного дополнитель-
ного источника (см. § 2-11).
Пусть цри коммутации в цепи
рис. 11-23,а точки а и & соединяются
накоротко.
Токи и напряжения, дополни-
тельно возникающие в результате
такой коммутации, равны токам -и
напряжениям, вызванным включе-
нием между узлами а и b дополни-
тельного источника с э. д. с. эъ=иаъ,
при отсутствии всех других источни-
ков и при нулевых начальных усло-
виях (рис. 11-23,6).
Алгебраическая сумма токов и на-
пряжений старого (fc, wc;) и дополни-
тельного (/д, и*) режимов равна то-
кам и напряжениям в действитель-
ной цепи после произведенной ком-
мутации:
w=wc + fza /=/с+/д (П-68)
Пример 11-21. Определить напряжение
и с в цепи рис. 11 -23, а при переходном ре-
жиме, выевайном замыканием рубильника.
До коммутации существовал установивший-
ся режим цепи с •источником постоянного
напряжения /7i=const.
Конденсатор к моменту коммутации был
заряжен до напряжения ис (—0)=200 в.
В индуктивности к моменту, коммутации су-
ществовал установившийся ток старого ре-
жима iL (—0) = Г71/(Г1+г2). Таким образом,
нужно рассчитать переходный процесс при
ненулевых начальных условиях.
Дано U] ==11110 в, остальные параметры
цепи те же, что в предыдущем примере.
Решен»е. Пользуясь только что изло-
женным методом, определяем сначала
что легко найти при постоянном напряже-
нии источника:
иаЬ = Ир; Г* - иС °) = -190 в-
Включая источник э„= каь=—190 в,
ищем напряжение идс- Составляя уравне-
ния в операторной форме, находим::
U% = 9V
Г1+_Г2_± Lp
CLr. [(р.4-а)2+Н
, nJO5 (1ЮЧ-0,lp)
Ь U Р (р+100)2+316® •
327
Промежуточные преобразования при вы-
воде этих формул пропущены. Мгновенное
значение напряжения
=—190(1 —е a/cos[tf)>
— 10 + 190^ a*cos[tf в.
Рассмотрим теперь коммутацию,
при которой производится разрыв
какой-либо ветви с током iG
(рис. 11-24,6»).
Такой разрыв равносилен тому,
что на старый режим налагается
режим, обусловленный включением
между точками разрыва дополни-
тельного источника тока Д(£)
(рис. 11-24,6). Ток этого источника
должен быть равен току старого
режима и направлен в про-
тивоположную сторону (см. также
§ 2-11).
Складывая алгебраически токи
и напряжения старого режима (zc,
uc) и дополнительного («гд, »гд), обу-
словленного включением источника
тока найдем токи и напряже-
ния действительного режима, уста-
навливающегося в -цепи после раз-
рыва ветви:
i = jc U = uG 4“66д.
Пример 11-22.' Требуется найти ток в
индуктивности цепи рис. 11-24,я в переход-
ном режиме, вызванном отключением источ-
ника. До коммутации существовал устано-
вившийся режим.
Дано: 671 = const=200 в, £=0,05 гн,
С=0,2 мкф, г =10 ом.
Решение. Следуя только что изло-
женному, ищем при включении в цепь
е)
Рис. 11-24.
дополнительного источника тока Zvi(£)=fe
(рис. 11-24,6). Заметим, что в этом режиме
не играет никакой роли левая часть схемы.
Зная, что ток источника распределяется по
параллельным ветвям обратно пропорцио-
нально их сопротивлениям, находим, что
r + pL + i/Cp
— 109-------------
_ [(р+«)2+₽2]р-
В нашем случае ic = 10 а = const, по-
этому операторное выражение дополнитель-
ного тока Jv (/?) =
Найденным операторным выражениям
соответствуют мгновенные значения
=»ю;[ 1 — (cos ₽/ 4- 0,01 sin e~at]
при a= 100 сек~1 и f — 104 сек~1.
Найдя из расчета старого режима
i = 10 а, получим для действительного
переходного режима
=icL — if — Ю (cos fit +0,01 sin fit) e~at~
Найденное значение соответствует то-
му, чего следует ожидать из физических со-
ображений: ток в индуктивности сразу по-
сле коммутации iL (+ 0) = 10 а равен току,
существовавшему до коммутации, (—0) =
= 10 а.
Интересно заметить, что при рассмо-
тренной коммутации напряжение на конден-
саторе может значительно превзойти напря-
жение установившегося режима: в резуль-
тате решения изложенным методом на-
ходим, что ис = исс—«дс='(1Ю0 cos р/—-
—5 000 sm^t)e~^ .
Рассмотренный метод замены
коммутаций дополнительными ис-
точниками применим и в случае «не-
корректных» задач, что иллюстри-
руется следующим примером.
Пример 14-23. В цепи рис. lil-25,a про-
исходит мгновенный разрыв ветви, шунти-
ровавшей одну из индуктивностей. Требует-
ся найти ток в цепи после разрыва ветви.
Дано: 67=100 в, £i=£2=0,01 гн, гх =
^./*3=10 ом.
Решение. Рассчитывая ток дополни-
тельного режима, приходим к цепи
рис. 14-25,6, в которой происходит включе-
ние источника тока Jv—i^ = const.
В получившейся схеме ю двумя пар ал-
лельными ветвями искомые токи
т Д _ V ____pL*_____
1 Р ri + Р (^i + ^2)*
д Ц ri + рЦ
2 Р Г1 4“ (£х + £2)
328
Рис. 1'1-25.
Действительные токи в цепи найдем,
сложив (с учетом выбранных положитель-
ных направлений) токи и ic. В -результа-
те найдем, что
: __1 -д • ____ -с -д
м — > *2 —• 12 — ’
Для приведенных числовых данных при
t 0 Zi == z2 — 10 -f- 5^"°>5fzz при t в милли-
секундах.
Очень важно обратить внима-
ние на следующее обстоятельство.
В тех случаях, когда в исходном
режиме цепи в ней существуют пе-
ременные токи и напряжения, на-
пряжение и ток дополнительных
источников 9V и Jv должны опреде-
ляться не значениями исаъ и /с, су-
ществовавшими в- момент коммута-
ции, а теми значениями исаЪ($) и
fc(£), которые существовали бы
в старой цепи, если бы в ней не про-
исходило коммутации, т. е.
= = (11-69)
Необходимость выполнения этого
условия делает метод более гро-
моздким при рассмотрении комму-
тации в цепях переменного тока.
Сказанное можно иллюстриро-
вать примером цепи рис. 11-24,я,
если в ней действует, например,
источник синусоидального напря-
жения щ и происходит разрыв
в момент прохождения тока через
нуль. При этом ток дополни-
тельного источника, конечно, нера-
вен нулю. Результирующий пере-
ходный режим можно найти изло-
женным выше методом только при*
условии включения дополнитель-
ного источника переменного тока.
Рассмотрению переходных про-
цессов в цепях синусоидального то-
ка посвящен следующий параграф.-
11-8. ЦЕПЬ С ГАРМОНИЧЕСКИМИ
ИСТОЧНИКАМИ
Г армоническими источниками^
здесь для краткости названы источ-
ники гармонических возмущений,
т. е. источники синусоидального*
напряжения или тока.
Переходные процессы в цепях
с гармоническими источниками
представляют очень важный класс
задач. Как и для других функций,,
расчеты можно вести, вводя изоб-
ражение гармонического напряже-
ния:
Um COS (со/ 4“ 7]) = Um (cos 7] COS О)/ —
Т7 р COST] — eosin7]
— sin n sin mt) ^Um----р2‘ + <а2-.
(11-70}
При этом, однако, расчетные
формулы становятся чрезмерно гро-
моздкими. Поэтому значительно
лучше пользоваться комплексным
представлением, полагая, например,
t7m cos (Wт]) — Re (11-71}
При этом можно рассматривать
процесс, протекающий при включе-
нии экспоненты, изображение кото-
рой достаточно просто:
—L-, (11-72}
jT J Ш
а в найденном результате перехо-
дить к интересующей нас вещест-
венной части1.
1 Как -отмечалось в § 4-2, в электротех-
нической литературе часто -принято счи-
тать, что мгновенное значение комплексно-
го выражения гар-монической функции .пред-
ставляется его мнимой частью. В этом слу-
чае, производя расчет для* включения нач
экспоненту, следует от найденного решения'
брать только мнимую часть. При этом сле-
дует быть особенно осторожным, если в ре-
шении содержатся вещественные состав-
ляющие обусловленные другими веществен-
ными источниками.
Пусть, например, необходимо
найти ток в контуре L, г при вклю-
чении напряжения
u(t)^Umc,QS С^ + 'п).
Рассматривая включение экспо-
ненциального напряжения, находим
операторное выражение для тока
и _____1_______—
т (P-J<*)(r+PL)
Um 1
L (р —»(р + л) *
Соответствующая функция времени
представляется комплексным выраже-
нием (формула 9 табл. 11-1)
Но нас интересует только веществен-
ная часть, которую легко выделить.
Действительно,
Um Um = Ume^-^
.£(« + /<») г + j&L z
№
z= <p = arctg^,
и, следовательно, искомое значение
тока
Z(Z)=Re/(/) —
= [cos (со/—J—TQ— <?)— cos (tj—(p)e~at}.
В электротехнической литерату-
ре часто в качестве Z(.Z) пишут не-
посредственно комплексное значе-
ние, подразумевая, что следует при-
нимать во внимание только вещест-
венную часть.
Ведя расчет изложенным мето-
дом, можно пользоваться всеми
формулами табл. 11-1, содержащи-
ми в знаменателе (р + 6) или (р+о)
и т. п., .полагая в них b = —ja) или
а=—/со и т. п. При этом, конечно,
напряжение. или ток источника
должны. представляться также
в комплексной форме (Оте^ или
те ), а в найденном результате
следует выделять только веществен-
ную часть.
Тем же методом можно рассчи-
тать и включение на затухающую
гармоническую функцию
и (/) Й= cos (со/ + т|),
представляя ее комплексной экспо-
нентной
1___
Р — Y ’
U
и т
где т = —« + /«> и Um=Ume?\
В простейшем случае для кон-
тура L, г находим:
ПР) L (p + r/L)(p_Y) •
Соответствующую комплексную
функцию времени легко найти по
формуле 9 табл. 114. Взяв от нее
только вещественную часть, найдем
действительный ток как функцию
времени.
Метод суперпозиции. Расчет пе-
реходных процессов в цепях гармо-
нического тока можно значительно
упростить, рассматривая результи-
рующий переходный режим как на-
ложение свободного режима на ус-
тановившийся.
Свободный режим удобно опре-
делять операторньим методом. При
этом следует рассчитывать цепь,
в которой отсутствуют источники,
однако существуют ненулевые на-
чальные условия для свободных со-
ставляющих тока в индуктивностях
Zlcb(O) и напряжения на конденса-
торах ^Ссв(О).
В общем случае эти составляю-
щие могут быть определены из ус-
ловия непрерывности изменения то-
ка в индуктивности
гЛ(-О) = г£пр(+О) + /Лсв(О) (11-73)
и напряжения на конденсаторах
«с(-о)=Ыспр(4-о) + «Ссв(0).
(11-74)
В этих формулах Zr(—0) и
^с(—0) —это ток и напряжение,
действительно существовавшие к мо-
менту коммутации; /ьщД+'О) и
^спр( + 0) — значения установивше-
го
гося (Цринужденного) режима в це-
пи после коммутации при /=0.
После того как свободные со-
ставляющие для момента коммута-
ции определены, дальнейший рас-
чет можно вести одним из методов,
изложенных в предыдущем пара-
графе (запись изображений с уче-
том предшествующего состояния,
введение эквивалентных источни-
ков).
Пример 11-24. В цепи рис. 11-26 до от-
ключения (рубильника Существовал устано-
вившийся режим. В момент /—О рубильник
разомкнулся и -в цепь был введен 'конденса-
тор; Напряжение источника
и = 100 У 2 cos (со/ — тс/4) при со =
=5 000 сек-1. Сопротивления трех элементов
1
г = 200 ом, xL = <£>L = 200 ом, хс~7лС —
=2400 ом.
Найти ток переходного режима.
Р е ш е н не. Рассчитав комплексным
методом 'старый и новый установившийся
режим, для (момента времени t—0 находим
действительный ток в индуктивности перед
коммутацией
»л(-0) = 4(0) =
{* 100 /2
= —т=----- cos (0 — л/4 — те/4) = 0
/2-200 v
я принужденный ток нового режима
‘лпр(+°) =
Очевидно, что ис (—0)=0. А из расчета
wCnp (+ °) °’ поэтому «Ссв (0) = 0.
Переходный процесс для свободного то-
ка 1МОЖ1НЮ найти, пользуясь эквивалентной
схемой р1йс. 11-27, или непосредственно из
дифференциального уравнения цепи. Опера-
торное выражение для свободного тока
£Q,Cb(0) --0,5^7
При а=2 500 сект1 .и $=6 600 сек~х.
.Соответствующая функция времени для
«Лев = — (cos ₽/ — 0,379 sin gi) =
= — 0,532е-2,5‘ cos (6,6Z + 20°45'),
здесь t — время в (миллисекундах.
На рис. 11-28 показан график всех со-
ставляющих тока.
100/2- - / те , те\
cos ( 0— т + 'Т ) = а-
/2-200 \ 4 4/
11-9. ФОРМУЛА РАЗЛОЖЕНИЯ
ХЕВИСАЙДА
Таким образом,
св (0) = Ч (- 0) - lL пр (+ °) = - °-5 «•
Мы уже несколько раз пользова*
лись простыми алгебраическими
приемами для разложения рацио-
нальных дробей
F{p)
Fi (Р)
PF2 (Р)
— Р{Рп + Ьгръ-1 + . . . + Ъп)
(11-75)
на элементарные составляющие Дв,
Ak
P — Pk
для которых известны .со-
1lc8 LiLC$(O}
Рис. 11-27.
ответствующие функции времени Ло,
А^‘.
Существуют, однако, и более об-
щие методы разложения.' Один из
них, применявшийся Хевисайдом,
331
получил широкое распространение
в электротехнической практике.
Пусть в формуле (11-75) т^п.
В этом случае при соответствующем
подборе коэффициентов Ло, Аг ...
правильную дробь (11-75) можно
представить суммой элементарных
дробей
F^=-^=iA‘+^
Однако при умножении (11-76) на
р — pk в левой части равенства ока-
зывается неопределенность [так как
по (11-77) Л(А) = 0]
которую легко раскрыть, пользуясь
правилом Лопиталя:
А2 । 1 Ап
Р— Р* ***' Р— Рп’
(11-76)
lim Ft (р)
р^-Рк
р--Тк
PFг. (р)
где pi, р2, • •Рп — корни уравнения
(11-81)
где
Л5(р)=0, (11-77)
Fr2 (Pk)
= dF1 (р)
dp
\Р=рк
не имеющего кратных корней1.
Если все коэффициенты Ао, ^i,
..., Ап известны, то легко записать
функцию времени f(tf), соответ-
ствующую заданному изображению
F(p):
Н0 = Ло + ДгЛ/+
Таким путем
находим, что
из (11-80) и (11-81)
д = Fi(pft)
h PkF'z (Рк)‘
(11-82)
При этом выражение (11-78) можно
записать так:
+ AzePai + --- + АпеРп'. (11-78)
Значение коэффициента Ао легко
находится: при р=0 в правой части
равенства (11-76), предварительно
умноженного на р, обращаются
в нуль все слагаемые, кроме По-
следовательно,
S" Л(Рь) Рк*
PkF'z(pk)
Й=1
©
(11-83)
Это и есть формула Хевисайда.
A0=pF(p) |^о-
(11-79)
Иллюстрируем применение этой фор-
мулы, рассмотрев включение цепи L, г к
постоянному напряжению UQ и к напряже-
-Yf 1
нию Uoe 1
Остальные коэффициенты А19..., Ап
можно найти следующим путем.
Умножая обе части равенства (11-76)
на р — Рп и полагая р -> pk9 полу-
чаем в правой части отличным от
нуля только одно слагаемое
В первом случае ток
и.
Р pL + г pF2 (р) ’
Iinl (f — а) = А-
р-*рк р Рк
Единственный корень уравнения F2 (р) ~
= 0 — это pi — — r/L. Поэтому по фор-
муле (11-83) для /^0
'<‘> = т+<=Дт «’-'-7о-о")
Все остальные слагаемые обращаются
в нуль:
Нт -А- (р—рь) = 0 при pi=£pk-
p-*pkp Pl
Во втором случае
и. Р
(р + Y) (Г + pL) р
1 (Приводимый вывод обычными в мате-
матике приемами 'Предельных переходов не-
трудно распространить и на случай кратных
корней.
Fi=Utp, F2 = (p + -{)(r+pL),
i (0) = 0, F’z (р) = 2pL + г +
Pi = — Y. Рг = r/L.
332
Поэтому для
(—r)g
(—Y)(—2?Ь+г + гО
Само собой разумеется, что при-
менение формулы Хевисайда к про-
стым выражениям F(p), для кото-
рых имеются простые табличные
формулы, нецелесообразно.
Интересно заметить, что форму-
ла Хевисайда (11-83) применима и
к тем случаям, когда Fv(p) и /^(р)
представляются не рациональными
алгебраическими, а некоторыми
трансцендентными функциями, на-
пример типа sha[Fp или сЬя ^/д
Формула Хевисайда для источни-
ков гармонических возмущений.
Пусть при воздействии постоянного
возмущения, скажем Uq~U$Ip, опе-
раторное выражение искомой функ-
ции имело вид:
F(p) = U,
7 0 pF2 (p)
В таком случае при гармониче-
ском возмущении Ume’wt ^Um 1
p — ja
Применяя преобразования, анало-
гичные предыдущим, можно прийти
к такому выражению соответствую-
щей функции времени:
f(/\— l) Fl (/») ei“>t
+ri с1-8®»
k=A
Действительное значение искомой
функции найдем, переходя к веще-
ственной части
если предполагается, что комплекс
представляет напряжение
tAn cos +
Определение начального и уста-
новившегося значения f (/) по ее опе-
раторному представлению F(p) в
случае гармонических источников.
В этом случае определение значе-
ния f(t) при £=0 не отличается от
ранее выведенного [формула
(1.1-22)].
Однако теперь, когда один из
корней имеет чисто мнимое значе-
ние, а остальные корни имеют отри-
цательную вещественную часть
Re(p&)<0, значение соответ-
ствующее установившемуся значе-
нию, ищется иначе. Обращаясь
к формуле (11-85), находим, что
очевидное комплексное представле-
ние синусоидальной функции при
установившемся режиме (/-> оо)
Теперь наша задача заключает-
ся в выделении этого выражения из
операторной функции F(p). Это
очень просто -сделать, обращаясь
к формуле (11-84). Действительно,
из нее очевидно, что
f __т'т Pl (J&)
= (/2-»^^)!^. (11-87)
11-10. ДАЛЬНЕЙШЕЕ РАСШИРЕНИЕ
ОПЕРАТОРНОГО МЕТОДА.
СВЕРТКА
В предыдущих параграфах изложены
лишь основы операторного метода. Даль-
нейшее развитие теории и ряд важных и до-
статочно простых теорем позволяют расши-
рить область применения этого (метода к ли-
нейным системам и найти соответствия
f(Y)/^iFi(p) для более широкого класса
функций.
Круг задач, которые могут ’быть реше-
ны операторным методом, чрезвычайно рас-
ширяется применением теоремы с в е р-
т ы в а н и я.
Пусть ft(f)~Fit(p) и /3(f) ~^2(Р),
в таком случае
(11-88)
333
выражается как « с в е ip т к а» функций
t
f (0= j fiG —0f2 CO dz =
о
t
== j /1(0 (t — ъ) dt.
о
(11-89)
Это легче всего доказать, предполагая,
что /1 (О представляет реакцию, например
ток i (I), при воздействии единичного воз-
мущения и (t) = 1 :
Ь(0-Л=рЛр
В таком случае реакция /(/) на (возму-
щение, изменяющееся по заданному закону
приходим к формулам (11-88) и (11-89); ко-
торые и требовалось доказать.
Приведем в заключение пример того,
как, пользуясь сверткой, можно найти ори-
гиналы, соответствующие дробным степе-
ням р.
Пусть в (11-88)
(11-95)
В таком случае
. ч t
ft (’) ft (t - ’) d-c. (11-96)
Q
В последнем интеграле можно заменить
переменную и на
а = т—• f/2, (11-97)
соответственно изменяя пределы; при этом
в операторной форме представляется равен-
ством
+t/2
-Ц2
da.
(11-98)
Hty^pF.U,
(11-90)
Полагая
а сама реакция f«(/) как функция (времени
может быть выражена через интеграл Дюа-
меля:
Ь(0 = у=~Л(р), (11-99)
t
/(О = Г(Ои(0)+
о
найдем, что
Замечая, что
(Н-91)
+t/2
№= J-
-Z/2
4е
V Z/2 4-s yt/2 — а
Г
fi(Oa(0) = pi(^ — х)м(т)а^, (11-92)
о
f/2
Г da
J к'(^/2)2 —g2
-Ц2
можем привести (11-91) к такому виду:
= arcsini72
o=f/2
== 7U.
a=—t/2
(11-100)
t
f (0 = Jfi(^ —-с)
О
[du । ч 1
Л+в(,)8 J
d'z.
(11-93)
Следовательно,
f (O = n^n/p = Ff(p) (11-101)
du
Здесь — простая производная, по-
этому .из основных формул операторного
исчисления [см. (11-5) и (11-6)] находим
[см. также (11-90) и (11-88)], . что
или
Fl (p)=V^/p ~ fl (0 =
(11-102)
> Ри (Р) = f, (р) - fz (0. (П-94)
Интегрируя в последней формуле пра-
вую часть в пределах от 0 до t и соответст-
венно деля левую часть на р, находим, что
. Выражая в (11-90) рЦ(р) как Гг(р) и
подставляя в (11-93) f2(x) =duldr+u(r)b,
(11-103)
334
ГЛАВА ДВЕНАДЦАТАЯ
ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
ФУРЬЕ И ЛАПЛАСА
12-1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
И СПЕКТРАЛЬНЫЕ (ЧАСТОТНЫЕ)
ПРЕДСТАВЛЕНИЯ
Рассмотрение переходных про-
цессов и в предыдущих главах
в значительной мере связывалось
с частотными характеристиками
(см. § 11-6). Действительно, если
система подвергалась какому-либо
возмущению, например в цепь вклю-
чалось напряжение
u(t)^U(p), (12-1)
то искомую реакцию, например ток
(12-2)
мы представляем через операторное
выражение
i (t) ^НР) = U,(p)fZ (р) = U(p)Y (/?),
(12-3)
в котором
Z(/’) = Z(7<o)|/e>=p
или
Г(р) = Г(»|/ю=р. (12-4)
При этом, комплексные сопро-
тивление Z (/со.) или .проводимость
Y(ja) — это функции от /со, т. е. ча-
стотные характеристики системы.
Совершенно аналогично записыва-
лись операторные выражения и
в том случае, когда реакция систе-
мы выражалась через передаточную
функцию, отличную от проводимо-
сти или сопротивления; например,
мы писали, что
Udp) = UMH(p), (12-5)
где
H(p) = H^)\i(O=p.
Таким образом, при определении
реакции системы на то или иное
возмущение свойства самой систе-
мы полностью определяются ее ча-
стотной характеристикой У (/со),
Я(/со).
Существование связи между ча-
стотными свойствами системы и ее
реакцией в переходном режиме оче-
видно из простых физических сооб-'
ражений: индуктивность, препят-
ствующая мгновенному изменению
тока, характеризуется ростом реак-
тивного сопротивления с частотой;
возможность существования соб-
ственных затухающих колебаний
в системе при переходном режиме
характеризуется резонансной зави-
симостью комплексного сопротивле-
ния от частоты и т. п.
Все операторные выражения ти-
па (12-3) и (12-5) совершенно ана-
логичны комплексным выражениям
для установившихся значений гар-
моник в цепях несинусоидальных то-
ков
/ (/со) = [7 (/со) У (/со), (12-6)
где величина /со могла принимать
ряд дискретных значений
/со = //2^, (12-7)
которым соответствуют гармониче-
ские составляющие напряжения и
тока
и Un = U (jn&J.
(12-8)
Дискретные значения гармони-
ческих составляющих тока 1п были
названы дискретным спектром то-
ка/(/).
Пользуясь формулой (J2-3)
/(p) = U(p)Y(p)
и заменяя в ней У (р) на
У(/Ш) = У(^)|г=уш,
можно было бы найти спектр тока
i(t), т. е. его гармонические состав-
ляющие /(/со), и в условиях переход-
ного режима, если бы мы знали, как
найти спектральный состав напря-
жения (возмущающей силы) по его
операторному выражению Щр).
335
Однако, рассматривая переход-
ные процессы, мы всегда имели де-
ло с апериодическими .возмущения-
ми
= u2(f) = le~at и т. п.,
^спектральный состав которых
у£/1(/со), {Л(Ло), ... оставался не-
раскрытым.
Наша задача теперь состоит
<в определении гармонических со-
ставляющих апериодической функ-
ции или ее спектра,
12-2. СПЕКТРЫ АПЕРИОДИЧЕСКИХ
ФУНКЦИЙ. ИНТЕГРАЛЬНЫЕ
ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Основная идея, на которой осно-
вано определение спектрального со-
става апериодической функции f(£),
заключается в возможности ее за-
мены периодически повторяющейся
функцией f(/) при достаточно боль-
шой длительности периода Т, хотя
бы при Т оо. Очевидно, что такая
замена возможна, если функция об-
ращается в нуль к концу периода,
т. е. f(t) —*0 при t^T, При рас-
смотрении переходных процессов
этому требованию должна удовле-
творять и функция, выражающая
•реакцию
На рис. 12-4,а показано, как апе-
риодическая функция /(/), обра-
щающаяся в нуль при Т, может
•быть заменена периодической f (/) =
= f(t+T). Что же касается спек-
трального состава любой периоди-
ческой функции, он может быть
найден известными методами (см.
'§ 9-6).
Повторим основные формулиров-
ки. Любая периодическая функция
может быть представлена в виде
симметричного комплексного ряда
Фурье
+ 00
= v Cnein^, (12-9)
п=—ОС
1 В «противном случае в начале нового
периода еще сохранится действие той же
функции от предыдущего или предыдущих
периодов и |результирую|щее значение пред-
ставится как /1(0 +f<(t+T)+f(t+2T) + . . .
{см. также следующую главу).
в котором комплексные амплитуды
определяются интегралом
772
= f fe)e~in^dT. (12-10)
х ~Т/2
Распределение комплексных амп-
литуд Сп по частотам характеризуется
спектральной функцией
F(jnm1) = — Сп
+7/2
= j f^e~ina>1Xd^
—T /2
(12-11)
Подставляя ’ (12-10) и (12-11)
в (12-9), находим, что
f(t)=
2тс в
или
+оо
f(f) = У
п——00
(12-12)
Применим теперь эти выраже-
ния к случаю апериодических функ-
ций, для чего достаточно считать
период Т неограниченно возрастаю-
щим. При Т —>оо основная частота
с01=2л/Т становится бесконечно ма-
лой, поэтому ее следует обозначить
rfo; интервал между соседними гар-
моническими определяется этой бес-
конечно малой величиной. Иначе го-
воря, теперь от дискретного спектра
мы переходим к сплошному. Часто-
ту п-й гармонической, т. е. пои, бу-
дем обозначать просто как часто-
ту -со, т. е. >co-=ncoi. Она может быть
конечной и даже неограниченно воз-
растать, поскольку суммируются все
гармонические ncoi при п -> оо.
При этом .вместо (‘12-10) мы по-
лучим, что
+ оо
dC (/<») = j f (г) (12-13)
—00
Теперь сами амплитуды бесконечно-
го числа гармоник, отличающихся
на бесконечно малую величину по
частоте (rfco), становятся бесконеч-
336
но малыми, что и выра-
жается записью dCfjto).
Соответственно сумму
в (12-9) следует заменить
интегралом
После подстановки в эту
формулу выражения (12-13)
для dC(ja) находим, что
<о =+оо
f(t)= J eimtdC(Jw).
W~—00
(12-14)
(12-15)
Lf(t) = f(t+T)
Рис. 12-1.
Запишем теперь спектральную
функцию F (jn^) = F (/<*>) для аперио-
дического импульса или его спект-
ральное представление. По определе-
нию (12-11) при /го)1 = сп
F (уш) = 2« j f (X) dz.
(12-16)
Эта функция характеризует спек-
тральную плотность бесконечно ма-
лых комплексных амплитуд, отне-
сенную к интервалу частот dco.
В тех случаях, когда f(t) =0 при
/<0, а это обычно и предполагается
при рассмотрении переходных про-
цессов, пределы интегрирования
в (12-16) могут быть заменены:
F (/«>) = / (*) £ dx
б
(12-17)
[так как f(r)=O при т<0].
Переходя в выражении (12-12)
от суммы к интегралу,^найдем вы-
ражение апериодической функции
/(/) по ее спектральному представ-
лению
4-оо
f{t) = -^-^F^)eiatd«>. (12-18)
—оо
Этот результат получается и не-
посредственно из (12-15), в кото-
ром квадратные скобки представля-
ют функцию F(jw),
Интегральные преобразования
(12-16) и (12-18) называют пря-
мым и обратным интеграль-
ными преобразованиями
Фурье.
В § 9-6 (рис. 9-15) был опреде-
лен спектральный состав функции,
изображенной на рис. 12-1,6. В том
же параграфе было показано, что
плотность линий дискретного спек-
тра возрастает с ростом Т. При
Г- оо апериодическая функция ха-
рактеризуется той же спектральной
функцией F(co) и ф(со) [формулы
(9-40) и (9-41).], однако* спектр ста-
новится непрерывным, а интервал
между соседними линиями, равный
(о1 = 2д/Т, стремится к нулю. •
12-3. ОПРЕДЕЛЕНИЕ СПЕКТРА
ФУНКЦИИ ХЕВИСАЙДА 1(f)
В первом параграфе этой главы
была поставлена задача определе-
ния спектрального состава, или, ко-
роче говоря, спектра, апериодиче-
ских функций и прежде всего функ-
ции Хевисайда. В следующем пара-
графе мы научились находить спек-
тральный состав апериодических
функций, обращающихся в нуль при
/ —► оо. Однако /(/) не удовлетворя-
ет этому основному условию — она
22 К. М. Поливанов
337
остается конечной при Z-*oo. Воз-
никшее препятствие можно обой-
ти, рассматривая функцию
= (12-19)
сколь угодно близкую 1 (/) для любого
конечного времени «X, если
т. е. 1.
Подставляя f (т) — е~^ в выраже-
ние (12-17), находим, что
О
— £— j(o I Р + У»’
о
так как
(12-20)
Полагая в последнем, выражение
£ 0, находим искомое спектральное
представление единичной функции
Хевисайда
(12-21)
12-4. СВЯЗЬ СПЕКТРАЛЬНОГО
ПРЕДСТАВЛЕНИЯ
АПЕРИОДИЧЕСКИХ ФУНКЦИЙ
С ОПЕРАТОРНЫМ ИЗОБРАЖЕНИЕМ
Если реакция на включение по-
стоянного напряжения l(t) выра-
жается в операторной форме равен-
ством
i^I=^Y(p), (12-22)
то по (12-6) спектральное представ-
ление того же тока выражается
формулой
' 1 = ТГ Y (12-23)
так как спектральное представле-
ние /(/) есть-Д-.
Из этого очевидного заключения
можно сделать важный вывод, осно-
вываясь на простом утверждении,
что найденные результаты не зави-
сят от применяемых буквенных обо-
значений.
Записывая (12-22) в виде
(12-24)
из (12-23)- находим, что f(t) имеет
спектральное представление:
F(j<o) = F (p)\p=Itt>,
(12-25)
при этом принято обозначение
F (уш) = F, (<u) — jF2(w).
Пример 12-1. Найти спектральное
представление функции
f (£)=/(/) Ае~а\
выразив отдельно вещественную и мнимую
части F(j^).
Решение; Как .известно (см. табл».
Н-1),
f (t) = Ае~<^ F (p) = A
следовательно,
F (ja>) = Fi (co) — /F2 (co) = А ;<i)^ fl-==
Aa . Aco
co2 -I- a2 J co2 -}- a2'
Характеристики Fx (co) и F2 (co) пред-
ставлены на рис. 12-2,а в нормированных
F
координатах F'= и со'= со/л. На
рис. 12-2,6 те же характеристики представ-
лены в полулогарифмическом масштабе.
Частотные характеристики часто
представляют как геометрическое
место концов вектора F(j<n) на комп-
лексной плоскости (годограф).
На рис. 12-3 представлены годографы
функций:
a) F—^Ae~at и
7 7 уСО —р- (2
б) П/»>)=(/<аХ<1р+р2 COS —
— a sin р 0 г-4
338
Рис. 12-4.
Рис. 12-3.
чае вычисление этого, интеграла
(12-18) может оказаться достаточ-
но сложным. Поэтому при решении
простых задач для перехода от
F(/co). к* fit) следует пользоваться
таблицами взаимно соответствую-
щих функций f(/)~F(/co) или таб-
лицами соответствий f(t) и F(p),
подставляя /со вместо р (табл. 11-1).
В ряде случаев спектр апериоди-
ческой функции легко найти и непо-
средственно из интеграла Фурье (12-16)
или (12-17).
Пример 12-2. Требуется, найти спект-
ральное представление функции f (t) = А
при 111 < 7'1/2 и f (О = 0 при 111 > 7i/2
(рис. 12-4,я).
Решение. Для заданной функции
интеграл (12-16) принимает вид:
Л/2
F (jo) = A j ё~,<0Т^т,
-Л/2
так как на этом интервале f (/)=Л = const,
а пои 11 | > Tj/2 по условию f (t) — 0.
Производя интегрирование и простые
преобразования, находим, что
sin(co7\/2)
F (/со) = 2 А-~-----L = Fr (со)
и
F2 (со) = 0
(рис. 12-4, (5).
Обратное преобразование Фурье.
Как уже говорилось, функция вре-
мени может быть найдена по ее
спектральному представлению
(12-18).
Выполняя действия, предписы-
ваемые этим интегралом (обратное
преобразование Фурье), над всеми
рассмотренными ранее функциями
F (ja), мы, разумеется, придем к
уже известным соответствующим
им выражениям /(£). В общем слу-
12-5. ЗНАЧЕНИЕ СПЕКТРАЛЬНЫХ
ХАРАКТЕРИСТИК. ПРИБЛИЖЕННЫЕ
МЕТОДЫ ОПРЕДЕЛЕНИЯ
ПЕРЕХОДНЫХ ПРОЦЕССОВ
Исключительное значение тео-
рии спектральных характеристик
заключается не только в возможно-
сти решения простых задач путем
интегрирования, которое предписы-
вается обратным интегралом Фурье.
Значительно важнее тот факт, что,
пользуясь изложенной теорией, лю-
бой однократный импульс (сигнал,
удар и т. п.) может быть представ-
лен своим спектром, а следователь-
но, при известной частотной харак-
теристике рассматриваемой системы
может быть найден спектральный
состав искомой реакции. Так, напри-
мер, зная частотную характеристи-
ку усилителя (способного усиливать
только в определенном диапазоне
частот), можно определить вноси-
мое им искажение при усилении то-
го или иного сигнала, имеющего
форму одиночного импульса.
Если входной сигнал представ-
ляется функцией Ui (/со), а отноше-
ние ^2(/co)/C7i(/co) выражается ком-
плексным коэффициентом усиления
Л (/со), то искомый спектральный
состав сигнала на выходе
t72(/co) = t/1(/<o)A(jco). (12-26)
22*
339
Чтобы получить выражение сиг-
нала на выходе в виде функции
времени, т. е. и2(/), надо подвер-
гнуть найденное выражение U2 (/’со)
преобразованию, предписываемому
обратным интегралом Фурье. Но
в некоторых случаях уже по виду
полученного спектра £72(/со) и по
его отличию от спектра входного
сигнала можно судить о степени
искажения.
Возможность правильной оценки
увеличивается по мере накопления
опыта в анализе расчетных или экс-
периментальных результатов.
Замена сплошного спектра ди-
скретным. В некоторых случаях по
заданной частотной характеристи-
ке системы и по заданному спектру
входного сигнала приближенная
оценка процесса может быть произ-
ведена путем замены сплошного
спектра дискретным с интервалами
(Di при соответствующей замене ин-
теграла Фурье рядом Фурье. Такая
замена существенно упрощает зада-
чу. Однако если не руководствовать-
ся правилами для выбора интерва-
вала (01 и числа гармонических со-
ставляющих, то полученный резуль-
тат может оказаться лишь грубо
приближенным. В пределах этого
курса мы не можем останавливать-
ся на изложении общих правил.
Покажем, что дает такой метод
в случае контура г, С (рис. 12-5,а),
когда выходное напряжение (на-
пряжение на сопротивлении) связа-
но с входным напряжением уравне-
нием
(12-27)
Пусть на вход поступает един-
ственный импульс постоянного на-
пряжения длительностью (рис.
12-5,6). Полагая этот импульс по-
вторяющимся с каким-либо перио-
дом Т, например Т=4Т1 на рис.
12-5,6, находим гармонические со-
.ставляющие входного сигнала
t/i(/n(Di) и соответствующие состав-
ляющие сигнала на выходе
и2 (M®i) = (jn »]) J jn^iCr ~-
(12-28)
С
0---1 j- | " 0
г H \u2(t)
0------1---0
a)
Суммируя их, находим приближен^
ное значение
+k
«2 (0 = V U2 (jnvj einait, (12-29)
п=—k
где k — порядок высшей гармониче-
ской, еще принимаемой во внима-
ние.
На рис. 12-5,в представлен при-
ближенный результат u'2(t) для
случая гС = ЗТ и T = 47'i, при том что
сумма ограничивается третьей гар-
моникой (£ = 3). На том же рисунке
показан действительный график
искомого напряжения и2 (/).
Экспериментальное определение
частотных характеристик. Для мно-
гих реальных систем аналитическое
выражение частотной характеристи-
ки неизвестно, однако есть возмож-
ность получить эту характеристику
340
из опыта. В таком случае по экспе-
риментально найденной характери-
стике всегда можно найти реакцию
системы на любое заданное возму-
щение, пользуясь изложенным ме-
тодом преобразований Фурье.
Действительно, если требуется
найти, например, ток в цепи с про-
водимостью У (/<»), возникающий
при воздействии напряжения u(t),
спектральное представление которо-
го U(jay) известно, то искомый ток
может быть найден на основании
обратного интегрального преобразо-
вания Фурье:
+ О0
i (0=2^" J и (/“DY
(12-30)
Трудности, возникающие при вы-
числении этого интеграла, делают
особенно важными специально раз-
работанные методы приближенных
вычислений.
Методы трапеций. Ограничимся
здесь изложением только двух гра-
фоаналитических методов— про-
стой и логарифмической трапеций.
Произведем прежде всего неко-
торые упрощения в формуле инте-
грального преобразования Фурье.
Полагая
F (№) = Fi («>) — jF2 (<о)
и
eJ(ot = cos mt j sin mt,
интеграл (12-18) представим в таком
виде:
+ оо
f W{ j * Н cos mt+
—00
-j- F2 (w) sin <»Z] dm -J“
+oo
4” / j [Л (ю) sin —
— F2 (<d) cos cdZ] dcoj.
Второй интеграл в фигурных
скобках должен быть равен нулю,
так как f(f) не может содержать
мнимой составляющей. Равенство
нулю этого интеграла следует так-
же из четного характера функции
Fi (о) и нечетного F2(co). Такой ха-
рактер этих функций вытекает и^
их определения через интеграл
(12-17) 1.
Из соображений четности функ-
ций Fi(g>) coscoZ и F2(co) sin о/ пер-
вый интеграл может быть заменен
удвоенным значением интеграла,,
взятого в пределах от 0 до оо. Та-
ким образом, получаем:
оо
f (О = J [fl (®) cos <Dt +
о
4-F2(a))sino>Z]d(o. (12-31)
В тех случаях, когда f (Z) =0 при
Z<0, выражение (12-31) может быть
подвергнуто дальнейшему упроще-
нию. В самом деле, изменяя в нем
знак t, получим по условию, что
оо
J [F1 (со) cos mt — F2 (оз) sin cdZ] dm —
о
=-f(— Z) = 0, (12-32)
где t— | Z |.
Складывая (12-31) и (12-32), нахо-
дим наиболее простое выражение
интегрального преобразования Фурье
[при условии f (Z) = 0 для Z <С 0]:
оо
2 (*
f (Z) — — I (со) cos gdZ dm. (12-33)
о
Обыкновенно FT (co) остается ко-
нечной при cd = 0 и Fj (cd) 0 при
со—>оо. в таком случае, применяя
’В самом деле, по (12-17)
F (j(°>) — iF2 (со) = f (z) e~i(olid^
о
замена —j на + / приводит к сопряжен-
ному комплексу
F (— /со) = Fi (со) + jF2 (со).
Однако изменение знака j под интегралом,
равносильно изменению знака со, следова-
тельно,
F (— /со) = Fx (— со) — jF2 (— со).
Сопоставление последних двух равенств:
показывает, что
Fi (<о) = Fi (— со) и F2 (со) — F2 (— со)„
34Ь
к (12-33) формулу интегрирования по
частям
оо
9 С ]
Z(0=— I — Л («) d (sin tot) —
<t>=0
оо
f • j. riFt (co)
--- I Sinco/------
J UC0
<o=0
получаем, что
оо
f /ух 2 f dFi (co) . , ,
/ (?) —-----r I —--------- Sill u>td<n.
nt ] aco
<0=0
(12-34)
Метод простой трапеции. До-
пустим, что Fr (о>) = gi (<о) представ-
ляет трапецию рис. 12-6. В таком
случае производная dFT ((o)/d<o отлична
ют нуля только в интервале
<0$—Д?- <С <0 <С (°г 4“ Дг,
где она имеет значение —g^l^^).
с достаточной степенью точности
аппроксимировать рядом трапеций
(рис. 12-7). Полагая
= (12-36)
i
находим, что
2 V sincoi? sinAi? /щ
=v L —rr • f12"37)
(Hit Lit
Замена 74 (co) даже небольшим
числом трапеций дает в ряде слу-
чаев хорошие результаты.
Метод логарифмической трапе-
ции. Если спад функции Т7! (со) с ча-
стотой происходит медленно, при-
Тогда
дам, что
ЛЮ
по формуле (12-34)
нахо-
2 Spi (*
nt J
со.—Д.
Рис. 12-8.
[cosfai + AiH —
— COS (<ог- — Дг) И =
__2 sinc0^ sin Дг? (12-35)
G>it Lit
При наличии табулированных функ-
ций —у- расчет по формуле (12-35)
•очень прост.
Приведенный здесь вывод был
сделан в предположении, что функ-
ция частоты имеет вид трапеции g\-(w)-
Однако любую функцию Fx (со) можно
нято прибегать к представлению ча-
стотной характеристики как функ-
ции логарифма частоты
2=1п<».
(12-38)
Если функция Т7! (со) в таком ло-
гарифмическом масштабе имеет вид
трапеции (рис. 12-8), то значение
производной отлично от нуля толь-
ко на наклонном участке, где
—g=const; (12-39)
342
ЗДеСЬ Л2 ill In ^*H2—
разность логарифмов конечной й на-
чальной частоты наклонного участка;
gQi — высота трапеции. Но
dF х (со)_ dFi (со) rfco
dK dm dK
и, значит,
(СО)_ got dK __ got 1
d (co) dm Af co *
так как
dl/dm — d (In m)/dm = 1 /co.
При малых значениях аргумента (х<^1)
можно считать Si(x)=^x. Таким образом,
при малых t
2 got
ft (О = (^Kt — <oHi) t. (12-42)
При больших значениях аргумента (х^> 1)
Si (х)
cos х
Следовательно, при больших t
t их ( C0S°Ht*
n Ad I mnit
cos coKiZ \
J
(12-43)
Очевидно, что на остальной части
логарифмической трапеции dF^mj/dm^
= 0. В таком случае по (12-34) на-
ходим, что
12-6. ИНТЕГРАЛЬНЫЕ
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
или
fi (0
___ 2 got
nt Ai
CO
Ki
(sin mt
co
dm
Обобщая преобразования Фурье
путем перехода к комплексной ча-
стоте
5==с+/со, (12-44)
получаем прямое и обратное
преобразования Лапласа:
f ?^d(®f) =
1 г v 7 nt Ai J mt v 7
А [Si (wKit) - Si (шнг-0], (12-40)
= (12-45)
о
если /(f) = 0 при /<<0, и
здесь Si (x)— J dx — интеграль-
0
ный синус.
Интегральный синус — табулиро-
ванная функция, ее график показан
на рис. 12-9.
В том случае, когда частотная
характеристика аппроксимируется
несколькими логарифмическими
трапециями,
I
(12-41)
НО =2^ J F(s)estds. (12-46)
Со—/оо
F (s) представляет собой конечную
аналитическую функцию комплексно-
го переменного при условии, что
f (о е~ Re <s<) -* 0 при оо.. (12-47)
Это условие выполняется при
(12-48)
где М — любое конечное число, если
Re(s)=c>Cb (12-49)
Вещественная часть комплексно-
го переменного в нижнем и верхнем
пределах интеграла (12-46) должна
удовлетворять условию
со>сь (12-50)
Обоснование необходимости и до-
статочности этих условий (впрочем,
их необходимость очевидна), а так-
343
же требований к виду функции f(t)
и к пути интегрирования на ком-
плексной плоскости в обратном пре-
образовании (12-46), наконец, раз-
работка методов вычисления инте-
гралов (12-45) и (12-46) составля-
ют предмет теории функций ком-
плексного переменного.
Функцию F(s) называют Лап-
ласовым изображением
/(/). С точностью до буквенных обо-
значений (s вместо /со) она совпа-
дает со спектральным представле-
нием функции f(t) по Фурье
F(s)\s=:Jfo = F(j^ (12-51)
<и с принятым в этой книге опера-
торным изображением (гл. 11).
Очень важно обратить внимание на то,
что формулы операторного изображения по
Хевисайду отличаются от изображений по
Лапласу и Фурье на множитель р. Поэто-
му, введя множитель s перед интегралом
(12-45), придем к интегральному преобразо-
ванию (оно носит имя Карсона), результат
которого тождественно совпадает с опера-
торным выражением по Хевисайду, в кото-
ром 1 (t) ~ 1, д^р.
Кроме того, следует иметь в виду раз-
личие в изображении производной. Если
df (О
0 ¥(0 =
то по Хевисайду
Ф(р) = ^(р)-Н0)],
по Лапласу
Ф (s) = sF (s) — f (0),
по Фурье
Ф (/со) = /coF (/со) — f (0).
Заметим в заключение, что су-
ществуют различные* методы инте-
грирования дифференциальных
уравнений, отличающиеся от изло-
женных здесь (например, метод ха-
рактеристических уравнений). Мно-
гие из них могут с успехом приме-
няться на практике и в достаточной
мере просты (хотя бы метод Лаг-
ранжа) .
В общих методах современного
анализа границы между классиче-
скими и операторными методами
практически стираются.
ГЛАВА ТРИНАДЦАТАЯ
ПЕРЕХОДНЫЕ И УСТАНОВИВШИЕСЯ РЕЖИМЫ
ПРИ ВОЗДЕЙСТВИИ СЕРИИ ВОЗМУЩЕНИЙ
13-1. РЕАКЦИЯ НА ЭШЕЛОН
ВОЗМУЩЕНИЙ
В ряде технических устройств
приходится встречаться с серией
одинаковых возмущений u(t), на-
лагаемых одно на другое через про-
межуток времени Т, начиная с не-
которого момента £=0.
В простейшем случае каждое из
возмущений представляет собой по-
стоянное напряжение U. Поэтому
для первого интервала k=\ или
€</<Т имеем u(t)=U, для второ-
го интервала k = 2 или T<t<2T по-
лучаем u(t)=2U и т. д., как по-
казано на рис. 13-1.
Условимся внутри каждого fe-ro
интервала (k—1) T<t<kT отсчиты-
вать время от начала этого интер-
вала, полагая
т=/—(А—1)Т, при 0<х<Т (13-1)
В таком случае для &-го интер-
вала результирующее возмущение
uk(x) выражается суммой k одина-
ковых функций u(t) с разными на-
чалами отсчета времени
(О = я[(£-1)Г + т] +
+ a[(k-2) 7' + т] + ... + «(т).
(13-2)
Первое слагаемое в этой форму-
ле выражает возмущение, которое
U(t) 4tf Г"
3U I
2U —--------------
U --------------
__ Zr=7 к-2 к=3
^1— тГДГ. г-Д
Рис. 13-1.
344
включилось в момент /=0 и дей-
ствует уже на протяжении времени
(k— 1) Т+т; второе слагаемое — воз-
мущение, включившееся в момент
t=T и действующее на протяжении
времени (k—2)Т+т, и т. д. Послед-
нее слагаемое и (т) —это возмуще-
ние, включившееся только в начале
рассматриваемого &-го интервала;
время его действия равно т, т. е.
времени, протекшему от начала k-w
интервала.
Функцию типа (13-2) называют
иногда лестничной функцией с ши-
риной ступени Т (по виду функции,
представленной на рис. 13-1); ее
можно назвать также эшелонной
функцией с интервалом Т между
звеньями эшелона.
Докажем простую, но очень важ-
ную теорему.
Если реакция на единственное
возмущение Ui(t) = u(t) выражает-
ся суммой экспоненты и постоянной
/\ (/) = D, (13-3)
то для k-ro интервала времени
(k—l)T<t<kT реакция на эшелон
возмущений ик(х) выражается функ-
цией
hW = A\=^e^+kD. (13-4)
Доказательство очень просто. Дей-
ствительно, зная (13-3), находим,
что для второго интервала, т. е. для
/г = 2,
f2 (г) = А (е“т(Г+х) + + 2D =
= А(е~хГ+ l)e~^ + 2D
и для любого k-ro интервала
fh^=A(e-^-l)T + e-uk~2)T +
+... + 1) е~1х+kD. (13-5)
Применяя известную формулу
для суммирования k членов геомет-
рической прогрессии, стоящей в
круглых скобках, приходим к (13-4).
Аналогичные выводы могут быть
проведены и для других простых
выражений реакции. Например, если
А(0 = Л^-Л '
то
Ш = А
I 1—g kJ^_(ke^ — #4-1) I
“Г (1 _ e-iTy |
(13-6)
Как частный случай (13-6) при у =0
имеем:
Л(/) = АЛ
№ = Ak
(13-7)
Последние выражения находятся
очень просто переходом от fi к f2,
/з и т. д.
В выражениях (13-3), (13-4), так
же как в (13-5) и (13-6), постоян-
ные А и у могут быть комплексны-
ми величинами. При этом, если иско-
мая функция h (/) представляется
как вещественная (или как мнимая)
часть выражения fi(f), то и в вы-
ражении для ffe(x) следует брать со-
ответственно только вещественную
часть (или только мнимую) для
определения /&(?).
Полученные выражения для
fk(x) при fi(Z), собранные в табл.
13-1, позволяют легко решать боль-
шое число простых задач, для кото-
рых операторные выражения реак-
ции Fi (р) выражаются в форме ра-
циональных дробей.
Формула 6 табл. 13-1 напомина-
ет, что ко всем линейным системам
применим принцип суперпозиции.
Пример 13-1. Напряжение источника
в цепи L, г (рис. 13-2,а) изменяется по за-
кону, представ ленному на рис. 13-1, т. е.
возрастает до U в момент /=0, а потом воз-
растает еще на U через каждый интервал
Т, оставаясь в пределах любого интервала
постоянным. Требуется найти ток &-го ин-
тервала.
Рис. 13-2.
23 К. М. Поливанов
345
Таблица 13-1
№ п/п. Реакция на единствен- ное возмущение (/) Реакция для &-го звена эшелона f к (x)
1 D kD
2 Ae~at I A1 р каГ — е~ах -е~аТ 6
3 Re (Аё~^) Re| \ А- 1 _ е~^т \ 2 -гГ~ е~1Х 1 — е~п 1
4 t k 1 2 7' + \)
5 te~at 1 — e~kaT ————— '.e~ax + ,..l -g-.tor + fe(l-gQr).e~Aar T _aT _ax
* ( 1 —. пТ 1 И Ь е~аТ)2
6 lim т — время, отсчитыва T — интервал между 1 — k, li 1 — e~^T aT-t емое от начала &-го звена; последовательными звеньями в эшелоне (ширина ступени); 1 _ е-^Т _|_ k ( i _ еаТ^ e-ka;- k—l (\-в~аТУ *
Решение. Ток «в цепи, обусловленный
единственным -напряжением и,] = 1 U,
h (0 = — 0 — e~at) при f>0,
где а = r/L.
В таком случае для k-ro интервала,
когда Т (k — 1)< < kT, ток имеет значе-
ние
и L 1—g~ftor _ах~
iuw = — k-
Пример 13-2. В цепи рис. 13-2,6 гене-
ратор посылает через интервал Т импульсы
высокого напряжения J7, длящиеся в тече-
ние малого промежутка времени 0, т. е.
6 Г, при том что 0 < \[at где \/а— по-
стоянная времени цепи (рис. 13-3,а). При
этом можно представлять эти импульсы
через d-функцию, полагая rz = Z70d. Тре-
буется найти напряжение на конденсаторе
в Интервале между k-м и (&+ 1)-м импуль-
сами.
Решение. При действии единствен-
ного импульса напряжение на конденсаторе
выражается в операторной форме равен-
ством
1
где
0 G 4- Г2
U^U^rc
Этому операторному .выражению соот-
ветствует функция времени
wCi (t) = Ume-at.
Следовательно, для любого k-ro интер-
вала (после воздействия k импульсов)
1 — e~~kaT
е-а\
На рис. 13-3,6 схематически показан
график этого напряжения.
Из полученной формулы и рис. 13-3,6
легко увидеть, что под влиянием каждого
очередного импульса напряжение .возраста-
ет именно на Um.
Максимальное напряжение, которое по-
является на конденсаторе после действия
большого числа импульсов, легко найти,
полагая kaT'^>l и, следовательно,
В начале импульса (т=0)
lim uCk (0) = Um - аТ .
&->оо 1 — е
При этом в течение любого интервала Т
конденсатор разряжается в точности на ве-
личину Z7„,.
346
Начиная с k^>l/(aT), в цепи устанавли-
вается практически периодический процесс.
Пример 13-3. На колебательный кон-
тур последовательно соединенных L, г, С
действует эшелон импульсов С76Ъ
(рис. 13-3,а). Интервал между импульса-
ми Т. Ищется ток в контуре.
Решение. П-ри действии единственно-
го импульса
Z>(p)=t/0------5----j- =
r+pL + pC
=t/0________p
L (p + y)(p + y) ’
где сопряженные корни знаменателя
Pi = —y=—«+/Р;
ps = —Y= —a—j₽
при
“~2L
1
LC~ “2-
Соответствующую функцию времени
можно представить экспонентой (см. фор-
мулу 17 табл. 11-1, стр. 308)
1г (t) = A Re [ei^e-'lt],
где
А = £76/(1, cos т]), cos т] = р/| у |.
Поэтому для k-го интервала
U (*) = A Re
\-ekiT
1 —е^т
е
Как видно из последней формулы, ре-
зультат существенно зависит от соотноше-
ния между периодом собственных колеба-
ний 70 = 2л/р и интервалом следования
импульсов. При Т — То и малом затухании
(«Г << 1) знаменатель в выражении для
тока принимает значение
1 — е~1Т = 1 — ё~а,т = аТ.
Рис. 13-4.
При неблагоприятном соотношении
между Т и То ток оказывается значительно
меньшим. На рис. 13-4 показан характер
тока при Т = То (а) и при Г = -^- То (б).
Последняя кривая построена в более
крупном масштабе (при одинаковом мас-
штабе скачкообразные изменения тока при
воздействии импульса одинаковы).
13-2. РЕАКЦИЯ НА ЭШЕЛОН
КОРОТКИХ ВОЗМУЩЕНИЙ1
Во многих случаях возмущения
£>(/), следующие при />0 одно за
другим через интервалы Т, длятся
настолько кратковременно, что к
концу интервала Т возмущение v(t)
обращается в нуль:
v(t) = O при t^T. (13-8)
Серию возмущений такого типа
можно назвать эшелоном коротких
возмущений. Примером такого типа
возмущений могут служить серии
импульсов, рассмотренные в приме-
ре 13-2 предыдущего параграфа
(рис. 13-3, а).
Очевидно, что в случае коротких
возмущений внутри любого А-го ин-
1 Излагаемый метод отличается только
формулировками и обозначениями от мето-
да {суммирования токов, обусловленных дей-
ствием отдельных импульсов напряжения,
уже много лет применяемого в Ленинград-
ском электротехническом институте име-
ни В. И. Ульянова (Ленина) [Л. 8].
23*
347
тервала они выражаются одинако-
выми функциями
= при 0<т< Т. (13-9)
Однако реакция, вызванная каж-
дым из таких возмущений, может
длиться дольше. Поэтому при /=
— Т+х еще существует реакция,
вызванная первым возмущением:
/(>1)^0 при / = Т + т;>7', (13-10)
здесь т отсчитывается от конца пер-
вого интервала.
Если бы реакция подчинялась
условию (13-8), весь процесс как
возмущения, так и реакции заканчи-
вался бы в пределах одного интер-
вала, и в каждом новом интервале
все повторялось бы заново.
Напротив, если реакция, .вызван-
ная действием короткого возмуще-
ния, затягивается, т. е. выполняет-
ся условие (13-10), то в любом 6-м
интервале на прямую реакцию дей-
ствующего короткого возмущения
накладывается эшелон затянувших-
ся реакций на все предшествовав-
шие возмущения.
Пусть в пределах интервала
0<£<Т реакция на единственное
короткое возмущение представ-
ляется функцией F\(t}\ будем обо-
значать ее большой буквой с индек-
сом 1 и называть прямой реак-
цией на короткое возмуще-
ние.
Пусть реакция на предшество-
вавшее единственное короткое воз-
мущение при t=T+x>T выражает-
ся функцией f(r); будем обозначать
ее малой буквой и называть оста-
точной или затянувшейся
реакцией.
В первом интервале п=1 или
0</<Т полная реакция совпадает
с прямой реакцией на короткое
возмущение
Л(т)=Л(/). (13-11)
Во втором интервале п=2 или
Г</<271 на прямую реакцию, вы-
званную новым коротким возму-
щением, накладывается затянув-
шаяся реакция на первое возму-
щение. Поэтому для этого интер-
вала полная реакция
Л(т) = Л(г) + /(-В), (13-12)
где время т отсчитывается от на-
чала интервала п=2.
Аналогично для третьего интерг
вала п=3, 27’</<37'
(13-13)
где х отсчитывается от начала ин-
тервала п=3.
Здесь на прямую реакцию,
вызванную новым коротким возму-
щением, накладываются затянув-
шиеся реакции от первого возму-
щения /(т+-Т) и от второго возму-
щения f(r).
Очевидно, что для любого ин-
тервала п полная реакция
Еп(-)=Л(-) + /[- + (^-1)Л +
+ Дт + (6-2)Л + --- + Н^
(13-14)
где 6 = п.—1. Время х отсчитывается
от начала рассматриваемого ин-
тервала п.
Из приведенного вывода сле-
дует, что во всех случаях, когда
f(r) совпадает с одной из функций
flf(f) (табл. 13-1), для интервала п
эшелон всех затянувшихся реакций
может быть выражен как ffe(x) той
же таблицы при k=n—1, т. е.
Fn (т) = Fi 004“ fn-i 0)- (13-15)
Пример 13-4. Напряжение, действую-
щее на контур L, г (рис. !13-2,а) при />-0,
представляется рядом треугольников (рис.
13-5,а); при этом U и Т известны. Требует-
ся найти ток 1п (х) для любого интервала п.
Решение. Единственное возмущение
г Л
вызывает прямую реакцию (ток), выражае-
мую операторным равенством
1 U 1
I(p) = U(p) r + pL 1Т-р*(р-\.аУ
где a —r/L, которому соответствует функ-.
ция времени
U Г t 1 1
Л(О=—
348
Остаточная реакция от ко-
роткого возмущения
(Т)е~ах
представляет собой свободный
ток 'в контуре L, г при -отсутст-
вии внешнего возмущения; его
начальное значение равно току,
достигнутому к концу первого
интервала.
Для любого n-го интервала
по формуле (113-15) полная ре-
акция
In Н = Л« +
1 — e~akT
+ 1^Г>\-^ге а'>
где k~n—'I.
Для большей конкретности
проведем вычисления при опре-
деленных числовых данных.
Пусть, например, U—1100 в, г—
=4 ом, 4=0,2 гн, 7=0,01 сек,
а=’5 сект1. Тогда
Iv(t) =400 [100 t—
—20(1——25 000 /2.
Этот результат мы получи-
ли, разлагая экспоненту в ряд
•и ограничиваясь первыми тре-
мя членами:
В такомГслучае (Г) ==
= 2,5/2. Следовательно, полная
реакция
1п (т) = 25 000ъ2 +
Таблица 13-2
п 7 (0) п ' ' /п(П ^п)мин
1 0 2,5 0
2 2,5 4,875 2,497
21 31,6 32,5 31,35
101 50 50 49,4
Ввиду того, что ах не превосходит зна-
чения <27=0,05, можно принять £ ~ ~ 1—
.—<2Т. В таком случае после простых алге-
браических преобразований находим, что
/п(т)=50(1—e-°’05fe)_250(1—e-°>o5fe)r+
4-25 000 т2.
Для интервала п=2, когда £=1,
/Дт) =<50 • 0,05—250 • 0,05 Т4-25 000 т2; для
интервала п=21, когда &=20,
/21’(т) =50 • 0,632—250 • 0,632т 4-25 000т2.
Цри очень больших значениях п, когда
е-о,о5л<^1} практически наступает устано
вившийся режим, и для любого интервала
1п (т) = 50—250т4-25 000 т2
Приведем в заключение значения тока
в амперах в начале и конце интервала и
минимальное значение внутри интервала
для нескольких интервалов (табл. 13-2).
13-3. ПЕРИОДИЧЕСКИЕ РЕЖИМЫ
В ЦЕПИ, ОПРЕДЕЛЯЕМЫЕ
МЕТОДОМ РАСЧЕТА РЕАКЦИИ
НА ЭШЕЛОН ВОЗМУЩЕНИЙ
Возмущения, периодически по-
вторяющиеся, начиная с момента
f=0, всегда можно представить или-
как эшелон коротких возмущений,
что было показано в двух предыду-
349
щих параграфах; или как эшелоны
специально подобранных функций;
или как наложение эшелона возму-
щений на ту или иную неповторяю-
щуюся функцию, включаемую в мо-
мент t=0.
Замечательно, что при этом рас-
чет реакции для установившегося
режима может оказаться более
простым и приводящим к более
точным результатам, чем расчет по
известному методу разложения
в ряд Фурье (гл. 9).
На рис. 13-5 представлены пе-
риодические функции. Первая из
них (пила) получается как раз-
ность неповторяющейся функции
^0(/) и эшелона постоян-
ных возмущений f (х) ——U с шири-
ной интервала Т при том, что пер-
вая ступень появляется в момент
/=Т (рис. 13-5,а).
Вторая функция (13-5,6) полу-
чается при однополупериодном вы-
прямлении синусоиды. Она может
быть представлена как эшелон си-
нусоид
с интервалом 7=Т0/2, где То =
= 2.тг/со — период синусоиды.
Третья (коммутированная си-
нусоида рис. 13-5,в) получается
как сумма синусоиды fo(O =
=Дз1псо/ и эшелона синусоид
двойной амплитуды fi (т) = 2Д sin сот,
включаемых, начиная с момента
/ = Т=Т0/2, через интервал Т, где
То —2л/со.
Очевидно, что каждая из при-
веденных здесь периодических
функций может быть представлена
и как эшелон коротких возмущений
(§ 13-2). При этом искомая реакция
может быть найдена методом, изло-
женным в предыдущем параграфе Ч
В следующем примере повто-
ряется расчет тока примера 13-3.
Однако пилообразное возмущение
рассматривается как разность не-
повторяющегося возмущения и эше-
1 Рациональность представления любых
периодических возмущений в виде эшелона
коротких возмущений и применения соответ-
ствующего метода расчета была указана
автору профессором Г. В. Зевеке.
лона постоянных возмущений, как
показано на рис. 13-5,а справа.
В тех случаях, когда представ-
ляет интерес спектральный состав
найденной периодической реакции-
(при установившемся режиме), для
нее могут быть найдены соответст-
вующие гармонические составляю-
щие (см. гл. 9).
Пример 13-5. Найти ток в цепи L, г при
действии пилообразного напряжения (рис.
13-5,а).
Решение. Ток содержит два слагае-
мых. Первое, определяемое линейно расту-
щим напряжением, найдено в примере 13-4:
U Г t 1 1
W “ [ ~Т О ~ *‘af) ] ’ (О
где а — r/L.
Второе слагаемое обусловлено эшело-
ном постоянных напряжений —JJ.
Для единственного возмущения
(б)
th (t)=
поэтому для £-й .ступени эшелона
Для первого периода 0</=т<7 весь
ток /(т) =г'б(т).
Для второго периода T<t=T+r<2T,
совпадающего с первым интервалом эшело-
на (&=1),
/(.) = /о (^ + П + йЛ) =
г
И т. д.
Для установившегося режима, когда
t = kT -f- т и kaT > 1, a e~kaT < 1, по фор-
мулам (а) и (в) находим:
/(г)=г„(т4-^) + ^ С0 =
U
---!—|-----е-'ах
Т аТ^-е-ат6
Во всех выражениях время т: отсчиты-
вается от начала рассматриваемого периода.
13-4. РЕАКЦИЯ
НА ЭШЕЛОН ВОЗМУЩЕНИЙ,
МОДУЛИРОВАННЫХ ПО АМПЛИТУДЕ
Методы, аналогичные изложен-
ным в этой главе, могут быть при-
менены и в случае, когда возмуще-
ния, следующие одно за другим
350
w Рис. 13-6.
через интервалы 7, различны и
подчиняются определенной зависи-
мости от порядкового номера.
В простейшем случае такая за-
висимость представляется дополни-
тельным множителем ап, завися-
щим от порядкового номера п.
Пусть, например, в момент t=0
включается постоянное возмущение
U, через интервал Т дополнительно
включается тоже постоянное возму-
щение avU, затем через такой же
интервал включается возмущение
a$U и т. д., как это показано на
рис. 13-6, причем
ап^е-пЪТ (13-16)
(рис. 13-7).
Такой эшелон можно назвать
модулированным по амплитуде.
Эшелон 6-функций, разделенных
интервалом Т, при том, что каждая
из них умножается на апА, также
можно назвать эшелоном модули-
рованных 6-функций; такой эшелон
схематически показан на рис. 13-8.
Точнее говоря, на рис. 13-8 пока-
заны интегральные характеристики
6-функций, т. е. импульсы, пропор-
циональные модулирующей функ-
ции,
~ Л—пЬТ Л—ПсТ /1 о 1 VX
ап — е '—е (13-17)
при 67=0,25 и с7=0,5.
Ограничимся здесь выводом
расчетной формулы для реакции на
эшелон модулированных возмуще-
ний, когда 1) реакция на единствен-
ное -BosMvnxeHHe представляется как
сумма экспоненты и константы
f(O = an(^-v + £), (13-18)
где ап — модулирующий множи-
тель, и 2) эшелон модулирован
экспонентой, т. е. каждое /г-е воз-
мущение выражается функциями,
отличающимися только множите-
лем (13-16).
Другими словами, если первое
возмущение выражается функцией
при />0, то второе возмуще-
ние, включившееся в момент
выражается функцией a\v(t—7),
третье — функцией а2^(^—27) и т. д.
Вывод очень прост: если в пер-
вом интервале 0<£<7 реакция
F1^) = Be~^ + D, (13-19)
где т отсчитывается от начала ин-
тервала, то во втором интервале
7<«27 полная реакция
+ e~bT + (13-20)
Здесь время т отсчитывается от
начала второго интервала, поэтому
для реакции, вызванной первым
возмущением, время /=7+т, тогда
как для реакции, вызванной вторым
возмущением, время равно т. Кро-
ме того, перед выражением реакции
от второго возмущения стоит мно-
житель е~ьт, так как именно во
столько раз второе возмущение
отлично от первого; в линейной си-
35 ।
стеме во столько же раз отличается
и реакция.
Полная реакция в k-м интервале
(k—1) T<t<kT выражается сум-
мой
Fk (t) = Вё~ т[х+(*-1)Г] + D +
+ е-6г (Ве-Т[х+(*~2)Г] + D) +
+ e~2bT (5е“т[х+(й“3)Л _|_р
+ e~(k-2)bT (Ве~^+Т)+£>) +
+ e-(*-1,M’(£e“r + 2))I (13-21)
здесь снова время г отсчитывается
от начала k-ro интервала.
•В этом выражении легко выде-
лить геометрическую прогрессию,
если вынести общий множитель
е^к-1)ът и отдельно сгруппиро-
вать множители при D.
В результате найдем, что
Fh (х) = Be~lk~lv’T [1 +е(Ь-т)7’ +... +
+ e(^-i)(ft-r)T]e-7x +
+ D[l+e-6r + ... + e-(fe-1)6r].
После суммирования геометриче-
ских прогрессий, стоящих внутри
прямых скобок, получаем
— ое . х_е(Ь-^т
или после простых преобразований
Fk(y) = B
e-kbT^e-k-tT
e-bT-e~^T
I — e~~kbT
I — e~bT ‘
(13-22)
е
цию и при гармоническом модули-
ровании эшелона. При этом, конеч-
но, следует переходить к веществен-
ной (или мнимой) части резуль-
тата, выполняя соответствующие
алгебраические преобразования.
Пример 13-6. Начиная с момента
на контур г, С поступает серия импуль-
сов, отделенных интервалом Т, причем
каждый импульс представляется 5-функ-
цией, умноженной на Ufte~nbT . Найти на-
пряжение на конденсаторе.
Дано (70 — 0,100 мв-сек, С~ 2-10~9 ф*
r = 106 ом, 7 = 0,20 мсек, ЬТ = $2§.
Решение. Напряжение на конденса-
торе в результате действия первого им-
пульса (70d выражается зависимостью
ис (О= где у = UrC = 500 сек~
Um — = 50 мв.
Применяя формулу (13-22) при D=09
находим, что
q-0,2Sfe _g — 0,lfe
UCk (Т) —50 £_о>25 _g-0,1 е \ Мв-
или после вычисления знаменателя
Uck (*с) = 410 -£-0,25&) 500-С,
Из этого выражения легко найти, что
максимальное напряжение на конденсаторе
появляется в начале 6-го интервала.
В тех случаях, когда на регу-
лярный эшелон возмущений накла-
дывается какое-то дополнительное
возмущение, последнее может рас-
сматриваться тоже как некоторая
модуляция эшелона.
На рис. 13-9 изображена серия
из пяти одинаковых импульсов при
том, что второй импульс отрицате-
лен. В этом случае можно считать,,
что на регулярный эшелон импуль-
сов накладывается действие удво-
енного отрицательного импульса,,
включаемого в момент t=T.
Для каждого конкретного слу-
чая подобной модуляции можно
Применяя принцип суперпози-
ции, расчет можно вести и в том
случае, когда реакция представ-
ляется двумя экспонентами, и в том
случае, когда модуляция представ-
ляется суммой или разностью
экспонент и т. п. Следовательно,
полагая b комплексным, можно по
той же формуле рассчитывать реак-
352
найти соответствующее видоизмене-
ние общего метода.
Ограничимся рассмотрением
конкретного примера, заимствован-
ного из сборника задач Ленинград-
ского электротехнического инсти-
тута имени В. И. Ульянова (Ле-
нина) Ч
Пример 13-7. В цепи последовательно
включенных г—10 ом, £«1100 мгн действует
группа импульсов, изображенная на рис.
13-9. Напряжение всех импульсов одинако-
во: U—1100 в.
Интервал между началами каждого из
пяти .импульсов Т==Ч мсек, продолжитель-
ность импульса 0,5 Т. Требуется найти ток
в цепи в интервале 2Т<£<10Г.
Решение. В интервале 2Т</<5Г
искомая 'реакция, т. е. ток, состоит: 1) из
прямой реакции на действующий импульс
Ai(t) ; 2) из затянувшейся реакции от преды-
дущих регулярных импульсов (+>U), обо-
значим ее как 3) из реакции на мо-
дулирующий отрицательный импульс двой-
ной величины '(—2U), обозначим эту реак-
цию как /мод(т).
Прямая реакция
f'1(T)=+1(^) = -^-(l-^x) ’
при 0 < т <С 0,5Г;
F", (t) = /", (т) = F'i (0,5>)
при 0,5Г < т < Т,
здесь у = r/L, время т отсчитывается от
начала интервала.
Затянувшаяся реакция от возмущения
в предыдущем интервале
f(^)=Z(T)=Fz,1
Сумма затянувшихся реакций для ин-
тервала п регулярного эшелона коротких
возмущений
1 — e~k^T
(г) = ^1(Г)----—т е-^.
1 — е 1
где k = п — 1.
Реакция на модулирующий отрицатель-
ный импульс (при />27’)
fM0H (-с) = — 2F"i (Т) е-т^+(«-3)Г]_
Производя вычисления, находим: U/r —
= 10 а, 7=100 сек-1 *, F\ (0,57')=0,488 а;
Г",(Г)=0,464а, уГ=О, 1, Z7", (Г)/(1—е~’<т)=
— 4,88 а.
1 См. п. 8 в (прилаженном списке лите-
ратуры.
Задача имеет номер 13, 104; авторы ре-
комендуют провести решение методом сум-
мирования токов. Именно этот метод в не-
сколько измененных формулировках изло-
жен в § 13-2. Текст примера 13-7 и постав-
ленное требование несколько отличны от со-
держащихся в цитированной задаче 13, 104.
В итоге находим, что при 2 < п =С 5
полная реакция
In (т) = Ft (t) -[ 4,88 (1 — e~1001 —
— 0,928г/ ~ *.’(« - 3 * * *)e~100x,
где Ft (t) = 10 (1—е 100т) при •с<0,57' и
Fi (ъ) = 0,488е-100(х~°’57') при 0,5Г< -с < Г.
Так, например, для интервала
4Т < t < 4,5Г, когда п — 5 и k == 4,
1п (т)= 10—(10-4,88-0,330 +
+ 0,928-0,819) е~100х = 10 —9,1б0~1СОх а.
’При t > 5 Г остается только действие
затянувшейся реакции на все предшество-
вавшие короткие возмущения. Отсчитывая
время т/ от конца 5-го интервала, находим„
что
/(х')=1,23е~100х',
причем т/ может быть и больше Т.
13-5. РЕЖИМ В ЦЕПИ
ПРИ ПЕРИОДИЧЕСКИ
ПОВТОРЯЮЩИХСЯ СТУПЕНЧАТЫХ
ИЗМЕНЕНИЯХ ЕЕ ПАРАМЕТРОВ
Исследование установившихся
процессов в таких цепях прово-
дится методами теории переходных
процессов.
Пусть, например, одна из ветвей
цепи периодически размыкается
в течение интервала времени Т\ и
остается замкнутой в течение сле-
дующего интервала Т2 (периодиче-
ская коммутация).
Для простоты рассмотрим кон-
кретную цепь рис. 13-10, в которой
контакты выключателя периоди-
чески размыкаются (на 7\) и замы-
каются (на Т2). Полный период
составляет Т\+Т2=Т. Такой про-
цесс соответствует периодической
подаче запирающих (отрицатель-
ных) импульсов на сетку лампы.
353
Напряжение на конденсаторе
в течение первого интервала вы-
ражается уравнением
zzc, = Ucl + АГаЛ (13-23)
тде UC,=UA; 2-=С(г + й); А —
постоянная; время т отсчитывается от
начала первого интервала, 0 < т < Tv
Для второго интервала (контакты
.замкнуты) 0 < т < Т2 напряжение на
том же конденсаторе выражается
аналогичной формулой
«C2=t/C2+^”^, (13-24)
но с другими значениями постоянных;
U = п
UA R 4-
время т отсчитывается от начала
второго интервала.
Постоянная интегрирования В
в выражении (13-24) пока остается
также неопределенной, как и А.
Эти постоянные длл первог©
цикла замыкания и размыкания
в общем случае отличаются от по-
стоянных для второго цикла и сле-
дующих. Но после того как рас-
смотренные коммутации повторятся
много раз, в цепи установится пе-
риодический процесс. Для такого
установившегося периодического
процесса начальные условия в на-
чале каждого интервала Ti будут
неизменными, так же как началь-
ные условия в начале каждого ин-
тервала Т2. А это значит, что
постоянные интегрирования А и В
приобретут также некоторые неиз-
менные значения (соответствующие
установившемуся периодическому
процессу).
Но по закону коммутации на-
пряжение на конденсаторе не мо-
жет изменяться скачком. Следова-
тельно, напряжение на конденса-
торе иС\ (0) в начале интервала 1\
равно напряжению на конденсаторе
^02(^2), достигнутому к концу ин-
тервала Т2. Сказанное позволяет
составить уравнение
«С1 (0) = ^с. +Л =
= ИС2 (Л) = Uc2 + Ве~а‘т\ (13-25)
Аналогично напряжение на кон-
денсаторе иС\ (Л) в конце интер-
вала 7\ должно равняться напря-
жению на конденсаторе ^сг(О)
в начале интервала Т2. Это позво-
ляет составить второе уравнение
«С1 (T1)=Ucl+Ae~aJ^
^uc2(P)^=Uc2+B. (13-26)
Совместное решение- этих урав-
нений позволяет определить постоян-
ные А и В для установившегося пе-
риодического режима:
_ 1
А— ^С2 ~~ UC\ ) ~еа^_е-ахТг ’
В — (Ucl UC2 ) ^ааГа __ ах?! е 8 а *
Аналогично проводится расчет
и для других цепей. Постоянные
интегрирования определяются при-
равниванием начальных условий
одного интервала и соответствую-
щих величин в конце предыдущего
интервала. Для цепи с индуктивно-
стью начальные условия определя-
ются значением тока в индуктивно-
сти
Для цепи, содержащей и ем-
кость С, и индуктивность А,
в уравнение для каждого интер-
вала входят две постоянные инте-
грирования. Соответственно для
границы между двумя интервалами
можно составить не одно, а два
уравнения, в которых приравнива-
ются значения ис и iL в начале
одного интервала и достигнутые
в конце предыдущего. При этом
нужно составить четыре уравнения
для определения четырех постоян-
ных. Расчеты получаются доста-
точно громоздкими.
Когда коммутации приводят
к некорректности начальных усло-
вий, условия для токов в индуктив*
354
костях и напряжений на конденса-
торах должны быть заменены усло-
виями для потокосцеплений и заря-
дов.
Во многих случаях .процессы в цепи при
серии ‘повторяющихся коммутаций могут
бцть найдены на основании .следующих со-
ображений: .равенства, выражающие иско-
мую функцию для двух перемежающихся
режимов, например равенства (1'3-23) и
(13-24), имеют неизменный вид для любого
цикла; от номера цикла зависят только вхо-
дящие в них постоянные. Так, в равенствах
(13-23) и (13-24)
4=А(л), В=В(п). (13-27)
Полагая известным режим до первой комму-
тации, можно найти значение постоянной
А (1) для первого цикла обычными мето-
дами расчета переходных процессов. В ре-
зультате оказывается известным и режим
к началу ‘второй коммутации, что позволяет
определить значение постоянной В (1) для
первого цикла, а следовательно, и режим
к началу второго цикла. Далее опять же
обычными методами можно установить зна-
чение постоянной для первой части второго
цикла А -(2) и т. д.
Продолжая такой расчет, обычно удает-
ся, после того как записаны .выражения для
постоянных второго (или третьего) цикла,
написать в общем виде зависимость этих
постоянных от номера цикла, т. е. А(п) и
В(п), Выражение для установившегося ре-
жима находится путем перехода к пределу
При П ~»ОО.
Этот метод применим и в том случае,
когда в равенство для первой части цикла
входит несколько постоянных, например две:
А1 и А2 (их число зависит от числа корней
характер’истического ур авнения).
Физическое изменение реактив-
ных параметров. Периодические из-
менения параметров цепи могут
происходить не только вследствие
коммутации, но и вследствие физи-
ческого изменения того или иного из
ее параметров. Если это реактивный
параметр (С, L, 7И), то воздействие
на цепь его физического изменения
существенно отличается от воздей-
ствия простой коммутации.
Поясним сказанное простым
примером (рис. 13-11). Пусть в це-
пи L, г, включенной к источнику
постоянного напряжения U, вели-
чина L внезапно уменьшается от
значения jLi + L2 до значения Ц.
Проще всего представить себе, что
это происходит, например, вследст-
вие выдергивания сердечника.
В уравнении такой цепи
(13-28)
вместо слагаемого L стоит про-
изводная от произведения Li, рав-
ного потокосцеплению, так как
теперь изменяются и L, и i.
Взяв интеграл от уравнения
(13-28) по времени за промежуток
А/, в течение которого индуктив-
ность изменяется, найдем, что
и м м
§ U dt=^ir dt-}- j d (Li).
ООО
(13-29)
Если Lt очень малая величина
(Lt—*O), то левую часть можно по-
лагать равной нулю:
д/
§ Udt = ULt — O при
о
Точно так же мож!но полагать
равным нулю и первый цнт^ррал пра-
вой части:
д/
J irdt —ir Lt = 0 при Lt -> 0.
о
В этом выражении i —qrrq из
значений остающегося конечным тока
i в интервале Lt (теорема о среднем).
В Таком случае из уравнения
(13-29) следует, что
д/
Jd(Lz) = L(4-0)z(+0) —
о
— L(— 0)/(— 0) = 0 (13-30)
или
Z(+O) = Z(-O)^=g, (13-31)
где аргумент ( + 0) соответствует
режиму, наступившему после изме-
нения индуктивности, а аргумент
(—0) — режиму, существовавшему
355
перед началом изменения индуктив-
ности.
Уравнения (13-30) и (13-31) вы-
ражают закон сохранения потока,
который был уже подробно разо-
бран' в § 10-10.
Очень важно определить изме-
нение энергии, происходящее в ре-
зультате рассмотренного физиче-
ского изменения индуктивности.
Можно, не записывая никаких урав-
нений, понять, что при уменьшении
индуктивности энергия, запасенная
в ее магнитном поле, должна уве-
личиваться. К этому выводу приво-
дит прежде всего такое соображе-
ние: выдергивая сердечник из
катушки с током, мы должны были
произвести работу против сил поля,
втягивающих сердечник в катушку.
Эта работа могла перейти только
в энергию магнитного поля.
Можно рассуждать и более
формально. Из условия сохранения
потокосцепления ясно, что, умень-
шая индуктивность, например,
вдвое, мы во столько же раз увели-
чиваем ток; но в формулу энергии
(й£/2) ток входит в квадрате, тогда
как индуктивность входит в первой
степени.
Обращаясь к уравнению (13-31),
найдем, что приращение энергии
/2(-0)£(-0)_
2 —
= wM(-0)-( l°L0L)(+P-1, (13-32)
где wM(—0) —значение энергии до
начала изменения индуктивности.
Из равенства (13-32) видно, что
энергия возрастает при уменьшении
индуктивности, т. е. при
L (—0)>L (+’0).
Переходный процесс в цепи
(рис. 13-11), после того как про-
изошло физическое изменение ин-
дуктивности, определяется уравне-
нием
= (13-33)
при начальном условии /(-}-0), от-
куда
/==Т-[7--г’(+°ф’а<’ <13'34*
где a—r!L\ и Li = L ( + 0).
Очевидно, что совершенно иной
* результат мы получим, рассматри-
вая цепь, в которой часть индуктив-
ности (Л2) замыкается накоротко
(рис. 13-12). Такая коммутация не
повлияет на ток, если перед комму-
тацией существовал установив-
шийся режим.
К аналогичному различию меж-
ду воздействием коммутации и воз-
действием физического изменения
емкости мы придем, рассматривая
цепь с источником постоянного на-
пряжения при последовательно
соединенных г и С (рис. 13-13).
При быстром физическом измене-
нии емкости С от С(—0)=Ci + C2
до С ( + 0) =СЬ хотя бы путем раз-
движения пластин конденсатора
(рис. 13-13,а), следует исходить из
закона сохранения заряда
q {—0)=<?(+0). (13-35)
Если изменение емкости проис-
ходит за время Д/, малое по сравне-
нию с постоянной времени контура
(г, С), то
йс(+0) = «с(-0)^Д$. (13-36)
Рис. 13-13.
356
При этом эйергия системы увели-
чивается на
л / ПХС(— 0) — С(+°)
Дауэ - (- о) g(+0;—.
(13-37)
Заметим, что пластины заря-
женного конденсатора взаимно при-
тягиваются; следовательно, раздви-
гая их, нужно было затратить
работу.
Пусть в рассматриваемом кон-
туре через каждые четверть пе-
риода индуктивность убывает на
AL, затем возрастает на A-А, вновь
убывает и т. д. (рис. 13-14,6).
Если в начальный момент суще-
ствовал какой-то небольшой ток
в индуктивности, то в результате
уменьшения индуктивности он не-
сколько возрастет и примет значе-
ние /о.
Как и в случае цепи с индуктив-
ностью А, к совсем иным результа-
там приводит уменьшение емкости
от Ci + C2 до Ci путем отключения
одного из параллельных конденса-
торов (рис. 13-13,6). В случае по-
стоянного напряжения источника
такое отключение вообще неощути-
мо, если до коммутации существо-
вал установившийся режим.
Применим изложенные сообра-
жения к колебательному контуру
L, R, С (рис. 13-14,а) высокой доб-
ротности. Для такого контура ча-
стота собственных колебаний
В течение следующей половины
периода ток будет изменяться по
закону
iL = IQe at cospA
По условию через 774 индуктив-
ность вновь увеличивается на ЛА
и принимает исходное значение Ао.
Но в этот момент ток равен
нулю, поэтому изменение индуктив-
ности не оказывает никакого влия-
ния на энергию цепи. К концу
половины периода (cos р t=—1)
ток достигает значения 1
p = 2'ir/7’ = l//LC>
^(7/2) = -/^-“г/2
коэффициент затухания
a = l/(2RC),
-Л(1
— —/ О——
2 J ° 1 • 2Q J ’
уменьшение амплитуды колебаний за
время одного периода
е—а.Т _ е~а2к/₽ _ tz/Q
где добротность.
q = R$C = R/$L) =
= RI\TLjC.
В этот момент индуктивность
вновь уменьшается и ток по абсо-
лютной величине возрастает на вели-
чину
AZ = /0e-“r/2^.
Л)
1 Влиянием малых изменений ДЛ на а
и р здесь пренебрегаем.
357
Если уменьшение тока за полпе-
риода, обусловленное затуханием ко-
лебаний в контуре, меньше, чем
возрастание, вызванное изменением
индуктивности, т. е.
/0 (1 — е~аТ'2') < 1йе~аТ12 4^
или
^0
то амплитуда колебаний в следую-
щую половину периода окажется
больше, чем в предыдущую.
При малых значениях аГ/2 по-
следнее неравенство можно запи-
сать в таком виде:
LL _______ тс
Lq 2 2Q
По мере повторения изменений
Д(Л колебательный контур раскачи-
вается (рис. 13-14,в), несмотря на
то, что в его' цепи отсутствуют
обычные источники питания. Огра-
ничение его раскачки в реальных
системах определяется только не-
линейностью системы.
Рассмотренное сейчас возбужде-
ние колебаний носит название
параметрического воз-
буждения, так как оно вызвано
периодическим изменением пара-
метра цепи L. Такое же возбужде-
ние колебаний можно получить и
при изменении С.
Из всего изложенного очевидно,
что периодическое изменение сопро-
тивления не связано с изменением
энергии цепи, а потому не может
служить для возбуждения колеба-
ний в контуре, не содержащем
источников питания (если сопро-
тивление положительно).
Параметрические явления игра-
ют большую роль в современной
электротехнике, но их более полное
рассмотрение возможно только
в теории нелинейных цепей.
ЛИТЕРАТУРА
1. Нейман Л. Р., Калантаров
А. Л., Теоретические основы электротехни-
ки, ч. I и И, Гооэнергоиздат, 1959.
2. 3 е в е к е Г. В., И о н к и ih П. А., Н е-
ту ш и л А. В., Ст р а х о в С. В., Основы
теории цепей, изд-во «Энергия», 1965.
3. Атабеков Г. И., Теория линейных
электрических целей, изд-во «Советское ра-
дио», 1960.
'4 . Балабан ян Н., Синтез электриче-
ских цепей, Гооэнергоиздат, 1961.
5. Шим о ни К.1, Теоретическая элек-
тротехника, изд-во «Мир», 1964.
1 В книге К. Шимони содержится большой
список литературы по теоретическим вопросам
электротехники.
6. Задачник по теоретическим основам
электротехники (теории цепей), под ред.
К. М. П о л и в а н о в а, Гооэнергоиздат,
1962.
7. Зайцев И. А. и Л у -р ь е А. Г., За-
дачник по теоретическим основам электро-
техники, Гооэнергоиз дат, 1960.
8. Башарина В. Н., Богданов
Е. И., Глазенап М. С., Григорьев
В. Т., Курен ев С. И., Мерзлютин
Ю. Б., «П и н е с М. И., Погодин А. С.,
Сборник задач по расчету электрических
цепей переменного тока, ЛЭТИ, Ленинград,
1958.
Поливанов Константин Михайлович
Теоретические основы электротехники,
ч. 1, Линейные электрические цепи с со-
средоточенными постоянными, М.—Л.,
издательство «Энергия», 1965, 360 с. с черт.
Тематический план 1965 г., № 72
* * *
Редактор Б. Я. Жуховицкий
Техн, редактор Г. Е. Ларионов
* * *
Сдано в набор 10/V 1965 г. Подп; к печати 27/VIII 1965 г.
Т-10290 Бумага 70Х10871в Печ. л. 31,5 Уч.-изд. л. 32,39
Тираж 40 000 экз. Цена в переплете № 7 — 1 р. 82 к.,
в переплете № 5—1 р. 77 к, Зак. 333
* * *
Московская типография № 10 Главполиграфпрома
Государственного комитета Совета Министров СССР
по печати.
Шлюзовая наб., 10.
Цена 1 р. 77 к.
О