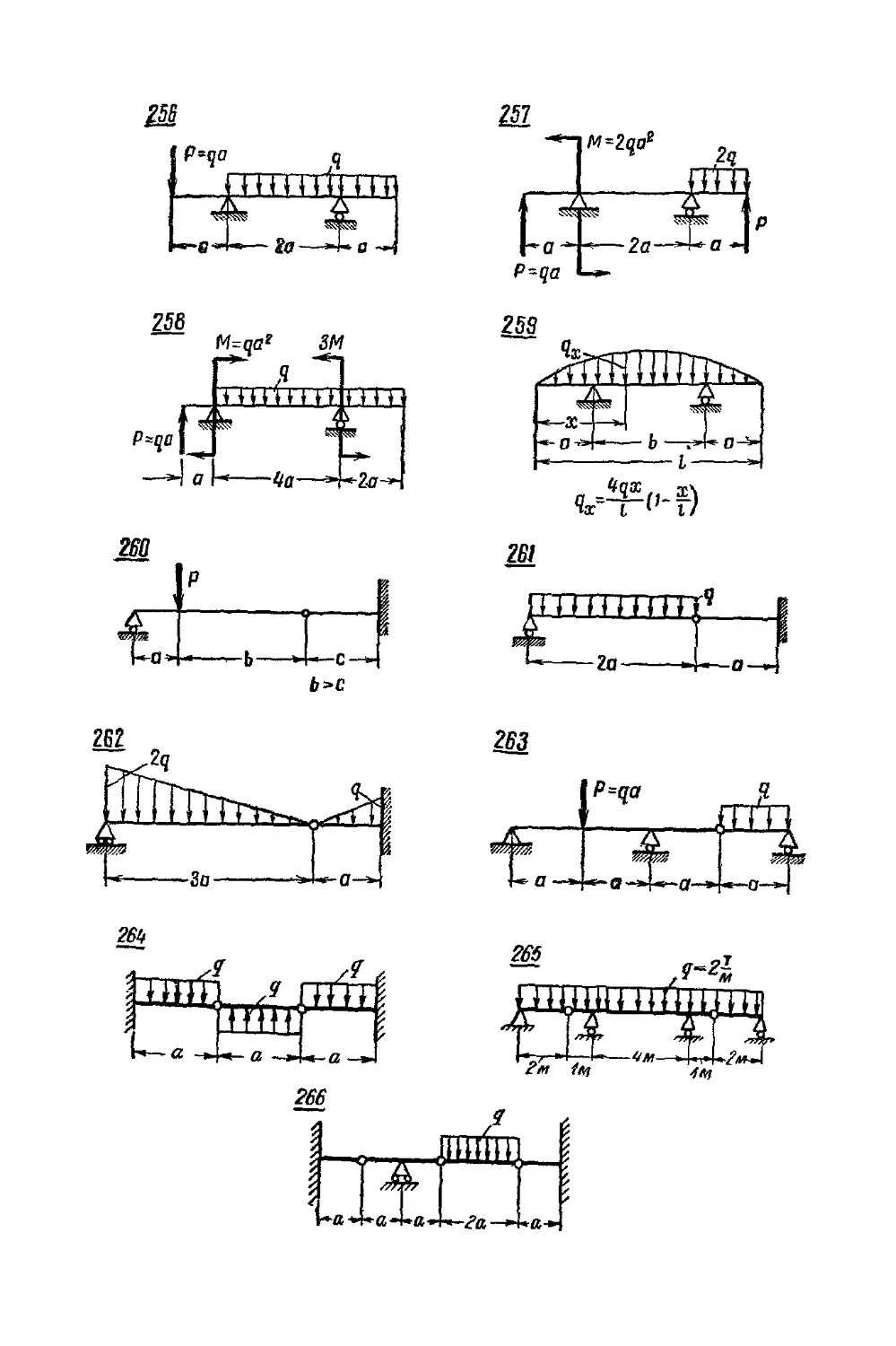
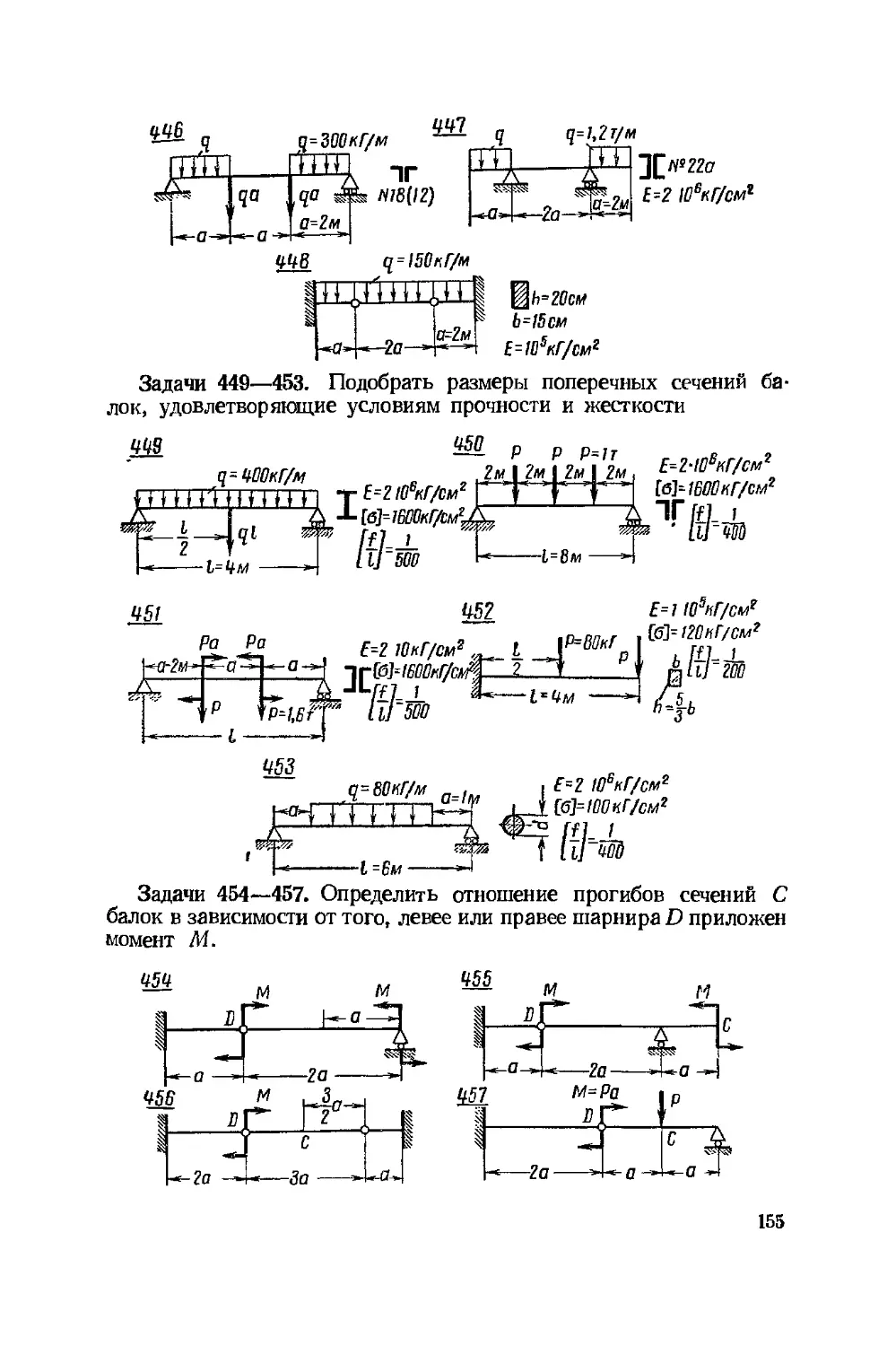
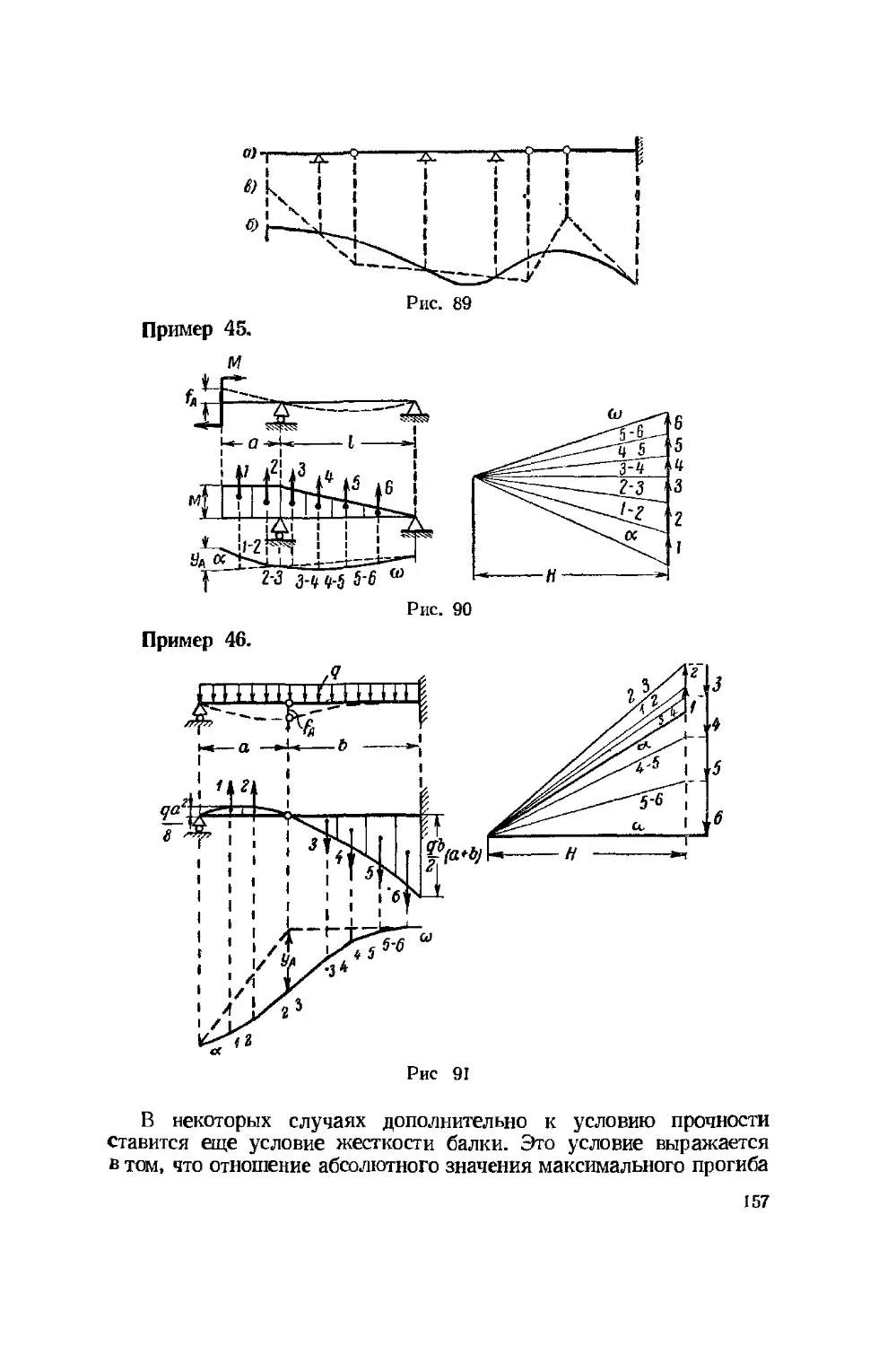
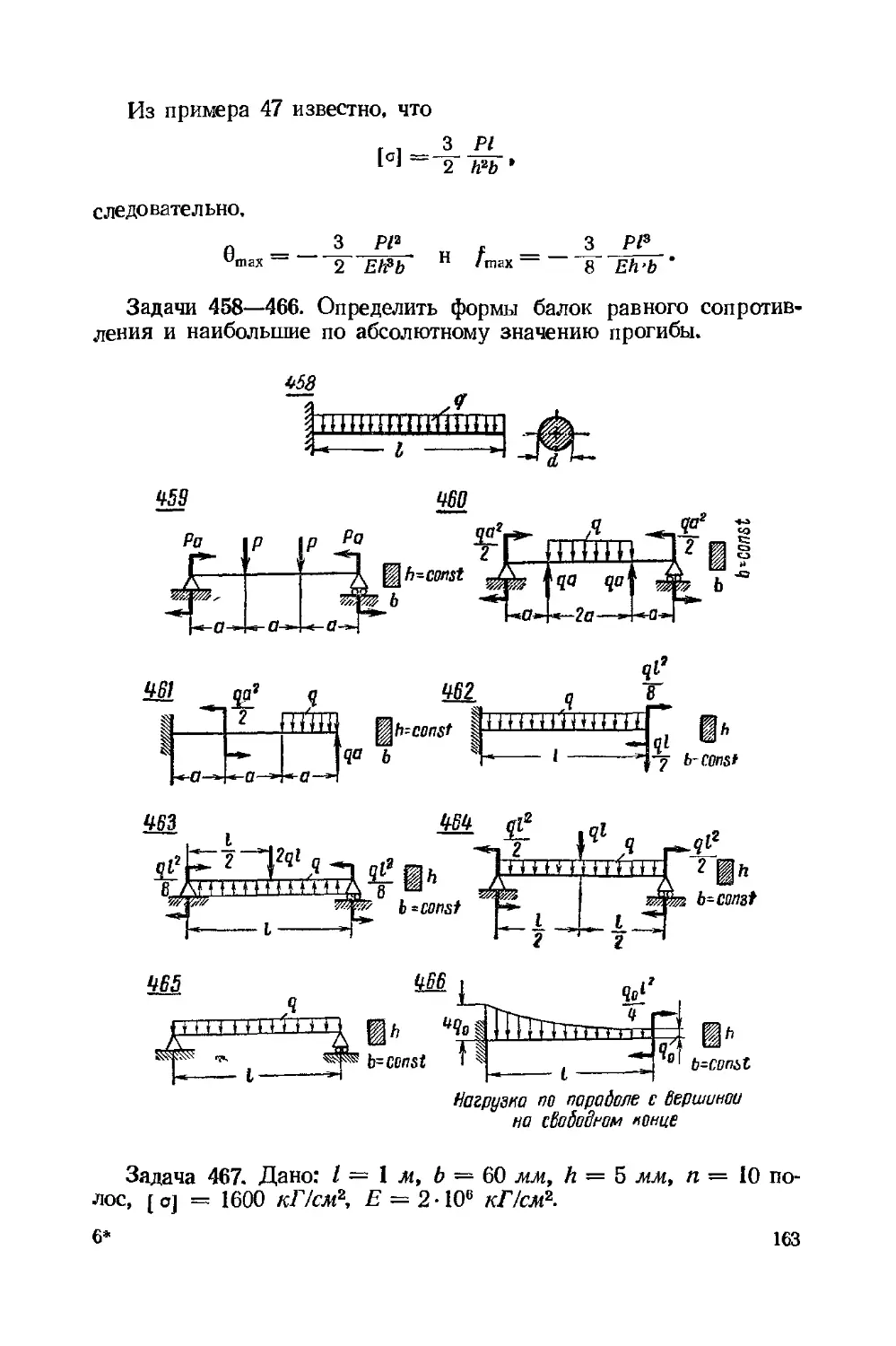
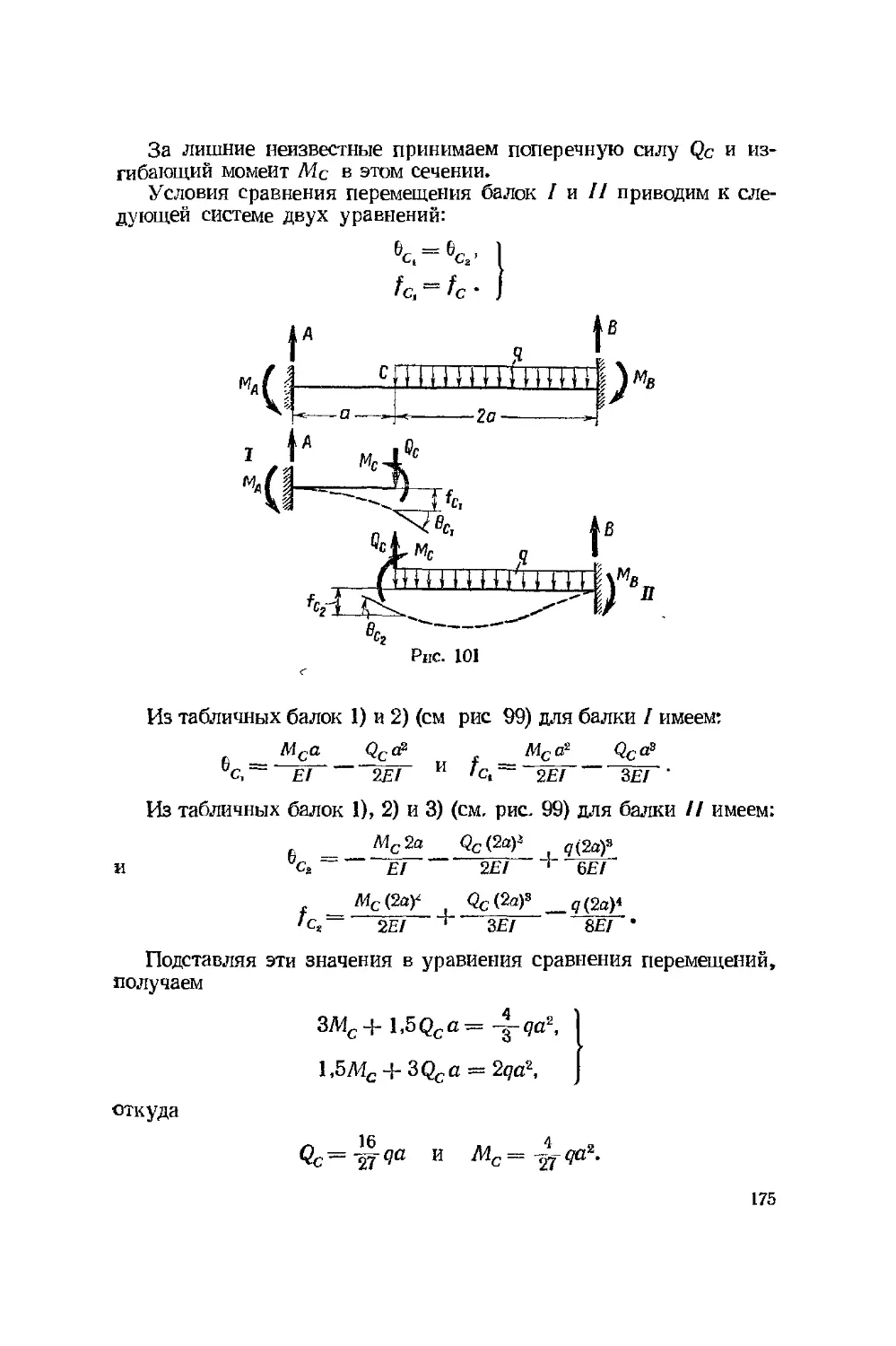
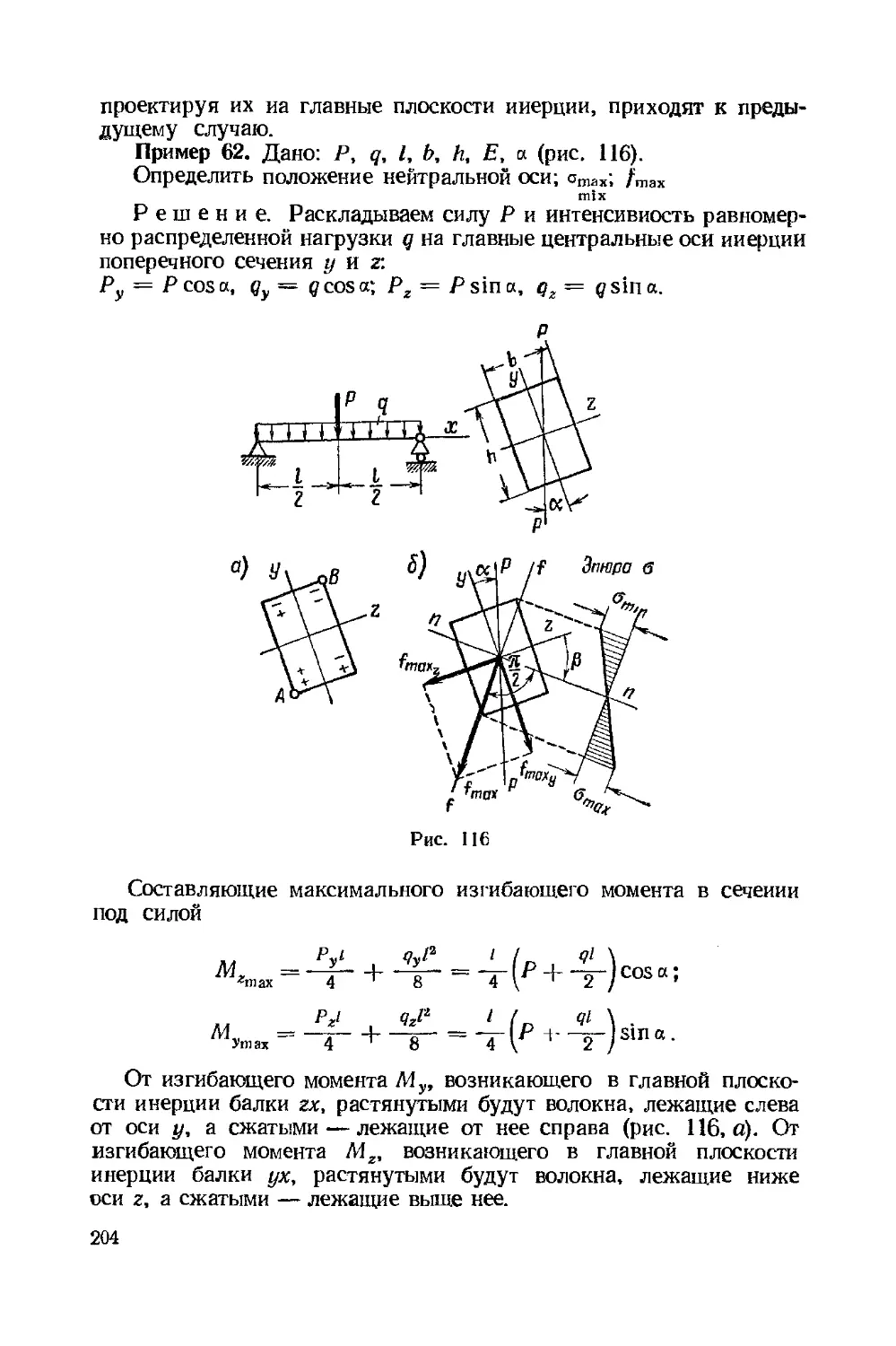
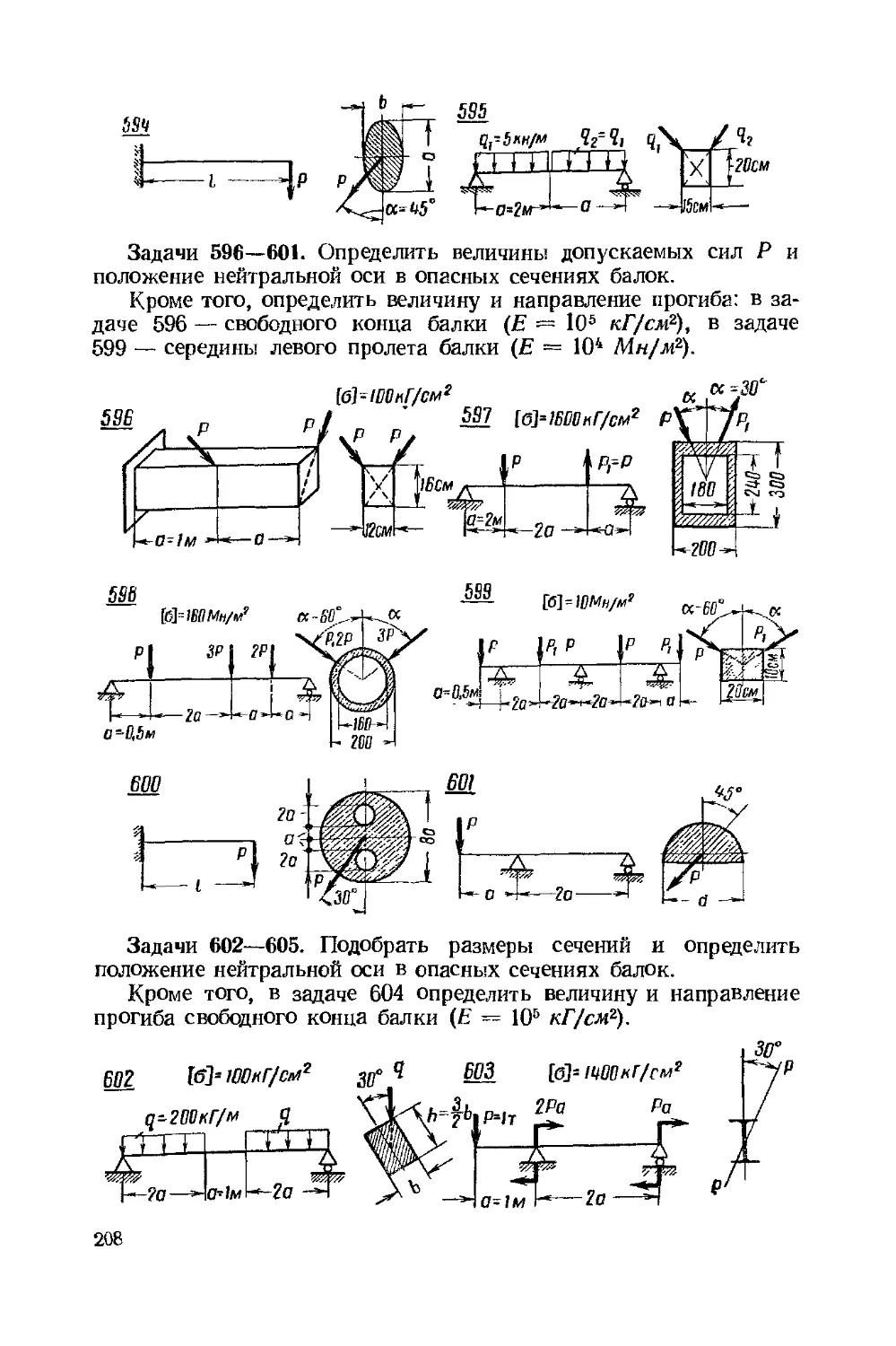
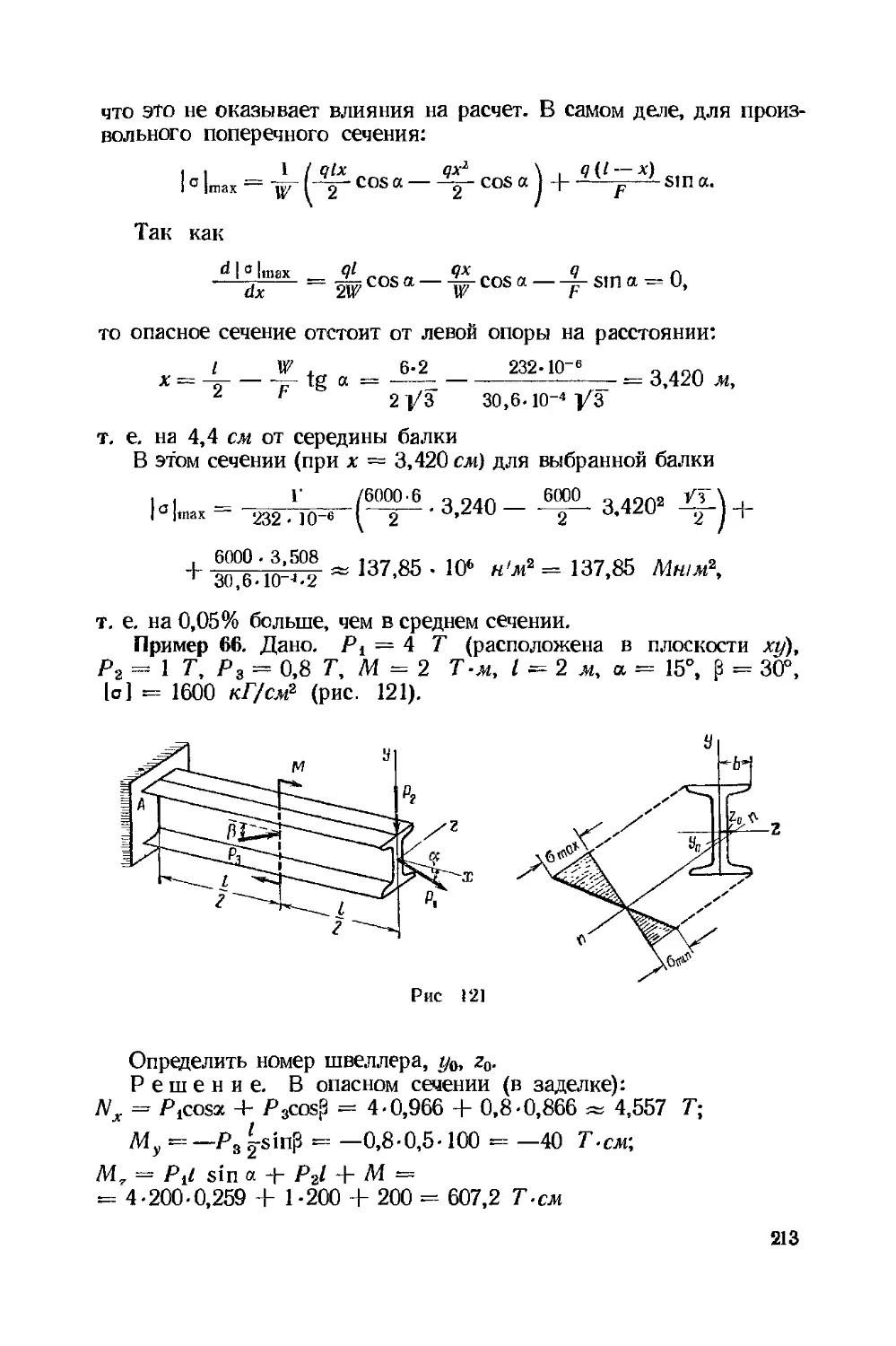
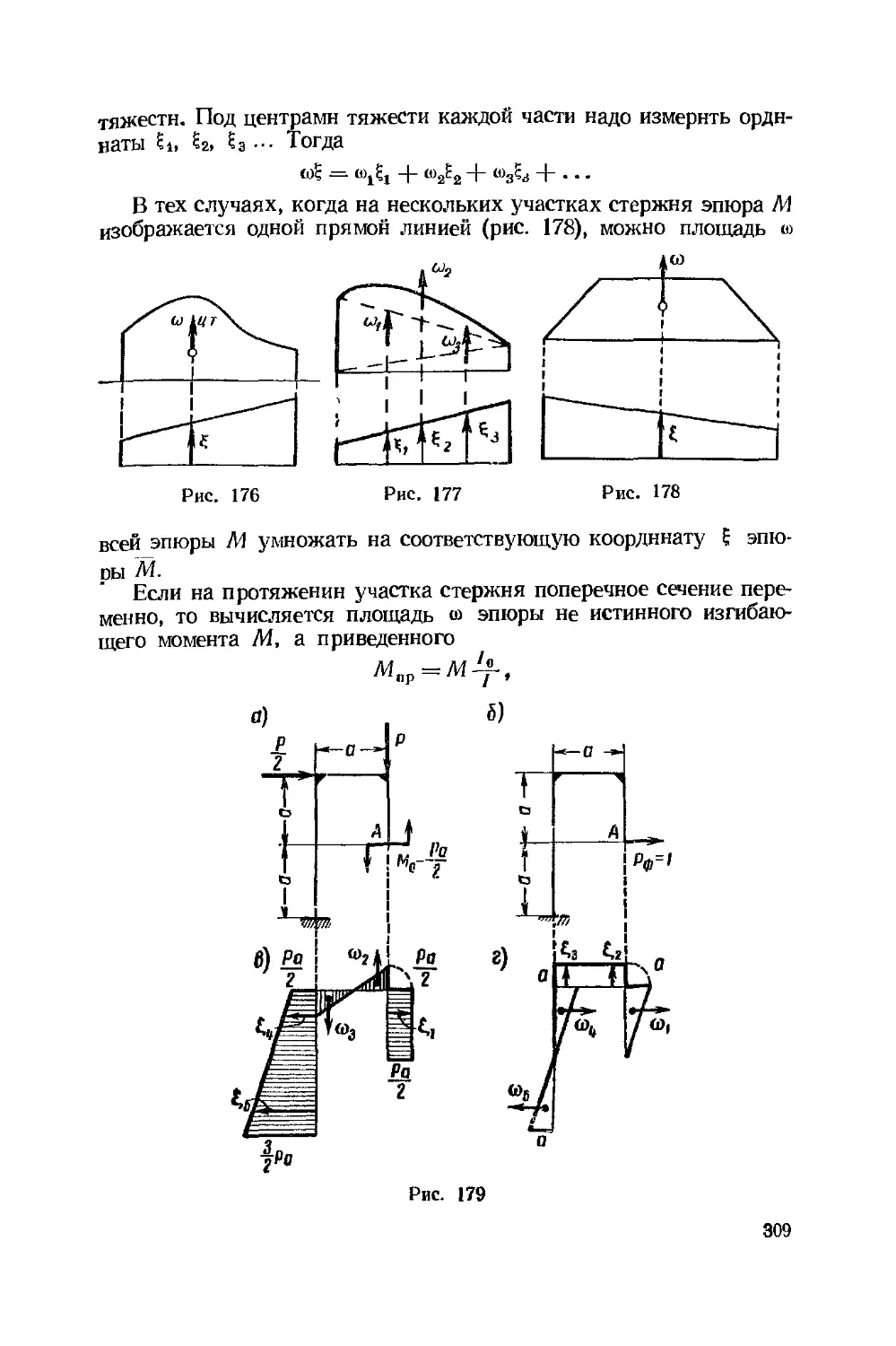
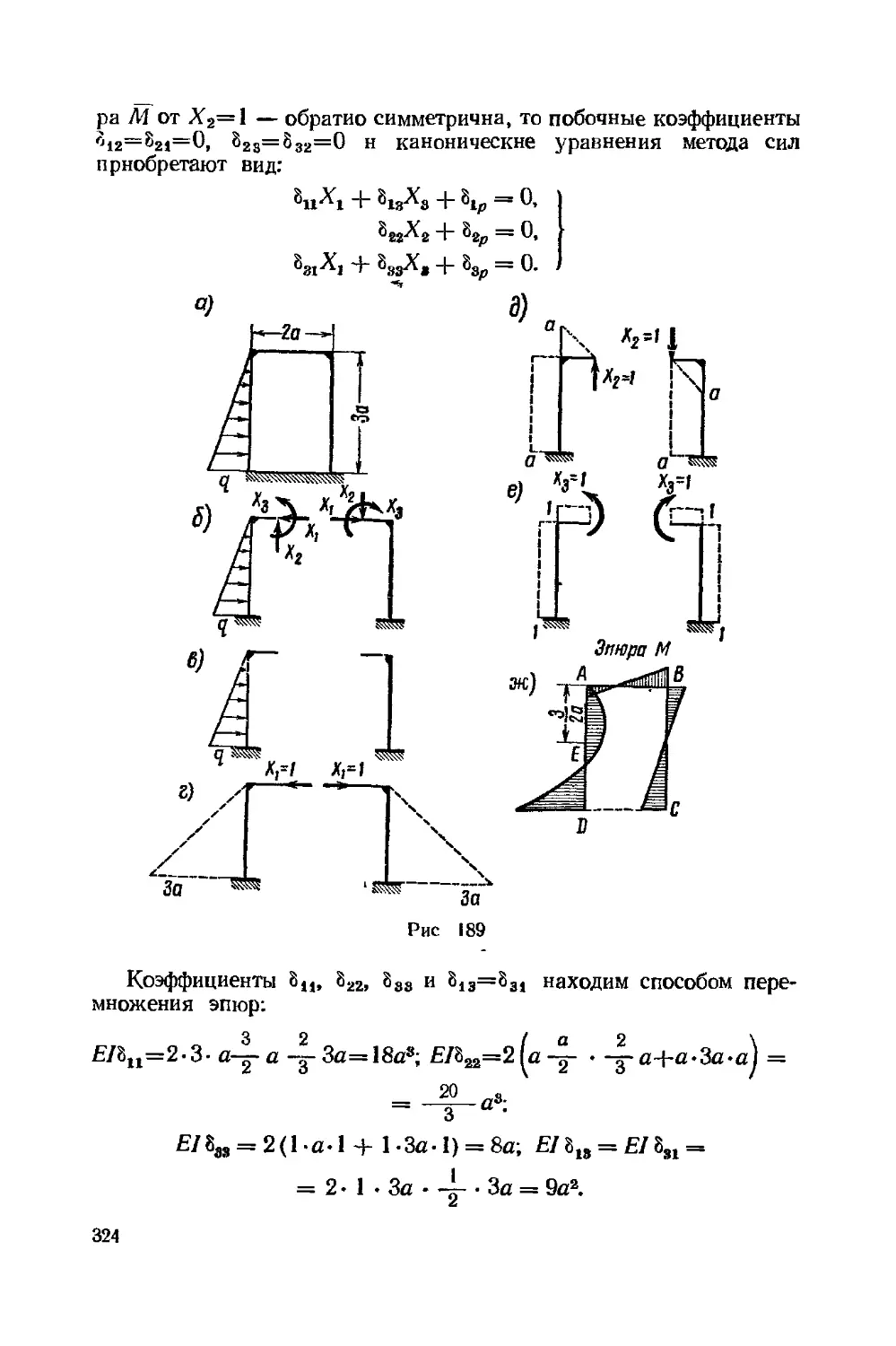
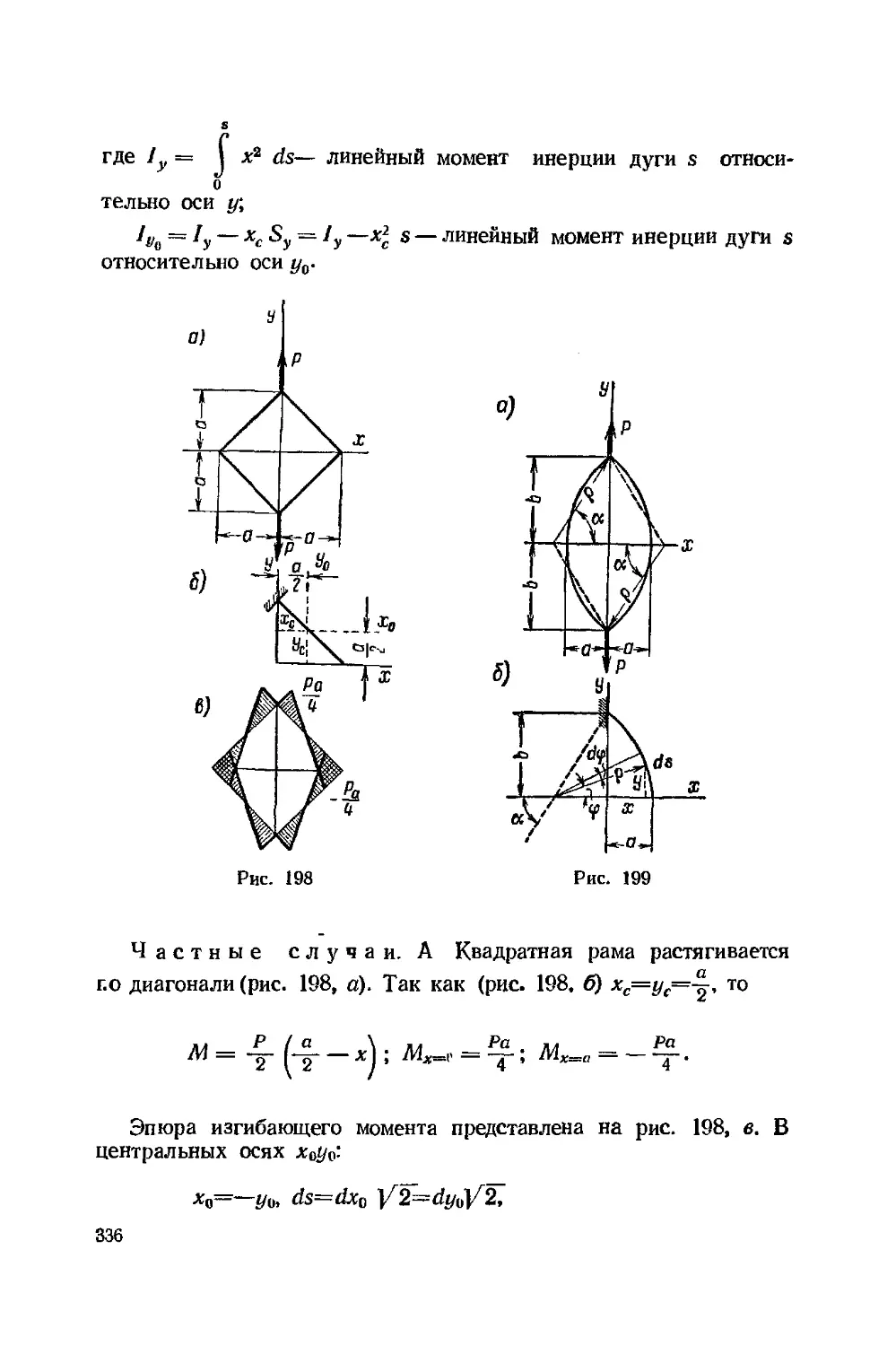
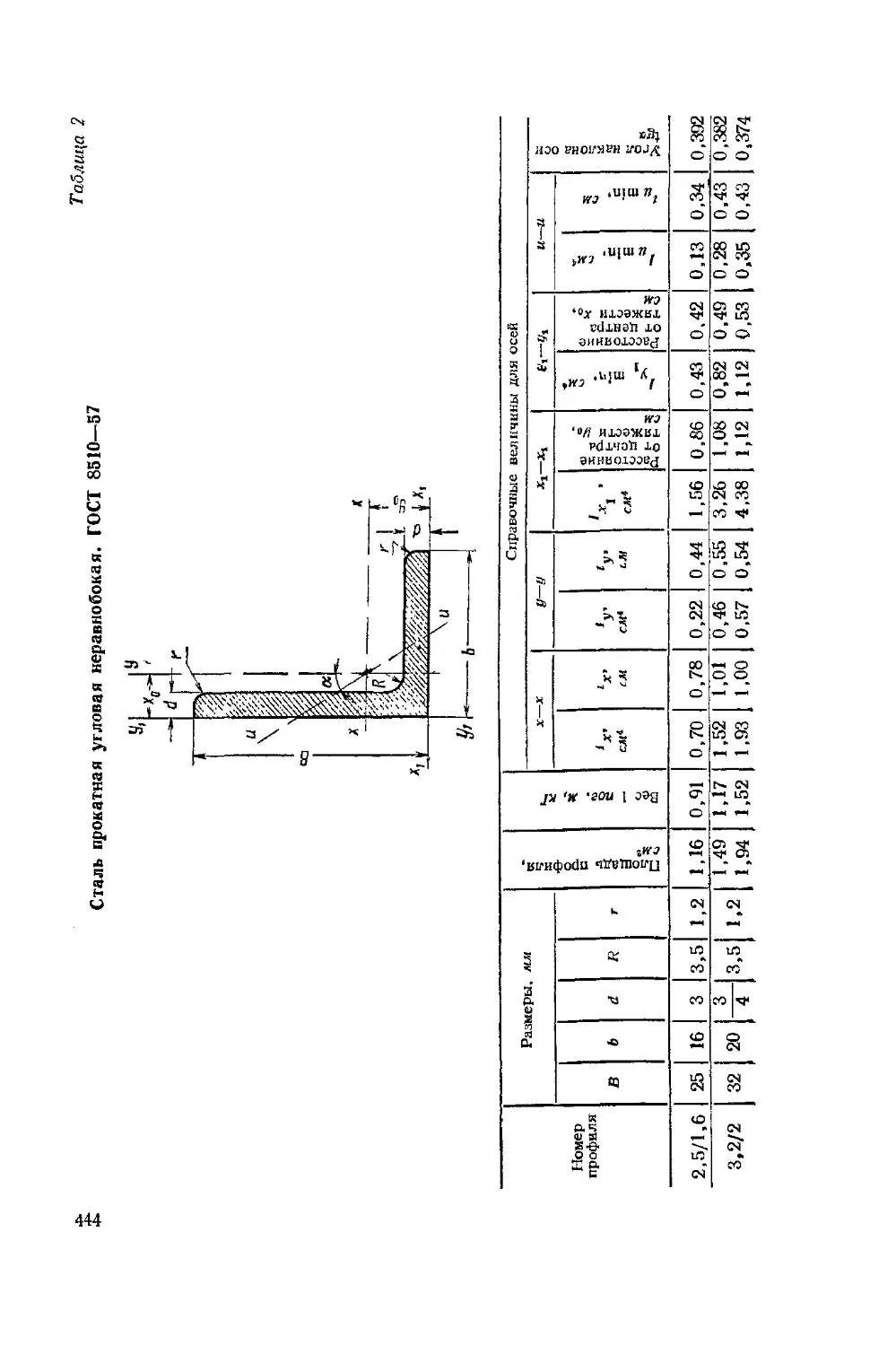
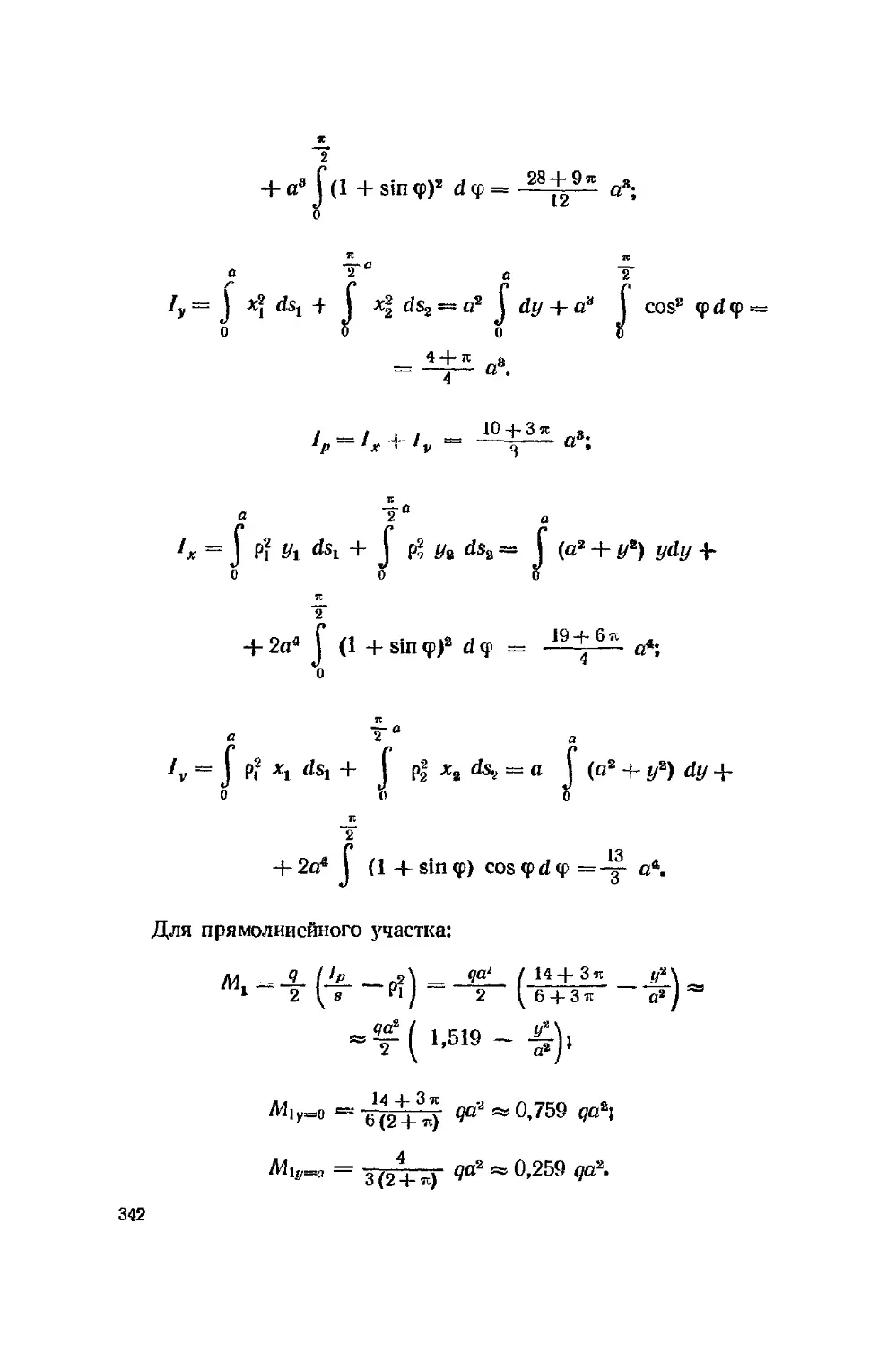Текст
И. Н. Миролюбов, С. А. Енгалычев, Н. Д. Сергиевский,
ф. 3. Алмаметов, Н. А. Курицьм, К. Г. Смирнов-Ввсильев,
Л. В. Яшина
ПОСОБИЕ
К РЕШЕНИЮ
ЗАДАЧ
ПО СОПРОТИВЛЕНИЮ
МАТЕРИАЛОВ
ИЗДАНИЕ ВТОРОЕ
ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебного пособия для студентов высших
технических учебных заведений
Пособие к решению задач по сопротивлению
материалов.
Миролюбов И. Н. и др. «Высшая школа», 1967.
Учебное пособие содержит краткое изложение
основных положений курса «Сопротивление материа-
материалов» , методические указания, примеры решения ти-
типовых задач. Имеется большой выбор задач для са-
самостоятельного решения. В конце книги даны ответы
на все задачи. В приложении приводится справочный
материал, необходимый для нх решения.
Предназначено для студентов машиностроитель-
машиностроительных и механических специальностей высших учебных
заведений Может быть использовано инженерно-тех-
инженерно-техническими работниками, занимающимися прочно-
прочностными расчетами.
Таблиц 23, иллюстраций 1393, библиографий 18.
Рецензент Г. М Ицкович
ПРЕДИСЛОВИЕ
У студентов, изучающих курс «Сопротивление материалов»,
наибольшие трудности обычно возникают при решении задач. На-
Настоящее пособие облегчит процесс изучения данного курса, а глав-
главное поможет овладеть методикой решения задач и получить необхо-
необходимый навык в их решении.
Пособие содержит материал, относящийся к разделам: растяже-
растяжение, сжатие, сдвиг, геометрические характеристики плоских фигур,
кручение, плоский поперечный изгиб, сложное сопротивление
прямых брусьев, продольный изгиб, энергетический метод расчета
упругих систем, кривые брусья, толстостенные трубы и динамиче-
динамическое действие сил.
В учебное пособие включены основные положения теории, не-
необходимые методические указания, примеры решения типовых за-
задач, задачи для самостоятельного решения, ответы к ним, а также
приложения со справочным материалом. Для удобства пользования
пособием и лучшего усвоения указанный материал расположен
концентрически в каждом небольшом, но самостоятельном разделе
курса; ответы же ко всем задачам и справочные данные помещены в
конце книги. Предусматривается, что студенты прежде всего должны
ознакомиться с теоретическими положениями, методическими ука-
указаниями и решениями иллюстративных примеров по рассматрива-
рассматриваемому разделу. Это позволит им восстановить в памяти, лучше
понять и освоить необходимые основы теории, осмыслить методику
решения задач данного типа и приобрести сведения, достаточные
для сознательного и самостоятельного их решения.
Условия всех задач, предназначенных для самостоятельного
решения, представлены схемами со значениями необходимых исход-
исходных величин. Так как каждая схема может характеризовать собой
аналогичную работу не одной какой-то конструкции, а несколь-
нескольких, иногда различных по назначению, то в подавляющем боль-
большинстве задач не приводятся словесные условия, ограничивающие
использование той или иной схемы для какого-нибудь отдельного
1* ч
случая и много раз повторяющие названия одних и тех же зада-
задаваемых и определяемых величин.
К каждой группе задач, относящихся к одной и той же теме и
имеющих одинаковое назначение, дается краткое указание цели,
которую нужно достигнуть в решении. Такая постановка задач,
не уменьшая ясности их содержания, должна заставить студентов
самостоятельно сформулировать условие и, следовательно, лучше
представить себе смысл разрешаемых вопросов и исходных данных.
Кроме того, отсутствие текста в условиях задач позволяет значи-
значительно увеличить число расчетных схем и рассмотреть достаточное
число разнообразных вопросов, не увеличивая объема пособия.
Разъяснение физического, механического или геометрического
смысла величин, обозначенных различными символами, дается в
таблице условных обозначений и в тех частях каждого параграфа,
в которых приводятся теоретические основы и методические ука-
указания.
Второе издание пособия к решению задач по сопротивлению
материалов по объему не отличается от предыдущего, но содержит
ряд изменений, дополнений и редакционных поправок. Задачи, не
представляющие большого интереса, исключены из настоящего
издания. В то же время добавлен новый материал, а именно, включен
продольно-поперечный изгиб. Пособие переработано с учетом новых
ГОСТов на прокатный материал.
Во втором издании нашла отражение Международная система
единиц (СИ). На ряде примеров показаны особенности решения
задач при использовании этой сисгамы. Даны также задачи для
самостоятельного решения в указанной системе. Для удобства
пользования сохранена нумерация большинства задач первого и
второго изданий.
В проверке решений и графического оформления отдельных
задач второго издания приняли участие преподаватели кафедры
сопротивления материалов Ленинградского механического инсти-
института М. Я. Водопьянов, Ю. Ф. Поляков и Л. С. Рамзина.
Авторы выражают особую благодарность проф. Н. И. Безухову
за исключительно тщательное рецензирование и ценные указания
по первому изданию пособия, а также благодарят всех лиц, при-
приславших свои замечания.
Одновременно авторы приносят искреннюю благодарность до-
доценту Г. М. Ицковичу за большой труд по рецензированию второго
издания и за целый ряд весьма полезных замечаний н советов.
Авторы будут весьма признательны за любые критические заме-
замечания, которые помогут улучшять настоящее пособие.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
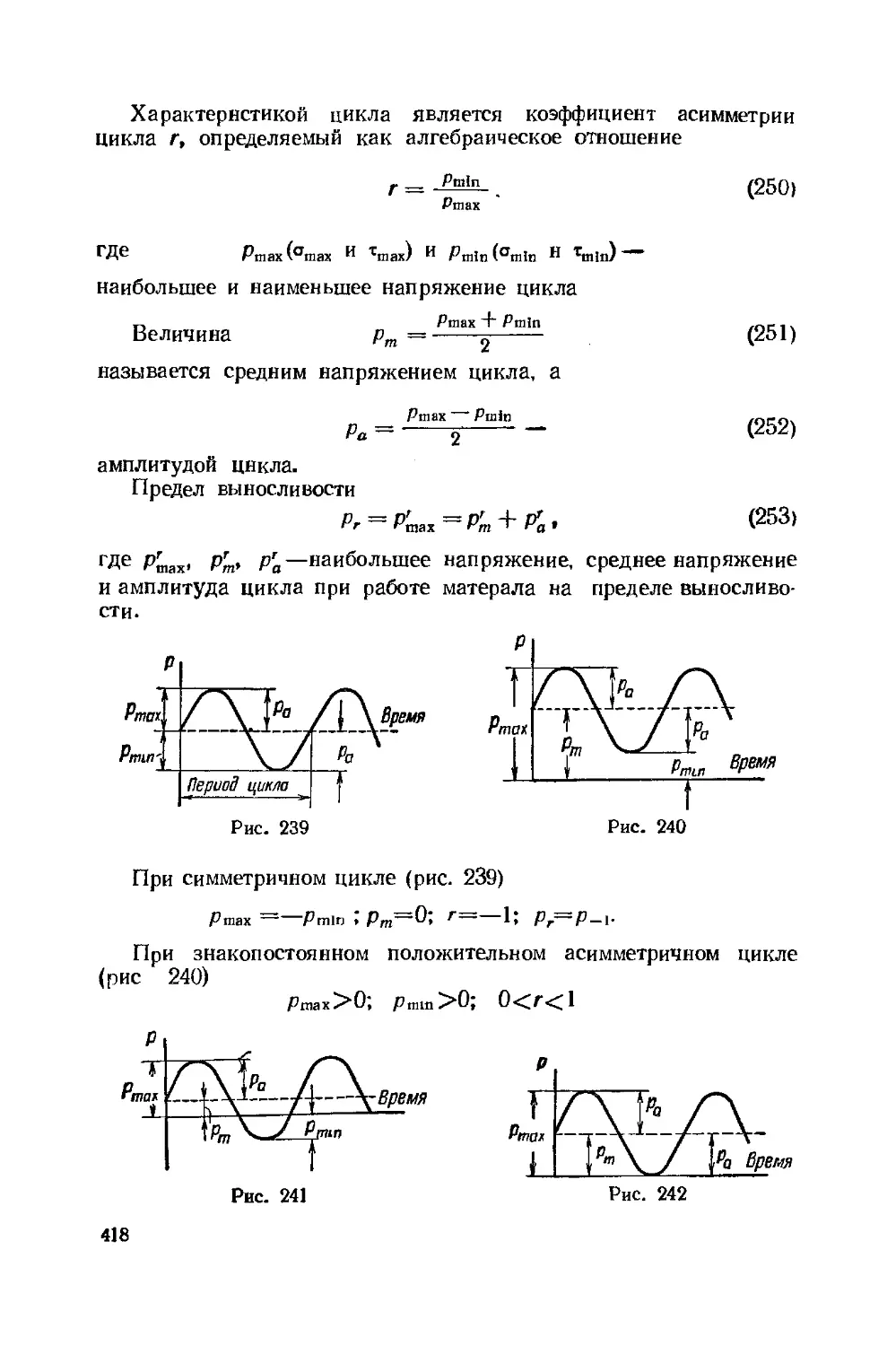
А—опорная реакция; амплитуда вынужденных колебание
а—длнна участка стержня; размер поперечного сечения; ус-
ускорение центра тяжести массы
В — опорная реакция; ширина поперечного сечення; длина
соединительной планки в составных колоннах
Ь—длина участка стержня; ширина сечения
С — жесткость стержня, системы
°С—градус по шкале Цельсия
D, d — диаметр
Е — модуль продольной упругости материала
е — расстояние, определяющее положение центра изгиба;
смещение нейтральной линии от центра тяжести при из-
изгибе кривого бруса
F, Fx— площадь поперечного сечения стержня
FCp, Fcu — площади среза, смятия
/, ft — прогиб балки
С — модуль сдвига материала
g — ускорение силы тяжести
h — высота прямоугольного сечения, высота падения груза
'zi lyi 'и> 'ч — радиусы инерции относительно осей г, у, и, v
i — минимальный радиус инерции поперечного сечения
Iz* ^у» ^и» ^v — осевые моменты инерции площади фигуры относительно
осей г, у, и, v
1р — полярный момент инерции площади фигуры
Imaii — главные моменты инерции площади фигуры
1ШП
/к — геометрическая характеристика жесткости сечения при
кручеини
1т — момент инерции массы относительно оси вращения
1г „—центробежный момент инерции площади фигуры относи-
относительно осей г, у
к — коэффициент формы, учитывающий влияние конфигурации
поперечного сечения на значение потенциальной энергии
от поперечной силы; коэффициент, учитывающий степень
кривизны витка пружины и влияние поперечной силы
Ад — динамический коэффициент
km — коэффициент приведения массы
/ — длина стержня (нли участок его длины)
*пр — приведенная длнна сжатого стержня
6
ДI —абсолютное изменение длины стержня
/й— длина (свободная) ветви колонны меж-
между планками
М — момент внешней сосредоточенной пары
сил
Мк — крутящий момент
М, Мх — изгибающий момент
Mrnex — наибольший по абсолютному значению
изгибающий момент
Мф —изгибающий момент фиктивной балки
Mz, My—из! ибающие моменты относительно глав-
главных центральных осей инерции сече-
сечения гну
Мэ11 , Л4Э///, Mstv, MsV —эквивалентные (расчетные) изгибающие
__ _ моменты по гипотезам прочности
М. (Мк) — изгибающий (крутящий) момент от дей-
действия единичной обобщенной силы
Л4пр—приведенный момент в балках перемен-
переменного сечення
Мп — динамический момент
т — погонный момент внешвих пар сил,
равномерно распределенных по длине;
масса груза, стержня
mnp — приведенная масса
¦U, Nx — продольное усилие; мощность в лоша-
лошадиных силах, вт, кет; частота колеба-
колебаний A/сек); число циклов
N — усилие от действия единичной обоб-
обобщенной силы
Л'д—динамическое продольное усилие
п—число оборотов в минуту; коэффнциен]
запаса прочности
пт, пв — коэффициент запаса прочности по пре
делам текучести и прочности
[п\—допускаемый коэффициент запаса
Пу — коэффициент запаса устойчивости
Р—сосредоточенная сила
Ркр — критическая сила
Pi —обобщенные силы
Рф—фиктивная обобщенная сила
Рд — динамическая сила
Рв — возмущающая сила
Pv — амплитуда возмущающей силы
р — интенсивность распределенной нагрузки
по площади; давление; полное (резуль-
(результирующее) напряжение
Ро —октаэдрическое результирующее напря-
напряжение; контактное давление между со-
составными цилиндрическими трубами
Ртах» Prnin» Pm — максимальное, минимальное и среднее
напряжение цикла
Ра — амплитуда цикла
Ртах* Р'т> Ра ~~ наибольшее, среднее напряжение и ам-
амплитуда цикла при работе на пределе
выносливости
рг — предел выносливости
Р-\ — предел выносливости при симметричном цикле
[p~j — допускаемое напряжение для цикла с коэффициентом асим-
асимметрии г
[p_t] — допускаемое напряжение при симметричном цикле
Q, Qx — вес стержня, груза; касательное усилие; поперечная сила
в сечении
<3ф —поперечная сила фиктивной балки
q Qz — поперечные силы, направленные по осям у, г
Q—поперечная сила от действия единичной обобщенной силы
Qo — вес ударяемого тела
q, qx — интенсивность распределенной нагрузки по длине
q — коэффициент чувствительности материала к концентрации
напряжений
г —- радиус; радиус кривизны нейтрального слоя кривого бруса;
коэффициент асимметрии цикла
Sz, Sy, (S)— статические моменты площади фигуры относительно осей
г, у (нейтральной)
s — размер по дуге, Длина кривой
ds—элемент длины геометрической оси участка
Т — период колебаний; кинетическая энергия
<°—температура в градусах Цельсия системы, стержня
t— время
V — потенциальная энергия упругих деформаций
ч> Мф| «об — удельная потенциальная энергия упругой деформации;
ее части, идущие на изменение формы и объема
V, v — начальный объем; обозначение оси
&V
&V,—у- — абсолютное; относительное изменение объема
Wр — полярный момент сопротивления круглого и кольцевого
сечения
WK — момент сопротивления сечения при кручении
W(Wt, W%) — момент сопротивления поперечного сечения балки относи-
относительно нейтральной оси (осевые моменты сопротивления
для растянутого, сжатого волокна)
Х,,Х„ Хп — лишние неизвестные
х, у, г — оси; координаты
а — угол; коэффициент линейного расширения материала; ко-
коэффициент распределения напряжений при изгибе кривого
бруса; коэффициент концентрации напряжений
аэ —эффективный коэффициент концентрации
(S — угол; коэффициент нарастания колебаний
1 — вес единицы объема материала; относительный сдвиг (угло-
(угловая деформация)
Tit Ъ> Тз —¦ главные угловые деформации
у0 — октаэдрический сдвиг
Д—линейная величина неточности изготовления упругого эле-
элемента системы; натяг составных труб
6 — упругое обобщенное перемещение; статическое перемещение
8z. 8у. К< 8г — проекции перемещения на оси г, у, на вертикаль и на гори-
горизонталь
Щ — допускаемое перемещение точки
blp> 8tt. hk — обобщенные перемещения; коэффициенты в уравнениях ме-
метода сил
Ъд—динамическое перемещение
6о —обобщенное перемещение точки подвеса груза при статиче-
статическом действии возмущающей силы
е — линейная деформация (относительное удлинение)
Нг еа» es — главные линейные деформации
е'—относительная поперечная деформация
ем — масштабный коэффициент
еп—коэффициент поверхностной чувствительности
О» Од. — угол поворота сечення балки
Од — динамический угол поворота
К — модуль объемной упругости материала
% —коэффициент сжимаемости материала
I — гибкость стержня
^к» ^в — гибкость колонны, ветви
^ —коэффициент Пуассона материала; коэффициент дли-
длины сжатого стержня прн продольном изгибе
р—расстояние от центра; раднус кривизны геометриче-
геометрической оси кривого бруса
Pt> Pm — радиусы кривизны окружного (кольцевого) н меридио-
меридионального сечений стенки сосуда
a^ ал* °а — нормальные напряжения
<*и °2> аз — главные напряжения в рассматриваемой точке
сп — предел пропорциональности
от — предел текучести
од—предел прочности (временное сопротивление)
[я]—допускаемое напряжение на растяжение и сжатие
со —октаэдрическое нормальное напряжение
[°рЬ 1°с1» [°и1> [асм1 — допускаемые нормальные напряжения на растяжение,
сжагие, нзгнб, смятие
сэ/ • °э/У» •••*G9v — эквивалентные (расчетные) напряжения по гипотезам
прочности: первой, второй... пятой (гипотезе О. Мора)
%р — критическое напряжение
[Оу] — допускаемое напряжение на устойчивость
сг, ct — радиальное н тангенциальное нормальные напряжения
в толстостенной трубе
Cf,cm — окружное и меридиональное напряжения в тонкостен-
тонкостенных сосудах
аг — предел выносливости
%axt offll са — наибольшее, среднее нормальное напряжение и ам-
плнтуда цикла
a_i—предел выносливости при симметричном изгибе
с_1р—предел выносливости при симметричном осевом растя-
жении-сжагии
[°г] — допускаемое нормальное напряжение при цикле с
коэффициентом асимметрии г
[о^,]—допускаемое нормальное напряжение при симметрич-
симметричном цикле
сд — динамическое нормальное напряжение
т, ia —касательное напряжение, "Сщах— наибольшее каса-
касательное напряжение
^1, ^2. "*з™экстремальные касательные напряжения
¦со — октаэдрическое касательное напряжение
М —допускаемое касательное напряжение
*to — динамическое касательное напряжение
тг — предел выносливости прн крученнн
•сшак, tm, та — наибольшее, среднее касательное напряжение и
амплитуда цикла
t_i — предел выносливости при симметричном кручений
[%г]—допускаемое напряжение прн кручении для цикла с
коэффициентом аснмметрнн г
[г_г] — допускаемое напряжение при симметричном цикле
^ — угол закручивания; коэффициент уменьшения допуска-
допускаемого напряжения при продольном изгибе
|<р] — допускаемый угол закручивания
со — площадь эпюр изгибающего момента, угловая ско-
скорость; круговая частота колебаний
ш, — круговая частота изменения возмущающей силы
ЕДИНИЦЫ ИЗМЕРЕНИЙ
Международная система единиц (СИ)
м, кг, сек—метр, килограмм, секунда; единицы длины, массы,
времени (основные единицы)
см, лш — дольные единицы длины (сантиметр, миллиметр)
н—иьютои, единица силы I 1к;«-g-gj-K/* = 0,102 кГ )
кн, Мн— дольные единицы силы: килоньютон, меганьютоиAкк=
= 103н; 1 Мн = 10е н)
н/м" — единица напряжения и дзвления A h/jus яа
ж 1,02.10 кГ/см')
Мн/м' — дольная единица напряжения и давления A М н/л4а =
KW2 t 10,2 кПсм»)
дж — джоуль, единица работы A дж х л g. кГ-м
х 0.102 кГ-1
вт; кет — ватт, киловатт; единицы мощности A кет ss
х 102 кГ-м/сек х 1,36 л. с.)
Техническая система единиц (МКГСС)
м, кГ, сек—метр, килограмм-сила, секунда A к/*«9,81 к)
Г —тонна-сила A Т = 103 кГ »9,8Ы08 к = 9,81 кн)
кГ/см" — единица напряжения и давления A кГ/см* х
Ж9.8Ы04 «Ли2«0,0981 Мн/м*)
бар — внесистемная единица давления
A бар = 106 h/jk2 «* 1,02 кГ/см*)
кГ-м — единица работы A кГ-м х 9,81 дж)
л. с. — внесистемная единица лошадиная сила
A л. о. = 75 кГ-м/сек =к 0,736 кет)
ОБЩИЕ ЗАМЕЧАНИЯ К УСЛОВИЯМ ЗАДАЧ
1. Во всех задачах величины, указанные на рисунках, считать заданны-
заданными, искомые величины (там, где это необходимо) отмечены вопросительным
анаком
2. Задачи, условия которых даны в Международной системе единиц
(СИ), предусмотрено решать в этой системе.
3. Если на рисунках ае указаны иаимеиования размеров, то считать
их в миллиметрах.
4. Элементы, указанные иа рисунках двумя линиями со штриховкой,
считать абсолютно жесткими.
5. Считать, что во всех элементах конструкций, испытывающих сжатие
(за исключением случаев, где это особо оговорено), устойчивость обеспечена.
9
I. РАСТЯЖЕНИЕ И СЖАТИЕ
§ 1. Продольное усилие
Равнодействующая нормальных сил упругости в сечении назы-
называется продольным усилием. Продольное усилие определяется ме-
методом сечений. Величина продольного усилия Ых в каком-нибудь
поперечном сеченни стержня равна алгебраической сумме всех
внешних продольных сил (сосредоточенных Р и распределенных
по произвольному закону с интенсивностью qx), действующих на
стержень по одну сторону от рассматриваемого сечения. Растяги-
Растягивающее усилие считается положительным, сжимающее — отри-
отрицательным.
Общая формула, по которой можно определить величину про-
продольного усилия в произвольном поперечном сечении стержня,
имеет следующий вид:
JV, = ЕР + v\qxdx. A)
Интегрирование производится по длине каждого участка, на
который действует распределенная сила, а суммирование — по
всем участкам, расположенным по одну сторону от рассматриваемого
сечения.
Если вектор продольного усилия Nx направлять в сторону от
рассматриваемого сечения, то условия равновесия отсеченной части
стержня, т. е. формула A), будет давать величину и соответствую-
соответствующий знак усилия.
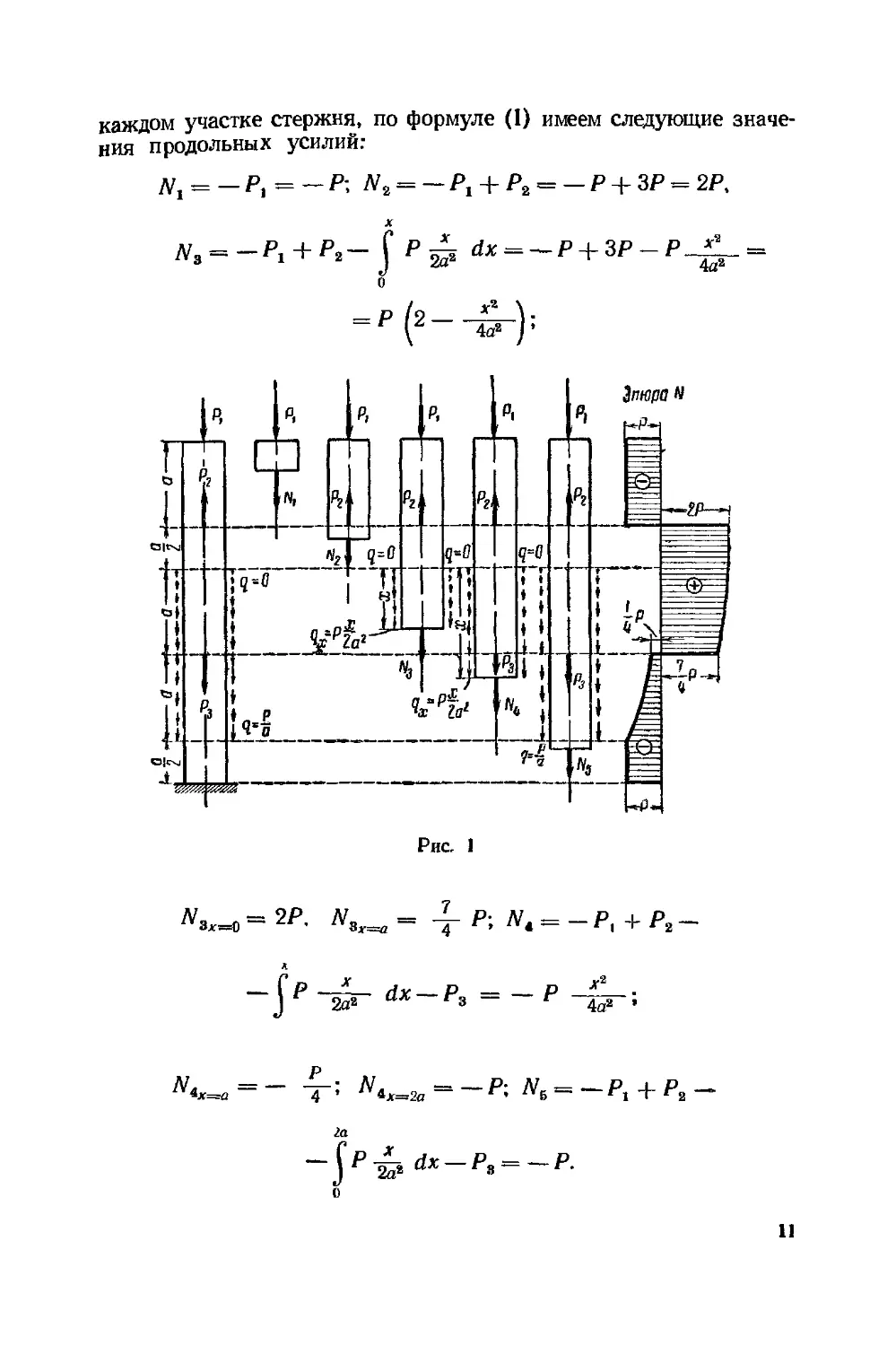
Пример 1. Дано Р,= Р, Р2= ЗР, Р3= 2Я; распределенная
г»
нагрузка qx изменяется по линейному закону от q = 0 до q =—
(рис. 1).
Построить эпюру N.
Решение. Проводя произвольное поперечное сечение на
10
каждом участке стержня, по формуле A) имеем следующие значе-
значения продольных усилий:
4а2
^з*=о = 2Р-
Рис, 1
, = -j- P\ NA = — Pt ¦+¦ Р2 —
Wy р — р * .
Л'.
~ "Г! ^*,=2о = -Р: Л6 = -Р, + Р2 -
11
Эпюра N изображена иа рис. 1.
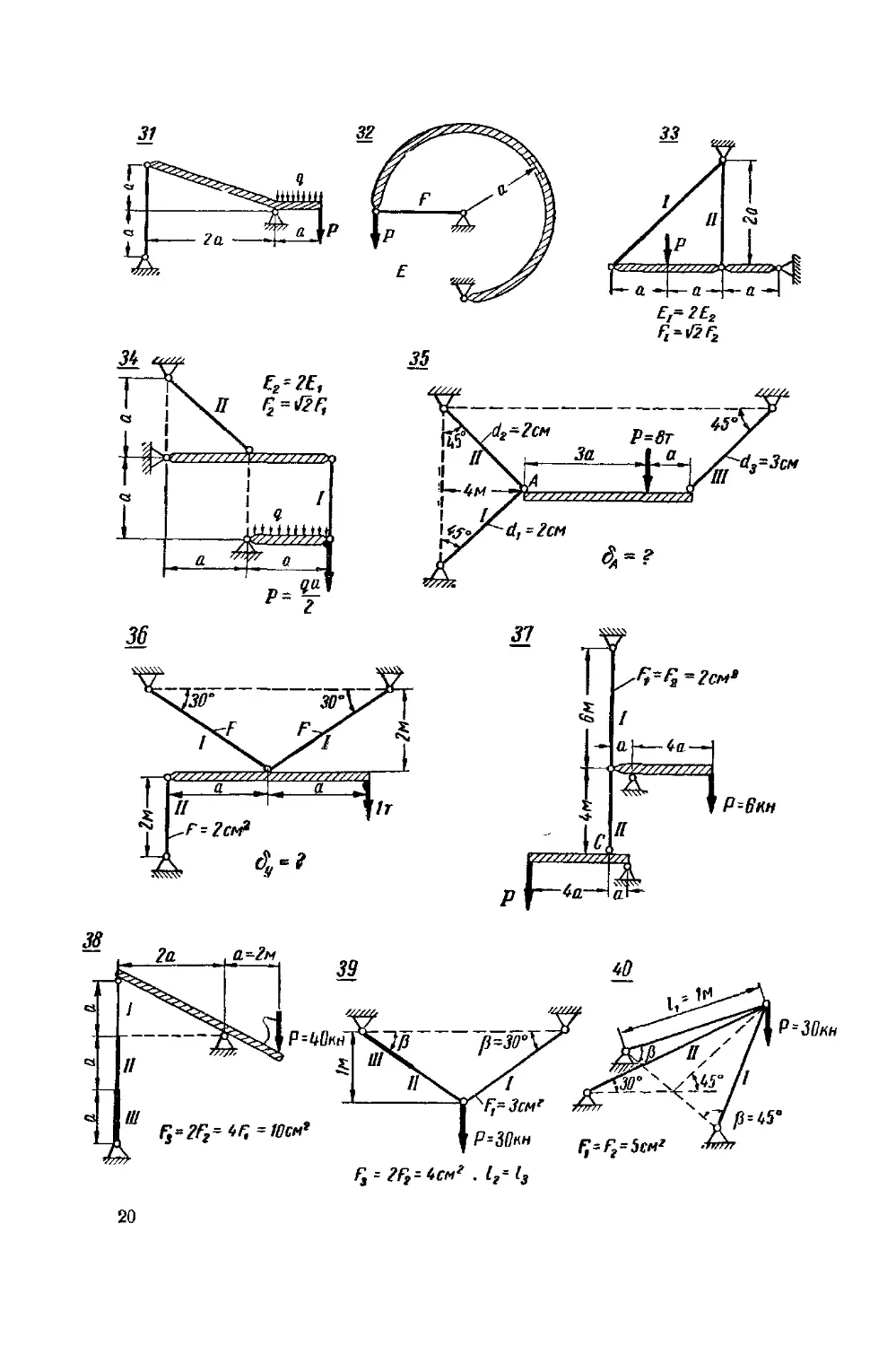
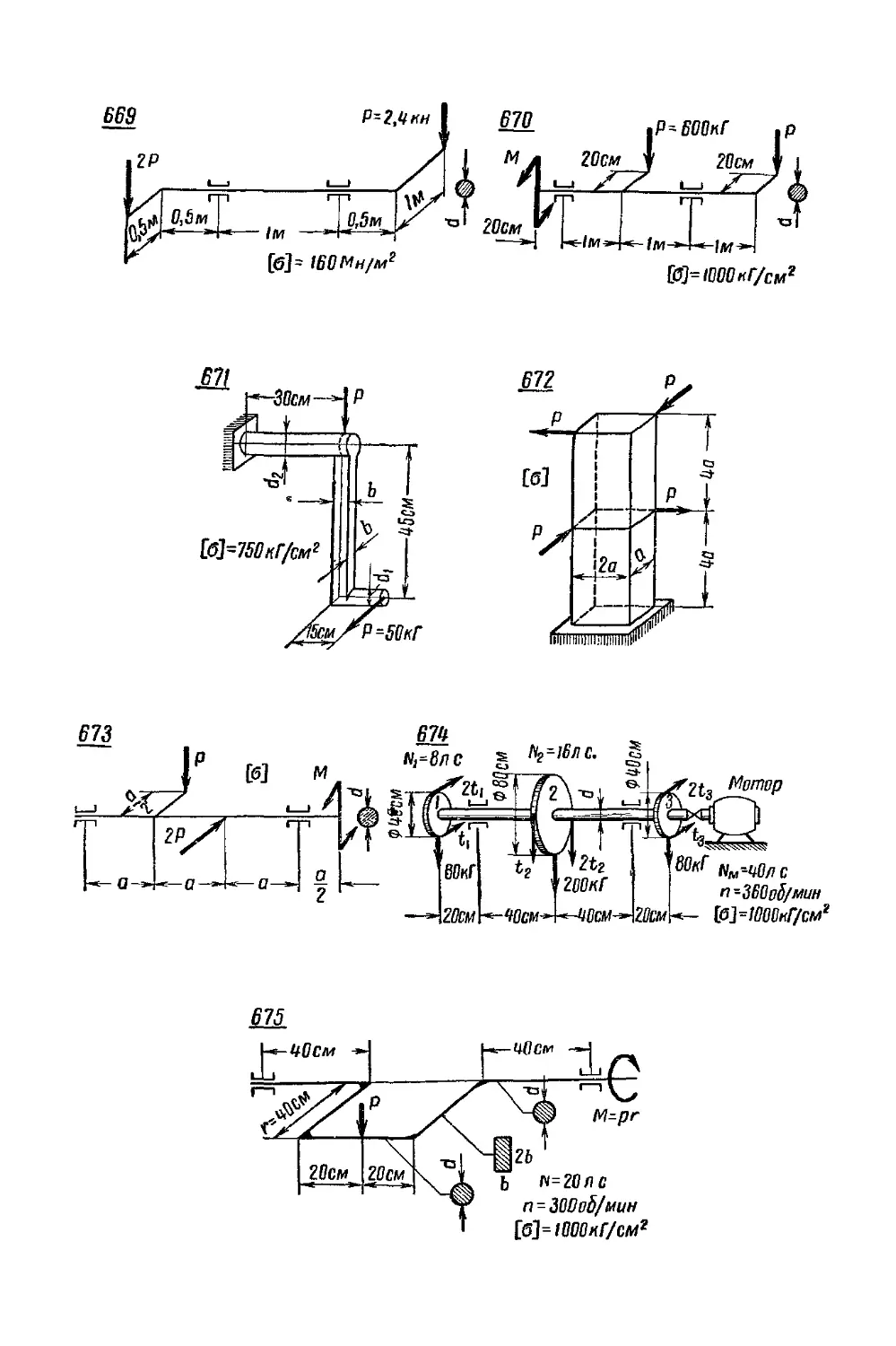
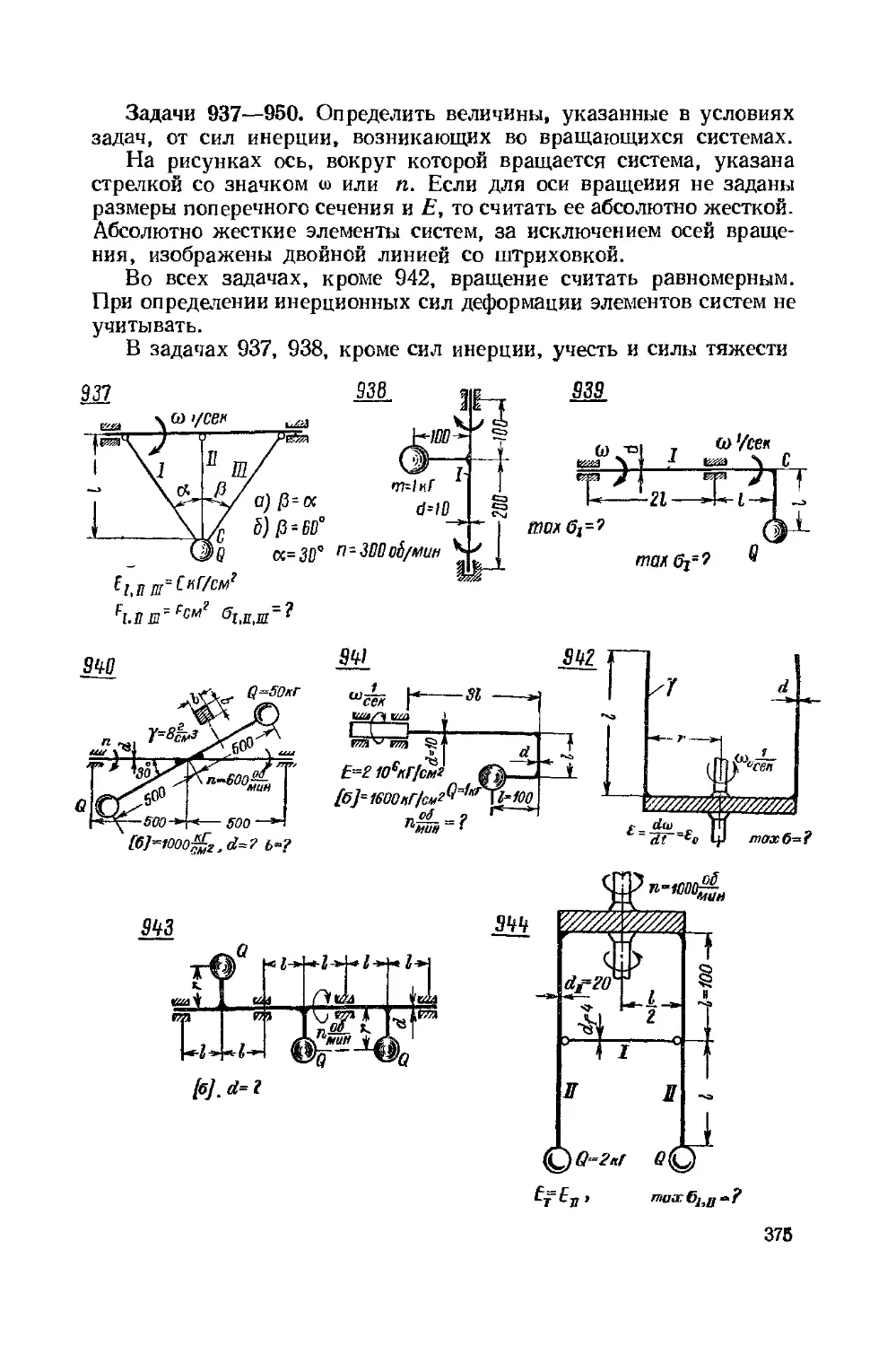
Задачи 1—8. Построить эпюры продольного усилия N.
В задачах 6, 7, 8 считать, что интенсивность распределенной
нагрузки qx изменяется по линейному закону.
I
Wto»
Щ/ня
¦3|СТЭ
\4°St/m f t У
2r
13т
=»
§ 2. Нормальные напряжения, абсолютное удлинение
и потенциальная энергия
Принимается, что во всех поперечных сечениях растянутых или
сжатых стержней (приближенно и для стержней переменного сече-
сечения) нормальные напряжения ох распределены равномерно.
Поэтому величина нормального напряжения в произвольном
поперечном сечении стержня определяется отношением продоль-
продольного усилия Nx в этом сечении к его площади Fx, т. е.
Считая материалы стержней подчиняющимися закону Гука,
12
величину абсолютного удлинения стержня можно определить по
следующей общей формуле:
где E — модуль продольной упругости материала стержня.
Интегрирование производится по длине каждого участка, а
суммирование — по всем участкам стержня.
Если на длине I стержня N и F постоянны, то Д/ = gp.
Общая формула для определения количества потенциальной
энергии упругой деформации 0, накопленной в стержне при растя-
растяжении и сжатии, имеет вид
// =
2EFX
D)
Эпюра бх
31,8
Мн/м*
Интегрирование и суммиро-
суммирование здесь производится так
же, как и при определении удли-
удлинения стержня.
Так как в пределах упругости
материала можно считать коли-
количество потенциальной энергии
равным работе внешних сил, то
для стержней, растянутых или
сжатых силами Р, приложен-
приложенными по концам,
U = ~РМ.
E)
Рис. 2
Пример 2. Дано: Р = 10 кн; / = 0,3 м; d — 0,01 м; d, =
= @,01 + л?) м; Е = 2-Ю5 М«/м2 (рис. 2).
Построить эпюру ох и определить Д/ и С/.
Решение. Продольное усилие в любом поперечном сече-
нин Л^ = Р = 10 кн. Площади поперечных сечеиий: в цилиндри-
цилиндрической части
F = J^!_ = 0,25 л- Ю-4 ж2;
в переходных частях
13
Нормальные напряжения: в цилиндрической части
ох = tf- = 0-25'°10-4 . нли ах » 1,273- 10s н/жа = 127,3
в переходных частях
Njc 4P 4-104
"~ 7i@,
127 3
о_п = 127,ЗУИ„/л«2; о ,= ¦ 127'3
i.~" A + 100-0,052)а
е
= 81,6 Mk/jh2; о , =31,8 Мн/мК
Эпюра ах изображена на рис. 2.
По формуле C) абсолютное удлинение стержня
Л / _ У С **** _ Pl j. 2Р f ^ _
'"'JJ ??дг ~ ZEF r .? J @,01 + *у ""
Р< 8Р I л- 1 '
3EF + 7t? 2@,01 + *2) " 0,1s
6TF arctS oTT
101030,3
3-2-10"-0,25n:-10-<
8-10' / 0,1 1 .\
+ 7t.210»|i2@,01+0,l2H,l2+ 2-0,1= arCtg }'
Д/ ж 1.46-10-» « = 0,0146 си.
По формуле E) количество потенциальной энергии упругой
деформации, заключенное в стержне,
., PAi ю* -1, 4б-10-«
I/ = ¦ g = ^^ = 0,73 дж я= 7,45 кГ-см.
Задачи 9—16. Построить эпюры нормальных напряжений о
и определить абсолютные изменения длин стержней Д/ и потен-
14
цнальные энергии упругих деформаций U, накопленные в стерж-
стержнях.
Считать ? = 2-105 Мн/м2- В задачах 11—14 принять Е =
= 2 - 10к кГ/см2.
9
Юли
20 кн
ЗВкн
W
t
t
t
t
t
•!
L
r~~
t
t
f
6) Шн
t
Л
IOkh
12
te-ЛА-
\21
IB
Wkh
5см
4 см
Wkh
§ 3. Поперечная деформация и изменение объема
Относительная продольная деформация е по закону Гука при
растяжении или сжатии равна
а относительная поперечная деформация
е'= — це = — [х -^-,
где |» — коэффициент Пуассона материала
G)
15
Относительное изменение площади поперечного сечения стержня
можно определить по формуле
(8)
Для определения абсолютного изменения объема стержня слу-
служит выражение
Nx их.
(9)
Интегрирование производится по длине каждого участка, сум-
суммирование — по всем участкам.
Если стержень растягивается или сжимается
силами Р, приложенными по концам, то
PL
A0)
Пример 3. Дано: Р, q, I, F^ E, v- (рис. 3).
Определить &х, * , Д V.
Решение. По формулам A) и B) продоль-
продольное усилие и нормальное напряжение в произ-
произвольном поперечном сечении будут:
Так как относительное удлинение по закону Гука имеет зна-
значение ех—~§-=РЕрЧХ' т0 по Ф°РмУле №) относительное изменение
площади поперечного сечения стержня равно
л Vti ^ v >t ' !•
Пользуясь формулой (9), определяем абсолютное изменение
объема стержня
LV--
16
(*+*)«¦
Задачи 17—24. Определить величины, указанные в условиях
задач.
В задаче 24 принять для стали Е = 2 • 106 кГ/смг; ц = 0,3.
§ 4. Перемещения точек шариирно-стержиеаых систем
Определение упругих перемещений точек шарнирно-стержне-
вой системы производится по следующей общей схеме.
Из условий статики находятся продольные усилия во всех упру-
упругих элементах системы По закону Гука устанавливаются величины
абсолютных удлинений элементов.
Считая, что элементы системы при деформации не разъединяют-
разъединяются, пользуясь методом засечек, составляются условия совместности
перемещений, т. е. геометрические зависимости между перемеще-
17
ниями элементен, составляющих систему. Из полученных зависимо-
зависимостей определяется величина искомого перемещения.
При использовании метода засечек надо иметь в виду, что каж-
каждый элемент системы, кроме осевой деформации, может еще пово-
поворачиваться вокруг соответствующего шарнира. Поэтому каждая
точка элемента может перемещаться вдоль осн элемента и по дуге
окружности соответствующего радиуса. Эти дуги (засечки) допу-
допустимо заменять перпендикулярами к радиусам вращения, поскольку
упругие удлинения элементов малы по сравнению с их длинами.
Рис. 4
Пример 4. Дано: Р, a, Et, Flt ?2. Р% (рис. 4, а).
Определить горизонтальную Ьх н вертикальную 8}, проекции
перемещения 8 точки приложения силы Р.
Решение. Расчленяем систему сечениями тяг / и // на две
системы (рис. 4, б).
Из условий статики Т,Мл =0 и Т.Мв = 0 определяем усилия
Р 2
в тягах Л', = -j- нЛ'а = -д-Р
Ра
2Ра
По закону Гука Д /, = 3? р— н Д /2 = 3? р—¦.
Пользуясь методом засечек (рис. 4, б), находим горизонтальное
перемещение точки С, равное Д/2, и перемещение точки С, перпен-
перпендикулярное линии ВС: ос = Д/2 У~2.
Точка D может перемещаться только горизонтально. Это пере-
га
мещение равно bD = 8С ^ .—= 2Д/2
Горизонтальное перемещение точки приложения силы Р сложит-
18
ся из горизонтального перемещения точки D и удлинения 1-й тяги,
т. е.
. = 2 Д /2 + Д /, =
АРа , 1
L_
Вертикальное перемещение точки приложения силы Р
Задачи 25—40. Определить перемещения 8 точек приложения
внешних сил Р (или других точек, указанных в условии) и нормаль-
нормальные напряжения в поперечных сечениях упругих стержней.
В задачах с буквенными условиями, в которых нет значений
Е и F, считать их известными и одинаковыми для всех упругих
элементов системы. В задачах 37—40 принять для всех стержней
Е = 2 105 Мн/м2. В задачах 35 и 36 принять Е = 2-Ю6 кГ/см2.
19
§ 5. Прочность и жесткость
Подбор необходимых размеров площади F поперечного сечения
растянутого или сжатого стержня постоянного поперечного сече-
сечения производится по расчетной формуле
F— N™&* МП
где Nmax — наибольшее по модулю продольное усилие в рассчиты-
рассчитываемом стержне, а [о]—допускаемое напряжение материала стерж-
стержня на растяжение—сжатие или на растяжение [cf], на сжатие [ос].
Для материалов, одинаково сопротивляющихся растяжению и
сжатию (для пластичных материалов),
[°р] = К1 = [о] = -^ , A2)
где от — предел текучести материала при растяжении (сжатии),
пт — коэффициент запаса прочности по пределу текучести.
Если дополнительно ставится условие, чтобы упругое переме-
перемещение 8 какой-нибудь точки системы не превосходило заданной
допускаемой величины [8 ], то производится проверка на жесткость
согласно неравенству
A3)
Пример 5. Дано: Р = \Т;а= 1 м; а= 30°; [ор h = 1000 кПсм?,
?, = 2-106 кГ/см2; [ос ]//= 100 кПсм2;
?2 = 0,Ы06 кГ/см*;
допускаемые горизонтальная [&х] и вертикальная [Ьу ] проекции
перемещения точки приложения силы Р: [8 ] = [Ь„ ] = 1 3 мм
(рнс. 5). У
Определить Fi и F2.
Решение. Из условий статики (рис. 5, a) ZX— 0 и EF = 0:
Nt = N2 = N; N = Р = 1 Т.
По формуле A1)
По закону Гука
л; Na, Ю3-Ю" г, пк . , Na
10».10s л1
=0,1 см.
0,1-10е-10
Из геометрического построения, полученного методом засечек
(рис. 5,6), следует, что Д/i равно сумме проекций Ьх и 8^, на направ-
21
ление стержня /, а Д/2 равно сумме проекций 8*- и Ву на направление
стержня //, т е
Д/, = 8у sina — S
Следовательно,
sin a -+- 8^ cos a.
мм.
/
Рис. 5
Рис. 6
Так как 8у>[8у]. то следует увеличить площади сечений стерж-
стержней.
Сохраняя площадь стержня / Ft = 1 см\ найдем необходимую
площадь стержня // — F2-
По условию жесткости
г
или
откуда
0,05 + А/, <0,13 см.
см и
22
При такой площади напряжение в стержне //
с„ = -?- = 80 кГ/см*,
а горизонтальное и вертикальное перемещение точки приложения
силы Р
Ьу = 1,3 мм; Ъх = -°'08~0'05 » 0,0173 еж = 0,173 лш.
Пример 6. Круглое кольцо внутренним радиусом г = 100 мм,
наружным радиусом R — 101 мм и длиной / подвергается действию
внутреннего равномерного радиального давления р = 20 бар
(рис. 6, а).
Определить увеличение радиуса кольца Лг и коэффициент за-
запаса прочности л„ с которым работает кольцо, если материал его
стенки имеет модуль продольной упругости Е = 2 • 105 Мн/м2 и
предел текучести от = 300 Мн/м2.
Решение. Для определения продольных растягивающих
усилий Л\ развивающихся в стенке кольца, рассекаем его диамет-
диаметральным сечением (рис. 6, б). Составляем условие равновесия полу-
полукольца как сумму проекций сил и усилий, которые для полукольца
будут внешними силами, на ось у; тогда
«/2
N = I plr sin ada = prl.
Нормальное напряжение в стенке кольца
N prl 20-105-10-Ю-2 „ ,„„ . , ПГ1Г1 ,. . „
° — —р— (Ц — А1 = —о 1 10-а— =-2• 1° н/жа= 200Мн/м2.
Коэффициент запаса прочности ит (по отношению к пределу
текучести материала)
300
Абсолютное увеличение внутреннего радиуса кольца Лг найдем
по закону Гука. Так как
E(R — r) I '
TO
Задачи 41—48. Подобрать размеры площадей F поперечных
сечений упругих элементов систем.
23
В задачах с буквенными условиями считать допускаемое напря-
напряжение [о] одинаковым на растяжение и сжатие для всех упругих
элементов системы. Если в условии задачи модуль упругости Е не
вздан, то считать его известным и одинаковым для всех стержней.
В задачах 45—46 принять для стали Е = 2- 10е кГ/см2.
24
Задачи 49—53. Определить допускаемую силу Р или вели-
величины, указанные в условиях.
50
Г=2смг,
[б] =Г20Мн/м
52
53
ZF
I i
\-—га —-4- и—Г
\б\ = 1500 кГЛм'
Чисм долтоё п=8
[С] =!00кГ/см';
§ 6. Учет собственного веса
Для призматического стержня при действии собственного веса и
сосредоточенной силы Р на свободном конце:
продольное усилие в поперечном сечении на расстоянии х ас сво-
свободного конца
Nx = P-\-yF x, A4)
A5)
нормальное напряжение в этом же сеченни
необходимая площадь поперечного сечения
F= p
абсолютное удлинение
A6)
A7)
25
где 7 — вес единицы объема материала стержня, / — длина стерж-
стержня и Q = -jFl — вес стержня.
Для бруса равного сопротивления, т. е, для стержня, у которого
в каждом поперечном сечении нормальные напряжения одинаковы,
подбор площади поперечного сечения производится по формуле
F = ¦
•ew , A8)
1 "i
где е — основание натурального логарифма.
Абсолютное удлинение бруса равного сопротивления опреде-
определяется выражением
Д/ =
[о]/
A9)
Для ступенчатого бруса площадь произвольной /-той ступени
Р Мм
' (M-T'i) (М-тгУ (М-т<«)
а абсолютное удлинение
Е
B0)
B1)
/э... — длины соответствующих ступеней бруса.
Пример 7. Дано Р = 16 Т;
7 = 8 Г/м3; [о] = 1600 кГ/см2;
Е= 2- 10е кГ/аФ, 1= 40 м (рис. 7).
Определить: площадь Fn, вес
Qn и абсолютное удлинение Д/п
призматического стержня; наи-
наибольшую площадь Fc ; вес Qc и
абсолютное удлинение А/с ступен-
ступенчатого бруса с 4 ступенями одина-
одинаковой длины; наибольшую пло-
площадь Fp. вес Qp и абсолютное
удлинение Л/р бруса равного со-
сопротивления.
Решение. Для призмати-
призматического стержня (рис. 7, а): пло-
площадь по формуле A6)
Рис. 7
16- 10s
16-102 — 8- Ю-3- 4-103
¦¦ 10,204 аи2",
вес
= 8-Ю-8-10,204-4- 10s «326,53 «Г,
абсолютное удлинение по формуле A7)
"'-- 2-Iff--10.204Г[ *" *" ' 2
Для ступенчатого бруса (рис. 7, б):
наибольшая площадь по формуле B0)
р _ ЯН3 ;
* г. —
l6-103 + ~\~ 3.168 СМ.
8^10-».4.10»\« ** 10,203 як»,
)
810
.6-10- A--4.
qc = [o1 Fc — P= 16-10s-10,203—16-103~ 324,8 к/\
абсолютное удлинение по формуле B1)
Д 'с =
» 3,192 аи.
Для бруса равного сопротивления (рис. 7, в):
наибольшая площадь по формуле A8)
вес
Qp = И Рр—Р = 16-Ю2-10,202 — 16-103 к323,3 кГ.
абсолютное удлинение по формуле A9)
Д / _ 1"Н l6-102-4-10'
Из полученных результатов видно, что для стального стержня
длиной в 40 м различие между призматическим, ступенчатым бру-
брусом и брусом равного сопротивления весьма незначительно.
Как видно из формулы A6), напряжение от собственного веса в
призматическом стержне достигает 5% от [о] при длине стержня
' > ' ¦ Если стержень стальной, то, считая [о] = 1600 кГ/см?
и 1 = 8 Г/см3,
I > —'8 |0_s = 104 см = 100 м.
27
Задачи 54—57. Определить величины, указанные в условиях
задач.
\@\-ЮкГ/с*Р Bfii/l равного
сспротидления
Г--И1ГЧ
§ 7. Статически неопределимые системы
Статически неопределимыми системами называются системы,
для которых, пользуясь только условиями статики, нельзя опре-
определить усилия во всех элементах. Для расчета статически неопре-
неопределимых систем используются условия статики и условия сов-
совместности перемещений, причем решение идет в следующем порядке.
Для рассматриваемой системы вначале записываются уравнения
статики и устанавливается степень статической неопределимости
системы; затем составляются условия совместности перемещений,
т. е. геометрические зависимости между удлинениями отдельных
элементов системы.
Удлинения элементов системы выражаются через усилия по
закону Гука и подставляются в условия совместности перемещений.
Решая составленные уравнения статики и уравнения совместно-
совместности перемещений, находят продольные усилия во всех элементах
системы.
Для определения температурных напряжений указанная схема
расчета сохраняется. В этом случае условия статики составляются
только для усилий, а величины изменений длин нагретых или
охлажденных элементов определяются алгебраическим суммирова-
суммированием приращений длин от усилий и от изменения температуры.
Абсолютное удлинение от изменения температуры подсчитывается
по формуле
Ы = late,
B2)
где / — длина стержня,
а — средний коэффициент линейного расширения материала
стержня,
28
At — изменение температуры.
Определение монтажных напряжений производится также из
условий статики и условий совместности перемещений. В этом слу-
случае при составлении условий совместности перемещений учиты-
учитывается наличие заданной неточности в длинах элементов системы.
Так как фактические длины элементов, полученные при изготовле-
изготовлении, весьма мало отличаются от предусмотренных в проекте, то
при определении абсолютных удлинений элементов по закону Гука
берутся их проектные длины, а не фактические.
При определении максимальной силы, безопасной из расчета по
допускаемому напряжению, полагают в наиболее нагруженном
стержне напряжение равным допускаемому значению. По найден-
найденному отсюда усилию устанавливают максимальную безопасную силу.
Расчет статически неопределимых систем по несущей способности
производится при помощи только условий статики. В этих условиях
продольные усилия принимаются равными произведениям допуска-
допускаемых напряжений на площади поперечных сечений во всех тех эле-
элементах, в которых достижение напряжениями значения предела
текучести материала приводит систему в геометрически изменяемое
состояние. Такая методика расчета основывается на замене дейст-
действительной диаграммы растяжения материала идеализированной
диаграммой Прандтля, в которой площадка текучести принимается
неограниченной.
Пример 8. Даио:
а) Е, = Е2 = Е3 = Е = 2-106 кГ/см2; [о] = 1600 кГ/см2 (в СИ
Е = 1,96-106 Мн/м*; [о] = 157 Мн/лР); а = 0,4 ж; Ь = 1,2 ж;
с = 0,4 ж; р4 = 45°; рг = 60°; р3 = 30°; F, = 12 си2; F2 = 14 еж2-
F3 = 16 см2 (рис. 8);
б) а, = а2 = а3 = я = 12,5- 10-в;
в) А2 = 1,2 мм — величина, на которую стержни // изготовлены
короче, чем следует.
о) Ч у ^л, 6)
\1
Рис 8
29
Определить; а) Р; Pmzx; б) ол;,,,„; в) о,,„,ш.
Решение, а) Расчет по допускаемому напряжению. Из
условия статики — сумма проекций на вертикальную ось сил и
усилий, действующих в выделенных узлах—(рис. 8, а):
2JV, sin 'ft = 2N2 sin p2; 2N2 sin p2 + 2JVS sin p3 = P.
Из условия совместности перемещеняй, т. е. равенства переме-
перемещений точки приложения силы Р от растяжения стержней lull
и от сжатия стержней /// (рис. 8, б):
По закону Гука
?„ f, sin P, ' *
Из геометрии системы
, Q i _ t i _
1 ~ sin p, ' 2 sin fcs ' *» ~
sin p3 *
После подстановки найденных величии условие совместности
перемещений принимает вид
Nl a Afa ь Н3 с
Е, f.sitfp, + Bj
Для заданных числовых значений
«п & ~-?L; sin р, = -??-. sin p, = -f;
12-2
120-4 80
faSin^Pj — 143 ~ 7 '""' f3sinsp3~ 16-1
В СИ:
о 0,4-4 2000 , ,
Мм;
_
F, sin2p, ~ 1210-4-2 ~ 3
1,2-4 8000
~ 14-10—»-3 ~ 7
с 0,4-4
\Im\
30
Подставляя эти величины' в уравнения статики и уравнения
совместности перемещений, получаем следующую систему трех
уравнений:
Л\ =
14 N,+24 W2 = 21 Ns.
Решение системы дает
Л^-с, F, = 0,332Р; N2 = с„ F2=0,
Л^с,,, FS-0.53P,
откуда
0/ = 0^. р » 0.0276Р; о„ = -^|L p » 0,0193 Р;
В СИ:
Так как наибольшее напряжение ат не должно превосходить
|о], то допускаемая сила
р< А •= S -48340 кГ«48-3 г-
При этой силе напряжения в стержнях системы будут иметь зна-
значения:
а, = 48,3-27,6 к 1334 кГ/сж2; о„ = 48,3-19,3 » 932
о„, = 1600 кГ/сжг.
В СИ:
р < -щ-= т ^О'475 Мн = 475 к«:
о, = 0,475-276 » 131 Мн/жй; o#J = 0,475-193 » 91,7 Мн/мг;
ош = 157
б) Расчет по несущей способности. Система приобретает геомет-
геометрически изменяемое состояние, когда «потекут» первые и третьи
3t
стержни. Условие статики, связывающее усилия в этих стержнях,
имеет вид
2Nt sin p, + 2 N3 sin р3 = P.
Полагая Ni = [о] Ft и iV3 = [о] F3 и подставляя их в условие
статики, определяем максимальную силу Яшах:
Лш,х = 2 [о] (Ft sinPi + Fg sinps) =
= 2-1600 (l2 ^~ + 16 -i-) » 52 750 кГ = 52,75 Т.
В СИ:
шах = 2-157 (l2-10-4 -J^- + 16- 10-i-)« 0,518 Мк =
Таким образом, грузоподъемность системы при расчете по несу-
несущей способности больше грузоподъемности при расчете по допускае-
допускаемому напряжению на
в) Определение температурных напряжений. Из условий статики
(рис. 9, а):
2 Nt sin pt= 2 W2sin p2; 2 W2sinp2 = 2JV3sin p3.
Из условия совместности перемещений (условие неизменности
высоты системы) (рис. 9, б):
В, + Ё2 4- В3 = 0.
Тяк кяк 8 — Д*1 g _ д/ Д'
laKKaKOj— sjn^ , os _
то условие совместности перемещений приобретает вид
Принимая во вииманяе, чтоЛ^ = о; Fit N2 =
и учитывая заданные числовые значения, условия статики и условие
совместности перемещений приводятся к следующим уравнениям:
32
В технической системе:
6 У~2 а, = 7 ]/ о„
7 \ГЪа„ =8о„,
о# + 2о„+2о/## =5000
В СИ:
а, = 7 1/ о„
З«„=8ош
а„ +2ош=490
Решая эту систему, получаем: о, ж 1105 кГ/смг, а„ « 774 кГ/см\
а,„ = 1172 кГ/см2
В СИ:
а, я= 108,5 Мн/м2, ап « 75,9 Мн/м2, а((, я= 115 Мн/м2.
а) 5)
«Л
1
1
1
Рис. 9
Рис. 10
г) Определение монтажных напряжений (рис. 10, а).
Из условий статики (рис. 10, б):
, sinp, = 2JV2sinp2; 2jV2sinp2 = 2p
Из условия совместности перемещений"
+
-I- ¦
или
а,а L 'н
sin2 р, sin2 р2 г sin2 р„ ~ sin» p2 *
Для заданных числовых значений условия статики и условие
совместности перемещений приводят к следующим уравнениям:
2 Заказ № 886 33
В СИ:
о, = 7
В технической системе:
8 о
Решая эту систему, находим о/ ж 886 кГ/см\ оц ж 620 кГ/см2,
- ~_ Q4Q tc Г/г яа2
Hi ^^ ЭО;? tvl/CJn
В СИ: о, « 86,8 Ми/л2, б„ = 60,4 Мн1м'\ °ш = 92 Мн/МК
Пример 9. На стальную цилиндрическую трубу / внутренним
радиусом rj = 40 мм и наружным радиусом Rt = 42 мм надета в
нагретом состоянии стальная
цилиндрическая труба // вну-
внутренним радиусом /2 =
=41,96 мм и наружным радиу-
радиусом /?2 = 43 мм (рис 11)
Определить напряжения в
стенке трубы /— о, ив стен-
Рис п ке трубы 11—о,,, которые
возникнут пря охлаждении
наружной трубы
Модуль продольной упругости материала труб Е — 2- ИN кГ/см2.
Решение Вместо труб рассматриваем кольца единичной
длины (см пример 6) Кольцо // при охлаждении будет оказывать
равномерное радиальное наружное давление р на кольцо / а послед-
последнее, сопротивляясь деформации, будет оказывать такое же давление,
но изнутри, на кольцо //. Величина давления р определится нз
условия, что изменение наружного радиуса кольца 1 ARt и измене-
изменение внутреннего радиуса кольца 11 Агг в сумме должны составить
величину, равную начальной разности /?, — г2
Так как (см. пример 6)
1 ~" ~Ё ' R,~r,
то условие совместности перемещений запишется в следующем виде:
откуда
EjRt-гг)
2-106-0,004
4,2*
~0Х
4,196г
~67Ю4~
= 31
34
Нормальные напряжения о; и аи определятся из формул (см
пример 6):
_р_г\ _ 31-4,2
u'~ «.-',
0,2
= 651 кГ/см?;
31-4,196 .ocr. rl „
= ПШГ ~ 125° кПсм-
Задачи 58—70. Определить нормальные напряжения в упругих
элементах систем от действия сил
Если в условии задачи модуль упругости Е ие задай, то считать
его одинаковым для всех упругих элементов системы
58
Ш
Wi
.2Г
If
f
59
III
16т
ЛПF
Е=Ю5кГ/см*
ВО
fi/
-
Si
1 \
63
Я7
Г,* 2см*
Ж
75 к/у/и
1\
-га -
\-Г, = Вснг
I
^
Задачи 71—73. Подобрать размеры поперечных сечений эле-
элементов системы
7/
72
\б\ -
'\
\р-гет
2й
d--?
Задачи 74—79. Определить монтажные напряжения.
Д — линейная величина неточности изготовления упругого
36
элемента системы Для стержней принять Е = 2- 10е кГ/см2 В за-
задачах 78, 79 принять Е = 2-105 Мн/м2
15 t За 1 JB
F
I
п
а-400
F
«а
it
а
1
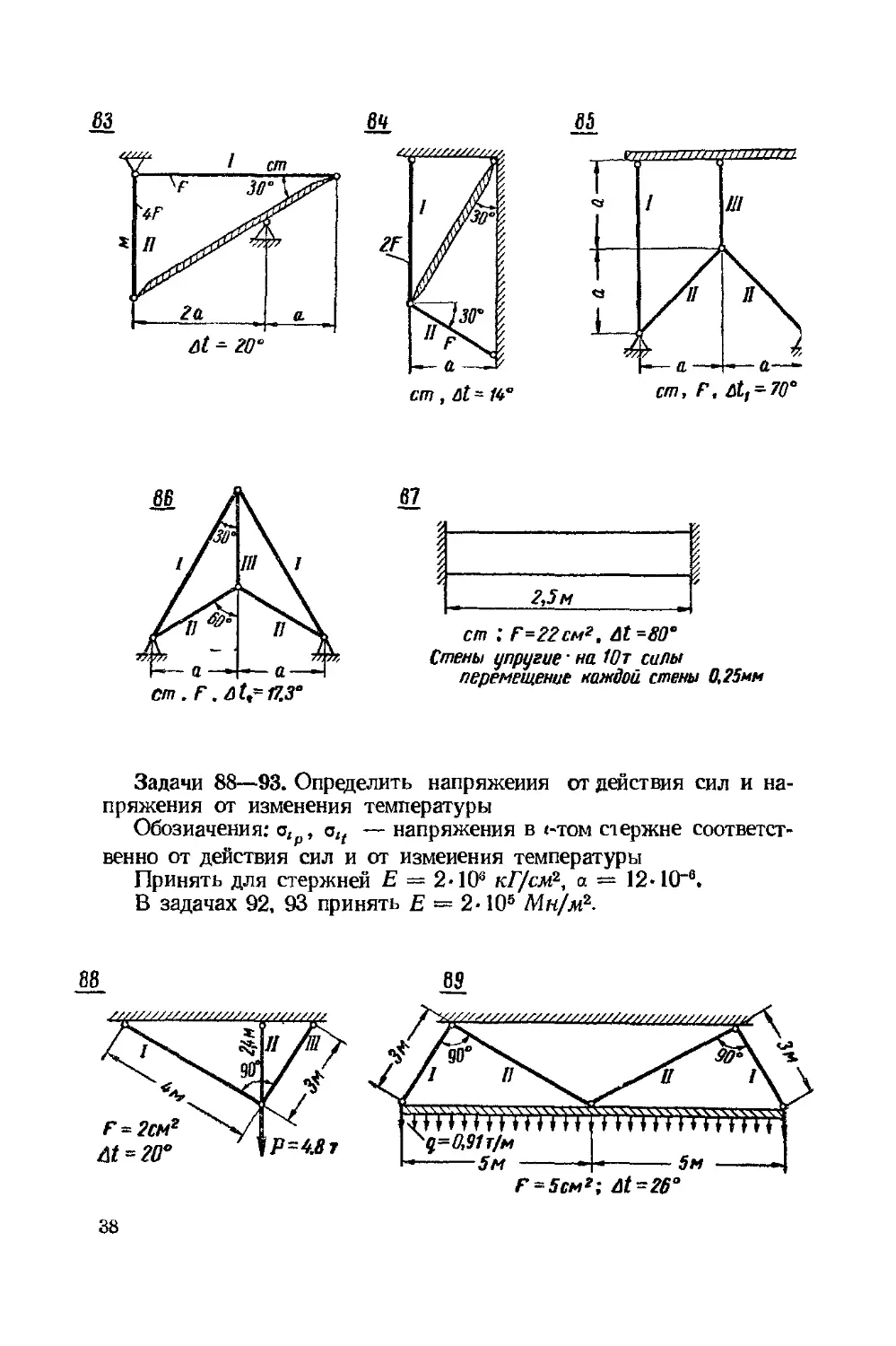
Задачи 80—87. Определить температурные напряжения.
Обозначения- At — изменение температуры в градусах Цельсия
всей системы; /Ц—изменение температуры /-того элемента системы;
ст — сталь; м — медь.
Принять: для стали Е = 2- Ю6 кГ/см2, а = 125-10;
для меди Е = 1-106 кГ/см2, а = 165-1 СИ.
В задачах 84, 86, 87 принять для стали Е = 2- Ю5 Мн/м2.
8? 8/
I
-F
cm
cm .F .At,-17.3°
2,5м
cm :F=Z2cm*. At =80°
Стены упругие" на Ют силы
перемещение каждой стены 0,25мм
Задачи 88—93. Определить напряжения от действия сил и на-
напряжения от изменения температуры
Обозначения: о,р, ач — напряжения в <-том стержне соответст-
соответственно от действия сил и от изменения температуры
Принять для стержней ? = 2- 10s кГ/см\ а = 12- 10Л
В задачах 92, 93 принять ? = 2-105 Мн/м2.
At = 20°
38
Г=2см' . /)t=/D"
ПТП7
W
Iff
*. а/ = -«-
Задачи 94—101. Определить допускаемые силы расчетом по
допускаемому напряжению [Р] и расчетом по несушей способности
'Р'\, а также определить монтажные о,м и температурные о2( напря-
напряжения в соответствии с условиями, данными на схеме
Для стержней принять [о] = 1600 кГ/см\ Е =2-10° кГ/см\
а = 12-10 « В задачах 99, 101 принять [о] = 160 Мн/м\ Е =
= 2-105 Мн/мК
at,*яг
39
96
97
а . I a
6L=iO°
Р
98.
'/////////у////////*"-"'/////////
ut,=10°
Задачи 102—107. Определить величины, указанные в условиях
для тонкостенных цилиндрических колец н труб.
Обозначения: р — давление по площади, q — интенсивность
распределенной нагрузки (кГ/см) между оправкой и кольцом нли
между кольцами.
Принять: для стали (ст) Е = 2-10° кГ/см2; а = 125-10"'; для
медн (м) Е — ЫО6 кГ/см2; а = 165-10~7; для алюминия (алюм)
Е = 0,7-106 кГ/см*.
В задачах 106 и 107 определить о при условии, что в результате
понижения температуры системы зазор Д перекрывается.
да
«=?,«= ?
=' 1200кГ/т>:
[.Г]=
PI
^уУуу^уу",
а
•о
we
/an
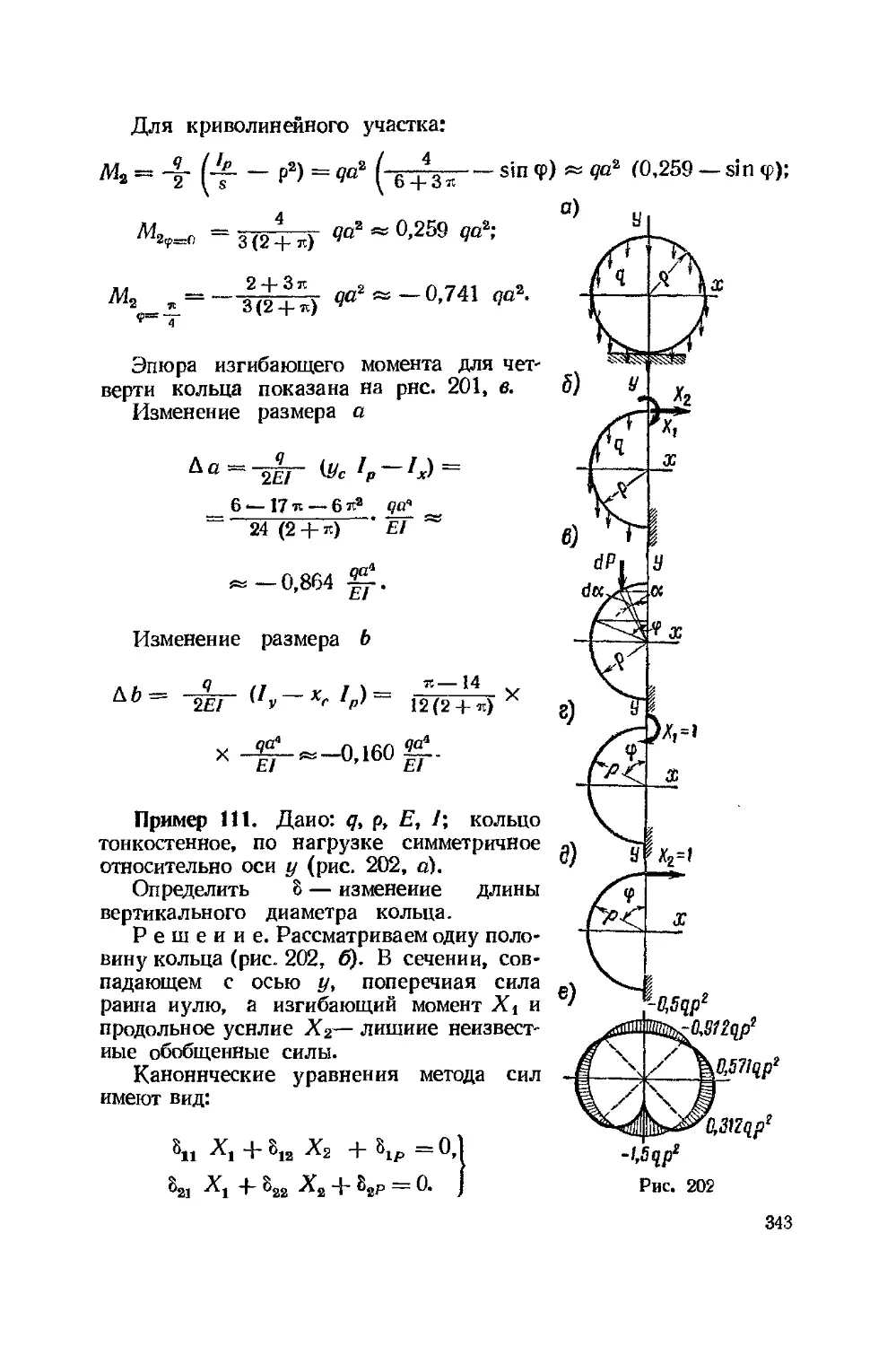
II. НАПРЯЖЕННЫЕ СОСТОЯНИЯ
И ГИПОТЕЗЫ ПРОЧНОСТИ
§ 1. Линейное, плоское и объемное
напряженные состояния
При объемном напряженном состоянии по граням элемента, выде-
выделенного около рассматриваемой точки тела, действуют три, отлич-
отличных от нуля, главных напряжения О( > ог>о3 (рис. 12, а). Площад-
Площадки, на которые действуют ot, o2 и о3 (на них нет касательных на-
напряжений), называются главными площадками напряжений. Оси
(Л //, ///), перпендикулярные этим площадкам, называются
главными осями напряжений.
41
Нормальные о, касательные т и результирующие р напряжения
в наклонных плоскостях сечений определяются по следующим
формулам:
в плоскостях, параллельных оси III (рис. 12, в),
р = Y °s + x2 = V of COS2 a + of sin2 a,
в плоскостях, параллельных оси /У (рис 13, а),
B4)
B5)
/1 itiZ%Z%; (\ 7
'иШШтт
= ог COS2 a
sin 2 и,
= у о?
cos2 а + og sin2 а,
t в плоскостях, параллельных оси
V / (рис. 14, с).
B6)
COS"
2
COS2
> + с3
Р+ о
smz p,
п2 В
з sin2 р.
Рис. 13
Графически эти напряжения устанавливаются по круговым
диаграммам в соответствии с построениями, указанными на
рис. 12, в, 13, 6, 14, 6. Общий вид круговой диаграммы напряжений
получается наложением трех диаграмм, изображенных на рис. 14, в.
Экстремальные касательные напряжения равны:
т, = ±
То = ±
г— °з
2 '
а, — о3
2 '
а, — аг
B7)
Рис 14
Они действуют в плоскостях, расположенных под углами в 45°
к направлениям главных напряжений: т,— в двух взаимно перпен-
перпендикулярных плоскостях, параллельных оси / (рис. 15, а); тг — в
двух взаимно перпендикулярных плоскостях, параллельных оси //
(рис 15. б), т3 — в двух взаимно перпендикулярных плоскостях,
параллельных оси /// (рис. 15, в)
Октаэдрические нормальные ао, касательные т0 и результирую-
результирующие р0 напряжения, которые действуют на площадку, равнонак-
лоненную к трем главным осям напряжений (рис 16), определяются
по формулам'
1 . .ч
Ра=-
02
B8)
Главные линейные деформации е4, е2, е3 (относительные удли-
удлинения, происходящие в направлениях действия главных напряже-
напряжений) имеют значения-
<Ч = -р- [о, - (Л (оа -(- о3) 1.
ег= -g- l^—V- К + Оц)],
°з = -?- l3s - I1 (°i + °а) 1-
f,
Рис IS
Отмосительиое изменение объема
~^г ~ si "Ь ^ т еэ
l—2t»
g-51"
Рис. 16
2 4- Од).
B9)
C0)
Величина 3 р~ * называется коэффициентом сжимаемости
— К называется моду-
модуматериала, а обратная ей величина gfgj
лем объёмной упругости материала.
Удельная потенциальная энергия упругой деформации
и = — (с, s,
= -^ [of
Ь
of — 2[i (о,
44
Удельная потенциальная энергия изменения формы
Мф = gc. f (°1 — ^г) "Ь (°а — °з) + (°в — aiJl* C2)
Удельная потенциальная энергия изменения объема
C3)
Все формулы, относящиеся к объемному напряженному состоя-
состоянию, могут быть применены и к плоскому напряженному состоянию,
если приравнять нулю одно главное на-
напряжение, и к линейному напряжен-
напряженному состоянию, если приравнять нулю
два главных напряжения тп^г/г. л 1 чип г/« »
Пример 10. Дано напряженное со- WMIlm ««ww тг^*
стояние, указанное на рис. 17,
?=2-10е кГ/см2, (х=0,3.
Определить аналитически и графичес-
графически Т) 2,з; о' и т' в плоскости, параллель-
параллельной оси /, при р = 30°; о" и -с" в плос- Рис
кости, параллельной оси //, при а =
=60°; о'" и х'" в плоскости, параллельной оси ///, при a = 30°;
Решение Так как главные напряжения о4 = 200 кГ/см\
о2 = —400 кГ/см2 и о3 = —800 кГ/см?, то по формулам B7) экстре-
экстремальные касательные напряжения
,д = ± -W00^ ± 200 кПсм-, ,,= ± 2OOt8OQ =
= ± 500 кГ/сж2;
По формулам B6) в плоскости, параллельной оси /, при р=30°
о' = _ 400 cos2 30° — 800 sin2 30° = — 500 кПсм*
, —400 + 800 . спо ,„„ „. „
t = y sin 60° ж 173 кПсмг.
По формулам B5) в плоскости, параллельной оси II, при а =60°
о" = 200 cos2 60° —800 sin2 60° = — 550 кГ/см\
sin 120° « 433 кПсм\
45
По формулам B4) в плоскости, параллельной оси ///, при а=30°
о'" = 200 cos2 30° —400 sm230° = 50 кПсм\
Графическое определение всех напряжении указано на круговой
диаграмме (рис 18)
Рис 18
По формулам B8) определяем октаэдрические напряжения:
ро = 100 \/~ D + 16 + 64) » 529 кГ1см\
°о= 4- B00 —400 —800) к -333 кГ/см2,
то = ~ У 9 + 4 + 100 » 354 кГ/смК
По формулам B9) находим главные линейные деформации!
100
0.3-1.2) - 2,8-
100
(—4 + 0,3-6)= 1,1-10-*,
¦§л55- (- 8 + 0,3- 2) = - 3,7 • 10А
2 I0*1
100
48
По формуле C0) определяем относительное изменение объема
-=^-= 10-4 B,8—1,1 —3.7) = —2-10-«
Удельную потенциальную энергию упругой деформации и
энергию изменения объема находим но формулам C1) и C3)
и = 100- 1G-*
B 2,8 4 1,1 8 3,7
Q T* О Г Q
] = 19,8-Ю-2
кГ см
uo6 =
B - 4 - 8J « 3,3 • 10-» кГ-см/см3
Удельная потенциальная энергия изменения формы
«Ф = и — ио6 = A9,8 — 3,3)-10-2= 16,5- 10-г к
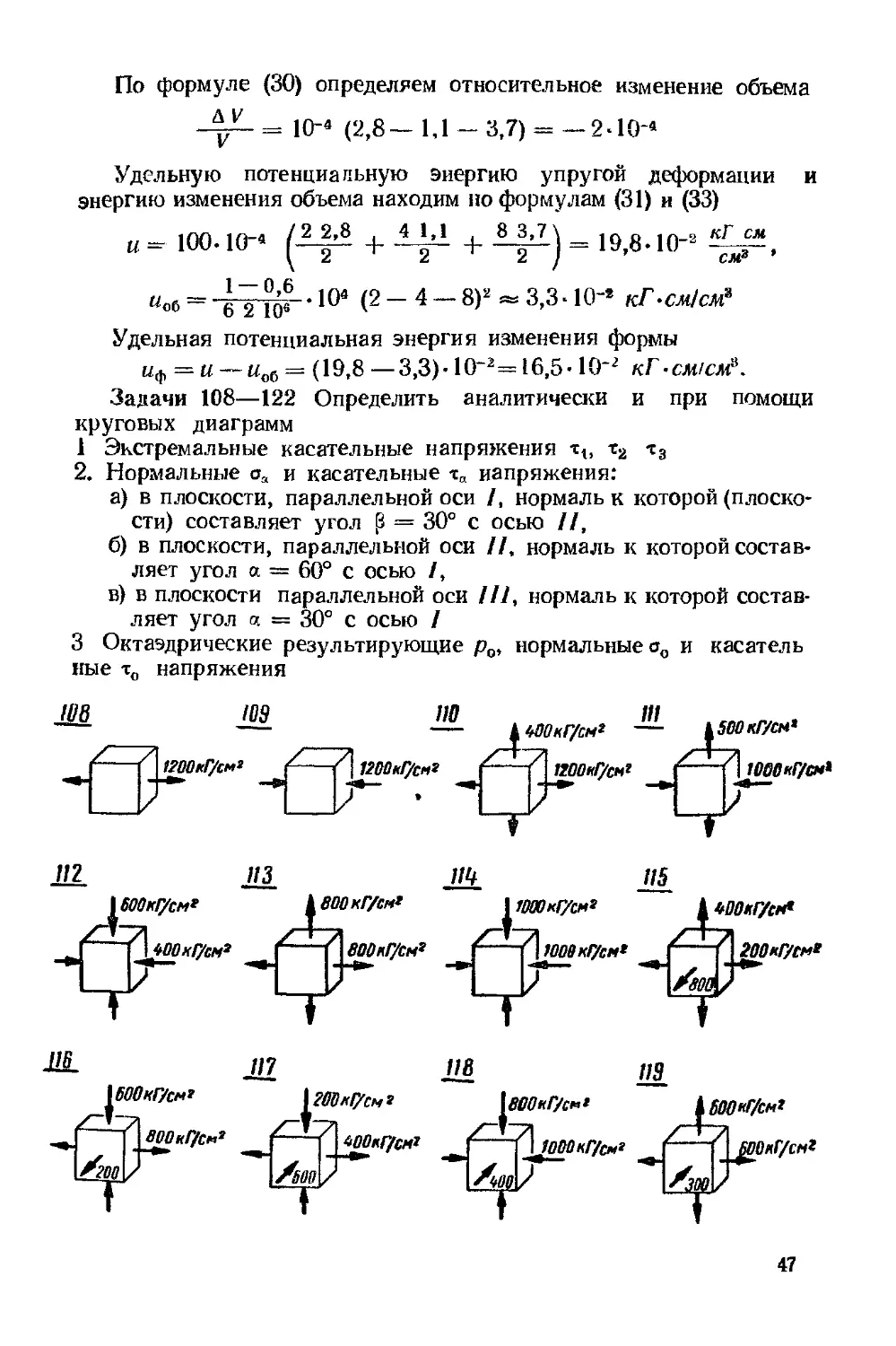
Задачи 108—122 Определить аналитически и при помощи
круговых диаграмм
1 Экстремальные касательные напряжения т,, т2 i3
2. Нормальные а, и касательные х„ напряжения:
а) в плоскости, параллельной оси /, нормаль к которой (плоско-
(плоскости) составляет угол р = 30° с осью //,
б) в плоскости, параллельной оси //, нормаль к которой состав-
составляет угол а = 60° с осью /,
в) в плоскости параллельной оси ///, нормаль к которой состав-
составляет угол а = 30° с осью 1
3 Октаэдрические результирующие р0, нормальные оо и касатель
ные х0 напряжения
108
ад //я
1200кГ/см' А /| ПМкГ/сн*
-^- к ШкГ/см*
А
500кГ/о**
I юввкг/е»*
из
ШОк/усм'
f Г \?00хГ/см3
ж
ZM.
ШпкГ/ск'
lilt
118
ЪЛ /-Ь|
47
Задачи 108'—122' Определить главные линейные деформации
AV
ei» е2, ез; относительное изменение объема -у- , удельную потен-
потенциальную энергию упругой деформации и и ее части, идущие на
изменение формы «ф и объема «о6.
Рассмотреть напряженные состояния, указанные в задачах
108—122
Принять ? = 2-10е кГ/см\ у. = 0,3. В задачах 120, 121, 122
принять ? = 2-106 Мн/лР.
§ 2. Гипотезы прочности
и эквивалентные напряжения
В гипотезах прочности предлагаются критерии, определяющие
прочность элемента материала, находящегося в сложном напряжен-
напряженном состоянии Соответственно этим критериям установлены экви-
эквивалентные напряжения (оэ), т е. напряжения одноосного растяжения
элемента материала, который равнопрочен тому же элементу при
сложном напряженном состоянии
Вне зависимости от принятой гипотезы условие технической
прочности элемента материала при любом напряженном состоянии
имеет вид
°S<K]- C4)
Для объемного напряженного состояния элемента эквивалент-
эквивалентные напряжения имеют следующие значения:
по гипотезе наибольших нормальных напряжений
оэ = о, при а, > 0*,
по гипотезе наибольших линейных деформаций
по гипотезе наибольших касательных напряжений
C5)
C6)
* Иногда на практике в тех случаях, когда |a3l>°i, расчет на проч-
прочность по 1-й теории производят по формулам
°i < [°pJ: I °з I <¦ М-
48
°э = О, — О,
C7)
по гипотезе удельной потенциальной энергии формоизменения
= \/ \ K«i -
по гипотезе предельных напряженных состояний
где
C8)
C9)
|ОС]
Пример И. Для объемного напряженного
состояния (рис 19) о,-= 200 кТ/сж2, о2=
=-400 кГ/сж2, о3= — 800к//см2 (в СИ: о4~
» 19,6 Мн/мК о2 » —39,2 Мн)м\ о3=
« —78,5 М«/ж2) и ц = 0,3
Определить эквивалентные напряжения
по всем теориям прочности.
При определении эквивалентного напря-
напряжения по гипотезе предельных напряженных
состояний принять v = 0,25.
бг
|б2
Рис. 19
Решение ОЭ/ = 200 кГ/см\ оэ„= 200 + 0.3 D00 + 800) =
¦¦ 560 кГ/см*. оэ,„= 200 -Ь 800 = 1000 кГ/см\
j/— Ш + 4J + (- 4 4- 8)г + (— 8 — 2J] »
~ 872 кГ/см\
в СИ:
100
оЭ(/ = 200 + 0,25 • 800 = 400
оЭ/=19,6 Мн1м\
аЭ/. = 19,6 + 0,3C9,2 4- 78,5) ^ 54,9 Мн/м*.
°э„. = 19,6 + 78,5 = 98,1 Мшм\
"IV
10
Т/у 1A.
96 + 3.92J + (— 3,92 + 7,85)* +
19,6 ¦+- 0,25 • 78,5 = 39,2 Мн/мК
49
Задачи 108"—122". Определить величины эквивалентных на-
напряжений по гипотезам прочности.
Рассмотреть напряженные состояния, указанные в задачах 108—
122. Принять A = 0,3. Для 5-й гипотезы — гипотезы предельных
напряженных состояний — считать v = 0,5.
Задачи 123—127. Определить величины, указаЛные в условиях.
Обозначения: к — коэффициент сжимаемости материала, К —
модуль объемной упругости, р — интенсивность распределенной
нагрузки по площади. Во всех случаях трением пренебречь.
В задаче 123 принять для стали Е = 2-10° кГ/см2, (i = 0,28;
для меди Е = 1 - 10е кГ/сФ, р = 0,34, для алюминия Е =
= 0,7-Ю6 кГ/см\ 11 = 0,33.
125
о) стань
tj) медь
В) аппюминий
50
III. ТОНКОСТЕННЫЕ СОСУДЫ
Для сосудов, имеющихформу тела вращения, стенки которых тон-
тонки, не имеют резких переходов и изломов при действии внутреннего,
нормального к стенкам, давления, обладающего осевой симметрией,
можно пользоваться безмоментной (мембранной) теорией расчета.
По этой теории из ус-
условия равновесия элемента,
выделенного около рас-
рассматриваемой точки стенки
сосуда бесконечно близ-
близкими меридиональными и
им перпендикулярными
сечениями (рис 20,а), по-
получается одно уравнение
(уравнение Лапласа) для
определения окружного с,
и меридионального ат нор-
нормальных напряжений
Рис 20
Р<
D1 >
где р, и рт — радиусы кривизны окружного (кольцевого) и мери-
меридионального сечений стенки сосуда на уровне рассматриваемой точки;
р — интенсивность внутреннего давления, являющегося функ-
функцией только координаты г,
8 — толщина стенки сосуда
Из условия равновесия части сосуда, отделенной сечениями,
перпендикулярными меридианам, на уровне рассматриваемой
точки (рис 20,6) получается второе уравнение
am8xcoso = S. D2>
гдех—радиус окружности сечения на рассматриваемом уровне,
а — угол между осью г и касательной к меридиану на том же
уровне, a S — сумма проекций на ось г сил, действующих на отсе-
отсеченную часть сосуда (S отнесено к дуге, равной радиусу),
S = J рх1 йхх.
D3>
Здесь xi — текущий радиус окружности сечения сосуда
Решение уравнений D1) и D2) дает следующие значения напря-
жении а, и о„
4 ~— 5 ~~~ "
D4>
8 р COS2 a
51
Частные случаи:
I- Рт — °°« Ре — Р — сосуд с прямолинейной образующей
6p cos2 я
2. р( = р,„ = р — сферический сосуд
Р9
D5)
О, = -!-i- ¦
Op COS о.
г) р = const (давление газа или пара)
28
25
При рт = с» и р,
ПРИ Р« = Рт = Р
о, = 2от = -^- .
D6)
D7)
D8)
D9)
E0)
6) р = i(h—г) (давление жидкости, рис 21),
где f — вес единицы объема жидкости, h — высота уровня жидкости
в сосуде, г — текущая ордината
Величина
S, = J гж rfx
E1)
E2)
легко определяется, если известно уравнение образующей сосуда
г = г (ж).
На внутренней поверхности стенок сосуда третье главное нор-
нормальное напряжение о, = —р В большинстве случаев оно весьма
мало по сравнению со,и от и им можно пренебречь прн расчете на
прочность.
52
Если стенкн сосуда имеют резкий излом (рис. 22,с), то в пере-
переходном сечении возникают краевые силы, могущие вызвать значитель-
значительные перенапряжения, которые не учитываются безмоментной теори-
теорией. Чтобы уменьшить влияние этих сил, стыковое сечение часто
упрочняют распорным кольцом
Если меридиональные нормальные напряжения в сеченни стыка
ат = о0 (рис 22,6), то погонная распорная сила
ft, = о08 sin<x0. E31
Рис 21
Рис 22
Необходимая площадь F распорного кольца радиуса г может
быть найдена по формуле
Ор8л sin a0
~" [«1
E4)
Пример 12. Дано -j = 1,2 г/см\ Л, = 4 м; г = 1 м; а = 60°;
[о] = 1000 кГ/см2 (рнс 23)
etS г От8
Рис 23
53
Определить 8, F.
Решение Для конической части сосуда
— z) = i(h— jcctga)
COS Ct
По формуле E2)
X
Sj = ctg a J ла dx = -^- = ctg a.
По формуле E1) вес жидкости в объеме отсеченной части сосуда
Окружные ot и меридиональные ат нормальные напряжения в
точках стенки конической части сосуда на произвольном уровне,
определяющемся координатой х, по формулам D5), равны
-у (h — х ctg а) х ix / h х \
6 cos а о \ cos а sin а /
1X4 — — ctg а
а = -¦- ' = 1Х ( х \
'" 6*cosn 6 \ 2cosn 3 Sinn /'
Так как
cos a cos а sin а
„ Q а =0 О = ^ ( Г \ 1Г^1
!а:=0 ' тх=Я ' *х=г В V COS а Sin а / 8 COS а '
51Па/
2B \ cos a 3si
При заданных числовых значениях
1,2. иг»-ш8-4.10». 2 96 г .,
'*„ = 1 = — кГ'ш<
= .
m«=r 25
.1О' /4.1Q..2 JO^X ^ JO^
V 1 3^3 / 6
=oo,
Для цилиндрической части сосуда (/i2<^z<^h) pm=,
^ = р = г, p = t(h — г), о. = 0 и S равно S конической части
при х = г, т.е. S^S^, = v2 (А_-i-ctg я).
54
Окружные at и меридиональные om нормальные напряжения в
точках стенки цилиндрической части сосуда по формулам D3) равны
При заданных числовых значениях
= 1,2-10--И»»-4 '«*
гг=Л. В 8
'¦2-1(r"-10S U ¦ 10= + -^ • 0.577^ « -^- кГ/сж*.
U. ю= + -151. 0,577) «
\ 3 '
Эпюры напряжений о, и от приведены на рис. 23,а.
Опасным сечением является верхнее сечение конической части
96 50,3
сосуда, где 0,= -^ и ат = —-—
Пользуясь 3-й гипотезой прочности, производим определение
толщины 8 стенки сосуда Считая о, = 0, имеем расчетное уравнение
Отсюда 8 = — = -^— = 0,096 см = 0,96 жж
[о] 1000
Берем 8=1 лш
В сеченни стыка конической части с цилиндрической (рис 23,6)
о0 = ат = 503 К//СА12
Так как ае — о = 60е, то площадь Z7 распорного кольца по фор-
формуле E2) должна быть равна
р 503-0,1 • 102-0,87 . . 2
с — — = 4,4 еж2.
10»
Найденные размеры 8 и F практически должны быть проверены
с учетом конструктивных соображений н устойчивости распорного
кольца
Задачи 128—133. Определить величины, указанные в условиях
Обозначения: р — внутреннее давление газа, f — удельный вес
Жидкости, 8 — толщина стенкн (8,;/ по 3-й, 8/у по 4-й гипотезе проч-
прочности), FK — площадь распорного кольца, d — диаметр одного бол-
55
та, п — число ботов, о,'23-_ главные напряжений в опасной
точке сферической части сосуда с^г.з— то же в цилиндрической
чаи и
Расчеты производить по безмоментной теории
В задаче 133 исследовать и построить графики изменений мери-
меридионального (от) и перпендикулярного ему (at) напряжений, а
также расчетного эквивалентного напряжения по 3-й теории проч-
прочности оэ„, в функции от координаты г.
Написать условие прочности
т
IV. ЧИСТЫЙ СДВИГ
Напряженное состояние, при котором по граням выделенного
элемента действуют только касательные напряжения, называется
чистым сдвигом. При чистом сдвиге происходит линейное смещение
двух параллельных граней элемента относительно друг друга.
Величина линейного смещения s (рис. 24) называется абсолютным
сдвигом.
Отношение абсолютного сдвига s к рассюянию / между смещаю-
смещающимися гранями
-j = tg т = 1 E5)
называется относительным сдвигом, или угловой дефдрмацией.
56
Главные угловые деформации ^и f2, -js (углы, на которые изме-
изменяются прямые углы между плоскостями действия одинаковых по
величине, но противоположных по знаку экстремальных каса-
касательных напряжений т4, т2, х3) определяются по закону Гука. Они
соответственно равны
^, E6)
¦ч
G '
/SL
А—л
7
Рис. 24
Рис 25
Л
\
Рис. 26
где
2A +у.)
E7)
— модуль сдвига или модуль касательной упругости материала.
Относительный сдвиг т0. происходящий под действием окта-
эдрического касательного напряжения то, называется октаэдрше-
ским сдвигом.
•V = — = J/ „2 I Т2 Л_ „2 /COj
При напряженном состоянии чистого сдвига (рис. 25) в плоскос-
плоскостях под углами в 45° главные напряжения
oi = — °з = *. E9)
57
главные линейные деформации
е = — т,
F0)
1+U.
е- = е = — т,
Е
главная угловая деформация
Т = 2е F1>
Круг напряжений имеет центр в начале координат (рис. 26)
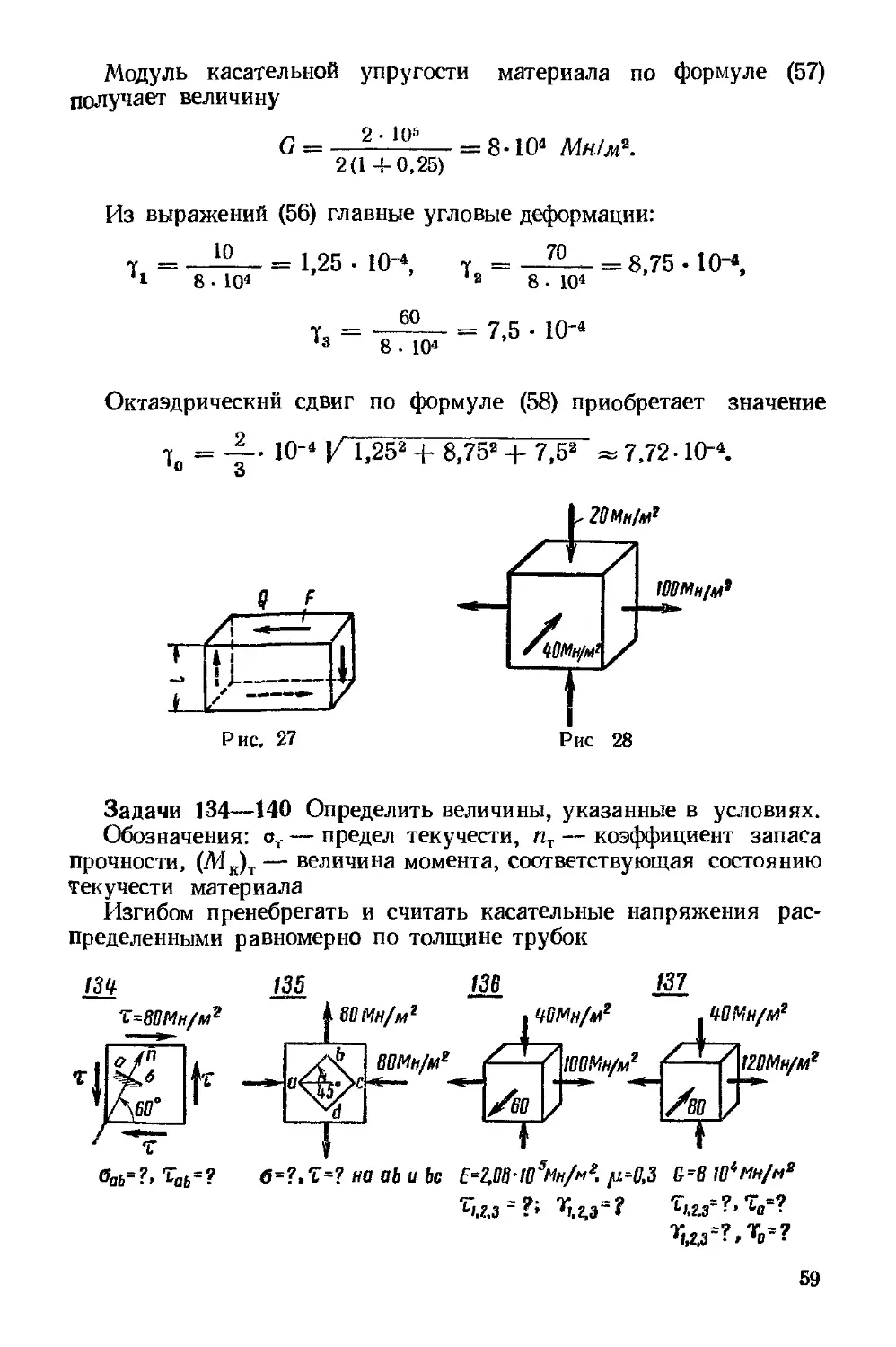
Если считать касательные напряжения равномерно распреде-
распределенными по площади F их действия (рис. 27), то касательное усилие
Q = xF F2)
Имея в виду формулы E5) и E6), закон Гука при сдвигеможно
записать следующим образом:
Потенциальная энергия упругой деформации при сдвиге опреде-
определяется формулой
Удельная потенциальная энергия при сдвиге
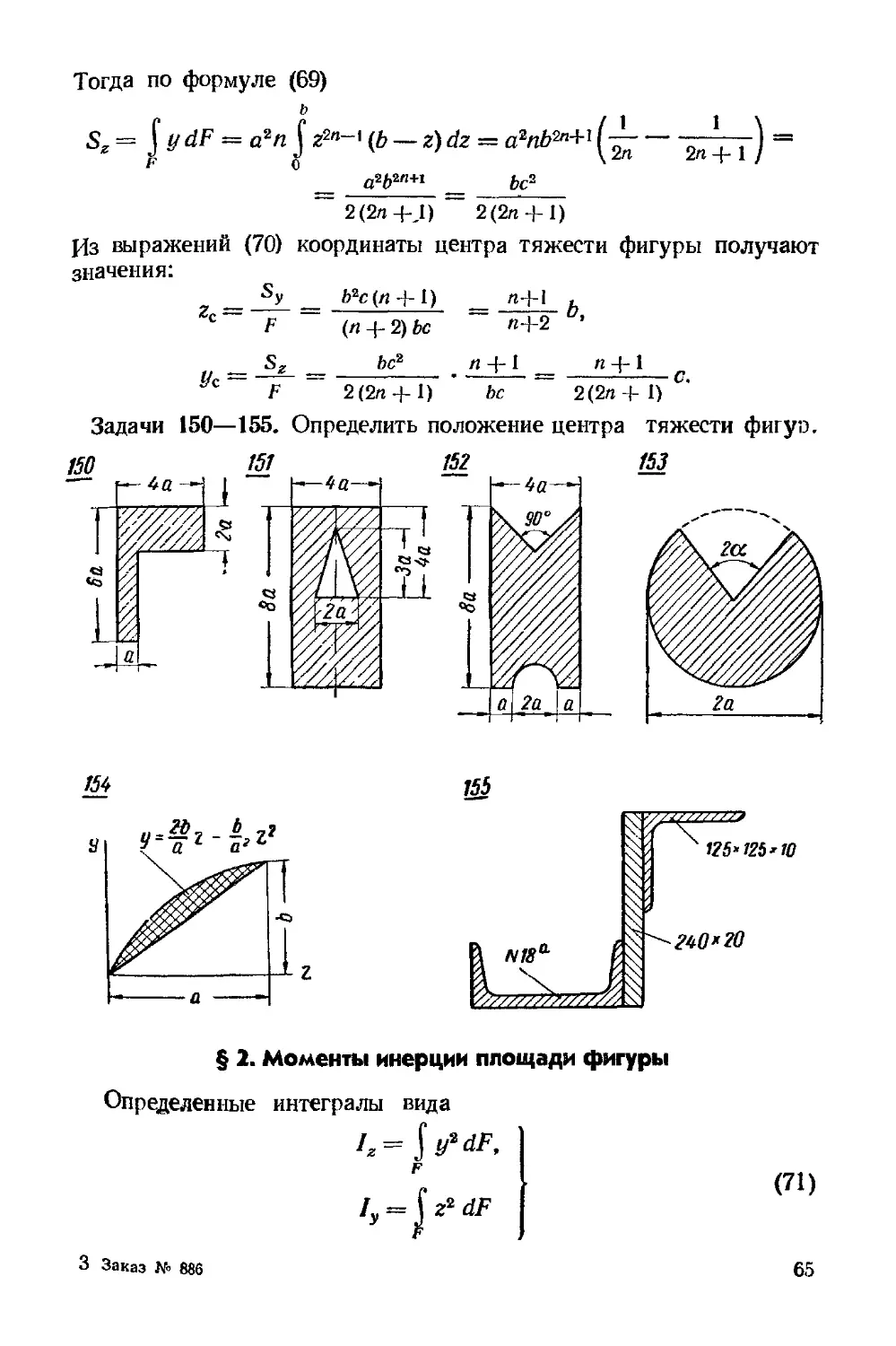
Пример 13. Для заданного напряженного состояния (рнс 28)
определить -^.г.з и f0, считая Е = 2- 10s Мн/м2 и [л = 0,25
Решение Главные напряжения в заданном объемном напря-
напряженном состоянии равны а, = 100 Мн/м2, о2 = —20 Мн/м2, оа =
= —40 Мн/м2
Экстремальные касательные напряжения, согласно формулам
27), имеют значения
10
2
"¦ = 60 Мнш".
•А
58
Модуль касательной упругости материала по формуле E7)
получает величину
8- 10*
2- 105
2A+0,25)
главные
. = 1,25 • 10-*,
= 8-10* Мн1м*.
Из выражений E6) главные угловые деформации:
10 , Пг ,«_, 70
60
8 • ю4
Та 8 • 10*
= 7.5 ¦ 10-*
= 8,75-10-4,
Октаэдрическнй сдвиг по формуле E8) приобретает значение
1о = — - 10-* У 1,252 + 8,75а + 7,52 « 7,72-10"*.
WDMh/m*
Рис. 27
Рис 28
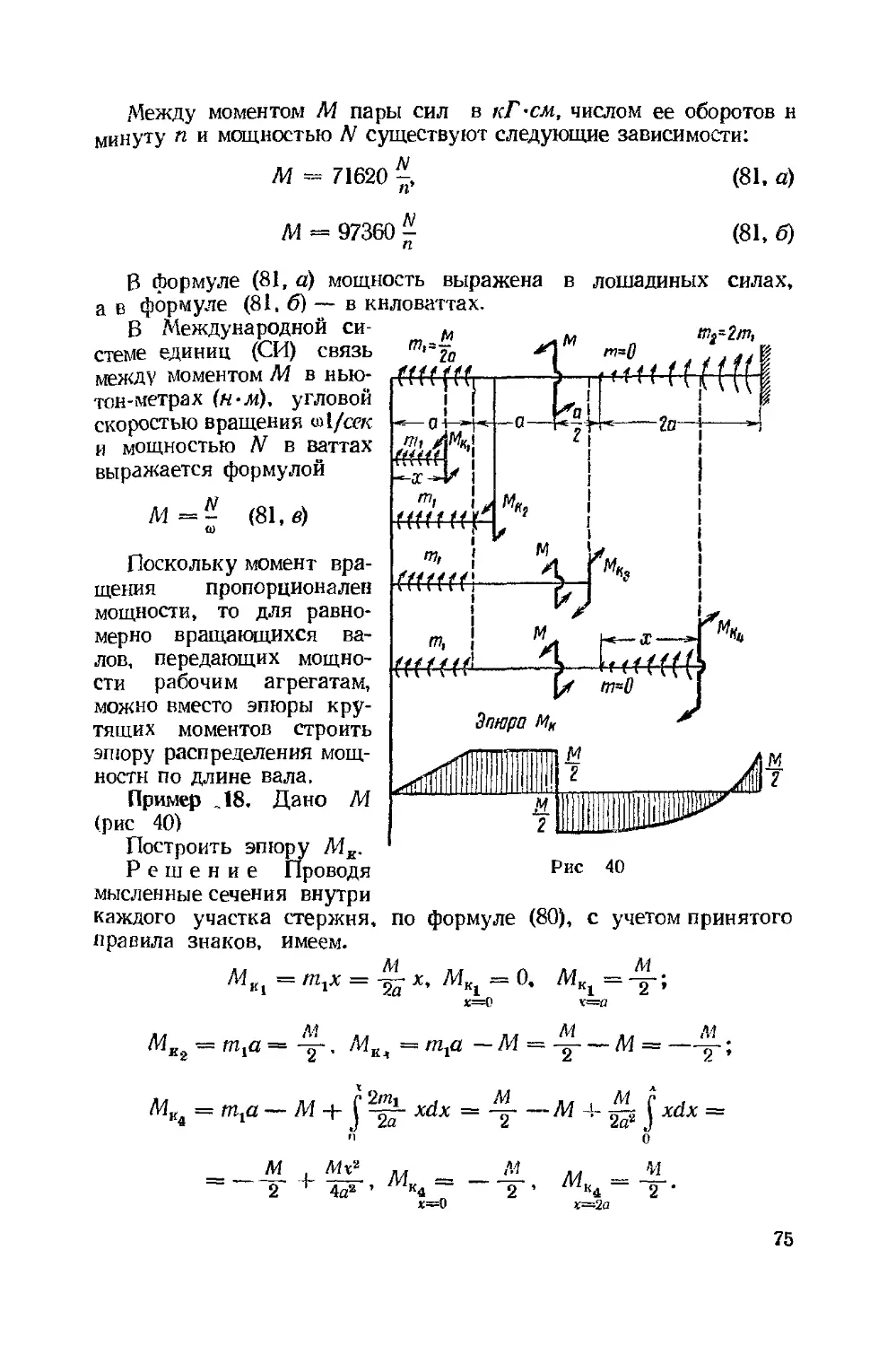
Задачи 134—140 Определить величины, указанные в условиях.
Обозначения: ог — предел текучести, пт — коэффициент запаса
прочности, (Мк)г — величина момента, соответствующая состоянию
текучести материала
Изгибом пренебрегать и считать касательные напряжения рас-
распределенными равномерно по толщине трубок
4 ВОМн/м*
80МН//И'
=? иоаЬиЬс
59
ш
St
A
1
В
С
s
[=2 Юек
б, = * бг
V. РАСЧЕТ ПРОСТЕЙШИХ
СОЕДИНЕНИИ ЭЛЕМЕНТОВ КОНСТРУКЦИИ
В различных соединениях (болтовых, шпилечных, шпоночных,
клиновых, заклепочных, сварных, деревянных врубках и т л ) по
разным плоскостям элементы испытывают растяжение, сжатие,
сдвиг и смятие
Если растяжение и сжатие обычно происходят в чистом виде,
то чистый сдвиг практически не встречается Сдвигу всегда сопут-
сопутствует либо изгиб, либо растяжение или сжатие, поэтому по плоскос-
плоскостям сдвига, кроме касательных, действуют еще и нормальные напря-
напряжения. Однако, поскольку величины этих нормальных напряжений
малы по сравнению с касательными напряжениями, технические
расчеты производятся только на сдвиг, который для металлических
элементов называют срезом, а для деревянных — скалыванием
Обычно считают, что по плошади среза или скалывания (Fcp) каса-
касательные напряжения распределены равномерно. Допущенные не-
неточности компенсируют величиной допускаемого касательного
напряжения [т ]
Смятие представляет собой местное (поверхностное) сжатие
давящих друг на друга элементов Так как точный закон распре-
распределения давлений по сминаемой поверхности неизвестен, то для
упрощения технических расчетов условно принимают давления
распределенными равномерно не по сминаемой поверхности, а по
площади (FCM), являющейся проекцией сминаемой поверхности на
плоскость, перпендикулярную направлению давящей силы Ясм.
Эта неточность также учитывается величиной допускаемого напряже-
напряжения на смятие [асм I.
Для рационального использования материала расчет соединений
должен производиться из условия равной прочности элементов,
60
входящих в соединение. При этом используются следующие рас-
расчетные формулы
1) на растяжение или сжатие
,>?: .ее» "
—15
2) на срез или скалывание
3) на смятие
г -ч. Рем
Сем]
F7)
F8)
Входящие в расчетные фор-
формулы площади являются площа-
площадями нетто, т. е площадями, в
которых учтено возможное осла-
ослабление за счет различного рода
отверстий, выкружек выточек
и т. п.
Если одна и та же площадь
рассчитывалась на срез и смя-
смятие, то берется большая пло-
площадь из полученных
Практически не всегда можно
выдерживагь условия равной
прочности элементов соедине-
соединений. Обычно вступают в силу
еще дополнительные конструк-
конструктивные соображения Они обос-
новываюгея в курсах деталей
машин, металлических и дере-
деревянных конструкций
Пример 14. Дано: Р = 4 Т;
1а] = 1600 кГ/см*. It] =
-1200 кГ/смг\ [осм]=3200 кГ/см*
(рис 29, а).
Определить d, 8, а, Ь.
Решение 1. Определение диаметра штыря d из
прочности на срез (рис 29, б)
Рис 29
условии
2 Определение толщины листа 8 нз условия прочности на
смятие (рис 29, в):
8d>
4- 1О>
1,46-32. 10я
= 0.86 яи.
3 Определение ширины полосы а из условия прочности на
разрыв (рис 29, г):
(с —d)8>—;
W
8[o]
0.86- 16- Ю2
1,46» 2,92cjm.
4. Определение длины fc конца полосы из условия прочности на
срез (вырез) (рис 29, д);
[t]
2S[t]
2-0,86- 12- 10s
Отсюда b = b' + — = 1,94 f 0,73 = 2,67 см
Задачи 141—149. Определить все размеры элементов соедине-
соединении, указанных на рисунках
Расчеты производить из условий равной прочности элементов,
В задачах 146—148 принять [о] = 1600 кГ/см2; [т] = 1200 кГ/см2;
[осм] = 3200 кГ/см2. В задачах 144, 145, 149 принять [о] =
= 160 Мн/м2; [т] = 120 Mh/mz; \а„] = 320 Мн/мК
/42
-Е2
$h-
к f
1Р=3,2т
[б] = 1800«Г/см', [Г] = 0.7[б] . [6CM]=2[6]i
|«JO__
[б] = ЮООкГ/см'
62
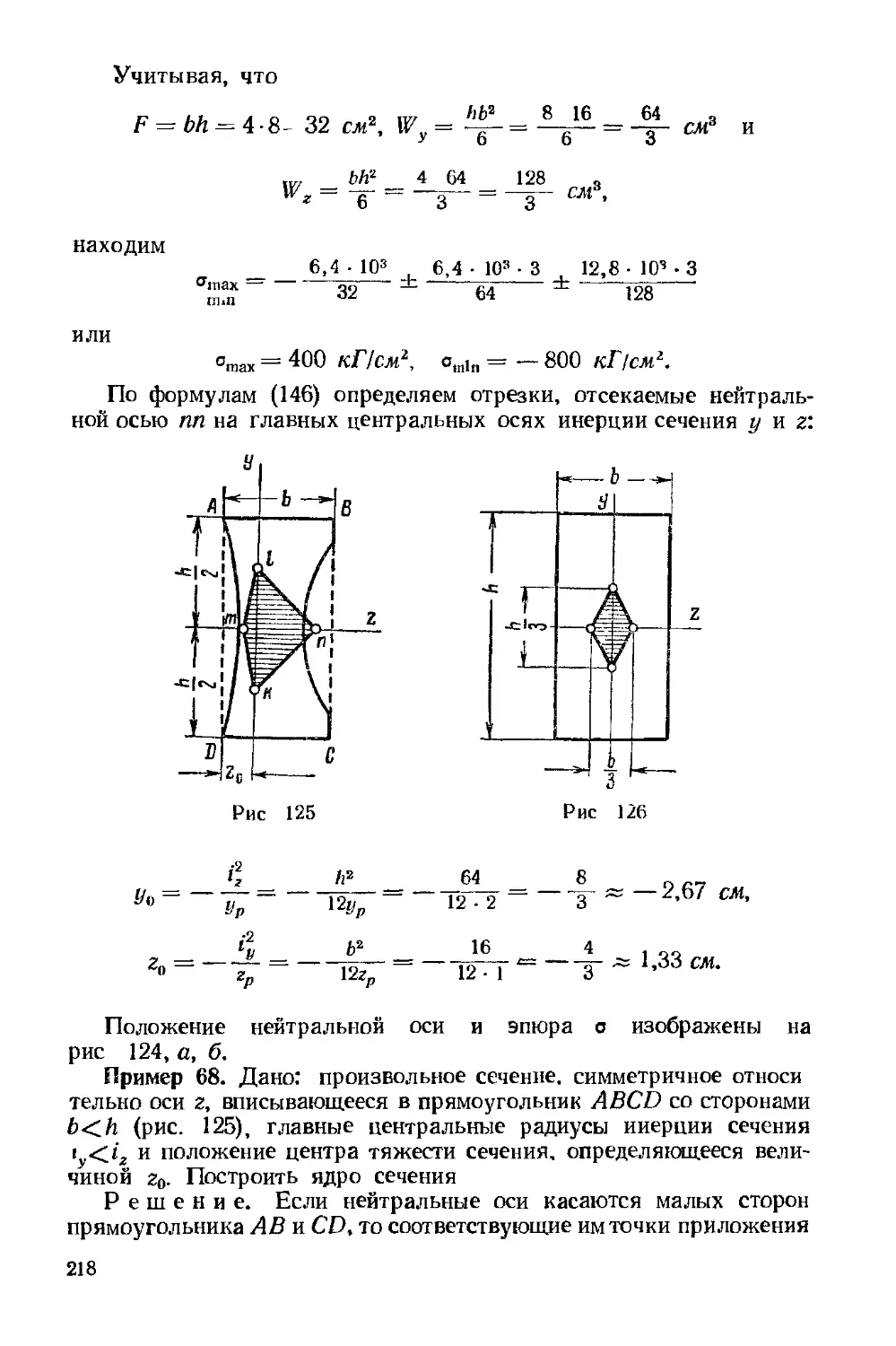
VI. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ ФИГУР
§ 1. Площади и их статические моменты
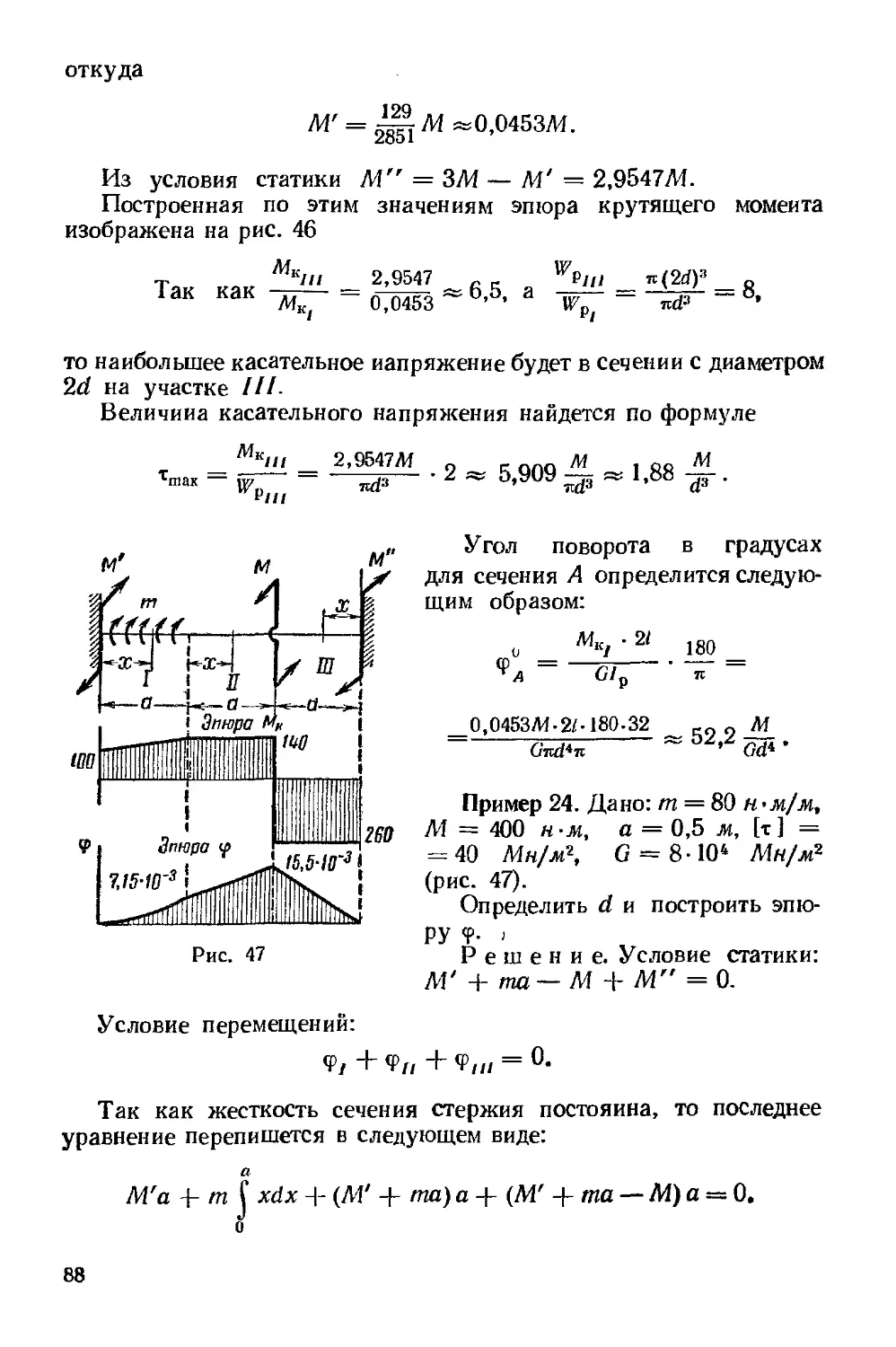
Статическими моментами площади фигуры относительно осей
и {/ ( рис 30) называются определенные интегралы вида
F9У
zdFy
63
где F — площадь фигуры, dF — ее элемент, а г и у координаты
этого элемента
Координаты центра тяжести фигуры zc и ус определяются отно-
отношениями
F
S2
F
G0)
Статические моменты площади фигуры относительно централь-
вых осей равны нулю.
л
I
1
z
Рис. 30
Пример 15. Определить координаты центра тяжести площади
фигуры, ограниченной прямолинейными отрезками Ь, с и параболой
у — az" (рис 31)
Решение. Берем элемент площади фигуры dF = ydz =
= az"dz, тогда площадь фигуры
zndz =
abn
п+\
be
п 4- 1
Статический момент площади F относительно оси у определяем
по формуле F9)
S \zdF = a
If о
l йг =
п+2 п+2
Для определения статического момента площади фигуры относи-
относительно оси г берем элемент площади
dF = (b — z)dy = an(b — г) г"-1 dz.
64
Тогда по формуле F9)
ь
(b
= «№+¦[~-
2Bл+,1) 2Bл+1)
Из выражений G0) координаты центра тяжести фигуры получают
значения:
__gy_ _. ь*с(п + \) __ «+I .
с ~ F ~ («+ 2) Ьс «+2 '
v с
F 2B/г + 1) be 2B/г+1)
Задачи 150—155. Определить положение центра тяжести фигуо.
N18°
У//////У/V/////.
125-125' 10
§ 2. Моменты инерции площади фигуры
Определенные интегралы вида
Iy = | г2 dF
3 Заказ № I
G1)
65
называются осевыми, линейными или экваториальными моментами
инерции площади фигуры (рис, 32) относительно оси г н оси у;
,= \yzdF
G2):
— центробежный момент инерции площади фигуры относительно
двух взаимно перпендикулярных осей гну;
G3)
— полярный момент инерции площади
фигуры относительно начала коорди-
координат О.
Моменты инерции для параллель-
параллельных осей, одни из которых
центральные (рис 33):
Рис. 32
G4)
Моменты инерции для повернутых осей (рис. 34):
—— cos2а — / sin 2а,
'в — 7. г
1уг
Л,=
г~ У
Л» =
* П
cos2а + /^sin2a,
i cos 2а>
G5)
Главные оси инерции плоской фигуры, т е две взаимно пер-
перпендикулярные оси, относительно которых центробежный момент
инерции площади фигуры равен нулю, занимают положение, опреде-
определяющееся уравнением
tg2a =
/у -U
G6)
66
Главные моменты инерции площади фигуры, т. е. осевые моменты
инерции, вычисленные относительно главных осей инерции,
имеют следующие экстремальные значения:
' max
ПИП
G7)
Если /уг<0, то главная ось, относительно которой момент инер-
инерции максимален, проходит через / и /// квадранты
Рис 33
Рис. 34
Если 1уг>0, то главная ось, относительно которой момент инер-
инерции максимален, проходит через // и IV квадранты.
Главные оси, проходящие через центр тяжести площади фигуры,
называются главными центральными осями, а моменты инерции
относительно этих осей — главными центральными моментами
инерции.
Положительные значения величии
G8)
называются радиусами инерции плоской фигуры относительно со-
соответствующей оси.
Эллипс, построенный по уравнению
— + — = 1, G9)
называется эллипсом инерции фигуры. Здесь оси у и г — главные
оси инерции фигуры Обычно эллипс инерции строится на глав-
главных центральных осях плоской фигуры.
Ось симметрии плоской фигуры является главной осью инерции
этой фигуры Любая ось. перпендикулярная оси симметрии, яв-
3* 67
ляется второй главной осью инерции фигуры для точки их взаимного
пересечения.
Если плоская фигура имеет хотя бы две оси симметрии, не пер-
перпендикулярные друг другу, то все оси, проходящие через центр
тяжести этой фигуры, являются ее главными центральными осями
инерции. Осевые моменты инерции площади фигуры, вычисленные
относительно этих осей, равны между
собой.
Пример 16. Для правильного «-уголь-
«-угольника со стороной а (рис.35) определить
главные центральные моменты инерции,
полярный момент инерции и построить
центральный эллипс инерции.
О
\ «
, и 1 1?"
щ
1 \ и
Рис. 35
Решение. Центральный угол, опирающийся на сторону а.
Радиус описанной окружности
Радиус вписанной окружности
г = R cos -^- .
Рассмотрим одни треугольник с углом а при вершине (рис. 36, а)
и найдем для него осевые моменты инерции /'„, I'v и полярный мо-
момент инерции /'р.
68
Площадь элементарной полоски толщиной dv
dF = atdv =—vdv.
Осевой момент инерции площади треугольника относительно
оси и
Площадь элементарной полоски толщиной du (рис. 36, б)
dF = /-j du = — (а — 2u)du.
Осевой момент инерции площади треугольника относительно
оси v
а/г
/ё= 2 J u3dF = 2 -?- j u?(a — 2u)du ==
48
Полярный момент инерции площади треугольника относительно
точки О
т 48 62
= -^— sin a B + COS a).
Так как все треугольники, на которые разбивается «-угольник,
равны между собой и опираются вершинами в точку О, то полярный
момент инерции площади всего л-угольника относительно точки О
/р = п1р = -^- sin a (cosa + 2) = -^- sin a (cos a + 2).
В правильном «-угольнике имеется не менее 2 осей симметрии,
которые не перпендикулярны друг к другу, поэтому все центральные
оси являются главными осями инерции и моменты инерции площади
многоугольника относительно них равны между собой и равны /,
отсюда
/ = -i- /р - -^ sin a (cos a + 2) = ^g- sin a (cos a + 2).
6S
Так как площадь п-угольника
Filar
— 2R2 sin — cos — = — Rs sin a.
2 2 2 2
то главные радиусы инерции многоугольника
IBO'ZO
tmB
2/3
Эллипс инерции представится окружно-
окружностью этого радиуса.
Пример 17. Для составной фигуры,
указанной на рис. 37, построить цент-
центральной эллипс инерции
Решение. Фигуру, вычерченную
в масштабе (рис. 38), относим к осям
координат гу, параллельным сторонам
контура фигуры.
Каждый элемент фигуры (уголок /,
швеллер 2, прямоугольник 3) относим к центральным осям z,#,-,
параллельным осям гу. Центр тяжести прямоугольника определя-
определяем, а координаты центров тяжести уголка г0 = 2,02 см и швеллера
гс = 2,46 см берем из сортамента прокатной стали.
70*70* В
Рис. 37
Рис 38
Дальнейшие вычисления удобно сводить в таблицы Все нужные
величины для прямоугольника легко подсчитываются, а для уголка
и швеллера берутся из сортамента. Так, например, для равнобокого
уголка с размерами 70x70x8 мм по сортаменту площадь
70
f, = Ю,7см2, для швеллера №22— F2= 28,8 см\ а для прямоуголь-
прямоугольника F3= 18X2 = 36 см2. Координаты центров тяжести каждого
элемента в осях уг будут иметь значения:
для уголка Zj = yt = 7—2,02 = 4,98 см,
для швеллера г2 = 11 см; у2 — 7 + 2,46 = 9,46 см,
для прямоугольника г3 = 22 + 1 = 23 еж; #3 = 7 + 9 = 16 еж.
/. Определение координат центра тяжести фигуры в осях zy
Номер
элемента
1
2
3
Площадь
а.
10,7
28,8
36
75,5
площадь
всей фигуры
Координаты ц. т. элемента
в осях ги
н
«1
см
4,98
II
23
4,98
9,46
16
Статические моменты
элемента для осей гну
см"
53,4
272,4
576
901,8
53,4
316,8
828
П98.2
для площади всей
фигуры
Координаты ц. т. фигуры
15>87 см> Ус^-Т = 5Ж ~ И'94
Относим фигуру к центральным осям гоуц, параллельным осям
Находим координаты центров тяжести элементов фигуры г0; ц^0(
В ОСЯХ Zo!/o:
для уголка
г01 = 4,98 — 15,87 = —10,89 ел,
//„1 = 4,98 - 11.94 = —6,96 см;
для швеллера
г02 = 11 — 15,87 = —4,87 см,
Уш = 9,46 - 11.94 = —2,48 см;
для прямоугольника
гоа = 23— 15,87 = 7,13 см.
Уоз= 16—11,94= 4,06 си
Находим моменты инерции элементов фигуры для их централь-
центральных осей ztyi
71
Для уголка (рис. 39) из сортамента:
IZi = /й = 48,2 смК
Пользуясь формулами для повернутых осей
-sin2( —45°) =
Рис. 39
~
76,4 — 20
2
(— 1) = - 28,2 аи*.
Оси ujt^i для уголка — главные оси
инерции, так как ось Ui — ось симметрии,
поэтому 1ил = 0. Значения /„, = 76,4 см1
и /о, = 20 еж4 приводятся в сортаменте.
Для швеллера из сортамента /г ,=
= 187 смк\ 1У% = 2330 см1; Itl!h = 0, так
как для швеллера оси г2, г/2— главные оси
инерции
Для прямоугольника подсчитываем:
972
12
= 12
2. Определение моментов инерции фигуры относительно осей гсу0
га
а
и
S
О.
I
1
2
3
см'
10,7
28,8
36
СМ
crCi3
^-6,96
—2,48
4,06
4f ?
187
972
48,2
2330
12
—28,2
0
0
С
CM
1269
683
1830
518,3
177,1
593,3
N°
С
811
347,8
1042
s
С
4
-г5
'¦**
и
о
566,5
364,1
1565,3
2496
1317,2
3013
1842
6172
й-
II =?
782,8
347,8
593,3
1724
для площади всей
|>игуры
3. Определение положения главных центральных осей инерции
фигуры uv.
По формуле G6)
2/ 2-1724
tg ~ /v -lz 6172-2496 - °'У<5°-
72
По таблицам тригонометрических функций 2а = 43°10', сле-
следовательно, а = 21°35'
Так как угол а>0, то откладываем его от оси г против часовой
стрелки. Проводим главные центральные оси инерции фигуры и
и v.
Поскольку /гог,о >0, ось с максимальным моментом инерции —
ось v — проходит через // и IV кнадранты.
4. Определение значений главных центральных моментов инер-
инерции фигуры.
В соответствии с формулой G7)
* max ' v
= .2496 + 6172. ± JL |/B496 - 6172J + 4-17242 =4334±2520сж4.
Таким образом,
/шах= /я = 6854 еж4; /min= /„ = 1814 см\
5. Определение главных радиусов инерции фигуры и построение
центрального эллипса инерции.
По формулам G8) главные радиусы инерции получают значения:
Г6854
fmin — hi— \ ~р~ —
^4,90 см.
X?
Так как уравнение эллипса инерции имеет вид~р"+г = 1.
V U
то полуосями эллипса инерции являются радиусы инерции ia на
оси v и iv на оси и. Откладывая найденные значения iu и iv, строим
на них эллипс инерции (см. рис. 38).
Задачи 156—158. Определить моменты инерции фигур относи-
относительно осей, указанных в условиях.
158
157
У
/
— ь
Г
/
J
2D0-
73
Задачи 159—163. Определить главные центральные моменты
инерции.
VII. КРУЧЕНИЕ
§ 1. Крутящий момент
Крутящий момент определяется методом сечений Величина кру-
крутящего момента Мк в каком-нибудь поперечном сечении стержня
равна алгебраической сумме моментов всех внешних пар снл (сос-
(сосредоточенных М и распределенных по длине с интенсивностью /и),
действующих относительно геометрической оси стержня по одну сто-
сторону от рассматриваемого сечения
Общая формула, по которой можно определить неличину крутя-
крутящего момента в произвольном поперечном сечении стержня, имеет
следующий вид:
Мх = ЪМ + I j" mdx.
(80)
Интегрирование производится по длине каждого участка, на
который действует распределенный момент, а суммирование — по
нсем участкам, расположенным по одну сторону от рассматриваемого
сечения
Крутящий момент, рассматриваемый со стороны ннешней нормали
к сечениф, условно будем считать положительным, если он направ-
направлен против часовой стрелки.
74
Между моментом М пары сил в кГ-см, числом ее оборотов н
минуту п и мощностью N существуют следующие зависимости:
М = 71620 j, (81, а)
(81,6)
в лошадиных силах.
М = 97360 I
В формуле (81, а) мощность выражена
а в формуле (81,6) — в киловаттах.
В Международной си-
системе единиц (СИ) связь
между моментом М в нью-
ньютон-метрах (н-м), угловой
скоростью вращения ml/сек
и мощностью /V в ваттах
выражается формулой
/И=? (81, в)
Поскольку момент вра-
вращения пропорционален
мощности, то для равно-
равномерно вращающихся ва-
валов, передающих мощно-
мощности рабочим агрегатам,
можно вместо эпюры кру-
крутящих моментов строить
эпюру распределения мощ-
мощности по длине вала.
Пример .18. Дано М
(рис 40)
Построить эпюру МЕ.
Решение Проводя Рис
мысленные сечения внутри
каждого участка стержня, по формуле (80), с учетом принятого
яравила знаков, имеем.
М.
= т.а ¦¦
Мк =1
Ki
1=С
М
м
¦Л-М:
4а2
2
75
Эпюра Мх изображена иа рис. 40.
Задачи 164—167. Построить эпюры крутящего момента.
§ 2. Касательные напряжения, угол закручивания
и потенциальная энергия упругой деформации
Для цилиндрического стержня круглого поперечного сечения
диаметром d = 2г касательные напряжения т в произвольной
точке поперечного сечения, находящейся на расстоянии р от центра,
определяются формулой
МкР
(82)
где /р=~- =-52" «0,ld4 — полярный момент инерции круг-
круглого сечения.
Максимальные касательные напряжения в точках, наиболее
удаленных от центра, имеют значение
'wn
(83)
W'p ТЕГ8
• полярный момент сопротив-
сопротивления круглого сечения.
Для стержней некруглого поперечного сечения максимальные
касательные напряжения определяются по формуле
*™.х = Ц. (84)
где WK — момент сопротивления сечения при кручении, значение
которого для различных форм сечения приводится в со-
76
ответствующих справочниках и в курсах сопротивления
материалов.
Угол закручивания <р на участке длиною /, где крутящий мо-
момент Ми сохраняет постоянное значение, определяется по формуле
закона Гука
»-$?• <85>
где /„—«момент инерции» поперечного сечения стержня при круче-
кручений, который для круглого сечения равен /р, а для других форм
сечения различен и приводится в справочниках и в курсах сопротив-
сопротивления материалов.
Если стержень имеет несколько участков, на длине которых М к
изменяется по тому или иному закону, то полный угол закручива-
закручивания (угол взаимного поворота концевых сечений стержня) опреде-
определяется из выражения
Интегрирование производится по длине каждого участка, а
суммирование по всем участкам стержня.
Для валов углы закручивания удобно отсчитывать в обе стороны
от сечения, где расположен ведущий шкив вала.
Общая формула для определения количества потенциальной
энергии упругой деформации, накопленной в стержне при кручении,
имеет вид
f* M2dx
?г~- <87>
Здесь интегрирование и суммирование производятся так же, как и
при определении угла закручинания.
Пример 19. Дано: М, a, d, G (рис. 41).
Построить эпюры Мк и <р; определить хшах/ и и U.
Решение. Крутящий момент на участке / Мк, = —М.
Крутящий момент в произвольном сечении участка //
/Ик^=— М + 2М— /л Bа— х2) = М—~Bа—х2) =
= М I—- —;
77
ЗМ; Мк
Для квадратного сечения со стороной с WK « 0,208 с3.
Так как с = -^ , toW, = 0,208 -^— « 0,0736 d3.
У2 /
Поэтому
м
If
м
Рис.41
Левое заделанное сечение не поворачивается, следовательно
целесообразно угол закручивания отсчитывать от левого конца
стержня
Для произвольного сечения участка //
78
Находим экстремум угла <?ц
2
Glp\ а
\ з
/ 2 2
9а \ 9 Ma 9 Ma «„
2~j ~ 4~57p = 4~GraF '
Длн произвольного сечения участка /
"с/р С/к"
Так как
/к « 0,1404с" = 0.1404 ~ « 0.035Ы4. и
,о0 о7
= -48,86^.
Количество потенциальной энергии упругой деформации, за-
заключенной в закручиваемом стержне, находится по формуле (87)
Задачи 168—173. Построить эпюры крутящего момента Л7Н,
угла закручивания <р и определить наибольшие касательные напря-
напряжения Тпии и потенциальную энергию деформации U, накопленную в
объеме стержня, Задачу 170 решить в системе СИ.
ум
С-
79
ш
/in /зп
&
—\fii-
СП
-1,51-
SM
CCCCG
-я-
Ш
„ I
§ 3. Прочность и жесткость
Для стержня постоянного поперечного сечения при кручении
размеры сечения подбираются по расчетной формуле
max MK
WK>-
(88)
где тахМк— наибольший крутящий момент по абсолютному зна-
значению.
Если дополнительно ставится условие, чтобы максимальный угол
закручивания отах не превосходил допускаемый угол закручивания
1<р], то подобранное сечение проверяется на жесткость согласно
выражению
max MKlp
(89)
где lp— расчетная длина, для которой задан допускаемый угол
закручивания.
В том случае, когда допускаемый угол закручивания задан в
градусах на метр длины [ <р°], его следует подставить в радианах
Нф] = 1?°] ~Ш~) в формулу (89) и считать /р = 100 см.
Если рассчитывается вал постоянного сечения, передающий
мощности, то в формулы (88) и (89) вместо тахМк подставляют одно
из выражений (81), в котором за расчетную мощность 7Vp принимают
наибольшую мощность из эпюры мощностей.
Для стержней круглого сплошного и круглого кольцевого сече-
сечений WK= Wp и /к = /р.
80
Пример 20. Дано: Nt = 40 л. с, Nz = 20 л. с, Ns = 30 л. с,
п= 1000 об/мин, а = А-= 0,6, [х] =450 k//oi2, [ <р°] = 2 грао/л,
0 = 8- 105/с//сж2(рис. 42).
Определить Dud
Решение. По эпюре мощностей (рис. 42) расчетная мощность
Wp = 50 л. с.
"Г С\
fVLf
Рис. 42
Так как полярный момент сопротивления круглого кольцевого
сечения
то, учтя зависимость (81, а), расчетная формула (88) примет вид
Отсюда
Так как допускаемый угол закручивания задан в градусах на
метр длины, то формула (89) запишется следующим образом:
Откуда
71620- 100- 180-32Л/п
71620Wp-100-180
nG [ф°] it
= 253,4 у H8.8.10».2-0,87 * 3,49 «4.
81
Следует принять
О = 3,64 см, d = 0,6-3.64 » 2.18 см
Пример 21. Дано: d = 4 ш, ш = 80 рад/сек, G = 8-104 М«/жа,
J т| =60 Мк/ж2, [ «pi =2-10 рад/м (рис 43).
Определить Л/о (кет).
Решение. По условию прочности (88), с учетом соотноше-
соотношения (81, в), расчетная мощность
mi* [т[ и
кD 10-гL 60-106-80
16
ж 60300 вт = 60,3 кет.
По условию жесткости (89), с учетом соотношения (81, в),
8 10Ю-2- 10-2п D-10-2L-80
/„
32/„
32
32200 вт=
= 32.2 кет.
Так как из эпюры мощностей (рис. 43) Nv — 5N — -^-Wo,
то
Л'о < 2iVp = 2-32,2 = 64,4 кет
Пример 22. Дано: d = 4 еж,
а = 40 еж, С = 8-Ю5
<Рв-с = 1° (рис 44).
Определить тшах,
<р°
Рис 44
Решение. Строим эпюру
крутящего момента (рис 44)
Угол поворота сечения В относи-
относительно сечения С определяется из
выражения:
п_ _ Ма_ Ша Ша
та ~~ е/к + о/к ~ е/„ •
Откуда
1 ~ 3 180 а *
Так как /K«0,1404d4, WK « 0,208d8, /p=w.
82
Wp = tj ~ 0,2rf3, т. e.
где Ми = SM. Поэтому
ЗА! _ ЗяС 0,1404d< ¦ 16
p, то опасным является участок,
G-0,1404 d-16
„ ~ 3 180 owf
8-105-0,1404-4-16
180а
.„„„
100°
= ШГТо
Угол поворота сечения А относительно сечения С найдется по
формуле
~Г + 2,86° = 3,86°.
Задачи 174—177. Определить необходимые размеры попереч-
поперечных сечений стержней из условий прочности и жесткости.
Во всех задачах этого и следующих параграфов, кроме задач,
решаемых в СИ, для которых величина G указана на чертеже, при-
принять G = 8-105/сГ/сл*2
Задачи 178—183. Определить необходимые размеры попереч-
поперечных сечений стержней и полный угол закручивания.
Во всех задачах этого и последующих параграфов численные
значения длин участков стержней указаны в метрах.
83
Задачи 184—201. Определить величины, указанные в условиях
задач.
В задаче 193 стержень АВ вращается с постоянной скоростью
в сопротивляющейся среде, которая создает реактивный момент,
распределенный равномерно по длине стержня.
В задаче 194 точка С, лежащая на поверхности, переместилась
на 0,5 мм.
В задаче 197 груз Q переместился на 2 см.
В задаче 198 стержни АВ и CD абсолютно жесткие.
В задаче 200 техническая прочность стержней одинакова.
В задаче 201 точка А лежит в наклонном сечении.
CTJ 2№1]сп'. CfJ-ОЗграв/м,
I.SM
ш
гм
/ЗН
84
D-M Ж
1 Мг=Ши« М,
м,-', ггао, = ?
ш
Л|
/
1 i
"-> g
•ё
^-
,S« —
А
к 1
[
-tu-
-turn
. Ль
•
[i]*WWcu', n од/мин^?
ISS
& Л
5 ffl
-31-
У
§ 4. Статически неопределимые задачи
Статически неопределимые задачи на кручение так же, как на
растяжение и сжатие, включают в себя системы, в которых реакции
закреплений и внутренние усилия не могут быть определены из
условий статики
Расчет таких систем производится путем использования надлежа-
надлежащих условий статики и условий совместности перемещений Послед-
Последние условия основаны на неразъединимости элементов, составляю-
составляющих систему, и представляют собой геометрические зависимости
между перемещениями элементов, входящих в систему
Если дополнительные связи абсолютно жесткие, то их деформа-
деформации равны нулю, а если дополнительные связи упругие, то их пе-
перемещения определяются через деформации, найденные по закону
Гука
Если все элементы статически неопределимой системы работают
только на кручение, упругие перемещения будут определяться
через углы закручивания. Если в системе часть элемв!тов работает
иа кручение, а часть на растяжение или сжатие, то для первой части
элементов перемещения определяются через углы закручивания,
а для второй части — через линейные продольные деформации
Для каждого вида статически неопределимой системы и условия
статики и условия совместности перемещения различны Однако для
некоторых типов систем эти условия в своей сущности одинаковы и
могут быть представлены в виде принципиально одинаковых урав-
уравнений.
86
Так, например, для систем, состоящих из нескольких прямоли-
прямолинейных элементов, соединенных соосно друг с другом, жестко заде-
заделанных по концам и нагруженных только внешними парами сил,
создающими кручение (рис. 45), условие статики представится
алгебраической суммой мо-
моментов всех заданных и ре- м- м< м м«
активных пар сил относитель-
относительно геометрической оси эле-
элементов Эта сумма моментов
должна равняться нулю.
Условие совместности пе-
перемещений представится
алгебраической суммой углов
закручивания на всех участ-
участках, которая в силу непово-
рачиваемости концевых се-
сечений тоже должна равнять-
равняться нулю.
Если одна из заделок стержня не жесткая, а упругая, то угол
поворота упруго заделанного конца не равен нулю, а пропорциона-
пропорционален величине реактивного момента Если обе заделки не жесткие, а
упругие, то полный угол закручивания должен равняться разности
углов поворота в закрепленных сечениях.
Пример 23. Дано: М, d, I, С (рис 46)
/
/
—1,-
у
—»-
/
Рис
-h-
45
У
Э»
у
и У^ш 3d /
*-ZL-
Определить тшаХ1 <р^.
Решение На участках /,
//, ///, IV полярные моменты
инерции круглых сечений
16/,,;
'"in
Эпшра М
ift/№53M |
г
'Ш53М
¦Я-
1 ^
а углы закручивания
М'21 . (АГ
16G/r
16С/„
Рис 46
<Р„
-L
•P'V - 8167р
По условию отсутствия угла
взаимного поворота концевых
сечений
= о,
87
откуда
М' = ^М «0.0453М.
Из условия статики М" = ЗМ — М' = 2.9547М.
Построенная по этим значениям эпюра крутящего момента
изображена на рис. 46
т
1ЗК КЗК
0,0453 '
КР/
_о
— »
то наибольшее касательное напряжение будет в сечении с диаметром
Id на участке ///.
Величина касательного напряжения найдется по формуле
Мк
ш 2.9547М
_ Q
5,909
м
1,88 ^дз" •
Рис. 47
Условие перемещении:
Угол поворота в градусах
для сечения А определится следую-
следующим образом:
М„. • 2<
180
0,0453М-2/-180-32 „ „ М
5^ /( Gd* '
Пример 24. Дано: т = 80 н-м/м,
М = 400 н-м, а = 0,5 м, [т] =
= 40 Мн/м\ G = 8-104 М«/ж2
(рис. 47).
Определить d и построить эпю-
эпюру <р. ,
Решение. Условие статики:
М' + та— М + М" = 0.
Ф„
= 0.
Так как жесткость сечения стержня постоянна, то последнее
уравнение перепишется в следующем виде:
М
'а + т f xdx + (M' + /па) а + (М' + та — М) а = 0.
88
Откуда SM'a = Ma — 2maa — m
$ = iD00 — 2,5-80-0.5)« 100 н-м.
Подставляя М' в уравнение статики, находим
М" = -y BM — 0,5ma) = -i- (800 — 0,5 • 80 ¦ 0,5) =s 260 н ¦ ж.
Строим эпюру крутящего момента (рис. 47), из котор*ои устанав-
устанавливаем, что max Мк = 260 н-м.
По расчетной формуле
Н7 _ !2*!
р ~ 16 ¦
Откуда
= 1 72 "*' 26°
400-10»
«3,2-Ю-2 ж = 3,2 см.
Находим углы закручивания:
м'х+~д-
100-0,5+4- -80-0,25
г^ ~°.°0715;
М'а + та» nnnvic i 100-0,5 +80-0,25
щ = O,OO/lb + 8.101о.о,Гз,2«-Ю-»
= 0,00715+0,00835 = 0,0155; Фн, = ^~\ 4>Wx=f) = 0;
М"а 26-10!-50
Фш« = 577 = 8-w-o.i-3.2T -
По этим данным строим эпюру угла закручивания (рис. 47).
Пример 25. Труба длиной 4а, диаметрами D и dзаделана нижним
концом С (рис. 48) В эту трубу сверху вставлен на длину 1а стер-
стержень круглого сечения диаметром d0 = -<r=-j-g Нижний конец В
стержня жестко скреплен с трубой, а верхний конец Е трубы жестко
скреплен со стержнем. Вокруг геометрической оси системы на кон-
концевом сечении А, выступающей части стержня,
действует пара с моментом М, а на верхнем се-
сечении Е трубы — пара с моментом 2М.
Определить тгоах/ в стержне и тп]М//в трубе,
а также <рд-С|если известно значение G матери-
материала стержня и трубы
Решение. На участке стержня А—Е
крутящий момент
Мк = М.
КАЕ
Так как в заделке С реактивный момент Мс =
— ЗМ, то крутящий момент на участке трубы
В—С М квс = 3 М.
Статически неопределимая система, состоя-
состоящая из стержня и трубы, на участке В—Е
подвергается по концам действию моментов ЗМ.
Рис 48 ^° Условию статики М/ + Мц = ЗМ, где Mi —
момент, передающийся через стержень, Мц —
момент, передающийся через трубу.
По условию совместности перемещений углы закручивания стерж-
стержня ft и трубы <ри на участке В—Е равны друг дру1 у, т е.
М, 2а Мц 2а
С/в
С/„
Отсюда
Подставляя это значение в условие статики, имеем
'р;;
М,\\Л-~\ = Ш или М, =
ЗМ
ЗМ
Так как
90
то
М, = -
= 0,287 М и М„« 2,713 М.
Наибольшие касательные напряжения будут:
для стержня на участке А — Е: хшах = —— = —- » 5,09 -4?- ,
для трубы на участке В — С:
ЗМ ЗМ
L
; 0,636т = 3.24 JL.
-jg
d-,,4,
16
• 0,58
Угол поворота сечения А относительно сечения С определится
следующим образом:
Ма п оо_ М2а
07^- + 0'287 -Щ^
Ж2а
О-9.46-/
Р|
« 22,5
Задачи 202—221. Определить величины, указанные в условиях
задач
В задачах 216—221 принять ? = 2 • 10е кГ/см2, G = 8 • 105 кГ/см\
В задаче 215 цилиндрические трубы расположены концентриче-
концентрически с зазорами и жестко связаны только по торцам.
ж
205
«ЗМ
V
ж
91
Ж
1,2м
М--1В!кГм АЩ,
ftto
О.Ви
Ж
-ЙЯм-
\\ я
*—в,<Ш Н-—й*/и »|- ftfi/и
VIII. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ
§ 1. Поперечная сила и изгибающий момент
Поперечная сила и изгибающий момент определяются методом
сечений.
Величина поперечной силы Qx в каком-нибудь сечении балки
равна алгебраической сумме проекций всех внешних сил (сосредото-
(сосредоточенных и распределенных), действующих на балку по одну сторону
от рассматриваемого сечения на одну из главных центральных осей
инерции сечения.
Величина изгибающего момента Мх в каком-нибудь сечении
балки равна алгебраической сумме моментов всех внешних сил,
действующих на балку по одну сторону от рассматриваемого сече-
сечения относительно одной из главных центральных осей инерции
сечения.
Положительными и отрицательными принято считать значения
Q и М, соответствующие тем направлениям, которые указаны на
рис. 49.
93
Если распределенная нагрузка оканчивается не доходя до рас-
рассматриваемого сечения (рис. 50), то ее можно заменить сосредото-
сосредоточенной силой, численно равной площади эпюры этой нагрузки
приложенной в сечении, проходящем через центр тяжести площади
эпюры распределенной нагрузки.
©
м
Рис 49
Рис. 50
Для нагрузок, изменяющихся по линейным законам, площади
и положения центров тяжести отсеченных частей определяются очень
просто по известным форму лам геометрии. Если нагрузки изменяются
по законам квадратной параболы ABC (рис. 51), то полезно иметь
-I, ч _ в виду следующие данные из ана-
аналитической геометрии Площадь
G параболы ABC = -| lh, центр тя-
тяжести О этой площади лежит на
вертикали BD; площадь парабо-
параболического сегмента FBE = -^h»
центр тяжести Ot этой площади
лежит на расстоянии ^lt от верти-
вертикали FN; площадь половины пара-
2 / 1
Рис 51
болы ABD и
центр тяжести О2 этой площади лежит на расстоянии -g • ~ = -« I
от линии BD; площадь прямоугольного треугольника CBG с пара-
параболической гипотенузой ВС = g- • g-ft =g7-h, центр тяжести О3
этой площади лежит на расстоянии 4- • g- = g7 от вертикали CG
Можно рекомендовать к сечению подходить с той стороны балки,
которая менее нагружена, и строить сначала эпюру Q, а потом
эпюру М.
94
Из определений величин Q и М в соответствии с принятым пра-
правилом их знаков вытекает, что для балок, симметричных по на-
нагрузке и способу закрепления, эпюра поперечной силы будет обратно
симметрична, а эпюра изгибающего момента — прямо симметрична
(рис 52, а).
Для балок обратно симметричных — наоборот, эпюра попереч-
поперечной силы будет прямо симметрична, а эпюра изгибающего момента—
обратно симметрична (рис. 52, б)
Из определения Q следует, что
в сечении, в котором приложена
сосредоточенная сила, на эпюре
поперечной силы должен быть ска-
скачок на величину этой внешней си-
силы (рис. 52, а и 52, б).
Из определения М следует, что
в сечении, в котором приложена
пара сил, на эпюре изгибающего
Рис 52
Рис 53
момента должен быть скачок на величину момента этой внешней
пары сил (рис 53)
Для балок на которые не действуют распределенные пары сил,
вызывающие изгнб, при построении эпюр Q и М, а также #ля про-
проверки их правильности, необходимо пользоваться дифференциаль-
дифференциальными зависимостями (90) и (91) между М, Q, д и следствиями, выте-
вытекающими из них:
<2=-^~. (90)
dQ
dx
(91)
95
Основные следствия из зависимостей (90) и (91):
1. Поперечная сила геометрически интерпретируется тангенсом
угла между касательной к эпюре изгибающего момента в рассматри-
рассматриваемом сечении с осью х (осью балки), а интенсивность распреде-
распределенной нагрузки — тангенсом угла между этой же осью и касатель-
касательной к эпюре поперечной силы.
2. Если функции изменения распределенных нагрузок алгебраи-
алгебраические, то на каждом участке балки порядок функции поперечной
силы на единицу выше порядка функции распределенной нагрузки
на этом же участке балки, а порядок функции изгибающего момента
на единицу выше порядка функции поперечной силы.
3. В том сечении балки, в котором поперечная сила равна нулю,
изгибающий момент имеет экстремальное значение, а в том сечении,
в котором поперечная сила скачкообразно переходит через
нулевое значение, эпюра изгибающего момента теряет свою моно-
монотонность.
4. В том сечении балки, в котором эпюра поперечной силы
имеет скачок, но не проходящий нулевое значение, эпюра изгибаю-
изгибающего момента претерпевает излом.
5. Если на всей длине балки или на какой-то ее части эпюра
поперечной силы обратно симметрична, то соответственно на тех же
длинах балки эпюра изгибающего момента прямо симметрична,
и наоборот.
6. На каждом участке балки изменение величины изгибающего
момента между какими-нибудь двумя сечениями равно площади
эпюры поперечной силы между теми же двумя сечениями.
7. Если ось х направлена влево от правого конца балки, то
8. Выпуклость криволинейной эпюры изгибающего момента
идет навстречу направлению интенсивности распределенной на-
нагрузки.
Полезно иметь в виду, что в поперечном сечении, совпадающем с
осью прямой симметрии балки, поперечная сила (обратно симметрич-
симметричная сила) равна нулю, а в сечении, совпадающем с осью обратной
симметрии балки, изгибающий момент (прямо симметричный момент)
равен нулю. Если по оси прямой симметрии на балку действует
внешняя сосредоточенная сила, то поперечные силы в сечении ле-
левее и правее оси симметрии численно равны половине этой силы.
Построение эпюр Q и М по их уравнениям
Пример 26. Дано: Mt= 2 Т-м, М2= 12 Т-м, <?j= 2 Т/м, д2^.
= 4 Т/м, Р = 12 Т, а = 3 м, Ь= 2 м, с = 1 м, d = 4 jk (рис. 54).]
Построить эпюры Q и М.
96
Решение. Определяем реакции А и В опор из условий ста>
тики как суммы моментов относительно правой и левой опоры:
+ b + c + d) — qfi (~ +c+d ) —M2+ Pd — q^-— = 0;
Л-10-2-2-6 — 12 + 12-4 — 4-4-2 = 0; А=*2 Т;
В. 10 — 4-4-8+12-6+ 12— 2-2-4=0; В = 6 Т.
В
Рис. 54
Для упрощения выражений, определяющих Q и М, сечения на
участках длиной а к b рассматриваем слева, а на участках d и с —
справа.
0 < хх < а;
<Зл, = Л = 2Т; М^ = — М1 + Ах1 = — 2 +2л:,; /W^=c = — 2Г-ж;
MXi=a=i= -2 + 2-3 = 4 Г-ж;
а < xz < а 4- 6;
&2 = Л — <7j(a;2— а) = 2— 2(л-2 — 3); (?Х2=а=г=2Г; Q^=a+i,=5 =
= 2 —2-2 = —2 Т;
Мх„ = _ М1 + Лд;2 - 9l i^^t = _ 2 + 2х2 ~ (Х2-З)г:
^=о=з =—2+6= 4 Г.л; /W^=a+i=5 = —2 + 2 -5 — 2г = 4 Г-ж.
4 Заказ Ян №6 97
Так как
QX2 = — 2х2 + 8 = 0 при х2 — 4ж, то max MXt=,4 — — 2 +
+ 2-4—1 =5 Т-м.
Qx, = — В + q2xs = — 6 + 4х3; &„=„ = — 6 Т; QXb=
= —6 + 4.4 = 10 Т;
Xt = ~ M,
— 2 + 6. 4 — 2- 42 = — 10 Г-ж.
Так как
Qx — — 6 + 4х3 = 0 при х3 = -g- ж, то
тахМ 8=— 2 + 6- -|-— 2 • -|- = 2.5 Т-м;
Q2d— P=— 6 + 4-4 —12 = — 2 Г;
4);
= — 2 + 6-4— 16-2= -10 Т-м, MXi=a+c=r,= — 2 +
+ 6-5—16-3+ 12-1 =—8 Г-ж.
Найдем, в каких сечениях MXl = —2 + 6jc3 — 2xi = Q;
xl-3xa+ 1 =0; xs = 4 ± У-?- ~ 1 = 4 ± -^T- -
~ 1,5 ± 1,118;
x3i = 2,618 м, xis = 0,382 м.
По полученным данным на рис 54 построены эпюры Q и М
Пример 27. Дано: q, I, P = 0,2 ?/ (рис 55)
Определить наивыгоднейшую длину консоли о и построить эпюры
Q и М
Решение Наивыгоднейшей длиной консоли балки называется
такая ее длина, при которой максимальный изгибающий момент
имеет наименьшую возможную величину. Длина наивыгоднейшей
консоли определяется из условия равенства абсолютных значений
изгибающего момента в сечении над опорой (Мт) и максимального
изгибающего момента внутри пролета балки между опорами (Мтах)
Так как балка симметрична относительно среднего сечения, то
VWmax B пролете будет посредине балки, а величины изгибающих
моментов в сечениях над опорами Моп будут одинаковы.
и
I Н И ИI Н WTTTTTT
Рис. 55
Условие для определения наивыгоднейшей длины консоли запи-
записывается так- |Моп| = |М|шах.
Найдем эти моменты Реакции опор будут
п~ а— 2^+2-
I —2a
По условию )Моа\ = |М|шах
J4
4
ЗРa
2
qia
2" '
Pa
99
или
Откуда
Знак «минус» перед радикалом отброшен, поскольку отношение -у
не может быть величиной отрицательной.
Построим эпюры Q и М.
Так как —= 0,2, то
а = ]^Ь±=!/~о,162/, Ь = 1 — 2а ~1 A—0,324) = 0,676/
и Л = В =
Поскольку по длине балки действует равномерно распределен-
распределенная нагрузка, то на всех участках балки эпюра Q будет линейной, а
эпюра М — параболической. В связи с прямой симметрией балки
эпюра Q будет обратно симметричной, а эпюра М — прямо симмет-
симметричной.
На левом свободном конце балки Q = —Р = —0,2 ql.
В крайнем правом сечении левой консоли
Q = —р _ Qa « — @,2 + 0,162) ql = — 0,362 ql
Над опорой за счет реакции А иа эпюре Q будет скачок.
Поэтому на левом конце пролета балки между опорами
Q = 0,362 ql + 0,8 ql = 0,438 ql.
При подходе к среднему сечению балки слева
Q = —0,2 ql + 0,8 ql — 0,5 ql = 0,1 ql.
По найденным значениям построена эпюра Q на рис 55.
На левом свободном конце балки изгибающей момент М — 0.
В сечении над опорой
Моп ^ — 0,2^-0,162 / — -|-@,162 /J= — 0,0455 qP.
Посредине балки
М гаах= |МОП| = 0,0455 qP.
Значение х0, при котором в пролете балки М = 0, находим сле-
следующим образом.
Из подобия треугольников
X
0,438?/—0,1?/ JL
2
100
или
Откуда
Q* — 0,1 ql 0,3381— х0
0,338 ql
0,338 г
Qx = @,438 / - хв) д.
Трапецеидальная площадь эпюры Q с высотой х0 равна измене-
изменению М при переходе от сечения над опорой к сечению на расстоянии
хк от опоры, т. е.
0,438 ql —
или
Откуда
хв = 0,0455 дР
@,438 / + 0,438 / — хв) хв = 0,091 Р.
х\ — 0,876 /х0 + 0,091 /2 = 0
хв = / @,438 ±/0,4382—0,091) = / @,438± /0,101).
М- 6
Так как х0 не может быть
больше ~= 0,338 I, то задаче
удовлетворяет лишь один корень
хо= / @,438 — /оТТбТ) «
«0,122/.
По этим данным на рис. 55 6)
построена эпюра М. А
Пример 28. Дано: Р, а (рис.
56, а).
Построить эпюры Q и М. i
Решение. Так как в се- г) \ \
чении В, проходящем через ви- 1_
сячий шарнир, изгибающий мо- о.
мент равен нулю, то балку мож-
можно представить в виде двух
балок (рис 56, б): левой °).
А В — перекидной балки и пра- 1
вой ВС — консоли.
Перекидная балка правым т
концом В опирается на левый '
свободный конец В консоли. Эти
две балки можно рассматривать
Рис. 56
101
отдельно (рис. 56, в). В перекидной балке реакции опор Л = В =Р.
Влияние перекидной балки на консоль выразится действием на
ее левый конец сверху вниз сосредоточенной силы В = Р.
Далее задача решается для каждой отдельной балки.
На левом участке перекидной балки Q = А = Р. На среднем
участке Q = 0 и на правом участке Q = —Р. На консоли Q = —Р.
Эпюра Q изображена на рис. 56, г.
На тех участках балки, на которых Q = const, изгибающий
момент изменяется по прямолинейному закону, а на участке, на
котором Q = О, М — const. Изменения величин М на участках
легко определить по площадям эпюры Q. На рис. 56, д показана
эпюра изгибающего момента.
Задачи 222—270. Построить эпюры поперечной силы Q и изги-
изгибающего момента М.
В задачах 251, 253, 255, 256 и 260 эпюры Q и М построить при
наивыгоднейших длинах консолей а
В задаче 252 эпюру М построить, не определяя реакций опор
и поперечных сил Q.
23/
кГсм\
I cm
-&,
102
ш
ЗР
. з) мг «м,
234
235
шш
I—.-^Д
, 1=0
M=Pff P, m
ТПТ111111 j 1111
]
-о—¦4-*— о—*4-*— о—
?o
I
—го —
a—I
р !р
24/
*=|; г) о={;
2)Р,=2РЪ а'С, Ь'2о
243
5Н
,я
ттттт
I-—о-
246
га
-0-J
т
p
-MRS?
**~~ 2
P
I
X
X
p .
Z
Z47
!S S?
гад
ттпн
^Za—'ha-
251
-1а-
*U (
ааг
М=2
-Зо-
?Ш
\P°qa
f 4
шннии
-»—2а—«4.о-<
Z56
M=qa'
-ца—».
ггга
Г.-
P=qa
-2о
-Ь «4—с
\* Зо-
Р=ца
ш 1
- а ¦»!¦« а »[¦¦ а-
?БЦ
jnnfm
г *1«а-»
e.uu q
гтт..'. ¦
Построение эпюр Q и М графическим методом
Эпюры изгибающего момента и поперечной силы можно построить
и графическим методом Этот метод особенно удобен при действии
на балку сложной системы внешних сил
При тщательном выполнении чертежа и надлежащем выборе
масштабов построения графический метод дает точность результа-
результатов вполне достаточную для практики. Этот метод построения эпюр
М и Q основан на известных из механики свойствах плана па-
параллельных сил и веревочного многоугольника
При графическом определении изгибающего момента Мх и по-
перечной силы Qx в произвольном сечении балки необходимо ^честЕ
масштаб длин р в котором вычерчена балка (? см длины балки со*
ответствует 1 см чертежа), и масштаб сил —, в котором изображен
план сил (tj кГ силы соответствует 1 см вектора на плане сил)
Поскольку полюсное расстояние Н на плане сил выражается
масштабе сил, а вертикальный отрезок у между веревочным многй
угольником и его замыкающей в рассматриваемом сечении балщ
выражается в масштабе длин, то истинные значения Мх и Q^
кГ-см, Qx = Qx{
где Qx — вектор на плане сил, соответствующий алгебраическо(
сумме векторов внешних сил, лежащих по одну сторон^
от рассматриваемого сечения балки
Замыкающая (замыкающие) веревочного MHoroyi ольника прово-
проводится (проводятся) по следующим правилам, соответствующим спо-
способу закрепления балки:
1) на свободном конце балки замыкающая — касательная к вере-
веревочному многоугольнику;
2) на шарнирной опоре в конце балки и в висячем шарнире за-
замыкающая пересекает веревочный многоугольник;
106
3) на шарнирной опоре в пролете балки замыкающая подверга-
подвергается излому (замыкающие при подходе к сечеиию над опорой справа
и слева пересекаются)
Если для заданной нагрузки построить веревочный многоуголь-
многоугольник и провести к нему замыкающую (замыкающие), соответствую-
соответствующую (соответствующие) способу закрепления балки, то получится
эпюра изгибающего момента
Масштабом для этой эпюры будет величина, показывающая,
что 1 см вертикального отрезка эпюры соответствует Н (Щ кГ-см
изгибающего момента
Прежде чем построить эпюру поперечной силы, необходимо
определить векторы, соответствующие реакциям опор На плане сил
эти векторы отсекаются линиями, параллельными замыкающим
(замыкающей) веревочного многоугольника, проведенными (про-
(проведенной) из полюса Эпюра поперечной силы строится путем пере-
переноса векторов плана сил в соответствующие точки линий нулевых
значений Q, параллельной геометрической оси балки. Масштабом
этой эпюры будет величина -, показывающая, что 1 см вертикального
отрезка эпюры соответствует tj кГ поперечной силы
При действии на балку распределенной нагрузки ее разбивают на
части линиями, перпендикулярными геометрической оси балки.
Площадь каждой части представляют вектором, приложенным в ее
центре тяжести С помощью этих векторов, как векторов сосредото-
сосредоточенных сил, строят и план сил, и веревочный многоугольник. По-
Полученную полигональную эпюру М уточняют путем проведения кри-
кривой, вписанной в полигон, а ступенчатую эпюру Q — путем
проведения кривой или прямой (в зависимости от порядка распреде-
распределенной нагрузки), проходящей через точки горизонтальных отрез-
отрезков ступенчатой эпюры, находящиеся против начала и конца
каждой части площади распределенной нагрузки.
При действии на балку сосредоточенных пар сил моменты М
этих пар сил откладывают на эпюре изгибающего момента в соответ-
м
ствующих сечениях в виде вертикальных отрезков у = „.. .
Для общности с аналитическим методом при графическом по-
построении эпюр М и Q будем считать положительными величинами
вертикальные отрезки, лежащие выше замыкающей веревочного
многоугольника для М и выше параллели геометрической оси
балки, принятой за линию нулевых значений Q.
Если условиться к рассматриваемому сечению балки подходить
слева и в этом же порядке откладывать векторы нагрузки на плане
сил, то для получения на эпюрах принятых знаков М и Q полюс сле-
Дует располагать слева от плана сил
В примерах 29, 30, 31, 32 и 33 указана методика графического
построения эпюр М и Q для балок с различным способом закрепле-
закрепления и нагружения
107
Пример 29. (рис. 57).
Рис. 57
Пример 30. (рис. 58).
и н_
L __«
ЩПЩ
Ш1 ,.
! f ¦ V \зща9 -Ц
[ ' ' ' ! !
Рис. 58
108
Пример 31. (рис. 59).
е
Пример 32. (рис. 60).
Рис. 60
109
Пример 33. (рис. 61).
С 1
Рис. 61
Задачи 271—275. Построить графическим методом эпюры по-
поперечной силы Q и изгибающего момента М
27/
т
тп
111
ТПТг
Hill
-1,5м
Пи
И
111
-15и
HI i
1м Ь< Зм-
Р,-8т
СП
Л-itr
1и
273
Ж
-Зм
P,-(F
3*
по
Задачи 276—285. Построить эпюры поперечных сил Q и опреде-
определить нагрузки, действующие на балки по заданным эпюрам изги-
изгибающих моментов М.
Ж Ш
Зтм
/1ара5оло
§ 2. Нормальные напряжения и подбор
поперечного сечения бапки
Нормальные напряжения в произвольной точке поперечного
сечення балки при изгибе определяются по формуле
0=^f., (92)
где М — изгибающий момент в рассматриваемом поперечном сече-
сечении;
/ — момент инерции площади этого сечения относительно
нейтральной оси;
у — координата рассматриваемой точки сечеиия до нейтраль-
нейтральной оси.
Наибольшие растягивающие и сжимающие нормальные напряже-
напряжения в данном поперечном сечении балки возникают в точках, наибо-
наиболее удаленных от нейтральной оси. Их определяют по формулам:
Myt М_
м
(93)
(94)
где yt и у2 — расстояния от нейтральной оси до наиболее
удаленных растянутого и сжатого волокон;
lPi=— и IF2=—— экваториальные или осевые моменты сопро-
сопротивления поперечного сечения балки (или
моменты сопротивления поперечного сечеиия
балки при изгибе) соответственно для растя-
растянутого и сжатого волокон.
Если в поперечном сечении
Л
У*. = Уг =-".
где h — высота сечения (например, для сечений, симметричных
относительно нейтральной оси, или сечений, центр тяжести которых
лежит посредине высоты — сечения рельса),
то 1^=1^= W =4- и °™x = -°nd« = -{r.
Необходимые размеры поперечного сечения балок при изгибе
подбираются по нормальным напряжениям, развивающимся в точ-
точках, наиболее удаленных от нейтральной оси.
Для балок, материал которых одинаково сопротивляется растя-
112
жению и сжатию, т. е. когда [ af] = [ сс], расчетная формула на из-
изгиб для подбора сечения записывается в следующем виде:
W--^p-. (95)
где W — минимальный момент сопротивления поперечного сечения
балки относительно нейтральной оси;
7Итах — наибольший по абсолютному значению изгибающий мо-
момент;
[ ои] — допускаемое напряжение материала балки на изгиб.
Отклонение от равенства (95) не должно превосходить ±5%.
При подборе сечений прокатных балок допускаются и более значи-
значительные отклонения в сторону увеличения запаса прочности. Для
балок из материалов, различно сопротивляющихся растяжению и
сжатию, должны удовлетворяться два условия:
^ = -Йг- (96)
Рациональное условие равной прочности материала балки в
крайних волокнах опасного сечения требует, чтобы поперечное сече-
сечение балки из материала, одинаково сопротивляющегося растяжению
и сжатию, было симметричным относительно нейтральной оси, а
поперечное сечение балки из материала, неодинаково сопротивляю-
сопротивляющегося растяжению и сжатию, было несимметричным относительно
нейтральной оси. При этом целесообразно стремиться к соблюдению
следующей пропорции:
[ОС] _ Г, _ fe /QR4
Наряду с условием прочности балка должна удовлетворять и
условию экономичности.
Так как прочность поперечного сечения балки при изгибе опре-
определяется величиной его момента сопротивления W, а вес балки
пропорционален площади ее поперечного сечения F, то степень
экономичности поперечного сечения балки можно оценивать отно-
W
шением \ — ~рт„ называемым удельным моментом сопротивления.
Чем больше это отношение при одинаковых площадях, тем эконо-
экономичнее сечение.
Пример 34. Дано: q = II кГ/см; Р = 1 Т; I = А м; о = 1 м;
К] = 1600 кГ/см2 (рис ъ'2)
В СИ: q = Ю,8 /см/ж; Р = 9,8 кн; I = 4 м; е = 1 м; [ а] =
= 157 Мн/м*.
113
Определить необходимые размеры круглого, квадратного, прямо-
прямоугольного и двутаврового прокатного сечений; отношение весов
балок этих сечений; нормальное напряжение в указанной точке А
сечения под силой для балки двутаврового сечения.
Решение. Так как балка симметрична относительно сред-
среднего сечения, то максимальный изгибающий момент будет в этом
сечении
Рис 62
От распределенной нагрузки эпюра М — параболическая с
mmq = \; от сосредоточенных сил эпюра М — трапецеидальная
с Мттр= Рс.
Поэтому
В СИ:
-1=3,2 Т-м.
I- 9,8-1 = 31,4 кн-м
По расчетной формуле (95) необходимый момент сопротивления
сечения должен иметь величину:
«г, Мтзк 3,2 1 О*
|а„1
16
В СИ:
W — 31'4 _ 9.
1К71П' ~
157- Ю
1. Для круглого сечения:
!= -^- = 200 еж3; d
ж8
= 12,68 см; F =
126,8 см\
114
2. Для квадратного сечения:
Wt = -^- = 200 СЛ13; а = ^200 • 6 = 10,63 см;
/7 = а2«113 см\
3. Для прямоугольного сечения:
Ws = ~- = -^- = 200 см3, h = ^2400 = 13,39 см,
F = bh=^- = 89,6 см*.
4 По сортаменту двутавровых балок:
для № 20 - W = 184 см3; для № 20а — W = 203 еж3.
Проверяем балку № 20
["..]
W
100 = 200~184 100 = 8,7 % перенапряжения.
Так как перенапряжение больше 5%, то двутавровую балку
20 брать нельзя
Проверяем балку № 20а
ЮО =
[а„1
= — 1,5 % недонапряжения.
100
Следовательно, принимаем балку № 20а, для которой F4 =
= 28,9 см'г, момент инерции относительно нейтральной оси / =
= 2030 смй и высота h = 20 см.
Поскольку вес балки пропорционален площади ее поперечного
сечения, то отношение весов балок будет равно отношению площадей
их сечений
Принимая площадь круглого сечения за условную единицу,
имеем: Ft : F2 : F3 : Fa « 1 : 0,89 : 0,71 : 0,23.
Таким образом, например, балка двутаврового сечения даже при
избыточных размерах площади (допущено недонапряжение на 1,5%)
приблизительно в 4,4 раза легче балки круглого поперечного се-
сечения.
115
Определяем изгибающий момент в сечении балки под силой:
1-1 =Цт-м.
В СИ:
М--
10.8-4-1
10.8-1
+ 9,8 ¦ 1 = 26 кн-м.
В точке А этого сечения, для которой у = j- = 5 см, нормаль-
нормальное напряжение будет сжимающим (балка выгибается вниз) и опре-
определится по формуле (92):
My —5,3-105-5
В СИ: ал
' / ~~ 2-2030
26-103-0,5-10-1
' 2030-Ю-»
~ ЬМ Kl ICM ¦
= — 64 ¦ 10s н/м2 = — 64 Мн/Л12.
— ь —
Рис.63
Так как
Пример 35. Балка П-образного сечения
(рис. 63) изготовлена из материала, у ко-
которого [ ос] =3 [ ор]. Известны размеры
Ь = 20 см и t = 1 см.
Определить рациональную высоту h се-
сечения.
Решение. Пусть ось z — нейтраль-
нейтральная и ее расстояние от крайних воло-
кои Л, и Л2.
По условию рационального использо-
использования материала (98) (условию равной
прочности крайних волокон):
А _ [°t] _ '
К ~ Ы ~ 3 •
, ТО Пх = —г- И А2 = -J- П.
Нейтральная ось z — центральная ось, а потому статический
момент площади сечения относительно оси должен быть равен нулю,
т. е.
= -(fc-20 2t
ft*
~2~
= 0.
Отсюда
116
18ft + 72 = 0 и h = 9 ± /9 = 9 ± 3.
Следовательно, высота сечения должна быть равна либо h = 12 см,
либо h = 6 см.
Задачи 286—306. Определить осевые моменты сопротивления
№г (г — горизонтальная центральная ось) поперечных сечений
балок. Размеры к задаче 306 взять из задачи 3C1.
287
UQ6H-1
го"
117
303
Задачи 307—313. Определить нормальные напряжения в точках
поперечных сечений балок (точки и сечения указаны в условиях
задач).
Обозначения: отах — наибольшее и наименьшее нормальное
min напряжение в опасном сечении,
шах ад — нормальное напряжение в точке А опас-
опасного сечения,
адтп — нормальное напряжение в точке А сече-
сечения тп,
f — вес единицы объема материала балки.
P-itr
118
Задачи 314—329. Подобрать необходимые размеры попереч-
поперечных сечений балок.
В задаче 319 определить необходимое число параллельно постав-
поставленных брусьев прямоугольного сечения заданных размеров.
В задаче 325 подобрать номера двутавровых балок при самом
неблагоприятном положении подвижных грузов.
В задачах 327—328 соответственно определить размеры Ь и h
из условия равной прочности растянутых и сжатых волокон.
Ш
315
=0,5га И
-*и—Ц Ы
tu
Ш
ЯпПпнпптН т
<nA~ 5m-
3J8
М'Зтм
fei-
IIIHIHf
h'O.Bh
119
ш
321
=езн
И = №Ш«Г/Ш* Ни
ш.
Т1ШПП
II
зги-
PSt
Ш#г
Р=26.6кн
II
-*-
a Zap la a
327
/o»
[6j=3[6j
120
10 10
I—?oo—1
HHIIHI1
Задачи 330—342. Определить величины допустимых нагрузок,
действующих на балки заданных размеров.
ш
г
—6м —I— 8м —IZ
8» 333
11 (и н
Z
Но ——~i a
[б)=Ш11кГ/мг
гтттт
q -0,5t/i*i
lltlltl
г!ЩУ*1'
J35
П liiltlll
N14
I—Z«—;
Ж
K-Im
[6\-WMh/m*
г».
J
Ш
121
'56см
=ШкГ/см1, [бс]=12Ш}«Г/см1
Ш
P
§ 3. Касательные напряжения, центр изгиба
и проверка прочности бапок по касатепьным напряжениям
В произвольной точке прямоугольного поперечного сечения
балки (рис 64) величину касательного напряжения определяют по
формуле Журавского Д. И.:
S =
где Q — поперечная сила в рассматриваемом сечении;
—4 У2 ) — статический момент относительно нейтраль-
нейтральной оси z части площади сечения, лежащей по
одну сторону от уровня у, на котором опреде-
определяется напряжение;
b — ширина сечения;
I — -7g—момент инерции площади сечения относитель-
относительно оси г
Наибольшие касательные напряжения получаются в точках
нейтральной оси Они имеют значение
где F = bh — площадь поперечного сечения балки.
По формуле (99) приближенно можно подсчитывать составляю-
составляющие касательных напряжений, перпендикулярные нейтральной
оси, и для балок непрямоугольного сечения, понимая под Ъ ширину
сечения на уровне рассматриваемой точки. Результирующие каса-
касательные напряжения в точках контура сечения направлены по каса-
касательным к контуру сечения, а в других точках сечения они наклоне-
наклонены к плоскости действия сил
122
Точно найти касательные напряжения в балках произвольной
формы сечения весьма сложно Приближенное их определение осно-
основано на некоторых произвольных допущениях о направлении каса-
касательных напряжений внутри сечения.
Для балок, поперечным, сечением которых является тонкостен-
тонкостенный открытый профиль (рис. 65), принимают, что касательные нап-
напряжения, направленные по касательным к средней линии стенки
сечения и по нормали (f) к ней, распределены равномерно. Формула,
1
1
-с
1
tm
— ь
tftt
—»
af fas
Рис. 64
Рис 65
определяющая касательное напряжение, в этом случае принимает
вид:
QS
A01)
где S — статический момент относительно нейтральной оси г части
сечения, лежащей по одну сторону от нормали t к средней линии
на уровне у рассматриваемой точки.
Если сечение балки несимметрично относительно главной цент-
центральной оси у, перпендикулярной нейтральной оси г, то возникают
касательные напряжения, создающие в этом сечении крутящий
момент. Чтобы кручения балки не было, поперечная сила должна
быть приложена не в центре тяжести сечения, а в точке, называю-
называющейся центром изгиба.
Для произвольной формы поперечного сечения балки определе-
определение положения центра изгиба представляет большие трудности.
Для тонкостенного сечения, симметричного относительно нейтраль-
нейтральной оси г (рис. 65), центр изгиба лежит на оси г, его расстояние от
центра тяжести сечения
1 с S
pdF,
A02)
123
где р — плечо элементарного касательного усилия xdF относительно
центра тяжести сечения;
F — площадь всего сечения.
Если толщина стенки профиля t постоянна, то выражение A02)
приобретает следующий более простой вид:
*'pds. A03)
Здесь Is — экваториальный момент инерции дуги средней линии
всего сечения относительно оси г;
Ss' — статический момент относительно оси z дуги s' сред-
средней линии части сечения, лежащий по одну сторону
от уровня у произвольной точки.
Интегрирование ведется не по площади сечения, а по дуге s.
Если профиль сечения состоит из нескольких частей разной, но
постоянной толщины t, то е можно найти суммированием выраже-
выражений A02), составленных для каждой отдельной части.
Прочность балки по касательным напряжениям проверяется в
точках с максимальными касательными напряжениями того попе-
поперечного сечения, в котором дейстнует наибольшая по абсолютному
значению поперечная сила Qmsx.
Проверке следует подвергать балки короткие, балки с тонкой и
нысокой стенкой сечения, балки, изготовленные из материала,
плохо сопротивляющегося сдвигу, и балки, несущие большие на-
нагрузки вблизи опор.
Проверочная формула имеет нид:
w = QT,St < М- A04)
где So — статический момент относительно нейтральной оси части
поперечного сечения, лежащей по одну сторону линии действия
Ьо — ширина сечения на линии действия тшах.
Для болышнстна проверяемых сечений тшах действует в точках
нейтральной оси.
Допускаемое касательное напряжение [т] обычно берут равным
0,5 — 0,7 от [ а]. Например, для Ст. ОС и Ст. 2 [ т] = 900 кГ/см2,
для Ст. 3 [ т] = 1000 кГ/см2, для сосны и ели [ х] =20 кГ/см2.
Пример 36. Дано: Mt = 40кн-м, Mz= 20кн-м, М3= 10 кн-м,
а = 1 м, 6 = 4 см, h = 12 см (рис. 66).
Определить ад и хл в сечении тп.
Решение. Реакции опор
= 40-20+ 10
Эпюры Q и М показаны на рис. 66.
124
В сечении тп М = — -~—= —25 кн-м; Q = 10 кн.
Так как точка Л находится в растянутой зоне сечеиия, то по
формуле (92)
\М\у
"л г
Для прямоугольного сечения
6ft3 4.12s
576 см1.
Зтм
2т«
Рис. 66
Для рассматриваемой точки А
у = —- = 3 см.
Поэтому
а
По формуле (99)
аА = ^(МО1""** 13°-106 н/м* = 130 Мн1м*-
4
10-103
16
= 2,34- 10е н/м2 = 2,34 Мн/м2.
8 bh ~ 8 0,04-0,12 '
Пример 37. Дано: Q = 8 7", Л = 12 ел, Ло= 8 см, b =--6 см,
Ь»~ 4 ел (рис. 67).
Построить эпюру условных касательных напряжений, перпенди-
перпендикулярных нейтральной оси (по формуле Журавского).
Решение. Найдем значения касательных напряжений в
точках / крайних волокон сечения, в точках 2 крайних волокон
125
полости, в точках 3, наиболее удаленных от нейтральной оси на
стенках полости, и в точках 4 на нейтральной оси z (рис. 67).
Для этого воспользуемся формулой (99).
Момент инерции относительно нейтральной оси г площади се-
сечения заданной формы:
12
12
= -?F.
13)
Рис 67
Для точек 4
-4
s) =
2080
CM*.
OB) = О —f,—I -H
Для точек / Si — 0, следова-
следовательно, и тA) = 0
Для точек 2
h—hpl
2^2 4
6-2F—1) = 60 см3
QSB,
TB) =
8-103-60-3
Ы
- -6T2080- ** 115'
Так как ширина сечения в
точках 3 равна i>—Ьй, то
т<3) - <Ь-Ь„)/
— тB)
* 115,4 •-r =
= 346,2 /сГ/сж2.
2-4-2 = 76 ел
«S.
D)
(Ь -
8-103-76-3
2-2080
438,5 кГ/см'
По этим результатам на рис. 67 построена эпюра т.
Пример 38. Дано: тонкостенное сечение в виде части кругового
кольца с центральным углом 2о, радиусом средней линии г и
постоянной толщиной t (рис. 68).
Определить положение центра изгиба А
Решение. Из чертежа видно, что элемент дуги средней
линии кольца d& = rdy; элемент площади стенки кольца dF =
= tds = rtdy; координаты центра тяжести элемента площади dF
в центральных осях уог:
у = г simp; г — г cosy — а,
126
где а—расстояние между осью у и осью у', проходящей через центр
кривизны сечения О,
Определяем положение центра тяжести О сечения на оси г.
Так как ось у — центральная ось сечения, то статический момент
площади сечения
а
Sy= \zdF=-2rt j(rcos(p — a)d<i> = 2rt (r sin о — aa) — 0.
Поэтому
Плечо р касательного уси-
усилия ttds по отношению к цент-
центру тяжести сечения имеет ве-
величину
р = г — a cos ф =
(. sin a \
1___СО5ф).
Момент инерции /* дуги
средней линии сечения отно-
относительно нейтральной оси г
Is =
\f sir
Рис. 68
= ^-Bа —sin 2а).
Статический момент 5s' относительно оси г части дуги средней
линии сечения, расположенной по одну сторону от произвольно
взятого элемента, определяющегося углом у. имеет значение:
= г2 (cos ф — cos a)
По формуле A03) расстояние е от центра тяжести сечеиия до
Центра изгиба А
6 ~ Is J Р = < Bз — sin 2а) Х
S
^ о
Я Sin a \
1 — cos ф 1 • (cos ф — cos а) ^ф,
127
или
е =
Чг
2а — sin Ъ-
-I sin а — 2 а cos а + — sin2 а cos а) .
Расстояние от центра кривизны сечения О' до центра изгиба А:
е = —sin a -f-
2а — sin 2a
(sin а — 2а COS а -] sin2 а COS а | =
\
4 (sin a — a COS а)
2 о — sin 2а
2ти
1т
Рис. 69
Мши = 2 Т-м,
Из расчетной формулы
Пример 39. Дано: Р = 4 Т,
М = 2 Т-м, а = 0,5 м, 1 = 4м,
[о]=1600 кГ/см*, [х]= 1000/сГ/сж2
(рис. 69).
Определить номер двутавра.
Решение. Эпюру изги-
изгибающего момента М легко по-
построить без вычислений, как
показано на рис. 69.
На консоли Q = const =
= —4 Т. В пролете между
опорами Q = const <0. Из эпю-
эпюры М
ДМ =2 T-m = —Q2 м.
Отсюда Q = — 1 Т.
Эпюра Q изображена на рис. 69.
Таким образом,
U = 4 Т.
По сортаменту: для двутавра № 16 W = 109 см3;
для двутавра № 18 W = 143 см3.
Проверяем двутавр № 16:
"max — j°l I nr
тЛ ' ) ' 100~ 15% (перенапряжение).
Проверяем двутавр № 18:
J^=M-. 100
я= — 12,5 % (недонапряжение).
128
Выбираем двутавр № 18, для него
10°
_ Mmw :
max y^ j^g
« 1400 /с/7сл2.
По сортаменту S = 81,4 см3; I = 1290 еж4; d = 0,51 см.
Следовательно,
_QimxS _ 4 - 10я -81,4
0,51 • 1290
dl
« 495 кГ/см* < [т]
и выбранный двутавр № 18 будет прочен и по нормальным, и по
касательным напряжениям.
Задачи 343—351. Построить эпюры касательных напряжений т,
перпендикулярных нейтральной (горизонтальной) оси, в частях от
наибольшего значения
сечения балок.
Для указанных форм поперечного
Ш Ml
i I
Задачи 352—357. Определить наибольшие касательные напряже-
напряжения тшах, установив предварительно (где нужно) необходимые раз-
размеры балок или безопасные нагрузки по заданным допускаемым
нормальным напряжениям.
Р'ШкГ
0,5м [е]* 100 к Г/см*
5 Заказ №
129
354
355
пЁ
•ЛпкГ/м \1В0«Г
¦Ви-
ашпшпп
2м | 1м
М'ЮСОкГ/см'
357
Тгда,
ж*ш
д,-10кн/м I
-Вм Л/J
J^Wkh/m P--W,
-Zm^\-^?m-4~-2m
е гь-гасм
Задачи 358—363. Определить расстояние е центра изгиба от
центра тяжести сечения (сечения считать тонкостенными).
356
353
говчоыо
звг
3B0
§ 4. Главные нвпряжения и полнвя
проверка прочности бвлки
В произвольной точке поперечного сечения балки, находящейся
на расстоянии у от нейтральной оси г, нормальные о и касательные
•с напряжения определяют по формулам (92) и (99)
130
Элемент, выделенный около этой точки бесконечно близкими
поперечными сечениями на расстоянии их друг от друга и бесконечно
близкими продольными сечениями, параллельными нейтральному
слою на расстоянии dy друг от друга, испытывает плоское напряжен-
напряженное состояние вида, указанного на рис. 70.
Нормальные о „ и касательные т „ напряжения в наклонной
плоскости сечения, проходящей через эту точку (рис. 71), имеют
значения.
о„ = oCOS2a — t sin 2a,
ta = -4- Sin 2a + i COS 2a.
A05)
Рис Tl
Две взаимно перпендикулярные наклонные плоскости являются
главными плоскостями напряжений в данной точке балки, когда
tg2a=
A06)
Величины главных напряжений о4 и о3 находятся из выражения
A07)
3
Экстремальные касательные напряжения определяются по фор-
формуле
A08)
Графическое определение величии и направлений главных на-
напряжений для четырех возможных вариантов напряженных состоя-
состояний элементов, выделенных из балки, показано на рис 72
Если в одном и том же поперечном сечении балки одновременно
Действуют максимальный изгибающий момент и максимальная
поперечная сила или величины М и Q, близкие к максимальным,
то в этом сечении производится проверка прочности балки по глав-
главным напряжениям.
5* 131
Прочность по главным напряжениям проверяется только для
балок, поперечное сечение которых имеет тонкую стенку, резко
уширяющуюся вблизи крайних волокон. Проверка прочности про-
производится в точках перехода от малой ширины сечения к большой.
Балки из пластичного материала проверяются по третьей гипо-
гипотезе прочности по формуле
°9ш = °1 - "э = У^ + № < ["]• <109)
Балки из хрупкого материала проверяются по первой гипотезе
прочности согласно условию:
(ПО)
Рис. 72
Полный расчет на прочность статически определимой балки
указан в примере 40.
Пример 40. Дано: Р = 4 Т, д = 3 Т/м, а = 0,8 м, I = 4 м,
1о] = 1600 кГ/см\ |х] = 1000 кГ/сл2 (рис. 73)
Определить номер двутавровой балки.
Решение 1. Определение опорных реакций:
-~Р—Ра
0'8 =5,2 Г.
2. Построение эпюр Q и М
132
На консоли 0 <^ хл <^ а:
Q*i =—P = —4T; MXi =—Pxt = — 4л:,; М^ = 0;
ЛЬ1=О = —4-0,8=—3,2 Г-ж.
В пролете между опорами 0<*2</:
Qxz — — В + цхг = — 5,2 + Зл-2; Qx =0 = _ 5,2 71;
Q*2~i = - 5,2 + 3 • 4 = 6,8 Т,
™*2 = 2 2~ хг ~ ^З** 2~ Х"г' ^х2=о = 0;
Л^2=г = 5,2 ¦ 4 — -|- • 16 = — 3,2 Т - м.
¦ ГПННШНИ
•с
в* 3
1
.1
\ 7.
1
h- Ь
4
в
9
Рис. 74
5,2
Рис. 73
Так как Q = — 5,2 + 3*» = 0 при к, = -^ = 1.73 ж, то
Л^та» =5,2- 1,73 -З.-ЦТЁ!- 4,5 Г-ж;
Х9*=*\ ,73 ^
* \
МХг = 5,2^2— -|- ^ = С когда х2 = ^^ = 3-47 м.
По этим данным на рис. 73 построены эпюры Q и М
133
3 Подбор сечения двутавровой балки.
Так как Мтю = 4,5 Т ¦ м, то W = ijsp. = A^fJ^- « 281 еж8.
По сортаменту для двутавра № 22а: W = 254 см3.
Щ=Ы . юо = W Ww° . юо = 281-254. ЮО = 10.6% > 5%
(перенапряжение).
Для двутавра № 24: W = 289 см
3
. ЮО = "»524 • 100 = ™^» . 100 «-2.7796
55=±1. ЮО =
(недонапряжение).
Выбираем двутавр № 24, для которого IF = 289 си*1*,
/ = 3460 см\ So = 163 еж3, Л = 24 см, b = 11,5 cjk, < = 0,95 еж,
d — Ьй = 0,56 еж, Ао = h — 2t = 22,1 еж (рис. 74). Этот двутавр
будет работать при максимальном нормальном напряжении в край-
крайнем волокне опасного сечения:
156°
4. Проверка сечения балки по касательным напряжениям.
Так как Qmax = 6,8 Г, то
QmsxSo 6,8- I03 • 163 .„„ г, „ ^, ,
W = -^7^ = 0,56-3460 * 570 КГ1СМ* < 1Т1-
5. Построение эпюр нормальных о, касательных т, главных
01,3 и экстремальных касательных ттах напряжений в неблаго-
min
приятном сечении балки и определение их направлений
В отношении главных напряжений неблагоприятным является
сечение над левой опорой (при подходе к ней справа), в котором
М = —3,2 7- м и Q = 6,8 Т.
Напряжения будем определять в девяти точках сечения, указан-
указанных на рис. 74.
Нормальное напряжение в произвольной точке, находящейся
на расстоянии у от нейтральной оси,
_ МУ — 3'2" Х№
°~ I ~ 3460 :
Статический момент площади полки относительно оси z
Sr = W А=±= цM. о,95 ?i^^« 126 см\
134
Статический момент части площади стенки по одну сторону от
ординаты у
Статический момент части сечения по одну сторону ординаты у
S = 5Г + Sc = 126 + 0,28 A22 — у2) « 160— 0,28#2
Касательные напряжения для точек полки согласно формуле (99)
а для точек стенки
21
QS
(б)
(в)
По формулам (а), (б), (в), A08), A07), A06) вычислены значения
о, t. ¦tmax, oi,3» tg2a, alt а2 для у, отвечающего девяти точкам
сечеиия.
Полученные значения сведены в следующую таблицу:
Номер
точек
1
2
3
4
5
6
7
8
9
V, см
12,00
11,05
11,05
5,52
0,00
— 5,52
-11,05
-11,05
-12,00
я
т
ттах
шт
кГ/см'
1110
1020
1020
510
0
— 510
—1020
— 1020
-1110
0
20
440
530
560
530
440
20
0
±555
±510
±670
±590
±560
±590
±670
±510
±555
1110
1020
1180
840
560
340
160
0
0
0
0
— 160
— 340
— 560
— 840
—1180
—1020
—1110
tg2o
0,00
—0,0392
—0,863
—2,08
оо
2,08
0,863
0,0392
0,00
0°0'
— 1 07
—20 24
—32 10
—45 0
32 10
20 24
1 07
0 0
«а
90э0'
88 53
69 36
57 50
45 0
122 10
ПО 24
91 07
90 0
Эпюры напряжений изображены на рис. 75.
Направления главных напряжений в рассмотренных точках
сечения показаны на рис. 76
На рис. 77 произведено графическое определение величин и на-
направления главных напряжений о, и о3 в точках 4, 5 к 6.
6. Проверка прочности балки по главным напряжениям.
Наиболее опасной точкой в неблагоприятном сечении является
точка 3. В этой точке oj = 1180 кГ/см? и о3=—160 кГ/см2. Прове-
135
63lif/CM!, б,
Рис. 75
В точке 4
Рис. 77
ряем прочность в этой точке по третьей гипотезе прочности согласно
неравенству
Так как 1180 + 160 = 1340 < 1600, то выбранное сечение проч-
прочно и по главным напряжениям.
Задачи 364—367. Определить (аналитически и графически)
величины и направления наибольших и наименьших главных
напряжений о, и о3 в указанных сечениях балок.
Обозначения: тахо, н mino3 — наибольшие и наименьшие
главные напряжения в самом неблагоприятном сечении балки по
длине в местах резкого изменения ширины сечеиия;
ашп и аЪтп — главные напряжения в тех же точках сечения тп.
В задаче 366 плоскость нагрузки проходит через линию центров
изгиба поперечных сечений.
60
Задачи 368—373. Подобрать поперечные сечения балок и про-
произвести полную проверку их прочности.
Принять [о] = 1600 кГ/ст2, [х] = 1000 кГ/см2 и третью гипо-
гипотезу прочности при проверке по главным напряжениям.
В задачах 372 и 373 принять [о] = 160 Мн/м2; [т] = 1Q0 Мн/м*.
В задаче 368 подобрать допускаемую нагрузку и произвести полную
проверку прочности балки.
№П0
0.5м
137
§ 5. Основы расчета балок на прочность
по несущей способности
Различие в расчете на прочность по допускаемому напряжению
и по несущей способности для пластичных материалов заключается
в разных стадиях деформированного состояния балки, которое при-
принимается за опасное состояние (
Расчет по несущей способности обычно производят по нормаль-
нормальным напряжениям без учета упрочнения материала балки от пла-
пластической деформации. За основу берут идеализированные диаграм-
диаграммы растяжения и сжатия материала балки (рис. 78)
При расчете по допускаемому напряжению за опасное состояние
балки принимают такое ее состояние, при котором в наиболее на-
напряженном крайнем волокне балки нормальное напряжение до-
достигает значения предела текучести материала от (рис. 79).
В соответствии с эпюрой о (рис. 79) изгибающий момент при
опасном состоянии балки
М7 = о, W.
A11)
Вводя коэффициент запаса, получают формулу для определения
допускаемого изгибающего момента:
MmM=l°llP. A12)
При расчете по несущей способности за опасное состояние балки
принимают такое ее состояние, при котором во всех точках опасного
сечения нормальные напряжения достигают значения предела теку-
текучести материала (рис. 80).
138
Это состояние в соответствии с эпюрой о (рис. 80) получается
при следующей определенной величине изгибающего момента
M't=2gtS, A13)
где S — статический момент половины площади поперечного
сечения балки относительно центральной оси Z.
Эпира б
Рис 78
Рис. 79
Так как дальнейшее увеличение изгибающего момента в этом
сечении невозможно, то говорят, что в сечении возник «пластический
шарнир» и балка стала геометрически изменяемой системой.
Расчетную формулу для определения допускаемого изгибаю-
изгибающего момента получают, вводя коэффициент запаса прочности
Mmax = 2[o]S. A14)
Из сравнения формул A12) и A14) видно, что допускаемый изги-
изгибающий момент М'тяк при расчете по несущей способности больше
допускаемого изгибающего момента Мтах при расчете по допускае-
допускаемому напряжению в vj раз, где
Ч
W
Величина yj зависит только от геометрии поперечного сечения
балки.
Пример 41. Дано: формы сечений, указанные на рис. 81.
Определить ¦»].
Р
Решение,
г\\ \у/ ОП о
4rs- 4
¦¦ 1,697.
3
4 = т
1,5.
8
= 1,5.
139
4) Так как W = -2[-. то T) = -^- = ^-ft.
По сортаменту, например, для двутавра № 20а:
' = 2030 еж4; S=*U4cms; ft = 20 см; •») = -Ц?^- ~ 1,12.
Б) W:
а42
• Л Г" Г
К2 „з.
ч) = -
= f B-/2);
'"~
«2,344.
Задачи 374—379. Определить отношения ij =х
максималь-
ных изгибающих моментов Л1^ахиЛ1тах , установленных рас-
расчетом по несущей способности и по допускаемому напряжению для
указанных форм поперечных сечений балок.
375
37В
/у///с
Л
ум1//.
1
1
140
877
378
Ьь-«а—'
Задачи 380—385. Определить необходимые размеры балок или
допускаемые нагрузки из расчета по допускаемому напряжению и
по несущей способности.
Обозначения: b, d, h, Ртя^, <7max — необходимые размеры попе-
поперечных сечений балок и допускаемые нагрузки из расчета по до-
допускаемому напряжению; b', d', h', Pmax, дтвх — то же, из расчета
по несущей способности.
1м h—Вм ~| 2м Н—
§6. Перемещения при изгибе
Перемещения сеченнй балок характеризуются:
1) линейными перемещениями центров тяжести поперечных се-
сечений в направлении, перпендикулярном геометрической оси балки
х, которые называются прогибами (JJ;
141
2) угловыми перемещениями поперечных сечений вокруг ней-
нейтральной оси г, которые называются углами поворота сечений FХ).
Прогиб fx считается положительным, если его направление
совпадает с положительным направлением оси у, перпендикулярной
геометрической оси балки к.
Угол поворота 6л. считается положительным, если поворот попе-
поперечного сечения балки вокруг нейтральной оси г происходит против
часовой стрелки.
Максимальные и минимальные прогибы fmta /шш и углы поворота
6шах, 6raln оцениваются по их абсолютным значениям.
Так как поперечная сила оказывает заметное влияние на дефор-
деформацию только коротких балок, то обычно /ив определяют лишь
от изгибающего момента.
/ив можно определять методом начальных параметров, графиче-
графическим, графо-аналитическим и другими методами.
Метод начальных параметров
За начальные параметры принимают прогиб /0 и угол поворота
60 поперечного сечения балки, в центре тяжести которого располо-
расположено начало координат.
Целесообразно начало координат располагать в центре тяжести
концевого поперечного сечения балки
Уравнения, определяющие fx и Qx в произвольном сечеиии балки,
находящемся на расстоянии к от начала координат (если интенсив-
интенсивности распределенных нагрузок дх являются степенными функция-
функциями), записываются в следующем виде:
EIfM-EIfa+EI %^
где E — модуль продольной упругости материала балки;
/ — момент инерции поперечного сечения балки относительно
нейтральной оси г;
М — моменты внешних пар сил;
142
ат — расстояния от начала координат до сечений, в которых
приложены пары сил (рис. 82, а);
Р — сосредоточенные поперечные силы (в том числе и реак-
реактивные);
ар — расстояния их точек приложения на оси балки от начала
координат (рис. 82. б);
а) 6) 6)
Рис. 82
q uij ,q'aq — соответственно значения qx первой и т. д. производных
qK по х при х = aQ, т. е. для поперечных сечений, с которых начи-
начинается действие распределенных сил (рис. 82, е);
q bq,q bq — соответственно значения qx первой и т. д. производных
qx по х при х = bQ, т. е. для поперечных сечений, в которых закан-
заканчивается действие распределенных сил перед рассматриваемыми
сечениями (рис. 82, е).
Если начало координат расположить в центре тяжести правого
концевого сечения балки и ось х направить влево, то при указанном
направлении нагрузок в формулах A16) и A17) у членов, отражаю-
отражающих влияние моментов внешних пар сил, знаки будут отрицатель-
отрицательными; направление поворота сечения балки, найденное по формуле
A17), окажется противоположным ранее принятому.
Можно помнить только одну формулу A16), из которой формула
A17) получается дифференцированием
Два начальных параметра /0 и 60 находятся из следующих усло-
условий закрепления балки:
1) в згделке прогиб и угол поворота сечения равны нулю;
2) на шарнирных опорах прогибы равны нулю
Для симметричных балок рассматривается одна их половина и
используются условия симметрии — равенства нулю угла поворота
сечения, совпадающего с осью прямой симметрии балки, или ра-
равенства нулю прогиба сечения, совпадающего с осью обратной сим-
симметрии балка.
Целесообразно записывать только одно уравнение A16) и одно
Уравнение A17) для произвольного сечения последнего участка
балки, включая нагрузки в той последовательности, в которой они
расположены от начала координат. Каждое из этнх уравнений при-
пригодно для определения fx и Ьх в любом участке балки, если в них
143
отчеркнуть число членов, соответствующих нагрузкам на предшест-
предшествующих участках
Пример 42. Дано: q, а, Р = Aqa, М = qa2. El (рис 83).
Определить f^ 6^.
Решение. Из условия статики 1>МВ = О
—да -|а + А-2а — Aqa-a + qa2 = 0; А = ^
Рис 83
По уравнению A16) для последнего правого участка балки:
*¦« 11 (х — а)" (х — сL (х—2аK
(f-^ + -j-qa g + <7 §4 ~ qa 6 ""
Ill
Для участка /: 0 ¦< х ^ а.
Для участка //: а ¦< к ^ 2а.
Для участка ///: 2а < х < За.
По условиям закрепления балки
на левой опоре:
на правой опоре:
24
= ?//„ + ?/в0 За + ¦? <?а4 - -f <?а4 - -^ <
1 = О,
т. е.
?//„+ ?/6^-^ = 0,
откуда
144
После подстановки
Следовательно, !о = ~ы ^Щ~ •
Уравнения, определяющие /^иб^в любом сечении любого участ-
участка, приобретают вид:
Elfx =4лЯа^ *Г Яа3х — ~дх*+^-да(х — аK + -^д (х—аL—
24
а<л:<2а|
l-qa(x-2af.
— 2?a (x — 2aJ.
Например,
угол поворота сечения над левой опорой
1 о 1
угол поворота сечения над правой опорой
qa> [ 1 27 44 8
прогиб балки под сосредоточенной силой
f —WLIA 1 l±_i__LL-l.Jl.^
'2a ~" ?/ ^ 24 6 24 + 24 "•" 24)
1 ?о«
24 El
На рис. 84 показаны примерный вид упругой линии балки (штри-
(штриховая линия) и найденные прогибы и углы поворотов сечений.
Следует иметь в виду, что в тех сеченнях балки, в которых изги-
изгибающий момент равен нулю, на упругой линии должна быть точка
перегиба. На участках балки, где изгибающий момент положителен,
выпуклость упругой линии направлена вниз, а где изгибающий
145
момент отрицателен, выпуклость упругой линии направлена вверх
(это отмечено на рис. 84).
Задачи 386—387. В задаче 386 определить прогибы f и углы
поворота G сечений балок методом интегрирования дифференциаль-
дифференциальных уравнений упругой линии:
1) в задачах 222—226 — прогибы и углы поворота свободных
концов;
qa*
Рис. 84
2) в задачах 228, 229, 231 — прогибы в серединах пролетов и
углы поворота на опорах;
3) в задачах 227 и 230 — наибольшие по абсолютному значению
прогибы и углы поворота на опорах.
Нагрузки, длины и жесткости сечений балок считать изнестными.
В задаче 387 установить, на сколько процентов и в какую сторону
прогиб середины пролета балки, указанной на рисунке, определен-
определенный по приближенному уравнению упругой линии, отличается от
прогиба, найденного точно по уравнению дуги окружности.
367
Р=?т
'ZmI
-5g
Tir-гг
Е-1106кГ/смг
Задачи 388—391. Определить, на сколько процентов наибольший
изгибающий момент и прогиб для балок, изображенных на
рис. 388—391, больше, чем для балки на двух опорах, нагруженной
такой же нагрузкой Q, но равномерно распределенной по длине.
146
388
389
• Порадело
3"/ Синусоиде (полволны)
и 1
Задачи 392—409. Определить прогибы fc сечений С н углы
поворота GD сечений D балок.
q, а, Е и / — считать известными.
392
зэз
ДГПТП"
a—a*—o-
tllltl |-тУтт
394
395
1Ш
J.t ( t
ЗЭЙ
3S9
-За
ШШ
147
402
qa
Ко—»
И
ц
адз
-2о
ш
ттттп п
Г h
-го—-Ко-
•с-
VCfi
— 30
Парадала
г*- о ¦ I * о*^ ¦•— о »I * о -»]
аде
loo
\
-.
1
t—
\
п-
\
¦^ а -
ад
—^j.
Графо-аналитический метод
Для заданной балки строят эпюру изгибающего момента. Эту
эпюру принимают за фиктивную распределенную нагрузку фиктив-
фиктивной балки. Угол поворота 6^. какого-нибудь сечення заданной балки
определяют как отношение поперечной силы фф,, в том же сеченни
фиктивной балки к жесткости сечения заданной балки, т. е.
143
Прогиб fx какого-нибудь сечения заданной балки определяют
как отношение изгибающего момента М Фх в том же сечении фиктив-
фиктивной балки к жесткости EI заданной балкн, т. е.
Мл,
Согласно формулам A18) и A19) деформационные условия в
закреплениях и на границах заданной балки должны переходить
в условия для фф и Л1ф фиктивной балки.
Чтобы получить фиктивную балку, соответствующую заданной
балке, необходимо соблюдать следующие правила-
т ?_ ° 2? -к б)
¦ ' ! ¦
а1) ' I 6 6 g ^
Рис. 85 Рис. 86
1) опора на конце заданной балки остается опорой на конце
фиктивной балки;
2) опора не на конце заданной балки переходит в висячий шар-
шарнир фиктивной балкн;
3) заделанный конец заданной балки становится свободным
концом фиктивной балки;
4) свободный конец заданной балкн становится заделанным кон-
концом фиктивной балки;
5) висячий шарнир заданной балки переходит в опору фиктивной
балки.
На рнс. 85 и 86 показано использование правил построения
фиктивных балок: а к б — заданные балки, а' к б' — соответствую-
соответствующие им* фиктивные балки.
Графо-аналитический метод удобен для определения перемещений
отдельных сечений балки тогда, когда легко находятся площади н
центры тяжести эпюр изгибающего момента от заданной нагрузки.
Чтобы соблюдались принятые условия знаков прогиба и угла
поворота сечения, положительную эпюру изгибающего момента
заданной балки следует принимать за фиктивную нагрузку, дейст-
действующую на фиктивную балку снизу вверх, а отрицательную эпюру
изгибающего момента заданной балки — за фиктивную нагрузку,
действующую на фиктивную балку сверху вниз.
Пример 43. Дано: Р, I, E, I (рис. 87).
Определить вс , вА , fA.
149
Решение. Эпюра изгибающего момента для заданной балки
ABC представляется отрицательным треугольником с высотой Р1
в сечении В.
Принимаем эту эпюру за фиктивную нагрузку для фиктивной
балки А'Л'С.
Из суммы моментов относи-
относительно висячего шарнира В'
(сил, расположенных от него
справа) находим реакцию
Г' - * Р/ ' ' _ Я/а
Рис. 87
Рис. 88
Следовательно,
Так как
В
то
с
Пример 44.
Определить
<?ФС.
El
j
Дано:
/max*
PI2
О/
и ~ 6 а
рр
- 6?/'
, М*А-
Га~ El
AJ, at E,
— Р1Ч
А =
1 (рис.
~ 3
' El
2 РР
3 El '
88).
РР
5
6
РР
EI
150
Решение. Фиктивная балка представляет собой балку
на двух опорах с фиктивной равномерно распределенной нагрузкой
интенсивности М на втором участке.
Из суммы моментов сил относительно опор А' к В' определяем
фиктивные реакции:
Эпюра фф представлена на рис. 88. В том сечении, в котором
Так как
1<2Ф | = А! — Мс = -~ Ма — Мс = О,
то
С == ""ё~ (X*
Следовательно,
—-g-a.
Находим МФшах:
шах:
Максимальный прогиб:
t 48
/max — "
El ~ 25 ?/
Задачи 410—421. Определить прогибы /с сечений С и углы
поворота 6D сечений D балок.
Р, q, М, а, Е, 1 — считать известными как в этом параграфе, так
и в последующих.
151
41?
М П I I |д
-га
2qa
Р
Pa
г
ШШЯ -*р\
м
-га——1
аде
1ТПТ1
р р
РО
1-—2
?0
t
пп \ 1 ) t
20
420
0—1* Зо-
Задачи 422—425. Определить прогибы /с сечений С и углы
поворота бд, и 6/>а сечений слева и справа от шарнира D балок.
411
423
5 f
Zo—-Кo-j»o
152
С D
«гэ
Задачи 426—433. Определить максимальные по абсолютному
значению прогибы |/|шах и углы поворота |6|шах сечений балок. Изоб-
Изобразить вид упругой линии балок.
Ч2Б
417
I—^04 Ufl*+»
-За
ЗРо
-2а
М-Ра
За
М'ЗРо
а —I—о-
433
7 --1* О > J п i
Задачи 434—443. Определить прогибы /, /ь /2 сечений С,
Сг и Сг балок, используя табличные значения прогибов и углов
поворота простейших балок (см. рис. 99).
153
чзч
lntt(nn
ишиптт
сг
чзв
qa2
тттп
U3]
я ш
-2о—-4—о-
лив.
-Зо-
J
лтттт
(tifll, НИ
Сг
ЧЧ-О
Задачи 444—448. Определить любым методом наибольшие по
абсолютному значению прогибы | / | тех балок
4=800 кГ/м
q-ВООкГ/м
а=1м
ттт
тгп
п
\qa
o4-o<
№27
I
154
tas.
nun
Я-ЗпО*Г/и — Я
qa
ПЩ ПГ
qa Mm N18A2)
а=2м
¦M*+*f—2a
][
Е '2 ШекГ/смг
Задачи 449—453. Подобрать размеры поперечных сечений ба-
балок, удовлетворяющие условиям прочности и жесткости
Ш 150
Задачи 454—457. Определить отношение прогибов сечений С
балок в зависимости от того, левее или правее шарнира D приложен
момент М.
W5
м м
V55
-о _^ц„ го
M
1±
го
с
¦За -
-о^Ц—го—4-о —j
_LClJ__
¦ia-
1
155
Графический метод
Если для фиктивной балки графически построить эпюры фиктив-
фиктивного изгибающего момента М^х и фиктивной поперечной силы Q$x,
то веревочная кривая (приближенно веревочный многоугольник)
будет представлять собой упругую линию заданной балки, а линия
поперечной силы — изменение угла поворота сечений.
Вертикальные отрезки ух между веревочной кривой и ее замы-
замыкающей дадут величины, пропорциональные прогибам fx заданной
балки, а вертикальные отрезки ухмежду линией фиктивной попереч-
поперечной силы и линией ее нулевых значений — величины, пропорцио-
пропорциональные углам поворота сечений 6^..
Так как
V*— El ~yx~W'
где Н — полюсное расстояние плана векторов, -= линейный
масштаб балки, масштаб векторов, определяющих площади
частей эпюры изгибающего момента заданной балки, EI — жест-
жесткость сечения последней, то масштабом прогибов будет величина
е , а масштабом угла поворота . Величины Н, ? и т\ следует
выбирать так, чтобы на чертеже ух и ух измерялись достаточно
точно.
Обычно графически строят только упругую линию балки. При
графическом методе фиктивной нагрузкой можно нагружать (и это
удобнее) не фиктивную балку, а заданную. Тогда для проведения
замыкающей (замыкающих) веревочного многоугольника необходимо
пользоваться следующими правилами, вытекающими из условий
закрепления балки:
1) в заделке замыкающая касательна к веревочному много-
многоугольнику;
2) на шарнирной опоре замыкающая пересекает веревочный
многоугольник;
3) в висячем шарнире замыкающая терпит излом (при подходе
к висячему шарниру слева и справа замыкающие пересекаются).
На рис. 89 показано использование правил проведения замыкаю-
замыкающей (замыкающих): а) заданная балка, б) веревочнаи кривая,
в) замыкающая.
В примерах 45 и 46 дано графическое построение упругой линии
балок.
156
Рис. 90
Пример 46.
'"HIIIDHHH
"--Кг
Рис 91
В некоторых случаях дополнительно к условию прочности
ставится еще условие жесткости балки. Это условие выражается
в том, что отношение абсолютного значения максимального прогиба
157
пах к пролету балки /фне должно превосходить заданную величину
¦, т. е.
В зависимости от назначения балки и ее материала допускаемая
величина — различна. Например, для стальных балок принимают
1 1.1
п 200 • 1000 *
§ 7. Балки переменного сечения
Если размеры поперечного сечения балки изменяются по длине
плавно и незначительно, то напряжения можно вычислять по форму-
формулам, установленным для балки постоянного сечения.
Рациональными являются балки равного сопротивления, у кото-
которых в крайних волокнах каждого поперечного сечения нормальные
напряжения одинаковы.
Построение балок разного сопротивления
При чистом изгибе балкой равного сопротивления является
балка постоянного сечения. В общем случае изгиба балка равного
сопротивления имеет переменное сечение, изменяющееся соответст-
соответственно уравнению
A23)
где Мх — изгибающий момент в произвольном сечении;
Wx — момент сопротивления этого сечения
Если в каком-нибудь поперечном сечении балки изгибающий
момент равен нулю или имеет малую величину, а поперечная сила
соответственно отлична от нуля или имеет большую величину, то
форма балки равного сопротивления, установленная по уравнению
A23), корректируется условием прочности A04) по касательным
напряжениям.
Ниже приводятся примеры построения балок равного сопро-
сопротивления.
158
Пример 47. Даио: Р, I, h = const, [ о], [ т] (рис. 92).
Определить Ьх.
Решение. Изгибающий момент в произвольном сечении
Рх
Момент сопротивления
этого сечення
" х— 6 •
По уравнению A23)
bxh* Ух
Рис. 92
откуда
ЪРх
3 Р1
-Чг~ 2
Так как в сечениях над опорами, где М = О, Q = у-, то нулевую
ширину сечения брать нельзя. Ширину сечения Ьо определяем из
условия прочности по касательным напряжениям:
3 Q
откуда
Форма балки равного сопротивления показана на рис 92.
Длина х0 концов балки с постоянной шириной Ьо находится из
условия
откуда
з Р _ Зрх0
АЛ
4 W
Так как [т] = @,5 ~ 0.6) [о], то х„ « @,5 ~ 0,42)h.
Пример 48. Дано: Р, I, [ о ], [tj (рис 93).
Определить dx
159
Решение. Мх = —Рх; Wx = -
По уравнению A18)
я^, Рх
32
М #
Следовательно
d,=
Рис. 93
Так как при х— О М = 0, a Q = —Р, то корректируем форму
балки равного сопротивления по условию прочности по касатель-
касательным напряжениям
, -. 4 1^1 4Р <ы
откуда
Зя|х]
Установленная форма балки равного сопротивления показана
на рис. 93, a
Длина Хо конца балки с постоянным диаметром d0 найдется из
условия
Зл Sx
9-.y4P.ro
160
откуда
Если балка равного сопротивления имеет сложную форму, то
изготовляют ступенчатую балку, описанную около балки равною
сопротивления. Зная величины dB и d, между ними берут диаметры,
произвольные по величине, например:
d0 < d, < d2 < ds < d.
Затем определяют
при которых d0, d,, d2 и d3 обеспечивают прочность
Откладывая на эпюре изгибающего момента (рис. 93, б) Мо,
Мъ М2 и Ж з, находят протяженность соответствующих ступеней
балки (рис 93, е)
Определение перемещений балок переменного сечения
Перемещения балок переменного сечения можно определять
аналитическим, графо-аналитическим и графическим методом
При аналитическом методе на каждом участке
балки составляют дифференциальное уравнение упругой линии:
Еу" = ^- A24)
где 1Х — переменный момент инерции сечений балки относительно
нейтральной оси
Двукратным интегрированием находят функции изменения
угла поворота сечений 6^ и прогиба fx
Евх = Еу' = {^dx+Cl A25)
и
?/, = Еу = J[ ('-^их]dx + Схх + С2. A26)
Постоянные интегрирования Cj и С2 определяют из условий
закрепления балки. При нескольких участках используются и гра-
граничные условия — условия равенства углов поворота и равенства
прогибов при подходе к границе участков слева и справа Участки
Должны разделяться не только по нагрузке, но и по законам изме-
изменения поперечных сечений балки.
6 Заказ № 886 161
Вместо уравнения A24) можно пользоваться и уравнением сле-
следующего вида:
Е10у" = Мх-^- = мпр, A27)
где /0 — момент инерции постоянного сечения, к которому условно
приводится балка;
Mnft — Мх -р — приведенный изгибающий момент
Пример 49. Дано: Р, I, h = const (балка равного сопротивления
прямоугольного сечения с постоянной высотой h и переменной
шириной Ьх, см. пример 47), Е (рис. 94).
а
г
Рис. 94
н,^
Определить ешах, /шах
Решение. В соответствии с примером 47
Р . _ Ьх№ _ Phx
2 х И 'х~ 12 ~ 4FaI
Поэтому уравнение A24) приобретает вид:
Еу =~i7 = -Jr или 2м^
Дважды интегрируем это уравнение
Так как при х — 0 t/ = 0 и при л = -| у'— 0, то Сг = О
Поэтому
/шах — '
162
Из примера 47 известно, что
следовательно.
Задачи 458—466. Определить формы балок равного сопротив-
сопротивления и наибольшие по абсолютному значению прогибы.
3
о
рр
E№b
3
2
PI
h*b>
/max ^
3
8
Pi
Eft
!3
¦b '
01 i=C0Wt
Нагрузка по параболе с вершиной
но свободном конце
Задача 467. Дано: I — \ м, Ъ = 60 мм, h = 5 лш, п = 10 по-
полос, [о] = 1600 кГ/см\ Е = 2- 10е /сГ/сл*2.
6* 163
Определить Рт№ \f\m!lx. Трение между полосами рессоры не
учитывать.
Задачи 468—469. Определить формы балок равного сопротивле-
сопротивления; влияние касательных напряжений на формы балок; прогибы
свободных концов балок; углы поворота концевых сечений балок
(объяснить получившиеся результаты).
9. '. ^шах. Е, /тах считать известными
Ц§8
ч-ез
uuurfumT
l=const
Задачи 470—475. Определить, в каком сечении балок возник-
возникнут наибольшие нормальные напряжения и во сколько раз огаах,
\f Lax и |6|шах- больше, чем в аналогичных балках постоянного (наи-
(наибольшего) сечения.
164
Задачи 476—477. Определить наибольшие нормальные напряже-
напряжения отахот собственного веса балок и положение опасного сечения.
Мтгх и И7гаах считать известными.
Ч-7В
-I
Задачи 478—481. Определить прогибы свободных концов балок
от собственного веса.
Вес балок Q, I, E и 1тах считать известными.
f
При графо-аналитическом методе определения
деформаций балки переменного сечения за фиктивную нагрузку
фиктивной балки принимается не истинный изгибающий момент
Мх, а приведенный
в соответствии с уравнением A27).
Угол поворота и прогиб произвольного сечения определяют
по формулам:
гДе Яфх и ^ф^ — фиктивная поперечная сила и фиктивный изги-
изгибающий момент фиктивной балки;
Е10 — жесткость постоянного сечения, к которому
условно приводится заданная балка.
Для балок равного сопротивления с постоянной высотой сече-
сечения, если за /0 принять момент инерции того поперечного сечения,
в котором действует Мтах, то приведенный изгибающий момент
Л1пр= Mmsx — const.
Пример 50. Дано: Р. а, М = 2Ра, Е, I (рис. 95).
Определить Од , 0s , fA , /с .
Решение. Изгибающие моменты иа участках заданной
балки имеют значения: MXl = —Pr, Mx, = MXt = Pa.
Выбираем /0= 21 и находим приведенные изгибающие моменты
на участках:
М — М 21 = — Ра М = М —Ра
Принимаем эпюру приведенного момента за фиктивную нагруз-
нагрузку фиктивной балки (рис. 95, а).
Расчленяем фиктивную балку на две основные (консоли) и пере-
перекидную балку (рис. 95, б). Так как
Вг = \Ра -а+Ра • -|- = 2Ра2;
\ = - Ра^; ^ = - Bt = - 2Раа;
Л1фд = 2Ра3 . а — Ра" ¦ -|- а = 4"
то
9з~ 2?/ = ?Г5
~т~— 16 ?/ •
16S
Пример 51. Дано: q, I, E, h = const; балка равного сопротив-
сопротивления, прямоугольного сечения, постоянной высоты h и переменной
ширины Ьх (рис. 96).
Определить G^ , fA .
Решение. Принимаем за
тогда
2 ' УA>А 2 ' — 2 '
4 •
Рис. 95
Рис. 96
Искомые перемещения приобретают значения:
Л— ?/.
4?/0 *
167
Задачи 482—485. Определить прогибы /с сечений С и углы пово-
поворота 6д сечений D балок.
Р, а, Е и /max считать известными.
ЧВ1
чвч
Задачи 486—491. Определить наибольшие по абсолютному зна-
значению прогибы и углы поворота сечений балок.
Р, М, а, Е и /max считать известными
/57"/лУ
168
Графический метод определения перемещения для
балок переменного сечения используется так же, как и для балок
постоянного сечения.
Различие заключается в том, что для балок переменного сечения
за фиктивную нагрузку фиктивной или заданной балки принимается
не истинный изгибающий момент Мх, а приведенный Мпр. Правила
проведения замыкающей (замыкающих) веревочного многоуголь-
многоугольника сохраняются.
Масштабом прогибов будет величина * , где /0— момент инер-
ции постоянного поперечного сечения, к которому условно приво-
приводится балка.
За фиктивную нагрузку можно принимать и истинный изгибаю-
изгибающий момент, но при условии, что полюсное расстояние плана векто-
векторов будет переменным и равным:
НХ=НО1±, A30)
где Яо — произвольное по величине полюсное расстояние, приня-
принятое для выбранного сечения с моментом инерции /о-
Пример 52. На рис 97, а, б, в показано графическое построение
упругой линии ступенчатой балки через приведенный изгибающий
момент, при котором принято /„ = /.
169
На рис. 97, г, д, е показано графическое построение упругой
линии той же балки через истинный изгибающий момент и через
переменное полюсное расстояние плана векторов. Принято
=Я, и Н, =
2/
§ 8. Статически неопределимые балки
Статически неопределимыми балками называются балки, для
которых из условий статики нельзя определить все реактивные
составляющие, возникающие в местах закрепления.
Степень статической неопределимости балки устанавливается
по числу лишних неизвестных, которые нельзя определить из усло-
условий статики.
Методы раскрытия статической
неопределимости балок
В
Метод начальных параметров. Для заданной
статически неопределимой балки составляются общие интегралы
дифференциальных уравнений
упругой линии через началь-
начальные параметры Начальные па-
раметры и реактивные состав-
ляющие определяются из усло-
вий закрепления балки и из
условий статики
Пример 53. Дано: q, I, Е, /
(рис 98)
Определить А, В, Мв,1х,
Решение Так как на
левой опоре /о = 0, то в соответ-
соответствии с уравнениями A16) и
A17) функции прогиба и угла
поворота запишутся следующим
образом:
-;
Рис. 98
I 24
По условиям закрепления балки ft = 0 и 6г = 0, т. е.
-% = о.
170
Откуда
, I2 ql3 . ql „ 1 IqP qP\ ql*
T = (Г ' То"И ° ~ W\2A ~ 0/ = ~ T20?7-
Таким образом,
EIfx = ~ T20" x + "go" x* ГТ20
и
Е1ЪХ = jgp- + Q- X j- ¦ -^- .
Полагая 6X — 0, из уравнения
находим х — —~т » 0,447/, при котором прогиб достигает макси-
максимального значения:
f _f 2 ql*
'mia~'x=_L~ 75 ~W"
Поперечная сила и изгибающий момент выражаются функциями:
— ql q Л3 я» ql q Xs
У*=Т0" г 2" И /MJr==To"JC { 6""
Полагая Мх—0, находим x=ly -g- ж 0,775/, при котором упру-
упругая линия имеет точку перегиба.
Полагая 0^=0, находим ж=-7= ~ 0,447/, при котором изги-
V 5
бающий момент достигает максимального значения:
д, g/3 _
По этим данным построены эпюры Q и М и упругая линия балки.
Задачи 492—495. Раскрыть статическую неопределимость балок.
171
В задачах 492 и 493 построить эпюры поперечной силы Q и из-
изгибающего момента М; в задаче 494 определить угол поворота сече-
сечения над опорой; в задаче 495 определить прогиб / сечения В.
Ш,
цзз
/W/J77
/7?777?
Ч-ЗЧ
з-.— i —4*—t
Метод сравнения перемещений. Рассматри-
Рассматриваемую статически неопределимую балку раскрепляют до статически
определимой, но геометрически неизменяемой, которую называют
основной. Основную балку сначала нагружают только заданными
силами и для нее в раскрепленных сечениях определяют перемеще-
перемещения, соответствующие отброшенным лишним неизвестным (силе —
прогиб, моменту — угол поворота). Ту же раскрепленную балку
(вспомогательную балку) нагружают затем только лишними неиз-
неизвестными и для нее в раскрепленных сечениях опять определяют
перемещения, соответствующие лишним неизвестным.
2Щ^
90,
JT
6)
BB =
<n~ 1F7
Pli
га
EL3
3E3
ill
6ЕЭ
.III
* t 'max
I
I
~6{J
Mil
16E3
v~e—im
Pi3
Рис. 99
172
Величины лишних неизвестных подбираются такими, чтобы
суммарные перемещения, найденные в раскрепленных сечениях
основной и вспомогательной балок, отвечали перемещениям в тех
же сечениях заданной статически неопределимой балки.
Этот метод удобен в тех случаях, когда основная и вспомога-
вспомогательная балки могут быть приведены к табличным балкам, для кото-
которых известны значения нужных
перемещений.
Полезно знать величины не-
которых перемещений хотя бы
для простейших табличных ба-
балок (рис. 99).
Пример 54. Дано: М, I, E, I
(рис. 100).
Определить А, В, Мв, Оа,
f i. Построить эпюры М и Q.
Решение. Принимаем за
лишнюю неизвестную реакцию А
опоры балки Основной балкой /
будет консоль, нагруженная за-
заданной парой сил с моментом М.
Перемещение (прогиб) основ-
ной балки в раскрепленном се-
сечении по табличной балке (рис.
99).
и =
2?/
Вспомогательная балка //
под нагрузкой неизвестной силы
А в раскрепленном сечении по-
получает прогиб (см. табличную балку 2 иа
Рис. 100
рис. 99).
АР
'а, ~~ 3EI "
Так как на опоре А заданной балки прогиб /л = 0, то из сравне-
сравнения суммарных перемещений балок / и // с перемещением заданной
балки имеем
или
откуда
МР АР __„
2Е1 3EI ~ '
А- 3 М
173
Поскольку в любом сечении заданной балки поперечная сила
Q = А, то эпюра поперечной силы представляет собой прямоуголь-
прямоугольник с высотой -щ. Реакция в заделке В = —А.
Эпюру изгибающего момента легко построить наложением эпюр
основной и вспомогательной балок. Для основной балки эпюра изги-
изгибающего момента — положительный прямоугольник с высотой М.
Для вспомогательной балки эпюра изгибающего момента — отри-
отрицательный треугольник с нулевой высотой на левом конце и
О
высотой g-M на правом конце.
Накладывая эти эпюры друг на друга, получаем результирую-
результирующую эпюру изгибающего момента для заданной балкн. Реактивный
момент в заделке:
Для определения перемещений балки используем графо-аналити-
ческий метод. Фиктивная балка и фиктивная нагрузка представ-
представлены на рис. 100, а
Так как
О _ м 1 пл ' - т
и
М,
то
*(/2 "" 12 { 2 9 J + 4 ' 12 ' 18 ~ 32 '
A— El ~ AEI hn— El ~ 32?/ '
Полезно обратить внимание на то обстоятельство, что фиктив-
фиктивная балка, будучи оперта только одним концом, должна находиться
в равновесии под фиктивной нагрузкой, т. е. момент фиктивной
нагрузки относительно левого конца фиктивной балки должен рав-
равняться нулю.
За лишние неизвестные можно принимать не только реактивные
составляющие в местах закрепления заданной балки, но и внутрен-
внутренние усилия Q н М в том поперечном сечении, в котором ее расчле-
расчленение приводит к балкам табличной формы
Пример 55. Дано: q, а (рис. 101).
Определить А, В, МА , Мв-
Решение. Раскрепляем заданную дважды статически не-
неопределимую балку путем расчленения на две балки (/ и //) в по-
поперечном сечении С.
174
За лишние неизвестные принимаем поперечную силу Qc и из-
изгибающий момент Мс в этом сечении.
Условия сравнения перемещения балок / и // приводим к сле-
следующей системе двух уравнений:
еСг
Рис. 101
Из табличных балок 1) и 2) (см рис 99) для балки / имеем:
с,— El 2EI
'с,— 2Е1 3?/ -
Из табличных балок 1), 2) и 3) (см. рис. 99) для балки // имеем:
__ Мс2а
С„ ~ El 2E/
МсBау
6?/
'с*"* 2EI + ЗВ/ BE/ '
Подставляя эти значения в уравнения сравнения перемещений,
получаем
ЗМС+ l,5Qca= -I?02
откуда
175
Реакция A = Qc=-^-qa, реактивный момент
Реакция В = 2qa — Qc
оо
реактивный момент
Мв = Qc 2а — Мс —
— 9 Я" ¦
Метод сравнения перемещения может быть использован и при
расчете статически неопределимых балочно-етержневых систем
(т. е. систем, состоящих из
балок, и шарнирно связан-
связанных с ними упругих стер-
стержней) и рамных систем
(т. е. стержневых систеэд с
жесткими узлами, в кото-
которых углы между стержнями
при деформации не изме-
изменяются).
При расчете рамных
систем обычно не учиты-
учитывают деформации растяже-
растяжения или сжатия элементов.
НЕ—По.
Рис 102
Рис 103
Пример 56. Дано: равномерно нагруженная консоль АВ и для
нее <7, /, Ei, /,; упругая тяга АС и для нее /2, ?2, F2 (рис 102).
Определить продольное усилие N в тяге.
Решение. Расчленяем заданную балочно-стержневую
систему в шарнирном узле А на балку АВ и упругую тягу АС.
Балка нагружена равномерно распределенной нагрузкой интен-
интенсивности q и неизвестной силой N Тяга нагружена только силой N.
Используем условие сравнения перемещений концов А балки и
тяги, которое должно иметь вид |/д,|= А/2.
Из табличных балок 2) и 3) (см. рис. 9S)
3?,/,
176
По закону Гука:
Д/„ =
Nl2
Подставляя /л, и Д/2 в условие сравнения перемещений, полу-
получаем:
ql\ JV/f Nlt
откуда
8E.I,
N =
Частные случаи (рис. 103)
2) ?2F2 =
N = 0.
Таким образом, в зависимости от жесткости упругой тяги уси-
усилие N может изменяться в пределах O^/V^-^/j, а изгибающий
момент Мв в заделке балки в
пределах
< МЕ
На рис. 102 изображена эпю-
эпюра изгибающего момента в бал-
балке при произвольно взятом зна-
значении Мв внутри указанного
интервала его изменения.
Пример 57. Дано: прямо-
прямоугольная рама со сторонами
а и Ь, жесткостью сечения на
изгиб El, нагруженная равно-
равномерным, нормальным к стенкам
внутренним давлением q (рис.
104).
Определить изменение рас-
расстояния 8 между средними сече-
сечениями Е—Е.
Решение. Расчленяем
раму на балки сечениями в
узлах. Так как рама симмет-
симметрична, то достаточно рассмот-
I)
-f-
itl
in
*-
H
fH
F
— »
НП
с
Рис. 104
177
реть две балки А В и ВС. Не учитывая растяжения стержней рамы,
каждую балку можно опереть по концам, считать нагруженной
распределенной нагрузкой интенсивности q и неизвестными мо-
моментами Мо в сечениях над опорами, обусловливающими собой
жесткость узлов рамы.
Так как углы рамы должны оставаться прямыми, условие срав-
сравнения перемещений запишем следующим образом: 6^, = 6Вг.
Из табличных балок 4) и 5) (см. рис. 99):
Моа „ М„Ь qbs
й — У"
Вх ~ 24?/
2?/
2?/
24?/
По условию сравнения перемещений
4?- = Me(a + 6),
12
•откуда
Из этих же табличных балок расхождение середин сторон а
будет:
El \ 384
-да*
16
Задачи 496—499. Раскрыть статическую неопределимость ба-
балок и построить эпюры М и Q.
Ж
Ж
Задачи 500—505. Раскрыть статическую неопределимость ба-
балок и определить величины допускаемых нагрузок.
Для всех балок принять длину равной 3 м; [а] = 1600 кГ/см2:
В задачах 500, 501 сечение балок круглое (d = 10 см);
178
в задачах 502,503 сечение балок кольцевое (D = 12 см, d =8 см);.
в задачах 504, 505 сечение балок квадратное A0 X10 см).
Ш
¦о-Ц«—?
Ж м м
47 -»|-.—2а-
'If
ьоь
_| J mTftttttl
'-« y> о -H a 4
Задачи 506—509. Подобрать номера двутаврового поперечного-
сечения.
Дано: Р = 2 Т, д = 2 Т/м, М = 3 Т ¦ м, 1 = 2 м^
[о] = 1600 кГ/см2.
Ж lp Д Ш
м м
508 р»-/и м
Задачи 510—513. Определить наибольший изгибающий момент
!-U-Zff
Ж
5/3.
8)НЦИ t t'HJH И
-2а
17D»
Задачи 514—519. Определить опускание у промежуточного
шарнира или ползуна.
-"у"
2а
I
• | •
f д'о
A3L
.516
Wia-
м Ж
-2а
а\а\ а
iTTTHHIlltl
Задачи 520—525. Определить продольные усилия Л' в тягах.
5?/
520
p-ij
522
/м-
Э0*30см
¦1м-
Д
380
Л13
м
$
¦i
525
м
г
ш
O'lM-
,=? WsMh/m*
30*30см
Л
2а
ш
Задачи 526—529. Определить в элементах балочно-стержневых
систем:
1) температурные напряжения (задачи 526 и 529);
2) монтажные напряжения (задачи 527 и 528).
52Б
?г=10"Мн/м2
ut,=-50°C
и,--12,5-10'*
181
Задачи 530—537. Раскрыть статическую неопределимость рам-
рамных систем и определить величины наибольших изгибающих мо-
моментов Мтак .
Деформации растяжения и сжатия стержней рам ие учитывать.
Жесткости на изгиб сечений всех стержней каждой рамы считать
одинаковыми.
В задачах 534, 535 деформации растянутых или сжатых элемен-
элементов учитывать.
530
ШкГ
I
и
_О—>
и
1,,,....,,,
*- а
1
„
182
Задачи 538—543. Определить опорные реакции или усилия N в
стяжках рамных систем, возникающих при монтаже E38, 539)
или при изменении температуры E40—543).
Принять: ?ст = 2 ¦ Юь кГ/см*, ?м = 10е кГ/см2,
ctCT = 12-10-\ 0,,= 16-10-6.
Стань
5i3
//
At>0
I ад=4
I a,=a
Метод уравнений трех моментов. Этот метод
удобен для расчета многопролетных неразрезных балок, т е балок,
перекрывающих несколько пролетов без соединительных шарниров.
Пусть рассчитывается n-пролетиая неразрезная балка
(рис. 105) постоянного сечения жесткости EI, у которой все опоры
лежат на одном уровне. Такая балка является балкой п — 1 раз
статически неопределимой.
183..
Раскрепление балки производится сечениями над опорами.
Получается п балочек, опертых по концам. За лишние неизвестные
принимаются изгибающие моменты в проведенных сечениях. Для
каждой пары двух смежных балочек с пролетами /,_| и 11
(рис. 106, а) составляется условие плавной сопряженности упругих
линий как равенство углов поворота сечений F)= 6)) на промежу-
промежуточной t-той опоре. В результате получается система п — 1 уравне-
уравнений трех моментов следующего канонического вида:
(в?
A31)
Рис 106
Здесь /W;-i, Л1, и M,+i — неизвестные три момента в сечениях
над опорами i—1, i и i'+l; 6J и Gj1 —углы поворота сечений над
<"-той опорой левой и правой балочек только от нагрузок в их
пролетах (рис 106, б). Значения Of и 6J1 могут быть определены
любым методом, который окажется целесообразным, или взяты из
табличных балок, если это окажется возможным
Подстановка в уравнение A31) вместо t значений 2, 3, 4, ... п
приводит к системе п—1 уравнений, решение которой даст величины
всех лишних неизвестных изгибающих моментов в сечениях над
опорами неразрезной балки.
При практическом использовании метода уравнений трех момен-
моментов полезно иметь в виду следующие замечания.
1. Углы 6J и 6J1 подставляют в уравнения со знаком «плюс»
при повороте сечеиий балочек в сторону, указанную иа рис. 106, б.
2. Если иеразрезная балка оканчивается нагруженной консолью
(рис. 107, а), то ее, как пролет, в уравнения трех моментов не вклю-
включают. Консоль заменяют моментом от приложенной к ней нагрузки,
184
вычисленным относительно ближайшей опоры и приложенным на
ней с соответствующим знаком (рис 107, 6). Этот момент целесооб-
целесообразно включать в левую часть уравнения трех моментов.
I 11
- М,=-Рс-М
Рис. 107
3 Если концевое сечение неразрезной балки заделано
(рис. 108, а), то его угол поворота равен нулю Fj = 0). В раскрытом
виде это условие можно представить через уравнение трех моментов,
заменив заделку фиктивным пролетом длиною /0 = 0 (рис. 108, б).
Рис 108
Рассматривая два смежных пролета /с и h по уравнению трех мо-
моментов, условие 6j = 0 записывается в виде
2ЛУ, + Мг/, = —6?/е". A32)
4. Если внешняя сосредоточенная пара сил приложена в сече-
сечении над промежуточной опорой неразрезной балки (рис. 109, я),
то момент М этой пары целесообразно относить в внутрипроле7ной
нагрузке.
Момент пары можно отнести либо к одному левому пролету
(рис. 109, б), либо к одному правому пролету (рис. 109, в), либо
одновременно и к левому, и к правому пролетам при расчленении
в произвольном отношении (рис. 109, г). Целесообразно момент пары
относить к одному пролету, который менее нагружен.
185
После того как из уравнений трех моментов будут найдены все
изгибающие моменты в сечениях иад опорами иеразрезной балки,
рассчитывают каждую отдельную балочку, опертую по концам от
нагрузки в ее пролете и от моментов, приложенных по концам.
Например, реакцию на f-той опоре неразрезной балки можно найти
как сумму реакций на t-тых опо-
опорах двух смежных балочек. Ка-
Каждую из них определяют из ус-
условий статики. Общая формула
для реакции на f-той опоре имеет
следующий вид:
At=A4+ ?'-i-Mi + A33)
где А°— суммарная реакция на
t-тых опорах двух смежных ба-
балочек только от заданных на-
нагрузок в пролетах;
—'~Y '— реакция на t-той
опоре левой балочки только от
~Ък~ моментов /И,_| и Mt;
——{ '—реакция на t-той опо»
ре правой балочки только от мо-
моментов /И(+1 и Mt.
При определении реакции в заделке фиктивный нулевой пролет
не учитывается.
При определении реакции опоры, за которой следует иагружеи-
ная коисоль, в величину А° включают результирующую всех внеш-
внешних сил, действующих на консоль
Эпюры поперечных сил и изгибающих моментов для неразрезной
балки можно строить отдельно для каждого пролета как балочки,
опертой по концам от заданных сил и от опорных моментов. Их можно
строить и методом наложения эпюр от моментов в сечениях иад
опорами и от заданных сил в каждом пролете.
Угол поворота и прогиб в произвольном сечении иеразрезной
балки целесообразно определять, рассматривая только один пролет
как балочку, опертую по концам под действием заданной нагрузки
в пролете и моментов в сечениях иад опорами. Здесь применимы все
методы, которые использовались при расчете статически опреде-
лимых балок.
186
Пример 58. Даио: Р — IT, Л4=4 Т-м, q = 6 Т/м, с=1л,
1г = Зм,12=2м,1с] = 1600кГ/см2, Е = 2• 10екГ/сл2(рис. 110, я).
Определить номер двутавровой балки и /„.
Решение. Расчленяем заданную балку иа две балочки с
пролетами h и 1% (рис. 110, б). Балочку пролетом /, нагружаем
на левой опоре моментом Mj
от силы Р, действующей на
коисоль, на правой опоре па-
парой сил с моментом М и не-
неизвестным изгибающим мо-
моментом М2.
Балочку пролетом /2 иа-
гружаем распределенной на-
нагрузкой интенсивности q, на
левой опоре — неизвестным
изгибающим моментом М2 и
на правой опоре — неизвест-
неизвестным изгибающим моментом
М,
Вместо заделки вводим
фиктивный пролет 13 — 0.
Для заданной дважды
статически неопределимой
балки два уравнения трех
моментов имеют следующий
вид:
МА
ЛА t CX71 /Д^ С\^\
Так как М 4 = — Ре =
=—2-1 ~—2 Т-м, а из таб-
табличных балок 4) и 5) (см. рис.
99), с учетом правила знаков,
?/ef :
Ш> 4'3 AT 2
EIQ1 --
= 2 Г-ж2,
то уравнения трех моментов приобретают вид
» = -30, 1
, = -6, }
10
откуда
Л» 2 + 2Л13
—2.667 Г-
М3 = —
-1,667 Т-м.
187
Пользуясь формулой A33), определяем реакции Аи А2 и А3 в за-
закрепленных сечениях:
л лО , М2 — Мх р М М2 — М,
4 Ч "т~ 9Я
= о -I- -5 I Z° 4 111 Т.
^ I 3 ' 3 - "9 d>U '•
Л2 — Лг -|- ^ ¦ Н ^ = yx 1 2 ""
-2 + А
, Мл— Ж2 Af3 — М2 4_ "*" 3
"*" /а "•¦ /, - з + °+ з "'"
5 о
~ ~3~ + ~3~ т
+ —2— = тг * 5>389 г=
) — JH4 G/9 , Ж9 i
о I"
к 2
__8_ _5_
=6+ ^2 = -г" = 5,5 Г.
Проверяем найденные реакции по сумме проекций на вертикаль»
ную ос|з
Ai+A2+Ar-P—ql2= 0; ^E6 + 97 f 99) — 2 —12 = 0.
Строим эпюру поперечной силы, как показано на рис ПО, в.
Эпюру изгибающего момента строим методом наложения От на-
нагрузок в пролетах эпюра для левой балочки — треугольная, а для
правой — параболическая (рис 110, г)
От моментов Мь М2 и М3 эпюра представляет собой ломаную
прямую, изображенную пунктиром (рис. 110, д). Пристраиваем к ней
прямолинейную эпюру на консоли от силы Р От пунктирных линий
в пролете откладываем ординаты эпюр в пролетах только от задан-
заданных сил. Учитывая знаки эпюр от моментов и от нагрузки, получаем
результирующую эпюру изгибающего момента
Находим х, при котором на правом пролете получается Мтпх ,
_ Q _ И7 , 0„
Так как
188
МтаХпр = 3,51 —f » 0,84 Т-м.
Как видно из эпюры,
М — — Т-м
'"шах 3
По расчетной формуле
/-«3
еж .
По сортаменту для двутавра № 18а
W = 159 см* и
Ж-
. 100 = -^Ц^9—• 100 = 4,8 '
(перенапряжение ^5%, что допустимо).
Выбираем двутавр № 18а, для него:
W
3 159
= 1667 кГ/см2 и /= 1430 ел4.
При определении прогиба /к воспользуемся методом наложения
табличными значениями прогибов балок 5) и 4) (см рис 99).
10»
16?/
16?/
0е 1,43 10а
х 6-16 + -JJ--4 + -^--4 j ж 0,058 см «0,58 мм.
Задачи 544—549. Раскрыть статическую неопределимость балок
E44, 545), подобрать необходимые размеры поперечных сечений
балок E46—549).
В задаче 549 определить и прогиб сечения С.
о - 1м
189
54В
Ч
ггп
M=qa}
547
°^d M
-2а
-2а -*И?^
546
8ШЗ
543
,°,
р=55
гщто
1
1В00кГ/смг
Задачи 550—555. Определить значение допускаемых нагрузок,
действующих на балки.
В задачах 551—553 считать [ о] = 1600 кГ/см2.
В задачах 554 и 555 считать [о] =160 Мн/м\
550
551
d гост q
-О- 1м *
HHIMt
ттпт
T/
55Z
м
553
-4
—го-
Г
1-
-30
/vie
ш
м
-а—Н*-о= 1/и -!«¦ о —»-
Г™'* I
ггпт.
14
190
Задачи 556—557. Определить прогибы сечений А ступенчатых
балок
557
Задача 558. Определить значения М, an b, при которых балка
указанного переменного сечения будет балкой равного сопротивле-
сопротивления.
Р м
Задача 559. Определить наибольший изгибающий момент для
балки, если средние опоры осядут на Д= 1 мм (Е = 2 ¦ 106 кГ/см2).
559
r-ti
Задачи 560—561. Определить зазоры Д, при которых наиболь-
наибольшие нормальные напряжения в балках заданной жесткости сечения
EI будут иметь наименьшие значения
56/
/щрт
191
Основы рвсчета статически неопределимых бвлок
по несущей способности
Предусматривается, что материал статически неопределимой
балки пластический с идеализированной диаграммой растяжения
и сжатия.
Поскольку несущая способность каждого пролета балки исчер-
исчерпывается, когда в нем возникнут три пластических шарнира (один
в пролетах и два в сечениях над опорами), то все пролеты можно
рассматривать отдельно и независимо друг от друга. Расчет балки
удобно производить методом выравнивания изгибающих моментов.
Если балка имеет постоянное поперечное сечение, то величина
допускаемого изгибающего момента тоже будет постоянна и найдется
по формуле A14)
ЛСч = 2 [о] S,
где S — статический момент половины площади поперечного сече-
сечения относительно его центральной оси.
Рис. 111
Окончательную (выравненную) зпюру изгибающего момента
строят для каждого пролета так, чтобы ее ординаты были равны
значениям M'mali в сечениях над опорами и в пролете. Из геометрии
полученных выравненных эпюр устанавливают М^а<, через нагрузки
в пролетах. Пользуясь выражением A14), определяют максималь-
максимальные допускаемые нагрузки каждого пролета.
Если конец балки закреплен на шарнирной опоре, то для пере-
перехода последнего пролета в геометрически изменяемое состояние
достаточно возникновения двух пластических шарниров (в пролете
и в сечении над промежуточной опорой). В этом случае изгибающий
момент на конце балки равен нулю, а в пролете и в сечении над
промежуточной опорой — М 'тах.
На рис. 111 показано построение эпюры выравненных изгибаю-
изгибающих моментов для неразрезной балки. Для ступенчатой балки с
192
заданными значениями 5 выравненную эпюру изгибающих моментов
строят на каждой ступени по своему значению М'тш.. Дальнейший
расчет производят так же, как и в балках постоянного сечения.
Если задана нагрузка и требуется подобрать поперечное сече-
сечение балки, то в тех сечениях каждого пролета, в которых должны
возникнуть пластические шарниры, через заданную нагрузку опре-
определяют допускаемые изгибающие моменты M'mai По максимальному
из них устанавливают 5 = ^
2[о|
Зпщрв Mrnot
и размеры поперечного сечения
НШИШ
Рис
При проектировании балки переменного сечения ее размеры
аналогично устанавливают для каждого пролета.
Пример 59. Дано: S, /,, /2, 1о] (рис 112)
Определить Р'вм; q^.
Решение. Строим эпюру «выравненного» допускаемого
изгибающего момента
М^х= 2 [оIS.
Так как из построенной эпюры
то максимальные допускаемые нагрузки в пролетах балки должны
иметь следующие значения:
Ряи* = 12 [а| -|- И ?тах = 32 М"^- •
Задачи 562—567. Определить допускаемые силы для балок и
систем.
7 Заказ № 886
193
ОС
В задачах 564—567 считать известными [a], a, W и 1Ч=~уу-
5П1 563
о—
10 см
II
[61=100 к Г/смг
«Zflo
о—г*- о~Н
565
Задачи 568—571. Определить размеры поперечных сечений
балок и систем
Сечение балок считать прямоугольным (Ь — 2Л), а материал
балок и тяг считать одинаковым.
588
Di
в я
563
У
^^
[61-100кГ/смг
194
570
\\
571
I
f, --1см'
Л
#,*?///.
(Г/ЛЮ.
Задачи 572—575. Определить коэффициенты запаса /?, (по на-
нагрузке), с которыми рассчитаны балки и системы
Принять предел текучести материала ог = 2400 кГ/см2
572
А
L—2
Р--Зт
573
<Z=«m
\N№
0-Im \^o
\мг
§ 9. Потенциальная энергия упругой
деформации при изгибе
Количество потенциальной энергии упругой деформации, sa-
ключенной в балке при плоском поперечном изгибе, определяют
по формуле
Q'dx
2GF •
7*
A34)
195
где
dF
A35)
— отвлеченный коэффициент, характеризующий неравномерность
распределения касательных напряжений по поперечному сечению
балки и зависящий от его формы.
В формуле A34) интегрирование про-
производится по длине каждого участка
балки, а суммирование по всем ее
участкам. В формуле A35) интегриро-
интегрирование производится по площади F попе-
поперечного сечения; S, Ъ и / имеют тот же
смысл, что и в формуле (99), определяю-
определяющей касательное напряжение; ? и С —
модули продольной и касательной упру-
упругости материала балки.
Пример 60. Дано: а, о0, h, 1ц> (рис.
113 ИЗ).
Определить k = F I ( -г\ dF
Решение. Площадь заданного сечения
F — ah — G(A,.
Экваториальный момент инерции площади сечения относительно
оси г
Для полок
Для стенок
= а-а0
Коэффициент неравномерности касательных напряжений
196
16 ^2 T) Y
2 (a — ae) " 3-8 5-32J/ "
Подставляя сюда значения F n I n производя некоторые преобра-
преобразования, получаем-
1 —-
к _ 6 °ft
Частные случаи.
1) ао=-а; А = -|" ¦
= ft0; ft =4--
Если, например. ao=—, то А=—^т-= 1,548.
3) Двутавр № 20
По сортаменту a = 6 = 10 см; h = 20 еж; о — о0 = d = 0,52 гж
a0 = 9.48 еж, Ло = h — 2^ = 20 — 2-0.84 = 18,32 см.
Так как -^- * 0,948 ; -^- = 0,916; -^- * 0,868;
П 7АП °°*0 п -7ОП Л" пес й|)/!0 п г 1 1
0,769; -^- ~ 0,729; -^- « 0,645 и -^- « 0,611,
197
то
— 30-0,769 + 7-0,645 + 8
-0,611)]}
2,51.
Для прокатного двутаврового сечения коэффициент неравномер-
неравномерности касательных напряжений при изгибе можно приближенно
определять по формуле
* = -
ah
о»
а
F
77'
где F — площадь сечения;
Fc — площадь стенки с высотой А, т е Fc = hd.
Пользуясь этой формулой, например для двутавра № 20,
находим F = 26,8 си2, Fc = 20-0,52 = 10,4 см2; k =|M.» 2,58.
Пример 61. Дано Р = 60 кн, q = 30 кн/м, а = 2 м, Е = 2х
Х1О5 Мн/м*, G = 8-Ю4 Жн/ж2; [а] = 160 Мн/м* (рис. 114).
Рис 114
Определить: номер двутавра и U.
Решение Из условий статики определяем реакции опор
) кн; В = P + 2qa — A = 100 кн.
2Р + 2да
'' 3
198
Составляем уравнения Q и М.
Qx> = А = 80 кн, Мх = Ахх = 80х, кк -ж; Л4*,=(, = 0;
/ЦХ|=-„ = 160 кн-,и;
Qx, = — В + qx2 = - 100 + 3O.v2; Qx^c = — 100 кн;
Qx,=lB = — 100 + 30-4 = 20 кн;
от? ЗОлк
М,г = Вх2 Y = 100*2 2^; ^«=0 = 0;
Л1^=2о= 100-4 ^--16= 160 кн-м.
Определяем Л1тах. Из условия
QXl = — 100 + 3O.v2 = 0, х2 = -^- «.
Следовательно,
,. .„„ 10 30 10! 500
По расчетной формуле
W = ^ = зТбо'-Ш^ -'042-Ю- *» » 1042 rf.
Из сортамента подбираем двутавр № 45, для которого
W =-¦ 1220 см3; I = 27450 ел4; F = 83,0 с.ч2; h = 45 еж;
d = 0,86 «и*=^= 45,0,8s - 2,14.
Потенциальную энергию упругой деформации балки найдем как
сумму энергий от изгибающего момента @м) и от поперечной силы
ш-
По формуле A34)
U 4U
I j" x\dXl +-i- JB0x2-3x! pxj- 10s =
0 II
199
10»
~2~2-10" -27450 10-е
. 72
«8 +-HL.8-120-16 +
~ 769,4 дж;
= 4gr[
64a + j(- 10
200a -
U =
= 2.8 102;,,'48з'°0в 10-< A28 + 400 - 480
+ 192)=* 38,7 дж,
+ Uo = 769,4 + 38,7 = 808,1 дж
Так как для нормальных балок потенциальная энергия от попе-
поперечной силы мала по сравнению с энергией от изгибающего момента,
то первую обычно не учитывают.
В этом примере
fe10° 1005%
Для коротких балок нельзя пренебрегать потенциальной энергией
от поперечной силы, поскольку она может достигнуть существенного
значения
Задачи 576—581. Определить потенциальную энергию U упру-
упругой деформации балок, учитывая только изгибающие моменты.
К задаче 576. Балки указаны в задачах 222—231. Для них счи-
считать известными нагрузки, длины / и жесткость сечений El.
577
\а=Ц5и
12см
200
?79
¦l,Sm—*
-1,5м—>-)
I"
o»Mj
2b'2b
f
16} ?. Ь, baima равного сопротиШенив
Задача 582. Определить, какое влияние оказывают закрепления
балки с силой посередине на величину потенциальной энергии от
изгибающего момента:
а) балка опирается по концам,
б) балка с одним заделанным и другим опирающимся концом,
в) балка с заделанными концами
Задача 583. Определить, как изменится потенциальная энергия
от изгибающего момента балки прямоугольного сечения на двух
опорах с силой Р посередине, если ее заменить балкой равного сопро-
сопротивления с постоянной высотой сечения.
Задача 584. Определить коэффициенты формы k сечений: 1) пря-
прямоугольного, 2) круглого, 3) треугольного с равными сторонами,
4) круглого кольцевого, 5) квадратного коробчатого, 6) двутаврового
№60 На последнем примере показать, что коэффициент k для дву-
двутаврового сечения может быть принят равным отношению площади
сечения к площади стенки с высотой профиля.
Задача 585. Для балок задач 577, 578 и 579 определить по-
потенциальную энергию от поперечной силы Оценить в процентах
степень влияния поперечной силы на потенциальную энергию изгиба.
IX. СЛОЖНОЕ СОПРОТИВЛЕНИЕ ПРЯМОГО
БРУСА БОЛЬШОЙ ЖЕСТКОСТИ
§ 1. Косой изгиб
При косом изгибе балки, представляющем собой сочетание двух
прямых поперечных изгибов, нормальное напряженнее в произволь-
произвольной точке поперечного сечения с координатами у и г (рис. 115) опре-
аеляют по формуле
¦» ?1 + ^11). (,зб)
201
где Iy и 1г — главные центральные моменты инерции поперечного
б
М
сечения балки;
у и Мг — изгибающие моменты относительно осей у и г, состав-
составляющие результирующего изгибающего момента М — V М% Л-Ml,
действующего в плоскости хр, расположенной под углом о.
к главной плоскости инерции балки ху.
Здесь и в дальнейшем
принято, что My и Mz поло-
положительны, если они опреде-
определяют растягивающие напря-
напряжения в точках первого
квадранта сечения.
Уравнение нейтральной
сси пп записывается следую-
следующим образом"
1,
У =
My
Рис 115
где
УИ„
, A37)
A38)
— тангенс угла наклона нейтральной оси пп к оси z.
Нейтральная ось пп всегда отклоняется от оси г на угол р в ту
же сторону, в которую след рр плоскости действия сил отклонен от
оси у на угол а.
Максимальные и минимальные нормальные напряжения подсчи-
тываются по формуле A36) с подстановкой координат (г/4) г, и г/2.
г2) точек касания к контуру сечения прямых, параллельных нейт-
нейтральной оси.
Если максимальвое или минимальное нормальное напряжение
возникает в точке, наиболее удаленной от обеих главных централь-
центральных осей инерции сечеиия, то
| My \ \MZ\
"max = ~~w I Я/ A39)
min \
\щ
\MZ\
A40)
где Wy и Wz — экваториальные моменты сопротивления сечения
относительно осей у к г.
202
Сечения балок при косом изгибе подбирают по нормальным
напряжениям пробами с последующей проверкой.
Первую пробу можно брать из расчета на плоский изгиб по тому
составляющему изгибающему моменту, который требует боль-
больших размеров
Для сечеиий, вписывающихся в прямоугольник, первую пробу
устанавливают по формуле
М,
где e = wf-
Для прямоугольного сечения с высотой h и основанием b
с = -г-; для прокатного двутавра можно принять с = 8, а для
швеллера с = 6.
Прогиб / и угол 6 поворота какого-нибудь сечения балки при
косом изгибе определяются как геометрические суммы прогибов
и углов поворота от составляющих изгибающего момента, действую-
действующих в главных плоскостях инерции балки, т. е.
- /; и в = г % + в; ,
где /у и /., — прогибы в направлении осей у и г;
6у и 6г — углы поворота сечения вокруг осей у к г.
Результирующий угол поворота происходит вокруг нейтральной
оси, а результирующий прогиб — в плоскости, перпендикулярной
нейтральной оси.
Если косой изгиб вызван двумя различными системами внешних
сил, лежащими в ее главных плоскостях инерции, то положение
нейтральной оси в каком-нибудь поперечном сечении надо опреде-
определять по формуле
а положение линии прогиба — по формуле
tgp = -K
h
поскольку угол р' между направлением результирующего прогиба
и осью у не равен углу р между нейтральной осью и осью г.
В этом случае упругая линия балки является пространствен-
пространственной кривой.
Если нагрузки, действующие на балку, расположены в несколь-
нескольких плоскостях, проходящих через геометрическую ось балки, то.
203
проектируя их иа главные плоскости инерции, приходят к преды-
предыдущему случаю.
Пример 62. Дано: Р, q, I, b, h, E, а (рис. 116).
Определить положение нейтральной оси; отм; /шах
mix
Решение. Раскладываем силу Р и интенсивность равномер-
равномерно распределенной нагрузки д на главные центральные оси инерции
поперечного сечения у и г:
Ру = Pcosa, ду — q cos а; Рг = Psina, gz = gsina.
а) У
Рис. 116
Составляющие максимального изгибающего момента в сечеиии
под силой
Sin a .
От изгибающего момента Му, возникающего в главной плоско-
плоскости инерции балки гх, растянутыми будут волокна, лежащие слева
от оси у, а сжатыми — лежащие от нее справа (рис. 116, а). От
изгибающего момента Мг, возникающего в главной плоскости
инерции балки ух, растянутыми будут волокна, лежащие ниже
оси г, а сжатыми — лежащие выше нее.
204
Таким образом, наибольшие растягивающие напряжения огаах
возникнут в точке А среднего сечения балки, а наибольшие сжимаю-
шие напряжения отш — в точке В. Они будут равны:
Положение нейтральной оси пп определится из уравнения
Отсюда видно, что чем больше отношение -^, тем больше угол р
отличается от угла о..
Если, например, плоскость действия сил рх будет диагональной
плоскостью балки, то tga = ^ и tg р = -^ = -ц, т. е, нейтраль-
нейтральная плоскость пх будет другой диагональной плоскостью балки.
В рассматриваемом случае ft>6, поэтому р>я, как это показано
на рис. 116, б. На этом же рисунке изображена и эпюра о.
Из табличных балок 5) и 6) (см. рис. 99) от М
Ely,
от Mz
384 Elz
5
Результирующая стрела
прогиба посередине балки
/max = ' ' 'max "^ ' em
p .—
/ Sin a COSaa
¦/ — \~ —
w о №
Направление прогибов по-
показано на рис. 116, б.
Пример 63. Дано: Р =
=240 кГ, д = 400 кГ/м, I =
= 2 де, a =30°,
Рис. П7
205
Е = 2-Ю6 кГ/см\ |о] = 1600 кГ/см* (рис. 117).
Определить номер двутавра; положение нейтральной оси; /шах.
Решение. Наибольшие изгибающие моменты в заделке
/М„шах= PI sin а = 240 • 2 -L = 240 кГ-л.
М =_?i- + P/cosa = -^P-+ 240-2-0,866» 1216 лГ-ж.
-'max z z
Для первой пробы принимаем с = 8
По формуле A41):
Проверяем ближайший меньший двутавр № 20, для которого
Wz = 184 см3 и Wy = 23,1 еж3.
В точках А к В заделанного сечения соответственно получается,
что сшах = — omm, поэтому
*»"« | Му™ 12160° 24000
184 "+ 23,1
17оо
°,„я* — [°1 1700—1600
Так как - , , -100 = Tcrir 100 « 6,2% > 5%,
то берем двутавр № 20а, для которого Wz = 203 смл, Wу — 28,
и
_ 121600 24000
°tnax — 203 + 28,2 =
Ti 1600—1450 ,„„ „ .„.
Недонапряжение составляет —^^— -100 ~ 9,4%.
Для двутавра № 20а /у = 155 см'*, a lz = 2030 еж4, поэтому в
заделанном сечении
На рис. 117, с проведена нейтральная ось пп и построена эпюра
нормального напряжения о для сечения в заделке
Максимальный прогиб будет на свободном конце балки. По
табличным балкам 2) и 3) (см. рис. 99):
г 1 i gl* P/3cosct\_ I /4.16-108
'Ушах "~ Elz ^~8 ' г! .) ~~ 2-10<!-203(Г { 8 ¦"
240-8 Юв-0,8С6
1 3
РР sino 240-8-10с-0,5
'«яах— ЗЕ1у 3-2-10"-155
206
] « 0,33 см,
-1,03 см.
Максимальвый результирующий прогиб:
/max = У ^max+ Дпах = У0^2 + L03' ~ 1,08 СМ.
Он будет направлен под углом р' к оси у, для которого
/г 1 .03
'У
= 3,12, т. е. р'= 72=14'.
Задачи 586—595. Определить наибольшие по абсолютному зна-
значению нормальные напряжения и положение нейтральной оси в
опасных сечениях балок.
Кроме того, в задаче 587 определить вертикальный /„ и гори-
горизонтальный /г прогиб сечения под силой, принимая Е = 2 ¦ 106 кГ/см2;
а в задаче 593 — величину и направление прогиба / под силой Рь
принимая ? = 104 Мн/мг.
fT1"!^7
Г№50
55о Р=!/)/)кГ
к =30°
Псм
207
I —
-
Задачи 596—601. Определить величины допускаемых сил Р и
положение нейтральной оси в опасных сечениях балок.
Кроме того, определить величину и направление прогиба: в за-
задаче 596 — свободного конца балки (Е = 106 кГ/смг), в задаче
599 — середины левого пролета балки (Е = 10* Мн/мг).
к =30"
Задачи 602—605. Подобрать размеры сечений и определить
положение нейтральной оси в опасных сечениях балок.
Кроме того, в задаче 604 определить величину и направление
прогиба свободного конца балки (Е = 10в кГ/смг).
3D'
208
вол
Ш.
р--
'2Р р'йШ ц-ШкГ/м
¦ с
^
Задача 606. Доказать, что при с^С^- и q2 ^ 9i "max не за-
зависит от величин а и д2.
?06 ф 9е v» йу №7
1 i /i \ I j
А
-гс —»J-tt
тп
Задача 607. Доказать, что при с^ а и q2 ^. qt a)n/!X не зависит
от величины <?2-
Задача 608. Дано: Р, = 1.63Р, Е, a, h = 26. Определить вели-
величину и направление [тлх.
BOB
а - arclg О Ь
Задача 609. Дано- Р, I, a, a — arctg 0,5. Определить огаах .
Задача 610. Дано: q, l, а. Определить апых .
Задача 611. Дано: Р, а, Ь, Е. Определить /гаах и угол отклонения
его от линии действия силы Р.
209
§ 2. Растяжение или сжатие и изгиб
В общем случае одновременной деформации растяжения или
сжатия и изгиба в произвольном поперечном сечении призматиче-
призматического стержня внутренние усилия приводятся к продольному уси-
усилию Nx, направленному по геомет-
геометрической оси стержня х, к изгиба-
изгибающим моментам Му и Mz в глав-
главных центральных плоскостях
инерции стержня хг и ху и к попе-
поперечным силам Qy и Qz, направлен-
направленным по осям у к г (рис. 118).
Нормальные напряжения в по-
поперечном сечении стержня опреде-
определяются следующим уравнением
плоскости, не проходящей через
начало координат:
Рис. 118
Mv
Mzy \
"А )'
A42)
где F — площадь поперечного сечения;
/у и 1г — его главные центральные моменты инерции;
iy и (г — его главные радиусы инерции;
у п г — координаты точки плоскости сечения.
Уравнение нейтральной оси имеет вид:
1 +
Муг
\ -
= 0.
A43)
Нормальные напряжения приобретают наибольшее и наимень-
наименьшее значения в точках касания контура сечения прямых, параллель-
параллельных нейтральной осн.
Результирующие касательные напряжения приближенно можно
определить путем геометрического сложения касательных напряже-
напряжений в данной точке сечения от Qy и Qz.
Как правило, эти напряжения невелики и не имеют существен-
существенного значения в практических расчетах.
Подбор поперечного сечения стержня производится по нормаль-
нормальным напряжениям пробами с последующей проверкой. Первую пробу
можно брать из расчета только на плоский изгиб по тому составляю-
составляющему изгибающему моменту, который требует больших размеров.
Взятая проба должна проверяться с учетом второго составляющего
изгибающего момента и продольного усилия. В подобранном сече-
сечении перенапряжение ие должно превосходить 5%.
210
Пример 64. Дано: q = 200 кГ/м, Ро = 24 Т, Pi = 16 Т,
р2 = 400 кГ, b = \2см, h= 16см, I = 2м (рис. 119).
' Определить оП1ах , о„„п и положение нейтральной оси.
Решение. В опасном закреплен-
закрепленном сечении бруса:
Nx = —Р„ — Р, = —24 • 103—
— 16-Ю3 = — 40-Ю3 кГ;
Му = Р1~+ Рг±-= 16-103 . 6+
+ 4-102-102 = 136-103кГ-сл1;
Мг= —Р1?—ч-?= —16-103-8 —
— 168-103 кГ-см
2-4'1
Знаки напряжений в точках опасного
сечения бруса от Nx, My и Mz указаны
на рис. 119, о.
Поэтому
-!t + ^-^~ 40-10"
136-10»
* 16-12й
168-10'
12-
-6«
•6±
475
— 891
кГ/см2.
В формуле A43) принято, что Nx >
> 0,' а от Му и Мг в первом квадранте
сечения о>0. В рассматриваемой задаче
Nx < 0, Му > 0, Мг < 0, а 4 = -? = 12 ^
и ^ = -^^21,3 см2.
Поэтому отрезки, отсекаемые нейтральной осью пп на осях гиг/,
будут:
"' " 12 =3,53 см,
Mv
136-10
40-10»
168-103
• 21,3 « — 5,07 см.
211
На рис. 119, а через концы этих отрезков проведена нейтраль-
нейтральная ось пи и построена эпюра нормальных напряжений.
Пример 65. Дано: q — 6 кн/м, L = 6 м, а = 30°,
Ы = 140 Мн/м2 (рис. 120).
Определить номер двутавра.
Решение. Проекции нагрузки д на оси хну (рис. 120, о):
qx =
Составляющая qx рав-
равномерно распределена по
длине I в левую сторону и
создает сжатие балки. Со-
ставляющая qy создает
плоский поперечный изгиб
балки.
Максимальный изгиба-
изгибающий момент в среднем
сечении балки равен:
8 cos о'
Первую пробу для подбора сечения берем по этому моменту.
Тогда
пп _ 'v'max
qL?
6000 • 36
8 [з] cos о
8-14-10'-0,866
^-=2,23-10 м3 =223 см3.
По сортаменту ближайший больший момент сопротивления имеет
двутавр № 22. Для него Wz = 232 см3, F = 30,6 см2.
В сечении, где действует Мшах, продольное сжимающее усилие
имеет величину:
N , =•
4x1
2
4-tg-
Проверяем подобранное сечение с учетом продольного усилия:
I I _ \N*\ 4- Мтах = 6000 • 6 х 6000 . 36 _
lalmax- F •+" Wz — 230 610_4^- + 8-232. 10-с. 0,866 ~
= 137,8 ¦ 106 н/м2 = 137,8 Мн1м2.
Недонапряжение составляет:
М-М.ш.х . 100 = 2^02 _ 100 __ j g%
[о] 140
В действительности сечение с максимальным напряжением лежит
несколько левее среднего сечения балки, но настолько близко,
212
что это не оказывает влияния на расчет. В самом деле, для произ-
произвольного поперечного сечения:
Так как
d I ° Imex _ <7< гп„
•—gj— — 2р —
? _
то опасное сечение отстоит от левой опоры на расстоянии:
232-10-"
¦ = 3,420 .«,
_ / W_ . _ 6-2
2 F 21/3
т. е. на 4,4 см от середины балки
В этом сечении (при х = 3,420 см) для выбранной балки
6000
3.4202 Ц-
1 I _ 1' /6000-6 о9д
И™* - 232 - 10-» \~?Г ' а'М" — 2
+ з™/^:^ ~ 137,85 • 106 н'м2 = 137,85 Мшм\
т. е. на 0,05% больше, чем в среднем сечении.
Пример 66. Дано. Pi — 4 Т (расположена в плоскости ху),
Лг = 1 Т, Р3 = 0,8 Т, М = 2 Т-м, I = 2 м, а. = 15°, р = 30°,
1о) = 1600 кГ/слР (рис. 121).
Рис 121
Определить номер швеллера, у0, z0.
Решение. В опасном сечении (в заделке):
Nx = /\cosa + P3cosp = 4-0,966 + 0,8-0,866 « 4,557 Г;
Ms = —P3 ^-sinp = —0,8-0,5-100 = —40 Т-см;
М, = Pil sin a + P2l + M =
= 4-200-0,259 + 1-200 + 200 = 607,2 Т-см
213
Первую пробу для размеров сечения берем из расчета на плоский
изгиб от момента Мг-
w _ JU _ 607,2 ¦ 10» _ з з
W*~ [a] ~ 16- 10» -MVCM.
По сортаменту ближайший больший момент сопротивления имеет
швеллер № 22, для которого W2 = 192 см3 Для двух швеллеров
Wz = 384 см3.
Принимая во внимание, что кроме Мг в балке возникают еще
большой по величине М „ и продольное усилие Л^, для проверки
берем швеллер № 24, для которого Wz = 242 см3;
Wz = 2 • 242 = 484 сма, F = 2F' = 2 • 30,6 = 61,2 сжа,
/у = 2/; = 2 • 387.2 = 774.4 см*. Wy = -^- = -^- = 86,0 см".
Проверяем прочность швеллеров № 24 в наиболее напряженной
точке А заделанного сечения:
_ N_x__^y_ . Мг _ 4557 40 ¦ 103 607,2-10J
°шах— р №\"~~?^~~ 61,2 + 86,0 + 484 ~
« 1794
Так как перенапряжение равно:
то швеллера № 24 не подходят
В качестве второй пробы берем швеллер № 24а. Для этого швел-
швеллера
W'z = 265 cms, Wz = 2 • 265 = 530 см", F = 2 ¦ 32,9 = 65,8 см2,
Iy = 2l'u = 2 • 488,5 = 977 см* и Wv = -j^- ж 102,8 еж3.
Проверяем сечение из этих швеллеров:
_ 4557 40 - 10J 607,2 ¦ 10°
°ии— 65,8 + 102,8 + 530 s
Перенапряжение составляет -jg-= 0,25%, что соответствует до-
допустимым нормам. Остановимся на швеллерах № 24а.
Переходим к определению положения нейтральной оси в опасном
сечении
Для швеллера № 24а: 1г = 9,84 см, & « 96,8 см2,
.2 _ /у 977 _ 14 о 2
214
По формуле A43) отрезки, отсекаемые нейтральной осью на
осях у и г, получаются следующими:
9G8 °73 см; z
У» = ~ "ёбГ? • 9G'8 ж ~ °'73 см; zo=- ~W •
= 1.69 см.
На рис. 121, а через концы этих отрезков проведена нейтраль-
нейтральная ось пп и построена эпюра нормальных напряжений.
Внецентренная на-
нагрузка. В общем случае вне-
центренного нагружения призма-
призматический стержень испытывает
одновременную деформацию рас-
растяжения или сжатия и чистого
косого изгиба.
Внутренние усилия в каждом
поперечном сечении стержня при-
приводятся к осевому продольному
усилию Nx = P и двум изгибающим
моментам Mv = Ргр н Mz = Рур,
возникающим в главных централь-
центральных плоскостях инерции хг и ху
стержня. Здесь Р — действующие
растягивающие (сжимающие) силы,
приложенные не в центре тяжести
концевых сечений стержня, а в
точках с координатами у. и г„
(рис. 122).
Нормальные напряжения в по-
поперечном сечении стержня опреде-
определяются следующим уравнением
плоскости, не проходящей через
начало координат:
Рис. 122
где F — площадь поперечного сечения;
1у и Iz — его главные центральные моменты инерции;
ij, и iz — его главные радиусы инерции;
у к г — координаты произвольной точки плоскости сечения.
Уравнение нейтральной оси пп запишем в виде:
= 0 или
= 1,
A45)
215
где
A46)
— отрезки, отсекаемые нейтральной осью на главных центральных
осях инерции г к у поперечного сечения стержня
Для точек линии, параллельной нейтральной оси и проходящей
через центр тяжести сечения, нормальные напряжения а = j.
Максимальные и минимальные нормальные напряжения возни-
возникают в точках касания к контуру сечения прямых, параллельных
нейтральной оси.
Для симметричных сечений, имеющих точки, наиболее удален-
удаленные от обеих главных центральных осей инерции, максимальные
напряжения возникают в этих точках
Поэтому для таких сечений
J_ + .??. + Je_V П47)
г у I
Если точка приложения силы перемещается по прямой рр,
проходящей через центр тяжести сечения О, то нейтральная ось геи,
не поворачиваясь, приближается к центру
тяжести или удаляется от него в зависи-
зависимости от того, удаляется от центра тяже-
тяжести или приближается к нему точка при-
приложения силы
На рис 122 показаны положения
нейтральных осей (ге^, и2гег и п3пз,
по"о — ушла в бесконечность) и соответ-
соответствующие им эпюры о для случаев, когда
растягивающая сила Р прикладывается в
точках 0, 1, 2 и 3 прямой рр
Если точка приложения силы пере-
перемещается по прямой рр (рис 123), не
проходящей через центр тяжести сечения,
то нейтральная ось вращается вокруг не-
неподвижной точки К с координатами:
Уо =* —
и 2o=-
Справедливо и обратное положение если нейтральная ось вра-
вращается вокруг неподвижной точки с координатами у0 и г0, то точка
приложения силы перемещается по прямой рр, не проходящей
через центр тяжести сечения, уравнение которой имеет вид:
Уо
-А
= 1.
216
Если точка приложения силы лежит на одной из главных цент-
центральных осей инерции сечения, то стержень испытывает одновремен-
одновременную деформацию осевого растяжения или сжатия и чистого плоского
изгиба. Все вышеуказанные формулы остаются справедливыми,
но в них надо положить либо гр = 0 (если точка приложения силы
лежит на оси у), либо у0 — О (если точка приложения силы лежит
на оси г).
Для обеспечения прочности стержней из хрупкого материала с
низким сопротивлением разрыву нужно, чтобы внецентренная ежи-
S)
Рис 124
маюшая сила не создавала в поперечном сечении растягивающих
напряжений
Часть плоскости поперечного сечения, окружающая центр
тяжести и ограниченная замкнутым контуром, внутри которого
приложенная сила создает напряжения одного знака во всех точках
поперечного сечения, называется ядром сечения.
Контуром ядра сечения является геометрическое место точек
приложения внецентренной силы, при котором нейтральные оси,
касаясь контура поперечного сечения, нигде его не пересекают.
Пример 67. Дано: Р = 6,4 Т, Ь = 4 см, h = 8 см, ур = 2 см,
гр = 1 см (рис. 124).
Определить ота„ отш, у0, г0
Решение. В поперечном сечении возникают усилия
Nx = —P = — 6,4 Т, Mv = — Рг„ = — 6,4- 1 = — 6,4 Тем
Мг= —Рур = —6,4-2 = — 12,8 Т-см.
Так как в 1 квадранте сечения от всех усилий напряжения
сжимающие, то о1ШП будет в правом верхнем углу сечения, а ошак в
левом нижнем углу (рис. 124, о)
При этом
IL
_
217
Учитывая, что
= bh = 4 • 8- 32 см2, IFV = -jj- = —Е— = -5- сма и
У о о о
,„, _ЬК1 _ 4 64 128 з
находим
или
6,4- Ю3 6,4 • 103 • 3 12,8 • 10' • 3
32 ± *
64
128
°шах = 400 кГ/сж2, ои1п = — 800 кГ\смг.
По формулам A46) определяем отрезки, отсекаемые нейтраль-
нейтральной осью пп на главных центральных осях инерции сечения у и г:
Рис 125
Рис 126
го = •
12г„
_64_
12 - 2
~ = — 2,67 СЖ,
q . ^— "*"~ л -^ 1 ,о
Положение нейтральной оси и эпюра о изображены на
рис 124, а, б.
Пример 68. Дано: произвольное сечение, симметричное относи
тельно оси г, вписывающееся в прямоугольник ABCD со сторонами
6<й (рис. 125), главные центральные радиусы инерции сечения
!j,<jj и положение центра тяжести сечения, определяющееся вели-
величиной г0. Построить ядро сечения
Решение. Если нейтральные оси касаются малых сторон
прямоугольника АВ и CD, то соответствующие им точки приложения
218
внедентренной силы (точки k и I контура ядра сечения) должны
2
лежать на оси у и определяться ординатами уа = q=i^.
Если нейтральные оси касаются больших сторон прямоуголь-
прямоугольника ВС и DA, то соответствующие им точки приложения внецент-
ренной силы (точки тип контура ядра сечения) должны лежать на
оси 2 и определяться абсциссами
;2 /2
,' '* . ¦," _ **
Так как горизонтальные положения нейтральной осн переходят
в вертикальные (и наоборот) путем вращения вокруг неподвижных
точек, совпадающих с вершинами прямоугольника, то при этих
вращениях нейтральной оси точка приложения внецентренной силы
должна .перемещаться по прямым линиям.
Соединяя точки k, I, m и п прямыми линиями, получаем ядро
сечеиия (на рис. 125 ядро сечения заштриховано горизонтальными
линиями).
Рве. 127
Рис. 128
Частные случаи: а) прямоугольное сечение со сторо-
нами 'о и h (рис. 126). Для прямоугольного сечения: 12г = тк- ,
12 '
2 '
;
Поэтому уя — Т
б) двутавровое сечение (двутавр №20а, рис. 127). Из сортамента
для двутавра № 20а: lz = 8,37 см., <у = 2,32 см, h — 20 еж, 6 = 11 см,
г0 =-'
2 '
219
Поэтому
— — 2 • 8'37"
У я t- 20
2 - 2,322
П
=F 0,979 см;
в) швеллерное сечение (швеллер № 22а, рис. 128). Из сорта-
сортамента Д1я швеллера № 22а: iz = 8,99 еж, iv = 2,55 еж, Л = 22сж,
Ь = 8,7 см, 2о = 2,46 еж Поэтому
2 ¦ 8,99'
22
2,55*
8,7 — 2,46
— 1,04 еж,
2,552
Задачи 612—620. Определигь наибольшие ошах и наименьшие
от1п нормальные напряжения и положение нейтральной оси в опас-
опасных сечениях прнмых брусьев
Ш
20см
Bit р--Вт
24см
А
у
Ввм
/
'Вт
ИПI1ШМ11!1111Ш!11
Я17 Р"ВТ
- 4
г ц
ШНШШНШИНШШ!"
220
Задачи 621—623. Определить наибольшее нормальное напряже-
напряжение от!1Х"и положение нейтральной оси в опасных сечениях брусьев.
621
бт„-э50кГ/см'
•¦4
Задачи 624—629. Определить наибольшие отах и наименьшие
°min нормальные напряжении в опасных сечениях брусьев и в тех
элементах систем, которые испытывают сложное сопротивление.
221
621 626
Задачи 630—635. Определить необходимые размеры попереч-
поперечных сечений брусьев, балок и элементов систем.
830
P Ш
Г
tT3 г
P-Zt
ш'',[есу\ШМ/см''
2Р
9-7-,
Р/," =t
м
Р'ЧВВн
222
Задача 636. Определить размер tt, при котором наибольшие
нормальные напряжения в полосах и в накладке будут одинаковы.
1 j ^__М _у
Задача 637. Дано: вес единицы объема матери-
материала сгойки 1 = 2,5 Т/м3 и боковое давление на
ее диаметральное сечение р = 90 к/Уж2.
Определить диаметр d поперечного сечения
сгойки из условия отсутствия в ней растягиваю-
растягивающих напряжений.
Задачи 638—647. Определить величины на-
наибольшей безопасной нагрузки Р.
ГГНТТТТТт'
за"
1ш,
Ш-ЩОкГ/сн
223
Задача 648. Определить, при каких значениях силы Pt в нижнем
сеченин бруса не будет растягивающих напряжений.
Задача 649. Определить значения силы Р4 и omIn нз условия,
что в брусе <w= 0.
§М Р'ЮОки
-йи»--
Задачи 650—655. Построить ядро св!ений.
650
651
1
}
а
Щ
1
1
щ
т
ш
- j
t
*¦
652
224
656
§ 3. Растяжение или сжатие и кручение
Если в поперечных сечениях стержня от действия внешних сил
возникают продольные усилия Nк и крутящие моменты Мк, то
стержень, испытывает деформацию одновременного растяжения
или сжатия и кручения.
х — геометрическая ось стержня, а у и г — главные централь-
центральные оси инерции его поперечного сечення.
В опасной точке (у, г) рассматриваемого поперечного сечення
сгержня от продольного усилия Nк возникают нормальные напря-
напряжения
где F — площадь сечення;
а от крутящего момента — касательные напряжения
WK •
где WK — момент сопротивления сечения при кручении.
Главные нормальные напряжения в этой точке находятся по
формуле A07)
°,=-2-l°±
Расчет на прочность производигся по гипотезам прочности.
Для пластичных материалов пользуются третьей или чегвертой
гипотезами прочности, согласно которым
A48)
"IV
A49)
Для материалов, различно сопротивляющихся растяжению и
сжатию, когда —j- = v, пользуются пятой гипотезой прочности
8 Заказ № i
225
По этой гипотезе
<^==„1_,а, = -Ц^о + -Ц^Уго« + 4* A50)
•sv — "t — ~, — 2 « -г 2
Если поперечное сечение стержня круглое с диаметром d,
с «d2 if/ if 7cd3
ТП Г — И U/ W = ¦
iu • 4 к Р 16
Пример 69. Дано: Р = 2 Г, М = 4 Г-еж, d = 4 еж, 1ор] =
= 350 кГ/сл2, lacl = 1400 к/Усл2 (рис. 129)
Определить, будет ли стержень прочным.
Решение. Продольное усилие
крутящий момент
Нормальные
i
мк = м =
напряжения
з - ^ -
= 4-
во
2 •
= —5
Ю3 к.
всех
103 • 4
! ¦ 103
Г-сж
точках сечения
^159
кГ/см2.
Максимальные касательные напряжения в точках контура
сечения:
Л1к 4 • Ю3 • 16 О1
тгаах = -Ж- = ZTTB— ~ 6i
Так как
l°pl 350
[°с] "~ W00 -""•"•
то эквивалентное напряжение по формуле A50) имеет величину.
Сэ =_ 1%0-25 159 + 1 + 0,25 yl5Q2 + 4-31g8 ^ 350 кГ/сжа =
Следовательно, стержень будет прочным.
Пример 70. Дано Р = 160кн, М = Акн-м, Л = 8еж, 6 = 4еж,
от= 360 /Мм/л* (рис 130).
Определить коэффициент запаса прочности ит
Решение Так как Nx= Р = 16-10* «, Л4К = М = 4х
Л о
х103н-жиг- = т= 2, то во всех точках поперечных сечений о =
226
= -у- = 0 О4'_о 08 = 50-106 н/мг = 50 Мн/м2, а в наиболее напря-
напряженных от кручения точках посредине больших сторон прямоуголь-
прямоугольника сеченнй левой половины стержня
4 ¦ 103 ¦ 10"
~ 127 • 10» н/ж2 = 127 Ми/ж2.
Рис. 129
Рис. 130
В опасных точках стержня эквивалентное напряжение по третьей
гипотезе прочности, согласно формуле A48), приобретает значение:
ааш = J/502 + 4 ¦ 1272 * 259 Мн/м2.
Коэффициент запаса прочности
„ _
360
259
§ 4. Кручение и изгиб
При одновременной деформации изгиба с кручением внутренние
усилия в поперечном сечении стержня приводятся к пяти компонен-
компонентам: крутящему моменту Мх — Мк относительно геометрической
оси стержня х (рис 131), изгибающим моментам Му и Мг относи-
относительно главных центральных осей инерции сечения у и г и попереч-
поперечным силам Qy и Qz, направленным по этим осям.
Если стержень имеет круглое поперечное сечение диаметром d,
то касательные напряжения, определяющие собой Qy и Qz, имеют
второстепенное значение, и их при расчете обычно не учитывают.
Касательные напряжения, определяющие крутящий момент,
достигают наибольшего и одинакового значения
_ «к _ 16М„
во всех точках контура сечения (рис. 132), а наибольшие нормаль-
нормальные напряжения, определяющие собой изгибающие моменты Му и
8* 227
Мг, получаются в двух точках {А и В) контура сечения, лежащих
на концах диаметра, перпендикулярного вектору результирующего
изгибающего момента М = У
М2„ + Ml ; они равны
М 32М
В опасных точках А и В главные нормальные напряжения о,
и о3 определяют по формуле A07), а условия прочности записывают
в виде неравенства A48), A49) и A50)
Рис 131
Рис 132
Учитывая значения о и т, а также, что Wp = 2 IF, расчетные
формулы приводятся к виду:
A51)
где Ms — эквивалентный (расчетный) изгибающий момент, равный
по третьей гипотезе прочности
Мзт = У М
по четвертой гипотезе прочности
м =У М2 +
по пятой гипотезе прочности
av 2 ' 2
где v s= -у—г- ¦
228
0.75М1 ,
- М -| Г «|2 1 я*2
; |/ "Г" К,
A52)
A53)
A54)
Если кручению с изгибом подвергают стержень некруглого сече-
сечения, то опасными точками будут также точки, расположенные на
контуре сечення. Однако, поскольку точки с наибольшими каса-
касательными напряжениями от кручення могут не совпадать с точками,
в которых возникнут наибольшие нормальные напряжения от изгиба,
опасными точками могут быть точки с наибольшими касательными
напряжениями, точки с наибольшими нормальными напряжениями
и какие-нибудь промежуточные точки контура сечення
Этими опасными точками (у, г) явятся те точки, в которых экви-
эквивалентное напряжение, составленное по выбранной гипотезе проч-
прочности, достигнет наибольшего значения
Рис 133
56 5т см
При составлении эквивалентного
подсчитывать по формулам:
напряжения следует о и т
м,.
где 7 — отвлеченный коэффициент, зависящий от формы и размеров
сечения н от координат (у, г) рассматриваемой точки контура се-
сечения
Для уточнения расчета могут быть учтены и касательные
напряжения от изгиба *Qi и те Тогда полное касательное напря-
напряжение должно определяться путем геометрического суммирования.
Пример 71. Дано: диаметры шкивов D' = 20 см; D" = 60 ел;
веса шкивов Р'о = 200 кГ; Ро" — 400 кГ; натяжения ремней Р\~
= 800 кГ; Р'г = 400 кГ; Р"t = 1000 кГ; Р'\ = 600 кГ; размер
229
длины вала 1 = 2 м; угол наклона ремней второго шкнва к оси г
а. = 45°; допускаемое напряжение материала вала [о] =
= 1000 кГ/смг (рис. 133).
Определить диаметр вала d
Решение Приводя силы натяжения ремней каждого шкнва
к центру сечення вала, находим в сечении первого и второго шкивов
моменты относительно оси х:
М'х = (P't — Р\)^ = 400-10 = 4-Ю3 кГ-см,
М"х = (Р", — Р)~ = 400-30 = 12-103кГ-сж.
Проектируя силы, действующие в сечении каждого шкива на
оси у и г, находим результирующие поперечные силы в направле-
направлениях этих осей:
Р'у = (P'i+P's) + Р'о=1200 -I- 200 = 1400 кГ, Р\ = 0,
Р"у= (P"l+P)cos45°+P ~ 1600-0,707+400 = 1530 кГ,
Р"г = (Р",+Р) sin 45* =* 1600-0,707 = ИЗО кГ
От действия М'х и М"х возникает кручение Эпюра крутящего
момента Мк построена на рис 133, а
От действия сил Р'у и Р"у вал изгибается в плоскости ху как
консольная балка (рис 133, б). Методом наложения эпюр строим
эпюру изгибающего момента Mz относительно оси г (рис. 133, в)
От действия силы Р"г вал изгибается в плоскости хг по схеме,
указанной на (рис 133, г). Эпюра изгибающего момента Mv относи-
относительно оси у приведена на рис 133, д.
Опасным сечением вала будет сечение, где расположен второй
шкив
Производим расчет по третьей гипотезе прочности Эквивалент-
Эквивалентный изгибающий момент находим по формуле A52):
+ м1= У Ml + Mi + Ml =
41,5s + 16s « 71,9 Т-см.
По расчетной формуле A51)
w »~0 1^-> Мэ'" - 71Ш0
w = 2" ~ и-ш > ~и~ ~ "Шоо"'
Диаметр вала
d>f/TT9"«4,2 см.
Пример 72. Дано: P. a, h = 2b, [о) (рис 134).
Определить bah.
Решение. Строим эпюры изгибающего М и крутящего Мк
моментов (рис 134, а, б)
230
Б точке А опасного сечения в заделке (рис 134, в):
0=^ = 4^ = 9% и т~, ? ~ 0.795, ^
Ь3
~3,23?.
0,4931Я>
По третьей гипотезе проч-
прочности
eili
=^-К 81 4-4-10,4
откуда
2,23
В точке В опасного сече-
сечения от изгибающего момента "
а — 0; от крутящего момента "
мк
ЧРа
По третьей гипотезе проч-
прочности
- . 2Ра . ,о)
0.49362
Рис 134
откуда
8,11
Ра
Точка Л оказывается более опасной, поэтому нужно взять
Проверим выбранные размеры ft и А расчетом в точке В, учитывая
касательные напряжения от изгиба.
231
Так как в опасном сечении поперечная сила Q = АР, то в точ-
точке В возникнут следующие касательные напряжения:
т -A Q .о р
С 2 ' Wi ~ ft2 '
Результирующее касательное напряжение в точке В
По третьей гипотезе прочности должно быть соблюдено условие:
поэтому
Pa ^ H
b" 2D,06 + 3-^
Расчетом в точке А было получено, что —Л- <J~\гш •
Таким образом, большие размеры сечения получатся при рас-
расчете в точке В, когда окажется, что —-,—— >гт<; ^'0J или
4,06 + 3— > 5,54. или — > -Ц^- « 0.493.
Это значит, что точка В будет опаснее точки А лишь при таких
малых длинах участков стержня, при которых а<п~лт~ ^ в-
Пример 73. Четыре призматических стержня длиной /, геомет-
геометрические оси которых лежат в одной плоскости, с одной стороны
заделаны, а с другой — связаны между собой абсолютно жесткой
планкой (рис. 135, а).
Определить угол ф поворота планки под влиянием приложен-
приложенного в ее плоскости момента Ме, если расстояния между осями стерж-
стержней а, бис; жесткости стержней на кручение Ct, С2, С3 и С4, а
их жесткости на изгиб J34, B2, В3 и б4.
Считать, что соединительная планка остается вертикальной, а
горизонтальная прямая, проходящая через центры тяжести концевых
сечений стержней, соответствует направлению одной из главных
центральных осей инерции стержней.
Решение. Так как соединительная планка жесткая, то она
повернетси в своей плоскости вокруг какой-то точки О (рис. 135, б)
232
на угол ф. Этот угол будет углом закручивания для каждого стерж-
стержня, т. е.
Поскольку
Ф1
мк
ЧЧ = Фз = Фз = Ф4 = Ф-
мк
Ч>4=
(а)
(б)
Рис. 135
где МК{ — крутящие моменты для каждого стержня
(жесткости С, = - ' ' J, то равенства (а) принимают вид:
С, Сч С3 С4
Принимая во внимание свойство равных отношений, имеем:
Мк, + Мк, + Мк, + Мк, - (С, + С3 + С3 + С4) Ф. (г)
233
Прогибы концов стержней должны лежать в плоскости соедини-
соединительной планки и быть равными (рис. 135, б).
--|-А!3| и /4 = (а + Ь + с -е)<р
где Я|, Я2, Я3, Я4 и Л4(, М2) Мъ, Мц — силы и моменты, приложен-
приложенные к концевым сечениям соответствующих стержней, а жесткости
Считая, что соединительная планка остается вертикальной,
углы поворота концевых сечений стержней от изгиба должны рав-
равняться нулю, т. е
<е)
Отсюда
Подставляя эти значения в уравнения (д) и решая последние
относительно Я,, находим:
Р1 = 46/9;
Из условия статики
j
+ а —e)q>; Я4= 4В4(а + 6 + с —e)q>. J
Я4 (и)
(к)
поэтому
234
Составляем сумму моментов относительно точки О
MK,+MK!+MKz+MKt+Ple+P2(e—a)+P3(a+b—e)+Pi(a+b+
+с—е) = Мо. (м)
Принимая во внимание (г) и (л), перепишем уравнение (м) сле-
следующим образом:
а)* + 4<?В 3
= Ми, (н)
откуда
Ф =
-a)a+B3 (a+b—eY +В,(а+Ь+с—еJ}' к '
Зная е и у, из выражений (б) определяем Л! К/. , из выражений
(з) — Pt, из выражений (ж) — М{.
Максимальные изгибающие моменты для каждого стержня полу-
получаются в концевых сечениях; они равны
max М, — P,-g.
Прочность каждого стержня устанавливают расчетом на круче-
кручение с изгибом.
Частный случай. Все стержни круглого сечения,
у них
dl=d2=dg=di—-d; a = b — о = d; I = 10 d;
с1 с1 с1 с1 с1. П П П П Г1 ^Е1
С( — С2—? 3—?* — ?» ^1—^2—^3—^4 —- ^ ^^ F"?
В этом случае:
В =в =в =б _ д ^ 3?/ _^ 15 G/p
Пользуясь формулами (л) (о), (в) и (з), соответственно находим
Л4о _Mgl_ 1_
Ч)- Glp Glp /J..J_ , J_a.^_\ G/p
4 -у- + 15 -7га ^4 4 4 ' 4 )
4 Mo/
~ 19" G/p '
235
MKl = МКг = Л?к. = MK, = MK = ^- Mo
4
19
AW 4
15
' 4
Glp
— p _
• 3 d
2 п
3 Mo
19 / '
19
0 /2
19
Максимальные изгибающие моменты в стержнях
Q О
max Ml = max Л44 = -gg- Л1О; max А42 = max /И3 = -^g- Mo.
Расчетные уравнения должны составляться для 1-го и 4-го
стержней. Пользуясь третьей гипотезой прочности, получаем:
MB
~ U,OI/ -==--
M-
Задачи 656—664. Построить эпюры крутящего момента (Л1К),
изгибающего момента М и определить величину эквивалентного
напряжения по третьей гипотезе прочности
п-ЖпВ/иии
236
Задача 665. Дано: Р = 60 кГ;
dt = 2 см; d2 = 1 см; а = 8 см;
/ = 20 еж; Е = |g = 2 ¦ Ю6 кГ/сжг;
планка Л б — абсолютно жесткая
и остается в вертикальной плоско-
плоскости Определить наибольшие и
наименьшие главные нормальные
напряжения в стержнях
и вертикальное перемещение
точки приложения силы Р
fin/,///
Задачи 666—680. Определить размеры поперечных сечений
стержней из расчета по третьей гипотезе прочности.
237
ZBCM | 20ш
¦Жм-МР
673
Мотор
675
*€
[б]=ЮООиГ/смг
„ .,„»,.. п=ЦООод/мин
Радисшыве давление--^ мрулнога усилю 16}- 750нГ/омг
Задачи 681—688. Построить эпюры крутящего и изгибающего
моментов и определить безопасную нагрузку из расчета по третьей
гипотезе прочности
В задаче 688 соединительная планка АВ абсолютно жесткая и
остается в вертикальной плоскости
239
§ 5. Общий случай сложного сопротивления
В общем случае пространственного действия сил на призмати-
призматический стержень внутренние усилия в поперечном сечении приво-
приводятся к шести компонентам: продольному усилию Nx, крутящему
моменту Мк, поперечным силам Qy,
Qz и изгибающим моментам Му, Мг
(рис. 136)
Если ось х — геометрическая ось
стержня, а оси у мг — главные цент-
центральные оси инерции поперечного
сечения, центр тяжести которого
совпадает с центром изгиба, то Qy и
Мг определяют собой поперечный
изгиб в плоскости ху, a Q2 и Му —
поперечный изгиб в плоскости хг Та-
Таким образом, стержень испытывает
одновременную деформацию растяжения или сжатия, кручения и
двух плоских поперечных изгибов.
В произвольной точке (у, г) поперечного сечения стержня нор-
нормальное напряжение определяют по формуле A42), а результирую-
результирующее касательное напряжение находят путем геометрического сложе-
сложения касательных напряжений от кручения и от изгиба.
240
136
Уравнение нейтральной оси представляем выражением A43).
Не всегда сразу можно установить положение опасной точки,
поэтому приходится сопоставлять степень опасности нескольких
точек контура сечения. Опасной точкой будет та
точка контура сечения, для которой эквивалент-
эквивалентное напряжение, составленное по выбранной ги-
гипотезе прочности, имеет наибольшее значение
Путем сравнения этого расчетного напряже-
напряжения с величиной допускаемого напряжения можно
либо определить размеры поперечного сечения
стержня, либо проверить прочность стержня при
заданных размерах сечения
Пример 74. Дано: Ро = 40 Т, Я, = 8 Т, Р2 =
= 4 Т, />„ = 2 Т, I = 1 м, h = 24 см, Ь = 8 см,
| о] = 1400 кГ/см? (рис 137).
Проверить прочность стержня.
Решение. В нижнем опасном сечении стер-
стержня усилия имеют следующие значения:
Nx = Рв + Р, = 40 + 8 = 48 Т;
М2 =Р, \ + Р21 = 8-12 + 4-100 = 496 Т.см- Рис. 137
Му = Рг~+ Р3-~-= 8-4 + 2-50 = 132 Т-см;
= 24
= 4 Г; Q2 =
2 Г
На рис. 138 изображены эпюры и величины нормальных и каса-
касательных напряжений, соответствующих найденным внутренним
усилиям
В угловой точке А нижнего сечения стержня (рис 137) возни-
возникают нормальные напряжения, достигающие наибольшего значения:
°эА = <W = о' + а" + о'" = 250 + 646 | 516 = 1412 кГ/см2.
В точке В посередине правой длинной стороны сечения возни-
возникают нормальные и касательные напряжения следующей величины:
о = о' + о'" = 250 + 516 = 766 кГ/см\
* = Ч max — *у = 59 — 31 = 28 КГ/СМ*
Эквивалентное напряжение по третьей гипотезе прочности
= l^7662 + 4 • 28* ж 768 кГ/см*.
241
В точке С посередине нижней малой стороны сечения возни-
возникают следующие нормальные и касательные напряжения:
а = о' + о" = 250 + 646 = 896 кГ/см\
* = 4+ *г = 44 + 16 = 60 кГ/см\
Эквивалентное напряжение по третьей гипотезе прочности
аэ = 1/8962 + 4 • 602 « 904 кГкж2.
я> U Fit/
mm*****.
Zlt-82 "
~51ВнГ/смг
2 г ьь
з г so3 .
~!ВкГ/Смг
Из сравнения величин оэ в опасных точках А, В и С видно, что
наиболее опасной является точка А.
Так как оЭд = 1412 кГ/смг превышает [ о] меньше чем на 1 %,
то можно считать стержень прочным.
Пример 75. Дано: Pt = 200 кГ; Р2 = 100 кГ; Р3 = 240 кГ;
h = 30 см; 12 = 40 см; 13 = 60 еж; /„ = 80 еж; [ о] = 1000 кГ/см?
(рис. 139).
Определить: a, h, Ь, d, d0.
Решение. 1. Определение реактивных составляющих в
заделке. Для этого пользуемся шестью условиями статики (рис. 140).
гу л р ft- Л р 9ПП irP-
LiSV — г\х л у U, г\х — Г| — uUU K-i (
vy л р г\. л р 1ПП й-Г*«
sz = — 4 + ^з = °; 4 = рз = 240 к/";
SiM ^ = МА — Р J.. = 0; МА = P..L = 240 • 0,6 =
= 144 кГ-л;
ел«у = Млу + р1/1 —^« = °;
242
Млг<= РХ13—
= 240 • 0,8 — 200 • 0,3 = 132 кГ- м;
- /уз + Р2 A4 — у = 0;
= 200 ¦ 0,6— 100@,8 —0,4) = 80 кГ-м.
2. Определение на участках продольных усилий Л', крутящих
моментов Мк и изгибающих моментов Мх, Му, Mz.
В Р,
4
Рис 139
Рис. 140
Участок 1. Считаем г = 0 в точке Е к г = lt в точке D.
Изгиб в плоскости хг.
Му = Ргг\
0;
= Р^ = 200 • 0,3 = 60 кГ-м.
Участок 2. Считаем х = 0 в точке D и х = 12 в точке С.
Растяжение и изгиб в плоскостях хг и ху:
N = Р1 = 200 кГ. Му = />,/, = 200 • 0,3 = 60 кГ-м; Mz = Р2х;
MZx=a = 0; М =Pj,2 = 100 ¦ 0,4 = 40 кГ-м.
Участок 3. Считаем у = 0 в точке С и у = /3 в точке В
Сжатие, кручение и изгиб в плоскостях уг и *#:
Л' = — Р2 = — 100 кГ; /Ик = /ух = 200 • 0,3 = 60 кГ-м;
=0;
= 240 - 0,6 = 144 кГ-м;
Mz = Р2/г = 100 ¦ 0,4 = 40 кГ-м;
Мг = Рг1г + P,ls = 100 • 0,4 + 200 • 0,6 = 160 кГ-м.
Участок 4. Считаем х = 0 в точке А и х = 1й в точке В.
243
Сжатие, кручение и изгиб в плоскостях хг и ху:
N = — Ах = — 200 кГ; Мк = МАх=Ш кГ-м;
Mv = МА = 132 кГ-м; Mv =МА — А^= 132 —
— 240-0,8 = —60 кГ-ж;
/Иг = /И 4г + i4y*; /И^^ = Maz = 80 кГ. ж;
Мг _ = МЛг-f Лу/4 = 80 + ЮО • 0,8 = 160 кГ-м.
а)
Зпара N
Pi
ft
wo ш
6) р,
Зпщра мн
в)
¦АУ -Jr-A
3 Построение эпюр Л', УИК, Мх, Му и УИг на участках.
В соответствии со значениями Л\ Мк, Мх, Му и Мг, найденными
для каждого участка системы, на рис. 141, о, б, в, г, д показаны
эпюры этих величии.
4 Подбор поперечных сечений участков.
Участок 1. Опасное сечение около точки D (рис. 141, е и 139)
Му = 60 кГ-м
244
Подбираем сечение из расчета на плоский поперечный изгиб:
ю
- =3-3 см-
Участок 2. Опасное сечение около точки С (рис. 141, ж и 139).
N = 200 кГ; Му = 60 кГ-ж; Л1г = 40 кГ-м.
Подбираем сечение из расчета на косой изгиб:
>~ 6 12' г 6 ~ 24'
А» - 6- 10»+ 2-4- 10» ,.
-jg-> 1jp5 =14;
Принимаем й = 5,6 еж; 6 = g- = 2,8 еж и проверяем сечение,
учитывая продапьное усилие:
F = bh = 2,8 • 5,6 » 15,7 еж2;
Й7у= -g. » 14,6 еж3; Wz = -^ » 7,3 еж3;
ЛГ . AJj- , М, 200 . 6-103 , 4-103
кГ1см-
Недонапряжение И^2й-Х ¦ 100 = -^j^- = 2,8%.
Участок 3. Опасное сечение около точки В (рис. 141, з и 139).
W = 100 кГ; Мк = 60 кГ-м; Мх= 144 кГ-ж; Мг = 160 кГ-ж.
Подбираем диаметр сечения из расчета на кручение н изгиб.
Эквивалентный изгибающий момент по третьей гипотезе прочности
= \/~м1 +М\+ Mf = / 602 + 1442 + 1602 « 223 кГ-ж,
Проверяем сечение, учитывая продольное усилие:
И7 = -W = 32 * 22'3 сж3: ^ = 247 = 44,6 еж3;
Изгибающий момент
Ж = Ym\ + М2г = К1442 + 160s « 215 /с Г.м.
245
Нормальное напряжение
_ Л _М_ _ 100 215 102
°~ F ~~ W ~ 29,2 + 22,3
Касательное напряжение
= 967 кГ,см2.
Мч 60 • 10е (О|- г. „
Т = ¦% = 44,6 « 135 кГ'СМ ¦
Эквивалентное напряжение по третьей гипотезе прочности:
оЭ/// = У а2 + 4т* = 1/ 9672 + 4 • 1352 =» 1004 кГ/см*.
Перенапряжение составляет 0,4%, что вполне допустимо.
Участок 4 Опасное сечение около точки В (рис. 141, и и 139).
N = 200 кГ; Мк = 144 кГ-м; Му = 60 кГ-м; Mz = 160 кГ-м
Подбираем диаметр сечения из расчета на кручение и изгиб
Эквивалентный момент по третьей гипотезе прочности:
М„ш = VK+K +М1 = КН42+602 + 1602 = 223 кГ-л.
Основываясь на расчете участка 3, берем йп = 6,1 сл< и прове-
проверяем сечение, учитывая продольное усилие:
W = 22,3 еж3; Wp = 44,6 еж3; f = 29.2 см2
Изгибающий момент
М = ]Л М\л-М\ = V602 + 1602 = 171
Нормальное напряжение
0 _ IL . Л*. _ J5°_ + 171 ' loa ~ 774
f "г U? ~ 29,2 +~ 22,3 ~ '
Касательное напряжение
T = ^ = iii_^ 323 кг еж*.
IVp 44,6
Эквивалентное напряжение по третьей гипотезе прочности:
о, = У 7742 -)- 4 • 3232 =s 1008 кГ/сж2.
Так как перенапряжение меньше 1 %, то можно взять d0 = 6,1 еж
246
Задачи 689—696. Определить эквивалентные напряжения по
третьей гипотезе прочности.
^т
|"П'ИГПИП
РеЧбОиГ/
30см-
-30см
U.
631
в=',2'
6SZ , гр
"Зш
—5d-
-1ВЧ-
'К*
f
Х-—Мм-
зо-
Задачи 693—695. Проверить прочность стержне'й из расчета по
третьей гипотезе прочности.
Задачи 696—698. Определить необходимые размеры попереч-
поперечных сечений стержней, используя третью гипотезу прочности.
696 P,=tW»r Б9в
§ 6. Витая цилиндрическая пружина
растяжения или сжатия
Витой цилиндрической пружиной называется призматический
стержень, навитый на круглый цилиндр постоянного радиуса
(рис. 142).
Рассмотрим пружину из стержня круглого поперечного сече-
сечения диаметром d. Средний диаметр витка обозначим D, а число
витков п. Шаг пружины определяется углом а наклона плоскости
витка (хг) к горизонтальной плоскости.
Рис. 142
Ось х касательна к средней линии витка, а ось у перпендику-
перпендикулярна плоскости хг.
Если концы стержня выведены в центры витков и подвергаются
вдоль оси пружины действию растягивающей силы Р, то н каждом
поперечном сечении стержня внутренние усилия приводятся к по-
постоянному растягивающему усилию Ns = Psina, поперечно-сре-
248
зывающей силе Qy = Pcosa, крутящему моменту Мк = PRcosa и
изгибающему моменту Му= PRsin а (рис. 143).
Опасной точкой сечения является точка А внутренней поверхно-
поверхности витка. В этой точке
Nj, му 16PD
°— ~T f u/ - ~Sd5~
И
Qy , мк 8PD /, d \ ..г-,..
т — —— -A ¦ = I 1 -A спя a A56)
— F W — nd3 I 2DJ У1'™)
По третьей гипотезе прочности расчетное условие пишется сле-
следующим образом:
[с,.
A57)
Если шаг пружины мал (а < 14°), а-^->10, то расчет произво-
производится только на кручение по формуле
При большой кривизне витка (-^-< 10) влияние кривизны и сило-
силовых факторов удобно учитывать коэффициентом
Цг — 0,25 „ „.г
й —' d
который включается в условие прочности
*-^-<М- A60)
Общее выражение, определяющее осевое перемещение свобод-
свободного конца пружины о, имеет следующий вид:
где Е и G — модули продольной и касательной упругости материала
стержня пружины.
Для пружины малого шага перемещение 8 можно определять с
достаточной точностью только от деформации кручения по формуле
8=^. A62,
249
Пример 76. Дано: D = 80 мм; d — 20 мм; а = 15";
п= 10 витков; ? = 2-Юе кГ/сж2; G = 8-105 кГ/сж2; | о] =
= 6000 кГ/см2 (рис. 144)
Определить Р и 8.
Решение Так как а>14°, то пользуемся формулой A57),
из которой допускаемое значение силы
D vi. 23 • 6000
. » 1050/сГ
16-8
0,067 + («+-278-) 0,933
Осевое перемещение свободного конца пружины 8 находим по
формуле A61). Подставляя в нее заданные числовые величины,
получаем
8 • 1050 ¦ 83 . 10
24 • 0,966
0,067
2- 106
Л . 2г N
« 3,54 см.
2а \ 0,9331
^ J
Если воспользоваться приближенной формулой A62), то
8 ¦ 1050 ¦ 8а • 10
8 ¦ 10" • 2"
- = 3,36 см.
Это значение приблизительно на 5% меньше действительного
перемещения.
Пример 77. Две витые цилиндрические иружи-
1ны малого шага вставлены одна в другую концен-
трически (рис. 145) На них действует сжимающая
шуджд осевая сила Р = 430 кГ. У наружной пружины
1 : Di = 160 мм; dt = 16 мм; п± = 8 витков. У внут-
внутренней пружины 2 : Di = 80 мм; d2 = 12 мм; я2=
= 12 витков. Модуль сдвига материала стержней
пружин G = 8-Ю5 кГ/смг.
Определить осадку пружин 8 и наибольшие
касательные напряжения xmaXi и tmaXj.
Решение. Если обозначить силы, действую-
действующие на пружины через Pt и Р2, то из условия
равновесия Pj -V Рг= Р
Условие совместности перемещений выража-
выражается в равенстве осадки первой (8t) и второй (82)
пружины, т. е 84 = 82.
Принимая во внимание, что обе пружины малого
шага, используем для осадки формулу A62) и пе-
перепишем последнее равенство в раскрытом виде:
250
откуда
Р - Р '"''
Следовательно,
Осадка пружин
g ВР^я,
Gdf
2 Р
!60 /сГ,
8Р2?>|л2
Gd2
16s • 8 •
в» - 12 -
f>2 —
! 8-
8
1,2а
1,6*
жр
160-
¦ 10s ¦
27
16
= 270
16s ¦ 8
1,6"
кГ.
-8 см.
Так как наружная пружина имеет малый шаг и у нее -? — 10,
то по формуле A58) определяем
8 -160 • 16
71- 1,6S
= 1590 кГ/см2.
Г) R
Внутренняя пружина имеет малый шаг, но у нее -^ = y-g
=к 6,67<10, поэтому tm,X2 определяем по формуле A60).
Так как поправочный коэффициент
_ 6,67-0,25 0,615
я— 6,67-1 ]"б
ТО
W. ='.224 ^Т^5* 3900
Задача 699. Пружина сжимается до исчезновения зазора между
витками. Определить величину необходимой силы Р и возникающие
iraax, если D — 50 мм, шаг витка t = 15 лш, п = 10, сторона квадрат-
квадратного сечения стержня пружины а = 5 лш, G = 8-Ю4 Мн/м2.
Задача 700. Две пружины сжимаются одинаковой по величине
силой Р.
Определить отношения ^Ь и il если известно, что Di=D2;
Задача 701. Дано: D,=D2 = 200 лш, di = 2rf2 = 20 лш,
«4 = 8, п2 = 5, Gt = Gz = 8-105 кГ/сж2; / > 8,.
Определить шах т,, max т2, 8= й^Зг-
Задача 702. Предохранительный клапан должен открываться
при давлении пара р = 5 атм Определить для пружины тшах,
п и 80, если известно, что Do = 80 мм; D = 60 лш, d = 10 жж,
251
t = 18 мм, G = 8-Ю5 кГ/см2; ход пружины до соприкосновения
витков 40 мм.
Предполагается, что при максимальном поднятии клапана (при
нарастании давления в процессе его открытия; должно остаться
20 мм в запасе.
70;
-21
¦ ш
Задача 703. Определить монтажные напряжения в пружинах,
если Д = 5 мм, ?>j = 60 мм, rf4 = 10 мм, я4 = 10, D2 = 50 мм
d2 = 8 мм, п2 = 8, Gi = G2 = 8-105 кГ/сл2.
Задача 704. Определить допускаемую силу Р, если для стержня
ABC I = 500 мм, b = 750 жж, d0 = 30 лл, [о| = 1600 кГ/см2,
расчетная формула по третьей гипотезе прочности; для пружины
D = 50 жж, й = 10 мм, п = 10, G = 8- 105кГ/м2, ? = 2 • 106 кГ/смг,
[х] = 4000 кГ/сж2.
Задача 705. Дано: D = 50 жж, rf = 10 лш. я = 2, G = 8 х
X105 кГ/см2, di = 50 жл, & = 500 лш, Р = 100 кГ. Стержень BE—
жесткий.
Определить, на сколько процентов пружина уменьшает напря-
напряжение в валике AD.
Задача 706. Дано: Р = 1,6 кн, D = 60 мм, й = 12 лш, /: = 15,
G = 8-104 jWw/jh2, Z = 500 мм, Ь = 50 лш, Е = 2-105 /
252
Определить силу Р предварительного поджатая пружины, чтобы
после ее установки в полураму напряжения в ней уменьшились в
2 раза.
К
\р
\ D
706
кГ,
D = 100 мм,
G = 8-105 кГ/
t = 182 мм,
л2, допускае-
допускаеЗадача 707. Дано: Р = 105
[о] = 4800 кГ/смг, Е = 2- 10е к1
мая осадка |8| = 100 мм.
Определить d и п, пользуясь четвертой гипотезой прочности.
Задача 708. Дано- ?>=100мм, с= 10 мм. /=182 лш, Ы =
=4800 кГ/см\
Определить Р, пользуясь третьей гипотезой прочности.
Задача 709. Определить осевое усилие Р в пру-
пружинах после их соединения, если известно, что
Д =60 мм, пружина / с большим шагом и для нее
Dl=\00 мм, Й1=10лш, П)=- 4, <,= 182 мм; пружина
// с малым шагом и для нее D2=80 mm, d2=8 мм,
и2=8, Ei=E2=2-10" кГ/см\ G,=G2=8-105 кГ/см2.
X. ПРОДОЛЬНЫЙ ИЗГИБ
§ 1. Критическая сила и критическое напряжение
При осевом сжатии призматического стержня в пределах про-
пропорциональности величину критической силы Р1ф определяют/- по
формуле Эйлера1
т?Е1
A63)
где Е — модуль продольной упругости материала стержня;
/ — минимальный момент инерции площади брутто F по-
поперечного сечения стержня,
'пр — V-1 — приведенная (свободная) длина стержня (длина, пря
которой стержень с шарнирно-закреплениыми кон-
253
цами эквивалентен по устойчивости стержню с задан-
заданным закреплением);
I — истинная длина стержня;
[г — коэффициент длины, зависящий от способа закреп-
закрепления и нагруження стержня.
На рис 146 указаны простейшие случаи сжатия стержней и соот-
соответствующие им значения коэффициента |х.
Критическое напряжение окр определяется по формуле
Ркр
т*Е
A64)
Рис 146
где Х= -SS- — гибкость стержня (отвлеченная величина, характе-
характеризующая склонность стержня к продольному изгибу); '—у у—
минимальный радиус инерции площади F поперечного сечения
стержня.
Так как критическое напряжение окр не должно превышать
предела пропорциональности материала стержня оп, то величину
гибкости X, при которой можно пользоваться формулами A63) и
A64), устанавливают из неравенства
A65)
Например, для стали марки Ст. 3 Х^ЛОО; для стали марки
Ст 5 >>85, для чугуна Х>80; для дерева >.>70 и г. д
Если продольный изгиб возникает в стержне только за пределом
пропорциональности его материала, то критическое напряжение
можно подсчитывать по эмпирической формуле Ясинского-
окр = с —ЬХ + сХ2, A66)
где а, Ь, с — опытные коэффициенты, зависящие от материала и
имеющие размерность напряжения.
254
с=0.
Для стали Ст. 3. с=3100 кГ/см\ 6=11,4 кГ/см2, с=0.
Для стали Ст. 5: с=4640 кГ/см2, 6=36.17 кГ/см2, с=0.
Для чугуна: с=7760 кГ/см2, 6=120 кГ/см2, с= 0,53 кГ/см2.
Для дерева: с=293 кГ/см2, 6=1,94 кГ/сл2, с0
Формулу A66) можно применять,
если окр меньше от для пластичного
материала и меньше ов для хрупкого
материала.
Пример 78. Дано: материал стер-
стержня—дюралюминий, ?=0,71 • 105 Мн/м2,
о„ =180 Мн/м2, 1=1,2 м, D = 4 см,
d= 3 см (рис. 147).
Определить Ркр, окр.
Решение. Момент инерции коль-
кольцевого круглого сечения стержня
' = ii(Di~di) = ж<256-81> =
175
Площадь поперечного сечения стер-
стержня
Рис. 148
Радиус инерции сечения
64.7
При заданном способе закрепления концов стержня коэффициент
длины [1 = 0,7.
Так как гибкость стержня
то критическую силу можно определять по формуле Эйлера:
Р =-"а?/ гг-. *а-0.7Ы05-Ю6-175*-10-° ?5 о Шя.. Ио
КР (ы./J 64@ 7-1,2J — oui° it» к — оо,о лт*.
Критическое напряжение
А-о 85,3-10'-4-10«
°кр = -р- = tS = 155" Ш6 Н/Л*2 = 155 M«/*2-
Пример 79. Дано- материал стержня — чугун, /=1,6 м,
d=6 еж, /=1 см (рис. 148)
255
Определить Рт, окр.
Решение. Момент инерции крестообразного сечения стержня
1-6<
12
12
5Л
12
221
Площадь поперечного сечения стержня
f=ai+ (а — 0^=6+5=11 еж2.
Радиус инерции сечения
^«1,294 см.
При заданном способе закрепления концов стержня у. =0,5.
Так как гибкость стержня X = -t- = -=—, -ggj- ~ 61,8 < 80,
то критическое напряжение следует подсчитывать по эмпирической
формуле
- окр = 7760— 120Х + 0.53Х2 = 7760— 120-61.8 + 0,53-61,8* »
~ 2370 кГ/см2.
Величина критической силы получается равной:
Ркр =
= 2370 • 11 = 26100 кГ.
Задачи 710—715. Определить величины критических сил Ркр
и критических напряжений окр для сжатых стержней.
Принять для материалов следующие округленные значения
модулей продольной упругости Е и пределов пропорциональности
о,
Материал
Е кГ/см2
о„ кГ/смг
Ст. г
2-W-
2000
Ст. 6
2-10"
2400
Чугун
1,2-10е
1800
Дуралю-
0,7-10'
1700
Дерево
(сосна)
1-Ю5
200
712
а) 1=24см
б) 1= 10см
СтЗ
256
Дерево
| (сеет)
§ 2. Расчет сжатых стержней на устойчивость
При расчете сжатых стержней, кроме условия прочности, долж-
должно соблюдаться и условие устойчивости:
[«у]
A67)
o=-f-<|oy]. A67')
Здесь Ркр — критическая сила, определяемая в зависимости от гиб-
гибкости формулой Эйлера A63) или формулой Ясинского A66), т. е
выражением Ркр = о|ф F=(a — bX+cX^F;
[оу] = —^— допускаемое напряжение на устойчивость;
[яу ] — допускаемый коэффициент запаса устойчивости. Этот
коэффициент всегда несколько больше основного коэффициента
запаса прочности, так как при расчете центрально-сжатых стерж-
стержней на устойчивость приходится учитывать дополнительные, неиз-
неизбежные на практике обстоятельства (эксцентриситет приложения
сжимающих сил, начальная кривизна и неоднородность материала
стержня), способствующие продольному изгибу.
Большие эксцентриситет и начальная кривизна рассчитываются
специально, малые же, не поддающиеся расчету и зависящие от
гибкости стержня, учитываются дополнительным коэффициентом
запаса, т. е. упомянутым увеличением коэффициента запаса на
устойчивость. Принимают: для стали [иуJ=l,8 — 3; для чугуна
lnyj=5 — 5,5; для дерева [пу]=2,8— 3,2.
Отношение |?*J = ср называется коэффициентом уменьшения
допускаемого напряжения при продольном изгибе или коэффициен-
коэффициентом продольного изгиба.
Зависимость значения f от X для различных материалов да-
дается либо в виде нормативных кривых, либо в виде таблиц (прило-
(приложение 3).
9 Заказ № 886 257
Расчет на устойчивость может проводиться в двух вариантах
(способах).
1. При заданном в условии коэффициенте запаса на устойчи-
устойчивость 1пу ].
2. С помощью таблиц коэффициентов уменьшения у(\).
Первый способ недостаточно точен, так как, строго говоря,
коэффициент запаса устойчивости не может быть заранее точно
задан, так как он зависит от гибкости стержня. Этот метод приме-
применяется при ориентировочных поверочных расчетах, а также в тех
случаях, когда отсутствуют таблицы и графики <?{).) (например,
в случае новых материалов или применения стержней с гибкостя-
ми, превышающими рекомендуемые).
Второй способ применяется повсеместно, являясь основным
методом расчета стержней на устойчивость Расчет ведется в этом
случае, исходя из уравнения
°=-?-<ф|ас|, A67")
с помощью только таблиц коэффициентов ср, не применяя ни фор-
формулы Эйлера, ни эмпирических формул Ясинского.
Определение допускаемой силы
Если для рассчитываемого стержня известны: длина /, способ
закрепления концов (;х), форма и размеры поперечного сечения
(F, I, i) и материал (Е, [ос]), то определение допускаемой сжимаю-
сжимающей силы [РI производится одним из следующих способов расчета.
Первый способ расчета (при заданном
lnyj): 1. Определяют гибкость стержня X = —. 2 Определяют кри-
критическую силу PKV(PKP—oKVf) по формуле Эйлера A63) или, ис-
исходя из формулы Ясинского A66), если условие A65) не удовлет-
удовлетворяется 3. Из формулы A67) находят допускаемую силу [Р\=
__ Ркр
Заметим, что если \пу J не задан, то его можно приближенно
подобрать в соответствии с материалом стержня, его назначением
и величиной гибкости X.
Второй способ расчета (с помощью таблиц
<р(Ц). 1. Определяют X =— 2. По нормативной кривой или из
таблиц <р(Х) с использованием интерполяции устанавливают коэф-
коэффициент продольного изгиба ср. 3. Определяют допускаемую сжи-
сжимающую силу lP]=loyjF= (j>lac]F.
258
Проверка стержней на устойчивость
Осуществляется в двух вариантах аналогично предыдущему
(т е аналогично определению допускаемой силы), исходя из урав-
уравнений A67') и A67").
Подбор поперечного сечения
Ясли для рассчитываемого стержня известны сжимающая сила
Р, длина /, способ закрепления концов fa), материал (?, [о, 1)
и форма сечения, то условие устойчивости A67") является неопре-
неопределенным, поскольку без размеров сечения нельзя найти /, а
следовательно, и q>. Нельзя также (при заданном коэффициенте
запаса [пу 1) воспользоваться уравнением A67), поскольку неизвест-
неизвестно какую формулу A63) или A66) надо применять при определении
Рло. Подбор сечения приходится производить пробами с последую-
последующей проверкой (одним из трех вариантов)
Первый вариант расчета (с заданным 1иу])
применяется редко, вследствие недостаточной точности, обуслов-
обусловленной тем, что величина [пу\, заданная безотносительно от вели-
величины X (которая еще неизвестна), чрезвычайно ненадежная. Расчет
в этом случае начинается от пробного предположения о справедли-
справедливости формулы Эйлера A63).
Находится момент инерции /, затем F, /, X. Если I оказывается
больше >0, то расчет считают законченным, если же меньше Хо,
то делается пересчет, исходя из формулы Ясинского A66).
Второй вариант расчета с помощью таблиц и
графиков ф(>) осуществляется в следующем порядке:
1. Задаются значением коэффициента ф=0,6 — 0,8
2. Устанавливают |оу J, F=t^-j , подбирают размеры сечения
или номер профиля (если стержень — прокатная сталь)
' 3 Находят /, / и К
4 Определяют новое значение q>j. Если ф1 значительно отли-
отличается от ф, то в качестве второй пробы берут ф2= -у
и повторяют расчет
Считают сечение подобранным удовлетворительно, если о и
[оу] отличаются не более чем на 5%.
Для стержней стандартного проката недонапряжение может
оказаться и больше 5%.
Третий вариант расчета (смешанный). Здесь
первая проба берется условно из формулы Эйлера, задаваясь коэф-
коэффициентом пу, а окончательный выбор осуществляется на основа-
основании условия устойчивости A67").
Порядок в этом случае следующий
9* 259
1. Задаются значением коэффициента пу, в соответствии с ма-
материалом стержня (для стали /гу« 2, для чугуна /гу»5, для де-
дерева Пу~3).
2. Находят минимальный момент инерции поперечного сече-
сечения, пользуясь формулой A63).
3. Подбирают размеры сечения или находят номер профиля
(для проката), а также F, i, X.
4. Определяют коэффициент ф, а затем [оу].
5. Составляют условие устойчивости A67").
6. Если условие A67") не соблюдается, подбор продолжают
либо путем варьирования коэффициентами <р (см второй вариант
расчета), либо варьирования размерами сечения (номерами про-
профиля для проката).
При практических расчетах на устойчивость не рекомендуется
брать стержни, гибкость которых превышает максимальную гиб-
гибкость, указанную в нормах для коэффициента <р. Если, однако,
следует определить допускаемую силу или подобрать сечение
при гибкости стержня, которая больше гибкости, рекомендуемой
нормами,, то расчет следует производить, пользуясь формулой Эй-
Эйлера с выбором коэффициента запаса устойчивости.
Пример 80. Дано: материал стержня — сосна (вдоль волокон),
[о]=100кГ/см2, 1=2м, |i=l, d=10cM (рис. 149,а).
Определить Р.
Решение. Для круглого сечения
i = -г = —г- = 2,5 см.
Гибкость стержня
Для дерева при Х=80 по табличным дан-
данным ф=0,48.
Поэтому [оу1 = ф |ст] = 0,48-100 =
= 48 кГ/см2 и допускаемая сила
Р = [Ov] F = 48 ~= 3770 кГ.
Рис. 149
Установим, с каким коэффициентом запаса будет работать стой-
стойка.
Так как Х=80>70, то по формуле A64)
10-МО» ок
156 Г/2
ок[|
802
156
8"
260
Пример 81. Дано: стойка из прокатной стали двутаврового
профиля, [о]=1600 кГ/см2, Р=40 Т, 1=2 м (рис. 149, б).
Определить номер двутавра.
Решение. Задаемся ф=0,6.
Тогда
[о | = Ф [о] = 0,6-1600 = 960 кГ/см*
По сортаменту ближайший двутавр № 27, для которого F=
=40,2 см2 и *„=2,54 см.
Гибкость стойки X = -^- = ' = 78,7.
ly Z,04
По таблице для Ст. 3: X = 70; ф = 0,81; X = 80; q> = 0,75,
поэтому для X = 78,7
Фи = 0,75 + 0,006-1,3 = 0,758.
Берем
Фа = 9 2^ ~ ~—2^ = °>679- -
Тогда
[оу] = 0,679-1600 = 1086 кГ/см2 и F = ^g^ « 36,8 ел2.
По сортаменту ближайший двутавр № 24, для которого F =
= 34,8 см" и ty = 2,3? см.
200
Гибкость стойки X = g-g« =s 84,5.
По таблице для Ст. 3: X = 80; ср = 0,75; X = 90; ср = 0,69.
Для Х = 84,5
Фз = 0,69 + 0,006-5,5 = 0,723.
Допускаемое напряжение
[Оу] = 0,723-1600 = 1157 кГ1см\
Действующее в стойке напряжение
40 ¦ ioj 11cfl r „
о = 34 8 « 1150 кГ/см2.
261
Рис 150
Перенапряжение
1157
¦¦ 0,8%.
Установим коэффициент запаса устойчивости
для рассчитанной стойки.
Поскольку Х=84,5< 100, то по формуле A66)
а = 3100 — 11,4 • 84,5 = 2137 кГ/см";
2137
1150
: 1.86.
Пример 82. Дано: составная колонна из двух
швеллеров с приваренными соединительными
планками. Р=35 Т, /=6л, [о]=1600 кГ/см2
(рис 150).
Определить номер швеллера, В, 10.
Решение. При увеличении расстояния а
между швеллерами момент инерции сечения ко-
колонны /у относительно оси у, перпендикуляр-
перпендикулярной плоскости планок, будет увеличиваться
Момент же инерции сечения колонны /г отно-
относительно оси z изменяться не будет и останется
равным /г=2/2-, где /г. — момент инерции се-
сечения одной ветви колонны относительно цент-
центральной оси швеллера г', совпадающей с осью
г. Поэтому в качестве минимального момента
инерции поперечного сечения колонны надо
взять /г.
Задаемся пу=2. Из формулы Эйлера
i __
РРПу
35-КР.36-10'-2
= 630 см\
По сортаменту прокатной стали ближайший
меньший швеллер имеет № 14а Для него:
h =545 см\ h =5,66 см, F= 17,0 см*
1Г,„
106.
Гибкость колонны
, I 600
iz' 5,66
По таблице для стали марки Ст. 3: >.= 100,
9=0.60, Х=1Ю, <р=0,52.
262
Для К = 106
Ф = 0,52 +- 0,008-4= 0,552.
Допускаемое напряжение
|ov] = 0,552 -1600 = 883 кГ/см\
Рабочее напряжение
Р 35-10' 1Г,ОГ, „, „
2F ~~ 2Л7Л) ~ b KIICM m
Перенапряжение составляет
10^~9Ш - 100% = 14,2% > 5%,
что недопустимо.
Выбираем швеллер № 16. Для него /г.=747 oi4, (г.=б,42 см,
f=18,l смг, /„.=63,3 см\ <,- = 1,87 см, 6=6,4 см, /=0,84 см,
го=1,80 см
Гибкость колонны
По таблице для стали марки Ст 3 Х=90, 9—0,69, х=100
Ч>=0,60.
Для Х=93,б
9=0,60+0,009-6,5=0,658.
Допускаемое напряжение
[оу 1=0,658-1600 = 1051 кГ/см2
Рабочее напряжение
Р 35- Ю' пс„ „, „
а = g^ = g7yg~j ж 967 кГ/смК
Недонапряжение составляет
1051 — 967
1051
100% = 7,99%.
Останавливаемся на швеллерах № 16.
Так как Х=93,5<100, то
ок=3100— 11,4X^2034 кГ/см*
263
н колонна будет работать с коэффициентом запаса
Рациональное расстояние а между ветвями устанавливается из
условия равной устойчивости колонны в главных плоскостях
инерции ху и хг.
Поскольку ветви колонны соединяются не абсолютно жесткими
планками, рекомендуется брать /у=A,15-г-1,2)/х.
Возьмем 1у — 1,15/г. Тогда
= 9,66 = 10 см
и искомая длина планки
В=а+26=Ю+2 -6,4=22,8 см.
Для обеспечения устойчивости отдельной ветви в плоскости ее
наименьшей жесткости хг', теоретически соединительные планки
надо расставить на такие расстояния 1т друг от друга, чтобы
гибкость всей колонны равнялась гибкости участка ветви между
плаиками, т. е., чтобы
Из этого условия теоретическая длина участка ветви
lm = ~ L' = И ¦ = 93,5-1,87 = 175 см.
ч
Практически ранее рекомендовалось брать /о=A/2"?4)'от-
Согласно новым нормам (см. Строительные нормы и правила, ч. II,
раздел В, гл. 3, 1962 г.), гибкость отдельных ветвей Хв на участке
между планками должна быть не более 40, т. е. /0<!40«V . В нашем
случае
/0=40-1,87=74,8 см..
Возьмем /0=75 см. Тогда длина колонны / разделится план-
планками на шесть равных участков, а 24 см останутся на закрепления.
Из конструктивных соображений можно принять:
Я=@,6+0,8)В, /0—Я=C^4)Я и <п=@,8-М)/.
Для рассматриваемого случая примем:
Я=0,8 ?=0,8-22,8=18 см и <„«<»0,8 см.
264
Обычно колонку с соединительными шгаиками проверяют на
расчетную гибкость
— для колонны, составленной из двух швеллеров или двух дву-
двутавров;
— для колонны, составлеииой из четырех уголков,
где >-„ — гибкость колонны относительно оси, перпендикулярной
плоскости планок;
XBil XBz — гибкости ветвей относительно собственных центральных
осей, перпендикулярных плоскостям планок.
Сделаем эту проверку.
Для всей колонны
<v = 1/ R + 20 + Tl = V 1<87* + О»8 + 5J « 7.05 CM>
, 600 „r .
Для ветви
v _ ± ZIL _ 40
'»
Поэтому
Хр = ^вб.Р + ад2 = 94,1.
По таблице для стали марки Ст. 3, интерполируя, находим для
94,1,
<?=0,60+0,009 • 4,1 =0,637.
Допускаемое напряжение
[ау ]=0,637-1600= 1019 кГ/смК
Недонапряжение составляет
1019 — 967
1019
•100% =5,1%.
Следовательно, колонна устойчива и относительно главной оси,
перпендикулярной планкам.
Следует иметь в виду, что при соблюдении условий: /у=1.2 /г
и Xt =40, величины X,, и *. всегда будут очень близкими друг к
аругу
265
Задачи 716—717. Определить величины коэффициентов запаса
устойчивости пу, при которых работают сжатые стержни в системах.
Задачи 718—720. Определить, при какой длине / системы поте-
потеряют устойчивость
Принять, что при заданной нагрузке и размерах поперечных
сечений стержней деформации происходят в пределах пропорцио-
пропорциональности. В задаче 720 деформацию сжатия стержня // при рас-
раскрытии статической неопределимости не учитывать.
7/S
W/M
Задача 721. Определить длину /, при которой сжатая стойка
из Ст. 3 круглого сечения диаметра d с шарнирно закрепленными
концами потеряет устойчивость
2t6
Принять: ?=2-10е кГ/смг, оп=1900 кГ/см\ о=2400 кГ/см\
а) й=\ см, Р=1 Т, б) d=l см, Р=1,8 Т.
Задачи 722—724. Определить, при каком повышении температу-
температуры (Д/° С) сжатые элементы систем потеряют устойчивость.
Принять: Сталь: ?=2-10е кГ/см*; а =12,5-10'6; оп =2000 кГ/смг
Медь: ?= 1.10е кГ/см*; а=16,5-10-6; оп=Ю00 кГ/смК
ж
'//9УУ>
Задачи 725—728. Подобрать поперечные сечения сжатых эле-
элементов в системах, основываясь на заданном коэффициенте запаса
устойчивости пу.
Все сжатые элементы изготовлены из Ст 3 для котосой
?•=2-10е кГ/см?, а„ =2000 кГ/см* '
В задаче 726 указанное положение шатуна считать наиболее
опасным
725
Задачи 729—733. Проверить на устойчивость сжатые стержни
и определить % их перенапряжения или недонапряжения. Здесь
267
и в последующем возможные крутильные деформации сжатых
стержней в расчетах не учитывать.
7Z9
L
Ш
Шва
Г
Т s
731
\~-ioo-A t
Р=1ВОт
Ш,
Cm3
Illllillll
Задачи 734—736. Определить грузоподъемность колонн. Ма-
Материал колонн Ст. 3 [о]=1600 кГ/см2.
Ш
73S
Г
щоноочо
N30
Задачи 737—739. Определить размер Ь в сечениях колонн из
условия их равной устойчивости относительно осей z и у.
268
737
Piy
u
1
1
— f
/
./vw
4
736 , 1J9
ЦишВри T~J
четий ]
шарнир
Шаровоп
шарнир
Цилиндрические
потки
Зппитичес-
кое сечение
Задачи 740—744. Подобрать поперечные размеры колони и
сжатых элементов систем.
Принять: для Ст. 3 [о] = 1600 кГ/см*, для дерева [о] =
= 100 кГ/см\
Ш
т
¦I
Cm,»
СтЗ
Задачи 745—748. Определить для составных колонн:
1) № профиля ветви колонны;
2) ширину сечения колонны Ь;
3) расстояние 10 между скрепляющими планками (в свету).
269
Для материала ветвей колонны принять ?=2-10* кГ/смг,
laj = 1600 кГ/см2.
в —i
Г
Ш р- wr
Н>-
§ 3. Продольно-поперечный изгиб
Стержни, находящиеся под действием продольных и попереч-
поперечных сил и моментов, рассчитывают приближенно, исходя из допу-
допущения, что упругая линия стержня близка к синусоиде.
О)
р
Рис 151
Для балок с шарнирно закрепленными концами (рис. 151),
которые в основном рассматриваются в этом параграфе, указан-
указанная синусоида описывается следующим уравнением'
/sin — .
A68)
При таком расчете (предусмотренном и в решении предлагаемых
задач) более точные результаты получаются для стержней с шар-
шарнирно закрепленными концами при поперечной нагрузке, направ-
270
ленной в одну сторону, и симметричной относительно середины
стержня.
Для таких стержней упругая линия о г поперечного изгиба не
имеет точек перегиба, т. е. имеет однозначную кривизну, а потому
может быть представлена полуволной синусоиды A68).
В этом случае посредине длины стержня максимальный прогиб
А=—Ц-. <168-а)
1 J.
p*
Наибольший изгибающий момент
- Pf = Мл + —^V~ • <169>
Наибольшее сжимающее напряжение
!д ^
max |o| = ~ +- ~p = -^- + ^ + —у^-нт, A70)
где Р — осевая сжимающая сила.
Рэ=—Yt Эйлерова сила, вычисленная при любой гиб-
гибкости стержня через главный центральный момент инерции /
площади F поперечного сечения относительно оси, перпендикуляр-
перпендикулярной плоскости действия поперечной нагрузки,
W — осевой момент сопротивления поперечного сечения
стержня относительно указанной оси,
/п и Ми— прогиб и изгибающий момент посредине длины /
стержня только от поперечной нагрузки.
Из формулы A70) видно, что принцип независимости действия
сил здесь неприменим и что напряжения при увеличении внешних
сил возрастают в этом случае значительно быстрее, чем сами внеш-
внешние силы.
Это требует перехода от проверки прочности по допускаемым
¦ напряжениям к расчету по допускаемым нагрузкам
Считаем, что рассматриваемая балочная система, испытывающая
продольно-поперечный изгиб, работает с заданным коэффициентом
запаса п, если при возрастании всех внешних сил в п раз она дости-
достигает опасного состояния, которое для пластических материалов
отождествляется с достижением наибольшим (по абсолютному зна-
значению) нормальным напряжением величины предела текучести
шах Н =
Приравнивая п допускаемому коэффициенту запаса прочности
\п\, получим расчетную формулу на прочность
271
max |o| =
\n\P_
¦ F
\v
\n\P\n\fa
A71, a)
Принимаем коэффициент запаса прочности 1п\ при расчете по
методу допускаемых нагрузок соответствующим тому, который
установлен для допускаемого напряжения по отношению к пределу
текучести, т. е.
[П] = 1Ц,
где
Тогда из формулы A71, а) получим следующую видоизмененную
расчетную формулу;
_Р_ , Мл , \п] Pfn
F w + v(i-.*L
A71, 6)
С несколько большей погрешностью формулы A68—171) можно
применять и для несимметричной поперечной нагрузки, если ее
асимметрия не очень близка к случаю косой симметрии.
Аналогичным образом ведется расчет на продольно-поперечный
изгиб для иных видов опорных креплений стержней, однако урав-
уравнение A68) должно быть в каждом частном случае видоизменено.
Так, например, для балки, защемленной одним концом (рис. 151, б),
упругую линию приближенно описывают функцией
Тем не менее расчетные формулы A69—171) остаются в силе,
если не считать того, что значение Эйлеровой силы Рэ меняется в
зависимости от вида опорных креплений стержня согласно форму-
формуле A63).
Если поперечная нагрузка действует в плоскости наибольшей
жесткости стержня, то его надо еще проверять и на устойчивость
в плоскости наименьшей жесткости.
Пример 83. Дано: Р=800 кГ; Р,= 100 кГ; 1=2 м; 6=2 см;
й=4 см; ?=2 -10" кГ/см2; ст =2400 кГ/см2 (рис. 152).
О /
Определить
Р
Л
щ
Пу
-——^»
р.
Рис.
1
Z
152
272
Решение. Так как
' - П - 12
то прогиб посредине балки от силы
_ ^2 з
"" 3 СМ •
'п - 18ЁГ ~ 48-2-№-32 ~ 2" ~ U'/tS1
Эйлерова сила
10-2-10в-32 16 1П,
Рэ=~р- = 4-104.3
Отношение
Р _ 800-3 _ 3 . Р_ _ . 3__ _17_
Т^ ~ 16-Ю3 ~ 20 И Ра ~ 20 "" 20 ¦
По формуле A68) искомый прогиб / = Ц- ^-=0,
Таким образом, /„от/ составляет gg--100%=85%.
Так как
М ^ 100200 5-Ю3 кГ.см.
п 4 4
4юах = 5-103 + 800-0,919 = 5735 кГ-см,
F = bh = 8 см2,
т, Ь№ 2-16 16 ч
w * — f. — ^ i^^rt )
то по формуле A70)
800 , 5735
»ты =^ + tjp • 3 = 1175 кГ1см\
Без учета изгиба от продольной силы
а'тах = -— + ^? = 100 + -^- • 3 = 1038
что от о„а„ составляет • 100% = 88%.
max п75
Коэффициент запаса прочности п (по отношению к пределу теку-
текучести), с которым работает балка, определяется из формулы A71)
W W I. пР^
273
или
n • 800 , n ¦ 15 ¦ IP3 • 3 . _n_- 800 • 3- n ¦ 0.781 _ „.„„
16
»(-тгт5?)
отсюда
n3 — 35,9n + 6t,6
A — 0.15л)
Решение этого уравнения дает два значения п:
«1=1,85 и п2=34,05.
Значение п2=34,05 не может быть решением задачи, так как
уже прн и=6,67 (Рои =п Р=5320 кГ) max |c| =оо, так как бином
1—тг-=A—0,15) обращается в нуль
Проверяем балку на устойчивость в плоскости наименьшей
жесткости. Поскольку
е = -51 = л. = ±
" 16 12 3
см' и к = — =
то по формуле A64)
10 ¦ 2 • 10«
3 • 4 • 10»
= 167 кГ/см\
800
только от силы Р напряжение сжатия о= ¦= ЮОкГ/сл9 Коэф-
Коэффициент запаса устойчивости балок
Задачи 749—751. Определить наибольший прогиб / и наиболь-
наибольшее сжимающее напряжение max |асж| для балок
274
Задачи 752—753. Определить /, max ]осж|, коэффициенты запаса
прочности п и запаса устойчивости пу, с которыми работают балки
f>i~?OO«r
№3.5
Задачи 754 — 755. Подобрать поперечные размеры сечения
балок.
XI. ПЛОСКИЕ КРИВЫЕ ЕРУСЬЯ
§ 1. Продольное усилие, поперечная сила
и изгибающий момент
Кривым брусом называется стержень, геометрическая ось ко-
которого криволинейна.
Рассматриваться будут кривые брусья, у которых: 1) геометри-
геометрическая ось — плоская кривая; 2) плоскость кривизны — плоскость
симметрии; 3) действующие силы лежат в плоскости кривизны;
4) материал подчиняется закону Гука; 5) жесткость достаточно
большая, чтобы применять принцип независимости действия сил
Внутренние усилия в поперечном сеченин кривого бруса опре-
определяются методом сечений. Они приводятся к продольному усилию
N, к поперечной силе Q и к изгибающему моменту М.
Принято считать положительными: растягивающее усилие N,
поперечную силу Q, направление которой совпадает с направле-
направлением растягивающего усилия N, повернутого на 90е по часовой
стрелке, изгибающий момент М, увеличивающий кривизну бруса
(рис. 153).
На эпюрах положительные значения N, Q и М условимся от-
откладывать перпендикулярно геометрической оси бруса в сторону
от центра его кривизны, а отрицательные значения — к центру
его кривизны Для брусьев, состоящих из криволинейных и пря-
прямолинейных участков, положительные н отрицательные эпюры на
275
прямолинейных участках лучше располагать в те же стороны от
геометрической оси, что и на криволинейных участках.
Вне зависимости от формы кривого бруса величины N, Q и М
в поперечном сечении, определяющемся координатами х, у и углом
P=arctg \J~\, устанавливаются одним и тем же методом.
Рис. 153
Рис. 164
Рассмотрим случаи, когда по одну сторону от сечения прило-
приложены различные нагрузки.
1. Сосредоточенная пара сил (рис. 154):
М=0; Q=0; M=M0.
2. Сосредоточенная сила (рис. 155, а).
Составляющие силы Р по осям х и у (рис. 155, б) равны:
Рх — Р cos а; Ру = Р sin а.
От составляющей Рх (рис. 155, в):
N' = Р cos a cos P; Q' = Р cos a sin Р; М = — Р у cos а.
От составляющей Ру (рис. 155, г):
N" = Р sin a sin P; Q" = — PsinacosP; M"=Pxs\na.
Результирующие усилия от силы Р:
N = Р (cos а cos р + sin asin P) = Рcos (а — Р);
Q = P (cos a sin р — sin a cos Р) = — Р sin (а — Р);
М = Р (a: sin а — #cosa).
3. Равномерно распределенная по прямой АВ и нормальная
к ней нагрузка (рис. 156, а).
Составляющие нагрузки q по осям х и у (аналогично предыду-
предыдущему случаю):
qx=q cos a; 9jr=9s'na-
От составляющей ^ (Рис- 156, б):
N'=qx cosa cos?; Q'= ?x cosa sin P; M' = — q xy cos a.
276
От составляющей qy (рнс. 156, е):
si
N" = qx sin a sin P; Q" = — qx sin a cos P; M" = q — sin o.
Рис. 155
Результирующие усилия от нагрузки q:
N = qx (cos a cos p + sin а sin P) = qx cos (а — p);
Q = qx (cos a sin p — sin a cos P) = — qx sin (и — P);
M = qx |— sin a — у cos a\ .
4. Равномерно распределенная по геометрической оси бруса
поперечная нагрузка (рис. 157, а).
От действия проекции отсеченной нагрузки на ось и
(рнс. 157, б, е):
—
N' = qxsin$; Q' = —
От действия проекции отсеченной нагрузки на ось х (рис. 157, а):
277
От совместного действия дх и q/.
; Q= — 9 (л: cos p + у sin p); М=-У-
5. Равномерно распределенная по геометрической оси бруса
параллельная нагрузка (рис 158, а)
278
Элементарная сила в сечении с координатами xtylt действующая
на элемент ds дуги геометрической оси бруса (рис. 158, б)
dP=qd&
Проекции силы dP на оси х и у:
dPx=dP sina =<7^s sin a; dPy=dP cos a=qds cos a.
Элементарные усилия от силы dPx в сечении с координатами
х, у и углом р (рис. 158, б):
dJV' =—dP xcos$=—qsmacosBds;dQ'=—dP x sinj3=—<7sinasinfids.
dM'=dPx(y — yi)=q(jy — yi) sina ds.
Элементарные усилия от силы dPy в том же сечении (рис. 158, в):
dN"=dPy<m$ = q cosa sin3 ds;
dQ"=—dPy cosp =—<7 cosa cosp ds;
dM"=dPy{x — Xi)=q(x — xj cosa ds.
Элементарные усилия от совместного действия сил dPx и dPy
в рассматриваемом сечении:
dN=—q(sina cos 3 — cos ж sin p)ds=—q sin (a — p)ds;
dQ=—^(sina sinp + cos a cos p)ds=—q cos (a — $)ds;
dM = q[(y — j/j) sina +(x — xt) cosa] ds.
¦ Полные усилия в рассматриваемом сечении, отсекающем дугу
s геометрической оси бруса:
S
N = — q sin (a — Р) j ds = — qs sin (a — P);
s
Q = — <7 cos (a — p) j ds = — 9s cos (a — P);
0
Л4 = 9 sina f # § ds— j j/jds 1 +cosa I x § ds —
s \
— J xxds 1=9 [sin a (j/s — Sx) -j- cos a (xs — Sy)] =
= <7« [(i' — f/c^ Sin a -f (д: — xc) COS a],
где
s s
Sx = J fids и Sy = j x,ds — статические моменты дуги s от-
0 С
носительно осей х и у;
S S
Ус = —- и хс = -^ координаты центра тяжести дуги s
6. Равномерно распределенная по геометрической оси бруса и
касательная к ней нагрузка (рис. 159. а).
279
Элементарная сила в поперечном сечении с координатами i/i
и углом р4 (рис. 159, б), действующая касательно к геометрической
оси бруса на элемент дуги ds:
dP=qds.
Элементарные усилия от действия силы dP в поперечном сече-
сечении с координатами х, у и углом р (рис. 159, б):
dN = — dP cos (pi — P) = — q cos (& — P) ds;
rfQ = dP sin (& — p) = ? sin (Pi - p) ds;
dM = —dP [(x — xt) sin px — (# — t/k) cos pj =
== Я К!/ — ^i) cos Рл — (j: — *,,) sin pj ds.
Полные усилия в рассматриваемом сечении, отсекающем дугу
s геометрической оси бруса:
S S
N = -q J costpt-PJds; Q = q J sin(p1-p)ds;
Lo
Пример 84. Дано: Р, р (рис. 160, a).
Построить эпюры N, Q и М.
Решение. Определяем Л', Q и М на участках бруса
(рис. 160, б).
Для первого участка: 0 <^ q>t <J -g- ,
N . « 0.707P; JV . = 0; Qfi=0 = 0;
Q ,«0,707Р; Q . = P;
M =0;M
Для второго участка:
= - 2Р sin ф2; Q^ = 2Р cos Ф2; М^ = Р р A + 2sin ф2);
0; ^ , « _ 1.414Р; ^ , 2Р; Q = 2Р;
Q . «1.414Р; Q ,=0;
М =Рр; М .«2.414РР; М 7[=ЗР.р.
280
Эпюры N, Q и М показаны на рис. 160 в, г, д.
Пример 85. Дано: Р, а, уравнения геометрических осей верх-
верхней и нижней ветвей пружины — параболы у = ±х[1—?-)
(рис. 161, а).
Построить эпюры Л', Q, М.
Решение. В силу симметрии системы относительно двух
взаимно перпендикулярных осей рассматриваем только половину
о)
Рис. 160
Рис. 161
281
одной ветвя пружины (рис. 161, б). Для произвольного поперечного
сечения на расстоянии х от левого конца:
Поэтому
2 / 2а-1 - 2ах +
Nx=k = _Lf_ p » 0.354P. N a = -J^~ P « 0.224P; Wt =o = 0;
= — J^-P = — 0.354P; Q o = ^-P~— 0.447P;
Q^=u = — 0,5P;
УИ,_П == 0; M „ = 0.25Pa; Mr=o = 0,5Pa.
Эпюры Л/, Q, AJ изображены на рис. 161, в, г, д.
Пример 86. Дано: q, а, Ь, кольцо изогнуто по дуге эллипса
(/= -]/2ах — х2 и имеет разрез в начале координат (рис 162, а)
Определить N, Q, М
Решение. Так как брус симметричен относительно оси х,
рассматриваем только его верхнюю половину
282
Пользуясь принципом наложения, от действия проекций на-
нагрузки qx и <7У (рис. 162, б) усялия в поперечном сечении с коорди-
натамя х, у и углом [3 (рис. 162, в, г)
N
Так как
то
sin В = -
qax
(й""
5)
m
Z. X
п
МИМ
¦*
Т х
6)
г I г
qx
qx
T
¦*—x-
ЧУ
г)
Если, например, а=6, то N=qx;
Q=qY2ax — x2; M=—qax. Эпю-
Эпюры W, Q, M показаны на рис. 163,
а, б, в.
Пример 87. Дано: q, p, верти-
вертикальная нагрузка интенсивностью
q равномерно распределена по дуге четверти окружности радиусом
р (рис. 164, а).
Построить эпюры N, Q и М.
283
Рис. 162
Зщра N
с\ Зпюро м
-IJ
Я1
2"г-7
о)
.NJ
Рис. 163
Рис. 164
Рис. 165
Решение. Усилия в поперечном сеченин под углом ф к
вертикали от элементарной силы dP=qds=qpda имеют значения
(рис. 164, б).
dN=—dP sin ф=<тр sin <pd(p;
dQ=dP cos ф=?р cos i
dM=dPp (яшф— sin a)=<7p2 (вшф— sinot) da.
Усилия от нагрузки, действующей на отсеченную часть бруса
9
Г da = — 9р ф sin ф;
Q = q p cos ф I d a =
i
T
И= op2 ( (sin ф — sin a) da = qp*(<f> вшф + ссвф— 1);
if
Л/9=0 =0; N __. « — ?p -^-0,707 = -0,5559P;
Q(pi=0 = 0; Q ^~0,5559p;Q ж=0;
= 0; M » ? p2 f — 0,707 + 0,707 — 1) » 0,262ц р2;
Эпюры Л', Q и /И изображены иа рис. 164, е, г, б.
Пример 88. Дано: q, p, нагрузка интенсивностью q равномер-
равномерно распределена по ауге полуокружности радиусом р и направле-
направлена по касательной к геометрической оси бруса (рис. 165, а).
Построить эпюры N, Q, М.
Решение. Элементарная сила в сечении под углом а к го-
горизонтали
dP=q ds=<
285
Элементарные усилия в поперечном сечении бруса под углом <f
к горизонтали от силы dP имеют значения (рис 165, б):
dN = —dPcos(<f —а) = —<?pcos(q> — a)da;
dQ = dPsm(<f —a) = q p sin (<p — a) d a;
dM = — dP[p — pcos(q) — o)J = —<?p2[l —cos (ф — о)] da.
Полные усилия от нагрузки, действующей на отсеченную часть
бруса
N =
= —<?р f
cos(<p — a)da = —
I*
Q — qp\ в1п(ф — a)da — qp(l—совф);
о
Г f t 1
M = —op2 f do— ГсовСф — a)da =ор2(в1Пф — ф);
L о J
= 0. N ж =—0,707qp; N n = — ?p; Л? 3
W = =0;
M=n=0, /И =— 0,078<?p2;
— 0,571<?p2;
; M = — 3,
/И
Эпюры N, Q к М показаны на рис 165, e, г, д.
Задачи 756—765. Построить эпюры продольного усилия N,
поперечной силы Q и изгибающего момента М.
286
758
Нагрузка распределено равномерно
по горизонтальной проекции
Нагрузка распределена
радномерно по касатепь ,
тй к дуге АРа
спираль
§ 2. Напряжения
Продольное усилие Л' и изгибающий момент М определяют нор-
нормальные напряжения ад/ и ам, а поперечная сила Q — касательные
напряжения х, развивающиеся в точках поперечного сечения
кривого бруса.
287
Напряжения од принимают распределенными равномерно по
площади поперечного сечения F, а напряжения ом по гиперболи-
гиперболическому закону; их подсчитывают по формулам:
м
г + У
A73)
где 5 — статический момент площади F относительно нейтральной
оси г, которая не проходит через центр тяжести сечения 00; г —
радиус кривизны нейтральной линии пп; у — координата рассмат-
рассматриваемой точки сечения от оси г (рис. 166).
Рис 166
Нейтральная линия пп смещена по отношению к геометрической
оси бруса к центру его кривизны на величину е~р — г. где р —
радиус кривизны геометрической оси бруса.
Радиус кривизны нейтральной линии бруса для каждой формы
его поперечного сечения устанавливают из выражения
г — -
dF
A74)
где и — координата рассматриваемой точки сечения от центральной
оси гс (рис. 166)
Для прямоугольного сечения
in —
288
для круглого
г = —
а для трапецеидального
г =
I-2-—(Ьв—Ьн)
где /¦„, /•„, Ьн и 6В — соответственно радиус кривизны и ширина на-
наружного и внутреннего волокон сечения.
Для некоторых других форм поперечных сечений значения г
приводятся в соответствующих справочниках и курсах сопротив-
сопротивления материалов.
Для брусьев не очень большой кривизны величина е может быть
найдена и по приближенной формуле
е = -^-, A75>
р
где i=y-p—радиус инерции поперечного сечения бруса отно-
относительно центральной оси г0
Лучшее приближение к точному решению формула A75) дает для
брусьев, поперечные сечения которых симметричны относительно
оси г0
Так как
г I
где и — расстояние рассматриваемой точки сечения от центральной
оси z0, то формула A73) переписывается следующим образом-
:У±.- Ш-^ИИИа. A76)
Здесь
a—^-g- A77)
р
10 Заказ № 886 289
является отвлеченной функцией координаты и, характеризует нели-
нелинейный закон распределения оЛ1по сечению и зависит от формы
последнего и начальной кривизны бруса Если •—-<-jq-, to а мало
отличаются от единицы и ом можно подсчитывать по формуле,
установленной для прямолинейной балки а =—у-.
Наибольшие и наименьшие нормальные напряжения получают-
получаются в крайних волокнах бруса при u=ha и и——Лв. Они равны
, М в
± — а
\Х>1 в
П78)
где W — экваториальный момент сопротивления сечения для на-
наружного волокна WH=-^- и для внутреннего волокна We=j-,
о)
1±
A79)
Значения коэффициентов а* для некото-
некоторых форм сечения приведены в таблицах
приложений 4.
Результирующее нормальное напряжение
о в произвольной точке поперечного сече-
сечения кривого бруса можно определить по
формуле
Ми
а
A80)
Рис. 167
в которую усилие N подставляется со своим
знаком. В большинстве случаев ад невели-
невелико по сравнению с ам
Касательные напряжения т, определяю-
определяющие поперечную силу Q, имеют второстепенное
значение и в расчеты обычно не включаются
Приближенно их можно подсчитать, как и
для прямолинейных балок, по формуле (99)
Пример 89. Дано: Р=\ Т; р=50 см; М=
~Рр; а=Ю см (рис. 167, а).
290
Определить maxoH, minoB, тшах, е.
Решение. В соответствии с эпюрами N, Q и М (рис. 167,
б, в, г) наибольшие нормальные напряжения будут в заде-
заделанном сечении бруса, где N — — Р = — 1 Т и М = 2Рр =
=2-1-50= 100 Т-см, а наибольшие касательные напряжения
будут в сечении свободного конца бруса, где Q=P~1 Т.
Для квадратного сечения
1±
6p
0,939
1,074"
Поэтому
¦¦ 553 кГ/см2;
10». 6
Ю3
= — 654 кПсм*;
1,074 — -{^- « — 644 — 10 =
_ 3 _Q 3 JO^
*W— 2 ' F — 2 " Ю»
15 кГ/см";
0,167 сж=1,67 мм.
Задачи 766—769. Определить наибольшие растягивающие отах>
наибольшие сжимающие omin и нормальные напряжения оа в
указанной точке А опасного сечения
IBS
10»
291
§ 3. Расчет на прочность
Для определения величины безопасной нагрузки, действующей
на кривой брус, и для проверки его прочности пользуются условием:
max о. ==
м _w_
W ав+ р
<["]¦
A81)
Необходимые размеры поперечного сечения бруса подбираются
пробами с последующей проверкой, Первую пробу можно брать
из расчета бруса как прямолинейной балки в соответствии с нера-
неравенством
^^-<[с\. A82)
Прочность сечения следует проверять с учетом кривизны бруса
и продольного усилия по формуле A81). Перенапряжение не дол-
должно быть более 5%.
Если материал бруса различно сопротивляется растяжению и
сжатию, то в опасном сечении условия прочности должны удовлет-
удовлетворяться и для внутреннего, и для наружного волокна в соответ-
соответствии с величинами допускаемых напряжений [ор] и 1ос].
Пример 90. Дано: 1о]==4000 кГ/см\ а=20 см; &=\ см; урав-
уравоси стержня пружины
у=—a sin —х
нение геометрическом
(рис. 168).
Определить Р.
Решение. Опасными сечениями стержня являются сечения
в вершинах синусоиды, где М=Ра=20Р кГ ¦ см, N=—Р кГ и
радиус кривизны геометрической оси
1 + я2 cos2 — :
я2
0,1а—2 см.
292
Для круглого сечения диаметра d
И7 = WB = W = O.ld3 = 0,1 см1; F=-?f- = ~~ 0,785 см2;
i-4r .- '
8-2
= 1,25.
1 —
2р
2- 2
\
2a
Рис. 168
По условию прочности A81):
, . Л! N 20Р
TTTtTT
-р—I
Рис. 169
Допускаемая сила
4000
.25 +
= 250Р<4000.
Пример 91. Дано: Р=6 кн, q = 12 кн/м, р=16-К)-2л, 6= |-А,
to]=200 Мн/л*2 (рис. 169).
Определить hub.
Решение. В опасном (заделанном) сечении бруса:
М = Рр + -§-<7Р2=6- Ю3-16-10-2+ -|- • 12.10». 162-10-4= 1421 н-м;
N = —р_(?р=_6. 103 — 12 - 103. 16. 10-г = 7920 н.
Пробные размеры сечения бруса определяем из расчета на изгиб
как для прямолинейной балки
откуда
> V. 1-8 =3,84 еж.
293
Учитывая кривизну бруса и наличие продольного усилия в
опасном сечении, берем Л=4 см и 6=3 см. При этих размерах:
Н7 =
J
= 8 см3, F = 3 • 4 = 12 см\
h A
6р
6-16
-«1,095.
1 —
2р
J
2- 16
Согласно формуле A81), расчетное напряжение во внутреннем
волокне бруса
М_ , N
W
max | оЕ | =
1421 1,095 + - 792°
12 ¦ 10-«
8-10"»
«201,1 -10е н!мг = 201,1
Так как перенапряжение составляет 0,55%, то можно считать
подбор сечения выполненным удовлетворительно.
Задачи 770—771. Определить величины допускаемых нагрузок
Р, М.
2) nig
х)
а =50см, Ь = 20аи
1б]р=500«Г/см1,
Задачи 772—773. Проверить прочность кривых брусье!
Считать допускаемое нормальное напряжение [а ]=1600 кГ/см'
294
XII. ЭНЕРГЕТИЧЕСКИЙ МЕТОД
РАСЧЕТА УПРУГИХ СИСТЕМ
§ 1. Определение упругих обобщенных перемещений
Метод фиктивной нулевой обобщенной силы
Выражение, определяющее количество потенциальной энергии
упругой деформации О, накопленной телом или системой при ста-
статическом действии сил, можно представить в виде однородной функ-
функции второго порядка, либо от обобщенных сил Рг, либо от обоб-
обобщенных перемещений 8,, если между последними существует ли-
линейная зависимость.
Обобщенные силы Р, представляют собой любые силовые воз-
воздействия (силы, моменты, группы сил, группы моментов и т. д),
которые удобно выделить для подсчета энергии.
Обобщенные перемещения 8г представляют собой величины, оп-
определяющие перемещения, на которых обобщенные силы совершают
работу (например, сосредоточенной силе соответствует линейное
перемещение, моменту — угловое перемещение и т. д.).
Упругое обобщенное перемещение ?, происходящее в теле илн
в системе под влиянием обобщенных сил, можно определить по
формуле Кастилиано:
где Рф— фиктивная обобщенная сила, соответствующая искомому
обобщенному перемещению Эта сила приложена к телу или сис-
системе в том месте, в котором определяется перемещение; ?/ф — по-
потенциальная энергия упругой деформации тела или системы, выра-
выраженная однородной функцией второго порядка от всех действующих
обобщенных сил Р, и от фиктивной обобщенной силы Рф,
Если в том месте, где определяется обобщенное перемещение,
имеется заданная обобщенная сила Р, соответствующая искомому
перемещению, то отпадает необходимость в приложении Рф и тогда
Если (-др-)р =0 > 0 (или -gp- > OJ, то направление обобщен-
обобщенного перемещения 6 совпадает с направлением действия Рф (или Р).
Если же ( д„ Iр _о<о(или ~gp- < 0), то направление обоб-
обобщенного перемещения 8 противоположно направлению действия
Рф (или Р).
Линейное перемещение, найденное по формуле Кастилиано,
представляет собой проекцию перемещения точки приложения
соответствующей силы на направление линии ее действия.
295
Метод фиктивной единичной обобщенной силы
В самом общем случае действия сил на упругую стержневую
систему, состоящую из прямолинейных элементов, обобщенные
перемещения удобно определять по формуле Максвелла-Мора:
A85)
где N, Mz, My, MK, Qy и Q2 — соответствующие усилия в произ-
произвольном поперечном сечении каждого участка системы от всех
действующих на систему обобщенных сил;
N, Мг, Му, Мк, Qy и Qz— такие же усилия, но от действия
на систему только фиктивной обобщенной силы, соответствующей
искомому обобщенному перемещению и равной безразмерной
единице;
Е и G — модули продольной и касательной упругости материала
участка элемента;
F — площадь поперечного сечеиия, где определяются усилия;
/г и /у—главные центральные моменты инерции площади F;
/к— момент инерции при кручении площади F; ky и kz— коэф-
коэффициенты формы сечения, характеризующие неравномерность каса-
касательных напряжений при изгибе, их — элемент геометрической
оси участка
Интегрирование производится по длине каждого участка,
суммирование — по всем участкам
Для плоских шарнирно-стержиевых систем с силами, прило-
приложенными в узлах.
"==Zj"gjr'> A"«)
где I — длины участков.
Для систем, участки которых испытывают только кручение,
8 = ?j^7^rf*- A87>
Для плоских балочно-рамных систем, у которых влияние на
деформацию усилий N и Q мало,
MM dx A88)
El
Для систем с элементами малой кривизны
*fdS, A89)
296
где ds — элемент геометрической оси криволинейного участка.
При уточненном расчете
pds+?J4rds- 090)
Пример 92. Даио: Р, а, I, Е, I (рис. 170, а).
Определить стрелу прогиба /.
Решение. Максималь- .р р
ный прогиб/ посередине бал- ц^_ < I ,[, I l_ _J
ки будем определять по фор- a) i z г~хг1 \ С i^2 t
муле A88), которую можно ЛГ ! Т ^ f т\
записать в следующем виде: f?j^J I J \
. t—~ а -*|*— Ь
f =-j^ У [ ММйх. I
Изгибающие моменты в В) УХ'*\ *\Хг
произвольных сечениях бал- Jj*^ '"'
ки имеют значения: Рис i70
от действия заданных сил Р
Ма = Pxt; М„ = Ра;
от действия фиктивной единичной силы Рф= 1 (рис. 170, б)
Величина искомого прогиба
2?/
[а 42—а
Установим влияние на прогиб поперечной силы. По формуле
A85) при прямом изгибе прогиб от поперечной силы
Так как на участках балки поперечные силы от заданной
фиктивной нагрузки соответственно равны:
где «а = -ir.
297
Принимая во внимание, что для изотропных материалов отно-
отношение-^- находится в пределах 2<^<3, отношение-у- будет
иметь следующие крайние значения:
kt'
¦^L = D8 — 72) -7-7—/5 ;
Если а -»• 0, то
если а = 4" • то
-^ = B4 -i- 36) А -^- = 1,5 G
Для второго случая (a=-j-), при котором поперечная сила ока-
оказывает на прогиб наибольшее влияние, рассмотрим балки прямо-
прямоугольного и круглого сечений.
Рис 171
Рис. 172
Так как для прямоугольника высотой h и круга диаметром d
соответственно Р = ^ или га= jg, A = -g и k =¦ ^, то для балок
прямоугольного сечения
А =B,4-3,6)"F
и круглого сечеиия
298
Отсюда видно, что /_может составить от / 5% и больше при
)d «F-5-7L
т. е. для не очень коротких балок.
Если же взять, например, двутавровую балку № 20а из прокат-
прокатной стали, то для нее g=2,5; ?=8,37 см; А=2,78 и
h - 04 2 78 2 5 8-37" 5840
Следовательно, /„ составит 5% от / уже при
Пример 93. Дано: Р, а, Ь, с, F, IK, E, G (рис. 171, а).
Определить 8 — вертикальное перемещение точки приложения
силы Р, учитывая все виды деформации стержня.
Решение Искомое перемещение о будем определять по
формуле A85)
Растяжение испытывает только участок Ь. Продольные усилия
от сил Р и Яф=1 (рис 171, б) равны N=P; N=l.
Изгиб испытывают все участки стержня Изгибающие моменты
и поперечные силы в произвольных поперечных сечениях участков
стержня от действия сил Р и Рф=1 соответственно равны:
Ma=Pxj_Ma=x; М„=Ра\ М„=а; Мс=Рх\ Ъс=х; QO=P; Qo=l;
Q6=0; Qb=0; QC=P; Qc=l.
Кручение испытывает только участок с Крутящие моменты от
действия сил Р и Рф=1 равны: Мк=Ра, Мк=а
Подставляя найденные усилия в формулу A85), получаем сле-
следующее значение искомого перемещения:
Пример 94. Дано: Р, р, ?, /, кривой брус малой кривизны
(рис. 172, а).
Определить 8с— вертикальное перемещение сечения С.
299
Решение. Чтобы не нарушать симметрии системы отно-
относительно вертикальной оси, проходящей через точку Е, приклады-
прикладываем Рф=1 в сечениях С и D (рис. 172, б) и рассматриваем только
одну половину системы.
В произвольных поперечных сечениях, определяющихся углами
ft и ?2, изгибающие моменты имеют значения:
от действия сил Р
М, = —/>рA—coscp,), М„ = — Ppj
от действия сил Рф=1
Л*, = —рA—cosq>,), М„ = —р.
По формуле A89) находим искомое перемещение:
Ж [f(l -со5ф)Мф+ рф2|=(Ая_2)^. « 1,927^ .
Пример 95. Дано q — интенсивность нагрузки, равномерно
распределенной по горизонтали, р, P=2qp, E, I, (рис 173, а).
Определить В — перемещение подвижной опоры.
Решение. Из условий статики для заданной системы:
Изгибающие моменты на участках системы от заданных сил:
Mi=Px = 2qpx; Л4„— —Яр A + sin q>) — Аур A —coscp) +
^ -^-(cos29 +6cosq) — 4sin9 — 11);
Из условий статики для вспомогательной системы (рис. 173, б)
Изгибающие моменты на участках вспомогательной системы:
Mt — х; Ми = —рA + sinq>)
— 2sin9 — 3); Ж,,, = х.
300
По формуле A89) искомое перемещение 8 получается равным!.
-4sinq> — ll)(cosq> —
+ 64 —
Г Р
j = —J 2<7р f х2 Лс +-^jp f (cos2<p
_ 2sin<p - 3) d<p + 4qPo j *• dx U -f? [-§- + -i- J-L я
0) У
Пример 96. Дано: Рл, Ру> s —
длина геометрической реи бруса, изо-
изогнутой по произвольной кривой, Е, I
(рис. 174, а).
Определить угол поворота G, го-
горизонтальное Вг и вертикальное 8у
%
Рис. 173
Рис. 174
перемещение сечения, в котором приложены силы Рх, Ру.
Решение. В произвольном поперечном сечении бруса с
координатами центра тяжести х, у и углом р наклона касательной
к оси х изгибающие моменты и продольные усилия имеют значения:
от действия заданных сил Рх и Ру (рис. 174, а)
М=Рху+Рух, N=—Px cos p+Pj, sin p;
301
от действия Мф=1 (рис. 174, б): М=\, N=0;
от действия Рфх—1 (рис. 174, в): М=у, N=—cos f);
от действия Р$у=\ (рис. 174, г): М=х, N=sm$.
По формуле A89) находим:
6 = ж (М yds+р> J **s)
ж (М yds+р> J **s) = ж
S j
где Sx= { yds и Sy = f xds — статические моменты дуги s относи-
о о
тельно осей х и у;
8
-EF(Р* 1
s s
где /л = f y2 ds и /лу = f xyds — линейный и центробежный мо-
моменты инерции дуги s относительно оси х и осей ху;
Ьу = Ж [Р* Iyxds + Ру 1
+ Py | sin2p ds j = -i (PA, + Vy) + ж (- 4 J sin 2^ ds +
J,
/
a
где /y = f x2ds — линейный момент инерции дуги s относительно
о
оси у.
Рассмотрим брус малой кривизны, геометрическая ось которого
изогнута по дуге параболы: у=—-^-; Рх=0; Ру=Р (рнс 175).
Так как
302
. х2 их = —
а
°= -? B 1/2 - 1);
SF
Рис. 175
Подставляя найденные величины в формулы, определяющие
0, о,, оу примера 96. получаем:
Е/
~и<о
8 =*"*>
EI
[в
ж** —0,161
^-«0,432
ЪТ'
Задачи 774—787. Определить обобщенные перемещения, ука-
указанные на рисунках.
Во всех задачах на определение обобщенных перемещений здесь
и в последующем считать известными жесткости сеченнй стержней.
Если нет дополнительных указаний, то полагать одинаковыми мо-
дулн упругости материала и геометрические характеристики сече-
30 3
ння всех элементов систем н всех участков стержней. В задачах
782, 783 установить прогиб с учетом поперечной силы.
774 Ш
779
-2а-
М
А
¦ntnut
?_
78;
\ :
г»- a >i« о
а —j-i« a
ft,-'
Ж
/it ННУИНЖ
'г*-8Ь
304
т
786
787
Зо
-fl^J-O-
B Л
Задачи 788—790. Определить изменение расстояний &лв между
сечениями А и В
788 Ш.
Задачи 791—793. Определить вертикальные перемещения 8
сечения А.
793
« А
//•»
Задачи 794—796. Определить линейные перемещения 8 сечения
А по направлению силы Р. приложенной в этом сечении
Л
c=ff
Задачи 797—805. Определить линейные вертикальные 8D, го-
горизонтальные 8Г и угловые 6 перемещения сечения С.
В задаче 801 определить угол поворота сечения слева от шарнира.
Задачи 806—811. Определить перемещения 8 подвижной опоры
и вертикальные перемещения 8В сечения С.
В задаче 811 определить только величину В.
306
А Нагрузка распределена равномерно
по Вертикальной проекции
Задачи 812—816. Определить вертикальные перемещении 8
сечения А.
Задачи 817—819. Определить изменения расстояний Ъдв между
течениями А и В.
вп
307
Задачи 820—821. Определить значение угла а, при котором
сечения С будут перемещаться только по вертикали.
Способ перемножения эпюр — правило
Верещагина
Если жесткость поперечного сечення стержня на участке по-
постоянна, то каждый интеграл формулы Максвелла—Мора A85)
можно подсчитывать через произведение площади о> эпюры усилии
от заданных сил (рис. 176) на координату с, эпюры такого же усн-
лня от единичной фиктивной обобщенной силы (обязательно прямо-
прямолинейной), приходящуюся против центра тяжести первой эпюры.
Практически это правило Верещагина применяется для опреде-
определения линейных и угловых перемещений в балочно-рамных систе-
системах от действия изгибающих моментов. Формула, определяющая
перемещение, записывается следующим образом:
-
A91)
где суммирование производится по всем участкам системы.
Участки следует различать не только по нагрузке, но и по знаку
эпюры М или М и по постоянству поперечного сечения. Для эпюр
М и М одинакового знака произведение <«1>0, для эпюр раз-
разного знака o>s<0.
Поэтому положение эпюр М и М относительно линий их нулевых
значений на участках может быть произвольным, но при одинаковом
знаке с одной стороны.
Если обе эпюры М и М прямолинейны, то безразлично, для
которой из них находить площадь ев или координату ?.
Эпюру М сложного очертания можно разбить на части, для
которых определяются площади <i>4, ш2, юз- (рис. 177) и центры
308
тяжести. Под центрами тяжести каждой части надо измерить орди-
ординаты 1\, ?2, S3 ¦•¦ Тогда
В тех случаях, когда на нескольких участках стержня эпюра М
изображается одной прямой линией (рис. 178), можно площадь ю
Рис. 176
Рис. 177
Рис. 178
всей эпюры М умножать на соответствующую координату 5 эпю-
эпюры М.
Если на протяжении участка стержня поперечное сечение пере-
переменно, то вычисляется площадь <о эпюры не истинного изгибаю-
изгибающего момента М, а приведенного
М„„=М
/о
Рис. 179
309
где /0— момент инерции постоянного сечения, к которому условно
приводится участок, а / — момент инерции переменного сечения
Пример 97. Дано: Р, а, Е, I (рис. 179, а).
Определить 8Л — горизонтальное перемещение сечения А.
Решение. На рис. 179, вне представлены эпюры изгибаю-
изгибающих моментов: заштрихованная — от заданных снл, незаштрихо-
ванная — от фиктивной силы Рф=1, приложенной в сеченни А
(рис. 179, б) и направленной по горизонтали вправо.
Так как
_ а* . t _ Ра . _ Раа > _ _ Ра2 е _
Ш1 —¦ 2 ' ч ~ ~~2~ > '"s — 8~~' 2 — а< Шз — 8—' 3 —
то, принимая во внимание правило знаков, по формуле A91)искомое
перемещение
Ь К? + «^ «^ Ы + ШУ
Пример 98. Дано: Р, а, Е, I (рис. 180, а)
Определить &д и /с.
Решение. На рис. 180, б представлена эпюра М от заданной
силы Р.
На рис. 180, в эпюра М от фиктивного момента Мф=1, прило-
приложенного в сеченни А и направленного по часовой стрелке, а на
рис. 180, г эпюра М от фиктивной силы Рф=1, приложенной в се-
сечении С и направленной по вертикали вниз
Так как
Pcfi ,
4 •
3
4 fl.
: 5 e'
1 — 6 ' I
РФ
h 4 .
a
~ 3 '
7
«3 — 12 .
-. «; =
2
3
a,
5
= 6
РФ
2
-a;
» ?
(B4
5
'2 Q
то (учитывая различие в моментах инерции сеченни на участках)
по формуле A91) искомые перемещения
1 Г г , 1 / г , t- , г Л 29 Ра"
Y0^ + (<^ + ю^ + «Л)J = 48"~?Г:
S4) J = -24 -?Г
Пример 99. Дано: /, ?, [о] — балка, равного сопротивления с
постоянной высотой Л (рис, 181, а).
310
Определить ВА , fA.
Решение. По условию построения балки равного сопротив-
сопротивления:
и? — '¦* — Мх
W* h \ч] •
В опасном сечении
S) \ЭгтроМ\ ыгк\ i6)« j "J
В) | j ЭПЮРОМ (При Mf I)
Рис. 180
Рис. 181
Если условно привести балку к постоянному опасному сечению,
то /0=/ и приведенный изгибающий момент
/
' X
Эпюра приведенного момента (рис. 181, б) представляет собой
прямоугольник высотой
На рис. 181, в, г изображены эпюры М от Мф—1 и Рф=1, при-
приложенных в сечении А и направленных против часовой стрелки
для Л1ф=1 и вертикально вниз для Рф=1.
Так как ш = Мтш I = —jj—-1; % = \ и {' = -я-, то искомые
311
перемещения
A El ~
El ~ El
Eh
El 1EI — Eh •
Задачи 822—826. Определить прогибы / и углы поворота в
сечения С.
ш т да? I «• /f
к-1,, a a f-^ -$Щ 1-гртЦ
¦^W /m» Tp I immi A 1 вир t/?=js »W»
82В
т
41
Задачи 827—830. Определить вертикальные 8В и горизонталь-
горизонтальные 8Г перемещения сечения, в котором приложена сила Р
827
628
W
623
630
У
-2а-
Задачи 831—833. Определить перемещения Ь подвижной шар-
шарнирной опоры
83/
632
тЬтт?
-2а-
633
р
2
-га
312
§ 2. Раскрытие статической неопределимости систем
Начало наименьшей работы
Раскрытие статической неопределимости упругих систем может
производиться по началу наименьшей работы. Согласно этому на-
началу лншнне неизвестные обобщенные силы имеют такие значения,
при которых обобщенные силы, действующие на систему, совер-
совершают наименьшую работу.
Решение задач выполняется по следующей общей схеме.
Статически неопределимая система раскрепляется до статичес-
статически определимой, но геометрически неизменяемой и называется
основной системой
Для эквивалентности заданной системы с основной последняя
нагружается всеми действующими Р-, и всеми лишними неизвест-
неизвестными Х-, обобщенными силами.
Далее определяется потенциальная энергия упругой деформа-
деформации основной системы как функция второго порядка от Р-, и X,.
Так как обобщенные перемещения, соответствующие лишним
неизвестным обобщенным силам, равны нулю, то составляются
¦уравнения вида:
|^=0(i = l,2,3...) A92)
Из этих уравнений определяются все лишние неизвестные обоб-
обобщенные силы X,.
Уравнения A92) и являются условиями минимума потенциаль-
потенциальной энергии упругой деформации системы как функции лишних
неизвестных обобщенных сил
Для стержневых систем уравнения начала наименьшей работы
могут быть выражены через формулу Максвелла—Мора
Если система состоит из прямолинейных элементов, испытываю-
испытывающих растяжение, сжатие, прямой изгиб и кручение, то каждое
уравнение A92) записывается следующим образом:
где N, M, Q и Мк— соответствующие усилия в произвольном
поперечном сечении каждого участка основной эквивалентной сис-
системы от всех заданных Р1 и всех лишних неизвестных Х; обобщен-
обобщенных сил;
N, М, Q н Мк— такие же усилия в основной системе, но от
действия только одной из лншннх неизвестных обобщенной силы
Х~1.
Таким образом, чтобы решить п раз статически неопределимую
задачу, систему следует рассмотреть в и+1 состоянии: основном
313
эквивалентном под действием всех Р, и X, ига вспомогательных
сил, каждая из которых находится под действием только одной
силы нз Xt—\.
Для плоских шарнирно-стержневых систем с силами, прило-
приложенными в узлах, уравнения A93) упрощаются до вида:
EF
A94)
а)
rJ Ч
rJ
/I*.
rJ
rJ
Рис 182
Рис 183
Для плоских балочно-рамных систем, в которых значение про-
продольных усилий N н поперечных сил Q мало, можно пользоваться
упрощенными уравнениями:
-Erdx=0. A95)
Для систем, элементы которых испытывают только кручение
t = 0. A96)
Для плоских статически неопределимых брусьев малой кривизны
мм d 0 A97)
EI
314
При уточнении расчета уравнения составляются с учетом про-
продольных усилий:
Раскрепление статически неопределимой системы должно про-
производиться так, чтобы основная система получалась наиболее прос-
простой и удобной для расчета.
Геометрически симметричные системы с прямоснмметричной
(рис. 182, а) и косо или обратно симметричной (рис. 183, а) нагруз-
нагрузкой целесообразно раскреплять путем их рассечения по плоскости
симметрии. Это приводит к снижению числа искомых лишних
неизвестных обобщенных снл и позволяет рассматривать только
одну отсеченную часть системы (рис. 182, б и рис. 183, б)
В сеченин, совпадающем с
плоскостью симметрии, при пря-
мосимметрнчной нагрузке обра-
обращаются в нуль кососимметрич-
ные усилия Q и Мк, а при
кососимметричной нагрузке —
прямосимметричные усилия ./V
и М (рис. 184).
Для прямолинейных элемен- рис
тов системы интегралы, входя-
входящие в уравнение A93), можно
раскрывать способом перемножения эпюр.
Если статическая неопределимость системы раскрыта, то обоб-
обобщенное перемещение какого-нибудь сечения можно определять
при рассмотрении или заданной, нлн любой возможной основной
эквивалентной системы. Целесообразно выбирать такую систему,
для которой проще всего определить усилия от фиктивной единич-
единичной обобщенной силы.
Пример 100. Дано: Р=8 Т, я=1 м, ^=30°, р2=60°, Е, =
=Е„ =Е„, = Е = 2-10е кГ/см2 (рис. 185, а).
Определить o;>/;>///i; ЪА .
Решение. Так как элементы заданной системы имеют оди-
одинаковую жесткость сечения и испытывают только растяжение уси-
усилиями, постоянными по длине, то для раскрытия статической неоп-
неопределимости используем упрощенное уравнение A94).
EAW/=0. (a)
За основную эквивалентную систему примем систему, изобра-
изображенную на рис. 185, б. Для нее из условий статики находим:
315
Из условий статики для вспомогательной системы (рис. 185, в)
получаем:
Принимая во внимание, что I, = ." = 2м, 1Ц — ° =
v sin р, ' sin p2
П 1 Q
для определения лишнего неизвестного усилия уравнение (а) пре-
преобразуем следующим образом:
2N,N, l, + 2N,,N,, hi + NuiN,,, hn = -2 -^=|=. -i- . 2 +
+ 2X -^ + X -^ = A [- 2P+ B+ 3 J/F) X] =0,
откуда
-0.278 Я
2Я
3P
Нормальные напряжения в поперечных сечениях элементов
системы:
X 0,278-8-103 N.
°и = °ш = Т~ ~ 2 =П12 кПсм2; о,= -у- »
0,417-8-10 1С/,О _, ,,
ж — = = 1668 кПсм1
Для определения вертикального перемещения 8^ узла А ис-
используем статически определимую систему.) представленную на
рис. 185, г.
ЪР
Так как в этой системеА'/ = —-—j=, а от фиктивной единичной
силы Рф=1, приложенной в узле А по вертикали вниз
N то искомое перемещение
2-10«-2-1,732
316
0,19 см.
ш
uL
4
П,
д)
Рис 186
Пример 101. Дано: q, I, Е, I (рис. 186, а).
Определить fA.
Решение. Так как жесткости поперечных сечений вертикаль-
вертикального и горизонтального участка полурамы одинаковы, то для рас-
раскрытия статической неопределимости системы используем упро-
упрощенное уравнение A95)
2>\ММ dx=0. (б)
Изгибающие моменты Mi и М_п на участках основной эквива-
эквивалентной системы (рис. 186, б) и Mi и М,, на участках вспомога-
вспомогательных систем (рис. 186, в, г) соответственно равны
Mi = Х^х ?|— , Мц = Х±
М, = х, Мц = 21,
М, = 0, Мц = х.
Составляем два уравнения (б):
a i
J ( Xvx — -%?-) xdx + 21 J (Xt2l + XiX — 2qi*—qx*)dx = 0,
о о
i
j (Xfil + X^c — 2ql* — qx*) xdx = 0.
После раскрытия интегралов эти уравнения принимают вид:
12Х,
о
откуда
v 35 , v 15 .
*. = -it ч'< Л2 = тг «Л
Для определения прогиба fA сечения А находим М для основ-
основной эквивалентной системы и М для вспомогательной системы
(рис. 186, д) в сечении, лежащем справа от сечения А на расстоя-
расстоянии х:
М = Х.21 + Xi(-±r + x\ — 2qP—q [~ + х\ =
44
318
По формуле A88) искомый прогиб / получается равным:
1/2
Пример 102. Дано: Р, р, Е, Iu=2Ii — брусья малой кривизны
(рис. 187, а)
а)
ЧРр
Определить горизонтальное Ъх и вертикальное %v перемещения
шарнира А и построить эпюры изгибающих моментов.
Решение. Так как брусья имеют малую кривизну и модули
продольной упругости их материалов одинаковы, для раскрытия
статической неопределимости системы используем упрощенную
формулу A97)
(в)
319
За лишнюю неизвестную X принимаем горизонтальную реакцию
на шарнирной опоре.
Пользуясь уравнениями статики и наличием висячего шарнира
А, выражаем реакции в креплениях основной эквивалентной сис-
системы (рис. 187, б) через заданную силу Р и лишнюю неизвест-
неизвестную X. На вспомогательной системе (рис. 187, е), загруженной
силой Х=\, возникает только горизонтальная реакция в заде-
заделанном сечении.
Изгибающие моменты на участках I и II основной эквивалентной
и вспомогательной систем получаются соответственно равными:
Mi = 4Рр —Р2р A—cos <р)—Х2р sin <р =2Рр A + cos <p) — 2Лр sin ф,
Мц = Лр sin tp, Mi = — 2р sin ф и Мц = р sin tp
Поскольку элементы геометрических осей брусьев имеют зна-
значения:
ds, = 2pdtp, dsn = pdtp, //; = 2/,,
то уравнение (в) принимает вид:
8 \ \X sin ф — Р A + cos (p)] sin tpd ф + -^ X \ sin2 (pdcp = 0.
о о
После раскрытая интегралов получаем:
-?-7tX-16P=0,
откуда
X = -fjr^- р ~ 1.198 Р.
Для определения горизонтального Ъх и вертикального 8}, пе-
перемещений шарнира А пользуемся вспомогательными системами,
изображенными соответственно на рис. 187, г и 187, д.
Поскольку на участке // этих систем усилия не возникают, то
рассматриваем только участок /. Для этого участка изгибающие
моменты:
от заданных сил:
/ 64 \
Mi = 2РрA +cosq>) — 2Xpsin(p =2Рр ^1+со8ф—"j7irs*'n4>yt
от горизонтально приложенной силы Рф=1:
320
н от вертикальной Яф=1:
М, = 4р — 2р A — cos <р) = 2р A + cos <p).
Следовательно, искомые перемещения:
Эпюры изгибающих моментов Mi и Ми представлены на
рис. 187, е.
Метод сил
Для раскрытия статической неопределимости упругих систем
методом сил составляют и решают канонические уравнения вида:
8 V i й V t й V
11Л1 + °12Л2 + °13Л3
й V I й V i й V
Ь21Л1 + Й22Л2 + Ь23Л3
г- 8зЛ
Ь1пХп
3„Х„
5.Р = 0,
Ч = о.
4, = о,
««Л +
= 0.
A99)
Каждое из этих уравнений выражает собой условие A92) —
равенство нулю обобщенного перемещения в статически неопреде-
неопределимой системе, соответствующего каждой лишней неизвестной
обобщенной силе Хь Xz> Xs, .., Хп
Свободные члены уравнений Ь1р и все коэффициенты 8Ш Ь1к
являются обобщенными перемещениями в основной системе в на-
направлении 1-той (указанной первым индексом) лишней неизвестной
обобщенной силы Х{. о(р— от действия всех заданных обобщенных
сил, Р, а Ьи и btk — от каждой единичной лишней неизвестной обоб-
обобщенной силы Х;=1 или Xk=l, указанной вторым индексом.
Все эти обобщенные перемещения можно определять любым из-
известным методом или брать их из таблиц, если это возможно.
11 Заказ Mi 886
321
Перемещения btp могут быть больше или меньше нуля и равными
нулю; онн зависят от заданных сил, геометрии системы и выбора
основной системы.
Перемещения Ьа и Ь№ не зависят от заданных сил, а полностью
определяются геометрией системы н выбором лишних неизвестных;
главные коэффициенты Ьи — величины существенно положительные
и отличные от нуля; побочные коэффициенты 8^= Ьы могут быть
больше нуля, меньше нуля и равны нулю.
При выборе основной системы следует стремиться к тому, чтобы
как можно больше побочных коэффициентов обратилось в нули.
Симметричные системы целесообразно раскреплять так, как это
указано на стр 315
Систему п раз статически неопределимую надо рассматривать
в п + 1 состоянии: основном от всех заданных обобщенных снл,
и п вспомогательных от каждой лишней неизвестной обобщенной
силы, равной единице.
Если статически неопределимая система подвергается только
изменению температуры, то свободными членами канонических
уравнений будут 8Й, представляющие собой обобщенные переме-
перемещения, соответствующие f-той лишней неизвестной обобщенной
силе в основной системе от изменения температуры. При одновре-
одновременном действии на систему нагрузки н изменения температуры
свободные члены в канонических уравнениях представляются
суммой 8,^+8;,.
Учет влияния неточности изготовления элементов системы при
ее монтаже производят введением в свободные члены канонических
уравнений величины biA, выражающей обобщенные перемещения,
соответствующие t-той лишней неизвестной обобщенной силе в
основной системе от неточности Д изготовления элементов.
Положительные нли отрицательные значения 8,., и 8М берут
н зависимости от того, совпадают нли противоположны направ-
направления этих перемещений с принятым направлением Xv
Для систем, один раз статически неопределимых, каноническое
уравнение метода сил принимает вид:
и, следовательно, лишняя неизвестная обобщенная сила получает
значение:
*.=-¦«?• B00>
Если рассчитываются один раз статически неопределимые плос-
плоские балочно-рамные системы или системы с криволинейными эле-
ментами малой кривизны, для которых роль продольного усилия и
поперечной силы мала, то
мм
, s V Г м*
ds, Ьи = 2jJ ?y-
B01)
где ds — элемент длины геометри-
геометрической оси участка.
Пример 103. Дано: Р, q, а (рис.
188, а).
Раскрыть статическую неопре-
неопределимость системы, учитывая де-
деформацию участков только от
изгибающего момента.
Решение Выбираем за
лишнюю неизвестную Xt реакцию
на подвижной опоре. Так как
MM=f=0 и Мгф0 только на участ-
участке длиной 2а н на этом участке
для основной (рис. 188, б) и вспомо-
вспомогательной (рис. 188, в) систем М=—Р(а+х)
формуле B01)
«)
Рис.
\ ММ их
МЧх
Р (о + х) +- -Г_ | хйх
хЧх
—
н /И=лг, то по
= -L ПР + Ъда).
Пример 104. Дано: д, а, Е, I (рис 189, а).
Построить эпюру изгибающего момента.
Решение. Для раскрытия статической неопределимости рас-
раскрепляем раму сечением посередине ригеля (рис. 189, б)
Основная система изображена на рнс 189, в, а вспомогательные
системы с эпюрами изгибающих моментов от Х1=1, Хг=\ и Xs=l
представлены на рис. 189, г, d, e
Так как эпюры М от ^(=1 и ^3=1 прямо симметричны, а эпю-
И* 323
pa M от Х2— 1 — обратно симметрична, то побочные коэффициенты
<512=82»=0, 82S=832=0 н канонические уравнения метода сил
приобретают вид:
Г"
р
ч
i__ _ !
а 5ЩЯ а ~$ш
f
Эпюра М
В
Коэффициенты 8И, 822, 8SS и 813=83, находим способом пере-
перемножения эпюр:
?/8и=2-3- a-^-
20
-а";
= 2- 1 -За
324
Свободные члены определяем через интегралы Мора:
За За
V
r qa*;
Подставляя найденные величины в канонические уравнения
и производя некоторые преобразования, получаем:
откуда
I 39a2 10
9 Чаг 64
20а 10
72а 64
192—90
1280—720
0.1821 да;
27
160
0,1688
560 а
180—216
560
qa? « — 0,0643
Пользуясь методом наложения, получаем эпюры изгибающего
момента М на всех участках рамы (рис. 189, ж):
н сеченни А М = 0,1688 qa ¦ а — 0,0643 qa2 • 1 =0,1045 qa2;
в сечении В М =—0,1688 qa-a — 0,0643 qa2-l=—0,2331 ga2;
в сечении С М = 0,1821 qa-За — 0,1688 <?a-a — 0,0643 qa? =
=0,3132 «г2;
в сеченни D М = 0,1821 qa-Ъа + 0,1688 ga-e — 0,06439a2 —
jl^-27 a3 = — 0,8492 ga2;
н сечении ? M= 0,1821 qa- 1,5a + 0,1688^a-a — 0,0643 <?aa—
ИГ f
Пример 105. Дано: а, 6, с, d, E, G |o], a, Д**>0 (рис. 190, a).
Состанить условие прочности системы на участке с.
Решение. Оснонная система с изменением ее геометрии
от повышения температуры на Д/ градусон представлена на
рис 190, б, а вспомогательная система — на рис. 190, в.
32Ь
Рис 190
Рис. 191
Э)
-ftiP
ада,
Так как
а
Ьи=,—аЬМ. a 8tI =-^- + ~/ f хЧх
Ь !/о' „, с3 \ azc
се ' гч о I u w 1 о I т^ /. г 1VJ
ab&t
W + -ЁГ (-у + °2fc+-3-) + -G7T
где г — —q~ , / g^- , a /p —
В опасном заделанном сечении участка в изгибающий момент
М=Х,с, крутящий момент Мк=Х,а
Условие прочности
где W=-^2~. 4= 1 по третьей или i\= j/0,75 по четвертой гипотезе
прочности
Пример 106. Дано: Р, р, ?/,//, ?//, Z7//, кривой брус малой
кривизны (рис. 191 ,а)
Определить 8 — перемещение подвижной опоры.
Решение. Раскрепляем систему путем разъединения эле-
элементов / и // в поднижном шарнире (рис. 191, б). Оснонная и вспо-
вспомогательная системы будут системами, представленными на
рнс. 191, в. »
Так как
I
то
327
Искомое перемещение S определится как абсолютное удлине-
удлинение стяжки //, т. е
Х,2р _ 2Рр 1
.+4
Е, I,
Если стяжка // отсутствует (т. е. ЕцРц=0), то
Если обе опоры неподвижны (т. е. EnFu=oo)t то
*.=
и 8 = 0.
Для первого случая (Ец Рц ==0) изгибающий момент в произ-
произвольном сечении
Эпюра М имеет вид, представленный на рис 191, д.
Для второго случая (Ец Fn = оо) изгибающий момент в произ-
произвольном сечении
Эпюра М имеет вид, представленный на рис 191, е.
§ 3. Расчет плоских тонкостенных колец
Под плоским тонкостенным кольцом понимается любая плоская
жесткозамкнутая упругая стержневая система, длины участков
которой значительно больше размеров
их поперечных сечений. Такая система
трижды статически неопределима. Ли-
шннми неизвестными являются нзгнба-
ющий момент Xt, продольное усилие
X? и поперечная сила Xs, т. е. внутрен-
ние усилия в поперечном сеченни, про-
веденном для раскрепления кольца (рис.
192) Поэтому жесткозамкнутые системы
относятся к системам внутренне стати-
чески неопределимым.
Статическую неопределимость колец
можно раскрыть, используя либо начало наименьшей работы,
либо (что удобнее) канонические уравнения метода сил В связи с
328
Рис. 192
тонкостенностью колец при составлении уравнений, раскрываю-
раскрывающих статическую неопределимость, достаточно учитывать только
деформацию от изгибающего момента.
Если кольцо по геометрии и нагрузке симметрично относи-
относительно одной осн (рис 193, а), то в поперечных сечеинях, совпадаю-
совпадающих с осью симметрии, поперечные силы равны нулю. Следователь-
Следовательно, лишними неизвестными в этих сеченнях будут изгибающий
момент (X, или Xt') и продольное усилие (Х2 или Х2')- Вместо
всего кольца можно рассматривать только одну его симметричную
половину (рис 193, а, б).
а)
Рис. 193
Рис 194
Если кольцо по геометрии и нагрузке симметрично отно-
относительно двух осей (рис 194, а), в сечениях, проходящих
через оси симметрии, поперечные силы равны нулю, а про-
продольные усилия можно определить из условия статики как
суммы проекций сил и усилий, приложенных к полукольцу, на
соответствующую ось симметрии. В этом случае лишним неизвест-
неизвестным будет только изгибающий момент (Х\ или Xt'). Вместо всего
кольца можно рассматривать одну его четверть, заключенную
между осями симметрии (рис. 194, б или е)
Если кольцо имеет более двух осей симметрии, то можно рас-
рассматривать только одну его часть, заключенную между сечениями,
совпадающими с соседними осями одинаковой симметрии.
329
В этих сечениях поперечные силы равны нулю, продольные уси-
усилия находятся из условия статики, а изгибающий момент будет
лишней неизвестной величиной
Пример 107. Дано: у, р, Е, 1;
кольцо тонкостенное и симметрич-
симметричное относительно осей х и у (рис.
195, а)
Определить 8 — сближение се-
середины прямолинейных участков
кольца.
Р е ш е .н и е. Рассматриваем
одну четверть кольца (рис. 195, 6).
В сечениях, совпадающих с осью
х, поперечная сила равна нулю,
продольное усилие равно qp, a
изгибающий момент Xt— лишняя
неизвестная обобщенная сила.
Изгибающие моменты в произ-
произвольных сеченнях участков / и /У
основной (рис. 195, в) и вспомога-
вспомогательной (рис. 195, г) систем
М, = — </ps A — cos ф),
2 •
M, = 1, Mn = 1.
В. Ч qp'
Так как
Рис. 195
hp = \Ml M,ds+ J M,,Mi, dx = — <yps J A — cos<p)d Ф —
i о - о
- я
* р те/2 р
Е/8„ = f/Й/rfs +- \M2,,dx =p ("Лр 1- ("<
0 0 0 0
+1).
330
то изгибающий момент Xi приобретает значение
После раскрытия статической неопределимости
М, = — <гр8 [l - 3^+|} - coscp 1 * - да8 @,26 — cos q>);
+ px — 0,5
поэтому
Mi =0 "= °-74 wS; w' * °-45 w2; Ж; ~ — °-26 w4;
M/;;c=f, « - 0,26 W2; MH » - 0,64да2; М//;с=/э = - 0,76 qf.
На рис 195, д представлена эпюра изгибающего момента.
Для определения величины сближения середин прямолинейных
участков кольца прикладываем в сечении, где действует qp, фиктив-
фиктивную силу Яф=1, направленную по вертикали вверх. От этой
силы н произвольных сечениях / и // участков четверти кольца
изгибающие моменты:
М, = — рA — cosq>)H М„ =
Следовательно, искомое перемещение
s
+ J М„Ми dx ) = ~- J @,26 — cos ф) х
J
х A —cos ф) йф + -|^- J@,26p2+px—
х (p+x)dx = 1,72-gT" •
Пример 108. Дано: Р, а (где 2а = ^), р, ?, /, F (рис 196, а).
Определить: Дрр, Др0— изменения радиусов кольца по линии
дейстния сил и посередине между силами
Решение. Рассматриваем часть стенки кольца, выделенную
Поперечными сечениями по серединам дуг между силами (рис. 196, б).
331
Поперечные силы в проведенных сечениях равны нулю, а про-
продольные усилия No определяются из суммы проекций сил и усилий
на вертикаль/V,,=g^ .
Изгибающие моменты и продольные усилия в произвольном се-
сечении основной (рис. 196, в) и вспомогательной (рис. 196, е) систем
соответственно равны:
Так как
1?_
2?/
1 Л
ina /'
то момент
2 \~Ш ~)-
Изгибающий момент в произвольном сечеиии кольпа
Рр
М
2 \ sin о sin a sin о "*" а ) 2
Для определения Дрр вместо силы Р прикладываем силу Рф
Тогда
- _ р / 1 cosy\ _ _ cosy
'" — 2 \ а ~ sin»/1 "
2sina
^~ 2EF sin2
332
- I cos8 <p d ср.
А х
р/г(хс-а)
Рис. 196
Рис. 197
Окончательно
РР
а \
Для определения Др„ прикладываем радиальную силу Рф—1
в сечении пол углом о к вертикали (рис. 196, д) Тогда
*У П cosy
2?/ Л sin а
— psincp, yv ¦¦
cosy 1 \ . Рр
Окончательно
i—l)l
Пример 109. Дано: Р, a, b, E, /; кольцо тонкостенное и симмет-
симметричное относительно осей у н х (рис. 197, а).
Определить Да, АЬ
Решение. Рассматриваем одну четверть кольца (рис. 197, б).
В сечениях, совпадающих с осью х, поперечная сила равна нулю,
р
а продольное усилие равно -у
Изгибающие моменты в произвольном поперечном сечеиии с
координатами центра тяжести х и у основной (рис. 197. в) и вспомо-
вспомогательной (рнс 197, г) систем соответственно равны:
8 8 S
Так как ?/81р = (MMds = ~ f (a— x)ds = -~-(а {ds —
С \ Р р I Sv\ Р
— J Jtrdsj = — (as—Sy)=-^-s\a f-J--g-s(a—*,,),
где s — длина дуги геометрической оси стенки четверти кольца,
s
Sv = J xds — статический момент дуги s относительно оси у и
ь
S
хс — -j абсцисса центра тяжести дуги s, а Е1Ьи = J M*ds =
о
s
= J ds = s, то изгибающий момент в сечении А
334
Изгибающий момент в произвольном сечении кольца
р [• р Е
"г
р
если а > *,., то Мк=а < 0; М*^ = 0; M*=o = -g- хс > 0.
На рнс. 197, д представлена эпюра изгибающего момента для
случая, когда а — хс<.хс
Чтобы определить изменение размера а, в сечении А четверти
кольца прикладываем горизонтальную силу Рф=1, направленную
к центру О
От этой силы М=у. Следовательно,
-^j- Uxc—x)yds = -i^j-l xc Г yds — f xyds ) =
0 (I 0
(х *У^ == 2?/ *
5
где S^ = j j/ds — статический момент дуги s относительно оси х;
s
1ху = J xyds — центробежный момент инерции дуги s относи-
о
тельно осей х, у;
/Вдо = 1ху — xlSx = Ixy—xcycs — центробежный момент инерции
дуги s относительно осей хоуа, проходнщих через центр тяжести
четверти кольца параллельно осям ху (рис. 197, б).
Для определения изменения размера Ъ в сечении А четверти
кольца прикладываем вертикальную силу Рф=1. направленную
вниз.
От этой силы М=а —х. Следовательно,
i
с-х) (а- х) ds = _JL_
S S 8
¦а Г xds — xc j xds + Г x'1 ds)
_ p
2Я/
335
s
где Iy = I a;2 us— линейный момент инерции дуги s относи-
о
тельно оси у;
1„о = 1у — xcSy = 1у —а:^ s — линейный момент инерции дуги s
относительно оси ув.
о)
е)
Рис. 198
Частные случаи. А Квадратная рама растягивается
г.о диагонали (рис. 198, а). Так как (рис. 198, 6) хс=ус=^, то
м = — D- —
^.; Мх
Ра
4 '
Эпюра изгибающего момента представлена на рис. 198, в. В
центральных осях хеу<>:
хо=—г/о, ds—dx0 }/2=Л/<,]/2,
336
поэтому
= -*1 f *J
—a/2
По формулам примера 109 укорочение горизонтальной и удли-
удлинение вертикальной полудиагоналей рамы по величине одинаковы
и равны
аа~ ~ШГ'~Т2~а ~~ 24 ' EI -
Б- Кольцо из двух дуг окружности радиуса р с центральным
углом 2а (рис. 199, а).
Так как (рис. 199, б)
ds — р d 9, s = р a, a = р A — cos о), 6 = р sin о, х = р (cos <p —cos о
и j/ = p sin а, то
Sy =
S а
Г xds = рг I (cos <р —cos а) d <р = рг (sinо — acosa);
о о
хс — — = — (sin а — о cos a);
s a
Sx = j j/ds = p2 1 sin <p d <p = pa A — cos a);
о о
& a
lxy = 1 *#ds = p3 I (cos <p — cos a) sin <p d <p =
о о
= ¦—- A — 2 cos a + cos2 a);
s a
/ = i x2ds = ps 1 (cos <p — cos aJ d<? =
о о
= -j- Ba + 4acos2 a —3 sin 2a).
По формулам примера 109
337
.. Р . . Р р / sin a
М= -т{хс — х)= —f- ^—- cos <
да p—lx S —I )- РрЭ / sing sin2a
Д6 = P A-х S)~ ~9—
v 2EI *y xc^y>- 2EI
Пример НО. Дано: а, Ь, Е, 1, q — внутреннее давление на стен-
стенку кольца, симметричного относительно осей х и у (рис 200. а).
Определить Да и ЛЬ.
Решение Рассматриваем одну четверть кольца (рис. 200, б).
В сечениях, совпадающих с осью х, поперечная сила равна нулю,
продольное усилие равно qa
Изгибающие моменты в произвольном поперечном сечении с
координатами центра тяжести х и у основной (рис 200, в) и вспо-
вспомогательной (рис 200, г) систем соответственно равны:
M=qa (а~х)~ -|" (а-х)* %- у%=
где р=]/л:2-|-#г — расстояние рассматриваемого сечения от начала
координат н 7W=1,
Так как
?/8Jp= Г мШэ^Л. f (с2 — р2) ds =
cJ ~ 2 cJ
= Л. (a j ds — J p2 ds W-f (as-/p),
где s — длина дуги геометрической оси четверти кольца;
s
/р= f p2rfs — полярный момент инерции дуги s относительно нача-
и
S S
ла координат, а величина ?/8и = f M2ds= f ds=s, то изгибающий
о о
момент в сечении А
338
0,25Sqal
0.75S qa'
Рис. 200
Рис 201
Изгибающий момент в произвольном сечении кольца:
Если р непрерывно возрастает от значения а до значения
Ь > а, то Л}р=а > 0; Mp=b < 0 и /И = 0.
На рис. 200, д представлена эпюра изгибающего момента для
случая Ьу-а.
Для определения изменения размера а в сечении А четверти
кольца прикладываем горизонтальную силу Рф=1, направленную
к центру О.
От этой силы М=у. Следовательно,
W-K-j yds- § f yds j =
f 'Р - J
Чет
где Sj. = I yds — статический момент дуги s относительно оси х;
о
о
ордината центра тяжести дуги s;
Для определения изменения размера 6 в сечении А четверти
кольца прикладываем вертикальную силу Яф=1, направленную
вниз
340
От этой силы М~а — х. Следовательно,
S ¦
—!f- J *Ь + J
о о
-a \p'ds—!f- J *Ь + J Р2
о о о
-а/р- ^
S S
где 1у = I р2 xds, Sy = I xds — статический момент дуги s
о о
с
относительно оси у; хс= — абсцисса центра тяжести дуги s.
Частный случай. Кольцо, составленное из двух полу-
полуокружностей радиуса а и двух прямых длиной 2а (рнс. 201, а).
Так как (рис. 201, б) s— —у— с; х, = с; у1— у; й^ = dj/,
х2 = a cos <р; #2 = а A 4- sin <p); ds2 =
pf = с2 + х/2; Pi = 2с2 A + sin ф),
то
а 2 fi я
= J ft rf«i + J 0s rfsa= J ydy + a2 J A +sin<p) dV =
о о
с2,
а 2 " a 2
SJI = J д;, ds, + J x2ds2=^a\ dy+a2
0 0 0
SJI J J
0 0
4a
2 "
у\ ds2
~< ¦ 6
341
а
+ sin<pJ d ф = ,„ as;
12
a 2 о 2
= f Jtf ds, + f x\ Ааг=*а* { dy + a* f
о У 8 8
2 a
I* = J Pi й dsi + J P? ^ dss= f («г + ^а) i/rf
T
4-2a" f A -f sin?J dy = 19 + 6tI o«;
о
Г"
lv = J Pf *i ^s, + J p| x8 dss = a J (os + i/2)
T
+ 2a* I (l+sinq>) cos<pd9=-^ a*.
Для прямолинейного участка:
0,759^
°>259 4°*-
342
Для криволинейного участка:
-. 0,259
Л12 =-
2 + Зя
0,741 <;а2.
Дс =
2?/
(Ус !Р — '
— 6 яа до'
24 B + 4)
«=—0,864 fp
Изменение размера 6
1 ?/
2?/
X
^ 0.160 g:.
sin ф);
3B +те) ч"
Эпюра изгибающего момента для чет-
четверти кольца показана на рнс. 201, в.
Изменение размера о
Л& явг- Uy — Xr !р)— 12B + 4) x г)
Пример 111. Даио: ^, р, Е, /; кольцо
тонкостенное, по нагрузке симметричное л
относительно оси у (рис. 202, о). '
Определить 8 — изменение длины
вертикального диаметра кольца.
Решение. Рассматриваем одну поло-
половину кольца (рис. 202, б). Б сечении, сов-
совпадающем с осью у, поперечная сила _ч
раина нулю, а изгибающий момент Xt и '
продольное усилие Х%— лишние неизвест-
неизвестные обобщенные силы.
Канонические уравнения метода сил
имеют вид:
-D,5qPz
C,gi2qp'
Рис. 202
343
Находим изгибающий момент в произвольном поперечном се-
чеиии,определяющемся углом <р, от заданной нагрузки q (рис. 202, в).
Так как элементарная сила, действующая на элемент дуги ds
геометрической оси стенки кольца, dp = q ds=q pda, то от нее
элементарный из! ибающий момент в сечении с углом <р
d/W=dpp (sin<p— sina)=qp2 (sin<p— sma) da.
Изгибающий момент в этом же сечеиии от всех сил, действующих
на дугу с центральным углом <р, получается равным
M=qp2 \ (sin <р—sin a) da = gp2 (tp sin tp + cos <p—1).
J
о
Для вспомогательных систем (рис. 22, г, д) изгибающие моменты
в том же сечении имеют значения Mt=l, М2=рA —cos <p).
Поскольку
8ip= I MM1 ds~qpa \
s ¦к
?•/82?=! MMs(fe = 9p4 (фsin<p + cos<p — 1) A —
о
о
— cos ф) d q> = j- q p4;
Ь It
El 8U = f M\ ds = p f d <p = я р;
о о
s it
= j Ml rfs = p8 |A-со5Ф)^ф=~ р3 и
о о
s к
Elbl2 = El821 =j 7Й, Мг ds = p2 | A — cosф) dф =
?/82
то канонические уравнения метода сил переписываются следующим
образом:
Х1+РЛ2=0,
Л1 +" РЛ2 = —^—
откуда
X q „х -
Л1 — 2 ИЛ2 —
344
Изгибающий момент в пронзиольном сеченни стенкн кольца
ф sin ф + cos ф — 1) — Ц- + Ц-
= <?ра (<р sin ф •+- -g- cos <р — 1).
М =qf (ф sin ф + cos ф — 1) — Ц- + Ц- A — cos ф) =
Поэтому
M
«—0.0912 qf;
Мр=!_я =
На рис. 202, e показана эпюра изгибающего момента.
Для определения величины изменения длины вертикального
диаметра кольца в сечении, совпадающем с осью у основной системы
(рис. 202, б), прикладываем вертикальную силу Рф—1, направ-
направленную вниз От этой силы в произвольном сечении изгибающий
момент
M=psin ср.
Следовательно, искомое перемещение
1 = — JMM ds = -|?- f f ф sin ф + -i- cos ф — l\ si
о о
sin q> йф =
A } El El
Задачи 834—835. Определить продольные усилия N в прону-
пронумерованных стержнях систем.
Жесткость EF одинакова для всех стержней.
В этих и последующих статически неопределимых задачах ис-
использовать (по желанию) начало наименьшей работы или метод сил.
вЗЧ 835
Ц
345
Задачи 836—837. Определить реактивные моменты в заделках
левых концов стержней
Ш И вз] _
Зто
Задачи 838—841. Определить реакции в закрепленных сече-
сечениях А и вертикальные перемещения 8 сечення С балок.
В задаче 841 определить и реактивный момент Мл и сечении Л.
Жесткости El считать известными.
Задачи 842—845. Определить реакции шарнирной опоры сис-
систем и линейные перемещения сечения С.
В задачах 842—843 Ьв— вертикальные, а в задачах 844—845 6Г —
горизонта льн ые*.
* В задачах 842—866 продольные деформации элементов системы не учи-
учитывать, и жесткости EI изгибаемы* элементов считать одинаковыми
346
Задачи 846—847. Определить реакции опоры А и вертикальные
перемещения 8 сечения на оси симметрии систем
Задачи 848—851. Определить горизонтальные реакции опор
в системах
646
U.
/7?///
вчз
Задачи 852—857. Определить составляющие реакции опоры А
систем
347
85?
853
651
I 1
_ШП
пттт
ИйййЭ
-га
II
856
я I
f
-a Zf о
р
Задачи 858—861. Определить наибольший по абсолютному зна-
значению изгибающий момент в рамных системах.
858
059
j*^W
Ъ t.
lit
flfifl
UllflUI
цЦЩШ
348
Задачи 862—870. Определить реактивные составляющие в за-
закрепленном сечении А систем.
В задачах 868—870 определить также вертикальные переме-
перемещения 8 сечения С, приняв, что сеченне на всех участках систем
круглое, а материал одинаков; G=0,4 E.
В62
вез
8В5
А
шли
¦Za-
it нищ
а к
8В7
f-
668
Задачи 871—875. Определить наибольшие нормальные напря-
напряжения, возникающие в элементах систем при повышении темпера-
температуры на Л/°С
Учитынать только деформацию изгиба. Симметричное сечение
с высотой h и материал с заданными Я и а у всех элементов каждой
системы одинаковы
349
871
87Z
2а
-ч— a -*d
873
-2а
ЪП 875
- а »|« а —».
Ч
Задачи 876—879. Определить наибольшие монтажные напря-
напряжения в системах, если длина элемента CD больше проектной на
величину Д
Учитывать только деформацию изгиба. Симметричное сечение
с высотой h и материал с заданным Е у всех элементов каждой сис-
системы одинаковы
87Й
677
С
1
в
1
I
- а *
-— а ».
¦
s
4
IS
4
-*
с
—На
*-
D
878
87S
ПТ) 77}
«- в
350
Г/1/IIII'
Задачи 880—884. Определить реакцию правой шарнирной опоры
и вертикальное перемещение 8 сечеиия С в системах*.
В задаче 882 нагрузка q равномерно распределена по горизон-
горизонтали.
680
881
Задачи 885—889. Определить реактивные составляющие в за-
закреплениях левого конца систем.
В85
* В задачах 880 — 915 учитывать только Деформации от изгибающего мо-
момента, и жесткости ?/ v всех элементов системы считать одинаковыми.
351
Задачи 890—895. Определить вертикальное перемещение сече-
ння, в котором к системам приложена сила Р.
Задачи 896—899. Определить изгибающие моменты в сечении С
систем.
Задачи 900—906. Определить реактивные составляющие в за-
закрепленном сечении А систем.
В задаче 902 — нагрузка д равномерно распределена по гори-
горизонтали.
352
Задачи 907—910. Определить, ио сколько раз в указанных сис-
системах наибольший по абсолютному значению изгибающий момент
и вертикальное перемещение среднего сечении меньше, чем в стати-
статически определимом кривом брусе (рис. задачи 907, а).
301 а \р
Задачи 911—913. Определить реактивные моменты в заделке
и вертикальные перемещения среднего сечении кривых брусьев.
Поперечные сечения стержней круглые; G=0,4 E.
Задачи 914—915. Определить необходимые размеры попереч-
поперечных сечений круговых колец.
Допускаемое нормальное наприжение материала колец [ol
12 Заказ № 886
353
XIII. РАСЧЕТ ТОЛСТОСТЕННЫХ ТРУБ
§ 1. Цилиндрическая труба
Для трубы неограниченной длины без днищ, подвергнутой дей-
действию внутреннего рг и наружного р2 равномерных радиальных
давлений (рис. 203), в произвольной точке стенки, находящейся на
расстоянии р от центра, окружные (тангенциальные) at н радиаль-
радиальные ог нормальные напряжения определяются по формулам:
B02)
i-'f
B03)
Напряжение ог < 0 при любых значениях р, и рг, а о^ может
быть больше и меньше нуля в зависимости от соотношения вели-
величин р, и р2.
— * 1 I, то о, > 0. В этом случае эпюры о, и о,
А )
по толщине стенки трубы имеют вид, представленный на рис. 204.
354
Наибольшие и наименьшие значения напряжений:
maxc, = cr(wi = — р.г,
min or = оГр=г_ = — р1,
Pi ( Л + 4 ) - 2рА
max о = о •= ——
min о, =
B04)
Если Pi ^ -М — + 1) , то mine, = 0.
2 V?
max a.
Рис 204
Рис 205
В опасных точках внутренней поверхности трубы (рис. 205)
расчетное уравнение по пятой гипотезе прочности (гипотезе
О. Мора) имеет внд
max о,— v min or <^ [ар],
откуда
где
Ы-A+ч)р.
B05)
Для материала, одинаково сопротивляющегося растяжению
и сжатию. [3pJ = [ocj = [о], v = 1 и расчетное уравнение B05)
будет следующим:
|/
Ч_ _ л! Щ
л, ' V [з] — 2р, -i-
B0G)
12*
Если р, < —^V , то at < 0. В этом случае эпюры о, и о, имеют
вид, указанный на рис. 206.
Наибольшие и наименьшие значения напряжений получаются
равными:
1118X0,= О, _ =
mm о, =сГ =
max a, = i
"p=r,
'I-'?
mm at — of _ = ¦
Pi
.2 s
f2— M
B07)
Если p, = —'^j-, то max of = 0.
6t
rm,n6t
Рис 206
Рис. 207
В опасных точках внутренней поверхности трубы (рис. 207)
расчетное уравнение по пятой теории прочности записывается сле-
следующим образом:
—V min ot = [ор],
откуда
356
Гг ~\f K1 — Pt
', К Ы + Л-2Р2 '
B08)
При соотношении давлений в интервале
значения at имеют разные знаки по толщине стенки трубы.
ЕСЛИ Pl=P2=P. Т° °/— аг~—Р-
Радиальное перемещение Ь произвольной точки стенкн трубы
определяется по формуле
B09)
где Б и [л — модуль продольной упругости и коэффициент Пуас-
Пуассона материала трубы.
Изменение внутреннего радиуса трубы
Изменение наружного радиуса трубы
B10)
B11)
Если на трубу действует только внутреннее давление рь то
в формулах B02—211) следует положить рг=0
Эпюры at и аг будут аналогичны
эпюрам, указанным на рис. 204, но
при рг=0
Если на трубу действует только на-
наружное давление р2, то в формулах
B02—-211) следует положить pi=0.
Эпюры at и оГ будут аналогичны эпю-
эпюрам, указанным на рис. 206, ио при
0
т
i
Пример 112. Дано: Рг=1 Мн/м2,
г,^=4 см, /-2=8 см, [oJ—ЗО Мн/м2,
[ос]=120Мн/м\ ?=1,2-10s Мн/м*,
Определить pi, hrt и Дг2, считая, что Pi
Решение. По расчетной формуле B05)
Рис 208
(рис. 208).
2рг
357
Так как v=;-Ej=0,25 и —=2, то, подставляй числа в воз-
[°с] П
водя обе части равенства в квадрат, имеем:
4 =
98
отсюда pi=j^=g-=17 Мн/м2.
По формуле B10)
30 + 0,75/5!
30 — 1,25р,+2'
4—16
=^0,99- 10-3 см «0.01 мм.
По формуле B11)
Л
2= 1,2-
2-17-
16
64—16
= 0,66- Ю-8 см» 0,007
Задачи 916—918. Определить величины, указанные в условиях
задач
В задачах 916, 917, 918,с использовать третью гипотезу проч-
прочности, а в задаче 918, б — пятую гипотезу прочности.
р, = ЖппГ/см*
г, -- Шм
[б]'6000кГ/смг
2-10вкГ/смг
"- 0.3
5)
jLt=fl,3
= ВВВВкГ/Ы'
г f=/7 wsmh/m*
ц--В,25
Иг7-
358
SIB
Задача 919. Абсолютно жесткий конический пуансон с неболь-
небольшим углом скоса р вгоняется в толстостенное кольцо длиной а.
Определить давление р0, возникающее между клином и кольцом в
среднем сечеиии кольца CD, когда клин продвинется на всю вы-
высоту кольца а. Найти также на-
наибольшие напряжения, возника-
возникающие в сечении CD кольца.
Задача 920. Определить, при
каком угле скоса р клинового
пуансона предыдущей задачи в
среднем сеченни кольца прои-
произойдет увеличение радиуса на-
наружной поверхности на величи-
величину Дг2 = 0,2 мм, если /•1=10 см,
/-а = 30 см, Е = 106 кГ/см*, [* =
= 0,34, а -¦ 5 см
Задача 921. Определить, при
каком угле р скоса конического
пуансона, вгоняемого во вну-
внутреннее отверстие на величину
а, перекроется зазор между
трубами /и Ни образуется
взаимное давление р= Ю0кГ/см2.
Расчет сделать для среднего
сечения CD, полагая, что rt
= 10 см, /-2=30 ем, г3=40 см,
?=106 кГ/см2, |i=0,34, а=5см,
Д=0,4 мм.
Задача 922. Определить дав-
давление ро между бетонной тру-
трубой и абсолютно жестким сердеч-
сердечником, а также проверить
прочность трубы, используя
пятую гипотезу прочности. Принять: ?6=2 • 105 кГ/см2, цо=О,16,
[ос]б=20 кГ/см2, [ор]6=4 кГ/см2.
demon
359
Задача 923. Определить величину наибольшего внутреннего
давления р, которое можно приложить к бетонной трубе, окружен-
окруженной абсолютно жесткой оболочкой, и граничное давление р0, если
?б=2-105 кГ/см\ |16=0,1б, Ы6=50 кГ/см\ [ср]6=5 кГ/смК
Задача 924. Определить граничное давление р0 между коль-
кольцом и абсолютно жесткой оболочкой, если известны значения q,
Л), л2 и ц. Считать, что модуль упругости материала кольца имеет
малую величину
925
Задача 925. Определить давление р0 между кольцом и абсолют-
абсолютно жестким сердечником, считая известным q, rit r2 и [а
§ 2. Составные цилиндрические трубы
При действии высокого внутреннего давления используют трубы,
составленные путем прессовой или горячей посадки, из двух и
более цилиндров. Прочность соединения цилиндров и возникно-
возникновение в их стенках начальных напряжений обусловливается тем,
что внутренний диаметр охватывающего цилиндра делается меньше
наружного диаметра охватываемого цилиндра на величину
натяга Д (рис 209).
При одинаковой длине соединяемых цилиндров контактное дав-
давление ро распределяется равномерно по посадочной поверхности
и имеет значение:
Ро =
B12)
где ?¦), Е2, (Aj, |i2— модули продольной упругости и коэффициенты
Пуассона материалов внутреннего и наружного цилиндров
300
Если цилиндры изготовлены из одного материала, то
Et = ?2 = Е, (ч = ft,
B13)
В стенках соединенных цилиндров начальные напряжения от
давления р0 определяют по формулам B02) и B03). При этом следует
учитывать, что для внутреннего цилиндра с радиусами ri и гг
контактное давление р0 является наружным (внутреннее давление
Рис. 209
Рис. 210
равно нулю), а для наружного цилиндра с радиусами г2 и г3 кон-
контактное давление р0 является внутренним (наружное давление
равно нулю).
Примерные эпюры а, и ог от давления р0 в соединенных цилин-
цилиндрах показаны на рис. 210 пунктирными линиями ab и ей.
От действия на составную трубу большого рабочего внутрен-
внутреннего Pi и небольшого наружного р2 давлений по формулам B02)
и B03) определяют напряжения а, и ог, как для монолитной трубы
с радиусами rt и г3.
Примерные эпюры этих напряжений показаны иа рис. 210 тон-
тонкими сплошными линиями ef.
361
Результирующие напряжения в составной трубе находят мето-
методом наложения напряжений, представленных эпюрами ab, cd и ef.
Примерные эпюры результирующих напряжении at и сг на
рис. 210 заштрихованы
Если составляющие трубу цилиндры изготовлены из материа-
материала, одинаково сопротивляющегося растяжению и сжатию, то
по третьей гипотезе прочности наивыгоднейшие соотношения
между радиусами и натигом устанавливают по формулам:
rt=VTJ7. B14)
Л= -^-(р, =- рг). B15)
Максимальное избыточное внутреннее давление:
max (р1 — р2) = r3~f' [о].
211
B16)
Методика расчета сохраняется и для
труб, составленных из трек и более ци-
цилиндров По натягу для первых двух
цилиндров определяют контактное давле-
давление между ними и через него — начальные
напряжения в этих цилиндрах. По второ-
второму натягу между блоком, состоящим из
двух цилиндров (как одного цилиндра с
общими размерами), и третьим цилиндром
аналогично определяют новое контактное
давление по посадочной поверхности и
через него — начальные напряжения в
блоке, состоящем из двух цилиндров и в
третьем цилиндре.
Результирующие начальные напряже-
напряжения в блоке, состоящем из трех цилинд-
цилиндров, получают методом наложения найден-
найденных начальных напряжений при первой
и второй посадке Напряжения от рабо-
рабочего давления в блоке, состоящем из
трех цилиндров, определяют как в одной
целой трубе с общими размерами. Алгеб-
Алгебраическая сумма найденных напряжений
дает расчетные значения, по которым
проверяют прочность.
Добавление четвертого и последующих
цилиндров приводит к необходимости на-
находить новое контактное давление и до-
дополнительные начальные напряжения.
362
При посадке полого цилиндра иа сплошной цилиндр без по-
полости контактное давление определяют по формуле B12) или
B13), при условии, что г, — 0.
Пример 113. Дано: pi = 2000 кГ/см\ рг ¦= 0, г1 = 8 см,
? = 2-10е кГ/см2, [а] =-3000 кГ/см* (рис. 211 а).
Спроектировать двойную составную трубу с рациональными
размерами и проверить ее прочность, пользуясь третьей гипоте-
гипотезой прочности
Решение. По формуле B16) определяем наружный радиус
составной трубы:
г, = '°"i - 3000-8 = 24 см
3 [а] — р, 3000 — 2000
По формуле B14) находим радиус посадочной поверхности
трубы:
VW V^7^ T [3,856cj«.
Для упрощения расчета берем г2 == 14 см. По формуле B15)
находим величину необходимого натяга
а по формуле B13) находим величину контактного давления
Ра =
(т)] _
414
Определяем начальные напряжения от контактного давления рв.
В стенке внутреннего цилиндра.
По формулам B07) при р, = 0 и р2 = р„
max а, = о, = - Р„ LiL— 500 ill « _ 985кГ/см\
I 4\г
— 1485 /сГ/слв,
363
r o,p=ri =0,
min or = orp_.g = — Po— — 500 кГ1см\
Эпюры ot и ar показаны на рис. 211, б, е пунктирными линиями
аЬ.
В стенке наружного цилиндра.
По формулам B04) при Pj=p0 и Рг=0, считая, что Гу=гг, r2~rs,
1 + Ьг 1 + Ы
max о, = olf=r = р0 y^w = 5°0 гт{г * 1Ш6
o,p=,.s= 2р0
шах о = о = 0,
min о, = о. = — р0 = — 500 кГ/см2.
р=г2
Эпюры о^ и ог показаны на рис. 211, б, в пунктирными лини-
линиями cd.
Определяем напряжения в стенке блока, состоящего из двух
цилиндров (как целой трубы), от действия внутреннего давления pt
По формулам B04) при pi=2000 кГ/см2 и р2=0, считая, что
/-,=/-, и r2=rs:
2.10"
mine, = о<= = 2р„ уу-^ = 2-2-Ю3да4п = 500 кПсм\
max ar = a. = 0,
min or = ог = — р„ = — 2000 кГ/см\
По формулам B02) и B03) при pf=2000 кГ/см? и р2=0, считая,
что ri=r, и ла=г3 для точек посадочной поверхности:
==2-10» з// «985
364
^ Ш 32 _j
Эпюры о,и огпоказаны на рис. 211, б, е сплошными линиями е/
Находим результирующие напряжения н стенке внутреннего
цилиндра:
atf=Tf = — 1485 + 2500 =1015 кПсм*; o,p_ri = — 985 + 985 = 0,
аг =—2000 кПсм2; о, =— 500 — 485 = — 985 кГ/см?;
в стенке наружного цилиндра:
о,^ = 1016 + 985 = 2001 кГ1ем\
«V», = 516 + 50° = 1016 кГ/см";
ог = — 500 — 485 = — 985 кГ/см^
О, =0.
Эпюры результирующих напряжений ot и ог на рис. 211, б, в
заштрихованы.
Эквивалентные напряжения по третьей гипотезе прочности
получаются следующими:
в точках внутренней поверхности внутреннего цилиндра
о9 =о, — аг =1015 + 2000 = 3015 кГ/см2.
аш 'e=-r< rp=r,
в точках внутренней поверхности наружного цилиндра
Незначительное отклонение от равной прочности материала
в опасных точках цилиндров получилось за счет округления раз-
размера г2.
Условие прочности оЭ]11— la] можно считать соблюденным, так
как перенапряжение составляет всего 0,5%.
Задачи 926—930. Определить радиальные о, и тангенциальные
о, нормальные напряжения и граничные давления р0 в составных
трубах от действия внутреннего давления pt (задачи 926, 927), от
нагрева на Ы° С (задача 928) и от прессовой посадки с натягом
А (задачи 929, 930).
В задачах 926—928 принять: ?„=2 -10е кГ/смг; |iCT =0,3;
»„= 12,5-Ю-6; ?м=Ы0в кГ/см*; цм =0,34; <*м = 16,5- 10"в;
rf=10 см; Л2=2О см; Л3=4О см.
365
В задачах 929, 930 определить только р0.
Ш Ш Ж
Задача 931. Определить для двойной составной трубы:
1) напряжения от прессовой посадки с натягом Д — 0,4 мм;
2) напряжения от внутреннего давления р0 =- 2000 кГ/см2;
3) суммарные напряжения;
4) процент уменьшения расчетного напряжения по третьей
гипотезе прочности в составной трубе по сравнению со сплошной
трубой тех же размеров. Принять л, = 10 см; г2 = 25 см; г3 = 50 см.
Задача 932. Спроектировать двойную составную трубу с ра-
рациональными размерами, используя третью гипотезу прочности.
Считать заданными rt = 10 см\ Е = 2-10в кПсм?; |i — 0,3;
[а] = 4000 кГ/см2; р =- 3000 кГ/см2.
Задача 933. Определить для тройной составной трубы:
1) напряжения от прессовых посадок Д,, Д2;
2) напряжения от внутреннего давления р;
3) расчетные напряжения по третьей гипотезе прочности;
366
4) процент уменьшения расчетных напряжений в составной
трубе по сравнению со сплошной трубой тех же размеров.
S33
33) —
-Ill
XIV. ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ СИЛ
§ 1. Расчет движущихся тел (систем)
с учетом сил инерции
Динамическое действие сил характеризуется наличием уско-
ускорений в элементах рассматриваемого тела (системы). В зависи-
зависимости от вида нозникающих ускорений изменяется характер
деформации и разрушения тела.
Наличие ускорений связано с возникновением сил инерции,
направленных в сторону, противоположную направлению уско-
ускорения. Величина элементарной силы инерции dPK определяется
произведением массы dm элементарного объема тела dV на его
ускорение а, т. е.
где f — вес единицы объема материала тела,
g—ускорение силы тяжести.
На рис. 212, а показано неравномерное поступательное движе-
движение, на рис. 212,6 — равномерное вращательное движение тела.
Если при движении элементы тела испытывают постоянные
ускорения, то никаких особенностей в поведении материала тела
не наблюдается В этом случае напряжения и деформации можно
определять как при статической нагрузке внешними силами
и силами инерции.
Если движение совершает тело (система) достаточной жестко-
жесткости, несущее на себе какие-то грузы, то по заданному движению
367
устанавливают ускорения элементов тела и грузов и через эти
ускорения определяют силы инерции. Присоединяя силы инер-
цин к весу грузов, собственному весу тела и всем действую-
действующим на него внешним силам, тело рассматривают как находя-
находящееся в покое и рассчитывают его по правилам, установленным
для статического нагружения.
Если вес грузов, несомых телом, велик по сравнению с его соб-
собственным весом, а инерционные силы от последнего малы по
сравнению с инерционными силами от
грузов, то при расчете тела на прочность
a) /fip,, ¦frfV1 Y"^ и жесткость влиянием его собственного
веса можно пренебречь.
В тех случаях, когда направления
ускорений а заданного движения тела
совпадают с линией действия ускорения
земного притяжения g, вид деформации
тела от инерционных сил соответствует
виду деформации от собственного веса
тела и от несомых им грузов. Если, кроме
последних, к телу не приложено иных на-
нагрузок, то обобщенные динамические уси-
усилия Ря, напряжения ря (нормальные оя
или касательные тд) и перемещения 8Д
(с учетом инерционных сил) удобно опре-
определять через соответствующие величины
Р, р н 8, отвечающие статической нагрузке (без инерционных
сил), и динамический коэффициент
Рис. 212
по формулам:
B17)
B18)
В тех случаях, когда направления ускорений а заданного дви-
движения тела не совпадают с линией действия ускорения земного
притяжения g, вид деформации тела от инерционных сил не
будет соответствовать виду деформации от его собственного неса
и от несомых им грузов. При расчете тела нужно учесть на-
напряжения и деформации от каждого из полученных видов
деформации, как это делается и при статических нагружениях.
Пример 114. Призматический стержень длиной / несет на себе
два груза весом Qr и Q2 и движется равноускоренно вертикаль-
вертикально вверх, проходя за первые t секунд путь S (рис. 213).
368
Определить необходимую площадь/7 поперечного сечения стерж-
стержня и его динамическое удлинение, если материал стержня имеет
вес единицы объема ?> модуль продольной упругости Е и допуска-
допускаемое напряжение на растяжение [о].
Решение. Наибольшее статическое продольное усилие в
верхнем сечении стержня:
Наибольшее статическое нормальное напря-
напряжение:
max Л'
2S
Так как ускорение заданного движения а =-—¦
направлено вертикально вверх, то динамический
коэффициент
л r g ' Рис. 213
Максимальное динамическое напряжение
max с„ = kn max о = hn i—^-f—— -Ь tl\,
По условию прочности
max о„ = ?д max о ¦< [о]
или
Отсюда необходимая площадь поперечного сечения стержня
Удлинение стержня площадью F при статическом действии
сил
Динамическое удлинение стержня Д/Д=?ДД/.
Пример 115. Винтовая цилиндрическая пружина малого шага
длиной /=30 см, радиусом витка i?=2 см и радиусом сечения
369
проволоки г=0,2 см с числом витков по=Ю имеет на своем конце
груз весом Q=l кГ и вращается в вертикальной плоскости вокруг
неподвижного шарнира, делая п=200 об/мин (рис. 214).
Определить наибольшее динамическое касательное напряжение
max тд в сечении проволоки пружины и наибольшее переме-
перемещение Л/ груза Q, если модуль сдвига материала
проволоки G=8-106 кГ/см2, а вес пружины весьма мал
по сравнению с весом груза Q.
Решение. При крайнем нижнем положении
груза Q на пружину будет действовать наибольшая
растягивающая динамическая сила Pa=kuQ.
Вследствие малой жесткости пружины при определе-
определении центробежной силы следует учесть растяжение оси
пружины
Поэтому динамический коэффициент
где угловая скорость
_ жп тс - 200
Ш ~ 3(Г~~ 30
о, -,/ ">8 212 „ .с .,
Gr* д 8-10е-16-Ю-4 4 €"Л1-
Таким образом,
= QH + 0,45C0 + 0,25Рд)]
отсюда
—0.I1Q
Максимальное динамическое касательное напряжение в попе-
поперечном сечении проволоки пружины
max ха =
- 2720 кПсмК
Наибольшее динамическое перемещение груза
М = — Р —
17,1
: 4,3 СМ.
Пример 116. Призматический стержень длиной / несет на верх-
верхнем конце груз весом Q, нижним концом заделан в абсолютно жест-
370
кой детали, которая движется под углом а к горизонтальной плос-
плоскости с постоянным ускорением а (рис. 215, а).
Определить наибольшее и наименьшее значение динамических
нормальных напряжений в опасном сечении стержня, если пло-
площадь и момент сопротивления на изгиб его сечения F и W, а вес
единицы длины q.
Решение. При движении системы на стержень действуют
вес груза Q и собственный вес q, направленные вертикально вниз;
Ъа
сосредоточенная инерционная сила — и равномерно распреде-
распределенная инерционная нагрузка —, направленные под углом |— а
к геометрической оси против направления движения (рис. 215, б)
Рис. 215
Рис. 216
В опасном заделанном сечении стержня действуют нормальные
напряжения: от сил тяжести Q и q, вызывающих осевое сжатие
от составляющих инерционных сил, действующих вдоль гео-
геометрической оси стержня, вызывающих осевое сжатие
„ _
_ _ (Q-\-ql)asma .
от составляющих инерционных сил, действующих перпендику-
перпендикулярно геометрической оси стержня, вызывающих изгиб
( Ql + -^-
371
Наибольшие и наименьшие значения динамических нормальных
напряжений в опасном сечеиии стержня
+4~ 4')alcosa пл
Пример 117. Стержень длиной /, наклоненный к горизонталь-
горизонтальной плоскости под углом о, несет на своем свободном конце груз
весом Q и вращается вокруг вертикальной оси 00 с постоянной
угловой скоростью ю (рис. 216, а).
Определить наибольшее динамическое нормальное напряжение
в опасном сечении стержня, если вес единицы длины стержня q,
площадь поперечного сечения F и момент сопротивления сечения
на изгиб W.
Решение. Учитывая возникающие центробежные силы,
представим расчетную схему в виде, изображенном на рис. 216, б.
В опасном заделанном сечении стержня будут действовать:
1) изгибающие моменты
от собственного веса стержня д
от веса груза Q
М2= Ql cos a;
01 сосредоточенной центробежной силы -чог / cos a
от распределенной по закону треугольника центробежной силы с
наибольшей интенсивностью ^- ю2 /cosa
2) сжимающие усилия
от собственного веса q
Nt=—ql sin a;
от веса груза Q
N2=—Q sin a;
3) растягивающие усилия
от сосредоточенной центробежной силы -^ ю8 / cos a
372
от распределенной по закону треугольника центробежной силы с
наибольшей интенсивностью —<и2 I cos <x
Результирующий изгибающий момент
= (Q + ±-
(<2+ -!¦
—
sin 2 а.
Результирующее продольное уснлне
Наибольшее динамическое нормальное напряжение в опасном
сечении стержня
Ь. =4"
Пример 118. Система, изображенная
на рис. 217, а, вращается вокруг верти-
вертикальной оси 00 с постоянной угловой
скоростью ш.
Определить допускаемое число п
оборотов вращения системы в минуту,
если т=\ кг, р=10 см, d=\ см, [о]=
160ЛГ/*
/
Собственным весом системы и влия-
влиянием изменения расстояния между гру-
грузами т на величину центробежной
силы пренебречь.
Решение. С учетом центробеж-
ной силы расчетную схему можно пред-
представить в виде, указанном на рис.
217, б.
В опасном заделанном сечении бу-
будут действовать продольное растягиваю-
растягивающее усилие Л?д=тю2р и изгибающий
момент
=mp(g + 2wap).
Рис. 217
373
Максимальное динамическое растягивающее напряжение во
внутреннем волокне заделанного сечения
¦
1
ав.
Так как при —- =-^ коэффициент ов = -г- да 1,
1 —
то условие прочности в опасном сечении
JL l
откуда
0)=зо<1/ —ГГ
w
-т
\ " I/
160 ¦ 10е —
1 -0.1 ¦ 9,81
0,1 ¦ 10-°
'
- lO
20-'Т
0,M0-6j
«1/750,
п =« — V750 « 270 об/жин.
Задачи 934—936. Определить нормальные напряжения о в
поперечных сечениях указанных элементов движущихся систем от
совместного действия сил тяжести и сил инерции.
На рисунках направление движения указано стрелкой со знач-
значком а
ГнГ/СМ3
а-дм/свк2
336
а=дм/сек
374
Задачи 937—950. Определить величины, указанные в условиях
задач, от сил инерции, возникающих во вращающихся системах.
На рисунках ось, вокруг которой вращается система, указана
стрелкой со значком и> или п. Если для оси вращения не заданы
размеры поперечного сечения и Е, то считать ее абсолютно жесткой.
Абсолютно жесткие элементы систем, за исключением осей враще-
вращения, изображены двойной линией со штриховкой.
Во всех задачах, кроме 942, вращение считать равномерным.
При определении инерционных сил деформации элементов систем не
учитывать.
В задачах 937, 938, кроме сил инерции, учесть и силы тяжести
933
Э«7
'¦ d=10
5H = 60°
<x=3D° л-ЗВВоб/мин
в=5ОкГ Ш1
т &> '/сек
/ ша \ С
1
I—J —
>
Ч "°" [eJ-Kooir/cfWjtioi
•*т«—да—«-1
=^6-?
/e/.rf^
37В
l=Z№
Sffi
Задачи 951—953. Опргделить угловую скорость ш l/сек (или
число оборотов в минуту п) вращения оси, при которой нарушится
устойчивость сжатого элемента систем.
Считать, что критические напряжения не превосходят предела
пропорциональности материала
376
SS7
952
§ 2. Упругие колебания
Упругими колебаниями называют периодические отклонения
упругой системы от положения устойчивого равновесия. Если сис-
система выведена из положения равновесия однократным воздействием
силового импульса, то возникающие колебания называют сво-
свободными или собственными. Если систему подвергают действию
обобщенной силы, периодически изменяющейся во времени (воз-
(возмущающей силы), то получающиеся колебания называют вынуж-
вынужденными.
Свободные колебания, вследствие наличия сил сопротивления,
являются колебаниями затухающими, т. е. происходящими с ам-
амплитудой, уменьшающейся во времени. Если частота собственных
колебаний равна частоте возмущающей силы, возникает резонанс —
явление быстрого и непрерывного возрастания амплитуды во вре-
времени. Так как увеличение амплитуды колебания связано с увели-
увеличением и напряжений, то резонанс может привести систему к преж-
преждевременному разрушению.
Всякая упругая система имеет бесчисленное множество степе-
степеней свободы, поскольку число независимых координат, опреде-
определяющих положение в пространстве, распределенных в элементах
системы масс, является бесконечно большим
Если собственную массу систем не учитывать совсем или учесть
приближенным приведением ее в одну или несколько точек, то
условно систему можно рассматривать как имеющую одну или
несколько степеней свободы Без учета собственной массы упругую
систему можно считать обладающей одной степенью свободы, если
система несет один груз, положение которого в пространстве опре-
определяется только одной координатой. С учетом собственной массы
систему условно считают обладающей одной степенью свободы,
если собственную массу системы с достаточным приближением
можно привести в точку подвеса груза.
377
Здесь рассматриваются только незатухающие колебания сис-
систем с одной степенью свободы без учета собственной массы. Соб-
Собственная масса будет учитываться лишь в простейших задачах,
относящихся к колебаниям призматических стержней.
Во всех случаях колеблющаяся масса считается постоянной,
а упругая система линейной, для которой возникающая в произ-
произвольный момент времени восстанавливающая обобщенная сила Р,
пропорциональна соответствующему обобщенному перемещению
Ъ, т. е.
Р=СЬ,
B19)
где С — жесткость системы, т. е. та обобщенная сила, которая
вызывает обобщенное перемещение, равное единице.
Вид деформированной системы при колебании принимается
такой же, как и при статическом нагружении этой системы соот-
соответствующей обобщенной силой, приложенной в точке подвеса
груза и действующей в направлении колебания.
Свободные колебания упругих систем
без учета собственной массы
Так как для линейно-деформи-
линейно-деформируемых систем обобщенное пере-
перемещение 8 точки подвеса груза при
статическом действии в этой же
точке соответствующей обобщенной
силы Р легко определить любым
из известных методов, то жест-
жесткость системы С находим из выра-
выражения
С = 4-. B20)
Жесткость систем с параллель-
параллельным, последовательным и смешан-
смешанным соединением упругих элемен-
элементов удобно определять, пользуясь
следующими известными положе-
положениями.
Если в системе упругие эле-
элементы с жесткостями С, соединены
параллельно (схемы указаны иа
рис 218, а, б), то жесткость сис-
системы
С =ТС, B21)
Рис. 218
378
Если в системе упругие элементы с жесткостями Сг соединены
последовательна (рис. 218, е), то жесткость системы
С =-
J
B22)
Если в системе смешанное соединение упругих элементов
(рис. 218, г), часть которых с жесткостями С1 соединены парал-
параллельно, а часть — с жесткостями С,' соединены последовательно,
то жесткость системы
С = -у-? р . B23)
+5:
Для систем без учета собственной массы круговую частоту сео-
бодных колебаний ю (число колебаний за время 2п секунд), час-
частоту колебаний Л' (число колебаний за одну секунду) и период
колебаний 7* (время одного полного колебания) определяют по
следующим формулам:
а) при возвратно-поступательном движении груза
V т Г В '
2п
B24)
где т=——масса груза весом Q, кГ-сек2/см (в СИ т — масса
груза кг определяется взвешиванием, т. е. сравнением
с эталонной массой в 1 кг; вес груза Q в ньютонах,
Q=mg);
Ь— линейное перемещение точки подвеса груза при ста-
статическом действии силы Q в направлении колеба-
колебания, см (м);
С—— жесткость системы, кГ/см (н/м или кн/м);
6) при возвратно-вращательном движении груза
B25)
Л/- ' l/C
379
где /„, = j р2 dm = -L \ psdV — момент инерции массы груза
носительно его оси вращения кГ-см-сек2 (в СИ /m = J
W кг-*»);
¦if — вес единицы объема груза V, кГ/см3;
р0— плотность, масса единицы объема V, кг/м3(ъ СИ);
р — расстояние элемента объема dV от оси вращения, см (м);
С= жесткость системы, кГ-см (н-м), где М — момент,
действующий статически в сечении подвеса груза в направлении
колебания кГ-см (н-м); <р — угловое перемещение сечения, в
котором приложен момент М от его статического действия, рад
Пример 119. Дано: Q=16 кГ, а=2 см, ?=2-10е кГ/см2,
Г=0,1 сек (рис. 219)
Определить /.
Решение. Так как период колебания Т = 2я |/ — , то
С другой стороны, от статического действия силы Q прогиб
свободного конца балки 8=-—-. Поэтому
QP __ T*g ._ VT2g-3E/ _ У" 1-981 -3-2- 10е-2« _ -~
ЗЕТ ~~ Аи И '—у 4n*Q — V 10W-4.16-12 ~ ° СМ'
Пример 120. Дано: т=20 кз, Ь=8 см, /=40 см, N=20 кол/сек,
G=8-104 Мн/м2 (рис. 220).
Определить а.
Решение. Так как ^ — ~^у ~ и lm — 2mb2, то
С = 4v2N2Im = &т?№тЬ\
С другой стороны, жесткость стержня при кручении
„ _ G/K G-0,i4o«
с —-у ~ j -,
где /н=0,14 а5— момент инерции при кручении квадратного се-
сечения со стороной а. Поэтому
0,14а*С _ о_яа7Я »,s -ш/ №№тЬЧ
V 8-10-4-10г-20"б4-10-4-40-10-2
~ V 0,14-8-10"
380
1,95 -10-2 = 1,95 см.
Пример 121. Дано: Q, a. I, E, I (рис. 221).
Определить «, /V, Т.
Решение. Так как угол поворота груза Q вокруг центра
шарнира левой опоры Ч~уГр го жесткость балки
_4-1
I —»-f
Рис. 219
Рис. 220
Рис. 221
Момент инерции массы груза относительно оси его поворота
По формулам B25) круговая частота колебания
частота колебания
период колебания
Пример 122. Дано: Q, I, у пружины: D, d,n(n — число виткоз),
G Стержень АВ — абсолютно жесткий и невесомый (рис. 222).
Определить круговую частоту колебания ю в функции от по-
положения груза Q, т. е. от расстояния х.
Решение. Растягивающая пружину сила P=Q-p
Вертикальное перемещение точки А:
g _ 8PD'n _ 8QD3n x
381
9L
Вертикальное перемещение точки С:
Круговая частота колебания груза
_
2Dx
2QDn
Рис 222
Рис. 223
Рис. 224
Эту задачу можно решить и иначе, исходя не из поступатель-
поступательного, а из вращательного движения груза Q. Тогда:
угловое перемещение груза <р = -j-;
восстанавливающий момент М=Р1;
М РР
жесткость системы С = — = =г—;
момент инерции массы груза относительно оси его вращения
/ Q 2
'т — ~тгх •
круговая частота колебания груза
2Dx
2QDn
Пример 123. Дано: для стержней h, di, Gu 1г, йъ G2; для
диска 1 (вес единицы объема), D, h (рис. 223).
Определить ю — круговую частоту колебания диска.
Решение. Жесткости стержней при кручении
С,:
32/,
нъ
382
Так как стержни соединены параллельно, то жесткость коле-
колеблющейся системы по формуле B21)
Момент инерции массы цилиндрического диска относительно
оси его вращения
1 j
U = -J- J
V
= -Г
1 2" Л j
О О
"2 g •
По формуле B25) круговая частота колебания диска
Пример 124. Дано: для балки lv Elt lt\ для стержня 1г,
Ег, F2, Q (рис. 224)
Определить Т.
Решение. Жесткость балки на двух опорах с изгибающей
силой посередине
48?,/,
Жесткость стержня при растяжении
Так как балка и стержень соединены последовательно, то по
формуле B24) жесткость колеблющейся системы
с= •
1 1
По формуле B24) период колебания системы
= 2я | ¦ -g- = 2те J/ — ^4g?i/i + ?^
383
Задачи 954—965. Определить величины, указанные в условиях
задач, для систем, испытывающих колебания.
На рисунках стрелкой около груза указано направление коле-
колебания.
357
FI
т=?
958
а
Е1
а-Л*—2а »С
т=?
Грузы д колеблются синхронна
384
Ш'иГ/см*
Свободные колебания упругих систем
с учетом собственной массы
При свободных колебаниях упругой системы распределенную
собственную массу те можно приближенно учесть, приведя ее в
точку подвеса груза и сложив с массой т последнего.
Приведенной массой тпр является такая масса, сосредоточенная
в точке подвеса груза, кинетическая энергия движения которой
равна кинетической энергии движения массы системы /«о- Вели-
Величина приведенной массы пропорциональна величине истинной
массы и определяется по формуле
B26)
*„, = :
Коэффициент приведения массы km, зависящий от закона из-
изменения скоростей движения элементов массы т0, устанавливается
из условия равенства кинетических энергий движения т„р и те,
которое приводит к выражению
1 Ч-^УЛ&Ло, B27)
те
где 8 и Ьх — обобщенные перемещения точки подвеса груза и про-
произвольной точки системы при статическом действии на иее обоб-
13 Заказ № 886
385
шейной силы, соответствующей виду деформации системы при
колебании и приложенной в точке подвеса груза в направлении
колебания.
Для прямолинейных стержней с постоянным поперечным се-
сечением коэффициенты приведения массы можно определять по
формуле
их,
B28)
где их — элемент длины стержня;
/ — его длина.
Круговая частота ш, частота Л' и период Т свободных колеба-
колебаний упругой системы с учетом собственной массы устанавливаются
по следующим формулам:
а) при возвратно-поступательном движении
JL,/JL '
2nV b'i+*J%
В> = 2, /4
B29)
где Q=mg и Qe=mog— вес груза и системы;
8=^—линейное перемещение точки подвеса груза при стати-
статическом действии иа систему силы Q в направлении колебания;
б) при возвратно-вращательном движении
'm0
г + "га'тй
Т _
B30)
386
где 1т и /Мл— моменты инерции массы груза т и массы системы
т0 относительно оси вращения.
Рассмотрим примеры учета собственной массы призматических
стержней для простейших видов их свободных колебаний.
Пример 125. Продольные колебания. Дано: Q, 7, F< a> &. E
(в СИ даио: масса груза т. кг, плотность стержня р0 кг/м3, F, а,
Ь, Е, рис. 225, a) oj
Определить Т.
Решение. При статическом действии гру-
груза Q отношения линейных перемещений (удлине-
(удлинений и укорочений) произвольных сечений (опре-
(определяющихся координатами х,, х^) и сечения, где
расположен груз, соответственно равны
5 — а 5 b ¦
На основании выражения B28) коэффициент
приведения массы
Так как участки стержня соединены параллель-
параллельно, то по формуле B21) жесткость системы
аЬ
Собственная масса стержня та=— (а+b), мас-
масса груза
Рас. 225
т = — [в
По формуле B29) период свободных колебаний системы
в СИ:
¦ТГ1 «
- 1 f Q
аЬ
Частные случаи (рассматриваются в технической сис-
системе).
13*
387
Если груз Q подвешен к стержню длиной а, а стержень с дли-
длиной Ь отсутствует (рис 225, б), то, полагая -у=0. получим
Если груз Q опирается на стержень длиной Ъ, а стержень
длиной а отсутствует (рис. 225, в), то
Рис. 226
8 -
ь*-
Пример 126. Поперечные коле-
колебания. Дано: Q, if, F, I, Е, I
(рис. 226).
Определить Т.
Решение. При статическом
действии груза Q линейное пере-
перемещение (прогиб) произвольного
сечения, находящегося на рассто-
расстоянии х от левой заделки, определя-
определяется методом начальных парамет-
параметров
1 /.. х* Q ха'
= W[Mo-2-~T"
Из условия симметрии балки
-S)-0 ¦*•-
*
Поэтому
8,=
QP
48EI
х*
х*
По формуле B28) коэффициент приведения массы балки
Собственный вес балки Q=-(Fl.
383
Период свободных колебаний балки находится из выражения
B29):
Пример 127. Крутильные колебания. Даио: Q, D, ?. d, a,
Ь, G (рис. 227, а)
Определить Т.
Решение. При статическом действии вращающего момента
в сечеиии подвеса диска отношения угловых перемещений (углов
поворота) произвольных сечений (определя-
(определяющихся координатами хи х^ и сечения подвеса ¦.
диска соответственно равны: I г%
%Л — ??i — iL ^?? — ?i? — 01.
Ь ср a S ф b
В соответствии с формулой B28) коэффициент ™
приведения массы стержня
Так как участки стержня соединены параллель-
параллельно, то по формуле B21) жесткость системы
Момент инерции массы цилиндрического стер-
стержня относительно его геометрической оси
Момент инерции массы цилиндрического диска весом Q и диа-
диаметром D
"»~ 8 ' 8 -
По формуле B30) период свободных колебаний системы
4 D -./"О
389
Частный случай. Если -jp=O (рис. 227, б), то
c-GJ±
±. I
а * то 32g
Задачи 966—970. Определить коэффициенты приведения массы
km балок, считая местом приведения массы сечение К
ЗБВ
SB7
-га
—За -4-0-
СкГ/см
Задачи 971—975. Определить периоды Т свободных колебаний
системы
87)
Ш «7= 5,/«г
Q--320*'
?73
? * (.96 W5Mh/m'
Ш. 1м
390
Вынужденные колебания без учета сил сопротивления
Если вынужденные колебания системы с одной степенью сво-
свободы вызваны приложенной к грузу гармонической возмущающей
обобщенной силой
PB = P0sinc1>0/, B31)
где Р„— максимальное значение возмущающей силы Рв;
«>с — круговая частота последней;
t — время,
то амплитуда вынужденных колебаний А определяется по формуле
А = —^4-=!$о- B32)
В формуле B32) 80— обобщенное перемещение точки подвеса
груза при статическом действии силы Ро, ш — круговая частота
собственных колебаний системы, а
р — коэффициент нарастания колебаний. B33)
_
-о
Если шо5>ш, то /4-*0 и груз на упругой системе практически
будет неподвижным
Если и>(,<ш, то А-ъЪо и колебания груза будут происходить
с амплитудой, равной его перемещению от статического действия
силы Рц-
Если ш0 приближается к ш, то амплитуда А быстро возрастает.
Когда иH=о), возникает резонанс и А — оо В действительности
из-за наличия сил сопротивления А не будет обращаться в беско-
бесконечность, но может достигнуть весьма большой величины.
В резонансной зоне, когда 0,7<J-2<J 1,3, сравнительно небольшие
возмущающие силы могут вызвать в элементах колеблющейся сис-
системы значительные деформации, а следовательно, и значительные
напряжения
Если частота возмущающей силы, увеличиваясь, проходит
резонансную зону быстро, то амплитуда ие успевает достигнуть
своего максимального значения.
Пример 128. К грузу Q= 100 кГ, укрепленному на конце приз-
призматического стержня длиной 1—1ми площадью поперечного се-
сечения F=\ смг, подвешен груз Qt-2 кГ, который вращается иа
плече р=8 ен, делая п-=2400 об/мин (рис. 228,а). Модуль продоль-
продольной упругости материала стержня ?—2 ¦ 10е кГ/см2.
Определить амплитуду вынужденных колебаний груза, не учи-
учитывая массу стержня и сил сопротивления.
391
Решение. Так как линейное перемещение (удлинение)
точки подвеса груза при статическом действии силы Q в направ-
направлении колебания
j. Qi 100-100 1
8 = W = -2Л0М- = 5HF =
см'
то по формуле B24) круговая частота свободных продольных коле-
колебаний
ш= ]/-?- = К981-2-10* «443-^Г- .
Рис. 229
При вращении неуравновешенного груза Qt возникает центро-
центробежная сила Р0=~~и$ р, составляющая которой в направлении
колебания будет гармонической вочмущающей силой (рис. 228, б)
Pb=Pq sin u>ot, вызывающей вынужденные колебания.
Угловая скорость вращения груза Qt является круговой часто-
частотой вынужденных колебаний и равна
п-2400
/сек-
Возмущающая сила имеет максимальное значение
Р % ,v п - 2'25'2-8 „ ючп КГ
*0 == ~7Г ^с Р ~оал 1UOU К1 .
От статического действия силы Ро в направлении колебания уд-
удлинение стержня равно:
s Р01 1030 100 _„„
0 = Ш ~ 2-ю6-1 ж "*™2 см.
392
Так как по формуле B33) коэффициент нарастания колебаний
Р = Ц-= 5§р-~1.47.
то амплитуда вынужденных колебаний системы приобретает зна-
значение
Л=р8о=1,47-О,О52«О,О8 см.
Пример 129. Посередине ригеля рамы, изображенной на
рнс. 229, а, расположен электромотор массой т=96 кг. Неурав-
Неуравновешенная часть мотора представляет собой сосредоточенный груз
массой /«1=4 кг, вращающийся иа плече р=4 см вокруг оси мотора,
делая «=1500 об/мин.
Определить амплитуду вынужденных колебаний рамы, если
/= 1 м, момент инерции поперечного сечения ригеля и стоек / =
=400 см1, а Е=2-105 Мн/м*.
Собственный вес рамы можно не учитывать.
Решение. Сила тяжести электромотора и его неуравнове-
неуравновешенной части будет:
Q=mgr=940 к; С,=т,§=39,2 н.
Горизонтальные реакции в опорах рамы от статического дей-
действия груза Q найдутся из формулы B00) канонического уравне-
уравнения метода сил Х,=^~- Так как
?/81р = -2 | %
a ?/8u =2 J % dXl + 214
Прогиб в точке подвеса груза Q от его статического действия
определяем методом единичной фиктивной силы
7 О4П 18
= 0,875-10-» л =0,875-10-s см.
96-2-10"-400-10-" '
393
Круговая частота свободных колебаний рамы
-< = 335
При вращении неуравновешенного груза Qt возникает центро-
центробежная сила P0=m1coozp. составляющая которой в направлении
колебаний (рис. 229, б) будет гармонической возмущающей силой
РЪ=РО sin <%'. создающей вынужденные колебания с круговой
частотой
таг
W
и-1500
; 30
= 157 '/се/с.
Наибольшее значение возмущающей силы
Р„=4-157г-4-Ю-г=3940 н.
От статического действия этой силы прогиб посередине ригеля
7-3940-1
7
96
Pol*
El
— = 3,7-Ю-4 ж.
96-2-10"-400-10-s
Так как коэффициент нарастания колебаний
1,28,
1 —
€0»
157'
3352
то амплитуда вынужденных колебаний системы получается равной
/4=р80=1.28-3,7-10-4=4,7-10-4 ж=0,047 см
Задача 976. Определить число оборотов п0 мотора (могущего
перемещаться в направляющих), на оси которого расположен эк-
эксцентрик весом Qt, если известна амплитуда А вынужденных ко-
колебаний мотора. Вес Q включает вес мотора и эксцентрика Qt.
Массу стержней не учитывать.
Q СкГ/см
Щш-
= I,SB-W5Mh/ih2 A=0,JSihm
Задача 977. Определить амплитуду А колебаний поршня инди-
индикатора паровой машины, двигающегося без трения в цилиндре диа-
диаметром D, если давление на поршень изменяется по закону
Рв=РсР+Ро sin <oof.
394
Задачи 978—980. Определить амплитуды А вынужденных коле-
колебаний систем.
В задачах 978. 979 учесть массу балок.
Задача 981. Точка подвеса винтовой пружины совершает гар-
гармоническое колебательное движение согласно уравнению: Хв =
10i20*
Определить амплитуду А вынужденных колебаний груза н ди-
динамические напряжения max тд, если диаметр внтка пружины
D=IQ см, диаметр проволоки пружины d—\ см, число витков
п=25 и G=8-10s кГ/см2.
880
1т-50кГо» сек'
xe=lllsinZOt
Определение напряжений и расчет на прочность
Динамическое обобщенное перемещение 8Д какой-нибудь точки
системы в произвольный момент времени t колебательного движе-
движения складывается из постоянного обобщенного перемещения 8,
соответствующего виду деформации системы при колебании от ста-
статического действия груза Q и собственного веса системы, и пере-
переменного обобщенного перемещения, вызванного возмущающей
силой
Р„ = Ро sin (оо t, т. е. \ = 8 + рао sin <%,'• B34)
Для линейных систем аналогично определяютсн и обобщенные
динамические напряжения рд(од или та) в точках элементов системы.
А именно:
sin
B35)
где р — обобщенное напряжение (о или т), соответствующее виду
деформации при колебании от статического действия груза Q и
собственного веса системы, а ре— обобщенное напряжение от ста-
статического действия наибольшей возмущающей силы Рв-
Экстремальные значения напряжений возникают в моменты наи-
наибольших отклонений системы от положения статического равнове-
равновесия и получаются равными
max
min
рц = р ±
B36)
Так как при колебаниях напряжения периодически изменяются
по величине (рис. 230), то в случае длительного процесса расчет
на прочность колеблющихся систем следует производить методами,
установленными в расчетах при циклической нагрузке.
\
|
1
\
Ч
та*рд
1
\
ттрд
Рис. 230
При кратковременных колебательных процессах, когда ампли-
амплитуда переменных напряжений I max рд ~~mw Рд \ невелика, рас-
расчет на прочность можно производить по максимальным напря-
напряжениям так же, как и при постоянной нагрузке.
Так как наибольшее динамическое обобщенное перемещение
тах8д
где
4-
B37)
B38)
— динамический коэффициент при колебаниях, то наибольшее ди-
динамическое обобщенное напряжение
max рд=рЛд. B39)
Условие прочности может быть записано в следующем виде:
B40)
396
-, B41)
где [р ]—допускаемое обобщенное напряжение (|о] или 1т 1).
Пример 130. Посередине балки прямоугольного сечения F=
=6X/z=12xl аи2 длиной 1-Х м расположен электромотор весом
<Э=20 кГ. Неуравновешенная вращающаяся часть мотора пред-
представляет собой сосредоточенный груз Qt=l кГ, укрепленный на
оси мотора на расстоянии р=4 см (рис. 231, а)
Определить число оборотов в минуту п оси мотора, при котором
наибольшие нормальные напряжения в балке достигнут значения
max од=2000 кГ/см2. Вес единицы объема материала балки i=
=SF/cms, модуль продольной упругости ?=2-106 кГ/см2.
Решение. Собственный вес балки
Q0=^F/=8- Ю-3-12-1 ¦ 102=9,6 кГ.
Момент инерции поперечного сечения балки относительно ней-
нейтральной оси и момент сопротивления соответственно равны:
При статическом действии на балку сосредоточенной силы Q
и распределенной силы Qe наибольшее нормальное напряжение
ошах и наибольший прогиб 8гаах имеют значении:
01 0?
/Ища» 4 8
Ога
гаах = —fr- = ^ - -Щ \Ч Л ~Y) — -4Т2
= 310 кГ1смг,
Q'8 ¦ 5 Qo'3 - <3 !п -1 5
TST + 384 El ~ 48?/ ^W + 8
Так как динамический коэффициент по формуле B38)
, , , A max о, 2000 „ . _
А„ = 1 + -> = ! = „,п « 6,45,
д «max Omax 310
то допускаемая амплитуда колебания
А = l^^i — 1) 8raaiI = 5,45 • 0,27 = 1,47 см.
\ ошах /
При статическом действии иа балку сосредоточенной силы
Q прогиб 8,. в произвольном сечении, находящемся на расстоянии
х от левой опоры, и прогиб 8 посередине балки соответственно
равны:
Qt" - 20 • 10" 5 с„
J ~ 48-2-10». Г -4
Поэтому
и коэффициент приведения массы балки по формуле B38)
Из выражения B29) находим круговую частоту свободных коле-
колебаний балки:
Вследствие неуравновешенности вращающегося груза Q, раз-
развивается центробежная сила Ро=— <»ор, вертикальная состав-
составляющая которой (рис. 231, б) РВ=РО sin <oof представляет собой
гармоническую возмущающую силу, вызывающую вынужденные
колебания балки. Здесь ^о^тя) является круговой частотой воз-
возмущающей силы, а Ро— наибольшим значением этой силы.
При статическом действии силы Ро наибольший прогиб балки
» Р0Р _ ftfp 2 _ 1-10|!-4 2 _ "о
о — 48?/ ~ 48?/g Шо " СЖ
о— 4&EI ~48EIg 0— 48-2- 10е-1-981 о 24-981
Исходя из формулы B32), записываем:
ш2 R1 (В ОJ
147 = - ¦ = . ° ss 0,162
/ Сил \ ^ ' 981 61 ,82 Сил 61,8
24-981 \1—5JT8*/
отсюда
2 61,8»-1,47 ., „i/ 147 coei/
юп = — ... — и ю0 = 61,8 I/ -тду ~ °8,6 Чсек.
Таким образом, искомое число оборотов в минуту
30 30 ¦ 58 6 __„ ,,
п = — щ0 = — » 560 об/мин.
Задачи 982—983. Определить максимальные динамические на-
напряжения в системах, испытывающих вынужденные колебания.
Вес Qo включен в вес Q.
§ 3. Удар
Явление удара возникает при резком изменении скоростей
движения соприкасающихся тел, систем или их частей.
Имеется в виду рассмотрение только простейших случаев со-
соударения движущегося тела (ударяющего тела) с неподвижным
телом или неподвижной системой (ударяемым телом) при следующих
допущениях:
1. Ударяющее тело абсолютно жесткое.
2. Ударяемое тело имеет одну степень свободы и его обобщенные
перемещения пропорциональны соответствующим обобщенным си-
силам при статическом и динамическом действии.
3. Удар неупругий, в процессе которого не происходит отделе-
отделения ударяющего тела от ударяемого, но общие деформации послед-
последнего упругие.
4. Вид деформации ударяемого тела такой же, как и при стати-
статическом нагружении соответствующей обобщенной силой, прило-
приложенной в месте соударения в направлении удара.
5. Скорость ударяющего тела мала по сравнению со скоростью
распространения ударных волн, а время соударения значительно
больше времени распространения этих волн по всему объему уда-
ударяемого тела.
При указанных допущениях обобщенные динамические усилия
Рд, напряжения рд и перемещения 8Д в ударяемом теле приближен-
приближенно могут быть найдены по формулам:
B42)
Здесь Р, р и 8 взяты при статическом действии на ударяемое
тело обобщенной силы, приложенной в месте соударения в направ-
399
лении удара, a kR — безразмерный динамический коэффициент,
больший единицы.
Если ударяющее тело весом Q при встрече с ударяемым телом
весом Qo движется в направлении силы тяжести со скоростью v<,
и вызывает в элементах последнего i/оступательные перемещения,
то динамический коэффициент
B43)
где 8= -g— линейное перемещение точки соударения при стати-
статическом действии груза Q в направлении удара;
С — жесткость ударяемого тела при данном виде его дефор-
деформации ;
km— коэффициент приведения массы ударяемого тела в точку
соударения, который определяется так же, как и при колебаниях;
Т=-Ц^— кинетическая энергия движения груза Q к моменту
соударения;
?/=-| потенциальная энергия упругой деформации уда-
ударяемого тела при статическом действии груза Q.
В СИ кинетическая энергия Т=—?р-, а отношение —jj- заме-
заменяется отношением -^-
m
Из формулы B43) видно, что чем больше жесткость С ударяе-
ударяемого тела, тем больше величина динамического коэффициента kK.
При внезапном приложении груза Q, когда Ро^О.
*д=2. B44)
При ударе без учета массы ударяемого тела, когда
B45)
Если не учитывать массу ударяемого тела, то увеличивается
динамический коэффициент по сравнению с его общим значением
B43), что дает расчет в запас прочности.
400
Если -т-= —-я—=-тг> Ю, то с погрешностью до 5%
go yg ч
динамический коэффициент можно подсчитывать по формуле
Если же —1->> ПО, то с погрешностью до 10% можно
принять
Следует иметь в виду, что пользование формулами B46) и B47)
дает расчет не в запас прочности.
В том случае, когда собственный вес ударяемого тела очень
велик (<2о-*°°). А„-*-2.
При горизонтальном ударе выражение B43) должно быть за-
заменено формулой
В этом случае ие учет массы ударяемого тела дает расчет в за-
запас прочности, хотя кл будет определяться по формуле B47)
Если собственный вес ударяемого тела мал, а на ием располо-
расположен тяжелый груз Qi, по которому производится удар грузом Q,
то в формулах B43) или B48) значение kmQ0 надо заменить зна-
значением Qt.
При расчете ударяемых систем с параллельным, последова-
последовательным или смешанным соединением элементов жесткость системы
С можно определять соответственно по формулам B21), B22),
B23).
Если ударяющее тело совершает вращательное движение и
создает в ударяемом теле деформации, определяющиеся угловыми
перемещениями, то можно пользоваться формулами, приведенны-
приведенными выше, но в них следует заменить линейную скорость v0 на угло-
угловую ю0, а массы— и ~ — на моменты инерции масс 1т и /mo
относительно осей их вращения
401
Расчет на прочность при ударе производят по формулам, ко-
которые установлены для статического нагружения.
Условие прочности можно зашгсать в следующем виде:
max рй = knpmayL < [рй], B49)
I
где max pK— наибольшее динамическое обобщенное
расчетное напряжение;
Ртах — наибольшее обобщенное напряжение при
статическом действии груза Q;
[рд] — соответствующее обобщенное динамичес-
динамическое допускаемое напряжение.
В практических расчетах следует учитывать, что
при ударном нагружении тело приобретает склон-
склонность к хрупкому разрушению, в сильной степени
зависящую от состава и структуры материала тела,
скорости нагружения, температуры и концентрации
напряжений.
В рассматриваемых задачах предполагают, что
указанные основные факторы, влияющие на проч-
прочность при ударе, учтены в заданных допускаемых
напряжениях.
Пример 131. Дано:т=10кг; h~4 см; 1{=20см;
Ft=2cM2;l2=40cM;Fz=4cm2; ?,=?2=?=2- 105Мн/ж2
(рис. 232, с). Собственный вес стержней не учи-
учитывать.
Определить ол1 , оЯг , 8Л.
Решение. Определяем вес ударяюшего груза
Q=mg= 10- 9,81 =98,1 н.
Так как стержни с жесткостями
EF,
EF,
и С„ =
соединены параллельно, то по форму-
формуле B21) жесткость системы
Рис. 232
С —
h
Учитывая, что к моменту удара скорость свободно падающего
груза Q с высоты h будет v0 = V%gh . имеем
Qe
2-4.10-г-4.10«
98,1
= 32-104.
402
Эта величина столь большая, что динамический коэффициент
вполне допустимо определять по формуле B47)
Так как при статическом действии груза Q перемещение его
. Q N, N.
точки приложения о = ^- = ¦—- = -^, то продольные усилия в
поперечных сечениях стержней
N - Q С Q и Л/ - Q Г - Q
Динамические нормальные напряжения в поперечных сечениях
стержней приобретают значения:
= 139-106н/ж2 = 139 Мм/ж2,
F. ж~~ К
= 70-10" н/м" = 70 Жм/ж2.
Динамическое перемещение точки соударения:
8 §* = 566 » 13
Частные случаи.
1) Если С2==0 (рис. 232, б), то
-0,02- 10-г « 2-108 к/л;
к 200 Мм/ж2;
1 = -^г • 4- Ю2 * 2- Ю-4ж ж 0,02еж.
403
2) Если С,=0 (рис. 232, в), то
С=С2 = -^- = g-^g— = 2-108н/л«; А* =4-10а;
О 1П Q Я1
% = -ji К = 4 •4°2 « 2-108 н/ж2 = 20(Шн/жа;
8Д = -§¦ *д - 2- 10-4ж = 2-Ю-2еж.
Пример 132. Дано: Q=4 кГ; А=4 еж; для пружин с малым
шагом ?>=2 см, d=0A см, п=4 витка, G=8-105 кГ/смг; для бал-
Рис. 233 Рис. 234
ки /=40см, я=3сж, 6=1 еж, Е=2- 10екГ/сжг(рис. 233). Собствен-
Собственный вес пружин и балки ие учитывать
Определить max тд в пружине, max од в балке, 8Д— перемеще-
перемещение точки соударения.
Решение. Так как пружины с жесткостями Cl=gg^ со-
соединены между собой параллельно, а балка с жесткостью С2=
= —р- соединена с ними последовательно, то по формуле B23)
жесткость системы как системы со смешанным соединением элемен-
элементов:
4D3n , /s 4-8-4
« 112 кГ/см.
_L , /s 4-8-4 64-1Q8-12
С2 СИ4 48?/ 8-106-256-10-4 48-2-10«-3-1
По формуле B45) динамический коэффициент
404
D 2
Так как -р = q-j = 5, то коэффициент увеличения напряжений
в пружине за счет кривизны витка
D
——~- — О 2*5
и d 0,615 4,75 , 0,615 , „,
ft = —D + -V- = -7- + -5-a!l-31-
Максимальные динамические напряжения в пружинах и балке
max тд = k4^-К « 1.31 Ju'-l(r*' 16 "" 334°
16 « 1280
Динамическое перемещение точки соударения
8д= -§-К = -щ-16
Если бы пружин не было, то С =С%= —р— = 375 кГ/см;
о-я=-т1т--28'4~2270
Пример 133. Дано: <?=20 кГ, й=2 см, р=4 см, /,=/2='з='=
=20 еж, d,= l,4 еж, da=l,2 еж, d3=l еж, С=2,8-105 кГ/см?
(рис. 234).
Собственный вес ступенчатого стержня ие учитывать
Определить \ — динамическое перемещение точки приложения
груза Q, max тД]11й1 — максимальные динамические касательные
напряжения на участках стержня.
Решение. Жесткости на кручение ступеней стержня соот-
соответственно равны:
С — —11- Г — з Г —
сч
Две первые ступени стержня соединены последовательно и их
общая жесткость
С'= _L,_L *
с, + сг
Так как в сечении, где прикладывается внешняя пара сил,
третья ступень стержня соединена с первыми двумя ступенями па-
405
раллельно, то общая жесткость всего стержня как системы с парал-
параллельным соединением элементов:
г г л. г L I г ' , С1рз
C=CO + CS = -^ _ + <;, = —j _ + __»_ =
С, + С2 G/^ +~Gf^~
= 0,1 -M_i2L/___!___ + , \ в 3290 «Г/с*.
Кинетическая энергия ударяющего груза к моменту удара
Т = —5-5-=гОА кГ-см.
Угол статического поворота сечения, где приложена- пара сил
с моментом M=Qp,
_ М __ Qp _ 20-4 _ 8 ,
У ~ С ~ ~С~ ~ 3290 ~~ 329 Р
Потенциальная энергия упругой деформации при статическом
кручении стержня
С/ = -
2 ~ 2С
Так как отношение
G ~ Qy ZO ~ Qf — 20-16 ~*1-1
невелико, то по формуле B46) динамический коэффициент
К = 1 +
Динамический угол поворота сечения стержня, где приложен
внешний момент от падающего груза,
Ф, = фАд=-^-« 0,182 рад.
Динамическое линейное перемещение груза Q
8Д = рфд = 0,182-4 = 0,73 см.
406
Реактивный момент в правой заделке стержня при статическом
действии внешней пары сил с моментом M=Qp
8 2,8.105-0,1
dp,
I
329
20
*34 кГ-см.
Реактивный момент в левой заделке стержня
М„=М — М„=20-4 — 34=46 кГ-см.
Максимальные динамические касательные напряжения на участ-
участках стержня:
М 46
^Ад « 0.2-1.4" 7-5 = 628
maxi4 = -
46
0,2-1.2»
7,5=986 кГ/см*;
¦ 1230
Пример 134. Дано: т=\ кг, vo=4 м/сек, яг4=20 кг, d=2 еж,
/=0,4 м, ?=|-G=2-105 Mw/ж2 (рис. 235).
Удар горизонтальный. Собственным весом
стержня пренебречь.
Определить тахол, max тДг, 8Д.
Решение. Определяем вес, соот-
соответствующий массе т: Q=mg=9,8l н.
Поскольку система подвергается удару
массой т, движущейся горизонтально, ди-
динамический коэффициент должен опреде-
определяться по формуле B48)* с заменой вели-
величины kmm0 величиной массы т1г т. е.
1
Рис. 235
т,
Так как горизонтальное перемещение точки соударения от за-
закручивания вертикального стержня статически действующей силой
<2 в направлении удара
ЛОЛР
то ударяемую систему можно рассматривать как систему с последо-
последовательным соединением горизонтального изгибаемого элемента,
* Так как задача решается в СИ, то в формуле B48) отношение —2р?.
заменяется на т°.
407
ОГ1
жесткость которого Ct= —я-, и вертикального закручиваемого
элемента, жесткость которого по отношению к линейному переме-
перемещению точки соударения С2-=—-?-.
По формуле B22) жесткость всей системы
С:
1 ПГ ~ j»_ _?<_ ~ р /»
С, + С2 3?/ + С/„ Б 1 + С/
8-1010.0,1.0,02<
*> , от » „а «16-Ю3 И/Л.
~ 1,27/3 ~ 1.27-0,43
Динамический коэффициент
д |/ 1-9,81 _20_
При статическом действии силы Q в направлении удара мак-
максимальное нормальное напряжение отах в горизонтальном стерж-
стержне, максимальное касательное напряжение ттах в вертикальном
стержне и линейное перемещение 8 точки соударения имеют зна-
значения:
= 5 Мн/м*.
¦W = -г- « о926оау ж 2-5> 1Ов н/ж8 = 2'5
8 = тг = жта» ~ 0>613' 10ж = °-0613 см-
Искомые динамические величины получаются равными!
max од = /глота1[ = 11,2-5 = 56 Мн1м2;
¦м2; \=кпЪ = 11,2-0,0613:
« 0,69 еж.
Если бы к системе не была присоединена масса mt, то
^ 51,6; max ол = 51,6-5 =
= 258 Мн/м2;
max *д = 51,6-2.5 = 129 Мщм\ 8, =51.6-0.0613 «3,16 см.
408
Пример 135. Продольный удар. Даио: Q=8 кГ, т=8 Г/см3,
1=2 м, F=i см2, Е=2- 10е кГ/см\ [од] = 1000 кГ/см* (рис. 236).
Определить h с учетом и без учета массы стержня.
Решение. Так как при статическом действии
груза Q
то по формуле B49) динамический коэффициент
*=JuL=J™ 500.
Рис. 236
С другой стороны, поскольку скорость движения груза Q к
моменту удара vo=\r2gh, жесткость стержня при растяжении
С=—, собственный вес стержня Q0=-\Fl и коэффициент приведе-
приведения массы стержня в точку соударения Ьт—-% (см. пример 125),
то по формуле B43)
k _i , / , , 2ft?F
Ql
= 1+
Л
1 /
a*-2-io'-4
8-2-10* 1 64
1+ з "Т
Поэтому 500 = 1 + т/ 1 -|- 3'10< h . откуда й =
г 3,8
D992—1)-3,8
з-ю*—-
Без учета массы стержня
и кпп Л Г V°C 1 Г
Ад =500 = |/ -^- = J/
8-2-108 — '" у "
Следовательно, й=25 см.
Это значит, что расчет, не учитывающий собственный вес стерж-
стержня, дает заниженное значение безопасной высоты падения груза на
-^¦Зпг^--ЮО «21%.
409
Пример 136. Поперечный удар. Дано: /г=5 см, 1=1 м, I—
=2000 см\ W=200 см3, Q0=25 кГ, ?=2-10" кГ/см\ [о.]==
= 1200 кГ/см2 (рис. 237).
Определить Q с учетом и без учета массы балки.
Решение. При статическом дейст-
действии груза Q прогиб свободного конца
балки 8 = ~^-; прогиб произвольного
сечения балки, находящегося на рассто-
расстоянии х от заделки, по формуле метода
начальных параметров
. 1 / Qlx* __ Qx<>\ _ Ql3 /JJ_ jp 1_ x3 \
*~ El \ 2 6 J 3?/ [ 2 " I" 2 ' P ) ¦
Поэтому коэффициент приведения массы балки в точку соу-
соударения
*™ =~г\ (~Г") dx =~ГJ ("a5 I5") ^ = "по"*
с с
Динамический коэффициент по формуле B43)
1+ Г\ л-
2h3El
33
1 + 140
= 1+-./ 1 +
2-5-3-2-10в-2
Q-10» _^
+ 140 '
12-10'
^ Q+6
С другой стороны, поскольку при статическом действии груза Q
наибольшее нормальное напряжение в балке
_ Ql _ Q-100 _ Q п ,
°шах — ~р 200~ 2~ '
то по формуле B49) динамический коэффициент
_ [ад] _ 1200-2 _ 2400
д~ "max ~ С ~ Q '
или
~ 2400 , , -, Г, Г
Следовательно, —^— = 1 + |/ 1 +
13Qa — 6 ¦ I02Q — 36 ¦ 102 =0.
410
откуда
Задаче удовлетворяет только один корень
Без учета массы балки
2-400
Поэтому
24»-10*.Р 24». 10'-10» _ла.гГ
2Л-3-И ~ 2-5-3-2-10»-2-10»
Таким образом, если не учесть массу балки, то безопасный вес
падаюшего груза снижается на —^— 100 «8%.
Рис. 238
Пример 137. Крутящий удар. Груз Q=3 кГ вращается на плече
р=8 см вокруг горизонтальной оси х с постоянной угловой ско-
скоростью соо и ударяет по выступающей части цилиндрического стер-
стержня длиной 1=40 см и диаметром rf=6 см (рис. 238).
Определить допустимое число оборотов п вращения груза Q в
минуту, если вес единицы объема материала стержня f=8 Г/см3,
модуль сдвига G=8-10s кГ/см2 и допускаемое касательное напря-
напряжение [хд 1=400 кГ/см2.
Решение При статическом действии груза Q на стержень,
в последнем возникают максимальные касательные напряжения
Динамический коэффициент
k = -М- = 40° 9 = 720
411
Так как момент инерции массы груза Q вокруг оси вращения
U = "f- P2 =4бГ
момент инерции массы стержня
' d4 01
коэффнциент приведения массы стержня (см. пример 127) km=-^,
кинетическая энергия вращательного движения груза
^ «0,1 «eg кГ-см
и потенциальная энергия упругой деформации кручения стержня
прн статическом действии груза
и - -2Й. ~ Q-64-40 - ' кг см
2Gfp ~ 2-8-10»-0,1-6* "~ 9-103 Л СМ'
то по формуле B43) динамический коэффициент
3-0,2
Сравнивая найденные динамические коэффициенты, получаем:
719 = |Л + 841ш? , откуда
= 25 н я = -^- -25 « 240
Без учета массы стержня
Поэтому
ю0 = -Щ- = ^- = 24 и п=-^р-«230 об/мин.
Таким образом, если не учитывать массу стержня, то допускае-
- 240—230
мое число оборотов ударяющего груза снижается на g^j х
X 100=4%.
412
= 720 = 1/ 4г = 30ш0.
Задачи 984—1003. Определить величины, указанные в усло-
условиях задач для упругих систем, подвергающихся удару.
Собственную массу элементов систем не учитывать В задачах,
которые решаются в общем виде, динамический коэффициент оп-
определять по приближенной формуле
k —
В рамных системах и в кривых брусьях учитывать только де-
деформацию изгиба.
ш
*U-a -4—0 —К а-А
Жесткость пружиныI-С, )кГ
Жесткость прутиныП-СИ1^м
see
а)
СкГ/см
Ш
?, f.[<jJ,W
п
413
331
-0,5 м
, w,
ЭЭ5
Т
f, I.
1
-2а-
[,I. W
ДИ
,X, W отел ва=?
10П0
шш
Зм-
0 /V
?.1
414
IBB!
Glp
Задача 1004. Доказать, что для указанных балок наибольшие
динамические напряжения без учета массы балки не зависят от
способа закрепления и величины а.
Считать А>8
г— а ~г^ Л
р i Н
Задача 1005. Определить о, при котором таход будут иметь
наименьшее значение. Массу балок не учитывать и считать h^>b.
Задача 1006. Определить тахтд в вале, вращающемся с угло-
угловой скоростью ш и несущем маховик с моментом инерции массы /т
при резком зажиме конца:
а) в одном подшипнике; б) в обоих подшипниках одновременно.
415
Задача 1007. Определить шахтд в вале передаточной системы
при резком торможении конца вала в подшипнике А.
Ж
(О л V////A
вкГ/смг
Задачи 1008—1011. Определить величины, указанные в усло-
условиях задач для систем, подвергающихся удару.
Учесть собственный вес тех элементов, для которых он указан.
В расчетах принять во внимание замечания, сделанные к задачам
984—1003.
W0B
1009
I
.=?
416
Задача 1012. Решить задачу 993 с учетом массы балки. Вес
балки Qo.
Задача 1013. Определить max тд в вале от крутящего удара,
вызванного включением муфты Мф. Муфта включения обеспечивает
соединение вращающейся системы правой части вала с неподвижной
левой частью.
Мф-муфто
включения
Задача 1014. Определить и сравнить оду, од//, оДу;у в стерж-
стержнях /, //, /// при ударе одним и тем же грузом Q, падающим с
одной и той же высоты А== 10 см.
XV. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ
В этой главе рассматриваются напряжения, периодически изме-
изменяющиеся в течение длительного времени.
Совокупность последовательных значений переменных напря-
напряжений за одни период процесса их изменения называется циклом
напряжений.
При систематическом действии на тело переменных напряже-
напряжений в местах их наибольшей концентрации могут возникнуть и
развиваться трещины, приводящие тело к хрупкому разрушению.
Процесс возникновения и развития в материале тела трещин от
действия переменных напряжений называется усталостью мате-
материала.
Сопротивляемость материала переменным напряжениям назы-
называется выносливостью материала. Наибольшее периодически из-
изменяющееся напряжение, которому материал противостоит неогра-
неограниченное время, называется пределом выносливости материала.
Обычно определяют условный (ограниченный) предел выносли-
выносливости, принимая за базу ограниченное число циклов изменения на-
напряжений, например, для черных металлов E-е-10) • 10е циклов,
для цветных металлов E0-j-lOO)-10е циклов и т. д
14 Заказ № 886
417
Характеристикой цикла является коэффициент асимметрии
цикла г, определяемый как алгебраическое отношение
Pmln
B50)
ГДе Ртах ("max И Тша]!) И рш1п (ош1п Н ТшШ) —
наибольшее и наименьшее напряжение цикла
Ртах ~Ь Pmln
Величина
Рт ="
называется средним напряжением цикла, а
Ртах — Pinin
Ро = - 2
амплитудой цикла.
Предел выносливости
B51)
B52)
B53)
где р'тд^, р^, р'а —наибольшее напряжение, среднее напряжение
и амплитуда цикла при работе матерала на пределе выносливо-
выносливости.
Рис. 239
Рис. 240
При симметричном цикле (рис. 239)
Ршах =—Pmln ; Рт=0; Г=—1; pr=p_i.
При знакопостоянном положительном асимметричном цикле
(рис 240)
0 0
Рис. 241
Рис. 242
418
Прн знакопеременном асимметричном цикле (рис. 241)
AW>0; Рш1„<0; -1<г<0.
При положительном отнулевом (пульсирующем) цикле (рис. 242)
Ртах > 0; рт,„ ==0; рт = ра-
Ртах
; г = 0, р, = р„.
§ 1. Основные факторы, влияющие
на выносливость материала*
Характер цикла и вид деформации
При симметричном цикле предел выносливости материала (прн
прочих равных условиях) имеет самое низкое значение. Величина
предела выносливости прн симметричном цикле p_i (o_i или т_])
определяется по кривой (рис. 243), которая строится на основании
'I N{ чиспо циклов)
Рис. 243
Рис. 244
опытных данных. Для этого к правой части кривой, переходящей
в горизонталь, проводится касательная. Ордината, отсекаемая
этой касательной, и принимается за условный предел выносливости.
Установлены следующие приближенные соотношения между
пределами выносливости при симметричном изгибе о_ь симмет-
симметричном осевом растяжении — сжатии о-i,,, симметричном кру-
кручении t_i н пределом прочности ов:
для стали
o_j »@,4 -^ 0,6) ов; а.1р »@,7 4- 0,8) о_1; т., « @,4 -J- 0,7) о_1;
для чугува
о.± « @,4 ^ 0,5) ов; т., « @,7 -г- 0,9) о^;
* Указываются только сведения, которые необходимы для решения задач,
помещенных в сборнике.
14 Заказ № 886
419
для цветных металлов
о.!» @,25 -f- 0,5) ав.
При асимметричном цикле предел выносливости можно опре-
определять по опытной кривой предельных амплитуд, построенной в
координатах: рт— ра (рис. 244).
На рисунке через рв обозначен предел прочности материала
при данном виде деформации тела.
При заданном коэффициенте асимметрии цикла г= р""п-
Ртах
устанавливают величину tgC =-^-=-рт7 и УТЛ& Р-
Из начала координат под углом C к оси р,п проводят прямую.
Складывая координаты prm и р'а точки пересечения прямой и
кривой, находят предел выносливости
Рт = Р'т + Ра •
Пример 138. Дано: сталь марки 40 в нормализованном состоя-
состоянии. Журнал наблюдений при испытании на выносливость изгибом
по симметричному циклу:
а Мн/м2 300; 290; 280; 270; 260; 250; 240; 235; 230; 230;
N-^ 0,52; 0,71; 1,21; 2,32; 3,44; 4,82; 5,85; 8,51; >10; >10
— два последних образца не разрушились.
Определить a_j.
Р е ш е н и е. По опытным данным строим кривую выносливости
в координатах а Мн/м2— ^ (N — число циклов) (рис. 245).
Проводя касательную к правой концевой части кривой, на оси
ординат устанавливаем значение условного предела выносливости
о.х » 232 Мн/м2.
Пример 139. Дано: материал — сталь марки Ст. 3; опытные
значения а„=38,8 кГ/мм2, с_,= 18,5 кГ/мм2 и предельных ампли-
амплитуд цикла За при заданных средних напряжениях <?,:
а'т, кГ/мм1 10 20 30;
а'а, кПмм2 17,5 14 8,5.
Определить а0, 25.
Решение. По опытным данным строим кривую предельных
амплитуд в координатах ат— аа (рис. 246).
Так как предел выносливости надо определить при коэффици-
коэффициенте асимметрии цикла г=0,25, то
420
Из начала координат проводим прямую под углом C=31° к
оси ат. Координаты точки пересечения этой прямой с кривой пре-
предельных амплитуд:
О«.25 я 22,5 кПмм* и <#25 я 13 кГ/мм2.
бМн/м*
300
б„ иГ/мм?
0 2 4 6 8 Ю 12 щ±
106
Рис. 245
Искомый предел выносливости
10 20
6т КГ/ММ1
30 10
Рис. 246
,25
= °?25 +
« 22,5 + 13 = 35,5 кГ/жма.
Концентрация напряжений
Концентрацией напряжений называется местное повышение
напряжений вблизи концентратора (т. е. местного изменения формы
тела в виде отверстия, выточки, надреза, галтели и т. п.).
Отношение максимального местного напряжения рм (ом или
ты) к номинальному р (о илн т) в ослабленном концентратором
сечении (но без учета концентрации), установленное при стати-
статической нагрузке в предположении идеальной однородности, изот-
изотропности и упругости материала, называется теоретическим коэф-
коэффициентом концентрации напряжений:
= -**-: (в.
и а.
B54)
Коэффициент с>1 отражает влияние только геометрии концен-
концентратора на величину максимального местного напряжения.
При переменных напряжениях вводится понятие эффективного
коэффициента концентрации напряжений:
Pi,
И rf=
14*
B55)
421
который представляет собой отношение предела выносливости при
симметричном цикле гладкого образца р_, к пределу выносливости
образца тех же размеров, но с концентратором pLt.
Коэффициент аэ отражает влияние на предел выносливости ие
только геометрии концентратора, но и материала образца.
Отношение
Я = -^=f- B56)
называется коэффициентом чувствительности материала к кон-
концентрации напряжений. Он изменяется в пределах 0<;<7<!1.
Для чугуна <7=0, для конструкционных сталей <7=0,6-г0,8
(где меньшие значения относятся к сталям средней прочности, а
большие — к сталям высокой прочности), для сталей с
ов >130 кГ/мм2, <7~1
(в приложении 5 на рис. 1 приведен график приближенных зна-
значений q для стали в зависимости от ов и а^, без учета влияния раз-
размеров тела).
Так как д зависит еще от формы и размеров тела, то в практи-
практических расчетах надежнее пользоваться значениями аэ, установ-
установленными при натурных испытаниях.
Масштабный фактор
Влияние абсолютных размеров тела на предел выносливости
называется масштабным фактором.
Уменьшение предела выносливости с увеличением абсолютных
размеров тела оценивается масштабным коэффициентом ем<1,
представляющим собой отношение предела выносливости образца
данного диаметра D к пределу выносливости стандартного образца
диаметром d:
ем = ^"ф- B57)
(P)
(в приложении 5 на рис. 2 приведен график значений ем в зависи-
зависимости от D для углеродистой и легированной стали при различной
обработке поверхности образцов. Этим графиком можно поль-
пользоваться для приближенного определения ем как при изгибе, так
и при кручении).
Если эффективный коэффициент концентрации взят из графика,
в котором учтен масштабный фактор, то вносить поправку на раз-
размеры тела не требуется.
422
Состояние поверхности
Влияние состояния поверхности тела на предел выносливос-
выносливости учитывается коэффициентом поверхностной чувствительности
еп<1, представляющим собой отношение предела выносливости
образца с заданным состоянием поверхности (р-\) к пределу вы-
выносливости такого же образца, ио с полированной поверхностю p~i
*п - -^ B58)
(в приложении 5 на рис. 3 приведена зависимость еп от оЕ для раз-
различных состояний поверхности образцов).
Упрочняющее влияние поверхностного иаклепа, поверхностной
закалки, цементации, азотирования и других технологических
факторов оценивается коэффициентом C, взятым из справочной ли-
литературы, который вводится сомножителем к коэффициенту еп.
§ 2. Расчет на прочность при линейном напряженном
состоянии и чистом сдвиге (кручении]
Предполагается, что с изменением нагрузки характер напряжен-
напряженного состояния в исследуемой точке тела не изменяется и циклы
изменений напряжений остаются подобными (/-=const)
При симметричном цикле переменных напря-
напряжений коэффициент запаса прочности устанавливается по величине
предела выносливости детали Влияние основных факторов (кон-
(концентрации напряжений, масштабного фактора и состояния поверх-
поверхности) на выносливость детали можно учесть общим коэффици-
коэффициентом
е = . е" Ре" ,. B59)
Поэтому коэффициент запаса прочности, с которым работает
деталь при симметричном цикле, можно оценить, пользуясь выра-
выражением
n=-i?i, B60)
Ртах
гае Ртах — максимальное (номинальное) напряжение в детали.
Условие прочности представится в виде
а величина допускаемого напряжения
1/Ч] = -^. B62)
[«I
где [я ] — допускаемый (рекомендуемый) коэффициент запаса.
423
При асимметричном цикле изменения напряже-
напряжений с заданным коэффициентом асимметрии г (или tg$=~^)
коэффициент запаса усталостной прочности можно установить,
пользуясь упрощенной диаграммой предельных амплитуд, постро-
построенной по пределу выносливости p_i при симметричном цикле и
пределу прочности рв при статическом растяжении (рис. 247).
Если рабочий цикл на
этой диаграмме характеризу-
характеризуется точкой С, а подобный
ему предельный цикл — точ-
точкой D, то графически коэф-
коэффициент запаса прочности вы-
0D
разится отношением п=—^-
или аналитически
B63)
Рис 247
При переменных напряжениях с небольшой амплитудой может
оказаться, что предельное состояние пластичного материала будет
определяться не усталостью, а текучестью (участок ЕМ) и тогда
коэффициент запаса прочности определится по пределу текучести
Рт
, - B64)
Ртах Рт "Г Ра
При проверке прочности рекомендуется сопоставить величины
запасов прочности, вычисленные по формулам B63) и B64), и при-
принять меньший из них. Принятый коэффициент запаса должен быть
не меньше допускаемого Из формулы B63), приравнивая п=[п ],
рт= 1рт] и ра— 1ра), величина допускаемого напряжения при
асимметричном цикле 1р,\ получается
Рт
Рв
B65)
где [р] ( [о] или [т]) — допускаемое напряжение при статической
нагрузке.
Условие прочности принимает вид:
= Рт + Ра
B66)
Для большего упрощения расчетов, но в сторону повышения
вапаса прочности, можно использовать спрямленную диаграмму до-
допускаемых напряжений Зодерберга (рис. 248).
424
По этой диаграмме коэффициент запаса прочности
р-1
Р-г
Рт
Ра
а величина допускаемого напряжения
B67)
B68)
Пример 140. Стержень кру-
круглого сечеиия диаметром d—
= 40 мм с гладко шлифован-
шлифованной поверхностью изготовлен
из стали марки Ст. 4, для ко-
торой ов =480 Мн/м2 и o_i=
=200 Мн/м2.
Определить коэффициент за-
запаса прочности п, с которым
будет работать стержень в усло-
условиях переменного изгиба по
симметричному циклу, если
•Мпмш =—Мт\„ =640 н-м.
Рис. 248
Решение. Наибольшее и наименьшее напряжение цикла
„ AW 640 _1П8 .,/„»—If
W
0,1.4» Ю-6
Из графика рис. 2 .приложения 5 для стержня круглого сечення
диаметром d=40 мм из углеродистой стали с гладко шлифованной
поверхностью масштабный коэффициент ем=0,86.
По формуле B60) коэффициент запаса прочности | Р
юо
Пример 141. Ступенчатый стержень круглого сече-
ния диаметрами С=80 мм и d=40 мм (рис. 249) изготов-
изготовлен из стали 40Х, для которой ов=1000 Мн/м2 и
с_|„=250 Мн/м2. В галтелн j-= 0,2. Поверхность стер-
жия тщательно полирована.
Определить наибольшее значение переменной осевой
силы Ршах, изменяющейся по симметричному циклу,
при которой будет обеспечен коэффициент запаса про-
прочности In 1=1,8.
Решение. Из графика рис. 4 приложения 5, при ^=0,2,
для стали с ов= 1000 Мн/м2 путем линейной интерполяции находим
425
эффективный коэффициент концентрации напряжений аэ=1,7.
При тщательной полировке еп= 1
Допускаемое напря»ение
(а 1 "-'" 25° —go Мн,м*
1 1 М ' "
(а 1
1 -IP1 ~ |п|аэ ~~ 1.8 1.7
Наименьшая площадь сечения стержня
F ^JL^L = ,1.4 « 12,6 сжа.
Наибольшая переменная осевая сила
Лпах= [a-lp]F = 82-\Ob-l2,6-Wr' = 103 000 н = 103 кн.
Пример 142. Вал круглого сечения
диаметром d=50 мм из углеродистой
стали ов=60 кГ/ммг и тщательно поли-
полированной поверхностью имеет сквозное
поперечное круглое отверстие диаметром
Ряс. 250 а= 10 мм и подвергается знакоперемен-
знакопеременному кручению по симметричному циклу
при max Мк——min Мк=90 кГ-м (рис. 250).
Определить коэффициент запаса прочности, с которым работает
вал.
Решение. Принимаем приближенно о_]=0,4 ов и
T.J = О.Бо.! = 0,2-60 = 12 кГ/мм2.
Из графика рис. 5 приложения 5 для стали с ов=60 кГ/мм2
устанавливаем эффективный коэффициент концентрации напря-
напряжений, учитывающий абсолютные размеры вала аэ=1,77.
Момент сопротивления при кручении круглого сечения, ослаб-
ослабленного отверстием при отношении ^-=0,2, согласно справочным
данным:
WK = -^|L 0,84 « 20,6 см3.
При действии max Мк=90 кГ-м
_ _ "ldA '"к au-m- , 437 кГ/гм*
WK 20,6
Искомый коэффициент запаса прочности
т., 12-Ю"
n = —— = ss; 1,00.
Сэ-Ъш 1,77-437
423
Пример 143. Определить допускаемое напряжение на пере-
переменный изгиб при характеристике цикла г——0,6, если рассчиты-
рассчитывается деталь из легированной конструкционной стали с ов=
= 100 кГ/ммг и от=80 кГ/мм2'пра коэффициенте запаса прочности
1и]=2 Деталь круглого сечеиия диаметром d—40 мм имеет кон-
концентратор, для которого теоретический коэффициент концентрации
напряжений аа =1,6 Коэффициент упрочнения от поверхностного
наклепа р= 1,4.
Решение. Принимаем о_,=0,4 ов=0,4-100=40 кГ/смг. По-
Полагая, коэффициент чувствительности материала <7=О,8, подсчи-
подсчитаем по формуле B56) эффективный коэффициент концентрации
напряжений
1„— 1)=Ц-0,8A,6- 1) = 1,48.
Масштабный коэффициент ем находим по кривой 5 для легиро-
легированной стали с умеренной концентрацией напряжений из графика
рис. 2 приложения 5, т. е. еы^0,65.
Допускаемое напряжение при постоянной нагрузке
[с] = -5_ = Ж = 40 кГ/мм\
М 2
По формуле B59) коэффициент влияния различных факторов
на выносливость при симметричном цикле
1,48
о 615
По формуле B62) -допускаемое напряжение при симметричном
цикле
г 1 ео 1 0,615-40 inn rt 8
[o_j] = -—— я^— = 12,3 кГ/мм .
По формуле B65) допускаемое напряжение при асимметричном
цикле с коэффициентом асимметрии г=—0,6 получается равным
A + 0,6) 40 + A — 0,6I2,3-0,8
Пример 144. Проверить прочность
ст упенчатого вала круглого сеченвя ди-
аметрами D=60 мм и d=30 мм (рис. М„ „ i м„
¦"¦"-¦ "- стали марки 45с г?" 1 kLJ CS
р
251) из углеродистой
ов=70 кГ/мм2, ъ=2
= 16 кГ/ммг при коэффициенте запаса
прочности In 1=1,6 В галтели -j=0,l Рис 2Б1
427
и коэффициент упрочнения от обдувки дробью р= 1,1. Вал испыты-
испытывает переменное кручение при max Ж„=48 кГ-м, min Мк=
=—24 кГ-м.
Решение. Допускаемое касательное напряжение при по-
постоянном кручении
Из графика рис. 6 приложения 5 путем линейной интерполяции
при -^=0,1 Для стали с о„=70 кГ/мм2 эффективный коэффициент
концентрации а*;=1,28.
Коэффициент влияния на выносливость всех факторов
8 1,1
1,28
; 0,86.
Допускаемое напряжение при симметричном цикле
г т El I 0,86' 16 г. ~
[т1=^=86
Характеристика заданного цикла
24
max MK 48
_ q 5
Допускаемое напряжение по формуле B68) при г=—0,5
г. ..,_.. 2WK.I _
« 23'8"8'6 « 9,5 кГ/мм* « 950 к/7сж».
A+ 0,5) 13,8 +A — 0,5)-8,6
От действия max MK рабочее максимальное напряжение
__ тахУИк 48-10*
16
Таким образом, прочность вала обеспечена.
§ 3. Расчет на прочность
при сложном напряженном состоянии
Рассмотрим только плоское напряженное состояние, показан-
показанное на рис. 252, для пластичного материала.
428
Условие прочности записывают в соответствии с третьей или
четвертой гипотезой прочности в следующей эллиптической форме:
j?=. + J^-<l. B69)
Здесь ошах = % + ой; тшах = тт 4- хй, а [ог] и [т,]—
допускаемые нормальное и касательное JI
напряжения, установленные по формуле B65
268)
б I '
р у фр
или 268) в соответствии с характеристиками
циклов изменения нормальных и касатель-
касательных напряжений.
Общий коэффициент запаса прочности п
детали при совместном действии на нее пе- рвс 252
ременных о и т определяется из выражения:
г-
6
B70)
где л„ и nz —частные коэффициенты запаса прочности от действия
на деталь соответственно только переменных о и только перемен-
переменных т. Эти частные коэффициенты запаса прочности устанавли-
устанавливаются по формуле B63) или B67).
Пример 145. Стальной нал (Ст. 5) подвергается действию пе-
периодически и синхронно изменяющихся изгибающих моментов
Л^пмх=400и-л, Мтш=—160 н -м и крутящих моментов max Мк =
=640 н-м, min MK =320 н-м. Вал ступенчатый диаметрами
D=50 мм и d=40 мм; радиус галтели р=0,25 см. Для Ст. 5:
ов=540 Мн/м\ от=280 Мн/м2, тв=350 Мн/м\ тт=180 Мн/м2,
о_,=240 Мн/м2, т_, = 140 Мн/м2.
Определить коэффициент запаса прочности п, с которым рабо-
работает вал.
Решение. Пользуясь линейной интерполяцией, из графиков
рис. 6 и 7 приложения 5 определяем коэффициенты концентрации
напряжений при -^-=-^=0,0625 для о„=540 Мн/м2
1,81 и а^о^ 1,42.
Так как в данном случае -j=^-=l,25<2, то надо сделать
поправку для осэо и «э,-
Из графика рис. 8 приложения Б находим поправочные коэффи-
коэффициенты Е, =0,83 и U =0,79.
Окончательные значения о|о и nj, устанавливаем по формуле,
указанной на рис. 8 приложения 5:
аэ = l +4aL-1)sI +0,83A,81 —1) = 1,67
429
al = l +K{al~ Ч*1 + 0,79A,42—1)« 1,33.
По кривой 3 графика, изображенного на рис. 3 приложения 5,
для ав=540 Мн/м2 определяем коэффициент поверхностной чув-
чувствительности е„ =0,88
Общие коэффициенты влияния на выносливость всех факторов
получаются равными:
. _ *п _ 0,88 ^O5g и е _%, =^88
Е" 1,67 z a* J,33
Наибольшие и наименьшие нормальные и касательные напря-
напряжения при переменном изгибе и кручении имеют значения:
<W = -^!SS- = Мшах = — ¦ = 64-10» н/м2 = 64 Мн/м2;
тах W п<Р 6,28-Ю-6
32
о = —!2!2- = —— ¦ = —25,5-106 н/м2 — —25,5 Мн/м2;
max
12,56. Ю-6
16
= 51 Мн/м2;
^°= 25,5-10» н/^ = 25,5 Мн/м2.
х =
тт Wp 12,56
Средние напряжения и амплитуды циклов нормальных и каса-
касательных напряжений получаются равными:
2
2
2
ттах Cmln
64
51
51
2
4-25
2
2
— 25
,5
5
,5
38,2
По формуле B63) находим коэффициенты запаса прочности па
нормальным и касательным напряжениям:
с-1 240
_
¦¦ 2,59;
-?41 13 4-
540 " +
3 4
540 " + 0,53
430
1Ц =
1-1
140
350
140
.38,2+
-4,06.
0,66
Общий коэффициент запаса прочности устанавливаем по фор-
формуле B70)
2,59 4,06
V п\ + п\
,Об2
да 2,18.
Пример 146. Деталь, изображенная на рис. 253, изготовлена
из стали марки Ст. 6, для которой ов=60 кГ/мм2, от=32 кГ/мм2,
тт=22 кГ/мм2, о_,=25 кГ/ммг и
т_,= 15 кГ/мм2, ?>=80 мм, d=
=40 мм, р=0,2 см, 1=40 см, а=
= 10 см, P0=const=16 кГ; Р изме-
изменяется по симметричному циклу
от Рта% до Ртт =— Ршах.
Определить допускаемое значе-
значение Pmsx, если для детали пре-
предусматривается коэффициент за-
паса прочности [п]=2. Поверх-
Поверхность детали грубо обточена
Решение Из графиков рис. 6 и 7 приложения 5 при
i = -Ы- = 0,05, -?- = 2 для ов = 60 кГ/лшг
d A d
определяем эффективные коэффициенты концентрации напряже-
напряжений в галтели
О° да 2,07, О' « 1,56.
По кривой 4 рис. 3 приложения Б для о„=60 кГ/мм* коэффи-
коэффициент поверхностной чувствительности еп=0,8 Общие коэффици-
коэффициенты влияния на выносливость всех факторов:
0,8
2,07
.0,386 и е, =
1,56
« 0,512.
Наибольшие и наименьшие нормальные напряжения в галтели
от переменного изгиба по асимметричному циклу имеют значения:
0 1• 64
"! 40 = 100 + 62,5Ртах кГ1см\
431
о = _Ро-Рп,гх г ^ _?б-ршт 40 = 100 — 62,5Ртах кГ/алК
W 0,1-64
Наибольшие и наименьшие касательные напряжения в гал-
галтели от переменного кручения по симметричному циклу приобре-
приобретают величину:
= 0,732Ршах кГ1см\
Wp - " 0,2.64 " шах
W = - -~^- a « - 0,732Pm
Средние напряжения и амплитуды циклов нормальных и каса-
касательных напряжений получаются равными:
= %,„ + «„»„ = шо
тт = 0; тй = 0,732Рт
По формуле B67) находим коэффициенты запаса прочности по
нормальным и касательным напряжениям:
25 25
А, = •
25 ,0,625 0,732 +1,62Ртах
32 ' ' + 0,386 та!!
^^-1 0,512-15 105
= -— ~-
to 0,0732Pmax ~ Яшах *
Так как общий коэффициент запаса прочности по формуле B70)
_2= п°п% —. 25-Ю5 х
"" ~ V^W, Ртах @,732+l,62Pmax)
1
105"
@,732+1,62Ртах
25-105
@,732 + 1,62Ртш)>
ТО
432
Ю52 @,732 +
ЯЛИ
+ 0,885Pmax — 58,1 = 0.
Отсюда искомая наибольшая допустимая сила
Рты « — 0,442 ± |/0,4422 + 58,1 » — 0,442 ± 7,63 кГ.
Так как задаче удовлетворяет только один корень уравнения,
то Ртахх7,2 кГ.
Задача 1015. Пользуясь нижними границами эмпирических
зависимостей, определить приближенное значение предела вынос-
выносливости при переменном кручении по симметричному циклу сталь-
стальных образцов с концентратором, если ов=960 Мн/м2, а, =1,6,
<7=О,9.
Задача 1016. Стальной ступенчатый стержень круглого сечения
диаметрами d=36 мм и D—72 мм подвергается переменному рас-
растяжению — сжатию при Рт^——Ртт—5 Т.
Определить минимальный допустимый радиус галтели р, если
известны о„=40 кГ/мм2, о_[Р =12 кГ/мм2 и нужно, чтобы коэф-
коэффициент запаса прочности [я] =2
Задача 1017. Ступенчатый стержень круглого сечения диамет-
диаметрами ?>=60 мм, dt—30 мм и d2=32 мм изготовлен из стали марки
20Х, для которой св=80 кГ/мм2 и o_ip=24 кГ/мм2.
В галтелях^5-=О,3 и -j-=0,l. Поверхность стержня
тщательно полирована.
Определить коэффициент запаса прочности п, с ко-
которым работает стержень в пресной воде при перемен-
переменной осевой силе Ртах =—Ртт =3 т, изменяющейся по
симметричному циклу.
Задача 1018. Определить максимальную изгибаю-
изгибающую силу Ртах, при которой стальной ступенчатый
вращающийся вал может работать по схеме, указанной
на рисунке, с коэффициентом запаса прочности [л] = 1,8.
Считать известными: ов= 1200 Мн/м2, o_i=360 Мн/мг,
433
О=70лш, d=50 мм, -^-=0,15, /=60 см, а = 40 еж. Поверхность
вала отшлифована
W18
м„
Задача 1019. Ступенчатый вал, имеющий D=60 mm, d=50 мм,
-^-=0,05, должен работать в пресной воде на знакопеременное
кручение по симметричному циклу с коэффициентом запаса [л ]=
= 1,5. Поверхность вала отшлифована. Установить, какой вал
будет прочнее: из стали марки Ст. 5, для которой св=52 кГ/ммг
и т_1 = 14 кГ/мм2, или из стали марки 40Х, для которой о„=
= 100 кГ/мм* и т_,=22 кГ/мм2.
Задача 1020. Дано: сталь марки ЗОХМ; опытные значения:
ов=90 кГ/мм2, о_1р=36 кГ/мм2 и предельных амплитуд </а при за-
заданных средних напряжениях агт
а'т кГ/мм2 20 40 60;
о? кГ/мм2 32 26 16.
Определить о±0,б.
Задача 1021. Определить о_о,., для стали, кривая предельных
амплитуд которой (при рассматриваемых циклах от>0) прибли-
приближенно описывается уравнением: а'а =20 1—I gm f •
L \ 40 / J
Задача 1022. Определить коэффициент запаса прочности, с
которым работает стальная деталь при переменных напряжениях
растяжения — сжатия, если ов=90 кГ/мм2, чТ =70 кГ/мм2, о_1р=
=30 кГ/мм2, ошах=16 кГ/мм2, ошш=—6 кГ/мм2, кэ= 1,5; ем =
=0.7; еп =0,9; р=1,3
Задача 1023. Стальная деталь должна работать при знакопере-
знакопеременном изгибе с амплитудой напряжений оо=200 Мн/м2 при коэф-
коэффициенте запаса прочности [я]=2. Каким должен быть коэффи-
коэффициент асимметрии цикла г, если оЕ=1Ю0 Мн/м2, от =906 Мн/м2;
о_, =480 Мн/м2; а„ =1,2; 9=0,9, ем=0,8; е„ =1; р= 1,4.
Задача 1024. Определить наименьшее значение допускаемого
напряжения для стальной детали, работающей на переменвое рас-
растяжение — сжатие при характеристике цикла г=—0,4 с коэффи-
коэффициентом запаса \п 1=1,4. Сталь — углеродистая, для которой
ов=50 кГ/мм2 и от=24 кГ/мм2. Деталь круглого сечения диаметром
434
d=30 мм с концентратором, для которого с,, =2. Коэффициевт
упрочнения от поверхностного наклепа р= 1,2.
Задача 1025*. Стальной вал круглого сечения диаметром d=
=40 мм имеет сквозное поперечное круглое отверстие диаметром
а=6 мм и должен работать при пульсирующем цикле (г=0) с коэф-
коэффициентом запаса In ]=1,8.
Определить величину максимального переменного крутящего
момента max MK, если известно, что вал изготовлен нз стали
марки ЗОХГСА, для которой ов=П0 кГ/мм2, тт=51 кГ/мм2
и x_l?=23 кГ/мм2.
1025
Задача 1026*. Определить коэффициент запаса прочности я,
с которым работает деталь на переменное растяжение и кручение,
если известно, что она изготовлена из стали марки 45: ов=60 кГ/мм2;
от=32 кГ/мм?; о_1Р=20 кГ/мм2; тт=22 кГ/мм2; х_,= 16 кГ/мм2;
D=1,7; <4=1,4; ем=0,7; е„ =1; р=1; отах =1000 кГ/см2; отт =
=200 кГ/см2; хтах =400 кГ/см2; хтт =—100 кГ/см2.
Задача 1027*. Стальной цилиндрический стержень круглого
сечеиия диаметром с1=30мм заделан по концам. Через выступаю-
выступающую часть на стержень действует сила Р, изменяющаяся по сим-
симметричному циклу.
Ш27
}
I ^
2
V//////////////
X/////////////
Определить величину максимальной силы Ршах, если известна
марка стали 40ХН, для которой ов=900 Мн/м2; с, =400 Мн/м2;
т_!=240 Мн/м2. Диаметр стержня в средней части ?>=60 мм;
¦^-=0,1; /=32 см; а=Ю см; р=1,2; [п]=1,6.
* При решении задач, отмеченных звездочкой,, использовать спрямленную
Диаграмму Зодерберга.
435
Задача 1028*. Стальной ступенчатый вал круглого сечения диа-
диаметрами D=60 мм, d=50 мм и радиусом переходной галтели
р=5 мм подвергается действию переменного изгиба и кручения.
Определить, с каким коэффициентом запаса п работает вал, если
в опасном переходном сечении от изгиба Л1шах =3 кн-м, Л1тш =
= 1,5 кн-м, от кручения шах Мк=2кн-м, min Мк =—0,5 кн-м.
Вал изготовлен из стали марки 40ХН, для которой ов=
=900 Мн/м2; от=750 Мн/м2; о_,=400 Мн/м2; \ =390 Мн/м2;
t_i=240 Мн/м2.
Упрочняющее влияние технологических факторов оценивается
коэффициентом р= 1,3.
ПРИЛОЖЕНИЯ
I
II
I
ft" я
о оо е- t*-
—ГсГо О
о о оо —'
О -# Г» С
¦«О* С1 Ш С
о о о о —i
оюооо
-^ ^Г (N СО
0J S3, iT
18 Г
a.
я щ о
s g a I.
III
ю
^Ш '
о
s -
I
Is
-* 8
438
i
i
i
l
|
?
?
ч
ч
ч
1
i
*
!*
•¦
я"
S
h
J
¦**
.,
- i
-
-
:
S
О
»
S
о
0,17
15
О
S
о
1Я
в
=
о
О)
СО
О
1,13
s
°
8
Я
о
0,22
R
О
78
о
1
58
о
S
о
1Я
-1
1.46
-р
из
а
с
о
57
™
49
а
0,34
S
о
-ч
О
СС
о
1,43
CD
о
II
Сч
00
о
0,44
S
о
62
-
сч
л
«
(N
20
я
с
0,48
84
с
S
-
1,62
2
ч-
И
я
со
IN
439
я
эл жен
Продс
«а
8
1
; величины
2
а
N и
1
\
1
к
-г в
Е*
О
К*
Eg
^ „
Площадь
профиля,
см?
Размеры, мм
о;
Номер
профиля
00 СП
о* о"
to сз
сч со
со -Ф
со сч
to из
о о
S 3
о о
8 Я
8 8
сч со
1>- СО
О) О5
ft СЧ
•3 сп
—. —.
00 ¦?
со
я
сч
со"
,99
,04
о —«
<о сч
о о
из из
о со
•" —<
S 55
¦* ю
1,10
1,09
S S
сч со
- эт
о ю
--
4,5
со
S3
to
,09
,13
8 S
to оо
s s
о о
t^ о
¦Ф СП
—I t-*
S S
S 8
1,23
1,22
Ю 00
со -Ф
1Я СЧ
СО •^1
1-н СЧ
1Я 00
со о
сч со
со
,21
,26
,30
S
СП
CN
со
12
CD О) СО
со со со
о
сч
сч
,75
о
74
CN
,74
о
Й
то
,72
со
со
1,39
со
о
1,38
3
CN
1.37
S
ю <о со
08
й
сч сч со
Ю СО СТ)
«э -ф сч
сч
СО
со
ю
,33
88*
,42
<^
8
1-Н
из
Si
о
О!
8
S
о
Ю О СО
СП 00 tD
сч
,95
со
,94
¦*
,92
со
si —
1,55
"I
1,54
сч
С)
1,53
CN
—
« 1Л N
со о г-
сч
со
со
СО СП О
СЛ СО 00
сч
со
¦*
со
со
S
»
,50
,52
со
со
S Я
сч
¦Ф 1Л
00
сч
со
сч
¦Ф 00
00
1,73
1,73 I 20
00
со
со
СО СО
00 СО
СО *f
сч
со"
33
440
1С
-
CN
1,10
о
со"
CD
CN
25,4
72
—
cd"
—
CO
-
33,1
1,25
45
CN
29,9
00
s
CO
CO
-
41,5
1.25
CN
o>"
CN
36,6
3
—
23,1
00
•»
CO
CO
-
50,0
1,24
;'n
CN
42,9
Ш
r^
CN
CN
Ю
CO
CN
C-.
2,3
CO
со
CD
CO
cd"
as
-
51,0
1,39
о
12
Й
CN
46,0
CD
CN
О
29,
Й
8
CD
Ы
-
56,7
1,39
CN
CO
CN
CN
50,7
CD
CN
Ol
31
8
CD
-
68,4
1,38
—
CN
59,6
CN
CO
37,
CO
в
00
ог
-
1.37
00
17
69
CN
68,2
CN
О
43,
CO
c-
CN
Ol
О
CN
91,9
1,37
о
20
00
CD
CN
76,4
CO
Of
CN
Й
00
о
cn"
4,5
1Л
8,0
CD
00
g
«-
s
CN
69,6
1.49
CD
CN
62,6
CN
S
s
Ю
о
CN
83,9
1,48
CO
2
g
CN
73,9
CN
CD
$
S
CO
e
00
CO
о
CN
98,3
4
L
a
CN
84,6
8
CN
CO
53
8
r»
o
CO
cn
CO
1,47
00
a
CN
94,9
CN
00
s
g
Ol
m
00
CN
127
1,46
Й
s
CN
105
й
CN
_.
О
00
CN
OJ
к
CN
93,2
1,59
oo
-
CO
83,6
CN
Й
00
s
00
ю.
CN
102
1,58
ю
a
=
CO
90,4
E?
CN
О
й
Г-
§§
СП
е-
с-
СО
CN
119
1,58
о
Й
S
СО
104
ю
CN
СО
00
00
о
CN
137
1,57
ее
о
СО
8
СО
116
CN
¦«•
S3
а
OJ
со
CN
00
s
CN
145
1,79
о
Е?
CN
169
1,78
О1
Я
ю
CN
194
1.77
00
со
в
CN
613
1,77
CD
й ^ ^ ^
со
130
00
CN
_
я
00
CD
О
*
со
150
Р:
CN
СО
ш
35
О)
со
CN
СГ
С
со
168
СО
CN
106
о
о
О)
со
00
со
186
к
CN
118
CN
со
g
а
441
¦к
X
ч
«г
о
Ь-
¦6
для
в
а
1
в
>1, ММ
а.
1
а.
Si
]
в
Si
1
кв
ч
к
(L)
гцадь
if
5
Л»
к
§
1
о:
•о
о.
1
к
§
СО
«О
CS
см
**•
s
со
193
S3
%
3
00
00
207
К
CS
гга
8
СО
Оз
~"
<2>
S
So
со
233
со
X)
CN
т
со
с^
1—*
„
84
со
284
от
CS
S
1—*
СП
86
00
во
331
85
(N
1-?
ж
~*
со
Si
78
СО
375
S
со
CN
3
$
1—*
112
с-
со
416
СО
122
о
со
2
ю
со
131
00
о
00
2
со
147
см
CS
со
ю
00
СО
179
м
см
о
в
со
209
от
00
?!
см
со
237
<с
СО
26,
CS
264
00
со
33 S
см
an
со
2
см
со
СО
СО
SS
см
00
со
о> со
^р .*
279
315
О О)
^» со
со
176
=
CS
ю
со
198
со
см
см
со
о
со
со
1С
01
см
я
СО
CS
а
CN
135
со
00
ю
со
о>
а
CN
149
S
S
со
со
^f
см
174
CN
00
S
со
СО
3>
200
S
00
со
со
*^
см
224
-* ^ ч- ^ •* <*
87
со
а
520
<о
00
со
со
СО
t.
о
571
S
со
1
S5
со
а
to
670
3
СО
422
г»
22
О!
764
§
со
482
СМ
853
00
!>.
СО
539
to
00
со
о
CN
<*<
to
125
CS
со
со
00
00
см
192
3
СО
•-Ч
СП
S
см
211
8
00
(^
о
см
248
* * 3
739
3
^*
466
1Д
814
СО
СО
512
ш
ю
957
со
602
ю
2 « й
*^
см
со
й
to
*^
1Л
CS
00
о
CS
140
^*
ю о> со ^ оч N й
СО ^ (fl О) - ¦CS
— _ _ _ CN C4CN
s r ffi
П ОТ П * Ю Ю Щ
a s
I S
Ю СО —< О —| 00 —¦
N 00 О) О "¦ И СО
CD СО СО NN NN
eg CN —i -Ф -Ф ^- СО
00 Ч1 О Й 1й N iO
00 О) О —' СО *# iO
Oi СО Ы <О *Р СОСЧ
со* со со со* со со со*
SCO
со* со*
Oi О) № Ф О О 00
CD *f CO —< Oi (Л
OV О) СП_ О) СО 00
со со со со со со со
2 5 й со ? ^§
СО СО СО ^ ^3" LQ и
Ч Щ. Я Ч -. ™2.
СО ^О СО ^О (О (О СО
8 S
N N*
—; со сч со ю
СО NN Ю Ю
SCO
1ft
СО Ю (N О) "ф О) Ю
N NN (D (О 1Л Ю
О) Oi О) О) О) Oi О
СО (О СО 1Л о *3" —"
О5 «-ч СО Ю СО О) Ю
СО —' СО N 1Л ^ СО
сч со со со ^ ic со
S S Щ ?
S О) м М
(D Ю ¦* W
СП Oi Ol Oi
S S
ю* ю
а я 8 ь з s 8
88 S
П ^ О! 1Я - О)
S S (О О <О Л
Ш (С Ю Ю Ю
to 1Л СЗ СП
¦ - о - Si»
00 СП "" ~ —¦ —|
CD N
CN CO
ш s & s к s
N СЧ N CN О N —i
4< Л Л (О N N СО
о ^ О 1Л О "Ч?
й" g S S 5>"
о oi oo h- — о <о
Й О) - п О Ю <С
м СО О И ^ Ч1 •"
tD CD N 00 О1 О «-ч
^p -ф -Ф CO -» CO -Ф
CO CO CO *# "sf ЮСО
—i O) CD О Ю CO
¦* CD
о со
CD CD
"sf N О —i N -» О
СО NN СО Oi CO CN
t^« CO O^ ^D ""^ СО ^"
443
—ч>
та
1
3
1
i
а,
О
ИЭО ВИО1ГЯВИ lfOJ^
1
f
7
?
ч
*°Х И1ЭЭЖВХ
annBoiooBcj
'"Л ИХ0ЭЖВ1
эиннмээад
а
3
к
<о
К
ё* а
S-&
С
392
о
со
о
со
о
см
о
43
о
СО
со
о
1,56
44
о
?!
О
К
о
о
|
о
CD
1.1
CS
1Л
со
со
CD
СЧ *^
до N.
СО 00
о о
со со
чф «^
о о
со ю
см то
о о
О) СО
о о
?2
о ~
GO CM
— ~
3,26
4,38
18 а
о о
$й
о о
— —
C*J СО
— —'
N. СМ
—. щ
— ~
см
1Я
со
СО W
S
444
3R5
о
A,54
8
о
0,59
1,58
381
о
а,54
о
0,63
2,15
CN h-
СО СО
—
ft:
со"
D.70
0,93
—
m
00
Q.69
1,18
—. —.
со со
со
со
—'
—•
1-й СМ
СО
О
00
9
4/2,5
см ел
оо !>¦
со со
о
0,61
о
D.60
02 |
О "—*
0,64
2,20 1
00
CD
2,98 1
—
9,02
3,79
1,32 1
со
12,1
?
1,69 |
OI
п"
— -
_
00
ю
ао О
СО CS
—'
CS
CS
CS
1.7
о
ш"
со
ОС
с-
*
ОС
о
U"
§3
о
R
00
-
0,72
3,26 1
S
о
s
-
4,42 |
IS
- -
^ CD
CN
),91
1,99 I
S
CO
D.90
2,56 1
s
- —
CD
°p
CS
CS
CO
CO
CO
<M
CO
s
5/3,2
li
о о
ее
in сп
—< CS
CS *J*
00 00
5,43
6,25
о <м
00 00
- —
CO CS
ss
Toz's
| OS'S
ее
- ¦*
2 Zl
CN c3
CO CO
О
OI
о
CD
""-I*
8
CD
404
о
3,78
CO
CN
D,88
3
CO
об
-
CM
a
1,01
4,48]
—•
00
2
CO
5,6/3,6
397
396
393
386
о
0,87
07 1
CO
D,91
8,51
03
cs
о
CO
CO
CO
5,16
о
CN
CO
CO
CO
о о
со CD
SS oo
CO П-
10,8
13,1
00 СЧ
CN CN
¦* OI
5?
CN —.
6,26
7,28
О С)
CS —'
СП CO
28
О) СО
СО *f
о
3,85
со
ш
m
17,9
CN
О)
СО
со
1,09
9,15
8
—
CD
S
СО
" 00 О 00
О Oi О CO
^ «* in r^
CO
CS
7,0
*
ш
со
s
3
с
с
*
407
о
S8
406
о
0,98
CO
¦^ ю
1,03
13,6 I
1,05
15,2 |
Ю 00
CN (N
CS
3
1,28
8.25 1
s
CS
00
s
1,27
9,05 |
s
CS
00
00
*
ЕЙ
m
ir
c^
IT
m
Ю
1
iff
436
435
430
о
о
о
1,09
1,08
1,07
CN
f~
1,17
20,8 1
00
1,21
25,2
О)
о
1,29
34,2
CO ^P Ю
CS
o.
8
1,43
12,5 1
en
00
CS
CO
CS
СП
?
1,42
14,6
8
CN
o>
CN
112
1,40
18,5
8
CN
CO "Г 1Л
e
CD
^ m i>
-
CD
•-
47
Cl
cn"
со
oo
s
S/9'Z
387
386
о
о
1,09
1,08
s
SB
l>- CO
1,13
20,8 1
CO
<M
CD
1,41
12,7 I
8
CS
tD
1,17
25,2 |
65
OI
102
1,40
14,8 |
В
CN
О
99
Si
36
Й
CO t^
CS
ОС
in
1
CO
s
s
8/5
384
384
380
о
.22
00
—
о
1,22
О
1.21
CO
to CO CD
Si cm Si
32,2 1
SS
1.58
19,7 I
§8
35,2
¦g
OI
¦*
1,58
21.2
S8
CS CS
CO
CD
CD
00
CD
g
CD
S
00
47,8
s
CO
1,56
27,1
a
CN
cn
8
00
00
CO
Oi
m
in
.o
00
to
8
9/5,6
445
ИЗО BUOl/HEH L
О
,*» '
HJU1 П
« 00 ** СО
2 8 8 8
Э S 8
о" о о
SSS
о> соьсо
СЧ C4JC0
ч* *# ^ "Sf
о о о" о*
8 Я й Ц
о" о" о" о
^ 00 СО 1Я
СО 00 Oi СЗ
¦* V Ю (О
СО 1Л |
ев1
СО СО (О СО
CN_ СЧ СО *_
CS СЧ СЧ СЧ
СО СО^ ТО
п-" о* сч"
1>- 00 О)
Я8Я:
Ю 1^. 1-н
со оо со
2 S3 й S
Ю Й Й 1Л
оо сч 43 со
ел со Ф со
—' О) ** О
<N со (О о:
'w 'sou 1
I
446
ф 00 (U Ч"
CS (М СЧ CS
<N СЧ* (N СЧ
Ю О <N «
со со со ¦*
е~ о
R 58 § й
1^> СО СЧ I
WM М I
Ю СО i-i 00
1Л |й Л Ю
Й i-i Ю Ю
О)" 1-Г CN Ю
О5 «3 СП
оо" оГ о*
i-h* CN* СО
IFF
О) СО
a" a
¦> » 2 3
со со
о о
сч* сч"
о о о о
Р- 00 О1 &
СЧ* СЧ* СЧ* СЧ*
S S fc Й
со со со со
00 Г^
00 СП
СО 4D (М —I
—' 00 СЧ <D
NN № О
N Ч" СО -|
О) —' CN СО
ts СО СО СО
00 00 CO CO
CO ID
ifl Ю
as
i СЧ —' N
1 00 1Я —'
^ Ю Ю
(D (D (D Ю
О) СП O> CO
<N со 1Я eo*\
§222/
1Я (D
8
н
т °
ЙеО Ю О GO C-1
СО 1Д t^ 00 —'
^ Ы in m ^
to со" i-h" -ф" оо"
— —< <-* CN
Oi О) О <О <О
l> t--" —* СО ci
1-н W >Ф 1Я СО
со п ¦? оо
Ч" Ю О S S
СО Ю 00 О
СЧ СО
1Я 00 C
2 з u s а
LO ilj in
<N СО Я К СО
1Л 1Л
N 00 OO ffl
<N C0_ 1Л CO —^
J0_ СП О -^
^ ^ 1Л 1Л
1С «Ф СО — О
Ю (D К СО О'
s s s
ч* lC_ t^ O^ "*
o: -<* со ifl'oo
О CN <t (D СО
448
s я & s й ш я s s в? e s ss э s s g t= s s s
осч1лао —'Son
ОС01>^<<1^.СМСГ)
^-* CO rO QG
^ OU ^5
со со о' го ст о = = « « т ч." «о со
о gj m
'^<СЧ1Л
1Л l>-
2 2 ° Zl "
N IN <N M W
00000000010101000—'
О *Г 00
CN CN W
о о о р 1Л irf
s я
s s e s" s s я ss
S S a
8 8 Я Й 3,8 й
S S § S 8
449
113
eg
со 01f- =00 51
1 О •—' CO 43 t~- CO
Ю СО 1Л (D CS
ts. (о г~ ^ m
CSCO ^f CD CO
- со ^ о\ ^f ю
— о ¦¦* со <?
sss
(N СО
Щ "H 00
ЧЭ h- 00* О* CO in t
ltd ex;
D(ONN 00 00
." E-J" Е-- Е-- tH CO CO"
Г-^"о0 О HcQ*
ё</ 8 S 2 о
.-< см ~- см* см
^r to ^r
CM CM CM
CN CN CM CM
—' CM OJ CM OJ CN
CM CN <N CN CN
— О CO CM CO «Э OO
2 2 ^ 8
ел —
CO 1Л
CO CM
•-^ ^r со — со
S Ю CO Is- 00
CD 2 CM
OODOCDO)
CO —i CN
О CN CO
g
= =i a § a
о о о
2 S 00
CO 5 Ю
г- «Л h- (N
2 2 S gj
CD О СМ Ю Ю чГ LO
со со со ^ ¦* ю S
Ю «Л «Л «О
CO 00 О O*
— CN ГО
ТГ О Is- CO О
?О CTi CO CJ) CD
Ю О I*- CO Ю
О -^ —* CM* ;o '
О О — -ч (N
LO О Ю
So о
о со
8 g-
со 9
CNCOCO4- ^rcOocDOOOt-DOLOOcO
¦^LOtDr^COO^-CN1* 1Л| t~- —i Ю ~- oo"
? 2 Э 2 8 S Я
s a
'/4 14*
451
Приложение 3
Гибкость, X
0
10
20
30
40
50
60
70
80
90
100
ПО
120
130
140
150
160
170
180
190
200
Коэффициент
стали марок
4. 3, 2,СС
1,00
0,99
0,96
0,94
0,92
0,89
0,86
0,81
0,75
0,69
0,60
0 52
0 45
0,40
0,36
0,32
0,29
0,26
0,23
0,21
0,19
стали м?
ки 5
1,00
0,98
0,95
0,92
0,89
0,86
0,82
0,76
0,70
0,62
0.51
0,43
0,36
0,33
0,29
0,26
0,24
0,21
0,19
0.17
0,16
продольного
Значения
р
чаля
СПК
1,00
0,97
0,95
0,91
0,87
0,83
0,79
0,72
0,65
0,55
0,43
0,35
0,30
0,26
0,23
0,21
0,19
0,17
0,15
0,14
0,13
изгиба
V Для
чугуна
1,00
0,97
0,91
0,81
0,69
0,57
0,44
0,34
0,26
0,20
0,16
—
дерева
1,00
0,99
0,97
0,93
0,87
0,80
0,71
0,60
0,48
0,38
0,31
0,25
0,22
0,18
0,16
0,14
0,12
0,11
0,10
0,09
0,08
|?
В в р
II
*и
8Ȥ
Sksi
О. U '
о"
в1
а*
Я
1
8
1
3
•а
i
1
1
-С
CD
+
1
CD
-VJ-
— V
"""
•с
-
1
1
CM
О.
CM
h
1
CD
T
_i
00
i
¦a
a-
X
4-
к
CN
-i
•a
¦a
16p
%
К
I
j
CM
1
1
f
Я
_1
1
+
S:
1
CM
a.
oo
1
4
1
1
CQ
H-
—г
t
_i
•e
Q-
Ш
-
+
+
J_
i"
a.
ID
+
e
D(
I,.
¦S
f
+
Is
-1
«a
+
e
e
|
Г
CN
CM
+
U- у
+
CM
+
s
CQ
+
a.
CQ
+
+
2°
+
3
+
ъ
Ц
I
-*-
CM
+
CM
—г
1
-1 С;
t3|fC
15 Заказ №. 886
453
ч
l0l
О.В
0.6
CM
0.2
О
J I,7_L\J
к
Lj
r
i
i
j
г,
_
i
1
ф
1
+
—
—
ш /г»
'ив ер
Рис. 1. Графики коэффици-
коэффициента чувствительности к
концентрации напряжений
для стали
=—-
¦^
"^
3
s
¦г
Приложение 5
Справочные даииые к расчетам на выносливость
1,0
O.S
c,ey
€35 Ю 20 30 т 50SO 80 100 d,MM
Рис 2. Графики масштабных коэф-
коэффициентов при изгибе:
/— углеродистая сталь, гладкая полировка;
2—углеродистая сталь, гладкая шлифовка;
3 — легированная сталь, гладкая полировка;
4 — легированная сталь, гладкая шлифовка;
углеродистая сталь с концентрацией напря-
зкений, Б — легированная стало с умеренной
концентрацией напряжений ( аа < 2\ ; б —
конструкционная сталь ( ав<Ъ5кГ/мм* или<*в
< 650 Мн/м*), вал с напрессованной деталью,
изготовленной из непрессованой стали, при
d < 60 мм — легированная сталь с резкой
концентрацией напряжений
60 во юв по но
мг (б8 ЮМн/н2)
<*$
IB
1,8
I.S
',¦
1.2
I.B
-
\
\
S
ч
---
_ 9
а
ол из ол о,5 о,б
Рис. 3. Графнки поверхностной
чувствительности для сталей:
/ — тщательная полировка, 2 — грубая
полировка; S —¦ тонкая шлифовка или
тонкая обточка; 4 — грубая шлифовка
или грубая обточка; 5 — испытание в
пресной воде при наличии концентрации
напряжений; 6 — испытание в пресной
воде при отсутствии концентрации на-
напряжений; 7 — испытание в морской во-
воде прн отсутствии концентрации напря-
напряжений
Рис. 4. Графнки эффективных коэффи-
коэффициентов концентрации напряжений для
ступенчатых валов при растяжении
(сжатии) с отношением ¦—¦ = 2 при
а
d = 30 -е- 50 мм:
/—для стали с ав =я 120 лГ/лл8 или етв <=
= 1200 /Им/л2; 2 — для стали с »в = 80 кГ/км*
или «в=800 Мн/м': 4—для стали < ов = 40 кГ/мм*
или ч„ = 400 Жи/л»
454
IB
',8
'.6
I.»
«
1С
-а—
-
Мл
1
С
И 5C Bl П 60 SO WO 1W
Рис. 5. График эффектив-
эффективного коэффициента концент-
рацин напряжений для ва-
валов с поперечным отвер-
отверстием при кручении:
— = 0,05 -i- 0,25; т =
й
* к нетто
-=-50 «Ж
при d=3(H-
3,0
ч'~
—
Т
0.1
0,2 0,3 BAp/d
Рис. 6. Графики эффективных
коэффициентов концентрации на-
напряжений для ступенчатых валов
при кручении с отношением
— =2 при d = 30 ч- 50 мм:
d
/ — для стали с ав= 120 кГ/мМ*
A200 Мн/мл); 2— для стали с (тв=я
== 50 КГ/Л1Л' E00 Мн/м').
1,0
OS p/d
Рис 7 Графики эффективных коэф-
коэффициентов концентрации напряжений
для ступенчатых валов при изгибе
D
с отношением —— = 2 при d =
а
= 30 -г 50 *.«:
/ — для стали с ов — 120 кГ/мм*
A200 Мн/м*У, 2— для стали с ов— 50 к/ /ЖЛ*1
E00 Мн/м?)
0,75
«5
0,25
/,0 1,25 1,5 V5v/il
Рис. 8. Графики поправоч-
поправочных коэффициентов иа от
ношеиие < 2 к рис. 6
а
и 7:
/ — изгиб, 2 — кручение
D
Если — < 2, то а9 следует
й
определить по формуле
где аэ —коэффициент, най-
найденный из графиков рнс. 6
или рис.7.
15*
455
9.— О 15 мм; 2,75 дж. 10. а) 0,5 мм; 3 33 дж; б) 0; 0 833 дж.
11. 1 мм; 120 кГ-см. 12. -0,531 мм; ~ 56,8 кГ-сл. 13. -0,833 мм;
— 76,7 кГ-см. 14. ~ 1,067 мм; 282,7 кГ-см. 15. —0,87 ли; — 4,35 дж;
16. -1,36 мм; -27,2 дж. 17. —^- . — 18. —?- Д Ь. 19.0.09 лш2;
0.003 жл. 20.
Ми/м?
456
/3.
•
кГ/см1
tern
нГ/см
23. -?-
' ~
7. 24. 3750 кГ. 25. 8y = .
26. 8V
w-o-^
v~r
Pa
~8?F~
A+3 1ЛГ);
~y ~ 1,36_mjm; 8Х =к 0,53 mm; -440; - 470 кГ/см2.
27 Bp + / 2 9° ) °. P + V~2~ <?a . P
?F ]Л2~ F ]/"T" • F
29. 8,
80. 8^
Ра
Ра
EF
B
2?F
3Po
EF,
BP + да) а
31 • 4?F :
1Р + да
4F
32. Ьх = Ъу =
l/ 2F
3
2
Pa
EF
Р
F
34.
10 Ра
4Р
. F, • F, ' F, -
35. 8^.s=5,4 жм; 8у~1,8лл; —900; —1800; ~ 1200 кГ/см2.
36. 8,5 лл; 1000; 500 кГ/см" 37. 3,9 жл; 30; 150 Мн/м* 38. 8у = 0,7 мм;
Ъх = 0,35 жл; 80; 40; 20 М«/л2 39. оу = 2,125 мм; Ъх = 0,08 л/и;
100; 150; 75 Мн/м\ 40. ~ 5,6 мм; - 142; 164 М«/л2. 41.
2/3 [о]
44. .7 *?" .;
2[о]
2Jo[
42.
[о]
43.
ЗР
V 3 [о]
р
4[а]
F, = Fs =-
7Р
5. 5 <
_ 2_
~ 4
2
[о]
49. 900 кГ 50. 6400
8[о] • '» ~ 4 ' [о]
51. 115 кГ. Б2. 2,07 ж. 53. 894 кГ/см* Б4. d = Л[ - ;
Г " ([°] — 7')
457
l
2P
55. ba =
а Г Р
= -g- \-jr
2 196 Т
617 я2; - 0,4 см. 57. 2500 см\ 2620 см2; 19,6 Т. 58. 600; 800,
56
56. 3 «>;
800 кГ/см2.
ээг
да
343;
22
59. —200;
61. max а
~ 1560 кГ/см*. 63. ,
65. —70,7, — 141,4 Мн/м2.
68. 23; 1000 Г8
300 кГ/см?.
Y а; min o;/
1164;
60. 130;
31
14
— 20, —120; 5 кГ/смг.
-ja. 62. ~ 1040;
875 кГ/см*.
Мн/мг.
- 452 кГ/см2.
—261 кГ/ст2. 7Б. 300; 200 кГ/см*. 76
2ДЕ
71. - 33 мм. 72. — 35,7 еж.
1091;
64. - 61; - 87 кГ/см2.
66. 120 Мн/мг. 67. —10; —7,1 Мн/м2.
399; - 312 кГ/ся2. 70. ~ 903; - 903;
74. - 739;
73.
-^т.
545 кГ/см*. 77.
Д Е
sin ft
78. - 16,4; — 15,4; — 16,4 Мн/м2. 79. 20; 40, 60 Мн/м2.
80. —764; -917, ~ 1070 кГ/см2 81. — 87; ~ 302 кГ/см1.
- 98; 1000 кГ/см2 83. - 596; — 43 кГ/см2 84. 35 Мн/м2
.2«- —" -¦ - -- - ¦- ---'--¦•-
600;
192
288;
93
322; 168 кГ/см2. 96. Р
aut = "in, ** 93 к/7™2-
280 кГ/см2. 97.
72 кГ/см2. 99.
82. — 172;
85. - 513;
14,ЗГ;
96. ~ 9,067*;
101. — 28,3 кн;
I? = 100 кГ/см.
4а Ь tg a
7.14Г;
— 63 кя;
32 кн;
103.
, яг 147 кГ/см*;
-11,537*; -220; -294;
8,747*; - 93; 93; 54 кГ/см2. 98. 5,27*; 6,47*;
-82 кн. 100. 2.05Г; 2,8Г; —300; 225 кГ/см2.
-16,3; -8,1; 5,4 Мн/м2. 102. 1000 кГ/см2;
2Е 2Е
б) 369°. 105. 60 кГ/см*. 106. ?
107. оу = znl — 1333 кГ/см2.
104. а) 217;
( «А'-
290 кГ/см2; 17,4 кГ/см2;
458
Но
задачи
108
109
НО
111
112
113
114
115
116
117
118
119
ч
<•
на площадках.
оси 1
оси
¦ч.
t
параллельных
OCF
3
Во
Ир
0
±600
±200
±500
+ 100
+400
0
±100
+ 400
±200
+ 100
±450
±600
+600
±600
±750
±300
+400
+500
±300
±700
±500
+300
±450
±600
0
+ 400
±250
±200
0
±500
+200
+300
+300
±200
0
0
—300
300
—250
—450
600
—1000
350
0
—300
—850
375
0
+520
173
+433
87
346
0
87
346
173
87
390
300
—900
300
—625
—450
200
-750
350
-250
—350
—850
—75
520
520
520
649
260
346
433
260
606
433
260
390
900
0
1000
375
—100
800
—250
700
650
250
—500
600
520
0
346
216
173
0
433
173
260
260
173
0
694
694
730
645
416
654
817
529
589
432
775
519
400
—400
533
—167
—333
533
—667
467
133
—133
—733
300
566
566
500
624
249
377
471
249
573
411
249
424
Е
9
a
Я
Номер
120
121
122
1
\
на
оси 1
'и
¦'и
глощадках, параллельны\
оси 2
ОСИ 3
0
МН/М*
0
0
0
+50
0
0
+50
0
0
—80
50
—70
0
0
0
—55
50
—70
43,3
0
0
—5
50
—70
43,3
0
0
66,5
50
70
—46,7
50
—70
47,1
0
0
Номер
задачи
108'
109'
ПО'
111'
112'
113'
114'
115'
116'
117'
118'
119'
е,
ч
LV
V
%
0,060
0,018
0,054
0,04
0,015
0,028
0,03
0,031
0,046
0,032
0,007
0,0255
—0,018
0,018
0,002
0,0075
—0,011
0,028
—0,035
0,005
0,007
—0,007
—0,019
0,0255
—0,018
—0,06
—0,024
—0,0575
—0,024
—0,024
—0,035
—0,008
—0,045
—0,033
—0,032
—0,033
0,024
-0,024
0,032
-0,010
—0,020
0,032
—0,04.
0,028
0,008
—0,008
—0,044
0.018
У»
0,36
0,36
0,328
0,388
0,094
0,224
0,350
0,126
0,326
0,170
0,222
0,202
Щ
КГ-СЛ1/СМ*
0,312
0,312
0,243
0,379
0,061
0,139
0,217
0,061
0,321
0,165
0,061
0,175
об
0,048
0,048
0,085
0,009
0,033
0,085
0,133
0,065
0,005
0,005
0,161
0,025
459
Номер
задачи
120'
121'
122'
0
0
—0
,034
01
,014
—0
с
—0
,031
,01
,014
—0,031
0,01
—0.014
AV
V
—0,028
0 03
—0,042
Со*
28,2
7,5
14,7
10»
Ю5
101
2I
,7
0
0
Ю3
123 а) 6,6 • Ю-6 мм'/кГ;
б) 9 6 Ю мм*/кГ;
в) 14 6 10~6 мм*/кГ;
124 0" —[лр,
A-
1,51 ¦ 104 кГ/мм*
1,04 ¦ 10" кГ/мж*
0,685 104кГ/лш2
P. —
— Р. — "
Е ***• Е
LFt + ЕфЬ + 4?,/
рЬ
6,5 10=
7,5 10»
14,7 10s
Номер
задачи
108"
109"
НО"
111"
112"
113"
114"
115"
116"
117"
118"
119"
1200
1200
500
800
800
800
400
600
1200
360
1080
800
300
560
600
620
920
640
140
510
"•///
кГ/см'
1200
1200
1200
1500
600
800
1000
600
1400
1000
600
900
1200
1200
1060
1320
530
800
1000
530
1220
870
530
900
1200
600
1200
1000
300
800
500
700
1100
700
100
750
Номер
задачи
120"
121"
122"
''IV
%v
Мн/м*
20
50
—
68
20
100
0
0
100
0
0
ьо
25
0
— V-P
= — р 127
Да :
1 — Л) Et
V-l)pn
?<!-!*>
126 а, = о2 =
— У-Р
= t_,, i °з= — Р.
128. а, = а2
460
= 1000 кГ /см2, as = 0, т, = та = 500 кГ /см1, т3 = 0, Д?> = 0,35 мм.
129. 2,5 м 130 2[g|cosa : ~??[^~ '3'. 15 лш, 11,1 еж2 132 <^*=
= erg* = 7Б кГ /см2, сг|Ф = 0 (для внутренней поверхности с~Ф =
= — 0,3 кГ/см2), о«= 100 кГ/см2, 0^ = 83 кГ/см2, о^ = 0 (для внут-
внутренней поверхности eS = —0,2 кГ/см2), ав — 67 кГ/см2 133
при 0 •
-ft 134 69, 3,
40 Мн/м2 135 0, ± 80 Мн/м2 136 50, 70, 20 Мн/м*, 0,625 10~3;
0,785 Ю-3, 0,25 10-» 137 20, 100, 80, 84,9 Мн/м2, 0,25 Ш, 1,25 Ю"8,
Ю-3, 1 061 • НГ3 138 500,0, — 500 кГ/см2, 0,625 10~3; 0,27 • 10~3
139 а) 12,5 кГ-см б) 0,86 кГ-см 140 о, = — о3 =
а = °;
[Мк] « 157 кГ м, (Мк)т да 236 кГ м 141. d0 ж 1,59 ел, d»I,35cж, S»
«0,74 см, Ь ~ 1,35 еж 142 d да 2,8 еж, а — 3 еж, Л = 6сж, 6 = 3,75 еж,
е= 1 бж, /= 1,25 еж, k= 1,25 еж 143 d = 4 еж, d, = 5,6 см, d2«6,9c«,
^ *^^ 2 см t '-"' 1 4 гм 144 d '^' 3 1 см dt z^ 4 ЗТ сл< с 'ч~' I 06 см
4,«4,88 еж 2 145* 2>да4,87сж, ся=5,97сл, 5да1,'99сж,' Лж7|97сж]
еда2,66 еж, (ж299сд1 146 а«3,16ел(, d»l,06c«, е«1,19ся,
*«9,46слB, /»11,56сж 147 а«3,16сж, сда1,06сл(, ^«3,87 еж,
ЬхЪсм, d«0,87 еж 148 dда3,57 еж, 8 «2,1 еж, Ь«21,4 еж, /да 13,1 еж
149 d»3,25 см, В,»1,92ел(, 82s=sl,44 см, 6«9,75 еж 150 лгс= 1,5 а, </с=4о
151 л^ = 2а, s/c = 3,9 a 152 jcc = 2а, </с = 3,71 а 153 хс = 0,5 а, ус =
2
- sin
154
Л? .^Ltt I^C l_ff ъ' 14
/ 2 \
г. — я — -^- sin a 1
_\ 3 /
a,
: = 0.6Ь. 155 хс= 17,79 еж,
4 7 5
ыс= 11,88 см 156 -тс-Ь1. 157 „к""*¦ "оя" о1- 15S /jc = 'v = 7869 e-«4;
/^ = 0 159 11,9 а», 12,4 а" 160 5,407а4. 5,382а4 161 0.726Я4, 0,678fi4,
162. 5.25 а4, 1,57 а4 163 5791 см*, 11591 см1 168 ~М~
Эпюра
Эпюра Мк
161
Эпюра
461
IBB. Зпюра Мк
Г
Эпюра У
ш
1.-Э- 54^ II1IIII1F
169.
4.06М . 1ШЧ
bs
SON
Cd4
172
I6M
7.85-
I552OT 15,3т/ ,
ъпла &•№ 171. ^я •
173
10m/
18,85
174 ~4 07 еж 175 ~4 еж 176 D = 6 84 см; d якЗ,42 см 177 ~3,64сл.
178. d[«2,94 см, d2=;4 ел, 9«9,2°. 179. dT = d,, ж 2,94 *л, d2sK3,72 ел;
462
9«= 1,05- Ю рад 180. as=2,88 см, d«2,94 см; <ря=0,41°
d2~5,9 еж, <ряа2,06° 182 d=s2 5 еж, <р«:0,98о. 183 d»2,5
184 490 об/мин; 126 кГ/сл2 185 ~ 5 л с; 127 кГ/сл2 186
181. djs=8 см;
184 490 об/мин; 126 кГ/сл2. 185 - 5 л с ; 127 кГ/сл2 186 - 4 48 кГ-л;
- 105 кГ/сж2 187 - 354 кГ/см2; 2,38° 188 - 70 кГ-м, -0 18°.
189. -363 н-м.; -77,2 Мн/м*. -З-Ю^рад. 190 81,25кГ-м; ~318кГ/сж2;
— 1,64° 191 —24,6 кет; 1,41-Ю рад. 192. — 194 об /мин; —1.18°.
195 7,
194 200 кГ/см?
1
19, т;
193 — 448 кГ/см'; — 2°
196 ~35кГ/сж2; -2°. 197 ~51,3 кж; ~27,5 Мн/л»2. 198 78,5 кГ; Ь мм
(вверх); 30 мм (вниз). 199. —425; ~ 123. 200 —0,98; —1,22
201. — 693 кГ/см'; ~ 400 кГ/см*. 202. d =
203 -3,94 еж, -0,48°. 204
т]
Згс [т]
1,97 см; 0. 205 -2 17 кн-м;
2М
148 - 1СГ=> ра^ __1б,1Лж 206 - 126 кГ-м, -0,215°; ~23 5кГ-сж.
207. ~573 кГ/см?, -0,41° 208. ~780кГ/сж2; -1,19°. 209 -33,3 Мн/м*;
-6,2. Ю~3 рад 210. 6ж|,28о. 211 270 кГ/см*. 212 - 390 н-м;
-2,81 • Ю-3 рад 213 ~12,7лш;~0. 214 -3,17 см; - 5,8 ¦ 10 рад.
215.
216. -306; -318кГ/сжг 217. —750 кГ/см*;
218 ~ 1000 кГ/см2; - 100 к/
м _ м
~ 37 кГ/см1; - 1,14°
я= 0,052 -^р-; а, я
220. - 402 кГ/см2; ~ 134 кГ/еж2; ~ 0,213°. 221
- 883 кГ/гж2 - 2,5°; - 2,13°
219
cmax =
Ma
-468,
-742,
dnwpo
i 1
1
0
463
I if hi
СО
8- ¦&§.
«I*.
oj см со ч; 1Я со r*«
Ю CO CO CO ^e CO CS
CM N (N CM CM C4 CM
§. а:
S5S m
§¦ §¦
t
• «¦
"ss
+
i
259.
2Б2.
Эпюра Q
2В9.
Зптро О
¦'"• Эпюра 0
j шшшнашрр
IIIHIIi
{ Эппра м
CJ.
286. 0.082 Н<
287. 0,0183 а8. 288. -Ц- bs.
289. -j- A — 1,5ft2 — 4*4). 290. 229 еж3. 291 0,0597 о3. 292. 0,0706 a».
293. 359,3 ел3: 294. 79 еж3. 295. 0,0425 a3. 296. 0 147 я3. 297. 0 74Я3
298. 205 ел3. 299 -737 еж3. 300. -663 еж3. 301. 0 560сл3. 302.0 470сл3.
303 1,865 еж3. 304. 0,780 еж3. 305. 1 478 еж3 306 2770 еж3
307. 1196 кГ/см'. 308. 91,7 кГ/см* 309. 865. —432 /сГ/сл2.
310. ^-Jp^ M. 311. -3,83—; 0.
312 12а„
313. ~0,0894о„.
317. ?> = 29,3 еж.
№ 14а. 322. № 45.
d3
314. а = 5 см. 315. b = 19 еж. 316. № 24а
318. Ь= 13,4 ел 319. я = 4 бруса. 320. № 33 321.
323. а = 3,42 ел. 324. 16 еж. 325. № 50. 326. а = 1 еж. 327. 6 = 20 еж.
328. А, = 177,7 еж. А2 = 38,3 ел. 329. а= 1 еж. 330. Р= 1067кГ. 331. Р =.
НЮ кГ. 332. Р = 453 кГ. 333. ? = 330 кГ/м. 334. Я ж 2,14 Т.
— 1,92 к«-ж. 337. Л4я=3,44 кн-м.
335. Рж2,16 Г. 336.
465
338. 9=9,36 кн/м 339. q = 3,75 кн/м 340 q = 38,4 кГ/см 341. Р = я2а0.
342 Р=1 У. 352. d = 8 см, хшах = 16 кГ/см%. 353. /г = 24 2 ел; тшах =>
= 5,6 кГ/смг. 354. № 27 с; хшах = 125 кГ/смг. 355. / = 3 ж; ттах =>
= 60.5 кГ/см2. Ш. 2.79 Мн/м*. 357. Я ж 8,0 еж; тшах= 1,82 Мн/м2.
343.
341
350 <Щ*°
358. 1,2 о 359. ~6 65сж 360. ~ 1.034а. 361. ~0,702«. 362. —0,5827г.
363 —0,762а. 364. 1745; —417кГ/см2; о = 26°. 365*. 11,3; — 120,3кГ/см*.
366*. 412; —47 кГ/см* 367*. 26; —0,4 кГ/см?. 368. Р = 49 Г. 369. № 24.
370. № 40. 371. Ь= 15,7 см. 372. № 55. 373. № 50. 374. 1,59. 375. 1 4.
376.3. 377. 1,28. 378 2.9. 379.4 380. Ь = 20мм; Ь'= 17,5 мм.
381. d = 10 см; d' = 8 4 см. 382. <? = 2,93 Г/ж; <?' = 4,16 Т/м. 383. Р =>
= 1,47 Т; Р'=1,66Г 384. ?= 10,7 кя/л; q'= 12,2 кн/м. 385. Р =
= 8,05 к«; Р'= 14,56 кл 387. Меньше на 0,05%. 388. 100%; 60%.
389. 33%; 28%. 390. 25%; 22% 391. 27,3%; 23,8%
Примечание. В ответах к задачам 392—443 приведены числовые
Ма* Ра3 да1 Ма
коэффициенты при ~р7~ ' pi или ~pl Для прогибов, и при
El
EI
El
Ра2 да'
~ЁТ или "?Г
— 23
— для углов поворота.
— 19 — 1
б»2
395. -
— 17
16
402 -
8
— 16
3 '
3 •
• ~ 2
— 5
3
-85
9' 72
— 1
12
— 59
24
-65
24
394
•25
— 5
— 3
. 397. —2;
403
72
— 7
400
— 5
— 7
36
4
— 13
12
401
9 404 12 ¦ 6
-2;
1
Т'
405
19
* Напряжения иайдеиы на стенке в месте резкого изменения ширины
сечения.
466
386.
Номер
задачи
f
6
Номер
задачи
f
222
91*
ЗОЕ/
qP
24Е/
га
— 0,000204-^—
qP
720Е/
+ 720Е/
223
7 ?/«
120 Е/
12Е/
228
ql*
-~ 0,00386-^—
qP
90Е/
72Е/
224
- 0, о7 ?/
qP
4яЕ/
22»
?''
л<Е/
qP
?/
225
13 ,?/«
180 Е/
ql'
WE/
230
<?'*
16я4Е/
8л Е/
226
тР
ЗБ/
тР
IE/
231
0
0
-тг 406
— 62
409 -4g-;
413.
417.
61
40
— 5 —I
10)
360
407
12 ' 2
12 ; 12
— 3 — 10
410.
414
418
— II
36
— 2
29
"ЗЙГ
; — 1 411
15
у
408 -§
— 1
421.
I
3
3 422.
0. 424 ~; ~
19
12
6 ' 2
-д- 415. 0; —-д- 416.
f 4Ш -г- -йг
7 —1 1
1 ~а
412. —7; 2.
¦11
425
— 17 — 1
423.
7
24 "
420.
-5
— 7
— 4
. 431.
— 71
24
12
426.
65
1
45
12 '
18 ; 2 ; 9
427 3; 2. 428. ~; -g-. 429. -д- ; -тр 430. -j-; ~^-
131 5 733 10 —23
432 "*Г! Т7 433' "^: "^ - « ¦
— II 436 J:3^-. 437. J=jf^-. 438. -^ 439
440• 4"; "i^"" 441- "~4^" • 442- "~Ш^"- 443- ~~lT~- 444' |'3|сл|
445 3.55 ел 446. 1,35 еж 447. 1,29 см 448. 1,6 еж 449. №22
; 2.
"_5_
162 • 9 '
435. —2;
I
467
450. № 22 A6) 451 № 27 452 12x20 см'. 453. 20 см. 454. -=- 455 тб •
144
456.-^—. 457.4,4 467 160 кГ; 4 см.
Ч5В
ЧБЗ.
)-trf о Г
Ч-БЧ-.
Ifln
2Ш-1 ql"
Elm
468
Касательные напряжения не влияют на формы балок. 6 = оо, так как
1 М
около свободных концов балок кривизна ~7~~ = ~f7~ велика, приближен-
приближенным уравнением упругой линии пользоваться нельзя.
470*. 1) -j- /; 2) 2; 3; 10. 471*. I) -g-1; 2) -j^-; -2,082; -2,912.
472*. I) -g- ; 2) - 1,10; -2,420; -3,251. 473*. I) -^- ; 2) -4-;
-2,841; -3,271; 474*. I) -4-; 2) -Щ-; 2; -rr . 475*. I) -|~; 2) -If-;
при x = 0,3826/. 477. 1,294
-2,898, 4 и 2. 476. 1.061 -j—^-
™^max ¦» max
при x = 0,2665/.
Примечание В ответах на задачи 478 — 491 приведены числовые
Qls Рая Моаг Ра?
коэффициенты при -ь—. , -р-, ¦ или -ъ—, — для прогибов, и при^т—¦
с/гаах с'тах ^-'тах ?'тах
М„а I 1 2
или -pj для углов поворота 478. -rx ¦ *79. -g— . 480. -5- C—41п2)=;
I 17 3 9 4 1
ж 0,1516. 481. -у-. 482 -jg-; -g- . 483. 10; -j-. 484 -j-; -j-¦
7 2 265 14 205
485. -s-; -,- 486. 3; 2. 487. -^-; -5- 488.
41
576 ¦
943 _
096" qa '
24 ¦ 49°- 72
•41
72 '
25 5
= 1T ?O. 493. |M|fflax =
63
. 495. /„ =
_98_
13
24
108
14
~9~
18 •
<?'4
- 496-
49
I Af
-g--^-
494 Ъ=
497. |M| иХ l32 ||m g^ ?
499. \М\тш = Ра; |Q|max = P. 500. [MJ = 3,14 Т-м. 501. [All = 2,85 Т-м.
502. [Р] = 7,73Г. 503. [Я] = 11.6 Т. 504. [<?] = 7,4 Т/м. 505. [<?) =
= 5,2 Г/л. 506. № 12. 507. № 14. 508. № 18. 509. № |0. 510. -^-М.
БИ. -jj- Pc 512.
7Ma* Pa?
516. ,2Я/ . 517. iE/
Ъ\ГЪ
9 3
¦я- <?a2. 513. -г- Pa. 514.
(?C4
32?/ •
515
20?/
518.
521.
24?/ •
522. 47 кГ. 523. 172 кГ. 524
519.
Рая
1217
I2M
5a
520. 720 кГ.
Т. 525 2,56; 3,2 кн.
526. ч1= Ю9 Мк/Л!2. 527. Ns= ¦ „ 3 . 528. —7,5; 15 Мн/м2. 529. 288,5;
* Расстояние указано от левого конца балки.
469
3
? кГ;
3
= 1440 кГ-см. 536. yv = -gg
43,3 кГ/см*. 530.
Мтах = Ра. 532. В
= -?¦ 534. W =
x = -^Pt. 531. Ву =
Р; Вх = ^Р;
7 Р
тт = -^Ра. 533. Вх = -g- ;
= 750 кГ-см; 535. JV = 98 к
11
/Итах =
/v = -§- Р;
Ра
538.
. 540. N==-
ТЧо2- 537. Давление в шарнире
48А?/" 3
4— 541. N=180 кГ. 542. В„ =
•. 543 ег =
M+3?c
\2aMEI
544 Над промежуточной опо-
М2 = 1,5 Т • м. 545 Над промежуточными опорами М2 =
-р^-Ра; /И3 =-д^-Ра 546. "|/ -~-. 547.|/ -j-y-. 548 №16.
,28Т/м 551. 5,9 Т/м. 552. -2,6 Т-м. 553. 1,86Г/л.
7Ра3 13 Р13
24,3 кн. 556. — "вБГ • 55?- — -ткя~ • рТ"- 558. 0J07PI;
549 № 18а 550. 6
554. 19,6 кн-л 555
0,293/; 0,707/. 559.
563. 3,65 Г. 564.
0,662 Т-м 560 - gg^ " Ш ' 561'
565
566.
+ - —) . 568.
571. 9,2 ел; 4,6 ел.
576.
562' 2 Г"
/
a a ¦ 567*. 2[о]I F +
17,6 см; 8,8 см. 569. 14 ел; 7 ел. 570. 9,2ел; 4,6 ел.
572. 1,97. 573. 1,62. 574. 3,06 575. 1,6
Номер
задачи
и
Номер
задачи
и
222
q*P
504?/
227
60480?/
223
18792;6
20160?/
228
2592?/
224
C + 8я2)?2/6
192я4?/
22»
qH<-
4п*Е/
225
13<73/6
1620?/
230
64?/
226
т2/3
6?/
231
0
577. 985 кГ-сл 578. 210 кГ-см. 579. 3565 кГ-см 580. д-^г^
581. ' у bq [а] 582. U^.U^.U^ = 1: -г^:0,25. 583. У балки равного
сопротивления f в 1,5 раза больше. 584. 1) 1,2; 2) -yf ; 3) -д-; 4) 2;
5) 2,4; 6) 1,8 585. E77) ^ =535 кГ-ея, т. е 35% от У; E78);
* Здесь F — площадь поперечного сечения диагонального стержня.
470
I/, =1 кГ-см, т е 0,5% от U; E79) Ц, = 314 кГ-см, т. е. 11,3% от U
586. 1104 кГ/сж2; р = 67°35'. 587. 1454 кГ/см\ р = 59°53'; /„ = 1.13 см;
/г = 0,65 см 588. 95 кГ/см2; Р = 61°38'. 589. 1059 кГ/см"; р = 44°31'.
590. 118,9 кГ/см2; р = 49=06'. 591. 1210 кГ/см2; Р = 74°35'. 592. 82,6 кГ/см*
Р = 16°06' 593. 9,13 Мн/м2; р = 82с59'; f, = 1,030 см; р, = 7°11,6' снаправ-
лением силы Р,. 594. ~ 4,025 -^; р=75° 595. 9 Мн/м2; р= 14°56'596. 160 кГ;
Р = 23°58'; f = 1,334 см; р, = 34°56' от вертикали 597. 9220 кГ; Р = 73°26'.
598. 47,5 к«; Р = 33°40' Б99 12,9 кн; Р = 75°37'; / = 0,377 см; р1 = 88°11'
от вертикали. 600. 44,9° \- ; Р = 26°47'. 601. 0,0295 ~^-; Р = 15°37'
602. ~ 12Х18 см2; р = 52°25' 603. №27; р»84°52'. 604. —18x24 еж2;
Р = 36°15'; /»1,94 см, р, =»41°30' 605. D ж 12 см; Р ж70°54'. 608. fmax=
Ра3 27 Р1
= 5,5—gri-;~45° к сторонам прямоугольника. 609. cmait = —— з при
3 дР
х = —т- I от свободного конца 610. ошах =5 0,453—j- при дгг= 0,317 / от опоры
Ра3
6". fmax—17.8 -gp-; ~ I5°42'
Примечание В ответах к задачам 612—620 положевие нейтральней
оси определено отрезками уа и г0, отсекаемыми нейтральной осью на глав-
главных осях инерции сечения.
612. 0; — 40 кГ/смг; у„ = оо; г„ = 15 см 613.—3,51; — 4,63 кГ/сМг; оо;
— 363 еж 614. 25; — 50 кг/см2; —6,67 еж,—8 еж 615. 65; — 286 кГ/см2;
-12.5сл;оо 616. 26,5-^-;—27,5-^-; -^-;— -^ 617.1285;
—1355 кГ/см2; 0,29 см; 1,47 см 618. 17,6; —14,4 Мн/м2; —0,834 еж;
0,625 еж 619. — 4,88 р; — 7,37р; 6,2 а; оо 620. 9,3;— 11,3 Мн/м2;— 4,67 см;
— 1,43 еж 621. 650 кГ/см*; г„ = — gj. 622. 44,7 кГ/см2; у0 = -Ц-; го= ~^-
623. 300 кГ/см2; уо = 8,3сж; го=7,8 еж 624. 85,8;— 80,8 кГ/сж2
625.79,3^-: —93,5-^- 626 58,4; — 63,6 Мн/м2. 627. 1122; — 1034 кГ/сжг.
Р 4Р 3 Р
628. 3afc при ах = За; — -3afc при ах = -у- о. 629. ¦ ^ при d^ =
125Р , / р~~
= 2d;— "gTiF при dt = 1'2 d- 630. о> 2 1/ . 631. а = 4 см
632. № 22 a; d= 1,26 еж. 633. № 27 634. d» 17 l/"—. 635. d«l ,5 еж.
Г [а)
636. <! ж 4,65 Л 637. й = 3л 638.64 кГ. 639. 9040 кГ 640. 2780 кГ
641. 19550 кГ. 642. 4180 кГ 643. 360 кГ 644. 6000 кГ 645. 368 кГ.
Jid2 lol
646. [7g J . 647. 4590 кГ 648. 8,68 кн < P < 12,15 кк 649. Р, = 8Р;
32Р
°ni!n = — "з^Г-
Примечание В ответах к задачам 650—655 даны координаты угло-
угловых точек контура ядра сечения в главных центральных осях инерции yz
(в еж).
650. Четырехугольник; 0,160а; 0;—0,072 с; 0; 0; ±0,166 о. 651. Четырех-
Четырехугольник; 0,697 с; 0;—0,650 с; 0; 0; ± 0,532а. 652. Восьмиугольник; 0;
±0,107а; ±0,107о; 0;±0,08а;±0,08а. 653. Шестиугольник; 0,226а; 0;—0,131а;
0; О, ±0,107о; 0,086а; а; ±0,113 а. 654. Прямоугольник; "^р; ± 12а;
471
a l/l 13 13 13 15
— —j2—;± 12а. 655. Четырехугольник;-^ Ь; 0; -^g-fc; 0;—j^q b; ± —gg— Ь.
656. 51 ^r 657. 1075 кГ/см2. 658. 91,6 -^ . 659. 78 -^-.
Р1
660. 1000 кГ/см2. 661. 95 М«/.и2 662. яг 4,9 — при л-гк 0,448 I от сво-
Ра
бодиого конца. 663. 19,4 -^ 664. ~ 1040 кГ/слР. 665. trmaXl =
= 827 кГ/см*; ст1п/ = — 223 кГ/rf; чтаХ//= 1755 кГ/сл2; %,1П// =
= — 35 кГ/сл2; 8. = 0,53 мм 666. d > 3,7 л/ _. 667. 6=3,35 |/ _ .
' М " I']
668. d«40 лл 669 ЛхбОмм 670. <fes
672. a = 3 I/ — 673. d>2,46 l/ —. 674. d~50M 675. dx38 м;
Г [а] Г [o]
Ьгк 22 лл 676. (^ = 54,5 мм; d2 x 64 и 677. с!гк70 лл 678. d>
> 1,84 l/~^ 679. d ж 24,2 лл 680. с!гк 80 мм 681. Р < М_^1. .
Г [а] 51а
682. (?< —-—^^—¦ 683. М< 0,026 [и] D3. 684. (?<1,4 кн/л
685. Р< 100 кГ. 686. Р< 0,556 [и] —. 687. М х 117 кГ-см 688. Р~6,4кГ,
689. 0//| = 47,4-^- 690. о/;;= 1240 кГ/сл2 691.0///= 1510 кГ/сл2
Р Р Р
692. а//; = 89 -^2 . 693. 96 -р- < [и] 694.8,14 -р- < [и]
695. 1570 кГ/сл2< 1600 кГ/см2 696. 6 = 12 ел; ft = 8,3 ел 697. с!,=;8,5сл;
d2»8,5 ел; <23»6,1 см 698. d, = 6c^ 6 = 3,63 ел, da = 5,71 см;
ТПЯХ Т. 8.
с = 2,72 ел 699. 715 «, ттах = 685 М«/л2. 700. ""*ХTl = 0,74; -»1- = 0,88
701. max ^ = 955 кГ/см?; max т2 = 2550 кГ /см2; 8 = 26 ел 702. тшэх =
= 4760 кГ/сж2; п = 15, 60 = 8,1 см 703. max Т! = 128 кГ/см?. max тг =
= 417 кГ/сж2 704. Р яг 800 кГ. 705. На 10%. 706. Р„ = 902 «. 707. d=l ел;
п=10 708. Р = 109 кГ. 709. р = 50 кГ. 710. 43 кГ; 20,5 кГ/см2.
711. 132,5 Г; 2630 кГ/сл2 712. а) 1070 кГ; 713 кГ/сл2; б) 3460 кГ;
2310 кГ/ел2. 713. а) 171 Г; 4530 кГ/сл2; б) 124 Т; 3300 кГ/см*. 714. 1210 вГ;
192 кГ/сл2- 715. 5,47Г; 17,1 кГ/см2. 716. 7,4 717. 2 718. -^-1/"E Cosa .
719.9.5 л 720. — ~\fT—.12\. а) 31,9 ел, б) 17,8 ел 722. 82°.
2 f qa
723. а) 37,5°; б) 10,1°. 724. 63° 725.d=13,5 см 726.</ = 6сл 727.4=6сл.
728. № 22а. 729. Перенапряжение 33%. 730. Перенапряжение 2,4%-
731. Недонапряжение 24%. 732. Недонапряжение 4,8% 733. Недонапря-
жеиие 14% 734. 9,1 Г. 735. 54,6 Т. 736. 177,6 Т 737.6 х 11,3 ел
738. 6 = 2,86 а 739. Ь = 2а. 740. № 30. 741. № 20 A6) 742. Ь= 10 ел.
743. 20 ел 744. d = 8 ел. 745. № 14; В =14 ел; /0 = 40 ел. 746. № 16;
В = 22 ел; /0 = 70 ел 747. № 10 A0); В = 39 ел; /0 = 60 ел (один из воз-
возможных вариантов при ^ = 0,81) 748. № 10 G); В = 34 ел; /0 = 60 см;
(один нз возможных вариантов при о> = 0,81) 749. 4,91 ел; 1462 кГ/см2;
750. 10,96 еж; 107,4 кГ/см2. 751. 1,30 ел; 67,1 кГ/см2 752. 0,303 ел;
1240 кГ/см*; 2,52; 1,84. 753. 229 ел; 1275 кГ/см*; 2,27; 1,78. 754.80x50x6
(один из возможных вариантов). 755. d= 16 ел.
Примечание В ответах иа задачи 756—765 приведены значения:
472
Л^ах. Qrcax и Мшах- 756. 2Р; IP; ^Ра. 757. Р; ЗР; ЗРа 758.
Р У~2; 2Ра. 759. «al/T; qaV2; 2AUqa\ 760.-^-; 4?-; -2|1
3 3 9
761. -g- Р; -g-P; 2Ра. 762. 2ga; Зда; -g- да2. 763. 2?а; да; 2да2.
764. qa; 2qa; 5,713 да2. 765. Р; Р; -g- Pq. 766. 127; —206; 111 кГ/см*.
767. 105; —87. —48 Мн/м*. 768. 1050; —700; —382 кГ/см*. 769. 805-
—403 кГ/см2 770. Р = 208ш 771. Л1, = 123 кГ-м\ М2 = 303 кГм-
М3 = 128 кГ-м; Л14 = 134 кГ-ж. 772. 782<1600 кГ/сл2. 773.360<1600 кГ/смК
774. -™_, -ЦГ,77, 2,,-|^; 3,6-1^.776.^.
777 44 4 Ш 778 — -^L 779 — — ¦ — W
777. 34,4 -^j- . 778. 3 G^ . 779. 24 ?/ - 6 El •
3
15?/ • 180-?/ • lbi' 3 El
В ответах на задачи 784—790, 797—819 и 822—833 даны коэффициенты
Л1о2 Pa3 qa* Ma
при —ft— , —pj— или —-p-j— для линейных перемещении н прн р. ,
Pa2 qcP I 1 / \
ИЛН EI для Угловых перемещений. 784. 16 l-g фр I; 8; 2.
(f ) ^): T- 787' ()
)- 788- 4C + w)- 789- 2 + "^~- 79°- 4"-
РФ Pas Pas 80Po3
791. 103,7-J2J-. 792. 85-g^. 793. 39,1 -g^j-. 794. -^j- X
170 Pa3 / i2 \ 56,9Pc3
™»-—Ёьг-^+Ттб?)- 796- —Ш^ х
) ^)
56Ьдо2 У 797. 13,6; 4"= 6-85- 798- T": 1>45; "I"- 7"-39;
19,1; 20,1. 800.0,36; -5- ; 0,57. 801. 0,071; 0; 0,142. 802. -^-; 0,010;
0,028. 803. 0,47; 0,85; 0,24. 804. 8; 37,4; 4it. 805. -j^-; 0,0927; 0,0181.
806. ~ 1,225. 807. -3-; 0,392. 808. 5,14, 3,14. 809. -|-; -g-.
810. 1, 1; -y. 811. 0,312. 812.0,071. 813.0,355. 814.0,0198 1 +
• 2 "I ОЙ 1
+3,57-^- . 815. 12,4. 816. -g- . 817. 3n. 818. -j-. 819. 7,24.
820. 45°. 821. 48°15'. 822. -^; -^ . 823. -i-; J-. 824. -|-[
2 _28_ / 44 7 / 23
-¦g-. 825. 3 + Q2/r » ^~ • 826. -"g— -f-2~~rfip~ • 2,5. 827. g—; 3«
828. 14; 8,5. 829. 0,5; 0. 830. 3; 1. 831. -|-. 832. -y. 833. ~ .
473
р р
834. 0; -jj-sinP; -g- cos ?. 835. 0,739 P; -0,369 P. 836. ma.
Sd7. Л.7/И. 8*58. g , 48 -g/ - »39. g ,o. 24 -gy-.
6M Ma» 25 ga* 23 P
84°- -^-5 -2ШГ- 841- * "ш": м «й! 842ш;
jjo^ J6_ ga» 3 Л1
84d 3 ; 9 ' ?/ • 844-
60E/ • 84d 3 ; 9 ' ?/ • 844- 8 " a ' ~ШГ ¦
845. -j- qa- -—¦ ¦ -^- . 846. -уЦ -0,137 -—. 847. ~P;
11 Pa3 15 45 3
Т5~~ШГ- ш- ~WP- 849- IT9"- E5°- ~°-162p- 851- "F9"-
P 9Л1 32 14
852. Ay = 0; Ax = -^-. 853. 4y = Л^ = -щ-. 854. Л, = -^ ?a: ^ = g 9°-
855. Ay = -^-qa; Ax= -gj- <?a. 856. Ду = -jgp-P; Д^ = -gg- P.
ga 3 3
857. Ay = Ax = -^-. 858. -g- Pa. 859. -^ Pa. 860. 0,164217a2.
op р^ 9
861. 0,0634 ga*. 862. Лу = 0, Ax = -jjt-\ MA =-j-. 863. 4y = -f]-ga;
57 P 3P 40 76
A* = 5" 9a- 864' АУ = T"; Л-«-= 2" ¦ 865- 4V = Г 90; A* = Г <?a-
11 ga ga2 P 15
866. <4y = -2o-W<4r = -fo-; УИЛ = -%-. 867. Л^-д-; Л^-jg-P.
44 68 Pa3 10 191 Pa3 19
868. -23- P;^ Ж.Ж. 869. -^-P; -^p . -%- . 870. -^ P,
-0,0722 ?° ¦. 871. 0,75?схДг— . 872. jj-?aA< —. 873. 0,3?<хД<— .
874.0,6 ?¦*/-?-. 875. -|f ?a Д< -§- . 876. ^ ^. 877.
878. ^~- 879- Щ^-- 88а Х; ^Г" ' ~Ж~- 881< °-0372 ^
ga4 5 it ga1 Pa3
0,1188-g;- . 882. -g-ga; -gj- . -|j-. 883. 0.0638P; 0,1052-gy-.
ga* ocr P
884. 0,1867 qa; 0,115 -—- . 885. Ry = -^-; ^ = 0,590 ga. 886. Ry = -yi
«JC = 0,786P. 887. ^v = 0; Rx=*-^-. 888. Ry=,wja. Rx = '6qa.
889. Rv = -y; ^ = 0.722P; /Ия = 1,077Pa. 890. 3,44 ~- .
2л Pa8 Pa3 РФ ¦ 2я Pa3
891. ~g- • -gj—. 892. 0,586 -gj-. 893. 0,25 -gj- . 894. -g- ¦ -gj- .
fas
895. 0,0994 896. 0,369 Pa. 897. 0,273<?аг. 898. 0,629Яа.
899. 1,152 Pa, 900. Ay = 0,216P; Лл-=0,433Р. 901. Лу=0,961 Р; <4л=0,774Р.
3 да Р
902. Л^-^да; Лл. = -^-. 903. Ау= 0,271 <?а; 4^=0,277 да. 904. Л^-g-;
Лл: = 0,0522Р; Af = 0,437P. 905. Ау=0,519да; ^=0,339^0 906. Лу=214 qa;
Ax = G,7G\qa\ MA — 0,569 да2. 907. 2,414; 2,515. 908. 2,75; 9,40. 909. 2,48;
8,52. 910.3,30; 15,26. 911. М„ = -у-; /Ик = -д^-; В = 0,298 ^°*- .
474
912. М„=
Pa
; УИК = 0,565Pa; 6=0,625 -gj-. 913. Мп=2даг; MK=0,9Mqa";
Ь = 1,435 _?_. 914.^,,362/|f. 9,5. ^1.371^.
916. rs = 17,3 еж; Дл,= 0,23 мм. 917. р2 = 111 Мк/жг; Дг2 = —0,19 жж
918. а) г2=14,1 еж; Дг, = 0,23жж; Дга = 0,19лл; б) р, = 24Мк/жа. 919.р,
= "^. г .2 . .2 , тт~з—Ж1: тах 1°«-1 = р* тах °< = Р'
1
920. р =
922. po=
Po = 3,8 кГ/см2. 924. p0 =
rf)J— 0,017
кГ/см2; osV = 17,4 кГ/см2. 923.
W
4+rl
А°. 921. р=0,0
. 925.р„=0.
l ,6°.
Номер
задачи
*
926
927
928
<
кГ/см2
Труба
I
[I
Точки
1
—2000
—2000
0
2
—577
—248
—173
3
0
0
0
°t, кГ/сл
Труба
I
11
Точки
1
1800
2670
—460
2
371
920
—290
2
962
413
290
3
385
165
115
кГ/см*
577
248
173
Номер
задачи
931
932
v кГ/см*
Труба
I
1 •
11
Точки
1
—2000
—3000
2
—825
—1500
3
0
0
°t, кГ/см*
Труба
I |
Точки
1
917
1000
*
—309
—500
2
1291
2500
3
517
1000
Уменьше-
Уменьшение
расчетно-
го напря-
напряжения
30%
2 = 20 см;
л, = 40 см;
Д = 0,6 мм
933
Оэ„, - кГ/см?
Труба
Точки
Одинарная труба
Составная труба
1
¦
5717
3615
2
3650
2304
II
2
3650
3624
3
1860
1852
ш
3
1860
3365
4
914
1654
475
где ni=-
Л =(!_„?
930.
934. тахс, = 37'; max с,, = 66 7/. 935. с, = 216 М«/л8; 0^=10,8 М«/л2.
кГ/см2. 937. а) с, = сш = o;J cosaa =
6) «;« =- °"
936. о, = 181 кГ/сл2; о,; =>
Qcos2.2
(l+2cos3a)F
Q
C-
e
У 3 I + /3
938. —66,8 M«/.m\ 939.
32 Qi
940. d = 14,3 см, b^ 12 см 941. 250 об/мин. 942. -il^! l/ ?0 + юо •
943
g [о]
945. ~ 1350 кГ/ш* 946.
:. -0,3 I/ - ^r/ . 944. max о, =1420кГ/сл2; max о,, =2220 к/7см2.
" g [°]
(Зл+8). 947. 195 об/мин; -1,59 еж.
948.
9. 4
-. 950. 4,9
gr.ds
-; 28,5
951- -яг
<?/¦
952.
«d2
32а
954. а) 501/сек; б) 5,6 1/сек. 955. 1/.
?57. -i!L
953. 672 об/мин.
956. 2 it tg a
960.
Elg
Ql
бГ/g -
958. 4 я "I/ Qg3 . 959. 1/40 сек
Г 3?/g
961. 0,106 сек. 962. 1,17 "J/-
Cg
963. 0,075 сек.
41
967.
968.
964.
333
d2
12R
2Qa '
965. 2,82 1/сек. 966.
Qcf
61
35 "
70 •
972. 0,147 сек. 973. 2тс
1 4
2240 • 969* ~3~- 970> Т* 971> °'144 СеК-
6ft3 ?g
q6
15Q )•
974.
976. 2000 об/мин. 977. Л = ¦
1+-
З/mg /"
_5 _Z
978. 1,65 мм.
979. 0,8 м.
gQ
980. 0,54 рад. 981. 20 см, 2160 кГ/см*. 982. 550 кГ/смг. 983. 510 кГ/смг.
984. 2,1 кГ. 985. 12,8 ел.
986. ow = -g- a =
476
-ш f 4Qha
V —зеГ
_. 988. a) -g- |
^ Vr,
2QEI
_?/. 902. 33,2 «Л 993. _LgL'
У ^f -. 996. 7,46 У~^§
-i Г 0,0379 Q qs~"
998. о
1000. 9,3 Ми/ж2. 1001.
§i§
1002.
1006.
1008.
1011.
h =
1013*
1014.
1016.
1020.
1022.
1026.
1003. 2
г тс Z
1005. 1) a = _; I
1007.
¦\ ~--
1260 кГ/сл2. Ю09. I/ -gp.
336 кГ/смК 1012. A = .." ''JJ
W4\gV I, . 13 Q
1010. 337 кГ/сж2; 0,78 жж.
13
35
6QEI У
•у/
35
4W[o]
5o V
21 „C
D + -t)
ад7 =336 кГ/сж2; од/; = 512 кГ/см?; алш =720 кГ/еж2.1015. 1 ,
~ 12 жж. 1017. —1,74. 1018. 6,25 кн. 1019. Прочнее вал из Ст. 5.
~1°38 1023. ~ —0,5 '1024. - 7,8 кГ/мм2. 1025. -118 кГ-м.
-1,3. 1027. —9,2 кн. 1028.-1,47.
Литература
Здесь приводится лишь небольшая часть учебной и научно техничес-
технической литературы для ознакомления читателей с некоторыми наиболее полны-
полными курсами сопротивления материалов, сборниками 'задач, методическими
руководствами и трудами по расчету на прочность.
1. БезуховН И Теория сопротивления материалов. Ч. 1 и
II. Издание Артиллерийской инженерной академии, 1959.
Полный курс сопротивления материалов, включающий основы теории
упругости, пластичности и строительной механики. В курсе приводятся
иллюстративные примеры и библиография к каждому разделу.
2. Б е з у х о в Н. И. Статически неопределимые системы. Госстрой-
издат, 1934.
В учебном пособии приводятся необходимые сведения по методам рас-
расчета статически неопределимых систем и большое число различных приме-
примеров. Для типовых примеров даются решения.
3. Б е л я е в Н. М. Сопротивление материалов. Гостехиздат, 1959.
Учебник охватывает все вопросы программы курса сопротивления ма-
материалов для машиностроительных и механических специальностей высших
технических учебных заведений; содержит примеры решения наиболее
характерных задач.
4. Беляев Н. М. Сборник задач по сопротивлению материалов.
Физматгиз, 1960.
Наряду с обычными задачами по курсу сопротивления материалов в
сборнике приводятся задачи на расчет тонкостенных стержней и элементов
конструкций на ползучесть. Для некоторых задач даны решения.
5. Г л у ш к о в Г. С. Моменты статические, инерции и сопротивле-
сопротивления, ГТТИ, 1932.
6. Г л у ш к о в Г. С. н С и н д е е в. В. А. Курс сопротивления ма-
материалов- Высшая школа, М., 1965.
Курс предназначен для студентов очного и заочного обучения; в нем
используется международная система единиц (СИ).
7. Иванов Н. И. Сборник задач по сопротивлению материалов.
Государственное издательство технико-теоретической литературы. М., 1948.
8. И з ю м о в С. М., Кудрявцев И. Н., О л и с о в Б. А.
Под редакцией М. М. Филоненко-Бородича. Сборник задач по сопротивлению
материалов. М.—Л., Стройиздат Наркомстроя, 1940.
9. Ицкович Г. М., Винокуров А. И., Минин Л. С.
Руководство к решению задач по сопротивлению материалов. Росвузиздат,
1963.
10. П и с а р е н к о Г. С. и др. Сопротивление материалов. ГИТЛ
УССР, 1963.
11. Пономареве. Д., Бидермаи В. Л., Лихарев К. К.,
Макушнн В. М., Малинин Н. Н., Феодосьев В. И. Рас-
478
четы на прочность в машиностроении. Машгнз, Т. I, 19S6, т. 11, 1958. т. III,
1960.
В трехтомном труде содержится полный материал по методам расчетов
на прочность в машиностроении. Приводятся примеры конкретных рас-
расчетов, сведения об экспериментальном исследовании механических свойств
материалов н большое количество справочных данных. После каждого раз-
раздела указывается библиография.
12. Р у б и и и н М. В. Руководство к практическим занятиям по
сопротивлению материалов. Росвузиздат, 1963.
В руководстве приводятся сведения нз теоретической части курса со-
сопротивления материалов и примеры решения типовых задач.
13. Се рейсе и С. В., Катаев В. П., Козлов Л. А.,
Шиейдеровнч Р. М. Несущая способность и расчеты деталей машнн.
Машгиз, 1954.
В книге излагаются вопросы несущей способности деталей машин прн
действии статических и переменных напряжений, а также соответствующие
расчеты на прочность ряда типовых деталей машин. Приводятся данные спра-
справочного характера по механическим характеристикам, по влиянию конструк-
конструктивных н технологических факторов на прочность.
14. У м а н с к и й А. А., Афанасьев А. М., В о л ь м и р А. С,
Григорьев Ю. П., Кодаиев А. И., Марьин В. А., При-
горовский Н. И. Сборник задач по сопротивлению материалов. «На-
«Наука», 1964.
15. Ф е о д о с ь е в В. И. Сопротивление материалов. Физматгнз,
1983.
Основной учебник по курсу сопротивления материалов для ВТУЗов.
1?. Феодосьев В. И. Избранные задачи и вопросы по сопротив-
сопротивлению материалов, ГИТЛ, 1950.
В книге приведены оригинальные и интересные задачи и вопросы из
области сопротивления материалов, рассчитанные на достаточно подготов-
подготовленных читателей. В конце книги приводятся решения задач и ответы на
вопросы.
17. Филоиенко-Бородич М. М., И з ю м о в С. М., О л и-
с о в Б. А., Кудрявцев И. Н., М а л ь г и н о в Л. И. Курс со-
сопротивления материалов. Ч. I и 11. Гостехиздат, 1955.
Первая часть содержит все основные вопросы курса сопротивления
материалов. Вторая часть включает материал, углубляющий трактовку
вопросов, излагаемых в первой части, а также основы теории упругости и
пластичности. В книгах имеются иллюстративные примеры.
18. Сборник задач по сопротивлению материалов. Кафедра сопротив-
сопротивления материалов МВТУ им. Баумана. Издание МВТУ, 1946.
Задачник предназначен для машиностроительных ВТУЗов. Для наиболее
сложных задач даются решения.
ОГЛАВЛЕНИЕ
Стр.
Предисловие 3
Основные обозначения ................ 5
Единицы измерений 9
Общие замечания к условиям задач 9
I. Растяжение и сжатие
§ 1. Продольное усилие . . 10
§ 2. Нормальные напряжения, абсолютное удлинение и потенциаль-
потенциальная энергия ..... ... 12
§ 3. Поперечная деформация н изменение объема 15
§ 4. Перемещения точек шарнирно-стержневых систем 17
§ 5. Прочность и жесткость . 21
§ 6. Учет собственного веса ....•...••.••. 25
§ 7. Статически неопределимые системы . . . 28
II. Напряженные состояния и гипотезы прочности
§ 1. Линейное, плоское и объемное напряженные состояния ... 41
§ 2. Гипотезы прочности и эквивалентные напряжения 48
111. Тонкостенные сосуды
IV. Чистый сдвиг
V. Расчет простейших соединений элементов конструкций
VI. Геометрические характеристики плоских фигур
§ 1. Площади и их статические моменты .•*...... 63
§ 2. Моменты инерции площади фигуры 65
VII. Кручение
§ 1. Крутящий момент 74
§ 2. Касательные напряжения, угол закручивания и потенциальная
энергия упругой деформации 76
§ 3. Прочность и жесткость . 80
§ 4. Статически неопределимые задачи 86
480
Стр.
VIII. Прямой поперечный изгиб
§ 1. Поперечная сила и изгибающий момент 93
§ 2. Нормальные напряжения и подбор поперечного сечения балки 112
§ 3. Касательные напряжения, центр изгиба и проверка прочности
балок по касательным напряжениям 122
§ 4. Главные напряжения и полная проверка прочности балки . . 130
§ 5. Основы расчета балок на прочность по несущей способности . . 138
§ 6. Перемещения при изгибе . 141
§ 7. Балки переменного сечения . 158
§ 8. Статически неопределимые балки 170
§ 9. Потенциальная энергия упругой деформации при изгибе . . 195
IX. Сложное сопротивление прямого бруса большой жесткости
§ 1. Косой изгиб . . 201
§ 2. Растяжение или сжатие и изгиб 210
§ 3. Растяжение нлн сжатие и кручение 225
§ 4. Кручение и изгиб 227
§ 5. Общий случай сложного сопротивления 240
§ 6. Витая цилиндрическая пружина растяжения или сжатия . . . 248
X. Продольный изгиб
§ 1. Критическая сила н критическое напряжение 253
§ 2. Расчет сжатых стержней на устойчивость 257
§ 3. Продольно-поперечный изгиб , 270
XI. Плоские кривые брусья
§ 1. Продольное усилие, поперечная сила и изгибающий момент 275
§ 2. Напряжения . .... 287
§ 3. Расчет на прочность .."¦.... .... 292
XII. Энергетический метоц расчета упругих систем
§ 1. Определение упругих обобщенных перемещений ..... 295
§ 2. Раскрытие статической неопределимости систем 313
§ 3. Расчет плоских тонкостенных колец ....... 328
5tlll Расчет толстостенных труе
. . 354
§ 1. Цилиндрическая труба 360
§ 2. Составные цилиндрические трубы
XIV. Динамическое действие сил
§ 1. Расчет движущихся тел (систем) с учетом сил инерции ... 367
§ 2. Упругие колебания 3gg
§ 3. Удар
481
XV. Переменные напряжения
§ 1. Основные факторы, влияющие иа выносливость материала . . 419
§ 2. Расчет на прочность при линейном напряженном состоянии и
чистом сдвиге (кручении) . . 423
§ 3. Расчет иа прочность при сложном напряженном состоянии . . 428
Приложение 1 438
Приложение 2 439
Приложение 3 452
Приложение 4 453
Приложение 5 454
Ответы к задачам 456
Литература 478
Игорь Николаевич Миролюбив,
Сергей Александрович Енгалычев,
Николай Дмитриевич Сергиевский,
Фотях Зайнулович Алмаметов,
Николай Александрович Курицын,
Константин Геннадиевич Смирнов-Васильев.
Людмила Васильевна Яшина
Пособие к решению задач по сопротивлению материалов
Редактор Н. Н. Ещенко
Переплет художника В. М Лукьянова
Художественный редактор Н. К. Гуторов
Технический редактор Е. М Лопухова
Корректор B.C. Кикоть
Т-10376 Сдано в набор 22/XI-66 г. Подп. к печати 2/Х-67 г. Формат 60X90'/ie. Объем
30,25 печ. л. Уч--изд. л. 26,03. Изд. № От -30/65. Тираж 50 000 экз. Цена S3 коп.
Тематический план издательства «Высшая школа» (вузы и техникумы) на 1967 г.
Позиция № 78
Москва, К-51, Неппннная ул., д 29/14,
издательство «Высшая школа»
Ярославский полиграфкомбииат Главполиграфпрома Комитета по печати при Совете Ми-
Министров СССР. Ярославль, ул. Свободы, 97. Зак. S86